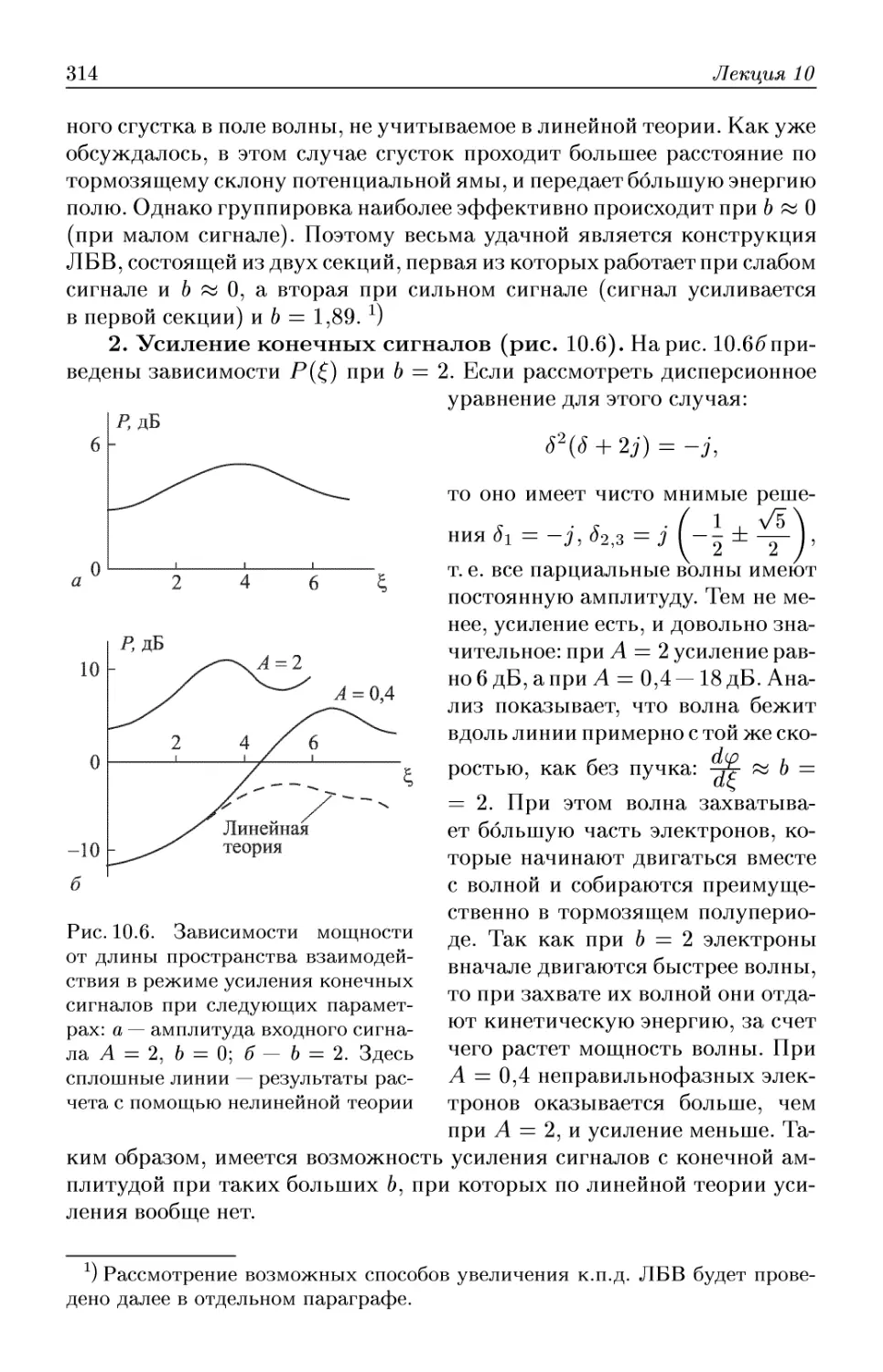
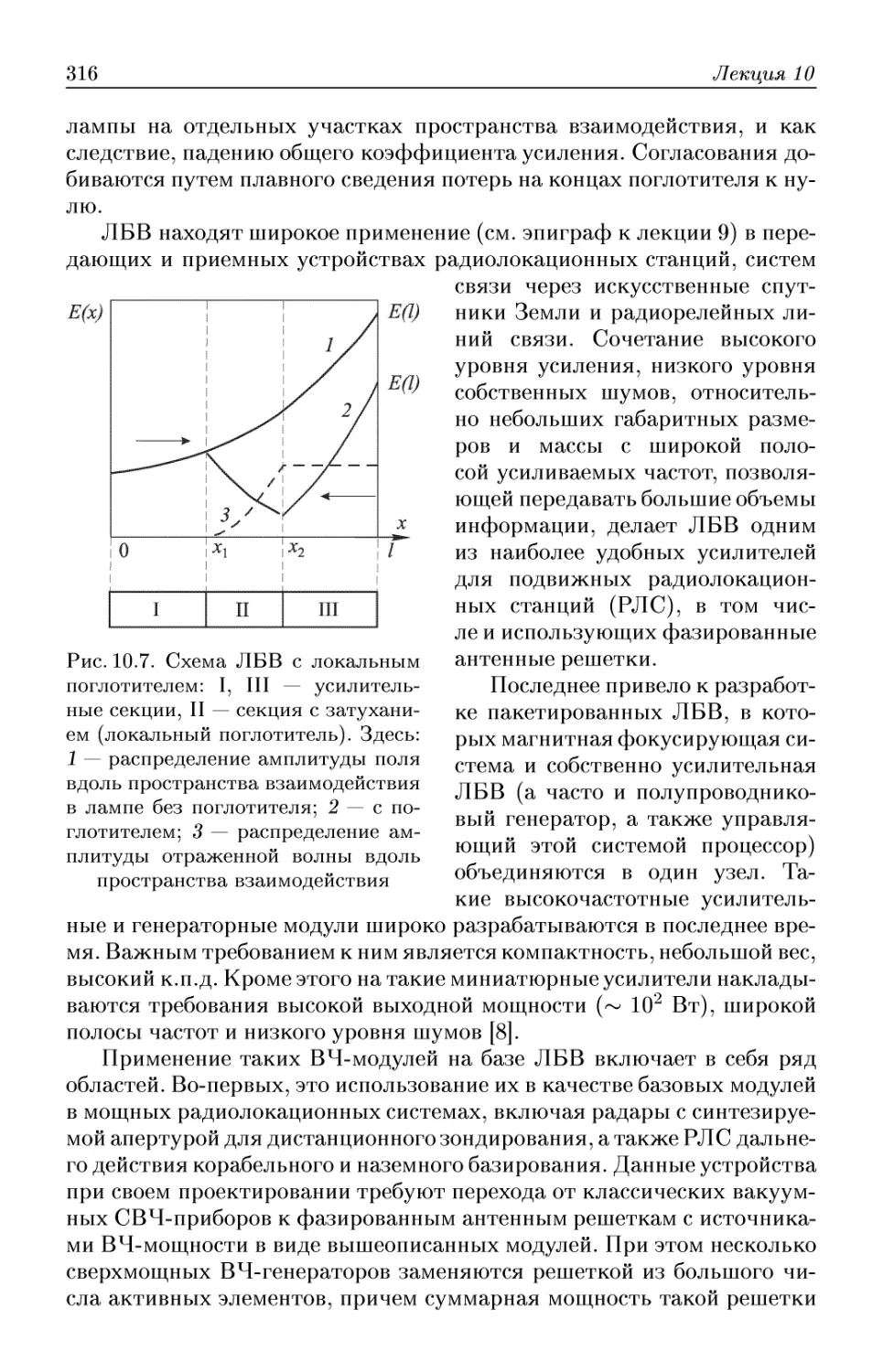
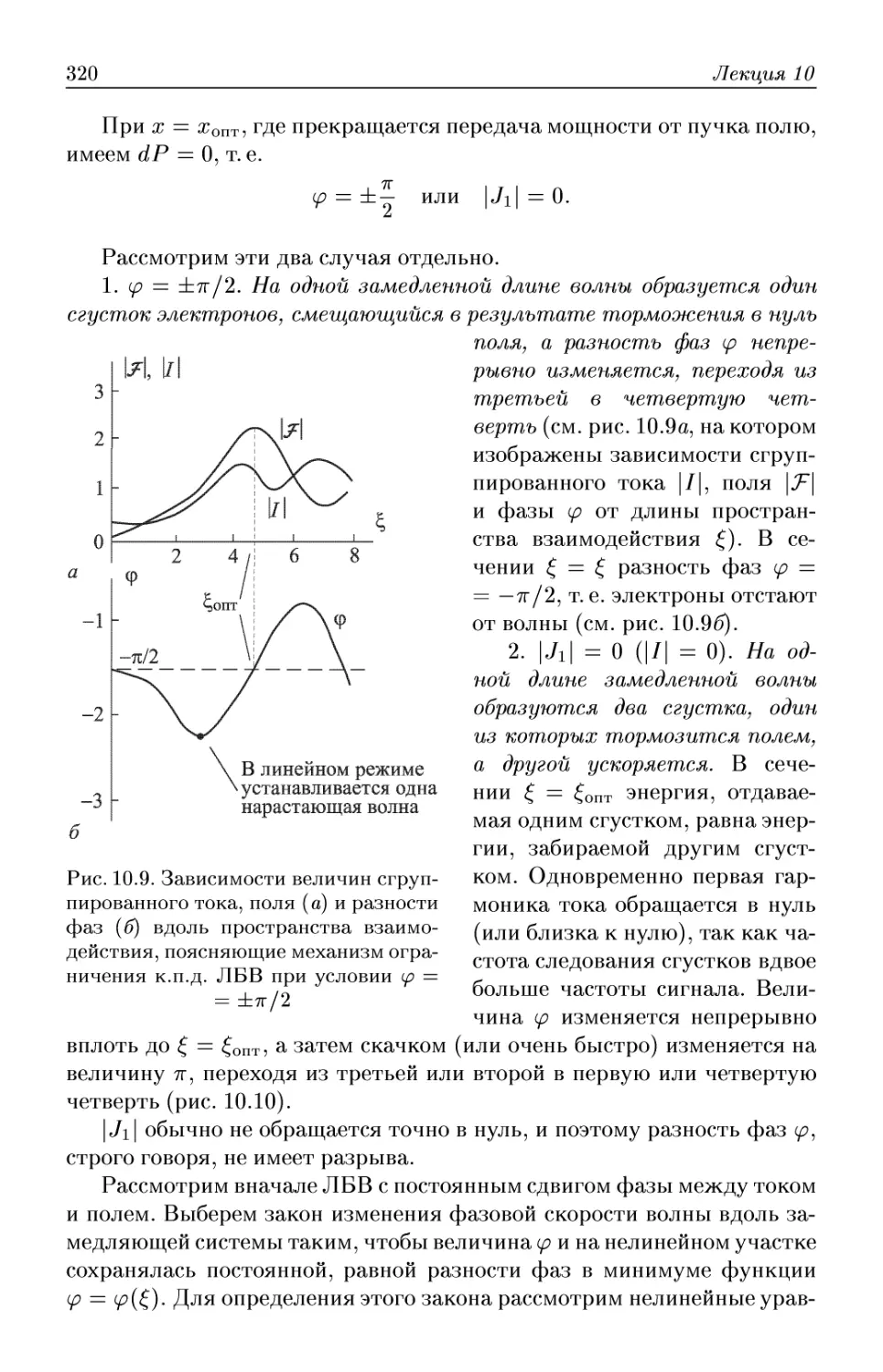
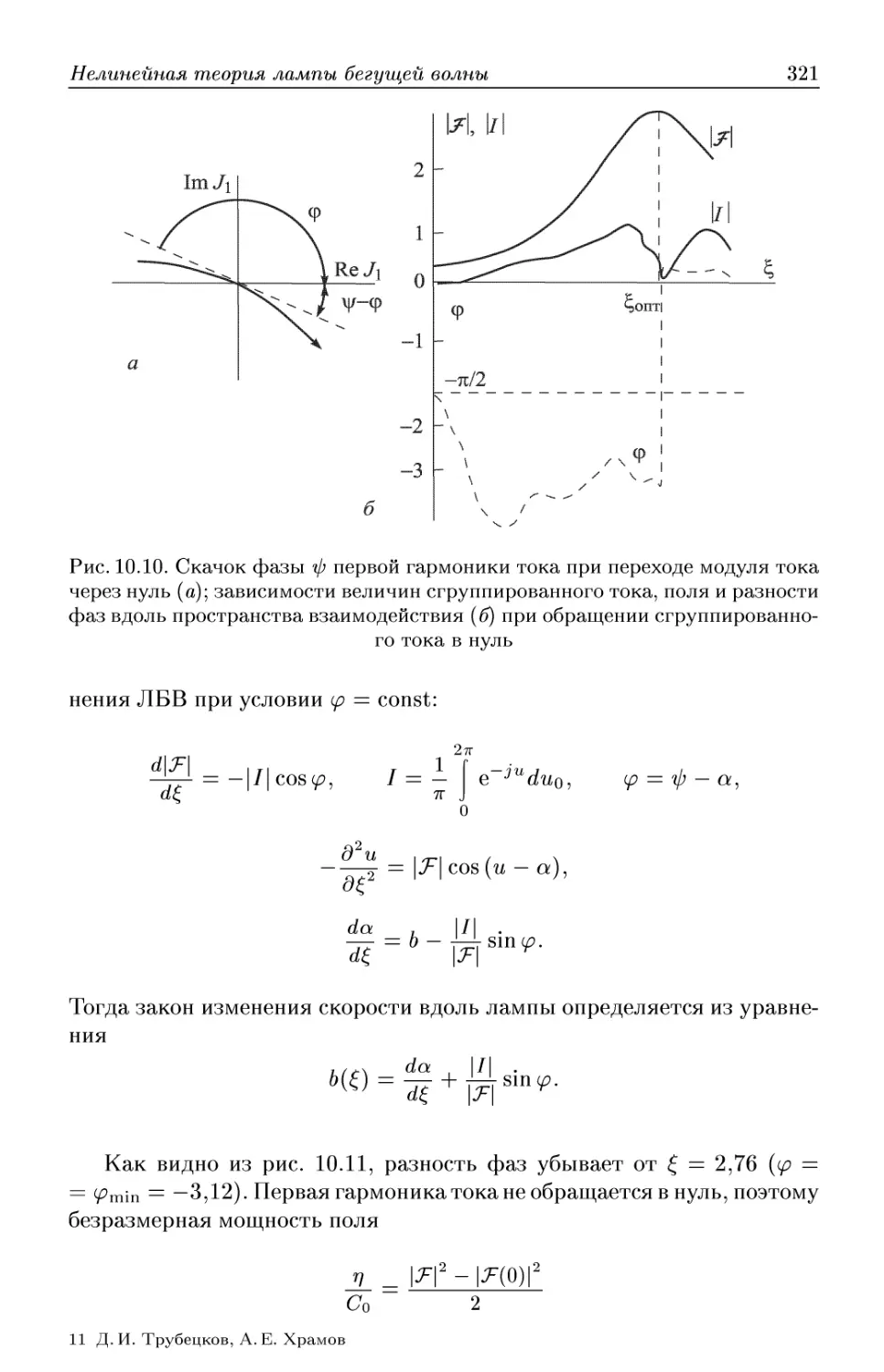
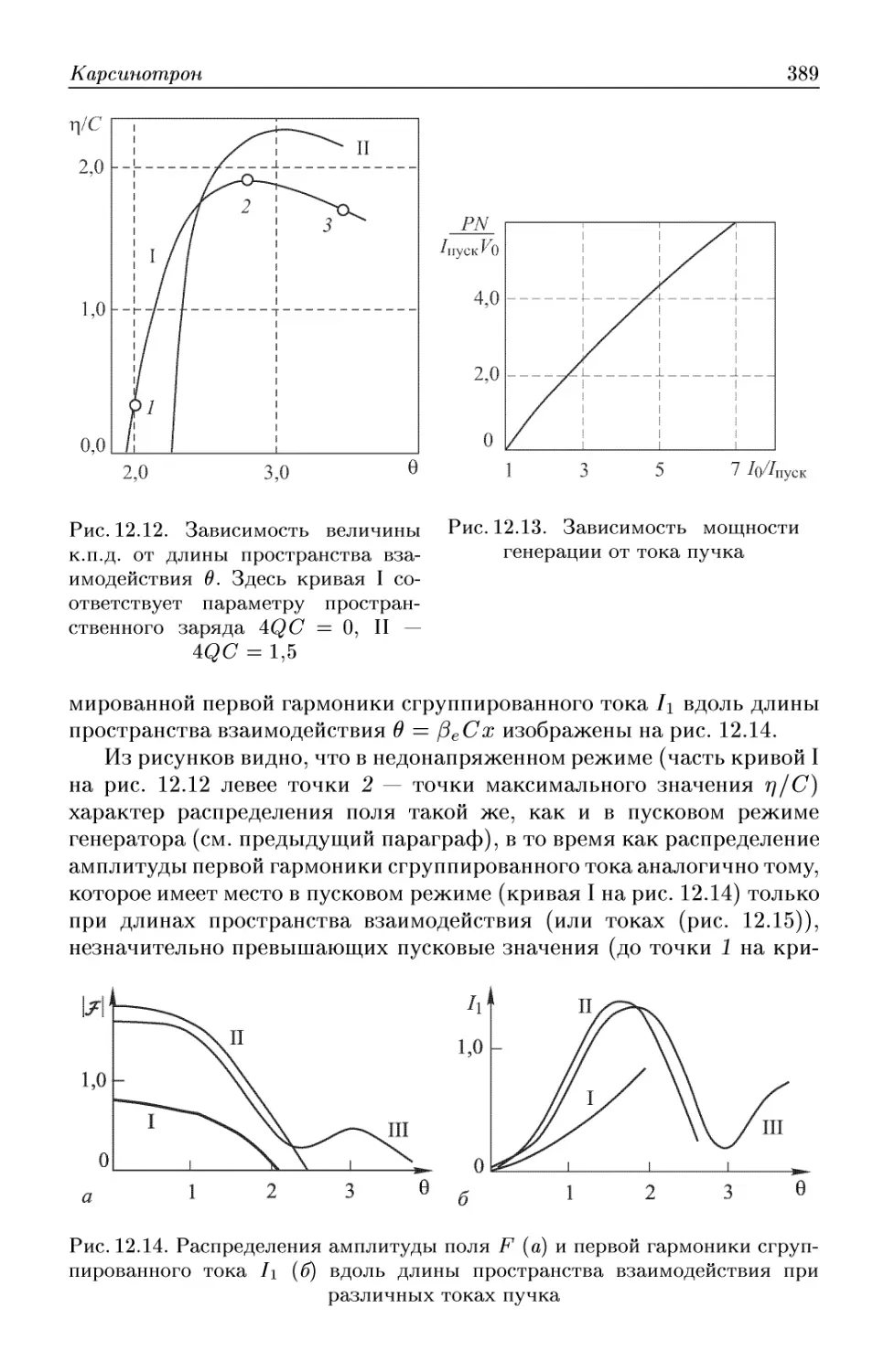
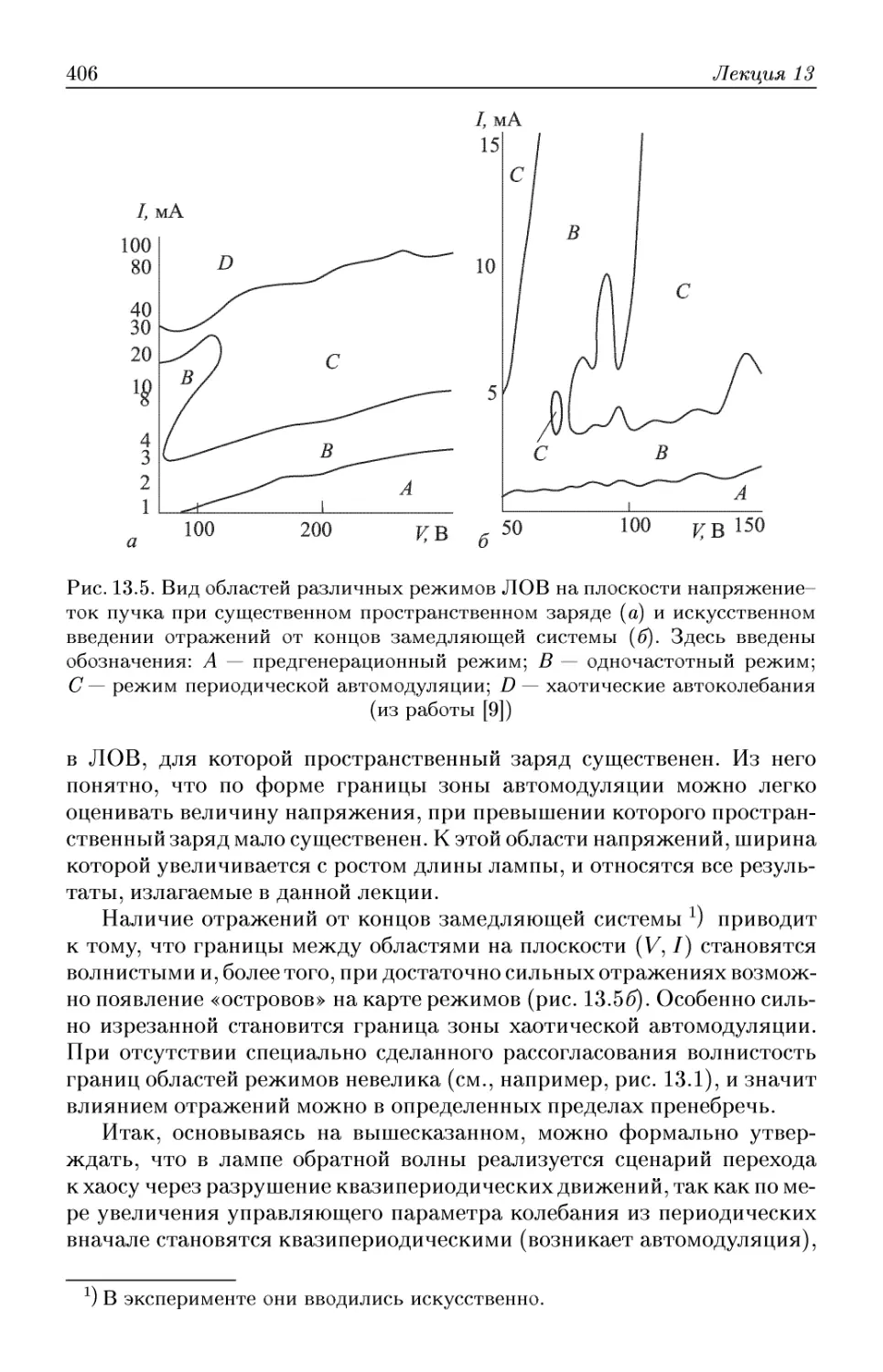
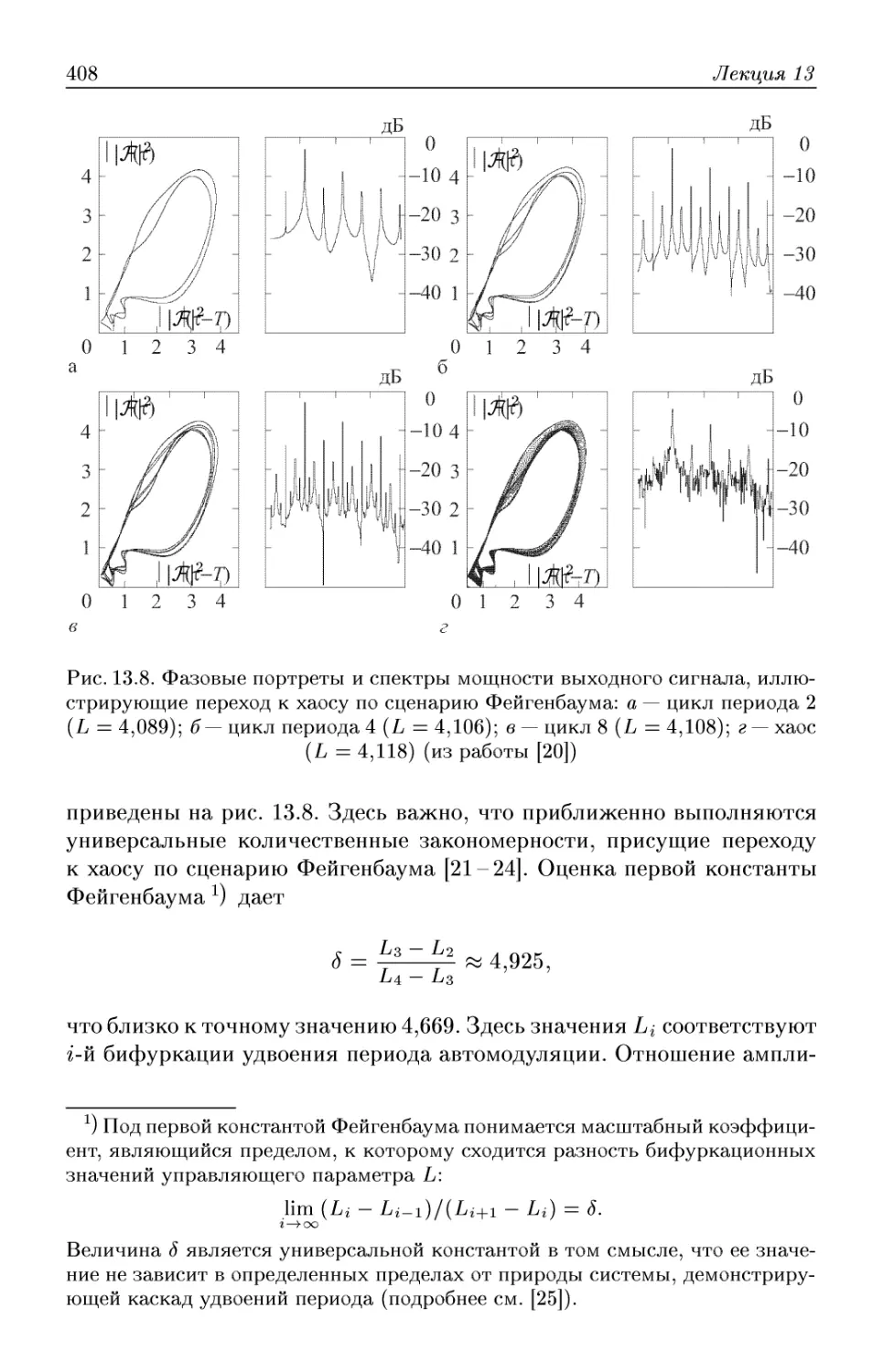
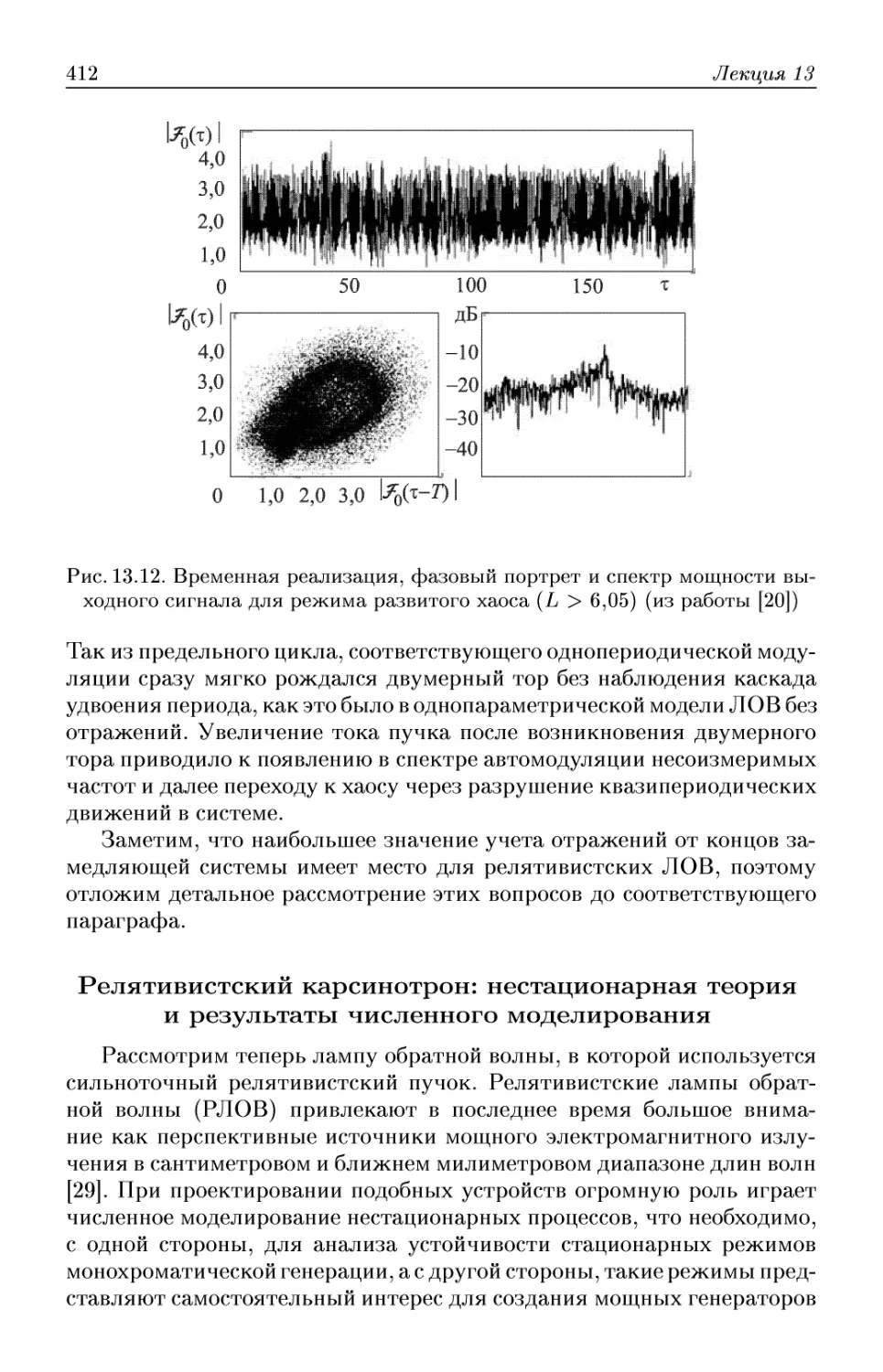
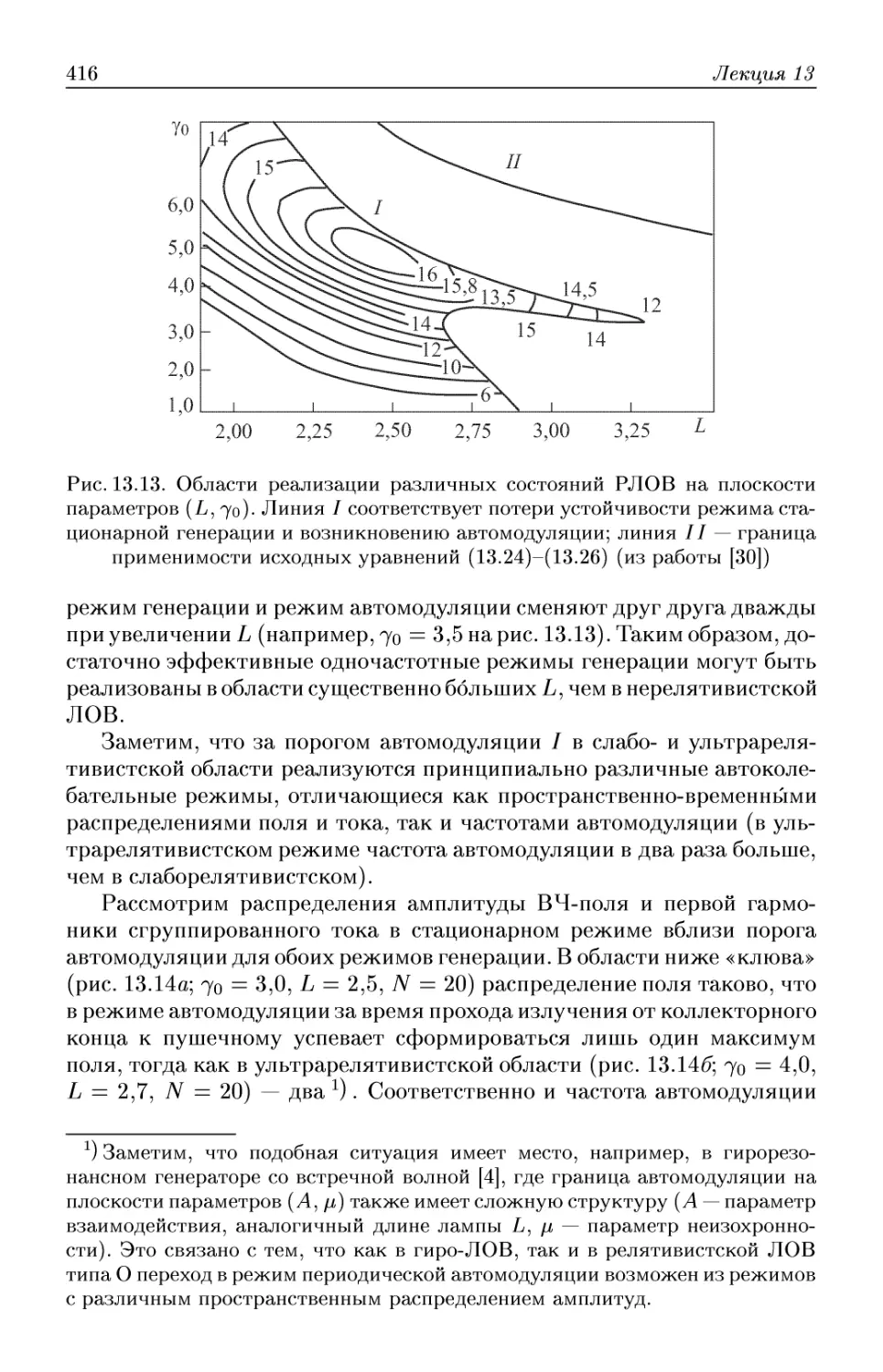
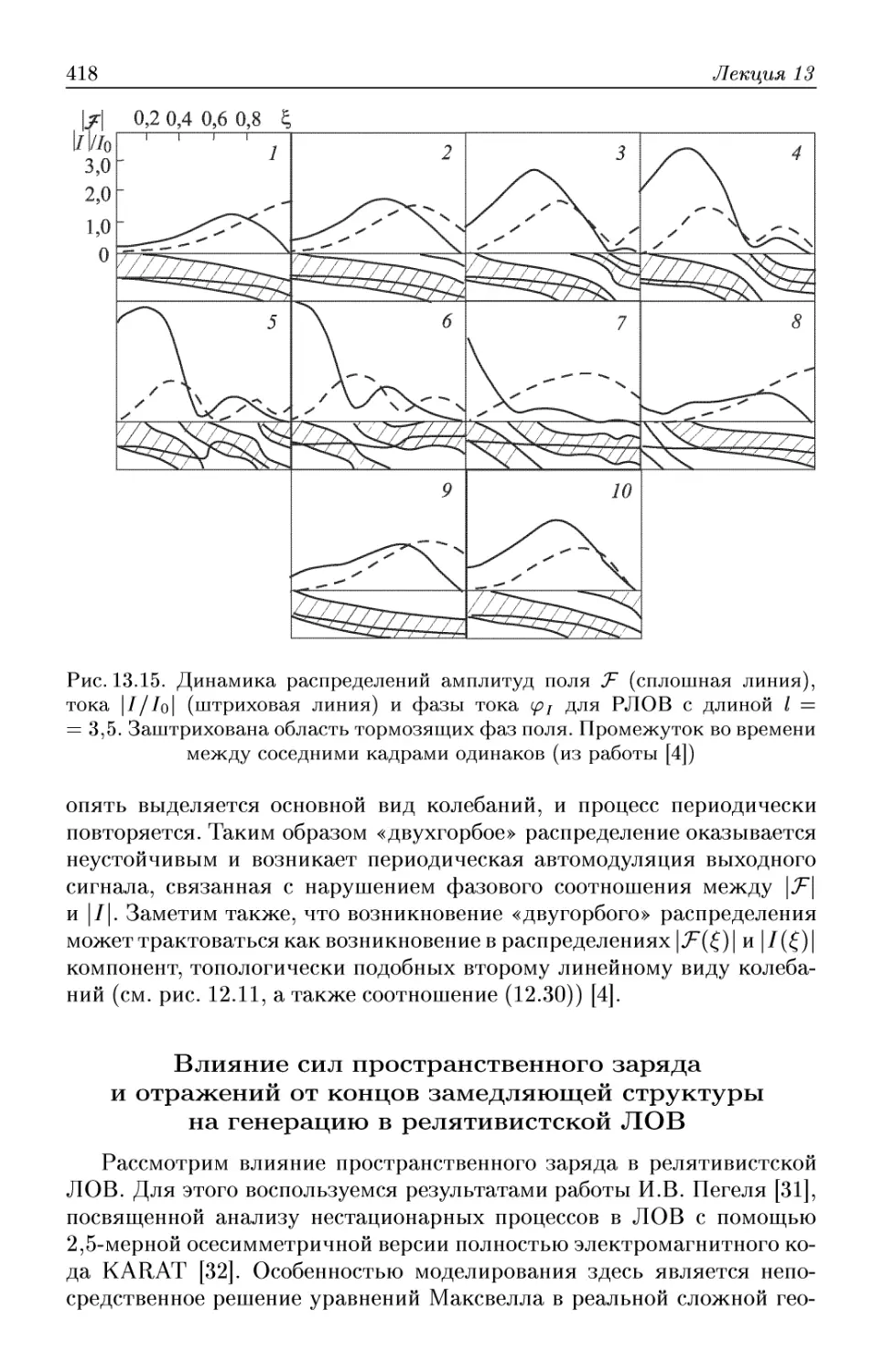
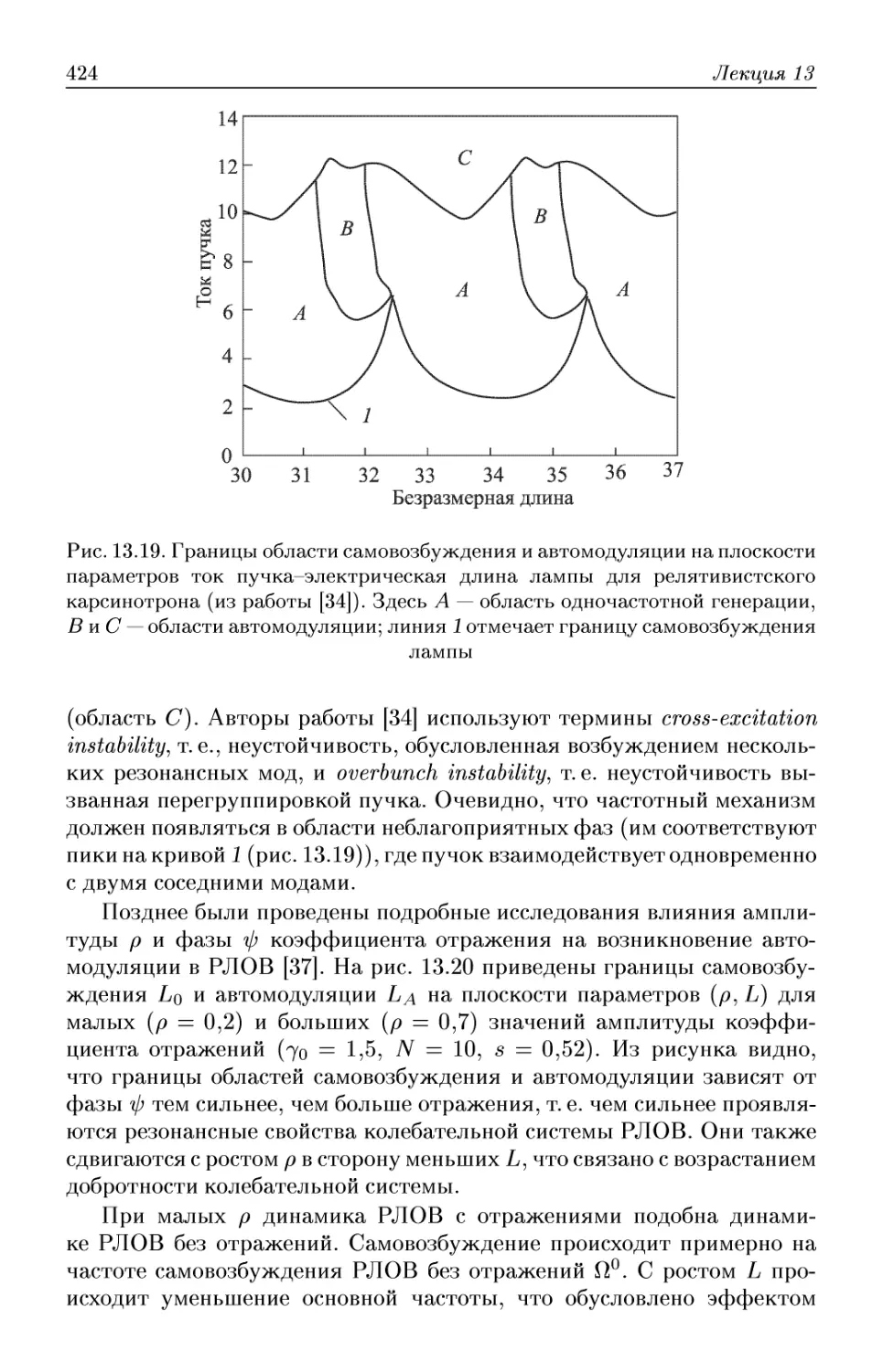
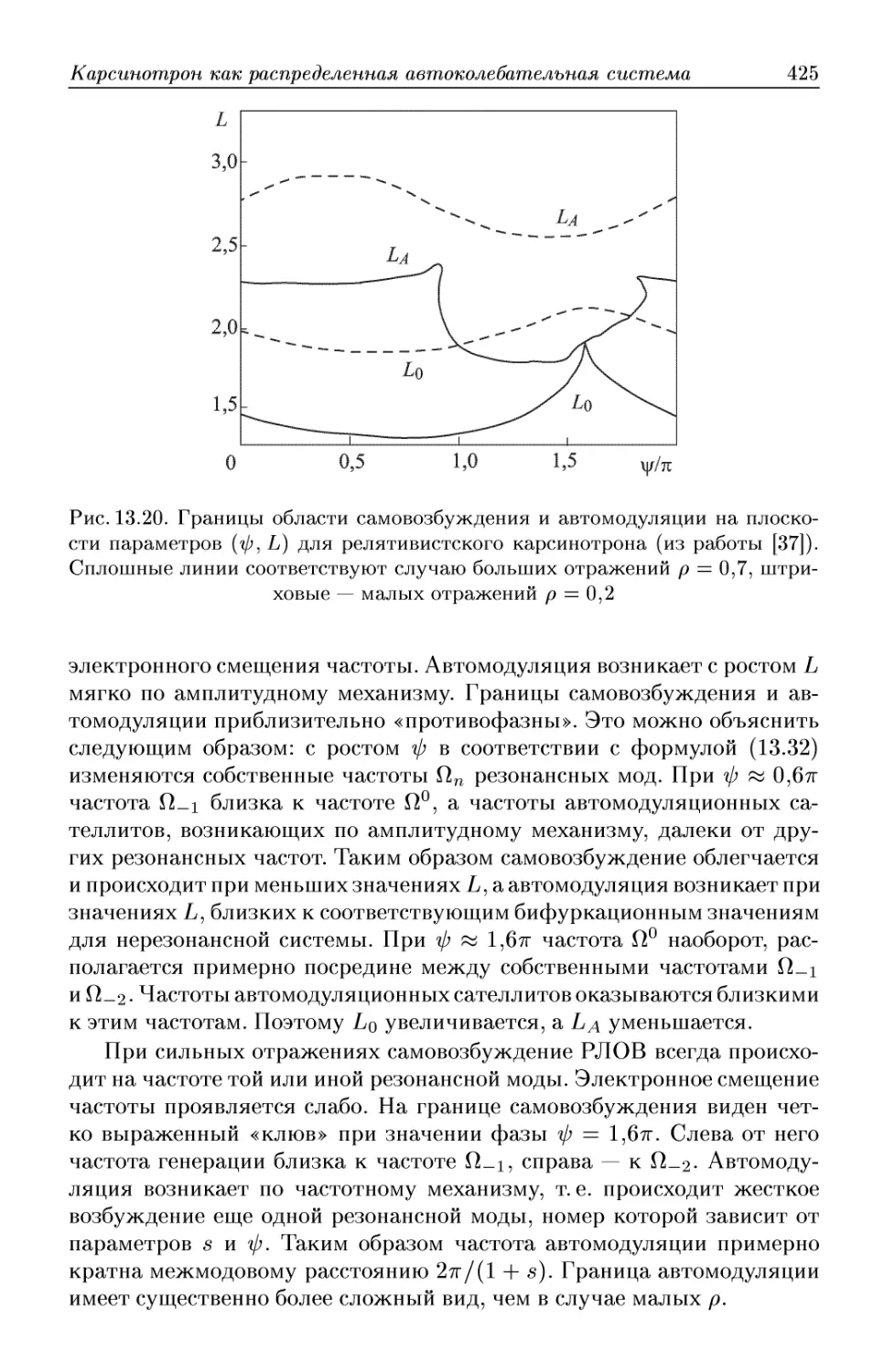
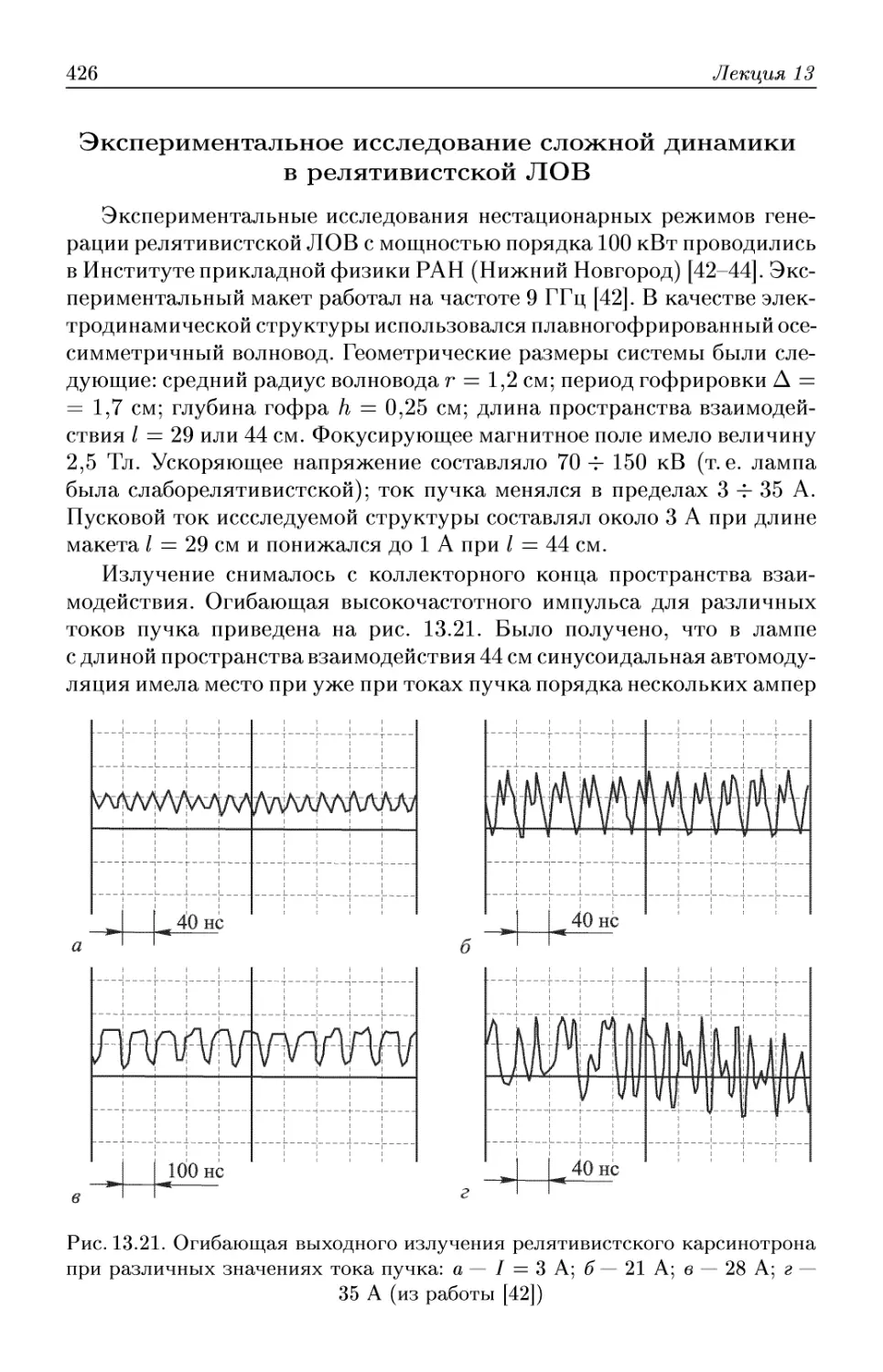
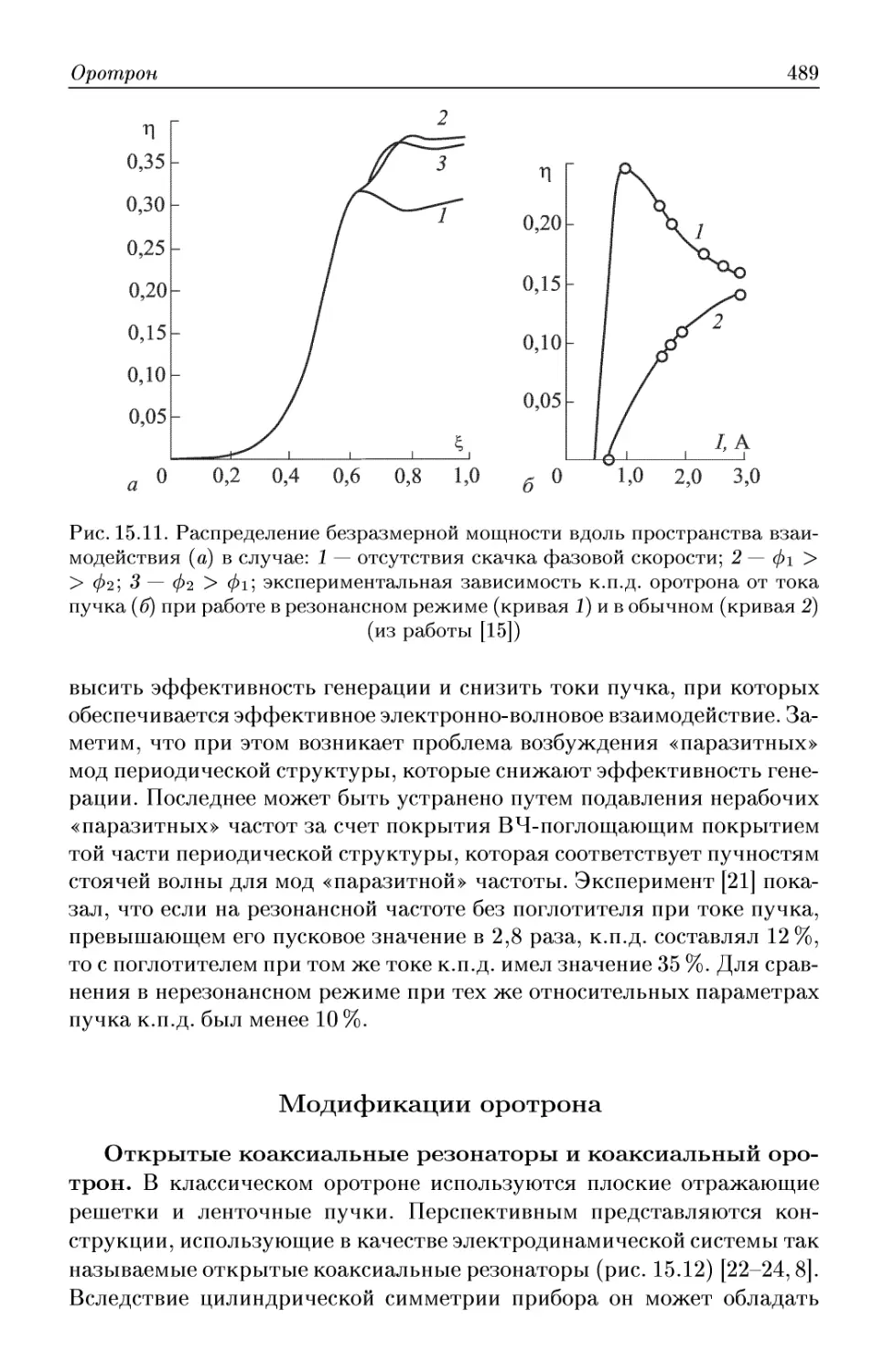
Автор: Трубецков Д.И. Храмов А.Е.
Теги: электронные и ионные явления физика электроника свч физика поля физматлит лекции по физике пособие для физиков
ISBN: 5-9221-0372-5
Год: 2003
УДК 537.5
ББК 22.333
Т77
Трубецков Д. И., Храмов А. Е. Лекции по сверхвысокоча-
сверхвысокочастотной электронике для физиков. В 2 т. Т. 1. — М.: ФИЗМАТЛИТ,
2003. - 496 с. - ISBN 5-9221-0372-5.
Современная сверхвысокочастотная электроника представлена в книге
не технической стороной с кратким описанием физики и основ теории раз-
различных электронных ламп, а детальным описанием основных физических
явлений, возникающих при взаимодействии электронных потоков с элек-
электромагнитными полями и лежащих в основе различных типов устройств
сверхвысоких частот. В книге уделено большое внимание математическому
моделированию на ЭВМ явлений в электронных потоках на сверхвысоких
частотах. Изложение ведется так, чтобы показать тесную связь сверхвысо-
сверхвысокочастотной электроники с современной нелинейной теорией колебаний и
волн и теорией излучения. Особенностью книги является то, что в ней опре-
определенное место занимает история СВЧ-электроники. В первом томе книги
излагаются основные понятия, методы и модели «классической» сверхвы-
сверхвысокочастотной электроники. Также в нем рассматриваются релятивистские
аналоги классических СВЧ-устройств: клистронов, ламп бегущей и обратной
волны, приборов со скрещенными полями.
Лекции предназначены для физиков различных специальностей, инте-
интересующихся процессами взаимодействия электронов с электромагнитными
полями, для научных работников, аспирантов и инженеров, проводящих
исследования в области вакуумной СВЧ-электроники, радиофизики, радио-
радиотехники и физики плазмы. Они могут быть полезны студентам старших
курсов соответствующих специальностей.
ISBN 5-9221-0372-5 (Т. 1)
ISBN 5-9221-0371-7 © физматлит, 2003
СОДЕРЖАНИЕ
Предисловие
Лекция 1. Вводная 9
Основные особенности сверхвысокочастотной электроники. Пять идей,
которые создали СВЧ-электронику. Индивидуальное излучение заря-
заряженных частиц (спонтанное излучение классических осцилляторов).
Индуцированное излучение ансамбля возбуэюденных классических осцил-
осцилляторов. Возбуждение резонансной системы заданным током. Стацио-
Стационарные уравнения возбуждения линии передачи электронным потоком.
Нестационарная теория возбуждения волновода током медленно меня-
меняющейся амплитуды.
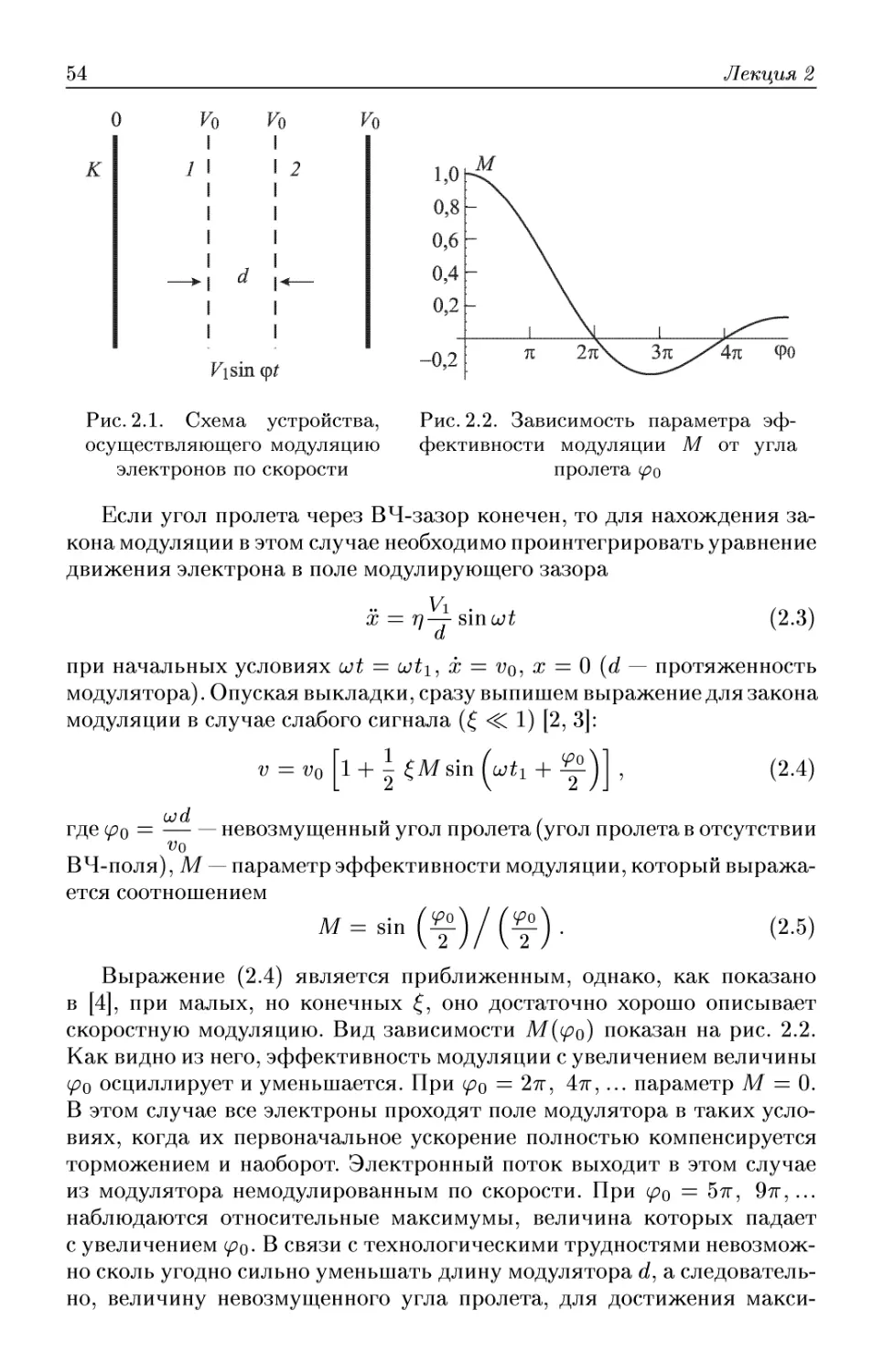
Лекция 2. Элементарная кинематическая теория клистронов . . 51
Модуляция электронного потока по скорости. Кинематический анализ
процесса группировки электронов в пространстве дрейфа. 100$ идея
братьев Вариан и Хансена. Клистронные усилители и умножители
частоты. Некоторые результаты теории резонансных автогенерато-
автогенераторов. Элементарная теория отражательного клистрона. Клистронный
генератор с запаздыванием: от режимов монохроматических колебаний
до режимов динамического хаоса.
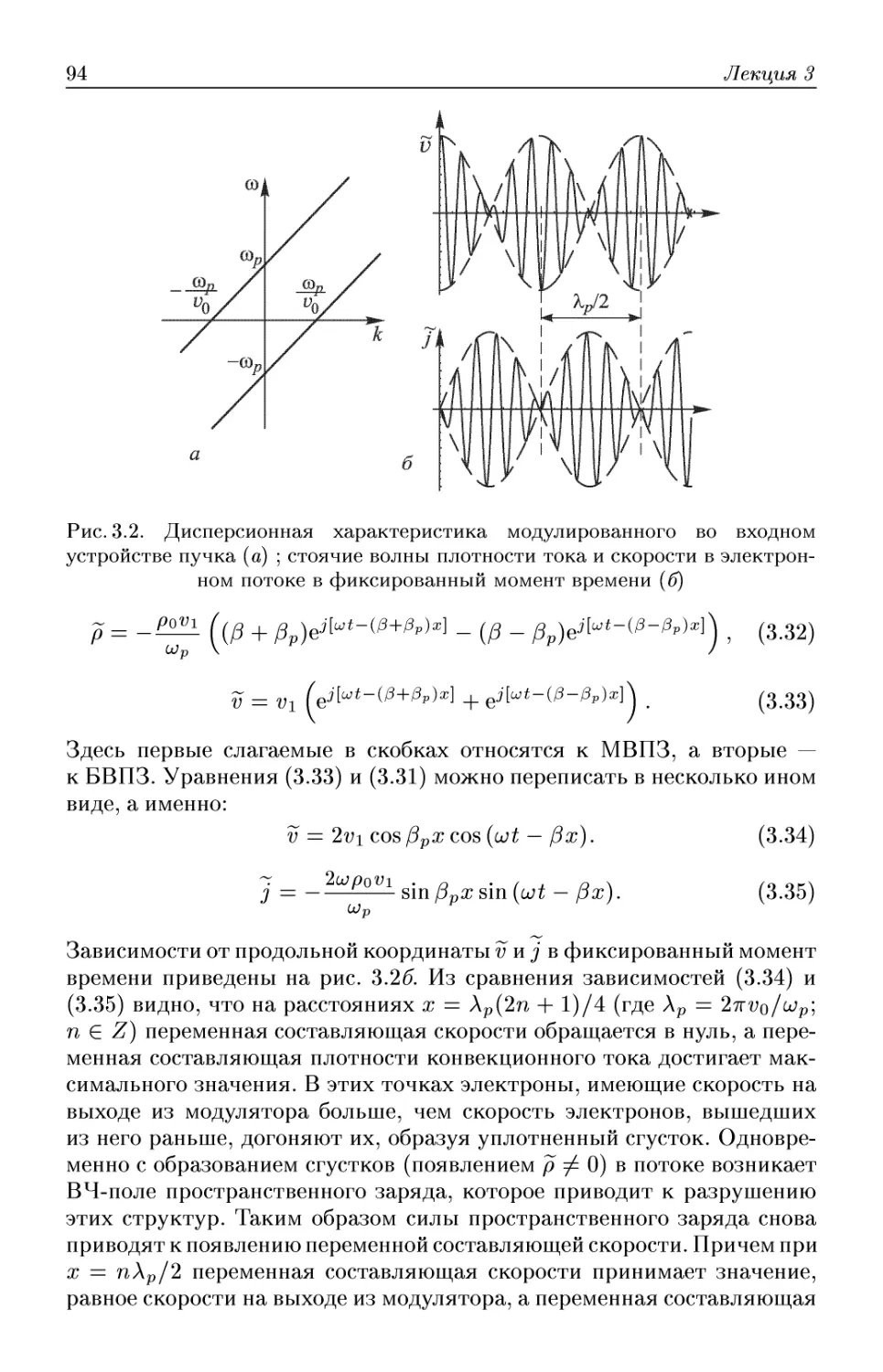
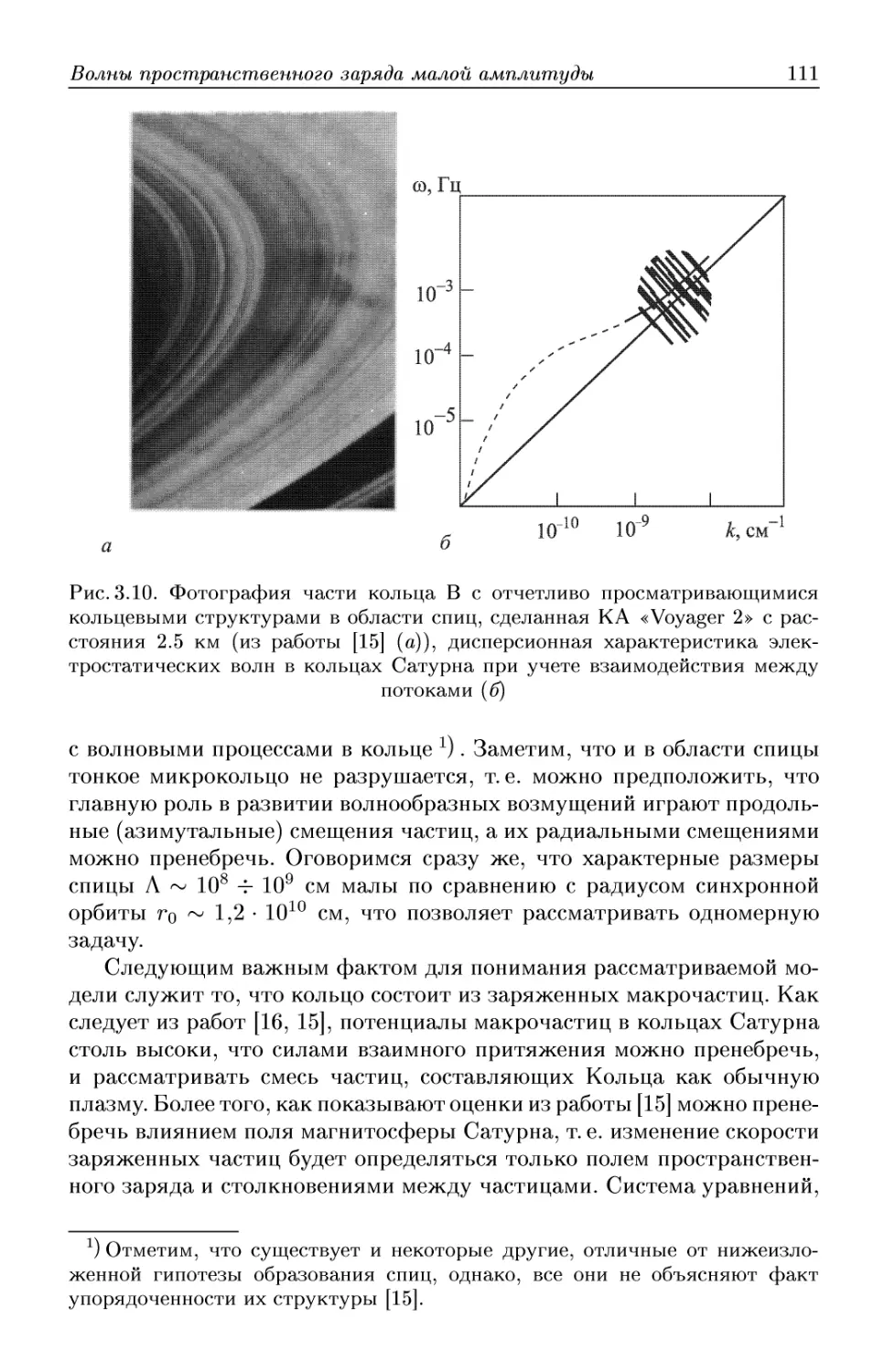
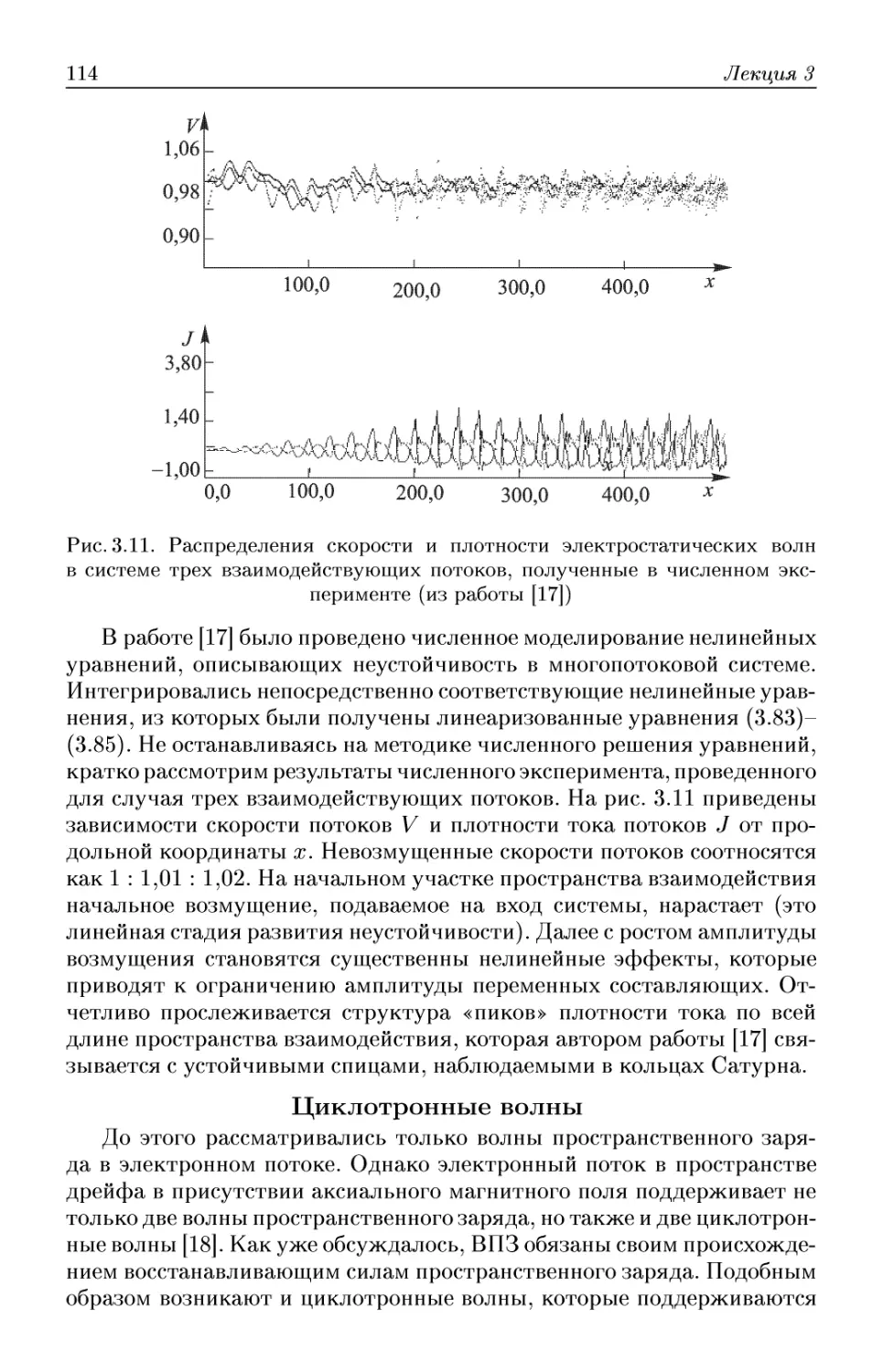
Лекция 3. Волны пространственного заряда малой амплитуды . 85
Гидродинамическое описание электронного потока. Волны простран-
пространственного заряда и группирование в пространстве дрейфа. Резистив-
ный усилитель. Волны пространственного заряда в электронном по-
потоке со столкновениями и диффузией. Двухлучевая неустойчивость
(абсолютная и конвективная неустойчивость; глобальная неустойчи-
неустойчивость). Неустойчивость Гельмгольца и об одной гипотезе образования
спиц в кольцах Сатурна (многопучковая неустойчивость). Циклотрон-
Циклотронные волны. Связанные волны.
Содержание
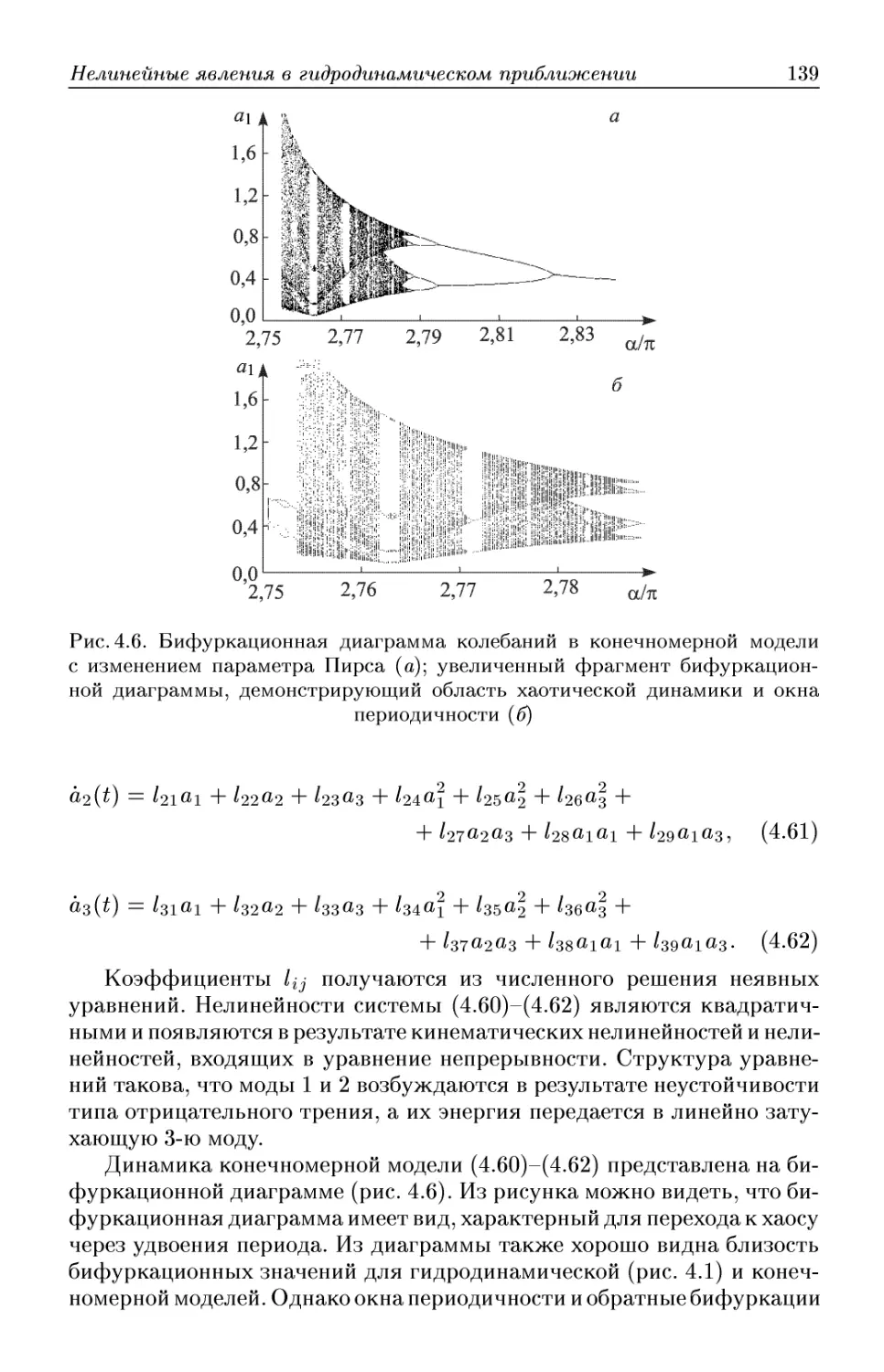
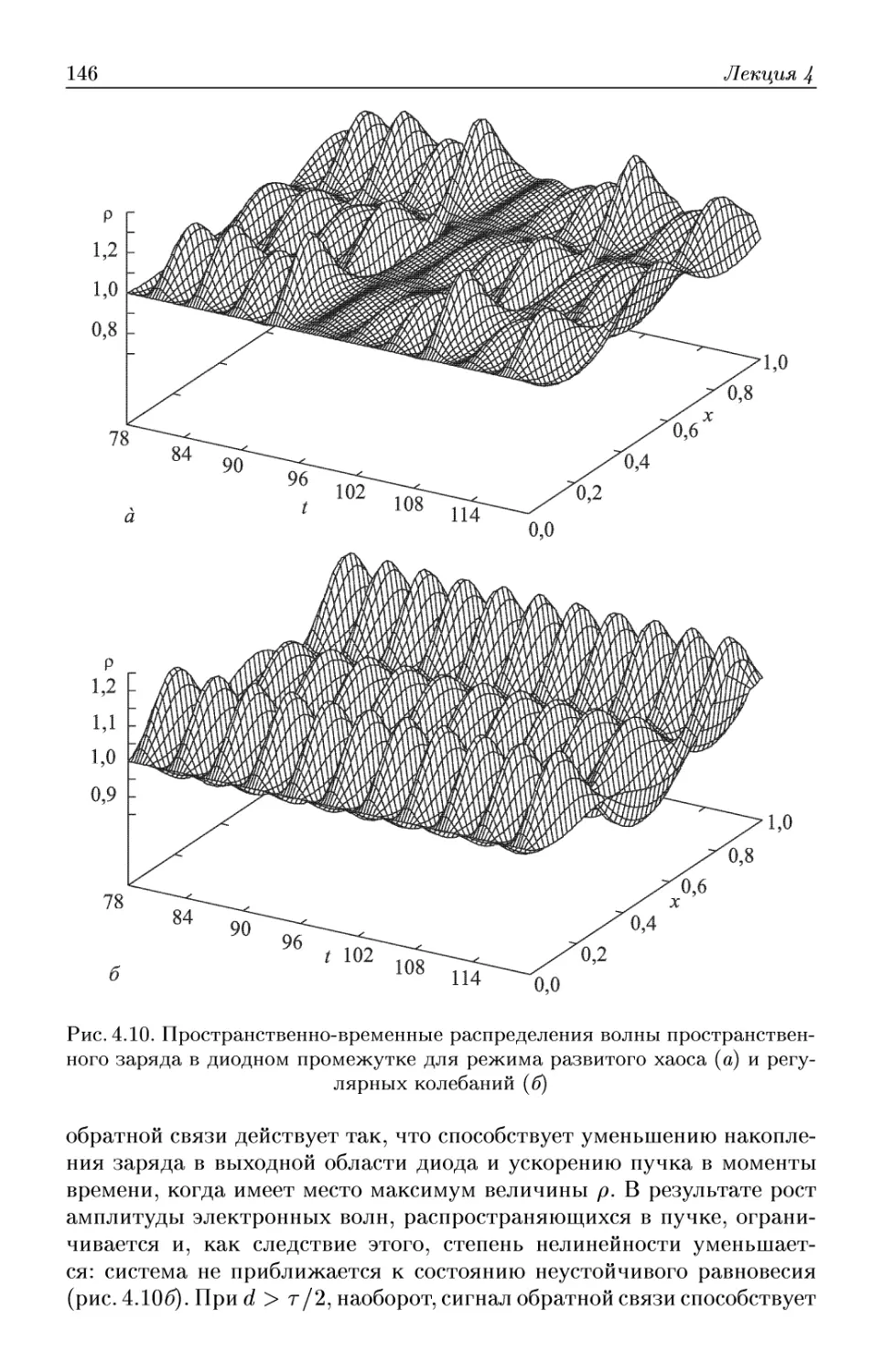
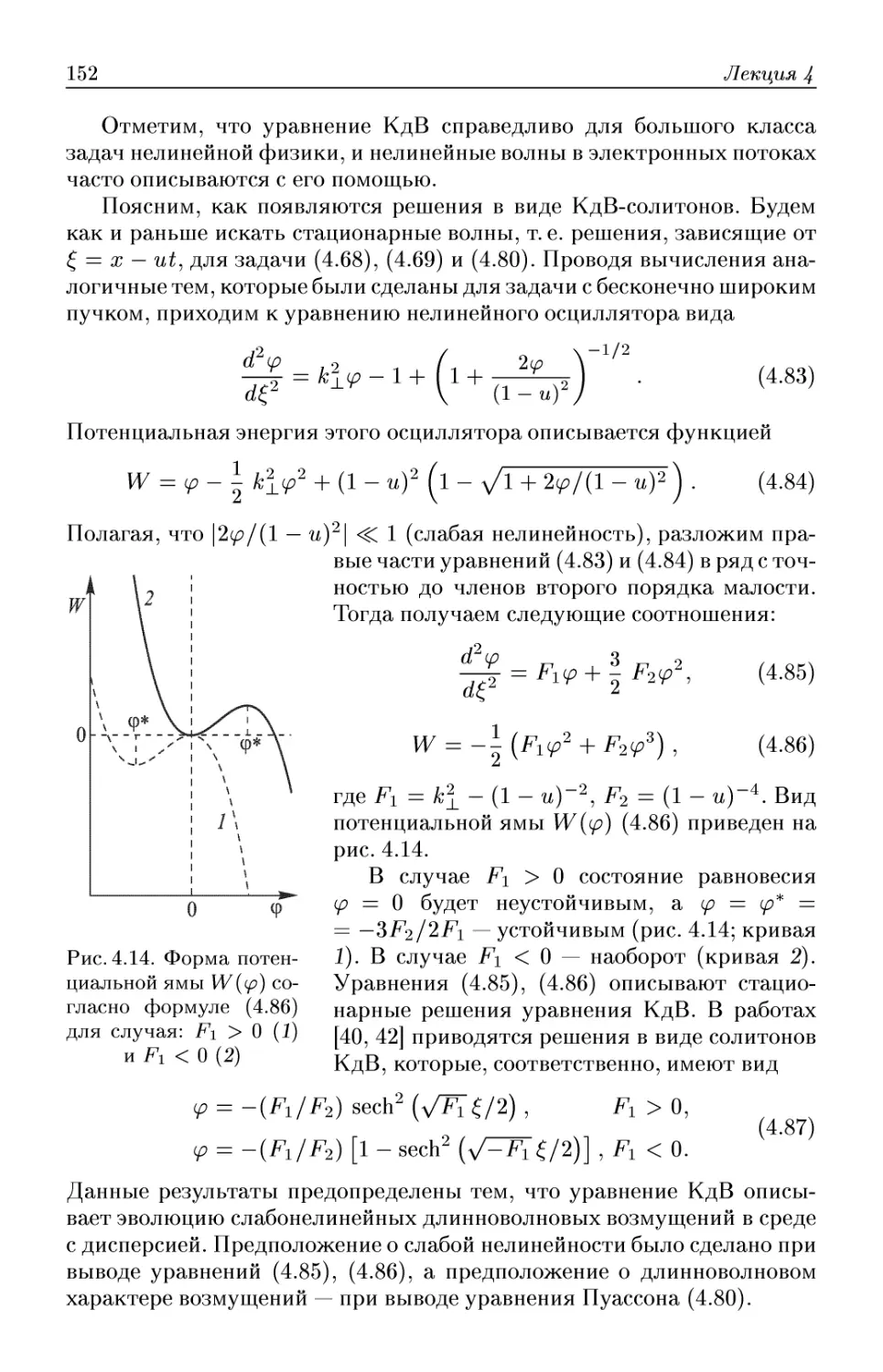
Лекция 4. Нелинейные явления в электронных потоках в гидро-
гидродинамическом приближении 120
Неизлунательная неустойчивость Пирса. Диод Пирса: от регулярных
автоколебаний к хаосу. Уравнения Годфри. Конечномерная модель ко-
колебаний в электронном потоке в диоде Пирса. Управление режимами
колебаний в диоде Пирса. Нелинейные волны пространственного заряда.
Моделирование нестационарных нелинейных процессов в клистроде с
помощью гидродинамических уравнений.
Лекция 5. Математическое моделирование нелинейных явлений
на ЭВМ и оптимизация параметров пролетных клистронов 164
Каскадное группирование электронного потока. Многорезонаторные
клистроны. Нелинейная двумерная модель взаимодействия элек-
электронного потока с ВЧ полями в клистроне. Уравнения одномерной
релятивистской теории многорезонаторного клистрона. Моделирова-
Моделирование и оптимизация многорезонаторных релятивистских клистронов.
Двумерные эффекты в многорезонаторных клистронных усилителях.
Многолучевые клистроны.
Лекция 6. Индуцированное и спонтанное излучение в резонанс-
резонансных автогенераторах 192
Индуцированное излучение в автогенераторах типа О. Спонтанное из-
излучение электрона при произвольном двиэюении через резонатор. Связь
между индуцированным и спонтанным излучением электрона в резо-
резонансных автогенераторах. Сравнение классического и квантового под-
подхода.
Лекция 7. Магнетрон, амплитрон и другие 201
Кинематическая дрейфовая теория движения электронов в скрещенных
статических электрическом и магнитном полях и в поле бегущей вол-
волны. Фазировка в скрещенных полях. Расчет мощности взаимодействия
и к.п. д. применительно к плоскому магнетрону. Что вносит цилин-
дричность в физику магнетрона. Цилиндрический магнетрон: история
создания от Хэлла до Бута и Рэндала. Вильям Браун и усилитель со
скрещенными полями. Карматрон и дематрон.
Лекция 8. Пространственный заряд в скрещенных полях 237
Пространственный заряд в скрещенных полях и три загадки магнетро-
магнетрона (свойства магнетрона при магнитном поле больше критического,
когда генерации нет; начало генерации в магнетроне; есть ли вооб-
вообще стационарный режим генерации в магнетроне). Неустойчивость
Содержание 5
электронного потока в скрещенных полях. Вычислительная физика и
магнетрон. Связь с проблемой турбулентности в электронном потоке.
Слоэюная динамика пространственного заряда в усилителе со скрещен-
скрещенными полями.
Лекция 9. История создания лампы бегущей волны и элемен-
элементарная теория взаимодействия электронного потока с бегущей
электромагнитной волной 269
История изобретения Рудольфом Компфнером лампы бегущей волны.
Роль Джона Пирса. Анализ взаимодействия электронного потока с
бегущей прямой электромагнитной волной на основе метода последова-
последовательных приближений. Квадратичная группировка. Качественное опи-
описание процесса группирования электронов в бегущей волне. Принципы
подобия для приборов с длительным взаимодействием (нерелятивист-
(нерелятивистские и ультрарелятивистские пучки).
Лекция 10. Нелинейная теория лампы бегущей волны 293
Нелинейные уравнения ЛЕВО. Линеаризация нелинейных уравнений
ЛЕВ. Дисперсионное уравнение ЛЕВ. Закон сохранения энергии в элек-
электронном потоке, взаимодействующем с бегущей электромагнитной
волной. Механизм фазировки в бегущей электромагнитной волне. Осо-
Особенности и результаты решения задачи на ЭВМ. Спиральная лампа
бегущей волны как основа усилительного модуля. Способы повышения
к.п.д. ЛЕВО.
Лекция 11. Лампа бегущей волны с цепочкой связанных резона-
резонаторов 330
Особенности физических процессов в ЛЕВО с цепочкой связанных резо-
резонаторов. Об особенностях физических процессов вблизи границ пропус-
пропускания периодической замедляющей системы. Дискретный и волновой
подход к анализу взаимодействия в ЛЕВО с цепочкой связанных резона-
резонаторов. Клистрон с бегущей волной. Линейные ускорители заряэюенных
частиц.
Лекция 12. Карсинотрон 367
Взаимодействие электронного потока с обратной электромагнитной
волной. Карсинотрон. "Чужие следы на песке... — история изобретения
лампы обратной волны Компфнером и Эпштейном. Теория пускового
реэюима лампы обратной волны в приблиэюении заданного поля. Нели-
Нелинейное поведение лампы обратной волны (результаты стационарной
нелинейной теории) Лампа обратной волны магнетронного типа.
6 Содержание
Лекция 13. Карсинотрон как распределенная автоколебательная
система 396
Натурный эксперимент и нестационарная теория ЛОВ: от монохрома-
монохроматических автоколебаний через автомодуляцию к динамическому хаосу.
Релятивистский карсинотрон: нестационарная теория и результаты
численного моделирования. Влияние сил пространственного заряда и
отражений от концов замедляющей структуры на генерацию в реляти-
релятивистской ЛОВ. Экспериментальное исследование сложной динамики в
релятивистской ЛОВ. Релятивистский карсинотрон и радиолокация.
Лекция 14. Некоторые методы решения нелинейных нестацио-
нестационарных задач электроники 434
Метод "частиц в ячейке1'. Учет влияния пространственного заряда.
Методы расчета полей в замедляющей системе: метод эквивалент-
эквивалентных схем и уравнение возбуждения. Конечно-разностный метод реше-
решения нестационарных уравнений релятивистского карсинотрона в ла-
гранжевых переменных. Математическое моделирование электронных
приборов с помощью самосогласованной системы уравнений Максвелла-
Власова. Применение метода функционального отображения к анализу
нестационарных процессов в ЛЕВ с запаздывающей обратной связью.
Лекция 15. Оротрон 470
Взаимодействие электронного потока с полями открытых резонато-
резонаторов. Излучение Смита-Парселла. Оротрон. Основные уравнения оро-
трона. Некоторые результаты теории оротрона. Нестационарные про-
процессы в оротроне. Методы повышения к.п. д. оротрона. Модификации
оротрона.
ПРЕДИСЛОВИЕ
Самый успешный путь обучения — проделать все
самому и учиться на собственных ошибках. Луч-
Лучше этого пути нет. Еще один хороший путь —
наблюдать, как кто-то проделывает это. Третий
путь — слушать лекции о том, как и что делать;
и последний стоящий путь — прочитать об этом.
Р. Компфнер
У книг по сверхвысокочастотной (СВЧ) электронике, в основном,
два стиля. Наиболее распространенный можно назвать техническим.
В соответствии с этим стилем большую часть книги занимает описа-
описание конструкций и параметров соответствующих приборов, разумеется,
с изложением основ их физики и элементов теории. Типичной книгой,
написанной в этом стиле, является известный учебник И.В. Лебедева
«Техника и приборы СВЧ» (Том I. Техника СВЧ, М.: Высшая школа,
1970 и Том П. Электровакуумные приборы СВЧ, М.: Высшая школа,
1972). Второй стиль — физический. По-настоящему в этом стиле напи-
написана, по нашему мнению, лишь одна книга — книга Л.А. Вайнштейна
и В.А. Солнцева «Лекции по сверхвысокочастотной электронике» (М.:
Сов. радио, 1973). Эта книга уникальна и останется на все времена,
пока существует СВЧ-электроника. Но с момента её издания прошло
почти тридцать лет. Книга не устарела, но стала неполной: она не
отражает сегодняшнего дня СВЧ-электроники. Кроме этого, с появле-
появлением вакуумной и плазменной релятивистской электроники, лазеров на
свободных электронах и вакуумной микроэлектроники к исследовани-
исследованиям подключились физики, не имеющие систематического образования
в СВЧ-электронике. Сказанное определило появление предлагаемых
читателю лекций. Это действительно лекции, которые в разном виде
(общий курс, спецкурсы) читались студентам-радиофизикам Саратов-
Саратовского государственного университета, на Саратовских школах-семина-
школах-семинарах по электронике СВЧ и радиофизике, на соответствующих предпри-
предприятиях и в НИИ. Поскольку в последнее время оба автора занимают-
занимаются нелинейной динамикой, под которой сами понимают современную
теорию колебаний и волн, в книге широко используются представле-
представления и методы этого нового междисциплинарного направления в науке.
В частности, использованы элементы курса лекций «Нелинейная дина-
динамика и сверхвысокочастотная электроника», который один из авторов
(Д.И. Трубецков) прочитал в июне 2001 года в Сеульском национальном
университете (Корея).
Ещё одна особенность лекций — в них определённое место зани-
занимает история сверхвысокочастотной электроники. М.В. Волькенштейн
8 Предисловие
в своей книге «Перекрестки науки» (М.: Наука, 1972) писал: «Есть
физики — и очень хорошие физики, которые не интересуются историей
своей науки. Мне это не импонирует. Мне всегда казалось, что знание
истории науки, более того, знание творческих индивидуальностей, её
развивающих, очень обогащает мысль. В отличие от искусства наука
объективна, она имеет дело с независимыми от человека законами
природы. Но наука так же как и искусство, создаётся людьми, она есть
и познание и творчество. Интересны не только окончательные резуль-
результаты исследования, но и путь, который к ним привёл, в особенности,
если этот путь был найден великим интеллектом». С этим трудно не
согласиться, тем более потому, что основные идеи СВЧ-электроники
выдвинули не только физики, но и лётчик Сигурд Вариан, гуманитарий
Хэлл и архитектор Компфнер.
Основное внимание в книге уделено детальному описанию физиче-
физических явлений, возникающих при взаимодействии электронных потоков
с электромагнитными полями. Математические выкладки приводятся
подробно. В ряде случаев даны алгоритмы численного решения задач
на ЭВМ. Последнее авторам кажется особенно важным, потому что
через всю книгу проходит попытка показать тесную связь сверхвысоко-
сверхвысокочастотной электроники с современной нелинейной теорией колебаний
и волн, которая невозможна без вычислительного эксперимента.
Список литературы к каждой лекции не является полностью ис-
исчерпывающим и охватывает, как правило, те работы, которые непо-
непосредственно использовались при написании лекции. В Предисловии
нет краткого изложения каждой лекции, поскольку дано расширенное
оглавление, повторяющееся перед текстом каждой из лекций.
Подчеркнём, что первая часть книги будет полезна как раз для фи-
физиков, которые не изучали систематически СВЧ-электронику в универ-
университете (книга получилась очень объёмной и пришлось разбить её на два
тома). В первом томе излагаются основные понятия, методы и модели
«классической» сверхвысокочастотной электроники. Рассматриваются
такие, уже ставшие привычными, приборы как клистроны, магнетроны,
лампы бегущей и обратной волны. Во втором томе пойдет речь о таких
современных областях иследований в электронике как взаимодействие
криволинейных электронных потоков с электромагнитными волнами;
лазеры на свободных электронах; сверхизлучение в электронных пото-
потоках; плазменная СВЧ-электроника; сверхмощные релятивистские гене-
генераторы высокочастотного излучения; вакуумная микроэлектроника.
Лекции предназначены для физиков различных специальностей,
интересующихся процессами взаимодействия электронов с электромаг-
электромагнитными полями (в том числе для тех, кто ранее не изучал СВЧ-элек-
СВЧ-электронику), для научных работников, аспирантов и инженеров, проводя-
проводящих исследования в области вакуумной СВЧ-электроники, радиофизи-
радиофизики, радиотехники и физики плазмы. Они могут быть полезны студентам
старших курсов соответствующих специальностей.
Д. И. Трубецков
А.Е. Храмов
Лекция 1
ВВОДНАЯ
Частоты электромагнитных колебаний, лежащие
в пределах от 3 • 108 до 3 • 1011 колебаний в секун-
секунду, принято называть сверхвысокими.
СД. Гвоздовер. Теория электронных
приборов сверхвысоких частот, М.:
Гос. изд-во технико-теоретической
литературы, 1956, с.9.
Прежде чем приступить к изложению, сделаем
несколько вводных замечаний.
Л.А. Вайнштейн, В.А. Солнцев. Лек-
Лекции по сверхвысокочастотной элек-
электронике, М.: Советское радио, 1973,
с.5.
Основные особенности сверхвысокочастотной электроники. Пять
идей, которые создали С В Ч-электронику. Индивидуальное излучение
заряженных частиц (спонтанное излучение классических осциллято-
осцилляторов). Индуцированное излучение ансамбля возбужденных классических
осцилляторов. Возбуждение резонансной системы заданным током.
Стационарные уравнения возбуждения линии передачи электронным
потоком. Нестационарная теория возбуждения волновода током
медленно меняющейся амплитуды.
Первая лекция настоящего лекционного курса сверхвысокочастот-
сверхвысокочастотной электроники для физиков посвящена вводным замечаниям об осо-
особенностях процессов взаимодействия носителей заряда с электромаг-
электромагнитными полями на сверхвысоких частотах (СВЧ), о связи сверх-
сверхвысокочастотной электроники с другими разделами физики и о тех
фундаментальных идеях, которые привели к развитию электроники
сверхвысоких частот как самостоятельной науки. Во вводной лекции
рассматриваются общие закономерности спонтанного и вынужденного
излучения заряженных частиц, вводится фундаментальное для ваку-
вакуумной СВЧ-электроники понятие фазировки (фазовой фокусировки,
группировки), а также выделяются случаи линейной и квадратичной
10
Лекция 1
группировки. В конце лекции выводятся уравнения возбуждения резо-
резонаторов и волноведущих структур заданными токами, которые будут
далее использоваться для описания явлений и процессов в сверхвысоко-
сверхвысокочастотных электронных приборах на протяжении всего курса лекций.
Основные особенности СВЧ-электроники.
Пять идей, которые создали СВЧ-электронику
В центре внимания электроники сверхвысоких частот как науки
находится изучение процессов взаимодействия потоков заряженных
частиц с переменными электромагнитными полями. При этом электро-
электроника СВЧ исследует преимущественно такие системы, в которых время
пролета электронов через пространство взаимодействия является срав-
сравнимым с длительностью периода возбуждаемых электронным потоком
колебаний или даже намного превосходит его.
В любом электронном приборе взаимодействие переменного элек-
электромагнитного поля (электромагнитных колебаний или волн) с элек-
электронами (свободными или связанными) является основным в его работе.
Поле воздействует на электронный поток, создает в нем переменный
ток, который, в свою очередь, изменяет поле. В физике такие систе-
системы называют самосогласованными. Разумеется, можно, да и нужно,
детализировать устройство электронного прибора. Но всегда имеется
связка поле-электроны (в более общем виде — поле-активная среда;
см. рис. 1.1).
Детализация: электродинамическая система,
Изующая поле нужного вида, ввод и вывод энергии
Колебательная или
волноведущая система
Электроны
(свободные или
связанные)
Детализация для вакуумных ламшэммитер (катод),
электронно-оптическая система, коллектор,
система фокусировки и формирования пучка
КОЛЕБАНИЯ ВОЛНЫ
(Могут быть аккустические,
а не только электромагнтные)
+
Взаимодействие
ЭЛЕКТРОНЫ
Рис. 1.1. Колебания, волны и электроны в электронных приборах
Одна из главных тенденций развития современной радиоэлектрони-
радиоэлектроники — повышение частоты («вечная» тенденция) и увеличение мощности
различных устройств. Электроника сверхвысоких частот возникла как
Вводная 11
развитие низкочастотной радиотехники по мере продвижения в сторону
все более высоких частот (или соответственно, все более коротких волн).
Такое продвижение было вполне закономерным следствием задач, кото-
которые стали возникать в конце 20-х-начале 30-х годов перед радиотехни-
радиотехникой. В первую очередь это были задачи, связанные с радиорелейной свя-
связью, радиолокацией, научными исследованиями. Одновременно с этим
выяснилось, что классические для низкочастотной техники методы
создания электронных устройств оказываются практически непримени-
неприменимыми на сверхвысоких частотах, т. е. на частотах, лежащих в диапазоне
/~ 0,3-=-3- 103 ГГц.
Это связано с тем, что для ламп, работающих на сравнительно низ-
низких частотах, имеет место выполнение двух принципиальных условий:
*Ж1, A.1)
где к = ojIс = 2тг/А — волновое число, D — характерный размер про-
пространства взаимодействия электронного устройства;
"*прол < 1, A-2)
где и — частота колебаний, ?Прол — время пролета электрона через
пространство взаимодействия.
Условие A.1) («полевое» условие) означает, что переменные поля
в лампе не должны проявлять своих волновых свойств: электронная
лампа должна быть элементом цепи с сосредоточенными параметрами.
Второе условие A.2), которое можно назвать «электронным», означает,
, [ах / / ,ч
что время пролета электрона tuv>OJl = —, г через лампу (v(x, t) —
J v(x,t)
xx
скорость электрона при его пролете через пространство взаимодействия
|#2 — х\\) много меньше периода колебаний электромагнитного поля.
Иными словами электрон при движении в лампе не должен проявлять
своей инерционности: величина Сс^прол? или как ее еЩе называют угол
пролета электрона, очень мала (можно считать её равной нулю).
В СВЧ-электронике эти условия уже не выполняются и заменяются
другими, часто противоположными условиям A.1) и A.2):
kD~l (&?>>1), A.3)
^прол ~ 1 Мпрол > 1). A-4)
Видимо, можно утверждать, что СВЧ-электроника, как самостоя-
самостоятельная наука, возникла тогда, когда было осознано, что попытки про-
продвижения приборов в высокочастотный диапазон, для работы которых
принципиальны условия A.1) и A.2), обречены на провал, и нужны
новые принципы и методы усиления и генерации электромагнитных
12 Лекция 1
волн на сверхвысоких частотах. Каковы же эти методы и как, кем
и когда они были предложены?
Впервые колебания на сверхвысоких частотах были получены
в 1919 году в аудионе (вакуумном триоде) — трехэлектродной лампе,
содержащей управляющую сетку между нитью накала и анодом. Триод
был сконструирован для работы на низких частотах, а СВЧ-колебания
имели место при наличии колебательного движения электронов
в межэлектродном пространстве при положительном потенциале на
сетке и отрицательном на аноде [1]. Вскоре были открыты и исследованы
колебания в простейших магнетронах — «гладком» и с разрезным
анодом, а затем в диодах — генераторах.
Далее новые идеи появлялись в изобилии, и их количество росло
по законам взрывной неустойчивости... Однако «развитие идей в элек-
электронике и производство электронных приборов далеко не всегда со-
соответствуют друг другу» [2, стр. 221-222]. Надо иметь в виду, что
приборам нового типа при завоевании «места под солнцем» — массо-
массового применения — приходится вести жесткую конкурентную борьбу
с приборами старых типов, технология которых хорошо отработана
и производство налажено. Лишь немногие новые приборы выдержива-
выдерживают эту борьбу: следя за развитием сверхвысокочастотной электроники,
нетрудно заметить, что ежегодно появляется несколько новых типов
приборов, которые, однако, изготавливаются в виде немногочисленных
опытных экземпляров для лабораторных исследований и затем оста-
остаются лишь вехами, отмечающими развитие научных идей. Массовое же
применение получают, как правило, только приборы с «выдающимися
свойствами» [2, стр. 221-222]. Очевидно, что выдающимися свойствами
обладают те приборы, в основе принципа действия которых лежат
и выдающиеся идеи — идеи «грубых» (в смысле, близком теории коле-
колебаний) механизмов взаимодействия электронных потоков со стоячими
или бегущими электромагнитными полями. Наверное, не будет большой
ошибкой утверждение, что в истории становления СВЧ-электроники
было пять выдающихся идей, которые и определили дальнейшее разви-
развитие этой науки.
Данный курс построен таким образом, что последовательно будет
рассматриваться каждая из этих идей, ее достоинства и недостатки,
а также те приборы, которые были реализованы на основе той или иной
идеи. Перечислим эти идеи с краткой их характеристикой.
Идея первая: модуляция электронов по скорости и груп-
группирование электронов в пространстве дрейфа. Условие A.4),
характерное для СВЧ-диапазона, сводило на нет все преимущества
и достоинства «статического» способа управления электронным по-
потоком, когда управляющий элемент воздействует непосредственно на
пространственный заряд электронного облака, создаваемого катодом.
Поэтому усилия исследователей были направлены на то, чтобы свести
к минимуму влияние инерционности электронов. Первыми, кто поняли,
Вводная 13
как превратить этот недостаток (инерционность) в достоинство, были
А. Арсеньева-Хейль и О. Хейль A933 г.), открывшие метод скоростной
модуляции, а первыми экспериментально реализовавшими новый при-
прибор (клистрон) были братья Вариан и их коллега по Станфордскому
университету Хансен (заметим, что они не знали до опубликования
своих результатов о работе Арсеньевой-Хейль и Хейль). Основная их
идея — разделить процесс скоростной модуляции потока (по схеме
она осуществлялась в узком зазоре объемного резонатора и приводила
к периодическому изменению скорости электронов без модуляции по
плотности электронного потока) и группирования, которое осуществля-
осуществлялось в пространстве дрейфа, свободном от каких-либо высокочастотных
полей. В результате группировки в потоке возникают электронные
уплотнения с частотой модулирующего напряжения. Это так называе-
называемый динамический способ управления электронным потоком.
Идея вторая: взаимодействие высокочастотных электро-
электромагнитных полей с электронами в скрещенных статических
электрическом и магнитном полях. Приборы, основанные на та-
таком взаимодействии, — магнетроны — являются одними из первых
нашедших широкое практическое применение приборов сверхвысоко-
сверхвысокочастотной электроники. Показательно, что одна из работ по истории
СВЧ-электроники (ее автор Д. Брайттейн, профессор истории науки
Института Технологии в Джорджии) называется «Магнетрон и начало
микроволнового века» [3]. Во время второй мировой войны и после
нее магнетрон стал «рабочей лошадкой» радиолокационных станций.
Заметим, что магнетрон не является единственным представителем,
реализующим данную идею: широко исследовались и разрабатывались
и другие приборы со скрещенными полями.
Идея третья: взаимодействие электронного потока с бегу-
бегущей прямой электромагнитной волной. Если мы не можем обеспе-
обеспечить малое время пролета электрона, чтобы поле за время его пролета
не изменялось, тогда пусть «... поле движется вместе с электронами».
Если фазовая скорость волны будет близка к скорости электронного
пучка (этого можно добиться путем замедления волны в той или иной
искусственной среде — замедляющей системе), то при определенных
условиях получим усиление электромагнитной волны в такой системе.
Осознание этого позволило в свое время создать Рудольфу Компфнеру,
чьи слова приведены в эпиграфе к предисловию к курсу лекций, элек-
электронные приборы с длительным взаимодействием, наиболее известный
из которых — лампа бегущей волны.
Идея четвертая: взаимодействие электронного потока
с обратной электромагнитной волной. В этом случае электронный
пучок как и в предыдущем случае пребывает в синхронизме (не
точном!) с электромагнитной волной, однако групповая скорость
волны (обратной пространственной гармоники) направлена навстречу
пучку. Отсюда и название прибора — карсинотрон (в переводе
14 Лекция 1
с греческого — «рак, пятящийся назад»), правда, более распространено
другое название — лампа обратной волны. Карсинотрон-генератор
стал в современной теории колебаний и волн эталонной моделью
распределенной автоколебательной системы.
Идея пятая: взаимодействие криволинейных электронных
потоков с электромагнитными полями. Мазеры на циклотронном
резонансе. Основная идея, которая привела к созданию мазеров на
циклотронном резонансе — это идея использования индуцированного
излучения в потоке электронов, вращающихся в магнитном поле. В этом
случае имеет место фазовая группировка, возникающая из-за неизо-
неизохронности электронов-осцилляторов, т. е. из-за зависимости частоты
вращения электрона в магнитном поле от энергии электрона.
Конечно, этот краткий обзор основных идей СВЧ-электроники да-
далеко не полон: сюда не вошел параметрический способ управления
электронным потоком, разработка которого привела к появлению ла-
лазеров на свободных электронах. Может быть ее следует считать
шестой идеей из создавших С1ВЧ-электронику'?'За рамками этих пяти
идей осталась идея использования эффекта сверхизлучения ансамбля
классических электронов-осцилляторов для генерации сверхмощных
импульсов СВЧ-излучения. Рассмотрению всех этих вопросов будет
уделено внимание в лекциях. В курсе лекций будут также рассмотрены
результаты численного моделирования различных систем СВЧ-элек-
СВЧ-электроники и, более того, в некоторых случаях будет обсуждаться методика
построения моделей и вычислительных схем.
В заключение вводной части отметим глубокую связь между
СВЧ-электроникой и такими областями фундаментальных исследо-
исследований как нелинейная теория колебаний и волн, теория излучения,
нелинейная динамика ([4-7]). Следует сказать, что специалисты
в области электроники сверхвысоких частот всегда использовали
язык теории колебаний и волн. Более того, электроника, наряду
с гидродинамикой, одной из первых стала «нелинейной» наукой,
применяя различные методы вычислительной физики. Огромна
роль в понимании работы различных электронных СВЧ-приборов
теории излучения. Так с точки зрения теории излучения все приборы
сверхвысокочастотной электроники основаны на различных типах
индуцированного излучения. Показательно, что началу разработки
и исследованию мазеров на циклотронном резонансе положили работы
именно по изучению индуцированного излучения (как в квантовой,
так и классической трактовке) потока электронов, движущихся
в магнитном поле. В последние годы успехи нелинейной динамики
«заставили» специалистов в области СВЧ-электроники искать типично
нелинейные феномены и явления в системах электронный поток-
электромагнитное поле: уединенные волны, режимы возникновения
динамического хаоса, синхронизацию автоколебаний, образование
Вводная 15
структур в электронных потоках. Вопросы исследования нестацио-
нестационарных процессов (в особенности сложной динамики) в электронных
системах кроме несомненного фундаментального значения имеют
и широкое практическое приложение в связи с необходимостью
создания мощных генераторов широкополосного сложного сигнала
для применения в системах радиолокации и радиопротиводействия,
в системах нагрева плазмы в установках управляемого термоядерного
синтеза и т. д.
Приведенный выше обзор основных особенностей сверхвысокоча-
сверхвысокочастотной электроники не претендует ни на полноту, ни на систематич-
систематичность. Скорее это аннотация того материала, который авторы нашли
нужным включить в лекции.
Индивидуальное излучение заряженных частиц
(спонтанное излучение классических осцилляторов)
Преобразование энергии направленного движения электронного по-
потока в электромагнитное излучение может происходить за счет резо-
резонансного взаимодействия отдельных электронов с полем монохрома-
монохроматической волны. В классической электродинамике для описания этих
процессов используется методика, основанная либо на нахождении по-
поля, возбужденного невозмущенным электроном-осциллятором, либо на
вычислении работы электромагнитного поля над электроном, соверша-
совершающим заданное движение, невозмущенное этим полем [8]. Однако более
изящным является подход к рассмотрению этих явлений на основе пред-
представлений квантовой электродинамики [10], причем при необходимости
всегда возможно сделать соответствующий переход к классическому
пределу.
Предположим, что электроны совершают периодическое (колеба-
(колебательное) движение около некоторого ведущего центра, который сам
движется со скоростью v± (состояние 1). При этом электрон отдает
энергию плоской электромагнитной волне с волновым вектором к, где
|к| = с^/^ф, Уф — фазовая скорость волны в данной среде. С квантовой
точки зрения в лабораторной системе отсчета электрон испускает квант
с энергией Ни и импульсом /ik, меняя импульс с pi на р2- Электрон-ос-
Электрон-осциллятор в системе отсчета ведущего центра можно рассматривать как
частицу с ненулевой внутренней энергией и массой mi, отличной от
массы то покоящегося электрона. Когда электрон-осциллятор пере-
переходит в состояние 2, в системе ведущего центра его масса становится
равной ?7i2, и частица переходит на соседний нижний энергетический
уровень с излучением кванта Ни о, где ujq — частота колебаний осцил-
16 Лекция 1
лятора в собственной системе отсчета. В этой системе закон сохранения
энергии запишется в виде:
mic2 — ГП2С2 = hojQ. A-5)
В лабораторной системе отсчета законы сохранения энергии и импульса
имеют следующий вид:
-- hu, A.6)
Pi-P2=ftk, A.7)
где
V\2 ',2*1,2 /-1 Q\
1,2 = , Pl,2 = , A.8)
Преобразуем соотношение A.6). Для этого перепишем первое слагаемое
в виде:
2 /-1 ,
/ L "Г
Аналогично для второго слагаемого в соотношении A.6) имеем
i/m|c4 +p|c2 . Тогда закон сохранения энергии A.6) примет вид:
z2 = Йо;, A.9)
В последнем соотношении квадратные корни представляют собой пол-
полные энергии частиц в состояниях 1 и 2. Исключим из соотношений A.5)-
A.9) ?7i2 и Р2- Соответственно из равенств A.5), A.7) и A.9) имеем:
A.10)
A.11)
т^с4 + р2с2 = (НиJ - 2hujJm\c4' + p\c2 + т\с4 + р\с2. A.12)
Подставляя соотношения A.10) и A.11) в равенство A.12) получаем:
J - 2hu>om1c2 + mic4 + pjc2 - 2H(p1k)c2 + /i2&2c2 =
2
/, Ч2 о?- ггцс
= (/го;) - ofc' ¦
Вводная 17
Окончательно находим, что
О О/ , ч ТП\С К / О О , О On /^ ^ „ч
wormi + c^(piki) - и; = - (u)q - oo + A:^c^). A.13)
Перейдем в выражении A.13) к классическому пределу, устремляя
>• 0. Тогда
COS в,
Последняя формула выражает эффект Доплера: излучение источ-
источника, имеющее частоту oj$ в системе отсчета, в которой он покоится,
воспринимается неподвижным наблюдателем как волна с частотой о;,
если источник движется со скоростью v\ под углом в к линии наблю-
наблюдения (угол измеряется в лабораторной системе отсчета). Соотношение
A.14) выражает условие резонанса при взаимодействии осциллятора
и высокочастотного поля с поправкой на эффект Доплера: собственная
частота осциллятора oj$ равна той частоте электромагнитной волны,
которую он «видит» в своей системе отсчета.
Рассмотрим некоторые важные частные случаи.
1. ujq =0. Изменение импульса в классическом пределе в соответ-
соответствии с формулой A.7) ничтожно мало. При излучении внутренняя
энергия электрона-осциллятора не меняется, поэтому он ведет себя по-
подобно заряженной частице, движущейся равномерно и прямолинейно.
В соответствии с соотношением A.14) и ф 0 лишь при обращении в нуль
знаменателя, т. е.
cos0 = ^. A.15)
Vl
Результат очевиден: соотношение A.15) — необходимое условие излу-
излучения Вавилова-Черенкова, которое наблюдается при v\ ^ Уф. Таким
образом излучение имеет место лишь при сверхсветовых скоростях дви-
движения частицы и возможно только для медленных электромагнитных
волн, т. е. при Уф < с.
2. ооо > 0. В этом случае знаменатель в соотношении A.14) должен
быть положителен, т. е.
v^ cos в '
что справедливо при vi/уф < 1. Таким образом возможно взаимодей-
взаимодействие осцилляторов с быстрыми электромагнитными волнами.
18 Лекция 1
3. ojo < 0. Как следует из закона сохранения энергии, осцилляторная
энергия частицы при излучении возрастает, что соответствует аномаль-
аномальному эффекту Доплера. Из формулы A.14) видно, что
Уф COS в '
а, следовательно, излучение будет лишь при v\ > Уф, т.е. осцилля-
осциллятор будет перемещаться со сверхсветовой скоростью. Любопытно, что
при аномальном эффекте Доплера осциллятор излучает, одновременно
увеличивая свою энергию. Ясно, что и излучаемую и колебательную
энергию он черпает из энергии дрейфового движения. Интересно, что
в область взаимодействия можно вводить и неосциллирующий пучок,
поскольку потом электроны могут «раскачаться».
Рассмотрим теперь пучок, образованный электронами, которые дви-
движутся в однородном магнитном поле. В системе отсчета, связанной с ве-
ведущим центром, частицы вращаются по окружностям. Циклотронная
частота (частота вращения или гирочастота) выражается формулой
еВ ujco ( ч
Шс = ^г = Т' ( 6)
где т — релятивистская масса, j = 1/д/1 — (v/сJ — релятивистский
фактор, В — магнитная индукция и ojc$ — нерелятивистская гирочасто-
гирочастота. Излучение таких электронов называется магнитотормозным. В со-
соответствии с квантовой теорией такие осцилляторы в нерелятивистском
случае имеют эквидистантный энергетический спектр с расстояниями
между соседними уровнями — «уровнями Ландау» — Hwco. У реляти-
релятивистского осциллятора расстояние между уровнями Ландау равно Hwc,
и, следовательно, спектр слабонеэквидистантен, что важно, например,
для создания мазеров на циклотронном резонансе.
Индуцированное излучение ансамбля возбужденных
классических осцилляторов
Итак, при вышесформулированных условиях электроны-осцилля-
электроны-осцилляторы в среде с высокочастотным полем будут излучать. Но без учета
реакции поля излучения поведение каждого осциллятора будет незави-
независимо от других, а электромагнитное поле некогерентно. Эффективность
энергообмена мала. В квантовой теории такое излучение называется
спонтанным. Когерентное излучение должно быть индуцированным,
в этом случае вероятность испускания квантов существенно зависит
от внешнего электромагнитного поля. Индуцированные процессы из-
излучения в вакуумной электронике связаны с группировкой (фазиров-
Вводная 19
кой) г) — образованием электронных сгустков в благоприятной (тормо-
(тормозящей) фазе высокочастотного поля. Фазировка происходит в результа-
результате действия поля на движение первоначально несфазированных частиц.
Найдем условия возникновения когерентного индуцированного из-
излучения в системе классических электронных осцилляторов, следуя
работам [10, 11]. Для этого рассмотрим совокупность большого числа
одинаковых осцилляторов, образованных электронами, совершающими
движение в одномерной потенциальной яме Uo(x). На осцилляторы
в этом случае действует сила Fq(x) = — dUo/dx, а также высокоча-
высокочастотное поле F(t). Последнее будем предполагать однородным, т.е. не
зависящим от координаты ж, и слабым, что позволит решать задачу
в линейном приближении. Уравнение движения электронов под дей-
действием указанных сил имеет вид
m^-f - F0(x) = F(t). A.17)
at
Невозмущенное периодическое движение электрона будет описываться
уравнением
т-
- F0(x^) = 0. A.18)
dt2
Решение последнего уравнения представляется рядом Фурье:
A.19)
Так как x^(t) является вещественной функцией, то X-k = х*к. В па-
параболической потенциальной яме невозмущенные колебания гармони-
гармонические, и в сумме A.19) отличны от нуля только слагаемые с к = =Ы.
В общем же случае все хи не равны нулю. Кроме того, при этом коле-
колебания неизохронны, т. е. частота ио зависит от энергии ? осциллятора:
где энергия
При данной постановке задачи осцилляторы могут отличаться только
фазой ifo.
Учитывая предполагаемую малость возмущения, вносимого высоко-
высокочастотным полем в движение электронов-осцилляторов, а также огра-
х) Понимание важности такого явления как группировка электронного по-
потока было впервые осознано Брюхе и Рекнагелем в связи с анализом динами-
динамического способа управления электронным потоком [9]. Они же впервые ввели
в электронику термин фазовая фокусировка.
20 Лекция 1
ничения на время жизни осцилляторов (на этом остановимся ниже),
представим решение A.17) в виде x(t) = x^\t) + x^(t), где \х^\ <С
<С |ж^|. Тогда, раскладывая силу Fq(x) в ряд Тейлора, получаем
A-20)
С учетом разложения A.20) и выражения A.18) уравнение A.17) стано-
становится линейным и принимает вид
(L21)
где dFo(x( ')/dx^ ' — известная функция времени.
Вспомним некоторые сведения из теории дифференциальных урав-
уравнений.
Теорема. Частное решение неоднородного линейного уравнения
второго порядка в действительных переменных
может быть представлено в виде
ъ
р
у = G(x, xf)f(xf) dx' (a < х < 6),
а
где G(x,x') есть функция Грина, дающая «фундаментальное» реше-
решение, причем
G(x, х') = - (y1(x)y2(xf) - у2(х)у1(х'))Н(х - х').
Здесь Н — функция Хевисайда, у\ и у2 — линейно независимые ре-
решения соответствующего однородного уравнения, W = У\{х)у2{х) —
— У2{х)у\{х) — вронскиан исходного уравнения. Для линейной неза-
независимости решений у\ и y<i необходимо и достаточно, чтобы W ф
= 0 М х е (а, Ь).
С учетом утверждения этой теоремы решение уравнения A.21) мо-
может быть записано в виде
*')] dt\ A.22)
to
Вводная 21
где у\ и г/2 — частные линейно независимые решения однородного
уравнения
dt2
В качестве у\ и ?/2 можно использовать частные производные
(Ц t)
л^ ' , где С некий параметр, определяющий невозмущенное ко-
колебание х(°'(С, t). Действительно, дифференцируя уравнение A.18)
частным образом по С, приходим к уравнению
'
эс
которое имеет вид A.23). В качестве С можно использовать любые два
параметра, связанные с начальными условиями, если для соответству-
соответствующих функций W ф 0. Примем за параметры энергию ? и фазу (ро.
Тогда
дх^ дх^ , ^
A.24)
Olfo ОС
Вронскиан в этом случае равен W = 1/muio ф 0, и выбранные значе-
значения у\ и ?/2 действительно линейно независимы.
Прямой путь исследования излучательных свойств ансамбля элек-
электронов-осцилляторов состоит в вычислении суммарного переменного
тока, возникающего при наложении высокочастотного поля, а затем
проводимости всей системы, как отношения тока к переменному напря-
напряжению. Здесь принципиальны два момента.
1. Электроны колеблются в разных фазах и воздействие переменного
поля на движение отдельной частицы может быть как тормозящим,
так и ускоряющим. Поэтому для нахождения суммарного эффекта
требуется усреднить найденный ток по фазам.
2. Необходимо учитывать конечность времени пребывания электро-
электрона в высокочастотном поле (время жизни осциллятора г). Понятно,
что при бесконечном времени жизни осцилляторы будут непрерывно
обмениваться энергией с полем и средний эффект окажется нулевым.
Рассмотрим вначале второй момент. Введем функцию распреде-
распределения частиц по временам жизни Ф(т). Если полное число частиц
в единице объема TVo, то число частиц dN, времена жизни которых
лежат в интервале (г, г + dr), равно dN = N^{r)dr. Плотность тока,
создаваемая всеми электронами:
j = -е
сю
dN = -e7V0 [ х{1)Ф(т) dr. A.25)
22 Лекция 1
Усредняя по начальным фазам, которые распределены равномерно
и явно входят в выражения для у\ и у2 (см. ниже), получаем выражение
для тока вида
2тг сю у- 2тг ч
(j) = — \ j d(fo = —eNo Ф{т) [ — ir1' d(fo ) dr =
2тг J J V 2тг J I
о oo
СЮ
= -e7V0 [ Ф(т)(х{1)) dr. A.26)
о
Задача сводится к вычислению (i^1)), где х^ определяется квадрату-
квадратурой A.22), т.е.
t 2тг
(?(!)) = ^ [ [ [y2(t)y1(tf)-y1(t)y2(tf)]F(tf)dtf dip0. A.27)
2тг J J
?о о
Найдем явные выражения для ?/i, ^/2, 2/1, 2/2 на основе ряда Фурье
A.19):
A.28)
^ = -000 Y^ k2xkejk{uJot^°\ A.29)
д_
д? ~ ^ ~д?
к= — оо
У2 = 5Z ^я7 ko^fcejfe(a;o^+(/?o)j , A.31)
А;= — сю
При подстановке этих рядов в выражение A.27) появятся интегралы
типа
2тг
сю
k= — oo
Очевидно, что отличны от нуля только те члены двойных рядов, для
которых к = I. Тогда с учетом соотношения
к= — оо к= — оо
Вводная 23
для интеграла A.27) по сро можно записать
2тг сю
к= — оо
х (-jk)x*k e~juJot' +oj0k2xkejkuJot-
oo o
E2 &
k= — oo
Если высокочастотное поле меняется по гармоническому закону (F(t) =
= — еЕ = —еЕ°е^шЬ), то из выражения A.27) находим:
to
dt' =
--и;ое 2^ — |
где Ао;^ = о; — kujo- Окончательно, учитывая, что t — to = т, получим:
= juoeE f^ к24с Ukfc|2l"^1 " f12)
г, ^^ L J
Для вычисления плотности тока по формуле A.26) необходимо за-
задать явный вид функции распределения электронов-осцилляторов по
временам жизни Ф(т). Зададимся для определенности следующим ви-
видом Ф(т) = ve~VT. Легко видеть, что среднее время жизни для принятой
функции (г) = 1/v.
Интегрируя выражение A.26) для (j) no r (при известном законе
Ф(т)), получаем плотность тока, а затем, деля результат на поле Е,
находим следующее выражение для проводимости среды, образованной
ансамблем осцилляторов:
д — " * 'U~u / ^ •" ЛС I „'Л, .. i ,. I * (l.OOJ
Проводимость в общем случае является комплексной величиной.
Рассмотрим некоторые частные случаи, представляющие физический
интерес.
24 Лекция 1
1. v — О (время жизни осцилляторов бесконечно). Согласно A.33)
проводимость при Auik ф 0 чисто реактивная. В системе электроны-ос-
электроны-осцилляторы-высокочастотное поле происходит перекачка энергии, од-
однако, энергия каждой из подсистем остается в среднем постоянной.
2. v = ос (время жизни осцилляторов равно нулю). В этом случае
а — О — взаимодействия нет.
3. Линейные осцилляторы. dojo/d? = 0, а х^ = x1e^()
+ а^е"-?^0*"^0). Энергия ? = 2mu>o\xi\2 и, следовательно, d|
= l/2mujQ. Тогда из уравнения A.33) получаем выражение для прово-
проводимости:
а = **> [, \ + , \ 1 - A-34)
Исследуем а вблизи резонанса, когда |До;| = \и — uq\ ^C о;о, а время
жизни существенно превышает период колебаний, т. е. г = l/i/ ^> 7q =
= 2тг/о;о, или // <шо. При указанных условиях первый (резонансный)
член в квадратных скобках намного больше второго, и а = af + ja"',
где
2 e2N0Auj
а = —= ;j=-, сг = -
2ш [До;2 + i/2] ' 2m [До;2 + и2] '
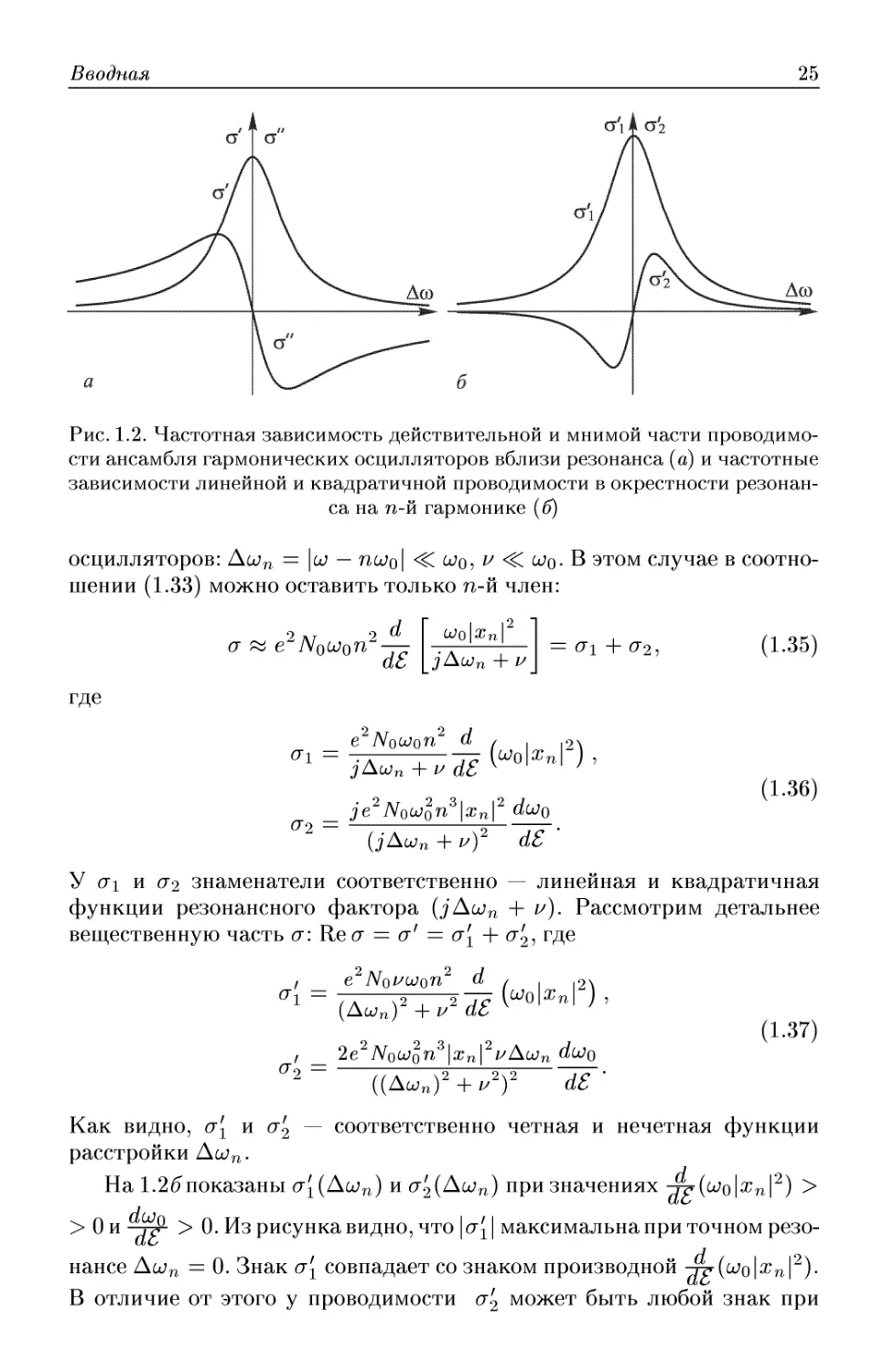
На рис. 1.2а показаны зависимости af(Aoj) и a/f(Aoj). Из рисунка видно,
что а' всегда положительна, т. е. гармонические осцилляторы в среднем
поглощают энергию электромагнитного поля. Частотная характериси-
ка cf((jj) носит типично резонансный характер. Максимум поглощения
^тах приходится на точный резонанс и; = ujo и растет с уменьшением г/,
т. е. с увеличением времени жизни. Ширина резонансной кривой по по-
половинным значениям равна 2v = 2/ (г). Физически такая зависимость
вполне прозрачна: чем больше время жизни осцилляторов, тем точнее
должен быть резонанс из-за накопления разности фаз между полем
и колебаниями осцилляторов за время их жизни.
Квантовая интерпретация поведения системы линейных осцилля-
осцилляторов как поглощающей среды состоит в следующем. Спектр гармо-
гармонического осциллятора является эквидистантным. В этом случае веро-
вероятность вынужденного перехода между соседними уровнями пропор-
пропорциональна энергии того уровня, на который попадает электрон после
перехода. Ясно, что вероятность перехода на более высокий уровень
больше, чем на нижний, и осцилляторы в среднем поглощают энергию
высокочастотного поля. С классической точки зрения этот эффект
связан с изохронностью колебаний линейных осцилляторов. Поэтому
взаимодействие протекает одинаково при любой их энергии, однако,
осцилляторы с нулевой энергией могут лишь поглощать излучение.
Рассмотрим теперь поведение ансамбля нелинейных осцилляторов,
для чего найдем величину а вблизи резонанса на n-й гармонике частоты
Вводная
25
Рис. 1.2. Частотная зависимость действительной и мнимой части проводимо-
проводимости ансамбля гармонических осцилляторов вблизи резонанса (а) и частотные
зависимости линейной и квадратичной проводимости в окрестности резонан-
резонанса на n-й гармонике (б)
осцилляторов: Аип = \и — пи^\ <С и)о, v <С с^о- В этом случае в соотно-
соотношении A.33) можно оставить только n-й член:
,d_
d?
= СП +СГ2,
где
A.35)
A.36)
d8
У <7i и G2 знаменатели соответственно — линейная и квадратичная
функции резонансного фактора (jAun + и). Рассмотрим детальнее
вещественную часть a: Re а = аг = а[ -\- аг2, где
A.37)
((AwnL/) d?
Как видно, a[ и а'2 — соответственно четная и нечетная функции
расстройки Аооп.
На 1.2?показаны <j[(Aujn) и cr2(Aujn) при значениях -jg(ujo\xn\2) >
> 0 и -рР- > 0. Из рисунка видно, что \а[ \ максимальна при точном резо-
резонансе Аиоп = 0. Знак а[ совпадает со знаком производной -4у{иоо\хп\2).
В отличие от этого у проводимости а2 может быть любой знак при
26 Лекция 1
произвольном характере неизохронности (знак производной -jfiP-)'- он
зависит от величины и знака расстройки. Максимум величины а2 до-
достигается при некоторой отстройке от резонанса, когда |До;п| ~ v.
Каково же фактическое поведение ансамбля нелинейных осцилля-
осцилляторов, описываемого суммарной величиной о~'1 Согласно соотношению
A.37), о~[ растет по модулю пропорционально времени жизни т, тогда
как @*2)тах является квадратичной функцией. Отсюда понятно, что
при больших временах жизни проводимость среды определяется сг2,
т. е. неизохронностью осцилляторов. Знак проводимости в этом случае
устанавливается расстройкой До;п, и, следовательно, при любом знаке
производной -х^Р- система осцилляторов может быть излучающей.
Рассмотрим в качестве примера движение электрона в магнитном
поле. Собственная частота ujq совпадает с циклотронной частотой: и =
= qjc = -^-qjCOj где ? = тс2, ?о = гпос2 — энергия покоя. Производная
с
= ~?- (L38)
Таким образом чтобы имело место индуцированное магнитотормозное
излучение, знак расстройки Аип следует установить положительным.
Возникает вопрос: почему система случайно распределенных по
начальной фазе осцилляторов обладает ненулевой проводимостью? Это
связано с группировкой осцилляторов по фазам их колебаний около
определенной фазы высокочастотного поля — фазовой группировкой.
Вычислим усредненное по начальным фазам и времени жизни значение
возмущения координаты осциллятора:
2тг оо
1
о о
Используя соотношение A.22) и значение вронскиана W = 1/тооо,
получаем
2тг оо t
О 0 to
A.39)
Подставляя в полученное выражение функции у\ и г/2 в виде рядов
Фурье A.28)—A.31) и учитывая вид распределения электронов по вре-
временам жизни Ф(т) = иеит', находим после интегрирования
k= — o
Вводная
27
Как и раньше выделим резонансный член и получим (х\ )/Е. Тогда
d\xn>2
jn
jn + и d?
+
d?
A.41)
Последняя формула показывает, что среднее смещение отлично от
нуля и осциллирует с частотой поля, т. е. имеет место фазовая группи-
группировка. Величина (щ ) /Е является комплексной, что свидетельствует
о наличии фазового смещения сгустка относительно фазы поля. Первый
член в выражении A.41) имеет величину порядка 1/г/, т.е. растет ли-
линейно со временем. Второй член, связанный с неизохронностью осцил-
осцилляторов, возрастает как \/ v2 и описывает квадратичную группировку.
Введем параметр неизохронности /i, который определим как отно-
отношение модулей активной проводимости при квадратичной и линейной
группировке:
A.42)
1
cr2max
/
°"lmax
и
d ,
Xu
2
2
)
Как уже обсуждалось, квадратичная группировка всегда может обес-
обеспечить излучение среды, состоящей из электронов-осцилляторов. Усло-
Условием индуцированного излучения при фазовой группировке неизохрон-
неизохронных осцилляторов является значение параметра неизохронности ц > 1.
В качестве примера вычислим значение ц для электрона в магнит-
магнитном поле при п = 1 в слаборелятивистском случае. Умножим числитель
и знаменатель выражения A.42) на величину тиос и внесем ее под
знак производной (это можно сделать, так как она не зависит от ?).
Учитывая соотношение A.38), в соответствии с которым
duc
d?
получим, что
—
Величина тш^х^2 = mv2^. В слаборелятивистском приближении ? =
= тс2 = гпос2 + гпоУ2/2. Отсюда -^- (ттгсс?^ |^i |2) « 2. В итоге получа-
получаем:
A.43)
2
где /Зц = V||/c, C± = v±/c, N — число оборотов, совершаемых электро-
электроном за время жизни г, L — длина пространства взаимодействия, г>ц и
28
Лекция 1
v± — соответственно продольная и поперечная скорости электронов-ос-
электронов-осцилляторов.
Рассмотрим теперь случай, когда времени жизни недостаточно для
развития квадратичной группировки и основной вклад в активную
проводимость A.37) вносит величина о~[. Условием излучения в этом
случае является неравенство
ИЛИ
d\xn\2
) d?
— x
d?
При положительной производной du$/d? для излучения необходимо,
чтобы d\xn\2/d? < О, что маловероятно. Следовательно, производная
duo/d? < 0, и кроме того, она должна быть достаточно большой. Это
может реализоваться в потенциальной яме с полочкой (рис. 1.3), где
duJo/dS отрицательна и велика по модулю. Если полочка имеет боль-
большую протяженность (штриховая линия), то эффект усиливается. Прак-
Практически, электрон, который оказыва-
оказывается на длинной полочке, перестает
колебаться, т.е. исключается из взаи-
модействия с высокочастотным полем.
Этот тип фазировки носит название
фазовой селекции. Эффект фазовой се-
селекции приводит к излучению, когда
из колебательного режима исключа-
исключаются «неправильнофазные» электро-
электроны, т. е. частицы, находящиеся в уско-
ускоряющей фазе высокочастотного поля.
Все результаты, полученные в дан-
ном разделе, предполагали простран-
пространственную однородность высокочастот-
Рис. 1.3. Потенциальная яма ного поля и одномерность движения
и ух) с полочкой частиц, что представляет собой суще-
существенную идеализацию. В случае отсутствия однородности поля могут
возникать существенно новые механизмы фазировки и индуцирован-
индуцированного излучения. Например, в работе [11] показано, что если высокоча-
высокочастотное поле знакопеременно на траектории частицы, то даже линейные
осцилляторы могут образовывать индуцированно излучающую систе-
систему.
Пусть частицы совершают невозмущенные колебания вдоль оси х
и дрейфуют вдоль у направления. Поместим систему таких осцилля-
осцилляторов в высокочастотное поле, имеющее компоненты Ех, Еу, и неод-
неоднородное в направлении х с масштабом неоднородности порядка ам-
амплитуды колебаний. В этом случае электроны дрейфуют вдоль оси у
со скоростью, зависящей от их фазы. В результате в направлении у
возникают сгустки, которые излучают за счет торможения полем Ех.
Вводная 29
Данная пространственная группировка является квадратичной, но не
связана с неизохронностью осцилляторов. Отметим, что пространствен-
пространственная группировка является также и «фазовой», так как имеет место обра-
образование сгустков в определенной фазе высокочастотного поля. Однако
при фазовой группировке, описанной выше, осцилляторы перемешаны
и невозможно заметить в пространстве каких-либо уплотнений.
Возбуждение резонансной системы заданным током
Задача о возбуждении резонансной системы заданными токами [2,
12] сводится к интегрированию уравнений Максвелла г):
A.45)
с граничными условиями вида [пЕ] = 0 на so (n — нормаль к поверх-
поверхности so) в случае, если резонатор ограничен идеально проводящей
поверхностью so- Здесь Е и Н — напряженности электрического и маг-
магнитного поля; D и В — векторы электрической и магнитной индукции,
j — вектор плотности электрического тока. Уравнения A.45) должны
быть дополнены материальными уравнениями, которые в простейшем
случае имеют вид:
D = еЕ, В = /iH, j = o-E, A.46)
где е, /л — соответственно электрическая и магнитная проницаемость
и а — проводимость, причем в вакууме е = €о, /i = /io-
Рассмотрим возбуждение объемного резонатора (колебательной си-
системы, все поле которой сосредоточено в объеме, ограниченном поверх-
поверхностью so, и не проникает за пределы so) монохроматическим током
с плотностью
j = Re{j(uj)ejwt}. A.47)
Ограничиваясь периодическими процессами, будем искать решение си-
системы уравнений A.45) в виде
U(uj)ejujt, A.48)
х) Здесь не рассматривается возбуждение резонатора магнитными токами,
что имеет место, например, в теории парамагнитных приборов СВЧ.
30 Лекция 1
где Еп(о;) и Нп(о;) — комплексные амплитуды полей на частоте о;,
которые удовлетворяют уравнениям
rotE = — jct;/i(ct;)H,
A.49)
rotH = juje{uj)'E + j.
Возможность ограничиться рассмотрением только первой гармоники
тока следует из допущения, что собственные частоты объемного резона-
резонатора лежат вдалеке от высших гармоник частоты и. Заметим также, что
в уравнениях A.45)—A.49) неявно предполагается зависимость токов
и полей от пространственных координат, а не только от^иш.
Далее предполагается, что известно решение задачи о собственных
колебаниях, т.е. известны собственные векторные функции Es и Hs,
которые характеризуют распределение в пространстве электрического
и магнитного поля s—го собственного колебания нагруженного резона-
резонатора. Поля Es и Hs удовлетворяют однородным уравнениям Максвелла
rotEs = -jsig,
A.50)
rotHs = juseEs,
Каждое из собственных колебаний характеризуется своей комплексной
частотой
u,s = oj's + ju,1: = w't(l + ^-) , w'J = u>'e/2Qa, A.51)
где Qs — нагруженная добротность резонатора. Набор {ojs} образует
дискретный спектр (дискретность спектра обусловлена тем, что поле
занимает конечный объем). Применение комплексной частоты A.51)
означает, что временной множитель exp (jut) = exp (joj'st) exp (—uj"t)
определяет поле, колеблющееся с частотой u's и имеющее затухание и".
Учитывая вышесказанное, решение задачи о вынужденных колебаниях
можно представить в виде:
Е = ^ ASES - grad<Z>, H = ^ BSUS, A.52)
где As и Bs — постоянные коэффициенты; Ф — квазистатический по-
потенциал поля пространственного заряда 1).
) Потенциал Ф удовлетворяет обобщенному уравнению Пуассона
div (sgrad#) = — о = —— divj, которое при е = const переходит в обычное
уравнение Пуассона.
Вводная 31
Опуская преобразования, для коэффициентов разложения A.52)
можно записать следующие соотношения:
A.53)
где
Ns = f eE28 dV = - [ ^
v v
есть норма s-го собственного колебания.
Если воспользоваться соотношениями
2
UJ — Шч
_ = I (_± l\ ,
2 2 \UJ — LOs U) + UK / '
то коэффициент As (формула A.53)) можно представить в виде суммы,
а коэффициент Bs — в виде разности двух других величин. Этим новым
величинам можно придать следующий смысл. Формально введем новые
функции, сопоставимые с векторными функциями Es и Hs и обознача-
обозначаемые индексом (—s), которые определяются формулами
W_s = -Ws, E_S=±ES, H_S = THS, N_S = NS. A.54)
Легко проверить, что они удовлетворяют уравнениям Максвелла A.50)
при замене s на (—s). Тогда выражение A.52) может быть представлено
как
Е =
где
A.56)
Данная запись более удобна для выделения резонансных слагаемых,
чем соотношения A.52)—A.53). Действительно, так как и > 0, в вы-
выражениях A.56) только коэффициенты Cs могут принимать большие
значения, a C-s всегда ограничены. Перепишем первое соотношение
32 Лекция 1
A.56) в виде:
^Juj)EsdV. A.57)
Меняющиеся во времени комплексные амплитуды Cs(oj) и }(и) можно
представить в виде интегралов Фурье
C.(w,t)= J Cs(oj
— сю
A.58)
причем функции Cs(oj + ?) и j(o; + ?) являются периодическими про-
процессами. Тогда, переписывая A.57) в виде
(" + 0 = ^ } J(w + ?)ES dV, A.59)
умножая его на exp (—j?t) и интегрируя по ?, получаем:
= 2^J J J(w.*)E»e-i€td^V. A.60)
V -сю
Учитывая интегралы A.58), окончательно получаем уравнение, кото-
которому удовлетворяют коэффициенты Cs:
Если резонатор возбуждается на частоте о;, которая лежит вблизи
какой-либо собственной частоты резонатора со ж cos и Qs ^> 1, то все
слагаемые в формуле A.55) кроме одного определяют свойства полей,
не имеющих в данном диапазоне частот резонансных свойств г), и лишь
члены CsEiS и CSHS окажутся резонансными (резонанс во времени).
Отметим также, что выводы теории возбуждения открытых резо-
резонаторов (колебательных систем, которые имеют достаточно высокую
х) Это так называемый «нерезонансный» фон, дающий динамические по-
поправки к полю пространственного заряда.
Вводная 33
добротность, и колебания в которых сопровождаются излучением в сво-
свободное пространство) заданными токами имеют много общего с соотно-
соотношениями A.55), A.56), формально совпадая с ними при определении
нормы собственных колебаний как
Ns = lim ej7 f eE28 dV = - lim ej7 \ /iH^ dV,
R J S R J S
где Vr — объем шара радиуса /2, a j выбирается так, чтобы интеграл
сходился. Изменяется также роль нерезонансного фона. В закрытых
добротных резонаторах на возбуждение колебаний практически не тра-
тратится активная мощность (это хорошо видно из формулы A.56)), и нере-
нерезонансный фон является реактивным. В открытых же резонаторах, где
нерезонансный фон связан с излучением энергии из объема резонатора,
на его возбуждение тратится активная мощность, причем эта мощность
может быть сравнима с мощностью, передаваемой резонансному коле-
колебанию. Вместе с тем формулы A.55)), A.56)) остаются справедливы,
и могут использоваться для анализа СВЧ-автогенераторов с открыты-
открытыми резонансными системами.
В заключение этого раздела отметим, что в СВЧ-электронике во
многих случаях стремятся работать на одном виде колебаний, чтобы
другие виды колебаний при этом не возбуждались. Если это не реали-
реализуется автоматически (в первую очередь это касается мощных генерато-
генераторов, где необходимо увеличение геометрических размеров пространства
взаимодействия) собственные частоты нежелательных колебаний либо
уводятся из рабочей полосы частот, либо снижается добротность этих
типов колебаний за счет специальным образом размещаемых диссипа-
тивных нагрузок.
Стационарные уравнения возбуждения линии
передачи электронным потоком
Будем рассматривать возбуждение однородного по оси х бесконеч-
бесконечного (или что тоже самое конечного, но идеально согласованного на
концах) волновода [12], пронизываемого прямолинейным электронным
потоком с плотностью тока j = \jx г), где 1 — единичный вектор в на-
направлении оси х. Под волноводом будем понимать любую передающую
линию, электромагнитное поле которой занимает в поперечном сечении
конечную площадь. В таком волноводе могут существовать волны,
распространяющиеся в направлениях ±ж. Волны, распространяющиеся
в волноводе, будут характеризоваться полями
E±s = E°±s(v±y^°x, H±s = Н^(г±)е^ж A-62)
х) Предполагаем, что плотность возбуждающего тока изменяется во време-
времени по закону е?шЬ.
2 Д. И. Трубецков, А. Е. Храмов
34 Лекция 1
и волновыми продольными числами /3±s. E±s, H±s — напряженности
электрического и магнитного полей собственной s-й волны в системе без
пучка, они удовлетворяют однородным уравнениям Максвелла. Здесь
верхний индекс отвечает за волны распространяющиеся в направлении
оси х (прямые волны), а нижний — против оси х (встречные волны).
Тогда электрическое поле в волноводе можно представить как две
группы волн: группа, в которой все волны распространяются вправо:
t = YtE>sej(ut~l3'x), A-63)
S
и группа волн, распространяющихся влево:
№+№, A.64)
где знаки «—У» и «•<—» соответствуют волнам, распространяющимся
соответственно вправо и влево; /3S — постоянная распространения s-й
волны в системе без пучка, причем будем полагать, что /3S одинаково
в обоих случаях.
Введем продольное волновое сопротивление s-й волны:
?г, A-65)
где Ps — активная мощность, переносимая s-й волной в направлении х.
Величина Ks часто называется сопротивлением связи. Действительно,
чем больше Ks, тем больше Е8^х, а следовательно, тем сильнее степень
взаимодействия распространяющейся в линии передачи волны с пото-
потоком электронов.
С учетом определения A.65) потоки мощности, переносимые s-й
волной вправо или влево от выбранной плоскости х = ж", выражаются
соответственно формулами
ф р Еф A }
Здесь «*» означает комплексно сопряженную величину.
Если в плоскости х — ~х амплитуда волны изменяется на величину
dE, то изменение потока мощности, переносимого волной, можно найти,
дифференцируя соотношение A.66):
A67)
Если теперь предположить, что изменение поля на величину dE в точке
х = ~х обусловлено током г (ж), то в точке х = ~х удовлетворяется равен-
равенство dE = dEs = dEs. Полное изменение мощности в линии передачи
Вводная 35
определяется изменением потоков мощности, текущих вправо и влево
и записывается как
dP = dt. + dts = ^ + ^ dE* + ^ + ^s dE. A.68)
Предполагаем далее, что ток i(Hc) связан с электронным пучком, возбу-
возбуждающим волновод. Тогда можно найти изменение мощности взаимо-
взаимодействия элемента тока i(x)d~x с полем Е8 + ES:
dP = -I Re (i(x)(l?8 + E)*) dx =
\ i*(x)(ts + %)dx. A.69)
Знак минус в выражении A.69) х) отражает тот факт, что увеличение
потока мощности в линии передачи происходит за счет мощности, от-
отдаваемой электронным потоком полю.
Приравнивая соотношения A.68) и A.69), получаем выражение,
известное в литературе как теорема «наведения»:
dE = -^y1 i{x)dx. A.70)
Отметим, что пучок возбуждает элементарные волны в любой точке
пространства взаимодействия и их необходимо суммировать по всей
длине линии передачи (см. рис. 1.4). В точке х = ~х поле будет склады-
складываться из волн, бегущих вправо от элементов тока, для которых ~х < х
(элемент 1 на рис. 1.4), и волнами, бегущими влево, для которых ж" > х
(элемент 2).
Используя соотношения A.63) и A.64) и теорему «наведения» A.70),
для напряженности наведенного поля в произвольной точке простран-
пространства взаимодействия получим:
dx -
A.71)
(I — длина пространства взаимодействия).
х) Поясним, как появляется соотношение A.69). Для выражения Re (ab*)/2
имеем: Re((ai + ja2)(b± + j&2))/2 = (a±bi + a2&2)/2; с другой стороны:
(ab* + a*6)/4 = (aibi + a2&2)/2. Сравнивая первое и второе выражение,
приходим к соотношению: Re (ab*)/2 = (ab* + a*b)/4.
36
Лекция 1
Ж
1"
= (р 2sKI2)i{x)dx
Рис. 1.4. Схема, поясняющая вывод уравнения возбуждения линии передачи
заданным гармоническим током
Обычно для простоты ограничиваются рассмотрением только одно-
одного вида волн, возбуждаемых в линии передачи сгруппированным током,
для которых s = О (основной вид волн). Тогда выражение A.71) для
полной напряженности поля можно переписать в виде:
x-x) dx -
i(x)ejMx-x) dx, A.72)
где E° — амплитуда входного сигнала. Здесь первое слагаемое — внеш-
внешняя приложенная напряженность поля в начале линии передачи, второе
слагаемое — интегральный эффект от составляющих между ~х — 0 и ~х —
= ж, третье — между ~х = х и ~х = I. Фактор e±JPo(x-x) уЧИТЫвает
конечную скорость изменения фазы волны: в данный момент в плос-
плоскость х приходят «элементарные» волны, возбужденные током г (ж) тем
раньше, чем дальше от плоскости х находится источник возбуждения.
Сопротивление связи Kq = К можно рассматривать как коэффициент,
связывающий ток i(x), и возбужденное им в плоскости ~х поле.
Перейдем от интегрального вида уравнения возбуждения линии
передачи к дифференциальному относительно возбужденной части по-
поля Ех. Для этого необходимо воспользоваться правилом Лейбница:
Правило Лейбница. Если функция f(x,y) и ее частная про-
производная df/dy непрерывны на прямоугольнике а^х^Ьис^у^е,
то
Вводная 37
Замечание. Для интеграла
Ф(у)
dy
Ф(у)
у которого функции ф(у) и ф(у) дифференцируемы на отрезке с ^
^ у ^ е и не выходят за пределы а ^ ф(у), Ф(у) ^ Ь по правилу
дифференцирования сложной функции имеем:
Ф(у)
dy J
Ф(у) ф(у)
Учитывая вышесказанное, соотношение A.72) легко свести к урав-
уравнению:
I. A.74)
Последнее соотношение является дифференциальным уравнением воз-
возбуждения линии передачи потоком. Оно справедливо для любых кон-
конфигураций линии передачи, поэтому задача заключается в правильном
вычислении сопротивления связи конкретной системы.
Отметим, что интегралы вида Т~ J i(~x)e~^oX dx, входящие в фор-
2 о
мулу A.72), допускают энергетическое толкование. Действительно, =F
=Ftt j i(T)E°e~jf3oX dx = ^Pe — средняя за период электронная мощ-
о
ность взаимодействия сгруппированного тока пучка с полем Е°е~^°х
волны в линии передачи без пучка. В соответствии с этим интегралы
Реа = Re |"l li(x)E°ej^x dx\, Per = Im |"i li(x)E°ej^x dx\
о о
A.75)
можно назвать соответственно активной и реактивной компонентами
электронной мощности взаимодействия.
Изложим теперь строгую стационарную теорию возбуждения волно-
волноводов заданными токами [2]. Будем рассматривать как и раньше волно-
волновод, однородный по оси ж, поле в котором отлично от нуля только внутри
цилиндра с поперечным сечением S± и образующими, параллельными
оси х. Волны, распространяющиеся в таком волноводе, характеризуют-
38 Лекция 1
ся полями, задаваемыми соотношениями A.62). Данные поля относятся
к фиксированной частоте возбуждения о;, причем волны различных на-
направлений при учете потерь в волноводе будут различаться следующим
образом:
lm/3S > О, Im/3_s < 0.
При этом индекс s, определяющий собственные волны в волноводе,
в силу изотропности всех веществ и выполнении теоремы взаимности
можно всегда выбрать так, чтобы выполнялось условие /3-s = — /3S.
Собственные волны в волноводе удовлетворяют условию ортого-
ортогональности [13, 2]:
{[EsUr]-[ErUs]}ldS = 0 при гф-s, A.76)
s±
где S± — поперечное сечение волновода х = const.
Искомые поля Е, Н, возбуждаемые монохроматическим электриче-
электрическим током, удовлетворяют неоднородным уравнениям Максвелла
rotE = jf,
A.77)
rotH = -jke~E+j.
Будем искать магнитное поле в виде
Н = ? (CSHS + C_SH-S), A.78)
s
где коэффициенты C±s зависят только от х. Так как величины C±s
постоянны при j = 0 (тогда формула A.78) дает общее решение однород-
однородных уравнений Максвелла — суперпозицию всех собственных волн), то
запись решения в виде A.78) представляет по существу метод вариаций
постоянных, позволяющий решить систему неоднородных линейных
дифференциальных уравнений, поскольку известно общее решение од-
однородных уравнений. Подставляя выражение A.78) во второе уравне-
уравнение A.77), получаем соответствующее выражение для электрического
поля
Е = ? (CSES + C_SE_S) -
— У
jke *-^ \ dx dx
где и) = ск. Для упрощения последнего соотношения подчиним функ-
функции C±8(z) дополнительному условию
= j*, A-80)
Вводная 39
в котором фигурирует поперечная составляющая плотности тока
ЛЬ(®13у>Зг)- Вся вторая строчка формулы A.79) не может быть
уничтожена по той причине, что векторы, стоящие в левой части
A.80), не имеют составляющих по оси х. Таким образом выражение
A.79) для поля Е принимает вид
^', A.81)
где jl(jXj 0,0) — продольная часть плотности тока.
Второе уравнение для C±s получаем, подставляя выражения A.78)
и A.81) в первое уравнение A.77), в виде:
dC' [IE.] + Щ^- [1E_S]) = -? rotJ-. A.82)
dx L SJ dx L ~ w e
Пользуясь соотношениями A.80) и A.82), несложно показать, что вели-
dC±8
чины | выражаются соотношениями
ах к
^ = -L [ jE_s dS, ^^ = -^ [ jEs dS, A.83)
аж vv5 J dx Ns }
s± s±
в которых
Ns = J {[ESH-^] - \E-8H8]}ldS A.84)
есть норма волны с индексом s, которая для волн, распространяющихся
без затухания, имеет четкий энергетический смысл — она пропорцио-
пропорциональна потоку мощности волны.
Если токи занимают отрезок волновода х\ < х < х^-, то из выраже-
выражений A.83) следует, что
X Х2
Cs(x) = ±-\dx\ jE_s dS, C.(x) = -L f dx I jEs dS. A.85)
Из формулы A.83), а также из уравнения возбуждения линии пе-
передачи в интегральной форме A.71) видно, что возбуждение волново-
волноводов происходит подобно возбуждению резонаторов. Единственное раз-
различие между возбуждением резонаторов и возбуждением волноводов
заключается в том, что если в первом случае имеет место резонанс
во времени, то во втором — резонанс в пространстве. Действительно,
если j = j°(y,z)e~^x, то в правой части в подинтегральных выра-
выражениях уравнения возбуждения в виде A.71) содержатся слагаемые
вида е~^^3~^х (аналогичный результат имеет место и в соотношении
A.83)). При равенстве /3 = /3S после интегрирования в правой части
40 Лекция 1
появятся слагаемые возрастающие пропорционально ж, это — резонанс
в пространстве, который полностью аналогичен резонансу во времени,
когда uj = u)s, и имеет место секулярный рост амплитуды колебаний,
пропорциональный t.
Развитая теория возбуждения гладких волноведущих систем может
быть достаточно просто обобщена на случай периодических волноводов,
для которых справедливы соотношения
е(х + nD, у, z) = е(х, у, z)\ fi(x + nD, у, z) = /х(ж, у, z)\ n e Z,
где D — период структуры. В этом случае зависимость собственных
волн от продольной координаты усложняется и определяется соотно-
соотношениями
Е,=Е°(Ж,у,ф^ж, Us=n°s(x,y,z)e^^, A.86)
где Е^, Н^ — периодические функции с периодом Z), а волновое число
/3S определяется не однозначно, так как всегда вместо /3S можно взять
% A-87)
Смысл формул A.86) и A.87) следующий: если разложить функции
Е^, Н^ в ряд Фурье по ж, то поле волны представится в виде суммы
пространственных гармоник, причем гармоника с индексом п будет
иметь волновое число, даваемое формулой A.87). Неоднозначность
связана с тем, что волновым вектором данной волны можно назвать
волновое число любой из пространственных гармоник. В целом же
теория возбуждения гладких волноводов переносится без изменений на
периодические волноводы, чем мы и воспользуемся при анализе прибо-
приборов с длительным взаимодействием в последующих лекциях. Следует,
однако, оговориться, что такой «перенос» не справедлив вблизи полосы
пропускания замедляющей системы [14] (см. также лекцию 11).
Нестационарная теория возбуждения волновода
током медленно меняющейся амплитуды
Пусть однородный и бесконечный вдоль оси х волновод возбужда-
возбуждается током
j(r,t) = Re{J(r,t)e^nt}, A.88)
где J(r, t) — медленно меняющаяся по сравнению с exp (jftt) функция
времени. С точки зрения спектральных характеристик предположение
о медленном изменении амплитуды означает, что спектр сигнала Aft
лежит в достаточно узком диапазоне вблизи некоторой частоты ft.
В этом случае достаточно знать главную часть возбуждаемого поля,
обусловленную частотами и « ft (точнее, \и — Щ < Aft), а побочными
частями вследствие их малой интенсивности можно пренебречь.
Вводная 41
Рассмотрим возбуждение волновода гармоническим током на ча-
частоте uj = ft + До;, следуя методике, используемой нами для вывода
уравнений возбуждения резонаторов. Введем собственные функции
периодического волновода (см. формулы A.62)):
E±s=E°±e(x,y,z,u)e^p-x; H±s=H°±s(x,y,z,oj)e^^x, A.89)
где E±s, H±s — периодические функции с периодом, равным периоду
волновода.
Если заменить E±s(#, у, z, uj) на E±s(#, у, z, ft), то мы совершим
ошибку порядка Аи. Если же заменить величину /3s(o;) на /3s(ft), то
ошибка в определении функций E±s, H±s (а значит и полей, которые
представляют собой линейные комбинации этих функций) имеет поря-
порядок (x/3fs(u))Au)), т.е. увеличивается по мере удаления от источника.
Поэтому учтем зависимость постоянной распространения f3s от часто-
частоты, пренебрегая вследствие малой ширины спектрального интервала
сигнала зависимостями от частоты функций E±s и H^_s.
Разложим постоянную распространения в ряд Тейлора вблизи ча-
частоты ft, учитывая, что она в общем случае комплексная 1):
+ \ ^'(fi)(AwJ + • • • A-90)
Тогда, учитывая малость До;, уравнение A.83) для коэффициентов C±s
dx NL
s±
можно переписать в виде
= ± 1 [ j^E^e^'^)^* dS A.91)
dx I s s 2 s
где
C±s = C±sexp \±jx(j48(il)+P'8(il)Au>
x) Заметим, что данную процедуру можно применять только вдали от гра-
границы пропускания волноведущей системы.
42 Лекция 1
Умножая обе части уравнения A.92) на exp [jAwt] и интегрируя по
До; от —оо до +00, а также учитывая, что C±s(Auj) ф О только при
малых Аи благодаря медленному изменению комплексной амплитуды
сигнала, получим
1 dC±s ± дС±8
vsrp at dx ' -"eV"' at
= ^ J J(W) [E%s]n dS = -j
A.93)
где (...) обозначает усреднение во времени;
+ ОО +ОО
б±, = [ 7J±s(Auj)ejAujt d(Au); J= [ j(^ + Au)ejAujt
^s rp = l//3fs(?l) — групповая скорость на частоте Г^.
Представим поля в волноведущей системе в соответствии с соотно-
соотношениями A.55) как
ЕМ = Е (CSES + C_SE_S) - т + Аш)?№ + До;), A-94)
H(w) = 2 (^Н« + C-SH-S) . A.95)
Здесь j/ — продольная составляющая тока.
Для нахождения непосредственно полей умножим эти соотношения
на е-?(^+Аа;^ и проинтегрируем по Аи от —оо до +оо, пренебрегая как
и раньше зависимостью медленно меняющихся функций Е^, Н^ от До;,
учитывая разложение в ряд постоянной распространения A.90), а также
связь между коэффициентами Сs и Cs, а затем возьмем действитель-
действительные части полученных выражений. Опуская элементарные выкладки,
получим, что
Е =
, [Е.]п + C-s [E_e]n) Je^nt + \ \ h dt, A.96)
— сю
;(<5s[Hs]Q + c_s[H_s]Q)}^m. A.97)
H = Re
Возьмем интеграл, стоящий в правой части уравнения A.96), учи-
учитывая, что j/ = Re J/ exp [?Ш], а также предполагая, что j —у 0 при
Вводная 43
t —У —оо. Тогда, интегрируя по частям, можно получить:
— сю
и т. д. Окончательно можно записать:
}"¦ (L98)
В данном разложении достаточно ограничиться только первым членом
разложения, делая при этом ошибку порядка Аи.
Вернемся к уравнению A.93) и выясним физический смысл каждого
из слагаемых в левой части уравнения. Для этого рассмотрим распро-
распространение волн в свободной от источников области волновода, когда
j = 0. Будем рассматривать задачу (берем для определенности верхние
знаки):
1 dC±s dC±s . ,(плдС±8 j д„^лд2С±8 ~
A.99)
с граничным условием
С(х = 0) = /(*), A.100)
где f(t) — произвольная медленно меняющаяся комплексная функция
времени. Если положить jfs(ft) = 0, /3"(Г?) = 0, то решение уравнения
A.99) хорошо известно и имеет вид:
Cs = f (t-^—)e-^x. A.101)
\ V3 гр У
Оно описывает волну комплексной амплитуды поля, распространяю-
распространяющуюся с групповой скоростью в сторону возрастания ж, без искажений,
но с затуханием. Аналогично можно показать, что волна C-s будет
распространяться подобным образом в противоположную сторону.
Наличие членов j's(ft), /3"(ft) в разложении A.90) и соответствую-
соответствующих членов в уравнении A.99) приводит к искажению профиля волны /
в процессе распространения её вдоль волновода [15, 16]. Эти эффекты
«расплывания» профиля волны становятся существенными на рассто-
расстояниях L rsj (--)/До;) и L rsj (/^(До;J) от источника. Поэтому при
выполнении условий
LYs(tt)Au; < 1, ЬР'ДЩАиJ < 1 A.102)
44 Лекция 1
можно пользоваться решением A.101), а, следовательно, и упрощенным
уравнением для коэффициентов:
^-Ж ± ТГ+ *<°>е- = Ж, |
A.103)
Если под L понимать длину прибора, то соотношения A.102) опреде-
определяют условия применимости нестационарного уравнения возбуждения
A.103) для этого прибора. Соотношения A.102) показывают, что урав-
уравнение возбуждения применимо, если характерное время изменения ам-
амплитуды сигнала 2тг/Дс<; мало по сравнению с периодом ВЧ-поля 2тг/с<;,
и, что характерное расстояние расплывания профиля волны амплитуды
(jgAcxj)'1 и (/^'(До;J) много больше длины L. Заметим, что при
этом не накладывается никаких ограничений на соотношение между
временем прохождения волной длины прибора L/vs гр и характерным
временем изменения амплитуды 2тг/Дс<;, их соотношение может быть
любым.
Рассмотрим энергетические соотношения, для чего умножим урав-
уравнение A.103) на С±8 и выделим отдельно действительные и мнимые
части. Тогда можно записать:
8W дР г
— + 2lsvs rpW = т^ - J (jE) dS, A.104)
s±
A.105)
где Р = — A^s|Cf±s|2/4 — поток мощности is-й волны; W = P/vs rp —
плотность энергии волны; ф — фаза волны C±s = |C±s|exp {j^}.
Здесь также полагается, что электрическое поле волны имеет вид Е =
= Re {c±sE±seiut} иЕ;= E_s.
Уравнение A.104) представляет собой закон сохранения энергии, ко-
который можно трактовать, как уравнение баланса активных мощностей
в элементарном объеме. Действительно, соотношение A.104) показыва-
показывает, что энергия волны, втекающая в элементарный объем, ограничива-
ограничиваемый двумя поперечными сечениями, расположенными на расстоянии
dx, и работа, совершаемая источниками в этом объеме (соответственно
первый и второй члены в правой части), идут на накопление энергии
поля и покрытие потерь в данном объеме (первый и второй члены
в левой части). Уравнение A.105) соответственно описывает баланс
реактивных мощностей.
Вводная 45
Выведенные выше нестационарные уравнения возбуждения волно-
волновода были впервые получены в работах [17, 18]. Однако изложенная
методика не обладает достаточной степенью строгости. Поэтому найдем
теперь, следуя работе Л.А. Вайнштейна [19], строгое решение задачи
о возбуждении произвольного однородного волновода заданным током
медленно меняющейся амплитуды.
Пусть периодический волновод возбуждается током j с медленно ме-
меняющейся амлитудой A.88). Представим плотность тока для удобства
расчета возбуждения s-и волны в волноводе (с комплексным волновым
числом ps(u))) в виде:
З(х, у, z, t) = 3„(х, у, z, e.)e-M-Mx-at\ A.106)
где Js — медленно изменяющаяся функция четвертого аргумента 6S =
= t — /3's(?l)x), /3's = d/3s/du>. Наиболее интересным является случай,
когда Js есть медленно изменяющаяся функция координаты х (по
сравнению с e^s^x), т.е. при синхронизме электронного потока с s
волной, но в общем случае это не предполагается.
Поля в волноведущей структуре, как обсуждалось выше, можно
представить выражениями A.78) и A.81). Если в них полагать функ-
функции Е8 и Hs зависящими только от у, z, о;, т.е. включить множитель
ejCs(u:)x B коэффициент Cs = Cs(x,lj), to последний будет удовлетво-
удовлетворять уравнению
^ - j/3s(u;)Cs = ь, is = -L [ jE_s ds. A.107)
ах Ns J
Пусть До; = ft — и), тогда введем вместо Сs и is новые функции Сs
и /s, которые определяются как
С,(х,ш) = Csi
A.108)
Уравнение A.107) относительно новых переменных примет вид
dCs . ~ ~
dx s s s
Аппроксимируя функцию /3s(uj) = f3s(?l + До;) при |До;| < ДГ^ рядом
Тейлора, перепишем уравнение A.109) в виде
... С. = /.. A.110)
46 Лекция 1
Функции Cs, Cs, /s, Is представим в виде
сю
C.(x,t)= f Cs(x,oj)ejut duj = Се(х,в.)е-М-Юх-т\
h(x,t) =
— сю
СЮ
A.1П)
C,(x,0.)=
— СЮ
СЮ
Здесь Cs и Is — медленно изменяющиеся функции 0S. Они связаны
меж;ду собой уравнением
ocs змы&с. /3'a"(u)d3ct ?
причем C-s и I-s связаны таким ж;е уравнением, в котором f3s заменено
Ha/3_s = —f3s- Ниже запишем выражения для функции Cs, соответству-
соответствующей волне, которая распространяется в положительном направлении
оси ж, для функции C-s справедливы аналогичные выражения.
Общее решение уравнения A.112) есть сумма общего решения одно-
однородного уравнения C®(x,6s) и частного решения неоднородного урав-
уравнения. Если частное решение удовлетворяет условию излучения, то
получим
X СЮ
с,(х,в.) = (%(х,ва)+ | | Gs(x-c,e.-e)Ts(<z,e)dedc, A.113)
— сю —сю
где Gs — функция Грина, которая при сохранении только первых
двух членов в левой части уравнения A.112) определяется выражением
вида [20]
Ga(x, 0) = (-2,тг#'(ВД~1/2 ехр ["щ
Если /3fJ(?l) = 0 и учитываются только первый и третий члены в левой
части уравнения A.112), то функция Грина для этого случая запишется
как
I 1/3
B/3's'(U)x/2)
1/3
A.115)
Вводная 47
где V(t) — функция Эйри. Если в левой части A.112) учитывать только
член dCs/dx, то формула A.113) примет вид
х
Cs(x,0s) = Cos@s)+ \ Ts((,O)d(, A.116)
причем С® не зависит от х.
Зная Cg(zx^6s), значения Cg(x,6s) при х ^ хо, можно вычислить
по формуле
сю
Cos(x,0s)= | Gs(x-xo,0s-e)C°s(xo,0)d0, A.117)
которая может быть применена к Cs, если Is = 0 при х = х$.
Существенно, что одна и та же функция Gs определяет изменение
комплексной огибающей Сs как в процессе свободного распространения
волны, так и процессе ее возбуждения сторонними токами. При доста-
достаточно малых х и вещественном значении Cfs(?l) выражения A.114) и
A.115) можно заменить дельта-функцией
G8(x,0) = 6@) (x>0), A.118)
приводящей к формуле A.116).
Непосредственный физический интерес представляет, однако, не
функция С8, а поле s-и волны
сю
E(x,y,z,t)= | Cs(x,w)F,s(y,z,w)ejutdt =
— СЮ
= Ев(я, у, z, в8)е-М-Юх-п», A.119)
где
Es(x,y,z,es)= | Cs(x,Aw)Es(y,z,tt + Aw)ejAue'd(Auj), A.120)
и, кроме того, нужно связать «возбуждающую» функцию 18 в правой
части A.112) с векторной функцией Js. Полагая, что Ns = 1, введем
векторные функции
A.121)
48 Лекция 1
Тогда для поля s-й волны получаем выражение
сю
Es(x,y,z,Os) = [ Cs(z,0s-0)E°s(y,z,0)d0, A.122)
Ts(x,es)= j dS | Ja(x,y,z,6a-6)E°_s{x,y,6)d6. A.123)
S± -OO
Таким образом поле s-й волны получается в результате свертки
функции Сs с векторной функцией Е^ по «групповому» времени 0 = t —
— /38 (il)x, а возбуждающая функция 18 — в результате такой же свертки
векторных функций Js и Е^_8 и интегрирования по поперечному сече-
сечению S±. Зависимость Е±8 от в различна для различных волн. Для чисто
поперечных волн в свободном пространстве, в плоскопараллельном
волноводе или в коаксиальной линии E±s и Ns не зависят от о;, тогда
E°±s=E±s(y,zMF), A.124)
так что выражения A.122) и A.123) упрощаются и принимают вид:
E8(x,y,z,08) = C8(x,08)E8(y,z),
г A.125)
I8(x,08)= J J8(x,y,z,O8)E-8(y,z)dS.
s±
Другие волны характеризуются конечным «временем поперечного
установления» Ats. г) Если Ats ^C А^, где Д# ~ I/Aft — характерное
время для комплексных огибающих токов и полей (т.е. Js и Cs), то
формулы A.125) остаются справедливыми при условии, что Es и E_s
взяты на несущей частоте fi. Последнее вытекает из соотношений
E\s{y,z,e)d6 = E±s{y,z,U). A.126)
Если Is(x,6s) есть медленно изменяющаяся функция ж, т.е., если
возбуждающий ток находится в синхронизме с данной волной, то соглас-
согласно формулам A.113) и A.116) по мере распространения волны (с ростом
продольной координаты х) происходит рост величины С8(х,08), кото-
которая может достичь больших значений. Таким образом мы опять пришли
к явлению пространственного резонанса, но теперь уже в нестационар-
нестационарных уравнениях возбуждения волноведущей системы. При отсутствии
х) Для волн в пустом волноводе с идеально проводящими стенками Ats
1/сс73, где (jjs — критическая частота.
Вводная 49
синхронизма Is(x,0s) — быстро изменяющаяся функция ж, такой же —
и при том малой — получается функция Снесли С® = 0). Влияние
второго и третьего члена в левой части A.112) тем меньше, чем больше
характерное время А0 (чем меньше АН).
Уравнение возбуждения A.103), по-существу, эквивалентно полу-
полученным строго соотношениям A.125) и A.126) и уравнениям A.112)
с одним первым членом в левой части. При этом мнимая часть Pfs(H),
ответственная за изменение формы энергетического спектра волны
и его смещение по оси частот (т. е. за сдвиг несущей частоты), в формуле
A.103) не учитывается. Второй член в левой части уравнения A.112)
позволяет учесть деформацию комплексной огибающей при распро-
распространении волны, например, растяжение и сжатие импульса [20].
Список литературы
1. Трубецков Д. И. История электронных ламп сверхвысоких частот /
В кн. Формирование радиоэлектроники. — М: Наука, 1998. Гл. 12,
С. 300-333.
2. Вайнштейн Л.А., Солнцев В.А. Лекции по сверхвысокочастотной
электронике. — М.: Сов. радио, 1973.
3. Brittain J.E. The magnetron and beginning of the microwave age //
Phys. Today. 1985. V. 33, № 7. P. 60.
4. Соколов Д.В., Трубецков Д.И. Нелинейные волны, динамический
хаос и некоторые задачи сверхвысокочастотной электроники / В
сб.: Проблемы физической электроники. — Л.: Изд-во ФТИ, 1986.
С. 7.
5. Трубецков Д.И., Шепелева Е.Я. Структуры (общий взгляд и за-
задачи электроники) / В сб.: Проблемы физической электроники. —
Л.: Изд-во ФТИ, 1988. С. 124.
6. Trubetskov D.I., Mchedlova E.S., Anfinogentov V.G., Ponomorenko
V.I.у Ryskin N.I. Nonlinear waves, chaos and patterns in microwave
devices // CHAOS. 1996. T. 6, № 3. С 358.
7. Трубецков Д.И., Анфиногентов В.Г., Рыскин Н.М., Титов В.Н.,
Храмов А.Е. Сложная динамика электронных приборов СВЧ
(нелинейная нестационарная теория с позиций нелинейной дина-
динамики) // Радиотехника. 1999. Т. 63, №4. С. 61.
8. Кузелев М.В., Рухадзе А.А. Электродинамика плотных электрон-
электронных пучков в плазме. — М.: Наука. 1990.
9. Briiche E., Recknagel A Uber die «Phasenfokussierung» bei der
Electronenbewegung in schnellveranderlichen elektrischen Feldern //
Ztsch. fur Physik. 1938. Bd. 108, H. 7-8. S. 459.
10. Цимринг Ш.Е. Мазеры на циклотронном резонансе. — Горький:
Изд-во Горьк. ун-та, 1988.
50 Лекция 1
11. Гапонов А.В., Петелин М.И., Юлпатов В. К. Индуцированное
излучение возбужденных классических осцилляторов и его ис-
использование в высокочастотной электронике // Изв. вузов. Радио-
Радиофизика. 1967. Т. 10, №9, 10. С. 1415.
12. Шевчик В.П., Трубецков Д. И. Аналитические методы в электро-
электронике СВЧ. — М.: Сов. радио, 1970.
13. Вайнштейн Л.А. Электромагнитные волны. — М.: Радио и связь,
1988.
14. Булгакова Л.В., Трубецков Д.И., Фишер В.Л., Шевчик В.И. Лек-
Лекции по электронике СВЧ приборов типа О. — Саратов: Изд-во СГУ.
1974.
15. Wainstein L.A. Propagation of quasi-monochromatic plane waves in
absorbing and amplifying media // In: the Proceedings of the Fifth
Colloquium of Microwave Communication. Budapest, 24-30 June,
1974. P. ET-429.
16. Вайнштейн Л.А. Распространение импульсов // Лекции по элек-
электронике СВЧ и радиофизике C-я зимняя школа-семинар инжене-
инженеров; книга V). Саратов: Изд-во СГУ, 1974.
17. Кузнецов СП., Трубецков Д.И. Две лекции по нестационарной те-
теории взаимодействия электронных пучков с электромагнитными
волнами // Лекции по электронике СВЧ и радиофизике C-я зим-
зимняя школа-семинар инженеров; книга V). Саратов: Изд-во СГУ,
1974, С. 88.
18. Кузнецов СП., Трубецков Д.И. Некоторые вопросы теории лам-
лампы обратной волны как распределенной автоколебательной си-
системы. В кн.: Электроника ламп с обратной волной // Под ред.
В.Н. Шевчика и Д.И. Трубецкова, Глава III. Саратов: Изд-во Са-
рат. ун-та, 1975.
19. Вайнштейн Л.А. Переходные процессы при возбуждении волно-
волноводов // Изв. вузов. Прикладная нелинейная динамика. 1998. Т. 6,
№ 1.С. 20.
20. Вайнштейн Л.А. // Успехи физич. наук. 1976. Т. 118, № 2. С. 339.
Лекция 2
ЭЛЕМЕНТАРНАЯ КИНЕМАТИЧЕСКАЯ ТЕОРИЯ
КЛИСТРОНОВ
«Опять клистроны, магнетроны, ЛБВ... —
вздохнёт кто-то, полистав книгу, — Что здесь
можно сказать нового?». Оргкомитет и лекторы
отвечают таким читателям строчками поэта
Д. Самойлова:
Люблю обычные слова,
Как неизведанные страны.
Они понятны лишь сперва,
Потом значенья их туманны.
Их протирают как стекло,
И в этом наше ремесло.
Лекции по электронике СВЧ и радио-
радиофизике F-я зимняя школа-семинар
инженеров), книга 1. Саратов: Изд-во
СГУ, 1983. с. 3
Модуляция электронного потока по скорости. Кинематический ана-
анализ процесса группировки электронов в пространстве дрейфа. 100$
идея братьев Вариан и Хансена. Клистронные усилители и умно-
умножители частоты. Некоторые результаты теории резонансных ав-
автогенераторов. Элементарная теория отражательного клистрона.
Клистронный генератор с запаздыванием: от режимов монохрома-
монохроматических колебаний до режимов динамического хаоса.
Как обсуждалось в первой лекции, характерной особенностью про-
процессов на сверхвысоких частотах является невозможность пренебречь
инерцией электронов. В низкочастотной электронике, где всегда выпол-
выполняется условие с^прол <^С 1 (о; — частота сигнала, ?Прол — время пролета
электрона через пространство взаимодействия), можно считать, что
в течение всего времени пролета ?Прол электронами промежутка \х2 —
— х\\ поле в нем не изменяется. В этом случае возможно применение
статического метода управления электронным потоком — модуляции
электронного потока по плотности, который заключается в том, что сет-
52 Лекция 2
ка лампы электростатически воздействует на пространственный заряд
электронного облака вблизи катода, изменяя в соответствии со своим
потенциалом электронный ток лампы от нуля до величины, равной току
насыщения. Понятно, что этот способ не будет работать, если имеет
место соотношение ojtnpojl ^> 1? когда поле сильно меняется за время
пролета, и инерцией электронов уже пренебречь нельзя г). Другим спо-
способом получения модулированного по плотности электронного пучка
является динамический способ управления. Главное в нем заключается
в разделении пространств модуляции электронного пучка по скорости
и по плотности. При этом управляющий сигнал воздействует не на
плотность, а на скорость электронов, периодически замедляя и ускоряя
их в переменном электрическом поле. Этот процесс получил название
модуляции электронного потока по скорости. Модуляция по скорости
переходит в модуляцию по плотности вследствие конечного угла проле-
пролета электронов в пространстве дрейфа, чем и решается вопрос создания
высокочастотной переменной компоненты тока пучка. В качестве мо-
модулирующего элемента может быть использован отрезок замедляющей
линии или объемный резонатор.
Анализ задачи о взаимодействии электронного потока с электро-
электромагнитным полем при динамическом способе управления может быть
разделен на три подзадачи:
1) анализ процесса модуляции электронов по скорости;
2) изучение процесса группировки электронов (модуляции электрон-
электронного потока по плотности);
3) описание процессов возбуждения резонансной системы сгруппи-
сгруппированным электронным потоком.
В данной лекции будут последовательно рассмотрены все эти во-
вопросы в кинематическом приближении, т. е. без учета кулоновских сил
расталкивания между электронами пучка 2). Полученные результа-
результаты применяются далее к построению элементарной теории клистрона
и определению его основных характеристик: выходной мощности, к.п.д.,
коэффициента усиления (для пролетного клистрона), зон колебаний
и электронной перестройки частоты (для отражательного клистрона).
Нелинейные процессы в клистронах и оптимизация их параметров бу-
будут изложены в лекции 5.
х) В последние годы электростатический метод управления электронным
потоком опять привлек внимание исследователей в связи с развитием ваку-
вакуумной микроэлектроники. Однако в приборах с автоэлектронной эмиссией
или фотоэмиссией, управляемой электромагнитным полем, правильней гово-
говорить не об электростатическом способе управления, а о модуляции эмиссии
[1].
2) Влияние сил пространственного заряда на колебательные процессы
в электронном пучке будет учтено в последующих лекциях.
Элементарная кинематическая теория клистронов 53
Модуляция электронного потока по скорости
Рассмотрим схему резонаторного модулирующего устройства, изоб-
изображенную на рис. 2.1, в котором однородный немодулированный по-
поток проходит через две сетки, идеально проницаемые для электро-
электронов и идеально непроницаемые для электрических полей. Между ка-
катодом К и сеткой 1 модулятора приложено постоянное ускоряющее
напряжение Vo (такое же напряжение между катодом и сеткой), так
что электроны попадают в модулятор с постоянной скоростью vo =
= л/ЩУо . Между сетками 1 и 2 действует переменное напряжение
V\ sino;?. За модулятором находится пространство, свободное от стати-
статических полей, которое будем называть пространством группирования
или пространством дрейфа. Предположим, что для описания процесса
модуляции можно пренебречь силами пространственного заряда. Будем
также считать, что время пролета электрона через модулятор мало по
сравнению с периодом колебаний ВЧ-поля, таким образом действую-
действующее на каждый электрон поле можно считать статическим. Тогда для
каждого из электронов можно записать закон сохранения энергии
mv2 2
1^ + e
где ut — фаза влета электрона в модулятор. Скорость электронов на
выходе из модулятора запишется в виде
v = vq\/\ + t^smut = vo \ 1 - — ?2 + - ^sincot + — ?2 sin2ujt + ...> ,
I 16 2 16 J
B.1)
где ? = Vi/Vo- Если воспользоваться приближением малого сигнала,
т. е. предполагать, что амплитудное значение переменного напряжение
мало по сравнению с ускоряющим напряжением Vo (С ^С 1), в выраже-
выражении B.1) можно ограничиться членами порядка ?. Тогда выражение
для скорости электронов примет вид:
) B.2)
где ut\ — фаза влета электрона в модулятор.
При больших амплитудах модуляции (нелинейная модуляция)
нельзя ограничиваться только первым членом в разложении скорости
в ряд, поэтому на выходе из ВЧ-зазора появляется периодическая во
времени переменная составляющая скорости, которая, кроме частоты
модулирующего напряжения, содержит еще и ее гармоники. Кроме
этого при нелинейной модуляции имеет место энергообмен между
потоком и полем модулятора. Действительно, если ограничиться
членами не первого, а второго порядка малости, то постоянная
составляющая скорости v = vq I 1 — — —^ ) становится функцией
V 16 Vo )
переменного напряжения.
54
Лекция 2
К
1 I
I 2
1,0
0,8
0,6
0,4
0,2
-0,2
M
\
\
" . \ i ^~
ж 2жЧ Зж/Чтг фо
Рис. 2.1. Схема устройства,
осуществляющего модуляцию
электронов по скорости
Рис. 2.2. Зависимость параметра эф-
эффективности модуляции М от угла
пролета (ро
Если угол пролета через ВЧ-зазор конечен, то для нахождения за-
закона модуляции в этом случае необходимо проинтегрировать уравнение
движения электрона в поле модулирующего зазора
х = г]—- sinoot
B.3)
при начальных условиях ut = u)ti, x = vo, x = 0 (d — протяженность
модулятора). Опуская выкладки, сразу выпишем выражение для закона
модуляции в случае слабого сигнала (? ^С 1) [2, 3]:
1
о = vo 1 + -
sin
B.4)
где у?о — — ~~ невозмущенный угол пролета (угол пролета в отсутствии
ВЧ-поля), М — параметр эффективности модуляции, который выража-
ется соотношением
"=*(?)/(?)•
B.5)
Выражение B.4) является приближенным, однако, как показано
в [4], при малых, но конечных ?, оно достаточно хорошо описывает
скоростную модуляцию. Вид зависимости М(сро) показан на рис. 2.2.
Как видно из него, эффективность модуляции с увеличением величины
сро осциллирует и уменьшается. При сро = 2тг, 4тг, ... параметр М = 0.
В этом случае все электроны проходят поле модулятора в таких усло-
условиях, когда их первоначальное ускорение полностью компенсируется
торможением и наоборот. Электронный поток выходит в этом случае
из модулятора немодулированным по скорости. При </?о = 5тг, 9тг, ...
наблюдаются относительные максимумы, величина которых падает
с увеличением (ро. В связи с технологическими трудностями невозмож-
невозможно сколь угодно сильно уменьшать длину модулятора ti, а следователь-
следовательно, величину невозмущенного угла пролета, для достижения макси-
Элементарная кинематическая теория клистронов
55
мального параметра эффективности модуляции. Поэтому в реальных
устройствах величина угла пролета лежит в пределах (/?о Е (тг/2, тг), что
соответствует М ~ 0,6 -г 0,9.
Кинематический анализ процесса группировки
электронов в пространстве дрейфа
Рассмотрим группировку (фазовую фокусировку) модулированного
по скорости электронного потока в пространстве дрейфа, свободном от
полей. Как и раньше будем проводить анализ группирования потока
в кинематическом приближении. Процесс группирования обусловлен
тем, что электроны, покинувшие модулятор раньше, но с большими
скоростями, догоняют электроны с меньшими скоростями, но вышед-
вышедшими из модулятора позже. Это приводит к образованию электрон-
электронных уплотнений, т.е. к модуляции потока по плотности. Наглядное
представление о группировании в трубе дрейфа дает пространственно-
временная диаграмма электронного потока на плоскости (x,u)ti),u)ti —
фаза влета электрона в трубу дрейфа (рис. 2.3). Каждая линия на ней
соответствует траектории движения одного электрона. До пересечения
с плоскостью модулятора поток однороден по плотности и скорости,
чему соответствует одинаковый наклон и одинаковые временные ин-
интервалы A(u)ti) между траекториями рассматриваемых электронов.
Воздействие управляющего гармонического напряжения (изображен-
(изображенного на рисунке штриховой линией) приводит к модуляции скорости
электронов — периодическому изменению наклона траекторий. Для
электронов типа 2 наклон траекторий не меняется, поскольку они пе-
Рис. 2.3. Пространственно-временная диаграмма группирования электронов
в пространстве дрейфа: 1 — электрон, который тормозится полем, 2 —
электрон, не испытывающий воздействия со стороны поля, 3 — электрон,
который ускоряется полем
56 Лекция 2
ресекают плоскость модулятора в момент времени, когда управляющее
напряжение равно нулю. Для электронов типа 1, попадающих в тор-
тормозящую фазу поля, наклон траекторий уменьшается, для электронов
типа 3 — увеличивается (они попадают в ускоряющую фазу поля).
За период высокочастотного воздействия траектории сходятся (что
соответствует образованию уплотнений) или расходятся (образуются
разряжения частиц), что и иллюстрирует процесс группирования.
Найдем угол пролета электрона до некоторой плоскости в простран-
пространстве дрейфа, находящейся на расстоянии / от середины модулятора.
В силу равномерного движения электронов время t прибытия их в за-
заданную плоскость, учитывая закон скоростной модуляции B.4) и ма-
малость ?, будет равно:
t = tx + l/v = h + * « h + A \
ri-L .7^ « h + A \
vo[l + (?Msino;?i)/2] v0 v 2
Тогда для угла пролета в пространстве дрейфа получим выражение
О = ut — ut\ = — — — • -— sin u)ti = во — X sin ut\. B.6)
Величина^ = -Ч— #о называется параметром группирования; во = —.
2 vo
Отметим, что хотя мы и полагали ^ < 1, параметр группирования мо-
может быть и не малым, так как #о ~ I может принимать любые значения.
Определим теперь зависимость сгруппированного тока от времени
в данной точке пространства /. Пусть /о — ток электронного пучка
до модулятора, %\ — сгруппированный ток. Тогда на основании закона
сохранения заряда для группы электронов, проходящих плоскость х =
= 0 за время dti, а затем плоскость х = / за время dt можно записать
B-8)
i(O,ti)dti = Iodti = i(l,t)dt, B-7)
откуда для сгруппированного тока получаем
г = /0
Дифференцируя выражение B.6) по переменной ?i, находим
B.9)
На рис. 2.4 представлены зависимости тока пучка от начальной фа-
фазы влета в пространство дрейфа для различных значений параметра
группирования. При X <$С 1 из формулы B.9) видно, что ток меняется
по гармоническому закону, амплитуда переменной составляющей мала.
Уравнение B.9) принимает вид:
г = /0A + Xcosoot!). B.10)
Элементарная кинематическая теория клистронов
57
1
/о
Л
х=
/о
и
х=
= 1,84
У
V
= 2,0
и
Рис. 2.4. Зависимость тока пучка от начальной фазы влета электронов для
различных параметров группирования. Видно, что при X ^ 1 наблюдается
обращение в бесконечность величины тока пучка
При X = 1,0 знаменатель выражения, стоящего в правой части урав-
уравнения B.9), при ujt\ = 2птг, п Е Z обращается в нуль, а ток — в бес-
бесконечность (такой нефизический результат связан с неучетом сил про-
пространственного заряда, приводящих к размытию сгустка). Если X > 1,
знаменатель дважды за период обращается в нуль и имеет место два
бесконечных пика тока.
Проведем гармонический анализ сгруппированного электронного
потока. Так как сгруппированный ток является периодической функ-
функцией времени, то ее можно представить в виде ряда Фурье
г = /о
- в0),
п=1
где Ап — амплитуда гармонических составляющих, которые представ-
представляются в виде:
2тг
1 Г
Ап — — i(t) cosn(ut — во)d(ujt).
7Г J
О
Учитывая закон сохранения заряда B.8) и выражение B.6) для угла
пролета сгруппированного тока, найдем
п = — I cosn(o;?i - X sinojti)d(ojti).
Последнее выражение является интегральным представлением функ-
функции Бесселя n-го порядка Jn(nX). Таким образом для коэффициентов
58
Лекция 2
i = 11+1*2+13
-1,2
Рис. 2.5. Зависимость амплитуды гармоник сгруппированного тока от вели-
величины параметра группирования
Фурье Ап получаем
An=2I0Jn(nX),
и сгруппированный ток может быть записан окончательно как
= /о A+ V 2Jn(nX) cosn(uit - в0]
n=l
B.11)
B.12)
На рис. 2.5 представлены соответствующие зависимости амплитуд
гармоник тока от величины параметра группировки. Максимум первой
гармоники приходится на параметр группирования X = 1,84. Амплиту-
Амплитуда тока первой гармоники при оптимальном параметре X составляет ве-
величину 1,16/о, т. е. имеют величину порядка постоянной составляющей
тока пучка. Из формулы B.12) также понятно появление бесконечного
пика тока при X = 1,0: дело в том, что этому значению парамет-
параметра группирования соответствует бесконечное большое число гармоник
с конечными амплитудами (см. кривую на рис. 2.5, соответствующую
сумме трех первых гармоник сгруппированного тока г = %\ + %^ + ^з)-
100$ идея братьев Вариан и Хансена
Итак, мы научились управлять электронным потоком на сверхвы-
сверхвысоких частотах, а именно получать сгруппированный по плотности
поток. Вывели закон скоростной модуляции и построили теорию кине-
кинематической группировки предварительно промодулированного пучка
в пространстве свободном от полей. Теперь нам остается научиться
использовать такой пучок для усиления и генерации СВЧ-сигналов.
Разместим в конце пространства дрейфа выходной элемент, связан-
связанный с высокодобротным колебательным контуром (объемным резона-
резонатором). Если частота ujq входного резонатора (или её гармоника
Элементарная кинематическая теория клистронов 59
^
Рис. 2.6. Фрагмент страницы из лабораторной книги для записей от 22-
35 июня 1937 г., на которой Рассел Вариан изобразил основную конструкцию
клистрона
близка к собственной частоте выходного резонатора о;, то соответству-
соответствующая гармоника сгруппированного тока (о; ~ oj$ или uj « tiujq) будет
возбуждать выходное устройство резонансным образом. Приборы, ра-
работающие по данной схеме, получили название «клистронов» (точнее
описанная нами конструкция соответствует схеме двухрезонаторного
пролетного клистрона). Слово «клистрон» происходит от греческого
слова хАг;?ё?г/, которое означает «прибой» (дословно «разбивание волн
на пляже»).
История изобретения клистрона стоит того, чтобы уделить ей неко-
некоторое время. Судя по воспоминаниям Э. Гинстона [5], прибор, ставший
прообразом современного клистрона (рис. 2.6), был изобретен летом
1937 г., а соответствующая статья братьев Вариан появилась в 1939 г.
и.
Статья начиналась так: «Очень эффективные ВЧ-резонаторы, опи-
описанные в этом журнале Хансеном, послужили основой для создания
усилителей и генераторов нового типа, в которых время пролета элек-
электронов, обычно рассматриваемое как источник серьезных трудностей
на очень высоких частотах, обращено на пользу конструкции» (имеется
в виду работа Хансена «Резонатор, предназначенный для клистронного
генератора» [7]). Такое начало звучит довольно скромно, но отражает
главное, а именно, применение в конструкции лампы объемного резо-
60 Лекция 2
натора. По поводу работы братьев Вариан удачно пишет Р. Компфнер
[8, стр. 6-7]:
«... Варианы применили очень эффективный контур, так называ-
называемый «румбатрон», который незадолго до этого предложил исследо-
исследователь из той же компании — Хансен. Он придумал то, что могло бы
стать резонатором с очень высокой добротностью, — резонатор в виде
двух конических сегментов сферы, которые почти касаются друг друга.
Румбатрон сыграл важную роль в схеме «клистрона», как его назвали
братья Вариан.»
Остановимся на обстоятельствах изобретения румбатрона. Хансен
занимался созданием рентгеновского излучателя и решил, что для
ускорения электронов, используемых в излучателе, можно применить
большие ВЧ-напряжения, которые образуются в резонансной системе.
По словам Хансена, он и Рассел Вариан много думали «над различ-
различными хитрыми способами, которые могли бы быть использованы для
получения большой скорости электронов без большой суммы денег»
[5, стр. 33]. Эксперименты и теоретические расчеты Хансена вскоре
показали, что резонатор, необходимый для рентгеновского излучателя,
должен обладать очень малыми потерями. Это заставило его отказаться
от резонаторов в виде отрезков коаксиальных линий и «выбросить» из
конструкции внутренний проводник. Последнее и привело к созданию
объемного резонатора (рис. 2.7). Следует заметить, что Рассел Вариан
также принимал участие в работе по рентгеновскому излучению и был
в деталях знаком с работой Хансена.
В эти же годы A933-1937) Сигурд Вариан был летчиком. Именно
он заинтересовал Р. Вариана задачей обнаружения воздушной цели
с земли в плохую погоду или ночью. Р. Вариан пришел к выводу, что
решение этой задачи состоит «в использовании радиоволн, и что точ-
точное определение направления с помощью оборудования, имеющего ра-
разумные размеры, потребует использования радиоволн сантиметрового
диапазона. К середине 1936 г., по счастливой для Рассела случайности,
новый резонатор Хансена — румбатрон — мог быть приспособлен для
генерации этих волн» [5, стр. 33-34].
Станфордский университет (физический факультет) предоставил
братьям Вариан возможность работать над созданием генератора в сво-
своих лабораториях, выделив 100 долларов в год на все нужды (отсюда
название статьи Гинзтона — «100-долларовая идея»). Причем универ-
университет оговорил, что потенциальная прибыль должна быть впоследствии
поровну разделена между им и братьями (позднее в эту маленькую
корпорацию вступил и Хансен). Руководство физического факульте-
факультета не ошиблось: университет получил более 2,5 миллионов долларов.
«Большая часть нынешней репутации Станфорда в электронике и фи-
физике может быть приписана совместным усилиям этих трех человек
и студентов, которые работали с ними», — писал в 1975 г. Эдвард
Гинзтон — один из упомянутых студентов.
Элементарная кинематическая теория клистронов
61
D
Рис. 2.7. Различные формы резонаторов для клистронов. Показано попереч-
поперечное сечение, так как резонаторы аксиально симметричны. Пучок электронов
должен двигаться параллельно оси симметрии. Тип (Л) весьма удобен для
практического использования, но труден для расчетов. Пунктиром показана
сфера и резонатор типа концентрической линии; (Л ) можно рассматривать
как искажение того или другого. (В) очень легко рассчитывается, (С) —
труднее, но тоже возможно рассчитать. Для (В) показана приближенная
картина линий электрического поля. Тип (D), аналогичный (Л), полезен
практически, но не может быть рассчитан точно (рисунок и подпись из [8])
Как были сделаны решающие шаги на пути изобретения клистрона,
лучше всего понять, обратившись к воспоминаниям Р.Вариана, которые
приводит Гинзтон [5, стр. 35-37] в разделе «Группировка —тринадцатая
идея».
«В один из дней, после того, как мы продумали множество вариан-
вариантов, я был занят разработкой классификации всех вариантов, которые
мы проработали, чтобы мы могли систематически изучать их все и не
обнаружить потом, что пропустили некоторые наиболее многообещаю-
многообещающие. В процессе разработки этой классификации я неожиданно подумал
о принципе скоростной группировки г). С психологической точки зре-
зрения скорее интересно, что эта попытка классификации действительно
привела к изобретению клистрона. Принцип скоростной группировки не
х) В оригинале [5, стр. 35-37] использован термин «velocity grouping»
рый мы переводим как «скоростная группировка».
кото-
62 Лекция 2
соответствовал ни одной схеме в классификации, которую я придумал,
и я скорее думаю, что идея пришла ко мне потому, что я бессознательно
пытался проверить справедливость моей классификации. Поэтому я
придумал исключение из классификации, которое в действительности
оказалось основной концепцией для клистрона». Далее Р.Вариан пояс-
поясняет термин «скоростная группировка» следующим образом. «Новый
метод» является вариантом сеточного управления, но ни один из элек-
электронов не избегает прохода через сетку. Они просто замедляются или
ускоряются... При этих условиях электроны после прохождения через
управляющие сетки будут иметь различные скорости в зависимости
от фазы в колебательной системе, когда электроны проходили через
нее. Если электроны движутся прямолинейно, то ускоренные будут
догонять отставшие, и поток электронов превращается из однородного
в состоящий из последовательности сгущений или волн электронов,
имеющих ту же частоту, что и возбуждающая».
Интересно, что, по воспоминаниям Гинзтона, прошло всего несколь-
несколько дней от обсуждения описанной выше концепции до начала кон-
конструкторской работы над новым прибором. Важнейшую роль в столь
быстром начале работы сыграло то, что объемный резонатор Хансена —
главная часть будущего прибора — уже существовал. Емкостную часть
резонатора (рис. 2.7) составили «крошечные шестиугольные сетки в ви-
виде сот» [5, стр. 36], которые были выполнены С. Варианом вручную
(рис. 2.8). Многочисленные трудности, которые пришлось преодолеть
изобретателям клистрона, пока не появилась первая лампа, живо опи-
описаны в неоднократно цитированной статье Гинзтона. Во всяком случае,
они потратили на создание первого макета ровно половину выделен-
выделенных ассигнований — 50 долларов. «Как указывал позднее Рассел, это
был, возможно, самый дешевый проект, из когда-либо выполненных
в электронике СВЧ» [5]. Кроме того, если следовать Гинзтону, то братья
Вариан и Хансен были первопроходцами во всем: от идей через теорети-
теоретическое обоснование до конструкции и экспериментального воплощения
прибора. «... До тех пор, пока их работа «Высокочастотный генератор
и усилитель» не была помещена в «Журнале прикладной физики»
в 1939 году, они не знали, что скоростная модуляция открыта в 1933 году
А. Арсеньевой-Хейль и Оскаром Хейлем в Европе» [5].
Когда первый клистрон был сделан, то возникла новая проблема:
как узнать, генерирует ли он? Пришлось изобретать и способ детек-
детектирования колебаний. Р.Вариан предложил следующую схему. Часть
электронного пучка проходила через отверстие во втором резонаторе
и в области за ним отклонялась магнитным полем так, что луч попадал
на ограниченную область флуоресцирующего экрана (рис. 2.8). Так
была создана достаточно чувствительная и оперативная детекторная
система для обнаружения колебаний. «Это изобретение было, возмож-
возможно, почти так же важно, как изобретение самого клистрона, потому что
Элементарная кинематическая теория клистронов
63
Рис. 2.8. Схема клистрона-генератора братьев Вариан: 1 — катод, 2 — уско-
ускоряющая сетка, 3 — фокусирующее кольцо, 4 — сетки, 5 — пространство груп-
группировки, 6 — элемент обратной связи, 7' — магнитное поле детектирующего
устройства, 8 — флуоресцирующий экран
без него мы, по-видимому, никогда не смогли бы обнаружить колебания,
хотя бы они, по-счастью, и имели место», — писал Р. Вариан [5, стр. 37].
И вот, наконец, наступило 19 августа 1937 года, когда заработал пер-
первый прибор. Сигурд Вариан впоследствии так писал об этом времени:
«Мы наблюдали повторяющиеся вспышки на экране нашего детектора,
но все выглядело очень нестабильно и весьма разочаровывающе. При-
Примерно 21 августа я отсоединил лампу от насоса и заменил вольфрамовые
проволочные сетки медными шестиугольными сетками и установил
микрометрический винт для подстройки. Это была главная операция.
На утро 30 августа 1937 года я был готов начать опять. Я повернул
выключатель, немного подстроил лампу и появились колебания по
всему флуоресцирующему экрану. Мы раскопали старый кристалли-
кристаллический детектор с кошачьими усами и гальванометр и начали измерять
ВЧ-энергию по всей комнате. Мы быстро определили частоту, двигая
кристаллический детектор через стоячие волны в комнате. К нашему
64 Лекция 2
удовольствию мы вычислили, что длина волны была 6,5 см, и были
очень смущены, когда должны были признать, что мы измерили по-
полуволны, т. е. правильная длина волны была 13 см» [5, стр. 37].
Несколько позднее за новым прибором закрепилось название «кли-
«клистрон», которое было предложено профессором факультета античной
литературы Станфордского университета Френкелем.
Два последующих года работы над клистроном продолжались в на-
направлении использования его в допплеровской радарной системе и си-
системе для посадки самолетов. К моменту публикации статьи братьев
Вариан их группа уже многого добилась: она уже хорошо понимала все
характеристики клистрона, имела в своем распоряжении клистроны-ге-
клистроны-генераторы (в том числе, отражательные), клистроны-усилители с двумя
и несколькими резонаторами, исследовала клистрон как компонент
сложной СВЧ-цепи. Как гордо пишет Гинзтон [5, стр. 38], который
подключился к работе в 1939 г., «мы смогли продемонстрировать, что
почти все, что можно сделать с обычными радиолампами могло быть
сделано с помощью клистрона в СВЧ-диапазоне». Интересно, что ма-
маленькая группа, реализовавшая 100-долларовую идею, превратилась
впоследствии в мощную Ассоциацию Вариан (основана в 1948 г.) —
фирму, хорошо известную в мире электроники г).
Изобретение клистрона сыграло важную роль для дальнейшего
развития электроники СВЧ, особенно для превращения её в самосто-
самостоятельную область индустрии. Клистрон использовался (в ряде слу-
случаев используется и сейчас) в навигационных системах гражданской
авиации, в системах спутников связи, в военной радиолокации и ра-
радиопротиводействии. Клистроны дали жизнь и многим ускорителям,
используемым в медицине и ядерной физике, в том числе знаменитому
станфордскому ускорителю, длиною в две мили (см. лекцию 11). Исто-
История клистрона — это еще и история удивительно удачного объединения
трех разных талантливых людей — физика и изобретателя Р. Вариана,
летчика и физика-экспериментатора, умеющего делать все С. Вариана,
физика (теоретика и экспериментатора) и педагога, опережавшего свое
время, В. Хансена 2).
х) В 1996 году эта фирма прекратила свое самостоятельное существование,
слившись с более мощной.
2) И хотя известный американский писатель Митчел Уилсон (в прошлом
физик, окончивший Колумбийский университет, работавший у Энрико Фер-
Ферми) весьма категорично заявляет: «В моих произведениях не бывает прото-
прототипов», его роман «Брат мой, враг мой» (М.: Мир. 1964. 440 с) несомненно
написан под впечателением работы братьев Вариан (уж очень сходны факты
из биографий реальных братьев и братьев Меллори — героев романа, кото-
которым впервые удалось осуществить телевизионную передачу движущегося
изображения).
Элементарная кинематическая теория клистронов 65
В Советском Союзе работы по созданию прямопролетных клистро-
клистронов были начаты в середине 30-х годов, и первые металлические усили-
усилительные клистроны на длину волны 13 -г 16 и 25 см и мощностью 50 Вт
были разработаны в 1940 году Н.Д. Девятковым и его группой [9, 10].
К этому же времени относятся работы Ю.А. Кацмана в Ленинградском
электротехническом институте им. В.И. Ульянова (Ленина) по разви-
развитию теории и разработке прямопролетных клистронов на длину волны
10см [11].
Клистронные усилители и умножители частоты
Прежде чем говорить о выходных характеристиках клистронных
усилителей, определим некоторые основные соотношения, характеризу-
характеризующие энергетическое взаимодействие электронного потока с перемен-
переменным электромагнитным полем.
Как уже отмечалось в первой лекции, энергетическое взаимодей-
взаимодействие между прямолинейным электронным потоком и электромагнит-
электромагнитным полем связано с изменением кинетической энергии электронов,
преобразующейся в энергию электромагнитного поля. В кинематиче-
кинематическом приближении рассматривается движение в заданном высокоча-
высокочастотном поле, при пренебрежении самосогласованного влияния элек-
электронов на само поле. Это означает, что энергия электронов идет не
на изменение поля, а на поддержание установившихся колебаний, т.е.
рассматриваются условия поддержания стационарных колебаний.
Пусть электрон движется прямолинейно в переменном поле Е, тогда
его уравнение движения имеет вид:
d(mv) ^ d (mv2\ ,_, ^dx
v y J = eE, или — = evE = eE — .
dt ' dt \ 2 J dt
Мощность взаимодействия с полем напряженности Е одного электрона
на пути dx, равная изменению кинетической энергии электрона в еди-
единицу времени, будет определяться как
Если п — концентрация электронов, то находящиеся на пути dx элек-
электроны (N = ndx) будут характеризоваться мощностью взаимодействия
PN = NPe = ne^p Edx = iEdx.
dt
Если конвекционный ток г и поле Е находятся в фазе, то кинетиче-
кинетическая энергия электронов увеличивается (поле отдает мощность элек-
электронному потоку). Противофазность г и Е соответствует обратному
процессу — пучок отдает мощность ВЧ-полю. В общем случае при
произвольном сдвиге фаз между г и Е мощность взаимодействия будет
3 Д. И. Трубецков, А. Е. Храмов
66
Лекция 2
комплексной величиной. Кроме активной мощности взаимодействия
появляется реактивная мощность, которая характеризует ту мощность,
которой периодически обменивается поле и электронный поток.
Предполагая гармонический характер изменения переменных вели-
величин и используя комплексные амплитуды, можно записать среднюю за
период мощность взаимодействия на пути / в виде
Ре = i iE* dx,
B.13)
Соответственно активная Реа и реактивная Рег мощности взаимодей-
взаимодействия принимают вид:
Реа = -
i
\iE* dx,
Per = - Im iE* dx.
о
B.14)
Определив понятие электронной мощности взаимодействия, можно
обратиться к эквивалентной схеме с сосредоточенными параметрами
для высокодобротной СВЧ-колебательной системы (объемного резона-
резонатора). Эквивалентная схема представляет собой обычный колебатель-
колебательный контур, составленный из сосредоточенных элементов. В частности,
в объемном тороидальном резонаторе клистрона и электронный пучок,
и электрическое поле колебательной системы находятся в узком зазоре,
так что зазор с высокой степенью точности эквивалентен конденсатору.
Если рабочая полоса частот резонатора достаточно узкая (в резо-
резонансной системе имеют место колебания только одного вида), то ре-
резонансные свойства можно опи-
описать введением в эквивалент-
эквивалентную схему (см. рис. 2.9) емко-
емкости С и индуктивности L. Экви-
Эквивалентные емкость и индуктив-
индуктивность вносят в схему реактивную
проводимость 6НК = шС — 1/ujL.
Поведение и свойства элемента
связи, а также нагрузки учиты-
Рис. 2.9. Эквивалентная схема сверх-
сверхвысокочастотного устройства с узко-
узкополосной резонансной системой
ваются включением в схему эк-
эквивалентной активной проводи-
проводимости (проводимости нагружен-
нагруженного контура) gHK [2]. Мощность потерь за период на gHK, как видно из
эквивалентной схемы, выражается соотношением
р -к К
1 нк — ь нк (у 1
B.15)
Элементарная кинематическая теория клистронов 67
где Vi — напряжение, воздействующее на пучок. Полная проводимость
резонансной системы без электронного пучка будет равна
Унк = ?нк + jbHK. B.16)
Понятие электронной мощности взаимодействия B.13) позволяет
ввести понятие электронной проводимости уе:
ye=ge+jbe = ^, Se = ^, be = ^. B.17)
Отсюда ясно, что когда активная мощность взаимодействия положи-
положительна, то пучок действует подобно дополнительной нагрузке (ge > 0).
Однако, если Реа < 0, то ge < 0, и существует возможность установле-
установления в колебательном контуре незатухающих колебаний. В установив-
установившемся режиме, когда амплитуда колебаний остается постоянной с тече-
течением времени, должно выполняться условие стационарных колебаний
Уе+Упк = 0 B.18)
или отдельно для активной и реактивной составляющих проводимости:
#е+#нк=0, B.19)
be + bHK = 0. B.20)
Выражение B.19) позволяет при известных параметрах резонансной
системы и нагрузки, а также известной электронной мощности взаимо-
взаимодействия определить амплитуду стационарных колебаний, а следова-
следовательно, мощность, отдаваемую в нагрузку. Формула B.20) определяет
частоту стационарных колебаний.
Однако вернемся к пролетному двухрезонаторному клистрону. Так
как теория взаимодействия сгруппированного тока с переменным элек-
электромагнитным полем (схема пролетного клистрона) достаточно подроб-
подробно и тщательно изложена в монографии [2], не будем останавливаться на
выводе выражения для электронной мощности взаимодействия, а сразу
выпишем окончательные соотношения:
Реа = 1ОУо?2ММХ)сОВ0о + \ ЛМ^/ДЫ, B-21)
Per = -IoVobMJi(X)Smeo + \ /oVb?i/r(?>o), B-22)
где ?i и ^2 — соответственно амплитуды ВЧ-напряжения, нормирован-
нормированные на ускоряющее напряжение Vo, в модулирующем ВЧ-промежутке
и выходном ВЧ-промежутке. Вторые слагаемые представляют собой
электронную мощность взаимодействия немодулированного электрон-
электронного потока с высокочастотным полем. Функции fa и /г носят на-
названия монотронных функций и определяют эффекты конечного угла
пролета </?о в модулирующем зазоре (их вид можно найти в монографии
68 Лекция 2
[2] г)). При условии d <1 вторыми слагаемыми в выражениях B.21)
и B.22) можно пренебречь.
Из формулы B.21) видно, что в зависимости от угла пролета во
взаимодействие характеризуется либо передачей энергии электронным
потоком ВЧ-полю, либо наоборот — поле отдает энергию электронам.
Знак активной компоненты мощ-
¦^ у^~^^т = ^~~^ ^_ ности определяется фазой тока,
\—<s ^^tfX ^ч"~"*^ входящего в выходной резонатор.
Реа<0 If/ Pea>^ Качественно это можно понять
ш^ с точки зрения взаимодействия
^^/^"^х^^уг^^х^^^/^^*^—»^ электронных уплотнений (струк-
ш тур в электронном потоке) с пе-
D О1П л ременным полем (рис. 2.10). Вид
Рис. 2.10. Схема, поясняющая энерго- к vk / ^
обмен электронного пучка и электро- взаимодействия зависит от то-
магнитного поля в выходном резона- г0> в какУю фазу поля попадают
торе в пролетном клистроне. электронные сгустки. Если сгуст-
сгустки проходят зазор в течение отри-
отрицательного полупериода, то электроны тормозятся и Реа < 0, при про-
прохождении положительного полупериода наблюдается ускорение элек-
электронов, и Реа > 0. Отметим, что реактивная компонента электронной
мощности взаимодействия B.22) сдвинута по фазе на угол тг/2 отно-
относительно Реа-, т-е- когда Реа максимальна, величина Рег равна нулю
и наоборот.
Предположим, что ^ < 1 (усиление слабых входных сигналов)
и cos#o = — 1 (оптимальные условия энергообмена), тогда из соотно-
соотношения B.21) и условия стационарных колебаний B.19) получим:
2MhJ1(X) _ ( .
где V<i — амплитуда ВЧ-колебаний в выходном резонаторе. Для малых
сигналов Ji(X) « Х/2 = ^Мво/А и коэффициент усиления напряже-
напряжения в режиме слабого сигнала имеет вид:
Ку = ? = 2у'°. B.24)
Реально реализуемые значения коэффициента усиления по напряже-
напряжению не превышают нескольких единиц, так как его увеличение связано
либо с увеличением длины пространства дрейфа, либо с уменьшени-
уменьшением величины входного сигнала. Однако и тот и другой способ ведут
к увеличению разгруппировки электронов, что ухудшает энергообмен
в выходной колебательной системе. Клистронные усилители слабого
сигнала кроме низкого коэффициента усиления характеризуются также
высоким уровнем шумов и узкой полосой усиливаемого сигнала.
х) См. формулы (Ш.4) и (III.5) на стр. 97 [2].
Элементарная кинематическая теория клистронов
69
В случае большого входного сигнала (усилитель мощности) из перво-
первого условия стационарных колебаний и формулы B.23) несложно найти,
что
_ У? _ BМ/оЛррJ
гнк — бнк 0 — 0
B.25)
Мощность во входном резонаторе Р\ = gkVi/2 (gk — проводимость
первого резонатора). Тогда для коэффициента усиления по мощности
получаем:
Кр = —- = 2 —^-. B.26)
Определим максимальный электронный к.п.д. двухрезонаторного
клистрона, воспользовавшись выражением B.21), в следующем виде:
B.27)
Подбирая оптимальные значения углов пролета (cos во = 1)? параметра
группировки (X = 1,84) и полагая М ~ 1, У^ = Vo (это соответствует
максимально возможной амплитуде напряжения, так как при дальней-
дальнейшем увеличении Уч электроны будут отражаться обратно в простран-
пространство дрейфа), получим максимальное значение к.п.д. равным 58 %.
Клистрон может быть эффективно использован и как умножитель
частоты. Это связано с тем, что в сгруппированном токе величина
амлитуд гармоник (гп = 2IoJn(nX)) основной частоты достаточно вы-
высока. В таблице 2.1 приведены величины отношения максимальных
значений гармоник гп к постоянной составляющей тока /о и к первой
гармонике %\.
Табл и ца 2.1
п
in/Io
in/h
1
1,16
1,00
2
0,96
0,83
3
0,86
0,75
5
0,74
0,64
10
0,60
0,52
15
0,54
0,47
20
0,48
0,42
Из таблицы видно, что максимальная величина гармоники убывает
достаточно медленно (отметим, что значения гармоник ВЧ-тока с уче-
учетом пространственного заряда получаются несколько хуже приведен-
приведенных в таблице). Это позволяет использовать клистрон как эффектив-
эффективный умножитель частоты, причем конструкция умножителя ничем не
отличается от конструкции усилителя, за исключением лишь того, что
выходной резонатор настраивается на частоту, кратную частоте моду-
модулирующего напряжения. Характерное отношение выходного к входно-
входному сигналу в умножителях частоты лежит в пределах 0,01 -г 0,1.
70 Лекция 2
Некоторые результаты теории резонансных
автогенераторов
В предыдущих разделах рассматривалось усиление ВЧ-сигнала
в приборах с динамическим управлением электронным потоком. Рас-
Рассмотрим теперь резонансный автогенератор, состоящий из объемного
резонатора и электронного потока г). Пусть резонатор является высо-
высокодобротным и возбуждается на одном колебании с индексом s.
Напомним, что уравнение возбуждения резонатора можно записать
в виде A.61) (см. также [3, 13]):
dCs +j(oo-us)Cs = JL [ j(w,*)Ee dV B.28)
dt JX *' * 2N,
v
(все обозначения совпадают с обозначениями лекции 1). Частота коле-
колебаний определяется (см. A.51)) как и = u's + ju)'J, где первое слагаемое
определяет частоту колебаний, а второе — декремент затухания этого
колебания.
Если ток j(o;) не гармоническая, а периодическая функция, то
в качестве j(c<;) в уравнении B.28) необходимо использовать первую
гармонику тока j(?)
2тг
1
j(w) = - j(t) exp (jut) d(ut) = 2j(t) exp (jut). B.29)
7Г J
0
Остальные гармоники резонансного возбуждения не дают и, как обсу-
обсуждалось в первой лекции, составляют так называемый нерезонансный
фон.
Используя формулу B.29) уравнение B.28) можно переписать в ви-
виде:
+ J{L° L°)C k\№№ext>tiwt)dV B.30)
причем для добротного резонатора можно считать, что вектор Es веще-
вещественный (т. е. пренебречь затуханием колебаний). Для Es в этом случае
будут выполняться соотношения:
Ев = Е* Ns = — [ E24dV > 0. B.31)
Vo
Величина
W = ^\CS\2NS B.32)
х) Характерным примером резонансного автогенератора является отража-
отражательный клистрон, который будет рассматриваться в следующем разделе.
Элементарная кинематическая теория клистронов 71
равна энергии s-ro вида колебаний в режиме генерации. Таким образом
норма резонансного колебания имеет четкий физический смысл — она
пропорциональна энергии этого колебания.
Рассмотрим следующий вопрос: на какой частоте и с какой ампли-
амплитудой происходят стационарные автоколебания системы электронный
поток — резонатор. При рассмотрении пролетного клистрона для ответа
на этот вопрос использовалось эквивалентное представление резона-
резонатора как колебательного контура. Понятно, что такое рассмотрение
не обладает необходимой общностью *). Получим общие соотношения
для любого резонансного генератора, используя выражения B.30) и
B.32). Из расмотрения пролетного клистрона ясно, что амплитуда будет
определяться энергетическим балансом в системе. Однако наиболее ин-
интересно найти поправку к частоте генерации относительно «холодной»
частоты резонатора и её зависимость от электронного потока, т. е. найти
электронную перестройку частоты.
Благодаря стационарности колебаний в системе, положим в формуле
B.30) —- = 0 и домножим обе ее части на C*NS:
s 2 J s
Взяв комплексно сопряженное от обоих частей выражения B.33) и ис-
используя B.32), получаем:
V. B.34)
V
Резонансная часть электрического поля равна
E(t) = Re {CSES exp (jut)} , B.35)
причем,
^Щ = Im {CSES exp {jut)} . B.36)
Таким образом из выражения B.35) с учетом формул B.35) и B.36)
получаем два соотношения соответственно для активной и реактивной
х) Л.А. Вайнштейну принадлежит замечательная фраза: «Когда мне рису-
рисуют эквивалентную схему, я чувствую, что меня обманывают.» Однако когда
в резонаторе рассматривается один тип колебаний, представление в виде
эквивалентной схемы правомерно.
72 Лекция 2
мощности взаимодействия:
\ J17dV = Ре„, B.37)
|dV = Per. B.38)
Формула B.37) есть формулировка закона сохранения энергии:
в правой части стоит мощность, отдаваемая электронами электромаг-
электромагнитному полю, в левой — мощность, выделяемая в нагрузке и в резонато-
резонаторе. Формула B.38) есть баланс реактивных мощностей, определяющий
частоту стационарных колебаний. Реактивная мощность обращается
в нуль при uj = u)fs, т. е. при точном резонансе, что согласуется с пре-
предыдущим рассмотрением.
Поделив выражение B.38) на B.37) получим формулу для частоты
стационарных колебаний:
^М = §^. B-39)
Последнее выражение определяет электронную перестройку ча-
частоты и справедливо для всех резонансных генераторов.
Элементарная теория отражательного клистрона
Отражательный клистрон представляет собой резонансный автоге-
автогенератор клистронного типа, в котором модуляция электронов по ско-
скорости и взаимодействие сгруппированного потока с ВЧ-полем проис-
происходят в единственном резонаторе. Схема отражательного клистрона
приведена на рис. 2.11. Группирование потока осуществляется в тор-
тормозящем поле между резонатором и специальным электродом — от-
отражателем, на который подается отрицательный относительно резо-
резонатора потенциал \Vr\- Отражательный клистрон представляет со-
собой генератор, в котором первоначальные колебания возникают за
счет шумовых флуктуации в пучке г). В предгенерационном режиме
сгруппированный ток характеризуется бесконечно большим набором
временных шумовых гармоник. Таким же числом гармоник обладает
и ток, наведенный во внешней цепи зазора. Однако так как резонатор
представляет собой колебательную систему с высокой добротностью,
он «выделяет» из бесконечного набора шумовых гармоник ту, частота
которой близка к его собственной частоте. Если в среднем за период
х) На языке теории излучения имеет место спонтанное переходное излуче-
излучение, которое после группирования пучка становится индуцированным.
Элементарная кинематическая теория клистронов
73
Катод
Резонатор
Отражатель
потери в резонаторе будут компенсироваться энергией, поступающей
от сгруппированного электронного потока, то в клистроне установится
режим стационарных колебаний. Мини-
Минимальное значение постоянной составля-
составляющей тока пучка /о, при котором воз-
возникают колебания на основной часто-
частоте, называют пусковым током, а ре-
режим возникновения стационарных коле-
колебаний называется пусковым.
Процесс группирования электронов
в однородном тормозящем поле мало
чем отличается от рассмотренного вы-
выше группирования в пространстве дрей-
дрейфа (см. рис. 2.3, на котором приведена
пространственно-временная диаграмма
электронного потока в пространстве
дрейфа пролетного клистрона). Если
тормозящий потенциал между второй
сеткой резонатора и отражателем линейно зависит от координаты
(а в кинематической теории, неучитывающей пространственный заряд
потока, распределение потенциала действительно линейно), то, очевид-
очевидно (см. рис. 2.12, на котором представлена пространственно-временная
диаграмма для этого случая), ускоренные в модуляторе электроны
пролетают дальше в пространстве сетка-отражатель, чем электроны,
затормозившиеся после прохождения модулятора. Центром сгруппи-
сгруппированного сгустка становятся электроны, вылетевшие из модулятора
с неизменившейся скоростью и пролетающие зазор в тот момент време-
времени, когда фаза ВЧ-поля изменяется с ускоряющейся на тормозящую.
При обратном движении потока от отражателя к высокочастотному
зазору резонатора поле, которое при прямом движении было ускоря-
ускоряющим, становится для электрона тормозящим. Центр сгустка будет
попадать в максимум тормозящего поля зазора (в этом случае, оче-
Рис. 2.11. Схематическое изоб-
изображение отражательного кли-
клистрона
во = Зя/2
во = 7я/2
00=1171/2'
Рис. 2.12. Пространственно-временная диаграмма группировки электронно-
электронного потока в тормозящем поле, поясняющая возникновение различных зон
генерации
74 Лекция 2
видно, Реа < 0), если невозмущенный угол пролета электрона в поле
отражателя
@о)опт = 2тг (п - ±) . B.40)
Здесь п — номер зоны колебаний (п = 1, 2, 3, . . .). Зона колебаний —
зависимость мощности от частоты или от величины потенциала от-
отражателя Vr. Зоне колебаний соответствует область во, где Реа < 0.
Выражение B.40) дает центр зоны колебаний. Из пространственно-
временной диаграммы несложно видеть, что границы зоны колебаний
будут определяться следующими значениями углов пролета:
(Oo)min = 2тг (п - 1/2) нижняя граница, , ,
(#о)шаж = 2тгп верхняя граница. ^ ' '
Рассмотрим процесс группировки потока в постоянном тормозящем
поле. Уравнение движения для электрона, вылетевшего из модулятора
в точке х = 0 в момент времени t = ti, имеет вид
X = v(t-t1)-a-{t-t1)\ а=ч(У° + \Уг\), B.42)
где D — расстояние между модулятором и отражателем.
Угол пролета электронов можно найти из соотношения B.42), поло-
положив х = 0 и отбросив тривиальное решение t = t\. Тогда
TWAlVo- B-43)
Невозмущенный угол пролета определяется выражением
vo
В предполож;ении, что электроны проходят центр модулирующего зазо-
зазора в момент времени t\ и модуляция слабая, закон модуляции запишется
в виде
v = v0 (l + ^ sin wtA . B.45)
Подставляя значение v в виде B.45) в формулу B.43), и учитывая выра-
выражение B.44) для угла пролета в пространстве группирования, находим,
что
2. B.46)
Используя, как и при рассмотрении теории пролетного клистрона, закон
сохранения заряда I^dti = idt, для сгруппированного тока получаем
соотношение
Элементарная кинематическая теория клистронов 75
Данная зависимость отличается лишь знаком при гармоническом члене
от соответствующего выражения B.9) теории пролетного клистрона.
Поэтому группировка оказывается сдвинутой по фазе относительно
группировки в пространстве дрейфа на величину тг, что, как уже отме-
отмечалось, объясняется особенностями группировки в каждой из систем.
Разложение в ряд Фурье дает для первой гармоники сгруппирован-
сгруппированного тока значение:
гх = 2/oJi(Xo) cos (cot- 0O), B.48)
где J\ — функция Бесселя 1-го порядка.
Проанализируем стационарный режим работы отражательного кли-
клистрона. Для этого воспользуемся выведенными в предыдущем разделе
энергетическими соотношениями для резонансных автогенераторов:
-Pea B.49)
о о
— баланс активных мощностей,
J ^i1{t)^dtdx -Per B.50)
О О
— баланс реактивных мощностей. Здесь E(t) = U(t)/l = V\ sinuit/l.
Используя выражение B.48) для первой гармоники сгруппированно-
сгруппированного тока и выражение для E(t), из соотношений B.49) и B.50) получаем
= -Реа, B.51)
-Per, B.52)
где
Ф = в0 - 2тг (п - 1/4) , п е Z.
Последние уравнения представляют собой уравнения стационарных
колебаний отражательного клистрона. Их удобнее переписать в ином
виде, используя эквивалентную схему резонатора. В этом случае урав-
уравнения B.51) и B.52) примут вид
Янк + ge = 0, B.53)
^ gHKQ + be=0. B.54)
2Р
где #нк = gk + gn = —y~ — результирующая активная проводимость
резонатора (gk) и нагрузки (gH).
76 Лекция 2
Учитывая вышеприведенные соотношения и выражение B.46)
для Хо, перепишем равенство B.53) следующим образом:
Jl(Xp) _ #нкУо /о кк\
Хо 1оМ29особФ
Последняя формула является уравнением для определения амплитуды
стационарных колебаний V±.
Пусковому режиму генератора соответствует бесконечно малая ве-
величина ВЧ-напряжения на зазоре резонатора (V\ —у 0) и оптимальное
значение угла пролета во (а? следовательно, Ф = 0, ge = (#е)мах)-
При этих условиях Хо -У 0, lim 1[r о) = -, а (#о)опт = 2тг (п - 1/4).
Тогда из соотношения B.55) находим для пускового тока
тгМ2(п-1/4) V ;
Из этого выраж;ения следует, что пусковой ток отражательного кли-
клистрона уменьшается с увеличением номера п зоны колебаний. Это свя-
связано с тем, что с ростом п (величины #о) электроны дольше находятся
в пространстве группирования, что облегчает образование электронных
сгустков при малых V\.
Мощность, отдаваемая электронным потоком электрическому по-
полю, выражается соотношением B.51). Выразив напряжение на зазоре V\
через параметр группирования Хо, можно записать:
^ B.57)
Понятно, что не вся мощность, определяемая этим выражением явля-
является полезной: часть ее идет на компенсацию потерь в стенках, диэлек-
диэлектрических вставках и т. д. Поэтому практический интерес представляет
мощность, выделяющаяся в нагрузку, которая определяется как Рн =
= ^нк(#н/#нк). Окончательно
Рн = Щ^ ХоЫХ0)со8Ф*±. B.58)
Соответственно к.п.д. отражательного клистрона выражается как
М ^-. B.59)
Обратимся теперь к анализу второго условия стационарных ко-
колебаний B.50), которое позволит нам определить частоту генерации.
Поделим уравнение B.50) на B.49). Тогда
OLip. = -^ = -tg<P B.60)
Элементарная кинематическая теория клистронов 77
или, используя определение добротности, получим
2("-;":) = -*?* B.61)
Из последнего соотношения находим для частоты генерируемых коле-
колебаний отражательного клистрона
i - b-f) ¦ B.62)
В центре каждой зоны (Ф = 0) частота генерируемых колебаний и в точ-
точности равна частоте u's резонатора. Частота генерируемых колебаний
будет меняться при изменении потенциала отражателя Vr в пределах
одной зоны, так как с изменением Vr меняется величина Ф. Данное
явление, как уже говорилось, носит название электронной перестройки
частоты. Электроная перестройка является одной из наиболее важных
характеристик отражательного клистрона. С точки зрения физики,
эффект изменения частоты с изменением Vr может быть связан с изме-
изменением диэлектрических свойств электронного облака [14]. Из рассмот-
рассмотрения формулы B.61) понятно, что диапазон электронной перестройки
существенно зависит от конкретной конструкции клистрона и величины
нагрузки (Q), а также от электрических параметров его работы {1%Ф =
= -Per/Pea)-
Клистронный генератор с запаздыванием: от режимов
монохроматических колебаний до режимов
динамического хаоса
Как уже обсуждалось в первой лекции, одним из направлений
современной сверхвысокочастотной электроники является разработка
и исследование генераторов, характеризующихся широкополосным шу-
моподобным выходным излучением. Генераторы хаотических автоко-
автоколебаний составляют важный класс приборов вакумной СВЧ-электро-
ники. Одной из таких систем, демонстрирующих сложную динамику,
является генератор на пролетном клистроне с внешней запаздывающей
обратной связью [15, 16]. Основным недостатком этого генератора яв-
является узкая рабочая полоса частот, что не позволяет создать шумовой
сигнал с полосой больше нескольких процентов. Вместе с тем, если такой
ширины полосы достаточно, то простота конструкции, а также высокий
к.п.д., свойственный клистрону, делают генератор хаотических колеба-
колебаний на клистроне весьма привлекательным.
Обратная связь в клистроне наиболее просто осуществляется за
счет ответвления части мощности с выхода прибора во входной моду-
модулирующей резонатор через внешнюю линию с задержкой во времени.
Цепь обратной связи характеризуется в этом случае коэффициентом
затухания сигнала А и задержкой d в цепи обратной связи.
78 Лекция 2
В работах [16, 17] изучена теоретическая модель, описывающая
сложную хаотическую динамику двухрезонаторного клистронного ге-
генератора с запаздывающей обратной связью. Выпишем уравнения мо-
модели без вывода.
Пусть напряжение на зазорах входного и выходного резонаторов
имеет вид
Vi,2 = Re
где Vi^(t) — медленно меняющиеся по сравнению с экспонентой ^ш°1
комплексные амплитуды, oj$ — собственная частота резонатора. Тогда
в кинематическом приближении и в предположении линейной моду-
модуляции по скорости электронного потока во входном резонаторе (т. е.
Vi/Vo <С 1; Vo — ускоряющее напряжение) система уравнений, описы-
описывающая исследуемую систему, записывается в виде [17]:
d F*1
-Н- + 71*1 =71*2, B-63)
ат
B.64)
где введены безразмерные медленно меняющиеся амплитуды колебаний
напряжений на зазорах входного F\(t) = V\ (tNo/2Vo и выходного F\ =
= AV2(r - o;od/^)#oe~ja;oG72V() резонатора; безразмерное время г =
= uJot/Ф; 71,2 = &/%Qi,2 — параметры затухания во входном и выходном
резонаторах; а = АК1^Фв^е~^ф+7Т/2Л>/2У^ — параметр пропорциональ-
пропорциональный току пучка; Ф = uJo(d + I/vq); I — расстояние между резонаторами;
К — волновое сопротивление резонатора [18]. Величина Ф равна набе-
набегу фазы за время распространения сигнала по петле обратной связи,
которое определяется как временем пролета l/vo электронами про-
пространства дрейфа, так и временем задержки в цепи обратной связи d.
Оптимальным для взаимодействия пучка с полем выходного резонатора
является значение Ф = 2тг(п — 1/4), которое соответствует центру зоны
генерации с номером п.
Отметим, что в случае 71 ^> 1 (малая добротность входного резона-
резонатора) система уравнений B.63), B.64) сводится к уравнению [15]
§ -1)\)$^>.г B.65)
которое справедливо также для простой модели гироклистрона с запаз-
запаздывающей обратной связью [19]
Найдем условия самовозбуждения колебаний в модели клистронно-
клистронного генератора с запаздыванием, ограничиваясь случаем оптимального
значения величины Ф = 2тг(п — 1/4). Последнее предположение позво-
позволяет считать параметр а вещественным.
Элементарная кинематическая теория клистронов 79
Характеристическое уравнение для системы B.63), B.64) получа-
получается при подстановке Fi^ ~ ехр (рт) и разложения функции Бесселя
в ряд J±(x) « х/2:
(Р + 7i)(P + 72) = аЪе~р. B.66)
Данное уравнение имеет бесконечное число комплексных корней, что
отражает наличие бесконечного числа собственных мод в системе. Обсу-
Обсудим вопрос об устойчивости этих мод. Так как в момент смены характе-
характера устойчивости величина корня характеристического уравнения чисто
мнимая (р = jlj), то из уравнения B.66) отдельно для действительной
и мнимой части получаем выражения:
—и2 + 7i72 — <^7i cos о;,
B.67)
cj(ji + 72) — —c^7i sin о;.
Поделив одно уравнение на другое, найдем уравнение для частот соб-
собственных мод:
^i±4 = -tg"- B-68)
77 Ш
Графическое решение уравнения B.68) в случае, когда добротности
резонаторов достаточно высоки (так что ^/тГТ2 < тг/2), приведено
на рис. 2.13а. Из него видно, что уравнение B.68) имеет бесконечное
число корней, соответствующих бесконечному числу собственных мод.
Поскольку параметры а и 71,2 считаются положительными, следует
учитывать лишь те корни уравнения B.68), для которых cos и > 0 (чер-
(черные точки на рис. 2.13а). Из рис. 2.13а также видно, что основная мода
имеет нулевую частоту, т. е. генерация возникает точно на собственной
частоте резонатора и® (реактивная мощность взаимодействия равна
нулю). Последнее справедливо только в центре зоны генерации.
Для основной моды условие самовозбуждения находится из первого
уравнения системы B.67) и имеет вид:
OL > 72-
Решения, соответствующие этому случаю, являются монохроматиче-
монохроматическими колебаниями с частотой о;о, их комплексная амплитуда имеет
вид Fi52 = Foeiv, где фаза ср произвольна, а амплитуда Fq находится
из решения уравнения
72Fo = 2aJi(Fo). B.69)
Понятно, что с ростом тока пучка (увеличением параметра а) число
вещественных корней этого уравнения увеличивается (см. рис. 2.13^, на
котором приведено графическое решение данного уравнения). Следова-
Следовательно, появляются все новые и новые стационарные состояния. Ситуа-
Ситуация, когда при одних и тех же значениях параметров задачи (в данном
Лекция 2
Рис. 2.13. Графическое решение уравнения B.68) для определения частот
собственных мод (а) и уравнения B.69) для нахождения стационарных со-
состояний (б) двухрезонаторного клистрона с запаздыванием
случае — а и 7) возможна реализация различных состояний, называется
мультистабильностью. Появление все новых стационарных режимов
обусловлено многократной перегруппировкой электронов (появлением
новых электронных структур (сгустков)) в пространстве дрейфа по
мере увеличения амплитуды поля во входном резонаторе. Однако не все
из них устойчивы. Седловые неустойчивые состояния равновесия рас-
располагаются на возрастающих участках функции Бесселя (обозначены
белыми точками на рис. 2.136), а устойчивые — на падающих участках
(черные точки).
Неустойчивые состояния равновесия в результате бифуркации
Андронова-Хопфа мягко теряют устойчивость с ростом а, т.е.
возникает предельный цикл, амплитуда которого растет с увеличением
надкритичности а. Эти колебания называются автомодуляционными,
так как они возбуждаются только на фоне автоколебаний на основной
моде с большой амплитудой. Физически причина возникновения
автомодуляции определяется кинематической разгруппировкой
(разрушением) электронных сгустков вследствии того, что амплитуда
колебаний, модулирующих по скорости электронный поток, достаточно
велика. В этом случае на амплитудной характеристике усилителя
появляется крутой падающий участок. Такой механизм модуляции
называется амплитудным [21].
Частоты, на которых возникает автомодуляция, также находятся из
уравнения B.67), но теперь уже при условии cos о; < 0. Будем называть
возмущения на этих частотах автомодуляционными модами, посколь-
поскольку они могут возбуждаться только на фоне стационарных колебаний
с достаточно большой амплитудой. Из рис. 2.13а видно, что частота fti
первой автомодуляционной моды лежит в пределах ^/тГТ2 < ^1 < тг/2.
Рассмотрим последовательность смены режимов колебаний в гене-
генераторе, происходящих по мере увеличения параметра а (т. е. с увеличе-
Элементарная кинематическая теория клистронов
81
22
Рис. 2.14. Бифуркационная диаграмма колебаний в теоретической модели
двухрезонаторного клистрона с запаздыванием (из работы [17])
нием тока пучка или коэффициента затухания в цепи обратной связи)
при постоянных параметрах потерь 71,2 = 1 [17]. Данные исследования
уже невозможно провести аналитически, поэтому рассмотрим резуль-
результаты численного моделирования системы уравнений B.64) и B.65).
С увеличением а последовательно наблюдались самовозбуждение
колебаний на основной моде (и = 0) и установление режима стаци-
стационарной генерации, а затем возникновение автомодуляции на первой
автомодуляционной моде (см. рис. 2.13а). Режимам периодической авто-
автомодуляции в фазовом пространстве соответствуют предельные циклы
различной формы. С изменением параметрам наблюдается усложнение
формы предельного цикла, а также жесткие переходы между различ-
различными циклами. При этом частота автомодуляции скачкообразно из-
изменяется. Такие жесткие переходы между колебательными режимами
объясняются наличием в системе мультистабильности (рис. 2.136).
При дальнейшем увеличении а происходит переход от периодиче-
периодической автомодуляции к хаотической. В области хаотических колебаний
наблюдается большое число окон периодической автомодуляции. Вы-
Вышесказанное иллюстрирует рис. 2.14, на котором представлена бифур-
бифуркационная диаграмма: на ней отложены положения максимумов ам-
амплитуды выходного сигнала F при различных значениях параметра а.
Режимам периодической автомодуляции на диаграмме соответствуют
линии, режимам хаотической динамики — сплошные черные области.
В работе [17] приводятся результаты экспериментального исследо-
исследования клистронного генератора с внешней обратной связью. Генератор
реализован на пролетном клистроне, выход которого соединен со вхо-
входом. В цепь обратной связи был включен поляризационный аттенюатор,
позволяющий в широких пределах изменять затухание в цепи обратной
связи L (т.е. изменять уровень мощности, который подается на вход
82
Лекция 2
Рис. 2.15. Спектры выходного излучения генератора, наблюдаемые в экспе-
эксперименте в режиме периодической модуляции (а), автомодуляции с удвоенным
периодом (б) и хаотических автоколебаний (в) (из работы [17])
клистрона с его выхода). Рассмотрим последовательность режимов ко-
колебаний, наблюдаемых в эксперименте при изменении затухания L при
неизменных значениях тока пучка /о и ускоряющего напряжения Vo-
Экспериментальные спектры выходного сигнала генератора при раз-
различных значениях L представлены на рис. 2.15.
При L « 10 дБ в автоколебательной системе возбуждались стаци-
стационарные гармонические колебания на частоте /о ~ 2,8 ГГц, близкой
к частоте максимального усиления исходного клистронного усилите-
леля в режиме малого входного сигнала. Уменьшение затухания при-
приводило вначале к росту амплитуды стационарных колебаний, а при
L « 7,6 дБ возникал режим периодической автомодуляции с частотой
/а ~ 3,5 МГц. В спектре выходного сигнала (рис. 2.15а) появлялись
частотные составляющие /о ± /а.
Если уменьшать L дальше, то при L « 3 дБ наблюдались удвоения
периода автомодуляции (рис. 2.156). В спектре генерации это соотвест-
вует появлению частотных составляющих /о ± /а/2п. И при L « 0,5 дБ
генерация становилась хаотической. Спектр генерации в данном слу-
случае является сплошным, хотя можно выделить в нем максимумы на
основной частоте /о, на частоте автомодуляции fa и ее субгармониках.
В натурном эксперименте как и в численном моделировании в режиме
хаотической динамики наблюдались окна периодической автомодуля-
автомодуляции с частотами /а/3 и /а/5. Таким образом результаты натурного
эксперимента качественно, а в ряде случае и количественно, соответ-
соответствуют теоретическим и численным расчетам. Например, частота пер-
Элементарная кинематическая теория клистронов 83
вой автомодуляционной моды, согласно теории (см. рис. 2.13а), лежит
в пределах 5 МГц < /а < 8,3 МГц, что близко к экспериментальному
значению 3,5 МГц. Оценки по результатам натурного эксперимента
значений параметра а, при которых происходит перестройка режимов
колебаний, также близки к соответствующим расчетным значениям.
Так экспериментальные значения параметра а, при которых происхо-
происходит самовозбуждение колебаний, возникновение автомодуляции и пер-
первое удвоение периода, соответственно равны а « 1,56, 2,73, 7,8, в то
время как численное моделирование дает а « 1,0, 4,0, 9,05. Заметим,
что в последнем случае можно требовать только качественного соответ-
соответствия, так как теория не учитывает целый ряд существенных факторов,
определяющих динамику генератора (влияние поля пространственного
заряда, особенности конкретной технической реализации генератора
и т. п.).
Список литературы
1. Трубецков Д.И., Рожнев А.Г., Соколов Д. В. Лекции по сверхвы-
сверхвысокочастотной вакуумной микроэлектронике. — Саратов: Изд-во
ГосУНЦ «Колледж», 1996.
2. Шевчик В.Н. Основы электроники сверхвысоких частот. — М.:
Сов. радио, 1959.
3. Шевчик В.Н., Трубецков Д.И. Аналитические методы в электро-
электронике СВЧ. — М.: Сов. радио, 1970.
4. Клеен В. Введение в электронику сверхвысоких частот. — М.: Сов.
радио,1963.
5. Ginston Е. The $100 idea // IEEE Spectrum. 1975. V. 12. P. 30.
6. Varian R., Varian S. High frequency oscillator and amplifier // Journal
of Appl. Phys. 1939. V. 10. P. 321.
7. Hansen W. W., Richtmayer R.D. On the resonator suitable for klystron
oscillator // Journal of Appl. Phys. 1939. V. 10. P. 189.
8. Kompfner R. The invention of the travelling-wave tube. — Sun
Franciscko Press. 1964.
9. Лобанов M.M. Из прошлого радиолокации. — M.: Военное изд-во
МО СССР, 1969.
10. Девятпков Н.Д., Данильцев Е.Н., Пискунов И.В. О колебательных
режимах клистрона // ЖТФ. 1941. Т. 11, № 15, 16. С. 1348.
11. Кацман Ю.А. Создание русского клистрона. — Санкт-Петербург,
1997.
12. Шевчик В.Н. Взаимодействие электронных пучков с электромаг-
электромагнитными полями. — Саратов: Изд-во СГУ. 1963.
13. Вайнштейн Л.А., Солнцев В.А. Лекции по сверхвысокочастотной
электронике. — М.: Сов. радио, 1973.
84 Лекция 2
14. Вайнштейн Л. А. Стабильность колебаний в генераторах магне-
тронного типа // В сб. «Электроника больших мощностей». М.:
Наука, 1964. Вып. 3. С. 36.
15. Афанасьева В.В., Лазерсон А.Г. Динамический хаос в двухрезо-
натрных клистронных генераторах с запаздывающей обратной
связью // Известия вузов. Прикладная нелинейная динамика. 1995.
Т.3,№5. С. 88.
16. Дмитриева Т.В., Рыскин Н.М., Титов В.Н., Шигаев A.M. Слож-
Сложная динамика простых моделей электронно-волновых систем //
Известия вузов. Прикладная нелинейная динамика. 1999. Т. 7, № 6.
С. 66.
17. Дмитриев B.C., Жарков Ю.Д., Рыскин Н.М., Шигаев A.M. Тео-
Теоретическое и экспериментальное исследование хаотических коле-
колебаний клистронного автогенератора с запаздыванием // Радиотех-
Радиотехника и электроника. 2001. Т. 46, № 5. С. 604.
18. Григорьев А.Д. Электродинамика и техника СВЧ. — М: Высшая
школа, 1990.
19. Ергаков B.C., Моисеев М.А. // Радиотехника и электроника. 1986.
Т. 31. С. 962.
20. Неймарк Ю.И., Ланда П.С. Стохастические и хаотические коле-
колебаний. — М.: Наука. 1987.
21. Блиох Ю.П., Бородкин А.В., Любарский А.Г., Онищенко Н.М.,
Файнберг Я.Б. Применение метода функционального отображе-
отображения для исследования ЛБВ-генератора с запаздывающей обратной
связью // Изв. вузов. Прикладная нелинейная динамика. 1993. Т. 1,
№1,2. С. 34.
Лекция 3
ВОЛНЫ ПРОСТРАНСТВЕННОГО ЗАРЯДА МАЛОЙ
АМПЛИТУДЫ
Существование «волн» как одной из форм, в кото-
которой проявляется движение, принадлежит к наи-
наиболее привычным свойствам физического мира;
их описание дает нам одну из нитей, связываю-
связывающих воедино различные разделы физики.
Из предисловия редакторов амери-
американского издания к книге «Нелиней-
«Нелинейные волны», М.: Мир, 1977, с.9.
Гидродинамическое описание электронного потока. Волны простран-
пространственного заряда и группирование в пространстве дрейфа. Резистив-
ный усилитель. Волны пространственного заряда в электронном по-
потоке со столкновениями и диффузией. Двухлучевая неустойчивость
(абсолютная и конвективная неустойчивость; глобальная неустойчи-
неустойчивость). Неустойчивость Гельмгольца и об одной гипотезе образования
спиц в кольцах Сатурна (многопучковая неустойчивость). Цикло-
Циклотронные волны. Связанные волны.
В данной лекции мы приступаем к рассмотрению волновых процес-
процессов в электронных пучках на сверхвысоких частотах, связанных с сила-
силами упругого взаимодействия, которые в первую очередь обусловлены
силами объемного пространственного заряда. Исторически изучение
этих вопросов связано с развитием теории СВЧ-приборов с модуляцией
электронного потока по скорости и последующей группировкой в про-
пространстве дрейфа. Первоначально описание явлений в электронном
потоке ограничивалось кинематическим приближением, т. е. движение
электрона рассматривалось без учета полей пространственного заряда
только под действием внешних сил. Хотя понятие волны пространствен-
пространственного заряда было введено практически одновременно с изобретением
клистрона в работах B.C. Хана и С. Рамо в 1939 г. [1, 2], значение
электронно-волновой теории выявилось значительно позднее, в 50-х
годах, когда была показана возможность нарастания при определенных
условиях амплитуд волн пространственного заряда вдоль пространства
86 Лекция 3
дрейфа. Дальнейшее развитие этой теории, которое привело к созда-
созданию электронно-лучевого усилителя — двухлучевой лампы, принцип
которой основывается на усилении волн пространственного заряда г).
Появился принципиально новый на тот момент подход к рассмотрению
явлений в электронном потоке — теория связанных волн и, как след-
следствие, к исследованию электронных приборов, принцип работы которых
основан на использовании колебательных и волновых явлений в самих
электронных пучках без использования каких-либо «материальных»
колебательных систем [3] 2).
Под волнами пространственного заряда (ВПЗ) будем понимать вол-
волнообразное распространение возмущений плотности, тока, напряжен-
напряженности поля пространственного заряда и скорости в электронном пучке,
причем скорость такого возмущения зависит от постоянной составля-
составляющей плотности пространственного заряда в потоке. В общем случае
существует много различных типов ВПЗ, в данной лекции ограничимся
подробным анализом линейной теории группирования электронного
потока в пространстве дрейфа и приложением ее к учету влияния
пространственного заряда в теории пролетного клистрона; рассмот-
рассмотрим двухлучевую неустойчивость, а также примеры ее использования
в электронике (двухлучевая лампа) и для возможного объяснения неко-
некоторых наблюдаемых явлений в астрофизике; укажем на одну из анало-
аналогий в гидродинамике жидкостей. В конце лекции кратко остановимся
на циклотронных волнах в электронных потоках, а также рассмотрим
аппарат связанных волн.
В основу рассмотрения волновых процессов в электронных потоках
положен гидродинамический анализ. Такой подход позволяет с единых
позиций рассмотреть широкий класс задач о поведении потоков заря-
заряженных частиц как в вакууме, так и твердом теле, а также о взаимодей-
взаимодействии электронных потоков с бегущими волнами различной природы
(см., например, [4]).
Гидродинамическое описание электронного потока
Возможность использования гидродинамической теории примени-
применительно к анализу процессов в электронных потоках связана с пере-
переходом от микроскопического описания уравнений дискретной среды
к макроскопическим уравнениям непрерывной среды, опирающимся на
следующие положения. Поток электронов в вакууме можно рассматри-
рассматривать как дрейфующую плазму. Поведение плазмы характеризуется по-
поведением ее микроскопических элементов. О коллективном поведении
плазмы можно говорить только в длинноволновом приближении, когда
г) Далее мы рассмотрим этот прибор достаточно подробно.
2) Монография [3] носит энциклопедический характер и до сих пор не
утратила своей значимости.
Волны пространственного заряда малой амплитуды 87
рассматриваются волновые процессы с длиной волны, много большей
значения дебаевского радиуса
^. C.1)
Здесь vT — средняя тепловая скорость электронов пучка, ир =
= y/vpo/'? ~ плазменная частота бесконечно широкого электронного
потока, г\ — удельный заряд электрона, ро — плотность заряда
и е — диэлектрическая проницаемость. Сверхвысокочастотные
волновые процессы удовлетворяют этому требованию, что позволяет
использовать классическую статистику и проводить анализ на основе
гидродинамической модели. Как показано в работе [5], результаты
гидродинамической теории совпадают с результатами кинетического
рассмотрения только при условии, что частота v соударений не
зависит от скорости носителей. При достаточно малом тепловом
разбросе по скоростям гидродинамическое описание электронного
потока применимо в широком интервале значений отношения v/oj
(и — частота высокочастотного возмущения). Более того, очень
часто используется приближение, в котором не учитывается тепловой
разброс скоростей электронов, а также столкновения и диффузия
в пучке. Именно в рамках этих предположений запишем основные
уравнения гидродинамической модели.
1. Уравнения Максвелла. При учете вихревых полей как в пучке,
так и в волноводной системе, в которой движется пучок, имеет место
обобщенное волновое уравнение:
ДЕ-«,/*?? =й)§ + ^, C-2)
dt (Ji so
где Е есть сумма напряженностей вихревого электрического поля, ко-
которое описывает собственное излучение электронов, собственные коле-
колебания резонаторов и волноводные моды, и потенциального электриче-
электрического поля. Если учитывается только потенциальное поле, связанное
с взаимодействием электронов через кулоновские поля, то решаются
совместно уравнение для полного тока и уравнение Пуассона:
дВ . _.
^0 а, Н~ J —JncwiH?
C.3)
Очевидно, что, введя уравнение непрерывности, которое выражает за-
закон сохранения заряда, вместо уравнений C.3) можно рассматривать
88 Лекция 3
эквивалентные системы уравнений вида
divE = A
"I C-4)
dlvJ = ~w
или
?() о. ~г J = ,1полн5
C-5)
j. . до
dlvJ = "в* ¦
2. Уравнение движения записывается следующим образом:
^ = ту (Е + [vH]), C.6)
оно представляет собой закон изменения скорости передвигающейся
в пространстве частицы. Поэтому так как уравнения поля характери-
характеризуют изменение полей в любой точке пространства с течением време-
времени, логично выразить производную —- через величины, относящиеся
к неподвижной точке пространства, т. е. перейти к переменным Эйлера.
Изменение скорости dv равно изменению скорости в данный точке
пространства за время dt (-p— dt) и разности скоростей в один и тот же
dt
момент времени в двух точках, разделенных расстоянием с/r, равным
пройденному частицей за то же время at (т— ах + -^г— ay + -p— dz =
удх ду dz
= (drV)v), т.е.
а следовательно, полная производная запишется как
? = ? + <W,v. ,„)
Окончательно уравнение движ;ения в переменных Эйлера имеет вид:
| + (vV)v = ,,(E + [vH]). C.8)
3. Уравнение для конвекционного тока выглядит так:
Jo+T= (po + p) '(vo+v), C.9)
где jo, рсь vo — постоянные составляющие плотности тока, плотности
заряда и скорости, a j, p, v — их переменные составляющие.
Рассмотрим теперь электронный поток, который бесконечен в на-
направлении у и z (т. е. -U- = -й- = 0) и движется вдоль оси ж, вдоль кото-
которой ориентировано бесконечное однородное постоянное магнитное поле.
Волны пространственного заряда малой амплитуды 89
Очевидно, что в этом случае в потоке могут распространяться только
продольные волны, а соответствующие переменные величины в рамках
гидродинамической модели будут иметь только ж-компоненты. Тогда
основные уравнения C.4), C.8) и C.9) гидродинамической модели для
бесконечно широкого потока запишутся как (индекс «ж» у переменных
величин опускаем)
где в общем случе поле Е = Евн + ЕПЗ ~~ сумма внешнего переменного
поля и поля пространственного заряда. Последнее определяется из
уравнения Пуассона, которое для одномерного случая имеет вид
дЕиз
дх
C.13)
Волны пространственного заряда и группирование
в пространстве дрейфа. Резистивный усилитель
Прежде чем переходить к рассмотрению волн пространственного
заряда, рассмотрим, к чему приводит попытка описания группировки
электронного потока в пространстве дрейфа в кинематическом прибли-
приближении в переменных Эйлера, а не Лагранжа, которые мы использовали
при построении теории пролетного и отражательного клистрона. Пусть
вдоль оси х движется поток невзаимодействующих частиц. Их скорость
удовлетворяет уравнению движения, которое в переменных Эйлера
имеет вид C.11)
Оно формально совпадает с уравнением, описывающим в теории волн
модель одноволнового приближения. Общий вид уравнения одноволно-
вого приближения таков:
? + f(.)?=0. CЛ5)
Это уравнение описывает плоскую бегущую волну в нелинейной среде
без диссипации и дисперсии. В общем случае V(v) — нелинейная функ-
функция.
Пусть в момент времени t = 0 пучок оказывается возмущенным по
скорости согласно закону a sin kx (пучок промодулирован по скорости).
90
Лекция 3
/ у \
-~'' 1
„ р
X.
V
2
X
—-- 2
с
Рис. 3.1. Эволюция во времени синусоидального возмущения в пучке невза-
невзаимодействующих частиц. Здесь сплошными линиями обозначена скорость,
штриховыми — плотность, а — начальное состояние, соответствующее сину-
синусоидальному возмущению скорости; 6— образование электронных уплотне-
уплотнений (группирование частиц около точек 1 и 2); в, г — опрокидывание волны
скорости и образование удвоенного числа особенностей на кривой р = р(х)
Перейдем в движущуюся со скоростью vq (vq — невозмущенная ско-
скорость потока) систему отсчета и рассмотрим в ней эволюцию начального
возмущения. Переход в новую систему отсчета эквивалентен замене
координат вида х = х' — v^t. Введем новую переменную: и = v — vo, где
и — переменная составляющая скорости. Тогда в движущейся системе
координат уравнение C.14) будет выглядеть следующим образом:
ди
ди
C.16)
Решение этого нелинейного уравнения есть так называемая простая
волна
и = U(t-x/u), C.17)
где явное выражение для функции U определяется видом начального
возмущения. При распространении такой волны в нелинейной среде ее
профиль меняется со временем, поскольку разные точки на профиле
бегут с разной скоростью. В случае пучка эт. е. следствие того, что
частицы смещаются относительно друг друга из-за разных скоростей,
причем одни частицы могут обогнать другие (это наблюдалось на
пространственно-временной диаграмме потока в кинематическом при-
приближении (см. рис. 2.3)), вследствие чего функция u(x,t) становится
неоднозначной. Проследим за пучком на фазовой плоскости (и,х),
на которой каждая точка движется со своей собственной скоростью.
Верхняя полуплоскость соответствует движению вправо, нижняя —
влево, причем скорость каждой точки пропорциональна удалению ее
от оси х. Рис. 3.1 иллюстрирует эволюцию пучка на фазовой плоскости.
Начальное состояние скоростей пучка — синусоида a smkx; здесь же
Волны пространственного заряда малой амплитуды 91
штриховой линией показана зависимость плотности пространственного
заряда пучка от продольной координаты. С течением времени происхо-
происходит искажение профиля волны: частицы с и > 0 уходят вперед, а с и < О
отстают от волны. Одновременно образуются сгущения частиц вблизи
точек 1 и 2, где и = 0, т. е. происходит группирование пучка (рис. 3.1а).
Волна постепенно становится круче (рис. 3.16), и в какой-то момент
времени производная ди/дх на переднем фронте обращается в беско-
бесконечность (в бесконечность также обращается плотность р(х) объемного
заряда пучка). В следующий момент времени происходит опрокидыва-
опрокидывание волны (рис. 3.1 в), и функция u(x,t) становится многозначной, у нее
появляется точка поворота, т.е. образуются встречные пучки. После
опрокидывания волны функция р(х) имеет удвоенное число особенно-
особенностей (рис. 3.1в;г). С дальнейшим течением времени структура волны
еще более усложняется.
Из нашего рассмотрения видно, что и в кинематическом анализе
существует возможность использовать уравнения в переменных Эйле-
Эйлера, однако такой подход является более сложным и менее наглядным,
чем описание процесса группирования в переменных Лагранжа, где не
возникает проблемы многозначности функций при обгоне и повороте
частиц.
Однако вернемся к рассмотрению волн в потоке взаимодействующих
через общее поле пространственного заряда частиц. Будем рассматри-
рассматривать бесконечно широкий поток, пространственный заряд которого пол-
полностью нейтрализован неподвижным ионным фоном. Наличие ионов
может быть объяснено присутствием в реальном приборе остаточных
газов, которые ионизируются пучком. Предположение о неподвижности
ионного фона связано с большой массой ионов (так протон почти в 2000
раз тяжелее электрона), что позволяет считать, что ионы не принимают
участия в колебательных процессах на сверхвысоких частотах.
В одномерном потоке в силу его бесконечной поперечной протяжен-
протяженности нет изменения потенциала, а значит и характеристик потока в по-
поперечном направлении. Пучок считается бесконечно длинным, так что
потенциал, vq и jo вдоль пучка не изменяются. Переменные величины
j и v изменяются только в продольном направлении. Тогда уравнение
движения C.11) запишется в виде
I („о + v) + Ы + ~V)l(V0 + ~V) = ft+ „og + *§§ = VE. C.18)
Используем предположение о малости сигнала, что даст возмож-
возможность пренебречь в исходных уравнениях членами второго и более
высокого порядка относительно малых переменных величин. Линеари-
Линеаризованные уравнения движения C.18), уравнение непрерывности C.10)
и уравнение для переменной составляющей плотности конвекционного
92 Лекция 3
тока C.12) запишутся соответственно в виде
¦pov. C.21)
Из уравнений C.19)—C.21) можно исключить риу и получить урав-
уравнение, связывающее j и Е. Разрешая уравнение для плотности конвек-
конвекционного тока C.21) относительно v, продифференцировав результат
по времени и используя уравнение C.20), приходим к соотношению
dv _ 1 dj vo dj
dt po dt po dx'
Продифференцировав уравнение C.19) по времени и используя полу-
полученное выше соотношение для dv/dt, найдем:
&.„ э*1 ,а*7 д~Е (з_22)
Уравнение C.22) связывает переменные составляющие плотности кон-
конвекционного тока и поля. Если Е создается переменными зарядами
в самом электронном потоке, то можно использовать уравнение полного
тока C.3) в виде
Подставляя его в соотношение C.22), получим окончательно уравнение
вида:
где величина fjpo/^o представляет собой квадрат плазменной частоты
ujp для бесконечно широкого потока.
Решение линейного дифференциального уравнения в частных про-
производных C.23) записывается в форме:
У= Aejujte~jkx. C.24)
Подставляя вид решения C.24) в уравнение C.23), получаем диспер-
дисперсионное уравнение, т. е. уравнение, связывающее частоту волны о; с ее
волновым числом к (к = 2тг/А, А — длина волны):
-со2 + 2voujk - v2k2 + oj2 =0. C.25)
Волны пространственного заряда малой амплитуды 93
Разрешая это уравнение относительно &, имеем
ku2 = -±^=l3±pp, C.26)
где uj — действительная величина, В = — fiv = —.
vo И vo
Решением уравнения C.23) будет действительная часть суммы
~2 = (А 1е-^"ж + A2ej0'x) e^-^, C.27)
где коэффициенты А\ и А<± определяются из начальных условий задачи.
Из уравнения непрерывности C.20) получаем выражение для р
в виде
р= (A1^e-jP*x + A2—ejP*x)ejlwt-Px). C.28)
Используя C.21) и соотношения C.27) и C.28), находим выражение
для v:
C.29)
oopo oopo '
Учитывая выражение C.26) можно сделать вывод, что переменные
величины j, р, v, определяемые выражениями C.27)-C.29), описывают-
описываются двумя волнами пространственного заряда с фазовыми скоростями:
= г,ф И)б =
C.30)
Волна, соответствующая знаку «+», имеет Уфм < vq и называется мед-
медленной волной пространственного заряда (МВПЗ), а со знаком « —» —
быстрой волной пространственного заряда (БВПЗ), для нее г>фб > vo.
Диаграмма Бриллюэна, соответствующая дисперсионному уравнению
C.26), приведена на рис. 3.2. Верхняя прямая соответствует МВПЗ,
нижняя — БВПЗ.
Полученные соотношения в рамках сделанных предположений яв-
являются достаточно общими. Применим их для анализа процессов груп-
группировки в пространстве дрейфа при наличии модуляции по скорости
(модуляция по плотности отсутствует). Пусть при х = 0 расположен
узкий высокочастотный зазор — модулятор. Тогда начальные условия
для уравнения C.23) запишутся в виде
У@) = 0, v = 2v1ejujt.
Подставив эти начальные условия в уравнения C.27)-C.29), определим
константы интегрирования А\ и А^ и получим следующие выражения
для 7, р и v:
у =
94
Лекция 3
Рис. 3.2. Дисперсионная характеристика модулированного во входном
устройстве пучка (а) ; стоячие волны плотности тока и скорости в электрон-
электронном потоке в фиксированный момент времени (б)
, C.32)
V =
C.33)
Здесь первые слагаемые в скобках относятся к МВПЗ, а вторые —
к БВПЗ. Уравнения C.33) и C.31) можно переписать в несколько ином
виде, а именно:
v = 2vi cos/Зрх cos (u)t — /Зх). C.34)
3 = —
LOp
sin Cpx sin (ojt — fix).
C.35)
Зависимости от продольной координаты v и j в фиксированный момент
времени приведены на рис. 3.2& Из сравнения зависимостей C.34) и
C.35) видно, что на расстояниях х = ХрBп + 1)/4 (где Хр = 27rvo/u}p;
п G Z) переменная составляющая скорости обращается в нуль, а пере-
переменная составляющая плотности конвекционного тока достигает мак-
максимального значения. В этих точках электроны, имеющие скорость на
выходе из модулятора больше, чем скорость электронов, вышедших
из него раньше, догоняют их, образуя уплотненный сгусток. Одновре-
Одновременно с образованием сгустков (появлением jo ф 0) в потоке возникает
ВЧ-поле пространственного заряда, которое приводит к разрушению
этих структур. Таким образом силы пространственного заряда снова
приводят к появлению переменной составляющей скорости. Причем при
х — пХр/2 переменная составляющая скорости принимает значение,
равное скорости на выходе из модулятора, а переменная составляющая
Волны пространственного заряда малой амплитуды 95
плотности тока обращается в нуль. С точки зрения закона сохранения
энергии в системе координат, перемещающейся с невозмущенной ско-
скоростью пучка vo, максимальное значение плотности тока соответствует
максимальной потенциальной энергии электронов (максимальному зна-
значению потенциала поля пространственного заряда). В точках, где мак-
максимальна переменная составляющая скорости, становится максималь-
максимальной и кинетическая энергия электронов. При возбуждении быстрой вол-
волны в потоке v и рсфазированы, т. е. преобладают электроны со скоростя-
скоростями больше vo, и результирующая кинетическая энергия, переносимая
пучком, больше энергии невозмущенного пучка. Если же возбуждена
медленная волна, то в тех местах, где наблюдаются сгущения, скорость
электронов меньше vo; она больше, где наблюдаются разряжения, т.е.
преобладают замедленные электроны, и энергия переносимая пучком,
меньше чем энергия пучка без волны.
Из рассмотрения понятно, что с ростом амплитуды МВПЗ сум-
суммарная энергия системы «электронный пучок-волна» уменьшается,
и наоборот: с ростом амплитуды БВПЗ энергия системы будет возрас-
возрастать. Волны, для которых выполняется условие уменьшения энергии
системы с увеличением их амплитуды, принято называть волнами с от-
отрицательной энергией, а волны, для которых наблюдается увеличение
энергии системы с ростом их амплитуды, — волнами с положительной
энергией г).
Получим выражение для плотности потока энергии в электронном
пучке, исходя непосредственно из уравнения движения электронного
потока и уравнения непрерывности. Для этого рассмотрим произведе-
произведение напряженности поля пространственного заряда на конвекционный
ток:
Если учесть здесь уравнение непрерывности dj/дх = —dp/dt, соотно-
соотношение C.36) принимает вид
х) Примеры волн с отрицательной и положительной энергией не исчерпыва-
исчерпываются только ВПЗ. Так П.А.Стэрроком (см. [9, 10]) было показано, что в среде,
движущейся со скоростью и, энергия быстрой и медленной волны, измеряе-
измеряемая неподвижным наблюдателем, выражается соотношениям VKM,6 = Wq{\ =F
=F и/Уф), где УфИ—Уф— скорости волн в подвижной системе координат, Wo —
энергия системы. Понятно, что при и > Уф величина WM < 0, в то время как
скорость переноса энергии (групповая скорость) обеих волн положительна.
Появление понятия о волнах с отрицательной энергией в СВЧ-электронике
связывается с работой [11], в которой выведена так называемая теорема Чу
о кинетической мощности.
96 Лекция 3
где плотность кинетической энергии
Wn = %f- C.38)
AT]
и плотность потока кинетической энергии
Sn = ^ = vWn. C.39)
Если теперь сделать предположение о малости возмущений, т.е. \v\ <С
<С vq и т.д., то, сохраняя в выражении C.38) члены второго порядка
малости, получим
Wu = hi [po(^ + 2vov + v2) + p(vl + 2vov)}. C.40)
Рассчитаем среднюю за период плотность кинетической энергии. Ес-
Если предположить, что пучок промодулирован на входе, то, как показано
выше, в нем будут распространяться волны пространственного заряда.
Для общности не будем конкретизировать вид модуляции, тогда рас-
распределения переменных величин тока, плотности и скорости по длине
пространства дрейфа будут определяться выражениями C.27)-C.30),
а поле пространственного заряда запишется как
(ut-(k+wp/v0)) _^_ ej(ut-(k+up/vo))\ ^ C.41)
где Eq как и раньше определяется начальным возмущением. Тогда из
выражения C.40) получим
х ' 2тг ) 2rj v ' 2тг
0 0 0
2тг 2тг
1 Г ~ 2 i P ~ ~
+ —- —— а{ш1) + — a{ujt).
2тг J 2r] 2тг J т/
о о
Первый интеграл — плотность энергии невозмущенного электронного
пучка, которую мы обозначим как (W®)- Так как v и р представляют
собой сумму гармонических составляющих, то второй и четвертый ин-
интегралы равны нулю. Таким образом нас интересует
2тг 2тг
S(Wn) = (Wn) - (W°) = ?±- j* v2 d(ut) + ^- f vpd(ut). C.42)
о о
Из уравнения Пуассона, которое может быть записано как дЕ/дх =
= —p/so, и уравнения движения легко получить связь между полем
и скоростью: v = rjE/(j(u) — kvo)). Тогда, учитывая вид переменных
Волны пространственного заряда малой амплитуды 97
составляющих плотности C.28) и скорости C.29), окончательно полу-
получим для быстрой и медленной ВПЗ
S(Wu6) « ?-ф- ^ > 0 5{WnM) « -*^° ^ < 0 C.43)
(здесь пренебрегли слагаемым, появившемся при вычислении первого
интеграла, так как при шр < w оно мало по сравнению со вторым
слагаемым).
Таким образом и из соотношений C.43) следует, что МВПЗ пере-
переносит отрицательный поток мощности, БВПЗ — положительный поток
мощности.
Какие же условия необходимы, чтобы в среде возбуждалась волна
с отрицательной энергией? Из закона сохранения энергии понятно, что
для возбуждения волны с отрицательной энергией необходима ситу-
ситуация, когда МВПЗ может отдавать свою энергию среде или другим
волнам.
Типичной иллюстрацией этого могут служить процессы в резистив-
ном усилителе [12, 9]. Схема прибора следующая (см. рис. 3.3): предва-
предварительно модулированный во входном устройстве электронный пучок
проходит через диэлектриче-
диэлектрическую трубку, внутренняя стен-
стенка который покрыта поглоща-
поглощающим слоем, и наводит в нем
переменный заряд. Поля, созда-
создаваемые наведенными зарядами,
в свою очередь, воздействуют
на электронный пучок и из- ^ о о ^
^ J Рис. 3.3. Схема резистивного усилите-
меняют переменную составля- ля: 1 _ резистивный слой; 2 _ ди_
ющую тока пучка. После прохо- электрическая трубка; 3 - электрон-
ждения трубки пучок попадает Ный поток; 4 и 5 - входное и выходное
в выходное устройство. Входное устройство
устройство возбуждает в пучке
две волны пространственного заряда, поля которых вызывают в ре-
зистивной стенке движение зарядов, что в свою очередь приводит
к джоулевым потерям энергии волн. Быстрая волна затухает (волна
с положительной энергией), а МВПЗ нарастает (т. е. увеличивает свою
амплитуду), отдавая энергию среде. Поэтому такая система выступает
как высокочастотный усилитель. Экспериментальное доказательство
нарастания МВПЗ в резистивном усилителе иллюстрирует рис. 3.4.
Теория резистивного усилителя здесь не приводится, так как она до-
достаточно подробно изложена в книгах [13, 9].
Если пучок является ограниченным в поперечном направлении
и окруженным металлическим экраном, то дисперсионное уравне-
уравнение для постоянных распространения ВПЗ является трансцендентным
и имеет бесконечное число решений, а, следовательно, число пар ВПЗ
4 Д. И. Трубецков, А. Е. Храмов
98
Лекция 3
20
10
-20
Рис. 3.4. Зависимость квадрата отно-
относительного сгруппированного тока от
ускоряющего напряжения [12]: 1 — ди-
диэлектрическая среда заменена метал-
металлической поверхностью (возбуждены
две ВПЗ с постоянными амплитуда-
амплитудами); 2 — пучок движется в резистив-
ной среде, но ток пучка мал (воз-
(возбуждены нарастающая и затухающая
волны); 3— ток большой (преобладает
нарастающая медленная волна)
450 550 650 V0,B
составляет в этом случае бесконечную последовательность (рис. 3.5) [3,
стр. 24-35]. С точки зрения решения соответствующей краевой задачи
это вполне понятный результат: появление бесконечного ряда волн
объясняется существованием граничных условий. Граничным условиям
для трубы дрейфа удовлетворяют все волны, у которых распределе-
распределение по радиусу таково, что на стенке трубы поле обращается в нуль.
Наибольший интерес представляют пары волн низшего порядка /3qi
и /Зо2, поля которых не имеют нулей внутри поперечного сечения элек-
электронного пучка. Это волны со скоростями, наиболее отличающимися
от невозмущенной скорости пучка vq. Им соответствует максимальная
энергия волн по сравнению с энер-
энергией пар волн высшего поряд-
порядка. Отметим, что распростране-
распространение волн в потоках конечного се-
сечения можно рассматривать по-
подобно рассмотрению ВПЗ в беско-
бесконечно широком пучке. Единствен-
Единственное различие заключается в необ-
необходимости пользоваться модифи-
ю
Poi
со
Щ
i
i
i
ю
Р
Р02
Рис. 3.5. Сравнение постоянных рас-
расцированной величиной постоян-
постоянной распространения [6, 7] /3q =
пространения /3 ВПЗ в бесконечно = R^ (и соответственно реду-
редушироком (а) и в цилиндрическом
пучке (б)
цированной плазменной частотой
ujq = Rojp), где R < 1 — коэффи-
коэффициент редукции. Уменьшение эф-
эффективной плазменной частоты для ограниченного канала связано
с тем, что часть силовых линий поля пространственного заряда замыка-
замыкается на стенках трубы дрейфа, а следовательно, продольная составляю-
Волны пространственного заряда малой амплитуды 99
щая поля уменьшается, что и учитывается соответствующим выбором
коэффициента редукции.
Уточним теперь линейную кинематическую теорию группирования,
изложенную в предыдущей лекции, учитывая силы пространственного
заряда. Ток пучка в пространстве дрейфа записывается в виде / = /о +
+ Re {i} (г = Sj,S — площадь поперечного сечения потока). Учитывая
выражение C.35), для тока пучка можно записать
/ = /0 [i + Re \j^-sin(PPx)^wt-0xA] . C.44)
L I v^ JJ
Из закона скоростной модуляции B.4) можно найти, что —— = — j-—.
vo 2
Тогда перепишем соотношение C.44) как
/ = /0 [l + L?- sin PPx cos (ut - fix)] . C.45)
Заметим, что при малых ? фаза влета электрона в модулятор ut\ « ut —
— /Зх. Тогда окончательно для сгруппированного тока получим
= /п
sin
C.46)
Напоминаем, что во = — — невозмущенный угол пролета электронов
в пространстве дрейфа. Величина
X =
носит название параметра группирования. При —^— —у 0 (простран-
(пространно
ственный заряд мал) соотношение C.46) переходит в выведенное в пре-
предыдущей лекции в рамках кинематической теории выражение для
сгруппированного тока B.10).
Из выражения C.46) также видно, что увеличение пространственно-
го заряда (увеличение —^—) приводит к уменьшению сгруппированного
vo
тока.
Волны пространственного заряда в электронном
потоке со столкновениями и диффузией
В предыдущем разделе рассматривались волновые процессы в элек-
электронных потоках в предположении отсутствия столкновений и диф-
диффузии носителей заряда. Рассмотрим теперь волны, которые распро-
100 Лекция 3
страняются в бесконечно широком электронном потоке в неподвижном
ионном фоне при наличии столкновений и диффузии.
В этом случае основные уравнения гидродинамической модели за-
запишутся в линеаризованном виде как [4, стр. 12]
% = vE-vv+*g. C.48)
dt ро дх
— уравнение движения, в правой части которого первое слагаемое
описывает влияние поля пространственного заряда, второе учитывает
столкновения, а третье — диффузию в электронном потоке (v — частота
соударений, vT — средняя квадратичная тепловая скорость);
^ = А C-49)
дх е0
# = "§, C-50)
дх dt
j = pv0 + pov C.51)
— уравнения Пуассона, непрерывности и уравнение для конвективного
тока. Предполагая, что все переменные величины изменяются по за-
закону eJ(ut-kx) ^ из системы уравнений C.48)-C.51) несложно получить
следующее дисперсионное уравнение:
A _ „?) ki _ 2рок A _ jV/2) + pi (I - jV) - 01 = 0, C.52)
где v^ = Vt/vo, v' — v 1^ч Ро = w/vo. Решение уравнения C.52) имеет
вид
^-^) }¦ C-53)
Проанализируем это решение в некоторых частных случаях.
1. vT = 0, v = 0. Электронный поток без столкновений и диффузии.
В этом случае решение дисперсионного уравнения C.53) переходит
в уже полученное нами решение C.26), которое показывает существова-
существование двух волн пространственного заряда — МВПЗ и БВПЗ (см. рис. 3.2).
Волны пространственного заряда малой амплитуды
101
Рис. 3.6. Дисперсионные характеристики ВПЗ при наличии редких столкно-
столкновений (а), частых столкновений (vT = 0) (б)
2. v'T = 0, v < 2ojp. При наличии редких столкновений обе волны,
МВПЗ и БВПЗ, становятся затухающими:
2шр) •"-" 2 '
C.54)
i,2 =Po- j'A>y A ± ^1 - (^
причем затухание пропорционально величине i//2vo, т. е. не зависит от
частоты и (рис. 3.6а).
3. v'T = 0, v > 2ир. В случае частых столкновений решение диспер-
дисперсионного уравнения принимает вид
C.55)
Из соотношения C.55) видно, что понятие быстрой и медленной вол-
волны пространственного заряда теряет смысл, так как фазовые скорости
обеих волн, распространяющихся в потоке, становятся равными скоро-
скорости электронов vo. Если v — 2ujp, то обе волны затухают одинаково:
k12 = /Зо — j/Зр. Когда v > 2ujp, ВПЗ имеют различные декременты
затухания Im к\ ф Im к2 (см. рис. 3.66). Чем больше становится v по
сравнению с 2ljp, тем быстрее происходит затухание одной из волн, и тем
медленнее затухает другая. Если и ^> 2ир, то
. ш
—
При условии v
(| Imfci| ^> | Re fci
> и волна с к\ практически не распространяется
). Вторую волну можно считать распространяющей-
102 Лекция 3
ся, если | Im &21 < | Re &21, т. е.
о \
4. vT ф 0 (v't < 1), v = 0, с^р < о;. Тогда
/2 \
C.56)
ВПЗ в таком потоке с диффузией, но без столкновений эквивалентны
ВПЗ в потоке без диффузии, но с меньшей статической скоростью
и большей плазменной частотой
vot = *>оA - Vt) < уо, и т
Можно показать, что фазовая скорость МВПЗ в потоке с диффу-
диффузией меньше, чем в потоке без диффузии. Физически объяснить повы-
повышение эквивалентной плазменной частоты за счет диффузии можно
следующим образом. Колебания частиц плазмы с плазменной часто-
частотой обусловлены появлением возвращающей силы — электрического
поля, вызванного создавшейся неоднородностью. Эта сила стремится
восстановить однородность плазмы так же, как возвращающая сила при
колебаниях гармонического осциллятора, например, маятника, стре-
стремится вернуть его в положение равновесия. Диффузия также приво-
приводит к устранению неоднородности плотности, т. е. увеличивает возвра-
возвращающую силу («упругую постоянную маятника») и, следовательно,
плазменную частоту. Действие столкновений эквивалентно появлению
сил трения, которые уменьшают возвращающую силу и эквивалентную
плазменную частоту.
Двухлучевая неустойчивость
(абсолютная и конвективная неустойчивость;
глобальная неустойчивость)
Гидродинамическое описание электронного потока, которое привело
нас к необходимости ввести понятие волн пространственного заряда,
распространяющихся в потоке заряженных частиц, позволило приме-
применительно к рассмотрению системы с предварительной скоростной мо-
модуляцией электронного пучка существенно уточнить линейную кинема-
кинематическую теорию пролетного клистрона. Рассмотрим теперь ситуацию,
в которой концепция ВПЗ не просто приведет к уточнению какой-либо
имеющейся теории, а позволит объяснить принцип работы двухлучевой
Волны пространственного заряда малой амплитуды 103
лампы — усилителя, в котором используются два электронных пучка
с немного различающими скоростями, движущихся параллельно друг
другу и сильно связанных через
общее поле пространственного за- Входной Выходной
ряда (см. рис. 3.7). Для улучше- с™ ^ g^™* '
ния связи между пучками в экс- _, | Vqi
периментах использовались като-
катоды, выполненные в виде плос- ~~1.,:,, ,v ¦..,-...-.: -,-,.-:-с,::..-.-=,.-.-.-,. -...-¦- .-.-.;¦ :.-..-.^ --\\
ких спиралей, которые вставля- —I """ ¦¦¦¦¦¦ ¦¦•¦¦¦ - - ¦//
лись друг в друга, в результа- 02 01
те потоки оказывались хорошо п о _ ~ ^
л. Рис. 3.7. Схематическое изображе-
смешанными. Усиливаемый сиг- Ние двухлучевого усилителя
нал вводился путем модуляцией
одного или обоих потоков за счет
размещаемого в начале пространства взаимодействия отрезка спирали.
Двухлучевой усилитель не состоялся как используемый в СВЧ-элек-
тронике прибор, так как с увеличением частоты необходимо уменьшать
разность скоростей потоков, а следовательно, при какой-то величине
разницы скоростей получим, что с учетом теплового разброса скоростей
два пучка просто неразличимы. Вместе с тем двухлучевой усилитель
является классическим примером рассмотрения различных неустойчи-
востей в теории волн.
Рассмотрим далее два ионно-скомпенсированных потока без столк-
столкновений и диффузии, которые будут описываться линеаризованны-
линеаризованными гидродинамическими уравнениями, связывающими конвекционный
ток и поле C.22), уравнениями для плотности конвекционного тока
C.21) и уравнением Пуассона C.13). Тогда имеем:
о2~ о2~ о2~ о т~1
at2 u iiZ dxdt u L'z дх2
jl,2 = Vo 1,2^1,2 + PO 1,2^1,2) C.58)
3F1 i
— = — (pi + p^i). C.59)
UX So
Здесь индекс «1» относится к первому, а «2» — ко второму потоку.
Используя стандартное предположение, что переменные величины ме-
меняются по закону eja;^, систему уравнений можно переписать в виде:
" l 'h+h), C.60)
JLO •
"-^± + 2j -^— ^ - ^— н 2 = jojso^^ E. C.61)
OX \V0 1,2j OX \V0 1,2j ' «0,1,2
104 Лекция 3
Получившаяся система уравнений представляет собой самосогла-
самосогласованную модель возбуждения электронного волновода электронными
пучками. Первое уравнение описывает возбуждение электронного вол-
волновода, два других — группирование электронного потока под действи-
действием поля пространственного заряда.
За счет предварительной модуляции потока с невозмущенной ско-
скоростью i?o,i < ^о,2 в нем за счет инерционной группировки наблюдается
модуляция по плотности пучка. Такая ситуация, как обсуждалось выше,
эквивалентна распространению в пучке двух волн пространственного
заряда — быстрой и медленной, фазовые скорости которых определя-
определяются соотношением C.30): Уф м^ = vo,i/(l ± ир/и). Второй, быстрый
пучок (г>о,2 > ^од) взаимодействует с продольной составляющей замед-
замедленной волны в первом потоке, в результате чего при соответствующем
выборе скорости г>о,2 второго потока последний будет отдавать энергию
ВЧ-полю, т. е. будет происходить усиление сигнала. Подставив из урав-
уравнения C.60) выражение для поля пространственного заряда в уравне-
уравнения C.61), окончательно получим систему уравнений относительно j\
и J2,:
^2~ / ., \ Я-i", Г//,\2 /,, \2~l_ /,, \2_
1Э [ — ) ~^Z - \\ — ) - ТГ" 31 - - [ — ) 32, C.62)
дх2 J \voiJ дх
ТГ^" + %3 ( — ) ~ъ ( — ) ~ ( ~^~ ) \ 32 = - ( ~^— ) 3i • C.63)
OX W02/ ОХ [4^02/ \ ^02 / J \ ^02 /
Данная система имеет решение j\ = j2 = 0, когда между потоками
нет взаимодействия. Однако возникает вопрос: будет ли такое решение
устойчивым? Для выяснения этого будем искать решение в виде
ji,2 = Vli2e~jkx. C.64)
Подставив соотношение C.64) в уравнения C.62) и C.63), получим
систему линейных алгебраических уравнений вида:
W2 = 0,
ф2 =
) 1 (
Условием разрешимости этой системы уравнений является равенство
нулю детерминанта системы, которое и дает дисперсионное уравнение
2 - (oj - kvOiJ(oj - kvO2J = 0. C.65)
Волны пространственного заряда малой амплитуды 105
Последнее можно переписать в виде:
——о = 1- C.66)
Как показано в [3], уравнение C.66) является общим видом диспер-
дисперсионного уравнения для N взаимодействующих электронных потоков
с дискретным распределением по скоростям {v}i,i = 1, ..., N.B анали-
анализируемом случае г = 1, 2.
Упростим дальнейшее рассмотрение, предположив, что потоки
идентичны (u)pi = соР2 = сор). Рассмотрим отдельно два случая: два
встречных потока и два потока, движущихся в одном направлении.
1. г>01 = —^02 = vq. Тогда из уравнения C.65) получаем, что
+4ш*к4* . C.67)
Неустойчивость может возникнуть только в том случае, если вели-
величина со будет комплексной, т. е.
k2v2
\к\ <V2^. C.68)
Vo
Или, перейдя от рассмотрения волновых чисел к длинам волн, получим,
что
Хр < V2 Л. C.69)
Последнее неравенство является условием того, что и — комплекс-
комплексная величина, т. е. и = Re со + j Imuj. Тогда exp [jut] = exp [(j Re со —
— Inid;)^]. Следовательно, при Imo; < 0 в системе будет иметь место
неустойчивость. Из соотношения C.69) видно, что в данном случае
неустойчивы только длинноволновые возмущения.
Рассмотрим дисперсионные характеристики двух взаимодейству-
взаимодействующих потоков. Как уже обсуждалось, для одного возмущенного по-
потока дисперсионные характеристики имеют вид, представленный на
рис. 3.2а. Тогда для двух невзаимодействующих потоков дисперсионная
характеристика будет иметь вид, показанный на рис. 3.8а (штрихо-
(штриховая линия). Дисперсионные характеристики, определяемые уравнени-
уравнением C.67), показаны на этом рисунке сплошными линиями. Понятно,
что ветви 1 дисперсионной характеристики соответствуют медленным
волнам, а 2 — быстрым волнам. Это легко установить рассматривая
асимптоты кривых, которыми являются прямые, соответствующие сво-
свободным ВПЗ.
106
Лекция 3
Рис. 3.8. Дисперсионные характеристики двух взаимодействующих потоков,
движущихся навстречу друг другу (а), движущихся в одном направлении (б).
Штриховыми линиями показаны дисперсионные характеристики невзаимо-
невзаимодействующих потоков. Заштрихованы области действительных значений &,
при которых имеют место комплексные значения ш
Из рисунка видно, что для быстрых волн неустойчивости быть
не может — любым действительным к соответствуют действительные
значения частоты и. Для медленных волн в диапазоне, определяемом
формулой C.68), частота будет комплексной, причем при lm oj < 0
возмущения будут нарастать во времени.
Таким образом в анализируемой консервативной системе существу-
существует неустойчивость. Энергия, необходимая для ее поддержания, оче-
очевидно, черпается из невозмущенного «неволнового» движения потоков,
движущихся с постоянными скоростями.
Как будет себя вести начальное возмущение со временем в такой си-
системе при выполнении условия C.69)? Оказывается возмущение возрас-
возрастает во времени, но не выходит за пределы некоторой области, в которую
оно было внесено. Такая неустойчивость носит название абсолютной
неустойчивости.
2. Электронные потоки, движущиеся в одном направлении (i?oi •
• V02 > 0). В этом случае, как видно из уравнения C.66), дисперсионное
уравнение имеет вид
(бе? —
=1-
C.70)
Диаграмма Бриллюэна для этого случая приведена на рис. 3.86". Диспер-
Дисперсионное уравнение по-прежнему имеет четыре решения, два из которых
не нарастают во времени (ветви 1), а два других (ветви 2) могут нарас-
нарастать, так как действительным к соответствует область (заштрихована
на рисунке) комплексных значений и.
Волны пространственного заряда малой амплитуды 107
Однако эта неустойчивость отлична от той, что в случае встречных
пучков, поскольку возмущение ведет себя иначе. Так как пучки имеют
скорости, направленные в одну сторону, возмущение сносится вместе
с пучком: имеет место нарастание только по длине пространства взаи-
взаимодействия (такназываемая конвективная неустойчивость). Отметим,
что классификация вида неустойчивости зависит от выбора системы от-
отсчета, в которой проводится анализ. Действительно, если в приведенном
примере перейти в систему координат, движущуюся вместе с пучком, то
неустойчивость в системе с попутными электронными потоками будет
уже абсолютной.
В заключение данного рассмотрения дадим формальное определе-
определение абсолютной и конвективной неустойчивостей.
Определение. Пусть функция u(x,t) характеризует некото-
некоторый волновой процесс, тогда, если имеет место соотношение
lim u(x,t) = 0 VxG(^i, ж2),
t—>-оо
то в системе имеет место конвективная неустойчивость.
Если функция u(x,t) характеризует некоторый волновой процесс
и имеет место соотношение
lim u(x,t) = ос Vx G (xi, ж2),
t—>-oo
то в системе имеет место абсолютная неустойчивость.
Для гиперболических систем существует следующий критерий уста-
установления неустойчивости, который иллюстрируется предыдущим рас-
рассмотрением: если асимптоты дисперсионных характеристик на плос-
плоскости (о;, к) направлены в одну сторону, то неустойчивость конвек-
конвективная, если в разные — абсолютная.
В заключение заметим, что если имеется система с конвективной
неустойчивостью, замкнутая в кольцо, то в этом случае иногда говорят
о глобальной неустойчивости. Примером системы с глобальной неустой-
неустойчивостью является лампа бегущей волны с запаздывающей обратной
связью, которая будет рассмотрена в последующих лекциях.
Неустойчивость Гельмгольца. Об одной гипотезе
образования спиц в кольцах Сатурна
(многопучковая неустойчивость)
Иногда можно встретить описания двухпучковой неустойчивости
(во всяком случае словесные), когда проводится аналогия с взаимо-
взаимодействием двух потоков жидкости. Эта аналогия неверна. Чтобы на-
наглядно доказать это, проанализируем ситуацию, в которой так же, как
и в предыдущем разделе, имеет место неустойчивость двух потоков
108
Лекция 3
Граница раздела встречных
потоков жидкости
Рис. 3.9. Неустойчивость Гельмгольца: а — возмущения границы раздела
нет — два слоя жидкости скользят по границе раздела навстречу друг другу;
6 — граница раздела возмущена — схематично показаны формы линий тока
и распределение давления вблизи возмущенной поверхности тангенциально-
тангенциального разрыва скорости
жидкости, движущихся навстречу друг другу; потоки предполагаются
несжимаемыми. Это реализуется, если рассматриваются два слоя иде-
идеальной несжимаемой жидкости г), которые скользят относительно друг
друга с постоянными и направленными в противоположные стороны
скоростями vi и V2, участок поверхности разрыва плоский, плотности
жидкости постоянны и равны pi и р2 (см. рис. 3.9а). При этих условиях
жидкость с каждой из сторон от поверхности разрыва описывается
уравнением Эйлера
=-Vp
C.71)
(р — давление) и уравнением непрерывности, которое в силу сжимае-
сжимаемости жидкости сводится к виду
divv = 0.
C.72)
Линеаризуя уравнения относительно малых возмущений v, p и р,
получим для верхнего слоя
dvxl dvxl
+ v
dt
дх
1 дрх1
р\ дх
C.73)
г) Под идеальной понимается жидкость, при движении которой вектор
напряжения в жидкости перпендикулярен любому элементу поверхности,
независимо от того, как он ориентирован в пространстве. Математически это
означает, что давление в жидкости есть скаляр, а не тензор [14]. В этом случае
в жидкости отсутствуют сдвиговые силы, и в частности, силы вязкости.
Волны пространственного заряда малой амплитуды 109
C.74)
1 дрУ1
dt pi ду
divv = O. C.75)
В уравнении C.74) учтено, что рассматривается поток жидкости, у ко-
которого постоянная составляющая скорости направлена по оси х. Приме-
Применяя к первому уравнению операцию div , и учитывая, что div grad = V2,
получим уравнение для переменной составляющей давления
1ГТ + ^ПГ = °- (З-76)
дх ду
Решение этого уравнения будем искать в виде
Pi = Pi(yy(ut-kx) ¦ C.77)
Тогда для pi(y) получается уравнение
dy
решение которого Ai ехр (—ку). Следовательно, решение уравнения
C.76) при у > 0, т. е. над границей раздела, имеет вид:
-~~-' а — ку j (uot — кх) / о т о \
Pi = /lie yeJK J. C.78)
Смещение границы задается в виде у = y(x,t) ~ ej(ut-kx)^ Тогда по
правилу дифференцирования сложной функции
yl li J \ li j i/1 J \ 01/ i/1 •
Из уравнения Эйлера для vy-R составляющей скорости имеем:
dvyi ., j \dy\ г., , ч~1 1 dpi
-jt=3("- *«oi)i" Ь(« ~ kvoM = ~ — W,
откуда:
Pi = -(и - кУог^рогуг/к. C.79)
Очевидно, что давление снизу от границы р^ равно величине, определя-
определяемой формулой, аналогичной формуле C.79), но с другим знаком, при
этом необходимо учесть, что г>02 направлено в сторону противополож-
противоположную Voi, т-е-
Р2 = (оо -\- куО2Jро2У2/к. C.80)
110 Лекция 3
Так как давления на границе должны быть равны (р± = ^2), то из
уравнений C.79) и C.80) приходим к дисперсионному уравнению
(ui-kvoiJ = -l^)(uj + kvO2J, C.81)
решение которого:
и
02) =Ь j(i?oi + ^02)л/~Рт~р02 ] • C.82)
Из решения C.82) видно, что частота является комплексной ве-
величиной, причем всегда выполняется условие 1т и < 0 при действи-
действительных к. Это и есть неустойчивость Гельмгольца, которая является,
очевидно, абсолютной. Физический механизм неустойчивости вполне
прозрачен (см. рис. 3.96). Если на границе возникает возмущение, то
линии тока искажаются, а следовательно, возникают поперечные гра-
градиенты давления. Из выражений для давления C.79) и C.80) видно,
что это приводит к усилению возмущения. Последнее в свою очередь
увеличивает градиент давления и т. д.
Легко видеть, что по физике явлений неустойчивость Гельмголь-
Гельмгольца отнюдь не аналогична неустойчивости двух взаимодействующих
электронных пучков. В частности, для нее принципиально решение
двумерой задачи.
Итак, оказывается, что в двухпотоковых системах могут наблю-
наблюдаться явления, связанные с возникновением неустойчивости и, как
следствие ее, имеет место рост амплитуды волн.
Применим аппарат, с которым познакомились, к одной из задач,
непосредственно не связанной с электроникой, но являющейся красивой
иллюстрацией вышеописанных явлений применительно к многопотоко-
многопотоковой системе. Задача связана с астрофизикой и касается объяснения на-
наблюдаемых в кольцах Сатурна азимутальных спицеобразных возмуще-
возмущений [15]. Кольца Сатурна представляют собой совокупность большого
числа узких колец, чередующихся со столь же узкими зазорами. Харак-
Характерное время образования такого микрокольца составляет несколько
десятков лет. На их фоне, как видно на фотографии (рис. 3.10а) (из
работы [15]), полученной космическим аппаратом «Вояджер-2», видны
азимутальные спицы, характерное время существования которых су-
существенно меньше времени образования кольца и составляет несколько
десятков минут. Данные неоднородности (спицы) имеют свойство обра-
образовывать устойчивые структуры, состоящие из нескольких спиц. Это
позволяет предположить, что образование неоднородностей связано
Волны пространственного заряда малой амплитуды
111
со, Гц
10
Рис. 3.10. Фотография части кольца В с отчетливо просматривающимися
кольцевыми структурами в области спиц, сделанная К A «Voyager 2» с рас-
расстояния 2.5 км (из работы [15] (а)), дисперсионная характеристика элек-
электростатических волн в кольцах Сатурна при учете взаимодействия между
потоками (б)
с волновыми процессами в кольце г). Заметим, что и в области спицы
тонкое микрокольцо не разрушается, т.е. можно предположить, что
главную роль в развитии волнообразных возмущений играют продоль-
продольные (азимутальные) смещения частиц, а их радиальными смещениями
можно пренебречь. Оговоримся сразу же, что характерные размеры
спицы Л ~ 108 -г- 109 см малы по сравнению с радиусом синхронной
орбиты го ~ 1,2 • 1010 см, что позволяет рассматривать одномерную
задачу.
Следующим важным фактом для понимания рассматриваемой мо-
модели служит то, что кольцо состоит из заряженных макрочастиц. Как
следует из работ [16, 15], потенциалы макрочастиц в кольцах Сатурна
столь высоки, что силами взаимного притяжения можно пренебречь,
и рассматривать смесь частиц, составляющих Кольца как обычную
плазму. Более того, как показывают оценки из работы [15] можно прене-
пренебречь влиянием поля магнитосферы Сатурна, т. е. изменение скорости
заряженных частиц будет определяться только полем пространствен-
пространственного заряда и столкновениями между частицами. Система уравнений,
) Отметим, что существует и некоторые другие, отличные от нижеизло-
нижеизложенной гипотезы образования спиц, однако, все они не объясняют факт
упорядоченности их структуры [15].
112 Лекция 3
описывающая в линейном приближении динамику возмущений состоит
из линеаризованных уравнений движения и непрерывности для частиц
разных сортов в отдельных потоках и уравнения Пуассона для самосо-
самосогласования задачи (уравнения записаны для одномерного случая), т. е.
имеем:
дх ' {6Ш)
C-84)
C-85)
Здесь индекс г указывает на сорт частиц, j — номер потока, vT —
средняя тепловая скорость движения частиц. Для простоты будем рас-
рассматривать только динамику макрочастиц, а ионами и электронными
компонентами в кольце пренебрежем. Это позволит, следуя [15], поло-
положить vT = 0. Тогда из системы уравнений C.83)-C.85) можно получить,
считая что все переменные величины изменяются по закону e3'(ut-kx)^
уравнение вида
~i l
Pi = —n
Потенциал ф$ можно представить так [15]:
где тензор {Sl-t} описывает вклад частиц сорта г из j-ro пучка в электри-
электрическое поле в области j-ro пучка. Учитывая выражение C.86), приходим
к системе линейных однородных уравнений относительно /5!:
Р) = ifli.i,*- C-87)
Условие равенства нулю детерминанта этой системы даст дисперсион-
дисперсионное уравнение, которое описывает азимутальные волны в многопотоко-
многопотоковой модели кольца при сделанных выше допущениях.
Рассмотрим отдельно два случая:
1. Случай невзаимодействующих потоков. Предположим, что рас-
расстояние между элементарными потоками столь велико, что можно
пренебречь взаимодействием между ними. Тогда в тензоре {*§]/}, как
Волны пространственного заряда малой амплитуды 113
несложно видеть, все недиагональные элементы равны нулю, так как
они описывают взаимодействие между потоками. Дисперсионное урав-
уравнение распадается на систему независимых уравнений, каждое из ко-
которых описывает волны в одном из потоков. Все уравнения однотипны
и имеют вид
/ г \2
Л V \шрз) _ 1 (о оо\
' 2^ 7 1 i \2 ~~ х> (б.ъъ)
i (и-куоз)
где Л — коэффициент, в который входят значения диагональных эле-
элементов матрицы {*Sj/}, u)pj — плазменная частота частиц сорта г в j-м
пучке. Сравнивая вид дисперсионного уравнения C.88) с дисперсион-
дисперсионным уравнением C.66), которое описывает взаимодействие двух элек-
электронных потоков, видим, что они полностью совпадают, если рассмат-
рассматривать величину y/~A(jjp как некоторую эффективную плазменную ча-
частоту.
Тогда все предыдущее рассмотрение неустойчивости в двухлуче-
вой лампе может быть перенесено на случай электростатических волн
в кольцах Сатурна в приближении слабой электростатической свя-
связи между отдельными микрокольцами. И можно предположить, что
в длинноволновом диапазоне (низкочастотные колебания, которые нас
и интересуют) возможно развитие конвективной неустойчивости.
2. Случай взаимодействующих потоков. Рассмотрим теперь более
интересный случай: волны во взаимодействующих потоках. В этом
случае в тензоре {S^} будет много ненулевых элементов. Анализ дис-
дисперсионного уравнения может быть произведен, если рассматривать
усредненные по сечению кольца возмущения плотности, т.е. просум-
просуммировать выражение C.87) по индексу j. Опуская выкладки, выпишем
сразу дисперсионное уравнение для этого случая:
— • In
OJ
_ (Ямин)
= 1, C.89)
где von- и von+ — невозмущенные средние скорости потоков на грани-
границах кольца, von- (ймин) и von+ (ймин) — соответственно невозмущенные
скорости для частиц с наименьшим геометрическим размером. Соответ-
Соответствующая диаграмма Бриллюена приведена на рис. 3.10& Пунктирной
линией отмечена область частот, где наше рассмотрение выходит за
границы сделанных предположений г). Штриховкой отмечена область
формирования спиц. Видно, что дисперсионная кривая лежит в этой
области, что подтверждает возможную связь образования «спиц» с рас-
рассматриваемыми волнами пространственного заряда в кольце.
г) Это связано с тем, что в уравнениях движения C.83) не учтены силы Ко-
риолиса, которые в диапазоне значений о; и /г, соответствующих пунктирной
линии, играют важную роль в динамике частиц, составляющих кольцо.
114
Лекция 3
1,06
0,98
0,90
J ^
3,80
1,40
-1,00 -
100,0
200,0
300,0 400,0
0,0
100,0
200,0
300,0 400,0
Рис. 3.11. Распределения скорости и плотности электростатических волн
в системе трех взаимодействующих потоков, полученные в численном экс-
эксперименте (из работы [17])
В работе [17] было проведено численное моделирование нелинейных
уравнений, описывающих неустойчивость в многопотоковой системе.
Интегрировались непосредственно соответствующие нелинейные урав-
уравнения, из которых были получены линеаризованные уравнения C.83)—
C.85). Не останавливаясь на методике численного решения уравнений,
кратко рассмотрим результаты численного эксперимента, проведенного
для случая трех взаимодействующих потоков. На рис. 3.11 приведены
зависимости скорости потоков V и плотности тока потоков J от про-
продольной координаты х. Невозмущенные скорости потоков соотносятся
как 1 : 1,01 : 1,02. На начальном участке пространства взаимодействия
начальное возмущение, подаваемое на вход системы, нарастает (это
линейная стадия развития неустойчивости). Далее с ростом амплитуды
возмущения становятся существенны нелинейные эффекты, которые
приводят к ограничению амплитуды переменных составляющих. От-
Отчетливо прослеживается структура «пиков» плотности тока по всей
длине пространства взаимодействия, которая автором работы [17] свя-
связывается с устойчивыми спицами, наблюдаемыми в кольцах Сатурна.
Циклотронные волны
До этого рассматривались только волны пространственного заря-
заряда в электронном потоке. Однако электронный поток в пространстве
дрейфа в присутствии аксиального магнитного поля поддерживает не
только две волны пространственного заряда, но также и две циклотрон-
циклотронные волны [18]. Как уже обсуждалось, ВПЗ обязаны своим происхожде-
происхождением восстанавливающим силам пространственного заряда. Подобным
образом возникают и циклотронные волны, которые поддерживаются
Волны пространственного заряда малой амплитуды 115
восстанавливающими магнитными силами. При этом циклотронные
волны требуют поперечного возбуждения в отличие от волн простран-
пространственного заряда, которые возбуждаются продольными возмущениями.
Чтобы получить выражения для фазовых скоростей циклотрон-
циклотронных волн, проанализируем поведение пучка в присутствии аксиального
магнитного поля. Причем, предположим, что силы пространственного
заряда пренебрежимо малы. Тогда уравнение движения электрона за-
запишется в виде
dv
_ + (vV)v = -^[v,B]. C.90)
Для модели, где х,у — переменные, a dz/dt = vo (постоянная про-
продольная скорость), уравнение C.90) распадается на уравнения для двух
компонент поперечной скорости:
^f+vo^f = -VvyB, C.91)
^+Vo^ = -VVxB. C.92)
Будем, как и раньше, искать решение в виде
vx = ио exp {jut — kz), vy = Avx. C.93)
Подставляя соотношения C.93) в уравнения C.91), C.92) и проводя
очевидные преобразования, получим
А = ±j, C.94)
juj — vok = TJ^cj C.95)
где ojc = г)В — циклотронная частота.
Из последнего выражения видно, что имеются два волновых ре-
решения, которые соответствуют двум волнам — медленной и быстрой.
Фазовые скорости этих волн соответственно равны
уф, м,б = Л , Vo . ¦ C.96)
Из последнего выражения видно, что разница в фазовых скоростях
волн вызвана присутствием магнитного поля — отсюда и название —
циклотронные волны.
Выведенные соотношения полностью аналогичны по своему виду
соответствующим соотношениям для ВПЗ, что подчеркивает общую
природу этих пар волн, обусловленную силами упругого взаимодей-
взаимодействия.
Воспользовавшись представлениями о потоке переменной мощно-
мощности, можно показать [18], что медленная циклотронная волна переносит
отрицательный поток мощности, а быстрая — равный ему по величине
положительный поток мощности. Аналогия с ВПЗ теперь полная, так
как оба типа волн имеют одинаковые характеристики потока мощности.
116 Лекция 3
Поэтому как и в случае ВПЗ существует возможность усиления как
медленной, так и быстрой циклотронных волн.
Заметим также, что циклотронные волны в отличие от ВПЗ, которые
являются продольными волнами, суть поперечные волны, а следова-
следовательно, можно говорить о поляризации циклотронных волн. Очевидно,
что поляризация будет определяться знаком аксиального магнитного
поля В.
Аппарат связанных волн
Рассмотрим теперь систему двух связанных волн, причем природу
волн конкретизировать не будем. Предположив, что связь слабая, урав-
уравнения для связанных волн можно записать в виде:
-р- = —k\x + с12а2, -р- = -к2х + c2iai, C.97)
dx dx
где &i52 — постоянные распространения волн, причем в силу слабой свя-
связи они не отличаются от постоянных распространения волн в отсутствии
связи, Ci2, C21 — коэффициенты связи. Затуханием волн пренебрегаем,
т. е. &i52 = ^/^ф1,2 — действительные величины. В случае слабой связи
общая средняя мощность приближенно равна сумме мощностей в несвя-
несвязанных системах:
Р = 2{|ai|2 ± |а2|2} « const, дР/дх = 0. C.98)
Знак +/— соответствует волне с положительной или отрицательной
энергией. Последнее выражение представляет собой выражение тео-
теоремы Чу о кинетической мощности в так называемом двухволновом
приближении. В частности, для электронного потока в пространстве
дрейфа, теорема Чу примет вид
Р = 2{\аб\2 - \ам\2} « const. C.99)
Поскольку а2 = аа*, из второй формулы C.98) следует, что
0- C-100)
Подставляя уравнения C.97) и комплексно-сопряженные им уравнения
в выражение C.100), находим
(±с*2 + c2i) aia* + (ci2 ± с*21) а\а2 = 0. C.101)
Последнее соотношение справедливо для любых а± и а2- Поэтому при
с12 = C2i и с2\ = с\2 получаем, что -j- (\а\\2 — \а2\2\ = 0 или
ах
Р = 2 (|oi|2 - Н2) = const = |fli@)|2 - |о2@)|2, C.102)
Волны пространственного заряда малой амплитуды
117
Таблица 3.1
(о;, &)-диаграмма
со*
i
/
/f
со
\
\
CO]
i
CO
V
¦//
/ *
!_/'¦
/ Л
\ *¦"
\
\
l'f<
4
Свойства системы
связанных волн
/г — действительная
величина для всех из
и наоборот; неустой-
неустойчивости нет
из — действитель-
действительная величина для
всех к; к — ком-
комплексная величина
для действительных
из] волны, затухаю-
затухающие в пространстве;
неустойчивости нет
из — действительная
величина для всех к
и наоборот; к имеет
значения, соответ-
соответствующие усилению,
для действительных
из; конвективная
неустойчивость
к — действительная
величина для всех
действительных из; из
— комплексная ве-
величина для действи-
действительных к; абсолют-
абсолютная неустойчивость
Примеры системы
связанных волн
Связь волн с положительной
или отрицательной энергией,
групповые скорости волн име-
имеют одно направление. Забегая
вперед отметим, что примером
такого взаимодействия являет-
является ЛБВ-подавитель, где имеет
место взаимодействие БВПЗ с
прямой волной в волноведу-
щей линии передачи (волной
с положительной энергией), в
результате которого происхо-
происходит полное подавление входно-
входного сигнал
Связь волн с положительной
или отрицательной энерги-
энергией, групповые скорости волн
противоположны. ЛОВ-пода-
витель; взаимодействие БВПЗ
с обратной волной в волнове-
дущей линии передачи (обе
волны с положительными
энергиями), полное подавле-
подавление входного сигнал возможно
на бесконечной длине про-
пространства взаимодействия
Связь волн с положительной и
отрицательной энергией, груп-
групповые скорости волн сонаправ-
лены. ЛБВ-усилитель; взаи-
взаимодействие МВПЗ с прямой
волной в волноведущей линии
передачи
Связь волн с положитель-
положительной и отрицательной энерги-
энергией, групповые скорости волн
противоположны. ЛОВ-усили-
тель, ЛОВ-генератор
118 Лекция 3
где ai(O) и ^@) — значения амплитуд связанных волн в начале
пространства взаимодействия. Из соотношения C.102) видно, что по
мере распространения вдоль пространства взаимодействия наблюда-
наблюдается либо одновременный рост амплитуд обеих волн, либо одновре-
одновременное их подавление. При с\2 — —с\± и с2\ — — с\2 получаем, что
^-(|а1|2 + |а2|2) =0или
Р = 2 (|ai|2 + |а2|2) = const = |ai@)|2 + |а2@)|2, C.103)
т. е. увеличение амплитуды одной из волн возможно только за счет
уменьшения амплитуды другой волны.
Предполагая, что ai, а2 ~ ej(ut-kx) ^ и ПрИНИмая в0 внимание форму-
формулы C.102) и C.103), из условия совместности системы уравнений C.97)
находим следующие дисперсионные уравнения:
для одинаково направленных потоков мощности
- oj/v2) = |c12|2; C.104)
для противоположно направленных потоков мощности
(к - и/у!)(к - uj/v2) = -|ci2|2. C.105)
В системе без потерь возможны четыре варианта связи взаимодей-
взаимодействующих волн (см. табл. 3.1) [19, 9]. Дисперсионные характеристики
соответствуют возможным вариантам связи.
Эффективное взаимодействие между связанными волнами возмож-
возможно только в случае, когда выполняются условия синхронизма, т. е. когда
фазовая скорость одной волны близка к скорости другой волны. Так,
например, при синхронном взаимодействии волны в линии передачи
с одной из циклотронных волн C.95) в пучке реализуется так называ-
называемый режим циклотронного резонанса. Понятно, что энергообмен при
этом будет зависеть от знака энергии волн.
Список литературы
1. Hahn W. Small signal theory of velocity modulated beams // General
Electric Rev. 1939. V. 42. P. 258.
2. Ramo S. Space charges and field waves in an electron beam // Phys.
Rev. 1939. V. 67. P. 276.
3. Шевчик В.Н., Шведов Г.Н., Соболева А.В. Волновые и колебатель-
колебательные явления в электронных потоках на сверхвысоких частотах. —
Саратов: Изд-во СГУ, 1963.
4. Гаврилов М.В., Трубецков Д.И., Шевчик В.Н. Волны в потоках
носителей заряда и их взаимодействие с волнами в линиях переда-
передачи / Обзоры по электронной технике. Сер. 1. Электроника СВЧ.
Вып. 11A28). - М.: ЦНИИ «Электроника», 1973.
5. Викулов И.К., Тагер А. С. О кинетическом и квазигидродинамиче-
ком методах решения задач СВЧ электроники при учете теплового
Волны пространственного заряда малой амплитуды 119
разброса скоростей электронов // Электронная техника, Сер. 1.
Электроника СВЧ. 1968. Т. 8. С. 3.
6. Шевчик В.Н., Шведов Г.Н. Волны пространственного заряда в
электронных потоках // Известия вузов СССР. Радиотехника.
1959. Т. 2. С. 511.
7. Шевчик В.Н., Трубецков Д. И. Аналитические методы в электро-
электронике СВЧ. — М.: Сов. радио, 1970.
8. Люиселл У. Связанные и параметрические колебания в электро-
электронике. — М.: Мир, 1963.
9. Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и
волн. — М.: Наука, 1984.
10. Sturrock P. A. In what sense do slow waves carry negative energy //
Journal Appl. Phys. 1960. V. 31. P. 2052.
11. Chu L.J. The kinetic power theorem. — IRE Electron Device
Conference, Univirsity of New Hempshire, June, 1951.
12. Birdsall C.K., Brewer G.R., Haeff A. V. The resistive wall amplifier //
Proc. IRE, 1953, V. 41. P. 865.
13. Шевчик В.Н. Основы электроники сверхвысоких частот. — М.:
Сов. радио, 1959.
14. Седов Л.И. Механика сплошной среды. — М.: Наука, 1970.
15. Блиох П.В., Ярошенко В.В. Электростатические волны в кольцах
Сатурна // Астрономический журнал. 1985. Т. 62, № 3. С. 569.
16. Альвен X. Космическая плазма. — М.: Мир, 1983.
17. Бессуднова И.О. К нелинейной теории электростатических волн в
кольцах Сатурна // Изв. вузов. Прикладная нелинейная динамика.
1994. Т. 2, №5. С. 109.
18. Johnson С.С. The theory of fast-wave parametric amplification //
J.Appl.Phys. 1960. V. 31. P. 1646.
19. Бекефи Дж. Радиационные процессы в плазме. — М.: Мир, 1971.
Лекция 4
НЕЛИНЕЙНЫЕ ЯВЛЕНИЯ В ЭЛЕКТРОННЫХ
ПОТОКАХ В ГИДРОДИНАМИЧЕСКОМ
ПРИБЛИЖЕНИИ
Однако не следует забывать, что линейные
уравнения для волн... получены в результате
упрощения (линеаризации) исходных нели-
нелинейных уравнений гидродинамики. Поэтому
представляется необходимым выяснить, при ка-
каких условиях оправдано линейное приближение
для волн, а также рассмотреть принципиально
новые эффекты, обусловленные нелинейностью
уравнений. Этим вопросам и посвящена
настоящая глава.
Л.М. Бреховский, В.В. Гончаров. Вве-
Введение в механику сплошных сред. М:
Наука, 1982. с. 291
Неизлунательная неустойчивость Пирса. Диод Пирса: от регулярных
автоколебаний к хаосу. Уравнения Годфри. Конечномерная модель ко-
колебаний в электронном потоке в диоде Пирса. Управление режимами
колебаний в диоде Пирса. Нелинейные волны пространственного заря-
заряда. Моделирование нестационарных нелинейных процессов в клистроде
с помощью гидродинамических уравнений.
В лекции 3 при рассмотрении многопучковой неустойчивости был
сделан закономерный переход от линейной теории, которая позволила
поставить и решить вопрос об устойчивости и типе неустойчивости
(если, конечно, она реализуется в системе), к нелинейной теории, ко-
которая позволяет анализировать динамику системы не только на на-
начальном (линейном) этапе развития неустойчивости, но и исследовать
пространственно-временную динамику систем в течение сколь угодно
длительных промежутков времени (пока, конечно, остаются справед-
справедливы гидродинамические уравнения для электронного потока). Здесь
нужно отметить, что применительно к рассмотрению пучков заряжен-
заряженных частиц, гидродинамический подход имеет существенное ограни-
ограничение. Дело в том, что уравнения движения в переменных Эйлера
Нелинейные явления в гидродинамическом приближении 121
C.11) справедливы только при рассмотрении электронного пучка как
сплошной среды — некоторой заряженной жидкости, скорость которой
является однозначной функцией координат и времени. В электронике
это не всегда имеет место. Очень часто оптимальные режимы работы
электронных ламп характеризуются наличием в пучке обгонов и отра-
отражений, что не позволяет использовать гидродинамический подход для
описания явлений. Вместе с тем для ряда задач гидродинамический
подход является наиболее оптимальным.
В данной лекции будет рассмотрена именно такая система — диод
Пирса, который позволяет при анализе некоторых режимов колеба-
колебаний ограничиться гидродинамическим описанием. Отметим, что диод
Пирса, являясь простейшей моделью электроники СВЧ, тем не менее
демонстрирует многие нелинейные явления, включая динамический
хаос, классический сценарий перехода к стохастичности, перестройку
хаотического аттрактора с изменением управляющего параметра, син-
синхронизацию хаотических колебаний внешним гармоническим сигналом.
Все это позволяет рассмативать диод Пирса как эталонную модель
возникновения «электронной турбулентности».
В конце лекции будет рассмотрен вопрос распространения в элек-
электронных потоках волновых возмущений большой амплитуды — нели-
нелинейных волн пространственного заряда, а также пример применения
гидродинамической теории к моделированию нестационарных нелиней-
нелинейных процессов в приборах с модуляцией эмиссии.
Неизлучательная неустойчивость Пирса
Диод Пирса представляет собой две бесконечных плоских парал-
параллельных сетки, пронизываемых моноэнергетическим бесконечно ши-
широким электронным потоком. Плотность заряда ро и скорость vo по-
потока на входе в диодный промежуток поддерживаются постоянными.
Пространство между сетками заполнено нейтрализующим фоном непо-
неподвижных ионов с плотностью pi. Плотность нейтрализующего заряда
равна по абсолютной величине невозмущенной плотности заряда в элек-
электронном потоке (ро = — pi).
В такой системе при определенных условиях возможно развитие
неизлунательной неустойчивости, которая носит название неустойчи-
неустойчивости Пирса [1]. Она связана с существованием внешней обратной связи
через цепь, соединяющую сетки, поскольку они заземлены [2]. Получим
условия развития неустойчивости Пирса.
Неустойчивость Пирса зависит от дисперсионной характеристики
колебаний пучка, которые, как было показано, определяется формулой
C.26). При k = ojp/vo одна из волн является стационарной (uj = 0).
В случае безграничного потока это тривиальный результат (если фа-
фазовая скорость волны меньше с, то всегда найдется система отсчета,
в которой существует стационарная волна). Однако в ограниченной
122 Лекция 4
системе существует выделенная система отсчета, в которой волны C.26)
являются стационарными, что приводит к сильной неустойчивости по-
потока [3].
Введем стационарное возмущение плотности пространственного за-
заряда потока, соответствующее волнам пространственного заряда (см.
C.26):
р(х) = psin (uipx/vo), D.1)
где р — некоторая амплитуда. Возмущение плотности пространствен-
пространственного заряда наводит на плоскостях диода статические заряды, которые,
в свою очередь, создают поле, возмущающее движение электронов.
Найдем его, воспользовавшись для этого уравнением Пуассона, при-
принимающим в одномерном случае с нулевыми граничными условиями
вид
dx2 so K }
Учитывая соотношение D.1) при граничных условиях ip@) = ip(L) = 0,
имеем
ер = — — [ — 1 sin ( —^— ) — — sin ( —^— ) . D.3)
?<э \Wp J L \ vo / L \ vo / ]
Первый член в формуле D.3) определяет потенциал плазменных колеба-
колебаний пучка, а второй — наведенное поле. Возмущение скорости электрона
может быть найдено из уравнения
dv р v2 . ((jjpL\
dt po L \ vo /
которое позволяет проанализировать вопрос об устойчивости движения
потока.
Пусть sin (ujpL/vo) > 0, т. е.
2тгп < ojpL/vo < 2тг(п + 1/2), п = 0, 1, 2,... D.5)
Если возмущение плотности пространственного заряда р > 0 (избыток
электронов), то dv/dt > 0. Следовательно, наведенное поле способству-
способствует уменьшению возмущения плотности пространственного заряда р,
и избыток электронов уменьшается. Если р < 0 (недостаток электро-
электронов), то dv/dt < 0, и недостаток электронов уменьшается. Следова-
Следовательно, при выполнении условия D.5) пучок устойчив.
Пусть теперь sin (ujpL/vo) < 0, т. е.
2тг(п + 1/2) < ojpL/vo < 2тг(п + 1), п = 0, 1, 2, ... D.6)
Если р > 0 (избыток электронов), то dv/dt < 0, и наведенное поле,
тормозя электроны, ведет к накоплению заряда. При р < 0 из соотно-
соотношения D.4) видно, что возмущение скорости dv/dt > 0, и недостаток
электронов возрастает.
Нелинейные явления в гидродинамическом приближении 123
Таким образом при выполнении условия D.6) электронный пучок
неустойчив. Как видно из соотношения D.4), характерное время разви-
развития неустойчивости (когда v становится порядка vq, f> ~ ро)
L Г . (jjpL~\
Vq I Vq J
-1
Отметим, что проведенный анализ позволяет лишь установить усло-
условия развития неустойчивости и оценить характерное время развития
неустойчивости. К чему же приводит неустойчивость, не совсем ясно,
так как заряд между плоскостями диода может либо накапливаться,
либо уменьшаться. В данном случае все определяется начальным воз-
возмущением, накладываемым на плотность пространственного заряда
потока. Различают в связи с этим мягкий и жесткий режим неустойчи-
неустойчивости Пирса. В первом случае наблюдается полное прохождение тока
и недостаток электронов в области между плоскостями диода. Во вто-
втором режиме образуется виртуальный катод — область в пространстве
взаимодействия с потенциалом, близким к ускоряющему, от которого
отражается часть электронного потока обратно к плоскости инжекции,
при этом наблюдается избыток электронов в диоде. Вместе с тем, при
величине а = upL/vq (так называемый параметр Пирса) порядка Зтг
возможно полное прохождение электронного потока х).
В последнем случае рост неустойчивости Пирса ограничивается
нелинейностью в системе, и в диоде наблюдается режим полного про-
прохождения потока. Таким образом существует возможность описания
системы в рамках гидродинамического подхода, чему и посвящен сле-
следующий раздел.
Диод Пирса: от регулярных автоколебаний к хаосу.
Уравнения Годфри
Система гидродинамических уравнений, описывающая нелинейные
нестационарные процессы в диоде Пирса, состоит из уравнений Пуас-
Пуассона, непрерывности и движения. Выпишем данные уравнения сразу
в безразмерном виде, так как при численном моделировании всегда
пользуются величинами, приведенными к безразмерному виду. Это
позволяет выделять комплексы безразмерных параметров (критерии
подобия), которые играют роль управляющих параметров системы, поз-
позволяя свести большое число параметров «размерной» системы уравне-
уравнений к нескольким параметрам для безразмерных уравнений. В данном
г) Увеличение параметра Пирса а при фиксированной длине системы L
и ускоряющем напряжении Vb (vo = y/2rjVo ) эквивалентно увеличению то-
тока / инжектируемого пучка. Токи, превышающие критическое значение /кр,
при котором в системе наблюдается неустойчивость, традиционно называют
сверхкритическими токами.
124 Лекция 4
случае имеем единственный управляющий параметр, а именно пара-
параметр Пирса се, представляющий собой невозмущенный угол пролета
по плазменной частоте. Проведем нормировку физических величин
(штрихи, стоящие над безразмерными величинами в дальнейшем будем
опускать) в следующей форме:
х' = Lx, t' = tot = Lt/vo-
Тогда система уравнений, описывающая диод Пирса, примет вид:
д\ ..2,. ^
дх2 ^ п
dp _ d{pv)
~dt = дх~'
dv dv dip
D.7)
D.8)
D.9)
dt dx dx'
Данные уравнения решаются при следующих граничных и начальных
условиях:
г?@, t) = 1, </?@, t) = 0, р@, t) = 1, ^A? t) = 0. D-Ю)
Система уравнений D.7)-D.10) интегрировалась численными мето-
методами в конечно-разностном представлении.
Построим численную схему для решения данной задачи. Во-первых,
необходимо ввести функции плотности, скорости и потенциала, задан-
заданные в дискретном времени и в дискретном пространстве. Для этого
зададим шаг во времени Д? и шаг пространственной сетки Ах = 1/iV,
где N — число узлов пространственной сетки. Будем строить явную
схему для интегрирования уравнений D.7)-D.10). Это означает, что
для нахождения значений функций на следующем шаге по времени
используются значения этих функций только на предыдущих шагах
по времени, и не используется значение функции на данном шаге г).
В начале рассмотрим уравнение движения D.9). Заменяя производ-
производную по времени конечной разностью вида
dv(x,t)
dt
AT
D.11)
х) В отличие от этого, неявные схемы подразумевают для нахождения
значений переменных на данном шаге п во времени использование значений
этих переменных не только на предыдущих шагах, но и на шаге п. Типичный
пример — широко известная схема Кранка-Никольсона (см. подробнее [4-6]).
Нелинейные явления в гидродинамическом приближении 125
где п — шаг во времени, Vj = v(xj), Xj = jAx, j = 1, ... N. Тогда
выражение D.9) в конечно-разностном виде можно записать как
\x,v,(p), D.12)
где Т — оператор, «переводящий» значения функции v на временном
слое п в значения на (п + 1) слое. Возникает вопрос: как корректно
перейти к конечно-разностному представлению оператора перехода Т
(так как можно самым различным образом записать пространственные
производные в разностном виде)? Основной критерий выбора той или
иной схемы — ее устойчивость г).
Для анализа устойчивости пользуются следующей методикой. Про-
Проводят линеаризацию оператора Т, и переходят к исследованию устой-
устойчивости возмущения вида и = иехр (jkx). Тогда уравнение D.11) сво-
сводится к уравнению вида:
nn+1 = un • G(At, Ax, и, </?), D.13)
где G называется коэффициентом перехода для уравнения D.12). Усло-
Условием устойчивости разностной схемы будет неравенство \G\ ^ 1.
Проанализируем устойчивость двух разностных схем, получаемых
из уравнения движения D.9) путем замены dv/dx центрированной
разностью [7] (схема «1»)
vn+1 _ vn nvn+1- vn_x (pn+1-(pn_1
— -\- v ¦ — — = —— — D.14)
l\Ti Al\X Al\X
и левой разностью (схема «2»)
A^ J i Ax Ax v '
Линеаризуем данные уравнения (т. е. скорость представим в виде
vq + v и будем отбрасывать члены второго порядка малости) и най-
найдем оператор перехода для случая ip(x,t) = 0 (понятно, что наличие
внешнего поля не окажет влияние на устойчивость разностной схемы).
Возмущение, относительно которого будем исследовать устойчивость
разностной схемы, зададим в виде uexp(jkxj). Тогда, для схемы «1»
(формула D.14)) имеем
„«+1 = „» - ^ („»+1 - и]_г) ,
x) При всей важности критерия устойчивости разностной схемы, это не
единственное требование, предъявляемое к виду Т. Другим, не менее важ-
важным требованием, является консервативность разностной схемы (т. е. выпол-
выполнение законов сохранения энергии и импульса), однако рассмотрение этих
вопросов выходит за рамки данного курса лекций.
126 Лекция 4
И окончательно
Найдем теперь величину |G|, которая примет вид
Таким образом получаем, что схема с центральными разностями абсо-
абсолютно неустойчива (\G\ > 1 для любых значений параметров) — при
любых сколь угодно малых величинах шага по времени и координате
любые ошибки и возмущения в данной схеме будут нарастать во времени
по экспоненциальному закону. Это далеко нетривиальный результат:
применение наиболее распространенной и привычной конечно-разност-
конечно-разностной аппроксимации производной приводит к «нефизическому» поведе-
поведению решения.
Если повторить выкладки для схемы «2», то мы придем к выраже-
выражению вида:
В этом случае условие, что \G\ ^ 1, принимает вид:
(^± - А A _ Cos k Ax) < 0. D.16)
Оценивая второй множитель своим максимальным значением
max {1 — cos&Ax} = 1 получаем условие, накладываемое на шаги по
времени и координате, при котором разностная схема D.14) устойчива
Д*<—. D.17)
vo
Соотношение D.17) в вычислительной математике называется усло-
условием Куранта. Условие Куранта определяет параметры сеточного раз-
разбиения (в нашем случае шага по времени At и шага по координате Ах),
при которых разностная схема устойчива.
Разностная схема D.15) в теории решения краевых задач разност-
разностными методами носит название схемы с разностями против потока [8].
Она имеет большое значение при исследовании различных потоковых
систем и широко используется для решения задач в вычислительной
гидродинамике, физике плазмы, электронике, метеорологии и т. д.
Заметим, что из рассмотрения условия Куранта может показать-
показаться, что можно брать сколь угодно большие шаги пространственно-
временной сетки, если они удовлетворяют D.17). На самом деле на Ах
также накадывается вполне определенное условие. Рассмотрим его, для
чего представим производную по продольной координате следующим
Нелинейные явления в гидродинамическом приближении 127
образом:
dv
~дх~
_ Vj+i - vj-i
3
Предположим, что v = ITexp (jkx). Тогда
dv -и
— — j i\j cte — j i\j и,
OX
а дискретное представление имеет вид:
dv
~dx~
_ jH3-i-)*x ., sin А-Ат si
= и — = -kueJ*Xj ——-r— = jkv —r-^-
2Аж j/еАж J kAx
Понятно, что дискретное представление стремится к непрерывному при
к Ах —у 0, когда —— —у 1. Это реализуется при к Ах ^С 1, т. е.
к Ах
Ах < 1/к - Л. D.18)
Последнее соотношение означает, что шаг пространственной сетки дол-
должен выбираться много меньше характерного пространственного мас-
масштаба возмущения Л; тогда временной шаг может быть выбран из
условия Куранта.
Уравнения непрерывности D.8) и Пуассона D.7) также записы-
записываются в конечно-разностном виде, причем первое с помощью схемы
разностей против потока, а второе в виде:
Соотношение D.19) представляет собой систему линейных алгебраиче-
алгебраических уравнений, которые решаются стандартными методами линейной
алгебры (см., например, [9, 10], а также лекцию 14).
Рассмотрим результаты численного моделирования с помощью вы-
вышеописанной методики сложной динамики в гидродинамической мо-
модели диода Пирса. На рис. 4.1 приведена бифуркационная диаграмма
колебаний плотности заряда в сечении системы х = 0,2. Бифуркаци-
Бифуркационная диаграмма представляет собой отложенные по оси ординат ве-
величины локальных максимумов временной реализации плотности при
фиксированном значении параметра Пирса, который откладывается
по оси абсцисс. Регулярным режимам на бифуркационной диаграмме
соответствуют линии; развилка линии соответствует удвоению периода
при переходе через некоторое критическое значение параметра. На
бифуркационной диаграмме легко выделяются две области.
При а большем 2,8575тг, динамика системы хорошо совпадает с ди-
динамикой универсального одномерного логистического отображения,
описывающего один из универсальных сценариев перехода к хаосу —
128
Лекция 4
1,0
2,8500
2,8625
2,8750
2,8875 а/я
Рис. 4.1. Бифуркационная диаграмма колебаний плотности пространствен-
пространственного заряда в диоде Пирса в точке х = 0,2
каскад удвоений периода Фейгенбаума [11]. Логистическое отображение
жп+1 = \хп A - хп) D.20)
является универсальной моделью, к которой сводится большое число
систем самой различной природы, общим в которых является наблюде-
наблюдение последовательности удвоений периода с изменением управляющих
параметров.
На рис. 4.2 показаны характеристики колебаний (временная
реализация, спектр мощности и фазовый портрет) плотности
пространственного заряда в сечении х = 0,2 для различных
уменьшающихся значений параметра а. Фазовый портрет строился
с помощью метода Такенса [11], который сводится к построению
фазовых векторов вида
R = {p(t),p(t
,... p(t + (n -
где Т — длительность задержки метода Такенса, an — размерность про-
пространства вложения (п = 2 соответствует проекции аттрактора колеба-
колебаний на плоскость). Первые четыре рисунка (а-г) демонстрируют каскад
удвоений периода: на них соответственно показаны режимы периода 1,
2, 4 и 8. На рис. 4.2д показан хаотический режим, возникающий после
каскада удвоений периода. Из рассмотрения восстановленного фазового
портрета видно, что аттрактор представляет собой узкую ленту в фа-
фазовом пространстве. В работе [12, 13] данный режим назван ленточным
хаосом. Характеристики ленточного хаоса подобны характеристикам
хаотической динамики в простых конечномерных системах, в которых
также наблюдается переход к хаосу через удвоения периода, например,
классической системе Ресслера [14].
При а < 2,8575тг размер аттрактора возрастает, и внешний вид
диаграммы уже не соответствует диаграмме, построенной для логи-
логистического отображения. В терминологии работы [12] это режим спи-
Нелинейные явления в гидродинамическом приближении
129
P(J)
-45
a
-90^
0,0
P(f)
-45
б
-90
0,0
W
-45
?-90
0,2
0,2
0,2
0,0 0,2
-45
?-90
0,0
W
-45
3-9O
p(/)o,o
-45
?-90
/
0,2 /
0,0 0,2 /
P0
1,9
0,9
Pit)
1,1
0,9
P©
1Д
0,9
P©
1,1
0,9
P©
1,1
0,9
P©
1Д
0,9
p(t+T)
Pjt+T)
pQ+T)
p(t+T>
122,9
Рис. 4.2. Спектр мощности, фазовый портрет и временная реализация
колебаний плотности заряда при следующих значениях параметра
Пирса: (а) а = 2,88тг — цикл периода 1; (б) а = 2,87тг — цикл периода 2;
(е) а = 2,8665тг — цикл периода 4; (г) а = 2,8655тт — цикл периода 8;
(д) а = 2,865тг — ленточный хаос; (е) а = 2,86тг — спиральный хаос
рального хаоса, который характеризуется существенным усложнением
колебаний в диоде (рис. 4.2е).
Покажем, что при определенных условиях из исходных гидроди-
гидродинамических уравнений, описывающих диод Пирса, можно получить
логистическое отображение. Для этого от системы дифференциальных
уравнений в частных производных перейдем к системе двух связанных
интегральных уравнений с запаздыванием относительно поля Eq на
входной сетке системы и времени пролета Т частиц через диодный
промежуток [15, 16].
5 Д. И. Трубецков, А. Е. Храмов
130 Лекция 4
Перепишем уравнение Пуассона в виде
0-ff-,,,,-,,. <4.И)
Граничное условие ср(О) = срA) = 0 можно записать как
1
\Edx = 0. D.22)
о
Продифференцируем D.21) по времени. Тогда
д дЕ 2др
т^ = ат- D23)
Подставляя этот результат в уравнение непрерывности получим
Ё1 = дЛЕ^1 = а2^ = А (±ЁЕ\ D 24)
= = а = (±
Эх дх dt дх\а2 dt
Из уравнения Пуассона можно найти выражение для плотности про-
пространственного заряда
Р=У^ + 1. D-25)
Подставляя выражение D.25) в уравнение D.24), получим:
дЕ ЭЕ
+
дх [а2 \" дх ' dt ' ' " ' ~ *" D6)
Учитывая, что полная производная записывается как
dE(x,t) дЕ дхдЕ дЕ ^Б
dt dt dt дх dt дх' [ ' '
из уравнения D.26) находим
f [Л f + §1 = О- D-28)
дх la dt dt]
Проинтегрировав это выражение по ж, и учитывая при нахождении
константы интегрирования соотношение D.24), получим:
±\Е 1 1 дЕ
+\^? dt
D.29)
где из условия нормировки следует, что poVo = 1, (дЕ(х, t)/ddt)x=o =
= dE0(t)/dt = dEo/dt.
Проинтегрировав уравнение D.29) по времени, учитывая из уравне-
уравнения движения, что Е = d2x/dt2, получим:
4 + ж = ^^4 + ^ = Л ВД) + (* - h). D.30)
a a at a
Нелинейные явления в гидродинамическом приближении 131
В качестве начальных условий здесь выбрано х = О, t = ti,
d2x
—— = Eo(ti). В принципе система уравнений D.9), D.30)
dt2 х=о
полностью эквивалентна исходной системе гидродинамических
уравнений. Однако она не дает устойчивых во времени решений при
численном моделировании. Поэтому обычно переписывают полученную
систему уравнений в другом виде.
Умножим левую и правую часть уравнения D.30) на функцию
sin (a(t — s)) и проинтегрируем от s = t\ до s = t. Выпишем отдельно
получающиеся интегралы в левой и правой частях D.30). Это с исполь-
использованием интегрирования по частям даёт
11Л
tl
— —2" sin (a(t — s)) ds + a x sin (a(? — s)) ds =
a dt J
= — —j sin (a(t — ti)) + ax, D.31)
(s - h) sin (a(t - s)) ds = -\ sin (a(t - h)) + a(t - h). D.32)
a
Окончательно из уравнения D.30) с учетом интегралов D.31) и D.32)
имеем:
t
x(t) = (t - h) + - [ E0(s) sin (a(t - s)) ds. D.33)
CM. J
tl
d2x
Такж;е из уравнения D.30), с учетом, что —^ = E(t), находим:
dt
t
E(t) = E0(t) - - [ E0(s) sin (a(t - s)) ds. D.34)
ti
Таким образом от системы уравнений Пуассона D.7), непрерывности
D.8) и движения D.9), пришли к системе связанных интегральных
уравнений D.33) и D.34). Чтобы ее решить, необходимо задаться соот-
соответствующими граничными условиями. Подставляя в D.33) граничные
условия х = 1, t = Т — ti (Т = T(t) — время пролета через диодный
промежуток), получим:
t
1 = Т + - \ E0(s)sin(a(t- s)) ds. D.35)
t-т
132 Лекция 4
Здесь Т и Eq — неизвестные функции времени. Подставим в уравнение
D.22) выражение для Е, полученное из соотношения D.30). Тогда
(t-t1)-a2x, D.36)
а а
1 1
2
_1 [ е dx = Щ± + [ (* -t1)dx- — = 0. D.37)
a J a J 2
о о
Вычислим интеграл в выражении D.37). Для этого перепишем его
в виде
](t-t1)dx=
о
Производную dx/dti найдем из D.33), и тогда
1
Ut-t1)dx = -
о i
2 *
= ^- + - f ^o(s)(*-s)sin(a(t-s)) ds. D.38)
2 a J
t-T
Объединяя выражения D.37) и D.38), окончательно получаем
2 Ь
E0(t) = ^(l-T2)-± J E0(s)(t-s)sin(a(t-s))ds. D.39)
t-т
Таким образом пришли к системе уравнений D.35) и D.39), которые
называются уравнениями Годфри. Получим из них логистическое отоб-
отображение, следуя работе [13]. Введем обозначения:
t
h = - \ E0(s)(t- s) sin (a(t- s)) ds,
t-T
t
I2 = — Eq(s) sin (a(t - s)) ds.
t-T
Тогда уравнения Годфри запишутся в виде:
1 = Т + ^/2, D.40)
lE0(t) = ^(l-T2)-±-h. D.41)
Предположим, что время пролета слабо меняется в пределах одно-
одного периода колебаний. В этом случае с точностью до членов первого
Нелинейные явления в гидродинамическом приближении 133
порядка малости можно считать, что Т « const. Это предположение
справедливо вблизи значений су, соответствующих границе устойчиво-
устойчивости, где движение потока близко к стационарному.
Из уравнения D.40) имеем
T = l-i /2. D.42)
Подставив соотношение D.42) в формулу D.41), находим
E0(t) = a(h-I1)-?. D.43)
Предполагая малое изменение величины Eq за время Т, легко полу-
получить для интегралов оценки вида
h « -(Т cos (аТ) - sin (аТ)/а)Ео№)/а = /3#o(*D>
h « -A - cosaT)E0(t*2)/a = 7^o(^),
где t* и t\ — некоторые моменты времени из интервала [t — T,t].
Далее предположим, что t\ ~ t\. Это очень сильное предположение,
однако, его справедливость в конечных пределах следует из результатов
численного моделирования. Тогда
E0(t) = a(-rE0(t - т) - 0Eo{t -r))-\ E%{t - т). D.44)
Обозначив Ai = аG — /5), А2 — 7 /2 перепишем последнее соотноше-
соотношение в виде
E0(t) = Ai??0(* - т) - A2E$(t - т). D.45)
Переходя к дискретному времени tn = п • т (п = 1, 2 . . .) и вводя
новую переменную E'Q = (A2/Ai)?ch придем к выражению, которое
совпадает по виду с логистическим отображением D.20). Действитель-
Действительно, имеем, что
E'0{tn+1) = Ai?U(in) (I - E'0(tn)). D.46)
Здесь величина Ai представляет собой управляющий параметр, экви-
эквивалентный параметру Л в логистическом отображении D.20).
Как следует из структуры уравнений D.44), величина 1^ опреде-
определяет нарастание плотности заряда в потоке, а 1\ — нелинейные свой-
свойства, связанные с воздействием формирующегося в потоке электрон-
электронного уплотнения на его движение. Квадратичное отображение D.46),
представляющее собой отображение с единственным максимумом (см
рис. 4.3а), определяет основные особенности превращений энергии
в гидродинамической модели. Из работы [17] следует, что отображе-
отображение жп+1 = g(xn) с функцией g(x), имеющей единственный максимум
134
Лекция 4
xn+i
0,50
(в рассматриваемом случае это логистическое отображение с g(xn) =
= ХхпA - хп) D.20)), характеризует процессы, в которых рост возму-
возмущений происходит при малых значениях переменной хп. Далее при пре-
превышении некоторого порога, равного максимуму функции g(x), проис-
происходит ограничение неустойчиво-
неустойчивости — уменьшение величины хп.
В рассматриваемой распределен-
распределенной системе этому соответству-
соответствуют, во-первых, рост возмущения
за счет торможения потока и, как
следствие, рост плотности заряда
в диодном промежутке при малых
значениях Eq. За счет накопле-
накопления заряда при этом наблюдает-
наблюдается увеличение напряженности по-
поля Eq. И, во-вторых, ограниче-
ограничение роста возмущения, связанное
с ускорением потока в возросшем
поле Eq. В результате этого плот-
плотность пространственного заряда
падает, и величина Eq уменьша-
0,0
0,50
0,87
0,78
0,70
3,40 3,45 3,50 3,55 3,60 3,65 X
Рис. 4.3. Вид квадратичного (логи-
(логистического) отображения D.20), по-
построенного при Л = 2,2 (а); бифур-
бифуркационная диаграмма для логисти-
логистического отображения (б)
ется. Далее процесс повторяется.
Итак, из уравнений гидро-
гидродинамической модели с помо-
помощью перехода к уравнениям Год-
Годфри было получено логистиче-
логистическое отображение. На рис. 4.3?
приведена бифуркационная диа-
диаграмма, полученная для логистического отображения D.20) с увели-
увеличением параметра Л. Величина Ai уменьшается с ростом параметра
Пирса су, следовательно, в отображении D.46) с увеличением а будет
наблюдаться обратный каскад удвоений периода.
Последний результат является очень интересным — удалось свя-
связать поведение сложной распределенной, а следовательно, бесконеч-
бесконечномерной системы с поведением универсального класса конечномер-
конечномерных систем — логистическим отображением, которое демонстрирует
некоторые особенности, присущие исходной распределенной системе,
описываемой уравнениями в частных производных.
Конечномерная модель колебаний
в электронном потоке в диоде Пирса
Анализ в гидродинамическом приближении движения в диодном
промежутке путем численного решения исходной системы дифферен-
дифференциальных уравнений D.7)-D.10) дает наиболее полную информацию
Нелинейные явления в гидродинамическом приближении 135
о процессах в этой системе. Однако естественным является стремле-
стремление получить более простое описание системы, например, с помощью
конечномерной аппроксимации уравнений. Подобный подход, конечно,
ограничивает область управляющих параметров, в которой можно ис-
использовать данное решение. Вместе с тем, переход от распределенной
системы, описываемой уравнениями в частных производных, к конеч-
конечномерной системе позволяет получить более ясное представление о фи-
физических процессах, происходящих в системе, упростить ее моделиро-
моделирование.
В конце предыдущего раздела был сделан переход от системы гид-
гидродинамических уравнений к системе двух связанных интегральных
уравнений с запаздыванием (уравнения Годфри). Далее на основе урав-
уравнений Годфри была построена простейшая модель динамики потока
в диоде Пирса — отображение, описывающее обратный каскад удвое-
удвоений периода с увеличением параметра а. Однако наряду с переходом
к уравнениям с запаздыванием и от них к простейшему нелинейному
отображению, возможно построение конечномерной модели из трех
обыкновенных дифференциальных уравнений, демонстрирующей ха-
характерные особенности процессов в диоде Пирса.
Для ее построения воспользуемся традиционным методом постро-
построения упрощенных моделей распределенных систем, а именно разло-
разложением движения в системе по характерным модам линейной задачи
[18, 19]. Впервые описание линейной динамики в диоде Пирса на языке
пространственных мод было дано в работах Куна [20, 21]. Хаотическая
динамика электронного потока в плазме в данном прибижении изу-
изучалось в работе [22], однако, выбор основных пространственных мод
в ней был произволен и не обоснован, и исследовались только условия
возникновения бифуркаций удвоения периода. Рассмотрим поэтому,
следуя работе [13], методику построения упрощенной конечномерной
модели динамики электронного потока в диоде Пирса на базе метода
Галеркина [5, 18].
В работе [20] показано, что в области изменения параметра Пирса
a Е Bтг, Зтг) в системе возбуждается бесконечное число мод с частотами,
определяемыми из дисперсионного уравнения
[{w2 + 1) sin a + 2jw cos a] +
v-2
- aw2 - 2jw}(w2 - 1) =0, D.47)
где w = oj/ojp. В случае диода Пирса линейные моды были определены
в работе [20]. Покажем связь линейных мод нашей задачи и наблюдае-
наблюдаемых пространственных распределений электронных волн, следуя этой
работе. Результаты решения дисперсионного уравнения D.47) представ-
представлены на рис. 4.4. При этом показаны только решения с наименьшим
значением Im ш, которым соответствуют наименее быстро затухающие
моды. В области значений параметра Пирса a Е Bтг,3тг) собственные
136
Лекция 4
Re ю/я
Im т/ж
0,0 0,5 1,0 1,5 2,0 2,5 о/тс 0,0 0,5 1,0 1,5 2,0 2,5 а/ж
Рис. 4.4. Решение дисперсионного уравнения для диода Пирса
значения нашей задачи имеют вид Ai52 = Retui52 — j Imvui^, A3 =
= 1тгоз, т.е. можно выделить два осциллирующих решения и одно
чисто затухающее.
Каждому собственному значению Xs соответствуют свои простран-
пространственные распределения мод. Так, например, для моды напряженности
поля пространственного заряда имеет место распределение
As —
-1
D.48)
и наблюдаемое распределение поля, соответствующее моде с номером s,
описывается функцией
Е = СЕ8(х,
+ к.с.
D.49)
Здесь С и 7 — действительные константы. Последнее уравнение с уче-
учетом выражения D.48) примет вид
Е = С [Re Es cos (Re uost + 7) + Im Es sin (Reojst + 7)]eImWe* +
+ jC [Re Es cos (Re ust + 7 + тг/2) +
+ Im #s sin (Reujst + 7 + тг/2)]е1тс^. D.50)
Из соотношения D.50) видно, что действительная и мнимая часть
каждой из мод в линейном приближении имеет одинаковую динамику
с различием в фазе на тг/2. Без потери общности при помощи выбора
констант С и 7 перейдем к чисто действительным модам, наблюдаемым
в численном эксперименте, а именно к
Е = [ReE8cos(Rew8t) + Im E8 sin (Rew8t)] elmuJst. D.51)
Собственные моды, соответствующие Ai52, демонстрируют одинаковое
поведение. Для них можно видеть, что наблюдаемая мода есть супер-
суперпозиция двух растущих стоячих волн с различным пространственным
Нелинейные явления в гидродинамическом приближении
137
60
2,0
-2,0
-6,0
-10,0
4
/*
/*
1
~2
4
\
"~~~~--A -" """" ~~ """^
" " \
\
\
„
Q6
распределением и сдвигом по фазе во времени тг/2 (см. рис. 4.5, кри-
кривые 1,2, на котором приведены пространственные распределения соб-
собственных мод). В результате
наблюдаемое пространственно-
временное распределение
величин представляет собой
распространяющийся волновой
пакет. Динамика этого пакета
определяется как мнимой,
так и действительной частью
величины Es. Мода, соответству-
соответствующая Аз, является затухающей,
и наблюдаемое распределение
(рис. 4.5, кривая 3) определяется
функцией ReEs. Аналогичный
вид имеют линейные моды и для
других переменных.
В качестве исходного базиса
(«пробного решения» в терминологии метода Галеркина) для конеч-
конечномерной аппроксимации используем набор собственных функций ли-
линейной задачи
з
8 = 1
Рис. 4.5. Собственные моды (про-
странственные распределения) ли-
нейной задачи о возбуждении коле-
бании электронного потока в диоде
Пирса; ^ 2 _ осциллирующие моды;
^ _ чист0 затухающая мода
D.52)
8 = 1
3
8 = 1
где Rs, Vs иФ8 — пространственные распределения, соответствующие
А..
Подставив пробное решение D.52) в исходную систему уравнений
D.7)—D.9), записанную относительно малых возмущений, будем иметь
отличный от нуля вектор невязки Ф = (Ф]_, Ф2, ^зM компоненты кото-
которого записываются в виде
Ol (Rlx + ^ж) + ^2 (R2x + ^2ж) +
a\{R1V1)x + о|(Д2
)x + a2a3(R2V3
)ж, D.53)
138 Лекция 4
Ф2 = oiVi + CL2V2 + ^3^3 + fll (Ф1Ж + Via;) + ^2 (^2Ж + ^2ж) +
+ аз (Фзх + Узх) + a\VxV\x + alV2V2x +
+ ^з^з^3ж + a1a2(V1V2x + V^Vi^) +
а2а3(К2К3ж + К3К2ж), D.54)
a2R2) + а3(^зжж + «2^3), D.55)
где введено обозначение (-)х = тг~(')-
Введем определение внутреннего произведения [5]:
1
(f*g)=\fgdx. D.56)
о
При обращении к методу Галеркина неизвестные коэффициенты as
находятся из решения матричного уравнения вида
х Ф2 =0. D.57)
Производя элементарные преобразования с учетом выражений D.53)—
D.55), получим матричное уравнение для определения коэффициен-
коэффициентов as в виде
MA + BA + D = 0, D.58)
где А — вектор, составленный из неизвестных коэффициентов а,{. Эле-
Элементы матриц М и В даются выражениями
niij = (Rj x R{) + (Vj x R{) ,
Элемент матрицы D соответствует формуле
di = E 4 KRkVk)x Ri +
A;
+ E E a/fefl/Kfi/feVi + ^V^^ + ^Vi^ + Vi^JVi]. D.59)
к /, /^fe
Разрешая уравнения D.58) относительно d^, получим явные уравнения:
Cbi(t) = /lltti + /12^2 + ^13^3 + ^14^1 + ^15^2 + ^16^3 +
+ /18^1^1 + /19^1^3, D.60)
Нелинейные явления в гидродинамическом приближении
139
2,77 2,79 2,81 2,83
Рис. 4.6. Бифуркационная диаграмма колебаний в конечномерной модели
с изменением параметра Пирса (а); увеличенный фрагмент бифуркацион-
бифуркационной диаграммы, демонстрирующий область хаотической динамики и окна
периодичности (б)
/270203 + 128СЦСЦ
, D.61)
+ /38^1^1 + /39^1^3- D.62)
Коэффициенты /^ получаются из численного решения неявных
уравнений. Нелинейности системы D.60)-D.62) являются квадратич-
квадратичными и появляются в результате кинематических нелинейностей и нели-
нейностей, входящих в уравнение непрерывности. Структура уравне-
уравнений такова, что моды 1 и 2 возбуждаются в результате неустойчивости
типа отрицательного трения, а их энергия передается в линейно зату-
затухающую 3-ю моду.
Динамика конечномерной модели D.60)-D.62) представлена на би-
бифуркационной диаграмме (рис. 4.6). Из рисунка можно видеть, что би-
бифуркационная диаграмма имеет вид, характерный для перехода к хаосу
через удвоения периода. Из диаграммы также хорошо видна близость
бифуркационных значений для гидродинамической (рис. 4.1) и конеч-
конечномерной моделей. Однако окна периодичности и обратные бифуркации
140 Лекция 4
удвоения периода, характерные для перехода к хаосу через каскад
удвоений периода, значительно лучше видны в конечномерной модели,
так как в этом случае учитывается взаимодействие только трех мод.
Как и в исходной системе, в модели сохраняются два типа хаотической
динамики — ленточный и спиральный хаос. Это можно заметить по
виду бифуркационной диаграммы: при а > 2,79тг динамика системы
характерна для перехода к хаосу через удвоения периода; при а « 2,78тг
наблюдается возрастание амплитуды колебаний, и система переходит
в режим спирального хаоса.
Таким образом конечномерная модель D.60)-D.62), полученная на
базе разложения Галеркина, демонстрирует динамику, которая как
качественно, так и количественно подобна поведению исходной рас-
распределенной системы. Из этого следует, что поведение электронного
потока в диоде Пирса в режиме полного прохождения определяется
взаимодействием небольшого числа мод. Моделирование динамики ко-
конечномерной модели может быть проведено существенно более просто
и с существенно меньшими затратами машинного времени, чем исход-
исходной системы гидродинамических уравнений D.7)-D.10). Последнее де-
делает перспективным использование таких моделей для изучения и опти-
оптимизации активных систем, представляющих собой несколько связанных
систем со сверхкритическим током г). На возможность такого модели-
моделирования указывает изложенное в следующем разделе описание влияния
обратной связи на процессы в диоде Пирса. Последнее рассматривается
на примере как гидродинамической, так и конечномерной модели дина-
динамики электронного потока со сверхкритическим током в диоде Пирса.
Управление режимами колебаний в диоде Пирса
Рассмотрим вопрос: возможно ли управлять сложными режимами
колебаний в диоде Пирса 2) ? По-видимому, одним из эффективных
способов управления является введение в систему управляемой обрат-
обратной связи. Впервые в электронике СВЧ это было сделано В.Я. Кис-
ловым [25, 26] для получения шумоподобных колебаний в ЛБВ с за-
запаздывающей обратной связью (подробнее этот прибор будет обсу-
) Такие системы привлекают большой интерес для различных приложе-
приложений, например, использование приборов с виртуальным катодом в качестве
модулей фазированных антенных решеток (см. работы [27]-[30]).
2) Кроме очевидного практического интереса к этому вопросу, связанного
с возможностью устранения нежелательных паразитных и шумоподобных
колебаний в случае возникновения в электронных и ионных потоках неустой-
неустойчивости Пирса, изложенное в данном разделе интересно с точки зрения
общих вопросов управления сложными режимами колебаний в распределен-
распределенной автоколебательной системе. Во многом интерес к этим исследованиям
стимулирован большими успехами в управлении хаосом в конечномерных
и дискретных системах (см., например, [23, 24]).
Нелинейные явления в гидродинамическом приближении 141
ждаться в лекции 14). В лекции 2 рассматривалась хаотизация ко-
колебаний в простой модели пролетного клистрона с обратной связью.
Не меньший интерес вызывает возможность разрушения хаотической
динамики в распределенной системе. В работах [31, 32] рассмотрено
влияние внешней обратной связи на сложные колебания в диоде Пирса.
В них показано, что при определенных параметрах обратной связи
возможно подавление хаотической динамики в диодном промежутке
и установление различных типов периодических колебаний. Изложим
приведенные в работах [31, 32] результаты.
Внешняя обратная связь в [31] вводится путем модуляции разно-
разности потенциалов между входной и выходной сетками диода сигналом,
снимаемым из некоторого сечения х = хос пространства взаимодей-
взаимодействия. В качестве такого сигнала используются колебания плотности
пространственного заряда р(хос, i) в межсеточном пространстве. Вве-
Введение такой обратной связи можно рассмотреть как подключение к про-
пространству взаимодействия цепи (волновода) обратной связи с линией
задержки.
В гидродинамической модели введение обратной связи приводит
к изменению граничного условия D.10) для потенциала на правой
границе системы, а именно
?>A, *) = foc(t) = Л • [р(хос, t -d)- po] • D.63)
Здесь А — коэффициент обратной связи, характеризующий какая часть
мощности колебаний ответвляется в цепь обратной связи, d — запазды-
запаздывание в цепи обратной связи. В этом случае требуется задать сигнал
в цепи обратной связи на временном интервале t Е [—d, 0). Считая, что
развитие процессов в системе начинается в момент времени t = 0, а при
t < 0 плотность пространственного заряда невозмущена p(x,t) = ро,
начальное распределение функции foc задается в виде
/oc|ieM,0)=0- D-64)
Точка подключения обратной связи в пространстве взаимодействия
не изменяется: хос = 0,2. Значение параметра Пирса, при котором
исследовалось влияние обратной связи, а = 2,86тг. При этом значении а
в системе без обратной связи наблюдается режим спирального хаоса (см.
рис. 4.2е).
Анализ зависимостей плотности пространственного заряда от вре-
времени в различных сечениях х = Жфикс диодного промежутка показал,
что характеристики колебаний (спектр мощности, фазовый портрет,
корреляционная размерность [33] и максимальный ляпуновский по-
показатель [34]), рассчитанные по временным реализациям р(хфИКС,г),
оставались постоянными с изменением координаты Жфикс. Это свиде-
свидетельствует об отсутствии пространственного хаоса и позволяет для ана-
142
Лекция 4
Рис. 4.7. Разбиение плоскости параметров длительность задержки d — ко-
коэффициент А обратной связи на различные режимы колебаний для гид-
гидродинамической модели диода Пирса. Символами Тп обозначены области
периодических колебаний с циклами периода п
лиза поведения системы рассматривать колебания р(хфИКС, t) в каком-
то одном сечении диодного промежутка.
На рис. 4.7 на плоскости управляющих параметров d и А выделены
области с различными колебательными режимами. Характерный вре-
временной масштаб колебаний в потоке без обратной связи в безразмерных
единицах времени г = 4,06.
При малых значениях коэффициента обратной связи А ^ 1 наблю-
наблюдаются хаотические колебания аналогичные колебаниям в диоде без
обратной связи. Временная динамика в этом случае сильно нерегуляр-
нерегулярна, однако, в спектре мощности на фоне высокого шумового пьедестала
наблюдается хорошо выделенная основная частота /о = 1/т и слабо вы-
выраженная её гармоника 2/q. Анализ аттрактора в фазовом пространстве
показывает, что вокруг состояния неустойчивого равновесия системы
образуется петля, на которой движение системы замедляется. При этом
область в фазовом пространстве, занимаемая остальным аттрактором,
плотно заполняется фазовой траекторией. Во временной реализации
также хорошо заметны периоды движения по петле возле состояния
однородного равновесия (с малой амплитудой колебаний плотности про-
пространственного заряда р(ж, t) « 0) и периоды движения по остальному
аттрактору (колебания с увеличивающейся во времени амплитудой).
Увеличение А приводит к различному поведению в зависимости
от длительности запаздывания в цепи обратной связи. При d > т/2
с увеличением А наблюдается увеличение сложности колебаний в элек-
электронном потоке; одновременно возрастает их амплитуда.
Нелинейные явления в гидродинамическом приближении 143
Дальнейшее увеличение А приводит к качественно иной динамике
системы. Амплитуда колебаний быстро растет с течением времени и,
начиная с какого-то момента, в потоке возникают отраженные элек-
электроны — в системе возникает колеблющийся во времени и простран-
пространстве виртуальный катод, от которого отражается часть электронно-
электронного потока обратно к плоскости инжекции. Колебательная динамика
в диодном промежутке определяется двумя основными механизмами —
развитием неустойчивости Пирса и ограничением её нелинейностью.
Введение обратной связи с А > 0,02 способствует разрушению меха-
механизма нелинейного ограничения и, как следствие, неограниченному
росту неустойчивости, заканчивающейся формированием виртуально-
виртуального катода. Гидродинамическая модель корректно описывает процессы
в потоке только при отсутствии в нем обгонов и отражений частиц,
в противном случае уравнения D.7)-D.9) становятся несправедливыми.
Критическое значение коэффициента обратной связи Лвк5 ПРИ котором
в диодном промежутке с обратной связью появляются отраженные
частицы и формируется виртуальный катод, зависит от длительности
запаздывания. Как видно из карты режимов, с увеличением d величина
^вк уменьшается.
При длительности запаздывания d < т/2 с ростом А сложность
колебаний в электронном потоке уменьшается; в диоде возникают ре-
регулярные колебания Тп.
Из рис. 4.7 видны особенности переходов от одних режимов к другим
при изменении параметров обратной связи. При небольших А колеба-
колебания в диоде остаются хаотическими, однако, их сложность уменьшается
по сравнению с колебаниями в диоде без обратной связи. Аттрактор
представляет собой узкую ленту в фазовом пространстве (режим лен-
ленточного хаоса). С ростом А в хаосе возникают окна периодичности
(например, режимы Тз и Т§). При А > 0.03 имеет место переход к пе-
периодическим колебаниям через обратный каскад удвоений периода . . .
... ->Ti6 ->Т8 -> ...->Ti.
Возникает вопрос: какие процессы, протекающие в электронном
потоке, определяют вышеописанную динамику исследуемой системы?
Исследование распространения электронных волн в пучке показыва-
показывает, что поведение системы определяется приближением её состояния
к однородному состоянию равновесия р(х) = ро, v(x) = vo, <р(х) = ipo.
Расстояние текущего состояния системы от неустойчивого равновесия
может быть определено как
\
2 + (<р(х t) ipJ + (v(x t) vJ
, t) - р0J + (<р(х, t) - ip0J + (v(x, t) - v0J } dx
D.65)
Рис. 4.8 иллюстрирует изменения величины отклонения системы от
неустойчивого состояния равновесия с течением времени в случае хао-
144
Лекция 4
1,0
а 100 120 140 160 180 200 220 t
S
2,0
1,0
б
120 140 160 180 200 220 t
Рис. 4.8. Зависимость расстояния S от текущего состояния системы до
неустойчивого равновесия
тических (режим спирального хаоса) (а) и регулярных (цикл периода 1)
(б) колебаний системы. Можно видеть, что в первом случае система
в некоторые моменты времени очень близко подходит к состоянию
равновесия (р(ж, t) « 0), и амплитуда волнового движения около него
близка к нулю. За счет неустойчивости происходит нарастание коле-
колебаний до ограничения их нелинейностью. Далее процесс повторяется.
Однако всякий раз значения величины S около положения равновесия
оказываются различными, также различными оказываются простран-
пространственные распределения величин около состояния равновесия. Поэтому
развитие неустойчивости начинается каждый раз с новых начальных
условий и динамика системы сильно нерегулярна.
Степень нелинейности системы можно проанализировать путем вы-
вычисления нелинейных энергетических функционалов [35]
dx - -,
/p = - pep dx,
о
D.66)
которые соответственно описывают переход энергии основного дви-
движения потока в кинетическую энергию волнового возмущения пучка
и потенциальную энергию поля пространственного заряда. В режимах
хаотической динамики максимальные значения функционалов больше,
чем для регулярных процессов: это указывает на большую степень нели-
Нелинейные явления в гидродинамическом приближении
145
-0,04
-0,08
Рис. 4.9. Зависимость разности энергий возмущения (Wp — Wk) от времени
для режима развитого хаоса (сплошная линия) и регулярных колебаний
периода 1 (штриховая линия)
нейности в режиме развитого хаоса. На рис. 4.9 показана зависимость
величины AW = Wv — Wk от времени, которая характеризует процес-
процессы преобразования различных видов энергии в процессе колебательно-
волновой динамики в пучке. В режиме периодической динамики видно
(штриховая линия на рис. 4.9), что энергия регулярно переходит из
кинетической в потенциальную, причем максимумы зависимости соот-
соответствуют накоплению заряда в межсеточном пространстве.
В режиме хаотической динамики на зависимости AW(t) (сплош-
(сплошная линия на рис. 4.9) видны моменты времени, когда AW « 0. Это
соответствует положению системы возле состояния неустойчивого рав-
равновесия. Далее энергия волнового движения опять начинает нарастать
во времени. Уменьшение энергии возмущения и длительное движение
около состояния неустойчивого равновесия наблюдается только после
резкого возрастания величины |AVK|. Физически это связано с тем, что
в этом случае в пучке возникает стоячая электронная волна, плотность
пространственного заряда которой в области выходной сетки резко
возрастает. Тогда тормозящее поле этого электронного уплотнения
сильно уменьшает скорость пучка ниже по координате, и как следствие,
диодный промежуток покидает значительно большее количество элек-
электронов, чем поступает в него. На рис. 4.10 показаны пространственно-
временные распределения волны пространственного заряда. Из него
видно, что в режиме спирального хаоса (рис. 4.10а) наблюдается рост
амплитуды волновых движений. После превышения амплитудой волны
критического значения наступает практически полное подавление ко-
колебаний в диоде. Далее, как уже обсуждалось, процесс повторяется, но
уже с новых «начальных условий».
Включение обратной связи позволяет разрушить данный механизм
хаотизации колебаний. При длительности задержки d < т/2 сигнал
146
Лекция 4
Рис. 4.10. Пространственно-временные распределения волны пространствен-
пространственного заряда в диодном промежутке для режима развитого хаоса (а) и регу-
регулярных колебаний (б)
обратной связи действует так, что способствует уменьшению накопле-
накопления заряда в выходной области диода и ускорению пучка в моменты
времени, когда имеет место максимум величины р. В результате рост
амплитуды электронных волн, распространяющихся в пучке, ограни-
ограничивается и, как следствие этого, степень нелинейности уменьшает-
уменьшается: система не приближается к состоянию неустойчивого равновесия
(рис. 4.106). При d > т/2, наоборот, сигнал обратной связи способствует
Нелинейные явления в гидродинамическом приближении
147
Колебания виртуального катода
Т\
Колебания
виртуального
катода
0,02
0,01
Хаос
0,0 0,50 1,00 1,50 d 2,00 2,50 3,00
Рис. 4.11. Разбиение плоскости параметров длительность задержки d — ко-
коэффициент А обратной связи на различные режимы колебаний для конеч-
конечномерной модели колебаний в гидродинамической модели диода Пирса
росту амплитуды электронных волн, и как следствие, за счет вышеопи-
вышеописанного механизма наблюдается усложнение динамики пучка, что при
больших А приводит к формированию виртуального катода.
Введение обратной связи в конечномерную модель производится
путем добавления в правую часть каждого из уравнений D.60)-D.62)
сигнала /осМ? который формируется следующим образом:
= А • [ai(t - d) + a2(t - d) + a3(t - d)] .
D.67)
Такая обратная связь во многом эквивалентна той обратной связи,
которая вводится в гидродинамическую модель диода Пирса. Сигнал
обратной связи в распределенной модели формируется как величина
плотности пространственного заряда в точке жос пространства взаимо-
взаимодействия. В соответствии с разложением D.52) сигнал обратной связи
в сосредоточенной модели должен быть взят как сумма амплитуд всех
трех высших мод. Одновременно, сигнал обратной связи воздействует
на каждую из мод, что отражается добавлением слагаемого /осМ
в каждое из уравнений конечномерной модели.
На рис. 4.11 представлена карта режимов на плоскости управляю-
управляющих параметров And при значении параметра Пирса а = 2,774тг. При
этом значении параметра Пирса в конечномерной модели без обратной
связи наблюдаются развитые хаотические колебания, фазовый портрет
которых подобен уже обсуждавшемуся выше спиральному хаосу. Из
рисунка видно, что при возрастании амплитуды обратной связи и зна-
значении задержки d < г/2 (где г = 1//о = 3,15; /о — основная частота
спектра) происходит подавление хаотических колебаний и установление
регулярного режима. Переход от хаотической динамики к регулярным
колебаниям периода 1 происходит как и в гидродинамической модели
148 Лекция 4
через каскад удвоений периода. В случае d > т/2 происходит неограни-
неограниченное нарастание амплитуды колебаний, что соответствует переходу
системы в режим формирования виртуального катода, где уравнения
конечномерной модели оказываются некорректными. Из сравнения ри-
рисунков 4.7 и 4.11 видно, что конечномерная модель, анализ которой
намного более прост, чем анализ гидродинамической системы, хорошо
описывает процессы, протекающие в распределенной системе и при
подключении обратной связи.
Нелинейные волны пространственного заряда
Перейдем теперь к обсуждению нелинейных волн пространственно-
пространственного заряда в неограниченных в продольном направлении электронных
потоках. Рассмотрим вначале бесконечно широкий электронный по-
поток полностью скомпенсированный ионным фоном. Вдоль оси системы
приложено сильное магнитное поле, так что исключается возможность
поперечных движений электронов. Такой пучок описывается уже зна-
знакомыми нам уравнениями, которые в безразмерном виде записываются
следующим образом:
dv dv dip ,л .
яТ + ^/Г = 7Г 4'68
at ох ох
— уравнение движения;
— уравнение непрерывности, а также уравнение Пуассона:
Здесь применена нормировка физических величин отличная от приме-
примененной в предыдущем разделе:
р' = Ро ' Р, v' = vo • v, ip' = ipo • ip = VQip/rj,
x = Up • x/vo, t = to • t = Upt.
Будем искать решение этой системы уравнений в виде стационарных
волн, т. е. решения, зависящие от комбинации ? = х — ut, где и = const —
скорость волны. Тогда
д__д_д^_д_ А-А^-_ А
дх~ д?дх~ дС dt~d?dt~ U дС
Нелинейные явления в гидродинамическом приближении 149
и система уравнений D.68)-D.70) сводится к системе обыкновенных
дифференциальных уравнений вида
dv dv dcp . А ^ ч
-и— + v— = -?, D.71)
dt, at, at,
D.73)
Проинтегрировав первые два уравнения, находим соотношения 1)
4> = \[(V- «J - A - «J] , D-74)
р=1-^. D.75)
v - и v у
Подставляя выражения D.74) и D.75) в уравнение D.73), получим
уравнение нелинейного консервативного осциллятора:
с потенциальной энергией VK((/?), где у? играет роль координаты, а ? —
времени. Проинтегрировав один раз D.76) с начальным условием
И/@) = 0, имеем:
W = if + A - uf (l - Л/1 + 2</?/A-пJ) • D.77)
Форма потенциальной ямы изображена на рис. 4.12. Из рисунка понят-
понятно, что решение будет носить колебательный характер, если величина ср
меняется в пределах
Нарушение этого условия эквивалентно опрокидыванию волны. Физи-
Физически это связано с тем, что дисперсия, которая приводит к распро-
распространению спектральных компонент волны с различными волновыми
г) Уравнение D.71) сводится к
1 d(v-lJ _ _dy_
а уравнение D.72) к
1 dp I dv
150
Лекция 4
числами с разной фазовой скоростью, в системе слаба. Поэтому остано-
остановить процесс укручения волны возможно только при достаточно малой
амплитуде, когда нелинейность
мала.
Найдем теперь точное решение
D.68)-D.70). Для этого перепи-
перепишем уравнение D.76) относитель-
относительно v, с учетом D.74). Тогда
v v — 1 ,л ^оЧ
— -vu\=- . D.78)
2 v — и
Умножим обе части D.78) на
d
Рис. 4.12. Форма потенциальной ямы
для нелинейного осциллятора D.76)
v
Y ~ vu
Интегрируя получившиеся выра-
выражение по частям, приходим к выражению вида:
d \ v
— — - vu \= ±y/G -(v- IJ ,
где G — постоянная интегрирования, которая имеет смысл квадра-
квадрата амплитуды волны [36]. Дальнейшее интегрирование даст решение
в неявном виде:
= ± \(и -
arcsin
J
D.79)
Здесь знак « —» соответствует БВПЗ, «+» — МВПЗ.
Решение D.79) описывает стационарную периодическую волну с ам-
амплитудой у/G . В работе [38] показана устойчивость этого решения.
Таким образом в бесконечно широком электронном пучке, не огра-
ограниченном в продольном направлении, нелинейные эффекты сводятся
лишь к укручению фронта волны.
Рассмотрим теперь к чему приводит учет ограниченности в попе-
поперечном направлении электронного пучка. Пусть цилиндрический элек-
электронный поток радиуса гь движется вдоль оси проводящей цилиндриче-
цилиндрической трубы радиуса R. В этом случае при условии гь ^ X ^ R, где Л —
характерный масштаб возмущения, уравнение Пуассона может быть
записано в виде
где
In {R/n)
D.80)
D.81)
Нелинейные явления в гидродинамическом приближении
151
Данные выражения получаются при разложении потенциала в попе-
поперечном направлении в ряд по мембранным функциям цилиндрического
волновода, если ограничиться только первым членом ряда. Фактически
это означает, что возмущенное поле пространственного заряда Ех имеет
в поперечном направлении распределение, совпадающее с распределе-
распределением TMqi моды цилиндрического волновода (Jo(^_i_^))-
Дисперсионное уравнение для этого случая выглядит так:
(ш - кГ =
D.82)
В области коротких длин волн к ^> к± это соотношение переходит
в соотношение для бесконечно широкого пучка C.26) V , однако, в длин-
длинноволновой области характеристики сильно различаются (см. рис. 4.13).
Для ограниченного потока рядом авторов (см., например, [39, 40])
была показана возможность существования решения в виде солитонов
уравнения Кортевега-де Вриза (КдВ).
Уравнение КдВ является эталонным
уравнением теории нелинейных волн
[41], описывающим эволюцию слабоне-
слабонелинейных длинноволновых возмуще-
возмущений в среде с дисперсией. Как известно,
оно имеет следующий вид:
ди
ди
Здесь второе слагаемое ответственно за
нелинейность, а последнее — за дис-
дисперсию. Данное уравнение допускает
решения в виде солитонов — уединен-
уединенных волн. Качественно их возникно-
возникновение связано с дисперсионным рас-
плыванием, которое компенсирует уже
упоминавшийся процесс опрокидыва-
опрокидывания волны. На спектральном языке это
объясняется тем, что фазовые скоро-
скорости гармонических составляющих с различными волновыми числами
неодинаковы и высшие гармоники, возникающие при искажении про-
профиля волны, не находятся в синхронизме с основной гармоникой, либо
обгоняя ее, либо отставая от нее. Поэтому при определенных условиях
возможна компенсация эффекта нелинейности дисперсионным расплы-
ванием, что и приводит к образованию солитона.
0
Рис. 4.13. Дисперсионные ха-
характеристики: 1 — ВПЗ в бес-
бесконечно широких потоках; 2 —
ВПЗ в потоке, ограниченном
в поперечном сечении
х) Здесь необходимо учесть, что уравнение D.82) записано в другой норми-
нормировке, чем та, которая использовались при выводе C.26).
152
Лекция 4
Отметим, что уравнение КдВ справедливо для большого класса
задач нелинейной физики, и нелинейные волны в электронных потоках
часто описываются с его помощью.
Поясним, как появляются решения в виде КдВ-солитонов. Будем
как и раньше искать стационарные волны, т. е. решения, зависящие от
? = х - ut, для задачи D.68), D.69) и D.80). Проводя вычисления ана-
аналогичные тем, которые были сделаны для задачи с бесконечно широким
пучком, приходим к уравнению нелинейного осциллятора вида
d2
-1/2
D.83)
Потенциальная энергия этого осциллятора описывается функцией
2 V /
Полагая, что |2у?/A — иJ\ <С 1 (слабая нелинейность), разложим пра-
правые части уравнений D.83) и D.84) в ряд с точ-
точностью до членов второго порядка малости.
Тогда получаем следующие соотношения:
W = -\
F2<p3) ,
D.85)
D.86)
Рис. 4.14. Форма потен-
потенциальной ямы W((p) со-
согласно формуле D.86)
для случая: F± > 0 A)
и Fi < 0 B)
где F1=k2±-A- и)'2, F2 = (l- и)'4. Вид
потенциальной ямы W(ip) D.86) приведен на
рис. 4.14.
В случае F\ > 0 состояние равновесия
ср = 0 будет неустойчивым, а ср = ip* =
= —3F2/2F1 — устойчивым (рис. 4.14; кривая
1). В случае F\ < 0 — наоборот (кривая 2).
Уравнения D.85), D.86) описывают стацио-
стационарные решения уравнения КдВ. В работах
[40, 42] приводятся решения в виде солитонов
КдВ, которые, соответственно, имеют вид
(р = -(F1/F2) sech2 (л/7п/2) , Fi > 0,
<р = -(Fi/F2) [1 - sech2 (У=7п/2)] , F, < 0.
D.87)
Данные результаты предопределены тем, что уравнение КдВ описы-
описывает эволюцию слабонелинейных длинноволновых возмущений в среде
с дисперсией. Предположение о слабой нелинейности было сделано при
выводе уравнений D.85), D.86), а предположение о длинноволновом
характере возмущений — при выводе уравнения Пуассона D.80).
Нелинейные явления в гидродинамическом приближении 153
Анализ уравнений D.83) с учетом D.84) показывает, что уединенная
волна может существовать и будет устойчива при 1 < k±\l — и\ < 2.
Отсюда следует, что скорость стационарной волны и должна удовле-
удовлетворять следующим неравенствам:
1 + kj1 < и < 1 + 2&J1
для быстрой волны пространственного заряда и
1 - 2k'1 < и < 1 - к'1
для медленной. Таким образом скорость быстрой уединенной волны
всегда больше, а скорость медленной — меньше, чем соответствующие
фазовые скорости линейных волн пространственного заряда. Действи-
Действительно, из дисперсионного уравнения D.82) следует, что фазовая ско-
скорость Уф лежит в пределах
1 - kj1 < Уф < 1 + kj1.
Точное решение может быть найдено лишь в неявной форме. Инте-
Интегрируя уравнение D.84), получаем
где G — постоянная интегрирования. Решение в виде уединенной волны
соответствует G = 0 (см. рис. 4.14). Тогда, выражая р через у при
помощи выражения D.74), приходим к уравнению
(и - у)^ = ±(у - 1)^к2±(у-2и + 1J /4-1, D.88)
где верхний знак соответствует БВПЗ, нижний — медленной. Интегри-
Интегрируя последнее соотношение, получаем решение в неявном виде:
D.89)
где М = k±\l — u\,V = k±\l — 2u + v\/2. Постоянная интегрированная
в решении D.89) выбрана так, что ? (vmax) = 0. Нетрудно показать, что
скорость и уединенной волны пропорциональна ее амплитуде vmax , но
связь между этими величинами другая, чем для КдВ солитонов, и имеет
вид
vmax =2и-1т2/к±. D.90)
С точки зрения физики процессов в пучке уединенная волна всегда
представляет собой сгусток электронов, поскольку в МВПЗ возмущения
скорости и плотности противофазны, а в БВПЗ — синфазны.
154
Лекция 4
Рис. 4.15. Образование уединенной волны и осциллирующего хвоста при
эволюции начального возмущения скорости (а) и плотности заряда(б)
Заметим, что анализ стационарных решений не позволяет понять:
реализуются ли полученные решения при эволюции произвольного на-
начального возмущения? Поэтому необходимо численное решение неста-
нестационарных уравнений системы D.68), D.69) и уравнения Пуассона.
Непосредственное численное решение исходных уравнений проводи-
проводилось в системе координат, которая движется со скоростью электронного
потока. На рис. 4.15 показан пример формирования быстрой уединенной
волны пространственного заряда и осциллирующего «хвоста» малой
амплитуды. На рисунке приведены пространственные распределения
скорости и плотности заряда в различные моменты времени. Вычис-
Вычислительный эксперимент показал, что в процессе эволюции достаточно
широкого класса начальных возмущений возникает одна или несколько
устойчивых уединенных волн, распространяющихся практически без
изменения их скорости и формы.
Мы не ставим себе здесь задачей подробно останавливаться на вопро-
вопросах применения методов теории нелинейных волн к задачам электрони-
электроники сверхвысоких частот. При подробном и строгом рассмотрении — это
тема не одной лекции, а, по-видимому, целого курса лекций. В заклю-
заключение нашего небольшого рассмотрения нелинейных волн простран-
пространственного заряда в неограниченых в продольном направлении потоках
отметим лишь несколько важных моментов. Во-первых, при анали-
аналитическом исследовании волновых уравнений обычно находят решения
в виде стационарных волн. В этом случае возрастает роль численного
моделирования нестационарных уравнений, которое позволяет решить
вопрос об устойчивости стационарных решений. Во-вторых, решения
обычно ищутся для бесконечно протяженных в продольном направ-
направлении потоков, хотя для электроники СВЧ принципиальный интерес
представляют решения краевых задач.
Нелинейные явления в гидродинамическом приближении
155
Моделирование нестационарных нелинейных
процессов в клистроде с помощью
гидродинамических уравнений
Удачным примером применения вышеразвитой теории к модели-
моделированию процессов в СВЧ-приборах является расчет характеристик
клистрода с помощью гидродинамических уравнений.
Клистрод — это мощный усилитель дециметрового диапазона, соче-
сочетающий принципы действия тетрода и пролетного клистрона. Схемати-
Схематически клистрод изображен на рис. 4.16. Клистрод относится к приборам
с модуляцией эмиссии [43, 44]. Лампа напоминает обычньй УВЧ-тетрод,
однако выходным контуром служит объемный резонатор.
^точное смещение
Анод
Трубы дрейфа
/ Коллектор
ВЧ-вход ВЧ-выходf
Рис. 4.16. Схематическое изображение клистрода
Между катодом и сеткой действует ВЧ-напряжение. Получающийся
модулированный по плотности электронный пучок ускоряется в направ-
направлении анода, находящегося под высоким потенциалом. Далее он с посто-
постоянной скоростью движется через трубу дрейфа, затем проходит через
зазор в объемном резонаторе, где возбуждаемое пучком электрическое
поле оказывается тормозящим. После этого пучок проходит вторую
трубу дрейфа, а затем попадает на коллектор. В настоящее время кли-
строды применяются в системах телевещания дециметрового диапазона
[45]. Возможно применение клистродов в качестве источников сигнала
в линейных ускорителях космического базирования [46, 47], так как
при столь же высоком уровне мощности и к.п.д., что и у современных
многорезонаторных пролетных клистронов, клистроды обладают зна-
значительно меньшими размерами и массой.
Оценки к.п.д. клистрода [44] в предположении, что имеет место ре-
режим ограничения тока пространственным зарядом г), дают максималь-
максимальный к.п.д. клистрода rjma^ = ji/jo ~ 82 %, где j\ — первая гармоника
г) В этом случае для плотности тока имеет место закон «3/2»: j =
где К = 2,33 • 10~6/d А~2В~3/2, d — расстояние между катодом и сеткой.
156 Лекция 4
плотности сгруппированного тока. Напомним, что максимальный к.п.д.
двухрезонаторного пролетного клистрона равен 58%, т.е. клистрод
оказывается значительно более эффективным, чем клистрон. К.п.д.
реальных приборов, разумеется, оказывается несколько ниже. Так, экс-
экспериментальный образец клистрода, используемый для телевещания,
имел г] « 60 % при коэффициенте усиления G = 20 дБ и выходной мощ-
мощности Р = 20 кВт на частоте / = 780 МГц [45]. Параметры клистрода,
предназначенного для космических систем следующие: г\ — 70%, G =
= 20 дБ, Р = 500 кВт на частоте / = 425 МГц [46, 47].
Использование гидродинамических уравнений представляется весь-
весьма выгодным, так как позволяет без труда моделировать процессы при
произвольном законе эмиссии, поскольку плотность заряда на входе
в пространство дрейфа в рамках гидродинамической модели можно
задавать в явном виде как функцию времени. Интерес к приборам с мо-
модуляцией эмиссии в значительной степени обусловлен созданием мат-
матричных автоэмиссионных катодов (МАЭК) и возникновением нового
направления — вакуумной микроэлектроники [43]. Поэтому интересно
исследование прибора, аналогичного клистроду, но на основе МАЭК.
При автоэлектронной эмиссии плотность тока определяется законом
Фаулера-Нордгейма [43, 44]
j = aV2e-b/y, где V(t) = Vb + Vm sin (u>ot), D.91)
Vb — напряжение смещения, а и b — величины, зависящие от геометрии
устройства и работы выхода. Анализ показывает [48], что в этом случае
можно получить более высокие значения гармоник тока, чем при эмис-
эмиссии, подчиняющейся закону 3/2, следовательно, применение МАЭК
позволит увеличить к.п.д. прибора. Клистрод с МАЭК был впервые
предложен в работе [49].
Для исследования нестационарных процессов в клистроде в работе
[50] предложена модель, представляющая ограниченный в попереч-
поперечном сечении поток. Движение электронов в нем предполагается од-
одномерным. Так как в приборах с модуляцией плотности (в частности,
в клистроде) начальная модуляция электронов по скорости отсутствует,
то можно ожидать, что обгоны электронами друг друга в пучке не
происходят, и можно воспользоваться гидродинамическими уравнени-
уравнениями D.68)-D.70). Эти уравнения необходимо дополнить граничными
условиями. В случае, когда для тока эмиссии можно воспользоваться
законом 3/2, имеем
О 7Г < U)t < 27Г.
Считая, что статический заряд электронного потока компенсирован
неподвижным ионным фоном и скоростная модуляция на входе от-
отсутствует, получаем граничные условия на входе в виде (нормировка
Нелинейные явления в гидродинамическом приближении 157
физических величин такая же, как в предыдущем разделе):
v(x = 0,0 = 1,
2 ,0 < ut < тг,
[0 7Г < Ut < 2?Г.
Очевидно, что для моделирования клистрода с МАЭК закон модуляции
плотности будет соответствовать формуле D.91) Фаулера-Нордгейма.
Представим продольную компоненту электрического поля резонато-
резонатора E(r, t) в виде Е = Re [Cs(t)Es(r)ejuJst], где Е8 и ujs — соответственно
распределение поля и частота собственного s-vo вида колебаний, Cs(t) —
медленно меняющаяся по сравнению с e^Ust амплитуда колебаний.
В нестационарном уравнении возбуждения резонатора A.61) в правой
части интегрирование по всему объему резонатора можно заменить ин-
интегрированием по объему, занимаемому током. Считая, что функции j
и Е8 зависят только от продольной координаты ж, получаем:
^Ж + %Ся = ~%\ °'(ж't)Es{x)) dV> D-93)
где х\ и Х2 — начальная и конечная координата зазора, Q — нагру-
нагруженная добротность резонатора и S± — площадь поперечного сечения
пучка. Введем функцию
Х2
= -JEs(x)dx, D.94)
и разделим в уравнении D.93) вещественную и мнимую части, полагая
Cs = Ле^. Тогда
2тг х2
dA ojsA S± Г , , Г ./ j.\dVs / . , /\ j (a (\n\
—г- + —тг = — dojst nx, t)—— cos iujst + w) dx, D.95)
dt 2Q 2ttNs J J dx
0 Xl
2тг X2
d4_ _ S±
dt ~
Z7T X2
Г Г dVs
dujst j(x,t)——sin (<jjst + ф) dx. D.96)
О Хг
Введем волновое сопротивление резонатора по формуле [51] К =
= V*KB/2u)sW, где КЭкв — эквивалентное напряжение на зазоре резо-
резонатора, W = NSA2/2 — энергия, запасенная в резонаторе за один пе-
период колебаний. Отнормируем собственную функцию Vs D.94) так, что
Vs(xi) — Vs(%2) — Vo, где Vo — ускоряющее напряжение. Тогда Уэкв =
= ЛУо, откуда следует, что Ns = Vq /ojsK. Очевидно, что зависимость
Es(x) может иметь самый различный вид в зависимости от геометрии
158 Лекция 4
резонатора, и рассматриваемая модель допускает исследование кли-
строда при любой форме Е8(х).
Перейдем в уравнениях D.95) и D.96) к безразмерным переменным,
нормируя К на величину /o/Vo, где /о — средний ток с катода:
dA usA мД/{" . ,
dt + 2Q
Здесь введены обозначения
2тг х2
dust j(x,t) cos (иst + ф) dx,
J
Х\ j
О хг
D.99)
2тг х2
dust j(x,t) sin (иst + ф) dx.
J
l[ = г
7Г(Ж2 - Xi)
О ял
Первая гармоника сгруппированного тока при этом определяется как
Активная и реактивная мощности равны Ра = Al[a'/2 и Рг = Л/^ /2,
причем при данной нормировке электронный к.п.д. клистрода rj = —Ра-
Уравнение движения D.68) в зазоре резонатора должно быть моди-
модифицировано следующим образом:
at ox ох
Заметим, что при выбранной нами нормировке величин все геомет-
геометрические размеры остаются неизменными при постоянном первеансе
пучка Р = Iq/Vq , так как нормируются на величину uip/vo ~ у/Р.
Коэффициент usK в правой части уравнений D.97) и D.98) также не
изменяется, так как он пропорционален Iq/ujpVq ~ у/Р . Таким образом
к.п.д. клистрода остается постоянным при постоянном первеансе, что
подтвержается экспериментальными данными [45].
В работе [50] и монографии [43, лекция 9; стр. 180] приведены
результаты моделирования процессов в клистроде с термоэмиссионным
катодом и МАЭК. Результаты моделирования и их сравнение с теорети-
теоретическими и экспериментальными исследованиями [45] свидетельствуют
о высокой эффективности применения рассмотренной гидродинамиче-
гидродинамической модели к моделированию нелинейных нестационарных процессов
в приборах с модуляцией эмиссии.
Нелинейные явления в гидродинамическом приближении
159
О 50 100 150 200 t 0,0 ОД 0,2 0,3 0,4 0,5 fо/тс
Рис. 4.17. Результаты моделирования нелинейных нестационарных процессов
в клистроде с термоэмиссионным катодом (из работы [50])
В качестве примера на рис. 4.17 приведены некоторые результаты
моделирования клистрода с термоэмиссионным катодом [50, 52]. Уста-
Установление колебаний в выходном резонаторе клистрода иллюстрирует
рис. 4.17а, на котором представлена зависимость электронного к.п.д.
клистрода г\ от времени. На рис. 4.176 приведены зависимости первой
гармоники сгруппированного тока от угла пролета в зазоре резонато-
резонатора ipQ. Как известно из теории возбуждения высокочастотного зазора
заданным током [53], амплитуда первой гармоники должна вести себя
согласно соотношению
Данная теоретическая зависимость приведена на рис. 4.176 в виде
кривой 1. Результаты численного моделирования с помощью вышеопи-
вышеописанной модели достаточно сильно отличаются от теории (кривые 2, 3).
Кривая 3 отличается от кривой 2 учетом сил пространственного за-
заряда. Кривая 2 рассчитана из кинематической теории, т.е. силы про-
пространственного заряда не учитываются, кривая 3 рассчитана с учетом
сил пространственного заряда. Видно, что рассхождение между ними
незначительно, что свидетельствует о возможности в данном случае
пользоваться более простой кинематической теорией, т. е. решать урав-
уравнения движения D.68) и непрерывности D.69) без уравнения Пуассо-
Пуассона D.71).
Мы не будем останавливаться здесь подробно на результатах моде-
моделирования нестационарных процессов в клистроде. Интересующимся
можно порекомендовать монографию [43], в которой изложены резуль-
результаты исследования процессов с помощью гидродинамической модели
в клистроде с МАЭК.
160 Лекция 4
Список литературы
1. Pierce J. Limiting currents in electron beam in presence ions //
J.Appl.Phys. 1944. V. 15. P. 721.
2. Незлин М.В. Динамика пучков в плазме. — М.: Энергоиздат, 1982.
3. Кузелев М.В., Рухадзе А.А. Электродинамика плотных электрон-
электронных пучков в плазме. — М.: Наука, 1990.
4. Фарлоу С. Уравнения с частными производными для научных
работников и инженеров. — М.: Мир, 1985.
5. Флетчер К. Численные методы на основе метода Галеркина. — М.:
Мир, 1988.
6. Флетчер К. Вычислительные методы в динамике жидкостей. —
М.: Мир, 1991.
7. Рихтмайер Р., Мортон К. Разностные методы решения краевых
задач. — М.: Мир, 1972.
8. Роуч П. Вычислительная гидродинамика. — М.: Мир, 1980.
9. Фадеев Д.К., Фадеева В.И. Вычислительные методы линейной
алгебры. — М.: Физматгиз. 1963.
10. Бахвалов Н. С. Численные методы (анализ, алгебра, обыкновенные
дифференциальные уравнения. — М.: Наука. 1973.
11. Шустер Г. Детерминированный хаос. — М.: Мир, 1988.
12. Анфиногентов В.Г., Трубецков Д.И. Хаотические колебания в
гидродинамической модели диода Пирса // Радиотехника и элек-
электроника. 1992. Т. 37. С. 2251.
13. Анфиногентов В.Г. Электронный поток в диодном промежутке
и пространстве дрейфа (нелинейные явления, хаос и образование
структур). — Дисс... к.ф.-м.н. Саратов, 1997.
14. Rossler O.E. An equation for continious chaos // Phys.Lett. 1976.
V. 57A. P. 397.
15. Godfrey B.B. Oscillatory nonlinear electron flow in Pierce diode //
Phys. Fluids. 1987. V. 30. P. 1553.
16. Lindsay P.A., Chen X., Xu M. Plasma-electromagnetic field
interaction and chaos // Int.J.Electronics. 1995. V. 79. P. 237.
17. Неймарк Ю.И. Стохастические движения динамических систем //
Динамика систем. Вып. 7. Горький: Изд-во ГГУ, 1974. С.З.
18. Канторович Л.В., Крылов В.И. Приближенные методы высшего
анализа. — М.: Физматгиз, 1962.
19. Любимов Д.И., Путин Г.Ф., Чернатынский В.И. Конвекция в
ячейке Хеле-Шоу при подогреве снизу // Гидродинамика, Том 10.
Пермь: Изд-во Перм. ГПИ, 1977.
Нелинейные явления в гидродинамическом приближении 161
20. Kuhn S. Linear longitudional oscillations in collisionless plasma diodes
with thin sheaths. Part II: Application to an extended Pierce-type
problem // Phys.Fluids. 1984. V. 27. P. 1834.
21. Kuhn S., Ender A. Oscillatory nonlinear flow and coherent structures
in Pierce-type diodes // J.Appl.Phys. 1990. V.68. P.732.
22. Wang N.Q. Chaotic behaviour in an electron beam plasma //
Phys.Lett. A. 1990. V. 145. P. 29.
23. Ott E., Grebogi C, Yorke J.A. Controlling chaos // Phys.Rev.Lett.
1990. V. 64, №11. P. 1196.
24. Badii R., Brun E., Finardi M. et al // Rev. of Modern Phys. 1994.
V. 66. P.732.
25. Кислое В.Я., Млсин Е.А., Залогин Н.Н. О нелинейной стохасти-
зации колебаний в электронно-волновом генераторе с задержан-
задержанной обратной связью // Радиотехника и электроника. 1979. Т. 25.
С. 2160.
26. Кислое В.Я. Теоретический анализ шумоподобных колебаний в
электронно-волновых система и автогенераторах с запаздывани-
запаздыванием // Лекции по электронике СВЧ и радиофизике E-я зимняя шко-
школа-семинар, Саратов,1981). Саратов: Изд-во Сарат. ун-та, 1981.
С. 78.
27. Magda I.I., Prokopenko Yu.V. Cooperative high-power radiation of
two beams at the dual vircator complex // In: the Proceedings of
the 11th International Conference on High Power Particle Beams
(BEAMS'96). (Prague, Czech Republic, June 10-14 1996), V.I.
Prague: 1996. P. 422.
28. Алехин Б.В., Дубиное А.Е., Селемир В.Д., Степанов Н.В.,
Шамро О.А., Шибалко К.В. Натурная имитация импульсной фа-
фазированной антенной решетки на основе виркаторов // Изв. вузов.
Прикладная нелинейная динамика. 1995. Т. 3, № 1. С. 28.
29. Hendricks К., Richard A., Noggle R. Experimental results of phase
locking of two virtual cathode oscillator // J.Appl.Phys. 1990. V.68,
№2. P. 820.
30. Храмов А.Е. Колебания в системе связанных генераторов на вир-
виртуальном катоде виртодного типа // Радиотехника и электроника.
1999. Т. 44, №2. С. 211.
31. Ремпен И.С, Храмов А.Е. Управление режимами колебаний в
электронном потоке со сверхкритическим током в диоде Пирса //
Известия РАН, Сер. физич. 2001. Т. 65, № 12. С. 1689.
32. Храмов А.Е., Ремпен И.С. Влияние обратной связи на сложную
динамику в гидродинамической модели диода Пирса // Радиотех-
Радиотехника и электроника. 2002. Т. 47, № 5. С. 732.
6 Д. И. Трубецков, А. Е. Храмов
162 Лекция 4
33. Grassberger P., Procaccia J. On the characterisation on strange
attractors // Phys.Rev.Lett. 1983. V. 50, № 5. P. 364.
34. Wolf A., Swift J., Swinney H.., Vastano J. Determining Lyapunov
exponents from a time series // Physica D. 1989. V. 16. P. 285.
35. Yagata H. Competition of the two unstable modes in the Rayleigh-
Benard convection // Progr. of Theoreical Phys. 1987. V. 78. P. 282.
36. Рыскин П.М., Трубецков Д. И. Нелинейные электронные волны.
Методы и результаты для приборов О-типа // Радиотехника и
электроника. 1993. Т. 38, № 2. С. 193.
37. Соколов Д.В., Трубецков Д.И. Нелинейные волны, динамический
хаос и некоторые задачи сверхвысокочастотной электроники / В
сб. сб.: Проблемы физической электроники. — Л.: Изд-во ФТИ,
1986. СС. 141-179.
38. Зайко Ю.П. Устойчивость нелинейных волн пространственного
заряда // ЖТФ. 1989. Т. 59, № 12. С. 137.
39. Канавец В.И., Ликунов В.М. Нелинейные волновые и колебатель-
колебательные процессы в протяженных электронных потоках // Радиотех-
Радиотехника и электроника. 1983. Т. 28, № 2. С. 326.
40. Ругпкевич Б.Н., Пащенко А.В., Федорченко В.Д., Муратов В.И.
Нелинейные волны объемного заряда в плазменном слое // ЖТФ.
1972. Т. 42, №3. С. 493.
41. Рыскин П.М., Трубецков Д.И. Нелинейные волны. — М.: Наука.
Физматлит, 2000.
42. Руткевич Б.Н., Пащенко А.В., Федорченко В.Д., Мазалов Ю.П.
Стационарные волны в ограниченной плазме // ЖТФ. 1977. Т. 47,
№ 1.С. 112.
43. Трубецков Д.П., Рожнев А.Г., Соколов Д.В. Лекции по сверхвы-
сверхвысокочастотной вакуумной микроэлектронике. — Саратов: Изд-во
ГосУНЦ «Колледж", 1996.
44. Исаев А.В., Соколов Д.В., Трубецков Д.И. Электронные СВЧ при-
приборы с электростатическим управлением и модуляцией эмиссии //
Радиотехника и электроника. 1990. V. 35, №11. Р. 2241.
45. Прист Д.Х., Шредер М.Б. Клистрод - необычно мощная лампа,
потенциально пригодная для ТВ-вещания в УВЧ-диапазоне //
ТИИЭР. 1982. Т. 70, № 11. С. 84.
46. Priest D.H., Shrader M.B. A high-power klystrode with potential for
space application // IEEE Trans, on El.Dev.. 1991. V. ED-38, №10.
P. 2205.
47. Nguen K., Warren CD., Ludeking L., Golphen B. Analysis of 425-
MHz klystrode // IEEE Trans, on El.Dev.. 1991. V. ED-38, №10.
P. 2212.
Нелинейные явления в гидродинамическом приближении 163
48. Шарбонье Ф.М., Барбур Дж.П., Гаррет Л. Ф., Дайк В.Р. Исследо-
Исследование природы и прикладных свойств холодной эмиссии на СВЧ //
ТИИЭР. 1963. Т. 51, № 7. С. 989.
49. Yokoo К., Shimawaki Н., Ono S. Proposal of a high efficiency
microwave power source using afield emission array // In: Techn. Digest
on VI International Vacuum Microelectronics Conf. 1993. P. 153.
50. Рыскин Н.М. Волновые взаимодействия в системах, содержащих
электронные потоки и электромагнитные поля (нелинейные вол-
волны, модуляционная и взрывная неустойчивость). — Дисс... к.ф.-
м.н. Саратов, 1996.
51. Григорьев А.Д. Электродинамика и техника СВЧ. — М: Высшая
школа, 1990.
52. Рыскин Н.М. Численное моделирование клистрода на основе гид-
гидродинамических уравнений // Изв. вузов. Радиофизика. 1997.
T.XL, №12. С.1511.
53. Шевчик В.Н. Основы электроники сверхвысоких частот. — М.:
Сов. радио, 1959.
Лекция 5
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
НЕЛИНЕЙНЫХ ЯВЛЕНИЙ НА ЭВМ
И ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ПРОЛЕТНЫХ
КЛИСТРОНОВ
Каковы же преимущества и неудобства числен-
численной модели? По отношению к эксперименту чис-
численные средства имеют то неудобство, что они
являются всего лишь моделями. Нужно уметь
отличать ту часть результатов, которая представ-
представляет теорию, от той, которая представлена осо-
особенностями численной модели... Численная мо-
модель особенно полезна при прогнозировании мало
изученных явлений в сложных системах.
К. Жаблон, Ж.-К. Симон. Примене-
Применение ЭВМ для численного моделирова-
моделирования в физике. М.: Наука, 1983. Гл. IX.
Каскадное группирование электронного потока. Многорезонаторные
клистроны. Нелинейная двумерная модель взаимодействия электрон-
электронного потока с ВЧ полями в клистроне. Уравнения одномерной ре-
релятивистской теории многорезонаторного клистрона. Моделирова-
Моделирование и оптимизация многорезонаторных релятивистских клистронов.
Двумерные эффекты в многорезонаторных клистронных усилителях.
Многолучевые клистроны.
Пролетные клистроны в основном конструируются как мощные
и сверхмощные усилители электромагнитных колебаний сантиметро-
сантиметрового и дециметрового диапазона. Во второй лекции рассматривалась
элементарная кинематическая теория двухрезонаторного клистрона-
усилителя, которая далее в третьей лекции уточнялась с учетом куло-
новского взаимодействия электронов в рамках линейной теории волн
пространственного заряда. Однако вышеизложенная теория позволяет
говорить лишь о качественном описании процессов в клистронных уси-
усилителях, так как не учитывает целый ряд важных факторов, оказываю-
оказывающих существенное влияние на процессы взаимодействия электронного
потока с высокочастотными полями в клистронах.
Моделирование и оптимизация на ЭВМ пролетных клистронов 165
В данной лекции описывается математическая модель и результаты
моделирования на ЭВМ нелинейных явлений и оптимизации парамет-
параметров клистронных усилителей.
Каскадное группирование электронного потока.
Многорезонаторные клистроны
Как обсуждалось во второй лекции, одним из недостатков двухрезо-
наторного клистрона является низкий коэффициент усиления. С этим
недостатком можно бороться путем каскадного соединения двухрезо-
наторных клистронов, когда выходной резонатор TV-го клистрона со-
соединяется со входным резонатором N + 1-го усилителя. Однако в этой
схеме имеется ряд недостатков: 1) задействовано много резонаторов,
выполняющих одинаковые функции; 2) используется много катодов —
велика мощность питания. Поэтому используют многорезонаторные
пролетные клистроны, в которых выходной резонатор (N — 1)-й сту-
ступени является входным для N-й ступени. В такой схеме пучок после-
последовательно проходит через ВЧ-промежутки, разделенные простран-
пространствами дрейфа — происходит каскадная группировка (группирование
электронного потока в результате последовательного и многократного
воздействия на него высокочастотных полей) [1, стр. 318-352]. Схема
каскадной группировки имеет ряд преимуществ.
1. В режиме малого сигнала существует возможность поднять коэф-
коэффициент усиления. Это достигается за счет возможности сильно умень-
уменьшить мощность входного сигнала. Существует эмпирическая зависи-
зависимость коэффициента усиления по мощности от числа резонаторов N:
КР = 15 + 20 -(N -2) [дБ].
Здесь необходимо заметить, что реально достижимы коэффициенты
усиления порядка 40 -г- 60 дБ, так как с ростом коэффициента усиления
растет вероятность самовозбуждения клистронного усилителя за счет
паразитной обратной связи.
2. В режиме большого входного сигнала каскадная группировка поз-
позволяет повысить не только коэффициент усиления, но и поднять к.п.д.
Для трехрезонаторного клистрона он составляет (^е)мах ~ 72,8 %.
Именно клистроны, использующие каскадную группировку (много-
(многорезонаторные клистроны), нашли широкое применение в самых раз-
различных областях радиофизики, физики и техники как мощные и сверх-
сверхмощные усилители СВЧ-колебаний сантиметрового и дециметрового
диапазона. Традиционное применение их связано с системами свя-
связи, радиолокации, радионавигации, установок промышленного нагрева
и сушки, ускорительной техники и т. п. Релятивистские многолучевые
клистроны в настоящее время активно разрабатываются и исследуют-
исследуются как перспективные усилители сигналов со сверхбольшой выходной
166 Лекция 5
Наведенное / у^у^ Наведен-
напряжение\ уу/ / ныйток
a Vi(t)
Рис. 5.1. Пространственно-временные диаграммы движения электронов
в трехрезонаторном клистроне для режима малого (а) и большого (б) вход-
входного сигнала
мощностью (до десятков и даже сотен МВт). Отметим, что клистро-
клистроны, наряду с тетродами и в последнее время появившимися мощными
полупроводниковыми усилителями, находят широкое применение как
усилители оконечных каскадов в телевизионных передатчиках [2]. Уни-
Уникальные выходные характеристики клистронов (высокий коэффициент
усиления (~ 60 дБ), большой к.п.д. (~ 80 %), высокие уровни выходной
мощности) делают клистрон одним из наиболее широко применяемых
приборов СВЧ-электроники.
Одна из основных задач конструирования и оптимизации клистрон-
ного усилителя заключается в достижении максимальной выходной
мощности и к.п.д. прибора. Для получения высокой выходной мощно-
мощности необходимо добиться появления достаточно большой переменной
составляющей конвекционного тока в области выходного резонатора.
Качественно рассмотрим как решается эта задача в многорезонаторном
клистроне, для чего проанализируем процесс группирования в трехре-
трехрезонаторном пролетном клистроне.
Рассмотрим случай малого входного сигнала. Пусть все резонато-
резонаторы настроены на одну частоту. Построим пространственно-временную
диаграмму для этого случая (рис. 5.1а). Электронный пучок модулиру-
модулируется в первом резонаторе и группируется в пространстве дрейфа перед
вторым резонатором. Так как частота второго резонатора равна частоте
колебаний в первом, то сдвиг фаз ф между возбуждаемым на ВЧ-зазоре
резонатора напряжением и возбуждающим током равен нулю. Прово-
Проводимость второго резонатора активная, и электронные сгустки наводят
Моделирование и оптимизация на ЭВМ пролетных клистронов
3 4 6 7 9 10
167
пШУШ
Рис. 5.2. Схема многорезонаторного клистрона: 1 — термокатод; 2 — фоку-
фокусирующий электрод; 3 — анод; 4 — входной резонатор; 5, 8 — пространства
дрейфа; 6 — второй резонатор; 7 — предпоследний резонатор; 9 — выходной
резонатор; 10 — коллектор с водяным охлаждением
в нем тормозящее поле. В результате скоростная модуляция во втором
резонаторе сдвинута на тг/2 (см. пространственно-временную диаграм-
диаграмму). Если увести резонансную частоту второго резонатора в область
больших частот, то группировка улучшится, но уменьшится амплитуда
вынужденных колебаний во втором резонаторе. При работе в режиме
недогруппированного потока основную роль играет амплитуда моду-
модулирующего сигнала. Поэтому в режиме слабого сигнала оптимальным
является режим синхронной настройки.
Если теперь рассмотреть режим большого входного сигнала, то
значительная группировка наблюдается уже в первом пространстве
дрейфа, и увеличивать скоростную модуляцию смысла нет. На первое
место выходит проблема согласования процессов группировки в первом
и втором пространстве дрейфа. Отстроим частоту второго резонатора
в большую сторону относительно первого резонатора. Тогда проводи-
проводимость этого резонатора имеет индуктивный характер, и возбуждаемое
ВЧ-напряжение опережает по фазе ток на величину ф < тг/2 [3]. Третий
резонатор имеет резонансную частоту равную частоте первого резона-
резонатора. Как видно из пространственно-временной диаграммы (рис. 5.16),
все электроны, включая тех, которые были раньше «нейтральными»
или имели слишком малую модуляцию, на входе в выходной резонатор
собираются в один электронный сгусток за счет «догруппировки» во
втором резонаторе. Первая гармоника тока достигает значения %\ =
= 1,46/о [4] (сравните со случаем двухрезонаторного клистрона, где
%\ = 1,16/о). Отсюда и рост к.п.д. системы (см. формулу B.27)).
Схема современного многорезонаторного клистрона приведена на
рис. 5.2. Электроны, эмиттируемые термокатодом 1 под действием
электрического поля, распределение которого задается фокусирующим
электродом 2 и анодом 3, а также под влиянием продольного фокуси-
фокусирующего магнитного поля, ускоряются и собираются в электронный
поток с нужными размерами поперечного сечения, движущийся вдоль
прибора с одинаковой для всех электронов скоростью v = v$. Проходя
через фокусирующую систему, электронный поток попадает в зазор
168 Лекция 5
тороидального входного резонатора 4. Электромагнитное поле входного
резонатора, возбуждаемое внешним источником (элементы связи на
рисунке не указаны), на основном типе колебаний распределено так,
что в зазоре резонатора оказывается максимум продольной компоненты
электрического поля.
Начальные каскады многорезонаторного усилительного клистрона
(входной и следующие за ним резонаторы, разделенные пространствами
дрейфа) настраиваются таким образом, чтобы достичь максимально
возможной величины %\ первой гармоники сгруппированного тока.
После модуляции пучка входным сигналом по скорости в первом
ВЧ-зазоре 4 происходит группирование электронного потока по плот-
плотности в трубе дрейфа 5 и появление переменной составляющей тока.
Благодаря этой составляющей происходит возбуждение второго резо-
резонатора б, который не связан с внешними цепями («холостой» резона-
резонатор). Если клистрон работает в режиме усиления большого сигнала,
то второй резонатор, в соответствии с вышесказанным, должен иметь
положительную отстройку относительно рабочей частоты (т. е. его ре-
резонансная частота о;о2 больше рабочей частоты uj). Тогда второй резо-
резонатор улучшает процесс модуляции и увеличивает величину %\ первой
гармоники сгруппированного тока. Последующие резонаторы также
настроены таким образом, чтобы улучшить группировку электронного
потока к выходному устройству.
На зазор предпоследнего резонатора 7 электронный пучок приходит
уже хорошо сгруппированным и соответствующая переменная состав-
составляющая тока велика. В случае необходимости обеспечения максималь-
максимального к.п.д. усилителя основная задача этого предпоследнего каскада
заключается в создании достаточно компактного электронного сгустка
в зазоре выходного резонатора 9. А это значит, что резонатор 7 дол-
должен обеспечить достаточные сжимающие силы в электронном сгустке,
противостоящие силам кулоновского расталкивания в хорошо сгруппи-
сгруппированном пучке. Эти сжимающие силы — силы инерции — возможно
увеличить только за счет увеличения модуляции электронов по скоро-
скорости, т. е. увеличения напряжения на зазоре предпоследнего резонатора.
Как следует из качественного рассмотрения трехрезонаторного кли-
клистрона, это возможно добиться путем уменьшения расстройки по часто-
частоте предпоследнего резонатора по сравнению с резонаторами начальных
каскадов. Длина последней трубы дрейфа 8 должна быть малой, так как
силы пространственного заряда быстро уничтожают модуляционный
разброс скоростей электронов потока. Последнее является и положи-
положительным эффектом, поскольку эффективность отбора энергии выход-
выходной резонансной системой повышается при уменьшении разброса по
скоростям электронов сформированного сгустка. После прохождения
выходного резонатора (элементы связи его с нагрузкой на рисунке не
указаны) заторможенный пучок поступает на коллектор 10, который
в мощных клистронах обычно имеет водяное охлаждение.
Моделирование и оптимизация на ЭВМ пролетных клистронов 169
Из вышесказанного понятно, что физическая сторона процессов
взаимодействия электронного потока с ВЧ-полями резонансных систем
оказывается качественно сравнительно простой. Однако математиче-
математическое описание нелинейных процессов в клистронах и оптимизация их
параметров является достаточно сложной задачей и требует для ее ре-
решения привлечения моделирования на ЭВМ [5-8]. Это связано с целым
рядом моментов, основные из которых перечислены ниже.
1. Из-за локального характера энергообмена электронного потока
с ВЧ полями большой ампитуды в режимах с высоким к.п.д. в кли-
клистроне возможно появление обратных и колеблющихся электронов. Это
требует проведения расчетов клистронов с высоким к.п.д. в системе
координат (?]_, ?), где t\ — время влета сечения электронного потока
в пространство взаимодействия, t — текущее время. Последнее суще-
существенно сложнее в плане численной реализации моделей, чем описание
динамики электронного потока в координатах (?]_, z), где z — продоль-
продольная координата. Однако при этом возможно описать не только обгоны
одних электронов другими, но и отражения в потоке.
2. Большой коэффициент усиления в многорезонаторном клистроне
приводит к тому, что незначительные ошибки и неточности в расчете
начальных каскадов определяют появление больших ошибок при опре-
определении выходных характеристик прибора.
3. Из-за необходимости согласования поля и возбуждающего тока
в протяженных зазорах резонатора оптимизация пролетного многорезо-
наторного клистрона с широкой полосой усиливаемых частот сводится
к решению краевой задачи.
4. Неодномерность движения электронного потока. В мощных кли-
клистронах используются резонаторы с бессеточными зазорами. В них
ВЧ-поля «провисают» к центральной части пучка. В этом случае мо-
модуляция электронного потока становится неоднородной в радиальном
направлении. К другим принципиально двумерным процессам в кли-
клистроне относятся пульсация пучка и динамическая расфокусировка.
При достаточно больших фокусирующих магнитных полях двумерные
эффекты сводятся к расслоению электронного потока в поперечном
к движению электронов направлении.
При построении нелинейной теории, которая может быть положена
в основу оптимизации клистронных усилителей, необходимо учитывать
такие факторы, существенно влияющие на процессы взаимодействия,
как нелинейность модуляции по скорости электронов в модуляторе, ре-
реальное распределение поля в протяженных зазорах резонаторов, обрат-
обратное и радиальное движение электронов, расслоение электронного пото-
потока по поперечной к направлению распространения пучка координате,
конечность фокусирующего магнитного поля, релятивистские эффек-
эффекты для релятивистских клистронов, нелинейные эффекты, связанные
с действием сил пространственного заряда.
170 Лекция 5
В следующем параграфе рассмотрена математическая модель [8],
учитывающая вышеприведенные факторы. Учитывая большую важ-
важность исследования мощных релятивистских клистронов, описана мо-
модель для релятивистского электронного пучка, которая учитывает ещё
и неодномерность движения электронного потока.
Нелинейная двумерная модель
взаимодействия электронного потока
с ВЧ-полями в клистроне
При построении модели пролетного клистрона будем предполагать
следующее: 1) электронный пучок (трубчатый или сплошной) имеет
азимутально-симметричное распределение плотности тока и располо-
расположен соосно с пролетными каналами; 2) ВЧ-зазоры резонаторов кли-
клистрона имеют аксиально-симметричную структуру (профиль их может
быть любой); 3) фокусирующее магнитостатическое поле азимутально-
симметрично, и осевая силовая линия совпадает с осью пучка (в про-
продольном направлении поле может быть и неоднородным). Тогда для
описания процессов взаимодействия электронного потока с ВЧ-полями
можно использовать двумерную модель, учитывающую азимутальную
симметрию полей.
Уравнение движения электрона во внешнем электромагнитном поле
без учета тормозного излучения, т. е. при скоростях v < 0,99с, имеет вид
и
^ = -^{E + [v,B]-v(v,E)/c2}, E.1)
где г]о — удельный заряд покоящегося электрона, j = l/y^l — v2/с2 —
релятивистский фактор. С учетом того, что для используемых в резо-
резонаторах клистронов i^-типов колебаний компонента Е^ = 0, уравнение
движения E.1) в цилиндрической системе координат запишется так:
г-гф2 = -^ {Ег + гфВг - zB^ - г (rEr + zEz) /с2} , E.2)
г
j? = -2° {Ez + rBv - гфВг - z (rEr + zEz) /с2} . E.3)
Полная скорость электрона v определяется в этом случае соотношением
v = i/r2 + (гфJ + z2 . E.4)
Будем также считать, что магнитостатическое поле слабо неодно-
неоднородное, поэтому при разложении радиальной и осевой составляющих
индукции В0 в ряд можно ограничиться только первыми членами.
Исключим величину ф, входящую в уравнения E.2) и E.3). Из
закона сохранения для азимутально-симметричных полей в случае
Моделирование и оптимизация на ЭВМ пролетных клистронов 171
слабонеоднородного магнитостатического поля следует [10, 11], что
г27о 2
где ис = eB°(zo)/mj, индексом «0» отмечены начальные значения при
z = zo соответствующих величин.
Высокочастотные поля в зазоре резонаторов представим в виде Е =
= Re {E0(r, z)ejujt}, В = Re {B0(r, z)ejujt}, где напряженность маг-
магнитного поля определяется из уравнения Максвелла rotE = — jc<;B.
Учитывая, что Е^ = 0 и <9Eq/<9</? = 0, находим
E.6)
дг dz
Учтем влияние пространственного заряда электронного потока, пе-
переходя от движущейся со скоростью электронного потока системы ко-
координат к неподвижной (лабораторной) системе. В подвижной системе
координат кулоновские поля являются чисто электрическими Ер. При
переходе к неподвижной системе координат электрические и магнитные
поля преобразуются в соответствии с преобразованиями Лоренца [9]:
К = 7 (К - [v, B'[]) , Bl = 7 (В* - [v, E'l] /с2) ,
где штрихом отмечены поля пространственного заряда Ер и Вр в по-
подвижной системе координат. Здесь также следует учесть, что продоль-
продольные отрезки при переходе из движущейся системы координат в непо-
неподвижную пересчитываются по формуле Az = jAzf.
В нашем случае составляющие поля пространственного заряда за-
запишутся в виде:
Ер = 0, Bfp = 0,
Щ = Е'р, Вр=7 (гЕ'р - zE'p) /с2, E.8)
т. е. поля пространственного заряда в двумерном релятивистском слу-
случае кроме Ер и Ер содержат азимутальную В^ и радиальную Вр
составляющие магнитного поля.
Статическую составляющую собственного магнитного поля В^0
электронного потока можно найти из закона Био-Савара-Лапласа. Для
случая трубчатого электронного пучка статическое магнитное поле
имеет только азимутальную составляющую В^°, вид которой приведен,
например, в монографии [8, стр. 92].
172 Лекция 5
Рис. 5.З. Модель электронного потока в виде «крупных частиц» (концентри-
(концентрических колец) в цилиндрической системе координат (г, г, у?). Серым цветом
выделена г-я частица j-vo слоя
Компоненты осесимметричного слабонерегулярного фокусирующе-
фокусирующего магнитостатического поля В0 = т$В® + яоВ® могут быть записаны
в виде
Полное магнитное поле, действующее на электрон, складывается
из фокусирующего поля E.9), из переменного магнитного поля зазора
резонатора E.6) и магнитного поля движущихся электронов пучка E.8).
Для нахождения тока пучка применим метод крупных частиц [12].
В предположении аксиальной симметрии системы представим элек-
электронный поток совокупностью концентрических заряженных колец (см.
рис. 5.3; на нём показано распределение крупных частиц (колец) в рас-
расчетной области), которые характеризуются в цилиндрической системе
координат составляющими скорости vz, vrj v^, координатами z, r,
а также внутренним г и внешним R радиусами. Заряд dq равномер-
равномерно распределен по объему кольца. Такое представление электронного
потока означает, что на все электроны в кольце с координатой z и со-
соответственно с внутреним и внешним радиусами г и R действует одно
и то же электромагнитное поле, усредненное по объему частицы. Тогда
все электроны, принадлежащие данной крупной частице (кольцу), дви-
движутся одинаково.
Вдоль длины пространства взаимодействия в потоке выделяют Mz
частиц (Mz G Z). Весь объем трубчатого электронного потока с вну-
внутренним гь и внешним радиусом Rb разбивается на Мг слоев (Mr G
G Z). Таким образом электронный поток моделируется всего Mz x
х Мг частицами, каждая из которых характеризуется продольным г
и радиальным j номером (г = 1, . . ., Mz, j = 1, . . ., Mr).
Моделирование и оптимизация на ЭВМ пролетных клистронов 173
Введем новые безразмерные переменные
2irz 2тгг л ш п
E.Ю)
о(*) , 1(x) , K
uj mo uj
где vo — начальная продольная скорость электронного потока.
В новых переменных величина U = v/vq, имеющая смысл относи-
относительной скорости электронов, с учетом закона сохранения E.5) и соот-
соотношения E.4) запишется как
EЛ1)
где Fx = loyo(v - Фо/2)/1/ + y*i/2, F2
Тогда с учетом выражения E.11) уравнения движения частиц E.2)
и E.3) в безразмерном виде принимают вид:
^ = -щ (?/г/73 + №/7) /wo ~Vo^ + Vo^ Br, E.12)
dO^ У ^7 ^7 dO
E.13)
Здесь введены обозначения f1 = — — lv -^ j -\——, /2 = Ро^штш?
/ 1 \ 2
/з = 1 + /3q f -т^-) . Релятивистский фактор в переменных E.10) запи-
сыватся следующим образом:
Уравнение возбуждения A.53) n-го резонатора клистрона на задан-
заданном s-виде колебаний периодическими во времени источниками в пере-
переменных E.10) записываются так:
27Г E.14)
тг (о; - ojsn) Nsn
v у о V
где Ct;sn = Ct;^n(l + j/2Qsn) и Qsn — соответственно комплексная часто-
частота и нагруженная добротность s-ro типа колебаний в TV-м резонаторе,
174 Лекция 5
jCT — плотность тока сторонних возбуждающих источников. Далее ин-
индекс «s» будем опускать.
Полагая, что все резонаторы клистрона высокодобротные, т.е.
1/Qn ^ 1 или Фп = 2 (шп — и) /ип <С 1, и используя закон сохранения
заряда для многослойной модели электронного пучка [10], получаем
уравнение возбуждения резонатора в виде
Лп — Лап + j Лгп —
Mr Mz
Qn 1 + i^nQn 2 v^ т v^
I VijE'dB, E.15)
где Ioj — ток j-го элементарного слоя, 6цj, @2ij — соответственно фазы
влета и вылета г-й крупной частицы слоя с номером j в зазоре п-го
резонатора.
Высокочастотные поля в зазоре резонаторов в безразмерных пере-
переменных E.10) запишутся в виде соотношений
2Gо-1) .,„.„,„. „.р.
/° , E-16)
2Go-l)
Здесь величина Z = Za + j Zr = —"! ° , Km — комплексная амплитуда
zujVod
ВЧ-напряжения на зазоре резонатора, Vb — ускоряющее напряжение,
d — ширина ВЧ-зазора, E°(r, z) — распределение напряженности элек-
электрического поля в зазоре резонатора.
С учетом соотношений E.16) уравнение возбуждения n-го резона-
резонатора в безразмерном виде примет вид:
dZan +jZrn _ KnQk
dO 120(d/a,
Mr M
xl^loJl^e [ и.й zn^ ли *rn
j=l 2=1
/ / ^oo
где ш = ojp/ojj ujp = W—-—о— ~~ плазменная частота электронного
у S
у
потока, Кп — волновое сопротивление резонатора.
Составляющие электрического поля крупной частицы с зарядом dq
запишем следующим образом:
^Ч , г), Е? = --^Ч Щ(*, г), E.18)
Моделирование и оптимизация на ЭВМ пролетных клистронов 175
где а — радиус проводящего экрана трубы дрейфа. Воспользовавшись
введенными переменными E.10), перепишем выражения E.18) в виде
wv _ тгсоурш2 Sj дФ _ тгсоурш2 Sj ,дФ ( .
r]oMzxe S dz r]oMzxe S дг
где распределения полей заряженной частицы E.18) представлены че-
через распределение потенциала Ф поля заряженной частицы:
4= в> = «
dz or
Здесь знак «штрих» у символа j означает принадлежность данной
величины частице-источнику.
В формуле E.19) также использованы следующие обозначения: S —
полная площадь поперечного сечения пучка, Sj — площадь сечения j-ro
слоя, Mz\ — число крупных частиц на одну электронную длину волну
Ле.
Магнитные поля, определяемые соотношениями E.6), E.8) и E.9),
в нормированных переменных выражаются следующим образом:
^, E.20)
7о dx
«о 2G0-1) s.n9 + ^cog ГдЕ* _ дЕ°
d(r/a) d(z/a)
«о 2G0-1) s.n9 + ^cog ГдЕ _ дЕ\
Vo yK \d(r/a) d(z/a)J
dx A ^
E lS's E-22)
Статическая составляющая собственного магнитного поля электронно-
электронного потока в безразмерных координатах в случае крупной частицы в виде
заряженного кольца имеет вид
Здесь уа = 2тга/Ае, Ayj = (у2 - у\-) [у\- - у\-), y±j, y2j — соответ-
соответственно внутренний и внешний нормированный радиус кольца крупной
частицы j-ro слоя в электронном потоке.
Учитывая соотношения E.19), E.20)-E.23) уравнения движения
крупной частицы с номером г из j-ro слоя в п-м резонаторе в безразмер-
безразмерных переменных E.10) окончательно запишутся в следующем виде:
(Zna cos в - Znr sin в) {E°zn/j2j - f2ijE*rn) +
176 Лекция 5
о мг mz
7o-l
х
cos
Mr M
P Slkl \ dO ^M dO rkl) Jlij 2 dxij
Mr Mz
k=l 1=1,l
'if = — - 1^L (Znacos6- Znrsin6)
E
syQ _ \ dxij
+ —о 7Г \Zka Sin в + Zbr COS в)
Система уравнений возбуждения E.17) и уравнений движения E.24)
и E.25) представляет собой полностью самосогласованную двумерную
нелинейную релятивистскую модель релятивистского многорезонатор-
ного пролетного клистрона. Эта модель описывает нелинейные и дву-
двумерные эффекты при взаимодействии электронных потоков с элек-
электромагнитными полями в многорезонаторных пролетных клистронах
в рамках сделанных упрощающих предположений, основные из кото-
которых связаны с аксиальной симметрией полей и возбуждением в резона-
резонаторах только одного вида колебаний.
Одним из основных критериев оптимизации мощных пролетных
клистронв является достижение максимального к.п.д. при заданных
параметрах пучка. Поэтому важно определить электронный к.п.д. г\е
многорезонаторного клистрона в нашей модели.
Как несложно показать, электронный к.п.д. в п-м каскаде клистрона
в безразмерных переменных E.10) может быть определен [13] либо по
Моделирование и оптимизация на ЭВМ пролетных клистронов 177
формуле
^ Mr Mz
ч«» = 7о-Г ' E-26)
либо по формуле
fft2 f [ <*КР 1±1Ф^\ Zn) * , E.27)
2^G0-1)
где (•)* означает комплексное сопряжение. Сравнение величин к.п.д.,
расчитываемых по формулам E.26) и E.27), дает критерий оценки
погрешности численного моделирования процессов в клистроне.
Уравнения одномерной релятивистской теории
многорезонаторного клистрона
Выведенные в предыдущем параграфе уравнения двумерной нели-
нелинейной релятивистской модели многорезонаторного клистрона описы-
описывают в предположении аксиальной симметрии высокочастотных и фо-
фокусирующих полей нелинейные процессы группирования релятивист-
релятивистского электронного пучка при каскадном взаимодействии с ВЧ-элек-
тромагнитными полями и полем пространственного заряда. Эта модель
позволяет также детально исследовать такие двумерные эффекты, как
расслоение, перемешивание слоев с различными радиусами, пульсации
электронного пучка. Вместе с тем, уравнения E.17), E.24) и E.25)
являются достаточно громоздкими и сложными для использования на
начальном этапе решения задачи оптимизации клистронного усилите-
усилителя. Ряд существенных нелинейных эффектов может быть описан в рам-
рамках более простой и наглядной одномерной теории. Поэтому целесооб-
целесообразно использовать одномерные модели, обеспечивающие существенно
меньшую трудоемкость расчетов, и лишь затем применять двумерную
модель для уточнения полученных результатов.
Переход к одномерной модели формально можно осуществить, по-
положив
ж = °- E-28)
Тогда система уравнений E.24), E.25) и E.17) будет описывать модель
электронного потока с расслоением. Такая модель, предполагающая
наличие фокусирующего магнитного поля с бесконечно большой на-
напряженностью, позволяет учесть различие в группировании электронов
по сечению. В этом случае электронный пучок в поперечном сечении
делится на Мг слоев, радиус которых в процессе взаимодействия не
изменяется, а в продольном направлении динамика слоев различна.
Модель с расслоением позволяет исследовать группировку в случае,
178 Лекция 5
когда поле в ВЧ-зазоре резонатора неоднородно по радиусу. Особенно
существенно это для резонаторов с бессеточными зазорами, которые
применяются в мощных клистронах г). Высокочастотные поля таких
зазоров «провисают» к центральной части пучка [5]. В результате возни-
возникающее различие в группировании отдельных слоев приводит к увели-
увеличению разброса скоростей электронов и уменьшению величины первой
гармоники сгруппированного тока ii, что уменьшает к.п.д. клистрона.
На основе исследования моделей с расслоением были разработаны спе-
специальные меры по компенсации этих эффектов [5] 2).
Простейшей одномерной моделью является однослойная модель,
в которой предполагается, что Мг = 1. При этом предположении и усло-
условии E.28) система уравнений движения E.24), E.25) и возбуждения
E.17) переходит в следующую:
^ Xi _ 2G0 - 1) п,0 по /7 je\ 1 ™ \^ т?Р (к 9Ch
-W-^!eTE-Re{Zke } + Л?Л'г' E-29)
n KnQk l + j<j>nQn w2/3o(lo - 1) v^ dx± Fo -jo
2
- -Е" е
dd 120(d/aJ 1 + (фпЯпJ Mz ^ dd zn
-1/2
Для заряженной частицы в форме кольца, усредняя поле по ради-
радиусу на интервале [г{, R{], для напряженности поля пространственного
заряда можно получить выражение [8]
8 = 1
Здесь
Bs = T1 [V2Ji(i
(все обозначения совпадают с обозначениями в предыдущем парагра-
фе).
В следующем параграфе рассмотрены результаты оптимизации
восьмирезонаторного релятивистского клистрона с помощью сформу-
сформулированной одномерной однослойной модели.
г) Это связано с тем, что любые другие резонаторы не выдерживают боль-
больших потоков мощности, заключенных в мощном электронном пучке.
2) Модели с расслоением электронного потока успешно применяются для
исследования не только клистронов, но и других приборов электроники СВЧ,
таких как ЛБВ [14, 8], виркаторы [15] и т. д.
Моделирование и оптимизация на ЭВМ пролетных клистронов
179
Моделирование и оптимизация многорезонаторных
релятивистских клистронов
Рассмотрим результаты оптимизации с помощью одномерной моде-
модели E.29)—E.31) восьмирезонаторного слаборелятивистского клистрона
при следующих заданных величинах d/a = 2,2, уа = 2тга/Хе = 0,616,
Уо = 2тга/Хе = 0,36, Vb = 6кВ (/?о = 0,152) и различных значениях
плотности пространственного заряда w — ир/и.
На рис. 5.4а приведены зависимости максимального к.п.д. кли-
клистронов от параметра пространственного заряда w при различном
числе резонаторов. Как следует из рисунка, в восьмирезонаторной
схеме клистрона (сплошная ли-
линия) высокое значение к.п.д. до-
достигается при малых значениях w
(г) = 0,903). С увеличением плот-
плотности тока величина к.п.д. мо-
монотонно понижатся. Для выясне-
выяснения причин этого проанализиру-
проанализируем зависимости скоростной моду-
модуляции Vi и фазовой группиров-
группировки Х{ на входе выходного каска-
каскада для случаев w — 0,186 (кри-
(кривая 1 на рис. 5.5) и w = 0,286
(кривая 2 на рис. 5.5). Из срав-
сравнения зависимостей видно, что
с увеличением величины w груп-
группировка в оптимальном режиме
ухудшается, а требуемая для под-
поддержания плотного электронно-
электронного сгустка скоростная модуляция
возрастает. Это требует повыше-
повышения ВЧ-напряжения на зазорах
резонаторов промежуточных кас-
каскадов, одновременно с этим увели-
увеличением необходимо сохранять оп-
оптимальным сдвиг фаз ф между то-
током и напряжением на зазорах.
Следует обратить внимание на
распределение оптимальных рас-
расстроек резонаторов промежуточ-
промежуточ0,0 0,5 1,0 1,5 2,0 2,5 3,0 d/a
Рис. 5.4. Зависимость максимально-
максимального к.п.д. от параметра простран-
пространственного заряда (а)(сплошная ли-
линия соответствует восьмирезонатор-
ному клистрону, штриховая — ше-
стирезонаторному клистрону) и от
ширины ВЧ-зазора выходного ре-
резонатора восьмирезонаторного кли-
клистрона (б) (построено по данным,
приведенным в [8])
ных каскадов клистрона. В по-
последних резонаторах расстройки в оптимальном по к.п.д. режиме моно-
монотонно понижаются (т. е. функция расстройки ф(п) является убывающей
с увеличением номера каскада п), что обеспечивает наилучшее распре-
180
Лекция 5
Щ
1,2
1,0
0,8
0,6
Xi
-5,0
13
21
29 i
13
21
29
деление ВЧ-напряжений в зазорах и, в итоге, наилучшую группировку
электронного потока.
Заметим также, что к.п.д. восьмирезонаторного клистрона суще-
существенно выше, чем к.п.д. шестирезонаторного клистрона (штриховая
линия на рис. 5.4а). Это связано
с тем, что с увеличением числа ре-
резонаторов удается повысить каче-
качество группирования и модуляции
по сравнению с шестирезонаторной
схемой.
На рис. 5А6 приведена зави-
зависимость максимального к.п.д. от
ширины d/a ВЧ-зазора выходного
резонатора при ш = 0,1 и шири-
шириной di+7/a = 2,2 ВЧ-зазоров ре-
резонаторов промежуточных каска-
каскадов. Из рисунка видно, что с уве-
увеличением ширины зазора до вели-
величины d/a «2,2 несколько снижа-
снижается к.п.д. клистронного усилите-
усилителя (примерно на 2%). При даль-
дальнейшем увеличении ширины зазора
(при d/a > 3,2) энергообмен меж-
между пучком и ВЧ-полем приобретает
знакопеременный характер (элек-
(электронный сгусток входит в зазор
в конце ускоряющей фазы). Догруппировка электронного сгустка в вы-
выходном сгустке ухудшается, в результате чего г]та^ заметно понижается.
Анализ физических процессов при увеличении ширины зазора показы-
показывает, что при этом наблюдаются следующие явления, сопровождающие
отбор энергии от электронного сгустка.
1. Непосредственно в области ВЧ-зазора (области энергообмена)
при всех величинах ширины зазора d/a наблюдается догруппировка
электронного потока и одновременное выравнивание скоростей, однако
при больших значениях d/a они выражены слабее из-за большого угла
пролета.
2. На выходе ВЧ-зазора сильно заторможенные электроны вновь
ускоряются, что имеет место в зазоре любой ширины и, соответственно,
несколько снижается электронный к.п.д.
3. С увеличением ширины зазора выходного резонатора имеет место
рост оптимальной амплитуды ВЧ-напряжения в нем. Это связано с тем,
что с ростом угла пролета электронов через зазор эффективное на-
напряжение, действующее на них, понижается, что и требует повышения
амплитуды ВЧ-напряжения для сохранения эффективности энергооб-
энергообмена.
Рис. 5.5. Зависимости скоростной
модуляции Vi и фазовой группиров-
группировки Xi для восьмирезонаторного оп-
оптимизированного по к.п.д. клистро-
клистрона при w = 0,186 A) и w = 0,286
B) (из работы [8])
Моделирование и оптимизация на ЭВМ пролетных клистронов 181
Рассмотрим теперь, что изменяется в физике взаимодействия элек-
электронного потока с ВЧ-полями в клистронном усилителе в случае силь-
сильного релятивизма. В работах [16,8] рассматривается оптимизированный
по к.п.д. восьмирезонаторный релятивистский клистрон. При модели-
моделировании при ряде заданных параметров (основные из которых ток пуч-
пучка, ускоряющее напряжение, геометрические размеры) определялись
оптимальные параметры расстройки фп, нагруженные добротности Qn
и амплитуды ВЧ-напряжения на зазоре каждого из восьми резонаторов,
а также оптимальные длины труб дрейфа 1п между резонаторами , при
которых достигается максимальный к.п.д. релятивистского клистрон-
ного усилителя.
Для клистрона с током пучка /о = 10 А, рабочей длиной волны Л =
= 12 см, радиусом трубы дрейфа а = 0,8 см, d/a = 2, Ki+7 = 100 Ом,
Kg = 150 Ом и ускоряющим напряжением Vb = 500 кВ (/?о = 0,863)
максимальный к.п.д. составил rje = 0,894 при коэффициенте усиления
С = 61дБ.
Для клистрона с ускоряющим напряжением Vb = 1000 кВ (/?о =
= 0,941) были выбраны параметры /0 = 50А, Л = 12 см, а = 1,0 см,
d/a = 2, Кг+7 = 100 Ом, К8 = 150 Ом. При них rje = 0,864, G = 59,5 дБ.
Оптимизация клистрона с теми же параметрами и с ускоряющим на-
напряжением Vo = 1500 кВ (/?о = 0,967) предсказывает к.п.д. г]е = 0,836
и коэффициент усиления G = 63,4 дБ.
Анализ скоростной модуляции показывает, что она очень мала по
сравнению со слаборелятивистским случаем, который рассматривался
выше. Так в последней трубе дрейфа максимальное отклонение ско-
скорости электронов от среднего значения не превышает 4%, в то время
как в клистроне с ускоряющим напряжением Vo = 50 кВ максимальное
отклонение скорости электронов от средней достигает 18 % при близ-
близких амплитудах ВЧ-напряжения на зазоре предпоследнего резонатора
в сильнорелятивистском и слаборелятивистском случаях. Малую глу-
глубину скоростной модуляции приходится компенсировать существенным
увеличением длин труб дрейфа релятивистских клистронов.
В релятивистских клистронах изменяется и характер энергообмена
между электронным сгустком и ВЧ-полем в выходном резонаторе.
Энергоотбор происходит в основном не за счет изменения скорости
электронов, а за счет изменения их массы при торможении в резонаторе.
Если в слаборелятивистском клистроне минимальные скорости элек-
электронов находятся в пределах 0,1 -г- 0,3 от средней, то в релятивистском
клистроне их значение лежит в пределах 0,5 -г- 0,8.
При величине ширины зазора выходного резонатора d/a = 2 вели-
величина напряженности ВЧ-поля в выходном зазоре в случае Vb = 500 кВ
имеет величину 312 кВ/см, в случае Vb = 1000 кВ — 500 кВ/см, в случае
Vb = 1500 кВ — 750кВ/см. Эти значения приближаются к пробив-
пробивным напряжениям для вакуума [17], которые составляют величины
^пробоя = 200 -г- 1000 кВ/см и зависят от материала, качества обработки
182
Лекция 5
0,2
0,0
-0,2
10
20
30
0,2
0,0
-о;
h
.5
§%§
,7
Ш
/71 ^йп
Ц
0
10
20
30
Рис. 5.6. Зависимости поперечных скоростей от продольной координаты (че-
(четыре последних каскада) для центров масс крупных частиц в слабореляти-
слаборелятивистском клистроне для внешнего (а) и внутреннего (б) слоев. Вертикальны-
Вертикальными линиями отмечены центры зазоров резонаторов 5-8 (из работы [13])
и формы поверхности и т. д. Поэтому важным представляется оптими-
оптимизация схем клистронов с увеличенной шириной ВЧ-зазоров последних
каскадов. Другим способом решения данной проблемы является приме-
применение распределенного отбирателя энергии типа отрезка замедляющей
системы (схема твистрона) [18]. Такие отбиратели энергии достаточно
высокоэффективны, поэтому можно ожидать незначительное снижение
к.п.д. усилителя в этом случае по сравнению с однозазорным выходным
резонатором.
Двумерные эффекты в многорезонаторных
клистронных усилителях
Рассмотрим, следуя работе [13], принципиально двумерные эффек-
эффекты в слаборелятивистском клистроне со следующими основными пара-
параметрами: d/a = 2,2, уа = 0,616, Ki+s = 76 0м, Vo = 6кВ (/30 = 0,152),
w = 0,1. Электронный к.п.д., рассчитанный в рамках одномерной мо-
модели, равен г]е = 0,89.
Использование двумерной модели E.17), E.24) и E.25) с числом
частиц Mz = 16 на одну электронную длину волны Ае, числом слоев
в поперечном направлении Мг = 3 и параметром фокусирующего маг-
магнитного поля Ф = 1 приводит к уменьшению к.п.д. до значения rje =
= 0,83, т.е. учет двумерных эффектов понижает расчетный к.п.д. на
6%.
На рис. 5.6 представлены зависимости поперечных скоростей vyij
от продольной координаты х центров масс крупных частиц, принад-
принадлежащих слоям с j = 1 (внутренний слой; рис. б) и j = 3 (внешний
Моделирование и оптимизация на ЭВМ пролетных клистронов
,5 ,6 ,7 ,8
183
Рис. 5.7. Траектории центров масс крупных частиц в координатах (ж, г/)
в слаборелятивистском клистроне всех трех слоев. Вертикальными линиями
отмечены центры зазоров резонаторов 5-8, горизонтальная штриховая линия
соответствует внутренней границе трубы дрейфа с радиусом уа = 0,616 (из
работы [13])
слой; рис. а). Как видно из рисунка, до седьмого резонатора пульсации
скорости имеют практически статический характер, причем амплитуда
этих пульсаций существенно больше во внутренних слоях электронного
потока. Модуляция в седьмом резонаторе приводит к появлению дина-
динамических пульсаций (поперечного колебательного движения основной
массы электронов, вызванного воздействием ВЧ-полей зазора резона-
резонатора и пространственного заряда), амплитуда которых увеличивается,
а период уменьшается. Из рис. 5.7, на котором представлены траекто-
траектории центров масс крупных частиц, видно, что имеет место частичное
перемешивание всех слоев. После седьмого резонатора за счет роста
пульсаций пучок расширяется. Расширение пучка можно оценить, ис-
используя интеграл движения граничного электрона для случая аксиаль-
аксиальной симметрии [10]
E.32)
Гд — v\ = const,
где го — радиус ведущего центра электронной орбиты, гс — ради-
радиус циклотронного вращения, определяемый поперечной скоростью v±
электронов (гс = v±/uc). Таким образом, как следует из соотношения
E.32), за счет действия радиального электрического и магнитного полей
резонатора возрастает не только радиус вращения гс, но и радиус веду-
ведущего центра го, т.е. пучок расширяется быстрее, чем растет величина
Г с-
Рис. 5.7 позволяет также проанализировать процесс токооседания
на стенки трубы дрейфа. Токооседание имеет место в области зазора
выходного резонатора, причем на стенку трубы дрейфа выходят элек-
электроны как внешних, так и средних слоев. Всего оседает около 12 % элек-
электронов. Токооседание может быть предотвращено за счет увеличения
радиуса выходной трубы дрейфа при том же значении фокусирующего
магнитного поля Ф, при этом к.п.д. прибора уменьшается всего на 3 %.
184 Лекция 5
Моделирование физических процессов в клистронном усилителе
в случае слабого релятивизма с помощью нелинейной двумерной модели
с тремя слоями (Мг = 3) выявило также следующие эффекты.
1. Из-за лучшей модуляции наиболее быстро вдоль пространства
дрейфа группировка электронов происходит во внешних слоях, однако,
после прохождения седьмого резонатора группировка во всех слоях
выравнивается.
2. Если рассчитать электронный к.п.д. отдельно для каждого слоя
77ej, то наибольший к.п.д. соответствует внешнему слою rjjMr = 0,89.
3. Наблюдается энергообмен между слоями через электрическое
поле пространственного заряда. Внешний слой несколько ускоряется за
счет торможения внутреннего. Данный эффект невелик — к.п.д. такого
энергообмена мал и составляет 1 Ч- 2 % (очевидно, что средний по слоям
к.п.д. такого энергообмена равен нулю).
Рассмотрим теперь, как влияет переход к сильнорелятивистским
электронным пучкам на двумерные эффекты. В работе [13] исследо-
исследовался релятивистский двенадцатирезонаторный клистрон с ускоряю-
ускоряющим напряжением Vo = 1000 кВ, током /q = 250 А и фокусирующим
магнитным полем Ф = 8,5. Резонаторы, в которых отбирается энергия
от пучка (нагруженные резонаторы), располагались в восьмом, десятом
и двеннадцатом каскадах. В промежуточных девятом и одиннадцатом
каскадах находились холостые резонаторы с достаточно большой рас-
расстройкой, которые предназначались для осуществления промежуточ-
промежуточной догруппировки в потоке и выравнивания скоростей электронов, что
важно для повышения эффективности энергообмена в многорезонатор-
ном выходном каскаде.
Как и в предыдущем случае число слоев в электронном потоке было
выбрано Мг = 3 и число частиц в продольном направлении на длине Ае
равно Mz = 16.
На рис. 5.8 приведены траектории центров масс крупных частиц для
всех трех слоев. Видно, что при большом фокусирующем магнитном
поле (Ф = 8,5) токооседание отсутствует. Статические пульсации пучка
малы, радиальные составляющие скорости электронов, обуславливаю-
обуславливающие динамические пульсации, появляются под воздействием попереч-
поперечных электрических и магнитных полей ВЧ-зазора шестого и особен-
особенно седьмого резонаторов. Динамические пульсации резко возрастают
после прохождения девятого и одиннадцатого холостого резонатора,
где поперечные скорости внешнего слоя достигают величин порядка
@,4 Ч- 0,6)^о. Вследствие этого пучок имеет значительные пульсации
в области выходных резонаторов. Сильная поперечная модуляция элек-
электронного потока связана с тем, что основная энергия электронов связана
с продольной скоростью vz, и для их торможения в зазорах выход-
выходных резонаторов необходимо поле высокой напряженности. Радиальные
Моделирование и оптимизация на ЭВМ пролетных клистронов
185
У
Уа
0,6
0,2
-
¦ i
7 1
L
1 ^ 1А!МА||Ц|№|Ам liiifU№№iii~tJi Hiii ш\
PI ШШш ШШ ill lillli Mil НИШ iilflii I4"*"" " *** ftflMlni IIT i Vi
1
? 9 10 Л 12
I ILL
I III
I 'ill
0
20
40
60
80
100 x
Рис. 5.8. Траектории центров масс заряженных колец для трех слоев с раз-
различными радиусами в шести последних каскадах в релятивистском двена-
двенадцати резонаторном клистроне. Вертикальными линиями отмечены центры
зазоров резонаторов 7-12, горизонтальная штриховая линия соответствует
внутренней границе трубы дрейфа с радиусом уа = 0,836 (из работы [13])
компоненты этого поля и обеспечивают высокий уровень ускорения
«поперечно-нерелятивистского» электрона.
Влияние двумерных эффектов на к.п.д. в данной схеме релятивист-
релятивистского клистрона мало. Так, для таких же параметров результаты расче-
расчета по одномерной однослойной модели дают значение к.п.д. г\е — 0,795,
а двумерная модель предсказывает величину г\е = 0,765. Это связано,
в первую очередь, с высоким значением фокусирующего магнитного по-
поля и спецификой отбора энергии у электронов в релятивистском случае.
Высокие к.п.д. достигаются при относительно небольшом изменении
средней скорости электронного потока, и поэтому преобразование про-
продольной скорости в поперечную не оказывает существенного влияния
на общем энергообмене.
В конце обсуждения физических процессов в многорезонаторных
клистронах заметим, что влияние пространственного заряда в сверх-
сверхмощных релятивистских клистронах на энергообмен между отдельным
электроном и электронным сгустком существенно выше, чем в нере-
нерелятивистских и слаборелятивистских клистронах. Это связано, во-
первых, с тем, что значительно возрастает погонный заряд пучка (ток
пучка /о быстро растет с увеличением ускоряющего напряжения Vb,
а скорость vq практически не меняется в случае сильного релятивиз-
релятивизма), и, во-вторых, релятивистский электрон более инерционен из-за
большой массы т = 7шо5 поэтому он большее время находится под
действием тормозящего или ускоряющего поля электронного сгустка,
находясь вблизи него.
186
Лекция 5
Многолучевые клистроны
Как уже обсуждалось в начале лекции, пролетные клистроны при-
применяются в радиофизике и технике, в первую очередь, как эффектив-
эффективные мощные усилители сантиметрового и дециметрового диапазона.
Однако клистроны, использующие в качестве активной среды один
электронный пучок, имеют для некоторых специальных приложений
целый ряд принципиальных недостатков и, в частности, неоптимальное
соотношение «размер/масса» прибора, высокое ускоряющее напряже-
напряжение и сравнительно узкую рабочую полосу частот. Эти недостатки
появляются ввиду принципиальных физических ограничений, прису-
присущих данным приборам. Одним из возможных способов преодоления их
является использование многолучевых клистронов.
Идея использования нескольких электронных потоков в пролетном
клистроне появляется почти сразу же после изобретения многорезона-
торного клистрона. В 60-х годах XX столетия были проведены первые
экспериментальные исследования многолучевых клистронов. Рассмат-
Рассматривались два основных типа приборов — многолучевой клистрон, ис-
использующий высшие рабочие моды резонаторов [20] и многолучевой
клистрон с бегущей волной [21]. Оба усилителя позволяют существенно
снизить рабочее напряжение. Однако если необходимо расширить по-
полосу усиливаемых частот А///, то клистронный усилитель с исполь-
использованием основной рабочей моды резонаторов более предпочтителен по
сравнению с однолучевым клистроном, а клистрон с бегущей волной
более эффективен для получения больших выходных мощностей (до
нескольких МВт).
Рис. 5.9. Схема многолучевого клистрона: 1 — электронная пушка, формиру-
формирующая многолучевой пучок; 2, 5 — проводящие экраны; 3 — резонаторы; 4 —
каналы дрейфа, через которые проходят отдельные пучки многолучевого
электронного потока; 6 — коллектор
На рис. 5.9 приведена схема многорезонаторного многолучевого
клистронного усилителя, работающего на основной моде резонаторов.
Особенностью конструкции прибора является использование несколько
соосных пролетных каналов 4 для электронных пучков, расположенных
в одной металлической многоканальной трубе дрейфа 5. В каждом
пролетном канале распространяется только один электронный пучок,
Моделирование и оптимизация на ЭВМ пролетных клистронов 187
причем между соседними пучками в пространстве дрейфа отсутству-
отсутствует какая-либо связь. Вместе с тем, они все пронизывают одни и те
же объемные резонаторы 3. Электронные пучки с небольшими перве-
ансами и токами легко фокусируются и удерживаются сравнительно
слабым внешним магнитным полем, в них происходит эффективное
группирование по плотности (за счет небольшой силы кулоновского
рассталкивания в пучке с небольшим током), они более эффективно
взаимодействуют, отдавая энергию ВЧ-полю выходного резонатора.
Выходная мощность многолучевого клистрона оказывается равной сум-
сумме мощностей, отбираемых от каждого в отдельности слаботочного
электронного пучка.
Ускоряющее напряжение в такой системе может быть существенно
понижено, что позволяет уменьшить размеры и вес прибора, а также
его источников питания. Кроме того, ширина полосы усиления может
быть увеличена за счет увеличения полного первеанса многолучевого
электронного пучка.
Многолучевой клистрон включает также в свою конструкцию мно-
многолучевую электронную пушку 1, фокусирующую магнитную систему
(не показана на рисунке) и коллектор 7.
В случае эквивалентных выходных мощностей многолучевого кли-
клистрона и обычного клистрона (PyvE = Pi), равных первеансах пучков
(Vn/N = T^part = V\) и равных нормированных радиусах каналов для
отдельных пучков, ширина полосы усиливаемых частот многолучевого
клистрона в 2 Ч- 2,5 раз больше, чем для клистрона с одним пучком [19].
Это связано с тем, что рабочая полоса частот может быть увеличена
за счет снижения усиления при расстройке резонаторов и снижения их
нагруженной добротности г). При увеличении нагрузки выходного ре-
резонатора (снижения его нагруженной добротности) полоса становится
шире, однако, при этом падает амплитуда ВЧ колебаний, что приводит
к снижению к.п.д. усилителя. С увеличением числа пучков N харак-
характеристическое сопротивление выходного резонатора увеличивается (за
счет увеличения электронной нагрузки в связи с тем, что многолучевой
электронный пучок вносит меньшую реактивную проводимость (ем-
(емкость) в полную проводимость резонатора) и, соответственно, умень-
уменьшается его нагруженная добротность, и тем самым увеличивается по-
полоса частот А/// при сохранении высоких значений к.п.д. клистрона.
Рабочее напряжение многолучевого клистрона уменьшается по срав-
сравнению с напряжением соответствующего однолучевого клистрона как
Vbi/Vow ~ iV2/5. Если величина суммарной площади поперечного сече-
сечения многолучевого электронного пучка равна площади сечения пучка
однолучевого клистрона, то ширина полосы многолучевого клистрона
расширяется более, чем в 6 -г 9 раз. Однако в этом случае ток много-
х) Заметим, что полоса усиления в многорезонаторном клистроне за счет
высокого коэффициента усиления в первую очередь определяется парамет-
параметрами выходного каскада.
188
Лекция 5
M, кг
D, мм
о
6
?
4
2
_l
! /
T ^
!
!
10JCM
! x
I ,
7 !/
П
L L_ J
0,05 0,5 5,0 30 100
Рис. 5.10. a — параметры многолучевого клистрона как функции числа пуч-
пучков N, рабочая длина волны оптимизируемого клистрона Л = 3 см, выходная
мощность 500 Вт, плотность тока с катода 15 А/см2; б— ширина усиливаемых
частот как функция выходной мощности многолучевого клистрона для раз-
различных рабочих длин волн Л, штриховая линия соответствует однолучевому
клистрону (из работы [19])
лучевого пучка должен быть увеличен (для увеличения первеанса) как
Son/Joi ~ ^2/5-
Рассмотрим некоторые результаты оптимизации многолучевых кли-
клистронов [19]. На рис. б.Юапоказаны зависимости ширины полосы А///,
ускоряющего напряжения Vb, ширины пролетного канала D и массы
фокусирующей магнитной системы М от числа лучей N многолучевого
пучка. Видно, что с увеличением числа пучков резко уменьшается
величина рабочего напряжения клистрона, одновренно имеет место
рост ширины полосы усиливаемого сигнала. На рис. 5.10? демонстри-
демонстрируется зависимость ширины полосы А/// многолучевого клистрона
как функция выходной мощности для различных рабочих длин волн
при плотности тока пучка с катода jo = 15 А/см2. В 3-сантиметро-
3-сантиметровом диапазоне многолучевой клистрон имеет ширину полосы порядка
2 Ч- 3% процентов при выходной мощности от сотен Вт до нескольких
десятков кВт. В дециметровом диапазоне ширина полосы расширяется
до величины А/// ~ 8 %. Увеличение первеанса пучка (плотности тока
пучка до j0N = 45 А/см2) приводит к расширению полосы до 15 % при
выходной мощности порядка 30 -г- 80 кВт (на рисунке не показано).
Размеры и масса усилителя на основе однолучевого клистрона во
многом определяются его магнитной фокусирующей системой. Как
правило, вес магнита в 4 Ч- 30 раз превосходит вес самого клистрона.
Оптимизация параметров многолучевого клистрона и его магнитной
фокусирующей системы позволила реально уменьшить вес прибора
примерно в 10 раз по сравнению с однолучевым аналогом. Это обеспечи-
обеспечивается главным образом за счет существенного уменьшения мощности
Моделирование и оптимизация на ЭВМ пролетных клистронов 189
источника питания прибора и суммарной длины дрейфового канала
электронных пучков [22].
Наряду с привлекательными свойствами многолучевых клистронов
(широкая полоса усиливаемых частот, сниженное рабочее напряжение,
небольшие масса и размеры), существуют и определенные технологиче-
технологические проблемы создания приборов этого класса. Наиболее значимые из
них связаны, во-первых, со сложностями получения мощных электрон-
электронных пучков с хорошей фокусировкой, а, увеличение числа пучков N
приводит к возникновению большого числа паразитных видов колеба-
колебаний.
Многолучевые клистроны активно разрабатываются и как источ-
источники коротких импульсов сверхмощного СВЧ-излучения, например,
для нужд ускорительной техники. Так для электрон-позитронного ли-
линейного коллайдера Станфордского центра линейных ускорителей раз-
разработан релятивистский многорезонаторный многолучевой клистрон
с выходной мощностью 2 ГВт [23]. В клистроне используется 10 пучков,
имеющих первеанс 1.4. Многолучевой электронный поток проходит
через четыре общих резонатора, и каждый отдельный пучок — через
10 дополнительных резонаторов для повышения полного к.п.д. прибора.
Некоторые характеристики данного прибора приведены в таблице 5.1.
Прибор может работать как в режиме усиления, так и в режиме генера-
генерации. В последнем случае в усилитель вводится внешняя обратная связь,
реализуемая за счет ответвления части мощности из второго резонатора
клистрона во входной резонатор.
Т а б л и ц а 5.1
Характеристики сверхмощного многолучевого клистрона [23]
Выходная мощность 2 ГВт
Длительность импульса СВЧ-излучения 1 мкс
К.п.д. 50%
Коэффициент усиления 30 дБ
Рабочая частота 1.5 ГГц
Рабочее напряжение 600 кВ
Ток многолучевого пучка 6.7 кА
Размеры 150 х 45 см
Вес клистрона без магнитной системы 81 кг
Список литературы
1. Гайдук В.И., Палатов К.И., Петров Д.М. Физические основы
электроники СВЧ. — М: Сов. радио, 1971.
2. Проектирование радиопередающих устройств / Под ред.
В. В. Шахгильдяна. — М.: Связь. 1976.
3. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. — М.:
Физматгиз. 1959.
190 Лекция 5
4. Шевчик В.П. Основы электроники сверхвысоких частот. — М.:
Сов. радио, 1959.
5. Канавец В.И., Лопухин В.М., Сандалов А.П. Нелинейные процес-
процессы в клистронах и оптимизация их параметров // Лекции по элек-
электронике СВЧ C-я зимняя школа-семинар инженеров), книга VII.
Саратов: Изд-во Сарат. ун-та, 1974.
6. Карнаух А.И., Карнаух В.А., Петров Д.М. Применение ЭВМ для
расчета многорезонаторного усилительного клистрона с сильной
магнитной фокусировкой (оптимизация в полосе частот) // Элек-
Электрон, техника. Сер. 1. Электроника СВЧ. 1972. No 6. С. 36.
7. Бороденко В.Г., Закурдлев А.Д., Малькова Н.Я., Победоносцев
А. С. Опыт проектирования с помощью ЭЦВМ усилительного кли-
клистрона сантиметрового диапазона // Электрон, техника. Сер. 1.
Электрника СВЧ. 1971. No 8. С. 18.
8. Кураев А.А., Байбурин В.В., Ильин Е.М. Математические модели
и методы оптимального проектирования СВЧ приборов. — Мн.:
Наука и техника, 1990.
9. Ландау Л.Д., Лифшиц Е.М. Теория поля. — М.: Наука, 1967.
10. Кураев А. А. Теория и оптимизация электронных приборов СВЧ. —
Мн.: Наука и техника, 1979.
11. Ковалев И.С, Кураев А.А., Колосов СВ. Законы сохранения в
приложении к теории и расчету электронных приборов // Доклады
АН БССР. 1973. Т. 17, № 7. С. 621.
12. Hockney R. W., Eastwood J. W. Computer simulation using particles. —
NY.: McGraw-Hill, 1981.
13. Аксенчик А.В., Кураев А.А. Двумерные эффекты в оптимизиро-
оптимизированных по КПД многорезонаторных клистронах // Радиотехника
и электроника. 1988. Т. 33, № 6. С. 1240.
14. Вайнштейн Л.А., Солнцев В.А. Лекции по сверхвысокочастотной
электронике. — М.: Сов. радио, 1973.
15. Anftnogentov V.G., Hramov A.E. Oscillation Conditions of the
Vircator-Klystron with External Delayed Feedback: A Computer
Simulation // J.Communication Technology and Electronics. 2001.
V.46, №5. P.546.
16. Аксенчик А.В., Колосов СВ., Кураев А.А., Шестакович В.П.
Результаты оптимизации КПД многорезонаторных клистронов //
Радиотехника и электроника. 1982. Т. 27, № 12. С. 2526.
17. Кухаркин Е. С, Сестрорецкий Б.В. Электрическая прочность вол-
новодных устройств. — М: Высшая школа, 1963.
18. Ковалев П.Ф., Кольчугин Б.Д., Кротова З.Н. Ультрарелятивист-
Ультрарелятивистский твистрон // Радиотехника и электроника. 1975. Т. 20, № 12.
С. 2636.
Моделирование и оптимизация на ЭВМ пролетных клистронов 191
19. Gelvich E.A., Borisov L.M., Zhary Y.V., Zakurdayev A.D.,
Pobedonostsev A.S., Poognin V.I. The new generation of high-power
multiple-beam klystrons // IEEE Trans, on Microwave Theory and
Techniques. 1993. V. 41, № 1. P. 15.
20. Boyd M.R., Dehn R.A., Rickey J.S., Mihran T.G. The multiple-beam
klystron // IRE Trans. Electron Dev. 1962. V. ED-9, №3. P. 247.
21. Pohl W.J. The design and demonstration of wide-band multiple-beam
travelling-wave klystron // IEEE Trans. Electron Dev. 1965. V. ED-12,
№6. P. 351.
22. Королев СВ. О возможности уменьшения веса и размеров про-
пролетного клистрона // Электронная техника, серия I: электрони-
электроника СВЧ. 1968. Вып. 9. С. 176.
23. Caryotakis G., Jonrewaard E., Phillips R., Scheitrum G., Tantawi S.,
Luhmann N.C. A 2-gigawatt, 1-microsecunde microwave source // In:
the Proc. of 11th Int. Conf. on High Power Particle Beams. Prague,
Czech Republic. June 10-14, 1996. V. 1. P. 406.
Лекция 6
ИНДУЦИРОВАННОЕ И СПОНТАННОЕ
ИЗЛУЧЕНИЕ В РЕЗОНАНСНЫХ
АВТОГЕНЕРАТОРАХ
ВЫНУЖДЕННОЕ ИЗЛУЧЕНИЕ (индуцирован-
(индуцированное излучение, стимулированное излучение), ис-
испускание эл.-магн. излучения квантовыми систе-
системами под действием внешнего (вынуждающего)
излучения; при В.И. частота, фаза, характер по-
поляризации и направление распространения ис-
испущенной эл.-магн. волны полностью совпада-
совпадают с соответствующими характеристиками внеш.
волны. В.И. принципиально отличается от спон-
спонтанного излучения, происходящего без внешнего
воздействия. Существование В.И. было постули-
постулировано А. Эйнштейном в 1916 при теоретическом
анализе процессов теплового излучения...
Электроника: Энциклопедический
словарь. М.: Сов. энциклопедия, 1991.
с. 72.
Индуцированное излучение в автогенераторах типа О. Спонтанное
излучение электрона при произвольном движении через резонатор.
Связь между индуцированным и спонтанным излучением электрона
в резонансных автогенераторах. Сравнение классического и квантово-
квантового подхода.
В квантовой электродинамике существуют простые соотношения,
связывающие спонтанное и индуцированное излучение связанных элек-
электронов, имеющих дискретный энергетический спектр. В данной лекции
рассмотрим соотношения, связывающие спонтанное и индуцированное
излучение свободных электронов (сплошной спектр излучения), проле-
пролетающих через объемный резонатор, имеющий дискретный энергетиче-
энергетический спектр. Будем следовать работе [1].
Излучение в резонансных автогенераторах 193
Индуцированное излучение в автогенераторах типа О
Рассмотрим взаимодействие прямолинейного электронного пучка
с электрическим полем собственного колебания в резонаторе. Поле
зададим в виде
E = Re{AeEee-^w*}. F.1)
Будем считать, что электроны движутся вдоль оси х. Ограничиваясь
приближением слабых сигналов, введем переменную плотность тока
следующим образом:
U = Re {ij(v±)J(x)e-^t} , Jv(rx)drx = 1, F.2)
где ф (rj_) — функция распределения плотности тока по поперечному се-
сечению пучка, J{x) — комплексная амплитуда тока в данном сечении х.
Далее введем
?.(х) = j Е.,хф* dr±, i=j№(rx)|2drx, F-3)
где ?8(х) — эффективное поле резонатора, S — эффективная площадь
сечения электронного потока.
Уравнение движения электрона в переменных Эйлера может быть
записано как (см. формулу C.11))
dv ( д д\^ ( д .
Поле пространственного заряда можно найти из уравнения Пуассона
=
дх so
Из уравнения непрерывности и уравнения для конвекционного тока (см.
уравнение C.3))
-^ = jwp, jx = Pov + pv F.6)
можно найти величину переменной плотности пространственного заря-
заряда:
Тогда уравнение F.5) перепишется в виде
дЕх,пз _ 1 djx
F-7)
F.8)
дх jooeo дх
откуда получаем выражение для поля пространственнного заряда:
Ех,пз = ^—3х. F-9)
JM?o
7 Д. И. Трубецков, А. Е. Храмов
194 Лекция 6
Перепишем уравнение для конвекционного тока F.6) так:
(ело)
Выражая из последней формулы v и подставляя в полученное выраже-
выражение F.4), находим
J k^ FЛ1)
Учитывая, что ujp = ^е2п/те^ — плазменная частота для бесконечно
широкого пучка (п — постоянная составляющая концентрации электро-
электронов в пучке), и используя формулы F.1)-F.3), получим
= -j'w^P ASS.,X. F.12)
Умножим последнее уравнение на \ф*\ и проинтегрируем по dr±, в итоге
для 3{х) получим дифференциальное уравнение
+ ША J(x) = -jw^- AsJs{x). F.13)
Решение уравнения F.13) можно найти воспользовавшись пред-
представлением решения через интеграл Дюамеля. Вспомним некоторые
сведения из теории дифференциальных уравнений.
Теорема. Общее решение неоднородного линейного дифференци-
дифференциального уравнения с постоянными коэффициентами
drv dr~xv rt ч
by = а0—? + fli-т^ + ...+ary = f(x)
at ax
можно представить в виде интеграла Дюамеля
X
у = \н+(х -x)f(x)dx,
о
если выполняется условие, что f(x) = 0 при х ^ 0 и Я+(ж — ~х) =
= 0 при х ^ ~х (фактически эти условия означают, что «будущие»
значения f(x) не могут воздействовать на «более ранние» значения
у(х), а также исключаются мгновенные влияния). Функция Я+ явля-
является частным случаем функции Грина, для нахождения ее необходимо
проинтегрировать однородное дифференциальное уравнение
Ь#+(ж)=0, х >0
при начальных условиях
Я+@) = Н'@) = ... = Я^)@) = 0, Я^}@) = —.
по
Излучение в резонансных автогенераторах 195
Предположим, что при х = 0 пучок не модулирован, т. е. J — О
dj п
и — = U, взаимодействие электронов с полем происходит на отрезке
О < х < L. Решение соответствующего однородного уравнения для
уравнения вида F.13) было получено в лекции 3: оно представляет
собой две волны пространственного заряда (медленная и быстрая),
распространяющихся с волновыми числами км^ = -. Тогда в со-
соответствии с теоремой решение уравнения F.13) имеет вид
2 х
j(x) = -JfL ^L As \?8(x) Ге-^*-^ - eJk^~x)] dx. F.14)
2шр mv j L J
Активная мощность, отдаваемая током F.14) резонаторному полю
F.1), определяется формулой
2
Lx
_ СО е ПР ,д |2 тз I \р*(г\р (-й\ \aJkM(x-x) jk6(x — x)\ j J777
AtOp mv J J L J
о о
F.15)
В двойном интеграле при замене х ^ х подынтегральная функция
заменяется комплексно сопряженной, ее вещественная часть не изме-
изменяется, и, следовательно, этот интеграл равен половине интеграла по
квадрату 0 < ж, ~х < L. Учтем сказанное и введем обозначения
L
I8(u>) = \es{x)e (^) dx, Fs{u) = e2|^)|2. F.16)
о
Тогда мощность Ps перепишется так:
Ра = Жаа/ , F.17)
mv 2ujp
где Ws — энергия собственного колебания F.1), Ns — его норма; при
этом
Wt = \\Ar\2Nt, Ns = ±-\\Es\2dV. F.18)
Таким образом за время Т = L/v (время пролета электронов через
пространство взаимодействия) энергия поля получает приращение
= N^-2^Fs{uJ + ^\-F^-w"), F.19)
196 Лекция 6
где TV = nSL — эффективное число электронов, находящихся в каждый
момент в пространстве взаимодействия.
Пусть через пространство взаимодействия пролетает только один
электрон. В этом случае в формуле F.19) надо положить N = 1, ир =
= 1, а под ?8{х) понимать составляющую Е8^х на прямой, по которой
электрон движется.
Имеем
SlWs = ^u,^l F.20)
— выражение для индуцированного излучения электрона, проходя-
проходящего через слабое поле F.1). Приращение 8\WS пропорционально
Ws — энергии резонаторного колебания, модулирующего движение
электрона.
Спонтанное излучение электрона при произвольном
движении через резонатор. Связь между
индуцированным и спонтанным излучением
электрона в резонансных автогенераторах
Пусть электрон движется по закону г = r(t) через резонатор, в кото-
котором при t = 0, когда электрон вступает в резонатор, поля нет. Покидая
резонатор в момент времени t = T, электрон оставляет в нем часть своей
энергии (весьма небольшую) в виде суперпозиции свободных колебаний
этого резонатора. Колебания возбуждаются током с плотностью
— сю
Для тока легко находим:
т т
J(o;,r)= \i(t,r)eju:t dt= \ er(t)S(r - r(t))ejujt dt. F.21)
о о
Электрическое поле колебания с индексом s, подобно току (см.
интеграл F.21)), может быть представлено в виде интеграла Фурье
F.22)
где векторная функция Es(r) не зависит от о; и представляет собой рас-
распределение поля собственного колебания резонатора. Согласно теории
возбуждения резонаторов (см. формулу A.53)), а также при использо-
Излучение в резонансных автогенераторах 197
вании формулы F.21), имеем
А.(ш) = ., 2Ш 2ч Ns \jE*sdV =
i
= Т 2 [ Es(rW)rWejc"^ dt. F.23)
Используем тот вариант теории, в котором для идеального резона-
резонатора условие ортогональности записывается в виде
\jE8E*dV = 4'irN868r. F.24)
Потери (омические или радиационные) будем учитывать только
собственной комплексной частотой us = u's — ш". Причем, cj'JT ^C 1,
т. е. потерями за время полета можно пренебречь.
Нас интересует поле Е(Т, г) и связанная с ним энергия
A0Ws = \\Vs\2Ns, F.25)
где
2тг
— сю
2тггУУ5 J
о
Последний интеграл G = Г_ —^ 2е Ja; ^и мож;етбыть взят
00 си oj
00 си — ojs
s
на основании теоремы о вычетах. Перейдем к интегрированию по конту-
контуру. В качестве контура интегрирования выберем контур, охватывающий
верхнюю полуплоскость. Найдем полюсы подинтегральной функции,
они являются решениями уравнения р(со) = и2 — u2s = 0: и\^ = =bo;s.
Корень — ujs нас не интересут, так как он лежит в нижней полуплоско-
полуплоскости. Найдем теперь вычет для интеграла G. Так как
то
Яыч - Шз
AUJS
Тогда
G = ^2тг
198 Лекция 6
т
о
где
т
18(ш) = [Es(r(?))r(?)e"ia;Td? F.27)
о
— интеграл взаимодействия, для прямолинейного движения согласую-
согласующийся с формулой F.15).
Условие uj'gT <С 1 означает, что в выражении F.26) можно считать
|e-jo;sT| = i и заменить ujs в функции I*(ujs) на uj's или же на любую
частоту 2, удовлетворяющую условию \и) — uis\T <^i 1 или \и) — us\ <
< ио". Величина F.25), таким образом, получается в виде
оWt =
F.28)
причем для прямолинейного движения электронная функция Fs(uj) та
же, что и в формуле F.16) для индуцированного излучения.
Итак, функция Fs(uj) из формулы F.16) определяет спонтанное из-
излучение электрона, пролетающего через резонатор, а выражение F.20)
устанавливает связь между индуцированным и спонтанным излучением
электрона в резонансных автогенераторах.
Заметим, что в модифицированном виде соотношение F.20) обобща-
обобщается на резонансные генераторы, в которых электроны под действием
статических полей движутся произвольным образом. Таким образом,
соотношения F.17) и F.19) обобщаются, но только при ир = 0: про-
пространственный заряд в приборах разного типа действует по-разному
и учитывать его так, как это принято в приборах типа О, в общем случае
нельзя.
Сравнение классического и квантового подходов
Преобразуем выражение F.20) с учетом того, что функции 1Г и Fr
зависят не только от частоты, но и от скорости v или, что то же, от
кинетической энергии ? = mv2/2. Используя полученное выражение
F.28), имеем:
dFr г (dir „ дГА F29)
Излучение в резонансных автогенераторах 199
Величины Is и dls/дио даются выражениями
18{и) = J ?8(x)e-jwx/vdx и ^Ll = -L J xs8eriu3X'v dx. F.30)
о о
Из соотношения F.29) получим:
®Fs — е [ — L [ Tf p-^x
дш ~ 2Ne\ v) s
4 о
А* +
° ¦ и j ° Is]'
о
С другой стороны
dFs_ = dFs 1 dFs
dS ~ d(mv2/2) ~ mv dv '
Тогда
dFs ez ( r* dls , T di: \ dls _ju; Г P -i(wi/e) ,
~r 7s ^.. ' ^„. ~ 2 xcse ax,
d8 mv2Ns \ s dv dv J ' dt? <y
откуда получаем
L
dFs _ -e2uj (j f f -j(u>x/v) dT , r _ J Г с*Жих)/у ,tT . r\
^ 2Nsmv2 \v ) s s v ) s *)
4 n n x
о о
F.32)
Сравнивая формулы F.31) и F.32), приходим к выражению вида
dFs со dFs ( ,
F.33)
^F 2 1
д? mv duo
И окончательно находим
F.34)
Для релятивистских электронов ? = ?тгс27,7 = A ~ v2/c2I/2,
а в формуле F.20) вместо m надо взять mj3 (продольную массу).
Соотношение F.29) при этом сохраняется.
В выражении F.1) частота и лежит в главной части резонансной
кривой, т. е. удовлетворяет условию \и — u's\ < и". В силу этого в фор-
формуле F.28) можно положить и) = о;, а полное приращение энергии Ws
данного колебания равно сумме
AWS = AOWS = Fs(w,?) - Ws^ (u,S). F.35)
Квантовая форма этого соотношения имеет вид [1]
AW, = (ns + l)Fs(w,S) - n,F,(w,S + Пш), F.36)
200 Лекция 6
где ns — число фотонов в s-м колебании, которое в силу условия и"Т <С
<С 1 можно уподобить идеальному гармоническому осциллятору; Ws =
= nsHu. Легко видеть, что при Ни —> 0 квантовое соотношение F.36)
переходит в классическое соотношение F.35). Действительно, устрем-
устремляя Ни к нулю, имеем выражение
AWS = nsFs(oj,?) + Fs(lj,?) - nshbjdFs(^S),
которое, если учесть, что Ws = nsHu, переходит в F.35).
Соотношение F.34) может быть применено для расчета пускового
тока. Если умножить обе части F.34) на число электронов Je, по-
поступающих в резонатор со случайными фазами (Je = J/e, где J —
ток пучка, поступающего в резонатор), то получим мощность отдавае-
мую пучком данному колебанию: Je Ws ^— • Поскольку мощность,
выделяющаяся в оболочке и в нагрузке, равна 2u"W (см. лекцию 2;
раздел, посвященный резонансным автогенераторам), то коэффициент
затухания s-ro колебания по энергии при наличии электронного пучка
запишется следующим образом:
= Ш s' (о.37)
Генерация возможна при ks < 0, а пусковой ток будет определяться
условием ks = 0.
В заключение лекции отметим, что классическая теория для резо-
резонансных автогенераторов дает индуцированное излучение в приближе-
приближении заданного поля, а спонтанное — в приближении заданного тока.
Формула F.36), полученная из квантовых представлений, определяет
суммарное излучение.
Список литературы
1. Вайнштейн В.А. Спонтанное и вынужденное излучение свобод-
свободных электронов // ЖЭТФ. 1988. Т. 94, № 5. С. 40.
Лекция 7
МАГНЕТРОН, АМПЛИТРОН И ДРУГИЕ
Тизард и Кокрофт привезли в Америку черный
кожанный чемодан, который мисс Джири, секре-
секретарша Тизарда, держала у себя под кроватью.
Она не знала, что в нем хранятся почти все новые
научные приборы военного назначения, создан-
созданные в Англии, и среди них новый магнетрон —
прибор совсем иной степени важности, чем все
остальные весьма важные изобретения...
Чарльз Сноу
Биографии тем и сильны,
Что объять позволяют за сутки
Двух любовниц, двух жен, две войны
И великую мысль в промежутке.
Даже беды великих людей
Дарят нас прибавлением жизни,
Звездным небом, рысцой лошадей
И вином при его дешевизне.
Л. Кушнер
Кинематическая дрейфовая теория движения электронов в скрещен-
скрещенных статических электрическом и магнитном полях и в поле бегущей
волны. Фазировка в скрещенных полях. Расчет мощности взаимодей-
взаимодействия и к.п. д. применительно к плоскому магнетрону. Что вносит
цилиндричность в физику магнетрона. Цилиндрический магнетрон:
история создания от Хэлла до Бута и Рэндала. Вильям Браун и уси-
усилитель со скрещенными полями. Карматрон и дематрон.
В этой и последующей лекциях будут рассматриваться некоторые
вопросы теории магнетронных приборов и, в первую очередь, магне-
тронных генераторов (магнетронов). Магнетроны — одни из первых
приборов сверхвысоких частот и наиболее широко распространенные
из приборов типа М, т.е. приборов, использующих взаимодействие
202
Лекция 7
Анодный блок Катод
Вывод
энергии
Связка
электронов с высокочастотным полем в скрещенных статических элек-
электрическом и магнитном полях. Магнетронные генераторы (магнетро-
(магнетроны) представляют собой автогенераторы резонансного типа, поэтому
для них справедливы те общие соотно-
соотношения, которые мы вывели в лекции 2
для автогенераторов резонансного ти-
типа.
С конструктивной точки зрения со-
современный многорезонаторный магне-
магнетрон состоит из трех основных частей
(см. рис. 7.1): 1) катода; 2) анодно-
анодного блока, содержащего колебательные
контуры, 3) вывода ВЧ-энергии. Рабо-
Рабочая поверхность катода располагает-
располагается строго коаксиально с рабочей по-
поверхностью анодного блока. Диаметр
катода составляет значительную часть
(порядка 50 %) диаметра рабочей по-
поверхности анодного блока. Характер-
Характерная особенность анодного блока состо-
состоит в том, что в нем располагается боль-
большое количество полостей, выполняю-
выполняющих роль колебательных контуров (ре-
(резонаторов). Форма этих полостей (ре-
(резонаторов) может быть весьма разно-
разнообразной, например, щель-отверстие,
сектор, щель и др. (см., например, [1]).
Каждая из полостей резонаторов со-
соединена щелью с пространством катод-
анод, и поэтому рабочая поверхность
анодного блока (т. е. поверхность, на
которую попадают вылетевшие из ка-
катода электроны) всегда разрезана на
ряд сегментов, отделенных друг от дру-
друга щелями. Между этими сегментами
при работе магнетрона возникает пере-
переменное напряжение высокой частоты.
При разработке многорезонатор-
ных магнетронов были эксперимен-
экспериментально обнаружены «перескоки» коле-
колебаний магнетрона с одной волны на другую. Эти перескоки вызывались
как изменением режима питания, так и изменениями высокочастотной
нагрузки магнетрона. Дело в том, что колебательная система магнетро-
магнетрона представляет собой замкнутую цепочку резонаторов. Она является
в \ Связка
Рис. 7.1. Схема цилиндриче-
цилиндрического магнетрона: а — маг-
магнетрон с резонаторами типа
«щель-отверстие» и с выводом
ВЧ-энергии с помощью петли;
б— анодный блок с резонатора-
резонаторами типа сектор, в котором чере-
чередуются резонаторы различного
размера, и с выводом ВЧ-энер-
ВЧ-энергии с помощью щели; в — схе-
схема соединения сегментов связ-
связками для получения колебаний
на тг-виде
Магнетрон, амплитрон и другие 203
неоднородной волноведущей структурой, в которой могут существовать
стоячие или бегущие волны. Из-за замкнутости системы в ней могут
распространяться только те волны, для которых выполнено условие
синфазности колебаний в начале и конце колебательной системы:
УУ</?0 = 2тгп, п = 1,2,3... G.1)
Здесь N — число резонаторов в замедляющей системе магнетрона, </?о —
сдвиг фазы на одном периоде системы, п — номер вида колебаний.
Видам колебаний с одинаковым по модулю значением п соответствуют
одинаковые частоты колебаний, т. е. в системе существует вырождение
по частоте. Введение элементов связи между отдельными резонаторами
нарушает симметрию колебательной системы и приводит к снятию
вырождения, при этом частоты колебаний, соответствующие п и — п,
близки. Поэтому в результате флуктуации, например, анодного напря-
напряжения, магнетрон может изменить частоту генерации.
Для устранения этого явления применяются либо анодные блоки,
в которых последовательно чередуются резонаторы двух типов, либо
анодные блоки с одинаковыми резонаторами, которые электрически
связаны между собой так называемыми «связками». Действительно,
усиление связи между отдельными узкополосными колебательными
системами, составляющими колебательную систему анодного блока,
приводит к удалению собственных частот друг от друга. Поэтому вве-
введение элементов, связывающих отдельные резонаторы, — связок —
приводит к увеличению устойчивости работы магнетрона. Одна из
конструкций связок, представляющих собой два металлических кольца,
одно из которых соединяет между собой все четные сегменты анодно-
анодного облака, а другое — все нечетные сегменты, показана на рис. 7.1 в.
Нормальная работа магнетрона при этом характеризуется тем, что
высокочастотные напряжения соседних сегментов сдвинуты по фазе
на 180°: это так называемый тг-вид колебаний (ему соответствует вид
колебания (см. формулу G.1)) п = N/2). В этом случае в различные
моменты времени одна связка заряжена положительно, другая заряже-
заряжена отрицательно и наоборот. Поэтому в случае колебаний тг-вида связ-
связки работают как обкладки конденсатора, увеличивая эквивалентную
емкость резонатора, что приводит к уменьшению частоты колебаний
тг-вида. При колебаниях других видов разность фаз между сегментами
колебательной системы отлична от нуля, и в результате по связкам течет
ток. При этом связки работают подобно индуктивностям, включенным
параллельно индуктивности резонатора, что приводит к увеличению
частоты колебаний. Кроме этого, из-за протекания тока по связкам
увеличиваются потери на любом виде колебаний, за исключением тг-
вида. Это способствует возбуждению именно тг-вида при возникновении
генерации. Кроме этого, при возбуждении только тг-вида колебаний
амплитуда высокочастотного поля будет иметь максимальное значение
204 Лекция 7
по сравнению с остальными видами. Это обеспечивает наиболее эффек-
эффективное взаимодействие электронного потока и поля высокочастотной
волны.
Вывод ВЧ-энергии из магнетронного генератора осуществляется
либо на коаксиальную линию с помощью петли в одном из резонато-
резонаторов, либо на волновод с помощью щели в одном из резонаторов (см.
рис. 7.1а,б).
Принципиальной особенностью приборов со скрещенными полями
является специфический характер энергообмена между электронным
потоком и ВЧ-полем, связанный с изменением потенциальной энер-
энергии электронов без изменения их кинетической энергии. В отличие
от приборов типа О, где в энергию ВЧ-поля в результате торможе-
торможения электронного потока переходит кинетическая энергия электронов,
в приборах типа М источником ВЧ-энергии служит потенциальная
энергия статического электрического поля. В процессе взаимодействия
электроны, практически не меняя своей средней кинетической энергии,
смещаются в область более высокого потенциала (к аноду) и уменьшают
свою потенциальную энергию, которая и переходит в энергию волны.
Важная черта приборов магнетронного типа — высокий к.п.д. Дело
в том, что энергообмен между пучком и полем начинается при дрей-
дрейфовых скоростях электронов, равных скорости волны в замедляющей
системе. Эта необходимая для взаимодействия синхронная скорость
сообщается электрону за счет статических полей и не меняется в процес-
процессе взаимодействия. Соотношение между долей потенциальной энергии
электрона, переходящей в энергию ВЧ-поля, и полной потенциальной
энергией, которой обладал электрон при выходе из катода, определяет
электронный к.п.д. прибора. Так как полная потенциальная энергия
может быть достаточно большой (она определяется потенциалом ано-
анода), а на создание синхронной скорости идет небольшая ее часть, то
к.п.д. приборов типа М может быть близок к единице. Высокий к.п.д.
в сочетании с низким сопротивлением электронного пучка (анодное
напряжение, деленное на ток) делает приборы магнетронного типа
особенно пригодными для получения больших выходных мощностей.
Кинематическая дрейфовая теория движения
электронов в скрещенных статических электрическом
и магнитном полях и в поле бегущей волны
Рассмотрим простейшую дрейфовую теорию взаимодействия элек-
электронов, движущихся в перпендикулярных электростатическом и посто-
постоянном магнитном полях, с высокочастотным электромагнитным полем
объемного резонатора. Будем анализировать плоскую модель магне-
магнетронного генератора (рис. 7.2а), которая, с одной стороны является
естественной аппроксимацией цилиндрической модели (рис. 7.26) (если
Магнетрон, амплитрон и другие
205
V=0
{
в ней радиус анода близок к радиусу катода), и, во-вторых, в некото-
некоторых случаях имеет самостоятельное значение (магнетронный прибор
с плоским пространством взаимо-
взаимодействия, планотрон и т.д.). На-
Наличие объемного резонатора силь-
сильно упрощает задачу — можно счи-
считать, что возбуждено только од-
одно колебание с известным рас-
распределением поля, но неизвестной
амплитудой и неизвестной часто-
частотой г). Заметим, что здесь не учи-
учитывается поле пространственного
Рис. 7.2. Схематическое изображе-
изображение пространства взаимодействия
плоского (а) и цилиндрического (б)
магнетрона
заряда (к чему приводит учет про-
пространственного заряда будет рас-
рассмотрено в следующей лекции). Другим упрощением является то, что
рассматривается только одна пространственная гармоника поля дан-
данного колебания резонатора. Фазовая скорость этой гармоники син-
синхронна с электронами; будем её далее называть просто синхронной
волной. Действием несинхронных пространственных гармоник мож-
можно пренебречь, за исключением случаев орбитальных резонансов (см.
подробнее [2]).
Уравнение движения электрона в геометрии, представленной на
рис. 7.2а, имеет вид
d2
i J k
х у z
BxByBz
G.2)
Здесь Вх = 0, Ву = 0, Bz = В = const — статическое магнитное поле,
Ех ф 0, Еу ф 0 и Ez = 0 — составляющие суммарного электрического
поля (статическое + сверхвысокочастотное). С учетом этого:
х = г]Ех + rjBy, у = г]Еу - г]Вх.
Введем новые обозначения fx = r\Ex и fy = f]Eyj а также величину
оос = г)В, называемую ларморовой или циклотронной частотой. Тогда
уравнение движения G.2) запишется в виде
х - ujcy = fx, y + ujcx = fy. G.3)
Уравнения G.3) можно приближенно решить, пользуясь так назы-
называемым дрейфовым приближением [2]. Рассмотрим вначале некоторые
частные случаи.
г) Вместе с тем о ней известно, что она достаточно близка к резонансной ча-
частоте колебательной системы, так как в противном случае данное колебание
будет возбуждаться с малой амплитудой и его нельзя считать единственным.
206 Лекция 7
Пусть fx = fy = 0, тогда уравнение G.3) имеет общее решение
х = х0 + го cos {-u)ct + (ро), у = уо + го sin {-u)ct + (po), G.4)
где жо, 2/о? го и </?о — некоторые постоянные. Физический смысл этого ре-
решения — движение по окружности радиуса го с центром в точке (хо, у о).
Это движение происходит с угловой скоростью ис (при ис > 0 — по
часовой стрелке, при ис < 0 — против) и линейной скоростью v = |о;с|го.
Период обращения 2тг/|а;с| называется циклотронным периодом.
При постоянных во времени и пространстве величинах fx и fy
уравнения G.3) имеют общее решение:
X = Хо + ^- t + Го COS (-U)ct + y?0)j
1 G-5)
2/ = 2/о t + r0 sin (-o;c? + tpo).
Данное решение можно интерпретировать как движение по окружно-
окружности, центр которой движется («дрейфует») с течением времени согласно
формулам
x = Xo + JjLt, y = yo-Lat, G.6)
UJC UJC
где х и у — координаты «ведущего центра», вокруг которого обращается
электрон с угловой скоростью ис.
Смысл термина «дрейф» заключается в том, что обычно это —
медленное движение, тем более медленное, чем больше \ис \, а движение
по окружности быстрое, причем тем более быстрое, чем больше \ис\.
Рассмотрим в качестве примера дрейф в плоском магнетроне под
действием постоянного поля с единственной составляющей Еу = Е° =
= const < 0. Этот дрейф определяется соотношениями
х = xo + vot, у = 2/о, ^о = -—• G.7)
LOc
Радиус окружности, по которой обращается электрон, зависит от
начальных условий. Если, например, при дрейфе, задаваемом форму-
формулами G.7), в начальный момент х = vo, у = 0, то го = 0 и движение
электрона сводится к чистому дрейфу. Если же в начальный момент
электрон покоится (х = у = 0), то
го = ^ = К G-8)
Шс UJC
и электрон движется по циклоиде, отходя от плоскости катода на рас-
расстояние 2го и затем возвращаясь назад. Если расстояние катод-анод
превышает 2го, то такое движение электрона называется движением в
«запертом» плоском магнетроне (магнитное поле больше критического,
когда электрон касается анода) в пренебрежении пространственным
зарядом.
Магнетрон, амплитрон и другие 207
Формулы G.6) показывают, что уравнение движения ведущего цен-
центра при постоянных fx и fy имеют вид:
i = t> y = ~t> G-9)
т. е. получаются из уравнений для электронов G.3) вычеркиванием
«инерционных» членов х и у. Таким образом, при приложении посто-
постоянного электрического поля ведущий центр движется в направлении
перпендикулярном этому полю.
В общем случае величины fx и fy не постоянны, а являются функ-
функциями координат ж, у и времени t. В этом случае для исследования
движения также можно применять дрейфовые уравнения G.9), так
называемое дрейфовое приближение.
Пусть теперь движение электронов происходит при наличии сверх-
сверхвысокочастотного поля. В этом случае даже слабое высокочастотное
поле, если оно имеет вид бегущей волны, синхронной с электронами
(т. е. если фазовая скорость волны Уф близка к дрейфовой скорости
электронов vo), радикально изменяет движение электронов, которое
ранее описывалось соотношениями G.5). Заметим, что если переменное
поле не синхронно, то оно заметно не изменяет движения электронов:
несинхронное поле приводит лишь к небольшим колебаниям, которые
накладываются на дрейф.
Рассмотрим дрейфовые уравнения G.9) при наличии наряду с од-
однородным электрическим полем синхронной волны, движущейся со
скоростью Уф ~ vo и имеющей частоту и {и — частота генерации).
Зависимость поля синхронной волны от времени и координаты опре-
определяется множителем exp (ut — /Зх), где Уф = uj/ /3. Для тг-колебания,
когда колебания в соседних щелях противофазны, /3 = тг/L, где L —
период структуры по оси х г).
Рассматривая нерелятивистские уравнения движения электронов,
полагаем, что
^Ф ~ ^о < с, G.10)
где с — скорость света. Тогда данная волна является электрической [3]
и описывается электрическим вектором Герца П с единственной состав-
составляющей Пж соотношением
Е = grad div П + &2П, G.11)
г) Заметим, что для других видов колебаний /3 другое, но зависимость
синхронной волны от координаты и времени такая же.
208 Лекция 7
Электрический вектор Герца является решением уравнения [3]
+
2 + 2
ох оу
2
k Ux = 0, G.13)
где подразумевается зависимость от времени в виде ехр (—jut), к =
= ojIс. В нашем случае для бегущей волны необходимо задать гранич-
граничное условие в виде Ех (у = 0) = 0, тогда выражение для поля этой волны
будет даваться соотношением
Ux = Aejpx sin L/k2 - f32y\ . G.14)
Здесь А — постоянная. Учитывая условие G.10), можно положить
j0y/l - (к/CJ = tfyjl - (Уф/сJ ss jp.
При этом совершается относительная ошибка порядка (уф/с) . Тогда
в уравнениях G.12) и G.13) можно пренебречь членом к2Их, и, положив
Г\тт
Ф = —wJL^ Для составляющих поля волны получим
ох
дФ дФ
* e <7151
Здесь Ф — скалярный потенциал, удовлетворяющий уравнению Лапласа
д2Ф д2Ф
^ + ^=0. G.16)
ох оу
В случае плоского магнетрона с гладким катодом (у = 0) будет
выполняться граничное условие Ех = 0 на катоде, поэтому для бегущей
волны возьмем скалярный потенциал в виде
Ф = ^ sin [^(ж - «ф*)] sh jfff/, G.17)
где Е > 0 — амплитуда составляющей Еу в плоскости у = 0. Тогда,
с учетом электростатического поля, дрейфовые уравнения G.9) пере-
перепишутся в виде
сдФ . сдФ
а оу н дх
Здесь ^о = сЕу/Н, как следует из соотношения G.9), есть скорость
дрейфа под действием статических полей в направлении оси х, а слага-
слагаемые, содержащие производные потенциала Ф, определяют дрейф под
действием электрического поля медленной волны.
Перейдем в систему координат, движущуюся со скоростью vo вместе
с бегущей волной G.14), для чего произведем замену переменных:
Магнетрон, амплитрон и другие 209
= -^ Ну + Ф = -[Еу)-^ H)y + -smPx'shPy. 7.20
с \ y с ) p
Здесь Ф' — эффективный потенциал, действующий на электроны в по-
подвижной системе координат и являющийся суммой электростатическо-
электростатического потенциала Еуу, соответствующего однородному полю
у ~ у ~ ~^~ ' \(-АЧ
которое определяет дрейф х) вдоль оси х со скоростью сЕу/Н = vo —
— г?ф, и сверхвысокочастотного потенциала G.15), который в рассмат-
рассматриваемой системе координат зависит только от координаты и не зависит
от времени.
Тогда в подвижной системе координат уравнения движения преоб-
преобразуются к более удобному виду:
с дФ' с дФ'
Н ду Н дх'
Данные уравнения определяют медленное движение — дрейф веду-
ведущих центров. Траектория этих движений совпадает с эквипотенциаля-
миФ' = const, так как согласно уравнениям движения G.22) мгновенная
скорость ведущего центра перпендикулярна вектору grad^. Если рас-
рассматривать движение ведущих центров, непрерывно распределенных
в пространстве, то их скорость (вектор с составляющими ж', у) как
функция координат х', у удовлетворяет уравнению
дх' ду
Это означает, что движение ведущих центров подобно движению несжи-
несжимаемой жидкости, поэтому плотность ведущих центров не изменяется
при движении по траекториям.
Фазировка в скрещенных полях. Расчет мощности
взаимодействия и к.п.д. применительно к плоскому
магнетрону
Как было показано выше, в системе координат, движущейся вместе
с волной, движение электронов складывается из дрейфа их ведущих
центров согласно уравнениям G.22) и орбитального движения — вра-
вращения вокруг ведущего центра с угловой скоростью ujc. При условии
точного синхронизма волны и электронов Уф = vq траектории ведущих
г) Заметим, что согласно релятивистским формулам преобразования элек-
электромагнитных полей, соотношение G.21) определяет электрическое поле,
которое действует на электрон в движущейся системе координат.
210
Лекция 7
Рис. 7.3. Эквипотенциали и траектории в плоском магнетроне
центров определяются уравнением
Ф = const или sin f3x' • sh /Зу = const, G.24)
т.е. совпадают с эквипотенциалями синхронной волны. Отметим, что
среди эквипотенциалей есть прямые линии: у = 0 (катод) и f3x' = 0, =Ь
±7Г, ±27Г.
На рис. 7.3 представлены траектории ведущих центров. Направле-
Направление движения по ним легко найти из второго уравнения G.22): при —
—тг/2 < /Зх' < тг/2 движение происходит вверх, от катода к аноду; при
—Зтг/2 < 13х' < —тг/2 — вниз, от анода к катоду. На рисунке приведены
все возможные траектории, фактическое же заполнение их ведущими
центрами определяется способом ин-
жекции электронов в пространство
взаимодействия.
Если электроны эмиттируются ка-
катодом, расположенным в плоскости
у = 0 (в пренебрежении простран-
пространственным зарядом и начальным раз-
разбросом по скоростям), то это означает,
что ведущие центры возникают в плос-
плоскости у = го, где го выражается соот-
соотношением G.8). Отсюда они и начина-
начинают движение вверх к аноду, образуя
при —тг/2 < 13х' < тг/2 спицу («язы-
(«язычок» по монографии [4]), заштрихованную на рис. 7.4. Поскольку за
время обращения 2тг/|а;с| ведущий центр смещается от катода, соответ-
соответствующие электроны не возвращаются к катоду и попадают на анод,
когда ведущий центр приближается к нему на расстояние го-
Вышеописанная картина справедлива, если расстояние D между
катодом и анодом больше 2го, и если время дрейфа Т через слой
-я/2
0
Рис. 7.4. Спица при точном син-
синхронизме
Магнетрон, амплитрон и другие 211
го < у < (D — го) высоты (D — 2го) существенно больше 1/|о;с|, т.е.
KIT » 1, G.25)
причем наименьшее время Т соответствует ведущим центрам, движу-
движущимся вертикально вверх (т. е. /3xf = 0), и равно [2]
Т = JL [in th ^~го) - In th Ы . G.26)
Условие D > 2го означает, что магнитное поле больше критического
и магнетрон заперт, т. е. анодный ток в статическом режиме отсутствует.
Ведущие центры, дрейфующие к катоду, соответствуют элек-
электронам, инжектируемым в пространство взаимодействия при
—Зтг/2 < /Зх* < —тг/2 и тг/2 < fix' < Зтг/2 и возвращающимся на катод
у = 0 после недолгого пребывания в пространстве взаимодействия:
совершая один оборот эти электроны оседают на катод. Они,
испытав ускорение со стороны высокочастотного поля, осуществляют
дополнительный разогрев катода. Далее эти электроны рассматривать
не будем. Заметим только, что для их рассмотрения анализа дрейфового
приближения недостаточно ввиду их малого времени пребывания
в пространстве взаимодействия.
Ведущие центры, дрейфующие вверх к аноду, составляют полови-
половину всех ведущих центров, возникающих в плоскости у = го- В связи
с этим, при исчезающе малом пространственном заряде анодный ток
составляет половину тока эмиссии. Формирование спиц происходит
и тогда, когда на движение электронов в прикатодной области влияет
пространственный заряд (вопросы влияния пространственного заряда
будут рассмотрены в следующей лекции).
Таким образом, как видно из рис. 7.3 и 7.4, при точном синхрониз-
синхронизме (^ф = vo) бегущая волна сколь угодно малой амплитуды отпирает
магнетрон — формируются спицы и появляется анодный ток /о > 0.
Анодное напряжение равно Vo = —EyD > 0, мощность, подводимая
к прибору, равна Ро = IqVq-
Найдем теперь мощность, отдаваемую электронами сверхвысокоча-
сверхвысокочастотному полю. Для этого будем предполагать, что электроны при своем
движении в поле волны сохраняют тот же радиус, что и при отсутствии
высокочастотного поля.
При отсутствии высокочастотного поля при эмиссии с нулевой ско-
скоростью радиус орбиты го = vo/ujc, причем в начальный момент скорость
дрейфа г>о как раз компенсирует скорость обращения исг$. По мере
удаления от катода потенциальная энергия электрона уменьшается,
а кинетическая соответственно возрастает до своего максимального
значения
= ^2^. G.27)
2
212 Лекция 7
Здесь в левой части стоит убыль потенциальной энергии от катода до
верхней точки циклоиды (расположенной при у = 2го), а в правой —
кинетическая энергия в верхней точке, где скорость дрейфа и скорость
обращения складываются, и скорость частицы равна 2г>о-
Слабое высокочастотное поле (Е <С \Еу\) не изменяет существенно
кинетической энергии, а, следовательно, энергия электрона при ударе
об анод та же, что и в верхней точке циклоиды. Величина ? = eE®D
характеризует убыль потенциальной энергии при перемещении элек-
электрона от катода к аноду, а энергия, которая тратится на бомбардировку
анода, равна 2r$?/D. Тогда на поддержку колебаний в резонаторе
(л 1гЛ с
остается энергия A — — 1 ?, и мощность, отдаваемая электронами
высокочастотному полю, равна
Р
= (l - ^) Р0. G.28)
Здесь множитель г\а = 1 — 2ro/ D является анодным коэффициентом
полезного действия. Он получается при эмиссии электронов с поверхно-
поверхности катода у = 0. При возвышении эмиттеров над плоскостью катода rja
падает, а при углублении — растет и может достичь значения ?7™ах =
= 1 - ro/2D [2, 4].
Из этого рассмотрения понятен механизм фазовой фокусировки
и энергетических превращений в магнетроне. Фазовая фокусировка
обусловлена тем, что заполнены лишь траектории, идущие от катода
к аноду, а траектории, идущие от анода к катоду (вблизи прямых /Зх' =
= ±тг на рис. 7.3), пусты. Заполненные траектории дают анодный ток,
поддерживающий колебания в резонаторе. Очевидно, что если бы были
заполнены все траектории, то наряду с этим током появился бы ток
противоположного направления, отбирающий энергию у колебаний.
Энергетические превращения в магнетроне обусловлены тем, что элек-
электроны при движении от катода к аноду теряют свою потенциальную
энергию. В отсутствие магнитного поля эта энергия бы превратилась
в кинетическую и выделилась бы в виде тепла при ударе электронов
об анод. Благодаря действию магнитного поля электроны разгоняются
постоянным электрическим полем Е® сравнительно мало (лишь до
кинетической энергии 2г^еЕуу). Остальная часть потенциальной энер-
энергии электронов непосредственно превращается в энергию электромаг-
электромагнитных колебаний. Это превращение происходит в результате фази-
ровки, благодаря которой в пространстве взаимодействия длительное
время присутствуют лишь «полезные» электроны, образующие спицы,
а электроны, отбирающие энергию у высокочастотного поля, быстро
выводятся из пространства взаимодействия.
Предыдущее рассмотрение соответствовало случаю идеальной фа-
зировки, т.е. точному синхронизму электронов и волны. Обсудим те-
теперь качественно ситуацию при отсутствии точного синхронизма, т. е.
Магнетрон, амплитрон и другие 213
^Ф Ф Щ- В этом случае траектория движения ведущих центров опреде-
определяется из уравнения G.20) при условии Ф' = const:
-а/Зу + sin /3x'sh /Зу = const, G.29)
где
а = (^-!*)Я = -^Л— G.30)
сЕ Е
характеризует расстройку скоростей. Первое слагаемое в выражении
G.29), пропорциональное у, определяет то постоянное поле в движу-
движущейся системе координат при отсутствии точного синхронизма, которое
обусловливает дополнительный дрейф траекторий ведущих центров,
исследованный выше: они «сносятся» в направлении оси х.
Этот дополнительный дрейф может уменьшить анодный ток и даже
воспрепятствовать образованию спиц. Действительно, при точном син-
синхронизме спица целиком расположена в полосе —тг/2 < fix' < тг/2, где
ведущие центры движутся от катода к аноду. Под влиянием дополни-
дополнительного дрейфа спица может выйти из этой полосы, и тогда она частич-
частично или полностью повернется к катоду, и анодный ток уменьшится или
станет равным нулю. При достаточно большом различии скоростей vq
и Уф вышеописанный простой механизм отпирания запертого магнетро-
магнетрона синхронной волной уже не работает [2].
Формулы G.29) и G.30) показывают, что форма траектории при
отсутствии синхронизма определяется параметром а ~ /ЗДж, где Ах =
= (уо — Уф)Т — дополнительное смещение ведущего центра в направ-
направлении оси х за время пролета Т. Можно показать (см., например [2]),
что анодный ток отличен от нуля при условии |сг| < ата^ ~ 1, а при
|сг| > атах спицы не образуются, и анодный ток равен нулю. На рис. 7.5
изображены спицы (траектории ведущих центров) для различных вели-
величин расстройки, причем вместо а взят пропорциональный ему параметр
7 _ а _ е'у G 31)
Ech/Зго
Здесь поле Е'у определяется формулой G.21), а величина Ech/Зго, как
можно видеть из соотношений G.15) и G.17), есть амплитуда составля-
составляющей Еу поля медленной волны в плоскости питания у = г^\
Еу = TEchPr0 при fix' = ±7г/2,у = г0. G.32)
Данная составляющая поля фазирует ведущие центры — смещает их
к вертикали /Зх' = 0, что приводит к образованию и сужению спицы.
Составляющая поля Ех определяет движение ведущих центров от ка-
катода к аноду и наоборот.
Рассмотрим более подробно результаты расчетов, представленных
на рис. 7.5. При — 1 ^ j ^ 1 (рис. 7.5а) спица искривляется, становится
асимметричной, но при этом анодный ток не изменяется, поскольку
214
Лекция 7
Рис. 7.5. Спицы при различной расстройке скоростей: a — j < 1; б — j = 1\
в — j > 1] г — j > 7max- Здесь простой штриховкой отмечены электроны,
возвращающиеся к катоду, а двойной — электроны, создающие анодный ток
все ведущие центры, начавшие свое движение при —тг/2 < /Зх' < тг/2,
приходят к аноду. Это связано с тем, что дефазирующее поле Е'у при
|7| < 1 меньше фазирующего поля G.32) на краях спицы, где она
всего ближе к граничным вертикалям /Зх' = ±тг/2, после пересечения
которых неизбежен дрейф обратно к катоду. Существенно именно фа-
фазирующее поле Еу при у = го, поскольку при дальнейшем движении
к аноду фазирующее поле (пропорциональное ch /Зу) монотонно растет,
а дефазирующее остается постоянным.
При 7 = 1 фазирующее поле еще удерживает правый край спицы
слева от вертикали /Зх' = тг/2 (рис. 7.56), при 7 > 1 этот край дрейфует
в область /Зх' > тг/2 (рис. 7.5в) и возвращается к плоскости у = го-
При достаточно больших значениях 7 (при I7I > 7max) в обратный
дрейф вовлекаются все ведущие центры, и анодный ток равен нулю.
Медленная волна в этом случае приводит лишь к образованию выступов
в прикатодном электронном слое, не достигающих анода (рис. 7.5г).
Что вносит цилиндричность в физику магнетрона?
При исследовании цилиндрической модели магнетрона (рис. 7.26)
также можно воспользоваться дрейфовыми уравнениями G.9), в кото-
которых от декартовых координат нетрудно перейти к полярным коорди-
координатам г, (/?. Однако электростатическое поле в цилиндрическом магне-
магнетроне не может быть постоянным, а убывает как 1/г, а следовательно,
Магнетрон, амплитрон и другие 215
скорость дрейфа Уо под действием электростатического поля зависит
от г по закону
v v
г
G.33)
Здесь U — скорость при г = г. Бегущая волна в новых координатах имеет
вид ехр (—j (гир + ujt)), поэтому фазовая скорость ее также зависит от г:
v* = v^ G.34)
где U — фазовая скорость при г = г. Выражения G.33) и G.34) свиде-
свидетельствуют, что в цилиндрической модели магнетрона точный синхро-
синхронизм электронов и волны во всем пространстве взаимодействия между
катодом и анодом невозможен: можно добиться точного синхронизма
лишь при г = г, где Уо = ^ф = "V- Тогда во всем пространстве взаимо-
взаимодействия при г > Т будет Уф > vo, а при г < г — Уф < vq. Величину г
обычно поэтому называют синхронным радиусом.
Невозможность точного синхронизма во всем пространстве взаимо-
взаимодействия приводит к тому, что появляется дополнительный дрейф спиц
в азимутальном направлении, причем скорость этого дрейфа зависит
от радиуса. Этот дрейф искривляет спицы, а при малых амплитудах
медленной волны, когда время дрейфа через пространство взаимодей-
взаимодействия велико, может уменьшить анодный ток, или даже привести к его
исчезновению (см., например, [2]).
Цилиндрический магнетрон: история создания
от Хэлла до Бута и Рэндала
Автоколебания на сверхвысоких частотах впервые были получены
в 1919 году в аудионе (вакуумном триоде) — трехэлектродной лампе,
содержащей управляющую сетку между нитью накала и анодом. Триод
был сконструирован для работы на низких частотах, а СВЧ-колебания
имели место при наличии колебательного движения электронов в меж-
межэлектродном пространстве при положительном потенциале на сетке
и отрицательном на аноде.
Вскоре были открыты и исследованы колебания в простейших маг-
магнетронах — «гладком» и с разрезным анодом, а затем в диодах —
генераторах.
Магнетрон занимает особое место среди СВЧ-автогенераторов. Ис-
Истории его создания посвящено много работ. Показательно название од-
одной из них, принадлежащей перу профессора истории науки Института
Технологии в Джорджии Джеймсу Брайттейну — «Магнетрон и начало
микроволнового века» [5].
В 1921 году Хэлл опубликовал работу, в которой была показана воз-
возможность управления движением электронов между коаксиальными
цилиндрами с помощью постоянного магнитного поля (регулируемого
216
Лекция 7
извне), перпендикулярного к постоянному электрическому полю между
цилиндрами. С этой работой обычно связывают открытие магнетрон-
ного принципа колебаний. Интересно, что Брайттейн датирует изобре-
изобретение магнетрона 1916 годом, хотя ссылается на публикацию 1921 года.
Подобно одному из братьев Вариан и Компфнеру, Хэлл тоже начинал
не как физик. Он окончил Иельский университет по специальности
греческий язык и второстепенному курсу социологии, учился несколько
лет в Академии в Олбэне, затем вернулся в Иель, чтобы окончить
университет с ученой степенью по физике.
Следует, однако, заметить, что Хэлл имел целью создание низко-
низкочастотного мощного генератора: в его экспериментах обмотка электро-
электромагнита была включена в колебательный контур магнетрона и в анод-
анодную цепь, так что его магнетрон был генератором звуковой часто-
частоты. Главным в экспериментах Хэлла было открытие докритического,
критического и закритического
статических режимов в магне-
магнетроне (рис. 7.6). Стало понятно,
что и в двухэлектродной лам-
лампе можно управлять электрона-
электронами, отклоняя их магнитным по-
полем (до этого было известно
лишь управляющее и отпираю-
отпирающее действие сетки в триоде).
Первые СВЧ-колебания в маг-
магнетроне с гладким анодом (кон-
(конструкция Хэлла) были получе-
В = О i В<Вкр iB=BKp \В>В}
'кр
Рис. 7.6. Зависимость тока /, прохо-
проходящего через цилиндрический маг-
магнетрон в статическом режиме, при
постоянном анодном напряжении от
индукции магнитного поля. Над
соответствующими точками кривой
изображены траектории электронов
для случая отсутствия магнитного
поля (В = 0), докритического режи-
режима (В < Вкр), критического (В =
= Вкр) и закритического (В > Вкр)
режимов работы магнетрона
ны в 1924 г. Жачеком. В осно-
основе работы лежал механизм фа-
фазовой сортировки электронов —
ускоренные высокочастотным по-
полем электроны сразу оседали на
катоде. Для удаления из про-
пространства взаимодействия магне-
магнетрона электронов, которые в тече-
течение нескольких периодов ВЧ-по-
ля тормозились и теряли свою
энергию вращательного движения, применялся наклон постоянного
магнитного поля относительно оси прибора или введение дополнитель-
дополнительных электродов на краях магнетрона (концевые диски). В том же 1924 г.
А.А. Слуцкиным и Д.С. Штейнбергом в Харьковском университете
были начаты работы, которые также привели к открытию магнетрон-
ного способа создания ВЧ-колебаний (эти работы были развернуты
по предложению и под руководством профессора Д.А. Рожанского).
Были разработаны магнетроны с разрезным анодом, генерировавшие
Магнетрон, амплитрон и другие 217
в сантиметровом и дециметровом диапазонах длин волн. Сначала ано-
аноды были двухразрезные (или двухсегментные), т.е. цилиндрический
анод магнетрона делился на две части щелями, параллельными оси
цилиндра. Эти щели составляли емкость колебательного контура маг-
магнетрона, а индуктивностью был металлический виток, присоединен-
присоединенный к половинкам анода. В дальнейшем появились и многосегментные
конструкции, достоинством которых были низкие анодные напряжения
и уменьшенные магнитные поля.
В 1935 г. Постумус предложил так называемый магнетрон с бегу-
бегущей волной (точнее это был новый режим работы магнетрона с раз-
разрезным анодом). В этом магнетроне угловая скорость одной из волн,
на которые можно было разложить высокочастотное поле в колеба-
колебательной системе, равнялась средней скорости азимутального вращения
электронного облака. До 1940 г. были сконструированы магнетронные
генераторы этого типа, работающие на волнах до 75 см и длиннее с к.п.д.
50 % и больше. Таким образом, в магнетроне с бегущей волной уже
был в известной мере заложен принцип будущего многорезонаторного
магнетрона. Но в магнетроне не было еще многоконтурной колеба-
колебательной системы, состоящей из многих резонаторов, хотя идея такого
контура уже существовала. Она впервые была предложена в 1929 г.
М.А. Бонч-Бруевичем. Приведем начало его патента. «В передатчи-
передатчиках большой мощности, в особенности для коротких волн, большие
затруднения вызывает устройство колебательной цепи последнего кас-
каскада, а также применение для этого каскада большого количества
ламп, включенных параллельно. Поэтому оказывается выгодным раз-
разбить колебательный контур на ряд отдельных контуров, соединенных
между собою таким образом, чтобы это со-
соединение обеспечило совместную правиль-
правильную работу всех контуров, входящих в кас-
каскад. Для осуществления этой цепи в изоб-
изображенном на чертеже ламповом генераторе
с несколькими парами катодных ламп (см.
рис. 7.7) колебательные контуры включе-
включены параллельно между собою таким обра-
образом, чтобы фазы в двух соседних контурах
были обратными». Впоследствии в 1935 г.
М.А. Бонч-Бруевич, став руководителем
магнетронного проекта, вернулся к этой рис> 7.7. Схема много-
идее на новом конструктивном уровне. контурного генератора,
Инженеры НИИ-9 (г. Ленинград) предложенного в патенте
Н.Ф. Алексеев и Е.Д. Маляров под его МА- Бонч-Бруевича
руководством создали такую конструкцию
магнетрона, в которой анодный блок был выполнен из целого куска меди
и содержал несколько (от четырех до восьми) полостей, играющих роль
218 Лекция 7
резонаторов. Первые приборы генерировали в непрерывном режиме
мощность 10 Вт на длине волны 9 см.
Рассмотренная нами выше кинематическая теория магнетрона в об-
общих чертах была известна и в 30-е годы.
В 1940 г. Н.Ф. Алексеев и Е.Д. Маляров опубликовали статью [6],
в которой описали многорезонаторный разборный магнетрон с четырь-
четырьмя контурами с водяным охлаждением, который генерировал на длине
волны 9 см колебания с мощностью до 300 Вт. Макет без водяного
охлаждения при прочих равных условиях давал мощность 100 Вт. В че-
тырехрезонаторном магнетроне были также получены колебания мощ-
мощностью 2 Вт на длине волны 2,6 см. Статья Н.Ф. Алексеева и Е.Д. Маля-
рова в 1944 г. была перепечатана в ведущем техническом журнале США
«Труды института электро-радио-инженеров» [6]. Приоритет указан-
указанных авторов признается во всем мире и отмечается практически во
всех исторических обзорах или книгах по магнетрону. Война прервала
исследования магнетрона в СССР, и интенсивные работы начались
лишь после окончания войны. Интересно, что истории изобретения
магнетрона в СССР посвящено художественное произведение (Бабат Г.,
Гарф А. Магнетрон. М.: Детгиз, 1957, 901 с), одним из авторов которого
был Георгий Ильич Бабат — известный советский изобретатель, приме-
применивший, в частности, многоконтурный блок для индукционного нагрева
и использовавший в нем связки в виде колец, подобные применяемым
в магнетроне.
В предисловии к книге Бабат и Гарф пишут, на основе чего она
была создана. «Работая над этой книгой, мы пользовались, помимо
собственных воспоминаний, различными литературными источниками:
комплектами советских и зарубежных технических журналов, рядом
советских и зарубежных монографий, посвященных магнетронам...
... Однако наша работа ни в коей мере не является исчерпывающей
историей магнетрона. Мы ограничили себя рассказом только об узком
круге тесно связанных между собой лиц». Разумеется, художественное
произведение — не исторический документ, но его чтение придает яркую
эмоциональную окраску легко узнаваемым историческим событиям.
С началом войны центр исследований магнетрона переместился
в Англию. Для борьбы с ночными бомбардировками необходимо было
иметь самолетные радиолокационные станции с большей мощностью,
чем обеспечивали применявшиеся тогда триоды. Ограничением на пу-
пути развития сантиметровой радиолокации было отсутствие подходя-
подходящего генератора. Наибольшего успеха добились ученые Бирмингам-
ского университета. «Британское Адмиралтейство — пишет уже упо-
упоминавшийся нами Р. Компфнер (более подробно его роль в развитии
СВЧ-электроники обсудим в лекциях, посвященных приборам с дли-
длительным взаимодействием типа О) — учредило здесь секретную группу
по исследованию ламп под руководством профессора М.Л.Олифанта
с целью практического создания сантиметрового радиолокатора — это
Магнетрон, амплитрон и другие 219
было общее задание и оно было разделено между различными подгруп-
подгруппами. Одни занимались детекторами, другие генераторами и усилите-
усилителями и так далее. Кто-нибудь еще напишет, как вот именно в такой
группе Бут и Рэндел создали многорезонаторный магнетрон».
Пророчества Компфнера сбылись: о создании магнетрона написали
сами Бут и Рэндол [7] и известный английский писатель Чарльз Сноу
[8]. Как ни странно, чувство справедливости покинуло Бута и Рэндола,
и они не сослались на работу Алексеева и Малярова. Приведем выдерж-
выдержку из написанного Сноу [8, стр. 93-94]. «Англичанам действительно
пришлось напрячь все свои силы ради того, чтобы выжить; неудиви-
неудивительно поэтому, что в большинстве вопросов, связанных с использо-
использованием науки в военных целях, они оказались более осведомленными.
В первую очередь это касалось радаров. Хотя английские, американские
и немецкие ученые начали заниматься радарами почти одновременно —
что, кстати, дает нам повод еще раз задуматься о природе «секретных»
открытий, — к 1940 году англичане значительно опередили всех осталь-
остальных.
Тизард и Кокрофт привезли в Америку черный кожаный чемодан,
который мисс Джири, секретарша Тизарда, держала у себя под кро-
кроватью. Она не знала, что в нем хранятся почти все новые научные
приборы военного назначения, созданные в Англии, и среди них новый
магнетрон — прибор совсем иной степени важности, чем все остальные
весьма важные изобретения...
Магнетрон, созданный Рэндолом и Бутом в лаборатории Олифан-
та в Бирмингеме, оказался, быть может, самым полезным прибором
в борьбе с Гитлером. Он произвел на американских ученых настолько
сильное впечатление, что они немедленно взялись за дело и трудились
все 16 месяцев, которые у них остались до вступления Соединенных
Штатов в войну».
Приведем еще одно, более компетентное, мнение об английском
магнетроне, принадлежащее президенту Института Радиоинженеров
США Ф.Б. Левеллину, когда он вспоминал о 6 октября 1940 г. — дне
демонстрации магнетрона. «Этот день запомнился. Лампа давала вы-
выходную импульсную мощность около 10 кВт на частоте около 3000 МГц.
Это была мощность почти в 5 раз больше даваемой триодами... и, бо-
более того, частота была в 4 раза выше. Можно представить себе наш
энтузиазм!». В лабораториях фирмы Белл была снята рентгенограмма
с английского магнетрона, и уже в середине ноября 1940 г. американцы
имели несколько работающих копий английской лампы.
В конце 50-х годов в США появился первый представитель нового
класса широкополосных приборов типа М с замкнутым электронным
пучком — платинотрон (амплитрон, усилитель со скрещенными поля-
полями). Истории его создания, а также описанию некоторых его характе-
характеристик, посвящен следующий параграф лекции.
220
Лекция 7
Вильям Браун и усилитель со скрещенными полями
В середине 1957 г. в журнале Electronics появилась реклама (она
приведена на рис. 7.8 *)) нового прибора, который назывался в ней
амплитроном. Тот же номер журнала содержал статью с названием
«Платинотрон увеличивает радиус
^¦1 действия поискового радара» [9]. За-
: ^ метьте, что в рекламе прибор не на-
называется платинотроном или усили-
усилителем со скрещенными полями, как
назвали его мы в заголовке раздела,
а «амплитроном». История этого при-
прибора начинается с некоторой путани-
путаницы в его названиях. Но лучше все-
всего эту ситуацию объяснит сам созда-
создатель амплитрона — Вильям Браун.
Вот как он пишет об этом в своих
воспоминаниях [10]: «Когда прибор
был изобретен, я обозначил его как
широкополосный усилитель. Мне ну-
I йш ' ^% * жен был какой-нибудь новый термин,
щ ~ заканчивающийся на «трон». В это
rf время суффикс «трон» применялся
ко всем электронным лампам. Было
также модно находить греческие или
латинские префиксы. Поэтому я про-
проконсультировался у ученого, знающе-
знающего греческий язык, и он посоветовал
мне греческое слово «платино», зна-
значение которого соответствует широ-
широким плато-подобным качествам лам-
лампы. С тех пор я использовал термин
платинотрон для этого прибора и использовал тот же термин в названии
заархивированной журнальной статьи «Описание и рабочие характери-
характеристики платинотрона — новой микроволновой лампы», опубликованной
в 1957 году в Трудах Института радиоинженеров [11].
Однако наш менеджер по рынку сбыта в Рэйшен 2) полагал, что
термин «амплитрон» будет более привлекателен для рынка, и термин
Рис. 7.8. Реклама фирмы Рейшен
в журнале Electronics от 1 авгу-
августа 1957, описывающая характе-
характеристики платинотрона, но назы-
называемого амплитроном (из работы
[Ю])
г) Практически все иллюстрации из этого раздела взяты из статьи [10], где
приведены соответствующие ссылки на оригинальные работы.
2) Raytheon — компания, в которой работал В. Браун. Он был принят в нее
в 1940 году и формально ушел из нее в 1984 году, продолжая работать в ней
дальше в качестве консультанта. Интересно, что по служебной лестнице Бра-
Браун поднялся до заместителя вице-президента компании, но после изобретения
Магнетрон, амплитрон и другие 221
«платинотрон» быстро ушел на задний план. К сожалению, термин
«амплитрон» был уже замаркирован, поэтому, когда соперники Рэйшен
вышли на арену, они заменили термин амплитрон и стали называть
этот прибор как «усилитель со скрещенными полями», и в конце концов
Рэйшен тоже начал использовать более общий термин. Я научился
жить с этими взаимозаменяемыми наименованиями, и надеюсь, чита-
читатель поймет, когда по ходу статьи я буду ссылаться на один и тот же
прибор, называя его платинотроном, амплитроном или усилителем со
скрещенными полями... ».
Возвращаясь к рекламе в Electronics можно сказать, что для про-
прочитавших её, прибор, описанный в ней, мог показаться «удачей одной
ночи». С чем же это было связано? Не будет большой натяжкой сказать,
что 1952 год был «годом усилителя». До этого времени магнетроны
были единственными СВЧ-лампами, использовавшимися в радарах во
время II мировой войны. Но это были генераторы, не пригодные для
новых улучшенных радаров, разработанных после II мировой войны,
которые требовали широкополосных усилителей с большей мощностью.
СВЧ-усилители в то время были большими, весьма неэффективными,
к тому же, у них была ограниченная полоса частот с падением мощности
и к.п.д. на краях. Поэтому это было очень подходящее время для пре-
преобразования обычного магнетронного генератора в широкополосный
усилитель, который бы сохранил все выдающиеся свойства магнетро-
магнетрона: высокий к.п.д., способность управления очень высокой максималь-
максимальной мощностью, простоту производства и относительно низкую цену,
небольшой размер и массу.
Первым, кто понял как преобразовать магнетронный генератор
в широкополосный усилитель, был Вильям Браун A916-1999) — заве-
заведующий лабораторией магнетронных разработок в компании Рэйшен.
Лаборатория начиналась с нескольких инженеров в начале II миро-
мировой войны, а уже вскоре после окончания войны насчитывала более
400 сотрудников, около 100 из которых были инженерами. В 1952 году
сотрудники лаборатории занимались разработкой второго поколения
магнетронов для радаров и контрольных измерений, поэтому времени
на исследование преобразования магнетронного генератора в широко-
широкополосный усилитель на работе у Брауна практически не оставалось. Од-
Однако уже тогда ему было ясно, что даже новый магнетронный генератор
был непригоден для будущих, более сложных радаров и устаревал, не
успев еще возникнуть.
Поэтому все работы над новым прибором В. Браун проводил
в небольшой, но хорошо оснащенной оборудованием для электронных
тестов мастерской у себя дома.
амплитрона добровольно отказался от управленческой должности, чтобы
руководить непосредственно исследованиями нового прибора.
222
Лекция 7
Проследим, что происходит при преобразовании магнетронного ге-
генератора в широкополосный усилитель. На рис. 7.9 схематично срав-
сравниваются магнетрон с платинотроном. Напомним, что магнетрон со-
содержит анодный блок, состоящий из полостей (резонаторов), который
окружает катод, эмитирующий электроны. Магнитное поле направ-
направлено параллельно оси системы. Чтобы прибор заработал, необходимо
подать постоянное напряжение
между катодом и анодным бло-
блоком. При увеличении ускоряюще-
ускоряющего напряжения электроны поки-
покидают катод и движутся в скре-
скрещенных полях. Если еще больше
увеличить напряжение, то дрей-
дрейфовая скорость электронов будет
равна фазовой скорости высоко-
высокочастотной волны в линии переда-
передачи. В последнем случае, происхо-
происходит эффективное взаимодействие
между синхронной волной и элек-
электронами, в результате чего фор-
формируются электронные структу-
структуры — спицы, которые в цилин-
цилиндрической конструкции вращают-
вращаются вокруг оси системы и отда-
отдают высокочастотную мощность
в линию передачи с медленной
волной. Эти спицы практически
идентичны у магнетрона и плати-
нотрона.
Как пишет сам Вильям Бра-
Браун: «Оглядываясь назад, трудно
понять, почему магнетрон не был
преобразован в широкополосный
усилитель раньше». Действитель-
Действительно, та кинематическая теория ко-
которая была изложена в этой лек-
лекции была в общих чертах известна еще в 30-х годах (мы уже упоми-
упоминали об этом в связи с идеей магнетрона с бегущей волной). Анодный
блок магнетрона в том виде, в каком он применялся в магнетронных
приборах, разрабатываемых в конце II мировой войны, по-существу
есть линия передачи, нагруженная последовательностью резонирую-
резонирующих полостей. Эта нагрузка превращает линию передачи в фильтр
с полосой пропускания значительной ширины с волновым сопротив-
сопротивлением, величина которого колеблется от бесконечной на краях поло-
полосы до значения, равного волновому сопротивлению выходного тракта,
Рис. 7.9. Основное конструктивное
различие между магнетронным гене-
генератором и платинотроном — нали-
наличие у платинотрона входного устрой-
устройства, а у магнетрона — его отсут-
отсутствие. Сама электродинамическая
система имеет свойства широкопо-
широкополосного полосового фильтра. Магне-
Магнетрон работает на нижнем краю по-
полосы пропускания, в то время, как
платинотрон — гораздо выше, где
фазовый сдвиг с частотой уменьша-
уменьшается, а характерное сопротивление
легко подобрать равным волновому
сопротивлению входной и выходной
ВЧ-линий связи
Магнетрон, амплитрон и другие 223
в середине полосы пропускания. Магнетроны, разработанные в Англии,
проектировались так, что работали на нижнем краю полосы пропуска-
пропускания, что делало их резонансными приборами. У магнетрона есть всего
один вывод энергии, свободно связанный с резонирующей цепью петлей
(или щелью). Отсюда понятно, что если разорвать замкнутую систему
магнетрона, присоединить входное и выходное устройство к разорван-
разорванным концам, как показано на рис. 7.9, и заставить полученный прибор
работать в частотной области ближе к середине полосы пропускания, то
можно получить мощный широкополосный усилитель со скрещенными
полями с замкнутым электронным пучком.
Однако в 1952 году никто не мог сказать, что произойдет, если
произвести такое простое механическое преобразование. В то время
акцент делался на приборы с продольным взаимодействием, такие, как
клистрон и лампа с бегущей волной, предложенная в 1942-1943 гг. Ру-
Рудольфом Компфнером. И тем более, никто не мог предсказать, в случае
создания такого прибора, который давал бы широкополосное усиление,
будет ли такой усилитель работать в линейном режиме или в режиме
насыщения, и будет ли он генерировать на частоте, отличной от ча-
частоты входного сигнала. В итоге удачным оказался усилитель, работа-
работающий в режиме насыщения, чья мощность слабо зависела от входного
ВЧ-сигнала. При этом оказалось, что коэффициент усиления ограничен
20 дБ, а в большинстве случаев достигает только 10 дБ. В то время это
совсем не соответствовало пониманию того, что такое усилитель. Тем
на менее, платинотронный прибор быстро завоевал рынок сбыта, где
были одновременно необходимы и высокая СВЧ-мощность, и большая
ширина полосы пропускания.
Обратим внимание на некоторые особенности резонансных колеба-
колебательных систем, использующихся в магнетроне, без знания которых
невозможно понимание свойств усилителя со скрещенными полями. Ко-
Колебательная система магнетронного генератора представляет собой, по
существу, широкополосную замедляющую систему того или иного вида,
свернутую в кольцо и замкнутую на себя. При этом колебательная систе-
система (анодный блок) приобретает резонансные свойства. При возбужде-
возбуждении в замкнутой колебательной системе устанавливается стоячая волна,
которая может быть представлена в виде двух вращающихся навстречу
друг другу бегущих волн. Условие G.1) определяет возможные виды
колебаний резонансной колебательной системы, характеризующиеся
различными фазовыми сдвигами на период </?о = 2тгп/7У, а следова-
следовательно, различными частотами и распределениями поля в пространстве
взаимодействия. Так как распределение поля каждой из бегущих волн,
образующих в колебательной системе стоячую волну, отличается от
гармонического, то каждая из этих волн может быть разложена в ряд
по пространственным гармоникам, которые имеют различную угловую
скорость и одинаковую частоту. Тогда, для фазового сдвига на один
224 Лекция 7
период замедляющей системы можно записать
(рт = ^0 + 27гш, т = 0,±1,±2,±3..., G.35)
где (рш — фазовый сдвиг т-й пространственной гармоники. Если ?1т —
угловая фазовая скорость m-й пространственной гармоники, то величи-
величина и/0>т — угловое волновое число. При сдвиге на один период систе-
системы азимутальная координата меняется на величину 2tt/7V — угловой
период системы, а, следовательно, фазовый сдвиг на период можно
представить в виде
Приравнивая соотношения G.35) и G.36) и учитывая формулу G.1),
для угловой скорости ттг-й пространственной гармоники n-го вида ко-
колебаний можно записать
п + Nm
где ujn — угловая частота n-го вида колебаний.
Для тг-вида колебаний (п = N/2) угловая скорость имеет вид:
Обычно в магнетроне используются гармоники с номерами О, ±1. Из со-
соотношения G.38) видно, что угловые скорости нулевой (т = 0) и первой
обратной (т = — 1) гармоник основного вида равны и противоположны
по направлению.
Как уже отмечалось в начале лекции, важным является добиться
стабильности работы магнетронного генератора. При работе на тг-виде
колебаний возможность возбуждения паразитного вида колебаний зна-
значительно уменьшается, если частота основного (п = А^/2) и первого
паразитного (п = 7V/2 — 1) видов колебаний достаточно разделены.
Наиболее эффективным способом такого разделения является примене-
применение в качестве колебательных систем магнетрона замедляющих струк-
структур с аномальной дисперсией. Такие структуры обеспечивают вблизи
частоты отсечки наибольшее разделение частот при переходе от основ-
основного вида колебаний к паразитным, в отличие от систем с нормальной
дисперсией [13, стр. 46; рис. 1.19]. Заметим, что типичными примерами
электродинамических структур с аномальной дисперсией, используе-
используемых в магнетронах, являются гребенка со связками (в дециметровом
и сантиметровом диапазоне; см. рис. 7.1 в) и разнорезонаторные гре-
гребенчатые системы (в нижней части сантиметрового и миллиметровом
диапазонах рис. 7.16).
Для нас наиболее важно то, что используемая в магнетронном гене-
генераторе, а следовательно, и в платинотронном усилителе колебательная
система обладает аномальной дисперсией, т. е. в ней распространяются
Магнетрон, амплитрон и другие 225
волны, фазовая и групповая скорости которых противоположно направ-
направлены. Это означает, что электронный пучок в амплитроне взаимодей-
взаимодействует с обратной волной, фазовая скорость которой равна дрейфовой
скорости электронов, а энергия распространяется навстречу пучку. По
существу, амплитрон является усилителем обратной волны.
Однако вернемся к истории создания амплитрона. Широкополосный
усилитель со скрещенными полями и с замкнутым электронным пучком
был создан в 1952 году. Как же был достигнут в итоге успех в создании
такого прибора? Обратимся опять к воспоминаниям В. Брауна [10]:
«За несколько лет до 1952 года я в принципе уже работал с простой
модификацией магнетрона. Но я не ожидал хорошего результата от
небольшого количества секций (соответствующих небольшому количе-
количеству резонаторов). В лаборатории мы создавали и испытывали лампы
с большим количеством секций, от 60 до 80. Эти лампы... делали... не
для того, чтобы создать усилитель.
На этом этапе создания прибора можно отметить, что «отчаяние —
мать изобретения». Настроенный таким образом, я решил попробо-
попробовать самую простую конструкцию, в которой было всего 11 секций.
Колебательная система была сконструирована так, чтобы получить
максимальное волновое сопротивление. Я решил проводить опыты сам,
чтобы отметить все нюансы, которые могли бы привести к лучшему
пониманию того, как можно преобразовать магнетронный генератор
в широкополосным усилитель.
Была сконструирована лампа, обозначенная как QK 403. Из-за своих
обязанностей менеджера мне приходилось проводить испытания только
по вечерам. Я начал испытывать лампу как генератор с нагрузкой
и изменяемым отражением на обоих концах.... я с удовольствием отме-
отметил большую разницу в выходной мощности, которая изменялась при
изменении полярности магнитного поля. Это очень обнадеживало, так
как указывало на направленное усиление. Однако было уже поздно,
поэтому я выключил прибор и пошел домой. На следующий вечер я
решил проверить предыдущие результаты прежде, чем продолжить
испытания усилителя, и был поражен, обнаружив, что не могу их вос-
воспроизвести. Затем последовало несколько вечеров интенсивной работы
по проверке каждого возможного изменения, которое могло произойти
во время испытания. Я начал думать, что то, что я видел раньше, было
иллюзией. И, наконец, с последней надеждой я снял колпак с лампы
и с облегчением обнаружил, что одна из лопастей расплавилась. Оче-
Очевидно, концы лопасти попались достаточно хрупкие, и так как я хотел
сохранить высокое сопротивление, расплавились как раз в тот момент,
когда я отключил прибор тем вечером. Была поспешно сконструирована
вторая лампа, и 18 декабря 1952 года мне удалось повторить прежние
наблюдения и продолжить получение новых данных по направленным
свойствам прибора ... [было] достигнуто усиление в 9 дБ при частоте
8 Д. И. Трубецков, А. Е. Храмов
226
Лекция 7
32
28
24
20
16
12
о
о
4
' DRIVE LEVEL POWER 2.6 KW
- DRIVE FREQ. 3821 MHZ
GAIN - 9.6Ш»
- QK304# y/
0 123456789 ^
QK 304 ANODE
a CURRENT-PEAKAMPERS б
Рис. 7.10. Первые данные, полученные от платинотрона QK 403, который
работал как усилитель и показал однонаправленное усиление (а); если маг-
магнитное поле изменялось так, чтобы поток электронов двигался в другом
направлении вокруг катода, вход и выход лампы менялись местами. Внешний
вид QK 403 [10] (б)
от 3780 до 3850 МГц. Максимальная мощность была 24 кВт, а к.п.д.
порядка 40 %. Эти данные показаны на рис. 7.10а».
Вильям Браун сохранил амплитрон QK 403, на котором были сдела-
сделаны первые измерения, и передал его в MTT-S историческую коллекцию
в 1987 году. Фотография лампы, позволяющая представить вид и раз-
размеры первого амплитрона, приведена на рис. 7.105.
Однако вначале новый усилитель не вызвал особого интереса и, как
утверждает Браун, «все могло закончиться крахом», если бы не по-
помощь войск связи США, которых заинтересовал новый прибор. В июне
1953 года в Оттаве на конференции по использованию электронных
ламп (мы еще упомянем эту конференцию в рассказе об изобретении
лампы бегущей волны: именно там Рудольф Компфнер «не узнает»
изобретенную им ЛБВ) платинотрон был рассмотрен экспертами армии
США, и группа сотрудников компании Рэйшен во главе с Брауном стала
разрабатывать платинотрон в качестве замены «рабочей лошадки»
радаров того времени — магнетрона 5J26. Именно эта конструкция
магнетрона стала прообразом амплитрона QK 434 (некоторые кон-
конструктивные части 5J26 непосредственно использовались в QK 434).
Получившаяся лампа показана на рис. 7.11: крышка QK 434 снята,
чтобы было видно его внутреннее устройство.
Именно эта лампа имела огромный успех. Амлитрон QK 434 был
продемонстрирован в качестве усилителя и высоко стабильного гене-
генератора (принцип стабилотрона) на специальном симпозиуме в Форте
Монмаут в 1954 году. Как пишет Вильям Браун, после этого симпози-
симпозиума всем стало ясно, что магнетронный генератор был преобразован
в широкополосный усилитель со многими желаемыми свойствами.
Магнетрон, амплитрон и другие
227
_ Резонатор
Фазовращатель
Отражающий
элемент
) = 2пп z^^-=
Рис. 7.11. (а) На фотографии представлен амплитрон QK 434; частота и мощ-
мощность такие же, как у QK 403, с которым он сравнивается на фотографии.
Разработанная в течение одного года, с 1953 по 1954, по контракту с вой-
войсками связи США, лампа QK 434 давала стабильное усиление до 16 дБ,
максимальные уровни мощности на выходе от нескольких сотен киловатт
до 3 МВт, средняя мощность порядка 1500 Вт; к.п.д. ~ 60 % для нормальных
диапазонов изменения мощности, и до ~ 76 % для высокомощных режимов
с низким усилением (из работы [10]). (б) Принципиальная схема стабило-
трона. (в) Зависимость фазового сдвига от частоты: штриховая линия —
нестабилизированная система, сплошная — стабилизированная внешним вы-
высокодобротным резонатором
По-видимому, самым удивительным свойством амплитрона являет-
является направленность усиления, которую теоретически первым объяснил
Домбровски (см., например, [13,14]). На языке теории возбуждения вол-
волновода заданным током это объяснение выглядит элементарно. Пред-
Предположим, что в электронном потоке амплитрона возникла волна тока
г = % ехр
G.39)
где vo = E°IВ, возбуждающая поле в колебательной системе прибора.
Для доказательства направленности усиления достаточно ограничить-
ограничиться приближением заданного тока и учесть, что амплитрон является
усилителем обратной волны. Подставляя выражение G.39) для тока г
228 Лекция 7
в уравнение возбуждения волновода A.72), получим:
Е(х) = Eoe
Здесь учтено, что в усилителе обратной волны входной сигнал Е°
поступает в конце пространства взаимодействия х = /, поэтому его
записывам в виде Е° ехр [—jРо(% — I)]-
Из уравнения возбуждения G.40) нетрудно видеть, что при условии
синхронизма uj/vo = /?о «резонансным» оказывается только первый
интеграл. Этим и доказывается однонаправленность усиления. Оче-
Очевидно, что при смене направления магнитного поля меняет знак vq и
«резонансным» становится второй интеграл.
Впервые усилитель со скрещенными полями был применен в по-
поисковом радаре в ракетной системе Hawk Missile System. Но там он
использовался как высоко стабилизированный генератор под названием
«стабилотрон» [12, 13]. Принцип стабилотрона был предложен Эрлом
Шелтоном. В этом приборе используется наиболее важное свойство
платинотрона— направленное усиление. Без подачи мощности питания
лампа прозрачна для высокочастотного сигнала в полосе пропускания,
где она работает. Сигнал, поступивший на один из элементов связи,
проходит к другому концу неизмененным, за исключением небольшого
затухания, которое вызывается «холодным» затуханием в СВЧ-цепи
(обычно десятая часть децибелла). Но если входной сигнал подается
на работающую лампу, то усиление происходит только в одном направ-
направлении, в зависимости от направления магнитного поля. Поэтому если
какая-то часть усиленного сигнала отражается от нагрузки выходного
тракта платинотрона, она проходит обратно по лампе, слабо взаимодей-
взаимодействуя со спицами, и достигает ввода энергии с небольшим ослаблением.
Отсюда очевидно, что если к отражению на выходе добавить полное
отражение на входе, то платинотрон превратится в генератор, частота
которого будет определяться фазовыми соотношениями в цепи обрат-
обратной связи. Для стабилизации спектральных характеристик такого гене-
генератора в цепь обратной связи вводится высокодобротный контур. Так
был создан стабилотрон.
Рассмотрим принцип его работы (рис. 7.116, [13]). Пусть на входе
платинотрона появляется шумовой сигнал. Часть сигнала отразится от
отражающего элемента в плоскости 1 и начнет двигаться в обратном
направлении. Эта отраженная мощность проходит без затухания через
замедляющую систему платинотрона, фазовращатель и попадает на
Магнетрон, амплитрон и другие 229
вход резонатора, расположенного в плоскости 2. Волна, отразившаяся
от плоскости 2, поступает на вход платинотрона, усиливается в нем,
и вновь попадает в выходную плоскость 1, где вновь отражается и т. д.
Таким образом цепь обратной связи замыкается, причем условия поло-
положительной обратной связи будут обеспечиваться только для тех частот,
для которых полный фазовый сдвиг в в цепи обратной связи равен 2тгп,
п = 1,2,3....
Основным элементом, стабилизирующим частоту генератора, явля-
является резонатор, подключенный к плоскости 2. Поскольку фаза коэффи-
коэффициента отражения от эквивалентной плоскости резонатора вблизи соб-
собственной частоты резонатора /о является быстропеременной функцией
частоты, полный фазовый сдвиг по замкнутому контуру генератора О
вблизи резонансной частоты /о испытывает резкий скачок. Для цепи
обратной связи без высокодобротной резонирующей нагрузки фазовый
сдвиг при изменении частоты меняется плавно и медленно. Тогда, если
условия положительной обратной связи выполняются как раз на резо-
резонансной частоте резонатора, то в этом случае стабилотрон устойчиво
генерирует на частоте /о.
Действительно, пусть (см. рис. 7.Не) в силу тех или иных причин
(изменение параметров нагрузки, линии передач и т. п.) полный фазо-
фазовый сдвиг в в системе изменился на некоторую величину АО. В неста-
билизированной системе это приведет к значительному изменению ча-
частоты А/нест, а в системе стабилизированной резонатором, благодаря
резкому скачку фазового сдвига вблизи резонанса, величина А/Ст <С
<С А/нест- Величина А/неСт/А/ст характеризует степень стабилизации
и имеет значение порядка 200 -г- 400 [11]. Отсюда также понятно, что для
изменения частоты генерации стабилотрона необходима одновременная
подстройка фазовращателя и стабилизирующего контура. Таким об-
образом, стабилотрон представляет собой генератор, высокоустойчивый
к различным как внешним, так и внутренним возмущениям.
Для сравнения в таблице 7.1 приведены данные по стабилотрону
QK 630, созданному на базе QK 434, и аналогичные параметры маг-
нетронного генератора 5J26 (см. рис. 7.12), выходные характеристики
(частота и мощность) которого аналогичны стабилотрону.
Следующим этапом разработки амплитрона под руководством Ви-
Вильяма Брауна стало исследование возможности создания сверхмощной
лампы на частоте порядка 3 ГГц, которая работала бы на уровне по-
постоянной мощности на выходе в 400 кВт [15]. Понятно, что разработка
таких устройств требует больших финансовых затрат. И здесь на по-
помощь Брауну приходит случай. Вот как он пишет об этом.
«Естественно, незатребованное предложение разработки такой
сверхмощной лампы вызвало бы мало поддержки со стороны прави-
правительства. Однако совершенно случайно, неожиданное международное
событие заставило правительство благоприятно отозваться на такое
230
Лекция 7
>-Л/\
Импульс тока A7 мкс)
118 1 -""•
МГц И
Спектр стабилотрона
1500 МГц »
Спектр магнетрона
Рис. 7.12. Показан яркий контраст в характеристиках обычного 5J26 магне-
магнетрона и платинотрона, действующего как стабилотрон при импульсе в 17 ми-
микросекунд с «плохой» формой импульса тока. Стабилотрон имеет почти тео-
теоретический спектр для импульса такой длительности, тогда как у магнетрона
5J26 он «рассыпался» на интервал 1500 МГц (из работы [10])
Таблица 7.1
Характеристики лампы
Затягивание частоты, МГц
Электронное смещение
частоты, кГц/А
Ток в импульсе, А
Напряжение в импульсе, кВ
Магнитное поле, Гс
К.п.д., %
Выходная мощность, кВт
Область механической
перестройки, МГц
Стабилотрон QK 630
0,4^-0,6
1 -=- 4
40
36
1150
52
650
1260 -=- 1350
Магнетрон 5J26
2^-2,5
50 -=- 100
46
28,2
1400
42
550
1220 -=- 1350
предложение. Этим событием был спутник, а ответом — Научно-
исследовательское Агенство по Передовым Технологиям Оборонного
характера (the Defence Advanced Research Projects Agency — DARPA).
Агенство занималось поиском передовых технологий. Рейшен, ведущая
фирма-новатор в области новых электронных технологий, представила
Агенству системное предложение, называемое RAMP, акроним
Raytheon Airborne Microwave Platform. Предложенный сверхмощный
амплитрон был ключевым компонентом этой системы, в которой
СВЧ-луч высокой мощности, сформированный на Земле, концентри-
концентрировался на платформе вертолета, действующего на высоте в 10 миль
над Землей, чтобы обеспечить вертолет энергией, осуществлять связь
и выполнять функции наблюдения. Этот проект получил некоторые
деньги на исследование, но разработка сверхмощного амплитрона была
финансирована полностью. На амплитрон с непрерывной мощностью
в 400 кВт и сверхмощный импульсный амплитрон с мощностью
50 МВт было выделено свыше шести миллионов долларов. В качестве
Магнетрон, амплитрон и другие 231
своего вклада в программу компания Рейшен построила лабораторию
по сверхмощным разработкам. Меня назначили руководителем
этой программы, в которую входили разработки не только по
сверхмощному амплитрону, но также и практическому применению
высокочастотной энергии, включая промышленную микроволновую
обработку материалов и первые разработки систем беспроводной
передачи энергии, о которой более подробно мы раскажем ниже.
Разработка мощного амплитрона непрерывного действия была
успешной: была создана лампа с мощностью 425 кВт при к.п.д. 76%
и шириной полосы пропускания 8 % ... Если посмотреть назад, то
можно считать программу по созданию сверхмощных источников
СВЧ-излучения аномальной, которая не часто возникает в мирное
время, и хотя полученные лампы было большим шагом вперед
в технологии, они не были такой насущной необходимостью, как
магнетроны во время II мировой войны... Поэтому вскоре эта
программа потускнела».
Интересно также то, что программа разработки сверхмощного ам-
амплитрона помешала Брауну организовать собственную компанию по
разработке и использованию маломощных платинотронов, для чего не
требовалось дорогостоящее и сложное оборудование, но вовлекла его
в еще один очень важный и новый проект. Дело в том, что когда уже
все было готово к его уходу из Рейшен, в дело вмешался «спутник»,
и Браун получает финансирование от министерства обороны США.
В результате он остается в компании Рейшен и через некоторое время
становится главой нового проекта, связанного теперь уже с лампа-
лампами низкой мощности. В нем амплитрон используется для передачи с
высоким качеством данных с приземлившегося на Луне космического
карабля Аполло на Землю. Но предоставим вновь слово Брауну [10].
«...в наши разработки в новой лаборатории я включил все до-
достижения, которых добился при работе над лампами с низкой мощ-
мощностью. В итоге, работа с низкими мощностями привела к предложе-
предложению использовать усилитель со скрещенными полями в передатчике...
... в лунном модуле программы Аполло. Мощность на выходе [разрабо-
[разработанного усилителя QKS 1300] была 24 Вт, что в несколько раз больше
того, чего надежно достигали твердотельные усилители в то время...
... Два усилителя со скрещенными полями включались каскадно (вход
второй лампы соединялся с выходом первой). Если катод одной из
ламп отказывал (самая вероятная неполадка), эта лампа все еще была
бы прозрачна либо для передачи входной мощности, либо выходной
мощности сопутствующей лампы. Фотография лампы QKS 1300 приве-
приведена на рис. 7.13. ... эта работа по программе Аполло была успешной.
Все высококлассные данные, включая видео, между Луной и Землей
передавались с помощью усилителя со скрещенными полями. Хотя
лампа успешно использовалась в программе Аполло, обнаружилось,
232
Лекция 7
что средняя продолжительность жизни ламп, апробированных в про-
процессе разработки программы до их применения в лунном модуле, была
всего 1000 часов. Неудача вы-
вызвана бомбардировкой электро-
электронов, разрушающей катод лампы.
Тогда мы не поняли, что этого
бы не произошло с цементиро-
цементированным торированным вольфра-
вольфрамовым катодом, таким, как тот,
который используется в обычном
магнетроне для микроволновой
печи. Если бы мы это поняли,
усилитель на скрещенных полях
с цементированным торирован-
торированным вольфрамовым катодом, воз-
возможно, сыграл бы значительную
роль в системах связи».
Что еще можно сказать об ам-
плитроне? Во-первых, он исполь-
использовался в качестве элементов це-
цепочек СВЧ-генераторов. Основ-
Основным недостатком усилителей со
скрещенными полями было низ-
низкое усиление, поэтому их приме-
Рис. 7.13. Амплитрон QKS 1300,
работающий в диапазоне частот
2,8 -г 3,2 ГГц, использовался для пе-
передачи высокого качества данных
с лунного модуля на Землю в про-
программе НАСА Аполло. Он обеспечи-
обеспечивал усиление в 17 дБ и выходную
мощность 25 Вт (из работы [10])
няют как элемент СВЧ-цепочки в
соединении с другим усилителем со скрещенными полями с низкой мощ-
мощностью, а затем с лампой бегущей волны с высоким усилением. В неко-
некоторых случаях лампа бегущей волны запускала оконечный усилитель
со скрещенными полями напрямую. Во-вторых, некоторые имеющиеся
перспективы повышения усиления платинотрона до 30 дБ (например,
использование в качестве катода эмиттирующей замедляющей систе-
системы; Джордж МакМастер) делают вполне логичным выбор амплитрона
в самых различных приложениях, где требуется высокое усиление при
достаточно высоком уровне мощности и к.п.д.
Вильям Браун в своей обзорной работе обращает внимание на
еще одну возможную область применения магнетрона как усилителя.
«Необычным изменением направления в технологии обычный магне-
тронный генератор может быть превращен при помощи внешней элек-
электронной схемы в регенеративный усилитель с высоким усилением C0 дБ
и выше)... и стать модулем в электронно-управляемой фазовой антен-
антенной решетке с целью беспроводной передачи мощности. Такие усили-
усилители — узкополосные, однако, беспроводная передача мощности будет
использовать только одну частоту, поэтому широкополосные устрой-
устройства и не требуются».
Магнетрон, амплитрон и другие 233
Осознавая важность исследований возможности беспроволочной пе-
передачи энергии с помощью СВЧ-излучения, Браун принял участие
в программе НАСА, целью которой было создание системы, передаю-
передающей со спутника на Землю до 5 миллионов ватт — энергию достаточную
для жизнеобеспечения среднего города. Им была разработана ключевая
часть этой системы — ректенна — устройство, поглощающее ВЧ-из-
лучение, превращая его в постоянный ток [16, 17]. Программа НАСА
была свернута в связи с недостаточностью финансирования, однако,
Вильям Браун продолжал работать над данной тематикой, но теперь
уже по контракту с ВВС США. В 1964 году, как уже упоминалось, он
продемонстрировал вертолет, движущийся за счет энергии, передавае-
передаваемой ему по СВЧ-лучу. Ключом к этому полету опять стала ректенна,
эффективность (т. е. отношение силы постоянного тока на выходе к силе
постоянного тока на входе ректенны) которой была существенно выше
разработанной им раньше. С 1969 по 1975 год Браун был техническим
директором программы Рейшен, направленной на создание системы
передачи энергии по СВЧ-лучу на расстояние одной мили, включающей
в себя мощный высокоэффективный передатчик СВЧ-энергии и ректен-
ну, которая перехватывала СВЧ-луч и превращала его в постоянный ток
с мощностью 30 кВт при к.п.д. 84 %. Вклад В. Брауна в разработки пере-
передачи энергии с помощью СВЧ-излучения был весьма велик. Так книга
«Solar Power Satellites: A Space Energy System for Earth» / Eds Glaser
Peter E., Davidson Frank Paul, and Csigi, Katinka I. Wiley Praxis Series in
Space Science and Thehnology A998), посвященная вопросам создания
электростанций в космосе и передаче с них энергии по СВЧ-лучу, была
посвящена Вильяму Брауну.
Заметим, что в программе разработки беспроводной передачи энер-
энергии ключевым элементом опять же было создание амплитрона, а, точ-
точнее, сверхмощного усилителя на скрещенных полях. Как уже отмеча-
отмечалось выше, только та часть программы, которая касалась амплитрона,
была профинансирована полностью.
Интересно, что Вильям Браун сыграл большую роль и в такой обла-
области применения СВЧ-техники, как создание нагревательных и других
СВЧ-устройств, не используемых для коммуникации. Браун принимал
участие в разработке идеи СВЧ-печи и других промышленных уста-
установок, связанных с СВЧ-нагревом. В середине 60-х годов Браун и его
коллеги основали Международный институт микроволновой энергии,
а в скором времени, сформировался успешно функционирующий рынок
СВЧ-печей [17].
В последние годы жизни Вильям Браун работал в своей домаш-
домашней лаборатории в первую очередь над развитием систем передачи
СВЧ-энергии. Он выступал и как популяризатор, проводя публичные
демонстрации такой передачи энергии на различных встречах и прие-
приемах, для телевидения. Эти работы Брауна не были до конца оценены
современниками. Однако в этом вопросе Браун нашел союзника в лице
234 Лекция 7
Петра Леонидовича Капицы. В начале 80-х годов Капица посетил ряд
научных учреждений США. Во время визита он произнес следующее
«пророчество», навеянное в том числе и работами Вильяма Брауна [17,
р. 44]: «Следует отметить, что раньше радиофизика и электроника со-
состояли на службе у энергетики и решали исключительно коммуникаци-
коммуникационные проблемы (телеграф и другие средства связи). В настоящее время
электроника используется в основном в сфере радиокоммуникаций, но
её будущее тесно связано с передачей энергии».
Карматрон и дематрон
Как обсуждалось выше, электронный пучок в амплитроне взаи-
взаимодействует с обратной волной, т.е. он представляет собой прибор,
в котором имеет место положительная обратная связь. Поэтому как
показал эксперимент, амплитрон при отсутствии внешнего сигнала или
в случае, когда внешний сигнал мал, имеет на выходе шумоподобный
сигнал, частота и амплитуда которого не зависят от входного сигнала.
Такое поведение связано с тем, что амплитрон находится в предге-
нерационном режиме и устанавливающаяся обратная связь случайна.
Действительно, скорость пучка, а следовательно, генерируемая частота
определяется анодным напряжением, которое, в свою очередь, зависит
от анодного тока. Как только в системе устанавливается некоторая
«случайная» волна, начинает протекать анодный ток, в результате ме-
меняется анодное напряжение, а также скорость пучка. Происходит срыв
генерации на одной частоте и установление нового режима, который
снова приводит к изменению анодного тока и т. д. Процесс усложняется
еще и тем, что электронный пучок замкнут и поддерживает волны
только с определенными характеристиками.
В работах [18, 19] обсуждается широкополосный генератор типа М
с замкнутым электронным пучком, схема которого ничем принципи-
принципиально не отличается от схемы амплитрона, работающего в вышеопи-
вышеописанном «генераторном» режиме. В этом приборе — карматроне — ис-
используется иная замедляющая система, чем в амплитроне — система
встречноштыревого типа [13], нагруженная на конце, где у амплитрона
располагается ввод усиливаемого сигнала, на согласованную нагруз-
нагрузку для предотвращения отражений от конца замедляющей системы.
В отличие от платинотрона, карматрон может стабильно генерировать
при достаточно высоком уровне выходной мощности. Такое различие
в характере генерации в амплитроне и карматроне связано с тем, что
замедляющая система последнего имеет большее сопротивление связи,
что позволяет при тех же характеристиках пучка перейти в режим
стацонарной генерации.
Экспериментальные исследования [19] показали, что карматрон об-
обладает достаточно высокими выходными характеристиками. При за-
заданном магнитном поле в приборе наблюдались интенсивные колеба-
Магнетрон, амплитрон и другие 235
ния, которые возрастали при подъеме анодного напряжения. При этом
с ростом выходной мощности увеличивался анодный ток и возраста-
возрастала частота генерируемых колебаний. Изменение анодного напряжения
позволяло перестраивать частоту примерно в 10 %-й полосе частот.
Наибольшая выходная мощность РВых — 2,6 кВт с к.п.д. около 70%
была достигнута на частоте 420 МГц. В работе [18] отмечено, что к.п.д.
карматрона повышается с ростом амплитуды ВЧ-поля (так же как
и в магнетроне). Это связано [13] с ростом сопротивления связи при
приближении пучка к замедляющей системе.
Таким образом карматрон может быть интересен как генератор,
сочетающий высокую выходную мощность с быстрой безинерционной
перестройкой частоты в небольших пределах.
Другим прибором, который, также как и карматрон, появился во
многом благодаря созданию платинотрона, является дематрон (или
ультрон) — широкополосный усилитель прямой волны с замкнутым
пучком [14]. Отличие ультрона от платинотрона в типе замедляющей
системы. В ультроне используется замедляющая система с нормаль-
нормальной дисперсией, для которой справедливо соотношение dv$/du < 0.
Использование системы с нормальной дисперсией позволяет ожидать
более широкую полосу усиливаемых частот, чем в амплитроне.
Экспериментальный ультрон SFD-202, разработанный фирмой CSF
во Франции, имел следующие выходные характеристики [13]:
Выходная мощность 1 МВт;
Частота 3 ГГц;
Усиление 15 дБ;
Полоса усиления 10 %;
к.п.д. 60%.
Список литературы
1. Коваленко В.Ф. Введение в электронику сверхвысоких частот. —
М.: Сов. радио, 1951.
2. Вайнштейн Л.А., Солнцев В.А. Лекции по сверхвысокочастотной
электронике. — М.: Сов. радио, 1973.
3. Вайнштейн Л.А. Электромагнитные волны. — М.: Сов. радио,
1957.
4. Капица П.Л. Электроника больших мощностей. — Изд-во АН
СССР, 1962.
5. Brittain J.E. The magnetron and beginning of the microwave age //
Phys. Today. 1985. V. 33, № 7. P. 60.
236 Лекция 7
6. Алексеев Н.В., Маляров Д.Е. Получение мощных колебаний маг-
магнетронов в сантиметровом диапазоне волн // ЖТФ. 1940. Т. 10,
№ 15. С. 1297. (Proc. IRE. 1944. V. 32. Р. 136).
7. Boot Н.А.Н., Randall J. Т. Historical notes on the cavity magnetron //
IEEE Trans, on ED. 1976. V. ED-23, № 7. P. 724.
8. Сноу Ч.П. Две культуры. — M.: Прогресс, 1973.
9. Brown W.C. Platinotron increases search radar renge // Electronics.
August 1, 1957
10. Brown W. С The History of the Crossed-field Amplifier // IEEE MTT-
S Newsletters. Fall 1995. V. 141. P. 29.
11. Brown W.C. Description and operating characteristics of the
platinotron — a new microwave tube device // Proceedings of the IRE.
September 1957. V. 45, № 9. P. 1209. (Существует русский перевод в
кн. [14]).
12. Brown W.C. The Platinotron: «Amplitron and Stabilotron». — in
Okress, Crossed Field Microwave Devices, Akademic Press, 1961. V. 2.
P. 165.
13. Стальмахов B.C. Основы электроники сверхвысокочастотных
приборов со скрещенными полями. — М.: Сов. радио, 1963.
14. Электронные сверхвысокочастотные приборы приборы со скре-
скрещенными полями / Пер. с англ. под ред. М.М. Федорова. — М.:
Изд-во иностр. лит., 1961, Том П.
15. Brown W. С. «The Amplitron: A super power microwave generator" //
Electron Progress. July/Aug 1960. V. 5, № 1. P. 1.
16. Brown W. С The history of power transmission by radio waves // IEEE
Trans. Microwave Theory Tech., Special Cenntennial Historical Issue.
1984. V. MTT-32, № 9. P. 1230.
17. Staecker P. William C. Browm: A Few Introductory Comments //
IEEE MTT-S Newsletters. Spring 1999. V. 151. P. 43.
18. Doehler O., Epsztein В., Arnaud J. Operation characteristics of the
Carmatron Tube // Proceedings of the IRE. 1958. V. 105B, № 10.
P. 529.
19. Warnecke R., Nalot J., Epsztein В., Doehler O. La carmatron, nouvel
oscilateur a large band d'accord electronique // Comptes Rendus. 1955,
Septembre. t. 241, No 11. P. 695.
Лекция 8
ПРОСТРАНСТВЕННЫЙ ЗАРЯД В СКРЕЩЕННЫХ
ПОЛЯХ
Вайнштейн с Рошалем были в новой роли:
В Саратов привезли на зимние гастроли
Свой вариант принцессы Турандот.
Бедняжка девою останется на троне,
Поскольку трех загадок в магнетроне
Принц-инженер Калаф не разберет.
Из фольклора 2-й зимней школы-се-
школы-семинара инженеров. Саратов, 1972.
Пространственный заряд в скрещенных полях и три загадки магне-
магнетрона (свойства магнетрона при магнитном поле больше критиче-
критического, когда генерации нет; начало генерации в магнетроне; есть ли
вообще стационарный режим генерации в магнетроне). Неустойчи-
Неустойчивость электронного потока в скрещенных полях. Вычислительная фи-
физика и магнетрон. Связь с проблемой турбулентности в электронном
потоке. Сложная динамика пространственного заряда в усилителе со
скрещенными полями.
Данная лекция посвящена рассмотрению вопросов учета влияния
пространственного заряда в теории магнетронных приборов. Вопросы
учета пространственного заряда в теории любого сверхвысокочастот-
сверхвысокочастотного прибора — самые сложные, требующие обычно привлечения чис-
численного моделирования [1]. Вместе с тем проблема пространственного
заряда, кроме очевидного физического интереса, черезвычайно важна
с практической точки зрения, так как позволяет определить предель-
предельные возможности прибора: для мощных приборов — максимальную
мощность (так как, например, в магнетроне слишком сильный про-
пространственный заряд в спицах приводит к их разрушению); для усили-
усилительных приборов — минимальный шум (вызываемый флуктуациями
в электронных потоках) и т. д.
В данной лекции мы остановимся на трех состояниях магнетрона:
1) негенерирующий магнетрон (магнитное поле больше критическо-
критического);
238 Лекция 8
2) магнетрон в начале генерации (переход от предгенерационного
режима в режим генерации);
3) магнетрон в режиме развитой генерации (когда сверхвысокоча-
сверхвысокочастотное поле является достаточно сильным). В первой половине лекции
будут перечислены вопросы, возникающие в связи с этими состояниями
(а в других состояниях магнетрон как таковой вообще находиться не мо-
может!) и представлены некоторые качественные рассмотрения, дающие
предварительную физическую трактовку в этих вопросах. Вторая часть
лекции посвящена рассмотрению того, что может дать вычислительная
физика в ответах на вышеобозначенные вопросы.
Хочется отметить, что в последние несколько лет появился ряд
работ (например, работа R.W. Lemke, Т.С. Genoni, Т.A. Spencer, 1999 г.
[2]), в которых на мощных вычислительных машинах решались задачи
полномасштабного моделирования магнетрона с помощью самосогласо-
самосогласованной системы уравнений Максвелла-Власова в 2,5 и даже 3-х измере-
измерениях, аналогичные рассмотренным в этой лекции. Однако результаты
и этих исследований оставляют ряд вопросов теории влияния простран-
пространственного заряда на работу магнетрона до сих пор открытыми. Вместе
с тем такие модели позволяют весьма точно рассчитывать реальные
приборы, проводя оптимизацию самых различных параметров проек-
проектируемых устройств [3, 4].
Пространственный заряд в скрещенных полях
и три загадки магнетрона. Неустойчивость
электронного потока в скрещенных полях
Прежде чем переходить к анализу влияния пространственного заря-
заряда на работу магнетрона, определим, что будет пониматься под сильным
пространственным зарядом [1]. Это заряд, плотность которого р ~ рс,
рс — критическая плотность, равная величине
_
Рс -
с
где Н — напряженность магнитного поля. Слабый пространственный
заряд имеет место в случае, когда р <С рс- Критическая плотность рс
имеет для магнетрона такое же важное значение как и критическое
значение магнитного поля Вкр. Физический смысл рс заключается
в следующем. Перепишем формулу (8.1) в виде
В правой части здесь стоит плотность магнитной энергии или давление
магнитного поля. Как известно, однородное магнитное поле оказывает
фокусирующее действие на протяженные пучки, направленные вдоль
Пространственный заряд в скрещенных полях 239
него, предохраняя их от разлетания под действием сил пространствен-
пространственного заряда (цилиндрические пучки при р < рс/2, плоские при р < рс).
Аналогичную функцию выполняет магнитное поле в магнетроне — оно
до некоторой степени компенсирует силы расталкивания в электрон-
электронных спицах, образующихся в работающем магнетроне. Соотношение
(8.2) показывает, до каких плотностей рс магнитное поле еще может
удержать электронные структуры от разрушения силами простран-
пространственного заряда. Иначе соотношение (8.1) может быть получено путем
приравнивания плазменной частоты электронного облака ljp, которая
определяется его плотностью, и циклотронной частоты о;с, соответству-
соответствующей магнитному полю в магнетроне. Плотность пространственного
заряда, существенно превышающая величину критической плотности,
существовать не может.
Первая загадка магнетрона — это его свойства при маг-
магнитном поле больше критического, когда генерации нет. В от-
отсутствии пространственного заряда все ясно — электроны в плоском
магнетроне возвращаются к катоду по циклоиде, в цилиндрическом —
по более сложной траектории. При сильном пространственном заряде
ситуация усложняется. Если принять, что движение электрона каче-
качественно такое же, как и при отсутствии пространственного заряда, и что
электрическое поле равно нулю на катоде, то расчет движения электро-
электронов приводит к следующим результатам [5,6]. Толщина d прикатодного
электронного слоя определяется выражением
(8.3)
где D — расстояние между катодом и анодом, U — анодное напряжение,
Uс — -2тгpcD2 (рс < 0) — критическое напряжение. Плотность заряда
р(у) в этом слое 0 < у < d сильно меняется с координатой, причем сред-
1 d
няя плотность — J p(y) dy — рс. Время пребывания электронов в про-
d 0
странстве взаимодействия удваивается по сравнению с циклоидальным
движением в магнетронном диоде при отсутствии пространственного
заряда. Это связано с тем, что под влиянием пространственного заряда
угловая скорость обращения электрона в магнитном поле уменьшается:
(84)
Отсюда видно, что при р ~ рс угловая скорость оказывается существен-
существенно меньшей, чем при р <С pc. Электронные структуры, у которых \р\ >
> \рс\, удерживаться магнитным полем не могут. Качественно анало-
аналогичные результаты были получены для цилиндрического магнетрона
[7, 8]. Суть данной теории заключается в том, что рассматривается
двухпоточное состояние электронного облака в запертом негенериру-
ющем магнетроне, т. е. предполагается по аналогии с движением при
240 Лекция 8
отсутствии пространственного заряда, что электронное облако состоит
из двух потоков электронов — движущихся от катода к внешней границе
и наоборот.
Чуть позже появились работы Бриллюэна [9], в которых были най-
найдены точные стационарные решения уравнения Пуассона и уравнений
движения для магнетрона, и показано, что электронное облако в запер-
запертом магнетроне находится в однопоточном состоянии (электроны дви-
движутся параллельно катоду со скоростями, соответствующими электро-
электронам, эмитированным катодом; в частности, скорость электронов у като-
катода равна нулю и максимальна у внешней границы облака). Плотность
заряда в этом решении постоянна и равна рс, толщина слоя d совпадает
с величиной, даваемой формулой (8.3). Правда, вопрос об установлении
однопоточного состояния оставался долгое время открытым.
Экспериментальные исследования, которые должны были дать от-
ответ на вопрос: какому состоянию (однопоточному или двухпоточному)
соответствует распределение заряда в запертом магнетроне, показали,
что не реализуется ни то, ни другое распределение. Экспериментально
были обнаружены нерегулярные колебания электронного облака с са-
самыми различными частотами. Наиболее четким и ясно наблюдаемым
явлением, не укладывающимся в рамки кинематической теории, ока-
оказывается легко измеряемый анодный ток, который, хотя и уменьшается
с увеличением магнитного поля, но делает это существенно медленнее,
чем это следует из расчетов, учитывающих реальный начальный теп-
тепловой разброс электронов по скоростям при термоэмиссии.
Вторая загадка магнетрона — это начало генерации в нем.
Как обсуждалось на прошлой лекции, механизм фазировки в магне-
магнетроне эффективен только при синхронизме электронов и волны. Сте-
Степень близости скоростей в стационарном режиме генерации определя-
определяется неравенством
где ojo = Cvo — частота, при которой скорость медленной волны точно
равна скорости электронов vo = сЕ®/Н (см. соотношение G.7)), Т —
время пролета электронов от анода к катоду. Так как перемещение
электронов от анода к катоду обусловлено дрейфом под действием поля
синхронной волны, то, следовательно, время Т обратно пропорциональ-
пропорционально амплитуде синхронной волны. Чем меньше амплитуда, тем ближе
должны быть величины Уф и vo (uj и ujo). Поэтому начало генерации
в плоском магнетроне можно представить так: волна весьма малой
амплитуды, возникающая в результате флуктуации на частоте, почти
равной и о, формирует спицы и при этом увеличивает свою амплитуду,
причем по мере роста амплитуды частоты шишо могут расходиться.
Однако в цилиндрическом магнетроне эти простые представления
о начале генерации неприменимы. Это связано с тем, что в соответствии
Пространственный заряд в скрещенных полях 241
с соотношениями G.33) и G.34) точный синхронизм между волной
и электронами во всем пространстве между катодом и анодом невоз-
невозможен, он реализуется только на окружности с синхронным радиусом
г. Отсутствие повсеместного синхронизма электронов и волны приво-
приводит к тому, что, например, при соотношении ra/rK = 1,5 (га и гк —
соответственно радиусы анода и катода) образование спиц невозможно
при амплитуде сверхвысокочастотного поля, всего на порядок меньшей
максимальной амплитуды, соответствующей стационарной генерации.
Эти аналитические результаты подтверждаются расчётами на ЭВМ:
волна достаточно малой амплитуды, «выпущенная» в пространство
взаимодействия цилиндрического магнетрона, неспособна (как бы ни
варьировать ее частоту и угловую скорость) сформировать спицы и за-
заметно увеличить свою амплитуду за счет энергии электронов.
Вышесказанное справедливо для теории магнетрона без учета про-
пространственного заряда. Видно, что эта теория неспособна описать про-
процесс самовозбуждения магнетронных генераторов, поскольку самовоз-
самовозбуждение должно начинаться с таких полей, которые неспособны сфор-
сформировать спицы, характерные для режима стационарной генерации.
То обстоятельство, что магнетронные генераторы все же легко само-
самовозбуждаются, объясняется действием пространственного заряда. Это
действие достаточно сложно, но без него самовозбуждения нет.
После того, как амплитуда синхронной волны приблизится к макси-
максимальной амплитуде, т. е. амплитуде волны при стационарной генерации,
роль пространственного заряда ослабевает. При высокой добротности
резонатора и малом токе эмиссии может оказаться, что поле простран-
пространственного заряда вообще несущественно и лишь слегка возмущает дви-
движение электронов; так может быть, например, в генераторах малой
мощности непрерывного действия, и тогда свойства магнетрона в раз-
развитом режиме генерации никаких загадок в себе не таят.
Третьей загадкой магнетрона являются его свойства в раз-
развитом режиме генерации при сильном пространственном за-
заряде, существенно влияющем на движение электронов. Первая
работа, посвященная численному исследованию переходных процессов
в магнетроне и ставшая классической, была опубликована еще в 1965 го-
году (О. Buneman, S.P. Yu, G.P. Koyers [10]). В ней в результате численного
эксперимента было показано, что стационарного режима генерации
в магнетроне нет: электронные потоки и анодный ток пульсируют,
причем характерное время пульсации существенно меньше времени
установления колебаний в резонаторе. Вследствие этого стационарное
состояние если и есть, то только по отношению к резонансному полю
объемного резонатора, но никак не в отношении электронного облака
и поля пространственного заряда.
Вместе с большой важностью решения третьей загадки магнетро-
магнетрона для теории приборов со скрещенными полями, обозначенный круг
242 Лекция 8
вопросов имеет и более широкое фундаментальное значение. Он непо-
непосредственно связан с проблемами динамического хаоса и турбулент-
турбулентности в электронных потоках. Так, экспериментально было установ-
установлено, что в магнетронных генераторах наблюдается избыточный шум,
на 5-6 порядков превышающий дробовой [12, 13]. Существует также
ряд экспериментальных результатов, свидетельствующих о связи этого
избыточного шума с динамическим хаосом. Рассмотрим результаты
экспериментальных исследований, приведенных в работе [14], и на-
направленных на прямую проверку связи электронной турбулентности
в скрещенных полях с проблемой детерминированного хаоса.
Избыточный шум и азимутальные колебания пространственного
заряда в магнетронных генераторах наблюдаются уже в предгенера-
ционном режиме, когда влияние резонаторной системы незначительно,
и магнетрон по существу является магнетронным диодом [15]. Поэтому
в экспериментах использовался магнетронный диод, в анодном бло-
блоке которого имелись емкостной зонд для наблюдения колебательных
процессов и окно для измерения температуры катода. Характеристики
пространства взаимодействия магнетронного диода следующие: га =
= 4,5 мм, гк = 2,15 мм, длина анода /а = 10 мм, катод прямонакаль-
ный, высокотемпературный, металлический, с малым коэффициентом
вторичной эмиссии. Все экспериментальные результаты были получены
при постоянных значениях анодного напряжения Vb = 2500 В и индук-
индукции магнитного поля В « 0,14 Тл (В/Вкр = 1,4).
Управляющим параметром являлась плотность пространственного
заряда р, зависящая от тока эмиссии /э. Величина /э в первую очередь
зависит от температуры катода Тк, которая регулировалась посред-
посредством изменения тока накала /н в пределах 0 ^ /н < /нб5 где ^нб —
ток, соответствующий резкому возрастанию обратной бомбардировки
катода. В этих режимах влияние обратной бомбардировки катода было
пренебрежимо мало, что подтверждалось измерением Тк. Соответству-
Соответствующие этой области значения анодного тока /а, протекающего через
магнетронный диод, не превышали сотен микроампер. При /н > /нб
резко возрастала мощность обратной бомбардировки, быстро повы-
повышалась температура катода и процесс становился неуправляемым: /а
скачком возрастал до величины 10 мА. В опытах с помощью СВЧ-ана-
лизатора спектра, подключенного к зонду, регистрировались колебания
пространственного заряда (спектры в логарифмическом масштабе при-
приведены на рис. 8.1 и 8.2; они слева) и низкочастотные процессы и шумы
в анодном блоке (на рисунках справа).
Исходным состоянием являлось /н = 0, р = 0. По мере увеличе-
увеличения р в формирующемся пространственном заряде при некотором зна-
значении р\ возникают гармонические азимутальные колебания простран-
пространственного заряда с частотами, кратными Д « 320 МГц. На рис. 8.1а
приведена вторая мода азимутальных колебаний (/2 ~ 640 МГц (цена
деления по оси абсцисс 10 МГц)), а на рис. 8.1 а' — осциллограмма
Пространственный заряд в скрещенных полях
243
-10 МГц
в'
Рис. 8.1. Спектры (слева) и осцил- Рис. 8.2. Разрушение хаотических
лограммы (справа) низкочастотных колебаний в магнетронном диоде
колебаний в анодном блоке маг- внешним гармоническим сигналом
нетронного диода с увеличением
плотности пространственного заря-
заряда в нем
НЧ-шумов анодного тока, полученная в этом же режиме г). На ос-
осциллограмме шумы не просматриваются, но специально проведенные
измерения показали, что их спектральная плотность близка к плотно-
плотности полного дробового шума, определяемого формулой Шотки Бш =
= 2е/аА/. По мере дальнейшего увеличения величины р интенсивность
колебаний возрастает, и при некотором значении р2 > pi возникает
автомодуляционная неустойчивость с частотой автомодуляции fa =
= 2,5 МГц. При последующем небольшом увеличении р частота ав-
автомодуляции возрастает до 6 МГц (рис. 8.16). В результате автоде-
автодетектирования гармонический сигнал этой же частоты обнаруживается
и в анодном токе магнетронного диода (рис. 8.15').
Дальнейшее увеличение р приводит к усложнению автомодуляции,
причем наблюдается две бифуркации удвоения, которые завершают-
завершаются возникновением стохастических колебаний (рис. 8.1 в), при кото-
которых спектральная мощность НЧ-шумов возрастает на 6 порядков (см.
рис. 8.1в', Ку =30дБ).
Шумовые измерения, проведенные в диапазоне частот 1 кГц -1 ГГц,
показали, что возникающий в режиме хаотических колебаний избыточ-
избыточный шум создает непрерывный пьедестал, верхняя граничная полоса
которого выходит за пределы данного диапазона. На фоне этого пье-
г) Осциллограммы НЧ-шумов снимались с выхода усилителя с полосой
пропускания (по уровню 3 дБ) 20 Гц... 1 МГц и коэффициентом усиления
Ку = 60 дБ.
244 Лекция 8
дестала хорошо просматриваются пики частот, кратных частоте / =
= 320 МГц (рис. 8.1в).
Детерминированность хаотических процессов в данном случае под-
подтверждается тем, что их удается разрушить гармоническим сигналом,
вводимым в катодную цепь магнетронного диода. Воздействие сигналом
с частотой, далекой от частоты / = 320 МГц, не оказывало существен-
существенного влияния на динамику пространственного заряда в магнетронном
диоде (рис. 8.2а и а'). При приближении частоты внешнего сигнала
к частоте / = 320 МГц хаотические колебания срывались и наблю-
наблюдался режим периодической автомодуляции с появлением дискретного
спектра (рис. 8.26). Шумы анодного тока при этом снижались до уров-
уровня дробовых (см. рис. 8.25', Ку = 30 дБ). И, наоборот, в отсутствии
внешнего сигнала, когда колебания пространственного заряда были
автомодулированными, введение внешнего сигнала с расстройкой по
частоте приводило к хаотизации колебаний анодного тока.
Для качественного понимания проблем, затронутых выше, обсудим
вопросы устойчивости двухпоточного или однопоточного состояния
магнетрона. Так в работе [16] показывается, что двухпоточное состояние
магнетрона неустойчиво по отношению к возмущениям, оставляющим
электронное облако симметричным. Если рассмотреть плоский магне-
магнетрон и пренебречь взаимодействием электронного слоя с катодом г), то
можно показать (см. [1, 16]), что в линейном приближении собственные
частоты симметричных колебаний такого слоя даются выражением
ш = ±пиос/2± jujcQ/2tt, 0« л/2 Inn. (8.5)
Выписанное значение 0 соответствует случаю нулевой начальной ско-
скорости электрона и равенству нулю поля на катоде. В режиме ограниче-
ограничения тока пространственным зарядом величина 0 дается выражением
[1]
0 = 1пС, где С>1. (8.6)
Рассмотрим теперь физический смысл формулы (8.5). Действительная
часть и является высокой гармоникой основной частоты невозмущен-
невозмущенного движения электронов (она равна о;с/2, так как период движения
равен 4тг/а;с — удвоенному циклотронному периоду). Мнимая часть uj
показывает, что за время 4тг/а;с амплитуда поля изменяется в е±2в раз,
т.е. при знаке « + » возрастает в С2 раз. Эта неустойчивость является
абсолютной и аналогична неустойчивости, имеющей место в двухлуче-
вой лампе (см., например, [17]): она вызвана наличием двух встречных
потоков, причем наибольший вклад в неустойчивость (в значение 0)
вносят области около катода и внешней границы, где скорости встреч-
х) Это означает, что электроны вблизи невозмущенной нижней границы
поворачивают и начинают новый период движения в этом слое.
Пространственный заряд в скрещенных полях 245
ных потоков близки (т. е. малы) г). В цилиндрическом магнетроне такая
область существует только вблизи катода, так как у внешней границы
слоя радиальное ускорение электронов не мало, однако в прикатод-
ной области, благодаря ограничению тока пространственным зарядом,
радиальное ускорение мало и величина 0 по-прежнему может быть
представлена в виде (8.6).
Взаимодействие с катодом приводит к обновлению электронов
в электронном слое. Поскольку часть электронов, испытавших
возмущение, поглощается катодом, а вновь эмиттированные электроны
возмущений скорости не имеют, учет взаимодействия приводит
к дополнительному затуханию колебаний слоя. Для оценки этого
затухания взаимодействие электронов с катодом можно учесть
с помощью «коэффициента зеркальности» ае @ ^ зэ ^ 1). В этом
случае предполагается, что из N приходящих к катоду электронов
TVae отражается и возвращается в слой, a 7VA — ае) поглощается
и заменяется новыми. Тогда вместо соотношения (8.5) получаем
соотношения
u> = ±n^±j^Q-j^ In!. (8.7)
2 J 2n J 4п ае v '
В реальном магнетроне примерно половина электронов возвращается
в слой, а половина — обновляется (в зависимости от фазы, определя-
определяющей смещение точки поворота у катода вверх или вниз). Поэтому
можно полагать, что в формуле (8.7) значение зэ ~ 1/2, а тогда до-
дополнительное затухание, вызванное обновлением электронов в слое не
изменит сильной неустойчивости, о которой говорилось выше и которая
приводит к возрастанию возмущений как С2 (С ^> 1) за время пролета
электронов.
Эта сильная неустойчивость приводит к тому, что двухпотоковое со-
состояние физически не реализуемо. Действительно, время установления
двухпоточного состояния во всяком случае не меньше 4тг/а;с, т. е. време-
времени пролета от катода до внешней границы электронного слоя и обратно,
а за это время начальное возмущение (обусловленное тем, что состояние
отлично от того, которое должно установиться) возрастёт настолько,
что двухпоточное состояние разрушится, не успев сформироваться.
Как показывают расчеты Хартри и Никольсона, вместо двухпоточ-
двухпоточного состояния возникает симметричное, близкое к однопоточному со-
состояние, когда составляющие скорости, нормальные к катоду, оказыва-
оказываются сильно подавленными. На рис. 8.3 показано радиальное движение
электронов в том случае, когда анодное напряжение Ua возрастает от
нуля за 4 циклотронных периода; при этом электроны выводятся на
траектории, близкие к круговым. Отсюда видно, что благодаря разви-
х) Заметим, что именно в этих областях р ^> рс, благодаря чему и происхо-
происходит быстрое разрушение состояния.
246
Лекция 8
12 3 4 5 mctl2%
тию неустойчивостей силы пространственного заряда почти полностью
выравнивают скорости встречных потоков и создают более упорядочен-
упорядоченные электронные потоки, близкие к ламинарным.
Однако и такие потоки оказываются неустойчивыми. Если рассмат-
рассматривать устойчивость однопоточного состояния относительно возмуще-
возмущения e-j(ut-px) ^ т0 оказывается, что при
вещественных и волновое число Р по-
получается комплексным, а при веще-
вещественных Р имеют место комплексные
величины uj. Для однопоточного элек-
электронного слоя, удаленного от анода,
получается следующее выражение для
«,[1]:
oj = ojc (Pd - 0,54 ± j0,06), (8.8)
которое справедливо для pd > 2, при
малых pd частота и вещественна, и од-
нопотоковое состояние устойчиво.
Для сравнения выражений (8.5) и
(8.8) необходимо учесть, что произве-
произведение pd принимает бесконечную по-
последовательность значений. Если рас-
5 mct/2n
Рис. 8.3. Установление состоя-
состояния, близкого к однопоточному
сматривать плоский магнетрон как некоторую аппроксимацию цилин-
цилиндрического, то, обозначая через г& радиус катода, мы должны подчи-
подчинить Р условию
Prk = га, га e Z, (8.9)
поскольку при обходе катода (увеличение х на 2тгг^) поле, пропорцио-
пропорциональное Q-Ji^t-Px) ^ должно принять прежнее значение; тогда
и значения Re о; из формул (8.5) и (8.8) образуют арифметические
прогрессии.
Что касается величины Im о;, то по формуле (8.8) для мнимой части
uj имеем
> О «0,4,
4тг
т. е. по сравнению с двухпоточным состоянием неустойчивость одно-
однопоточного состояния нарастает более медленно, благодаря чему оно
может быть осуществлено физически хотя бы на непродолжительное
время. Физическая причина неустойчивости в данном случае связана
с взаимодействием потоков с различными скоростями, распространя-
распространяющихся в одном направлении, однако связь между потоками с раз-
различными скоростями слабая (так как они пространственно разобщены)
Пространственный заряд в скрещенных полях 247
и неустойчивость также оказывается более слабой, чем в предыдущем
случае.
Характерная особенность неустойчивостей, обусловленных
пространственным зарядом, заключается в том, что, как видно из
соотношений (8.5) и (8.8), имеет место бесконечное число нарастающих
колебаний с различными частотами Re о;, но примерно равными
инкрементами нарастания Im и. Случайное начальное возмущение
возбуждает целый спектр таких несимметричных волн, которые
нарастают одинаково быстро. По достижению ими конечных амплитуд
начинается нелинейное взаимодействие между ними, в результате
которого электронное облако в негенерирующем магнетроне остается
симметричным только в статистическом смысле: оно ведет себя
хаотически, беспорядочно пульсирует, «выбрасывая» часть электронов
на анод (он расположен дальше от электронного облака, чем
катод, поэтому анодный ток на него меньше) и катод. При этом
наличие мелкомасштабных пульсаций не исключает возможность
существования крупномасштабных структур (например, волн
пространственного заряда). Данное качественное рассмотрение
подтверждается и полномасштабным численным моделированием,
на результатах которого мы остановимся в следующем разделе лекции.
Если одно из колебаний пространственного заряда находится в син-
синхронизме с колебанием резонансной системы, причем как частоты, так
и фазовые скорости колебаний близки, то развитие неустойчивости
происходит иначе. Согласно соотношению (8.8) фазовая скорость на-
нарастающей волны пространственного заряда равна
Reo; , Л 0,54 \ , Л
и = __ = Wcd^i - _ j , (8.10)
причем (см., например, [1, Лекция 1, задачи 1, 5])
bird = —^-i-,
где г>о — скорость дрейфа электронов при отсутствии пространствен-
пространственного заряда и том же анодном напряжении Ua = E° D. Отсюда видно,
что величина и того же порядка, что и скорость vq. Медленная волна
в резонансной системе, имеющая фазовую скорость г>ф, должна при
самовозбуждении синхронизоваться не с электронами, а с волной про-
пространственного заряда, т.е. условием синхронизма является v$ ы и,
а не Уф ~ vo\ Заметим, что структура поля волны пространственного
заряда (см. рис. 8.4) и волны в линии передач существенно различны.
Так как потенциал и поле обусловлены модуляцией электронного слоя и,
в частности, периодичностью границы, то при удалении от границы слоя
они экспоненциально убывают, в то время как поле синхронной волны
убывает при удалении от анода, т. е. в противоположном направлении.
248 Лекция 8
Этот результат дает качественный ответ на вторую загадку магне-
магнетрона: а именно, возбуждение цилиндрического магнетрона происходит
благодаря синхронизации двух вращаю-
вращающихся волн — волн пространственного
заряда и волны в резонансной системе.
Обе волны имеют зависимость от угла
<р и времени t в виде exp [j (тир — wt)],
и обе вращаются как «твердые тела», по-
Рис. 8.4. Эквипотенциали ЭТОМУ рассинхронизма, связанного с фор-
волн пространственного мулами G.33) и G.34), не возникает. Пока
заряда вблизи внешней амплитуда колебаний в резонаторе мала,
границы электронного слоя распределение поля близко к распределе-
распределению поля волны пространственного заря-
заряда, и, в частности, электроны начинают свое движение к аноду, стремясь
образовать расширяющиеся спицы в соответствии с рис. 8.4. По мере
нарастания амплитуды резонансного колебания оно во все большей
степени определяет распределение поля и движение частиц.
Здесь следует отметить, что соотношение (8.10) выписано в пред-
предположении, что генерация начинается с однопоточного состояния элек-
электронного облака. Однако скорее всего это не совсем так [1], поскольку
можно предположить (и ряд экспериментальных данных это подтвер-
подтверждает), что «кипящий» электронный слой также может поддерживать
волны пространственного заряда с фазовой скоростью того же порядка.
Кинематическая теория генерации в магнетроне, не учитывающая
действие сил пространственного заряда, приводит к тому, что обра-
образуются спицы, в которых сильно выражено орбитальное движение —
обращение с угловой скоростью ис вокруг ведущих центров. Сами же
ведущие центры дрейфуют упорядоченно — вдоль эквипотенциалей
синхронной волны (ламинарное течение). Каких изменений следует
ожидать при наличии сильного пространственного заряда? Суммируя
вышесказанное, перечислим важнейшее, что вносит пространственный
заряд в физику магнетрона.
1. Так как пространственный заряд перемещается вместе со спицами
и волной, то его поле накладывается на поле синхронной волны и спи-
спицы деформируются, поскольку эквипотенциали уже другие: они сами
теперь зависят от движения электронов, т. е. здесь необходимо решение
самосогласованной задачи.
2. При р ~ рс дрейфовое приближение неприменимо и необходимо
пользоваться полными уравнениями движения. Это видно из формулы
(8.4): при р ~ рс изменяется угловая скорость, а, следовательно, и все
движение.
3. По аналогии с результатами, полученными для двухпоточного со-
состояния, следует ожидать подавления орбитального движения в спицах
под действием пространственного заряда: движение самих электронов
Пространственный заряд в скрещенных полях 249
при учете их расталкивания должно быть более упорядоченным, более
близким к ламинарному течению.
4. Даже при чисто ламинарном течении электронной жидкости по
спицам, они должны быть неустойчивы по отношению к возмущениям,
бегущим вдоль спиц: в этом причина нестационарности спиц при «ста-
«стационарной генерации». Из-за конечного времени пролета электронов
от катода к аноду и непрерывного обновления электронов в спицах
неустойчивость не успевает развиться достаточно сильно, так что наря-
наряду с мелкомасштабной хаотической динамикой в движении электронов
наблюдается крупномасштабное упорядоченное движение.
Теоретические результаты, перечисленные выше дают лишь предва-
предварительную ориентировку в тех загадках, которые ставит перед иссле-
исследователями магнетрон. Полное количественное рассмотрение возможно
лишь в результате численного эксперимента. В следующем разделе мы
опишем некоторые результаты анализа нестационарных нелинейных
процессов в магнетроне с помощью численного моделирования зада-
задачи, в которой учитывается целый ряд факторов, которыми неизбежно
пренебрегали при аналитических исследованиях. В первую очередь это
касается корректного учета влияния пространственного заряда и нали-
наличия случайных процессов. Заметим также, что численный эксперимент
позволяет провести анализ полностью самосогласованной нестационар-
нестационарной задачи.
Вычислительная физика и магнетрон.
Связь с проблемой турбулентности в электронном
потоке
Из предыдущего раздела понятно, что корректный учет влияния
пространственного заряда на процессы, протекающие в магнетроне,
невозможен без решения нелинейной нестационарной полностью само-
самосогласованной задачи. Такая задача включает в себя интегрирование
полных уравнений движения совместно с уравнением Пуассона. Са-
Самосогласованность решения означает, что по найденным траекториям
движения электронов рассчитывается распределение пространственно-
пространственного заряда, а по нему уже находится из уравнения Пуассона поле, кото-
которое затем используется для расчета уравнений движения и так далее.
Решение таких задач невозможно без привлечения численного модели-
моделирования. Видимо поэтому магнетрон, наряду с диодным промежутком
со сверхкритическим током (см., например, С. Birdsall, W. Bridges [18]),
стал одним из первых приборов высокочастотной электроники, неста-
нестационарные процессы в котором были проанализированы с помощью
численного эксперимента (Хартри, Никольсон; О. Buneman, S.P. Yu,
G.P. Koyers).
В данном разделе обсудим некоторые результаты такого полномас-
полномасштабного численного моделирования с акцентом на роль простран-
250 Лекция 8
ственного заряда в физических процессах в магнетроне. Все результаты
в этом разделе, если не оговаривается особо, излагаются по лекциям
Л.А. Вайнштейна и А.С. Рошаля [1]. Здесь не будем останавливаться на
подробностях методики численного моделирования, отсылая интересу-
интересующихся к работам [1,10], а лишь отметим, что вычислительная процеду-
процедура заключается в одновременном решении уравнений поля и уравнений
движения.
В квазистатическом приближении и отсутствии сверхвысокочастот-
сверхвысокочастотной волны уравнение поля представляет собой уравнение Пуассона для
потенциала Ф и решается как разностное уравнение с использованием
быстрого преобразования Фурье [11]. Данная методика может приме-
применяться только в случае, когда задача допускает постановку периодиче-
периодических граничных условий для функции плотности р(х) и потенциала
Ф(х) пространственного заряда. Тогда функции р(х) и Ф(х) имеют
образы в Фурье пространстве — соответственно р(к) и Ф(к), где к —
волновой вектор в ядре Фурье преобразования ехр (—jkr). В Фурье
пространстве уравнение Пуассона сводится к виду [11]
Ф(к) =
?0К
т. е. соответствующий Фурье-образ потенциала находится из известного
из решения «электронной» части задачи Фурье-образа распределения
плотности пространственного заряда с помощью простой арифметиче-
арифметической операции — деления на квадрат волнового вектора к2.
В простейшем одномерном случае для численного решения урав-
уравнения Пуассона необходимо ввести пространственную сетку, в узлах
которой задаются значения плотности пространственного заряда p(xj)
и потенциала Ф(х^). Здесь Xj = jAx — координата j-ro узла про-
пространственной сетки, Ах — шаг пространственной сетки. Условие пе-
периодичности граничных условий накладывает следующее требование
к поведению какой-либо функции G(xj), заданной на сетке: G(xj) =
= G(xj + L), где L = N^Ax — пространственный период, определяе-
определяемый конкретными физическими условиями задачи. При моделирова-
моделировании процессов в магнетроне, работающем на тг-виде, в качестве такого
периода может выступать расстояние между соседними резонаторами
в анодном блоке. Тогда дискретное проебразование Фурье одномерной
функции G запишется как
G(k) = Ах J2 G(xj)e~jhXj, (8.12)
з=о
а обратное дискретное преобразование Фурье будет иметь вид
л NL/2-l
G(Xj) = j- J2 G(k)ejkxJ. (8.13)
n=-NL/2
Пространственный заряд в скрещенных полях 251
Окончательно, суммируя вышесказанное, алгоритм решения урав-
уравнения Пуассона можно представить следующей схемой:
/ ч FFT //Ч к2 Л/п IFFT ж, ч V^ п/ \
р(х) —у р(к) —у Ф(к) —у Ф(х) -^-у Е(х).
Таким образом, вначале из «электронной» части задачи находится рас-
распределение плотности заряда р(х) в пространстве. Далее рассчитывает-
рассчитывается в соответствии с определением (8.12) Фурье-образ р(к). При этом сум-
сумма, фигурирующая в формуле (8.12), может быть эффективно рассчита-
рассчитана с помощью применения процедуры быстрого преобразования Фурье
(FFT). По найденным значениям р(к) определяются соответствующие
значения Ф(к) из уравнения Пуассона (8.11), по которым с помощью
обратного преобразования Фурье (8.13) (IFFT) находится распреде-
распределение потенциала уже в «физическом» пространстве. Напряженность
поля пространственного заряда может быть найдена по распределению
потенциала в соответствии с определением Е = — \/ Ф.
Уравнение движения представим в виде разностных уравнений,
соответствующих приближению однородного поля [1]. Шаг расчета во
времени составит At = тг/4а;с, т. е. 1/8 циклотронного периода.
Вначале обсудим явления в негенерирующем магнетроне. Рассмот-
Рассмотрение одномерной задачи выявило картину, аналогичную расчетам Хар-
три и Никольсона (см. предыдущий раздел). Единственным отличием
от их расчетов был учет вторичной эмиссии с катода с коэффици-
коэффициентом вторичной эмиссии ош. Расчеты показали, что облако из N
«машинных» электронов распадается на относительно небольшое число
крупных слоев, что и приводит к флуктуациям. Флуктуации плотности
пространственного заряда в свою очередь приводят к возмущениям по-
потенциала, а, следовательно, и скорости. Описанное явление пропадает
при ош —у 0. Действительно, пусть все эмиттируемые электроны имеют
нулевые начальные скорости. Если поле вблизи катода в данный момент
времени не препятствует вылету электронов, то все термоэлектроны
и вторичные электроны, эмиттированные на данном шаге, поступают
в область взаимодействия, образуя компактный слой. При последова-
последовательных соударениях с катодом этот слой укрупняется тем быстрее, чем
больше ат. Если же ат « 0 или поле препятствует вылету электронов,
то слой поглощается катодом практически сразу и расслоения не на-
наблюдается.
Рассмотрим теперь двухмерную задачу. Размер исследуемой двух-
двухмерной области такой, что он соответствует паре резонаторов маг-
магнетрона 3-сантиметрового диапазона. В тангенциальном направлении
предполагается периодичность. В этом случае расчеты показывают,
что электронное облако по истечении некоторого переходного процесса
вступает в стационарное состояние, имеющее статистический характер.
Рассмотрим статистические характеристики этого состояния.
252
Лекция 8
Для каждого слоя в момент времени t вычислялись средние (по
электронам слоя) нормальные и тангенциальные скорости (vn) и (vT),
зависящие от нормальной безразмерной координаты ?/, а также нор-
нормальные и тангенциальные температуры потока
где к — постоянная Больцмана, и обычная температура
т
= (Тп+Тт)/2.
(8Л4)
(8.15)
Так как предполагается, что случайные процессы в потоке являются
стационарными и эргодическими, то для получения более достоверной
статистики производилось допол-
дополнительное усреднение этих вели-
величин за промежуток времени, пре-
превышающий обычное время пребы-
пребывания электрона в промежутке,
а именно за 4-6 циклотронных пе-
периодов.
Результаты расчета для цилин-
цилиндрического магнетрона приведены
на рис. 8.5а; б. Из них видно, что
тангенциальная скорость монотон-
монотонно возрастает от катода к аноду,
причем лишь вблизи катода это
возрастание нелинейно — наблю-
наблюдается перегиб кривой. Нормаль-
Нормальная скорость везде близка к нулю
36
У
Рис. 8.5. Электронные скорости,
плотность объемного заряда (а)
и электронная температура (б) в за-
запертом магнетроне
и лишь вблизи анода имеет место
некоторое направленное движение
к аноду. Этот результат подтвер-
подтверждает вывод предыдущего раздела
о том, что развитие несимметрич-
несимметричных неустойчивостей сглаживает различие в тангенциальных скоростях
различных слоев электронного облака.
Что касается плотности пространственного заряда, то она отлична
от нуля во всем пространстве взаимодействия, чем и объясняется не
равный нулю анодный ток г). Появление такого хвоста без сомнения
связано с ростом температуры электронного облака. Как следует из
х) Заметим, что если сравнить вид зависимости с решением Бриллюэна, то
окажется, что в прикатодной области р падает значительно быстрее, однако,
р ф 0 во всем пространстве взаимодействия, тогда как граница бриллюэнов-
ского потока в данном случае у = 12.
Пространственный заряд в скрещенных полях 253
расчетов (рис. 8.56), температура электронного потока Те в скрещенных
полях достигает нескольких миллионов градусов. Это указывает на
высокую степень неупорядоченности потока — электронный поток на-
находится в турбулентном состоянии. Вычисляя по известным функциям
распределения дисперсию скоростей эмиттируемых электронов, можно
по формуле (8.15) найти температуру электронов эмиссии: в данном
случае она составляет порядка 3 • 104 К, что на порядок ниже темпе-
температуры электронного облака в непосредственной близости вблизи като-
катода (в первом слое), где много возвращающихся электронов, имеющих
большой разброс по скоростям. С удалением от катода электронная
температура Те повышается. В рассматриваемом нами запертом магне-
магнетроне наиболее горячей является область электронного облака вблизи
анода. Заметим, что в уже упомянутой работе О. Buneman et al [10]
были получены аналогичные результаты, за исключением ряда несу-
несущественных деталей, связанных, видимо, с различными параметрами
моделируемого прибора.
Можно предполагать, что вследствие большого разброса электронов
по скоростям в запертом магнетроне облако пространственного заряда
сильно неоднородно и в нем хаотически образуются и разрушаются
электронные структуры. Для проверки этого предположения вычис-
вычислялась автокорреляционная функция плотности заряда и потенциала
вдоль той или иной тангенциальной линии у = const. При этом коор-
координаты у выбирались так, чтобы они располагались вблизи катода,
в середине или на границе облака.
В большинстве случаев плотность объемного пространственного
заряда оказывалась практически некоррелированной случайной функ-
функцией времени и координаты. Отсюда следует, что протяженность и дли-
длительность существования структур пространственного заряда через-
вычайна мала. Учитывая известную обратную связь между временем
корреляции и спектром процесса, можно заключить, что плотность
заряда обладает сплошным широким спектром. Здесь следует еще раз
отметить, что из-за ограниченности области моделирования не иссле-
исследовались крупномасштабные структуры (волны пространственного за-
заряда) в электронном облаке.
Пространственная протяженность неоднородностей потенциала
пространственного заряда существенно больше. Это связано с тем,
что потенциал является интегральной характеристикой плотности
заряда (соответствующая связь описывается уравнением Пуассона)
и дальнодействующие кулоновские поля в среднем сглаживают
потенциал. Вместе с тем, потенциалы в разных сечениях слабо
коррелированы друг с другом, т. е. существует быстро осциллирующее
поле пространственного заряда с широким спектром частот. Двигаясь
в таком быстро и нерегулярно осциллирующем поле, электроны
испытывают воздействие случайных, быстро меняющихся сил, которые
вызывают разогрев и турбулизацию потока, размывают границу
254 Лекция 8
электронного облака и могут вызывать попадание значительной части
электронов на анод даже при магнитном поле значительно больше
критического.
В заключение обсуждения вопросов динамики пространственного
заряда в запертом магнетроне отметим, что электронное облако в та-
такой системе является примером распределенной открытой нелинейной
системы, демонстрирующей сложную динамику, которая характери-
характеризуется формированием короткоживущих электронных структур раз-
различного масштаба. Все это позволяет говорить об электронном облаке
в магнетроне как об одной из моделей электронной турбулентности.
Рассмотрим теперь динамику электронного облака в слабом поле
синхронной волны. Очевидно, что эта задача связана со второй за-
загадкой магнетрона — анализом переходных процессов при установ-
установлении колебаний в магнетронном генераторе. Как и раньше, будем
рассматривать двухмерную задачу. Однако теперь электрическое поле
складывается из внешнего статического поля, поля пространственного
заряда и сверхвысокочастотного поля, создаваемого резонансной си-
системой. Как и в Лекции 5, будем предполагать, что электронный поток
взаимодействует с одной пространственной гармоникой поля синхрон-
синхронной волны, соответствующей тг-колебанию. Введем подвижную систему
координат, которая движется в тангенциальном направлении с фазо-
фазовой скоростью Уф = uj//3 выбранной пространственной гармоники —
синхронной волны с частотой uj и тангенциальным волновым числом
р. В подвижной системе координат электрическое поле синхронной
волны является электростатическим, и потенциал Ф имеет в танген-
тангенциальном направлении период Л = 2тг//3, т. е. при исследовании можно
ограничиться исследованием процессов в промежутке протяженностью
в одну длину волны Л синхронной волны (одной парой резонаторов
магнетрона). В цилиндрическом магнетроне движущаяся система коор-
координат должна вращаться с угловой скоростью uj/п и является неинер-
циальной. Переходя к движущейся системе координат, необходимо со-
соответствующим образом преобразовать и уравнения движения. Учет
поля резонансного колебания (оно имеет комплексную частоту ujs =
= uo's (I — j/2Qs), uo's — резонансная частота, Qs — нагруженная доброт-
добротность данного колебания) может быть проведен либо с помощью неста-
нестационарного уравнения возбуждения объемных резонаторов A.61), либо
с помощью балансов активных и реактивных мощностей B.37), B.38)
[1]. Именно последний метод и используется в данном случае в расчетах.
Проанализируем процесс самовозбуждения магнетронного генера-
генератора в соответствии с результатами численного моделирования. В на-
начальный момент времени, когда электронов в пространстве взаимодей-
взаимодействия нет, энергия колебания W имеет некоторое весьма малое началь-
начальное значение. Величину W удобно представить в виде
U8 = \C8\, (8.16)
Пространственный заряд в скрещенных полях
255
/la
а О 20 40 60 80 100 200 300
5 0 20 40 60 80 100 200 300 500 700
Рис. 8.6. Характеристики колебаний в зависимости от времени в режиме
установления колебаний в магнетронном генераторе
где Сs — комплексная амплитуда сверхвысокочастотного «напряже-
«напряжения» данного колебания, a F — коэффициент формы, имеющий раз-
размерность емкости. Последний можно связать с нормой данного резо-
резонансного колебания.
Предгенерационный режим характеризуется образованием элек-
электронного облака. В это время поле пространственного заряда мало
и не ограничивает тока эмиссии. С ростом пространственного заря-
заряда вылет эмиттируемых электронов уменьшается, и катод переходит
в режим ограничения тока пространственным зарядом. На рис. 8.6а
показаны соответствующие зависимости характеристик колебаний от
времени. Из него видно, что в начале происходит лавинообразный рост
тока Ik электронов, возвращающихся на катод и вторично-эмиссион-
вторично-эмиссионного тока Is. Величина суммарного объемного заряда qs в межэлек-
межэлектродном пространстве также быстро нарастает. Затем при переходе
в режим ограничения тока эмиссии пространственным зарядом (этот
момент можно определить по положению максимума Is) токи Is и /&
уменьшаются и достигают некоторого равновесного значения, при ко-
котором Is « Ik ~ const. Состояние равновесия продлевается до момен-
256 Лекция 8
та времени, когда появляется анодный ток /а. Снижение вторично-
эмиссионного тока приводит к некоторому уменьшению величины \qs .
Если не происходит разрушение облака пространственного заряда при
больших энергиях W, то в дальнейшем величина \qs\ может считать-
считаться постоянной. Тогда, пренебрегая током термоэмиссии по сравнению
с током вторичной эмиссии 1), можно записать
/««/* + 4,
так что коэффициент вторичной эмиссии
as = ^*l + ^. (8.17)
До появления анодного тока активная Ра и реактивная Рг элек-
электронные мощности взаимодействия (рис. 8.66) колеблются около ну-
нуля, так как электроны еще далеки от анода и электронное облако не
сгруппировано. В балансе активных мощностей B.37) Ра не может
скомпенсировать потерь и энергия колебания W падает. В это же время
формируются электронные спицы. После появления конвекционного
тока на анод /а наблюдается быстрый рост мощностей Ра и Рг.
Если начальное значение U8(t = 0) меньше некоторого порогового
значения, то спица не образуется, генерация не возникает и колебания
затухают (см. на рис. 8.6а ветвь кривой Us(t), отмеченную кружками).
Для возбуждения генерации в этом случае необходимо кратковремен-
кратковременное повышение величины постоянного анодного потенциала Ua на 10—
15 % в течение нескольких циклотронных периодов (момент повышения
напряжения отмечен стрелкой на кривой Us(t)). С повышением анодно-
анодного напряжения увеличивается эффективность взаимодействия электро-
электронов с волной, что и приводит к самовозбуждению. Реальный магнетрон,
благодаря наличию паразитных колебаний (в численном эксперименте
рассматривается одноволновое приближение), самовозбуждается и при
постоянном Ua. Однако возможно ли этим объяснить самовозбуждение
генератора при сколь угодно малой начальной амплитуде ?А?@), неиз-
неизвестно.
В момент касания спицы пространственного заряда анода (t = to)
(и соответственно появления анодного тока) предгенерационный режим
можно считать завершенным, и начинается установление режима гене-
генерации. В стационарном режиме постоянное значение энергии колебаний
определяется соотношением 2oj"W = Pa B.37).
С появлением анодного тока при t = to мощность Ра и амплиту-
амплитуда Us начинают экспоненциально нарастать. В начале предгенерацион-
ного режима активная мощность Ра в большинстве случаев несколь-
несколько превышает величину реактивной мощности Рг, но в дальнейшем
х) Это справедливо для многих типов катодов: платиновых, оксидно-
торриевых и др.
Пространственный заряд в скрещенных полях
257
У
0,8
0,4
0,0
У
0,8
0,4
0,0
У
0,8
0,4
0,0
/ "¦¦%
у ¦ Г Э
t = 2
-=?Т1 ¦.. ¦. L Л'"Г-=—
/V", 1 = 4
"' J" V ..
-к/2
я/2 -те/2
ж/2
Рис. 8.7. Процесс формирования спицы пространственного заряда
реактивная мощность нарастает быстрее активной. Качественно это
можно объяснить тем, что небольшие смещения спицы относительно
максимума тормозящего поля слабо влияют на величину активной мощ-
мощности взаимодействия и значительно сильнее — на величину реактивной
мощности взаимодействия, которая растет в результате быстрее Ра. Та-
Таким образом, опережающий рост реактивной мощности взаимодействия
означает увеличение разности фаз между током электронов и сверхвы-
сверхвысокочастотным полем, т. е. отставание электронной спицы от пучности
продольного тормозящего поля. Вследствие этого постепенно ухудша-
ухудшаются условия передачи энергии от электронов к полю, и амплитуда поля
достигает стационарного значения. Эти явления обусловлены силами
пространственного заряда, которые ограничивают плотность заряда
в спицах, анодный ток и генерируемую мощность.
Рассмотрим теперь непосредственно пространственно-временную
динамику электронного потока. Рис. 8.7 демонстрирует процесс фор-
формирования спицы. На нем показаны распределения электронов в про-
пространстве взаимодействия в последовательные моменты времени. Рас-
Распределения получены в результате наших расчетов с помощью мате-
математической модели, близкой к модели Л.А.Вайнштейна и А.С. Рошаля.
Из рисунка видно, как постоянно эмиттируемые катодом электроны по-
постепенно отклоняются от прямолинейного движения. Рост амплитуды
высокочастотной волны приводит к их группировке и началу цикло-
циклоидального движения. Электроны, попавшие в неблагоприятную фазу
высокочастотного поля, возвращаются обратно на катод, а находящиеся
Д. И. Трубецков, А. Е. Храмов
258
Лекция 8
12
0
106К
в благоприятной фазе формируют спицу пространственного заряда,
которая с течением времени начинает деформироваться.
Рис. 8.8 демонстрирует изменение температуры облака объемного
заряда в ходе самовозбуждения цилиндрического магнетрона. В начале
переходного процесса амплитуда колебаний мала, и сильно нагретый
край облака не достигает анода. Температура облака на границе мо-
может достигать 2 • 107 К (рис. 8.8, кривые 1, 2). С ростом амплитуды
синхронной волны и появлени-
появлением анодного тока горячий край
облака поглощается анодом, по-
поток в среднем охлаждается (кри-
(кривые 3-5) и распределение тем-
температуры становится более рав-
равномерным. Время перехода по-
потока от состояния, описываемо-
описываемого кривой 1, к состоянию 5 со-
составляет в представленном слу-
случае 400 циклотронных периодов.
Заметим, что продолжитель-
продолжительность предгенерационного ре-
12
24
36
У
Рис. 8.8. Изменение электронной тем-
температуры в процессе установления ко-
колебаний в магнетронном генераторе
(Тг <Т2< ... < Тъ)
жима определяется в основном
эмиссионными свойствами като-
катода, уровнем начальной амплиту-
амплитуды и затуханием резонансного колебания в резонаторе. Длительность
предгенерационного режима для трехсантиметрового магнетрона с пла-
платиновым катодом составляла около 25-60 циклотронных периодов. Вре-
Время установления генерации, как показывает численный эксперимент,
определяется только затуханием.
Необходимо также заметить, что все электронные процессы в маг-
магнетронном генераторе характеризуются сильными нерегулярными ко-
колебаниями соответствующих характеристик. На рисунках это не пока-
показано, так как зависимости предварительно усреднялись по некоторому
интервалу времени.
Вышеописанная картина относится к одному из возможных способов
генерации и, как отмечается в [1], скорее всего, фактически не реали-
реализуется. Дело в том, что «затравочное» поле с энергией VK(O), которое
группирует электроны и приводит к самовозбуждению, обычно вызы-
вызывается тепловыми флуктуациями в объемном резонаторе; заполнение
части резонатора кипящим электронным облаком сильно увеличивает
эти колебания и таким образом облегчает самовозбуждение. Вместе
с тем, дальнейший процесс установления режима развитой генерации
не зависит (или очень слабо зависит) от деталей, относящихся к пред-
генерационному режиму. Поэтому результаты, относящиеся к режиму
установления, имеют существенно большее значение.
Пространственный заряд в скрещенных полях
259
Перейдем теперь к анализу стационарного режима генерации. Как
уже понятно из вышесказанного, о стационарном режиме можно гово-
говорить лишь в смысле теории случайных процессов, т. е. как о процессе,
у которого математическое ожидание и корреляционная функция не
зависят от начала отсчета времени. Это связано с тем, что анодный ток
и другие характеристики не стремятся в процессе установления режима
генерации к постоянным значениям, а испытывают нерегулярные коле-
колебания около средних значений.
Режим генерации в магнетроне — намного лучше изученный про-
процесс, чем процесс возбуждения. Электронное облако в генерирую-
генерирующем магнетроне принимает форму вращающегося колеса. Прикатод-
ная часть образует втулку колеса. От втулки к аноду тянутся спи-
спицы облака — это электронные структуры, сгруппированные благода-
благодаря механизму автофазировки в области максимального торможения
тангенциального поля. Взаимодей-
Взаимодействуя с этим полем, электроны пере-
передают ему свою энергию и тем самым
поддерживают генерацию.
Рассмотрим некоторые результа-
результаты моделирования магнетрона трех-
трехсантиметрового диапазона в режи-
режиме ограничения тока пространствен-
пространственным зарядом [1]. На рис. 8.9 по-
показаны средние значения некото-
некоторых физических величин в режиме
стационарной генерации как функ-
функции Us (Ua = const). Кривая нагру-
нагруженной добротности Qs рассчитана
для плоского магнетрона, остальные
кривые — для цилиндрического. Ре-
Результаты расчетов для плоского и ци-
цилиндрического магнетрона в режи-
режиме генерации качественно подобны.
Из рисунка видно, что кривая Qs =
= QS(US) имеет две ветви, и одной
la
120
100
80
60
40
20
Qs
700
-600
-500
-400
-300
-200
-100
1
la
l\
i i j
\ //
1 1 1 1
Qs
7
-
-
i
Че
0,8
0,6
0,4
0 100 300 500 Us
Рис. 8.9. Средние значения нагру-
нагруженной добротности Qs в плос-
плоском магнетроне, к.п.д. г\е и анод-
анодного тока /а в цилиндрическом
магнетроне при постоянном анод-
анодном напряжении в режиме разви-
развитой генерации
и той же добротности соответствуют два значения Us. Физически оче-
очевидно, что устойчивой является ветвь, на которой с уменьшением потерь
(с увеличением Qs) амплитуда Us возрастает, т. е.
ди„
диа
dQs
> 0.
Следовательно, на левой ветви с меньшими величинами Us расположе-
расположены неустойчивые точки, а на правой ветви с большими значениями —
устойчивые.
260
Лекция 8
1,0
0,5
V
/
~Al—y—"^
— r* =¦ .T — — ]- "
,-^—*^. Ге>1°6к
7g «^ — —¦—._, s
"*" I i I
0
12
24
36
Рис. 8.10. Электронные скорости и температуры в цилиндрическом магне-
магнетроне в развитом режиме генерации
Анодный ток /а с ростом амплитуды волны быстро нарастает,
и в какой-то момент катод прибора переходит в режим термоэмиссии.
Перед этим наблюдается более быстрый рост анодного тока, а затем
анодный ток резко падает, так как в рассматриваемом магнетроне теп-
тепловая эмиссия мала для поддержания анодного тока. Переход в режим
термоэмиссии является следствием того, что электронное облако нес-
несколько удаляется от катода, механизм вторично-эмиссионного воспол-
восполнения электронов нарушается и развивается лавинообразный распад
облака пространственного заряда.
Зависимость электронного к.п.д. г\е — Ра/I&V& от амплитуды U8
также приведена на рис. 8.9. Максимум к.п.д. соответствует наиболее
благоприятному расположению спицы относительно максимума напря-
напряженности тормозящего поля синхронной волны.
При конструировании магнетронов обычно известным параметром
является не амплитуда колебаний, а нагруженная добротность. В этом
случае по кривой Qs на рис. 8.9 можно найти амплитуду Us, которая
установится в исследуемом магнетроне при заданной добротности Qs,
а затем по найденной величине Us исходя из остальных кривых, опре-
определить остальные параметры.
На рис. 8.10 изображены типичные зависимости средних
нормальной, тангенциальной и электронной скоростей, а также соответ-
соответствующих электронных температур в генерирующем цилиндрическом
магнетроне. При этом скорости нормированы на величину
уф = -г, (8.18)
р
т. е. на фазовую скорость синхронной волны при данном г. Здесь р —
количество пар резонаторов анодного блока.
Как видно из рисунка, с приближением к аноду нормальная скорость
движения (vn) монотонно возрастает. Зависимость (vT) оказывается
Пространственный заряд в скрещенных полях
261
более сложной. С удалением от катода тангенциальная скорость по-
постепенно (медленнее, чем по линейному закону) возрастает и достигает
максимума. При этом электроны движутся в среднем быстрее волны.
Ближе к аноду, благодаря взаимодействию с вращающейся синхронной
волной, поток в среднем снова замедляется и выпадает из синхронизма,
так как вблизи анода быстрые электроны скорее уходят из простран-
пространства взаимодействия. Точный синхронизм имеет место только при двух
значениях координаты у.
Как следует из расчетов, скорость (vT) хорошо аппроксимируется
выражением
2-а
VT =
— ¦ .
У/Упг +Ут - CL
U9)
Коэффициенты е, а, ут слабо зависят от межэлектродного расстояния.
Согласно выражению (8.19) vT имеет максимум ?Уф при у = ут. Обыч-
Обычно ? = 1,1 Ч- 1,3, а = 0,5 -г- 0,7, ут близко к половине межэлектродного
расстояния. На рис. 8.10 изображены зависимости при ? = 1,25, а =
= 0,6, ут = 23. Синхронизм потока и волны (vT = Уф) в соответствии
с выражением (8.19) достигается при
У = Ут \?i ±
?\ = ? + а-
1-е
?.
17
16
15
14
ЦкВ
-
i
i i i
Распределение электронной температуры Те зависит от геометриче-
геометрических и электрических параметров пространства взаимодействия, а так-
также характеристик эмиттера. Во многих случаях температура монотон-
монотонно нарастает в направлении от катода к аноду, причем вблизи анода
имеется область более быстрого ро-
роста Те. В других случаях максимум
температуры достигается внутри об-
облака. Очевидно, что максимум тем-
температуры соответствует тем частям
облака, где движение электронов наи-
наиболее нерегулярно. Обычно величи-
величина Те в генерирующем магнетроне со-
составляет несколько миллионов граду-
градусов.
Представляет большой интерес
сравнение результатов численных
расчетов с данными натурных экс-
экспериментов. На рис. 8.11 изображе-
изображены вольтамперные характеристики
плоского магнетрона, построенные по
результатам численного моделирования. Кружками на рисунке отмече-
отмечены соответствующие экспериментальные данные. Хорошее совпадение
0
12
24 36
Рис. 8.11. Вольтампетрные ха-
характеристики плоского магне-
магнетрона. Здесь кривая 1 соответ-
соответствует Qs = 150, 2 - Qs = 200,
3 - Qs = 250, 4 - Qs = 300.
Кружки соответствуют экспери-
экспериментальным данным
262 Лекция 8
служит подтверждением адекватности и достоверности полученных
численных результатов.
В работах [19, 20] описываются результаты компьютерного моде-
моделирования процесса автомодуляции пространственного заряда. Каче-
Качественно этот процесс можно описать следующим образом. Наложенное
на однородный статический электронный поток высокочастотное поле
резонаторной системы сначала приводит к образованию выпуклости,
на которую постепенно накручиваются новые слои электронов, обра-
образуя локальную вращающуюся втулку. Когда верхние слои этой втулки
поднимаются достаточно близко к аноду, они под действием высокоча-
высокочастотного поля резонаторной системы отрываются от локальной втулки
и постепенно в виде сгустков импульсами оседают на аноде. После оседа-
оседания сгустка локальная втулка постепенно восстанавливается и описан-
описанный процесс повторяется вновь. Нерегулярность этого процесса связана
с тем, что время образования локальной втулки не связано со временем
прохождения втулки от одной щели до другой. Поэтому процесс отрыва
порций заряда от локальной втулки каждый раз начинается при новом
исходном состоянии втулки. Вследствие этого от втулки каждый раз
отрываются разные порции заряда. Такая хаотическая автомодуляция
также является одной из причин возникновения высокого шумового
пьедестала в частотном спектре сигнала, генерируемого магнетроном.
Сложная динамика пространственного заряда
в усилителе со скрещенными полями
Сложная хаотическая динамика в усилителе со скрещенными поля-
полями (амплитроне) определяется возникающей обратной связью между
входом и выходом прибора [21]. Как уже говорилось в предыдущей
лекции в параграфах, посвященных амплитрону и карматрону, при
слабом входном сигнале амплитрон генерирует шумоподобный сигнал,
который не зависит от входного. При подаче значительного входного
сигнала в пространстве взаимодействия формируются спицы, и уста-
устанавливается режим усиления, при котором выходной сигнал «воспро-
«воспроизводит» входной сигнал. Однако при возникновении связи между
входом и выходом амплитрона может наблюдаться сильное искажение
выходного сигнала, которое, в первую очередь, проявляется в появле-
появлении флуктуации ВЧ-напряжения, ВЧ-фазы, анодного тока и других
характеристик около средних значений. Такая обратная связь возни-
возникает за счет вращения спиц пространственного заряда в пространстве
взаимодействия от выхода к входу усилителя, поэтому флуктуации на
выходе прибора переносятся на его вход, становясь начальными усло-
условиями. Такой механизм, по-видимому, является основным механизмом
возникновения избыточного шума в усилителе со скрещенными полями.
Рассмотрим, следуя работе [21], более подробно механизм возникно-
возникновения хаотической динамики в амплитроне. В работе [21] рассматрива-
Пространственный заряд в скрещенных полях
263
ется гидродинамическая модель динамики электронного потока в при-
приближении ведущего центра. Исследуется модель амплитрона с плос-
плоским пространством взаимодействия.
Предполагается, что имеет место вза-
взаимодействие только с одним видом ко-
колебаний резонансной системы (одномо-
довое приближение). В последнем слу-
случае описание динамики системы мож-
можно провести, используя только медленно
меняющиеся величины амплитуды V\
и фазы <р высокочастотного поля, а так-
также плотность пространственного заря-
заряда по во втулке спицы (см. рис. 8.12).
При этом форма и высота d втулки спи-
спицы считаются постоянными вдоль про-
пространства взаимодействия, а величи-
величина по считается постоянной по сечению
спицы, но медленно меняющейся вдоль
пространства взаимодействия. Величи-
Величина плотности заряда втулки по опреде-
определяется соотношением между процесса-
процессами вторичной эмиссии с катода и пе-
перехода электронов из вершины втулки
в область спицы. Движение электронов,
формирующих спицы, складывается из
дрейфового движения, которое проис-
происходит вдоль эквипотенциалей синхрон-
синхронной волны, и орбитального вращения
с частотой оос. Учитывая, что движение
ведущих центров подобно движению несжимаемой жидкости (см. со-
соотношение G.23)), можно использовать гидродинамические уравнения
для описания движения ведущих центров.
Использование медленно меняющихся амплитуды и фазы ВЧ-волны
позволяет исследовать сложную динамику в амплитроне только в узкой
полосе частот. Например, сдвиг фаз Aip при одном прохождении сигна-
сигнала через пространство взаимодействия, деленный на длину простран-
пространства взаимодействия /, определяет нелинейный сдвиг волнового числа
5C от значения /?о, соответствующего рабочей частоте uj$ в отсутствии
электронного пучка. При следующем прохождении сигнала через про-
пространство взаимодействия снова наблюдается сдвиг 5/3 и т. д. Поэтому
для понимания сложной динамики в усилителе на скрещенных полях,
обусловленной обратной связью между входом и выходом лампы, необ-
необходим анализ величин флуктуации выходных характеристик от одного
прохождения сигнала лампы к другому. Основными управляющими
О
Рис. 8.12. Схема спицы, ис-
используемая в гидродинамиче-
гидродинамической модели динамики элек-
электронного потока в скрещен-
скрещенных полях. Здесь D — расстоя-
расстояние «катод—анод», d — ширина
втулки спицы, определяющей
область, из которой эмитти-
руемые электроны возвраща-
возвращаются на катод; сплошные ли-
линии — эквипотенциали поля
синхронной волны в подвиж-
подвижной системе координат (ср.
с рис. 7.3 и 7.4)
264
Лекция 8
«О 20 40 60 80 N 6 0 20 40 60 80
г 0 20 40
60
80 N
Рис. 8.13. Зависимость анодного тока от числа прохождений сигнала через
пространство взаимодействия для увеличивающихся значений коэффициен-
коэффициента вторичной эмиссии aso (из работы [21])
параметрами, от которых зависит динамика системы, в этом случае
являются коэффициент вторичной эмиссии as, зависящий от материала
катода, и часть заряда An, несколько раз проходящая через простран-
пространство взаимодействия. Величина as определяется энергией электронов
?i, бомбадирующих катод, в соответствии с полуэмпирической форму-
формулой
?г
as —
ехр 1 -
(8.20)
где aso — максимальное значение коэффициента эмиссии при ударе
о катод электрона с максимальной энергией ?т.
На рис. 8.13 показаны результаты расчета зависимости анодного
тока 1а прибора от числа прохождений N сигнала через простран-
пространство взаимодействия при фиксированном значении величины An = 2/3
и различных величинах crso- Из рисунка видно, что с увеличением мак-
максимального коэффициента вторичной эмиссии система демонстрирует
последовательность переходов от стационарного состояния к периоди-
периодическим колебательным режимам и далее к развитому хаотическому
поведению.
При (jsq = 2,25 после нескольких первых прохождений лампы в си-
системе устанавливается стационарное состояние (рис. 8.13а), характе-
характеризуемое очень малыми флуктуациями выходных характеристик. При
Пространственный заряд в скрещенных полях
265
Рис. 8.14. Зависимость плотности пространственного заряда по от продоль-
продольной координаты ж/А (Л — длина волны, распространяющейся в линии пе-
передачи) для одного прохождения в режимах стационарного состояния (а)
(aso = 2,25) и хаотической динамики (б) (aso = 3,5) (из работы [21])
увеличении максимального коэффициента вторичной эмиссии до ве-
величины aso = 2,40 происходит потеря устойчивости стационарного со-
состояния. Из рис. 8.13?; с видно, что в системе устанавливаются пери-
периодические движения различных периодов. На рис. 8.13^, построенном
при aso = 2,40, показан цикл периода 2, на рис. 8.13с — цикл периода 10
(crso = 2,50). И, наконец, при достижении значения aso = 3,50 поведение
становится хаотическим (рис. 8.13г).
Таким образом наличие внутренней обратной связи в усилителе со
скрещенными полями приводит к разрушению стационарных режимов,
и при превышении некоторых критических значений параметров An
и aso происходит возникновение сначала периодических, а затем и ха-
хаотических режимов. При этом для данного значения An существует
максимальное значение коэффициента эмиссии, выше которого стаци-
стационарные состояния теряют устойчивость. Аналогично, существует мак-
максимальная величина An при фиксированном aso. Это свидетельствует,
что основная причина потери устойчивости и возникновения слож-
сложной динамики в усилителе связана с ростом величины накопленного
в пространстве взаимодействия заряда. Последнее способствует росту
влияния обратной связи. Заметим, что численное моделирование по-
показало сильную связь между флуктуациями выходных характеристик
усилителя за одно прохождение длины лампы и появлением больших
изменений плотности заряда в пространстве взаимодействия.
На рис. 8.14 показаны зависимости плотности заряда в спице по от
длины пространства взаимодействия в течение одного прохода для ре-
режима стационарных и хаотических колебаний. Зависимость плотности
от длины лампы меняется от гладкой кривой в стационарном режиме
до все более колебательной в хаотических режимах. Усложнение вида
зависимости по(х) делает динамику системы более чувствительной
к начальным условиям на входе усилителя, которые задаются вели-
величиной An, характеризующей внутреннюю обратную связь. Величина
266 Лекция 8
плотности пространственного заряда по влияет на два основных па-
параметра, характеризующих работу лампы: анодный ток и вторичную
эмиссию. Ширина спицы определяется отклонением скорости дрейфа
электронов от фазовой скорости волны (см. рис. 7.5). Поэтому любые
изменения пространственного заряда или электрического поля, приво-
приводящие к вариации дрейфовой скорости, влияют на анодный ток. Ко-
Коэффициент вторичной эмиссии определяется энергией столкновения,
которая, в свою очередь, зависит от величины как ВЧ-поля, так и посто-
постоянного поля на катоде. Взаимодействие между этими двумя факторами
приводит к сильным колебаниям величины по в том случае, когда
плотность заряда приближается к величине критической плотности рс,
а величина коэффициента вторичной эмиссии стремится к нулю.
Таким образом, основным механизмом возникновения сложной
нелинейной динамики в усилителе со скрещенными полями является
формирование внутренней обратной связи, связанной с неоднократным
прохождением некоторой части пространственного заряда через
пространство взаимодействия. Заметим, что изложенные результаты
работы [21] получены с помощью модели, которая не учитывает
целый ряд важных факторов, например, многомодовую конкуренцию
в резонансной системе и взаимодействие спиц. Однако, именно
изложенный механизм хаотизации динамики пространственного заряда
в амплитроне наиболее существенен, поэтому учет вышеназваных
факторов может лишь уточнить приведенную картину усложнения
колебаний.
Список литературы
1. Вайнштейн Л.А., Рошаль А.С. Пространственный заряд в скре-
скрещенных полях // Лекции по электронике СВЧ B-я зимняя школа-
семинар инженеров; книга III). Саратов: Изд-во СГУ, 1972, С. 2.
2. Lemke R.W., Genoni Т.С, Spencer Т.A. Three dimesional particle-
in-cell simulation study of a relativistic magnetron // Physics of
Plasmas. 1999. V. 6, № 2. P. 603.
3. Kypaee А.А., Байбурин В.Б., Ильин Е.М. Математические модели
и методы оптимального проектирования СВЧ приборов. — Мн.:
Наука и техника, 1990.
4. Байбурин В.Б., Терентьев А.А., Сысуев А.А., Шуколюков А.Н.,
Еремин В.П. Анализ процессов в магнетронах ММ-диапазона с
помощью численной многоволновой модели // Материалы между-
международной научно-технической конференции «Актуальные пробле-
Пространственный заряд в скрещенных полях 267
мы электронного приборостроения», 7-9 сентября 1998 г., Саратов,
Россия. Саратов: изд.-во СГТУ, 1998.
5. Брауде С. Я. Движение электрона в электрическом и магнитном
поле с учетом пространственного заряда // ЖЭТФ. 1935. Т. 5, № 7.
С. 621.
6. Брауде С.Я. К вопросу о действии магнитного поля на простран-
пространственный заряд в плоском и цилиндрическом диодах // ЖТФ. 1940.
Т. 10, №3. С. 216.
7. Гринберг Г.А., Болъкенштейн Б. С. Влияние однородного магнит-
магнитного поля на движение электронов между коаксиальными цилин-
цилиндрическими электродами // ЖТФ. 1938. Т. 8, № 1. С. 9.
8. Гринберг ГА. Избранные вопросы математической теории элек-
электрических и магнитных явлений. — М.: Изд-во АН СССР, 1948.
9. Теория магнетрона (по Бриллюэну). Сборник переводов. — М.:
Сов. радио, 1946.
10. Бипетап Ov Yu S.P., Koyers G.P. Time-dependent Computer
Analysis of Electron-Wave Interaction in Crossed Fields // Journal
of Appl.Phys. 1965. V. 35, № 8. P. 2550.
11. Бедселл Ч., Ленгдон А. Физика плазмы и численное моделирова-
моделирование. — М.: Атомиздат, 1985.
12. Sproull R.L II Journal of Appl. Phys. 1947. V. 18, № 3. P. 314.
13. Кандыбей Б.Г, Некрасов Л.Г, Смирнов А.Б., Усыченко Б.Г //
Электронная техника. Серия I. Электроника СВЧ. 1983. Вып. 11.
Сб.
14. Смирнов А.Б., Усыченко Б.Г Возникновение хаоса и избыточ-
избыточного шума в магнетроне // Радиотехника и электроника. 1988.
Т. XXXIII, №4. С. 883.
15. Тычинский Б.П., Деркач ЮЛ. Колебания облака пространствен-
пространственного заряда в цилиндрическом магнетроне // Радиотехника и элек-
электроника. 1956. Т. 1, № 2. С. 231.
16. Кадомцев Б.Б. Неустойчивость электронного облака в магне-
магнетроне // ЖТФ. 1959. Т. 29, № 7. С. 833.
17. Рабинович М.И., Трубецков Д. И. Введение в теорию колебаний и
волн. — М.: Наука, 1984.
18. Birdsall С, Bridges W. Electron Dynamics in Diode Regions. — NY:
Academic Press, 1966.
268 Лекция 8
19. Моносов Г.Г. Исследование электромагнитных шумов в магне-
магнетроне с помощью двумерного компьютерного моделирования //
Материалы международной межвузовской конференции «Совре-
«Современные проблемы электроники и радиофизики СВЧ". Саратов, 20-
24 марта 2001. Саратов: Изд-во ГосУНЦ «Колледж", 2001. С. 114.
20. Monossov H.G. The two-dimensional mathematical model of electron
enteraction with UHF field in a magnetron and high-voltage UHF
oscillations breakdowns // Proceedings of International University
Conference «Electronics and Radiophysics of Ultra-High Frequencies".
St. Petersburg, Russia. May 24-28, 1999. P. 97.
21. Riyopoulos S.A. Feedback-induced noise in crossed field devices //
IEEE Trans, on Plasma Sci. 1992. V. 20, № 3. P. 360.
Лекция 9
ИСТОРИЯ СОЗДАНИЯ ЛАМПЫ БЕГУЩЕЙ
ВОЛНЫ И ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
ВЗАИМОДЕЙСТВИЯ ЭЛЕКТРОННОГО ПОТОКА
С БЕГУЩЕЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНОЙ
Приборы СВЧ, в которых эффект усиления или
генерации основан на взаимодействии электрон-
электронного потока с замедленной волной, нашли широ-
широкое применение в системах связи, радиолокации
и многих других областях науки и техники.
A.M. Кац, Е.М. Ильина, И.А. Мань-
кип. Нелинейные явления в СВЧ-при-
борах О-типа с длительным взаимо-
взаимодействием
История изобретения Рудольфом Компфнером лампы бегущей волны.
Роль Джона Пирса. Анализ взаимодействия электронного потока
с бегущей прямой электромагнитной волной на основе метода последо-
последовательных приближений. Квадратичная группировка. Качественное
описание процесса группирования электронов в бегущей волне. Прин-
Принципы подобия для приборов с длительным взаимодействием (нереля-
(нерелятивистские и ультрарелятивистские пучки).
Рассмотренные в предыдущих лекциях сверхвысокочастотные
устройства являются принципиально узкополосными, так как
используемые в них резонансные контуры (объемные резонаторы)
позволяют получать усиление лишь в очень узкой полосе частот (около
1% относительно основной частоты). Если мы рассматриваем соот-
соответствующие генераторы, то ширина полосы генерируемого сигнала
и диапазон электронной перестройки частоты также малы. Поэтому
для реализации СВЧ-приборов с широкой рабочей полосой необходимо
отказаться от принципа обмена энергии между электронным потоком
и переменным электрическим полем, локализованном в «коротком»
зазоре высокодобротного резонатора, и заменить такую узкополосную
колебательную систему колебательной системой нерезонансного типа.
Такая колебательная система {замедляющая система) представляет
собой широкополосную электродинамическую структуру, способную
270 Лекция 9
уменьшить фазовую скорость электромагнитной волны по сравнению
со скоростью света.
Для нарастания амплитуды гармонической волны в пространстве
под действием внешней волны необходимо совпадение их волновых
чисел, т.е. в этом случае должен иметь место пространственный резо-
резонанс (резонанс волновых чисел) [1]. На самом деле, необходим резонанс
и частот, и волновых чисел, что выражается в равенстве фазовой ско-
скорости собственной волны в среде фазовой скорости внешней волны. Это
условие обычно называют условием синхронизма волн.
Применительно к электронике СВЧ это означает, что необходимо
транспортировать электронный пучок вдоль замедляющей системы,
и если скорость замедленной электромагнитной волны примерно равна
скорости электронов (условие синхронизма), то возможно кумулятив-
кумулятивное длительное взаимодействие между электронной волной и волной
в волноведущей структуре.
Данная идея — взаимодействие электронного потока с замедлен-
замедленной электромагнитной волной (как уже отмечалось в лекции 1) ле-
лежит в основе большой группы усилителей и генераторов, в которых
используются нерезонансные колебательные системы. Наиболее широ-
широко применяемыми и, даже можно сказать, классическими приборами
с длительным взаимодействием являются лампа бегущей волны (ЛБВ)
и лампа обратной волны (ЛОВ). В лекциях 9-11 рассматривается лампа
бегущей волны, в лекциях 12-13 — лампа обратной волны. Основное
различие этих двух устройств состоит в направлении потока мощности
в линии передачи. Если фазовая скорость волны и в том и другом
случае совпадает с направлением движения пучка, то поток мощности
(групповая скорость) в соответствии с разложением поля в ряд про-
пространственных гармоник (см. лекцию 1, формулы A.86) и A.87)) может
быть направлен как в направлении движения пучка, так и против.
Первый случай соответствует взаимодействию с прямой волной (ЛБВ),
второй случай — взаимодействию с обратной волной (ЛОВ).
Пусть имеет место выполнение условия синхронизма при взаимодей-
взаимодействии с прямой волной (рис. 9.1а). Тогда, если вблизи источника элек-
электронов вводить в линию передачи сигнал, то он приведет к модуляции
скорости электронов и последующей группировке, т. е. созданию в пучке
ВЧ-тока, который наводит в линии передачи ВЧ-поле. В результате
происходит сложение наведенного поля Енав с входным сигналом Е°.
Таким образом вдоль длины пространства взаимодействия происходит
усиление входного сигнала.
Рассмотрим в соответствии с рис. 9.1? устройство лампы бегущей
волны — усилителя. Она состоит из следующих основных частей: элек-
электронной пушки, входного устройства, усилительной секции, состоящей
из замедляющей системы, с продольной составляющей электрического
поля которой взаимодействует электронный поток, выходного устрой-
устройства и коллектора, на котором оседает электронный пучок. Фокусиров-
Лампы бегущей волны
271
Электронная
/ пушка
rj/T: Г: п 7. у: 7 \ у: у; z
^ Электронный пучок
З
Замедляющая т.
система Коллектор
\ Электронный
пучок
ВЧ-вход
ВЧ-выход
Рис. 9.1. Схема лампы бегущей волны со спиральной замедляющей системой
ка электронного пучка обычно осуществляется либо постоянным либо
периодическим магнитным полем. В качестве замедляющей системы
используются либо спирали, либо замедляющие системы типа цепочек
связанных резонаторов (ЦСР) или их
модификации (ЛБВ с ЦСР будет посвя-
посвящена отдельная Лекция 11).
Что касается спиральной замедляю-
замедляющей системы, то она объединяет свойст-
свойство малой дисперсии (см. рис. 9.2) с боль-
большим сопротивлением связи (см. Лек-
Лекцию 1), что позволяет добиться большо-
большого усиления в широкой полосе частот
[2]. Для прямых волн слабая дисперсия
имеет место, когда групповая и фазовая
скорости волны близки. С увеличением
групповой скорости vrp увеличивается
поток мощности Р, проходящий через
систему, что приводит к уменьшению сопротивления связи К =
Рис. 9.2. Дисперсионная ха-
характеристика спиральной за-
замедляющей системы. Диапа-
Диапазон длин волн Л G (Ai,A2)
соответствует области слабой
дисперсии, где г>ф(А) ~ const
20$ Р'
где Ех — продольная составляющая электрического поля замедленной
волны в области пучка; /3 = ojo/уф; Уф = vo. Поскольку Р = vrpW, то
для обеспечения в широкополосных замедляющих системах требуемой
272 Лекция 9
величины сопротивления связи К нужно по возможности уменьшить
запасенную в них энергию W (например, уменьшая объем, занимаемый
полем вне пучка). Спираль при распространении в ней прямой волны
в полной мере удовлетворяет этому требованию. Все результаты, кото-
которые представлены в этой и в следующей лекциях, будут относиться, если
не оговаривается особо, к ЛБВ со спиральной замедляющей системой.
Существенной чертой усилителя бегущей волны, отличающей его от
выше рассмотренных приборов типа клистрона и магнетрона, является
то, что электронный поток, сгруппировавшись, отдает свою энергию
электромагнитному полю на большой длине пространства взаимодей-
взаимодействия при относительно малой амплитуде поля.
История изобретения Рудольфом Компфнером
лампы бегущей волны. Роль Джона Пирса
Нет сомнения, что первый усилитель с бегущей волной разработал
Рудольф Компфнер в 1942-1943 гг., так же как нет сомнения в том, что
к моменту создания лампы он глубоко понимал особенности взаимодей-
взаимодействия электронного потока с замедленной электромагнитной волной 1).
История создания ЛБВ и сам ее создатель не менее удивительны, чем
100-долларовая идея братьев Вариан и Хансена.
Компфнер — фигура необычная для СВЧ-электроники. Он родился
в 1909 г. в Вене (Австрия) и получил диплом инженера-архитектора
в Венской Высшей технической школе в 1933 г. Начиная с 1934 г.,
вплоть до 1941 г. он продолжил учебу в области архитектуры в Англии,
совмещая ее с работой в архитектурной конторе. Однако Компфнер
всегда стремился стать физиком. «В начале войны он был интернирован
и тем самым имел удобный случай усовершенствовать свои знания
в области физики. В дальнейшем, еще во время войны, он освободился
от интернирования и работал над сверхвысокочастотными лампами для
Морского министерства» [5, с. 165].
Основные работы по ЛБВ были выполнены Компфнером в Бирмин-
гамском университете и позднее в Кларендонской лаборатории в Окс-
Оксфорде, где он получил ученую степень доктора физики. В 1951 г. он
переехал в США, где в лабораториях фирмы Белл продолжал работу
) Заметим, что идея о взаимодействии электронов с бегущей электромаг-
электромагнитной волной, фазовая скорость которой близка к скорости электронов,
упоминается в ряде патентов и до Компфнера. Варнеке и Генар изучали
этот вопрос. Ранняя история, точнее предыстория ЛБВ, отражена в обзоре
Варнеке [3, С. 50]. Отметим также, что к этой же идее, но не для усиления
электромагнитных волн, а в целях ускорения пучков заряженных частиц
пришли в середине 20-х годов специалисты в ускорительной технике (см.
Лекцию 11; раздел, посвященный линейным ускорителям заряженных ча-
частиц).
Лампы бегущей волны 273
над СВЧ-лампами, а позднее занимался исследованиями в области
квантовой электроники, космической связи с помощью спутников и оп-
оптической связи. С 1973 г. он преподавал на факультете прикладной
физики Станфордского университета. Умер Компфнер в 1977 г.
В 1941 г., когда Компфнер работал в Бирмингамском университете
(в секретной группе Олифанта, где был создан многорезонаторный
магнетрон), перед ним была поставлена задача разработать клистрон-
ный усилитель с коэффициентом шума значительно меньшим, чем
у усилителей, использовавшихся тогда в супергетеродинных приемни-
приемниках. Компфнер пишет, что мысль об использовании бегущей волны,
взаимодействующей с электронами, возникла у него, когда работа над
клистроном зашла в тупик. «Клистроны с хорошей связью между пуч-
пучком и резонаторами имели значительный коэффициент усиления, но
плохой коэффициент шума, если же коэффициент шума был хорошим,
то связь была слабой и усиление небольшим, так что от нескольких
каскадов шум снова был большим ... После двух лет работы над такими
лампами ... стало ясно, что это неправильный путь. Как бы то ни было,
в конце концов я подумал, раз время пролета через зазор представляет
такую серьезную трудность и взаимодействие со стационарным полем
получается таким слабым, то так и быть, — пусть поле движется вместе
с электронами, — мысль, в общем-то, достаточно очевидная» [4, с. 11-
12].
Компфнер сделал удивительный по смелости шаг: он отказался
от резонансного контура, благодаря которому были достигнуты столь
впечатляющие успехи как, например, создание клистронов. Пирс пишет
[5, с. 185]: «По-видимому, Компфнеру посчастливилось избавиться от
ограничения полосы частот в усилителях (что до него радиоспециа-
радиоспециалистам никак не удавалось) именно благодаря непредубежденности,
свежести взгляда на вещи человека, до этого работавшего в другой
области. Компфнер решил задачу просто, он построил эффективный
усилитель без резонансного контура».
Следует, однако, подчеркнуть — сам Компфнер не понял, что создал
широкополосный усилитель: «Я не понял, что имею прибор с потен-
потенциальной шириной полосы в несколько октав. Пирс понял.» [4, с. 29].
Да, Пирс понял: «Когда я в США начал работать с лампой бегущей
волны, на меня большое впечатление произвела ее огромная широко-
полосность» [5, с. 185] и сразу поставил перед собой задачу о создании
широкополосной лампы с высоким устойчивым коэффициентом усиле-
усиления, но это было много позже — в 1944 году.
Что же сделал Компфнер? На этот вопрос отвечает Пирс [5].
«Компфнер, который изобрел в конце войны лампу бегущей волны,
был исследователем в области малошумящих усилителей. Созданная
им лампа была очень нестабильна. Он пользовался спиралью с малыми
потерями, поэтому как только усиленная волна частично отражалась от
выхода, она шла ко входу и возбуждала генерацию в лампе. Тем не менее
274
Лекция 9
он добился усиления, а его измерения шумов дали результаты, которые
превосходили все то, что было достигнуто затем в течение нескольких
лет».
Эволюция размышлений Компфнера о приборе, в котором реализо-
вывалось бы взаимодействие электронов с бегущей волной, иллюстри-
иллюстрируют рисунки из его записной книжки (рис. 9.3-9.5). На двух последних
рисунках фигурирует спираль —
один из важнейших элементов бу-
будущей ЛБВ. К концу 1942 г.
Компфнер уже имел некоторую
информацию о свойствах спира-
спирали как замедляющей системы. «Я
имел несколько бесед с колле-
коллегами о том, как можно умень-
уменьшить скорость, и в ходе обсу-
обсуждений было высказано предпо-
предположение использовать спираль...
Рис. 9.3. Страничка из записной
книжки Компфнера, датированная
6 сентября 1942 г., со схемой откло-
отклоняющей системы ВЧ-осциллографа
из коаксиальной линии, скорость
волны в которой близка к скорости
электронов. Не приводится ориги-
оригинальный текст около рисунка [4]
... я взял немного медной про-
проволоки и стальной прут, зажал
прут в токарный станок и намотал
на него спираль. Витки касались
друг друга и я их немного раздвинул, чтобы не было короткого замыка-
замыкания. Затем я взял коаксиальный проводник от детектора стоячей волны,
вставил в него спираль, подал сигнал с длиной волны 10 см, и вдруг, —
о чудо! — я получил стоячую волну, конечно очень грубо, но когда я
измерил расстояние между максимумами и взял среднее, то оказалось,
что скорость уменьшилась в семь раз» [4].
Компфнер с трудом уходил от резонатора в конструкции лампы,
даже поняв свойства спирали. Характерен в этом смысле его ком-
комментарий к рис. 9.5 [4, с. 15]: «.. .я .. .заменил румбатрон другой си-
системой (рис. 9.3). Здесь в правой части тоже есть спираль, и выход
Рис. 9.4. Страничка записной книжки от 10 ноября 1942 г. В предлагаемом
усилителе полый пучок движется между спиралью и внешним проводником
к выходному резонатору, такому как в клистроне [4]
Лампы бегущей волны
275
Рис. 9.5. Страничка из записной книжки от 12 ноября 1942 г. Выходной резо-
резонатор заменен секцией со спиралью, что приводит Компфнера к неожидан-
неожиданному выводу: «Совершенно ненастроенный усилитель?» (рисунок и подпись
из [4])
сделан прямо от спирали. В записной книжке я пометил с недоумени-
недоумением: «Совершенно ненастроенный усилитель?» Это было невероятно —
усилитель несомненно был ненастроенным». Несколько месяцев было
потрачено на резонансные усилители с поперечным полем (Компфнер
по-существу возвратился к варианту скоростной модуляции, думая со-
создать бесшумный усилитель; см. рис. 9.6), пока «...понял, что шум
пучка все равно будет поступать
в резонатор, даже если электро-
электроны и не ударяются о него... »
Но в апреле 1943 года я вернул-
вернулся к тому, что теперь назвал бы
«спирально-коаксиальным усили-
усилителем» [4, с. 16].
Следует заметить, что все ра-
работы над будущей ЛБВ были «до-
«домашними упражнениями». На ра-
работе Компфнер продолжал зани-
заниматься клистронным усилителем.
Прежде, чем начать делать лам-
Рис. 9.6. Страничка от 13 ноября
1942 г. Пучок проходит через резона-
резонатор, не оседая на стенках, ни на сет-
сетках зазора, так что поперечное по от-
отношению к направлению движения
пучка ВЧ-поле приводит к его моду-
модуляции. Не приводится оригинальный
текст над и под рисунком [4]
пу, он по-существу построил до-
достаточно полную теорию усиления
слабого сигнала при взаимодей-
взаимодействии электронного потока с бегущей электромагнитной волной. В част-
частности, он научился рассчитывать сопротивление связи спирали, сумел
найти выражение для сгруппированного под действием поля волны
в спирали пучка и показал, что ток пропорционален квадрату расстоя-
расстояния (по современной терминологии Компфнер показал, что при взаимо-
взаимодействии типа О имеет место квадратичная группировка электронов).
В августе 1943 г. физическое отделение Бирмингамского универси-
университета распалось, поскольку большая часть сотрудников уехала в Лос-
Аламос (США), чтобы принять участие в работе над атомной бомбой.
Компфнер остался: ему разрешили официально заниматься усилите-
276
Лекция 9
Электронная
лампа
Фокусирующая
/ катушка
Внешний
проводник
Флюоресцирующий
экран
Спираль
Согласующий
румбатрон
Выход
Рис. 9.7. Экспериментальный макет, созданный Компфнером для демонстра-
демонстрации взаимодействия между бегущей волной и пучком [4]
лем с бегущей волной и, разумеется, он выбрал эту работу. Теперь он
поступил к экспериментальному созданию лампы. Вот, что представлял
собой по словам Компфнера первый прибор (рис. 9.7). «Использовался
пучок, созданный пушкой катодно-лучевой трубки, проходивший через
фокусирующую катушку и спираль и дающий пятно на флюоресцирую-
флюоресцирующем экране, которое можно было видеть снаружи. Спираль замедляла
волну примерно в 10 раз (при напряжении около 2500 В). С большим
нетерпением я ждал, что получится при подаче сигнала что-то около
100 мВт. К своему величайшему удовольствию я заметил как пятно
растянулось и превратилось в линию. Наверное это был один из самых
волнующих моментов в моей жизни. До сих пор я все-таки не верил,
что электроны можно на самом деле «одурачить». Все мои открытия до
этого были на бумаге; чтобы удостовериться нужен был эксперимент»
[4, с. 20]. Многочисленные (в ряде случаев весьма изящные) эксперимен-
эксперименты Компфнера шаг за шагом подтверждали его теорию. Эксперименты
продолжались на различных вариантах ламп, число которых перевали-
перевалило за первую десятку. Наконец, по воспоминаниям Компфнера в марте
1944 г. он «...получил наилучшие результаты, когда лампа показа-
показала следующие характеристики. Сорок из 50 микроампер доходили до
коллектора, имевшего потенциал 1800 вольт; ... усиление составляло
что-то около 10 дБ, а улучшение отношения сигнал/шум, когда лампа
включалась в цепь, равнялось 4 дБ. Коэффициент шума смесителя был
равен 13 дБ, т. е. коэффициент шума должен был быть порядка 10 дБ»
[4, с. 26].
Дальнейшая работа Компфнера проходила в Оксфордском универ-
университете. Здесь, в частности, он закончил свою теорию, получив легко
суммируемый бесконечный ряд для поля в спирали (ряд соответствовал
суммированию первичных, вторичных, третичных и т.д. волн). Были
получены точное и асимптотическое (для больших длин) выражения
Лампы бегущей волны 277
для возбужденного поля в спирали. В асимптотическом случае по-
поле росло с расстоянием экспоненциально. В это же время Компфнер
открыл экспериментально и объяснил теоретически явление полного
подавления сигнала в ЛБВ при определенных значениях тока и потен-
потенциала луча. Это явление носит название эффекта срыва Компфнера
(Kompfner dip condition) и используется для измерения дисперсионных
характеристик и сопротивления связи замедляющих систем.
Следующий важный шаг в развитии теории ЛБВ и осознании того,
что это — широкополосный усилитель, принадлежит Джону Пирсу.
Вот как оценивает роль Пирса в то время Компфнер [5, с. 27-28].
«...в 1944 г. доктор Джон Р.Пирс из «Белл Телефон Лэбораториз»
посетил Оксфорд. Он прочитал некоторые наши секретные заметки об
этой работе... И я помню, с какой живостью он проглотил все это,
а потом уехал назад и развил теорию, которая дала все результаты
строго, гораздо более изящно, чем сделал я суммированием членов, хотя
следует напомнить, что он, так сказать, заранее знал ответ, в то время
как мои первые теоретические шаги предвосхищали эксперименты...
В сущности его теория с самого начала правильно учитывала влияние
потерь в спирали и рассинхронизма между пучком и волной, его теория
предсказывала удивительные, по крайней мере для меня, вещи! Тот
факт, что в лампе с бегущей волной потери не только не вредны, но
даже очень полезны, был для меня совершенно неожиданным... При
первой возможности Пирс послал мне свою теорию еще задолго до того,
как она была опубликована. Несомненно, это был еще один волнующий
момент, когда я вдруг понял, как все оказывается просто и красиво».
Обстоятельства, связанные с войной, сложились так, что первые
публикации Компфнера появились только в 1946 г. и позднее, т. е.
практически одновременно с публикациями Пирса, хотя приоритет
Компфнера в создании ЛБВ очевиден из сказанного выше.
Джон Пирс родился 27 марта 1910 г. в штате Айова (США), в 1933 г.
окончил Калифорнийский университет, где в 1936 г. получил степень
доктора. После этого в течение 35 лет Пирс работал в американской
компании «Бэлл телефон лэбораториз», где занимался исследованием
и разработкой электровакуумных приборов, в том числе и ЛБВ (у него
88 изобретений, часть которых относится к ЛБВ). В 1955 г., т.е. за
два года до запуска в 1957 г. первого искусственного спутника Земли,
Пирс опубликовал статью «Орбитальные радиотрансляторы». В этой
работе были изложены теоретические основы для запуска пассивного
ретранслятора, который в 1960 г. был помещен на спутнике «Эхо-1»,
и активного ретранслятора, примененного на спутнике «Телстар» в 1962
г. Пирс — автор целого ряда известных монографий и научно-популяр-
научно-популярных книг. Он разносторонний человек — пишет научную фантастику,
стихи, сочиняет компьютерную музыку. После ухода из фирмы Белл
преподает в Калифорнийском технологическом институте.
278 Лекция 9
Анализ взаимодействия электронного потока
с бегущей прямой электромагнитной волной
на основе метода последовательных приближений
Прежде чем перейти непосредственно к количественному анализу
физических процессов при взаимодействии электронного потока с бе-
бегущей электромагнитной волной, перечислим основные предположе-
предположения, при которых строится простейшая теория приборов с длитель-
длительным взаимодействием. В отсутствии высокочастотного поля электроны
двигаются прямолинейно вдоль продольной оси х с некоторой посто-
постоянной скоростью г>о (т. е. электроны пучка полностью замагничены
сильным фокусирующим магнитным полем, которое приложено вдоль
пространства взаимодействия). Замедленная электромагнитная волна
распространяется только в положительном направлении оси х и имеет
только ^-компоненту напряженности электрического поля, так что
ВЧ-поперечными смещениями электронов пренебрегаем. В результате
возможно ограничиться построением одномерной теории взаимодей-
взаимодействия электронов с бегущей волной.
Проведем анализ взаимодействия с помощью метода последователь-
последовательных приближений. Сущность метода последовательных приближений
состоит в вычислении высокочастотной составляющей сгруппирован-
сгруппированного тока (или высокочастотных продольных смещений электронов),
возникающих под действием заданных высокочастотных полей, а затем
в вычислении поля, возбуждаемого в волноведущей системе током,
который считается теперь заданным. Далее процедуру можно повто-
повторять, получая приближения более высоких порядков. В качестве ну-
нулевого приближения задаются ВЧ-поля в волноведущей системе без
пучка. Важно, что для вычисления пусковых условий в ЛОВ доста-
достаточным оказалось первого приближения. Здесь нельзя не отметить,
что широкие возможности и высокая эффективность аппарата метода
последовательных приближений, впервые примененного Компфнером
к ЛБВ, была обоснована основателем Саратовской научной школы по
сверхвысокочастотной электронике профессором Владимиром Никола-
Николаевичем Шевчиком. Метод последовательных приближений применялся
впоследствии для решения широкого круга задач СВЧ-электроники
[7, 8] и, в первую очередь, применительно к анализу ЛОВ.
В качестве нулевого приближения («заданного поля») возьмем поле
невозмущенной волны, которая при х = 0 полагается равной входному
сигналу в ЛБВ, поскольку потери в линии передач не учитываются.
При этом задача разбивается на три части: 1) анализ модуляции элек-
электронного потока по скорости; 2) анализ группирования электронного
потока в бегущей волне постоянной амплитуды; 3) анализ взаимодей-
взаимодействия электронного потока с бегущей волной постоянной амплитуды.
Рассмотрим последовательно каждую из названных подзадач.
Лампы бегущей волны 279
1. Модуляция электронного потока по скорости в бегущей электро-
электромагнитной волне постоянной амплитуды. Пусть электронный поток
движется с постоянной скоростью г>о в положительном направлении
оси х. В том же направлении распространяется бегущая электромагнит-
электромагнитная волна с постоянной амплитудой. Продольная составляющая волны
имеет вид
ш. J ш. J 1 I Л/ j \^ f 7 C f 7 C • I \j • X )
где Уф — фазовая скорость волны, Е° — постоянная амплитуда волны
электрического поля г). В рамках теории малого сигнала уравнение для
переменной составляющей скорости электронов в Эйлеровых координа-
координатах, как было показано в Лекции 3, имеет вид C.19):
_^ _|_ v0— = rjE(x, t). (9.2)
Переменные величины будем предполагать изменяющимися по закону
QJut^ ТОГда уравнение (9.2) сводится к линейному неоднородному диф-
дифференциальному уравнению
dv(x) •о ~( \ V
dx vo
где введено обозначение f3e = lj/уо. Интегрируя последнее уравнение,
легко получить выражение для полной скорости
j j ЯПСУ d(\, (9.3)
где Vo = Vq/Bt]). Учитывая, что Е\(х) = Е°е~^°х, интеграл можно
представить в виде:
Э\Ре- РО)
п [{Ре - /Зо)Ж/2]
[(/3e-/30)/2] •
С учетом выражения (9.4) действительная часть формулы (9.3) запи-
запишется как
х) Предполагаем, что г^о ^С с, поэтому можно пренебречь ВЧ-магнитными
полями и релятивистскими эффектами.
280 Лекция 9
- E°l
При малых величинах ? = —— <С 1 (при этом для угла пролёта
справедливо приближение (ut — ujt\) & /Зех) и х = I соотношение (9.5)
принимает вид
Rev = v0 <1 + |mcos luh + ^1 1 . (9.6)
Здесь
?(*)(*) (,.7)
— невозмущенный относительный угол пролета в пространстве дрейфа,
характеризующий движение электронов относительно «холодной» вол-
волны; М = у— — коэффициент эффективности модуляции в бегущей
Фо/2
волне постоянной амплитуды (он схож; по своей форме с выражением
B.5) для коэффициента эффективности модуляции в ВЧ-зазоре).
Таким образом степень модуляции скорости электронов существен-
существенным образом зависит от относительного угла пролета Фо- Рассмотрим
физический смысл коэффициента М. Для этого будем считать, что при
движении электронов в волне на них действует эффективное поле МЕ°.
При Фо —> 0, т. е. когда vq « г>ф, электроны оказываются в поле данной
фазы волны все время пролета, что и обеспечивает хорошую модуляцию
скорости электронов полем волны. При увеличении Фо электроны за
время пролета длины лампы испытывают воздействие поля волны ме-
меняющейся фазы, а следовательно, проходят большое число ускоряющих
и тормозящих полуволн. Очевидно, что средний эффект воздействия
поля уменьшается и при Фо ^> 1 будет близок к нулю (М = 0). Отсюда
же следует, что для нерелятивистских пучков, эффективная модуляция
скорости электронов возможна лишь в замедленных электромагнитных
волнах, так как реально достижимые скорости электронов в нереляти-
нерелятивистских электронных приборах порядка 0,02 Ч- 0,1с, где с — скорость
света.
2. Кинематический анализ группирования электронов в поле бегу-
бегущей электромагнитной волны постоянной амплитуды. Для опреде-
определения тока пучка, сгруппированного в поле волны постоянной ампли-
амплитуды, воспользуемся уравнением, связывающим переменные величины
конвективного тока и поля, выведенного при рассмотрении гидродина-
гидродинамического описания электронного потока, а именно уравнением C.22):
дЧ дЧ 2д21 с, дЕ
s> (9-8)
где Se — площадь поперечного сечения электронного пучка.
Лампы бегущей волны 281
В предположении, что все величины меняются во времени по закону
ejujt, уравнение (9.8) сведется к виду
§д1-&=^ЕМ. (9.9)
Интегрируя данное неоднородное линейное уравнение и учитывая
вид Е(х, t) (см. формулу (9.1)), получим интегральное уравнение для
сгруппированного тока
C(* - С) d(. (9.10)
о
Подставляя Е\(х) = Е°е~^°х и проводя интегрирование, получим вы-
выражение для полного тока пучка
(9.11)
— E°l
При ? = —— <С 1 в конце пространства взаимодействия х = / соотно-
Vo
шение для полного тока пучка можно переписать в виде:
^7 С^^П Л^
где а = и — величина, аналогичная параметру группирования Aq,
который вводился при описании группировки в пространстве дрейфа
(см. Лекцию 2); Тр0 = /Зе1 — абсолютный угол пролета в пространстве
дрейфа.
Из формул (9.11) и (9.12) видно, что степень группирования X при
заданной амплитуде поля существенно зависит от длины пространства
взаимодействия (~ I ). Таким образом в потоке электронов, взаимо-
взаимодействующих с бегущей электромагнитной волной имеет место про-
пространственная квадратичная группировка, которая уже обсуждалась
нами в первой лекции. Такой характер группировки связан с тем, что,
с одной стороны, увеличение протяженности пространства взаимодей-
взаимодействия приводит у увеличению X за счет роста ? ~ I. Это приводит
к возможности получения эффективного взаимодействия электронного
потока с переменным полем в колебательной системе нерезонансного
типа. С другой стороны, X увеличивается с ростом / за счет роста
абсолютного угла пролета Тр0, так как для группирования электронов
существенно абсолютное время пребывания в пространстве взаимо-
взаимодействия, за которое одни электроны догоняют другие. Абсолютный
угол в системах с длительным взаимодействием может быть сделан
282 Лекция 9
существенно большим, чем в случае систем с резонансными колебатель-
колебательными системами (см. Лекцию 2). Это связано с тем, что в в системах
с резонансным взаимодействием увеличение сро связано с уменьшением
коэффициента М. В бегущей волне существует возможность сделать
малым относительный угол пролета Фо при условии синхронизма, а сле-
следовательно, величина М, определяющая величину эффективного поля,
может быть сделана близкой к единице при каких угодно больших
величинах длины пространства взаимодействия.
Из соотошений (9.11) и (9.12) можно получить выражение для пере-
переменной составляющей тока г в виде
Комплексное выражение в фигурных скобках можно представить в дру-
другой форме:
Выражение (9.15) представляет сдвиг фазы переменной составляющей
тока пучка относительно холодного поля E°e^ujt~^°l"). В частности, при
условии точного синхронизма ^о = ^ф (Фо = О),Фг = тг/2, из выражений
(9.14) и (9.15) следует
1_ = /ро;2/2 = /2тг/\2 /о = BтгЛр2 /0 ( ,
где N = I/X носит название электрической длины лампы. Видно, что
при точном синхронизме максимум сгруппированного тока образуется
там, где холодное поле равно нулю. Если, следуя монографии [8, 9],
назвать г/Е электронной проводимостью, то при условии точного син-
синхронизма она имеет характер положительной реактивной проводимо-
проводимости, что приводит к уменьшению фазовой скорости горячей волны (т. е.
волны в линии передачи с пучком) по сравнению со случаем точного
синхронизма: Уф = Vo.
3. Взаимодействие электронного потока с бегущей электромаг-
электромагнитной волной постоянной амплитуды. Для рассмотрения характери-
характеристик энергетического взаимодействия между потоком и бегущей волной
воспользуемся выведенным в первой лекции уравнением возбуждения
Лампы бегущей волны 283
волноведущей системы заданным током в интегральной форме A.72):
ox - Щ^- J i
Ех = E°e-j0ox - Щ^- J i(x)e-jl3^x-^ dx -
. (9.17)
При этом будем пренебрегать вторым интегралом, которому соответ-
соответствует обратное излучение к генератору сигнала. Это может быть сде-
сделано благодаря тому, что обратное излучение представляет собой ин-
интерференцию несфазированных элементарных волн. Тогда уравнение
возбуждения перепишется в виде
2
Ех = E°e-jCox - ^^- J i(x)e~jMx-^ dx. (9.18)
о
Подставим сюда выражение для сгруппированного тока (9.11), тогда
в конце пространства взаимодействия х = I имеем 1)
Е{1) = Eoe~j0J {1 - BttC7VK [Re F(<2>0) + j Im F(^o)]} • (9.19)
Здесь как и раньше предполагается, что ( < 1 и wt й ujt\ + f3ex.
Величина С = Со 1^-1 , Со = ( .,, ) носит название параметра
\Ре J V 4 Ко /
усиления Пирса. Величины Re F и Im F определяются следующими
выражениями:
0) = Fla = 2A
Ф0
Im F(*o) = Flr = 28тФо-ФоA + со8Ф0)_ (g 21)
Ф0
Учитывая соотношения A.75) и их связь с уравнением возбуждения
в интегральной форме (см. лекцию 1; стр. 37) для активной и реактивной
мощности взаимодействия можно записать:
Реа = \ IOVofvoFla@o), (9.22)
Pea = \ IoVofvoFlr@o), (9.23)
х) При выводе соотношения (9.19) удобнее перейти от интегрирования по
продольной координате х к интегрированию по относительному углу проле-
284
Лекция 9
-An
Фо
Рис. 9.8. Зависимость функций Fia, Fir от относительного угла пролета Фо
На рис. 9.8 приведены функции F\a и F\r в зависимости от относи-
относительного угла пролета Фо в предположении, что последний изменяется
благодаря изменению фазовой скорости волны при неизменных значе-
значениях /, U И Vq.
Интервалы изменения углов пролета Фо, при которых электрон-
электронный поток отдает энергию электромагнитной волне, соответствуют
заштрихованным областям, где Реа < 0. Незаштрихованные области
соответствуют отбору электронами энергии у волны (Реа > 0). Мак-
Максимальная передача энергии волне происходит при Фо = — тг. В этом
случае электроны, как видно из определения Фо, движутся несколько
быстрее волны. Электроны отдают энергию и в том случае, когда они
движутся существенно быстрее волны (например, Фо = — Зтг), однако,
эффективность такого энергообмена невелика. Заметим, что при Фо =
= 0 (условие точного синхронизма) активная составляющая мощности
взаимодействия равна нулю, в то время как реактивная мощность вза-
взаимодействия положительна и максимальна. В этом случае (Фо = 0) из
формулы (9.19) имеем
где
= /31 + arctg
(9.24)
(9.25)
— фаза горячей электромагнитной волны. По определению фазовая
скорость волны
. (9.26)
1 + arctg
Из последнего соотношения видно, что при условии точного синхро-
синхронизма электронов и холодной волны фазовая скорость горячей волны
Лампы бегущей волны 285
уменьшается по сравнению со скоростью электронов vo, т. е. взаимодей-
взаимодействие носит реактивный характер.
Электронная проводимость i/E(l), введенная в предыдущем разде-
разделе, в случае Фо = 0 дается выражением (оно следует из соотношений
(9.24) и (9.13)):
i _ /оBтгЛ02 = J ГBтгСЛ0я"" 1
4/3eVo "( [ 6
^o - aq i/. — 1 x ' I « I Г ^лн./ * *' (9.27)
,тг ^ i + ГBтгС7УK] тг
где 4*i = — + arctg — > —, т.е. электронная проводимость
является комплексной и имеет действительную часть с отрицательным
знаком.
В результате анализа взаимодействия электронного потока с бе-
бегущей прямой электромагнитной волной на основе метода последова-
последовательных приближений в кинематическом приближении получили до-
достаточно общие соотношения, которые далее будем использовать как
для анализа лампы бегущей волны, так и для анализа лампы обратной
волны (в частности, определения пусковых условий ЛОВ).
Качественное описание процесса группирования
электронов в бегущей волне
Проведенный элементарный анализ процесса взаимодействия элек-
электронов с бегущей электромагнитной волной позволяет весьма наглядно
интерпретировать этот процесс.
Привлечем для объяснения механическую модель (рис. 9.9), в кото-
которой электроны можно представить в виде шариков, а эффект действия
поля заменить действием гравитационных сил некоторой поверхности,
форма которой соответствует мгновенному распределению потенциала
ВЧ-поля вдоль длины пространства взаимодействия (см. рис. 9.9а).
Предположим, что в волноведущей линии без пучка распространяет-
распространяется волна с фазовой скоростью г?ф, в точности равной невозмущенной
скорости г>о электронов. На начальном участке пространства взаимо-
взаимодействия, когда энергообмен между электронами и волной невелик
(в механической модели это соответствует одинаковой высоте вершин
и глубине впадин: волна не меняет свою амплитуду), электроны-шарики
скатываются под действием силы тяжести по «склонам» потенциальной
поверхности и скапливаются в её «долинах» (рис. 9.96). То есть электро-
электроны группируются там, где поле волны равно нулю. Последнее означает,
что ток пучка опережает по фазе поле «холодной» волны на угол
тг/2. Этот результат полностью совпадает с выводами элементарной
теории (см. соотношение (9.24), которое будет выполняться не только
в конце пространства взаимодействия, но и в любой его точке в начале
пространства взаимодействия, где С N — мало; для нахождения Е(х)
286
Лекция 9
необходимо в уравнении (9.24) всюду осуществить замену х *-> /, в том
числе и в N и в Фо), Е(х) ~ Е^о,~^°х равно полю «холодной» волны
в линии передачи. Из формулы (9.16) следует, что сгруппированный
в поле волны постоянной амплитуды ток пучка опережает по фазе поле
на тг/2, достигая максимума там, где поле обращается в нуль. Сле-
Следовательно, вышеприведенные модельные представления полностью
соответствуют выводам элементарной теории.
По мере увеличения С N энергообмен между полем и электронами
становится все более значительным, и амплитуда поля Е(х), опре-
определяемая соотношением (9.24),
растет с ростом С N. В гравита-
гравитационной модели это означает, что
при продвижении в положитель-
положительном направлении оси х верши-
вершины поверхности становятся вы-
выше, а впадины глубже.
Одновременно, в результате
реактивного энергообмена фазо-
фазовая скорость Уф горячей вол-
волны становится меньше скоро-
скорости vq электронов. Поэтому сгу-
^ n n л/г сток электронов-шариков из «до-
Рис. 9.9. Механическая модель, по- к к
ясняющая процессы группирования лины» (см. рис. 9.9в) переме-
электронов в бегущей волне и взаи- щается на правый тормозящий
модействие с ней склон потенциальной поверхно-
поверхности (этот склон соответствует действию тормозящей фазы поля), где
продольная составляющая поля волны отлична от нуля.
Если сразу предположить, что vq > г>ф, а амплитуда волны растет
с расстоянием, то объяснение механизма усиления волны становится
совсем простым.
В системе координат, связанной с волной, вершины и впадины по-
потенциальной поверхности неподвижны относительно оси волноведущей
линии. Электроны-шарики на своем пути встречают области подъема
и спада потенциальной поверхности, поэтому они группируются на тор-
тормозящих («правых») склонах и разгруппировываются на ускоряющих
(«левых»). Следовательно, сгустки электронов-шариков формируются
на правых склонах, причем эффект торможения превосходит эффект
ускорения, поскольку было допущено существование волны с нараста-
нарастающей амплитудой. Энергия взаимодействия будет наибольшей, когда
электроны за время пролета пройдут весь тормозящий склон. Таким
образом, усиление волны происходит в результате непрерывного после-
Лампы бегущей волны 287
довательного отбора от электронного потока незначительных порций
энергии по всей длине пространства взаимодействия пучка с волной 1).
С позиций теории излучения описанное выше взаимодействие соот-
соответствует индуцированному излучению Черенкова. Отдельная частица,
двигаясь со скоростью vo, большей скорости света в среде (уф — скорость
света в замедляющей среде), излучает по Черенкову, а индуцирован-
ность излучения определяется существованием механизма группировки
электронов в волне.
В заключение следует указать, что вышеописанное взаимодействие
прямолинейного электронного потока с бегущей ЭМВ носит название
взаимодействия О-типа (от французского Vonde — волна). При этом
электроны отдают волне свою кинетическую энергию. Заметим, что
А.В. Гапонов-Грехов дал более широкое определение взаимодействия
типа О: он называет взаимодействием типа О любое, для которого
форма резонансной кривой совпадает с видом F\a (формула (9.20)).
Принципы подобия для приборов с длительным
взаимодействием
(нерелятивистские и ультрарелятивистские пучки).
Рассмотрим задачу нахождения критериев подобия для приборов
с длительным взаимодействием из соображений размерности [10]. Под
критерием подобия понимается безразмерное выражение, составленное
из параметров задачи, которое можно рассматривать как меру отно-
отношения интенсивностей двух физических эффектов, существенных для
исследуемого процесса [11]. Заметим, что мы фактически уже получа-
получали критерий подобия в задаче исследования развития неустойчивости
в диоде Пирса, когда после приведения уравнений процесса к безраз-
безразмерному виду получили единственный безразмерный управляющий
параметр задачи — параметр Пирса, который является критерием по-
подобия для этой физической задачи. В данном разделе будут получены
критерии подобия на основе анализа размерности. Дадим определение:
под размерностью той или иной физической величины понимается
выражение единиц измерения ее через физические величины, приня-
принятые за основные. Размерность физических величин представляет собой
произведение возведенных в степень размерностей величин, принятых
за основные [11]. Часто пользуются системой единиц «LMT»,t. e. в каче-
качестве основных выбирают единицы длины [L], массы [М] и времени [Т].
В этом случае размерность любой из физических величин [Р] может
г) Из аналогичных рассуждений понятно, что, если электронный поток
будет отставать от волны, то он будет забирать у нее энергию (электроны
группируются на «ускоряющих» склонах). Это приводит к затуханию волны,
а при определенных условиях к полному подавлению входного сигнала.
Одновременно электроны пучка будут ускоряться.
288 Лекция 9
быть представлена в виде:
где A, /i и т - некоторые рациональные дроби. Наиболее важно при
применении методов размерности правильно выделить физические эф-
эффекты, существенно влияющие на поведение исследуемой системы.
Рассмотрим движение нерелятивистского электронного пучка в по-
поле бегущей волны, при этом пренебрежем обратным влиянием пучка на
волну, а также силами пространственного заряда. В качестве опреде-
определяющих величин, от которых зависят физические процессы в системе,
выберем следующие величины: х — продольная координата (х = I —
длина пространства взаимодействия), и — частота поля, воздейству-
воздействующего на электронный пучок, Уф — фазовая скорость волны электро-
электромагнитного поля, воздействующего на пучок, Е° — амплитуда поля
волны в начале пространства взаимодействия х = 0 (причем Ех(х) =
= EQ fi(x)e^ujt~CoX^),ti — начальное время влета электрона в простран-
пространство взаимодействия, Vb — ускоряющее напряжение пучка, v(x,ti) —
скорость электрона в присутствии ВЧ-поля, зависящая от простран-
пространственной координаты и момента влета в пространство взаимодействия,
г] — удельный заряд электрона.
Заметим, что вместо Е° в число определяющих переменных можно
ввести значение амплитуды в любой точке пространства взаимодей-
взаимодействия, например, при х — I. Более того, можно задать ВЧ-поле в виде
Ех(х) = EQ fi{x)e^ujt~^eX\ где/?е = oj/уо (vo — скорость электронов на
входе пространства взаимодействия). Тогда, если считать функцию Д
комплексной, можно исключить Уф из определяющих величин. Однако
присутствие Уф делает выкладки более наглядными и физичными,
поэтому сохраним Уф среди определяющих величин. Введем безразмер-
безразмерную комбинацию ut\. Тогда вместо функции v(x,ti) можно определить
безразмерную величину
2тг
^ Ч (9.28)
— усредненный по начальным фазам влета электронов за один период
ВЧ-поля квадрат скорости в фиксированной точке пространства. Учи-
Учитывая соотношение (9.28), можно исключить из определяющих величин
время t\.
Связь между определяющими величинами можно записать в виде
следующего функционального выражения:
v = f{x,w,v^E\tuV^r)). (9.29)
Выпишем матрицу размерности в системе LMT:
Лампы бегущей волны 289
х и Уф Е° Vo v г) t\
L 1 0 1 -1/2 1/2 1 3/2 О
М О О О 1/2 1/2 О -1/2 О
Т О -1 -1 -1 -1 -1 -1 1
Здесь необходимо отметить, что число независимых критериев подобия
(фундаментальных критериев подобия), которые можно составить из
имеющихся определяющих величин, будет равно числу независимых
решений системы однородных линейных уравнений, соответствующей
матрицы подобия. Причем число независимых решений равно рангу
матрицы (см. [12, раздел 1.9-4]). Наибольший порядок, который могут
иметь миноры выписанной матрицы размерности, не равные нулю,
равен трем. Поэтому ранг матрицы равен трем, а, следовательно, число
фундаментальных критериев подобия равно трем, а всего можно соста-
составить пять критериев подобия.
Для решения задачи с учетом вышесказанного выберем следующие
новые первичные единицы: [со] = [Т], [уф] = [L] • [Т] и [Vo] = [L]3/2 •
• [М]1/2 • [Т]. Используя уравнение (9.29), можно записать:
= Ф
Используя матрицу размерности для первой безразмерной комбинации,
имеем:
~, . ГТ 1— 1— EХ — 17ж/2 ГДД]—17ж/2 ГгГ1СКа;+/За;+7а; 1
X . [LiJ • [1V1J * L J —
Отсюда получаем три уравнения для определения коэффициентов ах,
-1 - /Зх - 17ж/2 = 0, -17ж/2 = 0, аж + /Зх + 7ж = 0.
Тогда ах = — 1, /Зх = 1 и jx = 0, и критерий подобия выражается
комбинацией вида
Пж = ^. (9.30)
Аналогично находим остальные четыре критерия подобия:
-, 11^ = uiti, 1Ц = —2~. (9.о1)
Учитывая, что по определению оо/уф = 2тгЛ3ам (Азам — длина волны
в замедляющей системе), и, производя тождественные для критериев
подобия преобразования, получим систему критериев подобия (9.30) и
10 Д. И. Трубецков, А. Е. Храмов
290 Лекция 9
(9.31) в следующем виде:
V \ рг/ _ Е Азам
J П
(9.32)
В таком виде критерии подобия имеют вполне ясный физический
смысл: П^ — текущая длина пространства взаимодействия в замедлен-
замедленных длинах волн, П^ — безразмерная кинетическая энергия, П^о —
отношение ВЧ-напряжения к ускоряющему напряжению, П^ — на-
начальная фаза влета электронов в пространство взаимодействия, П^ —
параметр рассинхронизма электронов и волны.
Теперь понятно, в чем смысл введения новых основных единиц о;, Уф,
Vo — они являются характерными масштабами задачи: и /уф = 2тгА3ам
(определяет характерный масштаб длины), Vo (масштаб напряжения)
и л/ЩУо (масштаб скорости).
Предположим для простоты, что имеет место условие точного син-
синхронизма Уф = Vo, тогда на основании соотношений (9.32) и (9.29)
можно записать
v2 _ г (Е°Хзам х \ (а<\<\\
— - /1 I —77 ' Utl' 1 / ' (У.66)
Vq \ У 0 Азам J
где Д — некоторая функция.
Очевидно, что lim (v2/vq) = 1, поэтому уравнение (9.33) может
быть переписано как
?°Азам , X
при этом /2 @, wti, ж/Лзам) = 0. Усреднив полученное выражение по
wti, получим выражение для электронного к.п.д.:
v2
Е Азам
/1 и \ ? \ ^ Лзам о, 1 (с\ ъл\
Ve = ( 1 - — ) = /l —Г/ , -г • (9.34)
Если теперь предположить, что структура поля Ех(х) =
= E°fi(x)ej(ujt~l3oX"> зафиксирована, то при х = / имеем:
у2\ f [Ех\зам I \ ( ч
- — > = Л ( —Гг—j т— ) • (9-35)
V0 / V Vo Азам /
Величины ExX3am/V0 = (Ex\/y/Vo) • {у/Щ/с) и //Азам = A/Х) •
• (c/y/2rjVo ) (А — длина волны в свободном пространстве, с — скорость
света) являются критериями подобия, поэтому для их постоянства
необходимо
1) увеличивать — ~ \/Vo ;
А
Лампы бегущей волны 291
2) увеличивать ЕХХ ~ у/Vq .
Соотношение (9.34) можно получить сразу, если как указывалось
выше, вместо v сразу ввести в число определяющих величин (v2).
Рассмотрим теперь воздействие ВЧ-поля на ультрарелятивистский
электронный поток, скорость которого мало отличается от скорости
света. Для решения задачи перейдем в систему координат, движущуюся
со скоростью г>о электронов на входе в пространство взаимодействия.
В этой системе время Т' взаимодействия электронов с высокочастотным
полем на основе релятивистской формулы преобразования интервала
времени можно записать следующим образом:
Т' =
где ?Пок — энергия покоя электрона, ?q — полная энергия электрона
на входе в прибор. В ультрарелятивистском случае скорость электрона
мало отличается от скорости света, поэтому Т ~ -. Аналогично
А'= ^—=\^. (9.37)
В качестве определяющих величин в подвижной системе координат
выберем (?)utl — усредненную по начальным фазам энергию, ?o,Tf,\f,
с, еЕ° — силу, действующую на электрон на входе пространства взаи-
взаимодействия со стороны ВЧ-поля (Е° = {Е0}'). Таким образом искомая
функциональная зависимость может быть представлена в виде:
(?)шг1=/(?0,Т',Х',с,еЕ°). (9.38)
В качестве основных единиц выберем ?q, Т' и Л'. Тогда, повторяя
выкладки, сделанные нами для случая нерелятивистского электронно-
электронного потока, получим:
<?> = f
J
So
(
таккакД!^^ =0.
So
Если, как и в предыдущем случае, зафиксировать распределение
поля вдоль длины пространства взаимодействия, то для постоянства
критериев, стоящих под под знаком функции в правой части уравнения
(9.39), необходимо
1) увеличивать I/X пропорционально ?q ;
ю*
292 Лекция 9
2) увеличивать ЕХХ пропорционально ?о.
Отметим, что эти закономерности были впервые установлены
М.И. Петелиным для ультрарелятивистских пучков из других
соображений в работах [13, 14].
Список литературы
1. Рабинович М.И., Трубецков Д. И. Введение в теорию колебаний и
волн. — Москва-Ижевск: НИЦ «Регулярная и хаотическая дина-
динамика", 2000.
2. Силин Р. А., Сазонов В. П. Замедляющие системы. — М.:
Сов.Радио, 1966.
3. Варнеке. Эволюция принципов действия современных электрова-
электровакуумных приборов для СВЧ // В кн: Миллиметровые и субмил-
субмиллиметровые волны. М.: Изд-во иностранной литературы, 1959.
СС. 11-78.
4. Kompfner R. The invention of the travelling wave tube. — San
Francisco: San Francisco Press, 1964.
5. Пирс Дснс. Электроны, волны и сообщения. — М.: Госиздат.ФМЛ,
1964.
6. Пирс Дж. Лампа с бегущей волной. — М.: Сов.Радио, 1952.
7. Шевчик В.П. Взаимодействие электронных пучков с электромаг-
электромагнитными полями. — Саратов: Изд-во СГУ. 1963.
8. Шевчик В.Н., Трубецков Д.И. Аналитические методы расчета в
электронике СВЧ. — М.: Сов. радио, 1970.
9. Chodorow M., Susskind С Fundamentals of microwave electronics. —
NY.: McGraw-Hill, 1964.
10. Трубецков Д.И. Анализ размерностей, подобие и оценки в СВЧ
электронике // Лекции по электронике СВЧ и радиофизике D-
я зимняя школа-семинар инженеров), Книга V. Саратов: Изд-во
СГУ, 1978. С. 3.
11. Седов Л.И. Методы подобия и размерности в механике. — М.:
Наука, 1972.
12. Корн Г., Корн Т. Справочник по математике (для научных работ-
работников и инженеров). — М.: Наука, 1978.
13. Петелин М.И. Принцип подобия для высокочастотных приборов
с ультрарелятивистскими электронными потоками // Изв. вузов.
Радиофизика. 1970. Т. XIII, № 10. С. 1586.
14. Петелин М.И. Генерация когерентного излучения интенсивными
потоками заряженных электронов // Лекции по электронике СВЧ
и радиофизике C-я зимняя школа-семинар инженеров), Книга IV.
Саратов: Изд-во СГУ, 1974. С. 179.
Лекция 10
НЕЛИНЕЙНАЯ ТЕОРИЯ
ЛАМПЫ БЕГУЩЕЙ ВОЛНЫ
... Нелинейная теория ЛБВ занимает в электро-
электронике СВЧ особое положение. Определенный ин-
интерес она представляет и для понимания ряда
явлений в других системах, содержащих неравно-
неравновесные потоки заряженных частиц одинакового
или различных знаков. Во многом общими ока-
оказываются математические методы их описания.
Г.Ф. Филимонов, Ю.Н. Бадлевский.
Нелинейное взаимодействие элек-
электронных потоков и радиоволн в ЛБВ.
М.: Сов.радио, 1971. с. 7
Нелинейные уравнения ЛЕВО. Линеаризация нелинейных уравнений
ЛБВ. Дисперсионное уравнение ЛБВ. Закон сохранения энергии в элек-
электронном потоке, взаимодействующем с бегущей электромагнитной
волной. Механизм фазировки в бегущей электромагнитной волне. Осо-
Особенности и результаты решения задачи на ЭВМ. Спиральная лампа
бегущей волны как основа усилительного модуля. Способы повышения
к.п.д. ЛБВ О.
В прошлой лекции рассмотрен механизм взаимодействия электрон-
электронного потока с бегущей электромагнитной волной малой амплитуды
в рамках метода последовательных приближений, а также с помо-
помощью теории размерности выведены критерии подобия для электрон-
электронных пучков, взаимодействующих с бегущей электромагнитной волной,
в нерелятивистском и ультрарелятивистском приближении. В данной
лекции будет изложена нелинейная теория лампы бегущей волны со
спиральной замедляющей системой, которая, несмотря на ряд упро-
упрощающих предположений, позволит нам рассмотреть энергетические
характеристики взаимодействия пучка с полем, а также механизм фази-
фазировки при конечных амплитудах сверхвысокочастотного поля. В конце
лекции остановимся на некоторых практических аспектах разработки
усилителей бегущей волны, и в частности, методах повышения к.п.д.
ЛБВ.
294 Лекция 10
Нелинейные уравнения ЛЕВ
Выведем уравнения, описывающие взаимодействие электронного
потока с бегущей электромагнитной волной, которые будут учитывать
следующие нелинейные явления:
1) изменение средней скорости электронов при взаимодействии с по-
полем бегущей волны;
2) обгон одних электронов другими, группировку электронного по-
потока (образование сгустков, их деформацию и разрушение);
3) появление высших гармоник тока и поля на частотах пи (п =
= 1, 2, 3...).
При этом не будем рассматривать такие нелинейные явления как
расслоение электронного потока в поперечном направлении вследствие
неравномерной модуляции потока по сечению, вызванное неоднород-
неоднородностью поля замедленной волны и поля пространственного заряда;
остановка и отражение электронов; поперечные движения электронов.
Заметим, что учет последних явлений менее существенен при анализе
ЛБВ средней мощности и с небольшим к.п.д. г) Поэтому с практической
точки зрения можно ограничиться при выводе уравнений учетом только
первых трех нелинейных эффектов.
Уравнение движения запишется в виде
Tt="E> A(U)
где v — скорость какого-то выбранного сечения пучка, Е — усреднен-
усредненная по сечению пучка продольная составляющая электрического поля.
Перейдем в уравнении движения к переменным Лагранжа, выбрав в ка-
качестве независимых переменных текущую координату слоя х и время
влета t\. Выбор координаты х связан с тем, что все полевые харак-
характеристики определяются в пространстве и зависят от координаты х.
Введение в качестве второй независимой переменной времени влета t\
позволяет избавиться от сложностей при описании явлений, связанных
с взаимным обгоном электронов (точнее слоев в электронном потоке):
скорость электронов является однозначной функцией вплоть до начала
поворота частиц. В новых переменных траектория слоя электронного
потока, поступающего в момент времени t\ в пространство взаимодей-
взаимодействия, определяется уравнением t = t(x, t\). Тогда:
^ = _^^, (Ю.2)
dt fdt\
x) Далее мы покажем, что учет упомянутых явлений становится существен-
существенным при к.п.д. ЛБВ-усилителя большем, чем 60%.
Нелинейная теория лампы бегущей волны 295
и уравнение A0.1) в новых координатах записывается как
Текущую фазу электрона можно представить в виде
Ut = Wt! +/3eX + 0(?,?i),
где #(?, t\) — возмущение, вызванное полем Е. В предположении, что
параметр усиления Со мал, функция #(?, t\) является медленно меня-
меняющейся функцией координаты, т. е. зависит не от х, а от ? = Со/3ех.
Закон сохранения заряда в переменных (x,ti) имеет вид
Iodh = J(t,x)\dt\,
где dt\ > 0 — промежуток времени, за который через начальное се-
сечение лампы х = 0 проходят электроны, пересекающие сечение х >
> 0 за промежуток времени \dt\. Знак модуля поставлен в связи с тем,
что возможна ситуация, когда dt/dti < 0 и dt < 0, т. е. обгон одних
электронов другими.
Предположение об отсутствии в потоке отражений означает, что
функция t(x, t\) является однозначной, причем jp- = — г- > 0. Так
Ox v(x, t\)
как t(x, t±) является временем прибытия в точку х электрона, влетев-
влетевшего в начало пространства взаимодействия х = 0 в момент времени ?i,
то, очевидно, ?@, t\) = t\. Обратная функция ti(x,t) многозначна.
Действительно, если имеет место обгон, то в момент времени t в точку х
могут прибыть электроны, имеющее разное время влета t\.
Следует отметить, что рассматривается установившийся процесс,
поэтому два электрона, влетающие в моменты времени t\ wt\ -\- 2тгп/и
(п G Z), попадают в одну фазу поля и двигаются совершенно одина-
одинаково. Тогда величина u)t(x, t\) — uot\, а вместе с ней функции скорости
и ускорения электронов, являются периодическими функциями време-
времени влета t\. Это позволяет при дальнейшем анализе ограничиваться
рассмотрением интервала 0 ^ ujt\ ^ 2тг.
Так как рассматривается сильная группировка, то в нелинейном
режиме ток пучка при периодическом сигнале может быть разложен
в ряд Фурье. Для простоты выкладок ограничимся рассмотрением
только первой гармоники тока х):
сю
J(t,x) = /O + Re ? Jn(x)ejnujt ^/0 + Ji(x)ejuJ\ A0.4)
n=l
x) Заметим, что обобщить результат на случай учета любого числа гармоник
основной частоты не представляет сложности (см., например, [1]).
296 Лекция 10
2тг
jn(x) = I [ J(t,x)e-jnujtd(u;t). A0.5)
О
Ведя функцию и(^,щ) = uot — /Зех = ojt\ + #(?,?i) = и0 + 0(?,?i),
выражение A0.5) для первой гармоники сгруппированного тока можно
переписать в виде:
2тг
J^x) = I°e-j0'x \ e-jute>uo) du0 = IoI(O^~j0eX- (Ю.6)
7Г J
О
Теперь выпишем уравнения для полевой части задачи. Поле Е,
воздействующее на электронный поток, можно представить в виде
Е{х) = Re ? МяОе"""* " ?", (Ю.7)
п=1 °^Ж
где f n — поле синхронной волны на n-й гармонике (будем ограничивать-
ограничиваться, как и в случае вычисления сгруппированного тока, рассмотрением
только первой гармоники Е\ = ?), Ф — потенциал поля пространствен-
пространственного заряда. Не будем учитывать поля пространственного заряда, т. е.
предположим, что Ф = const. Заметим, что даже при учете влияния сил
пространственного заряда, их роль будет существенна только у конца
лампы, где поток уже сильно сгруппирован. В начале пространства
взаимодействия плотность пространственного заряда р = const и про-
продольные электростатические поля Ф = const, Я\— = 0.
Для нахождения ? воспользуемся уравнением возбуждения волно-
волновода (9.18) в форме, которая обсуждалось на прошлой лекции:
FT — ?Г®рь — ЗРоХ PqJ^O A(-^\Pk — j^o{x — x) J— /irk o\
J-Jx — Hi ъ lyXjKi UX. yL\J.Oj
0
Переходя к дифференциальному виду, как это делалось в первой лек-
лекции, получим
Введем безразмерную амплитуду синхронной волны
A0.10)
Тогда, учитывая, что -j- = -jF-fi- = PeCo-jF, уравнение A0.9) перепи-
CLX ^*C 0>Х ^*С
шется как
Нелинейная теория лампы бегущей волны 297
Введем обозначения:
V0CU/3e - Ро) _ j(/3e - Ро) _ , ( v
, _ (Ре - /?о) _ Уф - VQ
Ре Со Уф Со
— параметр холодного рассинхронизма;
( Ро\ С (Р\
0 \Ре
где учтено, что из уравнения A0.11) следуют равенства 1 —
= -ЬС0 > If
Окончательно уравнение возбуждения принимает вид:
A0.13)
2л-
= - I e-judu0. A0.14)
7Г J
О
Преобразуем уравнение движения A0.3):
1 Ре (?, h), h
Уо
dt _ 1 двЦеС0 _ 1 (дв
g2^ = ^Ср2 д2в
дх2 ш д?2'
Учитывая выражение для безразмерной амплитуды поля A0.10), а так-
также, что 0г? = tjtt, ^-^ = ^т^5 получим уравнение движения в виде
0. A0.16)
Таким образом получили систему нелинейных уравнений, которая, бу-
будучи дополненной начальными условиями
= 0, A0.17)
298
Лекция 10
Рис. 10.1. Модели лампы с бегущей волной
описывает упрощенную модель ЛБВ — бесконечно длинную замедляю-
замедляющую систему г) с полубесконечным в продольном направлении элек-
электронным пучком (рис. 10.1). Начальный сигнал представляет собой
волну, набегающую слева на сечение ? = 0. Еще раз отметим, что
система нелинейных уравнений A0.13)—A0.17) справедлива только при
малых параметрах усиления Со (Со ^ 0,2 [1, С. 151]). При её выводе не
учтены также потери в линии передачи и влияние пространственного
заряда.
Можно показать [2], что при учете пространственного заряда и по-
потерь нелинейные уравнения ЛБВ запишутся в виде
A0.18)
т = 12[е-'«
A0.19)
A0.20)
Здесь d = 7o/(/3eCo) — параметр холодных потерь, jo ~ постоянная
затухания, которая содержится в выражении для фазовой постоянной
распространения волны в линии передачи (/30 = Ро + J7o) и характери-
характеризует затухание волны на единицу длины, q = 4QCo = (f3p/(f3eCo)) —
параметр пространственного заряда.
Данная система уравнений не может быть проинтегрирована ана-
аналитически, поэтому для ее анализа используются те или иные при-
приближенные или численные методы решения [3]. Отметим также, что
выведенная система уравнений стационарна, и, следовательно, не поз-
позволяет исследовать нестационарные режимы работы ЛБВ (например,
переходные процессы). С помощью нее можно анализировать лишь
х) Вместо бесконечного волновода можно рассматривать конечной длины
идеально согласованный на концах волновод: дело в том, что наша модель
никак не учитывает отраженное поле от границ системы, что и требует
условия идеального согласования.
Нелинейная теория лампы бегущей волны 299
установившиеся стационарные режимы работы, определить мощность,
к.п.д., особенности группировки электронного потока.
Линеаризация нелинейных уравнений ЛЕВ.
Дисперсионное уравнение ЛЕВ
Линеаризуем систему нелинейных уравнений A0.18)—A0.20) и по-
получим дисперсионное уравнение ЛБВ в предположении малого сигнала
(в = \и - ио\ < 1, Со < 1, С0Щ < 1, exp (j6) « 1 - j6). Из уравнения
A0.19) получаем выражение для гармоники тока:
2тг
/
du0 =
О 2тг 2тг 2тг
= - [ eiwo duo + t [ e-jUo0duo = ^ [ e-juo0du0.
7Г J 7Г J 7Г J
0 0 О
Если рассмотреть это соотношение как уравнение относительно ?, то,
как несложно убедиться подстановкой, выражение
в =3- {-I(i)e~jUQ + /*@eJ'U0) A0.21)
2 v '
является его решением. Линеаризованное уравнение движения A0.20)
имеет вид
2 = Re(.F + jqI)(OeJU°- A0.22)
Подставляя выражение A0.21) в уравнение A0.22), получаем уравнение
относительно величины сгруппированного тока:
—- + ql = jT. A0.23)
Делая подстановку exp (jS?), из условия совместности системы уравне-
уравнений A0.23) и A0.18) получаем дисперсионное уравнение ЛБВ:
(S2 + q)(jS - b + jd) = A + ЬСоJ. A0.24)
Дисперсионное уравнение A0.24) совпадает с известным соотноше-
соотношением, полученным (см., например, [3]) из других соображений, что
является в определенной мере проверкой полученных нелинейных урав-
уравнений. Покажем это, для чего выведем дисперсионное уравнение ЛБВ,
воспользовавшись для этого уравнением возбуждения в дифферен-
дифференциальной форме (см. лекцию 1; формула A.74)) и уравнением для
конвекционного тока C.23), выведенным в лекц. 3). Будем искать их
п
решение в виде суммы парциальных волн: у(х) = ^ yi@)e~^iX, где
г=1
Pi — искомая постоянная распространения г-й парциальной волны, п —
300 Лекция 10
число парциальных волн. Из условия совместности системы уравнений
можно получить дисперсионное уравнение ЛБВ в виде
(/З2 - /302J [(/} - &J - $] = -2MIGI A0.25)
Данное уравнение является уравнением четвертой степени, т.е. соот-
соответствует четырем парциальным волнам, причем одна из волн соот-
соответствует встречному излучению. Если им пренебречь, то уравнение
возбуждения в форме A.72) переходит в интегральное уравнение вида
(9.18). Соответствующее ему дифференциальное уравнение с учетом
встречного излучения будет, в отличие от уравнения A.74), уравнением
первого порядка:
°b.+jfiEx = -?$fi(x). A0.26)
Тогда, если вместо уравнения A.74) взять уравнение A0.26), диспер-
дисперсионное уравнение примет вид
(Р2 - Pi) [(Р - Pef ~ Pi] = -2РеР30С$. A0.27)
Последнее выражение обычно записывают в нормированных пара-
параметрах Пирса: b (параметр холодного рассинхронизма), d (параметр
холодных потерь), 4QСо (параметр пространственного заряда). Введем
также новые обозначения: /3 = /ЗеA + jCoS), S = х + jy, х = j/(/3eCo),
у = (Ре — /3)/(/ЗеСо) ('у — усиление на единицу длины в линии передачи
с пучком, так называемая амплитудная постоянная). Тогда уравнение
A0.27) можно переписать в виде
S2 +4QC0= {] + ЬиСо),. A0.28)
jS — b + jd
Для сравнения см. уравнение A0.24).
Для определения искомого поля, даваемого суммой всех парциаль-
п
ных волн Е(х) = ^2 Ei@)e~^iX, необходимо найти величины Ei@).
г=1
Для этого воспользуемся начальными условиями
3 3 3
??/;@) = ?°, ?7@)= 0, E?(°) = o- A0-29)
г=1 г=1 г=1
Чтобы получить систему уравнений для определения амплитуд пар-
парциальных волн, необходимо воспользоваться соотношениями, связыва-
связывающими величины г, v и Е. Используя результаты лекции 4 (раздел,
посвященный диоду Пирса, где выведены соотношения, связывающие
величины скорости, тока и напряженности поля; также вывод уравне-
уравнений подробно описан в монографии [3, стр. 136-152]), несложно пока-
показать, что соответствующие выражения будут иметь вид:
v _ Е S 1 _ jE 1
г^ o 52 +4QC0'
Нелинейная теория лампы бегущей волны 301
Тогда в новых переменных система граничных условий A0.29), запи-
записанная относительно амплитуд парциальных волн, примет вид:
TEi@) = E°, У 2Ei{Q) = 0, У 2Ei@)di = 0. A0.30)
Разрешая уравнения A0.30) по правилу Крамера, находим, что
(Si - Sj)(Si - Sk)
Таким образом амплитуда для полного поля в линии передачи записы-
записывается как
°Т51 -;&(i+;ад*ь (ю.32)
Проанализируем дисперсионное уравнение, рассмотрев два важных
частных случая.
1. Пусть b = d = 4QCo = 0, т.е. «холодная» скорость волны рав-
равна скорости электронов, потери отсутствуют, пространственный заряд
пренебрежимо мал. Тогда дисперсионное уравнение принимает вид
S3 = -j, h=h h,z=^~\j- (Ю.ЗЗ)
Соответственно для постоянных распространения парциальных волн
имеем
Используя формулу A0.31) и выражение A0.33), легко получить
^@) = Е2@) = Я3@) = Я°/3. (Ю.34)
Подстановка соотношений A0.33) и A0.34) в формулу A0.32) приводит
к выражению, совпадающему с тем, которое может быть получено
на основе метода последовательных приближений с учетом высших
приближений (см. монографию [3, стр. 130; формула (III.26)]):
Е(Х) = ^!е"^ж {e^CN + е2*ст> + е2^*3) . A0.35)
о
2. Пусть d = 0, 4QCo ф 0 — случай больших пространственных
зарядов, Ъ ~ л/AQUq . В этом случае (см., например, [3]) достаточно
учитывать только две парциальные волны (двухволновое приближе-
приближение), и вместо дисперсионного уравнения третьей степени приходим
к уравнению второй степени. Постоянная распространения третьей пар-
парциальной волны остается такой же, как и в отсутствии взаимодействия
электронного потока с полем в линии передачи, т.е. #з ^
как видно из формулы A0.31), Е^@) « 0.
302
Лекция 10
В заключении рассмотрения линейной теории ЛБВ на основе мето-
метода дисперсионного уравнения проанализируем коэффициент усиления
ЛБВО. Коэффициент усиления по мощности определяется выражени-
выражением
= 101g
Е°
-201g
Е°
Поле Е(х) складывается из трех парциальных волн (Е = Е\ + Е^ +
+ Е%). Пусть имеет место точный синхронизм электромагнитной волны
с электронным потоком (Ь = 0, Фо = 0)- Если пренебречь потерями
в линии передачи (d — 0) и пространственным зарядом (q = 0), то
только одна из трех волн A0.33) с постоянной распространения 5s =
= д/З /2 — j/2 будет возрастать при распространении по длине лампы.
При условии (ЗеСх ^> 1 Е «
усиления может быть записан как
E л/з
= — ехр /ЗеСх, и коэффициент
о Ii
С[дБ] = 201gi + 20 • ^ ^ реС1 = -9,54 + 47,ЗСЛГ.
A0.36)
Выражение A0.36) носит название асимптотической формулы уси-
усиления ЛБВ. В более общем виде ее записывают как
С[дБ] = А + BCN, A0.37)
где А — параметр начальных потерь, связанный с расщеплением
входного сигнала на парциальные волны; В — характеризует
усиление на единицу нормированной
длины CN. В нашем случае име-
имеется три волны и А = —9,54 дБ,
В = 47,3 дБ. В общем случае А
и В являются функциями парамет-
параметров 6, d, q. На рис. 10.2 приведе-
приведена зависимость коэффициента уси-
усиления ЛБВ от С N. Сплошная линия
соответствует учету всех трех парци-
парциальных волн, штриховая — расчету
по формуле A0.36). Из рисунка вид-
видно, что при малых С N поле меняется
очень слабо, что связано с тем, что
пучок не сгруппирован, и эффектив-
эффективного взаимодействия с бегущей вол-
волной не происходит. С ростом С N ам-
амплитуда поля растет и при больших
С N волна с нарастающей амплиту-
CN
Рис. 10.2. Зависимость коэффици-
коэффициента усиления ЛБВ от парамет-
параметра С TV. Штриховая линия — рас-
расчет по асимптотической формуле
A0.36); сплошная — расчет с уче-
учетом всех парциальных волн
дой становится настолько большой, что влиянием двух других пар-
парциальных волн можно пренебречь — сплошная и пунктирная кривая
совпадают.
Нелинейная теория лампы бегущей волны 303
Закон сохранения энергии в электронном потоке,
взаимодействующем с бегущей электромагнитной
волной
Вернемся к анализу нелинейных уравнений ЛБВ, причем, как
и раньше, пренебрежем влиянием пространственного заряда и затуха-
затуханием в линии передачи, а также будем считать параметр усиления Со
малым. Тогда система нелинейных уравнений ЛБВ A0.18)—A0.20) суче-
том того, что Ц-рт — тт7!Г, принимает вид:
дТ
+jbFI, A0.38)
2тг
= - \ e-judu0, A0.39)
7Г J
A0.40)
Начальные условия A0.17) (поток на входе в пространство взаимодей-
взаимодействия не модулирован) имеют вид:
(У 11
и = и0, 7O = 0' F = A при ? = 0, A0.41)
где величина А характеризует амплитуду входного сигнала.
Как уже обсуждалось выше, нелинейные уравнения A0.38)—A0.40)
описывают две модели ЛБВ.
1. В бесконечном волноводе при ? = 0 распространяется волна с ам-
амплитудой А. В плоскости ? = 0 инжектируются электроны, и при ? > 0
в волноводе имеются взаимодействующие между собой пучок и волна
(см. рис. 10.1а).
2. Аналогичная система, но в плоскости ? = ?о находится коллектор,
собирающий все электроны, и при ? > ?о в волноводе также имеется
волна постоянной амплитуды, которую можно найти, решая систему
уравнений A0.38)-A0.41) (см. рис. 10.16).
Эффект усиления сигнала в ЛБВ связан с тем, что электроны тор-
тормозятся в поле бегущей волны, отдавая ей свою кинетическую энергию.
Этого нельзя видеть из линейной теории (см. лекцию 9), в которой
средняя скорость электронов предполагается постоянной. Нелинейная
теория позволяет проследить за энергетикой процесса даже без решения
исходных уравнений.
304 Лекция 10
Введем сокращенное обозначение для операции усреднения по на-
начальным фазам щ:
2тг
(/) = — [ fdu0. A0.42)
о
Применим операцию усреднения к уравнению движения A0.40),
учитывая, что из выражения A0.39) следует
2тг
^ ' 2тг
о
Тогда, воспользовавшись уравнением возбуждения и соотношением
Re (jJ~J~*) = 0, получим:
т. е.
2/^\ = i^L. A0.43)
Беря от обеих частей соотношения A0.43) интеграл по ? и учитывая
начальные условия A0.41), получим соотношение вида
Перейдем к размерным величинам:
A0.45)
Из определения потока мощности (см. формулу A.66)) получаем, что
??* 1 (Р\
где /Зе//30 « 1, так как Со < 1, и /30 = ^еA + 6С0). Окончательно,
мощность, переносимая синхронной волной, запишется как
l A0.46)
Нелинейная теория лампы бегущей волны 305
Мощность невозмущенного пучка: Р® = IoVo- Если Со <С 1, то из соот-
соотношения A0.15) следует, что
« « «о (l - Со||) , v2 = v* (l - 2<7о||) • (Ю.47)
По мере модуляции электронного потока скорость v все больше отли-
отличается от vo, в то время как ток /о остается постоянным. В общем случае,
если обозначить через V = (г>2) /2г] «эффективное» напряжение, то
Ре = iov = 10^1 = /оVo (I - 2С0 (ди/дО) • (Ю.48)
Умнож;им соотношение A0.44), выражающее закон сохранения энергии,
на Co/oVo, и прибавим к обеим частям постоянную величину IoVo-
Тогда
(/оVo - 2CoIoVo (dv/дО) + \ CoIoVo\F\2 =
= I CoIoVo\A\2 + IoVo = const, A0.49)
где
д у
I0V0-2C0I0V0— = Pe A0.50)
— мощность электронного потока,
\ C0I0V\F\2 = Р A0.51)
— мощность синхронной волны.
С учетом этого перепишем выражение A0.49) в виде
Ре + р = const, ^|p = 0. A0.52)
Последнее соотношение есть не что иное, как закон сохранения потока
мощности (теорема о кинетической мощности Чу, выведенная в лек-
лекции 3), который показывает, что в любом сечении лампы суммарный
поток мощности остается постоянным.
Вернемся к соотношению A0.47): v2 = Vq (I — 2Codu/d^) . Умно-
Умножим обе части его на т/2 и усредним по uq-
±Н:
( — - ~Y~) duo = -^2С0 (du/d?). A0.53)
306 Лекция 10
Используя выражение A0.43) с начальным условием
= 0, полу-
чим:
(du/d?) = -i J Re (ГГ) d?. A0.54)
о
Итак, окончательно имеем соотношения:
fJ/ЗеХ T*-jPeX n т*
Т = —^ , /* = ^- , TI* = ^ , A0.55)
где J\ есть первая гармоника сгруппированного тока (см. формулу
A0.6)).
Подставим выражения A0.55) и A0.54) в формулуA0.53):
2тг
2
UIV
О
ИЛИ
\ Т [^fJ* dx = -\±- \ке?Г dx, A0.56)
2тг
A0.57)
В последнем соотношении слева стоит разность кинетических энер-
энергий — на входе кинетическая энергия uivq/2, а на выходе, в результате
изменения скорости в связи с энергообменом в пространстве дрейфа,
энергия дается интегралом по фазам влета. Эта разность равна рабо-
работе поля, которая определяется интегралом, стоящим в правой части.
Численно этот интеграл равен энергии, переданной полю. Очевидно,
что если бы скорость не менялась (v = vq), to энергия взаимодействия
была бы равна нулю.
Механизм фазировки в бегущей электромагнитной
волне
В предыдущем разделе было доказано выполнение закона сохране-
сохранения энергии в модели, описывающей усиление сигналов в ЛБВ. Рас-
Рассмотрим теперь качественно механизм фазировки в слабых и сильных
полях. Будем исследовать случай, когда на вход лампы подается слабый
сигнал, который усиливается лампой до величины, при которой вблизи
выходного конца лампы создается существенно нелинейный режим.
Рассмотрение механизма фазировки произведем в предположении ма-
малых Со, причем будем пренебрегать не только слагаемыми порядка
Нелинейная теория лампы бегущей волны 307
Cq, но и слагаемыми порядка Со- Тогда уравнение движения A0.40)
перепишется в виде:
&-ТГ- <10-58>
<9? ои
где по определению
Г\ Т Т
—^ = ReFeju. A0.59)
ои
Поскольку Т — комплексная величина, то ее можно представить в виде:
F = |JT|e-^. Тогда
A0.60)
Vs = Re {-j\r\e3(«-<p)} = \p\ sin (u-(p).
Выясним физический смысл величины Vs, для чего остановимся на
интерпретации наших переменных и и ср. По определению:
и = (jjti + 0 = out — (Зех = —Ре(х — vot); ? = РеСох.
Рассмотрим явления в электронном потоке, взаимодействующем с бе-
бегущей электромагнитной волной, в двух системах отсчета — в непо-
неподвижной и движущейся со скоростью, равной невозмущенной скорости
потока.
1. В неподвижной системе отсчета ? есть безразмерная координата,
an — меняющаяся во времени фаза. Для фиксированной точки х
каждому значению и соответствует вполне определенное время t. Это
нетрудно видеть, если записать ии( через переменные х и t:
U = -Pe(x-VOt), ? = /3eC0X. A0.61)
2. Перейдем в подвижную систему отсчета с помощью преобразо-
преобразований х = х' + vot'] t = tf, тогда переменные ? и и выражаются через
новые переменные х' и t' как
U = -РеХ', С = РеСо(х' + VOt'). A0.62)
Из последних соотношений видно, что в подвижной системе отсче-
отсчета и есть безразмерная координата, а ? — меняющаяся во времени
и пространстве фаза. Для фиксированной точки х' каждому значению ?
соответствует однозначно определенное время t'.
Функция V8 зависит от и, и не зависит явно от ?, а значит и от
t'. Это позволяет рассматривать ее как безразмерную потенциальную
энергию в подвижной системе отсчета. Уравнение A0.58) выражает
тогда второй закон Ньютона для частицы, движущейся под действием
потенциальной силы, где Vs — это безразмерная потенциальная энергия
электрона в поле синхронной волны в подвижной системе отсчета.
308 Лекция 10
Пусть / = |/|e~JW*; T — \Т\оГ^^ тогда из уравнения возбуждения
A0.38) получаем
Щ ^ -|/|е^-«->. A0.63)
Выпишем отдельно действительную и мнимую части:
= -|/| cos
? A0.64)
Первое уравнение характеризует изменение амплитуды волны вдоль
системы. Для выяснения смысла второго уравнения преобразуем вели-
величину (dif/dt; - Ь).
Величина Т была введена так, что
TJ TJ
где Tp — Cex + (p — полная («горячая») фаза поля, (Зех — фаза «хо-
«холодной» волны, ер — добавка, обусловленная взаимодействием волны
с электронным потоком. Пусть /3 — постоянная распространения, аИф —
фазовая скорость «горячей» волны. Тогда
-о _ ш _ dip _ R dip _ п , о r dip _ и Л r dip
Р — =— — ~Г~ — Ре + -г- — Ре + Ре^О-ТТ — — I 1 + ^O-JT
Уф dx dx d^ vo \ d^
Отсюда имеем, что
A0.65)
Из определения величины b:
A0.66)
Используя полученные выражения для b A0.66) и -Ш- A0.65), нахо-
находим:
*"""', A0.67)
т. е. интересующая нас величина характеризует разность фазовых ско-
скоростей «холодной» и «горячей» волн.
Нелинейная теория лампы бегущей волны
309
Обратимся снова к первому уравнению системы A0.64), определяю-
определяющему изменение амплитуды поля вдоль пространства взаимодействия.
Очевидно, что условия нарастания волны вдоль системы есть —jrr^ > 0,
т. е.
— cos (и* — <р) > 0, — < ?/* — (/?< — тг. A0.68)
Если же \р * < 0, то волна затухает и
A0.69)
d\T\ Л
амплитуда
тт , 7Г . ЗТГ
Наконец, при п* — (/? = =Ь —, ±—,... имеем
волны не меняется.
Рассмотрим несколько иной подход к полученным условиям, опре-
определяющим направление энергообмена в системе. Можно показать, что
п* — это фаза, соответствующая центру сгустка электронов. Действи-
Действительно, если ограничиться первой гармоникой тока, то можно написать
J(x, t) = /о + Re Jie^* = /0 + Re
= /о (
= /о (l +
= /0(l + |/| cos (и - и*)). A0.70)
Ясно, что и — и* = 0 (и = п*) соответствует максимуму тока, а значит
и центру сгустка. На рис. 10.3 представлены графики Vs = \J-\ sin (и —
\ dV4 i^i / ч
— ip) и -W-2- = \j-\ cos (и — (р) в за-
зависимости от {и — ip). Тормозя-
Тормозящей фазе поля соответствует
дУа „ 7Г 37Г
-те/2
м—Ф
Результат взаимодействия зави-
зависит от того, в какую фазу попадет
центр сгустка и = и*.
Усиление будет происходить
при
-<и,-^<т, A0.71)
что согласуется с ранее получен-
полученным условием.
Остановимся на вопросе о вы-
выборе оптимального параметра рассинхронизма Ь. Если на начальном
участке лампы происходит усиление, то электроны группируются в тор-
тормозящей фазе поля. После того, как достигнуто насыщение первой
Рис. 10.3. Зависимость безразмерной
потенциальной энергии Vs и ее первой
производной dVs/du от фазы (и —
— (р). Заштрихована тормозящая фа-
фаза поля
310 Лекция 10
гармоники сгруппированного тока, дальнейшее взаимодействие опреде-
определяется движением сформированных сгустков в поле волны. Если пара-
параметр холодного рассинхронизма соответствует максимальному усиле-
усилению в линейном режиме b = 6ОПТ, то сгусток образуется вблизи максиму-
максимума тормозящего поля. Пусть теперь b > 6ОПТ, так что скорость электро-
электронов достаточно велика, и группировка происходит вблизи максимума
потенциала Vs. Тогда при прохождении сгустками тормозящего склона
потенциальной ямы полю будет передана энергия, большая, чем в пер-
первом случае. Значение ? в момент прохождения сгустком минимума Vs
соответствует максимуму мощности при данном Ь. Итак, режим макси-
максимума линейного усиления b = 6Опт неоптимален по выходной мощности.
Данный вывод может быть получен и из энергетических соображе-
соображений. Из закона сохранения энергии A0.44) видно, что по мере того как
энергия электронов передается полю, и его амплитуда \Т\ возрастает,
должна возрастать и величина (du/d?).
Ранее было выведено соотношение v = vo (I — Codu/d^). Усредняя
его, получаем (v) = vo (I — Со (du/d?)). Отсюда видно, что с увеличени-
увеличением величины du/dt; средняя скорость v уменьшается, и взаимодействие
перестает быть оптимальным, если величина параметра холодного рас-
рассинхронизма b = 6ОПТ. Для увеличения эффективности взаимодействия,
необходимо задать начальную скорость пучка vf0 > vq, а значит и b >
> Ьопт. Тогда уменьшение v приведет лишь к улучшению взаимодей-
взаимодействия.
Вернемся к рассмотрению движения сформированного сгустка в по-
поле волны. После достижения дна потенциальной ямы сгусток выходит
из тормозящего поля, проскакивает по инер-
инерции минимум Vg и попадает в область уско-
ускоряющего поля. Сгусток начинает ускорять-
ускоряться, v увеличивается, а, значит, величины
du/dt; и \Т\ уменьшаются. Через некоторое
время сгусток возвращается к минимуму,
продолжая совершать колебания около него.
При этом сгусток деформируется, и процесс
^ не является строго периодическим. Дефор-
Деформация эта тем больше, чем больше влияние
Рис. 10.4. Зависимость пространственного заряда. Если простран-
мощности 1^12 от длины ственный заряд велик, то сгусток распадется
пространства взаимодей- раньше, чем разовьётся колебательный про-
ствия цесс. Теоретическая зависимость \Т\2 от ?
представлена на рис. 10.4, которую можно
трактовать как зависимость мощности от длины пространства взаимо-
взаимодействия.
Итак, один из механизмов ограничения мощности в ЛБВ — отста-
отставание сгруппированного сгустка от бегущей волны.
Нелинейная теория лампы бегущей волны 311
Обсудим теперь второй механизм ограничения мощности, который
связан с нелинейностью модуляции электронного пучка, т. е. с нели-
нелинейной зависимостью первой гармоники сгруппированного тока J\ от
функции в = и — щ, определяющей изменение фазы электрона под
действием поля бегущей волны.
Учитывая, что в — периодическая функция щ, разложим ее в ряд
Фурье, ограничиваясь первой гармоникой:
0(?, «о) = Ш) + В@ sin («о + /5@), (Ю-72)
где (#(?)) ~~ среднее смещение электронов пучка, В(?) — параметр
группирования. Подставляя это выражение в формулу для сгруппи-
сгруппированного тока, получаем
Z7I
-hi
2тг
e~iu du0 =
о
2тг
= - \ exp {-j(u0 + <0(О> + В@ sin (щ + /3@))} duo. A0.73)
0
Известно, что для функции Бесселя справедливо интегральное соотно-
соотношение
2тг
Jn(x) = — exp {—j(nO — xsinO)} dO.
о
Тогда выражение A0.73) может быть переписано в виде:
/ = 2Л(?)ехр{-Л<0>-? + тг)}, \1\=2\МВ)\. A0.74)
При передаче энергии от электронов полю бегущей волны величи-
величина В возрастает, поэтому первая гармоника тока, пропорциональная
функции Бесселя 1-го порядка, сначала возрастает до величины В =
= 1,84, а затем начинает уменьшаться, обращаясь в нуль при В = 3,83,
что и дает второй механизм ограничения мощности. Преобладание того
или иного механизма ограничения мощности зависит, в первую очередь,
от режима работы ЛБВ [1].
Особенности и результаты решения
нелинейных уравнений ЛБВ на ЭВМ
Кратко обсудим методику численного решения нелинейных урав-
уравнений ЛБВ (более подробно родственные этой задаче численные схе-
схемы интегрирования нестационарных нелинейных уравнений ЛОВ бу-
будут рассмотрены на последующих лекциях). Большим преимуществом
численного решения уравнений ЛБВ является возможность не толь-
только получить интегральные характеристики прибора (максимальную
312 Лекция 10
мощность Pmax = - Co/oVblJ^I2, максимальный к.п.д. 7ymax = - С0|^|2,
оптимальную длину пространства взаимодействия хопт = ?Опт//ЗеСо),
но и проанализировать особенности движения электронов, т. е. найти
дифференциальные характеристики прибора, что является важным
для понимания процессов взаимодействия.
Система нелинейных уравнений A0.18)—A0.20) соответствует моде-
модели потока в виде сплошной среды с нелинейными волновыми свойства-
свойствами. При этом общее число степеней свободы бесконечно. Для численно-
численного решения необходимо свести её к системе обыкновенных дифференци-
дифференциальных уравнений, ограничиваясь конечным числом степеней свободы.
Наиболее удобным для данного класса задач является метод крупных
частиц, который уже рассматривался нами в лекции 5. Поэтому не будем
останавливаться на этих вопросах подробно. Электронный поток заме-
заменяется совокупностью конечного числа крупных частиц определенной
формы и размера, которые самосогласованно двигаются в ВЧ-поле.
Так как процессы периодические во времени, то достаточно проин-
проинтегрировать движение частиц за один период колебаний. Формально
введение частиц эквивалентно замене в уравнении A0.19) интеграла
суммой вида 1)
2 N
1 = дГ Y, exp(-jnn),
п=1
где вместо функции и = и(^щ) берется набор функций ип =
= ип(^иоп), где uon = 2тгп/УУ, n = l,...,7V, TV — число крупных
частиц, взятых вдоль пучка. В этом случае будем иметь B7V + 2)
уравнения. Множитель «2» появляется за счет того, что комплексное
уравнение разделяется на два уравнения относительно действительной
и мнимой части.
Поля пространственного заряда ^Пз вычисляются из уравнения
Пуассона, которое может быть записано как
div (e grad Ф) = —р.
Решение этого уравнения имеет вид
Ф(х, y,z)= J G(x, у, z, ж', у', z')p(x', у', z') dV',
V
где G — функция Грина. Физический смысл функции Грина заключает-
заключается в том, что она определяет взаимодействие между точечными заряда-
зарядами в данной системе, находящимися в точках (х,у, z) и (ж7, у', z'). Вид
г) Здесь рассмотрена численная схема без учета расслоения потока по попе-
поперечной координате, как это делалось при построении нелинейной двумерной
модели многорезонаторного клистрона (лекция 5; см. также [4]-[7]).
Нелинейная теория лампы бегущей волны
313
функции Грина зависит от выбора формы крупной частицы, а также
от соотношения геометрии волновода и пучка. Уравнение движения
запишется следующим образом:
Асимптотическая
Л2,, Р. дБ
п + ^пз.
0
-10
-20
-30
Р,
Л
ЦБ
2
4
/
/
/
/' формула
/б 8 10
а
10
1_Р,ДБ
Асимптотическая
/ формула
10
-10-
Обсудим некоторые результа-
результаты численного решения нелиней-
нелинейных уравнений ЛБВ. Все результа-
результаты были получены при числе ча-
частиц N = 24 и в пренебрежении вли-
влиянием сил пространственного заря-
заряда.
1. Усиление слабых сигна-
сигналов. На рис. 10.5 приведены зави-
зависимости мощности от длины про-
пространства взаимодействия Р(?). Из
них видно, что при увеличении ?
мощность волны сначала остает-
остается постоянной или даже убывает
(рис. 10.5а; 6), а затем модулирован-
модулированный начальным сигналом электрон-
электронный поток начинает отдавать энер-
энергию ВЧ-полю. В процессе усиле-
усиления начинает преобладать нараста-
нарастающая парциальная волна. Несмот-
Несмотря на малость входного сигна-
сигнала, возрастание мощности волны
при ее распространении вдоль лам-
лампы прекращается из-за нелинейных
эффектов. Достигнув максимума,
мощность убывает и становится ос-
осциллирующей при больших ?.
Интересно, что в некоторых слу-
случаях мощность, рассчитываемая из
нелинейной теории, превышает зна-
значение мощности, полученное из ли-
линейной теории. Это, например, име-
имеет место (см. рис. 10.5в) при b = 1,89
(в линейной теории этому соответ-
соответствует наличие в системе трех пар-
парциальных волн постоянной ампли-
амплитуды). Связано это с тем, что при такой величине параметра холодного
рассинхронизма особое значение приобретает движение сформирован-
10
-10
Р,ДБ
Нелинейная
теор
\ Линейная
теория
Рис. 10.5. Зависимости мощности
от длины пространства взаимодей-
взаимодействия в режиме усиления слабых
сигналов при следующих парамет-
параметрах: а — амплитуда входного сиг-
сигнала Л = 0,1, b = -1; б— Л = 0,2,
6 = 0; в- А = 0,3, Ь = 1,89
314
Лекция 10
ного сгустка в поле волны, не учитываемое в линейной теории. Как уже
обсуждалось, в этом случае сгусток проходит большее расстояние по
тормозящему склону потенциальной ямы, и передает большую энергию
полю. Однако группировка наиболее эффективно происходит при b « О
(при малом сигнале). Поэтому весьма удачной является конструкция
ЛБВ, состоящей из двух секций, первая из которых работает при слабом
сигнале и b « 0, а вторая при сильном сигнале (сигнал усиливается
в первой секции) и b = 1,89. *)
2. Усиление конечных сигналов (рис. 10.6). На рис. Ю.б^при-
ведены зависимости Р(?) при 6 = 2. Если рассмотреть дисперсионное
уравнение для этого случая:
Р, ДБ
то оно имеет чисто мнимые реше-
г ¦ s: • ( 1 , V^
ния Ji = -j, (Ь,з = J -- ± —-
\ I A
т. е. все парциальные волны имеют
постоянную амплитуду. Тем не ме-
менее, усиление есть, и довольно зна-
значительное: при А = 2 усиление рав-
равно 6 дБ, а при А = 0,4 — 18 дБ. Ана-
Анализ показывает, что волна бежит
вдоль линии примерно с той же ско-
скоростью, как без пучка: -?¦ « b =
= 2. При этом волна захватыва-
захватывает большую часть электронов, ко-
которые начинают двигаться вместе
с волной и собираются преимуще-
преимущественно в тормозящем полуперио-
полупериоде. Так как при 6 = 2 электроны
вначале двигаются быстрее волны,
то при захвате их волной они отда-
отдают кинетическую энергию, за счет
чего растет мощность волны. При
А = 0,4 неправильнофазных элек-
электронов оказывается больше, чем
при А = 2, и усиление меньше. Та-
Таким образом, имеется возможность усиления сигналов с конечной ам-
амплитудой при таких больших 6, при которых по линейной теории уси-
усиления вообще нет.
10
А = 2
А = 0,4
Линейная
теория
Рис. 10.6. Зависимости мощности
от длины пространства взаимодей-
взаимодействия в режиме усиления конечных
сигналов при следующих парамет-
параметрах: а — амплитуда входного сигна-
сигнала А = 2, b = 0; б — b = 2. Здесь
сплошные линии — результаты рас-
расчета с помощью нелинейной теории
х) Рассмотрение возможных способов увеличения к.п.д. ЛБВ будет прове-
проведено далее в отдельном параграфе.
Нелинейная теория лампы бегущей волны 315
Отметим ещё раз, что развитая нелинейная теория не учитывает
влияния пространственного заряда, потерь в линии передачи, двумер-
ность, отражения в электронном потоке. Эта теория дает большие
расхождения с экспериментом. Вместе с тем, полученные с помощью неё
результаты оказываются мощным средством для анализа путей опти-
оптимизации имеющихся приборов. В заключение можно сделать некоторые
выводы из результатов численного анализа.
1. Максимальный к.п.д. односекционной ЛБВ составляет около 50 %
и достигается при Со ^ 0,1; b « 1,8.
2. Усиление, как правило, уменьшается из-за действия нелинейных
эффектов, за исключением некоторых случаев (например, b = 1,5, Со <
< 0,05, 4QCq <С 1), когда появляется дополнительное нелинейное уси-
усиление.
Спиральная лампа бегущей волны
как основа усилительного модуля
Как уже отмечалось, основным достоинством ЛБВ по сравнению
с другими усилительными приборами (в первую очередь, клистрона-
клистронами и усилительными приборами магнетронного типа) является широ-
широкая полоса усиливаемых частот. Наиболее широкополосными являются
ЛБВ со спиральной замедляющей системой: скорость распространения
бегущей волны в них сохраняется постоянной при изменении частоты
входного сигнала в пределах 1-2 октав и более.
Для достижения больших коэффициентов усиления (до 30 -г- 50 дБ)
с целью предотвращения самовозбуждения за счет обратной связи,
обеспечиваемой отраженным сигналом за счет плохого согласования
с нагрузкой, вводят дополнительное затухание. Рассмотрим этот во-
вопрос более подробно. Если сделать затухание распределенным по длине
лампы, то в этом случае, очевидно, коэффициент усиления, резко упа-
упадет. Поэтому для «развязывания» входа и выхода лампы использует-
используется поглощающая локальная вставка, располагаемая на длине, равной
примерно 1/2 или 1/3 длины замедляющей системы, и создающая
затухание порядка 60 дБ. Поглотитель уничтожает отраженный сигнал,
при этом несколько падает и коэффициент усиления, но его изменение
можно скомпенсировать увеличением тока пучка.
На рис. 10.7 представлена схема ЛБВ с локальным поглотителем
и распределение поля вдоль длины пространства взаимодействия в этом
случае. В секции / происходит процесс усиления входного сигнала
при взаимодействии пучка с волной. После прохождения секции //
амплитуда сигнала близка к нулю, однако пучок по выходе из секции
// уже сильно сгруппирован. Поэтому при попадании в секцию /// он
возбуждает в линии передачи волну, амплитуда которой определяется
сгруппированным током. Отметим важную роль согласования самого
поглотителя, так как отражения от него могут привести к возбуждению
316
Лекция 10
лампы на отдельных участках пространства взаимодействия, и как
следствие, падению общего коэффициента усиления. Согласования до-
добиваются путем плавного сведения потерь на концах поглотителя к ну-
нулю.
ЛБВ находят широкое применение (см. эпиграф к лекции 9) в пере-
передающих и приемных устройствах радиолокационных станций, систем
связи через искусственные спут-
спутники Земли и радиорелейных ли-
линий связи. Сочетание высокого
уровня усиления, низкого уровня
собственных шумов, относитель-
относительно небольших габаритных разме-
размеров и массы с широкой поло-
полосой усиливаемых частот, позволя-
позволяющей передавать большие объемы
информации, делает ЛБВ одним
из наиболее удобных усилителей
для подвижных радиолокацион-
радиолокационных станций (РЛС), в том чис-
числе и использующих фазированные
антенные решетки.
Последнее привело к разработ-
разработке пакетированных ЛБВ, в кото-
которых магнитная фокусирующая си-
система и собственно усилительная
О
1
I
II
III
Рис. 10.7. Схема ЛБВ с локальным
поглотителем: I, III — усилитель-
усилительные секции, II — секция с затухани-
затуханием (локальный поглотитель). Здесь:
1 — распределение амплитуды поля
вдоль пространства взаимодействия
в лампе без поглотителя; 2-е по-
поглотителем; 3 — распределение ам-
амплитуды отраженной волны вдоль
пространства взаимодействия
ЛБВ (а часто и полупроводнико-
полупроводниковый генератор, а также управля-
управляющий этой системой процессор)
объединяются в один узел. Та-
Такие высокочастотные усилитель-
усилительные и генераторные модули широко разрабатываются в последнее вре-
время. Важным требованием к ним является компактность, небольшой вес,
высокий к.п.д. Кроме этого на такие миниатюрные усилители наклады-
накладываются требования высокой выходной мощности (~ 102 Вт), широкой
полосы частот и низкого уровня шумов [8].
Применение таких ВЧ-модулей на базе ЛБВ включает в себя ряд
областей. Во-первых, это использование их в качестве базовых модулей
в мощных радиолокационных системах, включая радары с синтезируе-
синтезируемой апертурой для дистанционного зондирования, а также РЛС дальне-
дальнего действия корабельного и наземного базирования. Данные устройства
при своем проектировании требуют перехода от классических вакуум-
вакуумных СВЧ-приборов к фазированным антенным решеткам с источника-
источниками ВЧ-мощности в виде вышеописанных модулей. При этом несколько
сверхмощных ВЧ-генераторов заменяются решеткой из большого чи-
числа активных элементов, причем суммарная мощность такой решетки
Нелинейная теория лампы бегущей волны
317
* , I
Рис. 10.8. Фотография интегрированного высокочастотного усилительного
модуля, включающего в себя миниатюрную ЛБВ-усилитель. Линейка внизу
фотографии проградуирована в дюймах (из работы [9])
может достигать мегаваттного уровня. Другие применения модульной
технологии включают в себя коммуникацию и передачу информации на
космических, воздушных и др. системах, решение задач электронного
и радиолокационного противодействия.
Усилительные ВЧ-модули включают в себя интегрированный источ-
источник питания, полупроводниковый усилитель и ЛБВ-усилитель, которые
собираются в одном корпусе. Особенностью модульной технологии яв-
является комбинация в них полупроводниковой и вакуумной СВЧ-тех-
ники, что позволяет существенно уменьшить размеры и массу модуля
по сравнению со стандартными вакуумными СВЧ-приборами. Одно-
Одновременно удается увеличить общий к.п.д. такого модуля, уменьшить
тепловые потери и требуемую мощность питания, уменьшить уровень
шумов. Высокий полный к.п.д., совместно с небольшими габаритными
размерами и массой, небольшой мощностью питания, делают такие мо-
модули особенно привлекательными для использования их в космических
и воздушных аппаратах, где накладываются строгие ограничения на
эти характеристики.
В работе [9] представлено описание и технические характеристики
усилительного ВЧ-модуля на базе ЛБВ. На рис. 10.8 демонстрируется
фотография модуля, на которой показаны высоковольтный блок пи-
питания, полупроводниковый усилитель, модулятор и ЛБВ. ЛБВ-усили-
ЛБВ-усилитель, показанный внизу фотографии, включает, если рассматривать фо-
318 Лекция 10
тографию слева направо, электронную пушку, периодическую магнит-
магнитную фокусирующую систему, вакуумное окно для вывода ВЧ-мощности
и коллектор. Полупроводниковый усилитель расположен слева сверху
на фотографии, напротив него справа — источник питания. Некоторые
характеристики модуля приведены в таблице 10.1. Представляется ин-
интересным теоретический анализ подобных усилительных модулей.
Таблица 10.1
Параметры ВЧ-усилительного модуля [9]
Диапазон частот
Выходная мощность
К.п.д. в непрерывном режиме
Коэффициент усиления малого сигнала
Коэффициент усиления в режиме насыщения
Напряжения питания
Потребляемый ток в режиме с
максимальной выходной мощности
Длина модуля
Ширина модуля
Высота модуля
Вес модуля
3,7 -=-5,3 ГГц
170 Вт
51%
68 дБ
53 дБ
270 В
1,2 А
19,8 см
15,2 см
2,5 см
1,4 кг
Способы повышения к.п.д. ЛЕВО
Одной из важных проблем разработки ламп бегущей волны явля-
является повышение их к.п.д. Здесь были достигнуты определенные успехи
и предложены определенные методы. Познакомимся с ними подробнее,
так как рассмотрение этих вопросов позволит глубже представить фи-
физику процессов в ЛБВ.
Рассмотрим каждый из методов повышения к.п.д. в отдельности.
Все результаты, приведенные в данном разделе, были получены разны-
разными авторами либо на основе анализа нелинейных уравнений ЛБВ, либо
на экспериментальных макетах.
1. Использование изохронности [10, стр. 452]. Основная идея
данного метода, предложенного еще в ранних работах Д. Пирса и Д.
Роу, состоит в сохранении синхронизма электронов и волны вдоль
всей длины лампы. Уменьшение средней скорости электронов к концу
пространства взаимодействия за счет передачи энергии электромаг-
электромагнитному полю компенсируется за счет уменьшения фазовой скорости
волны путем ввода дополнительной секции в замедляющую систему
или увеличением скорости электронов дополнительным ускоряющим
статическим полем.
Нелинейная теория лампы бегущей волны 319
Было установлено, что
а) при работе лампы в режиме максимального усиления с помо-
помощью изохронности удается увеличить к.п.д. до значений максимального
к.п.д. (при этом можно улучшить частотные характеристики прибора
и уменьшить длину лампы);
б) при работе ЛБВ в режиме максимального к.п.д, применение раз-
различных законов изохронности практически не приводит к дальнейшему
росту к.п.д.
2. Использование изофазности [11]. Под изофазной ЛБВ пони-
понимается такая, в которой закон изменения разности фаз р между первой
гармоникой тока пучка и полем системы задан вдоль всей лампы или
на некоторой ее части г). Для компенсации медленных уходов фазы
возможно, как и в изохронных ЛБВ, использовать изменение фазовой
скорости волны вдоль замедляющей системы. В ряде случаев изменение
фазы первой гармоники тока происходит быстро, почти скачкообразно
(режим максимального к.п.д.), поэтому разумно вводить скачки фазы
с помощью сосредоточенных фазовращателей. Остановимся подробнее
на картине физических процессов в изофазной ЛБВ.
Мощность взаимодействия электронного пучка с полем бегущей
волны имеет вид
/
Р = J dP,
о
где dP — мощность взаимодействия на элементе длины пространства
взаимодействия dx — дается выражением
dP = -ReJ1E*dx = - \^\\Е\ cosipdx, A0.75)
где J\ — первая гармоника сгруппированного тока; Е — продольная
составляющая поля; ip(x) — разность фаз между J\ и Е, при этом
Е = \Е(х)\ exp (ja(x)), Ji = | Ji(x)\ exp (j*l>(x)), A0.76)
(p(x) = ф(х)-а(х). A0.77)
Нахождение максимального к.п.д. требует нахождения максимума
функции, даваемой формулой A0.75).
В обычной ЛБВ пучок сначала отдает энергию полю, т. е. dP < 0;
E,Ji^0, поэтому cos if < 0. Такое соотношение фаз тока и поля соот-
соответствует образованию сгустка электронов в тормозящем полупериоде
медленной волны.
х) Величина (р определяет направление обмена энергией между электрон-
электронным пучком и замедленной волной.
320
Лекция 10
При х = жОпт, гДе прекращается передача мощности от пучка полю,
имеем dP = 0, т. е.
(р = ±—¦ или | Ji\ = 0.
Рассмотрим эти два случая отдельно.
1. ср = =Ьтг/2. На одной замедленной длине волны образуется один
сгусток электронов, смещающийся в результате торможения в нуль
W, 1/1
В линейном режиме
устанавливается одна
нарастающая волна
поля, а разность фаз <р непре-
непрерывно изменяется, переходя из
третьей в четвертую чет-
четверть (см. рис. 10.9а, на котором
изображены зависимости сгруп-
сгруппированного тока |/|, поля \Т\
и фазы (р от длины простран-
пространства взаимодействия ?). В се-
сечении ? = ? разность фаз ip =
= —тг/2, т. е. электроны отстают
от волны (см. рис. 10.96).
2. |Ji| = 0 (|/| = 0). На од-
одной длине замедленной волны
образуются два сгустка, один
из которых тормозится полем,
а другой ускоряется. В сече-
сечении ? = ?опт энергия, отдавае-
отдаваемая одним сгустком, равна энер-
энергии, забираемой другим сгуст-
сгустком. Одновременно первая гар-
гармоника тока обращается в нуль
(или близка к нулю), так как ча-
частота следования сгустков вдвое
больше частоты сигнала. Вели-
Рис. 10.9. Зависимости величин сгруп-
сгруппированного тока, поля (а) и разности
фаз (б) вдоль пространства взаимо-
взаимодействия, поясняющие механизм огра-
ограничения к.п.д. ЛБВ при условии (р =
= ±тг/2
чина <р изменяется непрерывно
вплоть до ? = ?опт, а затем скачком (или очень быстро) изменяется на
величину тг, переходя из третьей или второй в первую или четвертую
четверть (рис. 10.10).
| J\\ обычно не обращается точно в нуль, и поэтому разность фаз ср,
строго говоря, не имеет разрыва.
Рассмотрим вначале ЛБВ с постоянным сдвигом фазы между током
и полем. Выберем закон изменения фазовой скорости волны вдоль за-
замедляющей системы таким, чтобы величина ср и на нелинейном участке
сохранялась постоянной, равной разности фаз в минимуме функции
ср = (/?(?). Для определения этого закона рассмотрим нелинейные урав-
Нелинейная теория лампы бегущей волны
321
\|/-ф
2
1
п
и
-2
-3
\л и
ф
-я/2
\
~ \
\
\
\ х у
\ /- ^. ^
\ /
/
/
1
Ьопт
\ ^,
Л. I,
1/1
Рис. 10.10. Скачок фазы ф первой гармоники тока при переходе модуля тока
через нуль (а); зависимости величин сгруппированного тока, поля и разности
фаз вдоль пространства взаимодействия (б) при обращении сгруппированно-
сгруппированного тока в нуль
нения ЛБВ при условии (р = const:
J—1 =
at,
2тг
= -\e~Judu0,
тг J
о
д и
Тогда закон изменения скорости вдоль лампы определяется из уравне-
уравнения
Как видно из рис. 10.11, разность фаз убывает от ? = 2,76 (у? =
= ^min = —3,12). Первая гармоника тока не обращается в нуль, поэтому
безразмерная мощность поля
Со
11 Д. И. Трубецков, А. Е. Храмов
322
Лекция 10
л.
Со
5
4
3
2
1
О
-1
-2
-3
40
30
20
10
\6
4,8
4 4,8
Рис. 10.11. Нормированный к.п.д., сгруппированный ток, изменение парамет-
параметра холодного рассинхронизма b вдоль пространства взаимодействия ЛБВ
с постоянным сдвигом фаз между током и полем
непрерывно возрастает до г\/Со = 6,0, что соответствует г\ — 60 %. При
этом имеет место остановка электронов ( Щг —у ос I, и систему нелиней-
нелинейных уравнений нельзя использовать для дальнейших расчетов г).
В районе минимума тока пучка необходимо сделать резкий ска-
скачок фазы поля для компенсации быстрых изменений фазы тока (см.
рис. 10.11; зависимость параметра холодного рассинхронизма b от ко-
координаты пространства взаимодействия ?). В точке пространства вза-
взаимодействия ? = 4,8 к.п.д. равен г\ = 44 %, после скачка — 56 % в точке
с координатой ? = 5,25 (второй минимум тока), где необходим второй
скачок фазы.
3. Режим больших «6» (скорость электронов значительно
превышает скорость волны). Скачки «6» [12, 13]. Амплитуд-
Амплитудная характеристика ЛБВ в режиме большого рассинхронизма имеет
аномальный характер (рис. 10.12а): при некоторых значениях уровня
входного сигнала коэффициент усиления резко увеличивается (в рас-
рассматриваемом случае на 12 дБ).
х) Таким образом мы получили условие применимости выведенных нели-
нелинейных уравнений ЛБВ.
Нелинейная теория лампы бегущей волны
323
Рвых
,дБ -40 -30 -20 -10 0
Рис. 10.12. Амплитудная характеристика ЛБВ в режиме большого рассин-
рассинхронизма (а). Здесь сплошная кривая соответствует ? = 8,7, штриховая —
? = 5,3. Коэффициент усиления (б) и к.п.д. ЛБВ (в) со скачком величины 62
в конце пространства взаимодействия. Штриховые линии на рис. б, в соот-
соответствуют характеристикам «обычной» ЛБВ
Для увеличения коэффициента усиления ЛБВ (рис. 10.126), име-
имеющей аномальную амплитудную характеристику, имеет смысл ввести
на небольшой длине в конце участка взаимодействия режим сильного
рассинхронизма (участок с параметром холодного рассинхронизма 62),
а на всей остальной части режим экспоненциального усиления (с пара-
параметром холодного рассинхронизма Ь\). Тогда начальный участок с пара-
параметром Ь\ обеспечит достаточно высокое усиление в линейном режиме,
а участок с сильным рассинхронизмом даст аномальную амплитуд-
амплитудную характеристику. Анализ показывает, что режим рассинхронизма
на выходном участке прибора характеризуется более высоким к.п.д.
(см. рис. 10.12в, на котором представлена зависимость к.п.д. лампы от
параметра Ь\ при оптимальных значениях параметра холодного рассин-
рассинхронизма в конце пространства взаимодействия б2опт)• Как показывают
расчеты, для получения высокого значения к.п.д. скачок фазовой скоро-
скорости (уменьшение ее на 10%) нужно вводить ближе к выводу энергии.
и*
324
Лекция 10
Малые значения коэффициента усиления в линейном режиме и уве-
увеличение его в режиме насыщения позволяют использовать рассматри-
рассматриваемый режим для создания ЛБВ, устойчивых к возбуждению.
4. Режим больших входных сигналов [14]. В этом случае
к.п.д. может достигать значений rj « 45 % (см. рис. 10.13). Получение
высоких к.п.д. обусловлено воздействием на электроны пучка ВЧ-поля
большой амплитуды, которое приводит к более полному отбору энер-
энергии электронов, а также уменьшает влияние поля пространственного
заряда на процесс группировки. Заме-
Заметим, что при этом при значении ампли-
амплитуды входного сигнала Тъ^ соответ-
соответствующей максимальному к.п.д., су-
существенно падает коэффициент уси-
усиления G. И наоборот, при значении
J-BX, соответствующем Gmax , резко па-
падает к.п.д. лампы (rj ~ 20 %).
5. Введение гармоники [15] —
подача на вход ЛБВ, кроме основного
сигнала, сигнала удвоенной частоты.
По аналогии с клистронными усилите-
усилителями [16] можно ожидать увеличения
к.п.д. на основной частоте.
На рис. 10.14а приведена зависи-
зависимость выходной мощности сигналов
основной и удвоенной частот от соот-
соотношения фаз и амплитуд между ними
на входе (выходная мощность отнесе-
отнесена к ее значению на основной часто-
частоте, когда входной сигнал на удвоенной
частоте отсутствует). Кривые построены на длине участка взаимо-
взаимодействия, соответствующей насыщению мощности сигнала основной
частоты (? = 6,8).
Заметим, что подавая с выхода ЛБВ на ее вход сигнал удвоенной ча-
частоты с помощью цепи обратной связи, можно значительно уменьшить
величину его на выходе и увеличить выходную мощность на основной
частоте.
Кратко остановимся на физике процессов в этом случае (см.
рис. 10.14^, на котором приведены зависимости разности фаз (ф — ср) от
длины пространства взаимодействия). Эффективное взаимодействие
происходит, когда имеют место условия
ф — ср = тг (отбор энергии от пучка);
1,5 2,0 2,5 Fm
Рис. 10.13. Коэффициент усиле-
усиления (штриховая линия) и к.п.д.
(сплошная линия) ЛБВ в ре-
режиме большого входного сигна-
сигнала для случаев затухания: 1 —
7 = 0,1, 2 - 7 = 0,2. Другие
управляющие параметры име-
имеют следующие значения: d =
= 0, & = 2,4, Ъ = 2,5, до =
= (сор/соСоJ = Ю
ф — ср = тг/2(насыщение ВЧ-мощности).
Нелинейная теория лампы бегущей волны
325
5
О
-5
-10
-15
-20
-25
-30
-*ВЫХОТЕЬ
-
ДБ
«—-—¦
5 л
\
.—
i
ж
\
\
\
\
\
\
\
V 1,5и^
2 /
1 -" ^"""
/
/
/
2/ --
/
1
\
Аср
си
2ю
\|/-ф
4
2
0
\|/-ф
4
2
О
Ж
ж.
Ж
ш
ш
5,5 6,8
0
-^1,
//У/У//;
9///У//
ж
2т1,
V
¦
Рис. 10.14. Зависимость выходной мощности сигналов на основной и удво-
удвоенной частотах от соотношения фаз между ними на входе лампы (а) (вы-
(выходная мощность отнесена к ее значению на выходе лампы при отсутствии
на входе гармоники). Здесь кривая 1 соответствует РВХ2/Рв*1 = —3,6 дБ;
2 — РВх2/^Рвх1 = —5,3 дБ. Зависимость разности фаз (ф — ср) от длины
пространства взаимодействия ? (б) для случая РВХ2 = Ропт (сверху) и РВХ2 =
= 0 (снизу). Заштрихован полупериод, когда электроны отбирают энергию
у электромагнитной волны. Качественное поведение амплитуд гармоник то-
тока г и поля F вдоль пространства взаимодействия при подаче на вход ЛБВ (в)
для случаев РВХ2 = Ропт (слева) и РВХ2 = 0 (справа)
При наличии на входе сигнала Р2вх опт на удвоенной частоте 2и разность
фаз (ф — (рJш = тг/2 при ? = 5,5, тогда как насыщение на частоте и
происходит при ? = 6,8. Это означает, что электроны на длине ? = 5,5
начинают отбирать энергию у поля на удвоенной частоте. Это приводит
к улучшению группировки электронов и резкому возрастанию ампли-
амплитуды сгруппированного тока на основной и удвоенной частотах (см.
рис. 10.14в, на котором приведено качественное поведение амплитуд
гармоник вдоль пространства взаимодействия). Поскольку на основной
частоте электроны находятся в тормозящей фазе поля, они продолжают
отдавать свою энергию волне, причем, амплитуда ВЧ-поля на основной
частоте резко возрастает, тогда как на удвоенной она стремится к нулю.
326
Лекция 10
Рвх
Vi
v2
V02
40
30
20
10
Локальный
z b
i i
поглотитель
2,2 (Птах)
i i i
0,1 0,2 0,3 0,4 0,5 AF
Рис. 10.15. Экспериментальная схема ЛБВ со скачком скорости электро-
электронов (а), зависимость к.п.д. от величины скачка скорости AV (б) для раз-
различных значений параметра b
6. ЛБВ со скачком скорости электронов [17]. В эксперимен-
экспериментах исследовалась трехсекционная ЛБВ, схема которой приведена на
рис. 10.15а. Скачок скорости электронов помещался в точке насыщения
мощности.
Расчеты на основе нелинейных уравнений ЛБВ показывают, что при
введении скачка до точки насыщения или после неё к.п.д. ухудшается.
В теоретической модели [17] в точке насыщения скорость электронов
в электронвольтах изменялась на величину AV = V^ — У\- В расче-
расчетах проводилась необходимая коррекция электронного к.п.д. прибора,
связанная с учетом энергии, забираемой электронами от источника
питания, включенного между этими секциями.
Наибольшее увеличение к.п.д. имеет место при Ь = 0 со значением
ту = 17% (-ГГ- = 0) до — г] = 42,1 %. Для наибольшего коэффициента
усиления самым оптимальным является режим с b = 1 (см. рис. 10.156).
Скачок напряжения в случае 6 = 0 приводит к большим значениям
амплитуды сгруппированного тока и создает наиболее благоприятную
для взаимодействия фазировку поля и тока.
Основной причиной ограничения мощности в рассматриваемом
режиме является ухудшение фазировки между полем и током
(рис. 10.16в). Сам сгусток в точке насыщения еще достаточно хорошо
сгруппирован (///о ^ 1) (рис. 10.166), что позволяет рассчитывать
на дополнительное повышение к.п.д. введением повторного скачка
напряжения или скачка Уф.
Нелинейная теория лампы бегущей волны
327
3,0
2,0
1.0
0,6
0,5
= 0
i
hlh
1,5
1,0
Аср
Зз
2
0 0,5 1,0 1,5 2,0 ? 0 0,5 1,0 1,5 2,0 ? 0 0,5 1,0 1,5 2,0 %
а б в
Рис. 10.16. Зависимости амплитуды поля Т (а), первой гармоники сгруппи-
сгруппированного тока /i (б) и разности фаз Аср (в) вдоль пространства взаимодей-
взаимодействия ЛБВ со скачком скорости электронов
При работе входной секции в режиме максимального усиления в вы-
выходной секции также имеет место увеличение основной гармоники тока,
однако закон изменения тока оказывается таким же, как и в отсутствие
скачка напряжения. Основной выигрыш в к.п.д. в этом режиме получа-
получается за счет создания скачком
скорости электронов более опти-
оптимальных фазовых соотношений.
С увеличением амплитуды скач-
скачка, так же как и при 6 = 0, сгу-
сгусток вблизи точки насыщения на-
начинает разгруппировываться, на
что указывает падение величины
основной гармоники тока.
7. ЛБВ с увеличением Уф
в выходной секции [18, 19].
Рассмотрим лампу, у которой
имеется дополнительная секция
возле коллекторного конца, в ко-
которой 62 < Ь\ (см. рис. 10.17,
на котором приведена схема та-
ъ,
pBbmi
b2<bl
О
Рис. 10.17. Зависимость к.п.д. ЛБВ
с увеличенным значением г?ф в вы-
выходной секции от параметра холод-
холодного рассинхронизма в выходной сек-
секции для различных значений дли-
длины ? первой секции
кой лампы, а также зависимость
к.п.д. от параметра рассинхро-
рассинхронизма в дополнительной секции).
Наблюдаемое увеличение
к.п.д. при оптимальном значении
параметра холодного рассинхронизма в выходной секции Ь^ объ-
объясняется следующим. В режиме максимального к.п.д. «обычной»
ЛБВ насыщение связано с тем, что разность фаз Аср между полем
и первой гармоникой сгруппированного тока становится близкой к тг/2
328 Лекция 10
за счет замедления волны высокочастотного поля в линии передачи,
и следовательно, dP = 0. Поэтому для улучшения «фазировки»
поля и тока с целью повышения эффективности прибора необходимо
увеличивать скорость электромагнитной волны в выходной части
замедляющей системы (уменьшение величины 62).
Исследования показали, что оптимальные параметры, при которых
в данном случае реализуется максимальный к.п.д. следующие: Ь\ = 2,3,
62 = 1,<U = 7,9.
В заключение этой лекции отметим, что для повышения полного
к.п.д. ЛБВ используют такие достаточно аппробированные в вакуумной
СВЧ-электронике методики как рекуперацию электронов, коллектор
для сбора наиболее медленных электронов, демодуляцию.
Список литературы
1. Вайнштейн Л.А., Солнцев В. А. Лекции по сверхвысокочастотной
электронике. — М.: Сов. радио, 1973.
2. Цейтлин М.Б., Кац A.M. Лампа с бегущей волной. — М.: Сов.
радио,1964.
3. Шевчик В.Н., Трубецков Д. И. Аналитические методы расчета в
электронике СВЧ. — М.: Сов. радио, 1970.
4. Кураев А.А., Байбурин В.В., Ильин Е.М. Математические модели
и методы оптимального проектирования СВЧ приборов. — Мн.:
Наука и техника, 1990.
5. Ведяшкина К.А., Солнцев В.А. Расслоение электронного потока в
лампе с бегущей волной // Электронная техника, серия I: электро-
электроника СВЧ. 1972. Вып. 9. С. 3.
6. Журавлев СВ., Канавец СВ., Морозов Ю.Д., Сандалов A.M. Ква-
Квазитрехмерная теория электронных приборов с продольным дис-
дискретным взаимодействием // Радиотехника и электроника. 1978.
Т. 23, №7. С. 1557.
7. Ведяшкина К.А., Солнцев В.А. Двухмерные модели и нелинейные
уравнения аксиально-симметричных электронных пучков // Элек-
Электронная техника, серия I: электроника СВЧ. 1975. Вып. 2. С. 34.
8. Bress A., Dohler G., Groshart G., Pierce G., Weyrich R. Microwave
power module (MPM) development and results. — Int. Electron
Devices Meeting Dig. Washington, DC. 1993. P. 145.
9. Whaley D.R., Armstrong СМ., Gannon В., Groshart G., Hurt E.,
Hitchins J., Roscoe M., Antonsen T.M., Levush B. Sixty-Percent-
Efficient miniature C-Band vacuum power booster for the microwave
power module // IEEE Trans, on Plasma Sci. 1998. V. 26, № 3. P. 912.
10. Роу Дж. Теория нелинейных явлений в приборах СВЧ. — М.:
Сов.радио, 1969.
Нелинейная теория лампы бегущей волны 329
11. Солнцев В. А. Анализ изофазных ламп с бегущей волной // Элек-
Электронная техника, серия I: электроника СВЧ. 1971. Вып. П. С. 87.
12. Dournseif E.R., Roberts L.A. Modern Travelling-wave tubes for space
application // Microwave Journal. 1969. V. 12, №4. P. 55.
13. Кац A.M., Рыкшин Б. В. Особенности взаимодействия в ЛБВ при
скорости электронов, значительно превышающей скорость вол-
волны. — Электронная техника, серия I: электроника СВЧ. 1971.
Вып. 2. С. 64.
14. Калинин Ю.А., Кац A.M., Лесин Б.В. Исследование работы ЛБВ
при больших входных сигналах // Электронная техника, серия I:
электроника СВЧ. 1971. Вып. 6. С. 52.
15. Ильина Е.М. и др. Частный случай двухчастотного режима рабо-
работы ЛБВ // Электронная техника, серия I: электроника СВЧ. 1971.
Вып. 12. С.З.
16. Канавец В.И., Лопухин В.И., Сандалов А.И. Нелинейные процес-
процессы в мощных многорезонаторных клистронах и оптимизация их
параметров // Лекции по электронике СВЧ и радиофизике C-я
зимняя школа-семинар инженеров), Книга VII. Саратов: Изд-во
СГУ, 1974. С. 87.
17. Победоносцев А.С, Ровенский Г.В., Малькова П.Я. Исследование
ЛБВ со скачком скорости электронов и со скачком фазовой ско-
скорости волны в выходной части линии замедления // Электронная
техника, серия I: электроника СВЧ. 1970. Вып. 11. С. 12.
18. Победоносцев А. С, Ровенский Г.В., Малькова П.Я. Теоретический
анализ ЛБВ с увеличенной фазовой скоростью волны в выходной
секции замедляющей системы // Электронная техника, серия I:
электроника СВЧ. 1971. Вып. 4. С. 148.
19. Gerchberg R.W., Niclas К.В. The positively tapered travelling-wave
tube // IEEE Trans, on ED. 1969. V. ED-16, № 9. P. 827.
Лекция 11
ЛАМПА БЕГУЩЕЙ ВОЛНЫ С ЦЕПОЧКОЙ
СВЯЗАННЫХ РЕЗОНАТОРОВ
Универсальность замедляющих структур со свя-
связанными резонаторами подтверждается их ши-
широким применением на частотах от единиц до
десятков гигагерц, при этом выходные мощности
составляют от 1 до 500 кВт. Из общего числа ЛБВ
большой мощности количество ламп, в которых
используется этот тип замедляющих структур,
составляет, вероятно, около 90%.
Дж. Мендел. Мощные электроваку-
электровакуумные приборы СВЧ.
Особенности физических процессов в ЛБВО с цепочкой связанных ре-
резонаторов. Об особенностях физических процессов вблизи границ про-
пропускания периодической замедляющей системы. Дискретный и волно-
волновой подход к анализу взаимодействия в ЛБВО с цепочкой связанных
резонаторов. Клистрон с бегущей волной. Линейные ускорители заря-
заряженных частиц.
В первых лекциях были рассмотрены приборы клистронного типа,
которые описывались на основе дискретных представлений о взаимо-
взаимодействии электронного потока с высокочастотными полями. В этих
приборах используется динамический способ управления, когда элек-
электронный поток после модуляции по скорости в высокочастотном зазоре
движется в области, свободной от полей — пространстве дрейфа, где
быстрые электроны догоняют более медленные, образуя сгустки. Разви-
Развитие динамического способа управления привело, как уже обсуждалось,
к созданию целого класса приборов клистронного типа: пролетному
двухрезонаторному клистрону и клистрону-умножителю частоты, мно-
горезонаторному клистрону-усилителю 1), отражательному клистрону
и т. п. Основной особенностью таких моделей является то, что процессы
х) При введении той или иной обратной связи возможно говорить о соот-
соответствующих генераторах.
ЛБВ с цепочкой связанных резонаторов 331
модуляции электронного потока по скорости, процессы их группирова-
группирования и взаимодействия сгруппированного потока с ВЧ-полем разделены
во времени и пространстве. Кроме этого имеет место локализованное
в пространстве дискретное взаимодействие пучка с ВЧ-полем значи-
значительной амплитуды, которое обусловлено резонансными свойствами
колебательной системы. Конструкции всех вышеописанных приборов
состоят из различных сочетаний двух основных элементов: ВЧ-зазора
и пространства дрейфа. Причем в многорезонаторных клистронах мож-
можно говорить о многократном дискретном взаимодействии электронного
пучка с ВЧ-полем, что весьма существенно для последующего рассмот-
рассмотрения.
В ЛБВ, имеющей нерезонансную колебательную систему (напри-
(например, спиральную замедляющую систему), электронный пучок, возму-
возмущенный входным сигналом, сгруппировавшись, отдает свою кинети-
кинетическую энергию ВЧ-полю замедленной волны на большой длине про-
пространства взаимодействия при сравнительно малой амплитуде поля.
При выполнении условия синхронизма электроны все время находятся
в одной и той же фазе поля. Вследствие этого амплитуда поля замед-
замедленной волны нарастает в направлении движения пучка, что, в свою
очередь, улучшает взаимодействие электронов и волны. То есть, имеет
место выполнение условий пространственного резонанса.
Указанные выше особенности взаимодействия электронного пучка
с высокочастотным полем в приборах с длительным взаимодействием
привели к отказу от дискретного анализа ЛБВ и разработке теории
непрерывного взаимодействия электронного потока с полем бегущей
электромагнитной волны — волнового анализа, основанного на введе-
введении понятия о пространственных гармониках поля.
Однако появление мощных ЛБВ с периодическими замедляющими
системами, отличными от спиральных, привело к определенной транс-
трансформации взглядов на описание подобных конструкций. Для расчета
подобных систем часто используется подход, который был разработан
существенно раньше для приборов с дискретным взаимодействием.
Этот «старый» подход не требует новых представлений (например,
введения понятия о пространственных гармониках поля) при переходе
от теории резонансных СВЧ-приборов к теории приборов типа О с нере-
нерезонансными колебательными системами. В рамках этого подхода раз-
различные приборы (клистроны, ЛБВ, ЛОВ, оротрон и др.), по-существу,
можно описать едиными уравнениями. С точки зрения волновой теории
такой подход, основанный на дискретном взаимодействии электрон-
электронного потока с резонансными колебательными системами, учитывает
взаимодействие со всеми пространственными гармониками ВЧ-поля
одновременно. Рассмотрению вопросов описания приборов нерезонанс-
нерезонансного типа с периодическими замедляющими системами, отличными от
спиральных, и посвящена данная лекция.
332
Лекция 11
Об особенностях физических процессов вблизи границ
пропускания периодической замедляющей системы
Наиболее универсальной и широко используемой среди замедляю-
замедляющих систем периодического типа с характеристиками фильтра является
замедляющая система типа цепочки связанных резонаторов (ЦСР) х).
Название «цепочка связанных резонаторов» связано со сходством от-
отдельной ячейки замедляющей системы с объемным торроидальным
резонатором, применяемым в клистронах (см. рис. 11.1). Однако, в отли-
отличие от клистрона, здесь имеет место электродинамическая связь между
Отверстия
связи
ВЧ-зазор (резонатор)
¦ Пространство дрейфа
Отверстие связи
Рис. 11.1. Схематическое изображение замедляющей системы типа цепочки
связанных резонаторов с щелями связи, направленными противоположно
друг другу
ячейками через щель в стенке каждого резонатора. Как видно из рисун-
рисунка, замедляющая система типа ЦСР состоит из уже упомянутых в этой
лекции элементов: ВЧ-зазора и пространства дрейфа, только теперь
имеет место связь между соседними зазорами. Таким образом мы опять
приходим к дискретному и многократному взаимодействию. Это требу-
требует модификации описания свойств замедляющей системы по сравнению
с волновым анализом, основанном на введении пространственных гар-
гармоник продольной компоненты полного ВЧ-поля (см. Лекцию 1). В этом
случае дискретное по своей природе взаимодействие электронного пуч-
пучка с ВЧ-полем можно с определенной степенью точности заменить рас-
рассмотрением непрерывного взаимодействия с одной пространственной
гармоникой замедляющей системы. Это вполне оправдано при выпол-
выполнении условий пространственного резонанса, когда фазовая скорость
г) Это связано с простотой перестройки рабочей частоты, изменения мощ-
мощности и ширины полосы прибора с замедляющей системой типа ЦСР. За-
Заметим также, что ЦСР обеспечивает хороший теплоотвод, механическую
прочность, фокусировку, а также меньшее, чем у спирали, замедление при
высоком сопротивлении связи [1].
ЛЕВ с цепочкой связанных резонаторов
333
A/VV^n\/VVsA/^ny/VVVS/^^yjV^
«
б
-п/а
к/а
Рис. 11.2. Цепочка из одинаковых частиц массой т (а) и ее дисперсионная
характеристика (б), 7 — коэффициент упругости пружин, соединяющих
шарики. Здесь 1 — дисперсионная кривая дискретной цепочки; 2 — диспер-
дисперсионная кривая в случае ка <^ 1 (сплошная среда)
пространственной гармоники близка к невозмущенной скорости пучка.
Вместе с тем, при анализе процессов вблизи границ полосы пропуска-
пропускания замедляющей системы условие пространственного резонанса будет
выполняться одновременно для нескольких гармоник. Поэтому, в связи
с необходимостью анализа процессов вблизи границ полос пропускания
ЦСР, а также необходимостью исследования внеполосного излучения
в мощных ЛБВ, дискретное описание взаимодействия пучка с полями
нерезонансных колебательных систем нашло свое место как методика,
позволяющая учесть взаимодействие электронного пучка со всеми про-
пространственными гармониками ВЧ-поля одновременно.
Обсудим вначале наиболее общие свойства пространственно-
периодических структур (или как их еще называют, цепочек
(в одномерном) и решеток (в двухмерном случае)), к которым
относится и любая система типа ЦСР. Рассмотрим простейшую модель
такой системы — безграничную одномерную среду, составленную
из одинаковых, равноудаленных частиц массой т, связанных друг
с другом пружинами с жесткостью к (рис. 11.2а). Предполагая, что на
каждую п-ю частицу действуют только (n ± 1)-е частицы, уравнение
движения n-й частицы запишется как
тхп = -
- хп) =
Будем искать решение в виде волны хп = Ае^шЬ~пкаК Тогда
2 47 . 2 ка
UJ — —- Sin
т 2
)
A1.1)
A1.2)
Полученное выражение есть дисперсионная характеристика дискрет-
дискретной цепочки (рис. 11.2а). На рис. 11.26 представлен вид дисперсионной
кривой, из него видно, что всем возможным волновым числам соот-
соответствуют значения к G [—тг/а, тг/а] (первая зона Бриллюэна). Отсюда
334
Лекция 11
а
со
«о ;
ЛДЛ/
—ж/а
ж/а
Xi
Рис. 11.3. Цепочка одинаковых маятников (а) и ее дисперсионные характе-
характеристики: б — в области прозрачности; в — в области непрозрачности. Здесь
Xi = 2arcshyma^/47i/а
следует первое важное свойство такой дискретной цепочки: наличие
частоты отсечки иог = 2л^у~/т. Второе важное для нас свойство:
групповая скорость обращается в ноль при сдвиге фаз на период равный
тг. Действительно, по определению
dk
' 7 ka
i — a cos —
m 2
поэтому vrp = 0 при ka = =Ь/гтг, /г = 1, 2, 3 ...
Заметим, что при переходе к сплошной среде, т.е. ka
Л — длина волны возмущения), уравнение A1.3) дает:
/ т
vrD = \ — а = const,
F V m
A1.3)
1 (а ^С А,
A1.4)
и, следовательно, характерная для дискретной цепочки верхняя частота
отсечки при переходе к сплошной среде исчезает.
Если теперь рассмотреть цепочку (рис. 11.3), составленную из ма-
маятников, связанных друг с другом пружинами, то для дисперсионного
уравнения такой среды аналогично тому, как это было сделано выше,
можно получить:
• для действительных к
2
и =
47
-
ка
-¦
A1.5)
ЛЕВ с цепочкой связанных резонаторов
335
для мнимых k = jx-
UJ
2 _ .,2
_ .,2 47 1 2Ха.
A1.6)
ГУЛГУЛ ГУУУЛ ГТУУЛ ГУУУУ_
где изо — собственная частота маятника. Из уравнения A1.5), опре-
определяющего частоты от ооо до о;* = л/оо^ + Aj/m (см. рис. 11.3?;в),
следует, что волны с частотами со Е [ио, о;*] будут распространяться без
затухания (полоса прозрачности), в то время как вне этой полосы (см.
формулу A1.6)) — область непрозрачности — амплитуда волны спадает
экспоненциально с ростом номера п по мере распространения волны
вдоль цепочки.
Таким образом уже на примере простейших моделей понятны фи-
физические причины, которые приводят к появлению в пространственно-
периодических структурах полос
пропускания и непропускания.
Они связаны с наличием в це-
цепочке тех или иных собствен-
собственных пространственно-временных
масштабов.
Однако вернемся от механи-
механических сред-моделей к рассмат-
рассматриваемой замедляющей систе-
системе — цепочке связанных резона-
резонаторов. Простейшая модель такой
изображенной на рис. 11.1 структуры, когда щели между отдельными
резонаторами направлены противоположно друг другу, может быть
представлена эквивалентной схемой [4], изображенной на рис. 11.4. Ис-
Используя телеграфные уравнения, несложно показать, что она представ-
представляет собой фильтр промежуточных частот и описывается уравнением
для тока вида
4 1 L ^
Рис. 11.4. Простейшая эквивалентная
схема замедляюшей системы типа це-
цепочки связанных резонаторов
dtz
С
A1.7)
Представляя зависимость тока от времени и пространственной коорди-
координаты как In = /°eiM-n/ea) ^ получаем дисперсионное уравнение в виде
= Т-с + Тс8'1п2^> (и-8)
которое полностью совпадает с A1.5) при замене ио *-> \\JL\C,
j/m •<->¦ 1/LC, а следовательно, все выводы, сделанные относитель-
относительно цепочки связанных механических осцилляторов, полностью при-
применимы к электрической цепочке. Таким образом уже в простейшем
эквивалентном представлении ЦСР обнаруживается наличие полосы
прозрачности и непрозрачности. Заметим, что если в данном случае
перейти к пределу непрерывной среды (ка —у 0), то дисперсионная
336 Лекция 11
2 1 . ka
характеристика примет вид uj = + ——; это означает, что нижняя
LiC LC
частота отсечки сохраняется. Последнее связано с тем, что, положив
ka <С 1, мы «избавились» от пространственного масштаба, однако соб-
собственный временной масштаб среды (\/L\C) сохранился.
Заметим в связи с этим, что появление и разработка ЛБВ с ЦСР
представляются важным не только в связи с чисто прикладными вопро-
вопросами создания мощных усилителей. ЛБВ с ЦСР стала первой хорошо
изученной активной периодической структурой, под которой понима-
понимают систему «периодическая структура-активная среда». С начала 80-
х годов активно развиваются исследования и других периодических
активных сред применительно к вакуумной СВЧ-электронике. В пер-
первую очередь, имеются в виду системы, в которых в качестве активной
среды используется сильноточный релятивистский электронной пучок.
К ним следует отнести релятивистские карсинотроны, ЛБВ, оротро-
ны, генераторы поверхностных волн. В релятивистском карсинотроне
используются гофрированные волноводы или цепочки индуктивно свя-
связанных резонаторов, в релятивистских ЛБВ — волноводы, нагружен-
нагруженные дисками (системы с очень сильной дисперсией). Заметим также,
что активные периодические системы привлекательны не только для
вакуумной СВЧ-электроники: такие активные среды широко исполь-
используются в твердотельной электронике для создания активных антенн
отражательного типа, которые представляют собой гофрированные
поверхности, в каждую из щелей которых вводится полупроводниковый
усилитель (например, диод Ганна или ЛПД) [5], в квантовой электрони-
электронике, где разработаны лазеры с распределенной обратной связью (РОС-
лазеры) [6] и т. д. (основные направления этих исследований содержатся
в хорошем, хотя и несколько устаревшем, обзоре [7]).
Итак, характерным свойством периодических структур, как было
показано на простейших примерах пассивных сред-цепочек, является
наличие по крайней мере двух частот отсечек, разделяющих диапа-
диапазоны распространяющихся и нераспространяющихся в системе волн.
В полосе прозрачности волны распространяются без затухания (если,
конечно, рассматривается необладающая потерями цепочка), причем
дисперсионная характеристика определяется конкретным видом пери-
периодической структуры. В полосе непрозрачности имеет место реактивное
затухание, фазовая скорость является линейной функцией частоты, так
как фазовый сдвиг волны на период постоянен и равен тг или 0. Понятно,
что для пассивных устройств эта область не представляет интереса,
кроме как для использования соответствующих устройств в качестве
фильтров и аттенюаторов. Совсем другая ситуация складывается при
приближении к границе полосы прозрачности в активной среде.
Обратимся опять к механической аналогии. Рассмотрим систему
связанных маятников, изображенную на рис. 11.3. Если отвести все
маятники от положения равновесия на один угол, и предоставить им
ЛЕВ с цепочкой связанных резонаторов 337
возможность совершать свободные колебания, то (если пренебречь
трением) окажется, что колебания всех маятников будут синфазными
и незатухающими. Они будут происходить с частотой равной собствен-
собственной частоте и® несвязанного маятника. Это совершенно очевидно, так
как связывающие маятники пружины не испытывают никаких дефор-
деформаций. Эта собственная частота о;о, как мы показали раньше является
нижней частотой отсечки рассматриваемой механической передающей
линии-цепочки. Аналогичная ситуация наблюдается при противофаз-
противофазных колебаниях соседних маятников. Хотя в этом случае пружины
испытывают деформацию, последние исчезающе малы посередине пру-
пружины. Эти точки могут быть закреплены без внесения каких-либо воз-
возмущений в колебательный процесс. Энергия вдоль линии передачи не
распространяется, а частота противофазно колеблющихся маятников
(верхняя частота отсечки) совпадает с собственной частотой колеба-
колебательной системы, состоящей из маятника с пружинами половинной
длины а/2, закрепленными на концах. Таким образом передающая ме-
механическая линия-цепочка ведет себя подобно резонатору, накапливая
энергию.
В качестве еще одного примера резонансных явлений вблизи гра-
границы полосы пропускания можно рассмотреть распространение волн
в обычном гладком прямоугольном волноводе. Согласно концепции
Бриллюэна (концепции парциальных волн), распространение волн ти-
типов ТЕ и ТМ можно рассматривать как результат многократного отра-
отражения определенным образом поляризованных ТЕМ-волн от боковых
поверхностей волновода. Угол падения парциальных волн уменьшается
по мере приближения к частоте отсечки. В критическом случае волны
падают перпендикулярно отражающей поверхности (стенки волновода)
и, отражаясь от противоположной стенки, создают резонанс в попереч-
поперечном направлении. Переноса энергии в продольном направлении (вдоль
волновода) при этом не происходит. Наблюдается реактивное затухание
волны в продольном направлении. Наличие частоты отсечки в волно-
волноводе, таким образом, связано, как и в механической линии передачи,
с резонансными явлениями.
При возбуждении подобных пассивных сред (или цепочек в дискрет-
дискретном случае) можно получить лишь накопление энергии и безграничный
рост (при отсутствии диссипации) амплитуды колебаний во времени.
Энергия колебаний при этом не будет передаваться вдоль структуры.
Аналогичные явления наблюдаются и в периодической активной
среде типа ЦСР. Действительно, с приближением к частоте отсечки
в полосе прозрачности при неизменной передаваемой мощности резко
возрастает амплитуда полей в структуре, что позволяет увеличить эф-
эффективность взаимодействия электронного пучка с полями структуры.
В полосе непрозрачности взаимодействие носит в основном реактив-
реактивный характер, но электронный поток способен переносить информацию
вдоль структуры за счет движения электронов, хотя электромагнитные
338
Лекция 11
волны в системе и затухают. С другой стороны, реактивное взаимодей-
взаимодействие при определенных условиях может способствовать группировке
потока (вспомним наше рассмотрение трехрезонаторного клистрона,
когда расстройка по частоте промежуточного резонатора позволяла
существенно улучшить группировку электронного пучка).
Итак, периодические дискретные структуры (в том числе и цепочка
связанных резонаторов) характеризуются, во-первых, наличием полос
прозрачности — непрозрачности, а, во-вторых, на границах полосы
прозрачности наблюдаются резонансные явления, приводящие к росту
амплитуды колебаний. Какие из этого следуют особенности при рас-
рассмотрении явлений в ЛБВ с ЦСР рассмотрим в следующем разделе,
посвященном сравнению волнового и дискретного подхода к анализу
явлений в активных периодических средах.
Дискретный и волновой подход к анализу
взаимодействия в ЛБВ О с цепочкой
связанных резонаторов
Обсудим вопрос, как качественно объяснить физические процессы
взаимодействия пучка с полями нерезонансных колебательных систем
с точки зрения дискретного подхода? Для ответа на этот вопрос рас-
рассмотрим модель, представленную на рис. 11.5. Из рисунка видно, что
для многократного синхронного взаимодействия пучка с электромаг-
Электромаг-
нитная волна
Эдсктромаг-
нитный поток
D
Рис. 11.5. Модель изогнутой линии передачи, пронизываемой электронным
потоком, взаимодействующим с попутной электромагнитной волной
нитной волной, бегущей по изогнутой линии передачи со скоростью с,
необходимо, чтобы электроны пучка переместились из одного ВЧ-за-
зора (область 1) в следующий ВЧ-зазор (область 2), находящийся на
расстоянии d (аналог длины пространства дрейфа), за время, равное
времени распространения волны из области 1 в 2 по изогнутой линии
передачи. В этом случае электрон будет «видеть» в каждом зазоре поле
одной и той же фазы. Математически условие синхронизма выражается
формулой
d D + ^ + A(n
ЛБВ с цепочкой связанных резонаторов 339
где г>о — невозмущенная скорость электронов; Л — длина волны в сво-
свободном пространстве; п Е Z. Слагаемое Л(п + 1/2)/с появляется для
обеспечения правильной фазы поля в области 2 из-за наличия изгиба
в линии передачи и изменения направления поля. В данной модели
отчетливо прослеживается дискретный характер взаимодействия: поле
локализовано в области 1 и 2, а между ними отсутствует.
Если воспользоваться понятием пространственных гармоник, то
дискретное по своей природе взаимодействие электронного потока
с ВЧ-полем в ЛБВ с ЦСР можно с определенной степенью точности
заменить непрерывным взаимодействием пучка с одной пространствен-
пространственной гармоникой (как это было сделано при рассмотрении спиральной
ЛБВ). Такая замена вполне очевидна при близости фазовой скорости
пространственной гармоники поля к невозмущенной скорости пучка,
т. е. выполнения условия пространственного резонанса вдали от границ
полосы пропускания.
Возникает вопрос: возможно ли рассмотрение явлений в периодиче-
периодической структуре типа ЦСР с помощью одноволнового приближения, т. е.
когда в расчетах учитывается только одна прямая пространственная
гармоника, вблизи полосы пропускания? Оказывается, что сопротив-
сопротивление связи К, рассчитываемое в данном приближении, стремится
к бесконечности на границе полосы пропускания (так как групповая
скорость vrp становится равной нулю) [8], и уравнением возбуждения
в форме A.74) пользоваться нельзя, так как К является коэффициен-
коэффициентом при токе / в правой части уравнения A.74). В окрестности частоты
отсечки сопротивление связи остается конечным, но очень большим,
что эквивалентно в линейной теории большим коэффициентам уси-
усиления, которые не подтверждаются физическим экспериментом. Дело
в том [9], что по мере приближения к частоте отсечки одноволновое
приближение становится не корректным, так как синхронным с пучком
становится не только прямая гармоника, но и обратная. Действительно,
рассмотрим диаграмму Бриллюэна (рис. 11.6), на которой нанесена
дисперсионная характеристика периодической замедляющей системы
(штриховые линии относятся к областям, где vrp направлена навстречу
пучку). Прямые линии соответствуют электронному пучку и отражают
тот факт, что скорость электронного пучка не зависит от частоты. Точ-
Точка пересечения дисперсионных характеристик пучка и периодической
структуры определяет частоту, при которой имеет место синхронизм
для данной скорости пучка (для данного ускоряющего напряжения).
На рисунке выбраны значения скорости, соответствующие синхронизму
на границах полосы прозрачности для +1-й гармоники попутной вол-
волны. Очевидно, что для системы с положительной дисперсией нулевой
гармоники (рис. 11.6а) имеет место также синхронизм с —1-й гармони-
гармоникой встречной волны на низкочастотной границе полосы прозрачности
и с —2-й гармоникой встречной волны на высокочастотной границе.
Для систем с отрицательной дисперсией нулевой гармоники (рис. 11.66)
340
Лекция 11
Рис. 11.6. Диаграмма Бриллюэна для периодических структур: а — диспер-
дисперсия нулевой гармоники положительна; б — дисперсия нулевой гармоники
отрицательна. Сплошные кривые соответствуют положительному, а пунк-
пунктирные — отрицательному направлению групповой скорости. Прямые линии
соответствуют дисперсионной линии пучка, синхронного с +1-й простран-
пространственной гармоникой на высокочастотной и низкочастотной границе полосы
пропускания
имеет место синхронизм для + 1-й гармоники попутной волны и 0-й
гармоники встречной волны (на низкочастотной границе) и для + 1-й
гармоники попутной волны и —1-й гармоники встречной волны на
высокочастотной границе. Уже отсюда видно, что одноволновое при-
приближение не применимо у границ полосы пропускания и необходимо
использовать, по-крайней мере, двухволновое приближение.
Таким образом из всего вышесказанного понятно, что волновой ана-
анализ в классическом одноволновом приближении не способен корректно
описать явления вблизи границ полосы пропускания. Один из способов
решения задачи — использование модифицированного волнового подхо-
подхода, учитывающего взаимодействие с несколькими пространственными
гармониками поля периодической замедляющей системы.
В этом случае вид уравнений возбуждения остается тем же, что
и в случае гладких волноводов (формулы A.78) и A.81)), где собствен-
собственные функции Es и Hs удовлетворяют условиям A.86). Представим
функции Es и E-s в виде разложения в ряд по пространственным
гармоникам ВЧ-поля [22]:
<pa,n(y,
A1.10)
A1.11)
где D — период электродинамической структуры. Амплитуды встреч-
встречной и прямой волн полагаются здесь одинаковыми.
ЛЕВ с цепочкой связанных резонаторов 341
Если для рассматриваемой замедляющей системы справедливы со-
соотношения
Е-8(х, у, z) = Е8(-х, -у, -z),
H-S(x, у, z) = -Н8(-х, -у, -z),
то функции распределения y?s?n и ip-s,n электрического поля простран-
пространственных гармоник по поперечному сечению периодического волновода
связаны между собой соотношением
Переменную составляющую тока в периодической структуре также
можно представить в виде суммы соответствующих пространственных
гармоник
U = Io*ifix'Zi>m(v,z)ei2*nx/D, A1.12)
П
где фт — функции распределения пространственных гармоник тока по
поперечному сечению пучка, /3 — искомое волновое число.
Воспользовавшись вышеприведенными соотношениями можно по-
получить [2] выражение для ж-составляющей электрического поля в пе-
периодическом волноводе, возбуждаемом электрическим током, в виде
<Р
— s,q — m — n\y->ZIpm,s,n
/3 + /3, +2тг(т + п)/?>] j^^
где введены обозначения
Г Г
^m,s,n = Фт(У, z)(p8iTl(y, z) dy dz, R°s = --
, A1.13)
Полученное стационарное уравнение возбуждения периодической
структуры заданным током учитывает взаимодействие бесконечного
числа пространственных гармоник поля с гармониками тока.
При реальных расчетах учесть бесконечное число пространственных
гармоник невозможно, поэтому важным является вопрос о том, какое
же количество гармоник надо принять во внимание, чтобы получить,
хотя бы качественно, верную картину физических процессов на гра-
границе полосы пропускания и за ее пределами. Ясно, по крайней мере,
одно: при рассмотрении процессов вблизи граничных частот необходимо
учитывать не менее двух пространственных гармоник (см. рис. 11.6)
[10, 12, 13].
342 Лекция 11
Здесь следует отметить, что вышеизложенная методика волнового
анализа процессов в периодической замедляющей системе, как показы-
показывает анализ теоретических и экспериментальных результатов [2, 9, 10],
не позволяет подойти достаточно близко к границе полосы пропускания
и во многом сохраняет слабости общепринятого волнового анализа.
Другой подход к анализу процессов вблизи границ полосы пропус-
пропускания периодической структуры в рамках волновой теории был развит
в работах А.П. Кузнецова и СП. Кузнецова [14, 15, 18]. В основе этого
подхода лежит отказ от традиционной для электроники методики, осно-
основанной на разбиении поля в линии передачи на совокупность прямых
и встречных волн. В работе [15] получено нестационарное уравнение
возбуждения периодической структуры в рамках такого подхода
ае + щ^аЧ _ _кл|)М KtMJ, AU4|
где величины ? (ж, i) и 3{х, t) связаны с высокочастотным продольным
полем и током в периодической структуре соотношениями
E(x,t) = Re
I(x, t) = Re \j(x,t)ej^ot-jCox)] .
Здесь, как и раньше, (Зо и oj$ — волновое число и частота, соответству-
соответствующие границе полосы прозрачности. В уравнении возбуждения A1.14)
не появляется никаких особенностей на частоте oj$.
Нестационарное уравнение возбуждения A1.14) следует дополнить
уравнением движения электронов. В нестационарном гидродинамиче-
гидродинамическом приближении для слабых сигналов его можно записать в виде [15]
+ + ( ^)\ J ?. A1.15)
Если в системе уравнений A1.14) и A1.15) перейти к безразмер-
безразмерным переменным: ? = во/Зох, т = во/3^\и;//(/Зо)\г/2, I = J/1$, Т —
= Е/2/?oVo?oj ?о — ^o^(ySo)/2Vo и считать, что ео ^С 1, то получим си-
систему уравнений, описывающую взаимодействие электронного потока
с полем периодической структуры вблизи границы полосы пропуска-
пропускания:
1h*W = -l (ПЛ6)
д
— -jB) I = jF, A1.17)
ЛЕВ с цепочкой связанных резонаторов
343
где знак « —» соответствует высокочастотной границе полосы пропус-
пропускания периодической структуры, «+» — низкочастотной границе; В =
. При выводе системы нестационарных уравнении (II.16) и
р
A1.17) были сохранены только члены первого порядка малости по е$.
Самосогласованной системе уравнений A1.16) и A1.17) отвечает
дисперсионное уравнение
A1.18)
где верхний знак относится к высокочастотной границе полосы про-
прозрачности, нижний — к низкочастотной. Величины й = ш-шои^ =
= /3 — Ро имеют смысл безразмерных отстроек частоты и волнового
числа от значений и® и /?о, соответствующих границе полосы; В =
— параметр, характеризующий рассинхронизм электрон-
электронного потока и волны критической частоты (фактически, параметр В
управляет точкой пересечения
дисперсионных характеристик
электронного потока и периоди-
периодической структуры (см. рис. 11.7));
?0= y
Из анализа дисперсионного
уравнения A1.18) следует, что
вблизи границ полосы пропус-
пропускания возможно возникновение
абсолютной неустойчивости (ге-
(генерации) [14, 15]. Абсолютная
неустойчивость реализуется при
значении параметра В < 1,755
у высокочастотной границы про-
пропускания и при В > О у низко-
низкочастотной. В первом случае ге-
генерация возникает, когда точка
пересечения характеристик элек-
электронного потока и периодиче-
периодической структуры лежит еще на
ветви, соответствующей прямой
волне, а во втором — точно
в точке, соответствующей гра-
границе полосы пропускания. Физически этот факт понятен из рас-
рассмотрения диаграммы Бриллюэна. Как известно, электронный пу-
пучок отдает энергию электромагнитным волнам, фазовые скорости
которых меньше скорости пучка. На рис. 11.8 и 11.9, на которых пред-
представлены соответствующие диаграммы, область таких волн лежит спра-
Рис. 11.7. Взаимное расположение
дисперсионных характеристик пуч-
пучка и периодической структуры при
взаимодействии у высокочастотной
и низкочастотной границы полосы
пропускания для различных значе-
значений параметра В дисперсионного
уравнения A1.18)
344
Лекция 11
Рис. 11.8. Дисперсионная диаграмма
электронного потока и периодиче-
периодической структуры вблизи высокоча-
высокочастотной полосы пропускания: а —
В К О — неустойчивость абсолют-
абсолютная; б — 0 < В < 1,755 — неустойчи-
неустойчивость абсолютная; в — В > 1,755 —
неустойчивость конвективная. Пучок
отдает энергию электромагнитным
волнам, попавшим в заштрихован-
заштрихованную область
Рис. 11.9. Дисперсионная диаграм-
диаграмма электронного потока и периоди-
периодической структуры вблизи низкоко-
частотной полосы пропускания, а —
В > 0 — неустойчивость абсолют-
абсолютная; б — В < 0 — неустойчивость
конвективная Пучок отдает энер-
энергию электромагнитным волнам, по-
попавшим в заштрихованную область
ва от дисперсионной характеристики электронного потока и заштрихо-
заштрихована. У высокочастотной границы полосы пропускания в эту заштри-
заштрихованную область обратные волны попадают при любом положении
точки пересечения характеристик пучка и замедляющей структуры.
Если значения В не очень велики (рис. 11.8а;б), то поток будет отдавать
энергию этим волнам. В результате в системе возникает распределенная
обратная связь, и реализуется абсолютная неустойчивость (наблюдает-
(наблюдается самовозбуждение ЛБВ). При больших значениях В (рис. 11.8в) эф-
эффективного взаимодействия с обратной волной нет, происходит взаимо-
взаимодействие только с прямой волной в замедляющей системе — имеет место
конвективная неустойчивость (усиление сигнала). При взаимодействии
на низкочастотной границе ситуация иная. В этом случае обратные
волны оказываются в заштрихованной области только тогда, когда
точка пересечения дисперсионных характеристик лежит на обратной
ветви характеристики структуры, т.е. В > 0 (рис. 11.9).
Заметим также, что рассмотрение дисперсионного уравнения A1.18)
позволяет рассмотреть вопрос усиления сигнала в периодической струк-
структуре бесконечной длины. Пусть имеется источник с частотой, харак-
характеризуемой отстройкой ujq. Граница области усиления, как показано
в работах [14, 16, 17], подчиняется уравнениям 5о = ш(/3) и \±-*- = О,
которые для уравнения A1.18) выглядят как
1
1
A1.19)
Соотношения A1.19) на плоскости параметров Eо, В) определяют гра-
границы областей, в которых сохраняется знак мнимых частей корней
уравнения ujq = uj(/3). Анализируя динамику корней дисперсионного
ЛБВ с цепочкой связанных резонаторов
345
to
0
-2
-4
-6
А
-
^Ч П
К \
\
ш
4
2
0
-2
\
К
-
п
Ч
А
В -3
-2
-1
Рис. 11.10. Границы областей конвективной (К) и абсолютной (А) неустой-
неустойчивости, а также пропускания G7) для высокочастотной (а) и низкочастот-
низкочастотной (б) границы полосы пропускания периодической структуры
уравнения A1.18) в комплексных переменных 5 и /3, легко определить
характер решения в каждой из этих областей. На рис. 11.10 приве-
приведены полученные таким образом области абсолютной неустойчивости
(генерации), конвективной неустойчивости (усиления) и пропускания
сигнала для высокочастотной и низкочастотной границ полосы пропус-
пропускания. Из рисунка видно, что около низкочастотной границы полосы
пропускания реализуется внеполосное усиление сигнала, а у высокоча-
высокочастотной границы оно возможно только в узких интервалах значений
управляющих параметров.
В рамках волнового подхода, связанного с отказом от разбиения по-
поля на прямые и встречные волны, удалось, во-первых, описать процесс
и условия самовозбуждения ЛБВ с ЦСР вблизи границы прозрачности
[19], во-вторых, обнаружить ряд новых типов эффекта полного подав-
подавления сигнала [18, 20] и, в-третьих, — корректным образом сформули-
сформулировать граничные условия для поля на концах замедляющей системы,
учет которых принципиален при рассмотрении работы ЛБВ с ЦСР
вблизи границы полосы пропускания [21].
Последнее очень важно, так как коэффициент отражения от лю-
любой, даже малой неоднородности, резко возрастает при приближении
частоты к граничной частоте полосы пропускания. Поэтому оказыва-
оказывается невозможным обеспечить согласование в сколь-нибудь широком
частотном интервале, а, следовательно, необходимо учитывать отра-
отражения электромагнитной энергии от концов замедляющей структуры.
Попытка описать такие отражения путем учета конкретной частотной
зависимости модуля и фазы коэффициента отражения Г (о;), взятой
из эксперимента или численного расчета, приводит к потери общности
полученных таким образом результатов. В работе [21] предложен под-
подход, позволяющий описать отражения от концевых неоднородностей не
коэффициентом отражения, а новым параметром, плавно зависящим
от частоты даже у границы полосы пропускания.
346
Лекция 11
Рассмотрим простейший модельный пример: линию передачи,
нагруженную на активное сопротивление R. Эквивалентная схе-
схема линии передачи изображена на
L L L L/2 рИС 11.11 (см. также рис. 11.4).
Коэффициент отражения волн от
нагрузки дается соотношением
г^ = tg (Pa/2)-uL/R^
A1.20)
где волновое число /3 и частота
uj связаны дисперсионным урав-
уравнением A1.8). Разложив диспер-
дисперсионную характеристику в ряд по C около критической точки C$ =
= 2тг/а, получим
Рис. 11.11. Модельная линия переда-
передачи, нагруженная на активное сопро-
сопротивление
2 2
а
A1.21)
где uq = i/l/(LiC), к — y/l/(LC). Используя выражения A1.20)
и A1.21), можно найти закон поведения коэффициента отражения
в окрестности критической точки:
Г(о;) = -
A1.22)
Из последнего соотношения видно, что при и = и® коэффициент отра-
отражения имеет корневую особенность. Эта особенность является причи-
причиной сильной частотной зависимости коэффициента отражения вблизи
п „ dF(uj)
точки ujq. Действительно, —-т1—- —У оо при и —у loq.
Избавиться от этой особенности возможно, как и раньше, отказав-
отказавшись от разбиения поля на прямую и встречную волну, и выделять
полное синхронное с электронным потоком ВЧ-поле. В этом случае
удается избавиться от особенности в формулировке граничных условий
[21].
В отсутствии электронного потока амплитуда поля ?{х) подчиняет-
подчиняется уравнению A1.14) с отброшенной правой частью
A1.23)
поля меня-
л о2 2(ш — о;о) о
где Ар = „—-А Здесь предполагается, что амплитуда
w (?о)
ется по гармоническому закону. Запишем решение уравнения A1.23)
в виде суммы двух бегущих волн:
? =
- ?-о&
A1.24)
ЛЕВ с цепочкой связанных резонаторов 347
Продифференцируем соотношение A1.24) и положим х = 0. Тогда,
используя, что ?+о = Г?_о, получим
d? ( 1-Г\
= j(A/3±—-)?@). A1.25)
Граничное условие A1.25) содержит параметр
)?тЙы?» (и-26)
который вблизи граничной частоты может быть представлен в виде:
/ ч uj2L (' 2о;о /
«М «-j?-(l - ^ (« - «
т. е. функция а (о;) аналитична в точке о; = ujq.
Рассмотрим теперь общий случай. Пусть имеется стык однородной
волноведущей структуры с периодической структурой. Между ними
располагается неоднородность (в реальных устройствах с ЦСР — пере-
переходное устройство, с помощью которого подводящий волновод соединен
с периодической замедляющей системой). Амплитуды волн в однород-
однородной и периодической структурах связаны матрицей рассеяния А:
Л={а(и,)Ь(и>)\ ( }
\c(u)d(u))J ' v ;
где индексом «1» обозначена однородная, а индексом «2» — периодиче-
периодическая структура.
Вблизи граничных частот полосы пропускания каждая из компо-
компонент ?+ и ?- полного поля ? (см. формулу A1.24)) имеет особенность,
хотя полное поле особенностей не имеет. Поэтому опишем поле в пе-
периодической структуре с помощью вектора ( р, ), содержащего лишь
амплитуду синхронного поля ? и ее производную по координате ?'.
Переход к представлению поля через прямую и встречную волны осу-
осуществляется посредством матрицы Т:
ел _f(e\ _ 1 (i-i/jAp(u)\ (e\ ( ,
е-J ~ т {е'J ~ 2 [г 1/зА(Цш)) И2" ( 8)
Из уравнений A1.27) и A1.28) следует, что
. A1.29)
Матрица AT не имеет особенностей, поскольку не имеет особенно-
особенностей ни полное поле ?, ни его производная ?'. Поэтому зависимость
348 Лекция 11
элементов матрицы AT от частоты является плавной, и в неболь-
небольшой окрестности границы полосы пропускания можно считать, что
AT(и>) « const.
Предположим, что на некоторой фиксированной частоте и = и
сигнал проходит через систему без отражений (система идеально со-
согласована). Тогда AT (и) ~ AT (си), и матрица А имеет вид:
AL30)
где а = а(ш). Используя выражение A1.28), находим
_ 1 (а О \ (l-l/ja\ _ 1 / a -a/ja\
~ 2 \0а*) [l I/ja) ~ 2 \a*a*/ja) '
где введено обозначение а = А/3 (си). Заметим, что в соответствии со зна-
знаком А/3 вблизи высокочастотной границы полосы пропускания а < О,
а вблизи низкочастотной — а > 0.
Матрица AT несет полную информацию об отражениях и трансфор-
трансформации волн в переходных устройствах. Пусть ?вх — амплитуда входного
сигнала в подводящей волноведущей струкуре, ?отр — амплитуда волны,
отраженной от переходного устройства. Тогда из формул A1.29) и
A1.31) следует, что
?--з<*е] =-^?Вх, (Ц.32)
dx \х=0 п
тр. A1.33)
х=0 п
Проводя аналогичные рассуждения, легко получить подобные соотно-
соотношения и на выходном конце системы х = L:
=0^ (п-34)
x=L
ых. A1.35)
x=L п
Здесь ?Вых ~~ амплитуда выходного сигнала периодической структуры.
В соотношениях A1.32)—A1.35) входное и выходное устройство полага-
полагаются идентичными.
Полученные соотношения A1.32)—A1.35) дополняют уравнение воз-
возбуждения A1.14), и с помощью них можно сформулировать граничные
условия для типичных задач электроники в случае, когда рабочие
частоты лежат в окрестности границы полосы пропускания.
ЛБВ с цепочкой связанных резонаторов 349
1. В режиме самовозбуждения отсутствует внешний сигнал во вход-
входном тракте прибора: ?вх = 0. Уравнения A1.32) и A1.34) определяют
в этом случае требуемые граничные условия
d?_
dx
х=0
dx
= ja?(L). A1.36)
x=L
2. В режиме усиления при х = 0 нужно использовать граничное
условие A1.32), а при х = L — граничное условие A1.34). Соотношения
A1.32) и A1.35) позволяют записать выражение для коэффициента
усиления:
2aS(L)
= 201g
=201g
S'@)-jaS@)
A1.37)
3. В режиме полного подавления сигнала амплитуда поля в выход-
выходном тракте равна нулю: ?вых = 0. Складывая и вычитая соотношения
A1.34) и A1.35), получаем
§
= 0. A1.38)
x=L
Заметим, что в вышесформулированные граничные условия пара-
параметр а не вошел, поэтому с точки зрения взаимодействия электронного
потока с электромагнитным полем а является единственным парамет-
параметром, характеризующим постановку граничных условий для указанных
задач. Отметим также, что параметр а равен величине а (со) = ±
2(cj — о; о)
.. , лишь если частота согласования лежит в непосредствен-
w (Ро)
ной окрестности полосы пропускания. Если же точка удалена от грани-
границы полосы пропускания, то данное соотношение дает приблизительное
значение а, и для его уточнения требуются специальные измерения.
Наиболее важным в вышеописанной модификации волнового под-
подхода является то, что удается полностью избавиться от параметров,
сильно зависящих от частоты у границы полосы пропускания перио-
периодической структуры. Это позволяет проводить расчеты ЛБВ с ЦСР
во всем необходимом диапазоне управляющих параметров, в том числе
и непосредственно на границе полосы пропускания, в рамках волнового
подхода.
Однако существует и другой путь анализа явлений в активных
системах типа ЛБВ с ЦСР. Он связан с отказом от волнового анали-
анализа явлений в периодических структурах, и переходу к исследованию
взаимодействия поля и пучка на основе дискретного описания [1, 2].
В последнем случае «электронная» часть задачи сводится к анализу
каскадного группирования электронов (см., например, [2, 24]), после-
последовательно испытывающих действие высокочастотного поля, проходя
350
vk
I
Лекция 11
I
I
Рис. 11.12. Схематическое изображение последовательности к ВЧ-зазоров,
пронизываемых электронным потоком; / — период замедляющей системы,
d — ширина ВЧ-промежутка, г; о — скорость электронного потока на входе
в пространство взаимодействия
через некоторое число ВЧ-зазоров. В работе [23] была развита пол-
полная кинематическая теория дискретного взаимодействия электронов
с ВЧ-полями. Анализируемая модель представлена на рис. 11.12. При
расчетах полагается, что изменение кинетической энергии электрона,
пролетающего через ВЧ-поле к-vo зазора, выражается соотношением
mv\
= MeVk,
где Vk — скорость электрона на выходе из к-го зазора, Vk — напряжение
на к-м зазоре, М — коэффициент эффективности электронного вза-
взаимодействия (см. формулу B.5)). Изменение напряжения Vk от зазора
к зазору, с учетом того, что анализируется режим бегущей волны, будет
описываться выражением
Vk = Vie*7'^*"^
Здесь а = ut\ — фаза влёта электрона в первый зазор, </?о =
= — И — J — относительный угол пролета электронов и волны.
Последнее выражение было получено в предположении малости
амплитуды эффективного переменного напряжения MVk/Vo <С
<С 1. Пользуясь методикой, развитой в лекции 2 применительно
к двухрезонаторному пролетному клистрону, можно получить
выражение для сгруппированного тока в к-м зазоре:
гк = /0 A + jAkXeja) , A1.39)
где X — параметр группирования,
_ е^° - kejipo + к - 1
A-k — —
Зная величину сгруппированного тока, легко получить электронную
мощность взаимодействия электронного потока с бегущей волной в по-
_ A-
sin
- cos N(fo)
2(-
N(po sin (f(
i sin
N -
(fo -
-1K(
NA-
¦ 7VA
-f cos
— COS (fo
N<po)(l
) sin N(fo
— COS (fo)
ЛЕВ с цепочкой связанных резонаторов 351
следовательности N ВЧ-зазоров в виде
N N ~
Р - V Р.. - V ikMVk - р А-лр (лл лп)
к=1 к=1
Здесь
Pea = -l0X^Vl (N - lKfa(N, ^0), (П-41)
A1.42)
A1.43)
A1.44)
Осуществив в выражениях A1.41)—A1.44) предельный переход при
Id —у 0, получим формулы (9.22) и (9.23) для мощности взаимодействия
электронного потока с полем бегущей волны постоянной амплитуды. Та-
Таким образом, при большом числе ячеек N пространства взаимодействия
результаты каскадного и волнового анализа близки г). При уменьше-
уменьшении числа ячеек характер взаимодействия становится отличным от
предсказываемого волновым анализом и становится близким к тому,
что имеет место в многорезонаторном клистроне. При этом происходит
увеличение мощности взаимодействия:
fa{N,ipo)/Fia(<l>o) > 1,5 при N < 10,
где Fia(^o) определяется формулой (9.22), Фо = (N — 1)</?о-
Для обеспечения самосогласованности задачи необходимо в допол-
дополнение к «электронной» части уметь находить возбужденные поля в пе-
периодической структуре сгруппированным током. Дискретный анализ,
основанный на представлении реальных электродинамических струк-
структур эквивалентными схемами и формулировке уравнений возбужде-
возбуждения таких эквивалентных схем сгруппированным током, автоматически
учитывает взаимодействие со всеми пространственными гармониками.
Такой подход является эквивалентным интегрированию непосредствен-
непосредственно уравнений Максвелла. Более того, дискретный подход, как уже
отмечалось, позволяет, хотя бы в принципе, построить единую теорию
СВЧ-приборов типа О как резонансных, так и нерезонансных.
Построим дискретную модель периодической структуры типа ЦСР.
Цепочка связанных резонаторов, как уже обсуждалось нами ранее,
г) Это является свидетельством того, что в случае больших N электронный
поток взаимодействует преимущественно с одной пространственной гармони-
гармоникой ВЧ-поля.
352
Лекция 11
Рис. 11.13. Модель структуры со связанными резонаторами, нагруженной на
произвольные нагрузки, а также схемы, моделирующие работу генератора
на согласованную (слева) и несогласованную (справа) нагрузки
представляет цепочку идентичных электродинамических ячеек, при-
причем первая и последняя ячейки нагружены на произвольную нагрузку
либо связаны с генератором внешних сигналов. Полагаем, что элек-
электродинамическая связь имеет место только между соседними резона-
резонаторами, а взаимодействие полей в структуре с активной средой (элек-
(электронным потоком) происходит дискретно — в узком зазоре резонаторов,
образующих цепочку. Будем моделировать такую среду многозвенной
цепочкой шестиполюсников (см. рис. 11.13, на котором изображена
скелетная схема данной многозвенной цепочки), на входе которых дей-
действует ЭДС ? с заданным внутренним сопротивлением z0A, на выходе
цепочка нагружена на заданное сопротивление нагрузки z0B. Генератор
ЭДС и нагрузка связаны с цепочкой шестиполюсников посредством пас-
пассивных четырехполюсников. По отношению к СВЧ-устройствам ЭДС
? с внутренним сопротивлением z0A моделирует идеально развязанный
с внешней нагрузкой генератор, отдающий мощность в линию передачи
с волновым сопротивлением z0A. Введенная ЭДС должна быть связана
с мощностью, отдаваемой в нагрузку, или, что то же самое, с входной
мощностью, возбуждающей активную СВЧ-структуру. На рис. 11.13
приведены также схемы, моделирующие работу СВЧ-генератора на
согласованную и рассогласованную нагрузку. Пользуясь схемой, мо-
моделирующей согласованную нагрузку, можно рассчитать мощность,
выделяющуюся в нагрузке zH = z0A, и ввести ее как входную мощность
Рвх. Тогда Рвх = \?\2/Sz0A, откуда ? = 2^/2Pb^zoa • Модуль напряжения
в этом случае по длине линии не зависит от координаты и равен | ?/пад | =
= ?/2 = \/2PBxZoa • В случае несогласованной нагрузки напряжение
меняется вдоль линии и в плоскости эквивалентного представления
ЛЕВ с цепочкой связанных резонаторов 353
СВЧ-генератора источником ЭДС равно:
jj _|_ jj == ^
z^(x) + z0A'
^вх(^) — входное сопротивление в сечении х. На основании известного
соотношения, справедливого для любых линий передач (см., например,
[25]), имеем
Из двух последних соотношений следует, что |?/Пад| = ^/2 ~~ т0 же
самое, что и в случае согласованной нагрузки. В этом смысле ЭДС ?
с внутренним сопротивлением z0A моделирует идеально развязанный
генератор.
Два пассивных четырехполюсника А0 и AN+1, моделирующих
устройства связи, которые передают энергию от регулярной линии
к исследуемой периодической структуре и с выхода структуры к на-
нагрузке, будут характеризоваться заданием элементов матрицы передач.
В практических приложениях элементы матрицы передачи могут быть
определены экспериментально [26], либо рассчитаны теоретически при
известной эквивалентной схеме устройства связи.
Каждая ячейка периодической активной среды моделируется ше-
стиполюсником, где «боковые» клеммы служат для связи с соседними
элементами, а «верхние» — для «внутренней» связи с активной средой
(электронным потоком). Отметим, что напряжения и токи, изображен-
изображенные около каждой пары клемм, связаны с реально существующим элек-
электрическими и магнитными полями в структуре таким образом [27], что
величина комплексной мощности Р = - VI* равна величине комплекс-
ной мощности, переносимой через соответствующую поверхность в ре-
реальной структуре, т. е. - VI* = - J [E, H] dS. Таким образом величина
- Vkl% равна мощности, втекающей в реальную ячейку через левый
элемент связи, - V^+i/^+1 — вытекающая через правый элемент связи,
а - Uki% — комплексная мощность, передаваемая структуре активной
средой. Из условия баланса мощностей можно записать:
I Uki% = -Рвз,
где Рвз — мощность взаимодействия, которая находится из «электрон-
«электронной» части задачи, т.е. считается известной. Активную среду тогда
можно характеризовать некоторым током %k — — 2Рвз/?/?. С другой
12 Д. И. Трубецков, А. Е. Храмов
354 Лекция 11
стороны, Рвз = Ре = - J jE dV. Тогда
где в правой части стоят только заданные величины, т. е. ток г& можно
рассматривать как некоторый сторонний источник возбуждения.
Поскольку все источники возбуждения заданы, а сама структура не
содержит нелинейные элементы 1), то токи и напряжения, обозначен-
обозначенные на рис. 11.13, связаны между собой линейными соотношениями.
Любые три из шести токов и напряжений, как следует из теории цепей,
могут быть выражены через остальные три, образуя различные фор-
формы уравнений шестиполюсника. Запишем все напряжения через токи
в матричной форме:
Последнее выражение представляет собой уравнение возбуждения
шестиполюсника заданным током. Наибольшую сложность представ-
представляет собой нахождение коэффициентов матрицы zik для каждой ча-
частоты. Обычно их находят, представляя шестиполюсник эквивалент-
эквивалентной схемой, адекватной рассматриваемому типу электродинамической
структуры. При этом амплитуды и фазы напряжений и токов в рас-
рассматриваемой эквивалентной цепи должны вести себя подобно ам-
амплитудам и фазам полей и токов в реальной электродинамической
структуре. Важным также является количественное определение ве-
величин элементов цепи для конкретной геометрии ячейки. Часто для
определения этих параметров используют не геометрические размеры
структуры, а величины частот отсечки и другие «электрические» вели-
величины, которые можно измерить на «холодном», т.е. без электронного
пучка, макете [28].
Определение коэффициентов матрицы zik возможно и из строго-
строгого электродинамического расчета ячейки резонатора. Однако это су-
существенно более сложный путь, так как задача сводится к решению
дифракционной задачи для корректного учета связи между резона-
резонаторами.
Сформулированное матричное уравнение является разностным ана-
аналогом уравнения возбуждения гладкой электродинамической структу-
структуры в дифференциальной форме.
г) Фактически до сих пор использовались только уравнения Максвелла,
которые линейны. Нелинейность может появиться при включении в задачу
материальных уравнений, описывающих нелинейную среду.
ЛЕВ с цепочкой связанных резонаторов 355
Преобразуем матричное уравнение к более удобному виду. Очевид-
Очевидно, что матричное уравнение представляет собой систему трех алге-
алгебраических уравнений, содержащих три тока и три напряжения. Для
решения этой системы необходимо задать три из шести величин. Если
шестиполюсник возбуждается клеммами от шестиполюсника, располо-
расположенного слева (см. рис. 11.13), и сторонним током, то логично в ка-
качестве заданных выбрать величины V&, /& и гк и разрешить матричное
уравнение относительно трех остальных величин. В результате, проводя
несложные выкладки, получим:
к к к к к к к к к
У к = — V.к 1 h + 1 гк,
h = -^-Vk + ^h + ^ik, A1.46)
Z\2 Z12 Z12
к к к к к к к к к
Z32 т/ ^31^13 "" ^32^11 г | ^33^12 ""
f/A = ПГ Vk к 7* + Л %к'
Z\\ Z12 Z12
Задавая величины Vi, /1 и зная токи г^ из решения электронной
части задачи, можно последовательно определить напряжения и токи
всех шестиполюсников, двигаясь от ячейки к ячейке. Величины V\
и /i должны удовлетворять граничному условию Е' = V\ + hzf0Aj
а величины Vyy+i, /yv+i — граничному условию Vyy+i = In+iz'ob- Здесь
величины Е', Zq^, ZqB соответствуют величинам ?, 20д и 2;0Б, транс-
трансформированным четырехполюсниками связи Л° и AN+1.
Если записать уравнения A1.46) для & — 1, к и & + 1-го шестипо-
шестиполюсника, то получится девять уравнений, содержащих 14 напряжений
и токов (соответственно Vk-i, h-i, Uk-i, U-i, Vk, h, Uk, ik, Vfc+ъ 7fc+b
f/jfe+i, ijfe+i, V^+2, Ik+2)- Восемь любых напряжений и токов можно при
этом исключить, получив одно уравнение относительно шести напряже-
напряжений и токов. Сохранив напряжения ?/&+!, Uk-> Uk-i и токи г&
получим линейную связь меж;ду этими величинами:
AUk+1 + BUk + Сг/Л_1 = Dik+1 + ??u + Fik-U A1.47)
где коэффициенты при напряжениях и токах скомбинированы из эле-
элементов матрицы Zik каждого из трех рассмотренных шестиполюсни-
шестиполюсников.
Полученное разностное уравнение второго порядка A1.47) является
более удобной формой разностного уравнения возбуждения периодиче-
периодической структуры, чем матричное уравнение A1.45).
Именно теория дискретного взаимодействия электронного потока
с ВЧ-полями периодических замедляющих систем при использовании
метода эквивалентных схем в электродинамической части задачи дает
наиболее близкие к эксперименту результаты [2, 4].
12*
356 Лекция 11
Таким образом рассмотрение особенностей физических процессов
в приборах с длительным взаимодействием с периодическими замед-
замедляющими системами показало, что некоторые физические явления,
например поведение ЛБВ с ЦСР на границах полосы пропускания
замедляющей системы, невозможно описать в рамках волновой теории,
которая последовательно применялась в предыдущих лекциях к анали-
анализу ЛБВ со спиральной замедляющей структурой. Не спасает положение
и модифицированный волновой подход, учитывающий взаимодействие
электронного потока одновременно с несколькими пространственны-
пространственными гармониками поля периодической замедляющей системы. В связи
с этим более предпочтителен дискретный подход к анализу взаимодей-
взаимодействия электронного потока с ВЧ-полями периодических замедляющих
систем, который в состоянии объяснить упомянутые выше физиче-
физические явления. Вместе с тем волновой подход, основанный на отказе от
попытки разделить поле электродинамической структуры на прямую
и встречную волны, позволил сформулировать модель ЛБВ вблизи
границ полосы пропускания, использование которой предсказывает те
же результаты, что и применение дискретного подхода [29].
Дискретный подход с успехом применяется не только к расчетам
ЛБВ с ЦСР, но и таких приборов как клистрон с распределенным
взаимодействием (пролетный клистрон, у которого резонансная коле-
колебательная система заменена на волноведущую для обеспечения более
широкой полосы усиливаемых частот в сочетании с характерным для
многопролетных клистронов высоким значением к.п.д.) [30], усилитель
со скрещенными полями (амплитрон) [3, 31], многолучевой клистрон
с бегущей волной [32-34]. Последний прибор будет рассмотрен более
подробно в следующем параграфе.
Клистрон с бегущей волной
Рассмотрим устройство клистрона с бегущей волной (КБВ). КБВ
был предложен Р. Компфнером как клистрон, у которого резонансная
колебательная система заменена на волноведущую. Такой прибор долж-
должен был сочетать характерный для клистронов высокий к.п.д. с широкой
полосой пропускания, обусловленной использованием нерезонансной
колебательной системой. Однако, поскольку при расширении полосы
пропускания падает волновое сопротивление электродинамической си-
системы, для сохранения к.п.д. требуется пропорциональное увеличение
тока пучка. Конструктивно это не сложно, так как замена резонаторов
на волноводы открывает путь для использования в КБВ протяженных
ленточных электронных пучков или нескольких цилиндрических лу-
лучей.
Простейший двухкаскадный КБВ состоит из двух волноводов, ко-
которые разделены пространством дрейфа и пронизываются ленточным
электронным потоком (рис. 11.14). Скорость электронов перпендику-
ЛЕВ с цепочкой связанных резонаторов 357
Входной
сигнал
Выходной
сигнал
Рис. 11.14. Конструкция двухкаскадного клистрона с бегущей волной. Здесь
1 — протяженный ленточный электронный поток, 2— входной и 3 — выходной
волноводы, 4 — согласованный поглотитель
лярна направлению распространения электромагнитных волн в волно-
волноводах, поэтому КБВ относится к приборам с поперечным током. Вход-
Входной сигнал, распространяясь в первом (входном) волноводе, модулирует
электронный поток по скорости. В пространстве дрейфа электронный
пучок группируется по плотности как и в обычном клистроне, но,
поскольку модуляция электронного потока осуществляется бегущей
электромагнитной волной, формирование сгустков происходит с за-
запаздыванием вдоль волновода. Если входной и выходной волноводы
параллельны и идентичны, то волна тока, возбуждающая выходной
волновод, будет синхронна собственной волне этого волновода — пря-
прямые волны, излученные отдельными сгустками, складываются в фазе,
и прямая электромагнитная волна линейно нарастает вдоль выходного
волновода. Встречная электромагнитная волна не синхронна волне
в электронном пучке, и резонанс в пространстве для нее отсутству-
отсутствует, излучение в прямом направлении существенно преобладает над
встречным.
Линейное нарастание поля по длине пространства энергообмена
КБВ приводит к двукратному снижению к.п.д. по сравнению с к.п.д.
двухрезонаторного клистрона. Напомним, что высокий к.п.д. клистро-
клистрона достигается за счет того, что в узком зазоре выходного резонатора
электронный сгусток сильно тормозится полем большой амплитуды
(ВЧ-напряжение на зазоре близко к ускоряющему напряжению Vo),
при этом сгусток отдает большую часть своей кинетической энергии
ВЧ-полю. Напротив, по выходному волноводу КБВ поле линейно рас-
растет от нуля, достигая предельного значения (~ Vo) лишь для части
электронного луча, близкого к выходному концу волновода. Повысить
к.п.д. КБВ до уровня клистронного возможно путем осуществления на
значительном участке выходного волновода энергообмена электронного
потока с электромагнитной волной постоянной амплитуды, близкой
к предельной. Для этого продолжение выходного волновода долж-
должно иметь спадающее волновое сопротивление, чтобы при нарастании
мощности электромагнитной волны ее амплитуда поддерживалась на
постоянном предельном уровне.
Наиболее часто в качестве нерезонансной колебательной системы
в КБВ используются системы типа ЦСР, которые обладают большим
импедансом взаимодействия с пучком. Поскольку в таких системах
358 Лекция 11
электрическая компонента ВЧ-поля локализована в дискретных обла-
областях, использовать сплошной ленточный пучок нецелесообразно, и вме-
вместо него применяют большое число цилиндрических пучков. Сочета-
Сочетание колебательной системы в виде ЦСР и нескольких (порядка 10)
электронных лучей составляет многолучевую конструкцию клистрона
с бегущей волной (МКБВ).
В МКБВ с ЦСР, также как и в КБВ, существует проблема ограни-
ограничения к.п.д., связанная с нарастанием поля от ячейки к ячейке. Если
в процессе этого нарастания в какой-то ячейке ВЧ-напряжение V до-
достигнет оптимального значения (которое порядка ускоряющего напря-
напряжения Vo), то за счет взаимодействия с пучком в последующих ячейках
величина V превысит оптимальное значение. Это будет сопровождаться
отражением электрона, к.п.д. снизится, поэтому необходимо стремиться
к тому, чтобы поле стало оптимальным в последней ячейке. Но в этом
случае, как и раньше, к.п.д. МКБВ не превысит половинного значения
к.п.д. пролётного клистрона.
Как говорилось выше, для повышения к.п.д. необходимо понизить
волновое сопротивление тех ячеек, которые расположены дальше ячей-
ячейки, где достигается оптимальная величина поля. Оценим величину, на
которую следует понизить сопротивление. Пусть в ячейках с номерами
1тп волновое сопротивление равно величине zn, где п — ячейка,
в которой ВЧ-напряжение достигает оптимального значения Vn = Vo.
Тогда мощность, которая передается в следующую ячейку будет равна
Р = Vq /2zn. Эта мощность обеспечивает в этой ячейке амплитуду
ВЧ-напряжения V^+1 = ^2Pzn+\ , которое меньше Vo = \j2Pzn , но
к этому напряжению ещё добавится напряжение V^'+i = /zn+i/2 за
счет возбуждения колебаний током /n+i (последний известен из расчета
процесса группирования). Надо потребовать, чтобы V^+1 + Кн-i = Иь
и тогда уравнение
2Vo
определяет нужное соотношение между zn и zn+\.
Таким образом выходной каскад разделяется на две секции — сек-
секцию с постоянным волновым сопротивлением (секция усиления напря-
напряжения) и с уменьшающимся волновым сопротивлением (секция нарас-
нарастания мощности). К.п.д. прибора определяется соотношением числа
ячеек ЦСР, принадлежащих той или другой секции. Насколько большой
придется делать секцию усиления напряжения зависит в значитель-
значительной степени от модулирующей секции. Чем лучше будет сгруппирован
электронный пучок, тем короче будет секция усиления напряжения.
Повысить эффективность модулирующей секции (увеличить величину
первой гармоники сгруппированного тока) можно путем добавления
третьего каскада, аналогично тому, как это делается в многорезонатор-
ном клистроне (см. лекцию 5). Несколько первых ячеек промежуточно-
ЛЕВ с цепочкой связанных резонаторов
359
WWWWWWWWW W
Рис. 11.15. Схематическое изображение трехволноводного десятилучевого
КБВ
го каскада будут тогда секцией усиления напряжения, на протяжении
которых оно будет нарастать линейно. Когда напряжение достигнет
заданной величины, его дальнейший рост необходимо ограничить. Это
можно сделать, как и в выходном каскаде, путем уменьшения волнового
сопротивления. Однако в этом случае, хотя роста напряжения и не
будет, мощность, отдаваемая электронными пучками в последующих
ячейками, будет нарастать, а условия для дальнейшей группировки
пучка во втором пространстве дрейфа не будут оптимальными, так
как взаимодействие в промежуточном модулирующем каскаде должно
быть реактивным. Вышеописанная ситуация полностью аналогична
каскадной группировке в многорезонаторных клистронах, где реак-
реактивное взаимодействие в промежуточных каскадах обеспечивается на-
настройкой резонаторов на более высокую частоту, чем частота входного
и выходного каскада.
В работах [33, 34] экспериментально и численно исследуется МКБВ
с тремя цепочками связанных резонаторов. Рассмотрим конструкцию
исследуемой системы (рис. 11.15). В приборе три волновода и десять
электронных пучков A0 ячеек в каждом волноводе). Постоянная пе-
передачи одинакова у всех ячеек. После модуляции в зазорах первого
волновода электроны каждого пучка группируются в трубках дрейфа,
второй волновод возбуждается сгруппированными сгустками. Первые
три ячейки параллельны первому волноводу. Как показывают расче-
расчеты, уже в третьей ячейке напряжение на зазоре равно 0,4Vb. Далее
второй волновод изогнут, дрейф каждого следующего луча становится
все больше. Центры сгущений электронов проходят через зазоры этой
части волновода в тот момент, когда ВЧ-поле нулевое, что способствует
дальнейшей (в следующем пространстве дрейфа) группировке, ампли-
амплитуда сигнала здесь поддерживается примерно на постоянном уровне,
происходит реактивное взаимодействие. В выходном волноводе область
усиления сигнала включает в себя четыре секции, с пятой секции начи-
360
Лекция 11
Ф, рад
2,75 2,85 2,95 3,05/ГГц
а б
Рис. 11.16. К.п.д. и коэффициент усиления МКБВ в рабочей полосе частот
(а); коэффициент усиления и фаза выходного сигнала как функция мощности
входного сигнала (б) (из работы [3])
нается область нарастания мощности, в которой волновое сопротивле-
сопротивление ячеек последовательно уменьшается.
Численное исследование проводилось с помощью дискретного опи-
описания взаимодействия электронного потока с ВЧ-полями ЦСР, описан-
описанного в конце предыдущего параграфа. Особенностью расчетов являлся
учет нескольких пучков и нескольких пространств дрейфа [34]. Вна-
Вначале решались уравнения движения во всех пучках в зазоре первого
волновода. Последовательными расчетами рассчитывалось встречное
излучение по ячейкам. Затем рассматривался дрейф электронов каж-
каждого пучка до следующего волновода. Далее расчет повторяется для
следующего каскада.
На рис. 11.16а приведены рассчитанные выходные характеристики
трехволноводного МКБВ (коэффициент усиления и к.п.д.) в рабочем
диапазоне частот [3, 34]. Пунктиром нанесена экспериментально полу-
полученная зависимость коэффициента усиления [33]. На рис. 11.16^ пред-
представлены зависимости коэффициента усиления и фазы поля на выходе
от мощности входного сигнала, который достаточно слаб (линейный
режим). Заметим, что такие характеристики прибора как коэффициент
усиления, к.п.д. и фаза выходного сигнала не сильно меняются и при
изменении тока пучка. Таким образом характеристики МКБВ устойчи-
устойчивы к изменению режима в достаточно широком диапазон.
Линейные ускорители заряженных частиц
В СВЧ-приборах с длительным взаимодействием (ЛБВ, ЛОВ, оро-
трон, клистрон с распределенным взаимодействием и т. д.) имеет место
преобразование кинетической энергии электронного потока в энергию
электромагнитных волн, находящихся в синхронизме с электронами.
В результате скорость электронов пучка в среднем уменьшается, и на
ЛБВ с цепочкой связанных резонаторов 361
коллектор пучок «высаживается» со скоростью, существенно меньшей,
чем та, которую он имел на входе в пространство взаимодействия.
Однако из нашего рассмотрения (см. лекцию 8) понятно, что существует
принципиальная возможность изменить ситуацию: электроны могут
ускоряться за счет энергии электромагнитного поля в пространстве
взаимодействия и приходить на коллектор со скоростью большей, чем
на входе. Устройства, в которых имеет место такое ускорение электро-
электронов, называются линейными ускорителями. Коллектор таких приборов
обычно является специальной мишенью, сделанной из материала, свой-
свойства атомных ядер которого исследуются. В качестве примера можно
привести исследования распределения массы и заряда протона путем
бомбардировки мишени высокоэнергетичными электронами и дальней-
дальнейшего анализа рассеяния электронов на протонах. Для прохождения
через ядро атома электроны пучка должны преодолеть кулоновские
силы отталкивания между ними и положительно заряженным ядром,
поэтому необходимо ускорить электроны до как можно более высоких
энергий. Широко используются такие ускорители и в медицине. Обыч-
Обычно с помощью линейных ускорителей получают высокоэнергетичные
электронные пучки с релятивистскими скоростями.
Теория и детальный анализ процессов ускорения релятивистских
электронов в линейном ускорителе выходит за рамки наших лекций х).
Рассмотрим здесь только некоторые основные особенности устройства
и работы линейных ускорителей [35], которые позволили включить
данный раздел в лекцию, посвященную приборам с периодическими
электродинамическими структурами.
Из релятивисткой электродинамики известно, что в неподвижной
системе отсчета сила отталкивания Fx между двумя электронами, рас-
расположенными на оси х на расстоянии Ах друг от друга и движущихся
со скоростью v в положительном направлении оси ж, определяется
формулой
x =7
где 7 = l/i/l — (v/сJ — релятивистский фактор, е — заряд электрона.
Аналогично, сила отталкивания Fr между электронами, расположен-
расположенными на расстоянии Аг друг от друга на линии, перпендикулярной
направлению их движения, в неподвижной системе отсчета запишется
как
х) Теория, основные типы и области применения линейных ускорителей
достаточно подробно изложены в монографии [36].
362 Лекция 11
Заметим, что величины Fx и Fr стремятся к нулю при скорости
электрона v —> с. Это означает, что продольные и поперечные силы про-
пространственного заряда в пучке, движущемся с ультрарелятивистской
скоростью, в неподвижной системе координат малы. Поэтому в данном
случае для предотвращения «рассыпания» электронного пучка вслед-
вследствие кулоновского отталкивания достаточно сравнительно небольшого
фокусирующего магнитного поля.
В основе конструкции линейного ускорителя лежит ускорение
(вплоть до ультрарелятивистских скоростей) электронного пучка,
направленного вдоль периодической электродинамической структуры
и взаимодействующего в ней с синхронной электромагнитной
волной. Однако при увеличении скорости электрона одновременно
увеличивается и его масса те = то/т? гДе шо — масса покоя
электрона. При v —> с малые изменения скорости электрона будут
приводить к существенным изменениям массы те. Поэтому для
эффективного ускорения пучка электронов необходимо взаимодействие
его с электромагнитной волной, имеющей большую амплитуду.
Начальная скорость электронного пучка vo определяется ускоряю-
ускоряющим потенциалом электронной пушки. Так как скорость пучка меняется
от величины v = vo до величины v ~ с, то период D электродинами-
электродинамической структуры должен изменяться вдоль пространства взаимодей-
взаимодействия для сохранения условия синхронизма между пучком и волной.
Рис. 11.17 демонстрирует основные особенности конструкции ли-
линейного ускорителя. В качестве источника высокочастотной энергии
используются мощные клистро-
нь^ которые расположены на оди-
наковом расстоянии друг от дру-
друга вдоль пространства взаимодей-
взаимодействия (пространства ускорения).
Волновод, в который излучают
энергию клистронные усилители,
нагружен цилиндрическими дис-
\ч J ками с отверстиями посередине,
D которые служат для прохождения
^ ^ ^ „ _, ^ ускоряемого электронного пучка,
Рис. 11.17. Схематическое изображе-
/ Гок1ч движущегося вдоль оси симмет-
ние линейного ускорителя (из 1351) ^ j^ ^
рии системы. На все клистронные
усилители подается сигнал с одного магнетрона для того, чтобы выход-
выходные сигналы каждого из клистронов были сфазированы. Если ввести
соответствующий сдвиг фаз Аф между выходными сигналами, излуча-
излучаемыми в пространство ускорения соседними клистронами, то электро-
электромагнитная волна, распространяющаяся вдоль волноведущей структу-
ЛБВ с цепочкой связанных резонаторов 363
ры, может находиться в синхронизме с электронным пучком. Очевидно,
что оптимальными будут условия распространения синхронной волны,
при которых относительный угол пролета Фо будет поддерживаться
таким, что активная мощность взаимодействия Реа будет больше нуля
и максимальна. Заметим, что линейный ускоритель в виде нагруженно-
нагруженного дисками волновода не является единственной возможной конструк-
конструкцией; часто применяют ускорители, в которых пространство ускорения
представляет собой ряд сильно связанных между собой резонаторов.
Впервые идея линейного ускорителя была высказана в 1924 году
в работе Изинга [37]. Наиболее знаменитым линейным ускорителем
является Станфордский ускоритель г), длина которого составляет две
мили (три километра). Строительство его было закончено в 1966 году,
и на тот момент максимальная энергия электронных пучков, которые
можно было создавать на нем, составляла 20 ГэВ. Первые эксперименты
были проведены по бомбардировке высокоэнергетичным электронным
пучком неподвижной мишени в целях изучения внутренней структуры
атомного ядра. В дальнейшем была проведена модернизация ускорите-
ускорителя, позволившая достигать энергии электронов порядка 50 ГэВ.
Список литературы
1. Гаврилов М.В., Трубецков Д.И., Фишер В. Л. Теория цепочек ак-
активных многополюсников с электронным возбуждением (модель
взаимодействия электронного пучка с полями связанных резона-
резонаторов) // В кн: Лекции по электронике СВЧ и радиофизике E-я
зимняя школа-семинар инженеров). Кн. 1. Саратов: Изд-во Сарат.
ун-та, 1981. С. 173.
2. Булгакова Л.В., Трубецков Д.И., Фишер В.Л., Шевчик В.Н. Лек-
Лекции по электронике СВЧ приборов типа О. — Саратов: Изд-во СГУ.
1974.
3. Фишер В.Л. Теория возбуждения активных упорядоченных струк-
структур и ее применение к анализу колебательных и волновых явлений
в цепочках связанных резонаторов с электронным потоком. —
Дисс... к.ф.-м.н. Саратов, 1983.
г) В Internet существует большой WWW-сайт http:y/www.slac.stanford.edu,
посвященный деятельности Станфордского центра линейных ускорителей
(Stanford Linear Accelerator Center (SLAC)), которому и принадлежит Стан-
Станфордский линейный ускоритель. На этом сайте представлена информация
по истории создания центра, особенностям конструкции ускорителя и на-
научным исследованиям, ведущимся в центре. Кроме всего, этот сайт — сайт
Станфордского центра линейных ускорителей — был первым появившимся
в Internet WWW-сайтом, принадлежащим научной организации США.
364 Лекция 11
4. Стапранас А., Маккьюн Э., Рютц Дж. СВЧ электровакуумные
приборы большой мощности с линейным электронным пучком / В
сб.: Мощные электровакуумные приборы СВЧ. — М.: Мир. 1974.
5. Lee S. W., Fong Т. Т. Electromagnetic wave scattering from an active
corrugated structure // J. Appl. Phys. 1972. V. 43. P. 388.
6. Affolter E., Kneubiihl F.K. First experimental realization of a
distributed feedback gas laser // Phys. Lett. 1979. V. 74A, № 6. P. 407.
7. Элаши Ш. Волны в активных и пассивных периодических струк-
структурах. Обзор // ТИИЭР. 1976. Т. 64, № 12. С. 22.
8. Dow D.G. Behavior of travelling-wave tubes near circuit cut-off// IRE
Trans. 1960. V. ED-7, № 3. P. 123.
9. Рапопорт Г.П., Чайка В.Е. О поведении ЛБВ вблизи границ по-
полосы пропускания // Известия вузов СССР. Радиотехника. 1964.
Т. 7. С. 58.
10. Чайка В.Е. Исследование устойчивости ЛБВ вблизи границ поло-
полосы пропускания замедляющей системы // Известия вузов СССР.
Радиотехника. 1964. Т. 7. С. 58.
11. Шевчик В.П., Кураев А.А. Общее дисперсионное уравнение лам-
лампы с бегущей волной с периодической замедляющей системой //
Радиотехника и электроника. 1961. Т. 6, №9. С. 1519.
12. Осин А.В., Солнцев В.А. Анализ распространения электронных
волн внутри и вне полосы периодической структуры // Радиотех-
Радиотехника и электроника. 1982. Т. 27, № 11. С. 2207.
13. Осин А.В., Солнцев В.А. Исследование усиления ЛБВ вблизи
границы полосы пропускания на основе теории возбуждения пе-
периодических структур // Радиотехника и электроника. 1982. Т. 27,
№12. С. 2435.
14. Кузнецов А.П., Кузнецов СП. О характере неустойчивости в ЛБВ
вблизи границы полосы пропускания // Изв. вузов. Радиофизика.
1980. Т. 23, №9. С. 1104.
15. Кузнецов А.П., Кузнецов СП. Нелинейные нестационарные урав-
уравнения взаимодействия электронного потока с электромагнитным
полем вблизи границы зоны Бриллюэна // Изв. вузов. Радиофизи-
Радиофизика. 1984. Т. 27, №12. С. 1575.
16. Кузнецов А.П. Смена характера неустойчивости в системе двух
слабо связанных волн // Письма в ЖТФ. 1982. Т. 8, № 15. С. 941.
17. Кузнецов А.П. Определение характера неустойчивости вблизи по-
порога ее возникновения // В кн.: Лекции по электронике СВЧ и
радиофизике, кн. 2. Саратов: Изд-во СГУ, 1984. С. 106.
ЛБВ с цепочкой связанных резонаторов 365
18. Кузнецов А.П., Кузнецов СП. Режимы полного подавления сигна-
сигнала в ЛБВ, работающей вблизи границы пропускания // Изв. вузов.
Радиофизика. 1984. Т. 27, №8. С. 1049.
19. Кузнецов А.П., Рожнев А.Г. О самовозбуждении ЛБВ вблизи
границы полосы пропускания // Электронная техника. Сер. Элек-
Электроника СВЧ. 1985, No 9. С. 3.
20. Кузнецов А.П. Эффект реактивного подавления сигнала в ЛБВ //
Электронная техника. Сер. Электроника СВЧ. 1984, No 4. С. 7.
21. Кузнецов А.П. Граничные условия в волновой теории ЛБВ вблизи
частот отсечки замедляющей системы // Электронная техника.
Сер. Электроника СВЧ. 1984, No 7. С. 3.
22. Вайнштейн Л.А. Электронные волны в периодических структу-
структурах // ЖТФ. 1957. Т. 26, № 2. С. 237.
23. Шевчик В.П., Жарков Ю.Д. Каскадная группировка электронов
в применении к анализу взаимодействия электронного потока с
бегущей электромагнитной волной // Радиотехника и электроника.
1957. Т. 27, №10. С. 2342.
24. Шевчик В.П., Трубецков Д.И. Аналитические методы расчета в
электронике СВЧ. — М.: Сов. радио, 1970.
25. Гоноровский И.С. Основы радиотехники. — М.: Связьиздат. 1957.
26. Техника измерений на сантиметровых волнах. — М.: Сов. радио.
1949.
27. Альтман Дж. Устройства СВЧ. — М.: Мир. 1968.
28. Денисов A.M., Перекупко В.А., Рапопорт Г.И. Расчет приборов
О-типа на цепочках связанных неидентичных резонаторов в ли-
линейном режиме // Известия вузов. Радиоэлектроника. 1980. № 10.
С. 43.
29. Булгакова Л.В., Гаврилов М.В., Кузнецов А.П., Кузнецов СП.,
Рожнев А.Г., Фишер В.Л. Сопоставление результатов волнового
и дискретного подходов к расчету усиления ЛБВ вблизи границы
плосы прозрачности // Электронная техника. Сер. Электроника
СВЧ. 1985, No 6. С. 34.
30. Андрушкевич B.C., Вырский В.А., Гамаюнов В.Г. Усилительные
клистроны с распределенным взаимодействием. — Саратов: Изд-
во Сарат. ун-та, 1977.
31. Dombrowski G. Theory of the amplitron // Trans. IRE. 1959. V. ED-6,
№4. P. 419.
32. Гаврилов M.B., Перельман A.M., Пищик Л.А., Трубецков Д.И.
Клистрон с бегущей волной // В кн: Лекции по электронике СВЧ
366 Лекция 11
и радиофизике E-я зимняя школа-семинар инженеров). Кн. 1.
Саратов: Изд-во Сарат. ун-та, 1981. С. 216.
33. Pohl W.J. The design and demonstration of a wide-band multiple-
beam traveling-wave klystron // IEEE Trans. 1965. V. ED-12, №6.
P. 351.
34. Булгакова Л.В., Гаврилов М.В., Пищик Л.А., Трубецков Д.И.,
Фишер В.Л. Применение теории цепочек активных многополюс-
многополюсников к анализу ЛБВ и КБВ // В кн: Лекции по электронике СВЧ
и радиофизике E-я зимняя школа-семинар инженеров). Кн. 1.
Саратов: Изд-во Сарат. ун-та, 1981. С. 198.
35. Soohoo R.A. Microwave electronics. — Addisson-Wesley Publishing
Company, 1971.
36. Лебедев А.Н., Шальное А.В. Основы физики и техники ускорите-
ускорителей. — М.: Энергиздат, 1981.
37. Ising G. Prinzip einer Methode zur Herstellung von Kanalstrahlen
hoher Voltzahl // Ark. Mat. Astr. och Fys. 1925. V. 18, №30. P. 1.
Лекция 12
КАРСИНОТРОН
«...генератор обратной волны или карсино-
трон — это одно из тех изобретений, которые
были сделаны в разных местах, примерно в одно
и то же время и независимо друг от друга. Я
думаю, мои чувства по этому поводу смешались,
подобно чувствам Робинзона Крузо, когда он
обнаружил чужие следы на песке острова».
Р. Компфнер
Взаимодействие электронного потока с обратной электромагнитной
волной. Карсинотрон. « Чужие следы на песке... » — история изоб-
изобретения лампы обратной волны Компфнером и Эпштейном. Теория
пускового режима лампы обратной волны в приближении заданного
поля. Нелинейное поведение лампы обратной волны (результаты ста-
стационарной нелинейной теории) Лампа обратной волны магнетронного
типа.
В предыдущих лекциях подробно рассмотрено длительное взаимо-
взаимодействие электронного потока с попутной электромагнитной волной
и показано, что при подходящих соотношениях между vo и Уф (при их
близости) электрическое поле замедленной прямой волны эффективно
взаимодействует с электронами, которые практически все время «ви-
«видят» одну и ту же фазу поля. Поле прямой волны нарастает в направ-
направлении движения электронов, что обеспечивает увеличение эффектив-
эффективности взаимодействия электронов и волны. В отличие от этого в лампе
обратной волны групповая и фазовая скорость волны противоположно
направлены (противоположны направления распространения волны
и потока мощности, переносимой этой волной), причем, как и в ЛБВ,
направления распространения волны и электронного потока совпадают,
а, следовательно, поток мощности в приборе движется навстречу пучку
и нет нарастания поля в направлении движения электронов. Вопрос
о том, насколько эффективно может быть взаимодействие пучка с такой
обратной электромагнитной волной, становится далеко не тривиаль-
тривиальным.
368 Лекция 12
В распределенной активной системе «прямолинейный электронный
пучок, взаимодействующий с обратной электромагнитной волной» воз-
возникает распределенная обратная связь, что позволяет говорить о воз-
возможности генерации электромагнитного излучения. Напомним, что
в случае лампы бегущей волны мы говорили только об усилении сигна-
сигналов (чтобы усилитель бегущей волны сделать генератором, необходимо
тем или иным способом ввести обратную связь — либо внутреннюю
(за счет отражений от коллекторного конца), либо внешнюю (за счет
ответвления части мощности выходного сигнала на вход ЛБВ)).
Лампа обратной волны стала в сверхвысокочастотной электро-
электронике и нелинейной теории колебаний и волн классической моделью
распределенной автоколебательной системы. Именно с этих позиций
будем строить теорию ЛОВ — в основу изложения положим рассмотре-
рассмотрение нестационарных режимов генерации, что в свою очередь, потребует
построения нелинейной нестационарной теории лампы обратной волны.
Дальнейший вполне очевидный шаг — разработка методики интегриро-
интегрирования таких уравнений на ЭВМ и анализ результатов вычислительного
эксперимента. Последнее особенно интересно — численные [1—8], а так-
также натурные [1,9-11] исследования выявили, что ЛОВ демонстрирует
огромное число типично нелинейных динамических эффектов, включая
режимы детерминированного хаоса, классические сценарии перехода
к хаотической динамике, усложнение хаотических сигналов при прохо-
прохождении через ЛОВ-усилитель и т. п. г).
Данная лекция посвящена изложению истории создания ЛОВ, а так-
также рассмотрению пусковых условий генератора обратной волны на
основе метода последовательных приближений. В ней также будет
описана разновидность лампы обратной волны — ЛОВ М-типа. Вто-
Вторая лекция по теории ЛОВ (лекция 13) будет посвящена построению
простейшей нестационарной теории как нерелятивистского, так и реля-
релятивистского карсинотрона, а также изложению основных результатов,
полученных при экспериментальном исследовании карсинотрона и чис-
численном анализе нелинейных нестационарных уравнений, описывающих
взаимодействие электронного потока с обратной волной. Лекция 14
посвящена рассмотрению методов численного моделирования приборов
с длительным взаимодействием О-типа.
г) Многие исследования были выполнены в течение нескольких последних
лет: обратите внимание на даты опубликования работ [3-8]. Отметим, что
исследования нелинейной динамики ЛОВ начались более 20 лет назад — и до
сих пор ЛОВ как объект нелинейной динамики не перестает демонстрировать
новые явления.
Карсинотрон
369
Взаимодействие электронного потока
с обратной электромагнитной волной.
Лампа обратной волны или карсинотрон
Как уже отмечалось, лампа обратной волны обычно используется
либо как усилитель, либо как генератор. Схематические изображе-
изображения усилителя и генератора обратной волны приведены на рис. 12.1.
Для реализации противоположно направленных фазовой и групповой
скоростей в ЛОВ используются замедляющие системы с аномальной
дисперсией, для которых dv§/duo > 0. Это реализуется в определенных
диапазонах частот в самых различных электродинамических системах:
Выходное
.устройство
Входное
~~I i Электронная
пушка
Коллектор
Рис. 12.1. Схема ЛОВ-усилителя (а) и ЛОВ-генератора (б)
в цепях, имеющих распределенные параметры, в любых периодических
замедляющих системах (гребенки, системы типа «встречные штыри»
и т.д.), в ряде гладких волноведущих структур (спираль, плазменные
и ферритовые волноводы [12,13]). Главным в практическом применении
является то, чтобы либо основная волна замедляющей системы явля-
являлась обратной, либо в замедляющей системе была достаточно интенсив-
интенсивной обратная пространственная гармоника.
Как видно из рисунка, основное отличие ЛОВ генератора и усилите-
усилителя от ЛБВ заключено в том, что вывод энергии расположен у пушечного
конца ЛОВ, а входное устройство — у коллекторного. В генераторе
обратной волны на месте входной секции расположен поглотитель, роль
которого сводится к поглощению отраженной от вывода энергии волны
при неидеальном согласовании г).
х) Таким образом, поглотитель, как в лампе бегущей волны, служит для
устранения паразитной обратной связи, которая может приводить к ис-
370
Лекция 12
Электрон- •.••-. •
ный поток _
D
Электромаг-
I— нитная волна
Рис. 12.2. Модель линии передачи, пронизываемой электронным потоком, ко-
которая используется для объяснения синхронного взаимодействия электронов
с обратной волной
Для построения качественной картины взаимодействия электронов
с бегущей волной, обратимся к модели, введенной в лекции 10 и пред-
представляющей собой изогнутый волновод (см. рис. 12.2). Для условия
взаимодействия с прямой электромагнитной волной было получено
соотношение A1.9), которое выражало условие синхронизма электро-
электронов и прямой волны. В нашем случае электронный поток переносится
в изогнутой линии передач справа налево и навстречу электронам.
Проводя рассуждения, аналогично тому, как мы делали в лекции 10,
для поддержания эффективного многократного взаимодействия элек-
электронов с такой волной, можно получить фазовое условие вида
d _ Х(п + 1/2) -(D + d)
A2.1)
где Vo — невозмущенная скорость электронов; Л — длина волны в сво-
свободном пространстве; п Е Z.
Как можно представить себе процесс распространения волны, в ко-
которой фазовая скорость и поток мощности направлены в противо-
противоположные стороны? Простейшая аналогия — пример, предложенный
Флемингом: по плывущей барже бегут мальчики, спрыгивают с носа
в воду, проплывают под баржей, взбираются на корму и т.д. Если
мальчики бегут в сторону, противоположную движению баржи, то
мы и получим картину отрицательной групповой скорости (скорость
баржи).
Для более строго рассмотрения проанализируем схему с распреде-
распределенными параметрами, приведенную на рис. 12.3 [14]. Для нее можно
выписать телеграфные уравнения:
дх
dQ_
' dt '
dV_
дх
дФ
A2.2)
кажению частотной характеристики генератора, и даже к возникновению
колебаний на прямой волне.
Карсинотрон
371
которые, учитывая, что Ф = Ы, Q = CV, сведутся к виду (здесь V
и / — комплексные напряжение и ток в линии передач, L и С — погонные
индуктивность и емкость):
d2V _ l
dxdt ~ с '
dxdt
A2.3)
В предположении, что переменные величины изменяются по закону
eja;^, уравнения A2.3) примут вид
—
dx
dx
wL
A2.4)
Допуская, что закон изменения вдоль линии величин V и / имеет вид
е~^ж, дисперсионное уравнение запишется как /3 = \/ооу/LC. Тогда
фазовые скорости обратной (—) и прямой (+) волн в линии передачи
запишутся следующим образом:
а групповые скорости
A2.5)
A2.6)
А
Таким образом как для прямой, так и для встречной волн в линии
передачи, изображенной на рис. 12.3, фазовые и групповые скорости
направлены в противоположные направления.
Обсудим теперь механизм возникновения колебаний в лампе обрат-
обратной волны. На начальном этапе возникновения колебаний, за счет
флюктуации тока и скорости по-
потока, вдоль линии передачи воз-
возбуждаются шумовые электро-
электромагнитные волны, представля-
представляющие собой непрерывную со-
совокупность бесконечно большо-
большого числа гармонических коле-
колебаний различных частот. Шу-
Шумовые электромагнитные волны
распространяются как в прямом,
I+dl
Рис. 12.3. Эквивалентная линия пере-
передачи с распределенными параметра-
параметрами, в которой может распространять-
распространяться обратная волна
так и в обратном направлении
с различными скоростями, опре-
определяемыми дисперсионной ха-
характеристикой замедляющей си-
системы. Скорость же электронно-
электронного потока вполне однозначна и определяется ускоряющим напряжени-
напряжением. Из всей совокупности шумовых волн условия усиления в лампе
будут выполнены только для электромагнитной волны с частотой о;,
372 Лекция 12
для которой vo немного больше Уф(и). Шумовая пространственная
гармоника, для которой выполняется данное условие (ее частота равна
о;), по мере распространения к началу лампы вызывает нарастающую
к коллекторному концу модуляцию электронного потока по скорости,
и соответствующее ей образование электронных сгустков. Если ток
пучка таков, что электронная мощность взаимодействия пучка с этой
шумовой пространственной гармоникой окажется больше, чем мощ-
мощность, обусловленная потерями, то в лампе возникают незатухающие
колебания с частотой и (минимальное значение тока пучка, необходи-
необходимое для генерации, называется пусковым). Увеличение амплитуды этих
колебаний будет наблюдаться до тех пор, пока мощность на выходе
ЛОВ не достигнет мощности насыщения, соответствующей данному
току пучка *).
При изменении ускоряющего напряжения, а, следовательно, скоро-
скорости электронов, будет наблюдаться изменение частоты генерации. Это
связано с тем, что при разных скоростях электронного потока, условия
самовозбуждения в лампе будут выполняться на той же пространствен-
пространственной гармонике, если фазовая скорость Уф(со) будет несколько меньше
скорости электронного потока, а это, из-за наличия дисперсии, будет
уже на другой частоте. При этом, благодаря аномальности дисперсии,
с увеличением ускоряющего напряжения частота генерируемых коле-
колебаний будет всегда увеличиваться. Электронная перестройка частоты
ЛОВ возможна в очень широком диапазоне частот, достигающем окта-
октавы, и даже превосходящем ее 2).
Заметим, что некоторые генераторы на ЛБВ с обратной связью (см.
следующий раздел) также обладают свойствами перестройки генери-
генерируемой частоты в широком диапазоне, если не считать нежелательных
внезапных переходов с одного вида колебаний на другой. Это связано
с тем, что для сохранения одного вида колебаний, вдоль петли обратной
связи должно укладываться фиксированное целое число длин волн, что
с трудом выполняется для ЛБВ. В то же время для ЛОВ это условие
выполняется автоматически: лампа обратной волны представляется
) Исследования последних лет показали, что при дальнейшем увеличении
тока пучка и постоянном ускоряющем напряжении в ЛОВ наблюдается
цепочка бифуркаций с усложнением спектра выходного сигнала: колебаний
нет — одночастотные колебания — многочастотные колебания с дискретным
спектром — колебания со сплошным спектром (режим динамического хаоса).
Данные вопросы будут подробно обсуждаться в следующей лекции, где будут
изложены результаты исследований нелинейных нестационарных режимов
работы ЛОВ
2) Напоминаем, что октава — это такой диапазон частот, в котором частота
верхней границы диапазона ровно в два раза больше частоты нижней грани-
границы.
Карсинотрон 373
системой, которая имеет бесконечно большое число витков обратной
связи, каждый из который имеет бесконечно малую протяженность.
«Чужие следы на песке. . . » — история изобретения
лампы обратной волны Компфнером и Эпштейном
Работы по созданию лампы с обратной волной велись практиче-
практически одновременно в СССР [15] (М.Ф. Стельмах и его сотрудники),
в США [16] (Р. Компфнер, который начал эти работы в Великобри-
Великобритании, а заканчивал в США вместе с Н.Т.Вильямсом) и во Франции
[17] (Б. Эпштейн и другие сотрудники фирмы CSF). Интересно, что
все три группы исследователей шли к цели разными путями. Раньше
всех начал Компфнер, для которого «... путь от первой идеи к первым
экспериментальным наблюдениям был непростым» [16]. Сам Компфнер
считает, что для него работа над генератором обратной волны началась
с вопроса, который он задал в 1945 г. в Кларедонской лаборатории
Оксфорда своему сотруднику: «Как можно превратить ЛБВ в гене-
генератор, частота которого перестраивается при изменении напряжения
электронного потока?» [16]. В некотором смысле вопрос был странным.
Дело в том, что к тому времени ЛБВ была уже весьма широкополосным
усилителем, и Пирсу в лаборатории фирмы Белл удалось создать ста-
стабильные к самовозбуждению лампы. Было также известно, что если
охватить ЛБВ цепью внешней обратной связи, напрямую соединив
кабелем вход с выходом, то лампа будет генерировать на дискретных
частотах. Для самовозбуждения необходимо, как мы уже отмечали,
чтобы ЛБВ обеспечивала достаточно высокий коэффициент усиления
(усиление должно превышать потери) и чтобы вдоль всей цепи, включа-
включающей лампу и кабель обратной связи, укладывалось целое число длин
волн. Из-за того, что спираль — слабодисперсная замедляющая система,
при слабом изменении ускоряющего напряжения электронов (скорости
потока vq) частота генерации может меняться мало, поскольку вдоль
полной цепи по-прежнему должно укладываться целое число длин
волн. При большем изменении напряжения для выполнения фазовых
условий генерации должен быть скачок частоты, конечно, если усиление
превышает потери. Какой же путь выбирает Компфнер? «Скоро мы по-
поняли, — пишет он, — что из факта принципиального отсутствия диспер-
дисперсии у спирали следует трудность, если не невозможность, превратить
ЛБВ в генератор с электронной перестройкой, и это заставило нас ана-
анализировать системы, являющиеся в принципе дисперсными, которые
мы назвали системами с дискретным взаимодействием» (discontinous
interaction) [16]. В течение 1945-1946 гг. Компфнер подробно изучил
процессы в петлеобразном волноводе (рис. 9.5, 12.2), которые мы уже
неоднократно обсуждали.
Компфнер — архитектор, ставший физиком-самоучкой, с некото-
некоторой горечью пишет в своих воспоминаниях: «Может быть интерес-
374 Лекция 12
но заметить здесь, что догадки, представленные вышеприведенными
уравнениями [имеются ввиду соотношения A1.9) и A2.1)] заняли семь
месяцев в 1945 г., чтобы оформиться в моем сознании; теперь я знаю,
что они были «изобретенным велосипедом» х) для людей, знакомых
с многорезонаторными магнетронами, но были скрыты от меня, пото-
потому что были описаны на иностранном языке с использованием таких
слов, как постоянные распространения, волновые числа и компоненты
поля пространственной гармоники. Это то, во что вылилось для меня
отсутствие формального образования в области физики» [16]. Более
того, Компфнер не понял сразу важности соотношения A2.1) для со-
создания генератора с электронной перестройкой частоты. Он приду-
придумал генератор, но это была очень сложная конструкция. Вот путь его
рассуждений.
Пусть электронный поток проходит через последовательность бес-
бесконечно тонких ВЧ-зазоров, разделенных пространствами дрейфа дли-
длиной d. Тогда в простейшем случае для того, чтобы в каждом зазоре
электроны «видели» одну и ту же фазу ВЧ-поля, время, за которое
электрон двигается от одного зазора к другому, должно быть равно
времени, за которое волна с фазовой скоростью Уф продвинется в на-
направлении пучка электронов на целую длину волны Л плюс расстояние
между зазорами, т. е.
t = ± = ±±i A27)
Из соотношения A2.7) сразу следует, что
A2.8)
Таким образом как видно из формулы A2.8), изменение скорости элек-
электронов приводит к изменению длины волны (при поддержании условий
взаимодействия). Следовательно, линия передачи для волны должна
обладать дисперсией, чтобы можно было говорить о перестраиваемом
электрически генераторе, в котором сохранен принцип ЛБВ. Но нужно
было еще добиться, чтобы независимо от значения длины волны вдоль
полной замкнутой цепи всегда укладывалось целое число Л. Учитывая,
что Л = 27ГУф/с^, можно переписать выражение A2.8) в виде
^ = l-J-. A2.9)
cud vo Уф
Важен вывод Компфнера. «Если Уф постоянная величина (как это
приближенно должно быть в линии передачи типа коаксиальной), из
A2.9) видно, что когда vq увеличивается, то же самое должно быть
В подлиннике were old hat — «были старой шляпой»
Карсинотрон 375
и с о;» [16]. Такую зависимость Компфнер назвал «положительной»
дисперсией, считая ее типичной для подобного генератора.
Рассмотрим теперь ЛБВ-генератор, в котором электронный поток
дискретно взаимодействует с волной в линии передачи, обладающей по-
положительной дисперсией, причем, выход соединен со входом, например,
при помощи волновода с такими же свойствами в смысле распростране-
распространения волны. Пусть автоколебания установились на частоте, приближен-
приближенно удовлетворяющей соотношению A2.9), и вдоль цепи «дисперсная
ЛБВ — волновод обратной связи» укладывается целое число длин
волн. Если изменить напряжение электронного пучка незначительно,
то незначительно изменится и частота колебаний. Когда это изменение
мало (До; <С о;), из формулы Л = 2/kv^/u находим, что
Л + ДА = 2tt^V = ^— A " —) "> АА = -Л^. A2.10)
со + До; uj \ uj J uj
Но тогда изменится и общее число длин волн, укладывающихся по всей
цепи. Оно будет приблизительно равно
+ —\. A2.11)
uj J
Напомним, что для простоты было сделано предположение об одинако-
одинаковой положительной дисперсии вдоль всей цепи. Возник принципиаль-
принципиальный вопрос: «Можно ли добиться постоянства TV?» Ответ был положи-
положительным. «Да, если хотя бы часть замкнутой цепи имеет «отрицатель-
«отрицательную» дисперсию». Нужны были системы, в которых распространяется
волна, обладающая следующим свойством: число длин волн, укладыва-
укладывающихся на заданной длине, уменьшается с ростом частоты. Причем, это
уменьшение должно быть достаточно большим, чтобы скомпенсировать
аналогичное увеличение в системах с положительной дисперсией (име-
(имеется в виду, что замкнутая цепь генератора содержит элементы с обоими
видами дисперсии). Компфнер пишет, что с сотрудниками стал искать
системы, обладающие подходящими свойствами, и долго не мог ничего
найти. Он продолжает с сожалением: «Мы не знали, что они все время
«глядели» на нас, спрятанные в обобщение A2.1), согласно которому
электроны и волна движутся в противоположных направлениях» [16].
Изобретение ЛОВ опять откладывается!
Компфнер решил моделировать систему с отрицательной диспер-
дисперсией с помощью предварительно модулированного потока электронов,
движущегося в трубке дрейфа, в котором распространяются дисперс-
дисперсные волны пространственного заряда. Предложенный генератор пред-
представлен на рис. 12.4 [16]. По признанию самого Компфнера, это была
довольно сложная выдумка! При настройке генератора напряжением
пучка на тех участках, где он проходит через дисперсную линию пере-
передачи, необходимо изменять напряжение на трубке дрейфа (очевидно,
376
Лекция 12
Рис. 12.4. Схематическое изображение дисперситрона (в качестве элемента
цепи с отрицательной дисперсией используется электронный пучок, движу-
движущийся в трубе дрейфа [16])
в противоположную сторону изменению напряжения в секциях с дис-
дисперсными системами). Разумеется, это нужно делать в соответствии
с расчетами так, чтобы удерживать N = const.
В 1947 г. произошло событие, отодвинувшее для Компфнера все
идеи, связанные с дискретным взаимодействием электронов с ВЧ-по-
лями. Ему стала известна работа Пирса, где было доказано, что спи-
спираль обладает дисперсией, когда диаметр спирали намного меньше
длины волны (см., например, [18]). Конечно, Компфнер вновь с удо-
удовольствием обратился к спирали. Это было вполне естественным: он
добился преимущества перед другими исследователями при создании
ЛБВ исключительно благодаря тому, что применил спираль, и считал
ее настолько совершенной линией передачи для создания замедленной
волны, взаимодействующей с потоком электронов, «насколько можно
вообразить». Следует заметить, что занятия Компфнера генератором
были «домашними» (как в свое время работа над изобретением ЛБВ),
а в лаборатории он занимался всем тем, что делалось по ЛБВ в Вели-
Великобритании.
Карсинотрон 377
Следующий этап изобретения ЛОВ связан с участием Компфнера
летом 1947 г. в конференции по лампам, которая проводилась в Сираку-
Сиракузах в США. На предыдущей конференции электронный мир не только
узнал о ЛБВ (Дж. Хэттон изложил некоторые результаты, полученные
вместе с Компфнером), но и был поражен после доклада Дж. Пирса
тем, сколь далеко продвинулись в ее создании в лабораториях фирмы
Белл. Ситуацию на последующей конференции наиболее точно описы-
описывает сам Компфнер. «То, что я услышал на Сиракузской конференции
в 1947 г., сильно удивило меня. Работа над ЛБВ в Соединенных Штатах
развернулась во многих лабораториях и результаты, как теоретиче-
теоретические, так и экспериментальные, были не только многочисленны, они
были фундаментальны и значительны. Большая группа в лабораториях
фирмы Белл под руководством Пирса разработала почти новый язык
в этой области, и я с трудом понимал, о чем они говорили. Э.Б. Кал-
лик, представитель Британского Адмиралтейства в Вашингтоне в то
время, и я были глубоко поражены и обеспокоены. Это было изобре-
изобретение, сделанное в Британии только несколько лет назад, и теперь мы
смотрели на него со стороны. Мы были почти вне его. Нам казалось
безнадежным пытаться догнать американцев в исследованиях более или
менее обычных ЛБВ. Напротив, мы почувствовали, что если перенести
наши усилия на новые области подобно генератору, настраиваемому
напряжением, то это будет более эффективным использованием наших
талантов и ресурсов» [16]. Сразу же после возвращения в Англию,
Каллик и Компфнер встретились с представителями правительствен-
правительственных и промышленных организаций по исследованию СВЧ-ламп, чтобы
рассказать о Сиракузской конференции и обратить внимание на то, что
инициатива в СВЧ-электронике потеряна Великобританией. В приво-
приводимых в [16] «Пунктах для беседы, проведенной 8 августа 1947 г.», есть
такой текст:
«Лаборатории фирмы Белл — далеко впереди. Станфордский уни-
университет — второй. ... Какое счастье, если в конечном счете нам не
придется платить доллары за использование ЛБВ. Но как предотвра-
предотвратить повторение? Предложить оригинальные идеи и концентрировать
усилия на них. Я предлагаю две: а) дисперситрон, б) высокомощная
ЛБВ *). Что можно получить, если разработка окажется успешной?
а) Широкополосный генератор вплоть до 8 мм!
б) Мегаватный полосовой усилитель в диапазоне частот 2100-3950
МГц A550-5200 МГц), киловатты на 8 мм».
Результатом встречи было увеличение состава лаборатории, зани-
занимавшейся исследованием ЛБВ, на 100%. С Компфнером начал рабо-
работать Ф.Н.Х.Робинсон из SERL, которая имела прекрасные мастерские
х) Под дисперситронами понимались разные генераторы, перестраиваемые
напряжением, а высокомощная ЛБВ — клистрон с бегущей волной [19].
378
Лекция 12
I
-^-Э
Am+ti
,LU
Рис. 12.5. Схематическое изображение дисперситрона (используется внешняя
обратная связь в виде линии передачи с отрицательной дисперсией) [16]
и оборудование. К этому времени Компфнер придумал два генера-
генератора, схематически представленные на рис. 12.5 и 12.6 [16]. В SERL
была изготовлена лампа, соответствующая конструкции, схематически
представленной на рис. 12.4. 22 апреля 1948 г. Компфнер испытал
ее. Лампа генерировала на длине волны около 10 см, но выходная
мощность была незначительной, а электронная перестройка по частоте
составляла не более 30 МГц. Дисперситрон Марк II был изготовлен
в SERL. В этом генераторе электронный пучок дважды пересекает
дисперсную спираль — сначала в прямом направлении, затем после
прохождения областей дрейфа и отражателя — в обратном (конструк-
(конструкция соответствовала рис. 12.6). Генератор не был испытан, поскольку
лампа «натекла». К этому времени Компфнер охладел к дисперсным
спиралям, так как измерения показали, что в реальных спиралях,
окруженных диэлектриками, в случае положительной дисперсии диа-
диаметр спирали оказывался маленьким, что приводило к невозможности
Карсинотрон
379
Рис. 12.6. Дисперситрон Марк II содержит отражательный электрод, поэтому
обратная связь осуществляется целиком за счет потока электронов [16]
..
<9&i
Рис. 12.7. Принципиальная схема лампы, названной «сосиской» [16]
использовать в генераторах большие токи. В областях же с отрица-
отрицательной дисперсией последняя была столь малой, что ее было недо-
недостаточно для описанных выше «компенсацционных» целей. Компфнер
вновь обращается к дискретному взаимодействию. Первый результат —
«лампа-сосиска» (рис. 12.7). Название связано с тем, что электронный
пучок выстреливался в однородное продольное фокусирующее маг-
магнитное поле так, чтобы он принимал форму связки сосисок. Такой
пучок, двигаясь вдоль оси недисперсной спирали, эффективно взаи-
взаимодействует с электромагнитной волной там, где он близко подходит
к виткам спирали, где электрическое поле намного сильнее, чем на
оси. Любопытно, что спустя много лет другие английские исследова-
исследователи вновь предложили использовать эту идею, модифицировав ее:
у них пучок двигался в гладком волноводе и в ускоряющей фазе ухо-
уходил из области сильного электрического поля [20]. И вот, наконец, на
страничке записной книжки Компфнера от 2 мая 1948 г. появляется
рисунок лампы (рис. 12.8 [16]), которая вполне соответствует генера-
генератору обратной волны. На этой странице Компфнер записал: «Можно
380
Лекция 12
Stout *f ВЖО.
J /
Рис. 12.8. Схематическое изображение лампы обратной волны из записной
книжки Компфнера [16]
сделать дисперситрон без внешней обратной связи, с волной и пучком,
движущимися в противоположных направлениях, посредством схемы
с локальным взаимодействием?... Мы имеем здесь пучок, действующий
и как источник энергии и как цепь обратной связи одновременно. Здесь
нет одного замкнутого пути, вокруг которого должно укладываться
целое число длин волн. Вместо этого есть множество путей, каждый из
которых автоматически содержит целое число длин волн. Фактически
этот прибор должен иметь очень низкий стартовый ток» [16]. Компф-
нер был взволнован открытием, которое, наконец, далось ему в руки,
о чем свидетельствует его письмо Каллику в Вашингтон, написанное 30
ноября 1948 г., в котором есть следующий абзац [16].
«Испытывая самую последнюю холодную модель дисперситрона
(Марк V) на прошлой неделе, я действительно обнаружил сильную
отрицательную дисперсию... Эта самая последняя конструкция диспер-
дисперситрона, однако, не зависит от отрицательной дисперсии, поскольку
является системой с дискретным взаимодействием, в которой волна
и пучок движутся в противоположных направлениях. Я действительно
верю, что нашел теперь структуру, которая подойдет лучше любой
другой... Я очень боюсь, что Пирс и Миллмэн нападут теперь на эту
идею, потому что Пирс говорил мне, что его 6-миллиметровая лам-
лампа генерировала там, где пучок и волна двигались в противополож-
противоположных направлениях, и лампа с дискретным взаимодействием — это его
лампа» [16].
Оставалось сделать генератор, но этого не произошло. Компфнера
мучали сомнения: «В определенном смысле идея генератора обратной
волны казалась мне слишком хорошей, чтобы быть правильной. Приро-
Природа, конечно не могла быть настолько простой?! Пирс и Миллмэн разве не
Карсинотрон 381
наблюдают в своей лампе явление, которое должно породить эту идею?
Это казалось мне совершенно невероятным» [16]. После нескольких
неудачных попыток создать экспериментальный образец он забросил
работу. Более того Компфнер не запатентовал ни один из видов приду-
придуманных дисперситронов (впоследствии он объяснил это тем, что считал
некоторые идеи «сырыми», а отчасти нехваткой персонала в патент-
патентном отделе Адмиралтейства). У него не было широкой возможности
заниматься СВЧ-электроникой в Англии, поэтому почти без колебаний
Компфнер перешел в лаборатории фирмы Белл и 27 декабря 1951
г. присоединился к группе Джона Пирса. Там в лаборатории Нила
Вильямса велась работа над 6-мм ЛБВ-усилителем на пространствен-
пространственной гармонике. Это была та лампа, о которой рассказывал Компфне-
ру Пирс, упомянув о наблюдении паразитных колебаний на обратной
волне. Именно на этой лампе Компфнер и Вильяме впервые осмысленно
наблюдали генерацию на обратной волне. Они подсоединили трансфор-
трансформатор к катодному проводу, чтобы осуществить развертку напряжения
на несколько сотен вольт; подсоединили индикатор выходной мощно-
мощности к входному устройству, а к выходному — согласованную нагрузку
(ведь они превращали ЛБВ и ЛОВ!). Выходной сигнал отображался
на осциллографе, развертка которого была синхронизирована с раз-
разверткой напряжения электронного потока. Лампа загенерировала на
частоте, определяемой напряжением (причем, на неожиданно низких
напряжениях). Диапазон генерируемых частот при электронной пере-
перестройке был значительно больше, чем во всех известных генераторах.
Артур Карп пришел к выводу, что лампа генерировала на минус второй
пространственной гармонике ВЧ-поля замедляющей системы. Когда
напряжение подняли выше расчетного значения для усилителя прямой
волны, лампа стала генерировать большую мощность на минус первой
пространственной гармонике в диапазоне длин волн от 6 до 7,5 мм. На-
Напряжение, соответствующее перекрытию этого диапазона, изменялось
от 1800 до 4000 В. Как пишет Компфнер: «.. .на этом уровне лампа
долго не жила. Тем не менее генератор обратной волны был проде-
продемонстрирован, и никто не думал о потере лампы в те волнующие дни»
[16]. При уменьшении тока пучка ниже стартового лампа превращалась
в регенеративный усилитель обратной волны. По-существу, из-за очень
узкой полосы и высокого коэффициента усиления это был электрически
перестраиваемый активный фильтр. Компфнер и Вильяме доложили
об этой работе на конференции по электронным приборам Институ-
Института радиоинженеров в июне 1952 г. в Оттаве. На этой конференции
произошло еще одно важное событие. После доклада к Компфнеру
и Вильямсу подошел Бернард Эпштейн из CSF (Франция) и расска-
рассказал,что он и другие исследователи создали лампу со скрещенными элек-
электрическим и магнитным статическими полями, в которой реализуется
взаимодействие электронов с ВЧ-полем обратной пространственной
гармоники. Лампу назвали «карсинотрон» типа М (у нас принят термин
382 Лекция 12
ЛОВМ) от греческого Karcinox, что означает «рак, пятящийся на-
назад» *), и на прибор выдан патент [17]. Поведение Компфнера в данной
ситуации вызывает уважение. «Нам казалось важным, — вспомина-
вспоминает он, — чтобы в этих обстоятельствах Эпштейну была предоставле-
предоставлена возможность сообщить конференции о работе. Это было не легко
устроить, поскольку потребовалось несколько трансатлантических те-
телефонных переговоров и вмешательства служб правительства США; но
это было выполнено» [16].
Результаты французов были изложены в сообщении Эпштейна в От-
Оттаве и в последующих публикациях [21, 22]. В Оттаве речь шла о ЛОВМ,
которая на частоте 3000 МГц дала мощность в несколько сот ватт
и имела полосу электронной перестройки порядка 30 %.
В СССР генератор обратной волны, как уже указывалось, был со-
создан в 1948-49 гг. М.Ф. Стельмахом и его сотрудниками [15]. В заявке на
авторское свидетельство предлагалось устройство, в котором электрон-
электронный поток проходил над щелями цепочки резонаторов (одиночная или
сдвоенная гребенка) с целью генерирования СВЧ-колебаний. Следует
заметить, что и французские и советские исследователи, в отличие от
Компфнера, шли от концепции пространственных гармоник ВЧ-поля
в замедляющей системе.
Интересно, что все в той же записной книжке на странице от 2 мая
1948 г. Компфнер уже пытался сделать набросок теории ЛОВ, пока
лишь задавая вопросы самому себе: «Вопрос в том, какой вид волны
возбудит этот сгруппированный пучок? В каком фазовом соотношении
находится вторичная волна с первичной?» [16]. Далее Компфнер при-
признается, что на следующих страницах он пытался вычислить пусковые
условия, но «неэлегантно и безуспешно» [16].
Позднее наиболее полно на вопросы, поставленные Компфнером,
ответил профессор Саратовского университета Владимир Николаевич
Шевчик, который подробно обосновал целесообразность использова-
использования метода последовательных приближений, впервые примененного
Компфнером к ЛБВ, для решения широкого круга задач СВЧ-элек-
троники [24] и, в первую очередь, для ЛОВ [19].
Изложение этой любопытной страницы истории СВЧ-электроники
уместно закончить столь подходящими словами Компфнера: «Таким
образом оказывается, что генератор обратной волны или карсино-
х) Данное французскими исследователями название следует признать удач-
удачным, поскольку оно отмечает главное в приборе. Действительно, термин
«обратная волна» подчеркивает то обстоятельство, что групповая и фазовая
скорости волны противоположны (противоположны направления распро-
распространения волны и потока мощности, переносимого этой волной), поскольку
направления движения электронного потока и распространения волны совпа-
совпадают, мощность в приборе переносится от коллекторного к пушечному концу
лампы — «пятится назад».
Карсинотрон 383
трон — это одно из тех изобретений, которые были сделаны в раз-
разных местах, примерно в одно и то же время и независимо друг от
друга. Я думаю, мои чувства по этому поводу смешались, подобно
чувствам Робинзона Крузо, когда он обнаружил чужие следы на песке
острова» [16].
Теория пускового режима лампы обратной волны
в приближении заданного поля
Коэффициент усиления по полю лампы обратной волны при токе
меньше пускового может быть записан в виде
Условием генерации на обратной волне является условие обращения
коэффициента усиления в бесконечность или, как следует из опреде-
определения A2.12) и уравнения A.72), условие обращения в нуль поля на
коллекторном конце лампы:
Е{1) = 0. A2.13)
Это эквивалентно тому, что для ламп с определенной длиной /
и ускоряющим напряжением Vb (а, следовательно, и невозмущенной
скоростью потока vo = y/2Vo/rj) имеется значение тока пучка /пуск,
при котором параметр С N достигает критического значения СWnyCK,
а параметр холодного рассинхронизма b из формулы A0.11) (или Фо
из формулы (9.7)) достигает критического значения 6пуСк (Фо пуск),
необходимого для начала генерации.
Найдем пусковые условия ЛОВ, воспользовавшись уже знакомым
нам методом последовательных приближений, ограничившись первым
приближением (метод заданного поля). В лекции 7 для случая взаи-
взаимодействия с прямой волной для напряженности поля в конце линии
передачи было выведено соотношение (9.19):
Е[1) = E°e~jCJ {1 - BтгСЛ03 [Re F(<P0) + j I
которое получалось при комбинировании уравнения для сгруппирован-
сгруппированного тока (9.12) и уравнения возбуждения (9.18) для случая взаимодей-
взаимодействия с прямой волной без учета обратного излучения.
В усилителе обратной волны входной сигнал поступает в линию
передачи при х = /, поэтому выражение для него следует записать
в виде Е° ехр [—jfio(x — /)]. Кроме этого, в уравнении (9.17) теперь уже
X
первый интеграл (J ... dx) соответствует обратному излучению. Тогда,
о
в пренебрежении им, уравнение возбуждения в интегральной форме
384
Лекция 12
2sin#o
Рис. 12.9. Графическое решение уравнения A2.18), определяющего пусковое
значение Фопуск
для ЛОВ запишется в виде
Е(х) = E°e-iMx-
A2.14)
A2.15)
Используя соотношение для сгруппированного тока (9.12) и уравнение
возбуждения для обратной волны A2.15) и проводя выкладки, анало-
аналогичные проведенным в лекции 7, получим, что полное поле вдоль длины
пространства взаимодействия выражается соотношением
или, переходя к дифференциальной форме, будем иметь
-j-+JPoEx = -—— i{x).
Е(х) =
х-1) {1 + BтгСЛ03 [Re
F@O)]} , A2.16)
где действительные и мнимые части функции F даются соответственно
выражениями для F\a (9.20) и F\r (9.21).
Тогда, пусковое условие A2.13) может быть переписано в виде
BirCNKFla=0, Flr = 0,
или
BтгСА03
^Опуск
A2.18)
2sin<?OnycK = ^Опуск A
графическое решение которого приведено на рис. 12.9. Из него видно,
2sin^OnycK - ^0пускA + СОЯФопуск) = 0.
Последнее уравнение можно использовать для определения критиче-
критического значения Фоп^ск
Карсинотрон 385
что решением A2.18) является величина
допуск = -тгBп + 1), п е Z. A2.19)
Значение при п = 0 (Фопуск — —/тг) соответствует оптимальному углу
пролета, при котором происходит максимальная передача энергии
волне. Подставля это значение в уравнение A2.17), имеем
1 + BnCNfn уск-^-з = 0 -»• (CN)nyCK = 0,315, A2.20)
(-7Г)
Ф ^ 1,587. A2.21)
Точное значение, найденное из строгого решения дисперсионного урав-
уравнения и уравнений для парциальных волн, дает СNnyCK = 0,3141, 6пуСк =
= 1,522. Это свидетельствует о высокой эффективности метода после-
последовательных приближений: уже первое приближение дает результат
с точностью ~ 0,3 %.
Из выражения A2.19) следует, что при одном и том же значении
ускоряющего напряжения могут возбуждаться несколько волн, фазо-
фазовые скорости которых определяются из условия A2.19) с учетом опре-
определения угла пролета Фо (9.7):
^Ф = Цррт, neZ. A2.22)
1+ 27V
В этом случае в генераторе имеет место многочастотность, так как
волны с различными фазовыми скоростями имеют различные частоты.
Из выражений A2.20), A2.21), учитывая, что (С NK =
= (IoK /4Vo)N3 (Pe/Po) •> можно найти величину пускового тока
основного вида колебаний (п = 0). Проводя элементарные выкладки
для пускового тока получаем выражение
/ovckO — о~- A2.23)
Для расчета пусковых значений высших видов колебаний первого при-
приближения недостаточно. Более точный анализ показывает, что пусковой
ток первого высшего вида колебаний (п = 1) дается выражением:
/пуск! = /пускО • 6,3. A2.24)
Отсюда понятно, что для того, чтобы высшие виды колебаний не воз-
возбуждались необходимо выбирать такие значения рабочих токов, чтобы
выполнялось условие /о < /пуск1 • ;
х) Заметим, что формула A2.24) справедлива лишь в рамках линейной
теории. На самом деле паразитные колебания возбуждаются, когда ток
13 Д. И. Трубецков, А. Е. Храмов
386
Лекция 12
О
10
20 L, дБ
Рис. 12.10. Зависимость величины СNnyCK и Фопуск от затухания в линии
передачи. Здесь L = 8,6870/ дБ; Cq = -jrr
Рассмотрим как влияет наличие потерь в линии передачи и про-
пространственный заряд на пусковые условия генератора обратной волны.
Совершенно, очевидно, что наличие распределенного затухания 70 B ли-
линии передачи приводит к увеличению СWnyCK, так как часть мощности,
тратится на покрытие этих потерь, и к изменению Фопуск (генерируемой
частоты) (см. рис. 12.10).
В случае больших пространственных зарядов при Фд = ~0р =
= ojpl/vo (b = л/AQC) можно показать [25], что распределение поля
вдоль пространства взаимодействия дается простым выражением:
¦a irC N
(QCI/4
Тогда условие самовозбуждения ЛОВ A2.13) имеет вид
irCN
cos ¦
= 0,
(QOI/4
откуда следует, что
(CN)nyCK = (п + 1/2XQCI/4, п е Z,
A2.26)
A2.27)
A2.28)
Рассмотрим на основании этого более подробно высшие типы коле-
колебаний в ЛОВ. Учитывая, что /ЗеСх = ttCTV, условие A2.15) выразиться
в виде
откуда
тгBп
A2.29)
где /Пуск — длина пространства взаимодействия, соответствующая на-
началу генерации — пусковая длина лампы. Заметим, что при рассмотре-
превосходит значения соответствующие стационарному режиму генерации
(см. лекция 12), и условия их возбуждения следует находить из нелинейной
теории.
Карсинотрон
387
нии ЛОВ часто вместо пускового тока пользуются понятием пусковой
длины. С учетом соотношения A2.29) выражение для поля вдоль про-
пространства взаимодействия A2.25) можно представить в виде
Е{х) =
cos
A2.30)
Е(х)/Е(Щ
При п = 0 поле в линии передачи, как следует из A2.30), обращает-
обращается в нуль только в одной точке х = /Пуск в конце пространства вза-
взаимодействия. Понятно, что условие ЕAпуск) соответствует пусковым
условиям генератора. При п = 1 поле
обращается в нуль уже в двух точках х =
= ^пуск/3, х = /Пуск- При п = 2 пусковые
условия имеют место уже при /пуск/5,
З/пуск/5 и /пуск и т.д. Соответствующие
распределения полей вдоль простран-
пространства взаимодействия представлены на
рис. 12.11.
Из соотношения A2.27), возводя его
в четвертую степень и производя тожде-
тождественные преобразования, можно полу-
получить выражение вида
¦пуск
(CNny
16
Q_
Рис. 12.11. Распределение по-
полей различных видов колеба-
колебаний в лампе обратной волны
откуда следует общая формула для пусковых токов различных видов
колебаний:
'пуск n
4N3K
A2.31)
Для основного вида колебании Упуск0 = о —, откуда
4N К
/пуск „ = BП + 1L/Пуск0. A2.32)
В частности для основного и первого вида колебаний имеем
/пуск1 /Лгуско = 81. Сравнивая это соотношение с выражением для пус-
пускового тока первого вида колебаний в ЛОВ без учета пространственного
заряда (формула A2.24)), можно видеть, что пространственный заряд
приводит к увеличению пускового тока высших видов колебаний по
сравнению с пусковым током нулевого вида. Отсюда понятно, что,
следуя линейной теории, для создания ламп, устойчивых к возбужде-
возбуждению паразитных видов колебаний, необходимо увеличивать в них роль
пространственного заряда.
Как же соотносятся частоты различных видов колебаний? Формула
A2.28) представляет собой частотную характеристику генератора в пус-
13*
388 Лекция 12
ковом режиме. Используя A2.27), выражение A2.28) легко представить
в виде:
(А> - РеIпуск = тгBп + IJ (Q/N). A2.33)
Отсюда видно, что величина (/?о — /Зе)^пУск увеличивается с ростом но-
номера вида колебаний. Так как в ЛОВ используются замедляющие систе-
системы с аномальной дисперсией (увеличение \/3\ приводит к уменьшению
о;), то частота генерации высших видов колебаний будет меньше, чем
основного. Таким образом высшие виды колебаний должны появляться
на низкочастотном конце диапазона.
Нелинейное поведение лампы обратной волны
(результаты стационарной нелинейной теории)
Изложим теперь результаты, касающиеся нелинейного поведения
генератора обратной волны в рамках стационарной теории. Исходные
предположения и методика вывода нелинейных стационарных урав-
уравнений ЛОВ совпадают с принятыми в нелинейной теории ЛБВ (см.
лекцию 10). Прямолинейный электронный пучок представляется после-
последовательностью заряженных дисков, взаимодействующих с усреднен-
усредненной по поперечному сечению пучка продольной компонентой бегущей
электромагнитной волны. Электродинамическая система предполага-
предполагается полностью согласованной в отсутствии пучка с одной стороны —
с выходной нагрузкой, а с другой стороны — с поглощающей нагрузкой.
Плотность тока пучка считается неизменной по поперечному сечению
пучка, т. е. не учитываются поперечные движения электронов и рассло-
расслоение потока в поперечном направлении. Параметр усиления предпола-
предполагается малым (С <С 1).
При построении нелинейной теории ЛОВ ограничиваются учетом
взаимодействия электронного потока только с основным типом коле-
колебаний. Влияние сил пространственного заряда учитывается методом
функции Грина.
Не будем останавливаться на выводе нелинейных уравнений ЛОВ,
так как он в общих чертах совпадает с соответствующими выкладками
нелинейной теорией ЛБВ. Вывод уравнений подробно дан в работе [26],
где наиболее полно изложена стационарная нелинейная теория ЛОВ.
Приведем лишь некоторые результаты численного решения нелиней-
нелинейных стационарных уравнений.
На рис. 12.12 показана теоретическая зависимость нормализованно-
нормализованного к.п.д. tj/С от безразмерной длины пространства взаимодействия в =
= /ЗеС1 при отсутствии затухания в линии передачи [27]. На рис. 12.13
приведена зависимость нормализованной мощности PN/(InyCKVo) от
^о/^пуск (N — число замедленных длин волн на длине пространства вза-
взаимодействия). Распределения нормированной амплитуды поля F и нор-
Карсинотрон
389
ц/С
2,0
1,0 -
0,0
/г
f
01
~^"^ II
L
PN
4,0
2,0
2,0
3,0
1
7 /0//пу
Рис. 12.12. Зависимость величины Рис. 12.13. Зависимость мощности
к.п.д. от длины пространства вза- генерации от тока пучка
имодействия в. Здесь кривая I со-
соответствует параметру простран-
пространственного заряда 4QC = 0, II —
мированной первой гармоники сгруппированного тока 1\ вдоль длины
пространства взаимодействия в = /ЗеСх изображены на рис. 12.14.
Из рисунков видно, что в недонапряженном режиме (часть кривой I
на рис. 12.12 левее точки 2 — точки максимального значения Т)/С)
характер распределения поля такой же, как и в пусковом режиме
генератора (см. предыдущий параграф), в то время как распределение
амплитуды первой гармоники сгруппированного тока аналогично тому,
которое имеет место в пусковом режиме (кривая I на рис. 12.14) только
при длинах пространства взаимодействия (или токах (рис. 12.15)),
незначительно превышающих пусковые значения (до точки 1 на кри-
1,0
1,0
III
1
1
e
Рис. 12.14. Распределения амплитуды поля F (а) и первой гармоники сгруп-
сгруппированного тока 1\ (б) вдоль длины пространства взаимодействия при
различных токах пучка
390
Лекция 12
вой I (рис. 12.14)). При увеличении тока или длины пространства вза-
взаимодействия еще в пределах недонапряженного режима группировка
электронов становится оптимальной не в конце пространства взаимо-
взаимодействия, а в середине его.
Уже при значении #, соответствующем максимальному к.п.д., по-
появившийся при движении в сильном продольном поле разброс скоро-
скоростей электронов приводит к разгруппировке сгустков в сравнительно
малом поле непосредственно за
точкой обгона электронов (кри-
(кривые II на рис. 12.14). Данная
разгруппировка практически эк-
эквивалентна кинематической раз-
группировке пучка в простран-
пространстве дрейфа клистрона.
Стационарная нелинейная те-
теория предсказывает, что дальней-
дальнейшее увеличение длины простран-
пространства взаимодействия (тока пуч-
пучка) приводит к еще более сильной
разгруппировке сгустков. В конце
ц/С
1,5
1,0
0,5 -
0
/
Jo—
¦о
3
1
3
4 5 6
пуск
Рис. 12.15. Зависимость величины
к.п.д. от тока пучка
концов в некоторой точке вдоль
пространства взаимодействия амплитуда первой гармоники тока па-
падает почти до нуля и ее фаза изменяется приблизительно на 180°.
Затем вновь начинается процесс группировки, и электроны собираются
в сгустки. В результате этого возникает распределение поля с мини-
минимумом (кривые III на рис. 12.14). Генератор разделяется как бы на
два участка, работающих в противофазе, причем границей их является
точка в = #опт5 которая соответствует макимальному к.п.д.
Вышеописанный режим носит названия перенапряженного режима
работы лампы обратной волны. Как показали дальнейшие исследова-
исследования в рамках нестационарной теории ЛОВ, перенапряженный режим
не реализуется физически. При значениях параметров, соответствую-
соответствующих ему, стационарное решение становится неустойчивым, и система
переходит к нестационарным режимам генерации, которые характери-
характеризуются динамикой во времени как пространственных распределений ве-
величин вдоль пространства взаимодействия, так и выходного излучения.
Подробно нестационарные режимы работы ЛОВ будут обсуждаться
в следующей лекции. Пока лишь заметим, что данные режимы, полу-
получившие название автомодуляционных (выбор такого названия связан
с тем, что нестационарная динамика развивается на фоне колебаний
с частотой, примерно равной частоте генерации в стационарном ре-
режиме), наблюдаются при малых величинах пространственного заряда
и в достаточно длинных лампах.
Карсинотрон 391
Теоретические исследования нелинейных режимов в ЛОВ [14, 27,
28], а также экспериментальные результаты [29, 30] свидетельствуют
о том, что максимальный к.п.д. ЛОВ (г]/С при #Опт) растет при уве-
увеличении параметра пространственнного заряда AQC (см. кривую II на
рис. 12.12), если значение величины AQC достаточно мало.
Последнее связано с тем, что небольшие поля пространственного за-
заряда компенсируют кинематическую разгруппировку электронов и тем
самым увеличивают длину эффективного пространства отбора мощно-
мощности, что и приводит к увеличению значения максимального к.п.д. при
росте параметра пространственного заряда. Однако при больших зна-
значениях 4QC происходит ограничение переменной составляющей первой
гармоники сгруппированного тока, поэтому существует некоторое опти-
оптимальное значение параметра пространственного заряда DQC)onT, при
котором к.п.д. генератора максимален [26]. Расчеты работы [26] также
показали, что радиус пучка заметно влияет на к.п.д. лампы, причем при
данном параметре 4QC имеется некоторый оптимальный радиус, при
котором к.п.д. максимален.
Лампа обратной волны магнетронного типа
Лампа обратной волны М-типа является типичным представителем
лучевых приборов со скрещенными полями. Схема конструкции ЛОВМ
представлена на рис. 12.16а г). Отметим основные элементы конструк-
конструкции ЛОВМ:
1) замедляющая система, в которой может распространяться обрат-
обратная волна (обратная пространственная гармоника);
2) коаксиальный с замедляющей системой цилиндрический элек-
электрод, находящийся под отрицательным потенциалом относительно ка-
катода (его обычно называют «холодным катодом»);
3) электронная пушка со сложной электронной оптикой, которая
создает пучок с круговыми траекториями;
4) коллектор, собирающий электроны, не осевшие на замедляющую
систему, и расположенный около него согласованный поглотитель;
5) ВЧ-вывод энергии, соединяющий катодную часть замедляющей
системы с внешней нагрузкой.
Пространство взаимодействия помещается в однородное аксиальное
магнитное поле. Схема плоской конструкции такого генератора при-
приведена на рис. 12.166.
Возникновение колебаний в ЛОВМ практически ничем не отличает-
отличается от вышеописанных явлений в ЛОВО-генераторе. Основное отличие
х) Именно такая лампа была создана французами.
392
Лекция 12
Выход
Поглотитель
Замедляющая
/Ш77Ш7Ш7ШШШ7Ш7777ШШ777777777777777777'
Катод о Отрицательный электрод L
Рис. 12.16. Схема лампы обратной волны магнетронного типа: а— цилиндри-
цилиндрическая конструкция; б — плоская конструкция
состоит в том, что в ЛОВМ для начала генерации необходим точный
синхронизм между скоростью электронного потока и фазовой скоро-
скоростью холодной волны (vo = Уф). При определенном пусковом значении
тока пучка в лампе возникают колебания с частотой, которая опреде-
определяется дисперсией замедляющей системы и скоростью электронов.
Группирование электронов и их взаимодействие с ВЧ-полем анало-
аналогично процессам имеющим место в магнетронном усилителе: попереч-
поперечное ВЧ-поле приводит к группированию электронов в тормозящей фазе
продольного поля: электронный поток отдает ВЧ-полю свою потенци-
потенциальную энергию, смещаясь в среднем к замедляющей системе.
Мы не излагаем здесь теорию ЛОВМ, так как это достаточно хорошо
освещенный в литературе вопрос: в качестве источника, где детально
разработана общая теория лучевых приборов магнетронного типа (не
только ЛОВМ), можно порекомендовать издание лекций [31], прочитан-
прочитанных большим авторским коллективом на 2-й зимней школе-семинаре
по СВЧ-электронике (Саратов, 1972); некоторые вопросы линейной
теории ЛОВМ подробно изложены в монографии [25] (глава V); неста-
Карсинотрон 393
ционарная теория ЛОВМ и ее результаты приведены в коллективной
монографии [14] (глава III).
Список литературы
1. Безручко Б.П., Кузнецов СП., Трубецков Д. И. Стохастические
автоколебания в системе электронный пучок-обратная волна //
В сб.: «Нелинейные волны. Стохастичность и турбулентность».
Горький: АН СССР Институт прикладной физики, 1980, С. 29.
2. Гинзбург П.С, Кузнецов СП., Федосеева Т.Н. Теория переходных
процессов в релятивистской ЛОВ // Изв. вузов. Радиофизика. 1978.
Т. 21, №7. С. 1037.
3. Рыскин Н.М., Титов В.Н., Трубецков Д.И. Детали перехода к
хаосу в системе электронный пучок — обратная электромагнитная
волна // Доклады РАН. 1998. Т. 358. С. 620.
4. Рыскин Н.М., Титов В.П. О сценарии перехода к хаосу в одно-
параметрической модели лампы обратной волны // Изв. вузов.
Прикладная нелинейная динамика. 1998. Т. 6, № 1. С. 75.
5. Пегель И.В. Моделирование нестационарных процессов в реля-
релятивистской лампе обратной волны методом макрочастиц // Изв.
вузов. Физика. 1996. Т. 39, № 12. С. 62.
6. Рыскин Н.М., Титов В.П. Нелинейная динамика релятивист-
релятивистской лампы обратной волны // Труды VII Всероссийской школы-
семинара «Физика и применение микроволн», 24-30 мая 1999 г.,
Красновидово, Московская область. Том 1, С. 126.
7. Красичков Л.В., Рыскин Н.М. Прохождение детерминированного
хаотического сигнала через усилитель обратной волны // Труды
VII Всероссийской школы-семинара «Физика и применение ми-
микроволн», 24-30 мая 1999 г., Красновидово, Московская область.
Том 1, С. 100.
8. Трубецков Д.П., Анфиногентов В.Г., Рыскин П.М., Титов В.П.,
Храмов А.Е. Сложная динамика электронных приборов СВЧ
(нелинейная нестационарная теория с позиций нелинейной дина-
динамики) // Радиотехника. 1999. Т. 63, №4. С. 61.
9. Безручко Б.П., Кузнецов СП., Трубецков Д.И. Эксперименталь-
Экспериментальное наблюдение стохастических автоколебаний в динамической
системе электронный поток — обратная электромагнитная волна //
Письма в ЖЭТФ. 1979. Т. 29, № 3. С. 180.
10. Безручко Б.П., Булгакова Л.В., Кузнецов СП., Трубецков Д.И.
Экспериментальное и теоретическое исследование стохастических
автоколебаний в лампе обратной волны // Лекции по электронике
394 Лекция 12
СВЧ и радиофизике E-я зимняя школа-семинар инженеров). Са-
Саратов: Изд-во СГУ, 1980, С. 25.
11. Гинзбург Н.С., Зайцев Н.И., Иляков Е.В., Кулагин И. С, Новожи-
Новожилов Ю.В., Сергеев А.С, Ткаченко А.К. Наблюдение автомодуля-
автомодуляционных режимов генерации в мощной ЛОВ // Письма в ЖТФ.
1998. Т. 24, №20. С. 66.
12. Плазменные и электронные усилители и генераторы СВЧ. — М.:
Сов. радио, 1965.
13. Trivelpiece A.W. Interaction of electron beam with backward-wave
mode in a ferrite rod. — Internat. Microwellenrohren. Munchen, 1960,
251.
14. Электроника ламп с обратной волной / Под ред.В.Н.Шевчика и
Д.И. Трубецкова. — Саратов: Изд-во Сарат.ун-та, 1975.
15. Стелъмах М. Ф. Генераторное устройство микроволнового диапа-
диапазона. — Авторское свидетельство No 172364, 1948.
16. Kompfner R. The invention of travelling wave tubes // IEEE Trans, on
ED. 1976. V. ED-23, № 7. P. 730.
17. Epsztein B. Oscillateur tube a onde progressive avec propgation de 1
energie electromagnetique en sens inverse du faiseau. — Tranz. Patent
Anm. No 608149. V.13.4.1951.
18. Пирс Дж. Лампа с бегущей волной. — М.: Сов.радио, 1952.
19. Шевчик В.И. Основы электроники сверхвысоких частот. — М.:
Сов.радио, 1959.
20. Dyott R.B., Davies M.C. Interaction between an electron beam of
periodically varying diameter and EMwaves in cylindrical guide //
IEEE Trans, on ED. 1966. V. ED-13, № 3. P. 374.
21. Guenard P. Doehler O., Epsztein В., Warnecke R. Nouveaux
tubes oscillateurs a large bande d'accord electronique pour
huperfrequences // Comptes Rendus Acad. Sci. Paris. 1952. V. 235.
P. 236.
22. Warnecke R.R., Guenard P., Doehler O., Epsztein B. The «M»-type
carcinotron tube // PIRE. 1955. V. 43, № 4. P. 413.
23. Альтшулер Ю.Г., Татаренко А.С. Лампы малой мощности с
обратной волной. — М.: Сов.радио, 1963.
24. Шевчик В.И. Взаимодействие электронных пучков с электромаг-
электромагнитными волнами. — Саратов: Изд-во Сарат. университета, 1963.
25. Шевчик В.Н., Трубецков Д.И. Аналитические методы расчета в
электронике СВЧ. — М.: Сов. радио, 1970.
26. Рапопорт Г.Н. Нелинейная теория генератора обратной волны с
периодической замедляющей структурой // Радиотехника и элек-
электроника. 1964. Т. 9, № 3. С. 483.
Карсинотрон 395
27. Рапопорт Г.Н. Некоторые результаты нелинейной теории автоко-
автоколебаний лампы обратной волны с продольным полем // Доклады
АН СССР. 1957. Т. 117, № 3. С. 411.
28. Рапопорт Г.Н. О механизме возрастания к.п.д. генератора обрат-
обратной волны при увеличении параметра объемного заряда // Радио-
Радиотехника и электроника. 1958. Т. 1, № 5. С. 599.
29. Grow R., Watkins D.Q. Backward-wave oscillator efficiency // Proc.
IRE. 1955. V. 43, №7. P. 848.
30. Johnson H.R. Backward-wave oscillators // Proc. IRE. 1955. V.43.
P. 684.
31. Бочаров E.H., Гаврилов М.В., Левин Ю.И., Соколов Д.В., Тру-
бецков Д.И., Шараевский Ю.Н. Теория лучевых приборов магне-
тронного типа // Лекции по электронике СВЧ и радиофизике B-
я зимняя школа-семинар инженеров), Книга V. Саратов: Изд-во
СГУ, 1972.
Лекция 13
КАРСИНОТРОН КАК РАСПРЕДЕЛЕННАЯ
АВТОКОЛЕБАТЕЛЬНАЯ СИСТЕМА
Что ожидает нас в более сложных уравнениях,
если даже в таком простом уравнении с одним-
единственным параметром мы видим такое раз-
разнообразие возможностей!
Р. П. Фейнман
Натурный эксперимент и нестационарная теория ЛОВ: от монохро-
монохроматических автоколебаний через автомодуляцию к динамическому
хаосу. Релятивистский карсинотрон: нестационарная теория и ре-
результаты численного моделирования. Влияние сил пространственно-
пространственного заряда и отражений от концов замедляющей структуры на генера-
генерацию в релятивистской ЛОВ. Экспериментальное исследование слож-
сложной динамики в релятивистской ЛОВ. Релятивистский карсинотрон
и радиолокация.
Как уже указывалось выше, последовательная теория должна рас-
рассматривать лампу обратной волны как распределенную автоколеба-
автоколебательную систему. Целью теории должно быть исследование характера
изменения величин, описывающих поле и электронный поток как во
времени, так и в пространстве. В данной лекции изложим простейшую
нестационарную теорию ЛОВ, а также результаты, предсказываемые
ею, и их трактовку с позиций нелинейной динамики.
Нестационарная теория ЛОВ базируется на методе медленно меня-
меняющихся амплитуд. Поле обратной волны в линии передачи представ-
представляется функцией с комплексной амплитудой, медленно меняющейся
на протяжении временного и пространственного периода высокочас-
высокочастотного поля. Гармоника ВЧ-тока в этом случае также будет иметь,
в отличие от стационарной теории [1, 2], медленно меняющуюся ампли-
амплитуду. Остальные предположения полностью эквивалентны сделанным
нами в рамках рассмотрения стационарной нелинейной теории ЛБВ:
рассматривается одномерное движение электронного потока; учитыва-
учитывается взаимодействие с одной пространственной гармоникой ВЧ-поля,
Карсинотрон как распределенная автоколебательная система 397
причем параметр усиления полагается малым (С <С 1); не учитывается
расслоения потока в поперечном направлении и т. д.
Как и в предыдущих лекциях, для анализа выведенных нелинейных
нестационарных уравнений используется численное моделирование, на
конкретных особенностях которого остановимся в следующей лекции.
Натурный эксперимент и нестационарная теория ЛОВ:
от монохроматических автоколебаний через
автомодуляцию к динамическому хаосу
Будем рассматривать модель ЛОВ, которая представляет собой со-
согласованный на концах отрезок периодического волновода длины L,
пронизываемый электронным пучком с невозмущенной скоростью vo.
Не будем учитывать, как и при построении нелинейной теории ЛБВ
в лекции 10, такие явления как расслоение электронного потока в попе-
поперечном направлении, остановку и отражение электронов, поперечные
движения электронов.
Для построения нестационарной теории воспользуемся выведенны-
выведенными в первой лекции нестационарным уравнением A.103) возбуждения
линии передачи током медленно меняющейся амплитуды. В пренебре-
пренебрежении потерями в линии передачи (js = 0 в уравнении A.103)) уравне-
уравнение A.103) можно записать в виде
о~ Ш+2тг
Е
\
= Re (с_вЕ_ве^'ш) , A3.2)
где E±s = E±s(s,y, z)eT^sX — собственные функции is-й волны, Ns —
норма, численно равная учетверенному потоку мощности, переносимо-
переносимому волной при \C-S\ = lj^srp — l//?g(fi). Учитывать будем только одну
рабочую пространственную гармонику поля. Разложим собственную
функцию E±s в ряд:
+ ОО
Е°±, = Y, E±'"(V> z) ехР [
где d — период волновода. Теперь в соотношениях A3.1) и A3.2) необ-
необходимо вместо E±s взять соответствующий член ряда. Тогда, выбирая
нормировку собственной функции так, чтобы E±snx = =pl (в этом слу-
случае Ns > 0 [5]) и полагая, что j = j/ (jiS± = I(x,t), S± — площадь
поперечного сечения электронного пучка), вычислим интеграл в правой
части A3.1):
398 Лекция 13
Ш+2тг
- f db
тгАГ
1- J dS j j(r,t)Eee-^*d(m) =
Ш+2
s± nt
Ш-\-2тг
ttNs
nt
\ dS \ I(x,t)e-jn^-x/Vo)d(nt). A3.4)
S± nt
Введем, учитывая определение, сопротивление связи К =
а также обозначим C-s = Е. В итоге приходим к уравнению возбу-
возбуждения для обратной волны в форме
где
+/
7=- f I(x,t)e-jil(t-^vo)dt A3.6)
7Г J
— медленно меняющаяся амплитуда тока пучка. Граничное условие для
уравнения A3.5) в случае ЛОВ-генератора выражает равенство нулю
поля на коллекторном конце лампы Е(х = I) = О (I — длина лампы).
Продольное электрическое поле, воздействующее на электронный
поток, будет даваться в виде
# = Re |#0M)exp \jSl(t-x/v0)]}, A3.7)
где частота fi определяется из дисперсионного уравнения замедляющей
системы
=v0, A3.8)
а условие медленного изменения амплитуды волны по сравнению
с exp [jilt] определяется выражением
1 дЕ
~пЕ dt
1. A3.9)
Перейдем теперь к анализу движения электронов в поле бегущей
волны A3.7) и расчету создаваемого ими конвекционного тока. Будем
в дальнейшем пренебрегать учетом поля пространственного заряда.
Рассмотрим группу электронов, влетевших в пространство дрейфа за
время (ti,ti + 2тг/П). Будем полагать на основании условия медлен-
медленного изменения амплитуды поля во времени A3.9), что все электроны
Карсинотрон как распределенная автоколебательная система 399
движутся в поле одинаковой амплитуды Е(х, t\ + x/vq). Тогда можно
показать, аналогично тому, как это уже делали при выводе нелинейных
уравнений ЛБВ, что уравнение движения отдельного электрона дается
выражением A0.3):
-0-(?)'"¦
Как и в лекции 10, перейдем к зависимости не от координаты ж, а от
величины /ЗСх. Однако в данном случае выберем несколько другую
нормировку: ? = /ЗСх/l, т = / x[v°\ . Величина г называется
l(l/Vrp + 1/Vq)
безразмерным временем, хотя ее смысл в соответствии с определением
более сложен. Действительно, можно представить себе, что в каждой
точке с координатой х стоят свои часы, которые отстают от часов,
находящихся в начале координат на время At = x/vq. Несложно ви-
видеть, что показания таких часов пропорциональны т. Использование
переменной г вместо времени t удобно по двум причинам. Во-первых,
из числа управляющих параметров за счет выбора нормировки исклю-
исключается групповая скорость, а, во-вторых, вместо начальных условий для
поля и пучка необходимо задавать только начальные условия для поля.
Тогда, вводя медленно меняющуюся фазу электрона относительно
волны 0 = ?1 (t — x/vo), уравнение движения A3.10) и уравнение возбу-
возбуждения A3.5) могут быть представлены в новых переменных в виде
A3.11)
о
которые, будучи дополнены начальными и граничными условиями
ВО
^ 0) fc « 0H
представляют собой систему уравнений, описывающих простейшую
нестационарную нелинейную модель лампы с обратной волной. Здесь
Т — 2 ~~ нормированная амплитуда поля; Vb = Vq/2tj — ускоряю-
2/3 Vo С
щее напряжение. Величина L = ftCl/vo является единственным управ-
управляющим (бифуркационным) параметром рассматриваемой нелинейной
400 Лекция 13
системы уравнений. Поэтому система уравнений A3.11)—A3.13) часто
называется однопараметрической моделью лампы обратной волны г).
Полученная система уравнений является сильной идеализацией, не
учитывающей целый ряд важных факторов (в первую очередь, это
касается влияния сил пространственного заряда и отражений в лампе).
Вместе с тем, даже сильно упрощенная модель такой сложной рас-
распределенной системы, какой является карсинотрон, позволяет объяс-
объяснить целый ряд явлений, которые наблюдаются экпериментально. Нас
в первую очередь будут интересовать вопросы, связанные со сложной
нелинейной динамикой ЛОВ. Этот интерес определяется как фунда-
фундаментальными проблемами анализа сложной динамики распределенных
автоколебательных систем (среди которых ЛОВ является одной из
наиболее типичных систем электронной природы), так и прикладными
задачами разработки эффективных генераторов хаоса СВЧ-диапазона.
Ещё ранние теоретические и экспериментальные исследования лам-
лампы обратной волны (см. работы [6-11]) показали, что при увеличении
тока пучка (или увеличении параметра L в модели A3.11)—A3.13))
в ЛОВ режим стационарной одночастотной генерации сменяется двух-
частотным (т. е. выходной сигнал становится промоделированным) —
режим автомодуляции. Далее с увеличением тока наблюдается услож-
усложнение колебаний вплоть до возникновения режимов динамического ха-
хаоса. Как было показано в вышеназванных работах, причиной автомоду-
автомодуляции является перегруппировка электронов в поле электромагнитной
волны большой амплитуды и запаздывание реакции системы «элек-
«электронный поток — обратная волна» на начало действия нелинейности.
Обсудим основные результаты, полученные при экспериментальном
исследовании сложных режимов колебаний в ЛОВ [9]. Заметим, что
эксперименты проводились на специальных лабораторных макетах,
основные особенности и отличия которых от традиционных ЛОВ за-
заключаются в большей длине пространства взаимодействия (/3qI > 150)
и большем поперечном сечении пучка (до 3 см2). Важное внимание так-
также уделялось уменьшению потерь в замедляющей системе и отражений
от концов лампы. Применение многолучевой конструкции электронной
пушки и наличие отдельного пролетного канала для каждого луча
позволило значительно уменьшить провисание потенциала в пучке, что
в свою очередь, дало возможность существенно снизить статический
разброс электронов по скоростям.
Все вышеназванные особенности в конструкциии макетов позволили
получать значения параметра L от 0 до 10-12 при удовлетворитель-
удовлетворительном выполнении допущений, сделанных при выводе уравнений A3.11)—
г) Заметим, что данное название нельзя признать удачным: более точным
было бы название «модель лампы обратной волны с одним бифуркационным
параметром».
Карсинотрон как распределенная автоколебательная система
401
/,мА
Хаотическая
генерация
Периодическая
автомодуляция
A3.12). Здесь будут приведены результаты, полученные только на од-
одном экспериментальном макете ЛОВ. Более подробно данные резуль-
результаты изложены в работе [9], где также имеется сравнение результатов,
полученных на различных макетах.
При увеличении тока пучка / и постоянном напряжении V на-
наблюдается последовательность бифуркаций (при токах пучка h(V),
h(V) и т. д.), каждая из которых сопровождается усложнением спектра
выходного сигнала. На рис. 13.1
на плоскости управляющих па-
параметров (К, /) показаны об-
области существования различ-
различных динамических режимов; на
рис. 13.2 — соответствующие
спектры выходного сигнала. Рас-
Рассмотрим эти режимы.
При токах пучка I < 1\ ав-
автоколебания отсутствуют (пред-
генерационный режим в ЛОВ).
С увеличением тока пучка при
/ = 1\ в ЛОВ возникают автоко-
автоколебания (пусковой ток), и в диа-
диапазоне значений токов I<i > / >
> 1\ наблюдается генерация мо-
монохроматического сигнала с ча-
частотой и (рис. 13.2а). При /2 <
< / < /з реализуются много-
многочастотные автоколебания с дис-
дискретным спектром — режим ав-
автомодуляции (рис. 13.2?;в). Бо-
Боковые частотные составляющие
(сателлиты) возникают в резуль-
результате нормальной бифуркации,
мягким образом, их амплиту-
амплитуда (соответственно, глубина мо-
модуляции) постепенно возраста-
возрастает пропорционально квадратно-
квадратному корню из надкритичности (у/1 — 1^ ). Расстояние по частоте между
спектральными линиями иш (частота модуляции) намного меньше uj
и медленно увеличивается с ростом тока пучка. С ростом тока пучка
при / > 0,9/з наблюдается усложнение формы автомодуляции, чему
соответствует появление в спектре субсателлитов (рис. 13.2г), уровень
которых существенно ниже возникших ранее спектральных составля-
составляющих, а соответствующие частоты модуляции, как правило, кратны
ит/п (п — целое число, изменяющееся в зависимости от ускоряющего
1
0,6
0,4
Одночастотный
режим
2
Предгенерационный
режим
100
120
Рис. 13.1. Разбиение плоскости управ-
управляющих параметров (напряжение-
ток пучка) на области с различными
видами колебаний. Прямые линии —
линии равных значений параметра L
(из работы [9])
402
Лекция 13
ДБ
50
40
30
20
10
0
1,18
Ж
напряжения, условий формирования и транспортировки электронного
пучка и согласования лампы).
При / > /з возникают колебания со сплошным спектром (рис. 13.2д-
к). Если рассмотреть любую спектральную линию, существующую при
/ < /з, то для / > /з сосредо-
сосредоточенная в ней мощность пере-
перераспределяется в частотном ин-
интервале, ширина которого уве-
увеличивается с ростом тока пуч-
пучка, при этом интегральная мощ-
мощность практически не меняется.
При этом также повышается уро-
уровень шума на участках спектра,
не содержащих при / < /з дис-
дискретных составляющих.
Как уже отмечалось выше,
автомодуляция связана с нели-
нелинейными явлениями и запазды-
запаздыванием. Вместе с тем, в нача-
начале исследований данных вопро-
вопросов возникла и другая гипотеза:
автомодуляция является резуль-
результатом биений между видами ко-
колебаний ЛОВ, предсказываемы-
предсказываемыми теорией слабого сигнала (см.
предыдущую лекцию). Обсудим
специально поставленный экспе-
эксперимент [12], доказывающий, что
верно именно первое объясне-
объяснение: автомодуляция связана не
с возбуждением высших линей-
линейных видов колебаний, а с нели-
нелинейными свойствами автоколе-
автоколебательной системы. Исследова-
Рис. 13.2. Спектры выходного сигнала
ЛОВ в различных автоколебательных
режимах: а соответствует отношению
тока пучка к пусковому току равному
I/h = 1,5; б-Ъ\е- 15; г - 31; д -
31,2; е — 40; ж — 50; з — 70; и — 100;
к;-200 (из работы [9])
ния, как и в предыдущем слу-
случае, проводились на специаль-
специальных макетах ЛОВ, в которых бы-
было значительно ослаблено поле
пространственного заряда.
Частоты, на которых в ЛОВО при определенных значениях отно-
отношения рабочего тока к пусковому (///пуск) возникает неустойчивость
и происходит самовозбуждение, можно обнаружить, исследуя зависи-
зависимость коэффициента усиления G{u) от частоты слабого внешнего гар-
гармонического сигнала, поданного на коллекторный конец замедляющей
Карсинотрон как распределенная автоколебательная система
о/о
403
Рис. 13.3. Зависимость коэффициента усиления G слабого внешнего гармо-
гармонического сигнала от частоты ш при различных отношениях рабочего тока
к пусковому (из работы [12])
системы. Этим частотам соответствует максимум усиления (а непосред-
непосредственно перед самовозбуждением еще и максимум шума).
Рассмотрим зависимости G{u) для различных значений ///пуСк
(рис. 13.3). При ///пуск < 1 эти зависимости представляют собой ча-
частотные характеристики линейного усилителя (рис. 13.3, кривая 1). Вы-
Высокий максимум на частоте oj$ предшествует возбуждению основного
вида колебаний, предсказываемого линейной теорией (ему соответству-
соответствует невозмущенный угол пролета Фо = —к), а небольшой максимум на
частоте и^ — возбуждению высшего вида (Фо = ~~Зтг). Падение характе-
характеристики G(lj) на частотах, несколько больших ljq, связано с эффектом
противонаправленного подавления 1). При ///пуск > 1 ЛОВ возбужда-
возбуждается и генерирует квазигармонический сигнал на частоте ш'о, близкой
к частоте и® (отличие связано с электронным смещением частоты).
Присутствие мощного сигнала существенно влияет на вид зависимости
G{uj) (рис. 13.3, кривая 2). Максимум усиления на частоте о^ пропадает
и сменяется неглубоким подавлением. С увеличением ///пуСк подав-
х) В линейной теории наиболее ярко этот эффект (contradirectional dip)
проявляется при больших пространственных зарядах, когда быстрая волна
пространственного заряда находится в синхронизме с обратной электромаг-
электромагнитной волной [18, стр. 214].
404 Лекция 13
ление внешнего сигнала на частотах, удаленных от uf0, углубляется
и охватывает все более широкую полосу частот. Однако в небольшом
диапазоне частот, расположенных в низкочастотной области, примыка-
примыкающей к частоте и)'о, уже при при ///пуСк ~ 1 обнаруживается тенденция
к увеличению коэффициента усиления. С ростом ///пуСк в этом диапа-
диапазоне формируется ярко выраженный максимум G (рис. 13.3, кривая 3),
который затем смещается в область низких частот и увеличивается.
При ///пуск > 3 на частоте о;и, соответствующей этому максимуму,
возбуждается дополнительный сигнал. Его появление соответствует
возникновению в спектре выходного сигнала ЛОВ составляющих на
частоте 2ojfo — о;и и еще ряда уменьшающихся по амплитуде дискретных
составляющих, отстоящих друг от друга на частоту иш = ojfo — oju
(режим периодической автомодуляции; частота ит носит название ча-
частоты автомодуляции).
Таким образом наблюдаемый второй максимум в зависимости G{u)
соответствует выполнению фазового условия генерации низкочастот-
низкочастотной боковой составляющей в спектре выходного сигнала ЛОВ в режиме
автомодуляции. При ///пуСк > 3 оказывается выполненным и ампли-
амплитудное условие. Отсюда видно, что возникновение автомодуляционных
режимов «исторически» не связано с максимумом усиления на частоте
высшего вида линейной теории. Более того, существенно не совпадают
ни абсолютные значения частот и^ и ши, ни их отстройка от частоты
самовозбуждения uq (uq — col > uq — ии) и от частоты сигнала, на
котором происходит генерация со'о.
Возвращаясь к обсуждению экспериментальных результатов иссле-
исследования сложной динамики в ЛОВ остановимся на вопросе о детерми-
детерминированности хаотических режимов генерации в ней. Доказательством
того, что колебания со сплошным спектром обусловлены собственной
сложной динамикой системы служат следующие факты, наблюдаемые
в эксперименте.
1. Возникновение сплошного спектра имеет четко выраженный по-
порог / = /3. Если бы дело было просто в усилении шумов, то порога не
было бы — шум постепенно нарастал бы с увеличением надкритичности
(тока пучка).
2. Внешний гармонический сигнал, подаваемый на коллекторный
конец лампы, существенным образом влияет на форму спектра выход-
выходного сигнала. Если мощность внешнего сигнала Рвн на порядок меньше
выходной интегральной мощности РВых, то спектр просто сильно де-
деформируется. Если входная мощность достаточно велика, то возможна
дискретизация спектра под действием внешнего сигнала. Это явление
демонстрируется на рис. 13.4а; б, где приведены спектры автономной
генерации, внешнего сигнала и неавтономной генерации, и на рис. 13.4в,
где на плоскости частота-мощность внешнего сигнала приведены обла-
области, соответствующие дискретизации спектра.
Карсинотрон как распределенная автоколебательная система 405
30 г a s
Лл
20
10
о
40
30
20
10
о
f
-0,08 -0,04 0 /вн-/о
/о
Рис. 13.4. а, б — дискретизация спектра выходного сигнала ЛОВ внешним
сигналом (спектр 1) в режиме хаотической генерации (спектр 2) (///i =
= 100); в — спектр выходного сигнала (сверху) при I/Is = 1,15 (качественно)
и области значений частоты и мощности внешнего сигнала (отмечены серым
цветом), соответствующие дискретизации спектра (из работы [9])
3. Как видно из рис. 13.1, все границы раздела между областя-
областями различных режимов на плоскости (К, /) проходят примерно вдоль
линий L = const, что относится также к режиму стохастических ко-
колебаний г). Это является экспериментальным подтверждением закона
подобия, справедливого в рамках рассмотренной теоретической модели
(см. соотношения A3.11)—A3.13)). Поэтому естественно предположить,
что все наблюдаемые режимы и бифуркации обусловлены факторами,
«заложенными» в теоретическую модель, тогда как потери в замедляю-
замедляющей системе, поле пространственного заряда, отражение волн от концов
системы, шумы и т. д. в рассматриваемом случае имеют второстепенное
значение.
И в заключение рассмотрения результатов натурного исследования
сложных колебаний в ЛОВ кратко остановимся на влиянии простран-
пространственного заряда и отражений на характер автоколебаний в лампе
обратной волны.
При большом пространственном заряде в лампе постоянной длины
с увеличением тока пучка наблюдается следующее: режим монохро-
монохроматических автоколебаний сменяется режимом автомодуляции, а за-
затем опять устанавливается режим монохроматической генерации. При
больших токах пучка опять наблюдается возникновение автомодуляции
и хаотических автоколебаний. Это иллюстрируется рис. 13.5а, на кото-
котором показаны конфигурации областей различных режимов генерации
г) Значения сопротивления связи, необходимые для вычисления L, опреде-
определялись по стартовым условиям /пуСк = h(V) на основании линейной теории
[13].
406
Лекция 13
/, мА
KB 150
Рис. 13.5. Вид областей различных режимов ЛОВ на плоскости напряжение—
ток пучка при существенном пространственном заряде (а) и искусственном
введении отражений от концов замедляющей системы (б). Здесь введены
обозначения: А — предгенерационный режим; В — одночастотный режим;
С— режим периодической автомодуляции; D — хаотические автоколебания
(из работы [9])
в ЛОВ, для которой пространственный заряд существенен. Из него
понятно, что по форме границы зоны автомодуляции можно легко
оценивать величину напряжения, при превышении которого простран-
пространственный заряд мало существенен. К этой области напряжений, ширина
которой увеличивается с ростом длины лампы, и относятся все резуль-
результаты, излагаемые в данной лекции.
Наличие отражений от концов замедляющей системы г) приводит
к тому, что границы между областями на плоскости (К, /) становятся
волнистыми и, более того, при достаточно сильных отражениях возмож-
возможно появление «островов» на карте режимов (рис. 13.56). Особенно силь-
сильно изрезанной становится граница зоны хаотической автомодуляции.
При отсутствии специально сделанного рассогласования волнистость
границ областей режимов невелика (см., например, рис. 13.1), и значит
влиянием отражений можно в определенных пределах пренебречь.
Итак, основываясь на вышесказанном, можно формально утвер-
утверждать, что в лампе обратной волны реализуется сценарий перехода
к хаосу через разрушение квазипериодических движений, так как по ме-
мере увеличения управляющего параметра колебания из периодических
вначале становятся квазипериодическими (возникает автомодуляция),
> эксперименте они вводились искусственно.
Карсинотрон как распределенная автоколебательная система
•^ 'max
407
- а
ffvw
-/2,75
/2,5
2 -
1 -
0 123456789 Ют
4,200
4,025 4,050 4,075 4,100 L
Рис. 13.6. Зависимости амплитуды Рис. 13.7. Бифуркационная диаграм-
выходного сигнала ЛОВ от времени ма в области перехода к хаосу по сце-
в процессе установления колебаний нарию удвоения периода (из работы
при различных значениях парамет-
параметра L (из работы [20])
[20])
а затем в результате цепочки бифуркаций становятся хаотическими.
Вместе с тем, конкретный способ такого перехода даже в относительно
простейшей однопараметрической модели лампы обратной волны до
недавнего времени оставался до конца неизученным. В последующих
работах (Н.М. Рыскин, В.Н. Титов, Д.И. Трубецков [19, 20]) было
проведено детальное исследование перехода к хаосу в нерелятивистской
ЛОВ с помощью численного моделирования уравнений A3.11)—A3.13)
и выявлено, что при увеличении параметра L в системе реализуется
сложная последовательность переходов «порядок — хаос» и «хаос —
порядок», происходящих по различным сценариям. Изложем эти ре-
результаты, основываясь на работах [19, 20].
Исходя из модели A3.11)—A3.13) возбуждение автоколебаний воз-
возникает при L « 1,98. При L « 2,9 режим одночастотной генерации ста-
становится неустойчивым и сменяется двухчастотным: выходной сигнал
становится модулированным. Данное явление носит название автомо-
автомодуляции. На рис. 13.6 приведены характерные временные зависимости
амплитуды сигнала с выхода лампы |^-*@, т)|, полученные при различ-
различных L. Видно, что при L < 2,9 после переходного процесса, длитель-
длительность которого увеличивается с ростом L наблюдается установление
одночастотного режима, в то время как при превышении L « 2,9 имеет
место автомодуляция сигнала.
При увеличении управляющего параметра в очень узкой области
4,02 < L < 4,11 происходит переход к хаосу через последовательность
бифуркаций удвоения периода автомодуляции. На рис. 13.7 приведе-
приведена соответствующая бифуркационная диаграмма (положения макси-
максимумов ^(т)! в зависимости от параметра), на которой четко вид-
видна последовательность удвоений периода. Соответствующие фазовые
портреты и спектры мощности для различных значений параметра L
408
Лекция 13
ДБ
0
-10
-20
-30
-40
4
3
2
1
Ло ! г
- ff 1 -
"А / "
2 3 4
1
У
it
о
-10
-20
-30
-40
12 3 4
0 12 3
Рис. 13.8. Фазовые портреты и спектры мощности выходного сигнала, иллю-
иллюстрирующие переход к хаосу по сценарию Фейгенбаума: а — цикл периода 2
(L = 4,089); б— цикл периода 4 (L = 4,106); в — цикл 8 (L = 4,108); г — хаос
(L = 4,118) (из работы [20])
приведены на рис. 13.8. Здесь важно, что приближенно выполняются
универсальные количественные закономерности, присущие переходу
к хаосу по сценарию Фейгенбаума [21-24]. Оценка первой константы
Фейгенбаума 1) дает
8 =
L3- Ь2
L4 — Ls
: 4,925,
что близко к точному значению 4,669. Здесь значения Li соответствуют
г-й бифуркации удвоения периода автомодуляции. Отношение ампли-
г) Под первой константой Фейгенбаума понимается масштабный коэффици-
коэффициент, являющийся пределом, к которому сходится разность бифуркационных
значений управляющего параметра L:
Величина S является универсальной константой в том смысле, что ее значе-
значение не зависит в определенных пределах от природы системы, демонстриру-
демонстрирующей каскад удвоений периода (подробнее см. [25]).
Карсинотрон как распределенная автоколебательная система
409
3,400
4,150 4,175 4,200 4,225 4,250 4,275 4,300
Рис. 13.9. Бифуркационная диаграмма в области добавления периода (из
работы [20])
туд субгармоник, возникающих в результате последовательности би-
бифуркаций, также близко к универсальному значению (—13) дБ [25] х).
После перехода к хаосу через последовательность удвоений периода
в области 4,15 < L < 4,32 наблюдается достаточно большое число
окон периодичности в хаосе, период которых, начиная с трех, после-
последовательно увеличивается на единицу. На рис. 13.9 представлена би-
бифуркационная диаграмма, соответствующая этой области — области
добавления периода. Внутри окон периодичности имеется достаточно
сложная структура прямых и обратных бифуркаций удвоения периода.
При 4,32 < L < 4,333 происходит переход через перемежаемость
от хаотической автомодуляции к периодической. Кратко остановимся
на основных особенностях сценария перехода к хаосу через переме-
перемежаемость [21, 26, 27]. В этом случае переход к хаосу выглядит как
постепенное (при медленном изменении бифуркационного параметра)
исчезновение периодических колебаний за счет прерывания их стоха-
стохастическими всплесками. Возникновение перемежаемости связано с так
называемой касательной бифуркацией (см., например, [26, 27]), когда
в системе имеет место реализация двух периодических траекторий:
устойчивой и неустойчивой, которые при изменении управляющего
параметра сливаются и исчезают. В этом случае движение фазовой
траектории может быть разделено на две области: движение возле
исчезнувшей периодической траектории (длительная ламинарная фаза
движения, когда динамика системы близка к регулярной) и выход
г) Заметим, что в работах [14-17] также наблюдалось явление удвоения
периода в релятивистском карсинотроне, где данное явление связывалось
исключительно с релятивистскими эффектами.
410 Лекция 13
I \F\
О 150 200 250 30( ^ 0 ¦ 100 150 200 250 300 x
Рис. 13.10. Временные реализации выходного сигнала при перемежаемости:
L = 4,325 (о) и L = 4,3327 (б) (из работы [20])
из этой области, когда движение сильно неустойчиво по Ляпунову
(турбулентная фаза). После прохождения турбулентной фазы фазовая
траектория опять возвращается в область вблизи исчезнувшего перио-
периодического движения.
На рис. 13.10 приведены характерные временные реализации ^(т)!
для двух различных параметров L. Видно, что они имеют вид лами-
ламинарных фаз, динамика в которых близка к регулярным колебаниям,
прерываемых нерегулярными всплесками. Средняя длительность d ла-
ламинарных фаз увеличивается с ростом L по закону
d{L) = _?_, A3.14)
который характерен для перемежаемости I рода [27]. Здесь С и Lc —
константы, равные С « 0,4415 и Lc ~ 4,3333.
После этого перехода хаотический аттрактор в фазовом простран-
пространстве превращается в метастабильное хаотическое множество. В течение
переходного процесса фазовая траектория располагается вблизи этого
множества и временная реализация напоминает хаотическую, а затем
притягивается к устойчивому предельному циклу, после чего временная
реализация становится регулярной. Этот переходный процесс может
занимать достаточно долгое время.
При L > 4,3333 модуляция становится сначала периодической, а за-
затем — квазипериодической с двумя несоизмеримыми частотами. При
L « 4,63 происходит переход к хаосу через разрушение трехчастотного
квазипериодического движения. Образующийся странный аттрактор
существует в области параметров 4,63 < L < 4,90, после чего вновь
реализуются квазипериодические режимы. На рис. 13.11 приведена
бифуркационная диаграмма для этой области и увеличенный фрагмент,
соответствующий хаотическому режиму (на врезке). Из диаграммы
также видно, что внутри описываемой области имеют место явления
синхронизации и образования резонансных циклов на торе.
Карсинотрон как распределенная автоколебательная система
411
4,68 4,70 4,72 4,74 4,76 4,78
4,40 4,50
4,90
Рис. 13.11. Бифуркационная диаграмма в области перехода к хаосу через
разрушение квазипериодического движения (из работы [20])
При L > 6,05 имеют место сложные хаотические колебания. На фа-
фазовом портрете (рис. 13.12) не проявляется какая-либо крупномасштаб-
крупномасштабная структура, спектр мощности колебаний сильно зашумлен. Заметим,
что, уже начиная с L w 5,5, длительность переходного процесса суще-
ствено увеличивается, что связано с наличием уже упоминавшегося
нами метастабильного хаотического множества. В этом случае чрез-
чрезвычайно длительный переходный процесс выглядит как хаотический,
однако, на больших временах заканчивается установлением регулярных
колебаний.
Таким образом однопараметрическая модель ЛОВ A3.11)—A3.13)
позволяет предсказать и объяснить многие из экспериментальных ре-
результатов, обсуждаемых нами выше. Вместе с тем, данная модель не
учитывает целый ряд существенных явлений (влияние диссипации,
пространственного заряда и отражений), наиболее важным из которых
является невозможность идеального согласования ЛОВ и, как след-
следствие, важность учета электромагнитного поля, отраженного от концов
замедляющей системы, в сложных автомодуляционных режимах. Это
непосредственно следует из натурного эксперимента (см. рис. 13.5, на
котором демонстрируется искажение областей различных режимов при
наличии отражений в лампе).
В работе [28] были проведены теоретические и экспериментальные
исследования нерелятивистской ЛОВ с отражениями, из которых сле-
следует, что даже малые отражения от концов лампы приводят к принципи-
принципиальным изменениям вышеописанной последовательности бифуркаций.
412
Лекция 13
Рис. 13.12. Временная реализация, фазовый портрет и спектр мощности вы-
выходного сигнала для режима развитого хаоса (L > 6,05) (из работы [20])
Так из предельного цикла, соответствующего однопериодической моду-
модуляции сразу мягко рождался двумерный тор без наблюдения каскада
удвоения периода, как это было в однопараметрической модели ЛОВ без
отражений. Увеличение тока пучка после возникновения двумерного
тора приводило к появлению в спектре автомодуляции несоизмеримых
частот и далее переходу к хаосу через разрушение квазипериодических
движений в системе.
Заметим, что наибольшее значение учета отражений от концов за-
замедляющей системы имеет место для релятивистских ЛОВ, поэтому
отложим детальное рассмотрение этих вопросов до соответствующего
параграфа.
Релятивистский карсинотрон: нестационарная теория
и результаты численного моделирования
Рассмотрим теперь лампу обратной волны, в которой используется
сильноточный релятивистский пучок. Релятивистские лампы обрат-
обратной волны (РЛОВ) привлекают в последнее время большое внима-
внимание как перспективные источники мощного электромагнитного излу-
излучения в сантиметровом и ближнем милиметровом диапазоне длин волн
[29]. При проектировании подобных устройств огромную роль играет
численное моделирование нестационарных процессов, что необходимо,
с одной стороны, для анализа устойчивости стационарных режимов
монохроматической генерации, а с другой стороны, такие режимы пред-
представляют самостоятельный интерес для создания мощных генераторов
Карсинотрон как распределенная автоколебательная система 413
шумоподобных сигналов на базе релятивистского карсинотрона. Все это
делает необходимым остановиться на вопросах нестационарной теории
релятивистской лампы обратной волны г).
Рассмотрим как модифицируются уравнения лампы обратной вол-
волны при учете релятивистских эффектов. Понятно, что уравнение воз-
возбуждения останется неизменным, так как оно выведено из уравне-
уравнений Максвелла. Однако уравнение движения необходимо переписать
в соответствующем виде. Введем релятивистский фактор электрона
7 = 1/а/ 1 — (v2/с2) , который имеет физический смысл отношения
полной энергии электрона ? к энергии покоя (которая равна тс2).
Тогда, как и для «обычной» нерелятивистской ЛОВ, с учетом условия
A3.9), можно считать что все электроны, влетевшие в пространство
взаимодействия в промежуток времени (?]_, t\ + 2тг/П), движутся в по-
поле одинаковой амплитуды Е (x,ti + x/vq). Следовательно, уравнение
движения электрона можно записать в виде
Переписывая это уравнение относительно релятивистского фактора 7,
получим
|2 = ^ Re {E (x,h + —) eje} , A3.15)
ох с I V vo/ )
1(x = 0) = 7o, 0(x = 0) = 0o, A3.17)
где все обозначения совпадают с обозначениями в предыдущем разделе.
Используя формулу A3.6) и закон сохранения заряда Idt = /о \с16о/Щ,
несложно показать, что первая гармоника сгруппированного тока, ко-
который создается в сечении ж, когда туда приходит рассматриваемая
нами группа электронов (т.е. в момент времени t = t\ + x/vo), дается
выражением
2тг
ехр (-jO(x,t')) d00. A3.18)
0
2тг
7Г J
г) Заметим, что первые теоретические исследования нестационарной дина-
динамики в электронных приборах О-типа с длительным взаимодействием были
проведены именно для РЛОВ [6].
414 Лекция 13
Выберем нормировку физических величин, следуя работе [6] в виде
i = /ЗСх, т = nC(t-x/v0)
A3.19)
= с2 G I)/7? ускоряющее напряжение; С = (
где Vo = с2 G0 — I)/7? ~~ ускоряющее напряжение; С =
\ J
— модифицированный параметр усиления, который, как следует из
предположений, положенных в основу вывода уравнений возбуждения,
мал (С < 1). В результате, в новой нормировке уравнения A3.15)—
A3.18), A3.5) запишутся в виде
A3.20)
2тг
/9/9
где уравнение A3.20) получено из уравнений движения A3.15)—A3.17)
в предположении малости С. Здесь v = 2C(jq — 1). Система уравнений
A3.20)—A3.22) описывает релятивистскую лампу обратной волны при
тех же предположениях и упрощениях, что и система уравнений для
нерелятивистской ЛОВ. Вместе с тем, данная система существенно
сложнее. Действительно, система уравнений A3.20)—A3.22) зависит от
двух управляющих параметров: v (который можно трактовать как
нормированный квадрат релятивистского фактора пучка 7о) и I (дли-
(длина лампы). Таким образом учет релятивизма принципиально требует
рассмотрения системы как двухпараметрической (с двумя бифуркаци-
бифуркационными параметрами).
Возникает вопрос: при каких значениях релятивистского фактора 7о
полученные уравнения будут справедливы при описании взаимодей-
взаимодействия в системе «релятивистский электронный пучок-обратная элек-
электромагнитная волна»? В случае стационарной генерации к.п.д. ЛОВ
запишется в нормировке A3.19) как
0)|2. A3.23)
Карсинотрон как распределенная автоколебательная система 415
Отсюда ясно, что в слаборелятивистском случае G0 ~ 1) система
A3.20)—A3.22) справедлива только для генераторов с малым к.п.д., так
как из условия С <С 1 следует, что г\ <С 1. В ультрарелятивистском же
случае уравнения справедливы и для генераторов с высоким к.п.д., так
как малость С в формуле для к.п.д. A3.23) может быть компенсирована
большим значением 7о- Это связано с тем, что при выводе уравнений
РЛОВ неявно требовалось малое изменение скорости электронов при
пролете лампы. В случае слабого релятивизма это неизбежно ведет
к малому к.п.д., в то время как в случае 7о ^> 1 даже при малом
изменении скорости электронов изменение энергии пучка может быть
значительным.
В работе [30] предложены модифицированные уравнения нестацио-
нестационарной нелинейной теории релятивистской лампы обратной волны, ко-
которые справедливы для любых значений релятивистского фактора 7о-
Данная система уравнений записывается как
Aз-24)
од
и имеет три управляющих параметра: электрическую длину взаимодей-
взаимодействия N = 2тг//А, релятивистский фактор 7о = 1/л/1 ~~ ^о и параметр
L = 2тгСN/jq, пропорциональный току пучка.
Остановимся на результатах численного моделирования системы
уравнений A3.24)-A3.26), следуя работе [30]. Важным и интересным
результатом оказалось то, что форма границы автомодуляции на плос-
плоскости параметров (L, 7о) носит сложный характер. Это демонстрирует-
демонстрируется на рис. 13.13, на котором представлена карта режимов на плоскости
(L,7o) (N = 20). Здесь линией / обозначена граница автомодуляции,
// — линия, за которой начинается отражение частиц и исходные урав-
уравнения становятся неприменимы. В области стационарной генерации
приведены линии равного к.п.д. Из рисунка видно, что существуют
две области, где порог неустойчивости монотонно спадает с ростом 7о5
которые, следуя работе [30], назовем слабо- и ультрарелятивистскими.
Между ними на линии / имеется характерный «клюв», заходящий
далеко вглубь области автомодуляции. Для более коротких ламп этот
клюв располагается в области меньших 7о (То ~ 1,5 -г 2,0 при N = 5).
Существует и такая область значений 7о5 при которых стационарный
416
Лекция 13
Yo
Рис. 13.13. Области реализации различных состояний РЛОВ на плоскости
параметров (L, 70)• Линия / соответствует потери устойчивости режима ста-
стационарной генерации и возникновению автомодуляции; линия // — граница
применимости исходных уравнений A3.24)-A3.26) (из работы [30])
режим генерации и режим автомодуляции сменяют друг друга дважды
при увеличении L (например, 7о = 3,5 на рис. 13.13). Таким образом, до-
достаточно эффективные одночастотные режимы генерации могут быть
реализованы в области существенно больших L, чем в нерелятивистской
ЛОВ.
Заметим, что за порогом автомодуляции / в слабо- и ультрареля-
ультрарелятивистской области реализуются принципиально различные автоколе-
автоколебательные режимы, отличающиеся как пространственно-временными
распределениями поля и тока, так и частотами автомодуляции (в уль-
ультрарелятивистском режиме частота автомодуляции в два раза больше,
чем в слаборелятивистском).
Рассмотрим распределения амплитуды ВЧ-поля и первой гармо-
гармоники сгруппированного тока в стационарном режиме вблизи порога
автомодуляции для обоих режимов генерации. В области ниже «клюва»
(рис. 13.14а; 7о = 3,0, L = 2,5, N = 20) распределение поля таково, что
в режиме автомодуляции за время прохода излучения от коллекторного
конца к пушечному успевает сформироваться лишь один максимум
поля, тогда как в ультрарелятивистской области (рис. 13.14^; 7о = 4,0,
L = 2,7, N = 20) — два х). Соответственно и частота автомодуляции
г) Заметим, что подобная ситуация имеет место, например, в гирорезо-
нансном генераторе со встречной волной [4], где граница автомодуляции на
плоскости параметров (Л, /i) также имеет сложную структуру (А — параметр
взаимодействия, аналогичный длине лампы L, /л — параметр неизохронно-
неизохронности). Это связано с тем, что как в гиро-ЛОВ, так и в релятивистской ЛОВ
типа О переход в режим периодической автомодуляции возможен из режимов
с различным пространственным распределением амплитуд.
Карсинотрон как распределенная автоколебательная система
I
417
0,2 0,4 0,6 0,8
Рис. 13.14. Распределение амплитуды поля (сплошная линия) и первой гар-
гармоники сгруппированного тока (штриховая линия) для слабо- (а) и ультра-
ультрарелятивистской (б) областей на карте режимов (из работы [30])
оказывается в два раза больше. Физически переход ко второму режиму
автомодуляции связан с тем, что с ростом 7о происходит релятивист-
релятивистское увеличение массы электронов. Это замедляет процессы кинема-
кинематической разгруппировки электронных сгустков, что хорошо видно на
рис. 13.14. Амплитуда первой гармоники тока не падает до нуля, т.е.
полной разгруппировки не происходит. С увеличением 7о зависимости
/(?) в стационарном режиме становятся все более плавными, осцил-
осцилляции уменьшаются. Вследствии этого изменяются и стационарные
распределения амплитуды поля J-(?).
Как же возникает автомодуляция в ЛОВО? Ее возникновение свя-
связано с запаздывающей реакцией системы из-за её распределенности на
действие нелинейности [4]. Для примера рассмотрим эволюцию про-
пространственного распределения амплитуд волн и их фаз (рис. 13.15),
полученное при численном решении уравнений РЛОВ A3.20)—A3.22)
с длиной лампы / = 3,5 [17].
При малой амплитуде поля 1^@1 амплитуда тока |/(?)| монотонно
возрастает вдоль координаты, а ^(т)! имеет характерный «одногор-
«одногорбый» вид (кадр 1 на рис. 13.15). При увеличении амплитуды поля ампли-
амплитуда |/| в некоторой точке пространства достигает максимума, а затем
спадает — происходит разгруппировка электронов (кадр 2). При этом
1^(^I и распределение фаз качественно не меняются. Однако когда
амплитуда поля достигает такой величины, что вблизи коллекторного
конца системы ? = 1 амплитуда тока |/| падает почти до нуля, практиче-
практически скачком меняет фазу почти на тг и снова нарастает, происходит пере-
перегруппировка электронов (кадр 3). Образуется характерное «двугорбое»
распределение амплитуды тока и, вследствие нарушения фазового со-
соотношения между комплексными амплитудами \Т\ и |/|, «двугорбое»
распределение \3-(?) |. Затем вся картина смещается влево с групповой
скоростью, причем оба максимума растут при движении по величине из-
за взаимодействия с волной тока, пока не достигнут пушечного конца
лампы (кадры 4-10). Из оставшегося в системе распределения
14 Д. И. Трубецков, А. Е. Храмов
418
I/I//O
3,0
2,0
1,0
о
Лекция 13
0,2 0,4 0,6 0,8
1
/ \s
10
Рис. 13.15. Динамика распределений амплитуд поля Т (сплошная линия),
тока |///о| (штриховая линия) и фазы тока срг для РЛОВ с длиной / =
= 3,5. Заштрихована область тормозящих фаз поля. Промежуток во времени
между соседними кадрами одинаков (из работы [4])
опять выделяется основной вид колебаний, и процесс периодически
повторяется. Таким образом «двухгорбое» распределение оказывается
неустойчивым и возникает периодическая автомодуляция выходного
сигнала, связанная с нарушением фазового соотношения между \Т\
и |/|. Заметим также, что возникновение «двугорбого» распределения
может трактоваться как возникновение в распределениях 1^(^I и |/(?)|
компонент, топологически подобных второму линейному виду колеба-
колебаний (см. рис. 12.11, а также соотношение A2.30)) [4].
Влияние сил пространственного заряда
и отражений от концов замедляющей структуры
на генерацию в релятивистской ЛОВ
Рассмотрим влияние пространственного заряда в релятивистской
ЛОВ. Для этого воспользуемся результатами работы И.В. Пегеля [31],
посвященной анализу нестационарных процессов в ЛОВ с помощью
2,5-мерной осесимметричной версии полностью электромагнитного ко-
кода KARAT [32]. Особенностью моделирования здесь является непо-
непосредственное решение уравнений Максвелла в реальной сложной гео-
Карсинотрон как распределенная автоколебательная система
419
метрии прибора. Исследовалось взаимодействие электронного пучка
только с аксиально-симметричными модами замедляющей системы
типа гофрированный волновод. Основные параметры прибора, кото-
которые закладывались в расчеты, были следующие: рабочий диапазон 3-
сантиметровый; замедляющая система имела длину 12 см и состояла из
8 гофр с периодом гофрировки 1,48 см; радиус катода, формирующего
электронный пучок составлял 1,0 см. Сопротивление связи пучка с
— 1-й пространственной гармоникой волны Eqi составляло порядка 2 Ом
на рабочей частоте. Энергия инжекции электронного пучка на входе
в замедляющую систему составляла около 450 кэВ.
Наиболее интересным в полностью электромагнитном моделирова-
моделировании, в отличие от модели типа A3.24)-A3.26), является то, что учиты-
учитываются все без исключения пространственные гармоники. Кроме этого
в таких моделях существует возможность учесть двумерные эффекты
в пучке и, в частности, процессы токооседания на замедляющую струк-
структуру.
Одновременно в работе [31] исследовалась одномерная модель
РЛОВ, учитывающая взаимодействие электронного пучка только
с одной —1-й пространственной гармоникой. В этой модели для
исследования влияния пространственного заряда величины его поля,
вычисленные при фиксированных радиусах электронного пучка
и волноведущей структуры, учитывались с коэффициентом а, который
изменяется в пределах 0 -г 1. Другой способ исследования динамики
в ЛОВ при различных значениях величины пространственного
заряда — изменение радиусов волновода и пучка. Однако он
имеет ряд сложностей, связан-
связанных с изменением соотноше-
соотношений между амплитудами раз-
различных пространственных гар-
гармоник поля пространственного
заряда с изменением соотноше-
соотношений радиусов пучка и волнове-
волноведущей системы. Это вносит в ис-
исследуемую систему еще один до-
дополнительный фактор сложно-
сложности и, поэтому не использовался
в работе [31].
На рис. 13.16 приведена мощ-
мощность генерации в зависимости
от тока инжектируемого пучка.
Из рисунка видно, что мощность
генерации РЛОВ как функция
тока имеет четко выраженный максимум. Этот эффект можно объяс-
объяснить и в рамках одномерной модели, но с учетом объемного простран-
пространственного заряда [31].
0,5
0,4
0,3
0,2
0,1
о
~/>ГВт
Автомодуляция
7 I
/о,кА
Рис. 13.16. Зависимость мощности ге-
генерации в релятивистской ЛОВ (пол-
(полностью электромагнитное моделиро-
моделирование) от тока инжектируемого пучка
(из работы [31])
14*
420
Лекция 13
30
20
10
0,2
0,4
0,6
0,8
30
20
10
б 0
0,7
5,0
10,0
/, кА
Рис. 13.17. Зависимости электронного к.п.д., полученные в рамках одномер-
одномерной модели ЛОВ, для различных значений коэффициента пространственного
заряда а и тока пучка (из работы [31])
На рис. 13.17а [31] приведены зависимости электронного к.п.д., полу-
полученные в рамках одномерной модели ЛОВ, как функции коэффициента
пространственного заряда а при различных токах пучка. Из рисунка
видно, что кривые г)(а) имеют максимум, причем к.п.д. в максимуме
растет с увеличением тока пучка. Заметим, что падение г](а) справа от
максимума выражено тем более, чем больше ток пучка. На рис. 13.176
показана эффективность генерации как функция тока пучка для раз-
различных а. Из него видно, что зависимость мощности от тока пучка
в ЛОВ может быть существенно более сложной, чем приведенная на
рис. 13.16 кривая с одним максимумом. Поскольку одномерная модель
не учитывает изменение дисперсионных характеристик замедляющей
структуры в присутствии электронного пучка, единственным механиз-
механизмом влияния поля пространственного заряда на эффективность ЛОВ
является изменение продольных распределений амплитуды тока и его
фазы относительно волны. Действительно, интенсивность энергообме-
Карсинотрон как распределенная автоколебательная система
421
на на элементарную длину dx составляет
0,5я
^ = R
ах
где 0 = срi — (fjr — относительная фаза тока. Положение максимума
тока (а, следовательно, электронного сгустка) в тормозящей фазе поля
соответствует значениям 0 от тг/2 до Зтг/2.
На рис. 13.18 представлены продольные распределения относитель-
относительной фазы (а) и амплитуды тока пучка (б) в релятивистской лампе
обратной волны при токе пучка 12 кА. Увеличение коэффициента а
приводит к улучшению фази-
ровки ВЧ-тока, захватывающе-
захватывающему не только восходящие левые,
но и нисходящие правые ветви
кривых г](а). Отсюда следует,
что если рост эффективности
генерации на левых ветвях rj (a)
(рис. 13.17) обусловлен в том
числе и улучшением фазиров-
ки, то падение эффективности
генерации справа от максиму-
максимума никак с этим не связано.
Совершенно иным образом
ведет себя амплитуда тока пуч-
пучка / (рис. 13.186). При слабом
пространственном заряде (а ^
^ 0,4), её величина на второй
половине лампы значительно
возрастает, что ведет к росту
-0,5тг
5
4
3
2
1
0
I/I,
отн.ед. /^С
!/JS4a = 0x"
M65 V_^^
i i
6
4
i
10
см
Рис. 13.18. Продольные распределения
относительной фазы (а) и амплитуды
тока пучка (б) в ЛОВ для различных
коэффициентов пространственного за-
заряда а (из работы [31])
эффективности энергообмена.
Однако при дальнейшем увели-
увеличении а длина участка с нема-
немалой величиной |/| становится существенно меньше полной длины про-
пространства взаимодействия. Интенсивность энергообмена на коллектор-
коллекторном конце резко падает. Фактически происходит уменьшение эффектив-
эффективной длины прибора (рис. 13.18^; а = 0,65). Таким образом изменение
продольного распределения амплитуды тока и объясняет резкий спад
эффективности на правой части кривой if]{a). Оптимальное значение
величины пространственного заряда лежит в диапазоне 0,2 -г- 0,5.
Как уже обсуждалось выше, значительное влияние на динами-
динамику ЛОВ, особенно релятивистских, оказывает отражение излучения
от концов электродинамической замедляющей системы. Замедляющая
структура релятивистского карсиноторона представляет собой слабого-
фрированный волновод с запредельным сужением на пушечном конце.
422 Лекция 13
Отражаясь от запредельного сужения, волна распространяется в по-
попутном направлении с фазовой скоростью v^1 и излучается в сторону
коллектора [31, 34, 35]. Предполагая, что v^1 сильно отличается от ско-
скорости пучка г?о, так что взаимодействием с прямой гармоникой можно
пренебречь г), для её амплитуда Т+ можно записать уравнение вида
где s = A — vrp/vo) / A + ^гр/^о) — параметр, характеризующий от-
отличие групповой скорости волны от скорости электронного пучка.
Здесь считается, что фазовая скорость обратной гармоники v^1 = г>о,
и групповые скорости прямых и обратных гармоник равны по величине
и противоположно направлены.
Амплитуды прямой и обратной волны на границах системы связаны
соотношениями
= 0) = Ro?(Z = 0), F(Z = 1) = Rizj(k°-kl)lT+{ti = 1), A3.28)
где Ro и Ri — соответственно комплексные коэффициенты отражения
на левой и правой границах, ко = ujo/v^1 = ujo/vo, k\ = ujo/v^1 , ujq —
частота синхронизма. Поскольку решение уравнения A3.27) можно
представить следующим образом:
J-+(t,?)=.F+(t-s?,0), A3.29)
то исключим из рассмотрения прямую волну, переписав граничное
условие A3.26) для обратной волны в виде
Т{т, i = 1) = Т{т - s, ? = 0)ре^. A3.30)
Здесь вместо коэффициентов отражения, фигурирующих в соотноше-
соотношениях A3.28), введен единственный комплексный параметр
ре^ = RoR^^0'^1, 0 < р < 1. A3.31)
При больших коэффициентах отражения замедляющая структура
карсинотрона представляет собой резонансную колебательную систему,
собственные частоты которой без учета дисперсии групповой скорости
даются выражением [37]
пп = ^!L±1) A3.32)
г) Несмотря на сильный рассинхронизм, при определенных условиях вза-
взаимодействие с полем попутной волны может быть существенно за счет то-
того, что вблизи пушечного конца лампы, где пучок слабо сгруппирован, ее
амплитуда велика, так что она сообщает пучку значительную скоростную
модуляцию [36].
Карсинотрон как распределенная автоколебательная система 423
т. е. спектр собственных мод эквидистантный, причем межмодовое рас-
расстояние определяется величиной 2тг/A + s).
В работах [38-40] выделены два механизма перехода от режимов
стационарных колебаний к автомодуляции в распределенных электрон-
электронно-волновых автоколебательных системах. Первый из них, названный
автомодуляционным, связан, во-первых, с запаздывающим характером
обратной связи (т.е. распределенной природой системы) и, во-вторых,
с кинематической перегруппировкой электронных сгустков в сильном
поле (т.е. амплитудной нелинейностью системы). Второй механизм —
частотный — заключается в одновременном возбуждении нескольких
собственных мод высокодобротной колебательной системы, куда поме-
помещена активная среда. Конкуренция этих мод и определяет динамику
нестационарных процессов. При амплитудном механизме нарастают
главным образом возмущения амплитуды стационарного состояния,
при этом происходит модуляция только одной моды, остальные подав-
подавляются в результате конкуренции. При частотном механизме накапли-
накапливаются возмущения фазы. Частотный механизм характерен для резо-
резонансных автогенераторов (например лазеров на свободных электронах
[40] или ЛБВ-генераторов с запаздывающей обратной связью [38]).
Теоретические и экспериментальные исследования, приведенные
в работе [41], позволяют утверждать, что при малых отражениях в ЛОВ
реализуется амплитудный механизм, а при больших — частотный. В ней
показано, что при малых коэффициентах р < 0,3 отражения слабо
влияют на динамику системы. Увеличение р приводит к сильному изме-
изменению бифуркационных параметров, меняется и характер переходного
процесса. Вначале практически устанавливается режим стационарной
генерации, затем появляется медленно нарастающая во времени моду-
модуляция амплитуды. Как показано в работе [41], такое поведение связано
с жестким возбуждением соседней резонансной моды.
В работе [34] приведены результаты расчетов нестационарных про-
процессов в релятивистском карсинотроне в случае сильных отражений. На
рис. 13.19, взятом из этой работы, приведены границы областей самовоз-
самовозбуждения и автомодуляции на плоскости параметров нормированный
ток пучка-безразмерная длина системы k$l. Расчеты выполнены для
следующих параметров: 7о = 1,5, р = 0,7, vrp/vo = 0,32 (обычно для
релятивистских ЛОВ vrp значительно меньше vq). Фаза параметра
отражений ф линейно зависит от k$l в соответствии с формулой A3.31).
На границе области самовозбуждения (линия 1) видны характерные
пики, соответствующие неблагоприятным значениям ф. Граница воз-
возникновения автомодуляции имеет сложный вид. К пикам на границе
самовозбуждения вплотную примыкают области, в которых потеря
устойчивости происходит по частотному механизму (область В). Выше
расположена область, в которой реализуется амплитудный механизм
424
Лекция 13
14
12
Г 8
' 6
4
2 -
30 31
A
A
>
I
В \
с
A
4
\\ A
I I I
32 33 34 35 36
Безразмерная длина
37
Рис. 13.19. Границы области самовозбуждения и автомодуляции на плоскости
параметров ток пучка-электрическая длина лампы для релятивистского
карсинотрона (из работы [34]). Здесь А — область одночастотной генерации,
В и С — области автомодуляции; линия 1 отмечает границу самовозбуждения
лампы
(область С). Авторы работы [34] используют термины cross-excitation
instability, т.е., неустойчивость, обусловленная возбуждением несколь-
нескольких резонансных мод, и overbunch instability, т. е. неустойчивость вы-
вызванная перегруппировкой пучка. Очевидно, что частотный механизм
должен появляться в области неблагоприятных фаз (им соответствуют
пики на кривой 1 (рис. 13.19)), где пучок взаимодействует одновременно
с двумя соседними модами.
Позднее были проведены подробные исследования влияния ампли-
амплитуды р и фазы ф коэффициента отражения на возникновение авто-
автомодуляции в РЛОВ [37]. На рис. 13.20 приведены границы самовозбу-
самовозбуждения Lq и автомодуляции La на плоскости параметров (р, L) для
малых (р = 0,2) и больших (р = 0,7) значений амплитуды коэффи-
коэффициента отражений G0 = 1,5, N = 10, s = 0,52). Из рисунка видно,
что границы областей самовозбуждения и автомодуляции зависят от
фазы ф тем сильнее, чем больше отражения, т. е. чем сильнее проявля-
проявляются резонансные свойства колебательной системы РЛОВ. Они также
сдвигаются с ростом р в сторону меньших L, что связано с возрастанием
добротности колебательной системы.
При малых р динамика РЛОВ с отражениями подобна динами-
динамике РЛОВ без отражений. Самовозбуждение происходит примерно на
частоте самовозбуждения РЛОВ без отражений ?1°. С ростом L про-
происходит уменьшение основной частоты, что обусловлено эффектом
Карсинотрон как распределенная автоколебательная система
425
L
3,0
2,5
2,0
1,5
^-. La ^'''
Lo /V
о
0,5
1,0
1,5
Рис. 13.20. Границы области самовозбуждения и автомодуляции на плоско-
плоскости параметров (ф, L) для релятивистского карсинотрона (из работы [37]).
Сплошные линии соответствуют случаю больших отражений р = 0,7, штри-
штриховые — малых отражений р = 0,2
электронного смещения частоты. Автомодуляция возникает с ростом L
мягко по амплитудному механизму. Границы самовозбуждения и ав-
автомодуляции приблизительно «противофазны». Это можно объяснить
следующим образом: с ростом ф в соответствии с формулой A3.32)
изменяются собственные частоты ?1п резонансных мод. При ф « 0,6тг
частота fi_i близка к частоте QP, а частоты автомодуляционных са-
сателлитов, возникающих по амплитудному механизму, далеки от дру-
других резонансных частот. Таким образом самовозбуждение облегчается
и происходит при меньших значениях L, а автомодуляция возникает при
значениях L, близких к соответствующим бифуркационным значениям
для нерезонансной системы. При ф « 1,6тг частота ОР наоборот, рас-
располагается примерно посредине между собственными частотами fi_i
и ?1-2 - Частоты автомодуляционных сателлитов оказываются близкими
к этим частотам. Поэтому Lq увеличивается, a La уменьшается.
При сильных отражениях самовозбуждение РЛОВ всегда происхо-
происходит на частоте той или иной резонансной моды. Электронное смещение
частоты проявляется слабо. На границе самовозбуждения виден чет-
четко выраженный «клюв» при значении фазы ф = 1,6тг. Слева от него
частота генерации близка к частоте fi_i, справа — к ?1-2- Автомоду-
Автомодуляция возникает по частотному механизму, т. е. происходит жесткое
возбуждение еще одной резонансной моды, номер которой зависит от
параметров s и ф. Таким образом частота автомодуляции примерно
кратна межмодовому расстоянию 2тг/A + s). Граница автомодуляции
имеет существенно более сложный вид, чем в случае малых р.
426
Лекция 13
Экспериментальное исследование сложной динамики
в релятивистской ЛОВ
Экспериментальные исследования нестационарных режимов гене-
генерации релятивистской ЛОВ с мощностью порядка 100 кВт проводились
в Институте прикладной физики РАН (Нижний Новгород) [42-44]. Экс-
Экспериментальный макет работал на частоте 9 ГГц [42]. В качестве элек-
электродинамической структуры использовался плавногофрированный осе-
симметричный волновод. Геометрические размеры системы были сле-
следующие: средний радиус волновода г = 1,2 см; период гофрировки А =
= 1,7 см; глубина гофра h = 0,25 см; длина пространства взаимодей-
взаимодействия / = 29 или 44 см. Фокусирующее магнитное поле имело величину
2,5 Тл. Ускоряющее напряжение составляло 70 -г- 150 кВ (т.е. лампа
была слаборелятивистской); ток пучка менялся в пределах 3 -г 35 А.
Пусковой ток иссследуемой структуры составлял около 3 А при длине
макета / = 29 см и понижался до 1 А при / = 44 см.
Излучение снималось с коллекторного конца пространства взаи-
взаимодействия. Огибающая высокочастотного импульса для различных
токов пучка приведена на рис. 13.21. Было получено, что в лампе
с длиной пространства взаимодействия 44 см синусоидальная автомоду-
автомодуляция имела место при уже при токах пучка порядка нескольких ампер
^ММ/^^
^40 не
100 нс
Рис. 13.21. Огибающая выходного излучения релятивистского карсинотрона
при различных значениях тока пучка: а — I = 3 А; б — 21 А; в — 28 А; г —
35 А (из работы [42])
Карсинотрон как распределенная автоколебательная система 427
(рис. 13.21а). По мере увеличения тока пучка она становилась слож-
нопериодической (рис. 13.21 б, в), а затем при токах пучка более 30 А
автомодуляция превращается в хаотическую (рис. 13.21 г). Отсутствие
обнаруженных ранее режимов стационарной генерации объясняется
авторами работы [42] тем, что уменьшение тока пучка ниже 3 А было
сопряжено с большими техническими трудностями. Это также подтвер-
подтверждается тем, что в короткой лампе (/ = 29 см) стационарные режимы
генерации наблюдались при значениях тока пучка в диапазоне 3 -г 20 А.
Другая причина нестационарности процессов генерации связана с мед-
медленным изменением формы импульсов тока и ускоряющего напряжения
в течении импульса тока. Дело в том, что релятивистские ЛОВ исполь-
используют в качестве источника электронов сильноточные наносекундные
ускорители, действие которых основано на явлении взрывной эмиссии,
и длительность импульса тока которых невелика. Поэтому нестацио-
нестационарность формы импульсов тока и ускоряющего напряжения играет
принципиальную роль. Это было подтверждено в работах [33, 34], где
было проведено численное моделирование нестационарных процессов
в ЛОВ с длительностью импульса тока порядка 100 не и с учетом его
нестационарности.
Заметим также, что экспериментальное исследование режимов гене-
генерации при больших значениях тока пучка и энергии инжекции электро-
электронов наталкивалось на трудности, связанные с укорочением длительно-
длительности ВЧ-импульсов при уровнях мощности более 100 кВт [42]. Это укоро-
укорочение вызывается ВЧ-пробоями внутри электродинамической системы.
Релятивистский карсинотрон и радиолокация
Обсудим возможности и преимущества использования релятивист-
релятивистского карсинотрона в качестве источника мощности в радиолокацион-
радиолокационных станциях (РЛС) [29]. Информационные возможности РЛС зависят
от ряда параметров, основные из которых — величина средней мощно-
мощности передатчика и распределение мощности СВЧ-излучения в течение
импульса. Мощные короткие импульсы излучения, идущие с достаточно
большой частотой повторения, позволяют с высокой степенью точности
определять расстояние до объекта, получать высокую контрастность
радиолокационного изображения на фоне отражений от местных пред-
предметов, а обработка информации от серии импульсов позволяет опреде-
определить скорость движения объекта без использования эффекта Доплера
[45, 46]. В стандартной РЛС укорочение импульсов осуществляется,
в основном, в приемных трактах РЛС при пропускании частотно моду-
модулированных сигналов через оптимально сжимающие фильтры [29, 46].
Недостатком такого метода являются технические трудности сжатия
импульса более чем в 30-100 раз, а также наличие принципиально
428 Лекция 13
неустранимых боковых лепестков в корреляционной функции сигна-
сигналов, которые способны давать ложную информацию о местоположении
объекта.
Поэтому вызывает интерес получение мощных коротких электро-
электромагнитных импульсов непосредственно в передающей части РЛС, что
позволяет, во-первых, упростить всю радиотехническую схему станции
(отпадает необходимость введения частотной модуляции, излишними
становятся сжимающие фильтры), во-вторых, исключить появление
ложных сигналов, и, наконец, уменьшить мертвую зону перед РЛС
и существенно увеличить ее помехозащищенность.
Обсудим некоторые особенности конструкции РЛС, использующей
в качестве источника коротких электромагнитных импульсов реля-
релятивистскую ЛОВ, созданную в Институте прикладной физики РАН
(Нижний Новгород) [29]. Выбор в качестве генератора для РЛС ре-
релятивистского карсинотрона обусловлен простотой конструкции, адап-
адаптивностью, сравнительно высокой эффективностью при использовании
замедляющей системы с неоднородным сопротивлением связи [48, 49].
Особенностями конкретного генератора, используемого в радиолокаци-
радиолокационной станции, была возможность перестройки генерируемой частоты.
Выход генератора согласовывался с квазиоптическим преобразовате-
преобразователем типа волны, передающим электродинамическим трактом и облуча-
облучателем антенны. Для обеспечения надежной длительной работы коллек-
коллектор генератора был снабжен системой охлаждения, а сама релятивист-
релятивистская лампа обратной волны была помещена в поле сверхпроводящего
криомагнитного соленоида с напряженностью до 30 кЭ.
Приемная часть РЛС конструировалась с учетом принимаемого сиг-
сигнала—короткого и, соответственно, широкополосного импульса. Кроме
того, все входные цепи должны были быть защищены от перегрузок на
время генерации импульса, а также на случай близко расположенного
от станции отражающего объекта с большой эффективной площадью
отражения. Основная развязка между передающей и приемной частью
достигалась за счет использования раздельных антенн, работающих на
передачу и прием сигнала. Входной усилитель при перегрузках мог вно-
вносить дополнительное затухание в приемный тракт. Для эффективного
обнаружения объектов с малой эффективной поверхностью рассеяния
была предусмотрена система селекции движущихся целей, осуществля-
осуществляющаяся путем черезпериодного вычитания отраженных сигналов [45].
Локация различных объектов, проведенная в реальных условиях
натурных испытаний, показала высокую эффективность РЛС. Такие
объекты, как речные суда (даже малые) на фоне воды и берега были ясно
различимы на расстоянии в несколько десятков километров. Локация
самолетов (см. рис. 13.22) на тех же расстояниях на фоне облаков
и на фоне подстилающей поверхности при их движении вблизи линии
Карсинотрон как распределенная автоколебательная система 429
Самолет^;. ^ Самолет
Остров .:
Рис. 13.22. Радиолокационные сигналы, полученные на РЛС, использующей
релятивистский карсинотрон: а — сигнал, отраженный от острова и летящего
над ним на высоте 100 м самолета АН-2; б— те же сигналы, но с применением
черезпериодного вычитания. Интервал времени между соседними точками
соответствует времени запаздывания прихода отраженных сигналов, равно-
равному 5 не (из работы [29])
горизонта давала ясные изображения движущихся объектов. Отраже-
Отражения от местных предметов (деревьев, облаков и т. д.) на расстоянии
свыше нескольких километров были настолько малы, что позволяли
работать в ряде случаев без применения селекции движущихся целей.
Тем не менее, черезпериодное вычитание локационных сигналов поз-
позволяет избавиться и от изображений близко расположенных предметов
(одиноко стоящие деревья, специальные контрольные отражатели) (см.
рис. 13.216).
Список литературы
1. Рапопорт Г.И. Нелинейная теория генератора обратной волны с
периодической замедляющей структурой // Радиотехника и элек-
электроника. 1964. Т. 9, № 3. С. 483.
2. Электроника ламп с обратной волной / Под ред. В.Н. Шевчика и
Д.И. Трубецкова. — Саратов: Изд-во Сарат. ун-та, 1975.
3. Кузнецов СП., Трубецков Д. И. Нестационарные нелинейные яв-
явления при взаимодействии электронного потока, движущегося в
скрещенных полях, с обратной электромагнитной волной // Изв.
вузов. Радиофизика. 1977. Т. 20, № 2. С. 300.
4. Трубецков Д.И., Четвериков А. П. Автоколебания в распределен-
распределенных системах «электронный поток — встречная (обратная) элек-
электромагнитная волна» // Изв. вузов. Прикладная нелинейная ди-
динамика. 1994. Т. 2, №5. С. 9.
5. Вайнштейн Л.А., Солнцев В.А. Лекции по сверхвысокочастотной
электронике. — М.: Сов. радио, 1973.
430 Лекция 13
6. Гинзбург П.С, Кузнецов СП., Федосеева Т.Н. Теория переходных
процессов в релятивистской ЛОВ // Изв. вузов. Радиофизика. 1978.
Т. 21, №7. С. 1037.
7. Безручко Б.П., Кузнецов СП., Трубецков Д.И. Эксперименталь-
Экспериментальное наблюдение стохастических автоколебаний в динамической
системе электронный поток — обратная электромагнитная волна //
Письма в ЖЭТФ. 1979. Т. 29, № 3. С. 180.
8. Безручко Б.П., Кузнецов СП., Трубецков Д.И. Стохастические
автоколебания в системе электронный пучок-обратная волна // В
сб. Нелинейные волны. Стохастичность и турбулентность. Горь-
Горький: АН СССР Институт прикладной физики, 1980, С. 29.
9. Безручко Б.П., Булгаков Л.Б., Кузнецов СП., Трубецков Д.И.
Экспериментальное и теоретическое исследование стохастических
автоколебаний в лампе обратной волны // Лекции по электронике
СВЧ и радиофизике E-я зимняя школа-семинар инженеров). Са-
Саратов: Изд-во СГУ, 1980, С. 25.
10. Безручко Б.П., Булгаков Л.Б., Кузнецов СП., Трубецков Д.И.
Стохастические колебания и неустойчивость в лампе обратной
волны // Радиотехника и электроника. 1983. Т. 28, №6. С. 1136.
11. Гинзбург П.С, Кузнецов СП. Периодические и стохастические
автомодуляционные режимы в электронных генераторах с распре-
распределенным взаимодействием // Релятивистская высокочастотная
электроника. Горький: АН СССР Институт прикладной физики,
1981, С. 101.
12. Безручко Б.П. Экспериментальное исследование многочастотных
автоколебаний в ЛОВ типа О // Вопросы электроники СВЧ. Меж-
Межвузовский научный сборник (вып. II). Саратов: Изд-во СГУ, 1983,
С. 174.
13. Клеен Б., Пешль К. Введение в электронику СВЧ. — М: Сов.
радио, 1963, Т. 2.
14. Островский А.О., Ткач Ю.Б. К теории автомодуляционных про-
процессов в релятивистском карсинтроне // Письма в ЖТФ. 1991.
Т. 17, №18. С. 10.
15. Балакирев Б.А., Островский А.О., Ткач Ю.Б. К теории автомо-
автомодуляционной неустойчивости колебаний в связанных карсинотро-
нах // Письма в ЖТФ. 1990. Т. 16, № 19. С. 8.
16. Балакирев Б.А., Островский А.О., Ткач Ю.Б. К теории авто-
автомодуляционных процессов в системе связанных гофрированных
волноводов, возбуждаемых прямолинейными электронными пото-
потоками // ЖТФ. 1991. Т. 61, № 9. С. 94.
17. Безручко Б.П., Гинзбург П.С, Кузнецов СП. Теоретическое и
экспериментальное исследование переходных процессов в ЛОВО-
генераторе // Лекции по электронике СВЧ и радиофизике D-
Карсинотрон как распределенная автоколебательная система 431
я зимняя школа-семинар инженеров; книга V). Саратов: Изд-во
СГУ, 1978, С. 236.
18. Шевчик В.П., Трубецков Д. И. Аналитические методы в электро-
электронике СВЧ. — М.: Сов. радио, 1970.
19. Рыскин Н.М., Титов В.Н., Трубецков Д.И. Детали перехода к
хаосу в системе электронный пучок — обратная электромагнитная
волна // Доклады РАН. 1998. Т. 358. С. 620.
20. Рыскин П.М., Титов В. П. О сценарии перехода к хаосу в одно-
параметрической модели лампы обратной волны // Изв. вузов.
Прикладная нелинейная динамика. 1998. Т. 6, № 1. С. 75.
21. Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и
волн. — М.: Наука, 1984.
22. Неймарк Ю.И., Ланда П.С. Стохастические и периодические ко-
колебания. — М.: Наука, 1984.
23. Анищенко B.C. Сложные колебания в простых системах. — М.:
Наука, 1990.
24. Шустер Г. Детерминированный хаос. — М.: Мир, 1988.
25. Кузнецов А.П., Кузнецов СП., Сатаев И.Р. Критическая динами-
динамика одномерных отображений. Часть I. Сценарий Фейгенбаума //
Изв. вузов. Прикладная нелинейная динамика. 1993. Т. 1, №1.
С. 15.
26. Manneville P., Pomeau J. Different waves to turbulence in dissipative
dynamical systems // Physica D. 1980. V. 1. P. 219.
27. Берже П., Помо П., Видаль К. Порядок в хаосе. О детерминисти-
детерминистическом подходе к турбулентности. — М.: Мир, 1991.
28. Астахов С.А., Безручко Б.П., Зборовский А.В., Трубецков Д.И.
Исследование сложной динамики системы электронный поток -
обратная волна с отражениями (эксперимент и численное мо-
моделирование) // Материалы международной научно-технической
конференции «Актуальные проблемы электронного приборостро-
приборостроения», Том 1. 7-9 сентября 1998 г., Саратов, Россия. Саратов: изд.-
воСГТУ, 1998, С. 39.
29. Бункин Б.В., Гапонов-Грехов А.В., Ельчанинов А.С, Загулов
Ф.Я., Коровин С.Д., Месяц Г.А., Осипов М.Л., Отливанчик Е.А.,
Петелин М.И., Прохоров A.M., Ростов В.В., Сараев А.П., Си-
сакян И.П., Сморгонский А.В., Суворов В.А. Радиолокатор на
основе СВЧ-генератора с релятивистским электронным пучком //
Письма в ЖТФ. 1992. Т. 18, № 9. С. 61.
30. Трубецков Д.П., Анфиногентов В.Г., Рыскин Н.М., Титов В.П.,
Храмов А.Е. Сложная динамика электронных приборов СВЧ
(нелинейная нестационарная теория с позиций нелинейной дина-
динамики) // Радиотехника. 1999. Т. 63, №4. С. 61.
432 Лекция 13
31. Пегель И.В. Моделирование нестационарных процессов в реля-
релятивистской лампе обратной волны методом макрочастиц // Изв.
вузов. Физика. 1996. Т. ?, № 12. С. 62-83.
32. Tarakanov V.P. User's manual for code KARAT. — Springfield, VA.:
BRA, 1992.
33. Levush В., Antonsen T.M., Bromborsky A., Lou W.R., Carmel Y.
Relativistic backward wave oscillator: theory and experiment // Phys.
Fluids B. 1992. V. 4, № 7. P. 2293.
34. Levush В., Antonsen T.M., Bromborsky A., Lou W.R., Carmel Y.
Theory of relativistic backward wave oscillator with end reflections //
IEEE trans. Plasma Sci. 1992. V. 20, № 3. P. 263.
35. Levush В., Antonsen T.M., Vlasov A.N., Nusinovich G.S., Miller
S.M., Carmel Y., Granatstein V.L., Destler W.W., Bromborsky A.,
Schlesiger C, Abe D.K., Ludeking L. High-efficiency relativistic
backward wave oscillator: theory and design // IEEE trans. Plasma
Sci. 1996. V. 24, №3. P. 843.
36. Коровин С Д., Полевин С Д., Ройтман A.M., Ростов В. В. Влия-
Влияние попутной волны на эффективность генерации СВЧ излучения
в релятивистской ЛОВ // Изв. вузов. Физика. 1996. Т. 39, №12.
С. 49.
37. Титов В.Н. «Тонкая структура" процессов автомодуляции и пере-
перехода к хаосу в распределенной автоколебательной системе «элек-
«электронный поток — обратная электромагнитная волна". — Дисс...
... к.ф.-м.н. Саратов, 2000, 186с.
38. Блиох Ю.П., Бородкин А.В., Любарский А.Г., Онищенко Н.М.,
Файнберг Я.Б. Применение метода функционального отображе-
отображения для исследования ЛБВ-генератора с запаздывающей обрат-
обратной связью // Изв. вузов. Прикладная нелинейная динамика. 1993.
Т. 1,№1,2. С. 34.
39. Кузнецов СП. Сложная динамика генераторов с обратной свя-
связью // Изв. вузов. Радиофизика. 1982. Т. 25, № 12. С. 1410.
40. Antonsen T.M., Levush В. Mode competition and suppression in free
electron laser oscillators // Phys. Fluids B. 1989. V. 1, №5. P. 1097.
41. А миров Р.Ш., Безручко Б. П., Исаев В. А., Четвериков А. П. Вли-
Влияние отражений на нестационарные процессы в ЛОВО // Лекции
по электронике СВЧ и радиофизике F-я зимняя школа-семинар
инженеров) Кн. 2. Саратов: Изд-во СГУ, 1983, С. 90.
42. Гинзбург Н.С., Зайцев Н.И., Иляков Е.В., Кулагин И. С, Новожи-
Новожилов Ю.В., Сергеев А.С, Ткаченко А.К. Наблюдение автомодуля-
автомодуляционных режимов генерации в мощной ЛОВ // Письма в ЖТФ.
1998. Т. 24, №20. С. 66.
Карсинотрон как распределенная автоколебательная система 433
43. Гинзбург Н.С., Зайцев Н.И., Иляков Е.В., Кулагин И.С, Но-
Новожилов Ю.В., Сергеев А. С. Теоретические и эксперименталь-
экспериментальные исследования автомодуляционных режимов генерации 3-
сантиметровой ЛОВ с мегаваттным уровнем мощности // Изв.
вузов. Прикладная нелинейная динамика. 1999. Т. 7, № 5. С. 60.
44. Ginzburg N.S., Ilyakov E.I., Kulagin I.S., Novozhilova Yu.P.,
Sergeev A.S., Zaitsev N.I. Observation of self-modulation regimes of
generation in the powerfull BWO // In: the Proceedings of International
University Conference «Electronics and Radiophysics of Ultra-High
Frequencies», May 24-28, 1999, St. Petersburg, Russia, P. 186.
45. Дулевич B.E., Коростелев А.А., Мельник Ю.А. и dp. Теоретиче-
Теоретические основы радиолокации. — М.: Сов.радио, 1964.
46. Скольник М.И. Справочник по радиолокации. — М.: Сов.радио,
1976.
47. Радиолокация (Методы обработки и сжатия импульсов). Спецвы-
Спецвыпуск // Зарубежная радиоэлектроника. 1987. No 1.
48. Белоусов В.И., Бункин Б.В., Гапонов-Грехов А.В. и др. // Письма
в ЖТФ. 1978. Т. 4, № 23. С. 1443.
49. Ковалев Н.Ф., Петелин М.И., Райзер М.Д., Сморгонский А.В.
II В кн.: Релятивистская высокочастотная электроника. Горький,
1979, С. 76.
Лекция 14
НЕКОТОРЫЕ МЕТОДЫ РЕШЕНИЯ
НЕЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ ЗАДАЧ
ЭЛЕКТРОНИКИ
Высокоскоростные ЭВМ... сделали возможным
рассмотрение протекания взаимодействия во вре-
времени, и теперь нет необходимости искать усколь-
ускользающий. . .установившийся режим. Вместо этого
имеется возможность исследовать в динамиче-
динамических системах переходный процесс. В исследу-
исследуемых системах возможны, конечно, некоторые
установившиеся состояния...
Р. Хокней
И в вычислениях на логарифмической линейке
можно найти известную поэзию.
К.Ф. Гаусс
Метод «частиц в ячейке». Учет влияния пространственного заря-
заряда. Методы расчета полей в замедляющей системе: метод эквива-
эквивалентных схем и уравнение возбуждения. Конечно-разностный метод
решения нестационарных уравнений релятивистского карсинотрона
в лагранжевых переменных. Математическое моделирование элек-
электронных приборов с помощью самосогласованной системы уравнений
Максвелла-Власова. Применение метода функционального отображе-
отображения к анализу нестационарных процессов в ЛЕВ с запаздывающей
обратной связью.
В данной лекции рассмотрим различные методы численного анализа
нелинейных нестационарных уравнений электронных приборов с дли-
длительным взаимодействием. Эти задачи, как можно видеть из эпиграфа
к лекции, возникли из необходимости анализа устойчивости тех или
иных стационарных решений и рассмотрения переходных процессов
в тех или иных физических системах.
Изложение будет строиться на примере достаточно простых числен-
численных схем, базирующихся на математических моделях, учитывающих
только основные физические явления в исследуемых приборах. Зада-
Задача данной лекции продемонстрировать некоторые из таких моделей
Методы решения нелинейных нестационарных задач 435
приборов с длительным взаимодействием и способы построения со-
соответствующих конечно-разностных схем, удовлетворяющих условиям
устойчивости и выполнения законов сохранения.
В лекции будет изложена достаточно традиционная методика мо-
моделирования процессов в лампах бегущей и обратной волны с одним
исключением — в основу будет положен не метод крупных частиц в ла-
гранжевых переменных, ставший классическим в СВЧ-электронике,
а метод «частиц в ячейке», завоевывающий с развитием вычислитель-
вычислительной техники все большую популярность в электронике, физике плазмы,
гидродинамике и т. д. г). Далее кратко остановимся на рассмотрении
некоторых общих вопросов полномасштабного моделирования вакуум-
вакуумных сверхвысокочастотных приборов, следуя обзору [1]. В конце лекции
остановимся на результатах исследования ЛБВ-генератора с запазды-
запаздывающей обратной связью (шумотрона) с помощью метода функцио-
функционального отображения, предложенного Ю.П. Блиохом и др. [3], который
позволяет детально изучить механизм стохастизации в шумотроне.
Метод «частиц в ячейке». Учет влияния
пространственного заряда
Численное моделирование самосогласованных процессов взаимо-
взаимодействия электронного потока с бегущей как прямой, так и обратной
(встречной) электромагнитной волной, как уже указывалось, разбива-
разбивается на две части. С одной стороны, это нахождение величины сгруппи-
сгруппированного тока («электронная» часть задачи), с другой стороны — само-
самосогласованное решение «полевой» части: нахождение электромагнит-
электромагнитных полей, возбуждаемых в электродинамической структуре, и полей
пространственного заряда. Рассмотрим решение первой части задачи,
а именно нахождение величин сгруппированного тока и плотности про-
пространственного заряда, с помощью метода частиц в ячейке («particle-
in-cell»). Достоинство данного метода по сравнению с классическим ме-
методом крупных частиц в лагранжевых переменных (последний кратко
обсуждался в лекции 9 применительно к задаче решения стационарных
уравнений ЛБВ на ЭВМ) состоит в том, что благодаря использова-
использования переменных Эйлера, когда каждая макрочастица характеризует-
характеризуется только своими координатами и скоростью, можно легко строить
распределения плотностей токов и зарядов вдоль пространства взаи-
взаимодействия, а также при необходимости восстанавливать траектории
заряженных частиц (например, строить пространственно-временную
г) В то же время, кратко изложим классическую схему, базирующуюся на
методе макрочастиц в лагранжевых координатах, численного решения нели-
нелинейных нестационарных уравнений РЛОВ, использованную еще в первой
работе, посвященной исследованию сложных режимов генерации в РЛОВ
[2]
436 Лекция Ц
диаграмму движения электронов или находить различные функции
распределения электронов).
При использовании метода частиц в ячейке электронный поток
представляется в виде совокупности макрочастиц, которые характе-
характеризуются своими координатами в пространстве гт = (гхт,гут,ггт),
скоростями vm = (vxm, vyrn, vzrn) и зарядами qm (m — номер частицы).
Форма частиц определяется конкретной геометрией задачи. Так, если
мы рассматриваем плоскую геометрию, например, диодный промежу-
промежуток, то частица — плоский заряженный лист. В случае цилиндрического
волновода при наличии аксиальной симметрии частица — либо заря-
заряженный диск, либо кольцо, если рассматривается трубчатый пучок или
учитывается расслоение по поперечной координате. При рассмотрении
двух- и трехмерных задач форма макрочастиц может быть весьма
сложной.
Ограничимся в рамках данной лекции одномерным приближением,
т. е. будем предполагать, что частицы полностью замагничены внешним
продольным магнитным полем и двигаются только вдоль продольной
оси х. При этом каждая частица несет одинаковый заряд q. Тогда
каждая частица характеризуется скоростью v = vx, координатой в про-
пространстве взаимодействия х и зарядом q = е • Npj где Np — число
«реальных» электронов, «содержащихся» в одной макрочастице (е —
заряд электрона; понятно, что, если перейти к удельному заряду элек-
электрона г\ — е/т, то для макрочастицы он совпадет с удельным зарядом
электрона, поэтому в дальнейшем будем пользоваться параметром rj).
С учетом сделанных замечаний уравнение движения заряженной
частицы в нерелятивистстком случае запишется в виде
m) +En3(xm)), A4.1)
где E(xm) и En3(xm) — напряженность поля электромагнитной волны
и поля пространственного заряда в точке с координатой хш.
Численное нахождение поля электромагнитной волны будет рас-
рассматриваться в следующем разделе. Что касается поля пространствен-
пространственного заряда, то оно ищется в одномерном случае как Епз(хт) = —
— д(р(хт)/дх, где (р(х) есть решение уравнения Пуассона
§ = 0. A4.2)
Здесь pi — плотность пространственного заряда ионного фона, который
предполагается неподвижным, к± — поперечное волновое число, равное
в случае распространения Eqi-волны к± = 2,405/г^. Здесь распределе-
распределение поля в поперечном направлении задаваемое соотношением Ех(г) =
= Jo(k±r); гь — радиус пучка; предполагается, что пучок полностью
заполняет волноведущую структуру; Jq — функция Бесселя нулевого
Методы решения нелинейных нестационарных задач 437
порядка. Будем пользоваться такой же нормировкой физических вели-
величин, как и в лекции 4 (раздел, посвященный анализу гидродинамиче-
гидродинамической модели диода Пирса):
Р —> Pop, v —> ^0^5 ф ~~^ VoP/Vi E ~^ voE/Lrj, x —у Lx, t —у Lt/vo,
A4.3)
тогда уравнение Пуассона перепишется в безразмерных переменных
в виде
^-к2±<р = а2(р-п), р(О) = <рA) = 0, A4.4)
где п = pi/р — нормированная на невозмущенную плотность простран-
пространственного заряда пучка плотность пространственного заряда ионного
фона.
Введем пространственную сетку с шагом Ах = 1/УУ<7,где GV<7 + 1) —
число узлов сетки. В этом случае, аппроксимируя вторую производную
д2 /дх2 центральной разностью 2-го порядка, можно получить конеч-
конечно-разностный аналог уравнения Пуассона:
W+i-ayi + W-i-fc2yj = a2(pj_n)) ^0 = ^с=0. A4.5)
Для численного решения уравнений движения необходимо перейти
в них также к дискретной форме. Обозначим через t дискретное время,
toid — предыдущий момент времени, тогда tnew = гоЫ + At — следую-
следующий момент дискретного времени. Здесь Д? — шаг во времени. Введем
такой параметр вычислительной схемы как число частиц на ячейку
(т. е. на шаг пространственной сетки Ах) в невозмущенном состоя-
состоянии по- Тогда условия нормировки (читателю предлагается показать
это самостоятельно) требуют положить Д? = Ах/по. Для численного
интегрирования уравнений движения A4.1) используется схема с пере-
перешагиваниями. Введем в рассмотрение момент времени tav = t + At/2.
Выражение f(tav) означает, что значение некоторой переменной / бе-
берется в средний момент времени между tnew и to\d- С учетом введенных
обозначений формулировка метода с перешагиваниями применительно
к уравнениям движения записывается в виде
v(tnew) = v(toid) + a(tav)At, A4.6)
x{tnew) = x(toid) + v(tav)At, A4.7)
где а — ускорение частицы.
Возникает вопрос: зачем использовать схему с перешагиваниями,
а не ограничиться обычным методом Эйлера или методами Рунге-
Кутта более высокого порядка? Понятно, что использование методов
с большим объемом вычислений (каковыми являются методы Рунге-
Кутта высокого порядка) приведут к большим затратам машинного вре-
времени (число частиц может достигать достаточно большого значения).
438 Лекция Ц
Применение одношагового метода Эйлера приводит к неустойчивости
соответствующей разностной схемы [7]. Найдем границы устойчивости
метода с перешагиваниями. Для анализа этого будем решать методом
с перешагиваниями уравнение линейного осциллятора
d2a/dt2 = -со2а, A4.8)
аналитическое решение которого хорошо известно: а = ai(to)
+ ^2(^0) sino;o?. Тогда, в соответствии с соотношениями A4.6) и A4.7),
уравнения метода с перешагиваниями будут иметь вид
da/dt —у (at — a*-i) /At = ^t-i/2^
da/dt -+ (at+i - at) /At = vt+1/2,
dv/dt -+ (ut+i/2 - vt_1/2)/At = (at+i - 2at + at-i) /At2,
где через t ± 1 и t ± 1/2 обозначены моменты времени t ± At и i ± At/2
соответственно. Вычисления начинаются в некоторый момент време-
времени t с начальными значениями at, vt-\/2- Сначала по известному at
вычисляется сила, далее величина ^+1/2 рассчитывается из уравнения
для ускорения, а затем из уравнения для скорости определяется новое
значение a^+i. После этого процесс повторяется. Для устойчивости
уравнения центрированы во времени. Подставляя конечно-разностное
представление в уравнение линейного осциллятора A4.8), находим со-
соответствующий конечно-разностный аналог:
Q>t+i — %a>t + a>t-i
-± —2
A4.9)
Решение этого уравнения можно найти, полагая, что: ai = Лехр [—jut],
где А — начальное значение, а и — неизвестно. Делая подстановку
и проводя соответствующие тождественные преобразования, получаем
уравнение для частоты:
sin (иAt/2) = ±u0At/2. A4.10)
График зависимости и от и® A4.10) показан на рис. 14.1. Видно,
что для и At/2 <^i 1 величина и « и®, что и требуется. Однако при
uj^At > 2 полностью действительное решение для частоты становится
комплексным с нарастающими и затухающими корнями, что определя-
определяет численную неустойчивость. Определим величину фазовой ошибки
для малых uioAt (понятно, что амплитудная ошибка равна нулю при
выполнении условия uioAt < 2). При oo^At <^i 1 раскладывая и в ряд
получаем,что
со At « uj0At (I + l/6(ojoAt/2J + ...), A4.11)
Методы решения нелинейных нестационарных задач
439
что дает квадратичный член ошибки. Суммарная фаза после N шагов
равна uiNAt, т. е. суммарная ошибка будет иметь вид
Nu0At(uj0At/2J/6 = 1/24
A4.12)
©А*
Сделаем некоторые оценки. Если предположить, что максимально
допустимая ошибка равна 1/24 рад, то получаем для числа шагов
формулу N = l/(uioAtK, что при
u>0At = 0,1 составляет 1000 шагов
(или около 16 периодов), а при u$At =
= 0,3 — 37 шагов B периода). Ес-
Если можем позволить себе ошибку по-
порядка 1 рад, при uioAt = 0,1 ме-
метод дает верные результаты в тече-
течении 384 периодов, а при uj^At = 0,3
в течение 42 периодов. Таким обра-
образом при применении методов с пере-
перешагиванием надо четко представлять,
что увеличение шага интегрирования
при uioAt < 2 оставляет равной ну-
нулю амплитудную ошибку, но увели-
увеличивает фазовую ошибку как куб раз-
размера шага. При невыполнении усло-
условия uj^At < 2 решение начинает на-
нарастать во времени (появляется чис-
численная неустойчивость). Соответству-
Соответствующий анализ для схемы Эйлера пред-
предлагаем сделать самостоятельно и пока-
показать, что она неустойчива при любом
выборе величины шага во времени At.
Однако вернемся к решению урав-
уравнений движения A4.6) и A4.7). Ско-
Скорости и координаты частиц берутся
на различных временных сетках (см.
рис. 14.2, на котором представлено расположение временных шагов
для различных величин), сдвинутых относительно друг друга на At/2.
Поэтому уравнения движения для частиц запишутся в виде
Рис. 14.1. Зависимость ш от ujq
для уравнения гармоническо-
гармонического осциллятора, полученная ме-
методом с перешагиваниями для
уравнения в конечных разно-
разностях. Частота ш согласуется с loq
при малых uioAt, но она больше,
чем правильное значение при
увеличении cuoAt. Для cuoAt > 2
появляется численная неустой-
неустойчивость: одна ветвь распадает-
распадается на четные и нечетные шаги,
проявляя сдвиг фаз, равный тг
vt+l/2 t-1/2 _
E(xm)At,
A4.13)
Координаты частиц могут принимать любые значения в пределах
0 ^ хт ^ 1. В то же время такие величины как плотность простран-
пространственного заряда и тока, а также амплитуды полей определяются в уз-
узлах дискретной пространственной сетки. Плотность пространственного
заряда определяется с помощью процедуры «взвешивания». Рассмот-
Рассмотрим схему в которой используется наиболее распространенная в методе
440
Лекция Ц
частиц процедура билинейного взвешивания. Каждой частице присва-
присваивается элементарный заряд Q = 1/по- Если частица с номером т при-
принадлежит ячейке пространственной сетки, расположенной между j-м
и (j + 1)-м узлами, т. е.
jAx
\)Ах
A4.14)
(см. рис. 14.3), то вклады этой частицы в плотность заряда в j-м и (j +
+ 1)-м узлах равны:
= (xt
-jAx)Q. A4.15)
Понятно, что такое определение плотности пространственного заряда
означает, что pj определяется в моменты времени ^ + 1ит.д. Полная
плотность пространственного за-
заряда в j-м узле определяется
суммированием по всем части-
частицам, удовлетворяющим неравен-
неравенству A4.14), т. е.
t+l/2
J -
, „• —п.
A4.16)
f-1/2
x+Ax/2
Ток пучка задается в точках
пространства с координатами j +
+ Axj2 (j + 1/2) и в каждом узле
пространственной сетки определя-
определяется следующей процедурой. Нор-
Нормируя величину тока / на посто-
постоянный ток /о = poVoS (S — пло-
площадь поперечного сечения пучка),
находим, что каждая частица пере-
переносит элементарный ток, равный
J = I/no- Определяя ток пучка
в моменты времени t — At/2, t +
+ At/2 и т. д., получаем (см. рис. 14.3), что вклад частицы с номером j,
удовлетворяющей условию A4.14), в ток в j-м и j + 1-м узлах дается
выражением (аналогично выражению A4.15))
Рис. 14.2. Расположение временных
шагов, используемое в методе инте-
интегрирования с перешагиваниями
где величину хш ' проще всего определить как среднее арифметиче-
арифметическое между координатами частицы в моменты времени t и t — 1, т.е.
Методы решения нелинейных нестационарных задач
441
JAx
Рис. 14.3. Схема билинейного взвешивания плотности пространственного за-
заряда и тока электронного пучка в методе «частиц в ячейке»
х^ ' = {х1ш + ж^) /2 г). Полный ток в j-м узле определяется как
ft-l/2 _
3
= ?'
t-1/2
mj
A4.18)
(суммирование, как и в случае определения плотности пространствен-
пространственного заряда осуществляется только по частицам, удовлетворяющим
условию A4.14)).
Определенная с помощью билинейного взвешивания величина плот-
плотности пространственного заряда p(xj) используется для нахождения
распределения потенциала пространственного заряда. Будем рассмат-
рассматривать бесконечно широкий поток, т.е. к± = 0. Тогда уравнение A4.5)
упростится:
— 2(fj +
2
i\x
=0.
(Л Л Л(\\
A4.19)
Численное решение разностного уравнения A4.19) сводится к решению
системы уравнений относительно неизвестных функций cpj = cp(jAx).
Один из часто используемых методов для решения этой задачи —
метод функции Грина, обсужденный в лекции 9 (раздел, посвященный
численному решению нелинейных уравнений ЛБВ). Другой метод —
это применение той или иной разновидности метода прогонки [5, 7]
или спектральных методов, базирующихся на применении процедуры
быстрого преобразования Фурье [7]. Однако в ряде случае удается
решить уравнение Пуассона быстрее, чем методом прогонки, и при этом
значительно точнее, чем спектральными методами. Рассмотрим про-
простейший случай такой схемы, предложенный Дж. Роучем в монографии
[5], а именно метод распространения вектора ошибки (метод EVP),
который базируется на линейности уравнения Пуассона и сводится
к следующей процедуре.
х) Более подробно вопросы влияния на свойства расчетных схем способа
взвешивания тех или иных величин обсуждаются в монографии [7].
442 Лекция Ц
Пусть {(f}j — некоторые предварительные значения потенциала
в узлах сетки, за исключением <J?o = Фnc ~ ^> которые за счет гра-
граничных условий являются точными. Произвольно положим ф\ = фо =
= 0. Это значение (р\ отличается от истинного значения </?i на величину
ошибки е:
(р1 = ф1 + е. A4.20)
Тогда можно определить все предварительные значения cpj на осно-
основании соотношения A4.19) (напоминаем, что рассматривается случай
kj_ = 0) при первом обходе узлов, начиная с j = 2:
= Ax2a2(Pj - п) + 2<fj - fij-!. A4.21)
При этом
fij + ej =(pj. A4.22)
Подставляя A4.22) в уравнение Пуассона, получаем рекуррентную фор-
формулу для расчета распространения ошибки:
ej+1 =2ej-ej-1. A4.23)
Очевидно, что во = 0, e<i — е, тогда
Ч = 0" - 1)е. A4.24)
Ошибка е вычисляется в конце первого обхода с учетом граничного
условия на правой границе (р^с = 0:
e = -(pNc/{Nc-l). A4.25)
На втором проходе осуществляется исправление предварительных ве-
величин с использованием предыдущего соотношения
<Р> = Фз + U - 1)е- A4-26)
Поле Ej находится численным дифференцированием на основе цен-
центральных разностей в средних точках пространства взаимодействия:
и левых или правых разностей на границах пространства взаимодей-
взаимодействия:
Ах с Ах
Зная значение поля в узлах сетки, можно с помощью линейной
интерполяции вычислить поле, действующее на частицу с координа-
координатой хт, удовлетворяющей A4.14):
Е(хт) = Ej((j + 1)Дж - хт) + Ej+1(xm - jAx). A4.27)
Это значение затем подставляется в уравнения движения A4.13).
Методы решения нелинейных нестационарных задач
443
Итак, зная поле Е (см. следующий раздел) и Епз, можно с помощью
уравнений движения A4.6) вычислить координаты и скорости частиц
в следующий момент времени. На каждом временном шаге At в систему
инжектируется по новых частиц с начальными условиями
Частицы, для которых выполняется условие х1ш > 1, исключаются из
расчетной процедуры (оседают на коллекторе).
Методы расчета полей в замедляющей системе:
метод эквивалентных схем и уравнение возбуждения
Рассмотрим две методики для нахождения поля Е электромагнит-
электромагнитной волны в линии передач. Первая из них заключается в том, что
замедляющая система представ-
представляется в виде эквивалентной
длинной линии. Рассмотрим
такую схему применительно
к исследованию взаимодействия
электронного потока с прямой
волной (схема ЛБВ), следуя
работе И. Морейя и Ч. Б'дселла
[8]. Будем рассматривать ЛБВ
со спиральной замедляющей
системой. Эквивалентная схема
замедляющей системы, через
которую проходит электронный
поток, приведена на рис. 14.4. Элементы цепи выбираются из условия
соответствия фазовой скорости
Рис. 14.4. Эквивалентная схема за-
замедляющей системы ЛБВ, использу-
используемая в численном моделировании ме-
методом «частиц в ячейке» (из [8])
= l/y/LC
A4.29)
и поля волны в лабораторном макете в месте, где проходит электронный
пучок, и в эквивалентной схеме. Последнее выражается соотношением
Zo =
= V?/2P.
A4.30)
На рисунке обозначено: 1П — ток между (п — 1)-м и n-м узлами, Vn —
напряжение в n-м узле; Со = С do, Lq = Ldo — емкость и индуктивность
на ячейку Ах = do; qn — заряд электронного пучка, определяемый
методом частиц в ячейке.
Рассматриваемая длинная линия в предположении малости Аж, At
описывается телеграфными уравнениями, дополненными слагаемым,
описывающим возбуждение электромагнитных волн пучком:
dV _ 1 dl ус dq dl _ l dV
dt Co dx Co dt' dt Lo dx
A4.31)
444 Лекция Ц
Здесь к < 1 — параметр связи пучка с линией передачи, который
в общем случае зависит от частоты. Действительно, в модели ЛБВ,
ограниченной в поперечном направлении, движение пучка вызывает
токи смещения, что в свою очередь вызывает токи проводимости в за-
замедляющей системе. Определение функциональной зависимости к(оо)
достаточно сложно и зависит от соотношения радиусов пучка и замедля-
замедляющей системы, а также от вида конкретной моды, на которой работает
лампа.
Заметим, что возбуждение линии передач электронным пучком мо-
может быть учтено и несколько по-другому. Из уравнения непрерывности
можно записать
где 1ь — сгруппированнй ток пучка, определяемый методом частиц
в ячейке (индекс «6» введен для того, чтобы различать ток электронного
пучка и ток, наведенный в линии передачи). Следовательно, в уравне-
уравнении A4.31) вместо второго слагаемого надо записать выражение вида
к-тг-Ь-. Оба метода описания электронного потока полностью эквива-
эквивалентны и выбор конкретного соотношения определяется исключитель-
исключительно «качеством» взвешивания на сетке величины плотности простран-
пространственного заряда и тока пучка (см. монографии [9, 10]). Обычно, плот-
плотность заряда более удобна для вычисления, поэтому при разработке
конечно-разностных схем пользуются телеграфным уравнением в виде
A4.31).
Используя такую же, как и раньше, нормировку физических вели-
величин, уравнения A4.31) в дискретном виде запишим как
At С
rt-l/2 _ rt-1/2 * + l t
In-\-l/2 1n-l/2 Qn + 1/2 ~ Qn-1/2
Ax At
A4.33)
rt+Z/2 _ rt + 1/2 , vt _ vt
in in = --L V" + l Vn-1 A4.34)
A* ah Ax v }
где а безразмерный параметр, равный а = 2t]Io/vq.
Рассмотрим условия на пространственные и временные шаги, при
которых вышеописанная схема будет устойчива и, кроме этого, будут
выполняться условия A4.29), A4.30). Исключая второе слагаемое их
правой части уравнения A4.33) (слагаемое, определяемое сгруппиро-
сгруппированным током пучка) и полагая, что величины / и V меняются по закону
ехр [—j{ujiAt — кпАх)], получим, аналогично тому, как это делали
в лекции 4, что соотношения A4.33) и A4.34) примут вид
v_a шъ\п(кАх/2)
~ ~C кАх/2 '
v
uiAt/2 ~ C кАх/2
Методы решения нелинейных нестационарных задач 445
ш sin (ш At/2) j _ 1 о; sin (к Ах/2) у,
coAt/2 ~ ~^L кАх/2 '
Из условия разрешимости данной системы уравнений находим диспер-
дисперсионное уравнение «дискретной» линии передачи:
sm2(ujAt/2) = А* 2 sm2(kAx/2). A4.35)
V ' } LCAx2 V ' J K J
Отсюда сразу следует условие Куранта устойчивости разностной схе-
схемы, накладывающее ограничение на соотношение между временным
и пространственным шагом сетки:
At^\fbCAx. A4.36)
Перепишем теперь уравнение A4.35) в виде:
2 /оА2 1 fooAt/2\2 fsm2(kAx/2)\2 п л *>7\
"* = U) = 1С \кЩ2) UnaUt/2)J ' A4'37)
Отсюда следует, что равенство Уф = 1/y/LC A4.29) будет выполняться
только в случае, когда Уф = Ах/At. Таким образом, мы получили
условия, накладываемые на шаги на временной A4.36) и пространствен-
пространственной A4.37) сетке. Заметим, что представление замедляющей системы
в виде эквивалентной схемы позволяет достаточно просто учесть потери
в ней: достаточно добавить в схему элементарной ячейки активную
проводимость R.
На рис. 14.5 показаны некоторые типичные результаты моделирова-
моделирования ЛБВ с помощью программы IBC Code (И. Морей, Ч. Б'дселл, [8]),
использующей вышеописанную методику построения численной схе-
схемы г). Показаны зависимость скорости потока от длины пространства
взаимодействия, мощность взаимодействия и распределение электро-
электронов пучка по энергиям на коллекторе для следующих основных пара-
параметров лампы и численной схемы: L = 0,2 м; г>о = Ю7 м/с; Уф = 107 м/с;
/о = 10 мА; / = 500 МГц; гь = 1 мм; число узлов пространственной
сетки 7VC = 200.
Методика численного решения задачи о нестационарном возбужде-
возбуждении линии передач с помощью метода эквивалентных схем имеет ряд
достоинств, основное из которых связано с тем, что существует возмож-
возможность аппроксимации известной (например, из эксперимента) диспер-
дисперсионной характеристики во всей полосе частот, в том числе и вблизи
границ полос пропускания замедляющей системы. Вместе с тем вы-
вышеприведенная методика, основанная на применении эквивалентной
длинной линии, не дает достаточно общего описания явлений при вза-
взаимодействии с полем замедляющей системы.
х) Результаты получены авторами с помощью вышеназванной программы,
которая свободно распространяется в Internet (http://ptsg.eecs.berkeley.edu).
446
Лекция Ц
Ux-X Phase Space
: *
Position
LDglO(Powei> / Input Power)
Energy (eU)
1101
Рис. 14.5. Результаты моделирования ЛБВ-усилителя с помощью программы
IBC Code с параметрами, приведенными в тексте. На рисунке демонстрирует-
демонстрируется «снимок» экрана компьютера при выполнении расчета: сверху приведены
зависимости скорости заряженных частиц от продольной координаты. Вни-
Внизу показаны зависимость отношения мощности взаимодействия к входной
мощности в логарифмическом масштабе от координаты пространства взаи-
взаимодействия и энергетический спектр пучка на коллекторе
Рассмотрим поэтому другой подход к нахождению поля Е волны,
а именно использование нестационарной теории возбуждения волно-
волновода. Отметим сразу, что излагаемая ниже методика не может при-
применяться для сигналов с широким спектром и вблизи границ полос
пропускания. Проанализируем теперь случай взаимодействия потока
с обратной волной (схема ЛОВ).
В этом случае поле Е выражается как Е(х, t) = Re I Ее^шЬ~^°х^ L
где Е — медленно меняющаяся амплитуда. Уравнение возбуждения
обратной волны в размерных переменных имеет вид
^~Р dt дх
A4.38)
где / — Фурье-амплитуда первой гармоники сгруппированного тока.
При переходе к безразмерным переменным A4.3) уравнение A4.38)
принимает вид
дЕ дЕ
A4.39)
где ? = vrpril3QKLI0/vQ = 2vrpuj2LC3/v$, С3 = I0K/4V0 — параметр
Пирса.
Методы решения нелинейных нестационарных задач 447
Комплексные величины Е и I могут быть представлены через ве-
вещественные следующим образом. Введем
2тг
/cos = 1 Г цх t)co8(w(t-x))d(u>t),
2тг J
о
2тг
/sin = _L J I(x,t)8in(w(t-x))d(u>t),
0
E = #cos cos (u)(t - x)) - Es[n sin (u)(t - x)).
Здесь I(x,t) — ток пучка, определяемый с помощью вышеописанного
метода «частиц в ячейке». Тогда уравнение A4.39) в комплексных пере-
переменных перепишется в виде системы двух уравнений в действительных
величинах:
' дЁ*'ш „. дЁ*'ш
it гр дх ~ s' '
A4.40)
dEcos _ „, dEcos _
Особенностью интегрирования уравнений A4.40) совместно с уравнени-
уравнениями движ;ения макрочастиц является то, что уравнения возбуждения
решаются на другой пространственно-временной сетке, чем уравнения
движения. Действительно, так как Esm , Ecos, /sin, /cos — медленно
меняющиеся функции, то достаточно говорить об их изменении за время
порядка AT = 2тг/сс? и на расстояниях порядка АХ = 2тгг?ф/с(;. С учетом
этого конечно-разностная схема для уравнений A4.40) будет иметь вид
— — 77 — ^^ — г • / A441)
AT Vrp АХ ~ * 7х' li4<4ij
где используется уже ранее обсуждаемая нами схема разностей против
потока. При решении уравнений движения заряженных частиц величи-
величины {E}j в течение времени AT ^> А? считаются постоянными.
Конечно-разностный метод решения нестационарных
уравнений РЛОВ в лагранжевых переменных
В качестве исходных уравнений рассмотрим систему нестационар-
нестационарных уравнений релятивистского карсинотрона A3.20)—A3.22), которые
представим в несколько ином виде. Произведем замену переменных:
-1/2
A4.42)
448 Лекция Ц
Тогда уравнения A3.20)—A3.22) примут следующий вид (штрихи у без-
безразмерных переменных опускаем):
Щ = I (г - 1) = g(e), f| = /ReА<*° = /(Л,0),
27Г A4.43)
дА дА _ /г Г „—jo ли _ Kfi\
-rjj- - -щ - -11 J e J av0 - -J\P)i
•«-«•-*• &••
Численное решение системы уравнений A4.43) и A4.44) ищется как
и раньше в узлах двухмерной сетки на плоскости переменных (?,т)
с шагами Ах и Д? соответственно. Заменим электронный поток N круп-
крупными частицами, начальные фазы которых составяляют #о = 2тгп/УУ
(п = 1, . . . N). Тогда JF) может быть заменена суммой вида
т
п=0
Уравнения движения интегрируются по известным значениям вели-
величины поля А на предыдущем шаге по времени с помощью двухшаговой
схемы «предиктор—корректор» (см., например, [9, 10]). В этом случае
сначала делается прогноз:
?j+i/2 - ej + -
а затем это значение уточняется:
4+1 = 4 + дж/((л* + л*-+1)/2,в)+1/2), et+1 = в]
+ дж/((л + л+1)/2,в)+1/2), e = в]
Найденные значения в^ позволяют рассчитать значение функций Jj =
= Щ).
Что касается расчета комплексной амплитуды поля А1-, то уравне-
уравнение возбуждения можно интегрировать с помощью любой устойчивой
консервативной разностной схемы, например, с помощью уже использо-
использовавшейся схемы разностей против потока или с помощью более сложных
схем, например, можно применить схему Лакса-Вендроффа, имеющую
второй порядок точности [12, стр. 299-304]. Уравнения схемы Лакса-
Вендроффа получаются разложением функции А в ряд Тейлора по г:
Методы решения нелинейных нестационарных задач 449
Производная ЧА- в разложении A4.45) берется непосредственно из
уравнения возбуждения A4.43), а 2 находится путем диффиринци-
ОТ
рования уравнения возбуждения:
д2А _ д_ (дА_ _ Л _ д^А _ (dJ_ dJ_\
дт2 дт \di ) д?2 \дт дх) "
Далее производные по координате ? и по времени г аппроксимируются
конечно-разностными отношениями, что приводит к уравнению
- А, + At ( ^ ^ J +
^ A1 9 A2 J- A* I1 — ТЬ~г I1 I1
/ij + 1 — z/1.7 ~r Slj — 1 Jj Jj Jj ~ Jj-l
2
После несложных преобразований конечно-разностный аналог уравне-
уравнения возбуждения примет вид
a' + L (Ч AJ + <Л5 И + AU)
Коэффициент перехода (см. формулу D.13)) для полученного конечно-
разностного уравнения возбуждения имеет вид
G = 1- j^smkAx- ^ (I-cos к Ах), A4.47)
откуда условие Куранта:
At < Ах. A4.48)
Для окончательного определения задачи необходимо тем или иным
образом задать граничные и начальные условия. Из условия А(? = 1) =
= 0 получаем первое граничное условие
At = 0, A4.49)
где S — число узлов разностной схемы по координате. Второе граничное
условие получается, если учесть, что J(? = 0) = 0 (первая гармоника
сгруппированного тока в начале пространства взаимодействия равна
нулю), что дает
'дА ^ =0. A4.50)
15 Д. И. Трубецков, А. Е. Храмов
450 Лекция Ц
Аппроксимируя производные в уравнении A4.50) односторонними раз-
разностями в узле пространственной сетки j = 0, легко получить следую-
следующее граничное условие:
Данное выражение имеет первый порядок точности в отличие от урав-
уравнения A4.46), которое имеет второй порядок точности. Однако так как
оно используется только на одном шаге по координате, то это не будет
сильно сказываться на точности всей разностной схемы.
Вид начальных условий А(т = 0) = А°(?) не играет особой роли,
так как, если начальная амплитуда мала, то имеет место достаточно
длинный участок экспоненциального роста, где существует возмож-
возможность сшить решение, полученное из линейной теории и нелинейной
теории. Например, начальные условия можно задать в виде [2]
(А0 = const, 0< f < 0,9,
Л°(О = < A4.52)
[/L°sin2[57r(l-OL 0,9 <^< 1.
Именно с помощью схемы, подобной описанной в данном разделе,
были получены результаты, представленные в предыдущей лекции.
Математическое моделирование электронных
приборов с помощью самосогласованной системы
уравнений Максвелла—Власова
Современный уровень фундаментальных исследований в электрони-
электронике и задачи инженерного проектирования реальных устройств требуют
необходимости изучения физического прибора «как целого» с учетом
взаимосвязей всех процессов [1]. При проведении реальных физических
экспериментов на экспериментальных макетах такой подход является
естественным. Однако он требует больших затрат средств и времени,
а интерпретация полученных экспериментальных результатов оказы-
оказывается нередко затруднительной. Более того, часто оказывается невоз-
невозможно ответить на те или иные вопросы в результате только натурно-
натурного эксперимента. Поэтому возникает необходимость построения «гло-
«глобальных» математических моделей СВЧ-устройств (в первую очередь,
использующих сильноточные релятивистские электронные пучки), ко-
которые достаточно полно самосогласованным образом отражают работу
прибора в целом [13].
Одним из наиболее общих способов рассмотрения физических про-
процессов данного класса является рассмотрение самосогласованной си-
системы кинетических уравнений, описывающих динамику заряженных
частиц, совместно с полной нестационарной системой уравнений Макс-
Максвелла для эволюции электромагнитного поля [1, 13]. При анализе ди-
Методы решения нелинейных нестационарных задач 451
намики электронов пучка в вакуумных СВЧ-устройствах с большой
степенью точностью можно предполагать, что имеет место выполнение
условия бесстолкновительности, которое означает, что длина свобод-
свободного пробега электронов между столкновениями существенно больше,
чем характерный размер пространства взаимодействия. Тогда описание
движения электронного потока возможно провести с помощью кинети-
кинетического уравнения Власова:
i r i т i r i p/m
p = e\f dp, J = e /v dp, v = ^
Здесь /(?,r,p) — функция распределения частиц, имеющих заряд е
и массу покоя т.
Нестационарные электромагнитные поля описываются с помощью
уравнений Максвелла
— = -rotE, — = rotH - J, A4.54)
divD = p, divB = 0. A4.55)
Самосогласованнная система уравнений Максвелла-Власова, реша-
решаемая в двух- и трехмерном случае, позволяет наиболее полно описать
физические процессы в сверхвысокочастотных приборах с наибольшей
степенью общности. Например, моделирование приборов с длительным
взаимодействием с помощью уравнений Максвелла-Власова означает
учет взаимодействия пучка сразу со всеми пространственными гармо-
гармониками, отражения электромагнитных волн от концов замедляющей
системы, остановок и отражений электронов в потоке и т. д. Другим
важным аспектом таких моделей является их универсальность. Так
формулировка моделей для различных сверхвысокочастотных прибо-
приборов (например, магнетрон, лампа обратной волны, клистрон и т.д.)
при использовании системы уравнений Максвелла-Власова различа-
различается лишь формой расчетной области, т.е. постановкой граничных
условий для электромагнитных полей и способом инжекции электронов
в область взаимодействия прибора. Это позволяет создавать универ-
универсальные программные продукты для моделирования процессов в элек-
электронных приборах сверхвысоких частот, так называемые, электромаг-
электромагнитные коды.
Рассмотрим основные принципы, которые лежат в основе построе-
построения численной схемы на основе самосогласованной системы уравнений
Максвелла-Власова [1, 7].
Первой частью самосогласованной задачи является нахождение
распределения плотности тока и плотности пространственного заря-
15*
452 Лекция Ц
да в пространстве взаимодействия прибора, которое требует анализа
кинетического уравнения A4.53). Решение бесстолкновительного ки-
кинетического уравнения традиционно базируется на методе «макроча-
«макрочастиц», который в настоящее время является практически единственно
возможным методом расчета пространственно многомерной динамики
заряженных частиц в самосогласованных задачах [4, 7, 14].
Суть метода частиц, как уже обсуждалось нами выше, базирует-
базируется на том, что пучок заряженных частиц моделируется с помощью
конечного (и достаточно малого!) числа макрочастиц с одинаковым
удельным зарядом. Каждая из этих частиц движется вдоль харак-
характеристик кинетического уравнения. По результатам этого движения
вычисляются интегральные характеристики, такие как плотность за-
заряда, плотность тока и др. Интегральные характеристики находятся
с помощью взвешивания частиц на пространственно-временной сетке.
Простейший вариант такого взвешивания в одномерном случае описан
в первом параграфе данной лекции. Подробное описание метода частиц
можно найти в монографиях [4, 7, 10], где все эти вопросы рассмотрены
достаточно детально и с большим числом примеров. Там же приведены
удобные для расчетов формы записи уравнений движения заряженных
частиц в различных системах координат (цилиндрической, полярной
и т.д.). Найденные с помощью взвешивания на сетке интегральные
характеристики (плотность тока и пространственного заряда) далее
используются при нахождении электромагнитных полей в расчетной
области.
Заметим, что использование метода частиц позволяет достаточно
легко рассматривать и моделировать такие явления как эмиссию с за-
заданными законами, абсорбцию заряженных частиц на стенках про-
пространства взаимодействия, столкновительные процессы при взаимодей-
взаимодействии электронных пучков с плазмой и т. д. [1, 13].
Второй частью самосогласованной задачи является нахождение
электромагнитных полей непосредственно из решения уравнений Макс-
Максвелла, которое наиболее часто основывается на методе конечных раз-
разностей. Заметим, что если уравнения A4.55) выполняются в начальный
момент времени и в процессе решения закон сохранения электрического
заряда выполняется, то эти уравнения будут справедливы и во все
последующие моменты времени, как это видно из уравнений A4.54)
[15]. Таким образом если вышеуказанные условия соблюдены, то для
расчета полей достаточно решать уравнения A4.54), что значительно
упрощает вычислительную процедуру.
Пространственные и временные производные в уравнениях A4.54)
заменяются центральными конечными разностями. С этой целью в рас-
расчетной области вводятся пространственная и временная сетки, причем
значения различных составляющих электрического и магнитного полей
определяются в узлах сеток, сдвинутых друг относительно друга на
Методы решения нелинейных нестационарных задач
453
X
!
! ех
Ez
У i
i
\ez
ДС/+1
Xj
Xj-i
Zi+1
X
Рис. 14.6. Двумерная сетка для численного решения уравнений Максвел-
Максвелла (а); ячейка трехмерной сетки (б)
половину шага /г/2. При этом возможно использование как сеток с пря-
прямоугольными ячейками (прямоугольник в двумерном случае и парал-
параллелепипед — в трехмерном), так и криволинейных сеток и нескольких
сеток с различными шагами [16, 17].
Во временной области вводится сетка с шагом ht. При этом значения
вектора электрической индукции D и напряженности электрического
поля Е определяются в моменты времени tn = nht, n = 1,2,3, ...,
а вектора магнитной индукции В и напряженности магнитного поля
Н — в моменты ?n+i/2 = (п + 1/2)ht. Тогда уравнения A4.54) в конеч-
норазностном во времени виде запишутся так:
A4.56)
dt
dt
где предполагается, что диэлектрическая е и магнитная ц проницае-
проницаемости являются скалярами. В конечно-разностных уравнениях A4.56)
введены обозначения E(tn) = Еп, H(tn) = Нп.
Если рассмотреть двумерную по пространству расчетную область,
расположенную в плоскости (ж, z) декартовой системы координат, при-
причем вариации поля по третьей координате отсутствуют (д/ду = 0), то
координаты узлов (т. е. точек, в которых вычисляются значения со-
составляющих полей) определяются следующим образом (см рис. 14.6а):
для Ех Xj+x/2 = (j + 0,5)Лж, Z{ = ihz\ для Ez Xj = jhx, zi+1/2 = (i +
+ 0,5)hz; для Ну Xj+1/2 = (j + 0,5)Лж, Zi+1/2 = (« + 0,5)Лг. Здесь hx
и hz — шаги пространственной сетки по координатам х и z соответ-
454 Лекция Ц
ственно, индексы % и j характеризуют положение ячейки сетки в про-
пространстве. В случае границы области, несовпадающей с координатной
сеткой, ее обычно аппроксимируют ступенчатой линией, проходящей по
линиям сетки 1) .
Расчет «двумерных» электромагнитных полей легко обобщается на
расчет полей в соответствии с формулами A4.56) в трехмерных обла-
областях. На рис. Ы.бб изображены ячейка трехмерной пространственной
сетки и точки определения узловых значений, составляющих напряжен-
напряженности электрических и магнитных полей. Узлы электрического поля
расположены в середине ребер ячейки, а магнитного поля — в центре её
граней.
Вышеописанная схема интегрирования конечно-разностных анало-
аналогов уравнений Максвелла является полностью «явной», т.е. для нахо-
нахождения полей на (п + 1)-м шаге по времени необходимо использовать
значения соответствующих сеточных величин только на (п — 1)-м шаге.
Явные схемы, как обсуждалось выше, устойчивы только при выполне-
выполнении условия Куранта, которое для данной задачи имеет вид [1]
ht < ^% A4.57)
сл/3
где hm\n — минимальный шаг пространственной сетки. Коэффициент
л/3 появляется в трехмерном случае. При использовании двумерной
сетки он заменяется на коэффициент у2, и в одномерном случае —
на 1.
На рис. 14.7 приведена схема расчета на одном шаге At во времени
с помощью вышеописанной электромагнитной модели.
В настоящее время существует несколько широко используемых
коммерческих и свободно распространяемых электромагнитных кодов.
Наиболее известен 2,5-мерный 2) коммерческий код MAGIC [19]. Дан-
Данный код, накладывая существенно меньшие требования на вычисли-
вычислительные ресурсы, чем полностью трехмерные коды, позволяет решать
широкий круг задач вакуумной релятивистской сверхвысокочастотной
электроники. Ограничением здесь является необходимость формулиро-
формулировать решаемую задачу принципиально в двумерном виде. О затратах
машинного времени позволяет судить тот факт, что моделирование
переходных процессов в 5,5 ГГц лампе бегущей волны, которые длятся
около трех времен распространения сигнала вдоль пространства взаи-
взаимодействия, занимало около двух часов на персональном компьютере
с процессором Pentium II 300 МГц [1]. При этом для моделирования
используется около 11000 макрочастиц на каждом временном шаге.
х) Существуют и более точные методы аппроксимации криволинейных гра-
границ [18].
2) То есть предполагается, что поля имеют вариации только в двух измере-
измерениях, однако, рассчитываются все три компоненты полей и скоростей частиц.
Методы решения нелинейных нестационарных задач
455
Определ
действ
час
(Е,В)
ение полей,
ующих на
:тицы
—> F
Интегрирование уравнений
частиц, движение частиц
At
Интегрировано зфавнений
пиля на иегке
(p,J) ->(Д5)
)
Инжекци
абсорбция ч
расчет
столкнове
Взвешивание на
(x,v) —> (p,J)
яи
астиц,
НИИ
Рис. 14.7. Диаграмма расчета на одном шаге Д? во времени модели, основан-
основанной на решении самосогласованной системы уравнений Максвелла-Власова
с помощью метода частиц и явной схемы интегрирования уравнений Макс-
Максвелла
Другим электромагнитным кодом, широко используемым отече-
отечественными учеными, является код KARAT [20]. Свободно распростра-
распространяемым полностью электромагнитным кодом является код XOOPIC,
разработанный группой Ч. Бедселла [21] г).
Применение метода функционального отображения
к анализу нестационарных процессов в ЛЕВ
с запаздывающей обратной связью
ЛБВ-генератор с запаздывающей обратной связью (шумотрон)
представляет собой, как отмечалось в лекции 3, систему с глобальной
неустойчивостью. Шумотрон был первым СВЧ-генератором мощных
шумовых сигналов, предложенным в конце 60-х годов [22]. Системы
с обратной связью до сих пор привлекают внимание исследователей
как эффективные генераторы хаотических широкополосных сигналов
сантиметрового и миллиметрового диапазона (например, [23-
25]). Математический анализ таких систем обычно базируется на
полуаналитическом или численном решении нелинейных нестаци-
нестационарных уравнений генератора (например, ЛБВ с цепью обратной
связи), которые определяют поведение системы при различных
параметрах обратной связи и нелинейного усилителя. С одной
стороны, анализ таких широкоплосных систем затруднен в силу
отсутствия соответствующей простой теории: для численного анализа
х) Информация о данном программном продукте доступна в Internet по
адресу http://ptsg.eecs.berkeley.edu.
456 Лекция Ц
подобных систем требуется решение уравнений Максвелла-Власова).
С другой стороны, решение соответствующих нелинейных уравнений
в частных производных даже достаточно простых моделей (например,
изложенная выше нелинейная нестационарная теория ЛОВ) требует
существенных затрат машинного времени для детального изучения
явлений в приборе и оптимизации его характеристик в широком
диапазоне изменения управляющих параметров.
В данном разделе будет рассмотрен для анализа системы с распреде-
распределенными параметрами (ЛБВ с запаздывающей обратной связью) метод
функционального отображения, предложенный группой исследовате-
исследователей из Харьковского физико-технического института: Ю.П. Блиохом,
А.В. Бородкиным, М.Г. Любарским, И.Н. Онищенко и Я.Б. Файнбер-
гом [3, 28]. Данный метод позволяет с точки зрения вычислительной
математики резко сократить время численного анализа соответству-
соответствующих уравнений в частных производных, описывающих исследуемую
систему.
Из процедуры вывода нестационарного уравнения возбуждения вол-
волновода понятно, что его легко обобщить на случай взаимодействия
с прямой волной — это приведет только к изменению знака перед произ-
производной по времени т. Тогда система, описывающая нелинейный ЛБВ-
усилитель без учета пространственного заряда и потерь в безразмерных
переменных будет иметь вид:
±^+^=;, A4.58)
2л-
о
д2и
= Re{JreJU\ A4.60)
(vg — безразмерная групповая скорость) с граничными условиями:
и@,т) = ио, <9п@,т)/<9? = 0. A4.61)
Обратная связь описывается простым соотношением:
-), A4.62)
где L — длина лампы, О — время задержки в цепи обратной связи,
Z — коэффициент обратной связи. Чтобы полностью определить задачу
необходимо также задать величину ^(О) на отрезке [— @ + L), 0], что
эквивалентно заданию распределения поля в виде:
^(O,r)|rG[o,0+L]=^o(r). A4.63)
Понятно, что исследование системы с обратной связью существенно
упроститься, если определить нелинейный функционал U, который
Методы решения нелинейных нестационарных задач
457
Рис. 14.8. Структура пространственно-временных связей в ЛБВ-генераторе
будет давать по заданному входному сигналу J~o(t) значение выходного
сигнала J-(L, r), т. е.
t)}. A4.64)
Такая зависимость определяется тем, что информация переносится по
двум типам характеристик (г = const (пучок) и vgr — ? = const (волна);
см. рис. 14.8, на котором представлены пространственно-временные
связи в ЛБВ-генераторе). Значение сигнала на выходе усилителя опре-
определяется значениями функции ^(т), заданной на интервале времени
[г, г — L]. Это и означает, что Ы является функционалом.
Если известен функционал U, то генератор с запаздывающей обрат-
обратной связью с учетом соотношения A4.63) может быть описан функцио-
функциональным отображением вида
jro(r + 0) = ZU \Tq{t)\ . A4.65)
Запись A4.64) полностью эквивалентна исходной задаче в частных
производных, так как пока еще не сделано никаких упрощающих пред-
предположений (кроме тех, которые присущи исходной системе уравнений
Рассмотрим теперь структуру функционального отображения. Так
как исходная система не имеет общего аналитического решения, то для
получения зависимости Ы необходимо сделать некоторые упрощающие
предположения. Рассмотрим их.
Пусть имеем на входе ЛБВ-усилителя монохроматический сигнал
J-u exp [jct;r]. Тогда распределение поля в пространстве взаимодей-
взаимодействия может быть представлено в виде: J-(?, т) = J-u{?) exP [Jut] (cm.
лекцию 9; раздел посвященный численному исследованию нелиней-
нелинейных уравнений ЛБВ). Типичный вид функции J~u(?) представлен на
рис. 14.9. Из кривых этого рисунка видно, что выходной сигнал даже
458
Лекция Ц
bbl-
2,5
2,0
1,5
1,0
0
г 0,5
ro,o
1,0
-0,5
.-1,0
-1,5
6
4
2
24
16
24
Рис. 14.9. Зависимость амплитуды (а) и фазы (б) монохроматических сигна-
сигналов от координаты. Различные кривые соответствуют различным частотам из
в случае монохромотического входного сигнала сильно зависит как
от амплитуды, так и от частоты и. Поэтому в случае произвольно-
произвольного входного сигнала для нахождения выходного сигнала необходимо
рассматривать каждую спектральную гармонику отдельно, что и экви-
эквивалентно решению первичных уравнений. Однако при коэффициенте
связи Z <^\ решение задачи с большой степенью точности может быть
представлено в каждый момент времени монохроматическим сигналом,
амплитуда и фаза которого зависят от амплитуды и частоты входного
сигнала.
Действительно, при условии Z <С 1 входной сигнал генератора все-
всегда мал. Разобьем условно пространство взаимодействия на две части:
«линейную» (длиной Ьлин), где амплитуда поля мала и взаимодействие
пучка и волны описываются в рамках линейной терии, и «нелинейную»
(длиной L — Ьлин), где в качестве начального сигнала подается сигнал,
найденный из расчетов по линейной теории. В дальнейшем покажем,
что даже при широкоплосном сигнале на входе прибора линейная часть
формирует сигнал, близкий к гармоническому. Данное утверждение
тем точнее, чем длиннее линейная стадия, а, следовательно, меньше
Z.
Линеаризуем систему нелинейных нестационарных уравнений
A4.58)-A4.60). Представим и в следующим виде и = щ + ui, \ui\ <С
<С 1. Тогда, раскладывая в ряд Тейлора: ехр [—jui], получим, что
/ = —2juiexp[—juo]. Умножая уравнение A4.60) на ехр [—j
и усредняя по uq, получим систему линеаризованных уравнений:
A4.66)
Методы решения нелинейных нестационарных задач 459
рттр (Т) ^^ р J^O/ii., /77/n
Ф@,г) = по, <9Ф@,т)/<9? = 0. A4.68)
Предполагая, что на вход усилителя подается монохроматический
сигнал То = Тшезшт, будем искать решение A4.66) и A4.67) в виде Ф,
^г ~ ese?+jW Тогда из условия совместности получившейся системы
уравнений получим дисперсионное уравнение:
(зэ + jcovg)^2 =j/2. A4.69)
Будем искать собственные типы колебаний ЛБВ, т.е. такие решения,
которым соответствует неизменное распределение поля в пространстве
взаимодействия. Эти решения имеют вид
j~ (jj ^ ^, I ) — e j~ (jj у см. j у uj je , ^-Lti.iUJ
3
и, соответственно, для функции Ф:
;^-МС? A4.71)
A4.72)
где aej — корни характеристического уравнения A4.59), a clj(oj) —
коэффициенты разложения вектора начальных условий (У-ш, 0,0) по
собственным векторам системы A4.66)-A4.68).
Поскольку лишь один корень aej имеет положительную веществен-
вещественную часть (обозначим его как ае), то поведение решения на линейной
стадии взаимодействия быстро приобретает характер экспоненциаль-
экспоненциального роста. С увеличением ? вектор решения (У-Ш,ФШ, дФш/д^) экспо-
экспоненциально стремится к направлению, задаваемому вектором еш:
еш = A, Я«М +jvgu]J&(uj)[&(uj) +jvgw]),
так что пучковые компоненты при ? ^> 1 однозначно связаны с полем.
Если форма входного сигнала То произвольна, то общее решение
системы A4.66)-A4.68) может быть представлено с помощью функции
Грина
-Tf)Fo(T')dTf, A4.73)
где g^(r — т') — функция Грина системы уравнений A4.66)-A4.68).
460 Лекция Ц
Сравнивая решение для монохроматического входного сигнала и об-
общее решение, нетрудно видеть, что последнее определяет преобразо-
преобразование Фурье полевой компоненты функции Грина. Благодаря этому
существует возможность найти ее с помощью обратного преобразования
Фурье. В работе [3] приводится явный вид функции ^(т), полученный
асимптотическими методами (методом перевала) в предположении ? ^>
^> 1. Выпишем его без вывода:
где aeo = (—jvg + л/2) 2~4/3 — корень характеристического уравнения
A4.59) при о; = 0.
Аналогично асимптотическими методами могут быть найдены
и функции Грина g'^ и g'^ описывающие поведение функций Ф и <9Ф/<9?,
однако, можно воспользоваться и тем, что функция Грина по своему
определению является решением исходных уравнений. Тогда:
» д\ „ д ,
Из формулы A4.74) видно, что функция \g^ (г) | имеет максимум при
г = (vg/S)?, полуширина соответствующей кривой которого пропорци-
пропорциональна д/?. Из этого следует, что частоты |и \ ^ 1 /д/f, если они присут-
присутствуют в спектре входного сигнала То, существенно ослабляются после
прохождения линейной стадии взаимодействия, т.е. функция Грина
действует как фильтр промежуточной частоты, полоса пропускания
которого уменьшается с увеличением длины взаимодействия. При L ^>
> 1 к нелинейной стадии взаимодействия сигнал приходит близким
к монохроматическому, даже если на входе в ЛБВ он был широкопо-
широкополосным.
Для описания эволюции на нелинейной стадии (ЬЛИН < ? < L)
необходимо решить исходные уравнения, взяв в качестве граничного
условия поле Т{ЬЛУт, т) в конце линейной стадии.
При большой длине линейной стадии взаимодействия ЬЛИН эволюция
сигнала на нелинейной стадии зависит от двух параметров: амплитуды
и мгновенной частоты промежуточного сигнала 3-(ЬЛИН, г). Следующие
два момента позволяют упростить данную зависимость. Во-первых,
аргумент решения на нелинейной стадии меняется практически по тому
же закону, что и на линейной (см. рис. 14.9). Во-вторых, модуль выход-
выходного сигнала не зависит от фазы промежуточного сигнала Т(ЬЛИН, г),
что следует из инвариантности исходной системы относительно сдвига
фазы поля.
Методы решения нелинейных нестационарных задач 461
Исходя из этого, зависимость выходного сигнала от промежуточного
имеет вид
, г) = пЬ-Ьлин (№
х exp [jarg?L_L_ о ^(?лин, т)] . A4.75)
где U = Ы — вещественная функция.
Так как (L — ЬЛИН) <С ЬЛИН, то можно в соотношениях линейной
теории брать вместо ЬЛИН значение L, при этом частота о;(г) будет
даваться в этом случае с той же точностью, а модули полей в точках
ЬЛИН и L будут связаны очевидным соотношением
\QL о jTQ| =e**a(u)(L-Llm)\gL^ Q ^|_
Итак, суммируя все вышесказанное, получим окончательное соот-
соотношение, связывающее входной и выходной сигнал:
\Уь °*го{т)\
откуда, с учетом уравнения A4.65), функциональное отображение, опи-
описывающее ЛБВ-генератор с запаздывающей обратной связью, можно
записать в виде
Функция Ыь может быть задана в виде таблицы данных, полученных
из численного решения исходных уравнений в частных производных
A4.58)—A4.61), или аппроксимирована той или иной удобной для рабо-
работы функцией.
Перед дальнейшим обсуждением полученного соотношения A4.76)
перечислим еще раз основные особенности взаимодействия в генераторе
с бегущей волной и запаздывающей обратной связью, которые позволи-
позволили найти вид функционала^:
1) наличие двух пересекающихся семейств характеристик системы
уравнений A4.58)-A4.61);
2) наличие неустойчивости, приводящей к экспоненциальному росту
только одного из собственных решений линейной теории;
3) резонансный характер неустойчивости, т.е. зависимость про-
пространственного инкремента неустойчивости от частоты входного сиг-
сигнала;
4) малость коэффициента обратной связи, благодаря чему длинная
линейная стадия взаимодействия формирует стандартный вектор со-
состояния.
462 Лекция Ц
Исследуем теперь возможные механизмы потери устойчивости мо-
монохроматических режимов работы генераторов, описываемых отобра-
отображением A4.76). Численное решение уравнений A4.58)—A4.61) показы-
показывает, что с увеличением тока пучка после разрушения монохроматиче-
монохроматического режима быстро наступает режим стохастической автомодуляции.
Это указывает на совпадение механизма разрушения монохроматиче-
монохроматического режима с механизмом его стохастизации. Поэтому определение
условий и механизма потери устойчивости монохроматических решений
дает хорошую оценку снизу для тока стохастической автомодуляции
генератора и позволяет качественно описать основные спектральные
характеристики сигнала в этом режиме.
Будем рассматривать уравнение
Щт + Q)=U(\go Т{т)Ъ ш(т)) е^в^М, A4.77)
к которому легко перейти от A4.76) с помощью очевидных переобозна-
переобозначений. Функционал Q будем описывать его комплексной амплитудно-
частотной характеристикой а(о;), задаваемой соотношением
goejuJT = a(u)ejuJT. A4.78)
Уравнение A4.77) допускает монохроматические решения с часто-
частотами и)п, удовлетворяющими условию фазового баланса сигнала в цепи
обратной связи:
вип = arga(o;n) + 2тгп, п е Z, A4.79)
и амплитудами Т, определяемыми из уравнения
Tn=U{\a(ujn)\Tn,ujn). A4.80)
Исследуем устойчивость описанных решений, для чего представим J~(t)
в виде
Т{т)=Тпе^т{\ + и{т)), A4.81)
где |^(г)| <С 1 — малое возмущение.
Линеаризуя уравнение A4.77) вблизи невозмущенного монохрома-
монохроматического решения, получим уравнение для и(т), решение которого
в силу его линейности можно искать в виде
и(т) = e7r(n+eJ>r + u-e-j»T). A4.82)
Опуская выкладки, приведем характеристическое уравнение системы
линейных уравнений для функций n+, U-\
Методы решения нелинейных нестационарных задач
463
Здесь Л = 7 + J>, а>о(ь>п), a± = а(с^п ± /i), ^ и t^L — производные по
первому и второму аргументам функции Ы в точке (\a(ujn)\J-n, u)n).
Понятно, что монохроматический режим неустойчив, если хотя бы
один из корней Л характеристического уравнения расположен в правой
полуплоскости.
Рассмотрим сначала простейший случай, когда Ш^- = Ф*- = 0. При
этом уравнение A4.83) упростится:
е2Л0 _ е>
A4.84)
Уравнение A4.84) имеет два семейства корней:
,A)_А2пк , ,тгЛ (л г,,_Ш\ lnlaolieW/вя:
B)
к е z.
Корни первого семейства обладают вещественной частью, что дает
следующее условие неустойчивости монохроматического режима:
&и_
дх
> 1.
A4.85)
Заметим, что предположение о независимости функций Ы и а от
частоты и превращает отображение A4.77) в одномерное, для которого
условие A4.85) является, как известно [29], условием неустойчивости
неподвижной точки.
Учтем теперь зависимость функций Ы и а от частоты. Здесь в пер-
первую очередь следует обратить внимание на второе семейство корней
\B\ поскольку даже слабая зависимость упомянутых функций от и
может сдвинуть корни Л^ с мнимой оси, и безразличное равновесие
по соответствующему направлению будет нарушено. Семейство же А^1)
устойчиво к слабой зависимости от и.
Рассмотрим случай, когда изменение функций Ы и а на двух ближ-
ближних собственных частотах генератора невелико, что эквивалентно нера-
неравенствам
да_
дш
д\пЫ
A4.86)
Для ЛБВ-генератора первое условие, как следует из вида A4.74)
функции Грина, эквивалентно неравенству
A4.87)
464 Лекция Ц
Поскольку в безразмерных переменных, в которых записаны исходные
уравнения A4.58)-A4.60), 0 > L, ^^- - 1, то оба неравенства A4.87)
эквивалентны условию L ^> 1, выполнение которого предполагалось
ранее.
Рассмотрим сначала случай, когда от частоты и зависит только а.
Поскольку семейство А'2) в том приближении, в котором оно получено,
не зависит от вида функционала Ы, положим для простоты Ы = 1 (это
всегда можно сделать выбором соответствующей нормировки). В этом
случае решение характеристического уравнения имеет вид
B) .2тг/г ( 1 <9arga(g;n)\ 2ttV 1 д2\а(шп)\
Xk -^-^-l1 + ^ —. ) + —^Г~ |„Л. м ^~2 ' A4.88)
т. е. при
д-^Щ > 0 A4-89)
монохроматический режим неустойчив.
Таким образом монохроматический режим генератора, состоящего
из фильтра а(и) и идеального ограничителя Ы = 1 в качестве нелиней-
нелинейного элемента, неустойчив, если амплитудно-частотная характеристика
фильтра локально вогнутая. Этот результат хорошо известен в теории
цепей [30].
Следует подчеркнуть, что оба критерия (A4.86) и A4.89)) получены
из одного характеристического уравнения, т. е. функциональное отобра-
отображение содержит в себе оба механизма потери устойчивости. Будем назы-
называть первый механизм потери устойчивости амплитудным, а второй —
частотным, поскольку первый связан с функцией отображения ампли-
амплитуды и является простым обобщением механизма потери устойчивости
в точечном отображении, а второй обусловлен частотными свойствами
отображения.
Зависимость ^гВых(^Гвх) может быть получена решением исходных
уравнений в частных производных уравнений с различными начальны-
начальными условиями ^вх и сопоставлением соответствующих амплитуд выход-
выходного сигнала fBbIX = J-(L) (рис. 14.10).
Перейдем теперь к результатам численного решения уравнения
A4.76) с функцией U, описывающей ЛБВ-усилитель. Функция Ы стро-
строилась по численным решениям уравнений A4.58)—A4.61) с граничными
условиями То{т) = ^~о^шт с различными частотами uj.
При малых значениях параметра неравновесности (L —
— In \Z\/ Re {ae}) наблюдалось самовозбуждение генератора на одной
из собственных частот ип, значения которых хорошо согласуются
с заранее вычисленными по условию фазового баланса. Как уже
отмечалось, выбором граничного условия То(т), т G [0, 0 + L) можно
Методы решения нелинейных нестационарных задач
465
Рис. 14.10. Построение функции отображения ^7гВых(^гвх) по зависимости
1^@1- Кривые 1 и 2 отличаются начальной амплитудой JFbxi > ^гвх2- Рас-
Расстояние Д? определяется выражением Д? Reae = In (T^i/T^2)
добиться возбуждения генератора на той или иной из собственных
частот, лежащих вблизи максимума инкремента.
С ростом параметра надкритичности монохроматический режим
терял устойчивость и возникала автомодуляция. Существует простой
способ определения, какой из механизмов — амплитудный или частот-
частотный — приводит к потери устойчивости стационарного монохроматиче-
монохроматического режима генерации. Для этого достаточно определить положение
сателлитов в спектре сигнала, возникающих при превышении порога
неустойчивости, т. е. при автомодуляции. В случае амплитудного меха-
механизма ближайшие сателлиты расположены на расстоянии порядка тг/0
от основной частоты. В случае же частотного механизма расстояние до
сателлитов в два раза больше — 2тг/0. Это следует из вида мнимых
частей корней А'1) и А'2) характеристического уравнения.
Приведенные на рис. 14.11 примеры реализации {а, б) и характер-
характерного спектра (в) в развитом хаотическом режиме, полученные методом
функционального отображения, подтверждают, что именно частотный
механизм неустойчивости приводит к возникновению нерегулярной ав-
автомодуляции выходного сигнала ЛБВ-генератора с обратной связью.
Об этом свидетельствует спектр сигнала, в котором явно подчеркнуты
частоты, отстоящие друг от друга на расстоянии порядка 2тг/0. Харак-
Характерной особенностью рассматриваемой модели является переход к хаосу
через перемежаемость [26, 27], когда участки с плавноменяющейся
регулярной автомодуляцией сменяются участками с нерегулярным по-
поведением, длительность которых возрастает с увеличением параметра
надкритичности (см. рис. Ы.11а,б).
Спектральные характеристики стохастических сигналов содержат
в себе информацию о механизме неустойчивости. Для амплитудного
механизма характерны однородные компактные спектры, в которых
собственные частоты выделены незначительно. Частотному же меха-
механизму соответствуют спектры с хорошо выделенными собственными
466
Лекция Ц
частотами и широкий пьедестал со сплошным спектром. Различия
в ширине спектра обусловлены тем, что в первом случае сигнал мо-
модулирован, в основном, по амплитуде, а во втором случае — по частоте,
и только как следствие этого —
по амплитуде. Ширина же спек-
спектра при частотной модуляции
всегда больше, чем при ампли-
амплитудной модуляции [31].
Анализ полученных резуль-
результатов позволяет сделать следу-
следующий вывод о характере фи-
физических процессов, происходя-
происходящих в ЛБВ-генераторе с обрат-
обратной связью. При малом коэффи-
коэффициенте Z обратной связи в ре-
режиме развитой стохастической
автомодуляции взаимодействие
пучка с полем даже на нели-
нелинейной стадии носит одновол-
новой характер. Это означает,
что на нелинейной стадии в лю-
любой момент времени пучок вза-
взаимодействует с монохроматиче-
монохроматической волной, но частота и ам-
амплитуда волны различны в раз-
разные моменты времени. Разуме-
Разумеется, в этом утверждении содер-
содержится некоторая идеализация
происходящих процессов, одна-
однако такой подход является доста-
-2,0 -1,0
Рис. 14.11. Примеры временных реа-
реализаций сигнала генератора при уве-
увеличении тока пучка (а, б) и характер-
характерный спектр генерации в режиме раз-
развитого хаоса (в) (из работы [3])
точно точным. Численное реше-
решение исходных уравнений A4.58)-
A4.60) в частных производных показывает [3], что мгновенные функции
распределения частиц пучка по скоростям на выходе генератора оста-
остаются узкими, как и при одноволновом взаимодействии, даже в развитом
стохастическом режиме генерации, в то время как многоволновое взаи-
взаимодействие характеризуется в несколько раз более широкой функцией
распределения.
Завершая анализ результатов численных решений уравне-
уравнений A4.58)-A4.60) и отображения A4.76), отметим следующий
немаловажный факт. Если сравнить значения среднего квадрата
амплитуды сигнала генератора в стохастическом режиме и в режиме
монохроматической генерации, то оказывается, что в первом случае он
в 1,5-2 раза больше. Это означает, что коэффициент полезного действия
при переходе в режим стохастической автомодуляции генератора
Методы решения нелинейных нестационарных задач 467
возрастает в 1,5-2 раза. Это может быть объяснено тем, что при
автомодуляции точка, изображающая сигнал генератора, движется
вдоль кривой \J-(oj)|, т.е. значения ^(т)! бывают как больше, так
и меньше соответствующего значения для потерявшего устойчивость
монохроматического режима. Однако форма кривой ^(о;)! такова,
что I-T^t)! в среднем больше своего стационарного значения,
в чем легко убедиться, рассмотрев характерные для начальной
стадии развития неустойчивости малые гармонические колебания
частоты о;(г) вблизи исходной собственной частоты ujn. Заметим,
что аналогичное явление увеличения к.п.д. в режиме хаотической
генерации было обнаружено для уже рассмотренного нами в лекции 2
генератора на двухрезонаторном клистроне с обратной связью [32]. При
этом механизм повышения к.п.д. схож с вышеописанным: в режиме
хаотической автомодуляции величина электрического поля в выходном
резонаторе в среднем больше, чем в режиме регулярной автомодуляции,
что и приводит к возрастанию эффективности генератора [32].
Метод функционального отображения, предложенный в работах
[3, 28] и кратко проиллюстрированный в данной лекции, хорошо опи-
описывает ряд особенностей распределенных систем и, вместе с тем, поз-
позволяет существенно упростить численную процедуру исследования со-
соответствующих уравнений в частных производных. Авторы метода
особо подчеркивают, что функциональное отображение исследованного
вида применимо для описания нестационарных процессов не только
в ЛБВ-генераторе, но и в других генераторах, основанных на распре-
распределенном взаимодействии пучка заряженных частиц с собственной
волной электродинамической структуры [3].
Список литературы
1. Andersen Т.М., Mondelli A.A., Levush В, Verboncoeur J.P., Birdsall
С.К. Advances in modelling and Simulation of vacuum electron
devices // Proceedings of the IEEE. May 1999. V. 87, № 5. P. 804.
2. Гинзбург H.C., Кузнецов СП., Федосеева Т.Н. Теория переходных
процессов в релятивистской ЛОВ // Изв. вузов. Радиофизика. 1978.
Т. 21, №7. С. 1037.
3. Блиох Ю.П., Бородкин А.В., Любарский А.Г., Онищенко Н.М.,
Файнберг Я.Б. Применение метода функционального отображе-
отображения для исследования ЛБВ-генератора с запаздывающей обрат-
обратной связью // Изв. вузов. Прикладная нелинейная динамика. 1993.
Т.1,№1,2. С. 34.
4. Hockney R. W., Eastwood J. W. Computer simulation using particles. —
NY.: McGraw-Hill, 1981.
5. Роуч П. Вычислительная гидродинамика. — М.: Мир, 1980.
6. Поттер Д. Вычислительные методы в физике. — М: Мир, 1975.
468 Лекция Ц
7. Бедселл Ч., Ленгдон А. Физика плазмы и численное моделирова-
моделирование. — М.: Атомиздат, 1985.
8. Morey I.J., Birdsall С.К. Traveling-Wave-Tube simulation: the IBC
code // IEEE Trans, on Plasma Sci.. 1990. V. 18, № 3. P. 482.
9. Современные численные методы решения обыкновенных диффе-
дифференциальных уравнений / Под. ред. Дж. Холл и Дж. Уатт. — М.:
Мир, 1979.
10. Березин Ю.А., Вшивцов В.А. Метод частиц в динамике разрежен-
разреженной плазмы. — Новосибирск: Наука, 1987.
11. Анфиногентов В.Г., Храмов А.Е. Влияние распределенной обрат-
обратной связи на хаотические колебания виртуального катода // Изв.
вузов. Прикладная нелинейная динамика. 1998. Т. 6, № 1. С. 93.
12. Рихтмайер Р., Мортон К. Разностные методы решения краевых
задач. — М.: Мир, 1972.
13. Свешников А.Г., Якунин С.А. Численные модели бесстолкнови-
тельной плазмодинамики // Математическое моделирование. 1989.
Т.1,№4. С.1.
14. Сигов Ю.С Численные методы кинетической теории плазмы. —
М.: МФТИ, 1984.
15. Григорьев А.Д. Современные методы моделирования нестационар-
нестационарных электромагнитных полей // Изв. вузов. Прикладная нелиней-
нелинейная динамика. 1999. Т. 7, № 4. С. 48.
16. Monorchio A., Mittra R. Time-domain (FE/FDTD) technique for
solving complex electromagnetic problems // IEEE Microwave &
guided waves letters. 1998. V. 8, № 2. P. 93.
17. Kunz K.S., Luebbers R.J. The finite difference time domain method
for electromagnetics. — Roca Raton, FL: CRC Press, 1993.
18. Yang H., Railton CJ. Efficient and accurate FDTD algorithm for the
treatment of curved material boundaries // IEE Proc. MWAP. 1997.
V. 144, №5. P. 382.
19. Warren C, Ludeking L., Nguyen K., Smithe D., Goplen B.
Advances/applications of MAGIC and SOS // Computational
Accelarator Physics, AIP Conf. Proc. 1994. V. 297. P. 313.
20. Tarakanov V.P. User's manual for code KARAT. - Springfield, VA:
BRA, 1992.
21. Verboncoeur J.P., Langdon А.В., Gladd N.T. An object-oriented
electromagnetic PIC code // Comput. Phys. Commun. 1991. V. 64.
P. 252.
22. Кислое В.Я. Теоретический анализ шумоподобных колебаний в
электронно-волновых системах с запаздыванием // Лекции по
электронике СВЧ и радиофизике E-я зимняя школа-семинар ин-
инженеров). Саратов: Изд-во СГУ, 1981. С. 78.
Методы решения нелинейных нестационарных задач 469
23. Кузнецов СП. Сложная динамика генератора с запаздывающей
обратной связью // Изв. вузов. Радиофизика. 1982. Т. 25. С. 1410.
24. Манькин М.А., Школьников В.Г. Численное моделирование ав-
автоколебаний в системе электронный пучок — прямая электро-
электромагнитная волна с внешней обратной связью // Радиотехника и
электроника. 1984. Т. 29, № 2. С. 307.
25. Вакс В.Л., Сморгонский А.В., Шулешов А.О. Источники шума
миллиметрового диапазона длин волн на основе электронного уси-
усилителя // Радиотехника и электроника. 1992. Т. 37. С. 521.
26. Manneville P., Pomeau J. Different waves to turbulence in dissipative
dynamical systems // Physica D. 1980. V. 1. P. 219.
27. Берже П., Помо П., Видаль К. Порядок в хаосе. О детерминисти-
детерминистическом подходе к турбулентности. — М.: Мир, 1991.
28. Bliokh Уи.Р., Fainberg Уа.В., Lybarskii M.G., Podobinski V.O. The
investigation of the stohastization mechanisms of the beam generators
using the method of functional map // Preprint. Kharkov. 1994. 32p.
29. Кузнецов СП. Бифуркации удвоения в простой модели распре-
распределенной системы // Изв. вузов. Радиофизика. 1982. Т. 25, №11.
С. 1364.
30. Гоноровский И. С. К теории высокочастотных генераторов с запаз-
запаздывающей обратной связью // Радиотехника. 1958. Т. 13, № 5. С. 19.
31. Харкевич А.А. Спектры и анализ. — М.: Физматгиз, 1962.
32. Афанасьева В.В., Лазерсон А.Г. Динамический хаос в двухрезо-
натрных клистронных генераторах с запаздывающей обратной
связью // Изв. вузов. Прикладная нелинейная динамика. 1995. Т. 3,
. С. 88.
Лекция 15
ОРОТРОН
Открытые резонаторы используются в электро-
электронике еще мало. Одним из первых приборов такого
рода является оротрон — электронный автогене-
автогенератор миллиметровых и субмиллиметровых волн
с открытым резонатором и отражающей решет-
решеткой. ..
Л.А. Вайнштейн, В.А. Солнцев. Лек-
Лекции по сверхвысокочастотной элек-
электронике, М.: Советское радио, 1973,
с.38.
Взаимодействие электронного потока с полями открытых резона-
резонаторов. Излучение Смита-Парселла. Оротрон. Основные уравнения
оротрона. Некоторые результаты теории оротрона. Нестационарные
процессы в оротроне. Методы повышения к.п. д. оротрона. Модифика-
Модификации оротрона.
В данной лекции уделим внимание применению открытых резонато-
резонаторов в сверхвысокочастотной электронике. Открытые резонаторы при-
применяются в целом ряде приборов вакуумной электроники: оротронах,
гиротронах и различных вариантах лазеров на свободных электронах.
Гиротронам и лазерам на свободных электронах будут посвящены от-
отдельные лекции в следующем томе. В этой же лекции подробно будет
рассмотрен оротрон — прибор типа О с открытым резонатором и отра-
отражающей решёткой, генерирующий излучение в миллиметровом и суб-
субмиллиметровом диапазонах длин волн. На этот прибор в 1966 г. Ф.С.
Русину и Г.Д. Богомолову было выдано авторское свидетельство [1].
Генераторы типа оротрона изготовлялись и исследовались в Харькове
под названием «генераторы дифракционного излучения» [2]; в Япо-
Японии — под названием «электронные приборы с резонаторами Фабри-
Перо» и ледатронов [3, 4] и в США [5, 6], где сохранили первоначальное
название оротрон.
Оротрон
471
Взаимодействие электронного потока с полями
открытых резонаторов. Излучение Смита—Парселла
Открытый резонатор (ОР) оротрона образован двумя зеркалами —
вогнутым и плоским, между которыми могут существовать высокодо-
высокодобротные электромагнитные колебания (рис. 15.1). На плоском зеркале
нанесена периодическая замедляющая система — отражающая решет-
решетка. Период решетки существенно меньше длины волны, поэтому при
падении на нее плоской волны возникает только отраженная волна,
а дифракционные плоские волны не возникают. Электронный пучок,
двигаясь над зеркалом, взаимодействует с продольной компонентой
синхронной пространственной гармоники ВЧ электрического поля пе-
периодической системы, и, при определенных условиях в ОР устанавлива-
устанавливаются незатухающие колебания — оротрон становится автогенератором,
причем, поскольку используется ОР, прибор может эффективно рабо-
работать в миллиметровом и субмиллиметровом диапазоне длин волн.
Отличие оротрона от классических приборов типа О (ЛОВО, ЛБВО)
состоит в применении специфической электродинамической системы —
ОР. В ОР потери на джоулево тепло и потери на излучение не связаны
с электронами (они обусловлены полями вне пространства взаимодей-
взаимодействия) и поэтому во всех процессах взаимодействие электронов с пе-
переменным полем проявляется лишь суммарным образом. Заметим, что
применение ОР в качестве электродинамической системы не изменя-
изменяет механизм взаимодействия электронов с ВЧ-полями — он остается
полностью идентичным имеющему место в закрытых системах. Новое
заключается только в другом спектре собственных частот и волновых
чисел и в своеобразном распределении полей.
{Вывод энергии
Рис. 15.1. Схема оротрона и его дифракционной решетки. Здесь d — период
решетки; / — ширина канавки; а — глубина канавки
472
Лекция 15
Рис. 15.2. Излучение в плоскости (ж, г/), у — нормаль к решетке, расположен-
расположенной в плоскости у = const < О
В оротроне используется так называемое излучение Смита-
Парселла (дифракционное или варатронное излучение), которое
возникает, когда заряженная частица пролетает вблизи периодической
замедляющей системы (отсюда и уже упоминавшийся синоним
оротрона — генератор дифракционного излучения). Рассмотрим
элементарную теорию этого излучения. Для простоты рассмотрим
возбуждение двумерной периодической структуры (решетки) (см.
рис. 15.2) током
jx(t) = qvS(y)S(x - vt), jy = jz = 0,
A5.1)
соответствующим заряженной нити с погонным зарядом q, параллель-
параллельной оси z и движущейся со скоростью v в направлении оси х. В любой
фиксированной точке пространства поле заряженной нити исчезает при
времени t —У =Ьоо, поэтому для нахождения комплексной амплитуды то-
тока следует воспользоваться интегралом Фурье. В силу соотношения г)
i-oo i-oc
*\ 1 Г iu(x-vt) л r> ! Г
— vt) = — \ eJ y ' auj = Ke —
2тг J тги J
имеем
= -
]х{и) = ±8{уУшх'\
A5.2)
В рассматриваемой системе эта плотность тока возбуждает поле, кото-
которое имеет единственную составляющую векторного потенциала
*/\ A5.3)
где функция А(у) удовлетворяет волновому уравнению
^> -^ . 1 О л ^ 1 .1,1
dy2
A5.4)
Его легко проверить, пользуясь формулой обращения интеграла Фурье.
Оротрон 473
всюду, за исключением плоскости у = 0, в которой течет ток.
Решим сначала это уравнение для нити при отсутствии решетки.
Общее решение уравнения для А имеет вид
A = C1e>kyy + C2e-jkyy. A5.5)
Так как поле должно убывать при \у\ —у ос, то положим, что С\ — О при
у < О и Ci = 0 при у > 0. Так как функция А должна быть непрерывной
ЗА
при у = 0, а составляющая магнитного поля Hz = л х терпит скачок
'*l»=-o -.. ¦- п
nz\y=-o — nz\y=+o — —е
то при у < 0 будем иметь
я = JLei(-/^+W^ A5.6)
Если бы величина ку была вещественной (что имело бы место при
v > с, а это нереально), то формула A5.6) представляла бы плоскую
волну, падающую на решетку. В силу того, что v < с и ку = j\ky\,
соотношение A5.6) есть обобщенная (неоднородная) плоская волна,
которая характеризуется волновым вектором с составляющими
кх = ^ = &cos<9o, -ky, kz=0, (к = ^У A5.7)
Здесь чисто мнимый угол #о = j|^o| определяется соотношением
cos0о = ch|0o| = c/v > 1. A5.8)
Если бы вместо дифракционной решетки была плоскость у = const < 0,
то в результате отражения от этой плоскости возникла бы отраженная
волна, волновой вектор которой имел составляющие
кх = к cos во, ку = к sin #0, kz = 0. A5.9)
При наличии решетки с периодом d по оси х возбуждается бесконечное
число обобщенных плоских волн, волновые векторы которых имеют
составляющие
27ГП
(п = 0, ±1,...).
Возбуж;дающиеся волны мож;но трактовать как набор простран-
пространственных гармоник. Учитывая, что и/v — к - с [к — 2тг/Л), и вводя
474 Лекция 15
угол вп с помощью соотношения кх^п = к cos @n), получаем выражение
вида:
cos0n = - + ^. A5.11)
г; а
В том случае, когда по этой формуле получается, что (—1 < cos вп < 1),
имеет место излучение на n-й пространственной гармонике — излучение
Смита-Парселла. Это излучение можно рассматривать и как черенков-
ское излучение электрона, синхронного с одной из пространственных
гармоник периодической системы.
В оротроне обычно используется (—1)-я пространственная гармо-
гармоника, амплитуда которой максимальна. Условие синхронизма для нее
выражается соотношением oj/vo = 2тг/с( или vo = fd, где uj — частота
колебаний; vo — скорость электрона; d — период решетки (см. рис. 15.1);
/ = uj/2тг. Заметим, что то же самое можно сказать и о лампе обратной
волны, только там излучение на одной из пространственных гармоник
остается внутри закрытой электродинамической структуры. Чтобы ОР
эффективно возбуждался, необходимо, чтобы частота / = vo/d была
близка к одной из его собственных частот. Наличие ОР приводит к то-
тому, что излучение электронов носит индуцированный характер, т. е.
излучают не отдельные электроны (как в эффекте Смита — Парселла),
а электронный пучок группируется в сгустки под действием собствен-
собственного поля излучения, запасенного в ОР.
Таким образом для работы оротрона должны выполняться два усло-
условия:
1) синхронизм в пространстве, т. е. равенство скорости пучка и фа-
фазовой скорости одной из пространственных гармоник;
2) синхронизм во времени, т.е. равенство частоты, для которой
выполняется синхронизм в пространстве, одной из собственных частот
ОР.
Данные требования являются общими для всех резонансных генерато-
генераторов с длительным взаимодействием, к которым относится и оротрон.
Большая добротность колебаний, характерная для ОР (в реальных
приборах она может достигать нескольких тысяч), обусловливает важ-
важную особенность теории резонансных автогенераторов. Время пролета
электронов через пространство взаимодействия L равно Те ~ L/vo,
а характерное время изменения амплитуды колебаний в OP Tf ~ Q/ f
(Q — нагруженная добротность объемного резонатора). Для оротрона
Tf ^> Те, а, следовательно, электронный пучок практически не изме-
изменяет структуру поля собственного колебания в ОР, и, более того, каж-
каждый электрон движется в поле с практически постоянной амплитудой
и фазой даже в переходных процессах. Это позволяет построить теорию
оротрона в приближении заданного поля, которое при исследовании
Оротрон 475
приборов О-типа с закрытыми волноведущими структурами является
лишь первым приближением.
Основные уравнения оротрона
Теория оротрона г), как и любого другого электронного прибора,
требует решения двух задач: нахождение закона движения электрон-
электронного потока в электромагнитном поле и решение задачи возбуждения
электромагнитных волн в колебательной системе переменным током.
Рассмотрим вначале вторую задачу: возбуждение полей. Поскольку
колебательной системой оротрона является ОР, то при расчете полей
необходимо пользоваться теорией возбуждения открытых резонаторов,
которая (см. лекцию 1, а также [7, 8]) сводится к обычной теории
возбуждения закрытых систем.
Как уже обсуждалось в лекции 1, в общем случае, наряду с резо-
резонансным колебанием в ОР возбуждается нерезонансный фон, который
ответственен за излучение, уходящее из резонатора, т. е. на дифракци-
дифракционные потери. Для избежания их на практике применяются ОР с во-
вогнутым верхним зеркалом. Область канализации собственных типов
колебаний в таких устойчивых резонаторах ограничена каустической
поверхностью. Если каустика расположена далеко от краев зеркала,
то соответствующее колебание обладает исключительно малыми поте-
потерями на излучение (достаточно сказать, что добротность в реальных
ОР определяется в основном омическими потерями в самих зеркалах).
Наличие электронного пучка не изменяет этой картины из-за высокой
добротности колебаний. Пространственная структура поля очень слабо
изменяется, и она, в свою очередь, определяет модуляцию электронного
пучка, т. е. плотность переменного тока, возбуждающего резонатор.
Поэтому нерезонансный фон практически не возбуждается.
Учитывая сказанное, будем использовать при расчете полей обыч-
обычную теорию закрытых резонаторов, оставляя в формулах только один
член, соответствующий возбуждаемому в ОР собственному колебанию.
При определении нормы этого колебания можно ограничиться инте-
интегрированием по объему V между зеркалами. В этом случае, уравнение
возбуждения будет иметь вид (см. формулы A.55), A.61))
A5.12)
г) Заметим, что к приборам типа О с двойным синхронизмом (в простран-
пространстве и во времени) относятся кроме оротрона, также однорезонаторный
клистрон с распределенным взаимодействием, резонансные ЛБВ и ЛОВ,
ладдетрон. Поэтому излагаемая здесь теория является по существу теорией
большого класса резонансных автогенераторов.
476 Лекция 15
dC -j(oj-us)Cs = --L ijEsdV. A5.13)
dt
v
Здесь индекс s соответствует собственному колебанию, резонансно воз-
возбужденному в оротроне и характеризуемому полем Es, Cs(t) — ампли-
амплитуда колебаний, Ns = jv eE^ dV — норма s-vo колебания, us = u's —
— juo" = uo's A — j/2QS) — его комплексная собственная частота, Qs —
его нагруженная добротность.
Представим амплитуду Cs(t) в форме Cs = |Cs|e~J^s и, учитывая,
что W = \CS\ Ns/2 — энергия электромагнитного поля, запасенная
в данном колебании, из формул A5.12), A5.13) получаем соотношения
вида (аналогично см. лекцию 2, раздел, посвященный резонансным
автогенераторам):
A5.14)
где Реа и Рег — соответственно активная и реактивная составляющие
электронной мощности взаимодействия пучка с полем резонатора. Пер-
Первое из соотношений A5.14) есть закон сохранения энергии для нестаци-
нестационарных колебаний: активная электронная мощность расходуется на
увеличение энергии колебаний (слагаемое dW/dt) и на компенсацию
мощности ojfsW/Q, которая выделяется в нагрузке и в стенках резо-
резонатора, а также тратится на излучение. Второе соотношение — баланс
реактивных мощностей, определяющий мгновенную частоту резонанс-
резонансного поля. Левая часть его есть реактивная мощность резонансного
колебания, обращающаяся в нуль при точном равенстве мгновенной
частоты uj + ф8 и собственной частоты u)fs, а правая часть — реактивная
электронная мощность.
Полагая, что dW/dt = 0, ips = 0 и используя определение нагружен-
нагруженной добротности собственного колебания Qs = uj's/2uj", из соотношений
A5.14) получаем условия стационарных колебаний в оротроне:
%LW = -Pea, 2(ш-ш'3)\У = -Рег. A5.15)
Отсюда видно, что для определения пусковых параметров генератора
и его свойств в стационарном режиме достаточно вычислить мощность
взаимодействия электронного потока с высокочастотным полем, запа-
запасенную в резонаторе энергию и знать характеристики ОР. Причем,
как уже обсуждалось выше, для вычисления интегралов в уравнениях
A5.14), A5.15) достаточно знать сгруппированный ток в приближении
заданного поля, которое дает искомое решение для оротрона.
Оротрон 477
Обычно полагают, что амплитуда синхронной пучку пространствен-
пространственной гармоники в оротроне постоянна и собственное поле выражается
соотношением
, z) cos/Зож, 0 < х < L, , v
0, x>L,x< 0. A5Л6)
Здесь 4?(y,z) — функция, определяющая поперечное распределение
поля в оротроне. Она нормирована так, что jj Ч*(у, z) dy dz = 1;
Ро « 2тг/d — волновое число синхронной гармоники (т.е. пучок
синхронен с (—1)-й пространственной гармоникой). Представление
поля в виде A5.16) позволяет легко вычислить электронную мощность
взаимодействия и получить аналитически все результаты линейной
теории оротрона, а именно найти пусковые токи, пусковые частоты,
инкремент нарастания колебаний. Вместе с тем представление полей
A5.16) является сильной идеализацией, так как верхнее зеркало
является вогнутым, и вблизи решётки амплитуда поля меняется по
Гауссову закону:
Es = E1V(y,z)exp f-^j cos/^, A5.17)
где г определяет характерный размер поля на поверхности решетки.
Выражение A5.17) соответствует колебанию, у которого имеется один
максимум на плоском зеркале и которое наиболее часто используется
на практике.
Некоторые результаты теории оротрона
Обсудим вначале результаты линейной теории оротрона. Для ана-
анализа линейного процесса группировки электронного потока в резо-
резонансном поле удобно воспользоваться уравнением для конвекционного
тока C.22). Пусть 1\{х) — комплексная амплитуда первой гармоники
сгруппированного тока, а Е(х) — комплексная амплитуда продольной
компоненты электрического поля, тогда для 1\ (х) справедливо уравне-
уравнение (здесь подразумевается временная зависимость е^шЬ)
d2l^x) _ 24в dh^x) - (В2 - В2) U (г) - -iElM. EM A4 1Я)
dx2 jPe dx ^e Pp'll(x>- J2V^S~o (h { '
решение которого для нулевых начальных условий (пучок предвари-
предварительно не модулирован) дается интегральной формулой
x) = -JMf
h{x) = -JMf Ь/».(-0"°Д>(*-0 ВД<^. A5.19)
Здесь /о — полный ток пучка, So — поперечное сечение пучка, S —
эффективная площадь поперечного сечения пучка (величина, учиты-
учитывающая неоднородность в распределении поля в плоскости (y,z)), она
478 Лекция 15
определяется соотношением S = [jj Ф2(?/, z) dy dz] , ре = oo/ve, Pp =
= ojp/ve. Up — редуцированная плазменная частота. Нижний предел
интегрирования в интеграле A5.19) равен нулю, если распределение
поля в пространстве постоянно (см. формулу A5.16)), и — ос, если ам-
амплитуда изменяется по Гауссову закону (см. формулу A5.16)), а верхний
предел — координата х.
Для комплексной мощности взаимодействия Ре = Реа — j Рег пучка
с полем, как можно показать (см. подробнее [8, 9]), используя опреде-
определение электронной мощности взаимодействия B.13), формулу A5.19)
и выражения для полей A5.16) и A5.17), получается выражение вида
L
р
x
)* dx f ^" ft>(»
J Pp
О
A5.20)
для поля постоянной амплитуды и
для Гауссова распределения поля.
Рассмотрим сначала случай пренебрежимо малого пространствен-
пространственного заряда (Рр —у 0). Вычисление интеграла A5.20) приводит к выра-
выражению для электронной мощности взаимодействия, имеющему вид
— [/а(#о) - jfr(&o)] , A5.22)
гдеФо = (Ре — Po)L — относительный угол пролета электронов на длине
пространства взаимодействия. fa и fr — уже хорошо знакомые нам
функции (см. формулы (9.20), (9.21)), всегда встречающиеся в теории
приборов О-типа, основанной на методе последовательных приближе-
приближений. Они записываются в первом приближении следующим образом:
* (фп) -F. - 2A-со8Ф0)-
/г(ф0) = Flr = —o--ov^—оу A5<24)
Фо
и изображены на рис. 15.3а при (рр = 0.
Вычислим теперь интеграл A5.21) для случая Рр = 0. В этом случае,
введя обозначение а = Ро — /Зе, искомый интеграл можно представить
Оротрон
479
0,2 г fa
Рис. 15.3. Зависимость функций /а, fr (а) и /а, /г (б), которым пропорцио-
пропорциональны активная и реактивная мощность взаимодействия от относительного
угла пролета фо для различных значений параметра пространственного за-
заряда (fp
в виде
СЮ X
I = [ dx
— сю —сю
— сю —сю
Сделаем замену переменных и- = (х — ?)/2г, и+ = (х + ?)/2г, после
чего интеграл становится равным
о сю ж
JL
м- tin_.
480 Лекция 15
Отсюда окончательно получаем
[Я х
— [ cos2aru-e-j2rau~ du- -
да J
JO
¦J2r J
cos2aru-e i2rau- du- .
Оба интеграла в квадратных скобках являются табличными:
д
да J
f
cos2aru-e 3 rau- du- = —— ar e
4
cos2aru-e~j2rau- du- = Fi(l, 1/2, -a2r2),
— сю
где Fi(a, с, ж) — вырожденная гипергеометрическая функция, задава-
задаваемая своим разложением в ряд по степеням х:
Fx (а, с, х) - 1 + - ^ + ^^^ 2Г + с(с + 1)(с + 2) зГ + • • •
Обозначая Фо = —2аг = 2(^е — ^о)г — относительный угол проле-
пролета в случае Гауссова распределения поля, для мощности взаимодей-
взаимодействия Ре получаем выражение
w}sf Щ 1 Ы A5-25)
где
1(Фо) = I ФОе~фо/\ A5.26)
/г(Фо) = ^ Fi(l, 1/2, -Ф^/4). A5.27)
Функции fa и /г играют такую же роль, что и функции fa и fr
для поля постоянной амплитуды. Их график приведен на рис. 15.3?при
ipp = 0. Максимум энергии пучок отдает, когда Фо = —V2, при этом
fa(—л/2) ~ —0,337. Заметим, что для поля с постоянной амплитудой
максимальная отдача мощности от пучка к полю имеет место при Фо =
= —7Г, При ЭТОМ /а( —7Г) ~ —0,13.
Из приведенных формул следует, что в поле с Гауссовым распределе-
распределением взаимодействие пучка с полем происходит менее интенсивно, чем
в поле с постоянной амплитудой. Действительно, в реальном резонаторе
диаметр пятна 2г должен быть по крайней мере в два раза меньше
линейного размера резонатора для того, чтобы дифракционные потери
были малы. Поэтому множитель BгK, стоящий в формуле A5.25),
Оротрон 481
примерно на порядок меньше величины L3 в формуле A5.22). Следо-
Следовательно, взаимодействие пучка с полем с Гауссовым распределением
амплитуды значительно менее эффективно, чем в случае поля постоян-
постоянной амплитуды. Ещё одна причина отличия эффективности взаимодей-
взаимодействия в том, что электрон, входящий в пространство взаимодействия
с полем постоянной амплитуды, испытывает на границе толчок, кото-
который способствует в дальнейшем более интенсивной модуляции. В случае
поля с плавным изменением амплитуды такого толчка нет.
Учет пространственного заряда не вызывает особых сложностей.
Это приводит лишь к тому, что функции /а, /r, а также fa и /г, мо-
модифицируются и теперь зависят от двух переменных — относительного
угла пролета Фо и параметра пространственного заряда срр = /3PL для
поля постоянной амплитуды и срр = 2f3pr для Гауссова распределения
поля. Не будем выписывать соответствующие выражения для функций
вследствие их громоздкости (их вид приведен, например, в работе [8],
стр. 126). Вид этих функций при различных значениях срр для обоих
типов полей показан на рис. 15.3.
Из рисунков видно, что как и в случае приборов типа О с закрытыми
колебательными системами, влияние пространственного заряда умень-
уменьшает мощность взаимодействия пучка с полем и смещает оптимальные
значения угла пролета, увеличивая расстройку скоростей между элек-
электронами и волной.
Пусковые условия оротрона можно найти из уравнений A5.15) и
A5.22). Учитывая, что энергия, запасенная в резонаторе дается вы-
выражением W = 7Vs|Cs|2/2, для пускового тока и пусковой частоты
находим:
8u>'aVoSo ( Ns
( ,
A5.29)
Минимальный ток достигается при отсутствии пространственного за-
заряда (срр = 0) и при Фо = — л/2; он равен
/min = 23,81 Уо5° (-^Л • A5.30)
f}S{2f \QsEl) У }
Из последнего соотношения видно, что пусковой ток оротрона линейно
уменьшается с уменьшением отношения Ns/QsEf. Эта величина силь-
сильно зависит от параметров решетки и достигает минимума при / = d/2,
а = Л/4 (см. рис. 15.1) [8, 9].
Увеличение параметра пространственного заряда срр приводит к ро-
росту пускового тока. Соответствующая зависимость, построенная при
оптимальном угле пролета Фо, приведена на рис. 15.4. Видно, что при
16 Д. И. Трубецков, А. Е. Храмов
482
Лекция 15
--"¦пуск
6 - /min
о
2%
Рис. 15.4. Зависимость нор-
нормированного пускового то-
тока от параметра простран-
пространственного заряда. Угол про-
пролета Фо оптимальный
О -те/2
Рис. 15.5. Зависимость пускового
тока от угла пролета Фо- сплош-
сплошная кривая рассчитана без уче-
учета встречной волны, штриховая —
с учетом встречной волны
(срр > тг) /Пуск линейно увеличивается с ростом пространственного за-
заряда по закону /пуск/Ашп = 0,858у?р.
Интересно отметить, что если учесть в расчетах не только попутную,
но и встречную волну, то окажется, что /а@) Ф 0 — пусковой ток имеет
конечное значение даже при точном синхронизме скоростей электронов
и волны (см. рис. 15.5, на котором представлены зависимости пускового
тока от относительного угла пролета для расчетов только с попутной
волной (сплошная линия) и встречной волной (штриховая линия) (рас-
(расчеты выполнены для поля постоянной амплитуды)).
Рассмотрим теперь кратко нелинейную теорию оротрона.
Будем строить ее аналогично нелинейной теории ЛБВ (лекция 10).
Движение электронного потока описывается в переменных Лагранжа.
Пусть t = t(x, to) — время пролета электрона через точку х, если он
при невозмущенном полем резонатора движении, пролетает точку х =
= 0 (центр резонатора) в момент времени t = to. Введем текущую
фазу электрона ip(x,ipo) = ut — /Зох, tpo = wto. Если рассматривать
случай Гауссова распределения поля, то действующее на электрон поле
можно представить в виде Е = E\Cse~x '2r coscc^cos/Зож (начальная
фаза здесь выбрана равной нулю). Будем предполагать, что электрон
эффективно взаимодействует только с попутной волной. Тогда, проводя
выкладки аналогично тому, как это делали при выводе нелинейных
уравнений ЛБВ, получаем уравнение движения электрона:
*-V
COS If,
A5.31)
где ? = х/л/2г — медленно меняющаяся координата, Т —
= 2r2PoCsEi/4Vo — комплексная амплитуда поля, е = 1/л/2/?ог —
электрическая длина пространства взаимодействия. Обычно в оротроне
Оротрон 483
величина Рог порядка сотни и больше, поэтому во всех формулах
можно оставить первые неисчезающие по ? члены, что мы и будем
делать в дальнейшем. Уравнение движения в этом случае приобретает
вид
,2
_ _r. A5.32)
Это уравнение решается со следующими начальными условиями:
= 6, A5.33)
где параметр b определяет расстройку скоростей пучка и поля: b =
/ /
Первая гармоника сгруппированного тока выражается, как и рань-
раньше, интегралом вида
2тг
= - \e-jvdcp0. A5.34)
7Г J
Электронный к.п.д., определяемый соотношением
2тг
о
в безразмерных переменных и с учетом малости е принимает вид:
A5-36)
где (...) обозначает усреднение по начальным фазам у?о-
Построим приближенную теорию слабонелинейного режима работы
оротрона, используя уравнение A5.32) (см. работу [8], стр. 131-133). Для
этого будем искать его решение в виде разложения по степеням поля J-:
сю
<Р@ = Е ^ЫО- A5-37)
п=1
Для величин (рп(?) несложно с учетом уравнения A5.32) получить
систему зацепляющихся уравнений вида:
16*
484 Лекция 15
</?з = sin </?ое~^ у?2 - (l/2)cosy?0e~* у??,
у?4 = sin у?ое"^ </?з + (l/2)cos</?0e~^ 2y?iy?2 + A/6) si
Чтобы определить к.п.д., необходимо найти величину </?'(ос) =
= (//l^oo, для коэффициентов разложения которой в ряд по степеням
Т получаем:
сю
= - cos
оо С С
^(оо) = - J sinF^ + ^0)e-c2^ Jd?' J
— сю —сю
-b2/2
= _е W2
Ограничиваясь точностью до величин порядка Т2, находим для </?'(ос)
следующее выражение:
^'(оо) = Ь - Т^ cos^oe-/4 - ^2e-&2/2 (J 6 + 1^/| sin2
К.п.д. в этом приближении с учетом формулы A5.36) равен
v = -l?^be-b2/\ A5.38)
Данный результат показывает, что для rj > 0 необходимо, чтобы b < 0.
Вместе с тем выражение для к.п.д. A5.38) полностью совпадает с ре-
результатом, предсказываемым линейной теорией (это несложно увидеть,
если воспользоваться соотношениями A5.25)—A5.27)). Отсюда следует,
что необходимо найти, по крайней мере, четный коэффициент ряда *)
ф'±(оо). Однако соответствующий интеграл не берется аналитически,
поэтому приходится вычислять его численно. В результате для к.п.д.
в слабонелинейном режиме получаем выражение
rj = 2e [F2G2(b) + F4C4(b)] , A5.39)
где (?2 = —(тг/4Nе~6 /2, а график G^ приведен на рис. 15.6.
х) Несложно показать, что все нечетные коэффициенты ряда
обращаются в нуль при усреднении.
Оротрон
485
0,10
0,05
0,00
-0,05
-0,10
-0,15
10
8
6
4
2
F
-
b = -3,0
/^- -2,5
^^-—i.o
- —v^«^—"—0j5
,——-*^^ — — —
О
10
15
20
Рис. 15.6. Функция G±(b) в зависи- Рис. 15.7. Зависимость амплитуды ста-
мости от параметра расстройки b ционарных колебаний в оротроне от то-
тока пучка для различных значений пара-
параметра расстройки Ь. Сплошные линии
соответствуют устойчивым, а штрихо-
штриховые — неустойчивым состояниям систе-
системы
Найдем теперь амплитуду установившихся колебаний, используя
для этого закон сохранения энергии
u>'eW/Q. = r,IoVo.
В безразмерных переменных получаем выражение, которое устанав-
устанавливает связь между безразмерным током пучка 1\ и безразмерной
амплитудой поля в режиме стационарных колебаний:
A5.40)
Используя формулу A5.39), находим с необходимой точностью, что
1-
G4(b)
G2(b)
A5.41)
Это уравнение позволяет найти амплитуду стационарных колебаний
при заданном безразмерном токе 1\. Исследование полученного реше-
решения на устойчивость показывает [8], что при b > —1,4 (G^ib) < 0),
колебание с амплитудой J7, найденное из выражения A5.41) устой-
устойчиво и мягко возбуждается при превышении током пучка порогового
значения /п = 1/G±{b). Напротив, при b < -1,4 {G±{b) > 0) решение
уравнения A5.41) соответствует неустойчивому состоянию системы.
Это свидетельствует о наличие в системе жесткого возбуждения и ги-
гистерезиса. Поэтому представленной выше слабонелинейной теорией
оротрона можно пользоваться только при параметре b > —1,4, когда
в системе отсутствует гистерезис. Данные результаты подтверждаются
как численными расчетами уравнений в режиме сильной нелинейно-
нелинейности (см. рис. 15.7, на котором представлена зависимость амплитуды
486
Лекция 15
и2 и3
щ и2 и3 и
Рис. 15.8. Зависимость мощности колебаний (а) и амплитуды стационарных
колебаний (б) в оротроне от ускоряющего напряжения. Сплошные линии со-
соответствует устойчивым, а штриховые — неустойчивым состояниям системы
стационарных колебаний от тока пучка для различных значений па-
параметра расстройки 6), так и экспериментальными исследованиями
[10, 11] (рис. 15.8, на котором приведена экспериментальная зависи-
зависимость мощности генерации и амплитуды стационарных колебаний от
ускоряющего напряжения). На рисунках, соответствующих как числен-
численному, так и натурному эксперименту, штриховыми линиями обозначены
неустойчивые состояния системы. Из рисунков видно, что при больших
отрицательных расстройках (Ь < —1,4) связь поля с током носит гисте-
резисный характер.
Нестационарные процессы в оротроне.
Методы повышения к.п.д. оротрона
Перейдем к обсуждению нестационарных процессов в оротроне.
Нелинейные уравнения нестационарной теории оротрона представляют
собой уравнения A5.14) и A5.31). В работе [12] на основании этих
уравнений исследовалась эволюция начальной амплитуды колебаний
во времени при различных параметрах Фо (см. рис. 15.9). С ростом Фо
скорость нарастания амплитуды колебаний увеличивается и достигает
максимума при Фо = 5, а затем снова уменьшается. Максимальная
Рис. 15.9. Зависимость амплитуды колебаний в оротроне от времени для
различных относительных углов пролета Фо. Поле в резонаторе распределено
по Гауссовскому закону (из работы [9])
Оротрон
487
120 МГц
амплитуда колебаний достигается при значительно большем угле про-
пролета Фо (Фо — 9). Данные обстоятельства необходимо учитывать при
работе прибора в импульсном режиме, в котором желательно при мак-
максимальной крутизне фронтов иметь наибольший к.п.д. Для решения
этой проблемы в работе [13] было предложено использовать импульс
ускоряющего напряжения сложной ступенчатой формы так, чтобы на
начальном этапе реализовывался режим максимального инкремента,
а на последнем — режим максимального к.п.д.
В оротроне экспериментально наблюдались и автостохастические
колебания [14]. В эксперименте исследовался оротрон с многократным
пролетом электронного потока в пространстве взаимодействия (кол-
(коллектор заменялся отражателем, а электронная пушка одновременно
выполняла роль другого отражателя). Теоретические оценки показали,
что оротрон работал при семикратном пролете электронного потока,
так что отношение пусковых токов при однократном пролете (/oi) и ПРИ
семикратном пролете электронного потока (/07) составляло /oi//o7-
Это позволяло в широких пределах изменять величину отношения
рабочего тока /о к пусковому /07. При
lo/ Iqi > 60 и разных (вполне определенных)
значениях отношения VOTp/Va (К)Тр — напря-
напряжение на отражателе; Va — анодное напряже-
напряжение) наблюдались следующие переходы в ре-
режиме работы оротрона: монохроматические
колебания — многочастотные колебания —
стохастические колебания (рис. 15.10).
В экспериментах были также обнаруже-
обнаружены автостохастические колебания на прямой
поверхностной волне, что соответствует ре-
режиму ЛБВ-генератора с внутренней запаз-
запаздывающей обратной связью [8, 14]. При сры-
срыве стохастических «оротронных» колебаний
срываются колебания, соответствующие ре-
режиму ЛБВ-генератора. Это позволяет свя-
связать автостохастические колебания в оро-
оротроне с теми, которые характерны для нели-
нелинейных систем с запаздывающей обратной
связью (изменение VOT^ изменяет эту связь).
Рассмотрим методы повышения к.п.д.
оротрона [15], (раздел 5). Как и для ЛБВ,
одним из наиболее удачных способов повы-
повышения к.п.д. является использование допол-
дополнительной синхронизации электронов пучка с высокочастотным полем.
С практической точки зрения наибольший интерес представляет метод
повышения к.п.д. основанный на введении скачка фазовой скорости.
В этом случае периодическая структура состоит из двух участков
40
20
0
40
20
0
YV.
Рис. 15.10. Эволюция
спектра генерации в оро-
оротроне с многократным
пролетом электронного
потока в пространстве
взаимодействия при
изменении VOTp'- a —
Vo,P/Va = 1,317; б -
1,350; в - 1,352; г -
1,355 (/о//о 7 = const,
Va = const) (из работы
[14])
488 Лекция 15
с различными периодами. При отрицательном скачке фазовой скорости
период второго участка меньше периода первого участка (ф2 = b2L >
> ф1 = Ь\ L) [16]. Как мы уже обсуждали в лекции 8, этот способ широко
применяется для повышения к.п.д. в ЛБВ. При положительном скачке
фх > ф2. На рис. 15.11а представлено распределение безразмерной
мощности вдоль пространства взаимодействия для системы без скачка
(кривая 1; ф = ЬЬ = 16,5), системы с положительным скачком фазовой
скорости B; ф\ — 16,5, ф2 — 15,0) и отрицательным скачком C; ф\ —
= 16,5, ф2 = 23,0). Расчет был произведен без учета пространственного
заряда. Из рисунка видно, что положительный скачок приводит к су-
существенному увеличению электронного к.п.д. Заметим, что не всегда
положительный скачок наиболее оптимален. Так в работе [17] представ-
представлены результаты оптимизации мощного оротрона г), которые показы-
показывают возможность повышения к.п.д. с 25 % до 56%, причем наиболее
эффективен как раз отрицательный скачок фазовой скорости.
Другой метод повышения электронного к.п.д. оротрона связан с оп-
оптимизацией структуры высокочастотного поля. В работе [18] рассмат-
рассматривался вопрос оптимизации пространственного распределения ампли-
амплитуды высокочастотного поля для получения максимального к.п.д. Рас-
Рассматривался класс функций Гаусса /(?) = Ае~т (?~а) с максимумом
в точке а, причем а не обязательно совпадает с центром пространства
взаимодействия. В результате расчетов были определены оптимальные
значения параметров т и а, обеспечивающие величину г\ « 50 %. Вместе
с тем вопрос о реализации в оротроне заданного распределения поля
остается открытым.
Большое влияние на эффективность оротрона оказывают и условия
на границе периодической структуры. В работе [19] было показано,
что при определенных условиях на границе периодической структуры
электродинамическая система оротрона может рассматриваться как
система двух связанных резонаторов, один из которых — открытый,
а другой — периодическая структура. В этом случае оротрон работает
в так называемом резонансном режиме. При этом резонанс в периоди-
периодической структуре, определяемый соотношением частоты генерируемых
колебаний и ее поперечных геометрических размеров, существенным
образом влияет на пусковой ток и эффективность взаимодействия. На
рис. 15.11^ приведена зависимость к.п.д. от тока для оротрона 3-см
диапазона при работе в резонансном режиме (кривая 1) и в обычном,
когда концы ламелей периодической структуры вынесены за каустику
ОР и нагружены поглотителем (кривая 2) [15, 20]. Из рисунка видно,
что, используя резонансный режим работы оротрона, возможно по-
г) Отметим, что применение методов повышения к.п.д. актуально для оро-
тронов большой мощности, где к.п.д. является одним из наиболее существен-
существенных параметров.
Оротрон
489
л
0,35
0,30
0,25
0,20
0,15
0,10
0,05
2
1 —г
1
0 0,2 0,4 0,6 0,8 1,0
Рис. 15.11. Распределение безразмерной мощности вдоль пространства взаи-
взаимодействия (а) в случае: 1 — отсутствия скачка фазовой скорости; 2 — ф\ >
> фъ\ 3 — фъ > ф\\ экспериментальная зависимость к.п.д. оротрона от тока
пучка (б) при работе в резонансном режиме (кривая 1) и в обычном (кривая 2)
(из работы [15])
высить эффективность генерации и снизить токи пучка, при которых
обеспечивается эффективное электронно-волновое взаимодействие. За-
Заметим, что при этом возникает проблема возбуждения «паразитных»
мод периодической структуры, которые снижают эффективность гене-
генерации. Последнее может быть устранено путем подавления нерабочих
«паразитных» частот за счет покрытия ВЧ-поглощающим покрытием
той части периодической структуры, которая соответствует пучностям
стоячей волны для мод «паразитной» частоты. Эксперимент [21] пока-
показал, что если на резонансной частоте без поглотителя при токе пучка,
превышающем его пусковое значение в 2,8 раза, к.п.д. составлял 12 %,
то с поглотителем при том же токе к.п.д. имел значение 35 %. Для срав-
сравнения в нерезонансном режиме при тех же относительных параметрах
пучка к.п.д. был менее 10 %.
Модификации оротрона
Открытые коаксиальные резонаторы и коаксиальный оро-
оротрон. В классическом оротроне используются плоские отражающие
решетки и ленточные пучки. Перспективным представляются кон-
конструкции, использующие в качестве электродинамической системы так
называемые открытые коаксиальные резонаторы (рис. 15.12) [22-24, 8].
Вследствие цилиндрической симметрии прибора он может обладать
490 Лекция 15
рядом преимуществ по сравнению с обычными оротронами. К ним
можно отнести большую поверхность решетки, что позволяет получать
большую мощность, возмож-
возможность использования трубчатых
электронных потоков, удобство
создания магнитных фокуси-
фокусирующих систем. Расчеты по
оптимизации коаксиального
1 liMMiiiiii'HNNil I _1 оротрона показывают, что при
^ ^ оптимальной форме верхнего
зеркала (а, следовательно,
Рис. 15.12. Схема коаксиального оро- и оптимальном распределении
амплитуды поля в пространстве
взаимодействия) электронный к.п.д. может быть существенно повышен
и может достигать 58 %. Профиль образующей фокусирующего зеркала
при этом близок к эллиптическому.
Приборы типа ЛБВ с открытыми резонаторами. В работе
[25] предложен прибор, в котором прямолинейный электронный поток
взаимодействует с продольной составляющей Гауссова поля в ОР (коле-
(колебание TMoi). Для реализации этого используется резонатор, образован-
образованный, как и в оротроне, плоским и вогнутым зеркалами. Однако теперь
электронный пучок движется вдоль оси симметрии резонатора, пройдя
через отверстие в плоском зеркале. Электроны пучка взаимодействуют
с полем излучения в области каустики. В оптимальном случае при токе
пучка /о = 1 А, длине волны Л = 1 мм коэффициент усиления по мощ-
мощности такого прибора достигает величины 0,6 (при энергии электронов
50 кэВ) и 0,24 (при энергии электронов 0,25 МэВ). Основная сложность
здесь связана с необходимостью получить синхронизм электронного
потока и волны излучаемого поля, не используя ультрарелятивистские
пучки. Среди способов замедления фазовой скорости излучаемой волны
укажем следующие:
1) для малого замедления фазовой скорости волны возможно запол-
заполнить резонатор газом;
2) если не обращать внимание на изменение конфигурации полей,
то резонатор можно заполнить твердым диэлектриком с осевым отвер-
отверстием для пучка, но тогда это просто использование диэлектрического
волновода;
3) использовать между зеркалами периодическую металлическую
или диэлектрическую антенну (набор прямоугольных периодически
расположенных металлических или диэлектрических решеток (пла-
(пластин)). В случае пластин с отверстиями на оси такую структуру мож-
Оротрон 491
но рассматривать как набор ёмкостно связанных резонаторов Фабри-
Перо.
Оротрон-усилитель. Простейший вариант усилителя с открыты-
открытыми системами, аналогичного двухрезонаторному клистрону с распреде-
распределенным взаимодействием, представляет собой два открытых резонато-
резонатора, связанных электронным пучком. В этом случае первый резонатор
модулирует электронный пучок, а во втором резонаторе электроны,
сгруппированные в сгустки, отдают свою энергию высокочастотно-
высокочастотному полю. Линейная теория такого усилителя, развитая в работе [8],
предсказывает максимальный коэффициент усиления порядка 35 дБ.
Заметим также, что максимум усиления достигается при частотах сиг-
сигнала несколько меньших, чем собственная частота второго резонатора.
Поэтому для максимального усиления первый резонатор необходимо
расстраивать в меньшую сторону относительно частоты второго резо-
резонатора.
«Плоский оротрон». Данный прибор был предложен в США
(см. обзор [15], а также оригинальные работы [26-29]). Электроди-
Электродинамическая система «плоского оротрона» представляет собой четыре
зеркала: два плоских и два цилиндрических. На одном из плоских
зеркал нанесена узкая решетка, занимающая небольшую ее часть, над
которой вдоль ее оси х пролетает плоский электронный пучок. Второе
плоское зеркало — экран расположено над зеркалом с решеткой вдоль
оси у на расстоянии не более половины длины волны. В направлении
оси у (перпендикулярно направлению распространения электронного
потока) система не имеет отражающих поверхностей, т.е. является
открытой. В направлении движения электронного потока пространство
взаимодействия прибора ограничено цилиндрическими конфокальны-
конфокальными зеркалами, расположенными на входе и выходе в него электронного
потока и имеющими для этой цели соответствующие отверстия. Таким
образом, вдоль и поперек пространства взаимодействия генератора
реализуется колоколообразное распределение ж-компоненты высокоча-
высокочастотного электрического поля с максимумом в центре ОР.
Прибор работает на модах пространственных гармоник: электроны
взаимодействуют с волнами, бегущими вдоль оси ж, которые существу-
существуют над поверхностью решетки, и усиливают излучение в этом направле-
направлении. Прибор может работать как на прямой, так и обратной гармониках.
Таким образом прибор может рассматриваться как резонансная ЛБВ
или ЛОВ с той лишь разницей, что обратная связь в нем осуществля-
осуществляется с помощью конфокального цилиндрического ОР за счет быстрых
волн, распространяющихся вдоль оси и многократно отражающихся от
цилиндрических зеркал. В экспериментах с «плоским оротроном» [26]
492 Лекция 15
было получено излучение в диапазоне частот 30 -г-100 ГГц, с мощностью
2-^0,1кВтик.п.д. 7-1-1%.
Оротрон со скрещенными полями. В данном приборе гене-
генерация основана на взаимодействии М-типа [15,30-33]. В работе [30]
представлены экспериментальные результаты по возбуждению гене-
генерации в оротроне со скрещенными полями с длиной волны 8,05 мм;
напряженность магнитного поля составляла Bq = 0,23 Т; потенциал за-
замедляющей системы Ua = 20 кВ, коэффициент замедления vq/с = 0,2.
Результаты теории (как линейной, так и нелинейной) для оротрона М-
типа с инжектируемым пучком [31, 32] свидетельствуют о его перспек-
перспективности в качестве генератора миллиметрового диапазона длин волн
с высоким значением к.п.д. В результате взаимодействия электроны
отдают высокочастотному полю как кинетическую, так и потенциаль-
потенциальную энергию, причем в режиме максимального к.п.д. основной вклад
в энергообмен высокочастотного поля с пучком вносит потенциальная
энергия электронов. К недостаткам оротрона М-типа можно отнести
высокое значение пускового тока. Теоретически было показано, что вы-
выходная мощность оротрона со скрещенными полями может составлять
10 -г- 20 кВт при к.п.д. около 20 %.
Увеличение к.п.д. и генерируемой мощности в оротроне с инжек-
инжектируемым пучком связано с существенными трудностями, обусловлен-
обусловленными ограниченными эмиссионными свойствами катода, размеры ко-
которого ограничены весьма малой величиной. В этом отношении более
перспективным является оротрон типа М с эмиттером в пространстве
взаимодействия, в котором возможно использование большого рабочего
тока. Поскольку в оротроне обратная связь осуществляется открытым
резонатором, то пространство взаимодействия такого генератора может
быть выполнено как цилиндрическим, так и плоским. Интересующимся
теорией оротрона М-типа можно порекомендовать сборник [33].
И в заключение обсуждения модификаций оротрона подчеркнем
большую важность релятивистских оротронов [9]. Использование ре-
релятивистских электронных пучков позволяет достичь рекордных вы-
выходных мощностей прибора.
В работах [34, 35] представлены результаты эксперимента на лабора-
лабораторном макете релятивистского оротрона, генерирующего в миллимет-
миллиметровом и сантиметровом диапазоне длин волн. В работе [34] представ-
представлены результаты исследования осесимметричной конструкции (полый
цилиндрический пучок в отрезке многоволнового цилиндрического вол-
волновода с гофрированной стенкой), где на волне 9 мм достигнута мощ-
мощность около 70 МВт. Данная конструкция радикально отличается от
классического оротрона. В более поздней работе [35] в релятивистском
Оротрон 493
оротроне с двухзеркальным открытым резонатором на волне 2,4 см
получена мощность 300 МВт с к.п.д. порядка 14 %.
Список литературы
1. Русин Ф.С, Богомолов Г. Д. Электронный прибор для генерации
и усиления колебаний миллиметрового и субмиллиметрового диа-
диапазона волн // А.с. No 195557. Опубл. в Б.И. 1967. No 10. С. 49.
2. Шестопалов В.П. Дифракционная электроника. — Харьков: Вища
школа, 1976.
3. Mizino К., Опо S., Shibata У. // Sci. Inst. Tohoku Univ. B. Electr.
Commun. 1970. V., № 21. P. 113.
4. Mizino K., Ono S., Shibata Y. // IEEE Trans.. 1973. V. ED-20, №8.
P. 749.
5. Leavitt R.P., Wortman D.E., Dropkin H. // IEEE J. Quantum
Electronics. 1981. V. EQ-17, №8. P. 1333.
6. Leavitt R.P., Wortman D.E., Morrison CA. // Appl. Phys. Letters.
1979. V. 35, №5. P. 363.
7. Шевчик B.H., Трубецков Д. И. Аналитические методы расчета в
электронике СВЧ. — М.: Сов. радио, 1970.
8. Вайнштейн Л.А., Лесик Н.И., Рожнев А.Г., Трубецков Д.И. Ква-
Квазиоптические системы и их применение в сверхвысокочастотной
электронике // Лекции по электронике СВЧ и радиофизике F-
я зимняя школа-семинар инженеров; книга III, глава 7)Саратов:
Изд-воСГУ, 1983, С. 117.
9. Вайнштейн Л.А., Исаев В.А., Трубецков Д.И. Электронный гене-
генератор с открытым резонатором (обзор теоретических и экспери-
экспериментальных исследований) // Радиотехника и электроника. 1983.
Т. 28, №7. С. 1233.
10. Ревин И.Д. В кн.: II Всесоюзный симп. по миллиметровым и
субмиллиметровым волнам: Тез. докладов. — Харьков: ИРЭ АН
УССР, 1978. Том. 1, С. 21-22.
11. Бакай А.С, Лукин К.А., Шестопалов В.П. О природе гистерезиса
в резонансных автогенераторах с длительным взаимодействием //
Письма в ЖТФ. 1978. Т. 4, № 13. С. 789.
12. Бакай А.С, Лукин К.А., Шестопалов В.П. Нелинейная неста-
нестационарная теория генератора дифракционного типа // Препринт
No 94. Харьков: ИРЭ РАН УССР, 1978.
13. Ваврив Д.М., Третьяков В.О., Шматько А.А. К нелинейной
нестационарной теории резонансных генераторов с длительным
взаимодействием // Радиотехника и электроника. 1979. Т. 23, №4.
С. 812.
494 Лекция 15
14. Корнеенко В.К., Мирошниченко B.C., Цвык А.И., Шестопалов
В.К. О возбуждении стохастических колебаний в генераторе ди-
дифракционного излучения - лазере на свободных электронах //
ДАН УССР. Сер. физ-мат. и техн. наук. 1982. №5. С. 59.
15. Цейтлин М.Б., Мясин Е.А. Оротрон: анализ эффективных режи-
режимов (обзор) // Радиотехника и электроника. 1993. Т. 38, № 6. С. 962.
16. Цейтлин М.Б., Бернашевский Г.А., Котов В.Д., Нутович Л.М.
II Радиотехника и электроника. 1979. Т. 24, №6. С. 1164.
17. Цейтлин М.Б., Мясин Е.А., Нутович Л.М. Анализ основных
энергетических характеристик оротрона в нелинейном режиме //
Радиотехника и электроника. 1990. Т. 35, № 11. С. 2364.
18. Тарасов М.М., Третьяков О.А., Шматько А.А. Оптимизация
структуры поля в электронных резонансных генераторах О типа //
Радиотехника и электроника. 1988. Т. 33, № 1. С. 141.
19. Мясин Е.А., Чигарев С.Г. // Радиотехника и электроника. 1990.
Т. 35, №5. С. 1104.
20. Мясин Е.А., Чигарев С.Г., Евдокимов В.В. // XX Всесоюз. семинар
«Волновые и колебательные явления в электронных приборах О-
типа»: Тез. докл. Л.: 1990. С. 18.
21. Чигарев С.Г., Евдокимов В.В., Ильин А.Ю., Мазур Т.А., Мясин
Е.А. Повышение выходной мощности оротрона за счет подавления
собственных нерабочих частот периодической структуры // Меж-
Международная межвузовская конференция «Современные проблемы
электроники и радиофизики СВЧ" (Саратов, 20-24 марта 2001).
Материалы конференции. Саратов: Изд-во ГосУНЦ «Колледж»,
2001. С. 162.
22. Нефедов Е.И. Коаксиальный оротрон // Изв. вузов. Радиофизика.
1977. Т. 20, №11. С. 1740.
23. Кураев А.А., Нефедов Е.И., Оленин В.Д. и др. // Радиотехника и
электроника. 1983. Т. 28, № 7. С. 1442.
24. Нефедов Е.И. Открытые коаксиальные резонансные структуры. —
М.: 1982.
25. Davis J. W., Patsakos Y. // The 6th Int. Conf. Infrared and Millimeter
Waves, Maiami Beach, Fla, Dec. 7-12,1981. Conf. Digest, New York. -
N.Y.: 1981. P.F6.5/1.
26. Marshall E., Phillips P., Walsh J. // IEEE Trans. 1988. V. 16, №2.
P. 199.
27. Walsh J., Marshall E., Jackson J. et al // Proc. of SPTE. 1988. V. 873.
P. 125.
28. Price E., Walsh J. // Proc. of SPTE. 1990. V. 1514. P. 135.
29. Price E., Killoran J., Walsh J. // Proc. of SPTE. 1991. V. 1576. P. 557.
Оротрон 495
30. Поспелов А.А., Черенщиков С.А. Радиотехника. — Харьков: Вища
шк, 1978. Вып. 45. С. 80.
31. Цейтлин М.Б., Евдокимов В.В., Бернашевский Г.А., Русин Ф.С.
К вопросу о генерировании колебаний в оротроне со скрещенными
полями // Радиотехника и электроника. 1981. Т. 26, № 5. С. 1109.
32. Цейтлин М.Б., Евдокимов В.В., Нутович Л.М. Теория резонанс-
резонансных генераторов с длительным взаимодействием в скрещенных
полях // Радиотехника и электроника. 1981. Т. 26, №9. С. 1979.
33. Цейтлин М.Б., Мясин Е.А., Нутович Л.М. Электроника мил-
миллиметрового и субмиллиметрового диапазона. — Киев: Наукова
думка, 1988.
34. Александров А.Ф., Галузо С.Ю., Канавец В.И., Михеев В.В.,
Плетюшкин В.А. Исследование релятивисткого генератора ди-
дифракционного излучения миллиметрового диапазона // Письма в
ЖТФ. 1981. Т. 10, № 10. С. 587.
35. Зайцев Н.И., Ковалев Н.В., Кольчугин Б.Д., Кулагин И. С, Пете-
Петелин М.И. Возбуждение двухзеркального резонатора с гофрирован-
гофрированными стенками релятивистским электронным потоком // Письма
в ЖТФ. 1982. Т. 11, № 15. С. 911.
Научное издание
ТРУБЕЦКОВ Дмитрий Иванович
ХРАМОВ Александр Евгеньевич
ЛЕКЦИИ ПО СВЕРХВЫСОКОЧАСТОТНОЙ
ЭЛЕКТРОНИКЕ ДЛЯ ФИЗИКОВ
Том 1
Редактор О. В. Салецкая
Оригинал-макет: В. В. Дядичев
Оформление переплета: А.Ю. Алехина
ЛР №071930 от 06.07.99. Подписано в печать 24.12.02.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 31. Уч.-изд. л. 34,1. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с готовых диапозитивов в ФГУП «Московская
типография № 6» Министерства РФ по делам печати,
телерадиовещания и средств массовых коммуникаций.
115088 Москва, Ж-88, Южнопортовая ул., 24
3BBN 5-9221-0372-5
9 785922 103725