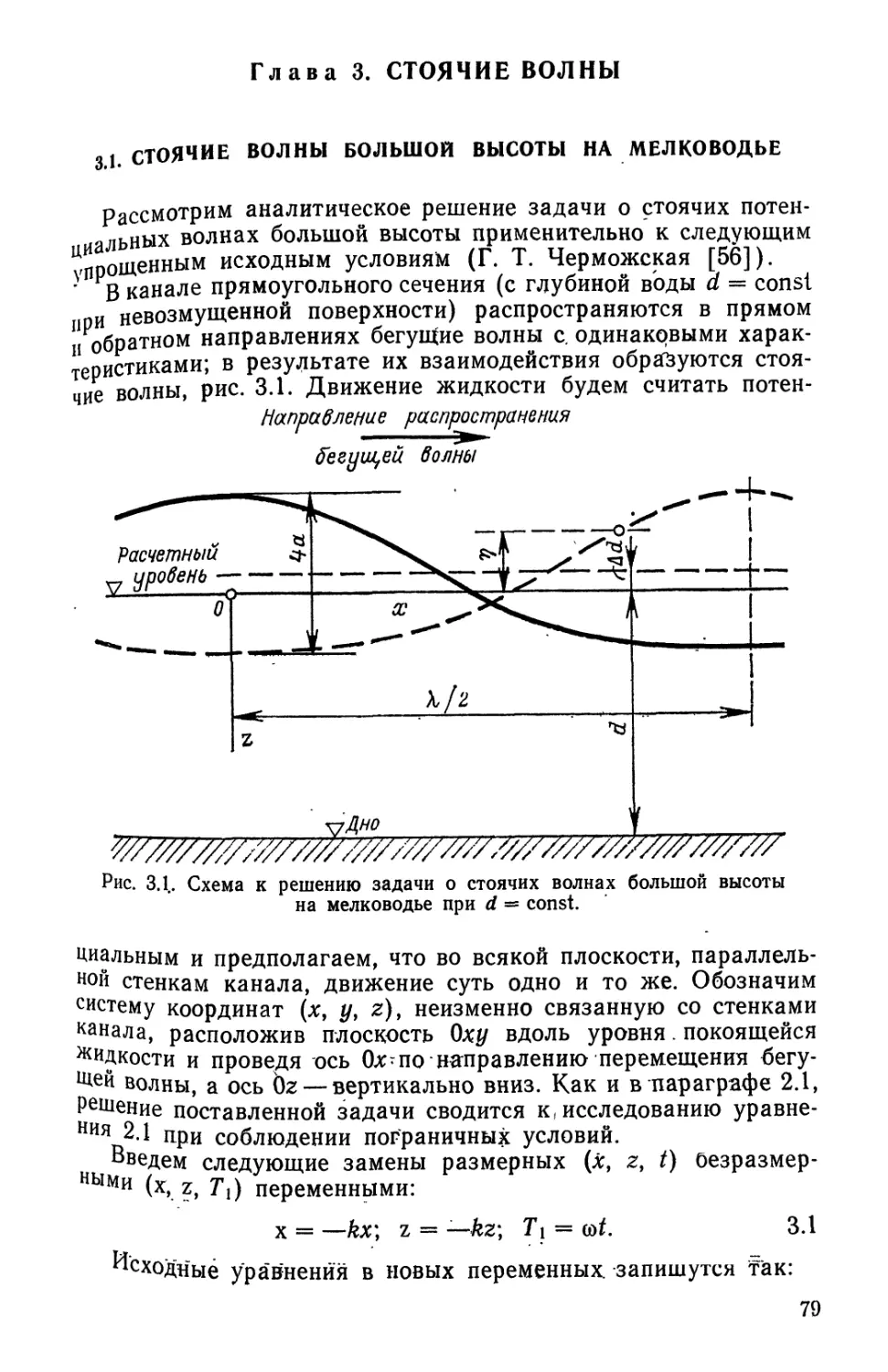
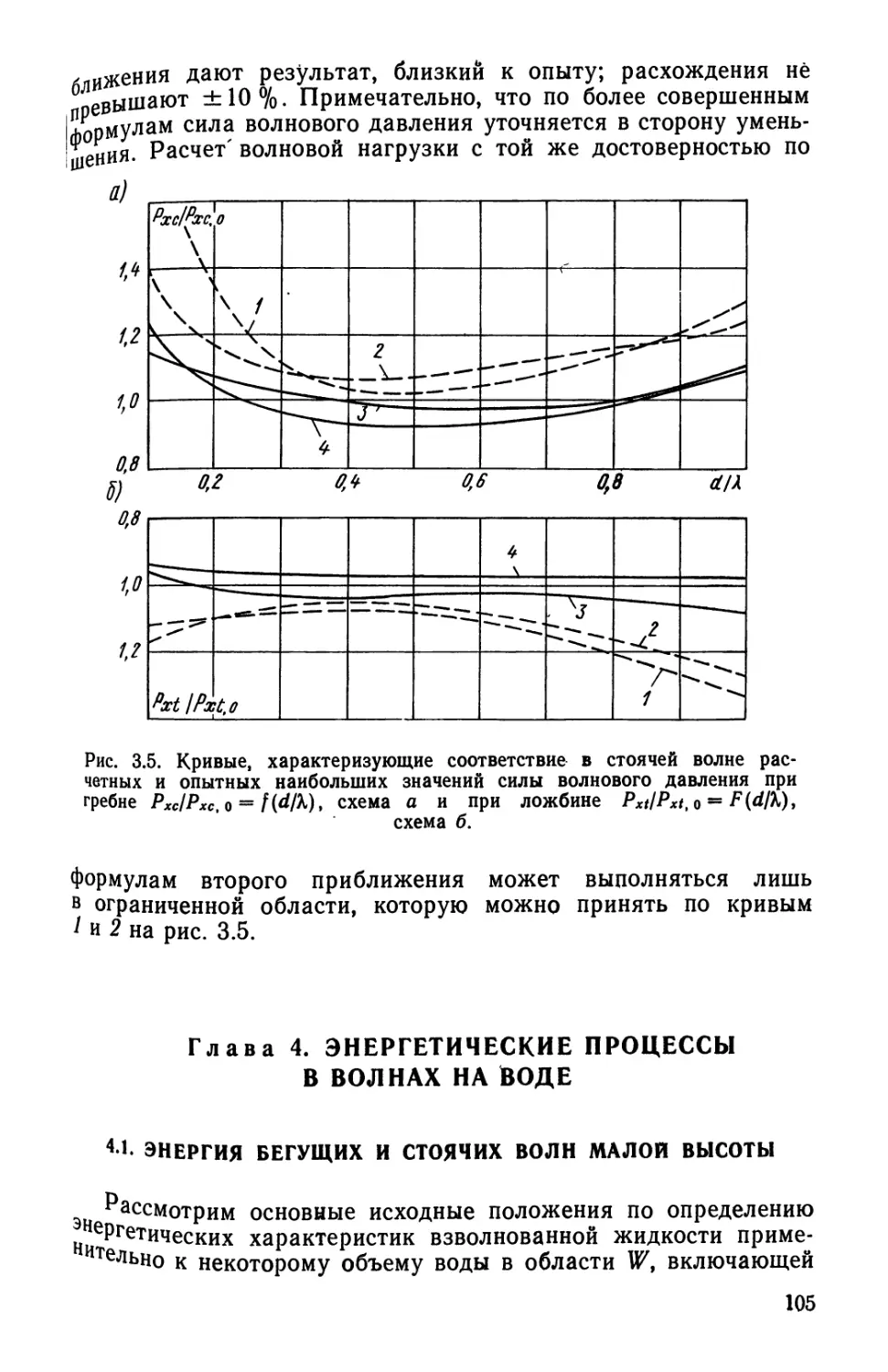
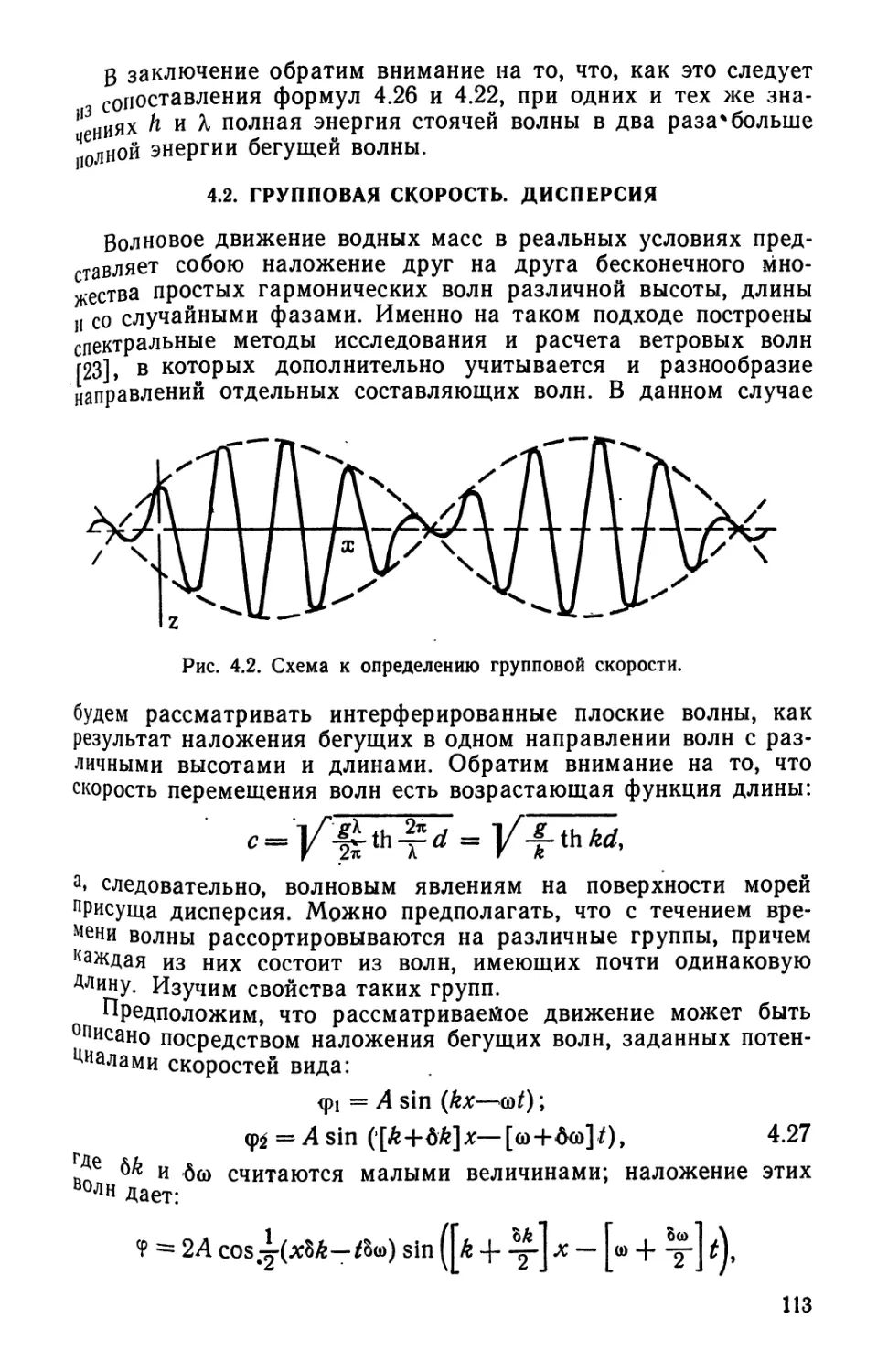
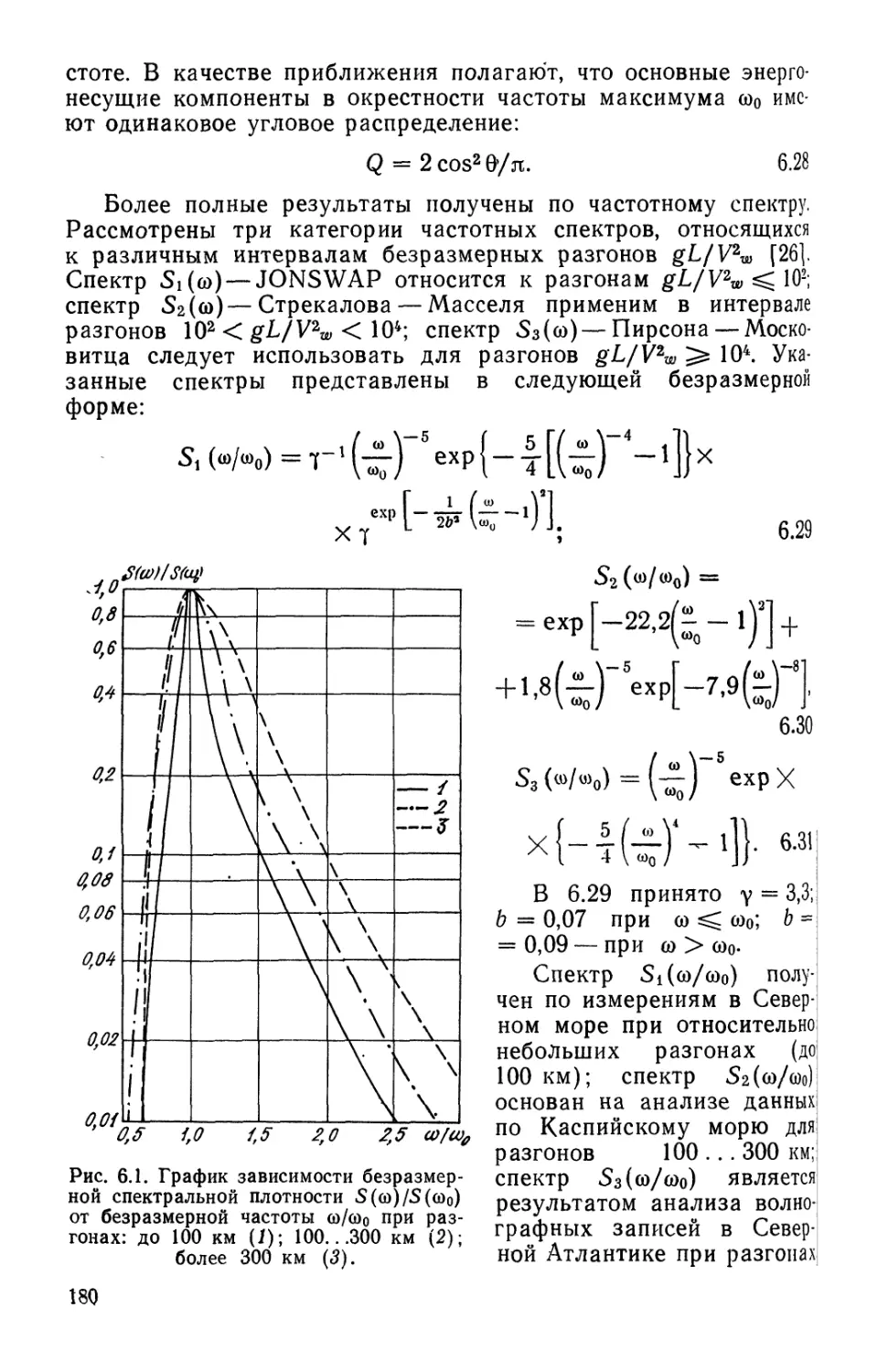
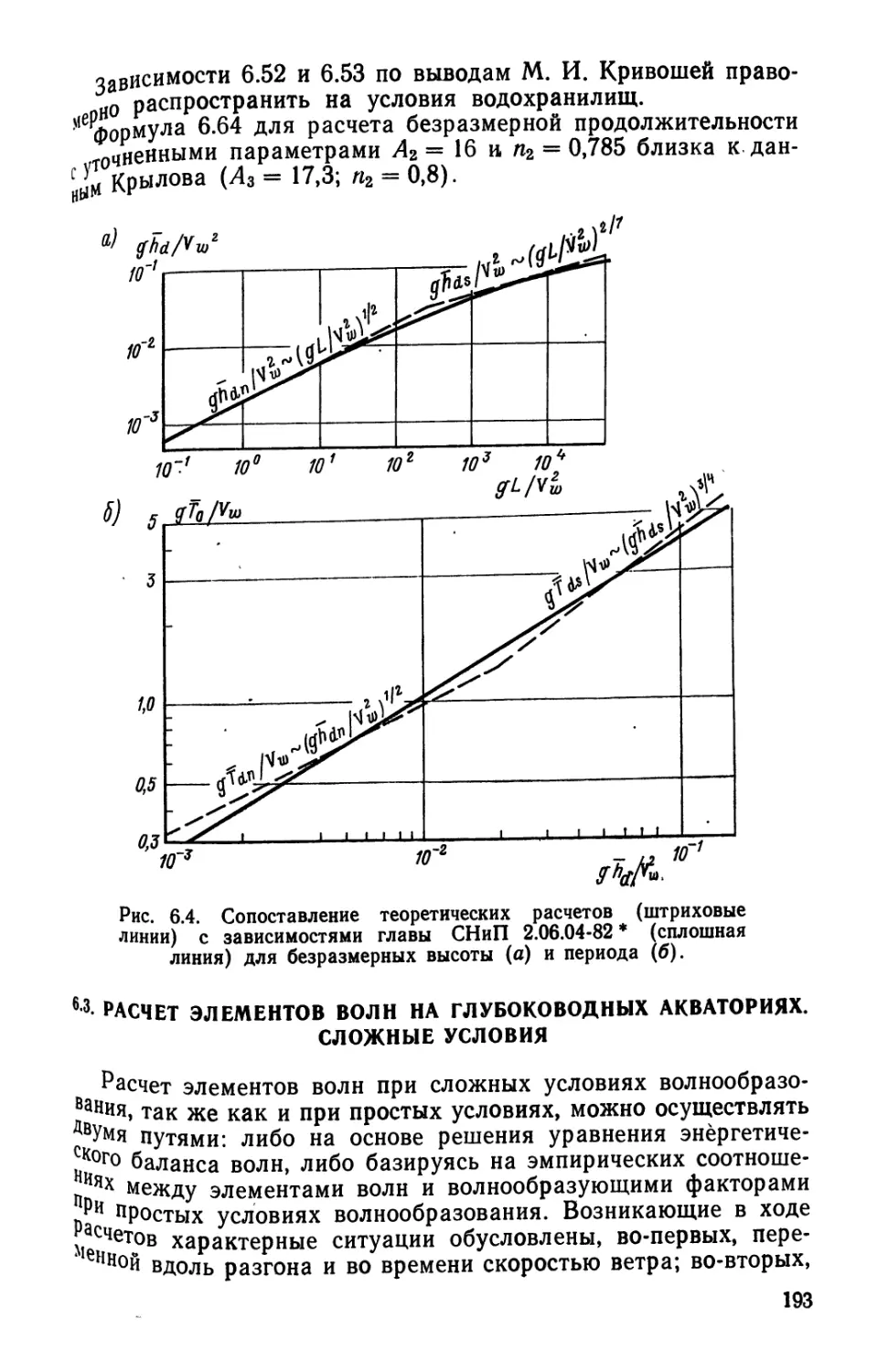
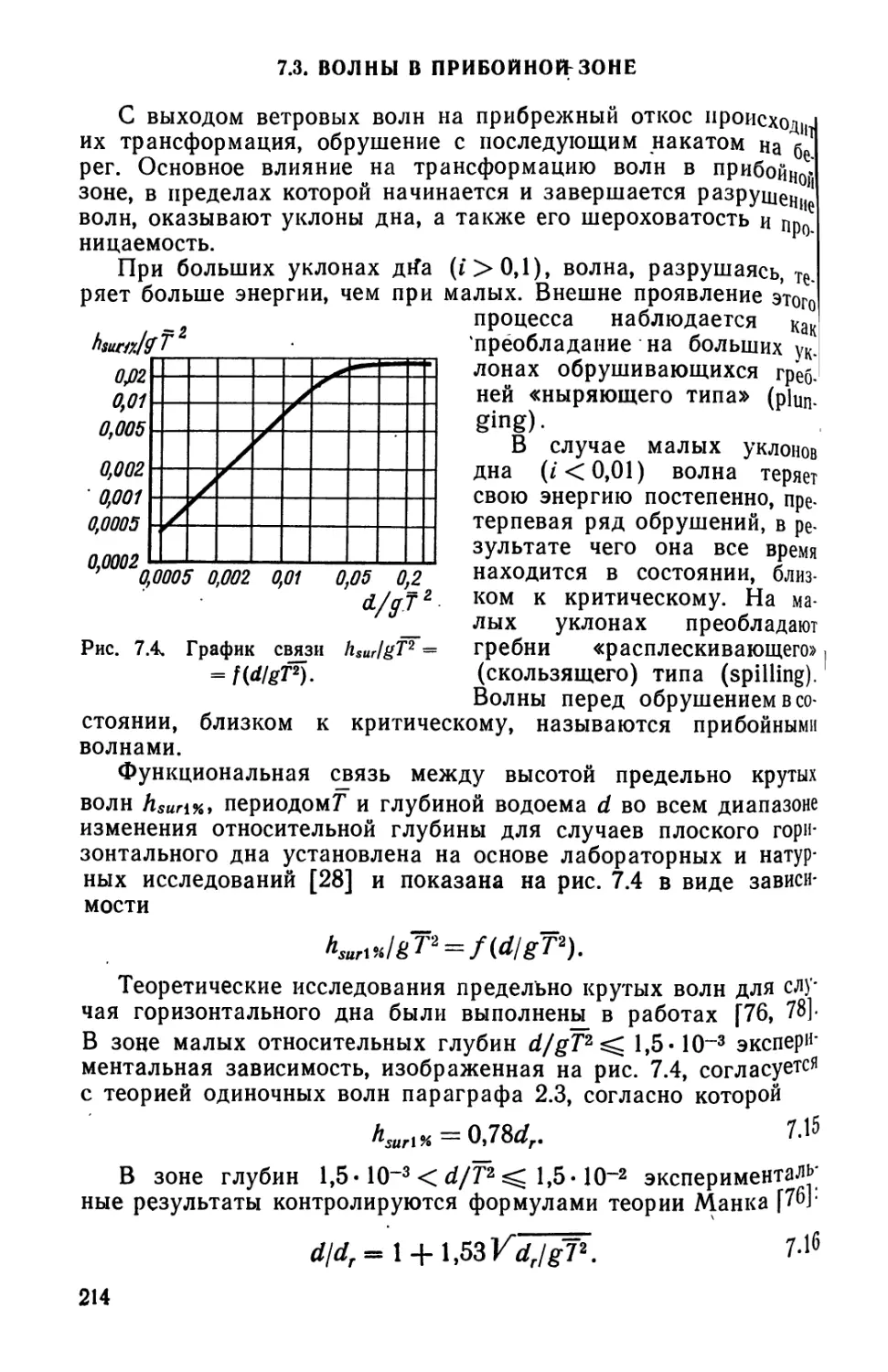
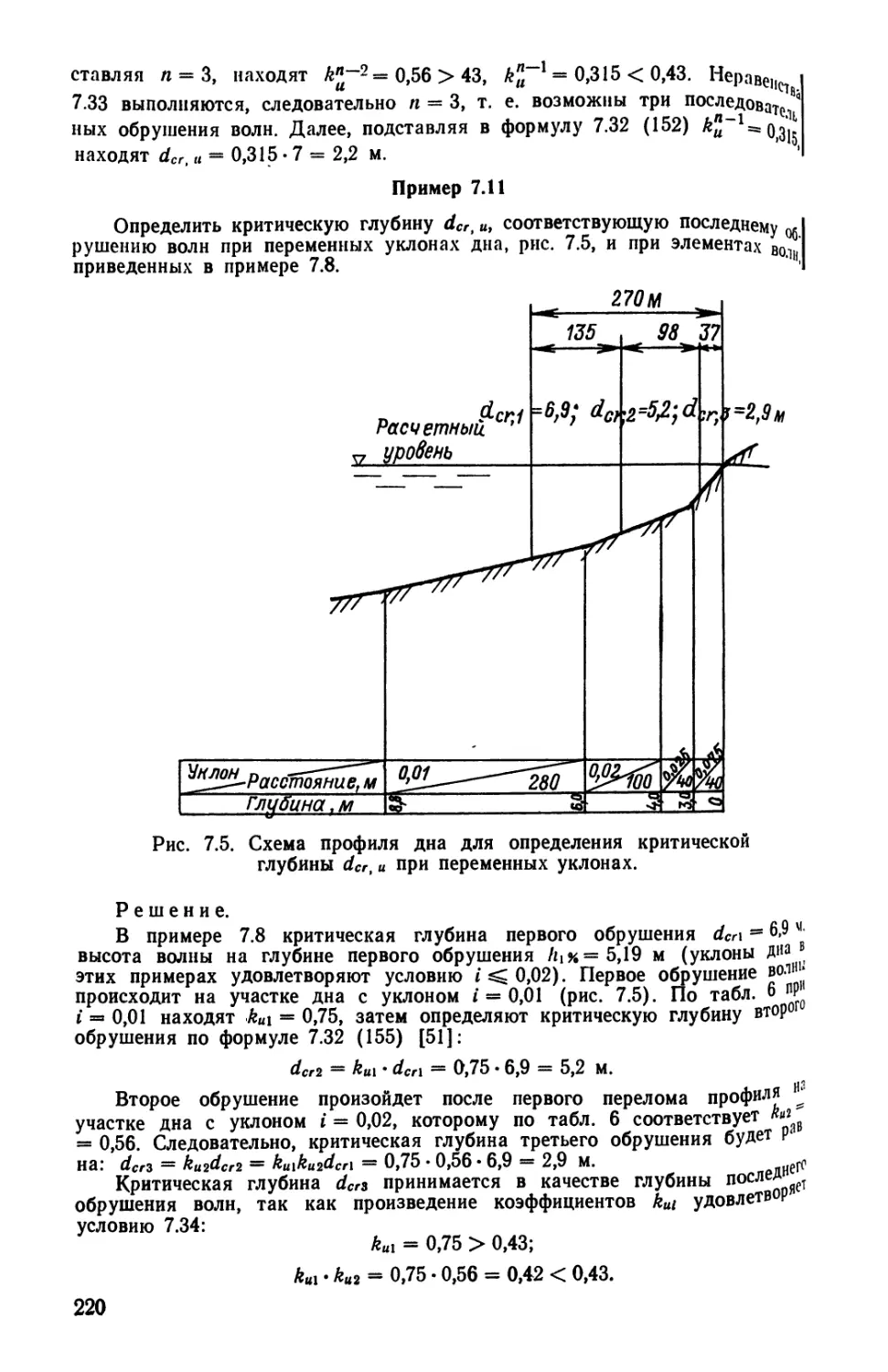
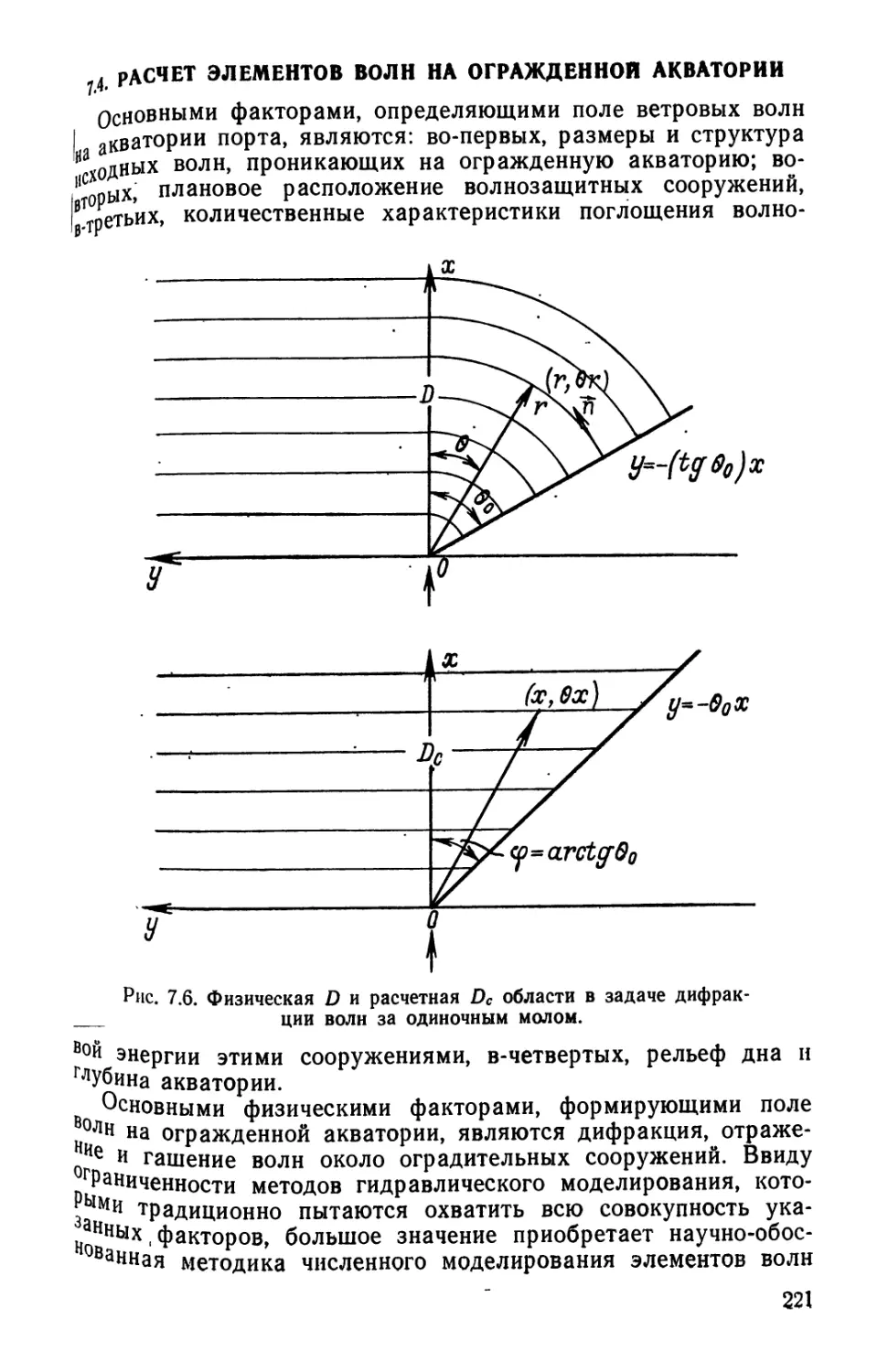
Текст
ВСЕСОЮЗНЫЙ
ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ ГИДРОТЕХНИКИ
имени Б. Е. ВЕДЕНЕЕВА
Д. Д. Лаппо, С. С. Стрекалов, В. К. Завьялов
НАГРУЗКИ И ВОЗДЕЙСТВИЯ ВЕТРОВЫХ ВОЛН
НА ГИДРОТЕХНИЧЕСКИЕ СООРУЖЕНИЯ
Теория. Инженерные методы. Расчеты
Под редакцией Д. Д. Лаппо
ЛЕНИНГРАД
1990
УДК 627.042.8 (083.74)
Кцига содержит сведения по теории и расчету элементов
регулярных и нерегулярных ветровых волн и методы
определения их воздействий на различные преграды в виде
традиционных гидротехнических сооружений и применяемых на
практике специальных конструкций для освоения природных
ресурсов морского дна. Особое внимание уделено примерам,
подобранным в качестве пояснений к общесоюзным
строительным нормам по расчету нагрузок и воздействий ветровых
волн на гидротехнические сооружения.
Предназначается для инженеров и специалистов,
связанных, с проектированием, возведением и эксплуатацией
сооружений на воде. Книга будет полезна научным работникам,
занимающимся исследованием ветровых волн и их
воздействий на различные преграды, а также студентам
гидротехнических факультетов вузов в качестве учебного пособия.
Д. Д. Лаппо, С. С. Стрекалов, В. К. Завьялов
НАГРУЗКИ И ВОЗДЕЙСТВИЯ ВЕТРОВЫХ ВОЛН
НА ГИДРОТЕХНИЧЕСКИЕ СООРУЖЕНИЯ
Теория. Инженерные методы. Расчеты
Под редакцией Д. Д. Лаппо
Редактор Е. Н. Боравскан
Технический редактор 7\ М. Бовичева
Корректор А. С. Каледкина
Младший редактор Я. В. Жердева
Сдано в набор 15.03.90. Подписано к печати 11.10.90.
Формат бумаги 60X90 Vie- Бумага типографская № 1.
Литературная гарнитура. Высокая печать. Усл. печ. л. 27,0. Усл. кр.-отт. 27,125.
Уч.-изд. л. 28,64. Тираж 2000. Заказ 196. Цена 6 р.
Типография ВНИИГ имени Б. Е. Веденеева. 195220 Ленинград, К-220, Гжатская ул.,21.
Издание осуществлено за счет ВНИИГ им. Б. Е. Веденеева,
Ленморниипроекта и Научно-исследовательского центра
капитального строительства
(6) ВНИИГ им, Б. Е. Веденеева, 1990 г.
ПРЕДИСЛОВИЕ
В последние годы в СССР и за рубежом издан ряд
монографий по теории и расчету ветрового волнения, среди которых
имеются фундаментальные труды крупнейших советских и
зарубежных ученых. Однако до настоящего времени не
издавалось таких книг, в которых вопросы теории волн были бы тесно
увязаны с нормированными методами расчета воздействий волн
на различные преграды в виде инженерных сооружений.
Следствием такого положения явилось то, что в практическом
использовании некоторых теорий волн допускаются разночтения,
которые приводят к погрешностям при определении волновых
нагрузок. Неоправданно мало внимания уделялось также
исследованию энергетических процессов в волнах, что затрудняло
изучение физики деформации волн на мелководье и воздействия
волн на некоторые сооружения.
Настоящая книга построена таким образом, чтобы читатель
без особого труда смог разобраться не только в рекомендуемых
для практики методах расчета характеристик волн и их
воздействия на различные преграды, но и получил бы возможность
убедиться в обоснованности те$ или иных аналитических
решений. В книге широко использованы графики и номограммы,
упрощающие и ускоряющие ведение расчетов. С помощью
приведенных графиков читатель сможет определить оптимальные
области использования теорий волн различной сложности и
степень достоверности результативных материалов. Авторы
считали необходимым содержание книги-пособия максимально
увязать с потребностями практики, а потому изложенные в ней
методы расчета параметров волн и их воздействия на
гидротехнические сооружения сопровождаются примерами расчета,
построенными применительно к содержанию действующего
СНиП 2.06.04-82* (П 44-89/ВНИИГ).
Расчеты нагрузок и воздействий ветровых волн на
гидротехнические сооружения базируются на той или иной теории
ветровых волн. Представилось уместным всесторонне
проанализировать принципиальные положения наиболее известных теорий
волн, положив в основу критерии их достоверности и
пригодности для использования в расчетах воздействия волн на соору-
а
жения, сохраняя по возможности однообразие в подходе и
методе решения частных задач.
Вопросы теории и расчета воздействия волн на портовые
гидротехнические сооружения, объекты гидроэнергетики и
специальные конструкции морских и океанских нефтепромыслов
изложены в десяти главах, объединенных в трех разделах:
первый раздел содержит информацию по основам теории волн на
воде; второй — посвящен отдельным положениям теории
возникновения и развития ветровых волн и расчету их элементов
на глубоководье и мелководье; последние три главы,
объединенные в третьем разделе, включают выборочные сведения из
теории и примеры расчета воздействий волн на инженерные
сооружения. Отдельные примеры расчета заимствованы из
Руководства [47].
Введение содержит краткую информацию по основным
направлениям развития и конструктивным формам
гидротехнических сооружений, подверженных воздействию ветровых
волн.
В главе 1 изложены общие сведения о волнах, принятая
терминология и классификация гравитационных волн. Приведен
обзор исследований в области гидродинамики волн, дана
постановка проблемы л о волнах на воде и отражены основные
особенности решения некоторых задач.
В главах 2 и 3 изложены основы теории бегущих и стоячих
волн, которые в дальнейшем используются в расчетах
сооружений, при этом более подробно рассмотрены решения теории по-,
тенциальных волн применительно к условиям ограниченной
глубины. Произведены сопоставления отдельных характеристик
волн, рассчитанных с помощью ЭВМ на основе рекомендуемых
теорий и, по формулам других наиболее известных решений.
Определены области применения аналитических формул
первого, второго и третьего приближений. Во второй главе уделено
внимание изложению основ теории уединенной волны, имея
в виду возможность использования отдельных выводов при
расчете воздействий прибойных волн и волн цунами на
сооружения.
В главе 4 приводится анализ энергетических процессов
в волнах на основе теорий волн малой и большой высоты.
Известно, что ветровые волны на воде возникают и
развиваются в результате поступления энергии от ветра,
движущегося над свободной поверхностью; вода является в некотором
смысле «проводником» энергии. Исследование энергетических
характеристик волн малой и большой высоты,
распределение энергии по длине волны и по глубине водоема, перенос
энергии бегущими волнами и знание других энергетических
процессов в волнах дает возможность с большей
достоверностью определять их взаимодействие с различными
преградами.
4
В главах 5, 6 и 7 освещаются вопросы возникновения и
развития ветровых волн. Анализируются волнообразующие
факторы и условия возникновения сильных штормов над
водоемами. Рассматриваются основные элементы взволнованной
поверхности воды. Обосновываются математические
представления характеристик нерегулярных ветровых волн через
энергетический спектр. Приводятся отдельные аналитические
выражения спектральной плотности волнения и дается их оценка.
В том же разделе содержится анализ методов и примеры
расчета элементов ветровых волн на глубоководных и мелководных
открытых акваториях при простых и сложных условиях
волнообразования. ' Исследуются особенности движения жидкости в
прибойной и в приурезовой зонах, приводятся рекомендации и
примеры определения элементов прибойных волн. Кратко
изложены вопросы теории и методика расчета волнения на
огражденной акватории порта. Ввиду сложности и многообразия
исходных условий эти задачи решаются преимущественно
полуэмпирически. Методы расчетов проиллюстрированы
соответствующими примерами.
В главе 8 представлена краткая информация о теории
расчета взаимодействия ветровых волн с сооружениями
вертикального профиля. Показано, что нерегулярность ветровых волн
не вносит существенных коррективов в значения волновой
нагрузки на вертикальную стену, рассчитанной на основе
детерминистических нелинейных теорий волн. Содержащаяся в [51]
методика расчета волнового давления и силы, действующей на
сооружения с вертикальной передней гранью, представлена в
виде простейших формул и облегчающих ведение расчетов
графиков, которые построены на основе большого объема
вычислений на ЭВМ.
Рассмотрены и некоторые наиболее характерные частные
задачи, в том числе определение волнового давления при
неполном отражении волн и при косом подходе волн, а также
расчет давления дифрагированных волн на тыльную грань
вертикальной стены со стороны огражденной акватории.
Приводятся приближенные формулы для определения воздействия
разбитых и прибойных волн на вертикальные стены и даются
соответствующие рекомендации по оценке воздействий волн на
основание и постель сооружения, в том числе и на берменные
массивы. В двух последних параграфах этой главы даны
рекомендации по не включенному в ([51] динамическому расчету
вертикальной стены, взаимодействующей с разбивающейся
волной, и определению нагрузок на крутонаклонные откосные
сооружения. По каждой из рассмотренных задач приведены
примеры расчетов.
Глава 9 содержит общий анализ материалов исследований
и конкретные указания по расчету воздействия волн на
оградительные сооружения откосного профиля и на различные
5
крепления откосов сооружения, в том числе крепление откосов
насыпных или намывных островов. Дается расчет высоты нака-i
та волн на откос с учетом нерегулярности ветровых волн и кон-!
струкции сооружения. Проанализирована физика явления воз-^
действия волн на сооружения с откосами, укрепленными моно-i
литными или разрезными плитами; изучены особенности этого!
явления, когда все сооружение выполнено из каменной или
массивовой наброски, а также случаи, когда откосные профили
из мелкого камня укреплены обыкновенными или фасонными
массивами. Применительно к разнообразным конструктивным
формам откосных сооружений изложена методика расчета со-'
оружений, проиллюстрированная рядом примеров.
Глава 10 содержит вопросы теории и расчета воздействий1
волн на отдельно стоящие обтекаемые преграды, сквозные co-j
оружения и подводные трубопроводы. К категории обтекаемых
преград отнесены такие сооружения или отдельные их элемен-ί
ты, которые только частично отражают или почти не отражают1
волн; набегающие волны огибают обтекаемые преграды,
существенно не изменяя своих параметров. Расчет волнового
давления с учетом явления обтекания должен производиться для
сквозных островных причалов, самоподнимающихся платформ,
погружных установок, крупноблочных островных сооружений!
морских нефтепромыслов и т. п. Анализ выполнен на базе
нелинейных теорий регулярных волн. Кроме того, даются
соображения по расчету силового воздействия нерегулярных волн на
обтекаемые преграды.
Предлагаемые для практики методы определения нагрузок
и воздействий волн на обтекаемые преграды систематизированы
и представлены в виде простейших формул и графиков,
облегчающих выполнение расчетов; даны характерные примеры.
В параграфе 10.8 приведен рекомендуемый, но не
содержащийся в [51] метод расчета нагрузок и воздействий волн на
произвольно ориентированную в пространстве обтекаемую преграду
ограниченных размеров, помещенную на глубину, равную или
больше половины высоты волны.
В приложении содержится библиотека программ
микрокалькулятора «Электроника Б3:34». С помощью 15 программ и
инструкций к ним без особых трудностей выполняются
практически все -расчеты нагрузок и воздействий ветровых волн на
гидротехнические сооружения, содержащиеся в [51]. Эти
программы пригодны не только для микрокалькуляторов типа
«Электроника БЗ-34», но и для «Электроники МК-52»,
«Электроники МК-54», «Электроники МК-56» и «Электроники МК-61»
с учетом оговоренных в приложении различий в некоторых
обозначениях.
Основные направления дальнейших научных исследований
по проблемам совершенствования теории и методов расчета
параметров ветровых волн в различных естественных условиях,
6
а также нагрузок и воздействий волн на гидротехнические
сооружения и берега изложены в заключении.
Нумерация формул, таблиц и рисунков в книге принята по
главам, но в отдельных случаях, там, где это сочтено
целесообразным, в круглых скобках дополнительно приведены
ссылки на номера соответствующих формул, таблиц или
рисунков из СНиП 2.06.04-82 *.
Настоящая книга написана коллективом авторов под
научным руководством и редакцией Д. Д. Лаппо;
непосредственные авторы-исполнители: Д. Д. Лаппо — предисловие, главы
1—4, 8, 10 и заключение; С. С. Стрекалов — главы 5—7;
β. /С. Завьялов — глава 9; Λί. £. Миронов — параграф 8.7 и
совместно с 5. В. Новиковым — приложение; 5. В. Каплун,
совместно с Д. Д. Лаппо, — параграфы 10.5—10.7 и 10.9;
А. Д. Лаппо — параграф 10.8. Введение написано
совместно Д. Д. Лаппо и Л. Б. Певзнером. В разработке ряда
предложений и написании глав 5—7 творческое участие принимали
Ю. Λί. Крылов, Б. А Дугинову С. В. Кривицкий, Ю. Я. Поляков,
Б. Г, Галенин; в составлении параграфа 8.7 участвовали
Я. Я. Кульман, В. 3. Филиппенок; в написании главы 9 —
Л. Λί. Жуковец и Д. Д. Лаппо. При написании данной книги
использовано также Руководство [47], в частности, в главах
6 и 7 учтены предложения Г. Ф. Красножона, Г. В. Матушев-
ского; в главе 8 — В. К. Штенцеля, Н.Н. Загрядской, Г. Т. Чер-
можской; в главе 9 —И. #. Попова, Л. А. Морозова,
Е. /С. Гречищева; в главе 10 —Д. Д. Лаппо, В. В. Каплуна,
С. β. Ивановой.
В рассмотрении рукописи книги принимали участие и дали
положительные письменные заключения доктора технических
наук: А £. Асарин, Б. В. Балашов, И. X. Костин, Я. Я. Кульман,
А. В. Мишу ев, Г. В. Симаков, С. Г. Шульман и доктор физ.-мат.
наук /С. Я. Шхинек, а также кандидаты технических наук:
β. С. Ермаков, УО. Д. Кравчук, Д. В. Марченко, Λί. £. Миронов,
С. С. Мищенко, В. Д. Ульянов, В. 3. Филиппенок.
Авторы книги выражают глубокую признательность всем
ученым, а также главному специалисту Гидропроекта им.
С. Я. Жука А Я. Жиркевичу и заместителю главного инженера
проекта В. Я. Τ у мило-Денисовичу за полезные замечания,
которые в основном учтены при доработке рукописи.
Отзывы и замечания просьба направлять по адресу: 195220,
Ленинград, Гжатская ул., 21, ВНИИГ им. Б. Е. Веденеева.
ВВЕДЕНИЕ
КОНСТРУКТИВНЫЕ ФОРМЫ
ГИДРОТЕХНИЧЕСКИХ СООРУЖЕНИЙ,
ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ ВЕТРОВЫХ ВОЛН
В последние годы гидротехническое строительство ведется
в широких масштабах у нас и за рубежом. Это обусловлено
развитием энергетики, в частности, гидроэнергетики,
интенсивным освоением шельфа морей и океанов.
В нашей стране завершается строительство Саяно-Шушен-
ской, Колымской и Бурейской ГЭС, Южно-Украинского
энергокомплекса, ведутся исследования и предпроектные
проработки одной из крупнейших ГЭС —Туруханской. Отметим,
что объекты гидро- и теплоэнергетики (плотины, подпорные
стены, дамбы обвалования, водосбросы, Деривационные и
судоходные каналы, туннели, шлюзы, судоподъемники,
водоприемники и водозаборы и т. д.) возводятся на реках и
водохранилищах, как правило, в зонах ограниченного волнового
воздействия. Однако при строительстве атомных
электростанций на морском побережье возникает необходимость
обеспечения гарантированной безопасности площадки АЭС от волнового
воздействия.
В настоящее время проводятся исследования и начато
практическое использование огромных запасов энергии,
заключенной в Мировом океане (приливно-отливные течения, ветровые
волны и т. д.). Достаточно заметить, что мощность
электростанций за счет использования волновой энергии Мирового океана
оценивается в 2,7 млрд. кВт, что составляет около 30 %
мощностей действующих в мире ГЭС. На некоторых участках
побережья США и Японии концентрация волновой энергии
достигает 40... 80 кВт · ч на один метр волнового фронта. Уже
эксплуатируются приливные станции Кислогубская в
Баренцевом море, во Франции на р. Ране и три станции в Канаде общей
мощностью 5600 кВт. Созданы первые установки на шельфе в
Англии, Японии и США по утилизации волновой энергии
Мирового океана.
8
Большое развитие получили специальные морские
гидротехнические сооружения (СМГТС), возводимые на шельфе и
используемые главным образом для разведки, добычи и
транспортировки нефти, газа и других полезных ископаемых. О широком
развертывании строительства СМГТС можно судить по
следующим цифрам. В мировых потенциальных запасах нефти около
70 % приходится на шельфовую зону. По прогнозу в 1990 г.
доля добычи нефти и газа на шельфе составит 45 % ,от общего
количества, а некоторые страны, например, Англия,
удовлетворяют свои потребности в нефти только за счет морской добычи.
В настоящее время в мире насчитывается более 4000
стационарных платформ и более 800 подвижных установок,
предназначенных для бурения. Конструкции платформ и установок
разнообразны в зависимости от естественных условий в месте
бурения. Для хранения и транспортировки нефти и газа
строятся хранилища и трубопроводы. Общая длина построенных
нефтегазопроводов превышает 30 тыс. км. Среди них следует
выделить: нефтепровод, соединяющий Африку и Италию;
в Шотландии — месторождение Фригг длиной 520 км;
нефтепроводы в Северном море. Для удаленных месторождений
оказывается экономичнее оборудовать нефтехранилища вблизи
газонефтепромыслов. В Северном море, в частности, установлен
целый ряд таких хранилищ, крупнейшее из них —на 840 тыс. т.
Большая работа ведется по освоению шельфовой зоны путем
строительства искусственных островов и плавучих сооружений
разного назначения. Одними из первых были созданы такие
искусственные территории у берегов Японии. На островах
площадью более 600 кв. км расположены три взлетно-посадочные
полосы, два рыбоперерабатывающих завода, три атомные
электростанции, завод по утилизации мусора. В море Бофорта
канадцами построено более 30 искусственных островов для
добычи нефти и газа.
В последние годы созданы крупные гидротехнические
транспортные сооружения для преодоления водных преград
(мосты и тоннели). Примером может служить мост через
Босфор, соединяющий Европу и Азию; он окупился в течение
трех лет эксплуатации. Построены мосты в Осакском и
Токийском заливах/ Проектируются мосты (или тоннели) через
Гибралтар и Ла-Манш.
Одними из интереснейших гидротехнических сооружений,
возводимых на Щельфе, являются подводные тоннели. В качестве
примера можно привести тоннель между Сицилией и материком
длиной 3,2 км; он заглублен на 40... 50 м под поверхностью
моря и состоит из трех железобетонных труб с наружным
диаметром 12,3 м при толщине стенок 0,75 м. Тоннели крепятся к
Дну с помощью якорных связей. Подводные тоннели имеют
существенные преимущества по сравнению с мостами и
подземными тоннелями, так как в данном случае не требуется строи-
9
тельство высоких опор (как в мостах) или выполнение
подземных выработок; они отличаются большей сейсмобезопасностью,
Акватории шельфов широко используются для размещения
навигационных установок и научно-исследовательских станций.!
Так, в США на Атлантическом побережье еще в 1950-х годах
воздвигнута целая сеть платформ, на которых расположены'
локаторы. Эта система платформ, вынесенных далеко в море и!
названных Техасскими башнями, предназначена для заблаго-,
временного обнаружения самолетов и не потеряла своего
значения до настоящего времени.
Из краткого рассмотрения основных направлений развития
гидротехнических сооружений следует, что они разнообразны
по назначению и конструктивному решению, а создание
специальных морских ГТС представляет собой прогрессивное на-ι
правление. Внешние оградительные сооружения, островные!
причалы, морские водозаборы, а также СМГТС возводят на
незащищенных акваториях, подверженных воздействию волн,1
течений, льда и т. д. Это является определяющим фдктором при
выборе типов сооружений и их конструктивных особенностей,
тесно связанных с условиями производства работ. Подводную
часть сооружений возводят, как правило, из заранее
изготовленных конструкций путем установки их в воду на подготовлен7
ное основание или погружением в грунт свай, шпунта, колонн-
оболочек с плавучих средств или пионерным способом,
используя уже построенную часть сооружения. ]
С условиями производства работ связана и другая важная:
особенность рассматриваемых гидротехнических сооружений—j
максимальное использование крупноблочных сборных
конструкций из заранее изготовленных элементов. Кстати, именно в
гидротехническом строительстве раньше всего появились и
получили наибольшее распространение сборные сооружения из
заранее изготовленных элементов. При возведении таких
сооружений на незащищенной акватории должно соблюдаться
важнейшее требование устойчивости их элементов на любой стадии
готовности. Кроме того, рассматриваемые конструкции должны
допускать возможность применения при «морских работах»
легко передвигаемого строительного оборудования: плавучих
кранов, копров и т. д.
Из традиционных портовых гидротехнических сооружений,
подверженных воздействию волн, в практике находят широкое
применение оградительные сооружения откосного и
вертикального профилей. Волны, набегающие на откосные сооружения
(рис. Ι,α), в основном гасятся, и поэтому отражение волн
практически отсутствует. Откосные сооружения могут быть
непроницаемыми для волн (с гладкой поверхностью) или
пористыми (набросными) — из рваного камня, бетонных блоков и
т. п.; в последнем случае в теле сооружения происходит
дополнительное гашение энергии волн.
10
Взаимодействие волн с оградительными сооружениями
вертикального профиля (рис. 1,6) характеризуется частичным или
полным отражением набегающих волн с образованием в
определенных условиях стоячих волн, что обусловливает необходи-
77Т77Г-77Г
$) М°Ре
//А/// л
ifegp
i?*a
Га бань
ι , ι
X
III
Л
W
^^^'^л^л
-5-?
у// /)/ /// φ//9/// ту/ ///
В) Море
У/ν /У/ ууу /// /А/
Рис. 1. Оградительные сооружения
а) откосного профиля, из наброски массивов; б) вертикального
профиля из массивовой кладки; в) сквозной мол-причал на колоннах
с двумя вертикальными экранами.
мость увеличения высоты всего сооружения или части его в
виде парапета. Нередко с внутренней стороны (со стороны
гавани) оградительного сооружения вертикального профиля
предусматривается швартовка судов. Тело сооружения верти-
11
кального профиля покоится на каменной постели, Которая Мб]
жет быть заглублена в грунт основания или возвышаться над
дном. В отдельных случаях представляется целесообразным
постель, возвышающуюся над дном, существенно увеличить nd
высоте, в результате чего получить конструкцию смешанного
типа в виде сооружения, включающего вертикальный и откос]
ный профили. Воздействие волн на такое сооружение иногда^
может иметь специфический характер: крупные волны могут]
разбиваться на нижней откосной части профиля и 'затем интен-1
сивно воздействовать на вертикальную стену и парапет соору-4
жения.
В определенном сочетании естественных условий, например]
при глубинах 15...20 м и относительно небольших параметрах!
волн, может оказаться целесообразным применять конструкции
оградительных сооружений по типу изображенных на рис. 1эв.
Характерной особенностью таких сооружений является, в
частности, то, что они способны в определенной степени отражать
энергию подходящих волн, т. е. выполнять функции
оградительного сооружения и одновременно служить причалом для
судов с большой осадкой.
В некоторых случаях, вблизи районов добычи нефти, руды!
и других полезных ископаемых, а также в пунктах их доставки]
создаются порт-пункты, состоящие из одного или нескольких!
глубоководных причалов для обслуживания крупнотоннажных^
судов. Характерным примером таких сооружений может
служить причал в Бантри-Бей (Ирландия), расположенный
параллельно берегу на расстоянии 365 м от него, предназначенный]
для одновременного приема танкера дедвейтом 312 тыс. τ cs
морской стороны и танкера меньших измерений — с противо-^
положной.
Иногда представляется целесообразным резервуары для
сбора и хранения нефти делать подводными, как
например, подводный железобетонный резервуар емкостью около
80 тыс. м3, построенный в Персидском заливе недалеко от
порта Дубай.
Стационарные сооружения морских нефтегазопромыслов по
способу обеспечения устойчивости делятся на гравитационные
и свайные. Гравитационные сооружения могут быть разделены
на мелководные и глубоководные (гравитационно-погружные).
Мелководные сооружения строятся, как правило, из грунта
в виде искусственных островов в районах с тяжелыми ледовыми
условиями при глубинах до 20.., 25 м. При глубинах до 40 м
применяют гравитационные сооружения в виде
массивов-гигантов или кессонов.
На больших глубинах возводят гравитационно-погружные
сооружения (платформы), которые удовлетворяют основным
принципам строительства в морских условиях: крупномодуль-
ность и минимальный срок установки. Основная идея, заложен-
12
ная в основу их конструкции, — изготовление сооружения в
удобном, месте, транспортировка к месту работы наплаву и
установка на месте бурения с учетом интервалов времени между
штормами.
Конструктивная схема сооружения включает следующие
элементы: верхнее строение, опорную часть (фундаментный
блок) и опорные колонны (рис. 2). В верхнем строении
располагаются технологическое оборудование, энергетические
установки и жилые помещения. Высота верхнего строения составля-
Рис. 2. Гравитационно-погружные платформы систем:
а) Кондин; б) Си-Тэнк; в) Сконека.
ет 10... 15 м, а площадь — 3000... 7000 м2. Как правило, оно
изготавливается из металла, однако есть установки и с
железобетонным верхним строением. Основа опорной части
сооружения—фундаментная плита толщиной 2...4 м. Сверху к плите
примыкают балластные отсеки, обеспечивающие плавучесть
основания в транспортном положении. Балластировкой этих
отсеков достигается погружение платформы на дно и ее
устойчивость в рабочем положении. Обычно балластнуе отсеки
объединяются с фундаментной плитой, образуя единое целое —
фундаментный блок. В большинстве случаев фундаментный блок
изготовляется из предварительно напряженного железобетона
и представляет собой либо объединение ячеистых элементов
13
(система Кондин), либо прямоугольный понтон, разделенный
переборками (системы Си-Тэнк, Фригг, Андок). После установ]
ки на дно балластные отсеки используются как нефтехранили]
ща, чем достигается многофункциональность платформы. На
нижней поверхности фундаментной плиты расположены pe6pd
для предотвращения сдвига в момент установки сооружения и
уменьшения размыва грунта основания.
Фундаментный блок соединяется с^ верхним строением при
помощи опорных колонн, число которых может быть от одной
до четырех, а в отдельных случаях — до четырнадцати. Опорь]
надлежит надежно крепить к верхнему строению. Различают]
два вида опор: имеющие волнозащиту и не имеющие ее.
В большей части платформ снижение волновых нагрузок
обеспечивается за счет применения колонн сравнительно не]
большого диаметра в области ватерлинии и уменьшения коли]
чества собственно опор (сооружения башенного типа). Высота
опор подбирается так, чтобы расчетные волны не достигали
верхнего строения, а диаметр (сечение) опор сужался к ватер]
линии. При изготовлении из металла опоры можно выполнитн
в виде ферм, обладающих меньшим волновым сопротивлением
Сооружения с волнозащитой в большинстве случаев исполь]
зуются также как нефтехранилища. Гашение волн в этих кон]
струкциях достигается за счет наличия в верхней части перфо]
рированной стены. При взаимодействии волны с такой преградой
часть волновой энергии отражается или гасится при про]
хождении сквозь отверстия, а часть переносится внутрь, воз]
действуя на опоры. При этом иногда достигается возможности
за счет рациональной конструктивной формы сооружения в два]
раза снизить волновые нагрузки.
Считается, что платформы с волнозащитой имеют преимут
щества перед сооружениями башенного типа при установке ил
на акваториях с глубинами до 70... 80 м. Гравитационно-по]
гружные платформы нашли применение в Северном море для
бурения и хранения нефти при глубинах до 150 м; существую^
проекты платформ для глубин до 300 м. Одим из достоинств
этих сооружений является возможность их быстрого монтажа
на месте эксплуатации; например,- установка платформы Си-1
Тэнк заняла 24 часа.
Сооружения свайного типа отличаются тем, что их устойчи-|
вость на морском дне обеспечивается креплением основания
с помощью забивки в грунт свай. Они получили широкое раз]
витие при освоении нефтепромыслов Каспийского моря, начиная
с 1936—1938 гг., впоследствии — нашли применение на аквато]
риях Мексики и Венесуэлы. Сооружения свайного типа включая
ют эстакады, искусственные острова и платформы. ]
Эстакады служат в основном в качестве транспортных
связей, соединяющих буровые установки между собой и берегом.1
Они возводятся пионерным способом (при глубинах до 15.. J
14
,.. 20 м) или с прмощью краново-монтажных судов,
грузоподъемность которых в СССР достигает 2500 т. Соответственно
применяются модули массой 40.. .50 т, позволяющие собирать
эстакады, платформы и искусственные острова на глубинах до 30...
... 35 м. Рассматриваемые сооружения нашли широкое
применение в Каспийском море, где на глубинах до 30... 40 м
возведено' 880 искусственных островов и более 300 км эстакад.
Принципиально иной вид конструкций платформ возник при
освоении больших глубин. Платформы (иногда их называют
сооружениями ферменного типа) состоят из трех основных
элементов: верхнего строения, опорного блока и свайного
основания. Эти элементы доставляются на место эксплуатации порознь
и монтируются на месте. Опорный блок представляет собой
решетчатую конструкцию из ферм пирамидального профиля,
рис. 3. Через опоры проходят сваи, забиваемые на расчетную
глубину (до 140 м) и образующие свайные основания. Сваи
изготавливаются из металлических труб наружным диаметром
до 2 м с толщиной стен до 25 мм. Верхнее строение обычно
металлическое, его масса достигает 10000 т. Самая
глубоководная из построенных платформ установлена в Мексиканском
заливе на глубине 300 м в удалении 19 км от берега. Она
рассчитана на воздействие ураганного ветра 70 м/с и волнение
высотой до 21 м. Нижняя секция имеет опорные муфты, через
которые забиты на глубину 138 м 24 стальные сваи диаметром
2,1 м (масса одной сваи 465 т). Платформы ферменного типа
отличаются индустриальностью, быстротой и удобством сборки
основания, сейсмостойкостью и устойчивостью основания от
размыва. Пространственная решетчатая конструкция
проницаема для ветровых волн и поэтому может возводиться на
открытых для волн акваториях. Следует отметить, что общая
стоимость при одинаковых внешних условиях комплекса с
сооружениями ферменного типа в 3-4 раза меньше стоимости
гравитационно-погружного. Время строительства сооружений
ферменного типа тоже существенно меньше. Однако при
эксплуатации в - течение 20... 25 лет железобетонные платформы
оказываются экономичнее за счет большей коррозионной
стойкости, меньшей подверженности действию льда и усталостным
разрушениям.
Разработаны комбинированные платформы, например,
конструкции итальянской фирмы «Техномаре». Платформа состоит
из фундаментной плиты, ферменной металлической опорной
части и трех металлических емкостей объемом 100 тыс. м3,
обеспечивающих плавучесть, балластировку и хранение нефти. Эти
платформы также" м'огут возводиться на незащищенных от
волнения акваториях благодаря проницаемой и обтекаемой для
ветровой волны конструктивной форме. >
15
7Ж77Г
If II II II II И
// II II \\
77П7ГЖ
/////////
/////Ш//Ш Щф///
IIII || || \\ \\
//////щшлм////
ι] ίί II II II И II
WW iff
У/////////// //////У/////////
Рис. 3. Платформы для глубин до 300 м (сооружения
ферменного типа).
16
Для глубин больше 300 м разрабатываются специальные
подводные устрбйства, обеспечивающие бурение и эксплуатацию
скважин в подводном положении. Они представляют собой
платформу с технологическими и жилыми помещениями,
расположенными под водой и соединенными с надводной фазой,
отличаются высоким уровнем использования автоматики,
телемеханики и робототехники. Поэтому характерно, что разработкой и
созданием их занимаются фирмы, связанные с авиацией и
космическими аппаратами (в США — известная авиационная
фирма «Локхид»). С точки
зрения волновых
воздействий такие сооружения
находятся в условиях,
при которых практически
исключаются нагрузки от
волн, и могут работать
при любых штормах на
поверхности моря.
Поэтому их целесообразно
использовать в морях
с суровыми
климатическими условиями.
Остановимся кратко
на конструкциях
подвижных буровых установок,
которые в период
эксплуатации опираются на
дно и
воспринимают.волновые нагрузки, как
стационарные сооружения.
К ним относятся
погружные и самоподъемные
буровые установки.
Погружные установки принципиально мало отличаются от
(уже рассмотренных гравитационно-погружных. Они, как.
правило, делаются металлическими/Верхнее строение опирается
чаще всего на колонны малого диаметра. Плавучесть
обеспечивается емкостью фундаментного блока, изготовленного в виде
понтона. Общий вид одной из конструкций погружных
установок приведен на рис. 4, на котором изображено треугольное
верхнее строение, покоящееся на бутылкообразных опорах,
заканчивающихся башмаками. Ее преимуществами являются
[простота установки на месте бурения и удобство размещения
технологического оборудования при проведении буровых работ.
|В настоящее время парк погружных установок составляет 38
единиц для бурения на мелководье с глубинами до 54 м.
Наибольшая высота волн, на которые они "рассчитаны; —12 м.
Рис. 4. Погружная подвижная буровая
установка.
17
Самоподъемные буровые установки (СПБУ), отличаются
тем, что положение их опор относительно верхнего строения
может изменяться, рис. 5: при буксировке опоры поднимаются
и понтоны объединяются с верхним строением (для уменьшения
буксировочного сопротивления); по прибытии на место
эксплуатации опоры опускаются на дно, верхнее строение
поднимается по ним на высоту, до которой не доходят волны, и тем
самым создаются хорошие условия для проведения буровьц
работ. СПБУ возводятся при глубинах до 100 м, но есть при·
α) ι л
Ж
Ж
^г
— -Ы
/// /// У/ /// ///у// /// /// /// /// /// ////////////////// //
б) I
я
11
ь2^1^ШШш^23
/// w /// ///////// ////// #/ л>/ /я;////;/////////;/////
Рнс. 5. Самоподъемные буровые установки:
в) с ломающимися опорами; б) двухъярусные; / — рабочее положение; II —
транспортное положение.
меры их применения на глубине до 115 м. К 1984 г. было
построено 435 единиц — в полтора раза больше, чем всех остальных
подвижных установок вместе взятых. Они могут работать при
волнении высотой до 9 м и выдерживать нагрузки от волн
высотой до 15 м при скорости ветра до 60 м/с.
Все стационарные вооружения, кроме грунтовых островов,
относятся, как правило, к обтекаемым преградам, т. е. таким,
поперечный размер которых меньше половины длины волны.
18
Раздел I. ОСНОВЫ ТЕОРИИ ВОЛН НЯ ВОДЕ
Глава 1. ОБЩИЕ ПОНЯТИЯ О ВОЛНАХ НА ВОДЕ.
ПОСТАНОВКА ЗАДАЧИ
1.1. ПРИЧИНЫ ВОЗНИКНОВЕНИЯ ВОЛН НА ВОДЕ.
КЛАССИФИКАЦИЯ ГРАВИТАЦИОННЫХ ВОЛН
В широком понимании волнами называется
неустановившееся движение среды, при котором скорость перемещения
формы среды отлична (обычно больше) от скорости движения
частиц самой среды. Волновые процессы сопровождают многие
явления природы, в частности, распространение энергии,
излучаемой солнцем, распространение звука, радиоволн и др.
Волновой характер имеют некоторые виды движения воды. Если
главную роль играют силы тяжести, то такие волны называют
гравитационными, в отличие от так называемых капиллярных
волн, в которых определяющими являются силы поверхностного
натяжения.
Возникновение и развитие ветровых волн на воде
сопровождается действием на воду непотенциальных сил, обусловленных
вязкостью. Поскольку вода обладает вязкостью, то, строго
говоря, реальные ветровые волны не могут быть потенциальными,
они будут вихревыми. Однако вязкость воды сравнительно
невелика и# как показывает опыт, ветровые гравитационные
волны, зародившись в одном месте, перемещаются по водной
поверхности на сотни и тысячи километров или продолжают
существовать в данном районе акватории после прекращения
действия ветра иногда сутки и более. К сказанному следует также
добавить, что гидромеханика до настоящего времени не
располагает приемлемым математическим аппаратом для изучения
ветровых волн с учетом вязкости воды. Естественно, что в целях
конкретизации практических задач их приходится решать
приближенно, применительно к упрощенным математическим
моделям явления. Одним из таких упрощений является
пренебрежение вязкостью воды, т. е. принятие условия потенщ^адьдости
движения в идеальной, лишенной трения жидкости.
В теории предполагается, что волны тяжелой жидкости ποι
лучаются в результате непостоянства действующих на нее сил
давления. Вязкость у идеальной жидкости отсутствует, каса-
тельные напряжения в ней' не возникают, и силы, обусловлен,
ные ими, на идеальную жидкость не действуют. В соответствии
с известными положениями гидромеханики волновое движение
идеальной жидкости, возникшее из состояния покоя, есть по.|
тенциальное движение, и оно не может быть вихревым.
Волны, в которых движение жидкости потенциальное, будеш
называть потенциальными, а следовательно, волны идеальной
жидкости — потенциальные. Принятием условия
потенциальности движения существенно облегчается аналитическое изучение
волн на воде, так как в этом случае может быть использован
хорошо разработанный аппарат кинематики и динамики потен|
циального движения жидкости.
В последующем будет показано, что основные результаты)
теории потенциальных волн удовлетворительно согласуются с
данными ряда натурных наблюдений. Заметим, однако, что при
рассмотрении перемещения волн на большие расстояния
вязкость следует учитывать в расчетах рассеивания волновой|
энергии.
Пренебрежение вязкостью воды и, как следствие, принятие)
условия потенциальности движения лишь частично облегчает]
решение задач о волнах на воде. Процессы, происходящие при
волновом движении жидкости, весьма сложны, и, несмотря на
серьезные теоретические и экспериментальные работы в этой
области, до сих пор нет единой удовлетворительной строгой
теории волн. Дальнейшее упрощение задачи сделано на основе
применения условия малости отношения высоты волны к ed
длине, при этом различают волны малой и большой высоты]
имея в виду уровень приближения аналитического решения.
В исходных уравнениях теории волн малой высоты сохран
няются лишь линейные слагаемые. Таким образом, к волнам
малой высоты следует относить волны высотой А, настолько
малой в сравнении с их длиной ιλ, что в исходных математиче]
ских выражениях теории волн допустимо пренебрегать величин
ной ν2 (квадратом скорости движения частиц жидкости по ори
битам), равно как и произведениями скорости на другие малыа
величины. Это, в свою очередь, дает основание в процессе pej
шения задачи и в некоторых окончательных расчетных зависи]
мостях (исключая, например, уравнение профиля волны) высотн
ную координату ζ частицы жидкости в волне заменять ее вын
сотной координатой в состоянии покоя io, имея в виду, что разН
ница между ними не превышает величины v%/2g> которая nq
условию пренебрежимо мала.
Использование отмеченных положений существенно ynpoj
щаёт разработку теории волн малой высоты и позволяет
получить конкретные результаты при решении задачи о волновом
20
движении жидкости. Однако такое упрощение достигнуто ценою
существенного ограничения области применения этой теории,
ι в ряде задач (применительно к прибрежной зоне) оно
окалывается даже лишено практического смысла. Если на глубоко-
зодье в отдельных случаях реальные ветровые волны и можно
г известным приближением отнести к категории волн малой
высоты, то при выходе этих же волн на мелководье, имея в виду,
что при этом крутизна волн увеличивается, использование
аппарата теории волн малой высоты может привести не только
к значительным количественным погрешностям, но и к
качественно неверным результатам.
Усилиями многих ученых разработан ряд более точных
решений теории волн большой высоты, в которых наряду с
линейными изучены и нелинейные члены уравнений волнового
движения жидкости. Волнами большой высоты принято называть
волны с такой высотой Λ, при которой уже нельзя пренебрегать
величиной ν2, равно как и произведениями скорости υ на
другие малые величины. Волны большой высоты могут иметь
любую крутизну Λ/ιλ, не превышающую предельное, наибольшее ее
значение Α/λ < .(Α/λ) um и могут существовать на любой
глубине d>dcr, где dCr — глубина, соответствующая обрушению
волн. Однако существующие теории волн большой высоты
недостаточно совершенны, так как каждая из них дает
удовлетворительный результат лишь в ограниченном диапазоне
параметров волн, за пределами которого ощутимо искажаются
характеристики волнового движения жидкости.
Нет определенной установленной числовой границы между
волнами малой и большой высоты. Тем не менее разделение
теорий на указанные две группы служит, по крайней мере,
качественной оценкой достоверности используемых тех или иных
формул. В дальнейшем будет показано, что отдельные
характеристики ветровых волн без большой погрешности могут
рассчитываться по довольно простым формулам линейной теории
волн. Современные спектральные методы расчета
характеристик ветрового волнения [4, 23, 68, 71, 81] базируются в
основном также на исходных формулах линейной теории волн. В то
же время в большинстве расчетов воздействий волн на
сооружения используются потенциальные теории волн второго и
третьего приближений.
Причины возникновения гравитационных волн на воде раз-,
нообразны, но в общем можно утверждать, что любое
мгновенное возмущение воды обуславливает возникновение одной
волны или системы волн. В соответствии с этим волны на воде
классифицируют следующим образом:
волны цунами — сейсмического происхождения,,
порожденные землетрясениями подводных участков земной коры или
вулканическими извержениями на морском дне и вблизи
берегов;
21
ветровые волны — возникающие от действия на свободную
поверхность воды ветра;
судовые волны (или корабельные) — возникающие при двин
жении на свободной поверхности воды судов;
приливные волны — обусловленные воздействием на водны^
массы Земли сил притяжения Луны и Солнца;
сейши — волны с периодом, равным или кратным (меньшим)!
периоду собственных колебаний рассматриваемого объема
воды, возникающие в замкнутых или неполностью замкнутых
водоемах в результате резкого изменения атмосферного
давления, ветрового нагона и воздействия низкочастотных
колебаний, наблюдающихся на подходах к порту;
тягун — низкочастотные (сейшевые) колебания воды на
акватории порта, приводящие к подвижкам пришвартованных у
причалов судов.
В последующем основное внимание будет уделено
гравитационным ветровым волнам, поскольку именно эти волны имеют
определяющее значение при выборе конструктивных форм
сооружений и в расчетах внешних нагрузок, действующих на
сооружение.
Классификация гравитационных волн, развернутая, в
основном, применительно к ветровым волнам, представлена на
рис. 1.1. В зависимости от того, возрастают, остаются
неизменными или убывают осредненные значения элементов не менее
100 волн, бегущих непосредственно одна за другой через
заданную точку акватории, ветровые волны подразделяются на
развивающиеся, развитые или установившиеся и затухающие.
В природе существуют вынужденные и свободные ветровые
волны: вынужденные ветровые волны — находящиеся все время
под действием породившего их ветра; свободные ветровые
волны— свободные от действия на них ветра вследствие того, что
они ушли из области акватории, над которой ветер
продолжается, либо ввиду прекращения ветра; свободные ветровые
волны называются волнами зыби, или просто зыбью.
Рассматривая в совокупности всю систему волнения на
данном участке акватории, волны назовем регулярными,
если в любой заданной точке акватории их форма и элементы
сохраняются приблизительно одними и теми же, и
нерегулярными, — если их форма и элементы изменяются
случайным образом от одной волны к другой.
Ветровые волны подразделяют также на двумерные (или
плоские) и трехмерные в зависимости от того, представляется
ли движение воды в них плоскопараллельным или нет. В
расчетах воздействий считают реальные ветровые волны
двумерными, если средняя длина гребней волн больше или равна
длине секции сооружения.
Строго говоря, все виды волн на воде относятся к категории
неустановившихся, так как элементы отдельных волн в фикси-
22
рованиый момент, как правило, в той или иной степени
неодинаковы—они изменяются во времени и пространстве. Однако
при сравнительно небольших изменениях во времени элементов
волн в процессе перемещения над горизонтальным дном их
принято относить к развитым, или волнам установившегося вида.
Волны
[ цунами |
[ Развиваю - 1
1 ш,иеся 1
Гравитационные волны
Ветровые
волны
Установившиеся
Вынужденные
Нерегулярные
Трехмерные
!
1 Судовые
| волны
1 дату хаю-\
| щие ι
Свободные
- "-
Регулярные I
Двухмерные 1
Стоячие
I Вихревые
I Малой 1
I высоты 1
Глубоководные
р
Приливные
волны \
Сейши
Тягун
Бегущие
Потенциальные
Большой,
высоты
Мелководные
*аевиваю-
-Ч ПриЛйные
Рис. 1.1. Схема классификации гравитационных волн.
В теории изучаются, главным образом, волны
установившегося вида, подразделяющиеся на бегущие и стоячие.
Бегущие волны представляются как порожденные ветром
чередующиеся валы и впадины на поверхности воды,
перемещающиеся в направлении породившего их ветра. При этом на
23
мелководье бегущие волны могут отклониться от направление
ветра вследствие рефракции волн.
Стоячие волны образуются, как правило, в результате слсм
жения противоположно направленных бегущих волн или сложЗ
ния набегающей (прямой) и отраженной (обратной) от верти]
кальной стены волны. Видимая форма стоячих волн ε
пространстве не перемещается; внешне такие волны выглядя]
в виде периодически возникающих и исчезающих на одних я
тех же местах валов и впадин. Один вал и одна соседняя с ниц
впадина представляют одну волну.
В процессе аналитического решения задач о волновых
движениях жидкости обычно принимаются те или иные
теоретические предпосылки, в соответствии с которыми, например,
-бегущие волны относятся к безвихревым (потенциальным) или
к вихревым, если в исследуемом движении воды вихрь
скорости равен нулю (потенциальное движение) или отличен от нуля
(вихревое движение).
В зависимости от соотношения между длиной волны и*
глубиной моря волны подразделяют на глубоководные· и
мелководные. Рельеф дна и наличие гидротехнических сооружений также
оказывают влияние на характер формирования волн. Так, при
пологом наклонном дне на глубинах, меньших критических
(rfcr), образуются прибойные волны, несущие на себе бурун и
по мере движения к берегу претерпевающие неоднократные
обрушения гребня. При подходе бегущих волн к сооружениям
с высокой постелью могут образовываться разбитые волны,
отличающиеся динамическим характером воздействия на
сооружения.
1.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ВОЛН НА ВОДЕ.
ТЕРМИНОЛОГИЯ И УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
В целях упорядочения изложения теории и расчетов
представляется целесообразным дать определения основным
характеристикам волн на воде, принять единую терминологию и
условные обозначения наиболее часто употребляемых
категорий и терминов. В качестве отправной схемы примем
изображенные на рис. 1.2 профили регулярных и нерегулярных
бегущих волн в водоеме ограниченной глубины с гладким
горизонтальным дном.
Расчетный уровень воды — уровень, назначаемый с учетом
сезонных и годовых колебаний, ветрового нагона воды,
приливов и отливов; d — глубина воды при расчетном уровне; ρ —
плотность воды; g — ускорение свободного падения.
Фронт волны — линия на плане взволнованной поверхности,
проходящая по вершинам гребня данной волны; луч волны —
линия, перпендикулярная фронту волны в данной точке (луч
направлен туда, куда бегутуволны).
24
Профиль волны — линия пересечения взволнованной
поверхности с вертикальной плоскостью в направлении луча волны;
средняя волновая линия — линия, пересекающая запись
волновых колебаний так, что суммарные площади выше и ниже этой
линии одинаковы. Для регулярной волны — горизонтальная
линия, проведенная на профиле волны на отметке, равной полу-
///у/у/;//;/ /// //?/////λ/// /// /// /// /// //////////////
δ)
Рис. 1.2. Профили и основные элементы регулярных (а) и нерегу-*
лярных (б) бегущих волн на ограниченной глубине
t — расчетный уровень; 2 — дно; ' 3 ·— средняя волновая линия; 4 — вершина
волны; 5 —подошва волны; 5 —гребень волны; 7 — ложбина волны; hlt h2,
Ьъ, ..., h — высоты и λι, Ха> λ3, . . ., λ — длины волн.
сумме отметок ее вершины и подошвы; гребень волны — часть
волны, расположенная выше средней волновой линии; ложбина
волны — часть волйы (площадь, не занятая водой), располо-
ркенная ниже средней волновой линии; вершина волны —
наивысшая точка гребня волны; подошва волны — наинизшая
точка ложбины волны.
25
Высота бегущей волны h — превышение вершины волны над
соседней подошвой на волновом профиле или разность отметок
наивысшего и следующего за ним наинизшего положения
взволнованной поверхности воды; высота гребня волны у\с —
превышение вершины волны над расчетным уровнем; высота подошвы
волны η* — понижение подошвы волны от расчетного уровня;
длина волны λ — горизонтальное расстояние между вершинами
двух смежных гребней на волновом профиле; k = 2π/λ—
волновое число.
Период волны Τ — интервал времени между прохождением
двух смежных вершин волн через фиксированную вертикаль;
ω = 2π/Τ — круговая частота волны; элементы волны — три
основные характеристики: /ι, λ и Г, через которые могут быть
выражены другие характеристики волнового движения
жидкости; крутизна волны — отношение высоты волны к ее длине
Λ/λ; пологость волны — отношение длины волны к ее высоте
λ//ι; склоны волны — участки профиля волны между ее
вершиной и ближайшими к ней подошвами; склон, движущийся перед
вершиной волны — передний (подветренный), за вершиной —
задний (наветренный); крутизна склона волны — отношение
высоты волны к длине горизонтальной проекции ее склона.
Скорость волны с — скорости перемещения гребня волны
в направлении ее распространения; волновое течение — перенос
воды в направлении перемещения волн.
Волновое давление ±р — доля (составляющая;
гидродинамического давления, обусловленная волнением на свободной
поверхности жидкости. Величина ρ определяется как разность
значений гидродинамического давления в данной точке
пространства, занятого жидкостью, при наличии волн и при их
отсутствии.
Полная энергия Ε одной волны — превышение полной
механической энергии воды на участке акватории (единичной
ширины) протяженностью вдоль луча волн в одну длину
волны при наличии волн над полной механической энергией воды
на этом же участке в состоянии покоя при спокойном уровне.
Разгон волн — протяженность охваченной ветром акватории;
измеряется по направлению ветра до расчетной точки.
Расчетная скорость ветра Vw — средняя на протяжении
всего разгона волн скорость ветра, измеренная на высоте 10 м над
расчетным уровнем воды; расчетный шторм — шторм,
наблюдающийся один раз в течение заданного ряда лет (25, 50 и 100)
с такой скоростью, направлением, разгоном и
продолжительностью действия ветра, при которых в расчетной точке
формируются волны с .максимальными за этот ряд лет элементами;
обеспеченность расчетного шторма (один раз в щ лет)
—характеристика по режиму, например, один раз в 50 лет, что
соответствует 2 % ·
26
Система"волн — ряд волн, последовательно бегущих одна за
другой и имеющих одно происхождение; статистические
характеристики волн — величины, определяющие волнение в целом
как совокупность нерегулярных волн; интегральная
функция распределения — вероятность превышения (обеспеченность)
заданных значений рассматриваемого элемента волн.
Обеспеченность элемента волны (/ι, λ или Т) в системе
волн — выраженное в процентах количество волн, у которых
числовое значение этого элемента равно или больше, чем у
остальных волн в ряду (не менее 100 волн), проходящих
непосредственно одна за другой через заданную точку акватории.
Значения элементов волн заданной обеспеченности
обозначаются индексом у соответствующего символа элемента,
например, высота волны h\%, h$% и т. д.; средняя высота Л, средняя
длина λ, средний период Г, средняя скорость перемещения волн
7— приближенно могут определяться как
среднеарифметические значения элементов нерегулярных волн.
Простые условия волнообразования — условия, при которых
элементы волн зависят только от основных волнообразующих
факторов (скорости ветра, продолжительности действия ветра
и разгона волн), от глубины воды и уклонов дна. Сложные
условия волнообразования — условия, при которых элементы волн
определяются в зависимости от основных волнообразующих
факторов с учетом контура береговой черты, наличия
препятствий на пути распространения волн, местных особенностей
рельефа дна и распределения ветра в пространстве.
Критическая глубина dcr — глубина воды, при которой
волны с данными значениями /ι, λ и Г, перемещающиеся по
мелководью, начинают разрушаться.
Трансформация волн — изменения высоты и длины волн при
их перемещении в пределах мелководной зоны водоема в
случае одинаковой глубины воды вдоль фронтов волн л плавко
меняющейся глубины вдоль лучей волн,; рефракция волн —
искривление фронтов и изменение высот бегущих волн на
мелководье, обусловленное плавным изменением глубины вдоль
фронтов волн; дифракция волн — искривление фронтов и
изменение высот бегущих волн, огибающих препятствия
(сооружения, острова, мысы и др.).
В общем случае в водоемах различают четыре зоны по
глубине, рис. 1.3: _
1) глубоководная, с глубиной d > λ<*/2, где дно водоема
практически не влияет на основные характеристики волн;
волны в этом случае называют глубоководными;
2) мелководная, с глубиной λί*/2 > d> dcr, где дно водоема
оказывает влияние на развитие волн и на основные их
характеристики; волны в этом случае называют мелководными; не-
27
обходимо отметить, что на характер волнения перед гидротех1
ническими сооружениями оказывают влияние и сами сооруже
ния, например, у оградительных сооружений типа вертикальной
стены при глубине до дна db ^ 1,5/г и глубине над бермой
dbr ^ 1,25/г образуются стоячие волны, а при подходе бегущих
волн к сооружениям с высокой постелью при глубине над бермой
dbr< 1,25/ι и глубине дна db ^ 1,5/г — разбитые волны, харак
теризующиеся динамическим эффектом воздействия на coopyj
жение;
3) прибойная, с постепенно уменьшающейся глубиной dcr Ξ^Ι
^ d ^ dcr, и, в пределах которой начинается и завершается раз^
рушение волн; волны в этом случае называют прибойными, xaJ
рактерной особенностью которых является то, что, пробегая nd
Рис. 1.3. Деление акватории на четыре зоны по глубине и
характерные створы
/ — глубоководная; 2 — мелководная; 3 —прибойная; 4 — приурезовая;
5—5 створ начала мелководья; 5—5 створ начала разрушения волн; 7—7 створ
завершения разрушения волн.
мелководью в направлении постепенного уменьшения глубины!
воды, они несут на своем переднем склоне бурун, образующий-!
ся вследствие их разрушения из-за недостаточной глубины;
- 4) приурезовая, с глубиной d<dCr,u, в пределах которой
поток от разрушенных волн периодически накатывается на!
берег.
В соответствии с влиянием глубины водоема на возникши
вение и развитие волнения различают два типа акваторий:
глубоководные, глубиной d>hd/2y где развитие волн не
ограничено глубиной;
мелководные, глубиной d ^ ,Г<*/2, где развитие волн
ограничивается влиянием глубины.
В заключение обратим внимание на то, что при определении)
характеристик ветровых волн и в расчетах их воздействий на'
сооружения следует учитывать два вида обеспеченностей эле-1
ментов волн: вероятность превышения в многолетнем разрезе!
(обеспеченность по режиму) и вероятность превышения при за-1
28
данном расчетном шторме (обеспеченность в системе).
Указанные обеспеченности параметров волн назначаются на основе
технологических и-других специфических требований,
предъявляемых к акваториям и возводимым на них гидротехническим
сооружениям.
1.3. ОБЗОР ИССЛЕДОВАНИЙ В ОБЛАСТИ ГИДРОДИНАМИКИ ВОЛН
Последние два столетия задачи поверхностных волн
привлекали внимание многих выдающихся математиков, начиная,
по-видимому, с Лагранжа. Чрезвычайно ценные исследования
принадлежат таким выдающимся зарубежным ученым, как
Герстнер, -Коши и Пуассон, Эри, Стоке, Рэлей, Ламб, Сен-Ве-
нан, Буссинеск, Сенфлу, Леви — Чивита, Миш и др. Ряд
значительных исследований теории волн выполнен крупнейшими
русскими и советскими учеными: М. В. Остроградским, А. Н.
Крыловым, Н. Е. Кочиным, М. А. Лаврентьевым, В. В. Шулейкинымг,
Л. Н. Сретенским, Я. И. Секерж-Зеньковичем, Ю. М.
Крыловым и др.
По-видимому, одним из первых Герстнер [72] получил
(1802 г.) решение, удовлетворяющее основным уравнениям
гидромеханики, согласно которому при d->oo частицы
жидкости в волнах движутся с одинаковой и неизменной во времени
угловой скоростью по замкнутым траекториям, имеющим форму
окружности, радиусы которых убывают по мере заглубления
частиц по экспоненциальному закону. Поскольку в этом случае
профиль волны имеет форму круговой трохоиды, полученное
решение обычно называют трохоидальной теорией волн.
Л. Н. Сретенский [53], Η. Ε. Кочин [22] и другие отмечают,
что решение Герстнера, несмотря на свою простоту, с позиций
теоретической гидромеханики несовершенно, так как полученное
движение оказывается вихревым, в то время как волновые
движения идеальной жидкости, обусловленные имеющими
потенциал силами, должны быть безвихревыми. М. П. Кожевников
[19] экспериментально доказал, что в действительности в
плоских волнах не наблюдается сколько-нибудь заметного вращения
частиц жидкости вокруг собственной оси.
Наиболее значительным достижением середины XIX века
в области исследований волновых движений жидкости явились
работы Коши и Пуассона по потенциальной теории волн малой
высоты. Линейная теория волн, содержащая ряд
противоречивых понятий, несмотря на явно приближенный характер
своих основных положений, неплохо согласуется с опытом
и практикой, а потому продолжает широко использоваться в
настоящее время при исследовании волновых процессов
спектральными методами и при решении некоторых инженерных
задач по взаимодействию волн с^преградами.
29
После опубликования теории волн малой высоты в 1863-J
64 гг. Ренкин [82] несколько отличным путем, чем это сделаЛ
Герстнер, получил основные формулы теории волн на глубоко]
водье. Свои рассуждения Ренкин построил, исходя из предпо!
ложения, что частицы жидкости в волнах движутся по замкну!
тым траекториям, имеющим форму окружности. Естественно
что работе Ренкина [82] свойственны те же недостатки, о ко
торых выше шла речь при оценке теории волн Герстнера [72]
Дальнейшее развитие теории трохоидальных волн сделал
Буссинеск [70]' в Г872 г., который, положив в основу результа
ты теории волн малой высоты в части формы траекторий частиц
жидкости, дал расчетные зависимости для определения элемен]
тов движения бегущих волн при d — оо и d = const и стоячим
волн при d = оо. Согласно Буссинеску, профиль бегущей волны
при d = const имеет форму эллиптической трохоиды. Важной
значение для инженерной практики имела также работа Сенфл^
[85], опубликованная в 1928 г., в которой дано дальнейшее
развитие теории Буссинеска применительно к условиям стоячим
волн при d = const. На основе решения ,Сенфлу были разрабо
таны методы расчета воздействий, волн на вертикальные стены
которые широко использовались на практике около двух десят
ков лет и не утратили своей ценности до настоящего времени
В 1944 г. была опубликована большая теоретическая рабо
та Миша [77], в которой получены в плоской постановке при
ближенные гидромеханические решения для вихревых и потен
циальных бегущих и стоячих волн. Рассмотрены случаи
водоемов с горизонтальным дном при ограниченной глубине и
с дном, имеющим наклон к горизонту <р = п/2т (где т — целой
число). В работе [77], в частности, Миш уточнил решение Сен
флу для определения давления стоячих волн на вертикальную
стену путем учета при интегрировании уравнений слагаемым
второго порядка, которыми обычно пренебрегали (в том числа
и Сенфлу). Существенным достижением работы Миша является
то, что в ней впервые обращено внимание на «седлообразную)]
форму хронограмм волнового давления. Опытные хронограммы
волнового давления оказались в удовлетворительном согласии
с теоретическими, если в теории должным образом учтены ела
гаемые второго (и выше) порядка малости. Отдельные положе
ния исследования Миша [77] получили развитие в трудах со]
ветских и зарубежных ученых [19, 63, 64, 71].
В 50-х годах В. В. Шулейкин разработал приближенную
теорию ветровых волн,-апробированную н# материалах иссле
дований в натурных и полигонных (в штормовом бассейне) ус
ловиях; основные положения этой теории изложены в моногра]
фии [64].
Первые" шаги в теории установившихся потенциальных воли
большой высоты на поверхности тяжелой жидкости были еде]
30
ланы Стоксом в 1847 г. [86]. Воспользовавшись интегралом
Лагранжа и решив приближенно уравнение Лапласа при
условии постоянства давления на свободной поверхности жидкости,
Стоке получил во втором приближении потенциал и все
формулы для расчета элементов волнового движения при
ограниченной и бесконечной глубинах жидкости. В более простом случае
бесконечно глубокого канала Стоке в своих приближениях
пошел дальше, учтя слагаемые третьего порядка. В работе [86]
получен ряд принципиально новых особенностей волнового
движения жидкости, в том числе, одним из самых интересных
результатов является установление формы траекторий частиц
жидкости. Именно на материалах' этих исследований впервые
было доказано, что в потенциальных волнах каждая частица
жидкости, помимо колебательного движения около некоторого
своего среднего положения, имеет также поступательное
перемещение в направлении движения волны. Результаты Стокса
были снова получены более простым путем Рэлеем, который
при этом в некоторой части усовершенствовал теорию.* В
частности, Рэлеем теоретически было доказано, что волновое
течение всегда существует и является следствием наличия
потенциала скоростей у рассматриваемого движения.
В уже упоминавшейся работе Миша [77] параллельно с
изложением теории вихревых волн содержится гидромеханическое
исследование потенциальных бегущих и стоячих волн большой
высоты во втором приближении, при этом автором
использовано несколько иное, чем у Стокса [86], представление функции
в виде степенного ряда. Среди попыток дальнейшего развития
рассматриваемого решения Миша заслуживает внимания
опубликованное в 1958 г. исследование Рундгрена [84], в котором
получены формулы для определения элементов волнового
движения в случае неполного отражения волн от вертикальной
стены и исследованы этим же методом некоторые другие
частные задачи. Следует, однако, заметить, что область применения
решений, учитывающих члены второго порядка, например,
решение Миша [77] и ему соответствующие, ограничивается
глубинами ί/^0,15λ. Одной из причин ограничения на мелководье
теории волн второго приближения является неправдоподобное
искажение профиля волны, за счет появление горба — второго
гребня — в ложбине волны.
Теоретическое решение задачи о стоячих волнах большой
высоты в плоской постановке было получено Я. И. Секерж-
Зеньковичем [50] в третьем приближении при d = оо (1974 г.)
и для случая ограниченной глубины d = const (1951 г).
Η. Η. Загрядская [16] уточнила и несколько развила
последнюю из этих работ; полученные ею расчетные формулы и
графики используются в инженерной практике [51] при
определении воздействий волн на вертикальную стену. В последние годы
31
появился ряд новых работ, в которых даны решения в перемен
ных Эйлера на уровне третьего приближения.
Перечисленные решения потенциальных волн большой вы
соты, как уже отмечалось, являются приближенными. Впервые
точное решение задачи об установившихся волнах большом
высоты было получено А. И. Некрасовым [42] в Г921 г. npJ
d = оо и в 1927 г. — для случая ограниченной глубины d =J
= const. За рубежом решение этой задачи другим методом, по]
лученное Леви — Чивита [75], опубликовано в 1925 г. Этим|
[42, 75] исследованиями строго теоретически доказана возмож
ность существования установившихся волн, что имело немало
важное значение, поскольку одно время эта возможность под
вергалась сомнению. Точные решения теории волн до настоя)
щего времени не применяются при разработке методов расчета
воздействий волн на сооружения из-за их чрезвычайной слож|
ности.
Оригинальное исследование потенциальных волн большой
высоты выполнено в начале 60-х годов М. П. Кожевниковым
[19] с помощью интегратора на основе сочетания метод]
электрогидродинамической аналогии (ЭГДА) с методом под]
бора.
Заканчивая краткий исторический обзор, обратим внимание
что литература о волнах на воде весьма обширная, включающа]
ряд монографий, подробно трактующих отдельные направлени]
исследований волн, и большое число мемуаров. Одной из фун
даментальных работ по гидродинамике является книга Ламб|
[30], в которой много внимания уделено гравитационным вол
нам; большую ценность имеет также монография Л. Н. Сретеч
ского [53].
По-видимому, нельзя должным образом познать основы тес]
рии волн без изучения в «Теоретической гидромеханике» [22
главы о волновых движениях идеальной жидкости, написанно
Н. Е. Кочиным. Одной из весьма полезных книг .о волнах н
воде является монография Дж. Дж. Стокера [54], содержаща
математические теории и их инженерные приложения, Болыыо
и хорошо систематизированный материал по теории и расчет]
ветровых волн обобщен в книге Кинсмана [74], в монографш
Ю. М. Крылова [23]; в последней работе основное внимани
уделено спектральным методам исследования и расчета ветр<|
вых волн. Естественно, что перечисленные труды не охватываю
всего разнообразия задач о волнах на воде и не могут удовле]
ворить все возрастающие потребности практики. Новые мат]
матические теории и их приложения, как правило, содержата
в материалах периодических изданий, в том числе в труда]
выходящих в свет после проведения научно-технических сов]
щаний и семинаров.
32
1.4. ПОСТАНОВКА ЗАДАЧИ О ВОЛНАХ НА ВОДЕ
И ОСОБЕННОСТИ ЕЕ РЕШЕНИЯ
Сформулируем, применительно к рис. 1.4, типичную задачу
Гидродинамики поверхностных волн следующим образом [54];
Пусть имеется водо.ем больших размеров в плане, с переменной
кпубиной d(x, у). Вода, находящаяся в состоянии покоя,
заполняет область: 0^jc<oo; — оо<у<оо; d(x,y)^z^0. В
некоторый момент времени t = 0 на поверхности воды, например,
Ьд областью А создается возмущение.
Расчетный
-/У?**!!'*) УР,о6е"ь
Рис. 1.4. Схема κ постановке задачи о волнах на воде.
Требуется определить- основные характеристики
обусловленного этим возмущением движения воды: форму свободной
поверхности η(*, у, t), проекции скорости орбитального движения
кастиц жидкости υχ{χ, у, zy /), vy(x, у, ζ, t) и vz(x, у, г, t);
распределение волнового давления р(ху у, z, t) и другие элементы
[движения жидкости.
Предполагается, что движение жидкости потенциальное
(вода лишена трения) и имеет постоянную плотность р. Известно,
что в природе нет идеальной жидкости, а следовательно,
изучаемое волновое движение, строго говоря, не может быть
потенциальным. Рядом исследователей [19, 22, 30, 42 и др.1 на
основе сопоставления теоретических и экспериментальных данных
показано, что решения основных задач с позиций теории
потенциальных волн приводят к результатам, хорошо
подтверждающимся практикой. Принятие же условия потенциальности
волнового движения существенно конкретизирует задачу, .так .как
обеспечивает, получение единственного .решения, при ..заданных
начальных. и пограничных: условиях. Отмеченная, особенность
33
выгодно отличает рассматриваемые решения от разнообразных
теорий вихревых волн.
В соответствии с классической гидродинамикой решение
поставленной задачи сводится к определению потенциала
скорости φ, удовлетворяющего, прежде всего, уравнению Лапласа:
#φ_ *£. + J5L-0 11
дх* ^ ду* ^ дг* ~~ υ 1Л
при
Х(У> *)<*< оо; — оо<у<оо;
d(x, У)>2^ц(х, у, t).
Здесь X(уу t)—абсцисса ватерлинии на берегу и η(*, у, t) —
возвышение свободной поверхности (заранее не известны, но
они должны быть определены в процессе решения задачи).
Функция φ должна удовлетворять следующим граничным
условиям:
кинематическому на дне моря
^ = 0 при z = d(x, у), 1.2
где η — нормаль к поверхности дна;
кинематическому на свободной взволнованной поверхности
при ζ = η (*, уу t)
дг ~ dt ι дх дх "*" ду ду ' bu
динамическому на свободной взволнованной поверхности
при ζ = η {χ, у, t)
где F{xy у у t) = О повсюду, за исключением области Л, в которой
создается возмущение. На бесконечности, т. е. при *->-оо и
\у\-+оо можно считать, что φ и η остаются ограниченными или
принимать, что эти функции (и некоторые из их производных)
стремятся к нулю.
Функция φ, кроме того, должна удовлетворять начальным
условиям, а именно при t = 0:
что соответствует состоянию покоя жидкости.
Для конкретизации решения задачи необходимо также
знать способ задания возмущения, т. е. знать над областью А
функцию F(Xy у, t) в условии 1.4.
Очевидно, что поставленная задача в общем случае —
нелинейная. Значительные трудности в ее решении обусловлены тем
34
обстоятельством, что-свободная поверхность не известна
заранее а следовательно, область, в которой должен быть
определен потенциал скорости <р, также неизвестна, особенно, если
учесть изменение границ этой области со временем. Следует
иметь в виду и то, что любая математическая формулировка
задачи, хотя бы в течение ограниченного времени
соответствующая обычно наблюдаемым фактам, связана с существованием
особенностей, распределение которых в пространстве и во
времени не известно. К таким особенностям, например, относятся
местные деформации волн под действием ветра, опрокидывания
и частичные разрушения гребней ветровых волн и т. п.
Учитывая изложенные трудности, не следует удивляться
тому, что до настоящего времени не создано единой физической
теории, удовлетворяющей потребностям инженерной практики.
Дж. Дж. Стокер [54] полагает, что еще в течение длительного
времени исследования задач о волновом движении жидкости в
полной нелинейной трактовке будут- иметь форму теорем только
для движений довольно специальной прирЪды.
Вполне естественно, что известные теоретические решения
волновых движений жидкости разработаны лишь
применительно к упрощенным исходным положениям на основе специальных
гипотез. Наибольшее распространение получили два
направления в теории, одно из которых базируется на допущении о
малом значении высоты волны по сравнению с длиной волны,
второе — на допущении о малом значении глубины моря по
сравнению с длиной волны. Классическим примером задач
первого типа является теория волн малой высоты. В настоящем
пособии допущение о малом значении отношения высоты к
длине волны использовано при решении задачи применительно к
волнам большой высоты в третьем приближении как для
бегущих, так и для стоячих волн. Второй тип задач — теория мел-
кой воды (или теория длинных волн)—получил развитие в
приближении низшего порядка при изучении приливов.
Дальнейшая конкретизация рассматриваемой задачи
достигается на основе метода последовательных приближений в
предположении, что скорость частиц воды, возвышение
свободной взволнованной поверхности и их производные являются
малыми величинами. В соответствии с этим потенциал скорости
φ и возвышение свободной поверхности η представляются в
виде разложений в степенные ряды по малому параметру ε:
φ = εφι+>ε2φιι+ ε3φια+ ...; 1.6
η = η0+€ηι + ε2ηιι + ε3ηιιι+ .... 1.7
При этом имеется в виду, что каждая из функций щ(х, у,
ζ> 0 является решением уравнения Лапласа, т. е.
Δ*ρ* = 0. . 1.8
35
Рассмотрение граничного условия на неподвижной
физической границе (на дне моря) приводит к равенству
% = °. ■·»
где д/дп — дифференцирование по нормали к пограничной
поверхности.
Динамическое условие на свободной поверхности при
давлении, равном атмосферному (может быть принято нулевым),
согласно 1.4 имеет вид:
После подстановки в 1.10 рядов 1.6 и 1.7 и рядов для ^,
(-Д-),... и т. д. по степеням ε получаем зависимости:
Ίο = 0;
чш+ши
711 —г^т =
1.11
1.12
0. 1.13
При этом следует обратить внимание на то, что функции
d^k/dt, dq>k/dx и т. д. должны быть вычислены для 2 = η(χ, у, t)
и что η, в свою очередь, должно быть разложено по степеням ε,
т.е. η=ηο + εηι + ε2ηιι+ ... Зависимости 1.11, 1.12 и 1.13 должны
удовлетворяться при ζ =η0; так как в силу 1.11 η0 = 0, то,
следовательно, 1.12, 1.13 и т.д. должны удовлетворяться на
первоначально невозмущенной поверхности воды при 2 = 0.
Кинематическое условие, характеризующее то, что частица
воды, находившаяся на свободной поверхности, на ней и
остается, выражается зависимостью 1.3; после подстановки в 1.3
выражений степенных рядов для φ и η получаем:
^- =0- 1 14
dt υ' ι
^±i!Liuoi.f!i^-i!i. lis
dt "*" дх дх "ϊ~ ду ду ~ дг ' 1ЛО
foil foil <?ηο , foil drj0 = foil foi foi
dt "* дх дх ' ду ду дг дх дх
foi foi
ду ду
которые также должны удовлетворяться при 2 = 0.
36
Принимая во внимание, что η0 = 0, динамические условия
яа свободной поверхности можно привести к виду:
ί*+ΤΓ = °·. 1Л7
g-Ίιι + Sf = - Τ [{Ж) + \W) + VST) J ηΐ ***·
^»+1Г = ^-ь Ь19
где символом /v-i обозначена некоторая комбинация функций
t\k и φ* при k^n— 1, и все зависимости должны
удовлетворяться при ζ'= 0.
Соответственно: кинематические условия на свободной
поверхности могут быть представлены в следующей форме:
1.20
1.21
ат)н
dt
дтц дЬ
dt ~~ дг>
дх дх ду ду
ЦЧп_—дЧп\п ,
1.22
где Grt-i зависит /только от функций η* и щ при k ^ η—1, и
все условия должны удовлетворяться при ζ = 0.
Решения в первом приближении получаются при обрыве
рядов 1.6 и 1.7 после членов εφι и εηι в предположении, чтоф =
= βφι и η = εηι. Ограничиваясь допущением на свободной
поверхности 1.17 и lt20 при ζ = 0, имеем:
£η
ι *р _ п. dY1 — ^1 - О
Исключив из этих двух соотношений η, получим
единственное выражение
dt* ^ ё дг ^
которое используется для определения φ из уравнения Δφ = 0
при ζ = 0, что и соответствует решению поставленной задачи
в первом приближении.
37
Глава 2. БЕГУЩИЕ ВОЛНЫ
2.1. БЕГУЩИЕ ВОЛНЫ БОЛЬШОЙ ВЫСОТЫ НА МЕЛКОВОДЬЕ
Рассмотрим решение задачи о бегущих потенциальных
волнах большой высоты применительно к следующим исходным
условиям. По поверхности жидкости в канале прямоугольного
сечения, имеющем при невозмущенной поверхности глубину
d = const, перемещаются с постоянной скоростью с волны без
изменения с течением времени своей формы, рис. 2.1. Движение
жидкости считается потенциальным; кроме того, предполагает-
Расчетный уродень
I уЛно
// /// /// /// /// /// /// /// /// /// /// //У /// /// /// /// ///
Рис. 2.1. Схема к аналитическому решению в третьем приближении
задачи о бегущих потенциальных волнах при ограниченной
глубине ά =.const
/ — средняя волновая линия.
ся, что во всякой плоскости, параллельной стенкам канала,
движение одно и то же.
Введем систему координат (х, */, ζ), неизменно связанную со
стенками канала, расположив плоскость Оху вдоль уровня
покоящейся жидкости и проведя ось Ох по направлению
перемещения волны, а ось Ог — вертикально вниз.
Решение поставленной задачи в соответствии с принятыми
обозначениями сводится к совместному исследованию уравнения
Лапласа и интеграла Лагранжа
дх* + dz*
0;
при соблюдении следующих граничных условий:
Р±
Ρ
2.1
38
кинематического, на дне
дг
кинематического, на свободной волновой поверхности
,,-„=°;
дг Utf*. t) " dt ** "ЗГ5
динамического, на свободной волновой поверхности (если
[принимать условно давление на свободной поверхности равным
рулю)
Заметим, что в данном случае предполагается периодич-
нрсть волн по χ и t. При известном,, значении потенциала
скорости φ не представляет особого труда определение-
аналитических выражений для расче.та основных элементов волнового
движения жидкости.
В целях сокращения записей формул произведем замену
переменных, обозначив
x = k(x — ct)\ z =—kz, 2.2
где k — волновое число, k = 2π/λ.
Благодаря этому преобразованию время t из исходных
уравнений исключается, и в новых переменных χ и ζ уравнения
2.1 запишутся так:
д2У ι &Г _ л.
2.3
2.4
?-*»+**-да+(*л+с·-
где через С обозначена произвольная постоянная.
Граничные условия приобретают следующий вид:
itl -о- _cii-μ*iiiL-iil
«Ч - **ΐ |_„ + "Τ pj + (i)"L-a, = C·
Как уже отмечалось, поставленная задача решается
методом последовательных приближений. В соответствии _ с этим
разложим выражения 2.4 в степенной ряд по ζ. При этом,
поскольку в последующем принимается ζ = — kx\ = 0, то, как
следствие, рассматриваемая теория является исследованием в
окрестности положения ^покоя находящейся в равновесии
жидкости. Соответствующие 2.4 ряды запишутся так:
39
-*ΐ+·*£(ί-+Α>.'+···)-
при ζ = 0;
η-4*+Α*4-τ*ν&-κ··)+
■+i[(*W+*M*M*n+···]-* у
при ζ = 0.
В дальнейшем будем исходить из представления искомы^
величин φ, η, с, pa и С в виде степенных рядов по малому па!
раметру ·ε, а именно:
φ = εφι + б^ц + е3срш + * . . = <Ρι + <р2 + ?з + . . ·;
η = εηι + ε2ηπ + ε3ηιιι + · · · = 4ι + Чг + η8 + · · .'. '
£ = ft + есц + s2cm + ... = έ?! + с2 + cs + ....; 2.7|
■Pd-P<f+ εΡι + *2/>π + ·8Λιι + · · · = Ре +Ρι + Ρ2 +Рз + ..-.;
С = еС, + в2Сц + в8Сщ + ... = Ct + C2 + C3 + '...
В соответствии с 2.7 и при условии, что задача решается!
в третьем приближении, выражения 2.5, 2.6 и нижнее из 2Д
приобретают вид:
+ s3(^»-Si + ^»-S') + TsV-S-) при2 = 0; 2А
dxdz "г
^ (εφι + ε2φιι + ε3φιιι) + ε2£ηι -^- + ε8 ^Ληι
+ Αγ1» Ж + lS* ν)] ~ кСпг [ж (·^ + в,?и) +
+ ε2*ηι "53i| ~ *t'Cl" ~dF + g (εΎί11 + ε3ηπΙ + εηι) +
при ζ = 0;
40
+ (ε ^L + ε2 ^ί + β»·^)1] + sCi + s2C„ + e»Cin. '2.10
В 2.8, 2.9 и 2.10 сгруппируем слагаемые, содержащие
множители ε, ε2 и ε3, и используем соответственно отобранное
уравнения для нахождения решения в первом приближении и для
определения дополнительных слагаемых, соответствующих
второму и третьему приближениям. Опустив написание символов
[малого параметра, получим следующие системы уравнений:
дщ_ __ <fyi
61 дх ~ dz
при ζ = 0;
при ζ = 0;
t + t--fz + ^^ + Ci; 2.11
при ζ = 0;
при 2 = 0;
— г дЪ __п дЪ —г *HL 1 и(дг[х <fy2 . <?η2 6ψχ . ,,
071 "дГ ^2 дх ^3 дх "*"к \ дх дх ^ дх дх "^
^Ληι дх 1Ш)- dz +Λνηι <^ +7]2 dz2 + 2 Λ7]ι dz3J
при ζ = 0;
-*°.&+*4-fe)-**& + <r%+ 2.13
41
при ζ = 0;
Зададимся искомым потенциалом скорости в виде функции
φι = А\ ch (z + kd) sin x 2.14
и решим совместно уравнения 2.11, приняв ЛА = ag/kci ch kd.
В результате удовлетворения уравнению Лапласа Δφι = 0 при
соблюдении пограничного условия dy\/dz\z = -kd = 0, получим
в первом приближении следующие выражения:
ag ch (z + kd) .
?* = lfr chM Slnx;·
^ = acosx; cx2 = -j-thkd;
. ch (z + Arf)
vzi = akcx —yshkd cos x;
vzt = a^Cj shltf sin x; ^'^
-^i - - atfc 2 5!liLt*£) cos x·
dt ~ aftCl shkd cosx'
p, ch (z + kd)
T=ag chL cos x·
Нетрудно убедиться в том, что, если возвратиться снова к
переменным (х, г, /) согласно 2.2, формулы 2.15 оказываются
тождественными результатам линейной теории '[22].
Воспользуемся решением в первом приближении 2.15.
Подставив значения φ4 и η4 в 2.12, получим, после преобразования]
уравнения:
ci дх
—
дх
№аЧ?
дг ~
+ ъ
-И -L-
^1
1
g
(Ч _
sin
С2
-Or
2х
=
4ι2
—
с2а
brf)
?2asinx;
•cos χ —
rn<2 9y1
4g sh2 kd'
2.16J
где по-прежнему полагаем ζ = 0.
Решая 2.16 применительно к нахождению φ2, получаем вы*
ражение
42
которое исследуется на основе уравнения Лапласа Δφ2 = 0 при
соблюдении пограничного условия дщ/дг \ ζ = -ы = 0. Заметим,
что в данном случае можно в 2.17 не рассматривать слагаемое
с множителем sinx, уже учтенное в решении 2.14,
соответствующем первому приближению,.а, следовательно, есть основание
считать С2 = 0. Таким образом, оказывается, что скорость
перемещения волны в первом и втором приближениях одна и та же.
В дальнейшем будем исходить из анализа для φ2 следующего
выражения:
φ2 = 42ch2(z + M)sin2x, 2.18
где
3 аЧс{
8 sh'toT
Заметим также, что для определения постоянной величины
С2 использовано условие
λ
η2 (х) dx as 0,
J'
из которого следует, что
Q — 8a2k
2 sh 2kd'
Формулы дополнительных к решению в первом приближении
слагаемых, характеризующих уточнение решения задачи до
второго порядка приближения, имеют следующий вид:
'^=^та(1+2сН2М>С082х:
*>*» _ 3 2,3 ,ch2(z + M) , » 2.19
__£!*£_ cos 2x4- a4g
2 sh 2Ы cos '* ^ 2 sh 2W*
43
Воспользуемся далее результатами решений задачи, в nej
вом 2.15 и втором 2.19 приближениях. Подставив значения φ
Ч?2, τ)ι, Лг и с2 = 0 в 2.13, получим после преобразования следу^
щие выражения:
__/> ^2з _^?L - с,а-\пх I аЧЧх (5сЬ*Ы 1
^ дх дг - c*asmx^8sh*kd (°сп>га"г
+ ch2 foty sin χ + 4"5Йй (3 ch4 Ы + 5 ch2 М - 2) sIn 2χ5
£*4з = *<?, η%~ + ~f- ^ cos χ — 2.2|
-||^(ch^~3ch2M + 3)cosx^
+ 4f^(ch^M + 3ch2^-5)cos3x + C3.
Из совместного решения уравнений 2.20 находится С3 и ис]
следуется выражение для φ3 в виде функции
q>3 = A3ch3(z+kd) sin3x, 2.21I
где
лз = бйга-(13-4сь2^),
Дополнительные к решению 2.15 слагаемые, характеризую
щие уточнение задачи до третьего приближения, с учетом 2.15
имеют следующий вид:
^ = -бйнш(13-4сН2Ы)сЬЗ(2 + ы)81п3х'
% = ^_^L_ {4 (2 ch6 Ы + 8 ch* Μ - 19 ch2 Ы + 9) cos χ-
— 3(H-8ch°Ai/)co's3xJ;
ν"=*τζ$Ια (13-4ch2^)ch3(z + M)cos3x;
^3 = -|i^(13-4ch2M)sh3(z + ^)sin3x; 2.22
T = ¥S(13-4ch2^ch3(z + M)sln3x:
^ = -¥SS(13-4ch2^sh3(z + ^cos3xi
13 — 4 chs kd
*=4г^*ялз£т*ь*(*+*а>«»**+
44
- иет lch 3 <z+M> c°"+ch <z+ω>c°s 3χ1 ·
Объединив 2.15, 2.19 и 2.22 и перейдя к переменным (л:, z, t)
Согласно 2.2, запишем в окончательном виде следующие
основные формулы теории бегущих потенциальных волн,
соответствующие решению поставленной задачи в третьем приближении:
ag ch k (d — г) . , , ,ч .
φ = , 6 > ·. . ■' Sin k (Χ — ct) 4-
T Ygk th kd ch kd
+1 a? Vgk th kd ch ^Jf- z) sin 2k (x - ct) +
+ ^uSlkd* (13 ~ 4 Ch2 M> ch 3k W ~ g> Sin U (x~ciY> 2·23
^ = /^1Ьм[1 + -Ш|^5-(8с^М-8сЬ2Ы + 9)]; 2.24
ri=-acosk(x-ct) [l + 16 f^a- (2 ch6 Ы + 8 ch4 Μ -
- 19 ch2 kd + 9)] - —- ~£ [ 1 + 2 ch2 kd] cos 2* (x - ct) -
-■li та Π + 8 ch° WI cos 3*-(* - «*); 2.25
t>, = α У g* th ferf ch till*} cos k (x - gQ +
u-__L
4 sh**tf
/g-* th JW· eh 2k (d — z) cos 2£ (x - ct)■+.
+ i|irel/"^thw[i3-4ch2;w]x
X ch bk (d -z)cos3k(x-ct); 2.26
v, = - aVgkthkd stlk{?Z2) sln* (* -ct) ~
sh kd
3 _2fc
f sra Vsk th M sh 2* ^ ~ г) sln 2/fe (* ~c')
^^yg*thfci[l3-4ch2*d]sh3£(a*-z)X
Xsin3£(.K — ct); 2.27
-^ = ate у gkthЫchh£-г) sln6 (x - ct) +
■+»SJ_iS_ffl'fat«-«e +
45
4^JTffi4«C-*W(-4 2.28
~f- = akc y'gkthkd Sh * ^7 г) cos k(x — ct) +
+ 11ш "31ьУ"·" Sh8t(rf-^)co,3*(x-C0; 2.29
Л* , , / .4 Г ch fe (ίί — г) .
^ = gz + cosk(x- ct) [ga с1;ы +
3fl»jbVch3*(<*-*>1 I
4 " κ δ sh3 /W sh 2*u(J ^
+ 2sh2*rf[ s№kd ijcosznyx ci)t
+ 4 sh3 kd sh 2Ы L 8 sh* Ы cn ** ^a Z)
-chk(d-z)}cos3k{x-ct) + ^^[\ -ch2k(d-z)l 2.30
Обратим внимание на то, что постоянную величину а,
входящую во все приведенные выше формулы, надлежит определять
из следующего уравнения:
A = 2a[l + TeiPlrf (2ch6M + 8ch4/ferf- 19сЬ3Ы + 9) +
+ ^ет('+8сН6Н' 2·25'
которое легко получается из 2.25, если положить в основу
условие h = Tlmax — ηηιίη.
Исследуем траектории частиц жидкости в бегущих
потенциальных волнах большой высоты. В связи с этим в некоторых
записанных выше формулах необходимо осуществить переход
от переменных Эйлера к переменным Лагранжа. Обратимся
снова к выражениям для горизонтальной 2.26 и вертикальной
2.27 проекций орбитальной скорости, переписав их в следующем
виде:
υχ = В{ ch k (d — ζ) cos k(x — ct) +
+ B2ch2k(d — z)cos2k(x — ct) +
+ B3ch3k(d — z)cos3k(x — ct); 2.31]
vz = B\ sh k{d — z)sin k{x — ct) +
+ B2 sh 2k (d — ζ) sin 2k (x — ct) +
+ B3 sh 3k (d — z) sin 3k (x — ct), 2.32
(где постоянные B\, B2 и В3 равны:
Произведем следующую замену переменных χ и ζ:
χ = *о+ξ4; ζ = ζ0 + η4, 2.34
при этом (#о, го) суть независимые от t координаты,
изменяющиеся только при переходе от одной частицы к другой, тогда
как (&» щ)—малые по сравнению с длиной волны величины,
характеризующие движение фиксированной частицы с течением
времени. Имея также в виду, что в этом случае υχ = d\jjdt и
Vz=dr\b/dty формулы 2.31 н 2.32 могут быть записаны так:
-^ = Вх ch k (d — z0 — η4) cos k (x0 + ξ4 — ct) +
+ B2 ch 2k (d.~ z0 — η4) cos 2k (x0 + ξ4 — ci) +
+ B3 ch ЗА (d — z0 — η4) cos 3ft (x0 + ?4 — ct)\ 2.35
-^ = Bx sh ft (rf - z0 - η4) sin ft (*0 + ?4 - <*) +
4- B2 sh 2ft (rf — z0 — η4) sin 2ft (x0 + ξ4 — c<) +
+ £3 sh 3ft (d — zQ — η4) sin 3ft (*0 + ξ4 — ct). 2.36
Разлагая 2.35 и 2.36 в степенной ряд Тэйлора и
ограничиваясь членами, содержащими а3, получаем:
-—*- = Вх ch ft (d — z0) cos ft (x0 ~ **) —
— Bxk\k ch ft (rf — z0) sin ft (λ:0 — ct) +.
+ Вхкг\к sh ft (tf — z0) cos ft (x0 — ci) — Z^ft2?^ sh ft (rf — z0) X
X sin ft (λγ0 — c<) + B2 ch 2ft (rf — z0) cos 2ft (*0 — ct) —
- 2£2ft£4 ch 2ft (d - z0) sin 2ft (x0 — rf) + 2B2k^ sh 2ft (rf — z0)X
X cos 2ft (#0 — ct) + £3 ch 3ft (d — z0) cos 3ft (л:0 — ct) +
+ члены 4-го и выше порядка; 2.37
-gjr = Вх sh ft (rf — z0) sin ft (лг0 — с/) + Bxk^ sh ft (rf — z0) X
X cos ft (л:0 — ct) + θι*η4 ch ft (d — z0) sin ft {x0 — ci) +
+ B\b\iu ch ft (rf — z0) cos ft (x0— rf) + Я2 sh 2ft (rf - z0) X
X sin 2ft (xQ — ct) + 252ft?4 sh 2ft (d — z0) cos 2ft (x0 — <*)■+
.+ 2e2ftvj4 ch 2ft (d — z0) sin 2ft (#0"- *0 +
47
+ Въ sh Sk (d — zQ) sin 3k (xQ — ct) +
+ члены 4-го и выше порядка. 2.38
Интегрируя последовательно слагаемые выражений 2.37 и
2.38, получаем для траектории движения частиц жидкости в
волнах большой высоты (третье приближение) следующие
уравнения:
jc ""-"" JCn — —* а ■
^ ch*sha*/o) [шя + τsh2 k^d ~ *) J «in· α (χ· - <*) +
+ 4sh»*d L ^ shTfed J sin ^ l*o - ct> +
+ *ЙЙт«*2*(<*-*о)
2 sh^ Ы
-igl[13-4chW] chaffj'fl) sin 3k (x0-ct); 2.39
+ ^ Sh'shf*70) [ώ + ί Ch2 * (rf - Zo)] ™° k (χ0 ~ Ct) -
q2fe sh 2fe (d — г0) Γ ι , ^ cos 2k (x0 — ct) 1
4 sh2 Ы L 2 sh2 kd J
-igl[13-4ch*Mj Sh3s^;"o) cos3»(*,-C<). 2.40
Из уравнения 2.39 следует, что, кроме периодического
движения, с течением времени частицы жидкости движутся по
направлению перемещения волны с постоянной скоростью и,
равной
и=211ЪсЬ2^-*о)· 2.41
Скорость волнового течения и, как это следует из 2.41,
зависит от координаты z0j при этом и быстро убывает при
увеличении глубины.
Следует обратить внимание на некоторую особенность
определения длин и периодов волн при наличии волнового
течения. Назовем, по-прежнему, длиной волны λ — расстояние
между вертикалями, проведенными через соседние вершины волн,
и периодом волны Τ — промежуток времени между моментами
прохождения через одну и ту же вертикаль бегущих одна за
другой вершин волн. Наличие волнового течения жидкости
обуславливает необходимость, наряду с понятием периода
волны Г, ввести' понятие «период частицы» Ts:, равный проме-
48
ккутку времени между моментами прохождения через данный
кфовень частицы в процессе движения ее по орбите. В общем
Случае Ts^T, и только для частиц, лежащих на свободной
взволнованной поверхности, Ts =Т.
В заключение заметим, что, если.в приведенных выше
формулах 2.23—2.30, а также в 2.39 и 2.40 ограничиться
рассмотрением только первых слагаемых правой части (подчеркнутых
гнизу сплошными линиями), получим соответствующие
расчетные зависимости для определения основных характеристик
теории бегущих волн малой высоты (первое приближение).
2.2. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ НАИБОЛЕЕ ИЗВЕСТНЫХ ТЕОРИЙ
И СОПОСТАВЛЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТА
НЕКОТОРЫХ ХАРАКТЕРИСТИК БЕГУЩИХ ВОЛН
В предыдущем параграфе рассмотрены задачи о бегущих
потенциальных волнах большой высоты методом
последовательных приближений. Некоторые трудности аналитического
решения обусловлены тем, что задача исследовалась' в третьем
приближении для условий ограниченной глубины жидкости
d = const. Стоксом [86] обстоятельно изучались бегущие
потенциальные волны при неограниченной глубине d = оо; в
работах Рэлея [83] отдельные характеристики волн получены
с точностью до пятого приближения и даже более точно;
Согласно ргоксу [86] при d = оо профиль волны в третьем
приближении определяется формулой
η с= a cos k (λ: — ct) — -^ ha1 cos 2k (x — ct):-{- .
+ -| k2a? cos 3ft (x - ct), 2.42
при этом начало координат принято на спокойном уровне, а ось
0z направлена вертикально вниз. Значение постоянной
величины а в уравнении 2.42 определяется обычным путем, исходя из
условия А==Лтах — т|т|п.
Нетрудно убедиться в том, что форма волны Стокса близка
к трохоидальной. Впадины этих волн имеют более пологое
очертание, чем гребни. С увеличением высоты (при данной дли-
не) гребни волн становятся все более заостренными; их
профиль приобретает предельную форму, характеризующуюся на:
личием угловой точки в вершине волны. Стоке доказал, что
У^ол между касательными в угловой точке всегда равен 120°.
Мичел [78] выполнил расчет профиля предельной волны Сток-
са и при этом получил, что крутизна этой волны Α:λ = 0,142,
или приблизительно 1 :7.
Решения Рэлея, в которых он последовательно развивал
метод Стокса, обладают достаточно большой степенью, точно-
49
2.4
сти и могут служить основой для полной уверенности в сущее
вовании установившихся волн. Точное исследование бегуцц
потенциальных волн было выполнено А. И. Некрасовым [42
который впервые строго теоретически доказал (1921 г.) сущее
вование установившихся волн большой высоты в случае неогр,
ничейной глубины d = оо, а затем развил (1927 г) теорию дл
ограниченной глубины d = const.
Применительно к расположению начала координат в ве|
шине волны и при направлении оси Ол: вправо, а оси Oz верт!
кально вниз, в случае d = оо, согласно А. И. Некрасову, пр(
фи ль волны определяется следующими уравнениями:
х _ ^L (о + b sin 0 + b2 sin 28 + -| Ьг sin 3β);
z = +rb[(l-cosO) + b(\ -cos2e) + |ft2(l -созЗв)],
где величина Ьу в свою очередь, рассчитывается так:
при этом вполне допустимо ограничиваться первыми трем
степенями разложения в ряд по параметру μ' = μ — 3.
Высота волны h и высота гребня волны цс связаны с вели
чиной b согласно формулам:
h = ±b(2 + W); ъ^Л^Ьф + Ь + ЗР).
Теорией волн А. И. Некрасова, являющейся строгим анали
тическим решением задачи о волновом движении жидкости
подтверждены правильность исходных положений и основны
расчетных формул приближенной теории волн Стокса. А. И. Не
красов корректно исследовал правомерность применения в за
дачах о волнах метода последовательных приближений, но са
мым главным в рассматриваемой теории [42]^ являете)
доказательство сходимости ряда последовательных приближе
ний, хотя это сделано только применительно к малым значени
ям параметра μ'. Л. Н. Сретенский [53] обращает внимание »
интереснейщую и вместе с тем чрезвычайно сложную проблем;
изучения свойств предложенного А. И. Некрасовым интеграль
ного уравнения
ε -
sin ~
. 6+l
sin—ό~
de
φ (*) = _£ s"?(e) in I
J 1 + μ f sin Φ dt
о о
для более широкого диапазона изменения параметра μ. В часТ
ности, крайне желательно выяснить возможность преобразова
5D
яия волн с заданными характеристиками в так называемые
предельные волны Стокса, однако эта задача представляется
настолько сложной, что трудно предположить возможность ее
решения в ближайшие годы.
Ограничиваясь анализом теоретических решений,
результаты которых получили наибольшее распространение в практике
расчета воздействий волн на сооружения, рассмотрим
несколько более подробно исходные положения и важнейшие
результаты теорий бегущих волн, предложенных Герстнером (при
условии d = оо) и Буссинеском (при условии ограниченной
глубины жидкости d = const).
А. ВОЛНЫ ГЕРСТНЕРА
Исследуем плоскопараллельное периодическое движение
идеальной жидкости в бегущих волнах в случае d = оо, не
накладывая условий малой высоты волн и потенциальности
движения. Примем начало правой системы координат на отметке
средней волновой линии, при
этом ось Ог направим
вертикально вверх, а ось 0* — вдоль
луча волн; координаты центров
замкнутых траекторий частиц
обозначим через х0 и z0.
Предположим, что в рас- ν
сматриваемых волнах
большой высоты частицы
жидкости движутся по траекториям,
имеющим форму окружности
2.44
с постоянной по величине
скоростью
v = mTe'
fiZ0 _
const, 2.45
Рис. 2.2. Схема движения частиц
жидкости в бегущей трохоидаль-
ной волне при d = оо.
где k = 2π/λ; ω = 2π/Γ, смысл которых уточнится
впоследствии.
Положение частицы жидкости на ее траектории
определяется углом (фазой) &= kxo — ωί, который не зависит от г0,
Учитывается от радиуса траектории, проведенного
вертикально вверх, и считается положительным в направлении против
часовой стрелки, рис. 2.2. Неизменные во времени радиусы г
траекторий частиц жидкости не зависят от координаты и
убывают по экспоненциальному закону г = -^efcz°y если переходить
Эт частицы к частице по вертикали вниз. Согласно рис. 2.2 ко-
°Рдинаты χ и ζ частицы Μ равны:
51
χ = Χο — r sin & = Xq — r sin (kx0 — ωί);
2.46
ζ = Zo + rcosQ = Zo + rcos (kxo — ωί).
Уравнение профиля волны запишем, приняв для простоты
t — 0 и соответственно θ = kx0 или х0 = θ/k и имея в виду, что
для точек профиля волны z0 = 0:
χ = -τ- — r0sin θ; z = r0cosB. 2.47
Уравнения 2.47 определяют кривую, получаемую
перемещением точки, расположенной на расстоянии г0 от центра круга
радиусом R = \/k\ при этом круг катится без скольжения по
ι л=тя ι ,
Рис. 2.3. Профили бегущих трохоидальных волн
/ — горизонтальная прямая; 2 — г0 = 0, горизонтальная линия; 3 и 4 — rQ < R,
круговая трохоида; 5 -- г0 = 0,45/?, круговая трохоида с наибольшей
крутизной волн Η/χ =в 1/7; б — г0 = Я, круговая циклоида; 7 — г0 > #, круговая
трохоида с петлями.
нижней стороне горизонтальной прямой линии /, которая выше
средней волновой линии 2 на величину R, рис. 2.3. С точки
зрения теории трохоидальных волн одинаково возможно
существование следующих профилей: при г0 = 0 — горизонтальная
линия 2; при /Ό <R — круговая трохоида 3 и 4\ при г0 = 0,45/? —
круговая трохоида 5; при /-0 ·= R — круговая циклоида 6.
Профиль волны согласно кривой 7 не может существовать, он
соответствует /Ό > R — круговой трохоиде с петлями.
Как известно, крутизна бегущих волн не превышает /ι/λ =
= 1/7, что соответствует г0 = 0,45/?. Поэтому физически
возможным предельным профилем следует считать трохоидальный
профиль 5 на рис. 2.3. Из этого же рисунка видно, что высота
волны h = 2r0, а длина волны λ =2π/? = 2π/£, следовательно
k = 2π/λ, τ. е. £ — характеризует длину волны.'Заметим здесь
же, . что для любого, определенного χ = const значения
sin (fejco — ωί) повторяются в моменты, для которых t разнятся
52
величину п = 2π/ω, где η — целое число. Соответственно
повторяются значения cos (kx0 — ωί) и ординаты ζ (при х0 =
consl). Промежуток времени между ближайшими такими мо-
ментами (при п= 1) равен периоду волны £ Отсюда следует,
что Τ = 2π/ω (или ω = 2π/Γ), т. е. ω —характеризует период
На рис. 2.4, α представлены профили волны, построенные по
круговой трохоиде 1 и косинусоиде %2У из сопоставления которых
следует, что гребень трохоидальной волны короче и острее ее
Рис. 2.4. Схемы к построению профиля бегущей трохоидальной волны (а)
при d = оо и к определению (б) возвышения средней волновой линии Δά
/ — круговая трохоида; 2— косинусоида; 3 — направление перемещения волн; 4 —
направление движения частиц жидкости; 5 —профиль волны; 6 — средняя волно-
' вая линия; 7 — направление вращения катящегося круга.
впадины. Поскольку в пределах одной волны объем жидкости
не изменяется, то линия, расчетного уровня должна быть, фас-
положена ниже средней волновой линии Ady рис. 2.4,6.
Возвышение Ad над спокойным уровнем определяется из условия ра:
венства суммы площадей фигур ABCDEFG и MNFG, а именно:
λ
Ad = 1 (QBCD - QABK - QDEL) = \^zdx = -^-. 2.48
о
Аналогичным образом можно показать, что возвышение
сР6дней волновой линии AdZQ для частицы жидкости,
находящейся в состоянии покоя на глубине z0> следует рассчитывать
По формуле
Ad -J^L*2**o
z° —?5Г
2.48'
53
Скорость волны с^К/Т = ω/A—const равна скорости переме!
щения центра круга радиусом /? = 1/Α=λ/2π. Применительно J
циклоидальному профилю 6 на рис. 2.3 для волн, движущих^!
вдоль положительной оси Оле, получаем, что поверхностные части]
цы жидкости в волне перемещаются по неподвижным, траекто!
риям — окружностям радиуса/?=Л/2 с неизменной по величина
скоростью υ = с, при этом в вершине волны имеем ( + с), в ло1
дошве— (—с). Если наложить на волновое движение встречной
волнам равномерное движение со скоростью — с, получим ус]
тановившийся поток, имеющий неподвижную свободную по]
верхность, для которого справедливо уравнение Бернулли]
В верхней точке свободной поверхности такого потока ско]
рость течения v\' = О и и2 = —2с — в нижней точке, а
давление во всех точках свободной поверхности одинаково. Запишем
уравнение Бернулли для точек профиля волны, который в рас'
сматриваемом потоке является линией тока:
Z\ — z2 + ~2ξ — z2 -f- "2^-;
откуда
n 2g » ° V 2 '
Имея в виду, что в круговой трохоиде h = λ/π, получаем
Результат 2.49 можно получить и в том случае, если проде·1]
лать такие же операции применительно к профилям, изображен
ным на рис. 2.3 (кривые 3 и 5), при этом несколько усложнятся
и выкладки.
Для определения частоты и периода волн Герстнера имеем:
ш = УГк;Т=УЦл.
Напомним уравнения Эйлера в целях использования их при
исследовании гидродинамического давления в трохоидальных
волнах:
Хдрд _ d?x a 1 dpd d*z
ρ дх ~ rf/2; ρ дг " * dP '
Осуществив во втором из этих уравнений переход от χ и г,
к лс0 и 2о, получаем:
1 dpd __ 1 (dpd дх dpd дг)_ d*x дх . / _<Mjg.
Ρ дг0 ~ ρ \ дх дх0 "*" дг дг0/ dt* дх0 ~*~ \ ё dt*) dz0'
h4
Использовав 2.46 и имея в виду, что г — -% екг\ после
подстановки производных и преобразований, запишем:
Jl^E± - _ ι J- π3/*3 ,>2^о
54
Интеграл этого уравнения с учетом 2.48 и 2.48' равен:
Ж = -гв-^(*-_г«) = -2Ь + М.-АА 2.50
Правая часть 2.50 есть заглубление покоящейся частицы
жидкости под горизонтальной свободной поверхностью при рас*
четном уровне, рис. 2.5; эта величина не зависит от времени.
Отсюда следует, что гидродинамическое давление,
испытываемое частицей идеальной жидкости во всех точках траектории
(круговой орбиты) с координатами z = f{t) в трохоидальной
Рис. 2.5. Эпюры гидродинамического и эолнового давлений в бегущей
трохоидальной волне при d = оо
/ — средняя волновая линия.
волне, равно гидростатическому давлению, которое испытывала
эта же частица в покое, находясь на горизонтальной
поверхности равного давления zcn =* const:
— Zcn = —z0+Ad2o—Arf. 2.51
На рис. 2.5 изображены эпюры гидродинамического и
волнового давлений в точках, проходящих через вершину при
cos (kx0 — cot) = +1 и через подошву при cos (kx0 — ωί) = — 1
бегущей трохоидальной волны в случае d = оо. Волновое
давление ρ определяется как разность значений гидродинамического
давления в данной точке пространства, занятого жидкостью, при
наличии волн pd и их отсутствии ps по формуле
Α = Αι-Α=±ρ*4**' 2·52
и откладывается по вертикали на расстояниях от оси 0х9 равных
пРи гребне z0 — r и z0+r — при впадине.
55
Рассмотрение основных положений теории волн Герстнер;
дает основание заключить, что эту теорию можно использоват,
как сравнительно простое гидромеханическое решение, в кото
ром, однако, имеет место принципиальное противоречие — вол
ны идеальной жидкости должны быть потенциальными, а в дан
ном случае они вихревые, т. е. непотенциальные. Как следств^
этого, в рассматриваемых волнах траектории частиц жидкости
суть замкнутые окружности, хотя, как уже отмечалось, в по
тенциальных волнах траектории частиц должны быть разомк
нуты ми.
Б. ВОЛНЫ БУССИНЕСКА
Исследуем теперь плоское движение жидкости в бегущщ
волнах в случае ограниченной глубины d = const, не наклады
вая условия потенциальности движения. Начало правой систе
мы координат по-прежнему расположим на отметке среднее
волновой линии, а оси ориентируем так: 0* — вдоль луча волнь
и Ог—вверх; координаты центров замкнутых траекторий
частиц обозначим через х0 и z0.
Примем, что в рассматриваемых бегущих волнах большой
высоты частицы жидкости движутся по траекториям, имеющим
форму эллипса:
где гх — горизонтальная и rz — вертикальная полуоси эллипса,
определяемые из следующих формул:
_ h_ ch k (го + rf). _ h_ sh к (**+ d) 9 ,,
Γχ~ 2 sh£d ' r*~ 2 sh£rf * ^
Здесь, как и в волнах Герстнера, остаются в силе значения
£ = -г-; ω = -=-; B = kx0 — ω/.
Схема движения частиц жидкости в трохоидальной волне
при d = const представлена на рис. 2.6, на котором изображены
две концентрические окружности: радиус одной из них равен
горизонтальнй полуоси, а другой — вертикальной полуоси
эллиптической траектории. Предположим, что по этим
окружностям движутся точки Μι и Λί2> все время находящиеся на одном
радиусе 0ΛίιΛί2, который вращается в направлении против
часовой стрелки с постоянной угловой скоростью и составляет в
данный момент угол θ = kx0 — ωί с радиусом, ориентированным
вертикально вверх. Точка Μ пересечения вертикали,
проведенной через точку Ми с горизонталью, проходящей через точку
М2, соответствует частице жидкости в волне. Движение точки Μ
происходит по эллипсу. На рис. 2.6 кружками обозначены
положения точки, соответствующие фиксированным моментам
через Т/16. Используя этот рисунок, можно записать
следующие формулы для координат χ и ζ точки М:
56
x = Χο — г χ sin & = χ0 — г χ sin (kx0 — ωή;
2.55
ζ = z0+rzcos& = z0+rzcos(kx0 — cot).
Из 2.55 легко записать уравнение профиля волны, приняв
[ля простоты t = 0. Имея в виду, что в этом случае х0 = &//г,
[ при z0 = 0, Гх *= Л/2 cth Μ, rz = /г/2» получаем:
x = -j ^cthArfsinS; г =-о· cos θ. 2.56
k 2 '2
Рис. 2.6. Схема движения частиц жидкости в бегущей трохоидальной
волне при ограниченной глубине ά = const.
Уравнение 2.56 определяет эллиптическую трохоиду —
кривую, получаемую при перемещении точки Λ1, если круг
радиусом # = i/£ c изображенными на нем точками М\ и Λί2,
Рнс 2.6, катится без скольжения по нижней стороне
горизонтальной прямой, параллельной лучу волн. Построение профиля
трохоидальной волны при d = const и сопоставление его с
косинусоидой дано на рис. 2.7, а, из которого следует, что гребень
_рохоидальной бегущей волны короче и острее ее впадины, а
57
следовательно, в этом случае средняя волновая линия
расположена выше расчетного уровня. Руководствуясь положением о
равенстве площадей фигур ABCDEFG и MNFG, рис. 2.7,6,
получаем, как и в теории волн Герстнера, что горизонтальная
линия расчетного уровня на профиле волны расположена ниже]
средней волновой линии на величину Ad:
Ld
= у (®bcd — ®авк — ®del) = γ \ zdx = γ rxrv
Рис. 2.7. Схемы к построению профиля бегущей трохоидальной волны
(а) при d = const и к определению (б) возвышения средней волновой
линии Ad
1 — эллиптическая трохоида; 2 — косинусоида; 3 — направление перемещения
волн; 4 — направление движения частиц жидкости в волне; 5 — профиль волны;
б —средняя волновая линия; 7 —расчетный уровень.
или
Μ = -^ cth kd.
2.57
Если произвести выкладки, аналогичные изложенным в
теории волн Герстнера, нетрудно получить, что скорость
перемещения трохоидальных волн при d = const определяется по
формуле
2.58
-V4
th^d,
а следовательно, в этом случае частота и период волн
определяются по зависимостям
ω = Ygk th kd\ T= ]/— λ cth kd.
2.59
Исследуем гидродинамическое давление в жидкости
трохоидальных волн при d = const, используя уравнение
1 др± __ J_ (др£ _дх_ дра_ дг \ _ _ сРх_ дх_ __ ( , j^£_ дг \
Ρ дг ~~ ρ V дх дх0 ^ дг дг0 / ~ dP дх0 \* ^ dP дг0 /'
58
которое подставим значения соответствующих производных
выражений 2.55 с учетом 2.54. После преобразований полу-
им:
1 д££ __ __ ι ι _ г г
9g дг*
— ί krx — ^-γ-j cos (kx0 — Ы).
gW
Интеграл этого уравнения
Pd _- , gT*_(r2 4π2λ2 h*\
— — г0 -f 2λ2 yrx g2?4t 4 j -f
+ (Г* Ш ~~ rJ C0S (Λ*° ~~ ωί)·
2.60
Легко убедиться в том, что при d-+oo 2.60 преобразуется
ι 2.50, равно как и все другие формулы волн Буссинеска. Од-
ако дальнейшие исследования уравнений 2.55 показывают, что
ни удовлетворяют условиям:
а) неразрывности, если пренебречь величиной k2(r2x — r\)\.
б) постоянства давления на свободной поверхности жидко-
ти, если принять k(r2x — r2z) = h2/d2.
Эти условия выполняются точно только в случае d->oo,
следовательно, рассматриваемое решение Буссинеска является
риближенным, и его погрешности возрастают с увеличением
араметра h/d.
В. СОПОСТАВЛЕНИЕ РЕЗУЛЬТАТОВ ИЗУЧЕНИЯ БЕГУЩИХ ВОЛН
Сравним между собою и некоторыми данными эксперимён-
ов отдельные результаты теоретического изучения волн раз-
Ю
-0,50
~0,25
0\—ι
щ
0,50\-
f/X
Рис· 2.8. Профили бегущей волны h = 20 см, λ — 200 см при d « оо
(схема а) и d =» 40 см (схема б)
4^5°> iHHeftHOft теории (косинусоида); 2 — по Герстнеру [72]; 3 —по Стоксу [86];
Г ιοί? ? И* НекРасову [42]; 5 —по формуле (2.25); 5 —по М. П. Кожевникову
1 ·>> ' — ПО данным Аптппргнгтпапнн ппгхЬиля волны в лабопатопных условиях.
• ' ι
4'J
1
II
>3
б'
Расчетный уробень
1 V I I 1
:^г^44 е
х/1
-по данным фоторегистрацни профиля волны в лабораторных условиях.
59
ι- ff
о,ю\
0,12
№
0,16
0,18
0,20
OyJU
0A0\
6,50
d
Я
h 5
λ
τ.
tjx
γ \
h
\ l__
1
6
\
\
1
^1
'&6
</
\ ι
тгА
[IK
m
>
ι
^
ill
*<-'
N
\ ' Ί
ч\
«5Г
^
.<=^
52
h
Рис. 2.9. Графики относительных значений постоянных величин
2а//г = /(Α/λ; d/λ) (схема а) и \L/Li\z=,o = F(h/K; dj(k) при ζ = О
(схема б)
i — граница разрушения бегущих волн; 2 — граница применения формул
третьего приближения.
60
ιιι—ι r-
^ δ
δ **
ι ι ι ι ι—ι—ι—г
o>
θς>
Γ 7
ff
о,ю
0//Z
0,Щ
0,f6
ом
0,20\- 5
0,30
0,50\-
λ
А
h
:\
- ^ч
-
_J
\ι ч
/
\
1
1
ЧЯИ:
1 1
ш
1
\
J J j j^K <»
ч!ж^^
,0,95'
ι -
1 I ■
δ)
Ч
\
\
I 1
Л
\
\
\
\
I
I 1
Ϊ3
§
^
^Ν
55
К
Рис. 2.10. Графики относительных величин наибольших значений
проекций орбитальных скоростей в бегущей волне при ζ =» 0;
горизонтальных Vxlvxi = /(Α/λ; dj%) (схема α) и вертикальных υζ\νζ\ =
= F(hl%\ dl%) (схема б).
^штрихованы области, в пределах которых в ложбинах волн появляются
вторичные гребни. / — граница разрушения бегущих волн; 2 — граница
применения формул третьего приближения,
61
личными путями. На основе этого попытаемся установить,
какая из теорий волн дает возможность получить наиболее
достоверные характеристики волнового движения жидкости. Имеет
смысл рассмотреть, например, следующие характеристики:
профили взволнованной поверхности; значения горизонтальной и
вертикальной проекций скорости и ускорения; величины
волнового давления в наиболее характерных точках пространства,
занятого взволнованной жидкостью; траектории движения
отдельных частиц жидкости в бегущей волне.
На рис. 2.8 представлены профили бегущей волны,
построенные по формулам различных теорий волн в условиях
глубоководья при d = оо (схема а) и мелководья при d = const
(схема б). Из этого рисунка следует, что большинство из
применяющихся на практике теорий волн, за исключением теории волн
малой высоты (кривые /), не дают сколько-нибудь
существенных различий в результатах расчета. При d = оо профили волн,
полученные по формулам теорий волн Герстнера и Стокса
(третье приближение), оказались практически тождественными
(кривые 2 и 3). Профиль 4, рассчитанный по точной теории волн
А. И. Некрасова, весьма незначительно отличается от кривых
2, 3: В случае d = const профили, построенные по формуле 2.25
(кривая 5) и по данным исследования М. П. Кожевникова [19]
на приборе ЭГДА (кривая б), наилучшим образом согласуются
с кривой 7, начерченной по данным фоторегистрации профиля
волны в лабораторных условиях.
На рис. 2.9 изображены две частные характеристики профиля
волны. Первая из них (схема а) — семейство кривых,
представляющих собою изменение отношения константы 2а к высоте
бегущей волны А. Кривые рассчитаны по формуле 2.25' в третьем
приближении для наиболее характерных диапазонов крутизны
волн h/λ и относительных глубин d/λ. Показательно, что, как
правило, во всех случаях, имеющих практический смысл,
отношение 2a/h меньше единицы, нередко составляет 0,75 и может
быть несколько меньшим. Заметим, что в решениях первого и
второго приближений значение отношения 2a/h всегда равно
единице.
Вторая частная характеристика профиля волны, рис. 2.9,6,—
семейство кривых, представляющее собой отношение L (ширины
гребня волны на уровне покоя), полученного по формуле 2.25 в
третьем приближении, к L\ (ширине гребня волны), рассчитан
ного по теории волн малой высоты^ Из этого рисунка однозначнс
следует, что всегда отношение (L/Lx)< 1, а в отдельных случая)
(вблизи границы обрушения волн) (L/Li) = 0,65.
На рис. 2.10 представлены два семейства кривых, характеры
зующих в системе прямоугольных координат (h/λ) и (d/λ) от
носительные значения (а) горизонтальной (νχ/νχί) и (б) верти
кальной (Vz/vZi) проекций орбитальной скорости, рассчитанны)
62
о формулам 2.26, 2.27 в третьем (vXj vz) и в первом (vxu vzi)
оиближениях для бегущих волн. Наибольшие значения проек-
ий скоростей определялись в точках с координатой ζ = 0.
Ц Из данного рисунка следует, что с уточнением теории
значения горизонтальной проекции скорости возрастают на 15... 30 %
лишь в области относительных глубин rf/λ ^ 0,14; в пределах
dl% > 0>20 в расчетах сооружений, по-видимому, можно
пользоваться в отдельных случаях более простыми формулами первого
приближения. Вертикальные проекции скорости без
существенных погрешностей можно рассчитывать по формулам первого
приближения практически во всех случаях, за исключением
небольшой зоны вблизи границы обрушения волн при ί//λ^0,12.
На рис. 2.11 представлены эпюры горизонтальных проекций
орбитальной скорости под гребнем и впадиной волн (схе-
мы а —г) для конкретных условий по формуле 2.26 в третьем
приближении. Результаты исследований М. П. Кожевникова
[19] с помощью прибора ЭГДА показаны пунктиром; точками
обозначены средние, замеренные в
опытах, значения скоростей,
полученные в большом и малом волновых
лотках. Нетрудно видеть, что почти
на всех четырех схемах расчетные и
опытные данные вполне
удовлетворительно согласуются между собою.
Исключение составляют эпюры
скоростей в схемах β и г, из которых
следует, что данные метода ЭГДА существенно отличаются от
результатов аналитических расчетов по формуле 2.26.
Расчетные данные в третьем приближении лучше других
соответствуют физическим "опытам (табл. 2.1).
Для более подробного сопоставления результатов расчета
проекций орбитальных скоростей по различным теориям с опыт-
Таблица 2.2
Схемы
а
б
в
г
h, см
48
33
25
20
Таблица 2.1
λ, см
940
470
250
230
d, см
400
400
83
5i
Номера
опытов
/
2
3
4
5
'6
7
8
9
10
d, см
ПО
по
17
ПО
30
130
30
150
30
83
Т, с
.6,82
4,82
1,48
3,54
1,6
2,9
1,33
2,43
1,0
1,28
λ, см
2202
1531
180
1098
250
982
200
774
140
250
Λ, см
69,8
47,5
6,8
64
12,0
66,6
12,0
58,5
9,3
25
dl\
0,05
0,072
0,094
0,10
0,12
0,132
0,15
0,194
0,21
0,33
λ/Λ
31
32
26,4
17
20,8
14
16,6
13,2
15.0
10,0
63
ными данными на рис. 2.12 приведены эпюры горизонтальных
проекций относительных скоростей в волне vx/(nh/T) при
относительной глубине d/λ от 0,05 до 0,33 и пологости волны λ/Α от
10 до 32 [8,9]. Опыты выполнялись в гидроволновых лотках^
&) Гребень бпабина S) Гребень Впадина
Ух.см1с 60 ΰ Οχ,οΦ 50 О
Расчетный , 1 4>iiib"H"i"H Расчетный
ъ уробень-эисщс
Рис. 2.11. Эпюры горизонтальных проекций орбитальной
скорости под гребнем и впадиной при значениях элементов волн,
приведенных в табл. 2.1
/ — по формуле (2.26); 2 — по М. П. Кожевникову [19]; 3 — средние
опытные значения по данным [5, 6].
с горизонтальным дном (табл. 2.2). Номера эпюр скоростей на]
рис. 2.12 соответствуют номерам опытов в таблице.
Из анализа рис. 2.12 следует, что при rf/λ < 0,15 проекции!
скорости ϋχ, рассчитанные по формуле 2.26 (третье приближе-1
G4
ν близко совпадают с опытными данными; определенные по
!Н82 (одиночная волна) — оказались выше опытных значений,
ρ хождения между результатами расчетов по 2.26 в третьем
еовом приближениях становятся существенными при d/λ ^
d
z ° z ***
US
ο\1
ш
Μ
-1-0,5 0 0,5 1 1,5 Ζ 4-0,5 0 0.5 1 1,5 - 1-0,5 0 0,5 1 йк
Рис. 2.12. Эпюры горизонтальных проекций относительной
орбитальной скорости υχ: nh/T под гребнем и ложбиной
t — по формуле (2.26) — третье приближение; 2 — то же — первое
приближение; 3 — по формуле (2.82) — одиночная волна; 4 — опытные значения [8, 9].
^0,2. Из этого следует, что при расчете скоростей на глубине
А > 0,2 с известным приближением допустимо пользоваться
Формулами линейной теории. Использование формул, основан-
ы* на теории одиночной волны, может быть оправдано лишь
для прибойных или разбивающихся волн.
65
тальных
Рис. 2.13, Графики относительных величин. наибольших значений
проекций орбитальных ускорений в бегущей волне при ζ = 0: горизон-
dvx Idv-r dvz /dv,t -■
-_/_^ = /(/*/λ; d/λ) (схема α) и вертикальных —-/Ц-f' А
at ι οι οι Ι οι
^E(hl%\dl%) (схема б).
Заштрихованы области, в пределах которых в ложбинах волн появляются
вторичные- гребни, / — граница разрушения бегущих - волн-; 2 —граница
применения формул третьего приближения,
т
На рис 2.13 представлены два семейства кривых, характе-
изуюших в системе прямоугольных координат (h/X) и (d/λ)
хносительные величины (а) горизонтальной (J^J^A и (б)
вертикальной ( -щ-ι ~^J проекций наибольших значений
локальных ускорений, рассчитанных в третьем \^"> -%f) по
формулам 2.28, 2,29 и в первом f-g^1 -gf) приближениях для
бегущих волн; ускорения определялись в точках с ординатой
Из этого же рисунка следует, что с уточнением теории
проекции локального ускорения существенно возрастают:
горизонтального при d/λ < 0,20 и вертикального при d/X <
< 0,25; на схеме а увеличения достигают двукратного, а на
схеме б —трехкратного. Таким образом, следует рекомендовать
локальное ускорение определять по более точным теориям
третьего приближения, и лишь в области d/X > 0,25 для не очень
точных расчетов можно использовать соответствующие формулы
первого приближения.
На рис. 2.14 (схема а) показано семейство кривых,
характеризующих отношения наибольшего волнового давления при
гребне волны, рассчитанного в третьем (р) и первом (pi)
приближениях для бегущих волн в точке, обведенной кружком на
схеме б, с координатой ζ = 0. Здесь же представлены эпюры
наибольших значений волнового /давления в створах вершины
и подошвы волны, рассчитанных для конкретных исходных
данных" в первом (кривая 7), втором (кривая 2) и третьем
(кривая 3) приближениях. Из рассмотрения рисунка следует,, что
при использовании расчетных формул теории волн третьего
приближения получается наиболее достоверный
количественный результат и соблюдается условие равенства нулю
волнового давления на гребне свободной взволнованной поверхности.
На рис. 2.15 изображены траектории частиц жидкости в
бегущей волне, построенные по формулам различных теорий
волн. Линии 1 и 2 представляют замкнутые кривые в виде
эллипсов одинаковых размеров, отличающихся тем, что центры
эллипсов 1 расположены на спокойном, а центры эллипсов 2 —
выше спокойного уровня, а 3 и 4 — разомкнутые кривые,
сходные между собою по начертанию, но существенно
отличающиеся по величине смещения данной частицы (в направлении
перемещения волн) за один период волны.
.По кривой 3 можно определить, что меченая частица,
совершив одиннадцать полных оборотов, переместится вдоль оси Ох
На расстояние, равное одной длине волны; если использовать
Результаты исследований на приборе ЭГДА, этот же путь ме-
еная частица пройдет, совершив лишь шесть с половиной
оборотов. На этом рисунке показано также, как изменяются на-
67
г «> · »Ч Vf> K^ Ч^
a*·
Си η
И
I"
CO
is
V
чертания траекторий частиц, заглубленных на различные рас-
стояния под уровень.
Заканчивая сопоставительный анализ результатов расчета
по формулам наиболее известных теорий волн и некоторых
экспериментальных данных, можно заключить, что в
исследованиях и расчетах сооружений на воздействие волн следует
отдавать предпочтение потенциальным нелинейным теориям волн.
Отдельные характеристики бегущих волн с достаточной
степенью точности допустимо рассчитывать и по упрощенным
формулам, руководствуясь представленными в данном
параграфе графиками.
2.3. ЭЛЕМЕНТАРНЫЕ ТЕОРИИ ОДИНОЧНОЙ (УЕДИНЕННОЙ) ВОЛНЫ]
Исследуем движение жидкости в канале прямоугольного
сечения с постоянной глубиной dy представляющее собою
отдельное возвышение поверхности (вал), перемещающееся
вдоль канала без изменения формы с постоянной скоростью с.
τρΎ// /у/ //у у/р у/^/// /// ν//γ///// /// /// /У/ /// /// УУУ
Рис. 2.16. Схема к решению задачи об одиночной волне.
Рассматриваемое движение изучалось рядом ученых
экспериментально и теоретически, в литературе <[30, 44, 53, 54]
оно'лолучило название одиночной (уединенной) волны, состо-|
ящей из одного гребня конечной высоты и бесконечной дли-|
ны. Основные сведения из истории развития этой теории из
ложёны в [54], где также показано, что одиночную волну мож-|
но получить как предельный случай кноидальной периодической]
волны при увеличении ее длины до бесконечности.
Остановимся кратко на тех решениях, которые получили]
наибольшее распространение на практике — главным образом
при разработке методов расчета сооружений, расположенных
в прибойной зоне: Исследуем, как и Л. Н. Сретенский [53], ре-!
70
ения Рэлея н Мак-Коуэна, использоваь дополнительно
отдельные положения статьи Манка [44].
расположим начало координат на дне канала, ось χ ориен-
руеМ по направлению, перемещения волны,, ось ζ—
вертикально вверх, рис. 2.16. Задача сводится к определению
элементов движения, при этом, по-прежнему, будем считать
жидкость идеальной, движение потенциальным, а плотность ρ —
постоянной величиной.
А. РЕШЕНИЕ РЭЛЕЯ
Сообщим всей массе жидкости скорость —с, обратную
скорости перемещения волны. Тогда волна будет неподвижной в
пространстве, а движение жидкости — установившимся.
Разложим горизонтальную υχ и вертикальную υζ проекции
скорости соответственно в ряд Маклорена по степеням ζ:
νχ = А0+Αιζ+Α2ζ2+ ... +Anzn
2.61
υχ = Βιζ + Β2ζ2+Β3ζ3+ ... +Bnzn +
где коэффициенты Л0, Au ..., Ап\ Β\9 Β2,^.,Βη являются
функциями х\ свободный член В0 в разложении υζ равен нулю, так
как Όζ = 0 при ζ = 0.
Найдем из 2.61 значения производных
dvx __ dA0 . dAt . dA2 ^ . « dAn ■ п ..
дх dx ' dx "*" dx * ' щ-%~ dx « · · ·»
-§- = Bt + 2B2z + .. . + nBnz»~* + (n-\)B„+1z» + ...
и подставим их в уравнение неразрывности
-&+-&-■&+*. + (#+**)»+·■.
■•· + [τηγ + <" + 1>α+1]*" + ·-· = 0·
Поскольку последнее равенство должно соблюдаться при
любых значениях ζ, то коэффициенты при степенях ζ должны
быть равны нулю. Отсюда находим следующее соотношение
между коэффициентами А и В:
~^--(я+1)Дл+ь 2.62
Где* = 0; 1;2;3;...
пол безвихревого движения, как известно, dvx/dz = dvz/dx\
втопТаВИВ в эт° Условие выражения для производных, получим
Рое соотношение между коэффициентами А и В:
»А» = ^ЧГ- 2·63
71
Учитывая, что β0 = 0, из совместного решения 2.62 и 2.63
имеем Αι = В2 = 0 и следующее выражение для Ап:
A l d2An~2 2 64
лп- п(п-\) dx* ' 1'щ
dnf
Обозначив A0 = f(x) и j^ = βη), с учетом 2.62—2.64, мож-]
но формулы 2.61 переписать так:
^ = /-|-/<2> + |-/<4)-...;
^=_*/<l)+*L/W_|./<5> + ... 2.651
Использовав замену νχ = -£- и νζ = — -^, из 2.65 получим:]
*=2/-ί/(2)+!-/(4)-···
На бесконечном удалении от начала координат на свободной
поверхности ψ = — cdy поэтому запишем первое основное
уравнение теории одиночной.волны в виде
*/- ΐ^(2)+ 4/(4) -... = -«*. 2.66
Для свободной поверхности гидродинамическое давление
равно нулю, и выражение интеграла Бернулли упрощается:
gz + ^ (vx2 + vz2) = const.
Поскольку в одиночной волне на бесконечном удалении от
гребня (при χ =.± оо) поверхность волны стремится к
положению невозмущенного уровня, то: ζ — dy- vx = с и νζ — 0, а
следовательно, const = gd + γ с2, и интеграл Бернулли перепишем
так
Ό*χ + ϋ*ζ = 2g(d — z) +c\ 2.67
На поверхности волны, являющейся линией тока, уравнение
которой — = —, левую часть 2.67 можно представить в таком
vx vz
виде:
«χ8+ «,· = «,» [l + (£/].
Из уравнения 2.67 в этом случае вытекает, что
2.681
« _ -, f*g &-*) + #
η
Подставив 2.68 в первое из уравнений 2.65 и умножив левую
и правую части на г} получим второе основное уравнение
теории одиночной волны:
*- 1> + £/(4)~ - = ]/iC2 + 2gdl^2^· 2·69.
Решим совместно уравнения 2.66 и 2.69; ограничиваясь
членами первого порядка, из 2.66 имеем:
2/=-£?rf;/(«) = -£?rf(l)(l,)f
что дает возможность при подстановке в 2.69 исключить
функцию / и записать одно уравнение ζ = ζ (χ) в виде:
--['-*(4Г+да--ь
Если считать волны настолько пологими, что третьим и
последующими членами в квадратной скобке можно пренебречь,
тогда из 2.70 следует:
l + (dx)
'■=2£-. 2.71
Подставив в 271 значение второй производной от \/z>.
равное
1 \(2) ~ ~d&
W=
*■&+*(#
*
после преобразований и исключения членов высоких порядков,
получим:
** I1 ~ τ {%] + τ * ш] = ^ + ^*2 ~ *#·
Умножив это выражение на *^ и проинтегрировав по #,
в результате имеем: *
3\dx]
Произвольная постоянная С определяется из условия
\dz/dx) = о и 2 = d при χ — ± оо, а именно:
W ^ β»/"·
73
Заметим, что метод определения произвольной постоянной
С обусловил особенности решения задачи применительно к
одиночной волне; возможны также решения уравнения 2.72
[30, 53, 54], которые используются при изучении периодических
волн.
Таким образом, в данном случае для производной dzjdx
получаем следующее окончательное уравнение:
dx
)'=3^(l-^). 2.73
Воспользовавшись условием равенства нулю dz/dx на
вершине волны, т. е. при ζ = d + h, запишем формулу скорости
перемещения волны:
c = Vg(d+h). 2.74
Точно такая же зависимость была получена эмпирически
С. Расселом на основе обработки экспериментальных данных
задолго до создания Рэлеем настоящей теории одиночной
волны [53].
Подставив 2.74 в 2.73, после преобразований имеем
ш-
откуда следует, что ζ не может быть больше (d+h), а
следовательно, одиночная волна без впадины — она всегда волна
возвышения (Zmax = d + U).
Проинтегрировав 2.75 и определив постоянную из условия
ζ = d+h при χ = 0 (ось ζ проходит через вершину волны),
получим уравнение профиля одиночной волны:
тле
z = d + hsch2~r, 2.76
ρ β £ij+*)e 2J7\
Отклонение η свободной поверхности от невозмущенного!
уровня равно:
h
\2d f a
=г-. 2.78
d + h)
Для одиночной волны, строго говоря, не существует понятия
длины волны, но нередко под этим термином понимается
расстояние между теми ее точками, в которых η = 0,1/ι; в таком
случае оказывается λ = 7,272β. Учитывая 2.77, можно
заключить, что чем больше высота волны /г, тем меньше значение λ;
«длина волны» возрастает при увеличении глубины d. Как
обычно, под длиной волны будем подразумевать λ = 2n/k.
74
Максимальная высота одиночной волны определена Рэлеем.
применительно к створу вершины волны (при z = d+/i) из
2 67 получим:
O2x + O*g = <* — 2gh.
Подставив сюда значение с2, согласно 2.74 имеем:
v2x + v*z = g(d-h),
и следовательно, выполняется условие h ^d9 т. е. высота
одиночной волны всегда меньше глубины; при h-*d волна
начинает разрушаться, и длина ее будет λ = 5,94d.
Б. РЕШЕНИЕ МАК-КОУЭНА
Обратимся снова к исходной формулировке задачи об
одиночной волне, сведя ее к исследованию установившегося
движения путем наложения на волновое движение поступательной
скорости — с. Потенциал скорости φ и функцию тока ψ
представим в виде следующего соотношения в комплексной форме:
оо
φ + ίψ = — <? (jc + iz) + с 2 оад+i th2'+l k/2 (χ + iz)\ 2.79
где #2/+i и k — неизвестные постоянные, причем kz < п.
Входящая в 2.79 бесконечная сумма обращается в нуль при
х-+± оо, а при ζ = 0 функция тока ψ = 0. Так как
гиперболический тангенс не содержит действительных периодов по
отношению к х, то зависимость 2.79 может быть .принята за
комплексный потенциал установившегося течения с наличием
одиночной волны.
Ограничившись рассмотрением только одного ^первого члена
суммы 2.79 применительно к рис. 2.16, получим:
φ -f /ψ = — с (χ + iz) -f- ас th -у (χ + iz). 2.80
Отделив действительную и мнимую части, имеем:
, sh kx
φ = —- ел: + ас г—;—г-г-;
1 cos kz + ch kxл
, . sin kz
ψ = — cz + ас
2.81
cos kz -f ch kx '
Горизонтальная υχ и вертикальная υζ проекции скорости
Равны:
v*~ dx~ C[ (cos, kz + ch kxy J' g2
υ - - U - rah sin^sh^
* ~" dx~ LLm .(cos te+ ch **)2 '
75
Очевидно, что Нтф = — Сг, при этом для свободной по-
верхности в той же области ψ = —cdy а следовательно
ц + са = сц, 2.83
где η — превышение свободной поверхности волны над линией
ζ = d.
Подставив 2.83 в 2.81, получаем уравнение для
определения η:
Sin k (d + η) J
η ~" u cos к (d + η) + ch kx · *Щ
В частности, при наибольшем возвышении свободной
поверхности i]max = ft, что соответствует χ = О, первое уравнение
связи постоянных α и /г имеет вид:
A = atg-5-(rf+A). 2.85
Запишем из 2.81 выражение для постоянной а и умножим
левую и правую части на k*
и k /, , л ν cos &г + ch £л: л 0 J
Αα=τ(ψ + «) ет . 2.86)
Найдем значение квадрата скорости υ2 на основе 2.82:
«2 _ u г . 7. г _ Г2 Г, . ^^-2^(l+costochto)1
ό — ^ -h^z -с j^i-t- (Cos^-fch^)2 J·
Подставим в эту формулу значение ka no 2.86, используем
также замену ψ + сг согласно 2.83 и, учитывая, что для свобод
ной поверхности ζ = d+ц, в результате
87
V2 = С2 {ΐ_- 2£η Ctg A (rf + η) + Λ2η2 [csch2 A (d + η - ^)] j. 2,
Из уравнения Бернулли 2.67, заменив ζ =d-f η, имеем
ϋ2 = C2_2gr\. 2.88
Решая совместно 2.87 и 2.88, после преобразований получим
уравнение
■^■ = ctgA(fli + 4)--|L[c8chI*(rf + 4)-^],
которое имеет смысл только при неизменном для данной волны
значении η; примем η = h и перепишем последнее уравнение
-fa = ctg Λ (d + η) - -£■ [csch2 Λ (rf + Λ) - A]. 2.891
Будем исследовать такое решение, для которого выражение^
в квадратных скобках равно нулю. Тогда можно записать в
дополнение к 2.85 второе уравнение связи постоянных а и k
ka=*2s\n2k{d+h). 2.90j
76
Цз зависимости 2.89 с учетом 2.90 получаем формулу для
пределения скорости перемещения волны:
c*=ftgk(d + h). 2.91
При совместном решении 2.85 и 2.90 находим связь между
высотой и длиной одиночной волны:
kh = 2 sin2 k (d + h) tg 4 (d + h). 2.92
Рассмотрим случай пологих волн, т. е. будем считать
k(d+h)—^j (d+h) малой величиной, позволяющей формулы
2.90, 2.91 и 2.92 упростить следующим образом:
ka^2k'2(d+hy; c*~g(d + h); kh &2k2 (d+ A)2-| (d + h).
Выражение для с2 тождественно 2.74, что свидетельствует
об ограниченности условий применения теории одиночной
волны Рэлея; из последней записи в результате преобразований
имеем:
г-ТгЬг.ь-Ь'УЩ
W 2.93
h
В случае пологих волн уравнение профиля волны 2.84
принимает близкий к 2.78 вид:
Ч- „ Ыг . 2.94
(d 4- h) ch2 —1/ - h
Определим условия разрушения одиночной волны.
Учитывая, что в момент обрушения ν2 = 0, из 2.88 имеем с2 = 2gh>
а следовательно, с учетом 2.91, получим
h = ±tgk(d + h). 2.95
В 2.82 при χ = 0 следует принимать vx = 0, тогда:
a£ = 2cos'-|-(d + A),
а после подстановки в' 2.85 —
*ft = sin*(d+A). 2.96
Решив совместно 2.95 и 2.96, в результате приходим к вы-
°°ДУ, что волны разрушаются при λ->6ό. Мак-Коуэн доказал,
1*7» Наибольшее возвышение вершины волны над дном равно
''<Ч а следовательно предельную высоту одиночной волны
°Жно принимать h = 0,78cf. При этом гребень волны по форме
77
представляет собою две ветви кривых, одинаково наклоненных
к линии дна и пересекающихся под углом 120°.
Заметим в заключение, что решение трансцендентных
уравнений 2.90 и 2.85, из которых определяются постоянные k и а,
может быть выполнено с помощью графиков, построенных по
этим формулам в преобразованном безразмерном виде:
ka = 2s\\Akd(\ + γ]\;
d kd l& L 2 V ^ d jy
2.90'
2.85'
В статье Манка [44] приводятся графики ka = f(h/d) и
kd = F(h/d), из которых цри заданном li/d находятся ka и Ы
и затем постоянные k и а, рис. 2.17. В этой же статье Манк
приводит в безразмерных координатах {z/dy x/d) графики,
например, для определения при заданном отношении h/d
проекций скоростей vx = /(-у; -7 J и v*= F\^-\ -J·). Однако другие
kdjka
основные характеристики
одиночной волны при известных
значениях постоянных к и а
могут быть рассчитаны без
особого труда по приведенным
выше аналитическим
формулам, в том числе: скорость
перемещения волны — по 2.91;
проекции скорости — по 2.82,
профиль волны — по 2.84 и
;Т. Д.
Заканчивая изложение
элементарных решений
одиночной волны, укажем на
интересный исторический обзор
развития теории,
содержащийся в монографии Стокера
[54], где, кроме этого,
подробно излагается более сложный
метод — теория Фридрихса и
Хайерса. Не останавливаясь
на ее разборе, отметим, чтс
полученное Фридрихсом и
Хайерсом выражение профиля
одиночной волны идентично формуле 2.78 из
приближенного решения Рэлея; по-видимому, нет. существенных
расхождений в результатах расчета других элементов одиночной волны
непростым и бол^ее? сложным теориям."
0,8
0.6
V*
0,2
Qfl
—
и.,... ^
J
/
....
г ·
-JC"
' ι
f \
I
L__
μ_._
s
„„
, J
>
—
k±
>0.
... 1 ,
—
!
!
1
i
1
l L -_ j
! 1 !
L _ |„ . j -4- -U J
_..J
_ -
1...
L.,., ,J
μ-
1
f -1
02
0Л
0,6 h/a
Рис. 2.17. Графики безразмерных
параметров kd = F(h/d) и ka*=f(hld),
используемых в расчетах элементов
одиночной волны.
78
Глава 3. СТОЯЧИЕ ВОЛНЫ
31. СТОЯЧИЕ ВОЛНЫ БОЛЬШОЙ ВЫСОТЫ НА МЕЛКОВОДЬЕ
рассмотрим аналитическое решение задачи о стоячих потен-
иальных волнах большой высоты применительно к следующим
упрощенным исходным условиям (Г. Т. Черможская [56]).
" В канале прямоугольного сечения (с глубиной воды а = const
при невозмущенной поверхности) распространяются в прямом
и обратном направлениях бегущие волны с. одинаковыми
характеристиками; в результате их взаимодействия образуются
стоячие волны, рис. 3.1. Движение жидкости будем считать потен-
Напрадление распространения
Расчетный
Х7 УР0бдНЬ "
о'
\
бегущей волны
^>**>^ — ι 0-
х ^^w^ ^
1/2
ХгДно '
I
\
■ ^т~
f
W///////////////////////////////^^^^
Рис. З.1.. Схема к решению задачи о стоячих волнах большой высоты
на мелководье при d = const.
Циальным и предполагаем, что во всякой плоскости,
параллельной стенкам канала, движение суть одно и то же. Обозначим
систему координат (х, у, ζ), неизменно связанную со стенками
канала, расположив плоскость Оху вдоль уровня. покоящейся
жидкости и проведя ось Ох-по направлению перемещения
бегучи волны, а ось Οζ — вертикально вниз. Как и в параграфе 2.1,
решение поставленной задачи сводится к (Исследованию уравне-
И\ П^и с°блюдении пограничных условий.
сведем следующие замены размерных (х, г, t) Оезразмер-
ныМи (χ, ь Tl) переменными:
χ = — кх\ ζ = — kz\ T\ = ωί. 3.1
^сходные уравнения в новых переменных, запишутся так:
79
Соответственно изменятся выражения пограничных условий:
ω д7\ + Я dx dx ~ * dz
при ζ = — Αη; 33
при Ζ= — £η.
Разложим 3.3 в степенной ряд по ζ, при этом члены
разложения будем определять при ζ = —kr\ = 0:
·Λ-+*·5(*-Α»4-·)-
-*[-* + -&*>-т-Й(*»ч-·].
при ζ = 0; 3.4,
при ζ = 0.
Будем исходить из представления искомых величин φ, η, ω,
pd и F в виде рядов по малому параметру ε:
<?~ь<?\ + е2<рн + ε3φπι + ... = 9t + φ2 + ?з + . · ·;
— η = εηΐ + β2ηπ + β3ηιπ + . . . = Щ + Ъ + η3 + . . . ;
ω = o)j -f- εωιι -f· ε?ωιιι -|~ .. . =. ω1 -j- ω2 -f- ω3 + . ..; 3.5
Pd = Pc + Vi + *2Ρη + **Pm + ·. · = Pc +Ρι +ρ2 +Рз + ·. -;
ρ = Вр1 + В2рп + Вгрш + ..Л = Р1+Р2 + РЪ + ...
В соответствии с 3.5 и при условии, что поставленная задача
решается в третьем приближении, выражения 3.4 и нижнее из]
3.2 примут вид:
<* д^ ι lrt drli ι irt dri2 ι lrt d*l2 , „ *h . m ^>1з ,
^Я \"Ж'"1Г^'Ж""Ж" + '1Г^+^^"1Г"ЖдГ-- 3.61
80
+ 2 ^ dzs
при ζ = 0;
*Сь + % + *) + -?Ш + »**] +
+ "Τ LUz / + ^ dz *ζ ] + й71'ГйГд^Г + dz dz»/ +
+ ι^ + -4ί!ϊ+·ιτί; + ·»ίί;+·.%+·ι4ί:+ 3.7
+ ^-TV3}?fe = ^ + /?, + /?.
при ζ = 0;
2 lUx / + \dz J J ω2 дГ, Шз дГ, ω· дГ,
-*2^^-*2^^ + ^1) + /^7'1) + F3(7\). 3.8
Используем отобранные из 3.6, 3.7 и 3.8 уравнения для
решения в первом приближении и определения дополнительных
слагаемых второго и третьего приближений, которые сгруппируем
следующим образом:
— решение в первом приближении
^Ж = к^дГ ПРИ ζ = 0;
ω* ΎΤ, +^t==/7i(71i) при z = 0;
f"^ + i?l(7;); 3·9
— определение дополнительных слагаемых второго
приближения
. при ζ = 0;
,^+^ + М*-Й5+ 3.10
°>1
при ζ = 0;
81
— определение дополнительных слагаемых третьего прибли-j
жения '
k дТ^ k дТ, dz ~r 2 dT\ ~~ к дх дх к дх дх
Я Ъ .dx dxdz + ^ dz* + Λ7»2 dz2 + 2 7?1 dz3
при z = 0;
Λ ^ι ^χ dxdz Λ ^ dz dz2
при ζ = 0;
Ρ* _ м дъ м *Ρι δψζ .2 aφ1 ду2 b2 д<?1 дъ ,ρ(Τ J
—- — ^-jf; - ω85τ7 - «ijjr — л "дх~'^'~~ ~dT~dz~ + r3l/ lj
Задавшись при исследовании системы уравнений 3.9 иско-1
мым потенциалом скорости в виде функции
φι = —Aich (z + kd) sin Γ ι cos x, 3.121
приняв Α\ ='m *^ьи , удовлетворив уравнению Лапласа Δφι = 0|
О, получим
ωχ ch kd
при соблюдении пограничного условия -д-
в первом приближении следующие выражения:
2а g ch (ζ + Ы) . -,
φ rs §. —v ^ sin /\ cos x;
TI ω, chkd l
ωι = Vgk th Ы; η! = 2α cos 7\ cos x;
«xl = 2*^ *<; + "> sinusitis; ЗЛЗ[
xl ωι ch kd l '
vzt = — 2a -^- s г , "t > sin Tt cos x;
ZI ωχ ch kd 1 '
/?i о ch (z + Ы) -.
T = 2gg chL cosT, cos x.
Нетрудно убедиться в том, что если возвратиться к пер^
менным (х, z, t) согласно 3.1, формулы 3.13 совпадут с соответ]
ствующими зависимостями линейной теории стоячих волн.
Подставив значения φι и η ι в 3.10 и полагая по ходу иссле·]
дования (02 = 0, после преобразований получаем для нахожде]
ния φ2 уравнение
82
JSL *!i + ω, *h = Jug" sm 27, cos x.
Зададимся теперь φ2 в виде функции
хр2 = А2 ch 2 (z+fcd) sin 2Γι cos 2x
проверим соответствие этой функции уравнению
дф2 = 0 при соблюдении пограничного условия ~^-
По ХОДУ решения определяются величины:
3.14
Лапласа
= 0.
z = -Atd
л2 =
3 а2щ
4 sh*kd
; /7.(3Γι) =
— a2£k
sh2kd
[(4 sh2 Μ+1) cos 27^-1].
Формулы для дополнительных к зависимостям. 3.13
слагаемым, характеризующим уточнение задачи до второго порядка
приближения, имеют вид:
Ъ = ~ Τ sh*kdch^(z + ^cos2x sin2^i»
η2
— 3ch2Arf+ l]cos2x;
■^Jch2(z + iW)sin27,1 sin2x;
3 a2^!
ΐλ
X2
3.15
v.
Г1
2 sh*M
sh 2 (z + Ы) sin 2'Λ cos 2x;
Ρ sh2£d
[(^^-cos27-,-l)ch2(z+M)-
— гснгмсозг^+г].
Покажем далее, как определяются дополнительные
слагаемые при решении задачи в третьем приближении. Рассмотрев
кинематическое и динамическое условия 3.11 и имея в виду, что
ω2*= 0, получим следующие уравнения:
0η3
ω3 дъ
щ1 с^з ι ω3 уд
k дТ^ k дТх
*-таЫ«*,«-
-И ch2 kd + 4) cos x sin Ί\ + (- 9 ch4 kd+9 ch2 Μ) cos 3x sin 7\ +
+ (ch4 kd — 3 ch2 Μ + 2) cos χ sin 3 Tx +
+ (-9ch*M— 15ch2M + 6)cos3xsin3ri;
(ei^ + <03^ + ^3-/?3(7'1) = |^th^[(7ch«^- ЗЛ6
- 13 ch4 kd + 5 ch2 (£rf — 2) cos χ cos Tt +
+ (9 ch6 kd — 5 ch4 Ы + ch2 kd - 2) cos 3x cos Τ, +
+ (13 ch6 Ы + ch4 kd - 11 ch2 kd) cos χ cos 37\ +
"+(3ch6/frf+9ch4^-15ch2/si/)cos3xcos371].
83
Исключив η3 из зависимостей 3.16, запишем для определения
φ3 одно уравнение
^ + Cth *£=<** С08Х81пГ,-
- a4^kkdd [(8ch6 kd - 24ch* kd + 9ch2 kd — 2) cos χ sin Tt +
+ (4 ch4 kd + ch2 Μ - 2) cos 3x sin Γ, -f
+ (40 chc kd - 31 ch2 fef) cos χ sin 3Γ, +
-f (12 ch4 kd - 39ch2 M) cos 3x sin 3Γ,] 3.16'
и будем искать φ3 в виде суммы произведений простейших
функций:
<рз = ch3 (z+kd) ΑΆ{ΤΧ) cos3x+ch (z + kd) Cs(Ti) cosx.
Подставив φ3 в выражение 3.16', приравняв коэффициенты
при cosx и cos3x в левой и правой частях, получаем два
дифференциальных уравнения второго порядка для определения
Л3(Г.) и С,(7\):
ch 3kdA3" (Г,) + 3 sh ША9 (Tt) cth kd =
-wbth^K4chi^+ch2M-2)sln
+ (12ch4JW-39ch3Ad)sIn37',];
ch^[C3"(^) + C3(r))] = -fesinri- ЗЛ7
- ££?1Ы th kd [ (8 ch6 kd - 24 ch* kd + 9 ch2 kd - 2) sin Tt +
+ (40 ch6 kd - 31 ch2 kd) sin 3Γι].
Заметим, что при решении последнего уравнения появляется
непериодический член вида Т\ sin Tu для исключения которого
коэффициент при sin Тг принят равным нулю; в результате
запишем выражение для ω3:
"з = ~ 4 shSh* <1Ы <8 Ch6 Ы ~ 24 Ch* М + 9 Ch2 kd ~ 2>· ЗЛ8
Из совместного анализа уравнений 3.17 для определения φ3
получим зависимость
<Рз = -Здаы- lch 3 <z + *rf) [ Wkd sin T> +
, 4ch3fcrf—13ch£d . 0~1 0 .
+ wu sm Щcos 3x +
+ ch (z + kd) [40 ch5 kd - 31 ch U\ cos χ sin ЗгД. 3.19
84
Подставив во второе из уравнений 3.16 выражение символов
ψ при ζ = О и <оз, получим для определения η3 и рз{Т\)
следующую формулу:
+ 5 ch2 kd — 2) cos x cos 7\ +
■{■ {9<±й kd -bctf kd + <±2 kd — 2) cos 3x cos η +
+ (3 ch6 kd + 9 ch* kd - 15 ch2 kd) cos 3x cos 37\ -
a3k»^ibkd {ch3M[2-4chc^7ch2^cos3xcos Tt +
32 she kd
+ 3 ет* cos 3x cos Щ +
+ 3ch kd (40 ch5 kd — 31 ch Ad) cos χ cos ЗгЛ —
_ -8fls3^2rf- th W (8ch6 Ы -24 ch4 Ы + 9 ch2 kd - 2) cos χ cos 7\.
2π
Использовав условие \ щах = 0, находим Fz[Ti)~0 и
Ό
в результате для η3 имеем зависимость
+ ch2 kd — 2) cos x cos Tx +
+ -^щз (24 ch8 Μ - 8 ch6 /и/ - 9 ch2 kd + 2) cos 3x cos 7\ +
+ (- 16 ch6 kd + 8 ch4 kd + 5ch2 kd) cos'x cos 3Tt +
+ -^ja(8chskd + ch2kd)cos3xcosSTl]. 3.20
Значения дополнительных слагаемых vx3 горизонтальной и
Vzs вертикальной проекций скорости при известном потенциале
319 определяются из выражений:
^-•ШЕГШь2й13сНЗ(2+МН ^ЕШ 8шГ»~
-^^J^^slnST-jslnSx-'
— ch (z + kd) [40 ch5 Ы - 31 ch kd) sin χ sin 3 τλ; 3.21
v„— aW<s>. (n , n. , , ,. Γ2 —4ch**d —chaArf _ ,
23-i6iET^iblwl3sh3(z + ^)[ ЕЕзы s,n^ +
+ 4ch3^3ch^sin3r1]cos3x +
+ sh (z + kd) [40 ch5 kd — 31 ch Ы] cos χ sin ЗГЛ.
85
Подставив в последнее из уравнений 3.11 соответствующие
значения символов, получим формулу для рз/р —
дополнительного слагаемого волнового давления в третьем приближении:
+ 9ch2kd-2) ch (ζ + kd) + 24ch2Mch 3 (ζ + M)]cos χ cos Γ, +|
+ ЖШ№ - 4ch«*d- chsW)ch3 (ζ + kd) -
- 24ch4 kd ch (z + kd)) cos 3x cos Tt +
+ [3 (40 ch5 kd - 31 ch kd) ch (z + kd) -
-24chMch3(z + M)]cosxcos37; +
+ [3 (4 ch3 kd— 13 ch kd) Α3^αΜ) +
+ 24ch kdch (z + kd)] cos 3x cos ЗгД. 3.22
Объединив 3.13, 3.15 и 3.18. ..3.22, перейдя согласно 3.1
к переменном (х, z, t), в результате преобразований получим
основные формулы теории потенциальных стоячих волн, coot-J
ветствующие решению задачи в третьем приближении:
2ag chk(d-z) . , ,
φ = . s -τ-η-}—- Sin tot COS kx —
/gk th kd ch kd
— -τ a3 ghi л.. ch Ik (d — z) sin 2Ы cos 2kx +
— 31 chkd] sin3iatcoskx + chSk(d—z) X
ч . [2 — 4 ch'M- chs kd . , .
X[ wm sino)' +
+ 4сЬ3^3сЬЫ sin З-ί] cos ЗА*}; 3.23
ω = VJkWkd [l - 4 sh2 ffshi 2Ы (8 ch° Μ -
-24ch*M + 9ch2fcrf-2)]; 3.24]
η = — 2a cos (o^ cos kx —
a2k , [(2 ch* kd + ch2 Ы) cos 2ωί + 2 ch4 kd -
sh* Ы sh 2kd l
- 3 ch* kd + 1 ] cos 2** - 8 sh2 *», ш X
X [4 (6 ch6 Ы — 2 ch* Μ + ch2 kd — 2) cos Ы cos 6* +
86
+■ ~d~& (2A c"8 kd ~8 ch6 kd ~9 ch'2 w+2>cos mt cos 3*л +
+ (- 16 ch° kd + 8 ch4 6d + 5 ch2 kd) cos 3ωί cos &c +
3
^g (8 ch8 kd + ch2 kd) cos 3co* cos 3b;];
lagk chk(d — z)
3.25
- -I a2k Vgkthkd ch2i{fb7z) sin 2o>* sin 2kx -
sh*kd
-ЙЙйгй^с-Ч
4ch*kd + c№kd — 2
Sin<i)f +
+
13 ch kd — 4 ch3 £rf ,
sh2 JW
Sin3o)/ Sin3^·
— ch Λ (rf - г) [40 ch5 kd — 31 ch kd] sin 3u>< sin *Ц; 3.26
2agk sh Л (rf — z)
Vz=YjkthTd chM sino)/cosbc +
+ ~a2£Vgkthkds~k^tb7~Z~ sin2ϋ)ίcos2Л;с -
^ifiSfe{»*»c-4
2 - 4 ch* Ы — ch2 Ы
ch3*d
Sin Ы +■
4 ch3 6rf — 13 ch A>rf
sh2 kd
Sin 3ω/ COS ЗЪс 4"
+ sh k (d - z) [40 ch5 Ы — 31 ch Ы] sin 3ω/ cos kx\\ 3.27
~ = 2agr СЬ^7г) cos ωί cos ** +
+ 5ЙЬ{сЬ2*(<1-г)[^йгсо.а.*-1]-
-2ch2^co8«< + 2}-gshiy;{taM-X
X {^ [4 (8 ch6 kd - 24 ch4 Ы + 9 ch2 kd - 2) ch k (d γ- ζ) +
+ 24 ch2 kd ch 36 (rf — z) ] cos ωί cos kx +
+ ^j^ [(2-4 ch4 kd - ch2 Ы) ch 3k (d - г)
— 24 ch4 kd chk(d — z)\ cos wt cos 3&л: +
+ [3(40сп5Ы-31спЫ)сп6(</-г)-
— 24 ch kd ch 3* (d — z)] cos 3ωί cos Awe -f
87
+ [з (4 ch3 kd - 13 ch kd) ch ^k^— + 24 ch kd ch 3k (rf - г)
X
'}
X cos 3ω£ cos 3£x . 3.2
Обратим внимание на то, что в первом и втором
приближениях константа 2а = h и высота стоячей волны оказывается
равной r]max->Timin = 2/г. Распространив это условие и на
решение в третьем приближении, использовав формулу 3.25,
получаем для определения 2а в третьем приближении уравнение:
и о Γι . tf2Wl04ch6^sh2 2^+132ch6^-41sh2 2£rf — 24\1 0 on
А==2а[1 + ТбЧ sh»Msh*2*f )\ 3·29
Из 3.29 следует, что, начиная с третьего приближения,
практически во всех случаях 2а < А.
Не производя выкладок, запишем для расчета траекторий
частиц жидкости в стоячей волне (во втором приближении)
следующие формулы:
χ —- х0 = — 2а -—Sh kd sin ω^ sin *x° "^
+ 4**Μ [2 sh2 Ы - 3 ch 2k (d - zQ)\ (1 + cos 2ω*) sin 2£*0;
ζ — 20 = 2α -—Jhkd cos ω* cos ^*° "^
3.30
a»*
4 sh* fcd
sh 2£ (d — z0) [(2 sh2 kd + 3 cos 2Λχ0) (1 + cos 2arf) +
cos2&x0 .
chs^rf ^°^Ло
Соответствующие зависимости для траекторий частиц
жидкости в стоячей волне в третьем приближении здесь не приведены
из-за их громоздкости.
В заключение заметим, что, если в выражениях 3.23.. .3.28 и
3.30 ограничиться рассмотрением только первых слагаемых
правой части после знака равенства (подчеркнутых снизу
сплошными линиями), получим расчетные зависимости для
определения основных характеристик теории стоячих волн малой высоты
(первое приближение).
3.2. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ НЕКОТОРЫХ НАИБОЛЕЕ
ИЗВЕСТНЫХ ТЕОРИЙ СТОЯЧИХ ВОЛН
Рассмотрим сначала приближенную теорию стоячих трохо-
идальных волн, а затем приведем основные сведения из других
решений, отличающихся большей точностью.
А. СТОЯЧИЕ ВОЛНЫ СЕНФЛУ
Исследуем плоскопараллельное периодическое движение
идеальной жидкости в стоячих волнах в случае ограниченной
гЛубины d = const, не накладывая условия малой высоты волн.
Примем начало правой системы координат на спокойном уровне,
ocb z направим вверх и обозначим независимые переменные
через Хо и го, которые суть координаты частицы в спокойном
состоянии.
Использовав некоторые результаты других теоретических
решений и данные экспериментов, Сенфлу [85] для определения
положения частиц в стоячих волнах предложил следующие
формулы:
х = Хо + 2rx cos kxo sin (ut;
3.31
ζ = 2o + 2rz sin kxo sin (ut + 2krxrz sin2 ω/,
где r χ и г г — полуоси эллипсов траекторий частиц бегущей
волны, рассчитываемые по формулам 2.54; k и ω —
по-прежнему, постоянные величины, равные:
, 2π 2π
к = -γ-; ω = -=-.
Докажем, что волновое движение жидкости,
характеризуемое уравнениями 3.31, совместимо в пределах некоторого
допустимого приближения с условиями неразрывности среды,
динамического равновесия, постоянства давления на свободной
поверхности и при вертикальной составляющей донной скорости,
равной нулю.
Подставим в уравнение неразрывности в переменных Лаг-
ранжа
дх дг ' дх дг , р(*\
дх0 дг0 дг0 &*0 * '
выражения частных производных от уравнений 3.31; в
результате получим:
1 + 2k2 (rx2—rz2) cos kx0 sin2 (ui—
—4khx (rx2 + rz2) sin**osin8<0f ^/ЧО·
Отсюда следует, что условие неразрывности жидкости в
данном случае удовлетворяется лишь приближенно, причем,
поскольку коэффициент при sin3 ωί имеет более высокий порядок
алости, степень погрешности определяется близостью к нулю
Сожителя при sin2 ωί:
2^(γχ«-γΛ = ^(Α)'. 3·32
π0γ тим» что в Данном случае ошибка в решении содержит
Решность, в два раза большую, чем в теории Буссинеска.
89
Обратимся к уравнениям динамического равновесия в пере!
менных Лагранжа:
__ д*х_ jhc_ __ ( , д*г\ дг _1_ <*£±.
дР дх0 \ё ·" дР ) дх0 ρ дх0 '
__ дЬс^ дх_ ( χ &ζ\ дг {_ дра_
дР дг0 \g + дР) дг0 ~~ ρ дг0 '
Подставив в них значения частных производных от исходны^
уравнений 3.31, в результате преобразований имеем:
— -р4- - 2 (со2гА. — gkrz) cos kx0 sin Ы —
— 8u2k2rxr22 cos kx0 cos 2ω^ sin ωί; 3.3^
— -^- = — g* + 2 (®2rz—gkrx) sin £x0 sin o)^ + 4&2krxrz sin2 ω* —
— 4и2кгхгг cos 2ωί - 2gk2 (rx2 + r/) sin2 ω* +
-f 4ω2£2/\, (г/ + гг2) sin £x0 sin3 at —
— 8&2k2rx2rz sin &x0 cos 2ωί sin ωί —
- 8ш2Л»/у, (г3, + г/) cos 2ω* sin2 ωΛ 3.3^
Используя 3.33 и имея в виду, что на свободной поверхности
дра/дхо = 0· при ζ0 = 0, получим равенство
12 (coV*—£&/'*) cos kx0 sin ωί—
—8(u2k2rxrz2 cos fcco cos 2ωί sin ω^ | *0=o = 0» 3.35
из которого следует, что условие постоянства давления на
свободной взволнованной поверхности удовлетворяется
приближенно, если пренебречь последним слагаемым как величиной
высшего порядка малости. В оставшемся первом слагаемом
множитель при произведении тригонометрических функций
должен быть равен нулю, т. е.:
I «>2г, — gkrz \г -о = О,
а это приводит к следующей формуле связи между постоянными
величинами ω и k:
(02 = gMhM. 3.36
В дальнейшем поставленную задачу Сенфлу [85] решил
при условии исключения из 3.33 и 3.34 слагаемых, содержащих
дробные множители более высокого порядка малости, чем
число ky что дало возможность существенно упростить решение,
а именно:
Τ Чг = 2 ^гх ~ Skr*) cos kx<>sin ω*;
P дХ° 3.37|
7 4z^ = ~ g + 2 (0)2r* — gkrx)sin kx°sin ωί§
90
Эти уравнения совместимы, в чем легко убедиться:
7 dxjio = 2k ^~Гг ~~ gkK^ C0S kX°Sin Ы;
7 Ш$Г0 = 2k ^r* ~ £*r-*) cos kx*sin ωί'
а следовательно в зависимостях 3.37 условие динамического
равновесия жидкости соблюдается.
При написании 3.31 имелось в виду, что последнее
слагаемое второго уравнения вида 2krxrz sin2 ωί характеризует
превышение середины колебания частиц над ее положением в покое
при данном z0f а именно:
u'=¥*"J?£d) «**·<- 3·38
Тогда возвышение средней волновой линии над спокойным
уровнем Ad при г0 = 0 равно
Ad = ^-cth kd sin2 ω/, 3.39
а соответственно наибольшее ее значение при sin ωί — ± 1
будет:
Д^шах - Щ- cth kd. 3.39'
Для получения аналитического выражения профиля волны
исключим из 3.31 переменную Хо и выразим ζ в явном виде
от χ при постоянном значении ζ0· В связи с этим обратим
внимание на то, что, как это следует из первого уравнения 3.31,
наибольшее значение (х—лго) = 2гх, а потому можно принять
k(x—χ0) = 2krx. Считая эту величину достаточно малой, без
большой погрешности запишем:
cos£ (χ—*о) « 1;· sin k (χ—χ0) « k (χ—χ0).
Сделаем еще следующие искусственные преобразования:
sin kxQ = srn k [χ— (χ—Xo) ] = sin kx cos k (x—x0) —
—cos to sin k (x—x0);
cos kx0 = cos k [x— (x—Xo) ] = cos kx cos k (x—Xo) +
+ sin kx sin k (x—*o),
a c учетом сказанного выше, имеем:
sintoo = sin fee—k (x—xo) cos to;
cos too = costo+i& (*—x0) sin kx.
Подставив значение cos too, в верхнее уравнение 3.31, пре-
орегая из-за малости по сравнению с единицей величиной
Rr*> получаем:
х—Хо « 2rx cos to sin ω/. 3.40
W
После подстановки sin^Xo во второе уравнение 3.31 с учетом
3.40 в результате преобразований окончательно запишем:
ζ = z0 + 2rz sin kx sin at—2krxrzcos 2kx sin2 ωί, 3.41
а это и есть искомое выражение кривой волновой поверхности
на любой глубине г0. Для свободной поверхности при г0 = О
имеем:
η = h sin kx sin o)£ — γ &Α2 cth Μ cos 2£x sin2 ω£. 3.42
Зависимости для расчета траекторий частиц жидкости в
рассматриваемой стоячей волне получаются путем исключения из
3.31 переменной t\
Ζ ζ<>- 2 cos2^jc0 Ι* *°' "+"
+ th А (ζ0 + d) tg £x0 (л: - x0), 3.43
или
(z — zQ+ gjJ4- sin2 £х0) -^ cos2 kx0 = (x — x0 + sul2^° J . 3.43'
Из этих уравнений следует, что в стоячих волнах частицы
жидкости совершают периодические движения по отрезкам
кривых; в узлах (при cos&Ko = ±1) эти отрезки близки к
горизонтальным прямым, а в пучностях (при sin£x0= ^1)—к
вертикальным прямым линиям. Последнее имеет место при
взаимодействии волн с вертикальной плоской поверхностью стены,
перпендикулярной лучу набегающих волн.
Исследование гидродинамического давления в стоячей волне
при ограниченной глубине d = const Сенфлу 1[85] выполнил на
основе второй из формул 3.37, которая после подстановки
значений гх и гг по 2.54, замены ω2 по 3.36 и умножения обеих
частей на р, перепишется так:
Разделив переменные и проинтегрировав это уравнение,
в результате получаем следующую формулу:
, , Г ch k (г0 + d)
_ shffi + d)] sin kx, sin ωί. 3.44
Экстремальные значения волнового давления в пучности
волны, т. е. в плоскости стены в точках с координатами
ζ = ζ« - χ r*r*± 2г*> 3·45
92
соответственно равны:
решение Сенфлу, как было показано, лишь приближенно
удовлетворяет уравнению неразрывности и пограничным
условиям, при этом погрешность увеличивается с уменьшением d/λ
и увеличением h/d. Известен ряд попыток [63, 77] уточнения
метода Сенфлу путем учета слагаемых, ранее отбрасывавшихся
из-за их малости.
Б. ИНТЕРФЕРИРОВАННЫЕ ВОЛНЫ МИША, БИЗЕЛЯ,
РУНДГРЕНА (второе приближение)
На основе анализа ранее выполненных исследований Миш
пришел к выводу о необходимости разработки более точной
теории волн. В опубликованной в 1944 г. работе [77] содержится
решение до второго порядка аппроксимации по высоте бегущей
волны, полученное в переменных Лагранжа, при этом отдельные
зависимости представлены в переменных Эйлера. Введено
понятие показателя завихренности в волнах, и тем самым
полученные в [77] формулы могут быть применены как для вихревого,
так и для безвихревого движений жидкости..
В 1952 г. Бизель '[67] перестроил теорию Миша полностью
в переменные Эйлера. Миш и Бизель исследовали волновое
движение жидкости, возникающее при интерференции прямой и
обратной бегущих волн, имеющих строго одинаковые высоты,
длины и периоды. В реальных условиях набегающие на
вертикальную стену волны отражаются неполностью, а следовательно
высоты обратных волн в большинстве случаев оказываются
меньше высот прямых волн. В 1958 г. Рундгрен [84]
опубликовал результаты своих теоретических и лабораторных
исследований волновых движений жидкости в случае неполного
отражения волн от стены; новое аналитическое решение в своей
основе представляет дальнейшее развитие теории Миша и
Бизеля.
В монографии [77] Миш представил уравнения движения
частиц жидкости в следующем виде:
. h , h* . , hn
Χ = X0 + γ cpt + -у- φ2 + · · · + -ψ Ψη>
h № hn
ζ = ζ0 + Ύ ψ! + -τ- ψ2 + · · · + w Ψ«·
3.47
де χ и ζ — координаты частиц жидкости в движении, а Хо и
^-трже в покое.
в Тд100ТветствУюЩее уравнение гидродинамического давления pd
ЧКе {х, ζ) записывается так:
93
Ρα ι h . . h2 . hn о AQ
-γ = - g*o + -yfci + χ 7.2 + . · · + -ψτΧη· 3.48
В приведенных формулах φ/, ψ/ и χ; (где ι = 1, 2,..., η)
суть некоторые функции (хо, 20, <), при определении которых
используется выражение потенциала скорости Φ из теории волн
малой высоты и вводится новая функция Ω — резольвента,
играющая роль потенциала смещений. Связь функций Φ
(потенциала скорости первого приближения) и Ωι (потенциала
смещения первого порядка) выражается зависимостью
φ=ζ±№ι_. 3 49
ν 2 df , о.™
соответственно для φι, ψι и χι в первом приближении имеем:
где /ι (/) находятся из соблюдения граничных условий.
Функции ψ2, ψ2 и χ2, с использованием которых дается
решение задачи во втором приближении, получаются на основе
потенциала смещения второго порядка Ω2 согласно следующим
формулам:
S + [ж)*\ +0)2 <*·2 + ^ +/* W- 3·52
Здесь 7^2 — гармоническая функция (xq, Zq) и периодическая
по /, которая, равно как и функция Ы0> определяется при
соблюдении граничных условий; скорость волнового течения и
рассчитывается по формуле
« = Т^<*°)· 3.53
где fu(zo) —является функцией только от zq.
В решении первого приближения движение всегда
безвихревое, однако во втором приближении имеет место вихрь с
напряженностью σ, равной
■ш
!t\ -Mil
8 L дг\
+ 2
3.54
По аналогии с соответствующим результатом теории волн
малой высоты для потенциала скорости Φ после замены χ и г
на Х(у и Zq принято следующее выражение:
Ф = Τ ί £ЧЙГ£) ΚΙ + Kref) Sin kx0 COS ω/ -
94
— (1 — Kref) cos kx0 sin 0)^, 3.55
где ω = 2π/Γ; Τ — период волны; Kref— коэффициент
отражения волн, равный отношению высоты отраженной href к высоте
исходной волны h.
Опустим промежуточные выкладки и напишем
заимствованные из работы [84] окончательные формулы для определения
на уровне второго при-ближения координат χ и ζ движущейся
частицы и волнового давления на глубине ζ:
х = Хо + \ Т^Г- [(1 + Кгв/) cos kx0 sin ω* -
— (1 — Krcf) sin kx0 cos ω^] —
X (3 cos 2ωί + th- kd)\ + (1 + /<rc/)2 sin 2£x0 [ - cos'-' «i +
I- СЬ?,£м<° (3cos2^-t^M)] +
+ (1 - ^e/)2 sin 2Ы cos 2^0 [l - |-£U^±iL]j +
+ f (1-^)(1-^/)^га[сЬ2А(г0 + й)-^]<; 3.56
^ = *o + 4 ^ *8h*fcd"rf> W + ^ref) sin *xo Sin at +
+ (1 -Kref) COS /tv0 COS Wt] + -jg S|;4J X
x {(1+/W)2 [sin2 ωί + -^|^(3 cos 2<oi + th«*d)] +
+ (1 - /<re/r [cos2 ωί + ^|^ (3 cos 2Ы - th2 kd) f
, 3· sill 2kx0 ". n J) 0 ~~
P=-pgh ^|g 1(1+ /Cy) sin £x0 sin Ы-\-(1-Кге/) cos /гх0 cos ωί] -
-wf^[o+^/),{ch*^+2rf)[48ln,e<+^S^L] +
+ 4thMsh£(z0 + 2tf)[l-3sin2«>i] +
+ ЗС0.2ЛХ.СО. 2-^-Ι*£&£-ΐ]} +
+ (l-A-re/)2{ch*(2o + 2ii)[4cos2o)i-^||^.] +
H-4thfo/sh6(20 + 2cO[l -3cos2o)2f] +
95
+ 3 cos 2 ,t cos 2**0 [*fe - 2^+"]} +
+ 6 (1 - A·,,«. 2**. s.„ a* [*& - »^1| 3.5»
В формуле 3.56 значится коэффициент μ, который введен
Мишем [77] в целях придания общности рассматриваемому
решению: при μ = 0 движение безвихревое и сопровождается
волновым течением со скоростью и, равной
« = |-0-О u£b[ch2*(*. + *) -^], 3.59
а в случае μ = 1 волновое движение вихревое, и при этом
отсутствует волновое течение.
Формулы 3.56—3.58 отличаются от аналогичных
зависимостей на уровне второго приближения несколько большей
общностью за счет учета коэффициентов Kref и μ, при этом
введение <з теорию Kref принадлежит Рундгрену [84], но метод
в целом разработан Мишем [77]. Последний впервые получил
двугорбые хронограммы волнового давления, обосновал
несовпадение во времени лгаксимума силы волнового давления и
наибольшего возвышения свободной взволнованной
поверхности, объединил в одном решении вихревые и потенциальные
волны, определил пределы применения расчетных формул
волнового движения жидкости, полученных на основе теории волн
второго приближения. Общность рассматриваемых формул
подтверждается тем, что при соответствующих ограничениях на их
основе можно получить зависимости Герстнера или Сенфлу.
В работах Бизеля [67] и Рундгрена [84] подробно
рассмотрены варианты теории волн Миша в переменных Эйлера приме-1
нительно к общей и частным задачам. В последующие годы
в печати появился ряд предложений по использованию в
практике в той или иной интерпретациях расчетных формул Миша,
Бизеля и Рундгрена.
Определенный интерес представляет статья В. К. Штенцеля
[63], в которой, как и в работе Миша [77], несколько уточнены
расчетные формулы теории Сенфлу.
В заключение заметим, что рассмотренным теориям на
уровне второго приближения присущи недостатки, обусловленные
некоторым их несовершенством, что в ряде случаев приводит
к расхождениям расчетных и опытных данных, особенно
в области малых относительных глубин.
В. СТОЯЧИЕ ВОЛНЫ СЕКЕРЖ-ЗЕНЬКОВИЧА
Одним из более точных исследований стоячих волн является
решение на уровне третьего приближения Я. И. Секерж-Зень-
ковича [50], развитое и дополненное И. Н. Загрядской [16].
96
η этоМ методе использованы общие уравнения движения жид-
ости и уравнение неразрывности в переменных Лагранжа. Вве-
к на вспомогательная функция Q, связанная с
гидродинамическим давлением зависимостью
(}=-&-.-gz- 3.60
Координаты (χ, ζ) фиксированной частицы представлены
ρ виде функций χ (a, b, t) и ζ (а, Ь, /); гидродинамическое
давление — функцией Pd{a> by t), где а и Ь — переменные параметры,
отмечающие индивидуальность частицы жидкости. В данном
случае линии а = const являются прямыми, параллельными оси
Oz, а линии Ь = const — кривыми, образующими второе
семейство линий координатной сетки, имеющей неизвестную заранее
форму в начальный момент. Профилю волны на поверхности
отвечает значение Ъ = 0; точно также получается, что в любой
момент дну будет соответствовать 6 = —6о — —d.
Решение задачи о стоячих волнах сведено автором [50]
к определению упомянутых выше функций, удовлетворяющих
исходным уравнениям гидродинамики и неразрывности в лаг-
ранжевой форме, уравнению 3.60, начальным и граничным
условиям; движение жидкости принято потенциальным.
Предположив периодичность движения по t и а, правомерно записать,
что Τ = 2π/ω и 'λ = 2π/&, при этом связь между ω и k должна
быть определена в процессе исследования.
В работе [50] применено понятие малого параметра ε,
в целях некоторого упрощения выкладок сделаны
соответствующие замены переменных, а также использованы отдельные
положения линейной теории. В результате достаточно строгого
решения при помощи рядов по степеням малого параметра
получены аналитические формулы для определения характеристик
стоячих волн первых трех приближений. Не останавливаясь на
довольно громоздких преобразованиях, приведем конечные
выражения на уровне третьего приближения для расчета
координат частиц жидкости χ и ζ, вспомогательной функции Q, связи
постоянной величины k = 2π/λ с амплитудой водны Л0, частотой
колебания ω и глубиной воды d> заимствованные из [16]:
χ = а + h. . ch k (b + d) cos ka sin Ы —
A^cthkd L 3
SgsWkd L* - ΊΜ ch 2k<<b + d^\sin 2ka sin2 »* +
, 4WcW kd /ΓΛ , 0 l~4ch2 kd\ * ь ,h . <. .
+ l3Z*2k7l ch3fe(6 + tf)]cosfea-
97
+ 4 ch2 kd) ch 3ft (ft + rf) cos 3fta j sin ω/ —
iwm- {[(105 -60ch2 M+27131U%4)ch *<*+Ή
. 3 7№kd+2
+ 4 ch2^sh2 2^rf
+
2 16
4 sh2 Ы
+
8 sha Ы
ch3^(6 + rf)]cos^ + [(^^-3)chA(* + rf) +
(2 ~ -2 8h*kd) Ch 3* Ψ + rf)] C0S 3*a} sin 3ω/ +
+
2 sh2 ^
Λ3ω* cth2 6rf
8£2 sh3 kd
(2ch2Ad-4-
2 + 7 ch2 fcd \ , - ,, , -v - . ,
shs 2kd—j C ' "^ ") C0S a Sin ωί'
3.61
42q)2Cthferf
8g shs W
sh &d
sh ft (b + d) sin ka sin ωί —
sh 2k (b + rf) [(2 - ^—) sin* «^ +
)
+ sh2 2*<* C0S im\ + 16^2 sh3^ Щ*-
8 ch2 Ы — 2
sh2 2^rf
X
xshfe(6 + rf) + (l + Li^^±i)sh3^(& + rf)]sinfta
+
+ L sh2 2^ Shk
21 ch2 fcrf + 6
8 ch2 kd — 2
sh2 2Ы
4ch2Airf
+
4 ch2 kd sh2 2fcd
A3a>±cth2£rf
(6+ *)-(■
j sh 3ft (6 + rf) J sin 3ftal sin ω* +
8^2 shs *>rf
sh»2M Jsl^(» + rf)X
(2 ch2 fttf - 4
X sinftasino^ —
+ 27-^^-)sh*(* + rf) +
+ (3+4#ы)8НЗ*(& + ^]81П^ + [
27 sh 6 {b + d)
4 shs kd
+
+
sh2£d
(2- 2sWkd)Sh3/fe<* + <*)] δίΠ3*alSin3<0t' 3i2^
Q=-
^g
ch kd
sin fta ch ft (b + rf) sin ω£ -f-
+ g~^j{[зcos2fta + 3ch2ft (b + d) - 1 -4sh2kd-
зЛ2к(Ь+Л cos2ka] cos2ωί - cos2£α - ch 2k(b + rf) - l) -
"[11lSw:1-2]ch^^rf)sin3to +
+ [3+7T^]T^rach3^6 + rf)sin34sin^+
16^ sh3 ftd
- [2 - шт] chk(b + d)sin3ka +
+ 1[97-60сЬ2Ы + 27 137sh4aC^Urf ] ch* (6 + rf) sinfca +
+ ■§■ [2- 2rt«*d] ch 3k (& + d^ sin 3*a} sin 3ωί; 3'63
<*" luuj . i42<*ecth3Arf Го t,tJ , 2 + 7ch2*d] 0 -.
ft= ycthW + -s___.|_2ch»W-4 ^rge-J· 3.64
Входящие в приведенные формулы ω2/#, ω4/#2 и ω6/#3
рассчитывают по следующим выражениям:
«« _ fc th ^ ** [о ch, ы 4 2 + 7 ch2 kd I
g — лт/га 4sh2ωу.сп /га 4 sh22kd j,
g2 -я.тп ш 4ch2^r - sh*2*rf J'
— =-#th'M- Mwtll^[2ch»fed-4-2^7ch,^1 365
^з -ЛШ Ш 8ch-'£rf L sh2 2^rf J' °-D0
Обратим внимание, что в данном случае, равно как и во
всех теориях волн третьего и выше приближений,
фиксированная константа А (или 2а) не равна высоте исходной бегущей
волны h или амплитуде стоячей волны А0. В параграфе 3.1 этот
вопрос рассмотрен подробнее на основе физического
представления об удвоении высоты бегущей волны, взаимодействующей
,е вертикальной стеной в случае образования стоячих волн.
Не останавливаясь на доказательствах некоторых других
положений теории стоячих волн Я. И. Секерж-Зеньковича,
папомним, что в работе [50] изучены известные особенности
ст°ячих волн большой высоты и сделаны следующие выводы:
""-неподвижных узлов нет;
^-максимальные амплитуды (пучности) находятся в точках
^ л/2 (вершина) и χ = 3π/2 (подошва), при t — π/2ω;
Πη 7" °Рднната вершины больше ординаты подошвы волны, а
Р°филь волны близок к трохоиде;
99
— профиль стоячей волны никогда не распрямляется;
— движение жидкости потенциальное.
Заканчивая изложение основных сведений из более строгие
теорий волн, упомянем об интересной работе Таджбакша и
Келлера [88], в которой содержится корректное математическое
исследование в переменных Эйлера задачи о стоячих волнах
на ограниченной глубине d = const. Конечные формулы этой
теории на уровне третьего приближения идентичны изложенным
в параграфе 3.1, достоверность которых подробно исследуется
ниже.
3.3. СОПОСТАВЛЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТА ОТДЕЛЬНЫХ
ХАРАКТЕРИСТИК СТОЯЧИХ ВОЛН ПО НАИБОЛЕЕ ИЗВЕСТНЫМ
ТЕОРИЯМ
Представляет интерес сопоставление результатов расчета
по разным теориям некоторых характеристик стоячих волн, а
в отдельных случаях — с имеющимися опытными данными.
В результате этого могут быть рекомендованы области
целесообразного применения простых и более сложных аналитических
формул. Ограничимся при этом рассмотрением важнейших
характеристик: волнового профиля, проекций скоростей и уско-
ч рений взволнованной жидкости, силы волнового давления при
гребне и ложбине стоячей волны.
На рис. 3.2, α представлены построенные по формулам
параграфа 3.1 графики равных значений относительных величин
ВОЗВЫШеНИЙ (Схема a, Tlmax/llmaxI И Tlmaxll/ilmaxl) И ПОНИЖеНИЙ
(схема б, r\t/t]tu ηπι/ηπ) вершины волны над спокойным
уровнем.
Из этого рисунка следует, что при использовании формул
второго приближения расхождения в расчетах по сравнению
с линейной теорией волн существенны на всем поле графиков;
третье приближение уточняет результат второго приближения
не столь существенно.
На основе сопоставления большого объема опытных и
расчетных данных Г. Т. Черможская [56] пришла к выводу, что
профили стоячих волн, построенные по формулам третьего
приближения как в переменных Эйлера, так и в переменных Лаг-
ранжа, совпадают между собою и согласуются с
экспериментом. Только при очень крутых волнах в области малых
относительных глубин точность решения задачи на уровне третьего
приближения оказывается недостаточной. Свидетельством этого
служит появление на расчетном профиле в области ложбины
волны вторичного гребня, существенно искажающего реальный
профиль, хотя небольшие горбы в ложбине иногда
обнаруживаются и на экспериментальном профиле стоячей волны.
На рис. 3.3 изображены графики относительных величин
наибольших значений проекций скоростей (сплошные кривые;
в момент при cos cot = 0) и локальных ускорений (пунктирные
100
Рис. 3.2. Графики равных значений отношений
возвышения (а) над расчетным уровнем вершины стоячей волны
В Третьем Приближении (СПЛОШНЫе КрИВЫе У\тих/У\тах, I =
= /(Λ/λ; 41%))\ во втором приближении (пунктирные кривые
Лтах, п/Лтах, ι = ^"(Λ/λ; d/λ)) к возвышению вершины
стоячей волны в первом приближении; понижения (б) от
спокойного уровня подошвы стоячей волны (η*/η*. ι = ДЛ/λ;
d/λ) nt\t,ulr\t,i = F(hl%; d/λ))
/ — граница разрушения бегущих волн,
101
ороч
OfiOA
Ο,δΟ
Рис. 3.3. Графики относительных величин наибольших
значений проекций скоростей (сплошные кривые, в момент
при cos at = 0) и локальных ускорений (пунктирные
кривые, в момент при.cos ω* = 1) в стоячей волне,
рассчитанных в третьем и первом приближениях: горизонтальных
dt I dt
=/?(/ζ/λ; rf/λ), схема а, и вертикальных (при х = 0, г = 0)
(при χ = λ/4, г = 0)vx/vXt { =/(Λ/λ; djl) и
^Κι=/(ΛΑ; d(k) и ^ll^l = F(hll; d/λ), схема б
/ — граница разрушения бегущих волн,
ό,δΟ
Рис. 3.4. Графики равных значений отношений:
наибольшей силы волнового давления в стоячей волне,
рассчитанной в третьем приближении, к замеренной в
лабораторных опытах (сплошные кривые) при гребне
PxclPXc,o = f(hlK\ d/λ), схема а, и при ложбине
Pxt/Pxt. о = F(hlK\ d/λ), схема б; то же, рассчитанной
в третьем и первом приближениях (пунктирные кривые)
при гребне Рхс/Рхс, ι = /(Λ/λ; d/λ) и при ложбине
Pxt/Pxt, ι = /\(Λ/λ; d/λ)
/ — граница разрушения бегущих волн,
кривые; в момент при cos ω/= 1) в стоячей волне, рассчитав
ных по формулам третьего и первого приближений в перемен!
ных Эйлера: горизонтальных (схема а) и вертикальных {Cxj
маб). ■ ^ |
Из этих графиков следует, что максимальные значения горщ
зонтальных и вертикальных проекций скоростей в стоячих вол]
нах консервативны; учет членов второго и третьего поряди
не приводит к уточнению их величины: расхождения не превы!
шают ±10%. Сопоставление наибольших величин горизонталь]
ной и вертикальной проекций ускорений жидкости в стоячей
волне, определенных в третьем и первом приближениях, позвоа
ляет установить существенные их различия во всей области граЗ
фиков; при малых относительных глубинах уточненные значе!
ния ускорений могут в полтора и более раз превышать
вычисленные в первом приближении.
Анализу расчетных и опытных значений силы волнового цщ
ления в стоячей волне при гребне и ложбине уделим несколько
больше внимания и проиллюстрируем этот материал двумя
рисунками. Кривые равных отношений наибольших сил волно!
вого давления, рассчитанных в третьем и первом приближениях]
изображены на рис. 3.4 пунктиром; сплошными кривыми пока]
заны отношения наибольших сил волнового давления,
полученных в третьем приближении, к замеренным в лабораторных'
опытах, соответственно при гребне (схема а) и ложбине
(схема б). Из рис. 3.4 следует, что расчетное значение силы
волнового давления в третьем по сравнению с первым приближением
или опытом могут различаться на ±30%.
Учитывая, что в нашей стране получили широкое
распространение формулы волнового давления на уровне второго
приближения, в целях уточнения границ области их применения на
рис. 3.5 представлены сопоставительные кривые расчетных и
опытных данных в широком диапазоне относительных глубин.
Значения силы волнового давления во втором приближении
(пунктирные кривые) определялись по формулам: 1 — Г. Г. Me·
телицыной в переменных Эйлера; 2—В. К. Штенцеля [63]
в переменных Лагранжа; то же в третьем приближении
(сплошные кривые) по формулам: 3 — Г. Т. Черможской [56] в
переменных Эйлера; 4 — Η. Η. Загрядской [16] в переменных
Лагранжа.
Использованы опубликованные в печати данные
экспериментов, выполненных разными исследователями за последние более
чем 25 лет. Горизонтальные линии на рис. 3.5 с делением на
вертикальных шкалах, равным единице, соответствуют
идеальному совпадению расчетных и опытных данных; реальные кри*
вые при гребне Рхс/Рхс,о = f(d/\k) (схема а) и при ложбине
Ρχί/Ρχί,ϋ=^(<ί/^) (схема б) свидетельствуют о том, что почти
во всей области относительно глубин (исключая переходную
зону к прибойным волнам) расчеты по формулам третьего при'
104
. йЖения дают результат, близкий к опыту; расхождения не
оевышают ±10%. Примечательно, что по более совершенным
!ьормУлам сила в°лнового давления уточняется в сторону
уменьшения. Расчет' волновой нагрузки с той же достоверностью по
а)
<♦
1.2
1.0
0.8
\PxclPxc,
\
1 \
\
\
1\ *>
1
0
V
ч
4
г
У^
.—■
---^
—»—·**"""*-·
-4^
Я
яг
«*
«*
4*
4*
лГ/Д
1^
|^/Λ
—.^
t,0
~ ——
—■=-"=:
^^^
4
\
^^X
~TT
-J.
"""">
/
"~^Γ"Ί
Рис. 3.5. Кривые, характеризующие соответствие в стоячей волне
расчетных и опытных наибольших значений силы волнового давления при
гребне PxclPxc,o = f(d/\), схема а и при ложбине Pxt/Pxt.o- F(dl%),
схема б.
формулам второго приближения может выполняться лишь
в ограниченной области, которую можно принять по кривым
1 и 2 на рис. 3.5.
Глава 4. ЭНЕРГЕТИЧЕСКИЕ ПРОЦЕССЫ
В ВОЛНАХ НА ВОДЕ
4·1. ЭНЕРГИЯ БЕГУЩИХ И СТОЯЧИХ ВОЛН МАЛОЙ ВЫСОТЫ
Рассмотрим основные исходные положения по определению
ергетических характеристик взволнованной жидкости приме-
Тельно к некоторому объему воды в области W, включающей
105
одну волну. Заметим также, что нас будет интересовать ποτ0ιΐ
энергии в направлении перемещения волны через вертикальну]
плоскость, ориентированную по нормали к лучу волн.
В общем случае энергия £, содержащаяся в области ty
состоит из кинетической энергии частиц воды этого объема и J
потенциальной энергии, обусловленной полем тяготения. Такц\
образом для Ε имеем следующее выражение:
w
Напомним, что для исследования потенциального неустано]
вившегося движения жидкости в гидромеханике использует^
интеграл Лагранжа
gz + f +* + !$. = F(t).
который, не меняя общности решения, можно записать так:
если положить
t
.Используем запись интеграла Лагранжа 4.2 и представим"
полную энергию Ε эквивалентным 4.1 выражением:
Будем предполагать, что в самом общем случаеобласть V
не обязательно фиксирована, т. е. она может зависеть от
времени t. Представим выражение Ε в виде
Ε = И /(х, у, г, t) dxdydz
w
и для вычисления dE/dt запишем следующую формулу
W S
где υη — нормальная скорость границы S области W, принимав
мая положительной в направлении внешней нормали к S.
Применим в рассматриваемой задаче формулу 4.4. ВоспоЛЬ'
зуемся зависимостями 4.1 для раскрытия первого (объемного)
106
нтеГрала и 4.3 для раскрытия второго (поверхностного)
интеграла; в результате получим:
~rfT~ PJJJ \дх dxdt + ду dydt + dz dzdtГ У
Η"
Используем формулу Грина и, имея в виду, что в данном
случае Δφ = 0, объемный интеграл в последней записи dE/dt
представим в виде
•я*-£<*.
5
где ду/дп — компонента скорости жидкости, взятая в
направлении нормали к S, ориентированной наружу относительно W.
Таким образом для скорости изменения энергии в объеме Wt
которую в общем случае назовем потоком энергии N, получаем
формулу:
"-£-ίί['ΐ(£-*·)-'Λ]*· м
Рассмотрим некоторые частные задачи, имеющие
практический смысл. Нередко, например, граничная поверхность S
области W состоит из отдельных участков, имеющих разные свойства
или для которых заданы различные условия. Предположим,
в частности, что часть Si поверхности S является «физической»
границей, состоящей всегда из одних и тех же частиц жидкости.
В этом случае ду/дп и υη совпадут между собой и,
следовательно:
"sx dt
= -JJ/W«. 4.6
Если, кроме того, поверхность S\ фиксирована в простран-
стве, т. е. vn = 0, то Nsx равен нулю. Это очевидно, так как
поток энергии сквозь фиксированную границу, всегда
содержащую одни и те же частицы жидкости* равен нулю. Аналогичный
Результат получим и в другом частном случае, когда S2 является
^вободной поверхностью, на которой давление ра равно нулю.
°следний результат согласуется с тем, что следует из физи-
ческих соображений.
Предположим далее, что S является «геометрической»
ВеРхностью, фиксированной в пространстве, но не обязательно
107
состоящей из одних и тех же частиц воды. В этом слуцал]
согласно условию υη = О, поток энергии сквозь S определите!
по зависимости
s ·/!
которая в последующем будет неоднократно использоватьел
для расчета потока волновой энергии через вертикальную пло.
скую поверхность 5, ортогональную к оси Ох. В отдельных слу.
чаях требуется исследовать поток волновой энергии через
поверхность S за некоторый отрезок времени, например, за
период волны Т\ обозначим его через Ντ и запишем:
t+T
t s
Осредненный поток волновой энергии Nm получим от
деления NT на период волны 7, а именно:
Применим полученные формулы к исследованию энергии
волн в предположении, что условия на свободной поверхности
линеаризированы, и при этом ограничимся рассмотрением
плоской задачи. Предположим сначала, что рассматриваемое
движение представляет собою наложение двух простых
гармонических по времени стоячих волн, характеризующихся
потенциалом скорости
φ = φι (χ, ζ) cos ω/+<ρ2(#, ζ) sin ωί. 4.10
Подставим частные производные от потенциала скорости 4.10
в формулу 4.8, в результате интегрирования за период волны
Τ = 2π/ω получим для определения потока волновой энергии Nr
следующую зависимость:
*-'-Μ'·£-*ΐ]Λ· 4·"
Из 4.11 следует, что поток энергии за период волны
нулю, если либо φι, либо <ψ2 обращается тождественно в нуль,
т. е. если движение представляет собою стоячую волну. По
условию в рассматриваемой задаче φι и <рг являются гармоническими
функциями. Поэтому, если S является неподвижной замкнутой
поверхностью, ограничивающей в жидкости область W, т0
согласно формуле Грина имеем:
Ш* ж - * -5гЦ- [Я1*** ~9МА dxdydz-
s V
108
учитывая, что φι и <рг не имеют особенностей в Wt например,
точников или стоков, получаем поток энергии равным нулю,
Ияк как Δφι = 0 и Δ«φ2 = 0. В другом случае, если S деформи-
т ТСЯ) не проходя через особенности, поток энергии через
вертикальную плоскость, проведенную нормально к лучу волны от
тна к свободной поверхности воды, будет один и тот же.
Д Предположим, что в условиях ограниченной глубины d =
== const движение жидкости характеризуется плоскими
гармоническими бегущими волнами малой высоты с потенциалом
скорости
hg ch£(*4- d) . ,и .ν
Используем это выражение потенциала скоростей для
расчета согласно формуле 4.8 потока энергии через вертикальную
полосу единичной ширины за время ί = Τ = 2π/ω:
t d
t+T η
= РфГет1 [^h*k(z + H)dz\cos'(kx-<»t)dt. 4.12
t d
Если положить в 4.12 верхний предел изменения ζ равным
нулю (т. е. η = 0) и таким образом не учитывать слагаемые
более высокого порядка малости по высоте волны А,
использовать известное соотношение ω2 = gkihkd, окончательно
получим:
Осредненный' за период волны поток энергии равен
= ^ = i^jLr1+JMj 4ЛЗ
1У<" Т 16 Τ ll ^ sh2kd\' ^lo
или в сокращенном виде:
Nm = ^.U, 4.14
где (У имеет размерность скорости и рассчитывается по
следующей формуле:
"ЧФ+агш]· 4·15
в которой применена замена λ/Τ = с.
хол Числим теперь при помощи 4.1 полную энергию Е> при-
МомЯ1ДУЮСЯ на ДЛИНУ волны λ = 2n/k в любой фиксированный
ент> рис. 4.1. Напомним, что полная механическая энергия
109
одной волны есть превышение полной механической энергИй
воды на участке акватории протяженностью вдоль луча в одн!
длину волны и единичной ширины при наличии волн £\ н'[
полной механической энергией воды на этом же^ участке £
в состоянии покоя при спокойном уровне. Таким образом"
в рассматриваемом случае согласно 4.1 имеем:
—d О
η λ
+ Ρ J j gzdxdz.
о о
4.16]
/////j^/s/s/trw////^
Рис. 4.1. Схема к определению полной механической
энергии одной волны.
Первый интеграл правой части 4.16 характеризует
кинетическую Eky а второй — потенциальную £р_ энергию одной волны.
Применим формулу Грина в выражении для определения
кинетической энергии, в результате запишем:
£*=4ρ]"τ
dL
4.17
где L — обозначает контур площади одной волны, изображенной
на рис. 4.1; η — внешняя нормаль к L.
Интеграл 4.17 может быть упрощен и сведен к определению!
его значения лишь на участке контура свободной поверхности
ОЛЯ, где направление внешней нормали можно принять при^
ближенно совпадающим с направлением оси Oz, arf/^^'
Таким образом, с учетом оговоренных допущений выражение
для Ek примет вид:
M*-S-
dx.
■4.1».
ПО
Действительно, в силу пограничного условия на участке CD
I оНтуРа "5я"= 0» а следовательно, интеграл 4.17 вдоль CD равен
лЮ. Поскольку значения функции φ в соответствующих точках
ертикалей 0D и ВС вследствие периодичности движения будут
одинаковыми, а значения δφ/δη будут отличаться только
знаком, результирующий интеграл 4-17 на участках 0D + BC также
будет равен нулю, т. е.:'
ί »*<«-<>·
OD-fBC
Подставим в формулу 4.18 значения φ и δφ/δζ для бегущей
волны с учетом того, что в первом приближении принимается
ζ «О, в результате получим:
χ
Е*=τ рдг *£ га ίsln2 <** - ·*> **·
о
или, после замены ω2 *= gkthkd, окончательно имеем:
Ek = Tg№№. 4.19
Потенциальная энергия бегущей волны, как это следует из
приведенного выше общего определения энергии, рассчитывается
следующим образом:
ηλ οχ λΓη1
Ер = р \ ) gzdxdz — p J J gzdxdz = ?g J J zrfz rfx, 4.20
-do -<*o о Lo J
что и соответствует второму интегралу в 4.16. Выполнив
согласно 4.20 интегрирование после подстановки для бегущей волны
малой высоты η =yCOs(£;t—ω/), запишем
λ
Ер= 1 pgA2 j [cos2 (Ax - ω/)] Лс = ^ ρ#Λ2λ. 4.21
о
Таким образом, из сопоставления 4.19 и 4.21 убеждаемся,
что в любой момент кинетическая энергия одной бегущей волны
малой высоты равна ее потенциальной энергии, а полная энер-
ГИя £, как результат суммы Ен и Ер, соответственно равна:
E = ^pgh2K 4.22
Среднюю энергию бегущей волны Ет, приходящуюся на
^Диницу длины в направлении оси 0^, получим от деления Ε/λ,
β = Εη = ψ. 4.23
111
Сравнив формулы 4.23 и 4.14, убеждаемся, что Ет равняет^
в точности коэффициенту при U для осредненного за пери0]
волны потока энергии через вертикальную полосу единично!
ширины, проведенную от дна до свободной поверхности. В силу
того, что энергия не создается и не исчезает внутри само[
жидкости, из 4.14 следует, что энергия переносится в направ]
лении распространения волн в среднем со скоростью V. \щ
это видно из формулы 4.15, скорость U отличается от скорости
перемещения волны с, при этом, как правило, U меньше с: npJ
d/K-+oo величина i/->c/2 и, соответственно, i7->c — npJ
d/λ-^Ο. '
Воспользуемся формулами 4.18 и 4.20 для определения кине·!
тической, потенциальной и полной энергии одной стоячей волнц|
малой высоты, потенциал скорости которой имеет вид:
• ω сп ка
Подставив в 4.18 значения φ и dq>/dzt взятые при 2 = 0,
запишем:
χ
υ
или после замены ω2 == gkthkd окончательно имеем:
Ek=£^-\cos2«>L 4.24I
Для определения потенциальной энергии одной стоячей
волны малой высоты выполним согласно 4.20 интегрирование,
после подстановки η = h sin ωί sin kx, получим следующую
формулу:
Ер = i|5? sin2 ω/ J sin2 kxdx = ίψ. λ sin2 ω/. 4.25
о
Полная энергия одной стоячей волны малой высоты
соответственно равна
Ε = Ек + Ер=-Ц^1. 4.26
Отметим два обстоятельства: во-первых, как это следует из
4.26, полная энергия одной стоячей волны малой высоты есть
величина постоянная; во-вторых, кинетическая и потенциальная
энергии переходят друг в друга, причем осредненные их
значения, взятые за промежуток времени, равный одному периоДУ
волны, одинаковы, так как
τ τ
J cos3 Ы dt = J sin2 <»tdt = -о-,
oo
112
В заключение обратим внимание на то, что, как это следует
з сопоставления формул 4.26 и 4.22, при одних и тех же зна-
11 еНИях h и λ полная энергия стоячей волны в два раза*больше
4 лНой энергии бегущей волны.
4.2. ГРУППОВАЯ СКОРОСТЬ. ДИСПЕРСИЯ
Волновое движение водных масс в реальных условиях
представляет собою наложение друг на друга бесконечного
множества простых гармонических волн различной высоты, длины
и со случайными фазами. Именно на таком подходе построены
спектральные методы исследования и расчета ветровых волн
[23], в которых дополнительно учитывается и разнообразие
направлений отдельных составляющих волн. В данном случае
Рис. 4.2. Схема к определению групповой скорости.
будем рассматривать интерферированные плоские волны, как
результат наложения бегущих в одном направлении волн с
различными высотами и длинами. Обратим внимание на то, что
скорость перемещения волн есть возрастающая функция длины:
а, следовательно, волновым явлениям на поверхности морей
присуща дисперсия. Можно предполагать, что с течением
времени волны рассортировываются на различные группы, причем
Каждая из них состоит из волн, имеющих почти одинаковую
Длину. Изучим свойства таких групп.
Предположим, что рассматриваемое движение может быть
описано посредством наложения бегущих волн, заданных
потенциалами скоростей вида:
<pi = A sin (kx—^at);
φ$ = A sin (;[k+bk]x—[(u+6<u]t)f 4.27
e об и δω считаются малыми величинами; наложение этих
*олн даеТ:
<Р = 2А COS Ι(*δ£-/δω) Sin ([& + Щ X - [ω + Щ *),
ИЗ
или
φ = β sin (k'x—ω'0>
4.28
где k = k + -γ-; ω' = ω + -^-.
Так как bk и δω малы, то функция В изменяется медленно
по χ и t. Отсюда следует, что φ характеризует амплитудно-
модулированную синусоидальную кривую в каждый момент
времени, рис. 4.2. Волны, характеризующиеся пунктирными
кривыми на этом
рисунке, будем называть
группой волн; скорость
их перемещения вдоль
оси Ох определяется
отношением δω/δί\
В рассматриваемой
задаче ω является
функцией от ky
следовательно скорость U группы
волн приближенно
равна άω/dk. Имея в виду,
что длина волны λ =
= 2π/&, а скорость
перемещения волн с = \
= ω/k, для
определения U получаем
следующую формулу:
О В
Рис. 4.3. График с = [(К).
X
U
_ d{kc) _
dk
= С-
dc
Ίλ
4.29
Этой формуле можно дать геометрическое толкование,
построив по приведенной в начале настоящего параграфа
зависимости для с график c = f(X)y рис. 4.3. Проведем касательную
к изображенной кривой в точке с координатами λ, с. В системе]
координат Ху ζ уравнение этой прямой будет иметь вид
dc / л ч dc ,
ζ — с = -рг- (х — λ), или ζ=χ -^γ- + с ■
d\
dc
Ж'
dc
откуда следует, что U = с—λ^ есть отрезок, отсекаемый этой
касательной на оси с. Полезно отметить, что угол ЛОВ на
рис. 4.3 определяет частоту колебаний ω. Действительно, tg β =
= c/λ = ω/2π, откуда
ω = 2jttgp.
4.3
Используем соотношение с2 =-^th-^-dn преобразуем 4.29J
в результате получим;
114
Обращает на себя внимание то, что формула групповой
скости 4.31 тождественна зависимости 4.15, т. е. скорость
распространения энергии равняется групповой скорости, а не
скорости перемещения волн. Однако по этому вопросу могут быть
и АРУгие толкования, о чем будет сказано несколько позже.
Здесь лишь заметим, что групповая скорость и скорость
переноса энергии могут существенно различаться, если в среде имеет
место рассеяние энергии.
При рассмотрении вопроса о групповой скорости
ограничимся для простоты сложением двух,волн одинаковой высоты
и приблизительно одинаковой длины. Для анализа
интерференции бесконечного числа волн с очень мало отличающимися
друг от друга высотами и длинами запишем следующее
выражение для потенциала скорости:
φ = j A(k) exp {/ (kx — ωί)} dk. 4.3£
K—«
Величина (kx—ωί) может быть представлена в виде
(kx—ωί) = kox—(oot+ (k—4io)x—((u—(uo)t.
Из 4.32 находим, что '
φ = С exp {i (/ζ0χ—ωοί)}, 4.33
где амплитудный множитель С определяется так:
С = j A (k) exp {/ \(k — k0) χ — (ω — ω0) t]} dk. 4.34
Найдем такую зависимость между переменными χ и t9 при
которой функция С представляет волну, распространяющуюся
с небольшим изменением формы, так как 4.33 будет тогда
Давать то, что мы назвали групповой скоростью. Поскольку χ
11 t встречаются только в экспоненциальном члене в 4.34,
интересующие значения таковы, когда этот член почти постоянен,
а именно:
[(k—\k0)x— (ω—ωο)4] α* const.
Отсюда следует, что скорость перемещения такой группы
Равна --^~- и, если только разность k—kc достаточно мала,
ПолУчаем формулу 4.29.
ΰ приведенном выше рассуждении о понятии групповой хжо-
JJ сти существенно то, что рассматриваемое движение должно
Р^дставлять собой интерференцию волн, мало отличающихся
и Частоте и амплитуде. Реальные волновые движения жидкости
* Я1отся результатом наложения волн, частоты и амплитуды
115
которых изменяются в широких пределах. Однако движение
в определенные моменты аппроксимируется с большой
точностью интегралом вида 4.32, где ε достаточно мало. В таких
случаях группы должны существовать, и изложенное
доказательство вполне уместно.
Итак, располагая кинематическим и динамическим
понятиями групповой скорости, формально можно обосновать то, что
скорость перемещения энергии равна групповой скорости, а не
скорости перемещения волн. Из предыдущего параграфа еле
дует, что понятие скорости переноса энергии может быть
получено независимо от наличия групп волн; в самом деле, эта
скорость получена для
случая волны,
имеющей всего одну
составляющую. В
действительности скорость
переноса энергии, по-
видимому, не равна
групповой скорости.
Покажем, это на
анализе переноса энергии
бегущими волнами на
глубоководье при d->
-»- оо.
Рис. 4.4. Схема к исследованию переноса энер- Рассмотрим какую-
гии бегущими волнами на глубоководье. либо вертикальную
плоскость OQt рис. 4.4.
Пусть фиксированная частица пересекает эту плоскость
при движении по окружности дважды за период волны в точках
В и А. Поскольку скорость движения частицы по орбите
постоянная, ее кинетическая энергия всегда одинаковая, следова
тельно, через плоскость OQ пройдет столько же кинетической
энергии в одну сторону, сколько в другую. Давление для этой
же частицы тоже все время постоянно, а потому работа сил
давления за время одного периода уничтожится, так как в точке
А будет совершаться такая же отрицательная работа, какая
в точке В совершалась положительная.
Не так обстоит дело с потенциальной энергией. Как частица
Ву так и частица В' будут проходить через плоскость OQ слева
направо над уровнем С С и, следовательно, будут переносить
потенциальную энергию. При этом очевидно, что эта энергия
будет перемещаться одновременно с формой волны, т. е.
скоростью с. Итак, в действительности, средняя волновая энергия
переносится в этом случае не со скоростью U =-*с, а со
скоростью перемещения волны. Ранее мы не обнаружили
противоречия в конечном результате лишь потому, что переносимая
116
отенциальная энергия составляет в точности половину полной
п ерГИи волны, на что уже обращалось внимание в 4.1 при
сопоставлении формул 4.19 и 4.21.
4 3 ИНТЕГРАЛЬНЫЕ И ДИФФЕРЕНЦИАЛЬНЫЕ ЭНЕРГЕТИЧЕСКИЕ
ХАРАКТЕРИСТИКИ СТОЯЧИХ ВОЛН БОЛЬШОЙ ВЫСОТЫ
рассмотрим интегральные и дифференциальные
характеристики механической энергии стоячих волн большой высоты при
гЛубине жидкости d = const (в плоской постановке)
применительно к схеме и обозначениям на рис. 4.1. Пусть указанный
объем жидкости ограничен двумя вертикалями, проведенными
на расстоянии друг от друга, равном длине волны λ, дном и
свободной поверхностью; размер, нормальный к плоскости
рисунка, примем равным единице длины.
Напомним, что в общем случае закон сохранения
механической энергии формулируется так: если все силы, приложенные
к системе материальных точек, потенциальны, то сумма
кинетической и потенциальной энергий системы должна быть
постоянной.
Применив для выделенной области W несжимаемой
жидкости уравнение энергии, нетрудно показать, что полная энергия
одной стоячей волны £, равная сумме кинетической Ek и
потенциальной Ер энергий, есть величина постоянная, а именно:
Ε = Ek + Ер = [ Ipd (av-x + tv,)dUtt + С, 4.35
где pd — в данном случае давление в центре участка контура
dl\ vx и υζ — проекции на оси координат скорости в центре
того же участка контура; α и β — косинусы углов,
образованных внешней нормалью; С — постоянная величина.
Действительно, в рассматриваемой области W стоячей волны
NPd{v,Ox+$Oz)dldt равен нулю, так как на свободной
поверхности pd = 0, на уровне дна υζ = О, а на вертикальных границах
П°А пучностями Όχ = 0. Таким образом из 4.35 следует, что
в Рассматриваемом случае
Ε = Ek + Ep ч= const,
34есь Ер — есть потенциальная волновая энергия, обусловленная
п°лем тяготения.
В 4.1 показано, что, руководствуясь интегралом Лагранжа,
ЦЛя некоторой области W жидкости, находящейся в потенциаль-
°м неустановившемся движении, полную энергию можно
опреть по следующим двум формально равноценным уравне-
117
E=N[[-pd + gF(t)-9£]dxdydz. 4.37
w
Используем эти уравнения для определения энергии стоячей
волны, исключив из 4.36 и 4.37 энергию рассматриваемого
объема жидкости в момент покоя. Значения кинетической Ek)
потенциальной Ер и полной Ε энергий одной стоячей волны
в объеме жидкости, ограниченном дном, свободной
поверхностью, вертикалями в пределах одной длины волны λ и
протяженностью по фронту 6, равной единице длины, определяются по
фор-мулам теории стоячих волн большой высоты в переменных
Эйлера при условии исключения слагаемых порядка а5 и выше,
что соответствует уровню второго приближения:
Е>=*ф-[\ -cos2»*+ 8Λ>£ν2ω [(32ch'M-8ch«M-
-14ch2M + 8)-
— /10 ch4 kd sh2 2kd + j sh2 2kd — 8 sh2 kd) cos 2ω/ +
+ (8 ch8 kd - 32 chfi kd + ch\kd + 5 ch2 kd) cos 4ωί]}, Дж/м, 4.38
X"[(48 ch8 kd ~ 72 che kd + 66 ch* kd - 36 ch2 kd+l2) +
+ (10 ch« kd sh2 2kd + \ sh2 2kd - 8 sh2 kd) cos 2ω* -
- (8 ch8 Ы — 32 ch6 kd + ch4 kd+δ ch2 Ы) cos 4ωί jl Дж/р
4.39
: = ρ^α2λ[
l + ,gb4wlo^(10ch4^sh22^ +
8 sh* W sh2 2Ы
+ 33ch4M--25ch2M+10)], Дж/м, 4.40
где 2а — константа, характеризующая высоту волны; параметры
Ьо) соответственно равны: k = 2π/λ; ω = 2π/7\
Заметим, что при написании формул 4.38—4.40 учтены все
слагаемые с множителями порядка до а4 включительно, кото-
рые получены при использовании решения теории волн третьего
приближения. Однако ограничиться результатами теории
стоячих волн на уровне второго приближения было бы недостаточно,
так как тогда не были бы учтены слагаемые как произведения
множителей, содержащих а3 и а. Если в вышеприведенных
формулах сохранить лишь слагаемые порядка а2, можно записать
-зависимость для определения интегральных энергетических
характеристик стоячей волны в первом приближении.
Обратим внимание на то, что в линейной теории и в теории
волн второго приближения всегда константа 2а = А, где ft —
высота бегущей волны. 3 формулах, полученных из решения
U8
0рии волн в третьем приближении, константа 2а < /г; частные
теацеНия 2а находятся из уравнения 2.25, имеющего вид:
! о Γΐ ι а2& ( 104che^sh2 2^ + 132che&rf-4lsh2 26tf — 24 VI
lt^2a\l+ 16 у sh*kdsh*2kd )[
В целях сопоставления результатов расчета кинетической,
потенциальной и полной энергий стоячих волн соответствующие
значения энергии могут быть определены другими способами.
Применим, например, метод численного интегрирования, введя
понятие так называемой удельной волновой энергии — энергии
элементарной области (6W) взволнованной жидкости,
отнесенной к весу этого же объема жидкости (pgbW). В связи с этим
составляющие и полная удельные энергии взволнованной
жидкости обозначим так:
е* = Vx*2gVz2> м» ер = — (* "" *о). м; 4.41
где е*-—удельная кинетическая энергия; ер — удельная
потенциальная энергия; е — удельная полная энергия.
Дифференциальные и интегральные энергетические
характеристики взволнованной жидкости в пределах одной стоячей
волны, рис. 4.1, могут быть в таком случае определены по
следующим зависимостям:
— применительно к элементарному объему 6W
bek = pgekbW; 6ep = pgep6W; be = pgebW; 4.43
— применительно к элементарному столбику с основанием
на дне водоема δχ
§-Р*2«*«*; b4r = PgZiepbW; -g- = PS2ebW; 4.44
—d —d —d °
— применительно к элементарному слою высотой bz в
фиксированном створе
χ χ χ
s-S-=p^2^r« δ-&·=ρ^Σ^δ^: ΐ-=ρ^Σ6δίΓ; 4·45
"— применительно к объему жидкости в одной стоячей волне
λ η λ η
£*=τ 22(β*,+·',)ίν: ^=p^55z8wr-
-γρ^λ;
119
λ η λ η 4.46
Ο d Ο if
Достоверность расчета по определению энергетических
характеристик в данном случае будет зависеть и от того, достаточно
ли малыми были приняты размеры элементарных объемов,
правильно ли были определены деформации граней и координаты
их центров тяжести, строго ли соблюдалось условие равенства
элементарных объемов жидкости в покое и во взволнованном
состоянии. Соблюдение последнего условия автоматически
обеспечивается, если, задаваясь координатами вершин и
центров тяжести элементарных объемов в состоянии покоя
(начальный момент), вычислять в любой данный момент времени
координаты этих же точек по уравнениям траекторий, которые
обычно записываются в переменных Лагранжа. Заметим, что
в большинстве случаев неправильное представление о
распределении по длине потенциальной энергии волн получается из-за
того, что сравниваются разные по величине элементарные
объемы жидкости в покое и во взволнованном состоянии.
С помощью ЭВМ были выполнены расчеты по определению
полной энергии (одной стоячей волны) и ее составляющих
в соответствии с формулами 4.38—4.40 в переменных Эйлера,
а также по зависимостям 4.46 и уравнениям траекторий частиц
из решения в переменных Лагранжа. Результаты этих расчетов
и отдельных опытов при й = 1 см представлены в табл. 4.1,
в которой приведены значения энергии в переменных Эйлера
на уровне первого приближения (графа 4, с точностью до (α/λ)2
при 2а = К) и второго приближения (графа 6, с точностью до
(α/λ)4 при 2α = /(ιΛ/λ; K/d)^h)> а также по зависимостям
4.46 и уравнениям траекторий частиц в переменных Лагранжа
(графы 5 и 7). Из анализа таблицы следует, что результаты
расчета по формулам 4.38—4.40 ближе к опытным данным, чем
по формуле 4.46.
Полная энергия, вычисленная в переменных Эйлера, строго
соответствует закону сохранения энергии. Естественно, что при
анализе свойств интегральных значений энергии стоячих волн
рекомендуется использовать численные величины, рассчитанные
по аналитическим зависимостям в переменных Эйлера. Вместе
с тем, дифференциальные характеристики (например,
распределение потенциальной энергии по длине волны и по глубине
водоема) представляется целесообразным получать, исходя из
выражений для траекторий частиц жидкости в переменных
Лагранжа. В таком случае дифференциальные характеристики
энергии волн оказываются более точными, чем интегральные,
120
Таблица 4.1
мальные значения потенциальной и кинетической энергий волны, Дж/см
Элементы волн, \
см \
1
Г 2~
λ = 271;
<f = 70
] Λ = 15,5;
λ = 271;
rf = 70
Ι Λ = 18,1;
λ = 271;
d = 70
Ι h = 13;
λ = 205;
\d = 70
Виды энергии
3
^k, max
**ρ, max
*k, max
1
Ε
**р, max J
™k% max
F
c,p% max
F
**k, max
/?
^/>, max
ί λ η Ι
0 ί/
λ
ί о
Σ Σ**
. 0 d
"fa*
0
Опыт
f ^ η
ΣΣ^ρ
0 d
λ
0
Ι Опыт
Ι λ η
0 d
Ι λ
0
[ Опыт
Порядок приближения, переменные
I
приближение
в
переменных
Эйлера
4
0,89
0,89
1,6
1.6
2,18
2,18
1 0,85
0,85
II приближение
в переменных
Лагранжа
5
0,88
0,88
0,85
1,56
1,56
1,46
1,49
2,12
2,12
1,92
2,04
0,82
0,82
0,77
0,71
Эйлера
6 J
0,85 1
0,85
1,47 1
1,47
1,97 |
1,97
0,79
0,79
III
приближение
в
переменных
Лагранжа
7
0,86
0,81
0,85
1,48
1,35
1,46
1,99
1,76
1,93
0,79
0,71
0,77
121
Продолжение таблицы 4 J
1
5
6
7
8
2 I 3
h = 16,4;
λ = 350;
d = 70
Λ =17,1;
λ = 287;
rf=40
h = 15,6;
λ = 156;
rf = 78
Λ = 1,56;
λ = 156;
rf = 78
ρ
*"kt max
F
*"p, max ·
ρ
^k, max
^p, max
^Λ, max
R
L'pt max
F
*■**, max
^p, max '
r λ ч
0 d
λ
0
Опыт
0 d
λ
0
Опыт
j ΣΣ**
| ϋ d
1 λ
Ι °
0 J
λ
0
4
2,31
2,31
2,06
2,06
0,93
0,93
0,0093
0,0093
5
2,29
2,29
2,12
2,16
2,02
2,02
1,50
1,64
0,87
0,87
0,0093
0,0093
6 | 7
2,14
2,15
1,65
1.71
0,8
0,8
0,0093
0,0093
2,14
2.0
2,14
1,6
1,46
1,67
0,82
0,67
0,0093
0,0093
В результате анализа табл. 4.1 можно также сделать
следующие заключения. Во-первых, полная энергия одной стоячей
волны, определенная на основе более точных теорий волн,
меньше, чем эта же величина, рассчитанная в первом
приближении; наибольшее расхождение составляет 20%. Замеренные
в опытах значения потенциальной энергии стоячих волн ближе
соответствуют результатам расчета по более точным
теоретическим решениям. Полученные выше формулы 4.38—4.40 на
уровне второго приближения (с учетом дополнительных членов
теории стоячих волн третьего приближения) приводят к
результату, практически совпадающему с данными численного
интегрирования на основе решения в третьем приближении в
переменных Лагранжа. Во-вторых, определенные по более точным
122
Ооиям максимальные значения потенциальной энергии одной
Тбоячей волны EPt max, Дж/м, всегда больше максимальных
знамений кинетической энергии £*,тах, Дж/м, на величину £р,тт,
гтж/м, — минимального значения потенциальной энергии; зна-
ения указанных составляющих энергиж~могут быть рассчитаны
по формулам:
ΕΌ
-р, max
o^ Γι . &Ь-1 10 ch* kd s№2kd + 33 ch* kd - 25 ch* kd + 10\1 , .-
*fg*+[l + -T-\ sh*kdsh*2kd /J5 4·47
EPt „i„ = pgflui [-j- ^ 8hiMsh,2to JJ; 4·48
£*, max —
= Ρ£α2λ[ΐ+—( gh4^gh»Md — JJ· 4·49
при этом соблюдается условие £Plmax = £p,min+£*,max, в чем
нетрудно убедиться.
Согласно зависимости 4.38—4.40 получаем, что, как и
в линейной теории волн, кинетическая энергия с течением
времени переходит в потенциальную, и наоборот. Однако на основе
более точных решений обнаруживается, что потенциальная
энергия одной стоячей волны в течение четверти периода изменяется
от максимума до минимума, но никогда не бывает равной нулю,
в то же время кинетическая энергия волны через каждую
половину периода оказывается равной нулю. Такая особенность
в изменении потенциальной энергии обусловлена тем, что
в нелинейных решениях профиль стоячей волны ни в один из
моментов не совпадает с уровнем покоя.
Хронограммы интегральных характеристик кинетической,
потенциальной и' полной энергии для двух стоячих волн из
табл. 4.1 представлены схемами α и б на рис. 4.5, на котором
кривые б, 4, 2 построены соответственно по формулам 4.38—4.40.
Перейдем теперь к исследованию уравнения 4.37, которое,
как уже отмечалось, формально равноценно с 4.36 и также
получено из интеграла Лагранжа. Проследим за характером
изменения каждой из составляющих 4.37, обозначив их
соответственно через ЕРу £? и EF\ в плоской постановке задачи для
определения этих величин имеем:
Ε = Ερ+Ει+ΕΡ\
λ η λ η
0 d 0 d
EP = pg$]F(t)dxdz. 4.50
123
Ограничиваясь для сокращения записей уровнем первого
приближения и имея в виду, что в этом случае константэ 2а=А,
для расчета EPt £φ и EF получаем:
Ер= ^^{kd+[sh2kd—{4sh^kd+l)kd]cos2o)t}; 4.51
£φ = Ρ£^ (l + cos2co/); 4.52
Рис. 4.5. Хронограммы интегральных характеристик кинетической Ek,
потенциальной Ер и полной Ε энергий стоячих волн и составляющих
Ер, Еу и Ef
а), в) для опыта 6 при Л= 17,1 см; Х — 287 см; d = 40 см; б) для опыта 5
при h = 16,4 см; χ = 350 см; d = 70 см;
lt2 — E\ 3,4— Ер) 5,6—Ek; 7 — Ер\ 8 — £<р ; 9~Ер.
Хронограммы ЕРу Εψ и EFy построенные по этим формулам
для двух стоячих волн из табл. 4.1, изображены на схеме в
(рис. 4.5) кривыми 7, 8 и 9. Из этого рисунка следует, что
каждая из упомянутых трех составляющих представляет собою
четко выраженную функцию времени. Очевидно, что только
сумма упомянутых трех составляющих дает постоянную
величину Е, численно равную значению полной энергии одной
стоячей волны.
Нетрудно показать, что любые другие сочетания слагаемых
интеграла Лагранжа, кроме рассмотренных здесь выражений
4.36 и 4.37, приведут к нарушению закона сохранения энергии
124
4.6. Графики равных значений потенциальной ер и кинетической е*
делЛЬНЫХ энеРгий в пределах одной стоячей полуволны и эпюры распре-
ения по глубине (в пучностях и узлах) значений удельной энергии,
а) отнесенных к высоте исходной бегущей волны h
= \bl .?ПЬ1Та 6 при Λ == 17,1 см, % = 287 см, d = 40 см;
1^6 см, λ =.156 см, d = 78cM; *
'-j
б) для опыта 7 при h =
β) для опыта 8 при h = 1,56 см, λ =156 см.
кинетНИИ равных значений удельной потенциальной энергии ер, см; 2 — то же
ности еской энергии ek, см; 3 — эпюры распределения по глубине в створе пуч-
«сходНО}?Лн-ы значений удельной потенциальной энергии, отнесенной к высоте
То Же в ст«Гу1Цей волнь1 Λ; 4 —то же кинетической в створе узла волны; 5 —
н°сти в ^JB0Pe пучности в момент наибольшего возвышения взволнованной поверх-
узле; б — дно; 7 — свободная взволнованная поверхность; 8 — спокойный
уровень.
125
в явном или неявном виде. Так, например, если, следуя
Η. Е. Кондратьеву '[20], представить полную анергию в виде
суммы кинетической энергии Ek, потенциальной энергии
положения Ер и потенциальной энергии давления Ерг, получим для Ε
на схеме в (рис. 4.5) вместо линии / совмещенную с ней
кривую 7, т.е. окажется, что £ = Ер+Ек—Ер,Фconst, а есть
некоторая функция времени. Н. Я. Фабрикант [59] считает, что
полная энергия потенциального неустановившегося движения
жидкости имеет четыре составляющие: Ek, Ер, Ерг и Εψ.
Обращаясь к рис. 4.5, убеждаемся, что и в этом случае Ε = Ek\
+ ЕР—Ер,—ΕуФ const, т. е. нарушается закон сохранения
энергии.
Рассмотрим дифференциальные энергетические характера
стики стоячих волн на конкретных примерах.
На рис. 4.6 представлены графики равных значений
потенциальной и кинетической удельных энергий в пределах одной
стоячей волны и эпюры распределения по глубине (в пучностях
и узлах) составляющих удельной энергии, рассчитанных по
формулам 4.41 и 4.42 в момент наибольшего возвышения
взволнованной поверхности. Графики построены применительно
к трем последним волнам из табл. 4.1: мелководной (схема а),
глубоководной крутой (схема б) и глубоководной пологой
(схема в).
Из рис. 4.6 следует, что удельная потенциальная энергия
в области гребней волн имеет положительные, а в области впа-'ι
дин волн — отрицательные значения; при этом, если для пологих
волн по абсолютной величине они примерно одинаковые, то для
крутых волн положительные значения удельной потенциальной
энергии существенно превосходят отрицательные (в полтора —
два раза). Эпюры распределения по глубине удельной потен-1
циальной энергии характеризуются быстрым затуханием ее
с глубиной; у дна во все моменты времени потенциальная
волновая энергия равна нулю.
Распределение удельной кинетической энергии существенно
зависит от крутизны волны и относительной глубины. В
мелководной волне, рис. 4.6, а, кинетическая энергия
концентрируется преимущественно в окрестности узлов, в то время как
для пологих волн на глубоководье удельная кинетическая
энергия распределена примерно равномерно. Характер изменения
удельной кинетической энергии по длине волны и глубине
водоема в других случаях представляется очевидным, рис. 4.6, и
не нуждается в комментариях.
На рис. 4.7 изображены графики распределения по длине
волны энергии элементарных столбиков с основанием на дне
водоема применительно к исходным волнам на рис. 4.6 и табл
4.1, построенные на основе зависимостей 4.44 с использованием
формул теории стоячих волн в первом, втором и третьем при
ближениях. Из рис. 4.7 следует, что характер распределен^
126
нииальной энергии в0 всех случаях отражает особенности
П°менения профиля взволнованной поверхности; в условиях
ЙлубоковоДья имеет место плавное увеличение кинетической
нергии На участках от пучностей до узлов. В случае мелко-
• 1 I
0,01
0,05
0,03
0,01
0
-0,01
- JA
~ r
-
δθ
л
-τ~'" ι
100
^5с—J7
n^. ι ι
~li0^«C
1 i
160
I
180
200 \,см
η„ι*χ,ηκ/*χ
0,05
w
0,01
0
-0,01
-0,03
x\
- />
Л
ySfi
ι 1 1 V\ U'l 1 1 1
50
r
60
70
*\S0 100 110 120
-0,03\-
,ic· 4.7. Графики распределения по длине стоячей волны потенциальной,
для кинетической и полной энергий
п°тенц!|^Т0В 6 ^α)ί 7 (б)'» 8 (*) (табл. 4.1); кривые 1—3 — наибольшие значения
и тРетьегЬН°^ энеРгии» рассчитанные соответственно по формулам первого, второго
его приближений теории стоячих волн; кривые 4—6 — то же. для
кинетической энергии/
Макс х волн отчетливо просматривается и то, что в момент
энергИМума кинетической энергии значения потенциальной
не гюИИ' Рассчитанные по более точным теориям, оказываются
Равными нулю, .
127
Характерной особенностью рис. 4.6 и 4.7 является то, что
во всех точках пространства в пределах одной стоячей волны
абсолютные значения удельной потенциальной энергии или
потенциальной энергии элементарных столбиков в несколько раз
превосходят соответствующие значения кинетической энергии.
Однако, если просуммировать составляющие энергии в объеме
одной волны, то не обнаруживается существенного различия
в численных значениях кинетической и потенциальной энергии.
Обратим внимание также и на недопустимость использования
в расчетах энергии волн формул первого приближения для
траекторий частиц и профиля волны в переменных Лагранжа, так
как в результате таких расчетов интегральное значение
потенциальной энергии получается равным нулю, что противоречит
действительности.
В заключении данного параграфа отметим, что правильный
результат в исследовании интегральных и дифференциальных
энергетических характеристик стоячих волн достигается только
на основе использования формул теории волн большой высоты
не ниже второго приближения.
4.4. УРАВНЕНИЕ БАЛАНСА ВОЛНОВОЙ ЭНЕРГИИ
Уравнение баланса волновой энергии предложено В. М. Мак-,
кавеевым в 1937 г.; оно плодотворно используется во многих
задачах, связанных с анализом энергетических процессов при
волнении.
С целью получения уравнения В. М. Маккавеева
воспользуемся законом живых сил для массы жидкости, находящейся
в момент времени t между расположенными на абсциссах χ и
х + дх вертикальными плоскостями, при этом объем, занятый
массой, предполагается распространяющимся на единицу
ширины и на всю глубину жидкости от ζ = —η (свободная
поверхность) и до дна при ζ = d. В момент времени / + dt эта масса
жидкости переместится в некоторое новое положение. Делением
уравнения закона живых сил на dt получим отдельные его
члены, отнесенные к единице времени; при этом секундное
изменение кинетической энергии будет равно секундной работе
внешних сил. Средние за период Τ значения отдельных членов
могут быть определены так '
τ
о
где f(t) —какой-либо из членов уравнения.
В дальнейшем будем опираться на зависимости линейной
теории бегущих волн. Таким образом, после применения
осреднения закон живых сил может быть записан в следующем виде
128
α / α . α \
^ έ/л = J pvxdz - ί J /^afe + jf ^pvxdzdx J -
—η \ —η -η /
дГ ^X + ^X — ^X' *'***
Левая часть уравнения 4.54 соответствует изменению
кинетической энергии за секунду. Первые три члена правой части
характеризуют значения работы сил гидродинамических
давлений за секунду, действующих по ограничивающим объем
вертикальным плоскостям. Четвертый член правой части выражает
работу сил тяжести за секунду, равную соответствующему
уменьшению потенциальной энергии. Последние два члена
характеризуют, с одной стороны, работу сил, увеличивающих
интенсивность волнового движения, и, с другой стороны, работу
сил сопротивления, например, сил трения у дна.
Используя формулы 4.19, 4.21 и 4.23, можно записать:
е — ek~\- ер — —g—.
Вычислив за период волны интеграл
d
§vxpdz,
после подстановки выражений для νχ и р, с учетом ранее
принятых обозначений, получим:
-η
а следовательно, после сокращения на dx уравнение 4.54 можно
представить так:
4(ЧР)+£[Ч?«('+;&)]-*;+*.-*
Или, при учете для групповой скорости формулы 4.15 или 4.31,
в виде:
Полученное уравнение 4.55 и есть уравнение баланса волно-
ои энергии В. М. Маккавеева, вывод которого сделан согласно
Работе [40].
г ^3 Уравнения 4.55 можно установить энергетический смысл
ир^повой скорости. Положив ~R\ = /?2 = 0, d = const, k = const
""" const, получим:
129
где U по условию 4.15 или 4.31 есть групповая скорость.
Введем новые независимые переменные Х\ и t\9 связанные)
с прежними χ и t зависимостями
U = t\ Х\ = χ—Ut
и соответственно будем иметь:
д ( ?g& \ д (?gv \ dt, , д1 ( ygto \ dx, _
dt { 8 J dtt \ 8 .) dt ~*~ дхг \ 8 J dt ~~
_ A {imILS ^uJL (mZL\
~~ dtA 8 ) u дхг \ 8 Г
πA(pg/l2) _ rr\JL(лЁ-) *к_мЛ~ (№h'2) dxA -
u dx\ 8 J * u[ dt, \ 8 ) dx ^ dx, \ 8 ) dx J ~
= tf J-(.£**.)
дхЛ .8 Г
Почленно складывая левые и правые части и учитывая зави]
симость 4.56, находим:
где / — получающаяся при интегрировании по U функция от
другой переменной Х\ = χ—Ui.
Условию постоянства во времени и пространстве некоторого]
значения волновой энергии pgh2/8 = const соответствуют:
dx
Х\ = const, dx — И dt = 0, -^- = U.
Таким образом, полная волновая энергия перемещается!
с групповой скоростью, т. е. волновая энергия группы волн]
переносится со скоростью перемещения этой группы.
Раздел II
РАСЧЕТ ПАРАМЕТРОВ ВЕТРОВЫХ ВОЛН
Глава 5. ВОЛНООБРАЗУЮЩИЕ ФАКТОРЫ.
ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ЭЛЕМЕНТОВ ВОЛН
5.1. ВОЛНООБРАЗУЮЩИЕ ФАКТОРЫ
Ветер, воздействуя на свободную поверхность водоема,
будь то океан, море, озеро или водохранилище, возбуждает
волновые движения с фазовыми скоростями, близкими κ
скорости ветра, — движения, называемые ветровыми волнами.
Количественные характеристики тех условий, которые
определяют параметры ветровых волн, называют волнообразующими
факторами.
Основными волнообразующими факторами открытой части
водоема являются: во-первых, кинематические характеристики,
структура, горизонтальные размеры и изменчивость во времени
полей ветра над водоемом; во-вторых, протяженность свободной
поверхности водоема и очертание береговой линии; в-третьих,
Рельеф дна.
Наиболее важными факторами, формирующими волны в
прибрежной зоне водоема, следует считать: параметры волн,
пришедших из открытой части водоема; конфигурацию изобат
вблизи берега; плановое расположение и конструктивные осо-
енности прибрежных гидротехнических, сооружений.
При определении характеристик поля ветра используют
понятие планетарного пограничного слоя. Под планетарным по-
Раничньщ слоем понимается слой атмосферы толщиной
с^МеРно 1000 м, в котором проявляется эффект трения о под-
лающую поверхность и на верхней границе которого турбу-
НепТНЫе потоки становятся пренебрежимо малыми. Слой,
Во 0еРедственно прилегающий к поверхности раздела вода —
Мос^х толщиной около 100 м, называют приводным слоем ат-
Ь1Ые Ы' ^ этом слое направление ветра, а также вертикаль-
тУрбулентные потоки импульса, тепла и влаги принимают
131
постоянными по высоте, что вносит существенные упрощения
в расчетные модели; при этом отклоняющей силой вращения
Земли (силой Кориолиса) в приводном слое пренебрегают.
К расчетным характеристикам ветра над водной
поверхностью относятся [26]:
а) скорость ветра Vw, м/с, в приводном слое на высоте г =
= 10 м над спокойным уровнем воды, осредненная за 10 мин;
эта скорость традиционно принимается в расчетах элементов
ветровых волн. Допускается использовать при определении Vw
как фактические измерения скорости ветра, в том числе и на
береговых метеостанциях, так и данные синоптических карт;
б) динамическая скорость щ, м/с, характеризующая
масштаб турбулентных скоростей вблизи водной поверхности; ее
находят по формуле
щ =(τ0/ρα),/2, 5.11
где το — тангенциальное напряжение ветра, Н/м2, приложенное
к единичной площади поверхности воды; ρα — плотность возду-|
ха, кг/м3;
в) тангенциальное напряжение ветра т0 определяем из за·]
висимости
То = paU2f = paCzV2(z), 5.2
где Cz — коэффициент сопротивления на высоте z\
V(z)—скорость ветра на высоте z\
г) коэффициент сопротивления Сг на высоте ζ
характеризует сопротивление шероховатой водной поверхности
обтекающему ее воздушному потоку; при логарифмическом профиле]
ветра Сг равно:
С, = (х-Чп^-)"2, 5.3]
где Zq — параметр шероховатости, м; κ = 0,4 — постоянная Кар-1
мана;
д) параметр шероховатости ζ0 представляет собой высоту
над спокойным уровнем воды, на которой средняя скорость
ветра обращается в нуль; его вычисляют по зависимости,
вытекающей из 5.3:
ζ0 = ζ exp (— *'VC2)\ 5.4
е) профиль средней горизонтальной скорости ветра V(z)\
отсчитывается от спокойного уровня водной поверхности до
верхней границы приводного слоя атмосферы (~100 м) и
определяется при нейтральной стратификации (больших
скоростях ветра) по формуле теории пограничного логарифмического]
слоя атмосферы:
1/(ζ)/^ = κ-4η (ζ/*,,). 5.Я
132
Параметр шероховатости z0 в условиях больших разгонов
(1> 10° км^ и СК0Р0СТей ветра (Vw > 15 м/с) на глубокой
воде равен
zQ = 0y02lu*f/g. 5.6
g этом случае коэффициент сопротивления при ζ = 10 м
[2б]' С10 ={*-' In (ггМ) +9,61-2. 5.7
Для удобства расчетов коэффициент сопротивления 5.7
приближенно может быть аппроксимирован в форме зависимости
от расчетной скорости ветра:
С10 = 7,1-10-^(1+0,1^/^), 5.8
где Va = 1 м/с.
В основу определения элементов волн положен следующий
простейший случай:'акватория имеет постоянную глубину, она
ограничена прямолинейной -береговой чертой, в начальный
момент времени свободная поверхность водоема неподвижна, и в
этот момент над всей акваторией внезапно возникает
постоянный по скорости и направлению ветер, дующий с берега
перпендикулярно урезу воды. Расстояние L от фиксированной
точки водоема до берега в этом случае называют разгоном волн
(см. параграф 5.2),
В целях предварительной оценки элементов волн на
обширных акваториях протяженностью 100 км и более значение
предельно допустимого разгона Lw для заданной расчетной
скорости ветра Vw определяют по обязательному приложению 1
норм [51], используя табл. 4. Среднее значение разгона Lm
вычисляют по формуле (150), полученной из предположения,
что масштаб турбулентных возмущений определяется числом
^Рейнольдса [26]:
Re = LVw/у —fovis,
гле £w* — коэффициент, принимаемый равным 5Ί011; ν
—коэффициент кинематической вязкости воздуха, принимаемый
Равным 10~5 м2/с
Элементы волн на обширных мелководных акваториях с
дубинами 10 м и менее (при уклонах дна 0,001 и менее)
допускается определять по измерениям скорости ветра в точке,
ез учета его пространственного распределения.
Дополнительно важным волнообразующим фактором явля-
зТся Уровень воды в водоеме: его определение — необходимое
jBeHo в расчетах элементов волн. При значительном (около
м и более) повышении уровня к гидротехническим сооруже-
iHM из-за увеличения глубины могут подходить более крупные
Лны, благодаря чему возрастают волновые нагрузки на со-
РУЖения. Понятие колебания уровня отнесем к таким возму-
ниям, период которых равен или превышает 1 мин. Спокой-
133
ным называется уровень, при котором отсутствуют ветровые
волны, но могут иметь место другие виды колебаний.
Различают такие виды колебаний уровня как приливы,
цунами, сейши, подъемы уровня, вызванные ветровыми волнами,
ветровые нагоны, климатические колебания уровня, вековые
колебания уровня. Первые пять видов колебаний характеризуются
периодами от нескольких минут до нескольких суток;
последние— охватывают периоды от сезона до многих лет.
Кратковременные колебания уровня воды, связанные с
воздействием ветра и атмосферного давления на водную
поверхность в виде повышения уровня воды — ветровой нагон, — могут
быть определены расчетным путем в тех случаях, когда
отсутствуют данные натурных наблюдений. Основной
характеристикой ветрового нагона является высота — расстояние по
вертикали отклонения поверхности воды от спокойного уровня
водоема, определенного с учетом других колебаний поверхности
воды.
Основными факторами, обусловливающими ветровой нагон,
являются скорость и направление ветра, величина отклонения
атмосферного давления от его среднего значения у
поверхности водоема, конфигурация береговой линии и рельеф дна и
прибрежной зоны водоема. В общем случае необходимо также
учитывать силу Кориолиса, течения и колебания уровня
другого происхождения, стратификацию воды и воздуха и другие
факторы.
5.2. ПАРАМЕТРЫ ВЕТРОВОГО ПОТОКА
НАД ВОДНОЙ ПОВЕРХНОСТЬЮ
Знание параметров ветрового потока над водной поверхно-ι
стью необходимо при решении многих инженерных задач, в том
числе, расчетах ветроволнового режима в районе строительства!
по данным синоптических карт и береговых наблюдений,
расчетах характеристик зон затопления побережий в результате
действия штормовых нагонов, при определении нагрузок от
ветра, волн и течений на гидротехнические сооружения^ пришвар-1
тованные суда.
Основные параметры воздушного потока: скорость ветра!
VWy коэффициент сопротивления CZi параметр шероховатости zl
и др. (см. параграф 5.1) могут быть получены с помощью
данных, снимаемых с приземных карт барической топографии
(синоптических карт), или стандартных гидрометеорологически»
наблюдений, выполненных на суше. При этом используют
методики, разработанные в [26].
Рассмотрим порядок расчета характеристик ветра по дан
ным синоптических карт. Расчет выполняют в два этапа. На
первом этапе определяют скорость градиентного ветра для
внешнего течения на границе планетарного пограничного сло^
134
моСферы, на втором — расчетную скорость ветра в приводном
слое.
Установившееся горизонтальное движение воздуха на
верхней границе планетарного пограничного слоя и выше по
криволинейной траектории при отсутствии сил трения называют
градиентным ветром. Скорость градиентного ветра Vg определяют
Из квадратного уравнения
-ί + ^νε±ψ-0, 5.9
где р — атмосферное давление; др/дп — барический градиент;
fk = 2Ω sin φ — параметр Кориолиса; Ω— угловая скорость
вращения Земли; φ — географическая широта; R — радиус
кривизны изобар; знак ( + ) перед третьим членом
соответствует ветру в циклоне, знак (—) —в антициклоне.
При градиентном ветре существует равновесие между
тремя силами, отнесенными к единице объема воздуха: барическим
градиентом др/дп\ силой Кориолиса pafkVg и центробежной
силой paV2g/R.
Барический градиент др/дп сообщает ускорение воздушному
потоку и является основной силой, вызывающей движение.
Сила Кориолиса pafkVg возникает во вращающейся системе
координат и связана с вращением Земли. При действии этой
силы воздушный поток получает относительно системы
координат поворотное ускорение,' направленное под прямым углом κ
скорости ветра. Эта'сила обращается в нуль у экватора и имеет
наибольшую величину на полюсе.
При криволинейном движении, кроме того, появляется
центробежная сила paV2g/R, которая направлена по радиусу от
центра циклонического образования.
Частным случаем градиентного ветра является
геострофический ветер, который представляет собой прямолинейное
равномерное движение воздуха вдоль изобар, происходящее таким
образом, что низкое давление остается слева от направления
Движения в северном полушарии (в южном —справа). Из
уравнения 5.9 для скорости геострофического ветра О (при R-+oo)
следует формула
G = -!_-^. 5.10
β тропической зоне океанов (при /л-^0) для ураганов и
тайфунов при круговых изобарах из 5.9 следует циклострофи-
Ческое приближение для скорости ветра:
β Циклоне с-круговыми изобарами (рис. 5.1, а) под
влияем барического градиента —др/дп частица воздуха получает
135
ускорение и начинает двигаться вдоль радиуса к центру. Как
следует из рисунка, барический градиент уравновешивает силу
Кориолиса и центробежную, а скорость движения частицы
направлена по касательной к изобаре против часовой стрелки в
северном полушарии (по часовой — в южном). Решение
уравнения 5.9 для циклонической кривизны изобар,
удовлетворяющее условию Vgc = 0 при др/дп = О, имеет вид
Vgc-
/?Λ/2 +
(ад2)2+£-ж
Ρα
1/2
5.12
PaWg-
В каждой точке
антициклона (рис. 5.1,6)
барический градиент направлен
вдоль радиуса от центра
к периферии. В случае
установившегося движения сила
Кориолиса уравновешивает
силу барического градиента
и центробежную. При этом
скорость ветра в каждой
точке антициклона
направлена по касательной к
изобаре по часовой стрелке
в северном полушарии
(против часовой стрелки —
в южном). Решение
уравнения 5.9,
удовлетворяющее УСЛОВИЮ Vga = 0 При
др/дп = 0 дли
антициклона, запишется следующим
образом:
^а = ЯЛ/2-
- [(ДА/2)2-f^f. 5.13
Формула 5.13 пригодна для расчета, когда удовлетворяется
неравенство
др/дп < Rfhpa/4
и скорость ветра не превысит максимально возможного
значения
(V*a)max = Я/*· 2.
Таким образом, при одном и том же расстоянии между
изобарами выполняется условие
PaWfr
Рис. 5.1. Градиентный ветер
а) циклон; б) антициклон.
Vga > G > Vgc.
136
Скорость ветра в циклонах, как правило, более высокая, чем
антициклонах, так как в циклонах барические градиенты
0 чНо превышают их значения в антициклонах.
Соотношения 5.12, 5.13 служат основой для расчета скорости
а над морем в циклонах и антициклонах по известному
ВоаДиенту атмосферного давления, снимаемому с приземных
синоптических карт. При этом осуществляется сращивание
решении ДлЯ скоростей градиентного (формулы 5.12, 5.13) и
приводного (5.5) ветра.
С учетом известных значении плотности воздуха ра =
= 1,25 кг/м3 (при температуре воздуха ta = 10°С), скорости
елового вращения Земли Ω = 7,29· Ю-5 с-1, длины градуса
меридиана, равной R = 60 т. mile, выражение для скорости
градиентного ветра в циклоне 5.12 принимает вид:
Vgc = axR sin (p+[(ai/? sin φ)2+α2(/?/α)]'/2, 5.14
где α— расстояние между изобарами, проведенными через
Др = 0,5кПа; R — радиус кривизны изобар, m.mile\ ab а2 —
размерные параметры.
Переход от скорости градиентного ветра Vgc к расчетной
скорости ветра Vw осуществляется с использованием
соотношения 5.5, а также трансцендентного уравнения
где А и В — эмпирические параметры, зависящие от условий
температурной стратификации атмосферы.
Уравнение 5.15 представляет собой известный закон
сопротивления Казанского — Монина.
Угол поворота приводного ветра относительно градиентного,
направление которого совпадает с осью х9 вычисляется по
формуле
sin a =
А Uf 5.16
Vgc*
Формулы 5.5, 5.6, 5.12, 5.15, 5.16 послужили основой для
Расчета скорости приводного ветра. По этим формулам,
относящимся к глубоководным акваториям (протяженностью более
W км), была построена номограмма для определения скорости
тетРа (на горизонте 10 м) Vw по данным, снимаемым с синоп-
ических карт приземной, барической топографии, а именно: по
Ηκ°°Ι>05ΙΗΗΚ) междУ изобарами a (m. mile) и по радиусу кривиз-
[5т ^т* т^е) (согласно рекомендуемому приложению 4*
тем Томограмма рассчитана для условий слабонеустойчивой
пературной стратификации, когда температура воздуха
д ЬЩе температуры воды, т. е. tw > ta> что чаще всего наблю-
Тся в условиях развития ветрового потока над океаном.
137
Поля скорости ветра по синоптическим картам приземной
барической топографии, когда над океанами и морями имеет
место слабоустойчивая или нейтральная температурная
стратификация, т. е. tw < ta, могут быть построены с использованием
номограммы, представленной на рис. 5.2.
Уи>,м/с
0,6 1 2 3 4 6 10 20 30 W 60 100 200 a,m.mile
Рис. 5.2. Номограмма для определения расчетной скорости ветра при
слабоустойчивой (и нейтральной) температурной стратификации по
данным синоптических карт при изобарах, проведенных через 0,5 кПа
я) φ > 50° с. ш.; б) φ = 35. . . 49° с. ш.
Номограмма^ (рис. 5.2, а) соответствует диапазону широт
φ ^ 50° с. ш., а номограмма (рис. 5.2,6) построена для φ =
= 35 ... 49° с. ш. Интервалы широт заданы таким образом, что
в их пределах скорость метра Vw меняется не более, чем
на 10 % из-за влияния параметра Кориолиса /*.
Расчеты по формуле 5.16 показывают, что в среднем для
условий океана направление ветра необходимо отклонять на
угол α = 15° от изобар в сторону низкого давления.
138
Скорость ветра в антициклоне обычно превышает не более,
чем на 10 % скорость геострофического ветра. Поэтому · без
больших погрешностей скорость ветра над морем при
антициклической кривизне изобар допустимо рассчитывать по
номограмме рекомендуемого в [511 приложения 4* и рис. 5.2 для
с^учая прямолинейных изобар (R = оо).
Пример 5.1
Требуется найти скорость ветра Vw на горизонте 10 м при
циклопической кривизне изобар, проведенных через 0,5 кПа для широты φ =
^ go0 с. ш. и tw — ta > 0; в окрестности расчетной .точки радиус кривизны
изобар Я = 600 т. mile, а расстояние между изобарами а = 60 т. mile.
Решение.
Входим, в номограмму приложения 4* [51] со значениями а = 60 m. mile,
β = 600 т. mile. Определяем значение Vw = 18 м/с.
Пример 5.2
Требуется найти скорость ветра Vw на высоте 10 м при
циклонической кривизне изобар, проведенных через 0,5 кПа. Широта φ = 60° с. ш.,
стратификация — слабоустойчивая, Δ/ = tw — ta < 0 °С; в окрестности
расчетной точки радиус кривизны изобар R = 600 m. mile, а
расстояние между изобарами а = 60 т. mile.
Решение.
Используя номограмму (рис. 5.2, а), по заданным величинам а =
= 60 т. mile и R = 600 т. mile определяем скорость ветра Vw = 14 м/с.
Пример 5.3
Требуется определить скорость ветра Vw при антициклонической
кривизне изобар (Δρ = 0,5 кПа) для широты φ = 40° с. ш. Значения
tw—ta, R, α —те же, что и в примере 5.2.
Решение.
Входим в номограмму (рис. 5.2, б) со значением а = 60 т. mile и
определяем при R = оо Vw в 22 м/с.
Пространственное распределение скорости ветра Vw,
вычисленное по картам приземной барической топографии, использу-
Ют при расчете элементов волн. Для расчета поля скорости
ветра акваторию равномерно покрывают сеткой с шагом 60...
•120 т. mile ц в каждом узле сетки рассчитывают скорость
ветра Vw по номограмме приложения 4* [51] для
слабонеустойчивой или по рис. 5.2 — для слабоустойчивой или нейтральной
гратификации атмосферы. Направление ветра в каждой точке
Уклоняют на угол 15° в сторону низкого давления. По резуль-
Татам расчета строят типовое поле скорости ветра.
При расчетах скорости ветра в прибрежной зоне необходимр
Учитывать горизонтально-неоднородные условия подстилающей
°верхности, ограниченные разгоны и встречающиеся обширные
елководные участки. В этом случае для определения скорости
етРа используют данные береговых метеостанций.
Пусть над исходной поверхностью суши характеристики воз-
УШного потока и подстилающей поверхности имеют следующие
и 0значения: скорость потока Vi{z)> динамическая скорость
п> тангенциальное трение τ0ι и параметр шероховатости гоь
139
Предположим, что переход к поверхности с новой
шероховатостью происходит скачком. Тогда исходный водный поток
деформируется и возникает внутренний пограничный слой (ВПС)
высотой δ, увеличивающийся вдоль потока. Выше слоя высотой
δ поток сохраняет свои первоначальные характеристики, а во
всей толще ВПС характеристики воздушного потока меняют
свои значения на V2{z), щг, тог- Профиль ветра над исходной
поверхностью и в слое ВПС зададим в виде логарифмического
(формула 5.5). Тогда:
Ух {г) = иП ΐη(*/*οι) ςΐ7
Иа(2г) ап Ιιιί*/^) ' ол'
Отношение динамических скоростей Uft/Uf2 определяют из
условия «склеивания» профилей скорости ветра на высоте
внутреннего пограничного слоя атмосферы ζ = δ, на которой
соблюдается равенство скоростей Vi(z) = 1^2(2). В этом случае
"/* = Jnjo/fog).
«/a In (*/*oO '
и из формулы 5.17 следует:
V\{z) _ Ιη(*/*ω) Ιπ(*/*οι) с ic
V2{z) ~ InCo/*01) hi (*/*,») - °Л
Соотношение 5.18 служит основой для определения скорости
ветра над водоемом по данным береговых станций.
Рассмотрим конкретный случай, когда ветровой поток
переходит с суши на поверхность водоема с характерной
протяженностью до 20 км; при этом скорость ветра Vw,
соответствующую десятиминутному интервалу осреднения, рассчитываем по
формуле
Vw^kfihVi, 5.19(149)*
где Vi — скорость ветра на высоте ζ = 10 м над поверхностью
суши; kfi — коэффициент пересчета данных по скоростям ветра,
измеренным по флюгеру; ki — коэффициент приведения
скорости ветра, измеренной на суше, к условиям водной поверхности.
Если скорость ветра Vi измерена с помощью анемометра
(или анеморумбографа) с десятиминутным осреднением над
водоемом, ровной песчаной, снежной, а также покрытой
гладким льдом поверхностью, то коэффициенты kfi — h = 1.
Коэффициент пересчета kfi данных по скоростям ветра,
измеренным по флюгеру, приводится к анемометрическим
измерениям (приложение 1, п. 9* [51])
kfi = Ofi75+Vo/Vi 5.20
при условии, что он не должен превышать единицу; V0 =
= 4,5 м/с.
При ветре, направленном с суши в сторону водоема, в
формуле 5.18 вводят следующие обозначения: V\(z)—Vi\ V2(z) =
140
703
ι/, ζοι = zos (где z0s — параметр шероховатости суши) и
Jzq. Тогда коэффициент ki рассчитываем из соотношения
*'~ У, ~ 1η(δ/*0) In (*/*<>*) '
5.21
По формуле 5.21 построен график на рис. 5.3 для нахожде-
коэффициента ki в зависимости от расстояния от берега L
Н скорости ветра на берегу Vi при данном типе местности.
И Параметр Zqs принимается в зависимости от типов
местности:
— тип А — открытые местности (степи, лесостепи, пустыни,
открытые побережья морей, озер и водохранилищ);
характерные значения Zqs = 0,035 м;
**г-
hO LjKm
Рис. 5.3. Зависимость коэффициента h при ветре со стороны
суши от величины разгона L и скорости ветра Vi при
параметре шероховатости суши zos'. 0,035 м— тип А\ 0,38 —
тип В\ 1,0 м —тип С.
— тип β — леса, сельские местности, территории больших,
кРУпных и крупнейших городов, застроенные зданиями высотой
*> 20 м; zos = 0,38 м;
тип С — территории больших, крупных и крупнейших го-
Родов
> застроенные зданиями высотой более 20 м; z0s = 1,0 м.
оысота пограничного слоя δ определена по эмпирической
формуле δ =:-0,25L0'54, где параметры δ и L даны в м.
с параметры шероховатости водной поверхности определяют
^Учетом последовательной смены режимов гладкого обтекания
На !!ачальных участках разгона, развивающейся шероховатости
зави Г0НН0м участке и полностью шероховатого обтекания по
зависи
мостям:
141
Zo =
m{u/L/vg
[m2u/lg
при
m0 == 43;
w1 = 2-10-11;
m2 = 0,021,
5.22
где ν — коэффициент кинематической вязкости воздуха.
Ориентировочные значения коэффициента ki для малых
водоемов (до 20 км) без учета влияния разгона приведены в
табл. 3* обязательного приложения 1 [51].
При ветре, направленном со стороны глубоководного
водоема большой протяженности на сушу, коэффициент ki в
формуле 5.19 (149) * определяют из графика рис. 5.4 по заданной
скорости ветра на берегу при данном типе местности. Графики
Таблица 5.1
Высота
ζ, м
2
4
6
8
10
12
14
16
18
20
30
40
50
100
Значение коэффициента kz
для типа
Μ
1,25
1.13
1,07
1,03
1,00
0,98
0,96
0,94
0,93
0,92
0,88
0,85
0,83
0,78
А
1,29
1,16
1,08
1,04
1,00
0,97
0,95
0,93
0,91
0,90
0,84
0,80
0,77
0,69
местности
В
1,42
1,22
1,12
1,05
1,00
0,96
0,93
0,90
0,88
0,86
0,78
0,74
0,70
0,60
с
1,70
1,35
1,18
1,08
1,00
0,94
0,89
0,86
0.83
0,80
0,70
0,63
0,59
0,47
tfi
12
т
10
15 20
25 30
ft
/\
35 Vi
Рис. 5.4. Зависимость коэффициента ki при
ветре со стороны акватории Vi при
параметре шероховатости суши z0s: 0,035 м —
тип Л; 0,1 м —тип Л'; 0,38 — тип В\ 1,0 м-
тип С.
рассчитаны по 5.18, в которой приняты обозначения: 20i = 2ц
Zo2 = zos\ Vi(z)= W, V2(z)=Vi. Параметр шероховатости
водной поверхности z0 вычислен по формуле 5.6, a z0s выбирался)
для заданного типа местности; высота приводного слоя б при!
ветре с водоема на сушу принята равной 200 м. |
Если скорость ветра измерена на любой высоте ζ на берегу)
для типов местности А, В, С, а также над открытой ровной
поверхностью, покрытой водой, снегом, песком, илом или гладким)
льдом (тип местности Λί, z0s = 0,0034 м), то приведение ее к
высоте ζ = 10 м выполняют по формуле Vi = kzVi{z), где kz —
коэффициент, принимаемый по табл. 5.1.
Пример 5.4
Скорость ветра Vi {ζ) = 25 м/с измерена на высоте ζ = 20 м по флюгер
ру; береговая метеостанция расположена на местности типа В. Требуется
определить скорость ветра Vw в пункте, расположенном на расстоянии L =|
= 30 км от берега, направление ветра —с суши.
142
решение.
ц0 табл. 5.1 для типа местности В определяем значение коэффициента
0 86; скорость ветра на высоте 10 м V/ = 25 · 0,86 = 21,5 м/с. Коэффи-
^/£// = 0,675+4,5/22 = 0,88 согласно 5.20. Коэффициент & = 1,25 опре-
и"ееН по графику рис. 5.3 для типа местности В, разгона L = 30 км и
скости ветра У ι = 21,5 м/с. Значение скорости ветра Vw над водоемом
Счисляем по формуле 5.19 (149)*: Vw = 0,88-1,25-21,5 = 23,6 м/с.
Пример 5.5
Скорость ветра на берегу Vi = 20 м/с измерена по флюгеру на высоте
Ю м. Требуется рассчитать скорость ветра над малым водоемом (до 20 км)
пон неизвестном разгоне и ветре с берега. Метеостанция расположена в
местности типа В.
решение.
Коэффициент кц = 0,675+4,5/20 = 0,9 согласно 5.20. Коэффициент ki =
- 1 26 определен по данным табл. 3* [51]. Значение скорости Vw вычисляем
,7о формУле 5Л9 (149> *: Vw = 20-0,9-1.26 = 22,7 м/с.
Пример 5.6
Требуется определить коэффициент ki и скорость ветра над
водоемом Vw при ветре, дующем^ со стороны водоема. Измеренная на берегу по
анемометру скорость ветра Vi = 20 м/с. Метеостанция расположена на
открытом побережье (тип местности Л).
Решение.
По графику рис. 5.4 определяем для типа местности А значение
коэффициента ki = 1,12. По формуле 5.19 (149)* находим значение скорости
ветра над водоемом: Vw = 1,12 · 20 = 22,4 м/с.
5.3. РАСЧЕТНЫЕ УРОВНИ ВОДЫ
Теоретической основой рекомендаций по расчету ветрового
нагона являются р.ешения уравнений гидродинамики в
приближении мелкой воды. Известно, что это приближение
выполняется тем лучше, чем меньше отношение глубины водоема d, м,
к длине волны λ, м, или к характерному горизонтальному
масштабу рассматриваемого процесса. В качестве такового в
случае ветрового нагона можно принять размеры атмосферных
барических образований, с которыми связаны изменения
атмосферного давления и скорости ветра. Оценку характерного
горизонтального масштаба можно выполнить, например, с помощью
Формулы (150) [51], которая связывает расчетную скорость
ветра VWf м, с соответствующим средним значением разгона
ч м. Из этой формулы следует, что даже при скоростях ветра
» = 50 м/с характерный горизонтальный масштаб L = 105 м
_ "ого больше, чем глубина океана. Таким образом применение
Уравнений мелкой воды к задачам о ветровом нагоне вполне
0пРавдано.
л fi я^опростых рекомендаций по расчету сгонно-нагонных ко-
аний уровня и, в частности, помещенных в [51], основан на
Шении уравнения следующего вида [10]:
143
где η — вертикальное смещение поверхности воды; d — глубина;
// = р/р; Δτ', = Δτ*/ρ; Ах'у = Аху/р;
ρ—атмосферное давление; ρ — плотность воды;
At* = %χ — Xxd) Аху = Ху — Xyd\
Vx> ty — компоненты тангенциального напряжения ветра на
поверхности воды; %Xd, τυα — компоненты тангенциального
напряжения у дна.
Решение 5.23 в общем виде возможно лишь численными
методами; заметим при этом, что здесь влияние силы Кориолиса
не учтено.
Важным этапом при разработке рекомендаций по расчету
высоты ветрового нагона на основе уравнения 5.23 является
задача определения тангенциальных напряжений на
поверхности воды и у дна. Тангенциальное напряжение ветра на
поверхности воды оценивают по формуле 5.2. Обычно используют
значения скорости ветра Vw и коэффициента сопротивления С*,
определенные на высоте г=10ы. В общем случае Cz зависит от
скорости ветра, разгона, стратификации приводного
пограничного слоя воздуха, а также от глубины водоема и других
факторов. Рекомендации по определению коэффициента
сопротивления Сг и тангенциального напряжения ветра τ0 содержатся
в параграфах 5.1 и 5.2.
Значительно меньше сведений имеется о тангенциальном
напряжении у дна Xd\ обычно его принимают равным Ο,ΐτο.
Расчет разности тангенциальных напряжений на поверхности и у
дна выполнен по формулам:
Δτο — xd = pkw V2W;
ft* = ««^-Ct0, 5.24
г
где aw = 0,85; pa/pw = 1,25· 10"3.
Коэффициент сопротивления d0 рассчитывают в
зависимости от скорости ветра по 5.8, а коэффициент kw — с учетом
соотношения 5.24. В зависимости от скорости ветра Vw коэф
фициент kw принимает значения, приведенные в табл. 2 * обя
зательного приложения 1 [51], с погрешностью до ±10%.
Рекомендации по определению тангенциальных напряжений
на поверхности воды и у дна были проверены в вычислению
высоты ветрового нагона при ураганах для некоторых пункта
побережья Кубы и Мексиканского залива. Проверка показала
U4
что
эти рекомендации значительно лучше удовлетворяют из-
ренным величинам высоты ветрового нагона, чем те, для ко-
рых первоначально было принято условие Сю = 2· 10-3 [26].
рассмотрим теперь частные случаи решения уравнения 5.23
соответствующие им примеры расчета высоты ветрового на-
11 на Процесс будем считать стационарным, т. е. атмосферное
г вление, скорость и направление ветра неизменными в течение
длительного промежутка времени. Предположим, кроме того,
что скорость и направление ветра не меняются по одной из
координатных осей (ось Оу).
В этой ситуации в урав- s&Vju ^
нении 5.23 можно пренеб- *■ АЬм±р
речь первым и третьим
членами в левой части и
вторым и четвертым членами —
в правой части. В
результате упрощений удается
получить решения,
относящиеся к следующим
случаям ветрового нагона.
1. Прибрежная
мелководная зона большого
водоема или континентальный
шельф имеют дно
постоянной глубины d\ ветер постоянной скорости Vw направлен в
сторону берега, и его направление составляет угол* aw с нормалью
к линии берега, рис. 5.5. В этом случае соответствующее
расчетное соотношение для определения высоты штормового нагона
&hset имеет вид '[10, 26]:
Vw*Lcosaw . + ДА
Рис. 5.5. Схема прибрежной
мелководной зоны постоянной глубины
/ — узловая точка.
Mset = ku
g
[d + ~2 Lhse4
5.25
гДе Ыгр = Δ/7/pg·; Δρ — отклонение атмосферного давления от
ег° средней величины.
Отклонение атмосферного давления от среднего значения на
*> кПа, вызывает статический подъем уровня Ahp = 0,1η, м.
Ь1соту ветрового нагона можно вычислить по формуле 5.25
Утем решения квадратного уравнения или последовательными
приближениями.
, При d^hhset и Δ/ΐ» = 0 (первое приближение) получаем
Формулу (148) [51].
Пример 5.7
τ
\щ обуется найти высоту ветрового нагона. Протяженность прибреж-
= Ю ^Лк°водной зоны от линии берега до свала глубин составляет L =
с n0D^M' ее глубина d = 5 м. Направление ветра составляет угол aw =■ 30°
м°сфепиЛЬЮ к линии берега, а его скорость Vw = 25 м/с. Отклонение ат-
Го давления от среднего значения на η составляет 1,2 кПа.
145
Решение.
Из табл. 2* [51] по значению скорости Vw = 25 м/с путем
интерполяции находим коэффициент kw = 2,55 · Ю-6. По величине отклонения
атмосферного давления от среднего значения (п = 1,2 кПа) находим величину
статического подъема уровня Ahp = 0,1 · 1,2 = 0,12 м. Положительный
квадратный корень уравнения 5.25 равен:
■(■
Г 2(kwVw*Lg-1 cos aw+Mipd)
■r-\
-l 5.26
Подстановка в 5.26 входящих в это соотношение величин дает:
В ЭТО СООТНО
λα /ς 0,12Ur2(2,5510-6252.104-9,81-1cos30o4-0,12.5) lt/2 ,1
ΔΛ^5-_^ (5^0Д2/2р +4 ~Τ
= 0,39 м.
Найдем теперь высоту ветрового нагона при тех же условиях методом
последовательных приближений. В этом случае соотношение 5.25 можно
записать так:
ΛΛ(ί)
Ληδ€ί
*(* + ±ы&1))
+ **,.
5.27
где /=1,2... — номер приближения. В первом приближении (i = 1)
полагают ΔΛ^7^= Δ^ρ*
Используя приведенные выше значения для величин, входящих в 5.27,
найдем в первом приближении
Во втором приближении
де=2,55.10-^1||^. +0,12 = 0,39 м.
Аналогично выполняется следующее приближение:
bhset = 0,39 м.
Таким образом, можно ограничиться вторым приближением.
2. Прибрежная
мелководная зона имеет дно с
постоянным уклоном т, рис. 5.6. Ветер
постоянной скорости Vw
направлен в сторону берега, и его
направление составляет угол
aw с нормалью к линии берега
При таких условиях расчетная
формула принимает вид [10.
26]:
Рис. 5.6. Схема прибрежной
мелководной зоны с постоянным уклоном
дна.
146
di — глубина, отвечающая кратчайшему расстоянию L от
Учетной точки до узловой; d — глубина в расчетной точке,
'глубину d\ и соответственно положение узловой точки оцени-
вают из условий:
gdx/V2w < 3, 5.29
(di—d)/L = m. 5.30
Соотношение 5.29 было получено с учетом предварительных
расчетов по формуле 5.28, которые показали, что для
большинства реальных ситуаций влияние глубоководной части на
высоту ветрового нагона около берега мало (не превышает 1 %).
расчет по формуле 5.28 выполняют методом
последовательных приближений, принимая в первом приближении Ш*^=Мр.
Пример 5.8
Необходимо найти высоту ветрового нагона на глубине d=l м при
скорости ветра Vw = 20 м/с. Прибрежная мелководная зона имеет постоян1
ный уклон дна /п/= 10~3, а с глубины rfi = 10 м дно резко понижается до
200 м и более. Ветер направлен по нормали к лини* берега. Отклонение
атмосферного давления от среднего значения составляет 1,5 кПа.
Решение.
Из табл. 2* [51] по значению скорости Vw = 20 м/с определяем
коэффициент kw = 2,1 · 10~6. По величине отклонения атмосферного давления от
среднего значения (п = 1,5 кПа) находим величину статического подъема
уровня Мр = 0,1 · 1,5 = 0,15 м. Вычисляем величину
_gg[L=9,8M0==0245
IV 202
и убеждаемся, что она удовлетворяет условию 5.29. С помощью
соотношения 5.30 находим расстояние от расчетной точки до узловой: .
d. — d 10—1
L=-±—-=-т—з- = 910з м.
Щ 10 3
С помощью формулы 5.28 находим в нервом приближении:
дед = 2,1.1(Г<2<Р-9.10»совО» ,„ ( 10 ) + 015 . 0>34 м;
Ш 9,81(10-1-0,15) U + 0,15/
во втором приближении имеем:
дМ2) = 2,Ь10-6.202.9.10з /_Ю_\ + 0>15 = 0>33 м.
set 9,81(10 — 1-0,34) \1 + 0,34/
"алогичным образом находим третье приближение:
Ш% = 0,33 м,
Как оно совпадает со вторым, принимаем его в качестве окончательного.
глубц!:рибрежная мелководная зона имеет дно с переменными
] Намц ветер постоянной скорости Vw направлен в сторону
147
берега под углом aw между нормалью и линией уреза. Изобаты
имеют прямолинейную форму и параллельны берегу;
атмосферное давление переменно в пространстве. В этом случае
формулу 5.28 можно преобразовать к виду:
m-'=Smv^
vsct
kwU)Vw(j)L(j)C0S aw
7+1
ΔΛ
seiij)]
In
*(/)
*<Ж) + *hset{j)
+
где / = 1, 2,..., η — номера участков
5.31
с постоянным уклоном
дна; L/ — протяженность /-го участка; άφ, d(/+i> — глубины со
ответственно в начале и конце /-го участка; Ahseta) —
возвышение уровня в начале /-го участка.
Величины kw(j), Vwu), Ahp(j) определяют как средние значе
ния на /-ом участке. В начале первого участка принимают зна
чения Ahset(Mi) = ΛΑρ(/=ΐ) или AhSet(j=ih если отклонение атмо
сферного давления от среднего не учитывается. Расчет пс
формуле 5.31 начинают либо с линии свала глубин, либо с
глубины, удовлетворяющей соотношению 5.29.
Пример 5.9
Необходимо оценить высоту ветрового нагона на линии берега, возмож
ную один раз в 10000 лет, на южном берегу залива в Средиземном море
где проектируется строительство АЭС.
Решение.
Поскольку .наибольшая величина ветрового нагона наблюдается πρι<
ветрах, направленных по нормали к линии берега, расчеты проведем для
штормов северо-восточных направлений. Режим этих ветров получен по ре
зультатам обработки синоптических карт погоды. Согласно полученному ре
жиму один раз в 10000 лет возможна скорость ветра Vw = 50 м/с. В соот
ветствии с табл. 4 обязательного приложения 1 [51] при этой скорости
ветра предельный разгон Lu = Ю5 м, что значительно превышает ширин\
прибрежного мелководья в заливе. Поэтому при расчетах можно принят!
Таблица 5.1
··»>
1
2
3
4
5
6
•^
ь?
50
·»*
3
4,8· 10" 3
а
V)
о
и
1
*
1,22· \0~в
ч"*
19200
4600
3100
1900
600
242
■ί"
100
50
25
20
10
5
+
ча*
50
25
20
10
5
0
>?
384
186
685
203
143
59
^
2,0
1,97
1,22
1,79
1,72
5,59
·«
Η
_с
0,693
0,678
0,199
0,631
0,545
1,720
-
0,325
0,153
0,166
0,156
0,095
0,124
11
< II
0,325
0,478
0,644
0,800
0,895
1,019
Примечание. Б таблице приняты следующие обозначения: Х= ^W{J)^w(jyS C0S7W
xl e Lu)ld(j) ~ d( Ж) - ΔΛω:
xd "" d( /)/(d( /+D + АА(У)):
r-X.XL.\nXd.
148
оость ветра постоянной на протяжении всего мелководья. Ветровой нагон
учитываем для нескольких профилей дна на участке побережья залива
Ра тяЖенностью около 25 км.
flP профили разбиваем на несколько участков с постоянными уклонами
Первый участок принимаем на глубине 100 м (начало свала глубин),
вторая удовлетворяет соотношению 5.29. Расчеты проводим по формуле
1\\ без учета статического подъема уровня ΔΛ,χ/), обусловленного
отклонением атмосферного давления от средней величины; результаты для одного
ιн1 профилей приведены в табл. 5.2, из которой следует, что высота ветрового
"агона составляет &hset^ 1,02 м.
4. Замкнутый водоем имеет прямоугольную форму и
постоянную глубину. Устойчивый по скорости ветер направлен вдоль
оси водоема, протяженность которого Ln, м. Отклонение уровня
за счет изменения атмосферного давления не учитывается,
рис. 5.7. Решение этой задачи можно получить так же, как
и решение предыдущих, используя уравнение 5.23.
4hset V
sys/ /// У// /// //у /s/ ν// /// //?.
._ L а
Рис. 5.7. Замкнутый водоем прямоугольной формы постоянной глубины
а) в плане; б) вертикальный разрез.
В замкнутом водоеме объем ограничен, и условие его
сохранения должно быть использовано при расчетах в явном виде.
Поставленная задача может быть решена на основе следующих
уравнений
(Ц kwVw* .
5.32
J (rf + η) d* = /,„</;
5.33
J (d + -n)ux = (Ln—xt)d9
5.34
где л;! —длина обнаженного участка дна, м.
Уравнение 5.32 непосредственно следует из 5.23.
Соотношения 5.33 и 5.34 выражают условия сохранения объема. Формула
·**-используется, когда все дно покрыто водой, а 5.34 — в том
в Учае, когда часть дна в результате перераспределения объема
Abi обнажается. Очевидно, что при Χι изменение уровня во-
η -!.Мпач СОставляет η = — d. Положение узловой точки (а: = х0 и
°) можно найти из соотношения
= 1-
Чтах = Ahset ПрИ X = L„.
1amax + 2т)Шах<*
2kwVw*Ln '
5.35
149
Решение приведенных выше уравнений можно получить
методом последовательных приближений, либо в графической
форме. В этом случае высота ветрового нагона определяется по
графикам рис. 5.8 следующим образом. По безразмерным
величинам
Ln* x~ g*
(L — разгон, расстояние от подветренного берега) из графика
рис. 5.8 получают безразмерную величину Ahset/d и вычисляют
высоту ветрового нагона Ahseu м.
Рис. 5.8. График для определения высоты ветрового нагона
khset.
В том случае, когда ветер направлен под углом aw к оси
водоема, величину/ι необходимо умножить на cosa^. Для
большинства реальных ситуаций дно водоема можно считать
горизонтальным, если выполняется условие
dmax/dmin < 1,5, 5.36
и при расчетах принять d = d, где d — средняя глубина
водоема, а rfmax, dmin — соответственно максимальная и минимальная
глубины.
150
Пример 5.10
требуется определить высоту ветрового нагона для замкнутого
ма без учета конфигурации береговой линии при следующих условиях.
ео со скоростью 25 м/с направлен под углом 30° к оси водоема,
протяжность которого Lrt = 5-104 м, расчетный створ находится иа расстоянии
_ 4 · Ю4 м от подветренного берега. Средняя глубина водоема d — 5 м,
1 ТСймальная dmzx = 6 м, минимальная dm\n = 4,5 м.
ма решение.
Находим отношение dmax/dmin - 6/4,5 = 1,33 < 1,5 и устанавливаем, что
водоема можно считать горизонтальным. Из табл. 2*· [51] находим
£■.2,55-10-· при V9 "~ ' ~
25 м/с. Рассчитываем безразмерные величины:
А = ±1°4 = о,8,
Ln 5-10*
/ - 2t55-l(r-6-253-5.10*cos30o = П9Я1
По графикам рис. 5.8 определяем khset/d«0,09, откуда находим вы-
:оту ветрового нагона khset = 0,09 · 5 = 0,45 м.
ца
й,Ч5
№1
-\
Рис. 5.9. График для определения положения узловой точки Хц.
5. Замкнутый водоем имеет сложную конфигурацию бере-
е°вой линии и переменные глубины; ветер направлен вдоль оси
водоема. В этом случае решение можно отыскать на основе
Уравнения 5.32, а в качестве условия сохранения объема
использовать следующее:
5.37
гДе θ —ширина водоема, м; W — полный объем водоема в от-
^Утствии нагона, м3.
Но Шение можно отыскивать либо численно с помощью соот-
°шений 5.32 и 5.37, либо методом последовательных прибли-
ений, используя рис. 5.8 и 5.9.
151
В первом приближении определяют среднюю глубину
водоема, и по величине Jx из графика рис. 5.9 находят x0/Ln и
положение узловой точки на оси водоема х0. Рассчитанные от
узловой точки в направлении высоты ветрового нагона Ahset
принимают положительные значения (нагон), а в противоположном
направлении — отрицательные (сгон). Начиная с х0, водоем
разбивают на отдельные участки таким образом, чтобы
учесть изменение его глубины и конфигурацию береговой
линии. Безразмерные величины Ahsetu)/^a) получают с помощью
рис. 5.8 при L/Ln = 1 и
__ kwVwtHLf
'2 1г
где /= ± 1; ±2 — номера участков, знак ± соответствует
нагону или сгону; аф — средняя глубина на /-ом участке с
учетом повышения (понижения) уровня на предыдущем участке.
Нарастания (убывания) уровня на /-ом участке &hs(n находят
из отношения Ак8ф/ац)\ высоту ветрового нагона (сгона) на
/-ом участке определяют по формуле
Последующие приближения выполняют аналогичным
образом; при этом положение узловой точки х0 рассчитывается из
соотношений:
Ww + WV) = 0, 5.39
j
^ш = 2А/МлА*(Л. 5.40
где В(/) — средняя ширина на /-ом участке, а знаки плюс и
минус означают суммирование соответственно с положительными
и отрицательными значениями AhSet{jy Расчет заканчивают при
выполнении условия
''Г'+'+Г<-'<0,1. Ml
которое позволяет получить расчетные величины с точностью
±5%..
Пример 5.11
Требуется определить высоту ветрового нагона в п. Μ водоема
(рис. 5.10); скорость ветра Vw = 25 м/с, направление — вдоль оси водоема.
Решение.
По табл. 2* обязательного приложения [51] принимаем коэффициент
kw = 2,55· Ю-6 при Vw = 25 м/с; в первом приближении определяем d и /2:
d = il±fk = 2A±±=:375M;J2= 2,55·10-6·252·5-10' = 057g
2 2 9.81-3.752
152
пим положение узловой точки: по графику рис. 5.д получаем x0/Ln =
^ал177 а следовательно х0 = 0,477-5. 104 = 2,38· 104 м. Разбиваем водоем
* той участка длиной AL(-d = 2,38- 104 м; Δί,(1) = 1,62- 104 м; Δί,(2) =
Η310·104 м и выполняем следующие вычисления:
J для первого участка
а/. ,) = 2,38· 104 м; d(-D = 5 м; £(-i) = 5- 103 м находим
при а ^
, = 2,55- ΙΟ"" 6·25?· 2,38 -10* = 0 155
2 9,81-52
затем из рис. 5.8 по значению /2 для L/Ln = 1 имеем
Mhen-i)ld(-i) = 0,09 или
Д/г*е/(-1) = —0,45;
— для второго участка
при AL(D = be2·104 м; ^c)-=5w;
β(1) = 5· 103 м находим
2j5.1Q-6-25M,62.10* = 0 105
J2- 9,8 Ь 52
и затем соответственно из рис. 5.8
имеем
ΔΑ5«/(ΐ>Λ*(ΐ> = 0,07 или
khset(i) = 0,35 м;
м
Уш=25м/с
*)
— для третьего участка
при AL(2) = 1,0· 10* м; d(2) = 2,5+ tf Λ
+ ΔΛ„/(ΐ) = 2,5 + 0,35 = 2,85 м; У[
β(2) = 2,5· 103 м находим
Λ
///, /V7, S//U/AU//U//
Β2=β5·10*Μ
/// ///
ιό
/// V// ///
/// ' ///.' //ΛΑ
j = 2,55 · ΙΟ"6· 252 .\.\qj = 0 20
2 9,8 Ь 2,85* ' „ Г1Л „
Рис. 5.10. Схема к определению высоты
и затем также из рис. 5.8 имеем ветрового нагона при переменной глу-
ДЛ,е/(2)/^(2) = 0,11 или бине и ширине водоема
А, а) вертикальный разрез; б) водоем в плане.
ΔΛ5β/(2) = 0,31 м.
Таким образом, (Miset)s = Miset(i)+Ahset{2) = 0,35+0,31 = 0,66 м.
Определяем значения Wi+) и №<->:
W<+) = θ(ΐ)ΔΛ,β/(ΐ)ΔΙ(ΐ)+θ(2)ΔΛίβ/(β)ΔΙ(2) = 5 - ΙΟ3 - 0,35 -1,62 · 104 +
+2,5 · ΙΟ3 · 0,66 · Ы04 = 4,5 · ΙΟ7 μ3;
№(_) = θ(-ΐ)ΔΛ,β/(-ΐ)ΔΙ(-ΐ) = —5,36- ΙΟ7 μ3.
Поскольку ! <±ΙΖ iizli = °;8^ = 0,19 > 0,1, выполняем расчет вто-
Wt
(+)
4,5
jj0r° приближения. Возьмем λτ0 = 2,2·104 μ, т. е. меньшую величину, чем
первом приближении. В этом случае имеем следующие три участка и со-
пп,*ТствУюш«ие им величины, которые определяем так же, как в первом
•фиближении:
Д{-(-1) = 2,2- 104 м; d{-x) = 5 м; В{-х) = 5- 103 м; ΔΑ,β/(-ι> = —0,425 м;
ΔΙ(ΐ) = 1,8- 104 м; d(i) = 5 м; В(1) = 5· 103 м; ΔΛ,β/(ΐ> = 0,375 м;
AL(2) = 104 м; dw = 2,5+0,375 = 2,875 м; Bi2) = 2,5 · 103 м;
AhSei(2) = 0,31 Μ,
0Т1<УАа (bhset)s = 0,375+0,31 = 0,685 м.
153
Находим величины:
W{+) = 5,09 . 107 м; UP(-, = — 4,68. ΙΟ7 м3.
Поскольку \W{+) + W(-)\IWi+) = 0,081 < 0,1 ограничимся расчетом
второго приближения и принимаем величину нагона в п. Μ (рис. 5.10): Ahset^
^0,68 м.
Расчетный уровень воды на акваториях, для которых
имеются многолетние ряды натурных наблюдений, определяют по
результатам статистической обработки. Обеспеченность
наивысших годовых и среднегодовых уровней рассчитывают по
формуле [47]:
_ (n + k)
п~~ (ЛГ + т)'
МПУ
7 нм ΑΛν
Рис. 5.11. Типы уровней
УНБ — уровень нижнего бьефа; УВБ — уровень
верхнего бьефа; ФПУ — форсированный
подпорный уровень; НПУ — нормальный подпорный
уровень; МПУ — минимальный подпорный уровень.
5.42
где я — номер члена
ряда, расположенного
в порядке убывания;
N — общее число
членов ряда; k = —0,3;
т = 0,4 — эмпирические
параметры.
Обычно на
водохранилищах различают уровень
верхнего бьефа (УВБ) —
по течению выше
плотины, и уровень нижнего
бьефа (УНБ) — ниже
плотины. В УВБ
рассматривают форсированный
подпорный уровень (ФПУ), нормальный подпорный уровень
(НПУ), минимальный подпорный уровень (МПУ). ФПУ
формируется во время паводка, МПУ наступает при минимальном
стоке, НПУ является характерным «рабочим» уровнем
водохранилища (см. схему на рис. 5.11).
Тип уровня учитывают при определении сочетания
обеспеченности уровня и скорости ветра согласно рекомендациям
п. 8* обязательного приложения 1 [51].
Пример 5.12
При проектировании берегоукрепления в виде бун (IV класс
капитальности), и в виде подпорной гравитационной волноотбойной стены (II класс
капитальности) требуется определить расчетный уровень. Период наблюдений
над уровнем 25 лет (число членов ряда N = 2Ь). Исходные данные
представлены в табл. 5.3 (столбцы 1—4).
Решение.
Согласно требованиям, приведенным в п. 5* обязательного приложения 1
[51], для берегоукрепления в виде буи (IV класс капитальности) необходимо
принимать отметки уровня с обеспеченностью 50 % по среднегодовым
уровням, а для подпорной гравитационной стены II класса — 1 % по наивысшим
годовым уровням.
154
Таблица 5.3
пп.
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Гол
2 |
1948
1949
1950
1951
1952
1953
1954
1955
1956
1957
1958
1959
1960
1961
1962
1963
1964
1965
1966
1907
1968
1969
1970
1971
1972
Уровни, ι
среднегодовые
3
-0,49
-0,44
-0,26
-0,17
—0,23
-0,18
-0,33
-0,23
-0,26
-0,32
-0,21
—0,24
-0,25
-0,26
—0,28
—0,21
-0,28
-0,19
—0,29
—0,24
-0,26
-0,16
-0,16
-0,23
-0,24
*hseV M
наивысшие
годовые
4
-0,09
-0,09
0,15
0,42
0,52
0,39
-0,01
0,11
0,06
-0,08
0,21
0,44
0.4
0,01
0,09
0,09
0,17
0,43
0,47
0,51
0,52
0,75
1 0,76
! 0,54
0,34
Уровни в порядке убывания
год
5
1969
1970
1951
1953
1965
1958
1963
1971
1955
1952
1959
1967
1972
1960
1950
1956
1961
1968
1962
1964
1966
1957
1954
1949
1948
среднегодовые
6
-0,16
-0,16
-0,17
-0,18
-0,19
-0,21
-0,21
-0,23
-0,23
-0,23
—0,24
—0,24
-0,24
-0,25
-0,26
-0,26
—0,26
-0,26
-0,28
—0,28
-0,29
—0,32 .
-0,33
^-0,44
-0,49
год
7
1970
1969
1971
1952
1968
1967
1966
1959
1955
1951
1960
1953
1972
1958
1964
1950
1955
1962
1963
1956
1961
1954
1957
1948
1949
наивысшие
годовые
8
0,76
0,75
0.54
0,52
0,52
0,51
0,47
0,44
0,43
0,42
0,4
0,39
0,34
0,21
0,17
0,15
0,11
0,09
0,09
0,06
0,01
-0,01
—0,08
-0,09
—0,09
Располагаем данные табл. 5.3
в порядке убывания уровней
(столбцы 5—8) и по формуле 5.42 для
каждого η определяем Fn. По
значениям Fn и соответствующим им
нанесшим годовым и среднегодовым
Уровням строим режимные функции,
Р»с. 5.12.
Экстраполируем режимные
функции в область малых обеспеченно-
стей и снимаем:
Аля F - 1 о/0 η = 0)95 м.
5 10 2030¥) 00 80 9095 F,%
Рис. 5.12. Обеспеченность годовых
уровней
/ — среднегодовые; 2 — наивысшие
годовые.
54. ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ЭЛЕМЕНТОВ ВОЛН
Изменчивость элементов волн в каком-либо фиксированном
стоп6 Любого водоема целесообразно рассматривать, с одной
де(Р°Ны> в пределах малого интервала времени, измеряемого
Не уТКами минут, в течение которого средние элементы волн
Успевают существенно измениться, и, с другой стороны, за
155
большие интервалы времени, измеряемые
десятками лет, в пределах которых
эволюционируют практически все
характерные для рассматриваемого района
штормовые ситуации. В первом случае
изменчивость элементов волн как случайных
объектов, описывают с помощью их
функций распределения в системе волн,
а во втором — с помощью режимных]
функций распределения.
Функцией распределения какого-либо!
элемента волн называют соотношение
устанавливающее функциональную связь
между возможными значениями этого
элемента и соответствующими им
вероятностями. Различают
дифференциальную функцию распределения или
плотность распределения f(x) случайной
величины X, характеризующую вероятность
того, что случайная величина X примет
значение в интервале между χ и χ+άχ\
и интегральную функцию распределения
или функцию обеспеченности ,F(x) той
же случайной величины; последняя
определяет вероятность того, что случайная
величина X примет значение, большее х\
Рассмотрим функции распределения!
элементов волн в системе.
Основными элементами нерегулярных!
волновых колебаний свободной поверх-ι
ности в фиксированной точке водоема
являются высота и период. Эти элемента
фигурируют при анализе волнограмм^
отрезков непрерывной волнообразной
кривой изменения во времени возвыше
ния свободной поверхности в фиксиро]
ванной точке водоема, рис. 5.13.
Высоту индивидуального колебание
на волиограмме определяют как расстоя
ние по вертикали от индивидуального
максимума (вершины), расположенного
над средней волновой линией, до бли
жайшего минимума (подошвы) ниже
той же линии. Периодом Τ индивидуаль
ного колебания на волнограмме назы
вают промежуток времени между двумя
соседними максимумами (вершинами)
и минимумами (подошвами), расположенными выше (или
^же) средней волновой линии.
1,11 Средняя волновая линия на волнограмме обладает тем
йством, что площадь, ограниченная ею и вышележащей
Састью кривой хода уровня, равна площади, ограниченной той
4 линией и нижележащей частью кривой.
Промежуток времени, охваченный анализируемой волно-
гРаммой, должен быть, с одной стороны, достаточно большим,
в нем должно укладываться такое количество индивидуальных
колебаний, которое позволило бы судить об их изменчивости
при данной силе волнения. С другой стороны, этот промежуток
времени должен быть настолько мал, чтобы в его пределах не
произошло значительное изменение средних элементов
волнения. Обычно продолжительность записи волн, удовлетворяющая
обоим требованиям, составляет 20.. .40 мин при средних
периодах волн 5... 10 с, если исследуется изменчивость какого-либо
одного элемента. Если же интересоваться совместной
изменчивостью высот и периодов, то необходимо выбирать условия,
когда средние элементы волн мало меняются в течение многих
часов, и производить значительно более продолжительные
записи в течение часа- и более. Аналогичные определения
относятся к длине волны. Главное направление распространения
волн определяют по направлению той вертикальной секущей
плоскости в сторону бега волн, для которой средняя длина волн
соответствующего волнового профиля минимальна. Профили
строят по сериям планшетов стереофотосъемки волнения,
выполняемой обычно с самолета. Для обработки используют
профили, содержащие около ста индивидуальных волн.
Функции распределения элементов (высоты, длины и
периода) индивидуальных волн в системе обычно представляют в
безразмерной форме. Для этого значение элемента с
фиксированной вероятностью принимают за единицу измерения и
выражают все другие значения элемента в долях от принятой
единицы. Обычно за единицу измерения берут среднее значение
элемента.
Установлено, что функция обеспеченности высот волн в
системе на глубокой воде совпадает с распределением Рэлея и,
бУДучи записанной в безразмерной форме, имеет вид [23]:
F (h/h) = ехр [- ^ (А/А)*], 5.43
пРи безразмерлых разгонах
gL/V*w^\,\-\0\ 5A4
Де ^--вероятность превышения безразмерной высоты h/h.
После логарифмирования функция 5.43 запишется в виде:
А/А = ^~V^^F^\J\2{-\gF)^. 5.45
У7·
157
Безразмерная функция обеспеченности высот волн
gL/V2w< 1,1 ·104 5.46
имеет более сложную структуру, отражающую ее зависимость
от безразмерного разгона [24, 55]:
F(h/h) = ехр [- Г* (Л- + l) (A/A)2*], 5.47!
где
0.5-103
{gLlV*w)w + 3,9.10»·
Г — гамма-функция.
Зависимость вида 5.47 называют распределением Вейбулла;
при φ= 1 оно переходит в 5.43 — распределение Рэлея.
Качественное отличие формул 5.47 и 5г48 от 5.43 состоит в том, что
они дают закономерное уменьшение изменчивости высот в
системе волн по мере уменьшения разгона. В количественном
отношении это уменьшение невелико, поскольку при уменьшении
параметра gL/V2w от 104 до 10 функция φ, учитывающая
влияние разгона, увеличивается от 1,0 до 1,3. Выражение 5.47 после
логарифмирования запишется так:
Α/Α = Γ-ι(^ + ΐ)[-1η^]2\
5.49
где зависимость параметра φ от величины безразмерного
разгона gL/V2w определяется формулой 5.48.
Функция распределения 5.43 выведена из теоретических
соображений и подтверждена многочисленными натурными
данными. Зависимость 5.47 для безразмерных разгонов gL/V2w
от 5 до 2-104 получена на основе анализа натурных измерений
в Черном и Баренцевом морях с помощью волнографов и
серийной стереофотосъемки, а также лабораторных данных в
ветроволновом лотке.
Функция распределения высот волн в прибрежной
мелководной зоне была получена в Государственном
океанографическом институте на основе анализа волнограмм в одном из
мелководных районов Каспийского моря, а затем проверена для
других морских районов [23, 24]; оказалось, что она зависит
от безразмерного параметра
hN = h/d 5.50
и удовлетворяет распределению Вейбулла следующего вида:
Р(ВД = ехр[- 4(,+· (А)-»"]
5.51
или
158
1-Лдг
A/A = [-^(l+0,4Aiv)ln/7] 2 . 5.52
Эту функцию рекомендуется использовать в расчетах волне-
I ,а прибрежной зоны глубоководных морей при уклонах дна
ft 0,02 ДО 0,002.
Введем коэффициент перехода от средней высоты h к высо-
те волн *%-ной обеспеченности:
Ь% = ^. 5.53
Λ
Тогда формулы 5.49 и 5.52 запишутся в виде:
ki% = Г-* [± + l) [—ln/+2 In 10p*, 5.54
Λ/Η = |.± (l + 0,4Алг) [-=- In i + 2 in 10]| 2 . 5.55
В расчетах обычно фигурируют высоты £%-ной
обеспеченности, где I = 0 1; 1,0; 2,0; 5,0; 13,0 %.
Высота /ΐο,ι?ί близка к наибольшей в данной системе воли;
ее используют, например, при назначении верхней отметки на-
Таблица 5.4
Коэффициенты (ki%)d в глубоководном водоеме
для /%-ной обеспеченности при gL\V*w
*W*w
ю.
50
• 100
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
5500
6000
6500
7000
7500
8000
8500
9000
9500
10000
10500
иооо
0,1
2,41
2,43
2,44
2,50
2.55
2,58
2,62
2,64
2,67
2,69
2,71
2,73
2,75
2,77
2,79
2,80
2,82
2,84
2,85
2,87
2,88
2,90
2,91
2,92
2,94
1,0
2,05
2,07
2,08
2,12
2,15
2,17
2,19
2,21
2,23
224
2,26
2,27
2,28
2,29
2,31
2,32
2,33
2,31
2,35
2,36
2,37
2,38
2,39
2,39
2,40
1%
2,0
1,93
1,94
1,94
1,98
2,01
2,03 '
2,04
2,06
2.07
2,08
2,10
2,11
2,12
2,13
2,14
2,15
2,15
2,16
2,17
2,18
2,19
2,19
2,20
2,21
2,22
5,0
1,73
1,74
1,75
1,77
1,79
1,81
1,82
1,83
1,84
1,85
1,86
1,86
1,87
1,88
1,89
1,89
1,90
1,90
1,91
1,92
1,92
1,93
1,93
1,94
1,94
13,0
1,49
1.50
1,50
1,5!
1,52
1,53
1,54
1,54
1,55
1,56
1,56
1,56
1,57
1,57
1,58
1,58
1,58
1,59
1,59
1,59
1,60
1,60
1,60
1,60
1,61
159
стила нефтедобывающих сооружений в море; h\% и Аг%
закладывают в расчеты волновых нагрузок и наката волн на
гидротехнические сооружения, а къ% — при анализе защищенности
портовых акваторий.
В табл. 5.4 приведены вычисленные по формулам 5.54 и
5.48 коэффициенты Ы% для указанных выше значений / и
различных-значений безразмерного разгона gL/V2w (см. рис. 2
обязательного приложения 1 [51]). '
В табл. 5.5 даны коэффициенты ki%, вычисленные по
формуле 5.55 для тех л<е обеспеченностей / % и различных
значений параметра км = h/d.
Таблица 5.5|
Коэффициенты kiK в прибрежной зоне
для *%-ной обеспеченности и Ttjd (при уклонах дна 0,02 .^0,002)
h\d
0,01
0,025
0,050
0,100
0,150
0,200
0,250
0,300
0.350
0,400
0.500
i%
0,1
2,94
2,90
2,84
2,71
2,59
2,47
2,34
2,23
2,12
2,01
1,81
*.ο
2,40
2,38
2,34
2,26
2,17
2,09
2,01
1,93
1,85
1,78
I 1,63
2,0
2,22 ί
2,20
2,16
2,10
2,03
1,96
1,89
1,82
1,76
1,69
I 1,56
5,0
1,94
1,93
1,89
1,86
1,81'
1,76
1,71
1,66
1,61
1,56
I 1,46
13,0
1,61
1,60
1,59
1,56
1,54
1,51
1,48
1,45
1,42
1,39
1,33
Данные табл. 5.5 служат для уточнения расчетов элементов
волн в прибрежной мелководной зоне глубоководного водоема,
выполняемых по нормам [51] с учетом обобщенного
коэффициента потерь ki (см. табл. 5 приложения 1). По определению,
обобщенный коэффициент потерь ki равен отношению
ki%l(ki%)di где ki%, \ki%)d — коэффициенты (см. формулу 5.53)
для условий мелководной прибрежной и глубоководной зон,
соответственно. Переход от значений h/d в табл. 5.5 к значениям
d/λ в табл. 5 [51] осуществляется из условия d/λ = h/K:h/d =
= 0,028- (h/d)-\ где Λ/λ"= 0,12-2π/5·22 = 0,028 определено по
графику рис. 1 приложения^ 1 при gL/V2w ^ 3· 104. Например,
при h/d = 0,4, находим d/λ = 0,028/0,4 = 0,07. Соответственно
при уклонах дна 0,02... 0,002, для которых справедлива
формула 5.54, получаем из табл. 5: h = 0,82 _при d/Kd = 0,07.
С другой стороны, согласно табл. 5.5 при h/d = 0,4, kn% -
= 1,78/2,40 = 0,74 (i % = 1); km%= 1,39/1,61 = 0,86 (/ % = 13).
Значения1 kt, найденные по нормам [51], с погрешностями,
не превышающими ±15%, согласуются с приведенными выше,
более точными вычислениями.
160
интегральную безразмерную функцию распределения высот
еТровых волн в мелководном водоеме с глубиной d
предлагается определять, используя формулы 5.47, 5.48, в которых без-
еазмерный разгон gL/V2w заменен на безразмерную глубину
L//W отвечающую той же безразмерной высоте волн [55].
Такой прием основан на гипотезе о том, что изменчивость высот
/в системе волн) в мелководном водоеме растет с увеличением
пазгона в соответствии с закономерностью на глубокой воде
Таблица 5.6
Коэффициенты kl% для мелководного водоема
при значениях /%-ной обеспеченности и gdjVw2
lvw
),025
),050
),075
),100
),125
),150
3,175
),200
3,225
3,250
3,275
),300
3,325
3,350
3,375
3,400
0,425
(3,450
0,475
0,500
0,525
0,550
0,575
0,600
0,625
0,650
0,675
0,700
0,725
0,750
3,775
3,800
),825
),850
Х875
5,900
Ч Лги-
ϋ.925
1 Пгл
и,950
У>975
1,000
1%
0,1
2,41
2,42
2,43
2,44
2,45
2,46т
2,46
2,47
2,48
2,49
2,50
2,51
2,52
2,53
2,54
2,55
2,57
2,58
2,59
2,60
2,61
2,62
2,64
2,65
2,66
2,68
2,69
2,71
2,72
2,74
2,76
2,77
2,79
2,81
2,83
2,85
2,87
2,89
2,92
2,94
1,0
2,05
2,06
2,07
2,07
2,08
2,09
2,09
2,10 '
2,10
2,11
2,12
2,12
2,13
2,14
2,14
2,15
2,16
2,17
2,17
2,18
2,19
2,20
2,21
2,22
2,22
2,23
2,24
2,25
2,26
2,27
2,29
2,30
2,31
2,32
2,33
2,35
2,36
2,38
2,39
2,40
2,0
1,93
1,93
1,94
1,94
1,95
1,95
1,96
1,96
1,97
1,97
1,98
1,99
1,99
2,00
2,00
2,01
2,01
2,02
2,03
2,03
2,04
2,05
2,05
2,06
2,07
2,08
2,08
2,09
2,10
2,11
2,12
2,13
2,14
2,15
2,16
2,17
2,18
2,19
2,21
2,22
5,0
1,73
1,74
J.74
1,75
1,75
1,75
1,76
1.76
1.77
1,77
1.77
1,78
1,78
1,79
1.79
1,79
1,80
1,80
1,81
1,81
1,82
1,82
1,83
1,83
1,84
1,84
1,85
1,86
1,86
1,87
1,87
1,88
1,89
1,89
1,90
1,91
1,92
1,93
1,94
1,95
13,0
1,49
1,49
1,50
1,50
1,50
1,50
1,50
1,51
1,51
1,51
1,51
1,52
1,52
1,52
1,52
1,53
1,53
1,53
1,53
1,54
1,54
1,54
1,54
1,55
1,55
1,55
1,56
1,56
1,56
1,57
1,57
1,57
1,58
1,58
1,58
1,59
1,59
1,60
1,60
1,61
161
вплоть до вполне определенной величины разгона, начиная с
которой элементы волн и их изменчивость в системе зависят
уже только от глубины и не зависят от разгона. В соответствии
с таким подходом функция распределения высот волн в
мелководном водоеме с глубиной d определяется той же формулой
5.47, в которой на этот раз
φ = 0,5103{2,8104[(ΐ ~ 0,625(^)°'8)"0,5--l] +3,9-102}""1. 5.56
Соответствующие коэффициенты перехода от h к /i/%,
вычисленные по формулам 5.54 и 5.56, представлены в табл. 5.6 и
на графиках рис. 2 приложения 1 [51].
Из формул 5.43—5.56 видно, что интегральные функции рас-,
пределения в системе волн позволяют рассчитывать
вероятность, т. е. частоту появления значения элемента волн,
превышающего заданное значение, в том случае, когда известно
среднее значение этого элемента в системе волн. Именно это
свойство функций обычно используют в практике гидротехнических
расчетов.
Формулы 5.43—5.56 кроме того указывают на то, что
структура этих функций зависит от условий волнообразования и,
в частности, от скорости ветра, разгона волн и глубины.
Приведем примеры, иллюстрирующие практическую пользу
формул 5.43—5.56.
Пример 5.13
При ветре V^ = 20 м/с с берега на расстоянии L = 600 км от берега
в глубоководном море сформировались ветровые волны со средней
высотой hd = 4,2 м. Требуется определить высоту волн 1 %-ной обеспеченности
в системе.
Решение.
Величина безразмерного разгона в данном случае, равная
gLIVj- »*'ун» =М7.,0<)
больше величины 1,1-104. Из последней строчки табл. 5.4, отвечающей
безразмерному разгону gL/V2& = 1,1 · 104, находим значение коэффициента
£1% = 2,40; с учетом формулы 5.53 получаем:
hi% ^~hdki% =4,2.2,40=10,1 м.
Пример 5.14
При ветре Vw = 32 м/с с берега на расстоянии L = 1 км от берега в
глубоком море сформировалась система ветровых волн со средней
высотой hd = 0,63 м. Требуется определить 1г1% в этой системе волн.
Решение.
В данном случае безразмерный разгон
gLI VV = 9>83У°3 = 9,58 < 1Д. 10*.
162
Согласно первой строчке табл. 5.4, соответствующей gL/V2w = 10, имеем:
- 2 05. Поэтому
h\% = k\%h(l = 2>05·°>63 = 1& м·
Пример 5.15
Требуется вычислить h0l%t hx% и Л5% в фиксированной точке прибреж-
а зоны с уклонами дна в пределах от 0,02 до 0,002 при шторме, если из-
стно, что средняя высота в этой точке h = 4,0 м, а глубина d = 16,0 м.
решение.
Вычисления необходимо проводить, используя табл. 5.5, описывающую
функцию распределения высот волн в прибрежной зоне с уклонами дна от
002 до 0,002. При безразмерном параметре hid = 4,0/16 = 0,25:
\х% = WA = 2,34-4,0 = 9,4 м.
Аналогично находим:
hl% = kl%h = 2,01 -4,0 = 8,0 м;
Лби=Аб*Л = 1,71-4,0 = 6,8 м.
Пример 5.16
При ветре Vw = 32 м/с в открытой части мелководного водоема с
глубиной d = 10 м сформировались ветровые волны с зысотой h = 1,6 м.
Параметры волн определяются глубиной водоема и скоростью ветра.
Требуется определить h^x%t hl%i h5%.
Решение.
Вычисляем значение безразмерной глубины gd/V2w = 9,81 · 10/322 ^ 0,096.
С помощью табл. 5.6 для gd/V2w = 0,096 находим к§л% =2,44; k{% =2,07;
*5% = 1,75. Следовательно, h0A% = 2,44 · 1,6 = 3,9 м; ' hx% =2,07 · 1,6 = 3,3 м;
hb% -1,75.1,6 = 2,8 м.
Помимо высоты, важной характеристикой волн является их
период Т. Интегральная безразмерная функция распределения
периодов и для глубоководного и для мелководного водоемов
описывается следующей формулой [23]:
F (Ti%l7d) = ехр [- Г* (5/4) (W]. 5.57
Коэффициенты перехода {ki%)T = TiyJTd для различных зна-
ений обеспеченности и %, вычисленные по формуле 5.57,
предъявлены в табл. 5.7.
Таблица 5.7
I
1,58
20
1,21
1,51
• 30
1,13
1,47
40
1,05
1,42
50
0,98
ю
1,33
75
0,79
.163
Пример 5.17
Средний период ветровых волн Td = 7,0 с. Требуется вычислить
наибольший период ста последовательно бегущих волн Тх%.
Решение.
Согласно табл. 5.7 имеем: Tl% = fd-1,58 = 7,0· 1,58 = 11,1 с.
Приведенные выше функции распределения высот и
периодов волн характеризуют изменчивость каждого из этих
элементов в отдельности за небольшой интервал времени (в несколь^
ко десятков минут) вне зависимости от значения другого
элемента. Между тем каждая индивидуальная волна на волно-
грамме характеризуется одновременно по крайней мере двумя
элементами: высотой и периодом. Поскольку волны с
различными высотами и периодами по разному воздействуют на
гидротехнические сооружения, важно уметь отвечать на вопрос:
какими периодами обладают волны с высотой 1%-ной
обеспеченности?
Для выяснения этого вопроса используют функции условных
распределений элементов волн:
а) дифференциальная функция условного распределения)
f(x/y) характеризует вероятность того, что случайная величина'
X примет значение в интервале между χ и x+dx при
фиксированной величине у\
б) интегральная функция условного распределения F{xty)
определяет вероятность того, что случайная величина X примет
значение, большее χ при фиксированной величине у.
Интегральные функции условного распределения периодов
волн F(T/h) при фиксированной высоте, равно как и
аналогичные функции высот волн F(h/T) при фиксированном периоде,
получены на основе обработки волнограмм, каждая из которых
содержала большое количество индивидуальных волн. Были
использованы волнограммы ветровых волн и зыби, на которых
зафиксировано около 25 тыс. волн f 13"|. В результате анализа,
во-первых, установлено, что функции F(T/h) и F(h/T)
подчинены распределению Вейбулла и, во-вторых, оценены
параметры распределений. В частности, было получено условное
распределение относительных
периодов для волн с различной
фиксированной относительной
высотой. Периоды и высоты
относили к их средним значениям
(табл. 5.8).
В первом столбце таблицы
указаны интервалы
относительных высот волн, которые
считаются фиксированными.
Например, интервал 1,8 ... 1,99
(четвертая строчка первого столбца)
Таблица 5.8
h\h
1,2... 1,39
1,4... 1,59
1,6... 1,79
1,8... 1,99
2,0... 2,19
2,2... 2,39
2,4 ... 2,59
Thlf
1,10
Ы1
1,13
1,14
1,16
1,18
1,19
kT
4,0
4,4
4,8
5,3
6,0
7,4
10,0
АТ
0,675
0,664
0,656
0,647
0.638
0,622
0,606
164
ι а3ь1вает на то, что в этой строчке рассматриваются волны с
относительными высотами в указанном интервале. Во втором
0 0Це помещены соответствующие относительные значения
соедних периодов, отвечающих данному интервалу
относительных высот. Например, относительному интервалу высот 1,8...
Н 199 соответствует относительный средний период, равный
ι 14*. В третьем и четвертом столбцах даны параметры кт и Ат
Iраспределения периодов волн для каждого фиксированного
'интервала относительных высот. Это распределение имеет вид:
F{T/Th) =ехр[^г(Г/ТЛ)*Ч, 5.58
т< е., как было указано, относится к распределению Вейбулла.
Например, относительные высоты в интервале 1,8... 1,99
имеют относительные периоды, которые подчиняются
распределению Вейбулла с параметрами kT = 5,3 и Ат = 0,647.
Поясним на конкретном примере процедуру использования
табл. 5.8.
Пример 5.18
При ветре 20 м/с с берега и £азгоне 600 км в глубоком море
сформировались волны средней высотой \и = 4,2 м и средним периодом Та = 9,4 с.
Требуется определить высоту /ι1% и соответствующие этой высоте средний
период, а также функцию распределения периодов.
Решение.
Вычисляем значение безразмерного разгона:
gL _ 3,81-6.10MQ3 -|47.1(ц
V*w 202 '
Поскольку это значение разгона больше 1,1-10*. с учетом табл. 5.4
получаем:
hl% = 2,4^ = 2,4-4,2 = 10,1 м.
Из табл. 5.8 по интервалу h/h от 2,4 до 2,59 находим Τ*χ%\Τά β 1,19,
откуда получаем средний период, соответствующий высоте hl% = 10,1 м:
Thl% = 1,197^ = 1,199,4= 11,2 с.
Из этой же строки табл. 5.8 выписываем параметры распределения 5.58:
kT = 10; Ат = 0,606.
Безразмерная функция обеспеченности периодов волн с высотой 10,1 м
Данном случае имеет* вид:
Z7 (Г/11,2) = ехр [-0,606 (Г/11,2)10].
Обратим теперь внимание на то обстоятельство, что ветро-
^Ые волны глубоководного водоема обычно формируются при
^ременном во времени и пространстве ветре и, кроме того,
0гАа в условиях сложного контура береговой черты. В этих
°Жных условиях то понятие разгона волн, которое было вве-
ВвНо вьние, теряет смысл. В этих ситуациях бывает полезным
еАение понятия «эквивалентного разгона Leq».
165
Величину Leq определяют, исходя, во-первых, из высоты
волн hdy вычисленной с учетом неоднородности поля ветра и
конфигурации береговой черты (см. параграф 6.3), и, во-вторых,
локальной скорости ветра Vw в окрестности расчетной точки.
Пользуясь зависимостью 6.52 между ghd/V2w и gL/V2w, величину
Leq находят по формуле
v*w
= 2,78-ΙΟ4 Γ L πό--ΐΓ>
5.59
или по верхней огибающей рис. 1 обязательного приложения 1
[51].
Определив Leqy высоту волн требуемой обеспеченности в
системе волн получают, пользуясь табл.. 5.4.
Пример 5.19
Требуется определить высоту волн 1 %-ной обеспеченности в системе
hl% для центральной части урагана. Согласно расчетам по синоптическим
картамч с учетом неоднородностей ветрового поля в области со скоростью
ветра Vw = 70 м/с, получена средняя высота ветровых волн ha = 10 м.
Решение.
По известным значениям /id и Vw вычисляем безразмерную высоту:
Согласно рис. 1 обязательного приложения 1 [51] для определения
элементов ветровых волн в глубоководной и мелководной зонах этому
значению безразмерной высоты соответствует безразмерный разгон gLeqIV2w =
= 125, а следовательно,
Lii=i2||900 =62,4-103 м.
Из табл. 5.4 получаем, что значению безразмерного разгона
соответствует &1%=2,08; таким образом, искомая высота волны hl% равна:
h1% = klyli = 2,08- 10 = 20,8 м.
Пример 5.20
Определить h5% в условиях сложного контура береговой черты
глубоководного водоема, если известно, что скорость ветра Vw = 20 м/с, а
средняя высота__волн при этой скорости в расчетной точке, полученная
расчетным путем, ha = 1,5 м.
Решение.
Вычисляем безразмерную высоту
ghdl VV = 9fAlf = 0,0368,
и, пользуясь рис. 1 обязательного приложения 1 [51], находим
£WV2W~6-102,
откуда
4.102.6-102
^-9,81 -**+*"·
166
ц3 табл. 5.4 получаем, что безразмерному разгону, равному 600, соот-
веТствует^5%=Ь77; поэтому
h5% = k5rTd = 1,77· 1,5 = 2,65 м.
рассмотрим теперь приемы расчета высот волн различной
обеспеченности в мелководном водоеме с переменными
глубинами, предполагая^ что скорость ветра над водоемом постоянна,
а средняя высота h в интересующей нас точке водоема получена
с учетом переменных глубин.
В случае, когда глубины вдоль расчетного створа
постоянные или увеличиваются, полезно ввести понятие эквивалентной
глубины deq аналогично тому, как ранее было введено понятие
эквивалентный разгон LeQ. Величину deq можно определить на
основе функциональной связи безразмерных высоты волн
gh/V2* и глубины gd/V2w при больших разгонах и постоянных
глубинах мелководного водоема по формуле *:
gh/VJ = 0,16 th {θ,62δ(-0)4/5}.
Величину deq определяют из последнего соотношения,
подставив туда величины h и Vw. После этого высоты волн i %-ной
обеспеченности в расчетной точке находят по табл. 5.6,
используя в качестве входного параметра величину gdeq/V2w-
Пример 5.21
При скорости ветра Vw = 32 м/с в. центральной части мелководного
водоема средняя высота волн, полученная расчетным путем, h = 1,6 м. Вдоль
расчетного створа глубины возрастают от 0 до 15 м. Требуется определить
Λ0,1χ в центральной части водоема.
Решение.
Безразмерная высота волн в центральной части водоема
^А/КТО'=9^М = 0,0153.
Согласно рис. 1 обязательного приложения 1 [51] этой безразмерной
высоте соответствует безразмерная глубина gd/V2w — 0,1, откуда находим
значение эквивалентной глубины:
0.1 IV ОД'322
deq = g = 9,81 = 10'4 М*
С помощью табл. 5.6 для gd/^w = 0,1 находим £0ti% = 2,44.
В итоге:
Λ0,ι% = *од*Л = 2'44·1»6 = 3>9 м·
Пример 5.22
определить высоту волн 1 %-ной обеспеченности и соответствующий
^ и высоте средний период Thx %t а также функцию распределения периодов
См. также зависимость 7.2 на стр. 205.
167
внутри обл_асти урагана, ограниченной скоростью ветра Vw = 70 м/с, где
hd = Ю м, Td= 12 с.
Решение.
Согласно расчетам, выполненным в примере 5.19, имеем:
hvfb^hx =2>08.
По табл. 5.8 находим, что относительной высоте hx%lh = 2,08 в интервале
от 2,0 до 2,19 соответствует средний относительный период ThiyJTd^\\^
откуда
Гш% =1,16.12 = 13,9 с.
По той же таблице относительных высот для интервала 2,0... 2,19
находим значения параметров распределения периодов:
kT = 6,0; At - 0,638,
а также функцию распределения периодов в безразмерной форме:
F(7713,9) = ехр [—0,638 (Г/13,9)6].
Перейдем к рассмотрению режимных функций
распределения элементов волн. Подобно тому как для количественного
описания разнообразия волн в системе выше были введены
функции распределения элементов волн, для описания
волнового режима любого конкретного района акватории используют
режимные функции распределения высоты, периода и длины
волн. Разница состоит только в ином выборе той совокупности
значений элемента, которая подвергается статистической
обработке. Выше такой совокупностью была последовательность
значений элементов, непрерывно наблюдаемых в данной точке
акватории в течение короткого интервала времени (в несколько
десятков минут). Теперь — это статистический ряд,
охватывающий десятки лет.
Статистические закономерности, которым подчиняются
параметры волн в данном районе акватории за большие
промежутки времени в десятки и сотни лет, называют волновым
режимом рассматриваемого района.
Итак, в отличие от'обычных функций распределения
элементов волн, изучение режимных функций следует производить
на основе результатов статистической обработки измерений,
выполненных либо непрерывно во время нештилевой погоды, либо
с перерывами, измеряемыми минутами или часами, но в любом
случае систематически в течение многих лет. Такие измерения
имеются в очень небольшом числе пунктов и охватывают
сравнительно непродолжительные периоды времени, что не
позволяет на основе статистической обработки этих измерений
установить какие-либо общие количественные t закономерности,
которым подчиняются режимные функции распределения
элементов волн в различных районах.
168
улученные в этом направлении выводы носят пока про-
речивый характер, что затрудняет их использование в ин-
тИнерной практике [13, 39]. Остается путь построения
режимных фУнкци" элементов в°лн для каждого конкретного района
дротехнического строительства. Решение этой задачи на ос-
Бе проведения многолетних измерений нереально из-за
ограненных сроков строительства. Поэтому, такие функции полу-
на10Т расчетным путем, используя многолетние фактические
данные о ветровом режиме в исследуемом районе.
рассмотрим более подробно приемы получения режимных
характеристик ветра, необходимых для расчета режима
элементов волн.
В тех случаях, когда разгоны волн для" интересующего
района по всем волноопасным направлениям не превышают
100 км или для мелководных акваторий любой протяженности
с глубинами менее или равными 10 м, характеристики ветра для
расчета режима ветровых волн в данном районе моря можно
определять по результатам многолетних наблюдений за ветром
на береговых метеостанциях. Предварительно в результаты этих
наблюдений необходимо внести поправки (согласно
рекомендациям параграфа 5.2).
Обработку наблюдений метеостанции производят за безлед-
ный период для волноопасных направлений. К одному типу
волноопасного направления относят все наблюдения за ветром,
при которых направление ветра совпадает с одним из основных
восьми румбов (С, СВ, В, ЮВ, Ю, ЮЗ, 3, СЗ) или
отличается от него менее чем на 22,5°, а скорость ветра равна или
превышает 5 м/с. Промежуточные румбы ССВ, ВСВ, ВЮВ,
ЮЮВ, ЮЮЗ, ЗЮЗ, ЗСЗ, ССЗ относят к предшествующим
Румбам, например, ССВ относят к направлению С.
По всей совокупности наблюдений за ветром на
метеостанции продолжительностью η лет определяют^ количество пу и
среднюю непрерывную продолжительность tv ситуаций, в
терние которых скорость ветра была равна или выше заданного
значения Vw (например, ^ 5, ^ 10, ^ 15 и т. д. м/с), после
Чего вычисляют обеспеченности Fv различных значений
скороди ветра VWy используя формулу:
Fv=A'™vnv< 5.60
v Nnp
Де tv — выражено в часах; N — средняя многолетняя продол-
стельность безледного периода в году, выраженная в сутках;
'^повторяемость данного типа волноопасного направления
тРа в долях единицы, Fv — выражено в процентах.
Число волноопасных ситуаций nv не должно быть очень ма
лым, иначе потеряется статистическая достоверность вычисляе
цых значений Fy. Обычно, как минимум, соблюдают условш
пу > 3. 5.61
При надлежащем обосновании допускается использованш
других методов обработки и расчета максимальных скоросте]
ветра.
Пример 5.23
Требуется определить обеспеченность волиоопасного северного вет
ра, имеющего скорость Vw = 20 м/с над водной поверхностью. В результат!
анализа наблюдений за ветром обнаружено пять случаев в безледный пе
1
Vw,Mfi>
40
30
20
10
9
8
7
6
^CJ^O
ОСЬ
г Г>
г
Ε
μιΜΊ
Hill
Η
и
ΓΙ I I
III Ι Ι—
π 1г4су
\
s
w
ty
к
X
>
*
Λτ
\
\
IlSSSsas^^^/ 2
88888 8§&§
10 20
30
Рис. 5.14. Режимная функция скорости ветра (сплошная линия);
штриховой линией изображена зависимость продолжительности
штормов от скорости ветра.
риод, когда скорость ветра северного направления (в секторе от —22,5° д
+22,5°) превышала 20 м/с, причем средняя продолжительность таких си
туаций оказалась равной 10 часам. Повторяемость северного ветра в доля
единицы для безледного периода по данным наблюдений за 25 лет состав
ляла 0,12, а средняя многолетняя продолжительность безледного периода
году —225 суток.
170
решение. ^_
g данном случае: Vw = 20 м/с; U = 10 ч, nv = 5, # = .225 сут; л =*
25 лет; ρ = 0,12. Подставляя эти величины в формулу 5.60, получаем:
ρ __ 4,17-10-5 _ng1(k:
^ 225-25-0,12 ~°>31%·
Вычисленные с помощью формулы 5.60 значения Fv для различных ско-
остей ветра наносят в виде точек на функциональную сетку,
изображению на рис. 5.14. На вертикальной оси этой сетки отложены отрезки, про-
0рЦИональные логарифмам^ указанных на оси чисел, а по горизонтали —
отрезки, пропорциональные билогарифмам чисел. По вертикальной оси
рисунка откладывают величину скорости ветра, а по горизонтальной — обеспе-
ценность в процентах. Соединяя точки на рис. 5.14 плавной линией, получают
режимную функцию скорости ветра.
Пример 5.24
Требуется построить режимную функцию скорости
северного ветра по данным обработки наблюдений за 25 лет
ции. Эти данные
представлены в табл. 5.9.
Средняя
продолжительность безледного
периода N = 225 сут, а
повторяемость волноопасного
северного ветра ρ=0,12.
Решение.
Используя формулу
5.60 применительно к
каждой строке табл. 5.9,
получают
последовательно:
ρ _ 4,17.29,2-139 „9ςΐο/.
Гъ~ 225-25-0,12 ~25Д%>
волноопасного
на метеостан-
Таблица 5.9
Градации
скорости
ветра Vw>
м/с
5... 9,9
10... 14,9
15... 19,9
20... 24,9
25 и более
Число ситуаций пу,
когда скорость ветра
в безледный период
превышала нижнюю
границу градации
139
48
16
5
2
Средняя
продолжительность таких
ситуаций, / у,
ч
29,2
20,2
13,6
10,0
6,0
/Чо =
4,17-20.2-48
225-25.0,12
= 5;
/Ί* =
4,17.13,6-16
225-25.0,12
1,34%;
Ρ __ 4,17-10-5 _п^<к
Данн
этой
т<>чки
ые самой нижней строки табл. 5.9 не используют, поскольку для
стРоки не выполняется условие 5.61. Наносят на сетку рис. 5.14 четыре
с координатами: 1) Fv = 25,1 %; Vw = 5 м/с; 2) Fv = 5,99 '
V.=
чяют
10 м/с; 3) Fv = 1,34 %; Vw = 15 м/с; 4) Fv = 0,31 %; Vw = 20 м/с — и соеди-
Рост линией. В итоге получают отрезок искомой режимной функции ско-
волноопасного северного ветра (сплошная линия на рис. 5.14).
171
Проектировщика интересует, прежде всего, так называемы)!
расчетный шторм — шторм, наблюдающийся в среднем одий
раз в течение заданного ряда лет (25, 50, 100 лет и т. д.) с та
кой скоростью, направлением, разгоном и продолжительностью
при которых в расчетной точке моря формируются волны с мак
симальными за этот ряд лет элементами.
В случае, когда разгон волн невелик (менее 100 км), скорости
ветра в расчетном шторме заданного направления находят πα
максимальным ежегодным значениям скоростей ветра: по упро
щенной или уточненной методике с помощью построения ре
жимной функции (отвечающей этому направлению ветра) ме
тодом последовательных приближений. При построении режим
ной функции в формуле 5.60 полагают ην = 1 и записывают]
ее в виде
где пс — число лет, в течение которых в среднем наблюдает^
расчетный шторм. Далее строят графическим способом
зависимость tv от Vw и экстраполируют ее в область больших скоро
стей ветра. С помощью этой связи при достаточно больших Уг
по 5.62 находят величину FVy и с помощью графика режимной
функции для экстраполированной области получают значение]
Vi (искомой скорости ветра в первом приближении),
наблюдающееся один раз в пс лет в расчетном шторме. По этой ве
личине Vi находят новое значение tv с помощью упомянуто^
выше графика и подставляют его в формулу 5.62, а затем по)
уточненной величине Fv из графика режимной функции получа]
ют второе приближение V2 искомой скорости ветра и т. д.
Пример 5.25
Требуется определить расчетную скорость ветра, наблюдаемую в|
среднем один раз в 50 лет по данным табл. 5.9.
Решение.
Строим режимную функцию скорости ветра (изложенным в примере 5.241
приемом) согласно данным табл. 5.9 и экстраполируем ее (рис. 5.14) в об
ласть больших скоростей ветра, имеющих малую обеспеченность. '
По данным табл. 5.9 на этом же рисунке строят, кроме того, график
зависимости средней продолжительности ситуаций (скорость ветра в без
ледный период превышает нижнюю границу градации) от нижней границы
и экстраполируют полученную кривую в область больших скоростей ветра
(рис. 5.14, пунктирная линия).
Расчетную скорость ветра, наблюдаемую один раз в 50 лет, вычисляют
методом последовательных приближений с помощью формулы 5.62, в кото
рой в данном случае (согласно условиям примеров 5.25 и 5.24) tf = 225cyT(
172
^ 012 и лс = 50. В первом приближении предполагают, что
продолжимость tv в формуле 5.62 отвечает скорости ветра Vw — 30 м/с. Согласно
т' роенному графику на рис. 5.14 получают tv = 4 ч. Подставляя вычис-
нные значения ΛΓ, /?, /гс и tv в формулу 5.62, находят
По полученному значению Fv = 0,012 из рис. 5.14 имеем, что один раз
50 лет V\ = 30 м/с. Расчет второго приближения в данном случае
отпадает, поскольку вычисленная скорость совпала с той, которая была принята
при определении tv.
В случаях, когда разгоны волн равны или более 100 км,
что обычно бывает, если район строительства расположен на
акватории моря, ре'жимные характеристики ветра для расчета
волн следует получать на основе анализа синоптических карт.
Выбор района перед портом и сортировку синоптических
карт производят с помощью заранее составленной таблицы.
Входными данными в таблицу служат: расстояние между
изобарами {т. mile) у радиус кривизны изобар (m. mile) и
характер кривизны изобар (циклоническая или антициклоническая),
а выходной информацией является та или иная градация
скорости ветра.
Затем производят сортировку всех синоптических карт по
основным волноопасным для данного района румбам и по
выбранным градациям скорости ветра: б... 10; 11... 15; 16...20;
21...25; более 25 м/с. ,
В итоге получают не более восьми типов карт, отвечающих
основным волноопасным румбам, и несколько групп для
каждого типа, соответствующих различным градациям скорости вет-
кРа. При этом синоптические карты в любой группе должны
относиться не менее, чем к трем различным штормам. Из
синоптических карт каждой группы выбирают характерную карту,
оптимально близкую ко всем картам данной группы.
Если в пределах какой-то группы синоптических карт не
Удается выделить одну характерную карту, необходимо
выделить несколько таких карт, при этом любая из них должна
пРедставлять группу карт, содержащих информацию не менее,
чем о трех различных штормах.
Каждую характерную синоптическую карту принимают за
**повую для карт, попавших в каждую группу, и, разделив эти
личества на общее число карт данного типа, получают ча-
в0тУ появления каждой типовой синоптической ситуации (%)
Рамках данного типа. Для каждой типовой синоптической си-
УаДии строят соответствующее типовое поле ветра и отмечают
каждом поле найденную выше частоту его появления, %.
173
Кроме того, путем просмотра массива синоптических карт
каждого типа определяют среднюю непрерывную
продолжительность штормовых ситуаций, в течение которых скорость
ветра в выбранном районе открытого моря перед портом
превышала нижнюю границу каждой градации скорости ветра
Далее строят в графической форме зависимость найденных
значений tv от Vw и экстраполируют eq в область больших
скоростей Vw.
Построенные по полям атмосферного давления типовые
поля ветра (см. параграф 5.2) вместе с зависимостью tv от Уг
принимают за основу последующих расчетов режима ветровых
волн перед портом.
Обратимся теперь к описанию практических приемов
построения режимных функций элементов волн но известным
режимным характеристикам ветра.
Построение режимных функций элементов волн в тех
случаях, когда разгоны волн по всем волноопасным направлениям
не превышают 100 км, ч выполняют следующим образом.
С графика режимной функции скорости ветра Vw для данного
волноопасного направления ветра снимают ряд значений У, и
соответствующих им
величин Fi. По снятым Vi для
данного волноопасного
направления в соответствии с
требованиями норм [51]
вычисляют значения вьхсог
А/, средних периодов Tt w
средних длин λ/ в системе
волн. Приписав вычислен
ным элементам волн
обеспеченности Flt на
функциональной сетке, изображен-
λ,/. ной на рис. 5.14, 5.15,
строям ят графики искомых ре-
SQ жимных функций.
£Q Пример 5.26
50 Требуется построить ре·
i*Q жимные функции hl%f h$0/o и ).
на входе в проектируемый порт]
с0 при северных штормах, по задан
ной режимной функции северноп|
волноопасного ветра, изображен
ной на рис. 5.14 сплошной линией]
Разгоны волн по всем волноопас
ным направлениям не превышают;
100 км. Продолжительность на
блюдений за ветром составляет]
25 лет.
ι
со
S.
2,0
1,0
0,5
Π11 kj
π iS
■I I Μ I I Ν)
hi I 1 I 1
\
ι lit 111
I
г
ГГТ
1
ιΚρ
1 f
Η
π -
г
w
I r
hf%
y%
>J
λ
s
N
Λ
V
X
>
J
4 1
s\
\4 ι
4
SgSgSS S3 § 0,10,2 0,5 1
2 5
Λ 7.
Рис. 5.15. Режимные функции высот
волн /i1%, h5% и длин волн λ.
174
решение.
q режимной функции ветра, изображенной на рис. 5.14 сплошной ли-
й для значений скорости ветра, равных 30; 25; 20; 15 м/с, снимают со-
"''ветствующие обеспеченности: 0,012; 0~06; 0,30; 1,41. Приемами, описанны-
оТ в главах 6 и 7, вычисляют для выбранных скоростей ветра требуемые
М,ементы волн. Результаты расчетов наносят на -функциональную сетку.
R1 итоге получают требуемые режимные функции (рис. 5.15).
расчеты режимных функций элементов волн для морских
оайонов, где разгоны волн превышают 100 км, обычно
выполняют по типовым полям ветра. Методика построения таких
полей была описана выше. Расчеты выполняют для каждого
типового поля ветра с учетом (если это необходимо) контура
береговой черты и морфометрии морского дна, пользуясь
приемами, описанными в главах 6 и 7. Вычисленным элементам
приписывают те режимные обеспеченности, которые имеют
соответствующие поля ветра, и таким образом получают режимные
функции элементов волн.
Глава 6. ЭЛЕМЕНТЫ ВЕТРОВЫХ ВОЛН
НА ГЛУБОКОВОДЬЕ
6.1. ЭНЕРГЕТИЧЕСКИЙ СПЕКТР ВОЛНЕНИЯ
Наиболее важное свойство взволнованной водной
поверхности—ее нерегулярность. Волнение рассматривают в
спектральном представлении как случайный процесс, стационарный для
сравнительно небольших промежутков времени (обычно 10...
•••20 мин при периоде волн 5... 10 с) и однородный для
небольших расстояний (до 10 км при длине волн —100 м). При
Этом используется свойство эргодичности, заключающееся в
Юм, что реализация (выборка) случайного процесса является
в статистическом смысле репрезентативной по отношению к
дРУпш реализациям, полученным в тех же самых условиях.
Задача описания нерегулярной водной поверхности
решается с помощью сравнительно простой модели, описывающей сло-
f2eHHe регулярных гармонических волн со случайными фазами
L ■!· В качестве регулярных гармонических составляющих вол-
^ового движения, в первом, приближении, принимают прогрес-
НооНЬ1е волны малой амплитуды, описываемые в рамках линей-
и гидродинамической теории, которая рассмотрена в
раздела и по в°Ан°й поверхности распространяется гармониче-
п0Лп^0лна> луч которой составляет угол θ с осью Оде, то форма
Рхности описывается уравнением
175
г(*> У у 0= acosfaf+4> —feOccosft+t/sine)"!, 61
где ω —частота; ψ —фаза; k = 2π/λ — волновое число.
Представим себе волновое поле, сформированное в
результате сложения спектральных составляющих (элементарных
гармонических волн типа 6.1), имеющих различные волновые
числа fa, частоты ω/ и направления распространения 0. Каждую
волну запишем в виде
*ν (χ·> У> t)**a (ω„ Oj) |/ΔωΔΘ cos [ω,ί + ψί7 —
— kt (χ cos 9y + у sin 9y)]. ' 6.2
Результат суммирования выражается формулой
Ν Μ
η (х, у, 0 = 2 2 a//cos К* + Ψ/y — ki (x cos е/+У sin ву)], 6.3
где α// — амплитуда; ψί;— случайная фаза спектральной
составляющей ij. Предполагается, что случайные фазы распределены
равномерно в интервале углов от 0 до 2π.
Формула 6.3 описывает взволнованную поверхность в виде
случайной функции координат и времени. При этом, в силу
имеющегося дисперсионного соотношения 2.59, волновому
числу k на глубокой воде соответствует частота ω и действует
следующая зависимость:
ω2 = gk. 6.4
При описании процесса колебаний в фиксированной точке
водоема функцию η(/) записывают в виде
N
Ч (0 = 2 а (ω*) V&® cos (ω,* + ψ,). 6.5
Определим полную энергию Ец спектральной составляющей
с индексом /у, приходящуюся на единицу площади
взволнованной водной поверхности. Согласно линейной гидродинамической
теории
Еи = -5· ?ga2 (ω., θ;·)ΔωΔθ. 6.6
Функцию 5(ω, θ) = α2(ω, θ) называют частотно-угловым
спектром возвышений, характеризующим распределение
удельной волновой энергии между составляющими с частотами от ω,
до ω*+Δω и направлениями распространения -от Θ/ до Θ/+Δ0.
Функцию двух переменных S(co, θ) относят к категории
двухмерных спектров. Результатом интегрирования частотно
углового спектра по частоте ω является угловой спектр
5(9) = J* S (ω, 9)d<o. 6.7
о
176
Частотный спектр получают путем интегрирования частотно-
углового спектра по углу
2π
5(ω)= fS(o>, θ)άθ.
6.8
Спектры 6.7 и 6.8 относят к категории одномерных спектров.
Наряду со спектрами 6.7, 6.8 рассматривают также
одномерный спектр модулей волновых чисел S{k) при k = 2π/λ = \k\ =
^(kzx+k2y)l,2y двухмерный спектр волновых чисел S(k, θ),
двухмерный спектр проекций волновых чисел S(kXi ky) при kx =
= fecos0, ky = Λ sin θ и др.
Связь между отдельными видами спектров для
глубоководных акваторий устанавливают с помощью формул линейной
теории [23]. Например, связи между -одномерным частотным
спектром S(g)) и спектром модулей волновых чисел S{k)
вытекают из дисперсионного соотношения 6.4 и имеют вид:
6.9
6.10
Соотношения между двухмерными спектрами проекций
волновых чисел S(kx, ky), частотно-угловым S(a>, θ) и двухмерным
спектром волновых чисел S(k, Q) определяют по табл. 6.1.
Таблица 6.1
Вид спектра
S(** ky)
S (ω, θ)
S(M)
S{kx, ky)
1
1
g1'2 (V + a^-W/2
θ = arctg (kylkx)
(V + VT1/2
* = (V+ V)"2
e = arctg(*y/*x)
S(u>, Θ)
2ω3/£
£χ = ω2 cos big
ky = ω2 sin b/g
1
1
2ω/^
θ = θ
S(k, 6)
£
kx — k cos θ
&У = A; sin θ
м+г ^
ω=(^)1/2
β = θ
1
1
c,lc °РяДок пользования табл. 6.1 следующий. Требуемый
ТР записан в верхней строке таблицы. Его получают путем
177
умножения заданного спектра, записанного в левой крайней
колонке, на множитель, приведенный в верхней горизонтальной
строке для требуемого спектра. При этом аргументы функций,
соответствующие выражению спектра в левой колонке, должны
быть заменены на аргументы, приведенные в нижней
горизонтальной строке таблицы на пересечении с требуемым спектром
в вертикальной строке. Например, спектр
5(ω, θ) = 2(dg~lS(ky θ); k = ω2/#, θ = θ
или
5 (ω, θ) = 2ω^"Ι5(ω2/^θ).
С целью установления зависимостей между спектральными
и статистическими характеристиками волн (дисперсией,
средним периодом и средней длиной) используют понятие о
моментах спектров [23]. Моменты спектра вычисляют по формулам:
т1п = JJ kJkynS (**' *у) dM*r 611
mr = JJa>'S(<», 0)d«)d0 = Jo/5(со) άω; 6.12
тя = J j KS (Α, Θ) dk d9 = j k«S (k) dk, 6.13
где ты — момент спектра S(kXt ky) порядка In; mr — момент
спектра S(co, θ) и S(co) порядка г; mq — момент спектра S(k, 0)-
и S(k) порядка q.
Момент нулевого порядка (//ι, г, <7) соответствует дисперсии
волновых ординат
/По = Ζλ), 6.14
а средняя высота волны hd связана с дисперсией Dr( формулами
Αι/ = (2ΐΓβη)Ι/2=(2π),%; 615
Οη = (2π)-»ΛΛ
где σ —среднеквадратичное отклонение возвышения.
В результате средняя высота волн hd для спектров S(kx,ky),
S(co, θ), 5(ω), S(&, θ), S(k) определяется с учетом 6.14 и 6.15
по формулам:
hd= ί~2π С \s{kx9 ky)dkxdky]m; 6.16
L kJy J
Γ π Π1/2 Γ οο ΠΙ/2
Ad = 2π(* |5(ω, θ)(1ωάθ = 2π J S (ω) do> '; 6,17
[π -11/2 Γ οο -11/2
2π| J5(A, 6)d/fed6 = 2*J$(A)d* . 6,18
178
Средний период Td находят с использованием моментов ну-
оГо и второго порядков т0 и т2:
Td = 2π [т0/т2]112. 6.19
Диалогичную формулу используют для определения сред-
й длины волны в направлений Θ:
λβ = 2π[/η0(θ)//Α2(θ)]1/2. 6.20
Средний период Td и среднюю длину волн λα в генеральном
(главном) направлении распространения волн 9ь, определяют
с помощью выражений 6.14, 6.15, 6.17—6.20:
[/ оо -П/2
jS(o))da)/ |ω25(ω)άω ; 6.21
λα = 2π J 5 (Л, θ0) dk / J £2S (Α, θβ) dk . 6.22
Характеристики спектрального максимума — длина λ0 и
частота ωό — связаны со средним периодом Та формулами:
ω0 = -4^-; 6.23
bmTd·
λ0 - *»«ΰ 6.24
где
F* = *?V/2«,*m=l,25 6.25
^-условная средняя длина волны, принимаемая в качестве
расчетной (см. формулу (151) [51]).
Таким образом, для вычисления статистических
характеристик волнения необходимо знание формы спектра.
Аппроксимация формы углового спектра вытекает из
рассмотрения частотно-углового спектра в виде
S(0, 0) = S(g>)Q(g>, Θ), 6.26
1де5(со)— частотный спектр.
Функция углового распределения энергии удовлетворяет ус-
π/2
JQK Θ)<1Θ = 1. 6.27
—π/2
Вол ГЛЫ ^ Ме^ду генеральным направлением распространения
ля» ^° И напРавлением распространения спектральных
составах заключены между —π/2 и +π/2.
^Sia? Фиксированного значения частоты m функция S(g)/,0) =
Щ определяет угловое распределение энергии на этой ча-
179
стоте. В качестве приближения полагают, что основные
энергонесущие компоненты в окрестности частоты максимума ω0
имеют одинаковое угловое распределение:
Q = 2cos2&/n. 6.28
Более полные результаты получены по частотному спектру.
Рассмотрены три категории частотных спектров, относящихся
к различным интервалам безразмерных разгонов gL/V2w [26].
Спектр Si (ω) — JONSWAP относится к разгонам gL/V2w < Ю2;
спектр S2(o))—Стрекалова — Масселя применим в интервале
разгонов 102< gL/V2w < Ю4; спектр 53(ω) — Пирсона — Моско-
витца следует использовать для разгонов gL/V2w ^ Ю4.
Указанные спектры представлены в следующей безразмерной
форме:
s.(-W-i-fe)",ep{-^[(ir-IBx
.-.[-±te-)l
χγ
6.29
S(w)ISH)
52(ω/ω0) =
= exp [-22,2^ -./] +
6.30
X
2,5 co/iVf
Рис. 6.1. График зависимости
безразмерной спектральной плотности S((u)/S(<u0)
от безразмерной частоты ω/ω0 при
разгонах: до 100 км (!); 100.. .300 км (2);
более 300 км (3).
S3(W«o) = (^) ехР
хИ(*)Ч}·*»,
В 6.29 принято γ = 3,3;
Ь = 0,07 при ω ^ со0; b =
= 0,09 —при ω > ω0·
Спектр 5ι(ω/ω0)
получен по измерениям в
Северном море при относительно]
небольших разгонах (до
100 км); спектр S2(<o/<do)
основан на анализе данных
по Каспийскому морю для
разгонов 100 ... 300 км;
спектр 53(ω/ωο) является
результатом анализа волно-
графных записей в
Северной Атлантике при разгонах|
180
,, ce 300 км. Обстоятельная проверка спектра 52(ω/ω0), вы-
^ненная по большому количеству данных измерений, показа-
п°леГ0 пригодность для использования в указанном диапазоне
Угонов.
I Перейдем к определению спектральных характеристик вол-
ния по графикам рис. 6.1 и 6.2. В качестве входных данных
НС рис. 6.1 используют значения безразмерной частоты ω/ωο,
Н3 которой определяют безразмерные ординаты S(g))/S(g)0)
П?я спектров типа Si, S2, S3 (линии 7, 2, 3). Размерную
ординату спектрального максимума S(g)o) определяют по
безразмерной ординате S (ω0) ω0/£>η (рис. 6.2). График на рис. 6.2
построен в виде зависимости 5(ω0)ω0/Οη= F(gL/V2w) для каждого
типа спектра Su S2 и S3 в выбранном интервале безразмерных
(разгонов gL/V2w с учетом формул 6.15 и 6.23 и рис. 1
обязательного приложения 1 [51]. Величины S((d0)(uo/£N определяют
10~SS(u)0) Ш0/Щ>
0,003
0,002
0,001
10 2 3 ϊ 6в*М 2 3 Ч 6 8/000 3 Ь 6 8/0000 J pi/v
»· ' ' ■ ' ""
.j ι ι ι ι ι μι
100
2 4 6 1000 2 <t 6 10000 2 4 6 gt/Vw
Рис. 6.2. График зависимости безразмерной спектральной
плотности на частоте максимума S(a>o) ω0/£η от безразмерных
разгона gL/Vw2 и продолжительности действия ветра gtlVw.
по вычисленным параметрам gL/V2w и gt/Vw\ при этом в
дальнейших расчетах используют наибольшую величину. Значения
Щ и Д) определяют по формулам 6.23 и 6.15 с учетом рис. .1,
а затем по величине S(g))g)0/£^ вычисляют S(g)0).
Пример 6.1
Требуется определить ординаты частотного спектра 5(ω). Скорость
ветра Vw = 18 м/с, разгон L = 350 км. Продолжительность действия ветра
' * 6 ч.
Решение.
Вычисляем величины gL/V2w = 10597, gt/Vw =11772. По графику
р,,с· 6.2 принимаем наибольшую величину 5(ω0)ω0/^η = 1,8, соответствую-
ЩУЮ параметру gt/Vw ^ 11772, а по графику рис^ 1 [51] — наименьшие ве-
Хпины «fo/V*· = 0,0825 и gTdIVw - 4,1, откуда h = 2,72 м, Тл = 7,52 с. По
п"Улам 6.15 и 6.23 находим:
ϋη = 7ГУ2я =2,722/2π = 1,18 м2,
ω0 = 0,8(2л)/7* = 0,8(2π)/7,52 - 0,67 рад/с.
181
Ордината спектра на частоте максимума 5(ω0) = lfiDJ(u0 ^ j I
Χ 1,18/0,67 = 3,17 м2-с/рад. Значению gt/Vw = Μ772 согласно рис. ι '1
ветствует величина gL/V2w = 6· ΙΟ3, или Ζ, = 198·103μ, т. е. ординаты r]
размерного спектра 5(ω)/5(ω0) определяем по кривой 2 рис. 6.1, относят*ί
ся к диапазону рйзгонов 100...300 км. Результаты расчетов привей 1
в табл. 6.2. mj
Таблица 6.2
ω/ω0
0,6
0,7
0,8
0,9
1,0
1,5
2,0
2,5
SH/SK)
2,9-10~2
1,4- ΙΟ"1
3,9- КГ1
8,0- Ю-1
1,0
1,8-ИГ1
5,3- Ю-2
1,8-10""2
ω,
рад/с
0,4
0,47
0,54
0,60
0,67
1,00
1,34
1,67
5(ω),
м9с/рад
9,19-ΙΟ"2
4,44-НГ1
1,24
2,54
3,17
5,71-10"1
1,68· ИГ1
5,71-Ю-2
6.2. РАСЧЕТ ЭЛЕМЕНТОВ ВОЛН НА ГЛУБОКОВОДНЫХ АКВАТОРИЯХ!
ПРОСТЫЕ УСЛОВИЯ
Расчеты элементов ветровых волн на глубоководных аква
ториях в мировой практике базируются на двух подходах. Пер
вый связан с вычислением элементов волн непосредственно из|
уравнения баланса энергии. Второй — основан на использова
нии обобщенных эмпирических зависимостей элементов волн от]
волнообразующих факторов. В качестве исходной модели,
описывающей развитие ветрового волнения, выбирают простые ус
ловия волнообразования: полагают, что ветер постоянной ско|
рости действует на водную поверхность в направлении, перпен
дикулярном прямолинейной подветренной береговой черте.
Рассмотрим основные соотношения для расчета элементов|
ветровых волн, базирующиеся на использовании уравнения ба-
ланса энергии, впервые полученного В. М. Маккавеевым *
1937 г. [40], вывод которого содержится в параграфе 4.4 пер
вого раздела. В спектральной форме это уравнение записал]
Хассельман [73]
dS
at
= a(£) + p(£)S--D + yV,
6.3
где t — время; L — горизонтальная координата; k — вектор в
нового числа; S(k> L, t)—пространственно-временной ЬпеЩ
волновых чисел, характеризующий распределение удельн^|
энергии волновых составляющих в интервале волновых чИС'
от к до k + dk^
Рассмотрим структуру правой части уравнения 6.32, в *<0
ром a(k) соответствует резонансному механизму Филлип ι
182
отвечает механизму индуцированного взаимодействия
у^айлза; D представляет потери энергии на диссипацию и,
наконец, N описывает нелинейные взаимодействия в спектре.
к физический смысл резонансного механизма состоит в
следующем. Турбулентный воздушный поток создает случайное
распределение давления над водной поверхностью, которое
распространяется с некоторой характерной скоростью. Спектр
пульсаций давления вызывает малые колебания водной
поверхности. При перемещении поля давления с той же скоростью,
что и скорость распространения волн, и при распределении
давления в противофазе с ходом уровня (пониженному
давлению отвечает повышенный уровень, и наоборот) происходит
резонансный рост волн. Спектральные составляющие
возрастают со временем по линейному закону.
Под действием механизма индуцированного взаимодействия
спектральные составляющие возрастают со временем по
экспоненциальному закону. Сущность механизма
экспоненциального роста (по Майлзу) заключается в следующем. В подвижной
системе координат, перемещающейся с фазовой скоростью волн
в направлении их распространения, воздушный поток,
характеризующийся в начальный #момент логарифмическим профилем
скорости, с течением времени преобразуется. Выше некоторого
уровня ζ > zc воздушный поток обгоняет волны. На уровне zCy
называемом уровнем совпадения, частицы воздуха неподвижны
относительно волнового профиля (Vc = с).
Ниже уровня совпадения zc воздушный ноток движемся в
направлении, противоположном распространению волн и
отстает от них. Циркуляционное движение возникает вблизи
уровня zc вокруг практически неподвижного слоя, ядро которого
смещено от вершины гребня по направлению распространения
волн. Линии тока приобретают асимметричное
относительно профиля волн распределение: они сближены перед
гребнем и разрежены за ним. Энергия передается волнам за счет
колебаний давления, изменяющегося в фазе с наклоном водной
поверхности.
Приведем аналитические выражения для коэффициентов α
и β, вытекающие из теории Филлипса — Майлза [13, 60].
Коэффициент, соответствующий резонансному механизму Филлип-
Са> имеет вид:
α = πΠ(Λ, со)/(р«,с)2, 6.33
а коэффициент β, отвечающий механизму индуцированного
Взаимодействия, записывается так:
-пространственно-временной спектр турбулентных флук-
атмосферного давления; с —фазовая скорость спект-
183
л
ральной составляющей; w — осредненная вертикальная ком
нента скорости воздушного потока, вызванная волнами; ρ, 0 °*
плотности воды и воздуха соответственно; dV/dz — наклгГ
d2V/dz2— кривизна профиля ветра; значения β по числена
модели Майлза даны в [13]. 0,i
Резонансный механизм и механизм индуцированного взаим
действия «работают» согласно обобщенной модели Филлилса^'
Майлза на всех стадиях.
От механизма индуцированного взаимодействия энергия ц0
ступает к волнам на основной стадии их развития. Влияние
резонансного механизма на рост волн наиболее существенно на
начальной стадии (пусковой механизм).
Основными факторами, обусловливающими диссипацию
энергии в спектре волн на глубокой воде (член D) являются
турбулентная вязкость, а также процессы обрушения гребней,
волн. По Хассельману [73] диссипация энергии из-за эффектов
турбулентной вязкости связана со спектром следующим
выражением:
D = 4k^tSf 6.35
где μ* — коэффициент турбулентной вязкости.
Связь между коэффициентом турбулентной вязкости μ* и
параметром взаимодействия в теории Майлза με имеет вид:
μ<=(ρ/2)μ^-3/'. . 6.36
Расчеты показывают, что оценка «сверху» для параметра
взаимодействия μ5 = 10~2.
Явление обрушения гребней волн ассоциируется с
существованием интерэала равновесия в спектре в области больших
частот (или волновых чисел) [60]:
S(g)) = αιβ"2ω~5 при ωΓ ^ ω ^ G)c, ^
где 5(ω) — частотный спектр; αϊ — безразмерная константа;
ωΓ — частота, соответствующая низкочастотной границе
степенного интервала 6.37; ω0— частота, соответствующая гранив
капиллярных волн. На начальных стадиях развития волн а>г~
~ω0, где ωο — частота максимума спектра. Выражения для
определения потерь энергии на диссипацию, учитывающие обрУ*
шение гребней, носят приближенный характер.
Явление нелинейных взаимодействий в спектре волн раС*
смотрено Хассельманом [13, 73].
Числовые оценки члена N в уравнении 6.32 для наибол*
простого случая, когда волны развиваются от прямолинейно
берега, были сопоставлены с результатами натурного экспер^
мента, проведенного в Северном море вдоль створа, ориентир
ванного по нормали к берегу. Результаты сопоставления по <
зали необходимость учета нелинейных процессов.
184
д/l. Μ. Заславский и В. Ε. Захаров [17] рассмотрели модель
звития спектра с учетом слабонелинейных взаимодействий.
^пользуется предположение о поступлении энергии от ветра к
оЛнам (накачке) в высокочастотной части спектра. С другой
сТОроны, предполагается, что интервал поступления энергии,
а также максимум спектра разнесены по шкале частот,
разделы так называемым интервалом «прозрачности».
Для оценки интегрального переноса энергии по спектру
использовано уравнение волнового действия, преобразованное из
уравнения баланса энергии 6.32 на основе понятия спектра
волнового действия W(k) = S(k)/<u. Установлено, что в результате
интегрального переноса в низкочастотную область энергия
накапливается в окрестности спектрального максимума.
Из анализа размерностей следует, что в области накопления
энергии выполняется закон
S (ω) = βιρ ν/3ω-11/3, ω0 < ω < ωη 6.38
где βι — безразмерная константа; ρ— параметр с размерностью
длины. Этот же закон получен другим способом Ю. П.
Поляковым в [26].
С. А. Китайгородский развил применительно к ветровым
волнам идеи А. Н. Колмогорова о передаче энергии
турбулентности из области низких частот к высоким и установил, что
S(<o) ~ ω~4, τ. е. этот вывод количественно близок к результату
6.38.
Уравнение баланса 6.32 можно решить аналитически лишь
для заведомо идеализированных случаев, например, когда
пренебрегают нелинейным членом Ν> что допустимо на самых
начальных стадиях развития волн. Во всех других случаях
используют численные методы решения уравнения. По
вычисленному из 6.32 спектру определяют основные характеристики
волн —среднюю высоту, среднюю длину и средний период волн.
При этом ввиду неоднозначного задания правой части
зачарую получают малосогласующиеся между собой результаты.
Упрощенный прием получения приближенных теоретических
3ависимостёй элементов волн от волнообразующих факторов
Для простых условий волнообразования основан на
использовании степенных зависимостей 6.37 и 6.38.
На ранних стадиях развития волн при сравнительно неболь-
Ши* разгонах модель' спектра представим в виде
Где 5ι(ω) = ^ω-5/ι(ω/(αο), 6.39
/1 ~ αϊ при 1 5ζ ω/ωο ^ g)c/g)o;
/ι ~ 0 при ω/ωο < 1 ·
"а более поздних стадиях при больших разгонах
S2 (ω) = ρ ν/3ω-»/,/2 (ω/ωο), 6.40
185
где
f2m β! при 1 < ω/ω0 ^ ωΓ/ω0,
/2 = О при ω/ω0< 1.
Связь между средней высотой волн на ранней hdn и заве
шающей стадиях has их развития с частотой максимума спектп]
ωθΛ и ωό* получают на _основе формулы 6.15 для определен^
средней высоты волны ha по заданной дисперсии £)η, а такж
модельных спектров 6.37—6.40:
при gL/VK,^(gL/V*w)cr
Α,Λ = (2πΗ|5(«))(1ο) ~aI/2(W/2)l^atf; 6.41|
npngL/V*w>(gL/V*w)cr
ΑΛ = (2*)1'21 J S (ω) dcol « β}'2 (8«/4)7Y^, 6.42I
где {gL/Vzw)cr—критическое число Рейнольдса, разделяющее
раннюю и позднюю стадии развития.
Из 6.41 и 6.42 с учетом 6.23 получим соотношения между
безразмерным средним периодом и безразмерной средней
высотой волны:
ΎΪ = А* [%-Υ> *№ < №IVJ)cn
*νζ- *= А« (-φ-)3'4'· *Lly· > (sUVJL·, б.«
где ρ—pg-V-^ = const;
An = 1,9*3/ν-·4; Asi = 2,\&fifiQ-**p-4*.
С другой стороны, воспользуемся соотношениями между
частотой максимума спектра и безразмерным разгоном, которые
следуют из теории [17, 21]:
up*gL/V*m^(gL/V*9)er
Vwmn/g~\gL/V*w)-4<\ 6.43'
при gL/V*w>(gL/Vzw)cr
Vwms/g~{gL/V*w)^<. 6.44'
Далее, исключая в 6.41 и 6.42 частоты аюп и щ5, получаем
зависимости между безразмерной средней высотой и безра3'
мерным разгоном:
при gL/VZv^igL/Vt^cr
6.43
gfian/VK, = knl(gL/V*w)4'; 6.45
186
npHgL/V*w>(gL/V*w)Cr
ghds/V*w = ksi (gL/V*wyt\ 6.46
Где Апи Л*ь knu ks\ — эмпирические параметры, подлежащие
определению.
Другой подход в разработке методики расчета элементов
волн базируется на обобщении материалов натурных наблюде-
ΗΙΙ^ относящихся к простым условиям волнообразования,
|с привлечением теории размерностей и математической
статистики [24].
| в случае дростых условий волнообразования для средней
высоты волн ha и среднего периода Td была выбрана система
определяющих параметров в виде Vw, ty Ly dy pfl, ρ, где t —
продолжительность действия ветра; d — глубина. На основе
теории подобия и размерностей записаны следующие
безразмерные зависимости:
^г,1/ 2 _ ρ IjL lL hL _lY
/ , \ 6.47
o-T/1/ - F l^L SL gd ρ
Для установившегося ветрового волнения на глубокой воде
при p/ρα = const соотношения 6.47 приобретают вид:
ihd{ IV = Fz {gH VJ); gTJ Vw = Λ (ёЦ VJ)
или
A^ = «W^!). 6.48
На первом этапе была исключена из рассмотрения^скорость
ветра. Вначале связь между исходными величинами ha и Та и
определяющими параметрами записывали в виде
hdIL = Fb(gLIVJ)\ gTd*!L = Ft(gLlVw*)9 6.49
откуда получены безразмерные зависимости, не содержащие
скорость ветра Vw:
hJL = F7 (gTSIL); hJgT/ = F8 (gTJIL). 6!50
Аналогично вводили скорость ветра в первой степени;
безразмерные зависимости для этих случаев:
hJL - ^9 (gTJVJ; hJgT/ = Fi0 (gTjVJ; g gl
gTJL = Fu(gTdIVw); hd/L = Ft2 (gTJVJ.
Последовательный анализ данных натурных наблюдений в
Рамках зависимостей 6.49—6.51 (включающих скорость ветра в
Улевой и первой степени) позволил в первую очередь исклю-
Ить те данные, которые содержали волны зыби, поскольку эле-
187
менты волн, не имеющие четкой связи со скоростью ветра, в
падали из совокупности. Также исключали из анализа и дан^1
относящиеся к сложным условиям волнообразования (резко /'
меняется скорость ветра, контур берега имеет сложные очерт·!]
ния.и т. п.). С этой целью была использована система фильт]
ров — сочетаний безразмерных зависимостей типа 6.49—6.51 I
соответствующими доверительными областями. 1
Фильтры были применены к большой совокупности данные
натурных измерений (~600), выполненных в морских уСЛо]
виях. Также использованы данные при специально подобранны)
«идеальных» условиях, включая измерения в аэрогидрокана
лах. В итоге функции, аппроксимирующие натурные и лабора·
торные данные, имеют вид (Стрекалов [55]):
S*t= 0 16 ίΐ- ί ! ΤΙ
ш
Формула 6.52 определяет количественную зависимость сред
ней высоты ветровых волн на глубокой воде от скорости ветра|
и разгона волн, а соотношение 6.53 — взаимосвязь между сред
ней высотой, средним периодом и скоростью ветра на горизонте]
10 м.
Верхняя огибающая номограммы рис. 1 обязательного при!
ложения 1 [51] рассчитана по формуле 6.52, а шкала периодов]
— по 6.53.
Пример 6.2
Требуется определить элементы ветровых волн ha, Та и Xd в точке Р|
глубоководной зоны. Ветер постоянен по скорости и направлению. Скорость]
ветра Vw = 18 м/с, волнение установившееся, разгон L = 350 км.
Решение.
Вычисляем величину gL/V2w = 10597. По верхней (огибающей^ кривой
графика рис. 1_приложения 1 [51] находим: (ghd/V2w)L = 0,10; (gTalVu)^
= 4,6. Откуда hd = 3,3 м, Та = 8,4 с.
По формуле (151) [51] средняя длина волны
χα = #ГУ2я = 9,81 · 70,56/(2 · 3,14) = 110 м.
Соотношение 6.53 представим в графической форме (п^|
Ю. М. Крылову). Откладывая по горизонтальнои_оси средне
период Tdy а по вертикальной — среднюю высоту haf получав
что каждой фиксированной скррости ветра Vw будет отвеЧ^Т!
своя зависимость между высотой и периодом. Такой граф*1]
представлен на рис. 6.3, на котором зависимости между cpeAi
ней высотой и средним периодом для скоростей ветра 10; Ί
20,..., 75; 80 м/с ограничены двумя предельными парабола^]
Верхняя граничная парабола / дает зависимость между сРед
188
ней
высотой и средним периодом для предельно крутых волн.
ггрИ ее построении принято, что
йод*/Г = 2*hotlo/olgTd2 = 1/7,
отКуДа с учетом приближенного равенства /ι0,ι%^3Λα получаем
для верхней параболы / такое уравнение:
h — -£-т 2
nd ~ 42π У <* ·
6.54
k,M
10
3
8
1
6
5
j
2
/
ι t ι
Средняя высота, м
ί
10j*
?.oJ^
35
Ч^
40 А
50>
'^ίί
10
/Ν
W
*0
6i
ύ
I
уф
•ir
70s
Υ////
1
^15
У^
75J\
ш
///h
'/ψ
Скорость ветра V
80 70 60 50 40
wjj
%л
й
/л
1I
ТА
V/
А
/Ύο
/А
V/
/
Л
//
'Δ
/
ю,н/с
'А
/25\
Td,c
Ζ 3 4 5 6 7 8 9 10 11 12 13 14 15 16
средний период, с
J ι_ι ι ι ι ι ι ι ι ι ι . ι ι г ι' ι ι 1 l ι
1 2 3 4 5 6 8 10 15 20 25 30 35 40 50 60 70 80 90 100 d м
Глудшна, м '
Pw. 6.3. Связь между средней высотой и средним периодом ветровых
волн при различных скоростях ветра
1и^АЛя пРеДельно крутых волн; // — для предельно развитых волн; /// — для
склонов; IV — для антициклонов; V — для циклонов и антициклонов в среднем.
Нижняя парабола // соответствует предельно развитым вол-
ам> для которых, согласно 6.52 и 6.53, выполняются соотно-
ghdIVw*^09l6; 6.55
g7rf/Vw^2ic.3fl (0,16F= 1,97*. 6.56
УРа ЛЮчая из этих зависимостей скорость ветра, получаем
*ие нижней параболы в виде
6.57
189
15
На рис. 6.3 изображены и другие зависимости между Вы
той и периодом, так кривая /// отвечает условиям типична
циклона, а кривая IV — типичного антициклона, V — осредНеГ°
ная (для циклона и антициклона). н'
Кривые ///—V на рис. 6.3 построены с учетом следующ
зависимостей между разгоном и скоростью ветра [26, 511·
11/^ = 4,28.1.0"; б58
11/^ = 5,76.10"; б59
ll/«;/v = 5.1011, 6.60(150)
где v~10~5m/c— коэффициент кинематической вязкости
воздуха.
Заменяя в формулах 6.52 и 6.53 значение разгона L
согласно 6.58, находим:
|^=0,1б(^1 - [ 14-/^28.1,9.103(^/^3)^ J );
# = 2..3,. (олв [l - l^^^Jj—-^^
Аналогичные преобразования можно выполнить в
формулах 6.52 и 6.53 с учетом 6.59 и 6.60; при этом числовой
множитель ]/Ч,28 заменяется на *|/~5,76 и 1^5,0 соответственно.
На рис. 6.3 каждую из кривых ///—V пересекает семейство
линий, характеризующих'связи между ha и Та для различных
скоростей ветра Vw. Графики ///—V позволяют приближенно
вычислить элементы ветровых волн в виде функции скорости
ветра для циклонов и антициклонов без учета влияния
продолжительности действия ветра, разгона и контура береговой
черты.
В качестве дополнительной на рис. 6.3 нанесена шкдла
глубины d\ если определенное из графика (по величине Та)
значение d оказывается большим, чем фактическая глубина, то
водоем следует отнести к мелководному.
Пример 6.3
Требуется определить элементы ветровых волн в фиксированной
удаленной от берегов, точке океана во время продолжительного ветра с I
скоростью Vw — 25 м/с.
Решение.
Расчет элементов волн производят с помощью графика на рис. 6.3. Щ
скольку в условии примера нет указаний о характере барического^ обра
вания, вызвавшего указанную скорость ветра, воспользуемся кривой V, Μ
торая соответствует элементам ветровых волн для циклонов и антициклон Ч
(в среднем). На графике изолиния Vw = 25 м/с пересекает_кривую V ъ1\
ке, координаты которой дают искомые элементы волн: Та = 9,35 с, '1(1 Ί
= 4,45 м.
190
Пример 6.4
Требуется оценить максимальные элементы ветровых волн в океане
прохождении тропического циклона, в центральной части которого мак-
Пильная скорость ветра (осредненная за 10 мин на горизонте 10 м)
'дожигала 60 м/с.
п решение.
3 данном примере указан характер барического образования — циклон;
помощью кривой /// на рис._6.3 находят_координаты пересечения с
изолинией 6° м/с· В итоге имеем: Td = 11,45 с, ha = 8,60 м.
Элементы неустановившегося ветрового волнения
определяют из 6.52, 6.53 с учетом соотношения из [60] между разгоном
I и продолжительностью действия ветра /:
/,// = йо(^) = -уСо, 6.62
где Uo(gr)y Со — групповая и фазовая скорость спектрального
максимума волн на глубокой воде.
Формула 6.62 получена из условия перемещения фронта
установившегося волнения со скоростью L/t, равной групповой
СКОРОСТИ U0(gr).
Безразмерную продолжительность действия ветра согласно
6.62 определяют в виде функции
где gTo/Vw — безразмерный период спектрального максимума.
Шкала безразмерной продолжительности действия ветра на
рис. 1 обязательного приложения 1 [51] построена по формуле:
d* -A (gL)nj
6.64
При этом параметры Л/ и щ найдены из условия равенства
фазовой скорости с0 = gT0/2n и скорости ветра Vw: >li == 2;
rti=l. Уточненное значение пг = 11/14 ~ 0,785 определено из
6.63; 6.64; 6.44; 6.44' и 6.46; коэффициент А2 = 16. В табл. 6.3
приведены значения безразмерного разгона и продолжительно-
сти действия ветра, вычисленные по формуле 6.64 с
параметрами А2 = 16, п2~ 0,785.
Таблица 6.3
SW*W
50
60
70
80
90
100
200
300
.400
stivw
345
398
449
. 498
547
594
1024
1408
1765
sUV\
500
600
700
800
900
1000
2000
3000
4000
*WW
2103
2426
2739
3041
3336
3623
6243
8583
10758
sWuw
5000
6000
7000
8000
9000
10000
20000
30000
35000
и более
**iv9 ·
12818
14790
16692
18537
20333
22086
38056
52319
60000
191
Шкалу безразмерной продолжительности на рис. 1 0бя
тельного приложения 1 [51] используют для условий, к0г3а'|
интервал времени между последовательно наблюденными и j
рассчитанными скоростями ветра составляет не менее 6 ч. гу
более подробной информации о ходе скорости ветра во времен!
рекомендуется использовать уточненные данные табл. 6.3. н'
Пример 6.5
Требуется определить элементы ветровых волн hd и Td в точке pi
глубоководной зоны. Ветер постоянен по скорости и направлению. Скород
ветра Vw = 18 м/с измерялась с интервалом 6 ч, разгон L = 350 км. ГЬ
должительность действия ветра / = 6ч.
Решение.
Вычисляем величины gL/V2w = 10597 и gt/Vw = 11772. По верхней оги·!
бающей кривой графика, приведенного на рис^ 1 приложения I находим
соответствующие значения (ghd/V2w) = 0,10, (ghdjy\v)t = 0,0825; (gTd/Vw)L^
= 4,6, (gTd/Vw)t = 4,1. Так как (ghd/V2w)t< (gh^w)^ то среднюю высоту!
волны haj= 2,72 м определяем по величине (ghd/^w) = 0,0825, а средний
период Td = 7,52,с — по величине (gTd/Vw)t = 4,1.
Пример 6.6
Требуется определить элементы ветровых волн ha и Та в точке Ρ
глубоководной зоны. Ветер постоянен по скорости и направлению. Скорость
ветра Vw = 18 м/с, интервал измерений 1 ч. Разгон L = 350 км,
продолжительность действия ветра / = 22 ч.
Решение.
Величина фактического безразмерного разгона gL/V2w = 10597 и
фактической безразмерной продолжительности gt/Vw = 43164. По табл. 6.3
определяем, что значению gt/Vw = 43164 соответствует безразмерный разгон
(£Ζ,/ν2«,)/^2,5·10*.
По верхней огибающей кривой рис. 1 приложения 1 [51] находим
соответствующие значения ghalV2w = 0,10^ и (ghd/V2tv)t = 0,12; gTd/Vw = 4^6 и
gTa/Vw = 5,2. Так как (ghd/V2w)<(ghdlVw)t, то среднюю высоту волны hi-
=3,30 м определяем по__величине ghd/V2w = 0,10, а средний период Td9
= 8,4 с — по величине (gTd/Vw) = 4,6.
В целом результаты расчетов элементов волн по
эмпирическим формулам согласуются с теоретическими расчетами. На
рис. 6.4 отрезками штриховых линий показаны теоретические
зависимости 6.45, 6.46 (а) и 6.43, 6.44 (б), а сплошной линией-
эмпирическая зависимость 6.52. Коэффициенты Ащ = 10, As\ *
= 28, km = 1,95· 10~3, ksi = 6,5· 10"3 подобраны из условия
совмещения теоретических расчетов с натурными зависимостями·
Предсказываем^^ темпы изменения безразмерных
характеристик gfd/Vw и ghd/V2w согласуются с вычисленными по
обобщенным эмпирическим формулам. Значение критического ра^'
гона (gL/V2w) = 2,7· 102; например,'для скорости ветра V*>*
= 20 м/с значение Lcr = 11 км. При L ^ 11 км Td и hd опр^Де'
ляют по формулам 6.43 и 6.45, а при L> 11 км период Td ]{
высоту ha вычисляют по формулам 6.44 и 6.46.
102
Зависимости 6.52 и 6.53 по выводам М. И. Кривошей право-
ерНО распространить на условия водохранилищ.
м формула 6.64 для расчета безразмерной продолжительности
тоЧненными параметрами Л2= 16 и, п2 = 0,785 близка к-дан-
Сным Крылова (Л3 = 17,3; п2 = 0,8).
1Q'1 10° 10 1 10г 103 10
6) sjIsJXi
SfL/vfo
1,0
0,5
0,3
s\K
^ рь
rf-ТдДЦ.^
tin
ш
'/
*У
л ι ι ι ι ι
10'
10'
ffyft»
10"
Рис. 6.4. Сопоставление теоретических расчетов (штриховые
линии) с зависимостями главы СНиП 2.06.04-82 * (сплошная
линия) для безразмерных высоты (а) и периода (б).
63 РАСЧЕТ ЭЛЕМЕНТОВ ВОЛН НА ГЛУБОКОВОДНЫХ АКВАТОРИЯХ.
СЛОЖНЫЕ УСЛОВИЯ
Расчет элементов волн при сложных условиях волнообразо-
двуИЯ' Так же как и ПРИ ПР0СТЫХ условиях, можно осуществлять
ско ПУТЯМИ: либо на основе решения уравнения энергетиче-
Нй Го баланса волн, либо базируясь на эмпирических соотноше-
Пр х между элементами волн и волнообразующими факторами
η*Λ. пР°стых условиях волнообразования. Возникающие в ходе
условиях волнообразования. Возникающие в ходе
МеннС1?в хаРактеРные ситуации обусловлены, во-первых, пере-
°и вдоль разгона и во времени скоростью ветра; во-вторых,
193
неоднородностью пространственно-временной структуры веГо ι
вых полей; в-третьих, сложным контуром береговой черты
рельефом дна. н
В тех случаях, когда скорость ветра вдоль разгона сущес
венно переменна, плавное ее изменение заменяют ступенчаты,
изменением таким образом, что при переходе от одной ступен,!
к соседней величина скорости терпит разрыв непрерывности1
а в пределах каждой ступени она остается постоянной. После
такой схематизации ветра расчет элементов волн производят
«шагами» от ступени к ступени на основе известных зависимо.
стей между элементами
волн и волнообразующимн
факторами. При этом
соблюдают условие непре-
рывности изменения
элементов волн в
пространстве и во времени.
При сложном поле
ветра и сложной
конфигурации береговой черты, т. е. в
тех случаях, когда понятие
разгона волн неприменимо,
приемы расчета
конструируют на основе анализа
спектральной линейной
модели формирования волн
при простых условиях и
обобщения этой модели на
сложные [23]. С этой целью
используют соотношение,
связывающее квадрат
средней высоты волн с угловым
спектром S (Θ; VWy L):
О N .
'/// /// /// /// /// /// /// /// /// /
Рис. 6.5. Схема формирования углового
спектра при ветре с берега.
hd2{Vw,L) = 2* j S(fl; Vw,L)dO.
6.65
-π/2
Величина SdQ равна энергии спектральных составляют^
распространяющихся в секторе углов от θ — 1/2 до &+1/2.
С помощью формулы 6.65 и гипотезы о том, что угловой
спектр в любой точке акватории при простых условиях
волнообразования пропорционален cos29 (параграф 6.1), получен0
условие нарастания энергии каждой спектральной
составляющей углового спектра вдоль луча NP; эта энергия в
произвольной точке Ρ пропорциональна величине h2a(Vw> L) в этой точке·
умноженной на cos2θ (рис. 6.5). .
Таким образом, принимая для условий глубокой водЫ1
S(9; V-V9L) = /(V«,, L) cos29,
194
I лучаем с учетом 6.65
ι. следовательно,
I S(θ; Vw, L) = ±-V(VW, I) cos2 θ. 6.66
Согласно полученной формуле энергия в расчетной точке
ρ спектральной составляющей, распространяющейся по лучу
Ор = г, при заданной скорости ветра полностью определяется
величиной проекции отрезка луча ΝΡ на направление ветра:
L = 0P = LS(9) cos θ.
Эта энергия с увеличением Ls(9)cos0. растет по тому же
закону, что и квадрат суммарной высоты, но с поправочным
множителем cos*0.
Таким образом, в простейшем случае волнообразования,
когда берег прямолинеен и вектор скорости ветра нормален к
нему, береговую черту можно рассматривать, как своеобразный
излучатель элементарных компонент углового спектра.
Изучив законы роста спектральных составляющих углового
спектра волн для простых условий волнообразования,
используют эти же законы в случаях сложного поля ветра и сложной
формы береговой черты. С этой целью сложное поле ветра
заменяют совокупностью областейс различными, но постоянными
скоростями ветра и применяют к ним полученные законы,
изменения энергии спектральных компонент, соблюдая при этом
условие непрерывности изменения энергии составляющих
углового спектра.
Таким образом, береговую черту будем, по-прежнему,
рассматривать как излучатель компонент углового спектра.
Принимаем, что энергия каждой компоненты углового спектра волн
в точке Ρ определяется проекцией отрезка луча этой
компоненты длиной Ls(9) на направление ветра. При этом закон
нарастания энергии каждой компоненты сохраним таким же, как
и в случае прямолинейного берега при ветре, перпендикулярном
береговой черте. Тогда функция углового распределения
энергии в точке Ρ при сложном контуре береговой черты запишется
По аналогии с формулой 6.66 таким образом:
S[B, Vw, Ls{m = -^hd*[Vw, ^WcosGJcos^, 6.67
a квадрат средней высоты волн по аналогии с формулой 6.65
впишется так:
V - -г ί VIv™ L* <θ>cos θ!cos2 θ άθ· 6·68
-π/2
195
При конкретных инженерных расчетах интегрирование
формуле 6.68 заменяют суммированием: в1
%л=Нг Σh*lVw'Lsn(UcosθηΙcos2ΘλΔΘΓ' 6·69'
где л —номер луча, проведенного из расчетной точки Ρ д0 Пе
ресечения с контуром берега; Qn — угол между лучом η и на*
правлением ветра: Lsn(Qn) — длина отрезка луча с номером п-
ΔΘ— угол между соседними лучами.
Обычно строят семь лучей в секторе от —π/2 до +π/2; глав-
ный луч в направлении ветра и 6 лучей под углами ±22,5°·
±45° и 67,5° —к главному лучу. В этом случае предыдущая
формула приобретает вид:
\ = 0,1 ]/25А? + 21(а! + А2-2) +*
+13 [hi + hU) + 3,5 [Я + hU), 6.70 (152)
где А, м — средние высоты, которые определяют по расчетной!
скорости ветра Vw и проекциям лучей Lrt, м, на направление)
главного луча.
Пример 6.7
Требуется определить элементы волн hdi Td% «λ* в точке Ρ
глубоководной акватории (рис. 6.6), имеющей сложный контур береговой черты, при
в£тре со скоростью Vw = 21 м/с.
Рис. 6.6. Схема к расчету высоты ветровых волн с учетом
сложного контура береговой черты.
Решение.
На схеме побережья выполняют необходимые построения, определяю
величины θ«, Ln и заносят их в табл. 6.4.
. В первом столбце таблицы записаны порядковые номера главного и б°'
ковых лучей, во втором —их направление, в третьем — величины проекий»
отрезков лучей Ln- Результаты расчетов приведены в столбцах 4—6. СреД'
няя высота волны определена по формуле 6.70 (152):
196
hd = 0,1 /25-1,803 + 21 (3,03a + 2,16*) + 13 (2.833+ 2,702) -f ~*
"+3,5(2,793 + 2.563) = 2,5 м.
Период волны определяем по значению jr/i/W= 9,81 · 2,5/212 = 0,056 из
. ι обязательного приложения 1 [51]: gTa/Vw = 3,2, откуда Та = 6,85 с.
формуле (151) определяем среднюю длину волны: Xd = 73 м.
Таблица 6.4
η
4
3
2
1
-2
—3
—4
ΘΛ, град
67,5
45
22,5
0
—22,5
-45
-67,5
Ln, км
93
111
128
31
49
Ι 90
76
2068
2469
1 2847
690
1090
ι 2000
1691
w
0,062
0,063
0,0675
0,04
0.048
0,06
0,057
Λη, μ
2,79
2,83
3,03
1,80
2,16
2,70
2,56
При учете большого количества препятствий, линейные
размеры которых значительно больше длины набегающих волн,
дополнительно делают следующие построения [27]. Из
расчетной точки Ρ в направлении подветренного берега и в пределах
каждого n-ого сектора от вп—уАО до β/ζ + γΔΘ проводят лучи,
касательные к препятствиям. В результате в п-м секторе
получают kn секторов с препятствиями и 1п секторов с
промежутками между ними. Средняя высота волн:
+ 2 h2nJ IV., Lnj (Kj) cos en;] cos* (θ„;) 8β JJ , 6.71
^e On/, θ«/, град — соответственно углы между отрезками лучей
Lnh Lni и направлением ветра Vw\ δθΛ/, δθ«/ — угловые размеры
^ответственно ί-го препятствия и /-го промежутка между
препятствиями (/ = 1, 2, 3,...., kn\ j = 1, 2, 3,..., In) в пределах л-го
<*ктора.
При использовании формулы 6.71 необходимо, чтобы
соблюдалось условие (δθΛί·+*θΛ/ΧΔΘ. Расчеты упрощаются, если
приближенно принять в пределах каждого сектора θΛ,~6Λ/ =
888 &л. В итоге выражение для сектора η записывается в виде
197
л,
*«« 42 "«л fк··L»' (θ«)cos β«ι +
U=i
'. U/2
+ 2 νΛ ί^ ^ <β«>cos θ-1 · 6·72 №)*
где hdn — средняя высота волн в секторе /г, хя/, vnj — соответст
венно угловые размеры /-го препятствия и /-го промежутка меж I
ду препятствиями в пределах /г-го сектора, отнесенные к y/J
ΔΘ, град; йя,·, АЛ/ — средние высоты волн, принимаемые по номо-
грамме рис. 1 обязательного приложения 1 [51] по расчетной
скорости ветра Vw и соответствующим проекциям отрезков лу-
чей на направление ветра. Лучи являются биссектрисами
углов, образованных касательными, проведенными из расчетной
точки к обеим сторонам /-го препятствия или у-го промежутка
между препятствиями в пределах /г-го сектора. Отрезки лучей
Lniy Lnj равны соответственно расстояниям от расчетной точки|
до пересечения с ι-м препятствием и максимальному разгону
в у-м промежутке.
Расчеты до формуле 6.72 (152а)* выполняют для каждого]
луча с номером п. Высоту волны в расчетной точке определяют
по формуле 6,71. При системе разбиения через- ΔΘ = 22,5, град,
для расчета средней высоты, ^олн в расчетной точке
используют формулу 6.70 (152). Если на каком-то из направлений θ
волны не достигли установившегося состояния, то высота волн
определяется не проекцией разгона, а продолжительностью!
действия ветра..
Пример 6.8
Выполнить необходимые построения для определения средней высоты]
волны hd при наличии большого числа островов, рис. 6.7.
Решение.
Из точки Ρ параллельно направлению ветра проводят..главный луч θι =
— 0°. От этого луча по часовой стрелке- со знаком плюс^ против часовой
стрелки — со знаком минус, проводят через 22,5 град шесть" боковых лучей.
Они обозначены на рис. 6.7 сплошными линиями. Около главного и
боковых лучей строят семь секторов (я= 1; ±2; ±3; ±4); углы при вершин^
равны 22,5°. Границы секторов отстоят от лучей на величину 11,25 град
Затем из точки Ρ проводят в границах каждого /г-го сектора лучи, касатель |
ные к береговой черте i-x препятствий (штрих-пунктирные линии). В Ρ'
зультате в я-ом секторе получают kn секторов с препятствиями (незаштр1'
хованные) и 1п секторов с промежутками между ними (заштрихованные)·
Система разбиения сектора η = — 2 на малые сектора с препятствиям
и промежутками показана на рис. 6.7. Для каждого сектора kn с препятМ
виями и и с промежутками последовательно (по часовой стрелке) onPeQM
ляют угловые размеры δθΛί· (препятствия) и 6Θ„/ (промежутка). При эт ·
обозначаем /= 1, 2, 3,... < kn\ / = 1, 2, 3,..., /„. Дополнительно измер*
198
езкй L,d и Lni у препятствий и промежутков, соответственно, являющиеся
с^рктрисами углов 69Я/ и б9яу. Далее вычисляют безразмерные параметры
6,1 ΓδθΛ//Δθ, vnJ = δθΛ//ΔΘ при Δθ = 22,5°.
Рис. 6.7. Схема к расчету высоты волн за большим количеством
островов.
Пример 6.9
Определить высоту волны hn в секторе η = —2 с учетом имеющихся
стровов и промежутков между ними, рис. 6.7. Расчетная скорость ветра
^ * 16 м/с.
Решение.
Результаты расчетов для сектора η = — 2 сводим в табл. 6.5.
Высоту Fnss=-2 определяют по формуле 6.72 (152а)* [51]:
*„=4
*-2 = 2*i#i+ Σ V«y= (0.17 + 0,48)^ = 0,81 м.
/-ι
/—1
199
Таб.
лща 6
град
Ап/
^П/С08вл,
Μ
bnl·
0,18
0,09
0,13
0,18
6900
3500
3300
3500
6400
3200
3000
3200
0,66
0,48
0,47
0.48
0,44
0,23
0,22
0,23
град
-η]
Lnj,u
£_,cos6„,
hny M
7-2
hnj>
W,
7.5
2,0
0,33
0,09
22000
22000
20300
20300
1,07
1,07
1,U
1,H
0,38
0,48
Рассмотрим случай, когда ветровое поле неоднородно [47]
Если скорость ветра меняется вдоль разгона, то весь разки!
делят на участки, в пределах которых скорость ветра изменя]
ется не более, чем на 5 м/с. В начале второго участка опреде
ляют разгон, при котором высота волн будет равна ее значению!
при скорости ветра на втором участке. Этот разгон суммируют)
с длиной второго участка разгона и по новому разгону и скоро
сти ветра на втором участке определяют высоту волны на
втором участке. Подобная процедура выполняется последовательно!
при переходе от одйого участка к другому до расчетной точки
' Если скорость ветра изменяется в поперечном направленш
более, чем на 5.м/с, и направление более, чем на 22,5°, то т
расчетной точки проводят лучи и при системе разбиения Δθ=ι
= 22,5° используют при расчете высоты волны формулу 6.70|
(152). Дальнейший расчет по каждому лучу выполняется так,
как это делалось в первом случае, при скорости ветра
переменной вдоль разгона.
Пример 6.10
Требуется найти среднюю высоту волны hd в точке Ρ глубоководно1
акватории на конце луча, направление которого совпадает с направление*
ветра, а скорость ветра переменна (рис. 6.8): на первом участке Ь\ *= 40 Щ
Vw\ = 20 м/с, на втором участке L2 = 60 км, VW2 = 25 м/с, на третье*!
участке 13 яв 50 км, VW3 = 30 м/с.
Решение.
Для первого участка ^1/^=981 и по рис. 1 обязательного при*°1
жения 1 [51] находим ghj V2W = 0,047, откуда Λχ = 1,92 м- Отноше«*4
gbil VI* = 0,030 и gUJ V%2 = 330.
Суммируем относительные разгоны:
gM*
gL
W2
V2o
Yw2
= 330 + 942=1272.
300
flo рис. 1 приложения 1 определяем значение £W V^,2 = 0,052, откуда
г ^3,31 м. Аналогичным образом £h2IVlz = °»036· Далее, gbL2l V^z = 510 и
fbMVU + 8L*lvl* = 510 + 544 - 1055. Соответственно #Л3/V'£3 = 0.0475
средняя высота волны в расчетной точке Р: Л3 = 4,36 м.
К.
AM Э
Рис. 6.8. Схема к расчету высоты волн при переменной вдоль
разгона скорости ветра.
Пример 6.11
Выполнить необходимые построения для определения элементов волн
в расчетной точке Ρ при переменной в пространстве скорости ветра, рис. 6.9.
Решение.
Из расчетной точки Ρ проводим главный луч (п = 1) в направлении,
овпадающем с точностью до 11,25 град с направлением ветра в
окрестности расчетной точки, и боковые лучи с интервалом в 22,5 град в секторе
** 67»5 град от главного луча. Каждый луч. делим на участки Lnb Ln2>
ηΖί·-·»£/ιί, в пределах которых скорость изменяется не более, чем на 5 м/с,
Управление — не более, чем на 22,5 град. Находим далее проекции
«ι cos θηι, ini cos 0n2f ,..tLni cos θΠί на направления ветра в выбранных
стках. Эти проекции рассматриваем в качестве расчетных отрезков раз-
а* На рис. 6.9 приведена указанная разбивка для одного луча η = — 2.
201
п=-Ч
77=-#
ηΙ_2 VW=1$M/C
,S
Л=2
77 = /
Рис. 6.9. Схема к расчету высоты волны по переменному!
в пространстве полю ветра. J
Пример 6.12
Определить высоту волны /zd, м в расчетной точке глубоководной зоны
при переменной в пространстве скорости ветра. Значения высот hn по лучам |
приведены "в табл. 6.6. :: " '
Таблица 66
Номер луча
Высота по лучу, м
—4
0,82
—3
0,94
—2
0,91
1
1,07
2
1,02
3
0,81
4
0,45
Решение.
Определяем среднюю высоту волны в расчетной точке Ρ по
6.70 (152):
hd = 0,1 ·/25· 1,072 4-21 (0,912 +1,022)+ 13(0,9Р + 0,812) + 3,5 (0,82* + Ц^ ''
= 0,95 м.
202
Глава 7.ЭЛЕМЕНТЫ ВОЛН НА МЕЛКОВОДЬЕ,
В ЗОНЕ ТРАНСФОРМАЦИИ
И НА ОГРАЖДЕННЫХ АКВАТОРИЯХ
7.1. РАСЧЕТ ЭЛЕМЕНТОВ ВОЛН НА МЕЛКОВОДЬЕ
На акваториях, где глубина относительно невелика, а дно —
горизонтально или слабо наклонно, (уклоны дна менее 0,001),
развитие волн под действием, ветра происходит вначале так же,
как и на глубокой воде, а затем начинает влиять глубина
водоема. Влияние глубины становится существенным, когда в
процессе развития волн их длина превышает удвоенную глубину
водоема. Этот факт является следствием того, что фазовая
скорость волн в водоемах с ограниченной глубиной
определяется соотношением 2.58:
где λ —длина волны, м; d — глубина, м.
Важным обстоятельством для развития ветровых волн в
водоеме ограниченной глубины является то, что в соответствии с
теорией [24, 26] генерация ветровых волн с помощью
резонансного механизма не всегда возможна в отличие от условий на
глубокой воде (параграф 6.2). Необходимым условием для
включения резонансного механизма генерации волн является
равенство скорости ветра фазовой скорости свободных волн на
поверхности водоема. Если на глубокой воде можно найти
компоненты спектра развивающихся волн, для которых выполняется
условие резонанса, то, как следует из 7.1, для водоема
ограниченной глубины такие условия возможны не всегда. В
последнем случае развитие волн существенно ограничивается глубиной
водоема. Это означает, что, начиная с некоторой величины,
скорость ветра практически перестает влиять на элементы
в°лн, развивающиеся на заданной глубине.
Другой механизм ограничения параметров волн на мелко-
в°Аных акваториях связан с нелинейными эффектами. Высота
ВОлн на мелководье не может превышать (0,6.. . 0,8)d,
поскольку Дальнейший рост невозможен из-за интенсивного обрушения
^олн. Дополнительными факторами, ограничивающими разви-
Ие волн на мелководье, являются придонное трение,
фильтрами* и т. п.
Рассмотрим качественно процесс развития волн в водоеме,
в ^ 7.1. Через некоторое время после начала действия ветра
м°мент tx поверхность водоема покрывается ветровыми вол-
Ми» высота h\ которых возрастает по мере увеличения раз-
а До некоторого значения Лг на расстоянии Li от берега
203
(рис. 7.1, α). Поверхность водоема оказывается разбитой
две зоны. В одной зоне, прилегающей к береговой черте (ι На|
^L2), высоты волн определяются длиной разгона, в друг5
удаленной от берега (L > L2), —высоты волн зависят тольу
от продолжительности действия ветра /2- В этих случаях глуб{
на водоема все еще не влияет на элементы волн. Однако, на J
hoh
Ihl·
it I I
у^\ ч
1 if
Рис. 7.1. Схема развития волн на акватории
а) глубоководной; б) мелководной.
котором расстоянии L\ (рис. 7.1,6) в момент времени tu на
волны сказывается влияние дна, и развитие их происходит меД*
леннее, чем в глубоководных водоемах. Рост высоты волн з^
медляется, а затем при разгоне L\ в момент времени t\ совс^
прекращается. С этого момента волнение становится установи
щимся на всей акватории. о ,,
Таким образом, в прилегающей к берегу зоне шириной ^
высоты волн при фиксированном значении скорости ветра
деляются только разгоном и совпадают с высотами волн
тех же условиях на глубоководных акваториях. В промежут
опре*
Пр,!
204
д зоне (L'%— L\) высота волн зависит и от разгона, и от
Шубины водоема, а в удаленной от берега части, где разгоны
*1г1ьше L'z, вплоть до наветренного берега высоты волн и опре-
*яются только глубиной. Это зона предельного развития волн
д мелководье. Аналогичные изменения претерпевают и другие
злементы волн (длина, период).
формулы для расчета элементов волн на мелководных
водоемах, содержащиеся в нормах [51], базируются на
фильтрационном анализе натурных данных [24, 55]. На первом этапе
использовали наблюдения, относящиеся к предельной
мелководной зоне водоема. Отбор был выполнен с помощью
безразмерных зависимостей 6.50, 6.51, в которых разгон L был
заменен глубиной d. На втором этапе были проанализированы
данные, относящиеся к промежуточной зоне водоема. Вначале
были зафиксированы (по интервалам) значения безразмерной
глубины gd/V2w и анализ был выполнен с помощью 6.50, 6.51,
а затем фиксировали безразмерные разгоны gL/Vzw и
использовали те же формулы, но с заменой в них L на d.
В результате получена обобщенная зависимость для расчета
средней высоты волн h с учетом скорости VW9 разгона L и
глубины водоема d при горизонтальном или слабонаклонном дне
с уклоном менее 0,001 (Стрекалов [55]):
Л =0,16(1 - [1 +6,0.10~3(^/l/w2)i/2]-2} χ
Xth[0№5'(gdjVw*)<>>*l\ - [1 +6,0.10-3(^VW2)1'2]-2}-1]. 7.2
Формула 7.2 переходит при gd/V2w-+°o в 6.52 для
глубоководных акваторий, а при gL/VzWT><x> она преобразуется в
зависимость для расчета средней высоты волны в зоне
предельного развития волн на мелководье:
Средний период волн Τ для мелководных водоемов в общем
слУчае, как и для глубокой воды, определяется по 6.53, а для
3°ны предельного развития:
f(d/g)-ll> = 4,6. 7.4
дл Ф°рмул 7.3 и 7.4 видно, что высота h и период волн Τ
^я зоны предельного развития не зависят от разгона L; при
а ^м их высота слабо зависит от скорости ветра (в степени 0,4),
ериод определяется только глубиной водоема.
среднюю длину волн на мелководных акваториях вычисля-
аквПо той же формуле (151) [51], что и для глубоководных
аторий, поскольку для_зоны предельного развития' поправоч-
1И множитель Ш(2я^Д)^1; (ίί/λ~0,3).
205
Рассмотрим наиболее часто встречающиеся на практц
случаи расчета элементов волн на мелководных акваториях. Ке
При любых постоянных уклонах дна, в том числе горИЗо
тальном, и глубинах, увеличивающихся вдоль разгона, расц!
параметров волн выполняют с учетом глубины водоема в расТ
четной точке с "помощью приведенных выше соотношений, либ
по графикам рис. 1 обязательного приложения 1 [51]. Тако?
подход основан на предположении о том, что при увеличении
глубины вдоль разгона трансформации волн не происходит, и
роль глубины заключается только в ее локальном влиянии'на
процесс генерации волн.
Аналогичное предположение относится к водоемам, где
глубина уменьшается вдоль разгона, но уклоны дна не превышают
0,001. Расчет параметров волн в этом случае выполняют так же,
как при увеличивающейся глубине или при горизонтальном
дне. Допускается также использовать графики рис. 6.3 для
расчета элементов волн А, м, и Г, с, по заданной скорости ветра
VWt м/с, и глубине d, м. На графике шкала d определена по
формуле 7.4 для заданного периода волн Т. При этом водоем
считается мелководным, если долученное по графику (по
величине глубоководного, периода Td) значение оказывается больше
фактической глубины 4е- Для мелководного водоема элементы
волн определяются по фактической глубине άε и заданной
скорости ветра Vw-
Пример) 7.1
Определить элементы волн Λ, λ, Τ и hx% в мелководном водоеме с
уклонами .дна- 0,001 при скорости ветра Vw = 18 м/с; разгон L■ — 5.· 105 м,
глубина d — 7 м.
Решение.
Находим безразмерные величины:
gL 9,81-5.105 __Гг,1?о.
τν = —т lo139·
gd ,9,81.7 __А?19
VV 18-
Далее по рис. 1 обязательного приложения 1 [51] определяем:
= 0,028 и gT/Vw = 2,15. _ ^
. Элементы волн соответственно равны: h = 0,028· 182/9,81 = 0,92 м; '"
= 2,15 · 18/9,81 =3,94 с.
Длина волн по формуле (151): λ = 9,81 ·3,92/6,28 = 24 м. Высоту волН^
1%-ной обеспеченности hl% определяют по вычисленным величинам gW *'^
= L5139 и gd/V2w = 0,122. Согласно табл. 5.4 и 5.6 (kl%)L = 2,40; (к\%*А*
= 2,10. Так как (k\%)L> (kl%)di то в расчет принимают коэфФиШ16^
(&1%"-)d = 2^0, учитывающий влияние глубины. Тогда h1% = 2,10 · 0,9^
= 1*93 м. -°
206.
При переменных глубинах вдоль разгона выделяют участки
различными уклонами дна (примерно одинаковыми в преде-
ах каждого из них). Если при этом для каждого участка
глуша либо возрастает, либо остается постоянной, либо умень-
ется, н0 уклон дна менее 0,001, то расчет выполняют
слегшим образом.
По заданной скорости ветра Vw, величине разгона L\ и
глубине di в конце первого участка определяют среднюю высоту
волн /*ι таким же образом, как это показано в примере 7.1.
Эту высоту принимают в качестве исходной для расчета
средней высоты волн на втором участке с разгоном L2 и глубиной
в конце участка d2. > _
По безразмерным величинам ghx/V2w и gd2/V2w определяют
величину дополнительного разгона ΔΙ с помощью рис. 1
обязательного приложения 1 [51]. Величина дололнительного
разгона AL соответствует эквивалентным условиям роста высоты
волн на первом участке до значения ft4 при той же скорости
ветра, но при глубине, отвечающей глубине на втором участке,
равной d2. Суммируя безразмерные величины дополнительного
разгона g&Li/V2w и разгона на втором участке gL2/V2w, найдем
безразмерную величину эквивалентного разгона для обоих
участков. По этой величине и безразмерной глубине gd2/V2w в
конце второго участка определим среднюю высоту волн в конце
второго участка \\2. На последующих участка^ расчеты
выполняют аналогичным образом. Средний период Τ, среднюю длину
волны λ и коэффициенты перехода ki% от средней высоты волн
к высотам волн *%-ной обеспеченности hi% определяют по
безразмерным величинам глубины gd/V2w и эквивалентного разгона
eq в расчетной точке.
Пример 7.2
Определить среднюю высоту волн h в точке Ρ мелководного водоема
•фи скорости ветра Vw = 25 м/с, рис. 7.2.
Решение.
Начиная от подветренного берега акватории, профиль дна разбиваем на
два участка с различными и примерно одинаковыми в пределах каждого из
Ш1 Х>ш
аг^5м
ΙΙ£· 7.2,. Схема к определению высоты волн при переменных вдоль
разгона глубинах.
207
них уклонами дна. По значениям gdi/V2w = 9,81 ·8/252 = 0,126 и gLlvi ,
9,81-3103
= 252 = 47,09 с помощью графика, приведенного на рис. 1 0бяз
тельного приложения 1 [51], находим, что в конце первого участкаig/ц/1/2
= 0,0113. Для второго участка gd2/V2w = 9,81- 5/252 = 0,0785; с помощи
того же графика и величины gh\IV2w = 0,0113 определяем величину дополни
тельного разгона gM\IV2w = 120, которую суммируем с безразмерным па,
гоном на втором участке: gbLJV*» = gL2IV2w = 120+78 = 198. н d'
Используя эту величину и величину безразмерной глубины в точке р|
gd2/V2w = 0,0785, определяем gh2IV2w = 0,012; откуда находим среднюю
высоту волн '
τ 0,012-252 A7f.
*=-w-e0,76M·
При сложной конфигурации береговой черты и переменных!
в пространстве поле ветра и рельефе дна расчеты элементов
волн выполняют с применением методики, изложенной в пара]
графе 6.3. При этом средние высоты волн для каждого луча
вычисляют как с учетом безразмерной проекции данного
участка на луче на направление ветра, так и с учетом безразмерной
глубины в конце каждого участка.
7.2. ТРАНСФОРМАЦИЯ ВОЛН НА МЕЛКОВОДЬЕ
При распространении ветровых волн из глубоководной
части водоема в мелководную зону происходит их трансформация,
обусловленная рефракцией, деформацией волн при уменьшении
глубины, трением о дно, обрушением из-за нелинейных
эффектов и другими особенностями. В том случае, когда уклоны дна1
равны или превышают 0,002, а глубина уменьшается вдоль
разгона, возникают условия для трансформации волн, которые
преобладают над процессом их роста под действием ветра.
Наиболее полное описание эволюции волн как в
глубоководной, так и в мелководной зонах может быть получено с
помощью уравнения баланса волновой энергии в спектральной
форме [13]. Аналитическое решение этого уравнения, как
указано в параграфе 5.2, затруднено даже для глубокой воды, тем
более трудной представляется задача его отыскания для
мелководной зоны. Поэтому исследованы только немногочисленные
частные задачи, причем большинство из них не доведено Д°
практического применения.
Основой для практического использования является задача,
исследованная Ю. М. Крыловым и др. [24]. Ее можно сформУ*
лировать следующим образом. Рассматривается прибрежий
мелководная зона с медленно изменяющимися глубинами (за
исключением прибойной зоны). Вместе с тем мелководная зон?
предполагается достаточно узкой, такой, что эффектами при1"0'
ка и оттока энергии, связанными с воздействием воздушН°г^
потока, и ее перераспределением из-за нелинейных взаимоД611'
208
вий можно пренебречь по сравнению с влиянием
изменяющейся глубины. Кроме того, считается, что можно пренебречь
Г еНием о дно, обрушением волн и другими диссипативными
ЛфеКтами, так что энергия волн полностью рассеивается вбли-
и береговой линии — в зоне прибоя.
3 Поток волновой энергии считается заданным в некоторой
точке пространства и в силу указанных условий остается
постоянным в направлении к берегу. В такой постановке задача
трансформации волн в прибрежной зоне рассматривается в
линейной постановке, что позволяет использовать классическое
решение задачи о рефракции волн, а в спектральном
представали— рассматривать каждую спектральную компоненту как
монохроматическую волну.
Основные результаты этой теории для монохроматических
волн можно записать следующим образом:
с _ s\nar* η -
cd sin ard
augrE = ddUgr dEdy 7.6
где с и ugr — фазовая и групповая скорость волны; аг — угол
между лучом волны и нормалью к изобате; Ε — энергия волны,
приходящаяся на единицу площади моря; а —расстояние
между соседними волновыми лучами; индекс d относится к
параметрам волн на глубокой воде.
Зависимость 7.5 выражает известный закон Снелла — закон
преломления волновых лучей, а 7.6 — условие постоянства
потока энергии между соседними волновыми лучами. Из
раздела I следуют соотношения:
^=TP£V;£=|pgA2;
8 rs d · ~ 8
_ 1
lgrd
-τ* *-M«+s§y··
„21 = дк. r7 = jL th ' 2nd
где ρ —плотность воды; λ и kd — средняя длина волны
соответственно в мелководной зоне и на глубокой воде.
Поэтому, предполагая, что период волн в зоне
трансформации остается таким же, как на глубокой воде, выражения
δ и 7.6 можно преобразовать к виду:
Ъ = ktkrhd; 7.8
209:
kr=Vad/a. 7Л 4154)
Здесь kt — коэффициент трансформации; kr — коэффицИе
рефракции. ,т1
Учитывая, что
hd,i = (ki%)dhd,
где {ki%)d и kt%— коэффициент перехода от средних выс0Т|
волн к высотам волн 1%-ной обеспеченности в системе
соответственно на глубокой воде и в зоне трансформации, выражение
7.8 можно переписать в виде формулы (153) [51]:
Λί = ΛΛ*Λ>Λ. 7.12(153)
где kt = ki%j(ki% )d — обобщенный коэффициент потерь,
учитывающий изменение функции распределения в зоне
трансформации по_сравнению с глубоководной зоной; значения (ki%)dt
CN = λ/λα представлены на рис.2, 4, a ki — в табл.5
обязательного приложения 1 [51]. При расчёте kt и С ν
использованы формулы 7.9; 7.10.
Описание методики определения коэффициентов ki% и k
содержится в параграфе 5.4. Значение kr можно получить либо
численными методами, либо путем построения плана
рефракции волн с помощью соотношения 7.5, которое преобразуется
к виду:
CNl+\ = Sin (iri + Aotr/) j и
CNi sinari
где_С#ж» Cni — величины, определяемые по 7.10 при di+\/%d и
di/λά] di+it di — глубины, отвечающие изобатам с
соответствующими номерами: ί+l, I; ari — угол между направлением луча
и нормалью к изобате с номером ί; Δώη· — угол преломления
луча на изобате с номером ί+l по отношению к углу аы-
Отклонение луча происходит в сторону меньших глубин
Таким образом формула 7.13 позволяет рассчитать значение
Δα,·/ по α,ί+ι/λά и di/hdy определенным на двух соседних
изобатах. Эта зависимость представлена в графическом виде на РиС
6 обязательного приложения 1 [51].
В случае прямолинейных изобат коэффициент рефракшп'
может быть определен в любой точке прибрежной зоны в
зависимости от относительной скорости См в этой точке и первой*"
чального угла подхода волны ad по формуле:
_ Г 1 — C^ysin^g^ τι/4 7(14
*'-[ ^^ J ·
Это соотношение следует из закона преломления 7.5 и УсЛ
210
п. ' COS СИи u
££. = C0Sflt , справедливого для мелководной зоны с прямо-
ценными изобатами.
111 Пример 7.3
Определить высоту волны 1%-ной обеспеченности Л1х при глубине d =
^ 5 м и приблизительно прямолинейных параллельных изобатах. Угол
подхода dd между нормалью и изобатами и направлением распространения волн
оставляет 60°; уклон дна 0,025. Элементы волн на глубокой воде: ha = 2,0 м;
£-50 м; *ιΚ-2,2.
решение.
Высоту волны hx% в расчетной точке определяем по обязательному
приложению 1: по табл. 5 и величине d/λα = 0,1 при i = 0,025 находим fe = 0,93,
а по рис. 5 —fejjj),93. С помощью нижней огибающей кривой на рис. 4
определяем Слг = λ/λ<ί = 0,7 и затем по формуле 7.14 вычисляем коэффициент
рефракции:
' L COS* 60° J
Подставляя в формулу 7.12 (153) найденные величины, получим: Λιχ =
= 0,93 -1,26- 0,93 · 2,2 · 2,0 = 4,8 м.
Пример 7.4
"Рассчитать коэффициент рефракции kr в мелководной зоне для глубинны
d = 20 м (рис. 7.3). Исходная длина воли на глубоководной акватории λ<* =
= 206 м.
%
Рис. 7,3, Схема к определению коэффициента рефракции,
211
Решение.
На основе предварительного построения плана рефракции, начиная
глубин d ^γΤα = 103 м, находим kr.
Расстояние между лучами 1 и 2 выбираем с таким расчетом, чтоб
они проходили по разные стороны от расчетной точки А. На плане выполи
но сглаживание изобат (штриховые линии на рис. 7.3) и обозначены пово
ротные точки в местах пересечения лучей с промежуточными изобатами
В этих точках последовательно находим величину угла art между направле
нием исходного луча и нормалью к промежуточной изобате. Определяем
отношение глубины на каждой изобате к исходной длине волны λα и по но
мограмме рис. 6 обязательного приложения 1 [51] находим угол поворота
луча Δον/. Откладываем значение Δα^.οτ направления исходного луча в
сторону меньших глубин и определяем направление рефрагированного луча
Расчеты сведены в табл. 7.1.
Таблица 7.1
Номер
луча
/
2
Номер
точки
1
2
3
4
5
6
7
8
9-
10
11
12
м
100
90
60
40
30
20
100
90
60
40
30
20
*i-\lld
0,48
0,44
0,29
0,19
0.15
0.1
0,48
0,44
0,26
0,19
0.15
0,1
di+\>
Μ
90
60
40
30
20
15
90
60
40
30
20
15
di+ifid
0,44
0,29
0,19
0,15
ОД
0,07
0,44
0,29
0,19
0,15
ο,ι
0,07
ari>
град
20
34
9
27
41
18
54
40
25
27
41
30
град
0,2
1,5
0,5
2.5
5
2,5
0.5
2
2
2,5
5
4,5
С построенного плана рефракции снимаем значения аа = 15 мм и я =
= 23 мм и по формуле 7.11 (154) вычисляем коэффициент рефракции
в точке Л: (kr)A = Κ~Ϊ5/23 = 0,81.
Приведенные соотношения получены на основе линейной
теории волн. Как показывают экспериментальные и
теоретические исследования, учет нелинейных эффектов приводит к
некоторому уменьшению расчетных высот волн в мелководна
зоне (за исключением прибойной). Поэтому, в первом прибли;
жении при расчетах трансформации высот волн в мелководна
зоне водоемов нелинейными эффектами можно пренебречь
Вместе с тем для таких параметров волн, как длина волны '■
или превышение вершины волны' над расчетным уровнем ικ·
учет нелинейности ветровых волн при их трансформации н'
мелководье оказывается более существенным (см. рис. 3,
обязательного приложения 1 [51].
Наиболее сильно нелинейные эффекты проявляются в ncKi|
жении формы волны, в асимметрии профиля волны как относ1
212
льно ее гребня, так и относительно уровня моря. На глубокой
де волны также асимметричны, но в меньшей степени, чем на
мелководье.
Параметр x\c/hiy определяющий асимметрию волн
относительно среднего уровня моря на глубокой воде, зависит от
величины hi/gT*d, характеризующей крутизну волн. При малой
крутизне (практически для hi/gT2d < 0,03) форма волн близка к
синусоидальной, и соответственно- x\c/hi = 0,5. С увеличением
крутизны, которая на глубоководье, согласно теории волн
конечной высоты, может составлять /ι/λ = 1/7, и асимметрия волн
достигает цс/Ы = СЦ376. Зависимость г\с/Ы = f(hi/gT*d) на
глубокой воде при d/λα > 0,5 соответствует теории Стокса [86].
В мелководной зоне параметр_г)с//1/_выражается более
сложной зависимостью η<?//ΐ/= f(hi/gT2, d/hd), которая получена на
основе анализа экспериментальных данных. Предельные
значения r\c/hi в мелководной зоне определяются только
безразмерной глубиной d/Kd [28].
Аналогичным образом получены зависимости λ/kd =
=s /(■ —2 , -=-), представленные на рис. 4 [51]: нижняя
огибающая кривая соответствует условиям трансформации длин
волн малой амплитуды, а верхняя — отвечает предельно крутым
волнам для данной безразмерной глубины.
Нример 7.5
Определить высоту волны 1%-ной обеспеченности Л1%, среднюю длину λ
и превышение вершины волны 1%-ной обеспеченности над расчетным
уровнем цс в точке с глубиной d = 7 м. Уклон дна акватории 0,01. Коэффициент
рефракции ^г = 0,8. Исходные элементы волн на глубокой воде (hd)\% =
= 5 м; λ^ = 80 м; Та = 7,2 с.
Решение.
Высоту волны hi% определяем по формуле 7.12 (153) обязательного
приложения 1 [51]. Коэффициент трансформации kt, входящий в эту формулу,
"аходим по рис. 5, где отношению d/λα = 7/80 = 0,087 соответствует значение
**^ 0,935. Обобщенный коэффициент потерь в соответствии с табл. 5 при
dlhd = 0,087 и уклоне дна / = 0,01 составляет ki = 0,85. Таким образом на-
х°Аим: hl% = 0,935-0,8-0,85·5 = 3,18 м. _
Длину волны определяем по рис. 4. _Используя величины d]%d = 0,087 и
h\%IgT* = 0,0062 по графику находим λ/λ^ = 0,71. Откуда λ = 0,71-80 =
"=57 м.
Превышение вершины волны 1%-ной обеспеченности над расчетным
Уровнем (r\c)i% определяем по графику, приведенному на рис. 3. Для значе-
Иий h\% 1ST"2 = 0,0062 и d/λα - 0,087 иэ рис. 3 находим (r\c)i% I hl% = 0.69,
0ТкУДа (η,)1% = 0,69 · 3,18 - 2,19 м.
213
7.3. ВОЛНЫ В ПРИБОЙНОЙ ЗОНЕ
hsum/if T
~2
η no Χ.
υμ/Ζτ
0 Π1ν
π πηΆ.
η η no V
UfUUcv
' ППП1Υ
UfUUI г
/7/7/7/75 L
nnnno L
0,0005 0,002 0,01
0,05 0,2
С выходом ветровых волн на прибрежный откос происходи
их трансформация, обрушение с последующим накатом на бе
per. Основное влияние на трансформацию волн в прибойноп
зоне, в пределах которой начинается и завершается разрущен'|
волн, оказывают уклоны дна, а также его шероховатость и пр0.
ницаемость.
При больших уклонах днГа (ί > 0,1), волна, разрушаясь, те.
ряет больше энергии, чем при малых. Внешне проявление этого
процесса наблюдается как
преобладание на больших ук.
лонах обрушивающихся греб.
ней «ныряющего типа» (plUn.
ging).
В случае малых уклонов
дна (/<0,01) волна теряет
свою энергию постепенно,
претерпевая ряд обрушений, в
результате чего она все время
находится в состоянии,
близком к критическому. На
малых уклонах преобладают
гребни «расплескивающего»,
(скользящего) типа (spilling).
Волны перед обрушением в
состоянии, близком к критическому, называются прибойными
волнами.
Функциональная связь между высотой предельно крутых
волн hsun%, периодомГ и глубиной водоема d во всем диапазоне
изменения относительной глубины для случаев плоского
горизонтального дна установлена на основе лабораторных и
натурных исследований [28] и показана на рис. 7.4 в виде
зависимости
Теоретические исследования предельно крутых волн для
случая горизонтального дна были выполнен^ в работах [76, 78].
В зоне малых относительных глубин d/gT2^. 1,5· 10~3
экспериментальная зависимость, изображенная на рис. 7.4, согласуется
с теорией одиночных волн параграфа 2.3, согласно которой
Л*п* = 0,7Мг. 7.15
В зоне глубин 1,5· 10~3 < d/T2 < 1,5-10"2 эксперимента^;
ные результаты контролируются формулами теории Манка [76J·
didr-i + i9saVdr/g7*. Мб
Рис. 7.4. График связи hsurlgT2 =
214
β зоне больших относительных глубин (cl/gT1 > 0,08) даи-
е лабораторных и натурных измерений подтверждаются тео-
"еТическими исследованиями Митчела для предельно крутых
волн:
ksurv,<Jgr2 = 0,023, 7.17
прН этом использовалось соотношение между длиной волны на
глубокой воде и ее периодом λα = gT2/2n.
Зависимость на рис. 7.4 была перестроена в следующем
виде
hsurirJgT^/Adlla) 7.18
и представлена на рис. 5 обязательного приложения 1 [51]
кривой 2. Результаты исследований для водоемов с
горизонтальным дном были распространены также на случай пологона-
клонного дна. Наибольшее значение уклона i = 0,02 принято из
условия, чтобы перепадом глубин на протяжении одной длины
волны можно было бы пренебречь. Таким образом, кривая 2,
изображенная на рис. 5,ч соответствует уклонам дна 0 ^ ί ^
^ 0,02; здесь же представлены аналогичные зависимости для
уклонов дна i = 0,05 и i = 0,2, полученные на основе
лабораторных исследований (кривые 3 и 4).
В итоге, с помощью кривых 2, 3 и 4 на рис. 5 обязательного
приложения 1 [51] можно определить высоту волны 1%-ной
обеспеченности в прибойной, зоне hSUri% в зависимости от
средней длины (или среднего периода) волн в глубоководной зоне,
глубины места и уклона дна. Понятно, что высота
глубоководной волны hdi% превышает значение высоты прибойной волны
hsunx при одном и том же периоде Та.
Пример 7.6
Требуется определить высоту волны hsur\% в прибойной зоне водоема
"а глубине d = 5 м, если известно, что уклон дна i = 0,02, длина волны на
глубоководной воде Id « 76 м, высота /zd,%= 6,5 м.
Решение.
η по кривой 2 на рис. 5 [51] при dfkd = 0,066 находят /2sttriWgP=0,008.
Рнод волны определяют по формуле
T=V2n\dlg = 6,28-76/9,81 = 7,0 с,
За т°гда hsurl% = 0,008 ·9,81·72 = 3,85 м. Высота исходных волн в 1,7 ра-
превышает высоту волн в прибойной зоне.
Другой важной характеристикой прибойных волн является
тепВЫШение веРшины волны над средним уровнем. Эту
характеристику выражают в виде отношения η<?, W1*» которое, как
взывают наблюдения, закономерно возрастает с уменьше-
215
В зоне глубин 0,01 <d/kd ^0tl применялись формулы теп
рии [76]:
нием относительной глубины водоема и определяется верхн>
огибающей кривой на рис. 3 приложения 1. _ е'!
При установлении зависимости i\c,sur/hi от d/Xd были j
пользованы следующие данные. 1с
В зоне малых глубин d/Xd^ 0,01 принята теория одиночны
волн, согласно которой v
-ncsur/hi&l. 7,|9
i/hd ^Oyl применялись формулы тео-
η*, surlhi = 2,28 — 1 $M\dr\ 7.20
d/dr = l+0fi\Vd^\ 7.21
из соотношений 7.20 и 7.21 найдена зависимость вида:
^.*η№ι = /*(<1β*)· 7.22
В зоне глубин 0,1 <d/Kd^ 0,5 связь между относительным
превышением вершины волны и относительной глубиной
водоема получена на основе анализа натурных измерений.
Наконец, в зоне больших относительных глубин rf/λ^ > 0,5
применена теория Стокса в третьем приближении [86],
согласно которой
г\с, sur/Ы = 0,676. 7.23
Обратимей теперь к рассмотрению изменения длины волн в
ПрибоЙНОЙ ЗОНе hsun
В зоне малых глубин d/λα ^ 0,01 для определения Ksur
используют соотношение теории одиночных волн
WT= 1,25/^2 7.24
и получают
Для зоны глубин в диапазоне 0,01 <d/Xa^ 0,1
использована теория [76], согласно которой:
^Λ = 3,34|/"ί/ζ. 7.26
Формула 7.26 с помощью соотношения 7.21, записанного *
виде
d/K=(dfid)(\+0fi\ydJd),
была пересчитана в зависимость
λ«Λ = Л (<*£*); 0,01 < d\\d < 0,1. 7·27
216
g зоне глубин 0,1 < ^Ad 2$: 0,5 построение зависимости от-
I цельной длины волны от относительной глубины водоема
ответвлено на основе применения равенства, полученного
1ЯоетШнайдером для предельно крутых волн [71]:
rlh
(2πά\
7.28
7.29
Зависимость
KurIK = Λ (di\), 0,1 < d/\d < 0,5 7.30
получают из соотношений между безразмерными параметрами
i\csar/hi и d/Xd на рис. 3, hSun%/gT2 и d/%d — на рис. 5 и
формул 7.28, 7.29.
На глубокой воде при d/λά > 0,5 согласно теории для
предельно крутых волн [78]
Kur = b2Xd. 7.31
Зависимости 7.25, 7.27, 7.30, 7.31 для всего диапазона
изменения относительной глубины водоема изображены
графически в виде верхней огибающей линии на рис. 4 обязательного
приложения 1 [51]. Эта линия служит для нахождения длины
прибойных волн в зависимости от длины волн на глубокой воде
и глубины водоема в прибойной зоне.
Пример 7.7
Определить превышение вершины волны над расчетным уровнем %, «ш-
и Алину волны в прибойной зоне hsur на глубине d = 5 м, если известно, что
"а глубокой воде высота волны /*<л% = 6,5 м, длина волны λα — 76 м,
период волны Та = 7 с. Уклон дна i = 0,02.
Решение.
По верхней огибающей кривой рис. 3 при dfkd = 5/76 = 0,066 находят
Ъ. W^х = 0,84. По графику 2 рис. 5 при d/λα = 0,066 получают:
'W.te?* = 0,008, тогда
hsun % = 0,008 - 9,81 - 49 = 3,85 м.
В итоге:
Лс sur = 3,85 - 0,84 « 3,23 м.
Длину прибойной волны Xsur рассчитывают по верхней _огибающей кри-
^.Рис. 4. При d/Kd = 0,066 находят К5иАа = 0,73, тогда λ5«, = 76 - 0,73 =
°ъ м.
Ма ^ассмотРИМ» наконец, методику определения глубины воДое-
"сг, на которой происходит обрушение волн. Расчет критйче-
217
ской глубины сводится к анализу трансформации волн и
стнжения ими в мелководной зоне предельной крутизны. С эт°·!
целью задаются рядом значений глубин и находят соответ]
. вующие им высоты и длины волн при перемещении их на мелГ
водье. По полученным величинам параметров выбирают такЛ
их сочетания, которые соответствуют предельной крутизне воЛ
на данной глубине — глубине первого и последующих обруШеН
ний волн.
Пример 7.8
Найти критическую глубину dcr при первом обрушении волны (без уЧет
рефракции при kr = 1). Высота глубоководной волны ha\% = 6,5 м, соответ3
ствующие длина волны λα — 76 м и период Та = 7 с. Уклон дна i = 0,02.
Решение.
Полагая в первом приближении А = Λ^ ·ί = 6,5 м^ в соответствии с
пп. 17 и 18 обязательного приложения 1 [51J при di/λα = 0,085, получают
коэффициенты ktl ki и высоту h\%\ kt = 0,945, £/ = 0,85, hx% = 0,945-085ν
Х6,5 = 5,22 м. _ _
По кривой 2 на рис. 5 при h\%lgT2 = 0,019 находят: dcr/λα = 0,092
откуда dcr =· 76- 0,092 = 6,99 м.
Принимая во втором приближении dn = 6,9 м, аналогично получают
dnTka = 0,091; £,_== 0,94; kt = 0,85; hl% = 0,94·0,85-6,5 = 5,19 м.
Тогда hi % /gT2 = 0,0108; dcr/λα = 0,091, откуда dcr = 6,9 — это
приближение считают окончательным.
Пример 7.9
Определить критическую глубину при первом обрушении с учетом реф
ракции волн. Высота волны ha\ % = 6,5 м, длина волны λα = 76 м, период
волны Та = 7 с. Уклон дна i = 0,02. Значения коэффициентов рефракции на
глубинах: d = 10 м, kr = 0,9; d = 8 м, kr = 0,7; d = 6 м, kr = 0,7; d = 4 м,
kr = 0,4; d = 2 μ, /ν = 0,5.
Решение.
Примем в первом приближении d\ — ha\%=* 6,5 \s_ в соответствии с
пп. 17 и 18 обязательного приложения 1 .[51], тогда di/λα = 0,085, kt = 0,945,
h = 0,85, kr = 0,7, Ы% = 0,945 · 0,85 · 0,7 · 6,5 = 3,65 м.
_По кривой 2 на рис. 5 при hx%/gT2 = 3,65/9,81 · 72 = 0,0076 находят
dCrlKa = 0,064, откуда dcr = 0,064 · 76 = 4,9 м. __
Во втором приближении при dn = 4,9 м получают: dn/λα == 0,064, kt ==
= 0,975, ki = 0,82, kr = 0,54 (по интерполяции для глубины dn = 4,9 м),
тогда: Λ ι* = 0,975 · 0,82 · 0,54 - 6,5 = 2,81 м._
Jlo кривой 2 на рис. 5 при hi%/gT2 = 2,81/9,81 ·72 = 0,0058 находя^
dcr/λα = 0,047, откуда dCr = 3,6 м. __
В третьем приближении при dm = 3,6 м имеем: dm/ha = 0,047, kt = 1" '
£/ = 0,79, Αν = 0,475, hi % = 1,03 - 0,79 - 0^475. 6,5 - 2,51. _
По графику на рис. 5 при hi%/gT2 = 0,0052 находят dcr/λα = 0,041, оТ'
куда dcr = 3,1 м. _
В четвертом приближении принимают div — 3,1 м, тогда div/Kd =* Щ:
£, = 1,05, fa = 0,78, kr = 0,45, Λι%= 2,40 м, hi%/gT2 - 0,0050, тогда <U^
= 0,04, откуда dcr = 3,04 м.
Это приближение, при котором diV и dcr отличаются на 2 %, принимз
за окончательное: dcr = 3,04 м.
218
Анализ результатов обработки лабораторных измерений
условиях постоянного уклона дна позволил количественно
\ тановить влияние уклонов на уменьшение высоты волны при
^рушении [28]. В результате в обязательном приложении 1
°пиведена формула (155) для расчета критической глубины,
Соответствующей последнему обрушению волн dcr,u:
dcr,u = knu-4cr, 7.32(155)
где ku--коэффициент, получаемый по уклону дна i из табл. 6
[51]; п —число обрушений, принимаемое из ряда η = 2, 3 и 4
Li выполнении неравенств
/^-2>0,43 и AS""1 < 0,43. 7.33
Из табл. 6 [51] и формул 7.32, 7.33 следует, что при
= 0,010...0,0140 л = 4;
= 0,0141...0,033 л = 3;
= 0,034.. .0,05 η = 2;
= 0,05 /ι=1.
В том случае, когда волна в прибрежной зоне
распространяется в условиях переменного уклона дна, критическую
глубину определяют путем последовательного расчета критических
глубин для участков дна с постоянным уклоном. Так, вначале,
определяют критическую глубину dcr,i и уклон участка дна t'i,
на котором произошло первое обрушение. Затем, по табл. 6
определяют коэффициент кии соответствующий уклону дна /,·.
Тогда второе обрушение произойдет на глубине, равной dCr,2 =
^Kidcn. Для этой глубины определяют уклон дна ί2> на
участие которого произошло второе обрушение, и т. д. Критическая
Шубина, соответствующая последнему обрушению,
определяется из условий, аналогичных условиям 7.33:
7.34
kul
kui
• kU2
'kU2
1
.. . ku(n-
. . . ku(n.
Пример
-i) < 0,43;
-2) > 0,43.
7.10
Определить критическую глубину йсг, ut соответствующую последнему
rni.is "Н**Ю ВОЛН ucrt и при постоянном уклоне дна i = 0,02. Критическая
Уоина в створе первого обрушения dcn = 7 м.
Решение.
волн ТИЧескую глУбинУ dcr, α, соответствующую последнему обрушению
фИц ПРИ постоянном уклоне дна, определяют по формуле 7.32 .(155). Коэф-
п * ент ku = 0,56 при уклоне дна i = 0,02 получают по табл. 6. Полагают
" 2 и проверяют соотношения knu~2 = 1 > 0,43, knu~l = 0,56. Неравенства
°бязательного приложения 1 [51] не выполняются (&2—1>0>43). Под-
219
ν
ставляя л = 3, находят И~2 = 0,56 > 43, k"~l = 0,315 < 0,43. Неравен
7.33 выполняются, следовательно η = 3, т. е. возможны три последовате
ных обрушения волн. Далее, подставляя в формулу 7.32 (152) ^S'^O^u
находят dcr, и = 0,315 · 7 = 2,2 м.
Пример 7.11
Определить критическую глубину dcr, α, соответствующую последнему^!
рушению волн при переменных уклонах дна, рис. 7.5, и при элементах во^|
приведенных в примере 7.8.
270М т
Расчетный
ъ уровень
dcniFW; dcU=5£;m
135
98 37\
—^*t**
У^!^Расстомшъм
Глуби на, м
Ж
Ъг,Ь=2,9м
Рис. 7.5. Схема профиля дна для определения критической
глубины dcr, и при переменных уклонах.
Решение.
В примере 7.8 критическая глубина первого обрушения dcr\ =* Wм
высота волны на глубине первого обрушения Λ ι κ = 5,19 м (уклоны диа в
этих примерах удовлетворяют условию /^0,02). Первое обрушение волни
происходит на участке дна с уклоном / = 0,01 (рис. 7.5). По табл. о пр
i = 0,01 находят ku\ = 0,75, затем определяют критическую глубину второ
обрушения по формуле 7.32 (155) [51]:
dCr2 = km - den = 0,75 · 6,9 = 5,2 м.
Второе обрушение произойдет после первого перелома профиля j
участке дна с уклоном i = 0,02, которому по табл. 6 соответствует &« ^
= 0,56. Следовательно, критическая глубина третьего обрушения будет Ρ
на: dCrz = ku2dCr2 = ku\kU2dCr\ = 0,75 · 0,56 · 6,9 = 2,9 м. еГо
Критическая глубина dcn принимается в качестве глубины поелед
обрушения волн, так как произведение коэффициентов kut удовлетвор
условию 7.34:
kui = 0,75 > 0,43;
ku\ · ku2 = 0,75 · 0,56 = 0,42 < 0,43.
220
?4 РАСЧЕТ ЭЛЕМЕНТОВ ВОЛН НА ОГРАЖДЕННОЙ АКВАТОРИИ
Основными факторами, определяющими поле ветровых волн
I акватории порта, являются: во-первых, размеры и структура
схоДных волн> проникающих на огражденную акваторию; во-
/торых, плановое расположение волнозащитных сооружений,
[.третьих, количественные характеристики поглощения волно-
У*-(Ч$0)х
(я,$х)
у=-о0х
.—. = L
" ί
1
\с—/ /
^yfy^<f=arctff-e0
1
1
Рис. 7.6. Физическая D и расчетная Dc области в задаче дифрак-
ции волн за одиночным молом.
^°и энергии этими сооружениями, в-четвертых, рельеф дна и
ГлУбина акватории.
Основными физическими факторами, формирующими поле
лн на огражденной акватории, являются дифракция, отраже-
* и гашение волн около оградительных сооружений. Ввиду
Раниченности методов гидравлического моделирования, кото-
3а1Ми традиционно пытаются охватить всю совокупность ука-
н НЬ1х, факторов, большое значение приобретает научно-обос-
анная методика численного моделирования элементов волн
221
на акваториях морских портов по заданным элементам волн
крытой акватории (А. М. Жуковец [6], В. К. Завьялов Гц?!
помещенная в обязательном приложении 1 '[51]. В настоят]
время используются также математические модели дифраКц
Г. Галениньщ \%i
и Н. Н. Загрядской [15]. μΊ
волн на акватории порта, разработанные Б.
Приведем некоторые результаты, полученные согласно Мо
дели [26], основанной на решении уравнения баланса волновой!
энергии для случая одиночного мола и двух сходящихся молов
Для случая одиночного мола отражающего или поглощаю!
щего типа при постоянной глубине жидкости d, решается кра^
вая задача (рис. 7.6):
дЕ т д*Е . п 4| ^ п
i>r = irw; х>0>у>°>
дЕ т д*Е Ε . Λ Λ^ - й
-W = -k-5W- — > r>0* 0>/>-β0τ,
7.351
где q = -2^-tg θ0 для отражающего мола и q = + с» для
поглощающего. Здесь Ε — плотность (количество на единицу
площади) волновой энергии, нормированное на исходное значение
~8Pgh20y где h0 — высота волны, подходящей к молу; (#,
у)—декартовы координаты, соответствующие волновым лучам и
фронтам в области падающих волн, причем ось χ совпадает с
направлением начального распространения волн; θο — угол между
осью χ и молом; (г, I) — цилиндрические координаты,
соответствующие волновым лучам и фронтам в области тени, / == ΘΓ·
где θ — полярный угол, 0 > θ > — θ0, θο ^ 0; k = 2π/λ —
волновое число; λ — длина исходной волны; т — безразмерный
параметр (по результатам экспериментальных исследований т = 2)
Коэффициент дифракции определяется формулой
kdif =VE. 7.36
Для упрощения решения дифракционной задачи перехода
от решения системы 7.35 в области D к решению краевой
задачи в «спрямленной области» DCi точки которой взаимно одн0'
значно соответствуют точкам области D. В области Dc задача
имеет вид [26]:
дЕ τη д^Е ч^ г\ ^ ^ л
-яг—т-зр'^0· °°>у>-^
Ε(χ, y)Uo = £O(y); 7·3
222
(■£-**),.-„-*
решение 7.37 в области Dc при однородном начальном ус-
1 в|1и £"о(£/) = 1 имеет вид:
^(^у)-4-[1 + ф(у/5)]±
±Техр(4-МУ+М)[^^ 7.38
φ (zt) = -т= J e at— табулированный интеграл ошибок
где
к;
(при i— If 2); знаки ( + ) и (—) соответствуют отражающему
„ поглощающему молам.
ис. 7.7. Физическая D и «спрямленная» Dc области в задаче
дифракции волн за сходящимися молами.
223
В физической области D решение имеет вид 7.38 для обл
сти прямолинейных падающих волн χ > О, у > О, а для облает
кольцевых волн г > О, 0>/>— θ0/' следует х, у в вырансет.!
для Ε заменить на г, /.
выРаженй
£о(у) '
У $
' yn9jyn-1 Уп-2
Уь-1 Уг
Рис. 7.8. Схема линейной аппроксимации неоднородного условия
на входе Е0(у).
Задача дифракции волн за сходящимися молами, рис. 7.7,
в области Dc формулируется в виде:
Л = ITS ПРИ Ψ + Q*x>y>-sl2- M;_
дх
k ду*
E(x,y)U=o = E0(y) при |y|<-f.
£-**)
[%+<*)
7.39
y = -sl2~tiX
= о,
y=>sl2+i,x
= 0 при qt = 2^- θ« или ?,— -f *>-
ί=1, 2.
224
решение задачи 7.39 при неоднородном условии на входе
с (у) (рис. 7.8) в случае линейной аппроксимации набором η
прЯмых вида
Ео(у) = α#+'β* при i = 1, 2,..., η 7.40
состоит из трех частей. Первая — описывает дифракционный
эффект, получаемый за счет условия на входе, и является
основной частью решения, а вторая и третья — описывают
дифракционные эффекты правого и левого молов, соответственно:
Е(х, у) = Е(ху у; 5, θ·ί, Θ2) = £*γ(*> У\ s)±Ert(x, у; s, θι)±
±Еи(х, y\ 5, θ2). 7.41
Знаки ( + ) и (—), как и в (7.38), соответствуют
отражающему и поглощающему молам. Конкретный вид каждой
составляющей решения таков:
η
Εν <*. у; s) = j1 [by + м [φ ((., -1 - у) У-&) -
><["p(-4ij(S'-'-f->')')-
-м-м*-т-уШ t·42
η
Ert(x, у; s, 61)=У]1ехр(-Ае1(| + у4-М))х
(-1
Χ {[Ρί - «, (У + s + 2Θ,*)] [Φ ((*, + у + У + 28,*) V^) -
-·((**-.+f+у+Н/Э]+
-exp(-4^(*, + i + y + 2elJC)·)]}. 7.43
fи(*, У; St. θ2) =Jiexp(^2({-y + м))Χ
|)<{lPi + al(e_y+2et*)][©((4s-sw-y + 2elJC)^5)-
225
-«ρ(-κτ(Ι*-'«'-ΐ'+2β»')')]}· ιμ
Здесь
^ = У| + 4» 7.45
где #,·— ί-я точка разбиения отрезка ~у» тИ на участке
аппроксимации, ί = 0, 1,..., п:
Уо — "2*> · · ·» У η — |<р τ· ^· ^о — и, ·· ·»
Р/ =
5Л — 5;
До(У|)-До(Ц_.1)
~ Л —Ум
У/До(У/-1)—.yj-i^o(y/)
У ι-У ι-\
7.46
По формулам 7.35—7.46 с помощью ЭВМ могут быть
рассчитаны волны на акватории морского порта, имеющего
сложное расположение оградительных сооружений в виде
одиночного мола, сходящихся молов, их комбинаций и др.
Методика расчета элементов волн на портовых акваториях,
содержащаяся в обязательном приложении 1 [51], основана на
результатах лабораторных исследований дифракции волн при
использовании уравнения баланса энергии (А. М. Жуковец [61,
В. К. Завьялов и др. [9, 14]). Положение волновых фронтов на
акватории определяют в соответствии с принципом Гюйгенса-
Френеля, согласно которому головные участки оградительных
сооружений служат источниками кольцевых волнч
Высоту дифрагированной волны определяют по зависимости
hdif = kdifhi, 7.47
где hi — высота исходной волны 1%-ной обеспеченности; kdu^
коэффициент дифракции. Вычисление коэффициента kdn oc·'
ществляют по формулам и номограммам, обобщающим данные
опытов.
В случае акватории, огражденной прямолинейным одино4'
ным молом (рис. 7.9), коэффициент дифракции равен
ь _ ~ 1 7.48
где а — параметр, характеризующий изменение коэффиии61**
kdius вдоль фронта волны: при а = О значение kdif,s = 1, а п"
а->оо: kdif,s-+0. Величина а дается выражением:
226
a = 0,5 th (θ,7 jj W (th φ)(ΐ + 0,9β γ j- cth φί >
7.49
где φ —Угол между лучом исходной волны и осью мола, град;
Ь^-угол между границей волновой тени и лучом, проведенным
L головы мола в расчетную точку (в зоне тени β > 0, вне зоны
тени β<0)> рад; г — расстояние от головы мола до расчетного
фронта, м. При а ^ О следует считать kdiftS = 1.
Зависимости 7.48 и 7.49 представлены в обязательном
приложении 1 [51] на рис. 7 в виде номограммы, с помощью кото-
Рис. 7.9. Схема к определению коэффициентов дифракции на
акватории, огражденной одиночным молом
* — луч исходных волн; // — граница волновой тени; /// — граница
дифракции; IV — фронт волн.
Р°и по известным φ, β, r/λ определяют значение kdif, s для ак-
ватории, огражденной одиночным прямолинейным молом.
Из условия а = 0 определяют границу, зоны той области
13°ны дифракции), в которой набегающие волны изменяются по
е^итуде и направлению под влиянием препятствия. Из 7.49
Ледует, что это условие выполняется, если
1+0,
·*γτ
Cth φ =0.
7.50
гра значим через / расстояние от границы волновой тени до
-ШШцы зоны дифракции. Тогда, как видно из рис. 7.9,
227
С учетом 7.50 выражение для определения границы зоны η, ι
фракции имеет вид: ДИ|
T=-ftg(1'1V/TtH)· 7.5,|
В зоне тени а->оо при г/%-+ оо и, следовательно, &</,[,s-*ol
Пример 7.12
Определить коэффициенты дифракции kdif, г и высоты волн Adif На
акватории, огражденной одиночным молом (рис. 7.9) в расчетных точках
J и 2. Глубина d постоянна. Элементы волн на подходах к порту: hb%*\
= 3,9 м, "λ = 60 м.
Решение.
Через голову мола проводят луч исходного направления волнения (грач
ницу волновой тени —ГВТ) и определяют угол φ между границей волновой
тени и осью мола (φ = 102°). Находят относительные расстояния гЛ от
исходного фронта волны до расчетных точек / и 2 и углы β,- между границей
волновой тени и лучами, проведенными от головы мола на расчетные точ-1
ки (табл. 7.2). __
Используя полученные значения гД, φ и β, по номограмме рис. 7
обязательного приложения 1 [51] согласно ключу определяют для каждой
расчетной точки значение коэффициента kdif.s и высоты hdif. Все данные сводят в
табл. 7.2.
Таблица 7.2
Номер
точки
/
2
Г γ М
720
1260
1
12
21
β,
град
65
—2
kdlf, s
0,09
0,73
hdif3=i
= 4%*dlf, s
0,35
2,85
В случае акватории, огражденной двумя сходящимися
прямолинейными молами (рис. 7.10, а), зону дифракции делят
главным лучом на зоны влияния левого и правого молов.
Главным лучом называют геометрическое место точек на акватории
с максимальными высотами волн, или, что эквивалентно,-
точек, в которых совпадают значения коэффициентов kdiu* °т
левого и правого молов:
ь ь 7.52
Kdif, 5(1) = Kdif, 5(2)·
Используя зависимости 7.48 и 7.49 для вычисления fc«f.s(£
kdif,S(2) в точках пересечения главного луча с расчетным фР°
том волны, получено следующее выражение для расстояния ^
м, по фронту волны от границы волновой тени, мола с углом Т1
до главного луча (φι < ψζ) [14]:
228
_ b |/ rf th <p, + 1,1 У{г1Г# th ?1 th?3 [(-{Jjjj - lJ
x у^Г^ЩЩ'5 '
ι де /; —ширина входа в порт, м, принимаемая равной проекции
'расстояния между головами молов на фронт исходной волны;
J! расстояние, м, от головы мол^а с углом φ! до расчетного
фронта.
Вычисление положения главного луча по 7.53 практически
совпадает с его расчетами по упрощенной зависимости [14]:
х= ν<*-ι*4*-*Κ 7.54(159)
Ail + 1>ач
в которой переменные величины /ί, φι, г2, φ2 заменены
величинами 1и lau 4, /α2· В 7.54 (159) U обозначает расстояние от
границы волновой тени мола с углом φι до границы дифракции
того же мола:
-f- = (f)tg(l,lyT^HT) 7.55
или по графикам рис. 9 обязательного приложения 1; Ιαι —
величины, определяемые по графикам рис. 9. Более простая
формула 7.54 по сравнению с 7.53 включена в обязательное
приложение 1 [51].
Коэффициент дифракции на акватории, огражденной
сходящимися молами, получен В.. К. Завьяловым на основе
результатов исследований дли одиночного мола с использованием
условия сохранения баланса энергии '[14]:
kdif, с = kdify s i|)c. 7.56 (157)
Здесь kdif,s — коэффициент дифракции в заданной точке
акватории для одиночного мола с углом φ;, в зоне дифракции
которого расположена расчетная точка; -фс — поправочный
коэффициент, учитывающий наличие двух молов:
= г 2 -11/2 у ^
[Де kdif,av определяют по 7.48 и 7.49 для точки пересечения
Явного луча с расчетным фронтом.
Коэффициент 1|)с может быть получен по графикам рис. 8
Нательного приложения 1. При.графическом определении t|)c
пользуется вспомогательный параметр dCi связанный с отно-
^ием (/i+./2)/& формулой
αο=τ{4τ+1)· 7.58(158)
229
Граница дифращии
Главный луч
Граница дифранциа
• | Луч исходных болн
Луч походных Волн
Рис. 7.10. Схемы к построению расчетных створов I, II, Ш
границ дифракции и главного луча (а); коэффициентов
дифракции на акватории, огражденной сходящимися молами (б).
230
Пример 7.13
Определить коэффициенты дифракции kdif,c в расчетных точках 1, 2 и
акватории, огражденной сходящимися молами, рис. 7.10. £лубина d по-
гоянна. Элементы волн на подходе к порту: Л5% = 3,9 м, λ = 60 м.
Ширина входа в порт. Ь =* 285 м.
решение.
Определение коэффициентов kdi\t с выполняют в следующем порядке.
1. Построение границ волновой тени. Через головы молов проводят
лучи параллельные лучам исходных волн. Эти лучи являются границами
волновой тени ГВТ (рис. 7.10). Определяют углы между границами волновой
тени и осями молов. Меньший угол обозначают через <рь больший
—через φ* Согласно рис. 7.10: φι = 50° и φ2 = 102°.
ν 2. Построение границ дифракции. Через расчетные точки У, 2, 3
проводят расчетные створы I, II, III. Измеряют расстояние г\ от головы мола I
иГ2 — от1 головы мола 2 до расчетных створов I, II и III (на рис. 7.10,а).
Эти расстояния обозначены через (η)ι, (п)ц, (ri)m и, (r2)i, (г2)ц,
Win· _ _
Вычисляют относительные расстояния rJK и г2Д, и далее по этим
расстояниям и углам φι и <р2, соответственно, находят по графикам,
приведенным на рис. 9 обязательного приложения 1 [51], значения относительных
величин /ι/λ, /2/λ и определяют расстояния 1\ и /2. Откладывают полученные
значения Λ по нормали к ГВТ мола 1 вдоль расчетных фронтов (Л)г, (Л)п,
(/|)ш. Полученные точки соединяют плавной линией с головой мола и таким
образом находят границу дифракции для мола 1 (рис. 7.10,а). Аналогично
по значениям /2 проводят границу дифракции для мола 2. Расчеты по
определению границ дифракции молов 1 и 2 сведены в табл. 7.3.
Таблица 7.3
Расчетные
створы
I
И
111
Г и Μ
795
1203
1335
т%> м
720
1128
1260
Τχ
λ
13,25
20,05
22,25
ra
λ
12,0
18,8
21,0
/,
λ
5,7
7,8
8,0
- h
λ
5,8
7,9
8,1
/„ Μ
3,42
468
480
/„, Μ
348
474
486
3. Построение главного луча. По графику, изображенному в виде
штриховой линии на рис. 9, для каждого отношения π/λ и г2/Я находят значения
Ό ι/λ и 1а2/К и величины 1а\ и 102· По вычисленным /i, /2, lau 1о2 и
^данному значению ширины входа Ь рассчитываются по формуле 7.54
Н59) величины χ для каждого расчетного створа. Откладывают значения
х \хи Хп, Хщ) вдоль расчетных створов по нормали к ГВТ для мола с
меньшим углом φ (мол 1 на рис. 7.10). Соединяют полученные точки и точку
пересечения границ дифракции Ρ плавной линией, которая и является главным
л^ч°м. Точки пересечения расчетных створов с главным лучом обозначают
Таблица 7.4
Расчетные
створы
I
II
III
Γι
λ
13,25
20,05
22,25
II
λ
12,0
18,8
21,0
1аг
λ
3,3
4,5
4,9
ια2
λ
3,0
4,2
4,7
l .. μ
*αν
198
270
294
/ Λ, μ
*β2* m
180
252
282
ΛΓ, Μ
130
128
132
23t
icpcd и, о, в (рис. 7.10,6). Главный луч делит акваторию на две зон J
волновой режим которых определяется дифракцией за соответствующе
молом. Главный луч отвечает максимальным высотам волн в любом р? ]
четном створе. Расчеты сводят в табл. 7.4. с
4. Определение коэффициентов дифракции волн kdif, с. Находят углы r
β<>, ββ между ГВТ одного из молов и направлением лучей из головы мот
на точки а, б, е. На рис. 7.10,6 эти построения выполнены для мола 2. уга
лы — отрицательные, так как отсчет ведется от ГВТ в сторону границ
Аиф.
ракции.
Из рис. 7 [51] по найденным значениям гг/λ, φ2 и соответствующим им
углам βα, ββ, ββ определяют коэффициенты дифракции kdif, αν для точек о б
в. Обозначают углы, измеренные между ГВТ мола 2 и направлением лучей
из головы мола на расчетные точки 1 и 2, через βι и β2, а угол между ГВТ
мола 1 и лучом из головы мола на расчетную точку 5 —через β3. уГЛЬ1
βι» β2, β3 — положительные, так как отсчет ведется от ГВТ в сторону
волновой тени.
Аналогично находят коэффициенты дифракции kdif, s для расчетных
точек 1 и 2 по значениям τ2/λ, φ2 и βι, β2, а для точки 3— по π/λ, φι и β3. По
формуле (158) рассчитывают dCi по значениям /ь /2 из табл. 7.3 и заданной
величине b — 285. Коэффициент ipc принимают из рис. 8 с учетом kdif, av и dc.
Коэффициенты дифракции kdif, с определяют по формуле (157), при этом
расчеты применительно к точкам У, 2, 3 сведены в табл. 7.5.
Таблица 7.5
Номера точек
расчетных
I
II
III
на
главном
луче
а
б
в
Г\
\
13,25
20,05
22,25
'а
X
12,0
18,8
21,0
**
те
ci
_^
03.
65
25
7
00
О.
ь
^
в
03.
—12
—8
-7
«о
ч .
^
*е
0,09
0,24
0,52
fS
α
<
^
•ее
0,91
0,86
0,84
s
ζ
«**
342
468
480
55
·.
***
348
474
486
V»
·«
1,71
2,15
2,19
«j
•э-
0.95
0,88
0,87
^
ц
•5
Λί
0,085
0,21
0,45
Величину yf>c для данных значений kdif, av* by /ь /2 можно также найти
по формуле 7.57.
Для акватории, огражденной волноломом, коэффициент
дифракции определяют по формуле
4*/.»-УЧл * + &/.-. 7.59 (160)
в которой kdif si — рассчитывается для головных участков
волнолома по 7.48 и 7.49 или по графику рис. 7 [51].
Согласно 7.59 (160.) энергия волн за волноломом равна
сумме энергий волн, пришедших с разных сторон, она рекоменДУ^
ется к применению в тех случаях, когда длина сооружения пре'
вышает 5λ.
Высоту дифрагированной волны с учетом ее отражения °
сооружений и преград находят по приближенной эмпирическо
формуле
kdif,r = (kdif+Uref)hi. 7.60 (^
232
|л1еСь kdif — коэффициент дифракции набегающей волны в
расчетной точке; kref— коэффициент отражения, определяемый по
прической зависимости
kref = kdiu S krkpkref, i exp (—0,08гД) (cos ΘΓ),/2; 7.61 (162)
l.. s — коэффициент дифракции набегающей волны в точке на
Сражающей поверхности; kr, kp — коэффициенты
шероховатости и проницаемости поверхности сооружения, определяемые по
табл. 6 п. 1.14* [51]; kref, ι — коэффициент отражения,
принимаемый по табл. 7 обязательного приложения 1 [51], при этом
1ля отражающей поверхности, наклоненной к горизонту более
45 град, kref,i = 1; ΘΓ — угол между фронтом волны и
отражающей поверхностью в точке отражения, град; г /λ —
относительное расстояние от точки отражения до расчетной точки по лучу
отраженной волны.
Точкой отражения называется точка, из которой лучи
отраженных волн приходят в расчетную точку. Положение ее
определяется так: за отражающей поверхностью или ее
продолжением строят зеркальное отображение расчетной точки и
проводят в полученную точку луч из головы мола. Точка пересечения
этого луча с отражающей поверхностью и есть точка отражения.
Пример 7.14
Определить высоту волны в
точке 1 акватории, огражденной
одиночным молом (рис. 7.11),
с учетом отражения волны от
внутреннего ^контура АВ
акватории. Откос АВ имеет жесткое
бетонное покрытие. Уклон
отражающей поверхности i = 0,5. Угол
между фронтом волны и
отражающей поверхностью ΘΓ=10°. Эле-
иенты волн на подходах к порту
Αΐχ = 4,0 м, λ - 60 м.
Решение.
Коэффициент kdif = 0,25 в
чке ι определяем по графи-
м рис. 7 обязательного прило-
ЛИя 1 [51] для значений:
*Q$ iφ = 102°: βι = 24°=
Найп (снимаем с рис. 7.11).
-- AfM точку отражения 1Ав и,
^я в нее луч гдв, получим:
1400 м; ΓΑΒ/λ = 23,5; βΑβ =
Рис. 7.11. Схема к определению высоты
дифрагированной волны с учетом ее
отражения от внутреннего контура
акватории.
^20°^
cornJl/9; kdif>s = °>29; h** = l>l6> %ih*v = 52>[ = °>5·
тзбт с асно π· 27 [51] krefi=L Далее для бетонного
6π· 1.14 [51] Λ,-1;^-0,9.
Далее
I 14 ГКП U _ 1. Ь _ЛО
Зове,
М Паи·. "~ "w*"" жло «j · · - .«..-J
М-ппоЫм' согласно формуле (162)
[ 0'08'4,6)(cosl0<y/2 = 0Л79.
покрытия по
этим Г°еАя из т°чки 1АВ луч г в точку /, имеем: г = 276 м; г/λ « 4,60. По
- ' ""' находят kref = 0,29-1 ·0,9· lexpX
233
Следовательно, согласно формуле (161), высота волны в точке / с
том отражения hdif,r = (0,25+0,179)-4,0 м = 1,72 м. Уч*
Результаты, помещенные в главе СНиП [51], относятся
волнам, имеющим крутизну Λιχ/λ примерно 0,1, т. е. характер!
зующим существенное влияние нелинейных эффектов.
Для уточнения расчетов элементов волн меньшей крутизну
допускается при-достаточном обосновании использовать поправ.
ки, полученные в результате теоретического решения [15]. щ
этом уточненный коэффициент дифракции kdif, sk в зоне волно-
h
^z
~V~~
/Г-0
5^
τ
3
Υ/\
rsinfi/k
кк1
0,8
0,6
0/t
0,2- 74=
2 0 ' г sin ρ/Κ. 6 4 2
Д-^
Τ
KOJ5
_L.
^
3
к κι
0,8
0,6
0Л
0,2
o,s
0,6
о,ч
rsinfi/λ 6 4 2 0 г sin β/Χ -6 4
А-
ν-
чг
Κ'2,5
■^
ι-
-S\f
λ
ά
kd
Τ
Κ=5
5^
2
<κ/
*>S
ίο
ο,δ
0,6
0,4
0,2
Рис. 7.12. Значения kui в зоне волновой тени одиночного
мола
/-при (/-Д)со8р=1;<2--при (г/λ) cosp=2; 3—при (r/r)cosp=4; 4—при
(г/λ) cos β -6; J—при (г/λ) cos β > 8.
вой тени акватории, огражденной одиночным молом, с учетом
крутизны исходного волнения следует вычислять по формуле
kdif, sk = kdif,s · kkl, "
где kdiu s определяется по 7.48, 7.49 настоящего пособия или
рис. 7 приложения 1 [51]. Коэффициенты kki принимаются η
рис. 7.12 в зависимости от относительного удаления расчетно[
точки от границы волновой тени г sin β/λ при заданном ^
учитывающем крутизну исходного волнения и относительна0
глубину на входе в акваторию. Значения К находят из рис
или по формуле
234
Ί'β
K= 4 / Ai«V8(сМЫ — cti*kd + 1,25)
V s№2kd)
7.63
гДе * = 2π/λ. При /С > 5 и вне области волновой тени следует
принимать kki = 1.
Учет влияния крутизны волн осуществляется как для
одиночного мола, так и для сходящихся молов и волнолома. При
этом используются значения kki для одиночного мола:
λ/d
8
\
Л
1
V
\
\*
/
\
V
)
W4
\2>
ч^
О 0,02 0,04 0,06 0,08 0,10 0,12 ЦПП^/Х
Рис: 7.13. Значения коэффициентов нелинейности К в
зависимости от крутизны волны h[%/K и относительной длины
Xjd.
Пример 7.15
Найти коэффициенты дифракции kdif, sk с учетом крутизны в расчетной
точке Л, расположенной на акватории, огражденной одиночным молом.
Исходное волнение с параметрами: высота h\% — 2,9 м; длина λ = 50 м;
волны подходят по нормали к оси мола. Глубина акватории // = 15,0 м;
координаты расчетной точки г/Г= 5; β = 20°.
Решение.
В соответствии с п. 24 обязательного приложения 1 [51] по графику
РИс· 7 при φ = 90°, r/λ = 5 и, β - 20° находим kdiU s = 0,4.
Затем, используя график на рис. 7.13 при Λ1Η/λ = 0,058 и λ/d = 3,3,
Случаем К = 2,5; а по графику из рис. 7.12 при К - 2,5, г sin β/λ =1,7,
г cos ВД = 4,7 имеем kM = 0,61.
Следовательно коэффициент дифракции с учетом крутизны исходного
волнения равен
kdtf t$k = 0,4-0,61 = 0,24.
д Таким образом, за счет учета крутизны исходного волнения коэффициент
АИФракции снижается примерно на 40 %.
235
Раздел III
РЯСЧЕТ НАГРУЗОК И ВОЗДЕЙСТВИЙ
ВЕТРОВЫХ ВОЛН ΗΛ ГИДРОТЕХНИЧЕСКИЕ
СООРУЖЕНИЯ И БЕРЕГЯ
Глава 8. НАГРУЗКИ И ВОЗДЕЙСТВИЯ ВЕТРОВЫХ ВОЛН
НА ГИДРОТЕХНИЧЕСКИЕ СООРУЖЕНИЯ
С ВЕРТИКАЛЬНОЙ ПЕРЕДНЕЙ ГРАНЬЮ
8.1. НАГРУЗКИ ОТ СТОЯЧИХ ВОЛН
НА СООРУЖЕНИЯ ВЕРТИКАЛЬНОГО ПРОФИЛЯ
В главе 3 выполнен сопоставительный анализ наиболее
известных теорий стоячих волн и в результате показано, что для
практических целей достоверная информация о нагрузках
получается при использовании формул теории стоячих волн на
уровне третьего приближения. В то же время некоторые
характеристики величин, используемых в расчетах, могут быть
получены, по более простым или даже эмпирическим зависимостям,
что и отражено в строительных нормах [51]. Так, в частности,
применительно к рис. 8.1 (1) учет влияния бермы на величину
нагрузки от стоячих волн допускается производить путем
назначения условной расчетной глубины d у сооружения по
зависимости
d = df + kbr(db — df)i 8.1 (1)
где df и аь — глубина над подошвой сооружения и глубина до
дна; кы — коэффициент, принимаемый по графикам рис. 8.2(2);
dbr — глубина воды над бермой.
Возвышение или понижение свободной волновой
поверхности у вертикальной стены над расчетным уровнем рекоменду-
* ется рассчитывать так:
η = — h cos ω/ ψ- cth kd cos2 со/, 8.2 (2)
236
[где А — высота бегущей волны; ω = 2п/Т — круговая частота
(волны; Τ—период волны; t — время; k = 2π/λ — волновое
число; λ —длина волны.
/V ///'/// /// \/// &S /Д /// /// /// /// /// /// ///
Расчетный
уробень
/// /// /// /// /// /// /// ///
Рис. 8.1 (1). Эпюры давления стоячих волн на
вертикальную стену со стороны открытой акватории
а).при гребне волны;, б) при ложбине волны (с эпюрами
взвешивающего волнового давления на берменные массивы).
При действии стоячей волны на вертикальную стену
необходимо предусматривать три случая определения η по формуле
8.2 (2) для следующих значений cos ωί:
a) cos ωί = 1 — при подходе к стене вершины волны,
возвышающейся над расчетным уровнем на цтах\
237
б) 1 ^ cos ωί > О — при максимальном значении
горизонтальной линейной волновой нагрузки Рхс для гребня волны,
возвышающегося над расчетным уровнем на η0 чему
соответствуют значения coso)£, рассчитанные по эмпирической
зависимости
cosut =
τζΗ (Akd — 3)
<1;
8.3 (3)
в) coso)i = — 1 — при максимальном значении
горизонтальной линейной нагрузки Pxt для подошвы волны, расположенной
ниже расчетного уровня на r\t.
kr
h:kzw
0,26
0,22
0,18
0,2
ОЛ
0,6
as
ж
ύ
щ
V,
й
ж
ψ>
уф.
^^
Ш
\>г
i
i
^>
'%>
Φ
О, Ht
0,10
0,06
1,0 0,9 0,8 0,7 0,6 0,5 Ο,ϊ 0,3 Ю
Рис. 8.2 (2). Графики значений коэффициента кы*
В СНиПе [51] содержатся указания по расчету нагрузок οτι
стоячих волн раздельно для глубоководья и мелководья. В глу
боководной зоне (при ώ>0,5λ), согласно исследованию!
В. К. Штенцеля [63], горизонтальную линейную нагрузку J
вертикальную стену при гребне или ложбине стоячей волны]
рис. 8.1, предлагается определять по эпюре, а величину ординат]
волнового давления ρ на глубине ζ— по формуле
p^pghe~kzcos Ы — pg -я- e~2kzcos2 ut —
• e-2k*) cos 2Ы
-pg-—(i
— Рё —о— е~ъкг cos 2ω< cos ω/,
8.4(4j
где ζ — ординаты точек {zt = цс; z2 = 0,..., ζη = d), отсчиты]
ваемые от расчетного уровня. Для гребня при zt = цс и для!
ложбины при z6 = 0 следует принимать давление ρ = 0.
В мелководной зоне (при d ^ 0,5λ) горизонтальную линеМ
ную нагрузку на вертикальную стену Рх при гребне и ложбин^
238
(стоячей волны, рис. 8.1, следует определять по эпюре,
построение использованием формул табл. 8.1; содержащиеся в ней
коэффициенты Л2, &з, &4, &5, ks и &9 — принимать из графиков
рис. 3, 4 и 5 норм [51]. В основу этого метода расчета положе-
Ео исследование Я. И. Секерж-Зеньковича [50], уточненное
Н.Н. Загрядской[16];
некоторые теоретиче- кюлицаб.!
ские аспекты научного
подхода к решению
займи содержатся в
параграфе 3.2, п. В.
Практически такой же
конечный результат
расчета можно
получить, если
воспользоваться решением
теории потенциальных
стоячих волн,
основные зависимости
которого приведены в
параграфе 3.1 и в
работах Г. Т. Черможской
[9,56].
Воспроизведем основные формулы в третьем приближении
[16, 50] для расчета волнового давления ρ в точках ниже
спокойного уровня с ординатой zty которой соответствует ордината
ι покоящейся жидкости:
Номера
точек
1
2
3
4
5
в
7
8
9
Заглубления
точек ζ
Значения βοίηοβογο
давления /;
При гребне
η
0
0,25^
0,50d
d
Pi = k2?gh
Рг = hPgh
Pi = k$gh
При ложбине
0
0,5d
d
P« = 0
Pi = ~ ?grlt
Ps = — ktfgh
Pv = — ktfgh
z, ^—z —
sli kd
§\\k(d— z) smut
Аы* ch kd
sh 2k (d - z) [(l + 2^j) (I - cos 2ω0 -
Sg sh3 kd
^!]-?1йЬ4»^-г)Ф'
21ch2^~ 3
sh3 2kd
+
1
+ i8h3A(rf-*)(n-liSSFi + 8D1,)]-
-fT§=?[-b*(^-«)(n-^»-^Sra) +
^sh3*(rf-z)(3+T^-3A,2)]};
rg^j {cos 2 ω/ [3 ch 2Λ (</ - z)cth2 kd-A ch2 &/] -
.ch2k(d-z)}-^^{sln.t[chHd~z)X
239
x(2-!iSSiu)+ch^-*)(2+iKii+D»)]-
+ ch 3k (d — ζ
)(s +
21
4 shs ftrf
A«
где
4chs
Μ7-
ch* Ы + 2
sh2 2Ы
+3
D22 =~(97~60ch2Ad +
+ 27
13- UcWkd
2 sh2 £rf
D*2 ~ 8s№M Г
2 sh2 kd
0,02 0,04 0,06
В приведенных формулах
величина А определяется в
зависимости от значений
элементов набегающих волн в дан-
Рис. 8.3. График значений A/h = Н0М СТВ0Ре Л> λ И d П0 РИС'8'3'
= /(Λ/λ· λ/d) на К0Т0Р0М представлены
кривые A/h = / (Α/λ; h/d).
8.2. ВЗАИМОДЕЙСТВИЯ НЕРЕГУЛЯРНЫХ ТРЕХМЕРНЫХ ВОЛН
С ЖЕСТКОЙ ВЕРТИКАЛЬНОЙ СТЕНОЙ
Определению нагрузок от волн на вертикальную стену с
учетом нерегулярности и трехмерности волн уделялось должное
внимание при отборе наиболее достоверного метода для
включения в нормативный документ [51]. В результате установлено,
что в рассматриваемой области заслуживают внимания
исследования [24, 25, 32, 33], с учетом которых и дается изложение
метода, разработанного С. М. Мищенко [33].
В общем случае при расчете гидротехнических сооружений
на воздействие нерегулярных волн под расчетной силой
понимается амплитуда Рс, ι этой величины, имеющая
обеспеченность i %. Если процесс является нормальным, а ширина
спектра настолько мала, что можно не учитывать вторичные
колебания, то согласно [25] имеем:
Pcti% = hP, 8.5
где Ρ — среднее значение амплитуды расчетной силы, связанное
с дисперсией DP соотношением
240
Ρ = у ]/2πΟΡ s 1,25 |/Dp; 8.6
значения кг представлены в табл. 8.2 или в нормах по графикам
рис. 2, приложение 1 [51].
Таблица 8.2
%
h
од
2,96
1
2,42
3
2,11
5
1,95
50
0,94
За расчетную высоту волны принимается ее величина,
соответствующая заданному проценту обеспеченности hi%:
hi% = kl%h = 2,5*,* ΥΊ7:, 8.7
где А — средняя высота бегущей волны, а Ζ)ζ—дисперсия
отклонений взволнованной поверхности в фиксированной точке.
Для линейных задач спектральная плотность нагрузки
связана со спектральной плотностью отклонений свободной
поверхности набегающих на сооружение волн [49] зависимостью:
5Ρ(ω) = |Φ(ω)|25ζ(ω), 8.8
где Φ (ω)—передаточная функция, равная амплитуде реакции
прн, набегании гармонических волн с частотой ω и единичной
амплитудой. Дисперсия колебаний определяется согласно [49]:
D = f Sc (ω) dco. 8.9
о
Таким образом, использовав соотношения 8.5—8.9, для
расчетного усилия Рс> i% получим формулу
Ρ,,/% = 1,25^ΐ/||Φ(ω)|2 5ζ(ω)(1ω, 8.10
из которой видно, что, отображая исходное волнение
различными спектральными функциями, можно получить
соответствующие им значения расчетных усилий.
В литературе [23, 33, 49] приводятся различные
аналитические выражения волновых спектров, которые в целях
сопоставления целесообразно привести к нормированному
безразмерному виду:
Sfr)= s<">D*w, 8Л1
где μ = ш/штах — относительная частота, т. е. отношение данной
частоты ω к частоте шШах, соответствующей максимуму
спектральной функции, а 5(μ) —безразмерная функция,
характеризующая форму спектра в зависимости от относительной
частоты.
241
На практике в расчетах преимущественно принимаются
волны со случайными амплитудами, распределенными по
закону Рэлея, и фиксированной частотой. Такой модели волнения
при линейном процессе соответствует спектральная плотность
в виде δ-функции:
5(ω) = ϋδ(ω — aw); 5(μ) = δ(μ—1). 8.12
Примем рассматриваемую модель за критерий сравнения.
Если на стену фронтально набегают волны высотой h с
волновым числом k, то амплитуда горизонтальной силы на стену
единичной длины при глубине d > 0,5λ равна
а, следовательно, передаточная функция запишется так:
Φ (ω) = *£е. 8.13
Подставив в 8.10 значение Φ (ω) согласно 8.13 и
использовав выражения 8.11 и 8.7, в результате получаем
Pe = -p-hl%K», 8.14
где Kw—коэффициент, характеризующий зависимость величины
расчетного усилия от формы безразмерного частотного спектра,
рассчитываемый по зависимости
д, =T/f£cjrtd_fo). 8.1
μ4
Вычислим теперь значения ΑΓω для различных
аналитических представлений волнового спектра, при этом заметим, что
для δ-образного спектра /<ω= 1. Исключим из дальнейшего
анализа спектральные плотности в виде дробно-линейных
функций по той причине, что они непригодны для
рассматриваемой задачи, как имеющие конечные ординаты при ω = 0,
вследствие чего дисперсия усилия оказывается бесконечной. В
литературе, например [23], наибольшее распространение получили
спектральные функции, имеющие вид формулы Барлинга:
Г-1
где Г — гамма-функция; г, η — параметры спектра
г(—)
242
Нормированные спектральные функции волнения
представлены на рис. 8.4. После подстановки в 8.15 выражения 8.16 в
результате интегрирования получаем:
/т(с±1) I
Вычисленные по 8.17 значения Κω для некоторых спектров,
имеющих наибольшее распространение на практике,
представлены в табл. 8,3.
Таблица 8.3
Λ'ω
0,99
0,90
0,91
Параметры
спектра
' 1 ·
6
5
7
2
4
5
Авторы формул 8.16
Нейман
Бретшнайдер
Крылов
Полученные значения Ко
относятся к тем случаям,
когда спектральная функция
имеет только один максимум, и
интеграл 8.15 существует.
Следует обратить внимание, что
различным аналитическим
представлениям спектральных
плотностей с одинаковой
видимой (эффективной) частотой соответствуют неодинаковые
и иногда существенно отличные частоты максимума спектра
Wmax; обоснованный выбор этих величин по данным
наблюдений весьма затруднен. Из рассмотрения табл. 8.3 нетрудно
убедиться в том, что значения Κω довольно близки к единице, а это
свидетельствует о достаточной достоверности значений сил,
рассчитываемых на основе детерминистических теорий волн.
Остановимся кратко на предложении Ю. М. Крылова [25]
по расчету взаимодействия нерегулярных волн с жесткой
вертикальной стеной. Предполагая известным двухмерный
энергетический спектр набегающих волн и считая сооружение
абсолютно жестким, решение задачи сведено к расчету
статистических характеристик волнового поля у сооружения и
определению статистических характеристик усилий, возникающих в
сооружении под действием волн. Сущность этого метода состо-
24а
0,5 1,0 1,5
Рис. 8.4. Нормированные
спектральные функции волнения
/ — спектр Неймана; 2 — спектр Брет-
шнайдера; 3 — спектр Крылова; 4 — спектр,
близкий к .^-функции.
ит в анализе процесса взаимодействия с сооружением отдельной
спектральной составляющей и в последующем суммировании
частных решений по формулам теории вероятностей. В
результате для определения максимальной силы воздействия Pir
нерегулярной трехмерной волны на стену получена приближенная
зависимость
Я/г = ЯАГвАГш, 8.18
-где Ρ — максимальная сила воздействия регулярной
двухмерной волны; К —коэффициент, учитывающий нерегулярный
трехмерный характер за счет углового спектра ветровых волн
(О — угол между спектральной составляющей и генеральным
направлением волн); Κω—сохраняет прежний смысл, как и в
8.14. Для установления значений /С9 и К предложены [32, 33]
формулы:
ΑΓθ =
"+«/2
Г S (Θ) sins (α Sin θ)
da
—π/2
sin3 6
+*/2
f 5(θ)άθ
-π/2
jl/2
8.19
Κω
2ъС2
1/2
%ι
8.20
8.21
где ω и k — средние значения круговой частоты и волнового
числа соответственно; / — длина секции сооружения, на
которую определяется нагрузка от волн; λπ^χ — максимальная
длина волны.
При фронтальном подходе волн угловой спектр может быть
аппроксимирован функцией вида cos^O; при этом для
глубоководья показатель степени q £ё 2. В рассматриваемом случае 8.19
приобретает следующий вид:
#. = ■
2Г|
ι+ι)
<7-1
у*{Ц±)
О-*2)
^ψ^άχ
1/2
8.22
Заметим, что обычно на практике рассчитывается секция
сооружения, протяженность которой / = 20 ... 25 м, а для
морских условий Лтах = 75 ... 100 м. Тогда, определяемая по 8.21
безразмерная величина а< 1, а исследование 8.19 или 8.22 по-
244
казывает, что при этом /CQ близко к единице. Изложенное поз*
воляет сделать вывод о том, что трехмерность ветровых волн
не оказывает существенного влияния на результирующую силу,
воспринимаемую одной секцией жесткой вертикальной стены.
В заключение обратим внимание на то, что, если
воспользоваться формулой 8.20, то можно для глубоководья получить
[23] значение Κω> 1. Правильный выбор критериев сравнения
должен базироваться на анализе процесса взаимодействия волн
с сооружением при частоте, соответствующей максимуму
плотности энергии, а не при средней частоте набегающих волн.
Итак, представляется доказанным, что расчет нагрузок от
волн на жесткую вертикальную стену с учетом нерегулярности
волн не приводит к уточнению этой нагрузки, определенной по
зависимостям, основанным на детерминистических
представлениях ветровых волн заданного процента обеспеченности.
8.3. ОСОБЫЕ СЛУЧАИ, ОПРЕДЕЛЕНИЯ НАГРУЗОК
И ВОЗДЕЙСТВИЙ ВОЛН
ΗΛ СООРУЖЕНИЯ ВЕРТИКАЛЬНОГО ПРОФИЛЯ И ИХ ЭЛЕМЕНТЫ
В числе особых случаев здесь рассматриваются
предложения по определению нагрузок от волн на сооружения
вертикального профиля неполной высоты (в недостроенном
состоянии), учету уменьшения нагрузки при косом подходе волн,
расчету нагрузок от дифрагированных волн, а также по
определению максимальных донных скоростей перед вертикальной
стеной. К сожалению перечисленные вопросы решались весьма
приближенно, и полученные расчетные зависимости следует
рассматривать как эмпирические.
При определении нагрузок от волн на вертикальную стену
в недостроенном состоянии, верх которой возвышается над
расчетным уровнем на величину zsup < Лтах, используются
зависимости как и для вертикальной стены полной высоты, но
значения ρ следует умножать на коэффициент kc:
Λβ = 0,76 ±0,19^, 8.23(5)
где знаки «плюс» и «минус» соответствуют положению верха
сооружения выше или ниже расчетного уровня воды. Этот же
прием используется при расчете возвышения или понижения
свободной волновой поверхности η согласно формуле 8.2(2).
Горизонтальная линейная волновая нагрузка Р'хс в
рассматриваемом случае определяется по площади эпюры волнового
давления в пределах высоты вертикальной стены.
В расчетах устойчивости сооружения и прочности грунтов
основания линейную волновую нагрузку на вертикальную стену
245
полной высоты, определенную при фронтальном подходе волн,
в случае набегающих волн с фронтом к сооружению под углом
а рекомендуется уменьшать путем умножения на коэффициент
kcs, принимаемый равным
а. град
kcs
45
1
60
0,9
75
0,7
о)
^Расчетный
Рис. 8.5 (6). Эпюра давлений дифрагированных
волн на вертикальную стену со стороны
огражденной акватории
а) при гребне волны; б) при ложбине волны.
Горизонтальную нагрузку от дифрагированных волн со
стороны огражденной акватории следует определять при
относительной длине секции сооружения Ι/λ < 0,8; при этом расчетную
-эпюру волнового давления со значениями ρ допускается строить
по трем точкам, рассматривая следующие случаи:
246
а) вершина волны совмещена с серединой секции
сооружения, рис. 8.5, а (6):
zx = т)тах = - ψ - k^f cth Μ, /;, « 0; 8.24 (6)
z2 = 0, p2 = *iPff(·
2 ~ 8
oXhkd
)■■
8.25(7)
8.26 (8)
б) подошва волны совмещена с серединой секции
сооружения, рис. 8.5, б:
г, = 0, pi = 0; 8.27 (9)
Ad// £АЛ*
га = Чг = -2 '
cth Ы, р2 = - ^pgvj,; 8.28 (10)
,з = d„ * = - ^ (^ + -^), 8.29 (11)
где hdif — высота дифрагированной волны, определяемая
согласно обязательному приложению 1 [51]; h — коэффициент,
.принимаемый по табл. 8.4 (2).
Таблица 8.4 (2)
Относительная длина
секции //Т
Коэффициент kj
0.1
0,98
0,2
0,92
0,3
0,85
0,4
0,76
0,5 0,6
0,64 J 0,51
0,7
0,38
0,8
0,26
При глубине со стороны огражденной акватории d ^ 0,3λ
следует строить треугольную эпюру волнового давления,
принимая на глубине г3 = 0,3λ волновое давление равным нулю,
рис. 8.5 (6).
Взвешивающее волновое давление в горизонтальных швах
массивной кладки й по подошве сооружения следует принимать
равным соответствующим величинам горизонтального
волнового давления в крайних точках (см. рис. ,8.1 (1) и 8.5(6)) при
линейном изменении его в пределах ширины сооружения.
В ряде случаев возникает необходимость проверки
возможности подмывов основания непосредственно перед сооружением.
С этой целью определяется максимальное значение донной ско-^
рости Vb, max в области, удаленной примерно на расстояние 0,25λ
от стены:
2kslKh
*Vb, max —
П
8.30(12)
λ sh 2kdb
где ksi — коэффициент, принимаемый по табл. 8.5(3).
247
Таблица 8.5 (3)
Пологость волн λ/Λ
Коэффициент ksl
8
0,6
10
0,7
15
0,75
20
0,8
30
1
Допускаемые значения неразмывающих донных скоростей
Уь, max для грунта крупностью фракций D следует принимать
по рис. 8.6 (7); при Vb,max>Vb,adm необходимо предусматривать
защиту от размыва основания. В случае использования для этих
V:
b,admi
Μ
1,6
1Л
0,8
0,6
ο,ϊ
0,2
ϋ
0,1 0,15 0,2 0,3 0,4- 0,60,81 2 3 4-568/0 20 30 40 6080100
Я 9 мм
Рис. 8.6 (7). График допускаемых значений донных скоростей.
целей горной массы, среднюю крупность камня, допускается
определять по следующей эмпирической формуле:
.л
*>
^
Л
s
1
1
"Г 1/1 1
>
У\
У
/^
Область
допускаем*.
скоростей.
н£
А,о =
vb, max
2^
8.31
где £>5о — условный диаметр шарообразных камней,
включающих, до 50 % (по весу) более мелких зерен; pgr и ρ —
соответственно, плотность материала зерен грунта и воды.
Нередко в качестве элементов крепления от размыва
основания непосредственно у сооружения используются берменные
массивы. Расчет устойчивости берменных массивов
производится на основе трапецеидальной эпюры взвешивающего волнового
давления, рис. 8.1, с ординатами ры, ι (при £= 1, 2 или 3),
определяемыми по эмпирической формуле
Ch k (d — df)
Рьг, ι = kbrpgh chkd cos kXiKP/j 8.32 (13)
где Xi — расстояние от стены до соответствующей грани
массива; kbr — коэффициент, принимаемый по табл. 8.6(4); pf —
волновое давление на уровне подошвы сооружения.
248
Таблица S.6 (4)
Относительная
глубина
Менее 0,27
От 0,27 до 0,32
Более 0,32
Коэффициент Л^г
при пологости λ/Λ
15 и менее
0,86
0,6
0,3
20 и более
0,64
0,44
0,3
8.4. ПРИМЕРЫ РАСЧЕТА НАГРУЗОК И ВОЗДЕЙСТВИЙ ВОЛН
НА СООРУЖЕНИЯ ВЕРТИКАЛЬНОГО ПРОФИЛЯ И ИХ ЭЛЕМЕНТЫ
Пример 8Л
Определить нагрузки и воздействия волн на оградительное
сооружение вертикального профиля из массивной кладки, рис. 8.7, расположенное
в мелководной зоне: .
а = 12,0
Расчетный
уробень
\/////У?//У//
Ьь-г6,0
Рис. 8.7. Эпюры бокового и взвешивающих давлений стоячей волны
со стороны открытой акватории при подходе гребня волны
(размеры, м; ординаты эпюр, кПа; силы давления, кН/м).
а) силы и опрокидывающие моменты от воздействия волн со стороны
открытой и защищенной акватории;
б) взвешивающее волновое давление по основанию и отдельным швам;
в) донные размывающие скорости с оценкой зернового состава грунта
основания;
г) взвешивающее волновое давление на берменные массивы.
249
Исходные данные: высота волны hx% =6 м; средняя длина волны λ =
= 100 м; естественная глубина у сооружения db = 15 м; глубина до верха
каменной постели df = 13 м; подводная часть сооружения состоит из шести
курсов массивов высотой 2,3 м; ширина сооружения по подошве а = 12 м;
ширина бермы Ъы = 6 м; длина секции сооружения / = 20 м.
Решение.
1. Определяем максимальную_донную скорость Vb, max по формуле (12),
при этом согласно табл. 3 для λ/Λ = 100/6 = 16,7 принимаем ksi = 0,76:
2·0,76.3,14·6 fto fft ,
. = 2,8 > 1,8 м/с.
У 9,81
100 sh4·3·14'15
100
Требуемый диаметр Dsq неразмываемых фракций определяем по чрормуле
8.31, принимая pgr = 2,6 т/м3; ρ = 1 т/м3; g = 9,81 м/с2:
В соответствии с п. 1.9 [51] перед сооружением на участке
протяженностью 0,4λ = 0,4· 100 = 40 м необходимо крепить дно камнем крупностью
£>5о ^ 0,25 м. Толщину защитного покрова с учетом обратного фильтра
принимаем равной 1,5 м. Тогда согласно пояснениям параграфа 8.1
расчетное значение db принимаем: db — 15 — 1,5 = 13,5 > 1,5Λ = 1,5'· 6 = 9 м
2. Над бермой, располагающейся в данном случае на 0,5 м выше
защитного покрова, предусмотрена укладка берменных массивов высотой ά\ —
— dbr =5=-0,25Λ— 0,25-6— -1,5 м; в соответствии с этим d6/= 13 — 1,5 =
= 11,5 > 1,25/г = 1,25-6 = 7,5 м.
При -у- = ^oq- =0,06, — = -^==0,96 находим из рис. 2 [51]
kbr — 0,95, а соответственно по формуле (1)—расчетную глубину: d = 13 г
+ 0,95(13,5 — 13) == 13,48 ξ 13,5 м, при этом γ = -щ = 0,135 < 0,5.
Следовательно, дальнейший расчет нагрузок от волн на
рассматриваемое сооружение следует производить для стоячих волн на мелководье.
3. Определяем расчетные моменты времени, оцениваемые значениями
cos ωί, повышение и понижение волновой поверхности у стены согласно
п. 1.2 [51]. _
Так как в данном случае d/λ = 0,135 < 0,2, то значение cos ω/,
соответствующее наибольшему значению горизонтальной волновой нагрузки Рхс при
гребне волны, равно единице. Таким образом, при определении действующих
на сооружение сил со стороны открытой акватории будем рассматривать
только случаи при coso)^=l и при cos ω/ =— 1, а этому соответствуют
при k - 2π/λ~= 6,28/100 - 0,0628:
η, = — 6-1 — °'06^8·62 cth (0,0628-13,5).Ρ = — 7,65 м;
η, = — 6.(-1) —-^^^ cth (0,0628-13,5) (—1)2 =4,35 м.
4. Ординаты эпюр волнового давления, необходимые для определения
линейной нагрузки от волн (для гребня Рхс и ложбины Pxt), вычисляем
согласно указаниям п. 1.4 [51]. Расчет ведется в табличной форме с
использованием графиков при Λ/λ « 6/100 = ,0,06 и yd = 100/13,5 = 7,4.
5. По данным табл. 8.7 строятся эпюры волнового давления при подходе
со " стороны открытой акватории к вертикальной стене гребня волны,
рис. 8.7, и подошвы, рис, 8.8; расчетные точки соединяются прямыми линиями.
250
Таблица 8.7
Номера
точек
Заглубление точек ζ,
м
Значения
коэффициентов кй. . . &9
Волновое давление р, кПа
О
*1/
0,5
d
При гребне
ι ·η
о
0,25^
0,5d
uf
—7,65
0
3,38
6,75
13,5
*2
*3
к,
*5
0,84
0,69
0,59
0,52
О
4,35
6,75
13,5
При подошве
0,58
0,52
Pi
Pi = k2?gh
Ръ = ktfgh
Pi = *4p£U
Рь - *5Р^Л
р? = — η/Ρ£
Р8 = — ^Pg^
А> = ~ *9Р£Л
о
49,4
40,6
34,7
30,6
О
-42,7
-34,1
—30,9
Расчетный,
ур одень
ЩШТТТт^
УУУ\УУ/Ш У// /У/
У/У УУУ УУУ
, У<* .
Рис. 8.8. Эпюры бокового и взвешивающих давлений стоячей волны
со стороны открытой акватории при подходе ложбины волны
(размеры, м; ординаты эпюр, кПа; силы давления, кН/м).
Суммируя площади эпюр волнового давления выше уровня подошвы
сооружения, получаем значения Рхс и Рхи при этом ординаты эпюры на уровне
подошвы рь и р% определяются путем линейной интерполяции:
d М—%) , Ρι+Рг d Pz + Pa
^хс— 9 ro A "+" 9
Т +
2
/_, d\ 49,4-7,65
ψ-Τ) = 2~ +
-251
+ Щ£& 3.38 + Щ^ 3.38 + %ψ* (13 - 6.75) - 672.5 кН/м;
Pxt =
Prtt
. Pt + Ръ Id \ Рн+Рэ (. d\
+ 2 ("2" — ^'j + 2 [df-T) = -
42,7-4,35
_!М+з4Д(6>75_4,35)_ 3M+309(13_675) = _3878 kH/m
6. Опрокидывающие моменты Мхс и Mxt сил волнового давления Рхс и
Pxt относительно внутреннего и внешнего ребер стены сооружения
определяем по эпюрам волнового давления, рис. 8.8, разбивая их на простые
фигуры: треугольники и прямоугольники. В результате получаем Мхе = 6415 кНм|
и Mxt = —2316 кНм.
Рис. 8.9. Эпюры бокового и взвешивающих давлений
дифрагированной волны со стороны огражденной акватории при подходе
гребня волны (размеры, м; ординаты эпюр, кПа; силы давления,
кН/м).
7. Так как _длина секции сооружения / = 20 м, в том числе и головной,
т. е. меньше 0,8λ = 80 м, то согласно п. 1.7 [5.1] следует учесть
горизонтальную нагрузку на вертикальную стену от дифрагированных волн со стороны
огражденной акватории, рис. 8.9. По формуле (1) и рис. 2 при btrl^-W
и df/d = 13/15 - 0,87 получаем kbr = 0,84, d - 13+0,84(15—13) = 14,68 м.
Тогда при £ = 0,0628: kd = 0,92; 2JW-1,84; сЬЫ- 1,454; cthiW-1,38;
sh 2kd ~ 3,07.
По табл. 2 при ί/λ — 20/100 = 0,2 значение коэффициента снижения £{ =
» 0,92. Высота дифрагированной волны hdif = 6 м. Волновое давление при
совмещении вершины волны с серединой секции сооружения рассчитывается
по формулам (6) —(8) [51]:
252
г\ — ^max — 2
6 62-0,0628
8
1,38 = —3,4 м; /?i^O;
*,=0, ρ9 - 0,92-1.9.81 (у - 0,06288'62 1,38) - 22,2 кПа;
/ 6 0,0628-62 \ |/%ле π
^з=13 μ, Λ=0,92· 1 -9,81 U. 1,454 " 4-3,07 j = Ι6'96 кПа'
Расчетный
уродень
%
/// ///
Bff=6,0
ιι Τ
игттттттгттПТПШ
255
^ττττττΤΤΤίΤίΤρ3
^V /^ лр уЦ/ /у/ ;& /s; ' УУУ л^ УУЛ
=^~
Pr.*~~1lZ
Bc = V,0
Рис. 8.10. Эпюры бокового и взвешивающих давлений
дифрагированной волны со стороны огражденной акватории при
подходе ложбины волны (размеры, м; ординаты эпюр, кПа; силы
давлений, кН/м).
Волновое давление при совмещении подошвы волны с серединой секции
ооружения вычисляется по зависимостям (9) — (11) [51]:
ζι = 0, р, = 0;
^ = η, = .|- °'06288'6' 1,38 = 2,6 м;р2 = - Ь9,8Ь2,6 = -25,5 кПа;
6 0,0627. бз\
г3= 13 м, /?з = —0,9219,
/ 6
>Sl[ 2-1,454
4-3,07
-J == — 20.;
3 кПа.
По вычисленным значениям /?,· и Zi строятся эпюры горизонтального вол-
ювого давления на сооружение дифрагированных волн со стороны ограж-
(енной акватории, рис. 8.9. Суммируя площади эпюр волнового давления,
входим значения сил волнового давления дифрагированных волн Рхс и Рхг.
при подходе к середине секции вершины дифрагированной волны
p^=M^2 + iM + 2^13 = 292>5KH/M;
253
при подходе к середине секции подошвы дифрагированной волны
Яг/ =
2,6-25,5 25,5 + 20,3
(13 —2,6) = -271,3 кН/ м.
^
Ж
.*Г+,<> .
Опрокидывающие моменты Мхс и Mxt сил волнового давления Рхс и PAj
дифрагированных волн соответственно относительно внешнего и внутреннего]
ребер сооружения определяют по эпюрам волнового давления дифрагиро
ванных воли, рис. 8.9 и 8.10. Тогда, разбивая их на плоские фигуры, полу
чаем:
Мхс = 2262,8 кНм; Mxt 1658,8 кНм.
8. Взвешивающее волновой
давление в горизонтальных швах]
массивовой кладки и по подошве
сооружения принимается равным|
соответствующим величинам го
ризонтального давления в край
них точках при линейном измене
нии его в пределах ширины со
оружения, рис. 1 [51]. В рас
сматриваемом примере силы
взвешивающего давления на подошву
сооружения оказываются равны
ми:
со стороны открытого мори,
рис. 8.8:
ψ///////////////////У/////////////////^
Рис. 8.11. Эпюры взвешивающего
волнового давления на берменные массивы
(размеры, м; ординаты эпюр, кПа).
: 2
30,9-12
= 184 кН/м;
Рж1 =
Р*а
.30,9 12
— 184кН/м.
Линии действия этих сил отстоят от внешней грани сооружения на
1/За = 4 м;
со стороны защищенной акватории от дифрагированных волн при
совмещении вершины волны с серединой секции, рис. 8.9:
ръа
17-12
^f- = —2~ = 102 кН/м,
а при совмещении подошвы волны с серединой секции, рис. 8.10:
р3а —20,3-12
zt ■
122 кН/м.
9. Ординаты эпюры взвешивающего волнового давления на берменные
массивы определяются согласно п. 1.10 по формуле (13) [51], рис. 8.11.
Расстояния _от стены до соответствующих граней массивов Х\ = 0 и х2 = 4 м.
При d/λ = 13,5/100 = 0,135 и λ/Λ = 100/6 = 16,7 по табл. 4 определяется
kbr = 0,79 путем линейной интерполяции.
В данном примере имеем: kd = 0,0628· 13,5 = 0,85; сЬЫ=1,38; k(d-
— df) =0,0628 (13,5 — 13) =0,0314; chk(d — df) = ch 0,0314 = 1,0005; chAX
X(d — df)/chkd= 1/1,38 = 0,73.
Подставляя эти значения в формулу (13), получаем рЬг, \ = 0,79· 1X
Х9,81-6-0,73-1 = 30,9 кПа при χι = 0. Далее результаты расчета
помещены в табл. 8.8.
254
Таблица 8.8
ι
1
2
Χ ρ Μ
0
—4
kx.
0
—0,271
cos kx^
1
0,963
Pf=Pf cos bx-v кПа
30,9
29,8
&пюра взвешивающего давления на бермениые массивы приведена на
|>ис. 8.11.
Пример 8.2
Определить нагрузки от волн на оградительное сооружение
вертикального профиля из массивовой кладки, расположенное в глубоководной
зоне:
а) боковое давление со стороны открытой и защищенной акваторий;
б) взвешивающее волновое давление по основанию; в) донные скорости
с оценкой зернового состава грунта.
Рис. 8.12. Волновые нагрузки на сооружение
о) при гребне волны с внешней стороны н ложбнне дифрагированной волны со -
стороны защищенной акватории; б) максимальная нагрузка на верхнее строение
в момент наивысшего подъема гребня волны (размеры, м; ординаты эпюр, кПа).
Исходные данные .применительно к рис. 8.12: высота волн /ιι% = 3 м;
редняя длина волн λ = 30 м; глубина у сооружения йъ — 18 м; глубина
ю верха каменной постели df = 15 м; подводная часть сооружения состоит
13 шести курсов массивов высотой 2,6 м; ширина сооружения по подошве
ι= 12 м; ширина бермы Ьы = 6 м; длина секции / = 20 м.
Решение.
J. Определяется условная расчетная глубина d по формуле (1). При
WU 6/30 = 0,2 и dfldb = 15/18 = 0,83 по рис. (2) находим kbr = 0,58,
а следовательно, dj= 15+0,58(18—15) = 16,7 м.
Отношение d/λ — 16,7/30 = 0,56 > 0,5, что соответствует условию
глубоководья.
2. Определяют ординаты эпюры наибольшего давления при гребне волны
30
со стороны открытой воды при cos (dt = 3 14- 3(8 3 14:-0 56 — 3ϊ ^ ®*^'
255
По формуле (4), принимая р = 1 т/м3; g· = 9,81 м/с3; hl%=3 м\ к =
2π 6,28
= — = -rfc- = 0,21; cos 2<ut = 2 cos2 ωί — 1 = 2·0,292 — 1 = — 0,83, получаем
ρ = 1 -9,81.3.«-°·21*-0,29 - 1 -9,81 ^^ *-2·°·21*.0,292 -
0,212-За
-1.9,81
0,21-32
(1
— Ρ-2·0,21Ζ'
)(—0,83)—1-9,81
·£
-3·0,21ζ
= 8,53<Г °·21* - 0,78<?-°'42* + 7.69 (1 - е~°>А22) + 1.4 е~°>6*2.
(—0,83)·0,29=
Дальнейшие расчеты сведены в табл. 8.9.
Возвышение свободной волновой поверхности в момент максимума го
ризонтального давления при гребне волны определяется по формуле (2) [51]
0,21-З2
η « — 3-0,29 — -— .0,29» = _о,95 м.
Таблица 8.9
Значения волнового
давления и его
составляющих р,
кПа
Ρ
0,21*
,-0,21*
8,53-^-°'21ζ
0,42*
e-0A2z
0,78.«-°'42ж
7,69.(1 -e-°A2z)
О.бЗг
е—0,63*
1.4 e-°>632
0
9.5
0
1
8.53
0
1
0,78
0
0
1
1,4
Заглубление точек
3
11,6
0,63
0,53
4,52
1,26
0,28
0,22
5,54
1.89
0,15
0.21
б
9,8
1.26
0,28
2,39
2,52
0.08
0.06
7,07
3,78
0,02
0,03
9
9,0
1,89
0,15
1,28
3,78
0,02
0,02
7,54
5,67
0,003
0
Ζ, Μ
12
8,5
2,52
0,08
0,68
5,04
0.01
0,01
7,61
7,6
0
0
16,7
8,2
3.51
0,03
0.26
7
0
0
7,69
10,5
0
0
3. Определяются ординаты эпюры давления при впадине волны со
стороны открытой воды по формуле 8.4(4) с подстановкой cosarf =— 1:
ρ = - 30.<?'-°'21г - 9,5*-°>42*- 9,5 (1 - *-°'42ζ) + 5,9*-°'63г =
= _ 30*-°'21г - 9,5 + 5,9<Г0'6Ч
Понижение свободной поверхности па 8.2 (2) равно
0,2 1-32
η»-3.(-1)-
(—1)2 = 2,05 м.
Все дальнейшие расчеты сведены в табл. 8.10.
Таблица 8.10
Ζ, Μ
6
9
12
16,7
е—0,21хГ
0,28
0.15
0,08
0,03
зо*-0'21*
8,4
4,5
2,4
0,9
g-О.бЗг
0,02
0
0
0
5,9ί?-0,63ζ
0.1 1
о
0
о 1
р, кПа
—17.8
-14,0
-11,9
-10,4
256
4. Определяются ординаты верхней части эпюры давления при гребне
волны в момент наивысшего подъема уровня (при cos ωί — 1) для расчета
устойчивости верхнего строения. При подстановке исходных величин в 8.4 (4)
получаем ρ = ЗОе-0-212 — 9,5 — 5,9е-°·632, при этом максимальное возвышение
0,21-32
►гребня волны равно η = —3— η—
ны в табл. 8.11.
= — 3,95 м. Расчеты ординат сведе-
Таблица 8.11
Ζ, Μ
0
3
6
„-0,21*
1
0,53
0,28
ЗОг-0,21*
30
15,9
8,4
е—0,632
1
0,15
0,02
5,9*-U,63z
5,9
0,9
0,1
р, кПа
14,6
5,5
-1,2
Расчетный
уробень
ν/;///////;//////А
12,0
Рис. 8.13. Волновые нагрузки на сооружение при ложбине с
внешней стороны и гребне дифрагированной волны со стороны
защищенной акватории (размеры, м; ординаты эпюр, кПа).
5. Так как отношение длины секции, в том числе головной, к длине
волны Ι/λ = 20/30 = 0,67 < 0,8, то, согласно п. 1.7 [51], необходимо
определить горизонтальную нагрузку от дифрагированных волн. Применительно к
головному участку оградительного сооружения haif — h — 3 м. Волновое
давление в верхних точках рассчитывается по зависимостям (6) и (7), а1 в
третьей точке, согласно примечанию к табл. 2 давление принимается равным
нулю на глубине ζ3 = 0,3λ = 9 м:
3 32-0,21
2ι = ηπΐ3χ = — у — § ·1 = — 1,74 м, /?! = <);
257
г2 = 0, /7, = 0,42-Ь9,81 fe
0,21-32
8
)..
3 кПа,
при этом коэффициент ki принят по интерполяции смежных значений из
табл. 2 [51].
При совмещении подошвы волны с серединой секции определяются по
формулам (9) и (10) [51] соответственно:
ζι = 0, /?ι = 0;
г2 = Άί = -| — Q<2g'32-1 = 1,26 м; р2 = —[0,42· 1-9,81 -1,26 = — 5,3 кПа;
23 = 9м, /?3 = 0.
6. По данным расчетов строятся эпюры нагрузок для следующих
случаев:
а) гребень волны с внешней стороны и впадина дифрагированной
волны— са стороны защищенной акватории, рис. 8.12, а;
б) эпюра максимальных нагрузок на верхнюю часть сооружения при
гребне со стороны открытой воды, рис. 8.12,6;
в) впадина волны с внешней стороны и гребень дифрагированной волны
со стороны защищенной акватории, рис. 8.13.
Эпюры взвешивающего давления по подошве сооружения строятся в
предположении линейного изменения нагрузки по ширине. Суммирование
нагрузок и определение сдвигающих сил или опрокидывающих моментов
пояснений не требуют.
ν
2.0,73,14-3
fy, max
У®"*(Ч£-п)
= 0,14 м/с,
а следовательно, обращаясь к рис. 7 [51], устанавливаем, что крепления дна
впереди стены не требуется.
Пример 8.3
Определить нагрузки от волн на плотину и ее затворы при
следующих исходных данных, рис. 8.14: высота волны h = 4 м, длина волны
Рис. 8.14. Расчетные волновые нагрузки к примеру 8.3
а) эпюры максимальных боковых нагрузок на плотину (в том числе и на нижний
затвор); б) эпюры максимальных боковых нагрузок на верхний за!вор (размеры,
м; ординаты эпюр, кПа),
258
Γ= 50 м, глубина у плотины d = 80 м, в верхней части плотины расположен
затвор, опускающийся ниже уровня воды на 10 м, а на уровне 10 м от дна
расположен низ донного отверстия высотой 8 м, перекрываемого затвором.
Решение.
1. Находим ординаты эпюры максимального давления при гребне волны
перед плотиной по формуле (4) в момент времени согласно формуле (3)
[51]:
COS (at :
50
■з-14.4(8.3,14§-з)
= 0,015;
cos 2ωέ = 2-0,1052 — 1 = — 0,98; k = -=£ = ^к^ = 0,13;
ρ = 1 -9,81 ·4β-°·13*·0,105 - 1 -9,81 °-^~е~°'26г■<).№* -
0,13 ·42
-1·9,81-4γ-(1
-о,2бг)(_0)98)_Ь9>81олз1±.х
χ β-°.39-'.(_0,98)-0,105 = 4,2е-°·132 - 0,11е-°'26г+ 10,2(1 -e-°·26*) +
+ 0,55е-°'-ш.
Дальнейшие расчеты сведены в табл. 8.12.
Таблица 8.12
Значения волнового
давления и его
составляющих р, кПа
Р,
0,13г
г-0ЛЧ .
4]2е-°'1гг '
0,2бг
β-0,26*
0tUe-°'26z
1 _ e-0,26z
10,2 (1 - *-°'26*)
0,39г
е~0,Ш
0,55^-°'39г
—
0
4,7
0
1
4,2
0
1
0,1
0
0
0
1
0,6
Заглубление
4
9,2
0,52
0,59
2,5
1,04
0,35
0
0,65
6,6
1,56
0,21
0,1
8
10,5
1,04
0,35
1,5
2,08
0,12
0
0,88
9
3,12
0,01
0
, точек ι
20
10,4
2,6
0,07
0,3
5,2
0,01
0
0,99
10,1
7,8
0
0
', М
40
10,2
5,2
0,01
0
10,4
0
0
1
10,2
15,6
0
0
80
10,2
10,4
0
0
20,8
0
0
1
10,2
31,2
0
0
Возвышение свободной волновой поверхности в этот момент по фор-
0,13-42
муле (2) равно: η = —4*0,105 — g ·0,1052 = —0,53 м.
2. Определяются ординаты эпюры максимального волнового давления
на верхний затвор при cosoi=l, при этом формула (4) преобразуется
к виду:
ρ = ?ghe-kz -9g-^-9g -ϊψ- e~3kz = 1.9,81.4<Г°>13* -
_ χ .9,81 ^^l2 _ ι .9,81 Щ^- е-°'т = 39,3<Г0'13* - 10,2 - 5,3<Г0·39*.
259
Дальнейшие расчеты сведены в табл. 8.13.
Таблица в. 13
Ζ, Μ
0
4
8
10
г-ОДЗ*
1
0,59
0,35
0,27
39,3έ?~0'13*
19,3
23,2
13,8
10,6
г-0,39г
1
0,21
0,04
0,02
5,3<?-0'39*
5,3
1,13
0,21
0,106
кПа
23,8
11,8
3,39
0,3
Возвышение свободной волновой поверхности, согласно формуле (2)1
0,13-42 '
при, cos ωέ = 1 равно η = — 4 — —g— — — 5,04 м.
По данным табл. 8.12 и 8.13 построены эпюры нагрузки от волн, которые
изображены на рис. 8.14, α и б.
Пример 8.4
Определить нагрузки от волн на сооружение с пониженной отмет]
кой верха, рис. 8.15,_при следующих исходных данных: высота волны h =\
= 3 м, длина волны λ = 60 м, глубина перед сооружением db — 20 м, глуби!
на над постелью df = 17 м, возвышение верха сооружения над спокойный
уровнем ZsuP = 0,5 м, высота бермеиных массивов 1 м.
1
II
V
J
«о
CSi
II
4}
J
' ^
\
II
•δ·
ί:
«о
С^
II
«о
4J
I
к
1
^
' ^~
'W
//////J
V///
w
i £/7.5-
Wgfr
\
I
&
^
~
,v
l|||||H|||llll_LLLi-Ui>
ГЧ5 ®
УУ/////////////////A
a
-* —»»
Расчетный
уровень
ι V
«"^
%\.
У/////////////////
Рис. 8.15. Эпюры бокового и взвешивающего давлений стоячих волн
на сооружение неполного профиля при подходе гребня волны
с внешней стороны (размеры, м; ординаты эпюр, кПа).
Решение.
1. Глубина над бермой dbr
17 — 1 = 16 м. В соответствии с
[51] перед сооружением наблюдается режим стоячих волн, так как db
= 20 м
: > 1,5-3 = 4,5 м; dbr = 16 м > 1,25 · 3 = 3,75 м.
260
2. Условная расчетная глубина определяется по формуле (1). При
Μλ~= 6/60 =0,1 и ^/<4 = 17/20 = 0,85 согласно рис. (2) kbr = 0,75, а
следовательно, d = 17+0,75(20 — 17) = 19,25 м.
Рассчитываемое сооружение расположено в мелководной зоне, поскольку
d= 19,25 < 0,5λ - 0,5-60 = 30 м.
3. Определяем по формуле (3) значение cos ω/, соответствующее
максимальной волновой нагрузке:
cos ωέ =
60
= 1,25 > 1,0;
3.14-3 ίβ·3,14-^--3
таком случае расчет следует вести при coso)/ = :i:l.
Расчетный
уродень
Рис. 8.16. Эпюры бокового и взвешивающего давлений на
сооружение неполного профиля при подходе ложбины волны с внешней
стороны (размеры, м; ординаты эпюр, кПа).
4. Положение волновой поверхности, рассчитываемое по формуле (2)
2π 6,28
при fc=—= -т^г-== 0,105, Ы = 2,03 и cth&d = l,04, оказывается равным:
а) при1 подходе к стене вершины волны
0,105-З2
"I max
= —3.1
. 1.04-12 == —3,5 м;
б) при подходе к стене подошвы волны
^ = — 3 (— 1) - 2lL^±L. 1)04 (-41Р = 2,5 м.
При сравнении отметок верха сооружения zsup = — 0,5 м и возвышения
вершины волны над расчетным уровнем r]max = — 3,5 м оказывается, что
данный волнолом относится к категории сооружений неполного профиля, и
261
через его верх происходит перелив волны. Рассчитываем волновое давление
согласно указаниям п. 1.4 [51] и полученные значения умножаем на
коэффициент kc, определенный по формуле__(5) в соответствии^ с п. 1.5*. Расчет
ведется в табличной форме при Λ/λ = 3/60 = 0,05 и λ/d = 60/19,25 * 3,1
с использованием п. 1.4 [51].
Эпюры волнового давления, построенные по данным табл. 8.14,
представлены на рис. 8.15 и 8.16.
Таблица 8 14
Номера
точек
/
/'
2
3
4
5
6
7
8
9
Ординаты ζ, м
*sup
0,25rf
0,5rf
d
0
0,5rf
d
—3,5
-0,5
0
4,81
9,63
19,25
0·
2,5
9,63
19,25
к,.. . *3;
*8
*9
0,72 '
0,44
0,27
0,18
0,49
0,38
Волновое давление
при полном профиле,
кПа
Pi
Psap
Pi^k^gh
P3 = bz?gh
p4 « k4pgh
Pb=h?gh
Pe
Pi = — ?gflt
Pb=—k8pgh
pQ=-k^gh
0
18
22
13
8
5,5
0
-25
—15
-11,5
kc
0,79
1
Волновое дав-
i ление при
неполном
профиле, кПа
Psap
Pzsup
Pzsup
Pisup
Pbsup
ни
14
17,5
10,4
6,5
4,5
0
-25
-15
-11,5
8.5. НАГРУЗКИ ОТ РАЗБИВАЮЩИХСЯ И ПРИБОЙНЫХ ВОЛН
НА СООРУЖЕНИЯ ВЕРТИКАЛЬНОГО ПРОФИЛЯ
В практике гидротехнического строительства нередки
случаи, когда сооружения в целом или отдельные их участки
подвергаются воздействию волн, разбивающихся при контакте с их
нижней частью (в виде относительно высокой постели), или
прибойных волн, разрушившихся на некотором удалении от
Рис. 8.17 (8). Эпюры давления разбивающихся волн на
вертикальную стену.
262
объекта. Достаточно строгих аналитических решений по расчету
нагрузок от волн для таких задач, к сожалению, еще не
получено, а потому в [51] рекомендованы к использованию
эмпирические зависимости.
Расчет сооружений на воздействие разбивающихся волн со
стороны открытой акватории рекомендуется производить при
глубине над бермой d&r<l,25ft и глубине до дна d& ^ 1,5/ι,
рис. 8.17(8). Горизонтальную линейную нагрузку Рхс, кН/м,
от разбивающихся волн следует определять по площади эпюры
бокового давления, при этом величины р, кПа, для значений
ординат 2, м:
zia=—ft, pi = 0; 8.33(14)
22 = 0, Р2= l,5pg7i; 8.34(15)
Ζ* = dp рг -
8.35(16)
ch kdf
Вертикальную линейную нагрузку Ргс, кН/м, от
разбивающихся волн следует принимать равной площади эпюры
взвешивающего волнового давления:
Ρ* = ν·
ръа
8.36(17)
где μ — коэффициент, принимаемый по табл. 8.15(5).
Таблица 8.15(5)
а
db — df
Коэффициент μ
<3
0,7
5
0,8
7
0,9
9
1
Максимальная скорость воды iff, max, м/с, над поверхностью
бермы перед вертикальной стеной при разбивающихся волнах
определяется по формуле
Ό/, max
-ν-
gh
с*г,· 8·37<18>
Расчет сооружений на воздействие прибойных волн со
стороны открытой акватории рекомендуется производить при
глубине db ^ dcr на примыкающем к стене участке дна
протяженностью не менее 0,5λ, м, рис. 8.18 (9); при этом возвышение
вершины максимальной прибойной волны ηίΜΓ> м, над расчетным
уровнем рассчитывается по зависимости:
r\c, sur = — 0,5df — hs
8.38(19)
где tisur — высота прибойной волны, м; dcr — критическая
глубина, м.
263
Горизонтальную линейную нагрузку Рхс, кН/м, от
воздействия прибойных волн следует принимать пр площади эпюры
бокового волнового давления, при этом величины р, кПа, для
значений ординат г, м:
Zi=-/W, Pi = 0; 8.39(20)
8.40(21)
8.41 (22)
z2 = -Thsun Рг = l>5pg-Aw;
3 "sur
*з = dn Ръ
?ghs
Ch — rf,
Λ.ΪΗ Г
где λίοΓ — средняя длина прибойной волны, м.
а)
Расчетный-hsup
. уробень "j
δ)
Расчетный я
уробень
-57--
Рис. 8.18 (9). Эпюры давления прибойных волн на
вертикальную стену
а) с верхом постели на уровне дна; б) с возвышающейся над дном
Вертикальную линейную нагрузку PZCt кН/м, от прибойных
волн следует принимать равной площади эпюры взвешивающего
волнового давления с высотой р3:
264
ρ -07^-
8.42(23)
Максимальная донная скорость прибойной волны Vbt max,
м/с, перед вертикальной стеной со стороны открытой акватории
определяется по зависимости
1>Ь, max =
8.43 (24)
Пример 8.5
Требуется определить нагрузки на оградительное сооружение
вертикального профиля, подвергающегося воздействию разбивающихся волн
при следующих исходных данных, рис. 8.19: высота волн /г = 5 м, средняя
Расчетный
уробень
гт
8,0
Рис. 8.19. Эпюры давления разбивающихся волн (размеры, м;
ординаты эпюр, кПа).
длина волн λ ~ 75 м, глубина перед сооружением db = 12 м, глубина до
верха каменной постели df = 7 м, ширина сооружения по подошве а = 8 м,
глубина до берменных массивов dbr = 5,7 м.
Решение.
1. В рассматриваемом примере dbr = 5,7 м, что меньше 1,25/г = 6,25 м;
4=12 м > 1,5/ι = 7,5 м. Поэтому, в соответствии с п. 1.11 [51],
производится расчет сооружения на воздействие разбивающихся волн.
2. Строится эпюра бокового давления, рассчитанного по формулам
(14)-(16)1 [51]:
Z\ = — h = — 5 м, pi = 0;
z2 = 0, р2 = 1,5 · 1 · 9,81 · 5 = 75 кПа;
*3 = rf =7mj3= 1'^8q11^ =42кПа;
. 2-3,14
ch-75-7
265
3. Суммарная сдвигающая сила равна
Рхс
75-5 75 — 42
+ 42-7 + о *7 = 5" кН/м·
2 -г^-'-г 2
4. Определяется линейная нагрузка от взвешивающего волнового дав-
а 8
ления по зависимости (17): . _. ~ 19 7 = ^ < **, а следовательно, по
табл. 8.15 (5) μ = 0,7 и соответственно
Р^ = 0,7—2~- = 118 кН/м.
5. Максимальная донная скорость над поверхностью бермы перед
вертикальной стеной рассчитывается по (18) [51]:
ν
/, max
V
9,81-5
, 2-3,14
= 6,5 м/с.
75
По эмпирической формуле 8.31 определяется крупность камня для
защитного покрова:
1 6,5^
D*
2.G —1 2-9,81
= 1,34 м.
Таким образом, условный диаметр шарообразных камней, включающих
до 50 % (по весу) более мелких зерен, D5o = 1,34 м.
Пример 8.6
Требуется найти нагрузки на оградительное сооружение вертикального
профиля, подвергающегося воздействию прибойных волн, рис. 8.20, при_сле-
дующих исходных данных: высота волн на глубоководье hd\% = b м и hd =
Рхс=273,0"%
PZ-60,0H%
.2,0
i =0,02 1
///////// ж;/л&>
<Ол» jjj Л> jjj »j »j j» Λν /л» Λν J
Расчетный
уровень
SL
Т7П'
6,0
Рис. 8.20. Эпюры давлений прибойных волнх (размеры, м;
ординаты эпюр, кПа).
266
= 2,3 м; средняя длина волн λα = 75 м; средний период Та = 6,9 с; глубина
перед сооружением df = 4,5 м; ширина сооружения о = бм; уклон дна / =
= 0,02.
Решение
1. Проверяется наличие режима прибойных волн. В соответствии с п. 21
обязательного приложения 1 [51] определяется критическая глубина. Полагая
в первом приближении —=г- = —=т" = "Qfti .6 92 = ^.0107. по КРИВ0И ^ Рис· 5
d
упомянутого приложения находится -^- — 0,087, откуда dcr = 0,087·75 =
= 6,5 м. Согласно π. 17 приложения по параметру -=^- = 0,087 с использо-
ванием рис. 5 и табл. 5 назначаются 'коэффициенты kt = 0,94 и k\ — 0,85.
Из условия задачи kly = - ° =5/2,3 = 2,2. По формуле (153) рассчиты-
0 hd
вается Λ/, при этом kr принято равным единице: Λ/ = 0,94-0,85-2,2-2,3 = 4 м.
ht 4
По уточненному значению —щ = q ^ §q2 = 0,0086 и по кривой 2
рис. 5 определяется dcr/hd = 0,07, и окончательно имеем dcr = dcr\\ = 0,07Х
Х75 == 5,3 м. Эта критическая глубина при уклоне дна i = 0,02 и глубине
перед сооружением df = 4,5 м будет отстоять от него на расстоянии
dcr — dt 5,3 — 4,5 Λ Γ. 75 ~„ ~
Выполнена проверка на возможность второго обрушения волн на подходе
к сооружению. Используя формулу (155) [51], получаем dcr, и = 0,56 · 5,3 =
= 3 м, при этом коэффициент ки = 0,56 принят по табл. 6 приложения 1. Так
как глубина перед сооружением df = 4,5 м больше вычисленной dcr, ц = 3м,
то второго обрушения не произойдет.
2. По указаниям π 20 приложения 1 [51] находим элементы прибойных
волн. Для условий d/Xd = 4,5/75 = 0,06 при i = 0,02 по графику 2 рис. 5
имеем carj_l% =0,007, а следовательно, hcur l% = 0,007-9,81 ·6,92 = 3,3 м;
gT'2
длина прибойной волны по ^огибающей кривой рис. 4 получается из
соотношения Xcurl^d = 0,7 равной Хсиг = 0,7.75 = 52,5 м.
3. Рассчитываются ординаты эпюр бокового давления по формулам
(20) —(22) [51], рис. 8.20:
z\ = —hcur = 3,3 м, pi — 0;
га = —уЗ,3 = —1,1 м, р2= 1,5.1.9,81-3,3 = 49 кПа;
1 ·9 81«3 3
2z = df= 4,5 м, /?3 = — 2 3 14 Ν = 29 кПа*
ch("W4'5j
Суммарная сдвигающая сила Рхс равна:
49(3,3—1,1) 49 — 29
/>« = -S-L2 — + 29(4,5+ 1,1) + —2—(4,5+1.1) =
= 54,5 + 160,5 + 58 = 273 кН/м.
4. Максимальное возвышение вершины прибойной волны у стены,
согласно зависимости (19) [51], равно: r\c, sur = —0,5-4,5—3,3 = —5,55 м.
267
[51]:
5. Вертикальная линейная нагрузка Ргс рассчитывается по формуле (23)
:0,7-
296
: 60 КН/М.
6. Максимальная донная скорость перед сооружением, согласно (24)
[51], равна:
ub, max
Г 9,81-3,3
-ш / /23,14 \
у ch(w4·5)
= 5,3 м/с.
В соответствии с эмпирической формулой 8.31 определяется крупность
камня для защитного покрова:
1 5 З2
D5o = 2,6-1 2-9,81 = °'9 м'
8.6. ДИНАМИЧЕСКИЙ РАСЧЕТ ВЕРТИКАЛЬНОЙ СТЕНЫ
ПРИ ДЕЙСТВИИ РАЗБИВАЮЩИХСЯ ВОЛН (РЕКОМЕНДУЕМЫЙ)
Эпюра импульса давлений
Эпюра навала
В п. 1.13 [51] отмечается, что при надлежащем обосновании
расчет воздействий разбивающихся и прибойных волн на
вертикальную стену
допускается, производить
динамическими методами,
учитывающими
импульсы давлений и
инерционные силы. Здесь
излагается один из
возможных методов расчета как
рекомендуемый,
включающий определение
нагрузок и методику
динамического расчета
устойчивости сооружения.
А. ОПРЕДЕЛЕНИЕ
НАГРУЗОК
1. Нагрузки на
сооружение при ударе волны о
стену изменяются во
времени согласно рис. 8.21.
Импульс давления характеризуется заштрихованной площадью
треугольника, величина навала давления ря выражается
максимальной ординатой эпюры навала. Возвышение вершины волны
над спокойным уровнем в момент удара принимается равным
Рис. 8.21.
Изменение нагрузок во времени
при ударе волны.
г]с, sur = — (0,55dbr + 0,1 h).
8.44
268
2. Эпюра импульса давлений имеет вид, представленный на
ис. 8.22. Величина импульса pim на единицу равна
А* = ^=Ю7,65а'с,Н-с/ма,
8.45
де а' находится по отно-
лению
T=1'6«>(£f-l,34)x
X sin-^< 1,1; 8.46
λ
с—скорость волны перед
ударом, равная
c=h2VJd;r. 8.47
3. Равнодействующая
величин импульса давлений
равна
fli*=ftmV(d/--5*i). H'C/M;
А
Расчетный /
„ UDOfiPHh r
Υ Уг
rf5
^
Π
1
I J
λ.
J
'
f
"Ί
\
f щ—
—^
•fsj
1
i
1
X
Zx = η.
7/Ъ
ДО
ί/
ft/2
0,10
0,08\
00
ом\
Щ
L о
J
I
V
1
/
1
/
У
ш*
+
^
*-*
·»—
:T
/rr.
T«lT- -
ft
41
Ofi W 2;0 CLbr/(l'
Рис. 8.23. Графики для определения Тп и Tq.
8.48 Рис. 8.22. Эпюра импульса давлений
в момент удара волны.
где k'ir — осредненный
коэффициент
пространственной неравномерности:
8.49
£., = 0,55 +ОЛ 5 th-^-;
I — длина омоноличенной
секции сооружения.
Точка приложения Rim
находится на расстоянии
от подошвы стены:
rlm —
df — zldf + :
2df-zx
-. 8.50
Полное время Тп действия силы Rim, а также время ее
нарастания Тд определяются по графикам, приведенным на рис.
8.23, где Г —период расчетной волны.
269
4. Эпюра давления навала строится по трем точкам, рис. 8.24:
при ζ = у\с, sur = — 0Jbdbr pq = 0;
при ζ = 0 pq0 = 0,65р^г; } 8.51
при ζ = df
pqf = 0,5tygrf*,.
По эпюре находится величина равнодействующей /?<? и точка
ее приложения. Если y\Clsur выше верха парапета, следует
вводить коэффициент снижения давлений в соответствии с
указаниями в п. 1.5* [51].
5. Для проверки устойчивости верхней части сооружения на
сдвиг (по швам массивовой кладки или надстройки над масси·
Расчетный /
v уровень /рао
;
'
\Rf>
1 '
1 Wf
Pf
π
"4 τ
1 %L
*4
η a
\U/J
¥
1
ζ
ΙΑ,
Рис. 8.24. Эпюра давления напапа.
Рис. 8.25. Эквивалентная эпюра
давления.
вом-гигантом) строится эквивалентная эпюра пикового
давления для статического расчета по четырем точкам, рис. 8.25.
Общая формула для расчета эквивалентного давления имеет вид:
тх
Pimbj/
\.т
где Pim — ординаты эпюры импульсов на соответствующих
отметках, рис. 8.22, значения коэффициентов для заданных точек
определяются следующим образом:
ти = О — на вершине волны (ζ = Ζ\);
mi2 = 5,0 — на расстоянии а'/2 от вершины волны;
я*1з = 3,0 — на расстоянии а! от вершины волны;
тн = 1,5 — под берменными массивами у подошвы стены.
Период собственных колебаний стены Тс = Т2 определяется
по указаниям пп. 8 и 9 настоящего параграфа.
6. Равнодействующая взвешивающего давления в подводных
швах массивовой кладки определяется по формуле
Я =0,6
Рже*г
5.53
270
де pze — ордината эпюры эквивалентного «пикового» давления
на уровне рассматриваемого шва; а2 — ширина сооружения по
шву.
7. Равнодействующая взвешивающего давления на подошву
(рис. 8.24) определяется только для навала волны:
Ρ =^· 8.54
ее момент относительно центра подошвы сооружения:
мжч = ржчт- 8-55
Б. ДИНАМИЧЕСКИЙ РАСЧЕТ УСТОЙЧИВОСТИ
ОГРАДИТЕЛЬНЫХ СООРУЖЕНИЙ ТИПА ВЕРТИКАЛЬНОЙ СТЕНЫ
ПРИ УДАРНОМ ВОЗДЕЙСТВИИ ВОЛН
8. Горизонтально-вращательные колебания стены под
волновым воздействием рассматриваются в главных формах, т. с.
как вращательные
колебания вокруг главных центров ι—ι 5^
Οι и 02 (рис. 8.26), лежа- ' ' Λ
щих на одной вертикали с
центром тяжести стены на
расстояниях г\ (выше
центра тяжести) и г2 (ниже
центра тяжести).
Эти расстояния
определяются по формуле
Расчетный
^6еН(
П,2 =
r/0cov
8.56 У//Ш////////У///////////////////Ш^
где ων =
2π
— ω1,2
угловая
ча-
Рис. 8.26. Положение главных центров
колебаний Οι и 02.
2π
rl,2
угловые
стота горизонтальных колебаний стены; соЬ2
частоты вращательных колебаний стены вокруг главных
центров колебаний:
·?. χ - <! [К -Ι" ·ϊ) ± /к + ^-^^к]; 8-57
θ— момент инерции массы сооружения относительно оси,
проходящей через центр тяжести перпендикулярно плоскости
чертежа; Θο = Θ + mh2o — момент инерции массы сооружения
относительно оси, проходящей через центр подошвы
перпендикулярно плоскости чертежа; т — масса сооружения; й0 — расстояние
(по вертикали) от центра тяжести до подошвы сооружения;
о><р—угловая частота собственных вращательных колебаний
271
стены относительно оси, проходящей через центр подошвы
сооружения:
ω
2_ <ν.
θη
ί.58
где / — момент инерции площади подошвы сооружения, а
другие обозначения поясняются ниже. Знак ( + ) перед корнем
в формуле 8.57 соответствует значению ω2ι. При построении
эквивалентных эпюр в расчет принимается наибольший период
Т2у соответствующий наименьшей частоте о)2, получаемой при
знаке (—) перед корнем в формуле 8.57.
9. Период собственных колебаний оградительных
сооружений типа вертикальной стены зависит от инерции мас.сы
сооружения и от жесткости основания, характеризующейся
величиной коэффициента постели.
Значения коэффициентов постели определяются по
формулам:
Сх = 0,7Сг;
с*=тт[1+2
A J V 2а '
8.59
где Со — основной коэффициент постели, определяемый по
данным натурных исследований сооружений или — приближенно —
по данным табл. 8.16 в зависимости от толщины каменной
постели гь, ширины стены по подошве а и грунтов основания; А =
= alc — площадь подошвы монолитной секции сооружения
между температурно-осадочными швами; Gb — вес 1 пог. м
сооружения с учетом гидростатического взвешивания, кН; Сх —
Таблица 8.16
Краткая характеристика основания
Основной
коэффициент постели
Со, кН/мя
Каменная постель малой толщины (гь/а ^ 0,25 ... 0,30) и
песчаная подушка на илистых грунтах или постель малой
толщины на заиленных песках
Каменная постель малой толщины на песках, глинах
средней плотности или каменная постель средней толщины (Zb/a=
= 0,31 ... 0,40) на слабых грунтах
Каменная постель средней толщины на грунтах средней
плотности
Мощная каменная постель (гь/а ^ 0,45) на грунтах
средней плотности
Плотные осадочные породы, гравий, галька, песок плотный
и мощная каменная постель
Бетон в мешках или кладка массивов для выравнивания
основания
Скальные основания
1226,2... 1471,5
1962... 2943
2452,5... 3924
3924 ... 5886
5886 ... 7848
10791... 12753
29430... 49050
272
шффициент постели при чистом сдвиге сооружения; С2—ко-
ффициент постели при равномерном сжатии основания; С<? =
коэффициент постели при неравномерном сжатии основания.
Если со стороны порта перед сооружением имеется
подсыпка камня выше подошвы стены, необходимо учитывать влияние
се отпора на положение главных центров. Для этого величину
Сх увеличивают на АСХ = 2452,5 кН/м3 из расчета 1 м
приведенной высоты подсыпки выше подошвы сооружения. Под
приведенной высотой подразумевается толщина слоя подсыпки с
учетом пригрузки берменным массивом.
Рис. 8.27. Графики для определения динамических коэффициентов
kdl И. &ίΠ.
10. Общая последовательность расчетов по определению
шболыыих отклонений стены от положения равновесия под
шовым воздействием такова:
-по формулам 8.58, 8.57 и 8.56 находятся положения
главок осей, проходящих через центры 0\ и 02 перпендикулярно
"оскости чертежа;
-определяются моменты равнодействующей импульса
давши М1ш и М11ш относительно осей Ои 02 соответственно;
-по величинам Тп и Тя% а также по Т\ = 2π/ω,ι и Гг = 2π/α)2,
вуясь графиком рис. 8.27, определяем динамические коэф-
чиенты kld и klld\
-по формулам
а=-^Г#иР=йТГ# 8·60
273
находим углы поворота вокруг С^ и 02 соответственно (в 8.60:
Ql = ® + тг2{ и в2 = 6 + тг22 — моменты инерции массы стены
относительно главных осей Οι и 02).
Наибольшее отклонение подошвы стены от положения
равновесия рассчитываем по зависимости
δ = β (/'2 — ho) — α (/'ι + ft0) · 8.61
Касательные напряжения и их равнодействующая но
подошве сооружения соответственно равны:
ts = Сх6; Rd = СхЬа. 8.62
t,/T2
1,0
Τς/Τη=Α5ΰ
0,5
—
■ '
ом
Щ
0;20
0,10
от_
^*
1Л
2fi
3,0
Тп/Тг
Рис. 8.28. Графики для определения значений t\.
11. Коэффициент устойчивости стены на сдвиг
рассчитывается так:
s~ " Rd + nRq
8.63
где Gb — вес 1 пог. м сооружения с учетом гидростатического!
взвешивания; \xs — коэффициент трения материала сооружения
по постели; /г = -яг-<;1; t{ находится из графиков на рис. 8.28.
Тп
Напряжения у граней подошвы определяются по формуле
-], 8.64
(Gb — nPzq)
<*1,2 = " ±
(α + β) Ύ С? + —ψ-
где ΣΛί — суммарный опрокидывающий момент относительно
оси, проходящей через центр подошвы стены перпендикулярно
274
плоскости чертежа, от давления навала, взвешивающего
давления и собственного веса стены; W = а2/6 — момент
сопротивления площади подошвы стены на 1 пог. м ее длины.
Пример 8.7,
Требуется произвести динамический расчет устойчивости
сооружения, подвергающегося воздействию разбивающихся волн при следующих
исходных данных: глубины на подходах к сооружению аь = 12 м, у стены
tff=7,0 м, над бермой dbr = 5J м; высота волн Л = 5 м, средняя длина
ъ-%0 .
//SS.///////S s//S W/S/S/W/V/SS/ ///λ JS/S J/M ////У/// /SS/ S/
Рис. 8.29. Эпюры давления разбивающихся волн на
вертикальную стену.
λ = 75 м, период Τ = 7,8 с. При заданных элементах волны разбиваются
непосредственно у стены, так как
.£*. = J2£ = 2,4> 1,5, а .£*£. = 5£ = 1Д4 < 1,25.
h 5,0 /г 5,0
Поперечное сечение рассчитываемого сооружения, подобранное на
основании статического расчета, показано на рис. 8.29. Длина секции с
монолитной надстройкой / = 15,0 м. Вес и масса 1 пог. м сооружения без учета
гидростатического взвешивания соответственно равны: G = 2020,9 кН, т =
= Gig = 206,0 т. Возвышение центра тяжести сооружения над его
подошвой h0 = 5,15 м. Момент инерции массы 1 пог. м сооружения относительно
275
оси, проходящей через центр тяжести перпендикулярно плоскости чертежа,
θ = 3027,4 тмс2. Вес 1 пог. м сооружения с учетом гидростатического
взвешивания Gb = 1471,5 кН.
Решение.
1. По 8.44 возвышение вершины разбивающейся волны над спокойным
уровнем равно цс, sur — ζ ι = —(0,55-5,7+0,1-5,0) = —3,64 м.
По 8.46 находим отношение — = 1,6 th(g~7 ~~" 1,341 sin "75" = *'6-0,39х
X 0,99 = 0,62, откуда я' = 0,62-5,0 = 3,1 м.
2. По 8.47 рассчитываем скорость волны перед ударом: с =
= 1,21/9,81-5,7 = 9,0 м/с.
По 8.45 значение импульса давлений на 1 пог. м стены равно: рш =»
= 637,65.3,1 · 9,0 = 17,8 кНс/м2.
По 8.49 при / = 15 м и kir = 0,55 + 0,15 th -jj = 0,598 = 0,60 находим
осредненный коэффициент пространственной неравномерности: ki/ =
0,6.3,14-1,3-0,6(7,0 + 3,65 — 3,1) Л^о
= 7 0 4- Я 65 = ' ' тогда по формуле 8.48 получим
/ 3,64\
равнодействующую импульса давлений: Rim = 17,8 · 0,73 f 7,0+ -у Ι =
72 + 3,64-7 + -^ψ-
= 114 кНс/м, а ее плечо, согласно 8.50: rltn = 2."7 4-3 64 == 4'^7 м"
dhr 5,7
По графикам из рис. 8.23 при —г- — -ττν = 1,85 находим полное время
действия импульса давлений Тп = 0,10 · Τ = 0,1 · 7,8 = 0,78 с, а время его
на~растания Tq = 0,5Г„ = 0,39 с.
3. Пользуясь формулами 8.51, вычислим ординаты и построим эпюру
давлений навала волны, рис. 8.29:
на уровне r\c, sur = — 0,75 · 5,7 = — 4,3 м
Ря = 0;
на уровне спокойной поверхности (ζ = 0)
pqo = 0,65 - 1,02 · 9,81 · 5,7 = 37,1 кН/м*;
на уровне подошвы стены (г = df)
pqf = 0,50 · 1,02 · 9,81 · 5,7 = 28,5 кН/м*;
находим равнодействующую давления навала:
Rg = 0,5 · 4,3 · 37,1 (37,14- 28,5) · 7,0 = 309 кН/м;
опрокидывающий момент силы навала относительно подошвы стены
равен:
- - - - 7,0
Xх
Mq = 0,5.4,3-37,1 (ψ + 7,θ] + 37,1 +28,5 70.
2-37,1 + 28,5
Х 37,1+28,5 = 1δ12 кН*м/м;
4,88 м;
плечо
__ Щ _ 1512 _
q Rq 309
по формуле 8.54 рассчитываем взвешивающее давление от навала:
28,5-8,0
Р2д = ' =114кН/м;
276
момент от взвешивающего давления навала относительно центра
подошвы стены согласно 8.55 равен:
114-8
Mzq = —g— = 152 κΗ·μ/μ.
4. По табл. 8.16 при zb/a = 5,0/8,0 = 0,625 > 0,45' и формулам 8.59
находим упругие характеристики основания
С0 = 4910 кН/мЗ;
^=491θΓΐ + 2 (8οΥ55)|ΐ/Γ21ί7οοι = 491°Π + 0.385)>3,06 = 20601 кН/мЗ;
Сх = 0,7 . 20601 = 14557 кН/м3;
Cf = 4910 (l + 2 8|j515)» j/gSIr " 49I0(1 + °'88>·3'06 = 28314 kH/m3·
5. По зависимостям 8.58, 8.57 и 8.56 определим частоты собственных
колебаний сооружения и положение главных центров колебаний Οι и 02,
рис. 8.26.
Θ0 = 3027,4 + 206-5,152 = 8491 тмс2;
, Ь8з <о о 28056,6-43 , r f
/= _ = 43 м±; ·» = 193>5 = Н5 1/с*
2 .14421-8 1_ _θ_ 3027,4
ωχ~ 206 -565С2; 0О - 8491 -°'3б>
wf 2 = _i~ [(565 + 145) ± /(565+ 145)2 —4-0,36.565· 145] =
' Ζ · U,«jO
= 1,39(710 ± 620); <*\ = 1,39-1330 = 1864 l/c»,
откуда
oh = 43 1/с; <4= 1,39.90 = 121 1/с»; ω8 = 11,2 1/с;
2π 6,28 Л1 „
^=^=1зГо = 0,146с;
2π 6,28
^=7, = .—= ^ = 0,57 с;
_ Λρω^ _ 5,15.565 _„оо7
1 ω2__ω2 565-1850
χ ι
Μ| = 5,15.565 =660м
2 ω2_ω2 565-125 '
Проверка:
θ 3027,4
Должно быть I rxr21 = — = 2Q6 = 14»70 м2> получили: | rxr2 \ = 2,27X
X 6,60 = 14,98 m2« 14,70 iA
6. Моменты равнодействующей импульса давления относительно Οι и 02
соответственно равны, рис. 8.26 и 8.29:
М\т = - 112,8 (2,27 + 5,15 — 4,45) = — 335,5 кН;
MVm = 112,8 (6,60 - 5,15 + 4,45) - 667,1 кН.
277
7. По значениям Tq, Tn, Г, и Т2 (пп. 2 и 5 настоящего параграфа)
определяем из графиков рис. 8.27 значения динамических коэффициентов для
0{ и 02:
kld = 1,0 при -Л = 0,50 и _? = -^ = 5,45 > 2,0;
fclJ = 1,35 при * = 0,50 и -£ = -L- = 1,39,
0,78
Гц 7\ 0,145
^ Л.Л ^_ 0J8
^ 0,56:
8. По 8.60 находим моменты инерции стены относительно 0{ и 02
углы ее поворота вокруг главных центров от удара волны:
0! = 3027,4+206·2,272 - 4089 Кн-м-с2;
θ2 = 3027,4+206·6,602 = 12000,8 Кн-м-с2;
п_ 21.(-335,5) __
4089-1850.0,78
2-1,35-667,1 _
0,00011 рад;
0,00162 рад.
г 12000,8 125-0,78
9. По 8.61 наибольшее отклонение подошвы стены от положения
равновесия составит
δ = 0,00162(6,6—5,15)+0,00011(5,15+2,09) = 0,00224+0,00079 = 0,00309 м.
Соответствующие касательные напряжения и их равнодействующая по
формулам 8.62 равны:
τ, = 14421 0,00303 = 437 кН/м2; Rd = 43,7-8 = 349,6 кН/м.
Τ 078 Τ
10. По значениям —--— = —1__ == 1,39 и —L == 0,5 с помощью рис. 8.28
Т2 0,56 ^
получаем -ψ— = 0,80, следовательно:
* 2
U 0,448
tx = 0,80Г2 = 0,80-0,56 = 0,448 с и η = γ- = -g^s" = °·57·
11. По 8.63 находим коэффициент устойчивости стены на сдвиг:
(1471,5 —0,57-114).0,6
349,6 + 0,57.311,0
= 1,58.
12. По 8.64 краевые напряжения у граней подошвы стены (угол
поворота φ = β+α = 0,00162—0,00011=0,00151 раД; момент сопротивления
1 пог. м подошвы W = 1 · 82/6 = 10,65 м3) равны: -
1471,5 — 0,57-114 ГЛЛЛ1Г1 8 Лло, 0,57(1512+ 162)
± 0,00151 -гг 28314 + -
у1, 2 - 8 ^ pwi«" 2 *°^ ^ 10,65
= 175,6 ± [171,3 + 89,3];
σι = 175,6+260,6 = 436,2 кН/м2 = 43,62 Н/см2;
σ2 = 175,6 — 260,6 = — 85,0 кН/м2 = —8,50 Н/м2.
Таким образом, раскрытие шва вдоль подошвы происходит на
протяжении 1,29 м. Здесь при определении напряжений принято, что собственный вес
сооружения приложен в середине его подошвы ввиду малости
эксцентриситета. Заметим, что при статическом расчете этого же сооружения в
рассматриваемых условиях получено: &* = 1,38, σι = 49,9 Н/см2; σ2 =
= — 16,2 Н/см2, а раскрытие шва вдоль подошвы равно примерно 2 м.
278
Использование динамического расчета позволило выявить некоторые
резервы устойчивости сооружения по сравнению с результатами статического
расчета.
13. Наиболее опасным при статическом расчете сооружения на сдвиг
является первый подводный шов на отметке —1,0 м. Вес части стены,
расположенной выше этого шва, составляет G\ = 836,8 кН/м с учетом
статического взвешивания.
Проведем расчет по эквивалентной эпюре, рис. 8.29. На расстоянии
а'/2 = 1,55 от вершины волны p2tm = 7,9 кН/м2 и рзш = 15,7 кН/м2 — на
расстоянии о! = 3,1 м — ниже расчетного уровня воды, в том числе у
подошвы рAim ~ 17,7 кН/м2. Соответствующие ординаты эквивалентной эпюры по
формуле 8.52 при ре = 0,73 (п. 2 расчета) равны:
5,0.7,9-0,73
Р2е = —оЗб— = 51»° кН'м'2;
3-15,7-0.73
Ръе = о^б— = 61,2 кН/м2;
1,5-17,7-0,73 л л ιτ
oie = Q^gg = 34,53 кН/м*.
На уровне первого подводного шва ордината давления по эквивалентной
эпюре ри = 54,9 кН/м2, а равнодействующая эквивалентного давления на
вышерасположенную часть стены:
511,55 51,0 + 61,2 , „г 61,2 + 54,9 , rr ftieo ttf
Rle = £— + —L-2—— 1,55 + * %—- 1,55 = 216,3 кН/м.
Равнодействующая взвешивающего давления по этому шву согласно
формуле 8.53 равна:
54,9-8
Rze = 0,6 —5— = 132,4 кН/м.
Коэффициент устойчивости на сдвиг по шву составляет
_ 0,5(836,8-132,4) _
*s~ 216,3 "" 1,°'5,
где μ = 0,5 — коэффициент трения бетона по бетону.
8.7. НАГРУЗКИ И ВОЗДЕЙСТВИЯ ВЕТРОВЫХ ВОЛН
НА КРУТОНАКЛОННЫЕ ОТКОСНЫЕ СООРУЖЕНИЯ
К крутонаклонным принято относить откосные сооружения,
угол наклона граней которых к горизонту составляет 90° > α >
> 45°. В таких случаях принимается условно, что у сооружения
образуется стоячая волна. Волновую нагрузку Ра, отнесенную
к единице длины крутонаклонной стены, рекомендуется
принимать по эпюре волнового давления, рис. 8.30. В качестве
исходных задаются значения /ι, λ, глубина d и угол наклона α
напорной грани к горизонту. Расчеты производятся в следующей
очередности:
— определяются ординаты эпюр волнового давления на
вертикальную стену полного профиля от действия стоячих волн;
279
— находятся поправочные коэффициенты, учитывающие
наклон напорной поверхности, и рассчитываются ординаты эпюр
давления на наклонную стену путем умножения ординат
давления для вертикальной стены на поправочные коэффициенты;
— строятся эпюры волнового давления.
Предварительно вы-
а)
Расчетный
τ-? уровень
Верх
сооружения
числяется
коэффициент отражения волн
Кс — krkpkref, 8.65
где kr и kp находятся
по табл. 6 [51], a kre\
следует из
зависимости:
λ
**./ =
π2Λ(1 -f ctg2«)·
8.66
Таблица 8.17
Верх
^сооружения
Номера
точек
*)
1
ti
ι
1
(
77/ ///
?}?
Расчетный
. Х7 уровень 6,
Ч1Р
$<^|^
у/; /// /V/ftv//7 ?/
/о
У '/// //?
Ζ
Заглубление
точек
ζ, м
Значения
ординат
волнового давления
/V кПа
/
2
3
4
δ
в
7
8
9
При
0
0,25d
0,5d
d
При
0
d
гребне
Ρτ* = к2оРг
РЗа=*кЗоРъ
P4* = k4aPi
P5a = k5aPb
ложбине
Ρη = knPi
Ρ8* — kSaP%
Ρ9* — k9<xP$
Рис. 8.30. Эпюры давления стоячих воли на
наклонную стену со стороны открытой
акватории
а) при гребне волны; б) при ложбине волны.
При Кс > 1 значение коэффициента Кс принимается равнык
1, в этом случае перед стеной образуются стоячие волны. В слу
чае, если Кс < 1, расчет следует вести на действие разбиваю
щихся волн в соответствии с пп. 1.11 и 1.12 [51].
Эпюры волнового давления на вертикальную стену строятся
в соответствии с требованиями пп. 1.3 и 1.4 [51] при заданные
элементах волн и глубине перед сооружением. Возвышения ηα
и понижения ηα/ уровня воды у наклонной стены находятся п<
формулам:
280
Здесь г\с и x\t — соответственно возвышения и понижения
ровня воды у вертикальной стены, а для коэффициента χ ре-
омендуется зависимость
1
У = —: .
8.68
Эпюры волнового давления на наклонную стену строятся
ipn гребне и ложбине волны, рис. 8.30, а, б, при этом ординаты
давления на глубине ζ должны вычисляться в соответствии
с табл. 8.17.
<Х = 75
5)
face
0,80
0,05
β)
0,80
0,60
0, Μ
020
0,05
сс=75
ol=60
I
~Υ-γ _
. f r
,
./.
a=45°
^Ξ3
i , . 1
0,15
0,25
0,35
a=75l
0,45 £
Л
•
N
4 ^
oc=45
^Ь
a^SO9
I u j
-H
Η
-
^4
|
0,15
0,25
0,35
0,45 ώ
Л
Рис. 8.31. Графики для определения
а) коэффициента k2a; б) коэффициента Лза; в) коэффициентов kAa, *ga.
281
Значения коэффициентов &2<χ.. .&5α, ^7α... k$* рекомендуется
принимать по графикам рис. 8.31 и 8.32. Здесь р2-5> Р7-9—
ординаты давления на стену вертикального профиля, а значения
'Пас и y\at следуют из формул 8.67 и 8.68.
а.)
1<5сс > ^ да
0,80
0,40
0,0
-0,40
-0,80l·
1,9.0
l4^
^
\\
^
ot=U5
О^Х
\
ч \
дс=75
\
\
О
сс=60
\
\
о
0.05
к 7 а
0,80
0,05
0,15
0,25
0,35 0,45
d//L
сс = 75°
сС = 60°
IS
СС='
Ч5°
I
0,15
0,25
0,35 0,45
d/λ
Рис. 8.32. Графики для определения
а) коэффициентов к5,г, к$а; б) коэффициента Л?а.
282
По эпюрам волнового давления определяются значения и
очки приложения равнодействующих Рас при гребне и Ρ «/при
тожбине стоячей волны.
Пример 8.8
Требуется определить волновую нагрузку на гладкую непроницае-
\ю наклонную стену при следующих исходных данных: высота волны h =
= 3м; средняя длина волны λ = 60 м; глубина, заложения низа стены d =
= 20 м; угол наклона стены к горизонту α = 45°, рис. 8.33.
Решение.
1. В соответствии с 8.66 имеем:
60Д)
Расчетгш.
уровень,
Kref~ π^ 3,0(1 -|-ctg245°)
δ)
Рис. 8.33. Эпюры волнового давления при гребне волны
а) на вертикальную стену; б) на наклонную стену (размеры, м;
ординаты эпюр, кПа; равнодействующие давления, кН).
Тогда по 8.65 Кс = 1,0 · 1,0 · 1,0 - 1,0.
Здесь принято kr = 1, kp = 1 как для гладкой непроницаемой
поверхности. Таким образом, перед преградой образуются стоячие волны.
По формуле (3) [51]:
cos ω' = τ. 3,0 (8π 20,60-3) = 1Д85 > h
В дальнейших расчетах принимается cos_oi = 1.
Согласно формуле (2) [51] при k = 2лД = 2π/60 = 0,105 м"1 и cos ωί =
= 1 возвышение х\с уровня воды при гребне волны:
η,=- 3,0 1—0,10593,0^ cth (0,105-20,0) 12 = -3,5 м;
понижение r\t при cos ω/ = —1 при ложбине волны:
0,105-3,02
η^_3,0(—Ι)--2—j
•cth (0,105-20,0)·(- Ι)2 = 2,5 м.
2. В соответствии с п. 3 приложения 1 [51] следует, что рассматривае-
мая преграда расположена в мелководной зоне, так как d — 20,0 м < 0,5λ =
283
= 0,5 · 60,0 = 30,0 м. Тогда ординаты эпюр волнового давления на верти!
кальную стену необходимо вычислять по п. 1.4 [51]. Расчеты сведены в
табл. 8.18, в которой значения коэффициентов k2... ks, k8 и_&9 определены
по графикам на рис. 3, 4, 5 [51] при Λ/λ = 3/60 = 0,05 и λ/d = 60/20 = 31
Построения эпюр давления на вертикальную стену при гребне и ложбине!
волны выполнены на рис. 8.33, а\ 8.34, а.
4
Расчетный
ъ уровень 6\
Рис. 8.34. Эпюры волнового давления при ложбине волны
а) на вертикальную стену; б) на наклонную стену (размеры, м; ординаты
эпюр, кПа; силы давления, кН/м).
Таблица 8.18-
Номера
точек
Заглубление
точек г, м
Значения
коэффициентов
Значения ординат волнового
давления р, кПа
При гребне
/
2
3
4
5
6
7
8
9
Чс
о
0,25d
0,5d
1 d
-3,5
0
5,0
10,0
20,0
_
ko,
*3
*4
*δ
-
0,72
0,43
0,27
0,17
Pi
Pi = k^gh
Pz = bz9gh
Pi = ktfgh
Рь = h?gh
При ложбине
0
Άί
ом
1 d
0
2,5
10,0
20,0
_
*«
*9
0,48
0,36 1
Ps = — b$gh
/>э = — btfgh
1
о
21,09
12,75
7,85
4,90
0
-24,52
-14,22
-10,79
3. По формуле 8.68 получаем: χ = sin ^0 = 1,41.
В соответствии с 8.67 изменения уровня воды у наклонной стены
cetera вляют:
— возвышение при гребне волны
Пае = W* = 1.41 (- 3.5) = - 4,95 м;
284
— понижение при ложбине волны
= 3,53 м.
4. Расчеты по определению ординат эпюр волнового давления на
нажую стену приведены в табл. 8.19, в которой приняты ^коэффициенты
а.../г5аи /г7а...£9а по графикам из рис. 8.31 и 8.32 при d/λ « 20/60 =0,33
α =45°; ρ — по данным расчета для вертикальной стены.
Таблица 8.19
Номера
точек
Заглубление
точек ζ, м
Значения
коэффициентов
Значения ординат волнового
давления ра, кПа
Час
0
0,25rf
0,5d
d
—4,95
0
5,0
10,0
20,0
При гребне
—
^2<х
^3α
*4«
*όα
0,88
0,83
0,54
-0,43
Pu
Pu = *з«Л
P\* = k4*Pi
Ры = кыРъ
При ложбине
о
ν
0,5rf
rf
0
3,53
10,0
20,0
^7α
Λ3α
*9α
0,87
0,54
—0,43
^6α
PU = k7aPi
Ръ-х = kSaP$
Р9л ^ ^9α^9
0
18,56
10,58
4,24
—2,11
0
-21,33
—7,68
4,64
Эпюры, давления на наклонную стену при гребне и ложбине стоячей вол-
д построены на рис. 8.33, б\ 8.34, б\ равнодействующие волновых давлений
родятся как площади эпюр давления.
Глава 9. НАГРУЗКИ И ВОЗДЕЙСТВИЯ
ВЕТРОВЫХ ВОЛН
НА СООРУЖЕНИЯ ОТКОСНОГО ПРОФИЛЯ И БЕРЕГА
Взаимодействия волн с откосами гидротехнических соору-
•ений и берегами сопровождаются периодическим обрушением
золи, подъемами и скатываниями масс воды по откосу. Эти
•вления следует рассматривать как сложные энергетические
поцессы, трудно поддающиеся теоретическому анализу, а
тому большинство содержащихся в этой главе рекоменда-
й для практики представляют собою эмпирические формулы,
лученные на материалах обобщения экспериментальных
/иных.
285
9.1. НАКАТ ВОЛН НА СООРУЖЕНИЯ ОТКОСНОГО ПРОФИЛЯ
И БЕРЕГА
Накат волн на сооружения и берега подлежит определению!
в решениях ряда инженерных задач, в том числе в расчетах'
нагрузок на откосы и назначении границ креплений откосов,
при прогнозировании динамики движения наносов и размывов
берегов в приурезовой зоне, подверженных воздействию раз
рушающихся волн и др.
Расчетно-теоретические зависимости метода определения
наката волн на прямолинейные откосы, укрепленные плитами,
разработанные Г. Ф. Красножоном [28, 56], легли в основу
п. 1.14* СНиП [51]; согласно этим указаниям высота наката
волн на откос рассчитывается по формуле (25) с использова
нием табл. 6.—9 и рис. 10*.
В связи с появлением в печати ряда работ, посвященных
исследованиям наката нерегулярных волн, возникла потреб·
Таблица 9.1
hl0, .м
I "о
0,5
0,75
1,0
1.5
2,0
'гип\%
10,5
6,5
5,0
4,5
иость в оценке достоверности рекомендаций [51]
применительно к реальному волнению. С этрй целью использованы
материалы экспериментов, выполнявшихся в последние годы
в США, Японии и СССР [6, 7, 62]. Остановимся кратко на
предложениях В. С. Шайтана [62], который для расчета высоты
наката нерегулярных волн обеспеченностью i (%, по накату)
на откосы, укрепленные плитами или наброской камнем,
использует формулу
hrwM% = Lran\ %^и%кЛгкрк{% tg φ, 9.1
где Lrun\% — относительная длина наката вероятностью превы
шения 1% в системе фронтальных волн, принимаемая пс
Таблица 9.2
*1К. м
До 1 2
>1,2
Величина функции
Lrunl%
kU%==r Г"
Lrun\%
Наибольшая
Средняя
Наибольшая
Средняя
Вероятность превышения длины наката
Lrunl%
2
0,99
0,96
0,98
0,94
5
0,98
0,88
0,91
0,85
7
0,97
0,86
0,88
0,82
10
0,96
0,82
0,81
0,78
50
0,78
0,68
0,56
0,53
286
:абл. 9.1; kLi% — функция связи Lrtm ι% относительной длины
фронтального наката вероятностью превышения i% с LrUn\% —
'ероятностью превышения 1 % при расчетном шторме, опреде-
шкал по табл. 9.2; ka—коэффициент, принимаемый по
габл. 9.3, учитывающий подход волн к откосу под углом ее,
рад; kr и kp — соответственно коэффициенты шероховатости и
проницаемости крепления, принимаемые для плит по табл. 6
[51]; φ — угол наклона откоса к горизонту, град.
Таблица 9.3
Угол а, град
Коэффициент ka
Наибольший
Средний
0
1
1
10
0,99
0,95
30
0,93
0,85
50
.0,82
0,75
70
0,7
0,65
90-
0.6
0,55
Сравнивая данные таблиц соответственно 9.2 и (8), 9.3 и (9)
\беждаемся в том, что в рекомендациях СНиП [51] учитывается
нерегулярность волнения, обеспеченность высот волн в системе
нпо накату,, а также косой подход волн к откосу. В табл. 9.4
приводятся сопоставительные данные расчета высоты наката
волн (обеспеченностью 1 % по накату) для фронтально подхо-
1ящих волн к откосам с пологостью ctg<p = 2; 4 и 10 при h\%'=
= 2 м, K/h]% = 10, 15, 20, полученные по [51] и формуле 9.1.
Таблица 9,4
Метод расчета
h r
"run 1%
СНиП [51]
Формула 9.1
4h\%
10
15
20
J0
15
I 20
Высота наката при пологостях откоса ctg φ
2
3,8
4,4
5,0
4,5
4
1,0
2,2
2,7
2,25
10
0,8
0,9
и
0,9
Из анализа табл. 9.4 можно установить следующее:
— в рекомендациях [51] по расчету высоты наката
учитывается как регулярный, так и нерегулярный характер волнения;
— расчетные значения высоты наката волн пологостью
ί./Αιχ=15 наилучшим образом соответствуют наблюдениям
в натуре; при пологости волн 10 и 20 между расчетом и
натурой существует пропорциональная зависимость; расхождения
287
находятся в пределах точности выполняемых измерений
в натуре.
В действующих нормах не содержится указаний по расчету
высоты наката волн на откосное сооружение при наличии берм.
В настоящее время в некоторых ведомственных нормативах
предлагается определять высоту наката волн на откос с бермой
hbrtrun по формуле (25) [51] с введением дополнительного
коэффициента kbrtrun', в таком случае можно записать
"br, run — Rbr, run"run I % ?
9.2
1520 30
Расчетный уровень
Рис. 9.1. Графики для определения
коэффициентов kbr, run (график 1) и kbr, m (гра-
фик 2).
где kbr, run —
коэффициент, определяемый по
графику / рис. 9.1;
hrun ι % — высота наката
волн на прямолинейный
откос без бермы
согласно формуле (25) [51].
При назначении &^,,„„
по рис. 9.1 входным
параметром _является
отношение bbr/Κ далее
следует двигаться по
«ключу» до λ/Λ ι ?0, затем —до
семейства линий
относительных величин dbr/db
и наконец до кривой /.
Здесь приняты
обозначения: Ьы — ширина
бермы; dbr — заглубление
бермы от расчетного
уровня; аь — глубина
воды у откосного
сооружения.
Остановимся кратко на определении высоты наката
судовых волн на прямолинейный откос. Увеличение ширины
современных каналов и скоростей движения судов по ним
обусловили необходимость некоторых уточнений прежних
рекомендаций норм по расчету высоты судовой волны hSh и высоты наката
hrsh судовой волны, которые сейчас представлены в виде
формул (84)* и (85)* [51]. Заметим, однако, что в случаях, когда
скорость движения судна по каналу vSh не ограничивается
эксплуатационными требованиями и превышает скорость
согласно (85)*, высоту судовой волны допускается рассчитывать
по зависимости
Кн = ΜνΥ&Α*ι ехр(~ °'15-|:)'
9.3
288
где L — расстояние по нормали от борта судна до расчетной
точки; mv — коэффициент продуцирования, принимаемый из
габл. 9.5 в зависимости от числа Фруда Fr:
Fr = r VsH ; 9.4
is я lu — осадка и длина судна; bs — ширина судна по миделе-
вому сечению; 6ι — коэффициент полноты миделевого сечения
судна, принимаемый для грузовых судов равным 0,95; для
пассажирских судов — 0,85; для прогулочных — 0,8.
Таблица 9.5
Fr
mv
0,4
0,18
0,6
0,31
0,8
0,47
1,0
0,57
1.2
0,58
1,6
0,56
2,0
0,53
При двухстороннем движении судов по каналу критическую
скорость расходящихся однотипных судов допускается
определять по упоминавшейся формуле (85)*, в которой
рекомендуется принимать увеличенным вдвое коэффициент ka>
характеризующий отношение подводной площади поперечного сечения
судна к площади живого сечения канала.
При отношении dSh/ds> 1,5 (где dsh — глубина воды
в канале) высоту судовой волны допускается назначать равной
наибольшему из значений величин, рассчитанных по (84)* [51]
и по зависимости
g{\-kaY*V h
где δ —коэффициент полноты водоизмещения судна.
Пример 9.1
Определить высоту наката волн на прямолинейный откос,
укрепленный железобетонными плитами. __
Исходные данные: расчетные элементы волн h\% = 3 м; λ = 30 м;
коэффициент откоса ctgcp = 4 при φ = 14°; глубина воды перед
сооружением d = б м; расчетная скорость ветра Vw = 10 м/с; подход волн к
сооружению фронтальный, α = 0; плиты с неомоноличенными швами;
обеспеченность по накату равна 1 %.
Решение.
Высоту наката волны на откос определим по формуле (25) [51] с
использованием таблиц 6—9:
hrun ι% = krkpkspk*kikrunh\% = 1 ·0,9· 1,1 -1-1-1 -3 = 2,97 м.
Принимаем hrun ι % = 3 м.
Пример 9.2
Определить высоту наката волн на откос с бермой, укрепленной
железобетонными плитами.
289
Исходные данные: элементы волн, пологость откоса, глубина
воды, скорость ветра даны в примере 9.1; берма шириной Ьы = 9 м распи
ложена на расчетном уровне воды, аы = 0.
Решение.
1. Коэффициент kbr.run определим по графику / на рис. 9.1 в
зависимости от безразмерных параметров:
λ -зо-од 7^ = Т = 10 и Т = Т = а
Его значение равно кы, run = 0,62.
2. Величину ΛΓ«/ιΐ%=3 м принимаем для прямолинейного откоса из
примера 9.1.
3. Подставив известные iirun \% = 3 м и kbr, run = 0,62 в формулу 9.2,
найдем высоту наката волн на откос с бермой:
hbr,run = 3-0,62 = 1,86 м.
Принимаем libr, run = 1,9 м.
Пример 9.3
Определить высоту наката судовых волн на откос, укрепленный
железобетонными плитами.
Исходные данные: канал III класса капитальности с размерами
Ь = 35 м, dSh = 3,0 м, ctgcp= 1,5; расчетное судно имеет размеры bs =
= 10 м, U = 60 м, ds = 1,8 м, δ = 0,85.
Решение.
1. Определим из (85)* [51] допускаемую по эксплуатационным требо
ваниям скорость судна:
53(35 + 26)
/"Г 3,14 4- arccos (1 — 0,2) 1 0,
Vadm = 0.9 Л/ 6 cos —- 3"^ -' - 2 (1 - 0.2) 9,81 -
10-1,8
где ка- 0,5-3(35 4-26) ~0'2·
2. По (84)* [51] высота судовой волны равна:
35
= 2,21 м/с,
**- 2^ΐΛ^ = 0,16 м.
* 9,81 Г 60
Поскольку rfsfc/rfs = 3/1,8 = 1,67 > 1,5, уточняем высоту судовой волны
по формуле 9.5:
h 1,6-2,21» |/ι
όΛ 9.81 (1 -0,2)'2'5 '
0,85-1,8 лп
ΊΒδ α23 Μ·
Для "дальнейших расчетов принимаем hsn = 0,23 м.
3. Определяем по (86) [51] высоту наката судовой волны на откос:
2 212
0,5-0,23+0,05-1,5-g-gj-
h-rsh = 1,4 ПГо^5Т5~^ = °'23 м·
Высота наката волн на сооружения откосного профиля,
укрепленные обыкновенными бетонными массивами и
фасонными блоками, обычно рассчитывается по формуле (25)
с использованием табл. 6—9 и рис. (10)* [51]. При этом
результаты расчетов оказываются нередко заниженными до отношс-
пню к данным экспериментов. Как показывает опыт, это
обусловлено недостаточно полным учетом влияния пористости
наброски при г//г1%>0,2. В настоящее время по материалам
обобщения данных лабораторных и натурных опытов
представляется возможным в таких случаях при неизменной величине
kr = 0J назначать численные значения коэффициента
проницаемости kp по формуле
*p = 1-w 9·6
где Π — пористость (в процентах), принимаемая для разных
элементов креплений из табл. 9.6; г — характерный размер
шероховатости, выраженный через размер ребра куба
согласно 9.30.
Таблица 9.6
Конструктивные формы блоков
для крепления откосов
Обыкновенные бетонные массивы
Тетраподы
Гексалеги
Гексабиты и пентаподы
Долосы
Массивы с прорезями
Пористость П,
%
41 . . .44
50
47
55
60
68 . . .72
Обратим внимание здесь и на то, что при наличии у
откосных сооружений бермы высота наката Ны,гип должна
определяться по формуле 9.2 с использованием рекомендаций по
назначению kbr,run согласно рис. 9.1.
Пример 9.4
Определить высоту наката волн на откос, укрепленный наброской
и* обыкновенных бетонных массивов.
Исходные данные: расчетные элементы волн h\% = 5 м, "λ = 100 м,
λ/Aj % = 20; откос ctgq)=l,5; плотность бетона рт = 2,3 т/м3; плотность
воды ρ = 1 т/м3; скорость ветра V«, = 10 м/с; подход волн к сооружению
фронтальный, α = 0; обеспеченность по накату i — 1 %.
Решение.
1. Вычисляем по рекомендациям п. 1.17* [51] массу и приведенный
размер бетонного массива":
3,16-0,021-2,3-53./20
т = ~"/о"з \з · = 18,7 т.
(ηΟ-Ι,ο) /1+1,53
С учетом коэффициента надежности γ/ = 1,2 масса массива равна 22,4 т.
Размер массива данной массы, приведенный к размеру куба, равен г =
= Vm/pm = 2,14 м.
2. Расшифруем значения символов, входящих в формулу (25) [51]:
— при r//i, «к = 2,14/5 = 0,43 из табл. 6 находим kr = 0,7 и по формуле
9.6 при Π = 44 %: kP - 1—44/100 = 0,56;
291
— далее принимаем по табл.7* ksp = 1,1; из рис.10* krun = 2,1.
по табл. 9 ka = 1,0.
3. Определяем по формуле (25) значение высоты наката волн на откос
hrun i?6 = 0,7-0,56-1,1-2,5· 1,0-5,0 = 5,4 м.
При распространении волн над дном с уклонами tg φ ^ 0,33
высоту наката волн на берег рекомендуется определять [56]:
для глубин d>2h\%—в зависимости от пологости волны
на глубокой воде λα/ha \%:
hrunx% = 1,35 tg <p {\dlhdl%)QA*hdX%\ 9.7
___ для глубин d<2h\% — в зависимости от пологости волны
λ/Ιΐι%, принимаемой на глубине d = Ш\%\
hrun 1% = 0,9 tg φ [Wi%)°'%%. 9.8
Формулы 9.7 и 9.8 были использованы Г. Ф. Красножоном
[56] при построении графиков рис. 10* [51]. С учетом
шероховатости и проницаемости наклонного дна, угла подхода фронта
волны к берегу, влияния скорости ветра и обеспеченности по
накату значение высоты наката волн, полученное по 9.7 и 9.8,
следует умножать на коэффициенты kr, kp, ksp, ki и &«,
принимаемые по табл. 6—9 [51].
При расчете высоты наката волн на берегоукрепительные
сооружения или высоты подъема взволнованной поверхности
воды у волноотбойных стен и других типов конструкций берего-
укреплений, в зависимости от места расположения их в
прибойной и приурезовой зонах, следует руководствоваться
рекомендациями пп. 3.3—3.6 '[51].
Возвышение верха волнозащитных стен z\, м, над расчетным
уровнем воды следует определять по формуле
Ζχ = Mlset + ric + a, 9.9
где khset — высота ветрового нагона, определяемая по (148)*
[51]; .а — запас высоты сооружения, принимается равным
0,1/1/о;;, но не менее 0,5 м; т)с — превышение гребня волны, м,
над расчетным уровнем в створе волнозащитной стены, рис. 27
[51], определяется в зависимости от места расположения
сооружения:
а) при расположении сооружения в створе последнего
обрушения прибойных волн, рис. 27, α [51], по формуле
ylc= -hbr (о,ОЗз4 + 0,75), 9.10(74; 75)
где hbr — высота разбивающихся (разрушающихся) воли, м;
б) при расположении сооружения в приурезовой зоне,
рис. 27,6 [51], по зависимости
Ъ = - К (θ,033 \ + 0,7б) (l - 0,3 Ц.)> 9.11 (76; 77)
292
где at — расстояние от створа последнего обрушения волн до
юоружения; ап — расстояние от створа последнего обрушения
золн до линии уреза (приурезовая зона);
в) при расположении сооружения на берегу за линией
уреза в пределах лаката волн, рис. 27, β [51]:
% = - К (θ,033 \ + 0,75) (l - jg-), 9.12 (78; 79)
где α/ — расстояние от линии уреза воды до сооружения; аг —
расстояние от линии уреза воды до границы наката на берег
разрушившихся волн (при отсутствии сооружения), равное
ar = Anmio6ctg<p, 9.13
''ш1°о — высота наката волн на берег, м, рассчитываемая по
и. 1.14* [51].
При расположении волнозащитной стены в прибойной зоне
возвышение вершины максимальной прибойной волны hc,sur, м,
над расчетным уровнем следует находить, согласно указаниям
п. 1.12 [51]:
К sur = - 0,5df — hsun 9.14
>де hsur — высота прибойной волны; df — глубина воды над
каменной постелью.
Превышение гребня волны г\с над расчетным уровнем воды
ν берегоукрепительных сооружений с криволинейным участком,
рис.29 [51], рекомендуется определять в зависимости от
расположения стены в различных створах приурезовой зоны по
формулам 9.10—9.14, как для вертикальной стены, п. 3.5 [51],
с ориентированием этой эпюры по нормали к криволинейной
поверхности.
Возвышение гребня волны у внешней η*?**, м, и у теневой
ι],„/, м, граней буны относительно расчетного уровня воды,
рис.30 [51], рекомендуется определять по формуле:
y\ex«int) = ^kji{\ +cos2a), 9.15(82; 83)
где Λα—коэффициент, принимаемый по табл.20 [51], в
зависимости от угла α подхода фронта волны к буне.
Пример 9.5
Определить возвышение верха волнозащитной стены,
расположенной в створе последнего обрушения прибойных волн.
Исходные данные: водоем имеет горизонтальное дно с глубиной
(1=10 м; скорость ветра Vw = 20 м/с; разгон 10 км; угол между
продольной осью водоема и направлением ветра <xw = 0; глубина воды перед
стенкой d = 10 м; высота волны в створе последнего обрушения кы = 3,0 м;
длина волны λ = 45 м.
293
Решение.
1. Определим по (148) * [51] величину
1Л-6 2.1-20,0-10000-1,0 ЛЛЛ
Lhset = 10 6 9,81-10.0 β °'09 м*
2. Отметку верха стены найдем по 9.9, предварительно определив
возвышение гребня волны по формуле 9.10 (74, 75):
а)
Άο = —. 3,0 (0,033-jq + 0,75) = — 2,7 м.
bsup
Расчетный уроВеньп\
δ)
л/h
15 20 JO ^ 0
Ζ sup I h
-0,05 0 0,1 0,3 0,5
0,7
10
w
\v
\ γ
\
k
§J
η
\\
l\W
\\\
ж
Λ....
\\
\\\
\\
\\\
/ \ \
SSi
\\
\
\\\
\\\
^j
tbsttf/л Ο,ϊ 0,£
о,г
ολ
0,6
nt,m
Рис. 9.2. Схема (а) и графики (б) для определения
коэффициента ПрОХОЖДеНИЯ ВОЛН, kt, т = f(bSuplh\ λ//Γ, Zsup/h)
через верх набросного сооружения неполного профиля
с ядром из несортированного камня.
При значении запаса высоты сооружения а = 0,5 м имеем Z\ = —(0,09+
+2,7+0,5) = —3,29 м; окончательно принимаем: z\ = —3,3 м.
Остановимся кратко на анализе перелива волн через гребень откосных
сооружений. Изучением взаимодействия волн с набросными сооружениями
неполного профиля занимались многие исследователи, в их числе Е. В. Кур-
лович, В. К. Завьялов и др. Экспериментально установлено, что высота
ht, m переливающейся волны зависит от возвышения (заглубления) верха
наброски zSUp/K над расчетным уровнем воды, от относительной ширины
294
.,)еГ)ия сооружения bsup/λ и от пологости исходных волн λ/Λ. Для расчета
высоты переливающейся волны Л*, т рекомендуется формула.
*Л » = */.**. 9.16
|де ktt т — коэффициент, определяемый по графикам на рис. 9.2 в
зависимое! и от безразмерных параметров bsup/λ; λ/Λ и zSUp/h.
Пример 9.6
Найти высоту волны ht> m, переливающейся через гребень набросного
сооружения, имеющего ширину гребня bsup = 10 м и отметку его
заглубления zsup = 2 м, при исходных параметрах волн Л = 5 м; λ — 100 м.
Решение.
1. Определим безразмерные параметры:
-1 = 129 = 20- *!ί!* =—=ov Zsap - 2
Л 5 ' I loo Л 5 "
2. Из графиков на рис. 9.2 имеем kt, m = 0,64.
3. По формуле 9.16 высота волны Л/, ,п — 0,64-5 = 3,2 м.
9.2. СКОРОСТИ ПРИ ВОЛНЕНИИ У ОТКОСНЫХ СООРУЖЕНИЙ.
ПРОНИЦАЕМОСТЬ НАБРОСНЫХ СООРУЖЕНИЙ
При назначении границ крепления откоса и разработке
мероприятий по обеспечению неразмываемости как собственно
крепления, так и грунтов основания требуется знать донные
скорости перед сооружением и скорости на поверхности
откосных сооружений. Дно перед сооружением будет устойчивым,
если максимальные донные скорости а&, max не превышают
допустимые скорости а&, adm для грунтов основания; в
противном случае перед сооружением следует предусматривать защиту
дна от размыва на полосе шириной (0,15. ..0,25)λ. Большее
значение ширины защищаемой полосы рекомендуется при более
слабых грунтах основания. Крепление дна от размыва
осуществляется отсыпкой гравелистого или щебеночного материала,
а также слоев каменной наброски с устройством обратного
фильтра. Средняя крупность фракций гравия, щебня или камня
ДОЛЖНа ПОДбираТЬСЯ ИЗ УСЛОВИЯ Ьь, adm > Vb, max.
Допускаемые значения неразмывающих донных скоростей
Vb,adm, м/с, для грунта крупностью фракций D ^ 100 мм
следует принимать по рис. 7 [51], а для грунта крупностью
фракций D > 100 мм — по формуле
*#,«!« = 1,52 ]/^ΕΞ. 9.17
Максимальные значения донных скоростей у основания
откосного сооружения при глубинах d > dcr рекомендуется
определять по зависимости
295
ν
nhksi
b, max
7sh~~T
9.18
где d — глубина воды перед сооружением; ksi — коэффициент,
принимаемый по табл. 9.7.
Таблица 9.7
Угол наклона
откоса а, град
14,5
26,5
45,0
67,5
Коэффициент Л j при пологости волны λ/Λ
i 10
0,8
0,82
0,93
1,0
15
0,83
0,91
1,07
1,12
20
0,88
1,08
1,2
1,2
30
1,04
1,34
1,5
1,5
40
1,08
1,46
1,5
1,5
Максимальные донные скорости в прибойной зоне при
глубине d ^ dcr допускается рассчитывать по формуле теории
одиночных волн:
v„
= kSurVg(hSur\%+d)>
9.19
где hSur\% — высота волны в прибойной зоне согласно [51];
ksur — коэффициент, принимаемый по табл. 9.8.
Таблица 9.8
h5Ur\%!d
"sur
0
0
0,1
! ο,ι
0.2
Ι 0,16
0,3
0,22
0,4
0,26
0,5
0,28
0,6
0.3
0,8
0,33
При назначении заглубления нижней границы крепления
используется выражение
d* = Ve+ 1,1<U 9.20
где VB — наинизший уровень воды; dxo—расчетная глубина
воды согласно 9.18 при vbtmzx = Vb,adm равна:
dm = τ- arcsh -^—~
*д:0
9.21
Jbt adm
Пример 9.7
Найти нижнюю границу крепления верхового откоса плотины,
укрепленного песчано-гравелистым грунтом средней крупностью D = 20 мм.
Исходные данные: пологость откоса ctgφ = 4; параметры волн
Л1%= 3 м, λ"= 30 м.
Решение.
1. Значение неразмывающей скорости для грунта D = 20 мм по
графику 7 [51] раВНО Vb, adm =1,1 М/С.
2. Определим по формуле 9.21 глубину dx0i на которой скорость Vb,max =
= Vb, adm, при этом ksi = 0,8 из табл. 9.7:
296
30 3,14.9,81.0,82.32
3. Отметка нижнего края крепления (при V6 = 0) согласно 9.20 равна:
= 0+1,1-7,2 = 7,9 м.
Рассмотрим вопросы, связанные с определением скоростей
iw набегании волн на непроницаемые и проницаемые поверх-
ости откосных сооружений. При взаимодействии волн с откос-
Рис. 9.3. Схема к определению характерных точек на откосе (а)
и эпюра максимальных скоростей при обрушении волны (б).
ными сооружениями, как установлено многими авторами [6, 7,
9, 46], волновые скорости различны в момент удара струи,
сбрасываемой с гребня волны, во время наката и ската
волнового заплеска, а также неодинаковы на сплошных и
проницаемых, крутых и пологих откосах [46].
Для прямолинейных непроницаемых откосов зоной
разрушения волны является участок от места обрушения волны до
встречи ее с откосом, рис. 9.3. Начало участка находится
297
в створе критической глубины, а заканчивается в створе удара
струи об откос [46]. Критическая глубина dcr при гладком
откосе определяется по формуле:
dcr = А = h (o,47 + 0,0231) !±||£*. 9.22 (29)
Струя движется от гребня под влиянием силы тяжести по
параболической траектории, рис. 9.3. Гребень волны
возвышается над спокойным уровнем на высоту
η, = β = д Го,95 - (0,84 ctg φ - 0,25) -γ| 9.23 (30)
Наибольшие скорости на откосе наблюдаются при
обрушении волны в зоне удара струи. Их значения вычисляются по
формуле
ν.> =
]/Ψ
+
ctg" <pg3 (dcr — dt)
9.24
где ζ — эмпирический· коэффициент, учитывающий уменьшение
скорости при растекании струи в слое воды, скатывающейся
с откоса, и принимаемый по табл. 9.9; vxc— горизонтальная
Таблица 9.9
Ctgcp
1,5
3
5
7
10
15
20
30
Л, м
1
0,995
0,97
0,94
0,9
0,85
0,77
0,68
0,51
2
0,99
0,94
0,87
0,8
0,7
0,53
0,36
0,02
3
0,981
0,91
0,81
0,7
0,55
0,3
0,04
—
4
0,978
0,88
0,74
0,6
0,4
0,06
—
—
5
0,97
0,85
0,68
0,5
0,25
—
—
—
проекция скорости движения струи в момент срыва ее с гребня
волны [46], рассчитываемая по зависимости ·
ν*
_ ghT
2λ Τ
4,7 4+3,4
Ctg φ
=.- - 0,85
9.25
λ vVi+ctg2<p
άι — заглубление точки 2, рис. 9.3, под расчетный уровень воды,
равное
,26
^ - - gWf V**e + 2* К + dcr) Ctg* φ +'^^ + d„. 9.:
Эпюра максимальных скоростей движения воды у
поверхности откоса в момент обрушения волны строится по значениям
скоростей в характерных точках, приведенных на схемах рис.
9.3. Для всех участков принимается линейный закон
изменения скорости.
298
В точке /, соответствующей расчетному уровню воды,
максимальная скорость определяется по формуле
krko-\0n 6/—=·
vx=9/rt„ У №. 9.27
В точке 2, в месте удара струи об откос, максимальная
скорость υ2 рассчитывается по 9.24 с использованием выражений
9.22 (29), 9.26 и данных табл. 9.9. В точке <?, соответствующей
максимальной высоте наката волн на откос, скорость
принимает нулевое значение. В точке 4, в створе критической
глубины максимальные скорости определяются интерполяцией
между ее значениями в точках 2 и 5, между которыми
принимается линейное распределение скоростей. В точке 5 при
расчетной глубине
db = lfR У'Ж 9.28
максимальные волновые скорости при d = d$ вычисляются по
9.18.
При глубине d> ds скорости определяются интерполяцией
между их значениями в точке 5 и на глубине d = 0,5λ, где
скорость равна нулю. Эпюра максимальных скоростей при
обрушении волны на гладком откосе показана на рис. 9.3, б.
Максимальные скорости при обрушении волны на
проницаемом откосе определяются умножением их значений,
рассчитанных для гладких откосов, на коэффициенты шероховатости kr
и проницаемости kP) принимаемые по рекомендациям
параграфа 9.1.
Пример 9.8
Определить волновые скорости в момент обрушения волны на
'огкосе. __
Исходные данные: расчетные элементы волн h\ = 3 м, λ = 45 м;
7=5,5 с, λ/Λ = 15; подход волн к сооружению фронтальный, а — 0; откос
(ctg φ = 2) укреплен плитами без омоноличивания швов; скорость ветра
Г„ = 20 м/с.
Решение.
1. Рассчитаем значения dcr\ vxc\ Цс и ζ по формулам 9.22 (29), 9.23 (30),
925 и табл. 9.9:
1 4-22
dcr = 3 (0,17 + 0,023-15) 22 = 3,06 м;
9,81» 3-5,5 45
Vjcc~ 2-45 + 5
I [4>7 i+3>4 (гт25- - °·85)] =5·55 *ι*
3
η, = 3-0,95 - (0,84-2 - 0,25) jg = 2,56 м; С = 0,96.
2. Найдем характерные точки 1.. .5 на откосе по 9.22 (29), 9.26 и 9.28:
— для точки / имеем d\ = 0;
— для точки 2 по 9.26:
299
5 552 5 55
d2 = 3(06 + 9^22 - 9^n5i У 5»55"J f 2·2'2·9»81 ί"2»56 + 3·06) = °.7? M;
— для точки 3 согласно п. 9.1:
dz=hranX% = 1,0.0,9·1,4·2,2.3,0 = 8,3 м;
— для точки 4 по 9.22 (29) имеем d4 = dcr = 3,06 м;
■для точки 5 по 9.28
А =
1,22
ctgo,82
■/3.45 = 8,1 м.
3. Выполним волновые скорости в характерных точках на откосе по!
9.27, 9.24 и 9.18:
„ _ 10-1.0,9/9,81 «,
2-3,14 + 2
/32-45=9,25 м/с;
/Г 243,06 — 0,77)2.9 81М
0,958 5,552 + —^ 55^, ; ' = 9,6 м/с;
*>з = 0;
vi =6,3 м/с.
*>* = '
0,75.3,14-3,0
^«•(ЧМ
= 0,84 м/с;
г/Л I 0,2 ОА 0.8 0.8 1.0 1.1
kttP 0,8 0,6 0А
/7 = 70%
300
Рис. 9.4. Графики для определения коэффициентов прохождения
волн kttP = f(r/h; d/λ; df/λ; Β/λ\ Π) сквозь однородное набросное
сооружение.
Вопросы проницаемости сооружений рассматриваются при
оценке волнового режима на ограждаемых акваториях. Для
набросных сооружений с ядром из несортированного камня, как
показывают исследования, проницаемостью можно пренебречь.
Однако для сооружений, образованных наброской
сортированного камня, бетонных массивов или фасонных блоков,
проницаемостью пренебрегать нельзя и ее необходимо оценивать
количественно.
Исследования набросных сооружений из камня,
обыкновенных бетонных блоков и фасонных массивов показали, что
проницаемость таких сооружений зависит от габаритов сооружения,
от размеров и формы защитных элементов, от параметров
исходного волнения и глубины воды перед сооружением и над
постелью. Для расчета высоты волны htiP, прошедшей сквозь
сооружение, разработана номограмма, которая представлена
на рис. 9.4.
Номограмма позволяет по известным исходным параметрам
волны (Л; λ), размерам сооружения (df/λ; d/λ; β/λ; r/h) и
пористости наброски Π определить коэффициент проницаемости
kt,p = httPlh, 9.29
где df — глубина воды над постелью; г — характерный размер
защитного элемента, приведенный к размеру ребра куба,
рассчитываемый через массу блока:
s - Vmhm. 9.30
Пример 9.9
Определить высоту волны Л/,р, прошедшей сквозь наброску из тет-
раподов на каменной постели. _
Исходные данные: расчетные элементы волн h2% = 5 м; λ = 80 м;
пологость откосов ctgq>=l; глубина воды перед сооружением d = 15 м;
глубина воды над постелью df = 6 м; ширина наброски на расчетном уровне
поды В = 14 м; перелив волн через гребень сооружения исключается;
гористость наброски Π из тетраподов согласно табл. 9.6 равна 50 %.
Решение.
1. Определим по формуле (33) * [51] массу тетрапода:"
3,16 -0,008 -2,3 -5з /80/5
т~~ /23 \з ^ —9,3 т.
С учетом коэффициента надежности yf = 1,15 принимаем т= 11 т.
2. Вычислим безразмерные параметры:
df 6 d 15 г 2/ТЩЗ 1,69
-f = — = 0,075; -=-= — = 0,19; — = }— J— = — = 0,34;
λ 80. λ 80 Л 5 5
В 14
Π = 50%; -γ =^ = 0,175.
301
на откос рассматривается как удар
3. Определим по номограмме рис. 9.4 коэффициент проницаемости с
учетом безразмерных параметров: kt,P — 0,21.
4. По формуле 9.29 вычислим высоту волны, прошедшей сквозь
наброску: ht,P = 0,21-5 = 1,05 м.
9.3. НАГРУЗКИ ОТ ВОЛН НА СООРУЖЕНИЯ ОТКОСНОГО
ПРОФИЛЯ И БЕРЕГОУКРЕПЛЕНИЯ
В инженерных расчетах откосных гидротехнических
сооружений на воздействия волн рассчитывается устойчивость
сооружений и прочность их элементов. При этом силовое воздействие
волн, проявляющийся
в начальной стадии
после обрушения, и
последующий навал
на откос; изучаются
также нагрузки при
скатывании с откоса
потока воды. При
построении эпюры
результирующей
нагрузки необходимо
учитывать давления как на
верхнюю, так и на
нижнюю поверхности
откосов.
Наиболее полные экспериментальные исследования
распределения волнового давления по поверхностям откосов в
широком диапазоне изменения параметров волн и при различных
заложениях откосбв выполнены И. Я. Поповым [6, 7]. Им же
разработан метод расчета, включенный в п. 1.15 [51]. Заметим
также, что в п. 1.16 [51] содержится указание, согласно
которому нагрузку от волн на откос, укрепленный плитами,
допускается определять методами, учитывающими нерегулярность
ветровых волн.
Рассмотрим в связи с этим рекомендации В. С. Шайтана,
опубликованные в трудах ВНИИВОДГЕО1. Применительно
к рис. 9.5 относительные отметки точек и значения ординат
эпюр давления в них могут быть определены при разрушении
нерегулярных волн на укрепленных плитами откосах с
заложением от 2 до 4 по данным табл. 9.10 и 9.11.
Рис. 9.5. Схема для построения эпюры
давления при воздействии на откос нерегулярных
волн.
1 Шайтан В. С. Стохастические закономерности волнового давления на)
откосы сооружений//Труды ин-та ВОДГЕО: Волновые воздействия на гид
ротехнические сооружения и берега. — М., 1987. — С. 4—14.
'302
Таблица 9.10
Высота волны
в шторме /i| %,
м
< 1,0
>1,5
Относительные отмсткп z\h\% точек приложения ординат эпюры
волнового давления
а
—0,9
—0,6
б
-0,6
-0,4
в | г | д
-0,3
-0,2
0.05
0,01
0,2
0,2
Таблица 9.11
Высота волны
в шторме /*!%,
м
<1,0
>1,5
Точки
приложения ординат
давления
на откос
а
б
в
г
д
а
б
в
г
д
Относительные ординаты волнового давления p\$gh\%
на откос при обеспеченности нагрузки (%) в шторме
0,5
0,34
0,55
2,5
0,4
0,24
0,37
0,63
2,0
0,46
0,26
1
0,31
0,5
2,3
0,36
0,2
0.33
0,56
1.8
0.4
0.22
2
0,28
0,47
2,1
0,32
0,16
0,3
0,5
1,62
0,36
0,18
5
0,25
0,42
1,86
0,28
0,13
0,27
0,44
1,4
0,31
0.15
10
0,22
0,38
1,66
0,25
0,22
0,24
0,4
1,24
0,28
0,13
30
0.17
0,29
1,22
0,19
0,09
0,18
1 0,32
ί 0,9
0,21
| 0,1
Сопоставление максимальных давлений в зонах ударов
гребней волн, разрушившихся на откосах, и суммарных
нагрузок от регулярных и нерегулярных волн обеспеченностью 1 %
в системе, рассчитанных по [51] и рекомендациям В. С.
Шайтана, представлено в табл. 9.12.
Таблица 9.12
h. „,
я1«»
1
4
ctg?
2
3
4
2
3
4
Максимальное
волновое давление,
кПл
СНнП jB. С. Шай-
[51]
33.4
29,9
27,5
78,5
72,5
66,8
тан
22.6
22,6
22.6
71,0
71,0
71,0
Суммарная нагрузка
на откос,
кН
СНиП
[51]
30,9
31,2
31,1
309,4
310,8
300,6
В. С.
Шайтан
23,0
32,4
42,4
216,9
336,8
400,1
Соотношение
давлений и нагрузок от
нерегулярной к
регулярной волне, %
максимальное
давление
68,0
75,8
82,4
90,5
98,0
104,5
суммарная
нагрузка
74,6
101,8
136,0
70,2
105.8
133,0.
Из анализа табл. 9.12 следует, что при ctgq> = 3 согласие
результатов можно считать удовлетворительным, хотя при
других заложениях откосов имеют место отдельные отклонения
(до 25. ..30%). Учитывая, что расчетные зависимости норм
получены на основе крупномасштабных опытов с волнами
высотой 1,5. ..2,0 м с помощью совершенной измерительной
аппаратуры, все положения п. 1.15 [51] без каких бы то ни было
изменений рекомендуются к использованию на практике.
Пример 9.10
Найти волновое давление и противодавление на откос пологостью
ctg<p = 4 (φ = 14°). _
Исходные данные: расчетные элементы волн hi % = 3 м; λ = 30 м;
подход волн к сооружению фронтальный, а = 0°; глубина воды перед
сооружением d — 8 м; скорость ветра Vw — 10 м/с.
Решение.
1. Определим ординаты zt точек приложения волновых давлений. В
соответствии с формулами (28) — (30) и рис. 11 СНиП [51] величины А и В,
а также ордината z2, м, точки приложения максимального расчетного
волнового давления равны:
/ 30\ 1 + 42
А = 3 ί 0,47 + 0,023 -И —ψ- = 2,2 м;
В = 3 ί 0,95 - (0,84-4 - 0,25) |J = 1,9 м;
г2 = 2,2 + 5г (1 - /2-4»+1) (2,2 + 1,9) = 1,5 м.
Согласно рекомендациям п, 1.14* [51] принимаем ординату:
*з = hrun l% = 1 -0,9.1,1.0,92-1 -3 = 2,7 м.
На участках крепления по откосу выше и ниже точки 2, рис. 11, опреде]
лнм расстояние /,· с использованием формул (31) [51]:
30-4
L= 4Г- =г=61,2 м;
ί/42—1
h = 0,0125-61,2 - 0,765 м; 12 = 0,0325-61,2 = 2м;
k = 0,0265-61,2 = 1,6 м; Ц = 0,0675-61,2 = 4,2 м.
2. Найдем волновое давление в характерных точках на откосе.
Максимальное расчетное волновое давление в точке 2 (точка максимального удара
волны) принимаем по (26), (27) с использованием табл. 10 и 11 [51]:
ks = 0,85 + 4,8~ + 4 (θ,028 - 1,15 ~) = 0,98;
pd=zp2=z 0,98-1 -1,8-9.81-3 = 52 кПа;
На расстояниях U и /3 получаем: /?i, з = 0,4-52 = 20,8 кПа; а на
расстояниях 12 и U получаем: ρ2ι 4 = 0,1-51 = 5,2 кПа; в точке Zz = hrUn\% имеем
р = 0.
3. Определим волновое противодавление, рс, кПа, на плиты крепления
откоса при длине ребра плиты bf = 6 м. Расчет противодавления сведен
в табл. 9.13.
304
Таблица 9.13
Расчетные величины
.С, Μ
к, Μ
jrflt
»//λ
Рсш по Рис· I2
[51]
ks по формуле (27)
[51]
fyno табл. 10 [51]
Л1?,, м
*Pc,rel> кПа
Нумерация плит
1
-10
30
-0,33
6
0,2
0
0,98
1,0
3
0
»
-4
30
—0,13
6
0,2
0,1
0,98
1,0
3
0,29
з
2
30
+0,07
6
0,2
0,18
0,98
1,0
3
0,53
4
8
30
+0,27
6
0,2
0,195
0,98
1,0
3
0,57
5
14
30
+0,67
6
0,2
0,16
0,98
1,0
3
0,47
6
20
30
+0,67
6
0,2
0,11
0,98
1.0
3
0,32
7
26
30
+0,87
6
0,2
0,083
0,98
1.0
3
0,24
Пример 9.11
Рассчитать ординаты эпюры давления 1 % -ной обеспеченности
в шторме при разрушении нерегулярных волн на откосе с пологостью
ctg<p = 4.
Исходные, данные: высота волны h\% =3м.
Решение.
1. Определим отметки точек приложения волнового давления, рис. 9.5.
По данным табл. 9.10 находим:
za « —0,6-3 « —1,8 м; Z6 = —0,4-3 = —1,2 м;
гв = —0,2-3 * —0,6 м; рг = 9,81-3 0,4 = 11,8 кПа:
Zd = 0,2-3 = 0,6 м.
2. Определим ординаты эпюры волнового давления с использованием
ланных табл. 9.11:
Ра = 9,81-3-0,33 « 9,7 кПа; рб = 9,81-3-0,56 = 16,5 кПа;
Ре = 9,81 -3-1,8.= 53 кПа; рг = 9,81 -3-0,4 - 11,8 кПа;
рд = 9,81-3-0,22 = 6,5 кПа.
Сравнивая максимальные волновые давления в точке удара на откосе,
рассчитанные для нерегулярного (рв = 53 кПа) и регулярного (р2 = 52 кПа)
волнения, легко .убедиться в том, что они практически совпадают.
Основные положения по расчету нагрузок от волн на
берегоукрепительные сооружения (пп. 3.1—3.6 [51]) разработаны по
материалам Черноморского отделения ЦНИИС, где в течение
нескольких десятилетий проводились натурные и
экспериментальные исследования нагрузок и воздействий волн на
подводные волноломы, вертикальные стены, расположенные в
прибойной и приурезовой зонах, буны и другие берегозащитные
сооружения.
Подводные волноломы. Лабораторные и натурные
исследования подводных волноломов показали, что при недостаточном
весе их подвижки всегда направлены в сторону моря. Это сви-
305
детельствует о том, что решающим является не лобовое
воздействие надвигающейся волны при подходе ее гребня, а
давление на береговую грань и подошву волнолома при подходе
ложбины волны. Схема волновых нагрузок, приведенная на
рис. 26 [51], соответствует моменту времени, когда подошва
волны расположена у передней наклонной грани волнолома, а
через гребень его происходит перелив воды в пространство за
волноломом. Наибольшее понижение поверхности воды перед
волноломом 22 и одновременно ее повышение z4 за ним
(относительно расчетного уровня воды) обуславливает расчетное
сочетание волновых давлений.
Если волнолом проектируется на отмелом берегу с
песчаными наносами при уклоне подводного склона в стометровой
полосе, считая от уреза моря (/^0,04), то максимальные
значения горизонтальной Рх и вертикальных Pz и Рс проекций
равнодействующей линейной нагрузки от волн на подводный
волнолом при ложбине волны следует определять по эпюрам
бокового и взвешивающего волнового давления, используя
рис. 26 и формулы (67) — (70) и (73) [51]. В случае, если
волноломы возводят на приглубых берегах с галечными наносами
при / > 0,04, нагрузки и давления должны рассчитываться по
(67), (68), (71) — (73). Заметим, что когда подводный
волнолом располагается в прибойной зоне, расчетную высоту волны
hsur следует принимать на глубине воды dcr перед волноломом
При расположении волнолома в приурезовой зоне, в пределах
которой поток от разрушенных волн периодически накатывается
на берег, величины hcr и dcr> и можно принимать в створе
последнего обрушения волн.
Пример 9.12
Волнолом из гравитационных массивов запроектирован на приглубом
участке берега со средним уклоном берегового склона в стометровой полосе
считая от уреза моря (t = 0,06). Подводный склон на участке волнолома
сложен размываемыми песчано-галечиыми грунтами. Глубина воды у
сооружения d = 4,5 м. Волнолом затоплен. Расстояние от расчетного уровня
воды; до гребня волнолома z\ = 0,5 м. Размеры сечения массива волнолома
даны на рис. 9.6. Класс капитальности волнолома — IV. Расчетная высота
волны h = 4,0 м имеет на участке возведения волнолома обеспеченное!!·
4 % в режиме и 5 % — в системе. Средняя длина волны λ — 75 м.
Расчетный уровень принят по среднегодовым уровням, обеспеченность его равна
50 о/о.
Требуется найти нагрузки от волн на грани волнолома.
Решение.
1. По табл. 16 [51] пои hfd = 4/4,5 = 0,89 находим: z2fd = 0.26, отк\ла
z2 = 0,26-4,5 « 1,17 м; zb\d = —0,32, откуда г5 = —0,32-4.5 = —1.44 м; krf-=
= 0,60.
Подставив найденные значения krd и z5, а также заданную величин
zx » 0.5 м в формулу (73) [51], получим: ζ* = 0,60 (0,5+1.44)— 0,5 = 0.66 ν
2. Определяем ординаты волнового давления, dhc. 9.6:
— на уровне верха сооружения при Z\ = 0,5 <: z2 — 1,17 м
рх * 1,03-9,81 (0,5+0,66) = 11,7 кПа — по формуле (67);
306
— на уровне подошвы волны при / = 0,06 !> 0,04
р2 = 1,03-9,81 (1,17+0,66) = 18,5 кПа —по (71);
— на уровне дна и по основанию волнолома
р3 = р2 = 18,5 кПа — по (72).
Море пущ Верег
0,75
Η
Рис. 9.6. Эпюры волнового давления на грани подводного волнолома
при уклоне дна ctg φ > 0,04
/ — боковое давление; 2 — взвешивающее давление; 3 — пригружающее
давление. Каменная постель под подошвой волнолома не показана (размеры, м;
ординаты эпюр, кПа; равнодействующие давления, кН).
3. Полное горизонтальное сдвигающее волновое давление на 1 м длины
волнолома равно площади эпюры, построенной по вычисленным ординатам,
рис. 9.6:
Р*= (d—Z2)P2+0,5(pi+pa)(z2—zi) = (4,5—1-17) 18,5+0,5(11,7+
+ 18,5) · (1,17—0,5) = 61,6+10,1 = 71,7 кН.
Взвешивающая нагрузка на подошву ED: Pz = 0,5-18,5-6,85 == 63,4 кН.
Нагрузка, пригружающая гребень волнолома: Рс = 0,5-0,75-11,7 = 4,4 кН.
Пример 9.13
Подводный волнолом из гравитационных массивов со скошенной
передней гранью и размерами, указанными на рис. 9.7, запроектирован на отме-
лом берегу (/ » 0,035) на глубине d — 3,5 м. Подводный склон на участке
расположения волнолома сложен песчаными отложениями. Волнолом
устанавливается на каменной постели. Глубина затопления гребня волнолома
Ζι = 0,6 м. Волнолом отнесен к гидротехническим сооружениям IV класса
капитальности, поэтому согласно приложению 1 [51] расчетная высота волны
для него къ% = 2,5 м принята с обеспеченностью 4 % в режиме и 5 % —
в системе. Средняя длина волны λ, соответствующая этой высоте, равна
35 м. Расчетный уровень моря для рассматриваемого волнолома вычислен
по средним годовым уровням с обеспеченностью 50%. Требуется определить
волновые нагрузки на грани волнолома.
307
Решение.
1. При hid = 2,5/3,5 = 0,71 находим по табл.16 [51]: —^ = 0,66;
z2/d = 0,22, откуда z2 =0,22tf = 0,22-3,5 = 0,77 м; zs/d = — 0,24, откуда z5 =
= —0,24-3,5 0,84 м.
По формуле (73) [51] ζ4 = 0,66(0,60+0,84)— 0,60 = 0,35 м.
2. Используя найденные и заданные величины,, определяем волновое
давление:
— на уровне подошвы волны при i = 0,035 <; 0,04
(ОС ОС Л СЛ\
0,0153^ + а23 ' Зб' )"~ i'03'9'81 (— °»35> =
= 12,1 кПа — ио формуле (69);
Море
Берег
Рис. 9.7. Эпюры волнового давления на грани подводного волнолома при
уклоне дна ctg φ < 0,04 (Размеры, м; ординаты эпюр, кПа;
равнодействующие давления, кН).
— на уровне гребня волнолома при Ζ\ = 0,60 < ζ2 = 0,77 м
pi = 1,03-9,81 (0,6+0,35) = 9,6 кПа —по (67);
— на уровне подошвы сооружения при λ/Λ = 35/2,5 = 14 и
соответственно по табл. (17) kw = 0,79.
р3 = 0,79· 12,1 =9,6 кПа.
3. Полное горизонтальное давление на 1 м длины подводного
волнолома равно площади эпюры, построенной по вычисленным ординатам
(рис. 9.7):
Рх = 0,5· (ρι+ρ2) · (*2+Ζι)+0,5· (р2+Рз) · (d—z2) =
= 0,5· (9,6+12,1) -0,17+0,5- (12,1+9,6) -2,73 = 31,5 кН.
308
Взвешивающая волновая нагрузка на подошву ED:
рг = 0,5-рз-5,0 = 0,5-9,6-5,0 = 24 кН/м.
Нагрузка, пригружающая гребень волнолома, равна
Ρ с = 0,5 -рг 0,6 = 0,5-9,6-0,6 = 2,9 кН/м.
Волнозащитные стены. Берегозащитные стены часто
подвергаются ударам разрушающихся волн. Разрушение волн
может происходить непосредственно на стене или на некотором
удалении от нее. В последнем случае на стену воздействует
поток, образовавшийся от разрушенной волны.
Общее давление, возникающее при ударе обрушающейся
волны о вертикальную стену, состоит из гидростатического и
гидродинамического давлений. Гидродинамическая часть
давления изменяется в зависимости от угла подхода волны к
вертикальной грани стены. При фронтальном расположении грани
относительно луча волны гидродинамическое давление
достигает максимального значения и составляет приблизительно
половину полной величины давления. Формулы (74), (76) и
(78), приведенные в пункте 3.3 [51], предназначены для
вычисления интенсивности давления при ударе о вертикальную грань
стены обрушающихся волн или прибойного потока,
подходящих к стене фронтально.
Очевидно, что в зоне прибойного потока величина давления
будет тем больше, чем больше скорость потока. Эта скорость
постепенно убывает от максимума в точке последнего
обрушения волны до нулевого значения на верхней границе наката
волны. На основании исследований принято, что интенсивность
давления волн на вертикальную грань стены также убывает —
от своего максимума ри в точке последнего обрушения волны до
нуля на верхней границе наката.
Принято также, что убывание интенсивности волнового
давления в зоне прибойного потока происходит по линейному
закону. Внутри зоны прибойного потока выделены два участка,
разграниченных линией уреза. На первом участке изменение
величины давления описывается формулой (76) [51], в которой
значение множителя (1—0,Зад/аЛ) изменяется от единицы
в точке последнего обрушения волны до 0,7 на урезе моря. На
втором участке, между урезом моря и верхней границей наката
волн, интенсивность давления соответственно уменьшается от
0,7ри до нуля.
Максимальные ординаты взвешивающего давления,
приложенного к подошве стены, равны, как показано на рис. 27 [51],
боковому давлению у внешнего ребра сооружения; дальше
взвешивающее давление уменьшается линейно до нулевого
значения у внутреннего ребра.
Максимальные значения горизонтальной Рх и вертикальной
Ρζ проекций равнодействующей линейной нагрузки от
разбивающихся (разрушающихся) волн на вертикальную волнозащитную
309
стену (при отсутствии·засыпки грунта со стороны берега)
необходимо принимать по эпюрам бокового и взвешивающего
волнового давлений, рис. 27 [51]. При этом значения ρ и цс должны
определяться в зависимости от месторасположения сооружения:
а) при расположении сооружения в створе последнего
обрушения прибойных волн, рис. 27, а, — по формуле (74);
б) при расположении сооружения в приурезовой зоне,
рис. 27, б, — по (76);
в) при расположении сооружения на берегу за линией уреза
в пределах наката волн, рис. 27, в,— по (78) и (80).
Если ордината верха сооружения Ζ\ ^ —0,ЗА, то величины
волнового давления, рассчитанные по (74), (76) и (78),
необходимо умножить на коэффициент kzat принимаемый по табл. 19
[51].
Нагрузки от прибойных волн на волнозащитные стены при
расположении их в прибойной зоне следует определять
согласно требованиям п. 1.12 [51].
Максимальные значения горизонтальной Рх и вертикальной
Pz проекций равнодействующей линейной нагрузки от
разрушившихся волн на вертикальную волнозащитную стену (с
засыпкой грунта со стороны берега) при откате волны необходимо
принимать по эпюрам бокового и взвешивающего волнового
давления, рис. 28 [51], при этом значение рг должно
определяться по формуле (81). В данном случае термин «нагрузки
разрушившихся волн» применен условно. Здесь имеется в виду
давление воды, попавшей в застенную засыпку в результате
воздействия волн расчетной высоты.
По (81) максимальное давление на 1 м2 задней грани стены
на уровне, определяемом величиной Azr> принято
эквивалентным гидростатическому давлению слоя воды толщиной (Δ2Γ—
—OJShbr). Понижение поверхности воды перед стеной
принимается равным нулю при наличии пляжа. Этим учитывается
разгружающее противодавление грунтовой воды, имеющейся
в толще пляжа перед стеной.
Волновое давление ρ на криволинейный участок стены
необходимо принимать по эпюре волнового давления на
вертикальную стену согласно п. 3.5 с ориентированием этой эпюры по
нормали к криволинейной поверхности, рис. 29, [51].
Пример 9.14
Найти величины волновых давлений на переднюю грань и подошву
берегозащитной стены, запроектированной на морском берегу, сложенном
десчано-галечными наносами.
Исходные данные: стена расположена по линии последнего
обрушения расчетной волны на глубине d = 5,0 м; IV класс капитальности;
высота волны h = 3,9 м при обеспеченности 5 % в системе и 4 % — в
режиме; длина волны λ = 52 м. Расчетный уровень моря получен по средним
годовым значениям; его обеспеченность 50 %. Исходя из недопустимости
перелива воды через гребень волноотбойной стены, его отметка принята
равной 7,0 м. Подошва стены заложена на глубине di = 8,0 м.
310
Решение.
1. По формуле (74) [51] волновое давление:
ра = 1,039,81 -3,9 f 0,033 у +.0,7б] = 43,1 кПа.
2. Возвышение гребня определено по (75):
33.1
"Чс —— 1,03-9,81 -~4>°> м·
На рис. 27, α [51] показаны схемы эпюр давлений на переднюю вертн-.
кальную грань и подошву стены.
Пример 9.15
Определить давление воды на заднюю грань берегозащитной стены;
ее гребень расположен на высоте 3,5 м относительно расчетного уровня моря.
Исходные условия для проектируемой стены аналогичны заданным в примере
9.14.
Решение.
1. Заданная отметка гребня стены меньше определенной в примере 9.14
величины у\с = 4,3 м; следовательно, возможен перелив воды.
Заданная ширина пляжа перед стеной, равная 4 м, меньше З/ι = 3-3,9 =
= 11,7 м, поэтому, согласно п. 3.4 [51], принимаем ΔζΓ = 0,2bhbr = 1,0 м.
2. По формуле (81) находим:
рг = 9,81-1,03-(0,75-3,9+1,0) = 39,7 кПа.
В соответствии с требованиями п. 3.4 давление рг приложено к задней
грани стены на отметке bzr = 1,0 м ниже расчетного уровня моря; ниже
этой отметки оно принимается постоянным и равным 39,7 кПа, а выше —
уменьшается до нулевого значения на отметке, соответствующей 0,75ft&r =
= 0,75-3,9 с^З м. Схема эпюр давления представлена на рис. 28 [51].
Пример 9.16
Определить равнодействующую волнового давления на
криволинейную грань стены, рис. 29 [51], с целью установления ее устойчивости
в условиях строительства при отсутствии засыпки за стеной. Исходные
данные приняты по примеру 9.14.
Решение.
Стена расположена примерно на середине расстояния, рис. 27, б, ah —
= 25 м между урезом моря и линией последнего обрушения расчетной волны
h = 3,9 м. Волновое давление ρ на криволинейный участок стены принимаем
по эпюре волнового давления на вертикальную стену (рис. 9.8, эпюра 1)
согласно требованиям п. 3.3 [51] с ориентированием ординат этой эпюры по
нормали к отрезкам, соединяющим точки излома поверхности волноотбойной
грани стены.
1. Криволинейная поверхность стены разбита на 10 участков, в пределах
каждого из которых кривая заменена прямой. Затем определены углы
наклона прямых отрезков относительно вертикали.
Углы наклона участков составляют:
0...1
1...2
2...3
3...4
4...5
0°
19°
51°
63°
49°
5...6
6...7
7...8
8...9
9...10
33,5'
13°
10,5'
34°
. 0°
311
2. Принимая ри по линии последнего обрушения равным 43,1 кПа (см.. ι
пример 9.14), по формуле (76) (51] находим интенсивность давления в створе]
расположения стены при ан = 12,5 м:
Pl = /l — 0,3 §Щ 43,1 = 36,6 кПа.
3. Превышение гребня волны над расчетным уровнем:
36,6
ТГ)С = "
1,03-9,81
= — 3,6 м.
Море
Берег
ЮоЯ-М—,
^ЩЩ\Щ№^
Рис. 9.8. Эпюра волнового давления на стену с криволинейной гранью
/ — эпюра давлений на стену с вертикальной гранью; 2 — эпюра давления на
криволинейную грань стены по п. 3.5 [51]; 3 — эпюра взвешивающего давления
на подошву стены.
4. Зная размеры отрезков стены по вертикали, вычисляем ординаты
эпюры давления и прикладываем их по нормали к серединам участков
криволинейной поверхности.
5. Горизонтальная составляющая общего давления, приложенная к
любому отрезку, выделенному на криволинейном профиле стены, равна
произведению интенсивности нормального давления на вертикальную проекцию
отрезка. Вычисленные таким образом горизонтальные составляющие РХ1
на 1 м длины стены имеют следующие значения (кН):
рдг.(0...1) = 36»6-0.5 = 18,3;
Рх (2_з) = 33,7-0,55 = 18,5;
Рх% (1_2) = 36,6-0,65 = 23,8; Рх (3 4) = 27,70,60 = 16,6;
312
Рл.>(4...5)= 20,2-0,85 = 17,2;
χ, (5...6)
= 12,3-15,65 = 8,0;
Χ, (7...8) ;
χ, (8...9)
= 0;
0;
Ρλγ,(6...7) = 4»4·0,85 = 3,7;
Ρχ, (9...10) — °>
Полная боковая (сдвигающая) волновая нагрузка на криволинейную
|оверхность стены:
ю
ρχ = ΣΡχ,ι=1^ κΗ·
6. Вертикальные составляющие давления Рг, ,· на 1 м длины стены равны:
Ζ, (0...1)
= 0;
г , (5...G)
= 8,0-0,662 = 5,3;
РжЛХлшЛ) =23,8.0,344 = 8,2;
Рг(б7)=: 3,0-0,231 =0,85;
ζ, (2...3)
= 18,5-1,235 = 22,8
Ρζ (3...4) = 16,6.2,050 = 34,0;
Рг(45) = 17,2-1,150 =19.7;
z, (7...S) :
г, (S...9)
^0;
= 0;
^г·, (9...10)— °*
Полная вертикальная волновая нагрузка на криволинейную поверхность
стен, направленная вниз:
Ю
ρζ=*Σρ2 / = 90,8 кН.
о
Эпюра взвешивающего давления на подошву стены, условно принятая
треугольной, рис. 9.8, с максимальной ординатой у внешнего ребра подошвы,
равной Р(о.. л) = 36,6 кПа. Таким образом, здесь сохраняется принцип
построения эпюры взвешивающего давления, принятый для стен с
вертикальными гранями.
Гравитационные буны. При взаимодействии волн с буной
все ее грани испытывают волновые нагрузки. Лабораторные и
натурные исследования показали, что в наиболее невыгодных
условиях воздействия волн находятся головные массивы бун
и промежуточные массивы, примыкающие непосредственно
к головным.
Для расчета устойчивости массивов определяется
критическая комбинация из следующих волновых нагрузок: нагрузка,
действующая на внешнюю боковую грань; одновременно
возникающее давление на противоположной (теневой) боковой
грани; взвешивающее давление на подошву буны.
Применительно к головному массиву, кроме указанной комбинации,
определяется вертикальная составляющая волновой нагрузки,
действующей на наклонную торцевую грань.
313
Максимальные значения горизонтальных Px,eXi, Рх,ш и
вертикальной Р-г проекций равнодействующей линейной нагрузки
от волн на элемент буны необходимо принимать по эпюрам
бокового и взвешивающего волнового давления, рис. 30; при
этом значения волнового давления на внешнюю Pext и теневую
Рш грани буны должны определяться по формуле (82), а
соответствующие возвышения гребня волны r\ext и г\ш — по
рекомендациям п. 3.6 ι[51].
Используемая в расчетах зависимость (82) представляет
собой произведение: l95pgA (давление разбитой волны при
фронтальном ударе о вертикальную стену); 0,5(l+cos2a) —
выражение, характеризующее косой подход волны, и \и
(коэффициент, учитывающий отставание по фазе и неравномерность
распределения давления на гранях буны). В формуле (82),
применяющейся для расчета бун гравитационного типа,
шероховатость граней не учитывается.
Волновое давление действует одновременно на обе
продольные грани буны; однако теневая грань оказывается при этом
менее нагруженной при косом подходе волны, что
обуславливает сдвигающую нагрузку Pext — Рш, перпендикулярную к оси
буны. Различия в давлениях на внешнюю и теневую грани
характеризуются эмпирическим коэффициентом £;, причем
одновременно учитываются неравномерность распределения
давления по длине буны и отставание по фазе давления на теневую
грань по сравнению с внешней. Взвешивающее давление у ребер
подошвы буны принимается равным соответствующим
значениям давления у дна по боковым граням. При
трапецеидальном поперечном сечении бун влияние наклона граней на
величину давления определяется введением в (82) соответствующей
поправки:
Ρ - ^k#gh(l + cos2 φ,cos2 β,), 9.31
здесь β& — угол наклона боковой грани к вертикали.
Следует подчеркнуть, что на конечный результат расчета
устойчивости головного массива буны большое влияние
оказывает учет наклона скошенной передней (торцевой) грани
массива.
При определении волновых нагрузок на головной массив
буны необходимо учитывать расположение массива
относительно линии последнего обрушения расчетной волны. В том
случае, когда головной массив выходит за линию обрушения
в прибойную зону с глубинами d > dcr необходимо иметь в виду,
что расчетная высота волны здесь может быть больше высоты
А, определенной по.линии последнего обрушения. Приближенно
для этого случая расчетная высота волны h может быть
принята равной глубине d по кромке передней грани массива, но
не больше высоты прибойной волны требуемой обеспеченности
(hsur) У ЭТОЙ КрОМКИ.
314
Пример 9.17
Определить волновые нагрузки на головной массив буны,
проектируемой на приглубом участке берега, сложенного песчано-галечнымн отложе-
Ипями. Согласно обязательному приложению 1 [51] расчетные обеспеченности
высот волн приняты равными 5 % в системе и 4 % — в режиме. Таким
образом, расчетная высота волны на участке_ расположения головного массива
h = 4,4 м и соответствующая ей длина λ = 75 м. Угол между продольной
осью буны и фронтом
расчетной волны α =
= 70°, рис. 30. Отметка
расчетного уровня
моря—0,25м имеет
обеспеченность 50% по
среднегодовым уровням.
Вид и размеры
головного массива
показаны на рис. 9.9.
Расчетная длина массива
I = 5,25 м. Наклон
боковых ' граней
относительно вертикали
составляет βΒ= 7°. Так как
cos 7° близок к единице,
то в данном расчете
наклон боковых граней не
учитываем.
Решение
1. Волновое
давление на 1 м2 боковой
внешней грани
головного массива буны
определяем по формуле (82)
с использованием табл.
20 [51]. После подстановки значений /г = 4,4 м, /га = 0,7 при //λ = 5,25/75 =
= 0,07; cos2 а = cos2 70° = 0,117, находим:
pext = 'j- °*7' 103-9,81.4,4(1 +.0,117) = 26,1 кПа.
Площади боковых граней головного массива в рассматриваемом случае
одинаковы и равны:
А = 0,5(0,5+3,5)5,25 = 10,5 м2.
Полная волновая нагрузка на боковую внешнюю грань головного
массива.
: 274 кН.
Рис. 9.9.
Каменная
Общий вид головного массива буны.
постель под подошвой буны не
показана (размеры, м).
х, ext
•Pext'A = 26.110,5:
2. Давление волн на боковую теневую грань головного массива
определяем также по (82) при //λ = 0,07 и 6ctga= 1,23 м; соответственно этому
*а=0,25:
3
Pint = J·0,25-1,03-9,81 -4,4.(1 + 0,117) = 9,3 кПа.
Полная волновая нагрузка на боковую теневую грань головного массива
Рх§ ш=Рш.А = 9,3-10.5 = 97.7 кН.
3. Полная сдвигающая нагрузка на головной массив буны
Рх — Ρχ, ext ΡX, int — 274 -
-97,7 = 176,3 кН.
315
4. Волновое давление на наклонную торцевую грань головного массива
определяем по (82); при этом угол α заменяем углом наклона торцевой
грани к вертикали βΤΟρ = 60° и по экспериментальным данным принимаем
ka t= 0,8, учитывая обтекание торца буны при ударе волны и затопленное
положение гребня головного массива. Подставляя в 9.31 значения р, g, //.
ka и cos2 βτορ находим:
^ = -^-.0,8.1,03-9,81-4,4(1 + 0,246) = 33,2 кПа.
Проекция площади торцевой грани на вертикальную плоскость:
/2,5 + 3,37\ п
, = ( 2 1-3,0 = 8,8 м2.
Вертикальная составляющая волновой нагрузки на наклонную торцевую
грань, направленная вниз, равна
РьАь tgProp = 33,2-8,8-1,75 = 511,3 кН.
5. При определении взвешивающего волнового давления на подошву
массива ординаты эпюры в угловых точках подошвы принимаются равными
соответствующим ординатам боковой нагрузки. Среднее взвешивающее
волновое давление на 1 м2 по подошве вычисляем как среднее
арифметическое из значений в угловых точках:
1РЪ + Pext + Pint 2-33,2 + 26,1 + 9,3
Pz — 4 ~~ 4 ~~ ' киа.
Площадь подошвы головного массива:
Af = 3,37-5,25= 17,7 м2.
Полная взвешивающая нагрузка, приложенная к подошве головного
массива буны:
рг = pzAf = 25,4-17,7 = 449,6 кН.
В рассматриваемом примере получилось, что суммарная вертикальная
составляющая волновой нагрузки на головной' массив буны пригружает его,
причем пригружающая сила равна:
Рь Аъ tg βτορ — Ρ ζ = 511,3—449,6 = 61,7 кН.
6. Расчет волновых нагрузок на блок буны, состоящей из нескольких
массивов, непосредственно примыкающих к головному и объединенных омоно-
личивающей плитой, выполняется по схеме, принятой в примере 9.17.
В данном случае, наряду с волновыми нагрузками, нужно знать моменты
сил, обусловленные и определяющие напряжения в материале омоноличи-
вающей плиты как несущего элемента в конструкции буны. Данный расчет
выполняется с целью выявления места возможного разрушения плиты.
При решении вопроса о размерах креплений откосов
судоходных каналов необходимо знать параметры судовых волн
и вызываемые ими нагрузки на откосы.
Максимальное значение линейной нагрузки от судовой волны
на крепления берегов каналов Ρ должно приниматься по
эпюрам волнового давления, рис. 31 [51], при этом значенияр
необходимо определять в зависимости от ординаты ζ для
следующих случаев:
а) при накате волны на откос, укрепленный плитами,
рис. 31 а;
316
б) при откате волны с откоса, укрепленного плитами,
рис. 31 б;
в) при ложбине волны у вертикальной стены, рис. 31 в.
Для них расчетными являются зависимости (87) — (96) [51].
Пример 9.18
Найти нагрузки от судовых волн на крепление откоса в виде
бетонных плит применительно к исходным данным примера 9.3, в котором
получено ka = 0,2; Vadm = 2,21 м/с; hSh = 0,16 м и hr sh = 0,23* м.
Решение.
Определяем ординаты эпюр волнового давления на крепление откоса
канала, вычисляя значения г и ρ по формулам (87) — (92) [51]:
а) при накате волн на откос
Zi = —0,23 м и рх = 0;
г2 = 0 и р2 = 1,34· 1,0-9,81-0,23 = 3 кПа;
^з= 1,50,23 7^1 + 1,52=0,62 м и ръ = 0,5-1,0-9,81 0,23 = 1,13 кПа;
б) при откате волны с откоса
г\ = 0,25-0,23 = 0,057 м и р, = 0;
г2 = 0,5-0,23 = 0,115 м и р2 = —1,0-9,81 (0,5-0,23—0,057) - — 0,57 кПа;
гъ = 2 м и р3 = —0,57 кПа.
Схемы эпюр волнового давления на откос показаны на рис. 31а, б [51].
9.4. РАСЧЕТ КРЕПЛЕНИЙ СООРУЖЕНИЙ ОТКОСНОГО ПРОФИЛЯ
Оградительные сооружения откосного профиля в виде
|наброски из камня, бетонных блоков или фасонных массивов
(получили большое распространение на практике при малых и
умеренных глубинах моря. С выходом сооружений на большие
(глубины целесообразность таких конструкций не всегда
оправдывается, даже при условии использования для крепления
откосов специальных бетонных блоков разной формы и
крупности.
Научные положения в обоснование устойчивости элементов
креплений откосных сооружений из несортированной каменной
наброски (пп. 1.18 и 1.19* [51] разработаны И. Я. Поповым.
Были использованы крупномасштабные,эксперименты,
результаты которых опубликованы, в частности, в трудах [6, 47] и
в ведомственных нормативах.
Обратим внимание на то, что на рис. 13 [51] верхняя и
нижняя кривые являются интегральными границами
распределения крупности фракций в горной массе, а следовательно,
только зерновой состав в заштрихованной зоне следует считать
пригодным для рассматриваемых сооружений.
При расчете допустимого содержания камня, крупность
которого находится в диапазоне от Dba, n до Dba,i2, применяется
следующий порядок вычислений:
— определяется расчетная масса камня и его крупность Dba',
317
— вычисляются по формуле (35) [51] значения
коэффициентов kgr, ί зернового состава для принятых крупностей камня
Dba, i\ И Dba, ίϊ,
— по верхней и нижней границам зоны допустимого
зернового состава, рис. 13, с учетом коэффициентов kgr\ и' кигч
принимаются по два их значения (максимальное и минимальное);
— определяются разности между максимальными и
минимальными значениями допустимого зернового состава.
Изложенный порядок вычисления допустимого содержания
камня, крупность которого находится в диапазоне от Dba, n до
Dba, i2, распространяется также и на другие диапазоны
крупностей, например/от Dba,K до Dba, и и т. д.
Часто в практике строительства грунтовых сооружений
(плотин, дамб обвалования водохранилищ ГЭС и бассейнов ГАЭС,
берегоукрепительных сооружений) экономически более
целесообразным является увеличение пологости откосов, так как
при этом используются мелкие фракции каменного материала,
попутно получаемого из карьеров или из полезных выемок,
разрабатываемых взрывным способом. В частности, при
строительстве грунтовых дамб, входящих в комплекс защиты
Ленинграда от наводнений, применялся камень крупностью 20...
...25см при пологости откосов ctgcp = 6...8. При
использовании песчано-гравийных смесей для укрепления откосов на
промежуточных этапах строительства устойчивость их
обеспечивается при пологостях ctg<p= 12. ..15. Поэтому в целях более
полного и рационального использования местных строительных
материалов полезно расширить диапазон расчетных
ограничений, что и рекомендовано в п. 1.19* [51].
Минимальное содержание фракций диаметров Dba,
соответствующее расчетной массе камня в несортированной разнозерни-
стой наброске, рекомендуется принимать согласно табл. 12, б"г*
[51] в зависимости от коэффициента разнозернистости D6o/Oio.
Пример 9.19
Определить вес камня и состав разнозернистого карьерного мак-
риала (горной массы) в основном креплении плотины. _
Исходные данные: расчетные элементы волн 1ц% =3 м; λ = 30 м;
пологость откоса ctg φ = 4; плотность материала камня рт = 2,6 τ/м3;
плотность воды ρ = 1,0 т/м3. Расчет выполним для участка основного крепления
от глубины ζ = OJhi % до гребня плотины.
Решение.
1. Определим по формуле (33)"* [51] массу камня в состоянии
предельного равновесия:
3,16-0.025.2,6.33 УЩ
т = —^6 \з = 0,38 т.
Вводя коэффициент надежности yf = 1,2, получаем т = 0,38-1,2 = 0,46 т.
318
2. Определим диаметр камня, приведенный к диаметру дтра:
Dba = 1,24 Ymfr = 1,24 "j/^ = 0,7 м.
3. Процентное содержание фракций в несортированной разнозернистой
смеси карьерного каменного материала определим по графику рис. 13 [51].
Результаты расчетов сведены в табл. 9.14.
Таблица 9.14
Диаметр
фракций,
см
> 70
50... 70
25... 50
10... 25
5...10
<5
Коэффициент
kgr,i
> 1,0
0,71 ....1,0
0,36.... 0,71
0,14.... 0,36
0,07.... 0,14
1 <о,об
Граничные значения, %,
по графикам
верхнему
92... 100
58... 92
28... 58
15...28
И...15
И
нижнему
27 ...100
20 ... 27
11 ...20
5...И
3...5
3
Допустимое содержание,
%
от
8
34
30
13
4
11
до
73
7
9
б
2
3
4. Для примера к табл. 9.14 определим допустимое процентное
содержание камня, например, крупностью 25.. .50 см. Диапазон изменения
коэффициентов kgr, ι определим по формуле (35) [51]:
ν = τδ· · -τό^0·36· · ·0'71·
Проведем вертикали через точки kgr = 0,36 и kgr = 0,71 до пересечения
их с верхней кривой и на оси ординат отсчитываем соответственно 28 и 58%.
Разность полученных значений даст максимальную величину допустимого
содержания фракций камня 25.. .50 см, а именно 58—28 = 30%.
Аналогичным образом определяем процентное содержание фракций
с крупностью 25.. .50 см по нижней кривой и соответствующие отсчеты на
вертикальной оси графика— 11 и 20 %. Разность их даст минимальную
величину допустимого содержания принятой фракции, равную 20—11 =9%.
Сооружения с применением сортировочного камня могут
оказаться более экономичными по сравнению с такой же
конструкцией из несортированного камня, особенно при возведении их
на больших глубинах и при интенсивном волнении. Однако,
как правило, при строительстве откосных набросных
сооружений возможности получения крупных глыб естественного камня
весьма ограничены, а порой и полностью отсутствуют; в таких
случаях рекомендуется применять искусственные бетонные или
железобетонные массивы или фасонные блоки.
Благодаря высокой сцепляемости блоков между собой и
с подстилающим их слоем камня, большой шероховатости и
проницаемости наброски появилась возможность снижения
массы блоков и повышения волногасящих качеств. В целом
применение фасонных массивов обеспечивает улучшение
экономических показателей набросных сооружений в связи с
уменьшением объемов наброски, использованием кранов меньшей
мощности и др. Указанные ^преимущества фасонных блоков
319
(массивов) явились причиной широкого применения их при
строительстве оградительных и берегозащитных сооружений.
Из анализа выполненных в разных странах исследований
фасонных блоков на устойчивость от воздействия волн
установлено, что наиболее оптимальными являются тетраподы, гекса-
леги, трибары, долосы и другие, рис. 9.10.
Известен ряд модификаций фасонных массивов, которые
успешно применяются на практике. В большинстве случаев
стремятся ядро откосного сооружения выполнять из каменной
наброски. Однако при строительстве сооружений в районах, где
Рис. 9.10. Конструктивные формы фасонных блоков (массивов)
/ — тетрапод; 2 — гексалег; 3 — гексабит; 4 — пентапод; 5 — долос; 6 —
массивы с прорезями.
отсутствует местный материал (камень для ядра), весь
профиль откосных сооружений отсыпается из обыкновенных или
фасонных массивов, но при этом должен учитываться эффект
проницаемости наброски.
Устойчивость камня и фасонных блоков при воздействии
волн исследовали многие отечественные и зарубежные ученые.
Наиболее достоверные и надежные результаты опубликованы
в работах [6, 7, &, 39, 47], которые были использованы при
составлении п. 1.16, включающего формулы (33) * и (34),
а также табл. 12* [51]. В качестве дополнительной
информации к табл. 12* можно рекомендовать величины
коэффициента kfr согласно табл. 9.15.
Массу элементов крепления откосов сооружений от действия
косоподходящих волн рекомендуется определять умножением
320
Таблица 9.15
Тип элементов крепления
Обыкновенные бетонные массивы
Массивы с прорезями
Тетраподы
Гексалеги
Гексабиты и пентаподы
Долосы
Коэффициент Λ.
при наброске
0,021
0,016
0,008
0,007
0,005
0.004
при укладке
0,006
0,004
0,004
0,003
массы элемента, рассчитанной от воздействия волн
фронтального подхода, на коэффициент ka, вычисляемый по
эмпирической формуле
ka= 0,4 + 0,6 cos α, 9.32
где а — угол между лучом исходных волн и нормалью к
сооружению.
Обратим также внимание и на то, что, если корневые участки
набросных сооружений расположены в зоне действия разбитых
и прибойных волн, массу элементов наброски, рассчитанную на
уровне расчетного горизонта воды по формуле (33) *,
рекомендуется увеличивать на 15%; элементы наброски с
максимальной расчетной массой целесообразно располагать по всей
длине откоса от гребня сооружения до его основания. При
наличии у набросного сооружения монолитной бетонной
надстройки с вертикальным парапетом расчетную массу элементов
крепления в этом случае следует увеличивать на 15%, если
отметка основания надстройки расположена выше горизонта
воды, и на 30% —при ее расположении ниже горизонта воды.
При проектировании защитного крепления сооружений
с бермой массу отдельного элемента mbr следует определять
умножением массы т или mz, полученной в соответствии с
формулами (33)* и (34) [51], на коэффициент kbr, m:
mbr = mkbr, m\ 9.33
ты, ζ = mzkbr> m. 9.34
Коэффициент kbr,m принимается согласно рис. 9.1:
— для участка откоса между точками / и 2 по графику 2
на том же рисунке в зависимости от безразмерных величин
bbjl\~i/h и dbr/d;
— для участка откоса между точками 3 и 4 равным кыхт =
= 1,0;
— на берме между точками 2 и 3 по интерполяции значений
з точках 2 и 3.
Пример 9.20
Η а и τ и массу гексалегов в защитном покрытии прямолинейного откоса
Hgff = 1,0) оградительного сооружения II класса капитальности (V/= 1,2).
321
Исходные данные: /г2% = 5м; λ = 100 м; ρ « 2,3 т/м3; р =
= 1,0 т/м3.
Решение*. (
1. Определим но табл. 9.15 для наброски из гексабитов коэффициент
kfr = 0,007.
2. Определим по формуле (33) * [51] массу гексалега
3,16-0,007^2,3-53 /Ϊ00/5 _
t$-U>JVT
+ 13
С учетом коэффициента надежности Vf = 1,2 расчетная масса гексалега
равна: т = 9,2-1,2 = 11 т.
Пример 9.21
Найти массу камня в защитном покрытии сооружения с бермой.
Исходные данные: параметры волн h2% = 5 м; λ = 100 м;
пологость откосов ctgqp=l,5; берма заглублена ниже расчетного уровня воды
на величину dbr — 1 м, ширина бермы Ьы = Ί0 м; глубина воды перед
сооружением d = 10 м; сооружение принимаем II класса капитальности (Vf = 1,2).
Решение.
1. Определим по графикам рис. 9.1 величину коэффициента kbr,m для
участка откоса выше бермы, используя для этого известные безразмерные
параметры:
-?*1_ϋ_οΐ· —-—-20· —г---01
λ "~100~ ' ' А ~~ 5 ~ ' <* -"ΊΟ"" ' "
По графику 2 рис. 9.1 имеем kbr, m == 0,7.
2. Рассчитаем по 9.33 массу камня на урезе воды (точка /, рис. 9.1):
3,16-0,025-2,6-53 Т/"-^
тьг = 0,7 __ _ L_L. - 9,4 т.
(^-..o)Vr
+ 1,53
С учетом коэффициента надежности γ^ = 1,2 расчетная масса камня на
урезе воды принимается равной: ты = 9,4-1,2 = 11,3 т.
3. Определим по 9.34 массу камня в нижней точке верхнего откоса
(точка 2, рис. 9.1):
3,16.0,025-2,6.53 l/Ip -<Ь^\
(ΐ75-ϊ.θ) /1 + 1,53
С учетом коэффициента ^ принимаем ты,г= 11,0 т.
4. Найдем массу камня для верхней точки нижнего откоса (точка #,
рис. 9.1), приняв коэффициент кы,т =1,0.
Массу камня определим по формуле (34) [51]:
3,16.0,025.2,6.53 1/100 _ П**\
L-L·, И00^ 13,2 т.
(р-1.0] /1 + 1,53
С учетом коэффициента Yf = 1,2 имеем: тг = 13,2-1,2 = 15,9 т.
322
5. Вычислим массу камня для нижней точки откоса (точка 4, рис. 9.1)
По (34) [51] при kor, m = 1,0:
. /7,5·1ϋ»\
3,16-0,025-2,6-53./100/5 ~ ТЛоо « А Л ЛЛО ОЛ
т2 = -тоб"2 Гз— -е ν ; = 13,4-0,223 = 3,0 т.
(ϊΐδ-ΙΛ) Vl + l&
С учетом коэффициента yf — 1,2 имеем: тг = 3-1,3 = 3,6 т.
Рассмотрим устойчивость элементов берегоукрепительных
сооружений. Волногасящие сооружения, предназначенные для
(защиты от волновых воздействий (ударов, всплесков и подмыва)
естественных береговых уступов, откосных укреплений, волно-
Рис. 9.11. Конструктивные формы берегоукрепительных набросных
сооружений
/ — существующий профиль берега; 2 — крепление из бетонных массивов;
3 — каменная постель; 4 — засыпка из несортированного камня; 5 —слои
обратного фильтра.
323
отбойных стен и других объектов, расположенных в прибойной
и приурезовой зонах моря, по конструкции делятся на три типа,
рис. 9.11:
— уложенные в виде призмы на горизонтальном или
слабонаклонном естественном основании, отодвинутые от стены или
берегового уступа, рис. 9.11, а;
— то же, прислоненные к стене или береговому уступу,
рис. 9.11,6;
— состоящие из каменного ядра и защитного покрытия из
камня или блоков, уложенных по откосу и гребню ядра,
рис. 9.11, е.
Основными факторами, определяющими волногасящий
эффект берегоукрепительных сооружений, являются: тип
защитного элемента, пологость и высота мористого откоса и процент
пустотности в теле сооружения. В качестве защитных
элементов могут быть использованы: камень, трибары, тетраподы,
гексалеги и другие фасонные блоки, рис. 9.10. Элементы могут
укладываться в виде произвольной наброски или по
определенным схемам.
Работоспособность берегоукрепительного сооружения
определяется устойчивостью отдельных защитных элементов на его
мористом откосе под воздействием расчетных параметров волн.
Масса отдельного защитного элемента га, т, соответствующая
состоянию его предельного равновесия, при воздействии воли,
обрушивающихся непосредственно на откосе сооружения,
расположенного на глубине dcr,«, рассчитывается по формуле
(33) * [51].
Если откос сооружения расположен на некотором
расстоянии χ от линии уреза воды и на него воздействует поток от
разрушенной волны, то масса тх защитного элемента определяется
так:
тх = kak2xm, 9.35
где ka — коэффициент, принимаемый по табл. 9.16,
характеризующий крутизну подводного склона;
Таблица 9.16
Ctga
Коэффициент ka
5
1,5
- ю
1,95
15
2,7
20
3,3
25
3,75
30
4,1
kx — коэффициент, зависящий от пологости подводного склона
ctga, расстояния χ и отношения h/λ:
где μι, μ2—безразмерные коэффициенты, определяемые
соответственно по графикам на рис. 9.12 и по табл. 9.17.
324
Таблица 9.17
Ctga
(Коэффициент μ2
5
4,2
7
6,7
10
10,6
15
М7.1
17
19,8
20
23,8
25
30,4
30
37
Значения χ для сооружений, расположенных выше линии
уреза, принимаются со знаком плюс, а мористее уреза — со
знаком минус. На глубине dCr,u, где завершается разрушение волн,
значение коэффициента kx
равно единице, а на верхней
границе наката волн — нулю.
Массу фасонных массивов на
приглубных берегах во всех
случаях следует принимать не
менее 3 т, а на отмелых
берегах— не менее 1 т.
Для ответственных
сооружений и при большой их
протяженности массу отдельного
защитного элемента, высоту и
ширину гребня следует
принимать по данным исследований
на моделях в лотках при
различных режимах волнения.
Для приближенного
определения высоты гребня
сооружения допускается принимать,
что высота наката волн на
покрытие вычисляется согласно
[51]. Ширина гребня сооружения принимается равной 3
мерам защитных элементов.
Пример 9.22
Определить- массу тетраподов в защитном покрытии откоса
берегоукрепительного сооружения, расположенного на расстоянии χ = —50 м от
уреза воды, при крутизне подводного склона ctg α = 30.
Исходные данные: параметры волн на глубине dcr, и равны hsur =
= 3 м; Ksur = 45 м; пологость откоса ctg φ = 1.
Решение.
1. Определим по формуле (33)* массу тетрапода на глубине:
3,16.0,008-2,3 · 33 УЩг
Рис.
9.12. Графики для определения
коэффициента μ1#
-5 раз-
(ίο-1·0)
= 2 т.
γΙ + V
С учетом коэффициента надежности yf = 1,2 принимаем т = 2-1,2 = 2,4 т.
2. Определим по формуле 9.35 массу тетраподов в сооружении,
возводимом на расстоянии χ — 50 м от уреза воды. Предварительно определим
из табл. 9.16, 9.17 и рис. 9.12 необходимые коэффициенты:
325
*« = 4,i; μ1== 0,175; μ2 = 37; *^ = 0,175 + ^ · -^ = 0,55.
Масса тетрапода будет равна тх = 2,4· 4,1· 0,55 = 2,9 т. Принимаем
тх = 3,0 т.
Глава 10. ВОЗДЕЙСТВИЕ ВЕТРОВЫХ ВОЛН
НА ОТДЕЛЬНО СТОЯЩИЕ ОБТЕКАЕМЫЕ ПРЕГРАДЫ,
СКВОЗНЫЕ СООРУЖЕНИЯ
И ПОДВОДНЫЕ ТРУБОПРОВОДЫ
10.1. ОБЩИЕ ИСХОДНЫЕ ПОЛОЖЕНИЯ.
ОСНОВНОЕ УРАВНЕНИЕ ДЛЯ РАСЧЕТА НАГРУЗОК ОТ ВОЛН
НА ОБТЕКАЕМУЮ ПРЕГРАДУ
К категории обтекаемых преград относятся такие
сооружения или отдельные их элементы, которые только частично
отражают или почти не отражают волн; набегающие волны огибают
обтекаемые преграды, существенно не изменяя своих
параметров. Если при взаимодействии волн с обтекаемой преградой
имеет место дифракция волн в вертикальной плоскости, преграду
принято называть горизонтальной, а при дифракции волн в
горизонтальной плоскости — вертикальной. К малым отнесены
горизонтальные и вертикальные обтекаемые преграды, имеющие
настолько малые по отношению к длине волны поперечные
размеры, что эффектом отражения при взаимодействии их с вол-1
нами можно прене0речь и рассчитывать нагрузки с учетом лишь!
одного явления обтекания. При анализе силового воздействия!
на обтекаемые преграды больших размеров отражением волн
пренебрегать нельзя, а следует учитывать как отражение, так и
обтекание преград волнами, что существенно усложняет
аналитический подход к решению задач.
В настоящее время можно говорить о трех направлениях
исследований взаимодействия волн с обтекаемыми преградами:
обтекание малых преград регулярными волнами, обтекание
сквозные конструкций из тонких элементов нерегулярными
волнами с учетом динамического эффекта и обтекание больших
преград регулярными волнами. Аналитические исследования,
как правило,· базируются на положении теории потенциальных
волн при соблюдении дополнительного пограничного условия
непроникания жидкости через поверхность преграды.
Используются также или потенциал обтекания тела
плоскопараллельным потоком или потенциал излучения (отражения) волн в слу]
чае применения дифракционной теории. Из опубликованных в
последние четыре десятилетия заслуживают внимания труды
326
следующих советских авторов: Ю. 3. Алешкова, Μ. Φ. bap-
штейна, М. В. Бухтояровой, Б. X. Глуховского, С. В. Ивановой,
А. А. Каспарсона, В. В. Каплуна, А. И. Кузнецова, Μ. Ф. Кур-
банова, Ю. М. Крылова, Д. Д. Лаппо, Ю. Б. Майорова,
С. С. Мищенко, С. И. Рогачко, И. Ш. Халфина, М. Д. Хаскинда,
10. Н. Шестакова и др. За рубежом чрезвычайно много
публикаций по данной проблеме, в том числе Бонефиля (Франция),
Вигеля (США), Года И. (Япония), Мак-Кеми (США), Могрид-
жа-Джемисона (Канада), Морисона (США), Рамана-Венката-
расайя (ФРГ), Р. Сильвестра (Австрия), С. Фонгвисессомджая
(Таиланд) и ряда других,
В этой главе представлено изложение теории и методов
расчета нагрузок от волн на обтекаемые преграды, построенные в
основном на материалах публикаций автора и его учеников
[31—37], с учетом работ упомянутых выше отечественных и
зарубежных ученых.
Общие научные положения исследований воздействия волн
на обтекаемые преграды сводятся к следующему:
—нагрузки от волн в общем случае должны определяться
как сумма скоростного и инерционного компонентов;
— в частных случаях достоверные результаты по
определению максимальных сил могут быть получены либо только по
скоростному (для малых преград), либо по инерционному (для
больших преград) компоненту;
— динамический эффект от воздействия нерегулярных волн
следует учитывать только в тех случаях, когда период
собственных колебаний сооружения соизмерим со средним периодом
набегающих волн.'
Основные задачи применительно к преградам с поперечным
сечением в виде эллипса или круга, рис. 10.1, решены
аналитически; расчетные зависимости применительно к обтекаемым
преградам с поперечным сечением в виде прямоугольника или
квадрата получены на базе решений основных задач с
введением эмпирических коэффициентов. В общем виде задачи
формулируются применительно к рис. 10.1 следующим образом.
Бегущие волны высотой h и длиной λ, перемещаясь по
водоему с постоянной глубиной dy встречают на своем, пути
обтекаемую преграду в виде вертикального (горизонтального)
эллиптического цилиндра, оси которого равны а и Ь, при этом
ось а ориентирована по лучу волн. Требуется определить силу,
действующую на участок обтекаемой преграды единичной
высоты (длины) — линейную нагрузку q (Px и Рг), суммарную
силу Q и линию ее действия — расстояние zq. Жидкость
идеальная, с постоянной плотностью р; движение безвихревое,
неустановившееся.
327
В целях получения основного уравнения для расчета!
нагрузок от волн на обтекаемую преграду воспользуемся
интегралом Лагранжа в следующей записи:
P + PgZ + PY + 9-fc
nth
а) Вершина
волны
Дно
///7////////,///
Средняя Волнобая
линия
Ά^ ι £ ι
ЮЛ.
Рис. 10.1. Схемы к определению волновых
нагрузок на обтекаемые преграды
а) вертикальные; б) горизонтальные.
где ρ, υ — давление и скорость в данной точке потока жидкости;
φ — потенциал скорости рассматриваемого потока; δφ/dt —
энергия единицы массы жидкости, обусловленная изменением
328
давления и других элементов движения с течением времени;
F(/).— некоторая функция времени, не зависящая от координат.
Применим уравнение 10.1 для исследуемого потока в точках
1 и 2 и таким образом исключим неизвестную-величину F(t)\
представим в итоге выражение для давления р2 на поверхности
преграды:
/'2 = /'1+Р^(г1-г2)+г4К2-^2) + Рр)1-(|)2]· 10·2
Воспользуемся теперь известным из гидромеханики [22, 30,
45] выражением для потенциала скорости φ при обтекании
эллиптического цилиндра плоскопараллельным потоком со
скоростью υ в бесконечности:
/а ■+- Ь [а — b . . а-\- b Л 0 1ЛО
т=ъ(—ге*+ ~т~ е~Jcos6> l0·3
где ε и θ—переменные в эллиптической системе координат, при
этом ε изменяется· от 0 до оо, а &—от 0 до 2π.
Используем известные связи между переменными (л:, у) и
(ε, θ); в виде
χ = — //chscos Θ; у ·= Я she sin θ; Η = -χ Υ α2 — b2
и найдем значение φ2 на контуре эллипса. Имея в виду, что
Щ+~1фГ=1 и й4; + Йт=1» получаем a = 2tfchs
и & = 2//shs, а следовательно,
е = ^Ь?· е~в- = —-· 10 4
с 2Н * 2И ш'*
После подстановки 10.4 в 10.3 получаем для φ2:
φ2 = Vit^- cos 8. 10.5
Скорость на контуре эллипса, в частности для точки 2,
выражается (dq)/ds)2j где ds— элемент длины контура. Имея в
виду, что χ = —а/2 cos θ и у = 6/2 sin & (d# = α/2 sin θί/θ, dy =
= 6/2cos6rf6) для элемента контура имеем:
ds = - }/V sin - 8 + &2 cos2 8 tf 8
или
rfS OS у а2 S|n2 θ + 62 COS2 θ
10.6
В результате дифференцирования по переменной 5
выражения 10.5 и подстановки 10.6 получаем выражение для скорости
на контуре α2·
329
10.7
ιο.ι
/d«\ (a + b) sin 0
\ ds /2 К & sin-' θ + 62 cos-' (J
Производная по времени от потенциала 10.5 равна:
Подставляя в 10.2 значения υ2 и (dy/dt)*, согласно 10.7 и
10.8, имея в виду, что (dq>/dt)i в данном случае равно нулю, а
для вертикальной преграды z\ = г2, в результате для давления
на контуре р2 окончательно получаем:
. 1 9Г, (а + by sin2 θ 1 ^tfl + ^A,fl mo
/>2 = Ρι+Τ^ [1"^^e + ^cotfoJ + Pir'-T""cos9- 10'9
Напрадлше распространения.болн .Сечение Η
УУУ УУУ УУУ УУУ УУУ УУУ
Рис. 10.2. Схемы к выводу основного уравнения для расчета
нагрузок от волн на обтекаемую преграду.
Элементарная удельная сила dq на цилиндр единичной
высоты, рис. 10.2, равна:
10.10
dq = p>ds cos α — ρ2 γ b cos θ άθ.
Линейная нагрузка от волн на вертикальный эллиптический
цилиндр q определяется интегрированием J0.10 по поверхности
преграды и представляется в виде суммы скоростного qv и
инерционного qi компонентов:
q = ρΎ CJkv<o\v\ + ρ — cikv-gr
b r> lo , ι Λ "tb п и ^υ
9υ = Ργ Cvklv\v\; qt - ρ— Cfiv-fi-'.
10.11I
в которых Cv и Ci — коэффициенты соответственно скоростного!
и инерционного сопротивлений, определяемые по следующим]
формулам:
330
2π cos 0 I cos β Ι - (1 + 2 -j) sin" β
C„ = 4r \ rr^ - cos9dB- 10.12
■*i
COS2 θ +
(τ)*8"13·
C,= l+—, 10.13
a
υ и cto/d/ — проекции локальных значений скорости и
ускорения волнового движения жидкости при отсутствии преграды
(индексы опущены); kv—коэффициент перехода от
действительных величин проекции скорости и ускорения к их средним
значениям по координате χ в пределах области жидкости,
интенсивно воздействующей на преграду.
Формула 10.11 представляет собою основное уравнение для
расчета нагрузок от волн на обтекаемую преграду,
теоретически и экспериментально обоснованное Д. Д. Лаппо в 1948 —
1949 гг., получившее широкое распространение на практике,
в том числе оно внедрено в общесоюзных нормативных
документах по строительству [51].
Нетрудно убедиться в том, что известное уравнение Мори-
сона [80] является частным решением 10.11, а именно при а =
= b = D и kv = 1 получаем:
D „ ... ~D* ^ dv
Я = Ρ -j-C^M + Ρ— Q-^·
В дальнейшем будут изложены особенности применения
уравнения 10.11 для расчета нагрузок и воздействий волн на
различные преграды, при этом даются обоснования входящих
в расчетные формулы коэффициентов и соответствующих
графиков.
10.2. СКОРОСТНОЙ И ИНЕРЦИОННЫЙ КОЭФФИЦИЕНТЫ
СОПРОТИВЛЕНИЯ И КОЭФФИЦИЕНТЫ ФОРМЫ.
КОРРЕКТИВ СКОРОСТИ
Входящие в основное уравнение 10.11 скоростной и
инерционный коэффициенты сопротивления, рассчитываемые по
10.12 и 10.13, могут быть определены и по экспериментальным
данным по формулам:
г - 2qv С. - ~4i 10 14
С*~ 9bkv*v\v\ · С'~ tt dv шл*
?izabkv -j£
Следует заметить, что в уравнении 10". 11 слагаемое,
характеризующее инерционный компонент, решается аналитически
точно, в то же время скоростной компонент в строгой постановке
дает нулевой результат (парадокс Даламбера). В
действительности скоростной компонент имеет конечное значение, и для
тонких преград максимальная нагрузка может определяться
331
этой составляющей. Однако в ряде практических задач при
расчете наибольшей нагрузки от волн на обтекаемую преграду
решающую роль играет инерционный компонент.
В специальной литературе [1] приводятся обоснования, как,
оставаясь в рамках представлений об идеальной жидкости,
можно построить теоретическую схему обтекания тела потоком
и получить при этом скоростной компонент, не равный нулю.
Рассматриваются физические модели струйного и вихревого
сопротивлений. Оказывается, что при струйной модели
обтекания, например, пластинки, получаются коэффициенты Cv
примерно в два раза меньше экспериментальных. Это, в свою
очередь, объясняется тем, что в струйной теории не учитывается
уменьшение давления с тыльной стороны обтекаемой преграды,
оно принимается постоянным и равным давлению на бесконеч-
дости.
Некоторое уточнение в физику процесса вносится при
анализе модели вихревого сопротивления; в этом случае
теоретические значения Cv почти совпадают с экспериментальными. По
теории вихревого сопротивления вследствие отрыва струй и
вихреобразования.на тыльной поверхности обтекаемой преграды
образуется разрежение, обуславливающее существенное
увеличение результирующей силы воздействия потока. Такое явление
наблюдалось многими исследователями; в книге [45] отмечено,
что в случае обтекания кругового цилиндра установившимся
потоком при больших числах Рейнольдса (Re>6,7-105)
давление разрежения на тыльной поверхности по абсолютной
величине достигает значений давления в лобовой критической точке.
Таким образом, из краткого анализа исследований обтекания
кругового цилиндра и тонкой пластинки установившимся
потоком можно заключить, что для плохо обтекаемых тел и тем
более для сваи, покрытой морскими обрастаниями, вполне
допустимо в практических расчетах принимать значение Cv
максимальным и постоянным, не зависящим от числа Рейнольдса.
Обтекание преград неустановившимся знакопеременным
потоком имеет ряд особенностей. На материалах специально
поставленных опытов [5, с 55] установлено, что в
рассматриваемом случае кризис сопротивления, наступает при меньших
числах Рейнольдса и эффект шероховатости проявляется
интенсивнее, рис. 10.3. При шероховатости &/D^l,5-10"2 (k —
абсолютный размер выступа шероховатости на круговом цилиндре
диаметром D) кризис сопротивления практически исчезает и
численные величины Cv могут быть приняты не зависящими от
числа Рейнольдса.
Обратимся к анализу приведенной в параграфе 10.1
формулы 10.12 для COt решение которой имеет следующий вид:
332
( /7|ri(ρ^γarctgК/2 - 1 - l) при/»>1;
: = J -|" при /2 = 1; Ю.15
где f = α/6.
ю* ζ 4 6 8 ios ζ ♦ β β ιο6 ζ ϊ $ βίο7
Re
Рис. 10.3. Экспериментальные значения и графики Су —
= f (Re; k/D) при обтекании кругового цилиндра
неустановившимся знакопеременным (штриховые линии) и
стационарным потоками (сплошные линии)
а) значения С0 для гладкого цилиндра (fc/D = 0), полученные ([5],
с. 55): / — на маятниковой установке; 2 — в волновом лотке; 3 —
в штормовом бассейне ЧОМГИ; то же для шероховатого цилиндра,
(k/D · 103 = 15. . .58); 4 — на маятниковой установке; 5 — в штормовом
бассейне; графики С0: 6 — для шероховатого; 7 — для гладкого
цилиндра—по ([5], с. 55); 5 —по Визельсбергеру; 9 — по Рошко [5];
б) то же по опытам Миллера [79] при k/D · 103 — 0. . .63; 6—7 — по
([5], с. 55).
333
Из 10.15 следует, что для круглоцилиндрическпх преград С
можно принимать равным 4/3. В нормативном документе [51]
содержатся дифференцированные рекомендации по назначению
величин Cv в зависимости от состояния поверхности подводной
и надводной частей и при различных отношениях а/Ь.
При симметричном обтекании волной горизонтальных
преград коэффициент скоростного сопротивления принимается
таким же, как и для
вертикальных отдельно
стоящих преград.
Однако по мере
нарушения условия
симметрии обтекания,
например, при приближении
трубопровода к дну на
расстояние, меньшее,
чем его наружный
диаметр, коэффициент Cv
увеличивается и
достигает на дне
величины 8/5 (вместо 4/3).
На рис. 10.4
изображены графики
коэффициентов
сопротивления в зависимости от
отношения а/Ь, из
которого следует, что при
увеличении этого
отношения как CO> так и
d уменьшаются.
Существенно осложняется вопрос о назначении величин
коэффициентов сопротивления для призматических преград и
элементов сооружений, имеющих более сложное поперечное
сечение. В табл. 10.1 представлены экспериментальные
значения Со и. Ci для применяющихся на практике преград, при
этом учтен также угол подхода волн.
На фактическом материале экспериментов с
призматическими преградами [5, 31, 34] установлено, что если к расчетным
величинам С*, согласно 10.15, и соответственно С/, согласно
10.13, ввести поправочные коэффициенты
то можно получить величины Cv и С/ для призматических npej
град пря любом отношении α/b, что изображено на рис. 10.4]
штриховыми линиями.
В последующем представляется целесообразным, как этс|
сделано в СНиПе [51], вместо коэффициентов сопротивление
Рис. 10.4. Графики скоростного Cv (кривые /
и 3) и инерционного & (кривые 2 и 4)
коэффициентов сопротивления для эллиптических
(сплошные) и призматических (штриховые
линии) преград.
334
Таблица 10 А
Форма сечения
а, град
Значения коэффициентов сопротивления
Су при поверхности
гладкой
*/О=0
шероховатой
Л/О=1/50
*№
Aj = 62
О
15
30
45
1,60
1,73
2,42
2,76
1,60
1,73
2,42
2,76
Aj =* ab
= 1,2
О
15
30
45
60
75
90
120
135
150
165
180
1,50
2,08
2,67
2,93
2,73
2,35
1,85
2,60
2,72
2,56
2,03
1,33
1,50
2,08
2,67
2,93
2,73
2,35
1,85
2,60
2,72
2,56
2,03
1,33
•Ε
тки1
%D*
4 = -г
1,4.
О
30
45
60
90
120
135
150
180
2,35
2,28
2,10
1,72
1,13
2,37
2,20
2,07
1,81
0,67
1,33
335
Продолжение таблицы 10.1
Форма сечения
-23
«7*
^ в _
4
b
* -1
■■ jFv
LJT
π£>2
Ь|
Η
и
2?
6
в-
1,4
1,6
н
-
"^
1
»Г*
^ίι
•J.
£■
II
1
±
α, град
' 0
30
45
80
90
0
15
30
45
60
75
90
105
120
135
150
165
180
0
90
0
90
0
180
Значения коэффициентов сопротивления
С при поверхности
гладкой
£/D=0
0,85
0,90
1,48
2,40
2,60
0,50
0,56
0,73
1,14
1,60
2,13
2,27
2,13
1,63
1,16
0,85
0,64
0,60
2,00
3,00
2,50
3,00
0,67
0,90
шероховатой
*//J=l/50
1,34
1,18
1,48
2,40
2,60
1,27
1,30
1,35
1,60
1,94
2,19
2,27
2,19
1,94
из
1,40
1,30
1,27
2,00
3,00
2,50
3,00
1,33
1,33
ci
1,80
2,08
2,12
2,20
2,20
1,65
1,90
2,09
1,90
1,61
—
—
—
Примечание. Значения Gy отнесены к размеру Ъ или D, С^-к площади основной
фигуры Α..
Со и Ci ввести понятия коэффициентов формы β^ и β;, при этом
взаимосвязь между ними выражается следующим образом:
А = Т/С|. Ь = с·· 10.16(39,40)
Остановимся кратко на вопросе о назначении величины
корректива скорости kv. Физический смысл этого коэффициента
состоит в обосновании перехода от расчетных значений скорости
или ускорения в данной точке пространства к их средним
значениям в пределах области жидкости, интенсивно
воздействующей на преграду.
По материалам экспериментов и на основании расчетов,
как это показано в [31], область существенных деформаций
движущейся жидкости может быть ограничена полутора —
двумя размерами обтекаемой преграды по данному направлению.
В результате интегрирования по переменной χ значений
скорости и замены ее средней скоростью одинаковой по величине в
пределах этой области получены значения kv, определяемые по
формуле 10.17 и представленные в табл. 10.2 для области
α/λ < 0,4:
Таблица 10.2
Относительный размер
преграды α/λ; D/λ
Ку
0,05
1
0,1
0,97
0,15
0,93
0.2
0,86
0,25
0,79
0,3
0,7
0,4
.0,52
Следует иметь в виду, что применительно к горизонтальным
обтекаемым преградам необходимо учитывать изменение
скорости по вертикали (от координаты ζ). В ряде практических задач
для преград с малым вертикальным поперечным размером
допустимо в расчет вводить значение скорости на уровне
геометрического центра преграды.
10.3. УЧЕТ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА ВЕТРОВЫХ ВОЛН
ПРИ РАСЧЕТЕ НАГРУЗОК НА ВЕРТИКАЛЬНЫЕ
КРУГЛОЦИЛИНДРИЧЕСКИЕ ОБТЕКАЕМЫЕ ПРЕГРАДЫ.
В последние годы предпринимался ряд попыток изучения
воздействия на обтекаемые преграды ветровых волн с учетом
их нерегулярности и трехмерности, среди которых заслужив-ают
внимания публикации Μ. Φ. Барштейна [2], Ю. 3. Алешкова и
Ю. Б. Майорова [5, 6], Ю. М. Крылова [24], Пирсона и
Холмса [81], Боргмана [68, 69] и др. Рассмотрим здесь лишь
принципиальные особенности этой сложной теоретической задачи,
положив в основу решение К)'. 3. Алешкова из [5, 6].
337
В качестве исходного, по-прежнему, принимается уравнение
10.11, которому в данном случае придан такой вид:
q(z, t)=Civ\u\+C2w9 10.18
где q(z> t) — линейная нагрузка с учетом нерегулярности и
трехмерности волн; υ (z, t) и w(zy t) = dv/dt — проекции на ось O.v
скорости и локального ускорения; при этом предполагается, что
зектор скорости одинаково направлен с осью О*; Ci и С2 —
постоянные величины, характеризующие связи неизменяющихся
параметров для конкретной задачи, а именно:
^ι = wpy; Рг = чр—'
где Cv и Ci — коэффициенты скоростного и кнерщгонного
сопротивлений, имеющие по условию неслучайные значения.
В дальнейшем согласно спектральной теории волн
принимается, что ό π w являются случайными стационарными по /
функциями с нормальным законом распределения для
фиксированных (z, t); средние значения этих величин и средние
значения их квадратов, т. е. математические ожидания (м. о.) равны:
м. о. \v(z9 t)) = 0; м. о. [ν2 (ζ, t)) = σ£;
V о. [w (ζ, t)} = 0; м. о. [ш7 (Ζ, t)} = σ£,
где ου и aw — суть среднеквадратичные значения υ и w.
В силу стационарности по t при фиксированном ζ величины
υ и w будут некоррелированы, а так как они распределены по
нормальному закону, то и независимы. Соответственно для
среднего значения линейной нагрузки и среднего значения се
квадрата имеем:
м. о. [q(z9 t)) = 0; м. о. [q* (ζ, t)) = 3C,V + Cf*w = *], 10.19
где oq — среднеквадратичное значение линейной нагрузки q.
Четвертый момент величины q равен [5, 6]:
!*4 = lOKVaJ + 18C^C2W + 3C,«Ci. 10.20
Решив систему уравнений 10.19 и 10.20 относительно С\а\ и
C2(Jw, получим:
,(CxolY = ^783V; (СаО* = σ£ -~(μ4-—3α^). 10.21
Заметим здесь, что 10.21 можно использовать для
определения величин Cv и С,·, если известны oq и μ4 = м. о. {<74(#, /)}·
Далее Ю. 3. Алешков [6] использовал прием линеаризации
уравнения 10.18 и, применив некоторые упрощения, получил для
силы от воздействия волн на круглоцилиндрическую
вертикальную преграду с учетом энергетического спектра выражение
ч/
d
338
а для спектральной плотности 5q(o), 0) функции Q следующую
зависимость:
Sq (·,β) = \£Ь)т К I J ch ft (rf - 2)«. (г) dz ] +
-d
+ C2a[jch*(i/-s)ds]
cos20S^<o, Ο). 10.23
Дальнейшие рассуждения ограничим рассмотрением
волнения, описываемого суперпозицией гармонических волн со
случайными высотами Л/, случайными фазами ε/, но с постоянной
частотой <оо, бегущих в разных направлениях Θ/. В таком случае
для возвышения взволнованной поверхности η и для горизонт
тальной проекции скорости υ будем иметь:
4(0 = ^Т"C0S (щ«* ~ е/)!
£* Ch £(<* — *) ^1 Λ;
*<*■ ^) = ·^ -^еш—J^tt008^008^""·/)·
Эти выражения для удобства последующих операций
представим в таком виде:
η = A cos (toot — Φ); 10.24
* = £^^*<™Κ<-ψ), Ю.25
ch^
где
10.26
tg φ ·.= i_l ,
2 -Jr COS г;
Τ 2
£2 = (S-y-cos θ,-cos ·,ή + (2-y cos 8, sin eyj ;
10.27
2j -j^- cos fly sin ε у
tg*"^—:—
2± ' cos θ;· cos г ι
Подставив 10.25 в 10.18, а затем в 10.22 (используя 10.24),
получим в данном случае для q(zy t) и Q(t) следующие
выражения:
*<«, 0=
C^&JЩУ^В'cosЫ-МсовЫ-turn
- C>8k ^ch^^ B sln (*o< - Ψ); Ю.28
- C*g 8".οΐ^7η) * sln К' - Ψ)· 10·29
Аппроксимируем 10.29 следующей зависимостью:
— C2g· th Ы5 sin (<o0* - ψ). 10.30
Наибольшее значение Q*max, соответствующее
зафиксированному Л = А,%/2, равно:
iC/^'-' + C^Ct'; £>#*;
С/В; В<В*=^ Ш·31
У max —
где
4 chs fcd
10.32
Величину Б, в силу ее определения, можно рассматривать
как модуль вектора с проекциями X и У, т. е. В = VX2+Y\
где X = 2 τ Λ/ cos By cos ε/, У = Σ -9- ft/ cos θ/ sin ε/. Если пред-
У ^ у ^
положить, что ft/ и ε/ — случайные независимые величины и ε/
распределена равномерно на отрезке (0,2π), то составляющие
X и У будут независимы. В этом случае величина β будет
распределена по закону Рэлея.
В силу 10.31 функция Q*max(£) является возрастающей, а
следовательно, чтобы получить то значение Q = Q/, вероятность
которого равна ί, нужно в 10.31 вместо В подставить β,- [5].
Ay
Дисперсия величины и=* Σ-*-cos fy cos (ωώ — ej) равна
A/ ' l
a2u = 2 τ cos2 θ. Если ввести обозначение Λ//4 = Sn (Θ/)ΔΘ/,
У
тогда:
^2 = Σ5η(θ;.)οο82θ;ΔΘ;^ί5η(θ)€θ82θάθ.
у в
Пусть спектр направлений при изменении —π/2^θ^π/2
имеет вид:
Sn(Q) = CscosnB,
где Cs — константа, определяемая с помощью дисперсии
ординат свободной поверхности согласно равенству σ2η -
340
= Cs j cos;i9d&, тогда среднее квадратическое значение вели-
-*/2
чины и будет равно:
10.33
*л = *гУЪ(п)>
где
Ь(«)
0,8
0,83
0,84
1
при этом η = оо соответствует плоскопараллельной
гармонической волне. Исходя из того, что величина и распределена по
нормальному закону с нулевым математическим ожиданием и
дисперсией σ2Μ, для величины. Ву которая будет распределена по
закону Рэлея, и соответственно для величины А можно
записать следующие выражения [5, 6]:
Bt; = ]Λ- 2δ(/*)1η icy, A% = V — 2 1ηίση.
Итак, расчетная нагрузка на вертикальный круговой
цилиндр Qmaxi(n) будет определяться по формуле 10.31, если в
нее вместо В подставить 5/, а именно:
{max i
(*)Ч
\C2'V — 2*(η)\ϊΐΙ*ύ
Д,(л)>Я·;
Bt{n)<B*.
10.34
Пример расчета
Дано: d = 24,9 м; D = 5,1 м; С0 = 4/3; d = 2; ρ - 1020 кг · с/м3;
g = 9,81 м/с2; λ= 102 м; σ* = 1,33 м; t = 0,01.
Требуется определить Qmaxi%.
Решение.
k = 0,0615 м-1; kd = 1,53; Ах% - 4,03 м; Я1% = 4,03/б^/Г); С2 =
= 510-3,14-26,1 = 41600 кг-м"1; d - 4/3-510-5,1 - 3460 кг-м~2; С2' =
= 416000,91 · 9,81 = 372000 кг. с~2; С/ = 3460'9'81 ^тУ£^= 35400 кг-
, о 372000 Δ
• м х.с '; θ* = ο-όΈΤηΤΓ = 5,25 м.
10,08
2-35400
В этом случае максимальная нагрузка 1%-ной обеспеченности будет
равна Отах1о/о =372000-4,03 Vb (я), Н, а именно:
η
Фтах1%» к^
3
1340
4
1370
δ
1380
>6
1500
Таким образом, в данном примере расхождения находятся в пределах
10% и менее.
В заключение заметим, что при учете энергетического
спектра ветровых волн можно использовать более полную
информацию о реальных волнах, если эта информация достоверна,
341
но при этом в теоретическом подходе приходится допускать
некоторые дополнительные упрощения. В настоящее время
получены и другие решения рассматриваемой задачи [24].
Многочисленные сопоставительные расчеты по различным
методам, основанным на спектральной и на детерминистической
теориях волн позволяют сделать следующие выводы:
— по сравнению с двумерными регулярными волнами
трехмерные ветровые волны оказывают меньшее силовое
воздействие на обтекаемую преграду, снижение может достигать 20%
для отдельно стоящих тонких свай;
— разнообразие двумерных волн по высотам и сдвигам фаз
не оказывает сколько-нибудь заметного влияния на результат
расчета силы на обтекаемую волной преграду.
Признавая полезность анализа по учету нерегулярности
волн в расчетах нагрузок, заметим, что в настоящее время
спектральная теория волн разработана в линейной постановке;
нет также достоверной статистики затухания с глубиной
скоростей и ускорений в нерегулярных волнах; отсутствует более или
менее универсальный и общепризнанный вид спектральной
плотности реального волнения.
Авторы считают возможным применить вероятностный
подход к назначению элементов расчетной волны и затем
определять нагрузку детерминистическими методами, а динамический
эффект учитывать соответствующими коэффициентами
применительно к воздействию на сооружение в целом отдельных
составляющих, обладающих более или менее значительным
энергосодержанием.
10.4 РАСЧЕТНЫЕ ФОРМУЛЫ И ГРАФИКИ
ДЛЯ ОПРЕДЕЛЕНИЯ НАГРУЗОК ОТ ВОЛН
НА ОТДЕЛЬНО СТОЯЩИЕ ОБТЕКАЕМЫЕ ПРЕГРАДЫ
Обратимся снова к полученному в параграфе ЮЛ
уравнению 10.11:
q = 9-jCvklv\v\ +Ртс~.СЛдр
Известные в СССР и за рубежом инженерные методы
расчета воздействия волн на обтекаемые преграды различаются
между собой главным образом тем, что в основу их решений
положены разные теории волн, дающие неодинаковые величины
проекций скорости и локального ускорения. Кроме того, до
настоящего времени нет единства в назначении численных
величин Су и С,. В первом разделе (глава 2) подобия показано, что
основные кинематические и динамические характеристики
бегущих волн при глубинах ύί^Ο,Ιλ с достаточной для
инженерных расчетов точностью можно определять по формулам
потенциальной теории волн на уровне третьего приближения.
342
Воспользуемся формулами 2.25—2.29 и запишем для
горизонтальной и вертикальной проекций скорости и локальных уско:
рений при χ — 0 следующие зависимости:
•'-^те 10·35
*> = Akc°wh> 10·36
&=-***£& 10·37
где
У-f-thftrf; 10.39
м = Ас, 11+Μ,]; 10.40
Α = 2Α[1+Λί21; 10.41
Bt = chk(d-z)cosu>t + ± ^~ch2k(d-z)cos2<»t +
+ -Jj- ет- (13-4 ch* kd) ch ЗА (<* - ζ) cos 3ωί; 10.42
Я, = sh k (d — z) sin Ы + -| ~^ sh 2A (rf — z) sin 2u>/ +
+ -|j- g^ (13-4 ch2 Arf) sh 3k (d - z) sin ЪЫ; 10.43
β, = ch k (d - z) sin mt + ·| ^-^- ch 2A (rf - г) sin 2wt +
+ ^ от 03-4 clinch з* (<*-*) sin 3ω<; 10·44
β4 = sh k (d - z) cos ωί + -| ji^- sh 2A (rf - г) cos 2ωί +
+ -J- ^^ (13 - 4 ch2 kd) sh Zk (d - z) cos Zmt; 10.45
Ж* = 1б1*ы <8 ch*Ы ~ 8 ch2 kd + 9>; XQM
M2 = 64^j (32 ch6 kd + 32 ch4 kd - 76 ch2 kd + 39). 10.47
Ординаты взволнованной поверхности согласно 2.25 могут
быть рассчитаны по формулам:
η = T\reih; 10.48
^w = -i{4cosW< + ^i^(2ch2*rf+l)cos2<^ +
343
+ 64^ГЫ [4 (2 ch° kd + 8 ch4 kd - 19 ch2 kd + 9) cos Ы +
+ 3(1 +8ch6fo/)cos3o>/]}. 10.49
Входящую в
приведенные формулы
величину А можно
также определить из
графиков на рис.
10.5, выражающих
зависимость 2A/h от
относительной
глубины d/λ и крутизны
волн Λ/λ; для
нахождения Г\ге1 В [51]
приведен рис. 20.
В уравнении 10.11
первое после знака
равенства слагаемое
есть скоростной
компонент нагрузки,
который равен
10.50
Щ 0,05 0,05 0,07 0f03 OJl 0J3 у
W050 20 !5 /0.8
Рис. 10.5.
7 Α
Графики относительной величины
2A/h = f(dlX; Λ/λ) по [8]
/ — граница обрушения волн.
%Ь № .о
4v = ?g-2Tkh'i
ъвлв,
'(1+Ai2)2sh2fcrf
при этом после исключения величин высшего порядка малости
с известным приближением можно принять, что
Bi\Bx\ =ch2£(d — ζ) cos ω* | cos ω* | +
+ |. ^^ohk(d--z)ch2k{d--z)[zo$<ut\cos2<»t\ +
ν +cos2io/|cosu>i|].
С учетом этого допущения, после подстановки в 10.50
выражений соответствующих символов, в результате преобразований
для максимального значения qV) max имеем:
^ηΐ3χ = ΤΡ^Τ^θ^
10.51 (43)
где ΘΧΌ — коэффициент скоростного компонента линейной
нагрузки от волн, определяемый при ί = 0πο^ формуле
о 3 В1\В1\
χν~~~ 4 (1 +Mtfsh2kd
10.52
или по рис. 19 [51] при частных значениях относительной
глубины Zrel = (d—Z)/d.
В СНиПе [51] рекомендовано β^ определять по графикам
рис. 17, на котором шероховатость учитывается тремя состоя-
344
нпями: сильно шероховатая преграда — кривая 7; гладкая (без
обрастаний) преграда — кривая 2\ шероховатая в подводной и
гладкая в надводной части преграда — кривая 3. Расчет
нагрузок на обтекаемые преграды должен, как правило,
производиться с учетом сильной шероховатости их поверхности, при
этом допускается использовать полученные экспериментально
значения Cv и β^, если они отличаются от рекомендованных
согласно [51], рис. 17.
Второе после знака равенства слагаемое уравнения 10.11
суть инерционный компонент нагрузки, который равен
4ι = - 98 "Г C^Ak iiw *з. Ю.53
После подстановки в 10.53 выражений соответствующих
символов, в результате преобразований для максимального
значения qit max имеем:
?*.««= Τ Ρ^'τ*·^'· 10.54(42)
где θ*/ — коэффициент инерционного компонента линейной
нагрузки от волн, определяемый по формуле
а - - ±±Ml -*»- 10.55
*'~~ \ + М2 chkd
или по рис. 19 [51] при частных значениях относительной
глубины Zrei = (d — z)/d.
Инерционный коэффициент формы связан с коэффициентом
инерционного сопротивления зависимостями:
— для эллиптической преграды (39) '[51]
Р« = IF С';
— для призматической преграды
Q = £-!&. 10.56
Обратим внимание на некоторые особенности определения
коэффициентов формы для обтекаемых преград с поперечным
сечением в виде прямоугольника или квадрата, кривые для
которых на рис. 17 изображены штриховыми линиями.
Общее решение уравнения 10.11 применительно к
вертикальной обтекаемой преграде с учетом изложенного подхода к
определению qv, max и qit max может быть предложено так:
? = *„,««*« + ?,, «.А». 10.57(41)
где δχΌ и ύχι — коэффициенты сочетания скоростного и
инерционного компонентов линейной нагрузки от волн, определяемые
из соотношений мгновенных значений скоростей и локальных
ускорений к их максимальным значениям:
345
Ζχν = ϊψΑ. Ю.58
"χ, max
- *^-.- 10.59
M (dvxldt)msix
По формулам 10.58 и 10.59 построены графики в виде
δ**=/(*=χ; d/X; λ!ή и ϊ^ = /^χ=*.; rf/λ; λ/*).
представленные на рис. 18 [51].
Для определения методом отбора максимальной силы от
воздействия волн на вертикальную обтекаемую преграду с
поперечными размерами а <: 0,4λ i\ b ^ 0,4λ при d>dcr в [51]
использовано выражение
Qmax — Qv, ma\°v + Q/,m«x8„ 10.60(36)
где Qv, max и Qi, max — соответственно скоростной и инерционный
компоненты силы от воздействия волн, определяемые по
формулам:
Qv, max - 72~ pgbh*klavfc 10.61 (38)
Qi, шах = \ №b2hkv4$i4 10.62 (37)
bv и δ/ — коэффициенты сочетания скоростного и инерционного
компонентов максимальной силы от воздействия волн,
определяемые по рис. 15 [511 или П0 зависимостям:
*„ = £ ; Ю.63
\ Β{\Βλ\άζ
d
ΪΒ302
[shkd
δ. = 4 , 10.64
sh kd
где Si в числителе 10.63 определяется для любого момента
времени, а в знаменателе — только для t = 0; в 10.64 в
числителе находится В3 также для любого значения /, а в
знаменателе при <7/, max на уровне г = 0 (ηι — ордината волновой
поверхности при qitmax); αΌ и α,— скоростной и инерционный
коэффициенты глубины, рассчитываемые, в свою очередь, так:
У
а, = 4* J θΧΌάζ; 10.65
346
a-i = k\Oxldz. 10.66
d
По 10.65 и 10.66 построены графики αΌ = ΐ(ά/λ, λ/Λ) и α,=
= F(d/K, λ/Λ), представленные в [511 на рис. 16. Расстояние
ZQ,max от расчетного уровня воды до точки приложения
максимальной силы Qmax от воздействия волн на вертикальную
обтекаемую преграду рекомендуется определять по формуле
Zq, max = л (Qi', max%2(?, ν + Ql, maxO^Q, /), 10.67 (46)
Vmax
где zQtV и zq, i — ординаты точек приложения соответственно
скоростного и инерционного компонентов сил:
ZQ,v = \KJiv,relk 10.68(48)
ZQ,l=*h.rel\ 10.69(47)
где ζΌ, rei и ζ/, rei — относительные ординаты точек приложения
скоростного и инерционного компонентов сил, принимаемые по
графикам рис. 21, а μΌ и μ; — скоростной и инерционный
коэффициенты фазы, принимаемые по рис. 22 [51]. Величины ζΌ,Γ3ΐ
и ζι trei могут быть найдены так:
J ^,тахг',г
С*, rei = —т ; 10.70
λ ί 1ν. max d*
j ?/, max z-
dz
W.r,/--^J Ю.71
Ml
λΙ <7i,maxd*
Скоростной и инерционный коэффициенты фазы μ^, и μ,-
можно рассчитать:
η \
^В1\В1\гаг J ^IBijd*
\\, = -* ^ ; 10.72
[Β,ΙΒ,Ιάζ Jb^B^zAz
η ηι
)ΒΖζάζ^ ΒΖάζ
Ρ' = "ϊ ΪΓ 10·73
^Β3άζ] Β3ζάζ
d d
Линейная нагрузка от волн на горизонтальную обтекаемую
преграду в отличие от вертикальной преграды складывается из
347
горизонтальной Рх и вертикальной Рг составляющих.
Максимальные значения Рт&х рассчитываются по формуле (49) [51]
для двух случаев:
. а) при РХу max и соответствующей этой фазе волны
вертикальной составляющей Рг\
б) при Рг, max и соответствующей этой фазе волны
горизонтальной составляющей Рх.
Максимальные значения горизонтальной составляющей
линейной нагрузки от волн PXt max на горизонтальную обтекаемую
преграду и вертикальной составляющей Pz, max следует
определять по зависимостям:
Рх. шах = Я,А* + PJjdi Ю-74 (50)
Ρ ζ, шах = Pzzfizv + ΡζίΚι- Ю.75 (53)
Скоростной Ρχυ и инерционный РХ1 компоненты
горизонтальной составляющей линейной нагрузки от волн находятся по
формулам:
р-х* = тк*ьтФ*Л» ю.7б(52)
Ptt^VVgW-rW*** 10,77(51)
аналогичным 10.51 и 10.54 для вертикальной преграды.
Скоростной Ρζυ и инерционный PZi компоненты
вертикальной составляющей линейной нагрузки от волн определяются
так:
Ршо = he*aTkl9«&» Ю.78 (55)
Р,1 = Ъ?&а*-£к№, 10.79(54)
где δζο и δζί — скоростной и инерционный коэффициенты
сочетания, находим по графикам 2 я 1 рис. 23 [51] или по
формулам
Κν= "''а*1; Ю.80
*«* = tatuS! ; 10·81
vz и duz/dt — проекции скорости и локального ускорения
частиц жидкости в волне, определяемые по 10.36 и 10.38; Qzv и
θ*/ — коэффициенты скоростного и инерционного компонентов
линейной нагрузки от волн, принимаемых по графикам г и в
рис. 19 [51] при значениях относительной ординаты zc,rei =
= (d—zc)/d или рассчитываемых по формулам:
348
При ty СООТВеТСТВуЮЩеМ B2max,
в« = Т(1+Д)»8Н2А^ 10·82
при t = О
θ .= !±4}ь-^ 10.83
2ί 1 -f Af2 ch Ы
Mb Af2, B2 и β4 определяются по 10.46, 10.47, 10.43 и 10.45.
10.5. НАГРУЗКИ И ВОЗДЕЙСТВИЯ ВОЛН НА ВЕРТИКАЛЬНЫЕ
ЦИЛИНДРИЧЕСКИЕ ОБТЕКАЕМЫЕ ПРЕГРАДЫ
МАЛЫХ И БОЛЬШИХ ПОПЕРЕЧНЫХ РАЗМЕРОВ
Расчетную обеспеченность высот волн в системе следует
принимать согласно п. 4 обязательного приложения 1 [51], а
именно: для сквозных сооружений и обтекаемых преград
класса 1—1 %; класса II —5%; классов III и IV—13%.
При определении нагрузок на сооружение необходимо
принимать высоту волны заданной обеспеченности^ створе
сооружения и длину волны в пределах от 0,8 до 1,4λ,
соответствующую максимальному волновому воздействию. Для назначения
высотных отметок сквозных сооружений, возводимых на
открытых акваториях, допускается расчетную обеспеченность высот
волн в системе принимать 0,1 % при надлежащем обосновании.
Размеры поперечного сечения преграды (а, &, D) следует
определять с учетом возможного увеличения их в период
эксплуатации за счет коррозии и обрастания морскими
организмами. При наличии опытных данных по снижению влияния
коррозии и морских обрастаний коэффициенты формы необходимо
определять для эллиптических преград по формулам (39) и
(40) [51]; для призматических преград вводится коэффициент
βϋ (также из формулы (40)) и коэффициент β,- по следующей
зависимости:
Р,-^С„ 10.84
где Cv и Ci — уточненные опытные значения коэффициентов
скоростного и инерционного сопротивлений; а и Ь —
соответствующие оси эллипса, вписанного в поперечное сечение
преграды.
Все необходимые зависимости для выполнения машинного
счета (ЭВМ) приведены в параграфе 10.4.
Для облегчения интерполяций по d/λ в данном случае
включены дополнительные графики расчетных коэффициентов
при d/λ = 0,1; 0,12; 0,15 и 0,25: графики r\rei — рис. 10.6;
графики б**· и δχν — рис. 10.7; 10.8; 10.9; графики б/ и δυ — рис.
10.10; 10.11; 10.12; 10.13; графики μ/ и μυ — рис. 10.14 и 10.15.
349
350
351
353
1 ^
II
to
\ Μ
^^λ\ /Ik
<r || *~ *^ ** *я *** ///fl
> >5^<л
Ж
Ш
Π
\
ψ\\\\\
f n s ε? ϊ? ^ §
ί ·£ν * '
^
V/
h
ca4
о
д
5
о
о,
о
«о
<5Г
I
00
I
•о
«si!
·θ<4
ее t3
α.
и к
2§
ёя
Ρ
Εί ϋ
cx»s
α> ω
£ ^
Κ to
Ο
κ η
ο s
ο ο
0 ffl
ο ο
Si Ο
К С
•Θ-S
*а
о
«ST
»s «
s Ξ
il
к
IS
CO
u
о
к
354
355
356
0,1 0,2 0,3 ОЛ
Рис. 10.14. Графики значений инерционного
μν коэффициентов фазы при d/λ = 0,
μ* и скоростного
,1.. .0,12.
0,1 0,2 0,3 0,Ь' х
Рис. 10:15. Графики значений инерционного μ* и скоростного μΌ
коэффициентов фазы при d/λ = 0,15.. .0,25;
Для упрощения расчетов при определении Qmax по
указаниям примечания 3 к п. 21. [51] рекомендуется пользоваться
графиками коэффициентов сочетаний δ, приведенными на
РИС. 10.16, В ЗаВИСИМОСТИ ОТ параметра X = Q/, max/Qt;,max ИЛИ
qi,max/qv, max — относительной глубины d/λ и — пологости
волны λ: h.
По параметру X находятся наибольшее относительное
удаление преграды от вершины волны κ = χ/λ в момент
максимума волновой нагрузки Qmax и коэффициенты сочетания ύι и δν.
Далее, задаваясь несколькими значениями κ, меньшими, чем
полученное по рис. 10.16, рассчитывают по формуле 10.60 (36)
Ι Ι Ι Ι Ι Ι Ι Ι Ι Ι Ι Ι ι ι ■ ι ι Ш #
οί4 ^ с^г сГ <гГ с^Г сгГ <5Г ζί ci ^ ς> ζί cs сз ^ сао^<гг=-> ^"
Рис. 10.16. Графики значений коэффициентов сочетаний δ и κ в
зависимости ОТ Параметра X =* Q/, max/Qv, max ИЛИ qt, maxAfr, max
i-bo 2-δΌ; 3-6xi; 4-βΧΌ.
значения Q, из которых выбирают наибольшее. При этом
коэффициенты сочетания б/ и &Ό для выбранного κ определяют
по рис. 10.16 или для соответствующей относительной глубины
по рис. (15), 10.10—10.13.
Для предварительных расчетов допускается принимать κ по
рис. 10.16, не варьируя, как выше указано, несколькими ее
значениями.
Для построения эпюры линейной волновой нагрузки по
высоте преграды, соответствующей Qmax, находим величину'κ для
этого момента времени (примечание 3, п. 2.1 [51]), а затем по
указаниям п. 2.2 —значения δχί и 6^. По п. 2.3 получаем
превышение взволнованной поверхности η с помощью графиков
рис. 10.6, по которым \\rei можно найти в более широком диапа-
359
зоне исходных параметров, чем по рис. 20 [51]. Затем по п. 2.2
определяем величины q при нескольких промежуточных г, в
том числе при ζ = d и η; и строим эпюру согласно рис. 10.1, α
(14).
Для расчета максимальной величины линейной нагрузки от
волн цтъъ на заданном заглублении г4 следует принять q no
формуле (41) [51] для ряда последовательных значений κ и
выбрать максимальное. Наибольшая величина κ находится из
рис. 10.16 по X = qit тгх/qv, max, а коэффициенты сочетания δ*,-
и δχν — из рис. 10.16 (или рис. 18 [51]) и рис. 10.7—10.9. В
общем случае для каждого ζ имеется свое значение κ,
соответствующее tfmax.
6) Расчетный в)
уровень
а)
' у |j
1
ζ
г ΥΉΐ
iv=j
S7zsup.f HH
"IfcN
L&
Ί I
[_
^__
В
/// /// /// /// ///
Рис. 10.17. Схема расчета нагрузки от волн на обтекаемые преграды
неполной высоты.
Нагрузку от волн на сооружения неполной высоты (рис.
10.17) можно получить по эпюре удельной нагрузки,
построенной в пределах смоченной высоты преграды:
— на преграды, не доходящие до дна, — от η до zsuPi\
(ординаты нижнего среза преграды, рис. 10.17, а);
— на затопленные преграды — от zsup (ординаты верхнего
среза преграды) до d (ординаты дна, рис 10.17,6);
— на затопленную преграду, не доходящую до дна,— от
Zsup до zSup, ι (рис. 10.17, β).
Ординаты точки приложения нагрузки от волн Q находят
по центру площади эпюры q\ Qmax — из ряда значений Q,
полученных при различных величинах κ.
При построении эпюры линейной волновой нагрузки
допускается принимать равными нулю скоростную составляющую
волнового давления на глубине 0,3λ и инерционную — на
глубине 0,5λ.
Следует заметить, что ζί|Γ** и ζυ, rei — относительные
ординаты точек приложения инерционного и скоростного компонен-
360
тов сил определены для величин κ, соответствующих
максимальным значениям этих компонентов. Изменение . ординат
точек приложения компонентов сил при любом κ
(положительном или отрицательном) учитывается коэффициентами фазы μ;
и μ^. Эти коэффициенты могут быть получены из графиков
на рис. 10.14 и 10.15 в более широком диапазоне изменения
исходных параметров, чем по графикам на рис. 22 [51].
Пример 10.1
Дано: d = 30 м; hd = 5,7 м; Τ = 10,6 с. Расчетная скорость ветра Vw =
= 28 м/с; изобаты перпендикулярны главному лучу i — 0,02. Требуется
определить максимальную нагрузку от волн Qmaxi и расстояние zq, max от
расчетного уровня воды до точки приложения максимальной нагрузки на
колонну D = 4 м, сооружения I класса, покрытую морскими обрастаниями в
подводной и гладкую в надводной частях.
Решение.
1. По формуле (151) [51] определяем среднюю длину волн в глубоковод-
- 9,81-10,62
ной зоне: λά — 9.3 14 = ^ м*
2. Расчетная обеспеченность высот волн в системе согласно табл. 1
обязательного приложения 1 [51] составляет 1 %. Определяем элементы волн
у сооружения:
а) высоту волны 1 %-ной обеспеченности вычисляем по формуле (153).
При d/kd = 30/175 = 0,171 из графика рис. 5 находим kt = 0,915; по условию
задачи kr = 1,0; при d/λά — 0,171 и i = 0,02 по табл. 5 лриложения 1 [51]
gd 9,8 Ь 30
находим ki = 0,9; при т,— = —9§ϋ— = 0»376 по графику на рис. 2
приложения 1 ki% = 2,28, тогда:
hl% = 0,915- 1,0-0,9.2,28.5,7= 10,7 м;
б) среднюю длину волны при d/Kd = 0,171 и -4^- = ■ = 0,01
gT- 9,81-10,62
(рис. 4 приложения 1) получаем λ/λά = 0,85, откуда
λ" =0,85- 175= 149 м.
_3. Максимальную нагрузку от волн Qmax определяем по п. 2.1 [51]. При
£/λ = 4/149 = 0,027 по табл. 13 находим kv = 1,0; при d/λ = 30/149 = 0,2 и
λ/Λ = 149/10,7 = 13,9 по графикам а и б рис. 16 снимаем щ = 0,88 и αΌ =
= 1,77. По графикам рис. 17 для круглоцилиндрической преграды имеем
ft= 1,0 и β0= 1,0.
Далее вычисляем по формулам (37), (38):
(?/linax=T'1,0'9,81,3'14,4»0210,7,1'00,88,1»0::::::1162'3 кН;
Qv, max = J2' 1.0.9,81 -4,0- 10J2-1,02.1,77-1,0 = 659,5 кН.
При X = Qi,mzxlQv, max = 1162,3/659,5 = 1,76 из рис. 10.16 находим
максимальное значение κ = 0,172 и значения коэффициентов δι и δ0 при d/λ =
= 0,2; λ/Λ = 13,9 (по интерполяции). По! формуле (36) ВЫЧИСЛЯеМ Qmax ДЛЯ
κ = 0,172 и ряда меньших значений κ; результаты сводим в табл. 10.3 и
выбираем наибольшее значение:
Qmax= 1345,5 при κ = 0,14.
361
Таблица 10.3
χ
0,172
0.14
0,13
δ.
ι
1,02
1,015
0,98
Qi, max* V
кН
1185,8
1180.9
1139,7
К
0,13
0,25
0,29
кН
86,2
164,6
191,1
Qmax'
кН
1272.0
1345.5
1330,84
4. Ординату zQt max точки приложения максимальной силы Qmax
определяем по п. 2.5 [51]: при d/X = 0,2 и X/h = 13,9 по_графикам / и2 рис. 21
находим ζ/, tei = 0,08 и ζ0, rei = 0,035. При κ = 0,14, λ/Α = 13,9 и d/X = 0,2 по
графикам рис. 22 имеем μι = 0,85 и μ0 = 1,7·.
По формулам (47), (48), (46) вычисляем
2·^ /== 0,85-0,08-149= 10,1 м;
zQtV = 1,7-0,035.149 = 8,85;
^Q,max:=:T345T(1162'3·1'015·10'1 "h 659·5·0.258»85) = 9.89 м-
Пример 10.2
Дано: d = 15 м, h5% = 6,5 м, λ = 65 м. Для сваи квадратного сечения
(а = 0,6 м) в составе эстакады (сооружение II класса) требуется
рассчитать Qmax, Zq, max и κ, а также волновую нагрузку Q для сваи второго ряда,
удаленного от первого на 7 м, в момент времени, соответствующий Qmax.
Решение.
1. Максимальную силу Qmax определяем по п. 2.1 [5JJ. При α/λ =
- 0,6/65 = 0,0924 по табл. 10.2 (13) находим kO = 1,0; при d/X = 15/65 = 0,23
и X/h = 65/6,5 = 10 по графикам а и б рис. 16 определяем щ = 0,88 и αΌ =
= 1,9. По параметру а/Ь = 1 из графиков рис. 17 принимаем β; =1,62 и
β. = 1,6.
По формулам (37) и (38) вычисляем:
О/.шах- -5"· 1.0-9,81.3,14-0,62-6,5-1,0-0,87-1.62 = 25.5 кН;
Qv, max = - "Ϊ2"· 1.0-9,81.0,6-6,52.1)0з. 1,9-1.6 = 62,7 кН.
При X = 25,5/62,7 = 0,41 из рис. 10.16 находим максимальное значение
κ = 0,033 и коэффициенты δ/ и δ0 (при d/X = 0,23 и X/h = 10). Далее по
зависимости (36) вычисляем Qmax для κ = 0,033 и ряда меньших ее значений.
Результаты приведены в табл. 10.4, из которой получаем наибольшее
значение Qmax = 67,3 КН.
Таблица 10.4
%
0,033
0,03
0,025
0,02
δ/
ι
0,38
0,35
0,29
0,23
Qi, max'V
• " кН
9,8
9,0
7,4
5,9
К
ν
0,91
0,93
0.95
0,96
Qv, max,5i;'
кН
57,2
58,3
59.6
60,3
^чпах'
кН
67,0
67,3
67,0
66.2
362
2. zQt max определяем по п. 2.5 [51]. При d/λ = 0,23 Η_λ/Λ = 10 из_рис.21
находим ζ,·, rei = 0,09 и ζβ. ге/ = 0,021; при κ = 0,03, d/λ = 0,23 и λ/Λ = 10
по рис. 22 — μι = 0,49 и μ0 = 1,10.
По формулам (47), (48) и (46) вычисляем
zQt ί = 0,49-0,09-65 = 2,87 м;
zQilf= 1,100,021 65- 1,50 м;
2Q, max = 67~3 (25,5 0.35-2,87 -f 62,7-0,93-1,50) = 1,68 м.
3. Для второго ряда свай, удаленных от вершины волны на
относительное расстояние κ2 = κ+7/65 = 0,138, определяем Q и zq. По рис. 15 при
κ2 = 0,138, d/λ = 0,23 и λ/Λ = 10 находим δ/= 1,05 и δ0 = 0,21, а по рис.
22 — μι = 0,75 и μ0 = 2,36.
По формулам (36) и (46) вычисляем
Q = 25,5- 1,05+62,7-0,21 = 40,0 кН,
zQ = щц (25,5-1,05-4,35 + 6,4-0,21 3,37) = 4,0 м.
Значения zQt ι = 4,35 и zQt Ό = 3,37 рассчитаны по (47) и (48).
Пример 10.3
Для естественных условий примера 10.1 требуется найти Qmax и zQi max
для колонны D = 3 м плавучей буровой установки, подверженной
периодической очистке от обрастания и коррозии (сооружение 1 класса). Опытные
значения С0 = 2/3 и С; = 2.
Решение.
1. Максимальную нагрузку от воли Qmax находим по п. 2.1 [51]. Для
отношения D/λ = 3/149 = 0,02 из табл. 10.2 (13) принимаем kv = 1,0.
Коэффициенты at- = 0,88 и <х0 = 1,77 (см. пример 10.1); β/ и β0 согласно
примечанию 1 п. 2.1 определяются по (39) и (40):
$. = JL.2 = 1,0; β;, = 0,67.
По формулам (37) н (38) имеем:
Qi, тах= Τ ЬО-адЬ3,14-32-10,7-1,00,88· 1,0 = 651,7 кН;
Qv тах = уз 1.0 9,81 -3-10,72.1,02.1,77-0,67 = 332,2 кН.
При X — 651,7/332,2 = 1,96 из рис. 10.16 находим максимальное
значение κ = 0,22, а из рис. 15 —значение δ/ = 0,95 и δ0 = 0,01 (при dfk = 0,2
Таблица 10.5
X
0.22
0.20
0,16
0,15
0,14
0.13
δ;
1
0,95
0,98
1,02
1,02
1,015
0.98
Ql, max'V
кН
619,4
638,0
664,4
664,4
661,5
638,0
ь*.
V
0,01
0,05
0,16
0,2
0,24
0,28
Qv, max*8i/'
кН
3,33
16,7
52,9
66,6
80.4
93,1
^гаах'
кН
622,7
654,7
717,3
731,0
741,9
731,1
363
и λ/h — 13,9). Далее по (36) вычисляем Q для κ = 0,22 и при меньших ее
значениях. Результаты вычислений даны в табл. 10.5, из которой получаем
Qmax - 741,9 КН.
2. Ординату zQ> max определяем по п. 2.5 [51]^ Согласно примеру 10.1
(и. 4) ζ/, re/= 0,08; ζ„. rei = 0,035. При κ = 0,14, λ/Α = 13,9 и rf/λ = 0,2 из
графиков рис. 22 следует, что μ; = 0,85 и μ0 = 1,7.
По формулам (47), (48) и (46) вычисляем:
zQ / = 0,85 0,08· 149 = 10,1 м;
zq,ν = 1.70,035-149 = 8,85 м;
ZQ, max = 74T¥(651'7'1,015'10·1 + 332.20.2-*-8.85) = 9.96 Μ·
Пример 10.4
Для условий примера 10.1 при ζ = 0 найти qmskX и κ, а также q в
момент времени, соответствующий Qmax- Построить эпюру q для того же
момента времени.
Решение.
1. Удельную нагрузку qmskX определяем по п. 2.2 [51]: при ζ = 0; z,ei =
= l—zld= 1; для отношений d/λ = 0,2; λ/h = 13,9 и zrei = 1 из графиков
рис. 19, а, б имеем θ*/ = 1,02 и Θ*» = 0,48. Значения коэффициентов kO, βί и
β0 получены в примере 10.1.
По формулам (42) и (43) вычисляем:
3,142-4а 10,7
?/, max = 1.<>.9,81-^—~П9 1.0.1,02.1,0 = 56,45 кН/м;
*v, max = 1.0 9,81 у 3,14-4 -^Г 1.00,48· 1,0 = 30,3 кН/м.
При X = 56,45/3,03 = 1,86 находим (рис. 10.16): κ = 0,194; δ* = 0,99
и δΧΌ = 0,06 при d/λ = 0,2 и λ/h = 13,9.
Далее по формуле (41) для κ = 0,194 и ряда меньших ее значений
вычисляем q. Результаты сводим в табл. 10.6 и выбираем из них qmax -
= 61,35 кН/м при κ = 0,15.
Таблица 10.6
0,194
0,18
0в16
0,15
0,14
xi
0,99
0.99
0,96
0,95
1 0,91
47, max·5*/'
кН/м
55,86
55,86
54,19
53,6
51,35
Jxv
0,06
0,09
0,20
0,26
0,31
Я ν, max*°jfu'
кН/м
1,82
2,65
5,98
7,74
9,21
Q>
к Η /м
57,68
58,51
60,17
61,34
60,56
2. Значение q при ζ = 0 в момент времени, соответствующий Qmax,
рассчитываем по формуле (41). Согласно примеру 10.1 Qmax соответствует κ =
= 0,14; из табл. 10.6 q = 60,56 кН/м при! κ = 0,14.
3. Для построения эпюры q при κ = 0,14; δχι = 0,91 и δΧΌ = 0,31
(согласно табл. 10.6) определим qi тлх и qv тях по (42) и (43) при ζ = η и
Zrei = 1; 0,8; 0,6; 0,4 и 0._
Из рис. 10.6 при d/λ = 0,2 и λ/h = 13,9 находим, что: v\rei = —0,28, а
по (44) имеем η = — 0,28 · 10,7 = — 3,02 м. Результаты расчетов см. в
табл. 10.7.
364
Таблица ΙΟΊ
zrel
1,1
1
0,8
0,6
0,4
0
г,
Μ
-3,02
0
6
12
18
30
θ .
цх1
1.17
1,02
0,81
0,68
0,58
051
Я ι, max»
кН/м
64,7
56,45
45,0
37,5
32,14
28,2
?i,max,8jri' !
кН/м
58,8
51,4
40.87
34,2
I 29,3
25,68
θ
"xv
Ofi
0,48
0,30
0.20
0,13
0,11
Qv, max»
fcH/m
37,93
30,3
18,8
12,64
8,23
6,96
Qv, max,5jft>' 1
кН/м
11,76
9,39
5,88
3,92
2,55
2,16
<7.
кН/м
70,56
60,79
46,75
38,12
31,85
ι 27,84
Эпюра <7 ^представлена на рис. 10.18.
Рассчитанная- по площади эпюры
волновая нагрузка Qmax — 1342,5 кН;
увеличение этого значения против
определенного по (36) составило 2,4 % за
счет погрешности при подсчете
площади по трапециям.
Пример 10.5
Дано: d = 30 м, Л, % = 10,7 м, Г=
= 149 м. Определить Qmax и zq, max на
затопленную, покрытую морскими
обрастаниями колонну диаметром 5 м с
верхним срезом zsup = 0,1 rf; Cv = 4/3.
Решение.
1. Построим эпюру q для
нескольких значений κ: 0,1; 0,12; 0,14 и 0,16,
для которых по графикам рис. 18
находим следующие расчетные величины
для bxi\ 0,74; 0,83; 0,92; 0,96 и для δχυ:
0,59; 0,45; 0,31; 0,19. По (40)
получаем β0 = Cv = 4/3; определяем q по
зависимости (41).
Величины Q и zq рассчитываем по
формулам:
q = 70,56 кн/м
\ 60,79
\ **6J5
\ SB, 12
\ 51,85
\г?№
-102 п .
' Расчетный,
ν уробень
0
6
12
16
30
Рис. 10.18.
Эпюра
10.4.
<? = ΣΔ(?*; 10·85 {
1 ^ 1
Результаты вычислений сводим в табл. 10.8.
=~οΣ^η*η.
q к примеру
10.86
Таблица 10.8
-»
Μ
3
6
12
18
24
30
zrel
0,9
0,8
0,6
0,4
0,2
0,0
Ki
χι
0,9
0,8
0,67
0,58
0,51
0,5
Βχν
0,37
0.30
0,21
0,15
0,13
0,12
tf/, max'
кн/м;
78,99
70,17
58,80
50,96
44,69
43,90
4v, max»
кН/м
40,18
32,14
22,54
16,07
13,62
12,84
Q, кН
2Q, max
Значения д, кН/м, при χ, равном
0,1
82,12
70,95
56,84
45,28
41,16
40,08
1435,99
14,8
0,12
80,62
72,81
58,99
49,59
43,22
42,24
1493,62
14,9
0,14
85,06
74,48
61,05
51,84
45,28
44,39
1544,97
14,95
0,16
83,49
73,40
60,76
ί 51,94
ι 45,47
1 33,59
1535,95
ί 14,99
365
Эпюры q приведены на рис. 10.19. Наибольшее значение Q получено при
κ = 0,U; Qfflax = 1544,97 кН, причем zQ. max = 14,95 м.
v Расчетный, уровень
σ= 82,12 кн/м Ύ^\ ry Z sup $=80,62 кн/м
Тп—z\3 * х~* \J
^Расчетный уровень
Х=0,1
v Расчетный уро день
а = 85,06кн/м
* =0,14
*«-»
12
18
1ч-
30
VРасчетный уровень
у =83,49 кН/Μ
*=0,16
Рис. 10.19. Эпюра q к примеру 10.5·.
Пример 10.6
Дано: d = 30 м, h\% = 10,7 м, λ = 149 м. Определить полный
максимальный опрокидывающий момент на круглоцилиндрическую преграду
диаметром D — 29,8 м, расположенную на каменнонабросном основании. По-
366
"строить эпюры волнового давления по первой (Θ = 0°) и второй (Θ = 60°)
образующим цилиндра в момент Qmax.
Решение.
1. Принимаем коэффициент опрокидывающего момента согласно
табл. 15а* (при D/λ = 0,2 и d/λ = 0,2) βρθΓ = 0,46 и рассчитываем величину
MZtPOr ιφ формуле 66а* п. 2.17* [51]:
ΜΖρρο,= γξ 1,0-9,81 · 10,7-29,83.0,46 = 79861,9 кН/м.
Рис. 10.20. Эпюры волнового давления ρ по передней образующей
цилиндрической преграды (в точках /, #, 5, 7, 0, θ = 0°) и по второй
образующей (в точках 2, 4, 6, 8, 10, θ = 60°); 7/ —уровень смоченной
поверхности на цилиндре в момент максимума горизонтальной силы
Момент от максимальной горизонтальной силы Qmax определяется по
пп. 2.1 и 2.5 [51]. По (37) при kO = 0,86; α,- = 0,88 находим:
Q. max = j 1,0-9,81 -3,14·29,82-10,7-0,86-0,88-1,0 = 55378 κΗ.
Согласно рис. 15 при dfk = 0,2; D/λ = 0,2 и λ/Ά= 13,9 максимум
инерционной компоненты наступает при κ = 0,18 и о\-=1,01, тогда по (36)
Qmax = 55378· 1,01 = 55932 кН. Скоростной компонентой можно пренебречь.
При κ = 0,18 (рис. 22) определяем μ,- = 0,97, тогда по формуле (47)
zQ ;=: 0,97 - 0,082 . 149 = 11,85 м.
Момент горизонтальной силы относительно центра днища равен:
Мх - 55932(30—11,85) = 1015166 кН/м.
Полный максимальный опрокидывающий момент, действующий на
преграду (рис. 10.20), можно записать так:
367
Μ = MZiPor+Mx = 79861,9+1015166 = 1095027,9 кН/м.
2. Уровень смоченной поверхности цилиндра ζ = %h в момент максимума
Qmax обозначен кривой //на рис. 10.20. Волновое давление ρ в точках
поверхности вертикальной круглоцилиндрической преграды в тот же момент
времени следует определять по формуле (ббб)^* [51]. Для точек /, 3, 5, 7, 9
первой (передней θ = 0°) образующей цилиндра и точек 2, 4, 6, 8, 10
второй образующей цилиндра (0 = 60°) рассчитываем значения chk(d — z) и
вычисляем р. Результаты расчетов даны вгтабл. 10.9 и на рис. 10.20.
Таблица 10.9
г
—7.8
—5,4
0
10
20
30
k(d-z)
1,264
0,842
0,421
0
ch k(d-z)
1,9110
1,3759
1,0899
1.00
ch k(d-z)
chkd
1,0
0,72
0,57
0,523
Значения р, кПа, в точках по образующим
первой
9
7
5
3
1
0
72,62
55,17
43,67
40,07
второй
10
8
6
4
2
0
52,48
37,79
29,91
27,45
Пример 10.7
Для условий примера 10.6 рассчитать максимальную донную скорость
Vb, max в точках, расположенных на контуре преграды (0 = 90°) и впереди
нее, на расстоянии 0,25λ.
Решение.
Из табл. 15в* [51] при D/λ = 0,2 находим значения коэффициентов qv
0,98 —на контуре и 0,67_—впереди преграды. При /г = 2-3,14/149 = 0,0422;
sh kd = sh 1,27 = 1,64 и Τ = 10,6 с по формуле (66в)"" определяем значение
максимальной донной скорости:
— на контуре преграды
3,14-10,7 1
vb, max = 2·°>98 ]0>6 Щ = 3,78 м/с;
— впереди преграды
3,14 10,7 1
vb, max = 2*0'67 Ю,6 Щ = 2'59 М/С·
10.6. НАГРУЗКИ И ВОЗДЕЙСТВИЯ ВОЛН
НА ГОРИЗОНТАЛЬНЫЕ ОБТЕКАЕМЫЕ ПРЕГРАДЫ
В общем случае положение элемента сквозного сооружения,
произвольно ориентированного в пространстве, определяется
координатами х> у> ζ какой-либо точки этого элемента и углами
<р и ψ, рис. 10.21. Горизонтальными обтекаемыми преградами
называют такие цилиндрические элементы, ось которых
составляет с вертикалью угол φ = 90°. В расчетах следует
рассматривать два положения горизонтальной преграды:
первое — угол ψ = 90°; при этом предполагается, что
направление оси О* совпадает с лучом волны, а начало координат —
с расчетным уровнем, ось 0ζ проходит через вершину волны и
направлена вниз; второе положение — угол ψ Φ 90°.
368
/J /6
6Γ Q,kH\
Рис. 10.21. Схемы сквозного сооружения и график нагру-
зок от волн на вертикальную колонну (пример 10.15)
а) расчетная схема: 1—16 — узлы сооружения; 17 — цилиндрический
элемент, произвольно ориентированный в пространстве; б)
упрощенная схема; в) график Q = f(^).
со
Си
и
со
О .
О
8-
О
и*
се С
jl
fee
д
g s
к 8
s? >»
α, α,
я со
к к
K»S
к о
д к
cO »S
Η CO
α> к
8*
о о
Ё5
α) ς
К СО
Pi «
s к
О)
л со
о ш
т
т
к £
а>
си
к с:
со £
о
к м
β~
со
К
Он
37Q
о
II
«<
•Q
S
α.
в
·&
ев
αχ
к
со
о
Η
я
3
S
Ef
S
•θ·
•θ-
<η
о
»s
к
и
9
ев
а
к
■Θ·
се
а.
со
CN
О
К
а.
371
372
ПервЬе положение преграды рассмотрено в [51], ниже
привод итсяогсример расчета. Для облегчения интерполяций по
параметру d/λ в пособие включены дополнительные графики
коэффициентов 6zi и δζυ при d/λ = 0,1 и 0,25 (рис. 10.22); 0,12
(рис. 10.23) и 0,15 (рис. 10.24).
Пример 10.8
Дано: глубина у сооружения d = 25 м; /ι,% = 6,7 м; λ = 100 м.
Требуется определить PXt max, Pz. max, соответствующие им значений Pz и Ρχ,
а также Ртах на горизонтальный элемент сквозного сооружения I класса,
расположенный на уровне zc = 5 м, D = 0,5 м, при ψ = 90°. По опытным
данным Со = 1,33.
Решение.
1. Максимальную величину горизонтальной составляющей нагрузки от
волн PXt max определяем по п. 2.7 [51]._При D/λ = 0,5/100_= 0,005 и из
табл. 10.2 (13) принимаем kv = 1,0. При d/λ = 25/100 = 0,25; λ/h = 100/6,7 =
= 15; zrei = 1—5/25 = 0,8 определяем по графикам рис. 19, а, б путем
интерполяции Qxi = 0,75 и βΧΌ = 0,25; по графикам на рис. 17 находим
βί =1,0, а по формуле (40) —значение β0 = 4/3.
По формулам 10.77 (51) и 10.76 (52) имеем:
Pxi = у 1,0-9,81.3,14-'.0,52 ^ 1,0-0,75· 1,0 = 0,608 кН/м;
ΡΧί, = у 1,09,8ЬЗ,14.0,5-щ-1,02-0,25.1,33 = 1,533 кН/м.
Задаваясь различными значениями κ, по графикам / и 2 на рис. 10.7
принимаем δχί и δΧΌ и далее по * 10.74 (50) вычисляем Рх,тах. Результаты
расчета сводим в табл. 10.10. Таким образом, Рх тах — 1,594 кН/м при κ =
= 0,03.
Таблица 10.10
X
0,01
0,02
0,03
0,04
0,29
~
°д7
0,05
0.13
0,20
0,25
1 0,94
Ρ ,-о .,
xi χι' \
кН/м j
0,03
0,079
0,122
0,152
| 0,572
δ™
XV
0,995
0,98
0,96
0,93
ί -0,06
Ρ -δ ,
XV XV'
кН/м
Ι 1,525
1,502
1,472
1,426
-0,092
ρ ,
χ'
кН/м
1,555
1,581
1,594
1,578
0,480
2. Максимальную величину вертикальной составляющей нагрузки от волн
определяем по п. 2.8 [51]. При d/λ = 0,25; λ/Λ = 15 и zrei = 0,8 по
графикам на рис. 19, в, г получаем θ2/ = 0,65 и 6го = 0,15.
По формулам 10.79 (54) и 10.78 (55) имеем:
1 6,7
Pzi = -j 1,0-9,81 3,142-0,52щ 1,0-0,65-1,0 = 0,527 кН/м;
2 6 72
Pzv = "J ^О*9'81 -3,140,5 -щ-1,02·0,15· 1,33 = 0,916 кН/м.
Задаваясь различными значениями κ, по графикам /и2«рис. 10.22
определяем 6Zi и б20, и далее по формуле 10.75(53) вычисляем Р*. max.
Результаты расчета сводим в табл. 10.11.
373
Таблица 10.11
χ
0,26
0,28
0,29
0,30
0,03
δ*;
Zl
—0,04
—0,18
-0,23
-0,28
0,99
ρζϊ\ν
кН/м
—0,021
—0,095
-0,121
—0,148
0,522
*..
ζν
-0,98
-0,96
—0,94
—0,89
—0,03
ζν ζν'
кН/м
—0,898
-0,879
—0,862
-0,815
-0,027
ρζ>
кН/м
-0,919
—0,974
-0,983
-0,963
0,495
Таким образом, как это следует из табл. 10.10 и 10.11, Рх тзх =
= 1,594 кН/м и Ρ г = 0,495 кН/м — при κ = 0,03, a Pz, max = 0,983 кН/м и
Р* = 0,480 кН/м — при κ = 0,29. Следовательно, согласно п. 2.6 [51],
максимальное значение равнодействующей линейной нагрузки от волн на
элемент 5—6 (рис. 10.21) равно:
— в первом случае
Лпах = К 1,5942 + 0,4952 * 1,583 кН/м;
— во втором ■
/0,4802 + 0,9832 = 1,094 кН/м.
Линейная нагрузка по всей длине элемента 5—6 постоянная, поскольку
для него значения χ и ζ также постоянны.
Пример 10.9
Для условий примера 10.8 определить волновые нагрузки, действующие
на стержень 6—8 (рис. 10.21) при zc = 5 м, ψ = 45°.
Решение.
Второе положение стержня относительно луча отличается от первого
тем, что при *ψ Φ 90° стержень обтекается потоком жидкости, скорость и
ускорение которого не перпендикулярны его оси. Если νχ и dvx/dt разложить
на две составляющие, одна из которых перпендикулярна, а вторая
параллельна оси стержня, то, как показали опыты, волновую нагрузку создают
лишь нормальные составляющие.
Нормальные составляющие к оси элемента 6—8 горизонтальных
проекций скорости υχ и ускорения dux/dt равны:
^,π^λ-^Ψ·
dvr n dvx
10.87
Нормальная составляющая линейной нагрузки от волн на элемент 6—8
имеет вид:
Ρ η = ΡχυδΧν sin2 ψ+Ρχίδχί sin ψ. 10.88
Определим значение Рп для двух случаев:
а) абсцисса точки 6 χ = 0,03Т:
Ρ п. 6 = 1,533 · 0,96 · 0,7072 +0,608 · 0,20 · 0,707 = 0,822 кН/м;
б) абсцисса точки 8 χ = 0,03λ+10 = 3+10 = 13 м; κ = 0,13; δΧΌ = 0,43*
δχΐ = 0,75:
Ρ η, a = 1,533 . 0,43 · 0,7072+0,608 · 0,75. 0,707 = 0,981 кН/м.
Составляющие линейной нагрузки от волн по осям Ох и Оу суть:
Рп.х = рп*1*Ь
η, у
Рп cos ψ.
10.89
374
-Доставляющие нагрузки от волн на элемент 6—8:
2 Рп> х = Ρ*·' + Ρ»>» sin ψ Lt; Σρη,ν= Ρ«·6\Ρη·8 cos ψ Ζ.,. 10.90
Подставляя значения символов в 10.90, получим
Σρη χ= 0,822 + 0,981 0707,1414 = 901 кН;
ЦРя,у = 0-822 + 0'9810.707.14,14 = 9.01кН.
Вертикальные составляющие линейной нагрузки от волн в точках 6 и 8
)пределяются по 10.75(53), 10.78(55) и 10.79(54). При κ = 0,03 и 0,13 из
ж. 10.22 находим δζυ и 62ί·:
а) в точке 6
Рг, б = 0,916(—0,027) +0,527(0,99) = 0,495 кН/м;
б) в точке 8
р2 8 = 0,916(— 0,5)4-0,527(0,69) = —0,094 кН/м.
Вертикальная составляющия нагрузки от волн на элемент 6—8 равна:
Σ Я2=°-^^ .4,14 = 2,84 к-Н.
Значения равнодействующей линейной нагрузки от волн по формуле
(49) [51] составят:
а) в точке 6
Д. = /0,8222 + 0,495* = 0,963 кН/м;
б) в точке 8
Р8 = /0,9812 + 0,0942 = 0,986 кН/м.
Равнодействующая Ρ находится в плоскости, перпендикулярной оси
стержня 6—8 под углом к горизонтали, равным —31° в точке 6 и +5,5° —
в точке 8.
Напомним, что горизонтальная и вертикальная составляющие нагрузки
от волн на элемент 5—6 в примере 10.8 составили:
ΣΡΧ= 1,594-10= 15,94 кН;
ΣΡΖ = 0,495 · 10 « 4,95 кН.
Пример 10.10
Бегущая волна (h\%*= 10,7 м; λ= 115 м) распространяется по акватории
глубиной d = 23 м. Требуется найти скорость жидкости на уровне гребня
волны.
Решение.
Из графика рис. 10.6 при d/λ = 0,2; λ//ι = 10,74 принимаем r\rei — -—0,62,
тогда η =—0,62· 10,7 =—6,63. При k = 0,0546; Ы = 1,256 определяем по
формуле 10.39:
Co=/ow0,85=12'358m/c·
По графику рис. 10.5 находим 2Л//г = 0,91, а следовательно, Л =
= 4,8685 м; Л2 = 23,7.
375
Рассчитываем аргументы и функции:
k(d — z) =0,0546(23+6,63) = 1,618;
chk(d — ζ) =2,6206; ch2k{d — z) = 12,706;
ch3k(d — ζ) =64,2; ch kd = 1,8981; sh kd = 1,6133.
По формуле 10.42 при ωί = 0 имеем:
= 2,6206 + 0,6033 — 0,01702 = 3,207.
Горизонтальную проекцию скорости на гребне υχ определяем по формуле
10.35:
3,207
Vje = 4,8685-0,0546.12,358 j-^узз = 6»53 м/с·
Для сравнения найдем υχ по формуле 2,26 в первом приближении:
νχ = UjjL /9,81 0,0546.0,85 ^gg = 5,86 м/с,
т. е. на 10 % меньше, чем при расчете по более точной формуле третьего
приближения.
При определении нагрузок от волн на лежащий на дне трубопровод
в соответствии с требованиями пп. 2.10 и 2.11 [51] следует учитывать
изложенные" здесь рекомендации.
1. При расчете волновых воздействий на подводные ^трубопроводы
надлежит выделять три участка трассы: глубоководный (с?Д>0,5);
мелководный (dcr < d ^ 0,5λ); прибрежный (d < dcr).
Трубопроводы, укладываемые на глубоководных участках трассы, на
волновые воздействия не рассчитываются. Значения горизонтальной
(боковой) Рх, cai и вертикальной (подъемной) Рг, cai составляющих линейной
нагрузки от волн и течений на свободно лежащий на дне трубопровод при
dcr < й < 0,5λ следует определять, рис. 10.1(14,6), по формулам:
Рх, cai = Pxktot COS» aw + Pxc cos* ac; 10.91
Pz, cai = Pzblot COS* aw + P2C COS* ac% 10.92
где Рх и Pz — горизонтальная и вертикальная проекции линейных нагрузок
от волн, рассчитываемые для двух случаев, согласно пп. 2.10 и 2.11
(формулы (56) — (59) [51]); Рхс и Pzc — горизонтальная и вертикальная
составляющие линейной нагрузки от действия на трубопровод течения,
определяемые по зависимостям:
Рхс = 0,6pDo2c; 10.931
Pzc = — 0fiPxc; 10.941
dw — угол подхода фронта волны к оси трубопровода или угол между нор-,
малью к оси трубопровода и лучом набегающей волны; ас — угол междэд
нормалью к оси трубопровода и направлением течения; vc — скорость
придонных течений на расстоянии D от дна; kiot — коэффициент снижения, учи-^
тывающий неодновременность действия нагрузки по длине трубопровода.]
определяемый по табл. 10.12.
2. Обеспеченность расчетной высоты. волны в системе следует прини-1
мать для магистральных трубопроводов 5 %, для ответвлений магистраль-!
ных трубопроводов — 13 %.
3. Горизонтальная и вертикальная проекции нагрузок от волн на сво^
бодно лежащий на дне трубопровод в пределах прибрежных участков трас]
376
Таблица 10.12
Расстояние между
опорными точками по трассе
трубопровода
Меньше
0,25λ
(0,25 ... 0,5) λ
(0,5... 1,0) λ
Больше
λ и без
опор
Коэффициент снижения
волновых нагрузок, ktot
0,8
0,7
0,6
0,5
сы (d s^ dcr) должны рассчитываться по указаниям 2.11 [51] при значениях
Ρχυ и Ρχί, полученных по (59) и (58) и умноженных на коэффициент kcr,
определяемый так:
*„=! +1,2
(hcr,i-hs»rV^
10.95
где her, ι — высота волн перед
обрушением (при dcr); hsur — высота
прибойной волны, которая определяется
по указаниям пп. 20 и 21
приложения 1 [51].
4. По полученным значениям
горизонтальной Рх, сл1 и вертикальной
Рг. ш составляющих линейной
нагрузки на свободно лежащий на дне
трубопровод выполняется расчет
устойчивости трубопровода в
соответствии с нормативами для проектиро-.
вания сооружений, подверженных
воздействию волн.
5. С целью упрощения
интерполяции рекомендуется скоростной Ρχυ
и инерционный Ρχι компоненты
горизонтальной составляющей линейной
нагрузки от волн, кН/м, определять
не по формулам (59) и (58) [51],
а по следующим зависимостям:
PXv = ?gDMxvp] 10.96
Pxi = ?gD''VxitP> 10.97
где коэффициенты линейной
нагрузки от врлн Οχυ,ρ и Θλγϊ,ρ, определя-
емые по графикам а и б рис. 10.25,
связаны с θ χυ И Όχι (10.52 и 10.55)
формулами:
χν, ρ '
: λ
10.98
χι, ρ
5)
βχί,ρ
0,5
0,3
0,1
0\ Ι Ι i^^t^a^L [ ί
0/0 0,20 0,30 0,40 0,50 λ
π
4
\
\.
*i
> Ν
S
#*
J5
25
№
0,10 0,20 0,30 0,^0 0,50
Рис. 10.25. Графики значений
коэффициентов линейной нагрузки от
волн θχο,ρ и θ*/, ρ для
цилиндрических преград, лежащих на дне.
3π2Λ
: 4λ "-"'·
10.99
6. При расчете нагрузки по второму случаю (п. 2.10 [51])
максимальную вертикальную Pz% max и соответствующую ей горизонтальную Рх
проекции линейной нагрузки от волн необходимо определять так:
377
Ρ — __ — ρ ·
Γζ, max — 5 XVt
г χ — л χν.
Пример 10.11
10.100
10.101
Дано: Морской глубоководный выпуск сточных вод. Наружный
диаметр трубопровода D = 0,45 м; план и профиль трассы представлены на
рис. 10.26; скорость придонного вдольберегового течения на возвышении
Направление \
вдольберегового
течений
АЛ
Расчетный уровень
SL·.
Рис. 10.26. Расчет нагрузок на подводный трубопровод
(пример 10.11) ♦
а) план рефракций волн по трассе трубопровода; б) профиль дна
по трассе трубопровода; / — трубопровод; 2 — линии фронта волн;
3 —луч волн.
верха трубопровода от уровня дна vc = 0,4 м/с; направление течения
перпендикулярно оси трубопровода; элементы расчетной волны на глубокой
воде: hds% = 5,5 м; Г= 100 м; Τ = 8 с; ρ = 1,03 т/м3; g = 9,81 м/с2.
Требуется определить нагрузку от волн и течений на лежащий на дне
трубопровод.
378
Решение.
Трасса трубопровода разбивается на ряд участков; для каждого из них
принимается средняя расчетная глубина моря. Затем на плане акватории
в районе трассы трубопровода по указаниям п. 18 приложения 1 [51]
строится план рефракции для определения углов подхода волн к трассе
трубопровода а», а по пп. 16—19 того же приложения выбираются значения
элементов волн 5%-ной обеспеченности (h5% и λ) для каждого участка.
Результаты расчетов приведены в табл. 10.13.
Таблица 10.13
Расчетные характеристики
участков трассы
Средняя расчетная глубина
моря d, м
Элементы расчетной волны
5%-ной обеспеченности:
Л5?-« м
λ, м
dfL
λ/ΑοΚ
Угол подхода волн aWt град
Значения расчетных характеристик для участков
1
5
3,8
56
0,09
14,7
65
2
14
4,9
81
0,173
16,5
50
з
20
5.1
87
0,230
17,0
45
«
27
5,2
92
0,294
17,7
40
5
35
5.3
96
0,365
18.1
35
Последовательность вычислении нагрузок на трубопровод проследим на
примере второго участка. По формулам 10.96 и 10.97 определяем скоростной
ΡΧυ и инерционный Ρχί компоненты горизонтальной составляющей нагрузки
от волн. Для этого по графикам рис. 10.25 при d/λ = 0,173 и λ//ι5% = 16,5
находим коэффициенты 0χυ,ρ = 0,033 и θ*,·,ρ = 0,27. Далее по 10.96 и 10.97
получаем:
ΡΧν = 1,03 - 9,81 · 0,45 · 4,9 - 0,033 = 0,735 кН/м;
Pxi = 1,03 · 9,81 · 0,452 - 0,27 = 0,552 кН/м.
По рис. 10.16 для параметра X =_0,552/0,735 =_0,75 находим значение
κ = 0,061 и по графикам 3 и 4 при d/λ = 0,173 и K/h5% = 16,5 определяем
δΧΌ = 0,79 и δχί = 0,55.
Согласно п. 2.10 [51] рассматриваем два случая сочетания нагрузок:
а) максимальная горизонтальная составляющая линейной нагрузки
Ρχ. max, кН/м, при соответствующем значении вертикальной составляющей
линейной нагрузки Рг, кН/м, формулы (56), (57)
Рх. max = 0,735. 0,79+0,552 · 0,55 = 0,885 кН/м;
9
Ρ ζ = —-§- 0,735- 0,79 = 1,045 кН/м;
б) максимальная вертикальная составляющая линейной нагрузки Рг тах,
кН/м, при соответствующем значении горизонтальной составляющей
линейной нагрузки Рх, кН/м, формулы 10.100 и 10.101:
Р:. max = ~ 5"0.735 = - 1,323 кН/м;
Рх = 0,735 кН/м.
По 10.93 и 10.94 находим горизонтальную и вертикальную составляющие
нагрузки от течения:
379
Pxc = 0,6 <ή^ 0,45-0,43 = 0,0445 kH/m;
pzc = — 0,6 · 0,0445 = — 0,0267 кН/м.
Расчетные значения горизонтальной PXt cai и вертикальной Рг, cai
составляющих линейной нагрузки от волн и течений определяются также для двух
случаев по формулам 10т91 и 10.92. Коэффициент ktot = 0,5 определяем по
табл. 10.12:
а)
Рх, cai = 0,885 · 0,5 cos2 50°+0,0445 · 1 = 0,2286 кН/м;
pz cal = — 1,045 · 0,5 · 0,416 — 0,0267 · 1 = — 0,244 кН/м;
б)
Рх, cat = 0,735 · 0,5 · 0,416+0,0445 · 1 = 0,1974 кН/м;
Pz, cai = — 1,323 · 0,5 · 0,416 — 0,0267 · 1 = — 0,302 кН/м.
По найденным расчетным значениям нагрузок от волн и течения далее
выполняется расчет устойчивости трубопровода на дне моря.
10.7. НАГРУЗКИ ОТ РАЗБИВАЮЩИХСЯ ВОЛН
НА ВЕРТИКАЛЬНУЮ ОБТЕКАЕМУЮ КРУГЛОЦИЛИНДРИЧЕСКУЮ
ПРЕГРАДУ
Максимальная сила от воздействия разбивающихся волн
Qcr, max на вертикальную цилиндрическую преграду, диаметр
которой D ^ 0,4dcr, имеет место, когда волны с высотой
обеспеченностью 1 % испытывают первое обрушение в створе
преграды при глубине d = dcr. Волны, которые разрушаются
позади или впереди преграды могут оказывать на преграду менее
интенсивное воздействие, чем волны, имеющие первое
обрушение в створе преграды.
Поэтому расчет волновой нагрузки на преграду по п. 2.12 и
2.13 должен производиться для волн с высотой 1 %-ной
обеспеченности, испытывающих первое обрушение в створе
преграды при глуби Не & — Clcr· Элементы этих волн определяются
по пп. 20, 21 приложения 1 [51]. При этом должны быть
рассмотрены два расчетных случая:
1) у преграды (d = dcr) происходит первое обрушение
глубоководных волн с высотой 1 %-ной обеспеченности в системе
расчетного шторма;
2) волны обрушаются впереди преграды {d<dcr),
сооружение подвергается воздействию прибойных волн. Здесь
рассматриваются волны 1 %-ной обеспеченности в системе при шторме
меньшей интенсивности.
Параметры глубоководных и разрушающихся волн для
условий таких штормов находятся подбором согласно
приложению 1 [51], пп. 13; 15*; 20; 21, npH.d = dCr, а значение h,ur
не должно превышать 0,8dt.
Если после определения высоты разрушающейся волны hsur
и глубины dt окажется, что отношение hSUr/dt > 0,8, то его сле-
380
дует принять равным 0,8. При этом расчетные значения dt
находим по формуле
dt=d+h8°ar 10Л02
с учетом того, что положение вершины гребня разрушающейся
волны не изменяется по высоте преграды.
Коэффициент 6v,cr всегда положительный, а коэффициент
6||СГ следует принимать положительным при x/dt>0 и
отрицательным— при x/dt<0. Положительные значения х отсчитыва-
ются от вершины волны в направлении ее распространения,
рис. 24, α [51].
Верхняя точка эпюры линейных нагрузок на преграду для
рассматриваемой фазы волны x/dt определяется по zrei,
выбираемому на уровне точки пересечения соответствующей кривой
на рис. 25,6 с ограничивающей кривой (пунктирная линия),
характеризующей профиль разрушающейся волны. Точка
приложения максимальной нагрузки Qcr, max принимается по эпюре
линейных волновых нагрузок, построенной согласно п. 2.13 для
фазы волны x/d(y соответствующей Qc,, max-
Пример 10.12
Дано: сооружение I класса капитальности; вертикальные сваи
диаметрами 0,5 и 1,6 м; глубина у сооружения d = 10 м; уклон дна χ = 0,01;
скорость ветра Vw = 20 м/с; разгон L = 675 км; рефракция отсутствует;
волнение установившееся. Требуется найти максимальные равнодействующие
волновых нагрузок и ординаты точек приложения этих нагрузок для
указанных свай.
Решение.
1. Определяем средние элементы волн на глубокой воде по приложе-
gL 9,81-675000 ,„ггл
нию 1 [51], п. 13, рис. 1. Вычисляем-γτ = gm —16550,тогда в соот-
ghd σψ — —
ветствии с рис. 1 имеем:-^ТГ = 0,110 и 4т- =4,82 и hd = 4,49 м и Τ =
Vw vw
= 9,83.
Высота глубоководной волны 1%-ной обеспеченности определяется по
п. 15* и рис. 2 [51]. Параметр gL/Vw — 16550 > 12000, и из рис. 2 получаем
kx% = 2,42; а следовательно, hd\% = 2,42· 4,49 = 10,85 м. Средняя длина
волн на глубокой воде вычисляется по формуле (151) при Τ — 9,83 с:
- 9,81-9,832 лсл
λ* = 2-3,14 = Ш М·
2. Определение элементов волн в месте расположения сооружения.
Случай 1. Находим критическую глубину dcr при первом обрушении
глубоководных волн расчетного шторма без учета рефракции (βΓ=1).
Согласно п. 21 и рис. 5 приложения 1 [51], принимая в первом приближении
hi hdl% 10,85
~~ψϊ =—ψΤ = g 81 ·9 832== °'0114 (уклон дна ί = 0,01, кривая 2), имеем
der/
==- = 0,096, тогда dcn = 0,096-151 = 14,5 м.
381
Глубоководная зона
V м'с
20
18
18.5
gL
vw
16550
20270
19300
*hd
v w
0,110
0,115
0,114
gT
w
4,82
4,97
4,95
V M
4,49
3,80
3,97
Vе
9,83
9,13
9.35
ld> μ
151
130
136
*1«
2,42
2,42
2,42
hd 1% ' M
10,85
9.20
9,60
По рис. 5, полагая во втором приближении — 2 =
В соответствии с пп. 17, 18 обязательного приложения 1 [51] при
dcr ι/λα = 0,096 из рис. 5 и табл. 5 получаем следующие значения
коэффициентов: kt = 0,933; ki = 0,856; kr = 1; kx% = 2,42.
По формуле (153) рассчитываем высоту волны на глубине dcr ι 1 %-Hoff
обеспеченности в системе: (hi%) dcr ι = 0,933· 1,0-0,856-2,42-4,49 = 8,68 м.
hi {h\%)dcri
gT " gT
8,68
= =0,00916 (уклон дна i = 0,01, кривая 2), определяем dCrlKd =
У,о1 ·9,οο~
0,08, тогда искомая критическая глубина dcr = 0,08· 151 = 12,1 м.
Так как первое обрушение глубоководных волн происходит на глубине,
большей, чем глубина у сооружения (12,1 > 10 м), то сооружение
оказывается в прибойной зоне, и расчет, следует выполнять для условий,
рассмотренных ниже. Результаты определения элементов волн для расчетного
шторма представлены в табл. 10.14, строка 1.
Случай 2. Определяем параметры обрушивающейся в створе
сооружения волны с высотой 1 %-ной обеспеченности в системе шторма, имеющего
меньшую интенсивность, чем расчетный, при той же длине разгона.
Задаваясь различными скоростями ветра, меньшими, чем 20 м/с, рассчитываем
значение критической глубины, добиваясь выполнения условия dcr = d = 10 м.
Результаты сводим в табл. 10.14 (строки 2, 3), из которой видно, что на
глубине dcr = 9,93 « 10_м будут обрушаться глубоководные волны, имеющие
следующие элементы: hd = 3,97 м; /idl%=9,60; Td = 9,35с; λ^ = 136 м.
3. Определение элементов волн в месте обрушения (d = dcr = 10 м).
Высоту волны 1 %-ной обеспеченности при первом обрушении hcr = hsur\%
находим по приложению 1, п. 20, рис.__5 [51]. При dlc/Xd = 10/136 = 0,0735
(ί = 0,01, кривая 2) получаем hsur] % /gT2 = 0,009, откуда высота
разрушающейся волны /icrl% = hsur\%= 0,009- 9,81·9,352 = 7,72 м. Дл^на этой волны
принимается по верхней огибающей кривой (рис. 4): при dcrfrd=0,0735 имеем
hsur/L· = 0,77, откуда λ*«Γ = 0,77- 136 = 105. м.
Возвышение гребня обрушающейся волны х\с,Сг с высотой 1 %-ной
обеспеченности в системе определяется по верхней огибающей кривой рнс. 3:
при drJXd=0,0735 получаем η0> СГ/ДСГ=0,83, откуда х\с, сг=0,83· 7,72=6,41 м.
Глубина от подошвы разрушающейся волны до дна равна: *=10 —
— (7,72 — 6,41) =8,69 м.
Отношение hcrldt = 7,72/8,69 = 0,888 > 0,8; принимая hcr\dt = 0,8,
получаем dt по формуле 10.102: dt = (10+6,4)/1,8 = 9,11 м. Тогда расчетная
величина hcr равна:
Лег = 0,8* = 0,8-9,11 =7,29 м.
4. Определение максимальной величины и точки приложения нагрузок
от разрушающихся волн на цилиндрические сваи.
382
Таблица 10 J 4
! Первое приближение
hd\%
*73
0,0114
0,0112
0,0112
dcr 1
0,096
0,092
0,092
dcrI, м
14,5
12.0
12,5
*t
0,933
0,94
0,94
kl
0,856
0,852
0,852
(hl%)dcrl· μ
8,68
7,35
7,67
Второе приближение
if*
(hl%)dcr I
gT2
0,00916
0,0090
0,00895
dcr
4
0,080
0,073
0,073
dcr> M
12,1
9,48
9.93
Свая диаметром D = 0,5 м. Рассчитываем наибольшие значения
скоростной QO, cr и инерционной Qt, cr составляющих волновой нагрузки по
п. 2.12 и рис. 24,6 [51]: при x/dt = 0 получаем δ0, cr max = 0,375 и δ;, cr max =
= ± 0,236 — при x/dt = ± 0,80.
По формулам (61) и (62) при ρ = 1 т/м3; g = 9,81 м/с2; d = dcr = 10 м,
dt — 9,1 Г м и r\c, cr = 6,41 μ, имеем:
Qi,cr, max = ±0,5- 1,0- 9,8b 3,14- 0,52( 10,0+6,41)0,236 = ± 14,9 кН;
Qv, cr, max = 0,4 · 1,0 · 9,81 · 0,5(10,0+6,41)9,11 - 0,375 = 110,0 кН.
Так как отношение Q/ cr, тах/Чсо, cr, max — 14,9/110 = 0,135 < 0,20, то,
согласно примечанию 3 к п. 2.1, за расчетную максимальную волновую
нагрузку принимаем Qv, cr, max = ПО кН. Построение эпюры удельных нагрузок
производим при учете только скоростной составляющей нагрузки qcr = qv, cr
и x[dt = 0. Согласно формуле (66) получаем:
qv, cr = 0,4 · 1,0 · 9,81 · 0,5(10,0 + 6,41 )е0, сг = 32,2εσ, сп кН/м.
Скоростной коэффициент ev, cr принимается по кривой x/dt = 0 рис. 25, б
[51] для различных величин относительной глубины zrei = (dcr—z)/dt.
Таблица 10.15
rel
l|
1.8
17
1.6
1,5
1,4
1,2
1,0
0,8
0,6
0,4
0,2
0,0
ζ
Ν
II
и
16,4
15,5
14,6
13,7
12,8
10,9
9,1
7,3
5,5
3,6
1,8
0,0
U)
0,588
0,477
0,394
0,332
0,281
0.216
0,174
0,146
0,136
0,117
0,1 Π
0,109
с\
со
55· U
19,28
15,60
12,90
10,87
9,32
7,08
5,71
4,79
4,46
3,84
3,64
3,57
+
+
Vi 2
«3- И
34,88
28,50
23,77
20,19
16,40
12,79
10,50'
9,25
8,30
7,48
7,21
2
+
1
1 ^
II ,**
-1 -*P*
~\a ||
0,45
0,45
0,45
0,45
0,95
0,95
0,90
0,90
0,95
0,90
0,90
x + ^7
II *> -
<i X +
15,70
12,83
10,70
9,10
15,60
12,15
9,45
8,32
7,88
6,74
6,48
-
N
<
+
+
N
II
С s
15,95
15,05
14,15
13,25
11,85
10,05
8,20
6,40
4,55
2,70
0,90
2
X
f\
250,6
"193,0
151,5
120,5
185,0
127,5
77,5
53,2
35,8
18,2
5,8
<?*, cr, max = 114,95 κΗ; Σ AQ^ = 1218,6 кН/м
383
Положения, над дном сечений рассчитываются по зависимости zt =
= dt'Zrei, м, и затем по вычисленным значениям qVt cr строится эпюра qv.cr,
находится величина и точка приложения Qv, cr, max над дном. Результаты
раСЧеТОВ СВОДЯТСЯ В Табл. 10.15; ПОЛОЖеННе ТОЧКИ ПрИЛОЖСИИЯ Qv.cr, max
равно:
Σ Qin 1218,6
*'·**.«= Qv.er.nui = Ш = 10'S6 Μ·
Свая диаметром D = 1,6 м. При тех же параметрах волн по формулам
(61), и (62) получаем:
Qt>cr>max = ±0,5. 1,0.9,81·3,14· 1,62(10,0+6,41)0,236 = 152,7 кН;
Qv,cr, max = 1,0 · 9,81 · 0,4 · 1,6(10+6,41)9,11 · 0,375 = 352,0 кН.
Так как отношение 152,7/352,0 = 0,434 > 0,20, то наибольшее значение
волновой нагрузки рассчитываем, как сумму скоростной и инерционной
составляющих для различных фаз волны (п. 2.12 [51]). В этом случае
инерционная составляющая волновой нагрузки определяется по формуле (61):
Qi,Cr = 0,5- 1,0-9,81 -3,14. 1,б2(10 + 6,4l)6t-.cr - 647,061·, сг, кН,
а скоростная составляющая — по формуле (62):
Qv,cr= 1,0- 9,81- 0,4- 1,6(10 + 6,41)9,11б0,с, = 938,6δ0. сг> кН.
Коэффициенты 6t·, cr и δ». с, получаем из рис. 24,6 [51] при различных
значениях x/du начиная с x/dt = 0, с интервалом через 0,1. Так как χ > 0,
то δυ, cr > 0 и 6t, cr > 0. Расчеты сведены в табл. 10.16.
Таблица 10.16
X
dt
0
0,10
0,20
0,30
0,40
0,50
δι>, с г
0,375
0,330
0,295
0,264
0,230
0,204
Й.
°i, сг
0
0,070
0,125
0,165
0,190
0,208
Qv, сг~
=938,6 -bOt сг, к Η
352,0
310,0
277,0
247,8
215,9
191,5
Qi, cr"647*5/, cr'
кН
0
45,3
80,9
106,8
122,9
132,0
β<τββ». "+
+Q/,cr» κΗ
352,0
355,3
357,9
35*,6
338,8
323,5
Расчетную величину волновой нагрузки принимаем Qcf, max ='357,9 кН
при x/dt = 0,20; для определения точки приложения Qcr, max следует
построить эпюру qcr = qv,cr + qi,cr для фазы волны x/dt = 0,2 (формулы 65, 66
[51]). Коэффициенты eVfCr и ε*, сг в этих формулах следует принимать из
рис. 25, а, б при различных значениях zrei для x/dt = 0,2. Вычисления
рекомендуется производить в табличной форме (аналогично табл. 10.15).
10.8. НАГРУЗКИ И ВОЗДЕЙСТВИЯ ВОЛН
НА ПОДВОДНЫЕ ОБТЕКАЕМЫЕ ПРЕГРАДЫ
ОГРАНИЧЕННЫХ РАЗМЕРОВ
Рассмотрим некоторые задачи о воздействии волн на распо-,
ложенные в толще воды произвольно ориентированные
преграды в виде эллипсоида вращения (вытянутого или сплющенного)
и цилиндра (со сферическими или плоскими торцами) или
половины этих преград, лежащих на дне так, что одна_.из осей
преград перпендикулярна поверхности воды, рис. 10.27. На чер-1
384
теже обозначено: ζ, η, ξ — оси локальной системы координат,
начало которой лежит в центре водоизмещения преграды — в
точке с; ось ζ совпадает с осью вращения преграды; η, ξ —
перпендикулярные ей главные оси преграды; х, у, ζ— оси основной
системы координат с нача- .
лом на расчетном уровне &'
воды. Точка 0 является
проекцией с на эту
плоскость, ось ζ направлена
вниз, а х — есть
горизонтальная проекция оси ζ;
γ — угол между осью χ и
лучом волн {—π<γ^π);
α — угол между осями χ и
ζ (Ο^α^π); d — глубина
воды; D и ζ — диаметр и
длина преграды; zc —
заглубление центра преграды.
В общем виде задача
формулируется следующим
образом. Бегущие волны
высотой h и длиной λ,
распространяясь по
поверхности жидкости с постоянной
глубиной dy встречают на
своем пути неподвижную
преграду в виде
эллипсоида вращения, центр
которого заглублен на величину
гс под поверхность
жидкости. Продольная ось
эллипсоида наклонена под углом
α к горизонту, а ее
проекция на горизонтальную
плоскость, совпадающая с
осью 0*, составляет угол у
с направлением подхода
волн. Как вариант,
рассматривается преграда в виде
половины эллипсоида
вращения, опирающегося на
дно плоскостью разреза.
Требуется определить
силы от воздействия волн на разные типы преград. Силы
считаются приложенными в центрах водоизмещения преград.
Жидкость идеальная, несжимаемая, с постоянной
плотностью р, движение безвихревое, неустановившееся. Используют-
Расчетный \
уровень
Рис. 10.27. Расчетные схемы подводных
обтекаемых преград, расположенных
в толще воды (а) и на дне (б).
385
ся формулы потенциальной теории волн на уровне 3-го
приближения. Свободная поверхность и дно не оказывают влияния на
процесс взаимодействия волн с преградой. Исходные волны,
воздействующие на преграду, заменяются нестационарными
плоскопараллельными потоками жидкости. Мгновенная
скорость каждого из них принимается равной соответствующей
компоненте скорости волнового движения, средней в пределах
некоторого объема жидкости.
Обтекание плоскопараллельным потоком жидкости
эллипсоидальных преград описывается известным "потенциалом скорости.
Вихри, образующиеся на тыльной стороне преграды, создают
характер движения, близкий к так называемому «кризису
сопротивления», вследствие чего считается, что нагрузки от
потока на переднюю и заднюю половины преграды равны по
величине и одинаково направлены.
Потенциалы скорости при обтекании эллипсоидов вращения
плоскопараллельными потоками жидкости приняты в виде [22,
38]:
при продольном обтекании вытянутого эллипсоида
/1 λ-Μ λ \
1 + i г" '
φ = ίΛ
2£2-
_ i*7,nL±£
10.103
при продольном обтекании сплющенного эллипсоида
φ = *Л
— — arcctgv I
arcsin YX—e^ — eYX — е'2 Г
при поперечном обтекании вытянутого эллипсоида
2£3
<Р = «Ср. j ГТ~£~;
Ε - 2£з _ -g- (l _ £2) in _2_
при поперечном обтекании сплющенного эллипсоида
• arcctgv
10.104
10.105
φ = Ui
1+-
1 ■+ ν*
1
arcsin V" 1 — en- — — (2 — *a) |/Ί
-62
10.106
Здесь и — скорость набегающего потока; ζ — текущая
координата по направлению потока; е = L/D (L< D)\ E = D/L
(D^L)\ μ, λ, ν — функции, зависящие от размеров
эллипсоида и координат рассматриваемой точки.
Сила от воздействия волн на подводную преграду находится
интегрированием по ее поверхности волнового давления,
определяемого в соответствии с интегралом Лагранжа — Коши:
386
где ρ — плотность воды; / — время; υ — скорость движения
жидкости в рассматриваемой точке.
Для преграды, расположенной в толще воды, искомая сила
от воздействия волн записывается в виде
Q = ]f (Qxt + Qxv)2 + (Qyl + Qyv)2 + (Qzi + О»)2, Ш08
а для входящих в выражение 10.108 инерционных и скоростных
компонентов нагрузки получены формулы:
Qxi = 2р£* Vy [BJxi (^„^cos2 α + μΟΙ$οι sin2 α) +
+ ΘΑ/ sin α cos α [vDl$Dl- V-LI$Ll)\ cos γ, 10.109
Qxv = 4 ρ^π Γ [9χ£ "-(Л^1о?*· cos2 α + Λοΐ*ωΡο» si"2 α) +
+ Θ*Α* sln α cos α (-Λομ-biP^ — ΛιΙ^οΜ] cos ?; Ю-1Ю
Qyi = 2ρδΤπ Vy θ^,βοι (:*DO cos-' α + p0i sin2 α) sin γ; 10.111
9 A2
Qy* — -gPSrwAo χ βχνΚνΡον (v-Id cos2 α + !xk si"2 a) sin Ή ЮЛ 12
Qii=2f>^KT|0iioii[(^UDsin-7-l-ixiDcos'-,T)pwCOS2a+ixioPtisln2a] +
+ΘΑ, sin a cos a [(jiDO sin2 γ -H*i0 cos2?) βο« - μΔΟβΐί]}; 10.113
9 /ϊ2
QzV= -3 Ρ^πΤ l8»8" [Ло O'od sln2 Τ +>Id cos2 Τ) Pdo cos2 a +
+ AL\>lD$LO sin2 a] -f θ ^δ^ sin a cos a [AD [\^DD sin2 γ +
+ ^Dcos27)pD, -A^iDP^]j. 10.114
Для преграды, находящейся на дне, выражение для силы
волнового воздействия записывается в виде
Q = \f{Qx< + Qxv)2 + (Qyi + Qyv)2 + (Qzl + Qzv + Q*,)2,10.115
где
/j2
(Pg^Az t^x^zPdl^dli если продольная ось
преграды вертикальна;
9gTzAz у Bxvbzl (aLD»A2d Cos2 γ + *DDi*2DD sin2 γ), если
продольная ось преграды горизонтальна.
В формулах 10.108—10.116 обозначено: Qxi, Qyil Q2ij QXZh
Qyv, Qzv — инерционные (i) и скоростные (υ) компоненты
составляющих нагрузки по осям координат; Qzi— подъемная си-
387
Qzl'
ла, направленная всегда вертикально вверх и возникающая при
обтекании преграды горизонтальным потоком; g — ускорение
свободного падения; V — объем тела; AL, AD, Az — площадь
проекции тела на плоскость, перпендикулярную продольной
(L) или одной из поперечных (D) осей эллипсоида, или на
горизонтальную плоскость (ζ) соответственно; θ**·, Qzi\ Q'xv> Qzv —
коэффициенты линейной нагрузки от волн, принимаемые из
графиков рис. 19 {51] в зависимости от относительной глубины
Zrei = (d—zc)Jd\ **ι = —|δ*υ|; Ъхи δ*ί, bxv, δζν — коэффициенты
сочетания инерционного и скоростного компонентов силы от
воздействия волн, принимаемые по графикам рис. 18 и 23 [511
в зависимости от относительного расстояния κ = //λ
(/—горизонтальная проекция удаления центра преграды от вершины
волны); μηη— коэффициент (табл. 10.17), зависящий от
относительных размеров преграды /π/λ и η/λ (каждая из величин
Таблица 10.17
m/λ
0,001
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,001
1,0
1.0
0,98
0,96
0,94
0,90
0,86
0,81
0,76
0,05
1.0
1,0
0,99
0,97
0,94
0,90
0,86
0,81
0,76
Значения коэффициента р.
0,10
1,02
1.01
1,0
0,98
0,95
0,91
0,87
0,82
0,77
0,15
1,04
1,03
1,02
1,0
0.97
0,93
0,89
0,84
0,78
0,20
1,07
1,06
1,05
1,03
1,0
0,96
0,91
0,86
0,80
0,25
1Д1
1,10
i.og
1,07
1,04
1.0
0,95
0,89
0,83
при л/λ, равном
0,30
1,15
1,15
1,14
1.11
1,08
1,04
0,99
0,93
j 0,87
0,35
1.21
1.21
1,19
1.17
1,136
1,09
1,04
0,98
0,92
0,40
1,28
1,28
1,26
1,24
1,20
1,16
1.10
1,04
0,97
/η, η принимает значения D или L); βζ)ί, βυ, §dv, βία —
инерционные и скоростные коэффициенты формы преграды, для
которых получены выражения:
при обтекании вытянутого эллипсоида
2(1-£*)ΐ/Τ="£3
$Di =
1 ,
(1 — 2£->) У 1 — £2 + £з in -g (I + у 1 -
(1 - £-) /Г=£*
Р/л = ;
-£2)
;
γ\ _ £2 _ £а |„ -g- (l + у\ _£2)
10.117
10.118
388
ϊο« = 2\ Q+w-mi+!B+**H*-2B+*>^_i\. lon9
1 3 (l-2£2)/l-£i+£4ng-(l+^l-£s) J
, ί 2(1—ff»)£Mn£ + (l-£»p
( [У Γ=1ϊ - Β» in j- (1 + jT^fi»)]
jfc. = 2]r aO-^g^ + a-gy 1[; ю.120
3D»
при обтекании сплющенного эллипсоида
2{ι-*>γτ=* 0
г б arcsin ]Л — β* — (2 — <?2) /l — ^
= ('-^'^ . ю.122
£ arcsin у \—ё> — ё*у\ —е*
>Г <1-*)а[2 + (1+«)»1 П. 10123
43(1 +ef[e arcsin }/Ί _^_J.(2_^/ι _^>J2 J»
г L(arcsin/1 -e^ — eYX—e^y J
odl, old, odd — коэффициенты подъемной силы. Значения
коэффициентов определяются по формулам:
при обтекании вытянутого эллипсоида
2(1 - £->) [(1 -£з) (1 - 2£*) -2Е?1η Ε] . 1П 10-
°dl — f ZZZI i -la "" *» lu.i^o
(1-2£2)/ΐ -£a + £2ing.(l + }Л-£2)
0ld = ^ __,; Ю.126
|V 1 - £2 - 22» In γ (1 + /1 - &)Y
. _ 4(l-£2)(£'-2£* + 2) 97
3 (1 -2£*) V\ —£2 + E* In g-(l + /1 —£2)
при обтекании сплющенного эллипсоида
_ 2 (1-g) [(1-«*)(?"-«»)+ 2* in «) .. 1ni9R
Di~ [βarcsin}ΓΓ=Ξ-(2-<*)УТ=ё\* ' υ·^°
0 «(2+ «)(!-gy
£D (e arcsin /l — <?-· — e= V 1 — e*)2 '
aflD= 4(1-^[1 + 2(1+,H 10130
DD 3 (1 + ^)2 [<? arcsin Υ1 — ^ — (2 — **) / 1 — ^]2
Для удобства значения коэффициентов сопротивления типа β
и подъемной силы типа σ представлены на рис. 10.28; при е <
<0,1 для вычисления $и и old можно пользоваться также
приближенными формулами:
2 8
389
dgHnunf]
*S
^
^ V-/-A—
\5> c^
390
Результаты могут быть использованы с некоторым
приближением для определения силового воздействия волн на
подводные преграды некоторых других форм, например, в виде
цилиндров со сферическими или плоскими торцами. Основные
расчетные формулы остаются теми же, а коэффициенты типа β и σ
могут быть получены «склейкой» их значений для составляющих
фигур — участка бесконечного цилиндра и двух торцевых
полусфер или половин диска. Рекомендуемые величины
коэффициентов типа е и σ в графическом виде представлены на рис. 10.29.
Для одиночных подводных обтекаемых преград полученные
выражения могут быть несколько упрощены за счет
пренебрежения малозначащими членами. Максимальную силу от
воздействия волн Qmax на расположенную в толще воды обтекаемую
преграду (рис. 10.27, а), заглубленную под поверхность воды
не менее, чем на Λ/2, и отстоящую от дна более, чем на половину
меньшего размера преграды (Д L), можно определить по
зависимости
Qmax = γΟ[+ % + Q\ Ю.131
для двух сочетаний проекций сил:
а) максимальное значение вертикальной составляющей силы
Qz при соответствующих ей составляющих Q*, Qy;
б) максимальное значение горизонтальной составляющей
VQx2+Qy2 при соответствующем ей Q*.
Составляющие силы от воздействия волн Qk на
расположенную в толще воды обтекаемую преграду конечных размеров
рассчитываются по формулам:
+ Qxv, max^xv) COS 7;
Qy = (Qy/, тш£д + Qr>. ««&„) sin 7; 10.132
Qz = Qzi, msL\°zi "Г Q?v, max^·
ЗдеСЬ Qxi> max*, Qyi, maxi Wzl> maxi Удг г», max ι W.yv, maxi **lzv, max* Qkl , max*
Qkv, max — максимальные инерционные и скоростные
компоненты составляющих сил от воздействия волн, рассчитываются так:
Qxi>m^^29g^V^bxl^LJucos2a + {xD^Dls\n2a); · 10.133
Qxv. max = 4 р£* γ *ΧΌ [AL^\D^Lv cos2 α + AD\?Dl}Dv sin2 α); 10.134
Qyi, max = 2ρ#π VT Qxl (jxDO cos2 α -f μβ, sin2 a) pD;; 10.135
Qyv, max = -j Pgnχ $xvAd$dv (v-2dd cos2 α + ji*,£ sin2 a); 10.136
Qzl, max = 2pg« V у θ^ [(μββ Sin2 7 + μLD COS4 7) 0Di COS2 α +
+ !^0PtiSin2aJ; 10.137
391
4днт/пГ)
Vl9Hh9H0X3S(?
«*
tf
л
1
4
'У
г
1Г:
*ъ <zs *ь Ъь
ЧГ сок ^ «si
къ VHTllUOVlfU tiVI/2fiCf)f ^
csT ^
i к2
Qzv, max = у pgKj- bzv [AD (у?т Sin2 7 + V\D COS2 7) $Dv COS2 α -f
где все обозначения те же, что и раньше
Аналогичным образом, по 10.131, рекомендуется определять
максимальную силу Qmax от воздействия волн на лежащую на
дне обтекаемую1 преграду (рис. 10.27,6), заглубленную под
поверхность воды не менее, чем на /ι/2. При этом составляющие
силы QXy Qy должны вычисляться по 10.132, a Qz — из выражения
Qz == Q:l, mnfizl + Qzv, max^w, + Qzl, max^/, 10.139
где компоненты вертикальной нагрузки Qzi,max рассчитываются
по формуле
xPS^z'x^xv^d^dL·'» если оси z и ^ параллельны,
Q2,'max= Рв*^тв„Кл0со8»т + р2,1,«»/,|,81п*т). если 10·140
1ось ζ параллельна одной из осей ξ или η.
Примечание. Расчет сил от воздействия волн на подводные преграды
должен производиться, как правило, с учетом шероховатости их
поверхности. При наличии специального обоснования снижения влияния коррозии и
морских обрастаний, коэффициенты формы типа β могут быть уменьшены
на основании соответствующих опытных данных.
Пример 10.13
Дано: <* = 24м; гс = 12 м; L = 12 м; D = 8 м; /ι = 3μ; λ = 48 μ;
α = 30°; ν = 60°.
Требуется найти максимальную силу от воздействия волн на
вытянутый эллипсоид вращения.
Решение
1. Определяются вспомогательные величины:
πΖ)2 8-8
AL = — = π -j- = 50,25 м2;
DL 8-12
AD = π -j- = π -£- = 75,45 Μ*;
V = -g- D2L = -g- π82.12 = 402 мЗ;
*"* - 24 " 0,5; λ - 48 "~ 1б: λ ~ 48 - °'5;
Ζ, 12 D 8 8
Т = 48~°'33> T = 48 = °'l7> ^ = Ϊ2=°>67·
По табл. 10.17:
V-dd = 1,0; \x.ld = 0,87; μ^ = 1,13.
По рис. 10.28 при Ε = 0,67 (правая часть графика):
$и - 1,30; βι,, = 1,63; β£0 = 0,14; β0ϋ = 0,35.
393
По графикам рйс. 19 [51]:
θχί = 0,23; θχ0 = 0,02; θχί = 0,20; 0ги = 0,02.
2. По 10.133—10.138 рассчитываются максимальные инерционные и
скоростные компоненты составляющих силы от воздействия волн:
3
Qxl> max = 2· 1,0-9,81 -3,14-402 jg 0,23 (0,87-1,30 cos* 30° +
+ l,13-l,63sin*30°)==466 kH;
2 3*
Qwmax = — 1,0-9,81 · 3,14 jg 0,02 (50,25 0,872.0,14 cos* 30° +
<?■
yl, max '
* yv, max
+ 75,45-1,132-0,35 cos* 30°) = 1 kH;
= 21,0-9,81 -3,14-4024 0,23 (1,0 cos* 30° + 1,13 sin? 30°) 1,63 = 599 kH;
33
3" 1,0-9,81-3,14^0,02-75,45-0,35 (1,02 cos2 30°+1,132 sin2 30°)=2 kH;
3
Qzi, max = 2· 1.0-9,81 -3,14-402 jg 0,20 [(1,0 sin* 60° + 0,87 cos* 60°) 1,63 cos* 30° +
<?*м
+ 0,87-1,30 sin2 30°] = 454 kH;
2 32
= -j 1,09,81 -3,14 5g0,02 [75,45 (1,0* sin260° + 0,87* cos* 60°)0,35 cos* 30°+
+ 50,25-0,87*-0,14 sin* 30°] =2 kH.
В соответствии с примечанием 3 к п. 2.1 [51] можно пренебречь
скоростными компонентами нагрузки, так как для всех составляющих
Vi. max
/Q. , max у** л.
3. Определяется максимальная сила от воздействия волн на подводную
преграду 10.131. Результаты вычислений} сведены в табл. 10.18.
Таблица 10.18
X
0,0
0,05
0,10
0,15
0,20
0,22
0,25
0,28
0,30
0*35
0,45
-0,45
—0,35
—0,25
—0,15
—0,05
ьх1
0
0,31
0,60
0,83
0,9+
0,97
1,0
0.98
0,95
0,80
0,31
-0,32
-0,81
-1,0
-0,81
—0,28
hi
1,0
0,95
0,81
0,59
0,32
0,20
0
—0,18
-0,29
-0,60
-0,94
—0,94
—0,59
0
0.60
0,95
QxV кн
0
72
140
193
219
226
233
228
221
186
72
—75
-189
—233
—189
-65
<?у,кН
0
161
311
430
488
503
519
508
493
415
161
—166
-420
—519
—420
—145
Qgi.*H
454
431
367
268
145
91
0
—82
—132
-272
—427
-427
—268
0
272
431
Q, кН
454
466
501
542
554
559
569
563
556
530
462
464
533
569
535
459
Таким образом, максимальная сила от воздействия волн на подводный
эллипсоид при κ = ± 0,25 равна 569 кН.
394
4. Для сравнения подсчитаем йеличину максимальной силы по более
точным формулам 10.108—10.114. В этом случае выражения для
компонентов составляющих волновой нагрузки имеют вид:
Qxi = 233б„+47б,£, κΗ;
1δχί+1δχϋ, κΗ;
Qyt = 519δ„, κΗ; QyO = 2δ„, κΗ;
Qzt = 454δ»ί+70δ,ί, κΗ;
Q„ = 2δζυ+2δΧΌ, κΗ.
Так же как и ранее, в дальнейших расчетах пренебрегаем скоростными
компонентами нагрузки ввиду их малости. Вычисления результирующей силы
волнового воздействия на эллипсоид сведены в табл. 10.19. В этом случае
максимальное значение силы волнового воздействия при κ = 0,16 равно 591.
Таблица 10.19
X
0,0
0,05
0,10
0,12
0,14
0,16
0,18
0,20
0,25
0,30
0,35
0,45
-0,45
—0,35
—0.25
—0,15
-0.05
ьх1
0
0,31
0,60
0,70
0,80
0 86
ο;9ΐ
0,94
1,0
0.95
0,80
0,31
-0.32
-0,81
-1,0
-0,81
-0,28
lzl
1.0
0,95
0,81
0.73
0,62
0,56
0,41
0,32
0
-0,29
—0,60
—0,94
-0,94"
—0,59
0
0.60
0.95
Qxi, кН
47
119
178
197
216
227
231
234
233
207
158
28
—118
; -227
—233
—161
1 -21
Qyi> «Η
0
161
311
363
415
446
472
488
519
493
415
1 161
1 —166
-420
-519
-420
1 —145
Qzi,KH !
454
453
409
380
337
314
249
211
70
-65
-216
—105
—449
-324
—70
216
I 412
Q, кИ
456
495
544
561
577
591
582
580
573
538
491
437
493
576
573
499
I 437
Из сравнения данных табл. 10.18 и 10.19 видно, что максимальные
значения сил волнового воздействия, рассчитанные по точным и упрощенным
формулам, практически совпадают (расхождение менее 4 %). В то же
время фазы этих нагрузок существенно разнятся. Поэтому упрощенные
формулы" рекомендуются для расчета волновых нагрузок только на одиночные
преграды.
Пример 10.14
Дано: d = 24 м; L = 12 м; D = 8 м; h = 3 м; λ = 48 м; у = 60°.
Требуется найти максимальную силу от воздействия волн на
лежащую на дне половину эллипсоида, разрезанного по главной
диаметральной плоскости τζη.
Решение.
1. Определяются вспомогательные величины:
1 D2 1 8-8
Л£ = у *-4-^у π-j- = 25,13 ^
1 DL 1 8 12 о
ло=у7С~==:"2"7С"Т" ==37'7 м2;
395
Ы 812 nr ^ o
Az — π -τ- = π —τ- = 75,45 Μ-;
V = y -g-*D2Z,=-2- -g-π 83.12 = 201 мз.
Удаление центра тяжести половины эллипсоида от плоскости разреза
3 п
равно -g-Д поэтому:
8 A=i.= L· £=Hi==o5·
*М- 24 =:0·13'' λ 48 Ϊ6' λ 48
L·. 1?--— D 8 — - 8
λ =48~
По табл. 10.17:
г==- = 0,33; —=48 = 0,17; £ = ^ = 0,67; a = 0°.
μοο = 1,0 при /η/λ = η/λ = D/λ = 0,17;
μιο = 0,87 при m/λ = L/λ = 0,33 и /ι/λ = D/λ = 0,17;
μβ£ = 1,13 при m/λ = D/λ = 0,17 и /ι/λ = L/λ = 0,33.
По рис. 10.28 при Ε = 0,67 (так как эллипсоид вытянутый, используется
правая часть графика):
βι« = 1,30; β,,ί = 1,63; βι* = 0,14; fiDv = 0,35.
По графикам рис. 19 [5l·]:
Qxi = 0,09; θ™ = 0; Θ2Ι· = 0,03; θ2ϋ = 0.
2. По 10.133—10.138 и 10.140 рассчитываются максимальные
инерционные и скоростные компоненты составляющих силы волнового воздействия:
<?лг/,тах = 2-1,0-9,81 ·3,14·201 |j 0,09 (0,87-1,30 cos* 0°+
+ I,131,63.sin2 0°)==79 кН;
4χν, max == ^yv, max == ^ZVi щах "»
3
Qy/ тах= 2-1,0-9,81 -3,14-201 jg0,09 (1,0 cos* 0° + 1,13 sin* 0°) = 70 кН;
Qzi max = 2-1,0-9,81 -3,14-201 ^0,03 [(1,0sin* 60° + 0,87 cos2 60°) 1,63 cos*0° +
+ 0,87-1,30 sin* 60°] =2 кН.
Так как ось ζ параллельна оси ζ (или η, что в данном случае не имеет зна-|
чения), вычисление компоненты вертикальной нагрузки Qzi, max производится
по второй из формул 10.140, но так как 0ΧΌ = 0, то Qzi = 0.
3. Определяется максимальная сила от воздействия волн иа подводную
преграду по 10.131. Результаты вычислений сведены в табл. 10.20, из которой
следует, что максимальная сила, действующая на лежащую на дне поло-1
вину эллипсоида, равна 76 кН при κ = ±0,25.
393
Таблица 10.20
χ
0,0
0,05
0,10
0.15
0.20
0.22
0.25
0.28
0,30
0,35
0,45
—0,45
—0,35
-0,25
—0,15
—0,05
bxl
0
0,31
0,60
0,83
0,94
0,97
1,0
0,9ί
0,95
0,80
0,31
-0,32
-0,81
—1,0
-0,81
-0,28
\i
1,0
0,95
0,81
0,59
0,32
0,20
0
-0,18
—0.29
-0,60
-0.94
-0.94
-0.59
0
0,60
0,95
QxV кн
0
21
41
57
64
66
68
67
65
55
21
-22
-55
-68
-55
—19
v kH
0
11
21
29
33
34
35
34
33
28
U
-11
—28
1 -35
—28
-10
qzV кн
2
2
2
1
1
0
0
0
0
—1
-2
-2
—1
0
1
2
Q, кн
2
24
46
64
72
74
76
75
73
62
24
25
62
76
62
21
10.9. НАГРУЗКИ ОТ ВОЛН НА СКВОЗНЫЕ СООРУЖЕНИЯ
ИЗ ОБТЕКАЕМЫХ ЭЛЕМЕНТОВ
Сквозные сооружения могут состоять:
— только из вертикальных колонн, соединенных вверху
ростверком или платформой;
— из вертикальных, горизонтальных и наклонных
обтекаемых элементов, образующих пространственную ферму;
— из решетчатых опор, соединенных вверху платформой.
Расчет нагрузки от волн на сквозное сооружение
складывается из определений:
— наиболее опасного положения сооружения относительно
вершины волны κι = Χ\/λ\
— суммарной нагрузки на элементы сквозного сооружения
для наиболее опасного его положения относительно вершины
волны;
— горизонтальной и вертикальной составляющих
максимальной статической волновой нагрузки на сооружение и
опрокидывающего момента относительно дна;
— расчетной нагрузки на сооружение от волн;
— расчетных нагрузок от волн на отдельные элементы
конструкции.
Максимальная нагрузка от волн на сооружение
рассчитывается методом последовательных приближений; при этом схема
сооружения рис. 10.21, заменяется упрощенной, в которой
оставлены только вертикальные элементы, поскольку они
являются ОПределЯЮЩИМИ При ОТЫСКаНИИ Qmax-
Для вертикальной колонны по формуле (36) с учетом
примечаний к п. 2.1 [51] строится график Q = /(x), (рис. 10.21, в),
397
при этом горизонтальные масштабы графика κ = χ/λ и
упрощенной схемы сооружения L/λ должны быть одинаковыми.
Затем на график Q = /(x) накладывается упрощенная схема
сооружения на таком относительном удалении от вершины волны
κ, чтобы нагрузка от волн на все вертикальные колонны была
бы наибольшей. Это достигается методом последовательных
попыток; при этом горизонтальная волновая нагрузка вычисляется
суммированием ординат графика Q = f(x), соответствующих
положению осей колонн. Наибольшие нагрузки от волн
определяются для полученного значения κ, затем выполняются
контрольные расчеты при больших и меньших κ с учетом разных
направлений подхода волн к сооружению.
Пример 10.15
Дано: d = 25 м; /г,% = 6,7 м; λ = 100 м; ρ = 1 т/м3; CO = 1,33.
Сооружение решетчатой конструкции из цилиндрических стоек D = 1,0 м,
горизонтальных, и наклонных элементов D = 0,5 м и L — 10 и 14,14 м.
Требуется определить значение κ при Qmax-
Ρ е ш е*н и е.
1. Выполняем расчет в соответствии с п. 2.14 [51] и указанными
дополнениями. Строим упрощенную схему блока в виде сооружения из двух
рядов вертикальных свай D = 1,0 м, расположенных на относительном
расстоянии L : λ = 10 : 100 = ОД (рис. 10.21, б). По зависимостям (37) и (38) опреде-
' ляем инерционный и скоростной компоненты нагрузки от врлн на сваю D =
= 1,0 м при d/λ =» 0,25 и λ/h = 14,9:
Q/|max= J 1,0.9,8b3,14-1,02-6,7-1,0-0,916-1,0 = 4,74 кН;
QOi max = j2 1.0-9,81 · 1,06,72· 1,02· 1,45-1,33 = 70,5 кН.
По формуле (36) для ряда значений κ находим Q. Результаты расчетов
сводим в табл. 10.21 и строим график Q = /(x), рис. 10.21, е.
Таблица 10.21
%
h
Qi. max*M<H
К
Qv, max5*" кН
Q, кН
—0,25
-0,97
-4,60
0
0
—4,60
-0,2
-1,04
-5,13
0,06
4,23
-0,90
-0,15
—0,98
-4,83
0,24
16,92
12,09
-0,1
-0,8
—3,94
0,55
38,78
34,84
-0,05
-0,46
-2,27
0t85
59,93
57,66
0
0
0
1
70,5
70,5
0,05
0,46
2,27
0,85
59,93
62,2
0,1
0,8
3,94
0,55
38,78
42,72
0.15
0,98
4,83
0,24
16,92
21,75
0,2
1,04
5,13
0,06
4,23
9,36
0,25
0,97
4,60
0
0
4,60
Для определения расчетного положения сооружения относительно
гребня волны κ наложим упрощенную схему его на график Q = /(x), рис. 10.21,
так, чтобы суммарная нагрузка от волн на первый и второй ряд свай была
наибольшей. В данном случае это достигается при одинаковой нагрузке на
сваи первого и второго ряда Q = 60 кН и относительном удалении их от
вершины волны κι = -— 0,045 и κ2 = 0,055.
398
Зная положение сооружения относительно вершины волны при Qmax,
приступаем к сбору нагрузок на обтекаемые элементы сооружения.
Нагрузки от волн на горизонтальные элементы сооружения
следует рассчитывать в соответствии с указаниями параграфа
10.6 для определенного κ — положения сооружения
относительно вершины волны.
Нагрузки от волн на произвольно ориентированный
цилиндрический элемент сквозного сооружения рис. 10.21,
определяются в предположении, что:
— волновое давление, нормальное к оси элемента,
рассчитывается с учетом величин составляющих скорости и ускорения,
нормальных к той же оси;
— ось χ совпадает с направлением луча волны и боковой
гранью сооружения;
— движение жидкости характеризуется проекциями скорости
υχ и υζ, а также локальных ускорений ах и az.
Положение наклонного элемента в толще воды
характеризуется координатами одного из его концов (χ, ί/, ζ) и углами
φ и ψ.
Линейную нагрузку от волн по осям х, у, ζ на наклонные
круглоцилиндрические элементы, например, на элемент 6—12,
рис. 10.21, получим:
1 D2
ρχ=γ pCvDv„vnx + рС,« т апх; 10.141
1 D2
ρζ=γ pCvDvnv„z + pCt« т а„; 10.142
1 D2
РУ = Τ ?CvDvnVny + PQ* χ anr 10·143
где ρ — плотность воды; Cv и Ct· — коэффициенты скоростного
и инерционного сопротивлений (табл. 10.1); υη — нормальная к
оси цилиндра скорость жидкости, выраженная через ее
проекции на оси координат:
vn = yvl + vl^(cxvx + c^\ 10.144
vnx = vx — cx(cxvx + czvz)\ 10.145
Όηζ = Vz — Cz(cxOx+CzOz)\ 10.146
vny = —cy(cxOx + czOz). 10.147
Символы cx, cz и Су находятся из выражении:
сх = sin φ cos ψ; ]
C(Z = cos^; I 10.148
cy — sin φ sin ψ. j
Составляющие ускорения жидкости, нормального к оси
цилиндра:
399
йпх = ax — cx(cxax + czaz); 10.149
anz = az — cz(cxax+czaz)\ 10.150
αΛί/ = —cy(cxax+czaz). 10.151
Проекции скорости и ускорения по осям χ и ζ можно
определять по формулам:
<,Χ«2ΑΛ„]/"^*; 10.152
vz = 2hkOY^S-\ 10.153
α, = ?4^5 10Л54
<ь=**4*А'· 10·155
Для расчета суммарных горизонтальной и вертикальной сил
от действия волн на элемент сооружения Рх и Ρζ можно их
значения получить по составляющим на концевых участках,
согласно зависимостям:
Рх элемента 6-12 = Р**+2Р™ ц 10.156
Ρζ элемента 6-12=* p** + p*« Lt. 10.157
Для расчета самого элемента суммарную нагрузку от волн
на единицу длины цилиндра запишем так:
Я= ± уР\ + Р; + Р]. 10.158
Опрокидывающий момент нагрузки от волн на сооружение
находится как сумма моментов всех горизонтальных и
вертикальных сил на элементы сквозного сооружения.
Указания п. 2.14 [51] об учете коэффициентов сближения
элементов сооружения по фронту и лучу волны следует
учитывать только при относительных расстояниях между осями
элементов 1/D < 3,0. _
При отношениях периодов 0,01 =^_ГС/Г ^ 0,3 (Тс — период
собственных колебаний сооружения, Τ — средний период
волны) следует полученную статическую нагрузку от волн
умножать на коэффициент динамичности kd, принимаемый согласно
табл. 15 [51]; при Тс/Т > 0,3 рекомендуется выполнять
динамический расчет сооружения.
Приложение
БИБЛИОТЕКА ПРОГРАММ НА ВХОДНОМ ЯЗЫКЕ
МИКРОКАЛЬКУЛЯТОРА „ЭЛЕКТРОНИКА БЗ-34"
Настоящие программы пригодны для микрокалькуляторов
«Электроника МК-52», «Электроника МК-54», «Электроника
МК-56», «Электроника МК-61» с учетом различий в некоторых
обозначениях, в том числе: х-+П вместо П, П-*х вместо ИП,
-«-* вместо XY и Bf вместо f; отличаются также символы
обратных тригонометрических функций sin-1, cos^1, tg-1 вместо
arcsin, arccos, arctg соответственно.
Принятые правила записи программ:
— запись осуществляется символами команд в табличной
форме с указанием адресов и кода команд;
— символы префиксных клавиш не указываются;
— порядок ввода исходных данных, пуска программы на
счет и вывода результатов описывается в инструкциях к
программам;
— к каждой программе прилагается контрольный пример с
указанием приближенного времени его счета.
Все операции, указанные в программах и инструкциях к
ним, нербходимо выполнять дословно при соблюдении
следующих правил.
1. Набор всех программ производится одинаково: после
включения микрокалькулятора следует нажать клавиши F и
ПРГ, при этом на индикаторе справа высвечивается 00. Затем
в строгом соответствии с программой нажать клавиши команд.
После окончания набора нажать клавиши F и АВТ, В/О,
дальнейшие действия выполнять в соответствии с инструкцией к
программе.
2. После нажатия клавиш F и АВТ любые нажатия других
клавиш на программе уже не отразятся. Программа вводится
в программную память микрокалькулятора только один раз.
В случае повторения расчета или изменения начальных
параметров набирать программу заново не надо.
401
3. Любое выключение микрокалькулятора приводит к
стиранию программы из памяти.
4. Если в процессе набора команд совершена ошибка, то
следует нажать клавишу ШГ и набрать правильную команду.
Если название команды состоит из двух частей, то "при
исправлении необходимо изменить обе части.
5. Введение чисел в регистры памяти следует осуществлять
набором требуемого числа, нажатием клавиши Π и набором
номера соответствующего регистра.
6. Содержание регистра извлекается из памяти нажатием
клавиши ИП и набором номера регистра.
7. Размещение исходных данных описывается в инструкциях
формулами вида: x-t = ΠΝ при вводе числа x-t в регистр Ν (Ν =
= 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А,, В, С, Д); xL = ПХ при вводе в
регистр X. Результаты yt счета ищутся в регистрах памяти с
помощью обозначений вида: ΠΝ = г//, ПХ = у ι.
Программа МК-1. Определение возвышений и понижений η
свободной волновой поверхности у вертикальной стенки.
Расчетная схема представлена на рис. 1 СНиП [51]. При
составлении программы использованы формулы (2) и (3) норм
[51]. В качестве исходных данных задаются:
h — высота бегущей волны, м; λ — средняя длина волны, м;
d — расчетная глубина воды, м.
Программа МК-1 приведена в табл. П1."
Ввод исходных данных и пуск программы на счет
производятся следующими командами: h\X\dy В/О, С/П.
Результаты расчета выводятся на индикатор командами:
НПО; nX = cosco/; ИПА; ПХ = г]тахЫ; ИПВ; ПХ = η*.
Контрольный пример. Исходные данные: h = 6,0 м; λ = 100 м;
d= 13,5 м. Время счета 30 с. Результаты расчета: cos ωί = 1; г\тгх =
= —7,64 м; r\t = 4,36 м.
Программа МК-2. Определение ординат ρ волновых
давлений на вертикальную стенку в глубоководной зоне. Расчетная
схема приведена на рис. 1 [51]. Использована формула (4)
[51]. Задаются следующие исходные данные:
ρ — плотность морской воды, т/м3; h — высота бегущей"
волны, м; k — волновое число, 1/м; cos ω^ — расчетный параметр,
характеризующий момент времени, для которого производится
определение волнового давления; ζ — ордината точки, м, в
которой определяется волновое давление.
Текст программы МК-2 представлен в табл. П2.
Ввод исходных данных и пуск программы на счет
производятся командами: В/О, pg; C/ΪΙ; А; С/П; k\ С/П; cos ω/; С/П;
г; С/П; С/П.
Результат расчета высвечивается на индикаторе и, кроме
того, выводится на индикатор командой ИПВ; ПХ = р.
402
Код
Команда
Адрес
Код
Команда
Адрес
Код
| Команда
Адрес
Код
Команда
Адрес
Код
Команда
Ε
ИП1
о
оо
СО
CD
ИПЗ
о
ю
см
со
ИП2
3
о
Л
8
со
"Ч*
со
СМ
1—*
X
см
X
5
СМ
X
5
00
ем
00
см
см
-f
1>>
4χ
о
+
см
00
1—*
см
СО
S
о
см
о
1—(
см
см
см
Τ см
1 с
о
'-'
со
00
о
ч—
со
СО
о
-
со
о
"Ч*
о
с:
со
см
см
0
1
<
"Ч*
00
со
см
Η
со
~
1
со
ю
см
^
&
СО tO—»Ю
Ю СОЬ- 00
00 00 00 00
о см со Ы см ^ *-·
г-* О»-· ОСМ 0*-«
+^ -I·-*- 1
Ю СО Г>» 00 <Л О «—ι
СО со со СО СО t- Ь-
σ> σ> ~ см со со -J
LOI'iOlNLOiO't
Α σ> 5 <ν Ε со GQ
Ю CO Ν 00 СП О '-
со -J О со ОСМ оо
Ю -Ч* LO СО СМ г-н О
lo со ь- оо о С"-<
-см см см см см со со
-« ОСМ СМ СМ СО -Ч«
^смог-^со —· "Ч*
^ см ^
т-< СО CM t^OCMCMO
СМ г-н r^ Tf СО СМ i-ч СО
^•l-xEgnxl
СМ<*О^ЮС01^.00С^»
О»—CMrfcMCMCO^
ЮСОСМСО — Ог-нСО
CMCO?^LOcOt^OOC75
LOlOLOLOLOLOtOLO
<МСО»- ^ ОСМ CM CO
_■ о^сссм*-* т-нсм
Хсо ι с * XXi
1 s
CMCO^MOcOt^OOCT»
сосососососососо
C0CMC0COLOC0»-H-J
СОСОгн-^оСМ^О
СО СМ ._ ^ -р-
о г-н см
О О О
-f LOCO ^ 00 О О г
О ОООООг-^т
CMCO^LOcOh-QOCTi
403
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
о*
X
о
00
«О
ИП1
о
CN
CN
с*
н
§
CN
X
о
CN
5
С
о
о
8
ипо
00
2
ипз
о*
X
5
J
■*
CQ
С
CN
s
с/п
1-*
CN
Χ
(Ν
00
CN
CN
Ч
CN
CO
Ю
CO
ИП5
CN
"4f
CO
s
s
a
CN
CN
CN
Q
CO
ИПВ
CO
00
CN
X
CO
со
о
~
co
4*
CO
ипз
CO
CN
О
LO
С/П
8
»—«
I
00
CN
CO
ИП2
rj«
1
4*
CN
X
CN
9
CO
о
о
/-/
LO
о
ч~
ю
CO
CQ
CO
00
CN
CN
*
CO
CO
S 8
ипо
1С
CN
CO
ИП2
Ю
CN
О
LO
С/П
о
с*
4
CO
"4f
CN
CN
*
CO
CN
О
О
CO
О
о
С/П
00
CN
X
СО
CN
О
CN
CN
X
1^
CN
О
LO
С/П
о
CN
X
00
со
CN
X
00
CN
О
CN
00
CN
I
<
00
о
CN
О
CN
a»
CO
о
~
a»
CO
+
CN
О
LO
С/П
a»
о
со
+
о
=
1
о
^
^f
о
со
CO
ИП1
о
со
СО
ипз
£
СО
СО
С
Ю
СО
со
ИПЗ
со
CN
СО
ИП2
~
1
СО
ИПА
CN
CN
X
CN
ю
1
СО
ИПА
CN
со
CN
X
CN
CN
X
со
1—*
1
со
ю
CN
X
со
со
со
со
ИПЗ
со
со
о
СО
ч*
ь-
СО
ИП4
8
CN
СО
1
СО
ИПА
ч*
CN
X
ю
CN
X
LO
ю
CN
X
LO
СО
CN
X
ю
о
/-/
СО
СО
ИПВ
СО
LO
О
/-/
СО
со
О
/-/
СО
СО
ч
-
1
1^
LO
СО
ч
<4>
со
СО
ч
<4>
t»-
CN
X
S
о
τ
оо
ю
LO
LO
00
со
CN
χ
00
CO
СО
ИП6
.J
4t
CQ
a
LO
о
CO
ИП0
CO
о
CO
ИП0
a
404
Контрольный пример. Исходные данные: pg = 10,1 т/м2 · с2; h =
= 3,0 м; k = 0,21 м-1; cos (dt = 0,29; ζ = 0. Время счета 35 с. Результат
расчета: ρ = 9,44 кПа.
Программа МК-3. Определение горизонтальных волновых
нагрузок на вертикальные стены по эпюрам волнового
давления.
Расчетная схема представлена на рис. 1 [51]. Программа
МК-3 вычисляет значения и координаты точек приложения
равнодействующих эпюр волнового давления РХу кН/м, на
единицу длины стены. Исходными данными являются:
pi — волновые давления, кПа, в точках стены (/= 1, 2, 3, 4
и, на уровне подошвы сооружений); Zi— координаты точек, м.
Программа МК-3 приведена в табл. ПЗ.
Ввод исходных данных и пуск программы на счет
производятся в следующей очередности: В/О, zH—г4; С/П; £4—^з; С/П;
zz-z2\ С/П; z2 — zx\ С/П; Pl; С/П; р2; С/П; р3; С/П; р4; С/П;
рн; С/П.
Результаты расчета выводятся на индикатор при помощи
команд: ИПС; ПХ = Рх\ ИПВ; ПХ = W; ИПА; ПХ = ε.
Здесь обозначено: Рх — равнодействующая эпюры волнового
давления, кН/м; W — опрокидывающий момент, кНм/м; ε —
плечо равнодействующей относительно подошвы вертикальной
стены, м.
Контрольный пример. Исходные данные: zH = df = 13,0 м; zA =
= d/2 = 6,75 м; z3 = rf/4 = 3,375 м; z2 = 0; г! = — цт&х = — 7,65 м; Pi =
= 0; /*2 = 50,5 кПа; /?3 = 41,9 кПа; р4 = 35,4 кПа; рн = 31,3 кПа. Время
счета 1 мин. Результаты расчета: Рх = 687,97 кН/м; UP = 6482,02 кНм/м; ε =
= 9,42 м.
Программа МК-4. Определение возвышений и понижений η
волнового профиля и ординат ρ волновых давлений от
дифрагированных волн.
Расчетная схема приведена на рис.6 [51]. При составлении
программы использованы формулы (6) — (11) [51]. Исходными
данными являются:
hdif — высота дифрагированной бегущей волны, м; λ —
средняя длина дифрагированной волны, м; d — расчетная глубина
со стороны огражденной акватории, м; / — длина секции
оградительного сооружения, м.
Предварительно по табл. 2 [51] находится коэффициент ki
в зависимости от относительной длины секции Ι/λ.
Программа МК-4 записывается в программную память
микрокалькулятора в соответствии с табл. П4.
Ввод исходных данных и пуск программы^ на счет выполня-.
ются при помощи команд: В/О, hdif, С/П; λ; С/П; d\ С/П; /;
С/П; ki\ С/П.
Результаты расчета выводятся на индикатор следующими
командами: ИП1; ПХ = η^; ИП2; ПХ = р2с\ ИПЗ; ПХ = рЪс\
ИП0; ПХ = η*; ИПА; ПХ = р2г, ИПВ; ПХ = pzt. Здесь буквен-
405
Код
Команда
ί Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес,
Код
Команда
Адрес
СО—'—·
*3
^ч-х
Or-*(N
00 00 00
5§2
Ем +
Or- (N
to to to
COt^Oi
ЮЮ to
333
О -*f ^f
Or-(N
SSS
85S
to
ИПД
CO
00
rf
^X
CO
to
о
+
9
о
ИП9
со
(Ν
О
ю
С/П
3
to ^^
^ i-OtO
00 00 00
(Ν (Ν Ш
-ι- — ©
Ι^Χ^
coto to
ст> Joo
Tf CO tO
rMOtO
Tf ^ -5f
to to ю
-i-LOtO
1 OJ
<E0Q
sss
1—*
00
to"
ИПС
to
to
ИП7
Ю
LO'
fc
о
LO
С/П
о
(Ν
Ю
В/О
00
00
о·—.
г-н <4*
. и
оо σ>
to to
C0t^
£10
σ>©
-г со
оо σ>
(Ν (Ν
^Ю
§8
ю
(Ν
0
о
to
ИП9
о
ю
со
со
ИПЗ
о
со
$
СО
о
-f
^Х
1^
о
+
ю'
СО
ИП4
СО
оо
оо
т-ч
—•О — CO(N(N
СО г-« СО *-" СО ·-.
i+l+i*
Οί СО ^ЮСО 1>.
Tj-СО гн rt Ю О
(N CO "* Ю CO l>.
ю ю ю ю ю ю
у^ю to*-« ^to
Csr j 2c:
(NCO -*ЮсО b-
со со CO CO CO CO
О TfiOO(NcO
С^ю C_oj со
£jE С qj С С
(Nco^iOOS
со
о
со
00
ю
CN
0
00
ю
ю
to
ИП5
00
со
о
ю
С/П
оо
СО
.1.
О)
о
н-
<7>
ю
со
СО
ИП6
(Я
СО
5
Ξ
о
Код
Команда
1
i Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
СМ
X
о
1
<
о
СО
см
X
о
о
-ί-
Ο
(Ν
-8
со
Π·
со
ОО
СО
СО
ИП6
СО
СО
ипд
5
а
^
см
S
с/п
о
00
СО
ИП8
СМ
оо
1^-
СО
ИП7
СМ
СО
СМ
О
СМ
СМ
О
+
СМ
СМ
?
Ξ
8
со
ИП9
S3
(Ν
СО
СО
СО
•1·
со
СМ
О
СМ
а
о
LO
С/П
8
см
X
оо
со
СМ
Н^
-ΙΟ
+
5
СО
·!·
СМ
СМ
(Ν
О
ю
оо
00
СО
ИП8
LO
СО
О
/-/
ю
о
-
LO
(Ν
О
LO
С/П
о
LO
С/П
СО
(Ν
Χ
СО
СО
5
Ε
S
СО
to
8
со
со
8 8
со
ИПД
1^
о
СО
ипд
(Ν
CM
CN
CO
ИП1
о
CN
О
см
00
СО
о
-]-
00
о
~
оо
СМ
со
•1·
оо
о
со
•1·
СО
о
о
с:
3
-
1
CN
О
LO
С/П
g
S
ИПб
о
о
-
о
LO
CM
I
о
со
С
о
со
Τ
b-
о
о
о
5
со
О
СМ
е
-
о
+
см
1
о
-
см
LO
со
•1·
см
со
см
о
см
см
о
/-/
СО
о
-
со
LO
to
ИПД
со
со
cni
X
со
оо
оо
со
ИП4
ю
см
см
со
to
ИП1
τί*
CO
ипд
LO
CM
X
a
LO
CO
ИП5
LO
CO
CO
•1·
LO
CO
ИПб
to
LO
CM
X
CO
CO
LO
LO
to
CO
•1·
^
b-
CM
X
LO
oo
о
00
CO
CM
CO
ИП2.
i>»
о
+
oo
см
-φ
CM
00
со
·ι·
оо
со
CM
χ
oo
<2?
CO
ИП9
ел
о
'Τ
оо
оо
а
СО
со
ч
^
<л
40?
ные обозначения с индексом с относятся к случаю нахождения
у середины секции вершины волны, а с индексом t — к случаю
нахождения у середины секции подошвы волны.
Контрольный пример. Исходные данные: haif = 6,0 м; λ = 100 м;
d = 13,0 м; I — 20,0 м; kt = 0,92. Время счета 30 с. Результаты расчета:
rimax = —3,42 м; р2е = 23,97 кПа; рзс = 18,48 кПа; η, = 2,58 м; p2t =
= —23,97 кПа; p3t = —22,74 кПа.
Программа МК-5. Определение максимального волнового
давления ра и ординаты е2 точки его приложения для
сооружений откосного профиля.
Расчетная схема представлена на рис. 11 [51]. Программа
составлена по формулам (26) — (30) [51]. Исходные данные для
расчета следующие: _
h — высота бегущей волны, м; λ — средняя длина волны, м;
cgtcp — заложение откоса.
Перед началом расчета по программе МК-5 в соответствии
с п. 1.15 [51] находятся: _
kf — по табл. 10 [51] в зависимости от пологости волны λ/Λ;
Prei — по табл. 11 [51] в зависимости от высоты волны h.
Текст программы МК-5 принимается по табл. П5.
Ввод исходных данных и пуск программы на счет
производятся командами: В/О, ctgcp = П1|Л = Π2|λ~; С/П; XY; kf\prei\
С/П. ~* '
Результаты расчета высвечиваются на индикаторе ПХ = ζι
и вызываются командой ИП4; ПХ = ра.
Контрольный пример. Исходные данные: ctg φ = 1,732; h = 2,0 м;,
λ = 37,4 μ; kf = 1,25; prei = 2,1. Время счета 1 мин. 20 с. Результаты расче-,
та: ζι = 0,1 Г м; ра = 55,6 кПа.
Программа МК-6. Определение массы m или тг массивов и
камней на откосах.
При составлении программы использованы формулы (33)*'
и (34) [51]. Исходными данными ^ля расчета являются:
h — высота бегущей волны, м; λ — средняя длина волны, м;
φ — угол наклона откоса к горизонту, рад; рт — плотность
материала элементов защиты откоса, т/м3; ζ — отметка точки, м,
для которой находится масса элемента наброски.
Предварительно по табл. 12* [51] находится коэффициент
kfr в зависимости от вида элемента крепления и способа его
устройства.
Программа МК-6 записана в табл. П6.
Ввод исходных данных и пуск программы на счет
осуществляются командами: В/О, kfr\ С/П; рт; С/П; h\ С/П; λ;
С/П; φ; С/П; г; С/П.
Результаты расчета появляются на индикаторе ПХ = mz или
вызываются командой ИПД, ПХ = т.
408
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
ч
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
о
+
о
о
^
о
1
о
*
о
о
+
см
со
1 *-*
•1·
8
СМ
1
СМ
X
СО
со
о
со
1—*
о
-
см
5
со
о
о
-
СМ
СМ
о
СМ
СМ
СМ
X
СМ
О
о
о
я
о
-
СМ
О
-
1
СО
ю
о
ю
со
СО
о
-*
3
о
о
о
со
СМ
о
-
со
о
о
/-/
Tf
-
1
δ
ь-
Tf
^
CO
■!·
см
LO
о
LO
s
со
•1·
Ю
00
CO
CO
ИПЗ
CO
о
+
LO
CO
CO
ИПЗ
Ю
CM
CM
X
s
CO
CM
Η
CO
CM
X
CO
CO
CM
CO
ИП2
CO
CO
CM
■Л
CO
CM
CM
о
CM
8
Tf
£t
ь-
о
σ>
CO
ΟΙ
Χ
$
ο
LO
С/П
οι
Ι
ο
-
ο
Ю
00
ИП5
00
00
Ю
ο
LO
00
CO
Ξ
ИП1
00
CM
Χ
00
см
8
00
οο
о
о
+
οο
=
I
8
CM
CM
с*
см
Χ
OS
CM
!-H
I
α»
о
см
X
о
о
/-/
о
о
-
о
LO
см
СО
ИП2
о
СО
СМ
X
о
ю
СО
ИП5
s
см
СО
ИП2
ί"Ξ
о
ч-
LO
СМ
X
со
О
/-/
-
о
+
см
см
X
см
о
-
см
LO
о
-
см
со
со
СО
ИПЗ
см
о
-
5S
s
ИП1
со
о
+
8
о
о
о
со
со
о
^
со
8
О
см
см
***
1>-
со
•1·
1
о
-
со
00
о
00
-ίο
о
о
LO
СП
о
ч—
LO
со
см
^
LO
LO
1—*
о
-
LO
со
8
о
ю
со о
С/П
СО Г»
ё 8
ч- ^
СО О-
CM LO
LO
X С
со ь~
LO LO
см ^
X С
СО 1>-
СО СО
см о
X +
СО Ь-
см
1—*
X
00
СО
ИП1
00
LO
1—*
1*
+х
00
со
8
оо
00
о
-
00
о
00
LO
CM
о
\а
со
3
ю
С75
409
Код
Команда
! Адрес
Код
1 СО
Ξ
СО
1 ~
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
CD
О
со
•Ιο
1
о
-
о
см
о
о
о
о
ю
СО
ИП5
S
CD
ИП4
5
о
-
см
8
С/П
о
см
см
с»
см
CD
ω
ьо
CM
CO
о
CD
CM
CM
"*
Ξ
8
o
r^
CO
CD
CO
CM
4^
CO
CM
X
a
s
С/П
8
1
о
-
CD
Ш
о
-
Tf
"*
CO
CO
ИПЗ
CM
CM
CM
С
о
ю
о
ю
ю
СО
см
см
см
СО
ИП2
ю
см
о
ю
с/п
ю-
о
см
X
CD
см
X
«
to
·!·
СО
см
СО
■4f
со
3
см
со
ИП2
со
о
~
1>-
см
1
см
о
ю
с/п
δ
со
СО
ИПЗ
00
СО
о
+
00
см
X
00
сч.
Ч"
■*
оо
о
см
X
СО
см
1
CD
ИП1
О»
CM
о
ю
с/п
о
со
•1·
о
1^
со
+
о
ю
о
~
о
со
ю
с
о
1
о
/-/
ь-
ю
1
о
*
со
о
СО
ИПО
-
СО
см
1^
см
СО
SUM
см
ю
о
о
о
см
со
СО
ИП1
см
СО
ипд
со
о
о
о
со
ю
СО
о
со
со
со
см
СО
ИП2
со
см
X
1
о
-
со
•1·
со
см
см
сн
rf
о
ю
с/п
о
ь-
ю
ю
о
-
ю
со
см
СО
ИП2
ю
U
СО
ИПД
со
см
X
СО
ю
f-«
1
СО
со
см
1—*
X
СО
о
ю
1^
1^
Ю
СО
с:
о
-
со
см
X
г-
-
1
00
ю
см
см
00
со
см
X
00
ю
о
V
см
X
С7>
со
8
со
О)
410
Контрольный пример. Исходные данные: kfr =Ό,008; pm =
= 2,4 т/м3; h = 4,63 м; λΓ= 65,0; φ = 0,524 рад; ζ = 0. Время счета 20 с.
Результат расчета: т = 3,86 т.
Программа МК-7. Определение волновой силы Q на
вертикальную обтекаемую преграду и координаты zQ точки ее
приложения.
Расчетная схема приведена на рис. 14 [51]. Использованы
формулы (36) —(38), (46) —(48) из [51]. Исходными данными
-являются: _
h — высота бегущей волны, м; λ — средняя длина волны, м;
а — размер преграды по лучу волны, м; Ь — размер" преграды
по нормали к лучу волны, м; d — глубина воды при расчетном
уровне, м.
Расчет по программе МК-7 производится с обращениями
к таблицам и рисункам [51].
Запись программы МК-7 в память микрокалькулятора
производится по табл. П7.
Ввод исходных данных и пуск программы на счет
обеспечиваются командами (все ссылки на таблицы и рисунки — см.
СНиП [51]): В/О; d; С/П; Л; С/П; λ; С/П; Ь\ С/П; а; С/П;
ΠΧ = α/λ; kO (табл. 13); С/П; ΠΧ = λ//τ, ΧΥ; ПХ = d/λ; ai\av
(рис. 16); С/П; ПХ = α/6; β/φβ0 (рис. 17)Гс/П; ПХ = ПВ =
= Q„; ПУ = ПА = <2,·; Xi; С/П; ПХ = κ г, б^б0 (рис. 15); С/П;
nX = nO = Qi; ζι,Γβί\μι (рис.21, 22); С/ПГ ζ0,Γβ^μ* (рис.21,
22); С/П; nX = 2Qfi; x2; С/П; ПХ = %2; б/фб^; С/П; ПХ =
= nO = Q2; ζί,Γ·/|μί; С/П*> Ur*ifav\ С/П; nX = zQ,2, ...
Результаты расчета высвечиваются на индикаторе в
процессе счета в соответствии с приведенной выше инструкцией по
вводу исходных данных и пуску программы.
Контрольный пример. Исходные данные: d = 30 м; h = 10,7 м;
λ*= 149 м; Ь = 4,0 м; а = 4,0 м; kv = 1,0; щ = 0,88; <х0 = 1,77; β/ = 1,0;
β0 = 1,0; jci = 25,63 м; δ* = 1,02; δ0 = 0,13; ξ*·, ге* = 0,08; μ£ = 0,85; ζ„, re/ =
= 0,035; μ0 = 1,7. Время счета 2 мин. Результаты расчета: Qi = 1294,4 кН/м;
zQt! = 10,05 м.
Программа МК-8. Определение удельного волнового
давления q на вертикальную обтекаемую преграду.
Расчетная схема представлена на рис. 14 [51]. Использованы
формулы (41) — (43) [51р. Исходные данные те же, что и в
программе МК-7.
Текст программы МК-8 приведен в табл. П8.
Ввод исходных данных и пуск программы на счет
производятся в следующей очередности (все ссылки на_таблицы и
рисунки—см. СНиП_[51]): В/О; d\ С/П; А; С/П; λ; С/П; Ь\ С/П;
а; С/П; ПХ = α/λ; kv (табл. 13); С/П; ПХ = α/ft;. β^βυ (рис.
17); С/П; 2; С/П; ΠΧ = λ//τ, XYj ПХ = 2ге/; θ,ί|θ,„ (рис. 19,α, б);
С/П;' ПХ = ПВ = ?„; ПУ = ПА^= qry хх\ С/П; ПХ = κ4; б*|б**
411
Код
Команда
Адрес
Код
Команда
Адрес
Код ι
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
со
СО
ИПЗ
о
s
со
О
СО
СМ
X
О
$
8
5
а
S
СМ
X
00
см
X
г-«
со
8
СМ
-+■
£t
см
S
α
о
СО
ИПС
СМ
00
J
^
CQ
см
«о
1
о
-
СМ
оо
00
с:
СМ
СМ
см
СМ
см
о
см
X
СО
00
S
С/П
со
СО
8
LO
3
ю
СО
ИП5
со
СМ
о
ю
С/П
S
rh
*χ
00
СО
ИПЗ
со
см
X
-*
^
СО
ИП4
см
5
со
о
СО
со
ИПЗ
LO
СО
•1·
ю
СО
1
<
СО
•1·
ю
см
о
С/П
§
см
X
со
00
о
ю
С/П
со
СО
OS
СО
ИП9
СО
О
С/П
8
5
СО
о
СО
ИПД
оо
СО
ИПВ
СО
СО
ИП7
см
о
ю
С/П
о
см
X
00
оо
см
X
00
со
см
X
00
^"
&1
оо
см
8
о
4-
1
00
^F1
со .
со
СО
ИП6
о
О
ел
см
со
СО
ипз
8
ό
СО
ипо
о
^
&t
о
1^
см
см
о
ю
оо
СО
ИП8
о
со
со
•Ιο
со
.,.
55
1
СО
ИПА
ь-
£ί
X
ю
см
X
со
О
ю
С/П
·—«
В
см
см
X
см
см
СО
ИП2
см
СО
СО
СО
С
5
см
со
СО
СО
а
см
СО
СО
СО
со
со
см
см
*
со
ю
см
X
я
СО
ИП1
со
о
+
-*
г-
см
X
ч*
ю
см
со
ИП2
СО
со
СО
1 ипз
Tt
о
о
1^
СО
ИП4
см
X
Ю
со
со
•1·
ю
S
С/П
о
см
X
18
'СО
ИП4
СО
со
СО
СО
ипз
СО
СМ
X
1^
8
О
N.
см
см
*
со
см
СО
ИП2
t^
о
ю
С/П
00
г-
1
о
00
ю
см
X
00
СО
со
•1·
00
см
X
8
00
8
8
Ы
со
8
I с/п
ел
412
Код
Команда
Адрес
Код
Команда
Адрес
Код
-Команда
Адрес
Кол
Команда
Адрес
Код
Команда
Адрес
ю
S
см
X
о
СО
СМ
X
о
о
ю
с/п
а
5
1—*
С
8
ел
СО
ел
со
со
а
s
СО
СО
ИП4
Tf
S
ИП1
СМ
о
ю
С/П
о
см
X
см
СО
О
см
и
см
1—*
1
см
см
см
см
см
о
8
СО
со
СО
см
1—·
X
со
о
/-/
со
см
о
ю
с/п
8
1
о
-
СО
см
см
'к
s
ИП1
CM
CO
CO
с
о
CO
о
СО
Ю
CM
X
3
CO
•1·
Ю
CM
о
С/П
о
о
ь-
co
CO
Ю
о
Ю
CO
CO
CO
ИПЗ
CO
CM
Tf
Tf
8
CM
X
CO
CM
1—*
X
CM
CO
ИП2
CM
о
С/П
о
4*
CQ
oo
CO
1
<
00
CO
1—t
•1·
00
CM
00
о
о
ю
с/п
ел
СО
-+
1551
ел
о
ю
С/П
ел
см
со
СО
ИПЗ
ел
о
СО
СО
ИПЗ
о
СО
ИП7
о
ю
3
ел
о
СО
со
·!·
О
СО
•1·
г^
см
X
LO
1—*
J,x
со
8
с/п
-
S
с/п
СМ
СО
СО
ИП6
см
ю
о
г °
S3
со
со
СО
см
СО
ИПВ
со
1>-
см
СО
ИП2
S
оо
СО
ИП8
со
СО
ю
СО
ИП5
со
СМ
X
см
X
СМ
X
со
со
ИП4
*#
^
&'
см
см
ю
ю
СО
СО
ИП6
ю
со
со
•1·
ю
I
СО
ИПА
СО
СО
СО
* ИПЗ
СО
ю
см
t—«
X
СО
со
О
ю
с/п
СО
СМ
X
со
•1·
см
СО
ИП2
1>-
со
^
Tf
г^
о
+
00
СМ
X
00
ю
со
СО
ИПЗ
оо
со
4Х
оо
τί*
и
ел
3
ИП4
ел
ю
со
+
Й
00
^ оо
ел
413
(рис. 18); С/П; ПХ = ПС = ^; х2\ С/П; ПХ = κ2; δ^δ,*; С/П;
ПХ = ПС = q2;...
Результаты расчета появляются на индикаторе в процессе
решения задачи в соответствии с приведенными выше
командами. Г
__ Контрольный пример. Исходные данные: d = 30,0 м; h = 10,7м;
λ = 149 м; Ъ = 4,0 м; α = 4,0 м; ΗΌ = 1,0; β,- = 1,0; β„ = 1,0; ζ = 0; 0χί = 1,02;
θ™ = 0,47; *, = 29,8 μ; δχί = 0,99; δχυ = 0,02. Время счета 2 мни. Результат
расчета: q = 57,86 кН/м.
Программа МК-9. Определение горизонтальной Рх и
вертикальной Pz составляющих волновой нагрузки на
горизонтальную обтекаемую преграду.
Расчетная схема приведена на рис.14 [51]. Использованы
формулы (50) — (55) [51]. Исходные данные должны быть
такие же, как и в программе МК-7.
Текст программы МК-9 совпадает с текстом программы
МК-8 в табл. П8.
Ввод исходных данных и пуск программы на счет при
определении Рх выполняются с помощью команд (все ссылки на
таблицы и рисунки —см. СНиП £51]): В/О; d\ С/П; А; С/П; λ;
С/П; Ь\ С/П; а; С/П; ПХ = α/λ; К (табл. 13);' С/П; ПХ = а/Ь\
β/|β„ (рис.17); С/П; zc\ С/П; ПХ = λ/Λ; ΧΫ; ΠΧ = ζ,|Γβί;
θΛί|θχσ (рис. 19, α, б); С/П; ПХ = ПВ = Ρχυ; Г1У = ПА = ΡΧί\
хх\ С/П; ΠΧ = κι; δ*;|δ*, (рис. 18); С/П; ПХ = ПС = Ρ*; ...
Ввод исходных данных и пуск программы на.счет при
определении Ρζ осуществляются командами (все ссылки на таблицы
и рисунки —см. СНиП_[51]): В/О; d\ С/П; А; С/П; λ; С/П; а;
С/П; 6; С/П; ПХ = ft/λ; *и (табл. ]3); С/П; ПХ = 6/α; β;|β,
(рис. 17); С/П; zc; С/П; ΠΧ=λ/Α; ΧΫ; ПХ==гС|Гв/; θ*ί|θ« (рис.
19,0,2); С/П; ПХ = ПВ = ΡΖϋ; ПУ^*ПА = Р*; *,; С/П; ПХ =
= хг, б*/|б«, (рис. 23)· С/П; ПХ = ПС = Р2; ...
Далее приводятся тексты программ, позволяющих
производить динамические расчеты вертикальных стен при действии
разбивающихся волн в соответствии с рекомендациями
параграфа 8.6.
Программа МК-10. Определение равнодействующей Яш
импульса давлений на вертикальную стену.
Изменение нагрузки во времени представлено на рис. 8.21.
Эпюра импульса давлений — на рис. 8.22. При составлении
программы использованы формулы (8.44) — (8.49).
В качестве исходных данных задаются: аы — глубина воды
над бермой, м; h — высота волны, м; λ — средняя длина волны,
м; / — длина секцииг м; d\ — глубина воды у стены, м; g —
ускорение свободного падения, м/с2.
4U
В результате расчета следуют:
zr — возвышение вершины разбивающейся волны над
свободным горизонтом, м; а! — параметр, м; рш— значение
импульса давлений на 1 п. м. стены, кНс/м2; Rim — значение
равнодействующей импульса давлений, кНс/м; k'ir — осредненный
коэффициент пространственной неравномерности.
Программа МК-10 приведена в табл. П9.
Ввод исходных данных и пуск программы на счет
производятся следующими командами: аы = ПО; h = ΠΙ; λ == П2; I =
= ПЗ; rff = n4; g = П5; 0,55 = П6; 0,1 = П7; 1,34 = П8; 1,2 =
= П9; 0,637 = ПА; 0,15 = ПВ; 1,3 = ПС; 1,6 = ПД; В/О; С/П.
Результаты расчета выводятся на индикатор командами:
ИП7; ПХ = г'; ИП8; ПХ = а'; ИП9; ПХ = pim\ ИПА; ПХ =
= Rim\ ИПС; ПХ = К*.
Контрольный пример. Исходные данные: dbr = 5,7 м; h = 5,0 м;
λ = 75,0 м; / = 15,0 м; df = 7,0 м; g = 9,81 м/с2. Время счета 45 с.
Результаты расчета: zr = —3,64 м; а' = 3,1 м; р-1т = 17,8 кНс/м2; Run = 114,0 кНс/м;
k'ir = 0,73.
Программа МК-И. Определение равнодействующей Rq
давления навала и координат точек приложения.
Расчетные схемы приведены на рис. 8.23—8.25. Использованы
формулы (8.50) — (8.55). Задаются следующие исходные данные:
dbr — глубина воды над бермой, м; df — глубина воды
у стены, м; а — ширина стены, м; г' — возвышение вершины
разбивающейся волны над уровнем свободной поверхности, м.
В результате расчета следуют:
rq — плечо равнодействующей навала относительно подошвы
стены, м; rim — плечо равнодействующей импульса давлений, м;
Rq — равнодействующая давления навала, кН/м; Pzq —
взвешивающее давление от навала, кН/м; Mzq — момент от
взвешивающего давления навала относительно центра подошвы стены,
кНм/м.
Программа МК-Н приведена в табл. П10.
Ввод исходных данных и пуск программы на сует
производятся следующими командами: аы = ПО; 0,65 = Π Г: 0,5 == П2;
10 = ПЗ; df = n4; 0,75 = П5; а = П6; ζ' = П7; В/О; С/П.
Результаты расчета выводятся на индикатор командами:
ИП2; ПХ = /у, ИП7; ПХ = r£m; ИПВ; ПХ = Л,; ИПС; ПХ =
= Pzq\ ИПД; ПХ = Mzq.
Контрольный пример. Исходные данные: аы = 5,7 м; df = 7,0 м;
а = 8,0 м; ζ = —3,64 м. Время счета 35 с. Результат расчета: rq = 4,88 м;
riin = 4,47 м; Rq = 309 кН/м; Pzq = 114 кН/м; Mzq = 152 кНм/м.
Программа МК-12. Определение частот и периодов колебаний
сооружения.
Расчетная схема приведена на рис. 8.26. В программе
использованы формулы (8.56) — (8.59). Задаются следующие
исходные данные:
415
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
СО
' ч*
S
-
1
о
СО
СМ
X
о
3
ИП1
о
см
СО
ИП1
S
о
ч-
1—*
оо
00
со
ИП8
СО
СМ
X
5
СМ
X
см
СО
ИП7
о
со
СМ
i
СМ
Π
I
(Ν
CO
a
9
CO
ИП1
(Ν
CM
(Ν
Χ
(Ν
Ο
»—*
•Ι
со
(Ν
Χ
СО
S
ИП1
со
о
(Ν
S
со
CM
О
CO
ИПО
со
о
8
СМ
со
о
+
СО
°2
СО
ИПЗ
(Ν
Г—i
χ
CM
со
СО
ИП6
о
со
•1·
00
СО
ИП4
со
со
•1·
00
о
00
ю
см
см
X
ю
о
ω
о
-
СО
00
СО
ИП7
СО
00
ю
а
со
СМ
X
СО
см
о
+
СО
о
см
с*
00
-
1
СО
о
оо
о
оо
ι**
<v3
СО
ИП2
см
ё
τ
о
о
~
00
00
СО
•1·
00
со
CO
ипв
00
со
•1·
оо
см
!?
а
00
о
о
+
С75
00
^г
и
СО
см
X
3
—
sin
OS
CM
СО
ИП1
о
CM
I
о
ся
СО
ИП9
о
СО
СО
ИП6
о
ю
см
X
о
со
8
см
о
со
S3
см
X
ь-
о
+
3
оо
00
с
со
см
X
-
см
ю
в/о
СО
ИП4
см
1^
00
СО
ИП8
см
ю
о
СО
ИПО
см
со
о
СО
о
а
5
см
СО
ИП7
S
■*
W
со
ю
Ю
СО
ИП5
, со
со
со
+
со
СМ
о
(М
ч*
ь-
см
X
см
X
со
00
СО
ИП8
Tf*
СО
•1·
о
CQ
см
1
-
1
ю
~
1
СО
<ΪΩ
5
СО
ИП9
СО
СО
СО
ю
а
с:
СО
СМ
X
ь-
г-
см
X
СМ
X
со
О
00
8
ь-
I
<
а
со
со
ИП4
°2
00
СО
ИП8
00
со
СО
ИПД
00
S
с/п
(75
1^
СО
ИП7
ю
ι
со
ИПА
аз
со
см
X
σ>
416
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
СО
ИПВ
о
со
о
со
о
СО
СО
СО
ИПЗ
о
-φ
s
ИП1
8
СО
ИП4
8
СО
·!·
00
со
•1·
3
о
+
Tf
см
X
см
см
см
сч
*
о
9
см
см
00
3
ИП1
см
СО
СО
ИП4
см
см
X
см
см
СО
ИП4
S
со
СО
ИПЗ
со
00
со
СО
ИПЗ
СО
СО
см
X
со
5
Ε
СО
см
СО
ИП7
со
о
«о
СО
ИП6
3
о
+
СО
СМ
о
см
О
СО
ИПО
см
см
X
S
см
X
Ю
СМ
X
ю
СО
со
+
со
СО
ИПЗ
Ю
СМ
-
1
о
см
о
см
СО
см
о
см
СО
СО
о
+
СО
*3-
см
СО
ИП2
со
см
1^
СО
1^
S
СО
о
со
•1·
оо
со
·!·
1>-
СО
J
Tf
со
t^
Tf
CM
χ
CM
CM
CM
*
о
тр"
00
00
Ю
CO
ИП5
00
CO
3
ИП1
00
CM
X
oo
CM
со
о
CO
о
CO
CO
CO
a
s
00
CO
о
CO
CO
CM
о
CM
4*
CO
•4F
CO
CM
CO
·!·
О
CM
X
S
CO
•1·
g
CM
X
о
Ю
о
CO
ИП0
о
CO
о
ΊΟ
CO
О
CD
^-1
со
ИП4
F^
CO
CO
ИПЗ
Ю
Ю
CD
ИП5
CO
4*
CO
ИП4
-
CO
.1.
CM
OS
о
+
CM
о
+
CM
CM
X
CM
CO
CM
о
CM
CM
^
с
CO
OS
3
ИП1
CO
3
ИП1
со
Ю
tO
a
CO
CO
CM
X
CO
s
С/П
CM
X
Tf
t^
CO
CD
ИПЗ
CM
CD
ИП2
CO
CD
S
^t-
Ю
CO
ИП5
o
+
Ю
CD
ИП5
CO
r~*
1
Ю
CM
1—<
X
CO
co
·!·
CO
Ю
CM
X
CO
CO
со
+
CO
CM
CD
ИП2
•4f
CO
ИП4
г-н
CD
ИП1
co
r»
CM
X
00
CM
CM
00
CM
Г—1
X
00
CO
о
CO
ИП0
oo
о
+
<Л
CM
X
о
со
СО
СО
ИПЗ
σ>
417
Co — основной коэффициент постели, определяется по табл.
8.16, кН/м3; а — ширина стены, м; I — длина секции стены, м;
Ge — вес 1 п. м сооружения с учетом гидростатического
взвешивания, кН; θ — момент инерции массы 1 п. м сооружения
относительно оси, проходящей через центр тяжести
перпендикулярно плоскости чертежа, тм-с2; га— масса 1 п. м сооружения, т;
Л0 — возвышение центра тяжести сооружения над его
подошвой, м.
Программа МК-12 приведена в табл. П11.
Ввод исходных данных и пуск программы на счет
производятся командами: Co/g = ПО; 0,7 = П1; а = П2; / = ПЗ; Ge =
= П4; Θ = Π5; га = П6; h = П7; 12,0 = П8; 2я = ПД; В/О;
С/П.
Результаты расчета выводятся на индикатор командами:
НПО; ПХ = С9; ИП1; ПХ = Сх\ ИПЗ; ПХ = 7\; ИП4; ПХ = Г2;
ИП6; ПХ = со2*; ИПС; ПХ = со2,; ИПВ; ПХ = ω22.
Контрольный пример. Исходные данные: С0 = 4910 кН/м3; а =
= 8,0 м; / = 15,0 м; Ge = 1475,1 кН; θ = 3024,7 тмс2; m = 206,0 τ; Ιι0 =
= 5,15 м. Время счета 50с. Результаты расчета: Οφ= 28315 кН/м3; Сх =
_ = 14558 кН/мЗ; Г, = 0,146 с; Т2 = 0,57 с; ω2* = 565 с-2; ω2, = 1864 с"2;
о>22= 121,1с-2.
Программа МК-13. Определение углов поворота α? β
сооружения вокруг главных центров и отклонения б подошвы от
положения равновесия.
Программа составлена по формулам (8.60), (8.61).
Предварительно определяются Тп — полное время действия
равнодействующей Rim импульса давлений и Tq — время ее
нарастания— по графикам на рис. 8.23, а также значения
динамических коэффициентов kla, kua по графикам на рис. 8.27.
Задаются следующие исходные данные:
Ло — возвышение центра тяжести сооружения над его
подошвой, м; ω2*; ω2ι, *о22 — частоты колебаний, с~2; Rim —
равнодействующая импульса давлений, кНс/м; пт — плечо
равнодействующей, м; θ — момент инерции массы 1 п. м сооружения
относительно оси, проходящей через центр тяжести
перпендикулярно плоскости чертежа, тмс2; т — масса 1 п. м сооружения, т;
kldy knd — коэффициенты динамичности; Тп — полное время
действия Rim, с.
Программа МК-13 приведена в табл. П12.
Ввод исходных данных и пуск программы на счет выполня-1
ются в соответствии с командами: h = ПО; ω2* = ΠΙ; ω2ι = П2:
ω22 = ПЗ; Rlm = П4; rim = П5; θ = П6; m = П7; kld = П8; klld=\
= П9; Тп = ΠΑ; В/О; С/П.
Результаты расчета выводятся командами: ИП8; ПХ = а;
ИП9; ПХ = β; ИПД; ПХ - δ.
Контрольный пример. Исходные данные: h0 = 5,15 м2; ω2λ =
= 565 с-2; ωι2 = 1864 с"2; ω22 = 121,1 с"2; Rtm = 114,0 кНс/м; rim = 4,47 м
θ = 3027,4 тмс2; m = 206,0 τ; kdl = 1,0; kdu = 1,35; Tn = 0,78 с. Время счетгУ
40 с. Результаты расчета: α = —0,000113 рад; β = 0,00162 рад; δ = 0,00309 м]
418
Код
Команда
Адрес
Код
Команда
| Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Кол !
Команда
Адрес
СМ
со
<м
С
S
о
σο
ю
СО
ю
а
S
S
о
+
о
CO
СО
со
S
8
ю
со
1 s
S
со
со
со
с
S
00
о
1—*
+
5
5
со
•1·
CN
о
-
о
СМ
X
СМ
оо
1
СО
<
S
СМ
СО
о
ч-
5i
СМ
X
СМ
СО
СО
со
S
8
СО
+
со
СО
+
со
СО
см
см
С1
3
СО
СО
СО
СМ
Г-
со
г-
С
5
S
СМ
О
СМ
00
V
и
СО
СО
а
s
со
О
со
(Ν
CM
CM
с»
·<*
о
см
Χ
ю
СО
ю
СО
о
-t
ю
СО
см
ю
см
см
Г·*
X
S
о
-
СО
со
Г-
со
г-
СО
СО
см
X
СО
см
СО
см
о
~г
СО
о
о
+
ΓΟΟ
со
с
Г-
СО
СО
СО
СО
а
S
г-
со
СО
со
с
г-
см
г-
г-
с
г-
о
о
СО
о
с
S
00
00
СО
CQ
S
00
со
см
X
оо
со
о
со
оо
см
со
·!·
00
о
см
X
00
со
ю
OS
со
00
СО
оо
с
S
3
см
X
см
?
§
со
-ι-
Ε
S
о
со
г-
со
Г-
о
г-
см
X
о
ю
со
ю
о
со
см
о
см
о
см
СО
см
С
5
σ>
Tf
Tf
Г-
***
1—*
I
1—*
ю
00
ΓΟΟ
ΓΟΟ
см
χ
-
со
·ι·
(Μ
ο
υ*
(Ν
Γ-
см
Ι
см
Ю
ο
ο
см
со
I
<
CM
см
О
CN
CO
OS
см
1
CO
Г-
5
1
CO
Ю
см
X
со
CO
CO
CO
s
CO
CO
+
U
CO
a
s
r-
О
*
CQ
00
CO
GO
s
CO
CO
ю
С
С
-*
см
ι
8
со
·ι·
Γ-
1—*
*Χ
Ю
Ю
со
1—*
·ι·
Ю
со
00
ΓΟΟ
ΓΙΟ
CM
ψ**
χ
«ο
со
см
СО
Γ-
ι
СО
<
1 S
СО
ю
г-
СО
г-
а
S
СО
со
СО
S
СО
о
со
г-
см
ю
О
ΓΟΟ
·ι·
ΓΙΟ
со
·ι·
fe
см
χ
г-
см
со
см
а
s
оо
г-
J
Tf
00
ю
00
00
оо
со
■**
С
00
о
+
OS
г-
•^
i^T
σι
ю
со
со
СО
С
S
со
см
СО
СМ
С
S
Оэ
419
Код
Команда
Адрес
Код .
[ Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
о
Команда
Адрес
о
+
о
00
СО
ИП1
о
СО
СМ
X
о
3
ИП1
8
см
СО
ИП2
о
ιΟ
В/О
ос
"*
&т
СО
СО
СО
ИП6
^
со
ю
с
см
со
ю
С
Π
о
-
1
CN
СО
СО
■1·
3
СО
СО
см
см
о
СО
о
со
см
о
S
ИП1
со
СО
со
СО
ипз
со
■4f
СО
со
со
СМ
J
^
CQ
со
о
о
СО
ипо
СО
со
■1·
оо
СО
ига
см
со
СО
ипз
о
см
X
ю
СО
1
СО
ИПА
Ю
см
о
см
см
СО
ю
ю
о
-φ
&I
со
СО
со
•1·
СО
СО-
ИПС
СО
о
СО
О
СО
СО
О
СО
■+
СО
ь-
"*
см
X
см
Tf
1—*
о
см
в/о
00
СО
СО
ИП1
00
см
X
00
см
СО
ИПВ
оо
о
§
ипо
СО
О
СО
ипо%.
3
ю
со
ИП5
СО
ю
о
-
1
о
-
1
о
ю
со
+
о
оо
СО
OS
со
о
Ю
СО
ИП5
Г--
см
X
ю
см
СО
ИП2
СО
"
и
-
о
+
см
оо
СО
ИП8
см
ю
со
•1·
я
СО
ИП1
см
СО
ИП4
со
СО
ИПВ
со
Ю
1
СО
ИПА
со
со
со
СО
см
X
"*
ь-
о
СО
ИПО
"β-
со
+
СО
СО
OS
СО
Tf
в/о
ю
1^.
1—1
1
00
00
ю
со
-*
ч*
ю
см
см
с*
СО
см
X
СО
ю
ел
СО
ИП9
СО
со
со
ипв
СО
1^
СО
ИП7
о
+
ю
см
о
см
1>-
со
со
ю
ь-
см
X
00
а
оо
ю
СО
ИП4
оо
СО
СО
СО
00
со
СО
ИП6
о
С/П
ю
см'
X
со
ю
ю
о
420
Программа МК-14. Определение коэффициента ks
устойчивости на сдвиг и напряжений σι, 2 под подошвой.
Программа составлена по формулам (8.63), (8.64). Перед
вводом исходных данных в память микрокалькулятора
необходимо по графику рис. 8.28 определить время ti и вычислить
параметр η = ti/Tn. Задаются следующие исходные данные:
Сх, Ср—коэффициенты постели, кН/м3; δ — отклонение
подошвы от положения равновесия, м; а — ширина стены, м; Ge —
вес 1 п. м стены с учетом взвешивания, кН; η— параметр;
Pzq — взвешивающее давление от навала, кН/м; μ8—
коэффициент трения материала сооружения по постели; Rq—
равнодействующая давления навала, кН/м; α, β — углы поворота
сооружения вокруг главных центров Оь 02 колебаний, рад; rq—
плечо равнодействующей давления навала, м; Mzq — момент
от взвешивающего давления навала относительно центра
подошвы стены, кНм/м.
Программа МК-14 приведена в табл. П13.
Ввод исходных данных и пуск программы на счет
производятся командами: Сх = ПО; δ = ΠΙ; а = П2; Ge = ПЗ; η = П4;
Р^ = П5; μ5 = Π6; Rq = П7; α = П8; β = П9; С* = ПА; гц =
ПВ; Mzq = ПС; В/О; С/П.
Результаты расчета извлекаются из регистров памяти
командами: ИП6;< UX = ks· ИП8; ΠΧ = σι; ИП9; ПХ - σ2; ИПД;
ПХ = U
Здесь /ш—раскрытие шва вдоль подошвы, м.
Контрольный пример. Исходные данные: Сх = 14558 кН/м3;
δ = 0,00309 м; Ge = 1471,5 кН; η = 0,57; Pzq = 114 кН/м; μ* = 0,6; Rq =
= 310кН/мЗ; α = —0,000113 рад; β = 0,00162 рад; (?φ= 28344 кН/м3; rq =
= 4,88 м; MZq — 152 кН/м. Время счета 25 с. Результаты расчета: ks =
= 1,58; σι = 435,5 кН/м2; σ2 = — 83,5 кН/м2; /ш = 1,29 м.
Программа МК-15. Определение коэффициента ks
устойчивости на сдвиг по первому подводному шву.
Расчет производится по эквивалентной эпюре (рис. 8.29).
Программа составлена по формулам (8.52), (8.53), (8.63),
(8.64). Задаются следующие исходные данные:
рш — импульс давлений на 1 п. м стены, кН/м2; а' —
параметр, м; k'ir — осредненный коэффициент пространственной
неравномерности; Т2 — период колебаний во 2-й главной форме,
с; df — глубина у стены, м; г' — возвышение вершины
разбивающихся волн над спокойным уровнем, м; dm — глубина первого
подводного шва, м; аш — ширина стены по первому подводному
шву, м; μ—коэффициент трения под водой бетона по бетону;
Gi — вес части стены, расположенной выше первого подводного
шва, с учетом статического взвешивания, кН/м.
Программа МК-15 приведена в табл. П14.
421
•Φ
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
00
СО
00
S
о
СО
to1
ИПС
о
со
СО
ИПЗ
8
8
ИПО
8
О)
СО
ИП9
СО
О
+
5
СО
ИП4
см
S
ИП1
о
-
1
см
СО
СО
ИП4
см
Ю
СО
ИП5
см
см
S3
СО
ИП2
см
о
со
•1·
,οο
со
см
X
3
см
X
85
см
X
со
О
ti
"φ
со
СО
о
СО
ч*
Tf
π
I
а
см
X
о
о
ю
С/П
ю
СО.
см
X
см
СО
ИП2
Ю
СМ
СО
ИП7
ю
о
см
СО
ИП2
СО
со
•1·
СО
СМ
СО
ИП4
СО
о
см
см
и
■rjr
см
CM
Χ
δ
со
■Ι-
со
00
СО
ИП8
00
CM
о
1—<
+
со
о
о
+
3
«О
ИП9
см
ю
со
ИП5
о
^
CJ
8
о
+
о
со
СО
ИП4
о
о
+
τ—Ι
Ю
СО
ИП2
со
СМ
X
~
со
00
см
X
см
со
со
ИПЗ
см
г.. |
СО
ИПД
со
ю
S
см
со
со
ч*1
&
со
о"
ИПС
со
•1·
·*
е<5
-
ί 1
·+
-
1
ю
1
СО
ИПА
ю
со
со
со
ИП6
ю
СП
СО
Ю
СМ
X
СО
СО
см
X
СО
СО
ИП2
СО
ИП7
со
1*1
г-
о
τ
00
ю
со
ИПВ
00
со
со
со
см
X
CN
X
СО
со
СО
σ>
422
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
Код
Команда
Адрес
I
со
ИПА
00
СО-
ИПС
о
со
см
X
5
со
ю
о
см
о
СО
ИПО
о
о
Tf
|х
00
СО
ИПВ
5
СО
ИПД
5
σ>
00
00
CM
1—ί
CO
ИП1
о
~
ί ι
oo
о
+
(Ν
CO
CO
ИП4
см
CO
ИП4
CM
CM
Ю
CO
ИП5
CM
о
OS
CO
ИП9
со
00
CO
ИП1
CO
CO
О
+
со
Tf
Ю
CO
ИП5
CO
CM
о
Τ
со
о
CM
Χ
00
(Ν
Χ
со
ю
СО
ИП5
5
Ξ
!
см
со
•1·
о
СО
СО
ИП6
Ю
оо
о
ч*
SS
~
1
ю
Tf
СО
ИП1
ю
см
см
X
ю
о
со
•1·
СО
00
со
·!·
СО
СО
сБ
ИП1
СО
Tf
~
ι
со
см
Tf
CQ
С
со
о
г-
ΓΟΟ
о
+
CD
Ξ
I
г-
Tf
-+
&ΐ
Γ-
CM
s
CM
о
о
ю
с/п
00
оо
со'
о
С
00
со
со
·!·
оо
Tf
СМ
X
00
СМ
со
τ—ι
·!·
оо
с?
СМ
X
OS
00
СО
ИП1
σ>
το
Li
-3*
С75
о
χ
CQ
σ>
CM
8
Ю
8
см
СО
ИП2
о
см
X
о
г-
СО
ИПВ
о
ю
СО
ИПВ
о
со
со
ю
о
см
X
05
О
Tf
г-
о
+
ю-
ч*
со
СО
ИПЗ
СМ
OS
СО
•1-
СМ
s
СМ
СМ
ю
/
~
βί ι
со
00
оо
s
СМ
со
тр*
и
С
СМ
СО
•1·
СО
о
+
со
Г-
со
·!·
со
ю
со
•1·
со
со
СО
ипв
со
см
ю
в/о
CD
со
СО
г-
СО
со
ИП6
«=3
со
со
о
со
■*
со
ИПД
ю
ΓΙΟ
со
ИП5
ю
ю
со
ИП4
"2
со
со
ю
ю
00
СО
ИП8
СО
Г-
»-^
I
со
ю
о
+
<5
со
О)
00
00
СО
г-
СО
ИП7
г-
г-
СО
ИП1
ΓΙΟ
со
со
ИП6
г-
со
CQ
г-
см
X
оо
Γι—·
1
оо
ю
=
1
оо
со
о
со
ипо
оо
см
X
г-
см
X
ю
СО
ипв
σι
со
г 1
СО
ипд
σι
423
Ввод исходных данных и пуск программы на счет
производятся командами: pim = ПО; а/ = П1; £'г> = П2; Т2 = ПЗ; df =
= П4; г' = П5; аш = П6; 0,3 = П7; аш = П8; μ = П9; G4 = ПА;
1,5 = ПД; В/О; СП.
Результаты расчета выводятся на индикатор командами
ИП7; ПХ = ks, а также высвечиваются на индикаторе при
окончании счета и остановке вычислений.
Контрольный пример. Исходные данные: p-im = 17,8 кНс/м2;
а' = 3,1 м; k'tr = 0,73; Г2 = 0,57 с; df = 7,0 м; *' = — 3,64 м; dm = 1,0 м;
аш = 8,0; μ = 0,5; Gi = 836,8 кН/м. Время счета 40 с. Результат расчета:
ks = 1,72.
ЗАКЛЮЧЕНИЕ
В последние десятилетия как в нашей стране, так и за
рубежом опубликовано много научных статей и ряд монографий
по расчету параметров, нагрузок и воздействий ветровых волн
на гидротехнические сооружения, в которых содержатся
новейшие достижения науки в данной области. При написании книги
тщательно анализировались результаты научных публикаций
и отбирались конкретные, проверенные теорией и практикой
методы расчета. Особое внимание при этом уделялось
необходимости учета нерегулярности ветровых волн. Можно
утверждать, что многое из достигнутого наукой нашло отражение
в книге применительно к расчету нагрузок и воздействий волн
на основные типы конструкций гидротехнических сооружений.
Авторы считают, что слабым местом в теории расчета
взаимодействия ветровых волн с гидротехническими сооружениями
является исходная теория волнового движения жидкости для
реальных условий, на базе которой и должны разрабатываться
конкретные предложения для практики. Несмотря на то, что за
последние десятилетия сделано немало в развитии
гидромеханической, спектральной и статистической теорий волн, эти
успехи привели главным образом к некоторому уточнению
количественных характеристик параметров ветровых волн.
Методы расчета нагрузок от волн и течений на
гидротехнические сооружения в большинстве своем создавались и
продолжают строиться на детерминистических представлениях о войнах
на воде. В некоторых практических задачах, в частности при
определении силы волнового давления на вертикальную стену
или на отдельно стоящую вертикальную обтекаемую преграду
малых поперечных размеров, теоретически и экспериментально
доказано,-что результаты расчетов по спектральным и
детерминистическим методам практически одинаковы, по крайней мере
в пределах точности определения исходных параметров
волнения. Однако эти результаты относятся к стационарным
массивным сооружениям или к сквозным малоподвижным обтекаемым
преградам.
425
В задачах, для которых подвижность сооружения
существенна или частота собственных колебаний» объектов соизмерима
с частотой преобладающих составляющих спектра, расчет
воздействий ветровых волн на сооружение должен выполняться
по методам, основанным на положениях теории нерегулярных
волн с учетом динамических характеристик объектов. К
сожалению, предлагавшиеся до настоящего времени методы
динамических расчетов гибких сквозных гидротехнических
сооружений весьма несовершенны.
Содержащиеся в книге методы расчета нагрузок от волн на
гидротехнические сооружения, хотя и нуждаются в более
глубоком теоретическом . обосновании, наиболее достоверны и
рекомендуются для использования на практике. Дальнейшие
научные исследования целесообразно направить прежде всего
на разработку более совершенной теории волновых движений
жидкости применительно к разнообразным граничным
условиям, особенно в прибрежной зоне, где волнение деформируется
за счет изменения глубины и может приобретать характер
прибойных волн.
Нередки случаи, когда ветровые волны взаимодействуют с
течениями: попутным, встречным или произвольно
ориентированным. В литературе содержится ряд предложений по этому
вопросу, но пока еще нет оснований отдавать предпочтение
какому-либо из них из-за недостаточной достоверности. В
отдельных опубликованных источниках распространен принципиально
неверный прием геометрического суммирования скоростей
течения с теоретически определенной скоростью взволнованной
жидкости на спокойной воде, что приводит, как правило, к
завышенным значениям расчетных нагрузок на элементы
гидротехнических сооружений. Если в ближайшее время появятся в
печати новые хорошо обоснованные теории волновых движений
жидкости, возникнет настоятельная необходимость в
пересмотре или разработке новых методов расчета нагрузок от волн и
течений на различные типы гидротехнических сооружений.
Содержащиеся в действующих нормах [51] методы расчета
воздействий прибойных и разбивающихся волн на
вертикальные стены и откосные сооружения, а также методы
определения нагрузок на берегоукрепительные сооружения и защиты
берегов от размывов их волнами- необходимо будет в первую
очередь подвергнуть дальнейшему совершенствованию.
Большое количество публикаций по расчету воздействий
ветровых волн и течений на обтекаемые преграды и сквозные
сооружения свидетельствует, с одной стороны, об актуальности
решений этих задач, а с другой стороны, — о
неоднозначности рассматриваемых предложений. Достаточно
упомянуть, что в рекомендуемых различными авторами значениях
коэффициентов скоростного и инерционного сопротивлений
426
расхождения достигают двух и более раз. Содержащиеся в этих
публикациях предложения относятся, как правило, к
простейшим формам преград с поперечным сечением в виде круга и
лишь в отдельных случаях — в виде квадрата или
прямоугольника.
Представляется целесообразным разработать общую теорию
воздействия ветровых волн и течений на различные типы
гидротехнических сооружений. На новой основе должны быть
получены решения задач по определению нагрузок от волн и
течений на вертикальную стену, обтекаемые преграды малых и
больших поперечных размеров и другие типы конструкций.
Естественно, что обобщенный подход к рассматриваемой проблеме
должен привести к более сложным математическим
зависимостям; возникающие при этом трудности могут быть преодолены
с помощью ЭВМ.
В некоторых случаях для определения нагрузок и
воздействий ветровых волн на гидротехнические сооружения удобно
пользоваться программируемыми микрокалькуляторами [18].
В связи с этим авторы сочли возможным привести в
приложении библиотеку программ для микрокалькулятора
«Электроника БЗ-34» и аналогичных ему. Упомянутые микрокалькуляторы
получили распространение на практике из-за относительной
простоты и доступности. Разработанные алгоритмы могут быть
также использованы при составлении программ для
персональных ЭВМ.
СПИСОК ЛИТЕРАТУРЫ
1. Аржаников Н. С, Мальцев В. Н. Аэродинамика. — М.: Оборонгиз,
1952. 480 с.
2. Барштейн Μ. Φ. Воздействие нерегулярной волны на сквозные
инженерные сооружения // Строительная механика и расчет сооружений, 1964.
№ 1.
3. Бигелоу Г., Эдмонсон В. Морские ветровые волны и прибой. — М.:
Изд-во иностр. лит., 1951. 212 с.
4. Ветровые волны // Сб. переводов с англ. под ред. и с вводной статьей
Крылова Ю. М. — М.: Изд-во иностр. лит., 1962. 442 с.
5. Волновые воздействия на обтекаемые преграды//Труды координац.
совещ. по гидротехнике. — Л.: Энергия, 1967. Вып. 34. 226 с.
6. Волны и их воздействия на сооружения // Труды координац. совещ.
по гидротехнике. — Л.: Энергия, 1969. Вып. 50. 772 с.
7. Волны и их воздействия на сооружения // Труды координац. совещ.
по гидротехнике. — Л.: Энергия, 1970. Вып. 61. 264 с.
8. Вопросы теории и расчета ветровых волн и их воздействий на
гидротехнические сооружения//Труды координац. совещ. по гидротехнике. — Л/.
Энергия, 1973. Вып. 84. 116 с.
427
9. Гидротехнические сооружения и волны на морях и водохранилищах//
Труды координац. совещ. по гидротехнике. Л.: Энергия, 1972. Вып. 75.
(Основная часть 208 с; дополнительные материалы — 116 с).
10. Гидродинамика береговой зоны и эстуариев / Монография в переводе
с английского. —Л.: Гидрометеоиздат, 1970. 396 с.
11. Гнеденко Б. В. Курс теории вероятностей. —М.: Гос. изд-во физ.-мат.
лит., 1961. 408 с.
12. Горюнов Б. Ф., Шихиев Φ. Μ. Морские порты и портовые
сооружения. — М.: Транспорт, 1970. 448 с.
13. Давидан И. Н., Лопатухин Л. И., Рожков В. А. Ветровое волнение
в мировом океане.— Л.: Гидрометеоиздат, 1985. 256 с.
14. Завьялов В. К., Семенов С. П. Использование метода Юнга в
исследованиях дифракции волн за разными преградами // Сб. трудов молодых
научных работников. — Л.: ЛИВТ, 1975. С. 144—155.
15. Загрядская Η. Η. Учет крутизны при дифракции волн на акваториях
портов водохранилищ//Гидротехническое строительство, 1988. № 4. С. 25—
27.
16. Загрядская Η. Η. Расчет нагрузки от волн на гидротехнические
сооружения вертикального профиля (Рекомендации для проектирования).—
Л.: Энергия, 1975. 94 с.
17. Заславский М. М., Захаров В. Е. К теории прогноза ветровых волн//
ДАН СССР, 1982. Т. 265. № 3. С. 567—571.
18. Заритовский Н. Г., Миронов М. Е., Новиков В. В. Типовые расчеты
морских гидротехнических сооружений с применением программируемых
микрокалькуляторов. — Л.: ЛВВИСКУ, 1988. 116 с.
19. Кожевников М. П. Гидравлика ветровых волн. — М.: Энергия, 1972.
264 с.
20 Кондратьев Η. Ε. Расчеты ветрового волнения и переформирования
берегов водохранилищ. — Л.: Гидрометеоиздат, 1953. 109 с.
21. Коненкова Г. Е., Показеев К. В. Динамика морских волн. — М.:
Изд-во МГУ им. М., В. Ломоносова, 1985. 298 с.
22. Кочин Н. Е., Кибель И. Α., Розе Н. В. Теоретическая гидромеханика.
Ч. I. —M.: Физматгиз, 1963. 536 с.
23. Крылов Ю. М. Спектральные методы исследования и расчета
ветровых волн. — Л.: Гидрометеоиздат, 1966. 256 с.
24. Крылов Ю. М., Стрекалов С. С, Цыплухин В. Ф. Ветровые волны и
их воздействия на сооружения. — Л.: Гидрометеоиздат, 1976. 256 с.
25. Крылов Ю. М. Линейная теория взаимодействия нерегулярных
трехмерных волн с жесткой вертикальной стеной // Труды по портовому
гидротехническому строительству / Союзморниипроект — М.: Транспорт, 1969. №27
(33). С. 95—111.
26. Крылов Ю. М. и др. Ветер, волны и морские порты. — Л.:
Гидрометеоиздат, 1986. 264 с.
27. Крылов Ю. М., Леденев В. В., Марков В. В. Расчет высоты ветровых
волн на глубокой воде при наличии препятствий малых размеров/В кн.:
Вопросы совершенствования конструкций морских береговых сооружений.—
М.: Транспорт, 1984. С. 102—107.
28. Красножон Г. Ф., Сидорова А. Г. Трансформация волн на
мелководье/В кн.: Управление поверхностными и подземными водными ресурсами
и их использование. — М.: Изд-во АН СССР, 1961. С. 161—208.
29. Кульмач П. П. Морские гидротехнические сооружения. Ч. I. Основы
морской гидрологии и оградительные сооружения. — Л.: ЛВВИСКУ, 1975.
260 с.
30. Ламб Г. Гидродинамика. —М.: Гостехиздат, 1947. 928 с.
31. Л anno Д. Д. Силовое воздействие волн при обтекании
гидротехнических сооружений. — М.: Изд-во АН СССР, 1962. 115 с.
32. Лаппо Д. Д., Загрядская Η. Η. Исследование давления и энергии
стоячих волн//Американское общество гражданских инженеров. Водные пути
и порты. Август, 1977. Т. 103. С. 335—347.
428
33. Лаппо Д. Д., Мищенко С. М. Некоторые принципиальные уточнения
взаимодействия нерегулярных трехмерных волн с жесткой вертикальной
стеной //Труды координац. совещ. по гидротехнике. — Л.: Энергия, 1973. Вып.
84. С. 43—49.
34. Лаппо Д. Д., Каплун В. В., Шестаков Ю. Н. Исследование
коэффициентов сопротивления при обтекании волной сквозных гидротехнических
сооружений//Известия ВИИИГ им. Б. Ε Веденеева, 1980. Т. 138. С. 84—93.
35. Лаппо Д. Д. Воздействие волн на подводные гидротехнические
сооружения малых поперечных размеров // Известия ВНИИГ им. Б. Е.
Веденеева, 1981. Т. 145. С. 112—119.
36. Лаппо Д. Д., Лаппо А. Д. Воздействие волн при обтекании
подводных сооружений в виде эллипсоида или шара // Известия ВНИИГ им.
Б. Е. Веденеева, 1982. Т. 154. С. 96—102.
37. Лаппо Д. Д. Теоретические основы нормированных методов расчета
воздействия волн на гидротехнические сооружения // Известия ВНИИГ им.
Б. Е. Веденеева, 1983. Т. 168. С. 24—35.
38. Лойцянский Л. Г. Механика жидкости и газа. — М: Наука, 1973.
848 с.
39. Методы исследований и расчетов волновых воздействий на
гидротехнические сооружения и берега // Материалы конференций и совещаний по
гидротехнике. — Л.: Энергоиздат, 1982. 240 с
40. Маккавеев В. М., Коновалов И. М. Гидравлика. — М. — Л.: Речиздат,
1940. 644 с.
41. Марченко Д. В., Симаков Г. В., Смолко С. Я. Современные рейдовые
причалы для обслуживания супертанкеров. — Л.: Энергия, 1973. 26 с.
у 42. Некрасов А. И. Точная теория волн установившегося вида на
поверхности тяжелой жидкости. — М.: Изд-во АН СССР, 1951. 96 с.
43. Нелинейная теория распространения волн / Перевод с англ. под ред
Баренблатта Г. И. —М.: Мир, 1970. 232 с.
44. Основы предсказания ветровых! волн, зыби и прибоя/Сб. переводов
под ред. Штокмана В. В. —М.: Изд-ва иностр. лит., 1951. 488 с
45. Патрашев А. Н. Гидромеханика. — М.: Военмориздат, 1953. 720 с.
46. Порты и портовые сооружения / Г. Н. Смирнов, Б. Ф. Горюнов,
Е. В. Курлович, С. Н. Левачев, А. Г. Сидорова. —М.: Стройиздат, 1979.
608 с.
47. Руководство по определению нагрузок и воздействий на
гидротехнические сооружения (волновых, ледовых и от судов). — Л.: Π 58-76/ВНИИГ
им. Б. Е. Веденеева, 1977. 316 с.
48. Риман . Н. С., Крепе Р. Л. Присоединенные массы тел различной
формы//Труды ЦАГИ, 1947. № 635. 46 с.
49. Свешников А. А. Прикладные методы теории случайных функций. —
М.: Наука, 1968. 463 с.
50. Секерж-Зенькович Я. И. К теории стоячих волн конечной амплитуды
на поверхности тяжелой жидкости конечной глубины. — М.: Известия АН
СССР. Т. XV, № 1. Серия географическая и геофизическая, 1951. С. 57—73.
51. СНиП 2.06.04-82*. Нагрузки и воздействия на гидротехнические
сооружения (волновые, ледовые и от судов). —М.: ЦИТП Госстроя СССР,
1986. 40 с.
52. Смирнов В. И. Курс высшей математики. — М.: Наука, 1967. Т. 1.
479 с. Т. 2. 655 с. Т. 3, Ч. I. 323 с.
53. Сретенский Л. Н. Теория волновых движений жидкости. — М.:
Наука, 1977. 816 с.
54. Стокер Дж. Дж. Волны на воде. Математическая теория и
приложения.—М.: Изд-во иностр. лит., 1959. 617 с.
55. Стрекалов С. С. Обобщенный метод расчета параметров ветровых
волн//Тр. Союзморниипроекта, 1974. Вып. 36. С. 135—146.
56. Теория волн и расчет гидротехнических сооружений / Сб.. АН СССР,
Ин-т водных проблем. — М.: Наука, 1975. 192 с.
57. Теория поверхностных волн / Сб. переводов под ред.
Красносельского М. А. и Моисеева Н. Н. — М.: Изд-во иностр. лит., 1959. 366 с.
429
58. Титов Л. Φ. Ветровые волны — Л.: Гидрометеоиздат, 1969. 294 с.
59. Фабрикант Н. Я. Аэродинамика. — М: Наука, 1964/816 с.
60. Филлипс О. М. Динамика верхнего слоя океана / Перевод с англ. —*
Л.: Гидрометеоиздат, 1980. 319 с.
61. Хаскинд М. Д. Гидродинамическая теория качки корабля. — Μ.Ι
Наука, 1973. 328 с.
62. Шайтан В. С. Проектирование креплений земляных откосов на водо|
хранилищах. — М.: Стройиздат, 1986. 216 с.
63. Штенцель В. К. Определение воздействия неразбитой стоячей волн^
на вертикальную стенку//Труды ЛИВТ, 1967. Вып. 88. С. 131—139.
64. Шулейкин В. В. Теория морских волн//Труды МГИ АН СССР, 195б!
Т. IX. 141 с.
65. Шулейкин В. В. Физика моря. —М.: Изд-во АН СССР, 1953. 989 α
. 66. Шуляк Б. Л. Физика волн на поверхности сыпучей среды и жидкости]
— М.: Наука, 1971. 400 с.
67. Biesel F. Study of wave propagation in water of gradually varying
depth. U. S. National Bureau of Standards, Gravity Waves, NBS Circular 521
1952.
68. Borgman L. E. Wave forces on piling for narrow band spectr
Journ. of the Waterways and Harbour Div., v. 91, № 6, 1965.
69. Borgman L. Ё. Spectral analysis Jof ocean wave forces on pilin
Journ. of the Waterways and Harbour Div., v. 93, № 2, 1967.
70. Boussinesq J. Theorie des ondes liquides periodiques. Mem. prese
tees par divers sav. a 1'Akademie des Sc. XX, Paris, 1872.
71. Bretschneider C. L. Selection of design wave for offshore structures
Proc. ASCE, v. 85, № 3, Part 1, 1959.
72. Gerstner F. Theorie der Wellen. Gilberts Annalen der Physik, Bd. Ц
1809.
73. Hasselman K. Grundgleichungen der Secgangvoraussage. Schiffslecll
nik, Bd. 7, H. 39, i960.
74. Kinsman B. Wind waves, their generation and propagation on thi
ocean surface. Prentice-Hall. Inc., Englewood Cliffs, New Jersey, 1965. I
75. Levi-Civita T. Determination rigoureuse des ondes permanentd
d'ampleur finie. Math. An., 93, p. 264—314, 1925.
76. Munk W. H. Solitary wave theory. Ann. N. Y. Acad. Sci., v. 51. 1941
77. Miche M. Mouvements ondulatoires de la mer en profondeur constanl
ou decroissante. Ann. des Ponts et Chaussees, 114, 1, 2, 3, 4. 1944.
78. Michel J. H. The highest waves in water. Phil. M. (5). 36, p. 430-1
437, 1893.
79. Miller B. L. The hydrodynamic drag of roughened circular cylinde^l
the naval architect. Journ. of the Royal Institution of Naval Architect]
March, № 2, London, p. 55—61, 1977.
80. Morison J. R. et al. The forces exerted by surface waves on pile]
Journ. of Petroleum Technology, v. 2, № 5, 1950.
81. Pirson W. J., Holmes P. irregular wave forces on a pile. Journ. <j
the Waterways and Harbour Div., v. 91, № 4, 1965.
82. Rankine W. On the exact form of waves near the surface of de^
water. Phil. Trans., v. 153, 1863—1864.
83. Rayleigh, Lord. On periodic irrotational waves at the surface <j
deep water. Phil. M. (6), 33, p. 381—389, 191Ϋ.
84. Rundgren L. Water wave forces (a theoretical and laboratory stud}1
Bull, of the Institute of Hydraulics, № 5t, Stockholm, 1958.
85. Sainflou. Essai sur les digues maritimes verticales. Ann. des Ponl
et Chaussees, № 4, 1928.
86. Stokes G. G. On the theory of oscillatory waves. Trans. Camb. Ph|
Soc. 441, 1847 (also in Mathematical and Physical Papers, v. 1, Londoij
Cambridge University Press, 1880).
87. Wiegel R. L. Oceanographical engineering. Prentice-Hall, Incj
Englewood Cliffs, N. Y., 1964.
88. Tadjbakhsh Ϊ., Keller J. B. Standing waves finite amplitude, Joun
of Fluid Mechanics, v. 8, Pt 3, July, 1960.
89. Shore Protection Manual, v. II, Department of the Army Corps 5
Engineers, 1973.
СОДЕРЖАНИЕ
Предисловие 3
Введение. Конструктивные формы гидротехнических сооружений,
подверженных воздействию ветровых волн ....... 8
РАЗДЕЛ I. ОСНОВЫ ТЕОРИИ ВОЛН НА ВОДЕ
Глава 1. Общие понятия о волнах на воде. Постановка задачи 19
1.1. Причины возникновения волн на воде. Классификация
гравитационных волн '9
1.2. Основные характеристики волн на воде. Терминология и
условные обозначения 24
1.3. Обзор исследований в области гидродинамики волн . . ^У
1.4. Постановка задачи о волнах на воде и особенности ее
решения 33
Глава 2. Бегущие волны 38
2.1. Бегущие волны большой высоты на мелководье ... 38
2.2. Основные сведения из наиболее известных теорий и
сопоставление результатов расчета некоторых характеристик
бегущих волн 49
2.3. Элементарные теории одиночной (уединенной) волны . . 70
Γι а в а 3 Стоячие волны 79
3.1. Стоячие волны большой высоты на мелководье . 79
3.2. Основные сведения из некоторых наиболее известных
теорий стоячих волн 88
3.3. Сопоставление результатов расчета отдельных
характеристик стоячих волн по наиболее известным теориям . . 100
Гллва 4. Энергетические процессы в волнах на воде .... 105
4.1. Энергия бегущих и стоячих волн малой высоты 105
4.2. Групповая скорость. Дисперсия 113
4.3. Интегральные и дифференциальные энергетические
характеристики стоячих волн большой высоты . . . . . П7
4 4. Уравнение баланса волновой энергии 128
РАЗДЕЛ II. РАСЧЕТ ПАРАМЕТРОВ ВЕТРОВЫХ ВОЛН
Глава 5. Волнообразующие факторы. Функции распределения
элементов волн . ч 131
5.1. Волнообразующие факторы 131
5.2. Параметры ветрового потока над водной поверхностью 134
5.3. Расчетные уровни воды 143
5.4. Функции распределения элементов волн 155
Глава 6. Элементы ветровых волн на глубоководье . ... 175
6.1. Энергетический спектр волнения 175
6.2. Расчет элементов волн на глубоководных акваториях.
Простые условия 182
6.3. Расчет элементов волн на глубоководных акваториях.
Сложные условия 193
Глава 7. Элементы воли на мелководье, в зоне трансформации и
на огражденных* акваториях 203
7.1. Расчет элементов воли на мелководье * . 203
7.2. Трансформация волн на мелководье 208
431
7.3. Волны в прибойной зоне 214
7.4. Расчет элементов волн на огражденной акватории . . 221
РАЗДЕЛ III. РАСЧЕТ НАГРУЗОК И ВОЗДЕЙСТВИЙ ВЕТРОВЫХ ВОЛН
НА' ГИДРОТЕХНИЧЕСКИЕ СООРУЖЕНИЯ И БЕРЕГА
Глава 8. Нагрузки и воздействия ветровых волн на
гидротехнические сооружения с вертикальной t передней гранью . . ^36
8.1 Нагрузки от стоячих волн на сооружения вертикального
профиля 236
8.2. Взаимодействия нерегулярных трехмерных волн с жесткой
вертикальной стеной ..." 240
8.3. Особые случаи определения нагрузок и воздействий волн
на сооружения вертикального профиля и их элементы 245
8.4. Примеры расчета нагрузок и воздействий волн на
сооружения вертикального профиля и их элементы .... 249
8.5. Нагрузки от разбивающихся и прибойных волн на
сооружения вертикального профиля 262
8.6. Динамический расчет вертикальной стены при действии
разбивающихся волн (рекомендуемый) 268
8.7. Нагрузки и воздействия ветровых волн на крутонаклонные
откосные сооружения 279
Глава 9. Нагрузки и воздействия ветровых волн на сооружения
откосного профиля и берега 285
9.1. Накат волн на сооружения откосного профиля и берега 285
9.2. Скорости при волнении у откосных сооружений.
Проницаемость набросных сооружений 295
9.3. Нагрузки от волн на сооружения откосного профиля и
берегоукрепления 302
9.4. Расчет креплений сооружений откосного профиля . . 317
Глава 10. Воздействие ветровых волн на отдельно стоящие
обтекаемые преграды, сквозные сооружения и подводные
трубопроводы . 326
10.1. Общие исходные положения. Основное уравнение для
расчета нагрузок от волн на обтекаемую преграду .... 326
10.2. Скоростной и инерционный коэффициенты сопротивления
и коэффициенты формы. Корректив скорости .... 331
10.3. Учет энергетического спектра ветровых волн при расчете
нагрузок на вертикальные круглоцилиндрические
обтекаемые преграды 337
10.4. Расчетные формулы и графики для определения нагрузок
от волн на отдельно стоящие обтекаемые преграды . . 342
10.5. Нагрузки и воздействия волн на вертикальные
круглоцилиндрические обтекаемые преграды малых и больших
поперечных размеров 319
10.6. Нагрузки и воздействия волн на горизонтальные
обтекаемые преграды 368
10.7. Нагрузки от разбивающихся волн на вертикальную
обтекаемую круглоцилиндрическую преграду ...·.. 380
10.8. Нагрузки и воздействия волн на подводные обтекаемые
преграды ограниченных размеров 384
10.9. Нагрузки от волн на сквозные сооружения из обтекаемых
элементов 397
Приложение. Библиотека программ на входном языке
микрокалькулятора «Электроника БЗ-34» 401
Заключение . . . ·. 425
Список литературы ,_ . 427
Μ
g
>>
η
>>
4
ο
π)
Я
α.
α
•θ-
•θ-
•θ-
to
ο
α,