Л. А. СКОРНЯКОВ
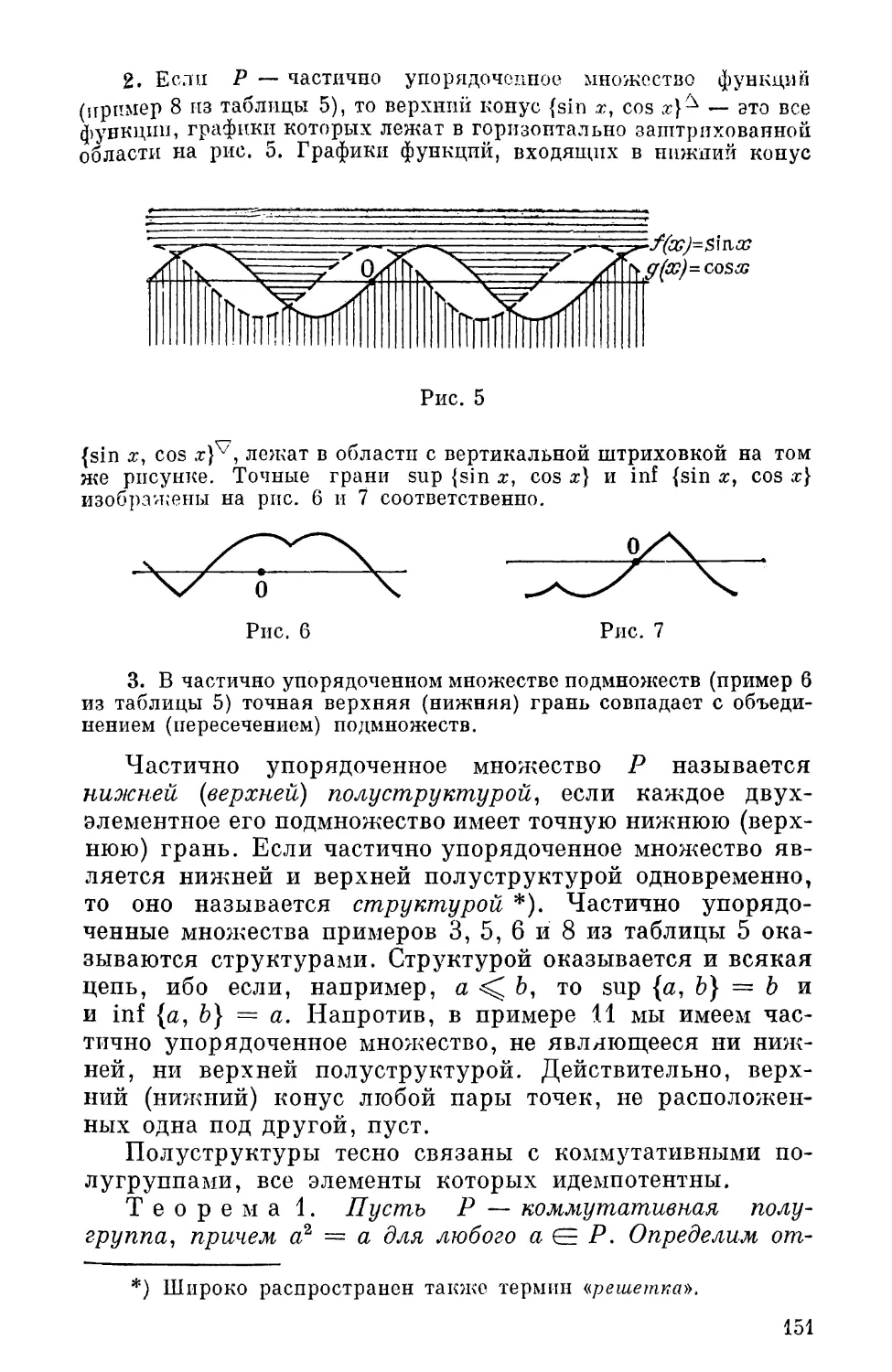
ЭЛЕМЕНТЫ АЛГЕБРЫ
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ
Допущено Министерством высшего
и среднего специального образования СССР
в качестве учебного пособия
для. (ризико-математических специальных вузов
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 8 6

ББК 22.14
С44
УДК 512 (075.8)
С к о р н я к о в Л. А. Элементы алгебры: Учеб, пособие для
вузов.—2-е изд.— М.: Наука. Гл. ред. физ.-мат. лит., 1986.— 240 с.
В основу учебного пособия положен курс лекций по высшей
алгебре, читавшийся в течение ряда лёт на механико-математиче¬
ском факультете и отделении структурной лингвистики филологи¬
ческого факультета Московского университета.
В книге содержатся следующие разделы: матрицы и системы
лииейпых уравнений, элементы общей алгебры, представления
конечных групп. При этом учение о системах линейных уравнений
излагается без использования понятия линейной зависимости, а из¬
ложение теории представлений конечных групп имеет теоретико¬
кольцевую направленность. Уделено внимание и упражнениям,
помогающим овладеть изложенными в пособии понятиями.
1-е издание выходило в 1980 г.
Для студентов младших курсов университетов и педагогичес¬
ких институтов.
Рецензент
доктор физико-математических наук профессор 3. И. Боревич
Лев Анатольевич Скорняков
ЭЛЕМЕНТЫ АЛГЕБРЫ
Редактор Ф. И. Кизнер
Художественный редактор Т. Н. Кольченко
Технический редактор Е. В. Морозова
Корректор Н. Б. Румянцева
И Б № 12923
Сдано в набор 09.04.86. Подписано к печати 27.08.86,
Формат 84x108/32. Бумага тип. № 2.
Гарнитура обыкновенная. Печать высокая.
Усл. печ. л. 12,6. Усл. кр.-отт. 12,92. Уч.-изд. л. 13.13.
Тираж 21000 экз. Заказ № 2453. Цена 45 кои.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
2-я типография издательства «Наука»
121099 Москва Г-99, Шубинский нср., 6.
^ 1702030000—173
С 053(02)-86
© Издательство «Наука».
Главная редакция
физико-математической
литературы, 1980;
с изменениями, 1986

ОГЛАВЛЕНИЕ
Предисловие ко второму изданию	♦	4
Предисловие к первому изданию . 		 5
Глава I. Системы линейных уравнений	 7
§ 1, Матрицы и их элементарные преобразова¬
ния 	 7
§ 2.	Определители	 16
§ 3.	Алгебра матриц	 30
Глава II* Элементы общей алгебры .		 47
§ 1.	Отображения и операции	 47
§ 2. Полугруппы	  .	56
§ 3.	Группы 	 71
§ 4.	Кольца	 90
§ 5.	Модули	 105
§ 6.	Правые идеалы в кольцах	 124
§ 7.	Абелевы, разрешимые и простые группы 130
§ 8.	Структуры и булевы алгебры	 147
Глава III. Линейные пространства и линейные алгебры 168
§ 1. Линейные пространства	 168
§ 2. Линейные алгебры и модули над ними . ,	190
Глава IV. Представления конечных групп	 207
§ 1. Основы теории представлений	 207
§ 2. Приложение теории представлений	 224
Указатель расположения теорем	 236
Предметный указатель 	 237
Указатель обозначений	 240

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Наиболее фундаментальное изменение по сравнению
с первым изданием состоит в том, что ряд результатов, не
зависящих от теории представлений, перенесен из главы
IV в главу II, где вместе с теоремой о строении конечно
порожденных абелевых групп они составили новый пара¬
граф. Здесь же дано прямое доказательство разрешимости
д-групп и групп порядка pq, а также намечено доказатель¬
ство простоты группы SO (3). Остальные изменения сво¬
дятся к улучшению деталей изложения.
По техническим причинам в настоящем издании не уда¬
лось привести список литературы для дальнейшего изу¬
чения общей алгебры. В качестве первого чтения здесь
может быть рекомендована книга автора «Элементы об¬
щей алгебры» (М.: Наука, 1983), где имеются и необхо¬
димые литературные указания. Изложение учения о сис¬
темах линейных уравнений, более элементарное, чем в
настоящем пособии, можно найти в брошюре автора «Си¬
стемы линейных уравнений» (М.: Наука, 1986).

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Настоящее учебное пособие ставит своей целью позна¬
комить читателя с основами алгебры. Здесь излагается
общая теория линейных уравнений (включая теорию оп¬
ределителей и алгебру матриц), элементы общей алгебры
(а именно простейшие свойства полугрупп, групп, колец,
модулей и структур (решеток)) и основы теории представле¬
ний конечных групп, включая необходимые факты из тео¬
рии линейных пространств и полупростых конечномер¬
ных алгебр. При этом основы теории линейных пространств
излагаются как частный случай теории правых модулой
над кольцом. Разумеется, читатели, изучившие линейные
пространства по каким-либо другим источникам, могут
пропустить § 1 главы III. В главах III и IV не использу¬
ются результаты § 7 главы II. С другой стороны, в этих
главах необходимы некоторые сведения из теории много¬
членов, не затрагиваемой в настоящем пособии. В этих
случаях даны точные ссылки па соответствующие места
из учебников А. Г. Куроша и А. И. Кострпкина *). С рас¬
четом на студентов младших курсов в пособие не включе¬
ны результаты, в доказательствах которых используется
трансфинитная индукция или лемма Куратовского —
Цорна. Именно поэтому речь идет о конечномерных алгеб¬
рах, а не о кольцах с условием минимальности. Сознавая
архаичность такого изложения, можно утешать себя
мыслью, что оно дает лишний повод для использования тео¬
рии линейных пространств.
Настоящее пособие, хотя и имеет в виду университет¬
ский курс алгебры, не может заменить существующие ру¬
ководства и не претендует па это. Однако оно дает возмож¬
ность преподающим и изучающим алгебру познакомиться
с изложением материала, отличающимся от предлагаемо¬
го упоминавшимися выше учебниками А. Г. Куроша
*) К у р о ш Л. Г. Курс высшей алгебры.— ll-о изд.— М.:
Паука, 1975; Кос т р и к и и Л. И. Введение в алгебру.— М.:
Паука, 1977.

и А, И. Кострикина. Именно, в главе I излагается учение
о системах линейных уравнений без использования поня¬
тия линейной зависимости, а в главе IV предлагается
изложение теории представлений, имеющее теоретико¬
кольцевую направленность.
Автор глубоко благодарен 3. И. Боревичу, А. В. Ми¬
халеву, А. П. Мишиной и Р. А. Шмидту, прочитавшим
рукопись и сделавшим ряд полезных замечаний, а также
Т. А. Гуровой за большую помощь при оформлении ру¬
кописи,

ГЛАВА I
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Задачей настоящей главы является разработка мето¬
дов, позволяющих исследовать и решать системы линей¬
ных уравнений. Аппаратом для этого служат матрицы
п определители, изучаемые в этой главе.
§ 1. Матрицы и их элементарные преобразования
Понятие п-мерной строки действительных чисел яв¬
ляется неопределяемым. Если дана строка (дх, . . ., дп) *),
то числа at называются ее координатами или компонен¬
тами. Строки (дх, . . ., ат) и (6Х, . . ., Ъп) считаются рав¬
ными, если т = п и at = для всех I.
На множестве n-мерпых строк действительных чисел
можно определить сложение и умножение на действи¬
тельное число X по следующим правилам:
(«ь • • -х ап) 4- (blt . . Ьп) = (а, + Ьи . . ап + Ьп)
и
А (дх, . . ., дп) (Адх, . . ., Адп).
Строка, состоящая из одних нулей, называется нулевой
и обозначается через 0. Легко проверяется справедли¬
вость следующих свойств:
а 4“ b = Ъ 4~ а,
(а + Ь) + с = а + (Ь + е),;
а 0 ~ 0 -J- а ~ а,
уравнение а + я = 0 разре¬
шимо для любой строки а,
(здесь а, Ь, с — строки, а X и
А (а 4~ Ь) — Ад 4~ А&,-
(X 4- ц) а = Ад 4-
(Хц) а = А (цд)г
1д = д
ц — числа) **).
*) Употребляются такие термины «строка длины п», «п-мерный
вектор» и «кортеж длины п» над множеством действительных чисел.
**) Обратим внимание на то, что во втором равенстве правого
столбца знак 4~ в его левой и правой частях имеет различный смысл:
слева он означает сложение чисел, а справа — сложение строк.
Различный смысл имеет и подразумеваемый символ умножения в
третьем равенстве этого столбца: Хц означает произведение чисел,
а в остальных случаях мы имеем дело с умножением строки на
число,
7

Докажем, например, равенство X (а + Ь) = ка + АЬ.
С этой целью заметим, что i-ми координатами строк, стоя¬
щих в левой и правой частях этого равенства, являются
A (at + и Аа, + Xbi соответственно и их совпадение
вытекает из справедливости закона дистрибутивности для
действительных чисел.
Таблицу, представляющую собой несколько п-мерных
строк, записанных одна под другой, называют матри¬
цей, Матрица
«11
«12
«21
«22
Д —
Л 1

ППЛ
ат2 • '
содержит т строк и п столбцов. Будем говорить также,
что она имеет размер т X п. Строка является матрицей
размера 1 X п. Столбец можно рассматривать как матри¬
цу размера т X 1. Матрицу размера п X п называют
квадратной матрицей порядка п, Матрица, состоящая
из нулевых строк, называется нулевой и обозначается О,
а матрица
1
0 ..
, . о
0
1 . .
> . о
0
о . ,
,. 1
— единичной. Подчеркнем, что для каждого числа п
существует своя единичная матрица порядка п, а для
каждого размера т X п — своя нулевая матрица. Две
матрицы считаются равными, если они имеют одинаковые
размеры и их элементы, стоящие на соответствующих
местах, совпадают.
В дальнейшем элементы матрицы, обозначенной неко¬
торой большой буквой (скажем, Л), будем, как правило^
без специальных оговорок обозначать соответствующей
малой буквой с индексами (в нашем случае обозначаю¬
щими помер строки и столбца соответственно.
Ступенчатой называется матрица А, обладающая сле¬
дующими свойствами:
(1)	Если Z-я строка нулевая, то (Z + 1)-я строка также
нулевая.
(2)	Если первые ненулевые элементы i-й и (I -|- 1)-й
строк располагаются в столбцах с номерами и khl
соответственно, то
/Г; <
8

Наглядно эти свойства означают, что ниже нулевой
строки могут располагаться лишь пулевые строки, а все
элементы^ располагающиеся влево и вниз от первого не¬
нулевого элемента какой-либо строки, являются нулями.
Происхождение названия нетрудно объяснит^ рассмат¬
ривая, например, ступенчатую матрицу
0 1
1 1
2
0
3
1
0
0
о|
I2
0
0
0
0
0
ч
L
2
0
0
0
0
0
(1
|0
0
0
0
0
0
где кл = 2, к2 = 4 и к3 = 5.
Под преобразованием матрицы понимается переход
от одной матрицы к другой, осуществленный по опреде¬
ленным правилам. Будем рассматривать следующие пре¬
образования, называемые элементарными преобразования¬
ми строк:
Элементарное преобразование первого типа — перемела
местами двух строк матрицы.
Элементарное преобразование второго типа—прибав¬
ление к какой-либо строке матрицы другой ее строк и
умноженной на некоторое число.
Аналогично определяются элементарные преобразова¬
ния столбцов.
Иногда оказывается полезным
Элементарное преобразование третьего типа —умножение
некоторой строки на отличное от нуля число.
Решающую роль для построения нужной нам теории
играет следующий факт.
Теорема 1. Всякую матрицу конечным числом
элементарных преобразований строк можно превратить
в ступенчатую матрицу.
Доказательство. Проведем доказательство
индукцией по числу строк матрицы. Если имеется всего
одна строка, то матрица уже ступенчатая, ибо оба усло¬
вия, входящие в определение ступенчатой матрицы, вы¬
полнены тривиальным образом (ввиду отсутствия второй
строки). Пусть теперь матрица А содержит т строк, где
т 2. Предположим, что матрицу с числом строк, мень¬
шим т, можно привести к ступенчатому виду. Если А — О,
то она ступенчатая. Если А ненулевая, то в ней есть хоть
один ненулевой элемент. Ненулевой элемент располагает¬
9

ся в какой-то строке. Значит, в нашей матрице есть нену¬
левые строки. Выберем ту, в которой первый ненулевой
элемент располагается в столбце с наименьшим номером,
скажем, с номером кг. Применив преобразование первого
типа, перенесем эту строку на первое место, Тогда матри¬
ца примет вид
0 .
.. о
о . ,
.. о
••
о . .
.. о
причем ¥= 0. Теперь будем применять преобразования
второго типа: ко второй строке прибавим первую, умно-
1
женную на —-—- , к третьей строке — первую, умножеп-
ную на — т—, и т. д. После применения т — 1 таких эле-
ментарных преобразований добьемся того, что в АрМ столб¬
це всюду, кроме первой строки, будут пули:
0 . ,
.. о
•••
0 . ,
о
0
0 . ,
.. о
о
Отбросим первую строку. Оставшаяся матрица имеет т —
— 1 строку. По индуктивному предположению ее можно
привести к ступенчатому виду:
0 . .
.. о
0
G =
D
0 .
.. о
0
Пусть первые ненулевые элементы строк ступенчатой мат¬
рицы G располагаются в столбцах с номерами к2, . . .
. . ., кТ. Тогда к2 <С . . . <1 кг по определению ступенча¬
той матрицы. Но осуществляя элементарные преобразо¬
вания уменьшенной матрицы, можно считать, что мы де¬
лаем элементарные преобразования матрицы С, не ис¬
пользующие первой строки. Поскольку при выполнении
этих элементарных преобразований нули, стоявшие в пер¬
вых к± столбцах матрицы С, не могли исчезнуть, то к± <
10 .

< &2* ^аким образом, мы получили матрицу
0
... о
1
к • • •
•
0
... 0
0
D
0
... о
0
удовлетворяющую условию (2) из определения ступен¬
чатой матрицы. Если же в Н имеется нулевая строка, то
она не совпадает с первой строкой, так как blkt 4= 0 и,
значит, лежит в матрице G. Но G ступенчатая. Следова¬
тельно, ниже нулевой строки лежат только нулевые стро¬
ки. Таким образом, Н — ступенчатая матрица.
Теорема 2. Если от матрицы А к матрице В
можно перейти конечным числом элементарных преобра¬
зований строк, то и от В к А также можно перейти ко¬
нечным числом элементарных преобразований строк.
Доказательство. Если для перехода от А
к В использовано одно элементарное преобразование пер¬
вого типа, то утверждение очевидно. Допустим, что от
А к В перешли, используя одно элементарное преобра¬
зование второго типа, т. е. (Z-я строка в В) = (Z-я стро¬
ка в Л) + X (/-я строка в Л), а каждая из остальных строк
матрицы В совпадает с соответствующей строкой матри¬
цы А. Таким образом, bik = aik kajk и bjk = а^ для
каждого номера к. Если теперь к i-й строке матрицы В
прибавить ее у-ю строку, умноженную на —X, то в полу¬
чившейся после этого матрице на месте (/, к) окажется
элемент
bin + (—^) bjk = (aik + kajk) + (■—lkajk) = aik.
Поскольку элементы получившейся матрицы, располо¬
женные в строках, отличных от Z-й, совпадают с соответ¬
ствующими элементами матрицы А, то и вся она совпадает
с А, так что справедливость теоремы в случае примене¬
ния одного элементарного преобразования полностью
доказана. Допустим теперь, что переход от А к В осу¬
ществлен с использованием t элементарных преобразова¬
ний, где £^>1. Обозначим через С матрицу, возникшую
после применения первого из этих элементарных преоб¬
разований. Тогда от С к В перешли, используя t — 1 эле¬
ментарное преобразование. В силу индуктивного пред¬
положения, используя элементарные преобразования,
можно перейти от В к С, а как установлено в начале до¬
казательства, точно так же можно перейти и от С к А.
11

Таким образом, применение элементарных преобразований
позволяет перейти от В к А, что и требовалось.
Полученные результаты дают возможность предло¬
жить метод решения любой системы линейных уравнений
вида
aii^i + (ЧгХ-i Ц- . .
. -1-	= />t,
«21Д1 -|- «22-^2 4~ • ■
. . -I- аг„х„ = bt,
• • "I" ^mn^n -— btn.
Эта система однозначно определяется матрицей
aLl
«12
••• “in
bl
II
«21
«22
b2
“mt
^7712
• • • amn
которая называется расширенной матрицей системы..
Матрица, стоящая левее вертикальной черты, называется
матрицей системы.
Строка (а1? а2, . .	а„) считается решением выписан¬
ной выше системы, если для всех i справедливы числовые
равенства
+ й/2а2 Н" . . • + ainan ~ bi.
Две системы линейных уравнений называются эквива¬
лентными, если всякое решение первой системы является
решением второй системы и наоборот. Поэтому вместо
данной системы можно решать ей эквивалентную.
Теорема 3. Если от матрицы А к матрице В
можно перейти конечным числом элементарных преоб¬
разований строк, то соответствующие системы линейных
уравнений эквивалентны.
Предварительно докажем следующую лемму.
Лемма. Если от матрицы Л к матрице В можно
перейти конечным числом элементарных преобразований
строк, то всякое решение системы, соответствующей
матрице А, служит решением системы, соответствую¬
щей матрице Ё.
Ясно, что лемму достаточно доказать для случая, ког¬
да применяется одно элементарное преобразование, ибо
переход к общему случаю легко осуществляется индук¬
цией. Если применено элементарное преобразование пер¬
вого типа, т. е. переставлены местами строки, наши урав¬
нения только меняются местами. Конечно, старые решения
12

по-прежнему будут им удовлетворять. При элемен¬
тарных преобразованиях второго типа к f-й строке при¬
бавляем у-ю строку,; умноженную на X, Следовательно,
г-я строка матрицы В имеет вид
(«и 4* jit * * ^in + hajn | bi + ^bjY
Пусть (alt а2,; . . ап) — решение системы с матрицей
А, т. е. решение каждого из ее уравнений. Будет ли оно
решением системы с матрицей В? Сомнение может вызвать
только i-e уравнение этой системы. Но
(«И + ^«д) «1 + • • . + («in + ^«jn) ап =
«= («iiCtj 4“ • • » 4“ «in^n) 4-	(«ji^i + » • • 4“ «jn^n) '■
= bi +
Переходя к доказательству теоремы, заметим, что
согласно лемме каждое решение системы А (т. е. системы,
соответствующей матрице А) служит решением системы /?.
С другой стороны, в силу теоремы 2 от матрицы В к мат¬
рице А можно перейти с помощью элементарных пре¬
образований. Следовательно, применив лемму еще раз,
видим, что каждое решение системы В служит решением
системы А. Таким образом, эти системы эквивалентны.
Теперь ясно, что для нахождения решений любой си¬
стемы линейных уравнений достаточно уметь находить
решения ступенчатой системы (т. е. системы, матрица ко¬
торой является ступенчатой), так как любую матрицу мож¬
но привести к ступенчатому виду, а после элементарных
преобразований получается эквивалентная система урав¬
нений.
Пусть нам дана ступенчатая матрица, соответствую¬
щая системе т линейных уравнений с п неизвестными.
Возможны следующие два случая.
I.	Существует строка, в которой первый ненулевой
элемент находится на последнем месте.
II.	Такой строки нет.
В первом случае соответствующая система уравнений
содержит уравнение вида 0-ад 4" • * • 4~ 0-яп = Ь, где
b 0. Ясно, что никакой набор значений xt не может
удовлетворять этому уравнению, а тем более всем урав¬
нениям системы. Значит, система уравнений не имеет ре¬
шений *).
*) Про систему, не имеющую решений, говорят, что она несов¬
местна.
13

Для анализа второго случая допустим, что рассмат¬
риваемая ступенчатая матрица содержит г ненулевых
строк и что первые ненулевые элементы этих строк распо¬
лагаются в столбцах с номерами	кг. По определе¬
нию ступенчатой матрицы
1 < fcj < /г2< > • • <Л < 72.
Неизвестные , . . ., назовем главными, а все осталь¬
ные (если они есть) — свободными. Кроме того, отбросим
уравнения, соответствующие нулевым строкам, что, как
легко видеть, приведет к системе, эквивалентной исходной.
Допустим сначала, что свободных неизвестных нет.
Тогда
г = п,
= 1, Л?2 = 2, » . кп =
п
рассматриваемая
система имеет вид
+ ai2Z2 +
• • • + #1п-1^?г-1	4- а\пхп
<722^2 4"
• • • 4" #2 п-1хп-1	4- а2пхп
г. Ь>.
<
#71-1 п-1хп-1 Ч- #?i-i7i^n —
#7'171^'71	==-
причем ап, а22, . . ., апп отличны от нуля. Поскольку
апп 0, из последнего уравнения однозначно определя¬
ется хп. После этого предпоследнее уравнение позволяет
однозначно определить хп^ и т. д. Таким образом, в вы¬
деленном случае рассматриваемая система имеет единст¬
венное решение,
Предположим теперь, что свободные неизвестные есть.
В этом случае обозначим через сумму свободных не¬
известных, умноженных на стоящие перед нами коэффи¬
циенты i-ro уравнения, и, перенося свободные неизвестные
в правую часть, придем к системе
'	+ «1Л + • • • + а1А',ЛА> =	~ Л,
а2кгХ1Гг + • • • + «2А-,.^А.Г = Ь-г 	 Lz,
&гкгхкг
где коэффициенты alfri, а2^, . . ., агк отличны от нуля.
Как и выше, мы можем последовательно определять
xkri хкг^ и т. Дч если придадим свободным неизвестным
какие-либо определенные значения. При этом главные
14

неизвестные определяются однозначно. Придавая свобод¬
ным неизвестным всевозм.оясные значения, мы найдем
все решен ня данной системы, т. е. решим ее. Поскольку
свободным неизвестным можно придавать различные зна¬
чения, система в рассматриваемом случае имеет более од¬
ного решения.
Система линейных уравнений называется однородной,
если все ее правые части равны нулю. Однородная система
всегда имеет решение, например нулевую строку. Поэто¬
му интересно выяснить, когда имеются и ненулевые ре¬
шения.
Т е о р е м а 4. Если число уравнений однородной си¬
стемы линейных уравнений меньше числа, неизвестных,
то она имеет хотя бы одно ненулевое решение.
Доказательство. Приведем данную однород¬
ную систему к ступенчатому виду. Разумеется, она оста¬
нется однородной. Ясно, что число главных неизвестных
не может превысить числа строк. Следовательно, сущест¬
вуют свободные неизвестные, что обеспечивает существо¬
вание ненулевых решений.
Таким образом, мы располагаем методом, позволяю¬
щим решить любую систему линейных уравнений, т. е.
или установить, что она не имеет решений, или указать
ее единственное решение, или, выбрав свободные неиз¬
вестные, выразить через них остальные *). Однако оста¬
ется неясным, не зависит ли число свободных неизвест¬
ных от способа решения. Более того, даже в случае, если
такой зависимости нет, остается открытым вопрос: сущест¬
вует ли для данного набора неизвестных способ решения,,
при котором именно эти неизвестные окажутся свобод¬
ными? Например, если (ап а2, а3, а4) — решение системы
J Х1 -|- х% х% х$ = 4,
I ^1 + %2  ^3 + ~ 2,
то а3 = 1, т. е. неизвестное х3 ни при каком способе ре¬
шения не может оказаться свободным.
Решить эти вопросы позволяет теория, развиваемая
в последующих параграфах этой главы (см. также конец
§ 1 гл. III). Отметим, что изучаемые в этих параграфах
понятия находят широкое применение и в других вопро¬
сах, как внутриматематических, так и прикладных.
*) Этот метод часто называют методом Гаусса или методом по¬
следовательного исключения неизвестных.
15

У пражнения
1.	Доказать, что элементарными преобразованиями строк и
столбцов любую матрицу можно привести к диагональному виду
(матрица D называется диагональной, если йц = 0 при i =/=!)•
Привести пример, показывающий, что существуют матрицы, которые
нельзя привести к диагональному виду элементарными преобразо¬
ваниями только строк.
2.	Доказать, что, присоединяя к расширенной матрице системы
линейных уравнений нулевую строку, мы получим систему линей¬
ных уравнений, эквивалентную исходной.
3.	Говорят, что строка а является линейной комбинацией
строк а,, .... ат, если а =	+ . . . + Xmam для некоторых
чисел Хн . . ., Хт. Доказать, что, отбросив строку расширенной ма¬
трицы системы линейных уравнений, являющуюся линейной комби¬
нацией остальных, мы получим систему линейных уравнений,
эквивалентную исходной. Использовать этот результат для решения
упражнения 2.
4.	Доказать, что система линейных уравнений однородна тогда
и только тогда, когда нулевая строка является ее решением.
5.	Сформулировать и доказать условия на элементы расширен¬
ной матрицы системы линейных уравнений с п неизвестными, необ¬
ходимые и достаточные для того, чтобы всякая строка длины п
служила решением этой системы.
6.	Доказать аналог теоремы 2 для элементарных преобразова¬
ний третьего типа, а аналоги теорем 1 и 2 — для элементарных
преобразований столбцов.
7.	Может ли система линейных уравнений с действительными
коэффициентами иметь в точности два различных решения?
8.	Доказать утверждение: если матрица В получена из матри¬
цы А конечным числом элементарных преобразований строк, то
каждая строка матрицы В является линейной комбинацией строк
матрицы А. У к а з а н и с: провести индукцию по числу использо¬
ванных преобразований.
9.	Показать, что первые ненулевые элементы строк ступен¬
чатых матриц, полученных конечным числом элементарных преоб¬
разований строк из одной и тон же матрицы, располагаются в одних
п тех же столбцах. У казаки е: использовать упражнение 8.;
§ 2. Определители
Отображение F множества квадратных матриц порядка
п в множество действительных чисел называется опреде¬
лителем, если оно удовлетворяет следующим условиям.
J. Если матрица А имеет две одинаковые строки, то
Л’(И) = 0.
Дь
(ivi
а1п
г	н	г
а и "1" aiL а 12
' • ат	а iu
а1Ь,
ап2
is

(другими словами, если некоторая строка матрицы пред¬
ставлена в виде суммы двух строк, то определитель этой
матрицы *) равен сумме определителей двух матриц, по¬
лученных из данной заменой строки, являющейся суммой
двух строк, ее слагаемыми).
III.
строке, можно выносить за знак определителя).
IV.
1
0. ,
. .0
0
1..
, .0
0
0. ,
.. 1
Подчеркнем, что вопрос о существовании и единст¬
венности определителя пока остается для нас открытым.
Однако всякое отображение F, удовлетворяющее усло¬
виям I—IV, должно обладать также следующими свойст¬
вами:
1.	Если матрица А содержит нулевую строку, то
F(A) = 0.
2.	Если от матрицы А к матрице В можно перейти с по¬
мощью одного элементарного преобразования первого
типа, то F (В) = — F (Л).
3.	Если от матрицы А к матрице В можно перейти с по¬
мощью одного элементарного преобразования второго
типа, то F (В) = F (Л).
4.	Если S — ступенчатая матрица порядка /г, то
F (S) =	. snn, где в соответствии с нашим соглаше¬
нием Sij — элемент матрицы 5, стоящий на пересечении
i-й строки и /-го столбца.
*) Говоря «определитель матрицы Л», мы имеем в виду число,
соответствующее матрице А при отображении Л.
17

Доказате л ь с г в о.
2.	Предположим, что при переходе от А к В перемене¬
ны местами i-я и /-я строка. Рассмотрим вспомогательную
матрицу С, в которой в z-й и в у-й строках стоит сумма
i-й и у-й строк матрицы А. Согласно условию I, F (С) = 0.
Так как г-я строка выражена в виде суммы двух строк,
то, вводя обозначение ак = (аки . . ., акп) и воспользо¬
вавшись условием II, напишем
si + sj
“г
Во вновь полученных матрицах у-е строки представлены
в виде суммы двух строк. Можно еще раз воспользоваться
условием II:
Отсюда с помощью условия I получим
0 = F (Л) + F (5).
Следовательно,
F (Л) = —F (5),
что и требовалось доказать.
3.	Допустим, что матрица В получена из А прибав¬
лением к i-й строке матрицы А ее у-й строки, умноженной
на X. Используя условия II и III и обозначения ак =
18

= (fl/,1, • • ■ ak„), получаем
F(B)
Последняя матрица содержит две одинаковые строки.
Значит, по условию I последнее слагаемое обращается
в нуль, откуда F (В) = F (А).
4.	Пусть А — ступенчатая матрица. Если она содер¬
жит пулевую строку, то, с одной стороны, F (А) = 0 по
свойству 1, а с другой — хотя бы одно из чисел ап, а22, • • •
, . ., апп равно нулю, чем и доказывается справедливость
свойства 4 в рассматриваемом случае. При отсутствии в
матрице А пулевых строк она имеет вид
«и
«12 • ■
• • аь,
0
«22 •
• • “‘2„
0
0 .
. . (1
■п п
где яп, я22, . . ., апп =£= 0 (так как равенство ati ~ 0 за¬
ведомо ведет к появлению нулевой строки). Такая матри¬
ца называется треугольной. Прибавив к первой строке
матрицы А ее последнюю строку, умноженную на	—,
о	О 2
ко второй — последнюю строку, умноженную на	,
апп
и т. д., добьемся того, что все элементы последнего столб¬
ца, кроме апп, обратятся в нуль. При этом элементы ос¬
тальных столбцов останутся без изменения. Далее, при¬
бавив к первой, второй и последующим строкам получив¬
шейся матрицы ее предпоследнюю строку, умноженную
па подходящие числа, превратим в нули все элементы
предпоследнего столбца, кроме ап_хп_х. Аналогично по¬
ступая с третьим от конца столбцом и т. д., придем к
19

матрице
«П
0 .
. . 0
в=
0
«22 • ■
.. о
0
0 . .
Используя свойства 3, III и IV, получаем
/у (Л) = /у (В) —	(-®) = ^11^22 • ‘ * ^пп>
Теорема 1 (теорема единственности). Существует
не более одной функции, удовлетворяющей условиям I — IV.
Доказательство. Предположим, что есть две
такие функции F и G. Надо доказать, что F = G, т. е.
установить, что F (Л) = G (Л) для любой матрицы Л.
В силу теоремы 1 из § 1, матрицу Л можно привести
к ступенчатому виду S конечным числом элементарных
преобразований. Допустим, что при этом использовано
к элементарных преобразований первого типа. Ввиду
свойств 2, 3 и 4
F (А) = (-1/F (5) = (-1ЛП.?22 . . . s,m.
Поскольку те же самые соображения справедливы и для
функции G, а матрица Л была приведена к ступенчатому
виду независимо от функций, то
G (Л) = (-1/G (S) = (-1)W;2 • • • U
т. е. F (Л) - G (Л).
Теорема 2 (теорема существования). Функция F,
удовлетворяющая условиям I — IV, существует.
Д о к а з а т е л ь с т в о. Установим справедливость
следующего утверждения, равносильного утверждению
теоремы 2.
Для всякого натурального п существует функция F,
отображающая множество квадратных матриц порядка
п в множество действительных чисел и удовлетворяющая
условиям 1 — IV.
Из пего, очевидно, вытекает справедливость теоремы 2.
Но такая формулировка позволяет провести индукцию
во п. Для матриц первого порядка достаточно положить
F (а) = а. Предположим, что высказанное утверждение
справедливо для матриц, порядок которых меньше н.
Возьмем произвольную матрицу порядка п;
«11
«12 • •
• а1п
«21
«22 • <
■ • а2п
« 1
711
(1 п .
/14
’ • апп
20

Матрицу, полученную из матрицы А вычеркиванием Z-й
строки и /-го столбца, назовем подматрицей матрицы А
и будем обозначать через а если ясно, о какой матрице
А идет речь, то через Мц. В силу индуктивного предпо¬
ложения для каждой из этих подматриц определено число
которое называется минором или, точное'-
дополнительным минором элемента ац. Число Ац =
= (—l)ilJ’F (Mtj) назовем алгебраическим дополнением
элемента в матрице А, Положим
= aAi^li + a2i^2l + • • • +
(пока можно ожидать, что F2, . . Fn — различные
функции!). Теперь зафиксируем i (т. е. номер столбца)
и положим F = Ft. Убедимся, что функция F удовлетво¬
ряет условиям I —IV.
I.	Пусть s-я и t-я строки матрицы А совпадают. Тогда
во всех минорах Mri, кроме Msi и	встречаются оди¬
наковые строки. Поэтому, учитывая индуктивное предпо¬
ложение, имеем
F (Л) = aSi Ast -р atiAti =
= asi(- 1)”гЛ’(М5/) + ан(- l)f^F(M(i).
Допустим для определенности, что 5 < Z. Тогда t-я стро¬
ка матрицы А (с выброшенной координатой а,£-), равная
ее 5-й строке (с выброшенной координатой в матрице
располагается на (Z — 1)-м месте. Та же самая строка
встречается и в матрице Мц, но располагается в ней на
5-м месте. Все остальные строки матриц Msi и Mti одни
и те же и располагаются в одном и том же порядке. Таким
образом, для того чтобы матрицу МГ/ превратить в мат¬
рицу	достаточно передвинуть ее 5-ю строку па (Z —
— 1)-е место, не меняя взаимного расположения осталь¬
ных строк. Для этого придется Z — 1 — 5 раз менять мес¬
тами соседние строки матрицы. В силу свойства 2
F = (-1)' 1 /•
откуда
М) = «si [(- 1)-<■' ' (Mti) (- 1)' ■ 7- (Мн)] =
=	(- l)!li (- F (Mti) +	= 0.
21

II.	Положим
ац
«12
ain
a'sl + Ч
«6-2 + as2 * *
• аяп + asn
ani	аи2 • '
■ •	апп	I
а-и.
«12 • •
• а1п
«11
«12 •
• •
А' --=
asi
a.s2 • ■
• а8П
п Л" =
Я81
а >82 *
• • <4
ап2 ■ ’
’ * апп
а>.1
ап2 ’
♦ • а/т
Далее обозначим через Акц А'м и A/-i алгебраические до¬
полнения элемента, стоящего на месте (к, I) в матрицах
Л, А' и А" соответственно. Аналогичные обозначения бу¬
дем применять и для подматриц. Заметим, что Asi =
= Asi = ASi, так как при вычеркивании 5-й строки во
всех трех случаях остается одна и та же подматрица. Если
же t Ф s, то, в силу индуктивного предположения и усло¬
вия II, имеем
= (- i)t+i (F (Ми) + F (Ми)) = Аи + Аи-
Поэтому
F (Л)	diiAn 4“ . . . “р (&si 4" ^si) Л§г | . . . —J ^niAni —
= а,ц (Л1г- 4- Лц)	(aSi 4~ asi) Л3(-, 4~ • • •
.. . 4" ani (Ant 4" Ani) = (ацАц 4- ... 4- asi Л8г- 4~ • • •
• • • 4" ani^ni) 4- (ацА±г 4- — • + ^siAsi + •••
. . . 4~ aniAni) — F (А ) 4- F (А ).
III.	Пусть
«11
«12 • •
•а1п
«21
«22 • •
• а2п
°81
as2 * ‘
’ • asn
flni
Яп2-
• • апп
«11
«12 .
• • °1>г
«21
«22 •
• ■ а2п
Kasl
Чг .
• ■ Чп
ап1
ап2 •
. . а
пи
Обозначения Лж Л^, Mki и М'м будем использовать
в том же смысле^ как и выше. Тогда, учитывая индуктив-
22

ное предположение и условие III, получим
Ль
если I — s,
если l=£s.
Поэтому
F (А) — иц Ац	(hasi) Ast 4- . . . -f- аП|ЛПг~
— tf i; (Мн) 4- • • • + (Xasi) Asi 4- ... 4- ani (ХЛП{) =
= X (ацАп + . . . 4" aSiASi + • • • 4~ aniAni) — ^F (Л).
IV.	Учитывая индуктивное предположение, имеем
0. . .0
1 ... о
О ... 1
Таким образом, каждая из функций Ft удовлетворяет ус¬
ловиям I — IV, т. е. является определителем. Этим закан¬
чивается доказательство теоремы 2.
Из теорем 1 и 2 вытекает, что каждой матрице А со¬
ответствует вполне определенное число F (Л), которое
будем называть определителем матрицы А и обозначать
через | Л |.
Поскольку согласно теореме 1 для функций Fh рас¬
сматривавшихся при доказательстве теоремы 2, имеем
F± = F2 = . . . = Fn, нами заодно доказана
Теорема 3 (теорема о разложении по столбцу).
I	Л | = «1/Лн- 4- ••• 4- aniAni.
Если дана матрица А = ||	||, то условимся обозна¬
чать через Л* матрицу, определяемую условиями а* =
= aji. Про эту матрицу будем говорить, что она получена
из матрицы Л транспонированием. Заметим, что строки
матрицы А служат столбцами матрицы Л*, а столбцы —
строками.
Условимся обозначать через I*, II* и т. д. условия 1,:
II и т. д., в которых слово «строка» заменено на «стол¬
бец». Аналогичный смысл имеют свойства 1*, 2* и т. д.
Убедимся, что определитель удовлетворяет условиям I* —
III* и обладает свойствами 1*—3*.
I*. Проведем доказательство индукцией по порядку
матрицы. Если он равен 1, то утверждение тривиально,
а для матрицы второго порядка оно проверяется непо¬
средственным подсчетом. Если кроме двух равных столб¬
цов имеется хотя бы еще один, то разложим определи¬
23

тель но этому столбцу и рассмотрим алгебраические до¬
полнения его элементов. В каждой из соответствующих
подматриц остались одинаковые столбцы. Определители
этих подматриц, будучи определителями порядка п — .1,
равны нулю по индуктивному предположению. Но тогда
и сами алгебраические дополнения равны 0, а значит,
равен нулю и определитель.
Справедливость условий II* и III* сразу следует из
теоремы о разложении по столбцу.
Что касается свойств 1*—3*, то они могут быть вы¬
ведены из условий I* — III* дословным повторением рас-
суждений, использованных при выведении свойств 1 — 3
из условий I — IV.
Теорема 4 (теорема о транспонировании). | Л* |
-М |.
Доказательство. Положим F (Л) = | Л* !.
Определенное таким образом отображение F удовлетво¬
ряет условиям I —III, поскольку эти свойства отображе¬
ния F относительно строк матрицы А превращаются в ус¬
ловия 1* —III* для определителя матрицы Л*, которые,
как уже установлено, справедливы. Кроме того, F (Е)
— ] Е* | = | Е | = 1. В силу теоремы единственности,
отображение F совпадает с определителем, т. е.
|Л* I = F (A) = I А |.
Теорема 5 (теорема о разложении по строке).
I Л j (ijjAii	(11цА[а,
Док а з а г е л ь с т в о. Заметим, что подматрица
Л7* матрицы Л*, полученная удалением 1-й строки и /-го
столбца, может быть получена транспонированием под¬
матрицы МЛ матрицы Л, полученной удалением /-й стро¬
ки и i-го столбца. В силу теоремы 4, | Л/* | = | М ц |.
Используя теоремы 3 и 4, получаем
|Л|_|Л*| = а*(-1)^|Л/* | + ...
• • • +	(- l)"+i | Afni | = «i! (- I)1' ' | Л/i! | + • • •
. . . -|- а,„ (— 1)',!; | Л/,„ | = ааАц Н . . + а;„ЛЬ1.
Теорема 6 (теорема об умножении на чужие ал¬
гебраические дополнения). Если i j, т0 auAji + . . «
. . . -|- ainAjn 0 и	(L)tiAnj 0.
Д о к а з а т е л ь с т в о. Достаточно заметить, что
первая из сумм совпадает с разложением по у-й строке оп¬
24

ределителя *), некотором все строим матрицы Л, кроме
оставлены без изменения, а вместо ;-й подставлена
/-я. Ио такой определитель имеет две одинаковые строки и,
следовательно, равен нулю по свойству I. Второе соотно¬
шение доказывается аналогично.
Теорема 7 (об определителе с нулями в правом
верхнем углу). Если А и В — квадратные матрицы, то
Л : О
с\в
Доказательство. Обозначим через к поря¬
док матрицы А и будем вести индукцию по числу к. Если
к = 1, то, разложив по первой строке, получим
что и требовалось. В общем случае, разложив определитель
А =
Л 1 о
с’\в
по первой строке, получим
А = апЛп + . . » +
где A{S означает алгебраическое дополнение элемента
в определителе А. Аналогично используются обозначения
Л-t М*, Имеем
| м*\, где 6- = 1, 2, . . к.
Правый верхний угол матрицы М£ч заполнен нулями,
причем порядок матрицы, стоящей в ее левом верхнем
углу, равен к — 1. Применив индуктивное предположе¬
ние, получим
I М* I = I М* I I в |.
*) Говоря о строках, столбцах или элементах определителя,
мы имеем в виду строки, столбцы и элементы рассматриваемой мат¬
рицы.
25

Отсюда
+£ = (-1)1+3 | М* I = (-1)1+3 I М* | | в I = Л* I В |.
Поэтому
Д = аиЛЙ I в | + а12А* I В | + . . . + «н^. | В | =
= I Л II В
Остановимся еще на одном способе вычисления опре¬
делителя. Используя разложение по первой строке^ мож¬
но записать
и
«11
Й21
^12 I
= #11^22 	 ^12^21
«22 1
«11
«12
«13
«21
«22
«23
«>2
= ^11
«23
«21
	 ^12
«23
+ «13 Г21
«31
«32
«33
1 «32
«33 |
1 «31
«33 1
1 а;!1
= &11<222#33 “Ь ^12^23^31 + ^13^21^32 —
— аца3заз2 — «12а21«зз — «1з« 22^.31.
Таким образом, для определителей второго и третьего
порядка существуют формулы, выражающие их через эле¬
менты соответствующих матриц *). Убедимся, что подоб¬
ные формулы имеют место для определителей любого по¬
рядка. С этой целью рассмотрим отображение о множество
чисел {1,2, . . ., п} на себя, при котором различные чис¬
ла переходят в различные (т. е. если i =/= j, то о (i) о (/)).
Такое отображение называется подстановкой на множест¬
ве {1, 2, . . ., п}. Подстановки пит на множестве
{1, 2, . . ., /г} считаются равными, если о (Z) = т (i) для
каждого i. Подстановку о удобно записывать в виде
таблицы
/1 2 . . . п \
(1)	<5 (2)	... б pi)/’
Число
Пб (i) — б (/)
• _ • • =
(б (1) - б (2)) . . . (6 (1) - б (п)) (б (2) - б (3)) . . .(б (/г - 1) - 6 (л.))
(1 — 2) ... (1 — п) (2 — 3) ... (2 — п) ... ((/г — 1) — п)
*) Для запоминания этих формул удобно следующее геометри¬
ческое представление: «положительные» произведения получаются,
если идти по стрелкам, изображенным на рис. 1, а «отрицатель¬
ные» — на рис. 2.
26

называется знаком подстановки. Легко заметить, что аб¬
солютная величина как числителя, так и знаменателя
выписанной дроби равна 1! 2! ... (п — 1)!. Следователь¬
но, знак подстановки может быть равен 1 или —1. В пер¬
вом случае подстановка называется четной, а во вто-
а11 а12
X
а21
Рис. 2
ром — нечетной. Например, если о задается таблицей
то
1	2 3 4\
4 1 3 2р
sgn о =
3.1.2.(-2) (- 1)-1
(- 1) (- 2) (- 3) (- 1) (- 2) (- 1)
= 1,
т. е. эта подстановка четная.
Скажем, что подстановки о и т отличаются на транс¬
позицию (j, /), если
о(/с) =
т (7с),
если
/»
* (/)<
если
к = 1,
если
k = j.
27

При записи этих подстановок в виде таблицы нетрудно
заметить, что одна из них получается из другой переменой
местами чисел, стоящих на z-м и /-м местах нижней строки.
Теорема 8. Если подстановки о и т отличаются
на транспозицию (i, j), то
Доказательство,
получим
sgn О' = —sgn т.
Группируя сомножители,
SgttfJ =
П	■ П
fryO, j
j
fry-г, j
. 3(0
—	g (/■)
—	z
= П 1
<1<м
j
П П(')
— T (&)
т (/’) — т (k)
k -1
T (/) — T (/)
/ —/с
i — к
T (Zc) — T (I)
' — i
fc-У-г, ;
п
l<fr<Z<n
fr^i, j
)
k — l
i — к
•	.(— 1) = (— 1) sgn т.
используется) несколько иной подход
(и обычно
четности подстановки. Именно: говорят, что пара
. ., п} и
Возможен
к определению
(о (г), ст (;)), где о — подстановка на множестве {1,2,..., п} * и
i < /, образует инверсию, если о (I) > о (j). После этого четность
подстановки определяется как четность числа инверсий в ней.
Убедимся, что это определение совпадает с нашим. В самом деле,
пара (о (i), о (/)) образует инверсию тогда и только тогда, когда
g(0 — з (?)
i — /
и, следовательно, sgn о = (—!)', где t — число инверсий в под¬
становке о.
Т е о р е м а 9. | /1 I 3 sgn <*«10(1) • • ■ «woo, где <»
(V
пробегает все подстановки на множестве чисел {1, 2, . . 4
. .	и}.
Доказательство. Рассмотрим функцию
F (А) = 2	°	• ♦ • ^na(n)
о
и убедимся, что она удовлетворяет условиям I —IV.
Тогда из теоремы о единственности определителя будем
иметь F (Л) = | А | , что и требуется. Начнем с проверки
последнего условия.
28

IV. Пусть Л = Z?. Если подстановка	% ’ * п г-
,г0 o(j)	г для некоторого i. Поэтому произведение а10(г) . ..
Мпо(п) содержит элемент	= 0 и, следовательно,
равно нулю. Значит, остается только одно слагаемое^ т. е.
A(/l) = sgn^ 2	”)«и«22 • • • апп~ 1.
III. Если матрица А' получена из А умножением
.s й строки на X, то
F (Л )— О’ «10(1) • • • (X<l.sr)(.s)) • • • «/io(n) ~
о
X Sg’ll О О-ЮЦ) - • . «80(8) • • • ^U<7(?i)== XX (Л).
<7
II. Если Л, Л' и А" имеют тот же смысл, что и на
с. 22, то
(Л) = Ssgn О «10(1) . . . («8О(8) + «80(б)) • • • «7Ш(/1) =
о
= 2lSgU О «10(1) • • • «80(8) • • • «П0(П) +
0
-|- 2sgn О й10(1). . . aso(s) . . . art0(n) = F (Л') + F (Л").
о
I. Допустим, что .s-я строка матрицы Л совпадает
с Z-й, причем s <Z t. Возьмем четную подстановку
\	/	1	. . . S . . . t . . . п \
U (1) ... О (8) ... б Ц) ... б («)/ ’
Этой подстановке соответствует произведение
«10(1) •	•	• «80(8) •	•	• «(©(/) • •	• «П0(П)«	(*)
Рассмотрим подстановку т, полученную из о применением
транспозиции (5, Z). Согласно теореме 8, подстановка т
нечетная и, следовательно, ей соответствует произведение
«1Ц1) • • • «8Т(8) • • • «(Т(/) • • • «ПТ(П)«	(**)
Согласно определению транспозиции, a (Z) = т (/), если
i =?*= 5, С су ($) — х (t) и (j(t) = т ($). Отсюда, поскольку 5-Я
строка матрицы Л равна ее t-й строке, имеем	~
«11(07 если I 5,	/,	с>о(8) ~ «1©(8) — «1т(о и «/о(/)
«so(0 = «st(s). Следовательно, произведения (*) и (**)
отличаются только знаком. Поэтому их сумма равна нулю.
Допустим, что таким образом перебраны все четные
2‘J

подстановки. Если сумма
5 Sg£l О' fl-Kj(i) • . • ^no(n)
а
отлична от нуля, то должна остаться нерассмотренной
какая-то нечетная подстановка. Но применив к ней транс
позицию (5, £), придем к нерассмотренной четной подста¬
новке , Полученное противоречие завершает доказатель¬
ство®
У п р а ж н е и и я
1.	Если F и G — две функции со свойствами I — III и G (Л)
=/= 0 для некоторой матрицы Л, то существует такое число X, что
F (X) = kG (X) для любой матрицы X.
2.	Определитель матрицы Л равен нулю тогда и только тогда,
когда хотя бы одна из ее строк (или столбцов) является линейной
комбинацией остальных.
3.	Если Л — матрица нечетного порядка и Л* = —Л (через
—Л обозначена матрица, полученная из Л изменением знака всех ее
элементов на противоположный), то | Л | = 0.
4.	Сформулировать и доказать для определителя свойство
столбцов, аналогичное свойству 4 для строк.
5.	Какова связь между определителями матрицы Л и матрицы,
полученной из строк (столбцов) матрицы Л, расположенных в об¬
ратном порядке (т. е. первая строка (столбец) ставится па послед¬
нее место, вторая — на предпоследнее и т. д.)?
6.	Чему равен определитель, у которого сумма строк с четны¬
ми номерами равна сумме строк с нечетными номерами?
7.	Доказать, что существует п! различных подстановок на
множестве (1, 2, . . ., п}. Указание: провести индукцию по п.
8.	Чему равно произведение знаков всех подстановок на мно¬
жестве {1,2,..., п}?
§ 3. Алгебра матриц
Если в матрице А отметить какие-нибудь к строк и к
столбцов, то элементы, стоящие на пересечении отмечен¬
ных строк и столбцов, образуют квадратную матрицу по¬
рядка к — подматрицу матрицы А. Определитель каждой
из таких матриц называется минором порядка к матри¬
цы А, Таким образом, миноры, о которых говорилось
в § 2, оказываются минорами порядка п — 1 в смысле дан¬
ного определения. Наивысший порядок отличных от нуля
миноров матрицы А называется ее рангом. Разумеется,
ранг матрицы размера т X п не превосходит наименьшего
из чисел т и п. Заметим, что у нулевой матрицы ненуле¬
вых миноров нет. Поэтому ее ранг естественно положить
равным нулю.
30

Теорема 1. Ранг ступенчатой матрицы равен
числу ее ненулевых строк.
Доказательство. Пусть ступенчатая матрица
Л содержит г ненулевых строк. Тогда, отметив ненулевые
строки и столбцы, в которых располагаются первые нену¬
левые элементы этих строк, получим треугольную матрицу.
Ее определитель равен произведению диагональных элемен¬
тов, отличных от нуля, и, следовательно, отличен от нуля,
так что матрица А содержит ненулевой минор порядка г.
Всякий же минор большего порядка содержит нулевую
строку и поэтому обращается в нуль. Таким образом,
рангЛ = г.
Теорема 2. ранг А = ранг Л*.
Доказательство. Пусть ранг Л = г. Рассмот¬
рим в матрице Л* произвольный минор порядка г.
Пусть он является определителем подматрицы М. Тогда
М* — подматрица матрицы Л*. Поскольку ее порядок
больше г, то минор | М* | = 0, а значит, и | М | = О
(см. теорему 4 из § 2). Таким образом, все миноры матрицы
Л*, порядок которых больше г, обращаются в нуль. Сле¬
довательно, ранг Л* г — ранг Л. Это же неравенство
для матрицы Л* дает ранг Л = ранг Л** ранг Л*.
Таким образом, ранг Л* ранг Л ранг Л*, т. е.
ранг Л = ранг Л*.
Теорема 3. Ранг матрицы не меняется при эле¬
ментарных преобразованиях строк (столбцов).
Сначала будет доказана
Лемм а. Если от матрицы А к матрице В можно
перейти конечным числом элементарных преобразований
строк, то ранг В ранг Л.
Доказательство леммы будем вести индукцией по
числу примененных элементарных преобразований. До¬
пустим, что использовано только одно элементарное пре¬
образование. Пусть ранг Л = г. Для доказательства
леммы достаточно убедиться, что всякий минор | М |
матрицы В порядка, большего чем г, равен нулю. Если
от матрицы Л к матрице В перешли переменой местами
двух строк, то подматрица М либо совпадает с некоторой
подматрицей Мг матрицы Л, порядок которой больше
чем г, либо отличается от такой подматрицы М' только
порядком строк. Поскольку ранг Л — г, то | М' | = О,
в значит, | М | = + | М' | = 0. Допустим теперь, что
переход к матрице В осуществлен прибавлением к i-й
строке матрицы Л ее у-й строки, умноженной на X. Воз¬
можны три случая: 1) i-я строка не проходит через под-
31

матрицу М\ 2) как t-я, так и /-я строки проходят через
подматрицу М; 3) t-я строка проходит через подматрицу
М, а /-я не проходит. В первом случае подматрица М сов¬
падает с соответствующей подматрицей матрицы А и, сле¬
довательно, | М | = 0. Во втором случае имеем
aikt +	•
ail^ -
11 Hl ’
• • aiks
ибо последний определитель является минором матрицы At.
В третьем случае запишем
|М| =
+Kajkt • • • (ln;s И'
ai',-	’
■ • ♦
-1 - A
a
4 1 (
•S
./" i
s
Но первый из этих определителей является минором ма¬
трицы 4, а второй лишь порядком строк отличается от
некоторого минора матрицы А. Следовательно, оба этих
определителя равны нулю, откуда | М | = 0. Таким
образом, для случая, когда использовано лишь одно
элементарное преобразование, лемма доказана. Допу¬
стим, что использовано т преобразований. Пусть С —
матрица, полученная после осуществления т — 1 пре
образования. Учитывая индуктивное предположение,)
имеем
ранг В ранг С ранг Л,
что и требовалось.
Д о к а з а т е л ь с т в о т е о р е м ы. Допустим, что
огг матрицы А к матрице В перешли конечным числом
элементарных преобразований строк. Ввиду леммы ранг В^С
ранг А. Но если элементарные преобразования позво¬
ляют перейти от А к В, то, согласно теореме 2 из § 1,
от В к А также можно перейти конечным числом элементар¬
ных преобразований. Еще раз применяя лемму, получаем,
что ранг А ранг В. Нужное равенство сразу следует
из полученных неравенств. Справедливость теоремы для
столбцов легко вывести из теоремы 2.
Теорема 4 (теорема Кропекера—Капелли). Систе¬
ма линейных уравнений совместна (т. е. имеет решение)
32

тогда и только тогда, когда ранг матрацы системы
>авен рангу ее расширенной матрицы.
t Доказательств о. Поскольку, согласно теоре¬
мам 1 и 3 из § 1, от каждой системы линейных уравнений
можно перейти к эквивалентной ей ступенчатой системе t
а ранги матрицы системы и ее расширенной матрицы,
в силу теоремы 3, при этом меняться не будут, то достаточ¬
но установить справедливость теоремы 4 для ступенчатой
системы. Для ступенчатой же системы, в силу теоремы 1,
ранги матрицы системы и ее расширенной матрицы равны
тогда и только тогда, когда эти матрицы имеют одинако¬
вое число ненулевых строк, или, что то же самое, тогда и
только тогда, когда первый ненулевой элемент последней
ненулевой строки расширенной матрицы не располагается
в столбце свободных членов. Из анализа ступенчатой
системы, проведенного в § 1, известно, что это имеет мосто
тогда и только тогда, когда система совместна.
Теорема 5. Совместная система линейных урав¬
нений от п неизвестных с матрицей А имеет, единственное
решение тогда и только тогда, когда ранг А = п.
Доказательств о. В силу теорем 1 и 3 ранг А —
п тогда и только тогда, когда данная система приводит¬
ся к треугольному виду (т. е. к системе с треугольной ма¬
трицей). С другой стороны, ступенчатая система имеет
единственное решение в том и только том случае, когда она
треугольна.
Следствие. Однородная система п линейных
уравнений с п неизвестными обладает ненулевыми реше¬
ниями тогда и только тогда, когда определитель этой
системы равен нулю.
Когда в § 1 мы говорили о главных и свободных не¬
известных, эти понятия зависели от способа приведения
расширенной матрицы системы к ступенчатому виду.
Для решения задач, обсуждавшихся в конце § 1, необ¬
ходимо иметь определение, зависящее лишь от данной
системы линейных уравнений. С этой целью, если дана
система линейных уравнений относительно неизвестных
. ., хп, условимся говорить, что неизвестные . . .
• • •.» можно объявить главными, если при любом
задании остальных неизвестных значения этих неизвест¬
ных определяются однозначно. Про эти остальные неиз¬
вестные будем говорить, что их можно объявить свобод¬
ными. Подчеркнем, что в последних двух фразах опреде¬
ляются термины «можно объявить главными» и «можно
ооъявить свободными»^ а не понятия «главное неизвестное»
2 Л. а. Скорняков	33
и «свободное неизвестное». Неизвестные становятся глав¬
ными или свободными лишь после того, как мы, реализуя
имеющуюся возможность, объявим их таковыми. Ясцо,
что главные и свободные неизвестные в смысле, опреде¬
ленном в § 1, можно объявить такими и в смысле нового
определения.
Центральным результатом нашей теории является
Теорема 6. Пусть имеется совместная система т
линейных уравнений с п неизвестными, А — расширен¬
ная матрица этой системы и ранг А = г. Тогда неизвест¬
ные х^, . . ., xik можно объявить главными в том и толь¬
ко том случае, когда к = г и в столбцах матрицы А с но¬
мерами ilr . . ., ц- располагается ненулевой минор поряд¬
ка г.
Доказательство. Допустим, что к — г и что
в столбцах с указанными номерами располагается ненуле¬
вой минор порядка г. Тогда ранг матрицы
1Ц
в1»2 •
'2 ? t
й24	•
гтг\
ami2 •
' * amir
размера т X г равен г. В силу теорем 1 и 3, приведя
эту матрицу к ступенчатому виду, получим матрицу
"14
0
"14 •
"24 •
•	ч 1
•	"2!Г
0
0 ••• ч
0
0 .
. 0
0
0 .
. 0
где	. * .у brir у= 0. Применив те же самые элемен¬
тарные преобразов ания к матрице А, получим матрицу
• • • "14
••• "14
•••ч •••
... 0
•• • ">4
... ...
... 0
... о
. . . b ; ...
с
Т
... о
. . . о
. . . о ...
с ,
Г+1
... 0
... 0
... 0 ...
ст
34

Подчеркнем, что эта запись не означает, что все строки
матрицы 5, начиная с (г + 1)-й, нулевые: в столбах с но¬
мерами, отличными от i2, . . jr, могут встретиться
ненулевые элементы, стоящие в этих строках. Однако на
самом деле все строки матрицы 5, начиная с (г + 1)-й,
нулевые. Действительно, допустим, что это не так, т. о.
b'pq #= 0 для некоторых р и д, где г + 1 < р < т. Конеч-
н0?	ц, . , ., Однако может случиться, что q —
= п + 1, т. е. bpq = ср. Пусть М — минор матрицы В
порядка г + 1, расположенный в строках с номерами
1, 2,. . г, р и столбцах с номерами . ., ir, q. Пере¬
ставляя, если нужно, столбцы этого минора, получим
М-=±
Но тогда
Ч
6в, ■■
•• ч
0
Ь2г, ■
•• ч
b2q
0
0 . ,
.. Ч
ЬГЧ
0
0 .
. . 0
bvo
= ± blix. . . brzrbPQ о.
ранг А — ранг 2J > г + 1,,
что противоречит условию. Таким образом, система ли®
нейных уравнений, соответствующая матрице 5, экви¬
валентна исходной системе и содержит г уравнений, не
считая уравнений вида (kq + . , » 4~ 0хп = 0, Придавая
неизвестным, отличным от	xir-9. произвольные
значения и перенося их в правую часть, легко убедиться,
что неизвестные xiix я . xir однозначно определяются
одно за другим, начиная с последнего. Таким образом, их
можно объявить главными.
Допустим теперь, что неизвестные xixi » * *, xik можно
объявить главными. Положив остальные неизвестные рав¬
ными нулю, придем к системе
'	+ • • • + ank^ik = bi,
‘	’ (*)
Ч~ • • • 4“	==
имеющей единственное решение, В силу теоремы 5Л ранг
матрицы этой системы равен к» Следовательно,; к г
и в столбцах	располагается ненулевой минор
порядка к, Допустим,, что к < г* Заметим^ что система (*)
приводится к треугольному виду, и применим к исходной
системе те же самые элементарные преобразования, Тогда
2*
35

расширенная
матрица системы приобретает вид
••• ьи. ■
• • ч •
• • Ьик • • •
С1
... о .
•• Ь2,- •
. . Ь •	. . .
с2
... 0 .
0 .
Ь;	...
с
' ч-
г
... 0 .
. . о .
. . о
... о
. . о .
. . о
Ст
В силу теоремы Кронекера — Капелли, ранг матри-
цы системы равен г > к. Поэтому среди строк (bilr . . .
. . ., bia), где к <Z i т, есть ненулевые. Следовательно,
найдется bpq О, где р > к. Если теперь положить
равными нулю все неизвестные с номерами, отличными
от 1^, . . ., ifc, 7, то получим xq = cylbpq. Следовательно,
хч не может быть взят произвольным, что противоречит
возможности объявить xit, . . ., х-ч, главными неизвест¬
ными. Следовательно, к = г, чем и завершается доказа¬
тельство.
Пример. В системе
Г хх 4- х2 + л’з + Ч = 4,
1 21 + Х'2, — 2'3 4~ 24 = 2
главными можно объявить следующие пары неизвестных: (^, я3),
(22, 23), (ля, х4). Пары же (^, х2), (^, х^) и (j?2, х^) объявить главными
нельзя.
Пусть даны .матрица А размера тп X п и матрица В
размера п X р, Другими словами, число столбцов мат¬
рицы А равно числу строк матрицы В. Произведением
АВ матриц А и В называется матрица С размера m X р,
элементы которой вычисляются по следующему правилу:
п
<--ц = S	—	j = 1, ..., р).
/г=1
Подчеркнем, что в соответствии с этим определением
(и в отличие от чисел) произведение двух матриц существует
не всегда. Целесообразность предложенного определе¬
ния подтверждается дальнейшим развитием теории, изла¬
гаемой в настоящем параграфе и в гл. III. Попутно заме¬
тим, что рассмотрение произведения матриц оказывается
полезным во многих вопросах теоретической и приклад¬
ной математики.
36

т е орем а 7. (АВ) С - А (НС) и (АВ)* - /?*Л*
(написанные равенства означают, в частности, что правая
и левая части каждого из них существуют одновременно).
Д о к а з а т е л ь с т в о. Сначала убеждаемся, что из
существования левой части каждого из этих равенств
следует существование правой и наоборот. Например,
если существует произведение (АВ) С, то матрицы А и
В имеют размеры т X п и п X р соответственно. Но
тогда АВ имеет размеры т X /?, откуда вытекает, что
матрица С должна иметь размеры р X д. После этого
ясно, что произведение ВС существует и имеет размеры
п :< д. По тогда су1цествует и произведение А (ВС).
При этом как (АВ) С, так и А (ВС) имеют размеры
т X д. Далее полагаем U = АВ, V = ВС, S — (АВ) С\
Т — А (ВС) и убеждаемся, что
р	р	п	п	р
Sij= uUelj— S 3 aik^klclj =	3 aik^klclj~
1=1	1=1	k=i	k=i	i-.=i
n	p	n
3 aik ( 3	^klclj}	~ X aik^k i~t i. p
k=l	1=1	k=i
Этим доказано первое равенство. Для доказательства
второго положим С — АВ и D — В*А*. Как и выше,;
нетрудно убедиться, что произведение D = В*А* су¬
ществует и что матрицы С и D имеют одинаковые размеры.
Кроме того,
с*	3 а1кЪкг= 2	2j	= dih
к=1	к=1	А—1
что и требовалось.
Котя для произведения нескольких чисел и употреб¬
лялась запись ал . . . ап, она, строго говоря, бессмысленна,,
ибо определено лишь произведение двух чисел. Да ив
в самом деле, для того, чтобы вычислить это произведе¬
ние, мы всегда (правда, мысленно) расставляли скобки.
Употребление же приведенной выше записи объясняется
тем, что результат вычисления не зависит от расстановки
скобок. Докажем аналогичный результат для матриц,,
что даст нам возможность использовать запись Лх . . . Ли
без скобок.
Теорема 8. Пусть произведение матриц
к = лили... (л^лд..))
Ърцествует. Тогда произведение At ... Ап существует
при любой расстановке скобоксводящей вычисление к вы¬
37

числению произведений, содержащих лишь два сомножите¬
ля, и всякий раз равно К.
Доказательство. Произведение одного пли
двух сомножителей скобок не содержит, и потому справед¬
ливость доказываемой теоремы тривиальна. Для трех
сомножителей это утверждение совпадает с первой частью
теоремы 7. Допустим, что теорема доказана, если число
сомножителей меньше п, Рассмотрим произведение А± . . ,
. . ,Ап с некоторой расстановкой скобок. Выделяя скобки,
соответствующие последнему умножению, имеем следую¬
щие варианты:
Вг = Aj (А2. . •
В2 = (А±А2) Из • • •
В п-1	Hi • • • ^п-1) Л-П’
Разумеется, предполагается, что внутри данных скобок
задана некоторая расстановка скобок. Ясно, что Вг = К,
ибо в силу индуктивного предположения произведение
А2 . . . Ап от расстановки скобок не зависит. Допустим,
что доказаны равенства
К = В. = ... = в^.
Тогда
В{-\=— (^1 • • • Ai-i) (А}А i+i... Яп) —;
= (ЛХ...	Лп)) =
= ((Л1...Аг-_1) /10(Л,+1... /1П) =
= (Л!... Ai)(Ai+1...An) = Bi
в силу теоремы 7 и индуктивного предположения. Про¬
должая этот процесс, убедимся, что
К = В1 = . . . = Вп^.
А это и требовалось.
Теорема 9. Умножение матрицы А слева (справа)
на диагональную матрицу
dx
0
. . . о
0
d2
. . . о
0
0 ,
, . . d
’	n
равносильно умножению строк (столбцов) матрицы А
на элементы d±, d2,t » • dn соответственноs
38

Доказательство. Если DA = С, то
п
Су =■ 2 dikakj = duCLjj = d^a^
7f=l
для каждого i. Утверждение, касающееся столбцов, до¬
казывается аналогично.
Следствие. Если
11
0 .
.. о


0
1 .,
.. о
0
0 .
.. 1
то АЕ = А и ЕВ = В всякий раз, когда умножение
возможно.
Следствие объясняет, почему матрица Е была названа
единичной.
Назовем элементарными матрицы, полученные из
матрицы Е примененном одного элементарного преобра¬
зования. Это будут матрицы вида
1 .
i
J
■•1 : '•
1 ;
: 1
i
... 0 ... 1 ...
. 1
i
..'.1 .
: ’1 :
. • L
J
... 1 ... 0 ...
J
... 0 .
.. i...]
. 1
: • 11
матрицы могут быть описаны так:
эти
Формально
SPQ.

i,
1,
О
если p = q^=
если p = i, q = j или p — B Я~В
в остальных случаях;
1, если p = q,
X, если p — i, q — B
О в остальных случаях.
Примерами элементарных матриц служат
5(2, 4) =
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
1
0
X
0
0
0
1
0
0
и T{2, 4,X) =
0
0
1
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
1
39

Теорем а 10. Умножение матрицы А на матрицу
S (i, у) слева (справа) равносильно перемене местами
1-й и j-й строк (l-го и j-го столбцов),
Доказательство. Положив С = S (i, j) -А-х
будем иметь
X:ia.iq = aiq, если р = I,
sJta:q = a}q, если р = /,
s[>Pai‘q = av<i> если P^iJ-
Утверждение, касающееся столбцов, доказывается ана¬
логично.
Т е о р е м а 11. Умножение матрицы А на матрицу
Т (i, у, X) слева (справа) равносильно прибавлению к i-й
строке (j-му столбцу) матрицы А ее j-й строки (i-го
столбца), умноженной на X.
Дока з а т е л ь с т в о. Положив С = Т (г, /, X) Аэ.
будем иметь
ii^iq + ^xj^jq == ^\q 4“	вСЛИ р =
Cpq — ZitpKdKq — (	=a,)q,	если p=£i.
Утверждение, касающееся столбцов, доказывается анало¬
гично.
Таким образом, применение элементарных преобразо¬
ваний к строкам матрицы равносильно ее умножению сле¬
ва на элементарные матрицы.
Теорема 12. Ранг произведения не превосходит
рангов сомножителей.
Доказательство. Допустим, что матрица А
имеет размеры т X п, а В — размеры п X р. Докажем
сначала, что (ранг АВ) (ранг Л). Это очевидно, если
(ранг Л) = т, ибо матрица АВ имеет размеры т X р.
Если же (ранг Л) = г < т, то приведем матрицу Л
к ступенчатому виду S, используя элементарные преобра¬
зования строк. Ввиду теорем 8, 10 и 11 можем записать
5 = 1\ . , . UkA,
где Ux, . . Uj( — элементарные матрицы. Но тогда
SB = иг . . . и^АВ.
и теоремы 10 и 11 позволяют заключить, что от матрицы
АВ к матрице SB можно перейти, осуществляя элемен¬
тарные преобразования строк. В силу теоремы 3
ранг SB = ращ" АВЛ
40

Далее, из теорем 1 1ГЗ вытекает, что все строки матрицы 5,
начиная с (г + 1 )-й, нулевые. Простой подсчет показывает,
что то же самое верно и для строк матрицы SB, Следова¬
тельно,
ранг АВ = ранг SB г ранг А.
Теперь, учитывая теоремы 2 и 7, а также доказанное
неравенство, получаем
ранг АВ = ранг (АВ)* = ранг В* А* << ранг В* =
= ранг В,
Теорема 13. Если А — квадратная матрица по¬
рядка пи | Л | =^= О, то существует одна и только одна
матрица В такая, что АВ = В А = Е.
Д оказате ль ст в о. Как известно, производя
элементарные преобразования над строками, можно от
матрицы А перейти к некоторой диагональной матрице D
(см. рассуждения, использованные при доказательстве
свойства 4 на с. 19). Ввиду теорем 10 и 11
D = t/j . . . UkA,
где Uri . . ., Uк — элементарные матрицы. С другой
стороны, согласно теореме 3, имеем
ранг Z)=pa нг А—п,
т. е. j D | =/= 0. Следовательно,
dl
0 .
. . 0
0
d2 . ,
,. о
0
0 . .
•• dn
- где все dt отличны от 0. Положим
0
0
0
d.;1	..
,. о
0
0 .
• •
и В = UUX . . . U1(. Учитывая теорему 8, получим
BA = UU1 . , , ЩА - UD = Е.
Но |Л* | #= 0. В силу доказанного
СА* = Е
Для некоторой матрицы С. Ввиду теоремы 7
ЛС* - (СА*)* - Е* = Е.
41

Отсюда
т. е.
В = BE = ВАС* = ЕС* = С*,
АВ =-- Е = ВА.
Если АХ = Е = ХА для какой-нибудь матрицы X, то
X = ХЕ = ХАВ = ЕВ = В,
чем доказывается единственность матрицы В.
Матрица В, рассмотренная в теореме 13, называется
обратной *) для матрицы А и обозначается через А"1.
Заметим, что в качестве А'1 можно взять матрицу
Ли
A:i
Ml
Ml
• • Ml
/112
Л22
Ai2
Ml
Ml ••
• "Ml
А,П
Ain
Ann
Ml
Ml •
•• Ml
где через Ац обозначено алгебраическое дополнение эле¬
мента ац в матрице А. Действительно, если С = АВ
и D = В А, то, учитывая теоремы 3, 5 и 6 из § 2, получаем
aikb];j —
п
ТлТ X а^-А.л- =
4=1
если
если
i	=	Л
i-	Ф	Л
п
4=1
п
1
I • 11
если
если
? == h
' # Л
Таким образом, С — D = Е, т. е. В = Л"1. ЭтихМ еще раз
доказано существование обратной для всякой матрицы
с ненулевым определителем.
Рассуждения, приведенные при доказательстве теоремы 13,
можно использовать и для получения еще одного способа вычислена з
обратной матрицы, Действительно, мы имеем равенство
UL\ , . , UkA = Е,
*) Матрицу, определитель которой отличен от нуля (равен hj-
лю), обычно называют невырожденной (вырожденной). Поэтому тео¬
рему 13 можно сформулировать так: каждая невырожденная матри¬
ца имеет обратную, и притом только одну. Устанавливаемому ни¬
же следствию теоремы 14 можно придать такую форму: вырожден¬
ная матрица не имеет обратной^
42

умножая его справа на А \ получим
UUt . . . UhE = Л~Ч
Это равенство показывает, что для вычисления матрицы Л-1 доста¬
точно применить к матрице Е те же элементарные преобразования,
которые применялись к матрице Л при превращении ее в единичную.
Поэтому, преобразуя матрицу (Л | Е) размера п X 2п так, чтобы
матрица Л превратилась в единичную, придем к матрице (£ | Л~]).
Теорема 14. Если А и В — квадратные матрицы,
то \ АВ \= \ А \ \В
Доказательство. Допустим сначала, что |Л | =
= 0. Ввиду теоремы 12 (ранг АВ) < (ранг Л) < (порядок
Д) = (порядок А В). Следовательно, | АВ | = 0 = |Л| |7?j,
что и требовалось. Теперь можно считать, что | А |	0.
Допутим2 что А диагональна, т. е.
с?!
0 .
.. о
0
d2 .
.. о
0
0 .
.Учитывая теорему 9 и свойство III определителя, получаем
|ЛВ| =
= di. . . dn\В \ = \ А\\В\.
П1
пп
Переходя к общему случаю, вспомним (см. с. 19), что
элементарными преобразованиями строк матрицу А
с ненулевым определителем можно привести к диагональ¬
ному виду D. При этом | А | = (—l)?f \D\, где к —
число осуществленных при этом приведении перемен
местами строк. В силу теорем 8, 10 и 11 имеем D *= 1/А,
где U — произведение элементарных матриц. Если
к матрице АВ применить те же самые элементарные цре-
образования, то получим матрицу U (АВ), прцчем
I U (АВ) | = (—l)fe | АВ |. Учитывая, что в случае ди¬
агональной матрицы А теорема верна, имеем
| АВ | = (-1 )к | U (ЛВ)| = (—1)* | DB | =
= (-1)* | D | | В | = | А | | В |г
что и требовалось.
Следствие. Если | А | = 02 то матрица А не
имеет обратной,
43

Действительно, если | А \ ■■= 0 и АВ = Е, то
О - \А \\В \АВ\ = \Е\ = 1,
что невозможно.
Умножение матриц можно использовать для полу^
чения правила Крамера, позволяющего решать системы
линейных уравнений. Нетрудно понять, что всякая система
линейных уравнений может быть записана в форме, исполь¬
зующей произведение матриц:
(*)
Ь,
?
а
Т1
61
И
— столбцы,
Ьп
со¬
где А — матрица системы,
стоящие из неизвестных и свободных членов соответст¬
венно. Допустим, что А — квадратная матрица, причем
| А | #= 0* Тогда рассмотрим столбец
Если этим столбцом заменить столбец неизвестных, то
уравнения системы (*) обращаются в тождества. Сле¬
довательно, столбец С является решением системы
Если столбец D также является решением, то имеем
&1
АС =
Ьп
= AD. Умножая слева на А \
получаем
С = D, чем доказана единственность решения. Наконец,
обозначая через элементы матрицы Л”1, получим
формулы для вычисления значений неизвестных:
А-=1
1Л!
«и • •
. . bi . .
• • ащ
anl • •
• Ьп	•
* ’ апп
п
МТ
где	располагаются в f-м столбце. Это и есть
правило Крамера,
44

Как и для строк, для двух матриц А и В одинакового
размера можно определить их сумму С = А + В как
матрниу того же размера, где си = аи Ъи, Можно
определить и произведение кА матрицы А на действи¬
тельное число X как матрицу того же размера, элемен¬
тами которой служат числа ка^. Так же, как для строк,
легко проверяются следующие свойства:
А + В =- В + А,	А (Л -1- В) = кА + кВ,
(Л + В) -г С = А + (В + С), (А + р) Л — кА 4- рЛ,
А + о = 0 + Л - Л,	(Ар) Л - к (рЛ),
уравнение Л + X О	1Л - Л
разрешимо,
(здесь Л, В, С — матрицы, а к и р — числа). Замеча¬
ния по поводу смысла используемых знаков, высказанные
в примечании **) на с. 7, сохраняют свою силу и здесь.
Умножение и сложение связаны дистрибутивными законами:
Л (В + С) = АВ + АС и (Л + В) С - АС + ВС,
причем из существования одной из частей этих равенств
следует существование другой. Допустим, например, что
существует Л (В + С). Тогда матрицы Л, В и С должны
иметь размеры т X п, п X р и п X р соответственно. Но
тогда произведения АВ и АС существуют и имеют разме¬
ры т X р, а значит^ существует и их сумма. Элементами,
стоящими на месте (i, у) в левой и правой частях этого
равенства, служат суммы
2	+ c>j)
/f
И
2 aikblfj + 2 aikckj^
к	k
совпадающие ввиду свойств операций над действительны¬
ми числами.
Без труда проверяются и равенства
к (АВ) - (кА) В = А (кВ).
У и р а ж н е и и я
1. Доказать, что ранг матрицы не меняется при элементарных
преобразованиях столбцов первого и второго типа. Изменяется ли
ранг матрицы при элементарных преобразованиях третьего типа?
2- Доказать, что, применяя элементарные преобразования строк
и-столбцов всех трех типов, любую матрицу ранга г можно превра¬
тить в такую матрицу D, что dn = . , . — drr = .1, а на всех
остальных местах стоят нули.
45

3. Если
(строк), то
А и В — матрицы с одинаковым числом
столбцов
< ранг А 4- ранг В
(ранг || А В ||) < ранг А + ранг В,
4.	Если А и В — матрицы порядка п, то АВ — ВА Ф /?
Указание: вычислить суммы диагональных элементов матрщ
АВ и В А.
5.	Если | А |, | В | =/= 0, то (АВУ1 =
6.	Если | А | =/= 0, то (А*)”1 = (А х)*.
7.	Если А и В — ненулевые матрицы порядка п и АВ — О
то | х | = | в | = 0 (здесь утверждается больше, чем «| А | - (
или | В | = О»!).
8.	Если | А | = 0, то определитель матрицы, составление;]
из алгебраических дополнений элементов матрицы А, также pauei
нулю.
9.	Если | А | ф 0, то ранг АВ — ранг В и ранг С А =
= ранг С всякий раз, когда эти произведения существуют.
10.	ранг (А + В) < ранг А + ранг В. Указа н и с: испод,
зовать упражнение 3.
И. Если А — матрица размера тх п и ранг/1 =//?, то су¬
ществует такая матрица В, что
1
о . . .
0
о . ,
. . о !
0
1 ...
0
0 . ,
.. И
0
о .. .
1
0 . ,
.. о
12.	Если А — матрица размера т X п н ранг А = т, то су
ществует такая матрица В, что АВ = Е.
13.	Если А — матрица размера т X п и ранг А = п, то су¬
ществует такая матрица В, что BA = Е,
14.	Любую матрицу А ранга г можно представить в виде суммь
г матриц ранга 1 и нельзя представить в виде суммы меньшего чист?
таких матриц, Указание: представить матрицу А в виде А =
— US, где S — ступенчатая матрица, затем матрицу S представки
как сумму г однострочных матриц в воспользоваться теореме!
о ранге произведения,
1о. Решить систему линейных уравнений:
+ ^2 = О,
Х-2 + &Л = О,
*П-1 +	~ О»

ГЛАВА II
ЭЛЕМЕНТЫ ОБЩЕЙ АЛГЕБРЫ
Под общей алгеброй понимается часть алгебры, зани¬
мающаяся изучением алгебраических систем, т. е*
множеств, на которых заданы те или иные операции и от¬
ношения. В настоящей главе излагаются определения и
простейшие свойства таких алгебраических систем, как
полугруппы и группы, кольца и модули, структуры
(решетки) и булевы алгебры.
§ 1. Отображения и операции
Скажем, что задано отображение ср из множества А
в множество В, если каждому элементу из множества А
поставлен в соответствие некоторый вполне определенный
элемент из множества В. Подчеркнем, что данное выска¬
зывание не является определением. Понятие отображения
является неопределяемым. Для обозначения отображения
Ф из А в В употребляются символы ср: А -> В и А —> В.
Если а ЕЕ А, то поставленный ему в соответствие элемент
из В будем обозначать через ср (а) и называть его образом
элемента а при отображении ср. Если Ъ ЕЕ В, то всякий
элемент а из А, для которого справедливо равенство
Ь = <р (а), называется прообразом элемента Ь. Множество
А называется началом отображения ср, а множество В —
его концом. Разумеется, каждый элемент из начала отоб¬
ражения ср имеет в точности один образ. Однако не у каж¬
дого элемента из конца этого отображения должен быть
прообраз. С другой стороны, конец отображения может
содержать элементы, имеющие несколько прообразов. На¬
пример, если А — множество действительных чисел и ср:
А А, где ф (х) = х2, то 1 и — 1 служат прообразами
элемента 1, а —1 прообразов не имеет. Подмножество
конца отображения ф, состоящее из всех его элементов,,
имеющих прообраз (или, другими словами, таких элемен¬
тов Ь, что b ~ ф (а) для некоторого а ЕЕ А), называется
образом отображения ф и обозначается 1ш ф. Отображе-
47

пие ср считается равным отображению ф, если начала и
концы этих отображений совпадают и для каждого элемеж
та х, принадлежащего их общему началу, справедливо рж
земство ср (х) = гр (х). Подчеркнем, что с точки зрении
итого определения отображения ф: А -> /1 и ф: /1 А,
/де А — множество всех действительных чисел, В —
множество положительных действительных чисел и
Ф (.г) == гр (х) = 2х для всех х ЕЕ А, различны.
Отображение ф: А -+В называется • вложением, если
каждый элемент из В имеет не более одного прообраза,
г. е. ф (а') = ф (а") влечет за собой а' = а". Если
каждый элемент из В имеет хотя бы один прообраз (или,
другими словами, если Im ф = Z?), то отображение ф
называется наложением. Имея наложение ф: А -> В,
часто говорят, что ф — отображение А на В. Отображение,
являющееся одновременно вложением и наложением,
называется взаимно однозначным *). ПримерохМ взаимно
однозначного отображения служат подстановки, являю¬
щиеся отображениями множества {1, 2, . . ., п} на себя
и рассматривавшиеся в конце § 2 гл. I. Важным примером
взаимно однозначного отображения является тождествен¬
ное отображение множества А на себя, определяемое ус¬
ловием: ф (х) = х для всех х ЕЕ А. Это отображение будем
обозначать через 1А. Одним из таких отображений являет¬
ся тождественная подстановка
1	2	... п
1	2	. . . п
,Если конец отображения ф совпадает с началом отоб¬
ражения гр, то можно определить произведение фгр **).
Именно, если ф: А В, a гр: В -> С, то фгр, по определе¬
нию, отображает А в С, причем фф (х) = тр(ф (х)) для
каждого хЕЕА. Предложенное определение выглядит
более естественным, если образ элемента х при отображе¬
нии ф записывать не как ф (я), а как а?ф. Тогда имеем
г (<ргр) = (адр) гр, Эта запись выглядит как ассоциативный
закон, но это чисто внешнее сходство. В дальнейшем,
юли мы не имеем дела с умножением отображений, часто
будем использовать и запись ф (х). Если ф: А -> В, то
*) Вложение часто называют инъективным отображением-,
наложение — сюръективным, а взаимно однозначное отображение —
биективным.
**) Заметим, что многие авторы говорят в этом случае о произ¬
ведении фф. Если стать на эту точку зрения, то формулировка не¬
которых результатов изменяется.
-8

легко проверяется справедливость равенств 1Лср = ср ~
(plАссоциативность произведения отображений фор-
мVлируется следующим образом.
Теорема 1. Если ср, ф и % — отображения, то
(срф) X = СР (Фх) (написанное равенство означает, в част¬
ности, что его левая и правая части существуют одновре¬
менно).
Д о к а з а т е л ь с т в о. Пусть левая часть сущест¬
вует и <р:	-> В. Ввиду существования произведения (рф
имеем ф: В -> С. Из определения произведения вытекает,
что (рф: А -> С. Существование левой части дает
Q	D, после чего последовательно получаем (<рф) х:
Д	D, фх« В -> D и ср (ф%): А D. Таким образом, из
существования левой части вытекает существование пра¬
вой, причем начала и концы отображений, стоящих в этих
частях, совпадают. К аналогичным выводам можно прий¬
ти, предполагая существование правой части. Если теперь
а. Е-2 А, то, используя определение произведения, получаем
цепочку равенств
а ((фф) X) = (« (фФ)) X = ((йф) Ф) X = («ф) (Фх) =
= а (ф (Фх))-
Ввиду произвольности а это доказывает теорему.
Повторяя почти дословно доказательство теоремы
1.3.8 *), можно установить следующий факт.
Т е о р е м а 2. Если произведение отображений (ри
(р2, • • <рп существует при некоторой расстановке ско¬
бок, то оно существует и при любой другой расстановке
скобок, причем результат не зависит от выбора этой
расстановки.
Этот результат позволяет использовать запись ср^. . .
. . ,срп не расставляя скобок.
Замечание. Если (р и ф — отображения множества А
в себя, то существуют как фф, так и фср. Однако, вообще говоря, эти
произведения не совпадают. Например, если
то
2 3\
1 2/ 1
2	3\
3	О
Следующие две теоремы позволяют охарактеризовать
вложение и наложение, используя свойства некоторых
произведений.
*) Это означает, что имеется в виду теорема 8 из § 3 гл. I.
49

Теорем а 3. Отображение ср является вложением
тогда и только тогда, когда из каждого равенства вида
л|хр = yjp, где ф и % —- некоторые отображения, вытекает,
что ф =
Доказательство. Пусть ф: А -> В — вло¬
жение и фф = хф. Тогда как ф, так и х отображают неко¬
торое множество С в А. Если с ЕЕ С, то имеем (сф) ф =
= с Сфф) = с (хф) ~ (с%) ф. Поскольку ф — вложение, от¬
сюда вытекает, что еф = с%. Ввиду произвольности с
это означает, что ф —х« Допустим теперь, что для отобра¬
жения ф справедлива указанная в формулировке имплика¬
ция, но ф не является вложением. Тогда найдутся а',
а" ЕЕ А такие, что а' а", но а'ф = а" ср. Рассмотрим ото¬
бражения ф и х множества А в себя, определяемые усло¬
виями аф = а' и а% = а" для всех а ЕЕ А. Тогда для
всех а ЕЕ А имеем
а (фф) = (аф) ф = a'q> = а" ср = (а%) (р = а (хф)«
Следовательно, фф = ХФ, откуда, в силу условия, выте¬
кает гр = х,? что невозможно.
Теорема 4. Отображение ф является наложе¬
нием тогда и только тогда, когда из каждого равенства
вида фф = фх, где уЬ их — некоторые отображения, выте¬
кает, что ф =
Доказательство. Пусть ф: А В — наложе¬
ние и фф = фх- Тогда как ф, как и х отображают В в не¬
которое множество С. Если b ЕЕ В, то, поскольку гр —
наложение, имеем Ъ = аф для некоторого а Е Л, Отсюда
= (a<p) i|> = а (фхр) = а (фх) = (Яф)х = Ь%,
что ввиду произвольности элемента Ъ влечет ф = х- До¬
пустим теперь, что для ф справедлива указанная в фор¬
мулировке импликация, но ф не является наложением.
Тогда найдется элемент b ЕЕ В такой, что аср у= b для
всех а ЕЕ А. Зафиксируем в В элемент b0 =/= Ъ и рассмо¬
трим отображение ф: В -> В, определяемое условием:
если х^АЪ,
если х = Ь.
Ясно, что ф 1в, что в силу условия влечет фф ф1д
Однако для всех а ЕЕ А имеем
а (фф) = W) ф = аф = (аф) 1в = а (ф!в).
Противоречие,
БО

Непосредственным подсчетом или с использованием
теорем 3 и 4 может быть доказана
Теорема 5. Если ф и ф — вложения, наложения
или взаимно однозначные отображения, то то же самое
справедливо и для произведения фф.
Если ф: А В — взаимно однозначное отображение,
то можно определить отображение ф”1: ВА, приняв
за г/ф 1 Для каждого у GE В прообраз элемента у при
отображении ф. Это определение имеет смысл, ибо каждый
элемент из В имеет прообраз и притом только один. Обоз¬
начение объясняется следующей теоремой *).
Теорема 6. Если ф ~ взаимно однозначное ото¬
бражение множества А на множество В, то фф-1 = 1А
и ф'-’ф — 1в-
Доказательство. Ясно, что фф 1 отображает
А в себя, а ф_1ф отображает В в себя. Если х ЕЕ А и
= Уг то
я (фф'1) = 0 ф) Ф~] = #Ф-1 = z = х1А
и
У (ф'Хф) = G/ф'1) ф = Тф = у = ytp.
Ввиду произвольности элемента х из А, первое равен¬
ство влечет фф*1 = Соотношение ф'‘2ф — 1В вытекает
из второго равенства, если принять во внимание, что
каждый элемент у из В может быть записан как у —
= х’ф для некоторого х ЕЕ А,
Система S непустых подмножеств множества А назы¬
вается разбиением, если каждый элемент из А принад¬
лежит одному и только одному подмножеству системы.
Подмножества, входящие в разбиение, называются
смежными классами разбиения. Смежный класс разбие¬
ния 2, содержащий элемент а, условимся обозначать
через [а]у или — если ясно, о каком разбиении идет
речь,— через [а]. Множество смежных классов разбиения
S множества А называется фактормножеством множест¬
ва А по разбиению S и обозначается через A/S.
Пример ы. 1. А — множество зерен, насыпанных в мошки,
2 — система подмножеств, каждое из которых ость множество
всех зерен, насыпанных в данный мешок, Л/5— мн о же с та о мешков.
2.	А — множество все?. целых чисел, Ло и Aj — множества
всех четных и нечетных чисел соответственно, S состоит из 40
и A,, A/'S — двухэлементное множество, элементами которого
*) По той же причине отображение ф”х называет обратным
отображению ф.
51

служат Л0 и Лг При этом, например, [0] - - [2] = [300] = [—4] =
= Ло, а [II - [-1] - 12051 - А}.
3.	Пусть А — множество всех действительных чисел. Положим
Л() = {0}, а для каждого положительного а образуем двухэлемент¬
ное множество Аа = {а, —а}. Ясно, что система 2, состоящая из
Ло и всех Аа, является разбиением. Фактормножество Л/S можно
отождествить с множеством неотрицательных действительных чисел,
отображая смежный класс Аа на число а.
Отображение я, при котором каждому элементу из
А ставится в соответствие смежный класс, в котором
этот элемент лежит, называется естественным. Ясно,
что естественное отображение является наложением.
В рассмотренных выше примерах имеем: 1) л (j,j — мешок,
в котором лежит зерно х\ 2) л (х} = Л(), если х четное, и л (.,■) =
= лп если х нечетное; 3) л (.г) — двухэлементное множество {.г,
—а?}, если х 0, и л (0) — множество, состоящее из одного нуля.
Пусть теперь ср: А -> В — наложение. Обозначим
через Аь, где b В, множество всех прообразов элемен¬
та Ь. Нетрудно проверить, что система подмножеств
| b ЕЕ В} является разбиением множества А. Это раз¬
биение называется ядром отображения (р и обозначается
через Кег ср.
Теорема 7 («теорема о гомоморфизме» для мно¬
жеств). Если ср: А-+В — наложение и л: Л->Л/Кег ip-
естественное отображение, то существует взаимно одно¬
значное отображение В А/Кег ср такое, что срх —
= л (см. рис, 3).
Доказательство. Если аеЛ, то ап обозна¬
чает смежный класс разбиения Кег ср, которому этот эле¬
мент а принадлежит. Если Ь ЕЕ В, то, поскольку ср —
наложение, Ь = а(р для некоторого а ЕЕ А. Положим
6% = ап. Предложенное определение отображения х
корректно, т. е. не зависит от случайного выбора элемен¬
та а. В самом деле, если Ъ = а'ср, то ап = а'п в силу опре¬
деления разбиения Кег ср. Таким образом^ х оказывается
52

Справедливы ли
законы
05 л
05
Е-	Н
05 ф 05 ф
н
ф
05 05
н
ф
£
н
ф
Е->
Ф
Г; Н
гсгс
ГС
г<:г -(X
X
Г[Г[
ж
ж
К
§ и
о? 3
ГСМ
□3 05
Oj
6-
Л D Л Л
05
Л ф
05
Л
05
Н
Ф
а®
с и
О£
а>.О'
я
3 о о
5 - *
СЦ ZU ф
К ^£2
£
И
6 о
& а
55 С
со
5-' -и
*
1
1
ос °?
□ н
53

отображением из В в Л/Кег ср. Если а ЕЕ Л , то
« (ФХ) = («Ф) X = ал,
т. е. <рх = л. Если В'х = то, выбрав а', а" ЕЕ А так,
что Ь'= а'ср и Ъ” = а"ср, заметим, что ап <= а”п. В силу
определения разбиения Кег ср, отсюда вытекает, что
Ь' — а'ср — а" ср = Ъ".
Следовательно, х ~~ вложение. Наконец, произвольный
элемент из Л/Кег ср имеет вид ап, где а ЕЕ А: Поэтому
уже доказанное равенство ап = (аср) х показывает, что
X — наложение. Таким образом, х — взаимно однознач-
ное отображение, что и требовалось.
Если А — некоторое множество, то обозначим через
А X А множество всех пар вида (а, 6), где а, b ЕЕ А.
Операцией на множестве А называется всякое отобра¬
жение множества А X А в множество А. Образ пары
(а, Ь) называют произведением и обозначают через ab.
Иногда вместо «произведения» говорят «сумма» и пи
шут а + Ь. Используются и другие обозначения (напри¬
мер, а о Ь, а * Ъ и т. и.). Многочисленные примеры мно¬
жеств с разнообразными операциями собраны в таблицу 1.
Элемент е ЕЕ А называется единицей (относительно
данной операции), если ае = еа — а для всех а ЕЕ А.
Единица существует не всегда. Однако:
Теорема 8. Множество с заданной операцией со¬
держит не более одной единицы.
Доказательство. Пусть е и / — единицы. По¬
скольку е — единица, то ej — f. Но ef — е, поскольку
/ — единица. Таким образом,
/ = ef = e.
Если операцию называют сложением, то единицу обыч¬
но называют нулем и обозначают 0.
Если (ab) с = а (Ьс) для любых а, Ъ, с ЕЕ А, то опера¬
ция называется ассоциативной, а если ab — Ьа для
всех а, Ь ЕЕ А, то коммутативной.
Если множество А с заданной операцией содержит
единицу е, то элемент Ь ЕЕ А называется обратным эле¬
менту а А, если аЬ = Ьа = е.
Теорема 9. Если множество А с заданной ассо¬
циативной операцией содержит единицу е, то каждый
элемент из А имеет не более одного обратного.
Доказательство. Пусть Ъ и с — обратные эле¬
менту а, Тогда,; учитывая определения единицы и об-
М

ратного элемента, имеем
b — be — b (ас) = (Ьа) с — ес = с.
Замечав и е. Требование ассоциативности существенно.
Действительно, рассмотрим трехэлементное множество {с, а, 6}
с умножением, задаваемым таблицей
• 1
1е
а
b
с
е
а
b
а
а
е
е
b
b
е
е
и
Ъ являются обратными к а.
Здесь е — единица, а как а, так
У и р а ж нения
1. Рассмотрим следующие отображения ср: А В:
А
в
<р(х)
1
Целые числа
{0, 1}
0, если х четное, 1,
если х нечетное
2
Действительные
числа
Отрезок [0, 1]
Дробная часть чис¬
ла х
3
Действительные
числа
Целые числа
Целая часть числа х
4
Квадратные мат¬
рицы
Действительные
числа
Определитель м а т ри-
цы х
5
Целые числа
Р, 1}
0 для всех х
6
Целые числа
{0}
0 для всех х
7
Матрицы размера
тХп
Действительные
числа
Сумма всех элемен¬
тов матрицы х
8
Матрицы размера
мХм
п-мерные строки
Первая строка мат¬
рицы X
< Какие из этих отображений являются наложениями (вложения¬
ми)? Найти ядра этих отображений. Рассмотреть фактормножество
по ядру и указать отображение /, упоминаемое в формулировке
теоремы 7.
2.	Если фф — вложение, то ф — вложение.
3.	Если фф- — наложение, то ф — наложение.
4.	Пусть V — множество всех n-мерных строк, А — квадратная
матрица порядка п и ф — отображение множества V в себя, задавае¬
мое равенством
ф (.?!, . . хп) = (zj, . . ., zn) 4.
Доказать эквивалентность следующих утверждений: а) | А | =/= 0;
о) ф ■— вложение; в) ф — наложение; г) ф — взаимно однозначное
отображение.
55

5. Рассмотрим следующие операции на множестве Л:
Множество
Операция ху
1
Положительные целые числа
ху
2
Матрицы порядка п
ху — ух
3
Неотрицательные целые числа
И. 0. д. (х, у)
4
Неотрицательные целые числа
н. о. к. (х. у)
5
Неотрицательные целые числа
min (т, у)
6
Произвольное множество
X
В примерах 3 и 4 считается, что 0 делится на 0. Какие из этих
операций ассоциативны пли коммутативны? В каких случаях су¬
ществуют единица и обратные элементы?
§ 2. Полугруппы
Непустое множество А с заданной на нем ассоциатив¬
ной операцией называется полугруппой. Все множества
с операциями, приведенные в таблице 1, кроме 5, 10 и 14,
оказываются полугруппами.
Рассуждения, применявшиеся для доказательства
теоремы 1.3.8 и теоремы 2 из § 1 позволяют доказать
следующее:
Теорема 1. 11 роизведение нескольких элементов
полугруппы не зависит от расстановки скобок.
Этот результат позволяет использовать запись
ara2. . .аи, не расставляя скобок. Заметим, что, в отли¬
чие от произведения матриц и отображений, это произ¬
ведение существует всегда. Поэтому вышеупомянутые
теоремы 1.3.8 и 2 из §1 не являются следствиями теоремы I.
Если операция полугруппы А не только ассоциативна,
но и коммутативна, то полугруппа А называется ком¬
мутативной (или абелевой'). Полугруппы 1, 2, 3, 4, 6, 9
из таблицы 1 коммутативны.
Теорема 2. Если а}, . . ., ап — такие элементы
полугруппы, что a^Uj — a/ti для любых i и ], то
#]#2 . . . <1п *= #О(])#О(2) • • • й0(п),
где о — произвольная подстановка на множеств
{1, 2, . .	п).
Доказательство. При п = 2 утверждение тео¬
ремы справедливо по условию. Допустим, что теорем а
верна для п — 1 сомножителей. Если о (п) = п, то, учи¬
тывая теорему 1 и индуктивное предположение, имеем
#0(1) • ♦ • #О(Ц-1)#н “ (^0(1) • * • ^O(n-l)) #ц = #1 * . .
50

Если n = о (к), где к < п, то
«0(1) ’ • • flo(A-i)«zt«o(/fH) • * • Go(n) =
—	(«о(1) • • • «о(/г-1)) («п(«а(Ач-1) • • • «о(п))) --
—	(ttG(l) * ’ * «О(А-1)) ((«0(A+1) • • • «0(h)) a") ~
= «o(D . . . «o(fr-i)«o(/f+i) • • • «u(/<)6ZH ~ tli • • • «/).
D силу доказанного выше,
Следствие. Для любых элементов aL, а2, . . ., ап
коммутативной полугруппы и любой подстановки о на
множестве {1, 2, , . ., п} справедливо равенство
<ца2 * • • ап = «о(1)^о(2) • • • «сон*
Таким образом, в коммутативной полугруппе, вы¬
числяя произведение нескольких сомножителей, можно не
только ставить скобки произвольным образом, по и распо¬
лагать сомножители в любом порядке.
Непустое подмножество Н полугруппы называется
подполугруппой, если произведение любых двух эле¬
ментов из Н снова лежит в Н. Это, в частности, означает,
что всякая подполугруппа является полугруппой отно¬
сительно операции, определенной в исходной полугруппе.
Например, четные числа образуют подполугруппы полу¬
групп 1, 2 и 4 из таблицы 1, а множество { — 1, 0, 1} —
подполугруппу полугруппы 2 из той же таблицы. Но для
полугруппы 1 это подмножество подполугруппой не яв¬
ляется.
Теорема 3. Непустое пересечение любого множества
подполугрупп является подполугруппой.
Доказательство. Пусть U — пересечение не¬
которого множества подполугрупп. Если х, у ЕЕ U, то х
и у лежат в каждой из подполугрупп рассматриваемого
множества. Но тогда в каждой из них лежит и произведе¬
ние ху, а значит, ху ЕЕ U.
Замечание. Требование непустоты пересечения в теореме 3
существенно. Действительно, в примере 4 из таблицы 1 как положи¬
тельные, так и отрицательные числа образуют подполугруппы, и пе¬
ресечение этих подполугрупп пусто.
Отображение ср полугруппы А в полугруппу В на¬
зывается гомоморфизмом, если ср (ху) (р (х) ср (у) для
любых хцеА. Подчеркнем, что здесь ху обозначает
операцию в полугруппе Л, а ср (х) ср (у) — операцию в по¬
лугруппе В. Гомоморфизм, являющийся вложением (на¬
ложением), называется гомоморфным вложением (гомомор¬
фным наложением), а взаимно однозвднньш гомоморфизм —
57

Гомоморфизмы ср:
Ml, У 2, . . ., Ум)
н>7
1 04
"Г •
ф
>ч —
н сч
£
е-Н
о
Н
9- В
©•
9*
9
58

*) Если х,	то возможны четыре случая: -а) х и у четные; б) х и у нечетные; в) х четное. а у нечетное; г) х нечетное,
а у четное. В случае а) имеем ф(я4-у)-—1-—1’1=ф(х)ф(у), а в случае б) ф(я-Н/)=1=(—1)(—1)—Ф(а)(р(у). В случае в) получаем
Ф(х+у)= —1=1 •(—1)=Ф(х)ф(г/). Случай г) рассматривается аналогично.
**) fl» если
sgn х= 4	0, если х—О,
59

изоморфизмом. Если существует изоморфизм полу,
группы А па полугруппу В, то эти полугруппу
называются изоморфными *). Примеры гомоморфизмов
приведены в таблице 2.
Теорема 4. Если ср: А -> В — гомоморфное на.
ложение полугрупп и е — единица в А,' то (р (<?)• — еда^
ница в В.
Д о к а з а т е л ь с т в о. Если b ЕЕ В, то, поскольку
ф — наложение, имеем b =. q? (а) для некоторого а ЕЕ А,
Отсюда
Ь<р (е) = ф (а) ф (е) = ф (ас) = q> (а) = Ь,
поскольку ф — гомоморфизм. Аналогично проверяется, что
ф (е) Ъ = Ь для всех Ъ ЕЕ В.
В силу теоремы 9 из § 1, каждый элемент а из данной
полугруппы имеет не более одного обратного. Если такой
обратный существует, то условимся обозначать его через а~[.
Т е о р е м а 5. Если ф: А —> В — гомоморфное на¬
ложение полугрупп, аЕА и а~г существует, то ф (а'1)
= (<Р (я))”1-
Доказательство. Ввиду теоремы 4, ф (е) —
единица полугруппы В, если е — единица полугруппы А.
Остается вспомнить определение обратного элемента и
заметить, что
Ф (а~1) ф (а) = ф (а~1а) = ф (е) = ф («а'1) = ср (а) ср (г/-1).
*) Говоря «полугруппы А и В изоморфны», мы, на первый
взгляд, вступаем в противоречие с. определением изоморфизм»,
в котором полугруппы А и В не равноправны. Однако если ф: А -
~В — изоморфизм, то существует обратное взаимно однозначнее
отображение ф-1: В А. При этом, каковы бы ни были Ъ', Ь" с=-.
е В, для некоторых а', a" е А имеем Ь' = Еср и b" = a"q>. Следз-
т ательно,
(b'b”) ф”1 = (а'ф>я"ф) ф-1 = ((а'а"} ф) ф“1 = а'а" = 6'ф-1. Ь"ф-1,
т. е. ф-1 оказывается гомоморфизмом, а значит, и изоморфизмом. Та¬
ким образом, на самом деле полугруппы А и В равноправны. Далее,
если ф: А —> В и ф: В С — гомоморфизмы полугрупп, то дли
любых а , а" е А имеем
(а'а") (фф) = ((а'а") ф) ф = ((а'ф) (а"ф)) ф = (а'ф) ф-(«"ф) ф =
= а> (фф) -л" (ффГ
Следовательно, фф — гомоморфизм полугруппы А в полугруппу
С. В силу теоремы 5 из § 1, отсюда вытекает, что произведение изо¬
морфизмов — изоморфизм. Это, в частности, означает, что если но-
лугруппа А изоморфна полугруппе В, а полугруппа В — полугруи-
п С, то полугруппы А и С изоморфны.
60

Замечание. Для справедливости теорем 4 и 5 существен-
0 что <р — наложение. Действительно, для гомоморфизма 9 из
"аблииы 2 имеем
Ф (1) -
jfc).neo того, матрицы, обратной к <р (1), не существует.
Теорем а 6. Если <р: А -> В — гомоморфизм полу-
,руппп, то Im ср — подполугруппа полугруппы В,
'Доказательство. Если у, у' ее Im ф, то у --
ф (х) и у' = ф (х') для некоторых х, х' ЕЕ Л. Но тогда
<р и') = ф (О ф (X) = УУ', т. е. уу' (= Im <р.
Разбиение S полугруппы А называется допустимым.Г1
если из того, что х и и принадлежат какому-то одному
смежному классу разбиения S, а у и v также принадлежат
одному смежному классу этого разбиения, вытекает, что
ху и uv лежат в одном смежном классе.
Примеры. 1. Пусть А — полугруппа целых чисел отно¬
сительно сложения и S — ее разбиение, состоящее из двух классов,
один из которых содержит все четные числа, а второй — все нечет¬
ные. Для J?, у, и и е, упоминаемых в определении, возможны сле¬
дующие четыре случая:
Л’ и и
У И V
х у
и -1г у
1
четные
четные
четное
четное
2
четные
нечетные
нечетное
нечетное
.3
нечетные
четные
нечетное
нечетное
4
нечетные
нечетные
четное
четное
Как видно, во всех случаях х Д- у и и -| е попадают в один и
тог же смежный класс, т. е. разбиение S допустимое.
2.	Пусть А — полугруппа целых чисел относительно умноже¬
ния и S — ее разбиение,состоящее из трех классов: все положитель¬
ные числа, нуль и все отрицательные числа. Допустимость разбие¬
ния видна из таблицы, приведенной па следующей странице.
3.	Если А — полугруппа целых чисел относительно сложения,
то разбиение, рассмотренное в предыдущем примере, допустимым
не является. Действительно, 5 и 3 лежит в одном классе этого раз¬
биения. То же самое верно для —4 и — 3. Однако 5	(—4)
= 1 и 3 ф (—3) = 0 принадлежат различным классам этого раз¬
биения.
Если S — допустимое разбиение, то па фактормно¬
жестве A/S можно определить операцию, полагая
[х] [*/] = [хг/],
61

X и и
у и V
ху
UV
1
>0
>0
>0
>0
2
>0
=0
=0
=0
3
>0
<0
<0
<0
4
=0
>0
=0
=0
5
=0
=0
=0
=0
6
=0
<0
=0
==0
7
<0
>0
<0
<0
8
<0
=0
=0
=0
9
<0
<0
>0
>0
где через [id обозначен смежный класс разбиения 2,
содержащий элемент х. Это определение корректно.
Действительно, из равенств Ld — [и] и [г/] = [г;] выте¬
кает, что как х и н, так и у и v располагаются в одних
и тех же классах разбиения S. Ввиду его допустимости,
ху и ии также лежат в одном смежнохм классе^ что дает
[.ry] = [uv]t
Из равенств
([ж! [?/]) [z] = Ixy] [z] == [(.rz/) z] — [.г (z/z)] =
= id [yz] == Ы ([г/] [г])
вытекает^ что операция, определенная на фактормно¬
жестве, ассоциативна. Следовательно, фактормножество
становится полугруппой, которая называется фактор-
полу группой полугруппы А по допустимому разбиению 2.
Если л: А А/S — естественное отображение^ то
л (ху) — 1ху} = [х] [#] = л (х) л (у).
Следовательно, л оказывается гомоморфизмом (даже гомо¬
морфным наложением) и потому называется
гомоморфизмом.
Для рассмотренных выше допустимых разбиений фактормноже¬
ства состоят из двух и трех элементов соответственно, Обозначив
элементы первого множества как чет и нечет, а второго как [1], [0]
и [—1], получим следующие таблицы умножения:
-
чет
нечепг
•
[1]
[0]
[-1]
чет
чет
нечет
[1]
[Ч
[0]
[-1]
нечет
нечет
чет
[0] '
[0]
[0]
[0]
(-1]
[-1]
[0]
[1]
62

Естественные гомоморфизмы определяются как
л (х) = {
чет, если х четное,
не чет, если х нечетное
D первом случае п как
[	[1], если х^>0,
л (ж) —
■!	[0], если х = 0,
1 [— •!]» если я<0,
во втором.
Теорема 7. Если <р: А В — гомоморфизм по-
лугрупп, то разбиение Кег ср (оно называется ядром го¬
моморфизма ср) допустимо.
Доказательство. Если х и и располагаются
в одном смежном классе этого разбиения и то же самое
справедливо для элементов у и и, то по определению раз¬
биения Кег ср имеем ср (х) = ср (и) и ср (у) = ср (о). Отсюда,
поскольку ср — гомоморфизм, вытекает, что
ф (ху) = ф (ж) <р (у) = ф («) ф (0 = ф (uv)
и, следовательно, ху и ии располагаются в одном классе
разбиения Кег ср.
Таким образом, таблица 2 доставляет нам ряд при¬
меров допустимых разбиений. Заметим еще, что всякое
допустимое разбиение совпадает с Кег л, где л — естест¬
венный гомоморфизм.
Теорема 8 (теорема о гомоморфизме для полугрупп).
Если ср: А -> В — гомоморфное наложение полугрупп и
л: А -> А/Кег ср — естественный гомоморфизм, то су¬
ществует изоморфизм %: 5 А/Кег ср такой, что ср% =
== л.
Доказательство. Рассмотрим взаимно одно¬
значное отображение %, существование которого доказано
в теореме 7 из § 1. Для доказательства теоремы достаточ¬
но установить, что % — гомоморфизм. Но если Ъ', Ь" ЕЕ
ЕЕ В, то для некоторых а , а!' ЕЕ А имеем Ъ' = ср (д') и
Ъ" = <р (д"). Вспоминая определение отображения % и
учитывая равенство ср (а'а") = ф (а') ф (а") = b'b", получим
X (Ь')Х (&") = п Ю л (а") л (а'а) = % (b'b"),
что и требовалось.
Если А — полугруппа и а ЕЕ А, то для всякого на¬
турального п положим
а11 = а ... а.
п раз
Если А содержит единицу то полагаем а0 = е.
63

Теорема 9. ат-ап = ат+п для всех т, п > 0.
Д о к а з а т е л ь ст в о. Ввиду теоремы 1
ат-ап = (а ... а) (а ... а) = а ... а — ат'1П.
т раз п раз т+п раз
Полугруппа А называется моногенной, если в ней
содержится такой элемент а, что всякий элемент х из
А может быть записан в форме х = ап для некоторого
п 0. Элемент а называется образующим (или порождаю¬
щим) моногенной полугруппы. Важнейшим примером мчь
посевной полугруппы является полугруппа Р положитель-
пых целых чисел относительно сложения. Ее образующим
служит 1. Зафиксируем положительные числа п и d и
рассмотрим разбиение S (я, d) множества Р, состоящее
из одноэлементных классов [1] = {1},	[2] = {2}, . . .
. . ., [d — 1] = {d — 1} и бесконечных классов
Ml = {d, б/ + /?, <7 + 2п, . . ., d + Aw, . . .
Id + 11 =--- {d + 1, d + 1 + n, d + 1 + 2n, . . .
. . ., d -|- 1 + kn, . . .
(б/ + (n — 1)1 = {d + (n — 1), d +	(n	—	1) + n,
d + (n — 1) + 2n, . . ., б/	-(-	(/?	— 1) 4~ kn,	.	. .}•
Убедимся, что это разбиение допустимо. В самохм деле,
пусть т, и p[il и у1 и С- I/], где 1	<	f,	] < d 4 п.	Воз¬
можны следующие четыре случая:	1)	г,	/ <; d\ 2) i	«<	е,
/ О б/; 3) i d, / <С б/; 4) f, / d. В первом случае имеем
X и — i и у = V = 7, откуда [х + ?/] = [и -4- г], по¬
скольку х 4- У ~ и 4- V. Во втором случае х = и = Z, у =
7 + кп и v = / 4- In для подходящих к и Z. Исполь¬
зуя деление с остатком, запишем
i 4- 7 — d — sn 4- r7)
где 0 < г < п. Тогда
х 4- У = i 4- 7 + кп = d 4- G + 7 — d) 4- кп =
= d 4- г 4- (s 4- к) п
и
и 4"	? 4" / 4" In == d 4* (Z 4" j — d) 4~ In =
= d 4- г 4- (5 4- I) nt
откуда [x 4- у] = M 4- г] = [и 4- v]. Третий случай рас¬
сматривается аналогично., В четвертом случаел используя
оДределение смежных классов, можно записать
х = i	+	кп	=	d	+	(i	—	d)	+	kn,
и = i	+	In	~	d	+	(i	—	d)	-|-	In,
У = j	+	Im	---=	d	-|-	(7	—	d)	+	pn
v = 7	+	qn	---=	d,	+	(j	—	d)	+	qn.
Тогда
x + У = d + (d + (i — d) + (7 — d) ) 4- (k + p) n
и + v — d + (d (Z — d) 4- (7 — d)) 4~ G + q) n„
Разделив с остатком, получим
d + (Z — d) 4- (7 — d) sn + г
где О с <C n. Отсюда
x 4- У — d T r I - (/c 4- p + 0 n
и
и 4- v ~ d -\- r + (/ 4- q s) n,}
т. e. [,r -r N = [d 4- r| -■ [n 4- H.
Факторполугрупну полугруппы P по рассмотренному
разбиению называют циклом с хвостом (см. рис. 4). При
Рис. 4
d^ 1 хвост оказывается пустым. Такую полугруппу на-
3Ывают циклом.
Теорема 10. Всякая моногениая полугруппа изо-
М()Рфна или аддитивной полугруппе Р положительных
4 и се л, или некоторому циклу с хвостом (возможно, пустым).
3 л.
А. Скорняков
65

Доказательство. Пусть А — моногеяпая по,
лугруппа с образующим а. Рассмотрим ото^рааюпие ио.
лугруппы Р в полугруппу 4, определяемое условие^
ср (т) — ат.
Ввиду моногенности полугруппы 4, ср оказывается па.
ложением. В силу теоремы 9
ср (пг + п) — ап+п — ат-ан—Ц) (т) ср (л),
т. е. ср является гомоморфизмом. Из теоремы 8 вытекает,
что А изоморфна факторполугруппе Р/^, где S — Кег ф.
Если все классы разбиения S одноэлементны,
то А изоморфна Р. В противном случае обозначим
через d наименьшее целое число, входящее в неодноэле-
ментный класс, а число п выберем так, чтобы d + п
было наименьшим числом, отличным от d, но входящим
в один класс с d. Тогда имеем классы [1], [2], . . ., [d — 1],
[cZ], [d + 11, . • {d + п — 1], среди которых первые
d — 1 одноэлементные и [rf] [d + Z] при t = 1, 2, . . .
. . ., п — 1. Докажем, что
[с? 4- i] = [d + i + кп\	(*)
при любых i и к, В силу определения разбиения S, для
этого достаточно установить, что
ср (cZ + i) = ср (d + i + kri).	(**)
При к = 0 это очевидно. Допустим, что (**) доказано
при всех i и к = 0, 1, . . ., t — 1. Тогда, вспоминая, что
ср (d) = ср (d + тг), получаем
ср (d -f- i -р	Z/2) = ср (d 4~ i + (Z	— 1) 72 4" 72) ==
—	cp (d	4~ i + (Z — 1) /г) ср (n) = ср (cl 4~ Z)	ф	(n)	—
—	cp (d	4- i + 72) = cp (d 4-	/г) cp (Z) = cp (d)	cp	(Z)	=
= cp (d + /),
Тем самым равенство (**), а значит и (*), доказано. Остает¬
ся убедиться, что разбиение S совпадает с разбиением
S (?2, d). С этой целью заметим, что одноэлементные клас¬
сы этих разбиений совпадают. Ввиду равенства (*), для
доказательства совпадения бесконечных классов доста¬
точно установить, что смежные классы [d + i] и [d 4- /]
разбиения S, где 0 i < / << 72, различны. Но если
Id 4- Z] = [d + /1, то
[d] = \d 4" 72] = \d 4- /1 + [72 — j] =
= [d 4- Z] + [/2 — j] — [d 4- (72 — (7 — Z))]
66

поскольку 0 < п — (/ — i)<Z п, мы вступаем в проти¬
воречие с выбором числа п.
Пусть S — полугруппа, а X — ее непустое подмноже¬
ство. Пересечение Т всех подполугрупп полугруппы 5,
содержащих X, называется подполугруппой, порожденной
пно^есгг1вом Существование полугруппы Т вытекает
п3 теоремы 3, поскольку подполугруппы, содержащие
множество X, существуют (например, сама полугруппа 5)
и пересечение их непусто (все они содержат X). Ясно, что
р — это наименьшая среди подполугрупп полугруппы 5,
содержащих множество X * *). Если эта наименьшая под¬
полугруппа совпадает с 5, то говорят, что полугруппа S
порождается множеством X. В частности, моногенная
полугруппа порождается своим образующим.
Полугруппа S = S (X) называется свободной полу¬
группой со свободно порождающим множеством X, если
(1)	S порождается множеством X;
(2)	для любого отображения (р: X -> А, где А —
произвольная полугруппа, существует гомоморфизм ф:
S (X) А такой, что <р (х) = ср (х) для любого х €= X.
Для доказательства существования свободных полу¬
групп возьмем произвольное непустое множество X,
которое будем называть алфавитом. Всякую конечную
последовательность хд . . . хт, где х^_ Е=Х, назовем словом
в алфавите X. Пусть W = W (X) — множество всех не¬
пустых слов в алфавите X. Определим произведение двух
слов и и v из W (X) как слово, равное написанным подряд
без пробела словам и и и. Эта операция ассоциативна и
превращает W в полугруппу.
Теорема 11 (теорема существования свободной
полугруппы). W — W (X) — свободная полугруппа, со сво¬
бодно порождающим множеством X.
Доказательство. Назовем длиной I (ш) слова
w количество входящих в него букв, причем каждая
буква считается столько раз, сколько раз она входит в сло¬
во w. Оба свойства (1) и (2) из определения свободной по¬
лугруппы проверим индукцией по I (to).
(1) Пусть Т — подполугруппа полугруппы Wr по¬
рожденная множеством X. Тогда любое слово w W
лежит в Т. Действительно, если I (w) = 1, то w Г—
S X CZ Т. Если I (w) > 1, то w = w'x, где I (и/) <Z
I (w) и х GE X. Следовательно, w', х GE Т по предполо-
*) Нетрудно доказать также, что подполугруппа Т совпадает
с множеством всех элементов полугруппы S, представимых в формо
*1 • • • где xi <= X.
3*
67

желто индукции. Так как Т — подполугруппа, a w
произведение двух ее элементов wr и х, то weT. Ноэтс^
IV Е Т. Обратное включение очевидно. Итак, Т т= !р
(2) Пусть ср — произвольное отображение множеств;
X в некоторую полугруппу А с операцией о. Определи
элемент ф (w) полугруппы А индукцией по I (w). Ес.д
I (w) = 1, то w Е X, и мы положим
ф (tr) = ф (w).	(*
Если / (и?) > 1, то ш = w'x, где Z (и/) <С I (п?), а х Е X
Тогда ip (и?') и ф (х) уже определены. Положим
ф (ш) = Ф (и/) о ф (х).	(т*
Покажем, что отображение ф: W —А является гомо
морфизмом, т. е. что ф (u\w2) = Ф (wi) ° Ф (^>) Для любы?
w2 СЕ W. Проведем индукцию по длине второго со
множителя п;2. Если /(ш2) = 1,то доказываемое следуе
из равенства (**). Если же I (w2)	1, то w2 = w2x, гд»
I (wz) < Z (^2) и х АС. Поэтому, учитывая (**) и индук
тивное предположение, получаем
Ф (wiw2x) = ф (?гц4) ■' Ф (х) = (ф о ф (нл2)) с ф (х) =
= ф (?/’].) о (ф (1Г2) о ф (х)) = ф (щД) о ф (^
Кроме того, если х Е X, то ф (х) = ф(;г) в силу равен
ства (*). Итак, условия (1) и (2) выполнены.
Т е о р е м а 12 (свойство универсальности свободно!
полугруппы). Для всякой полугруппы А найдутся сводах
пая полугруппа S и гомоморфное наложение ф: S —> /I
Д о к а з а т е л ь с т в о. Пусть 5 — свободная полу
группа со свободно порождающим множеством А. В си.т
свойства (2) из определения свободной полугруппы
тождественное отображение множества А на себя продол
жается до гомоморфизма (р: 5 —> А, который в дан по.'
с л уча е о к а з ы в а е тс я на л о же и и ем.
Т е о р е м а 13 (теорема единственности свободно
полугруппы). Если S — S (X) — свободная полугруппа с
свободно порождающим множеством X, то существуем
изоморфизм ф полугруппы S на полугруппу W = W (А
слов в алфавите X, причем ф (х) — х для всех хЕ А
Д о к а з а т е л ь с т в о. Согласно теореме 11 и свой
ству (2) из определения свободной полугруппы, тож:^
ствепное отображение множества X на себя продолжав тс
до гомоморфизмов ф: S —> W и ф: W —> S, приме;
Ф (г) — Ф (т) = х для всех х СЕ X, Таким образов
68

-- jni (р и X с~ Im ф. Ввиду теоремы 6 и свойства (1)
з определения свободной полугруппы, 1щф=(У и
|т ф	т’ е' КаК (Р’ так и оказь|каются наложениями.
]эолее того, поскольку х (фср) = х для всех х<=Х, не¬
трудно заметить, что w (фср) = w для всякого слова w
’|,кЬавите X, т. е. фср — lVv. Если яф = 1л\' для некого-
ры'х a,b^w, то
а — лх|?ср — />фср - - ft.
Следовательно, ф- — влечение, а значит, и изоморфизм.
У и р а ж пени я
1.	Убедиться, что множество всех подмножеств некоторого
множества с операцией пересечения (объединения) является ком¬
мутативной полугруппой. Есть ли у этих полугрупп единицы?
Для каких элементов этих полугрупп существуют обратные? Дока¬
зать, что отображение ср, где (р (Л7) — дополнение подмножества Л7,
является изоморфизмом одной из этих полугрупп на другую.
2.	Доказать, что как вырожденные, так и невырожденные ма¬
трицы образуют подполугруппы полугруппы матриц относительно
умножения.
3.	Доказать, что всякое непустое подмножество полугруппы
5 упражнения 5 из § 1 является подполугруппой.
4.	На множестве действительных чисел определим операцию,
наложив ту — 0 для любых х и ?/. Доказать, что это полугруппа.
Найти все ее подполугруппы.
5.	На множестве четырехмерных строк определим операцию
U. 6, с, rf) (.s, t, и, v) = (a, b, it, г). Доказать, что это полугруппа
и что все ее элементы являются идемпотентами (элемент е полу¬
группы называется идемпотентом, если е1 ~ с).
6.	Доказать, что множество всех идемпотентов коммутативной
полугруппы с единицей является подполугруппой.
7.	Пусть А \\ В — полугруппы. На множестве А X В всех
пар (а, Ь), где а <= А, Ъ €= В, определим операцию
(a, b)(a',b') — (аа', ЪЬ').
Доказать, что А X В — полугруппа, причем она содержит единицу
тогда и только тогда, когда единицы существуют в полугруппах
А ц В. Указать какой-либо гомоморфизм полугруппы А X В на по¬
лугруппу А и найти его ядро. Доказать, что если полугруппа R
содержит единицу, то существует гомоморфное вложение полу¬
группы А в полугруппу А X В.
Будут ли гомоморфизмами полугрупп отображения ср: Л —> В
113 приводимой на следующей странице таблицы? В случае
Положительного ответа найти их ядра.
Пусть А и В — полугруппы т- п n-мерпых строк соответст¬
венно относительно сложения, причем т < п. Доказать, что су¬
ществуют гомоморфное вложение полугруппы А в полугруппу Z? и
Н)моморфное наложение полугруппы В на полугруппу А. Указать
яДро найденного наложения. Доказать, что В изоморфна полу¬
группе А 4' С (см. упражнение 7), где С — полугруппа (п — т)-
м*рных строк.
09

А
В
ср
->
1
1
n-мерные строки от-
Действительные
гр («1, . . • ,
cz.7J) —
носительно сложе-
числа о:носитель-
= «1 + . •.
• “Г ап
нпя
но сложения
2
Действительные чпс-
Целые числа от-
ф (х) = (целон Ча-
ла относительно ело-
носительно ело-
сти числа
•а
жен и я
жен ия
3
Д ейст в п те л ьп ые чис¬
Целые числа от¬
То же
ла относительно
несите л ьно умно¬
умножения
жения
4
Полугруппа слов
Полугруппа слов
ср (х) — X2
5
Произвольная полу¬
Произвольная по¬
ср (.г) =1
группа
лугруппа с еди¬
для всех х <= Л
ницей
6
лМатрицы вида
Д е й ст в и т е л ы-i ы е
/II 1 I
Що 1
n = z
II1 х ||
числа относитель¬
IU
1° Ч
но ело ;кенпя
относительно умно¬
жения
10. Доказать, что полугруппа слов в алфавите, состоящем из
одной буквы, изоморфна полугруппе положительных целых чисел
относительно сложения.
И. Убедиться, что двухэлементная полугруппа {— 1, 1} с опе¬
рацией умножения не изоморфна полугруппе с таблицей умножения
•
а
b
а
а
b
b
b
b
12.	Доказать, что факторполугруппа, возникающая из допус¬
тимого разбиения примера 2 на с. 61, не изоморфна полугруппам с
таблицами умножения
•
0
1
2
• 1
1°
1
2
0
0
1
2
0
0
0
0
1
1
2
о u
1
0
1
2
2
2
0
1
2
0
2
2
13.	Доказать, что моногенные полугруппы P/S (jn, с) и P/S (/ь
d) изоморфны тогда и только тогда, когда т = п и с = d.
14.	Доказать, что для каждого непустого множества X суще¬
ствует коммутативная полугруппа S, обладающая следующими
свойствами: a) S порождается множеством X; б) для любого ото¬
бражения ср: X -+А, где А — произвольная коммутативная полу
группа, существует гомоморфизм ф: S А такой, что ср (л) = ф (х)
для всех х е X.
15.	Доказать, что для каждого непустого множества X суще¬
ствует полугруппа S с единицей, обладающая следующими свойст¬
вами: а) 5 порождается объединением {1} 'J X; б) для каждого
70

Сражения ср: X —* А , где А —-Произвольная полугруппа с еди¬
ницей, существует гомоморфизм ср: S ■_* А такой, что ф (х) = ср (х)
и ня всех х (= X.
16.	Доказать, что для каждого непустого множества X сущест¬
вует коммутативная полугруппа S, обладающая следующими свой¬
ствами: a) s2 = s для всех ,?е5;б) 5 порождается множеством X;
в) для каждого отображения ср: X -* А, где А — коммутативная
полугруппа и а2 = а_ для всех аеЛ, существует гомоморфизм
ф: 5 А такой, что ср (х) = ср (х) для всех х <= X.
§ 3. Группы
Полугруппа называется группой, если она содержит
единицу и для каждого ее элемента существует обратный.
Среди полугрупп, приведенных в таблице 1, группами
оказываются, например, полугруппы 1, 3, 4, 8 и 12.
Подмножество Н группы G называется подгруппой,
если II является подполугруппой (т. е. непусто и вместе
с любыми двумя элементами содержит их произведение)
и вместе с каждым элементом содержит обратный к нему.
Всякая подгруппа Н группы G содержит единицу груп¬
пы G. Действительно, по условию существует элгемент
h ЕЕ Н. По тогда /г-1 ЕЕ II, что в свою очередь влечет
1 = /г/г"1 £Е II. Нетрудно понять, что всякая подгруппа
является группой относительно операций, определенных
в исходной группе.
Подгруппами группы отличных от нуля действительных чисел
(группа 3 из таблицы 1) будут, например, подмножество всех по¬
ложительных действительных чисел, подмножество, состоящее из
1 и —1, совокупность всех степеней 2т, где т — произвольное це¬
лое число. Однако, например, множество всех отличных от нуля
целых чисел подгруппой не является. В группе целых чисел по сло¬
жению (группа 4 из таблицы 1) подгруппу образуют, например,
четные числа (но не нечетные!). В группе невырожденных матриц
(группа 8 из таблицы 1) можно указать подгруппу, состоящую из
нсех матриц с определителем, равным 1 (принять во внимание тео-
Р°му 1.3.14), и подгруппу, состоящую из всех невырожденных диа¬
гональных матриц.
Во всякой группе существуют две тривиальные под¬
группы*. вся группа и единичная подгруппа, состоящая из
одной единицы.
Теорема 1. Пересечение любого множества под-
гРУпп является подгруппой.
Доказательство. Пусть U — пересечение не¬
которого множества подгрупп. Так как каждая из этих
Подгрупп содержит единицу 1, то 1 ЕЕ U, т. е. U непусто.
Ьвиду теоремы 3 из § 2, U — подполугруппа. Если g СЕ
U, то g принадлежит всем подгруппам рассматриваемо¬
71

го множества. По тогда каждая из них содержит ; i
а значит, 1 ЕЕ U.
Если II — подгруппа группы G и g — пекоторы]
элемент из 6\ то множество всех произведений вида
где h ЕЕ Н, называется левым смежным классом по под
группе Я, определенным элементом g, и обозначается черо
gll. Аналогично определяется правый смежный класс Н%
Если g ЕЕ II, то gll = II. Действительно, gll ЕЕ Я, hq.
скольку II — подгруппа. Если теперь h ЕЕ Н, то, носко, ц
ку Н — подгруппа, имеем g~vh ЕЕ Н. Отсюда h = g (g'Mi)^
ЕЕ gll, т. е. II El gll. Из полученных включений вы те-
кает равенство gH — II. Другие примеры смежных клас¬
сов приводятся в таблице 3.
Т а б л и ц а
Группа 6
Подгруппа Л
Элемент g
Смежный и л .и <•
#//
1
Действ итель-
Положите ль-
—
О
Все отрица¬
ные числа, от¬
личные от 0
ные действи¬
тельные дейст¬
тельные числа
вительные чис¬
(группа 3 из
таблицы 2)
ла
2
То же
{Г -1}
-
3
{-3,-3}
3
Целые числа
Четные числа
—
3
Все нечетные
(группа 4 из
таблицы 2)
числа
4
II евы рожден¬
Матрицы с
|1.!
2||
Все матрицы с
ные матрицы
определителем,
б||
определителем.
второго поряд¬
равным I
равным 2
ка (группа 8 из
таблицы 2)
5
То же
Матрицы вида
II1
21|
Все матрицы
АЛ’, где X — лю¬
II
б ||
вида
бое отличное
от 0 действи¬
тельное число
6
Взаимно одно¬
Все такт? ото¬
/1 2
3
Все такт? ото¬
значные ото¬
бражения ([',
\2 3
4 1J
бражен ня ср,
бражения мно¬
ч ГО
что
жества (1, 2, 3,
<г(1) = 1
Ч'(4) = 1
4} на себя
(группа 12 из
таблицы 2)
Т е о рема 2. Множество левых смежных классе
группы G по подгруппе Н образует разбиение группы С
Дока з а т е л ь с т в о. Если g ЕЕ G, то g = g'l i
поскольку 1 ЕЕ II у имеем g ЕЕ gll. Поэтому для до к азател!
72

с-гва теоремы достаточно установить, что два различных
сМежных класса не пересекаются. Для этого достаточно
доказать, что два смежных класса, имеющие общий эле¬
мент, совпадают. Но если х ЕЕ аН ЬН, где a, b G,
,г0 ;Г. ah} = bh2, где /гп h2 ЕЕ Н. Отсюда а — (6Л2) 1ц.
Если, далее, g ЕЕЕ аН, то g = ah, где h ЕЕ Н. Поэтому
g — ah = ((bh2) h^1) h ~ b (h2h^h).
Из определения подгруппы вытекает, что h2h\ xh //.
Следовательно, g ЕЕ ЬН. В силу произвольности g это
означает, что all cz ЬН. Обратное включение доказывает¬
ся аналогично.
Разбиение группы G па левые смежные классы ио
подгруппе II называется левым разбиением по подгруппе II.
Аналогично, доказав правый аналог теоремы 2, можно
говорить о правом разбиении по подгруппе Н.
Т е о р е м а 3 (теорема Лагранжа). Если II — под¬
группа конечной группы G, то число элементов подгруппы II
является делителем числа элементов группы G *).
Докажем более сильное утверждение.
Теорема 3'. Если п — число элементов группы
G, т — число элементов ее подгруппы II и к — число
правых смежных классов группы G по подгруппе Н, то
п = кт.
Д о к а з а т е л ь с т в о. Пусть h}, . . ., hfn — элемен¬
ты подгруппы Н. Смежный класс Hg содержит элементы
Kg, ■ ■ ■, >>,„g- Гели /г,/? - • к#, то
К =~- (Kg} g~' = (hjg} g~r = hj.
Таким образом, элементы htg, . . hmg различны, т. о.
каждый смежный класс по подгруппе II содержит т
элементов. Ввиду теоремы 2, п = кт.
Для случая групп теоремы 4 и 5 из § 2 могут быть
усилены.
Т е о р е м а 4. Если ср: G G' — гомоморфизм групп
и 1 — единица группы G, то (р (1) — единица группы G/
и Ф (/Г1) (ф (А')Г1 для всех g ЕЕ G.
Дока з а т е л ь с т в о. Имеем ср (!) ср (1) ф (1 • 1) - -
— Ф (1), откуда
Ф (1) = (ф (1) ср (1)) (ср (I))’1 ф (1) (ф (1)Г - 1',
*) Число элементов группы G часто называют порядком. группы
Тогда теорема 3 звучит так: порядок подгруппы делит порядок
гРуппы.
73

где 1' — единица группы Gr. Далее,
ф (g_1) ф (g) =ф (g“’g) = ф (1) = 1' = ф (1) =
= ф (gg’1) = ф (g) ф (g_1),
откуда ср (g-1) = (ф (g))'1 по определению обратного эле.
мента.
Из теорем 4, 5 и 6 из § 2 получаем:
Теорема 5. Если ф: G —G' — гомоморфизм /< о,
лугрупп и G -— группа, то 1т ф — группа.
Следствие. Если ф: G -> G' — гомоморфное на¬
ложение полугрупп и G — группа, то G' — группа.
Применяя это следствие к естественному гомомор,
физму, убеждаемся, что факторпол у группа группы я в,
ляется группой. Поэтому ее естественно назвать фак¬
торгруппой.
В случае групп оказывается возможным получить
более прозрачное описание допустимых разбиений, чем
для произвольных полугрупп. Введем важное определен! г?:
подгруппа Н группы G называется нормальной, если
ghg~x ЕЕ Н для любых h ЕЕ Н и g ЕЕ G. Если группа ком¬
мутативна, то, ввиду следствия теоремы 2 из § 2, ghg'A -
= h (gg"1) — hi = h, т. e. любая подгруппа коммутатив¬
ной группы нормальна.
Примером нормальной подгруппы может служить подгруппа
матриц с определителем, равным 1, в группе невырожденных мат¬
риц (см. пример 4 из таблицы 3). Действительно, если | А | = 1, то
для любой невырожденной матрицы В, учитывая теорему 1.3.14,
имеем
| BAB'* | = | В | | Л | | Я-Ч = | В | | 5-1 | = | Е | = 1.
Напротив, подгруппа D диагональных матриц в группе невырож¬
денных матриц второго порядка нормальной не является. Дейсж
вительно,
111' 111 111 ОII 111 1Ц-1 I|1 1||||1 0||||l —1||
||o 11111° 2 IIII0 1||	II0 1 || || 0 2 [I || 0	1II
-II1 ll1 “ЧМ1 'Ik^
II o 2 Illi 0	1|| || 0 2 IP
Теорема 6. Следующие свойства подгруппы 11
группы G равносильны:
(1)	Н — нормальная подгруппа'1,
(2)	gH = Hg для всех g ЕЕ G *);
*) Это свойство, в частности, означает, что левое и правое раз¬
биения по нормальной подгруппе Н совпадают.
74

(3)	левое разбиение по подгруппе Н допустимо;
(4)	правое разбиение по подгруппе Н допустимо.
Доказательство. Достаточно доказать спра¬
ведливость следующих импликаций:
(1)	=> (2). Если х ЕЕ gH, то х = gh, где h ЕЕ Н. За¬
пишем
я = (ghg'1) g
и заметим, что ghg~x Е Я по определению нормальной
подгруппы. Следовательно, х ЕЕ Hg. Ввиду произволь¬
ности х имеем gH ее Hg. Обратное включение доказывает¬
ся аналогично.
(2)	=> (3). Пусть х, и ЕЕ аН и у, v ЕЕ ЪН, где а, Ъ ЕЕ G.
Тогда х ?= а/г15 и = ah2, у = дЛ3, и — bh4, где Л2, /г3,
/г4 е Н. Отсюда ху = ahrbh3 и uv — ah^bh^. Поскольку
Hb = ЬН, то h±b bh' и h2b = bh", где h', h' е Н.
Следовательно,
ху = abh Я3 Е~ {ub^ Н
и
uv .= abhr,h4 ЕЕ (ab} Н,
что и доказывает допустимость левого разложения по Н.
(2)	=> (4). Аналогично.
(3)	=> (1). Ясно, что при любом h EE Н элементы gh
и g принадлежат одному смежному классу левого раз¬
биения по подгруппе Н. В силу допустимости этого раз¬
биения, элементы ghg~Y и gg"1 1 также должны принад¬
лежать одному смежному классу. Но 1 ЕЕ Н и, следова¬
тельно, ghg~l е Н.
(4)	=Ф (1). Аналогично.
Теорема 7. Всякое допустимое разбиение группы
С является левым *) разбиением по некоторой нормальной
подгруппе. Этой нормальной подгруппой является смеж¬
ный класс разбиения, содержащий единицу.
*) А в силу примечания на с. 74 также и правым.
75

Доказате л ьство. Пусть S —допустимое разбиение
группы G и Н — смежный класс этого разбиения, Содер¬
жащий 1. Если /гг, h2 ЕЕ Н, то, обозначив через [.г] смеж¬
ный класс разбиения 2, содержащий элемент .г, будем
иметь [TiJ [Л2] —- [1]. Из допустимости разбиения выте¬
кает, что
[ад п и Ш
Таким образом, h}h2 Н, т. е. Н — подполугруппа. Если
h ЕЕ Н, то [ZJ — [1|. Из допустимости разбиения Е
вытекает, что
[/Г1] - [1-/Г1] - ШГ1] = [11 - Я,
т. е. /Г1 ЕЕ Н. Следовательно, Н — подгруппа. Если К --
некоторый класс разбиения S, то зафиксируем в К не¬
который элемент /с. Тогда [ZJ = /<, и для всякого h ЕЕ Я
имеем, что [А7г] --- [Л • Г| — [/>:], т. е. khEEK. Следова¬
тельно, кН ЕЕ К. Если х ЕЕ К, то [Аг_1.г] — [7г_17с] = [1 L
Следовательно, k~lx — h ЕЕ Н, откуда х = kh ЕЕ кН. Та¬
ким образом, К СЕ кН, а значит, К = кН. Этим доказано,
что разбиение S совпадает с разбиением по подгруппе//.
Ее нормальность вытекает из теоремы 6.
Теорема 7 показывает, что вместо того, чтобы гово¬
рить о факторгруппе группы G по допустимому разбие¬
нию S, можно говорить о факторгруппе группы G по нор¬
мальной подгруппе Н. В силу теоремы 7, эта нормальная
подгруппа совпадает со смежным классом разбиения, со¬
держащим единицу. С другой стороны, если q: G G' -
юмоморфиое наложение групп, то, в силу теоремы 7 из
§ 2, разбиение Кег ф допустимо и по той же причине оп-
} оделяется нормальной подгруппой, состоящей из всех
прообразов единицы 1' группы G'. Поэтому в теории групп
ядром гомоморфизма называют эту нормальную подгруп¬
пу и через Кег ф обозначают именно ее, т. е. Кег ф
= {g | g ЕЕ G, ф (g) = 1'}. В связи с этим теорему 8 ю
§ 2 it случае групп можно переформулировать следующим,
образом.
Теорема 8 (теорема о гомоморфизме для групп).
Если ф: G -> G' — гомоморфное наложение групп, Кег ф —
нормальная подгруппа, являющаяся ядром этого гомомор¬
физма, и л: G -> 67Кег q? — естественный гомоморфизм,
то существует изоморфизм G' G/Kct ф такой, что
мх л-
76

Т е о р е
Д о к а з
Если g -
полагаем )
- элемент
группы
6, а 1
ч — целое числе
ё
если
П > о,
п раз
gll= <
1,
если
п = 0,
1. ..g'1,
если
п < 0.
pi | раз
м а 9.
■ ё‘
"■ё“ - ё
1ГНП
аге л
\ ь
с Т В О.
Если
т ~ 0, то
ё"
= 14'" =
■ ё" -
Г'1.
о
Случай, когда п = 0, рассматривается аналогично. Если
же /п, п Ф 0, то возможны следующие случаи:
т
п
1
>0
>0
2
>0
<0
3
<0
>0
4
<о
<0
В случае 1, учитывая теорему 1 из § 2, имеем (ср. с тео¬
ремой 9 из § 2)
г • g"=(g^g) (g_^g)=g_._g=g"1+".
7?i раз а раз	mtn раз
Случай 2 распадается на подслучаи: а) т > I и I;
б) т = | п в) /??С | п |. При этом согласно правилам сло¬
жения чисел имеем tn + п = т — | п |, т + /г = О и
т -}- п ~ — (| п | — т) соответственно. Но тогда, по¬
скольку gg"'1 = 1, имеем
g"‘ • g“ = (g_g) (g-ь ■ . . g-1) = g_.^g = g»H"l = g”'+",
пг раз	pi| раз	m-|n| раз
g'” • g" = (g^g) (g-o.-g-1) = 1 = g” = g'n+n
m раз	pi| раз
*) Если операция в группе G записывается как сложение, то
приводимое ниже определение выглядит так:
g + • • • -1- g.
если
п > 0,
п раз
0,
если
п - 0,
(-£) + ... +(- g),
если
п <0.
pi| раз
^°гДа доказываемые ниже теоремы 9 и 10 формулируются как mg Е
пё ~ (т + п) g и п (mg) — (inn) g соответственно.
77

или
gm-gn=(g j)(g-1---gj)-rW1 = g-';|ni”,:) - g'"
m раз	|?i| раз	|n|— m раз
Случай 3 рассматривается аналогично.
В случае 4 имеем т п = — (\ т \ + | м |), откуда
|m| раз	|п| раз
= g'*1 . . . g~1 = g~(bnl+|n|)= gw П'
|m| + |n| раз
Теорема 10. (g’T = gm".
Доказательство. Если m = 0, то
(g«)n = 1” = 1 = g” = g'-Л
Если n = 0, to
(gm)° = 1 = g» = g-o.
Если m, n > 0, to
(g’T = (g-;-g) • • • (g---g) = g^g = g”'”-
m раз	m раз	mn раз
- ■	Ц -	"
n раз
Далее, в силу теоремы 9 для любого целого числа к полу¬
чаем
gkg-k = g~'!gk = li
откуда
(g'T1 = g-k-
Поэтому если п < 0, а значит, п = — | п I, то для лю¬
бого целого числа т имеем
(gm)n = (gw)-ln| = ((g™)|n|)_1 = (g™1"1)’1 = g~™lnl = gm'\
Если же m < 0, но n > 0, то
(g’T = (g-|m|r -(g^-.-g-1)" = ((g-1)1™1)” = (g-1)1™1" =
|?a| раз
_ g-|rn|n —- g™
Группа G называется циклической, если в ней суще¬
ствует такой элемент g, что для всякого х из G найдется
такое целое число п, что х = gn. Этот элемент g называет¬
ся образующим (или порождающим) циклической группы б-
Из теоремы 9 вытекает, что всякая циклическая грущ
па коммутативна. В случае группы Z целых чисел по
78

Г107кению в качестве образующего можно взять 1 ила
		|5 так что аддитивная группа целых чисел циклична.
рели пг — некоторое положительное целое число, то
множество Zin всех целых чисел, делящихся на т, ока¬
зывается подгруппой. В силу коммутативности группы
эта подгруппа является нормальной. Поэтому можно
рассмотреть факторгруппу ZlZm, которая называется
группой вычетов по модулю т. Группа вычетов по модулю
т содержит смежные классы [01, [11, [21, . . ., [т — 11.
Все эти классы различны, ибо I — j Zm, если 0	<
< i < т. Убедимся, что других элементов в ней нет.
Действительно, любое целое число и можно записать в
виде и = mq Я- г, где 0 г < т. Учитывая равенство
\mq\ = [01, вытекающее из включения mq EE Zm, и оп¬
ределение операций в факторгруппе, получаем
[zz] = [mq + г] = [mq] + [г] = [0] + [г] = [г].
Таким образом, группа вычетов по модулю т содержит
в точности т элементов. Класс [11 служит ее образующим.
Естественно спросить: какие другие классы вычетов яв¬
ляются образующими этой группы? На этот вопрос отве¬
чает
Теорема 11. Класс [А*], где 0 к <Z т, является
образующим группы вычетов по модулю т тогда и только
тогда, когда числа кит взаимно просты.
Доказательству теоремы предпошлем следующую
лемму:
Лемма. Всякая ненулевая подгруппа группы Z сов¬
падает с Zm для некоторого т.
Доказательство. Пусть II — ненулевая под¬
группа группы Z. Тогда Н содержит положительные це¬
лые числа. Пусть т — наименьшее среди них. Тогд-1
Zm cz Н. Если же х — произвольный элемент из II, то,
разделив х на т с остатком, будем иметь х = qm 4- г,
где 0 г <Z т. Ясно, что г = х — qm GE II. Если г 0,
'го вступаем в противоречие с выбором числа т. Следова¬
тельно, г = 0. Отсюда х = qm ЕЕ Zm, т. е. II cz Zm.
Таким образом, II = Zm, что и требовалось.
Доказательство теоремы И. Допустим,
Что класс [А] является образующим группы вычетов по
Модулю т. Если к и т не взаимно просты, то к — k'd и
гп = m'd, Yj\e d > 1. Тогда
[т'к] = [m'k'dl = [mk'l = [01,;
73

ибо ink' ( - Zm. Далее рассмотрим классы
[01, [/fl, [2/f|, . .	{(т' - 1) /fl.
Так как f/}> 1, их меньше чем т. С другой стороны, д.-.я
! *'якого целого я имеем s — qm' + г, где q — некотор
целое число и 0 < г < т'. Отсюда
Ш = [(qm' + r)k] = [qm'k] + [r/fl = [qm'k'd] +
+ [r/f| - [Q/fW + [r/fl - 10Ц- Irk] = \rk\,
поскольку qk'm GE Zm. Следовательно, выписанными вы¬
ше классами исчерпываются все элементы группы выче¬
тов по модулю /??, что невозможно. Допустим теперь, что
к и т взаимно просты. Тогда найдутся целые числа и и
и такие, что ит -|- vk — 1 *).
Отсюда
[11 - [ит] [гА| [01 -Т Ш [к/d.
Поэтому для любого |.s-| GE ZIZm (напомним, что 0 s <.
<Z т)
[Д - 5 [II - X Irk] - l.sr/fl - (st) [k]**)r
т. e. I/f| оказывается образующим.
Строение циклических групп описывается следующей
теоремой.
Т е о р е м а 12. Всякая циклическая группа изоморф¬
на или группе целых чисел по сложению, или группе вычетов
по некоторому модулю т.
Д о к а з а т е л ь с т в о. Пусть G — циклическая
группа с образующим g. Рассмотрим отображение (р:
*) Это является следствием следующего утверждения:
Если т и п — целые числа и d = н. о. д. (пц п) (т. е. наиболь¬
ший общий делитель т и п), то найдутся такие целые числа и и с,
что ит + vn ~~ d.
Для доказательства рассмотрим множества I всех целых чисел,
представимых в форме sm + tn, где .9 и t — какие-то целые числа.
Легко проверяется, что множество I является подгруппой группы
Z и, в силу леммы, совпадает с Zd' для некоторого целого положи¬
тельного d'. Поскольку т — 1 -т + 0-п <= I и п = 0-т -|- 1 •/?
ее У, имеем т ~ m'd' и п — п'сГ для подходящих т' и п'. Следова¬
тельно, d' оказывается общим делителем чисел т и п. Если же d" --
какой-либо общий делитель этих чисел, то т = m,"d" и п = n"d"
для подходящих т" и п". Поскольку d' е= I, то d' = ит + vn для
некоторых целых чисел и и г. Поэтому
d' -- ит -J- гн — um"d" + vn'd" — (ит" + vn") d",
т. е. d' оказывается наибольшим общим делителем чисел т и п.
Отсюда d -- -\^d', чем и заканчивается доказательство.
**) См. примечание на с. 77.
80

определяемое равенством ср (п) — gn. Из циклич¬
ности группы G вытекает, что ср — наложение. В силу
теоремы 9
ф (к -|- I) = g^1 = g'!-gl = ф (к) ср (Z),
. е, ср оказывается гомоморфизмом. В силу теоремы 8,
, руппа G изоморфна фактогруппе Z/Ker ср. Если Кег (р
{0}, то все смежные классы по подгруппе Кег ср од1 о
элементные. Следовательно, Z/Ker ср совпадает с Z и,
значит, G изоморфна Z. Если же Кег (р 0, то в силу
/геммы, предпосланной доказательству теоремы И,
Кег ср --Zm для некоторого т и, следовательно, Z/Ker (р
является группой вычетов по модулю т, которой и изо¬
морфна группа G.
Как уже отмечалось (полугруппа 12 из таблицы 1),
множество всех взаимно однозначных отображений не¬
которого множества на себя является группой. Эта груп¬
па является в некотором смысле универсальной, как по¬
казывает следующая
Теорема 13 (теорема Кэли). Для всякой группы,
G существует гомоморфное вложение ее в группу Q взаимно
однозначных отображений множества, G на себя *).
Доказательст в о. Если g ЕЕ G, то обозначим
через ср (g) отображение множества G в себя, определяем; е
равенством х (ср (g)) = xg для всех х ЕЕ G. Так как
а? =	(g)),
то ср (g) оказывается наложением. Если х (ср (g))	-
= У (ф (g)), то
X = (xg) g~l = (х (ф (g))) g'L = (у (ф (g)))g~l = (yg)g~l g,
т. е. ср (g) является вложением множества G в себя.
Таким образом, ср (g) — взаимно однозначное отображе¬
ние множества G на себя, т. с. ср отображает G в Q. Есио
ф (gi) — ф (g.,), то
gl I (ф (gl))	1 (ф (g>))
е.. ср оказывается вложением. Из равенств
х (ф (g'l) Ф (g.>)) = (х (ф	(g2)) =
= (-Tg|) g-2 -= X (gtg2) ---= X (ф (g^)),,
*) Ввиду теоремы 5, эта теорема допускает и такую формули¬
ровку: всякая группа изоморфна подгруппе группы взаимно одп.о-
иылс отображений некоторого множества на себя.
81

где х — произвольный элемент из G, вытекает, что
ф (gl) ф (g2) = ф (glg2)f
чем доказывается, что ср — гомоморфизм.
П р и м е р. Пусть G = Z/3Z. Тогда группа Q, рассмотрении;!
в теореме 13,— это группа подстановок множества {0, 1,2}, и вло.
жение ср, описанное в ходе доказательства теоремы 13, выгляди
следующим об разом:
Из доказательства теоремы 13 видно, что всякая кж
печная группа вкладывается в группу взаимно одноз¬
начных отображений конечного множества на себя, т. о.
в группу подстановок множества {1,2, . . ., п] для не¬
которого п. Эту группу называют симметрической группой
степени п и обозначают ®п. Симметрическая группа сте¬
пени п содержит п\ элементов. Остановимся на некото¬
рых из ее свойств.
Назовем циклом и обозначим (G . . . ik), где ilf . . .
. . ., ijf — некоторые различные числа из множества
{1, 2, . . . 2 п}, такую подстановку ст, что
i, если i =^=	j7.,
если i = ih и h /с,
Ц, если i = ik.
Например, в группе 6б имеем
2 3 4
2 5 4
5 6 \
1 (J ‘
Двухэлементный цикл называется транспозицией. Транс¬
позицией будет, например, подстановка
/1 2 3 4 5 6\
(35)=	2 5 4 3 6./
В дальнейшем термин цикл и символ (Ц . . . ц.) обозначают
как определенную выше подстановку, так и подмножест¬
во {Ц, . . ., ik} множества {1,2,..., п}. Циклы, не со¬
держащие общих элементов, называются независимыми.
Например, в группе ®0 независимыми циклами будут
(126) и (35).
Теорема 14. Если р п о — независимые циклы г то
ро = ор.
82

Доказательство. Заметим, что i Е р влечет
р, ip а и I о. Аналогично, io е о, 1$ р и
j jgp, если i Е а. Поэтому
i (Р°) = (ф) ° =
Ш = ?,
ip,
если t р IJ о,
если i Е р,
io, если i Е о,
ip = i,
i (op) = (io) р =
ip,
io,
если i p (J о,
если i E p,
если i E a.
и
Таким образом, i (po) = i (op) для всех i, т. e. po = op.
Теорема 14 вместе с теоремой 2 из § 2 дает.
Теорема 15. Если циклы о17 . . ., ош попарно не¬
зависимы, то
. Om ^n(l) • • • tf.n(ni)
для любой подстановки л Е ®/п.
Теорема 16. Каждая подстановка х представля¬
ется в виде произведения попарно независимых циклов.
Доказательство. Для каждого i рассмотрим
множество {i = ix°, ix, ix2, ix3, . . .}. Так как ixfc E
E {1, 2, . . ., n}, то существует такое m, что ixm — ix™+/l
для некоторого h 0. Отсюда, учитывая теоремы 9 и 10,
получаем
i = (ixm) (xm)_1 = i (xm-ll~m) = ixh.
Можно считать h выбранным так, что числа i, ix, . . ., ix/!_1
различиы. Про цикл о = (i (ix) . . . (ix/l_1)) скажем, что
он является орбитой подстановки х, порожденной элемен¬
том i. Если и — произвольное целое число, то, записав
и = hq + г, где 0 г h, получим
ixu = i (x,l7xr) = (i ((x/l)7)) xr = ixr E o.
Л e м м а 1. Две орбиты подстановки х или не пере¬
секаются, или совпадают.
Действительно, если орбиты or = (i (ix) . . . (ix/,_L)) и
P (/ (/T) . . . (/tz_1)) содержат число d, то cl ixs -
7’V, где, скажем, t s. Но тогда
i = (/x^XxT1 = ГЕр,
°ткуда о E p. Аналогично получаем, что p E о. Таким
образом, о = р.
83

Л е м м а 2. Если о — орбита подстановки т и i Е а
то at = io (не забудьте о двусмысленности слова «цикл
В самом деле, пусть о = (к (А’т) . . . (/ттг~1)). Тогда
z = А’т\ где 0 < h < г, откуда
ш = (кть) о =
( к = ктг —■ (Л'т^1) т — 1т, если к = г—1,
( кт11 1 --- (кть) т — ат ,	если О /а <> — 1,
Возвращаясь к доказательству теоремы, допустим, что
О], . . .,от — все неодноэлементные орбиты подстановки
т. Если I di (J . . .[J от, то iOfr = i для всех к, откуда
В противном случае, ввиду леммы 1, i ЕЕ о5 в точности
для одной орбиты os. Поэтому i Oj (J . . . [J as_i в,
значит, 1аА — , . . = io^-i ~ i. Кроме того, ат ЕЕ о6., от¬
куда at (T.s+i [J . . . (J от и, следовательно, (at)osi -
= . . .
= (гт)о,п
— АТ.
Отсюда,
учитывая лемму
2, ио-
лучаем
AOj . . .
Os_1O$(J.sh1 .
• • О т
= (ios) о
s+l • • • От =
(ат) О§+1 . • . От - АТ,
Таким
образом,
АТ
i (а, .
• • о7Н)
для всех /, т. е.
Т = 0
1 . . . от.
Независимость
циклов
оп • • •
, от вытекает из
леммы.
Теорема 17. Каждая подстановка представляется
в виде произведения транспозиций.
Д о к а з а т е л ь с т в о. Ввиду теоремы 16 достаточ¬
но установить равенство
(«!••• ').) = (Ш(Мз) • • •	(*)
По i ((/ц?) • . • 0Д\)) — Ь если а =£ аь . .	а\. Если
i — ih, то
i	. (zjij.)) = ik (i^.) = zv
Если же a — ?tS, где 1 s < /f, to
a ((A1A2) . . . (/]//..)) — is ((Al/,) (a'iUi) . . . (hh))
— h (Gia.s-i i) • • . (iiiitY) = W ((<1^2) . . . (й/Л)) = M-
Таким образом,
А ((/цЛ) . . .	= i (G . . . А\)
для всех а, т. е. равенство (*) справедливо.
84

Поскольку орбиты подстановки определены однознач-
из доказательства теоремы 16 можно усмотреть, что
•тждая подстановка представляется в виде произведения
попарно независимых циклов однозначно с точностью до
порядка сомножителей. Для представления подстановки
и виде произведения транспозиций это пе так, ибо из ра¬
венства (*) вытекает
(13)(15) = (135) - (351) - (35)(31).
Правда, (13) = (31), но (15) у= (35). Некоторым утеше¬
нием может служить следующая теорема.
Теорема 18. Четность подстановки равна чет¬
ности числа транспозиций, входящих в ее представление.
Д о к а з а т е л ь с т в о. ('начала будет установлена
Лемма. Для любой подстановки т и транспозиции
(ij) подстановки т и (if) т имеют различные четности.
Действительно,
А- ((,/) т)
Таким образом, если
/гт, если	f
/т,	если k — i,
б*т, если k — /,
2
..	п \
т(2)
. .	г(п)/’
i
1
. .	п
Т (/)	• •
. т (')	•
■ ■ т (г/)
и лемма вытекает из теоремы 1.2.8.
Теперь, если т ~ ть . . тш, где Т/, — транспозиции,
нужное утверждение следует из очевидного равенства
т = Tj . . . тте, где е — тождественная подстановка, яв¬
ляющаяся, конечно, четной. Надо только принять во
внимание, что, ввиду леммы, при умножении на каждую
113 тл четность меняется.
Теорема 19. Четные подстановки образуют нор¬
мальную подгруппу ЭДП группы
Доказательство. Пусть ЭДН — совокупность
нсех четных подстановок из ®,(. Нетто, что тождествен¬
ная подстановка принадлежит ЭД^. Если о, тЕ ЭДП, то
ат ЕЕ ЭДввиду теорем 17 и 18. Имеет место
Л е м м а. Если ор . . ., ст гп — транспозиции, то
(Oi . . . om) 1 =- <Зпг . . . О,.
85

Для доказательства заметим, что = 8, где е
тождественная подстановка. Отсюда
ОД • • • OmOm • • . О] 8 о 7Г1 . . . од од . . «от.
Если теперь о ЕЕ то, ввиду леммы, из теорем 17
и 18 вытекает, что о-1 ЕЕ Таким образом, 9(п — под,
группа в ®п. Если, наконец, о ЕЕ 9fn и.р = Pi . . . pm (g
ЕЕ где рг- — транспозиции, то, ввиду леммы,
pop-1 = Pj . . . pmaprn . . . рР
По тогда из теоремы 18 вытекает, что
(четность pop-1) = (четность о) + 2т — (четность о),
т. е. pop-1 ЕЕ если о ЕЕ ЭДП.
Группу 9fn часто называют знакопеременной группой,
Вернемся к рассмотрению произвольных групп.
Элемент z группы G называется центральным, если
zg = gz для всех g ЕЕ G. Множество всех центральных
элементов группы G называется ее центром.
Т е о р е м а 20. Центр Z группы G является ее под¬
группой, и каждая подгруппа группы Z оказывается нор¬
мальной подгруппой группы G.
Доказательство. Ясно, что Z содержит еди¬
ницу. Если z', z" ЕЕ Z, то для любого g ЕЕ G имеем
(z'z")g = z'(z'T) =z'(gz") = (z'g)z" = (gz')z" = g(z'z"),
t. e. z'z" e Z. Если z ЕЕ Z, to gz — zg для всех g EE G.
Отсюда
z-1g = z^gzzP1 = z"1zgz~1 = gz'1,
t. e. z'1 EE Z. Таким образом, Z — подгруппа. Наконец,
если Н — подгруппа группы Z, g ЕЕ G и h ЕЕ Н, то
ghg'1 = hgg~l =hE Н.
Если а — элемент группы G, то про всякий элемент
вида gag~\ где g ЕЕ G, скажем, что он сопряжен с элемен¬
том а. Множество всех элементов, сопряженных с эле¬
ментом а, называется его классом сопряженности. Ясно,
что любой элемент содержится в своем классе сопряжен¬
ности (достаточно взять g = 1) и что класс сопряженности
центрального элемента никаких других элементов не
содержит.
Теорема 21. Два класса сопряженности группы G
или не пересекаются, или совпадают, т. е. классы сопря*
женности группы G образуют разбиение.
86

Доказательство. Пусть К и L — классы со¬
пряженности элементов а и b соответственно, и пусть
К я L. Тогда и = gag'1 = hbh'1, где g, /iE= 6'.
Если v К, то и = сас'1 для некоторого с	G. Отсюда
v = cg'higc'1 = cg'Uibh'^gc'1 = (cg'lh)b(cg'4T)~l <= L.
Таким образом, К ст L. Обратное включение доказыва¬
ется аналогично.
П р и м е р. Непосредственным подсчетом можно убедиться,
что группа £3 распадается на следующие три класса сопряжен-
no сти*
к; I анс з зК ? м з :))■
К з М 5 3)-
Т е о р е м а 22. Пусть конечная группа G содержит п
элементов и g СЕ G. Тогда gn = 1, и если gm = 1, но
g* 1 при 1 Л <С т, то т делит п.
Доказательство. Пусть g ЕЕ G, gm = 1 и
gk 1, если 1 к <Е т. Для любого целого положитель¬
ного числа s имеем s = qm 4~ г, где 0 г <Z т. В силу
теорем 9 и 10,
g’ = (gW = igr = g”.
Кроме тою, если 0 <Е k <i т, то g1'gm"k = 1 и 0 <Е т —
— к <С т. Следовательно, {1, g, ... ., g™} — подгруппа
группы G, содержащая т элементов. По теореме 3, т
делит п. Этим доказано второе утверждение теоремы.
Для доказательства первого рассмотрим множество {g,
g2, g\ • • • }• Ввиду конечности группы G, найдется такое
число т, что gk = gl +m для некоторого т Е> 0. Можно
считать, что среди элементов g\ gA+1, . . . ., g/l+nl~1 нет
одинаковых. В силу теорем 9 и 10, отсюда вытекает, что
1 == gJ'g-K~ = gl!+mg-k = gm
11 что среди элементов l,g, g2, . . ., gw_1 нет одинаковых.
Как доказано выше, отсюда вытекает, что п = qm для не¬
которого целого числа д, и, следовательно, gn = (gm)(/ =
l7 = 1 в силу теоремы 10.
В дальнейшем условимся обозначать через | X | число
элементов множества X (не путать с определителем мат¬
рицы!).
Теорема 23. Пусть К (g) — класс сопряженности
элемента g группы G и С (g) — множество всех таких
87

элементов ос (=~- G, что xg — gx. Тогда С -(g) .— подгрупп(1
группы G и | К (g) И. С (g) | = | G
Доказательство. Положим L = С (g). Ясно,
/Что 1 GE L. Если х, у ЕЕ Л, то
(ху) g = х (yg) = х (gy) = (xg) у = (gx) у = g (xy)
II
x_1g = x~Jg(xx~') (x~'(gx))x'1 = (x'^xg^x'1 = gx'1,
t. e. xy и x_1 принадлежат L. Следовательно, L — под-
группа. Обозначим через GiL множество правых смежных
классов группы G по подгруппе L (подчеркнем, что, по¬
скольку подгруппа L не предполагается нормальной, это
нс обязательно факторгруппа!) и определим отображение
<р: К (g) -> G;L, полагая
cp.(u_1giz) = Lu*
Если iT'gu =-■ v~}gv для некоторых и, veG, то (viT^g -
g^viE1). Отсюда viL1 Gz L. Поэтому v G= Lu, а значит,
Lu Lv. Этим доказана корректность определения отоб¬
ражения ср. Ясно, что это наложение. Если ср (zz_1gu) -
ф (^_1gb), то Lu ~ Lv. Отсюда и = lv для некоторого
I ЕЕ L, а значит,
U~igU = v~1l~lglv = v~1l~1lgv = v~lgv.
Таким образом, ср — вложение, а значит, и взаимно од¬
нозначное отображение. Учитывая теорему 3\ получаем
| К (g) \\ L | = \G/L || L | = |G |.
Теорем a 24. Центр группы G, где | G | = p^
причем p — простое число и к Ее 1, соде россит более одного
элемента.
Доказате л ь с т в о. Допустим, что 1 — единст¬
венный нейтральный элемент группы G, a gn . . ., g( -
представители всех остальных классов сопряженность
Положим Lt — С (gt). Ввиду теоремы 22, получаем
| К (gi) I I ц I =
Отсюда | L{ | --= р\ где О k-t к, а значит,
I К (gt) | =
Если к = kf для некоторого i, то | Lt | — | G |. Отсюда
Lt =-- G, т. е. gt оказывается центральным элементом вег
нреки его выбору. Таким образом, к — kt 1 для всех о
88

Крсдстанляя группу G в виде объединения классов со-
иря51;еивости (см. теорему 21), получаем
рк - • I С j == 1 + | X (gi)| + . . . + | К (gt) | =
= 1 +	+ . . . -1- /Л',
т. с.
1 = р (р*-1 - р*-*'-1 - ... - р*-^1),
что невозможно.
У it р а ас н е п и я
1.	Доказать, что если А и В — группы, то Л X В — группа
'см. упражнение 7 из § 2), причем А \\ В изоморфны некоторым из
ее нормальных подгрупп, а факторгруппа (4 X В)! 11, где 11 —
{(а, 1) | а = А }, изоморфна группе В.
2.	Показать, что (ab)~L ~ Ь'1а~1 для любых элементов а и b
из группы. Обобщить на произведен не п элементов.
3.	Доказать, что пересечение любого множества нормальных
подгрупп является нормальной подгруппой.
4.	Доказать, что множество матриц вида ХЕ, где X — отличное
от нуля число, является нормальной подгруппой группы невырож¬
денных матриц, а подгруппа примера 6 из таблицы 3 нормальной
п с является.
5.	Доказать утверждение: если // и К — подгруппы G, содер¬
жащие т п и элементов соответственно, а числа пь и п взаимно
иросты, то II П К ~ {1}.
6.	Пусть ср: G —* G' — гомоморфизм групп, II — подгруппа
группы G, ср (II) — множество всех элементов вида ср (/г), где К <=
i= 11. Доказать а) ср (II) — подгруппа группы G'; б) если ср — на¬
ложение, а подгруппа II нормальна, то подгруппа <р (11) также нор¬
мальна; в) если 1Г — подгруппа группы G' и ср — наложение, то
существует такая подгруппа II группы G, что ср (II) ~- 1Г; г) если
11 и К — подгруппы группы G, содержащие Кег ср, то ср (Il f i К) -
- ср (II) А ф (/<).
7.	Доказать, что всякая факторгруппа и всякая подгруппа
циклической группы является циклической группой.
8.	Доказать, что группы (Z/2Z) X (Z/2Z) и Z/4Z не изоморфны.
9.	Группа G не содержит подгрупп, отличных от G и от еди¬
ничной, тогда и только тогда, когда она содержит р элементов, где
Р — простое число или 1, и, в частности, изоморфна группе выче¬
тов но модулю р.
10.	Пусть G — группа и а <= G. На множестве G определим
Новую операцию о, полагая хоу — лау. Доказать, что множество
G с этой операцией является группой и что отображение ср: G -- 6’,
где ср (./) — хаГ1, является изоморфизмом старой группы на новую.
11.	Группа G называется периодической, если для всякого t> из G
найдется натуральное число п такое, что — 1. Доказать, что для
■•побей группы G и ее нормальной подгруппы II из периодичности
групп II и G/П вытекает периодичность группы G.
12.	Пусть G — группа положительных рациональных чисел по
Умножению и II — множество всех рациональных чисел, предста¬
вимых в виде отношения двух положительных нечетных чисел.
Доказать, что II — подгруппа и что факторгруппа G/11 изоморфна
группе Z.
89

13.	Доказать, что ие существует гомоморфного наложения
группы всех рациональных чисел по сложению на группу всех це.
лых чисел.
14.	Осуществить вложение групп, указанных в упражнении 8,
в группу (g4.
15.	Пусть ср — отображение группы в группу невырои^
денных матриц порядка п, определяемое условием ср (о) = А, где
если з (i) = /,
в противном случае.
Доказать, что ср — гомоморфное вложение.
16.	Доказать, что центр группы состоит из одной тождест¬
венной подстановки, а центр группы невырожденных матриц сов-
падает с множеством матриц вида ХЕ, где X — отличное от нуля
число.
17.	Если G — группа, Z — ее центр и | G | = ph', где р -
простое число, то | Z | р.
18.	Если факторгруппа группы G по ее центру циклическая,
то G коммутативна.
§ 4. Кольца
Множество R с двумя операциями — сложением п
умножением — называется кольцом, если
(1)	R образует коммутативную группу относительно
сложения (она называется аддитивной группой кольца);
(2)	R. образует полугруппу относительно умноженья
(она называется мультипликативной полугруппой кольца);
(3)	сложение и умножение связаны дистрибутивным п
законами (а + Ь)с = ас + Ьс и а (Ъ + с) = ab + ас.
Ввиду (1), кольцо содержит нуль. Единица мульти¬
пликативной полугруппы (если она существует) назы¬
вается единицей кольца. Вместо а + ( — Ъ) обычно пишут
а — Ь. Кольцо называется коммутативным, если комму¬
тативна его мультипликативная полугруппа. Примерами
колец служат целые, четные, рациональные и действитель¬
ные числа с обычными операциями. Ввиду изложенною
в конце гл. I, кольцо образуют квадратные матрицы по¬
рядка п. В отличие от перечисленных выше, это кольцо
ие коммутативно. За исключением кольца четных чисел,
все вышеупомянутые кольца обладают единицей. Всякую
коммутативную группу А можно превратить в кольцо,
положив ab = 0 для любых а, b ЕЕ А. Это кольцо назы¬
вается кольцом с нулевым умном ением. Оно коммутативно,
по без единицы. Коммутативное кольцо образуют дейст¬
вительные функции с обычными операциями. Его едини¬
цей служит функция, тождественно равная 1.
Из определения кольца можно вывести следующие
свойства:
90

(а)	0-л — л-О О;
(б)	л ( — Ь)	(—a) b = — ab\
(в)	(л — Ь) с — ас — be, a (b — с) — ab — ас.
Действительно, учитывая свойства нуля и дистрибу¬
тивность, имеем
0-а = (0 + 0) а = Оа + Оа.
Прибавив к обеим частям —Ол, получим 0 = Ол. Анало¬
гично доказывается, что аО = 0. Далее, равенство
а b) = —ab вытекает из соотношения
ab -г а (—Ь) = а (Ь + ( — Ь)) = аО = О,
получаемого с учетом (а). Аналогично получаем, что
(~а) b = —ab. Наконец, учитывая (б) и определение
разности а — Ь, выводим
(а — Ь) с = (а + (—/?)) с = ас + ( — Ь)с =
= ас + ( — Ьс) ас — Ъс
и, аналогично,
a (b — с) — ab — ас.
Подмножество II кольца R называется подкольцом,
если оно является подгруппой его аддитивной группы и
подполугруппой его мультипликативной полугруппы.
Ясно, что подкольцо является кольцом относительно
операций, определенных в исходном кольце. В качестве
примеров можно указать кольцо четных чисел как под¬
кольцо кольца целых чисел, а последнее как подкольцо
колец рациональных и действительных чисел. Диаго¬
нальные матрицы образуют подкольцо кольца матриц.
Всякая подгруппа аддитивной группы кольца с нулевым
умножением является подкольцом.
Согласно теоремам 3 из § 2 и 1 из § 3, справедлива
Теорема 1. Пересечение любого множества подколец
является подкольцом.
Отображение ср кольца R в кольцо R' называется го¬
моморфизмом, если (р (х + у) = ср (х) + ср (у) и ср (ху) —
== ср (х) ср (у) для любых х, у ЕЕ R- Таким образом, коль¬
цевой гомоморфизм является как гомоморфизмом адди¬
тивных групп, так и гомоморфизмом мультипликативных
полугрупп. Взаимно однозначный гомоморфизм называет-
Ся изоморфизмом. Если существует изоморфизм кольца /?
11а кольцо R', то эти кольца называются изоморфными *).
*) См. примечание на с. 60.
91

В качестве примеров укажем гомоморфизмы кольца дп;^
зональных матриц второго порядка'и кольца действитель¬
ных функций в кольцо действительных чисел, определяе¬
мые условиями
(\\а °1!\
ф (||0 б|} ='а "	<7(•'»- /(’О
соответственно.
Согласно теоремам 6 из § 2 и 5 из § 3, справедлива
Т е о р е м а 2. Если ср: R —> R' — гомоморфизм ко¬
лец, то I ш <р — подкольцо кольца R.
Разбиение кольца R называется допустимым, если
оно является допустимым как для его аддитивной группы,
так и для его мультипликативной полугруппы. Другими
словами, разбиение 2 кольца R допустимо, если из того,
что одному его смежному классу принадлежат как х и
и и, так и у и v, вытекает, что в одном и том же смежном
классе лежат х + у и и -I- v и, кроме того, что в одном
смежном классе лежат ху и uv.
Разбиение множества целых чисел, описанное в при¬
мере 1 из § 2, является допустимым разбиением кольт
целых чисел, ибо приведенную там таблицу можно допол-
нить следующими столбцами:
ху
1
четное
четное
2
четное
четыое
3
четное
чет нос
4
нечетное
нечетное
Если S — допустимое разбиение кольца то па фак¬
тормножестве 7?/S определим операции
Ы + [г/1 = U + у\
и
[dfz/l = [л^г/1.
Допустимость разбиения позволяет доказать коррек!-
кость этих определений (см. с. 62). После этого нетрудно
проверить справедливость свойств (1) —(3) из опредо
леиия кольца. Таким образом, фактормножество R/У;
оказывается кольцом. Это кольцо называется фактор -
кольцом кольца R по разбиению S. Отображение, ставя¬
щее в соответствие каждому элементу из R содержащий его
92

смежный класс разбиения, оказывается кольцевым гомо¬
морфизмом. Этот гомоморфизм называется естественным.
Для рассмотренного выше допустимого разбиения кольца це¬
лых чисел факторкольцо состоит из двух элементов. Обозначив их
чет и нечет, получим следующие таблицы сложения и умножения:
чет,
нечет
• 1
чет
нечет
чет
чет
н?ч( т
чет
чет
чет
нечет
нечет
чет
нечет |
чет
неч т
Нулем этого кольца служит чет, а единицей — нечет.
Согласно теореме 7 из § 3, допустимое разбиение коль¬
ца, будучи допустимым разбиением его аддитивной груп¬
пы, является разбиением на смежные классы по некото¬
рой ее подгруппе. По какой же именно? Назовем под¬
кольцо / кольца R идеалом, если произведения хг и гх
лежат в / при любых х ЕЕ / и г ЕЕ Л. Идеалом кольца
целых чисел будет, например, кольцо четных чисел.
В кольце действительных функций идеалом является,
например, множество всех таких функций /, что / (0) =
= 0. Ответ на поставленный вопрос дает
Т е о р е м а 3. Разбиение 2 кольца R допустимо тогда
и'только тогда, когда оно является разбиением его адди¬
тивной группы по некоторому идеалу. Этот идеал оказы¬
вается смежным классом, разбиения содержащим 0.
Доказательств о. Так как идеал вследствие
коммутативности аддитивной группы кольца является
ее нормальной подгруппой, то, согласно теореме б из
§ 3, разбиение кольца па смежные классы по идеалу яв¬
ляется допустимым разбиением его аддитивной группы.
Если как а и с, так и b и d располагаются в одном классе,
то а = с г х и b — d + у, где х и у — какие-то элементы
из идеала. Отсюда
аЬ = \с -|- x}(d + у) ~ cd + (су + xd + ху).
Так как элемент су + xd -|- ху лежит в идеале, то ab и
cd располагаются в одном смежном классе по этому идеа¬
лу. Следовательно, разбиение по идеалу оказывается до¬
пустимым разбиением и для мультипликативной полу¬
группы. Пусть теперь 2 — произвольное допустимое
Разбиение кольца R. Ввиду теоремы 7 из § 3, это разбие¬
ние является разбиением по некоторой подгруппе / ад¬
дитивной группы кольца R. Если х ЕЕ /, то х и 0 лежат
13 одном смежном классе разбиения 2. Если г ЕЕ R, то,
поскольку г лежит в одном смежном классе с самим собой,
а разбиение 2 допустимо^ хг и Or 0 попадают в один
93

смежнтчй класс разбиения S. Следовательно, хг /,
Аналогично проверяется, что гх СЕ /. Стало быть, /
идеал.
Теорема 3 показывает, что вместо того, чтобы говорить
о факторкольце кольца R по допустимому разбиение,
можно говорить о факторкольце кольца R по некоторому
идеалу. В силу теоремы 3, этот идеал совпадает со смеж¬
ным классом разбиения, содержащим 0. С другой сто¬
роны, если ср: R -> R' — гомоморфное наложение колец,
то разбиение Кег ср по той же причине определяется идеа¬
лом К, состоящим из всех прообразов нуля кольца /Г,
т. е. К= {г\г ЕЕ R, ср (г) = 0'}. Поэтому в теории колец
ядром гомоморфизма называют этот идеал и через Кег ср
обозначают именно его (ср. с. 76). Еще раз подчеркнем, что
если I — идеал, то смежный класс, определяемый эле¬
ментом г, имеет вид г + I.
Теорема 4 (теорема о гомоморфизме для колец).
Если ср: R R' — гомоморфное наложение колец, Кег ср —
идеал, являющийся ядром этого гомоморфизма, и л:
R 7?/Кег ср — естественный гомоморфизм, то сущест¬
вует изоморфизм %: R' -> 7?/Кег ср такой, что ср% = л.
Доказательство. Пусть % — групповой изо¬
морфизм, существующий в силу теоремы 8 из § 3. Ес.ли
теперь х , у' ЕЕ R', то, поскольку ср — наложение, имеем
х' = хц) и у' = z/cp, где х, у ЕЕ R. Напомним, что хп —
это смежный класс по Кег ср. Поэтому, принимая во вни¬
мание определение отображения % (см. доказательство
теоремы 7 из § 1) и учитывая, что ср и л — гомоморфизмы
колец, получаем
(Ту') х = ((ху) ср) х = (ху) п = хп-уп = х'^-у'х-
Следовательно, % — кольцевой гомоморфизм, а значит,
и кольцевой изоморфизм.
Легко проверяется, что подгруппы Zn являются
идеалами кольца целых чисел. Поэтому факторгруппа
ZIZn оказывается кольцом, которое называется кольцом
вычетов по модулю п.
Легко проверить, что если ср: R -> R' — гомоморфное
наложение колец и кольцо R коммутативно, то кольцо
R' также коммутативно. В частности, факторкольцо ком¬
мутативного кольца коммутативно. Поэтому коммутатив¬
ными оказываются все кольца вычетов.
Ненулевой элемент а некоторого кольца называется
делителем нуля, если аЪ — 0 или Ъа = 0 для некоторого
94

называется обратимым, если ab — 1 = Ьа для некоторого
Ь
Теорема 5. Обратимый элемент кольца не может
быть делителем нуля.
Д о к а з а т е л ь с т в о. Допустим, что обратимый
элемент а кольца R оказался делителем нуля. Тогда
для некоторого b ~Е R имеем ab = 1 = Ьа, а для некото¬
рого ненулевого с ЕЕ R — ас = О или са = 0. Учитывая
свойство (а), установленное в начале параграфа, полу¬
чаем с = (Ьа) с = ЬО = 0 или с = с (ab)— 0Ь— 0. Про¬
тиворечие.
Коммутативное кольцо Р называется полем, если
оно содержит единицу, отличную от нуля, и каждый
ненулевой элемент из Р обратим. В силу теоремы 5,
в поле нет делителей нуля. Отсюда и из определения
поля, в частности, вытекает, что ненулевые элементы
поля образуют коммутативную группу относительно
умножения. Примерами полей служат кольца рацио¬
нальных и действительных чисел. В дальнейшем будут
приведены и другие примеры.
Заметим еще, что все полученные ранее результаты
о матрицах и определителях над поле^м действительных
чисел остаются справедливыми для матриц и определите¬
лей над произвольным полем, ибо в соответствующих до¬
казательствах специфика поля действительных чисел ни¬
когда не использовалась. Более того, теоремы 1.3.7 и
1.3.8 остаются справедливыми для матриц с элементами из
любого кольца. Как и выше, доказательства остаются
прежними.
Теорема 6. Кольцо вычетов по модулю п является
полем тогда и только тогда, когда п — простое число.
Доказательство. Пусть R — кольцо вычетов
по модулю п. Допустим, что R — поле. Если п не является
простым, то п = kl, где 0 <С k, I <С п. Тогда классы [А] и
1Л отличны от нуля. Но [7Д [Z] = [л] = [0]. Следовательно,
— делитель нуля, что невозможно, поскольку R —
поле. Предположим теперь, что п — простое число. Если
'^'1 ¥= [0], то 0 < к < ft. Поскольку п делится лишь
1 и па ft, то н.о.д. (к, п) = 1. Следовательно, найдут¬
ся такие целые числа и и v, что ик + vn = 1 (см. приме¬
чание на с. 80). Отсюда
[и] [7с] = [п7с] 4- [0] = [н7Д + [vn] = [ик + vn] — [1 ],
е. все ненулевые элементы из R обратимы.
95

Пусть Р — поле. Положительное число р-называется
характеристикой поля Р, если 1 4- ... 4-- 1 — 0 и никакое
/’ раз
положительное число, меньшее р, этим свойством не обла¬
дает. Если указанное свойство не имеет места ни для ка¬
кого положительного числа, то говорят, что ноле имеет
характеристику 0. Полем характеристики нуль .являет¬
ся, например, поле действительных чисел. Характеристику
р, где р — простое число, имеет поле вычетов п.о модулю р,
Имеет место
Теорема 7. X арактеристикой поля может быть
только 0 или простое число.
Д о к а з а те л ь с т в о. Если п — kl, г де 1 <С k,
I <Zn, является характеристикой поля Р, то а = 1 * . . . 4 1
V раз
и Ъ~ 1 -|- . . .	1 отличны от пуля. Однако ab
/ раз
—- 1 I . . . -Н 1=0, что противоречит отсутствию в поле
п XI раз
делителей нуля.
Теорема 8. Всякое коммутативное кольцо с еди¬
ницей и без делителей нуля вкладывается в поле.
Дока з а т е л ь с т в о. Пусть R — коммутативное
кольцо с единицей без делителей нуля. Обозначим через О
множество всех символов-^- , где а, b ЕЕ R, причем
Положим
Убедимся, что подмножества
множества Q. Поскольку ЕЕ
образуют разбиение
, для этого достаточна'
и,
г
г
//
установить, что два таких множества, имеющие общин
элемент, совпадают. Чтобы это доказать, допустим, чт >
Нт
Нт
, то ау — Ьх. Докажем, что су = dx. Действо-
тельпо,
(7ж) (су — dx) — bduy — vdya = avdy — vdya = 0.
Поскольку в R нет делителей нуля и Ъ, и =/= 0, отсюда
вытекает, что су — dx = 0. Следовательно, су = dx, т. с.

['т] ‘ Таким образом, -1- | cz |	| . Обратнее
включение доказывается аналогично. Обозначим полу¬
ченное разбиение через 2 и рассмотрим фактормн -
я<ество Q/'Z. Определим па нем операции 4- и • , полагчя
а | | Г с |	[ (}(^ ~1--	|
т I	I J
и
Г а I Г с I	[ а': I
| ~ Г I T J	\~bd I
Ввиду отсутствия в /-? делителей нуля, правые части этих
равенств имеют смысл. Убедимся, что определения кор-
ректны. Допустим, что [-£-] = [v] и ["г] = И •
Надо убедиться, что
НП-гН-НН-]-
Но, по условию, av — Ъи и cz — dw. Отсюда
(bd) (uz + wv) — bduz + bdwv =
= advz + bczv (uz) (ad -|- be)
u
(ac) (uz) — budw ~ (bd) (uw),
ЧТЭ и требовалось. После этого легко убедиться, что
умножение ассоциативно и коммутативно, а сложение
коммутативно. Ассоциативность сложения вытекает из
равенств
([т] +	+
	 Г ad с -|- bcu -|- bdu 3
|_	bdu	]
И
bdv
]■
из равенств
И
ab — ab
62
4 Л. а. Скорняков
и
97

выводим, что — коммутативная группа относительно
сложения. Кроме того, имеем
/ Г а 1	. Г с 1 \ Г и “I Г (ad + be) и “| Г (ad + be) uv "I
UvJ	[—wv—J = L——J
Следовательно, — кольцо. Заметим, что второй закон
дистрибутивности легко вывести из первого, поскольку
умножение коммутативно. Кроме того,
К] [т] = Н].
т. е.	~* единица кольца QI1L. Если	#= ["Т"] »
то а Ф 0. Следовательно,	ЕЕ <2/2. Но	[“4"]
=	• Значит, — поле. Определим отображение <р;
R-+Q/S, положив <2ф —	• Поскольку	= [~г]
влечет а = Ь, это отображение является вложением,
а из равенств
(a -J- 6)ср= [-а-у-~] = [-р] + [-р] =а<Р + Ь<Р
(ай)ср = [-у-] =	[-J-J = аср• &ср
вытекает, что ср — гомоморфизм. Следовательно, ср осу¬
ществляет гомоморфное вложение кольца R в поле (?/2,
что и требовалось.
Построим еще одно поле. Пусть С — множество мат¬
риц вида
|| а — & ||
|| b а ||
над полем действительных чисел. Из равенств
|| а	—	b	||	|| с	—	d	||	||	а с	— (b -р d)	||
|| b	а	||	'	Ц d	с	||	||	b	-р d	а -|- с	||
II
|| а	•—	Ь	||||	с	—	d ||	||	ас —	bd —	(ad -|- be)	|]
|| b	а	|| ||	d	с ||	||	ad	be	ас — bd	||
98

ридно, что С — подкольцо кольца матриц второго порядка,
ибо
II 0
II 0
и
Хотя само кольцо матриц не
оказывается коммутативным,
II с
— d || || а — b
с II 6 а
са — db
da 4~ cb
коммутативно, подкольцо О
поскольку
— (da 4- cb) II
си — db ||
II а
HI Ь
— b
а || || d
с
— d
с
ТО
Более того, Е ЕЕ С, и если
|| а — b
II b а
а2 + Ъ2 ф 0 и
II	II0	0II
Г о	о ’
а
ь
a* -I- bi
а2 4-
b
а
— а3 + 62
а2 4- Ь'2
II 1
II 0
т. е. каждый ненулевой элемент из С обратим, причем об¬
ратный элемент также лежит в С. Таким образом, С ока¬
зывается полем, которое называется полем комплексных
чисел. Матрицы, входящие в поле С, будем называть
комплексными числами. Поле действительных чисел вкла¬
дывается в поле С с помощью гомоморфного вложения <р,
где
II а
Ф (я) = о
о II
Г I
я || •
Чтобы получить традиционную запись комплексных
чисел, условимся отождествлять комплексное число
II а 0 II
л с действительным числом а и положим
II и а ||
II 0 ~ 1 II
Тогда
li — .1	0 1!
II ь
0 II
II 0
-1
о _1 h
=-i,
Но
b
1
0
11°
Ь О II
и,, следовательно,
а
b
- b II
|| = а bi.
а
Г
99

Если z а -|- bi — комплексное число, то комплекс,
вое число F а — bi называется сопряженным с г
11епосредственньш подсчетом проверяется
Т е о р е ма 9. Отображение <р: С -> С, где <р (z)
~ z,— изоморфизм, и z = z тогда и только тогда, когда
z — действительное число.
Еслиг - а г bi — комплексное число, то zz = а2 4 &
и, следовательно, является неотрицательным действитель
ным числом. Число [ z | = р zz назовем нормой комю
лексного числа z (не путать с обозначениями определителя
матрицы и числа элементов множества) *).
Норма обладает следующими свойствами:
(1)	| и |	0 тогда и только тогда, когда и = 0;
(2)	| ни | - | и | I и |;
(3)	| и -\- и | < | и. | 4- I v |.
Действительно, пусть и = а 4- bi и v = с 4~ di. Свой¬
ство (1) очевидно. Свойство (2) вытекает из соотношений
| ио Г2 = (ас - bd)2 + (ad 4- be)2 =
-- а2с2 — 2abcd 4~ b2d2 + a2d2 4~ 2abcd 4- b2c2 =
---- (a2 + b2) (c2 + d2) = \u |2 \v |\
Для проверки	неравенства	(3)	заметим, что
(I и | 4-	I и |)2	— | и 4- и Г2	=	| и Г2 +	| и I2 4- 2 | и 11 v | -
— (и	и) (и	v) — ий 4-	ио	+ 2 | и	| | v | — ий — w —
— (ио 4- йи)	=	2 | и | |	v | — (ио + йо). (*)
Далее,
uv + йо (а 4~ bi) (с — di) -|- (а — bi) (с + di) =
-■= ас 4- bd 4- (be — ad)i 4~ ас 4- bd — (be — ad)i --
- 2 (ас 4- 'О
и, следовательно,
(2 | и | | о |)2 — (ио 4- йп)2 — Аийио — 4 (ас + bd)2 —
- 4 ((а2 4- Ь2) (с2 4- d2) - (ас 4- bd)2) -
= 4 (а2с2 4~ Ь2с2 4- a2d2 4- b2d2 — а2с2 — 2abcd — b2d2) -
= 4 (a2d2 4- b2c2 — 2abcd) ~ 4 (ad — be)2 0-
Поскольку 2 | и | | v |	0, отсюда вытекает, что
2	| и | I и | uo 4- йи.
*) Вместо «норма» часто говорят «модуль» или «абсолютная ; "
личина».
100

Используя (*), получаем
(I W | + I г I)2 — I и + V Г' > и,.
чТ0 доказывает неравенство (3).
Кольцо с единицей, отличной от пуля, называется те-
лОм, если каждый его ненулевой элемент обратим. Ком¬
мутативные тела — это в точности поля. Для построения
примера некоммутативного тела рассмотрим множество К
Бсех матриц вида
II U V II
II — v й И
над полем комплексных чисел. Как и выше, легко про¬
веряется, что К — подкольцо кольца матриц. Оно не
коммутативно, поскольку,	ввиду I	= —	К	имеем
II 1	° 11'1 ° 1 II II 0 _1 II	II 0	1 II II	0	1 1111 1	0 II
II о — i 11II i О II II 1 О II	II —1	О И ~ II	I	о ИII 0	— И ■
Однако Е ЕК,и если и =	а + Ы	и и —	с	+ di, то	ий +
+ vv = а2 + Ь2 + с2 + d2 — неотрицательное действи¬
тельное число. Поэтому
II и v II II 0 0II
II — V й р II О ОII
влечет за собой ии	w	0.
Следовательно,
имеем
и
и
II u Ml
ии,	ub	ии -|- VV
1 1 0 II
II — v а II
V
и
II 0 1 11
ии	VV	ии -}- VV
и
и
ий 4
- vv	ий	vv
II “ ч
V
и
II — V и || ’
ий
- vv	ий -|- vv
т. е. каждая ненулевая матрица из К обладает обратной,
принадлежащей К. Таким образом, К оказывается телом.
Оно называется телом кватернионов, а его элементы —
кватернионами.
Нетрудно проверить, что отображение
II а II
^(«>=||о ah
где а — действительное число, является гомоморфным
вложением поля действительных чисел в тело кватернио-
101

|| а 0 ||
нов. Отождествляя ас L и полагая
|| и а ||
11 i О ||	’ || 0 1 || II 0 Ч
i==||o —i||’	= jj — 1 О II’ Л==||/ о ||’
получаем следующую таблицу умножения:
•
1
i
3
к
1
1
1
3
к
г
i
-1
к
-з
j
3
— к
— 1
i
к
к
3
— i
-1
Если а — действительное число, то а = а. Поэтому
|| ib и || || аи av ||
а у — v й || || — av ай || ’
и, следовательно, если и = а + bi, а и = с di, то
Il и v II
_	_ = а + bi + с j 4- dk.
|| — v а ||	1	| t/ I
Кольцо R с единицей, отличной от нуля, называется
простым, если оно не содержит идеалов, отличных от
О и R. Легко проверить, что поле (и даже тело) является
простым кольцом. Более того, справедлива
Теорема 10. Кольцо матриц над телом простое.
Доказательство. Пусть R — кольцо матриц
порядка п над телом D. Обозначим через аЕц матрицу,
у которой на месте (Z, /) стоит элемент а, а на остальных
местах — нули. Непосредственным подсчетом прове¬
ряется, что
[(аЬ)Еи, если i = k,
аЕ^ЬЕк1=\ ’	(*)
3	[	0, если у /£,	v
и что для любой матрицы В имеем
(**)
4	7
Пусть I — ненулевой идеал кольца R. Тогда I содержит
ненулевую матрицу А. Разумеется, apq ф 0 для некото¬
рых р и q. Учитывая (*) и (**), получаем
ЬцЕц ~ ((bijapq)E)EipAEqp
Ввиду (**) отсюда вытекает, что I содержит произволь¬
ную матрицу В, а значит, / = R,
102

Элемент z кольца R называется центральным, если
za = az Д*у,я всех а ЕЕ R. Совокупность Z всех централь¬
ных элементов кольца называется его центром.
Теорема 11. Центр кольца является подкольцом.
Доказательство. Ясно, что О ЕЕ Z. Пусть х,
у Z, т. е. для любого а ЕЕ R имеем ха *= ах и уа ау.
Тогда
(х Ч- у)а *= ха + уа ах + ау — а (х + У),
(—х)а	—ха	—ах	а (—х)
и
Оу)а = х(уа) = х(ау) = (ха)у — (ах)у а(ху).
Следовательно, х + у ее Z, — хЕ^ и ал/ Z, значит^
Z — подкольцо.
Теорема 12. Центр Z кольца матриц над полем
Р совпадает с множеством матриц вида КЕ, где X ЕЕ Р.
Доказательств о. Для любой матрицы А в
силу формул, приведенных в конце § 3 гл. I, имеем
(ХЕ)Л - Е(ХЛ) — (ХЛ) ЦА)Е = А ЦЕ),
т. е. ХЕ ЕЕ Z. Допустим теперь, что Л ЕЕ Z. Используя
обозначения и формулы, рассмотренные при доказа¬
тельстве теоремы 10, имеем
0 . .
0
0
ail ••
• aii
••• ain
0
0 .
... о
= AEa
= auEu
Отсюда
<ht -
. . . — a
е.
+ • • • Ч~ —
всех Z, т.
Условии
1-1 i ^i+lj ’
= ^иЕц 4- . . . 4~ а
in?
7. — 17
-"in -1—	11
Л =
0
‘ • • aLi
0
0
••• aii
0
0
••• ani
0
flm = 0
для
матрица Л диагональная. Поскольку при этом
—3	=Pij(^\dkiEki) = ЕиА —
z	k,l
АЕц ~ (^akiEi;i) Ejj = ^flktEkj (t'iiEц
k,l	k
Для любых i и Д to au = ?	ann ~ Xx т, e. A — XE.
ao.3

У is р а ж к е it и
1.	Пусть /? Li /?' — кольца. Па множестве В X И' (см. упраж¬
нение 7 из § 2) он ределим операции
(г, г') -|- ($, Л-') = (г + 5, г' + s')
И
(г, r')(x, s') --- (гл*, r's').
Доказать, что В х /?' становится кольцом, кольца В и В' изоморф¬
ны некоторым идеалам этого кольца, а факторкольцо (В X В')/!>
где /	{(г, 0) | г е /?}, изоморфно кольцу В'.
2.	Доказать, что пересечение любого множества идеалов неко¬
торого кольца также является идеалом этого кольца.
3.	Доказать, что делителями нуля в кольце матриц над полем
являются матрицы с нулевым определителем и только они. Вывести
отсюда, что в кольце матриц всякий нецелитель нуля обратим.
4.	/(оказать, что в кольце функций всякий нецелитель нуля
обратим.
5.	Найти все делители нуля кольца В X В' из упражнения 1
для случая, когда В и В' — поля.
6.	Если идеал / кольца В содержит обратимый элемент
частности, если 1 е /), то I = В.
7.	Пусть Z?, I и II — множества всех матриц вида
а b с
0 g h\\
0	1 2т
0 d е
0 0 27с и
0	0 2п
0 0 /
0 0 о И
ООО
/, g, h, к, I,
с, d,
т,
е,
соответственно, где а, Ь,
г-
в
п — целые числа.
Доказать, что В — кольцо, / — идеал кольца/?, II — идеал коль¬
ца /, но 11 не является идеалом кольца В, являясь, однако, его
левым идеалом (см. с. 107).
8.	Доказать, что коммутативное кольцо с единицей, отличной
от нуля, не имеющее идеалов, отличных от нуля и всего кольца, яв¬
ляется полем. Показать, что нельзя отказаться от требования суще¬
ствования единицы.
9.	Кольцо В называется ниль-колъцом, если для всякого эле¬
мента ос из В найдется такое натуральное число п, что хп~ *
Пусть В — некоторое кольцо, I — его идеал такой, что кольцо
и факторкольцо В/1 являются нпль-кольцами. Доказать, что В
та кже пил ь-кол ьцо.
10.	Какие теоремы из гл. I остаются справедливыми для ма
риц с элементами из произвольного коммутативного кольца и,
частности, из кольца целых чисел?
II z 0 '1
И. Доказать, что, полагая ср (z) ~ I — I , мы получаем гом<
II0 z II
морфное вложение поля комплексных чисел в тело кватернионе
12.	Доказать, что матрицы вида II а , где а и b — рацн<;-
II 2Ъ а\\
нальные числа, образуют поле, изоморфное полю, образованному
действительными числами вида а -|-	где а и Ь — рациональные
числа.
104

13.	Тело кватернионов изоморфно кольцу, состоя тему из всех
матриц вида
..J	а "Ь с d
b a —d с
~-с d а b
— d —с — Ъ а
над полем действительных чисел.
14.	Доказать, что центр кольца матриц над телом D совпадает
с множеством всех матриц вида КЕ, где л принадлежит центру
тела D.
15.	Если I — идеал кольца матриц над кольцом /?, то найдет¬
ся такой идеал U кольца R, что I совпадает с множеством всех мат¬
риц, элементы которых принадлежат U.
§ 5. Модули
Правым модулем над кольцом R с единицей или пра¬
вым R-модулем называется коммутативная группа М, для
которой определены произведения ar ЕЕ М для любых
а GE М и / ’ GE 77, причем
(1)	(а -1- Ь)г =- аг + Ьг,}
(2)	a(r + s) = ar + asr
(3)	a(r.s) = (ar)s,
(4)	al — а
для любых а, b ЕЕ Л7 и г, s ЕЕ R. Подчеркнем, что сим¬
вол + в левой и правой частях равенства (2) имеет
различный смысл: слева он означает сложение элемен¬
тов кольца 77, а справа — сложение элементов группы М.
Различный смысл имеет также подразумеваемый в форму-
! ле (3) символ умножения: rs означает произведение эле¬
ментов кольца 7?, a ar, (ar)s и a(rs) — произведение эле¬
мента из группы М на элемент кольца 77. Примеры пра¬
вых модулей приведены в таблице 4. Элементы модуля для
краткости условимся называть векторами (ср. § 1 гл. III).
Аналогично определяются левые модули, где произведе¬
ние записывав гея как га. Если кольцо 77 коммутативно, то
разницы между правыми и левыми модулями нет. Дей¬
ствительно, пусть Л/ — правый модуль над коммутатив¬
ным кольцом 77. Если г F- R и яЕЕЛ/, то положим г о а
аг. Тогда
г?(а + b) — (а -|- Ь)г	аг + Ьг = г* а г^Ъ,
(г s)°a = а(г + *') — ar + as — r^a + s^a,
(rs)ca = a(rs) ~ a(sr) = (as) г — г о (so a)
i 05..

Таблица
a
К
СП
2
S
' II
II
QJ
S
и
Оч
ф
ф
ф
С
—
ГС
ГС
Оч
—
о>
1 й
ф
ф
о
ф
до a
1
те
со
«
те
ь
о
1
3
1 а
S
о
о
о
1
а
а
Е-
CD
ф
У до
С
С
cS
c
к
p*»
a
'th C>1 CQ
•<f LQ
Г- ОС
106

И
lea = ai = а
для любых a, b ЕЕ М и г, s ЕЕ R, т- е. М оказывается ле¬
вым Л-модулем. Подчеркнем, что коммутативность кольца
ft использована лишь при доказательстве третьего равен¬
ства (ср. замечание на с. 112 — ИЗ).
Рассуждениями, аналогичными проводившимся на
с. 91 для колец, устанавливается справедливость следу¬
ющих свойств:
(а)	аО = Or = О,
(б)	(—а)г — а(—г) — — аг,
(в)	(а — b)r = ar — br, a(r — s) =* ат — as,
где cl, Ъ ЕЕ Мч Е s (ЕЕ R>
Заметим, что символ 0 в формуле (а) обозначает как
нуль кольца R, так и нуль группы М. Точно так же
в различных смыслах в формулах (б) и (в) используется
символ —.
Подмножество N правого модуля М над кольцом R
называется подмодулем, если a, Ъ ЕЕ N влечет а + Ъ ЕЕ 1V
и ar ЕЕ N для всех г ЕЕ R.
Подгруппа Н аддитивной группы кольца R называет¬
ся правым идеалом, если ar ЕЕ Н для любых а ЕЕ Н и
г Ez R. Другими словами, правый идеал — это подмодуль
правого /?-модуля R. Левый идеал определяется анало¬
гично. Правый идеал кольца матриц образуют, например,
матрицы, у которых все строки, кроме первой, нулевые
(см. пример 6 в таблице 4). Идеал — это правый идеал,
одновременно являющийся и левым. Поэтому его часто
называют двусторонним идеалом.
Аналогично теоремам 3 из § 2, 1 из § 3 и 1 из § 4 доказы¬
вается
Теорема 1. Пересечение любого множества под¬
модулей л вл лет с я подмодулем.
Если М — правый Л-модуль, то выражение вида
а1г1 + . . . + С1тГmi
вде at ЕЕ М и rt Ez R, будем называть линейной комбина¬
цией векторов а±,. . ., ат. Если все гг- = 0, то линейная
Комбинация называется тривиальной. Если вектор равен
линейной комбинации векторов ах,. . ., ат, то гово¬
рят, что он выражается через систему ЭД = {<21?. . ., ат}.
Например, в модуле 3-мерных строк (пример 2 из таб¬
лицы 4) каждый вектор выражается через систему {(1,0, 0),
107

Если систем^ ЭД
[О, 1, О), (О, О, 1)}, а в модуле примера 4 из той же
(||1 ОII || О — 1 '
таблицы 4 — через систему^ t , || t Q
бесконечна, то выражаемость элемента через систему ЭД
определяется как его выражаемость через некоторую ко¬
нечную подсистему системы ЭД. Если каждый вектор си¬
стемы ЭД выражается через систему ЭД', то скажем, что
счстема ЭД выражается через систему ЭД'.
Теорема 2 (о транзитивности линейной выражай-
мости). Если система ЭД выражается через систему ЭД ,
а система ЭД' — через систему ЭД", то система ЭД выража¬
ется через систему ЭД".
Доказательство. Если а ЕЕ ЭД, то а — У,
где а\. ЕЕ ЭД', rt ЕЕ Ii, ибо ЭД выражается через ЭД'. Пэ
а, —	где а} ЕЕ ЭД", ЕЕ /?, поскольку ЭД' выра-
жается через ЭД". Отсюда
а = X (2	/у = 3 aj (3 G/i) >
I j	)	I
т. e. а выражается через ЭД".	'
Если ЭД — некоторая система векторов, то обозначим
через 5Z (ЭД) и назовем линейной оболочкой системы ЭД
множество всех векторов, выражающихся через систему ЭД.
Линейную оболочку системы, состоящей из одного векто¬
ра а, будем обозначать также через aR.
Т е о р е м а 3. Линейная оболочка любой системы
(екторов ЭД является подмодулем.
Доказательство. Если «,ЬеЖ (ЭД), то а -;
b =	где at ЕЕ ЭД, г,, St ЕЕ Ft. Отсюда
г	i
а 1>	(П + s.)
И
ar = '£1al (rjr)
для любого г Ft, что и требовалось.
Теорема 4. Линейная оболочка системы векто¬
ров ЭД совпадает с пересечением всех подмодулей, содерг
жащих ЭД.
Доказательство. Пусть U — пересечение,
указанное в формулировке. Поскольку ЭДcz U, то 2ДЭД)СЕ
се U по определению подмодуля. С другой стороны, ввиду
теоремы 3, X (ЭД) — один из подмодулей, содержащих ЭД,
и, следовательно, U се X (ЭД),
108

Отображение ср правого модуля М над кольцом R
я правый модуль Л/' над тем же кольцом называется
гомоморфизмом, если
Ф (а + Ь) = (р (а) + (р (6)
и
<р (аг) = (р (а)г
для любых a, Ъ ЕЕ М и г ЕЕ R. Взаимно однозначный го¬
моморфизм называется изоморфизмом. Если существует
изоморфизм модуля М на модуль М', то эти модули назы¬
ваются изоморфными*).
В качестве примеров гомоморфизма модулей укажем отобра¬
жения:
а)	множества матриц порядка п над произвольным полем в мно¬
жество «-мерных строк, где
ср (Д)	- (яп, . . ., а]п);
б)	множества матриц порядка 2 в множество четырехмерных
строк, где
41“ dll)=i(e’6’c’d,;
в)	множества «-мерных строк над полем Р в себя, определяем о
равенством
X (А, • • •> Лг) — (z1? . . яп) А ,
где А — некоторая фиксированная матрица порядка п над полем р.
Изоморфизмом оказывается гомоморфизм ф. Гомоморфизм /
является изоморфизмом тогда и только тогда, когда матрица А но¬
вы рождена (см. упражнение 4 из § 1).
Аналогично теоремам 6 из § 2, 5 из § 3 и 2 из § 4 доказы¬
вается
Теорема 5. Если ср — гомоморфизм правого i
модуля М в правый R-модуль М', то Im ср — подмодули
модуля М'.
Разбиение S правого модуля М над кольцом R на¬
зывается допустимым, если оно является допустимым
разбиением группы М и из того, что векторы а и b из
М принадлежат одному смежному классу разбиения
вытекает, что для любого г Е- R векторы аг п Ъг также ле¬
жат в одном смежном классе. Если 2 — допустимое раз¬
биение модуля 717, то на фактормножестве A//S определим
операции
[а] + [61 ~ 1а 6]
в [п|г - [цг] (а. Ъс=_М, г ЕЕ R).
*) См. примечание па с. 60.

Допустимость разбиения позволяет доказать коррект-
ность этих определений (см. с. 62). После этого нетрудно
проверить, что фактормножество оказывается коммута¬
тивной группой относительно сложения и что справед¬
ливы свойства (1) —(4) из определения модуля. Таким об¬
разом, фактормножество Л/72 становится правым /2-моду¬
лем, который называется фактормодулем модуля М ио
разбиению 2. Отображение, ставящее в соответствие каж¬
дому вектору из М содержащий его смежный класс раз¬
биения 2, оказывается модульным гомоморфизмом. Этот
гомоморфизм называется естественным.
Теорема 6. Разбиение 2 правого модуля М над
кольцом R допустимо тогда и только тогда, когда оно
является разбиением группы М по некоторому подмодулю.
Этот подмодуль оказывается смежным классом разбие¬
ния 2, содержащим 0.
Доказательство. Допустим, что 2 — разбие¬
ние модуля М на смежные классы по некоторому под¬
модулю N. Согласно теореме 6 из § 3, 2 — допустимое
разбиение группы М. Если а и b располагаются в одном
классе разбиения 2, то а = b 4- х для некоторого х ЕЕ N.
Поэтому для1 произвольного г ЕЕ R имеем
аг == (b + x)r Ьг 4- хг.
Поскольку хг ЕЕ N, то аг и Ьг располагаются в одно й
смежном классе разбиения 2, что доказывает его дону
стимость. ' Пусть теперь X — произвольное допустимое
разбиение модуля М. Ввиду теоремы 7 из § 3, это раз¬
биение является разбиением по некоторой подгруппе /7
коммутативной группы М. Если a GE N, то из вк люден пн
а, 0,ЕЕ N и допустимости разбиения 2 вытекает, что
аг и Or = 0, где г — произвольный элемент из /2, распо¬
лагаются в одном смежном классе. Следовательно, аг ЕЕ N,
т. е. N — подмодуль модуля М.
Теорема 6 показывает, что вместо того, чтобы говорит;’
о фактормодуле модуля М по допустимому разбиению,
можно говорить о фактормодуле модуля М по некоторо¬
му подмодулю. В силу теоремы 6, этот подмодуль совпа¬
дает со смежным классом разбиения, содержащим (б
С другой стороны, если ср: М М' — гомоморфизм пра¬
вых 72-модулей, то разбиение Кег ср по той же причине
определяется подмодулем К, состоящим из всех прообра¬
зов нуля модуля АГ, т. е. К = {а| а ЕЕ М, ф (а) — ()';•
Поэтому в теории модулей ядром гомоморфизма <р назы¬
110

вают этот подмодуль и через Кег ср обозначают именно
его (ср. с. 76, 94).
Теорема 7 (теорема о гомоморфизме для модулей).
Если ср: М -+■ М' — гомоморфное наложение правых мо¬
дулей над кольцом R, Кег ср — подмодуль модуля М,
являющийся ядром этого гомоморфизма, и л: М —>•
М/Кю ср — естественный гомоморфизм, то сущест¬
вует изоморфизм М' —ТИ/Ker ср такой, что ср/ л,
Доказательство. Пусть % — групповой изо¬
морфизм из М' на ТИ/Кег ср, существующий в силу теоре¬
мы 8 из § 3. Если теперь х' ЕЕ М', то, поскольку ср — на¬
ложение, имеем х' = хер для некоторого хЕЕ М. Напом¬
ним, что а-л — это смежный класс но Кег ср. Поэтому,
принимая во внимание определение отображения % (су«
доказательство теоремы 7 из § 1), для произвольного х' ЕЕ
ЕЕ М' получаем
(.г'г)х ((ялр)г)х = (^г)срх — (хг)л = (хл)г =
Следовательно, х — модульный гомоморфизм, а значит,,
и модульный изоморфизм.
Теорема 8. Множество Hom (М, М') всех гомо¬
морфизмов правого R-модуля М в правый R-модуль М'
становится коммутативной группой, если для ф, ф ЕЕ
E Hom (М, М') положить
х (ср + ф) = хер + яф
для всех х ЕЕ М.
Доказательство. Равенства
(я + У) (ф + Ф) = (^ + У)Ч> + (^ + */)ф =
— х(р + у<р + яф + г/ф = х<р + хф + г/Ф + г/ф =
= х (ф + ф) + у (ф + ф)
и
(хг)(ф + ф) = (хг)ф + (гсг)ф = (xq)r + (#ф)г =
= (яф + гсф)г = (х (ф + ф))г,
где х, у СЕ М и г G Я, показывают, что ф 4- ф ЕЕ
ЕЕ Hom (М, М'). Отображение 0, переводящее все век¬
торы из L в 0, очевидно, лежит в Hom (М, М'), и
ср + О = О + ф = ф
Для всех ф ЕЕ Нот (М, М'). Положив х (—ф) = —хф
Д'ля всех х ЕЕ М, как и выше, убеждаемся, что ( — ф) ЕЕ
Нот (М, М'), При этом ф + (—ф) = 0, поскольку
х (ф 'Г (—ф)) — х<р 4- (—Х<р) == О
ш

д 1я всех х Е М. Из равенств
х ((<р -I- ф) х) х (<р + ф) + %Х = ^'Ф + ГФ + Х’Х =
— ;/ (р + X (q) + х) = X (ф + (ф + х))
П
х ((р А- Ф) ГФ 0~ ^‘Ф "=	= х + ф)’
справедливых для всех х ЕЕ М и любых ф, ф, X г
Е Пот (А/, А/'), вытекает, что Hom (Af, М') является
к о м м у т а т и в 11 о й г р у п п о й.
Теорем а 9. Если М — правый R-модулъ, т ■>
Пот (Af, М) — кольцо с единицей, где сложение определи-
но в теореме 8, а умножение — в начале § 1 *).
Д о к а з а т е л ь с т в о. Ввиду теоремы	8,
Пот (А/, М) — коммутативная группа. Если ф, ф Е-
СЕ Hom (М, А/), то для любых a, b Е М и г Е R имеем
(а + Ь) (фф) = ((« А- b)q) ф = (тр + 6ф)Ф =
= (mp) ф A- (МФ = а (фф) + b (фф;
п
(М (фФ) = (М ф)Ф = ((М ОФ = ((М Ф) г = (« (фФ)) '■
Следовательно, фф Е Hom (М, М), т. е Hom (М, М>
является полугруппой по умножению (см. теорему С
из § 1). Поскольку для любых х Е М и ф, ф, х GJ
Е Нот (А/, М) имеет место
х ((ф + Ф)х) = О (<р + '1’))х = (w + М) х =
= U<P)X + (М)х = X (фх) + х (ipx) = х (фх + 4>х)
и
X (ф (ф + х)) = (ЛР) (Ф + х) = е<р)ф + (лр)Х =
= * (ф'Р) + х (фх) = х (фф + фх),
Hom (М, М) оказывается кольцом. Единицей этого кольца
является тождественное отображение 1М.
Пусть М — правый 2?-модуль. Его аддитивную группу можно
рассматривать как модуль над кольцом целых чисел (см. пример 3
из таблицы 4), и теорема 9 позволяет говорить о кольце эндомор
физмов этой группы, которое, в отличие от Hom (М, М), будем
обозначать через Hom^ (М, М). Рассмотрим отображение Ф: В —»
Ilomz (М, А/), где хФ (г) = хг для любых х <= М и г <=: В.
Равенство
(х + у)Ф (г) = (х А- у) г = хг уг = х Ф (г) + г/Ф (г)
*) Гомоморфизмы модуля М в себя обычно называются эндо¬
морфизмами. Поэтому кольцо Hom (М, М) называется кольцом
эндоморфизмов модуля М. Аналогичная терминология использует-
«я для групп, полугрупп, колец и др.
112

доказывает, что Ф (г) действительно лежит в ftoinz (М, М). Из ра-
В ‘ЯСТВ
лФ (/■ + 5) ~ х (r “I" #) ~~ тг -|- ху --- .гФ (г) -|- гФ (.у) '
== х (Ф (г) |- ф (у))
П
а?Ф (rs) — х (rs) — (xr) s ~ (x Ф (г))Ф (s) ~ x (Ф (г)Ф (s)),
r i.0 x ge M, r, s ее 77, вытекает, что Ф — гомоморфизм колец. Заме-
тдм, что если G — произвольная коммутативная группа и Ф —
г моморфизм кольца R в кольцо Homz(G, G), то, полагая хг .тФ(г)
ля любых ,т Е G и г<= R, мы, как легко проверить, превращаем
Ь в правый 7?-модуль. Тем самым установленгг тесная связь между
правыми 77-модулями и гомоморфизмами кольца 77 в кольца эндо¬
морфизмов коммутативных групп. Если 37 — левый 77-модуль, то
можно определить гомоморфизм Ч7 аддитивной группы кольпа 77. в
аддитивную группу кольца Honiz (Л/, Л/), положив гЧ7 (г) гх
для любых х е М и г ее R. Но тогда
тЧ7 (Z'S) - (rs) X = г (sx) - (.г Ч7 (s))47 (г) - ,г(Ч7 (.у) Ч7 (г)),
откуда
Ч7 (rs) - Ч7 (.у) Ч7 (г).
Следовательно, если кольцо 7? не коммутативно, то отображение Ч7
по является гомоморфизмом колец. Однако можно проверить, что
это отображение Ч7 станет кольцевым гомоморфизмом, если исполь¬
зовать другое определение произведения отображений (см. приме¬
чание на с. 48). Действительно,
Ч7 (rs)(x) = (rs) х = г (sx) = Ч7 (г)(Ч7 (s)(.r)) - (Ч7 (г) Ч7 (s))(x)
для любых х е М и г, ss77. Разумеется, если кольцо R комму¬
тативно, то отображение Ч7 оказывается гомоморфимом колец, и
никаких затруднений не возникает. Тем самым еще раз показано,
что для коммутативного кольца разницы между правыми и левыми
модулями нет.
Теорема 10. Правый R-модулъ М является правым
модулем над кольцом Нот (71/, 71/), если произведенье
«ср, где а ЕЕ М, ср ЕЕ Нот (Л/, 71/), определить как образ
элемета а при отображении ср.
Доказательство. Поскольку М — коммута¬
тивная группа по сложению, справедливость теоремы вы¬
текает из равенств
(« + Ь) ср = «ср + d(p,j
а (ф + Ф) = а(Р + «ф
а (<рф) = (а<р)ф
и
а 1м = а,
а и b — произвольные элементы из 7И, а ф и ф —
произвольные отображения из Нот (71/, М). Сами же
эти равенства непосредственно следуют из определений.
113

Суммой подмодулей назовем линейную оболочку их
теоретико-множественного объединения. Сумму подмоду¬
лей Sn. . Sm будем обозначать через Sx + . . . + Sn].
Теорема И. Подмодуль Sr + . . . + Sm совпадает,
с множеством векторов, представимых в виде sr © . . .
. . . + stn, где st ЕЕ Si.
Доказательство. Пусть S — Sx +	...
. . . + Sm и S' — множество, упоминаемое в формулировке.
Ясно2 что S' — подмодуль и что
S' ст ж (Sx и ... U Sm) - S.
С другой стороны, поскольку Si (J ... [J Sm ст: S', то
согласно теореме 4 имеем S т S'.
Сумма St + . . . + Sm называется прямой суммой,
если каждое слагаемое имеет нулевое пересечение с сум¬
мой остальных, т. е.
(Sx + . . . + Si-! 4- Si}.i + . . . + Srn) n Si = о
для каждого i. Прямую сумму подмодулей Slv . ., Sm
условимся обозначать через
Ввиду теоремы 11 сумма и, в частности, прямая сумма
не зависят от порядка слагаемых.
Теорема 12. Пусть S = Sj + . . . + Sm. Тогда
эквивалентны следующие свойства:
(1)	S - sx © ... Э sm;
(2)	(Sx + . . . + SO n SiKL = 0 при i - 1,	2,. . .
. . ., n — 1;
(3)	каждый вектор s из S единственным способом пред¬
ставляется в форме
S	Sx + . . . © Sm,-
где St GE S ;
(4)	если Si tE Si и
Si ® ... ® sm — 0,j
mo Si — О для всех i.
Доказательство. (1) => (2) тривиально.
(2)	=> (3). Допустим, что
sx © . . . © sm ?= sj + . . . © s'm,
где Si, s',; EE Si. Если sz © s'L для некоторого i, то среди
таких номеров I выберем наибольший. Тогда Sj ~ sj
114

при 7 > * и
$/—	— ($1 — $1) + • ♦ • + (Si-1 — si-l) £=
П (‘S’l + • . . 4-
Ввиду (2), s'i — st — 0, t. e. st — s[ вопреки допущению.
(3)	=? (4). Достаточно заметить, что 0 — 0 + . . . + 0,
где 0 ЕЕ Sj.
(4)	==> (1). Предположим, что
О #= я ЕЕ Sj П (51 + . . . +	+ S+ . . . +5m),j
т. е.
Z ~ 5] + . . . +	+ 5И1 + . . . + Smi
где sk Sk. Отсюда
$1 + . . . +	+ (— х) +	. + Sm — О
и, следовательно, х = 0 ввиду (4). Противоречие.
Следствие. Сумма S + Т двух подмодулей яв¬
ляется прямой тогда и только тогда, когда S р| Т — 0.
Теорема 13 (о транзитивности разложения в пря-
мую сумму). Пусть S — 5Г © .
ма. Тогда
• • © Sm
— прямая сум
5 = (5хф. ..©Фф©
(© © • • •
© Sm)
для каждого i, и если
S - 5i © . . .
© sm
и
Sr = stl® . . .
© Siki
для каждого i, то
S == Л 11 (4 • • • ф ^l/f, © 5-21 ® • • • (
В ^2/,-, © .
• • © 5 mi © , . .
• • • Ф Smi,m,
Доказательство. Допустим, что
X ЕЕ (S, + . . . + 5,_т) п (5, + . . . + 5Ш),
Тогда для подходящих sk Е имеем
х ~ S1 + • • • + 5i-l — - Si + • • • + sm ~ Si + . . .
.. . + Si»! + 0 -|- ... 4- 0 = 0	0 -|-	+ . . . sm.
nt—t4-i раз	г—1 раз
В силу свойства (3) теоремы 12 отсюда вытекает, что sk ~ 0
Для всех /с. Следовательно, ж — 0,и первое утверждение
115

доказываемой теоремы вытекает из следствия теоремы 12.
Для доказательства второго утверждения заметим, ч то
если х ЕЕ S, то s = Ч- . . . -|- sm, где sL ЕЕ Далее,
-I- ... ч- SjA-p где s}j Sij. Отсюда
S 6'п + . . . + 51/fl + Л-21 + . . . + s2kz + , , г
• • • Ч~ sml 4“ • • • +
т. е.
5 - 5П + . . . + 51/fl + 521 +	+ S21{2 + . : .
• • •- + Snil + . . . + Smkm. (*)
Если
Sjl + • . . "I" Sjfrl + $21 + . . . + S21fi + . . .
. • • + sml + . . . + $mkm — 0,
где Sij EE Sij, то, поскольку сумма Sj + . . . + Sm пря¬
мая, по свойству (4) теоремы 12 имеем
s<i + . . • +	>= 0
для каждого i. Поскольку сумма + . . . + Siki пря¬
мая, отсюда следует, что Sjj — 0 для каждого /. Таким
образом, su =--- 0 для любых i и /, и сумма (*) оказывает¬
ся прямой по свойству (4) теоремы 12.
Если N — подмодуль модуля М и ср: М М' —
1 омоморфизм модулей, то положим
ср (N) = {ср (с) I х Л}.
Легко проверить, что ср (Аг) — подмодуль модуля ЛГ.
Если N ~ Ч/, то, как легко видеть, ср (N) — 1т ср.
Т е о р е м а 14. Если ср: М М' — изоморфизм
модулей и SY ф • • • ® Sm — прямая сумма подмодулей
модуля М, то сумма ср (*$]) + . . . + ср (5т) также пря¬
мая.
Д о к а з а т е л ь с т в о. Пусть sj + . . . + s’m --- 0.
где 6-; ЕЕ ср (SJ. Тогда = ср где st ЕЕ Sh и
ср (ад + . . . 4- .Sm) —: .Si -|- . . . + sm = 0.
Отсюда лд -|- . . . -г sm г т 0 и, в силу свойства (4) теоремы
12, st : - 0 для всех I. Но тогда .ьд ~ 0 для всех г, и по топ
же теореме 12 сумма ср (5\) + . . . + ср (Sт) оказывае т¬
ся прямой.
Разлагая модуль 15 прямую сумму подмодулей, мы,
грубо говоря, представляем данный большой модуль в ви¬
де суммы маленьких. Естественна обратная задача: как
116

из данных маленьких модулей построить новый больший
модуль-
Пусть Мг, . . Мт — некоторые правые модули чад
кольцом R (не обязательно различные!). Рассмотрим мно¬
жество всех строк вида (аь . . ат), где af 71/,. Это
множество при покомпопеитиохм определении операций
превращается в правый модуль над кольцохм /?, который
называется внешней прямой суммой модулей и обозначает¬
ся Л/i Ф . . • ф М пг или 2Ф7к7ф Приводимый ниже резуль¬
тат показывает, что эти обозначения согласуются с упот-
реб л я в ш имися р а н ып е.
Т е о р е м а 15. Пусть М — внешняя прямая сумма
модулей ММт и St,i = 1, 2, . . ., ш,— множество
всех строк вида (0, . . О, а^, 0, . .	0), где at ЕЕМф Тогда
Si — подмодули модуля М, модули Mt и Sf изоморфны
для каждого i и М разлагается в прямую сумму подмоду¬
лей Sf.
Д о к а з а т е л ь с т в о. Ясно, что Si — подмодули
и что каждый из них имеет нулевое пересечение с суммой
остальных. Изоморфизм ср: Мt -> 5, можно установить,
положив ф (а) = (0, . . ., а, . . ., 0) для каждого а ЕЕ М
Наконец, равенство
• . •, am)	Э, . . ., 0/ Н
Ф (0, а2,. . ., 0) Ф . . . ф (0, 0, . . ., а„)
показывает, что М = 5,1 ф . . . ф Sm.
Т е о р е м а 16. Если М = ф . . . ф Мт, Nz —
подмодуль в М i и N t ф ... ф N т, то фактормодуль
MIN изоморфен внешней прямой сумме (MJNX) ф . . .
• • • Ф (7Иm/Nт).
Доказательство. Рассмотрим отображение
ср: М -	ф . . . ф (А/т/Аф),
определяемое условием
ф (^1 ф . . ♦ ф ^т)	(|ф1Ь • • •’
где [aj — смежный класс из фактормодуля МJNсо¬
держащий элемент at. Ввиду свойства (3) из теоремы 12,
это определение корректно. Ясно, что ф — гомоморфное
наложение. Если а = аг ф . . . ф ат и ф (а) = 0, ю
а4 ее Ni для всех i. Но тогда a^N, т. е. Кег ф cz ;V.
Ясно, что N СЕ Кег ф. Таким образом, N = Кег ф, и ис¬
комый изоморфизм вытекает из теоремы 7.
Если п = 2, Nl = 0 и N2 ■= М.,' то получаем
117

Следствие. (Мг ф М2)/М2 = Mi,
Будем говорить, что подмодуль S модуля М выделяет¬
ся прямым слагаемым, если М — S @ Н для некоторого
подмодуля Н, Из приведенного выше следствия вытекает
Теорема 17. Если подмодуль S модуля М выделя¬
ется прямым слагаемым, то М содержит подмодуль, изо¬
морфный фактормодулю M/S.
Подмодуль М модуля L называется минимальным,
если М 0 и соотношение Ocz NQ М*), где N'— подмо-
дуль модуля L, влечет за собой N = 0. В частности, пра-
вый идеал кольца R минимален, если он отличен от нуля
и не содержит ненулевых правых идеалов кольца R, от¬
личных от него самого. Модуль, являющийся своим ми¬
нимальным подмодулем, называется неприводимым. Дру¬
гими словами, неприводимым называется модуль, отлич¬
ный от нуля и не содержащий никаких подмодулей, кроме
себя самого и нулевого. Примером неприводимого модуля
над кольцом целых чисел служат группы простого поряд¬
ка (см. упражнение 9 из § 3). Поле (и даже тело) является
неприводимым модулем над самим собой. Минимальными
идеалами кольца Р х Р, где Р — поле (см. упражнения I
и 6 из § 4), служат множества {(х, 0) | х ЕЕ Р}, {(0, х) | хЕ
GE Р} и {(х, х) | х ЕЕ Р}. Менее тривиальный пример до¬
ставляет следующая теорема.
Теорема 18. Пусть R — кольцо матриц порядка
п над телом D и Мt — множество всех матриц, у которых
все элементы, расположенные вне i-й строки, равны 0.
Тогда — минимальный правый идеал кольца R,
Доказательство. Легко проверить, что Mt —
правый идеал кольца R. Рассмотрим ненулевой правый
идеал II кольца R, лежащий в М t. Правый идеал Н со¬
держит ненулевую матрицу, скажем, А, Тогда aiq 0 для
некоторого q. Используя обозначения и формулы (*) и
(**) из доказательства теоремы 10 из § 4, для любой мат¬
рицы В ЕЕ Мi будем иметь
ijEij = AEqi (diqbij) Е е II
Но тогда В ЕЕ Мt влечет за собой
п
В = bijEij ЕЕ И,
т. е. II = Mt,
*) Символ X С У означает, что X — подмножество множества
Y и X =/= Y, Отметим, что некоторые авторы используют знак С
в том же смысле, что и CZ.
118

Теорема 19. Правый R-модулъ М неприводим тогда,
и, только тогда, когда М = aR для любого ненулевого эле-
меюпа а ЕЕ М.
Доказательство. Если модуль М неприводим
й 0 а Е~: М, то aR — ненулевой подмодуль модуля М
и, следовательно, aR = М. Если же модуль М не являет¬
ся неприводимым, то он содержит такой подмодуль II,
чт0 {0} =# II СЕ Л/. Если теперь 0 й Е Я, то aR се II
и, следовательно, М ф aR.
Подмодуль W модуля L называется максимальным,
если W L и соотношение W СЕ N cz L, где N — под¬
модуль модуля L, влечет за собой N = L. В частности,
правый идеал кольца R максимален, если он отличен от R
и не содержится ни в каком правом идеале кольца R, от¬
личном от него самого и от R. Примером максимального
подмодуля служит нулевой подмодуль неприводимого
модуля. Минимальные идеалы кольца Р X Р, рассмотрен¬
ного выше, максимальны.
Теорема 20. Фактормодуль МП! правого R-моду-
ля М неприводим тогда и только тогда, когда Н — макси¬
мальный подмодуль.
Доказательс т в о. Если II — максимальный
подмодуль и [0] =/= la] М!Н, где [а], каки раньше, обоз¬
начает смежный класс, содержащий элемент а ЕЕ М, то
а EfE II. Отсюда Н (ЕЕ Н + aR се М, что, ввиду макси¬
мальности подмодуля И, влечет II + aR = М. Если те¬
перь х ЕЕ М, то х ■= у аг, где у ЕЕ II и г ЕЕ R. Отсюда
Ы = [аг] = [а\г, т. е. МП! = [а] R, и неприводимость
фактормодуля Mill вытекает из теоремы 19. Если, наобо¬
рот, М!Н — неприводимый модуль, II СЕ К cz М и h
ЕЕ К \ II *), то, по теореме 19, Mill — [Я] R. Если те¬
перь х ЕЕ М, то Ы ЕЕ [Я] R, т. е. х = hr + у, где г ЕЕ R
и у ЕЕ Н СЕ К. Следовательно, х ЕЕ К. Таким образом,
М — К, чем и завершается доказательство.
Теорема 21. Правый модуль над кольцом R непри¬
водим тогда и только тогда, когда он изоморфен фактор-
моду лю RiM, где М — максимальный правый идеал коль¬
ца R.
Доказательство. Если М — максимальный
правый идеал, то неприводимость фактормодуля RiM вы¬
текает из теоремы 20. Если же А — неприводимый правый
Я-модуль, то, по теореме 19, А — aR, где 0 а ЕЕ А.
*) Через U \ V обозначается множество всех элементов мно¬
жества U, не принадлежащих множеству Г,
119

Определим отображение <р: 7? —>Л, положив ф(г). == аг
для всех г ее R. Нетрудно проверить, что (р — гомоморф,
ное наложение модулей. По теореме 7, А Rilfav ср, при-,
чем, в силу теоремы 20, Кег <р — максимальный правый
идеал кольца R.
3 а м е ч а и и е. Пусть R — кольцо матриц порядка
п над телом/), Wt — множество всех матриц с нулевой ыц
строкой и АЦ — множество всех матриц, у которых все
строки, кроме z’-й, нулевые. Тогда и Al t — правые идеа¬
лы кольца R. В силу следствия теоремы 12 7? = Мt @ В г.
Отсюда, ввиду следствия теоремы 16, имеем М t ~ R/И- h
и из теорем 18 и 20 вытекает, что Wt — максимальный
идеал кольца R,
Модуль называется вполне приводимым, если он разла¬
гается в прямую сумму конечного числа неприводимых
подмодулей. Вполне приводимым правым модулем будет,
например, внешняя прямая сумма минимальных правых
идеалов. Конечные вполне приводимые модули над коль¬
цом целых чисел описаны в упражнении 21. Другие при¬
меры будут приведены в следующем параграфе.
Т е о р е м а 22. Пусть М — вполне приводимый пра¬
вый модуль и
М --- АЦ ®	. ,ф А1п
— одно из его разложений в прямую сумму неприводимых
подмодулей. Тогда все ненулевые подмодули и факте; -
модули модуля AI вполне приводимы, причем каждое из и.с
неприводимых слагаемых изоморфно одному из модулей Мр
Каждый подмодуль модуля М выделяется прямым-слага-
мым. Каждый фактормодуль модуля AI изоморфен его
подмодулю.
Д о к а з а т о л ь с т в о. Предварительно уставов! м
две леммы.
Л е м м а 1. Если II — подмодуль модуля А1 и II Л/\
то при подходящей нумерации имеем
м - н е ац со.. ло мк,
..<£) Ми
и
м н л/1 а. . • -в 'I,.
Для доказательства, изменив, если нужно, нумерацию,
имеем Л?! (JL Н. Но тогда Aly Q II CZ Му, откуда
вследствие неприводимости модуля Л/j вытекает, что Мл. [)
р| II = 0. Если II •+ Му-/- М', то, как и выше, получи^
d 20

(Н + М}) П М2 = 0. Продолжая описанное построение^
ддд некоторого натурального числа к будем иметь
•"‘,1	(II Н- Л/, ф Л72) П Л/3 О,
(II ф м} л/2 -I- л/3) п ац - о,
(// ф л/т © ... ф М^) п Л/. = О
л ф м. ф . . . ф л/,„т + Aik - м.
В силу свойства (2) из теоремы 12 отсюда вытекает, что
М = II ф АЦ ф ... ф А1к.
Первая часть тео-ремы 13 позволяет записать
Л/ - 11 ф (АЦ + . . .ф Л/,),
т. е. 11 выделяется прямым слагаемым. Используя след¬
ствие теоремы 16 и первую часть теоремы 13, получаем
М/Н ЛЛф ... ф Мк
и
Н М !(М\ ф . . . ф Л/^) = ((А1\ Ф . • • Ф Д/\)ф
ф (Мл-+1+ • • • Ф Мu))l(AIi ф . . . ф Мк)	М/гнф . . . ф Мп.
Лемма 2. Если U — неприводимый подмодуль мо¬
дуля М, то U Al i для некоторого i.
Действительно, по лемме 1, U А1к[1 ф . . . ф Л/„.
Но поскольку U неприводим, то эта прямая сумма содер¬
жит лишь одно слагаемое.
Возвращаясь к доказательству теоремы, заметим, что
полная приводимость подмодулей и фактормодулей мо¬
дуля AI сразу следует из леммы 1. Применив к ним лем¬
му 2, убедимся, что любой неприводимый подмодуль этих
модулей изоморфен одному из Л/ф Из леммы 1 вытекает
также, что каждый подмодуль модуля AI выделяется из
него прямым слагаемым, а каждый фактормодуль модуля
AI изоморфен некоторому подмодулю модуля Л/.
3 а м е ч а и и е. Если
М = Ah ф . . . © А1т - Л/; ф . . . © А1п
— два разложения вполне приводимого правого модуля Л/
и 'прямую сумму неприводимых подмодулей, то каждый
Из модулей Ah изоморфен некоторому модулю М$ и на¬
оборот. Можно доказать, что т = п и что число модулей,
изоморфных данному модулю, одно и то же в обоих разло¬
•121

жениях. Это, однако, не означает совпадения слагаемых.
Например, если А и В — группы вычетов по модулю ?
то А е В = А е С, где С = {(0, 0), (1, 1)}.
Правый /?-модуль называется конечно порожденные,.
если он является линейной облочкой некоторой конечн чт
системы векторов.
Примером конечно порожденного модуля служит моду ij,
n-мерных строк над произвольным кольцом R. Действительно, об¬
ложив
1,0,
г-1
для любой строки а = (гх, . . ., гп), rt €= 7?, будем иметь
а = ехгх + . . . + епгп.
Для получения примера модуля, не являющегося конечно порох:-
денным, рассмотрим множество всех счетных последовательное! й
элементов некоторого кольца R и определим на нем онерацн *,
полагая
(ах,а2, . . . ) + (bx, Ь21 . , . ) = (ах + &х, <?2 + Ь2, • • • )
и
(лх, а2, . , , ) г — (алг, а2г2, . .
Нетрудно проверить, что таким образом возникает правый 7?-м >-
дуль W. Далее обозначим через V множество всех таких последова¬
тельностей из W, почти все (т. е. все, за исключением конечного
числа) члены которых равны нулю. Легко видеть, что V — под¬
модуль модуля W, Допустим, что V — линейная оболочка после¬
довательностей рх, . . vm е V. Но тогда найдется такой номер
что все члены этих последовательностей, начиная с (п + 1)-го, рав¬
ны нулю. Следовательно, равенство
n-hl
вопреки допущеппю не имеет места ни пои каких г? В. Таким
образом, модуль V не конечно порожден. Несколько сложнее дока¬
зывается, что и сам модуль W не является конечно порожденным.
Можно доказать также, что группа рациональных чисел не конеч¬
но порождена как модуль над кольцом целых чисел (см. упражне¬
ние 4).
Теорема 23. Каждый конечно порожденный правый
R-модулъ М изоморфен фактормодулю правого модуля // -
мерных строк над кольцом R для подходящего натураль¬
ного числа п.
Доказательство. По определению, модуль Л/
совпадает с линейной оболочкой некоторой конечной си¬
стемы векторов, скажем, ах, . .	<%. Пусть V — модуль
/г-мерных строк. Определим отображение <р:	М,
122

полагая
Ф (г,, . .	r„) = a^j + . . . + ангп.
Легко проверяется, что ср — гомоморфизм модулей. Если
то
а = а1г1 + . . . + а,ьгп
для некоторых rt ЕЕ R. Отсюда
<Р (^1, - -	^г) = а.
т. е. ф оказывается наложением. По теореме 7, модуль М
изоморфен V/Кег ф.
У пражнения
1.	Убедиться, что ситуация, описанная в примере 8 таблицы \ ,
возникает, если S — кольцо матриц порядка 2, а R — множеств0
II а 0 ||
всех матриц вида q q -Указать единицу кольца 7?.
2.	Доказать, что множество n-мерных строк, сумма координат
каждой из которых равна нулю, образует подмодуль модуля строк.
3.	Используя запись комплексных чисел в форме а -|- bi, где
а и b — действительные числа, можно отождествить множество ком¬
плексных чисел с множеством всех точек действительной плоско¬
сти. Доказать, что всякая прямая, проходящая через начало коор¬
динат, является подмодулем модуля комплексных чисел над полем
действительных чисел (пример 4 из таблицы 4) и что это не так,
если комплексные числа рассматривать как модуль над собой (при¬
мер 1 из таблицы 4).
4.	Доказать, что линейная оболочка любого конечного множе¬
ства рациональных чисел не совпадает со всей группой рациональ¬
ных чисел по сложению, рассматриваемой как модуль над кольцом
целых чисел (пример 3 из таблицы 4). Убедиться, что эта группа
конечно порождена как модуль над полем рациональных чисел.
5.	Доказать, что линейная оболочка двух целых чисел совпа¬
дает со всем кольцом целых чисел, рассматриваемым как модуль
над собой (пример 1 из таблицы 4), тогда и только тогда, когда эти
числа взаимно просты.
6.	Пусть R — множество счетных последовательностей элемен¬
тов из поля Р с операциями
(«1, я2, . . . ) + (^i, Ь2, . . . ) = (ях + а2 +	• • • )
и
(«X, я2, . . . YJ^bz, . . . ) = (Ях^х, а2Ь2, . . . ).
Доказать, что 7? — коммутативное кольцо и что множество Н, cq-
стоящее из всех последовательностей из 77, у которых все члены, за
исключением конечного числа, равны нулю, образует идеал кольца
Я. Доказать, что 77 не является конечно порожденным R-модулем,
Хотя R конечно порождено как 7?-модуль.
7.	Фактормодуль конечно порожденного модуля конечно по¬
рожден.
123

8.	Пусть N — подмодуль модуля М. Доказать, что из коиед,
noii порождснпостп модулей N и Mi N вытекает конечная порожден-
НОГТЬ модуля М.
9.	Сумма конечного множества конечно порожденных подмо¬
дулей конечно порождена.
10.	Если /1, В, С — подмодули модуля М, A CZ В, Л + С
= В 4- С и А П С = В П С, то А = В.
11.	Если А, В, С — подмодули модуля М и A CZ С, то (Л <-
-| В) П С ~ А 4- В П С. Убедиться, что равенство (Л -I- В) J
р (.' “ А р| С + В Р С не имеет места, если М — модуль дву¬
мерных строк над кольцом В (см. пример 2 из таблицы 4), а Л, В
и С — все строки вида (0, г), (г, 0) и (г, г) соответственно.
12.	Если Л и В — подмодули модуля М, то фактормодуль
(Л }- В)!А р В изоморфен внешней прямой сумме (Л/(Л р В)} ф
Ф (Bi(A р В)).
13.	Если М и М' — модули над коммутативном кольцом /*,
т<» определение .г (гф) = г (.гф), где х е М, г ЕЕ В, ф е Пот (М,
Мпревращает Hom (М, Л/') в левый Я-модуль. Убедиться, чк»
к•••ммутатнвность кольца В существенна.
14.	Если М — М' ф М"	и Пот (М', М") = Нот (М", М')	~~
-	0, то кольцо Нот (Л/, Л7)	изоморфно кольцу Нот (Mf, М')	X
X Пот (М", М") (см. упражнение 1 из § 4).
15.	Пусть М — модуль, ф	е Нот (М, М) и ф2 = ф. Доказать,
чт	»	М — Кег ф ф 1т ф. У к	азан и е: каждый элемент х <=	М
представить в форме х = (х — .гф) + 2ф.
16.	Доказать, что кольцо целых чисел не содержит минималь¬
ных идеалов.
17.	Пусть В — кольцо действительных функций и W — мно¬
жество функций, обращающихся в нуль в точке а. Доказать, что
Е — максимальный идеал кольца В.
18.	Доказать, что идеал кольца целых чисел максимален тогда
п только тогда, когда он порождается простым числом.
19.	Модуль /г-мерпых строк над полем (и даже над телом)
вполне приводим.
20.	Правый В -модуль М изоморфен правому модулю п-мерных
строк над кольцом В тогда и только тогда, когда М содержит эле¬
менты г/1;. . ., ап, обладающие следующими свойствами: а) М сов¬
падает с линейной оболочкой системы j^,. . ., ап}; б) если Л -•
пр -извольный правый Я-модуль, то, каковы бы ни были элементы
. ., Ьп е //, существует гомоморфизм ф: М В такой, чт<>
ф (a,) — bj для каждого i.
21.	Конечная коммутативная группа G вполне приводима как
модуль над кольцом целых чисел тогда и только тогда, когда для
любого a число элементов подгруппы Za свободно от квадратов
(т. о. равно рх . . . рт, где pi — различные простые числа).
§ 6. Правые идеалы в кольцах
Элемент е кольца R называется идемпотентом, если
е2, ••= е. Идемпотенты е и / называются ортогональными,
если ej = fe = 0. В качестве примера можно указать ор¬
тогональные идемпотенты Ец и Ejj, где i ], в кольце
матриц (см. доказательство теоремы 10 из § 4). Про правый
идеал eR скажем, что он порождается идемпотентом е.
124

Правый идеал Н кольца R пазовом правым идеалом с ну¬
левым умножением, если ху ----- 0 для любых х, у 6= II.
3 а м е ч а и и е. Если е — идемпотент кольца R, то
х Её eR тогда, и только тогда, когда х = ех.
Действительно, ясно, что ex ЕЕ eR. Если же х ЕЕ eR, го
х = ег для некоторого г R. Отсюда
х — ег -■= е2г ~ е (ег) ~ ех.
В дальнейшем этот факт будет часто использоваться без
специальных ссылок.
Теорема 1. Если R — кольцо с единицей и R -----
= Я] ф . • . ф IIп — разложение в прямую сумму пра¬
вых идеалов, то найдутся такие идемпотенты е}, . . еа,
что Hi — etR для каждого I, e.ej ■	0, если i 7, и 1 -
— О +	• • •+ ен.
Доказате л ь с т в о. В силу теоремы 11 из § 5
1 — е} -у-	. . . ф etl, где с, ЕЕ IE. Умножая справа на et
и используя определение прямой суммы, получаем
е, — е* =	+ ... + f	+ • • • + е
Е tf, П (Я. + • • ■ + Я.-i -I- Яьх T • • • + Нп) = Г,
т. е. <?, — идемпотенты. По тем же соображениям имеем
ej = e\ej ф ... ф Ф ej Ф fyify Ф . . . Ф енер
Отсюда
e^ej Ф ... -j- Ф ерлв] Ф . . . Ф enej 0
и, используя свойство (4) теоремы 12 из § 5, получаем
ep?j = ... = ej-iej -= ej^ej --•= . . .= euej — О,
т. е. dCj --= 0 при i Ф Е Если х ЕЕ II {, то
х --- ах ф . . . -|- еих,
откуда, как и выше,
х — е,х — CiX ф . . . ф е^х ф в/^х ф . . . ф епх ЕЕ
е И. П UE ф .. • Ф Н^ ф /Ел ф ... + н,д - V
Таким образом, х =--- е.х Ё= с,/?, т. е. 1Ц СЕ eLR. Посколь¬
ку ei ЕЕ И. влечет eiR се Hi, то //, =•= e(R.
Т е о р е м а 2. Сумма правых идеалов кольца R с еди¬
ницей, порожденных попарно ортогональными идемпотен-
t Игами, прямая.
Доказательство. Пусть ei, . . ., еп — попар¬
но ортогональные идемпотенты и 0 = Xi ф ... ф хп,
125

где xt ЕЕ e{R. По замечанию, х{ = etXi, а значит, ejxt =
— ejeiXi = 0, если i Ф j. Следовательно,
О С[ (<24 ~|“ . . . ~НX-п)	в[Xi	Xi
и, согласно свойству (4) теоремы 12 из § 5, сумма
e±R +	... +enR оказывается прямой.
Напомним, что правый идеал Л/ кольца R называется
минимальным, если из соотношений 0 =# Я cz. М, где
И — правый идеал кольца 7?, вытекает, что II =■ М. Дру¬
гими словами, минимальный правый идеал — это непри¬
водимый подмодуль правого 7?-модуля R.
Теорема 3. Минимальный правый идеал кольца R
с единицей или является правым идеалом с нулевым умно¬
жением, или порождается ненулевым идемпотентом.
Доказательство. Пусть М — минимальный
правый идеал кольца R. Если он не является правым
идеалом с нулевым умножением, то ab Ф 0 для некоторых
а, b ЕЕ М. Нетрудно проверить, что аМ — правый идеал
кольца R. При этом 0 =/= ab ЕЕ аМ и, следовательно, 0
аМ ее М. В силу минимальности правого идеала М
имеем аМ — М. В частности, а ~ ае для некоторого е ЕЕ
ЕЕ М. Конечно, е =# 0. Рассмотрим множество
II — {х \х EEE R, ах = 0},
т. е. совокупность всех х ЕЕ R таких, что ах = 0. Лег¬
ко проверяется, что II — правый идеал кольца R. Ввиду
теоремы 1 из § 5, II М — также правый идеал кольца R.
При этом II р| М СЕ М. Но II р| М у= М, поскольку b
лежит в М, но не лежит в II. Из минимальности правого
идеала М вытекает, что II М 0. Но е — е2 ЕЕ М и
а (е — <?2) ае. — ае2 = а ~ ае ~ 0,
т. е. е — с2 ЕЕ М р| II 0. Следовательно, е = е2. Нако¬
нец, из соотношения 0 =?е eR ее М, в силу минимальности
правого идеала М, вытекает, что eR ~ М.
Теорема 4. Если кольцо R с единицей не содержит
ненулевых двусторонних идеалов с нулевым умножением, то
оно не содержит и ненулевых правых идеалов с нулевым ум¬
ножением..
Доказательство. Предположим, что кольцо R
содержит ненулевой правый идеал М с нулевым умноже¬
нием, Рассмотрим множество I всевозможных сумм вида
Г1Ш1 + , ,
126

где rt ЕЕ 7?, GE М. Легко проверяется, что I — двусто¬
ронний идеал. Поскольку М cz: I, то I Ф 0. Однако, учи¬
тывая, что	М, если г'-	7?, и что М — правый
идеал с нулевым умножением, получаем
(rLmi + • • • + rkmk)(rpnl + . . . + rim'i) =
г, э
Таким образом, I оказывается ненулевым двусторонним
идеалом с нулевым умножением, что противоречит усло¬
вию.
Кольцо R с единицей называется вполне приводимым
справа, если 7? — вполне приводимый правый 7?-модуль.
Другими словами, кольцо вполне приводимо справа, ес¬
ли оно разлагается в прямую сумму конечного числа своих
минимальных правых идеалов. Вполне приводимым спра¬
ва кольцом является каждое поле, а также конечная пря¬
мая сумма полей. Нетривиальный пример доставляет сле¬
дующая теорема.
Теорема 5. Кольцо матриц над телом вполне при¬
водимо справа.
Доказательство. Пусть 7? — кольцо матриц
псрядка п над телом D. Используя теорему 12 из § 5 и
обозначения, использованные в теореме 18 из § 5, имеем
7? = М± © . . .© Мп.
Остается заметить, что по той же теореме 18 Mt — мини¬
мальные правые идеалы кольца 7?.
Теорема 6. Каждый правый идеал II вполне при¬
водимого справа кольца R порождается идемпотентом.
Этот идемпотент может быть выбран в центре кольца R
(такой идемпотент называется центральным) тогда и
только тогда, когда II — двусторонний идеал.
Доказательство. Ввиду теоремы 22 из § 5
R = 77 © 1Г, где 77' — правый идеал кольца 7?, и первое
утверждение доказываемой теоремы вытекает из теоремы 1.
При этом 1 = е + f, где е2 = е, /2 = /, ef = fe = 0, Н =■=
= eR и 77' = fR. Если 77 — двусторонний идеал, то для
любого г ЕЕ R имеем ге ЕЕ II = eR и, следовательно, ге —
= ег' для некоторого г ЕЕ R. Отсюда
fre = fer' = 0	(*)
для любого г ЕЕ R. Далее, правый идеал er/R в силу уже
доказанного порождается идемпотентом, т. е. erfR = gR,
где g2 = g, Отсюда erf = gerf и g = erfs для некоторого
127

S CE /i. Ввиду (*)
g — g2 - crfserfs — 0
r, следовательно,
erf gerf 0.	(**)
Учтивая ортогональность e и /,	(*) и (**), получаем
Cl- — гс - = (е -г /) {er — ге) (е + /) ere + fere -|- erf -j
ferj — ere —jre — eref — fref = ere — ere ~ 0
дчи любого r ЕЛ /?, т. e. e оказывается центральным идем¬
потентом. Наоборот, если е — центральный идемпотент,,
то равенство г {ел} ~ е {гл}, справедливое для любых х,
г ЕЛ R, показывает, что <:7? — двусторонний идеал.
Т е о р е м а 7. Пусть е — центральный идемпотент
кол1ца R с единицей. Тогда
(1)	eR — кольцо с единицей е, причем всякий правый
(левый, двусторонний} идеал кольца eR оказывается пра¬
вым {левым, двусторонним) идеалом кольца R;
(2)	каждый минимальный правый идеал кольца R, ле¬
жащий в eR, является минимальным правым идеалом коль¬
ца eR;
(3)	если кольцо R вполне приводимо справа, то кольцо
eR также вполне приводимо справа.
Д о к а зательст в о. Поскольку
ех {ее}х е{ех) е {хе} {ех}с
для любого х R, то е оказывается единицей кольца eR.
Если // — правый идеал кольца eR и h ЕЛ II, то h — ей.
Отсюда
hr — {eh} г (he) г h (er) ЕЕ II
для любого г ЕЕ R, ибо er ЕЕ eR. Следовательно, Н — пра¬
вый идеал кольца R. Соответствующие утверждения для
левых и двусторонних идеалов доказываются аналогично
Если, далее, М — минимальный правый идеал кольца R
н .М c~z eR, то рассмотрим соотношение 0#= // С Л/, где
И — правый идеал кольца < R. В силу утверждения (1), П —
правый идеал кольца R, что ввиду минимальности право¬
го идеала М влечет// =-- М. Следовательно, М —минималь¬
ный правый идеал кольца eR. Наконец, если кольцо R впол¬
не приводимо справа, то согласно теореме 22 из § 5 имеем
eR ~ М \	® А/mi
128

где Mt — минимальные правые идеалы кольца R. В силу
утверждения (2),	— минимальные правые идеалы коль¬
ца еВ, что доказывает утверждение (3).
Теорема 8. Все ненулевые кошчно порожденные пра¬
вые модули над вполне приводимым спрс ва кольцом В вполне
приводимы. Каково бы ни было разложение кольца в пря¬
мую сумму минимальных правых идее лев, каждый непри¬
водимый правый модуль над таким кольцом изоморфен од¬
ному из минимальных правых идеалов, встречающихся в
этом разложении.
Доказательство. Пусть L — произвольный
конечно порожденный правый /?-модуль. По теореме; 23
из § 5, модуль L изоморфен фактормодулю VIK, где V —
модуль ту?-мерных строк для некоторого натурального т.
Согласно теореме 15 из § 5, модуль V изоморфен внешней
прямой сумме
В^...^В .
'		/
т раз
Если теперь
В =	(£) . . . ф Мп
— некоторое представление кольца В в виде прямой сум¬
мы минимальных правых идеалов, то, в силу теоремы 13
из § 5, модуль V изоморфен прямой сумме
Ml ф . . . ф Мп Ф Mi ф . . . Ф Мп ф . . . ® Ml ф . . . ф мп.
По теореме 22 из § 5, модуль V/K, а значит и модуль L,
вполне приводим, причем в его представлении в виде пря¬
мой суммы неприводимых модулей встречаются лишь моду¬
ли, изоморфные каким-либо правым идеалам М\. В част¬
ности, поскольку неприводимый модуль неразложим в
прямую сумму, он должен быть изоморфен одному из этих
минимальных правых идеалов.
Следствие. Каждый конечно порожденный пра¬
вый модуль над вполне приводимым справа кольцом изомор¬
фен внешней прямой сумме некоторых минимальных пра¬
вых идеалов этого кольца.
Теорема 9. Каждый неприводимый правый модуль
над вполне приводимым справа кольцом изоморфен некото¬
рому минимальному правому идеалу этого кольца.
Доказательство. Поскольку каждое кольцо
с единицей является конечно порожденным правым мо¬
дулем над собой (оно порождается единицей), то, ввиду
5 Л. Л. Скорняков
129

теоремы 19 из § 5, каждый неприводимый модуль конечно
порожден. Теперь остается лишь применить только что
сформулированное следствие.
У п р а ж и е и и я
1.	Кольцо R называется нильпотентным, если существует Та
кое натуральное п, что произведение любых п элементов из R рав¬
но нулю. Доказать, что кольцо не содержит ненулевых правых (ле¬
вых, двусторонних) идеалов с нулевым умножением тогда и только
тогда, когда оно не содержит ненулевых нильпотентных правых
(левых, двусторонних) идеалов.
2.	Элемент а кольца R называется нильпотентным, если ап ~
= 0 для некоторого натурального п. Доказать, что коммутативное
кольцо не содержит ненулевых нильпотентных идеалов тогда и
только тогда, когда оно не содержит ненулевых нильпотентных эле¬
ментов. Рассматривая кольцо матриц второго порядка над полем,
убедиться, что это неверно в некоммутативном случае.
3.	Пусть R — кольцо, I — его идеал, а кольцо I п фактор-
кольцо R/I нильпотентны. Доказать, что кольцо R также нильпо-
тентно.
4.	Доказать, что сумма нильпотентных правых идеалов пиль-
потентна.
5.	Доказать, что всякое коммутативное вполне приводимое
кольцо с единицей является прямой суммой полей.
6.	Если все идемпотенты вполне приводимого справа кольца
центральны, то все его правые идеалы являются двусторонними.
7.	Доказать, что кольцо D X D, где D — тело (см. упражнение
1 из § 4), вполне приводимо справа.
§ 7. Абелевы, разрешимые и простые группы
В этом параграфе рассматриваются группы, обладаю¬
щие некоторыми дополнительными свойствами. Попутно
устанавливаются некоторые важные свойства конечных
групп (например, теорема Силова).
Начнем наше исследование с коммутативных или, что
то же самое, абелевых групп. Как уже отмечалось, они
являются модулями над кольцом целых чисел Z (см. при¬
мер 3 из таблицы 4). Поскольку кольцо Z коммутативно,
то левые и правые модули можно не различать (см. с. 105,
—107), и мы будем придерживаться левой записи.
Элемент а абелевой группы А называется периодиче¬
ским, если па = 0 для некоторого ненулевого п ЕЕ Z.
Совокупность всех периодических элементов группы А
называется ее периодической частью и обозначается через
Т (А). Ясно, что Т (Z) = {0}. Если А — конечная груп¬
па, то Т (А) = А в силу теоремы 22 из § 3.
Теорема 1. Если А — абелева группа, mo Т (А) - -
ее подгруппа и Т (А/Т (А)) = {0},
130

Доказательство, Ясно, что 0 е Т (Л). Если
.г, у Т (Л), то тх пу = 0, где 0 =/= т, пё Z. Учи¬
тывая аддитивную форму теорем 9 и 10 из § 3 (см. приме¬
чание на с. 77), получаем
тп (х + у) = п (тх) + т (пу) = 0
и
т (~х) = —тх = 0.
Следовательно, х + у и — х принадлежат Т (Л), т. е.
Т (Л) — подгруппа. Как и всякая подгруппа коммута¬
тивной группы, она нормальна, что дает возмож¬
ность рассмотреть факторгруппу Л!Т (Л). Если Ы @
ЕЕ Т (А/Т (Л)) (как всегда, Ы обозначает смежный
класс, содержащий элемент х), то для некоторого ненуле¬
вого п ЕЕ Z имеем п Ы = [0]. Отсюда [пх\ = [0], т. е.
пх ЕЕ Т (Л). Поскольку пх — периодический элемент, то
m (пх) = 0 для некоторого ненулевого m ЕЕ Z. Поскольку
тп Ф 0, то х ЕЕ Т( Л) и, следовательно, [я] = [0].
Если Л — абелева группа, то система {е1? . . ., еп} эле¬
ментов из Л называется базой, если для любого а ЕЕ А
найдутся такие к1ч . . ., кп ЕЕ Z, что а = к1е1 + * . >
. . . + kmem, а равенство 11е1 + . . . + 1пеп = 0, где
Zi, . . ., 1п ЕЕ Z, влечет за собой	. = 1п = 0. В ка¬
честве примера заметим, что строки е±, . . ., еп, где et =»
= (0, . . . ., 0, 1, 0, . . ., 0), образуют базу группы строк
г-1 раз
с координатами из группы Z,
Теорема 2. Если {t^, . . ., еп} — база абелевой
группы F, кг, . . ., кп, к{, . . .,	и
^iei + . . . + кпеп = к1е1 + , . . + kne.ni
mo кЛ = к[, . . ., kn = k'n.
Доказательство. Если
a = k1e1 + . . .+ knen = k,1e1 + . . . + knen,
то, принимая во внимание основные свойства модулей
(см. с. 107), получаем
(ki — к[) ei + . • • + (кп — кп) = 0?
откуда к± — к{ = . . . = кп — к'п = 0, т. е. кх = к{, . . .
, кп = кп.
Если ег — периодический элемент, то те± = 0 для не¬
которого ненулевого т ЕЕ Z. Отсюда
те1 -|- Об?2 + • • • + 0гп — 0,
134

что противоречит определению базы. Таким образом, ба¬
за не может содержать периодических элементов. Ввиду
теоремы 22 из § 3, отсюда вытекает, что конечная группа
не может иметь базы.
Абелеву группу, обладающую базой, назовем сво¬
бодной.
Теорем а 3 (лемма о базе). Если F — свободная абе¬
лева группа с базой {/и . . ., /т,.} и II — ее ненулевая под¬
группа, то группа F обладает такой базой	еп},
что se} ЕЕ Н для некоторого ненулевого s ЕЕ Z, а включение
k^e^ -В ^2^2 “В • • • “В knen (ЕЕ II%де к±, . . ., kn Е—- Z, вле¬
чет за собой, что к± делит s.
Доказательство. Если $ =	. . ., сп} —
некоторая база группы F, то обозначим через Г ($) наи¬
меньшее из таких целых положительных чисел к, что при
подходящих целых числах к2, . . ., кп справедливо вклю¬
чение
ксх + 71’2с2 + . . . -г кпсп GE Н.
Будем считать, что база выбрана так, что Г (^) Г (®)
для любой базы ® группы F, состоящей из п элементов.
Пусть
h — Г (^’)с1 + к2с2 + . . .+ кпсп ЕЕ II.
Осуществив деление с остатком, будем иметь
kt = Г (%) qt + rt (i = 2, . . ., п)7)
где 0 <; rt < Г (®). Положим
с ~ с± q2c2 + . . .+ q^cn
{^7	^2?	•	•	•?
Если g ЕЕ F, то для подходящих 1±, . . .. ln ЕЕ Z имеем
g = 11с1 + 12с2 + . . . + 1псп =
~ 1\С	^17г) ^2 “В . < . ~В (7n КЯп)
С другой стороны, если
I^С ~В 72^2 “В • • • —В	3),;
где Z1? 12, . . ., ln ЕЕ Z, то
ZjCj -В (/2 + ^1^2) с2 ~В ... ~В (7n + ^1Яп) сп ~ О,
Поскольку $ — база, то отсюда вытекает, что
Zi — Z2 ~В l^q2 — ♦ • • — Zn -В l±qn = Qi
132

откуда Zx = l2 = . . . = ln = 0. Таким образом, %>' ока¬
зывается базой группы F. Предположим, что щ 0 для
некоторого i. Ясно, что
$ = {С‘?	С 2* • * •» С-Р ^i+1’ • • •» ^п}
является базой группы F. При этом
h = Г (®)(с — q2c2 — ... — qncn) + k2c2 + • • • +	=
= Г (9?) с -С г2с2 -Т ... 4- гпсп =
= ЕС 4” Г (71) с 4“ Г2С-2 + . . . 4~	-1 "Н
ПцС 1+1 + . . • СЕп.-1
Следовательно, Г ($") щ << Г ($), в то время как
Г ($) <; Г ($") по выбору базы с$. Таким образом, г2 = . . .
. . . = г„ = 0 и h = Г ($) с, т. е. база $ обладает
первым из требуемых свойств.
Если, далее,
g — клс + к2с.2 + . . • “I" kucfl GE Н
и
7fx = Г ('С) q + r,j
где 0^ г < Г (??), то
гс — к2с2 — ... — кГ1сп =
= (#Г ($) — кл)с — к^2 — ... — к„си - -
— qT ((&)с — g GE Я,
что противоречит выбору числа Г ($).
Теорема 4. Следующие свойства конечно порож¬
денной абелевой группы F эквивалентны: (1) F свободна;
(2)	F изоморфна группе п-мерных строк с координатами из
группы Z для подходящего целого положительно числа п;
(3)	F изоморфна внешней прямой сумме п экземпляров
группы Z для подходящего целого положительного числа п\
(4)	Т (/’) = {0}.
Доказательство. (1) =ф (2). Если {е1? . . .
. . ., ел} — база группы F, a G — группа п-мсрпых строк
с координатами из Z, то определим отображение ср: G
—> F, положив
Ф (Агх, . . ., kn) = к1е1 + . . . -I- ktte,t.
Нетрудно проверить, что ср — гомоморфное наложение
групп. Если ср (к1У . . ., /сп) = ср (A-j, . . ., кп), то, ввиду
теоремы 2, кА = к{, к2 — к2, . . кп — к’п, т. е. ср оказы¬
вается вложением и, следовательно, изоморфизмом.
‘ 133

(2) => (4). Если т, кл, . .	к}1 ЕЕ. Z, т=^ 0 и т (kL, . . .
. . ., кп) — (О, . . ., О), то, очевидно, кг = . . . — кп = 0.
(4) ==> (1). Поскольку F конечно порождена, то F -
== Zar + . . . + Zan, причем можно считать, что п выбра¬
но наименьшим из возможных. Пусть G — абелева груп¬
па, обладающая базой {Д, . . ., fn} (например, группа м-мер-
ных строк с координатами из группы Z). Определим
отображение ср: G —> F, положив
ф (^i/i “Ь	knfn) к^а-^	• » • + кпап.
В силу теоремы 2, это определение корректно. Ясно, что
Ф — гомоморфное наложение групп. По теореме 8 из § 3,
F G/Ker ф. Если Кег ф = {0}, то все доказано. В про¬
тивном случае теорема 3 позволяет найти такую базу
{б?!, . . ., еп} группы G, что se± ЕЕ Кег ф, где 0 s ЕЕ Z.
Если [еД — смежный класс, содержащий элемент еА,
то 5 [ех] =	= [0], откуда [еД = [0], поскольку
Т (GIK.& ф) = {[0]}. Если теперь g ЕЕ F, то для подхо¬
дящих . ., кп ЕЕ Z имеем
g = Ф (*i^i + . . . + кпеп) = k2q (е2) + . . . + &пф (еп).
Следовательно,
F = Zф (е2) + . . . + ^Ф (еп),
что противоречит выбору числа п.
Остается заметить, что эквивалентность свойств (2)
и (3) является следствием теоремы 15 из § 5.
Теорема 5. Всякая конечно порожденная абелева
группа А разлагается в прямую сумму свободной и конеч¬
ной групп.
Доказательство. Из конечной порожденное™
группы А нетрудно вывести, что факторгруппа А!Т(А)
также конечно порождена. Ввиду теорем 1 и 4, отсюда вы¬
текает, что AIT (Л) — свободная группа. Пусть {[еД, . . .
. . ., [еп]} — база этой факторгруппы (как обычно, через
[а] обозначается смежный класс, содержащий элемент а).
Пусть F = Ze± + . . . + Zen. Если /г1е1 + . . . + кпеп = 0,,
где . ., кп е Z, то к± [еД + . . . + кп [е.Д = [0], от¬
куда кг = . . . = кп = 0 по определению базы. Следова¬
тельно, F — свободная группа с базой (еи . , еп}. Далее,,
если а ЕЕ А, то
[а] = kr [еД + . . . + кп [еп[,:
где къ . . ., кп Z, откуда
Ъ = а — к1е1 — . , . — кпеп Т (А).
134

Следовательно, а = и + b, где и СЕ F и Ъ ЕЕ Т (Л), т. о.
А F+ Т (Л). Ввиду теоремы 4, F (Д Т (Л) = {0} и
Л = F ф Т (Л) по следствию теоремы 12 из § 5. По след¬
ствию теоремы 16 из § 5, Т (А) А/F, откуда, как уже
отмечалось, вытекает конечная порожденность группы
Т (Л), т. е. Т (Л) = Zbr + . . . + Zbm для некоторых
bi, . . ., bm ЕЕ Т (Л). Ясно, что Zfej, . . ., Zbm — конеч¬
ные группы. Но тогда оказывается конечной и группа
Т (Л), ибо
| Т (Л) |< \Zbr I . . . \Zbm |.
Примаркой циклической группой называется группа
вычетов по модулю где р — простое число.
Теорема 6. Всякая конечная абелева группа изо¬
морфна внешней прямой сумме примарных циклических
групп.
Доказательство. Предварительно установим
две леммы.
Л е м м а 1. Всякая конечная абелева группа изоморф)-
на прямой сумме циклических подгрупп.
Проведем доказательство индукцией по числу элемен¬
тов рассматриваемой группы Л. При | Л | = 1 доказывае¬
мое утверждение тривиально. Пусть | Л | > 2. В силу тео¬
ремы 4 и теоремы 23 из § 5, Л F/Н, где F — свободная
абелева группа. Пусть п ~ число элементов, входящих
в базу этой группы. Можно считать, что группа F выбрана
так, что число п является наименьшим из возможных.
Если бы подгруппа Н была нулевой, то группа А оказа¬
лась бы бесконечной. Если же Н {0}, то применима
теорема 3. Пусть {е?х, . . ., еп} и 5 имеют тот же смысл, что
и в этой теореме. Тогда для любого h ЕЕ II имеем
h = k^e-L + k2e2 + . . . + k^en,
где /q, . . ., knEE Z. Поскольку ser ЕЕ H, то
^2^2	кпеп ЕЕ Н Р| F ,
где F' = Ze2 + . . . + Zen. Другими словами,;
II = Zser + Н Д Г.
С другой стороны, ясно, что
F = Zei @ F'.
Но теореме 16 из § 5 отсюда вытекает, что
Л FHI @ F'/H П F\
135

где С] = Zej/Zsej, Первое слагаемое, очевидно, является
циклической группой. Если оно равно нулю, то мы всту¬
паем в противоречие с выбором числа п, поскольку ясно,
что F’ — свободная абелева группа с базой {е2, . . ., еп}.
В противном случае | F'/II р| F' | < | А | и, в силу ин¬
дуктивного предположения,
F'/II П F' С2 ф . . . ф ст,
где С2, . , ,, Ст — циклические группы. По теореме 13
из § б,
А Ci ф С2 ф . . . ф Ст.
Лемма 2. Всякая циклическая группа С изоморфна
прямой сумме примарных циклических групп.
Действительно, по теореме 12 из § 3, С Z,,, где
Zn — группа вычетов по модулю п. Пусть п = р\* . . .
. . . р^1, где /jj, . . ., рт — различные простые числа.
Если пг = 1, то С примарна. Пусть in > 1. Ясно, что
II.о.д. (rx, у/™) = 1, где г = Pl' . . . р'^11- Отсюда иг -|-
ф up*™ = 1 для некоторых и, v ЕЕ Z (см. примечание па
с.	80). Поэтому для любого g ЕЕ С имеем
g = и (rg) + V (р1^) ё s Cl + С2,
т.	с.
С == ф С2,
где = гС и С2 = р\}пС. Кроме того, по теореме 22
из § 3,
p^Ci I С I С = {0}
и
гС2 - | С | С = {0}.	(♦)
Поэтому если х ЕЕ Сг (Д С2, то
X --= и (гх) ф V (р^х) = (X
В силу следствия теоремы 12 из § 5,
С = Ci ф С2.
Если С3 == {0}, то С = С2 и, ввиду (*), гС = {0}, хотя
г 11] = [г] =/= 10], где [/с] — элемент группы вычетов Zn,
содержащий число к, ибо ()</'< п. Следовательно,
С] ф {0}. Аналогично доказывается, что С2 {0}. По¬
136

этому I Cj I, | C2 | <C | С I, а из следствия теоремы 16
из § 5 нетрудно вывести, что С} и С2 — циклические груп¬
пы/Следовательно, к этим группам применимо индуктив¬
ное предположение, т. е.
Di ф . . . ф
и
С2 Di ф ... ф
где Z?j, . . ., Di>, Di, . . ., Dt" — примарные циклические
группы. Отсюда
С -2^ ф . . . ф Dt' ф Dr Ф . . . ф Di"
по теореме 13 из § 5.
Справедливость теоремы является следствием лемм 1
и 2 и теоремы 13 из § 5.
Следствие. Если число элементов конечной абе¬
левой группы А делится на простое число р, то А содержит
подгруппу, состоящую из р элементов.
Действительно, по теореме 6, А Сх ф . . . <ф Ст,
где Cj, . . ., Ст — примарные циклические группы, отку¬
да | А | = | Сх | ... | Ст |. Поэтому, например, |	|
делится на р. В силу теоремы 12 из § 3, С1 Zpk, а груп¬
па Zpk содержит подгруппу {[01, [рА'“1], 12/2/с_11, 1(р —
— 1)	содержащую в точности р элементов.
Для установленного выше разложения конечной абелевой
группы в прямую сумму прпмарных циклических групп имеет место
теорема единственности (см. § 67 учебника А. Г. Куроша или § 5
гл. 7 учебника А. И. Кострикйна). Из этой теоремы единственности
следует, например, что группы 12-го порядка = Z4®Z3 п А2 ;-
~ Z2®Z2®Z3, где Z^, Z3 и Z4 — группы вычетов по модулю 2,
3 и 4 соответственно, не изоморфны. Именно поэтому мы не огра¬
ничились установленной в лемме 1 разложимостью в прямую сум¬
му циклических групп. Впрочем, во многих случаях неизоморфность
прямых сумм можно установить и непосредственно. Например, в
рассмотренной выше группе ф имеется элемент at — (1, 0) поряд¬
ка 4 (т. е. 4ах = (0, 0), но =j= (0, 0), если 0 < к < 4). Если Аг~ А
то найдется элемент а2 = (и', и", и'") порядка 4. Однако 4я2 ~ (0,
0, 0) влечет и"' = 4 и'" = 0. Следовательно, а2 — (и', и", 0), откуда
2а2 — (0, 0, 0). В силу теоремы 22 из § 3 примарные циклические
слагаемые группы порядка 12 могут иметь порядок 2, 3 или 4.
Следовательно, существуют в точности две абелевых группы поряд¬
ка 12.
Из теорем 4, 5 и 6, ввиду теоремы 13 из § 5, вытекает
Т еорема 7. Всякая конечно порожденная абелева
группа изоморфна внешней прямой, сумме примерных цик¬
лических групп и некоторого множества экземпляров груп¬
пы Z.
137

Вернемся к рассмотрению произвольных групп. От¬
метим следующий интересный факт:
Теорема 8 (первая теорема Силова). Если G —
группа, р — простое число и | G | = ркт, где к 1, то
G содержит такую подгруппу Н, что | Н | = рк.
Доказательство. Если | G | = р, то теорема
тривиально справедлива. Поэтому можно предположить,
что она верна для всех таких групп G', где | G' | < | G |,
и что | G |	2. Пусть z±, . . zs — все центральные эле¬
менты группы G, a . ., g( — представители всех ос¬
тальных классов сопряженности. Применяя теорему 23
из § 3, получим
I |C(g.) I = |G|,	(*)
Отсюда
I C (gi) I = pkimt,	(**)
0	к. Допустим сначала, что kt = к для неко¬
торого i. Если | С (gi) | = | G |, то С (gj) = G и gt во¬
преки предположению оказывается центральным элемен¬
том. Следовательно, | С (gi) | < | G |. Но тогда, в силу
индуктивного предположения, группа С (gt), а значит,
и группа G, содержит подгруппу, состоящую из рк элемен¬
тов. Таким образом, можно предполагать, что kt < к
для всех i. Ввиду (*) и (**) отсюда следует, что | К (gt) |
делится на р для каждого I. Далее, воспользовавшись
теоремой 21 из § 3, представим G в виде объединения клас¬
сов сопряженности. Поскольку | К (zj) | = 1, то, обозна¬
чив через Z центр группы G, получим
Ркт = | G | = | Z | + | К (gl) | + . . . + | К (gt) |,
откуда вытекает, что | Z | делится на р. В силу следствия
теоремы 6, Z содержит такую подгруппу U, что | U | = р.
По теореме 20 из § 3, U — нормальная подгруппа группы
G и, следовательно, существует факторгруппа G/U. По
теореме 3' из § 3
|G/t7| = -^L=p^.
В силу индуктивного предположения, группа G/U содер¬
жит такую подгруппу 7/, что | Н | = рк~г. Обозначим
через Н множество всех^аких элементов Е G, что смеж¬
ный класс [fe] = hU Е Н. Легко проверить, jito Н — под¬
группа группы G и что отображение ср: Н Н, где ф (К) —
= [/г],— гомоморфное наложение групп. При этом
138

Кег ср — U, В силу теорем 3' и 8 из § 3,
I Н I = I Н I I [7| = р'^р = р\
что и требовалось.
Замечание. На первую теорему Силова можно смотреть
как на частичное обращение теоремы Лагранжа (теорема 3 из § 3).
Полное же обращение теоремы Лагранжа невозможно. Так, напри¬
мер, группа 5(4, состоящая из 12 подстановок, не содержит подгрупп
порядка 6. Другие теоремы Силова см. в § 4 гл. 7 учебника А. И. Ко-
стрикина.
Элемент группы G называется коммутатором, если он
представим в форме a^b^ab, где а, b ЕЕ G. Множество
G', состоящее из всевозможных произведений коммутато¬
ров группы G, называется ее коммутантом. Ясно, что
1 ЕЕ G' и что произведение двух элементов из G' снова ле¬
жит в G'. Поскольку (а_16“1а6)"1 = Ь^аГ^Ъа и (и1 . . .
• • ♦ ит) 1 ~ ит . » • Ui1, то и ЕЕ G' влечет и"1 ЕЕ G'. Та¬
ким образом, G' — подгруппа группы G. Высшие комму¬
танты группы G определяются равенствами G^ —
= (G'Y, G<3> = (G^Y и т. д. Так возникает ряд комму¬
тантов:
G з G' з G& э G<3) з .
Т е о р е м а 9.	(1) Все коммутанты G^ являются
нормальными подгруппами группы G. (2) Если Н — под¬
группа группы G, то £ G^ для всех i. (3) Если Н —
нормальная подгруппа группы G, то х ЕЕ G^H тогда
и только тогда, когда [.г] ЕЕ (GIH)^ (как и раньше, Ы —
= хН). (4) Если Н — нормальная подгруппа группы G,
то факторгруппа G/Н коммутативна в том и только том
случае, когда G' CZ Н.
Доказательство. (1) Проведем индукцию по
i. Положив = G, заметим, что доказываемое утверж¬
дение справедливо при i = 0. Пусть Z > 1. Как уже от¬
мечалось, G^> — подгруппа группы	Если а, b ЕЕ
ЕЕ G^'1), то, в силу индуктивного предположения, g~rag,
g~rbg Е	для любого g ЕЕ G. Отсюда
g-1 (а'Ч^аЬ) g = (g_1a_1g)	(g^ag^g^bg).^
= (g^ag)-1 (g^bg)"1 \g~rag) (g^bg) G (G(i_1))' = G'}.
Если uL, u2, . . ., um — коммутаторы группы G^1^, то
g-1 (U1U2 . . . Ur) g = (g'^g) (g'^g) . . .Jg^Umg) G= Gb\
поскольку, как только что показано, g H^g Е G^ для
k = 1, . . ., т. Таким образом, G^ — нормальная под¬
группа группы 6г,
139

(2)	Ясно, что Я(0) = .Яс G = G(0). Если доказаны
включения се G{Q\ H<v> ст G(1) , . . .	ст С<г_1), то
коммутаторы группы 1) оказываются коммутаторами
группы G(l_1), откуда Н{г} — (Н{г~1})' с:	= С(г).
(3)	Как и выше, положим G(0) = G и проведем индук¬
цию по г. Справедливость доказываемого утверждения
очевидна при i = 0. Пусть i 1. Если х — uh, где и ЕЕ
СЕ и hEH, то u = uL , . . um, где uk = 'aklbklakbk
(к = 1, . . ., т) для некоторых ак, Ьк EEG(i_1). Заметив, что
ак = ак*1 и применив индуктивное предположение, полу¬
чим kJ ЕЕ (G/Iiy1 Аналогично [Ьк] ЕЕ (GHiy1^. Отсюда
[u] = kJ . . . [ит] ее ((G/ny^y = (G/iry^,
ибо kJ = kJ”1 kJ”1 kJ [bk] — коммутаторы группы
(G/7Z)(i_1) и, следовательно,
[d = kJ |Л] - [и] е (G/H)^.
Наоборот, если [d (С/Я)<г), то [d = kJ . . . kw1, где
kJ = kJ”1 kJ”1 kJ kJ (k = 1, . . ., m) для некото¬
рых kJ, kJ EE (G'7Z/)(i~1). В силу индуктивного предпо¬
ложения, ак = cksk и bk = dktk для некоторых ск, dk ЕЕ
ЕЕ G6-1) и sk, tk ЕЕ II. Заметим, что = c^d^c^ ЕЕ
ЕЕ	= G(i). С другой стороны, для некоторого s ЕЕ
е н имеем
Щ. =	s = sYcY'tfdYci^dY^s.
Отсюда = [cfr]-1[rf/(.]-1[cft.][cZft] = [г?7с], ибо [sj = 17J =
= 11], и, следовательно,
[d = kJ . . . k7J = [^jJ . . . km] = [px . . . vm].
Таким образом, x = vL . . . vmh для некоторого h ЕЕ II,
причем	. vm EE G(i).
(4)	Если G'eeH, to a~vo~labEEH для любых a, b^G,
откуда [fe] [a] = [6] [a] [a^b^ab] = [a] [6]. Наоборот, если
Gill коммутативна, то abEEball. Отсюда аТЧ^аЪ ЕЕ II. Сле¬
довательно, Н содержит все коммутаторы, а значит, G' сс II.
Группа G называется разрешимой, если ряд ее комму¬
тантов обрывается на конечном шаге, т. е. Gw = {1} для
некоторого ш.
Название объясняется связью разрешимых групп с возможно¬
стью выразить корни многочлена через радикалы (см., например,
Скорняков Л. А. Элементы общей алгебры.— М.: Наука,
1983, гл. VI, §2, или Постников М. М. Теория Галуа.— М.:
.140

Физматгиз, 1963, с. 89—90). Разрешимой является всякая комму¬
тативная группа. Некоммутативной разрешимой группой оказы¬
вается, например, @3. Действительно, поскольку группа ©3 не
коммутативна, а факторгруппа ®а/513 коммутативна, то | @8 | =к 1
и, в силу теоремы 9 (4) Зз CZ 513. Но | 513 | = 3 и, значит,
= по теореме Лагранжа (теорема 3 из § 3). Наконец, 5(з	{!},
т. е. = {1}. Разрешимость группы вытекает также из до¬
казываемой далее теоремы 12. Другие примеры доставляют теоремы
11 и 13.
Теорема 10. Пусть G — конечная группа и II —
ее подгруппа. Тогда'. (1) если G разрешима, то II
разрешима', (2) если G разрешима и Н нормальна, то G/II
разрешима', (3) если II нормальна и разрешима, a GII раз¬
решима, то G разрешима.
Доказательст в о. (1) Если	— {!}, то
j/(m) = {1} по теореме 9(2).
(2)	По условию, = {1} для некоторого т. Поэто¬
му, если 1x1 G= (G/Hym\ то, по теореме 9 (3), х G: G^II =
= II, т. е. [х| = [01. Таким образом, (G//7)<m) = {HI}.
(3)	Допустим, что (б/Я)(А) = {[11} и Н<Т> = {!}. Если
у Gz G(/f), т. е. у = у Л, где 1 ЕЕ Н, то по теореме 9(3),
I?/] Gz (G/HyM. Следовательно, [z/l=[lI, т. е. у Gz Н. Таким
образом, G(Zl‘) се II, откуда
G(/i‘+Z) = (gOyz) 27(О = {1}
по теореме 9 (2).
Т е о р е м а И. Если G — группа и | G | = р\ где
р — простое число и k 1, то G разрешима.
Доказательство. Если к = 1, то G, будучи
абелевой группой, разрешима. То же самое можно ска¬
зать, если G совпадает со своим центр ом Z. Поэтому, учи¬
тывая теоремы 3, 20 и 24 из § 3, при к I можно пред¬
полагать, что | Z | = р1, где 0 <С I < к. Теорема 20 из
§ 3 позволяет рассмотреть факторгруппу G/Z, причем
| G/Z | = рК~1 <С рк в силу теоремы 3' из § 3. Но индук¬
тивному предположению, группа G/Z разрешима. По¬
скольку группа Z коммутативна, разрешимость группы G
вытекает из теоремы 10(3).
Теорема 12. Если G — группа и | G | = pq, где
р и q — простые числа, то G разрешима.
Доказательство. Ввиду теоремы 11, можно
считать, что р q. По теореме 8, G содержит такие под¬
группы А и В, что | А | = р и | В | — q. Теоремы 1 и 3
из § 3 позволяют заключить, что
А П В = {!)-	(*)
141

Рассмотрим множество
II = {ab | а ЕЕ А, Ъ В}.
Если й]., #2 ЕЕ А, Ьх, В и ciyby = $2^2’ то
^2	= ^2^11 Е- A Q В — {1}?
откуда аг = а2 и by = Ь2. Следовательно, | Н | = pq и,
значит, II = G. Рассмотрим множество
С = {х | х А, x'rbx е В для всех Ъ В}.
Нетрудно проверить, что С — подгруппа группы А. По
теореме 3 из § 3, С = {1} или С = А. Допустим сначала,
что С = А. Если g ЕЕ G, то, поскольку G = Я, имеем
g = ab^ где а ЕЕ A nb^EB. Поэтому для любого b ЕЕ В
получаем
g^bg = ih1 (а-1^) \ S В,
т. е. подгруппа В оказывается нормальной. Следовательно,
рассмотрев факторгруппу G/В и заметив, что, ввиду тео¬
ремы 3' из § 3, равенства | G/В | = р и | В | = q обеспе¬
чивают коммутативность групп GIB и В, получаем, что
группа G разрешима по теореме 10 (3). Обратимся к слу¬
чаю, когда С = {1}. Если а СЕ Л, то, как легко проверить,
множество Ва = а'1 В а оказывается подгруппой группы
G, причем | Ва | = q. Поэтому, допустив, что а2 ЕЕ А
и | BQi П Bai | > 1, и принимая во внимание теоремы 1
и 3 из § 3, получим, что | Bat Q Вао | = q, т, е. Ва1 =
= Ва2. Если теперь b ЕЕ В, то а^Ьау = а?Ь'а2 для не¬
которого Ъ' ЕЕ В, откуда
(piyCiz ) * b (ciydz } == b СЕ В.
Ввиду произвольности выбора элемента Ь, получаем, что
dyd)1 ЕЕ В = {1},
т. е. dy = а2. Таким образом, если А = {а1, а2, , . ар}
и Bt = a^Bdi, то Bt П Bj = {1} при i /, а, ввиду тео¬
ремы 3 из § 3, А р| Bi = {1} для всех i. Следовательно,
U U By и . . . U Вр I = (р - 1) + р (q - 1) + 1 = pq,
т, е.
A U By и . . . и Вр = G,
Если теперь g ЕЕ G, то g~rAg — подгруппа и | g~xAg | =
= р. Поэтому	р| Bi = {1} для всех откуда
g^Ag cz: А. Этим доказана нормальность подгруппы А,
142

Как п выше, применив к G'A п А теорему 10(3), убедимся
в разрешимости группы G.
Замечанп е. Существенным обобщением теорем И и 12
является теорема 3 из § 2 гл. IV.
Пример бесконечной некоммутативной разрешимой
с группы доставляет следующий результат.
Теорема 13. Совокупность G всех матриц вида
Я11
012
•	‘	а1п
0
022 •
• •	а2п
0
0 . ,
’ *	апп
над произвольным полем Р, где ап, а22, . < ., апп 0,
является разрешимой группой.
Доказательство. Непосредственный подсчет
показывает, что G — группа. Непосредственным же под¬
счетом проверяется
Лемма 1. Если А и U — матрицы порядка A, D
и Z — матрицы порядка Z, С и V — матрицы размера
kxluDuW — матрицы размера I X к, то
и
С 1
|| и V ||	|
AU + CW
AV J- CZ
II в
D 1
|| Р7 Z II = I
BU + DW
BV 4- DZ
леммы
1
вытекает
Лемма 2.
|| Е СЦЦЯ V ||	|| Я £+и||
II О Е || || О Е И= II О Е || '
Л е м м а 3. Совокупность Тп всех таких матриц из
G, что ап = а22 = ... = апп = 1, является разрешимой
группой.
Для доказательства сначала простым подсчетом убе¬
димся, что Н — подгруппа в G. Далее заметим, что Тг =
= {1}. Это позволяет вести индукцию по п. Если п 2,
то рассмотрим отображение ср: Тп-+	где
(здесь 0 — (zz — 1)-мерная нулевая строка, а с — (п —
— 1)-мериый столбец). Учитывая лемму 1, нетрудно про¬
верить, что ср — гомоморфное наложение. Ясно также, что
143

Ker q) состоит из всех матриц вида
Е
с
7
1
Поскольку 7’п_1 разрешима по индуктивному предполо¬
жению, а из леммы 2 нетрудно вывести, что Кег ср — ком¬
мутативная группа, то разрешимость группы G вытекает
из теоремы 10 (3).
Л е м м а 4. G' С2 Тп.
Действительно, при п = 1 это очевидно. Если же п >
> 2, то, используя лемму 1, получаем
А 1 | с
1
в-1 i d
А\с I
_ _i

I В | d
A'1 B"1 AB j “
	1
0 i а-1
TijF
Oja 1
0 ■ 1
ибо А~ЧГ1АВ ЕЕ по индуктивному предположению*
Возвращаясь к доказательству теоремы, заметим, что
факторгруппа G/G' коммутативна по теореме 9(4), а раз¬
решимость группы вытекает из леммы 3 и теоремы 10(1).
Остается принять во внимание теорему 10(3).
Чтобы установить существование неразрешимых групп,
заметим, что неразрешима всякая некоммутативная прос¬
тая группа, т. е. неединичная группа, не содержащая
нормальных подгрупп, отличных от {1} и всей группы.
Действительно, если G — простая группа, то G' = {1}
или G. В первом случае G коммутативна по теореме 9 (4),
а во втором {1} =^= G = G' = G" = . . . Таким образом,
поставленную задачу решает
Теорема 14. Знакопеременная группа проста
и некоммут ат иена.
Доказательство. Сначала установим три
леммы.
Лемма 1. Если подгруппа II группы содержит
все циклы длины 3, то II = ЭД5.
В самом деле, для произведения двух транспозиций
имеем
(0) (О) = (0’0
и
(Z/) (kl) = (ijk) (ilk),
где i, j, knl — различные числа. Следовательно, всякий
элемент из ЭД5, будучи, согласно теореме 18из§3, представив
мым в виде произведения четного числа транспозиций,
представим и в виде произведения циклов длины 3, а сле¬
довательно, принадлежит II.
144

JI e м м a 2. Если нормальная подгруппа II группы
ЭД5 содержит хотя бы один цикл длины 3, то Н — ЭД5.
Для доказательства, согласно лемме 1, достаточно ус^
тановить, что Н содержит все циклы длины 3. Допустим,
что (Z/A) ЕЕ Я, a (pqr) — произвольный цикл длины 3.
В силу теоремы 1.2.8 * *), одна из подстановок
i	/	k	s t \ fi	/	к	s	t
р	q	г	и v /	И \	q	г	v	и
где
{i, j, к, s, t} = {р, q, г, и, v} = {1, 2, 3, 4, 5},
четная. Обозначим ее через о. Если о — первая из вы¬
писанных подстановок, то для т = о-1 (ijk) о из равенств
т(р) = Qi т (q) = г, т (г) = р,х (и) = и и т (0 = v вытекает,
что т — (pqr). Но т = о-1 (ijk) о ЕЕ Я. Аналогично рас¬
сматривается второй случай.
Лемма 3. Если нормальная подгруппа II группы
ЭД5 содержит хотя бы один цикл длины 5, то II = ЭД5.
В самом деле, допустим, что (ijklm) ЕЕ Я. Поскольку
(ikj) = (ik) (ij) е ЭД5, то
(i/l) = (imlkj) (ikj) (ijklm) (ijk) =
= (ijklm,)"1 (Z/Vc)-1 (ijklm) (ijk) e Я
и II = ЭД5 по лемме 2.
Возвращаясь к доказательству теоремы, допустим,
что нормальная подгруппа Я группы ЭД5 отлична от ЭД5
и содержит нетождественную подстановку ст. Согласно
теореме 16 из § 3, о представляется как произведение
циклов, причем, в силу лемм 2 и 3, о ие может быть цик¬
лом длины 3 или 5. Следовательно, ст = (ij) (kl), или о =
- (ij) или ст = (ijk) (Im) = (ij) (ik) (1т), или о = (ijkl) =
= (ij) (ik) (И). Но во всех случаях, кроме первого, о ЭД5
в силу теоремы J.3.18. В первом же случае, имея {/, /, к,
Z, т}= {1, 2, 3, 4, 5}, и учитывая, что
(ijm)"1^ (ijm) = (imj) (ij) (kl) (ijm) = (jm) (kl) ЕЕ Я,
получим
(Zm/) - (ij) (kl) (jm) (kl) E Я,
вопреки лемме 2. Некоммутативпость группы ЭД5 видна
из соотношений
Z1 2 3 4 5\
U 5 2 3 V —
—= ((1 3)(2 5))((1 2)(3 4)).
*) См. примечание на с. 49.
«12)(3 4))((13)(2 5)) = С 3412)
145

В качестве примера бесконечной простой группы укажем груп¬
пу SO (3), состоящую из всех ортогональных матриц порядка 3
с определителем, равным 1. Правда, соответствующее доказатель¬
ство нуждается в сведениях о линейных пространствах, выходящих
за рамки изложенного в следующей главе. Для доказательства на¬
помним, что если А е SO (3), то существует такая ортогональная
матрица £/, что
U-iA U = Г (ф),	(*)
где
1
0
0
Г(ч>) =
0
COS ф
—sin ф
0
sin ф
COS ф
(см. например: К о с т р и к и н А. И., М а н и н 10. И. Линейная
алгебра и геометрия.— М.: Наука, 1986, с. 136, теорема 46);
с. 32, п. 8в)). Поскольку | — U | = — | U |, то можно считать, что
в равенстве (*) имеем U е SO (3). Допустим, что Н — неодпоэле-
ментная нормальная подгруппа группы SO (3). Тогда найдется не¬
единичная матрица A е= Н. В силу сделанного замечания, из фор¬
мулы (*) вытекает, что для некоторого ф0 =/= 2л7с имеем Т (ф0) е Н.
Положим s = sin фо, с = cos ф0 и
а
-д
0
b
а
0
0
0
1
где а — любое число из отрезка [0, 1], a b = ]/~ 1 — а2. Ясно, чю
В (а) е= SO (3), откуда D (а) = (В (а)^Т (ф0)~1 В (а))Т (ф0) е Н,
Заметив, что Т (ф0)-1 = Т (—ф0), а
а	b	01|
— b	а	0	,
О	0	1||
В (а)"* =
будем иметь
а Ъ 0
1 0 0
О(а) =
—Ь а 0
0	с s
0 0 1
0	—s с
а -
Ь
-ъ
а
0
0
1
0
0
с
0
— S


0
0
1
0
S
с
а
Ьс
bs
а
— Ьс
bs
=
— Ь
ас
as
b
ас
—as
0
-S
с
0
S
с
Вычислим след Tr (D (а)) матрицы D (а) (см. цитированную выше
книгу А. И. Кострикина и 10. И. Манина, с. 33, и. 9):
Tr (D («)) = а2 + Ъ2с + Ъ2с + а2с2 + as2 + as2 + с2 =
= а2 + 2 (1 - а2) с + а2 с2 + 2а (1 - с2) + с2 =
= а2 (1 — с)2 + 2а (1 — с2) + 2с + Л
Как уже отмечалось, для подходящей матрицы V ЕЕ SO (3) имеем
V^D (a)V = Т (ф (а)).
Учитывая инвариантность следа при изменении базы (см. цитиро¬
ванную выше книгу А. И. Кострикина и 10. И.Манина, с. 33, и. 9),
146

= 2(1 — с)>0,
1а=1
получаем
с0,, („) „
	а2 (1 — с)2 2а (1 — с2)	(2с -| ■ с2 — I)
—
Поскольку
COS ф (1) = 1
II
d cos (ф (q)) I _2a (1 -c)2-|-2(l — c2)
da L=i	2
то найдется такое число 6 > О, что cos ф (а) =f= 0 для всех а е [1 —
— 6, 1]. В силу непрерывности функции cos ф (а) ее значения запол¬
няют весь отрезок [cos ф (1 — б), 1]. Но тогда углы ф (а) заполняют
отрезок [0, с] для некоторого е > 0. Следовательно, найдется такое
целое положительное чизло п, что 0 < ф < 2п!п влечет Т (ф) е= Н.
Поэтому если В произвольная матрица из SO (3) и W~^BW =
= Т (ф), где W е SO (3), то Т (ф/n) е Я, откуда
В = WT (ф) W’1 = W (Т (ф/тг))п1Г-1 е Я.
У п р а ж н е н и я
1.	Сколько существует неизоморфных абелевых групп поряд¬
ков 10, 18, 24 и 105?
2.	Для каких чисел п все абелевы группы порядка п цикличес¬
кие? (Разумеется, все эти группы изоморфны между собой.)
3.	Прямая сумма двух конечных циклических групп является
циклической группой тогда и только тогда, когда порядки слагаемых
взаимно просты.
4.	Свободная абелева группа является циклической тогда и
только тогда, когда опа изоморфна Z.
5.	Все базы свободной абелевой группы содержат одно и то же
число элементов.
6.	Если G и Я — разрешимые группы, то и группа G X Я раз¬
решима.
7.	Доказать, что группа @5 неразрешима.
8.	Пусть Я — кольцо с единицей, I — идеал кольца Я и про¬
изведение любых п элементов из I равно нулю (другими словами,
идеал I нильпотентен). Доказать, что множество всех элементов
вида 1 + х, где х е /, является разрешимой группой по умноже¬
нию. Используя этот результат, получить новое доказательство
теоремы 13.
9.	Если центр группы порядка pqr, где р, q и г — простые чис¬
ла, пеодноэлементиый, то эта группа разрешима.
10.	Знакопеременная группа ?(п проста тогда и только тогда,
когда п > 5.
§ 8. Структуры и булевы алгебры
Пусть Р — произвольное непустое множество. Отно¬
шением на множестве Р называется подмножество р пря¬
мого произведения Р X Р. Вместо (а, Ь) р часто пишет-
147

Т а б л и ц а 5
Множество Р
Отношение р
1
Произвольное
(«, Ь) е р, если а = Ъ
2
Произвол иное
(a, b) е р, если а и b лежат в
одном смежном классе данного
разбиения X множества Р
3
Целые числа
(т, п) е р, если т п
4
Целые числа
(т, п) р, если т делит п
(считается, что 0 делит 0)
5
Н е о т р и ц а т е л т»и ы е целые
числа
(т, п) е р, если т делит п
6
Все подмножества данного
множества
(А, В) е р, если А с: В
7
Все подмножества данного
множества
(А, В) ер, если А р) В непу¬
сто
8
Множество действительных
функций
(/, g) е= р, если / (.г) < g (.*•)
для всех х
о.
1 и о ж е с т в о д ей с т ви т е л ьны х
функций
(/, Цер, если / (я) < g (я)
для некоторого х
10
Множество точек плоско¬
сти
(Л/, /V) е р, если Л/ = N или
прямая MN параллельна оси х
11
Множество точек плоско¬
сти
(Л/, Лг) ер, если М — N или
прямая MN перпендикулярна
оси х и точка М расположе¬
на ниже точки N
ся apb. Примеры отношений приведены в таблице 5. От¬
ношение на множестве Р называется порядком, если
(1)	а а для всех а GE Р (рефлексивность);
(2)	если а b и b с, то а с (транзитивность);
(3)	если a b и b а, то а = b (антисимметричность).
Порядком являются отношения в примерах 1, 3, 5, 6,
8 и 11 (см. таблицу 5). Отношение р примера 4 порядком
не является, поскольку, например 3 =^= —3, хотя (3, —3)
и (—3, 3) принадлежат р, т. е. для этого отношения не
выполнено свойство (3). Свойство (3) не имеет места и для
отношений из примеров 2 и 10. Отношения примеров 7
(если множество содержит не менее двух элементов) и 9
также не являются порядком, ибо для них не выполнено
свойство транзитивности. Порядок, указанный в приме¬
ре 1, называется тривиальным.
Множество Р называется частично упорядоченным,
если оно непусто и на нем зафиксирован некоторый поря¬
док. Разумеется, на одном и том же множестве можно за¬
148

фиксировать различные порядки. Возникающие при этом
частично упорядоченные множества считаются различ¬
ными (например, множество неотрицательных целых чисел
с порядками, описанными в примерах 3 и 5 из таблицы 5).
Множество с тривиальным порядком называется три¬
виальным частично упорядоченным множеством. Всякое
подмножество частично упорядоченного множества явля¬
ется частично упорядоченным множеством относительно
того же порядка.
Частично упорядоченные множества Р и Р’ называют¬
ся изсм>рфными, если существует взаимно однозначное
отображение <р множества Р на множество Р' такое, что
'а С & имеет место тогда и только тогда, когда ф (а)
ср (6) *). Отображение ср частично упорядоченного мно¬
жества Р в частично упорядоченное множество Р' назы¬
вается изотопным, если а b влечет ср (а) ср (6).
Элементы а и Ъ частично упорядоченного множества
называются сравнимыми, если имеет место а Ъ или
b С а- Два элемента тривиального частично упорядо¬
ченного множества, очевидно, сравнимы тогда и только
тогда, когда они совпадают.
Если любые два элемента частично упорядоченного
множества сравнимы, то оно называется цепыо (или ли¬
нейно упорядоченным множеством). Цепыо является, на¬
пример, частично упорядоченное множество примера 3
из таблицы 5. Элемент и частично упорядоченного множе¬
ства Р называется наибольшим, если х v для всех х ЕЕ
6= Р. Если же и х для всех х ЕЕ Р, то элемент и назы¬
вается наименьшим. Наибольший элемент часто называют
единицей, а наименьший — нулем. Конечно, частично упо¬
рядоченное множество может не содержать ни нуля, ни
единицы. Таким, в частности, будет иеодноэлемеитиое
тривиальное частично упорядоченное множество. Однако
более одного наибольшего элемента частично упорядо¬
ченное множество содержать не может. В самом деле,
если и и и' — наибольшие элементы частично упорядочен¬
ного множества Р, то v^v' ни' и, а, следовательно, v =
= vf по свойству антисимметричности. Аналогично уста¬
навливается единственность наименьшего элемента. Эле¬
мент w частично упорядоченного множества Р называет¬
ся максимальным, если из w х для некоторого х ЕЕ Р
вытекает х ~ w. Если из х т для некоторого х ЕЕ Р
следует, что х = т, то т называется минимальным эле-
*.) См. примечание на с. 60.
449

ментом. Легко проверяется, что всякий наибольший эле¬
мент является максимальным, а всякий наименьший эле¬
мент — минимальным. Обратное, вообще говоря, места
не имеет. Так, например, в тривиальном частично упоря¬
доченном множестве всякий элемент является как макси¬
мальным, так и минимальным. Другой пример минималь¬
ных, но не наименьших элементов дают простые числа в
множестве целых положительных чисел, отличных от 1,
упорядоченном по делимости (см. пример 5 из таблицы 5).
Наибольшим и наименьшим элементами в частично упоря¬
доченном множестве подмножеств (пример 6 из таблицы
5) являются все данное множество и пустое подмножество
соответственно. Частично упорядоченные множества при¬
меров 3 и 11 из таблицы 5 ни наибольшего, ни наимень¬
шего элементов не содержат.
Заметим, что определение наименьшего элемента получается из
определения наибольшего элемента простой заменой символа на
символ >. Точно таким же образом связаны понятия минимального
и максимального элементов. Вообще, имея какое-либо высказыва¬
ние о частично упорядоченном множестве и заменяя на >, полу¬
чаем новое высказывание. Высказывания, связанные таким образом,
называются двойственными.
Если А — непустое подмножество частично упоря¬
доченного множества Р, то верхним (нижним) конусом
множества А назовем множество всех таких элементов
х GE Р, что а х (х а) для всех a А. Верхний и ниж¬
ний конусы множества Л будем обозначать символами А'^
и А^ соответственно. Наименьший (наибольший) элемент
верхнего (нижнего) конуса множества А (если он сущест¬
вует) называется точной верхней (нижней) гранью мно¬
жества А. Точную верхнюю (нижнюю) грань множества А
в частично упорядоченном множестве Р будем обозначать
йирРЛ (infpJl). Впрочем, индекс Р часто будет опускать¬
ся. Подчеркнем, что supP?l и inf РЛ — однозначно опре¬
деленные элементы множества Р, ибо, как было отмечено
на с. 149, Лл (Л^) содержит не более одного наименьшего
(наибольшего) элемента.
П р и м еры. 1. Если Р — частично упорядоченное множество
неотрицательных целых чисел, упорядоченных по делимости (при¬
мер 5 из таблицы 5), то
{18, 12 }л= {множество всех чисел из Р, делящихся на 18
и 12 одновременно^{36/г, п = 0, 1, 2,. . .},
{18, 12}v=множество всех чисел из Р, делящих 18 и 12 одно¬
временно}^!, 2, 3, 6},
sup{18, 12}=36 и inf {18, 12} = 6.
150

2. Если Р — частично упорядоченное множество функций
(пример 8 из таблицы 5), то верхний конус {sin г, cos — это все
функции, графики которых лежат в горизонтально заштрихованной
области на рис. 5. Графики функций, входящих в нижний конус
{sin х, cos х}^, лежат в области с вертикальной штриховкой на том
же рисунке. Точные грани sup {sin х, cos х} и inf {sin х, cos #}
изображены на рис. 6 и 7 соответственно.
Рис. 6	Рис. 7
3. В частично упорядоченном множестве подмножеств (пример 6
из таблицы 5) точная верхняя (нижняя) грань совпадает с объеди¬
нением (пересечением) подмножеств.
Частично упорядоченное множество Р называется
нижней (верхней) полуструктурой, если каждое двух¬
элементное его подмножество имеет точную нижнюю (верх¬
нюю) грань. Если частично упорядоченное множество яв¬
ляется нижней и верхней полуструктурой одновременно,
то оно называется структурой *). Частично упорядо¬
ченные множества примеров 3, 5, 6 и 8 из таблицы 5 ока¬
зываются структурами. Структурой оказывается и всякая
цепь, ибо если, например, а Ъ, то sup {а, 6} = b и
и inf {а, Ь} = а. Напротив, в примере 11 мы имеем час¬
тично упорядоченное множество, не являющееся ни ниж¬
ней, ни верхней полуструктурой. Действительно, верх¬
ний (нижний) конус любой пары точек, не расположен¬
ных одна под другой, пуст.
Полуструктуры тесно связаны с коммутативными по¬
лугруппами, все элементы которых идемпотентны.
Теорема 1. Пусть Р — коммутативная полу¬
группа, причем а2 = а для любого а ЕЕ Р. Определим от-
*) Широко распространен также термин «решетка».
151

ношения
а Ь, если а = аЬ,
и
а ^3 Ь, если Ь ~ аЬ.
Тогда каждое из этих отношений оказывается порядком
и множество Р с порядком (с порядком оказывается
нижней (верхней) полуструктурой, причем
inf {a, Ь} = ab (sup {a, Ь} = аЬ).
Доказательство. Рефлексивность обоих от¬
ношений вытекает из равенства а2 ~ а. Если а <4 Ь и Ь С
^с(а^ЬиЬ^с), то а — аЬ и b ■— Ьс (Ь =■■= аЬ и с ~ Ьс).,
Учитывая ассоциативность умножения, получаем
а ^аЬ = a (be) ~ (ab) с = ас
(с = be = (ab) с = а (Ьс) = ас),
т. е. а с (а ^3 с). Таким образом, оба отношения тран-
зитивны. Если а^ЬнЬ^а(а^ЬнЬ^а),тоа = аЬ
и Ь = Ьа (Ь = аЬ и а ~ Ьа), откуда а, = Ь в силу комму¬
тативности умножения. Таким образом, -С и — по¬
рядки. Из равенств (ab) а = a (ab) = a2b = ab и (ab) Ь
== ab2 = ab вытекает, что ab ЕЕ {а, Ь}^ относительно по¬
рядка Если хЕЕ {а, Ь)Ъ, то х <; а и х Ь, т. е. х = ха
и х = хЪ. Отсюда
х (аЬ) ~ (ха) Ь = хЬ ~ х,
т. е. х ab. Следовательно, ab — наибольший элемент
нижнего конуса {«, Ь}^, т. е. ab = inf (а, Ь}. Чтобы до¬
казать, что аЬ ЕЕ {а, Ь}& относительно порядка обра¬
тим внимание на равенства а (ab) *= а2Ь = аЬ и Ь (аЬ) —
(Ьа) Ь = (аЬ) Ь — ab2 = ab, откуда а ab и Ь аЬ.
Кроме того, если х ЕЕ {а, Ь}\ то а х и Ь х, т. е.
х — ах и х = Ьх. Отсюда
(аЬ) х = а (Ьх) = ах = х,
т. е. аЬ х. Следовательно, аЬ — наименьший элемент
верхнего конуса (а, Ъ}^ относительно порядка <], т. е.
ab = sup {а, Ь}.
Теорема 2. Если L — структура, то полагая,
а Ь = sup {а, Ь],
ab = inf {а, 6},
152

имеем'.
(1)	(a+b) + c = а + (Ь + с); (Г)
(2)	а	4-	b	= b 4-	а;	(2 )
(3)	а	+	а	-=	а;	(3')
(4)	(а	-И	Ь)	а	= а;	(4')
(ab) с а (Ьс);
ab = Ьа\
аа — а;
аЪ + а = а.
Доказательство. Как было отмечено на с. 150,
a -j- Ь и аЬ — однозначно определенные элементы мно¬
жества L. Другими словами, + и • — операции на мно¬
жестве L. Свойства (2) и (2') очевидны. Для доказательства
свойств (3) и (3') достаточно заметить, что {а, а)Л ==. а^
и {а, a}v =	. Для доказательства свойства (1) поло¬
жим а -|- b = s, b + с = С 5 4- с и и а + t — v. Тогда
s и и с и, ибо и ЕЕ {.v, с}Л. Кроме того, а s и
поскольку s ЕЕ {а, 6}Л. Учитывая транзитивность порядка,
имеем а и, Ъ -С и и с и, т. ё. и Е=Е {я, Ъ, Если
х ЕЕ {а, Ъ, с}-\ то а х, b х и с	х и, в частности,
х ЕЕ {а, Ъ}&. Поскольку s — наименьший элемент верхне¬
го конуса {а, д}Л, то $ х. Вместе с с х это дает, что
х СЕ {е с}А. Но и — наименьший элемент верхнего кону¬
са {.s*, и, следовательно, и х. Этим доказано, что
и — наименьший элемент верхнего конуса {а, Ъ, с}Л.
С другой стороны, из неравенств а и, b t v и с
<С -С вытекает, что v ЕЕ {а, Ъ, с}Л. Если же х ЕЕ {«,
5, с}^, то а <^ х, Ъ х и с х. Отсюда х ЕЕ {Ъ, с}Л,
а значит, I х. Вместе с а х это дает, что х ЕЕ {а, Z}\
а значит, и х. Следовательно, и — наименьший элемент
верхнего конуса {а, 5, с}^. Поскольку и — также наи¬
меньший элемент этого верхнего конуса, то, как отмеча¬
лось на с. 149, и = v. Тем самым доказана справедливость
свойства (1). Свойство (Г) доказывается двойственным рас¬
суждением (т. е. вместо верхних конусов следует рас¬
сматривать нижние). Переходя к доказательств у свойства
(4), заметим, что а а 4~ Ъ и, следовательно, а ЕЕ {а,
а -4 Ь}^. Но если х ЕЕ {а, а + 6}v, то х	а, т. е. а -—
наибольший элемент нижнего конуса {а, а	Ь}^' и по оп¬
ределению а — (а 4- Ь) а. Двойственным рассуждением
устанавливается свойство (4').
Замечание. Проанализировав доказательство теоремы 2,
нетрудно понять, что свойства (1) —(3) ((!') — (3')) остаются, спра¬
ведливыми для любой верхней (нижней) полуструктуры.
Из свойств (1), (2), (1') и (2') видно, что структура является ком¬
мутативной полугруппой как относительно операции ►(-, так и
относительно операции •,
153

Теорема 2 допускает следующее обращение.
Теорема 3. Всякое множество Р с двумя операция¬
ми + и обладающими свойствами (1) —(4) и (Г)—(4'),
можно превратить в структуру, положи
а Ь, если а = аЪ.
При этом
ab = inf {я, Ъ},
а + b = sup {а, Ь}
и неравенство а Ъ имеет место тогда и только тогда,
когда а Ъ = Ь.
Доказательство. В силу теоремы 1, Р — час¬
тично упорядоченное множество, причем ab — inf {а, Ь},
Ввиду а (а + Ь) = а и
b (а + b) = b (Ь + а) = b
имеем а Ъ ЕЕ {а, Ъ}\ Если х ЕЕ {а, Ь}\ то ах = а и
Ьх = Ъ, откуда по (4'), (2) и (2') получаем
х = х-[-ха = х-[-ах = х-\-а,
х ~ х + xb = х + Ьх = х + Ъ.
Но тогда, учитывая (3), (1), (2), (2') и (4), имеем
(а ± Ь) х = (а + Ь) (х х) = (а + Ь) (х а х Ь) =
= .{а + Ь) (х + (а + Ь)) = а 4-' Ь,
т. е.
а + Ъ х.
Таким образом, а + Ь — наименьший элемент верхнего
конуса {а, Ь}£\ т. е.
а + b = sup {а, Ь}.
Поэтому, если а 6, то Ь оказывается наименьшим элемен¬
том верхнего конуса {а, Ь}^ и, значит, а + b = Ь. Если
же а + Ъ = Ь, то Ъ ЕЕ {а, Ь}^, откуда а Ь.
Из определения операций + и •, учитывая, что
sup {a, b} (inf {а, Ь}) — это наименьший (наибольший)
элемент верхнего (нижнего) конуса {а, Ь}^ ({а, 6р),
получаем:
Следствие 1. Если а, b с, то а + Ъ с,
Следствие 2. Если с а, Ъ, то с аЬ-
Замечая, что а b и с <; d влечет b + d ЕЕ {а,
и ас ЕЕ {b, d}v, выводим:
С л е д с т в и е 3. Если а и с	то а -|- с
b + d и ас bd.
154

Если в соответствии с теоремой 2 от структуры перейти к мно¬
жеству с двумя операциями, а от него к структуре в соответствии
с теоремой 3, то, как нетрудно проверить, возникает исходная
структура. То же самое имеет место и при переходе от множества
с операциями к структуре, а затем снова к множеству с операциями.
Отображение ср структуры L в структуру L' называет¬
ся гомоморфизмом, если ср (а 4- Ь) = ср (а) ср (6) и
<р (ab) = ср (а) ср (Ь) для всех а, Ь ЕЕ L. Взаимно однознач¬
ный гомоморфизм называется изоморфизмом. Если L —
структура функций (пример 8 из таблицы 5), а Л' — струк¬
тура действительных чисел с обычным порядком и ср (/) =
= / (0), то ср оказывается гомоморфизмом. Действитель¬
но, если, например, / (0) g (0), то
<Р (supL (/, g)) = g (0) = SUPl- (f (0), g (0)} =
= SUPi/ {<p (/), ф U)},
Ф (infL (/, g)) = /(0) = inft, {/ (0),g (0)} == {cp (/), <P (g)}-
Гомоморфизм структур является изотопным отображе¬
нием. Действительно, если ср — гомоморфизм структур
и а Ь, то согласно теореме 3 а — ab. Отсюда ср (а) =
= ср (а)-ср (Ъ), т. е. ср (а) ср (Ь). Однако изотопное ото¬
бражение не обязано быть структурным гомоморфизмом
Например, пусть L — структура подмножеств множества
М = {1, 2, . . ., п}, где w > 3 (пример 6 из таблицы 5),
L' — структура целых чисел с обычным порядком и
ср (Л) = {число точек подмножества Л}.
Изотонность этого отображения очевидна. Однако
ср (stipL ({1, 2}, {3})) = ср ({1, 2, 3}) = 3 ф 2 =
= supL< {2, 1} = supz/ {ф ({1, 2}), ф ({3})}.
Непустое подмножество Н структуры L называется
подструктурой, если а, Ъ ЕЕ Н влечет за собой а + Ъ ЕЕ Н
и ab ЕЕ Н. Любое подмножество цепи оказывается под¬
структурой. Совокупность конечных подмножеств струк¬
туры всех подмножеств бесконечного множества (пример 6
из таблицы 5) также оказывается подструктурой.
Аналогично теоремам 6 из § 2, 5 из § 3, 2 из § 4 и 5 из
§ 5 доказывается.
Теорема 4. Если ср — гомоморфизм структуры L
в структуру L', то Im ср — подструктура структуры L'.
Структура L называется дистрибутивной, если для
любых a, b, с ЕЕ L имеет место (а + Ь)с = ас + Ъс.
155

Теорема 5. Структура всех подмножеств некото¬
рого множества (пример 6 из таблицы 5) дистрибутивна.
Доказательство. Если А, В и С — подмноже¬
ства множества М и х е= (A (J В) р| С, то х ЕЕ С и, кроме
того, х ЕЕ А или х ЕЕ В. Таким образом, х Е: А р| С или
хеВ С, т. е. х е (А П С) U (В Q С). Наоборот, ес¬
ли х (А р| С) U (В П С), то х Е А С или х Е
Е В Q С. В обоих случаях х Е С и, кроме того, х Е А
или х ЕЕ В. Значит, х Е (A [J В) Q С.
В качестве другого примера дистрибутивной структуры укажем
произвольную цепь. Действительно, если а, Ъ, с — элементы цепи,
то имеет место а Ъ с, а с Ь, & < а < с, b с < а,
с < я < & или с С & С а- В этих случаях имеем
а-|-Ь
(а-\-Ь)с
ас
Ьс
ас -h Ьс.
1
ъ
ь
а
b
b
2
ъ
с
а
с
с
3
а
а
а
b
а
4
а
с
с
Ь
с
5
Ь
с
с
с
с
6
а
с
с
с
с
Таким образом, (а -р Ь)с — ас -|- Ьс во всех случаях.
Примером недистрибутивной структуры служит нятиэлемент-
пое множество {О, 1, а, Ъ, с} с порядком, задаваемым условиями
и0<с^1 (см. рис. 8). Здесь (а + Ь) с =
= 1с = с, но ас + Ьс = 0 + 0 = 0.
Теорема 6. Следующие свойства структуры L
эквивалентны:
(1)	L дистрибутивна;
(2)	аЬ А~ с = (а А~ с) (Ь А~ с) для любых а, Ъ, с ЕЕ L;
(3)	аЬ + ас + Ьс ~ (а + Ь) (а + с) (Ь + с) для любых
a, b, с Е L.
Доказательство. (1) => (2). Имеем
(а А~ с) (Ь А~ с) = (а А~ с) b А~ с = ab А~ Ьс А~ с = ab А~ с*
(2)	=е (3). Действительно,
аЬ + ас + be = аЬ А~ (ас + Ьс) ==
= (а 4-	ас	+	Ьс) (Ь	А~ ас А~ Ьс) =
= (а +	Ьс)	(Ь + ас)	=	(а	+	Ь)	(а + с) (Ь + а)	(Ъ +	с) =
= (а + Ь) (а А~	с) (Ь	4-е).
(3)	=>	(1). Если а	с,	то	ас	= а = а + аЬ = ab	А~ 'de*
156

Поэтому
ас + be = ab 4~ ас + be =
— (а + b) (а + с) (b + с) = (а + Ь) с (fe + с) (а + fe) с,
поскольку с Ь 4- с. Таким образом, доказываемое со¬
отношение дистрибутивности установ¬
лено в предположении, что а с*.
Чтобы установить его справедли¬
вость в общем случае, положим
и = аЬ + ас + Ьс
и
v = (а -ь Ь) (а + с) (Ь + с).
Из теоремы 3 и ее следствия 1 выте¬
кает, что ас + Ьс с. Используя	Q
уже доказанный частный случай ди-	рИс. 8
стрибутивиого закона, получим
си = с (ab -|- (ас -|- Ьс)) =
= cab + с (ас + Ьс) — аЬс + ас -Т Ьс ас 4- fee,.
cv = с (а 4- Ь) (а 4- с) (Ь 4~ с) = (а 4- Ь) с.
Но и = и по условию. Поэтому
(а 4- Ь) с — си> — си = ас Ьс.
Пусть D — дистрибутивная структура. Непустое под¬
множество I структуры D называется идеалом, если х,
у ЕЕ / влечет х 4" У ЕЕ I и xd ЕЕ I для всякого d из D.
Теорема 7. Если нижний конус некоторого под¬
множества дистрибутивной структуры не пуст, то он
является идеалом *).
Доказательство. Если х, у ЕЕ Av, то х а и
у а для каждого а ЕЕ А. Ввиду следствия 1 теоремы 3
х 4“ У а для каждого а ЕЕ А, и, кроме того, если d ЕЕ D,
то xd х а для каждого а ЕЕ А. Таким образом, х у
и xd лежат в А^', т. е. А^ — идеал.
Теорема 8. Если I и J — идеалы дистрибутивной
структуры D, то идеалом в D является и множество всех
сумм вида х 4~ У. еде х ЕЕ I, у ЕЕ J.
Доказательство. Если х. х ЕЕ I, у. у' ЕЕ J и
d ЕЕ D, то
(# 4- у) 4- (х 4- у')= (х 4- х) + (у + у')
♦) Эта теорема справедлива для произвольной структуры при
(том*же самом определении идеала.
157

(I
(.!• -|- у) d = xd + ydf
причем x + xf, xd GE I и у 4- у', yd ЕЕ Л
Идеал, рассмотренный в теореме 8, называется суммой
идеалов I и J и обозначается через 1 4“ J-
Теор е м а 9. Всякая конечная дистрибутивная струк¬
тура изоморфна подструктуре структуры всех подмно¬
жеств некоторого конечного множества.
Доказательство. Пусть а и Ъ — два различ¬
ных элемента конечной дистрибутивной структры D. Если
а Ъ и Ъ <1 а, то а — Ъ. Следовательно, имеем а Ъ или
Ъ а. Допустим, что Ъ а. (Случай, когда а. Ь, рас¬
сматривается аналогично.) Существуют идеалы струк¬
туры D, которые содержат а, по не содержат Ь. Ввиду
теоремы 7 таким будет, например, нижний конус а^.
Поскольку структура конечна, то среди таких идеалов
есть максимальные, т. е. не вкладывающиеся в строго
больший идеал, обладающий указанным свойством. Пусть
1а,ь — один из таких максимальных идеалов.
Лемма 1. Если с 1а,ъ, то Ъ = и 4" s, где и с и
s ЕЕ Ia,v
Для доказательства положим I = 1а,ъ и рассмотрим
идеал с^ 4- I- Поскольку структура D конечна, она со¬
держит наименьший элемент 0. Поскольку 0d = 0 для
всех d ЕЕ D, элемент 0 принадлежит любому идеалу струк¬
туры D. Отсюда х = 0 4	4: + / для всех х GE Z,
т. е. I се & 4~ Z, и с = с 4~ 0 GE с^ 4- Z. Следовательно,
Z ЕС с^ 4- Z. Отсюда ЪЕЕ 4- Z, ибо I максимален среди
идеалов, содержащих а, но не содержащих Ъ. Приняв
во внимание определение суммы идеалов, получаем, что
Ъ = и 4- 5, где и GE cv, т. е. и с, и s GE Z.
Лем м а 2. Если х, у Iа, ь, то ху 1а, ъ-
Действительно, ввиду леммы 1 имеем Ъ == и 4- 5 =
= и 4- t, где и х, v у и s, t ЕЕ 1а, ъ- Ввиду теоремы 2
и следствия 3 теоремы 3 отсюда следует
Ъ = Ъ- = (и 4- 5) (и 4- t) < (х 4- {у 4- 0 =
= ху 4- (xt 4- sy 4- st).
Поскольку xt 4- sy 4~ st GE 1а,ъ, то предположение, что
ху GE Iа,ъ, влечет Ъ ЕЕ 1а,ь, вопреки выбору идеала 1а ь*
Пусть 2 = {0, 1} — двухэлементная цепь, где 0 1Й
и
fl, если x^D\Iaibl
Фа, ъ (х)	если х ц ь.
158

Л е м м а 3. ф<ьЬ — гомоморфное наложение структу¬
ры D на структуру 2.
Для доказательства достаточно заметить, что 1а>ъ =/=
-z- D, и установить, что, условившись писать ср и I вместо
11 Льо соответственно, имеем
<р 0 + у) = ф (*) + ф (г/)
II
Ф Оу) = <р (ж) ф (г/)
для любых х, yE=D. Возможны следующие четыре слу-
чая:
1) х, у ЕЕ 1\ 2) х (ЕЕ I, у е£ I; 3) х	I, у ЕЕ I, 4) х, у I.
Заметим, что х + у ЕЕ Z влечет х — х (х + у) ЕЕ I и
у = у (х + у) ЕЕ I. Поэтому в первых трех случаях имеем
ф(х + у) = 0 = 0 + 0 — ф (х) + ф (у)г
Ф (ху) = 0 = 0-0 = ф (х) ф (у),
Ф (х + у) = 1 = 0 + 1 = ф (х) + ф (уД
Ф (ху) = 0 = 0-1 = ф (х)ф (у)
и
Ф (х + у) = 1 = 1 + 0 = ф (х) + ф (у),
Ф (.г’У) = 0 = 1 -0 = ф (х) ф (у)
соответственно. В четвертом случае, учитывая лемму 2,
получаем
Ф (х + у) = 1 = 1 + 1 = ф (х) + ф (у)
п
ф (ху) = 1 = 1.1 = ф (х) ф (у).
Теперь обозначим через М множество всех пар («, 6),
где а, Ъ ЕЕ D и а Ъ, а через Р — структуру всех под¬
множеств множества М. Для доказательства теоремы
укажехМ гомоморфное вложение структуры D в структуру
Р. С этой целью для всякого х из D положим:
ф (х) = {(а, Ь) ЕЕ М ] х 1а,ъ} =
= {(а, Ь) ЕЕ М | фглЬ (х) = 1}.
Ясно, что Ф — отображение множества D в множество Р.
Если х у, то имеем, например, у х, Но тогда х ЕЕ
ЕЕ /х,?/ и у	т. е. (х, у) Ф (х), но (х, у) Е Ф (у),
Следовательно, Ф (х) =^= Ф (у), т. е. Ф — вложение.
Остается доказать, что
Ф (х + у) = Ф (х) U Ф (У)
159

и
Ф (ху) = Ф (х) П Ф (у).
Но если (а, Ъ) ЕЕ Ф (х + у), то, учитывая лемму 3, имеем
1 = Фа, Ь	+ У) = Фа, 0 (^) + Фа,Ь (у) •
Отсюда фа)Ь (.г) = 1 или сра?ь (z/) = 1, т. е. или (а, Ъ) ЕЕ
ЕЕ Ф (х), или (а, Ь) ЕЕ Ф (у)> Последнее означает, что
(а, Ь) (ЕЕ Ф (.г) [J Ф (у). Таким образом, Ф (х у) ее
ее ф (ж) [J Ф (у)- Если же (а, Ь) ЕЕ Ф (х) |J Ф (у), то
имеем, например, (a, b) ЕЕ Ф (х). Отсюда
Фа,Ь + У) = Фа,Ь (*) + Фа, Ъ (У) = 1 + Фа, !> (У) = Л,
т. с. (а, 6) ЕЕ Ф (х + у). Таким образом, Ф (,т) [J Ф (у) ее
ее Ф (х + у), и первое из нужных соотношений доказано.
Если теперь (а, Ъ) ЕЕ Ф (ху), то, принимая во внимание
лемму 3, имеем
1 = Фа.Ь (*У) = (ра,ь(х)<Ра,Ь (У)г
что возможно лишь при (рП)Ь (х) — cpoj, (у) = I. Но тогда
(а, Ь) ЕЕ Ф (х) П Ф (у), т. е. Ф (ху) ст ф (.г) р| ср (у). Если,,
наконец, (а, Ь) ЕЕ Ф (х) р| Ф (у), то
Фа, Ь М = Ч>а,Ъ О)фа,Ь ((/) = 1 • 1 = 1,
т. е. (а, Ь) ЕЕ Ф (ху). Таким образом, Ф (х) р| Ф (у) ЕЕ
ее ср (ху), чем и заканчивается доказательство, так как
Jin Ф — подструктура структуры Р согласно теореме 4.
Дистрибутивная структура В с нулем и единицей назы¬
вается булевой алгеброй, если для каждого элемента а из
В найдется такой элемент а ЕЕ В, что а + а' = 1 и аа' —
—0. Этот элемент называется дополнением элемента в.
Структура всех подмножеств любого множества является
булевой алгеброй. Цепь же, содержащая более двух эле¬
ментов, булевой алгеброй не является.
Теорема 10. Каждый элемент булевой алгебры име¬
ет только одно дополнение.
Доказательство. Если а' и Ъ — дополнения
элемента а, то
а' = а -1 = а' (а + Ь) — а а + а'Ь = 0 + а'Ъ —
— ab + а'Ь = (а + а') b = 1-Ъ = Ь9
160

Теорема 11. Z> булевой алгебре справедливы сле¬
дующие соотношения:
{а + b)f = а'Ь',
(аЬ)' — а' + Ь\
а" = а,
О' = 1, Г = 0.
Доказательство. Равенство а — а сразу сле¬
дует из теоремы 10. Учитывая теорему 6, получаем
(а + Ь) + а b = (а + b + а) (а b b ) = 1 • 1 = 1 т
(а + b) (a'b') = aa'b' + ba'b' = 0 + 0 = 0.
Отсюда в силу теоремы 10 имеем (а + Ь)' — а'Ь'. Далее,
учитывая уже доказанные соотношения, получаем
(ab)' = (a"b")' = ((а' + b')')' — а + Ь'.
Наконец, из равенств 1 + 0=1 и 1-0 = Ои теоремы 10
вытекают последние два соотношения.
Теорема 12. Всякая конечная булева алгебра изо¬
морфна структуре всех подмножеств некоторого конечно¬
го множества.
Доказательство. Пусть В — конечная булева
алгебра. Элемент р из В называется атомом, если р + 0
и 0 =# х + р влечет х = р*). Обозначим через М множе¬
ство всех атомов булевой алгебры В, а через Р — булеву
алгебру всех подмножеств множества М.
Л е м м а 1. Если 0 х Ei В, то найдется такой атом
р, что р <; х.
Для доказательства положим х0 = х. Допустим, что
найдены различные ненулевые элементы xQ, х1г . . ., хт ее
ЕЕ В, такие, что
Хт < • • • <	< до¬
вели хт — атом, то можно положить р = хт.® В про¬
тивном случае найдется элемент	ЕЕ В такой, что
+пч-1 Хт, ^т+1	%т+1 0* ВСЛИ Xm+i = ГД0
0 < i < т, то xt = хт+1 < xm < Xt, откуда xt = хт в
силу антисимметричности. Следовательно, ,г0,	х±, ...
. . ., хт, хт+1 — различные элементы из В. Остается за¬
метить, что, ввиду конечности множества В, описанный
процесс построения элементов Xi не может продолжаться
бесконечно.
*) Другими словами, р — минимальный элемент частично упо¬
рядоченного множества ненулевых элементов булевой алгебры В
6 Л. Л. Скорняков	101

Л е м м а 2. Каждый ненулевой элемент х из В равен
сумме всех атомов, лежащих в нижнем конусе xv.
В самом деле, если х ЕЕ В, то пусть р1У . . рп — все
атомы, принадлежащие нижнему конусу х^, и у =
=	+ . . . + рп. В силу следствия 1 теоремы 3, у 4^ х.
Поэтому
X = X (у + у') = ху + ху' = у + ху'.	(*)
Допустим, что ху' Ф 0. Тогда по лемме 1 найдется атом
Р ху'- Ио ху' <7 х. Следовательно, р х, а значит,
р = pi для некоторого I. Кроме того, pi <7 у. По следст¬
вию 3 теоремы 3
Pt = PPi < (ху')у < У'У = 0,;
т. е. pi = 0, что невозможно. Таким образом, ху' — 0,;
что вместе с (*) дает х = у.
Теперь определим отображение Ф множества В в мно¬
жество Р, полагая
Ф (х) = М р|
Если Ф (х) = Ф (z/), то из леммы 2 сразу следует, что
х = у, т. е. Ф оказывается вложением. Пусть теперь U —’
некоторое подмножество из М. Если U пусто, то 77 =
= Ф (0). В противном случае обозначим через х сумму
всех атомов, лежащих в U. Ясно, что U сс ф (х). Если
q Ei Ф (х), то из равенства
q = xq = 3 PQ
вытекает, что pq Ф 0 для некоторого р ЕЕ U. Но тогда
0 pq < р
И
0 РУ Учу
откуда в силу определения атома следует
У — РУ = Р ^Е U,
Таким образом, Ф (х) — U, т. е. Ф является наложением.
Для дальнейшего понадобится
Лемма 3. Если х у, то Ф (х) ст Ф (г/).
Действительно, если х<р у, то х^ ст у^, откуда
Ф (х) = М Q xv ст Л/ р] zp7 = Ф (у).
162

Остается убедиться в справедливости равенств
ф (^ + у) = ф (х) U Ф (у)
и
Ф (т?/) = Ф (х) П Ф (у)
для всех х, у ЕЕ В. Из леммы 3 вытекают включения
Ф (я) U Ф (у) ф + у)
и
Ф (%у) с ф (х) п Ф (у).
Если р £= Ф (% + у), то р х + у. Отсюда
р = р (х + у) = рх + РУ.
Следовательно, рх 0 или ру у= 0. В первом случае
имеем
0 < рх < р,
откуда рх — р, а значит, р х, что означает р ЕЕ Ф (х).
Во втором случае получаем, что р ЕЕ Ф (у). Таким обра¬
зом, Ф (х + у) cz ф (х) U Ф (у) и, следовательно,;
Ф (х 4- z/) = Ф (ж) U Ф (у). Наконец, включение р d
ЕЕ Ф (х) р] Ф (у) влечет р х и р у. Отсюда р <; ху,
т. е. р ЕФ (ху). Следовательно, Ф (.г) Q Ф (у) се ф (ху),-
а значит, и Ф (ху) = Ф (х) П Ф (у).
Остановимся на связи булевых алгебр с кольцаАми.
Кольцо В называется булевым, если а2 = а для всех
7а из R.
Теорема 13. Булево кольцо коммутативно, и а +
+ а = 0 (/;?. е. а. — — а) для всех элементов а»
Док а вате л ь с т в о. Во-первых,
а а — (а 4- а)2 = 6/2 + а~ + а2 4- а2 = а 4~ а 4 -> г а,
откуда а лг ci ~ 0- Во-вторых,
а + Ъ = (а + б)2 — сг 4- аЬ 4- Ьа 4- Ъ* =
= а 4- Ъ 4- ab 4- Ьа.
Отсюда ab 4“ Ьа — 0. Учитывая доказанное выше, полу¬
чаем
ab = ab 4- (Ьа 4- Ьа) = (аЬ + Ьа) 4- Ьа = Ьа.
Тео р е м а 14. Пусть В — булева алгебра. Для лю¬
бых а, Ь ЕЕ В положим
а Ь = аЬг 4" & Ь
*63

и
aob — ab.
Tогда В становится булевым кольцом с единицей.
Доказательство. Равенство а2 = а, ассоциа¬
тивность умножения, наличие единицы и коммутативность
обеих операций очевидны. Далее, учитывая теорему 113
имеем
(а * Ь) * с —	+ а'Ь) с''+ (ab' + а'Ь)' с —
= ab'c' -р а'Ьс ~Р (а -р 6) (а Ч- 6х) с =*
= ab'c' -|- а'Ьс' + а'Ь'с -р Ьас =
= a (b'c' + be) + a' (be + b'c) =
= а (Ь' + с) (Ь + с') + a' (be + b'c) =
= a (be' 4- b'c)' + a (be' + Ъ'с) — а * (Ъ ф с)э
а # 0 = аОх + а'О = а-1 = а
и
а а = аа' -Р а а = О,
т. е. В оказывается абелевой группой по сложению. На¬
конец,
(а 4Р b)oc = (ab' + а'Ь) с = ab'c + ab'c =
= ас (b' + с') + (а + с') Ъс = (ас) (be)' + (ас)'(be) —
= аос Ьос.
Теорема 15. Пусть В — булево кольцо с единицей
относительно операций 4k w Положим
a+b = a^b^ а°Ь
и
ab = а°Ь.
Тогда В становится булевой алгеброй В. Кольцо, получае¬
мое из алгебры В с помощью теоремы 14, совпадает с В.
Применение только что описанной конструкции к кольцу,
указанному в теореме 14, приводит к исходной булевой
алгебре.
Доказательство. Ассоциативность операций
+ и •, а также равенство аа — а проверяются непо¬
средственным подсчетом. Коммутативность булева кольца,
установленная в теореме 13, обеспечивает коммута,
тивиость этих операций. Кроме того, о ф а = 0 по
164

теореме 13. Поэтому
а + а — а 44 а 44 а°а ~ а,
(а + Ь) а — (а * Ъ * а°Ь)оа = сюа * а°Ь а^Ь^а
= аоа 44	44 а°Ь а
и
а + ab = а * a°b '44 ао(а°Ь) = а 44 а<>Ъ 44 а°Ь — а.
В силу теоремы 3, В оказывается структурой. Ясно, что
al = а и аО = 0 для всех а ЕЕ В, т. е. структура В облада¬
ет нулем и единицей. Из равенств
а (1 44 а) — «°1 44 а°а ~ а 44 а = О
и
« + (1 # а) = a 1 4|= а # ао(1. * а) =
= a4f=l#a#«#a = l
вытекает, что!? — структура с дополнениями. Ее дистри¬
бутивность проверяется следующим образом:
(а + Ь) с = (a 44 b 44 ab)°c=ac 44 Ьс 44 ас^Ьс = ас + Ьс.
Заключительные утверждения теоремы вытекают из ра¬
венств
аЬ' + а'Ь =
= ао (1 44 ь) 44 (1 44	44	(1 44 ^)°^° (1 44^) =
= а 44 аЬ 44	44	44	44 а^а 44 аЪЬ 44 аЬаЬ = а 44
(а 44 &) 44 a°b =	+ а'Ь) №)' 4“ (ab' + ab)'ab —
= (ab' 4- а'Ь) (а' + Ь') + (а' + b) (а + Ь')аЬ =
= аЬ' 4- а'Ь + ab = ab' + ab + а'Ь + аЬ =
а (Ь' Ь) (а 4- а) Ь = а 4~ Ь*
У н р а ж нения
1.	Какие из отношений, приводимых в таблице на следующей
странице, являются порядками?
2.	Пусть Р — множество неотрицательных целых чисел с обыч¬
ным порядком, а Р' — то же самое множество, упорядоченное по де^
лимости (пример 5 из таблицы 5), ср: Р —> Р' и *ф: Р' —> Р — тож¬
дественные отображения. Является ли какое-нибудь из них изотоп¬
ным?
3.	Если <р: Р Р' — изоморфизм частично упорядоченных
множеств, то элемент а является наименьшим, наибольшим, мини¬
мальным или максимальным элементом частично упорядоченного
множества Р тогда и только тогда, когда соответствующим свойст¬
вом обладает элемент ф (а) частично упорядоченного множест¬
ва Р'. Построить примеры, показывающие, что это не всегда так,
если <р изотопное отображение.
165

Множество
Отношение р
1
Подмодули модуля А
Включение (ср. пример 6 из
таблицы 5)
2
Треугольники на плоско¬
сти
арЬ, если площадь треуголь¬
ника а не превосходит пло¬
щади треугольника Ь
3
Слова (включая пустое)
арЬ, если Ь = ци для некото¬
рого слова и
4
То же
арЬ, если Ъ = иаи для некото¬
рых слов и и V
5
Слова от двух или болео
букв
арЬ, если существуют такие
слова и и v, что аи = Ьо
6
Слова от одной буквы
То же
4.	Доказать, что существуют в точности два неизоморфпых
двухэлементных частично упорядоченных множества.
5.	В конечном частично упорядоченном множестве всегда суще¬
ствуют как минимальные, так и максимальные элементы. Однако
наибольший (наименьший) элемент может не существовать.
6.	Элемент а максимален (минимален) тогда и только тогда,
когда = {а} (когда аУ = {а}).
7.	Доказать следующие свойства конусов: а) если A CZ В, то
2 Bv;6) A СЛ^7 П	в) Лд =	г)Л? =
= 4^av; д) (4 (J В)Л = 4Л П е) (4 (J S)v =	(“] 5V.
8.	Элемент, являющийся максимальным и минимальным одно¬
временно, не сравним ни с каким отличным от него элементом.
9.	Если а и Ь — максимальные элементы, то точная верхняя
грань множества {а, Ь] существует тогда и только тогда, когда а = Ь.
10.	Найти точные верхние и точные нижние грани (или доказать
их отсутствие) двухэлементных подмножеств в частично упорядо¬
ченных множествах примеров 3, 5 и 8 из таблицы 5 и 1, 3 и 4 из уп¬
ражнения 1. В тех случаях, когда частично упорядоченное множе¬
ство оказывается структурой, выяснить, является ли она дис¬
трибутивной.
11.	Всякий минимальный (максимальный) элемент структуры
является наименьшим (наибольшим).
12.	Если а, Ь, с — элементы структуры и а + Ь + с = abc,
то а = Ь = с.
13.	Доказать равносильность следующих свойств структуры L:
a) L — цепь; б) все непустые подмножества из L являются подструк¬
турами; в) а = Ьс влечет а = Ь или а = с.
14.	Изотонное отображение цепи в любую структуру является
гомоморфизмом структур.
15.	Доказать, что дистрибутивность структуры L равносильна
каждому из следующих свойств: а) неравенство а Ь имеет место
тогда и только тогда, когда ас^5сиа + с^5 + с для некоторого
с е L\ б) (а + 5) (с + аЬ) = аЪ + ас + Ьс для любых а, 6, с е L;
в) (а -|- Ь)с < а + Ьс для любых а, b, с е L.
16.	Идеал I дистрибутивной структуры D называется простым,,
если аЬ <= I влечёт за собой а е I или Ь е 1. Доказать, что всякий
169

максимальный идеал М дистрибутивной структуры D (т. о. идеал,
отличный от D и не содержащийся ни в каком ее идеале, отличном
от М и D) прост и что нижний Конус является простым идеалом
тогда и только тогда, когда а = Ьс влечет за собой а — Ь или а = с.
17.	Следующие утверждения об элементах а и Ь из булевой ал¬
гебры равносильны: а) а Ь; б) аЬ' = 0; в) а' + Ъ — 1.
18.	Всякое допустимое разбиение булевой алгебры является
допустимым разбиением соответствующего булева кольца и на¬
оборот.
19.	Булево кольцо является полем тогда и только тогда, когда
оно двухэлементно.
20.	Идемпотенты любого коммутативного кольца образуют бу¬
лево кольцо относительно операций
е + / = е + f — ef,
е о f = ef.
21.	Убедиться, что подгруппы группы (Z/2Z)®(Z/2Z) об¬
разует структуру, изоморфную структуре, изображенной на рис. 8
(см. с. 157).

ГЛАВА III
ЛИНЕЙНЫЕ ПРОСТРАНСТВА
И ЛИНЕЙНЫЕ АЛГЕБРЫ
Общая теория линейных пространств излагается здесь
в минимальном объеме. Поэтому некоторые факты, обычно
выводимые из общей теории, сопровождаются специальны¬
ми доказательствами. Как правило, приводятся лишь ре¬
зультаты, необходимые для дальнейшего. Исключение сде¬
лано для теорем, освещающих связь теории линейных про¬
странств с системами линейных уравнений. Результаты,,
справедливые для произвольных модулей, изложены в§5
предыдущей главы и, разумеется, широко используются
здесь. Что касается линейных алгебр, то в качестве основ¬
ного объекта изучения выступают конечномерные вполне
приводимые алгебры.
Отбор результатов диктуется потребностями теории
представлений конечных групп, излагаемой в гл. IV.
В связи с этим конечность размерности линейной алгебры
включена в определение. Значительное место уделено ал¬
гебре линейных преобразований линейного пространства.
§ 1. Линейные пространства
Модуль над полем Р называется линейным простран¬
ством. Поскольку коммутативность поля позволяет не
различать правые и левые модули, будем записывать ли¬
нейные пространстве^ как левые модули. Подмодуль и
фактормодуль линейного пространства будем называть
подпространством и факторпространством соответст¬
венно.
Отметим простой, но важный факт.
Теорема 1. Если L — линейное пространство над
полем Р, а ЕЕ L, 0 h ЕЕ Р и да = 0, то а = 0.
Доказательство. Поскольку X 0, а Р —
ноле, то существует элемент V1. Вспоминая определение
и простейшие свойства модуля, получаем
а — la =	а = V1 (да) = V1 0 = 0.,
1G8

Линейное пространство называется конечномерным,
если оно является линейной оболочкой некоторого конеч¬
ного множества векторов, т. е. конечно порожденным мо¬
дулем. Конечномерным оказывается, например, простран¬
ство /г-мерных строк вад полем (см. с. 122). Линейное про¬
странство, не являющееся конечномерным, называется
бесконечномерным. Бесконечномерным пространством яв¬
ляется, например, множество всех таких счетномерных
строк над полем, у которых почти все координаты равны
нулю (см. с. 122).
Теорема 2. Линейное пространство L над полем Р
является неприводимым Р-модулем тогда и только тогда.,
когда L = Ра для некоторого ненулевого вектора a ЕЕ.!..
Доказательство. Если L — неприводимый
P-модуль и Q а ЕЕ L, то Ра, будучи ненулевым подмо¬
дулем модуля L, совпадает с L (ср. теорема II.5.19). Если
же L = Ра, где а, 0, и L' — ненулевой подмодуль мо¬
дуля L, то найдется ненулевой вектор Ъ ЕЕ L'. Поскольку
b = Ха, где О X Р, то
а = 1а = (Х_1Х) а == V1 (Ха) Х~]Ь ЕЕ £',
откуда L cz L', т. е. £ = £*'.
Конечная система векторов линейного пространства
называется линейно зависимой, если существует их нетри¬
виальная линейная комбинация, равная нулю. Другими
словами, система векторов {а1? . . ., ат} называется ли¬
нейно зависимой, если существуют элементы Хп . . ., Хт ЕЕ
ЕЕ Р, из которых хотя бы один отличен от нуля, такие, чго
^1Й1 +	. . . + Хтат = 0. Система, не являющаяся ли¬
нейно зависимой, называется линейно независимой. Ли¬
нейно независимую систему образуют, например, векчо-
ры . . ., еп из пространства тг-мерных строк (см. с. 122).
Действительно, если	. . .+ Хпеп = 0 для неко¬
торых Xt ЕЕ Р, то (Хп . . ., Х.п) = 0, т. е. все Xt равны нулю.
Система, содержащая нулевой вектор, всегда линейно за¬
висима. Действительно, если {0, aL, . . ., ат} — такая си¬
стема, то в качестве равной пулю нетривиальной линей¬
ной комбинации можно взять 1-0 + Обгх -|-	...	0аП1.
Теорема 3. Система, состоящая из одного вектора,
линейно зависима тогда и только тогда, когда этот век¬
тор нулевой.
Доказательство. Если система {а} линейно
зависима, то Ха = 0, где 0 X (= Р, и а 0 согласно
теореме 1. Если а = 0, то система {а} линейно зависима,
поскольку 1-а = а = 0.
469

Теорема 4. Система, содержащая два или более
векторов линейного пространства, линейно зависима в том
и только в том случае, когда хотя бы один из векторов си¬
стемы линейно выражается через остальные.
Доказательство. Допустим, что система век¬
торов	ап}, где п > 2, линейно зависима, т. е.
Н- • • •	О»
причем Kt 0 для некоторого I. Тогда
"4=	й1+ • • • + (	+
+	"v) fli+i + • • • + (- ■ 77)
Следовательно, вектор at линейно выражается через ос¬
тальные. С другой стороны, если
а^ =	+ 'Kt-iai-x Xf+itti+i 4~ • » •
то
Х1Д1 4" • • • 4“ ^г-\_а^ 4“ (— 1) Щ 4- ^г+l^i+l 4~ • • • 4- ^п^п. — О,,
где Kt = —1 =# 0, т. е. система {a17 . . ., ап} линейно за¬
висима.
Теорема 5. Сумма Ра± 4- • • • +	где а^ — нену¬
левые векторы, является прямой тогда и только тогда,
когда система векторов ЭД = (а15 . . ., ат} линейно не¬
зависима.
Доказательство. Допустим, что сумма пря¬
мая, но система ЭД линейно зависима. Тогда для подходя¬
щих Kt ЕЕ Р имеем
^1^1	• • • + ^тат — О,
причем хотя бы одно из скажем Кр, отлично от нуля.
Но Кщ} ЕЕ Pat и, согласно свойству (4) теоремы II.5.12,
Kia-i — 0 для всех i. В частности, Крар — 0. Ввиду теоремы 1
ар — 0, вопреки условию. Наоборот, если система ЭД ли¬
нейно независима и 0 = х± + . . . 4~ хт, где ЕЕ Pai,
то хл = KiUi для некоторого Kt ЕЕ Р. Таким образом,
. + Ктат = 0. Из линейной независимости си¬
стемы ЭД вытекает = . . .= Кт = 0, т. е. х± = . . .
. . хт = 0. Остается еще раз применить теорему
II.5.12.
Линейно независимая система векторов, линейная
оболочка которой совпадает со всем пространством (под-
170

пространством), называется базой этого пространства
(подпространства). Например, упоминавшиеся выше век¬
торы	£п} образуют базу пространства V п-мерных
строк, ибо, как уже отмечалось, они линейно независимы,
а V совпадает с их линейной оболочкой (см. с. 122).
Теорема 6. Всякое ненулевое конечномерное линей¬
ное пространство L над полем Р обладает базой, причем
все его базы содержат одно и то же число векторов. Если
^п} — база пространства L, а ЕЕ L и а =
—	+ . . . + то числа ЕЕ Р определяются одно¬
значно.
Доказательство. По определению конечно¬
мерного пространства, L = X (а1? . . ., ат) = Ра± + . . ,
Рат, причем а^ Ф 0 для некоторого I. Если т = 1,
то система {аД является базой пространства L в силу тео¬
ремы 3. Если т > 1, то можно предполагать, что для ли¬
нейной оболочки меньшего числа векторов существование
базы уже доказано. Если векторы alf . . ., ат линейно не¬
зависимы, то они и образуют базу пространства L. В про¬
тивном случае из теоремы 4 вытекает, что, например,
ат ЕЕ X (а^ . . ., ^m-i). Следовательно, L = X (ап . . .
. . ., am_j), и база пространства L существует по индук¬
тивному предположению*). Допустим теперь, что как
{е1, . . ., еп}, так и {Д, . . .,_ fm} — базы линейного прост¬
ранства L, причем т < п. Запишем
т
ej ==	г>
2=1
где atj ЕЕ Р (/ = 1, . . ., п) и составим систему линейных
уравнений:
011^1 + «1-^2 -|- . . . -Г Я1?Лг = 0,
. amiXl ^m2^2 “Ь • • • + ^тп^п ~
*) Приведем другое доказательство, в некотором смысле более
поучительное. Именно, заметим, что поскольку Р = Р-1, то, в си¬
лу теоремы 2, поле Р является неприводимым, а значит, вполне
приводимым Р-модулем. Поэтому, согласно теореме II.6.8, L ока¬
зывается вполне приводимым P-модулем. Учитывая теорему 2, по¬
лучаем, что
L = Рег ф . . . ф Реп,
где — ненулевые векторы из L. Из определения суммы подмоду¬
лей вытекает, что L = X (ех, . . ., еп), а теорема 5 обеспечивает
линейную независимость системы	еп}. Таким обрл
,, у еп} база пространства L.
171

Поскольку число неизвестных больше числа уравнений/
эта система согласно теореме 1.1.4 имеет ненулевое реше¬
ние, скажем, (а1? . . ., ап). Отсюда	■
п	п т	т п	п
3	= 3 “j 3 aiifi =3(3 №j} fi= S 0/{ = 0.
j=4	1=1	г=1 ; = t	1=1
Поскольку aj Ф 0 для некоторого /, это противоречит ли¬
нейной независимости системы . . ., еп}. Для доказа¬
тельства последнего утверждения теоремы допустим, что
а =	+ . . . + ИЛ, где р,, Р. Тогда после вычита¬
ния получаем
(А/£ pi) е^	(А,п рп) еп 0,
Ввиду линейной независимости системы {е17 . . еп} от¬
сюда вытекает, что Хг- — рг- = 0, т. е.	щ для всех i._
Однозначно определяемые числа Хг«, упоминающиеся
в формулировке теоремы 6, называются координатами
вектора а в базе {^17 . . ., еп}.
Линейное пространство называется п-мерным (или
имеющим размерность п), если оно обладает базой, состоя¬
щей из п векторов. По теореме 6, п векторов содержит лю¬
бая база ^-мерного линейного пространства. Размерность
линейного пространства L условимся обозначать через
di п L. Как и следовало ожидать, размерность линейно-
ю пространства дг-мерных строк равна дг, ибо, как уже от¬
мечалось, система {^1? . . . , еп} служит его базой.
Согласно теоремам 2 и 5, каждое ненулевое конечно¬
мерное линейное пространство вполне приводимо. Поэто¬
му из теоремы II.5.22 вытекает
Теорема 7. Всякое подпространство конечномер¬
ного линейного пространства выделяется прямым слагае¬
мым.
Теорема 8. Следующие свойства суммы подпро¬
странств S = Sr 4- •••+ S т некоторого линейного про¬
странства эквивалентны:
(1)	сумма является прямой;
(2)	объединение любых баз линейных пространств St
служит базой линейного пространства S;
(3)	объединение некоторых баз линейных пространств
служит базой линейного пространстеа S.
Доказательство. (1)	(2). Допустим, что
S =	© . . . ®Sm. Если {eily . . ., ein..} — произволь¬
ная база подпространства Sто согласно теореме 5	~
172

=3= Рец ф . . . ф P^ini* Теперь остается использовать гео-
рему П.5.13 и еще раз теорему 5.
Импликация (2) ==> (3) тривиальна.
(3) =Ф (1). Предположим теперь, что {^п, . .	?. } —
некоторые базы подпространств Sh
&	{^11» • • ч ^1пг1	^21’ ’ • • 1	1 & mYi • ‘ ’i ^тчт}
— база подпространства S и
+ . . . + Sm = О,
где Si €5 Тогда
Т" • • • Т ^т^т.
для подходящих kij ЕЕ Р, откуда
^11^11 +•••“!“ \nAni + ^21^21 + • • •
• • • 4“ ^2п2^2П2 + • • • Н~ ^ml^rnl 4~ • ♦ • Н~ ^тптетп1п ~ О*
Поскольку система & линейно независима, отсюда следу¬
ет, что ки == 0 для всех i и /. Но тогда s* = 0 для всех i и
S = S± ® ... @ Sm ъ силу свойства (4) теоремы II.5.12.
Теорема 9. Следующие свойства линейного прост¬
ранства L над полем Р эквивалентны:
(1)	dim L = п;
(2)	L изоморфно линейному пространству п-мерных
строк;
(3)	L представляется в виде прямой суммы п одномер¬
ных подпространств.
Доказательство. (1)	(2). Пусть {/г, . . .
. . fn} — база пространства L и V — пространство п-
мериых строк. Определим отображение (pc V —> L, пола¬
гая
ф (^1, • • Ч ^п) = W1 +	• •. •+
Легко проверяется, что это — гомоморфизм. Поскольку
L ~ X (/л, . . ., /,п), он оказывается наложением. Из пос¬
леднего утверждения теоремы 6 вытекает, что ф —
вложение. Таким образом, ср — изоморфизм, что и тре¬
бовалось.
(2) -—> (1). Пусть V — пространство n-мерных строк,
q=(0, ...,0,1,0, ...,0)
j-l
I о

и ср: V —> L — изоморфизм. Если а ЕЕ L, то для некото¬
рого v £= V имеем
а = ф (у) = Ср ( S ^iei) = S М (ег)>
2=1 2=1
т. е> L = <2 (ср (ег), . . >, ср (еп)). Если A,xcp (^) + > » ®
, 4 . + X/ncp(en) = О для некоторых X/ GE Р, то
ф (^it • *	^п) 2=5 Ф (^1^1 4“ • • • 4“ Кг^п) =
= ^1Ф (#i) “И • • » 4“ кф(^п) ~
Отсюда (Хх, ■, . ,, Хп) = 0, т. е. = 0 для всех i. Следова¬
тельно, {ср (ej, . . Ф (еп)} — база пространства L.
Поскольку линейное пространство одномерно /огда и
только тогда, когда оно обладает базой, состоящей из од¬
ного вектора, то импликация (3)	(1) сразу следует из
теоремы 8, а импликация (1) => (3) — из теоремы 5.
Ввиду свойства (2) теоремы 9 имеем
Следствие 1. Изоморфные конечномерные линей¬
ные пространства имеют одинаковую размерность.
Из свойства (3) теоремы 9 и теоремы о транзитивности
разложения в прямую сумму (теорема II.5.13) вытекает
Следствие 2.
dim (L.J ® . . . ф Am) = dim Lr 4- . .» , + dim Lm>
Следствие 3. Если dim L = n и alt , . ., an+l GE
GE L, то система {at, . . ., an+1} линейно зависима.
Действительно, если система {a1? . .	линейно не¬
зависима и L' = X (а1? . . «па), то dim Lf = п 4- 1.-
В силу теоремы 7, L = L' ф Н для некоторого Н, и, сог¬
ласно следствию 2, п = п 4- 1 4- dim Н, что невозможно.
Теорема 10. Если L' — подпространство линей¬
ного пространства L и dim Л' = dim А, то L ~ L'.
Доказательство. Если L L', то, согласно
теореме 7, L « L' ф Я, где Н 0. Ввиду теоремы 8, ба¬
за пространства L содержит больше векторов, чем база
пространства I/, Следовательно, dim L dim L'.
Гомоморфизмы линейных пространств будем называть
линейными отображениями i а линейные отображения ли¬
нейного пространства в себя — линейными преобразова¬
ниями.
Теорема 11. Множество Пот L') всех линей¬
ных отображений линейного пространства L над полем Р
в линейное пространство L' над полем Р становится ли¬
нейным пространством1 если для ср, ф GE Нот (Ех L') и
174

X, Е Р положить
X (ф + г|>) = Хф +
и
х (Аф) = А (яф)
для всех х ЕЕ L.
Доказательство. Ввиду теоремы II.5.8,
Нот (Л, L') является абелевой группой. Из равенств
(х -I- у) (Хф) = х ((ж + у) ф) = X (жф + !/ф) =*
= X (жф) + X (г/ф) = х (Хф) 4- у (Хф)
И
(£г) (Хф) = X ((£ж) ф) = X (I (жф)) =
= (Х£) (жф) = (£Х) (жф) = |(Х (жф)) = t (ж (Хф)),.
где х, ijEL и § ЕЕ Р, вытекает, что Аф ЕЕ Hom (Д [/)<
Равенства же
х (А (ф + гр)) = I (х (ф + гр)) = А (яф + #гр) =:
= X (бсф) + А (хгр) = х (Аф) + £(Агр) == х (Аф + Агр),.
х ((А + ц) Ф) = (А + р) (бсф) = А (хф) + р (#ф) =
= х (Аф) + х (рф) = х (Аф+ рф),.
х ((Ар) ф) = (Ар) (.гф) = А (р (гф)) = к(х (рф)) = х(К (рф))
п
X (1ф) = 1 (бСф) = £ф,;
справедливые для всех х ЕЕ L, любых ф, гр Е- Hom (A, L')
и А, р ЕЕ Р, показывают, что Нот (L, L') оказывается
линейным пространством.
Столбец
е —
еп 1
где et — векторы, назовем вектор-столбцом. Вектор-
столбец называется независимым (базисным), если входя¬
щие в него векторы линейно независимы (образуют базу
пространства). Если А — матрица размера т X п, а е —
вектор-столбец длины и, то естественным образом опреде¬
ляется произведение Ае, являющееся вектор-столбцом
длины т. Простой подсчет показывает, что (АВ) е =
= А (Be), причем из существования одной из частей это¬
го равенства следует существование друзей.
175

Теорема 12. Если вектор-столбец е независим, то
из равенства Ае — Be вытекает, что А = В.
Доказательство. Данное равенство означает,,
что
#zl^l 4" • • *	~ ^il^L 4“ • • • 4“ б[пвп
для каждого I и, следовательно, а^ = для всех / по
теореме 6.
Пусть теперь ср — линейное отображение линейного
пространства L в линейное пространство L'. В простран¬
ствах L и I/ зафиксируем базисные вектор-столбцьт е и е/
соответственно. Будем предполагать, что dim L = т и
dim А' = п, Положим
ср (в) =
ФЙ
ф(*т'
Матрица А размера т X п, строками которой служат ко¬
ординаты векторов, входящих в ср (е), в базе е', называется
матрицей линейного отображения ср в базах {е, е'}. Таким
образом, если А — матрица линейного отображения ср
в базах {е, е'}, то
ср (е) = Ае'.
Если теперь (gn . . .,	— координаты вектора х в базе е,,
а (£1, • • •> 5п) — координаты вектора ср (х) в базе е', то
m
Qi,... Х)е' = ф(Х ^i) =
2=1
m
= S Qi) = Qi, • • •, gm) <P Q) = Qi,... Лго) Ae',
2=1
откуда
•> U — (£i>
m) Л
в силу теоремы 12. Это равенство носит название формулы
для вычисления образа вектора при линейном отображении
с матрицей А.
Пример. Пусть L — линейное пространство матриц размера
2x3 над некоторым полем Р, L' — пространство 3-мерных строк
над тем же полем, Ец — матрица, у которой на месте (i, /) стоит 1,
176

а на остальных местах — пуль,
(1,
о,
0)
е' ?=
(1,
1,
0)
(1,
1,
n
ср (X) ~ (2, 1) X для всех X е L.
Нетрудно проверить, что ср — линейпое отображение и что
ср (е) =
(2.
(О,
(О,
(1,
(О,
(О,
О,
2,
О,
О,
1,
О,
0)
0)
2)
0)
«)
1)
Легко проверяемые равенства
(2, 0,	0)	=	2 (1, 0,	0)	+ 0 (1, 1, 0) + 0(1, 1, 1),
(О, 2,	0)	=	—2(1, 0, 0) + 2 (1, 1, 0) + 0 (1, 1, 1),
(О, 0,	2)	=	0 (1, 0,	0)	+ (-2) (1, 1, 0) + 2 (1, 1, 1),
(1, 0,	0)	=	1 (1, 0,	0)	+ О (1, 1, 0) + 0 (1, 1, 1),
(О, 1,	0)	=	—1 (1,	0,	0) + 1 (1, 1, 0) + 0(1, 1, 1),
(О, О, 1) = О (1, 0, 0) + (-1) (1, 1, 0) -I- 1 (1, 1, 1)
показывает, что матрица
2
0
0
—2
2
0
0
—2
2
1
0
0
-1
1
0
0
— 1
1
служит матрицей линейного отображения ср в базах [е, е'}. Исполь¬
зуя формулу для вычисления образа вектора, можно, например, по¬
лучить
Ф(||1 0 ;||) = Ф((2.3>0>110,1)е) = (2,3,0,1,0,1)Д^ =
= (-1, 5,1) е' = (-1) (1, 0, 0) + 5 (1,1, 0) + (1,1, 1) = (5,6,1).
Убедимся теперь, что при фиксированных базах е
и в' всякая матрица размера т X п служит матрицей
одного и только одного линейного отображения ср G
Е?' Hom (L, L'). В самом деле, если дана матрица А, то
положим
т	пт
ф (S £а) = S (S «.A) «i.
' i=l	j=l i-1
17'/

Простой подсчет показывает, что ф ЕЕ Нот (Л, L') и что
матрица линейного отображения ф в базах {е, е'} совпа¬
дает с А. Если ф — другое линейное отображение с той же
самой матрицей Л, то по формуле вычисления образа век¬
тора имеем
Ф (*) = (£1,. ■ • ■, 1т) Ав' = 'Р (*)
для всех х ЕЕ L, откуда ф = ф.
Теорема 13. Если зафиксированы базы е и е' в
пространствах L и L' над полем Р соответственноf
dim L = т и dim L' = тг, то отображение Ф, ставящее
в соответствие каждому линейному отображению ф ЕЕ
ЕЕ Нот (Л, L') его матрицу в базах {е, е'}, является изо¬
морфизмом линейного пространства Нот (Л, L') на ли¬
нейное пространство Ртхп всех матриц размера т X п
над полем Р.
Доказательство. Проведенными выше рас¬
смотрениями уже установлено, что Ф осуществляет взаим¬
но однозначное отображение множества Нот (Л, L') на
множество Ртхп всех матриц размера т х п. Если те¬
перь ср, фЕ Hom (Л, L'), X- == ф + ф, Е Р, Хф = со,}
Ф (ф) = А, Ф (ф) = 5, Ф (X) = С и Ф (со) = D, то, учи¬
тывая определение операций в пространстве Нот (Л, L')$
и меем
Се' = % (е) — ф (е) + ф (е) = Aef + Be' = (Л + В) е'
и
De' = со (е) = (Хф) (е) - X (ф (е)) = X (Ле') = (ХЛ) е',
откуда С = А + В и D = ХЛ по теореме 12. Таким об¬
разом, Ф оказывается гомоморфизмом, а следовательно,
и изоморфизмом линейных пространств.
Теорема 14. Пусть L, L' и L" — линейные прост¬
ранства над полем Р, ф ЕЕ Hom (L, L'), ф ее Нот (Z/, L"),
А — матрица линейного отображения ф в базах {е, е'},
В — матрица линейного отображения ф в базах {е‘, е") и
С — матрица линейного отображения фф в базах {е, е"}.
Тогда С = АВ.
Доказательство. Достаточно заметить, что
Се" = е (фф) = (еф) ф = (Ле')ф —
= А (е'ф) = А (Be") = (АВ) е\
и принять во внимание теорему 12.
Если теперь L — линейное пространство над полем Р,}
то линейное преобразование фЕЕ Hom (L, L) является линей¬
178

ным отображением L в L. Матрица этого линейного ото¬
бражения в базах {е, е}, где е — некоторая база прост¬
ранства А, называется матрицей линейного преобразова¬
ния ф в базе е.
Пример. Пусть L — линейное пространство матриц второ¬
го порядка над некоторым полем Р, {^ц, Е12, Е21, Е22} — база про¬
странства L и <р (X) = X* для всякой матрицы X из L. Тогда
и, следовательно,
Е{1
е21
Е12
Е-2-2
1
0
0
0
0
0
1
0
0
1
0
0
0
0
0
1
матрица линейного преобразования ф в данной базе. По формуле
вычисления образа вектора имеем
ф(|1 о|) = (2’2’11О)Ле = (2’112’О)е = ||2 о|>
как п следовало ожидать.
Теорем а15. Если в п-мерном линейном пространст¬
ве L над полем Р зафиксирована база е, то отображение Ф,
ставящее в соответствие каждому линейному преобра¬
зованию ф GE Hom (L, L) его матрицу в базе е, является
изоморфизмом кольца Нот (£, L) на кольцо Рпквадратных
матриц порядка п над полем Р.
Доказательство. Согласно теореме II.5.9,
Нот (Л, L) является кольцом. В силу теоремы 13, Ф осу¬
ществляет изоморфизм абелевых групп (и даже линейных
пространств), а из теоремы 14 вытекает, что Ф (фф) =
= Ф (ф)Ф (ф).
Если в линейном пространстве L зафиксирован базис-
ный вектор-столбец е, то, ввиду теоремы 6, каждому век¬
тору х из L однозначно соответствует строка	gn),
составленная из его координат в базе в. При этом
~ (^1, • • М 5п)
Пусть теперь е и f — два базисных вектор-столбца и
Т — матрица, строками которой служат координаты век¬
торов, входящих в /,вбазе е. Матрица Т называется мат¬
рицей переходабазы е к базе f. При этом имеет место ра¬
венство / = Те, Если U — матрица перехода от базы f
179

к базе <?, то е = Uf. Отсюда
Ее = е = Uf = U (Те) = (UT) е
и, согласно теореме 12, UT = Е. Ввиду теоремы 1.3.14,,
матрица перехода всегда невырожденная. Наоборот, если
дана невырожденная матрица Т и базисный вектор-стол¬
бец е, то рассмотрим вектор-столбец
f = Те.
Если векторы, входящие в /, линейно зависимы, то най3
дется ненулевая строка (Хт, . . ., Хп) такая, что
(^,.. .,м/ - 0.
Отсюда (0, . .	0) е = (Х1? . . ., Лп) Те, т. е., сог таено
теореме 12, (0, . . ., 0) = (Хх, . . ., Хп) Г, а значит, (Хх, . . .
. . ., %п) = (0, . .	0) Т'1 = (0, . . ., 0), что противоречит
выбору строки (Хп . . ., 1П). Таким образом, вектор-стол¬
бец / независим. Следовательно, dim (X (/х, . . ., fn)) =
и, ввиду теоремы 10, X (Д, . .	/п) = L. Таким образом^,
/ оказывается базисным вектор-столбцом, причем Т слу¬
жит матрицей перехода от базы е к базе f. Этим доказано,,
что всякая невырожденная матрица служит матрицей
перехода.
Если Т — матрица перехода от базы е к базе е',
(51, • • •, 5п) — координаты вектора х в базе е, а
(51, • • • , 5п) — его координаты в базе е', то
е' = Те и х = (li, . . L) е = (&, . .	£„) е',;
Отсюда
(Ъ, . .	£„) Те
и, следовательно,
(51, • •	5п) = (51, . .	5п,) Т.
Эта формула называется формулой изменения координат
при изменении базы.
Пусть L — линейное пространство над полем Р, ср е=
СЕ Hom (L, L), а А и В — матрицы линейного преобразо¬
вания ср в базах е и / соответственно. Если Т — матрица
перехода от базы е к базе /, то
Bf = ср (/) - ср (Те) = Т<р(е) = ТАе = TAT^f,
откуда, согласно теореме 12, В = ТАТ'1. Эта формула
носит название формулы изменения матрицы линейного
преобразования при изменении базы.
180

Пусть ф — линейное преобразование ^-мерного ли¬
нейного пространства L над полем Р и А — матрица этого
линейного преобразования в базе е. Определитель | А —
__ tE | оказывается многочленом степени п над полем Р
относительно t. Если В — матрица того же самого линей¬
ного преобразования ф в базе /, то, как только что пока¬
зано, В = ТАТ'1, где Т — матрица перехода от е к
В силу теоремы 1.3.14 и соотношений, установленных в
конце § 3 гл. I,
| А __ tE | = | Т | | А - tE | | Т'1 | - | Т (А - tE yi"1 | -
Таким образом, многочлен | А — tE | не меняется при
изменении базы, что позволяет назвать его характери¬
стическим многочленом линейного преобразования ф. Кор¬
ни характеристического многочлена линейного преобра¬
зования ф называются характеристическими корнями это¬
го линейного преобразования.
Допустим теперь, что рассматривается n-мерное ли¬
нейное пространство над полем комплексных чисел С.
Тогда каждое линейное преобразование ф имеет в точно¬
сти п характеристических корней (если каждый корень
считать столько раз, какова его кратность) *). Сумма
всех этих корней называется следом линейного преобра¬
зования ф и обозначается через Тг ф **). По формуле Вие¬
та ***) сумма всех характеристических корней равняется
коэффициенту характеристического многочлена, стояще-
стороны, если А — матрица линейного преобразования
Ф в некоторой базе, то, вычисляя определитель | А — tE |
с помощью теоремы 1.2.9, нетрудно заметить, что воз¬
никает лишь при вычислении произведения элементов,
стоящих на главной диагонали. Г1оскольку это произве¬
дение равно (яп — £)... (апп — t), то коэффициент при
Г’1 равен (-1)"'1 (ап + . . . -|- апп) = (-1)^ Тг ф.
*) См. с. 157 учебника А. Г. Куроша или с. 273 учебника
А. И. Кострикина.
**) Чтобы эти определения были пригодны для любого поля,
надо рассматривать корни в поле разложения характеристического
многочлена (см. с. 304 учебника А. Г. Куроша или с. 276 учебника
А. И. Кострикина).
***) См. с. 159 и 305 учебника А. Г. Куроша или с. 253 учеб¬
ника А. И. Кострикина,
181

Поскольку, как было отмечено, характеристический мц0
гочлен от базы не зависит, нами доказана
Теорема 16. След линейного преобразования
нейного пространства над полем С равен сумме диагональ
них элементов матрицы этого линейного преобразования
в любой базе.
Теорема 17. Пусть ср — линейное преобразование
линейного пространства L над полем С. Число ^ЕЕ С яв¬
ляется характеристическим корнем линейного преобра¬
зования ср тогда и только тогда, когда существует нену^
левой вектор иЕ L такой, что ср (и) = Хи *).
Доказательство. Пусть А — матрица линей¬
ного преобразования в некоторой базе е и X ЕЕ С. Рас¬
смотрим систему линейных уравнений:
О
О
(Л - ХЕ)*
(*)
Из теоремы 1.3.7 легко вывести, что строка	. ,,
... , ссп) — решение этой системы тогда и только тогда, когда
(а1г . . ., ап)(А — ХЕ) = (0, . . ., 0).
Ввиду теоремы 15, (Л — ХЕ) — матрица линейного пре¬
образования ср — ML в базе е. Поэтому формула для вы¬
числения образа вектора показывает, что вектор
v = а1е1 + . . . +
удовлетворяет соотношению (ср — ML)(i?) = 0 или, что
то же самое, ср (и) = Xv тогда и только тогда, когда
(а1? . . ., ап) — решение системы (*). Значит, согласно
следствию теоремы 1.3.5, вектор и может быть выбран
ненулевым в том и только в том случае, когда \А — ХЕ |===
= 0, или, что то же самое, когда X — характеристический
корень линейного преобразования ср.
Теорема 18. Если Хг, . . ., Хп — все характери¬
стические корни взаимно однозначного линейного преобра¬
зования ср линейного пространства над полем С, причем
каждый корень выписывается столько раз, какова его крат¬
ность, то ХД . . ., Х^ — все характеристические кор¬
ни линейного преобразования ср-1, причем каждый корень
выписывается столько раз, какова его кратность.
*) Вектор v называется собственным вектором линейного пре¬
образования <р, отвечающим характеристическому корню X. В свя¬
зи с этим число X часто называют собственным значением линейного
преобразования (р.
182

доказательство. Поскольку Ker ср = 0, то,
иду теоремы 17, X; =7^ О для всех i. Пусть А — матрица
Инейного преобразования (р в некоторой базе. Тогда *)
I а - tE | = (-i)na - м) м-
С гласно теореме 15, А'1 служит матрицей линейного
пеобразования ср'1 в той же базе. Ведя вычисления в
поле рациональных дробей **) и принимая во внимание
свойство III определителя и теорему 1.3.14, получаем
= £"| Л’ЧС— 1)п| А	е|=
= (- 1)« | А-11 Xi.. лп (t - V)V).
чем и завершается доказательство.
Теорема 19. Если Х1? . . ., Хп — все характери¬
стические корпи линейного преобразования ср линейного
пространства L над полем €, причем каждый корень
выписывается столько раз, какова его кратность, | ХЛ. | =
_ 1 ***) $ля всех р и | Тг ф | = п, то Хх = ... = Хп.
Доказательство. Сначала установим следую¬
щее утверждение.
Л е м м а. Если | X | = | ц | = 1 и | К -И ц | = 2,
то X = р,.
Действительно,
4 + |Х — И|2 = |Х + р|2 + |Х-ир =
_ = С + н)С + й) + С —	— й) =
— XX Zu + Хр. рр J- XX — Хр — Хр рр —
= 2(|Х|* + |р|2) = 4.
Отсюда | X— р | = 0, а значит, X — р по свойству (1)
нормы (см. с. 100).
Обратимся к доказательству теоремы. Если | X/t. -f-
+ Ч’+i I < 2 для некоторого то, ввиду свойства (3)
р .	) Как известно, если ХА, . . ., Хп — все корпи многочлена
(0 со старшим коэффициентом а, причем каждый корень выписы-
ается столько раз, какова его кратность, то F (0 -- a (t — XJ . . .
‘	Хп) (см. с. 156 учебника А. Г. Куроша или с. 282 учеб-
Кострикина).
vtT г.' ) См. § 50 гл. X учебника А. Г. Куроша или и. 2 § 4 гл. 5
У	А‘ И- Кострикина.
) Здесь | z | — норма комплексного числа z.
183

нормы,
п = I Tr <р | = I kj + ... + Хп |<
I ^-1 + • • • + ^Jr-1 I + I ^Jr + ^'+1 | + | ^Л'+2 4* • • • + Kl | <4
<; (/c — 1) + 2 + (n — (/c 4- 1)) == n,
что невозможно. Следовательно, |	+ X7(+i | = 2 для всех
к и, согласно лемме, Z/f = X^+i. Таким образом, Хх == .
. . . = Хп, что и требовалось.
Теорема 20. Если ср — линейное пре? бразоеание
п-мерного линейного пространства L над полем С, срт =
= Il для некоторого т и все характеристические корни
линейного преобразования ср равны X, то ср = X1L, а X ока¬
зывается корнем степени т из единицы.
Доказательство. Пусть А — матрица линей¬
ного преобразования ср в некоторой базе. Если	.
. . .,	— все корни степени т из единицы, то имеем ра¬
венство многочленов *)
(t -	. (t - U) = tm - 1.
Поскольку Ат = Е по теореме 15, то попарная переста¬
новочность матриц А, ^1Л', . . ., ЪтЕ, вытекающая из тео¬
ремы II.4.12, позволяет записать
(А - £х£) ... (А - lmE) = Ат - Е = 0.	(*)
В силу теоремы 1.3.14 отсюда следует, что, скажем,;
| А — ZrE | = 0. Но тогда Ех = X, | А — %iE\ Ф 0 при
i > 2, и по теореме 1.3.13 существуют матрицы (А —
—	Умножая равенство (*) справа на
(А -	... (А -
получим
А —	= 0,
откуда в силу теоремы 15 имеем ср = £x1l, что и требова¬
лось.
Теорема 21 (теорема о ранге). Ранг матрицы ра¬
вен размерности линейной оболочки ее строк.
Д о к а з а т е л ь с т в о. Если А — матрица, то обо-
значим через Ж (А) линейную оболочку ее строк.
Л е м м а 1. Если от матрицы А к матрице В перешли
конечным числом элементарных преобразований строк,,
пх X (В) cz X (А).
*) См. примечание *) на с. 183.

g самом деле, очевидно, достаточно доказать лемму
случая, когда применено только одно элементарное
•^образование. Если это перемена местами двух строк,,
утверждение леммы тривиально, ибо матрицы А и В
Т°стоят из одних и тех же строк. Если же к i-й строке a-L
СаТрицы А прибавлена ее /-я строка а$, умноженная на
X то для i-й строки bt матрицы В имеем bt = at + G
^$(Л) и <2(5)cz^(X) в силу теоремы II.5.2.
Из леммы 1 и теоремы 1.1.2 вытекает
Лемма 2. Если от матрицы А к матрице В перешли
конечным числом элементарных преобразований строк,
то	= £ (А).
Л е м м а 3. Если ступенчатая матрица S содержит
г ненулевых строк, то dim X (5) = г.
Для доказательства, очевидно, достаточно установить
линейную независимость ненулевых строк . . ., .s> мат¬
рицы S. Но если
si (5ili • • •, sin)i
sihi — первый ненулевой элемент строки Si и
+ . . . + K-Sr “ О,;
то
^1*17;, = О,
= 0 ч
^1^1/fr_j +	+ Tlr-iSr-! frr_x — 0,
hlSikr 2v2S2/fr + . . . + Xr_i5r_1 k? -|- hrSrkr — 0?
откуда последовательно получаем, что = 0, Л2 = 0, . . .
• • — 0, = 0.
Теперь для доказательства теоремы замечаем, что,
согласно лемме 2, для данной матрицы А имеем X (Л) ---
X (5), где S — ступенчатая матрица, к которой
согласно теореме 1.1.1 можно перейти от А элементарны¬
ми преобразованиями строк. Из теорем 1.3.1 и 1.3.3 и
леммы 3 получаем
ранг Л = ранг S = dim Ж (S) = dim X (Л).
Если V — подпространство линейного пространства
J и а — вектор из L, то смежный класс а + V называется
Шейным многообразием.
Те о рем а 22. Совокупностъ всех решений одно-
^°оной (произвольной) системы т линейных уравнений
аад

от п неизвестных с коэффициентами из поля Р образуем
подпространство (пусто или образует линейное многоо(Р
разие) пространства п-мерных строк над полем Р. Pq3„
мерность пространства решений равна п — г, где г
ранг матрицы данной системы.
Доказательство. Если А — матрица данной
однородной системы линейных уравнений с п неизвест¬
ными над полем Р, А ЕЕ Р, а а = (cq, . . ап) и
b = (рь . . рп) — решения этой системы, то, подстав¬
ляя строки а + Ъ и ка в i-е уравнение данной системы,
получаем
Pl)	‘ ^in («п + Pn) ’
= (а^! + . . . +	+ (fl^Pi + . . . + ^mPn) =
=0+0-0
и
^il(^^l) + * » » + ^in (^^n) =	+ • • » + ^in^n) ~
= M) = 0.
Таким образом, a + b и ka оказываются решениями, что
и доказывает справедливость первого утверждения тео¬
ремы об однородных системах. Если дана неоднородная
система и она несовместна, то множество ее решений
пусто. Если же она совместна, то выберем одно из ее
решений, скажем строку с, и обозначим через W прост¬
ранство решений однородной системы, полученной из
данной системы заменой свободных членов нулями. Лег¬
ко проверить, что каждый вектор из линейного многооб¬
разия с + W служит решением данной системы. Наобо¬
рот, если и — произвольное решение этой системы, то
разность и — с оказывается решением соответствующей
однородной системы, т. е. и — с ЕЕ 17, откуда и ЕЕ с +
+ W. Для доказательства второго утверждения теоремы
заметим, что, согласно теореме 1.3.6, п — г неизвестных
нашей системы являются свободными. Поскольку нуме¬
рация неизвестных не имеет значения, можно считать, что
главными являются неизвестные х^ . . ., хг. Пусть V —
пространство (п — г)-мерных строк. Если и = (и^ . . •
. . ., un-r), то обозначим через ср (и) то единственное ре¬
шение данной системы, которое получается после прида¬
ния свободным неизвестным значений и1ч . . ., ип_г. По¬
скольку
<р (и) ■= (. . и.г, . . ип.г),
486

называется взаимно однозначным отображением про-
°аНства V на пространство решений. Пусть теперь и,,
сТР yt Поскольку решения ф (и) + ф (р) и ф (и + и)
^меют одни и те же значения свободных неизвестных, они
должны совпадать, т. е.
ср (и + у) = Ср (и) + Ср (и).
Аналогично доказывается, что ф (Хи) = Хф (и) для лю¬
бого X ЕЕ Р- Таким образом, отображение ф линейно, т. е.
оказывается изоморфизмом. Остается принять во внима¬
ние следствие 1 теоремы 9.
Базу пространства решений однородной системы линейных
уравнений часто называют фундаментальной системой решений.
Теорема 23. Всякое подпространство S простран¬
ства п-мерных строк V над полем Р служит пространст¬
вом решений некоторой однородной системы линейных
уравнений от п неизвестных с коэффициентами из поля Р.
Доказательство. По теореме 7 V = S @ Т,
где Т — некоторое подпространство пространства V.
Если / и g — базы пространств 5 и Т соответственно, то
по теореме 8 их объединение служит базой пространства
V. Как отмечено на с. 177, существует линейное преоб¬
разование ф пространства V такое, что ф (/) = 0 для всех
/ ЕЕ f и ф (g) = g для всех g ЕЕ g. Ясно, что ф (я) = 0 для
всех х ЕЕ S и ф (у) — у для всех у ЕЕ Т. Если же ф (и) = О
для некоторого v ЕЕ V, то, записав v = s + tx где
S и t ЕЕ Т, получим
о = ф (») = ф (5) т ф (0 = о + i = t,
откуда и ЕЕ S. Таким образом, и ЕЕ S тогда и только
тогда, когда ф (и) = 0. Теперь обозначим через А матрицу
линейного преобразования ф в базе е = {е1г . . ., еп}, где
ci = (0, ...,0,1,0,..., 0).
г-1
Используя формулу для вычисления образа вектора (см.
с- 176), заметим, что равенство
Ф ((<%!, . . ., ап)) = (рг, . . рп)
Равносильно равенству
(«1, . .., ап) А = (р1? . . .,pn)?J
187

которое в силу второго утверждения теоремы 1.3.7 равц0;
сильно равенству
ai
?!
=
®п
?п
Следовательно, (ап . . а-п) 8 тогда и только тогда
когда
at
0
.
ап
0
т. е. тогда и только тогда, когда (ах, . . ап) служит
решением однородной системы линейных уравнений:
1 *
• + а1п*п
= 0,
-1- • •
■ • “1" аппХп
= 0.
Теорема 24. Всякое линейное многообразие npch
с пранства п-мерных строк над полем Р служит много¬
образием решений некоторой системы линейных уравнений,
от п неизвестных с коэффициентами из поля Р.
Доказательство. Рассмотрим многообразно
М = b + S, где b — вектор, a S — подпространств).
В силу теоремы 23, подпространство S служит прост¬
ранством решений системы
/
*1
0
А
—
X
п
0
Пусть b = (р1т * . рп). Простой подсчет показывает^
что М совпадает с многообразием решений системы
XI
?!
А
= А
Хп
Рп
Действительно, если а = (ах, . . ., ап) — решение этой
системы, то вектор $ = (аг — рх, . . ., ап — рп), буду1*1'1
решением системы (*), лежит в S. Следовательно, а = ft +
-F М. Если же а = (ах, , : ап) ЕЕ М, то а — b +
188

4- s, где s	• • • Л») e 5. Отсюда
Л
ai
= А
01
+ 4
= А
01
ап
0„
0„
ибо (?i, • • •’ £n) — решение системы (*).
у И р а ж Н с н и я
1.	Если линейное пространство бесконечномерно, то оно содер¬
жит подпространства любой конечной размерности.
2.	Если система векторов {аг, . . ат} линейно независима, а
система {ах, . . ат, Ь15 . . ., Ьп} линейно зависима, то хотя бы один
из добавленных векторов линейно выражается через все отличные
от него (но не обязательно через аг, . . ., ат).
3.	Если V — подпространство линейного пространства L, то
dim L = dim V + dim (L/V).
4.	Если U и V — подпространства линейного пространства
Т° dim (U + V) + dim (U Q V) dim U + dim V.
5.	Пусть V — линейное пространство «-мерных строк над по¬
лем Риф — изоморфизм поля Р на себя. Определим новое умноже¬
ние элементов из Р на элементы из V, полагая Хор ~ ф (X) р. Убе¬
диться, что это определение превращает абелеву группу У в линей¬
ное пространство V' над полем Р, и привести конкретный изомор¬
физм линейного пространства V на пространство V'.
6.	Если L и L' — линейные пространства и L — U ф V, то
линейное пространство Hom (L, L') изоморфно внешней прямой
сумме Нот (U, L') ф Нот (У, L'), а линейное пространство
Hom (Lf, L) — внешней прямой сумме Нот (Z/, U) ф Нот (L', V).
Кроме того, кольцо Нот (L, L) изоморфно кольцу матриц вида
II Ф II
II х	р II1
W ф (= Нот (U, U), ф с= Нот (t7, У), % е= Нот (V, U), ре
е Нот (V, У), а операции определены так же, как для обычных
матриц.
7.	Линейное преобразование ф линейного пространства L над
полем Р имеет одну и ту же матрицу во всех базах тогда и только
тогда, когда ф =. Х1£ для некоторого X е Р.
8.	Пусть ср — линейное преобразование линейного простран¬
ства L над полем комплексных чисел С. Если X е С, то положим
| 2' е L, ф (х) — Х.т}. Доказать, что У (X) — подпро¬
странство и что У (X) р| У (pi) = 0, если X =)= р.
9.	Если линейное преобразование ф линейного пространства
П^Д полем комплексных чисел нилыютентпо (т. е. фт = 0 для не¬
которого т), то все его характеристические корни равны нулю.
Установить справедливость обратного утверждения.
Ю. Доказа ть, что Тг (фф) = Тг (фф) для любых линейных пре¬
образований ф и ф.
И. Пусть а -|- U и Ь + У — линейные многообразия. Дока-
ать, что а U = Ь + У тогда и только тогда, когда U — У и
а - Ъ <= и.
1Я9

12.	Доказать, что непустое подмножество М линейного прост>
ранства L над полем Р является линейным многообразием тогда ц
только тогда, когда из соотношений
а1, • • •> ат €= М ч	Хх, • • •,	Р
П
Хх + . . . + кт = 1
вытекает, что
+ • • • + ^тат М.
13.	Пересечение двух (и даже любого множества) линейных мно¬
гообразий или пусто, или является линейньш многообразием.
14.	Если М' и М" — линейные многообразия, то среди линей¬
ных многообразий, содержащих объединение М' U М", сущест¬
вует наименьшее.
15.	Указать систему линейных уравнений, описывающую пере-
сечение линейных подпространств S П Т, если указаны системы ли¬
нейных уравнений, описывающие подпространства S и Т.
§ 2. Линейные алгебры и модули над ними
Если кольцо R является конечномерным линейным
пространством над полем Р и для любых к ЕЕ Р и х, у ЕЕ
GE R имеет место (Хх) у = к (ху) = х (Ху), то R называется
линейной алгеброй над полем Р *). Нетрудно убедиться,
что поле комплексных чисел является алгеброй над по¬
лем действительных чисел. Другой пример доставляют
квадратные матрицы над полем.
Теорема 1. Линейная алгебра R над полем Р, об¬
ладающая единицей 1, отличной от. О, содержит подполе
Р-1, изоморфное полю Р,
Доказательство. Построим отображение ф
поля Р в алгебру R, полагая ср (X) — XI. Тогда
ф (X + |1) = (X + р)1 = XI + |11 = ф (X) + ф (р)
н
Ф (Хц) - (Хц)1 = X(|il) = Х(1 • (|И)) == (XI)-(ц1) ==
= ф (Х)-ф (р\.
т. е. ф — гомоморфизм колец. Если ф (X) = ф (ц), т. е*
XI = рЛ, то Х^ |л ввиду теоремы! из § 1. Следовательно.,
Ф — гомоморфной вложение. Но тогда ясно, что поле Р
и кольцо 1ш ф Р1 изоморфны.
Подмножество U линейной алгебры R над полем Р
называется подалгеброй, если оно является подкольцом
кольца R и подпространством линейного пространства R-
*) В современной литературе требование конечности размер-
пости в определение линейной алгебры не включается.
190

Ясно, что подалгебра является линейной алгеброй отно¬
сительно операций, определенных в исходной алгебре.
Цз теорем II.4.1 и II.5.1 вытекает
Теорема 2. Пересечение любого множества подал¬
гебр является подалгеброй.
Левым, правым и двусторонним идеалом линейной
алгебры R над полем Р назовем соответственно левый,
правый и двусторонний идеал кольца R, являющийся
подпространством линейного пространства R. Вообще
говоря, идеал кольца не обязан быть идеалом алгебры.
J3 самом деле, пусть R — множество действительных чи¬
сел, рассматриваемое как линейное пространство над по¬
лем действительных чисел. Положив аЪ = 0 для всех
а b 6= R, превратим R в алгебру над полем действитель¬
ных чисел. Тогда множество всех целых чисел оказывает¬
ся идеалом кольца К, хотя идеалом алгебры R не явля¬
ется. Однако положение меняется, если R — алгебра с
единицей. Действительно, согласно теореме 1, линейная
алгебра R с единицей над полем Р содержит поле Р. Сле¬
довательно, для каждого правого или левого модуля над
кольцом 7? и, в частности, для любого левого или правого
идеала кольца R определено умножение на элементы поля
Р. Имея в виду это умножение, получаем следующее ут¬
верждение.
Теорема 3. Пусть R — линейная алгебра с еди¬
ницей над полем Р. Тогда всякий левый, правый и двусто¬
ронний идеал кольца R является соответственно левым,
правым и двусторонним идеалом алгебры R. Всякий пра¬
вый (левый) модуль над кольцом R является линейным
пространством над полем Р, причем
X (аг) = (Ка) г = а (V)	(X (га) = г (\а) = (Хг) а)
для любых а А, г (= R, К Р.
Отображение ср линейной алгебры R над полем Р в
линейную алгебру R' над тем же полем называется го¬
моморфизмом линейных алгебр, если ср является гомомор¬
физмом колец и гомоморфизмом линейных пространств
одновременно. Взаимно однозначный гомоморфизм назы-
лается изоморфизмом. Если существует изоморфизм ли¬
нейной алгебры R на линейную алгебру то эти алгебры
называются изоморфными *).
Из теорем II.4.2 и II.5.5 вытекает
*) См. примечание на с. 60.
191

Т ео-рема 4. Если ср: R -> Rr — гомоморфизм Л1и
не иных алгебр, то Im ф — подалгебра линейной алгебр^
R'.
Ввиду теорем 3, II.4.3 и II.5.6 имеем следующее ут,
верждение.
Теорема 5. Допустимыми разбиениями линейноц
алгебры R с единицей являются разбиения по некоторому
идеалу кольца R. Факторкольцо линейной алгебры над
голем Р по любому идеалу оказывается линейной алгеброй
над тем же самым полем. (Это факторкольцо естественно
называть факторалгеброй.)
Из теорем II.4.4 и II.5.7 вытекает
Теорема 6 (теорема о гомоморфизме для линей¬
ных алгебр). Если ср: R -> R' — гомоморфное наложение
линейных алгебр, Кег ф — идеал, являющийся ядром этого
гомоморфизма, и л: R Л/Кег ф — естественный го¬
моморфизм, то существует изоморфизм х« R' 7?/Кег ср
такой, что ф% = я.
Теорема 7. Пусть L — линейное пространство
над полем Р. Тогда Hom (L, L) — линейная алгебра над
полем Р. Если dim L = п и е — база линейного прост¬
ранства L, то отображение Ф, ставящее в соответствие
каждому линейному преобразованию ф ЕЕ Hom (L, L)' его
матрицу в базе е, является изоморфизмом линейной ал¬
гебры Нот (L, L) на линейную алгебру Рп квадратных
матриц порядка п над полем Р.
Доказательство. В силу теорем II.5.9 и И
из § 1, множество Hom (L, L) является как кольцом, так
и линейным пространством над полем Р. При этом
dim Hom (L, L) = п2 в силу теоремы 13 из § 1. Кроме
того, для любых х ЕЕ L, ф, ip Е Hom (L, L) и X ЕЕ Р
X ((Хф)ф) = (х (Хф)) ф = (X (Жф)) ф =
= ((Ха;) ф) ф ■= (кс)(фф) = х (X (фф))
И
X (ф (Хф)) = (хф)(Хф) = X ((а;ф)ф) = X (х (фф)) = х (X (<рф)).
Следовательно, Hom (L, L) — линейная алгебра над
полем Р. В силу теоремы 13 из § 1, Ф осуществляет изо¬
морфизм линейных пространств, а из теоремы 15 из § 1
вытекает, что Ф — изоморфизм колец. Таким образом,:
Ф оказывается изоморфизмом линейных алгебр.
Пусть G — конечная группа и Р — некоторое поле.
Рассмотрим линейное пространство PG над полем
приняв элементы группы G за базу. Таким образом,
192

элементами пространства PG служат линейные комбина¬
ции S	где	Поскольку базисные элементы
g&G
можно перемножать как элементы группы, это умножение
можно распространить на произвольные элементы линей¬
ного пространства PG, полагая
( S м)( S V-hh}= s	= 3
g&G	h^G	g, h(=G	k&G
где v/f = S	Легко проверяется, что это опреде-
g, h^G
gh-^k
ление превращает линейное пространство PG в линейную
алгебру над полем Р, которая называется групповой ал¬
геброй группы G над полем Р.
Теорема 8. Элемент а =	групповой ал-
p^g
гебры PG конечной группы С лад полем Р лежит в центре
Z алгебры PG тогда и только тогда, когда *ки = для
любой пары сопряженных элементов и и v из G. Размер¬
ность центра Z *) групповой алгебры равна числу классов
сопряженности группы G.
Доказательство. Пусть а ЕЕ Z, и, и ЕЕ G и
v= wuur1 для некоторого w ЕЕ G. Тогда aw= wa, откуда
^gg ~ a — waw~l = X {wguf1').
g^G	g^G
Сравнивая коэффициенты при и, убеждаемся, что =
= Хи. Наоборот, если а удовлетворяет указанному ус¬
ловию, то для любых w, g ЕЕ G имеем = Kogw-*- Отсюда
wattT1 = X /■.„ (wgw-1) = X K»gu~l (wgw-1) — X hhh — a,
g&G &	gsG	h^G
поскольку, когда g пробегает группу G, элементы wguP1
также пробегают всю эту группу. Таким образом, wa =
= aw для всех w ЕЕ G. Если теперь я = 2 £ww— произ-
вольный элемент из PG, то
ха — X ^w(wa)= 3 lw(aw) = a X ^,ww — ax,
w^G	w^G	w^G
*) Под центром линейной алгебры R понимается центр кольца
•Я- Если алгебра R содержит единицу, то, как легко проверить, ее
Центр оказывается подпространством линейного пространства R
следовательно, является подалгеброй алгебры R.
7 Л. Д. Сборников
193

т. е. а ЕЕ Z. Пусть, далее, Кг, . . ., Кт — различны^
классы сопряженных элементов группы G. В силу теОх
ремы II.3.21, эти классы попарно не пересекаются. Пус-ц
Wi — сумма всех элементов из класса Къ (разумеется,
вычисляемая в алгебре PG). Если
“Ь • • • КгЕЕ О,
где ЕЕ Р, то, очевидно, = . . . =	= О, ибо элем сю
ты группы G по определению образуют базу пространства
PG. Следовательно, система {и\, . . ., wm} линейно ню
зависима. Поскольку, согласно первой части теоремы,
коэффициенты элемента а из Z при элементах группы,
принадлежащих одному классу сопряженности, совпадают.
а = М S' £)+••• “г Мп ( S g) =	+ • • • J - Мп"', ,•
Таким образом, элементы шх, . . ., wm образуют базу
пространства Z и, следовательно, dim Z = т.
Теорема 9. Если линейная алгебра D над полем
комплексных чисел С является телом, лто D = С.
Доказательство. Ввиду теоремы 1 можно
считать, что С cz D. Если z ЕЕ D, то, согласно следствию
3 теоремы 10 из § 1, для подходящего номера п элементы
1, z, . . ., zn оказываются линейно зависимыми над С.
Следовательно, найдутся комплексные числа л0, Хх, . ..
. . ., Хп, не все равные нулю и такие, что
Хо + Xxz + . . . + К zn =
Другими словами, z оказывается корнем многочлена
F (0 ~	^1 + . . . + ‘kntn
с комплексными коэффициентами. Не ограничивая общ¬
ности, можно считать, что %п = 1. Согласно следствию
основной теоремы алгебры многочленов *),
F (t) = (t — ctj) . . .(£ — а„),
где ЕЕ С. Отсюда
(z — ах) ... (z — ап) = 0
и, поскольку, согласно теореме II.4.5, в теле D пет дели¬
телей нуля, для некоторого i получаем z = ЕЕ С.
В соответствии с определением, данным на с. 127.
линейная алгебра R называется вполне приводимой
*) См. примечание *) на с. 183.
194

спраеа' если она разлагается в прямую сумму минималь¬
ных правых идеалов. В силу теорем 3 и II.6.5, вполне
приводимой справа линейной алгеброй оказывается коль¬
цо матриц над полом.
Теорема 10. Если R — вполне приводимая справа
алгебра с единицей над полем Р, то существуют такие
попарно ортогональные центральные идемпотенты е1? . . .
. . что
1 = е± + . . . + еп и R = eLR Q . . . © eaR,
где OtR — двусторонние идеалы, каждый из которых
является простой алгеброй с единицей.
Доказате л ь с т в о. Напомним, что теорема 3
позволяет по различать идеалы алгебры R и кольца R.
Далее, для сокращения речи условимся называть идем¬
потент е алгебры R простым, если е — ненулевой цент¬
ральный идемпотент и eR — простая алгебра.
Лемма. Каждый пену лесой двусторонний идеал I ал¬
гебры R содержит простой идемпотент.
Действительно, пусть Л/ — ненулевой двусторонний
идеал алгебры R, лежащий в I и как линейное прост¬
ранство над полем Р имеющий наименьшую размерность
среди ненулевых двусторонних идеалов алгебры R, ле¬
жащих в I. В силу теоремы 10 из § 1, М не содержит не¬
нулевых двусторонних идеалов алгебры R. Согласно тео¬
реме II.6.6, идеал М порождается центральным идемпо¬
тентом, скажем е. Если алгебра М не является простой,
то она содержит двусторонний идеал, отличный от 0 и от
М. Но, согласно теореме II.6.7, этот идеал должен быть
идеалом алгебры R, что невозможно. Таким образом,
е оказывается простым идемпотентом.
Ввиду леммы, алгебра R содержит простой идемпо¬
тент. В силу теорем II.6.2 и 8 из § 1, а также следствия 3
теоремы 9 из § 1, она не может содержать бесконечного
множества попарно ортогональных идемпотентов. Поэтому
в ней существует множество {ег, . . ., еп} попарно орто¬
гональных простых идемпотентов, которое не может быть
вложено в большее множество попарно ортогональных
простых идемпотентов. Положим
е = т . . . + еп.
Учитывая ортогональность идемпотентов et, нетрудно
подсчитать, что е2 ~ е и е,е = е, для каждого I. Если
е =/= 1, то (1 — е)2 1 — е — е + е = 1 — еп, в силу
теоремы II.6.6,	(1 — е) R — ненулевой двусторонний
7*
195

идеал алгебры R. Согласно лемме найдется простой идедь
потент /ЕЕ (1 — e)R. Поскольку / централен и / = (1 — е у
для некоторого г ЕЕ Л, то fet = erf = ete (1 — е) г = о.
Следовательно, множество {е15 . . еп}, вопреки допущу
нию, вкладывается в большее множество {е1? . . .,еп,/} по¬
парно ортогональных простых идемпотентов. Таким
образом, е = 1 и, ввиду теоремы II.6.2,
R — l’-R = e^R ф • • • ©
По определению простого идемпотента, алгебры etR прос¬
тые. В силу теоремы II.6.6, они являются двусторонними
идеалами алгебры R.
Теорема 11. Линейная алгебра R с единицей над
полем Р, не содержащая ненулевых двусторонних идеалов
с нулевым умножением,, вполне приводима справа.
Доказательство. Напомним, что теорема 3
позволяет не различать правые идеалы алгебры R и коль¬
ца R. Для сокращения речи условимся называть идем¬
потент е алгебры R минимальным' если eR — минималь¬
ный правый идеал.
Л е м м а. Каждый ненулевой правый идеал II алгебры
R содержит минимальный идемпотент.
Действительно, пусть М — ненулевой правый идеал
алгебры R' лежащий в Н и как линейное пространство над
полем Р имеющий наименьшую размерность среди нену¬
левых правых идеалов алгебры Я, лежащих в Я. В силу
теоремы 10 из § 1, М оказывается минимальным правым
идеалом алгебры R. Ввиду теоремы II.6.4, М не является
правым идеалом с нулевым умножением и, согласно тео¬
реме II.6.3, порождается идемпотентом в. Конечно, идем¬
потент е минимален и е ~ II.
Возвращаясь к доказательству теоремы, заметим, что,
согласно лемме, алгебра R содержит минимальный идем¬
потент. Но, в силу теорем II.6.2 и 8 из § 1, а также след¬
ствия 3 теоремы 9 из § Дона не может содержать беско¬
нечного множества попарно ортогональных идемпотен¬
тов. Поэтому в ней существует множество {е1? . . . , ен}
попарно ортогональных минимальных идемпотентов, ко¬
торое не может быть вложено в большее множество по¬
парно ортогональных минимальных идемпотентов. По¬
ложим
е = ег	еп.
Учитывая ортогональность идемпотентов eh нетрудно
подсчитать, что е2 — е и ete = e-L = eet для каждого ?.
196

Допустим, что еф 1. Тогда правый идеал (1 — e)R от¬
личен от нуля и, согласно лемме, содержит минимальный
идемпотент /. Поскольку f <= (1 — e)R, то f = (1 — в) г
для некоторого г ЕЕ R. Отсюда
eif =	= ete (1 — е) г = eflr = 0.
Если fe = 0, то
= feet =	= 0
для каждого i и, вопреки допущению, множество	.
еп} вкладывается в большее множество {ех, . . . , еп,
/} попарно ортогональных минимальных идемпотентов.
Таким образом, fe^= 0, по ef = 0. Рассмотрим элемент
g = / (1 — е). Равенство
Г = / (1 - e)f (1 - е) = f(f - е/)(1 - е) =
= f2 (1 — е) = / (1 — е) = g
показывает, что g — идемпонент. Если g = 0, то / = fe,
откуда
O^f = f=fef = fO = 0,
что невозможно. Если же g 0, то из соотношения
0 =/= gR се fR и минимальности правого идеала fR выте¬
кает, что gR = fR. Следовательно, g — минимальный
идемпотент. Но
etg = С7(1 — в) = 0 (1 — 6?) = 0
и
get = f (1 — е) ei = f (1 — е) eet = fOeL = 0,
и мы опять сумели вложить множество {^17 . . ., еп} в
большее множество {е1У .. еп, g} попарно ортогональных
минимальных идемпотентов. Полученное противоречие
показывает, что е =1. Ввиду теоремы II.6.2
R = 1-R = e±R © . . . © enR,
что и требовалось.
Следствие. Простая линейная алгебра (т. е.
линейная алгебра, являющаяся простым кольцом) с еди¬
ницей вполне приводима справа.
Теорема 12. Все минимальные правые идеалы
простой линейной алгебры R с единицей изоморфны друг
°Ругу как правые R-модули.
Доказательство. Пусть М и ТУ — минималь¬
ные правые идеалы алгебры R. Из теорем 3, II.6.3 и
197

II.6.4 вытекает, что М eR и N = fR, где е~ = с ц
/2 = /. Нетрудно проверить, что множество I всевозмо;^
ных сумм вида
’Z.riesi (rit St е R)
оказывается двусторонним идеалом алгебры R. При этом
/ #= О, поскольку 0^ е Е /. Следовательно, I = R,
а значит,
1
для подходящих тд, Si ЕЕ R. Из равенства
о #= / = ^frieSi
следует, что frte Ф 0 при некотором i. Определим ото¬
бражение ср: М , полагая
Ф (er) = frter.
Легко видеть, что ср — гомоморфизм правых 7?-модулей.
Поскольку ср (е) = frte =/= 0, имеем Кет ср CZ М, откуда
Кег ср = 0 в силу минимальности правого идеала М. Из
минимальности правого идеала N и соотношения
О frte ЕЕ Im ф cz N
вытекает, что 1т ср = N. Таким образом, ф, будучи вло¬
жением и наложением одновременно, оказывается изомор¬
физмом.
Т е о р е м а 13. Пусть R — простая линейная алгебра
с единицей над полем комплексных чисел С и R =
= М\ Э • • . & Мп — ее представление в виде прямой
суммы минимальных правых идеалов. Тогда dim М t = п
для каждого I и dim R = п1.
Доказательство. Согласно теореме II.6.1
1 = ^1 + • • • + еп,
где е] = в/, etej = 0 при I / и Mt = etR.
Л е м м а 1. eiRei —линейное пространство над полем
С, изоморфное одномерному пространству С.
Действительно, ясно, что e^Rei — подкольцо кольца /?•
Равенство X	= et	где л СЕ С, г ЕЕ пока¬
зывает, что это подпространство пространства 1?, а следо¬
вательно, и подалгебра алгебры R. Единицей этой подал¬
гебры служит е^. Если ер'е^ 0, то из соотношения
0 ф eireiR се eLR
198

минимальности правого идеала
11' я = e;R. Следовательно,
et = е^ге^
etR вытекает, что
дня некоторого sE й. Отсюда
е; = е2 = (е^ге;)(е;хег).
Цо по тем же соображениям
(etse^eitei) = et
для некоторого Е Я, откуда
= (etre^et = (е^е^е^е^е^) = е^.
Таким образом,	обратим в алгебре eiRe^ т. е. e^Rei
оказывается телом, и справедливость леммы вытекает из
теоремы 9.
Лемма 2. etRej — одномерное подпространство ли¬
нейного пространства R.
В самом деле, без труда проверяется, что etRej — под¬
пространство. Согласно теореме 12 существует изоморфизм
правых /^-модулей ср: e$R etR. Тогда
О ¥= ф Н = ф	= ф (ej)ej е etRej.
Следовательно, etRe^ 0. Если у ЕЕ etRej, то у = ф (я),
где х ЕЕ ejR. Отсюда, учитывая включение xej ЕЕ ejRej и
принимая во внимание лемму 1, получаем
У = ytj = <Р (^)ej = ср (хе}) = ср (Ае;) = Хер (е;)
для некоторого X ЕЕ С. Кроме того, ф (е7) ЕЕ е^в]. Сле¬
довательно, {ф (е7)} — база пространства eiRe^
Л е м м а 3. etR = (е^е^) ф ... ф (ez/?en).
Действительно, для всякого г её R имеем
п
е,г = е4г1 = e j-ег -f- . . . + еуеп ЕЕ 3 eiRej-
5=1
Если же
е^пеп = 0,
то> умножая справа на получаем еу^ ±= 0 для каждо¬
го /. Остается принять во внимание свойство (4) теоремы
П.5.12.
Возвращаясь к доказательству теоремы, заметим, что,
в силу свойства (3) теоремы 9 из § 1, леммы 2 и 3 обес-
печивают справедливость равенства dim e^R = п. После
199

этого равенство dim R = п2 вытекает из следствия 2 тео¬
ремы 9 из § 1.
Т е о р е м а 14. Простая алгебра R с единицей над по^
лем комплексных чисел С изоморфна алгебре матриц над
полем С.
Доказательство. В силу следствия из тео¬
ремы 11, алгебра R вполне приводима справа, т. е. пред-
ставима в форме
R — Мг @ . . . ф Мп,
где Mt — минимальные правые идеалы. Согласно теореме
13, dim Mt = п. Пусть R' — алгебра линейных преобра¬
зований линейного пространства М±. Определим отоб¬
ражение Ф алгебры R в алгебру R', положив
аФ (г) = хг
для всякого х ЕЕ Мг и г ЕЕ R. Из равенств
(х + у) Ф (г) = {х + у) г = хг + уг = хФ (г) + уФ {г)
и
{Хх) Ф (г) = {Хх) г = X {хг) = X (аФ (г)),
справедливых для любых х, у ЕЕ М± и Л Е С, вытекает,
что Ф (г) ЕЕ R'. Равенства
яФ (г + 5) = X (г + s) = ХГ + XS =
= хФ {г) + аФ ($) = X (Ф {г) + Ф ($)),
хФ {rs) = х {rs) = {xr)s = (пФ (г))Ф ($) = X (Ф (г)Ф ($))
и
хФ (Хг) = х (Хг) = X {хг) = X (яФ (г)) = х (ХФ (г)),
справедливые для любых хЕЕМъ г, s ЕЕ R w X ЕЕ С, по¬
казывают, что
Ф {г + $) = Ф (г) + Ф ($),
Ф {rs) = Ф {г) Ф (s),
Ф (Хг) = ХФ (г).
Следовательно, Ф — гомоморфизм линейных алгебр.
Поскольку Ф (1) — тождественное отображение, ядро
Кег Ф =т<= R и, будучи двусторонним идеалом алгебры 7?,
равно нулю. Следовательно,Ф— гомоморфное вложение
алгебр. Поскольку, ввиду теорем 7 и 13,
dim (Im Ф) = dim R = п~ = dim Rr,
200

лз теоремы 10 из § 1 вытекает, что Im Ф = R'. Следова¬
тельно, Ф — наложение, а значит, изоморфизм. Остает¬
ся еще раз принять во внимание теорему 7.
Теорема 15. Пусть R — вполне приводимая справа
алгебра с единицей над полем комплексных чисел С. Тогда
ц допускает представление
R = R±Q) • • • @ Rm
в виде прямой суммы двусторонних идеалов, причем спра¬
ведливы следующие утверждения:
(1)	RtRj = 0, если i
(2)	каждый из двусторонних идеалов Rt изоморфен ал¬
гебре матриц над полем С;
(3)	каждый минимальный правый идеал алегбры R
лежит в одном из идеалов Rt, и два минимальных правых
идеала алегбры R изоморфны как правые R-модули тогда и
только тогда, когда они леэхат в одном и том же идеале
R6
(4)	каждый неприводимый правый R-модуль изоморфен
некоторому минимальному правому идеалу алегебры R-,
(5)	если Mt, . . ., Мт — все неизоморфные неприводи¬
мые правые R-модули и dim Мt = nt, то R как правый R-
модулъ изоморфен внешней прямой сумме
ф (М2ф...фМ2) ф ...
nt раз	п2 раз
. . . ф (Мт ф . ® Мт);
пт раз
(6)	элемент z алгебры R принадлежат ее центру Z *)
тогда и только тогда, когда z = zx + ... + где zt
принадлежит центру ZL алгебры Rt;
(7)	центр Z алгебры R имеет размерность т.
Доказательство. Будем иметь в виду, что,
согласно теореме 3, каждый правый 7?-модуль является
линейным пространством над полем С и что та же теоре¬
ма позволяет не делать различия между правыми идеала¬
ми алгебры R и кольца R. То же самое верно и для дву¬
сторонних идеалов. По теореме 10
R = ф « . . ф Rm,
гДе Rt — двусторонние идеалы алгебры R, каждый из
Которых является простой алгеброй с единицей. После
*) См. примечание на с. 193.
201

этого утверждение (2) сразу следует из теоремы 14. Дли
доказательства утверждения (1) достаточно заметить, что
RiRj Ri П Rj = 0, поскольку сумма прямая. Если,
далее, М — минимальный правый идеал алгебры R и О
У= х ЕЕ М, то в обозначениях теоремы 10 имеем
X — \х	“4^ • • • Ч- ^тп) е1х ~|~ • • • ~СтХ,
причем е^х =/= 0 для некоторого i. Поскольку
ечх = xet ERi^M,
то
0 Ф Rt П М.
Ввиду теоремы II.5.1, Rt Q М -— правый идеал алгебры
R, и из минимальности правого идеала М вытекает, что
Rt П М = М. Последнее означает, что М cz Rt, т. е.
справедливость первой части утверждения (3). Если же
М и М' — минимальные правые идеалы алгебры R, ле¬
жащие в идеале Rt, то, будучи согласно теореме II.6.7
минимальными правыми идеалами кольца Rt, они в силу
теоремы 12 изоморфны как правые Rrмодули. Если ср:
М М' — этот изоморфизм, то для любых г ЕЕ R и
х ЕЕ М, записав г =	+ . . . + гп, где г; ЕЕ Rj, и при¬
нимая во внимание (1), получаем
ср (хг) = ср (хгЕ) = ср (х) rt = ср (х) г.
Следовательно, ср оказывается изоморфизмом правых
Л-модулей. Допустим теперь, что М и М' — минималь¬
ные правые идеалы алгебры R, М ЕЕ Ri, М' cz R^ t j
и ср: М -> М' — изоморфизм правых A-модулей. Затем
выберем в М элемент х 0 и, вспоминая, что et ЕЕ Z,
запишем его как х = ety = yeh где yER. Поскольку
ср (х) ЕЕ Rj, то, учитывая (1), получаем
Ф (я) = Ф (г/ег) = ф (г/е?) = ф (г/е;) ег = ф (х)	= 0,
чего не может быть при изоморфизме. Тем самым уста¬
новлена справедливость утверждения (3). Утверждение
(4) содержится в теореме II.6.9. Из этой же теоремы и
утверждения (3) вытекает, что при подходящей нумерации
каждый из модулей Мь упоминаемых в утверждении (5),
изоморфен некоторому минимальному правому идеалу
алгебры R, являющемуся, как это следует из теорем 10
и II.6.7, минимальным правым идеалом алгебры Rt. Из
утверждения (3) и теоремы 13 вытекает, что Rt как
202

лравый Я-модуль изоморфен внешней прямой сумме
ХЦ . . . <^ Л Л,
s'
11г раз
откуда непосредственно следует (5). Допустим теперь,
что z =	+ . . . + znJ, где zt ЕЕ Zt. Записав произволь¬
ный элемент г ЕЕ R в форме г — 1\ + . . . + гт, где
Г[ ЕЕ Ri, и используя (1), получаем
rz -=	+	. . .	+ rmZm -= Z1r1 + . . . + Wn = 2Г,
т. е. z Z, Наоборот, если zEEZwz = zl-[-...-\- zml
где Zi ЕЕ Rj, то для любого rt ЕЕ Rt имеем
= rtz = zrt = z^,
т. e. Zi EE Zt. Таким образом, доказано утверждение (6).
Отсюда и из теоремы II. 5.12 вытекает, что
Z = Z± (Е) . . . Ф Zm.
В силу теоремы II.4.12 dim Z-t = 1, и утверждение (7)
вытекает из следствия 2 теоремы 9 из § 1.
Замечание. Теорема 15 позволяет решить зада¬
чу: сколько существует не изоморфных друг другу вполне
приводимых справа алгебр над полем комплексных чисел,
имеющих данную размерность п! Например, если п = 12,
то, ввиду свойства (2), каждой такой алгебре соответствует
представление числа 12 в виде суммы квадратов. Таких
представлений имеется пять:
12 - 1 + 1 + ... +1,
12 = 4 + 1 + 1 + . . . + 1,
12 = 4 + 4 + 1 + 1 + 1 + 1,
12 - 4 + 4 + 4,
12-9 + 1+1+1.
Первому из этих представлений соответствует комму¬
тативная алгебра, являющаяся прямой суммой 12 эк¬
земпляров поля комплексных чисел, второму — прямая
■сумма алгебры двумерных матриц и 8 экземпляров поля
комплексных чисел, трем оставшимся — прямые суммы
алгебр матриц порядков 2, 2, 1, 1, 1 и 1, затем 2, 2 и 2
и, наконец, 3, 1, 1 и 1 соответственно. Алгебры эти не
изоморфны, поскольку согласно утверждению (7) раз¬
мерности их центров равны 12, 9, 6, 3 и 4 соответственно.
Правда, иногда доказательство неизоморфности требует
203

более тонких рассуждений (например, для 27 = 9 + 9 4- 9
и 27 = 25 + 1 + 1).
Теорема 16 (теорема Машке). Групповая алгебра
CG конечной группы G над полем комплексных чисел С
вполне приводится справа.
Доказательство. Если
х = s МеСС,
g^G
то положим
g&G
Ясно, что х** = х. Если теперь
У — 3 Р/Л £= CG,
hf=G
ТО
ху= 3 VfcA:,
freG
где vk = У	В силу теоремы П.4.9, vjt = У
g, h^G	gy feG
gh=k	gh=k
Поэтому
Gz/)* = 5 vfcA:_1= 3 ( S	= y*x*.
k^G	k^kG gy hzgG
gh=k
Далее,
xx* = 3 kgkhgh~z = (3 mJ 14-...,
g, AeG	g^G
т. e. коэффициент при единице группы G равен v —
— 3 ^g^g- ЕслиХ^= ag -Н bgi, где ag, bg — действитель¬
нее
ные числа, то v = 2 (ag + &g) и, следовательно, v =/= (’.z
geG
если х =/= 0. Таким образом, хх* =# 0, если х 0. Пред¬
положим теперь, что I — ненулевой идеал алгебры CG с
нулевым умножением. Если 04= ^Е/, то хх* ЕЕ I ж
следовательно,
(хх*}(рхх*}* = (хх*)(х**х*) = (хх*)(хх*) = 0,
хотя хх* Ф 0. Таким образом, алгебра CG не содержит
ненулевых идеалов с нулевым умножением и ее полнил
приводимость вытекает из теоремы 11.
204

Теорема 17. Число неизоморфных неприводимых
правых модулей над групповой алгеброй CG конечной груп¬
пы G над полем комплексных чисел С равно числу классов
сопряженности группы G.
Доказательство. 13 силу теоремы 16, алгебра CG
вполне приводима справа. Поэтому из теоремы II.6.8
вытекает, что каждый неприводимый правый CG-
модуль изоморфен некоторому минимальному право¬
му идеалу алгебры CG. Сопоставляя утверждения (3)
и (7) теоремы 15, видим, что число неизоморфных ми¬
нимальных правых CG-модулей равно размерности центра
алгебры CG. Согласно же< теореме 8, последняя равна чис¬
лу классов сопряженности группы G.
Из теорем 15 (5) и 16, учитывая следствие 2 теоремы 9
из § 1, выводим следующее утверждение.
Теорема 18. Если Мг, . . ., Мт — все неизоморф¬
ные неприводимые правые модули над групповой алгеброй
CG конечной группы G над полем комплексных чисел С, то
\G\ = (dim + . . . + (dim Mm)2.
У пражнения
1.	Поле действительных чисел не является конечномерной ал¬
геброй над полем рациональных чисел.
2.	Указать в линейной алгебре матриц над полем Р подполе,
изоморфное полю Р, но отличное от РЕ, где Е — единичная мат¬
рица.
3.	Убедиться, что групповая алгебра группы @3 над полем вы¬
четов по модулю 3 не является вполне приводимой справа.
4.	Убедиться, что алгебра верхних треугольных матриц (т. е.
таких, у которых члены, расположенные иод главной диагональю,
нулевые) не является вполне приводимой справа.
5.	Коммутативная алгебра над полем С вполне приводима спра¬
ва тогда и только тогда, когда она изоморфна прямой сумме несколь¬
ких экземпляров поля С.
6.	Вполне приводимая справа алгебра пад полем Сне содержит
делителей нуля тогда и только тогда, когда она изоморфна С.
7.	Если все идемпотенты вполне приводимой справа алгебры
н^д полем С центральны пли если она не содержит ненулевых нилъ-
)готентных элементов (т. е. таких элементов а, что ат = 0 для не¬
которого т), то она коммутативна.
8.	Пусть S — кольцо матриц второго порядка пад кольцом В
е н	II 1 0 II II 1 U II
ъ единицей. Доказать изоморфизм колец В и | g о п 10 0 1
9.	Сколько существует попарно не изоморфных вполне приво¬
димых справа алгебр над полем комплексных чисел размерностей 3,
4- 5, 6, 10, 20?
_	10. Доказать, что групповые алгебры групп ZlkZ и Z/2Z СВ
Z12Z над полем комплексных чисел изоморфны, хотя сами эти
РУппы не изоморфны.
205

11.	Пусть Н — вполне приводимая справа алгебра л е- ~ е
е Н. Доказать, что правый I?-модуль еН неприводим тогда п только
тогда, когда неприводим левый 72-модуль Не.
12.	Доказать, что всякая вполне приводимая справа алгебра
вполне приводима слева.
13.	Указать для групповой алгебры группы G пад полем С раз¬
ложение, существующее согласно теоремам 15 и 16, для следующих
групп G: а) группы вычетов по модулю 2 или 3; б) (Z/2Z) X (Z/2Z};
в) @3; г) ?(4 (см. конец § 3 гл. II).
14.	Доказать, что групповая алгебра группы G над полем С
проста тогда и только тогда, когда G—одноэлементная группа.

ГЛАВА IV
ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
В первом параграфе настоящей главы излагаются
основные определения теории представлений конечных
групп и устанавливаются результаты, касающиеся связи
числа неприводимых представлений и их размерности с по¬
рядком группы G. Во втором параграфе эти результаты
используются для доказательства разрешимости некото¬
рых конечных групп. На протяжении этой главы под груп¬
пой всегда понимается конечная группа.
§ 1. Основы теории представлений
Представлением конечной группы G называется гомо¬
морфизм этой группы в группу взаимно однозначных ли¬
нейных преобразований линейного пространства V над
полем комплексных чисел С*), которая называется ли¬
нейной группой пространства V и обозначается через GL(V).
Таким образом, представление группы G — это гомомор¬
физм Ф: G—^GL (У). Пространство V называется прост¬
ранством представления Ф. Размерностью представле¬
ния Ф (в обозначениях dim Ф) называется размерность
пространства представления. Учитывая связь между ли¬
нейными преобразованиями и матрицами (см. теоремы
1.3.13, 1.3.14 и III.1.15), нетрудно вывести, что если
dim V = п, то группа GL (У) изоморфна группе невырож¬
денных матриц порядка п. При п = 1 группа GL (1) изо¬
морфна группе отличных от нуля комплексных чисел
по умножению. Эту группу будем называть мультипли¬
кативной группой поля С. Групповую алгебру группы G
над полем С, как и раньше, обозначим через CG.
Если У — пространство представления Ф группы G,
то определим произведение vg для v У и g G,
*) Таким образом, мы говорим о комплексном представлении
группы. Разумеется, можно рассматривать представления, исполь¬
зующие линейные пространства над другими нолями.
207

положив
vg = иФ (g).
Тогда для любых g, /гЕ G и е С имеем
v (gh) = уф (gh) = у (Ф (£)Ф (Л)) = (уф (£))ф (h) = (vg) h
Е) g = (М Ф (g) = Л, (уФ (g)) = % (Vg).
Теперь можно превратить V в правый модуль над алгеб¬
рой CG. положив
v ( 3 \g) = 3	(vg),
gEG	gEG
где Xg ЕЕ С, v ЕЕ V, g ЕЕ G. Действительно, учитывая оп¬
ределение операций в алгебре Hom (V, V) и в алгебре
CG, для любых %, Xg, piZl ЕЕ С, g, h е G и и, и ЕЕ V имеем
(и + 0(3 М) = 3 \ ((w + v) g) =
gEG	gEG
= Ъ E ((» + v) Ф (g)) = Xg (иФ (g) + РФ (g)) =
= 3 E (ug) + 3 E (vg)—u (3 Eg) + v (3 kgg),
g&G	gEG	gEG	gEG
V	( 3 ^gg + S Hg#) —
geG	geG
=v (3 (E + pg) g) = 3 E + pg)(vg) =
geG	geG
= 3 (vg) + 3 Pg (vg) = v ( 3 Eg) + V ( 3 p«g),
geG	geG	geG	geG
V	( 3 Eg‘ 5 Р/Л) = v( 3 ElE)(gh)) =
geG	heG	g, heG
= 3 E^h)(v(gh))=^ 3 EMvg) h) =
g, hEG	g, hEG
= (3 4M)( 3 p^) = M 3 \»g))( 3 pXi,
geG	hEG	gEG	hEG
Полученный таким образом модуль называется моду¬
лем представления, Ф.
С другой стороны, если М — правый модуль над груп¬
повой алгеброй CG, то, поскольку CG содержит С, М яв¬
ляется линейным пространством над полем С, и можно
определить гомоморфизм Ф: G-+GL(M), положив
.гФ (g) = +g для всех х ЕЕ М и g ЕЕ G. Таким образом ,
с модулем над групповой алгеброй CG связано вполне оп¬
ределенное представление группы G.
208

Представления Ф и Чт группы G с пространствами
представлений V и W соответственно называются экви¬
валентными, если существует изоморфизм линейных про¬
странств ср: V W такой, что
Ф fe) = фЧТ (^)ф-1
для всех g Е^_ G.
Теорема 1. Два представления группы G эквива¬
лентны тогда и только тогда, когда изоморфны их модули
представления.
Доказательство. Пусть Ф и Чг — представле¬
ния группы G, V и W — модули этих представлений. До¬
пустим, что Ф и ¥ эквивалентны, и рассмотрим соответ¬
ствующий изоморфизм ф линейных пространств. Если
г	Kg — элемент групповой алгебры CG, то для любого
Kg
v ЕЕ V имеем
(w)<r	( Е ^g(vg))<P =
( X Ч (уф fe))) <р = У [у (ф'^ fe) ф_1ф)1 =
g^.G 1	g^G
= X [(уф) fe)l = (уф)( У М) = (уф) г>
g<=G	g~G
т. е. ф оказывается изоморфизмом левых CG-модулей.
Наоборот, если имеется изоморфизм ф модуля V на модуль
W, то ф, очевидно, является изоморфизмом линейных
пространств, и для любых g СЕ G и v ЕЕ V имеем
у (ф4^ fe)) = (уф) (g) = (уф) g =
= (у#)ф = (уф fe))<p = у (Ф fe)<p).
Отсюда
фТ fe) = Ф fe)cp
и, следовательно,
ф (g) = срТ (g)fp-l
Для всех g ЕЕ G, т. е. Ф~и Т — эквивалентные представле¬
ния.
Если Фь. . ., Ф7П — представления группы G и
^i,. • •» Vm — пространства этих представлений, то об¬
разуем внешнюю прямую сумму
v = уг @ . .е vm
и Для каждого g ЕЕ G положим
(Уп- • ■, »т) Ф fe) = (y^j fe),. . УтФт fe)).
5 Л. А. Скорняков
209

Легко проверяется, что Ф (#) FE GL (V) и что Ф — го¬
моморфизм группы G в группу GL (У). Следовательно,
Ф — представление группы G. Оно называется прямой
суммой представлений Ф; и обозначается через Фх ф . . .
• • -Ф Фпг-
Подпространство U пространства V представления ф
называется инвариант!ш, если нФ (g) Е= U для любых
и U и g ЕЕ G. Представление Ф называется неприво¬
димым, если единственные его инвариантные подпрост¬
ранства — нуль и все пространство У.
Теорема 2. Представление неприводимо тогда и
только тогда, когда неприводим его модуль.
Доказательство. Пусть Ф — представление
группы G и V — пространство этого представления.
Если представление Ф неприводимо, Н — подмодуль
CG-модуля V, 0=^=HcV и хеН, то xg G= Н для всех
g £= G cz CG. Отсюда яФ (g) = xg ЕII для всех g Е G.
Следовательно, II — инвариантное подпространство про¬
странства V, отличное от 0 и V, что противоречит непри¬
водимости представления Ф. Наоборот, если V — непри¬
водимый CG-модуль и й — отличное от 0 и У инвариант
ное подпространство пространства V, то для любого
и Е U и г = 2 ЕЕ CG имеем
g^G
иг=Е1 = У X (иф (g)) и-
g^G	gOLG
Следовательно, U — отличный от 0 и У подмодуль модул я
У, что противоречит неприводимости последнего.
Теорема 3. Число неэквивалентных неприводимых
представлений конечной группы G равно числи классов
сопряженности этой группы.
Доказательство. Из теорем 1 и 2 вытекает,
что число неэквивалентных неприводимых представле
ний группы G равно числу неизоморфных неприводимых
модулей над алгеброй CG. По, в силу следствия теоремы
III.2.17, число неприводимых модулей над алгеброй СО
равно числу классов сопряженности группы G.
Теорема 3 в ряде случаев позволяет подсчитать количество не¬
приводимых представлений данной конечной группы. С другой сто¬
роны, ввиду теорем 2 и II. 6.8, все остальные представления этой
группы могут, быть сконструированы из неприводимых. В ряде слу¬
чаев построенная теория дает также возможность определить не
только число неприводимых представлений, но и их размерность.
Правда, никакого алгоритма для решения этой задачи она не дает.
Примеры. 1. G — коммутативная группа. В этом случае
алгебра CG коммутативна. Значит, все алгебры матриц, входящие в
210

ее разложение, описываемое теоремой III. 2.15, коммутативны и,
следовательно, это матрицы первого порядка. В силу теорем III.2.13
я II. 6.8, каждый неприводимый С G-модуль одномерен. В силу
теоремы 2, все неприводимые представления группы G одномерны.
В силу теоремы 3, число их равно порядку группы G. В частности,
если G — группа вычетов по модулю 3, а 1, £,	— все корни степе¬
ни 3 из 1, то ее неприводимыми представлениями будут (вместо ли¬
нейных преобразований пишутся матрицы порядка 1):
Фо: Фо U) = 1 Для всех g <= G,
Фх: Фх (0) = 1, Фх (1) = £, Фх (2) = £2,
Ф2: Ф2 (0) = 1, Ф2 (1) = £2, Ф2 (2) = ? -
Всякое другое представление — это прямая сумма перечисленных.
Например,
Ф = Фо ф Фх 0 Фх Ф Ф2
— четырехмерное представление, где
Ф(0) = £, Ф (1)
1
0
0
0 1
0
‘Q
0
0
0
0
5-
о
0
0
0
0
Г'2
ъ
2. Группа @3. Групповая алгебра шестимерна. Группа @3
имеет три класса сопряженности. В силу теоремы 3 существуют три
неизоморфных неприводимых представления, среди которых — од¬
номерное единичное представление ф0, где ф0 (g) = 1 для всех g е
е @3. Если пх и и2 — размерности двух других представлений, то,
учитывая строение алгебры С@3 (см. теоремы 111.2.15(2) и III.2.16),
имеем
6 = 1 +
Отсюда nx = 1 и /г2 = 2. Таким образом, группа Оз имеет еще одно
одномерное неприводимое представление Фх и одно двумерное не¬
приводимое представление Ф2. Теорема II.3.19 позволяет положить
(?) = I
Фх
1, если g — четная подстановка,
—1, если g— нечетная подстановка.
Представление Ф2 можно определить так:
8*
211

Теорема 4. Если Ф — представление конечной
группы G и g ЕЕ G, то Ф (g)m для некоторого натурального
т оказывается тождественным преобразованием и каждый
характеристический корень линейного преобразования
ф(£) является корнем из единицы.
Доказательство. В силу теоремы II.3.22,
имеем gm = 1 для некоторого т, откуда Ф (g)m — тожде¬
ственное преобразование. Если X — характеристический
корень линейного преобразования Ф (g), то, согласно
теореме III.1.17, кФ (g) = Xv для некоторого ненулевого
вектора v. Отсюда
v = кФ (g). .. ф (g) — 'k'mv.
т раз
Поскольку v 0, то X™ = 1 в силу теоремы III.1.1.
Если Ф — представление группы G, то отображение
%ф группы G в поле С, определяемое равенством
Хф (?) = Тг Ф (g)
для всех g ЕЕ G, называется характером представления Ф.
Таблицы характеров рассмотренных выше представлений выг¬
лядят следующим образом:
1. Группа вычетов по модулю 3.
0
1
2
Хфо
1
1
1
ХФ1
1
е
Хф2
1
с
Хф
4
с
2.
Группа ©3.
fl 2 3\	,
<1 2 3\
i 2 3\	,
fl 2 3)
fl2 3\
fl 2 3.
(12 3)	1
а з 2)
V
1 2 1) 1
(2 1 3)
(2 3 1)
(3 1 2)
Хфо
1
1
1
1
1
1
1
—1
—1
—1
1
1
^ф2
2
0
0
0
—1
—1
212

Теорема 5. Если Ф — представление группы G
и g, h ЕЕ G, то хф (ghg-1) = хф (h).
Доказательство. Как уже отмечалось, теоре¬
мы 1.3.13, 1.3.14 и III.1.15 позволяют смотреть па Ф (g)
как на невырожденную матрицу. Но тогда равенство
ф (ghg'1) = Ф (£)Ф (Л)Ф (g)’1
я формула изменения матрицы линейного преобразования
при изменении базы (см. с. 180) показывают, что Ф (ghg~l)
и ф (/г) — это матрицы одного и того же линейного пре¬
образования в разных базах. Согласно теореме III.1.16,
следы этих матриц равны, что и требовалось.
Теорема 6. Если Ф и Т* — эквивалентные пред¬
ставления группы G, то %ф =
Доказательство. Пусть V и W — простран¬
ства представлений Ф и Т соответственно. Если пред¬
ставления Ф и Т эквивалентны и g ЕЕ G, то Ф (g) =
= срТ (g)cp'1, где ср: V W — изоморфизм линейных про¬
странств. Пусть
е =
— базисный вектор-столбец из V.
е
п
Если Хх (ехф) + . . . + Хп (епф) = 0 для некоторых X, ЕЕ С,
то (Vi + . . . + 1пеп) (р = 0, откуда Х^ + . . . + Хпеп = 0,
а значит, = . . . = Хп = 0. Таким образом, вектор-
столбец еф *) линейно независим. Из теоремы III.1.10
вытекает, что он базисный. Обозначим через А матрицу
линейного преобразования Ф (g) в базе в, а через
В — матрицу линейного преобразования Т (g) в базе еф.
Тогда
В (вф) = (еф) T (g) = (еФ (g)) ср = (Ле) ср = А (еср) **),
откуда А = В по теореме III.1.12. Следовательно,
Хф (ё) = Тг А = Тг В = Xv (g).
Ввиду произвольности элемента g ЕЕ G имеем хф — Xv>
что и требовалось.
*) Если <р — линейное отображение, то, как уже отмечалось,
<?icp
еФ означает вектор-столбец
**) Равенство (Ае) ср = А (еср) проверяется непосредственным
Подсчетом, использующим линейность отображения ср.
213

Наша ближайшая цель — доказать, что и, наоборот,
из равенства характеров вытекает эквивалентность пре/ь
став лений.
Тео р е м а 7. Если Ф — представление группы G,
то Хф (# 1) — Хф (g) для каждого g ЕЕ G.
Доказательство. Если Х15 . . Хп — собствен-
пые значения линейного преобразования Ф (g), то
Хф (g) = Тг Ф (g) = И + • • • + К-
Согласно теореме 4,	— корень из единицы. Но тогда
— положительный действительный корень из еди’
ницы (см. с. 100), откуда = 1, т. е. = X?1. Вви¬
ду теоремы III.1.18
Хф (Г1) = Тг (1) (Г1) = Тг (Ф (g)f1 = _
= V + • • • + V? = И -Г • • • -Г Е = Тг Ф (g) = Хф (g).
Теорема 8. Если
Ф = Фг ф . . . ф Фт,
где Ф, Ф^ — представления группы G, то
Хф = ХФ1 + • • • + Хф?п-
Доказательство. Если Vf — пространство
представления Ф^ и (вц, . . ., ein.} — его база, то
V= V,®. . .ф vm
—	пространство представления Ф и, согласно теореме
П1.1.8,
^21» • • •» ^2П2, • • •»	• •» Епт}
—	его база. Если g ЕЕ G, то поскольку «</Ф (g) = etfl>i(g)
для каждого Z, матрицей линейного преобразования Ф (g)
в этой базе будет матрица
где At — матрица линейного преобразования Ф/ (g) в ба¬
зе . . ., eini}. Ввиду теоремы III.1.16
Хф (") = ТгФ (g) = ТгФх (g) + . . . + Тг Фт (g) =
= ХФх (g) + • • • + Хфш (g)-
214

Теорема 9. Пусть Ф1?. . ., Фт — все эквивалент¬
ные неприводимые представления группы G, dim Ф, =
= nt и 1 =^= g G. Тогда
(£) + •••+ «тХФ,„ (?) = 0.
Доказательство. Групповая алгебра CG, бу¬
дучи модулем над собой, может рассматриваться как
пространство некоторого представления Ф. Приняв эле¬
менты группы G за базу этого пространства, заметим, что
линейное преобразование Ф (g) переводит каждый элемент
h этой базы в отличный от h элемент hg той же базы. Сле¬
довательно, на главной диагонали матрицы линейного
преобразования Ф (g) в этой базе стоят нули, и
%Ф (g) = о
потеореме III.1.16. Сдругой стороны, из теорем2, III.2.16
и III.2.15 (5) вытекает, что
ф=(фх ф... е фх) ® (ф2 ф ... ф ф2) ф ...
	'	4	ЧЛ	'
пх раз	п2 раз
... © (Фпг© -j . ©Ф,Д
пт Раз
В силу теоремы 8
о = ХФ (g) = «1Хф, (g) + «2Хф2 (g) + • • • + «тХФт(^)-
Если g ЕЕ G, то обозначим через К (g) множество всех
элементов группы G, сопряженных с g, через | К (g) |—
число элементов множества К (g) и через zg — элемент
групповой алгебры CG, равный сумме всех элементов из
К (g). В силу теоремы III.2.8, zg— центральный элемент
алгебры CG. Теоремы III.2.15 (2) и III.2.16 позволяют
указать изоморфизм ср алгебры CG на внешнюю прямую
сумму
R1 © ••• Ф Rm
алгебр матриц над полем С. Ввиду теорем II.4.12 и
III.2.15 (6)
Ф (Zg) =	(g) А’, . .	(g)A’),	(*)
где (g) — комплексные числа. Если, далее, Ф — не¬
приводимое представление группы G и М — модуль
представления Ф, то, по теореме 2, М — неприводимый
Правый CG-модуль. Теоремы II.6.8 и III.2.15 (3) позво¬
ляют считать, что М — минимальный правый идеал ал¬
гебры CG, причем ср (М) принадлежит в точности одному
215

прямому слагаемому Rt. Комплексное число (g) из фор¬
мулы (❖) назовем центральной Ф-компонентой элемет
та g и будем обозначать через Хф (g). Наконец, если г
ЕЕ CG, то обозначим через Т (г) линейное преобразование
линейного пространства М, определяемое равенством
хТ (г) = хг
для всех х ЕЕ М. Поскольку пространство М является
правым CG-модулем, то Т (г) действительно оказывается
линейным преобразованием пространства М.
Теорема 10. Для любого неприводимого представ¬
ления Ф группы G имеем
Tr Т (Zg) = | К (g) | ХФ (g) =	(g) dim Ф.
Доказательство. В силу теорем 2, III.2.13
и III.2.15 (3), dim Ф равна порядку матрицы Хф (g) Е
в формуле (*). Пусть для определенности Хф (g)
Ч (#) М- Если х ЕЕ М, то, вспоминая, что ср (М) се
cz Ra, можно записать
ср (х) - (Л, 0,. . ., 0),
где А — некоторая матрица. Поэтому
<р (xzg) = ср (ж)ср (z.«) = (Л, 0, . .	0) (?ч (g)E, Х2 (g)E, . . .
. .	(g)E) = Xj (Л,	0, . .	0) = Xjcp (х) = ср (Хрг),
откуда, поскольку ср — изоморфизм, получаем
хТ (zg) = xzg = k±x.
Следовательно, %1Л', где Е — единичная матрица порядка
dim Ф, служит матрицей линейного преобразования
Т (zg) в любой базе, и по теореме III.1.16
TrT (zg) ~ Xi-dim Ф.
С другой стороны, из теорем III.1.15 и III.1.16 вытекает,
что след суммы линейных преобразований равен сумме
следов слагаемых. Поэтому
TrT(zg)= 3 Тг7т(х) =	3 Xo(x) = |^(g)| Хф(?),
ибо %ф (х) = хф (g) по теореме 5.
Теорема 11. Если Ф — неприводимое представле¬
ние группы G, dim Ф = п и а, Ъ ЕЕ G, то
Zazb = S
ces
216

где 8 — множество представителей классов сопряжен¬
ности группы G, а ХЙ — целые числа,
Хф (а) Хф (Ь) —- ХаьХф(с),
cceS
Хф(1) = 1
и
I К (a) I I К (&) | Хф (а) Хф (&) = п 3 2$ | К (с) | Хф (с).
Доказательство. В силу теоремы III.2.8,
элементы гс, где с пробегает S, образуют базу центра Z
алгебры CG. Поскольку zazb ЕЕ Z, то
ZaZb = S
ceS
для некоторых Х^ сЕ С. Ясно, что в левой части этого ра¬
венства коэффициентами при элементах группы G служат
целые числа. В силу единственности выражения элемента
линейного пространства через базу, то же самое верно
и для правой части равенства, т. е. Х^ должны быть це¬
лыми числами. Далее, ввиду равенства (*) на с. 215,
имеем
(Xi (a) Xi (b)E, .. ., Xm (a)	(b) Е) —
= (Хх (а) Е • Хх (Ъ) Е, . . ., Хт И Е • Хт (&) 7?) =
= Ф (za) ф (z6) = ф (znZ6) = ф ( ^abZc) =
eeS
= 3 ^‘ьФ (zc) = 3 (Хг (с) /<;, . . . , Х,п (с) Е).
cc-S	c&S
Отсюда, поскольку в силу определения Хф (g) = Хг (g)
для всех g ЕЕ G при некотором i, вытекает, что
Хф(а)Хф(5)-= 3 2>ф(с).
c^S
Используя теорему 10, получаем
IК (а) 11 К (Ъ) | хф («) Хф (Ь) = %Ф (а) Хф (&) п* =
= S	(с) п2 — п У, Еъ | К (с) | хф (с).
ces	c&s
Наконец, поскольку 2, = 1 и ср (1) =	(1) Е,. . .
• . Xm (1) Е) (Е,. . ., Е), имеем Хф (1) ~ 1, ибо, как
Уже отмечалось, Хф (1) = Xf (1) для некоторого номера I.
Теорема 12. Пусть Ф1?. . ., Ф7П — все неэквива¬
лентные неприводимые представления группы G, а, Ъ ЕЕ
217

EE G и | G | — число элементов группы G. Тогда
Хфх («) Хф, (Ь) 4- • • • Н- Хф,„ («) Хфш W =
0, если Ь~г К {dp
= 1тмЖ’ если ъ'1-кс-
Доказательство. Согласно теореме 11
IК (а) 11 А' (Ь) | Хф. (а) /Ф. (ft) =
= ««2 ^|А(с)|ХФ{(с)	(*)
CtrS
для каждого I, где nt = dim ФР
(а)	Если Ъ~х е£ r {ар то х(аь = 0.
Действительно,
^abZc = ZeZ6= 3	gh.
czES	g^K(a) h^K(b)
Если Хдь y= 0, to gh = 1 для некоторых g ЕЕ К (а) и
h ЕЕ К (&). Если g = иаи"1 и h = vbv~\ где и, v ЕЕ G, то
uau^vbv'1 = 1, откуда
Ь~г = и~1иаи''1и = (и^и) а (р-1^)”1 (ЕЕ К {а),
вопреки условию.
(б)	Если b~Y ЕЕ К (а), то /Г1 ЕЕ К (а) для всех h (ЕЕ К U))
и = I К (a) I = I К (Ь) |.
В самом деле, если b г = иаи 1 и h ~= vbv \ где и,
v ЕЕ G, то
h"1 = vuau~1v~'1 — {vu)a(vu)~'1 ЕЕ К {а).
Таким образом, положив К (Ь)'1 =-- {х1 \ х ЕЕ К (£)}, име¬
ем К (Ь)"1 ее. К (а). Аналогично получаем, что К (a)-1 £
се К (Ъ) и, следовательно, К (а) се К (Ъ)"1. Отсюда
К (а) = К (Ь)-1, а значит,
I К (b) I I К (Ъ)~х I = I К {а) |.
Далее, учитывая теорему 11, получаем
2(Е>Ь = 2	2 ^abZc
/i&K(b)	l^c&S
и, следовательно, = | К (а) | = | К (Ь) |.
218

Суммируя равенства (*) по i и используя теорему 9,
будем иметь
7П	ТП
I к (а) IИ (b) I 3 Хф,; (а) %ф{ (&) = 3 № I К (с) | 3 "»Хф{ (с)=
1	г=1	1	L	ces	г=1	г
т	7п
- 2$ IК (1) I з ПЛФ. (1) - хй У «1.
2=1	2=1
Ввиду (а) и (б) отсюда вытекает, что
| к (a) 11 К (b) I jg ХФг (а) Хф4 (Ь) =
' 0, если Ъ"1 К (а),
= ‘ Л& § п} = | к (а) 11G |, если б"1 е К (а),
2=1
т
поскольку | G ] = 2 л? в силу теорем 2 и III.2.18. Ос-
2=1
тается разделить полученное равенство на | К (а) || К(Ь)\.
Теорема 13. Если Ф1?. . Фт — все неприводимые
представления группы G, то
	f|G|, если 1=-р
o^G	[О, если i Ф j.
Доказательство. В силу теоремы 3, группа G
распадается на т классов сопряженности. Пусть . .
. . ., gm — представители всех этих классов. Положим
%2=ХФр <Ej = Ki(gj) и
| К (g.) |
| G |
Рассмотрим матрицы А = || atj ||, В = || Ъц || и С = В А.
Ввиду теорем 7 и 12
т	т
СИ = У,bit!akj = -jg-j- У I К (gi) I Xfc (gi) Xi- (g>) -=
/>=1	A’=l
= W^(gi)l12Zfc(g71)z't(^==[o’
если i = /,
если i=^= j.
Таким образом, BA = E. Но тогда AB = E, t. e.
m	7П
■[су У K (Sk) '/Л (gk) Xi(gk) = У dikbkj=
A'=l	A’=l
1, если
О, если
219

Ввиду теоремы 5 отсюда вытекает
„		 S		 (|<Ц если i=/,
3	7..Й1ЛН Х|КШ|Х.(г,)Ь(Л) = [ о, если l^f.
Теорема 14. Если Ф и Т* — представления груп¬
пы G и %ф = то представления Ф и эквивалентны.
Доказательство. Пусть М и N — модули
представлений Ф и Т соответственно. Ввиду следствия
теоремы II.6.8, из теоремы III.2.16 вытекает, что модули
М и N изоморфны внешним прямым суммам минималь¬
ных правых идеалов алгебры CG, скажем,
(Ж ©... э Мг) © (м2 ©... © м2) ©...
Ч— .. ■	—Ч_			-
h-t раз	А-2 раз
•	• • © (Мтф... ©Мт)
© ₽аз
И
(Л/i ® .. . ф Л£1) ® (Мг ф •. • ф Л/г) © • • •
4	.	—	Ч. ...	.-ы	-<
li раз	12 раз
•	• • Ф (Мт ф . -. ф мт)
1т ₽аз
соответственно. Если Ф^ — неприводимое представление
с модулем представления Mt (учесть теорему 2), то в силу
теоремы 8
ХФ {g) = *1ХФ, (?) + ••• + *тХФт (?)
для всех g ЕЕ G. В силу теоремы 13
S Хф(?)Хф{(?) = ^|^|.
g=G	г
По тем же соображениям
3 X'F(g)%oi (g) = ^l G|-
g(=G	г
Отсюда
2j Хф (g) ХФ.(О 2j Хч'(£) Хф.(^)
I. _ g^G	L _ g^G	1		 7
г~~	\G\	~~	|G|
Следовательно, модули представлений Ф и Y изоморфны,
а значит, сами представления эквивалентны по теореме 1.
Наконец, докажем, что размерность неприводимого
представления делит порядок группы. С этой целью на¬
220

зовем комплексное число S целым алгебраическим, если
+ . . . + ап_£ + ап = О,
где ах,. . ап — целые числа.
Теорема 15. Если рациональное число является
целым алгебраическим, то оно целое.
Доказательство. Пусть ~	несократимое
представление рационального целого алгебраического
числа. Тогда
где а±,. . ., а,г — цельте числа. Отсюда
— (aLpn'1q + . . . + a^pq71"1 + anqn),
т. е. рп делится на q, что противоречит взаимной простоте
чисел р и q.
Теорема 16. Целые алгебраические числа образуют
подкольцо поля комплексных чисел.
Доказательство. Сначала установим:
Лем м а. Если . ., сот ЕЕ С zz группа
М = ^(l)1 + . . . + Z(dm
является подкольцом поля С, то М состоит из целых ал¬
гебраических чисел.
Действительно, если со1 = . . . = сот = 0, то М = О,
и лемма справедлива. Допустим, что не все со, равны 0.
Если а ЕЕ М, то
Е «у»;
5=1
для некоторых целых чисел ац. Тогда система линейных
уравнений:
($11	0^) Х1 ^12*^2 Т • • . р МутУт —
^21^1 + (#22 — &) #2 ~Г • • • "Г а2т^т = 0,
^7721*^'1	#7712*^2	*^т —
имеет ненулевое решение (со1, . . ., com). В силу следствия
теоремы 1.3.5, определитель | А — аЕ |'= 0, т. е. а ока¬
зывается корнем многочлена | А — tE | с целыми коэф¬
фициентами, причем коэффициент при старшем члене ра¬
вен +1. А это и означает, что сх — целое алгебраическое
число.
221

Для доказательства теоремы допустим, что а и (3 —
целые алгебраические числа. Тогда
а191 +	1 4- • • • + ат — 0	(*)
и
рп +	. + bn = 0,	(**)
где аг, . . ат, bi, . . Ъп — целые числа. Рассмотрим множе¬
ство М всех комплексных чисел, представимых в форме
У Cij^3,
г, 3
где 0 i < ттг, О / < 77, а — целые числа. Равен¬
ства (*) и (**) позволяют показать, что	ЕЕ М при
любых неотрицательных целых к и I (для этого достаточно
заметить, что соотношения (*) и (**) позволяют выра¬
зить ак и pz, где к т и I > тг, через меньшие степени а
и Р соответственно). Следовательно, М — подкольцо
поля С. В силу леммы, все его элементы и, в частности,
а + р, 0 — а и оср — целые алгебраические числа, что
и доказывает теорему.
Теорема 17. Если Ф — неприводимое представле¬
ние группы G и g Е G, то центральная Ф-компонента
Хф (g) элемента g является^целым алгебраическим числом.
Доказательство. Пусть gx, . . ., gm — пред¬
ставители всех классов сопряженности группы G. В силу
теоремы 11
^(g)^(gi) = S МтАф(£>)>
fc=l
(g.)
где Мк =	— целые числа. Тогда строка
(М> (#1), • . . Дф (gm))
служит решением системы линейных уравнений:
(Ml — ^Ф (g)) Х1 + Мг-Г2 4~ • • • 4” Mm^m = О,
Mi^i 4~ (Мг — ^ф (g)) х2 + • • • + ^2тхт = О,
ч 4' ^7712^2 + • • • 4	^Ф (g)) хт —
В силу теоремы 11 Хф (1) = 1, т. е. рассматриваемая си¬
стема имеет ненулевое решение. Пусть А — || Му II- В силу
следствия теоремы 1.3.5, определитель \А — Хф (g) Е\
= 0. Следовательно, (g), являясь корнем многочлена
| А — IE | — 0 с целыми коэффициентами и коэффициен¬
222

том +1 при старшем члене, оказывается целым алгебраи¬
ческим числом.
Теорема 18. Если Ф — представление группы G
и g ЕЕ 6, то /ф (g) — целое алгебраическое число, причем
I %ф (g) I < dim Ф.
Доказательство. Допустим, что dim Ф = п.
Если fe,. . Хп — все характеристические корни линей¬
ного преобразования Ф (g) (здесь каждый корень выпи¬
сан столько раз, какова его кратность), то
Хф fe) = fe + • • • + би¬
согласно теореме 4, fe — корни из единицы, т. е. целые
алгебраические числа. В силу теоремы 16, хф (g) также
целое алгебраические число. Далее, ввиду свойства (2)
нормы комплексного числа (см. с. 100), | fe | = 1. Поэто¬
му, в силу свойства (3) нормы комплексного числа (там же),
имеем
I Хф fe) I < I 611 + . . . + | Кп I = П = dim Ф.
Теорема 19. Если Ф — неприводимое представле¬
ние группы G, то число dim Ф делит |G |.
Доказательство. В силу теорем 10 и 17
I К (g) I Хф (g)
dimCD	/v®fe)
— целое алгебраическое число для всякого g ЕЕ G. По
теореме 18 целым алгебраическим является и число хф (g).
Число /ф (g), будучи корнем того же самого целочислен¬
ного многочлена*), является целым алгебраическим. При¬
меняя теорему 16, убеждаемся, что
I К (g) I Хф (g)
dim Ф
• Хф (g)
— целое алгебраическое число для всякого gEzG. Отсюда,
обозначив через gn . . ., gm представители всех классов
сопряженности группы G и снова применяя теорему 16,
видим, что
I К fe) I Хф fe) Хф fe)
dim Ф
*) Здесь используется тот факт, что число, сопряженное корню
многочлена с действительными коэффициентами, является корнем
того же самого многочлена (см. с. 160 учебника А. Г. Куроша или
с. 282 учебника А. И. Кострикина).
223

— целое алгебраическое число. Ввиду теорем 5 и 13,
целым алгебраическим оказывается и число
т

2i ^ф '	/.ф (ё})
I G |	__ a’^g		 2=1

сИтФ	dimO	сИтФ
Но число	, будучи рациональным, должно быть
целым в силу теоремы 15. А это н означает, что число
| G | делится на dim Ф.
У п р а ж н е н и я
1.	Доказать, что конечная группа коммутативна тогда и толь¬
ко тогда, когда все ее непроводимые представления одномерны.
2.	Составить таблицы характеров для следующих групп:
ZlkZi, (Z/2Z) X(Z/2Z), Z/6Z, знакопеременные группы $(3 и 5(4
(см. конец § 3 гл. II), группа кватернионов, т. е. подгруппа {+1,
^Н,	dz/c} мультипликативной группы тела кватернионов (см.
конец § 4, гл. II). При составлении таблицы полезно пользоваться
«соотношениями ортогональности», установленными в теоремах 12
и 13. Найти неприводимые представления этих групп.
3.	Доказать, что наименьшая некоммутативная группа содер¬
жит 6 элементов.
4.	Пусть Ф — представление группы G. Рассматривая Ф (g)
как матрицу, положим V(g) = (Ф (g-1))* для всех g G. Доказать,
что Т — представление группы G и что представления Ф и Т эквива¬
лентны тогда и только тогда, когда %ф (g) — действительное число
для всех g G. Установить, что представление неприводимо тог¬
да и только тогда, когда неприводимо представление Ф.
5.	Доказать, что группа, порожденная двумя элементами а
и Ь, для которых справедливы равенства а° = 1, b2 — 1 и abab = 1,
содержит 10 элементов. Найти неприводимые представления этой
группы.
6.	Доказать, что группа, порожденная двумя элементами а и
д, для которых справедливы равенства а4=1, &2 = 1 и abab — 1,
содержит 8 элементов. Найти неприводимые представления этой
группы. Доказать, что она не изоморфна группе кватернионов (см.
упраждение 2).
§ 2. Приложение теории представлений
В качестве одного из приложений установим достаточ¬
ное условие разрешимости, обобщающее теоремы 11.7.11
и II.7.12. Однако для этого нам понадобятся некоторые
дополнительные свойства целых алгебраических чисел.
Пусть Q —поле рациональных чисел, Н — комплекс¬
ное число и Q [£]—линейная оболочка системы {1, 3,
S2,. . .} в поле комплексных чисел, рассматриваемом как
224

линейное пространство над полем Q. Легко проверяется,
что Q [£| — подкольцо поля комплексных чисел.
Т е о р е м а 1. Пусть w0 — целое алгебраическое чис¬
ло, Тогда cyiuecmeyem неприводимый над полем Q много¬
член f с целыми коэффициентами *) такой, что коэффи¬
циент при его старшем члене равен 1 и /(со0) = 0. Если
со — какой-либо корень многочлена /, то существует изо¬
морфизм ср кольца Q [со0] на кольцо Q [col такой, что
ср (соо) = со и ср (г) ~ г для всех rE Q-
Доказательство. Напомним, что многочлен g
с целыми коэффициентами называется примитивным,
если не существует простого числа р, на которое делятся
все его коэффициенты. Поскольку соо — целое алгебраи¬
ческое число, то, по определению, существует многочлен g
с целыми коэффициентами такой, что коэффициент при его
старшем члене равен Ing (со0) = 0. Многочлен g можно
представить как g = g3 . . . gm, где gt — многочлены,
неприводимые над полем Q **). Отсюда
gl (®о) • • • gm (®0) = g (®0) = 0,
значит, например, g± (со0) = 0. Можно считать, что много¬
член gr примитивен. Положимg2 . ..	— где г и s —
взаимно простые целые числа, причем г Е> 0, а 1г — при¬
митивный многочлен. По лемме Гаусса***) многочлен
gAh примитивен. Поэтому из равенства
Я? = sgv . . .	-- I'gjt
вытекает, что s 1. Поскольку коэффициент при старшем
члене многочлена g равен 1, то то же самое верно и для
многочлена Положив / = gx, убедимся в справедливо¬
сти первого утверждения теоремы. Далее, для любых
Го, 7’1, . . ., rm GE Q положим
т	т
Ф ( X = X г fit.
1 0	2=0
т	т
Если У 7\се>о = 0, то рассмотрим многочлен g = тцх1.
1=0	1=0
Если d н.о.д. (/, g), то d = uf + vg для некоторых мио-
*) Напомним, что многочлеп над полом Р называется неприво¬
димым, если он нс может быть представлен в виде произведения
многочленов с коэффициентами из Р, имеющих мепыную степень.
**) См. с. 290 учебника А. Г. Куроша пли с. 229 учебника
А. И. Кострпкппа.
***) См. с. 351 учебника А. Г. Куротпа пли с. 230 учебника
А. II. Кострпкппа.
225

точленов и и р*). Отсюда
d (®0) = и (со,,)/ (®0) -Н v (со0) g (®0) — 0.
Следовательно, степень многочлена d 1. Но f ~ dh
для некоторого многочлена h, и поскольку / неприводим
над полем Q, то 0 й ЕЕ Q. С другой стороны, g = dk
для некоторого многочлена /с, откуда g jkh"1 = fq,
где q = kh~l. Но тогда
m	т
ф ( S 4®о) = 3 ’’i®’ = g (®) = f (®) 7 (®) = О,
?=0	i=i)
что доказывает корректность определения отображения ср
кольца Q [со0] в кольцо Q [со]. Простые выкладки показы¬
вают, что это гомоморфное наложение кольца Q [соо]
на кольцо Q [со]. Если
т
ф ( S Г1®о) = о,
1=0
то, как и выше, убеждаемся, что g fq для некоторого
многочлена q, откуда g (со0) = / (соо) q (соо) = 0. Тем са¬
мым доказано, что ср — изоморфизм колец.
Теорема 2 (критерий непросто™). Если класс
сопряженности элемента g группы G содержит pd эле¬
ментов, где р простое и dk^ 1, то группа G содержит нор¬
мальную подгруппу, отличную от G и от единичной под¬
группы (т. е. группа G не является простой).
Доказательство. Допустим, что группа G
не содержит нетривиальных нормальных подгрупп. Обо¬
значим через К класс сопряженности элемента g. По
скольку | К | =# 1, то группа G не коммутативна.
Л е м м а. Если Ф — не единичное неприводимое
представление группы G и п = dim Ф, то
п-У.ф (ё) =
где сс — целое алгебраическое число.
Действительно, справедливость леммы тривиальна,
если /ф (g) = 0, и вытекает из теорем 16 и 18 из § 1,
если п делится на р. Если это не так, то
и.о.д. (I К I, п) = и.о.д. (у/, п) = 1.
Следовательно,
и-п + и | К | = 1
*) См. с. 140 учебника А. Г. Куроша или с. 227 учебника
А. И. Кострикпиа.
226

для некоторых целых и и и*). В силу теорем 10 и 17 из
§ 1,
I ДГ| Хф (g)
п
= ^ф (g)
— целое алгебраическое число. Ввиду теорем 16 и 18
из § 1, целым алгебраическим оказывается и число
со
 Хф (g)
п
= (?) - !-
I | уф (g)
п
Допустим, что | хф (g) | = dim Ф, т. е. | Тг Ф (g) | =
= dim Ф. Но, ввиду теоремы 4 из § 1, норма характери¬
стических корней линейного преобразования Ф (g) рав¬
на 1. Поэтому из той же теоремы 4 вместе с теоремами
III.1.19 и III.1.20 вытекает, что Ф (g) = Хо 1у, где V —
пространство представления Ф и Хо Е7 С. Обозначив через
II множество всех таких элементов х из G, что Ф (х-) =
= Му для некоторого 1Е С, нетрудно заметить, что II —
нормальная подгруппа группы G. Поскольку g ЕЕ//, то
Н {1} и в силу допущения Н = G. Таким образом, Ф —
гомоморфизм группы G в группу всех линейных преобразо¬
ваний вида Му. Без труда проверяется, что эта группа
коммутативна. Если Кег Ф = {1}, то коммутативной
должна быть и группа G, что несовместимо с | К |=# 1.
Следовательно, Кег Ф = G, т. е., вопреки условию леммы,
представление Ф оказывается единичным. Тем самым
установлено, что | /ф (g) I Ф dim Ф, а значит, | хф (g) I <
< dim Ф = п по теореме 18 из § 1. Допустим, что все
характеристические корни линейного преобразования
Ф (g) совпадают. Тогда из теоремы II 1.1.20 и теоремы 4
из § 1 вытекает, что Ф (g) = Му, где X ЕЕ С. Отсюда, учиты¬
вая ту же теорему 4 и свойство (2) нормы (см. с. 100),
получаем
n > I Хф (g) I = I Тг Ф (g) I = I пк I = п I X I = п,
что невозможно. Следовательно,
= Хф (?) = М + • • • + М,
где %!,. . ., М — корни степени п из единицы, среди
которых есть различные. Ввиду теоремы 1 существует не¬
приводимый над полем рациональных чисел многочлен /
с целыми коэффициентами такой, что его коэффициент
при старшем члене равен 1 и / (со) = 0. Если со' — ка¬
*) См. примечание па с. 80.
227

кой-либо другой корень многочлена /, то в силу той же
теоремы 1 существует описанный там изоморфизм ф,
для которого ср (со) со'. Отсюда
по/ = ф (тгсо) = ф (^i) + . . . + ф (^г)«
Поскольку
(<Р (М)" = Ф С") = ф (1) = 1,
то лгсо' равен сумме корней степени п из единицы, среди
которых есть различные. Используя лемму, установлен¬
ную при доказательстве теоремы III.1.19, нетрудно по¬
лучить, что | псо' | < п, а значит, | со' | < 1. Таким
образом, нормы всех корней многочлена / меньше 1. В си¬
лу формул Виета* *) и свойства (2) нормы комплексного
числа (см. с. 100), то же самое верно и для свободного чле¬
на этого многочлена. Поскольку этот свободный член —
целое число, он равен нулю, вопреки неприводимости мно¬
гочлена /. Полученное противоречие доказывает лемму.
Возвращаясь к доказательству теоремы, обозначим
через Фо единичное, а через Фх, . . ., Фт все остальные
неприводимые представления группы 6', положим пt =
= dim Ф/ и, воспользовавшись теоремой 9 из § 1, запи¬
шем
1 + ^1X01 (#)+•••+ пт%Фт (£■) = 0-
Ввиду леммы	(g) = pah где — целое алгебраиче¬
ское число, для i = 1, . . ., т. Ввиду теоремы 16 из § 1
1 .
	— = CZ1 + • . • - Г
— целое алгебраическое число, вопреки теореме 15 из
§ 1. Полученное противоречие завершает доказательство
теоремы.
Теорема 3 (теорема Бернсайда). Если G — группа
и | G | = pm(f^ где р и q простые, то группа G разрешима.
Доказательство. Будем вести индукцию по
т + п. Если т + п = 1, то | G | — простое число. В си¬
лу теоремы II.3.3, G не содержит нетривиальных под¬
групп. Следовательно, она циклическая, а значит, ком¬
мутативная.
Л е м м а. Если т + п 1, то G или коммутативная,
или содержит нетривиальную нормальную подгруппу.
*) Имепно: что произведение корней многочлена со старшим
коэффициентом 1 с точностью до знака совпадает с произведением
корней (см. примечание ***) на с. 181).
228

Действительно, допустим для определенности, что
п 1. Тогда по теореме II.7.8, G содержит такую подгруп¬
пу Я, что | II | = qn. В силу теоремы II.3.24, центр
группы II содержит элемент 1. По теореме II.3.23.
| К (z) | | С (z) | - | G |,
где К (z) — класс сопряженности элемента z в группе G.
Кроме того, II ст, С (z). Ввиду теоремы 1.3.3' | С (z) | =
= pdqn, где 0 cl т, а значит, | К (z) | = pm~d. Если
т — d у> 0, то применима теорема 2. Если же т — d = О,
то | К (z) | = 1, т. е. z принадлежит центру Z группы G.
Если 6r = Z, то G коммутативна. В противном случае
Z оказывается нетривиальной нормальной подгруппой
группы G в силу теоремы II.3.20.
Для доказательства теоремы заметим, что если G
не коммутативна, то она согласно лемме содержит не¬
тривиальную нормальную подгруппу II. В силу теоремы
II.3.3', как число элементов группы II, так и число эле¬
ментов факторгруппы GUI являются произведением
степеней не более чем двух простых чисел. В силу индук¬
тивного предположения, обе они разрешимы, и разреши¬
мость группы G вытекает из теоремы II.7.9.
Замечание. Отметим, что только в самое последнее время
удалось найти доказательство теоремы Бернсайда, не использующее
теории представлений (см. Га ген Т. М. Некоторые вопросы тео¬
рии конечных групп, § 8—9.//К теории конечных групп: Пер. с
англ./Под ред. А. И. Кострикина.— М.: Мир, 1979).
В заключение опишем группы, содержащие не более
10 элементов.
Подгруппа {±1,	± fc} мультипликативной
группы тела кватернионов (см. с. 102) называется группой
кватернионов.
Условимся говорить, что группа G порождается
своим подмножеством X, если никакая отличная от G
подгруппа группы G не содержит множества X. Нетрудно
доказать, что в этом случае каждый элемент g группы G
может быть представлен в форме
р„>
g ~ х! ... X т,
где Xf ЕЕ X и = Ч- 1, вообще говоря, различными спо¬
собами.
Теорема 4. Группа G изоморфна группе кватер¬
нионов тогда и только тогда, когда | G | = 8 и G порож¬
дается элементами а и Ь, удовлетворяющими условиям
а1 = 1, а2 = Ь2 и aba = b.
229

Доказательство. Если G — группа кватер¬
нионов, то из таблицы умножения, приведенной нас. 102,
видно, что — 1 = г2, 1 == г4, — i = г3, — j —	& =
= ij и — k = i?j, т.е. G порождается множеством {i, j},
С помощью той же таблицы умножения получаем г2 =
- —1 =--= J2n iji = j. Пусть теперь G — группа, удовлет¬
воряющая условиям теоремы. Тогда Ъа = a3b, bab =
= а3Ь2 = а5 -= а и abab = а2, т. е. возникает следующая
таблица умножения:
1
а
Ъ
ab
1
1
а
Ъ
ab
а
а
а2
ab
а2Ъ
b
b
a2(ab)
а2
а
ab
ab
b
а2 а
а2
Сравнивая ее с таблицей умножения, приведенной на
с. 102, и замечая, что а2 лежит в центре группы G, нетрудно
убедиться, что отображение ф группы кватернионов Q
в группу G, задаваемое таблицей
X
1	i	j
к
-1
— 1
-J -1с
<р(ж)
1
а
b
ab
а2
а2а
a2b	a2(ab)
оказывается гомоморфизмом. Поскольку a, b FE Im ср,
то ввиду теоремы II.3.5 Im ф = G, т. е. ф является нало¬
жением. Поскольку | Q | — 8 = | G |, то отображение ф
взаимно однозначно, т. е. изоморфизм.
*2 д,
Пусть 0—	• Простой подсчет показывает, что мат¬
рицы
Il cos АО — sin АО ||	|| cos АО — sin АО ||
[I sin АО cos АО ||’ II—sin АО —cos АО || (к — 0, 1, . . ., п — 1)
образуют подгруппу группы невырожденных матриц вто¬
рого порядка над полем действительных чисел. Эта под¬
группа называется группой диэдра и обозначается через
Dn. Можно показать, что группа Dn изоморфна группе
симметрий правильного тг-угольника (см. К о ст р и-
к и н А. И. Введение в алгебру.— М.: Наука, 1977,
с. 327-328).
Теорема 5. Группа G изоморфна группе диэдра
Dn тогда и только тогда, когда | G | = 2п и G порож¬
дается элементами g и а, удовлетворяющими условиям
gn = а1 = agag = 1.
230

Доказательство. Если G = Dn, то, как легко
видеть, указанные соотношения справедливы для эле¬
ментов
II cos 0 — sin 0 ||	|| 1	01|
II sin 0 cos 01|	|| 0 — 11|
Пусть теперь G — группа, удовлетворяющая условиям
теоремы. Тогда ga = agn~\ откуда легко вывести
g*a = ag^\
g'-ag1 -
• ag* = gs<"-i)+»
И
ag'-ag' = g^" = g"9 = 1,
где s, t = 1, 2,. . ., n — 1. Эти равенства показывают,
что
н = {1, g,. .	g”-1, a, ag,. . agn_1}
— подгруппа группы G. Поскольку a, g (ЕЕ Н, то G ~ Н.
Положим
„  || cos £0 — sin ЛО11	. || 1	01|
— II sin kQ	соаЛеЦ И Л	|| 0 — 11| •
Тогда
.Xi  || cos/cO — sin 7с0 ||
к	|| _ sin Л-0 — cos kQ || *
Далее определим наложение ф: Dtl -> G, положив
Ф (G/,) = gh' и ср (Л€?а) = agl;.
Поскольку | Dn\ = 2п = | G |, то <р — взаимно однознач¬
ное отображение. Равенства
Ф (£&£/) = Ф (&k+i) = gll+l = ф (fib) Ф
<р (G^-AGi) = ф (ЛС;_,) = ag^ = gk-agl = ср (Gft) ф (4GZ),
ф(Лад) = Ф(4СЛН) — ag/,+z = ag'- .g1 = ф (ЛС,,.) ср (Gz)
И
Ф (AG.AG,) = Ф (Gz_ft) = gM' = ag,; -ag1 - ср (AGk) ср (ЛС;)
показывают, что ф — изоморфизм.
Сведем вместе некоторые факты, касающиеся размер¬
ности неприводимых представлений.
Теорема 6. Пусть G — конечная группа и к)г —
число ее п-мерных неприводимых представлений. Тогда'.
231

(1)	| G | =- /fj + 22/r2 !- 32^3 + . . ., причем k^i и
kn ~ 0, если n не делит, j G |;
(2)	группа G коммутативна тогда и только тогда,
когда kL 0 для всех i 2;
(3)	если | G j 5, то группа G коммутативна',
(4)	Лх = | GlG' |;
(5)	если | G | = р2, где р — нечетное простое число,
то группа G коммутативна.
Доказательство. (1). Каждая группа допус¬
кает одномерное представление Ф, где Ф (g) = 1 для
всех g ее G. Следовательно, Ад 1. Если п не делит
| G то кп = 0 по теореме 19 из § 1. В силу теоремы 2
из § 1 размерность неприводимых представлений груп¬
пы G совпадает с размерностью неприводимых правых мо¬
дулей над групповой алгеброй CG. По теореме III.2.16
эта алгебра вполне приводима справа. В силу теорем
III.2.15 (2), (3), (4) каждому 7г-мерпому неприводимому
модулю над такой алгеброй соответствует прямое слагае¬
мое, имеющее размерность п2 согласно теореме III.2.13.
Учитывая строение алгебры CG (теорема III.2.15) и след¬
ствие 2 теоремы III.1.9, можно записать
| G | - dim CG = kr + 22Ад + 3% + . . .
(2)	Ввиду (1) из теоремы 3 в § 1 вытекает, что комму¬
тативность группы G равносильна равенству
/ft -|- . . . + klt == | G | кк -|- 4//2 -|- . . . -|- т2кт,
возможному лишь при к2 ... -- кпг = 0.
(3)	Если G некоммутативна, то, согласно (2), kt 0
для некоторого i 2 и, следовательно, | G | > 1 +
+ i2ki > 5 в силу (1).
(4)	Ввиду (2) из теоремы 11.7.9(4) вытекает, что все
неприводимые представления группы G/G' одномерны.
Следовательно, если Ф — неприводимое представление
группы G/G' и л: G -> GIG' — естественный гомоморфизм,
то лФ — одномерное неприводимое представление груп¬
пы G. Если же Ф — одномерное неприводимое представле¬
ние группы G, то для каждого g CZ G положим
Ф (gn) = Ф (g).
Если gn = g^, то в силу теоремы 11.7.9 (4)
gg?1 Е= Кет л = G' cz Кег Ф,
откуда Ф (g) = Ф (gx). Таким образом, Ф определено кор¬
ректно и оказывается представлением группы GIG'. Ра¬
232

зумеется, лФ = Ф. Поскольку лФ = лФх влечет за собой
Ф = Фх в силу теоремы 11.1.4, нами установлено взаимно
однозначное соответствие между всеми неприводимыми
представлениями группы GIG' и всеми одномерными не¬
приводимыми представлениями группы G. Остается заме¬
тить, что число неприводимых представлений группы G/G'
равно | G/G' | в силу теоремы 3 из § 1.
(5)	Если | G | = р2, где р — нечетное простое число,
то ввиду теоремы 19 из § 1 равенство (1) превращается
в р2	+ крр2, где > 1. Отсюда кр 0, и остается
лишь применить свойство (2).
Теорема 7. Если G — группа и | G | — 2р. где
р — нечетное простое число, то G или коммутативна или
изоморфна группе диэдра D2p.
Доказательство. Ввиду теоремы 6 (1)
2/? = /q + 4Л2 + р2кр,
откуда кр ~ 0. В силу теорем 6 (4) и 11.3.3', к± -= 1, 2
или р. Но равенства 2р = 1 -|- 4*2 и 2р = р -|- 4*2, оче¬
видно, невозможны. Следовательно, | GIG' | = 2 и
| G' | — р по теореме II.3.3. Из теоремы II.3.3 нетрудно
вывести, что G' — циклическая группа. Обозначим че¬
рез g ее образующий. Кроме того, согласно теореме 11.7.8Ж
G содержит двуэлементную циклическую подгруппу /£,
скажем, с образующим а. Таким образом, gp = а2 = 1.
Рассмотрим множество
II = {1, g,. .	g1"1, a, ag,. .	agi"1}-
Если gl — ag\ то
1 ф а - gi+1>~j е G' П К - 1,
ибо | G' Г| К | = 1 в силу теоремы II.3.3. Следователь¬
но, | II | = 2р. Отсюда G = II и, в частности, G порож¬
дается элементами а и g. Ввиду теоремы II.7.9 (4)
aga ~ a~rga ЕЕ G',
т. е. aga = g*, где 0 s < р. Отсюда
g = agsa = (aga)8 = g*\
Следовательно, gs2~x = 1 и, как легко вывести из тео¬
ремы II.3.3, р делит s2 — 1 = (s — 1) (5 + 1). Но это
возможно лишь при 5 = 1 или р — 1. В первом случае
имеем aga = g, откуда ag = ga, т. е. группа G оказы¬
вается коммутативной. Во втором случае получаем aga =
233

• = g73'1, откуда agag — 1, u остается лишь применить
теорему 5.
Теорема 8. Если G — некоммутативная груп¬
па и | G | = 8, то G изоморфна или группе кватернионов
или группе диэдра.
Доказательство. Разумеется, группа G не
циклическая. Если х2 = 1 Для всех х ЕЕ G, то для лю¬
бых х, yr G получим хуху = 1. Отсюда ху = ух, во¬
преки некоммутативности группы G. Поэтому, учиты¬
вая теорему II.3.3, получаем, что G содержит четырех-
элемепгпую циклическую группу II, скажем, с образую¬
щим g. Если а $Е II, то ввиду теоремы II.3.2
G = {1, g, g\ g3, a, ag, ag3, ag3},	(*)
откуда a2 — ag8 или gs, где 0 5 3. Однако первое
предположение влечет а = gs, что несовместимо с (*).
Если а2 = g или g3, то
G = {1, а, а2, а3, а1, а5, а*, а1},
что противоречит некоммутативности группы G. Следо¬
вательно, а2 = 1 или g2. В первом случае имеем g4 =
= а2 = 1 и gag = gs или ag8, где 0 5 3. Если
gag = gs, то а = g®+6 = g842, вопреки (*). Следова¬
тельно,
gag = ag8,	(**)
откуда aga = g8”1. Но тогда
g = ag8'1a = (aga)8'1 = gC^DC8"1) =	= g8(8'2)+ij
t. e. g8(8-2) = 1. Поэтому 4 делит 5 (5 — 2) и, следова¬
тельно, 5 = 0 или 2. Если s = 2, то (**) превращается
в gag = ag2, откуда ga = ag, вопреки Гпекоммутативно-
сти группы GJ Если же $ = 0, то (**) принимает вид
gag = а. Отсюда agag = 1, и G изоморфна D4 по тео¬
реме 5. Обратимся к случаю, когда g4 = 1 и а2 = g2.
Кроме того, имеем ga = gs или ags, где 0 s 3. При
первом предположении получим а = g8+3, что противо¬
речит (*). Следовательно, ga = ag1. Если 5 = 0, то
1 g = 1. Если 5 = 1, то возникает противоречие с не-
коммутативностью группы G. Если 5 = 2, то ga = ag2 =
= а3, откуда g2 g = а2 = g2. Таким образом, 5 = 3,
т. е. ga = ag3. Отсюда gag = а, и G изоморфна группе
кватернионов по теореме 4.
В приведенной ниже таблице через Zm обозначена
группа вычетов по модулю т, а через Q — группа ква¬
234

тернионов. При ее составлении использованы теоремы
6—8 и II.7.6. Кроме того, используется тот факт, что груп¬
па, содержащая р элементов, где р — простое число, цик¬
лическая. Это может быть выведено из теоремы II.3.3.
Группы, содержащие не более 10 элементов
Число
элементов
Коммутативные группы
Нс к оммутативные
группы
2
z2
3
z3
—
4
Zi, z2®z2
—
5
Zb
	.
6
Zt
D3^Q3
7
Z-,


8
Z„	Z2®Z2®Z2
Dit Q
9
Z<), Z3@Z3
	,
10
Zia
Db
Число групп, содержащих не более 20 элементов
Число элементов
2 3 4
5
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Число
групп
1
1
2
1
2
1 5
2
2
1
5
1
2
1
14
1
5
1
5
В том числе не¬
коммутативных
0
0
0
0
1
0 2
0
1
0
3
0
1
0
9
0
3
0
3
Проверка правильности заполнения последней табли¬
цы не составляет труда, если число элементов отлично
от 12, 16, 18 и 20. На основании материала, имеющегося
в настоящем пособии, можно исследовать случаи 12,
18 и 20 элементов. Случай же 16 элементов требует более
мощных средств.
Упражнения
1.	Найти центр и коммутант групп, рассмотренных в упражне¬
ниях 2 — 4 пз § 1. Какие из них разрешимы?
2.	Доказать, что для любого одномерного представления Ф
группы G найдется такое одномерное представление 'К группы G/G',
что Ф (g) = Т (gG') для всех g е G.
3.	Доказать, что существует лишь одна (с точностью до изо¬
морфизма) некоммутативная группа, состоящая из 10 элементов.
Найти ее центр, коммутант, неприводимые представления и их ха¬
рактеры (ср. упражнение 5 из § 1).
4.	Доказать, что некоммутативная простая группа содержит
не менее 30 элементов.
5.	Доказать, что некоммутативная простая группа имеет лишь
одно одномерное представление. У казание: принять во внима¬
ние теорему II.7.9 (4) и упражнение 2.
235

УКАЗАТЕЛЬ РАСПОЛОЖЕНИЯ ТЕОРЕМ
Глава I
§ 1 1
9
§ 2 1 20
6
26
§3 1
31
8
37
9
11
2 20
7
25
2
31
9
38
3
12
3 23
8
28
3
31
10
40
4
15
4 U
9
28
4
32
И
40
5 24
5
33
12
40
6	34	13 41
7	37
Глава II
§1
1
49
§ 2
1 56
£
■ 3	1 71
13 81
§ 4	1
91
2
49
2 56
2 72
14 82
2
92
3
50
3 57
3 73
15 83
3
93
4
50
4 60
3' 73
16 83
4
94
5
51
5 60
4 73
17 84
5
95
6
51
6 61
5 74
18 85
6
95
7
52
7 63
6 74
19 85
7
96
8
54
8 63
7 75
20 86
8
96
9
54
9 64
8 76
21 86
9
100
10 65
9 77
22 87
10
102
И 67
10 78
23 87
И
103
12 68
И 79
24 88
12
103
13 68
12 80
§ 5
1
107
9
112
17
118 §
6 1 125
8 129
2
108
10
V3
18
118
2 125
9 129
3
108
И
114
19
119
3 126
4
108
12
114
20
119
4 126
5
109
13
115
21
119
5 127
6
110
14
116
22
120
6 127
7
111
15
117
23
122
7 128
8
111
16
117
§7
1
130
9
139
§8
1 151
9 158
2
131
10
141
2 152
10 160
3
132
И
141
3 154
11 161
4
133
12
141
4 155
12 161
5
134
13
143
5 156
13 163
6
135
14
144
6 156
14 163
7
137
7 157
15 164
8
138
8 157
Глава III
§ 1 1 168
9 173
17 182
§2 1 190
8 193
15
201
2 169
10 174
18 182
2 191
9 194
16
204
3 169
И 174
19 183
3 191
10 195
17
205
4 170
12 176
20 184
4 192
И 196
18
205
5 170
13 178
21 184
5 192
12 197
6 171
14 178
22 185
6 192
13 198
7 172
15 179
23 187
7 192
14 200
8 172
16 182
24 188
Глава IV
§1 1 209
8 214
15 221
§ 2 1 225
6 231
2 210
9 215
16 221
2 226
7 233
3 210
10 216
17 222
3 228
8 234
4 212
И 216
18 223
4 229
5 213
12 217
19 223
5 230
6 213
13 219
7 214
14 220

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аддитивная группа кольца 90
Алгебраическое дополнение 21
Алфавит О7
Атом булевой алгебры 161
База 131, 171
Булева алгебра 160
Вектор 105
—, выражающийся через систему век¬
торов 107
Вектор-столбец 17 5
—	базисный 175
—	независимый 175
Вложение А 8
Гомоморфизм колец 91
—	— естественный 93
—	линейных алгебр 191
—	модулей 109
—	— естественный 110
—	полугрупп 57
—	— естественный 62
—	структур 155
Гомоморфное вложение (наложение)
полугрупп 57
Группа 71
—	абелева 130
—	вычетов 79
—	диэдра 230
—	знакопеременная 86
—	кватернионов 224, 229
—	периодическая 89
—, порожденная множеством 229
—	примарная циклическая 135
—	простая 144
—	разрешимая 140
—	симметрическая 82
—	циклическая 78
Групповая алгебра 193
Делитель нуля 94
Длина слова 67
Дополнение элемента в структуре 160
Единица 54
—	кольца 90
—	частично упорядоченного множе¬
ства 149
Знак подстановки 27
Идеал алгебры (двусторонний, ле¬
вый, правый) 191
—	дистрибутивной структуры 157
—	— — простой 166
—	кольца (двусторонний, левый, пра¬
вый) 93, 107
—	— правый максимальный 119
—	— — минимальный 118, 126
—	— — с нулевым умножением 125
Идемпотент 69, 124
—	центральный 127
Идемпотенты ортогональные 124
Изоморфизм колец 91
—	линейных алгебр 191
—	модулей 109
—	полугрупп 57
—	структур 155
Инвариантное подпространство про¬
странства представления 210
Кватернион 101
Класс сопряженности 86
Кольца изоморфные 91
Кольцо 90
—булево 163
—	вполне приводимое справа 127
—	вычетов 94
—	коммутативное 90
—	нильпотентное 130
—	простое 102
—	с нулевым умножением 90
—	эндоморфизмов модуля 112
Коммутант 139
Коммутатор 139
Комплексное число 99
Компонента строки 7
Конец отображения 47
Конус (верхний, нижний) 150
Координата вектора 172
—	строки 7
Критерий непростоты группы 226
Лемма о базе 132
Линейная алгебра 190
—	—, вполне приводимая справа 194
—	— простая 197
—	комбинация векторов 107
—	— — тривиальная 107
—	— строк 16
—	оболочка 108
Линейно зависимая система векторов
169
—	независимая система векторов 169
—	упорядоченное множество 149
Линейное многообразие 185
—	отображение 174
237

Линейное преобразование 174
—	пространство 168
—	— бесконечномерное 169
—	— конечномерное 169
—	— п-мерное 172
Линейные алгебры изоморфные 191
Максимальный элеме нт частично упо¬
рядоченного МПОЛл ства 149
Матрица 8
—	вырожденная 42
—	диагональная ig
—	единичная \ 39
—	квадратная 8	__
—	линейною отображения 176
—	— пр< -образования 179
—	невырожденная 42, 53
—	ну. '; вая 8
—	обратная 42
—	перехода 179
—	размера т X п 8
—	системы 12
	 — расширенная 12
—	ступенчатая 8
—	треугольная 19
—	элементарная 39
Матрицы равные 8
Минимальный элемент частично упо¬
рядоченного множества 149
Минор 21. 30
Многочлен неприводимый 225
Модули изоморфные 109
Модуль (правый, левый) 105
—	вполне приводимый 120
—	конечно порожденный 122
—	неприводимый 118
—	представления 208
Мультипликативная группа поля 207
—	полугруппа кольца 90
Наибольший элемент частично упо¬
рядоченного множества 149
Наименьший элемент частично упо¬
рядоченного множества 149
Наложение 48
Начало отображения 47
Неизвестные главные 14» 33
—, которые можно объявить глав¬
ными 33
—, — — — свободными 33
—	свободные 14, 33
Нилькольцо 104
Нильпотентный элемент 130. 205
Норма комплексного числа 100
Нуль 54
—	частично упорядоченного множе¬
ства 149
Образ отображения 47
—	элемента 47
Образующий монотонной полугруп¬
пы 64
—	циклической группы 78
Обратимый элемент кольца 95
Обратный элемент 54
Операция 54
—	ассоциативная 54
—	коммутативная 54
Определитель 16
—	матрицы 23
Орбита подстановки 83
Отношение 147
Отношение антисимметричное 148
рефлексивное 148
	 транзитивное 148
Отображение 47
—	биективное 48
—	взаимно однозначное 48
—	естественное 52
—	изотопное 149
—	инъективное 48
—	на 48
—	обратное 51
—	сюръективное 48
—	тождественное 48
Отображения равные 48
Периодическая часть 130
Периодический элемент 130
Подалгебра 190
Подгруппа 71
—	единичная 71
—	нормальная 74
—	тривиальная 71
Подкольцо 91
Подматрица 21, 30
Подмодуль 107
—, выделяющийся прямым слагае¬
мым 118
—	максимальный 119
—	минимальный 118
Подполугруппа 57
—, порожденная множеством 67
Подпространство 168
Подстановка 26
—	нечетная 27
—	тождественная 48
—	четная 27
Подстановки, отличающиеся на транс¬
позицию 27
—	равные 26
Подструктура 155
Поле 95
—	комплексных чисел 99
Полугруппа 56
—	абелева 56
—	коммутативная 56
—	монотонная 64
—, порожденная множеством 67
—	свободная 67
Полугруппы изоморфные 60
Полурешетка — см. Полуструктура
Полуструктура (верхняя, нижняя)
151
Порядок 148
—	группы 73
—	тривиальный 148
Правило Крамера 44
Правый идеал 107, 191
—	— максимальный 119
—	— минимальный 118, 126
—	—, порожденный идемпотентом
124
—	— с нулевым умножением 125
Представление конечной группы 207
—	— — неприводимое 210
Представления конечной группы эк¬
вивалентные 209
Произведение 54
—	гомоморфизмов модулей 112
—	— полугрупп 60
—	матриц 36
—	матрицы на число 45
—	отображений 48
—	строки на число 7
Прообраз 47
238

Пространство представления 207
Прямая сумма модулей внешняя 117
—	— подмодулей 114
—	— представлений 210
Разбиение группы допустимое 75
—	— по подгруппе (правое, левое)
73
—	кольца допустимое 92
—	множества 51
—	модуля допустимое 109
—	полугруппы допустимое 61
Размерность линейного пространства
172
—	представления 207
Ранг матрицы 30
Решение системы линейных уравне¬
ний 12
Решетка — см. Структура.
Свойство универсальности свободной
полугруппы 68
Система векторов, выражающаяся че¬
рез другую систему векторов 108
		линейно зависимая 169
—	— — независимая 169
—	линейных уравнений несовместная
13
—	— — однородная 15
—	— — совместная 32
Системы линейных уравнений экви¬
валентные 12
След линейного преобразования 181
Слово 67
Смежный класс 51
—	— по подгруппе (левый, правый)
72
Собственное значение 182
Собственный вектор 182
Сопряженные комплексные числа 100
—	элементы группы 86
Сравнимые элементы частично упоря¬
доченного множества 149
Строка нулевая 7
—	п-мерная 7
Строки равные 7
Структура 151, 152, 154
—	дистрибутивная 155
Сумма гомоморфизмов модулей 111
—	идеалов структуры 158
—	матриц 45
—	подмодулей 114
—	— прямая 114
—	строк 7
Теорема о ранге 184
—	— транзитивности линейной вы-
ражаемости 108
—	— — разложения в прямую сум¬
му 115
—	— транспонировании 24
—	об определителе с нулями в пра¬
вом верхнем углу 25
—	— умножении на чужие алгебра¬
ические дополнения 24
—	Силова (первая) 138
—	существования определителя 20
—	— свободной полугруппы 67
Точная верхняя грань 150
—	нижняя грань 150
Транспозиция 82
Транспонирование матрицы 23
Факторалгсбра 192
Факторгруппа 74, 76
Факторкольцо 92
Фактормножество 51
Фактормодуль 110
Факторполугруппа 62
Факторпространство 168
Формула для вычисления образа век¬
тора 176
—	изменения координат при измене¬
нии базы 180
—	— матрицы линейного преобразо¬
вания при изменении базы 180
Фундаментальная система решений
* 187
Характер представления 212
Характеристика поля 96
Характеристический корень 181
— многочлен 181
Целое алгебраическое число 221
Центр группы 86
—	кольца 103
—	линейной алгебры 193
Центральная Ф-компонспта элемен¬
та 216
Центральный элемент группы 86
—	— кольца 103
Цепь 149
Цикл 65, 82
—	с хвостом 65
Циклы независимые 82
Тело 101
—	кватернионов 101
Теорема Бернсайда 228
—	единственности определителя 20
—	— свободной полугруппы 68
—	Кронекера — Капелли 32
—	Кэли 81
—	Лагранжа 73
—	Машке 204
—	о гомоморфизме для групп 76
	 	 — — колец 94
—	— — — линейных алгебр 192
—	— — — множеств 52
—	— — — модулей 111
—	— — — полугрупп 63
—	— разложении по столбцу 23
—	— — — строке 24
Частично упорядоченное множество
148
— — — тривиальное 149
Частично упорядоченные множества
изоморфные 149
Элементарное преобразование строк
(столбцов) 9
Эндоморфизм модуля 112
Ядро гомоморфизма групп 76
—	— колец 94
—	— модулей 110
—	— полугрупп 63
—	отображения 52

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
Е 8
М;;, М$, Ау 21
I А I (определитель матрицы)
А* 23
А-1 42
Ф
<р: А -> В, А В 47
хф 47
Im Ф 47
1л 48
Ф-» 51
[а]^, Lal 51
A/S 51
Кег ф 52, 7G, 94, 111
ап 63, 77
JP
Г (n, d) 64
А X В 69
па 77
Z, Zm 79
®п 82
«п 86
I X | (мощность множества) 87
K(g) 87, 215
C(g) 87
а — Ъ 90
С 99
z 100
I z I (норма комплексного числа) 100
К 101
(Ю 108
Hom (М, М') 111
Sx + • * • + Sm 114
St © ... © Sm 114, 117
cz 118
17 \ V 119
T(A) 130
T(^) 132
G' 139
G V 139
SO(3) 146
Тг Ф 146, 181
A\ A^ 150
supp A, sup A 150
infp A, inf A 150
2 158
dim L 172
(A) 184
R 191
PG, CG 193
GL (V) 207
dim Ф 207
Ф1 © • • • © Фт 210
ХФ 212
215
(g) 216
T (r) 216
Q 224
230