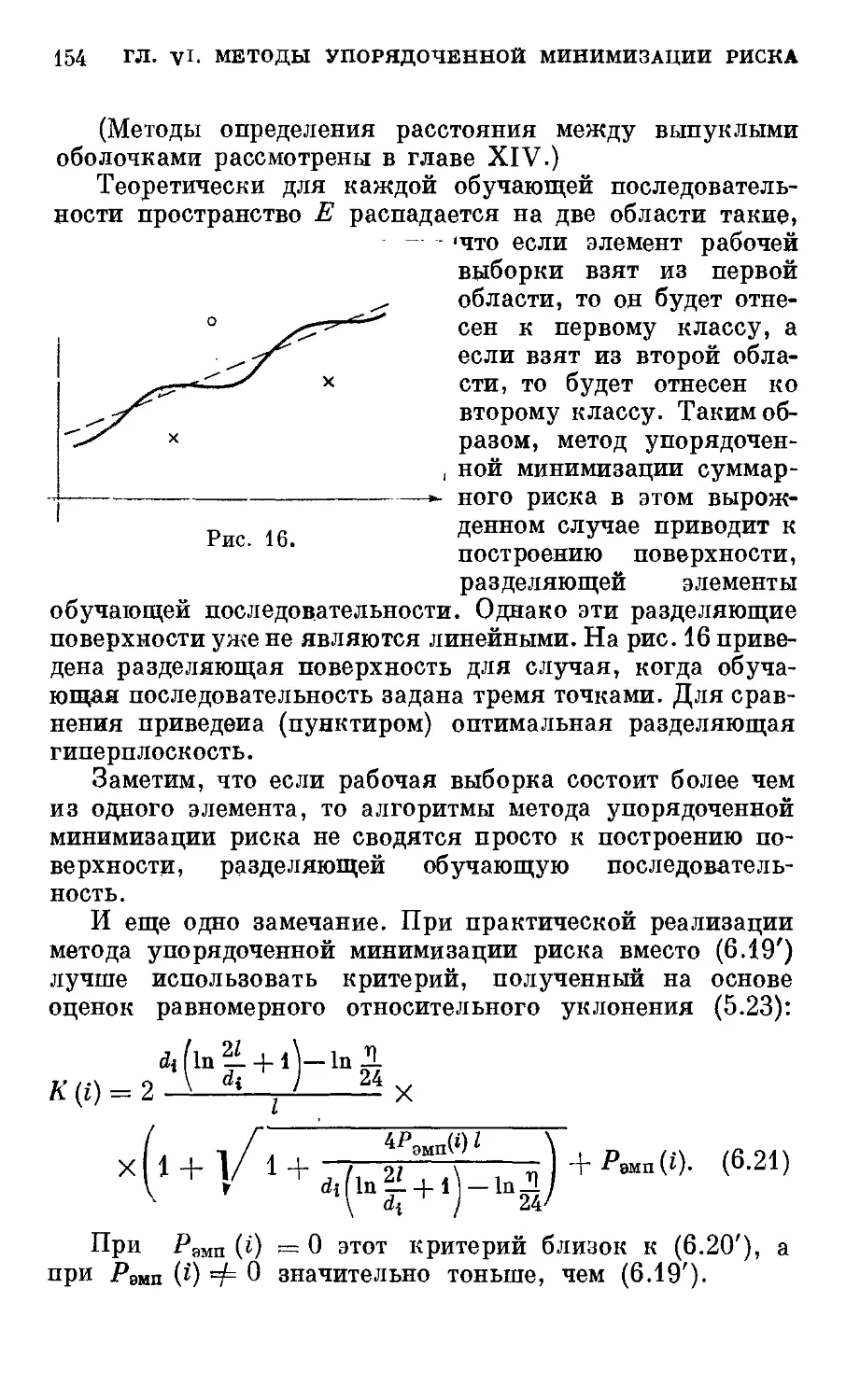
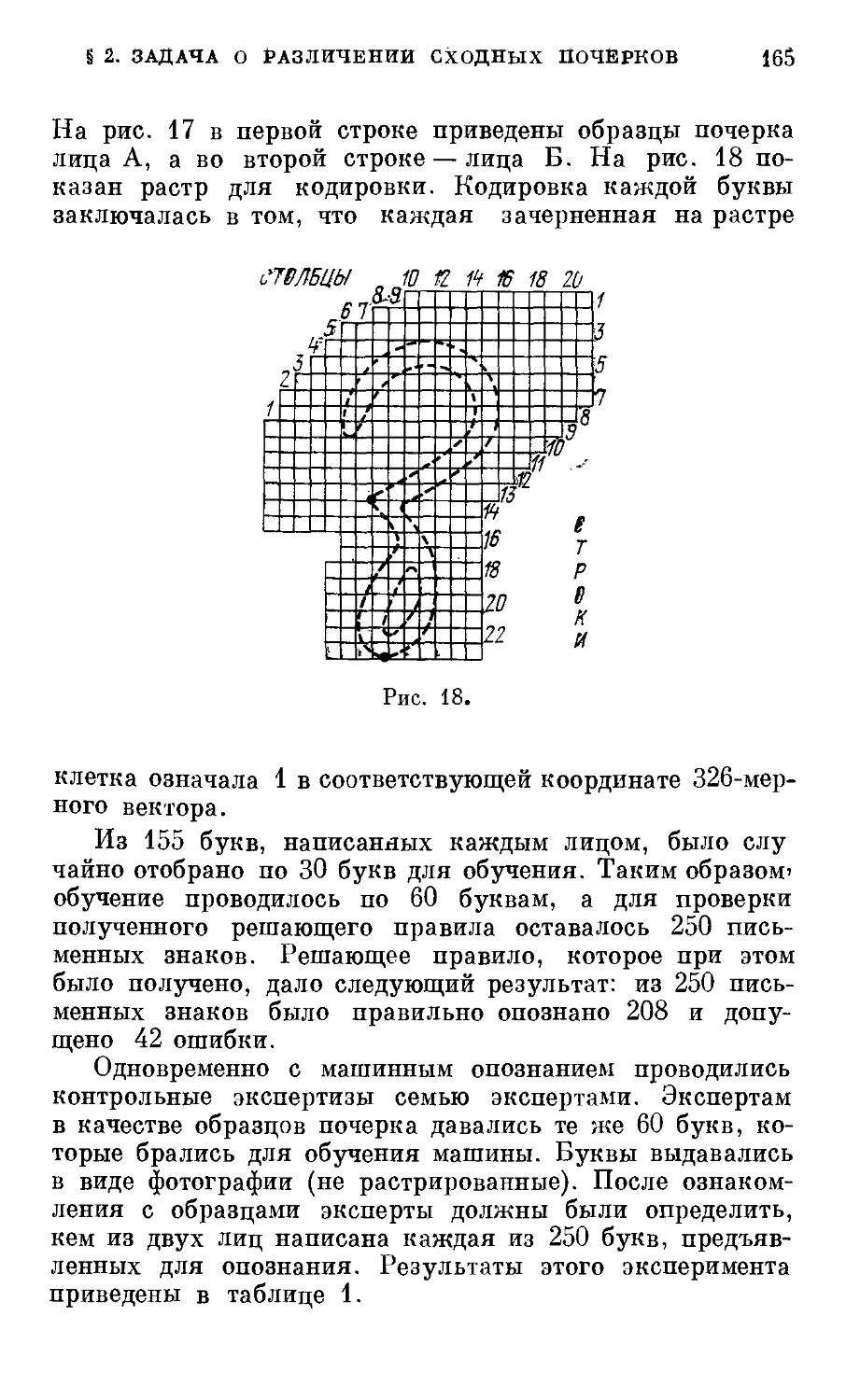
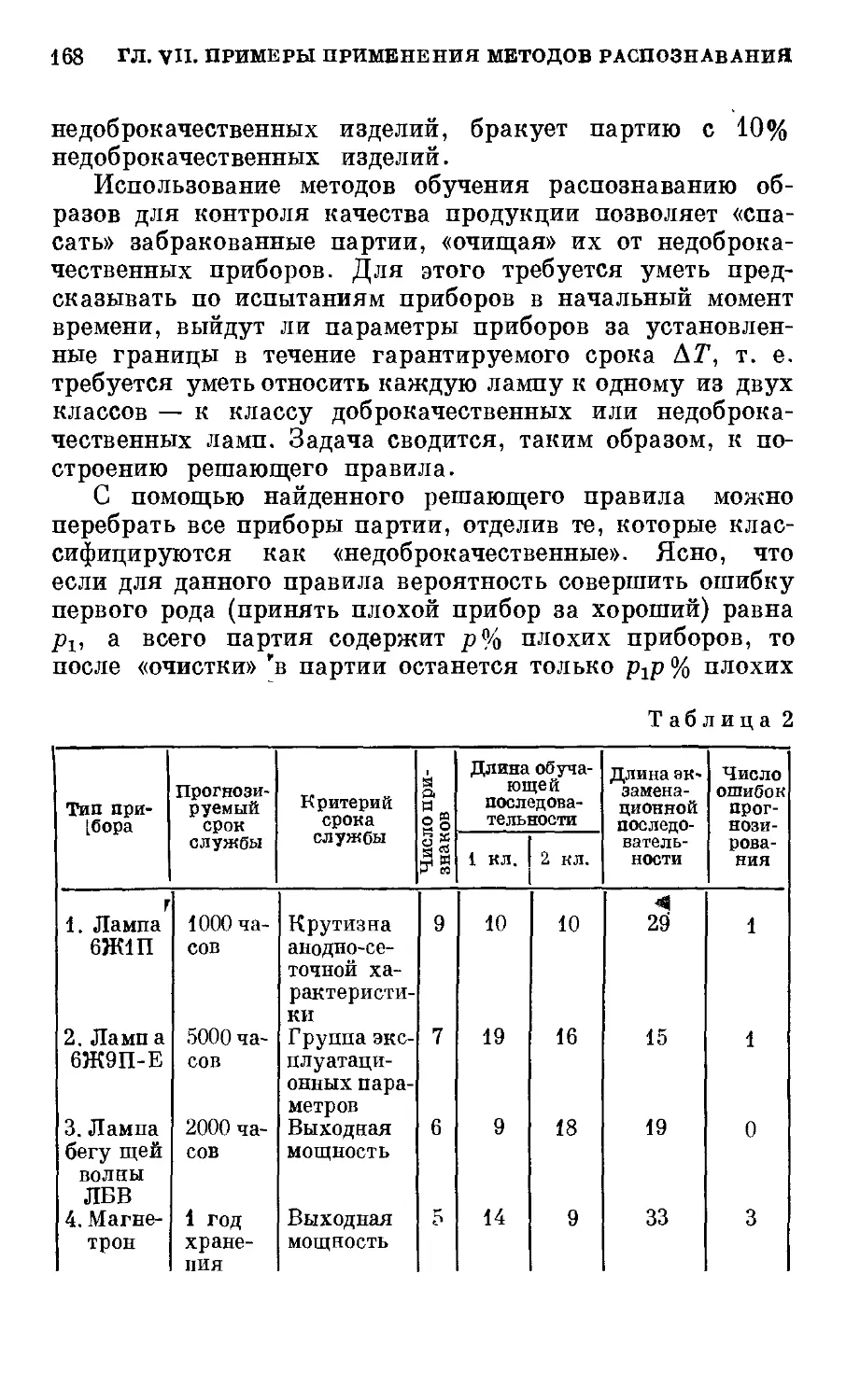
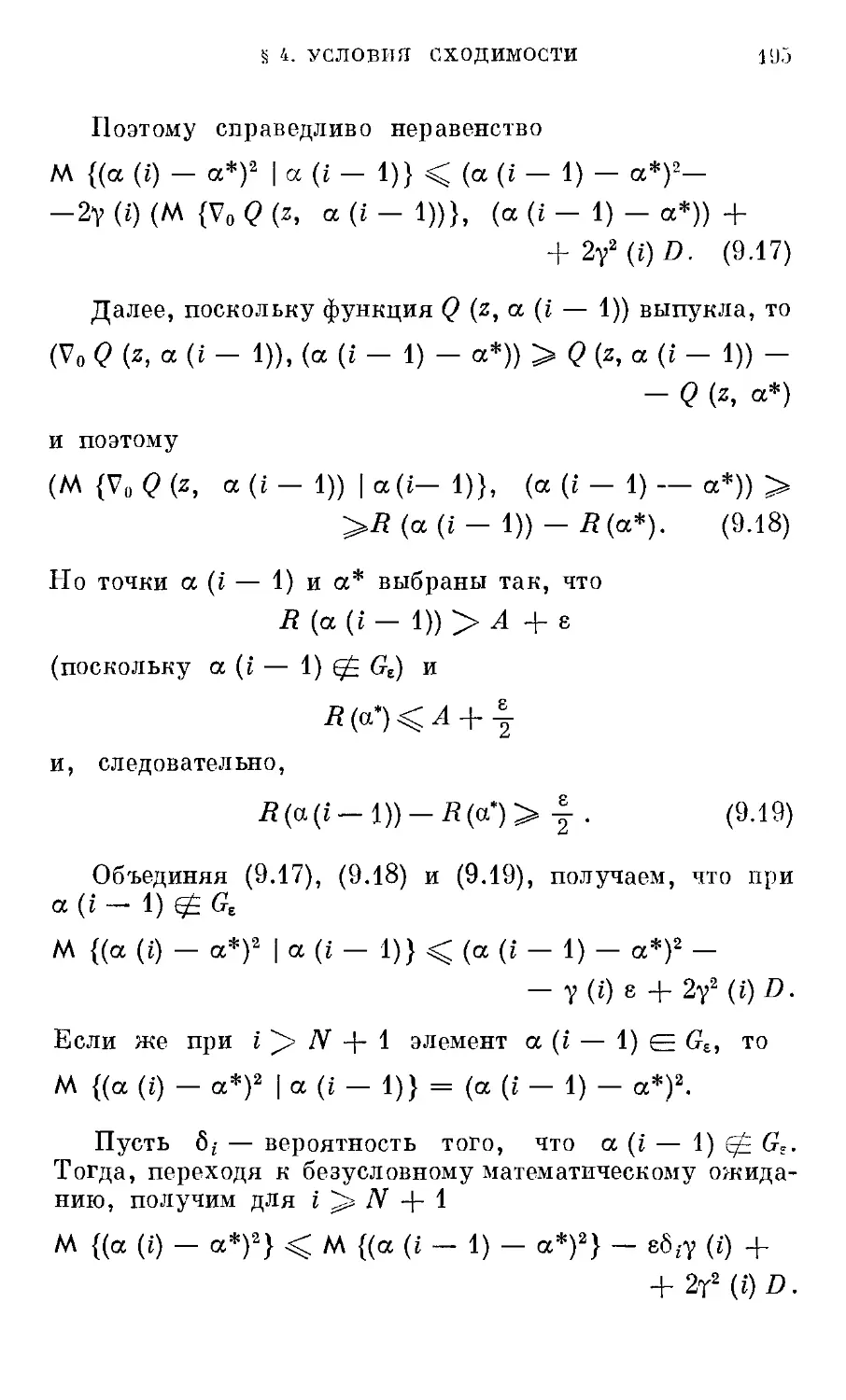Текст
В. Н. ВАПНИК, А. Я. ЧЕРВОНЕНКИС
ТЕОРИЯ
РАСПОЗНАВАНИЯ
ОБРАЗОВ
СТАТИСТИЧЕСКИЕ ПРОБЛЕМЫ ОБУЧЕНИЯ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1974
6 ф 6.5
В 17
УДК 62-50
Теория распознавания образов (статистические проблемы обу-
обучения), В. Н. Вапник, А. Я. Червоненкис. Издатель-
Издательство «Наука», Главная редакция физико-математической литерату-
литературы, М., 1974, 416 стр.
Книга посвящена изложению статистической теории распоз-
распознавания образов.
В первой части книги задача распознавания образов рассмат-
рассматривается с точки зрения проблемы минимизации среднего риска.
Показано, как далеко можно продвинуться в решении задачи обу-
обучения распознаванию образов, следуя по каждому из существующих
в статистике путей минимизации риска, и к каким алгоритмам они
приводят. Вторая часть посвящена исследованию математических
проблем обучения. Изложена теория равномерной сходимости час-
частот появлений событий к их вероятностям, которая является пре-
предельным обобщением теоремы Гливенко. Третья часть посвящена
алгоритмам построения линейных и кусочно-линейных решающих
правил.
Книга рассчитана на студентов старших курсов, аспирантов,
инженеров и научных сотрудников, занятых в области теоретиче-
теоретической и технической кибернетики. Она будет также интересна специа-
специалистам по теории вероятностей и математической статистике.
Илл. 28. Библ. 96 назв.
Издательство «Наука», 1974.
30501-048
053 @1)-74 172~74
ОГЛАВЛЕНИЕ
Предисловие 9
ЧАСТЬ ПЕРВАЯ
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
Глава I. Персептрон Розенблатта 16
§ 1. Феномен восприятия 16
§ 2. Физиологическая модель восприятия 17
§ 3. Техническая модель. Персептрон 19
§ 4. Математическая модель 20
§ 5. Обобщенная математическая модель 23
§ 6. Теорема Новикова 25
§ 7. Доказательство теоремы Новикова 28
§ 8. Двухуровневая схема распознавания 30
Глава II. Задача обучения машин распознаванию образов 34
§ 1. Задача имитации 34
§ 2 Качество обучения 35
§ 3. Надежность обучения 37
§ 4. Обучение — задача выбора 38
§ 5. Две задачи конструирования обучающихся уст-
устройств 39
§ 6. Математическая постановка задачи обучения . 41
§ 7. Три пути решения задачи о минимизации средне-
среднего риска 43
§ 8. Задача обучения распознаванию образов и методы
минимизации среднего риска 47
Глава III. Методы обучения, основанные на восстановле-
восстановлении распределения вероятностей 49
§ 1. О восстановлении распределения вероятностей 49
§ 2. Классификация оценок 52
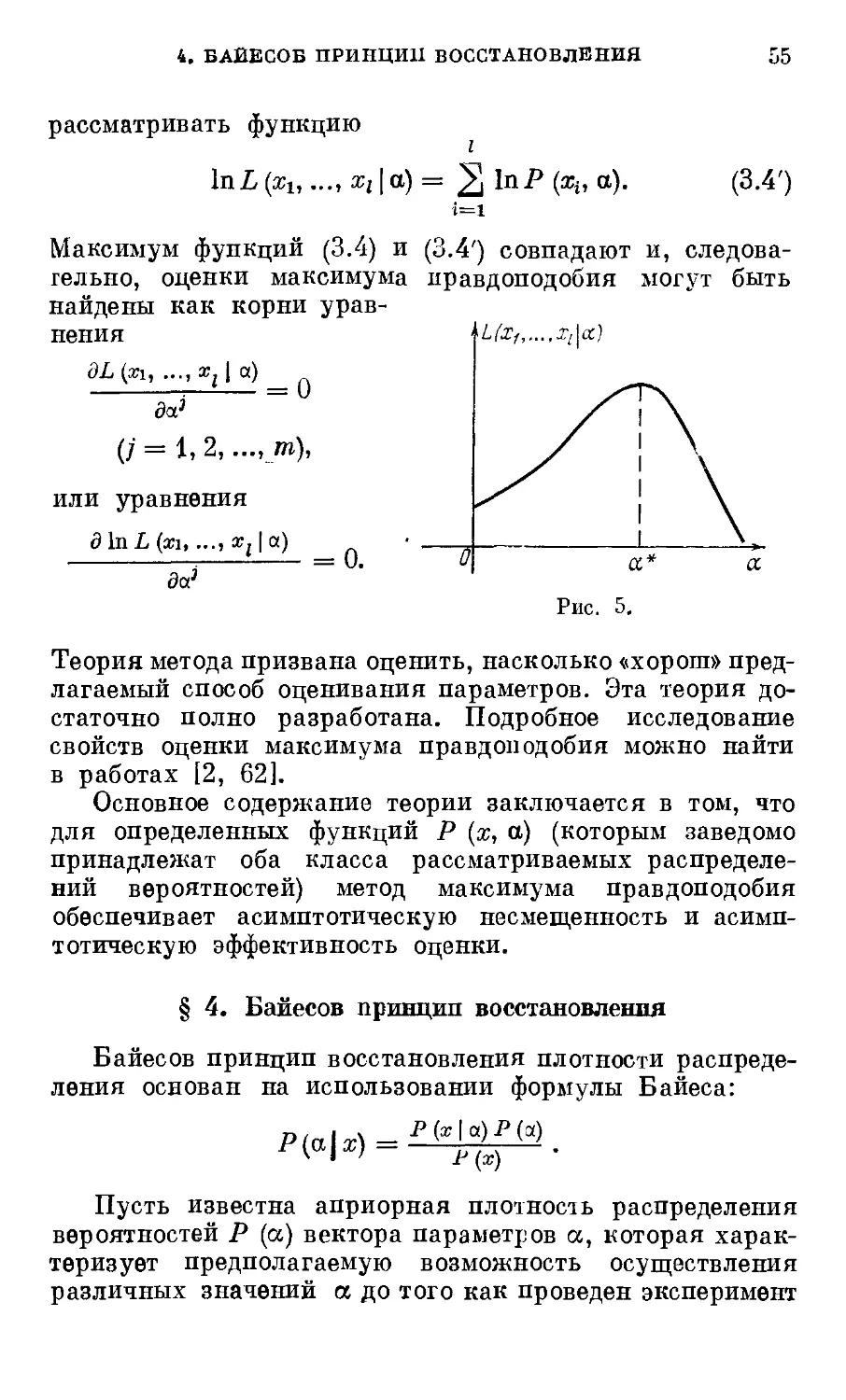
§ 3. Метод максимума правдоподобия 54
4 ОГЛАВЛЕНИЕ
§ 4. Байесов принцип восстановления 55
§ 5. Сравнение байесова метода оценивания и оцени-
оценивания методом максимума правдоподобия ... 59
§ 6. Оценка параметров распределения дискретных не-
независимых признаков 60
§ 7. Байесовы оценки параметров распределения дис-
дискретных независимых признаков> 63
§ 8. Восстановление параметров нормального распре-
распределения методом максимума правдоподобия .... 65
§ 9. Байесов метод восстановления нормального рас-
распределения 67
Глава IV. Рекуррентные алгоритмы обучения распозна-
распознаванию образов 72
§ 1. Метод стохастической аппроксимации 72
§ 2. Детерминистская и стохастическая постановки
задачи обучения распознаванию образов ... 73
§ 3. Конечно-сходящиеся рекуррентные процедуры 78
§ 4. Теоремы об останове 80
§ 5. Метод циклического повторения обучающей по-
последовательности .... 84
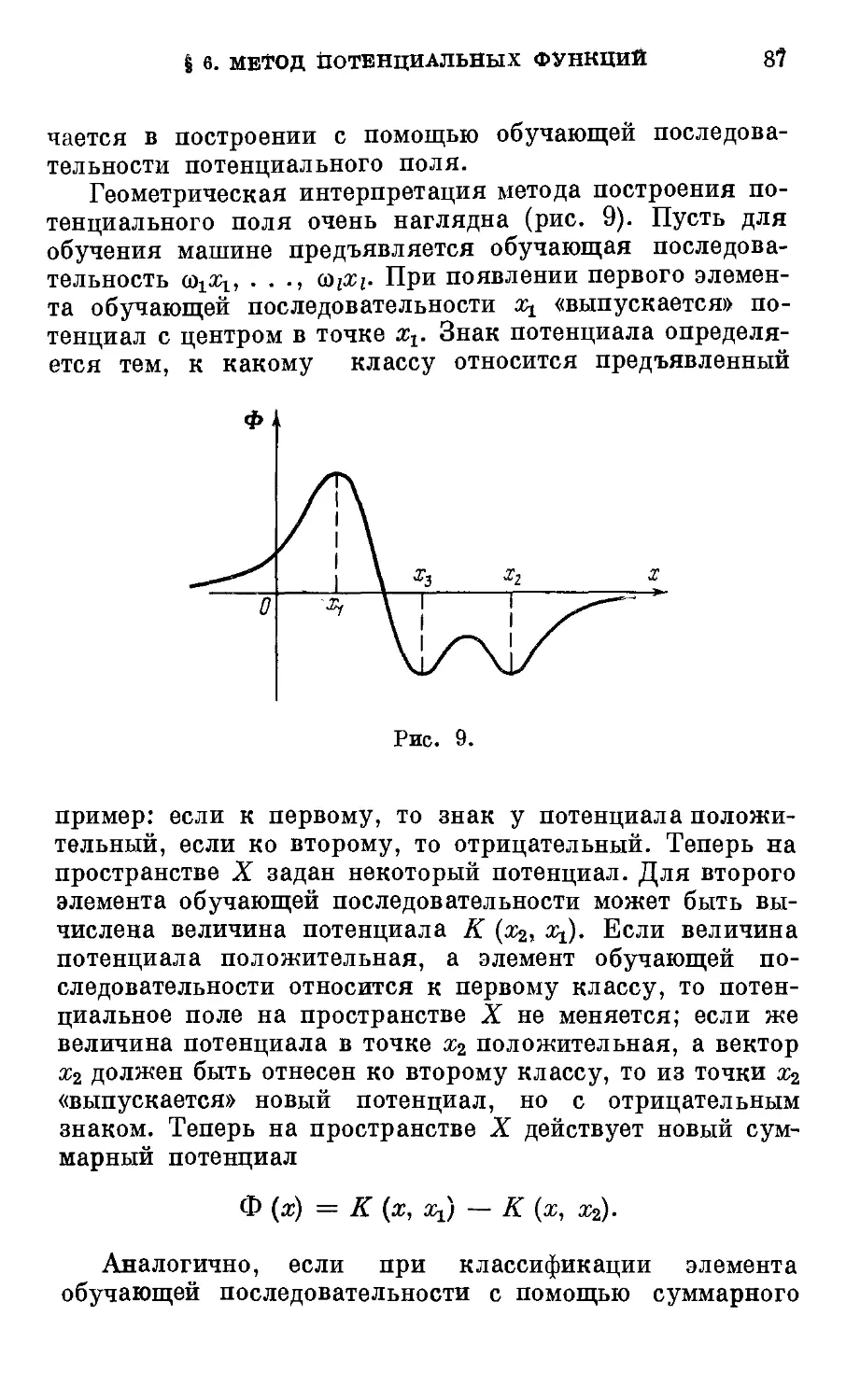
§ 6. Метод потенциальных функций 86
Глава V. Алгоритмы, минимизирующие эмпирический
риск 89
§ 1. Метод минимизации эмпирического риска ... 89
§ 2. Равномерная сходимость частот появления со-
событий к их вероятностям 90
§ 3. Теорема Гливенко 92
§ 4. Частный случай 93
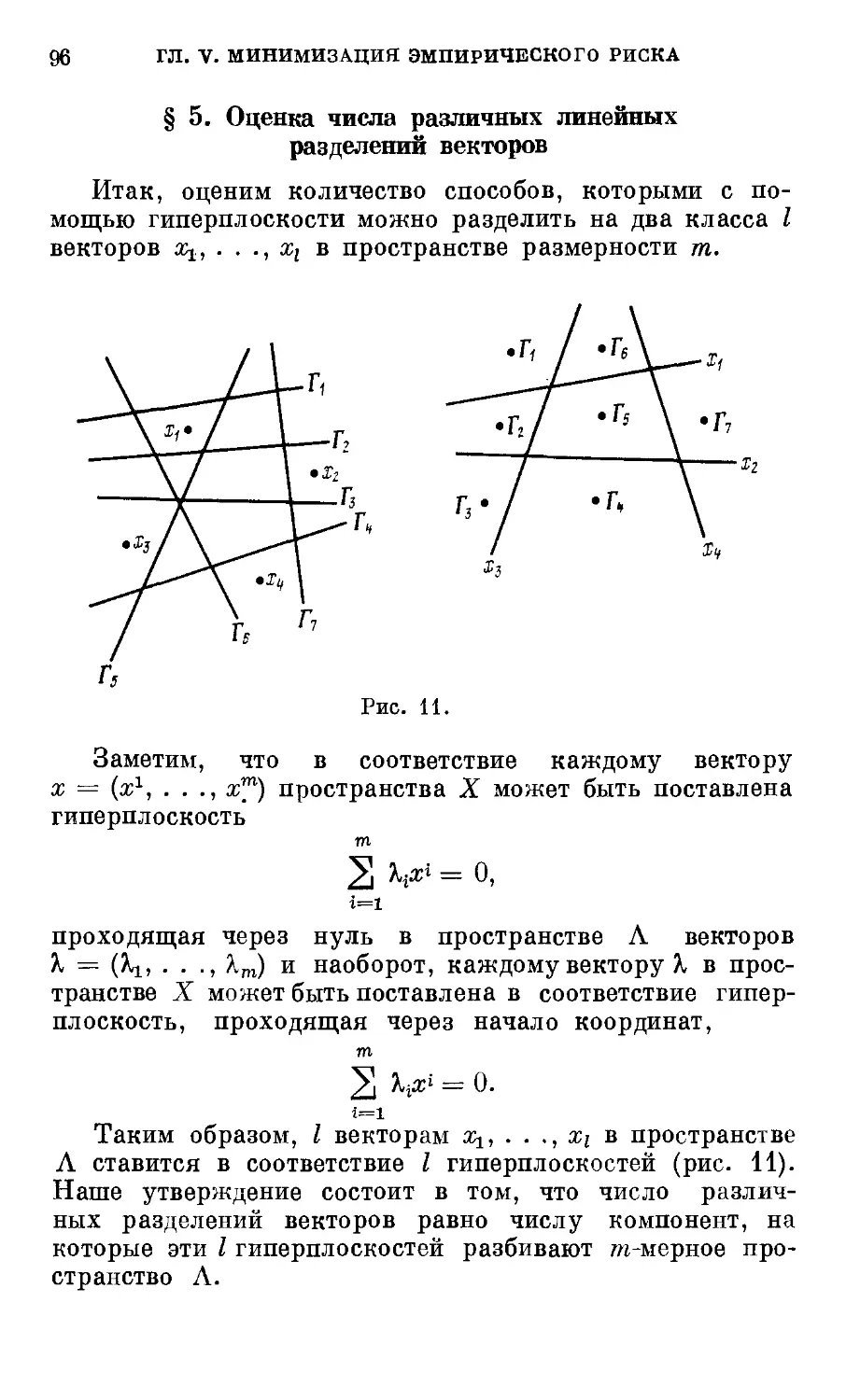
§ 5. Оценка числа различных линейных разделений
векторов 96
§ 6. Условия равномерной сходимости частот появле-
появления событий к их вероятностям 99
§ 7. Свойства функции роста 101
§ 8. Оценка уклонения эмпирически оптимального ре-
решающего правила 102
§ 9. Метод минимизации эмпирического риска в де-
детерминистской постановке задачи обучения рас-
распознаванию образов 104
§ 10. Замечание об оценке скорости равномерной схо-
сходимости частот появления событий к их вероят-
вероятностям 107
ОГЛАВЛЕНИЕ 5
§ 11. Замечания об особенностях метода минимизации
эмпирического риска 111
§ 12. Алгоритмы метода обобщенного портрета . . . 113
§ 13. Алгоритм Кора 115
Глава VI. Метод упорядоченной минимизации риска 118
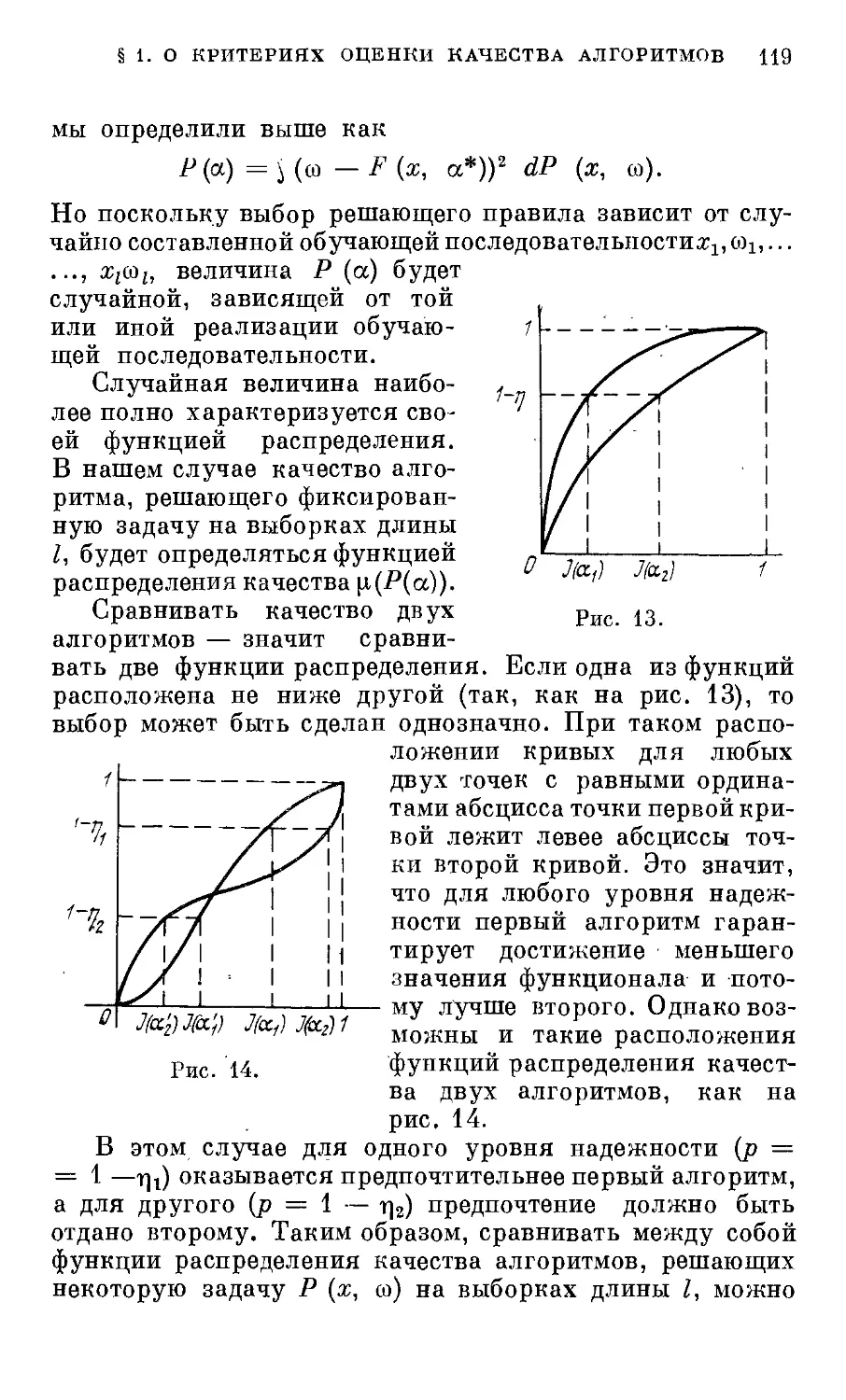
§ 1.0 критериях оценки качества алгоритмов . . . 118
§ 2. Минимаксный критерий 121
§ 3. Критерий минимакса потерь 123
§ 4. Критерий Байеса 126
§ 5. Упорядочение классов решающих правил . . . 127
§ 6. О критериях выбора 129
§ 7. Несмещенность оценки скользящего контроля . 130
§ 8. Упорядочение по размерностям 132
§ 9. Упорядочение по относительным расстояниям 134
§ 10. Упорядочение по эмпирическим оценкам относи-
относительного расстояния и задача минимизации сум-
суммарного риска 139
§ И. О выборе оптимальной совокупности признаков 147
§ 12. Алгоритмы упорядоченной минимизации суммар-
суммарного риска 151
§ 13. Алгоритмы построения экстремальных кусочно-
линейных решающих правил 155
§ 14. Приложение к главе VI 156
Глава VII. Примеры применения методов обучения распоз-
распознаванию образов 161
§ 1. Задача о различении нефтеносных и водоносных
пластов в скважине 161
§ 2. Задача о различении сходных почерков .... 164
§ 3. Задача о контроле качества продукции .... 166
§ 4. Задача о прогнозе погоды 169
§ 5. Применение методов обучения распознаванию обра-
образов в медицине 171
§ 6. Замечания о применениях методов обучения рас-
распознаванию образов 176
Глава VIII. Несколько общих замечаний 178
§ 1. Еще раз о постановке задачи 178
§ 2. Физики об интуиции 180
§ 3. Машинная интуиция 181
§ 4. О мире, в котором возможна интуиция 181
б ОГЛАВЛЕНИЕ
ЧАСТЬ ВТОРАЯ
СТАТИСТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
Глава IX. О сходимости рекуррентных алгоритмов обу-
обучения распознаванию образов 184
§ 1. Определение понятия сходимости 184
§ 2. Выпуклые функции 187
§ 3. Обобщенный градиент 188
§ 4. Условия сходимости рекуррентных алгоритмов 190
§ 5. Еще одно условие сходимости рекуррентных ал-
алгоритмов 200
Глава X. Достаточные условия равномерной сходимости
частот к вероятностям по классу событий . . . 203
§1.0 близости минимума эмпирического риска к ми-
минимуму среднего риска 203
§ 2. Определение равномерной сходимости частот
к вероятностям 206
§ 3. Определение функции роста 211
§ 4. Свойство функции роста 213
§ 5. Основная лемма 219
§ 6. Вывод достаточных условий равномерной сходи-
сходимости частот к вероятностям по классу событий 223
§ 7. О равномерной сходимости с вероятностью единица 229
§ 8. Примеры и дополнительные замечания 231
§ 9. Приложение к главе X 236
Глава XI. Необходимые и достаточные условия равно-
равномерной сходимости частот к вероятностям по
классу событий 240
§ 1. Энтропия системы событий 240
§ 2. Асимптотические свойства энтропии 242
§ 3. Необходимые и достаточные условия равномерной
сходимости (доказательство достаточности) . . . 248
§ 4. Доказательство необходимости условий равно-
равномерной сходимости 251
§ 5. Примеры и дополнительные критерии 261
Глава XII. Оценки равномерного относительного укло-
уклонения частот от вероятностей в классе событий 267
§ 1. О равномерном относительном уклонении . . . 267
§ 2. Оценка равномерного относительного уклонения
частот в двух полувыборках 269
ОГЛАВЛЕНИЕ
§ 3. Оценка равномерного относительного уклонения
частот от вероятностей 272
Глава XIII. Применение теории равномерной сходимости
к методам минимизации эмпирического риска 276
§ 1. Оценка достаточной длины обучающей последова-
последовательности в задачах обучения распознаванию . . 276
§ 2. Равномерная сходимость средних к математиче-
математическим ожиданиям 285
ЧАСТЬ ТРЕТЬЯ
МЕТОДЫ ПОСТРОЕНИЯ РАЗДЕЛЯЮЩИХ
ПОВЕРХНОСТЕЙ
Глава XIV. Построение разделяющей гиперплоскости
(метод обобщенного портрета) 292
§ 1. Оптимальная разделяющая гиперплоскость . . 292
§ 2. Однопараметрическое семейство разделяющих
гиперплоскостей 295
§ 3. Некоторые свойства обобщенного портрета . . 299
§ 4. Двойственная задача 302
§ 5. Алгоритмы персептронного типа 306
§ 6. Градиентные методы построения разделяющей
гиперплоскости (вычисление обобщенного пор-
портрета) 310
§ 7. Теория оптимальной разделяющей гиперплос-
гиперплоскости 316
§ 8. Двойственная задача 318
§ 9. Методы вычисления оптимальной разделяющей
гиперплоскости 322
§ 10. Построение оптимальной разделяющей гипер-
гиперплоскости модифицированным методом Гаусса—
Зайделя 324
§ 11. Применение метода обобщенного портрета для
нахождения оптимальной разделяющей гипер-
гиперплоскости 326
§ 12. Некоторые статистические особенности метода
обобщенного портрета 328
§ 13. Приложение к главе XIV 335
Глава XV. Алгоритмы обучения распознаванию обра-
образов, реализующие метод обобщенного портрета 344
§ 1. Способы представления информации 344
§ 2. Алгоритм построения разделяющей гиперплос-
гиперплоскости 349
ОГЛАВЛЕНИЕ
§ 3. Алгоритм построения разделяющей гиперплос-
гиперплоскости, минимизирующей число ошибочно клас-
классифицируемых векторов 359
§ 4. Алгоритм построения кусочно-линейной разде-
разделяющей поверхности 360
§ 5. Алгоритмы построения разделяющей гиперплос-
гиперплоскости в пространстве минимального числа приз-
признаков 362
§ 6. Алгоритм построения экстремальной линейной
разделяющей поверхности 365
§ 7. Алгоритм построения экстремальной кусочно-
линейной разделяющей поверхности 367
§ 8. Алгоритм построения разделяющей гиперплос-
гиперплоскости с оценкой ее качества методом скользяще-
скользящего контроля 368
§ 9. Алгоритмы построения экстремальных разделя-
разделяющих гиперповерхностей с помощью процедуры
скользящий контроль 370
§ 10. О работе с алгоритмами 371
Глава XVI. Метод сопряженных направлений 373
§ 1. Идея метода 373
§ 2. Метод сопряженных градиентов 380
§ 3. Метод параллельных касательных (партаи) . . 387
§ 4. Анализ погрешностей метода 391
Комментарии 397
Литература 410
Мир выглядит молодой красавицей или
Брокенской ведьмой в зависимости от
того, через какие очки на него смотришь.
Г. Гейне
ПРЕДИСЛОВИЕ
Задаче обучения машин распознаванию образов уже
более пятнадцати лет.
За это время иные идеи оформились в самостоятельное
научное направление, а задача обучения распознаванию
образов все еще не обрела формальной постановки, которая
удовлетворила бы всех исследователей. И не потому, что
ей уделялось мало внимания.
Содержательная (а не формальная) постановка задачи
появилась в конце 50-х годов и заключалась в том, чтобы
построить машину, способную обучаться классификации
ситуаций так же, как это делают живые существа. Такое
широкое понимание проблемы привело к возникновению
различных направлений исследования. Одни ученые счи-
считали главным построение модели процесса восприятия,
другие видели основное содержание проблемы в ее утили-
утилитарном проявлении — создании алгоритмов обучения рас-
распознаванию образов для решения конкретных задач прак-
практики, третьи искали в этой задаче постановки новых мате-
математических проблем.
Сначала исследование задачи обучения распознаванию
образов шло чрезвычайно успешно. Сразу же по всем на-
направлениям удалось сделать значительный шаг: были по-
построены модели, которые на первых порах вполне удовлет-
удовлетворяли исследователей, решено несколько практических
задач, которые никак не удавалось решить другими мето-
10 ПРЕДИСЛОВИЕ
дами, наконец, были доказаны первые теоремы об
алгоритмах обучения.
Начало 60-х годов казалось весьма обнадеживающим.
Однако время шло, а второй шаг так и не был сделан:
усложнение моделей ничего не добавило к объяснению тон-
тонких эффектов восприятия, не удалось построить более
эффективных алгоритмов распознавания.
С этого момента, пожалуй, впервые стал серьезно про-
проявляться интерес к теории. Теория призвана была выяс-
выяснить, существуют ли общие принципы обучения, которым
должен был бы следовать любой алгоритм, или любая мо-
модель процесса восприятия. Словом, как это всегда бывает,
к теории обратились тогда, когда выяснилось, что никакие
изобретения не позволяют улучшить существующие ал-
алгоритмы. От теории ожидали новых принципов, которые
позволили бы строить более эффективные алгоритмы обуче-
обучения. Для построения теории прежде всего надо найти фор-
формальную схему, в которую можно было бы вложить задачу
обучения распознаванию образов. Это-то и оказалось труд-
трудно сделать.
Одни специалисты видели проблему в том, чтобы, ис-
используя априорные сведения о свойствах образов, найти
такое их описание, при котором отыскание принципа клас-
классификации не составляло бы труда. Другие, напротив, счи-
считали выбор системы описания внешним моментом в поста-
постановке задачи и видели основную проблему в отыскании
правила классификации среди заданного множества воз-
возможных правил.
Эти две точки зрения являются диаметрально противо-
противоположными. В первом случае постановка должна быть на-
нацелена на выявление общих принципов использования
априорной информации при составлении адекватного опи-
описания образов. При этом важно, что априорные сведения
об образах различной природы разные, а принцип их учета
один и тот же.
ПРЕДИСЛОВИЕ И
Во втором случае проблема получения описания выно-
выносится за рамки общей постановки и теория обучения машин
распознаванию образов сводится к проблеме минимизации
риска в специальном классе решающих правил.
По существу, различные точки зрения на постановку
задачи распознавания образов определяются ответом на
вопрос: возможны ли единые принципы построения адек-
адекватного описания образов различной природы или же кон-
конструирование языка описания есть каждый раз задача
специалистов конкретных областей знаний?
Если да, то выявление этих принципов должно соста-
составить основное направление исследования задачи распозна-
распознавания образов. Основное потому, что такое направление
исследований явилось бы и общим и принципиально новым.
Если же нет, то задача обучения распознаванию обра-
образов приводится к задаче минимизации среднего риска в
специальном классе решающих правил и может рассматри-
рассматриваться как одно из направлений прикладной статистики.
Ответа на этот вопрос до сих пор нет и потому выбор
постановки задачи является пока вопросом веры. Боль-
Большинство исследователей, однако, приняли вторую точку
зрения, и под теорией распознавания образов принято
сейчас понимать теорию минимизации риска в специальном
классе решающих правил.
В этой книге мы также будем придерживаться того, что
теория обучения машин распознаванию образов сводится к
проблеме минимизации среднего риска *).
Методы минимизации среднего риска являются тради-
традиционным предметом исследования теории статистических
решений, и поэтому проблема заключается в том, чтобы
суметь применить их для соответствующего класса решаю-
решающих функций. На этом пути существовали известные труд-
*) Чтобы подчеркнуть это, мы дали книге второе название —
«Статистические проблемы обучения», а соответствующую теорию
назвали статистической теорией.
12 предисловие
ности, но довольно быстро их удалось преодолеть и к сере-
середине 60-х годов появилась общая теория обучения распоз-
распознаванию образов. Эта теория одновременно с удовлетворе-
удовлетворением принесла и некоторое разочарование. Общий прин-
принцип построения алгоритма был чересчур широким: ему
удовлетворяло очень много алгоритмов обучения; кроме то-
того, можно было найти регулярным способом (и было пока-
показано каким именно) огромное количество конкретных алго-
алгоритмов обучения распознаванию образов, которые на прак-
практике оказывались ничуть не лучше существующих.
Таким образом, сложилась кризисная ситуация: каза-
казалось, что задача обучения распознаванию образов в статис-
статистической постановке себя исчерпала.
Вероятно, это было бы действительно так, если бы не од.
но обстоятельство. Дело в том, что конструктивные методы
минимизации среднего риска, разработанные в теории ста-
статистических решений, в основном носят асимптотический ха-
характер, т. е. метод, минимизирующий величину среднего ри-
риска на основе выборки, считается состоятельным, если с рос-
ростом объема выборки с помощью этого метода можно как уго-
угодно близко подойти к оптимальному решению. Вот эти-то
асимптотически-оптимальные методы минимизации риска
и применялись для решения задачи обучения распознава-
распознаванию образов. На практике же всегда используются вы-
выборки ограниченного объема, которые никак нельзя счи-
считать настолько большими, чгобы применять асимптотичес-
асимптотические методы.
Поэтому возникает надежда построить более содержа-
содержательную теорию применением к нашей специальной задаче
минимизации среднего риска, образующей статистическую
задачу обучения распознаванию образов, методов миними-
минимизации риска на конечных выборках, т. е. построить не аси-
асимптотически-оптимальную теорию алгоритмов обучения,
а конечно-оптимальную теорию. Но оказалось, что в тео-
теории статистических решений нет достаточно общих конст-
ПРЕДИСЛОВИЕ 13
руктивных конечно-оптимальных методов минимизации
риска. И не потому, что математики не подозревали о суще-
существовании такой проблемы; напротив, необходимость созда-
создания конструктивных конечно-оптимальных алгоритмов
давно была известна, но все попытки построить теорию та-
таких алгоритмов наталкивались на значительные трудности.
Итак, исследование задачи обучения распознаванию
образов вывело на нерешенную проблему. Но теперь эта
проблема стоит не во всем объеме, а лишь для специаль-
специального класса задач. Конечно-оптимальная теория алгорит-
алгоритмов обучения распознаванию образов еще не построена.
Однако вне зависимости от того, насколько удачными ока-
окажутся попытки построить такую теорию, идея создания
конечно-оптимальных методов минимизации риска для
специального класса решающих правил уже принесла свои
плоды: были найдены новые достаточно общие процедуры
поиска оптимальных решений.
Что же сейчас составляет статистическую теорию обу-
обучения распознаванию образов? Вероятно, правильно было
бы видеть в задаче обучения распознаванию образов три
линии развития.
Первая линия связана со становлением задачи. В ней
можно проследить, как из физиологической модели вос-
восприятия возникают алгоритмы опознания образов, как за-
задача обучения формулируется в четких математических
терминах, как она вливается в традиционные задачи мате-
математической статистики, какие новые идеи она порождает,
как способствует решению задач практики.
Вторая линия отражает влияние задачи обучения рас-
распознаванию образов на развитие аппарата математической
статистики. Здесь можно проследить, как сначала
использовались известные методы статистики, как затем
образовывались новые понятия, и, наконец, можно уви-
увидеть влияние этих новых идей на развитие традиционных
направлений исследований в статистике.
14 ПРЕДИСЛОВИЕ
Третья линия отражает развитие конструктивных идей
построения алгоритмов. Сначала это были некоторые эв-
эвристические процедуры, единственным обоснованием ко-
которых была ссылка на аналогию с физиологическими мо-
моделями восприятия, затем это были различные методы по-
построения разделяющих поверхностей и, наконец, это —
методы выбора экстремальных подпространств и построе-
построения на них различных решающих правил.
В монографии нашли отражение все три линии разви-
развития теории. Первая линия сконцентрирована в основном в
первой части книги — «Элементарная теория», вторая —
во второй части — «Статистические основы теории» и
третья — в третьей части книги — «Методы построения
разделяющих поверхностей».
Первая часть книги носит сравнительно элементарный
характер. В ней основной упор сделан на изложение идей
статистической теории обучения распознаванию образов.
Для чтения этой части книги достаточно знания математи-
математики в объеме курса втуза.
Чтение второй части книги требует знания основ теории
вероятностей в объеме университетского курса и предпо-
предполагает известную математическую культуру.
Третья часть книги посвящена изложению группы ал-
алгоритмов, основанных на методе обобщенного портрета.
Она написана так, чтобы ее могли использовать читатели,
цель которых выбрать и запрограммировать нужный им
алгоритм обучения.
Книга ни в коей мере не является обзором теории обу-
обучения распознаванию образов. В ней, сильно сказывают-
сказываются научные интересы и пристрастия авторов. Тем не менее
мы надеемся, что она окажется интересной и полезной
читателю.
Авторы
Часть первая
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
В этой части книги задача обучения распознаванию об-
образов рассматривается с точки зрения проблемы миними-
минимизации среднего риска для специальных классов функций
потерь.
В современной статистике существуют три пути ми-
минимизации среднего риска.
Первый путь связан с восстановлением функции распре-
распределения вероятностей, второй — с организацией рекур-
рекуррентной процедуры поиска решения и третий — с метода-
методами минимизации эмпирического риска. Здесь показано, как
далеко можно продвинуться в решении задачи обучения рас-
распознаванию, следуя по каждому из этих направлений, и к
каким конструктивным алгоритмам они приводят. На-
Наконец, здесь рассмотрен еще один метод минимизации рис-
риска — метод упорядоченной минимизации и получены соот-
соответствующие алгоритмы распознавания.
В заключение этой части приведены примеры примене-
применения методов обучения для решения задач практики.
Глава I
ПВТСВПТТОН РОЗЕНБЛАТТА
§ 1. Феномен восприятия
Известно, что человек, сталкиваясь с новыми явления-
явлениями или предметами, очень часто их узнает, т. е. без особых
затруднений относит к тому или иному понятию (клас-
(классу). Так, впервые увидев лощадь незнакомой масти
или собаку необычной породы, человек определяет
в них уже известных ему животных. Человек может
читать рукописи, написанные разными людьми, хотя каж-
каждый почерк имеет свои особенности. Каждый из нас легко
узнает своих знакомых, даже если они изменили прическу
или одежду. Эта особенность человека называется феноме-
феноменом восприятия.
Феномен восприятия проявляется во всех сферах чело-
человеческой деятельности, а многие профессии связаны исклю-
исключительно с умением правильно классифицировать ситуации.
Так врачи умеют диагностировать заболевания, экспер-
эксперты-криминалисты различают сходные почерки, ар-
археологи устанавливают принадлежность найденных пред-
предметов определенной эпохе, геологи по косвенным дан-
данным определяют характер месторождения и т. д.
Всюду здесь проявляется умение человека правильно
относить наблюдаемый объект к тому или иному понятию,
к тому или иному классу.
Человек умеет вырабатывать на основе опыта и новые
понятия, обучаться новой системе классификации.
Существуют два различных метода обучения: один из
них — объяснение, другой, более интересный,— обучение
на примерах. Первый метод предполагает существование
достаточно простых правил, простых настолько, что их
§ 2. ФИЗИОЛОГИЧЕСКАЯ МОДЕЛЬ ВОСПРИЯТИЯ 17
можно изложить так, чтобы, действуя сообразно этим
правилам, каждый раз получать требуемый результат.
Однако во многих случаях учитель, проводящий
обучение, не может сформулировать правило, по кото-
которому он действует, и тогда первый способ обучения
неприменим и обучение проводят на примерах. Так,
нельзя указать четких правил для такого, казалось бы,
простого случая, как различение рукописных знаков.
В этом случае при обучении пользуются вторым ме-
методом. Обучающемуся показывают рукописные знаки и сооб-
сообщают, какие это буквы, т. е. к каким классам данные знаки
относятся. В результате у учепика вырабатываются нуж-
нужные понятия, он приобретает умение правильно относить
каждую новую букву к тому или иному классу. Точно так
же студентов-медиков учат диагностировать заболевания.
Возможность использования такого метода обучения
определяется заложенным в человеке внутренним меха-
механизмом построения правила, позволяющего распознавать
нужные понятия.
§ 2. Физиологическая модель восприятия
В 1957 году американский физиолог Ф. Розенблатт
предпринял попытку технически реализовать физиологи-
физиологическую модель восприятия. Он исходил из предположения,
что восприятие осуществляется сетью нейронов. Согласно
распространенной и наиболее простой модели нейрона
(модели Мак-Калока —
Питса), нейрон — это нер-
вная клетка, которая име-
имеет несколько входов —
дендритов и один выход —
аксон. Входы бывают либо
возбуждающие, либо тор-
тормозящие. Нейрон возбуж-
возбуждается и посылает импуль-
импульсы в том случае, если число Рис. 1.
сигналов, пришедших по
возбуждающим входам, превосходит число сигналов, при-
пришедших по тормозящим входам пейрона. Модель восприя-
восприятия состоит из рецепторного слоя 5, слоя преобразующих
нейронов А и слоя реагирующих нейронов В (рис. 1).
18 ГЛ. I. ПЕРСЕПТРОН РОЗЕНБЛАТТА
Внешнее раздражение воспринимается рецепторами.
Каждый рецептор связан с одним или несколькими ней-
нейронами преобразующего слоя, при этом каждый нейрон
преобразующего слоя может быть связан с несколькими
рецепторами.
Выходы преобразующих (ассоциативных) нейронов в
свою очередь соединяются с входами нейронов третьего
слоя. Нейроны этого слоя — реагирующие — тоже имеют
несколько входов (дендритов) и один выход (аксон), кото-
который возбуждается, если суммарная величина входных сиг-
сигналов превосходит порог срабатывания. Но в отличие от
нейронов второго слоя, где суммируются сигналы с одним
и тем же коэффициентом усиления (но, возможно, разными
знаками), для реагирующих нейронов коэффициенты сум-
суммирования различны по величине и, возможно, по знаку.
Каждый рецептор может находиться в одном из двух
состояний: возбужденном или невозбужденном. В зависи-
зависимости от характера внешнего раздражения в рецепторном
слое образуется тот или иной букет импульсов, который,
распространяясь по нервным путям, достигает слоя преоб-
преобразующих нейронов. Здесь в соответствии с букетом при-
пришедших импульсов образуется букет импульсов второго
слоя, который поступает на входы реагирующих нейронов.
Восприятие какого-либо объекта определяется воз-
возбуждением соответствующего нейрона третьего слоя, при-
причем различным букетам импульсов рецепторного слоя мо-
может соответствовать возбуждение одного и того же реаги-
реагирующего нейрона. Гипотеза как раз и состоит в том, что
коэффициенты усиления реагирующего нейрона подобра-
подобраны так, чтобы в случае, когда объекты принадлежат к од-
одному классу, отвечающие им букеты импульсов возбуж-
возбуждали бы один и тот же нейрон реагирующего слоя. Напри-
Например, наблюдая какой-нибудь предмет в разных ракурсах,
человек отождествляет увиденное, так как каждый раз на
различные внешние раздражения реагирует один и тот же
нейрон, ответственный за узнавание этого предмета.
Среди огромного числа (порядка 1010) нейронов чело-
человека, обеспечивающих восприятие, лишь некоторая часть
занята сформированными уже понятиями, другая служит
для образования новых. Формирование нового понятия,
по существу, заключается в установлении коэффициентов
усиления реагирующего нейрона. Процесс установления
$ 3. ТЕХНИЧЕСКАЯ МОДЕЛЬ. ПЕРСЕПТРОН 19
коэффициентов усиления реагирующих нейронов в схеме
описывается Розенблаттом в терминах поощрения и нака-
наказания.
Предположим, что появился букет импульсов, соответ-
соответствующий вновь вырабатываемому понятию. Если при его
появлении нужный реагирующий нейрон не возбудился
(пришедший сигнал не отнесен к данному понятию), то
реагирующий нейрон «штрафуется»: коэффициенты усиле-
усиления тех его входов, по которым проходил импульс, увели-
увеличиваются на единицу. Если нейрон правильно реагировал
на пришедшие импульсы, то коэффициенты усиления не
меняются. Если же окажется, что некоторый набор сигна-
сигналов будет ошибочно отнесен к данному понятию, то нейрон
тоже «штрафуется»: в этом случае коэффициенты усиления
тех входов, по которым пришел импульс, уменьшаются на
единицу. Такая модель восприятия проста и может быть
реализована на однородных элементах — пороговых эле-
элементах.
§ 3. Техническая модель. Персептрон
Пороговым называется элемент, имеющий п входов:
х1, ..., хп, и один выход у, причем сигнал на выходе у мо-
может принимать только два значения, 0 и 1, и связан с вхо-
входами х1, ..., хп соотношением
п
1, если ^ Х-гх1 ^> Хо,
7 A.1)
О, если ^ ^.{2;* <^ Ко,
1=1
где Хи ..., Хп — коэффициенты усиления сигналов х1, ...
..., хп, а Ко — величина порога срабатывания элемента.
Моделью преобразующего нейрона может служить по-
пороговый элемент, у которого Яг = + 1, а моделью реаги-
реагирующего нейрона служит пороговый элемент, у которого
коэффициенты X — некоторые настраиваемые числа.
Техническую модель зрительного анализатора Розенб-
латт назвал персептроном (от слова «персепция» —
восприятие). Первый, рецепторньш слой 5 модели
20 ГЛ. I. ПЕРСПЕТРОН РОЗЕНБЛАТТА
Розенблатта состоял из набора 400 фотоэлементов, которые
образовывали полз рецепторов B0 X 20). Сигнал с фотоэле-
фотоэлементов поступал на входы пороговых элементов—нейронов
преобразующего слоя (элементов А). Всего в модели Ро-
Розенблатта было 512 элементов. Каждый элемент А имел 10
входов, которые случайным образом были соединены с ре-
рецепторами — фотоэлементами. Половина входов считалась
тормозящими и имела коэффициент усиления — 1,адругая
половина — возбуждающими с коэффициентом усиления 1.
Порог срабатывания нейрона принимался равным нулю.
Наконец, сигналы с выходов элементов А поступали на
входы реагирующего нейрона — элемента В (см. рис. 1).
Персептрон предназначался для работы в двух режи-
режимах: в режиме обучения и в режиме эксплуатации. В режи-
режиме обучения у персептрона по описанному выше прин-
принципу вырабатывались величины коэффициентов Хъ ..., Хп
реагирующих нейронов. В ходе эксплуатации персептрон
классифицировал предъявленные ему ситуации: если воз-
возбуждался р-ш реагирующий элемент и не возбуждались
остальные /?-элементы, то ситуация относилась к р-му
классу. Эта машина, получившая название «Марк-1», была
создана для экспериментальной проверки способности
персептрона образовывать понятия.
§ 4. Математическая модель
Появление машины, способной образовывать новые по-
понятия, оказалось чрезвычайно интересным не только для
физиологов, но и для представителей других областей зна-
знаний и в первую очередь для математиков. Ведь как только
стала ясна схема будущей экспериментальной установки,
персептрон перестал быть только техническим аналогом
физиологического феномена, он стал математической мо-
моделью процесса восприятия.
Определение закона образования нового понятия — вы-
выработка коэффициентов усиления каждого из элементов
В — означало задание алгоритма, решающего некоторую
формальную задачу.
Идея персептрона была осуществлена технически в ма-
машине «Марк-1». Однако для моделирования процесса вос-
восприятия вовсе нет необходимости строить специальную ма-
машину. Схема персептрона легко реализуется на ЦВМ, до-
I 4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ 21
статочно написать соответствующую программу. В даль-
дальнейшем изучение феномена восприятия пошло по пути мо-
моделирования обучающихся машин средствами ЦВМ, т. е.
по пути создания обучающихся программ.
Обратимся к математической модели персептрона:
1. В рецепторном поле образуется сигнал, соответству-
соответствующий внешнему раздражителю, который изображается
некоторым вектором х. Розенблатт отмечает, что каждое
нервное окончание передает достаточно простой сигнал —
либо посылает импульс, либо не посылает его. Это означа-
означает, что вектор х бинарный, т. е. его координаты могут при-
принимать только два значения: 0 и 1.
2. Букет импульсов распространяется до тех пор, пока
с помощью нейронов второго слоя не будет преобразован в
новый букет импульсов (бинарный вектор х преобразуется
в бинарный вектор у). Розенблатт уточняет характер пре-
преобразований у = / (х):
а) преобразование осуществляется пороговыми элемен-
элементами;
б) входы преобразующих пороговых элементов соеди-
соединены с рецепторами случайно.
3. Считается, что персептрон относит входной вектор к
р-ыу понятию, если возбуждается р-й реагирующий нейрон
и не возбуждаются другие реагирующие нейроны. Фор-
Формально это означает, что для вектора у = (у1, ..., ?/т) вы-
выполняется система неравенств:
для всех
В этих неравенствах %{, ..., 11т — коэффициенты усиле-
усиления ^-го реагирующего нейрона.
4. Формирование понятий в схеме Розенблатта сводится
к образованию коэффициентов (весов) каждого из элемен-
элементов К. Процедура построения весов элементов В такова.
Пусть к данному моменту существуют некоторые веса
элементов Д и ^, .,., ^ веса р-то элемента Кр. В момент
времени х для классификации на вход персептрона посту-
поступает сигнал, описываемый вектором жт. Вектор жт может
22 ГЛ. I. ПЕРСЕПТРОН.РОЗЕНБЛАТТА
либо соответствовать понятию р, либо не соответствовать
ему. Рассмотрим оба этих случая.
Случай первый. Вектор х соответствует по-
понятию р. Тогда правильной реакцией элемента Кр на сиг-
сигнал х должно быть возбуждение, т. е. должно выполнять-
выполняться неравенство
т
2 ^ > о.
г=1
Если веса элемента Вр обеспечивают правильную реак-
реакцию на вектор х, то они не меняются. Если же веса не обес-
обеспечивают правильной реакции элемента Кр, т. е. они тако-
таковы, что
г=1
то веса элемента Вр изменяются по правилу
1.1 (новое) = Л| (старое) + у1 (I = 1, 2, ..., т).
Случай второй. Вектор х не соответствует по-
понятию р. Тогда элемент Нр не должен возбудиться, т. е.
должно выполниться неравенство
г=1
Если веса элемента Вр обеспечивают правильную реак-
реакцию этого элемента на вектор х, то они не меняются. Если
же веса элемента Вр не обеспечивают правильной реак-
реакции, т. е.
то веса Х^, ..., Хт изменяются по правилу
^ (новое) = 'Ц (старое) — у1 (I = 1, 2, ..., т).
При обучении аналогично меняются веса всех элементов
Л персептрона.
$ 5. ОБОБЩЕННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ 23
§ 5. Обобщенная математическая модель
Ф. Розенблатт надеялся, что его персептрон моделиру-
ег существенные черты человеческого восприятия, в осо-
особенности восприятия зрительных образов. Он полагал, что
персептрон легко можно будет обучить узнаванию одного
и того же изображения независимо от масштаба изображе-
изображения, существенных сдвигов его в рецепторном поле и дру-
других преобразований, при которых человек относит изобра-
изображение к одному и тому же понятию. Ипыми словами, пред-
предполагалось, что персептрон будет узнавать предметы
инвариантно по отношению к определенным группам пре-
преобразований.
В действительности же теоретические и эксперименталь-
экспериментальные исследования персептрона Ф. Розенблатта показали
его неспособность к такому обобщению.
Последовали всевозможные усложнения схемы пер-
персептрона. Строились персептроны с большим числом ней-
нейронных слоев, допускалась пастройка коэффициентов уси-
усиления не только на верхнем слое, по и на промежуточных
уровнях, предлагалось вводить перекрестные и обратные
связи.
Теоретическое исследование таких сложных персепт-
ронных схем чрезвычайно затруднительно. На практике
же при распознавании зрительных образов эти модели ока-
оказались малоэффективными, в конце концов от них приш-
пришлось отказаться и пойти другим путем.
Основная идея нового направления состоит в том, что-
чтобы, опираясь на известные свойства зрительных образов,
найти такую систему признаков пли, общее, такой язык
описания изображения, которые уже сами по себе обеспе-
обеспечивают инвариантность по отношению к требуемым преоб-
преобразованиям. Таким образом, при построении обучающего-
обучающегося устройства закладываются априорные сведения отно-
относительно того, по каким именно преобразованиям должна
достигаться инвариантность.
Если предположить, что физиологическая модель чело-
человеческого восприятия действительно аналогична персепт-
рону, то следует допустить, что связи преобразующих А-
элементов с рецепторами (а вероятнее, нескольких слоев
таких элементов) отнюдь не случайны, а построены имеп-
но так, чтобы обеспечить новое описание изображения,
24 И1. I. ПЕРСЕПТРОН РОЗЕНВЛАТТА
содержащее уже требуемые инварианты. Математически
эго означает, что преобразование
у=1{х)
таково, что среди координат вектора у есть такие, которые
не меняются при определенных преобразованиях век-
вектора х.
Возможно, что человек вовсе и не учится находить эти
инварианты. Способность использовать их дана ему от
рождения и заложена в «схеме» зрительного анализатора,
возникшего в процессе эволюции. Во всяком случае экспе-
эксперименты с персептронами, где в процессе обучения выби-
выбиралось и отображение у = / (х), не доказали способности
персептрона к выработке такого рода инвариантов.
Поэтому, оставляя в стороне вопрос о том, как устроено
отображение, будем рассматривать более общую схему
персептрона. Будем считать, что дано некоторое преобра-
преобразование у = / (х) или, в координатной форме,
У1 = Ф1 (х)> ■■-. УШ = 4>т (X).
Здесь х — входной вектор, соответствующий исходному
описанию объекта. Преобразование / (х) ставит ему в соот-
соответствие некоторое новое описание у. Это преобразование
выбирается до начала обучения и может быть построено на
основании известных сведений о природе данной задачи
распознавания.
Координаты вектора у теперь в общем случае — дейст-
действительные числа, не обязательно 0 или 1.
Для простоты будем считать, что различаются всего два
понятия. Тогда персептрон отнесет вектор х к первому
понятию, если выполнится неравенство
A.2)
а в противном случае — ко второму.
Такая схема имеет простую геометрическую интерпре-
интерпретацию: в пространстве X задана гиперповерхность
т
2Мй(*) = 0, A.3)
§ 6. ТЕОРЕМА НОВИКОВА
25
которая делит пространство на два полупространства. Счи-
Считается, что если вектор х находится по одну сторону от по-
поверхности (это значит, что для него выполняется неравен-
неравенство A.2)), то он соответст-
соответствует первому понятию, Хг Т(х)>0
если же по другую от нее
сторону, то второму. Та-
Такие гиперповерхности на-
называются разделяющими
(рис. 2). п
Для образования ново- —
го понятия надо построить —-"
соответствующую разделя- Рис 2.
ющую гиперповерхность. /
Каждой гиперповерхности у
A.3) пространства X в пространстве У с координатами
у1 = фх (х), ..., ут=(рт (х) соответствует гиперплоскость
Г(х)<0
= о.
г=1
A.4)
Введение пространства У позволяет заменять рассмот-
рассмотрение разделяющих гиперповерхностей A.3) разделяющи-
разделяющими гиперплоскостями A.4). Поэтому пространство векто-
векторов У получило название спрямляющего. В спрямляющем
пространстве изучается следующая схема. Каждому объ-
объекту ставится в соответствие вектор у = (у1,. .., ут). Этот
вектор относится к первому классу, если он лежит по одну
сторону от разделяющей гиперплоскости
т
2 № = о.
и ко второму, если по другую.
§ 6. Теорема Новикова
Естественно, что первый же вопрос, который возник
при изучении персептрона,— насколько эффективен пред-
предложенный Розенблаттом алгоритм построения разделяю-
разделяющей гиперплоскости, т. е. всегда ли с помощью этого алго-
алгоритма может быть построена гиперплоскость, разделяющая
26 ГЛ. I. ПЕРСЕПТРОН РОЗЕНБЛАТТА
два множества векторов уи ..., уа и уг, ..., уь. Конечно,
имеются в виду случаи, когда такая гиперплоскость в
принципе существует.
В 1960 году американский ученый А. Новиков показал,
что если последовательность, составленную из всех эле-
элементов множеств у1, ..., уа и у\, ..., уъ, предъявить пер-
септрону достаточное число раз, то он, в конце концов, раз-
разделит ее (конечно, если разделение с помощью гиперплос-
гиперплоскости в принципе возможно). Это утверждение оказалось
чрезвычайно важным для развития теории обучающихся
программ. Использованные для его доказательства поня-
понятия оказались полезными и при установлении более тон-
тонких свойств алгоритмов обучения. Рассмотрим их под-
подробнее.
Утверждение Новикова относится к случаю, когда в
пространстве У существует гиперплоскость, проходящая
через начало координат и разделяющая два множества
векторов^, ..., у а11 У11 •••. I'ь > т. е. когда существует такой
вектор А, что выполняются неравенства
{уи Л) > 0, г = 1, 2, ..., а,
(у}, Л)<0, / =1,2, ... ,Ь. A.5)
Здесь использовано обозначение
т
(У, Л)= %у%.
г=1
Рассмотрим множество \У, состоящее из всех векторов
Уи •••> Уа и — Уъ ■■■■> — Уъ- Тогда система неравенств A.5)
примет вид
(у, Л) ^> 0 для всех у (= Ш.
Если обозначить
т1п ТХТ = р (Л)'
вир р (Л) = р0,
Л
то условие разделимости векторов уи ..., уа и уи ..., уь
может быть формально выражено так: р0 ^> 0.
6. теорема Новикова
27
Рис. Э.
Величине р0 может быть дана следующая геометричес-
геометрическая интерпретация. Пусть, как на рис. 3, множество векто-
векторов {у} обозначено крестиками, а множество векторов {у}
кружками. Утверждение о том, что два множества векто-
векторов разделимы гиперплоскостью, проходящей через начало
координат, эквивалентно тому, что выпуклая оболочка
векторов ух, ..., уа, — у\, ..., —уъ
не содержит нуля или, что то же
самое, расстояние от начала коор-
координат до выпуклой оболочки мно-
множества Ш отлично от нуля *). Ве-
Величина р0 как раз и равна рассто-
расстоянию от выпуклой оболочки мно-
множества Ш до начала координат.
Особенность алгоритма персеп-
трона, состоящая в том, что раз-
разделяющая гиперплоскость прохо-
проходит через начало координат, не
является серьезным ограничением
при построении произвольной раз-
разделяющей гиперплоскости (в том
числе и не проходящей через начало координат). Если
для разделения классов необходима гиперплоскость, не
проходящая через начало координат, то достаточно рас-
расширить пространство У, добавив к векторам уи ..., уа,
у\, ..., уь еще одну координату и положить ее равной 1.
Тогда нетрудно видеть, что в новом пространстве множе-
множества разделимы гиперплоскостью, проходящей через на-
начало координат. Итак, пусть расстояние от начала коор-
координат до выпуклой оболочки множества ]У отлично от
нуля и равно р0, а расстояние от начала координчт до
конца самого далекого вектора этого множества равно/).
Тогда, как показал Новиков, после многократного
предъявления обучающей последовательности, составлен-
составленной из элементов множеств {у} и {7, }, будет проведено не
более к = — исправлений коэффициентов (символ [а]
I Ро \
означает целую часть числа а).
*) Выпуклой оболочкой множества пазывается минимальное
выпуклое множество, содержащее эти элементы. В свою очередь
выпуклым множеством называется множество, которое наряду
с любыми двумя точками содержит отрезок их соединяющий.
Й8 ГЛ. I. ПЕРСЕПТРОН РОЗЁНБЛАТТА
§ 7. Доказательство теоремы Новикова
Докажем теорему Новикова в несколько более общей
формулировке.
Теорема 1.1. Пусть дана произвольная бесконечная огра-
ограниченная по модулю последовательность векторов уъ ...
..., т/г, ..., принадлежащих множествам {у} и {у}. Пусть
существует гиперплоскость, проходящая через начало коор-
координат и разделяющая множества {у} и {у}, т. е. сущест-
существует единичный вектор Л* такой, что
(т/г, Л*) > р0 для всех уг е {у},
(у;, Л*) < — р0 для всех у; е {у}
и
зир_ \у\ = ,0<оо.
Тогда при использовании «персептронной» процедуры
построения разделяющей гиперплоскости с начальными ве-
весами Я-длемента, равными нулю, число исправлений оши-
ошибок не превзойдет числа
Эта теорема утверждает, что если существует гипер-
гиперплоскость, разделяющая множества {у} и {у}, то персепт-
рон после конечного числа исправлений ошибок построит
разделяющую гиперплоскость (которая безошибочно бу-
будет делить весь бесконечный оставшийся хвост последова-
последовательности).
Доказательство. Рассмотрим новую последо-
последовательность уи ..., г/*, ..., которая отличается от исходной
только тем, что векторы т/г, принадлежащие {у}, заменены
на — г/г- Тогда работа персептрона может быть описана
так. Обозначим через Л; вектор, координатами которого
являются веса /?-элемента после просмотра I членов после-
последовательности.
Если очередной вектор опознается правильно, т. е.
{У 1+и Аг) > °.
| 7. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ НОВИКОВА 29
то изменения настройки не происходит, т. е.
Лг+1 = Лг.
Если же произошла ошибка, т. е.
{У 1+и Лг) < 0, A.6)
производится исправление:
А-г+1 = Лг + </г+1.
Начальный вектор Ло = 0.
Оценим модуль вектора Л( после к исправлений. Если
в момент г + 1 произошло исправление, то
2 =
2 (уН1, Дг) + \у1+1
Учитывая A.6), а также то обстоятельство, что
\у1+1 | <#,
имеем
|Лг+1 |2< |Л, |2 + Д2.
Таким образом, если к моменту I произошло ровно к ис-
исправлений, то
I Л, | 2 < 1Л2, A.7)
поскольку Ло = 0.
Далее, по условию теоремы существует единичный век-
вектор Л* такой, что для всех {
(У1, Л*) > р0.
Оценим величину (Лг, Л*). В начальный момент (Ло, Л*) =
= 0. Если в момент 1 + 1 происходит исправление, то
(Лг+1, Л*) = (Л«, Л*) + (у{+1, Л*) > (Л,, Л*) + р0.
В противном случае (Лг-+1, Л*) = (Лг, Л*). Таким образом,
если к моменту I произошло к исправлений, то
(Л„Л*)>/сРо. A.8)
30 ГЛ. I. ПЕРСЕПТРОН РОЗЕНБЛАТТА
В силу неравенства Коши
(Л(, Л*)< | Л( | • | Л* | = | Л, |
и, следовательно, справедливо неравенство
| Л, | > йр0. A.9)
Сопоставляя A.7) и A.9), убеждаемся, что эти неравенства
могут одновременно выполняться только при
Следовательно, число исправлении не превосходит—,
после чего все остальные члены последовательности будут
опознаваться правильно. Теорема доказана.
Теорема Новикова была первой теоремой в теории обу-
обучения распознаванию образов. В начале 60-х годов она
казалась чрезвычайно интересной и была предсказана
многими авторами: ведь согласно этой теореме алгоритм,
подсмотренный у природы и вначале сформулированный в
традиционных для физиологов терминах поощрения и нака-
наказания, получил простую геометрическую интерпретацию.
Интересной казалась и оценка, полученная в этой тео-
теореме: если спрямляющее пространство персептрона бинар-
бинарное, то величина Б2 не превосходит величины размерности
пространства п. В этом случае справедлива оценка
к
1-Ро .1
Интересно в этой оценке то, что число коррекций растет с
ростом размерности пространства не быстрее чем линейно.
Такой медленный рост числа коррекций позволял надеять-
надеяться, что удастся построить алгоритмы, эффективно решаю-
решающие задачи достаточно большой размерности.
§ 8. Двухуровневая схема распознавания
Итак, исследование персептрона приводит к рассмотре-
рассмотрению двухуровневой модели. На первом уровне осуществля-
осуществляется отображение исходного пространства описаний X в
новое пространство V. На втором уровне реализуется алго-
§ 8. ДВУХУРОВНЕВАЯ СХЕМА РАСПОЗНАВАНИЯ 31
ритм обучения — построение разделяющей гиперплоскос-
гиперплоскости в этом новом пространстве на основании обучающей по-
последовательности.
Для того чтобы вторая часть могла решать свою задачу,
необходимо, чтобы после отображения у = / (х) множества
векторов, соответствующие разным классам, были раздели-
разделимы гиперплоскостью.
Возникает естественный вопрос, насколько универсаль-
универсальна идея персептрона, т. е. существует ли такое отображе-
отображение, при котором любые два непересекающихся в исход-
исходном пространстве множества были бы разделимы в новом
пространстве гиперплоскостью.
Оказывается, да — универсальна. При не слишком сте-
стеснительных ограничениях, например, считая исходное про-
пространство бинарным, такое отображение действительно
ножно построить. В. А. Якубович показал даже, что пре-
преобразование
У1 = Ф1(Ж), •••, Ут = Фя, (X)
может быть осуществлено с помощью пороговых функций,
т. е. буквально можно построить универсальный пер-
септрон.
Беда лишь в том, что у универсального персептрона:
а) размерность спрямляющего пространства оказыва-
оказывается огромной,
б) почти для всех пар непересекающихся в исходном
пространстве множеств отношение Б2/р2 в спрямляющем
пространстве чрезмерно велико.
Как будет показано ниже, это приводит к катастрофи-
катастрофически большой оценке необходимой длины обучающей по-
последовательности.
Поэтому всякая реальная машина должна использо-
использовать специализированное отображение у = / (х), при кото-
котором лишь относительно немногие пары непересекающихся в
исходном пространстве множеств переходят в разделимые
гиперплоскостью.
Выбор такого отображения тесно связан со спецификой
данной задачи обучения и должен делаться в нашей схеме
до начала обучения, т. е. опираться на априорные сведения
о природе распознаваемых образов.
Например, при распознавании изображений в качестве
функций фг (х) берутся такие функции, которые по набору
32 ГЛ. I. ИЕРСЕПТРОН РОЗЕНВЛАТТА
чисел х, характеризующих яркость точек рецепторного по-
поля, строят новые описания в терминах кривых, пересече-
пересечений, кривизны и т. п.
Совсем иные преобразования могут понадобиться при
применении распознавания, скажем, в медицине или геоло-
геологии. В каждой конкретной области приложений выбор
отображения чрезвычайно сильно связан с конкретными
особенностями этой области знаний *).
В пределе наилучшее отображение будет таким, когда
все точки, относящиеся к одному классу в исходном про-
пространстве, перейдут в одну точку (а разные классы, есте-
естественно, в разные точки). При таком отображении задача
обучения совсем вырождается, так как для обучения до-
достаточно показать по одному представителю каждого клас-
класса. Построение такого пространства является недосягае-
недосягаемой мечтой всякого, кто строит отображения по априорным
данным.
На практике же оказывается, что построение даже
«хорошего» спрямляющего пространства представляет со-
собой чрезвычайно сложную задачу. Поэтому часто в по-
построенном пространстве целесообразно искать разделение
не с помощью гиперплоскостей, а с помощью более слож-
сложных разделяющих поверхностей. Строго говоря, такая схе-
схема уже не является персептронной. Однако это обстоя-
обстоятельство никак не меняет основного принципа построения
машины, обучающейся распознаванию образов: машина
реализует двухэтапную систему обучения, где на первом
этапе по априорным данным задается класс возможных
решающих правил, а на втором этапе из заданного множе-
множества решающих правил выбирается нужное. С этой точки
зрения персептрон Розенблатта реализует некоторые ку-
кусочно-линейные решающие правила: задание отображения
определяет возможные для данного персептрона кусочно-
линейные решающие правила, а алгоритм настройки весов
позволяет выбрать в заданном множестве решающих пра-
правил нужное.
Итак, задача обучения машин распознаванию образов
приводит к двухэтапной схеме распознавания. В эту
*) В этом отношении распознавание зрительных образов при-
приводит к некоторым иллюзиям, поскольку, как правило, каждый
специалист по распознаванию является и специалистом по геометрии
плоскости.
§ 8. ДВУХУРОВНЕВАЯ СХЕМА РАСПОЗНАВАНИЯ 33
схему укладываются отнюдь не только персептроноподоб-
ные распознающие машины — во всякой программе рас-
распознавания априори заложен некоторый запас решающих
правил, выбранный из тех или иных соображений (напри-
(например, решающие правила, реализуемые булевыми функция-
функциями определенного вида, пороговыми функциями, функция-
функциями, инвариантными относительно определенных преобра-
преобразований, и т. д.). И только из этого запаса с помощью обу-
обучающей последовательности выбирается нужное правило.
В дальнейших главах книги мы ограничимся исследова-
исследованием второго этапа решения задачи. Именно эта часть зада-
задачи была предметом исследования большинства (если не
всех) теоретических работ по распознаванию, не привязан-
привязанных к конкретным приложениям.
Проблемы, возникающие здесь, тесно переплетаются с
задачами математической статистики. С точки зрения ма-
математической статистики не очень существенно, какова
природа решающих правил. Как будет показано, основ-
основную роль здесь играют некоторые общие статистические ха-
характеристики класса решающих правил в целом.
Глава II
ЗАДАЛА ОБУЧЕНИЯ МАШИН
РАСЛОЗНАВАНИЮ ОБРАЗОВ
§ 1. Задача имитации
Какую же задачу решает программа, моделирующая
процесс выработки понятий? Попытаемся формализовать
постановку такой задачи.
Некто, для определенности будем говорить учитель,
предъявляет машине ситуации и о каждой сообщает, к ка
кому из к классов она относится. Для простоты будем по-
полагать к = 2, так как при любом другом числе классов
последовательный разделением на два класса можно пост-
построить разделение и на к классов. Для этого достаточно
провести к разделений по принципу: первое — отделяет
элементы первого класса ог всех остальных, а /-е — эле-
элементы /-го класса от всех остальных.
Будем считать, что входная ситуация описывается
вектором х. Координаты этого вектора могут выражать
яркости точек изображения при распознавании зритель-
зрительных образов, энергию в различных полосах спектра для
звуковых образов, значения симптомов в задачах меди-
медицинской диагностики, значения параметров систем в тех-
технических задачах распознавания и т. д.
Последовательность ситуаций с указанием, к какому
классу они относятся, называется обучающий последова-
последовательностью.
Задача заключается в том, чтобы построить такую про-
программу, которая, используя обучающую последователь-
последовательность, вырабатывала бы правило, позволяющее классифи-
классифицировать вновь предъявляемые «незнакомые» ситуации
(вообще говоря, отличные от входивших в обучающую по-
последовательность) примерно так жэ, как учитель.
| 2. КАЧЕСТВО ОБУЧЕНИЯ 35
Иначе говоря, программа должна имитировать учи-
учителя.
Слово «учитель» здесь понимается широко. В частности,
это может быть человек (например, при обучении распозна-
распознаванию рукописных знаков). Здесь цель обучения — клас-
классифицировать рукописные знаки примерно так, как это
умеет человек. Под учителем может пониматься и природа.
Так, одной из важных задач медицинской дифференциаль-
дифференциальной диагностики является различение центрального рака
легкого от воспаления легкого по рентгенологическим дан-
данным и клинической картине болезни.
Здесь в качестве материала обучения берутся случаи с
точно установленными диагнозами (верифицированные).
Цель обучения — выработать правило, позволяющее по
клиническим данным дифференцировать заболевания при-
примерно так же, как с помощью верификации.
§ 2. Качество обучения
Какие же требования предъявляются к обучающему
устройству? Попытаемся в первую очередь уточнить, какой
смысл вкладывается в понятие «хорошее» решающее пра-
правило, т. е. каков смысл утверждения «решающее правило
классифицирует ситуации так же, как учитель».
Очевидно, оно должно означать, что между классифи-
классификацией учителя и тем, как ее проводит машина, несовпаде-
несовпадения составляют небольшой процент. Однако если сущест-
существует хотя бы одна ситуация, которую машина и «учитель»
классифицируют по-разному, то процент несовпадения в
ответах существенно зависит от той последовательности
ситуаций, по которой он будет исчисляться. Например, ес-
если в последовательности много раз встречается ситуация,
которую машина классифицирует не так, как учитель,
то процент несовпадений будет велик, в то время как
ПРИ другом составе последовательности он может ока-
оказаться мал.
Поэтому необходимо заранее условиться, как будет оп-
определяться качество решающего правила, т. е. по какой по-
последовательности будет исчисляться процент несовпадений.
Можно условиться, чтобы процент несовпадений вычислял-
вычислялся по отношению ко всем возможным входным ситуациям.
Однако такое определение качества решающего правила не
36 ГЛ. II. ОБУЧЕНИЕ МАШИН РАСПОЗНАВАНИЮ ОБРАЗОВ
является удовлетворительным: в жизни требуется пра-
правильно распознавать как можно больший процент встреча-
встречающихся, а не всех возможных ситуаций. Различие здесь
заключается в том, что некоторые ситуации встречаются ча-
чаще, их желательно классифицировать правильно, другие
ситуации, хотя и возможны, но встречаются сравнительно
редко, ошибка (так дальше будем называть несовпадение в
классификациях учителя и машины) в последнем случае
менее опасна.
Такое положение идеализирует гипотеза о том, что на
множестве всех возможных ситуаций X задана функция
распределения вероятностей Р (х). Иначе говоря, считает-
считается, что в соответствие каждой возможной ситуации ставит-
ставится вероятность появления ее среди элементов, подлежащих
классификации. Тогда «потери» от ошибки на ситуации х
могут быть оценены величиной, пропорциональной веро-
вероятности появления этой ситуации. Для каждого решаю-
решающего правила можно подсчитать средние потери от всех его
ошибок. Хорошим решающим правилом следует считать в
этом случае то, которое дает минимальные средние потери,
т. е. обеспечивает минимальную вероятность ошибок при
классификации *).
Гипотеза о существовании функции распределения ве-
вероятностей Р (х) вовсе не предполагает, что она нам извест-
известна. Важно лишь то, что она существует и что ситуации,
предъявляемые для классификации, появляются случайно
согласно этой функции. Образно говоря, функция Р (х)
является характеристикой среды, в которой будет работать
классифицирующее устройство. Качество решающего пра-
правила определяется вероятностью ошибок при работе в этой
среде.
Несмотря на то, что функция Р (х) нам не известна, ка-
качество любого решающего правила может быть оценено
эмпирически.
Для этого случайно и независимо отбирается некоторое
количество примеров, относительно которых выясняется,
к какому классу отнес их учитель. Такое множество при-
примеров принято называть экзаменационной последователь-
последовательностью. На экзаменационной последовательности опреде-
*) Иногда учитывают различные цены ошибок первого и вто-
второго родов. Однако это принципиально не меняет существа дела.
§ 3. НАДЕЖНОСТЬ ОБУЧЕНИЯ 37
ляется процент несовпадений в классификациях учителя и
машины. Найденный процент характеризует качество ре-
решающего правила точно так же, как вычисленная по ко-
конечной выборке частота характеризует вероятность.
§ 3. Надежность обучения
Следующий вопрос о том, на каких примерах учить, т. е.
как подбирать элементы обучающей последовательности.
Ведь от того, какие элементы содержатся в материале
обучения, зависит, насколько хорошо будет в дальней-
дальнейшем работать решающее правило, т. е. каково будет
качество.
Чтобы обеспечить высокое качество решающего прави-
правила, надо предвидеть свойства среды, в которой предстоит
работать устройству после обучения (т. е. какова функция
Р (х)). Однако задача такова, что вероятность Р (х) неиз-
неизвестна. Существует поэтому единственная возможность —
выбирать примеры для обучения случайно и независимо,
согласно тому же распределению, при котором будет ра-
работать обучившееся устройство. Так поступать целесооб-
целесообразно еще и потому, что во многих задачах обучения нель-
нельзя конструировать примеры, а приходится довольство-
довольствоваться только теми, которые уже существуют, т. е. фак-
фактически случайной выборкой из множества возможных
примеров.
Так, во многих задачах дифференциальной медицинской
диагностики совокупность верифицированных случаев,
представленных для обучения, часто есть случайная вы-
выборка из множества всех случаев заболеваний.
Итак, в задаче обучения распознаванию образов при-
принято, что обучающая последовательность составлена из
элементов, выбранных случайно и независимо из той среды,
для которой будет оцениваться качество полученного ре-
решающего правила.
Однако при случайном подборе элементов обуча-
обучающей последовательности уже нельзя требовать, чтобы
обучение было безусловно успешным; ведь не исключе-
исключена вероятность того, что обучающая последователь-
последовательность будет составлена только из «нетипичных» случаев.
Поэтому успех в обучении может быть гарантирован не на-
наверняка, а лишь с некоторой вероятностью. Иначе говоря,
38 ГЛ. II. ОБУЧЕНИЕ МАШИН РАСПОЗНАВАНИЮ ОБРАЗОВ
так как элементы обучающей последовательности за-
заданы случайно, то способность устройства обучаться опре-
определяется тем, как часто оно строит решающее правило с
заданным качеством, т. е. надежностью получения решаю-
решающего правила с заданным качеством.
Таким образом, способность к обучению характеризу-
характеризуется двумя понятиями:
1) качеством полученного решающего правила (вероят-
(вероятностью неправильных ответов; чем меньше эта вероятность,
тем выше качество);
2) надежностью получения решающего правила с за-
заданным качеством (вероятностью получения заданного ка-
качества; чем выше эта вероятность, тем выше надежность ус-
успешного обучения).
Задача сводится к созданию такого обучающегося уст-
устройства, которое по обучающей последовательности строи-
строило бы решающее правило, качество которого с заданной на-
надежностью было бы не ниже требуемого.
§ 4. Обучение — задача выбора
Но и в такой формулировке содержится некоторая не-
нечеткость: непонятно, что значит строить решающее прави-
правило по обучающей последовательности.
Слова «строить решающее правило» надо понимать так:
задано (конструкцией устройства) множество решающих
правил. Из этого множества правил выбирается то, кото-
которое удовлетворяет определенным требованиям. Условие,
которому должно удовлетворять выбранное правило, и
определяет алгоритм обучения.
В таком понимании обучения акцент делается на том,
что множество возможных решающих правил определено
заранее, а задача обучения заключается в том, чтобы уметь
выбрать среди них нужное. В персептроне, например,
множество всех возможных правил задано структурой
персептрона: коммутацией элементов $ и элементов А. С
помощью элементов А осуществляется отображение
У1 = Ф« (х) (* = 1, 2, •••, т)-
Множество возможных решающих правил персептрона
§ 5. ДВЕ ЗАДАЧИ КОНСТРУИРОВАНИЯ 39
может быть записано так:
т
/(*,*) = 8 (З^Ф)- B-1)
Символ 9 B) в формуле означает, что
й 2>0)
9B) = (о, 2<о.
В B.1) значения параметров %г определяют конкретный
вид решающего правила. Тот факт, что правила будут
иметь вид B.1), определен заранее коммутацией элементов
персептрона.
§ 5. Две задачи конструирования обучающихся
устройств
Итак, перед конструктором обучающихся устройств
стоят две задачи:
— какой набор решающих правил заложить в обучаю-
обучающееся устройство;
— как среди множества решающих правил выбирать
нужное.
Трудности при решении данных задач носят различный
характер. Так, первая задача неформальная: класс функ-
функций определяется конструктором на основании имеющихся
в его распоряжении сведений о тех задачах, которые пред-
предстоит решать обучающемуся устройству. '
Вторая, напротив, может быть формализована я имеет
строгие схемы решения. По существу, то, что в настоящее
время называется теорией обучения распознаванию обра-
образов,— это теоретические вопросы, связанные с решением
второй задачи.
К сожалению, пока нет сколько-нибудь общих принци-
принципов выбора класса решающих правил. Правда, иногда су-
существует возможность «подсмотреть», каким классом реша-
решающих правил природа снабдила живые существа. Так, при
изучении зрительного анализатора лягушки были обна-
обнаружены нейроны, которые возбуждаются при появлении
отдельных геометрических фигур, таких как «прямая» или
«угол».
40 ГЛ. II. ОБУЧЕНИЕ МАШИН РАСПОЗНАВАНИЮ ОБРАЗОВ
В рамках схемы Розенблатта это значит, что существу-
существуют элементы А, реагирующие на появление элементарных
геометрических объектов. Такие «нейроны» можно предус-
предусмотреть в искусственном зрительном анализаторе.
Но как выяснить, какие решающие правила могут ока-
оказаться полезными при классификации абстрактных обра-
образов, например при постановке диагнозов?
Если методика поиска класса функции, предназначен-
предназначенного для решения задач классификации зрительной или
акустической информации, сводится к тому, чтобы по воз-
возможности выяснить, какой класс функций используют жи-
живые существа, то для задач классификации абстрактной
информации такой путь неприемлем. Ведь если умение
классифицировать зрительные и акустические сигналы вы-
вырабатывалось в процессе эволюции с момента появления
первых живых существ и формирование нужных для этого
классов функций проходило многие миллионы лет, то не-
необходимость классификации абстрактных понятий воз-
возникла у человека всего лишь несколько тысяч лет назад и
вряд ли за столь короткий период у человека произошли
значительные эволюционные изменения. Поэтому при поис-
поиске класса решающих правил, специализированных для ре-
решения задач классификации абстрактных образов, вряд
ли стоит выяснять, какой класс решающих правил ис-
использует человек. Скорее следует искать класс решающих
правил, отличный от <<человеческого>>.
Забегая вперед, отметим, что, как показали экспери-
эксперименты, человек недостаточно хорошо справляется с клас-
классификацией абстрактной информации. Так, если при реше-
решении «человеческих» задач, таких как классификация гео-
геометрических фигур, классификация мелодий, ни одна из
существующих узнающих машин не может сравниваться с
аппаратом восприятия человека, то при классификации
абстрактной информации интуиция человека уступает
машине.
Подобные примеры будут приведены ниже.
Определение класса решающих правил выходит за пре-
пределы статистического аспекта теории распознавания обра-
образов. В дальнейшем будем полагать, что класс решающих
функций определен, а задача заключается в том, чтобы най-
найти в нем нужную функцию, используя обучающую после-
последовательность фиксированной длины.
§ 8. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ ОБУЧЕНИЯ 41
§ 6. Математическая постановка задачи обучения
Такая постановка задачи на формальном языке имеет
простое выражение. В среде, которая характеризуется рас-
распределением вероятностей Р (х), случайно и независимо
появляются ситуации х. Существует «учитель», который
классифицирует их, т. е. относит к одному из к классов
(для простоты к — 2). Пусть он делает это согласно услов-
условной вероятности Р (© | х), где со = 1 означает, что вектор
х отнесен к первому классу, со = 0 — ко второму. Ни ха-
характеристика среды Р (х), ни правило классификации
Р (со \х) нам не известны. Однако известно, что обе функ-
функции существуют, т. е. существует совместное распределе-
распределение вероятностей
Р (со, х) = Р (х)-Р (со | х).
Пусть теперь определено множество й решающих пра-
правил Р (х, а). В этом множестве каждое правило определя-
определяется заданием параметра а (иногда удобно понимать пара-
параметр а как вектор). Все правила Р (х, а) — характеристи-
характеристические функции, т. е. могут принимать только одно из двух
значений: нуль или единица (наполним: нуль означает,
что вектор х отнесен к первому классу, а единица — ко вто-
второму). Для каждой функции Р (ж, а) может быть определе-
определено качество Р (а) как вероятность различных классифика-
классификаций ситуаций х учителем (с помощью правила Р (со | х) и с
помощью характеристической функции Р (х, а). На фор-
формальном языке качество Р (а) функции Р (х, а) определя-
определяется так:
а) в случае, когда пространство X дискретно и состоит
из точек Хх, ..., хн,
г N
Р (п\ ^ ^ /гл Р (г гЛ\2 Р (г\ Р ((,Л I Т-\ (9 1 '^
ш=0 1=1
где Р (хг) — вероятность возникновения ситуации х-ь\
б) в случае, когда в пространстве X существует плот-
плотность распределения Р (х),
Р(а) = 2 $ (а - Р{х, а)JР (х) Р(а\х)их; B.1")
а>=0
42 ГЛ. II. ОБУЧЕНИЕ МАШИН РАСПОЗНАВАНИЮ ОБРАЗОВ
в) в общем случае можно считать, что в пространстве
X, со задана вероятностная мера Р (х, со). При этом Р (а)
выражается так:
Среди всех функций Р (х, а) есть такая Р (х, а0), кото-
которая минимизирует вероятность ошибок. Эту-то наилучшую
в классе функцию (или близкую к ней, т. е. функцию с ка-
качеством, отличным от Р (а0) не более чем на малую вели-
величину е) и следует найти. Однако, поскольку совместное
распределение вероятностей Р (х, ©) неизвестно, поиск ве-
ведется с использованием обучающей последовательности
^1»! Ж,©,,
т. е. случайной и независимой выборки примеров фиксиро-
фиксированной длины I. Как уже указывалось, нельзя найти алго-
алгоритм, который по конечной выборке безусловно гарантиро-
гарантировал бы успех поиска. Успех можно гарантировать лишь с
некоторой вероятностью 1 — т).
Таким образом, задача заключается в том, чтобы для
любой функции Р (х, со) среди характеристических функ-
функций Р (х, а) найти по обучающей последовательности фик-
фиксированной длины I такую функцию Р (х, а *), о которой с
надежностью, не меньшей 1 — ц, можно было бы утверж-
утверждать, что ее качество отличается от качества лучшей функ-
функции Р (ж, а0) на величину, не превышающую е.
Для персептрона в соответствии с B.1) качество реша-
решающего правила определяется так:
т
Р (X) = 5 (ш - 9 ( 2 ?чФ1 (*))Jс1Р (х, ш).
Задача заключается в том, чтобы по обучающей после-
последовательности найти решающее правило, которое доставля-
доставляет либо минимум Р (к), либо значение, близкое к мини-
минимальному.
Такая задача не является новой в математике. Она из-
известна в более общей постановке: требуется найти минимум
по а функционала
$, B.2)
§ 7. ТРИ ПУТИ МИНИМИЗАЦИИ РИСКА 43
если неизвестна функция распределения Р (г), но зато дана
случайная и независимая выборка %, ..., гг. Эта задача по-
получила название задачи о минимизации величины среднего
риска. Она имеет простую интерпретацию: функция
(? (г, а) для всякого фиксированного значения параметра а
определяет величину потерь при появлении сигнала г.
Средняя по 2 величина потерь для фиксированного значе-
значения параметра определяется согласно B.2).
Задача заключается в том, чтобы выяснить, при каких
значениях параметра а средняя величина потерь (чаще го-
говорят: величина среднего риска) будет минимальной.
Задача обучения распознаванию образов есть частный
случай задачи о минимизации среднего риска. Особенность
ее заключается в том, что функция @ (г, а) (эту функцию
двух переменных часто называют функцией потерь) не об-
обладает таким произволом, как в общей постановке задачи и
минимизации риска. На функцию (? (г, а) наложены огра-
ограничения:
вектор 2 задается п 4- 1 координатами: координатой со
и координатами х1, ..., я!"',
Функция потерь (? (г, а) задана в виде (со — Р (х, а)) 2,
где Р (х, а) — характеристическая функция множеств.
§ 7. Три пути решения задачи о минимизации
среднего риска
Существуют три традиционных пути решения задачи
минимизации среднего риска.
Первый путь связан с идеей восстановления функции
распределения вероятностей. Предположим, что наряду с
функцией распределения Р (х, со) существуют ус-
условные плотности распределения Р (х | со = 0),
Р (х | со= 1) и вероятности Р (со = 0), Р (со = 1). Здесь
Р (х | со = 1) — плотность распределения вероятностей
векторов первого класса, а Р (х | со = 0) — плотность
распределения вероятностей векторов второго класса.
Величины Р (со = 1), Р (ш= 0) определяют вероятность
появления векторов * соответственно первого и второго
классов.
Зная эти функции, можно с помощью формулы Байеса
определить вероятность принадлежности вектора х
44 ГЛ. II. ОБУЧЕНИЕ МАШИН РАСПОЗНАВАНИЮ ОБРАЗОВ
первому или второму классу:
Р (ш = 1 | х) = сР (х | ш = 1) Р (<о = 1),
Р (ш = 0 | х) = сР (х | ш = 0) Р (<о = 0). B.3)
В формуле B.3)
1
С =
Р (а; | со = 0) Р (со = 0) + Р (ж I со = 1) Р (со = 1)
— нормирующий множитель.
Нетрудно понять, что минимальные потери будут по-
получены при такой классификации векторов, при которой
вектор х будет отнесен к первому классу в случае выпол-
выполнения неравенства
Р (ш = 0 | ж)< Р (ш = 1 | х)
(т. е. если более вероятно, что он принадлежит к первому
классу чем ко второму) и относится ко второму классу в
противном случае.
Иначе говоря, учитывая B.3), вектор х должен быть от-
отнесен к первому классу, если выполняется неравенство
Р(ж|со = 0) ^ Р(со = 1)
Р (х | со = 1) ^ Р (со = 0) '
или, что то же самое, оптимальная классификация векто-
векторов производится с помощью характеристической функции
B.4)
Такие характеристические функции иногда называют дис-
кримипантными. Таким образом, знание плотностей ус-
условных распределений Р (х \ со =0), Р (х | со =1) и ве-
вероятностей Р (со = 1), Р (со = 0) гарантирует отыскание
оптимального правила классификации.
Первый путь заключается в том, чтобы сначала
восстановить по выборке неизвестные функции распреде-
распределения векторов первого и второго классов, а затем по вос-
восстановленным функциям распределения построить дис-
криминантную функцию.
§ 7. ТРИ ПУТИ МИНИМИЗАЦИИ РИСКА 45
Однако следует заметить, что в этом случае решение
сравнительно простой задачи — построение дискриминант-
ной функции — подменяется решением значительно более
сложной задачи — задачи о восстановлении функции рас-
распределения. Ведь восстанавливаемые функции распределе-
распределения вероятностей составляют исчерпывающие сведения о
классах векторов, в то время как нужная нам дискрими-
нантная функция отражает только одну из характеристик
взаимного расположения векторов различных классов.
Поэтому, вообще говоря, решать задачу обучения рас-
распознаванию образов, восстанавливая неизвестные функ-
функции распределения вероятностей, нерационально. Исклю-
Исключения составляют случаи, когда задачи о восстановлении
многомерных функций распределений сильно вырожда-
вырождаются. Например, когда функция распределения такова,
что координаты вектора х = х1, ..., хп распределены не-
независимо, т. е.
Р (х | <о) = Р (х1 | <о) ... Р (хп | со).
В этом случае задача о восстановлении двух п-мерных
функций распределения вероятностей вырождается в зада-
задачу о восстановлении 2 п одномерных функций
Р (ж* | ш = 0), Р (ж* | со = 1) (I = 1, 2, ..., п).
Второй путь связан с организацией рекуррент-
рекуррентной процедуры поиска параметра а, доставляющего ми-
минимум функционалу B.2).
Если бы функция распределения вероятностей Р (г)
была известна, то при определенных условиях рекуррент-
рекуррентная процедура поиска минимума могла бы быть организо-
организована с помощью градиентного спуска по функции В (а).
В данном случае градиент может быть найден так:
§га<1а К (а) = § §гайа(? (г, а) йР (г).
Процедура спуска представляла бы собой следующее пра-
правило:
а (г + 1) = а (г) - у (г + 1) §га<1 В (а (г)), B.5)
где у (г) — величина г-го шага.
Прямым обобщением градиентного метода поиска ми-
минимума функции В (а) на случай неизвестной функции
46 ГЛ. II. ОБУЧЕНИЕ МАШИН РАСПОЗНАВАНИЮ ОБРАЗОВ
распределения вероятностей Р (г) является процедура ме-
метода стохастической аппроксимации
а (I + 1) = а (I) - у (I + 1) д (а (I), 2|+1), B.6)
где вектор-функцию д (а, г) можно понимать как градиент
по а функции (? (г, а) в точке 2;+1, а (V).
В B.6) вектор д (а, г) определяет направление движе-
движения. В отличие от B.5) направление, вдоль которого будет
происходить изменение вектора а, зависит не только от
предыдущего значения а (I), но и от случайной величины
2г+1. Таким образом, вектор д (а, г) определяет стохастичес-
стохастический градиент — направление, случайное вследствие влия-
влияния переменной г. В зтой процедуре сходимость к мини-
минимуму обеспечивает такая последовательность величин ша-
шагов у (I) > 0, что
(эти условия обеспечивают возможность, во-первых, по-
подойти к точке минимума из сколь угодно «далекой* точки
пространства а, а во-вторых, приблизиться к точке мини-
минимума как угодно близко).
Теория таких итерационных методов поиска минимума
направлена на то, чтобы выяснить, каким условиям долж-
должны подчиняться функция двух групп переменных () (г, а),
вектор-функция д (а, г) и константы у (I), чтобы с помощью
процедуры B.6) можно было обеспечить сходимость после-
последовательности а (г) к значению а0, на котором достигается
минимум функционала В (а). Используя эту теорию, мож-
можно для определенных (не для любых!) функций потерь
(? (г, а) строить рекуррентную процедуру поиска нужных
значений вектора параметров а.
Второй путь как раз и связан с построением итерацион-
ной"процедуры B.6) для поиска минимума В (а).
Наконец, третий путь связан с идеей замены
неизвестного функционала
В (а) = ^ <? B, а) ЛР (г)
§ 8. РАСПОЗНАВАНИЕ ОБРАЗОВ И МИНИМИЗАЦИЯ РИСКА 47
функцией
1=1
построенной по случайной и независимой выборке 2Х, ...
..., 2г.
Функция Ктп (а) получила название функции, исчис-
исчисляющей величину эмпирического риска. Для каждого
фиксированного значения параметра а она определяет
среднюю величину потерь на выборке 21( ... ,%\.
Идея метода состоит в том, чтобы найти значение пара-
параметров а = аэ*, обеспечивающих минимум функции эмпи-
эмпирического риска, а затем в качестве решения задачи о ми-
минимизации среднего риска предложить функцию с этими
значениями параметров, т. е. () (г, аэ*).
Такой метод решения задачи называется методом мини-
минимизации эмпирического риска. Теория метода минимиза-
минимизации эмпирического риска призвана ответить на вопросы,
когда (для каких функций () (г, а)) такая подмена возмож-
возможна и какая при этом совершается ошибка.
Развитие методов обучения распознаванию образов
пошло по всем трем путям минимизации среднего риска.
§ 8. Задача обучения распознаванию образов
и методы минимизации среднего риска
Итак, задача обучения распознаванию образов сводится
к задаче о минимизации среднего риска и существуют три
традиционных пути решения этой задачи.
Казалось бы, чтобы получить соответствующие алго-
алгоритмы обучения распознаванию образов, достаточно в
этом частном случае применить общие методы минимиза-
минимизации риска.
Однако на самом деле ситуация не такая уж простая.
Методы минимизации риска недостаточно разработаны.
Первый путь приводит к необходимости восстанавли-
восстанавливать многомерную функцию. Эффективные методы восста-
восстановления функции разработаны лишь для случая, когда
функция задана с точностью до значения небольшого числа
параметров. Восстановить функцию значит определить
значения параметров.
48 ГД. II. ОБУЧЕНИЕ МАШИН РАСПОЗНАВАНИЮ ОБРАЗОВ
Два других метода минимизации риска могут быть при-
применены не для всяких функций потерь (? (г, а).
Теоретические исследования этих методов минимиза-
минимизации риска как раз и направлены на то, чтобы установить
классы функций (? B, а), для которых эти методы при-
применимы. Специфика задачи обучения распознаванию
образов состоит в том, что функции Р (х, а) характери-
характеристические. Оказалось, что для таких функций теория ми-
минимизации риска не могла гарантировать успех примене-
применения методов минимизации.
По существу, задача обучения распознаванию образов
есть теория минимизации среднего риска специального
вида функций потерь. Ниже, в главах III, IV, V, примени-
применительно к задаче обучения машин распознаванию образов
будут рассмотрены все три пути мипимизации риска.
Глава III
МЕТОДЫ ОБУЧЕНИЯ, ОСНОВАННЫЕ
НА ВОССТАНОВЛЕНИИ
РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
§ 1. О восстановлении распределения вероятностей
В задачах математической статистики чрезвычайно
важным является случай, когда функция распределения
вероятностей известна с точностью до значения параме-
параметров. В этом случае восстановление распределения веро-
вероятностей сводится к установлению значений параметров
на основе имеющейся выборки. Методы исследования,
разработанные здесь, получили название методов пара-
параметрической статистики.
Выше было указано, что задача обучения распозна-
распознаванию образов может быть решена путем построения дис-
криминантной функции по восстановленным функциям
распределения вероятностей различных классов объек-
объектов. В этой главе будут рассмотрены такие параметриче-
параметрические методы решения задачи. Как уже указывалось,
идея решения задачи обучения распознаванию путем вос-
восстановления распределения вероятностей, вообще гово-
говоря, кажется малопривлекательной и реальных успехов
на этом пути можно ждать лишь для вырожденных
случаев.
Параметрические методы решения задач обучения рас-
распознаванию связаны с двумя классами функций распре-
распределения.
Первый класс распределений. Рас-
Распределение вероятностей для каждого класса векторов
Р (х, р), зависящее от вектора параметров р, таково,
что координаты вектора х = (х1, . . ., хп) распределены
50 ГЛ. III. МЕТОДЫ ВОССТАНОВЛЕНИЯ РАСПРЕДЕЛЕНИЙ
независимо, т. е.
Р (х, р) = Р(х\р1) X ... X Р (хп, рп), C.1)
и, кроме того, каждая координата ж* вектора х может
принимать лишь фиксированное число значений. Для
определенности будем считать, что каждая координата ж1
принимает хг значений с1 A), . . ., с* (т4).
Таким образом, рассматривается случай, когда распре-
распределение вероятностей для каждого класса объектов
задано выражением C.1), где функция Р [х{, р{) может
быть записана так:
1р{(\), если ж4 = с{A),
C.1')
р*(т{), если х{ = с1(тг),
2
3=1
Здесь р1 (к) есть вероятность того, что х1 примет значение
с{ (к). Восстановить распределение вероятностей C.1')
значит найти значения параметров/?» (к) (к = 1, 2, . . .,Т;).
Второй класс распределений. Плот-
Плотность распределения вероятностей для каждого класса
объектов задана нормальным законом
Р {Х^ А) 6ХР [ (Т
Восстановить плотности распределения вероятностей зна-
значит найти вектор средних (г и ковариационную матрицу
А для каждого класса объектов. Однако часто решение
такой задачи на выборках ограниченного объема оказы-
оказывается недостаточно точным и поэтому рассматриваются
еще более узкие постановки, где наложены ограничения
на свойства ковариационных матриц А (например, счита-
считается, что ковариационные матрицы различных классов
равны либо являются диагональными или даже единич-
единичными). Согласно формуле B.4) знание плотностей распре-
распределения вероятностей векторов для различных классов
объектов и вероятностей появления представителя каж-
каждого класса дают возможность немедленно определить
оптимальное решающее правило.
§ 1. ВОССТАНОВЛЕНИЕ АСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ 51
Представим, как это часто принято в теории обучения
распознаванию образов, п-мерный вектор х, каждая ко-
координата которого может принимать лишь тг значений,
как бинарный вектор X = {Xх, . . ., Xх) размерности
т == 2т;- Эт0 делается так. Каждой координате ж* ста-
г=1
вится в соответствие вектор $1, координаты которого
х\, . . ., 2{* определяются следующим образом:
к Г 0, если х1фс1{к),
Хг ~\ 1, если х1 = с*(/с).
Например, если координата х1 может принимать че-
четыре значения и имеет значение с{ C), то соответствую-
соответствующий вектор Х{ равен @, 0, 1, 0).
Координаты векторов &г {I = 1, 2, . . ., п) записыва-
записываются подряд, образуя новый вектор X = {х1, . . ., У),
так что первые %х координат зтого вектора совпадают
с хг, следующие т2 — образуют х2 и т. д.
Тогда для первого класса функций, согласно B.4),
оптимальным решающим правилом является линейная
дискриминантная функция
где рт и рп — соответственно вероятности появления
векторов первого и второго классов; р\ — вероятность
того, что Я* = 1 для векторов ч первого класса; р\ —
вероятности того, что хк = V для векторов второго
класса. С^_-»?^ ^К*«*«^-- - *
Для нормальных распределений оптимальное решаю-
решающее правило, согласно B.4), оказывается, вообще говоря,
квадратичной дискриминантнои функцией
Р(х) = В ((х - ц2)Г А (х - [х2) - (х - ^ГДГ1 (х - н) -
52 ГЛ. III. МЕТОДЫ ВОССТАНОВЛЕНИЯ РАСПРЕДЕЛЕНИЙ
где [1(и Д, — параметры плотности распределения векто-
векторов первого класса, а ц2 и А2 — векторов второго класса.
Таким образом, задача построения решающего прави-
правила сводится к нахождению соответствующих параметров
плотностей распределения вероятностей.
Среди параметрических методов восстановления плот-
плотности распределения вероятностей наиболее эффективны-
эффективными являются метод максимума правдоподобия и методы,
основанные на байесовой оценке. Применение этих двух
методов для восстановления плотностей распределения
вероятностей в описанных классах и составляет содержа-
содержание теории параметрических методов обучения распозна-
распознаванию образов. Прежде чем перейти к изложению этой
теории, напомним некоторые понятия статистической
теории оценивания.
§ 2. Классификация оценок
Итак, задача состоит в том, чтобы, используя случай-
случайную и независимую выборку хъ . . ., хг фиксированной
длины I, полученную согласно плотности распределения
вероятностей Р (х, а0), восстановить значение вектора-
параметров а0.
Иначе говоря, задача заключается в том, чтобы найти
функцию, которая по каждой выборке векторов х1, . . ., хг
вычисляла бы вектор а {хъ . . ., х{), который мы примем
за приближение вектора-параметров а, т. е. найти
функцию
а = а (хъ . . ., Х[). C.3)
Функция C.3) получила название оценки параме-
параметров а0. Так как векторы хи ... , хг случайны, то оцен-
оценка а (хъ . . ., хг) является случайной величиной, обла-
обладающей такими характеристиками случайной величины,
как функция плотности распределения К (а), математи-
математическое ожидание
а = \ а/г. (а) йа,
дисперсия
В (а) = ^ (а — аJ К (а) йа.
!2. КЛАССИФИКАЦИЯ ОЦЕНОК
53
В математической статистике приняты следующие
характеристики оценок.
Несмещенной называется такая оценка, для которой
математическое ожидание оценки равно самой определяе-
определяемой величине.
Эффективной оценкой называется несмещенная оценка
с минимальной дисперсией т. е. наиболее точная из всех
Оценки с асимпто-
асимптотической эффек-
эффективностью
Асимптотически
зффек/пиднй/е
б)
Рис. 4.
несмещенных оценок. Для остальных (неэффективных
оценок) вводится количественная мера точности оценки
е<С 1, называемая эффективностью оценки, которая опре-
определяется отношением дисперсии эффективной оценки к дис-
дисперсии данной оценки. Очевидно, что эффективность эф-
эффективной оценки равна 1, а для остальных оценок е ■< 1.
На основе этих определений можно ввести первоначальную
классификацию оценок (рис. 4, а).
54 ГЛ. III. МЕТОДЫ ВОССТАНОВЛЕНИЯ РАСПРЕДЕЛЕНИЙ
Эта классификация предназначена для характеристик
оценок, полученных на выборках малого объема. Для
выборок большого объема предлагается несколько иная
система классификации, в которую введены понятия
асимптотически несмещенных, состоятельных и эффектив-
эффективных оценок.
Асимптотически несмещенной называется оценка, для
которой
а («!, . . ., хг) -> а0 при /-> оо.
Состоятельной называется оценка, для которой
Р (| а — а0 | > е) -> 0 при I -> оо для всех е > 0.
Асимптотически эффективной называется оценка,
для которой е -*■ 1 при /->оо. Такая классификация
оценок представлена на рис. 4, б.
§ 3. Метод максимума правдоподобия
Метод максимума правдоподобия в задаче о восстанов-
восстановлении плотности распределения вероятностей в классе
функций Р (х, ос) связан с исследованием так называемой
функции правдоподобия Фишера. Функция правдопо-
правдоподобия задается на выборке хъ . . ., хг и имеет вид
Ь(хъ..., х1\а) = ЦР(х1,а). C.4)
1=1
Если величины х дискретны, то функция Ь (хг, ...
. . . , XI | а) для каждого а определяет вероятность
случайной и независимой выборки образовать после-
последовательность хг, . . ., XI. Если же Ж|, . . ., тг — непре-
непрерывные величины, то функция Ь (хг, . . ., х; \ а) может
быть истолкована как плотность совместного распределе-
распределения величин хи . . ., хг.\
Таким образом, каждой выборке может быть поставле-
поставлена в соответствие функция правдоподобия (рис. 5). Метод
максимума правдоподобия состоит в том, чтобы в качестве
восстановленного значения параметра а выбирать
то, которое доставляет максимум функции правдопо-
правдоподобия. Наряду с функцией Ь (хи . . ., жг| а)] принято
4, БАЕКСОБ ПРИНЦИП ВОССТАНОВЛЕНИЯ
рассматривать функцию
1пЬ (хъ ..., х11 а) = ^ 1пр
C.4')
Максимум функций C.4) и C.4') совпадают и, следова-
следовательно, оценки максимума правдоподобия могут быть
найдены как корни урав-
уравнения Цх1,...,х[\сс)
да3
() = 1, 2, ...,_!»),
или уравнения
д 1п Ь (х1,..., х^\а)
—-
= 0.
Рис. 5.
Теория метода призвана оценить, насколько «хорош» пред-
предлагаемый способ оценивания параметров. Эта теория до-
достаточно полно разработана. Подробное исследование
свойств оценки максимума правдоподобия можно найти
в работах [2, 62].
Основное содержание теории заключается в том, что
для определенных функций Р (х, а) (которым заведомо
принадлежат оба класса рассматриваемых распределе-
распределений вероятностей) метод максимума правдоподобия
обеспечивает асимптотическую несмещенность и асимп-
асимптотическую эффективность оценки.
§ 4. Байесов принцип восстановления
Байесов принцип восстановления плотности распреде-
распределения основан на использовании формулы Байеса:
Пусть известна априорная плотность распределения
вероятностей Р (а) вектора параметров а, которая харак-
характеризует предполагаемую возможность осуществления
различных значений а до того как проведен эксперимент
56 ГЛ. III. МЕТОДЫ ВОССТАНОВЛЕНИЯ РАСПРЕДЕЛЕНИИ
(дана выборка). Апостериорная вероятность Р (а | хъ . . .
. . ., х{) характеризует возможность осуществления раз-
различных значений а после того, как к априорному знанию
добавлено знание, извлеченное из экспериментальных
данных ж1, . . ., хг. В этом случае формула Байеса ут-
утверждает, что апостериорная вероятность параметра а
получается умножением априорной вероятности на функ-
функцию правдоподобия
г
Ь {хъ ..., жг | о) = \[Р {хг | а)
1=1
и делением на вероятность данного эксперимента
Р {х1, . . ., хг).
Иначе говоря, справедлива формула
Ь(х1,...,х1\а)Р{а)
Р{а\хъ ..., хг) = —
где
Р {хх,..., хг) = ^ Ь {хъ ..., х11 а) Р (а) йа,
если параметры а непрерывны, и
Р{х1г..., хг) =^Ь{х1,..., хг\ак)Р (ай),
к
если значения параметра а дискретны.
Таким образом, с помощью формулы Байеса по апри-
априорному распределению вероятностей параметров а и ре-
результатам эксперимента может быть вычислена плотность
апостериорного распределения вероятностей Р (а | хъ . . .
. . ., х{).
Теперь задача заключается в том, чтобы, зная плот-
плотность Р {а | хъ . . ., х{), определить искомый параметр.
Здесь может быть несколько идей оценивания.
1. В качестве искомого значения вектора параметров
выбирается такое а, которое доставляет максимум функ-
функции Р {а | хг, . . ., Хг).
I 2. В качестве искомого значения вектора параметров
выбирается математическое ожидание значения а, т. е.
а = \ аР (а | хх,..., х{) йа.
§ 4. ВАЙЕСОВ ПРИНЦИП ВОССТАНОВЛЕНИЯ 57
3. Принята и такая идея восстановления, когда с по-
помощью плотности распределения Р (а | хъ . . ., хг) кон-
конструируется плотность Р (х) по правилу
Р(х) = ^Р (х\а) Р (а\хъ ..., хг)йа =
= ^(»|а)Р(ая,...,»,|а)Да
^Р(ЭДх\а)Р(а)йя ' (
т. е. в качестве оценки выбирается математическое ожи-
ожидание плотности Р (х | а). Вообще говоря, полученная
в результате восстановления C.5) плотность Р (х) вовсе
не должна принадлежать рассматриваемому параметри-
параметрическому семейству Р (х, а). Поэтому, строго говоря,
рассматриваемый метод конструирования плотности Р (х)
нельзя называть восстановлением функции в классе
Р (х, а), тем не менее он получил название байесовой стра-
стратегии восстановления функции Р (х).
Байесова оценка плотности распределения вероят-
вероятностей обладает замечательной особенностью, делающей
получение ее крайне желательной. Она реализует опти-
оптимальную стратегию в следующей игре с «природой».
Игра состоит в том, чтобы «угадать» ход, сделанный при-
природой. Функция Р (а) задает вероятность того, что при-
природа назначит вектор а = а0 в качестве параметра плот-
плотности распределения Р (х, а). Пусть теперь дана выборка
длины I из генеральной совокупности с плотностью
Р (х, а0). Стратегия игрока заключается в том, чтобы
задать такую функцию п (х; а^, . . ., х{), которая была бы
как можно «ближе» к Р (х, а0). «Партия» в такой игре
определяется стратегией природы а = а0, стратегией
игрока п (х; хъ . . ., хг) и случайной выборкой хи . . ., хг.
Величина проигрыша в этой игре
В (а; хъ ..., ж,) = $ (Р (х | а) - п (х; хъ ..., х,))* их. C.6)
Средний проигрыш игрока в игре определяется выраже-
выражением
= §1>(<х; жх,..., хг) Р(а)Р{хъ ..., ж, |а)йжх,..., йхгйа, C.7)
58 ГЛ. III. МЕТОДЫ ВОССТАНОВЛЕНИЯ РАСПРЕДЕЛЕНИЙ
т. е. C.7) получается усреднением C.6) по стратегиям
природы и всевозможным реализациям выборки.
Замечательное свойство байесовой оценки заключается
в том, что она минимизирует средний проигрыш игрока,
который знает смешанную стратегию природы Р (а).
Иначе говоря, оптимальная стратегия игрока определя-
определяется как
. . . \Р(х\*)Р(х1 *, | а) Р (а) Ах
Л [X. Хл* .... X] ) ^ я .
$ Р (*!,..., х1\а)Р(а)йа
Докажем это важное для понимания значения байесо-
вых оценок утверждение.
Итак, требуется найти такое я (х; хи . . ., х,), которое
минимизирует функционал
/ = 5 ... ^ (Р (х\а) — %{х- хъ ..., хг))* Р (хи ..., х,\а)Р (а) X
X йайхйхх... йхг. C.8)
Обозначим
Ф(х; хъ ..., хг) = 5(Р(ж|о) — п{х-хъ ..., х1)JР(х1,..., ж,|а)Х
X Р (а) йа
и изменим порядок интегрирования, после чего C.8)
примет вид
I = \ . . . I Ф {х; хъ . . ., хг) <1х <1хх йх% . . . йхь
Преобразуем теперь функцию Ф (х; хъ . . ., хг):'
Ф (х; хи . . ., хг) = I Р2 (х\ а)Р (хъ . . ., х,\ а)Р(а) да -
—2я (х; хъ . . ., хг) ^ Р (х\ а)Р (хи . . ., хг \ а)Р (а) йа +
+ я2 (х; хъ . . ., х{) \ Р(хи . . ., хг \ а)Р (а) 6а.
Обозначим
с (хъ . . ., хг) == .( Р (хи . . ., хг\ а)Р (а) йа,
$ 5. СРАВНЕНИЕ МЕТОДОВ ОЦЕНИВАНИЯ 59
Справедливо равенство
Ф (ж; хъ . . ., жг) = | Р2 (ж] а)Р (хг, . . ., хг | а)Р (а) йа —
—Р2 (х)с (хи . . ., х,) + [Р (х) — я (ж; Ж!, . . ., жг)Р X
X с (жх, . . ., жг).
Таким образом, функционал / распадается на два сла-
слагаемых
/ = 1х + А,
где
А = 1 II ^2 (я I «)Р (ж1( . . ., ж, | а)Р (а) йа -
— с (ж!, . . ., жг)Р2 (ж)] йх йхх . . . йхи
1г = ] \Р (х) — я (ж; жъ . . ., жг)]2 с (жь . . ., хг) йх йхг ...
. . . йхх.
Первое слагаемое не зависит от функции п (х; хх, . . ., х{).
Поэтому минимизация / эквивалентна минимизации вто-
второго слагаемого /2.
Минимум этого слагаемого равен нулю и достигается
тогда, когда
п (х', хъ . . ., ж,) = Р (х).
§ 5. Сравнение байесова метода оценивания
и оценивания методом максимума правдоподобия
Рассмотренные методы оценивания не являются рав-
равнозначными ни по сложности их реализации, ни по эф-
эффекту, который может быть с их помощью получен. Наи-
Наибольшую трудность в реализации метода максимума прав-
правдоподобия представляет отыскание решения системы
уравнений
дЬ (х\ х, I а)
Хотя система уравнений, вообще говоря, не является
линейной, численное решение ее не составляет принци-
принципиальной трудности, тем более что для широкого класса
функций существует лишь единственное решение C.9).
Реализация байесовой стратегии — задача значитель-
значительно более трудная. Как правило, эта стратегия может быть
реализована лишь тогда, когда удается провести
60 ГЛ. III. МЕТОДЫ ВОССТАНОВЛЕНИЯ РАСПРЕДЕЛЕНИЙ
аналитическое интегрирование выражения
Численное интегрирование C.10) — задача чрезвы-
чрезвычайно трудоемкая из-за высокой кратности интеграла
(вектор а обычно имеет большую размерность).
В свою очередь метод максимума правдоподобия менее
привлекателен чем байесов: теория гарантирует лишь
асимптотическую эффективность метода.
Байесова процедура имеет интерпретацию оптимальной
стратегии в игре с известной смешанной стратегией про-
противника. Правда, при ее реализации требуются сведения о
плотности априорного распределения параметров а, что
не всегда имеется у исследователя. Однако известно
(теорема С. Н. Бернштейна), что влияние априорных
сведений на получение апостериорной плотности распре-
распределения вероятностей падает с ростом объема выборки.
В случае, когда нет никаких иных сведений, обычно поль-
пользуются равномерным законом априорных распределений
параметров а. Таким образом, ситуация такова, что при
оценивании плотности распределения желательно полу-
получить байесову оценку, хотя найти ее часто бывает крайне
трудно. Когда получение байесовой оценки невозможно,
используются оценки метода максимума правдоподобия.
Ниже, для первого класса распределений будут при-
приведены оценки параметров методом максимума правдо-
правдоподобия и байесовы оценки. Для второго класса распре-
распределений будут приведены оценки параметров методом
максимума правдоподобия; будет показано, в чем состоят
трудности при получении байесовых оценок, и, наконец,
будут найдены байесовы оценки для некоторых специ-
специальных видов ковариационных матриц А.
§ 6. Оценка параметров распределения дискретных
независимых признаков
Итак, пусть координаты вектора х распределены не-
независимо и, кроме того, каждая координата х вектора х
может принимать т, значений, т. е. известно, что
Р(х,р)=
1=1
§ 6. СЛУЧАЙ НЕЗАВИСИМЫХ ПРИЗНАКОВ 61
где
|р*A), если ж1 = с1A),
(З.Н)
р'х (т4), если хг = с1 (т^),
;=1
Составим функцию правдоподобия
г п
х-/ ^1, ..., Х^ р) — II II г уХк) р ^,
где ^й — значение г-й координаты к-то вектора обучаю-
обучающей последовательности.
Переставив порядок сомножителей, получим
п г
Ь(хъ ..., х,, р)= П П Р(х\> Р1)-
г=1 К=1
Перейдем к функции 1п Ь:
N I
1п Ь (хъ ..., хь р)= 2 2 1п р (х*> Р1)-
1=1 К=1
Рассмотрим теперь величину
(С=1
Согласно C.11) она может быть представлена в виде
где т; (/) — число векторов выборки, у которых коорди-
координата принимает значение жг" = с* (/); / — объем выборки,
62 ГЛ. III. МЕТОДЫ ВОССТАНОВЛЕНИЯ РАСПРЕДЕЛЕНИЙ
Таким образом, логарифм функции правдоподобия
равен
% %рЧ]). C.12)
1=1 3=1
Найдем максимум по р1 (/) функции 1п Ь (хъ . . ., хь р)
при ограничениях^р'(у) = 1. Для этого воспользуемся
методом множителей Лагранжа.
Составим функцию Лагранжа Ф (р, %):
п ^
ф(рД)=2 2 и 0Iп р* 01 - ^ ('»•
1=1 3=1
где %1 — множители Лагранжа.
Вектор р, доставляющий максимум функции Ф (р, %),
определяется из системы уравнений
Из C.13), учитывая условия нормировки
3=1
получаем
Таким образом, рекомендации метода максимума прав-
правдоподобия состоят в том, чтобы в качестве функции распре-
распределения вероятностей использовать ее эмпирическую
оценку, т. е.
р1 A) = —-,—, если х1 = & A),
(ЗЛ4)
А*\)= —т~^ > если 'х' = с* (т0-
§ 7. БАИЕСОВЫ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ 63
§ 7. Баиесовы оценки параметров распределения
дискретных независимых признаков
Ниже будет показано, что при минимальных априор-
априорных сведениях относительно значения параметров рас-
распределения Р (х{, р1) (параметры рг = {р{ A) , . . ., р4(т{)}
•ч
распределены равномерно на симплексе 2 Р1 (/) —1> Р{ (/) ^»
> 0) байесова оценка имеет вид з=1
Р(х\ р*) =
C.15)
Согласно § 5 баиесовы оценки являются наиболее точ-
точными. В случае, когда объем выборки I мал — соизмерим с
числом градаций т; — эти оценки могут значительно отли-
отличаться от оценок максимума правдоподобия C.14).
Поэтому для построения дискриминантной функции
по малым выборкам лучше пользоваться не оценками
C.14), а оценками C.15).
Получпм баиесовы оценки распределения.
Для этого вычислим сначала нормировочную
с (хи .. .,х1) = \)Ь(х1,...,х1,'р)Р (р) йр.
константу
где Ь (хт, . . ., XI, р) — функция правдоподобия, Р (р) — апри-
априорная плотность. Подставляя сюда функцию правдоподобия и учи-
учитывая, что параметры р1 (/) распределены равпомерно, получим
где а = Р (р) = сопя1 п
с (а?1, . . . , тг) =
1=1
2 ргC)
3=1
Рг(з)>о
1=1
1 хгУ>
п
-!). C.16)
64 ГЛ. Ш. МЕТОДЫ ВОССТАНОВЛЕНИЯ РАСПРЕДЕЛЕНИЙ
Известно [57], что определенный интеграл C.16) может быть
вычислен
где Г (п) — гамма-функция. Для целых п она равна Г (п) =
= (п - 1)!
Таким образом, нормировочная константа равна
Найдем теперь байесову оценку функции распределения вероят-
вероятностей. Согласно C.5) она равна
X
Х_
С1 (XI, ...,*;)
Обозначим каждый сомножитель произведения Р (ж*). Учитывая,
что функция Р (ж* | р) представлена в виде C.11), вычислим зна-
значение Р (х1) при ж* = с1 (к). Легко видеть, что аналогично инте-
интегралу C.16)
■ч-1
I П[
3=1
х»—1
5=1
С1 (XI, ..., Хг)
Г(т1(к)+2)ТA+Х1) т.(к)
Таким образом,
Р (/) =
Г(т,(*)-М)Г(/ + Т.
/» A) = —, . — , если а; = с A),
если ж ^с
Заметим, что оценки, полученные байесовым методом C.17), от-
отличаются от оценок, полученных методом максимума правдо-
правдоподобия C.14).
Отличаются эти оценки тем больше, чем меньше объем выбор-
выборки и чем большее число значений т& могут принимать координаты
вектора х{.
§ 8. ВОССТАНОВЛЕНИЕ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ 65
§ 8. Восстановление параметров нормального
распределения методом максимума правдоподобия
В случае, когда функция плотности распределения
вероятностей задана нормальным законом
I*)] '
где ^ = ^г1, . . ., ^п — п-мерный вектор параметров,
а А — матрица параметров п X п, функция правдоподо-
правдоподобия оказывается равной
Ь(хъ..., хг, \1, Д) =
г
4
4
(^ -1*)] • C.18)
Логарифм функции правдоподобия равен величине
1п Ь(хъ ..., хь \1, А) =
г
1=1
Оказывается, что максимум C.18), а следовательно, и
C.19) достигается, когда вектор параметров ^ есть оценка
математического ожидания вектора Х(, т. е.
г
г=1
а матрица А есть оценка ковариационной матрицы, т. е.
II а II = || 4- 2 D - 4) D - 4) | = I к* |. C.20)
Доказательство этого факта имеется во всех руковод-
руководствах по многомерному статистическому анализу [2]. Оно
в векторной форме буквально повторяет очевидное для
одномерного случая утверждение: максимум функции
66 ГЛ. III. МЕТОДЫ ВОССТАНОВЛЕНИЯ РАСПРЕДКЛЕНИИ
достигается при
— 2 хь <з9 = ]/ 4" 2 (хг—жэJ.
1=1 1=1
Как уже указывалось, по оценке параметров плотно-
плотности распределения обоих классов векторов: \лг, Дх и ^2,
Д2, немедленно находится решающее правило
? (х - М -
Особенность этого правила заключается в том, что
оно образовано с помощью операции обращения
У = А-1^.
Известно, что к использованию операции обращения ма-
матриц следует относиться с большой осторожностью: воз-
возможны случаи, когда достаточно малой ошибке при за-
задании матрицы А соответствуют значительные ошибки
величины У. В нашем случае, когда в качестве матрицы А
берется ее эмпирическая оценка, такие ошибки тем более
вероятны, чем меньше объем выборки, по которой строи-
строилась оценка, и чем хуже обусловленность самой ковариа-
ковариационной матрицы.
Поэтому может оказаться, что для построения надеж-
надежного решающего правила потребуется такая точность
в оценке ковариационных матриц, которая при заданном
объеме выборки не может быть гарантирована. Вот по-
почему на практике применяются частные постановки,
использующие особенности ковариационных матриц. При-
Принято пять вариантов таких постановок.^ I Р* Г1
1 вариант. На матрицы Ах и А2 не наложено
никаких дополнительных ограничений. В этом случае
решающее правило оказывается квадратичной дискрими-
нантной функцией.
2 вариант. Считается, что коварицаионные ма-
матрицы векторов обоих классов равны, т. е. Аг = А2 = А.
В качестве оценки такой матрицы берется среднее ариф-
арифметическое матриц, полученных соответственно для
9. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, БАЙВСОВ МЕТОД 67
векторов первого и второго классов:
д Д1 + Аа
2
В этом случае решающее правило оказывается линейной
дискриминантной функцией (функцией Фишера)
Р (х) = 9^ - |ч)т А-1* + 4" (^А">2 - ^А-^0 + 1п-
3 вариант. Считается, что ковариационные ма-
матрицы векторов разных классов различны, но диаго-
диагональны:
<зи 0 ... О
О ам ... О
О 0 ... с,
Этому варианту соответствует случай, когда координаты
векторов х распределены независимо по нормальному
закону с дисперсией^. [При этом решающее правило
оказывается^квадратичной^дискриминантной формой.
4 вариант. Считается, что ковариационные ма-
матрицы векторов различных классов равны и диагональны.
В этом^случае решающее правило оказывается линейной
дискриминантной функцией.
5 вариант. Считается, что ковариационные матри-
цы^векторов обоих, классов^ единичные. К этому варианту
приводится случай известных одинаковых ковариацион-
ковариационных матриц. При этом решающее правило оказывается
линейной дискриминантной функцией.
Ясно, что каждый последующий вариант более «по-
«помехоустойчив», чем предыдущий.
§ 9. Байесов^метод восстановления нормального
распределения
К сожалению, восстановить методом Байеса распре-
распределение вероятностей в многомерном случае не удается.
Как уже указывалось, это связано с тем, что не удается
вычислить аналитически соответствующие кратные интег-
68 ГЛ. Ш. МЕТОДЫ ВОССТАНОВЛЕНИЯ РАСПРЕДЕЛЕНИЙ ^
ралы. Не удается аналитически получить байесову оценку
даже для случая, когда вектор х имеет размерность 2.
Ниже мы покажем, что при минимальной априорной
информации байесова оценка плотности нормального рас-
распределения случайной величины х имеет вид
^ . 11
2
г=1 г=1
Интересно, что эта оценка плотности нормального распре-
распределения оказалась не принадлежащей классу нормаль-
нормальных. Однако читатель легко может убедиться, что при
I —*■ ос справедливо
(х-хэ)>
2
« , . 1 . «"в
Использование более точных байесовых оценок плот-
плотности для построения дискриминантных функций при-
приводит к тому, что дискриминантная функция оказывается
не квадратичной, а более сложного вида.
Сравним дискриминантные функции, полученные для
третьего варианта постановки на основе байесовых оценок
и оценок максимума правдоподобия:
1п —-
Р
9. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, БАЙЕСОВ МЕТОД 69
где хгВ1, Жэ2 — соответственно эмпирическая оценка мате-
математического ожидания г-й координаты векторов пер-
первого и второго классов, а\ъ Сд2 — эмпирическая оценка
дисперсии 1-й координаты векторов первого и второго
классов. Эти функции различаются тем больше, чем
меньше объем выборки. Однако в пределе при I —*■ оо
Гв (х) -* Рк (х).
Итак, пусть известно, что величина х распределена по нормаль-
нормальному закону
(х —
Кроме того, пусть априорное распределение параметров ц и а
подчиняется равномерному закону на интервале —Г^ц-^+Г
и 0 ^ а ^ N. Функция правдоподобия в этом случае будет равна
^ (ж{ — р,)
1=1
•••''• |*'°'-B*)^ "'
Байесова оценка плотности распределения вероятностей равна
Т IV
Р(х)= ^-1У • C-21)
\ \ Ь (хл х \х, с) Щх йс
1т \
Мы будем считать, что интервалы [ — Т, Т] и [О, Щ столь
велики, что пределы интегрирования в C.21) могут быть расширены
до [ — оо, оо] и [0, оо]. Это' во всяком случае можно сделать, если
I > 2 (так как при I >■ 2 интегралы в выражении C.21) сходятся).
Вычислим интеграл
со оо
1
70 ГЛ. III. МКТОДЫ ВОССТАНОВЛЕНИЯ РАС «ЕДЕЛЕНИЙ
Обозначим
1=1 °
Тогда интеграл C.22) перепишется в виде
ОО у*
Обозначим
где С (I) не зависит ни от ц, ни от а.
Итак, интеграл может быть представлен в виде
C.23)
Преобразуем теперь выражение Т (ц). Для этого заметим, что
г=1
ГДе хв — -г- 2 Хи сэ = -у- 2 (хг ~ х^2' Соответственно
г=1 г=1
Т {р) = /а| + / (|1 - ос*J + {х- VJ.
Положим теперь
Тогда Т (A) может быть представлено в виде
% 9. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, ВАЙЕСОВ МЕТОД 71
Запишем теперь интеграл / в виде
оо
/(*) = С(/Д 1 ^ !- =
сA)
[г + 1 аэ+ (г +1)
Заметим, что подынтегральное выражение не зависит от парамет-
параметров. Таким образом, оказывается, что
с' <1) о" (I, а8)
'(*) = г=г = г=г-« C.24)
Нам остается нормировать к единице выражение C.24):
Известно [57], что интеграл в знаменателе C.25) равен следующему
выражению:
р р с" (I, а8) их
77
4-
Обовначим
Е{1) =
г I ^") г 1~2~
Таким образом, окончательно находим
*. . 1 1
Глава IV
РЕКУРРЕНТНЫЕ АЛГОРИТМЫ
ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ
§ 1. Метод стохастической аппроксимации
Метод стохастической аппроксимации применительно
к задаче о минимизации среднего риска состоит в том,
что для отыскания минимума по а функционала
В (а) = ^ Я B> °0 йр B)
используется рекуррентная процедура
а @ = а (I - 1) - у (г)д (ги а (г - 1)). D.1)
Теория этого метода устанавливает, когда (при каких
(? (г, а), д (г, а), у (I)) рекуррентная процедура приводит
к успеху. Оказывается, итерационный процесс D.1) при-
приводит к успеху (см. главу IX), если:
вектор-функция д (г, а) является градиентом по а
функции () (г, а) при фиксированном г (или обобщенным
градиентом *) этой функции);
последовательность положительных чисел у A), . . .
. . ., у (г), . . . такова, что
г=1 1=1
*) Обобщенным градиентом функции Р (х) называется вектор-
функция / (ж), которая определяет некоторый вектор, совпадающий
с градиентом функции Р (х) в тех точках, где градиент существует, и
которая специально определяется в тех точках, где градиент не
существует. Обобщенный градиент может быть определен по для
всех функций Р (х). Точное определение см. в главе IX.
§ 1. МЕТОД СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ 73
(примером такой последовательности может служить гар-
11 1
моническии ряд -—- , -у- , • • • , — ,•••)•
& О 71 у
Если при любом фиксированном 2 функция () (г, а)
одноэкстремальна по а, то с помощью процедуры D.1)
может быть достигнут минимум функционала К (а).
Если же функция не одноэкстремальна, то можно га-
гарантировать лишь достижение локального минимума (под-
(подробнее см. главу IX).
Рис. 6.
Попытка применить метод стохастической аппрокси-
аппроксимации непосредственно для решения задачи обучения
распознаванию образов к успеху не приводит. Функция
потерь этой задачи
ф = (а - Р (х, а)J D.2)
такова, что поиск нужного значения а этим методом не-
невозможен. На рис. 6 приведена функция потерь при фик-
фиксированных значениях ш и х. Во всех точках прямой,
кроме точки а = а*, градиент этой функции равен нулю,
а в точке а = а* его не существует. Отыскание решения
для такой функции потерь должно проходить согласно
процедуре D.1). В нашем случае вектор д (г, а) либо
равен нулю, либо не определен. Таким образом, проце-
процедура D.1) оказывается невозможной.
§ 2. Детерминистская и стохастическая постановки
задачи обучения распознаванию образов
Идея применения метода стохастической аппроксима-
аппроксимации для решения задачи обучения распознаванию обра-
образов связана с заменой функции потерь D.2) другой функци-
функцией, такой, чтобы по ней была возможна организация ре-
74 ГЛ. IV. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ ОБУЧЕНИЙ
куррентной процедуры. Замена функции потерь, по суще-
существу, означает, что задача об обучении распознаванию
образов подменяется некоторой другой задачей. В одних
случаях такая подмена приемлема, а в других — непри-
неприемлема, так как дает результаты, значительно отличаю-
отличающиеся от оптимальных. Чтобы разделять эти случаи,
принято различать два варианта постановки задачи обу-
обучения распознаванию образов — детерминистскую поста-
постановку и стохастическую *). В детерминистской постанов-
постановке предполагается, что среди характеристических функ-
функций Р (х, а) есть такая, которая идеально решает задачу
классификации, т. е. существует такое а = а0,
что Р (а0) = 0. Стохастическая постановка предусма-
предусматривает случай, когда идеальное решение задачи не-
невозможно.
Оказывается, что в первом случае удается построить
такую функцию потерь, что, с одной стороны, минимум
соответствующего функционала достигается на той же
функции Р (х, а0), которая обеспечивает безошибочное
разделение классов, а с другой стороны, для введенной
функции потерь может быть организована рекуррентная
процедура поиска.
В качестве примера вновь обратимся к классу решаю-
решающих правил персептрона. Вспомним, что для перспептрона
Розенблатта может быть выписан функционал, миними-
минимизация которого составляет суть задачи обучения. В коор-
координатах спрямляющего пространства функционал имеет
вид
( )у (со,
Предположим, что существует точное решение задачи
распознавания, т. е. существует такое X = %°, что
р (Х°) = 0, и, кроме того, для всех векторов у первого
класса справедливо
(Ь°, У) > « > 0,
а для векторов второго класса
(Ь°, У) < -8-
*) Термины здесь выбраны неудачно, так как и в той и в другой
постановке задача остается статистической. Однако эти термины
широко распространены и поэтому будем их придерживаться.
| 2. ДЕТЕРМИНИСТСКАЯ ПОСТАНОВКА ЗАДАЧИ
75
Построим новый функционал, например, со следующей
функцией потерь:
Ф (ш, у1\)=*^
' еслисо = 0,
1
3=1
3=1
т
1=1
' —б. если ш = 1.
D.3)
График этой функции при фиксированных ш и у при-
приведен на рис. 7. Введенная функция потерь имеет простой
смысл: для каждого X она
определяет величину по-
потери в зависимости от то-
го,|как расположен вектор
у относительно разделяю-
разделяющей гиперплоскости
т
2 ^ = о-
3=1
Если с помощью разде-
разделяющей гиперплоскости
вектор у классифицирует-
классифицируется правильно, то штраф равен нулю, если, же классифи-
классификация проводится неправильно, то величина штрафа на-
назначается пропорционально расстоянию от этого век-
вектора до разделяющей гиперплоскости. Например, если
вектор должен быть отнесен^к первому классу, а
Рис. 7.
3=1
то штраф численно равен 2 | с |; если же у должен быть
отнесен ко второму классу, а
3=1
то величина штрафа численно равна 2с (сравним с
76
ГЛ. IV. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ ОБУЧЕНИЯ
функцией потерь персептрона, где при любой ошибке
штраф равен единице).
Используя эту функцию потерь, можно подменить
задачу о минимизации функционала Р (к) задачей о ми-
минимизации другого функционала
СО, I/)
= $ Ф (СО, 1/
на том основании, что точка минимума нового фукнцио-
нала доставляет минимум исходному функционалу.
Для функции потерь Ф (и, у, X) может быть най-
найден обобщенный градиент и, следовательно, выписана
рекуррентная процедура. Обобщенный градиент
равен
О, если ш = 1 и 2
И (со, у, X) =
0, если со = 0 и
3=1
у, если и = 1 и 2 ^У1 <С $,
— у, если в = 0 I ^ ^у3>—б.
3=1
Соответствующая рекуррентная процедура
Я, @ = Я, (» - 1) + V (*)П (ш*« 2/ь Я, (I - 1))
означает, что если вектор у правильно классифицируется
построенной к этому времени разделяющей гиперплос-
гиперплоскостью, то вектор коэффициентов X (I — 1) не меняется.
Если же совершается ошибка одного рода (вектор при-
принадлежит первому классу, а относится правилом ко вто-
второму), то к вектору коэффициентов к (г — 1) прибавляется
вектор у A)у1. Если же совершается ошибка другого рода
§ 2. ДЕТЕРМИНИСТСКАЯ ПОСТАНОВКА ЗАДАЧИ
77
(вектор у% второго класса отнесен к первому), то из векто-
вектора X (I — 1) вычитается вектор у {г)у.
Полученный алгоритм поиска характеристической
функции очень напоминает алгоритм построения коэффи-
коэффициентов элемента В в персептроне Розенблатта. Разли-
Различаются алгоритмы лишь тем, что у Розенблатта у (г) = 1
и б =0.
Конечно, Рх (X) не единственный функционал, которым
можно подменить функционал Р (X). Можно рассмотреть,
например, функционал, который задается такой функ-
функцией потерь:
Ф (ш, у,Х) =
[ 12 ЪУ} + 61 + 2 № + б J5 если со = 0,
\ г=1 г=1 '
I х 3=1
3=1
если со = 1.
D.4)
График этой функции потерь для фиксированных ш, у
приведен на рис. 8.
Для такого функционала определяется рекуррентная
процедура
Я, @ = X (I - 1) + у (ОП (щ, уи X (I - 1)),
78 ГЛ. IV. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ ОБУЧЕНИЯ
в которой вектор-функция П (ш, у, X) имеет вид
т
О, если со = 1 и 2 ^■У3 ^ б,
Гт
0, если ш = 0 и 2 ^#3 <С — б,
3=1
ЧУ + о) у, если ш = 1 и 2| л;-г
4=1 5=1
т т
— B к}У} — *) 2/, если со = 0 и 2 Ь}У* > — б.
Такой алгоритм (при условии, что т{ (г) = -=—р- и б = 0)
предложил в свое время американский ученый Уидроу
для настройки весов сконструированных им пороговых
элементов (адалинов).
Существует много различных функционалов (разли-
(различающихся функциями потерь), для каждого из которых
стандартная процедура D.1) порождает рекуррентный ал-
алгоритм обучения распознаванию образов.
Исторически, однако, алгоритмы обучения распозна-
распознаванию образов были получены не так. АвторьГкаждого
из алгоритмов находили законы поиска разделяющей
гиперплоскости, исходя из различных соображений. По-
Поэтому сразу же после сообщений о персептроне Розенблат-
та появился целый ряд алгоритмов, обеспечивающих выбор
нужной гиперплоскости. Только в середине 60-х годов
Я. 3. Цыпкин заметил, что все эти алгоритмы могут быть
получены по одной и той же схеме и различаются между
собой так как различаются функционалы, экстре-
экстремум которых достигается на одной и той же решающей
функции.
§ 3. Конечно-сходящиеся рекуррентные процедуры
Итак, существует универсальная процедура D.1), по-
порождающая различные рекуррентные алгоритмы построе-
построения разделяющей гиперплоскости. Однако эти алгоритмы
гарантируют успех лишь при неограниченном увеличе-
$ 3. КОНЕЧНО-СХОДЯЩИЕСЯ ПРОЦЕДУРЫ 79
нии выборки. Это связано с тем, что процедура D.1) доста-
достаточно универсальна, и потому поиск нужных коэффици-
коэффициентов X ведется весьма осторожно: вспомним, что величи-
величина шага у (г) быстро падает с ростом I (последовательность
00
у A),..., у (I),... такова, что 2 ТЧ&Х!00)- Такая осто-
1=1
рожность иногда может оказаться чрезмерной. Пусть,
например, класс решающих правил задан в виде
'3=1
По-прежнему рассматривается детерминистская поста-
постановка задачи; геометрически это значит, что множества
векторов {у} и {у}, которые должны быть отнесены
к первому и второму классам соответственно, разделяются
гиперплоскостью
т
3=1
(иначе говоря, выпуклые оболочки этих множеств не пе-
пересекаются). Исключая из рассмотрения те задачи, для
которых расстояние между выпуклыми оболочками мно-
множеств {у} и {у} равно нулю, рассмотрим только такие
задачи, для которых это расстояние отлично от нуля
(равно некоторой положительной величине р0). Кроме
того, будем считать, что диаметр объединенного множества
{у} и {у} ограничен и равен 3.
В данных условиях поиск функции, минимизирующей
функционал Р (X), можно вести менее осторожно.
В частности, для рекуррентной процедуры D.1) шаг
у (г) может быть выбран равным постоянной величине,
например у (() = 1, и тогда можно гарантировать, что
минимум функционала будет найден после того, как про-
произойдет конечное число М изменений величин %. При этом
величина М заведомо ограничена числом Х>а/р5 (теорема
Новикова). Алгоритмы, с помощью которых можно за
конечное число исправлений найти нужное решающее
правило, получили название конечно-сходящихся.
Конечно-сходящиеся' алгоритмы гарантируют также,
что минимум функционала будет найден с помощью обу-
обучающей последовательности конечной длины.» Однако
80 ГЛ. IV. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ ОБУЧЕНИЯ
в общем случае оценить длину обучающей последова-
последовательности оказывается невозможно.
Можно представить себе такой вариант обучающей
последовательности, где исправление коэффициентов раз-
разделяющей гиперплоскости будет происходить на каждом
ее элементе (возможно, искусство педагога и заключается
в умении так подобрать материал обучения). Длина такой
обучающей последовательности равна необходимому чис-
числу исправлений. Возможен и такой состав обучающей
последовательности, когда между двумя элементами, на
которых происходят исправления, находится некоторое
число элементов, не приводящих к изменению коэффици-
коэффициентов. В этом случае длина обучающей последовательно-
последовательности, на которой произойдут все необходимые исправления,
будет значительно больше числа исправлений. В случае,
когда на обучающей последовательности произойдут все
необходимые исправления, полученная решающая гипер-
гиперплоскость обеспечит нуль функционалу Р (X).
Однако в нашей постановке задачи требуется отыска-
отыскание не оптимальной, а близкой к ней гиперплоскости,
притом отыскание такой гиперплоскости должно произой-
произойти не безусловно, а лишь с заданной вероятностью.
Такое решение задачи можно гарантировать на обу-
обучающей последовательности фиксированной длины. Ниже
будет показано, что если алгоритм конечно-сходящийся,
то для любых е и г] существует такое число шагов
I = N (е, г\, М), на котором хотя бы однажды будет по-
получено решающее правило требуемого качества. Поэтому
возникает необходимость' установить, в какой момент
(после какого шага рекуррентной процедуры) с вероят-
вероятностью 1 — г] можно утверждать, что построено требуемое
решающее правило.!
Теоремы, устанавливающие этот момент, т. е. момент
окончания процесса обучения, получили название теорем
об останове рекуррентных алгоритмов.
§ 4. Теоремы об останове
Пусть одновременно с построением разделяющей ги-
гиперплоскости будет выясняться качество построенной к
данному моменту гиперплоскости. Если оно высоко, то
обучение прекращается; в противном случае обучение
§ 4. ТЕОРЕМЫ ОБ ОСТАНОВЕ 81
продолжается. Таким образом, кроме алгоритма построе-
построения разделяющей гиперплоскости имеется алгоритм
проверки качества построенной гиперплоскости. Бу-
Будем пользоваться следующим критерием: процесс обуче-
обучения заканчивается, как только после некоторого (к-то)
исправления решающего правила очередные тп (к) эле-
элементов обучающей последовательности не приводят к из-
изменению решающего правила. Теория останова, по су-
существу, исследует два вопроса:
1) какими должны быть величина тп (к), чтобы в слу-
случае, если останов произойдет, можно было бы утверждать,
что с заданной вероятностью качество построенного ре-
решающего правила будет не хуже требуемого;
2) на какой длине обучающей последовательности за-
заведомо произойдет останов.
Ответ на эти два вопроса дают следующие теоремы.
Теорема 4.1. Если в соответствии с критерием оста-
останова процесс обучения закончится, то с вероятностью,
большей 1 — т), можно утверждать, что построенное ре-
решающее правило характеризуется качеством е при усло-
условии, что
у ' 1п A — е) '
где 0 <; г] < 1; п — любая константа, большая 1;
с() 2Л
1=1 *
Доказательство. Пусть в процессе обучения
сменяются решающие правила
Р (х, а), . . ., Р {х, ак), . . .
Оценим вероятность того, что останов произойдет в тот
момент, когда выбрано правило Р (х, а) с качеством
Р (а) > в.
Пусть, например, после к-то исправления выбрано пра-
правило Р (х, ак) с качеством Р (ак) ^> е; при этом условии
вероятность Рк того, что останов произойдет после к-то
(но до (к •{- 1)-го) исправления, равна вероятности
того, что за этим исправлением последует т (к) безо-
безошибочных опознаний, т. е.
рк = A _ р (ак))тЮ < A - е)т(*>.
82 ГЛ. IV. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ ОБУЧЕНИЯ
Тогда вероятность Р того, что останов произойдет
после одного из исправлений, когда Р (ак) ^> е, оцени-
оценивается так:
Таким образом, справедлива оценка;
Выберем теперь функцию т (к) такую, что
A_е)™№) = « . D.5)
/С
Из равенства D.5) может быть найдено, что
/7Ч 1па— л1п к
Остается определить величину а. Найдем ее из условия
т. е.
оо 1
где
Из этого соотношения находим, что
1п а = 1п г] - 1п С (л). D.7)
$ 4, ТЕОРЕМЫ ОБ ОСТАНОВЕ 83
Таким образом, из D.6) и D.7) следует, что при
вероятность Р меньше требуемой величины т]. Оценка D.8)
справедлива для любого п ^> 1. В частности, при п = 2
$B)=^-, откуда
я2
1п т) — 21п к — 1п -я-
"»<*> = ЩГ=7) "
Теорема доказана.
Теорема 4.2. Пусть конечно-сходящийся алгоритм та-
таков, что число коррекций не превосходит величину М, а в
качестве т (к) взята функция D.8), описанная в условии
теоремы 4.1; тогда можно утверждать, что останов
заведомо произойдет на обучающей последовательности
длины
, 1пт) — 1п ^ — л 1п М у.
1п A — е)
Доказательство теоремы очевидно.
Для персептрона Розенблатта в силу теоремы Новико-
Новикова М <С ——, поэтому останов произойдет на обучающей
последовательности длины
В
1п т) — 1п I (л) — 2л 1п —
1 =
Существует некоторая тонкость в понимании приве-
приведенных теорем об останове. Эти теоремы никак не гаран-
гарантируют, что после того, как будет сделано I шагов, по-
построенная разделяющая гиперплоскость окажется тре-
требуемого качества. Теоремы гарантируют лишь то, что
до 2-го шага обязательно произойдет останов и что в мо-
момент останова построенная гиперплоскость окажется за-
заданного качества.
Если же алгоритм не остановить, то, вообще говоря,
может случиться, что последующие коррекции ухудшат
качество решающего правила и к 1-му шагу это качество
будет ниже требуемого.
84 ГЛ. IV. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ ОБУЧЕНИЯ
§ 5. Метод циклического повторения обучающей
последовательности
Итак, конечно-сходящиеся алгоритмы способны обу-
обучаться, используя последовательность примеров фикси-
фиксированной длины. Оценка длины такой последовательно-
последовательности позволяет, хотя и грубо, составить представление
о том, приемлем ли алгоритм для практического ис-
использования; ведь на практике редко встречаются зада-
задачи, где на обучение выделено больше нескольких сотен
примеров.
Какова же достаточная длина последовательности
примеров для персептрона Розенблатта?
Выше мы установили, что длина обучающей последо-
последовательности пропорциональна числу необходимых ис-
исправлений коэффициентов X и определяется величи-
величиной (—г")- Для персептрона Розенблатта величина В2
легко оценивается, если учесть, что векторы у бинарные,
В2 ^ т, т. е. величина В не превосходит размерности про-
пространства. Для величины ро — расстояния между непе-
непересекающимися выпуклыми оболочками двух групп би-
бинарных векторов — существует оценка снизу. Это рас-
расстояние может быть достаточно малым (<~ 2~т, где т —
размерность пространства), и тогда оценка числа исправ-
исправлений становится большой: ~ 2т.
Конечно, это оценка пессимистическая. Существуют
и такие множества векторов, для которых расстояния
между выпуклыми оболочками довольно большие, напри-
например имеют порядок 1/т. Однако такие пары множеств
составляют скорее исключение, чем правило.
Казалось бы, в данной ситуации обучение на реальном
числе примеров (несколько сотен) возможно лишь в ис-
исключительных случаях. Вспомним, однако, что выше нас
всюду интересовало только число исправлений, независи-
независимо от того, на каком материале они происходили. При этом
оказывалось, что если только нужное число исправлений
проведено, то можно гарантировать, что искомое решаю-
решающее правило найдено. А раз так, возникает мысль исполь-
использовать одну и ту же обучающую последовательность не-
несколько раз: предъявлять ее обучающемуся устройству
до тех пор, пока при очередном предъявлении не будет
§ 5. МЕТОД ЦИКЛИЧЕСКОГО ПОВТОРЕНИЯ 85
ни одного исправления коэффициентов. Прекращение
исправлений решающего правила как раз и будет озна-
означать, что обучающая последовательность разделена пра-
правильно. Но это-то и означает также, что реализуется метод
минимизации эмпирического риска.
Таким образом, попытка уменьшить длину обучающей
последовательности приводит к тому, что рекуррентную
процедуру приходится заменять более сложной — рекур-
рекуррентной процедурой с циклическим повторением обучаю-
обучающей последовательности, что приводит к методу миними-
минимизации эмпирического риска. Однако теперь приходится
помнить всю обучающую последовательность. Это об-
обстоятельство лишает рекуррентную процедуру ее основ-
основного удобства.
Наличие памяти у обучающегося устройства сущест-
существенно меняет его возможности. Теперь в процессе обуче-
обучения целесообразно различать два момента. Во-первых,
сколько элементов обучающей последовательности доста-
достаточно хранить в памяти, чтобы, в конце концов, гаран-
гарантировать выбор нужного решающего правила. И, во-
вторых, сколько раз должна просматриваться обучающая
последовательность, прежде чем будет выбрано решающее
правило, безошибочно ее разделяющее.
Таким образом, при конструировании обучающихся
машин с памятью приходится отвечать на два вопроса:
какой должен быть информационный массив, достаточный
для выбора нужного решения, и как долго этот массив
будет обрабатываться.
У персептрона Розенблатта на каждом шаге вычисли-
вычислительной процедуры использовался один элемент обучаю-
обучающей последовательности, и поэтому здесь информационный
массив равен количеству шагов, необходимых для выбора
нужного правила. Оценка достаточной длины обучающей
последовательности персептрона, по существу, устанавли-
устанавливает и достаточное количество шагов для вычисления ре-
шаюшего правила.
Если же модифицировать персептрон Розенблатта,
снабдив его памятью, а при обучении элементы обучаю-
обучающей последовательности циклически повторять до тех пор,
пока не перестанут меняться коэффициенты К, то доста-
достаточный информационный массив такого персептрона,
как будет показано в главе V, пропорционален величине
86 ГЛ. IV. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ ОБУЧЕНИЯ
т (т — размерность спрямляющего пространства), а чис-
число шагов, необходимое для выбора нужного правила, про-
пропорционально величине —^ .
Важно, что при р -> 0 информационный массив (длина
обучающей последовательности) не увеличивается, а уве-
увеличивается лишь объем вычислений. При наличии совре-
современных вычислительных средств увеличение объема вы-
вычислений не является принципиальной трудностью для
решения задач обучения распознаванию образов, в то
время как увеличение информационного массива сопря-
сопряжено с трудностями отыскания новой информации.
§ 6. Метод потенциальных функций
В 60-х годах М. А. Айзерман, Э. М. Браверман,
Л. И. Розоноэр предложили для решения задач обучения
распознаванию образов использовать разработанный ими
метод потенциальных функций [1]. Этот метод также реа-
реализует идею рекуррентной процедуры минимизации сред-
среднего риска. Применительно к задаче обучения распо-
распознаванию образов суть метода заключается в следующем.
На пространстве входных векторов х задается функция,
которая называется «потенциалом». Потенциал определя-
определяет близость двух точек, х, х0, и обычно задается как функ-
функция расстояния между точками. Потенциальная функция,
как правило, такова, что она монотонно уменьшается
с увеличением расстояния. Примерами потенциальной
функции могут служить
К (*, х0) = 1 +'гаа , К (х, х0) = е~'\
где г = 1/ 2 (хо — ?1J—расстояние от точки х0 = (х\,...
1=1
..., ж") до точки х1 = (#1, . . ., х1); а — константа.
С помощью таких функций на пространстве X образует-
образуется потенциальное поле. Считается, что вектор х относится
к первому классу, если потенциал поля в точке х поло-
положителен; в противном случае вектор х относится ко вто-
второму классу. Процесс обучения, таким образом, заклю-
| 6. МЕТОД ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ 8?
чается в построении с помощью обучающей последова-
последовательности потенциального поля.
Геометрическая интерпретация метода построения по-
потенциального поля очень наглядна (рис. 9). Пусть для
обучения машине предъявляется обучающая последова-
последовательность щхг, . . ., шгх1. При появлении первого элемен-
элемента обучающей последовательности % «выпускается» по-
потенциал с центром в точке х1. Знак потенциала определя-
определяется тем, к какому классу относится предъявленный
Ф\
Рис. 9.
пример: если к первому, то знак у потенциала положи-
положительный, если ко второму, то отрицательный. Теперь на
пространстве X задан некоторый потенциал. Для второго
элемента обучающей последовательности может быть вы-
вычислена величина потенциала К (я2, %). Если величина
потенциала положительная, а элемент обучающей по-
последовательности относится к первому классу, то потен-
потенциальное поле на пространстве X не меняется; если же
величина потенциала в точке х% положительная, а вектор
х2 должен быть отнесен ко второму классу, то из точки х%
«выпускается» новый потенциал, но с отрицательным
знаком. Теперь на пространстве X действует новый сум-
суммарный потенциал
Ф(х)=К (х, Хг)~К (х, хг).
Аналогично, если при классификации элемента
обучающей последовательности с помощью суммарного
88 ГЛ. IV. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ ОБУЧЕНИЯ
потенциала совершается ошибка, потенциал меняетсятак,
чтобы по возможности выправить ошибку.
Таким образом, результатом обучения в методе по-
потенциальных функций является построение на простран-
пространстве X потенциального поля
(здесь штрих у суммы означает, что суммирование про-
проводится не по всем элементам обучающей последователь-
последовательности, а лишь по тем, на которых совершалась «ошибка»).
Это поле разбивает все пространство на две части:
часть пространства X, где значение суммарного потен-
потенциала положительно (все точки в этой части пространства
считаются принадлежащими первому классу), и части,
где значения потенциала отрицательны (точки в этой
части пространства считаются принадлежащими второму
классу). Поверхность, на которой потенциал принимает
нулевые значения, является разделяющей поверхностью.
Оказывается, что для всякого вида потенциала суще-
существует система функций щ (х), . . . ук (х), . . . (вообще
говоря, бесконечная!) такая, что все возможные разделяю-
разделяющие поверхности, которые могут быть получены с помощью
метода потенциальных функций, могут быть получены
с помощью персептрона Розенблатта, где соответствующее
спрямляющее пространство задается преобразованиями
фх (х), . . ., фт (х), .... С другой стороны, для каждого
персептрона легко находится соответствующая потен-
потенциальная функция.
Таким образом, метод потенциальных функций близок
к персептронным методам Розенблатта. Для метода по-
потенциальных функций возможны те же модификации,
что и для персептрона Розенблатта.
Глава V
АЛГОРИТМЫ, МИНИМИЗИРУЮЩИЕ
ЭМПИРИЧЕСКИЙ РИСЕ
§ 1. Метод минимизации эмпирического риска
Выше было установлено, что рекуррентные алгоритмы
обучения распознаванию образов приводят к успеху, но
при этом необходимо использовать достаточно большую
обучающую последовательность. Длину последователь-
последовательности можно сократить, но тогда обучающееся устройство
должно иметь память и помнить всю обучающую последо-
последовательность. Последовательность должна использоваться
многократно до тех пор, пока коэффициенты разделяющей
гиперплоскости не перестанут меняться, т. е. до тех пор,
пока элементы обучающей последовательности не будут
разделены гиперплоскостью безошибочно. Безошибочное
разделение обучающей последовательности означает, что
выбрано решающее правило, минимизирующее эмпири-
эмпирический риск.
Таким образом, оказалось, что попытка уменьшить
достаточную для обучения длину последовательности при-
привела к минимизации эмпирического риска. Возникает
вопрос, всегда ли в задаче обучения распознаванию обра-
образов метод минимизации эмпирического риска приводит
к успеху?
Нет, это не так. Вот пример обучающегося устройства,
которое минимизирует эмпирический риск, но не способ-
способно обучаться. Устройство запоминает элементы обучаю-
обучающей последовательности, а каждую ситуацию, предъяв-
предъявленную для распознавания, сравнивает с примерами,
хранящимися в памяти. Если предъявленная ситуация
совпадает с одним из хранящихся в памяти примеров,
то она будет отнесена к тому классу, к которому относится
90 ГЛ. V- МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
пример. Если же в памяти устройства нет аналогичного
примера, то ситуации классифицируются наудачу (на-
(например, с помощью бросания монеты). Понятно, что это
устройство, вообще говоря, не может ничему научиться,
так как в обучающую последовательность обычно входит
лишь ничтожная доля ситуаций, которые могут возник-
возникнуть при контроле. А вместе с тем такое устройство клас-
классифицирует элементы обучающей последовательности безо-
безошибочно.
Как же различить, когда метод минимизации эмпири-
эмпирического риска может быть успешно применен в задаче
обучения распознаванию образов, а когда нет? Ответ на
вопрос и составляет содержание теории алгоритмов обу-
обучения распознаванию образов, минимизирующих эмпи-
эмпирический риск.
§ 2. Равномерная сходимость частот появления
событий к их вероятностям
Рассмотрим снова функционал, минимизация которого
в нашей постановке составляет суть задачи обучения рас-
распознаванию,
Р(а) =1(а-Р(х, а)JЙР(со, х).
Как уже указывалось, этот функционал для каждого
решающего правила Р (х, а) определяет вероятность
ошибочной классификации. Эмпирическая оценка функ-
функционала, вычисленная на обучающей последовательности
I
Рэмп (а) = у(а) = у2(щ1-^ (*'а)J
1=1
для каждого решающего правила Р (х, а), определяет
частоту неправильной классификации на обучающей по-
последовательности.
Согласно классическим теоремам теории вероятностей
частота появления любого события сходится к вероятно-
вероятности этого события при неограниченном увеличении числа
испытаний. Однако из этих теорем никак не следует, что
решающее правило Р (х, а*), которое имеет минималь-
минимальную частоту ошибок V (а), будет иметь минимальную (среди
этих же правил) или близкую к минимальной вероятность
§ 2. РАВНОМЕРНАЯ СХОДИМОСТЬ ЧАСТОТ К ВЕРОЯТНОСТЯМ 91
ошибки. Это утверждение является очень важным и по-
поэтому разберем его подробнее.
Предположим для наглядности, что решающие правила
Р (х, а) задаются скаляром а, который может принимать
значения от 0 до 1. Каждому значению а ставится в соот-
соответствие решающее правило, для котогого существует
вероятность ошибки Р (а).
Таким образом, каждому
а может быть поставлено
в соответствие число Р(а).
Рассмотрим функцию Р (а)
(рис. 10). Наряду с этой
функцией может быть по-
построена и функпия V (а),
которая для каждого а
определяет частоту оши-
ошибочной классификации с Рис, 10.
помощью правила Р (х,а),
вычисленную на обучающей последовательности.
Метод минимизации эмпирического риска предлагает
по минимуму функции V (а) судить о минимуме функции
Р (а). Для того чтобы по точке минимума и минималь-
минимальному значению функции V (а) можно было судить о точке
минимума функции Р (а) и о ее минимальном значении,
достаточно, чтобы кривая V (а) находилась внутри
е-трубки кривой Р (а). Напротив, выброс хотя бы в од-
одной точке (как на рис. 10) может привести к тому, что
в качестве минимального значения Р (а) будет выбрана
точка выброса. В этом случае минимум V (а) никак не
характеризует минимум функции Р (а). Если же функция
V (а) приближает Р (а) равномерно по а с точностью е,
то качество эмпирически оптимального решающего пра-
правила отличается от качества истинно оптимального пра-
правила не более чем на 2е.
Формально это означает, что нас интересуют не клас-
классические условия, когда для любых а и е имеет место
Р {IV (а) -Р(а) |>е}->0,
а более сильные условия, когда для любого е справедливо
Р {зир|у(а) -Р(а) | > е}-> 0. E.1)
92 ГЛ. V. МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
В случае, когда выполняется E.1), говорят, что имеет
место равномерная сходимость частот к вероятностям по
классу $ событий А (а). Каждое событие А (а) в классе $
задается решающим правилом Р (х, а) как множество
векторов х, которое это правило ошибочно классифи-
классифицирует.
Таким образом, эффективность решения задачи обуче-
обучения распознаванию образов методом минимизации эмпи-
эмпирического риска оказалась связанной с существованием
равномерной сходимости частот к вероятностям по классу
событий $.
§ 3. Теорема Гливенко
В классической математике уже однажды решалась
задача о равномерной сходимости. В 30-х годах замеча-
замечательный советский математик В. И. Гливенко доказал
теорему, согласно которой с ростом объема выборки эм-
эмпирическая кривая распределения сходится к функции
распределения равномерно.
Теорема Гливенко может быть сформулирована еще и
так: на прямой х задана система решающих правил
Р (х, а). Правило Р (х, а) относит точку х к первому
классу, если х ^ а, и относит ко второму, если х ^> а.
В соответствие этому правилу может быть поставлено
событие А (а), которое состоит в том, что точка х
отнесена к первому классу. Теорема утверждает, что ча-
частоты сходятся к вероятностям равномерно по всем собы-
событиям А (а) ЕЕ $1-
Однако с помощью этой теоремы можно обосновывать
правомочность замены среднего риска эмпирическим лишь
при поиске решений среди самых примитивных решаю-
решающих правил, таких, которые позволяют классифицировать
'только одномерные векторы по принципу: вектор х отно-
относится к первому классу, если х ^ а*, и ко второму,
если х > а*.
Чтобы гарантировать успех в применении метода ми-
минимизации эмпирического риска в классе линейных ре-
решающих правил, надо установить равномерную сходи-
сходимость частот к вероятностям для более сложного класса
событий 8т. Подобно тому как класс событий 5]. в теореме
Гливенко задавался всеми возможными полупрямыми,
§ 4, ЧАСТНЫЙ СЛУЧАЙ 93
класс событий 8т определяется всеми возможными полу-
полупространствами га-мерного векторного пространства х.
Здесь, аналогично одномерному случаю, каждое событие
задается неравенством
г=1
В этом смысле теорема, доказывающая равномерную
сходимость частот к вероятностям по классу событий 8т,
явилась бы прямым обобщением теоремы Гливенко на
многомерный случай. Для обоснования же применения
метода минимизации эмпирического риска в задаче
обучения распознаванию образов (не только для случая
линейных решающих правил!) надо найти условия, при
которых можно гарантировать равномерную сходимость
частот к вероятностям для различных классов событий.
§ 4. Частный случай
Рассмотрим простой случай: множество б1 конечно и
состоит из ./V событий Ах, . . ., А^. Для каждого фикси-
фиксированного события справедлив закон больших чисел (ча-
(частота сходится к вероятности при неограниченном увели-
увеличении числа испытаний). Одним из выражений этого за-
закона является оценка
Р {\у(А)-Р(А) |>е}<е-»". E.2)
Нас, однако, интересует случай равномерной сходи-
сходимости, т. е. вероятность одновременного выполнения
всех неравенств | V (Аг) — Р (Аг) | ^ е (ь = 1, 2, . . ., И).
Такая вероятность может быть оценена, коль скоро оце-
оценена вероятность выполнения отдельно каждого неравен-
неравенства E.2), а именно
Р{8ир \ч{Аг)-Р{Аг) | > е} <
Учитывая E.2), получим
Р {вир | V (Аг) - Р (Аг) | > е} <Лге~2е!'. E.3)
94 ГЛ. V- МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
Неравенство E.3) означает, что имеет место равномер-
равномерная сходимость
Р{8ир \у{А1)-Р(А1) | > е} 7_^ 0.
Потребуем теперь, чтобы вероятность
не превосходила величины т), т. е.
Р {зир \у(А1)-Р(А1) |>е}<г!. E.4)
Неравенство E.4) во всяком случае будет иметь место,
если величины И, е, т), / связаны соотношением
Ые-™ = 1\. E.5)
Разрешая равенство E.5) относительно е, найдем для
данных Лг, /, г] оценку максимального уклонения частоты
от вероятности в рассматриваемом классе событий:
../I
1п N — 1п т)
и •
Разрешая равенство E.5) относительно /, найдем, какова
должна быть длина обучающей последовательности, чтобы
с вероятностью, не меньшей 1 — т], можно было утвер-
утверждать, что минимум вероятности по классу событий 5
отличается от минимума частоты по этому же классу
событий на величину, не превосходящую е;
, 1п N — 1п т)
1= 2^ •
Иначе говоря, выше была доказана следующая теорема.
Теорема 5.1. Если из множества, состоящего из N ре-
решающих правил, выбирается решающее правило, частота
ошибок которого на обучающей последовательности рав-
равна V, то с вероятностью 1 — г\ можно утверждать, что
вероятность ошибочной классификации с помощью вы-
выбранного правила составит величину, меньшую V + е,
если длина обучающей последовательности не меньше
E.6)
§ 4. ЧАСТНЫЙ СЛУЧАЙ 95
В теореме важно, что достаточная длина обучающей
последовательности лишь логарифмически зависит от
числа событий в классе N.
Число решающих правил является весьма гру-
грубой характеристикой разнообразия класса решающих
правил (такая характеристика, например, никак не учи-
учитывает, состоит ли класс из одних и тех же или «близких»
элементов или же он состоит из существенно «различных»
функций). Однако качественные выводы, которые можно
сделать из этой оценки, довольно хорошо отра-
отражают существо дела — чем меньше емкость класса, тем
меньшей может быть длина обучающей последователь-
последовательности. Наоборот, чем универсальнее обучающееся ус-
устройство, тем большая информация необходима ему для
обучения.
Используя формулу E.6), можно получать достаточные
оценки длин обучающих последовательностей для различ-
различных алгоритмов, реализующих метод минимизации эм-
эмпирического риска. Так может быть получена оценка
длины обучающей последовательности для персептрона
с памятью (метод обучения с циклическим повторением
обучающей последовательности). Для этого достаточно
оценить число N различных решающих правил персеп-
персептрона. Для бинарного спрямляющего пространства число
различных векторов не превосходит 2т. Существует 22
способов разделения 2т векторов на два класса.
Однако персептрон делит множество векторов не всеми
способами, а только с помощью линейных дискриминант-
ных функций.
Число различных способов разделений с помощью
линейных дискриминантных функций N значительно мень-
те чем 22 •
Ниже будет показано, что Лг<2т2, и тогда, соглас-
согласно теореме, оценка достаточной длины обучающей по-
последовательности будет равна
, т? — 1п т)
1 - 2е» '
т. е. обучающая последовательность пропорциональна т2
(сразу же заметим, что эта оценка завышена; ниже будет
показано, что справедлива оценка / ~ т).
96
ГЛ. V. МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
§ 5. Оценка числа различных линейных
разделений векторов
Итак, оценим количество способов, которыми с по-
помощью гиперплоскости можно разделить на два класса /
векторов х1, . . ., хх в пространстве размерности т.
Г7
Рис. И.
Заметим, что в соответствие каждому вектору
ж = (ж1, . . ., ж™) пространства X может быть поставлена
гиперплоскость
2
1=1
= о,
проходящая через нуль в пространстве Л векторов
К = C^, . . ., Хт) и наоборот, каждому вектору X в прос-
пространстве X может быть поставлена в соответствие гипер-
гиперплоскость, проходящая через начало координат,
т
2 м = о.
1=1
Таким образом, / векторам х1, . . ., жг в пространстве
Л ставится в соответствие / гиперплоскостей (рис. 11).
Наше утверждение состоит в том, что число различ-
различных разделений векторов равно числу компонент, на
которые эти / гиперплоскостей разбивают т-мерное про-
пространство Л.
§ 5. ОЦЕНКА ЧИСЛА ЛИНЕЙНЫХ РАЗДЕЛЕНИЙ 97
В самом деле, поставим в соответствие каждой гипер-
гиперплоскости в пространстве X вектор X пространства А,
равный направляющему вектору гиперплоскости. При
этом непрерывному вращению разделяющей гиперплос-
гиперплоскости в X, не изменяющему разделение точек хх, . . ., .-г,,
соответствует в Л непрерывная траектория движения
точки к внутри одной из компонент пространства.
Оценим теперь, на какое число компонент могут раз-
разбить т-мерное пространство / гиперплоскостей, проходя-
проходящих через начало координат. Обозначим через Ф (т, I)
максимальное число компонент, на которое / гипер-
гиперплоскостей делят пространство размерности т, и
определим рекуррентную процедуру поиска числа ком-
компонент.
Очевидно, что в одномерном случае справедливо
Ф A, /) = 2.
Одна гиперплоскость делит пространство размерно-
размерности т на две части, т. е. справедливо
Ф (т, 1) = 2.
Пусть известно, что / — 1 гиперплоскость Г!, . . ., Гц
делит га-мерное пространство не более чем на Ф (т, I — 1)
компонент. Добавим новую гиперплоскость Гг. Если эта
гиперплоскость проходит через одну из «старых» компо-
компонент, то она дробит ее надвое. В противном случае старая
компонента сохраняется. Таким образом, при проведении
гиперплоскости Г, число компонент увеличится на столь-
столько, сколько компонент окажется разделено надвое.
В свою очередь каждая такая компонента К{ оставляет
на Г^след.^ |~| Г;. Число таких следов в точности равно
числу компонент, на которое гиперплоскости Гц . . ., Г,^
дробят новую гиперплоскость Г,. Поскольку размерность
Гг равна т — 1, число следов не превосходит Ф (т — 1,
Таким образом, мы получим следующее рекуррентное
уравнение:
Ф (т, I) = Ф (т, I — 1) + Ф (т — 1, I - 1),
Ф (т, 1) - 2, E.7)
Ф A, I) = 2.
98 ГЛ. V. МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
Решением уравнения E.7) является выражение
Ф (т, I) =
т.—1
2 2 с\-ъ если
2', если т^> I.
Нам, однако, удобнее будет пользоваться не этой
формулой, а" ее оценкой сверху (см. главу X)
или даже более грубой оценкой
Ф (т, I) < Г.
Число различных бинарных векторов не превосходит
2т и, следовательно, справедлива еще более грубая оцен-
оценка числа различных разделяющих гиперплоскостей:
N <Ф (т, 2т)< 2т2.
Эта-то оценка используется для получения оценки
длины обучающей последовательности.
Подставляя оценку N в E.6), получаем
_ т? — Ы ц
т. е. длина обучающей последовательности должна быть
пропорциональна т2.
. Как уже отмечалось, число различных решающих
Правил является слишком грубой характеристикой клас-
класса. Уже простейшие классы решающих правил содержат
бесконечное число элементов. Например, если только
в персептроне спрямляющее пространство не бинарное,
то число различных гиперплоскостей, разделяющих точки
этого пространства, бесконечно. Для такого класса ре-
решающих правил проблема возможности замены миними-
минимизации среднего риска минимизацией его эмпирической
оценки оставалась открытой и, как уже отмечалось, сво-
сводилась к исследованию обобщенной теоремы Гливенко.
5 6. УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ 99
§ 6. Условия равномерной сходимости частот появления
событий к их вероятностям
Обобщение теоремы Гливенко и построение теории
равномерной сходимости частот появления событий к их
вероятностям стали возможны благодаря введению более
тонкой меры разнообразия класса функций, чем число
функций в классе. Вот как она определяется.
Пусть задана система й решающих функций Р (х, а).
Рассмотрим класс событий
А (а) = {х : Р (х, а) = 1}.
Рассмотрим, далее, выборку хх, . . ., ж;. Известно, что,
вообще говоря, эта выборка может быть разделена на два
класса 21 способами. Однако нас будут интересовать толь-
только те способы разделения выборки, которые могут быть
реализованы с помощью решающих правил Р (х, а).
Число таких разделений зависит как от класса решающих
правил, так и от состава выборки. Будем обозначать это
число
А8 (хг,. . ., хг).
Так как хх, . . ., хг — случайная и независимая вы-
выборка, то число разделений — величина случайная, т. е.
случайной величиной будет А8 (хг, . . ., х{).
Разнообразие класса решающих правил будем изме-
изменять величиной математического ожидания 1д2 А8 (хг, ...
. . ., х{). Эту величину будем называть энтропией класса 8
решающих правил на выборках длины I и обозначать
Я8 (I) = М {1&2 А8 (хи . . ., х^}. E.8)
Оказывается, что для существования равномерной
сходимости частот V (а) появления событий к их вероят-
вероятностям Р (а) по классу событий $ необходимо и доста-
достаточно, чтобы последовательность
Д8A) Я8B) Я8 (О
стремилась к нулю при неограниченном увеличении длины
выборки /. Стремление к нулю отношения —г^- означа-
означает, что класс решающих правил состоит из «не слишком
100 ГЛ. V- МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РЙбЙА
разнообразного множества функций». Доказательство
этих утверждений дано в главах X и XI.
Как и всякие исчерпывающие условия, приведенные
необходимые и достаточные условия равномерной сходи-
сходимости частот появления событий к их вероятностям ис-
используют довольно тонкие понятия. На практике проверка
таких условий представляет значительные трудности.
В нашем случае трудности связаны с тем, что характер
распределения неизвестен, в то время как проверке под-
подвергается свойство энтропии, которая конструктируется
с помощью распределения Р (х).
Поэтому для использования на практике условий
равномерной сходимости целесообразно из данных усло-
условий получить более грубые достаточные условия, которые
не зависели бы от свойств распределения Р (х). Такие
условия могут быть получепы абстрагированием от свойств
распределения. Иначе говоря, на практике нас будут ин-
интересовать те условия, которым должен удовлетворять
класс решающих правил, чтобы при любой функции рас-
распределения можно было гарантировать существование
равномерной сходимости.
Огрубление необходимых и достаточных условий за-
заключается в том, что вместо энтропии функции Р (х, а)
рассматривается логарифм функции
т5 (I) = шах А6 (хъ .. . , хг),
*1 *1
где максимум определяется по всем возможным выборкам
длины I. Функцию т8 (I) назовем функцией роста класса
Р (х, а).
Функция роста построена так, что она не зависит от
распределения Р (х), и, кроме того, всегда выполняется
неравенство
1&2 т* (I) > ЯЗ @.
Теперь, если окажется, что величина
I
стремится к нулю с ростом /, то отношение
I
% 1. СВОЙСТВА ФУНКЦИИ РОСТА 101
й подавно устремится к нулю. Поэтому условие
11Ш : = У
является достаточным условием существования равно-
равномерной сходимости. Это условие может быть легко про-
проверено для различных классов решающих правил.
§ 7. Свойства функции роста
Функция роста класса решающих правил имеет про-
простой смысл: она равна максимальному числу способов
разделения I точек на два класса с помощью решающих
правил Р (х, а).
В главе X будет показано, что функция роста обладает
одним замечательным свойством, которое дает возмож-
возможность ее легко оценивать: она либо тождественно равна 21,
либо мажорируется степенной функцией 1,5 — т-т-, где
(п — 1I
п — минимальное число, при котором нарушается равен-
равенство т8 (I) = 21.
В первом случае для любого I найдется комбинация
точек хг, . . ., XI такая, что ее можно разбить всеми воз-
возможными способами на два класса с помощью решающих
правил Р (х, а).
Во втором случае это не всегда возможно. Существует
максимальное число точек п — 1, которое еще разбива-
разбивается всеми возможными способами с помощью правил
Р (х, а), но уже никакие п точек этим свойством не обла-
обладают. Оказывается, что при этом функция роста мажори-
мажорируется степенной функцией с показателем роста п — 1.
Число п —■ 1, таким образом, может служить мерой
разнообразия решающих правил в классе Й. Мы будем
называть его емкостью класса й (при т5 (Г) = 2х считаем
емкость бесконечной).
Нетрудно убедиться, что, если емкость класса конечна,
всегда имеет место равномерная сходимость частот к ве-
вероятностям. В самом деле, при этом
11т
и достаточное условие выполнено.
102 ГЛ. V. МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
Найдем функцию роста для класса линейных решаю-
решающих функций. Для этого достаточно определить макси-
максимальное число точек в пространстве размерности т, ко-
которые с помощью гиперплоскости можно разбить всеми
возможными способами на два класса. Известно, что это
число равно т + 1. Поэтому
"" ^7«=*." (то+ 1I *
Тот факт, что емкость класса линейных правил конеч-
конечна (равна т + 1), доказывает обобщенную теорему Гли-
венко. Отметим, что для гиперплоскостей, проходящих
через начало координат, более точная оценка функции
роста фактически была выведена в предыдущем параграфе.
§ 8. Оценка уклонения эмпирически оптимального
решающего правила
В главе X будет получена оценка скорости равномер-
равномерной сходимости. Оказывается, что
Оценка имеет тот же вид, что и для конечной системы
событий, но вместо числа событий ./V в правой части нера-
неравенства стоит функция роста. Таким образом, функция
роста служит мерой разнообразия класса событий.
Если емкость класса бесконечна (т8 (I) = 2'), оценка
E.9).тривиальна, так как правая часть неравенства боль-
больше единицы при всех I.
Если же емкость г конечна, оценка приобретает вид
E.10)
Правая часть неравенства стремится к нулю при
I —> оо и притом тем быстрее, чем меньше г. Можно по-
потребовать, чтобы вероятность Р {зир [ Р (а)—-V (а) [ ^> е}
а
не превышала заданное значение т].
§ 8. ОЦЕНКА УКЛОНЕНИЯ ЮЗ
Это во всяком случае произойдет, если
, с B1) I
4,5-у-е =т\.
Это равенство можно разрешить относительно е. Таким
образом, справедливо утверждение: с вероятностью, не
превышающей 1 —■ г\, максимальное по классу 5 укло-
уклонение частоты выпадения событий от вероятности не пре-
превосходит
А( )'пТ E.11)
Отсюда, в силу сказанного в § 2, непосредственно сле-
следует, что с вероятностью, превышающей 1 —■ г\, качество
эмпирически оптимального решающего правила отлича-
отличается от качества истинно оптимального не более чем на
А = 2е, т. е.
1-1П-3-
д I \1 \ г ■ I О
где I — длина обучающей выборки, а г — емкость класса
решающих правил, из которого осуществляется выбор.
В частности, для линейных решающих правил в простран-
пространстве размерности т
А =
Таким образом, при заданной длине обучающей вы-
выборки качество решающего правила, выбранного алго-
алгоритмом, тем ближе к наилучшему в классе, чем меньше
емкость класса й. Но следует помнить, что качество наи-
наилучшего в классе й решающего правила, вообще говоря,
напротив, тем выше, чем шире класс й.
Разрешая равенство E.11) относительно I, можно
оценить для фиксированной точности и надежности до-
достаточную длину обучающей последовательности (см.
главу XIII). Оказывается, что качество эмпирически
оптимального решающего правила с вероятностью,
104 ГЛ. V. МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
превышающей 1—г|, отличается от наилучшего в классе й
не более чем на е, если только длина обучающей выборки
достигает
Следовательно, достаточная длина выборки пропор-
пропорциональна емкости класса решающих функций. В част-
частности, для линейных решающих функций в т-мерном
спрямляющем пространстве достаточная длина пропор-
пропорциональна размерности т.
§ 9. Метод минимизации эмпирического риска
в детерминистской постановке задачи обучения
распознаванию образов
До сих пор при исследовании методов минимизации
эмпирического риска в задаче обучения распознаванию
образов не возникала необходимость различать две по-
постановки — детерминистскую и стохастическую, как при
исследовании методов стохастической аппроксимации.
Однако, вообще говоря, применение методов мини-
минимизации эмпирического риска в детерминистском вариан-
варианте задачи обучения распознаванию образов дает более
эффективные результаты. Во всяком случае, оценки ско-
скорости равномерной сходимости указывают на более быст-
быструю сходимость. Чтобы выяснить, почему это происходит,
вернемся сначала к частному случаю, рассмотренному
в § 4.
: Итак, пусть класс решающих правил состоит из конеч-
конечного числа N элементов {Р (х, аг)} A = 1,2,..., Ы).
Особенность детерминистской постановки заключается
в том, что по предположению среди этих решающих пра-
правил есть то, которое идеально решает задачу. Его-то или
близкое к нему правило и предлагается найти, используя
выборку Хъ . . ., XI.
■ ■■$ Искать такое решающее правило будем'методом мини-
минимизации эмпирического риска. Так как среди функций
{Р (х, аг)} есть та, которая идеально решает задачу,
то заведомо ясно, что на любой выборке хх, . . ., хг зна-
значение минимума эмпирического риска будет равно нулю.
Однако этот минимум может достигаться на многих
функциях. Поэтому возникает необходимость оценить ве-
§ 9. МИНИМИЗАЦИЯ РИСКА В ДЕТЕРМИНИСТСКОЙ ЗАДАЧЕ 105
роятность того, что при выборе любой функции, достав-
доставляющей нуль величине эмпирического риска, можно га-
гарантировать, что выбрана функция, качество которой не
хуже заданного е.
- Введем функцию
Г1, если 2 = 0,
6 B) = ( 0, если 2 > 0.
Тогда формально оценка скорости равномерной схо-
сходимости частот к вероятностям по множеству правил, для
которых частота ошибок равна нулю, связана с оценкой
вероятности следующего события:
{зир \у1-Р1 |-в (V,) > е}.
г
Так как число функций, на которых достигается нуль
величины эмпирического риска, не превосходит N —
числа всех элементов в классе, то справедливо неравен-
неравенство
Р{вир | V, - Р41 -в (V,) > е} <NР^, E.13)
г
где Рс — вероятность того, что решающее правило, для
которого вероятность совершить ошибку есть величина,
большая е, правильно классифицирует все векторы обу-
обучающей последовательности. Эту вероятность легко оце-
оценить:
Подставляя оценку Р[ в E.13), получим
Р {зир [ V, - Рг | .9 (V,) > е} < N A - вI.
г
Для того чтобы вероятность Р{зир | V/ — Р{\-^ (V,) ^> е}
I
не превосходила величину т|, достаточно выполнения
условия
ЛГ A _ е)' = т]. E.14)
Разрешая относительно I это равенство, получим
106 ГЛ. V. МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
Так как для малых е справедливо —1п A — е) ~ е,
то формула E.15) может быть представлена в виде
В отличие от оценки E.6) здесь знаменатель равен е,
а не е2. Разрешая E.14) относительно е, аналогично
получим
Таким образом, справедлива следующая теорема.
Теорема 5.2. Если из множества, состоящего из N ре-
решающих правил, выбирается такое правило, которое на
обучающей последовательности не совершает ни одной
ошибки, то с вероятностью 1 — т] можно утверждать,
что ^вероятность ошибочной классификации с помощью
выбранного правила составит величину, меньшую е,
если длина обучающей последовательности не меньше
, _ 1п N — 1п т)
— 1пA— е) -
В общем случае, когда класс решающих правил 5
состоит из бесконечного числа элементов, оценка
скорости равномерной сходимости для тех правил, на
которых частота равна нулю, имеет ту же структуру, что
и E.6) (см. главу XIII):
где т5 (I) — функция роста класса решающих правил 5.
В E.18) величина т5 (I) играет роль «числа элементов»
в классе.
Если объем класса ограничен:
1'" г! '
т. е. выполнены достаточные условия равномерной
5 10. ЗАМЕЧАНИЕ ОБ ОЦЕНКЕ СКОРОСТИ СХОДИМОСТИ Ю7
сходимости, то можно потребовать, чтобы вероятность
не превосходила заданное значепие т|.
Это заведомо произойдет, если величины I, е, г\, г
будут связаны соотношением
1H (г)! е ~ Т1-
Разрешая это равенство относительно I, можно получить
(см. главу XIII)
7 ~ г г~ 1пт1 / 1Р^
'дост — с [О.1.У)
С
(в отличие от E.12) здесь знаменатель не е2, а е). Разре-
Разрешим еще это же равенство относительно е. Заменяя г!
по формуле Стирлинга, получаем
с_о
21
E.19')
Таким образом, в детерминистском варианте поста-
постановки задачи оценки оказываются лучше, чем в общем
случае.
§ 10. Замечание об оценке скорости равномерной
сходимости частот появления событий
к их вероятностям
Почему же оценки, полученные для детерминистского
и стохастического вариантов постановки задачи, так
сильно различаются
Объяснение этому частично дано в предыдущем пара-
параграфе, где формулы E.3), E.10) и E.13), E.18) определяют
скорости равномерной сходимости частот появления
событий к их вероятностям по различным классам
событий $.
В детерминистском варианте постановки учитывают-
учитываются только те события исходного множества событий 5,
частоты которых равны нулю. Обозначим эт от подкласс
108 ГЛ. V. МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
^о- В стохастическом варианте задачи уклонение оцени-
оценивалось для всех событий исходного класса событий 5.
Формально этот факт находит свое отражение в струк-
структуре формул, задающих оценку равномерной сходимости,
E.10), E.18). Правая часть неравенств E.10), E.18) со-
состоит из двух сомножителей. Первый сомножитель ха-
характеризует емкость класса событий (он идентичен, как в
случае E.10), так и в E.18)), второй сомножитель оцени-
оценивает вероятность уложиться в заданное уклонение е
частоты от вероятности для любого события заданного
класса (в детерминистской постановке этот класс есть 5,),
в стохастической — этот класс совпадает с 5).
Оказывается, удается существенно по-разному оценить
этот второй сомножитель. Так как при стохастическом
варианте постановки априори не известны никакие ха-
характеристики вероятностей событий класса 5, то оценка
уклонения частоты от вероятности для любого события А,
принадлежащего 5, производится в условиях наиболее
неблагоприятного случая, когда Р (А) = -*■. Поэтому
возможна лишь оценка E.10).
Для детерминистского варианта постановки наиболее
неблагоприятное событие в классе 5 то, для которого
Р (А) = е. Для оценки уклонения частоты от вероятно-
вероятности этого события возможна более тонкая оценка E.14).
Таким образом, оценки, полученные для детерминист-
детерминистского и стохастического вариантов постановки задачи,
различаются так, как различаются оценки уклонения
частот от вероятностей в двух событиях: в событии А,
для которого Р (А) близко к нулю, и в событии А', для
которого Р (А') близко к 1/г-
Это обстоятельство заставляет внимательно отнестись
к тем требованиям, которые предъявляются к величинам
уклонения частот от вероятностей.
В задаче обучения распознаванию образов можно
ослабить требования к характеру сходимости: разумно
требовать не равномерного отклонения частот от вероят-
вероятностей для всех событий, а разрешить большее уклонение
для тех событий, которым соответствует вероятность,
близкая к 7г > и мепынее для событий с вероятностями,
близкими к нулю. Рассмотрим снова функции Р (а) и
V (а) (рис. 12), где Р (а) — вероятность ошибки для ре-
§ 10. ЗАМЕЧАНИЕ ОБ ОЦЕНКЕ СКОРОСТИ СХОДИМОСТИ Ю9
шающего правила Р (х, а), V (а) — частота ошибок этого
правила на выборке хх, . . . , хх.
Допустим, что оптимальным является правило Р (х, а0),
т. е. при а = а0 достигается минимум функции Р (а).
Для того чтобы гарантировать, что качество решающего
правила Р(х, ах), выбранного
из условия минимума числа
ошибок, отличается от опти-
оптимального не более чем на е, не-
необходимо и достаточно, чтобы
этот минимум лежал в области,
где Р (о)< Р (о0) + е.
Учтем далее, что сходимость
частот к вероятностям для фик-
фиксированного значения а проис-
происходит значительно быстрее,
чем равномерная сходимость по
всем значениям параметра. Поэтому уже при сравнительно
небольшой длине выборки можно принять, что Р (а0) с^.
^V (а0). Тогда е — близость качества правил Р (х, ах)
и р (х, а0) будет гарантирована, если потребовать, чтобы
для всех а, для которых Р (а) ^> Р (а0) + е> частота
V (а) была бы больше чем V (а0) ж Р (а0).
Оценим требующуюся для этого длину выборки. В гла-
главе XII будет показано, что справедлива односторонняя
оценка:
Р|зир
Положим
УР(л)
б =
Л\ <1Вт8
E.20)
Тогда из условия
зир
Р (а) — V (а)
E.21)
следует, что
V (а) > Р (а) г.
При Р (а) > Р (а0) + е получаем
V (а) > Р (а0) ж V I
НО ГЛ. V. МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
Таким образом, условия E.21) достаточно для е-бли-
зости эмпирически оптимального решающего правила к
истинно оптимальному. Подставляя значение б в E.20),
получаем
~ 4<Р(ао)+Е) . E.22)
В детерминистском случае Р (а0) = 0 и мы получаем
оценку, близкую к E.18), а при Р (а) ~ 7г — оценку,
близкую к E.10).
Результаты главы XII позволяют получить и другую
оценку качества решающего правила. Допустим, что
выполняется E.21). Тогда, разрешая E.21) относитель-
относительно Р (а), получим
E.22')
Потребуем теперь, чтобы E.21) выполнялось для всех
а с вероятностью, превышающей 1 —■ г\. Для .этого до-
достаточно правую часть E.20) приравнять ц;
ьч
1Ът3B1)е 4 = п.
Разрешая это уравнение относительно б и подставляя
найденное значение в E.22'), получаем окончательно
1а т3 B1) — 1п -Лг /
1п т3 B1) — \а -^г ,
+ V(а)
При /
а(Р <2-^ ^ — х
хA+1/1+ , 21^{а\1 -^4-V (а). E.23)
§ 11. ЗАМЕЧАНИЯ ОБ ОСОБЕННОСТЯХ МЕТОДА Ц1
Как и раньше, примем, что в точке а0
V (а0) ж Р (а0).
Заметим, что для эмпирически оптимального ах справед-
справедливо
V (а,) < V (о0) = Р (а0).
Тогда с вероятностью 1 — т]
I 21 \ т]
г 1а — + 1 -1П-5Г
/
X
2ГТ
г[1п — + 1)-
Используя E.22), можно получить оценку длины обу-
обучающей последовательности, которая в одном предельном
случае (при Р (а0) = 0) совпадает с оценкой E.19), а в
другом предельном случае (Р (а0) ж у2) — с оценкой
E.12). Для этого достаточно правую часть неравенства
E.22) приравнять т] и разрешить относительно I. Получаем
В этой главе были приведены качественные оценки
длины обучающей последовательности. Строгие оценки
получены в главе XIII. Однако при использовании оце-
оценок важно не столько их конкретное выражение (ведь
оценки получены в предположении наиболее неблаго-
неблагоприятных условий), сколько структура связи основных
параметров
г, I, е, Р (а0), т).
§ 11. Замечания об особенностях метода
минимизации эмпирического риска
Характерной особенностью изложенной теории мини-
минимизации эмпирического риска является полное отсутст-
отсутствие каких бы то ни было указаний на конструктивную воз-
возможность построения алгоритма. Это обстоятельство име-
имеет как свои недостатки, так и преимущества. Недостаток
заключается в том, что построенная теория не указывает
112 гл. у. минимизация эмпирического риска
на регулярные процедуры, которые должна реализовать
обучающая программа, как было в теории рекуррентных
алгоритмов. Здесь исследователю каждый раз приходится
изобретать алгоритмы, подчиняющиеся определенным об-
общим правилам.
Преимущество такой теории — ее общность. Так, при
исследовании задачи обучения распознаванию образов не
возникает необходимости различать две постановки зада-
задачи — детерминистскую и стохастическую. И если все су-
существующие рекуррентные алгоритмы обучения распозна-
распознаванию образов, по существу, строят в спрямляющем про-
пространстве разделяющую гиперплоскость, то конструк-
конструктивные идеи алгоритмов обучения распознаванию образов,
использующих метод минимизации эмпирического риска,
значительно богаче. В частности, метод минимизации
эмпирического риска может быть применен в классе ку-
кусочно-ломаных функций, логических функций опреде-
определенного вида и др.
Все эти преимущества связаны с тем, что метод мини-
минимизации эмпирического риска отвечает на вопрос «что
надо делать», оставляя в стороне вопрос о том, «как это
сделать». Поэтому для минимизации эмпирического рис-
риска широко могут быть использованы различные методы,
в том числе и эвристические.
Применение эвристических методов в этом случае име-
имеет теоретическое оправдание: если в классе решающих
правил, емкость которого невелика, выбрать правило,
которое хотя и не минимизирует эмпирический риск, но
доставляет ему достаточно малую величину, то в силу рав-
равномерной сходимости выбранное правило будет иметь до-
достаточно высокое качество.
Таким образом, алгоритм заведомо способен обучаться,
если:
1) емкость класса решающих правил алгоритма неве-
невелика,
2) выбирается правило, которое доставляет величине
эмпирического риска малое значение.
Конструктивные идеи таких алгоритмов имеют чрез-
чрезвычайно наглядную геометрическую интерпретацию: в
пространстве надо построить гиперповерность, принадле-
принадлежащую заданному классу гиперповерхностей (характер
класса гиперповерхностей существенно определяет осо-
; 12. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА ИЗ
бенность алгоритма), которая по возможности с мень-
меньшим количеством ошибок, разделяет векторы обучающей
последовательности одного класса от векторов обучающей
последовательности второго класса. Методы построения
таких разделяющих поверхностей и составляют кон-
конструктивную особенность алгоритмов обучения распозна-
распознаванию образов. При этом принято различать два класса
алгоритмов: алгоритмы, строящие «гладкие» разделяющие
гиперповерхности, и алгоритмы, строящие «не глад-
гладкие» разделяющие поверхности. Методы построения
гладких разделяющих поверхностей основаны на
построении разделяющей гиперплоскости в соответ-
соответствующем спрямляющем пространстве. Один из них —
метод обобщенного портрета будет подробно рассмотрен
в третьей части книги. Методы построения «не гладких»
разделяющих гиперповерхностей берут свое начало с работ
М. М. Бонгарда и М. Н. Вайнцвайга, предложивших один
из наиболее популярных алгоритмов обучения такого
типа — алгоритм «Кора» [4, 9].
§ 12. Алгоритмы метода обобщенного портрета
Алгоритмы метода обобщенного портрета реализуют
идею минимизации эмпирического риска в классе линей-
линейных и кусочно-линейных функций.
Сам метод обобщенного портрета состоит в специальном
способе построения разделяющей гиперплоскости. В слу-
случае, если обучающая последовательность может быть
разделена гиперплоскостью, существует целое семейство
разделяющих гиперплоскостей. Особенность метода зак-
заключается в том, что с его помощью строится оптимальная
разделяющая гиперплоскость (т. е. гиперплоскость, ко-
которая из всех разделяющих гиперплоскостей наиболее
далеко отстоит от ближайшего к ней элемента обучающей
последовательности). Важной особенностью метода обоб-
обобщенного портрета является возможность установить (в
случае, если это так), что «безошибочного» разделения
элементов обучающей последовательности не существует.
Различные алгоритмы, реализующие метод построения
обобщенного портрета, предназначены для построения
разделяющей гиперплоскости в условиях, когда безоши-
безошибочное разделение векторов невозможно. В этих случаях
114 ГЛ. V. МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
используются алгоритмы, минимизирующие эмпиричес-
эмпирический риск в классе линейных или кусочно-линейных ре-
решающих правил.
В качестве примера приведем здесь идею двух таких
алгоритмов (подробно система алгоритмов метода обоб-
обобщенного портрета будет рассмотрена в третьей части
книги).
Если обучающая последовательность не может быть
безошибочно разделена на два класса, среди векторов обу-
обучающей последовательности определяется тот, который
наиболее «препятствует» разделению. Он исключается из
обучающей последовательности, а оставшиеся векторы
вновь разделяются гиперплоскостью. Если разделение все
еще невозможно, то исключается еще один вектор, и так
до тех пор, пока множество оставшихся векторов не будет
разделено. При этом считается, что число исключенных
векторов минимально (или близко к нему). Правило
удалений определяется эвристическим понятием «вектора,
наиболее препятствующего разделению». Удаленные из
обучающей последовательности векторы как раз и со-
составляют множество неправильно опознанных векторов.
Отношение числа этих векторов к числу всех векторов
обучающей последовательности определяет величину
эмпирического риска для выбранного решающего пра-
правила (обобщенного портрета). Величина же истинного
риска для найденного правила с вероятностью 1 —т) отли-
отличается от эмпирического риска не более чем на е, где е
определяется согласно E.11).
Если с помощью приведенного алгоритма будет пост-
построена разделяющая гиперплоскость, которая неправильно
классифицирует слишком много векторов обучающей по-
последовательности, то считается, что в классе линейных
решающих правил нет удовлетворительного правила,
и делается попытка отыскать такое правило в классе ку-
кусочно-линейных правил. Для этого сначала строится раз-
разделяющая гиперплоскость, минимизирующая число оши-
ошибок, а затем к ней «пристраивается» еще одна гиперплос-
гиперплоскость, с тем чтобы с помощью гиперповерхности, состав-
составленной из двух кусков гиперплоскостей, минимизировать
число ошибок при разделении обучающей последователь-
последовательности. Если ошибок все еще много, то достраивается еще
одна гиперплоскость и т. д.
§ 13. АЛГОРИТМ КОРА 115
С увеличением числа к кусков гиперплоскостей умень-
уменьшается количество неправильно опознанных векторов,
т. е. уменьшается величина эмпирического риска. Однако
величина ей гарантированного уклонения истинного риска
от эмпирического растет с ростом числа кусков гипер-
гиперплоскостей по линейному закону
гк — кг.
Отсюда следует, что желательно разделить обучающую
последовательность с помощью минимального числа кус-
кусков гиперплоскостей.
Различные алгоритмы реализуют разные идеи построе-
построения такого кусочно^линейного правила, которое миними-
минимизирует сумму величины эмпирического риска и величины
гарантированного уклонения.
§ 13. Алгоритм Кора
Все рассмотренные до сих пор конструктивные идеи
алгоритмов обучения распознаванию образов были свя-
связаны с построением в спрямляющем пространстве разде-
разделяющей гиперплоскости. Алгоритм обучения распознава-
распознаванию образов «Кора») исходит из иных конструктивных
идей.
Пусть обучающая последовательность распадается на
два множества векторов — множество векторов первого
класса {х} и множество векторов второго, класса {%}.
Задается множество характеристических функций 1|} (х, т),
которые называются признаками. Из множества при-
признаков алгоритм выделяет так называемые достаточные
признаки. Достаточным признаком для векторов первого
класса называется признак 1|) (х, т*), который на всех
векторах второго класса принимает значение 0, а на не-
некоторых векторах первого класса 1.
Аналогично определяются достаточные признаки вто-
второго класса. Алгоритм выбирает I достаточных признаков
первого класса и I достаточных признаков второго клас-
класса, так, чтобы для каждого вектора обучающей после-
последовательности нашлось несколько достаточных призна-
признаков, принимающих на этом векторе значение 1. Иными
словами, признаки должны «покрывать» все множество
примеров.
116 ГЛ. V- МИНИМИЗАЦИЯ ЭМПИРИЧЕСКОГО РИСКА
Опознание вектора, не участвовавшего в обучении,
проводится так: подсчитывается, сколько достаточных
признаков первого класса на этом векторе приняли зна-
значение единица и сколько достаточных признаков второго
класса приняли значение единица. Вектор относится к
тому классу, для которого число достаточных признаков,
принявших значение единица, больше.
Особенность алгоритма «Кора» состоит в том, что рас-
рассматривается бинарное пространство X. В качестве клас-
класса характеристических функций 1|) (х, х) берутся все воз-
возможные конъюнкции двух-трех переменных.
Для каждого класса отбор конъюнкций (признаков)
производится по следующим правилам:
1. Из всех возможных признаков (конъюнкций трех
переменных) отбираются достаточные признаки. Доста-
Достаточные признаки упорядочиваются: считается, что при-
признак 1|) (х, хг) лучше, чем 1|) (х, т2), если число векторов
обучающей последовательности, обладающих этим при-
признаком (т. е. векторов, для которых 1|) (х, тх) = 1), больше
числа векторов, обладающих признаком 1|) (х, т2).
2. Из найденного множества достаточных признаков
исключаются «подчиненные». Признак^ (х, т2) называется
«подчиненным» признаку 1|) (х, т1), если множество векто-
векторов обучающей последовательности {х:^.(х, х1) = \),
обладающих признаком я|э (х, т,), включает в себя мно-
множество векторов {х:^.(х, т,) = 1}, обладающих при-
признаком 1|? (х, т2). Подчиненность признаков легко про-
проверяется от старшего в упорядоченном ряду признака
к младшему.
3. Из оставшихся достаточных признаков произво-
производится окончательный отбор I признаков. Принцип отбора
таков, чтобы в окончательный набор вошли признаки,
которые «покрывают» все множество примеров, данное на
обучение, и чтобы, по возможности, все примеры обладали
приблизительно одинаковым количеством признаков
(признаки должны «покрывать» множество примеров «рав-
«равномерно»).
Характерной особенностью алгоритма «Кора» являются
небольшая емкость класса решающих правил и чрезвы-
чрезвычайно простой метод (хотя и эвристический) поиска пра-
правила, минимизирующего эмпирический риск. Заметим,
что указать класс функций малой емкости, в котором
§ 13. АЛГОРИТМ КОРА Ц7
можно найти достаточно хорошее решающее правило,
значительно труднее, чем класс функций большой ем-
емкости.
Оценим число возможных решающих правил для алго-
алгоритма «Кора». Пусть бинарное пространство X имеет раз-
размерность п, тогда число возможных троек координат рав-
равно Сп- На каждой тройке с помощью конъюнкции может
быть задано восемь функций алгебры логики. Таким об-
образом, всего возможно Т = 8 Сп различных признаков.
Из возможных признаков должно быть отобрано I доста-
достаточных признаков первого класса и I достаточных призна-
признаков второго класса. Так как существует не более Ст спо-
способов выбрать I признаков из множества, содержащего Т
элементов, то число различных решающих правил N
ограничено величиной
N < (8 СтJ.
Следовательно, N <. ге6' и, согласно E.17), в случае,
если величина эмпирического риска близка к нулю, ве-
вероятность неправильной классификации с помощью най-
найденного правила уклонится от эмпирической оценки не
более чем на величину
п — 1п Т1
е =
I
Заметим, что величина уклонения пропорциональна
только логарифму размерности пространства. В этом и
есть замечательная особенность рассмотренного класса
не гладких решающих правил.
Глава VI
МЕТОД УПОРЯДОЧЕННОЙ
МИНИМИЗАЦИИ РИСКА
§ 1. О критериях оценки качества алгоритмов
До сих пор мы интересовались только тем, каким усло-
условиям должен удовлетворять алгоритм, чтобы обеспечить
машине способность обучаться. Были рассмотрены рекур-
рекуррентные алгоритмы. Оказалось, что они требуют достаточ-
достаточно большой обучающей последовательности. Поэтому бы-
была рассмотрена их модернизация, которая заключалась
в запоминании обучающей последовательности и много-
многократном ее использовании. Суть этой модернизации со-
состояла в том, что задача решалась методом минимизации
эмпирического риска. Были найдены условия, при кото-
которых алгоритмы минимизации эмпирического риска при-
приводят к успеху, и тем самым получена возможность
строить различные алгоритмы, способные обучаться рас-
распознаванию образов. Какой же алгоритм выбрать теперт
для решения конкретных задач? Какой из алгоритмов обу-
обучения распознаванию образов будет лучше работать на
выборках фиксированной длины I?
Для того чтобы строить наилучшие алгоритмы на вы-
выборках фиксированной длины (конечно-оптимальные ал-
алгоритмы), надо прежде всего договориться о том, как
оценивать качество алгоритма (т. е. о том, каков критерий
оптимизации).
Качество алгоритма обучения при решении конкрет-
конкретной задачи естественно определять как качество решаю-
решающего правила, выбранного им по обучающей последова-
последовательности. Качество же решающего правила Р (х, а*)
для конкретной задачи, заданной распределением Р (х, со),
§ 1. О КРИТЕРИЯХ ОЦЕНКИ КАЧЕСТВА АЛГОРИТМОВ Ц9
Рис. 13.
мы определили выше как
Р(а) = $ (и - Р (х, а*)J йР (х, со).
Но поскольку выбор решающего правила зависит от слу-
случайно составленной обучающей последовательности;^,«!,...
..., хг&1, величина Р (а) будет
случайной, зависящей от той
или иной реализации обучаю-
обучающей последовательности.
Случайная величина наибо-
наиболее полно характеризуется сво-
своей функцией распределения.
В нашем случае качество алго-
алгоритма, решающего фиксирован-
фиксированную задачу на выборках длины
I, будет определяться функцией
распределения качества \х(Р(а)).
Сравнивать качество двух
алгоритмов — значит сравни-
сравнивать две функции распределения. Если одна из функций
расположена не ниже другой (так, как на рис. 13), то
выбор может быть сделан однозначно. При таком распо-
расположении кривых для любых
двух точек с равными ордина-
ординатами абсцисса точки первой кри-
кривой лежит левее абсциссы точ-
точки второй кривой. Это значит,
что для любого уровня надеж-
надежности первый алгоритм гаран-
гарантирует достижение меньшего
значения функционала и пото-
потому лучше второго. Однако воз-
возможны и такие расположения
функций распределения качест-
качества двух алгоритмов, как на
рис. 14.
В этом случае для одного уровня надежности (р =
= 1 —т)х) оказывается предпочтительнее первый алгоритм,
а для другого (р = 1 — т]г) предпочтение должно быть
отдано второму. Таким образом, сравнивать между собой
функции распределения качества алгоритмов, решающих
некоторую задачу Р {х, со) на выборках длины I, можно
Рис. 14.
120 ГЛ. VI. МЕТОД УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
только при фиксированном уровне надежности. Это соз-
создает некоторые неудобства, поэтому будем иногда харак-
характеризовать качество алгоритма не функцией распределе-
распределения ц (Р (а)), а математическим ожиданием качества
В = 1 Р (а) ^ (Р (а)).
Теперь для решения предложенной задачи на выборках
длины / будем считать тот алгоритм лучшим, для которого
соответствующая величина математического ожидания
меньше.
Обозначим через А алгоритм обучения, а через Т кон-
конкретную задачу; тогда качество алгоритма А, решающего
задачу обучения распознавания образов Т на выборках
длины I, можно записать как функцию двух переменных
Вг(А, Т).
Итак, определено, как должно измеряться качество
ВI (А, Т) для любой фиксированной задачи Т. Далее сле-
следует договориться, как измерять качество алгоритма,
предназначенного для решения класса задач {Т}.
Разрешению этой трудности посвящена теория стати-
статистических решений. В этой теории для сравнения различ-
различных алгоритмов предлагаются следующие три критерия:
а) критерий Байеса,
б) критерий минимакса,
в) критерий минимакса потерь.
Критерий Байеса предлагает вычислять для каждого
алгоритма среднее по множеству всех задач качество.
Для этого надо знать закон, который указывал бы, с
какой вероятностью придется решать ту или иную зада-
задачу, т. е. знать функцию распределения Р (Т). Тогда
критерий Байеса определяется так:
Л) = 1 Н1 (А, Т) йР (Т).
Критерий минимакса наиболее осторожен. Он пред-
предлагает оценивать качество алгоритма как качество ре-
решения наиболее неблагоприятной для данного алгоритма
задачи. При таком критерии, напротив, совершенно не
принимается во внимание, какова вероятность того, что
на практике придется решать эту неблагоприятную за-
задачу. Поэтому может оказаться так, что качество алго-
алгоритма определяет задача, которая на практике никогда
§ 2. МИНИМАКСНЫЙ КРИТЕРИЙ 121
не встретится. Иначе говоря, этот критерий конструирует-
конструируется так:
1(А, Т).
Критерий минимакса потерь предполагает минимиза-
минимизацию наибольшей величины потери качества, ко-
которая возникает из-за применения данного алгоритма для
решения разных задач по сравнению с применением опти-
оптимального для каждой из задач алгоритма. Иначе говоря,
критерий минимакса потерь конструируется по правилу:
Дн.п (А) = шах(Я1 (А,Т)— шш Вг (А, Т)).
Т А
Эта глава посвящена сравнению различных алгорит-
алгоритмов обучения распознаванию образов. В ней будут рас-
рассмотрены оптимальные с точки зрения различных крите-
критериев алгоритмы, установлена близость алгоритмов, ми-
минимизирующих эмпирический риск, к оптимальным с точки
зрения минимаксного критерия и критерия минимакса
потерь. Однако алгоритмы, оптимальные по этим двум
критериям, не столь интересны, как алгоритмы, оптими-
оптимизирующие критерий Байеса. Построение же оптимальных
по критерию Байеса алгоритмов — задача, практически
неосуществимая из-за чрезвычайно громоздких вычис-
вычислений. Поэтому представляют интерес квазибайесовы про-
процедуры, которые сохраняют ценные свойства байесовых
процедур, но не столь громоздки. В этой главе будут рас-
рассмотрены алгоритмы упорядоченной минимизации риска,
которые реализуют такие процедуры.
Рассмотрение оптимальных алгоритмов начнем с ис-
исследования алгоритмов, оптимальных по минимаксному
критерию.
§ 2. Минимаксный критерий
Как было указано выше, в этом случае алгоритмы срав-
сравниваются по тому, как они решают наихудшую для себя
задачу. Используя этот критерий для выбора оптимально-
оптимального алгоритма, мы будем .действовать наиболее осторожно.
Следует отметить, что применение этого критерия бессмыс-
бессмысленно в случае, когда на круг решаемых задач заранее
не наложено ограничений. Дело в том, что всегда
122 ГЛ. VI. МЕТОД УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
существуют задачи, которым не может обучиться никакой
алгоритм (например, если Р {а>\х), независимо от х, равно
0,5 при со = 1 и при со = 0), и именно эти задачи и будут
наиболее неблагоприятными для всякого алгоритма обу-
обучения, а потому все алгоритмы будут оценены одинаково.
Если же круг задач заранее ограничен, минимаксный
критерий может представлять интерес.
Пусть, например, заранее известно, что все задачи та-
таковы, что для каждой из них в классе $ существует без-
безошибочное разделяющее правило (детерминистский слу-
случай). Тогда, как установлено в предыдущей главе, для лю-
любой задачи алгоритм А, основанный на минимизации эм-
эмпирического риска, с вероятностью, превышающей 1 — -п,
построит по обучающей последовательности длины I
решающее правило с качеством не хуже
где п — показатель функции роста класса 5. Полагая
т) = 1/1 и переходя к математическому ожиданию, полу-
получим, что
шш Пг (Д Т) < 2 »даа-1п» + 1) + 1+
А 1
для любой задачи Т рассматриваемого типа.
Следовательно,
С другой стороны, как показано в приложении, сущест-
существует и оценка снизу:
тш тах Вг (А, Т) >
А Т
0,5 1 — , ) , если г<п,
— ^1--^^ 0,2 ттг, еслиг>п.
Таким образом, в этом случае любой алгоритм, осно
ванный на минимизации эмпирического риска, довольно
близок к минимаксному. Кроме того, при конечном п
§ 3. КРИТЕРИЙ МИНИМАКСА ПОТЕРЬ 123
минимакс стремится к нулю при I -*- оо, но тем медленнее,
чем больше п.
Отметим, что непосредственное конструирование оп-
оптимального сточки зрения минимаксного критерия алго-
алгоритма обучения для заданного круга задач,—вообще гово-
говоря, проблема чрезвычайно сложная и, вероятно, не-
неблагодарная.
§ 3. Критерий минимакса потерь
Рассмотренный в предыдущем параграфе критерий тре-
требует предварительного явного выделения определенного
круга задач. Это не всегда удобно. Чаще ситуация такова,
что задан определенный класс решающих правил $ и
рассчитывают на задачи, для которых в этом классе есть
«достаточно хорошие» разделяющие правила. Критерий
минимакса потерь позволяет не определять явно, что зна-
значит «достаточно хорошие» правила.
Идея этого критерия состоит в следующем. Для задан-
заданного набора алгоритмов () потери я определяются как раз-
разность между качеством данного алгоритма А для данной
задачи и качеством наилучшего для этой задачи алгорит-
алгоритма из набора ():
я (А, Т) = Я, (А, Т) — тга /?, (А, Т).
А®
В дальнейшем будем считать, что () состоит из всевозмож-
всевозможных алгоритмов обучения, выбирающих решающие пра-
правила из класса $. Тогда, как нетрудно убедиться,
я (А, Т) = Пг {А, Т) — шш Р (а, Т),
где Р (а, Т) — качество решающего правила Р (х, а)
для задачи Т, и следовательно,
тш Р (а, Т)
8
— это качество наилучшего для данной задачи решающе-
решающего правила из класса $.
Таким образом, потери оценивают степень «недоучен-
ности», тогда как тш/^а, Т) — это тот процент ошибок,
8
который неизбежен даже при идеальной обученности.
124 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
Максимум потерь определяется как потери на наибо-
наиболее неблагоприятной с этой точки зрения задаче. Заме-
Заметим, что в случае минимаксного критерия задача счи-
считается «плохой», если выбранный алгоритм дает большое
число ошибок на экзамене независимо от того, сущест-
существует ли вообще в данном наборе алгоритм, который хо-
хорошо решает задачу. В случае же минимакса потерь за-
задача считается «плохой», если выбранный алгоритм
работает плохо, но существует другой алгоритм из
данного набора, который эту конкретную задачу решает
хорошо.
Результаты предыдущей главы могут быть применены
для оценки сверху величины минимакса потерь алгорит-
алгоритмов, минимизирующих эмпирический риск. В соответ-
соответствии с оценкой E.11) для любой задачи распознавания
алгоритм А, основанный на минимизации эмпирического
риска, с вероятностью 1 — т| выберет решающее правило,
отличающееся от оптимального в классе $ пе более чем на
-*/-■ -,_-,
Aп 21 — 1а п + 1) — 1а т]/5
Положив т] = -г, перейдем к математическому ожиданию;
получим, учитывая, что Р (а) <^ 1,
1а2г-1п';+1)+1п5г +4--
Следовательно,
С другой стороны, можно установить оценку снизу (см.
приложение)
тш тах я (/4, Т) >
0,5е п, если ^<!п,
/0,25 + 4-)е-''п, если гс<2<22,
8л к
-у- A — ег! A)), если ^ > 2ге,
$ 3. Критерий мийимакса потерь 12§
для алгоритмов А, выбирающих разделяющее правило из
класса $, и любых задач распознавания.
Таким образом, алгоритмы, минимизирующие эмпи-
эмпирический риск, оказываются довольно близкими к опти-
оптимальным по критерию минимакса потерь. Очевидно, что
минимакс потерь при конечном п стремится к нулю при
/ ->■ оо. Если же функция роста т5 (Г) = 2', то максималь-
максимальные потери вообще не убывают с ростом I, оставаясь рав-
равным 0,5, т. е. обучение не происходит.
Как было показано в главе V, величина п, входящая
как в верхнюю, так и в нижнюю оценку минимакса по-
потерь, является мерой объема класса $. Таким образом,
минимакс потерь тем больше, чем шире класс решающих
правил, из которого осуществляется выбор. Это несколь-
несколько парадоксальное заключение легко понять, если учесть,
что мы фактически рассматриваем только такие задачи,
для которых в классе $ есть решающее правило, удов-
удовлетворительно разделяющее классы. Это значит, что
с увеличением класса $ расширяется и круг задач, из
которого выбирается наиболее трудная для данного
алгоритма.
Вообще для данного алгоритма А и задачи Т средний
риск (т. е. качество) распадается на три составляющие:
Н (А, Т) = л (А, Т) + Аг (Т, 8) + Л2 (Т).
Здесь А2 — это неизбежная составляющая риска, которая
остается даже при использовании самого лучшего решаю-
решающего правила для данной задачи, выбранного без всяких
ограничений. Величина Ах + А2 определяет качество наи-
наилучшего решающего правила в классе 5; таким образом,
Ах — это потери, связанные с ограничением, заставляю-
заставляющим выбирать правило только из класса $ (в детерминист-
детерминистской постановке Л2 + Дх = 0). Наконец, л — это потери
в смысле, определенном выше; они отражают то, насколь-
насколько решающее правило, выбираемое алгоритмом А в ходе
обучения, близко к оптимальному в классе $•
Величина А2 (Т) зависит только от задачи распознава-
распознавания. Величина Ах (Т, А) зависит уже от класса 5, но не
зависит от алгоритма обучения. Потери же л (А, Т) за-
зависят от задачи, класса 5 и конкретного алгоритма обу-
обучения.
126 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
§ 4. Критерий Байеса
Пусть априорные сведения о природе задач, на кото-
которые рассчитывается алгоритм обучения, задаются как ап-
априорная вероятность тех или иных задач. В этом случае
теория статистических решений предлагает метод построе-
построения оптимального алгоритма обучения в смысле средне-
среднего качества по ансамблю задач, т. е. метод минимизации
критерия Байеса
ДБ-,Песд(-4) = 2^апрG>Я((Л, 7').
Следующая схема реализует оптимальную по критерию
Байеса процедуру обучения.
1. Пусть дана обучающая последовательность х^а^. . .
. . . , хь а>1. По этой последовательности для каждой
задачи Т вычисляется апостериорная вероятность Рапост (Т)
того, что алгоритм столкнулся именно с этой задачей:
Лшр
(■* ) = I
р
Т г=1
где Рапр (Т) — априорная вероятность задачи Т.
Здесь Рт (х, ш) — распределение, соответствующее за-
задаче Т.
2. Для каждой ситуации х вычисляется апостериор-
апостериорная вероятность того, что она будет отнесена (учителем)
к классу ш:
Рапост (й) \х) = 2 Рт ((й\х) Рапост {Т).
т
3. Наконец, строится решающее правило Р (х), ра-
работающее следующим образом:
V _ /1, если Рапост A|ж) > 0,5,
^ ^ - \0, еСЛИ Рапост (Цх) < 0,5.
Несмотря на всю привлекательность байесовой стра-
стратегии обучения, она оказывается практически неосущест-
неосуществимой, так как, за исключением простейших случаев,
приводит к чрезвычайно громоздким вычислениям. Кроме
§ 5. УПОРЯДОЧЕНИЕ КЛАССОВ РЕШАЮЩИХ ПРАВИЛ 127
того, сведения об априорной вероятности различных за-
задач весьма расплывчаты, поэтому точное следование оп-
оптимальной по Байесу процедуре'может оказаться нецелесо-
нецелесообразным. Представляют интерес «квазибайесовы» про-
процедуры, которые сохраняют ее ценные свойства и не столь
громоздки.
Необходимо отметить, что, в отличие от других приме-
применений байесовой процедуры, в задачах распознавания об-
образов априорные сведения о задачах, которые предстоит
решать, существенны и от них сильно зависит выбираемое
решающее правило. В частности, можно показать, что
эффективно могут работать лишь алгоритмы, рассчитан-
рассчитанные на достаточно узкий класс задач по сравнению со все-
всеми возможными. Поэтому, для того чтобы байесова стра-
стратегия была эффективной, необходимы такие априорные
вероятности задач, чтобы огромное большинство задач
было в совокупности маловероятно, а ничтожное мень-
меньшинство образовывало множество, вероятность которого
близка к единице.
§ 5. Упорядочение классов решающих правил
Последнее замечание предыдущего параграфа можно
записать следующим образом. Пусть () — множество
всех возможных задач. Тогда из этого множества может
быть выделена система вложенных подмножеств
^с^с... аBпс:A F.1)
такая, что вероятность Р ((^д встретить задачу из (I об-
образует систему неравенств
Рт<РЮг)<-~<РШ<1. F.2)
Суть замечания состоит в том, что при переходе от (); к
(?1+х количество задач должно резко возрастать, в то вре-
время как величины
АР; = Р ((?{+1) - Р ((^
монотонно уменьшаются.
Задание системы вложенных множеств F.1) и вероят-
вероятностей F.2) составляют априорные сведения о тех зада-
задачах, которые предстоит решать.
128 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
Огрубление байесовой стратегии обучения мы начнем
с того, что будем использовать априорную информацию,
заданную не двумя условиями F.1) и F.2), а одним усло-
условием F.1), полагая, что АР* уменьшаются. Особенностью
байесовой стратегии является то, что она с большим весом
учитывает гипотезы, априори более вероятные. Поэтому,
учитывая, что АР* монотонно уменьшаются, следующую
стратегию можно понимать как некоторую квазибайесо-
ву стратегию.
К обучающей последовательности применяется сна-
сначала алгоритм, рассчитанный на задачи из класса Bг.
Только в том случае, если он дает неудовлетворительные
результаты, применяется алгоритм, рассчитанный на
задачи из класса (J, и т. д.
Назовем такую стратегию методом упорядоченной ми-
минимизации риска.
Схема реализации этого метода такова. В классе ре-
решающих правил $ вводится упорядочение, т. е. строится
система вложенных множеств
^С^С ...С Я* = 5.
Затем в классе ^ ищется правило, минимизирующее
эмпирический риск. Если найденное решающее правило
оценивается как неудовлетворительное, то ищется пра-
правило, минимизирующее эмпирический риск в классе 82,
и т. д. Процедура поиска оканчивается, когда будет най-
найдено удовлетворительное решающее правило.
Заметим, что решения, полученные методом упорядо-
упорядоченной минимизации риска, вообще говоря, отличаются
от решений, полученных методом минимизации эмпири-
эмпирического риска.
В первом случае выбирается правило, минимизирую-
минимизирующее эмпирический риск лишь в классе функций 5; (Г <$,
в то время как во втором случае правило минимизирует
эмпирический риск в 5.
Метод упорядоченной минимизации риска удобно рас-
рассматривать как двухуровневую процедуру обучения. На
первом уровне к обучающей последовательности приме-
применяется N алгоритмов Аъ . . ., Лдг, каждый из которых
выбирает решающее правило, минимизирующее эмпи-
эмпирический риск в классах $;. На втором уровне из N ото-
§ 6. О КРИТЕРИЯХ ВЫБОРА 129
бранных решающих правил выбирается то, которое ми-
минимизирует заданный критерий выбора*).
Для конструктивного задания алгоритмов метода упо-
упорядоченной минимизации риска необходимо определить:
1. Каков критерий выбора решающего правила (т. е.
задать алгоритм второго уровня).
2. Как вводить упорядочение класса решающих пра-
правил 5.
Теория метода упорядоченной минимизации риска
должна ответить на вопрос, какова эффективность мето-
метода (например, по сравнению с методом минимизации эм-
эмпирического риска).
§ 6. О критериях выбора
Известны две процедуры второго уровня. Обе они
существенно используют то, что на втором уровне выбор
решающего правила производится из небольшого числа
правил (порядка десятков или сотен) и поэтому пробле-
проблема равномерной сходимости здесь не стоит остро. Первая
идея связана с использованием оценки качества, полу-
полученной в главе V, E.11)
/п. Aа 21 — 1а п. + 1) — 1п т)/5
— т^гг1 —' F-3)
где Р8МП @ — величина минимума эмпирического рис-
риска в классе 5,-, та,- — показатель емкости класса 5$.
Величина
задает доверительный интервал для класса 5* и моно-
монотонно растет с номером I. Напротив, величина Рша (г)
не возрастает с ростом I, поскольку эмпирически опти-
оптимальное правило из 1$1 содержится во всех 5; (/ ^> I).
В качестве критерия выбора может быть взята правая
*) Разумеется, в практических реализациях метода упорядо-
упорядоченной минимизации риска эти два этапа могут сливаться, что,
однако, не меняет существа дела.
130 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
часть оценки, т. е.
К (а) = Р9МП (а) + 2 1/"РпИ-1пп + 1)-1пт|/5 # F4)
Правило, минимизирующее F.4), обеспечивает мини-
минимальную гарантированную величину вероятности оши-
ошибочной классификации.
Второй способ выбора решающего правила основан
на использовании следующего приема оценивания, кото-
который получил название скользящий контроль*). Идея
этого приема такова: для того чтобы оценить качество
работы каждого алгоритма низшего уровня, процедура
второго уровня выделяет из обучающей последователь-
последовательности один элемент и предлагает каждому из алгоритмов
обучиться на оставшейся части последовательности и
классифицировать выделенный элемент, затем выде-
выделяется другой элемент (а первый возвращается) и снова
проводится обучение и экзамен на этом одном элементе;
и так поочередно перебираются все элементы обучающей
последовательности. После этого подсчитывается, сколь-
сколько раз каждый алгоритм ошибался при классификации
выделенных элементов. Отношение числа ошибочных
классификаций к числу примеров, выделенных для обу-
обучения, и оценивает качество решающего правила, вы-
выбранного каждым из N алгоритмов.
§ 7. Несмещенность оценки скользящего контроля
Покажем, что оценки скользящего контроля являют-
являются несмещенными, т. е. математическое ожидание ре-
результата контроля равно истинной величине качества.
Для удобства обозначим через
Р (х; хг, (аъ . . . ; хи юг)
решающее правило, найденное по выборке длины I,
через
Р {хъ (йх; . . . ; хь юг) =
= У (ю — Р (х; хъ ©х;. . . ; хи юг))г йР (х, ю)
*) Процедура скользящего контроля, вероятно, впервые была
предложена М. Н. Вайнцвайгом.
§ 7. НЕСМЕЩЕННОСТЬ ОЦЕНКИ СКО ЙЬЗЯЩЕГО КОНТРОЛЯ 131
качество решающего правила, найденного по выборке
хъ щ; . . . ; хь а>1.
Кроме того, введем обозначения
Р1 = 11 ••• 1 Р {ХП ©1,' • • -,' ХЬ ©,) йР (Ж1? Шл)...
... йР(жг, ©,)>
/
р = -у- 2 К — Р (*»; жц ©х;. ..; х\, ©4; ...; жг, ©,)J.
5=1
Здесь «х, ©х;...; гг, йг; . . . ; жг, о>г — выборка, по-
полученная из Жх, ©х» • • •» хь ©г исключением элемента
хи а>1-
Нам надо показать, что
Мр = рг_ъ
где М — символ математического ожидания. Доказатель-
Доказательством этого утверждения является следующая цепочка
преобразований:
М^ =«и#-- ОТ" 2 К — Р(Х»Х1> ©х,-...
5=1
.. .; жь щ;. ..; жг, ©,)JйР(жх, ©х).. .йР(жг, ©г) =
I
= \ • • • \Т 2 и03! ~ Р (ж» Ж1' Ш1' • • •' ^' ®*' • • •' хь мг)J X
X АР (хг, и») ЙР (Жх, ©х)... йР (жг, ©г) =
I
х, ©1+х) ... ЙР (жг, ©,) = -р
1=1
Однако свойство несмещенности оценки недостаточно пол-
полно характеризует оценку. Необходимо знать еще и дис-
дисперсию оценки р. В случае, когда известна дисперсия
оценки скользящего контроля, можно оценить сверху
качество решающего правила:
Р<уе + г (Ч), F.5)
132 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
где V,. — оценка скользящего контроля, е (т]) = у (ц) У Б,
В — дисперсия] оценки,* т (у\) — константа, зависящая от
надежности, с которой требуется выполнение F.5).
Есть основания полагать (и многочисленные экспери-
эксперименты это подтверждают), что для большинства практи-
практически важных случаев дисперсия оценки «скользящий
контроль» стремится к нулю с ростом I примерно так же
быстро, как дисперсия «экзамена», но строгого доказа-
доказательства этого утверждения не известно. Любопытно, что
существуют примеры алгоритмов обучения, когда оно не-
неверно [45], хотя, видимо, для всех «разумных» алгорит-
алгоритмов обучения это утверждение справедливо.
Таким образом, алгоритмы выбора лучшего решающе-
решающего правила по критерию «скользящего контроля» в настоя-
настоящее время являются эвристическими и будут оставаться
таковыми до тех пор, пока не удастся получить оценку
дисперсии «скользящего контроля». Отыскание диспер-
дисперсии оценки метода «скользящего контроля» является од-
одной из наиболее актуальных задач не только теории обу-
обучения распознаванию образов, но и теоретической ста-
статистики. Знание этой оценки позволит выбрать на-
настоящее правило, минимизирующее верхнюю оценку ве-
величины р, и тем самым позволит гарантировать опре-
определенное качество выбранному решающему правилу.
В дальнейшем будут рассмотрены алгоритмы второго
уровня, использующие лишь оценки типа F.4).
Для того чтобы задать алгоритмы упорядоченной
минимизации риска, нам осталось определить способы
упорядочения классов решающих правил. Ограничимся
исследованием принципов упорядочения линейных ре-
решающих правил.
§ 8. Упорядочение по размерностям
Наиболее простым принципом упорядочения класса
линейных решающих правил является принцип упоря-
упорядочения по размерностям.
Рассмотрим класс линейных решающих правил
=1
| 8. УПОРЯДОЧЕНИЕ НО РАЗМЕРНОСТЯМ 133
Выстроим признаки ср4 (х) в порядке уменьшения ап-
априорной вероятности того, что этот признак понадобится
при классификации. Упорядоченная система линейных
решающих правил
строится так: в класс ^ попадут решающие правила,
где все ^1 = О, за исключением Я,1; в класс 82 — такие,
что только Я,х и К2 могут быть отличны от нуля, и т. д.
Такое упорядочение имеет следующий смысл. В первый
класс попадают решающие правила, которые при распоз-
распознавании используют только первый признак, во второй
класс те, что используют первый и второй признаки
и т. д. Показатель емкости каждого из этих классов,
как было установлено в предыдущей главе, равен т -\- 1,
где т — число используемых признаков.
Процедура высшего уровня в алгоритме упорядочен-
упорядоченной минимизации риска в данном случае будет выбирать
решающее правило, минимизирующее критерий
К(т) = Рэмп (ат) + 2 у("> + 1)ап21-1п0п +
F.6).
Рассмотренный выше способ упорядочения класса
линейных решающих правил страдает одним недостат-
недостатком — он требует априорной ранжировки признаков.
В том случае, когда такой ранжировки нет, можно
ввести другой принцип упорядочения по размерностям:
в класс включать все линейные решающие правила, ис-
использующие не более т признаков. Функция роста та-
такого класса решающих правил, как нетрудно убедиться,
оценивается величиной
где п — размерность исходного пространства, откуда
следует, что процедура высшего уровня должна мини-
минимизировать критерий
ф
т-{1)(\п21-\п(т + 1) + 1)-\пг]/5 + \пС%
. F.7)
134 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
Трудность реализации такого алгоритма состоит в
том, что при больших т не известно эффективных мето-
методов минимизации риска в 8т.
Как уже указывалось в главе V, оценка доверитель-
доверительного интервала E.11) является пессимистической и до-
достигается лишь в случае, когда вероятность ошибок
близка к Чг- Для решающих правил, оценки вероятно-
вероятностей ошибок которых малы (—0,1, 0,2), лучше пользо-
пользоваться более тонким критерием E.23):
вместо оценки F.6) и аналогичным критерием
Л (тп) —
хА+Т/^!
+ -Рэмп («т)
вместо F.7). Эти критерии не столь наглядны, но зато
более точны.
§ 9. Упорядочение по относительным расстояниям
Приведенные выше метод упорядочения по размерно-
размерностям и вытекающие из него рекомендации для построе-
построения оптимального алгоритма представляются достаточно
грубыми: они учитывают только внешнюю характерис-
характеристику задачи — размерность и никак не принимают^во
внимание более тонкие ее характеристики, например
геометрию расположения разделяемых множеств. О су-
| 9. УПОРЯДОЧЕНИЕ ПО ОТНОСИТЕЛЬНЫМ РАССТОЯНИЯМ 135
ществовании иных и, возможно, более эффективных ме-
методов упорядочения свидетельствуют также и оценки
качества решающего правила, которые могут быть по-
получены для персептрона, использующего многократно
обучающую последовательность. Рассмотрим такие оцен-
оценки качества.
В главе I была доказана теорема Новикова, утверж-
утверждающая, что если в спрямляющем пространстве два мно-
множества векторов разделимы гиперплоскостью, расстоя-
расстояние от начала координат до выпуклой оболочки множеств
{х}, {—Я} больше р = р0 ^> 0, а максимальная длина век-
вектора не превосходит Б, то персептрон разделит обучаю-
обучающую последовательность (при циклическом ее повторе-
повторении), сделав не более (.О/рJ исправлений. При этом он
реализует один из алгоритмов минимизации эмпиричес-
эмпирического риска. Оценим качество персептронного алгоритма
с многократным просмотром последовательности, иду-
идущим до полного разделения, для задач с известными
величинами р и В. Качество В (А, Т) алгоритма А для
данной задачи Т было определено как математическое
ожидание относительного числа "ошибок на экзамене
после обучения на обучающей последовательности дли-
длины I. Справедлива следующая теорема.
Теорема 6.1. Качество персептронного алгоритма А с
многократным повторением обучающей последователь-
последовательности для задачи Т с фиксированными О ир0 оценивается
неравенством
Доказательство. Доказательство этой теоре-
теоремы основывается на доказанном в § 7 утверждении о не-
несмещенности оценок, полученных с помощью процедуры
«скользящий контроль». Поэтому вместо оценки качест-
качества нам достаточно оценить математическое ожидание
частоты ошибок при скользящем контроле. При сколь-
скользящем контроле иэ обучающей последовательности вы-
выделяется один элемент, на оставшейся части проводится
обучение, строится решающее правило и затем прове-
проверяется классификация выделенного элемента этим ре-
решающим правилом. Эта операция проделывается с каж-
каждым элементом.!
136 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
Если при использовании полной обучающей после-
последовательности в ходе обучения персептрон всегда пра-
правильно опознает элемент хк, т. е. ни одно исправление
не происходит при просмотре хк, то работа алгоритма
на последовательности, из которой элемент хк выделен,
ничем не отличается от обучения по полной последова-
последовательности. Следовательно, этот элемент будет правильно
опознан при контроле. Таким образом, число ошибочно
опознанных элементов при скользящем контроле не пре-
превосходит число 10 таких элементов, на которых проис-
происходит хоть одно исправление при обучении по полной
последовательности. В свою очередь общее число ис-
исправлений, согласно теореме Новикова, не превосходит
величины
а значит, и
р°
Итак, для любой обучающей последовательности число
ошибок при скользящем контроле не превосходит
°21
Следовательно, математическое ожидание частоты оши-
ошибок в этом случае оценивается
Теорема доказана/
Теорема может быть несколько усилена. Рассмотрим
выпуклые оболочки Кг и К2 точек из обучающей] после-
последовательности длины I, принадлежащих соответственно
первому и второму классам. Обозначим через
1
математическое ожидание отношения —— , где ^^—диа-
метр множеств Кх и Кг, а р,— расстояние между ними.
По существу, не меняя доказательства, убеждаемся, что
$ 9. УПОРЯДОЧЕНИЕ ПО ОТНОСИТЕЛЬНЫМ РАССТОЯНИЯМ 137
Аналогичные утверждения справедливы и для не-
некоторых других (но не для любых!) алгоритмов построе-
построения разделяющей гиперплоскости, основанных на ми-
минимизации эмпирического риска, в частности, для ме-
метода обобщенного портрета (см. главу XIV).
Доказанное здесь утверждение показывает, что эф-
эффективность обучения тем выше, чем больше относитель-
относительное расстояние между классами.
Рассмотрим теперь два подпространства Ех и Ег ис-
исходного пространства Е. Пусть в этих подпространствах
обучающая последовательность может быть разделена
гиперплоскостью и, кроме того, отношения —ттгт- под-
подчинены следующему неравенству:
Согласно теореме, качество решения задачи в первом
подпространстве оценивается величиной
в то время как качество решения во втором — вели-
величиной
Поскольку никаких иных сведений о качестве решаю-
решающих правил нет, то, очевидно, следует предпочесть то
БЕ
правило, для которого отношение —^—- меньше.
Таким образом, критерий —^щ- позволяет оцени-
оценивать качество подпространств при построении линейных
решающих правил. На практике же пользоваться этим
критерием трудно: как правило, нам не известны вели-
величины В (Е) и р (Е).
Конечно, можно их оценить по выборке и с помощью
соответствующих оценок вычислять качество подпрост-
подпространств. Однако такой прием будет уже эвристическим.
Теорема 6.1 справедлива не для оценок величин В (Е)
и р (Е), а для точных их значений.
138 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
Хотелось бы построить метод, который позволял бы
оценивать качества подпространств не по величинам
В (Е) и р (Е), а по их оценкам.
Такому методу будут посвящены следующие параг-
параграфы. В них будет приведен метод, позволяющий эф-
эффективно выделять экстремальные подпространства.
Однако подобные алгоритмы решения задачи обучения
распознаванию образов возможны лишь в постановке,
отличной от той, которую мы рассматривали до сих пор.
В заключение этого параграфа обратим внимание
читателя на интересную аналогию, которая может быть
проведена между рассматриваемым здесь] критерием
упорядочения и хорошо изученным в классическом диск-
риминантном анализе понятием — расстоянием Маха-
Махаланобиса [62].
Пусть требуется построить гиперплоскость, разде-
разделяющую два множества векторов {х} и {х}, каждое из
которых подчиняется нормальному распределению с па-
параметрами цг, 2 и ц2, 2 (ковариационные матрицы рав-
равны). Тогда, как указывалось в главе III, оптимальным
решающим правилом (т. е. правилом, минимизирующим
вероятность ошибки) является линейная дискриминант-
ная функция.
Расстояние Махаланобиса
позволяет вычислить вероятность правильной класси-
классификации оптимального решающего правила
д
р = 4-
Геометрически расстояние Махаланобиса выражает от-
отношение расстояния между математическими ожидания-
ожиданиями векторов двух различных классов к дисперсии ве-
величины проекции векторов каждого класса на направ-
направляющий вектор разделяющей гиперплоскости:
$ 10. УПОРЯДОЧЕНИЕ ПО ЭМПИРИЧЕСКИМ ОЦЕНКАМ 139
Структура расстояния Махаланобиса F.8), F.9)
очень напоминает структуру ранее исследованного отно-
отношения
И расстояние Махаланобиса и число V характери-
характеризуют взаимное расположение множеств с помощью
относительного расстояния. В первом случае это относи-
относительное расстояние между «центрами» множеств, во
втором случае — относительное расстояние между
выпуклыми оболочками непересекающихся множеств.
Однако, в отличие от характеристики «разделимости»
Махаланобиса, характеристика V с уменьшением раз-
размерности пространства может расти, а вместе с ним (сог-
(согласно теореме) растет и оценка математического ожида-
ожидания вероятности правильной классификации с помощью
гиперплоскости, построенной по выборке фиксирован-
фиксированного объема.
Характеристика разделимости Махаланобиса уменьша-
уменьшается с уменьшением размерности пространства и вместе
с ней уменьшается вероятность правильной класси-
классификации с помощью оптимального в этом подпространст-
подпространстве линейного решающего правила.
Заметим, что расстояние Махаланобиса характери-
характеризует нижнюю оценку качества решающего правила, по-
построенного по выборкам фиксированного объема, а чис-
число V — верхнюю оценку этого качества. То, что оценки
по своей структуре близки, свидетельствует об эффек-
эффективности полученного критерия оптимизации.
§ 10. Упорядочение по эмпирическим оценкам
относительного расстояния и задача минимизации
суммарного риска
В этом параграфе мы рассмотрим постановку задачи
обучения распознаванию образов, которая отличается
от рассматриваемой до сих пор, но которая для многих
случаев, встречающихся на практике, может оказаться
более естественной. Для этой постановки задачи будут
построены некоторые априори упорядоченные классы
140 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
решающих правил и применен метод упорядоченной ми-
минимизации риска.
Итак, до сих пор исследовалась постановка задачи
обучения распознаванию образов, согласно которой в
классе характеристических функций Р (х, а) нужно
было найти функцию, доставляющую минимум функцио-
функционалу
Р(*)=1(а-Р(х, а)J ЛР(х, со),
если функция Р (со, х) неизвестна, но зато дана случай-
случайная и независимая выборка пар (обучающая последова-
последовательность)
Величина со могла быть равна либо нулю, либо единице.
Особенность рассматриваемой здесь постановки [со-
[состоит в том, что наряду с обучающей последовательно-
последовательностью задается выборка векторов
#1 ,. . ., Хр ,
которую будем называть рабочей выборкой. Рабочая вы-
выборка получена из выборки пар, найденной при случай-
случайных и независимых испытаниях, согласно распределе-
распределению Р (х, со):
(Из этой выборки пар отбираются только элементы х*,
элементы ш* считаются неизвестными). Задача состоит
в том, чтобы, используя обучающую последовательность
и рабочую выборку, найти в классе характеристических
функций Р (х, а) такую функцию, которая минимизи-
минимизировала бы функционал
г=1
Таким образом, разница в постановках состоит в том,
что в одном случае требуется найти функцию Р (х, а),
минимизирующую средний риск, а в другом случае ищет-
ищется функция, минимизирующая суммарный риск класси-
классификации элементов рабочей выборки.
§ 10. УПОРЯДОЧЕНИЕ ПО ЭМПИРИЧЕСКИМ ОЦЕНКАМ 141
Если наша цель состоит в том, чтобы классифициро-
классифицировать некоторые векторы (а не в том, чтобы найти общее
решающее правило!), предлагаемая постановка кажется
более разумной.
Итак, будем решать задачу обучения распознаванию
образов в постановке, которая требует с помощью правил
из класса 5 минимизировать суммарный риск на элемен-
элементах рабочей выборки.
В этой постановке задачи обучения распознаванию об-
образов также будем различать два варианта постановок —
детерминистскую и стохастическую. Детерминистская по-
постановка предполагает, что решающее правило Р (х, а)
должно быть выбрано из правил, безошибочно разделяю-
разделяющих множество векторов первого и второго классов обу-
обучающей последовательности. Стохастическая постанов-
постановка предполагает, что может быть выбрано правило, не
обязательно безошибочно делящее элементы обучающей
последовательности.
Замечательная особенность задачи минимизации сум-
суммарного риска состоит в том, что можно считать, что до
начала обучения (до начала поиска решающего правила)
множество Р (х, а) распадается на конечное число классов
эквивалентных с точки зрения обучающей и рабочей вы-
выборок разделяющих гиперплоскостей (эквивалентными
разделяющими гиперплоскостями называются гиперплос-
гиперплоскости, одинаково разделяющие элементы обучающей и
рабочей выборок).
Нетрудно понять, что число классов эквивалентных
разделяющих гиперплоскостей для / векторов совпадает
с числом способов разделения / векторов и оценивается
величиной
где т — размерность пространства.
В нашем случае число классов эквивалентных гипер-
гиперплоскостей оценивается величиной
1,5
(т + 1)! '
где I — длина обучающей, а р — рабочей выборок.
142 ГЛ. VI- МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
В дальнейшем для упрощения выкладок будем считать, что
длины обучающей и рабочей выборок равны, т. е.
Р = 1.
Итак, путь дана выборка длины 21
. . , Х21,
состоящая из векторов х, принадлежащих обучающей по-
последовательности и рабочей выборке. Определим диаметр
этой выборки как наибольшее расстояние между ее эле-
элементами
В = тах||ач — щ\
Упорядочим теперь класс линейных решающих пра-
правил по следующему принципу. К первому классу ^
отнесем такие решающие правила, для которых выпол-
выполняется равенствэ
где р — расстояние от гиперплоскости до ближайшей из
точек разделяемых множеств. К классу 5^ — те гипер-
гиперплоскости, для которых
Заметим, что упорядочение решающих правил прово-
проводится по известным значениям х-г A <; I ^ 21), но без
учета соответствующих значений со г.
Справедливы следующие две теоремы.
Теорема 6.2. Вероятность того, что хотя бы для
одного решающего правила из 8г частоты ошибок на обу-
обучающей и рабочей выборках отклонятся более чем на г,
не превосходит
^), F.10)
где
й = шш (I + 2, п + 1) ,
п — размерность пространства.
Теорема 6.3. Вероятность того, что найдется решаю-
решающее правило из 81г безошибочно делящее обучающую выбор-
$ 10. УПОРЯДОЧЕНИЕ ПО ЭМПИРИЧЕСКИМ ОЦЕНКАМ 143
ку и ошибающееся на рабочей с частотой, превосходящей е,
меньше
F.11)
где
, п+ 1) .
Доказательство. Число различных разбие-
разбиений выборки хъ . . . , х21 с помощью правил из $< конечно.
Обозначим его числом N1, значение которого оценим ни-
ниже. Вероятность того, что для фиксированного решающе-
решающего правила частота ошибок на обучающей и рабочей вы-
выборках уклонится более чем на е, в условиях теоремы
равна
2Ьт'ЬИ-т
с1 '
где к пробегает значения, удовлетворяющие неравен-
неравенству
к т — к
~1
I
здесь т — число ошибок на полной выборке, к — число
ошибок на обучающей выборке, т — к — число ошибок
к т — к
1 I
— отклонение частот
на рабочей выборке,
ошибок в двух полувыборках.
Как показано в приложении к главе X, при любом
О <| т <; 21 имеет место оценка
Поэтому вероятность Р (г) того, что хотя бы для одного
решающего правила из дУг частоты ошибок уклонятся бо-
более чем на е, оценивается величиной
144 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
Аналогично для теоремы 6.3 показывается, что для
фиксированного решающего правила вероятность Р того,
что на обучающей последовательности ошибок не будет,
а на рабочей частота их превзойдет е, равна
1С™
-фг прит>е/,
О при т^е/,
где т — число ошибок на полной выборке. В свою оче-
очередь
С™ 2/... (/ + 1)
и соответственно при т ^> е/
_ т_\1
21/
Тогда вероятность Р (е) того, что найдется решающее
правило из 5,, безошибочно делящее обучающую выбор-
выборку и ошибающееся на рабочей с частотой, превосходящей
е, оценивается как
Для доказательства теорем остается оценить число Л^.
Оно равно числу разбиений точек выборки хъ. . . , х21
на два класса таких, что расстояние между их выпуклыми
оболочками больше или равно 2р( = —г= {условие I). Как
показано в главе X, это число не превосходит
где в, — максимальное число точек выборки, для которых
любое разбиение на два класса удовлетворяет условию I.
Отметим, что если условие I выполняется, то разбиение
заведомо осуществимо с помощью гиперплоскости;
поэтому заведомо Л <^ п + 1, где п размерность прост-
пространства.
{ 10. УПОРЯДОЧЕНИИ ПО ЭМПИРИЧЕСКИМ ОЦЕНКАМ 145
Пусть теперь дано к точек ху,. . . , хк и 1\,. . . , Т2н —
всевозможные разбиения этих точек на два класса; р (Тк)—
расстояние между выпуклыми оболочками классов при
разбиении Тк.
Тот факт, что условие I выполняется для всякого Т\,
можно записать так:
ттрG';) > 2р;.
Тогда число Л пе превосходит максимальное число к (к ^
^ п +1). при котором еще выполняется неравенство:
1(к)= шах пнп р (Г,) > 2р =-^= F.12)
хь...,х4 г У г
Из соображения симметрии ясно, что
I (к) — шах ттрG\),
/ х, | < Б/2
достигается, когда жг, . . . , х^ располагаются в вершинах
правильного (к—1)-мерного симплекса, вписанного в шар
радиуса Б/2, а Т — разбиение на два подсимплекса раз-
к . ,
мерности —} 1 для четных к и два подсимплекса размер-
т. л т. о
ности —г— и -=— для нечетных к. При этом путем эле-
ментарных расчетов может быть найдено, что
Т) для четных к,
Ук~\ F-13)
Б-,—;—, для нечетных к ~> 1.
*-1 Ук+1 ^
Начиная с к ~^> 2, для всех к справедливо
'=*-• F-14)
146 ГЛ. VI- МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ .РИСКА
Из F.12) и F.14) следует, что г не превосходит величины
2. F.15)
Окончательно, учитывая, что разбиение осуществляется
гиперплоскостью, имеем
й<Ш1П^ + 2, п + 1) F.16)
и соответственно
Оценка величины N завершает доказательство обеих
теорем.
Эти теоремы дают возможность вычислить доверитель-
доверительные интервалы оценок качества правила класса &( при
решении задачи обучения распознаванию образов в общей
детерминистской постановке.
Приравнивая правые части F.10) и F.11) к величине
т] и разрешая соответствующие уравнения относительно
е, найдем
е = 2 Т/^1112*-111^1)-1111-)/5 F.17)
для общего случая и
е = 2 <*Aп2г-1а<* + 1)-1пт1/2 6 18
для детерминистского случая. В формулах F.17) и F.18)
д, равно минимальному значению двух величин: п + 1 и
]
Таким образом, с вероятностью 1 — т] для всех ре-
решающих правил Р (х, а) класса $( справедливы соотно-
соотношения
Р («) < Ршп (а) + 2
при решении задачи в общей постановке и
Р (а) < 2 *д"И-1п«Н-1)-1пт|/2
в детерминистской постановке.
§ 11. ОБ ОПТИМАЛЬНОЙ СОВОКУПНОСТИ ПРИЗНАКОВ 147
Существование оценок F.19) и F.20) позволяет
построить упорядоченную процедуру 1 минимизации
риска.
Для детерминистской постановки задача состоит в том,
чтобы так отнести элементы рабочей выборки к'пер-
вому и второму классам, чтобы, во-первых, разделение
множества векторов первого и второго классов, со-
состоящих из элементов обучающей^и рабочей последова-
последовательностей, было возможно, а во-вторых, расстояние ме-
между выпуклыми оболочками объединенных множеств бы-
было бы максимальным (по сравнению с другими варианта-
вариантами разделения рабочей выборки на два класса). При этом
качество полученного решающего правила оценивается
с помощью функционала F.20).
В общем случае проводится индексация не только ра-
рабочей выборки, но и переиндексация элементов обучаю-
обучающей последовательности. При этом количество переиндек-
переиндексированных векторов задает число ошибочных классифи-
классификаций материала обучения. Задача состоит в том, чтобы
так индексировать рабочую выборку и переиндексировать
обучающую последовательность, чтобы^минимизировать
функционал F.19).
§ 11. О выборе оптимальной совокупности признаков
Соображения предыдущего параграфа указывают на
то, что при построении конечно-оптимальных решающих
правил следует учитывать не только число ошибок на
обучающей _ последовательности и размерность выбирае-
выбираемого подпространства, но и относительное расстояние ме-
между проекциями классов на подпространство.
Для того чтобы учесть все зти особенности, рассмот-
рассмотрим двухступенчатую схему упорядочения класса решаю-
решающих правил. Пусть сначала задана ранжировка системы
признаков. Как и ранее, разобъем класс 5 линейных ре-
решающих правил на вложенные подклассы ^ так, что в
подкласс д^г попадают правила, использующие только
первые г признаков, т. е. работающие в подпростран-
подпространстве Ег.
Рассмотрим сначала задачу в детерминистской поста-
постановке. Пусть дана обучающая выборка хг,. . ■ , #г- Алго-
Алгоритмы первого уровня, используя упорядоченный поиск,
148 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
выберут каждый в своем классе 5* из числа безошибочных
решающих правил правило Р (х, а) (если оно есть) с мак-
максимальным р. Процедура второго уровня должна выбрать
наилучшее из предложенных первым уровнем решающих
правил.
Теперь естественно принять в качестве критерия выбо-
выбора величину доверительного интервала
е = 2
где
Здесь как величина Б (Е^ , так и р (Ег) зависят от под-
подпространства Е-г, поскольку и расстояние между выпук-
выпуклыми оболочками классов и их диаметры изменяются
при проектировании в подпространство. Процедура вто-
второго уровня должна выбрать то решающее правило из
числа предложенных первым уровнем, для которого оцен-
оценка F.20') минимальна.
Оценка доверительного интервала F.20') меняется,
вообще говоря, не монотонно с ростом размерности под-
подпространства. Поэтому выбранное процедурой второго
уровня подпространство может содержать больше при-
признаков, чем минимально необходимо для разделения
классов.
Описанная процедура эквивалентна упорядоченному
поиску при одноступенчатом упорядочении, определенном
следующим образом.
К первому классу относятся либо все те решающие
правила, которые либо производят разделение в подпро-
подпространстве, заданном первым признаком, либо такие, ко-
которые характеризуются числом
Ко второму классу относятся разделяющие гиперплоско-
гиперплоскости, которые либо производят разделение в подпрост-
подпространстве, заданном первыми двумя признаками, либо
§ 11. ОБ ОПТИМАЛЬНОЙ СОВОКУПНОСТИ ПРИЗНАКОВ 149
характеризуются числом
и т. д.
Иначе говоря, к й-му классу относятся такие гипер-
гиперплоскости, для которых минимум двух величин равен й,
т. е.
шш
^] + 2) = й.
В общей постановке не требуется, чтобы выбираемое
правило было безошибочным на материале обучающей по-
последовательности. Обозначим Рэмп (а) частоту ошибок на
материале обучения для решающего правила Р (х, а).
Пусть правила {Р (х, аг)} доставляют минимум Ржп (а)
в подклассе 5*. Процедура высшего уровня выбирает
наилучшее правило из {Р (х, аг)} по критерию
К @ = Рэмп (а,) + 2
В том случае, когда априорная ранжировка признаков
не задана, упорядочение класса линейных правил произ-
производится по следующему правилу: к 1-му классу относятся
гиперплоскости, заданные в подпространстве Ег размер-
размерности тг.
В случае детерминистской постановки задачи алгорит-
алгоритмы первого уровня выбирают каждый в своем классе ре-
решающее правило, которое правильно классифицирует
материал обучения (если такое есть) и при этом доставляет
максимум величине р (Е{).
Алгоритм высшего уровня выбирает из числа предло-
предложенных алгоритмами первого уровня такое решающее
правило, для которого минимальна величина
К (I) = 2 -Л_* '—;—*. , F.20")
где
150 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
В общем случае алгоритмы первого уровня действуют
так, как это было описано', в конце предыдущего па-
параграфа, а на втором уровне выбор проводится по кри-
критерию
/в, Aп 21 — Ы й+1) — 1пт|/5 + 1п С™
При использовании некоторых алгоритмов построения
линейных разделяющих гиперплоскостей (в частности,
алгоритмов метода обобщенного портрета) можно ввести
такой способ упорядочения, при котором достигается бо-
более глубокий гарантированный минимум.
Идея этого способа упорядочения связана с тем, что
в формуле F.19') п можно понимать не как размерность
координатного пространства, а как размерность линей-
линейной оболочки множества векторов обучающей рабочей
выборки. Размерность же линейной оболочки векторов
может оказаться меньше размерности координатного про-
пространства. Поэтому при введении порядка в классе ли-
линейных решающих правил можно учесть это обстоятель-
обстоятельство.
Рассмотрим следующий способ упорядочения: к й-му
классу отнесем те правила, для которых выполняется ра-
равенство
([^|] + 2, т + и Л-
т. е. минимум трех величин равен й. Здесь символ к опре-
определяет минимальное число векторов обучающей последо-
последовательности, по которым раскладывается вектор направ-
направляющих косинусов разделяющей гиперплоскости.
При таком способе упорядочения оценка качества вы-
выбранного решающего правила также определяется крите-
критериями F.19), F.20).
Итак, рассмотрено три способа упорядочения класса
линейных решающих правил. Каждый следующий способ
позволял достичь, вообще говоря, более глубокого гаран-
гарантированного минимума. Это происходило за счет того,
что разделяющая гиперплоскость строилась не в исходном
пространстве признаков, а в некотором его подпростран-
подпространстве, обладающем экстремальными свойствами.
5 12. АЛГОРИТМЫ МИНИМИЗАЦИИ СУММАРНОГО РИСКА 151
Таким образом, оказалось, что попытка построить по
выборке фиксированного объема наилучшее решающее
правило приводит к выбору того или иного набора призна-
признаков из фиксированного множества признаков и построе-
построению в пространстве выбранных признаков разделяющей
гиперплоскости.
Часто множество отобранных признаков называют ин-
информативным набором признаков. «Информативность»
этого набора может быть оценена числом, равным мини-
минимальной величине критерия F.19'), которая достигается
и пространстве этих признаков. Можно оценивать «вклад»
каждого признака в информативность набора признаков
как разность между величиной оценки набора признаков,
из которого исключен данный признак, и информативно-
информативностью набора признаков.
Однако, вероятно, понятие «информативность набора
признаков» или «информативность данного признака»
не несет достаточно глубокого содержания. И вот по-
почему:
1) понятие «информативность пространства призна-
признаков» определяется не само по себе, а в связи с конкретным
алгоритмом опознания;
2) информативность набора признаков зависит от конк-
конкретной обучающей последовательности.
Ясно, что чем больше объем выборки, тем большим бу-
будет, вообще говоря, информативный набор признаков. Тем
не менее можно привести примеры задач, когда информа-
информативный набор признаков, найденный по выборке мень-
меньшего объема, и информативный набор признаков, най-
найденный по обучающей последовательности большего объ-
объема, не имеют ни одного общего элемента.
§ 12. Алгоритмы упорядоченной минимизации
суммарного риска
Итак, рекомендации метода упорядоченной минимиза-
минимизации суммарного риска состояли в том, чтобы так индекси-
индексировать точки рабочей выборки и выбрать такое подпро-
подпространство исходного пространства, чтобы для построенной
разделяющей гиперплоскости оценка качества F.19')
принимала минимальное значение.
152 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
При детерминистской постановке задачи предлагалось
так индексировать точки рабочей выборки и отыскать
такое подпространство, чтобы точки обучающей и рабочей
выборок, индексированные первым классом, и точки
обучающей и рабочей выборок, индексированные вторым
классом, были разделимы гиперплоскостью и при этом
достигал минимума функционал F.20").
Разницу в решениях детерминистской задачи мини-
минимизации суммарного риска методом минимизации эмпири-
эмпирического риска и методом упорядоченной минимизации ил-
иллюстрирует следующий пример (рис. 15).
Рис. 15.
Пусть требуется, используя обучающую последователь-
последовательность (на рисунке векторы, принадлежащие первому клас-
классу, обозначены крестиками, а векторы, принадлежащие
второму классу,— кружками), построить гиперплоскость,
минимизирующую число ошибок на векторах рабочей вы-
выборки (на рисунке соответствующие векторы обозначены
черными точками).
Решение этой задачи методом минимизации эмпири-
эмпирического риска заключается в том, чтобы построить гипер-
гиперплоскость, разделяющую векторы первого и второго клас-
классов с минимальным числом ошибок, а затем классифици-
классифицировать с помощью построенной гиперплоскости точки ра-
рабочей выборки. В нашем случае возможно безошибочное
разделение векторов обучающей последовательности, по-
поэтому существует целое семейство разделяющих гипер-
$ 12. АЛГОРИТМЫ МИНИМИЗАЦИИ СУММАРНОГО РИСКА 153
плоскостей. Выберем среди них оптимальную Го (см. главу
XIV). Теперь те векторы рабочей выборки, которые ле-
лежат по разные стороны гиперплоскости, отнесем различ-
различным классам. Таково решение методом минимизации эм-
эмпирического риска.
Для решения этой задачи методом упорядоченной ми-
минимизации следует ввести априорное упорядочение клас-
класса линейных решающих правил. Рассмотрим упорядоче-
упорядочение по критерию Б /р. Поскольку диаметр множества для
всех подклассов при таком упорядочении окажется одним
и тем же, то решение задачи заключается в том, чтобы
так индексировать точки рабочей выборки первым и
вторым классом, чтобы точки первого класса обучающей
и рабочей выборок и точки второго класса обучающей
и рабочей выборок были разделимы гиперплоскостью,
наиболее удаленной от ближайшего из разделяемых
классов.
Решением этой задачи является построение гиперплос-
гиперплоскости 1\. (Гиперплоскость Гх обеспечивает расстояние до
ближайшего из разделяемых классов рг, в то время как
гиперплоскость Го — лишь р0.) Как видно из рисунка,
полученные решения могут достаточно сильно различать-
различаться между собой.
Основные трудности в решении задачи распознавания
методом упорядоченной минимизации риска связаны с
проведением перебора по способам индексации рабочей
выборки. (В случае, когда упорядочение ведется по кри-
терию ', перебор проводится еще и по подпростран-
подпространствам.) Однако чем меньше элементов в рабочей выбор-
выборке, тем меньше перебор и в пределе; когда рабочая выбор-
выборка состоит из одного элемента, алгоритм метода упорядо-
упорядоченной минимизации риска состоит в следующем:
1) элемент рабочей выборки присоединяется к первому
классу и определяется расстояние р2 между выпуклыми
оболочками разделяемых множеств;
2) элемент рабочей выборки присоединяется ко второ-
второму классу и определяется расстояние р2 между выпуклыми
оболочками разделяемых множеств;
3) элемент рабочей выборки относится к первому
классу, если р2 ^> р2, и ко второму классу, если
Ра > Р1-
154 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
Рис. 16.
(Методы определения расстояния между выпуклыми
оболочками рассмотрены в главе XIV.)
Теоретически для каждой обучающей последователь-
последовательности пространство Е распадается на две области такие,
— 1ЧТ0 если элемент рабочей
выборки взят из первой
области, то он будет отне-
отнесен к первому классу, а
если взят из второй обла-
области, то будет отнесен ко
второму классу. Таким об-
образом, метод упорядочен-
, ной минимизации суммар-
-*- ного риска в этом вырож-
вырожденном случае приводит к
построению поверхности,
разделяющей элементы
обучающей последовательности. Однако эти разделяющие
поверхности уже не являются линейными. На рис. 16 приве-
приведена разделяющая поверхность для случая, когда обуча-
обучающая последовательность задана тремя точками. Для срав-
сравнения приведена (пунктиром) оптимальная разделяющая
гиперплоскость.
Заметим, что если рабочая выборка состоит более чем
из одного элемента, то алгоритмы метода упорядоченной
минимизации риска не сводятся просто к построению по-
поверхности, разделяющей обучающую последователь-
последовательность.
И еще одно замечание. При практической реализации
метода упорядоченной минимизации риска вместо F.19')
лучше использовать критерий, полученный на основе
оценок равномерного относительного уклонения E.23):
0- F.21)
При Рашп (г) = 0 этот критерий близок к F.20'), а
при Р8ИП (г) ф 0 значительно тоньше, чем F.19').
| 13. ЭКСТРЕМАЛЬНЫЕ КУСОЧНО-ЛИНЕЙНЫЕ ПРАВИЛА 15й
§ 13. Алгоритмы построения экстремальных
кусочно-линейных решающих правил
В 50-х годах Фикс и Ходжес рассмотрели~следующий
алгоритм построения дискриминационного решающего
правила [78].
Пусть заданы обучающая последовательность
хг, ыъ. . . ; хь со;
и рабочий элемент х. Пусть в пространстве X определена
метрика р (х, у).
Упорядочим элементы обучающей последовательности
по близости к вектору X в метрике р (х, у). Соответствую-
Соответствующим образом перенумеруем эти векторы. Затем рассмот-
рассмотрим первые к элементов перенумерованной последователь-
последовательности (к — параметр алгоритма; определение к и состав-
составляет предмет исследований теоретиков этого метода).
Вектор X относится к первому классу, если среди к эле-
элементов преобладали элементы первого класса, и относит-
относится ко второму классу в противном случае.
Основная идея алгоритма Фикса — Ходжеса состоит
в том, чтобы строить решающее правило не по всей выбор-
выборке, а лишь по выборке, попадающей в окрестность дискри-
дискриминируемой точки. Фикс и Ходжес рассмотрели самый
простой тип «локального» решающего правила — кон-
константу и все внимание сконцентрировали на определении
величины «окрестности».
Пользуясь оценками F.19) и F.21), можно определить
величину экстремальной окрестности для локальных ли-
линейных решающих правил и тем самым строить не экстре-
экстремальные кусочно-постоянные решающие правила, а более
содержательные экстремальные куеочно-линейные реша-
решающие правила. Вот как это можно сделать.
Упорядочим элементы обучающей последовательности
по близости к элементу х. Затем последовательно рас-
рассмотрим I экстремальных гиперплоскостей, разделяющих
соответственно 1, 2, . . ., / элементов упорядоченной
обучающей последовательности. Качество каждой из I
построенных разделяющих гиперплоскостей может быть
оценено с помощью критериев F.20') и F.21) (соответст-
(соответственно для детерминистского и стохастического вариантов
задачи). Вектор х относится к тому классу, к которому
156 ГЛ. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
его относит гиперплоскость с наилучшей оценкой каче-
качества.
Таким образом, построение экстремальной кусочно-
линейной разделяющей поверхности связано не только
с минимизацией критериев F.19), F.21) ко параметрам
р, В, п, й, но и с минимизацией по параметру I.
§ 14. Приложение к главе VI
Оценим снизу величину минимакса потерь в задачах обучения
распознаванию образов.
Пусть задан класс решающих правил Р (х, а), а €Е 5. Рас-
Рассмотрим некоторый круг задач обучения <?, совокупность К ал-
алгоритмов, выбирающих по обучающей последовательности решаю-
решающее правило вида Р (х, а). Величина минимакса потерь Мо опреде-
определена так:
Мо = тт тах л (А, Т),
А т
л (А, Т) = Н(Л,Т) — тт В (а, Т),
а.е.8
где Е (А, Т) — качество алгоритма А при решении задачи Т,
Я (а, Т) — качество решающего правила Р (х, а) для задачи Т.
Примем что алгоритм Ао оптимален в смысле минимакса потерь,
г. е.
Мо— тахя(Ло, Т).
Пусть теперь известно, что задачи Гд, . . ., Т^ из () могут
появиться с вероятностью Рд, . . ., Рк BР,- = 1) и алгоритм
А\ 5 К оптимален в смысле средней величины потерь при решении
этих задач, т. е.
Нетрудно
Мх = тт
убедиться,
В самом деле,
Мх = тт
А
N
г=1
ЧТО
Мх «
Л,-
N
г=1
0-
(П.1)
тах я
Пусть, наконец, ^42 — оптимальный по Байесу алгоритм для задач
2*1, . . ., Тп, появляющихся с вероятностями рх, . . ., рп, и М% —
средние потери для этого алгоритма (алгоритм Л2 не обязательно
§ 14. ПРИЛОЖЕНИЕ К ГЛАВЕ VI 157
принадлежит К). Тогда
М% < М\ (П.2)
(равенство достигается, если ^ 6 X).
Таким образом, из (П.1), (П.2) получаем
Мо > Л/2 (П.З)
и для оценки снизу минимакса потерь достаточно рассмотреть
некоторую совокупность задач с заданными вероятностями появ-
появления, построить оптимальный по Байесу алгоритм и найти в этом
случае среднюю величину потерь М^.
Случай 1. Оценим величину Мо для задач обучения в де-
детерминистской постановке, когда допустимы только такие задачи,
что вклассе 5 есть безошибочное решающее правило (тт Р (а, Т) = О
е8
для любой задачи Т).
Пусть п характеризует емкость класса 5; тогда (см. главы
V, X) существует п точек х\, . . ., хп таких, что правила из 5
разбивают их всеми возможными способами. Поставим каждому
разбиению Л; точек от, . . ., хп в соответствие задачу Т{ (всего
2П задач) следующим образом.
Полагаем, что вероятностная мера Р (х) сосредоточена в точках
хг, . . ., хп, причем точка х\ имеет вероятность 1 — р, а остальные
Р
равновероятны и имеют вероятности — . .
Точка х^ принадлежит первому классу, если разбиением Л,
она отнесена к первому классу, и принадлежит второму классу,
если разбиением Л,- она отнесена ко второму классу. Иными словами,
Г Р @ | хк) = О,
\РA \х1с) = 1,
если хк отнесена разбиением В; к первому классу;
Р @ | а*) - 1,
Р A | хн) = О,
если ль отнесена разбиением Л,- ко второму классу. Этими соотно-
соотношениями задача Тг задана полностью. Очевидно, что для каждой
задачи Т{ в классе 5 есть безошибочное решающее правило.
Предположим далее, что задачи Тг появляются с равной веро-
вероятностью.
Можно убедиться, что оптимальный по Байесу алгоритм для
этой совокупности задач таков.
Пусть дана обучающая последовательность длины I; с вероят-
вероятностью 1 в ней встречаются только точки из набора х\, ..., хп.
Точки из набора XI, . . ., хп, встретившиеся в обучающей последо-
158 Гл. VI. МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИЙ РИСКА
вательности, следует относить к тому классу, к которому они от-
отнесены в материале обучения. Классификация остальных точек
безразлична. При этом средние потери равны
М* (/>) = 0,5 A - р) р1 + 0,5 (п - 1) [~т) A - ~1
)г/'- (П.4)
Здесь 0,5 A — р) — средние потери при классификации точки
х\ при условии, что она не встретится в обучении; р1 — вероят-
р
ность того, что она не встретится в обучении; аналогично 0,5 . —
средние потери при Классификации точки ж, (г =/= 1) при условии,
р у
п-1)
что она не встретится обучении, а A — п_ц ) — вероятность осу-
осуществления этого условия.
Найдем значение /? (О ^ /? -^ 1), при котором выражение
достигает максимума. Это произойдет, если
!1 при I <; п — 2,
п — 1
Подставляя р в (П. 4) и учитывая (П.З), получаем
Ма — шш тах л (А, Т) >
А
я —1 / 1\г л +1
Случай 2. Пусть теперь задачи Т произвольны, а
алгоритмы А выбирают по-прежнему из класса 5 емкости п
(задача в вероятностной постановке). Оценим величину минимакса
потерь Ма.
Пусть XI, . . . , хп, как и ранее, совокупность точек, разби-
разбиваемых правилами из 5 всеми возможными способами. Поставим
в соответствие каждому разбиению К( задачу Г; следующим об-
образом.
1. Вероятность Р (х) сосредоточена в точках х%, . . ., хп,
причем все точки равновероятны: Р (х^ = —^- .
§ 14. ПРИЛОЖЕНИЕ К ГЛАВЕ VI 159
2. Условная вероятность Р (со | х) в точках XI, . . ., хп задана
так:
р (О I ж 1 = / ^'** ~ ^' если Х1( отнесено К{ к первому классу,
^ ' й' \ 0,5 -)- А, если а:^ отнесено Л, ко второму классу!
р 1\ \ \ — /0M + Д) если а:^ отнесено Лг- к первому классу,
^ I хк) \ 0,5 — Д, если х^ отнесено Лг- ко второму классу.
Оптимальным решающим правилом в классе 5 для задачи
Т, очевидно, является такое правило Р (х, а), которое классифи-
классифицирует точки XI, . . ., хп в соответствии с разбиением Л,-. При этом
качество
Л (а, Т) = 0,5 — Д.
Оптимальная по Байесу стратегия обучения Аа в случае слу-
случае оказывается следующей:
а) Допустим, что точка х встречалась в материале обучения,
причем п\ (х) раз была отнесена к первому классу и л2 (а:) раз ко
второму. Тогда точку х следует отнести к первому классу, если
п\ (х) > я2 (а:), и ко второму, если п\ {х) < я2 (а:). При п\ = л2
классификация безразлична (выбирается на удачу).
б) Если точка х не встречалась в обучающей последостельности,
ее классификация безразлична (выбирается на удачу).
Потери при решении каждой задачи Т{ по этому алгоритму
равны между собой и задаются выражением
Г 2Д Д 1
где 2Д/га — потери, если точка а:,-, относимая разбиением Л; к перво-
первому классу, будет отнесена после обучения ко второму (щ (а:) <
<[ л2 (а:)), или соответственно, наоборот, точка, относимая Лг-
ко второму, будет отнесена в результате обучения к первому классу
(щ (х) > п2 (а:)); Д/га — потери в случае, когда щ (а:) — щ (х);
рг — вероятность того, что щ (х) < л2 (а:) при Р A | а:) > Р @ | х)
или п\ {х) > га2 (а:) при Р A | ж) < Р @ | ж); р% — вероятность
того, что щ {х) = л2 (а:). Точные значения рг и р2 задаются форму-
формулами:
„ 2! / 1 \п3 /о,5 + А\". /0,5-А\п2
п I \ п
0,5 —Д
А
т!п2!пз! \ л
^^ (П.6)
При I <! п положим Д = 0,5. Тогда
Л/о> 0,5 И — -^-]'«0,5е" "". (П.7)
160 ГЛ. VI- МЕТОДЫ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
При л < I ^ 2л положим Д = 0,25. В этом случае учтем только
первые члены суммы (П.5) и (П.6) (в первой сумме гг2 = 1, во вто-
второй щ = л2 = 0):
(^г)~. (П.8)
При I > 2л положим
Д = -2-К "Г
Л1 — Лз
и аппроксимируем распределение величины -, = 9 нормаль-
нормальным законом (для определенности считаем, что Р A | х) > 0,5). Эта
величина имеет математическое ожидание и дисперсию
2Д
М (8)= — ,
Таким образом, нормальное распределение имеет вид
откуда
1=Р(9<0)= 1-егГ BД]/ -^-Ь
1 1/1Г
при Д = — К ~Г
Таким образом,
рг = 1 - егГ A).
А/о> у -у" A — егГ A)).
Итак из (П.7), (П.8), (П.9) следует, что
0,5е п при
0,25 + ^-1 е п при л < г < 2л,
—т- A — еН A)) при I ^ 2п:
(П.9)
Глава VII
ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДОВ
ОБУЧЕНИЯ РАСПОЗНАВАНИЮ
ОБРАЗОВ*)
§ 1. Задача о различении нефтеносных и водоносных
пластов в скважине
Одной из первых задач, где применялся метод обуче-
обучения распознаванию, была решенная в 1963 году задача
о различении нефтеносных и водоносных пластов в
скважине.
Залегающая в недрах нефть пропитывает пористые
слои земной породы. Такие, подобные смоченной губке,
пласты называются коллекторными. Они могут быть на-
наполнены не только нефтью, но и водой и обычно череду-
чередуются с неколлекторными пластами. Жидкость, пропиты-
пропитывающая породу, испытывает значительное давление, по-
поэтому при бурении в скважину нагнетается глинистый
буровой раствор. Каждый пройденный участок одевается
трубами, которые цементируются. В результате^много-
километровая скважина надежно изолирована.
Теперь относительно тех пород, через которые про-
проходит скважина; эксплуатационникам предстоит решить:
во-первых, какие из пластов коллекторные и, во-вторых,
какие из коллекторных пластов наполнены нефтью (неф-
(нефтеносные пласты подлежат вскрытию; в определенном
месте скважина пробивается специальным снарядом, и
*) В этой главе рассказано о примерах применения метода обоб-
обобщенного портрета, наиболее знакомых авторам. Некоторые резуль-
результаты практического применения других методов к этим же задачам
упомянуты в комментариях к главе.
162 ГЛ. VII. ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДОВ РАСПОЗНАВАНИЯ
нефть по трубам поступает в нефтеприемник). Число кол-
коллекторных пластов в скважине может достичь нескольких
десятков и среди них возможны самые различные отно-
отношения нефтеносных и водоносных.
При классификации коллекторных пластов на нефте-
нефтеносные и водоносные существует опасность ошибок двух
родов.
Ошибка первого рода приводит к тому, что вскрытый
пласт оказывается не нефтеносным (и в нефтеприемник
поступает вода). В этом случае скважина требует ремонта:
заделывание вскрытого пласта — дорогая и трудоемкая
операция.
При ошибках второго рода вскрыты бывают не все
нефтеносные пласты скважины и эксплуатационный эф-
эффект скважины снижается. Чтобы избежать таких оши-
ошибок, с самого начала разработки скважины производится
геофизическое исследование пластов, идея которого до-
довольно проста.
Известно, что земные породы обладают сравни-
сравнительно большим электрическим сопротивлением и по-
поэтому в скважину накачивается раствор с заведомо
малым электрическим сопротивлением. Непористые слои
породы, не впитав в себя бурового раствора, не изменят
свое электрическое сопротивление, в то время как кол-
коллекторные пласты, впитав буровой раствор, покажут малое
электрическое сопротивление. Кроме того, нефть обладает
более высоким электрическим сопротивлением, нежели
вода, и поэтому коллекторный пласт, насыщенный нефтью,
в свою очередь покажет более высокое сопротивление,
чем коллекторный пласт, содержащий воду.
В общем, такие соображения как-то оправдываются.
Действительно, на коллекторных пластах отмечается
резкое падение сопротивления. Среди самих же коллек-
коллекторных пластов электрическое сопротивление нефтеносных
пластов бывает в среднем несколько выше, чем водо-
водоносных .
На практике же оказалось, что геофизические методы
позволяют сравнительно надежно различать коллектор-
коллекторные пласты от неколлекторных, в то время как ни один
из геофизических методов не позволяет достаточно надеж-
надежно классифицировать коллекторные пласты на нефтенос-
нефтеносные и водоносные.
§ 1. ЗАДАЧА О РАЗЛИЧЕНИЙ ПЛАСТОВ В СКЙАЖИНЁ Ш
Почему же это не удается сделать? Во-первых, сами
коллекторные пласты бывают разных толщин (от одного
до десятков метров) и, чем меньше толщина пласта, тем
труднее его классифицировать — сильнее сказываются
случайные влияния, вкрапления других пород и т. п.;
во-вторых, пористость породы может быть различная,
поэтому степень заполнения породы раствором разная и,
следовательно, возможно различное сопротивление по-
породы. Классифицировать коллекторные пласты можно
было бы, учитывая косвенные влияния на сопротивление
породы, т. е., по существу, используя не один параметр,
а набор их. Такой набор геофизических параметров со-
составляет стандартный комплекс обследования скважин.
Он включает в себя измерения:
1) кажущихся электрических сопротивлений пород при
измерениях зондами различной длины D зонда);
2) потенциалов собственной поляризации,
3) интенсивности естественного гамма-излучения пород,
4) интенсивности гамма-лучей захвата при облучении
нейтронами,
5) диаметра скважины,
6) сопротивления бурового раствора.
По этим измерениям эксперты принимали решения
принадлежности пласта к числу нефтеносных. Однако
надежность получения таким образом классификации не
превосходила 75—85%.
Поэтому и возникла задача классификации средствами
распознавания образов.
Эксперимент ставился на нефтеносных месторожде-
месторождениях Башкирии и Татарии (основной материал относился
к девонским песчаникам Татарии). Были собраны све-
сведения о геофизических комплексах 300 вскрытых пластов
и 100 примеров пластов E0 водоносных и 50 нефтеносных)
были выделены для выработки решающего правила, а
200 — для оценки его качества.
Такое правило было получено, и качество его было
оценено как три ошибки на 200 случаев. Так примерно
это правило и работало в условиях промышленной экс-
эксплуатации.
Надо сказать, что методы обучения распознаванию
образов нашли очень широкое применение во многих раз-
разделах геологии.
164 ГЛ. VII. ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДОВ РАСПОЗНАВАНИЙ
§ 2. Задача о различении сходных почерков
В криминалистике существует задача о дифференциал
ции сходных почерков, когда известно, что запись вы-
выполнена одним из нескольких лиц, и необходимо выяснить,
каким именно лицом она была сделана.
I .., л
Рис. 17.
Такую задачу решает эксперт, которому предъявля-
предъявляются исследуемый текст и образцы почерка, выполнен-
выполненные подозреваемыми лицами. Эксперт, исследуя эти
документы, высказывает свое мнение о том, кому при-
принадлежит исследуемая запись.
Интересно было бы выяснить, в состоянии ли обуча-
обучающаяся программа конкурировать с экспертами-почерко-
экспертами-почерковедами в задаче о различении сходных почерков.
Для эксперимента были отобраны два лица со сход-
сходными почерками и было сфотографировано по 155 букв
«б», написанных в связных текстах каждым из них. Фото-
Фотоснимки букв были выполнены одинаковыми по размеру *).
*) Криминалисты указали две характерные точки в начертании
букв, по которым проводились масштабирование, центрирование и
ориентация изображений.
§ 2. задача о Различении сходных Почерков
165
На рис. 17 в первой строке приведены образцы почерка
лица А, а во второй строке — лица Б. На рис. 18 по-
показан растр для кодировки. Кодировка каждой буквы
заключалась в том, что каждая зачерненная на растре
1
V
1
//
}
Ы
■г
Л
_
>
6
7
а-
!«•
/
э
}
Ч)
•
\
V
Д
к
•
14
\
1
п
16
И
7
7
*>
и
у
1
7
1Ь
Ь
20
«
(
т
р
в
к
0
1
1
Ч
'1
Рис. 18.
клетка означала 1 в соответствующей координате 326-мер-
326-мерного вектора.
Из 155 букв, написанных каждым лицом, было слу
чайно отобрано по 30 букв для обучения. Таким образом»
обучение проводилось по 60 буквам, а для проверки
полученного решающего правила оставалось 250 пись-
письменных знаков. Решающее правило, которое при этом
было получено, дало следующий результат: из 250 пись-
письменных знаков было правильно опознано 208 и допу-
допущено 42 ошибки.
Одновременно с машинным опознанием проводились
контрольные экспертизы семью экспертами. Экспертам
в качестве образцов почерка давались те же 60 букв, ко-
которые брались для обучения машины. Буквы выдавались
в виде фотографии (не растрированные). После ознаком-
ознакомления с образцами эксперты должны были определить,
кем из двух лиц написана каждая из 250 букв, предъяв-
предъявленных для опознания. Результаты этого эксперимента
приведены в таблице 1.
166 ГЛ. VII. ПРИМЕРЫ ПРИМЕНЕНИЙ МЕТОДОВ РАСПОЗНАВАНИЯ
Таблица 1
Эксперт
№
1
2
3
4
5
6
7
Верных отве-
ответов на 250
226
229
200
223
220
237
217
Ошибок
на 251)
24
21
50
22
30
13
33
% опознания
90,4
91,4
80
91,2
88
94,6
86,8
Средний процент опознания семью экспертами соста-
составил 88%; процент же правильных ответов, полученных
с помощью ЭВМ, составил 83%.
Таким образом, надежность экспертизы с помощью
машины и традиционным способом имеет один и тот же
порядок. При этом надо иметь в виду, что машина и экс-
эксперты пользовались, по существу, различной информа-
информацией. Эксперты проводили опознание по фотографиям
букв, в то время как машина опознавала рукописные
знаки по растру, никак не отражающему все многообра-
многообразие графического очертания знака.
Несомненно, что кодирование растрированием не яв-
является лучшим для целей экспертизы. Существуют спо-
способы кодирования, приспособленные для того, чтобы со-
сохранять индивидуальность в начертании знаков. Поэтому
возможности вычислительных машин в применении их
к задачам почерковой экспертизы далеко не исчерпаны.
Проведенный эксперимент показал, что уже при уни-
универсальном (а потому плохом) способе кодирования ка-
качество экспертизы, полученной с помощью машины и
традиционным способом, соизмеримы. Специализиро-
Специализированный способ кодирования буквенных знаков безуслов-
безусловно повысит надежность успешной экспертизы. Создание
такого специализированного способа кодирования состав-
составляет предмет исследования криминалистов-почерковедов.
§ 3. Задача о контроле качества продукции
В настоящее время одной из важнейших проблем
в промышленности является контроль качества продукции.
В частности, такая проблема возникает при проверке
качества электронных ламп.
$ 2. ЗАДАЧА О РАЗЛИЧЕНИИ СХОДНЫХ ПОЧЕРКОВ 167
Специфика понятия качества применительно к элек-
электронным лампам состоит в том, что они должны удовлет-
удовлетворять двум требованиям:
параметры ламп должны находиться в заданных пре-
пределах;
параметры прибора должны не выходить из заданных
пределов на протяжении заданного промежутка време-
времени АТ.
Контроль над выполнением первого требования обыч-
обычно не вызывает принципиальных затруднений: всегда
можно предусмотреть пост технического контроля в конце
технологической линии производства, который проверяет
все без исключения приборы, отбраковывая не удовлетво-
удовлетворяющие стандарту.
Гарантировать выполнение второго требования зна-
значительно сложнее. Для этого принят статистический кон-
контроль качества выпущенной продукции. Статистический кон-
контроль качества обосновывается так: поскольку приборы
выпускаются партиями, считается, что внутри партии
отклонение от некоторого фиксированного значения ка-
качества есть явление случайное. Поэтому в каждой партии
может быть определено событие, которое выражается
в том, что долговечность прибора окажется менее тре-
требуемых АТ часов. Оценить вероятность такого события
можно следующим образом: из партии извлекаются I
приборов, которые ставятся на испытания, имитирую-
имитирующие реальные условия. Испытания проводятся в течение
АТ часов. Вероятность встретить нестандартный прибор
в партии оценивается как
где п — число нестандартных приборов, выявленных во
время испытания.
Партия принимается или отклоняется в зависимости
от величины V.
Конечно, хорошо, если партия принята, но как быть,
если по результатам статистических испытаний партия
должна быть забракована. Досадно бывает, когда партия,
большая часть приборов которой доброкачественная,
бракуется целиком. Обычным бывает, например, такой
случай, когда заказчик, согласный принять партию с 5%
168 ГЛ. VII. ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДОВ РАСПОЗНАВАНИЯ
недоброкачественных изделий, бракует партию с 10%
недоброкачественных изделий.
Использование методов обучения распознаванию об-
образов для контроля качества продукции позволяет «спа-
«спасать» забракованные партии, «очищая» их от недоброка-
недоброкачественных приборов. Для этого требуется уметь пред-
предсказывать по испытаниям приборов в начальный момент
времени, выйдут ли параметры приборов за установлен-
установленные границы в течение гарантируемого срока АГ, т. е.
требуется уметь относить каждую лампу к одному из двух
классов — к классу доброкачественных или недоброка-
недоброкачественных ламп. Задача сводится, таким образом, к по-
построению решающего правила.
С помощью найденного решающего правила можно
перебрать все приборы партии, отделив те, которые клас-
классифицируются как «недоброкачественные». Ясно, что
если для данного правила вероятность совершить ошибку
первого рода (принять плохой прибор за хороший) равна
Рх, а всего партия содержит р% плохих приборов, то
после «очистки» 'в партии останется только рхр % плохих
Таблица 2
Тип при-
прибора
Г
1. Лампа
6Ж1П
2. Лампа
6Ж9П-Е
3. Лампа
бегу щей
волны
ЛБВ
4. Магне-
Магнетрон
Прогнози-
Прогнозируемый
срок
службы
1000 ча-
часов
5000 ча-
часов
2000 ча-
часов
1 год
хране-
хранения
Критерий
срока
службы
Крутизна
анодпо-се-
точпой ха-
рактеристи-
рактеристики
Группа экс-
плуатаци-
плуатационных пара-
Выходная
мощность
Выходная
мощность
а
и
§8
!«
9
7
6
5
Длина обуча-
обучающей
последова-
последовательности
1 кл.
10
19
9
14
2 кл.
10
16
18
9
Длина эк-
замена-
заменационной
последо-
ватель-
вательности
щ
29
15
19
33
Число
ошибок
прог-
нози-
рова-
ния
1
1
0
3
§ 3. ЗАДАЧА О КОНТРОЛЕ КАЧЕСТВА ПРОДУКЦИИ 169
приборов. Конечно, из партии будет изъято и A00—р)х
Хр2% хороших приборов (р2—вероятность ошибок вто-
второго рода), но с этим ничего не поделаешь — такова
плата за отбраковку приборов партии. Такой метод от-
отбраковки в настоящее время успешно применяется для
многих типов электронных ламп.
Результаты отбраковки для некоторых типов элек-
электронных ламп проведены в таблице 2.
После исключения из партии ламп прогностически
недоброкачественных приборов снова может быть про-
произведен статистический контроль партии. Партия опять
либо принимается, либо не принимается. В последнем
случае может быть снова построено решающее правило
по расширенной обучающей последовательности, про-
проведена новая очистка партии и т. д.
Комбинация методов обучения распознаванию обра-
образов с методами статистического контроля открывает
возможность построения интереснейших схем отбора и
оценки партий доброкачественных приборов.
§ 4. Задача о прогнозе погоды
Эта традиционная задача прогнозирования всегда
решалась специалистами-синоптиками с использованием
чисто синоптических качественных методов прогноза.
Относительно недавно для прогноза погоды стали при-
применяться точные методы, где развитие синоптической
ситуации представлено в виде модели, которая может быть
описана уравнениями. Полученное на ЭВМ решение
такого уравнения, где начальные условия — метеоро-
метеорологическая ситуация в момент времени I определяет про-
прогноз для различных моментов времени I + А;. Однако
качество прогнозов, даваемых по расчетным моделям,
пока уступает качеству прогнозов, полученных тради-
традиционными методами. И сейчас прогнозы, по существу,
даются синоптиками, использующими сведения о машин-
машинном прогнозе лишь как консультативный материал.
Для получения прогноза в настоящее время на земном
шаре существует широко разветвленная сеть метеостанций,
которые фиксируют значения различных метеорологиче-
метеорологических параметров. Эти данные поступают в центральные
метеорологические учреждения, где составляются карты
170 ГЛ. VII. ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДОВ РАСПОЗНАВАНИЯ
метеорологических ситуаций. Синоптики, исследуя эти
карты, и дают прогноз погоды. Прогноз погоды состоит
из нескольких элементов, таких как прогноз осадков, тем-
температуры, ветра и т. д. Особенно важно уметь прогно-
прогнозировать опасные явления погоды, такие как заморозки,
шквал, гололед, грозы.
Для всех этих опасных явлений погоды в настоящее
время средствами обучения распознаванию образов по-
получены решающие правила. Вероятно, первое такое реша-
решающее правило было получено в
Западно-Сибирском региональ-
региональном гидрометцентре для реше-
решения чрезвычайно важной для
сельского хозяйства задачи —
прогноза заморозков для лет-
летних месяцев (июль — август).
Прогноз минимальной тем-
пературы (заморозков) давался
по данным Новосибирска и ше-
шести станций, расположенных в
радиусе 1000 км. Данные состо-
состояли из сведений о значениях следующих шести пара-
параметров:
1) температуры воздуха у поверхности Земли,
2) температуры воздуха на изобарической поверх-
поверхности 850 миллибар,
3) давления у поверхности Земли,
4) высоты изобарической поверхности 850 миллибар,
5) скорости ветра на уровне 850 миллибар.
6) направления ветра на уровне 880 миллибар.
В отличие от предыдущих задач решалась задача раз-
разделения не на 2, а на 18 классов. Результаты испытания
полученных решающих правил приведены на рис. 19.
На этом рисунке сравниваются распределения вероят-
вероятностей ошибок прогноза ЭВМ (кривая 1) и синоптика
(кривая 2).
По оси абсцисс графика отложена величина ошибки,
по оси ординат вероятность этой ошибки. Согласно этому
графику малые ошибки при получении прогноза сред-
средствами обучения распознаванию образов менее вероят-
вероятны, чем при прогнозе синоптика. Наоборот, машина
несколько чаще делает грубые ошибки, которых синоп-
5. МЕТОДЫ РАСПОЗНАВАНИЯ В МЕДИЦИНЕ 171
тик избегает. Это объясняется тем, что информация о
метеорологических ситуациях собиралась только от шести
станций, расположенных на расстоянии 1000 км. А на
таком сравнительно небольшом расстоянии нельзя учесть
быстрых и резких изменений в развитии атмосферных
процессов; они могут быть учтены лишь при наблюдении
за большим участком земной поверхности. Тем не менее
показательно то, что уже по данным шести станций про-
прогнозы ЭВМ оказались в среднем не хуже прогнозов синоп-
синоптиков.
Схема прогноза гололеда средствами обучения рас-
распознаванию образов была построена в Гидрометцентре
СССР.
Прогностическая схема была построена по шести пара-
параметрам:
1) температура воздуха у поверхности Земли,
2) температура воздуха на изобарической поверхности
850 миллибар,
3) суммарный дефицит точки росы у поверхности земли
и на уровне 850 миллибар,
4) лапласиан температуры на уровне 850 миллибар,
5) скорость ветра у поверхности земли,
6) разность между скоростями ветра у поверхности
земли и на уровне 850 миллибар.
Надежность прогноза гололеда с помощью построен-
построенной схемы составила 90 %. Это намного выше, чем синоп-
синоптический прогноз.
Аналогичные схемы прогноза были построены в Гид-
Гидрометцентре СССР для предсказания гроз и шквалов. Эти
явления прогнозировались по большому числу парамет-
параметров B6 для шквалов и 80 для гроз). И здесь оправдыва-
емость прогнозов, полученных с помощью решающих
правил, оказалась выше, чем оправдываемость прогно-
прогнозов, даваемых синоптиками.
§ 5. Применение метода обучения распознаванию
образов в медицине
Вероятно, наибольший интерес у специалистов в об-
области построения обучающихся программ вызывают при-
приложения, связанные с^внедрением методов распознавания
в медицину. Оказалось, что почти на всех участках своей
172 ГЛ. VII. ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДОВ РАСПОЗНАВАНИЯ
деятельности врач так или иначе связан с необходимостью
классифицировать различные ситуации. Внедрение мето-
методов распознавания в медицину началось уже в первой
половине 60-х годов. В настоящее время существуют
десятки задач, решенных методами обучения распозна-
распознаванию образов. При этом оказалось, что в сопоставимых
условиях, как правило, классификации с помощью ма-
машин значительно точнее классификаций, которые про-
проводит врач.
Методы обучения распознаванию образов использу-
используются для решения следующих задач.
А. Дифференциальная диагностика.
Б. Прогнозирование осложнений при лечении.
В. Прогнозирование отдаленных результатов лечения.
Г. Выявление людей, «предрасположенных» к забо-
заболеванию (эпидемиологические задачи).
А. Задачи дифференциальной диа-
диагностики. Дифференциальная диагностика — одна
из наиболее трудных задач медицины. Она состоит в том,
чтобы поставить больному диагноз тогда, когда имеюща-
имеющаяся симптоматика может проявляться при различных
болезнях. Часто при этом окончательный диагноз корен-
коренным образом меняет тактику лечения. Например, чрезвы-
чрезвычайно трудно различать такие сходно текущие заболе-
заболевания, как рак легкого и центральное воспаление легкого.
А между тем в первом случае желательно срочное опера-
оперативное вмешательство, тогда как во втором необхо-
необходимо консервативное лечение. Для различных трудно
дифференцируемых заболеваний строятся решающие
правила.
В качестве исходной информации о больном берется
анамнез, данные обследования: лабораторных анализов,
рентгенограммы, кардиограммы и т. д.
Все эти данные определенным образом кодируются.
Для этого составляется стандартный перечень вопросов,
который для каждого больного заполняется ответами.
Часть вопросов требует ответов в виде утверждения «да»
(отрицания «нет»), на другие вопросы ответ дается в виде
числа. Уславливаются, что ответ «да» — наличие при-
признака — обозначется 1, а «нет» — 0. Таким образом,
набор ответов для[_ такого вопросника — вектор, 1-я
координата которого есть ответ на 2-й вопрос перечня.
§ 5. МЕТОДЫ РАСПОЗНАВАНИЯ В МЕДИЦИНЕ
173
Для примера в таблице 3 приведена часть вопросника,
составленного в связи с диагностикой заболеваний
желудка.
Таблица 3
№
1
2
3
4
5
6
7
8
9
Й1
кг
Наименование признака
Пол
Возраст
Наличие болей
Боли ноющие
Боли приступообразные
Боли голодные
Боли возникают сразу после еды
Возникают через 30 мин после еды
Возникают через 2—3 часа после еды
На сколько кг похудел больной
за последние 0,5 года
Гемоглобин в крови
Наличие молочной кислоты и т. д.
Характер ответа
мужской A) женский @)
целое число
да A) нет @)
да A) нет @)
да (\) нет @)
да A) нет @)
да A) нет @)
да A) нет @)
да A) нет @)
ответ в виде числа
ответ в виде числа
есть A) нет @)
Обучающая последовательность составляется из век-
векторов, соответствующих больным с установленным диаг-
диагнозом; полученное с помощью этой последовательности
решающее правило и используется в дальнейшем для
установления характера заболевания.
Такие решающие правила получены для дифферен-
дифференциальной диагностики болезней желудка (язва желудка,
рак желудка, полипы, гастриты), для дифференциальной
диагностики болезней пищевода (кардиоспазм, рак пи-
пищевода, рубцовые сужения и т. п.), заболеваний легких
и других заболеваний. Как уже указывалось, точность
правильной классификации с помощью этих правил выше,
чем точность врачебной диагностики.
Б. Задачи прогнозирования ослож-
осложнений. Умение прогнозировать осложнения очень
важно при выборе схемы лечения. При хирургических
вмешательствах существует опасность, связанная с та-
таким, например, осложнением, как тромбофлебит, и было
174 ГЛ. VII. ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДОВ РАСПОЗНАВАНИЯ
бы очень заманчиво для каждого больного уметь прогно-
прогнозировать эту опасность. При других заболеваниях какие-
то схемы лечения могут у некоторых больных вызвать
аллергию, а ее тоже надо уметь предсказывать.
Подобные задачи решаются по той же схеме, что и
задачи дифференциальной диагностики. Для каждой
такой задачи составляется свой перечень вопросов, со-
содержание которых должно отражать причины, вызыва-
вызывающие осложнение. Затем формируется обучающая после-
последовательность: к одному классу этой последовательности
относят тех больных, которые прошли данный курс
лечения, не имея осложнений; к другому — больных, пе-
перенесших осложнения. По этой последовательности стро-
строится правило, которое, учитывая индивидуальные осо-
особенности больного, должно прогнозировать возможности
осложнения при заданной методике лечения.
В.Прогнозирование отдаленных ре-
результатов лечения. Прогнозирование отдален-
отдаленных результатов лечения является определяющим фак-
фактором при выборе методов лечения. По существу, реша-
решается вопрос об эффективности для данного больного
некоторой схемы лечения. Обычно принятие решения
о применении определенного метода лечения связано с вы-
выбором одного из «конкурирующих» методов. Например,
для многих заболеваний существуют радикальные (опе-
(оперативные) и консервативные способы лечения, при этом
каждый вариант может иметь различные отдаленные ре-
результаты. Для простоты будем считать, что лечение при-
приводит к одному из трех исходов: 1) полное выздоровление,
2) инвалидность, 3) смерть (в действительности сущест-
существуют различные степени инвалидности).
Предположим, что для каждого метода лечения у нас
есть правило, с помощью которого с большой точностью
может быть осуществлено отдаленное прогнозирование
результатов лечения. Естественно тогда выбирать такую
методику лечения, которая дает для данного больного
прогностически наиболее благоприятный результат.
Такое прогностическое правило может быть получено
средствами обучения распознаванию образов.
Для этого также составляется вопросник, учитывающий
индивидуальные особенности больного и особенности те-
течения его заболевания. По такому вопроснику состав-
§ 5. МЕТОДЫ РАСПОЗНАВАНИЯ В МЕДИЦИНЕ 175
ляется обучающая последовательность, т. е. для каждого
метода лечения отбирается группа людей, для которых
известен результат лечения. Такая группа людей распа-
распадается на несколько классов, соответствующих результа-
результату лечения. По этой обучающей последовательности стро-
строится решающее правило, прогнозирующее попадание
каждого больного после лечения в соответствующую
категорию.
Такие решающие правила строятся для каждого ме-
метода лечения. А затем метод лечения для данного больного
выбирается исходя из наиболее благоприятного прогноза
результатов лечения.
Подобные методы Тпринятия решения чрезвычайно
эффективны. Обычно, чем большее число параметров не-
необходимо обработать для принятия решения, тем сильнее
сказываются преимущества машин в сравнении с челове-
человеком. Уже задача о дифференциальной диагностике забо-
заболевания выявляет значительное преимущество вычисли-
вычислительных методов в точности и надежности классификации.
Задача о выборе методов лечения исходя из наибольшей
прогностической эффективности по структуре значитель-
значительно сложней задач дифференциальной диагностики. Имен-
Именно поэтому здесь должны сказаться преимущества точного
расчета.
Г. Эпидемиологические задачи. По-
Появление методов обучения распознаванию образов позво-
позволило поставить в медицинской практике принципиально
новые и чрезвычайно важные задачи эпидемиологического
плана. Вот примеры таких задач.
Известно, что бывают так называемые вредные произ-
производства. Вредными их называют потому, что, несмотря
на принятые меры предосторожности, часть рабочих,
занятых на этом производстве, заболевает определенным
заболеванием (они называются профессиональными).
Между тем рядом с этими заболевшими рабочими работают
их [товарищи, для которых то же самое производство не
опасно. Спрашивается, можно ли при приеме на работу
по^различным особенностям организма рабочего, его пре-
предыдущей жизни, особенностям, связанным с привычками,
и т. п. прогнозировать, заболеет ли он профессиональной
болезнью. Естественно, что людям, для которых ответ
прогностически неблагоприятен, следует рекомендовать
176 ГЛ. VII- ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДОЙ РАСПОЗНАВАНИЯ
не поступать на эту работу. Такая задача решается так
же, как и обычная задача прогноза.
Чрезвычайно важна задача по выделению среди насе-
населения так называемых групп риска. Известно, например,
что различные психофизиологические особенности чело-
человека, его образ жизни как-то связаны с вероятностью
заболеть той или иной болезнью. Так, например, среди
заболевших инфарктом миокарда чаще отмечаются люди
с такими психофизиологическими особенностями: это
люди сангвистического темперамента, с преобладающими
отрицательными эмоциями, предрасположенными к пол-
полноте, чаще — занятые умственным трудом и т. д.
Возникает вопрос, нельзя ли средствами обучения рас-
распознаванию образов построить такое правило, которое
по данным о психофизиологических особенностях чело-
человека, об особенностях его жизненных условий и его нас-
наследственности прогнозировало бы для него вероятность
заболевания той или иной болезнью.
Людей с неблагоприятным прогнозом можно было бы.
объединить в «группы риска» и для каждой из них пы-
пытаться выработать некоторые профилактические меро-
мероприятия.
В настоящее время уже существуют решающие пра-
правила, с помощью которых можно выделять группы риска
по поводу некоторых онкологических и кардиологических
заболеваний.
§ 6. Замечания о применениях методов обучения
распознаванию образов
В приведенных выше примерах можно проследить
одну и ту же схему: для каждой конкретной проблемы спе-
специалисты указывают формальный способ описания ситуа-
ситуаций, в соответствии с которым образуются векторы, под
лежащие классификации. Составляется соответствующая
обучающая последовательность, а затем с помощью од-
одного из универсальных алгоритмов обучения распозна-
распознаванию образов строится нужное решающее правило. Часто
оказывается, что полученное правило классификации
позволяет разделять ситуации точнее, чем это делают
специалисты. Может возникнуть иллюзия, что уже одно
применение алгоритмов обучения распознаванию образов
8 6. О ПРИМЕНЕНИЯХ МЕТОДОВ РАСПОЗНАВАНИЯ 177
само по себе гарантирует успех в решении задач класси-
классификации. Это далеко не так.
Прежде всего, заметим, что из пяти приведенных при-
примеров четыре относятся к классификации так называемых
абстрактных ситуаций. Как уже отмечалось, структура
человеческого распознающего устройства, видимо, не
приспособлена к распознаванию абстрактных образов.
Кажущаяся легкость выбора системы формальных
описаний ситуаций в приведенных примерах объясняется
отнюдь не безразличием к способам формализации инфор-
информации, а тем, что в рассмотренных примерах существует
единственная возможность «разумной» формализации.
Так, в задаче о классификации нефтеносных пластов ком-
комплекс геофизических измерений был уже определен, в за-
задаче прогнозирования срока службы ламп определены
эксплуатационные параметры приборов, в задаче о про-
прогнозе погоды определены синоптические параметры, при
составлении программированной истории болезни широко
использовались разработки реальных историй болезни.
Итак, оказалось, что во всех приведенных задачах уже
задолго до появления методов обучения распознаванию
образов было ясно, какая информация нужна для клас-
классификации и как данная информация может быть фор-
формально представлена. Именно этим во многом и объяс-
объясняется успех применения методов распознавания.
Однако не везде методы распознавания позволили
достигнуть успеха в решении конкретных задач. Оказа-
Оказалось, что наиболее трудны для решения такие задачи, как
создание буквочитающего автомата и автомата, распо-
распознающего речь (акустические сигналы). В различении
рукописных знаков ни один из существующих буквочита-
ющих автоматов не может сравниться с искусством раз-
различения рукописных знаков человеком.
Чем это можно объяснить? Вероятно тем, что руко-
рукописные знаки придумывали сами люди и, естественно,
создавали их максимально удобными для своего распо-
распознающего аппарата. Теперь, для того чтобы состязаться
•с человеком в различении рукописных знаков, надо по-
повторить в программе «человеческую распознающую
■структуру».
Глава VIII
НЕСКОЛЬКО ОБЩИХ ЗАМЕЧАНИЙ
§ 1. Еще раз о постановке задачи
Почему же задача обучения распознаванию обра-
образов вот уже более пятнадцати лет вызывает такой боль-
большой интерес у ученых различных специальностей? Ко-
Конечно, отвечая на вопрос, можно было бы сослаться на ту
пользу, которая может быть достигнута при использова-
использовании идей и методов распознавания.
Однако основная притягательная сила задачи обу-
обучения распознаванию образов не в этом. Вот уже более
пятнадцати лет ученые пытаются понять, какую же за-
задачу они решают. Иногда удается нарисовать общую,
а потому поверхностную схему, в которую укладывается
постановка задачи распознавания образов, например
такую, какая проводится в данной книге. При
несколько прямолинейном взгляде на мир можно
утверждать, что задача обучения распознаванию образов
является примитивной задачей о минимизации среднего
риска. Примитивной потому, что решающие правила,
среди которых отыскивается нужное,— просто характе-
характеристические функции. Более того, это, возможно, просто
линейные дискриминантные функции.
Если стать на традиционную в математике точку зре-
зрения о том, что задание класса функций, в котором ищется
нужная функция, является внешним моментом в поста-
постановке задачи, то задача обучения распознаванию обра-
образов есть частный случай задачи о минимизации среднего
риска. Правда, оказалось, что для решения такой част-
частной задачи соответствующая математическая теория была
недостаточно развита. Поэтому в связи с задачей обучения
распознаванию образов были проведены исследования
§ 1. ЕЩЕ РАЗ О ПОСТАНОВКЕ ЗАДАЧИ 179
некоторых вопросов теории вероятностей и математиче-
математической статистики, таких как теория стохастической аппро-
аппроксимации, теория равномерной сходимости частот появ-
появления событий к их вероятностям. Однако необходимость
в развитии этих вопросов могла появиться и сама
по себе, а вовсе не в связи с задачей распознавания
образов.
Что же нового ищут в задаче обучения распозна-
распознаванию образов исследователи? Какую специфику они
пытаются вложить в формализацию понятия обучения?
Вероятно, в разное время основными в исследовании
обучения оказывались разные аспекты этой проблемы.
Всего 15—17 лет назад во времена первых работ Розен-
блатта обучение казалось таинственным феноменом, при-
присущим живым существам, и методика работ по исследо-
исследованию обучения напоминала нынешние работы по био-
бионике; считалось, что надо подсмотреть у живых существ
технологию обучения и перенести ее, как алгоритмы, на
ЭВМ.
Затем была поставлена задача обучения распозна-
распознаванию образов как задача минимизации риска. Следствием
такой постановки оказалось появление огромного коли-
количества алгоритмов, поток которых и в настоящее время
все еще достаточно широк. Однако вскоре удалось уста-
установить одну и ту же природу этих алгоритмов обучения
(связанную либо с идеей стохастической аппроксимации,
либо с идеей минимизации эмпирического риска).
Такая общность в природе алгоритмов немедленно была
связана с мыслью о появлении кризиса идей в теории рас-
распознавания .
Как же понимается задача об обучении распознаванию
образов сейчас? В чем специфика постановки задачи, в чем
ее отличие от общей задачи минимизации риска? Оче-
Очевидно, что вся специфика задачи обучения распознаванию
образов должна проистекать из того, что класс решающих
правил чрезвычайно прост. Применительно к такому
простому классу решающих правил надо найти тонкие
свойства методов минимизации риска, такие свойства,
которые присущи только этому классу и никак не явля-
являются общими свойствами методов минимизации риска.
В этом смысле единственная глава, которая была посвя-
посвящена обучению распознаванию образов,— это глава VI.
180 ГЛ. VIII. НЕСКОЛЬКО ОБЩИХ ЗАМЕЧАНИЙ
К сожалению, в настоящее время еще не найдена та-
такая постановка задачи, которая в рамках классической
теории минимизации среднего риска определила бы спе-
специфику задачи обучения. Таким образом, оказалось, что
содержание книги отражает в большей части не то, что
составляет сейчас предмет исследования, а скорее то,
где этот предмет должен находиться. Тем не менее можно
попытаться описать тот круг вопросов, который, очевид-
очевидно, должен составлять^специфику задач обучения.
§ 2. Физики об интуиции
Получилось так, что большинство законов, сформули-
сформулированных на основе наблюдений за феноменами природы,
принадлежат физикам. При этом обычная схема физиче-
физических открытий, в общем, всегда примерно одна и та же:
существует ряд экспериментов или наблюдаемых явлений,
которые не могут быть объяснены в рамках старой тео-
теории, поэтому на смену старой теории приходит новая,
которая объясняет и старые факты и новые факты, про-
противоречащие старой теории.
Удивительно в этой схеме не то, что отыскивается
новая теория, а то, что построенная по такой схеме теория
является правильной (способна предсказывать новые
явления). Действительно, в принципе существует огром-
огромное число формальных «законов», которые могли бы объяс-
объяснить все известные факты, но которые ничего общего не
имели бы с истинными законами природы.
Так, чтобы построить теорию относительности, надо
было построить теорию, которая содержала бы в себе
классическую механику и объясняла бы еще два-три
факта, главный из которых опыт Майкельсона. Формаль-
Формально таких теорий много. Как же нашел Эйнштейн свою
знаменитую теорию?
В общем, физики единодушны в объяснении этого
феномена — они ссылаются на интуицию ученого. Однако
даже проявление интуиции (не говоря уже о том, что такое
интуиция) физики определяют по-разному. Одни говорят,
что с их точки зрения теория должна быть наиболее кра-
красивой, другие — необычной, третьи, напротив, считают,
что теория должна быть наиболее простым правилом,
объясняющим мир. Иначе говоря, физики понимают, что
§ 4. О МИРЕ, В КОТОРОМ ВОЗМОЖНА ИНТУИЦИЯ 181
для выбора правильной теории одного объяснения фактов
явно недостаточно, и поэтому теория, объясняющая мир,
должна, по их мнению, удовлетворять еще и некоторому
экстремальному свойству (одни называют его красотой,
другие — необычностью, третьи — простотой и т. д.).
§ 3. Машинная интуиция
В главе VI мы столкнулись с проявлением «машинной
интуиции»: среди множества правил, правильно класси-
классифицирующих примеры, надо было выбрать лучшее.
Оказалось, что уже в рамках теории минимизации
среднего риска удается сформулировать экстремальные
свойства, которым должно удовлетворять выбираемое
решение. Более того, возможно сформулировать раз-
различные экстремальные принципы, одни из которых могут
оказаться более «глубокими», чем другие. Значит, можно
строить машины, различающиеся степенью «интуиции»,
и возможна машина, превосходящая другие «глубиной
интуиции».
§ 4. О мире, в котором возможна интуиция
При тех способах рассуждения, которые были про-
проведены, «глубина интуиции» определяется введением
априорного порядка среди решающих правил. Может
показаться, что введение порядка целиком зависит от
нашего произвола. На самом деле это далеко не так уж
очевидно.
При проведении упорядочения мы задаем классы
функций не перечислением их элементов, а рекурсивным
способом (заданием правила получения таких функций).
Правила получения функций задаются конструктивным,
а потому простым способом. Насколько разнообразны
способы упорядочения? В каких терминах можно опре-
определить разнообразие? Все это вопросы, на которые пока
нет ответа. Хотелось бы думать, что способы упорядоче-
упорядочения не слишком разнообразны и что всякое упорядоче-
упорядочение отражает расслоение функций по сложности.
Тогда интуицию можно объяснить, если принять ги-
гипотезу о «мире, где все явления имеют простую функцио-
182 ГЛ. VIII. НЕСКОЛЬКО ОБЩИХ ЗАМЕЧАНИИ
нальную связь» *), в то время как большая часть функций
отражает сложные зависимости. В таком мире, исследуя
явления природы, неразумно искать объясняющий их
закон в классе сложных функций, это и бесполезно,
потому что не хватит экспериментального материала,
чтобы его найти, и в этом, по сути, нет необходимости,
так как мир «прост». Принятие гипотезы о простом мире
позволяет, отбросив подавляющую часть всех функций —
сложные функции, искать решение в сравнительно мало-
малочисленном классе простых функций.
Найти наиболее простое правило, объясняющее на-
наблюдаемые явления или факты, задача весьма трудная.
Наверное поэтому найденное простое правило часто ка-
кажется неожиданным. В нашем человеческом понимании
простота тесно связана с понятием красоты. Может быть,
поэтому свойства «простота», «неожиданность», «красота»,
которые используют физики для объяснения причины
выбора того или иного закона, являются отражением
разных сторон одного и того же функционала. Не это
ли имел в виду Эйнштейн, когда заметил, что бог изо-
изощрен, но не злонамерен. Изощрен, потому что трудно
найти экстремальные принципы познания, и не злонаме-
злонамерен, потому что мир познаваем с помощью тех средств,
которые нам доступны. Хотя в принципе можно предста-
представить себе такой мир, для познания которого у нас просто
никогда не хватило бы опыта.
*) Заметим, что само понятие простоты и сложности функций
в математике до сих пор четко не определено. Поэтому в данном
случае приходится апеллировать к интуиции читателя.
Часть вторая
СТАТИСТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
В первой части книги задача обучения машин распо-
распознаванию образов рассматривалась с точки зрения про-
проблемы минимизации среднего риска. Последняя формули-
формулируется так: найти минимум функционала
2, а) ЛР (г),
причем функция (? (г, а) считается известной, вероятност-
вероятностная же мера Р (г) заранее неизвестна, но зато дана слу-
случайная выборка ги . . ., 2Ь полученная в результате неза-
независимых испытаний с неизменным распределением Р (г).
В этой части книги будет приведено математическое
обоснование двух путей решения этой задачи: рекуррентных
методов поиска минимума функционала В (а) и методов,
основанных на замене функционала В (а) его эмпирической
оценкой
г=1
Будет установлено, при каких условиях эти методы
приводят к успешному решению задачи.
Глава IX
О СХОДИМОСТИ РЕКУРРЕНТНЫХ
АЛГОРИТМОВ ОБУЧЕНИЯ
РАСПОЗНАВАНИЮ ОБРАЗОВ
§ 1. Определение понятия сходимости
В первой части книги задача обучения распознаванию
образов была рассмотрена с точки зрения проблемы ми-
минимизации среднего риска, т. е. приводилась к следующей
постановке: найти минимум функционала
аNР(г), (9.1)
если функция Р (г) неизвестна, но зато дана случайная
и независимая выборка 2ь. .., 2,.
Было установлено, что решение зтой задачи может
быть получено с помощью рекуррентных процедур вида
се @ = а (г - 1) - г (!) д (*й аA- 1)). (9.2)
Каждая такая процедура позволяет получать последо-
последовательность значений параметров а:
а A), . . ., а (п), . . ., (9.3)
которая определяет последовательность величин
В (а A)), . ... Л (а (п)), . . . (9.4)
Как последовательность (9.3), так и последовательность
(9.4) суть случайные последовательности, которые порож-
порождаются реализацией случайного процесса (9.2).
Исследование сходимости алгоритмов, минимизиру-
минимизирующих средний риск, сводится, таким образом, к исследо-
исследованию сходимости последовательностей (9.3) и (9.4).
§ 1. ОПРЕДЕЛЕНИЕ ПОНЯТИЯ СХОДИМОСТИ 185
Существуют различные понятия сходимости случайных
последовательностей. Ниже будут использованы два по-
понятия: сходимость по вероятности и сходимость с вероят-
вероятностью единица.
Определение 1. Последовательность случайных век-
векторов |х, . . ., |„, . . . сходится к вектору ^0 по вероят-
вероятности, если, каково бы ни было г ^> 0, вероятность вы-
полнения неравенства
II 1п — 1о К е
при п-у оо стремится к единице, т. е-
Факт сходимости по вероятности записывается так:
Определение 2. Последовательность случайных векто-
векторов 1и ...,!„,... сходится к вектору 10 почти наверное
(иногда говорят также с вероятностью единица), если,
каковв бы ни было г ^> 0, вероятность выпвлнения нера-
неравенства
при п -*■ оо стремится к единице, т. е.
Сходимость почти наверное принято обозначать так:
ёг * 60-
Приведенные определения сходимости случайных по-
последовательностей отражают различные требования к по-
понятию сходимости.
В первом случае событие {| \п — |01 ^ 8) выделяет мно-
множество последовательностей, для которых выполняется
условие \\п — ^01^8 для заданного фиксированного п.
При этом каждая последовательность с ростом п может
то удовлетворять этому условию, то не удовлетворять
ему. Сходимость по вероятности есть в некотором смысле
186 ГЛ. IX. О СХОДИМОСТИ РЕКУРРЕНТНЫХ АЛГОРИТМОВ
«слабая» сходимость — она не дает никаких гарантий
того, что каждая конкретная реализация |х, . . ., \п, . . .,
сходится в обычном смысле.
Напротив, сходимость почти наверное есть понятие
«сильной» сходимости. Оно означает, что почти все реа-
реализации сходятся в обычном смысле. Сходимость почти
наверное может быть определена еще и так.
Определение 2а. Последовательность случайных ве-
величин |г, . . ., |п, ... сходится почти наверное к %0,
если вероятность множества реализаций, для которых
существует предел
Нт 1п = |о,
равна единице, т. е-
Легко видеть, что из сходимости почти наверное сле-
следует сходимость по вероятности. В самом деле, так как
для любого п справедливо неравенство
Р (|б„ - бо|| < е) > Р (зир |& - &„К в),
то из условия
следует
Обратное утверждение, вообще говоря, неверно.
Нашей целью является установление условий схо-
сходимости случайных последовательностей (9.3), (9.4).
Для непрерывных В (а) из сходимости последователь-
последовательности (9.3) следует сходимость последовательности (9.4).
Обратное утверждение, однако, неверно: может случиться
так, что существует множество Ао точек |, на котором
функционал (9.1) достигает минимума. В этом случае
различные реализации процесса (9.2) могут сходиться
к различным элементам | е Ао, в то время как пос-
последовательность (9.4) будет сходиться к одной и той же
реличине,
§ 2. ВЫПУКЛЫЕ ФУНКЦИИ 18?
Постановка задачи обучения распознаванию образов
сводится к минимизации функционала (9.1). Таким обра-
образом, исследованию подлежит сходимость последователь-
последовательности (9.4). В том случае, когда точка минимума функ-
функционала (9.1) единственна, из сходимости (9.3) следует
сходимость (9.4) и, наоборот, из сходимости (9.4) сле-
следует сходимость (9.3).
Итак, будем исследовать сходимость ряда (9.4), т. е.
наша цель — определить условия, при которых
в том случае, когда т! В (а) существует.
§ 2. Выпуклые функции
Непрерывная функция Р (х) скалярного аргумента х
называется выпуклой, если для любой пары точек хг
и х2 справедливо неравенство
ХР (хг) + A — Ц Р (хъ) ^ Р (Кхг + A — к) х2),
0<А,<1. (9.5)
Приведенное определение выпуклой функции имеет про-
простой геометрический смысл. Прежде всего, отметим, что
выражение х = Кхг + A — Ц х2, 0 < Я<^ 1 для вся-
всякого фиксированного X опре-
определяет точку х, которая ло- у.
жит на отрезке, соединяющем
хх и х2. Обратно, каждое число „
х может быть разложено по хх г
и х2 единственным образом, „
причем '
-.ц=х-И?1 . (9.6)
2 XI
Если рассмотреть график функции Р (х) (рис. 20) и его
дугу между точками (ххуг), (х^г), где уг = Р (х^) и у2 =
= Р (х2), то неравенство (9.5) означает, что дуга гра-
188 ГЛ. IX. О СХОДИМОСТИ РЕКУРРЕНТНЫХ АЛГОРИТМОВ
фика лежит под хордой, соединяющей любые две точки
графика:
3?2 *^1 «С 2 &1
Аналогично определяется выпуклая функция в случае
векторного аргумента: для любой точки х, лежащей на
отрезке, соединяющем две точки хх и х2, имеет место не-
неравенство
> Р (х). (9.8)
§ 3. Обобщенный градиент
Вернемся к процедуре (9.2). Здесь обычно в случае,
когда функция (? (г, а) дифференцируема по а, в качестве
вектора <? (гг, а ({ — 1)) берется градиент по а функции
(? (г, а) при г = гг, а = а (I — 1). Градиент фУнкЦии
/ (а) будем обозначать V/1 (а). Таким образом, (9.2)
имеет вид
а @ = а (г - 1) - V (I) V. 0 (г,, а (г - 1)). (9.9)
Как известно, градиентом функции Р (а) в точке а0
называется вектор д такой, что функция (д, (а — а0))
является главной линейной частью приращения
= Р(а)-Р (а0),
АР = (д, (а - а0)) + о (а - а0), (9.10)
где о (а — а0) — величина более высокого порядка ма-
малости по сравнению с | а — а0 |.
Известно, что понятие градиента может быть обоб-
обобщено для недифференцируемых выпуклых функций следу-
следующим образом. Обобщенным градиентом У0Р выпуклой
функции Р (а) в точке а0 назывется такой вектор д (а0),
что для всех а
АР = р (а) - Р (а0) >(д, (а - а0)). (9.11)
Существование обобщенного градиента для выпук-
выпуклых функций в любой точке а показано, например, в
работе [27].
| 3. ОБОБЩЕННЫЙ ГРАДИЕНТ 189
Очевидно, что во всех точках, где выпуклая функция
дифференцируема, обобщенный градиент совпадает с обыч-
обычным. В самом деле, допустим, что в некоторой точке а0
V/1 (а0) Ф У0Р (а0). Тогда существует вектор е такой,
что
Положим
а (I) = а0 + 1е.
Тогда
Р (а0) - Р (а (*)) = {\Р, еIЛ-о Ц) =
= (V,/, е)*-а + о Ц). (9.12)
Поскольку с ^> 0, а о {I) — величина второго порядка
малости, при достаточно малых I ^> 0 обе части равенст-
равенства (9.12) становятся меньше, чем (Уо Р, е), что противо-
противоречит (9.11).
Рассмотрим пример выпуклой функции, которая не
всюду дифференцируема:
Ф (а) = | (а, 2) - с |,
где 2 — некоторый фиксированный вектор, ас — фикси-
фиксированный скаляр. Эта функция имеет градиент всюду,
за исключением многообразия
{а: (а, г) = с}.
Определим обобщенный градиент следующим образом:
( 2 при (ай, г)>с,
\Ф (а0) = 0 при (а0, г) = с,
| —2 при (а0, 2)<с.
При (а0, г) =?ь с сообщенный градиент совпадает с обыч-
обычным, а при (а0, г) — с условие (9.11), очевидно, выпол-
выполняется, поскольку при этом
(УоФ (а,), (а - а0)) = О,
в то время как
Ф (а) - Ф (а0) = Ф (а) > 0.
190 ГЛ. IX. О СХОДИМОСТИ РЕКУРРЕНТНЫХ АЛГОРИТМОВ
В главе IV была введена в рассмотрение функция
потерь
п п
() (г, а) = ^ а;гг -\- с -\- ( 2а сцгг -{■ I
г=1 ^ г=1
Как нетрудно убедиться, в качестве обобщенного гра-
градиента суммы функций можно взять сумму обобщенных
градиентов.
Поэтому для этой функции обобщенный градиент можно
положить равным
22 при
2 При
0 при
г=1
1=1
= с>
с-
В дальнейшем будем рассматривать только выпуклые
по а функции потерь. Это будет означать, что для таких
функций всегда существует обобщенный градиент и вы-
выполнены условия
<? B, а)-<? B, а„) > (Уо <? B, а0), (а - а0)).
§ 4. Условия сходимости рекуррентных алгоритмов
Итак, пусть задана выпуклая по а при любом фиксиро-
фиксированном 2 функция потерь () (г, а) и определена процедура
получения последовательности а A), . . ., а (п), . . .:
а @ = а (I - 1) + у (I) Уо (? (гг, а (I - 1)).
Рассмотрим несколько более общую, чем в главе IV,
процедуру образования последовательности
а @ = а (г - 1) + у (О [Уо <? (я,, а (I - 1)) + Ы, (9.13)
отличающуюся тем, что |$ — случайная помеха при изме-
измерении обобщенного градиента, которая удовлетворяет
§ 4. УСЛОВИЯ СХОДИМОСТИ 191
условиям
М (%\ а, г) = О,
М(^2 \а, 2)<#<оо.
Будем считать, что величины у (г) ^> О, образующие
бесконечную последовательность неотрицательных чисел,
таковы, что
2 т@ = °с.
1=1
1=1
Процедура (9.13) для заданного начального условия а —
= анач определяет случайный процесс. Реализации
этого случайного процесса индуцируются последователь-
последовательностями точек 2Ь . . ., гп, . . ., которые появляются неза-
независимо в соответствии с распределением Р (г). Распре-
Распределение же Р (г) таково, что для любого а существует
В (а) = ^ <? B, а) йР B) = М2 {<? B, а)}
Д (а) = $ | УоA B, а) |2 йР (г) = М2 {| Уо<1 (г, а) |2}.
Справедлива теорема
Теорема 9.1. (Б. М. Литваков [44]): Если:
1) функционал Н (а) ограничен снизу,
2) функция Б (а) ограничена сверху, т. е- В (а) <^ В,
3) дисперсия помехи \ ограничена сверху, т. е. В (^) <;
^ Б, то при любом начальном векторе анач последователь-
последовательность В [а (г)] —> т! В (а) с вероятностью 1.
г-»оэ а
Доказательство теоремы опирается на следующие
леммы.
Лемма 1. Для любых N и б ^> 0 можно подобрать такое
г ^> 0, чтобы вероятность того, что вектор а (ЛГ) ока-
окажется внутри гипершара Ом с центром в анет и радиусом
г, была больше 1 — б.
Доказательство. Покажем сначала, что для
любого I существует ограниченная величина Г (г) —
192 ГЛ. IX. О СХОДИМОСТИ РЕКУРРЕНТНЫХ АЛГОРИТМОВ
«= М{(а (г) — аначJ} *). Согласно процедуре (9.13) спра-
справедливо равенство
М {(а @ - аначJ} = М {(а A-1)- аначJ} - 2у (I) X
X М {((а (I - 1) - анач), (Уо () B„ а (I - 1)) + Ш +
+ У2 (ОМ {\Ч0(? BЬ а (г - 1)) + в I 2}- (9-14)
Увеличим правую часть этого равенства. Согласно условию
■теоремы
М {Б | а, 2 } = О,
М {[Уо <? B,, а (г - I))]2} < Л,
М {^2 |а(г-1), гг}<Д.
Поэтому Т2 (ОМ {[Уо (? (г,, а (г - 1)) + Ы2} < 2Т2 (г) Д.
Кроме того, используя то, что для выпуклой функции
и любых г, аг и а2 справедливо неравенство
(К - а2), Уо <? (г, ах)) > <? (г, в1) - <? (г, а2),
оценим величину М {((а (г — 1) — анач), Уо <? B> а (I —
- 1)))}:
М {((а (г - 1) - амч), Уо<?B, а (г - 1)))} >
> М {<? (г, а (г - 1))}- М {<? (г, анач)} =
= Е(аA — 1)) -В (анач) > Л - ^? (анач),
где Л = т! ^? (а).
а
Таким образом, оказывается справедливым неравенство
М {(а @ - аначJ} < М {[а (г - 1) - а„ачР} + с (I), (9.15)
где с @ = 2у (») (Л (анач) - А) + 2Ду2 (О-
Используя неравенство (9.15) и учитывая, что
М {(а A) - апачJ} = сA),
непосредственно получаем, что
N
М {(а (ТУ) - аначJ} < 2 с @ = ГА'-
т. е. величина М {(а (/V) — аначJ} ограничена числом Г у,
*) Для сокращения записи здесь и дальше используются обоз,
начения а2 = (а-а).
§ 4. УСЛОВИЯ СХОДИМОСТИ 193
Для доказательства леммы воспользуемся неравен-
неравенством Чебышева для нецентрированных случайных ве-
величин
Р(|а(Л0-анач|>г)<
М{|а(Л')-аначр}
Усилим это неравенство; учитывая, что
М{|а(УУ)-анач|2}<Г]У,
получим
Потребуем, чтобы эта вероятность не превосходила б.
Это произойдет, если величины г, Глг, б будут связаны
соотношением
откуда следует, что с вероятностью, превышающей 1 — б,
точка а (/V) будет находиться внутри гипершара С с цен-
центром в <Хнач и радиусом
г =
Лемма 1 доказана.
Пусть, далее,
А = 5п! Я (а).
а
Обозначим через Ог область значений а:
Ог = {а: В («)< А + г}.
Лемма 2. Для любых г ^> 0 и N последовательность
<хъ . . ., <хЛ', . . ., а-г, . . . с вероятностью 1 хоть раз вой-
войдет в область Сг при I ^> N.
Утверждение леммы 2 эквивалентно такому: вероят-
вероятность того, что подпоследовательность <х#, • • ., сс« ни
разу не заходит в область С€, стремится к нулю при I —>■ оо.
Доказательство. Для доказательства удоб-
удобно рассмотреть процедуру, отличающуюся от (9.13)
только тем, что если последовательность при I ^> N
входит в область О€, то она там и остается.
194 ГЛ. IX. О СХОДИМОСТИ РЕКУРРЕНТНЫХ АЛГОРИТМОВ
Для этого будем считать, что соотношение
а @ = а (I - 1) - у (I) [Уо <? (г, а (г - 1)) + Ы
выполняется всегда при г <^ /V + 1, а при I ^> N + 1 —
лишь для а (г — 1) ф Сг. В случае же, когда при I ^>
^> /V + 1 элемент а (I — 1) принадлежит Се, последова-
последовательность «залипает», т. е.
а (г) = а (г — 1).
Очевидно, что если последовательность а A), ..., а (/V), ...
..., а@, построенная в силу исходного алгоритма, ни разу
не заходит в Сг при I 1> /V, то последовательность, постро-
построенная по новому правилу, ничем не отличается от исход-
исходной и, в частности, не заходит в Сг при I 1> N. Поэтому
достаточно оценить вероятность того, что новая последо-
последовательность ни разу не войдет в СЕ при I ^> N.
В области Ог выберем точку а*, для которой
(это всегда можно сделать), и оценим величину М {(а (г)—
— а*J} для процедуры
(а (г — 1), если I > N + 1 и аA-1)ЕСг,
а@= а^-!)-^)^^.^-!)^;] (9-16)
[ в противном случае.
Согласно этой процедуре при а (г — 1) (^ё Ог
М {(а @ - а*J | а (г — 1)} = (а (I — 1) - а*J -
-2у (О [М {У„<? B, а (г - 1)) | а (г - 1)}, (а (I - 1) -
- а*)] - 2у (О [М {Ъ | а (г - 1)}, (а (*• - 1) - а*)] +
+ У2 (О М {^2 + [Уо (? B, а (I - 1))]г| а (г - 1)}.
В силу условий теоремы
М {Ь | а} = О,
а также
М {ГУ0 <? (г, а)]2} <СиМ{?!|а}<й.
§ 4. УСЛОВИЯ СХОДИМОСТИ 1УЗ
Поэтому справедливо неравенство
М {(а @ - а*J | а (I — 1)} < (а (I — 1) - а*J-
-2у (О (М {Уо (} B, а (г- 1))}, (а (г - 1) - а*)) +
+ 2Т2@#. (9.17)
Далее, поскольку функция (? (г, а (I — 1)) выпукла, то
(Уо (} (г, а (I - 1)), (а (I - 1) - а*)) >(? (г, а (* - 1)) -
- <? (г, а*)
и поэтому
(М{У0<?B, «(г-1)) |а(г-1)}, (а (I - 1) — а*)) >
>Д(а(г-1))-Д(а*). (9.18)
Но точки а (I — 1) и а* выбраны так, что
В (а (I - 1)) > А + 8
(поскольку а (^ — 1) §ё Се) и
Д(а-)<Л + |
и, следовательно,
Д(а(г_1))-Д(а*)>|. (9.19)
Объединяя (9.17), (9.18) и (9.19), получаем, что при
а (I ~ 1) ^ Се
М {(а (г) - а*J | а (г - 1)} < (а (I - 1) - а*J -
Если же при I ^> /V + 1 элемент а B — 1) ЕЕ Сг, то
М {(а @ - а*J | а (г — 1)} = (а (I - 1) - а*J.
Пусть 6г- — вероятность того, что а (I — 1) §Ё О..
Тогда, переходя к безусловному математическому ожида-
ожиданию, получим для г ;> N + 1
М {(а @ - а*J} < М {(а (I - 1) - а*J} - еб^ @ +
196 ГЛ. IX. О СХОДИМОСТИ РЕКУРРЕНТНЫХ АЛГОРИТМОВ
Из этого рекуррентного соотношения, очевидно, сле-
следует, что при г > N + 1
М {(а @ - а'J} < М {(а (Л') - а*J} -
В силу леммы 1 величина
М (а (/V) — а*J
ограничена, и по условию теоремы ряд 2 Т2 (О СХ°-
{=N+1
дится. Поэтому
г
(9-20)
где с — константа, не зависящая от I,
Далее, поскольку процедура (9.16) организована так,
что, попав в Ог, последовательность «залипает», вероят-
вероятность 6^ не возрастает с ростом I.
Если бы при этом 6г оставалась больше некоторого
б ^> 0, то величина
г
2 »,-т(/)
/=N+1
с ростом I неограниченно возрастала, поскольку при
этом
2
а ряд 2 тО)Расх°Дится-
Но это невозможно, потому что тогда правая часть
неравенства (9.20) становилась бы отрицательной при
достаточно больших г, тогда как левая часть положитель-
положительна. Следовательно, последовательность бг стремится
к нулю при г -*■ оо.
Остается отметить, что последовательность а (г) орга-
организована процедурой (9.16) так, что если она хоть раз
§ 4. УСЛОВИЯ СХОДИМОСТИ 197
войдет в Ог при I > N + 1, то она там и останется к мо-
моменту I. Следовательно, вероятность того, что последо-
последовательность (Хлг, . . ., сх.1 ни разу не заходит в Сг, равна
бг и стремится к нулю при г->■ оо.
Лемма доказана.
Лемма 3. Для любых г ^> 0 и б ^> 0 существует такое
/Уь что при всех N ^> Ыг вероятность последователь-
последовательности ах, . . ., <хи . . . выйти из области
О2€ = {а: В (а) < А + 2г},
при условии а (/V) ЕЕ О€, меньше б.
Доказательство. Оценим вероятность 6^ того,
что в последовательности а,\, . . ., а-ь хотя бы один эле-
элемент не принадлежит О2г при условии, что а^ ЕЕ Ог.
Для этого изменим процедуру (9.13) при I > N + 1,
положив
а (г — 1), если а (I — 1)„§= С2е,
если а (г — 1) ЕЕ С2е.
Очевидно, что величина бг равна вероятности того, что
а; 0. С2г при условии а.н ЕЕ Се, если, начиная с I =
= N + 1, действует процедура (9.21).
Обозначим через ае (г) точку множества Се, ближай-
ближайшую к а (г), и оценим величину
М {(а @ - ае (ОJ}.
Очевидно, справедливо неравенство
(а @ - ае (ОJ < [а (г) - а, (г - I)]2.
Поэтому при а (I — 1) ЕЕ С2е в силу процедуры (9.21)
М {(а (г) - ае (ОJ | а (г - 1)} < М {(а @ -
- ае (I - I)J | а (г - 1)} < (а A-1)- аг (I - I)J -
-27 (О (М {Уо<? (г, а (г - 1))}, (а (I -1) - а. (г - 1))) +
+ 2Ду2 (г).
В силу выпуклости (^ (г, а) справедливо неравенство
(М {Уо<? (г, а (г - 1))}, (а (г - 1) - ае (г - 1))) >
> Д (а (I - 1)) - В (а, (г - 1)).
198 ГЛ. IX. О СХОДИМОСТИ РЕКУРРЕНТНЫХ АЛГОРИТМОВ
Но при а (I — 1) ЕЕ СЕ элементы а (г) и аг (г) совпадают,
а при а (г — 1) §ё Се
В (а (I - 1)) > В (ае (* - 1)).
Поэтому
В(аA— 1)) - Д (а8 (I - 1)) > 0.
Следовательно,
М {(а @ - ае (ОJ | а (I - 1)} < (а (I - 1) -
-а. (г- 1))»+27*@Л-
Если же а (г — 1) §Ё С2г при г ^> N + 1» то
М {(а (г) - аг (ОJ | а (г - 1)} = (а A-1) -а, (( - 1))\
Таким образом, всегда
М {(а @ - а. @) |а A-1)}<
^ (а (I _ 1) _ «, (г _ 1))» +27а@^-
Из этого рекуррентного соотношения следует, что при
г ^> /V справедливо
<2Д 2 Т2(/), (9.22)
3=Л'+1
поскольку при а (/V) 6Е Сг имеет место
(а (^) - ае (Лг)J = 0.
Далее, оценим расстояние Л между произвольным эле-
элементом а ^ С2г и множеством Се, т. е. ширину зоны,
которую должна пройти точка а (г), чтобы из Сг уйти
за пределы Сгг. Так как функция Д (а) выпукла,
У0Я(а) =М{|У0(?B, а) |}
для всякой точлп а (ЕЕ Сг выполняется неравенство
Л (а)< Л + е
и для всякой точки а ^Е Сге — неравенство
Я (а) > А + 2е,
§ 4. УСЛОВИЯ СХОДИМОСТИ 199
то
(9.23)
Поэтому
бг = Р (а @ ф О2г | а (/V) ЕЕ С.) <
< Р {(| а (г) - а. (О I > Л) | а (-
Воспользуемся неравенством Чебышева
Учитывая далее (9.22) и (9.23), получаем
{=N+1
Правая часть неравенства не зависит от I, поэтому, выбрав
N достаточно большим, можно добиться, чтобы бг было
меньше б при всех I ^> /V, а это и значит, что последова-
последовательность выходит из Сгг с вероятностью, меньшей б.
Лемма доказана.
Докажем теперь теорему 9.1.
Для заданных е и б подберем Ых так, чтобы для всякого
N ^> /У\ вероятность последовательности выйти за пре-
пределы области
С2е = {а: Я (а)< А + 2е}
при условии, что а (/V) ЕЕ Ог, была меньше б. Это можно
сделать в силу леммы 3.
Далее, в силу леммы 2 последовательность а A),...
. . ., а (/V), ... с вероятностью 1 хоть раз войдет в Ог
после момента /У\ и, следовательно, выйдет из С2е с ве-
вероятностью, меньшей б. Ввиду произвольности б и 8
это означает, что
К (а (г)) т-> И11 Я (а)
г~*со а
с вероятностью единица.
Теорема доказана.
200 ГЛ. IX. О СХОДИМОСТИ РЕКУРРЕНТНЫХ АЛГОРИТМОВ
§ 5. Еще одно условие сходимости рекуррентных
алгоритмов
В условиях теоремы 1 не предполагалось, что сущест-
существует минимум функционала В (а). Достаточно было того,
что функционал ограничен снизу и, следовательно, су-
существует точная нижняя грань. Сходимость к точной
нижней грани и утверждала теорема.
Сейчас будем предполагать, что минимум функционала
существует. Это позволит ослабить требования к порядку
роста модуля градиента функции потерь.
Теорема 9.2. (Б. М. Литваков [44]). Пусть выполнены
следующие условия:
1) функционал В (а) ограничен снизу и существует
непустое множество Т = {а: В (а) = т! В (а.)},
2) М{|У0<?B, а)р}<ДA +|а|2),
3) М{|» |а}<Д A + |а|2).
Тогда при любом анач с вероятностью единица
справедливо: В (а {I)) —> т! В (а).
Доказательство. Выберем произвольную
точку а0 ЕЕ Т. Оценим долю б тех последовательностей,
которые хоть раз выйдут из гипершара О с центром в а0
и радиуса г. Для этого положим, что рекуррентные соот-
соотношения (9.13) выполняются лишь для | а — а0 | ^ г
и вне гипершара С последовательность «залипает», т. е.
( а (г — 1), если | а (г — 1) — а0 \ > г,
а @ = а (г - 1) - V @ [V,, <? (г, а (* - 1)) + Ы,
1. если | а (г — 1) — а0 |< г.
Таким образом, последовательность, выйдя из гипершара,
не может войти обратно.
Аналогично теореме 9.1, учитывая условия выпукло-
выпуклости (^ (г, а) и условия теоремы 9.2, можно показать, что
справедливо неравенство
М {(а (г) - а0J} < М {(а ({ - 1) - а0)*} +
+ 2у2 A)ДМ {A + а2 (г - 1))}. (9.24)
Усилим неравенство (9.24), для чего оценим величину
М {1 + о? (г- 1)} = 1 + М {а2 (* — 1)}.
§ 5. ЕЩЕ ОДНО УСЛОВИЕ СХОДИМОСТИ 201
Воспользовавшись неравенством а2 ^ 2 (а — ЬJ -\- 2№,
получим
М {1 + а2 (I - 1)} < 1 + 2М {(а (I - 1) - а0J} +
+ 2а2. (9.25)
Подставляя (9.25) в (9.24), получим
М {(а (I) - а0J} < A + 4у2 @ Д)М {(а (I - 1)- аоJ}+
+ 2у2 (*)Л A + 2а1). (9.26)
Из неравенства (9.26) следует, что величина М {(а (г) —
—а0J} ограничена числом Ь, не зависящим от номера I.
Покажем это.
Обозначим (анач — а0J = а, 2Д A + 2а2,) = Ъ. По-
Покажем, что справедливо неравенство
М {(а @ - а0)*} < П A + 4т2 (/) О)(а+Ь^ ^ (/)). (9.27)
3=1 ' 3=1 '
Для I = 1 справедливость неравенства легко проверяется:
М {(аA)-аоJ}<A + 4Т2 A) Б) а + у2 A) Ь <
По индукции легко доказывается справедливость нера-
неравенства и для любого I, если оно справедливо для I — 1:
1—1
М {(а @ - а0J} < A + 4Т2 ({) О) Ц A + 4Т2 (/) Б) х
г—1 г г
X (а + Ь 2 Т2 (/)) +Ьг'(О< П A +4Т2(/)Д) (а + Ь 2 Т2 (/)) ■
)
' з=1
Остается показать, что величина М {(а (I) — а0J}
ограничена, т. е.
П A + 4Т2 (/) 0) (а + Ъ 2 Г2 (/)) < I- (9.28)
В самом деле, в произведении (9.28) сомножитель
(а -)- Ь 2 Т2(/)) ограничен, так как 2 Т2(/)<С °°-
202 ГЛ. IX. О СХОДИМОСТИ РЕКУРРЕНТНЫХ АЛГОРИТМОВ
Сомножитель
ПA+4Т2(/)Г)
3=1
также ограничен, так как бесконечное произведение
3=1
ограничено тогда и только тогда, когда сумма
оо
3=1
ограничена.
Таким образом,
Используя неравенство Чебышева, можно получить
неравенство о <^ — .
На множестве С функция М {(^ (г, а)} ограничена.
Рассмотрим процесс, отличающийся от (9.13) лишь тем,
что при выходе за пределы С он «залипает». Очевидно, что
все реализации исходного процесса, не покидающие О,
при этом сохранятся и вероятность «залипания» меньше
б. Применительно к новому процессу можно повторить
все рассуждения теоремы (9.1) и показать, что с вероят-
вероятностью, превышающей 1 — б, для этого процесса
Я (а (г)) —> т! Н (а).
Отлично лишь в том, что в леммо 2 величина бг есть
вероятность того, что процесс за первые I шагов ни разу
не вышел из области С и не вошел в Сг. Получая, далее,
что Нтб1 = 0, приходим к выводу, что с вероятностью,
превышающей 1 — б, процесс входит в Сг. Остальные
рассуждения повторяются, по существу, без изменения.
Далее, соответствующим выбором г величина б может
быть сделана сколь угодно малой, откуда и следует ут-
утверждение теоремы.
Глава X
ДОСТАТОЧНЫЕ УСЛОВИЯ
РАВНОМЕРНОЙ СХОДИМОСТИ ЧАСТОТ
К ВЕРОЯТНОСТЯМ ПО КЛАССУ
СОБЫТИЙ
§ 1. О близости минимума эмпирического риска
к минимуму среднего риска
Перейдем теперь к анализу методов, основанных на
минимизации эмпирического риска. Пусть задана выборка
полученная в серии независимых испытании при неизмен-
неизменном распределении Р (г), и известна функция (? (г, а).
Требуется найти минимум функционала
>B, а) AР (г).
В дальнейшем будем полагать, что минимум В (а) суще-
существует и достигается при а =■- ап.
Рассматриваются методы, где в качестве приближения
берется значение а*, доставляющее минимум функции
I
1=1
Естественно, в качестве меры близости <х0 и а* взять
разность значений функционала В (а) в этих точках:
р (ая, с/.*) - В (а*) - В (а,).
Как было указано в главе V, близость значений сс0
и а* в этом смысле может быть гарантирована, если
204 гл. х. достаточные условия равномерной сходимости
функция Вшп (а) равномерно по параметру а приближает
функцию Л (а). В самом деле, если
вир \К (а) — Вшп (а) | < 8,
а
то Л (а*) - Кшп (а*) < е, A0.1)
Вта (<*„) - В (а0) < 8. A0.2)
Кроме того, поскольку а0 и а* — точки минимума
соответственно функций Л (а) и Вжп (а), то
В (а0) < Л (а*), (Ю.З)
Яэмп (а*) < Яэмп («;). A0.4)
Из A0.1) — A0.4) непосредственно вытекает, что
Л (а*) - В (а0) < 2е.
Или, иначе,
Д (а*) - Л (а0) < 2 вир | Л (а) - ЛВИП (а) |. A0.5)
а
Таким образом, если отклонение функций Втп (а)
и Н (а) при всех значениях параметра не превосходит
8, то значение истинного риска В (а) в точке эмпириче
ского оптимума а* не более чем на 2е отклоняется от
минимального. Если же максимальное по а уклонение
риска В (а) и его эмпирической оценки велико, то, вообще
говоря, замена истинного минимума эмпирическим может
привести к большим ошибкам.
В задаче обучения распознаванию образов функция
() (г, а) в функционале К (а) имеет специальный вид.
Здесь каждый элемент г есть пара х, со, где х — описание
ситуации, а со — указатель класса, к которому в действи-
действительности относится эта ситуация. Обычно число классов
невелико, т. е. со может принимать конечное небольшое
число значений 0, 1, . . ., к. Каждому значению параметра
а соответствует решающее правило Р (х, а), причем
функция Р (х, а) принимает те же дискретные значения,
что и со.
В качестве критерия В (а) обычно берется вероятность
неправильной классификации с помощью правила
Р (х,а). Это значит, что определена функция штрафа
,, . „. @ при со = Р,
Ф (со, Р) = |1 при со ^ ^
§ 1. ОБ УКЛОНЕНИИ МИНИМУМА ЭМПИРИЧЕСКОГО РИСКА 205
и функционал Л (а) задан в виде
К (а) =1Ф(со, Р (х, а)) д,Р (х, со).
Функция Ф (со, Р) есть характеристическая функция
множества
Та = {х, со: Е (х, ос) ф со}.
Соответственно функционал Л (а) при каждом значении а
есть вероятность события Та1
К (а) = Р {Р (х, со) ф со} = Р (Та).
Эмпирическая оценка Вжп (а) равна частоте V (Та)
появлений этого события в обучающей выборке, т. е.
частоте ошибок на материале обучения. Пусть теперь
параметр а принимает всевозможные допустимые значе-
значения а ЕЕ (^- Соответствующие события Та образуют класс
событий 5. Равномерная близость функций Н (а) и -йЭМп(с)
означает равномерную близость частот и вероятностей
событий Та по классу 5.
Применяя формулу A0.5) в данном случае, имеем
Н (а*) - Л (а0) < 2 вир | V (Та) - Р (Та) |. A0.5')
тае8
В более общем случае проблема равномерной сходи-
сходимости функций ЛЭмп (с) и Л (с) также может быть све-
сведена к равномерной сходимости частот к вероятностям
в определенном классе событий (§ 2 главы XIII).
Перейдем теперь к выводу условий, которым должен
удовлетворять класс событий 5 для того, чтобы выполня-
выполнялась равномерная по классу сходимость частот появления
событий к их вероятностям. Существенно, что при опре-
определенных условиях удается получить оценку равномерной
близости частот к вероятностям, не зависящую от рас-
распределения Р (х, со), которое обычно неизвестно, и опре-
определяемую только внутренней структурой класса 5. Эта
оценка не содержит произвольных констант и позволяет
эффективно оценить близость эмпирического оптималь-
оптимального решающего правила к истинному для заданного
класса решающих правил при фиксированной длине
обучающей последовательности.
206 ГЛ, X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
§ 2. Определение равномерной сходимости частот
к вероятностям
Согласно классической теореме Бернулли, частота
появления некоторого события А сходится (по вероят-
вероятности) в последовательности независимых испытаний
к вероятности этого события. Выше мы убедились, что
возникает необходимость судить одновременно о вероят-
вероятностях событий целого класса 5 по одной и той же вы-
выборке. При этом требуется, чтобы частота событий схо-
сходилась к вероятности равномерно по всем событиям клас-
класса 5. Точнее, требуется, чтобы вероятность того, что
максимальное по классу уклонение частоты от вероят-
вероятности превзойдет заданную сколь угодно малую поло-
положительную константу, стремилась к нулю при неограни-
неограниченном увеличении числа испытаний.
Оказывается, что даже в простейших примерах такая
равномерная сходимость может не иметь места. Поэтому
хотелось бы найти критерий, по которому можно было
бы судить, есть ли такая сходимость или же ее нет.
В этой главе будут найдены достаточные условия
такой равномерной сходимости, не зависящие от свойства
распределения, и дана оценка скорости такой сходимости.
В главе XI мы введем необходимые и достаточные усло-
условия равномерной сходимости частоты к вероятностям. Эти
условия уже будут зависеть от свойств распределения.
Пусть X — множество элементарных событий, на ко-
котором задана вероятностная мера Р (х). Пусть 5 — неко-
некоторая совокупность случайных событий, т. е. подмножеств
пространства X, измеримых относительно меры Р (.х)
E включается в а-алгебру случайных событий, но не обя-
обязательно совпадает с ней). Обозначим через X (I) про-
пространство выборок из X длины /. Тот факт, что выборка
является повторной, т. е. получена в последовательности
независимых испытаний при неизменном распределении,
формализуется заданием вероятностной продукт-меры на
X (I) из условия
Р \А1 х . . . х А,] = Р (Аг) . . . Р (А{),
где А — измеримые подмножества X.
Для каждой выборки X1 = хх, . . ., х1 и события
А (= 8 определена частота выпадения событий А, равная
§ 2. ОПРЕДЕЛЕНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ 207
отношению числа п (А) элементов выборки, принадлежа-
принадлежащих А, к общей длине выборку
ч/х Х\
Теорема Бернулли утверждает, что при фиксирован-
фиксированном событии А уклонение частоты от вероятности стре-
стремится к нулю (по вероятности) с ростом объема выборки,
т. е. для любого А справедливо:
Р {\Р(А) -х(А) |>8}-^0.
Нас же будет интересовать максимальное по классу 5
уклонение частоты от вероятности:
я (I) = вир | V' (А) — Р (А) |.
А8
Величина я (I) является функцией точки в простран-
пространстве X (I). Будем предполагать, что эта функция измерима
относительно меры в X (I), т. е. что я (I) есть случайная
величина.
Если величина л (I) стремится по вероятности к нулю
при неограниченном увеличении длины выборки I, то
говорят, что частота событий А ЕЕ 8 стремится (по веро-
вероятности) к вероятности этих событий равномерно по
классу 5. Дальнейшие теоремы посвящены оценкам ве-
вероятности события
{л (I) > е}
и выяснению условий, когда для любого е^> 0 справед-
справедливо
Нт Р {л (I) > е} = 0.
В отличие от обычного закона больших чисел равно-
равномерная сходимость частот к вероятностям может иметь
или не иметь места в зависимости от того, как выбрано
множество 5 и задана вероятностная мера Р (х). Приве-
Приведем простейший пример, когда равномерной сходимости
нет.
Пусть X — интервал @, 1) и на нем задано равномер-
равномерное распределение вероятностей, т. е.
Р {х<а} = а; @<а<1).
208 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
В качестве системы 5 рассмотрим любую совокупность
событий (измеримых подмножеств X), содержащую все ко-
конечные подмножества интервала @,1). Очевидно, что ве-
вероятностная мера Р (А) каждого события, состоящего
лишь из конечного числа элементов, в нашем случае равна
нулю.
Пусть теперь дана выборка хх, ..., х,\. Рассмотрим ко-
конечное множество Л*е5, состоящее из тех и только тех
элементов х, которые встретились в этой выборке. Очевид-
Очевидно, что
/ Л* \ П (А*) л
у(А;хъ...,х1) = -^ = 1,
в то время как Р (А*) = 0.
Учитывая, что всегда
\Р(А) -ч(А) | <1,
получаем
вир | V (А; хъ ..., ж,) — Р (А) | = 1.
А8
Это соотношение выполняется тождественно для любой
выборки любой длины. Таким образом, в данном случае
величина
я8 (хх, ..., х,) = 1
и не стремится к нулю ни в каком смысле.
Совершенно аналогично показывается, что
Я8 (.X!, ..., Хх) = 1
и в более общем случае, когда X есть «-мерное евклидово
пространство, Р (х) — любое распределение, обладающее
плотностью, а 5 — любая система событий, включающая
все события, состоящие из конечного числа элементов.
В частности, при этих предположениях в качестве 5 мож-
можно взять полную систему событий, составляющую всю
0-алгебру; тогда
Я (Хг, ..., Ж;) = 1
и равномерной сходимости нет. Таким образом, во многих
случаях равномерная сходимость частот к вероятностям
не имеет места для полной системы событий. Для того
чтобы такая сходимость происходила, приходится в каче-
8.2. ОПРЕДЕЛЕНИЕ РАВНОМЕРНОЙ СХОДИМОСТИ 209
стве 5 рассматривать более узкие (не полные) системы со-
событий.
Примеры систем 5, для которых выполняются условия
равномерной сходимости частот к вероятностям, будут
приведены ниже. Отметим лишь то, что для конечных сис-
систем 5, содержащих N событий, равномерная сходимость
всегда имеет место. В самом деле, из усиленного закона
больших чисел известно, что для каждого А последова-
последовательность
л (А; хг, ..., а-,) = \ Р (А) - \1 (А) \
стремится к нулю с вероятностью единица при I —>■ оо.
Поскольку число событий в 5 конечно,
я8 (%., .... х\) = тах л [Аи %г, •••> -^г)
Ах, ..., Ар;
и также стремится к нулю с вероятностью 1.
Выведем оценку вероятности
Р {л8 (хг, ..., ж,) > 8}
для случая конечной системы 5. Величина V (А) распре-
распределена по биномиальному закону
Р (V (А)) = С\Р (Л)*(А>< A - Р
Поэтому
Р { | V (А) - Р (А) | > 8} = 2' ЯР* (А) A - Р
где штрих у суммы означает, что к пробегает значения,
удовлетворяющие неравенству
Событие я8 (I) ^> 8 означает, что по крайней мере для
одного из событий Ах,..., АК справедливо IV (А) — Р (А) |^>
^> 8. Поэтому по теореме о сложении вероятностей
Р {вир | V (А) - Р (А) | > 8} < N 2' С^Р* (А) A - Р (А)I~\
A0.6)
210 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
В силу интегральной теоремы Муавра — Лапласа
тая часть неравенства A0.6) при больших I может
у
правая часть
быть оценена так:
где
оА = УР(А)A-Р(А)).
Величина оА достигает максимального значения при
Р (А) = -я- и равна в этом случае х/2. Поэтому
ПрИ 1 > 2я?~ полУчаем
Р {вир | V (А) — Р (А) I > 8} < -/Уе^2'. A0.7)
Ае8
Таким образом, остается выяснить, для каких беско-
бесконечных систем 5 выполняется равномерная сходимость
частот к вероятностям.
Основная идея выводимых ниже условий равномерной
сходимости связана с тем, что и в том случае, когда систе-
система 5 бесконечна, лишь конечное число групп событий раз-
различимо на конечной выборке *). Правда, это число не по-
постоянно и зависит от выборки. Грубо говоря, идея состоит
в том, чтобы подставить в оценку A0.7) переменное число
N, зависящее от выборки. Если при этом N возрастает с
длиной выборки достаточно медленно (медленнее любой
показательной функции), то правая часть оценки A0.7)
при I —>■ оо стремится к нулю при любом г ^> 0 и, следова-
следовательно, равномерная сходимость частот к вероятностям
имеет место.
*) Два события считаются различными на выборке щ, . . ., х\,
если в этой выборке найдется элемент х\, принадлежащий одному и
не принадлежащий другому.
§ 3. ОПРЕДЕЛЕНИЕ ФУНКЦИИ РОСТА 211
§ 3. Определение функции роста
В этом параграфе будет введена характеристика клас-
класса событий, достаточная для выяснения факта равномер-
равномерной сходимости.
Пусть X — множество, 5 — некоторая система его
подмножеств, X1 = %, ..., х\ — последовательность эле-
элементов X длины I, Каждое множество А ЕЕ 5 определя-
определяет подпоследовательность Хд этой последовательности,
состоящую из тех и только тех элементов, которые принад-
принадлежат А. Будем говорить, что А индуцирует ХА на после-
последовательности X1. Обозначим через
А8(хъ ..., хг)
число различных подпоследовательностей Ха, индуциро-
индуцированных множествами 4е5. Очевидно, что
Число А8 (хг, ..., хг) будем называть индексом системы
8 относительно выборки хг, ..., хх.
Определение индекса системы можно сформулировать
и иначе. Будем считать, что Ах^ 3 эквивалентно А2 {= 5
относительно выборки х1, ..., Х\, если Ха, = Ха2- Тогда
индекс А8 (хи ..., ж() есть число классов эквивалентности,
на которые система 5 разбивается этим отношением экви-
эквивалентности.
Очевидно, что эти два определения равносильны.
Функцию
т8 (I) = шах А8 (а*, .... х{), A0.8)
XI,..., X}
где максимум берется по всем последовательностям дли-
длины /, назовем функцией роста системы 5. Здесь максимум
всегда достигается, так как индекс А8 (хг, ..., х{) принима-
принимает лишь целые значения. Используя функцию роста, сфор-
сформулируем ниже достаточные условия равномерной схо-
сходимости частот к вероятностям по классу событий и дадим
соответствующие оценки.
В заключение этого параграфа приведем несколь-
несколько примеров функций роста для различных классов
событий.
Пример 1. Пусть X — прямая, а 5 — множество
всех лучей вида х ^ а. Найдем функцию роста.
212 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
Пусть дана последовательность точек хи ..., хх без пов-
повторений. Изменив порядок последовательности, можно
добиться того, что
Очевидно, что каждое множество А вида
{х : х ^ а)
при хх ^ а <С ЗГ'1 индуцирует подпоследовательность
ХХ, Хг, ..., Х{
такую, что XI ^ а
При а < жх индуцируется пустая подпоследователь-
подпоследовательность, а при а Г> Ж{ — вся последовательность ж1г ..., Ж;.
Ясно, что число различных последовательностей, индуци-
индуцируемых множествами А е= 5, равно I + 1. Таким образом,
Д8(Ж1, ..., ж,) = 1 + 1.
Если в последовательности есть повторения, то индекс
А8 (хх, ..., х{) разве лишь уменьшается.
Поэтому
твA) = 1+ 1. A0.9)
Пример 2. Пусть X — сегмент [0, 1],а 5 состоит
из всех множеств, каждое из которых представляет собой
объединение конечного числа непересекающихся сегмен-
сегментов с рациональными концами. Если X1 = ж1г ..., х\ —
— последовательность точек из сегмента [0, 1] без повто-
повторений, то для всякой подпоследовательности X* найдется
множество из 5, включающее только те точки X1, кото-
которые входят в Хк Для этого достаточно покрыть точки X1
достаточно малыми сегментами с рациональными концами
и взять их объединение. Поэтому в данном случае
т8 (I) = 2'
(отметим, что система 5 содержит лишь счетное число эле-
элементов).
П р и м е р 3. Пусть X — 71-мерное (п 3> 1) евклидово
пространство, 5 — система всех подмножеств вида
{Хг(х, Ф)>0} (ф^О).
§ 4. СВОЙСТВА ФУНКЦИИ РОСТА 213
Тогда индекс А8 (хг, ..., х{) определяет число различ-
различных разбиений / векторов х1,...,Х1 на два класса с помо-
помощью гиперплоскостей, проходящих через начало коор-
координат. Как было показано в главе V,
п—1
1=1
откуда следует
п—1
г=1
Можно показать, что в действительности
п—1
г=1
Аналогично показывается, что если X — «-мерное евкли-
евклидово пространство, а 5 — система подмножеств вида
{х : (х, ф) > с},
где ф — произвольный вектор, ас — произвольная ска-
скалярная величина, то
п
т8а) = 2 у, си.
§ 4. Свойства функции роста
Функция роста класса событий 5 обладает следующим
замечательным свойством.
Теорема 10.1. Функция роста либо тождественно рав-
равна 2', либо, если это не так, мажорируется функцией
11-1
2 С], где п — минимальное число I, при котором
т8 A)^21.
()
Иначе говоря,
г либо=. 21,
т" (I) = \ \л
■ ' либо гс; 2л
214 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
Для доказательства этого утверждения нам понадо-
понадобится следующая лемма.
Лемма. Если для некоторой последовательности хъ ...
..., XI и некоторого п ^ 1
п-1
А8(г1,...,г,)>2й,
г=0
то существует подпоследовательность Хп длины п такая,
что
А8 (Хп) = 2".
Доказательство. Обозначим
п—1
2С} = Ф(Л, I)
г=0
(здесь и дальше считаем, что при г ^> I С\ = 0). Для
этой функции, как легко убедиться, выполняются соотно-
соотношения
ФA, I) = 1,
Ф(п, Т) = 2* при / < « — 1, A0.11)
Ф («, I) = Ф (/г, г - 1) + Ф(« - 1, г - 1)
при /г > 1,/ > 1.
Эти соотношения в свою очередь однозначно определяют
функцию Ф (п, I) при I > 0 и и > 0.
Будем доказывать лемму индукцией по I и п. Для
п = 1 и любого / ^> 0 утверждение леммы очевидно. Дей-
Действительно, в этом случае из
следует, что существует элемент последовательности х{
такой, что для некоторого Ах ЕЕ 5 выполняется ж1 ЕЕ ^1,
а для некоторого другого А2 ЕЕ 5 выполняется хг ^ 4г и,
следовательно,
А» (,тг) = 2.
Для I <С п утверждение леммы верно ввиду ложности
посылки. Действительно, в этом случае посылка есть
| 4. СВОЙСТВА ФУНКЦИИ РОСТА 215
что невозможно, так как
Дв (ах, ..., ж,)<2'.
Наконец, допустим, что лемма верна для п ^ п0 (п0 ]>
^> 1) при всех /. Рассмотрим теперь случай п = п0 ~\- 1.
Покажем, что лемма верна и в этом случае для всех I.
Зафиксируем п = п0 -\- 1 и проведем индукцию по I.
Для I < ?г0 -г 1, как указывалось, лемма верна. Предпо-
Предположим, что она верна при / <^ 10, и покажем, что она спра-
справедлива для I — 10 + 1. Действительно, пусть для некото-
некоторой последовательности
Х1> •••» Х1>> х1а+1
справедливо условие леммы:
А8(Ж1, ..., хго+1)>Ф(«о + 1, 10 + 1).
Найдем подпоследовательность длины п0 + 1:
такую, что
А8^, ..., .тПо+1) =
Рассмотрим подпоследовательность Х1« — х1г ..., хи.
Возможны два случая;
а) А8(Х1, ..., Жго)>ф(„о + 1, д,
б) А8 (жх, ..., хго) < Ф («о + 1,г0).
В случае а) в силу предположения индукции существует
подпоследовательность длины /го+1 такая,что А8 (ХщП) =
= 2"»+1, что и требуется.
Для случая б) разделим подпоследовательности после-
последовательности X1», индуцируемые множествами из 5,
на два типа. К первому типу отнесем такие подпоследова-
подпоследовательности Хт, что на полной последовательности Х1»+1
индуцируется как Хт, так и Хт, Ж;оИ. Ко второму — такие
Хг, что на последовательности Х1«+1 индуцируется либо
Хг, либо Хг, х(о+1. Обозначим число подпоследова-
подпоследовательностей первого типа К1г а второго типа К2. Легко
видеть, что
Д8 (%, .-, хО = Кг + Кг; АЦХ1, ..., хш) = 2К, + Кг%
216 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
и следовательно,
А8 Ы, .... хш) = Д8 (а*, ..., хи) + К,. A0.12)
Обозначим через 5" систему всех подмножеств 4ё5
таких, что на последовательности X1" они индуцируют
подпоследовательности первого типа. Тогда, если
б') Кг = А8'(%, -,хО>Ф(по, 10),
то в силу предположения индукции существует подпосле-
подпоследовательность Хп° = хA, ..., хг такая, что
Но тогда для последовательности х1г, ...,хг , ,х(о+1 имеем
так как для каждой подпоследовательности Xе1, индуциро-
индуцированной на последовательности Хп°, найдутся две подпо-
подпоследовательности, индуцированные на Хщ, Ж;о+1, а имен-
именно Ха и Хч, х,10+1. Таким образом, в случае б') искомая под-
подпоследовательность найдена.
Если же
б") Кг = А8'(%, -,хгс)<Ф(п0, /0),
то получим в силу A0.12) и б)
А8 (хи ..., х;0+1)<Ф(«0+ 1, ^0) + Ф («о. ^о).
откуда в силу свойств A0.11) функции Ф (п, I)
А8 (хи ..., ж,0+1) < Ф (п0 + 1, 10+ 1)
в противоречии с предположением, т. е. б") невозможно.
Лемма доказана.
Теперь докажем теорему. Как уже отмечалось, т8A) <^
^ 2'. Пусть т8 (I) не равно тождественно 2г и пусть п —
первое значение I, при котором т8 (I) ф 2г.
Тогда для любой выборки длины I, большей п, спра-
справедливо
А8(хи ..., *,)<ФК I).
§ 4. СВОЙСТВА ФУНКЦИИ РОСТА
217
Действительно, в противном случае на основании утверж-
утверждения леммы нашлась бы такая подвыборка х1, ..., хп, что
^(Х1,...,хп) = 2".
Но это равенство невозможно, так как по допущению
т8 (п)ф 2".
Таким образом, функция т8 (Г) либо тождественно рав-
равна 2', либо мажорируется Ф (п, I).
Теорема доказана.
Замечание 1. Функция Ф (п, I) может быть оценена
сверху при п Г> 1 и 1~^> п следующим образом;
п—1
Ф (га, I) =
A0.13)
г=0
Поскольку для функции Ф (п, Г) выполняются соотно-
соотношения A0.11), для доказательства A0.13) достаточно убе-
убедиться, что при п ]> 1 и /1> п справедливо неравенство
1п . (I +1)"
A0.14)
и проверить A0.13) на границе, т. е. при п — I, 1 = п -\- I.
Неравенство A0.14), очевидно, равносильно неравен-
неравенству
Г-1 („ + [) - (I + 1)" ^ о,
справедливость которого следует из формулы бинома
Ньютона.
Остается проверить соотношение A0.13) на границе.
При п = 1 оно проверяется непосредственно. Далее про-
проверим оценку при малых п и I;
1
= п
„Ф(га
5 1
' (»
+ 1
,1)
п-1
-1)!
1
1
1
,5
2
4
4
3
И
12
.41
26
I1/!
5
57
Г
218 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
Теперь, чтобы проверить A0.13) при п> 5, восполь-
воспользуемся формулой Стирлпнга для оценки сверху Л:
2!«
откуда при I = п + 1
г"-1 (г-1),
(« - 1)! " '
и, далее, при /!>6
2п Г 2 е 1+ т
П
A — 1) I —
С другой стороны, всегда
Ф (п, I) < 2'.
Поэтому достаточно проверить, что при I ;> 6
2г<1,2—4^ег.
/27
С ростом I (при I ^> 2) это неравенство усиливается и по-
поэтому достаточно его проверить при I = 6, в чем и убеж-
убеждаемся непосредственно.
Итак, оказывается, что
функция роста либо тож-
тождественно равна 2', либо
при некотором п впервые
нарушается равенство, т.е.
т8 (I) =?=■ 21, и тогда при
1~^> п функция роста ма-
мажорируется степенной
функцией
1,5
тП-1
A0.15)
Рис. 21.
Это положение проиллюстрировано на рис. 21, где
сплошной линией изображен график 1§2 тп8{1) для случая,
когда тп8 (Г) = 21, а пунктирными — мажорирующие
функции для различных п.
§ 5. ОСНОВНАЯ ЛЕММА 219
Таким образом, для того чтобы оценить поведение
функции роста, достаточно выяснить, каково минималь-
минимальное число п такое, что ни на одной последовательности
длины п система 6' не индуцирует все возможные подпо-
подпоследовательности.
Замечание 2. Существуют примеры класса событий 8,
для которых
71—1
т8A)= 2 С',
где п — первое число, при котором
Пусть X — произвольное бесконечное множество, а 5
состоит из всех его конечных подмножеств с числом эле-
элементов, меньшим п. Очевидно, что
т8 (I) = 21 при I < п,
71—1
т8A) = 2 С\ при 2>га.
г=0
Таким образом, оценка теоремы для функций т8 (Г), не
равных тождественно 2г, может достигаться.
§ 5. Основная лемма
В конце § 2, было сказано, что основная идея, на кото-
которой строятся условия равномерной сходимости частот к
вероятностям, состоит в том, что бесконечная система со-
событий 5 заменяется конечной подсистемой, состоящей из
таких событий, которые различимы на конечной выборке.
Для того чтобы сделать такой переход корректным, ока-
оказывается необходимым заменить исходную проблему рав-
равномерной близости частот событий к их вероятностям проб-
проблемой равномерной близости частот в двух следующих
друг за другом выборках одинаковой длины.
Оказывается, что равномерная сходимость к нулю раз-
разности частот в двух полувыборках является необходимой
и достаточной для равномерной сходимости частот к ве-
вероятностям и из оценок скорости одной сходимости сле-
следуют оценки для другой.
220 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
Итак, пусть взята выборка длины 11:
и подсчитаны частоты выпадения события А (ЕЕ 5 на пер-
первой полувыборке Х[ = хх, ■ ■■, х^г и второй полувыборке
Х[ = х;+1, ..., хг\- Обозначим соответственно частоты че-
че' ( " (
рез V' (.4) и V" (А) и рассмотрим отклонение этих величин:
Ра(х1,...!х21) = \ V'(А) - V (А) \.
Нас будет интересовать максимальное отклонение ча-
частот по всем событиям класса 6":
р8 (х19 ...,х1) = вир рд (хи ..., х21).
Ае8
Напомним, что через я8 (х\, ..., х{) мы обозначили
Далее будем полагать, что как зх8 (хц ■ . ., хг), так и
р8 (хц ..., Х2г) —измеримые функции.
Основная лемма. Распределения величин я8 (х1г ...
..., х{) и р8 (х,\,..., Х21) связаны следующими соотношениями:
а) Р{пВ(Х1,.{}
только I > — ;
8
б)
Доказательство. Доказательство утверждения
а) построено по следующей схеме. Представим себе, что
полувыборки XI, ..., х\ и х1+х, ..., х<ц берутся последова-
последовательно и независимо. Допустим, что первая полувыборка
оказалась такой, что
8ир | V' (А; хъ ...,хг)-Р (А) \ > е. A0.16)
Аез
Это значит, что в классе 5 имеется событие А* такое, что
[V (А*) — Р (Л*) | > е.
На второй полувыборке будем следить за отклонением
§ 5. ОСНОВНАЯ ЛЕММА 221
частоты от вероятности лишь для этого фиксированного
события А*. Так как нас интересует всего одно событие,
то можно воспользоваться обычным законом больших чи-
чисел. Поэтому при достаточно большом I с достаточно вы-
высокой вероятностью частота V" (А*) близка к вероятности
Р(А*):
и, следовательно,
\у'(А')-*(А*)\>±. ир8(ц г,)>|. A0.17)
Таким образом, условная вероятность A0.17) при усло-
условии A0.16) становится достаточно большой при соответст-
соответствующих I. Это и позволяет доказать утверждение а).
Перейдем к формальному доказательству.
По определению
где
/1 при 2>0,
Учитывая, что пространство X B1) выборок длины 21
есть прямое произведение Хг (I) и Х2 (I) полувыборок дли-
длины I, согласно теореме Фуббини [36] для любой измери-
измеримой функции ф (хи ... )
Поэтому имеем
= ^ йР(Х[)
(во внутреннем интеграле первая полувыборка
222 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
фиксируется). Обозначим через () событие пространства
ХгA)
{л (ж1, ..., ж,) > е}
и, ограничивая интегрирование, получим
х,...,хг1)-~-\аР{Х1ъ). A0.18)
Оценим внутренний интеграл правой части неравенст-
неравенства, обозначив его через /. Здесь хх, ..., хг фиксировано и
таково, что л (хх, ..., х{) ^> е. Следовательно, существует
А* ЕЕ 5 такое, что
| Р (А*) — V (А*; хг, ..., а-г) | > е.
Тогда
/
Пусть, например,
у'(Л»; Ж!,..., х,)<Р(А*)-г
(аналогично рассматривается случай V' (Л*)^>Р (Л*) + е).
Тогда для выполнения условия
| у'{А'; хъ . . .,Х1)-у"(А'; хм,.. .,ж2()|>-|-
достаточно потребовать, чтобы выполнялось соотношение
откуда
§ 6. ВЫВОД ДОСТАТОЧНЫХ УСЛОВИЙ 223
Как известно, последняя сумма превосходит 1/2, если
2 2
только 1^>- . Возвращаясь к A0.18), получим для /^>—:
= Т-Р{я8(х1, ...,ж,)>е},
что и требуется.
Утверждение б) непосредственно следует из того, что
если
| V' (А; хх, ..., ж() — V" (А; х1+1, ..., х2() | > е,
то
либо
либо
Учитывая, что при этом полувыборки Х± и Хг независимы,
получаем:
Р {зир | V' (А; хъ . .., х{) — V (А; х1+1, .. ., х21) | > е} <
А
{р | () - V'(Л; *!,..., *;)| >-|-}) х
X A Р { \
и поэтому
A - Р {зир \Р(А)- у" (А; х1+1,..., х21) \ > -^-
< 2Р(пЦхъ .. .,х,)У-^ -
Лемма доказана.
§ 6. Вывод достаточных условий равномерной сходимости
частот к вероятностям по классу событий
Итак, задача может быть сведена к оценке равномер-
равномерной близости частот в двух последующих полувыборках.
Схему сравнения частот выпадения событий в двух полу-
полувыборках можно представить себе так. Берется выборка
224 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
двойной длины X21 и затем делится случайным образом
на две полувыборки равной длины. Будем считать, что вы-
выборка X21 зафиксирована. Если два события А1 и А2 не-
неразличимы на выборке X2', т. е. всякий элемент этой вы-
выборки, принадлежащий Аг, принадлежит А2 и наоборот,
то частоты выпадения этих событий на всякой подвыбор-
ке одинаковы. Поэтому для оценки максимального укло-
уклонения частот достаточно из каждой группы неразличимых
событий взять по одному. Число таких событий будет ко-
конечно и равно индексу А8 (хг, ..., х21) системы $ относи-
относительно выборки Хх, ..., х21. Рассмотрим одно из таких со-
событий А и, по-прежнему считая выборку X21 фиксирован-
фиксированной, разобьем ее случайно на две равные полувыборки и
оценим уклонение частот этого события в двух полувыбор-
полувыборках. Эта схема равноценна схеме с невозвращаемыми ша-
шарами, а поэтому (см. [64])
, \ \ к т. — к
где т — число элементов А в выборке X21, к — число эле-
элементов А в первой полувыборке.
Как показано в приложении к главе X, правая часть
равенства может быть оценена сверху:
Ч1т-
Таким образом,
Р{\у' (А; хи ..., х,) -V" (А; хп1, ..., х21) | >
>е}<3ехр[-е2B- 1)].
Вероятность того, что хотя бы для одного события А, из
числа выбранных, окажется
| V' (А; х17 ..., Х[) — V (А; х1п, ..., х21) \ > е,
§ 6. ВЫВОД ДОСТАТОЧНЫХ УСЛОВИЙ 225
по теореме о сложении вероятностей оценивается:
Р {зир | V' (А; хь..., хг) — V (А; х1+1,..., хг1) | > е} <
< ЗА8 (*!,...,;г2гКег(М).
В свою очередь по определению функции роста
А8 (а*, .... х2г)<т8B0
и, таким образом,
Р {зир | V' (А; хъ ..., х21) — V (А; х1+1,..., х2,)| > е} <
Очевидно, что если функция ш5 (I) растет лишь степенным
образом, то правая часть неравенства стремится к пулю
при I -V с». Это и дает достаточные условия равномерной
сходимости (по вероятности).
Перейдем к строгой формулировке и доказательству
достаточных условий.
Теорема 10.2. Вероятность того, что частоты всех
событий класса 8 уклонятся от соответствующих вероят-
вероятностей в эксперименте длины I более чем на е, удовлетво-
удовлетворяет неравенству
Р{я5 (хг, ..., ж,) > е} < 6т8 B1)е 4 . A0.19)
Следствие. Для того чтобы частоты событий клас-
класса 8 сходились (по вероятности) к соответствующим ве-
вероятностям равномерно по классу 8, достаточно сущест-
существования такого конечного п, что
Доказательство. В силу с основной леммы
достаточно оценить величину
Рассмотрим отображение пространства X B1) на себя,
•получаемое некоторой перестановкой Т1 элементов
226 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
последовательности X2'. В силу симметрии определения
продукт-меры имеет место следующее равенство:
X B1) ХB1)
для любой интегрируемой функции / (х).
Поэтому
B0!
2
$ ——ш
ХB1)
где сумма берется по всем B/)! перестановкам.
Заметим, прежде всего, что
йР{хг1)> A0-20)
= 0 (зир | V' {А; хъ ..., хч) — Vя (А; хиъ ..., х21) \ > —) =
(8 \
А;х1+1, ...,х21)\ —-у .
Очевидно, что если два множества Ах и Аг индуцируют на
выборке хх, ..., XI, ж(+1, ..., х2г одну и ту же подвыборку,
то справедливо
V' D15 ТЬХ*1) = V' (Л2; Г
V" (Л1; ГД2') = V" (А2; Т{
и, следовательно,
для любой перестановки 1'*.
Иными словами, если два события эквивалентны отно-
относительно выборки хх, ..., х,21, то уклонение частот для этих
событий одинаковы при всех перестановках Т{. Поэтому,
если из каждого класса эквивалентности взять по одному
$ 6. ВЫВОД ДОСТАТОЧНЫХ УСЛОВИЙ 227
множеству и образовать конечную систему 8', то
Число событий в системе 8' конечно и было обозначено
А8 (%, ..., хц). Поэтому, заменяя операцию зир суммиро-
суммированием, получаем
вир 0 (рд (Г;Х2') — —\ = зир 0 (рд (Т{Х21) — ~\
Эти соотношения позволяют оценить подынтегральное
выражение в A0.20):
1=1
B/)!
Выражение в квадратных скобках означает отношение
числа порядков в выборке (при фиксированном составе),
для которых
к общему числу перестановок. Легко видеть, что оно рав-
равно
■р \1
где пг равно числу элементов выборки х1г ..., хгь принад-
принадлежащих А.
228 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
В приложении к этой главе показано, что
е* д-р
Г<3е * .
Таким образом,
— 5] еГо^г-х2')-—!■
B/I /1°[Р Нгл / 2 ]'
г=1
е« ((-1)
2 зг -5-
■ Ае8'
= ЗА8(ж1, ...,
Подставляя эту оценку в интеграл A0.20), имеем
Р {р« (хъ ..., х21) > 4"} < 3™8 B0 е""■^1~,
откуда в силу основной леммы
е' A-1)
Р{п8(хъ ...,х,)
Теорема доказана.
Доказательство следствия. Пусть су-
существует такое п, что
тп8 (п) ф 2п .
Как было доказано в § 4, если только функция т8(п) не
равна 2™, то при I ^> п справедливо:
Поэтому:
т. е. имеет место равномерная сходимость по вероятности.
Полученное достаточное условие не зависит от свойств
распределения (единственное требование — это измери-
измеримость функций я и р), а зависит от внутренних свойств
системы $.
§ 7. О СХОДИМОСТИ С ВЕРОЯТНОСТЬЮ ЕДИНИЦА 229
§ 7. О равномерной сходимости с вероятностью единица
В предыдущем параграфе мы указали на достаточные
условия равномерной сходимости (по вероятности) частот
к вероятностям по классу событий 5.
Здесь мы покажем, что полученные условия гаранти-
гарантируют также равномерную сходимость с вероятностью еди-
единица. Доказательство этого утверждения основывается
на использовании известной из теории вероятностей лем-
леммы [21].
Лемма. Если для случайной последовательности ^, ...
..., ^п, ... найдется такое ^0, что для любого ^ ^> 0 спра-
справедливо неравенство
1=1
то последовательность \\, , ..., ^п, ... сходится к ^0 с ве-
вероятностью единица.
Доказательство. Обозначим через ЕТп собы-
событие, состоящее в том, что выполняется неравенство
| 1п — ^о | > — (г — целое число).
Рассмотрим событие 8гп, состоящее в том, что выполняется
хотя бы одно из событий Егп, Еп+1, ..., Еп+н, •••, т. е.
п [] пн
1=1
Оценим вероятность этого события:
оо оо
Р {&} < 2 Р {Егпн} = 2 Р \Aг - Бо) > 4"} • (Ю-21)
Но так как в силу условия леммы ряд A0.21) сходится, то
НтР{,5';} = 0. A0.22)
П—*оо
Рассмотрим теперь событие 5Г
ЯГ = П ^п.
п=»1
230 гл, х. достаточные условия равномерной сходимости
Из того, что событие 8Г влечет за собой любое из событий
8п, в силу A0.22) получаем
Р (8Г) = 0. A0.23)
Наконец, положим
Как нетрудно установить, это событие означает, что
найдется такое г, что для каждого п (п = 1, 2, ...) хо-
хотя бы при одном к (к = к (п) ) будут выполняться нера-
неравенства
| %п+к — %о | > — •
Так как
то в силу A0.23)
Р {8} - 0,
что я требовалось доказать.
Теорема 10.3. Если существует такое число п ^> 0,
что при I ^> п функция т8 (I) <С Г, то справедливо
Доказательство. В силу теоремы 10.2
Р {лз (тй, ..., хг) > е} < 6/га8B0е г".
Пусть п — такое число, что при I ^> п
т8 {1)< Г.
Выберем целое число I* так, чтобы оно превосходило и п.
Тогда
(=1
§ 8. ПРИМЕРЫ И ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 231
Первое слагаемое в правой части равенства не превосхо-
превосходит I*, а второе слагаемое
B1?е
сходится, как известно, при любом е ^> 0.
Поэтому
и, согласно приведенной лемме,
Теорема доказана.
§ 8. Примеры и дополнительные замечания
В примере 1 § 3 в качестве пространства X взята пря-
прямая, а в качестве системы 5 — множество всех лучей вида
х <^ а. В этом случае
Р (А) = Р{х < а} = Ф (а)
есть функция распределения случайной величины х,
V (А; х1г ..., ж() = Р (а) есть эмпирическая функция рас-
распределения этой случайной величины, построенная по
выборке хг, ..., ж(.
Согласно теореме 10.2
_ & A-1)
Р {вир | Р (а) - Ф (а) | > е}< 6/и8B/)е~ * .
Поскольку в соответствии с A0.9) в данном случае т8 (I) <^
< (I + 1), то
(')
()
а) — Ф(а)|>е}<6Bг + 1)е 2
а
и имеет место равномерная сходимость эмпирических
функций к функциям распределения почти наверное.
Это — известная теорема Гливенко.
В примере 3 § 3 X — 7г-мерное пространство, 5 — сис-
система подмножеств вида
(х, Ф) > 0 (Ф ф 0).
232 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
В соответствии с формулами A0.19), A0.10) иA0.15) при
любом задании распределения в пространстве X
Р {вир | Р (Ф) - V (Ф; хх хг) | > е}<18 {П{~^ е"^1,
где Р (ф) и V (ф) — соответственно частота и вероятность
события {(хц>) ;> 0}, и следовательно, при I -*■ оо величина
зир | Р (ф) — V (ф) |
сремится к нулю с вероятностью единица. Аналогично,
если система $ состоит из множеств вида
(Жф) > С,
то
21-IV1 е'('~"
1)
и, очевидно, также с вероятностью 1 имеет место равно-
равномерная сходимость частот к вероятностям.
Это весьма существенный для приложений результат.
В известном смысле он может рассматриваться как обоб-
обобщение теоремы Гливенко.
Замечание 1. Пусть дано конечное число систем
для каждой из которых известна функция роста т " (I).
Пусть далее, система событий 80 такова, что каждое со-
событие 4ё50 есть пересечение некоторых событий
А =А11] А
2
где событие А1 принадлежит соответственно систе-
системе 8{.
Тогда
В самом деле, для произвольной выборки хп ..., хг в каж-
каждой системе $1 найдется не более т {(I) неэквивалентных
событий. Рассматривая всевозможные их пересечения,
| 8. ПРИМЕРЫ И ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 233
получим, что
п
1=1
При этом, если каждая из функций т8{ (I) растет не быст-
быстрее, чем степенным образом, то и функция то8» (I) растет
не быстрее некоторой степени.
П^р и м е р 4. Обобщение теоремы Гливенко на га-
мерный случай в ином смысле имеет место, если в качестве
X взять Еп, а в качестве $ — систему множеств вида
х1 < «ц, ..., Xй < ап.
В силу приведенного замечания в этом случае
т8 @ < (I + 1)"
и, таким образом, равномерная сходимость также имеет
место.
Пример 5. Пусть X — га-мерное евклидово прост-
пространство, I? — любые выпуклые многогранники с числом
граней, не превосходящим к.
Тогда
так как каждый такой многогранник может рассматри-
рассматриваться как пересечение к множеств вида
{(х, 1|>) > с}.
Следовательно, и для этой системы имеет место равно-
равномерная сходимость частот к вероятностям.
В примере 2 § 3 т8 (I) = 21 и наши условия не гаран-
гарантируют равномерную сходимость частот к вероятностям.
И действительно, как легко убедиться, например, при рав-
равномерном распределении (и любом непрерывном) такой
сходимости нет.
Замечание 2. Выше было установлено, что для всех
систем событий 8, у которых функция роста не равна тож-
тождественно 21, всегда имеет место равномерная сходимость
частот событий к вероятностям независимо от вероятно-
вероятностной меры Р (х). При этом формула A0.19) позволяет
оценить величину максимального по классу 8 уклонения
234 гл. х. достаточные условия равномерной сходимости
частот от вероятностей независимо от распределения
Р(х).
В случае же, когда т8 A) = 21, величина максимального
по классу 8 уклонения частоты от вероятности не может
быть оценена нетривиальным образом, ни при каком
конечном I, если не используются сведения о распределе-
распределении Р (х).
С одной стороны, существуют распределения, при ко-
которых величина
я8 (хъ .. ., хг) = вир | V (А; хь ...,х()—Р (А) \
с вероятностью 1 равна нулю при I !> 1; таким будет рас-
распределение, сосредоточенное в какой-либо одной точке
х0. Это означает, что вероятностная мера задается усло-
условиями:
Р (А) = 1, если хо^А,
Р (А) = 0, если х0 ф А
(для простоты будем считать, что одноточечное множество
{х0} измеримо, хотя эта оговорка не принципиальна).
Тогда с вероятностью 1 выборка будет состоять только
из повторяющегося элемента х0
X = Хо, ..., Ха.
Очевидно, что при этом для всех А
V (А; х0, ..., х0) = 1, если хй <= А,
V (А; х0, ..., х0) = 0,- если х0 ф А
и, следовательно,
зир | V (А; хъ ..., хг) — Р (А) \ = О,
АеЗ
каков бы ни был класс 5.
С другой стороны, если т8 (I) = 21, то существуют та-
такие распределения, что величина
со сколь угодно большой достоверностью сколь угодно
близка к единице.
Тем не менее, как будет показано в главе XI, сущест-
существуют примеры систем, для которых т8 (I) = 21 и все же
§ 8. ПРИМЕРЫ И ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 235
при любом распределении имеет место равномерная схо-
сходимость. Поэтому настоящее замечание означает, что при
т8 (I) ~ 21 без сведений о распределении Р (х) невозмож-
невозможно оценить скорость равномерной сходимости.
В заключение этого параграфа докажем теорему.
Теорема 10.4. Допустим, что все одноточечные мно-
множества пространства X измеримы и задана система со-
событий 8 такая, что
т8 (I) ~ 2'.
Тогда по заданным I, е можно указать такое распределе-
распределение Р (х), что с вероятностью 1 будет выполняться не-
неравенство
Л)— Р(А)\>{ — е.
Доказательство. Выберем любое целое число
п, превышающее I I е. Поскольку т8 (п) = 2п, можно ука-
указать п точек
х^, ..., хп
так, что события А ЕЕ 5 индуцируют на этой последова-
последовательности все подпоследовательности. Обозначим через
Хп конечное множество, состоящее из точек х1г ..., хп.
Определим распределение Р (х) следующим образом:
распределение Р (х) сосредоточено в точках хх, ..., хп,
причем все они равновероятны; иными словами,
р ,д\ _
0, если А не содержит ни одной точки из Аг,
—, если А содержит только одну точку,
1, если А содержит все точки Хп.
Пусть теперь дана выборка хЛ, ..., х1. С вероятностью 1
эта выборка состоит лишь из элементов X". Рассмотрим
конечное множество X', состоящее из всех тех точек мно-
множества Хп, которые не вошли в выборку. Очевидно, что
их число не меньше чем п — I.
Поскольку
найдется событие Ао ЕЕ <5\ которое содержит все точки из
множества X' и ни одной из выборки хх, ..., хх. Это
236 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
V (Ао) = О
значит, что
и в то же время
В силу выбора числа п, получаем
| V (Ао) - Р (Ао) | >
и, следовательно, с вероятностью 1
зир \\(А;х1,...,х1)
- е
— е.
§ 9. Приложение к главе X
Оценим величину
г _ V тьч1-т
~ Ь Ы >
где к пробегает значения, удовлетворяющие неравенствам
к т, — к
I
I
> 8 и тах @, т — I) <^ к ^ тщ (т, I)
или, что то же самое, неравенствам
ъ1
~2~ и тах@,т—/)^&^1ШП (т, I),
к—
а I и т ^. 21 — произвольные положительные целые числа.
Разложим Г на два слагаемых:
Г = Гх + Г2,
Г, —
11-
гпьч1-т
при
+
г
Введем обозначения:
р(к
р(к) ~ (к
- т)
§ 9. ПРИЛОЖЕНИЕ К ГЛАВЕ X 237
ДНЯ
тах (О, т — /) ^ к <^ пнп (т, /).
Далее обозначим
5 = тш (т, /), Т = тах @, т — /),
5
«(*) = 2*Ю'
1 к
Очевидно, что имеет место соотношение
8 8—1 8-1
«(*+1)= 2 р^= %р(ь+1)= 2^(')»(')• (п-3)
Далее из (П.2) непосредственно следует что при !</
Я С) > Я (/).
т. е.. <? (*) монотонно убывает. Поэтому из (П.З) следует неравенство
5-1 8
и, по определению а (к), имеем
а (к + 1)< а (Л) д (к).
Применяя последовательно это соотношение, получим для произ-
произвольных к и /, удовлетворяющих условию Т < / < к ^ 5,
&-1
«(*)<«(/■) П «о-
Наконец, поскольку а (/) ^ 1,
к-1
«(Щ<1\я(Ц, (П.4)
где / — любое целое число, меньшее чем к.
Положим
т — 1
тогда
238 ГЛ. X. ДОСТАТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ
При этом, очевидно, пока Т < к < 5,
/ пг + 1 т — 1
| * |< тш I 2— > ' — —2—
Для аппроксимации д (к) исследуем функцию
а—г Ь—1
Р ^= г + а ' Ъ-\-1 '
считая, что а и Ь больше нуля.
При | I | < тт (а, Ь)
1п Р (г) = 1п (а — г) + 1п (Ь — I) — 1п (* + а) — 1п (* + Ь).
Далее,
1п Р @) = 0,
Л . Г 1 1 1
г + + +
Г 2а 2Ь И
= - [ аг _ B + Ьа _ р ].
Отсюда следует, что при | * | < тш (а, Ъ)
Соответственно при 1*1*^ т1п (о, ^) и I ^ 0
1 1
— + —
Возвращаясь к д (*), получаем, что при * > 0
Оценим теперь
к-1\
Д
т-1 .
считая, что о— ^ / <С * — 1 '•
Возвращаясь к (П.4), получим
§ 9. ПРИЛОЖЕНИЕ К ГЛАВЕ X
239
т — 1
здесь / — любое число меньшее к. Поэтому для к >—^— можно
т — 1
положить / = ц для т нечетного и / = т/2 для т четного, полу-
получив наиболее сильную оценку. Суммируя, далее, арифметическую
прогрессию, получим
1п а (к) <
4(/ + 1) / т. \а
<
4A + 1)
"Т + *] ДЛЯ четного т'
т-1 , \/ т-1
для нечетного т.
Наконец, 14 есть а (к) при к первом целом таком, что
т еЧ
откуда
- 1).
Точно так же оценивается величина Г2, так как распределение
(П.1) симметрично с центром т/2.
Таким образом,
ехр [-
Далее, рассмотрим сначала случай, когда е2 (/ — 1) ^ 1
(О < 8 ^ 1). При этом заведомо 1^2и е2/2 ^ 2.
Правая часть (П.5) в этом случае достигает максимума при
т = I и, следовательно,
[еЧ 1 П
- тн-гу + т+т] < 3е"Ч1'1)- (п-6)
При 82 (/—1)< 1 оценка (П.6) тривиальна, поскольку левая
часть неравенства не превосходит единицу, а правая всегда боль-
больше единицы.
Таким образом, оценка (П.6) справедлива при любых целых
2 и 8 в пределах 0 < 8 < 1.
Г лава XI
НЕОБХОДИМЫЕ Ж ДОСТАТОЧНЫЕ
УСЛОВИЯ РАВНОМЕРНОЙ
СХОДИМОСТИ ЧАСТОТ
К ВЕРОЯТНОСТЯМ ЛО КЛАССУ
СОБЫТИЙ
§ 1. Энтропия системы событий
Большинство практически интересных приложений*ох-
ватывается изложенными в предыдущей главе достаточ-
достаточными условиями. Интересно, однако, получить и исчер-
исчерпывающие необходимые и достаточные условия. Сущест-
Существенно, что это удается сделать в терминах, введенных в
§ 3 главы X.
В отличие^от достаточных условий, сформулирован-
сформулированных в § 6 главы X, необходимые и достаточные условия,
вообще говоря, зависят от задания вероятностной меры
на множестве X, но схема, по которой они строятся, оста-
остается прежней. Идея, как и раньше, состоит в том, чтобы
заменить бесконечную систему событий $ конечной под-
подсистемой, состоящей лишь из различимых на выборке со-
событий. Число таких событий зависит от выборки и равно
индексу системы $ относительно выборки
А8(х1, ..., хг).
При выводе достаточных условий использовалась функция
роста т8 (I), оценивающая сверху значение индекса для
выборок длины /. Такая оценка оказывается слишком
грубой для получения необходимых и достаточных усло-
условий. Последние удается сформулировать, если ввести не-
некоторую усредненную характеристику величины Д8^
{
§ 1. ЭНТРОПИЯ СИСТЕМЫ СОБЫТИЙ 241
Рассмотрим функцию
Н*A) =М 1е%АВ(х1, .... хг)
(М — символ математического ожидания).
Здесь и дальше предполагается, что функция Д5 (%,...
..., х{) измерима и этого достаточно для существования
математического ожидания, поскольку
Д< Д8(а;1, ..., гг)<2'
и соответственно
0<1в,Дв(ж1, ..., *,)</. A1.1)
В силу этих же соотношений очевидно, что
О < Я8 (I) < I.
*"" Функция Н8 (I) обладает свойством полуаддитивности,
что позволяет назвать ее энтропией системы событий
8 относительно выборок длины I.
В самом деле, рассмотрим выборку
Х^, ..., #й) #й+1> ..., Х\.
Каждая подвыборка, индуцированная некоторым собы-
событием 4б5на этой выборке, состоит из подвыборки, ин-
индуцированной А на
Х]_ч • • • , Х^ч
и подвыборки, индуцированной А на
Поэтому число А8 (хг, ..., хк, хк+1, ..., х{) не превосхо-
превосходит числа пар подвыборок, каждая из которых состоит из
одной подвыборки, индуцированной некоторым А ^ 8
на хг, ..., хк, и одной подвыборки, индуцированной на
1, ..., Х\. Следовательно,
, ..., хк, хк+1, ..., хг) < Д8(ж1, ...,хк)А8(хк+1, ..., хг)
A1.2)
и соответственно
1&г Д8(ж1, .... хк, хк+1, ..., жг)< 1§2 А8 (хг, ..., хк) +
+ \§2А*(хк+1, ..., хО. (И.З)
242 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
Усредняя соотношение (И.З), получим
Н8 & + к) < Н8 (У + Н8 (/,), A1.4)
т. е. свойство полу аддитивности.
Применяя A1.4) многократно, получаем
Я8 (п1) < пН8 (I). A1.5)
§ 2. Асимптотические свойства энтропии
Энтропия системы событий относительно выборки х1>...
..., Х\ обладает рядом свойств, аналогичных свойствам
энтропии гс-членных цепочек, рассматриваемых в теории
информации. В этом параграфе будет сформулировано и
доказано несколько утверждений относительно асимпто-
асимптотического поведения и оценок энтропии, которые пона-
понадобятся при выводе необходимых и достаточных условий
равномерной сходимости.
Я8 (п
Лемма 1. Последовательность —-^-имеет при I -> оо
предел с @ < с <; 1).
Приводимое доказательство совпадает с доказатель-
доказательством аналогичного утверждения для энтропии п-член-
п-членных цепочек в теории информации [66].
Доказательство. В самом деле, поскольку
„ . Я8 (/) . .
0<,—р^- <^ 1,то существует нижний предел
с = Цщ-^Л @ < с < 1).
I—*оо
^ Тогда для любого е > 0 найдется 10 такое, что
^<С + г. A1.6)
Произвольное 1^> 10 представим в виде
I =п10 + к,
где п > 0 и к < 10.
Далее, в силу A1.2), A1.4) и A1.5)
Н8 (I) = Н8 (п10 + к) < Н8 (п10) + Я6 (к) <
(г0) + Я» (к) < пН8 A0) + к.
§ 2. АСИМПТОТИЧЕСКИЕ СВОЙСТВА ЭНТРОПИИ 243
Поэтому
Н8A) пН8 (к) + к . пН8(к) + 1п _ Я5 (/о) _1_
I ^ пк + к <~ га/0 ~" 13 + п '
Воспользовавшись теперь условием A1.6), получим
Далее, поскольку при / -> оо также и гс->-оо, имеем
г:— Я8 (/) / .
г—оо '
и ввиду произвольности е
8 (I)
^! = с.
Я8
Лемма доказана.
тэ х на)
В теории информации величину—±-*- называют энтро-
энтропией на символ. Сохраним зтот термин и для величины
—р-'-. Несмещенной оценкой этой величины служит слу-
случайная величина
г8 (*!,..., гг) = ^-1§а А8 (*!,...,*г).
Покажем, что эта случайная величина стремится по
Я^ (I)
вероятности при / -> схэ к тому же пределу, что и —-~
(аналогичное утверждение для эргодических источников
доказывается и в теории информации, но на этот раз до-
доказательства различны).
Я8 {1\
Лемма 2. Пусть —^- —> с, тогда
8 1в А5 (*!,...,*,)
г ~ /
сходится к с по вероятности, т. е.
Пах Р {\ г8 (хъ .. ., х,) — с I > е} = О,
г—«=о
244 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
Более того, если обозначить
Р+(г, I) =Р{г8(Ж1, ...,ж,)-с>в},
Р- (е, I) = Р{с-г8 (хг, .... хг) > е},
то
Доказательство. Оценим сначала Р+ (е, I),
Поскольку
найдется 10 такое, что
г0 <-с+ з
Рассмотрим случайную последовательность
п—1
Я (и) = -^
г= 2 г(х1Ш> • • •. ж(«+1)го) •
г=0
Таким образом, д (п)/п есть среднее арифметическое слу-
случайной величины г8 (х1У ..., жго), полученное в серии неза-
независимых испытаний длины п.
Математическое ожидание г8 (ж1, ..., ж^) равно
Н8A0)/10, поэтому математическое ожидание ^ (п) /п также
рд&во Н8 A0)/10', случайная величина г^ (хг, ..., х1о) огра-
ограничена @ <^ г -^ 1) и потому обладает центральными мо-
кейтами любого порядка. Пусть В2 и /L — ее централь-
центральные моменты соответственно второго и четвертого порядка.
Очевидно, что 1L и Ю2 меньше 1. Тогда центральный мо-
момент четвертого порядка величины ^ (п)/п есть
Применяя неравенство Чебышева для моментов чет-
четвертого порядка, получим при любом б ^> О
12. АСИМПТОТИЧЕСКИЕ СВОЙСТВА ЭНТРОПИИ 245
Далее, в силу (И.З)
1 1 л5 ^
—у- 1д2 А (хъ ..., Хп1) <^ —т-
п—1
1=0
т. е.
г (Ж!, ..
Поэтому, тем более,
Полагая б = -$ и учитывая, что
получим
{^>« + -т}<-§-, A1.7)
где через <? обозначено -^-.
Наконец, для произвольного 1^> 1й положим I = п10 +
+ к, где п = [///0], а к <. 10-
В силу A1.2)
Поэтому
г (ж1(. .., хг) = -т- 1§а А (хъ ..., х
Усиливая неравенство, получим
A1.8)
Предположим, что I настолько велико, что
_1_ ._е_
Тогда из A1.7) и A1.8) следует, что
1- A1.9)
246 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
Поскольку при I -> оо имеет место ге-> оо, то
ПтР+(е, /) = 0.
I—*оо
Кроме того,
Действительно, достаточно оценить сумму, начиная с до-
достаточно больших /, для которых выполняется A1.9).
Тогда
г=г*
п=1
Остается показать, что Р~ (е, /) -> 0 при /-у схэ. Пусть
10 таково, что для всех / ^> 10
Н8A)
I
— С
8
2 *
Из свойств математического ожидания и того факта,
что Н8 {1I I есть математическое ожидание г8 (хл, ..., хг),
имеем
г=НA)/(
г=0
5
г=Н8A)/1
Обозначая первую часть равенства Дх, а вторую ^?а и по-
полагая I ^> 10, получим
Г=С—6
*!>-!-$ <1Р (X) =-I-Р~ (г, I). A1.10)
г=0
Далее, пусть б ]> 0 — произвольное число. Тогда
г=с+5 _ „ г=1
г=с+5
X
г=1
+
$ 2. АСИМПТОТИЧЕСКИЕ СВОЙСТВА ЭНТРОПИИ 247
или, иначе,
с+ б —
я8 (О
г
Объединяя A1.10) и A1.11), имеем
Н8A)
Переходя к пределу при I-*■ оо,
г
и, поскольку б ]> 0 произвольно, а Р~ (г, I) Г> 0,
Лемма доказана.
Замечание 1. В отличие от последовательности
(г)
тах 1&2 А8
которая в силу результата § 4 главы X гс/ш / -> схэ стре-
стремится либо к нулю, либо к единице, последовательность
Н8 (I) .. 1&2 А8 (XI X)
—~ = м г
может стремится к любому пределу с @ <^ с <^ 1).
Например, пусть X — сегмент [0, 1]. В качестве сис-
системы 5 рассмотрим все измеримые множества А, которые
включаются в сегмент [0, с]. Распределение Р (х) поло-
положим равномерным. Тогда на последовательности хг, ...,хг
(без повторов) будут индуцироваться множествами А
те и только те подпоследовательности, которые целиком
укладываются в сегмент [0, с]. Значит, их число равно
, ...,Х1) =2",
нтов последовав
м
Н8 (I) = М 1§аЛ8 (х1г .... хг) = М (и) = с1
где п — число элементов последовательности, принадле-
принадлежащих [0, с]. При этом
248 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
и, следовательно,
Заметим, однако, что поскольку всегда
1цтЗA)^Н8A),
то предел
Пт —у-"-
может быть отличен от нуля только в том случае, когда
или, что то же самое,
д8
Замечание 2. Значение функции —р-^- при любом I
служит оценкой сверху для величины
г—«.
т. е.
44
Доказательство этого утверждения аналогично доказа-
доказательству леммы 1.
Отсюда следует, что если с = 1, то
Н8{1) _,
~г~ — *•
т. е. индекс Д5 (хг, ..., хг) равен 2' с вероятностью 1.
§ 3. Необходимые и достаточные условия
равномерной сходимости (доказательство достаточности)
Введенное в предыдущих параграфах понятие энтро-
энтропии системы событий позволяет полностью охарактери-
охарактеризовать те случаи, когда имеет место равномерная сходи-
сходимость частот к вероятностям по классу событий. Оказыва-
§ 3. ДОКАЗАТЕЛЬСТВО ДОСТАТОЧНОСТИ 249
ется, что для этого необходимо и достаточно, чтобы энтро-
энтропия на символ последовательности стремилась к нулю с
ростом длины выборки.
Теорема 11.1. Допустим, что функции л8 (хг, ..., хг),
р8 (х1г ..., ж;) и А8 (жц ..., хг) измеримы при всех I. Тогда
Н8 (I)
а) если Пт—р-^- = 0, то имеет место равномерная
г—оо '
сходимость частот к вероятностям с вероятностью 1;
Н® (I)
б) если Ит —р^- = с > 0, то существует число б (с) > О,
г-»оо *
не зависящее от I, такое, что
ПтР {я8(ж1,.. .,ж,)>б} = 1,
г-»оо
т. е. вероятность того, что максимальное по классу 8
уклонение частоты от вероятности превзойдет б, стре-
стремится к 1.
Таким образом, необходимым и достаточным условием
равномерной сходимости частот к вероятностям по классу
событий в этом смысле является условие
1ип—г^- = 0.
Доказательство достаточности (ут-
(утверждения а)). Это доказательство аналогично вы-
выводу достаточных условий главы X.
Итак, пусть
11т
Оценим величину
В силу основной леммы (§ 5 главы X)
Р {л! > е} < 2Р [Р8(х1,..., хг) > -1].
В свою очередь, как было показано при доказательстве
теоремы 10.2,
ВД)
250 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
где У* — всевозможные перестановки последовательности
хг, ..., хг1. Кроме того,
№ = ~;о"т\
Очевидно также, что & <^ 1.
Разобьем область интегрирования на область Хг, где
1^2 А5 К ...,хг1) „^
21 ^ 8
и область Х2, где
1^2 А5 (XI Хп) ^ г2
21 ^ 8 '
Тогда, заменяя к мажорирующими выражениями, по-
получим
A1.12)
В обозначениях леммы 2 предыдущего параграфа
поскольку
1-мо '
Учтем также, что в области Хг
Тогда
{!Ц^е-^ + Р*(-^-,21у A1.13)
Первый член суммы стремится при / -> схэ к нулю экспо-
экспоненциально, второй член также стремится к нулю соглас-
согласно лемме 2. Более того, поскольку в соответствии с этой
§ 4. ДОКАЗАТЕЛЬСТВО НЕОБХОДИМОСТИ 251
леммой
г=1
то и
г=1
а следовательно, и
1=1
Отсюда следует равномерная сходимость частот к ве-
вероятностям почти наверное.
Утверждение а) доказано (заметим, что в оценке A1.13)
только член Р+ (е, /) зависит от распределения).
§ 4. Доказательство необходимости условий
равномерной сходимости
Пусть теперь
Н8 (I) . А
^ >0
(-•оо '
В силу основной леммы (§ 5, гл. X), если только
ПтР{р8(х1, ...,жаг)>2б} = 1, A1.14)
г-«о
то и
Таким образом, достаточно показать справедливость
A1.14) при некотором б (с) ^> 0.
1. Рассмотрим сначала для пояснения общего доказа-
доказательства частный случай, когда
1ип—р^- = 1.
В этом случае, как было указано в замечании 2 § 2,
П8 @ _ м
252 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
и, поскольку —— есть математическое ожидание вели-
величины
18» А8 (ад,...,*,)
<ч !
то
р |^А (*ь •••.*,) = Д = 4>
Следовательно, для всякого ^ с вероятностью 1
т. е. с вероятностью 1 всякая выборка такова, что на ней
индуцируются системой $ все возможные подвыборки.
В частности, для выборки хг, ..., хгХ можно найти такое
А* 6= 5, что х1 е= А* для I = 1, ..., / и х1 ф А* для
I =1+1, ..., 21. Тогда V1 (А*) = 1, V"(Л*) = 0 и, сле-
следовательно, с вероятностью 1
зир| V (А) — т
Тогда и подавно для всех б -< 0,5
Нш Р {зир | V' {А) — V" (А) | > 26} = 1.
1 Лев
Идея доказательства утверждения б) в общем случае
основана на том, что при
почти из всякой выборки длины I можно выделить подвы-
борку, на которой индуцированы все подвыборки и дли-
длина которой растет пропорционально /.
2. Для этого нам понадобится следующая
о
Лемма 3. Если при некотором а @ < а ^ 1) и 1^> —
для некоторой выборки хг, ..., хг оказывается, что
то найдется подвыборка
хи,
I 4. ДОКАЗАТЕЛЬСТВО ЙЁОЁ&ОДИМОСТИ 253
длины г= [<?Л, гЗед(а) = ^4- (е — основание натуральных
логарифмов), такая, что
Дв (х„ ..., х.т) = 2Г.
Доказательство. В силу леммы § 4 главы X
требуемая подвыборка заведомо существует, если
г—1
Чтобы убедиться в последнем, достаточно проверить нера-
неравенство
2аг > Ф (/, г). A1.15)
Поскольку при наших условиях г Г> 2 и 1^> г + 1, то
можно воспользоваться оценкой функции Ф (г, I), полу-
полученной в замечании 1 § 4 главы X: . ; ,
В свою очередь это неравенство можно усилить, применяя
формулу Стирлинга:
Нетрудно убедиться, что функция (—) монотонно воз-
растает по х при х < I. Следовательно, справедливо так-
также неравенство
так как
г = [д, Л < д^.
Поэтому отношение A1.15) будет установлено, если спра-
справедливо неравенство
254 ГЛ. XI. необходимые и достаточные условия
Логарифмированием и сокращением на / это неравенство
преобразуется к следующему виду:
A1.16)
При 2 ]> 0 справедливо неравенство
Оно непосредственно следует из того, что функция -Щ4-
V г
достигает максимума в точке 2 = е2 и равна при этом
—гИ. Поэтому A1.16) следует из неравенства
Подставляя сюда значение д = —т— , непосредственно убеж-
У
даемся в справедливости выражения
Лемма доказана.
Напомним, что, согласно лемме 2 § 2, при
оказывается, что с ростом
стремится к единице (б ]> 0). Следовательно, при доста-
достаточно больших / с вероятностью, сколь угодно близкой к
единице,
1§^8(х1,...,х1)>2* A1.17)
и, согласно только что доказанной лемме, в каждой выбор-
выборке, удовлетворяющей условию A1.17), найдется подвы-
борна длины
§ 4. ДОКАЗАТЕЛЬСТВО НЕОБХОДИМОСТИ 255
на которой система # индуцирует все подвыборки. Длина
этой подвыборки возрастает пропорционально /.
3. Схема доказательства (утвержде-
(утверждения б)). Сравнение частот выпадения событий в двух
полувыборках может вестись следующим образом: берет-
берется выборка длины 21 и случайным образом делится на две
полувыборки равной длины, после чего по дочитывается
и сравнивается число появления каждого события клас-
класса # на первой и второй полувыборках.
Рассмотрим несколько измененную схему. Допустим,
что выборка двойной длины хх, ..., жаг удовлетворяет усло-
условию A1.17), т. е.
Тогда в ней можно указать подвыборку Хг длины
на которой индуцированы все подвыборки. Теперь разде-
разделим случайно на две полувыборки сначала подвыборку
Хг, а затем (независимо) остаток ХЧХГ. Пусть Х[ и
XI — две полувыборки, на которые распалась Хг. По
построению найдется событие А* ЕЕ 5 такое, что все эле-
элементы Х[ принадлежат А*, а все элементы Х\ не принад-
принадлежат А*. Для этого события «разбаланс» частот достига-
достигает наибольшего значения. Допустим, что в оставшейся
части последовательности элементы из Л* встречаются
т раз. При случайном разбиении остатка примерно т/2
из них попадет в первую полувыборку и столько же во
вторую. Тогда
и, следовательно,
Поскольку число 5 ]> 0 не зависит от длины выборки, то
равномерной сходимости нет.
Измененная схема не вполне эквивалентна исходной,
так как в действительности подвыборка Хг и остаток не
256 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
обязательно делятся точно пополам при делении полной
выборки X1, но при достаточно больших / (а значит, и г)
это условие почти всегда выполняется достаточно точно.
Приводимое дальше формальное доказательство позволя-
позволяет строго учесть все сделанные здесь допущения и прибли-
приближения.
4. Доказательство утверждения б).
Итак, пусть
При доказательстве достаточных условий (§ 6 главы X)
было установлено, что
A1.18)
где Тг — всевозможные перестановки последовательности
хг, ..., х21. Обозначив через К (х1г ..., х21) подынтеграль-
подынтегральное выражение, сократим область интегрирования:
) с
7
Оценим величину К, полагая, что
21
т. е.
При этом выберем -у > ц (с) ^> 0 так, чтобы в соот-
соответствии с леммой 3 при достаточно больших / существо-
существовала подвыборка Хп длины п ]> д/, на которой система $
индуцирует все возможные подвыборки (т. е. Д8 (х1} ...
..., хп) =2"), и положим б (с) = -^-\ Примем, что п ^ /,
и заметим, что числа д и б не зависят от I.
§ 4. ДОКАЗАТЕЛЬСТВО НЕОБХОДИМОСТИ 257
Сгруппируем перестановки Г, так, что в каждую груп-
группу /?5 входят перестановки, соответствующие одному и
тому же разбиению на первую и вторую" полувыборку.
Очевидно, что
'D; Тгхъ..., х{) — \"(А\ Тг-хг,..., хи)\
зависит только от /?5 и в пределах 'каждой группы постоян-
постоянна. Поэтому
к = -±- ^е [р8 (Д.; »1 »«) - 2б].
Сумма берется по всем возможным разбиениям хъ . . .
. . ., х21 на первую и вторую полувыборки.
Пусть, далее, Хп — та самая подвыборка длины п, на
которой 5 индуцирует все возможные подвыборки. Обоз-
Обозначим ее дополнение в Хгг через X (длина X равна
21- п).
Разбиение ,йв будет полностью задано, если заданы
разбиение Н^ подвыборки Хп на часть, попадающую в
первую полувыборку, и часть, попадающую во вторую
полувыборку, и соответствующие разбиение .й; подвы-
подвыборки X.
Обозначим для данного разбиения число элементов из
Хп, попадающее в первую полувыборку, через г и пред-
представим К (X1) в следующей форме:
4
°аг
-2*]. ~
Здесь суммирование по г ведется в пределах 0 ^ г ^ п.
Суммирование по к ведется по всем разбиениям Хп таким,
что к первой полувыборке | относится точно г элементов
из'-Х™, суммирование по / — по всем разбиениям X таким,
что к первой полувыборке относится I — г элементов из X.
Для фиксированного к, т. е. разбиения подвыборки
Хп, найдется такое А (к) ЕЕ. 8, что все элементы жг, отно-
относимые этим разбиением к первой полувыборке, принадле-
принадлежат А (к), а все элементы х-{, отнесенные ко второй
полувыборке, не принадлежат А (к). Это следует из того,
258 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
что $ индуцирует на Хп все подвыборки. При этом
р« (НкНг, Хг, . . ., Х21) > р« (А (к); НкН}; хх , . . . ,х21)
и, следовательно,
К > -?г222<э [Р8 (А(&); ВД; хи.-, хл1) - 26].
Пусть, далее, Р (к) — число элементов подвыборки Ж,
принадлежащих А (к), и { — число элементов подвыборки
X, принадлежащих А (к) и отнесенных разбиением Н] к
первой полувыборке. Тогда для фиксированных г, к, /
*) = 1+1
I
); х1+и ..., х21) = ^=
Соответственно
1, если
) —26] = '
О, если
Наконец, сгруппируем разбиения В^ соответствующие
одному и тому же I (при фиксированных г и к). Число
таких разбиений равно
\-т-1
Тогда оценка для К примет вид
После элементарных преобразований получим
где суммирование по I ведется в пределах, задаваемых
выражением
1,г + 2г-^1>2б| A1.20)
§ 4. ДОКАЗАТЕЛЬСТВО НЕОБХОДИМОСТИ
259
Положим теперь0 <^ е <^-^г- и рассмотрим величину К',
отличающуюся от правой части A1.19) лишь иными
пределами суммирования,
Г1Т Г11—Т
где г и I пробегают значения, удовлетворяющие следую-
следующим неравенствам:
ей, A1.21)
г —
2
21 —п
A1.22)
При г и {, удовлетворяющих A1.21) и A1.22), автомати-
автоматически выполняется A1.20). Действительно, при этом
Поскольку было принято, что'^1 <Г гс <Г /, 6= —, е <Гтг- »
8 20
ТО
г + 2г—р 1 Г га , Л _ Ч _ „«,
Так как область суммирования в выражении для К' вкла-
вкладывается в область суммирования A1.19), то
Далее, для всякого г\ > 0 найдется 1й, зависящее
только от т} и 5, такое, что для всех / > 10
\1 п а/-" -у^ л /л л по\
(суммирование ведется по г, удовлетворяющим A1.21)) и
2 С*$Г" > * - 1 (И.24)
а;-п
(суммирование ведется по г, удовлетворяющим A1.22)).
260 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
Действительно,
1?
есть вероятность вынуть г черных шаров из урны, содер-
содержащей п черных и 21 — п белых шаров, когда вынимается
случайно I шаров без возвращения. При этом математи-
математическое ожидание числа черных шаров в выборке равно
гс/2 и правая часть формулы A1.23) выражает вероят-
вероятность того, что число черных шаров в выборке отклонит-
отклонится от математического ожидания более чем на гп. Пос-
Поскольку для схемы без возвращения справедлив закон
больших чисел, формула A1.23) верна, начиная с дос-
достаточно больших /.
Аналогично
есть вероятность вынуть { черных шаров из урны, содер-
содержащей р черных и 11 — п — р белых шаров, когда
вынимается 1^> г шаров, опять-таки без возвращения.
Математическое ожидание черных шаров в выборке равно
гРA-г)
^21 — п—р
и, следовательно, формула A1.24) выражает зако боль-
больших чисел в этом случае.
Тогда, учитывая что число разбиений Вк подвыборки
Хп для фиксированного г равно Сгп, получим при 1^> 10
К > A - п)а.
Окончательно для / ;> 10 и б (с) = -|-
ё, А5 Оч,..., *а;; с_
%1 а
§ 5. ПРИМЕРЫ И ДОПОЛНИТЕЛЬНЫЕ КРИТЕРИИ 261
Поскольку, согласно лемме 2,
имеем
ИтР-(-|-, 0 =
V
Ит Р {р8(Л1,..., хаг)> 26} >A -
!->оо
Ввиду произвольной малости г]
1ш Р {р8 (хь ..., ха;) > 26} = 1.
Теорема доказана.
§ 5. Примеры и дополнительные критерии
При выводе необходимых и достаточных условий по-
попутно было установлено (§ 4), что если
Я5 B7)._ .
2/ ~~ х'
то
р;{аир|^И)
лез
и соответственно
{\
Лез
т. е. в зтом случае максимальное отклонение частоты от
вероятности остается большим даже при сколь угодно
длинных выборках.
1. В примере 2 § 3 главы X было принято, что X —
сегмент [0, 1], система 5 состоит из всех множеств, каж-
каждое из которых является объединением конечного числа
замкнутых сегментов с рациональными концами. Система
1? счетна. Было установлено, что
если только выборка не содержит повторений.
При любом непрерывном распределении выборка с
вероятностью 1 не содержит повторений. Поэтому
262 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
и, следовательно, с вероятностью 1
зир\у(А)—
(в действительности нетрудно убедиться, что в данном
случае почти наверное зир | V (А) — Р (А) | = 1).
Таким образом, равномерной сходимости нет, несмот-
несмотря на то, что система $ содержит лишь счетное число
событий.
2. В примере 3 § 3 главы X рассматриваются гс-мер-
ное пространство Еп и система событий вида
{х:(х, ф)>0}
при всевозможных ф (ф ф 0).
Нетрудно убедиться, что если точки хг, . . ., хг1 на-
находятся в общем положении при 21 <^ п, то
Дз (х, , . . ., хг1) = 2а<.
При любом непрерывном распределении, как известно,
с вероятностью 1 выборка удовлетворяет условию общ-
общности положения. Поэтому при / <С -к-
2/
аир IV (Л) —
Аез
с вероятностью 1. Таким образом, пока длина выборки
меньше половины размерности пространства, максималь-
максимальное уклонение частоты от вероятности остается большим.
3. Установим еще один критерий, который позволяет
судить о наличии равномерной сходимости в тех случаях,
когда достаточные условия не выполняются.
Теорема 11.2. Пусть в пространстве X заданы веро-
вероятностная мера Р (х) и система событий 8. Допустим,
что для всякого е ^> 0 можно указать системы З^е) и
82(ь), удовлетворяющие условию равномерной сходимости,
так что для всякого множества А е= 5 найдутся мно-
множества В СЕ #1 и С СЕ #2 такие, что
В -^ А =э С
§ о. ПРИМЕРЫ И ДОПОЛНИТЕЛЬНЫЕ КРИТЕРИИ 263
\Р(А)- Р(В)\ < е, \Р(А)-Р (С) | < е.
Тогда для системы 8 также имеет место равномерная
сходимость частот к вероятностям (по вероятности).
Доказательство. В самом деле, пусть 8 > О
и г] > 0 — произвольные числа. Выберем такое /„, чтобы
выполнялось
Р\ вир \^}
) ' A1.25)
Р( 8ир \1(АIР(А)\>±}<
для всех / > 10.
Возьмем произвольное событие А (^ 8 и найдем дли
него события В ЕЕ #1 и С ЕЕ 82 такие, что Йц4 гз С и
^Г. A1.26)
Тогда
V (В) > V (А) > V (С). A1.27)
Сопоставляя A1.25), A1.26) и A1.27), получаем, что
Р {зир | V1 (А) - Р (А) | > 8} < 2л-
лез
Теорема доказана.
4. Приведем два примера, где применяется этот кри-
критерий.
Пусть X — счетное множество, на котором задана
вероятностная мера Р (х), $ — произвольная система
подмножеств. Занумеруем каким-либо образом элементы
X. Поскольку
1=1
то по всякому 8 > 0 можно указать п такое, что
1=1.
264 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
Обозначим конечное множество хх , . . ., хп через X (п).
В качестве системы 82 возьмем все подмножества X (п), а
в качестве ^ — все множества вида
<?и (х/хп),
где (? произвольное подмножество X (п).
При этом для каждого А ^ 8 можно указать В <= 8г
и Сё 8 2, удовлетворяющие условию теоремы, а именно:
С = А
X (п),
[) (Х\Х (п)).
Поскольку системы б^ и 82 конечны, для них выпол-
выполняется равномерная сходимость, а следовательно, она
имеет место и для системы 5. Таким образом, если X — счет-
счетное множество, то равномерная
сходимость частот к вероятнос-
вероятностям имеет место всегда. При
этом система $ может быть та-
такой, что т8 (I) = 2'. В этом
случае скорость сходимости мо-
может быть сколь угодно низкой.
5. Рассмотрим еще один лю-
любопытный пример. Пусть X —
двумерная плоскость, а систе-
система $ состоит из всех выпуклых
замкнутых множеств на плос-
плоскости. В зтом случае
т8 (/) = 2'.
Рис. 22.
В самом деле, разместим / точек хъ . . ., хх на окружно-
окружности (рис. 22). Рассмотрим любую подпоследовательность
х-г , . . . , х1г (на рисунке эти точки отмечены крестиками,
а остальные — кружками). Вписанный замкнутый вы-
выпуклый многогранник с вершинами в точках ж4 , . . ., х-1Т,
очевидно, содержит эти точки и не содержит никаких
других из числа хх , . . . , Х\. Значит, система $ инду-
индуцирует на хх , . . . , х; любую подвыборку:
Дз (*!,.. ., *,) = 2'
§ 5. ПРИМЕРЫ И ДОПОЛНИТЕЛЬНЫЕ КРИТЕРИИ 205
и поэтому
тз (I) = 21.
Таким образом, в этом примере достаточные условия не
выполнены.
Равномерная сходимость по классу событий $ может
выполняться или нет в зависимости от распределения.
Например, если вероятностная мера сосредоточена на не-
некоторой окружности и равномерно распределена по ней,
то с вероятностью 1
как бы длинна ни была выборка.
В самом деле, с вероятностью 1 все точки выборки
х1 , . . ., Х\ лягут на окружность. Натянем на них вы-
выпуклую оболочку. Она представляет собой вписанный
многогранник А с вершинами х1 , . . . , Х\. Этот много-
многогранник содержит все точки хъ . . ., Х\ и пересекается с
окружностью на множестве меры нуль.
Если же вероятность равномерно распределена в не-
некотором круге О, то равномерная сходимость имеет место.
Действительно, в этом случае достаточно рассмотреть сис-
систему $*, состоящую из выпуклых замкнутых множеств,
целиком вкладывающихся в круг О. Дело в том, что с
вероятностью 1 все точки выборки лежат в круге. Поэ-
Поэтому для произвольного А ЕЕ 5 и В = А[]О оказывается
ч(А) = ч(В), Р(А) = Р(В).
В свою очередь В = А р) О будет замкнутым выпуклым
множеством и вкладывается в круг О.
Таким образом, с вероятностью 1
зир \\(А) — Р(А)\ = вир \ч(А) — Р(А)\.
лез Аез*
Далее, элементарным построением можно показать,
что по заданному е > 0 для всякого выпуклого множества
из <?* можно найти вложенный в него и объемлющий его
/с-сторонние многоугольники, так что их мера отличается
не более чем на е, причем число к можно зафиксировать
для данного е.
260 ГЛ. XI. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
Следовательно, выполнены условия теоремы настоя-
настоящего параграфа, так как для систем 8г, 82, состоящих
из выпуклых многоугольников с фиксированным числом
сторон, равномерная сходимость установлена (пример 5
§ 8 главы X).
Значит, равномерная сходимость имеет место при
исследуемом распределении и для произвольных выпук-
выпуклых множеств.
Отметим, что во всех рассмотренных ранее примерах
непрерывное распределение было наиболее неблагоприят-
неблагоприятным, а в данном случае ситуация обратная.
Глава XII
ОЦЕНКИ РАВНОМЕРНОГО
ОТНОСИТЕЛЬНОГО УКЛОНЕНИЯ
ЧАСТОТ ОТ ВЕРОЯТНОСТЕЙ
В КЛАССЕ СОБЫТИЙ
§ 1. О равномерном относительном уклонении
Полученные в главе X оценки скорости равномерной
сходимости в действительности оказываются завышенны-
завышенными. Это связано с тем, что пришлось пойти на завыше-
завышение оценок во избежание чрезмерной громоздкости
самих оценок и технических сложностей при их вы-
выводе. Но в еще большей степени это вызано тем, что,
желая получить общий результат, пришлось ориентиро-
ориентироваться на наихудший случай (с точки зрения оценивае-
оцениваемой величины) по тем параметрам, которые не входят
явно в оценку.
В частности, для того чтобы уложиться в заданное
абсолютное уклонение частоты от вероятности для не-
некоторого события А, придется взять большую выборку,
если вероятносгь А близка к 1/2, и меньшую при Р (А),
близком к 0 или 1. В самом деле, для Р (А) = 0,5 и до-
допустимого уклонения в 1% (т. е. V (А) = Р (А) ± 0,01)
необходимо ~ 104 показов, тогда как при Р (А) = 0,01
и том же допустимом уклонении достаточна длина вы-
выборки ~ 100 -и- 200. Если же необходимо получить оцен-
оценку сверху, не зависящую от Р (А), то приходится ориен-
ориентироваться на наихудший случай, т. е. Р (А) = 0,5.
В нашем доказательстве тоже фактически необходимо
было ориентироваться на тот случай, когда вероятности
Р (А) всех событий близки к 1/2.
Вообще известно, что для фиксированного события А
отклонение частоты от вероятности имеет порядок е, если
268 ГЛ. XII. ОЦЕНКИ ОТНОСИТЕЛЬНОГО УКЛОНЕНИЯ
среднеквадратичное уклонение а частоты имеет порядок
е. В свою очередь
т. е. при фиксированном I отклонение пропорционально
У
-Р)-
Поэтому естественно было бы и равномерное уклоне-
уклонение измерять в относительных единицах, т. е. потребо-
потребовать, чтобы
V(^) — Р(А)
зир
' А
г-с
Однако такого рода оценку при разумных предпо-
предположениях удается получить только для равномерного
уклонения частот в дзух последующих полувыборках,
нормированного к эмпирической оценке величины
УР (А) A — Р (А)) по всей выборке. А именно, в следу-
следующем параграфе будет выведена оценка:
Р|вир \У<Л)-ч"(А)\ . ., .
< 4т8 B1) е * ,
где V' (А) и V" (А) — частоты выпадения события А со-
соответственно на первой и второй полувыборках, а у(А) =
V (А)-\-у" (А) .
= —ч ' — частота выпадени А на полной вы-
борке.
При этом достигается определенное «равноправие» со-
событий класса <?. Что же касается равномерного относи-
относительного уклонения частот от вероятностей, то здесь
удается получить одностороннюю оценку:
Р { зир Р (Л)^1.(-4> > Л < 16т» B1) е~~ т . A2.1)
Нормирующий делитель УР (А) при малых Р (А)
близок к величине УР (А) A — Р (А)).
§ 2. УКЛОНЕНИЕ ЧАСТОТ В ДВУХ ПОЛУВЫБОРКАХ 269
Эта оценка существенно отличается от полученных в
главах X и XI только при малых Р (А), когда ]/ Р (А)<§^
<^ 1. В то же время при очень малых Р (А) <^ еа оценка
тривиальна, так как при этом всегда
Справедлива и симметричная односторонняя оценка,
работающая при Р (А), близких к единице:
Р\ вир—. -—- **> рл ^ 1 Вт5 (Я/) <» *.
I лез У\-Р(А) )
В главе V было показано, что для применения в тео-
теории обучения существенны именно односторонние отно-
относительные оценки уклонения частот от вероятностей.
§ 2. Оценка равномерного относительного уклонения
частот в двух полувыборках
Схема вывода оценок относительного уклонения час-
частот событий от их вероятностей остается той же, что и в
главе X. Но теперь сначала получим оценку относитель-
относительного уклонения в двух полувыборках, а затем применим
ее для оценки максимального по классу относительного
уклонения частоты от вероятности.
Теорема 12.1. Пусть задана система событий 8 и ее
функция роста т8A). В серии независимых испытаний
получена выборка хг, . . ., х2г и для каждого события А
подсчитаны частоты V' (А) выпадения этого события в
полувыборке хх. . . ., хь Vм {А) выпадения события А в
полувыборке хг+р..., х21 и \ (А) — У ' г ^ ' вы-
падения этого события на всей выборке хъ . . ., х2ь
Справедлива оценка:
]у'(А)—у"(А)\
вир
. A2.2)
270 ГЛ. XII. ОЦЕНКИ ОТНОСИТЕЛЬНОГО УКЛОНЕНИЯ
Доказательство. Точно так же как при дока-
доказательстве теоремы 10.2, сведем дело к рассмотрению
относительного уклонения частот для одного фиксиро-
фиксированного события.
Обозначим через На (хи . . ., х2г) = На (яаг) величину
Тогда оцениваемая вероятность равна
Р = ^ 9 [зир | НА (ха<) — е |] ЙР (хаг),
где
( 1 при х> О,
\ 0 при х<^ 0.
Рассмотрим опять всевозможные перестановки Ть после-
последовательности хг, . . ., хг1. Тогда
B)
р = Ш 2 5 0 1зиР I Яд G\х*0 - е |1 ЙР (^') =
(а()!
= 5 Ш 2 аир 9 | ЕА (?>*) - е | йР (а*'). A2.3)
Далее исследуется подынтегральное выражение.
Теперь, так как выборка фиксирована, можно вместо $
рассматривать конечную систему 8', куда входят по
одному представителю из каждого класса эквивалентно-
эквивалентности. Таким образом,
B0!
рткг 2 8иР е I еа G>20 — е | йР (хаг) <
< 2 \ш 2 01 па (Т<хи) — е;|} . A2.4)
Ае.8' 1—1
Выражение в фигурных скобках и есть вероятность
уклонения частот в двух полувыборках для фиксиро-
фиксированного события А для данного состава полной выборки.
§ 2. УКЛОНЕНИЕ ЧАСТОТ В ДВУХ ПОЛУВЫБОРКАХ 271
Оно равно
•р _ у °т'^Ы-т
1 —Д 7п '
где т — число выпадений событий А в полной выборке,
а к — число выпадения событий в перзой полувыборке.
Оно пробегает значения, удовлетворяющие неравенствам
шах @, т — I) <; к < пип (т, /),
к т — к
I I
/№
1_'»-1
■ 8.
11
Обозначим через б величину
Теперь можно воспользоваться неравенством (П.5), вы-
выведенным в приложении к главе X:
2
Подставляя сюда значение б, получим,
(отметим, что эта оценка слабо зависит от т, что и оз-
означает «равноправие» событий).
Правая часть неравенства! достигает максимума при
т = 0 или т = 11. Поэтому
1+1
Г<2е * +а(+1;
откуда при 0< е< 1, учитывая, что всегда Г< 1,
Возвращаясь теперь к A2.4), получаем
г=1
272 ГЛ. XII. ОЦЕНКИ ОТНОСИТЕЛЬНОГО УКЛОНЕНИЯ
Переходя к A2.2), получаем искомую оценку. Теорема
доказана.!
Замечание.' Точно так же можно получить оценку
<4т8B0е *. A2.5)
( | V' (А) — V" (А)
Р зир ' ) ' \>
Аез
I
Отличие состоит лишь в том, что теперь
б = 8
Подставляя эту величину в (П. 5), получаем
2
4-
4-
2B1 — т + 1р (т + 1) B/ - т + 1)
Первая часть неравенства достигает максимума при
т = 0, откуда
и, далее, при 0 < е <^ 1, учитывая, что всегда Г ^ \$
Г<4е *.
Далее, повторяя рассуждения теоремы 12.1, получаем
требуемую оценку.
§ 3. Оценка равномерного относительного уклонения
частот от вероятностей
Переход от оценок относительного уклонения частот
в двух полувыборках к относительному уклонению час-
частот от вероятностей ведется по той же схеме, что и при
доказательстве основной леммы § 5 главы X. Трудность
здесь состоит в том, что нормирующие делители УР (А)
и у\ (А) A — V (А)) могут сильно отличаться при малых
Р (А) для «наихудшего») события в классе. Поэтому вы-
выводится лишь односторонняя оценка, котораяв как уже
указывалось, фактически касается только событий, ве-
§ 3. уклонение ЧасТот от вероятностей 273
роятность которых больше е2 (при Р (А) «^ е2 оценка
тривиальна).
Теорема 12.2/Пусть 8 — система событий А,Тт8 {I) —
функция роста системы^8^ хг , . . . , Ж[ — выборка, по-
полученная в серии независимых испытаний с неизменным
распределением. Тогда справедлива односторонняя оценка
зир р(А)~^А) > 8) < 16тЗ B/) в" "*". A2.6)
Доказательство. Обозначим через (^ собы-
событие, вероятность которого нам предстоит оценить:
<?! = { зир
УР(А)
Предположим теперь, что выборка продолжена до 11, и
обозначим через <?2 событие, вероятность которого оце-
оценена в предыдущем параграфе A2.5):
| у' (Л) - у"(А) | -
Г"
Аез
У ^(А)+1г
Покажем, что при определенных предположениях из (^
следует (?2- Допустим, что событие (^ произошло. Это
значит, что существует такое А* €Е- 8, что на первой по-
полувыборке
Поскольку V (А*) ^ 0, то отсюда следует, что
Р (А*) > е2.
Допустим теперь, что на второй полувыборке частота
выпадения события А* превзошла вероятность, т. е.
V" (А*)>Р(А*). A2.7)
Примем еще, что / ^>-^г • При этих условиях обязатель-
обязательно выполняется событие] <?2.
Действительно, оценим величину
Г 1
У у>(А')+ж
274 гл. хп. оценки относительного уклонения
при условиях
V' {А*) < Р (А*) — &УР (Л*),
V" (А*) > Р (А*); Р (А*) > еа.
Для этого найдем минимум функции
т Х—у
в области 0< а <^ а; <^ 1, 0 < г/ <; 6, с > 0. Имеем
13 3 1
дТ _ Т^ + ^-У + с дт - —х-^-у-с
дх ~ (х-\-у-\- с)'" ^ ' ду - (х + у + с)''г ^ '
следовательно, Т достигает минимума в допустимой об-
области при х = а, у = Ъ.
Поэтому величина ^ будет оценена снизу, если в A2.8)
V' (А*) заменить на Р (А*) — е"|/> (А*), а V" (А) заме-
заменить на Р (А*). Таким образом
Г У
У 2Р(А*)-еУР(А')+-г
Далее, поскольку Р (А*) > еа и / > —^ , имеем
. е У2Р (А*)
/ 2Р(А*) — еа + е3
Таким образом, при выполнении Bг, а также условий
Р (А*) < V" (А*) и / "> —г- выполняется и (?2.
Заметим, далее, что вторая полувыборка выбирается
независимо от первой и, как известно, при / ^> ,. час-
частота выпадения события А с вероятностью, большей 0,25,
превышает Р (А).
Поэтому событие A2.7) выполняется при условии (I с
вероятностью, большей '/4, если только 1~^>—. Значит,
и событие <?2 выполняется при этих условиях с вероят-
вероятностью, большей 74.
§ 3. УКЛОНЕНИЕ ЧАСТОТ ОТ ВЕРОЯТНОСТЕЙ 275
Итак, при 1^>—— выполняется неравенство
Но вероятность события <?2 оценена выражением A2.5).
Таким образом,
^>—^-. Но при ^<^ — оценка тривиальна, так как
Р (<?!) всегда не превосходит 1. Теорема доказана.
В заключение приведем простейший пример, показы-
показывающий принципиальную односторонность оценок видя
A2.1).
Пусть х — интервал @, 1) и на нем задано равномер-
равномерное распределение. Система # состоит из всевозможных
множеств А, каждое из которых есть интервал (а, Ъ) та-
такой, что 0 <^ а <С Ъ <^ 1; при этом пусть мера каждого
из А больше нуля. Покажем, что неравенство
I Ух - Ра I ^
вир — ^С 8
хез УРА ^
не выполняется ни при каком / > 0 и ни при каком е ^> 0.
Действително, пусть хх , . . . ,Х[ — выборка. Рассмот-
Рассмотрим интервал А* = (хг — б, хх + б) при б > 0. Частота
V (А*) не меньше 1/1, вероятность при достаточно малых
б > 0 равна
Р (А*) = 26.
Теперь при
получаем
V {А*) —Р(А*)>-&УР {А*).
В то же зремя в главе X было показано, что равномер-
равномерная сходимость к нулю ненормированных уклонений
имеет место. В силу теоремы 12.2 сходимость к нулю
односторонних нормированных уклонений в этом при-
примере также имеет место.
Глава XIII
ПРИМЕНЕНИЕ ТЕОРИИ
РАВНОМЕРНОЙ СХОДИМОСТИ
К МЕТОДАМ МИНИМИЗАЦИИ
ЭМПИРИЧЕСКОГО РИСКА
§ 1. Оценка достаточной длины обучающей
последовательности в задачах обучения распознаванию
1. В главе X было показано, что значения риска Н (а)
в точках истинного и эмпирического минимумов заведомо
отличаются не более чем на е, если выполнено условие
8ир|Д(а)-Д0МП(а)|<-^-.
Далее было показано, что в задачах распознавания об-
образов с функцией штрафа
0 при со = Р,
это условие переходит в следующее:
где Та — событие {(со, х): Р (х, а) Ф со}, Р (х, а) —
решающее правило с параметром а, () — множество до-
допустимых значений параметра а.
Таким образом, проблема оценки близости истинно
оптимального и эмпирически оптимального решающего
правила непосредственно сводится к исследованной в
предыдущих главах проблеме равномерной сходимости
частот к вероятностям по классу событий.
1. ОЦЕНКА ДЛИНЫ ОБУЧАЮЩЕЙ ПОСЛЕДОВАТЕЛЬНОСТИ 277
Обозначим, как и ранее, через сс0 значение параметра,
доставляющего минимум функции]
Н (а) = $ Ф (« - Р (х, а)) йР[(х, ю),
а через а* значение параметра, при котором достигается
минимум функции
Яэмп (а) = -|- 2 ф К - р (*ь а)),
1=1
где «!, а?! , . . ., соI, хI — обучающая последовательность.
Тогда на основании формулы A0.19) получаем
Р {В (а*) — Е (а„) > 8} < 6т« B1) е " , A3.1)
где т8 (?) — функция роста класса событий вида
Та = {(со, х): афР (х, а)}.
В этой формуле функция роста берется для событий,
заданных в пространстве пар со, х.
Рассмотрим число различных разбиений выборки
хъ . . ., Х\ на классы с помощью решающих правил
Р (х, а). Обозначим это число
Иными словами, будем считать два решающих пра-
правила Р (х, аг) и Р (х, аг) эквивалентными относительно
выборки хь . . ., хг, если для всех я, A <] I <[ /)
Р {хи ах) - Р{хи а2). A3.2)
Тогда число N (хъ . . ., хг) равно числу классов экви-
эквивалентности, на которые разбивается множество решаю-
решающих правил этим отношением.
С другой стороны, два множества Га1 и 7'Я2, в соответ-
соответствии с соглашением главы X, считаем эквивалентными
относительно выборки соь хг, . . ., соь х;, если для всех
[со, ф Р (хг-, аг)] ~ [а>1 ^г= Р (хг, ос2)], A3.3)
причем Д8 (х1У 001, •••»*!> со г) есть число классов
эквивалентности. Очевидно, что A3.3) следует из A3.2), а
278 ГЛ. XIII. ПРИМЕНЕНИЕ ТЕОРИИ РАВНОМЕРНОЙ СХОДИМОСТИ
в случае, когда « и Р принимают всего два значения 0 и
1, и соотношение A3.2) следует из A3.3). Поэтому
А8 (хъ Й1, • . ., хи аг) < N (хъ . . ., ж,),
т8 (/) ^ шах N (хъ . . ., Ж[).
Соответственно из A3.1) следует, что
а*) —Я(ао)>е}<6 тах 7У(хь ..., хг)е 1в . A3.4)
*1 Ж;
Рассмотрим более подробно дихотомический случай,
когда распознаются два класса. При этом как со, так и
функция Р могут принимать всего два значения: 0 и 1.
Пусть система 8' состоит из событий
А = {х: Р (х, а) = 1}
при всевозможных а €Е <?.
Тогда очевидно, что число разбиений выборки хъ . . .
..., Х\ на классы с помощью решающих правил Р (х, а) рав-
равно числу подвыборок, индуцируемых 8' на х1У . . ., х1у
т. е.
N (х1У . . ., ж,) = А8 (Ж!, . . ., хг).
Кроме того, как указано выше, в дихотомическом слу-
случае соотношения A3.2) и A3.3) равносильны. Поэтому
А8 (Х1У СОЬ . . ., XI, СО;) == N (Ж1? . . ., Хг) =
= А8'(^1 , • ■ • , Хг),
т8 A)= т8' (I)
и соответственно
(а*) - Е (а) > е} < 6тЗ' (/)е 1в ,
где т8' (I) — функция роста для системы 8' событий вида
{х: Р (х, а) = 1}.
2. Ограничиваясь, далее, случаем дихотомии, оценим
длину обучающей последовательности, достаточную для
того, чтобы решающее правило, выбранное произвольным
§ 1. ОЦЕНКА ДЛИНЫ ОБУЧАЮЩЕЙ ПОСЛЕДОВАТЕЛЬНОСТИ 279
алгоритмом обучения рассматриваемого типа, отличалось
от оптимального не более чем на е, с вероятностью боль-
большей, чем 1 — ц. Для этого, в соответствии с A3.1), дос-
достаточно положить
)
ц > 6т8 B/) е «
и разрешить это неравенство относительно /.
Допустим, что т8 (I) ф. 2е, и пусть п — такое число,
что т8 (п) = 2", а т8 (п + 1) < 2П+1; тогда, в соответ-
соответствии с замечанием 1 к теореме 10.1,
или, заменяя гс! по формуле Стирлинга,
Здесь п — это максимальная длина последователь-
последовательности, которую можно разбить всеми возможными спо-
способами с помощью решающих правил из (?.
Разрешим относительно / неравенство
еп-е 1в .
Логарифмируем:
1п-д-^>п1п( — 1 + п— ' —'-. A3.5)
Обозначим
еЧ _
"ШГ "Х-
Тогда
„5 1П "о" „»
и соответственно
280 ГЛ. XIII. ПРИМЕНЕНИЕ ТЕОРИИ РАВНОМЕРНОЙ СХОДИМОСТИ
Разрешим это неравенство относительно х. Учитывая, что
1п х < 0,5 х,
получаем
( л А II \
откуда
( 1 -3_ ^1
32га . ш 6 16 , е2
Эта оценка, однако, завышена.
Более точную оценку получим из следующих сооб-
соображений.
Пусть обучение проведено на последовательности длины
I, а затем устроен экзамен на последовательности такой
же длины. Оценим вероятность того, что частота ошибок
на обучении и на экзамене будет отличаться более чем на
е для решающего правила, выбранного произвольным
алгоритмом, из класса (? по обучающей последовательности.
Эта вероятность во всяком случае меньше, чем
Р {вир | V {А; %,..., ж,) — V (А; х1+1 , . . ., жн) | > е}.
А&8
где А — событие вида {« Ф- Р (х, а)}.
Но для этой величины оценка получена при выводе
теоремы 10.2:
Р {вир |>' (А) ~ V" (А) | > е} < Зтз B1)е~^1~11
А
Отсюда, аналогично выводу A3.6), получаем, что для
того, чтобы с вероятностью, большей 1 — т}, частота оши-
ошибок на материале обучения и на экзамене отличалась
меньше чем на е, достаточно, чтобы
_1П^1, A3.7)
где п — максимальная] длина последовательности
§ 1. ОЦЕНКА ДЛИНЫ ОБУЧАЮЩЕЙ ПОСЛЕДОВАТЕЛЬНОСТИ 281
хх , . . ., хп такой, что ее можно разбить всеми возмож-
возможными способами с помощью правил из (?.
Обе оценки зависят только от свойств класса решаю-
решающих функций и никак не связаны с распределением ве-
вероятностей на множестве пар х, со. Требуется лишь,
чтобы ситуации возникали независимо и с неизменным
распределением. Получим еще оценку для задачитобу-
чения распознаванию в детерминированной постановке.
В этом случае среди решающих правил заведомо есть
правило, обеспечивающее безошибочное распознавание.
Алгоритм, минимизирующий эмпирический риск, выбе-
выберет решающее правило, которое всю обучающую после-
последовательность классифицирует безошибочно. Оценим ве-
вероятность Р (е, I) того, что решающее правило, выбран-
выбранное таким алгоритмом по обучающей последовательности
длины I, сделает более г1 ошибок на экзамене длины I.
Очевидно, что вероятность Р (е, Т) не превосходит
Р {вир (V [А; хг, . . ., х{) = 0) и (V (А; х1+1, . . ., х21) > г)},
т. е. вероятность того, что найдется событие А вида
{х, со: Р (х, а) ф со}
такое, что частота его выпадения на первой, полувыборке
равна 0, а частота выпадения на второй полувыборке пре-
превышает е. Для "одного события А вероятность того, что
\'(А) = 0, а у"(Л)>8, равна
Р (я 1\ — СЫ-т — B? —/»)...(? —/те+ 1)
гА[*,Ч- ^ - 21.B1-1)...A + 1) '
если число т элементов А в выборке хъ ..., хп превос-
превосходит г1, и нулю в противном случае.
Поэтому во всех случаях
В общем случае, как и при доказательстве условий
равномерной сходимости, достаточно учесть* конечное
число событий А, различимых на выборке хх , . . . ,а:2;.
282 ГЛ. XIII. ПРИМЕНЕНИЕ ТЕОРИИ РАВНОМЕРНОЙ СХОДИМОСТИ
Поэтому
Р (8,1) < т3 B1) A - -|- < /п8 B/) е « .
Опять-таки аналогично выводу A3.6), получаем, что
длина обучающей последовательности, достаточная для
того, чтобы с вероятностью 1 — т] частота ошибок на
экзамене такой же длины не превышала е, равна
, Ач I. те , т)
'дост — ~ 1-1 Ш —^ АП —
где п определяется, как и раньше, как максимальная
длина последовательности, которую еще можно разбить
всеми возможными способами с помощью правил из <?.
Эта величина является характеристической. Все оценки
при фиксированных е и т] являются линейными функция-
функциями п. В ряде случаев оказывается, что с вероятностью 1
А3 (хх , . . . ,х{) = т3 (Г). В этом случае, рассуждая
аналогично доказательству необходимости в теореме
11.1, можно показать, что с вероятностью, близкой к
единице, максимальное по классу 5 уклонение частот в
двух следующих друг за другом полувыборках длины I
не меньше п/21 при 21 > п и равно 1 при 21 < п. Поэтому
без дополнительных предположений нельзя получить
оценку лучшую, чем
3. Выясним, наконец, чему равна функция т3 (Г)
для наиболее часто используемых классов решающих
функций.
Линейные решающие правила в случае двух классов
(случай большего числа классов сводится к последова-
последовательной дихотомии) имеют вид:
х относится к I классу, если (х, <р) ^ с,
х относится ко II классу, если (х, ц>) <; с.
Здесь /г-мерный вектор <р и константа с являются па-
параметрами класса решающих функций.
Нас интересует функция т8 (I) для системы событий
вида
{{х, <р) > с}.
§ 1. ОЦЕНКА ДЛИНЫ ОБУЧАЮЩЕЙ ПОСЛЕДОВАТЕЛЬНОСТИ 283
Для случая с = О функция т8 (Г) была найдена в
примере 3 § 3 главы X. Она равна
1=0
где п — размерность пространства.
Случай произвольного с сводится к предыдущему пу-
путем введения дополнительной координаты, причем раз-
размерность увеличивается на единицу. Таким образом, для
линейных решающих правил
где п — размерность пространства.
Отсюда следует, что в оценках длины обучающей
последовательности, полученных в предыдущем пункте
для линейных решающих правил, п — это размерность
пространства.
К этому же случаю сводятся алгоритмы решающих
правил, основанных на переходе к спрямляющему про-
пространству и построении в этом новом пространстве линей-
линейного решающего правила. Соответствующие правила
имеют вид:
п
X ОТНОСИТСЯ К I КЛаССу, еСЛИ 2 ^гФг (Х) > С>
г=1
п
х относится ко II классу, если 2 ^гФН^)*^^
г=1
Здесь набор функций <рг (х) фиксирован для данного клас-
класса решаюших правил, а параметры кг и с задают конкрет-
конкретное решающее правило в классе. В этом случае оценки
те же, что для линейных правил, но п — это размерность
спрямляющего пространства (число функций <р* (х)).
Рассмотрим более сложный вид решающего правила:
1Е1, если К (9,,^! (х, е^.фг (х,в2), . . . , фА (*,вй)) > 0,
если К (во,(^1(х, вг), цJ(х, 92), ..., фА (х, еА))<0.
284 ГЛ. XIII. ПРИМЕНЕНИЕ ТЕОРИИ РАВНОМЕРНОЙ СХОДИМОСТИ
сдесь функции К и <рг фиксированы для класса решаю-
решающих правил, а параметры 0О, 0!, ... ,0А (скалярные или
векторные) задают конкретное решающее правило. Кро-
Кроме того, предположим, что функции <рг принимают лишь
два значения: —1 и +1.
Тогда, если известны функции
т8а (Г) для класса событий {у: К F0, уъ . . ., ук) > 0}, . . .,
т?1 (Г) для класса событий {х: <рг (ж0,-) = 1}.
то интересующая нас функция т8 (I) оценивается
В частности, пусть х — тп-мерный вектор, а функции
,- и К — линейные пороговые функции, т. е.
у. = фДя)
3=1
где 0{ и 0ц — настраиваемые параметры,
[— 1 при 2^0
1 при 2
-Г
Тогда
т3 {I) < [Ф (/га, I)]11 Ф {к, I),
где
т
Ф (т, I) = 2 2 СЦ.
1=1
/С
Ф(А,г) = 22с{_1.
1=1
Порядок роста функции т8 (Г) равен тк -\- к и, сле-
следовательно, в оценках длины обучающей последователь-
последовательности, полученных в предыдущем пункте, в качестве п
для этого случая можно взять
п = тк -\- к.
§ 2. СХОДИМОСТЬ К МАТЕМАТИЧЕСКИМ ОЖИДАНИЯМ 285
Этот класс решающих функций используется при
настройке многослойных персептронов, в машинах типа
«Маделин» и вообще при построении кусочно-линейных
решающих правил.
Во всех рассмотренных случаях оказалось, что за
число п в оценках предыдущего пункта может быть при-
принято число настраиваемых параметров данного алгорит-
алгоритма обучения распознаванию образов. Видимо, и вообще,
за исключением патологических случаев, эти оценки
справедливы для алгоритмов обучения распознаванию
при п, равном числу настраиваемых параметров.
§ 2. Равномерная сходимость средних
к математическим ожиданиям
1. В общем случае вопрос о равномерной близости
функций К (а) и Я,та (а) сводится к равномерной по пара-
параметру а сходимости средних к математическим ожиданиям.
В самом деле, функция
Д(а) =
есть математическое ожидание функции потерь () (г, а),
тогда как
(«) = — 2 <?кB{, а)
1=1
есть среднее арифметическое зтой случайной величины,
вычисленное по выборке 2г , . . . ,гг.
Сформулируем в точных терминах проблему равно-
равномерной сходимости средних к математическим ожиданиям.
Пусть х — элементарное событие из пространства X,
Р (х) — вероятностная мера в нем, а — некоторый абст-
абстрактный параметр, Е (х, а) — некоторая функция, измери-
измеримая при всех а относительно меры Р (х) в пространстве X.
Предположим, что существует математическое ожи-
ожидание этой функции при всех а
М (а) = [Р (х, а) ЛР (х).
Пусть, далее, задана повторная выборка Х1= хх , ...
. . . ,х1 из пространства X, т. е. выборка, полученная в
286 ГЛ. XIII. ПРИМЕНЕНИЕ ТЕОРИИ РАВНОМЕРНОЙ СХОДИМОСТИ
последовательности независимых испытаний при неиз-
неизменном распределении. Тогда для каждого а по этой
выборке можно вычислить среднее значение
Мэмп(а)==-1-2
1=1
Если бы а была постоянной величиной, то сходимость
среднего к математическому ожиданию обеспечивалась
бы законом больших чисел. Но если параметр а может
изменяться в пределах некоторого множества О, то воз-
возникает вопрос о равномерности по параметру а оценки
математического ожидания средним значением. Точнее,
обозначим через Р (X1) вероятностную меру в простран-
пространстве выборок длины I. Тогда равномерность близости
средних к математическим ожиданиям может быть оце-
оценена величиной I
Рг(п,1) = Р {вир | М (а) - Мэмп (X1, а) | > е},
т. е. вероятностью того, что максимальное по а уклоне-
уклонение средневыборочного значения от математического
ожидания превзойдет е.
Говорят, что имеет место равномерная по параметру
сходимость средних к математическим ожиданиям, если
случайная величина вир | М (а) — Мэмп (X1, а) I стремится к
нулю соответственно по вероятности или почти навер-
наверное при I -> оо.
Приводимые ниже достаточные критерии такой схо-
сходимости (за исключением последнего) сводят при опре-
определенных условиях вопрос о равномерной сходимости
средних к математическим ожиданиям к исследованной
в предыдущих главах проблеме равномерной сходимости
частот к вероятностям в некотором классе событий.
Теорема 13.1. Пусть Р (х, а) (а ё й) - семейство
измеримых на X. функций, причем выполнено условие
О <; Р (х, а) <^ а (число а не зависит от х и а). Рассмот-
Рассмотрим систему 8 событий вида
А = {х:Р (х, а) > с)
для всевозможных а и с.
§ 2. СХОДИМОСТЬ К МАТЕМАТИЧЕСКИМ ОЖИДАНИЯМ 287
Тогда равномерная сходимость частот к вероятнос-
вероятностям по классу событий 8 является достаточным усло-
ем для равномерной сходимости средних к математичес-
математическим ожиданиям. При этом выполняется соотношение
вир | М (а) - Мэмп (а) |< а вир | Р (А) - V (А) |.
Доказательство. Действительно, согласно
определению интеграла Лебега
Аналогично
п
Обозначим событие
через 4(лё5. Тогда
п
|М(а)-М^п(а)|<11т 2^"!^ (Ат) - VD) И
чем и доказывается наше утверждение.
Кроме того, получаем
Р{вир |М (а) - М^мп (а) |> ае}<Р{вир \ Р(А) ~ ч(А)\>г}.
Тем самым из оценок для равномерной сходимости
частот к вероятностям по классу событий можно всегда
получить оценки для равномерной сходимости средних
к математическим ожиданиям для равномерно ограничен-
ограниченных функций Р (х, а).
Следствие. В силу полученных в главах X и XI условий
равномерной сходимости частот к вероятностям в слу-
случае, когда
О < Р (х, а) <; а,
288 ГЛ. XIII. ПРИМЕНЕНИЕ ТЕОРИИ РАВНОМЕРНОЙ СХОДИМОСТИ
для равномерной сходимости средних к математическим
ожиданиям (почти наверное) достаточно, чтобы т8 (I) ^
■ф 21 или (более слабое условие)
Н8A) А
где 8 — определенная выше совокупность событий.
При этом справедлива оценка:
Р {вир | М (а) — /<мп (а) | > ае} < 6т8 B1) е~ 4 . A3.8)
Отметим, что необходимые и достаточные условия
равномерной сходимости частот к вероятностям перехо-
переходят здесь лишь в достаточные условия равномерной схо-
сходимости средних к математическим ожиданиям.
Замечание. Равномерная ограниченность функции
Р (х, а) в этом рассуждении существенна, так как в про-
противном случае можно построить примеры, где равномер-
равномерная по классу 8 сходимость частот к вероятностям имеет
место, тогда как равномерной сходимости средних к ма-
математическим ожиданиям нет.
Однако это требование может быть ослаблено. В ряде
случаев существенно не абсолютное, а относительное ук-
уклонение средних от математических ожиданий. В этом
случае из допущения, что
вир Р (х, а)
где к не зависит от а и х, аналогично доказанной теореме
выводится неравенство
где система 5 определена как и раньше. Отсюда следуют
аналогичные оценки и условия сходимости. I .
Применим полученный результат для оценки алгорит-
алгоритмов, основанных на минимизации эмпирического риска.
Допустим, что функция потерь () (х, а) неотрицательна и
равномерно ограничена. Тогда из A3.8) следует, что
Р{Н (а*) - В (а„) >е} < 6т8 B^ 1ва!
§ 2. СХОДИМОСТЬ 1; МАТЕМАТИЧЕСКИМ ОЖИДАНИЯМ 289
где 5 — система событий вида
А = {г: (} (г, а) > с}
при всевозможных а и 0 < с < оо.
Свойством равномерной ограниченности обладают
функции потерь в задачах распознавания образов при
произвольной функции штрафа за ошибку.
2. Пусть существует функция К (х), не зависящая от
а такая, что
О < К (х, а)<К (х), \ К (х) ЛР (*)< эо.
Тогда для равномерной сходимости средних к математи-
математическим ожиданиям (почти наверное) достаточна равно-
равномерная сходимость частот к вероятностям по классу 8
событий вида
А = {х: Р (х, а) > с}.
Пусть е^>0. Выберем с таким, чтобы выполнялось
и положим
лл. \ 1С) ИХ)И /\_ 1 ОС) ^* С
Р' (г „ч _ /° ПРИ ^ (ж) > С'
г ух, а) — ^ ^ ач при д- ^ч ^ с
Тогда
I мэмп (о-) — М (о) | < | Мэид (а) - М' (а) | + Кша + -|-,
где М' (а) и Мэмп (а) — соответственно математическое
ожидание и среднее функции Р' (х, а), а
А эмп — ~7~ 2^ "■
_1_ Я1
I
290 ГЛ. XIII. ПРИМЕНЕНИЕ ТЕОРИИ РАВНОМЕРНОЙ СХОДИМОСТИ
Поскольку Р (х, а) равномерно ограничена, в силу
предыдущего результата с вероятностью 1 найдется 1г
такое, что при I > 1г
Кроме того, из усиленного закона больших чисел следует,
что с вероятностью 1 найдется 1г такое, что при 1> 1г
Но тогда при I > 10 = шах AХ, 1%)
вир | М (а) — МэмП (а) | < е,
а
что и требуется.
3. Ле-Кам [84, 85], основываясь на идеях Вальда,
получил следующий результат.
Пусть Р (х, а) — измеримая по х функция, непрерыв-
непрерывная по а почти для всех х, а изменяется в пределах мет-
метрического компакта С и существует К (х) такая, что
Е (х, а)<К (х), ^ К (х) ЛР (х) < оо.
Тогда, если математическое ожидание Р (х, а) существует
для всех а, то
Нт вир | Р (х, а) — Рвш (х, а) \ — 0,
т. е. имеет место равномерная по параметру сходимость
средних к математическим ожиданиям.
Этот результат не перекрывает изложенные выше хотя
бы потому, что здесь требуется непрерывность, тогда как
предыдущие критерии включали также и разрывные
функции, обычно используемые в распознавании. Кроме
того, в рамках идей Вальда — Ле-Кама, видимо, трудно
получить какие-либо оценки.
Часть третья
МЕТОДЫ ПОСТРОЕНИЯ РАЗДЕЛЯЮЩИХ
ПОВЕРХНОСТЕЙ
В этой части книги исследуются методы построения
гиперповерхностей, разделяющих два конечных множества
векторов. Ключом к решению такой задачи служат эф-
эффективные методы построения разделяющей гиперплос-
гиперплоскости.
Оказывается, что построение оптимальной в опреде-
определенном смысле разделяющей гиперплоскости эквивалент-
эквивалентно максимизации некоторой квадратичной формы в по-
положительном квадранте. С этой точки зрения алгоритмы
персептронного типа реализуют модифицированный метод
подъема Гаусса — Зайделя.
Однако известно, что более эффективными методами
поиска экстремума являются методы сопряженных на-
направлений, позволяющие отыскивать максимум за п шагов
(п — размерность квадратичной формы).
Рассмотрению методов сопряженных направлений,
созданию на их базе конструктивных алгоритмов пост-
построения разделяющей гиперплоскости и кусочно-линей-
кусочно-линейных разделяющих поверхностей посвящена третья часть
книги.
Глава XIV
ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ
ГИПЕРПЛОСКОСТИ (МЕТОД
ОБОБЩЕННОГО ЛОРТРЕТЛ)
§ 1. Оптимальная разделяющая гиперплоскость
Выше было показано, что конкретные алгоритмы обу-
обучения машин распознаванию образов могут быть по-
построены по следующей схеме: из класса решающих пра-
правил подходящей емкости выбирается правило, мини-
минимизирующее количество неправильных классификаций
элементов обучающей последовательности.
При этом чрезвычайно важным оказывается способ
задания класса решающих правил. Во многих случаях
этот класс задается параметрически, т. е. считается,
что функции известны с точностью до значения конеч-
конечного числа параметров. Более того, класс функций за-
задается линейно по параметру, т. е. в тшдо
Выбрать функцию из этого класса—значит найти
соответствующие а или, что тоже самое, построить
соответствующую разделяющую гиперповерхность
2 а^х) =0.
г=1
На практике такая задача решается путем построения
гиперплоскости, разделяющей в соответствующем сирям-
§ 1. ОПТИМАЛЬНАЯ РАЗДЕЛЯЮЩАЯ ГИПЕРПЛОСКОСТЬ 293
ляющем пространстве V (уг — ц:1 \х) уп = ф„ (х))
два конечных множества векторов: множества векторов
обучающей последовательности, относящихся к первому
и ко второму классам.
В этой главе будут рассмотрены методы построения
разделяющих гиперплоскостей. Однако следует иметь
в виду, что рассмотренные здесь методы немедленно могут
быть использованы для выбора решающего правила пл
заданного множества линейных по параметру решающих
правил.
Два конечных множества .векторов: множество
X = {хг , . . . , ха) и множество X = (лх , . . . , У-,,} раз-
разделимы гиперплоскостью, если существуют такой единич-
единичный вектор ф и такое число с, что для любого векторе!
хг ЕЕ X справедливо неравенство
Ф)>с, A4.1)
а для любого вектора г; €Е X — неравенство
(х„ ф)<с. A4.2)
В случае, когда выполняются A4.1) и A4.2), говорят
также, что множество X отделимо от множества X гипер-
гиперплоскостью
(х, ф) = с.
Определим для любого единичного вектора ф две вели-
величины сг (ф) и с2 (ф):
С, (ф) ■=-- ШШ (Х;, ф),
с2 (ф) = гпах (ж3-, ф).
Согласно определению величин сг (ф) и с2 (ф) всегда спра-
справедливы неравенства
0*1, ф) > ^ (ф) A = 1,2,..., а),
(X;, ф) < С2 (ф) (/ = 1, 2, . . ., Ь).
Ясно, что если
сх (ф) > с, (Ф), A4.2')
294 ГЛ. XIV- ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
С1 (ф) 4- а (ф)
то пара ф, — ,—^- определяет гиперплоскость
(х, ф) = -^—^-^— ,
отделяющую множество X от множества X.
Заметим, что функции сг (ф) и с2 (ф) непрерывны. По-
Поэтому из существования одной гиперплоскости,разделяю-
гиперплоскости,разделяющей два конечных множества векторов X и X, следует
существование целого множества гиперплоскостей, раз-
разделяющих X и Ж.
Будем выделять ив множества разделяющих гипер-
гиперплоскостей оптимальную.
Определение. Назовем оптимальной разделяющей гипер-
гиперплоскостью такую разделяющую гиперплоскость, кото-
которая определяется следующей парой: единичным вектором
доставляющим максимум функции
п (ф) = С1 (ф) — С2
и числом
С* (Фопт) + С2 (фопт)
2
Справедлива теорема
Теорема 14.1. Если два множества векторов разделимы
гиперплоскостью, то существует единственная опти-
оптимальная разделяющая гиперплоскость.
Доказательство. Очевидно, достаточно пока-
показать, что функция П (ф) на множестве | ф | <^ 1 имеет
единственный максимум, который достигается на границе,
т. е. при | <р | *= 1.
Существование максимума следует из того, что функ-
функция П (ф) непрерывна, а множество | <р | ^ 1 ограниче-
ограничено и замкнуто.
Допустим, что максимум достигается не на границе,
а в некоторой точке ф*, для которой |ф*|-<1. Тогда
Ф*
значение функции в точке ф** = —;— равно
1<Р I
откуда следует противоречие:
П (Ф**) > П (Ф*).
§ 2. ОДНОПАРАМЕТРИЧЕСКОЕ СЕМЕЙСТВО
295
Остается показать единственность. Пусть максимум П (ф)
достигается в двух граничных точках: ф! и фа. Тогда в
силу выпуклости функции — П (ф) максимум должен дос-
достигаться и на всем отрезке, соединяющем ф! и ф2, т. е. на
внутренних точках множества |<р| <; 1, что по
доказанному невозможно.
Теорема доказана.
Геометрически величи-
величина П (ф)- равна расстоянию
между проекциями , мно-
множеств X и X на направле-
направление ф (рис. 23). Вектор фопт
задает такое направление,
для которого эта величина
максимальна. Сама же оп-
оптимальная разделяющая
гиперплоскость
С1 (Фопт) ■
(А, фопт)=
2
Рис. 23.
обладает тем свойством, что в классе разделяющих гипер-
гиперплоскостей она максимально удалена от ближайшего из
множеств X, X.
В § 9 будут указаны алгоритмы построения оптималь-
оптимальной разделяющей гиперплоскости. А пока рассмотрим
однопараметрическое семейство разделяющих гипер-
гиперплоскостей, содержащее оптимальную разделяющую ги-
гиперплоскость.
§ 2. Однопараметрическое семейство разделяющих
гиперплоскостей
Введем еще одно определение.
Определение. Будем говорить, что пара ф, С1 "X*Са
определяет нормально ориентированную разделяющую
гиперплоскость, если наряду с неравенством A4.2') выпол-
выполняется условие
сг (ф) > 0.
Нетрудно видеть, что если два конечных множества
векторов X и X разделимы гиперплоскостью, то сущест-
290 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
вует нормально ориентированная гиперплоскость, кото-
которая отделяет либо множество X от множества А', либо
множество X от X.
Рассмотрим систему неравенств
(хи г|:) > 1 A = 1,..., а),
{X}, я|з)<Л {1 = 1, ...,Ь).
Будем считать величину к допустимой, если система A4.3)
имеет хотя бы одно решение. Очевидно, что если кй — до-
допустимое значение параметра, то и любое значение к ^> к0
также допустимо.
Каждому значению о|з, удовлетворяющему A4.3), по-
поставим к соответствие гиперплоскость
(*,щ = !+*..
Очевидно, что при к < 1 эта гиперплоскость нормально
ориентирована и отделяет X от X. Обратно, если множе-
множества X ш X разделимы нормально ориентированной гипер-
гиперплоскостью, то существует допустимое значение к < 1.
Действительно, пусть ср — направляющий вектор этой
гиперплоскости; при этом с1 (<р) > 0 и сд (<р) > с2 (ф).
Тогда
■ф = ф и к = сг ^
4 с] (ф) а. (ф)
удовлетворяют A4.3), причем к < 1.
Определение. Назовем минимальный по модулю вектор
о|з, удовлетворяющий неравенствам A4.3) при заданном
допустимом к, обобщенном портретом множества X от-
относительно X для данного значения к.
Поясним это понятие. _
Рассмотрим случай, когда класс X пуст. Тогда ми-
минимальный по модулю вектор, удовлетворяющий нера-
неравенствам
(Л,Ю>1, A4.4)
коллинеареп единичному вектору <р, доставляющему
шах тщ (ф, Ж;) = тах с^ (ф) *)
М ||
*) Дейстг.пгелыю, поставим в соответствие всякому едшшчпо-
му вектору ср, для которого сх(ф) ^> 0, вектор ^|; == , . . Очевидно,
§ 2. ОДНОПАРЛМЕТРИЧЕСКОЕ СЕМЕЙСТВО 2!>7
Иными словами, вектор 1р задает среднее в минимакс-
минимаксном смысле направление Викторов класса .V (рис. 2'*).
Это обстоятельство оправдывает ла.чпаипе «обобщенный
портрет».
Приведенное определение обобщенного портрета явля-
является естественным обобщением этого понятия на случай,
когда в обучающей выборке продотянле-
ны оба класса. :-'
Теорема 14.2. При каждом допусти- ■*■
мом значении к обобщенный портрет су- I
ществует и единствен.
Доказательство. Поскольку
значение к допустимо, найдется вектор
1|5*, удовлетворяющий A4.3). Рассмотрим
множество векторов о|з, удовлетворяющих
наряду с A4.3) условию | о|з | <; |1|>,*|.
Это множество не пусто, ограничено, зам-
замкнуто и выпукло. Поэтому сильно выпук- и
лая функция (о|з, \|з) имеет на нем единст- Рис- 24-
венный минимум ^0. Очевидно также, что
вне шара 1^1^ Iе1!5*! все векторы имеют модуль боль-
больше о|з0. Отсюда следует доказываемое утверждение.
Таким образом, обобщенные портреты, имеющие раз-
различные к, образуют однопараметрическое семейство, ко-
которое мы условимся обозначать о|з (к).
При к < 1 ему соответствует семейство разделяющих
гиперплоскостей
±±±. A4.5)
что получившийся вектор 5'ДовлетвоРяет неравенствам A4.4).
Обратно, всякому вектору я|з, удовлетворяющему A4.4) и такому,
что по крайней мере одно из неравенств переходит в равенство, по-
ставим в соответствие единичный вектор <р = т-т-г. При этом с\ (ср) —
= ГХТ- Нетрудно убедиться, что эти соответствия взапмно обратим.
Далее, поскольку минимум (-ф, -ф) при ограничениях A4.'1)
достигается на границе ограничений, то для обоощенного портрета
по крайней мере одно из неравенств действительно переходит в ра-
1
венство. Поэтому максимуму сг (ф) соответствует максимум т^г-;.
т. е, минимум (-ф, я)з).
298 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
Теорема 14.3. Если оптимальная разделяющая гипер-
гиперплоскость нормально ориентирована, то она принадлежит
однопараметрическому семейству A4.5).
Доказательство. Пусть <ропт — направляю-
направляющий вектор оптимальной разделяющей гиперплоскости и
при этом сх (фопт) > 0. Положим
Ао = Ц<1| яК- ?\ A4-6)
с' (Фопт) ^ «(Фопт) '
и покажем, что вектор $* совпадает с обобщенным порт-
портретом *ф (к0).
Прежде всего, убедимся, что пара Ц>*, к0 удовлетворя-
удовлетворяет A4.3). Действительно,
1Г
Далее, если ф* ф^р (к0), то в силу единственности обоб-
обобщенного портрета
1Ф* 1>Ж*о)|. A4.7)
Рассмотрим вектор ф0 = . ^ ^.. . Из A4.3) следует, что
и, значит,
П ^гп ^ -^ 1~к° - С1 (фопт) — °2 (Фопт) П (Фопт)
Далее, в силу A4.7)
П(Фо)>-
(Фопт)
Окончательно, поскольку |т|)* | = — -, получаемП(фо)>
> П (фопт), что противоречит определению оптимальной
разделяющей гиперплоскости. Итак, \|з,* = \|з (А;о). Теперь
§ 3. НЕКОТОРЫЕ СВОЙСТВА ОБОБЩЕННОГО ПОРТРЕТА 299
из определения /с и \]5* A4.6) немедленно следует, что
гиперплоскости
= !
и
(Фопт) +
(фонт, X) =
совпадают. Теорема доказана.
Замечание. Из доказательства теоремы следует, что
П (фопт) =
§ 3. Некоторые свойства обобщенного портрета
Нахождение обобщенного портрета, очевидно, сво-
сводится к задаче квадратичного программирования: найти
минимум функции (\|з, г|з) при линейных ограничениях
A4.3).
В настоящее время известны алгоритмы решения об-
общей задачи квадратичного программирования. Однако,
опираясь на некоторые особенности обобщенного порт-
портрета, удается привести задачу о его нахождении к прос-
простому частному варианту задачи квадратичного програм-
программирования и найти для этого частного варианта эффек-
эффективные методы решения.
Для дальнейшего нам понадобится следующая теорема.
Теорема 14.4 (Куна — Таккера). Пусть заданы диф-
дифференцируемая выпуклая функция Р (х) и линейные функ-
функции /{ (х); 1 = 1,...,/. Пусть х0 доставляет минимум
Р (х) при ограничениях
П(х)>0 A = 1,2,. . .,1). A4.8)
Тогда существуют такие числа X; ^> 0, удовлетворяю-
удовлетворяющие условиям
41 (х) =0 (* = 1, 2, . . ., I), A4.9)
что справедливо равенство
I
У;<>-„)-2ШгЫ A4.10)
1=1
(V — знак оператора градиента).
300 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
И обратно, если для некоторой точки х0 выполняются
условия A4.8) и можно найти числа Х;2>0, удовлетворяю-
удовлетворяющие условиям A4.9) и A4.10), то в точке х0 достигается
условный минимум Р (х) при ограничениях A4.8).
Доказательство этой теоремы приведено в приложении.
Введем еще одно определение.
Определение. Будем говорить, что вектор хг (ж;-) явля-
является крайним вектором множества X (X) для вектора а|з,
удовлетворяющего A4.3) при константе к, если вы-
выполняется равенство
(B;, Ю = к).
Справедлива следующая важная для дальнейшего
теорема.
Теорема 14.5. Обобщенный портрет может быть
представлен в виде линейной комбинации крайних векто-
векторов. Причем крайние векторы множества X входят в это
разложение вектора с неотрицательными коэффициента-
коэффициентами, а крайние векторы множества X — с неположитель-
неположительными коэффициентами.
Иначе говоря, минимальный по модулю вектор 1|), удов-
удовлетворяющий A4.3) может быть представлен как
г=1 ;=1
а{ > 0 (г = 1,2,..., а),
рг>0 (/- 1,2, ...,Ь), A4Л1)
причем
а< ((*«. 11') — !) =^ ° (' ^ 1. 2, . . ., а), A4.12)
РИА - (*;, Ч>)) = 0 (/- 1,2, . . ., Ь).
Доказательство. Для доказательства тео-
теоремы 14.5 воспользуемся теоремой 14.4, где положим
Р<$) = (!>, Ю,
/.(*) = ((^, Ю-1)>0 (I = 1,2 а),
/; №) - (Ао - («;- *)) > 0 (/ = 1,2 , Ъ).
§ 3. НЕКОТОРЫЕ СВОЙСТВА ОБОБЩЕННОГО ПОРТРЕТА 301
Согласно утверждению теоремы 14.4 существуют такие
неотрицательные %г A <^ г <^ а) и %] A <; / <; Ь), что
%1 ((х1, г|з) — 1) = 0 (г = 1, 2, . . ., а),
^ (^ — (^л 'Ф)) = 0 (/ = 1, 2, . . ., Ь)
и
а Ь
Вычисляя градиент, имеем
а Ь
■^т '— 2л ЛЛ — ^1 Л;''з-
Полагая
получаем
а Ь
Г *^~ / I ^>1р^х ~~ / I [^^1 *
„ --. А
<Х; -г> V,
Р/ > 0;
Ру [А; — (ж^)! = 0.
Теорема доказана.
Справедлива обратная теорема.
Теорема 14.6. Всякий вектор^, удовлетворяющий A4.3)
м допускающий разложение вида A4.11) по своим крайним
векторам, совпадает с обобщенным портретом.
Доказательство немедленно следует из об-
обратного утверждения теоремы 14.4 (Куна — Таккера) и
единственности обобщенного портрета, если функции
Р (х) и /г (х) интерпретировать так же, как при доказатель-
доказательстве предыдущей теоремы.
Замечание. В теореме 14.2 была доказана един-
единственность обобщенного портрета. Однако обобщенный
портрет, вообще говоря, не единственным образом разла-
разлагается по своим крайним вектора.^ в виде A4.11).
302 ГЛ. XIV- ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
§ 4. Двойственная задача
В этом параграфе будет рассмотрена частная задача
квадратичного программирования, решение которой эк-
эквивалентно построению обобщенного портрета.
Введем пространство параметров а, Р и рассмотрим в
нем функцию
а Ъ
уу («. Р) = 2 °ч —к 2 в —2~^' ^'
г=1 }=1
где вектор \|з есть
а Ь
I ^ ^ й —
1=1 )=1
Будем искать максимум этой функции в положитель-
положительном квадранте аг ^> 0, Р^ > 0.
Для построения разделяющих гиперплоскостей су-
щественпым оказывается то, что точка максимума а0, ро
функции И7 (а, Р) в положительном квадранте определяет
обобщенный портрет для заданного параметра к, а значе-
значение максимума И7 (а0, р0) определяет расстояние между
проекциями векторов первого и второго классов на нап-
направление обобщенного портрета.
Итак, рассмотрим точку максимума а, Р функции
И7 (а, Р) в положительном квадранте.
Необходимыми и достаточными условиями максимума
функции И7 (а, Р) в точке а? > 0, Р? > 0 являются ус-
условия:
[ 0, если а? ^> 0,
|< 0, если а" = 0,
0, если Р?>0,
<^ 0, если Р° = 0.
Выпишем эти условия, обозначив
§ 4. ДВОЙСТВЕННАЯ ЗАДАЧА 303
получим
О, если аг = О,
О, если р°>0,
' ' |<0, если р,°=0.
Условия A4.13) могут быть переписаны в виде нера-
неравенств A4.3)
(XI, *°)>1,
{х}, цо) < А;
и равенств A4.12)
- 1) = О,
Согласно утверждению теоремы 14.6, эти условия одно-
однозначно определяют обобщенный портрет о|э°.
Таким образом, связь между обобщенным портретом
и максимумом функции \У (а, |3) в положительном квад-
квадранте устанавливает следующая теорема.
Теорема 14.7. Для того чтобы функция Ш (а, Р) била
ограничена сверху в положительном квадранте, необхо-
необходимо и достаточно, чтобы к имело допустимое значение.
При допустимом к точка а0, |30, в которой достигается
условный максимум \У{а, Р) в положительном квадранте,
задает обобщенный портрет соотношением
а Ь
$ (Щ =2 «1*1-2 Р°ЖГ
1=1 3=1
Существует также связь между значением этого мак-
максимума И7 (а, Р) и модулем обобщенного портрета.
Теорема 14.8. При допустимом к максимум функции
\У (а, Р) в положительном квадранте равен половине квад-
квадрата модуля обобщенного портрета г|з (к).
Доказательство. Действительно, по теоре-
теореме 14.7
1=1 1=1
304 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
поэтому
а Ь
г-1 3=1
и, вспоминая, что отличны от нуля лишь коэффициенты
при крайних векторах х и ж, имеем
1=1 3=1
Таким образом,
г—1 3=1
(
2(
4=1 }=1
Теорема доказана.
Из теоремы 14.8 вытекает важное для конструирования
алгоритмов построения разделяющих гиперплоскостей
следствие.
Следствие. В случае, когда среди крайних векторов обоб-
обобщенного портрета г|з. (к) встречаются векторы обоих клас-
классов, справедливо соотношение
A4Л4)
причем равенство достигается при а = а0, Р = Ро-
Здесь П|-пгщу есть расстояние между проекциями
классов X и а на направление обобщенного портрета.
Действительно, в силу теоремы 14.8
Далее, по условию
ш
ф \ _
§ 4. двойственная задача 305
Поэтому
Отсюда, зачитывая, что
1—к
„, Ро),
получаем A4.14).
Это следствие используется для конструирования кри-
критерия неделения. В самом деле, будем считать, что два мно-
множества X и X не могут быть разделены с допустимым «за-
«зазором» с помощью обобщенного портрета \|з (к), (к < 1),
если соответствующая величина П т-у-г- меньше заданной
константы р ^> 0.
Тогда существование такой точки а!>0, р>0, что
\У (а, Р) > -<Ц=*>1 , A4.15)
и будет означать, что множества неразделимы с заданным
зазором с помощью обобщенного портрета т|з (А)»
Итак, согласно теоремам 14.7 и 14.8, максимум
\У (а, Р) в положительном квадранте определяет обобщен-
обобщенный портрет, а, согласно следствию, тот факт, что при
\У (а, Р) = В максимум еще не достигнут, означает,
что множества неразделимы с зазором, большим, чем
угв
Таким образом, проблема построения обобщенного
портрета свелась к поиску максимума функции IV (а, |3)
в положительном квадранте или оценке снизу величины
максимума этой функции.
Оказывается, что и другие методы построения
разделяющей гиперплоскости в определенном смысле
реализует различные алгоритмы поиска максимума
функции IV (а, Р) в положительном квадранте. Это об-
обстоятельство дает возможность сравнивать их между
собой: тот алгоритм построения разделяющей гипер-
гиперплоскости эффективнее, в основе которого лежит бо-
более эффективная процедура максимизации функции
306 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
§ 5. Алгоритмы нерсептронного типа
1. В главе I был сформулирован алгоритм построения
разделяющей гиперплоскости персептрона. В этом па-
параграфе рассмотрим различные модификации метода Га-
Гаусса—Зайделя для поиска максимума У/ (а, Р) в положи-
положительном квадранте и покажем, что алгоритм построения
разделяющей гиперплоскости персептрона отражает одну
иэ модификаций этого метода.
Итак, пусть задана функция Р (г1, . . ., 2П) от п аргу-
аргументов г1, . . ., 2П. Поиск максимума функции методом
Гаусса — Зайделя состоит в следующем: из начальной
точки 2о, . . ., 2о делается первый шаг вдоль первой ко-
координаты при фиксированных значениях остальных ко-
координат до достижения функцией Р (г) условного макси-
максимума по этому направлению, затем ищется условный мак-
максимум по второй координате при фиксированных значе-
значениях остальных координат и т. д. После того как сделаны
шаги вдоль всех координат, поиск максимума вновь на-
начинается по первой координате и т. д. Процесс поиска
максимума оканчивается, когда выполняется система
неравенств
<е A = 1,2 »).
Рассмотрим модифицированный метод Гаусса—Зайделя.
Модификация метода направлена на то, чтобы искать макси-
максимум функции Р (г1, . . ., 2П) в положительном квадранте.
Изменение метода Гаусса—Зайделя состоит в следующем:
1) в качестве начальной точки выбирается точка, рас-
расположенная в положительном квадранте (в дальнейшем
всегда в качестве такой точки будем выбирать начало ко-
координат);
2) движение вдоль каждой из координат происходит
либо до точки, где достигается максимум функции на этом
направлении, либо, если этот максимум достигается при
отрицательном значении координаты, до обращения в нуль
этой координаты;
3) процесс поиска максимума прекращается, когда вы-
выполнятся неравенства
О, если 21>0,
§ 5. АЛГОРИТМЫ ПЕРСЕПТРОННОГО ТИПА 307
ох
2. Применение модифицированного метода Гаусса—
Зайделя для максимизации функции \У (а, |3) в области
<%1 > 0, ^ > 0 приводит к следующему алгоритму по-
построения обобщенного портрета. Если на ^-м шаге произ-
производится движение вдоль координаты аг, то
аг (I) = аг (I — 1) + Даг.
Аналогично в случае движения вдоль координаты $^
Значения остальных координат сохраняются.
Приращения Ааг (Ар^), доставляющие максимум по
направлению шага, определяются из условий
= 0
= [1 - (яНг - 1), *;)] - Ы
- 1), ж,) - А] - | ^ |2 Ар,- = 0)
где положено
г=1
Учитывая, что шаг не должен выводить за пределы огра-
ограничений, получаем
—/с
, — Р»(<—1)) -
Процесс подъема продолжается до тех пор, пока не бу-
будет построен обобщенный портрет, либо не будет установ-
установлено, что множества не могут быть разделены с помощью
обобщенного портрета о|? (к) с допустимым зазором (§ 4).
308 ГЛ. XIV- ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
В первом случае останов производится по условию
| 1 — (х1г \|з) | < е, если аг ^> 0,
1 — (хь г|з) < е, если аг = 0
(\ (% У) — к\<. е, если Р^ > 0,\
^ (жг, •§) — к <; е, если Р; = 0 / *
Во втором случае критерием останова служит выпол-
выполнение неравенства A4.15)
где р — допустимый зазор.
Алгоритм можно реализовать и в такой форме:
•V]) (() = \|5 (( — 1) + хгАа{ при движении вдоль аг,
г|з (I) = \|з (I — 1) — Ж./ДC;- при движении вдоль ^.
3. С помощью метода Гаусса — Зайделя удается до-
достигнуть максимума IV (а, Р) и тем самым построить обоб-
обобщенный портрет. Однако часто требуется найти просто
разделяющую гиперплоскость (х, "ф) = с (не обязательно
экстремальную) такую, что
A4.16)
Построение такой гиперплоскости обеспечит следую-
следующая огрубленная модификация метода Гаусса — Зай-
Зайделя:
1) движение вдоль каждой из координат ссг ф;) проис-
происходит только в сторону от ограничений тогда, когда
В случае выполнения этих условий значение вектора
вычисляется по формулам
я|3 (;) = ^ (; — 1) 4-
(•ф (;) = \|з (I — 1) —
§ 5. АЛГОРИТМЫ ПБРСБПТРОННОГО ТИПА 309
где шаг по-прежнему выбирается из условия максимизации
функции \У (а, Р) по направлению
Д(Хг= П
2) процесс подъема по функции И7 (а, |3) прекращает-
прекращается, когда будут выполнены все неравенства A4.16). Легко
видеть, что при к = —1 полученный алгоритм совпадает
с алгоритмом построения разделяющей гиперплоскости,
предложенным Уидроу (см. главу IV).
Нетрудно убедиться, что после каждого изменения
вектора а|} функция У/ (а, Р) возрастает на величину
где
В = шах Aа;, |, | х,\).
Поэтому, учитывая, что, согласно A4.14),
где р — расстояние между проекциями классов на на-
направление обобщенного портрета^ (к), получаем, что мак-
максимальное число исправлений в алгоритме Уидроу ог-
ограничено величиной
тахИЧз, 3)
4Л-
ппп
(Здесь принято, что а @) = |3 @) — 0.) Оценка аналогич-
аналогична оценке числа исправлений для персептрона (глава I,
теорема Новикова).
4. Еще более грубая модификация метода Гаусса —
Зайделя приводит к алгоритму построения разделяющей
гиперплоскости, использованному в персептроне. Этот
алгоритм получается сразу из рассмотренного в преды-
предыдущем пункте, если положить к = —1 и^Даг!= ДC, = 1.
310 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
§ 6. Градиентные методы построения разделяющей
гиперплоскости (вычисление обобщенного портрета)
В предыдущем параграфе мы рассмотрели различные
модификации метода Гаусса — Зайделя. Известно, что,
вообще говоря, метод Гаусса — Зайделя является мало-
малоэффективным средством поиска максимума квадратичной
формы. Поэтому хотелось бы использовать для построения
разделяющей гиперплоскости более эффективные моди-
модификации методов поиска максимума квадратичной формы.
В настоящее время наиболее эффективным методом мак-
максимизации квадратичной формы считается метод сопря-
сопряженных направлений. Особенность метода состоит в том,
что с его помощью гарантируется достижение точного мак-
максимума за п шагов (п — размерность квадратичной фор-
формы). Подробно остановимся на методе сопряженных гра-
градиентов в главе XVI, а в этом параграфе рассмотрим мо-
модификации этого метода для поиска максимума квадра-
квадратичной формы в положительном квадранте.
Рассмотрим метод сопряженных градиентов для по-
поиска максимума квадратичной функции Р (х) = Ьх —
— (х, Ах); здесь А — положительно определенная мат-
матрица. Согласно этому методу поиск максимума функции
начинается в произвольной точке х @). Первый шаг де-
делается в направлении градиента функции в этой точке.
Обозначим градиент функции в точке х @) через д A),
направление движения из точки х @) через 2 A). Таким
образом,
2A) = ?A).
Шаг делается в направлении г A) до достижения мак-
максимума по этому направлению. Согласно формуле A6.26)
главы XVI точка х A), доставляющая этот максимум, за-
задается выражением
где А — матрица квадратичной формы функции Р (х). За-
Затем последовательно находятся точки х B), . . ., х (к).
В общем случае направление движения из точки х (к)
(к ^> 1) определяется A6.25) вектором
1)+ |*|(* + р)|* *(*), A4.17)
§ 6. ГРАДИЕНТНЫЕ МЕТОДЫ 311
где 8 (к -\- 1) и д (к) — соответственно градиенты функции
Р (х) в точках х (к) ж х (к — 1), а 2 (к) — направление дви-
движения из точки х (к — 1).
Движение по направлению г (к + 1) ведется до до-
достижения условного максимума. Точка х (к + 1), достав-
доставляющая этот максимум, находится A6.26) из выражения
Формулы A4.17) и A4.18) задают, таким образом, алго
ритм поиска максимума квадратичной функции Р (х).
Как уже указывалось, этот метод гарантирует отыскание
максимума за п шагов.
Для вычисления максимума функции Р (х) в поло-
положительном квадранте можно использовать модификации
метода сопряженных градиентов. Модификации направ-
направлены на то, чтобы ограничить область поиска максимума
положительным квадрантом. При этом число шагов,
необходимых для достижения максимума, может быть
большим п, однако оно остается конечным.
Рассмотрим следующую модификацию метода сопря-
сопряженных градиентов:
1) Поиск максимума функции Р (х) в области х1 >
> О, . . ., хп > 0 начинается с точки х @) = (х1 @) >
> 0, . . ., хп @) > 0). При этом движение в соответствии
с формулами A4.17) и A4.18) происходит лишь до тех
пор, пока точка х (к) находится внутри области х1 3> 0.
Если траектория движения не выводит за ограничения, то
не более чем за п шагов максимум будет найден.
2) Если же на некотором шаге к оказывается, что точ-
точка, в которой достигается условный максимум по направ-
направлению, лежит за пределами ограничений, то величина ша-
шага должна быть сокращена. Нетрудно убедиться, что при
этом максимально допустимая величина шага определяет-
определяется формулой
/ 1(/) П(к) \ ......
(/) A4Л9)
где минимум берется лишь по тем координатам I, для ко-
которых г{ < 0. При этом для всех I оказывается
х% (к + 1) > 0,
312 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
но по крайней мере для одной координаты х: окажется, что
х? — О, т. е. движение происходит до выхода на ограни-
ограничение.
Итак, в этом случае
х (к -!■ 1) -■- х(к) -V кг (к + 1).
3) Если на некотором таге к траектория выводит на
ограничение, т. е. величину шага приходится уменьшать
но формуле A4.19), то некоторые координаты хи, . . ., хт
обратятся в нуль. Дальнейший поиск максимума ве-
ведется в положительном квадранте координатного под-
подпространства Еп-т размерности п — т, задаваемого
уравнениями
х1' = 0, . . ., хт = 0.
Для этого действуем снова в соответствии с пп. 1) и 2),
по уже в подпространстве Еп..т. При этом либо условный
максимум функции в этом подпространстве будет пайден
не более чем за я — т шагов, либо при поиске еще раз
будут нарушены ограничения. В последнем случае вновь
сокращается размерность пространства и ищется услов-
условный максимум функции в положительном квадранте но-
нового подпространства.
4) Так продолжается до тех пор, пока в положительном
квадранте некоторого координатного подпространства
хх, . . ., хп не будет найден условный максимум функции.
Пусть он достигается в точке %. Если при этом выполня-
выполняются условия:
дР (х)
дР (х)
дх1
если х1 ^> О,
если х'1 — О (г = 1, .. ., п),
то в действительности точка х доставляет условный мак-
максимум функции и в положительном квадранте исходного
пространства Еп. В противном случае точка х берется за
начальную и поиск максимума продолжается по той же
схеме, начиная с п. 1).
Легко убедиться в том, что при подобной модификации
метода сопряженных градиентов максимум функции Р (х)
§ 6. ГРАДИЕНТНЫЕ МЕТОДЫ 313
будет найден за конечное число шагов. В самом деле,
в силу алгоритма каждый раз за конечное число шагов бу-
будет достигаться условный максимум на соответствующем
подпространстве Еп.т, причем каждый раз условный
максимум будет достигаться на разных координатпых под-
подпространствах. Конечность числа шагов следует из того,
что число различных координатных подпространств ко-
конечно.
Рассмотрим еще одну модификацию метода сопряжен-
сопряженных градиентов.
Определим следующую функцию (х):
дР (х) ъ , Л (I<"(х) ^
—\->~ , если хк ■-=!= О или —■ ^> О,
ду, дхК
О, если а* = 0 и Шф- < 0.
дхК
Вектор "§ (х) есть условный градиент функции Р (х) на
множестве хг ]> 0 (см. формулу (П. 8) приложения).
Будем теперь совершать восхождение к максимуму, ис-
используя A4.17), A4.18), A4.19), где § (х) заменено на
условный градиент ^ (х). Движение начинается из про-
произвольной точки положительного квадранта и происхо-
происходит до момента нарушения ограничения в точке х0. Тогда
снова начинается восхождение по методу сопряженных
градиентов из точки х0 и т. д. Поиск максимума закан-
заканчивается, когда выполнятся неравенства
I & (X) | < 8.
Важной особенностью модифицированного метода по-
поиска максимума функции Р (х) в положительном кпад-
ранте является то обстоятельство, что он допускает по-
последовательную процедуру поиска. Пусть пространство
Еп имеет координаты х1, . . ., х\ хЫ1, . . ., х11. Можно
сначала найти условный максимум функции при огра-
ограничениях х1 > 0, . . ., х1 > 0 и хи1 = 0, . . ., хп = 0.
Затем, используя найденную точку максимума как на-
начальную точку, найти максимум.?1 (х) в области х1 ~> 0, ...
. . ., *п>0.
Применим вторую модификацию метода сопряженных
градиентов к задаче нахождения обобщенного портрета.
314 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
Максимизируемая функция IV (а, |3) имеет вид
а Ь а Ь
1=1
г=1
Квадратичная часть этой функции есть
а Ь
2 а^~ 2 Р^
г=1 э=1
Обозначим составляющие условного градиента через
^ = I "^-=1 — (хь ^), если сц>0 или A —(^, о|з)>
I
0 в противном случае,
в- =
Ж = ^'' ^ ~ А' если ^ ^ ° или
О в противном случае,
а Ь
где положено я|) = 2 агхг— 2 Р>^# Обозначимсоставляю-
г=1 /=1
щие вектора г (I), задающего направление движения на
^-м шаге, через аг, р;-.
При вычислении величины шага по формуле A4.18)
необходимо вычислять величину (г (<), Аг @)>т- е. значе-
значение квадратичной функции Р (х) при подстановке в нее
вектора г. В нашем случае
B, Аг) = 2 °№ — 2
г=1 )=1
2 _
I
где обозначено
Таким образом, заменяя формулы A4.17), A4.18) и
A4.19) в соответствии с введенными обозначениями, при-
приходим к следующему алгоритму.
Находится условный градиент в точке а (I), $ (I):
оц (* + !) =
1 — (х^ (()), если а @ > 0 или 1 — (х$ (I)) > О,
О в противном случае,
6. ГРАДИЕНТНЫЕ МЕТОДЫ 315
= {(^, т|? ({)) — к, если р, (*) > 0 или (а^ (<)) —А > О,
\ О в противном случае.
Определяется направление движения:
а, (^ + 1) = а, (* + 1) + б {I + 1) аг {I),
где
2
г=1
Далее вычисляется
а
г=1 )=1
Новое значение а^ и $^ находится по формулам
аг (* + 1) = а, (I) + аг (I + 1) к (I + 1),
Здесь к (I + 1) — величина шага, определяемая из усло-
условия достижения максимума по направлению или выхода
на ограничение:
к {I + 1) = шш (То (* + 1), Тг {I + 1), Т,- (* + 1))»
где
г , если а* (I + 1) <* О,
оо, если
— , если
оо, если р,-(г!4-1)>0.
316 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
Наконец,
Ч? (* + 1) = Ч> @ +^ (* + 1) к (I + 1).
Первый шаг (I = 0) отличается от общего лишь тем,
что значения аг A), |3/ A) задаются следующим образоом
«I A) = <*, A),
Р; A) = & A).
Критерий останова: | с*г | < е и | (^ | < е или
\У(<х, Р)>Б.
В главе XV будет подробно рассмотрена структура ал-
алгоритма построения обобщенного портрета на основе ме-
метода сопряженных градиентов в первой модификации.
§ 7. Теория оптимальной разделяющей гиперплоскости
Напомним, что оптимальной разделяющей гиперпло-
гиперплоскостью была названа плоскость
[X, фопт) = сопт
где фопт — единичный вектор, доставляющий максимум
функции
П (ф) = С] (ф) — с2 (ф) = шш (х, фопт) — шах (X, ф),
х X
. с' (Фопт) +с* (Фопт)
"опт — 2 •
Рассмотрим теперь минимальный по модулю вектор
1|з (доставляющий минимум функции (г|з, я|))), удовлетворяю-
удовлетворяющий неравенствам
(хг, г|?) > 1 + с,
A4.20)
(Хц У) < — 1 + с.
Параметр с считается допустимым, если неравенства A4.20)
совместны. Нетрудно убедиться, что если множества
X и X разделимы гиперплоскостью, то множество допу-
допустимых с не пусто. Будем искать минимум функции A|), \|з)
§ 7 ОПТИМАЛ ЬНАЯ РАЗДЕЛЯЮЩАЯ ГИПЕРПЛОСКОСТЬ 317
при ограничениях A4.20), считая переменными как век-
вектор 1|з, так и параметр с. Оказывается, что решение этой
задачи равносильно отысканию оптимальной разделяющей
гиперплоскости.
Теорема 14.9. Если множества X и X разделимы ги-
гиперплоскостью, то минимум функции (г|з, г|з) при ограни-
ограничениях A4.20) существует, единственен и достигается при
С1(Фопт)-с2(Фопг) '
где фопт — направляющий вектор оптимальной разде-
разделяющей гиперплоскости.
Доказательство. Покажем, что для любого
вектора г|з, удовлетворяющего A4.20), справедливо не-
неравенство
П(*Ь.2
ж)>т!г <14-2»
Действительно, поскольку нуль не удовлетворяет A4.20),
знаменатель в нуль не обращается. Далее, в силу A4.20)
с
и, значит,
причем равенство достигается только в том случае, когда
с ( * \ -с+1
и
Теперь, учитывая, что
A4.22)
318 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
получаем для любого вектора^, удовлетворяющего A4.20),
В силу единственности оптимальной разделяющей
гиперплоскости (теорема 14.1) неравенства A4.21) и A4.22)
переходят в равенство для векторов, удовлетворяющих
A4.20), только при
■ — фопт>
A4.24)
2
IЧ» I '
Только при этих условиях, очевидно, достигается равен-
равенство и в A4.23).
Разрешая эти равенства относительно о|з и с, получаем
что минимум (а|э, а|з) при ограничениях A4.20) достигается
только в точке
С1(Фопт)-с2(Фопт) '
°~~ С1(Фопт)-с2(Фопт)
Теорема доказана.
Таким образом, вектор 1|з0, доставляющий максимум
A|з, о|^) при ограничениях A4.20), всегда коллинеарен (г0Пт
и оптимальная разделяющая гиперплоскость может быть
задана в виде
§ 8. Двойственная задача
Точно так же как при нахождении обобщенного порт-
портрета, здесь оказывается удобным перейти к двойственной
задаче. Воспользуемся условиями Куна — Таккера.
Согласно теореме 14.4, для того чтобы величина (г|з, я|)),
рассматриваемая как функция 1|з и с, достигала минимума
при ограничениях A4.20) в точке г|з0, с0, необходимо и до-
достаточно, чтобы
§ 8. ДВОЙСТВЕННАЯ ЗАДАЧА 319
а) точка 1|з0. с0 удовлетворяла A4.20) и
б) градиент функции в этой точке раскладывался с по-
положительными коэффициентами по градиентам ограни-
ограничений, которые достигаются в точке 1|з0, с0.
Иными словами, необходимо и достаточно, чтобы су-
существовали такие числа с^ ^ 0 и Р^ :> 0, что
а Ь
ч>0 = 2 од - 2 Рл- (I4-25)
г=1 )=1
и, кроме того,
Ь
д-с— = Ъ «г — ^ ^ = и>
г=1 )=1
причем
а, A + с0 — (яро, ««)) = 0,
A4.26)
*>) + 1 - с0) = 0.
Рассмотрим теперь функцию
г=1
где положено
г=1 )=1
Будем искать максимум этой функции при ограниче-
ограничениях
а, > 0, р, > 0,
а Ь
2 «г = 2 Щ- A4.27)
г=1 5=1
Согласно условиям Куна — Таккера, для того чтобы мак-
максимум функции IV (а, |3) при ограничениях A4.27) до-
достигался в точке а0, C°, необходимо и достаточно, чтобы:
а) точка а0, C° удовлетворяла условиям A4.27) и
320 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
б) существовали числа дг ^ 0, . . ., да ^ 0, цх ^ 0, . . .
. . ., дь ^ 0; с *) такие, что
-§^ = A - №„ *0) - Я1-с, "^ = A + (%, *})) = 7,- + с
а Ь
и дгаг=0, д7Р7- — 0. где положено ^о = 2 а1х1 + 2 Р°^"-
1=1 )=1
Ввиду произвольности положительных чисел дг, д;-
условие б) равносильно существованию числа с такого,
что
(*«, ^о) >с + 1,
14- , A4.28)
и
A + с - (т|H, Ж|)) о? - 0,
A4.29)
A-е + (т|H, г,)) р? = 0.
Сопоставляя условия Куна — Таккера для минимума
функции Aр,1|з) при ограничениях A4.20) и для максимума
функции Ш (а, Р) при ограничениях A4.27), получаем
следующую теорему.
Теорема 14.10. Точка а", р°, в которой достигается мак-
максимум функции ТУ (а, Р) при ограничениях A4.27), и век-
вектор а|з0, доставляющий минимум функции (\|з, \|з) при огра-
ограничениях A4.20), связаны соотношением
г=1 У=1
Таким образом, для нахождения оптимальной разде-
разделяющей гиперплоскости достаточно найти максимум
функции V/ (а, Р) при ограничениях A4.27), определить
\|;п из A4.30) и задать гиперплоскость уравнением
тш (х., 1|з0) + тах (х-, г(.о)
(яг, Ь) - -1 И •
а Ь
*) Условие ^ а{ = ^ р. можно рассматривать как два нера
иенотва 2щ — 2р\; > 0 и 2а{ — 2р, <0.
§ 8. ДВОЙСТВЕННАЯ ЗАДАЧА 321
Отметим, что функция \У (а, Р) имеет, вообще говоря,
не единственный максимум. Но все точки а0, Р°, достав-
доставляющие максимум этой функции при ограничениях
A4.27), соответствуют одному и тому же вектору я|з0.
Значение максимума функции \У (а, Р) позволяет су-
судить о расстоянии между выпуклыми оболочками мно-
множеств X и X, которое равно
Действительно,
Напомним, что значения а0 и C° отличны от нуля толь-
только для тех векторов хг (ж;-), для которых
(*|. Ч?о) = с + !
Поэтому с учетом A4.27)
г=1 )=1 4=1 )=1 ' г=1 )=1
Следовательно,
а Ь
Ж (*о, Ро) = 2 «? + 2 Р° - 4-(^0' ^) = -Т ^«' ^о)-
г=1 )=1
Наконец,
П (фо11Т^ = ТФЙ" = У
Последнее соотношение позволяет в ходе практиче-
практического вычисления оптимальной разделяющей гиперпло-
гиперплоскости оценивать зазор между разделяемыми множествами.
А именно, если найдена точка а, р\ удовлетворяющая ус-
условиям A4.27), и значение функции ТУ (а, Р) в этой точке
равно Б, то «зазор» не превосходит у ^.
Для множеств, не разделимых гиперплоскостью, т. е.
таких, выпуклые оболочки которых пересекаются, функ-
функция ТУ (а, р) в области, определяемой соотношениями
A4.27), возрастает неограниченно.
322 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
§ 9. Методы вычисления оптимальной разделяющей
гиперплоскости
Вычислять оптимальную разделяющую гиперплоскость
на ЦВМ не многим сложнее, чем находить обобщенный
портрет.
Для этого достаточно в градиентных методах макси-
максимизации функции IV (а, В) заменить условный градиент
функции IV(а, В) в положительном квадранте на условный
градиент функции при ограничениях
«I >0, Р, >0 (I = 1, 2, . . ., а) (/ = 1, 2, . . ., Ъ),
2 «* = 2 в*
и в качестве начальной точки выбрать точку, удовлетво-
удовлетворяющую A4.27). В соответствии с теоремой П. 4, дока-
доказанной в приложении, условный градиент функции
IV (а, В) на многообразии, задаваемом условиями A4.27),
однозначно определяется формулой
Л—(хи \|э)+ й, если 1 — (хь
0 в противном случае,
( 1+ (% 40 - й, если \+(Х}, Ч?) - A4<31)
(«, Р) = | -с2>0,Вг>0,
[ 0 в противном случае
при условии
Теперь остается подобрать величину й так, чтобы это
ловие выполнялось. Будем рассма
A4.31) как функции в, и обозначим
условие выполнялось. Будем рассматривать УуСЛ, VуСл в
A431) ф
Очевидно, что для нахождения условного градиента до-
достаточно найти корень уравнения
Ь F) = 0=
§ 9. ВЫЧИСЛЕНИЕ ОПТИМАЛЬНОЙ ГИПЕРПЛОСКОСТИ 323
Из определения следует, что функция Ь (А) — моно-
монотонно возрастающая непрерывная кусочно-линейная
функция. Кроме того, при А —>■ оо она неограниченно убы-
убывает. Поэтому корень заведомо есть. Функция Ь (А) может
иметь изломы (разрывы первой произвольной) только в
точках
Поэтому корень Ь (А) можно определить так: найти ли-
линейный кусок, на котором лежит корень, а затем найти
корень линейной функции, совпадающий с Ь (А) на этом
куске.
Таким образом, приходим к следующему алгоритму.
1. Вычисляется значение функции Ь в точках А( (А}).
2. Если при всех Аг (А}) функция Ь (А) > 0, то корень
лежит на луче А ^ тш (А{, <1}) и равен
где 2' берется по всем векторам хг, для которых а,- ^> 0;
2" берется по всем векторам х^ а' — число векторов XI,
для которых аг ^> 0; Ъ' — число векторов X].
3. Если при некоторых д,г (А]) функция меньше нуля,
то следует найти максимальное А{ (А^, при котором
Ь (А) < 0. Обозначим его через А*.
Тогда корень уравнения Ь (А) = 0 лежит на участке,
прилегающем справа к точке А*, и равен
а' + V
где 2' берется по тем векторам хх, для которых а^ ^> 0
или 1 — {хи 1|з) + А* > 0; 2" берется по тем векторам
3/, для которых (^ > 0, или 1 — А*— (Ж;, т|з) > 0; а' и
Ь' — соответственно числа слагаемых в сумме 2' и 2".
4. |3начение ЛуСЛ И7 вычисляется путем подстановки
в A4.31) корня уравнения Ь (А) = 0. :*?
Подробнее структура алгоритма построения оптималь-
оптимальной разделяющей гиперплоскости будет рассмотрена в
главе XV.
324 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
§ 10. Построение оптимальной разделяющей
гиперплоскости модифицированным методом
Гаусса — Зайделя
Рассмотрим еще один метод построения оптимальной
разделяющей гиперплоскости. Идея метода основана на
том, что оптимальная разделяющая гиперплоскость орто-
ортогональна отрезку, соединяющему ближайшие точки вы-
выпуклых оболочек X и X, и проходит через его середину.
Точка х* принадлежит выпуклой оболочке векторов
хг, . . ., ха, если
х = 2а^г, 2аг = 1, аг > 0.
Аналогично точка х* принадлежит выпуклой оболочке
векторов хъ . . ., Хъ, если
Х* = Щ%1, 2^=1, Р;>0.
Поэтому, для того чтобы найти оптимальную разделяю-
разделяющую гиперплоскость, достаточно найти минимум квадра-
квадратичной формы (о|з, о|з), где
в области
2а1 = 1, аг >0,
A4.32)
2C, = 1, $}>0.
Вектор о|з, доставляющий минимум, будет направляющим
вектором оптимальной гиперплоскости.
В вычислительном плане эта задача никак не проще
той, которая рассмотрена в предыдущем параграфе.
Здесь ограничения задаются двумя условиями типа ра-
равенства, тогда как там входило лишь одно такое условие.
Рассмотрим модифицированный метод Гаусса —
Зайделя для поиска максимума (о|з, о|з) в области A4.32).
Модификация метода Гаусса — Зайделя направлена на
то, чтобы при движении вдоль выбранной координаты,
во-первых, не выйти за пределы положительного квад-
квадранта, а во-вторых, все время оставаться на многообра-
многообразии 2аг = 1 (или 2C; = 1).
Итак, пусть в <-й момент времени точка а (I — 1),
Р (I — 1) удовлетворяет условию A4.32) и совершается
§ 10. ПОСТРОЕНИЕ МЕТОДОМ ГАУССА — ЗАЙДЕЛЯ
325
шаг вдоль координаты а,. Тогда величина шага Да,
модифицированного метода Гаусса — Зайделя опреде-
определяется из условия
шах | х* (I — 1) A — Да,) + Аа,х( — х* (I — 1) |2, A4.33)
где
а Ь
4=1 3-1
Минимум величины A4.33) находится при шаге
О, если (х*{1 — \) — х\1—\), х* (I— 1)— ж,)< О,
Да( =
1, если
(X 11—1) — :
(х A—1) — х{, х ({—1) — х{)
—г в остальных случаях.
Таким образом, рекуррентная процедура поиска оп-
оптимальной разделяющей гиперплоскости задается так:
х* @ = х* (I — 1) A - Да,) + х,Аа,. A4.34)
Аналогично находится значение х* (<) в случае движе-
движения по РA
х* (I) = Х* (I) A - ДРУ) + г,Др„
где
0, если (х* (I — 1) — х* (/ — 1), х( — х* (I — 1))<0,
1, если
^7
*-г ({-1), ^-г ({-1))
* ({-!)-г* ({-!))
г, _ 5;* ({ - 1), ?( - ^ ({ - 1))
в остальных
случаях.
A4.35)
Зная х* и х*, нетрудно построить оптимальную разде-
разделяющую гиперплоскость. Она задается парой
■ф = х* — %\ с =
(г х\ (х х\
[X , X ) — [X , X )
326 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
Рекуррентная процедура A4.34), по существу, есть
алгоритм Б. Н. Козинца для построения оптимальной
разделяющей гиперплоскости.
Замечательная особенность этого алгоритма — пре-
предельная простота реализации. Однако существуют за-
задачи (особенно при большой размерности вектора х), для
которых скорость сходимости алгоритма оказывается мед-
медленной (вспомним, что скорость поиска максимума в этом
алгоритме определяет метод Гаусса — Зайделя). Именно
для таких задач и строят значительно более сложные ал-
алгоритмы, в которых для увеличения скорости сходимости
используются более эффективные методы поиска максиму-
максимума квадратичной формы.
§ 11. Применение метода обобщенного портрета
для нахождения оптимальной разделяющей
гиперплоскости
Задача нахождения обобщенного портрета при задан-
заданном к несколько проще, чем задача нахождения оптималь-
оптимальной разделяющей гиперплоскости. В частности, при ре-
решении двойственной задачи в случае поиска обобщенного
портрета отсутствует ограничение вида 2 а, = 2C^.
Существует два способа применить метод обобщенного
портрета для отыскания оптимальной разделяющей ги-
гиперплоскости.
Первый способ основан на последовательном построе-
построении обобщенных портретов при разных к и подборе к,
близкого к к0 (теорема 14.3).
При подборе к можно исходить непосредственно из
критерия
V И3 (к)\
шах П ,;;,:. = шах
V И3 (к)\
и искать максимум по к одним из известных способов по-
поиска экстремума функции одной переменной. Можно так-
также подбирать к из условия 2 а, = 2 0,, где а} ■> 0 и C, >
^ О — коэффициенты разложения обобщенного портре-
портрета по крайним векторам. При выполнении этого условия,
как нетрудно убедиться, обобщенный портрет а|з (к) кол-
лине арен фош>
§ 11. ПРИМЕНЕНИЕ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА 327
Второй способ основан на следующем свойстве вектора
Фопт. Рассмотрим всевозможные разности вида
У и = Х1 — %1 {хг <= X, X] <= X
При этом вектор фопт обладает свойством
гаш(фопт, уц) = тах тт(<р, уц)
г,3 |ф|=1 1,3
и поэтому, как было указано в § 2, он коллинеарен обоб-
обобщенному портрету о|з класса У = {у^} при пустом втором
классе. Число векторов уц обычно много больше, чем дли-
длина обучающей выборки. Поэтому непосредственное по-
построение обобщенного портрета о|з затруднительно. Вместо
этого можно воспользоваться следующей итеративной про-
процедурой.
1. Берется произвольная пара векторов х^, х^. Обра-
Образуется класс Уг всего из одного вектора уг = хи — х^.
Строится обобщенный портрет \рг этого класса (при пустом
втором классе).
2. Допустим, что на 1-й шаге построены класс векто-
векторов У( и его обобщенный портрет о|з(. В обучающей по-
последовательности находится вектор Х((+1 такой, что
(■*(. хч+1) = Ш.1П №. хд>
и вектор Х}1+1 такой, что
№. Ч+1) = тах №. Ч-
Образуется вектор у(+1 = хг{+1 — х^+1.
3. Если (а|з(, у(+1) <1 — е(е>0 — параметр про-
процедуры), то класс Уг пополняется вектором у1+1. Далее
находится обобщенный портрет а|з(+1 образовавшегося
класса У/+1 и процесс продолжается дальше.
Если же (о|з(, у{+1) > 1 — е, то процесс заканчивается
и за приближение оптимальной разделяющей гиперпло-
гиперплоскости принимается гиперплоскость
(.Р 11)() +тах
х) = -! =—*
328 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
При 6 = 0 процесс за конечное число итераций приво-
приводит к нахождению обобщенного портрета класса У =
— {Уц}' а следовательно, и оптимальной разделяющей по-
поверхности.
При реализации этой процедуры удобно на каждой
итерации при образовании класса У(+1 из У( удалять
все векторы у, входящие с нулевым весом в разложение
обобщенного портрета а|з(.
§ 12. Некоторые статистические особенности метода
обобщенного портрета
В главе VI были получены оценки качества алгоритмов,
строящих разделяющие гиперплоскости методом миними-
минимизации эмпирического риска.
В частности, было показано, что для детерминист-
детерминистского случая математическое ожидание вероятности оши-
ошибочной классификации с помощью решающего правила,
построенного по выборке длины /, не может быть меньше
где с — константа, п — емкость класса.
Были получены и верхние оценки качества. Верхние
оценки были двух типов — зависящие от размерности про-
пространства (эти оценки следует из общей теории равномер-
равномерной сходимости) и оценки, зависящие от относительного
расстояния (эти оценки следуют из обобщенной теоремы
Новикова 6.2).
В этом параграфе будут исследованы оценки качества
алгоритмов, реализующих метод обобщенного портрета.
Будет показано, что для этих алгоритмов справедливы
одновременно оценки обоих типов (тем самым выполняет-
выполняется лучшая из них). При этом существенно то, что верхняя
оценка, зависящая от размерности, значительно ближе к
нижней с -у-, чем оценки для произвольных алгоритмов,
строящих разделяющую гиперплоскость на основе ми-
минимума эмпирического риска. Тем самым будут показа-
показаны особые статистические свойства метода обобщенного
портрета.
§ 12. СТАТИСТИЧЕСКИЕ ОСОБЕННОСТИ МЕТОДА 329
Итак, пусть задача такова, что для любой выборки дли-
длины / при заданном параметре к < 1 существует обобщен-
обобщенный портрет множества X относительно X.
Оказывается, что при этом качество И алгоритма, ис-
использующего метод обобщенного портрета, может быть оце-
оценено:
Д<ГТТ' (I4-36)
где п — размерность пространства.
Эта оценка может быть еще усилена. В § 3 было пока-
показано, что обобщенный портрет ар всегда может быть разло-
разложен по своим крайним векторам в виде
1=1 У=1
Это разложение, вообще говоря, не единственно. Назовем
крайний вектор информативным, если он входит с нену-
ненулевым весом во все разложения вектора ар. Обозначим че-
через т — математическое ожидание числа информативных
векторов в выборке длины 2 + 1. Ниже будет показано,
что справедлива оценка
/?<т|г. A4.37)
Будет показано также, что всегда имеет место неравен-
неравенство
ш ^ п.
В практических задачах часто оказывается, что ш мно-
много меньше п, и тогда методом обобщенного портрета
удается по выборке, соизмеримой с размерностью про-
пространства, построить разделяющую гиперплоскость, га-
гарантирующую малую вероятность ошибочной класси-
классификации.
Для вывода оценок A4.36) и A4.37) воспользуемся
свойством несмещенности оценки скользящего контроля
(см. § 7 главы VI). Несмещенность означает, что мате-
математическое ожидание частоты ошибок на экзамене после
обучения на последовательности длины / равпо матема-
математическому ожиданию частоты ошибок при скользящем
330 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
контроле на последовательности длины I -\- 1. Приме-
Применительно к методу обобщенного портрета скользящий кон-
контроль проводится так: из обучающей выборки последова-
последовательно (каждый раз по одному) удаляются векторы хр (хр);
по оставшейся части выборки строится обобщенный порт-
портрет о|зр и проверяется правильность опознания удаленного
вектора; после этого подсчитывается частота ошибок.
Справедлива теорема
Теорема 14.11. Число ошибок при скользящем контроле
не превосходит числа информативных векторов обобщен-
обобщенного портрета 1|з (к), построенного по всей выборке.
Доказательство. Достаточно показать, что
при удалении неинформативного вектора из обучающей
выборки в ходе скользящего контроля ошибки на этом
векторе не произойдет.
В самом деле, если вектор хр (хр) не является инфор-
информативным, то существует разложение обобщенного порт-
портрета
1=1 }=1
а*>0;Р;>0, (а;/,т|з)>1, (х}, т|з) < к, A4.38)
щ A - (хг, Ю) = О, р, (к - (х}, т|))) = О,
в которое вектор хр (Хр) входит с нулевым весом. Но это
значит, что вектор о|з является одновременно обобщенным
портретом и для выборки, из которой вектор хр удален,
так как для него выполняются все условия теоремы 14.6
применительно к укороченной выборке, т. е. \|з =1|)р.
Следо вательно,
(хр, т|зр) = (хр, т|з) > 1
или
(гр,о|з) =(хр,у) < к,
а значит, удаленный вектор опознается правильно. Тео-
Теорема доказана.
Из теоремы, с учетом несмещенности оценки сколь-
скользящего контроля, немедленно вытекает неравенство
A4.37).
Покажем еще, что число информативных векторов ни-
никогда не превосходит размерность пространства п. Для
§ 12. СТАТИСТИЧЕСКИЕ ОСОБЕННОСТИ МЕТОДА 331
этого достаточно построить разложение вида A4.38),
в которое с ненулевым весом входит не более п векторов.
Действительно, если в разложении A4.38) входит бо-
более п векторов, то всегда можно построить разложение
того же вида, в которое входит меньшее число векторов.
Всякая система из т ^> п векторов линейно зависима.
Поэтому существуют числа уг (^) такие, что
а Ь
1=1 3=1
причем в это разложение входят только те векторы, кото-
которые входят в A4.38) с ненулевым весом, и по крайней мере
одно 7г (Т./) положительно.
Тогда выражение
а Ъ
1> = Е («»- *Ъ) Щ ~ 2 (в - *п) *} A4.39)
задает семейство разложений обобщенного портрета по
своим крайним векторам. Поскольку все а и |3 положи-
положительны, то при достаточно малых по модулю I все коэф-
коэффициенты остаются положительными. В хо же время,
поскольку среди чисел т{ (у;-) есть положительные, при
достаточно большом I ^> 0 некоторые коэффициенты ста-
станут отрицательными. Значит, найдется 1= ^т;п, при кото-
котором впервые один или несколько коэффициентов разло-
разложения A4.39) обратятся в нуль, в то время как остальные
сохранят положительное значение. Применяя это построе-
построение, если нужно, несколько раз получим искомое разло-
разложение .
Для метода обобщенного портрета при к < 0 удается
получить также оценку качества, зависящую от относи-
относительного расстояния между классами. При к = — 1
оценка совпадает с выведенной в главе VI (теорема 6.2)
оценкой качества для персептронного алгоритма с много-
многократным повторением обучающей последовательности, а
именно:
332 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
где
р — расстояние от начала координат до выпуклой оболоч-
оболочки множества векторов хг, . . ., ха, хг, . . ., хъ. Математи-
Математическое ожидание берется по всем выборкам фиксирован-
фиксированной длины.
Нетрудно убедиться, что число р и модуль обобщенного
портрета, полученного при к = — 1, связаны соотноше-
соотношением
1
Если, как и раньше, воспользоваться несмещенностью
оценки скользящего контроля, то для вывода A4.40)
достаточно доказать следующую теорему.
Теорема 14.12. Число ошибок при скользящем контроле
для метода обобщенного портрета при к — — 1 не превосхо-
превосходит О2 |о|з(— 1) | 2.
Доказательство. Пусть дана обучающая по-
последовательность хъ . . ., ха, хг, . . ., хь и максимум соот-
соответствующей функции Ц^(а, Р) при а>0; Р>0 достига-
достигается в точке а; = оц°, $] = Ру°.
Соответственно о|з = Ъа(хг — 2|}^ — обобщенный пор-
портрет. Обозначим через ар, |}р точку, доставляющую
максимум функции IV (а, |}) на множестве а( > 0, ^ ^ 0,
ар = 0. Очевидно, что ей соответствует обобщенный порт-
портрет, построенный по выборке без вектора хр:
г=1 1—1
Обозначим через \УР значение функции \У (ее, Р) в точке
а{ — а\ {I =^ р), ар = 0, |};- = Р°. Очевидно, что
IV (ар, рр) > 1УР
и одновременно
Ш (ар, рр) < И7 (а0 р0)-
Поэтому
И7 (а0, р°) - И7 (ар, рр) < И7 (а0, р°) - Шр. A4.41)
§ 12. СТАТИСТИЧЕСКИЕ ОСОБЕННОСТИ МЕТОДА 333
Далее,
Иг (а0, ро) _ игр = ао _ ^_№> ^ + _1_ | ^ _ ^
Для крайнего вектора хр
цг (ао; р0) _ {^р = _1_ (ао у | ^ |2_ A4.42)
Будем считать далее, что обобщенный портрет а|зр непра-
неправильно опознает вектор хр. Это значит, что
Кроме того, как было показано при доказательстве преды-
предыдущей теоремы, это возможно только в том случае, когда
хр является крайним вектором обобщенного портрета о|з0.
Исследуем теперь левую часть неравенства A4.41).
Для этого рассмотрим один шаг максимизации функции
И7 (ее, Р) из точки ар, |}р вдоль оси ар ^> 0 и выберем
оптимальное значение ар. Имеем
Ц? (а, р) = |
Отсюда получаем оптимальное значение сср;
Увеличение ТУ (ее, Р) на этом шаге составит
\Хр\*
Так как А]УР не больше, чем приращение функции при
полной максимизации, то
\У (а0, р°) - ТУ « рр) > АРГР = A ~ ^7",.?р)) ■ A4.44)
I жр I
Объединяя A4.41), A4.42), A4.44), получим
334 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
откуда, учитывая A4.43)
р
I ~Р1
Аналогично оценивается |}р:
г, ^ 1 — к
Учитывая, что \ хр \ <; О, \ хр \ <^ Б, имеем
^ 1— к
1 —
Пусть теперь при скользящем контроле число непра-
неправильно опознаваемых векторов первого и второго классов
равно соответственно 1г и 1г. Тогда в силу теоремы 14.10
при отрицательном к
а Ъ а Ъ
A>,ч>) = 2«1-*2 в>2'«1-й2"в.
г=1 ;=1 г=1 ;=1
где Е' и 2" берутся только по тем векторам, которые
неправильно опознаются при скользящем контроле.
Далее,
Окончательно при &"-< —1
При 0 > А; > — 1
В случае А; = — 1
Теорема доказана.
§ 13. ПРИЛОЖЕНИЕ К ГЛАВЕ XIV 335
§ 13. Приложение к главе XIV
1. Рассмотрим в евклидовом пространстве Еп конечную си-
систему векторов X = хъ . . ., хк.
Множество Г векторов х, представимых в виде
{=1
г=1
образует минимальный выпуклый конус, содержащий систему
векторов X, или, иначе, выпуклый конус, порожденный системой
векторов X.
Определение 1. Система векторов X не развернута, если
порожденный ею выпуклый конус не содержит нуля.
Определение 2. Система векторов X сильно развернута, ес-
если порожденный ею выпуклый конус Г содержит все пространство Еп.
Определения 1 и 2 эквивалентны следующим двум определениям.
Определение 1'. Система векторов X не развернута, если
существует такой вектор ф €Е Еп, что для всех ж;.6Е X
(хг, ф) > 0.
Определение 2'. Система векторов X сильно- развернута,
если Зля всякого ф 6Е Еп найдется такой вектор ж; СЕ X, что
(XI, Ф) < 0.
Докажем, что определения 1 и 2 эквивалентны 1' и 2'.
Теорема П.1. Определение 1' эквивалентно 1.
Доказательство. Пусть система векторов не развер-
развернута в смысле 1'. Значит, существует такое ф, что
(*1,Ф) >0
для всех XI 6Е X.
Рассмотрим произвольный элемент х выпуклого конуса, по-
порожденного системой х\, . . ., хк'.
к
1=1
Умножим скалярно (П. 1) слева и справа на
(х, ф) = 2Т1(*г, ф).
336 гл. XIV. Построение разделяющей Гиперплоскости
Так как (хи ф) > 0 и по крайней мере одно у{ > 0, то
(*, Ф) > О,
т. е. х Ф 0.
Таким образом, из Г следует 1.
Пусть теперь система векторов X выпукла в смысле определе-
определения 1. Рассмотрим выпуклую оболочку X системы X, т. е. множество
векторов х, представимых в виде
к
х = 2 ТЛ (*< е Х)'
1=1
ъ > о,
2Т1=1.
Согласно определению 1, это множество не содержит нуля. Кроме
того, оно замкнуто и ограничено. Поэтому вектор х0, на котором
достигается тт |ж|, не равен нулю и принадлежит множеству X.
Покажем теперь, что для любого 1*б!
(х*, х0) > 0.
Рассмотрим отрезок
A — 1)х0 + 1х* A»б1, 0 < I < 1).
Легко видеть, что этот отрезок принадлежит X. Найдем модуль
произвольного вектора х, конец которого лежит на отрезке
A - 1)х0 + 1х*:
- {) х0 + Ьх*, A - {) х0
где о (I) — величина второго порядка малости по {.
Так как | х \ ^ | х0 |, то коэффициент при линейном члене должен
быть неположительным, т. е.
| х0 |* - (х*, х0) < 0,
откуда следует
(х*, х0) > | х0 |2 > 0.
Последнее неравенство справедливо для любого х* 6Е X, а следо-
следовательно, и для XI, . . ., хп. Значит, условие определения 1 выпол-
выполнено.
Таким образом, эквивалентность 1 и 1' показана.
Теорема П.2. Определения 2' и 2 эквивалентны.
Доказательство. Пусть справедливо 2. Это значит,
что произвольный вектор —ср =/= 0 может быть представлен в виде
-Ф = 2Т№,
где
1=1
§ 13. ПРИЛОЖЕНИЕ К ГЛАВЕ XIV 337
Умножим скалярно последнее равенство на ф:
- |ф|2= 2Тг(*г, Ф)- (П.2)
Учитывая, что у; ^. 0, из равенства (П.2) имеем, что по крайней
мере для одного I
{Щ, Ф) < О,
т. е. система строго невыпукла в определении 2'.
Покажем теперь, что из 2' следует 2. Допустим, что не сущест-
существует вектора <р ф 0 такого, что для всех х{
(хи Ф) > 0.
Отсюда следует, что нуль принадлежит выпуклому конусу, порож-
порожденному XI, . . ., х%, так как в противном случае в силу эквива-
эквивалентности 1 и 1' найдется вектор <р такой, что для всех ж;
(*г,Ф) >0,
в противоречии с 2'.
Назовем вектор хц базовым, если существует представление
нуля вида
в которое вектор х^ входит с ненулевым весом (т. е. ун ф 0).
Выпуклый конус, порожденный всеми базовыми векторами
из X, совпадает с гиперпространством Е^, порожденным этими век-
векторами. Действительно, если вектор % базовый, то вектор — х^
принадлежит конусу, порожденному базовыми векторами пз X,
так как из соотношения
0 = 2т,-*,- (УкфО, У]>0)
следует, что
Произвольный вектор у пространства Ец, порожденного базо-
базовыми векторами из X, представим в виде
у =- Ъ*%хи
где XI — базовые векторы; здесь некоторые о^ могут быть отрица-
отрицательными.
Представим все члены суммы с отрицательными коэффициента-
коэффициентами аг в виде | аг | (—24), а (—хг) в соответствии с (П.З) разложим
по базовым векторам с неотрицательными коэффициентами.
Таким образом, получим представление
6г>0, 26; > 0
для произвольного у 6Е Е^.
Далее рассмотрим следующие возможности.
А. Пространство Ек, порожденное базовыми векторами, сов-
совпадает со всем пространством Еп. В этом случае, как только что
338 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
показано, выпуклый конус, порожденный X, совпадает с Еп, т. е.
выполняются условия определения 2.
Б. Пространство Е% имеет размерность меньшую, чем Еп,
и при этом все векторы из X базовые. В этом случае рассмотрим
произвольный вектор ср из Еп, ортогональный Е^. Очевидно, что
при этом для всех х-ъ 6Е X выполняется равенство
(Щ, Ф) = О
в противоречии с определением 2'.
В. Пространство Е^ имеет размерность меньшую, чем Еп,
и не все векторы X базовые.
Тогда пространство Еп представим в виде произведения двух
ортогональных подпространств
Еп= ЕкХ Еп-*
Рассмотрим множество проекций У небазовых векторов в
пространстве Еп-%.
Утверждается, что множество У образует неразвернутую си-
систему векторов. Действительно, если это не так, то, как уже было
показано, выпуклый конус, порожденный У, содержит 0, т. е.
существуют такие бг > 0, 2бг>0. что
2Й11Я = О,
гДе VI — проекции небазовых векторов в Еп-^.
Рассмотрим вектор
х=Щхи (П.4)
где XI — небазовые векторы, проекции Которых равны соответствен-
соответственно у и
Тогда
й х = 2бг2/г = 0.
Следовательно, вектор х принадлежит пространству Е^. Поэ-
Поэтому вектор —х может быть представлен как линейная комбинация
базовых векторов х-ъ с неотрицательными коэффициентами
— х = 2т*ж*. (П.5)
Суммируя (П.4) и (П.5), имеем
0 = Щхг + 2тК- (П.6)
Легко видеть, что в разложении нуля (П.6) хотя бы один не-
небазовый вектор х участвует с ненулевым весом.
Полученное противоречие доказывает, что множество проекций
У не развернуто.
Покажем теперь, что это утверждение находится в противо-
противоречии с тем, что множество векторов X сильно развернуто в смысле
определения 2'.
Поскольку множество У не пусто и не развернуто, то, согласно
определению 1', в Еп-к существует такой вектор ф0) что
(Уг, Фо) > 0, (П.7)
§ 13. ПРИЛОЖЕНИЕ К ГЛАВЕ XIV 339
а Следовательно,
(*,. ф0) = О (П.8)
для базовых векторов и
(х\, Фо) = (уи Фо) > О
для небазовых векторов, в противоречии с определением 2'. Эк-
Эквивалентность определений 2 и 2 доказана.
Фактически попутно доказана следующая теорема.
Теорема П.З. Если минимальный выпуклый конус, порож-
порожденный конечной системой векторов {п, . . ., х^} = X, не совпа-
совпадает со всем пространством Еп, то существует вектор ф ф О
такой, что для всех х$
(хи Ф) > О, (П.9)
причем для небазовых векторов неравенство переходит в строгое
(XI, ф) > 0. Если же система векторов X сильно развернута, то
всякий ее вектор является базовым.
Замечание. Если ф ф 0 — произвольный вектор такой, что
Зля всех I выполняется (П.9), то Зля всякого бавового вектора х^
неравенство переходит в равенство, т. е.
(х}, Ф) = 0.
Действительно, пусть х$ — базовый вектор. В силу (П.9)
(х), ф) >0. (П. 10)
В то же время, как показано выше ((П.З)), вектор —щ разложим
по базовым векторам с неотрицательными коэффициентами
; 7{г (И > О)-
Следовательно,
- (х,, ф) = 2в (*!, Фг) > о. (П.И)
Из (П.10) и (П.И) получаем
(х-:, Ф) = 0.
2. Из теоремы П.З легко следует известная теорема Куна —
Таккера.
Теорема П.4 (Куна — Таккера). Пусть заданы дифференци-
дифференцируемая функция Р(х) и линейные функции (х, /;) при 1=1,2, ...
. . ., п. Пусть х0 доставляет условный минимум Р (х0) при ограни-
ограничениях
(я, /г) > сг.
Тогда существуют такие числа %1 ^ 0, что выполняются условия:
Ч ((*оЛ) - с,) = 0 ({=1,2 п). (П.12)
Доказательство. Если ЧР (х0) равен нулю, то утвер-
утверждение леммы тривиально, так как можно положить все Я,- равны-
равными нулю.
Занумеруем от 1 до р те ограничения, для которых
(х0, /г) = сг.
340 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
Допустим, что ЧР (х0) ф 0 и утверждение теоремы неверно.
Это значит, что система векторов
-V/1 (*0), Д /р
такова, что — V? (х0) не является базовым вектором системы.
Действительно, если бы вектор — ЧР (х0) был базовым, то су-
существовало бы представление
р
0 = 2 VI-7/" (*•>)'
{=1
а значит, и представление (П.12).
Следовательно, в соответствии с теоремой П.З, существует
вектор ф такой, что
(Ф. П) > 0
для всех г A ^ г ^ I) и
(УР (*0), Ф) < 0. (П.13)
Рассмотрим точку х (I) = х0 -\- Щ. При достаточно малом 1^-0
ограничения не нарушатся, так как при 1^1^/»
(х0 + {ф, /) = { (ф, /г) > 0,
а при р < г < г
(*о. /г) > 0
и, следовательно, по непрерывности
({ф + х0) > 0
при достаточно малых {.
В то же время
Р (х ({)) = Р (х0) + (V/1, ф){ + о (I)
и, следовательно, в силу (П.13) при достаточно малых положитель-
положительных {
Р (х ({)) < Р (х0)
в противоречии с условиями теоремы. Теорема доказана.
Замечание. Теорема обобщается и на случай, когда среди ог-
ограничений есть ограничения вида равенств
(*,,ф) = 0. (П. 14)
Действительно, ограничение (П.14) равносильно двум огра-
ограничениям:
(аг,-, ф) > 0 и (—хг, ф) >0.
Поэтому условия (П. 12) сохраняются, но Ц, соответствую-
соответствующие ограничениям вида равенств, могут быть отрицательными.
В случае, когда функция Р (х) дифференцируема и выпукла,
условия (П. 12) становятся не только необходимыми, но и достаточ-
достаточными условиями минимума.
§ 13. ПРИЛОЖЕНИЕ К ГЛАВЕ Х1у 341
Теорема П.5. Пусть функция Р (х) дифференцируема и вы-
выпукла. Если в точке х0, удовлетворяющей неравенствам
(*о, /;) > с; (г = 1,2,..., п),
выполняются условия (П.12), т. е. существуют такие ^;, чт.о
УР (х0) = 2^/ь
^г ((хо> /г) — сг) = О,
то точка х0 доставляет условный минимум функции Р (х) при ог-
ограничениях
(х,П)>С(- (П.15)
Доказательство. Пусть х0 — точка, о которой гово-
говорится в условии теоремы. Если теорема неверна, то найдется точка
XI, удовлетворяющая (П. 15), такая, что
Р (Х1)< Р (х0). (П.16)
Рассмотрим отрезок
х = х0 + X (XI — х0) при 0 ^ X ^ 1.
В силу выпуклости допустимой области этот отрезок целиком лежит
в пределах ограничений. Кроме того, из выпуклости Р(х) следует
(см. § 2 главы IX), что
Р (XI) - Р (ХО) > (XI - Х0) V Р (ХО)
и, следовательно,
(—УР (хо), (XI — х0)) > 0. (П.17)
Как и раньше, будем считать, что от 1 до р занумерованы
те ограничения, которые достигаются в точке ж0, т. е.
(*о, /г) = Ч A < I < Р),
Тогда, поскольку отрезок х\ -г- х0 целиком лежит в пределах ог-
ограничений, имеем
(и - *о, П) > 0 A < I < Р). (П.18)
Из (П.17) и (П.18), учитывая замечание к теореме П.3, получаем,
что вектор — УР (х0) не является базовым в системе
-Р (х0), Д, . . ., /р
и, следовательно, не существует представления
1=1
(Х( ^ 0) в противоречии с условием теоремы. Теорема доказана.
3. Пусть точка х0 удовлетворяет системе ограничений Г:
(/ь жо) = ^ A < г < р),
(/г, хо) > с; (Р + 1 < I < п),
т. е. первые р ограничений достигаются в точке х0.
342 ГЛ. XIV. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ
Назовем единичный вектор ср допустимым направлением в
точке х, если существует I > 0 такое, что (х0 + ФТ) С Г при
О ^ т ^ {. Нетрудно убедиться, что допустимыми в х0 являются те
и только те направления ср, для которых выполняются неравенства
Условный градиент в точке х0 определяется так. Прежде всего,
находится направление ф0 наибольшего возрастания функции среди
допустимых, т. е.
(У/"-фо)= тах (V/1,ф),
|ф|=1
где максимум берется по допустимым направлениям. При этом мо-
может оказаться, что
(У^-фоХО.
Это означает, что по всякому допустимому направлению функция
не возрастает. В этом случае условный градиент считается равным
нулю.
Если же
(V Р, ф0) > О,
то в качестве условного градиента берется вектор, по направлению
совпадающий с ф0, а по модулю равный (ЧР, ф0).
Таким образом,
утр _ Л?- Фо)Фо> если (V/1, ф0) > О,
у^усл \о, если (УР, ф0) < 0.
Справедлива теорема.
Теорема П.6 Условный градиент в точке х0 представим в виде
г=1
причем
п' ' " - ' " ч (П.20)
и обратно, всякий вектор, удовлетворяющий (П.19), (П.20), яв-
является условным градиентом.
Доказательство. Допустим, что VуслР = 0; тогда
по теореме Куна — Таккера существует представление
р
1=1
и, следовательно,
1=1
Что и требуется.
13. ПРИЛОЖЕНИЕ К ГЛАВЕ XIV 343
Обратно, пусть справедливо (П. 21); в этом случае раз-
разложение (П. 19) может задавать только нулевой вектор. Дей-
Действительно, пусть
р
Ч> = V? - 2 М»,
1 1
к М>, /г) = О,
(*. /г) > 0.
Тогда
Если при этом
ф 1) (V/1 |5) > 0,
то ф/|^| есть допустимое направление, по которому функция Р
возрастает в противоречии с допущением. Таким образом, (-ф, лр) = 0
Допустим теперь, что | ^уС11Р\ > 0. Тогда, как нетрудно убе-
убедиться, направление <р0 совпадает с направлением обобщенного
портрета класса X, состоящего из одного вектора УР, относитель-
относительно класса Ж., состоящего из векторов —/1, . . ., —/р для к = 0.
Действительно, прн этом <р есть единичный вектор, на котором
достигается максимум
(^, Ф)
при ограничениях
(/г-ф)>0,
причем заведомо известно, что а (ф) > 0.
Поэтому в силу теорем, доказанных выше, вектор фо однознач-
однозначно задается разложением
Р
<ро=аУ*-+2 Р,-/,-. (П-22)
3=1
а>0, р,- > 0, р,- (/;, ф0) = 0, (/,-, Фо) > 0.
Умножим равенство скалярно на ф0:
1 = (Фо- Фо) = « (У?, Фо) 4- 2Р,- (/,-, ф0) = а (V/1, Фо),
откуда
1
Поэтому
Vусл^ = Фо (Фо, ЧР) = ЧР + 2р,- (Фо, V/)/,-.
Полагая Я,г = (ф0, УР), получим разложение (П.19). Теорема
доказана.
Глава XV
АЛГОРИТМЫ ОБУЧЕНИЯ
РАСПОЗНАВАНИЮ ОБРАЗОВ,
РЕАЛИЗУЮЩИЕ МЕТОД
ОБОБЩЕННОГО ПОРТРЕТА
В этой главе дано описание алгоритмов обучения рас-
распознаванию образов, строящих разделяющие поверхно-
поверхности методом обобщенного портрета.
С помощью первого алгоритма ОП-1 строится гипер-
гиперплоскость, разделяющая два множества векторов.
Алгоритм ОП-2 предназначен для построения разде-
разделяющей гиперплоскости, минимизирующей число ошибок
разделения. С помощью алгоритма ОП-3 строится кусочно-
линейная разделяющая гиперповерхность. Алгоритмы
ОП-4, ОП-5 предназначены для отыскания разделяющей
гиперплоскости в пространстве минимального числа приз-
признаков.
Алгоритмы ОП-6, ОП-7 строят экстремальную разделя-
разделяющую гиперплоскость и кусочно-линейную поверхность.
Наконец, алгоритмы ОП-8, ОП-9, ОП-10 используют
процедуру «скользящий контроль» для оценки качества
построенной гиперплоскости, построения экстремальной
гиперплоскости и экстремальной кусочно-линейной раз-
разделяющей поверхности.
Кроме того, в этой главе приведен алгоритм разбивки
значений признака па градации.
§ 1. Способы представления информации
В задачах обучения распознаванию образов принято
два способа представления информации — непрерывный
и дискретный. При непрерывном способе представления
все координаты вектора х могут принимать любые значе-
§ 1. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ 345
ния числовой оси. При дискретном способе каждая коор-
координата вектора х может принимать лишь фиксированное
число значений.
Оба способа представления информации имеют как свои
сильные, так и слабые стороны.
Сильной стороной непрерывного способа является точ-
точность задания значений координат. Каждая координата
вектора здесь равна тому значению параметра, которое
было замерено. Однако при таком способе представления
информации для хранения значения каждого параметра
требуется одна ячейка памяти вычислительной машины.
А так как в задачах распознавания ситуация описывает-
описывается большим числом параметров (вектор х имеет размер-
размерность порядка десятков и сотен), то хранение одной ситу-
ситуации в памяти машины требует слишком большого объема
памяти. Кроме того, часто, например в задачах медицин-
медицинской диагностики, ситуации описываются признаками,
которые не имеют точного количественного выражения
(например, надо отразить, что у данного больного повы-
повышена «бледность кожных покровов»). В этом случае при-
принят следующий способ записи такой информации. Дого-
Договариваются, что единица означает наличие данного приз-
признака, нуль — его отсутствие.
Возможен способ записи информации, при котором
кодируется не только наличие или отсутствие некоторого
признака, но и степень проявления признака. Например,
следующие характеристики: «бледность кожного покрова
не выражена», «бледность кожного покрова выражена
слабо», «бледность кожного покрова сильно выражена» —
могут иметь соответствующие коды 100, 010, 001.
Таким образом, наличие качественных признаков опи-
описания объекта предопределяет дискретный способ пред-
представления информации.
В задачах обучения распознаванию образов принято
дискретно кодировать не только признаки, отражающие
качественную характеристику объекта, но и параметры,
которые принимают непрерывные значения. При этом
пользуются следующим способом представления дискрет-
дискретной информации.
Весь диапазон значений параметра разбивается на
ряд градаций. Единицей кодируется /-й разряд кода приз-
признака, если значение параметра принадлежит ;-й градации;
346 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
если же значение параметра не принадлежит /-й градации,
то в /-м разряде проставляется нуль.
Пример. Пусть значение параметра х* принадлежит отрез-
отрезку [—5, +8] и этот отрезок разбивается на пять градаций:
ж < 0; 0 < ж < 2; 2 < х < 4; 4 < х < 6; х > 6.
Кодом 10000 обозначаются величины х < 0, 01000 — величины
0 < х < 2, 00100 — величипы 2 < х < 4, 00010 — величины 4 <^
< х < 6, 00001 — величины х > 6.
Рассмотренный дискретный способ представления ин-
информации замечателен не только тем, что позволяет ком-
компактно записывать информацию. Дискретизация вели-
величины х есть нелинейная операция, с помощью которой век-
вектор х переводится в бинарный вектор х'.
Поэтому увеличение числа градаций при кодировке
значения параметра эквивалентно использованию более
разнообразного класса разделяющих поверхностей в про-
пространстве X. Однако, как было установлено в первой ча-
части книги, чрезмерная емкость класса решающих правил
при ограниченном объеме обучающей последовательности
недопустима и поэтому возникает проблема экстремальной
разбивки на градации непрерывных признаков.
В этом параграфе будет приведен алгоритм опреде-
определения экстремальной разбивки значения признаков на
градации. Принцип, который реализует алгоритм, заклю-
заключается в следующем: необходимо так разбить значения па-
параметра, чтобы оценка неопределенности (энтропии) при
классификации с помощью этого признака была мини-
минимальной или близка к минимальной (оценка энтропии
производится с помощью элементов обучающей последо-
последовательности).
Итак, пусть признак х может принимать значения из
интервала [а <^ х <] Ь] и пусть вектор, обладающий этим
признаком, принадлежит одному? из к классов. Будем
считать, что существуют условные вероятности принадлеж-
принадлежности к каждому классу
Р A | х), . . ., Р (к | х).
Для каждого фиксированного значения признака х = X
может быть определена мера неопределенности (энтропия)
$ 1. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ 347
принадлежности к тому или иному классу. Она равна
к
г=1
Среднее значение по мере Р (х) энтропии вычисляется
так:
к
Н = \ Н (х) Р {х)их = — 2 ^ Р(I|я) 1§2 Р{г\х) Р(х) их.
Пусть теперь параметр х разбит на т градаций. Тогда
средняя энтропия может быть записана в виде
к -с
Н (X) = - 2 2 Р A\ х-) 1& Р A\х}) Р (X}). A5.1)
1=1 3=1
Воспользуемся теперь формулой Байеса
Р (х-1 п Р и)
РР\Х})= рщ • A5-2)
Подставляя A5.2) в A5.1), получим
г=13=1
Подставляя теперь байесовы оценки Р [х] \ г), Р (г), Р (х^,
найденные по обучающей последовательности (см. главу
III), получим
где I (г) — число векторов 1-го класса в обучающей вы-
выборке, ГП] (I) — число векторов 1-го класса, у которых
к
х — Х]\ Ь — 2 I @ —длина выборки.
{=1
Формула A5.3) получена в предположении, что априор-
априорные значения Р (х} | I), Р (I) равновероятно распределены
348 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
на симплексах:
= 1, Р(х}\1)>0;
A5.4)
1 = 1
В более общем случае целесообразно рассмотреть фор-
формулу
к т
V V '
1=1 3=1
X
ах
& х
ак
7'
1=1
, A5.5)
где параметр а определяется характером априорной ин-
информации.
Реализация сформулированного принципа состоит в та-
таком подборе разбивки на градации, чтобы обеспечить ми-
минимум A5.5).
Алгоритм удобно реализовать в следующей форме:
сначала разбить параметр на большое число градаций, а
затем, «склеивая» соседние градации, добиваться мини-
минимизации значения Н (т).
Можно оценить и количество информации /(т) о при-
принадлежности объекта к тому или иному классу, которое
несет сведение о значении параметра
где
/(т)=--#апр-#(т),
_ у* 1A) +а ,„ г @ 4-а
апр- — 2_| Ь + ка 1§2 Ь + ка
1=1
Часто разумно продолжать «склеивать» градации и пос-
после достижения минимума по т функции Я(т), но лишь до
тех пор, пока величина / (т) не уменьшится в 1 — р. раз
(е, так же как и а, — параметры алгоритма).
2. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ 349
ОП-1/1
РазбиВка на
группы
пкоп-1/г
Образование
дыделеннои
группы
Печать ф и о
и 0П~1/3
Нахождение
обобщенного
портрета
Информация с
'неделении
§ 2. Алгоритм построения разделяющей гиперплоскости
Алгоритм ОП-1 предназначен для построения гипер-
гиперплоскости, разделяющей два конечных множества век-
векторов, либо для выяснения того факта, что безошибочное
линейное разделение невозможно.
Данный алгоритм имеет две модификации. В одной из
них он позволяет найти обобщенный портрет при задан-
заданном параметре /с; во второй мо-
дификации алгоритм находит
оптимальную разделяющую ги-
гиперплоскость (см. главу XIV).
Алгоритм строит плоскость, ре-
решая двойственную задачу, как
это было описано в предыдущей
главе. Однако часто длина обу-
обучающей последовательности на-
настолько велика, что обработка
сразу всего материала обучения
привела бы к задаче слишком
высокой размерности. Поэтому
обработка обучающей последо-
последовательности ведется итеративно.
На каждой итерации из обуча-
обучающей последовательности выде-
выделяется группа векторов, кот >-
рую будем называть выделенной
группой, строится разделяю-
разделяющая плоскость для этой группы путем решения двой-
двойственной задачи (либо устанавливается неразделимость).
Затем из группы исключаются векторы, которые входят
в разложение направляющего вектора гиперплоскости
с нулевым весом, и добавляются векторы, неправильно
опознаваемые построенной гиперплоскостью на остав-
оставшейся части обучающей последовательности. После этого
снова обрабатывается выделенная группа. Так продол-
продолжается до тех пор пока
либо после очередной итерации все векторы обуча-
обучающей последовательности не будут опознаны правильно,
либо на очередной итерации не будет установлена не-
неразделимость выделенной группы.
Рис. 25. Блок-схема
алгоритма ОП-1.
350 ГЛ. XV- АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
Блок ОП-1/1
Этот блок подсчитывает количество векторов, данных
на обучение, разбивает их на группы заранее фиксиро-
фиксированной длины М и определяет число ц, получившихся
групп. Обычно в каждой группе встречаются векторы как
первого, так и второго классов- Последняя группа может
быть неполной.
Блок ОП-1/2
Этот блок ведает формированием выделенной группы
векторов.
1. На первой итерации выделенная группа образуется
из векторов первой группы, которая возникнет после раз-
разбиения материала обучения блоком ОП-1/1.
2. На очередной, 1-й, итерации, т. е. при очередном об-
обращении к^блоку ОП-1/2, блок просматривает векторы
первых г групп, если число г не превосходит число групп
[х, или весь материал обучения в противном случае. При
этом к выделенной группе добавляются те векторы, кото-
которые неправильно опознаются с помощью решающего пра-
правила, построенного на предыдущей (I — 1)-й итерации,
или опознаются правильно, но с недостаточным превы-
превышением порога.
В зависимости от того, используется ли алгоритм
для построения обобщенного портрета при заданном па-
параметре к или для построения оптимальной разделяющей
гиперплоскости, добавление вектора идет по следующим
правилам:
а) в случае построения обобщенного портрета вектор
заносится в выделенную группу, если
(х, я|э) < 1 — б и х е X,
или
где -ф — обобщенный портрет, построенный на пре-
предыдущей итерации, б и к — заданные параметры,
причем
$ 2. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ 351
б) в случае построения оптимальной разделяющей
гиперплоскости вектор х заносится в выделенную группу,
если
(х, 1}з) < 1 + с — е и 1ЕХ|
или
(X, 1|з) > — 1 + с 4- е и 16^,
где яр и с направляющий вектор и порог разделяющей пло-
плоскости, построенной на предыдущей итерации.
Если при просмотре всего материала обучения ока-
оказывается, что блок не выделяет ни одного нового вектора,
то гиперплоскость, построенная на предыдущей итера-
итерации, совпадает с искомой, ее параметры выводятся на
печать и алгоритм прекращает работу.
Блок ОП-1/3
Блок строит обобщенный портрет либо оптимальную
решающую плоскость для выделенной системы векторов
путем решения двойственной задачи. Подробнее обе мо-
модификации (ОП-1/За и ОП-1/36) описаны ниже. В резуль-
результате работы блока либо устанавливается неразделимость
векторов системы (в этом случае алгоритм прекращает
работу, сообщая о неудаче), либо вычисляются направ-
направляющий вектор гиперплоскости 1}> и его разложение
а Ь
V = 2 «Л - 2 Ы A5-6)
1=1 3=1
по векторам выделенной группы (а в случае оптимальной
гиперплоскости определяется еще и константа с).
Блок ОП-1/4
Этот блок исключает из выделенной группы те векторы,
которые входят в разложение A5.6) с нулевым весом и
передает управление блоку ОП-1/2.
Перейдем к подробному описанию блока ОП-1/3 в двух
модификациях.
352 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО НСЛ'ТГКТА
Блок ОП-1/За
Нахождение обобщенного портрета модифицированным
методом сопряженных градиентов (рис. 26).
нет
вычисление
градиента
г
Восстановление
размернисти
1
начальные
условия
нет
да .
Печать <р
\ нет
Вычисление
я,/
♦
10
Вычисление <р
11
Вычисление Ь„р^
11
Вычисление Ь
да
нет
да
Т
16
Вычисление IV
—
15
Вычисление ф
*-
13
Снижение
размерности
| I
п
Вычисление а,/
Информация о неделении
Рис. 26.
Целью работы этого блока является нахождение в по-
положительном квадранте максимума функции
а Ь
[V (а, Р) = 2 <** - * 2 Р; - 4" №. 10.
где
= 2 аЛ — 2 Р;гл
3=1
§ 2, ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ 353
а — число векторов первого класса, Ь — число векторов
второго класса в выделенной группе.
Каждому вектору хг и г у ставится в соответствие бинар-
бинарная переменная Лг (соответственно йу) *). Кроме того,
номер текущего шага обозначен через I.
В этом блоке:
1. Устанавливается ч|) @) = 0, -ф @) = 0, I = 0.
2. Полагается для всех I и / йг = 1, йу =1 (восстанов-
(восстановление размерности пространства).
3. ^ =^+ \.
4. Производится вычисление градиента функции
}У (а, Р) и квадрата его модуля в соответствующем коорди-
координатном подпространстве по формулам
<*, (*) = [1 - A|з (* - 1), хг)] 6{,
Р'у («) = К* С - 1). *у) - И ^-
^2 Ц) = 24? (*) + 2$ (*)•
5. Проверяется условие: для всех г и/
или а; (г) < е и аг (г — 1) = 0, A5.7)
или р;- (г) < б и Ру (г - 1) = 0;
6. Если условия A5.7) выполнены и
а Ь
2 ^г + 2 Л} = а + Ь,
т. е. найден максимум функции в положительном квад-
квадранте всего пространства, то блок заканчивает работу,
вектор -ф (* — 1) принимается за обобщенный портрет
1}з0 с разложением
3=1
*) С помощью этих переменных задаются координатные прост-
пространства, в которых ведется поиск.
354 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
7. Если условия A5.7) выполнепы и
а Ъ
2 й\ + 2 Л, < а + Ь
1=1 1-Х
(максимум найден в подпространстве), осуществляется
переход к п. 2 (для восстановления размерности).
8. Если условие A5.7) не выполнено, исполняется п. 9.
9. Если ^ B — 1) =0, то
а, @ = л, (о, Р1 (*) = р;- @;
в противном случае
а, (*) = а, @ + б (г) а, (« - 1),
Р1 (*) = Р^ @ + б @ р, (^ - 1),
где
10. Находится вектор
Ь
г=1 г=1
11. Вычисляется пробная величина шага
12. Определяется истинная величина шага
где минимум берется лишь по тем I и /, для которых а, <0
или р^ < 0.
13. Если минимум достигается при к = кцроб, то ис-
исполняется п. 14, если же минимум достигается при
то устанавливается й,- = 0 (й^ = 0) и яр B) = 0 и далее
исполняется п. 14.
§ 2. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ 355
14. Находятся новые значения коэффициентов а и |3:
щ(г) =а, (* — 1) + Аи, (*),
р . (г) = р. (г - 1) + Ару (*).
15. Находится новый вектор
' 1|з{I — 1) + йлр (г), если А =
' еСЛИ
16. Осуществляется проверка на неразделимость груп-
группы векторов. Для этого вычисляется значение функции
а Ь
ш (а (о, ^ @) = 2 а< @ - * 2 Р; о -4-01' (*), ^ (*))•
Если И7(а, Р) <^ 5, осуществляется переход к п. 3),
в противном случае принимается решение о неразделимо-
неразделимости группы векторов и блок заканчивает работу.
Модификация ОП-1/36
Эта модификация предназначена для отыскания опти-
оптимальной разделяющей гиперплоскости путем решения
двойственной задачи модифицированным методом сопря-
сопряженных градиентов (рис. 27).
От ОП-1/За отличаются только первые пункты.
1. Устанавливается
1|? @) = 0, Щ @) = 0, I = 0.
2. Полагается для всех I и /
й, =1; 1] =1.
Кроме того, вводится бинарная переменная д и устанав-
устанавливается
д= 1
(указатель работы во всем пространстве или в гиперпро-
гиперпространстве).
3. I = 1-\- 1.
356 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
Начальное
услоВа'я
Восстансдление
размерности
4.1
Вычисление
градиента
4.5
Вычисление
условного
градиента.
нет
да
информация о неделени
Рис. 27,
§ 2. ПОСТРОЕНИЕ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ 357
4.1. Находится градиент функции И7 (а, Р):
<*; (о = 1 - (ж,, ^ (* - !))>
E; @ =(*,, ^(*— 1)) -Ь 1.
4.2. Если д = 1 исполняется 4.3, в противном слу-
случае 4.4.
4.3. а) Определяются функции от аргумента р
1а1{*) + Р, если а{({— 1)">0,
щ (р) =
{Р{а;,{1) + р) если а{(* —1)<0,
РДО-Р, если
К (&'(*)-/>). если р;(*-1)<0,
где
' (х) - \0 при х < О,
и функция
1=1 3=1
б) Вычисляются числа
Ьг = Ь (- аО, ^ = Ь (р:).
в) Если все Ьг и Ь;- < 0, то устанавливается
^ =0
для всех у, при которых |3,- = 0. Осуществляется переход
к 4.4.
г) Если не все Ьг, Ь1 < 0, то находится
Ьа = тш (Ц, Ц),
где минимум берется лишь по тем г и у, для которых
^>0и^> 0.
д) Устанавливается
й; = 0, если аг = 0 и Ь; ^ Ьо,
й] = 0, если р,- = 0 и Ь] < Ьо.
Далее исполняется 4.4.
358 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
4.4. Вычисляется
а Ъ
— У а'-(()а. ±у р'(«) I.
1=1 3=1
1=1 з'=1
4.5. Вычисляется условный градиент функции XV
*> (*) = (*; (*) + ^ (*)) ^,
Р; @ = (Й (*) + ^ (*)) ^-
4.6. Вычисляется квадрат условного градиента
5. Проверяются условия
I 4< (*) I < б, A5.8)
I Р; (*) I < Б.
6. Если условия A5.8) выполнены и д = 1, то услов-
условный максимум функции IV (а, Р) при ограничениях
A4.27) найден. Вектор
1=1 3=1
принимается за направляющий вектор т]з0 оптимальной
гиперплоскости. Константа
7. Если условия A5.8) выполнены и д = 0, то услов-
условный максимум найден только в координатном подпростран-
подпространстве. В этом случае осуществляется переход к п.2 (восста-
(восстановление размерности).
8. Если условия A5.8) не выполнены, то устанавли-
устанавливается
д =0
и исполняется п. 9.
Остальные пункты совпадают с модификацией ОП-1/За.
§ 3, АЛГОРИТМ, МИНИМИЗИРУЮЩИЙ ЧИСЛО ОШИБОК 359
§ 3. Алгоритм построения разделяющей гиперплоскости,
минимизирующей число ошибочно классифицируемых
векторов
В результате работы программ ОП-1 либо будет по-
построена разделяющая гиперплоскость, либо будет установ-
установлено, что построить разделяющую гиперплоскость невоз-
невозможно. В последнем случае необходимо построить разде-
разделяющую гиперплоскость, минимизирующую число не-
неправильно классифицируемых векторов.
Такая задача принципиально может быть решена, од-
однако требует достаточно большого объема вычислений.
В самом деле, если установлено, что а векторов первого
класса и Ъ векторов второго класса не могут быть разде-
разделены гиперплоскостью, то возникает естественная идея
исключить из обучающей последовательности минималь-
минимальное число векторов с тем, чтобы оставшиеся векторы
могли быть разделены гиперплоскостью.
Найти минимальное число векторов, которые надо
исключить, можно с помощью следующей процедуры.
Исключить из обучающей последовательности последо-
последовательно по одному все векторы и каждый раз пытаться
оставшееся множество векторов разделить гиперплоско-
гиперплоскостью. При этом либо однажды разделяющая гиперплос-
гиперплоскость будет построена, либо будет установлено, что разде-
разделение обучающей последовательности с одной ошибкой
невозможно. В последнем случае может быть предпринята
попытка построить разделяющую гиперплоскость, которая
делит обучающую последовательность с двумя ошибками.
После С\ последовательных попыток разделения обу-
обучающей последовательности без двух элементов будет
либо найдена такая гиперплоскость, либо установлено,
что такой гиперплоскости невозможно построить.
Тогда может быть предпринята попытка построить
гиперплоскость, с помощью которой на материале обучаю-
обучающей последовательности совершается только три ошибки.
Для выяснения возможности построения такой гиперпло-
гиперплоскости необходимо, вообще говоря, С\ раз использовать
программу ОП-1.
Ясно, что, действуя согласно этой процедуре, в конце
концов, можно будет найти гиперплоскость, минимизирую-
минимизирующую число ошибок на материале обучения.
360 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
Однако рассмотренный алгоритм требует организации
перебора, соизмеримого с полным перебором по всем
возможным подмножествам множества обучающих векторов.
Для современных вычислительных машин такое количе-
количество операций является чрезмерным.
Поэтому для решения этой задачи используются эври-
эвристические приемы, позволяющие сократить число вычис-
вычислений.
Алгоритм ОП-2 использует следующий стандартный
эвристический прием: из множества векторов обучающей
последовательности исключается один элемент, «наиболее
препятствующий разделению», затем, если разделение
невозможно, из оставшегося множества исключается еще
один элемент и т. д.
Специфика алгоритма заключается в определении эле-
элемента, «наиболее препятствующего разделению множеств».
В качестве такого элемента определяется вектор х (или
х), неправильно классифицируемый построенной к мо-
моменту останова гиперплоскостью, и наиболее далеко от
нее отстоящий, т. е. вектор х (или %), которому соответст-
соответствует максимальное значение а или р.
Программа ОП-2 исключает из множества векторов
вектор, «наиболее препятствующий разделению», делит
оставшееся множество векторов и, если разделение все
еще невозможно, исключает очередной вектор, делит ос-
ставшиеся и т. д.
Программа ОП-2 включает в себя как составную часть
ОП-1.
§ 4. Алгоритм построения кусочно-линейной
разделяющей поверхности
Во многих приложениях возникает необходимость раз-
разделить элементы обучающей последовательности с помощью
гиперповерхности, образованной кусками гиперплоско-
гиперплоскостей. Известно, что если среди векторов обучающей после-
последовательности нет двух тождественных векторов, принад-
принадлежащих разным классам, то всегда найдется такая раз-
разделяющая гиперповерхность, составленная пз кусков
гиперплоскостей, которая безошибочно разделит векторы
обучающей последовательности.
§ 4. ПОСТРОЕНИЕ КУСОЧНО-ЛИНЕЙНОЙ ПОВЕРХНОСТИ 361
Однако желательно, чтобы разделяющая гиперповерх-
гиперповерхность состояла из минимального числа кусков гиперплос-
гиперплоскостей.
Принципиально можно предложить переборную схе-
схему, с помощью которой, в конце концов, удастся построить
разделяющую гиперповерхность, образованную минималь-
минимальным числом кусков гиперповерхностей. Однако ее реали-
реализация требует слишком большого объема вычислений.
Поэтому при решении такой задачи также применяют-
применяются эвристические приемы. В частности, используется
тот же стандартный прием, что и в алгоритме ОП-2.
Сначала строится одна, в некотором смысле «наилучшая»,
разделяющая гиперплоскость. Затем к ней достраивается
еще одна «наилучшая» гиперплоскость и т. д.
Алгоритм ОП-3 основан на том, что в качестве наилуч-
наилучшей гиперплоскости выбирается такая ориентированная
гиперплоскость, которая делит обучающую последователь-
последовательность с минимальным числом ошибок (гиперплоскость
строится с помощью алгоритма ОП-2). Затем эта гипер-
гиперплоскость фиксируется и к ней достраивается еще одна
(также с помощью алгоритма ОП-2).
Достраивается «наилучшая» разделяющая гиперплос-
гиперплоскость по следующему правилу.
Пусть к моменту времени т построена (с помощью
ОП-2) разделяющая гиперплоскость, которая на части
векторов обучающей последовательности делает ошибки.
Образуем с помощью построенной разделяющей гипер-
гиперплоскости и векторов обучающей последовательности но-
новый массив векторов размерности т + 2 по следующему
правилу.
Каждому вектору х обучающей последовательности
становится в соответствие вектор х в пространстве раз-
размерности т -\- 2, у которого первые т координат совпа-
совпадают с координатами вектора х, а77г+1и7?г + 2 коорди-
координаты суть соответственно 1,0, если вектор х лежит по одну
сторону от построенной гиперплоскости (т.е. (х, $г) )> с),
или 0,1, если вектор х лежит по другую от нее сторону
((ам|>г)<с).
Полученное множество векторов {х} проиндексируем
по правилу: вектор х относится к первому классу, если
соответствующий ему вектор х принадлежал первому
362 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
классу, вектор х относится ко второму классу, если
вектор х принадлежал ко второму классу.
Разделим теперь множество векторов {2} на два клас-
класса с помощью гиперплоскости
(х,Ц) =с.
В пространстве размерности т этому разделению соответ-
соответствует разделение векторов {х} с помощью гиперповерх-
гиперповерхности, составленной из кусков гиперплоскостей с направ-
направляющими векторами 1|зх и 1|за (вектор 1}з2 коллинеарен
т-мерному вектору, образованному первыми т координа-
координатами вектора ар).
Если же и с помощью гиперповерхности, образованной
кусками двух гиперплоскостей, безошибочное разделение
невозможно, то обучающая последовательность делится
с помощью гиперповерхности, образованной из кусков
трех гиперплоскостей, для чего, аналогично предыдуще-
предыдущему, образуется множество векторов размерности т + 4,
которое делится гиперплоскостью.
Классификация векторов с помощью построенной раз-
разделяющей поверхности, образованной кусками гиперплос-
гиперплоскостей, происходит по следующему правилу.
Сначала по вектору х и первой разделяющей гипер-
гиперплоскости вычисляется вектор $. Затем в новом простран-
пространстве Ет+г с помощью второй разделяющей гиперплоско-
гиперплоскости строится вектор х и т. д. Наконец, вектор относится
к первому классу, если (х, ■$) ^> с, и ко второму, если
(х, ф) < с.
Алгоритм ОП-3 включает в себя как составную часть
ОП-2.
§ 5. Алгоритмы построения разделяющей гиперплоскости
в пространстве минимального числа признаков
Алгоритм ОП-4 предназначен для поиска минималь-
минимальной размерности, в котором множества векторов обучаю-
обучающей последовательности могут быть разделены гиперпло-
гиперплоскостью так, чтобы расстояние между выпуклыми обо-
оболочками множеств было больше р0.
Так же как и две предыдущие задачи, эта задача в прин-
принципе может быть точно решена, однако точное ее решение
5. АЛГОРИТМЫ, МИНИМИЗИРУЮЩИЕ ЧИСЛО ПРИЗНАКОВ 363
сопряжено с необходимостью организации полного пере-
перебора по всем возможным подпространствам исходного
пространства. Для достаточно большой размерности ис-
исходного пространства (~ 10—30) такой перебор неприем-
неприемлем и поэтому, так же как и в предыдущих случаях, кон-
конструктивное решение задачи сопряжено с заменой пол-
полного перебора эвристической схемой поиска решения.
Примем все тот же эвристический прием поиска реше-
решения: из множества признаков исключаем «наименее ин-
информативный признак»; затем из оставшегося множества
опять исключаем наименее информативный признак и т. д.
Процесс исключения признаков будем продолжать до тех
пор, пока не выяснится, что множество векторов обучаю-
обучающей последовательности не может быть разделено на два
класса.
Таким образом, поиск минимального подпространства
определяется введенным понятием «наименее информатив-
информативный признак». Определим его следующим образом. Пусть
в пространстве Еп {п признаков) заданы два множества
векторов обучающей последовательности — множество
векторов хг, . . ., ха и множество векторов Хг, . . ., Жь.
В пространстве Еп могут быть построены выпуклая
оболочка множества хг, . . ., ха и выпуклая оболочка
множества хъ . . , хь. Пусть расстояние между выпуклы-
выпуклыми оболочками будет р (Еп).
Рассмотрим теперь пространство Еп-1{к), образованное
п — 1 признаком (исключен признак к). В этом простран-
пространстве могут быть построены выпуклые оболочки множеств
{х} и {х} (векторы % и X суть проекции векторов хигна
подпространство Еп_х (к)) и вычислено расстояние между
выпуклыми оболочками. Пусть оно равно р (Еп-\(к)). Если
расстояние между оболочками больше р0, то будем считать,
что в этом пространстве возможно построение разделяю-
разделяющей гиперплоскости, в противном случае будем пола-
полагать, что разделение гиперплоскостью векторов {х} и
{%} невозможно.
Рассмотрим теперь величину Ар (Е^^к)) = р (Еп) —
— р(Еп-1(к)). Эта величина показывает, насколько умень-
уменьшится расстояние между выпуклыми оболочками векто-
векторов в пространстве Еп_х(к) (с исключением к-то признака).
Будем считать тот признак наименее информативным,
364 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
с удалением которого расстояние между выпуклыми обо-
оболочками уменьшается на минимальную величину.
Таким образом, для того чтобы организовать поиск
подпространства минимальной размерности, в котором
возможно разделение двух множеств векторов обучающей
последовательности по предложенной эвристической схе-
схеме, надо уметь определять расстояния между выпуклыми
оболочками двух множеств векторов. В этом случае, для
того чтобы исключить один из п признаков (или устано-
установить, что исключение невозможно), надо определить рас-
расстояние между выпуклыми оболочками в ге-мерном под-
подпространстве. Определить расстояние между выпуклыми
оболочками можно с помощью программы ОП-1 (где ищет-
ищется оптимальная разделяющая гиперплоскость).
Расстояние между выпуклыми оболочками определяет-
определяется по формуле
где 1}з — обобщенный портрет, соответствующий оптималь-
оптимальному к0. Однако, даже несмотря на то, что для поиска
«наименее информативного признака» происходит п раз
вычислять расстояние между выпуклыми оболочками,
такой способ исключения признака не является чрезмер-
чрезмерно трудоемким.
Удобно проводить поиск наименее информативного из
признаков по следующей схеме.
Сначала в пространстве Еп (п признаков) строится оп-
оптимальная разделяющая гиперплоскость и определяется
расстояние между выпуклыми оболочками двух множеств
(это делается с помощью соответствующей модификации
программы ОП-1). Пусть 1}з — найденный обобщенный
портрет, ос-р . . ., аа; рг, . . ., рь — соответствующие ко-
коэффициенты разложения вектора т|) по информативным
векторам обучающей последовательности.
Спроектируем вектор 1}з и векторы обучающей последо-
последовательности на подпространство 2?„_г(р).Для этого доста-
достаточно в те разряды ячеек, где записаны значения р-й
координаты вектора 1}з и векторов х, (х), заслать нули.
Затем построим оптимальную разделяющую гипер-
гиперплоскость в подпространстве Еп-1{р) (также с помощью
ОП-1). Однако за начальные условия следует брать не
§ 6. ПОСТРОЕНИЕ ЭКСТРЕМАЛЬНОЙ ПОВЕРХНОСТИ 365
ах = . . . = аа = рг, . . ., рь = 0, а те значения ссг, . . .
..., аа и рг, . . ., Рь! которые были найдены при построении
разделяющей гиперплоскости в пространстве размерно-
размерности тг. При таких начальных условиях отыскание вектора
произойдет значительно быстрее.
Программа ОП-4 использует как составную часть про-
программу ОП-1.
Алгоритм ОП-5 используется для поиска минималь-
минимальной размерности, в котором разделяющая гиперплос-
гиперплоскость делит обучающую последовательность, совершая не
более I ошибок (г — параметр алгоритма). Структура
алгоритма ОП-5 аналогична структуре алгоритма ОП-4.
Разница заключается лишь в том, что алгоритм ОП-4 пре-
прекращает поиск соответствующего подпространства, когда
выясняется, что построение разделяющей гиперплоскости
становится невозможным, в то время как алгоритм ОП-5
исключает I векторов, «препятствующих» построению
разделяющей гиперплоскости, и только после этого пре-
прекращает поиск минимального подпространства.
В соответствии с этим алгоритм ОП-5 использует
в качестве составной части не алгоритм ОП-1, а ОП-2.
§ 6. Алгоритм построения экстремальной линейной
разделяющей поверхности
Алгоритм ОП-6 реализует идею упорядоченной мини-
минимизации риска при построении гиперплоскости, разделяю-
разделяющей два множества векторов {х} и {х} (см. главу VI).
С помощью этого алгоритма строится гиперплоскость, раз-
разделяющая два множества векторов в подпространстве Ет
исходного пространства Еп, в котором достигается минимум
величины
й = тш [т + 1, [Щ + 2, К + 1) , A5.9)
где т — размерность подпространства Ет, И — диаметр
векторов в Ет, р — расстояние между выпуклыми обо-
оболочками векторов в Ет, К — число векторов, участвовав-
участвовавших в разложении вектора 1}з с ненулевым весом.
Найти минимум A5.9), не используя полный перебор
по подпространствам, невозможно, поэтому в алгоритме
используется тот же прием локального поиска минимума,
который использовался выше.
366 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
Пусть в начальный момент ситуация описывается
«-мерным бинарным вектором, который образован раз-
разбивкой т параметров на градации A-й параметр имеет
д{ градаций). На каждом шаге алгоритм ищет такой спо-
способ «объединения» соседних градаций одного параметра,
чтобы максимально увеличить величину критерия й.
Для этого в векторах обучающей последовательности
вместо координат Т; и Т;+1 (обе координаты соответствуют
различным градациям одного параметра) определяется
новая координата т* по правилу
т. е. координата т* принимает значение единица, если
одна из координат тг или тг+1 равна единице, нуль, если
одновременно тг и т;+1 равны нулю. Если в результате
многократного объединения градаций параметр кодиру-
кодируется только одной градацией, то он исключается из рас-
рассмотрения (кодировка параметра одной градацией в слу-
случае, если исходная кодировка проводилась рассмотренным
в § 1 способом, означает, что всегда значение этой единст-
единственной градации будет равна единице). Для каждого па-
параметра возможны дг — 1 способов объединения.
Таким образом, для установления одного оптималь-
т
ного «объединения» проводится 2 (<?г — 1) построений оп-
г=1
тимальных разделяющих гиперплоскостей (построение
оптимального обобщенного портрета необходимо для по-
построения критерия сГ).
Итак, уменьшение размерности исходного пространст-
пространства на единицу в этом алгоритме требует построения боль-
большого числа разделяющих гиперплоскостей, однако постро-
построение каждой разделяющей гиперплоскости может быть
проведено довольно быстро. Для этого надо в исходном
пространстве построить оптимальную разделяющую ги-
гиперплоскость. Пусть такая гиперплоскость есть (х,1}з) = с,
где вектор 1}з разлагается по векторам хх, • . ., ха; X, . . ., Хь
с коэффициентами аг, . . ., аа; рг, . . ., рь. Теперь, после
объединения двух градаций, для построения оптимальной
разделяющей гиперплоскости в новом пространстве сле-
следует в качестве начальной группы векторов выбрать
векторы, соответствующие векторам х\, . . ., х^х^, . . ., Х*ь,
§ 7. ЭКСТРЕМАЛЬНАЯ КУСОЧНО-ЛИНЕЙНАЯ ПОВЕРХНОСТЬ 367
а в качестве начальных условии взять соответствующие
значения аг, . . ., аа; р1( . . ., рь.
В результате работы программы ОП-6 должно быть
найдено экспериментальное подпространство, в котором
будет построена оптимальная разделяющая гиперплос-
гиперплоскость. Программа ОП-6 включает в себя как составную
часть программу ОП-1.
§ 7. Алгоритм построения экстремальной
кусочно-линейной разделяющей поверхности
Алгоритм ОП-7 подробно описан в § 11 главы VI.
Идея алгоритма состоит в том, что каждый раз для клас-
классификации вектора х строится свое экстремальное
решающее правило. Для этого с помощью метрики р (х, у)
упорядочиваются элементы обучающей последовательно-
последовательности по близости к вектору х.
Затем рассматривается сначала экстремальная гипер-
гиперплоскость, построенная по двум элементам обучающей
последовательности, затем по трем элементам, и, наконец,
гиперплоскость, построенная по I элементам. В каждом
случае получим свою оценку качества построенной гипер-
гиперплоскости. Оценка пропорциональна
/, А й Aп 2г — 1п
[п, I) —
I '
где Л определяется A5.9). Естественно считать ту гипер-
гиперплоскость наилучшей, для которой величина V (й, Г)
минимальна.
Таким образом, алгоритм построения экстремальной
кусочнолинейной разделяющей гиперповерхности экви-
эквивалентен построению для каждого вектора своей раз-
разделяющей гиперплоскости и состоит в следующем:
1) для каждого вектора, подлежащего классификации,
производится упорядочение элементов обучающей после-
последовательности;
2) выбирается экстремальный объем выборки и стро-
строится соответствующая разделяющая гиперплоскость.
При этом может оказаться, что экстремальная кусоч-
кусочно-линейная разделяющая гиперповерхность есть гипер-
гиперплоскость. Алгоритм ОП-7 включает в себя как составную
часть алгоритм ОП-6.
368 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
§ 8. Алгоритм построения разделяющей гиперплоскости
с оценкой ее качества методом скользящего контроля
Алгоритм ОП-8 предусматривает одновременно с по-
построением обобщенного портрета оценку его качества
методом скользящего контроля.
Согласно процедуре скользящего контроля оценка ли-
линейного решающего правила должна проходить следу-
следующим образом. Сначала из обучающей последовательно-
последовательности изымается первый элемент, а по остальным I — 1
элементам строится решающее правило, затем с помощью
построенного решающего правила классифицируется изъя-
изъятый и не участвовавший в обучении вектор. Затем этот век-
вектор возвращается в обучающую последовательность, а
из нее исключается второй элемент. Вновь по I — 1 эле-
элементам обучающей последовательности строится обобщен-
обобщенный портрет, а этот исключенный элемент классифици-
классифицируется и т. д. Всего происходит I исключений векторов и I
классификаций исключенных векторов. Отношение числа
правильно опознанных исключенных векторов к I характе-
характеризует математическое ожидание качества решающего
правила, построенного по обучающей последовательности
длины I.
В результате работы алгоритма ОП-8 кроме разделяю-
разделяющей гиперплоскости будет найдена еще оценка.
Однако ввиду особенностей метода «обобщенного порт-
портрета» процедура проведения скользящего контроля мо-
может быть упрощена.
В самом деле, согласно главе XIV, вектор 1|з, задающий
направление разделяющей гиперплоскости, образуется ли-
линейной комбинацией части векторов обучающей последо-
последовательности. Эти векторы обучающей последовательности
назывались крайними. Напомним, что среди векторов обу-
обучающей последовательности крайними векторами для по-
построенной разделяющей гиперплоскости назывались те,
на которых достигалось равенство
или
(X], 1|з) = к,
а крайними векторами обучающей последовательно-
последовательности — остальные векторы, -г, е. те, для которых
§ 8. ОЦЕНКА МЕТОДОМ СКОЛЬЗЯЩЕГО КОНТРОЛЯ 369
выполнялось неравенство
(*„1Ю>1
или
(Х}, 1|3) < к.
Поэтому, если удалить из обучающей последовательно-
последовательности вектор, который заведомо не является крайним, то,
во-первых, по такой укороченной обучающей последо-
последовательности будет построена та же самая разделяющая
гиперплоскость, а во-вторых, построенная разделяющая
гиперплоскость будет правильно классифицировать уда-
удаленный из обучающей последовательности вектор.
Таким образом, в нашей случае заранее известно, что
при проведении скользящего контроля все не крайние
векторы обучающей последовательности будут опознаны
правильно и поэтому скользящий контроль следует про-
проводить только на крайних векторах. Это обстоятельство
значительно сокращает время проведения скользящего
контроля (обычно число крайних векторов в несколько
раз E—7 раз) меньше числа всех векторов обучающей
последовательности).
Кроме того, программу скользящего контроля удобно
реализовать по такой схеме.
1. Сначала по обучающей последовательности строит-
строится разделяющаяся гиперплоскость (программа ОП-1).
В результате построения будут найдены векторы т!р,
крайние векторы хх, . . ., ха; хх, . . ., хь и соответствую-
соответствующие веса аи . . ., аа; рг, . . ., рь.
2. Затем из множества крайних векторов исключается
первый крайний вектор (этот вектор исключается также
и из обучающей последовательности). На место исклю-
исключенного крайнего вектора х записывается ближайший
к нему вектор х* обучающей последовательности.
3. Строится новая разделяющая гиперплоскость, при-
причем в качестве начальных условий выбирается вектор 1}з,
полученный как линейная комбинация векторов хг, . . ., х*,
..., ха; хг, ..., хь (здесь вектор х* заменил вектор х) с весами
<хХ1 . . ., аа; рг, . . ., Рь- При таких начальных условиях
поиск новой разделяющей гиперплоскости проводится
значительно быстрее.
370 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
4. С помощью построенной разделяющей гиперплос-
гиперплоскости проводится классификация исключенного вектора.
Затеи исключается второй крайний вектор. Он заме-
заменяется ближайшим из оставшихся, образуются соот-
соответствующие начальные условия, ищется новая разделяю-
разделяющая гиперплоскость, классифицируется исключенный
крайний вектор и т. д.
Алгоритм ОП-8 использует алгоритм ОП-1.
§ 9. Алгоритмы построения экстремальных разделяющих
гиперповерхностей с помощью процедуры
скользящий контроль
Алгоритм ОП-9 предназначен для построения гипер-
гиперплоскости в экстремальном подпространстве признаков,
т. е. преследует те же цели, что и алгоритм ОП-6. Разница
заключается в том, что при поиске экстремального решаю-
решающего правила в алгоритме ОП-6 использовалась верхняя
оценка качества решающего правила в соответствующих
подпространствах, в то время как в алгоритме ОП-9 оцен-
оценка качества решающего правила проводится методом
скользящего контроля.
Схема алгоритма ОП-9, таким образом, аналогична
схеме алгоритма ОП-6. В исходном бинарном пространст-
пространстве методом перебора ищется такое «объединение» соседних
градаций параметра, при котором «качество» полученного
решающего правила наилучшее. Оценка качества, как
уже указывалось, проводится методом скользящего конт-
контроля (а не по формуле A5.9), как в алгоритме ОП-6).
Алгоритмически это осуществляется следующим образом;
1) объединяются соседние градации параметра (пере-
(перекодируются аналогично ОП-6 векторы обучающей после-
последовательности) ;
2) строится разделяющая гиперплоскость (ОП-1);
3) оценивается качество построенной разделяющей
гиперплоскости методом скользящего контроля (ОП-8);
4) выбирается такое объединение градаций, при кото-
котором качество получаемой гиперплоскости наивысшее;
5) процесс объединения градаций продолжается до тех
пор, пока любое объединение не приведет к ухудшению
качества получаемой разделяющей гиперплоскости (при
этом, если в ходе объединения градаций какой-либо пара-
§ 10. О РАБОТЕ С АЛГОРИТМАМИ 371
метр кодируется только одной градацией, то этот пара-
параметр исключается).
Алгоритм ОП-9 включает в себя как составную часть
алгоритм ОП-8.
Алгоритм ОП-10 аналогичен алгоритму ОП-7. С его
помощью, так же как и с помощью ОП-7, строится экстре-
экстремальная кусочно-линейная разделяющая гиперповерх-
гиперповерхность. Отличие заключается лишь в том, что в этих алго-
алгоритмах по-разному оценивается качество отыскиваемой
гиперплоскости: в алгоритме ОП-7 используется оценка
сверху, с помощью формулы, в то время как в алгоритме
ОП-10 качество оценивается методом скользящего конт-
контроля.
Алгоритм ОП-10 реализует такую последовательность
операций:
1) упорядочиваются элементы обучающей последова-
последовательности по расстоянию до вектора х, подлежащего клас-
классификации;
2) для обучающей последовательности строится экст-
экстремальная гиперплоскость и оценивается методом сколь-
скользящего контроля ее качество;
3) определяется гиперплоскость, построенная по та-
такому объему выборки, для которого оценка качества най-
найденного решающего правила наилучшая;
4) с помощью найденного правила классифицируется
вектор.
Алгоритм ОП-10 включает в себя как составную часть
алгоритм ОП-9.
§ 10. О работе с алгоритмами
Выше была рассмотрена группа алгоритмов, реализую-
реализующих метод обобщенного портрета. Среди алгоритмов
группы есть алгоритмы, учитывающие достаточно тонкие
критерии построения разделяющих поверхностей, и алго-
алгоритмы, использующие простые критерии. Естественно, что
первые требуют для своей реализации больших вычисли-
вычислительных мощностей, чем вторые.
Самым простым в реализации является алгоритм ОП-1,
строящий обобщенный портрет для заданного фиксиро-
фиксированного к (к — параметр алгоритма). Наиболее слож-
сложным является алгоритм ОП-10, который строит экстре-
372 ГЛ. XV. АЛГОРИТМЫ МЕТОДА ОБОБЩЕННОГО ПОРТРЕТА
мальные кусочно-линейные разделяющие поверхности,
используя оценку «скользящий контроль».
Какой же алгоритм выбрать для решения конкретной
задачи? Выбор того или иного алгоритма зависит от раз-
разных причин. Если заранее известен весь материал экзаме-
экзаменационной последовательности и имеются достаточно мощ-
мощные вычислительные средства, то, вероятно, разумней
всего использовать алгоритм ОП-10. Этот алгоритм строит
экстремальные кусочно-линейные решающие прави-
правила, пытаясь полностью учесть особенности данной кон-
конкретной задачи. При этом теоретически не исключена
возможность, что рекомендация, полученная с помощью
ОП-10, полностью совпадет с рекомендацией, получен-
полученной с помощью ОП-1.
Менее трудоемким является алгоритм построения эк-
экстремальной кусочно-линейной разделяющей поверхно-
поверхности ОП-7. Реализация этого алгоритма упрощается тем,
что вместо процедуры скользящий контроль в нем исполь-
используется оценка качества решающего правила с помощью
формул.
В том случае, когда заранее не дана экзаменационная
последовательность и необходимо построить решающее
правило, которое будет в дальнейшем использоваться для
классификации различных векторов, следует применять
алгоритмы построения экстремальной разделяющей гипер-
гиперплоскости, а в том случае, когда гиперплоскость разделяет
векторы обучающей последовательности, совершая доста-
достаточно много ошибок, строить кусочно-линейную разде-
разделяющую поверхность. Среди алгоритмов метода «обобщен-
«обобщенный портрет» есть такие, которые строят разделяющую
гиперплоскость в пространстве минимальной размерно-
размерности. Часто возникает необходимость строить такие решаю-
решающие правила, однако при этом следует иметь в виду, что,
вообще говоря, критерий минимизации размерности про-
пространства является более грубым, чем критерий A5.9).
Как и всякие алгоритмы, система алгоритмов ОП
имеет свои константы, которые необходимо задать при
использовании той или иной программы. Величины этих
констант следует задавать, исходя из класса вычисли-
вычислительных машин.
Глава XVI
МЕТОД СОПРЯЖЕННЫХ
НАПРАВЛЕНИЙ
§ 1. Идея метода
Рассмотрим задачу о нахождении максимума квадра-
квадратичной функции
где х и Ъ — «-мерные векторы евклидова пространства
Еп, (х, Ах) — положительно определенная квадратичная
форма, задаваемая матрицей А.
Сначала заметим, что градиент \Р (х) функции Р (х)
равен Ъ — Ах и точка максимума функции может быть
найдена из уравнения
Ъ — Ах = 0.
Выводимые ниже алгоритмы позволяют отыскивать
максимум, минуя решение системы линейных уравнений
или получение обратной матрицы. Напротив, эти алгорит-
алгоритмы могут быть использованы для решения систем урав-
уравнений.
1. Рассмотрим сначала процесс, отнюдь не являющий-
являющийся алгоритмом для нахождения минимума квадратичной
функции, но из которого легко следуют весьма эффек-
эффективные алгоритмы — метод сопряженных градиентов и
метод параллельных касательных.
Пусть х0 — произвольная точка пространства Еп. Обо-
Обозначим §х — градиент функции Р (х) в точке х0. Пусть
Ех — одномерное гиперпространство, прямая, прохо-
проходящая через х0 в направлении §х, т. е. иными словами,
множество векторов вида х0 + Х§ (— оо <; X < + оо).
374 ГЛ. XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
Найдем точку хг, в которой достигается условный мак-
максимум функции Р (х) на прямой Ех. Продолжим это по-
построение по индукции. Пусть уже построено /с-мерное
гиперпространство Ек и в нем найдена точка хк, в которой
функция Р (х) достигает условного максимума.
Обозначим #ь+1 = Ъ — Ахк градиент функции Р (х)
в точке хк. Примем, далее, за гиперпространство Ек+1 про-
пространство, натянутое на Ек и прямую, проходящую через
хк в направлении §к+1. Пространство Ек+1 состоит из век-
векторов вида
у = х + Хёк+1, A6.1)
где х ЕЕ Ек, а скаляр % пробегает значения от — оо до
Наконец, хк+1— это точка, в которой Р(х) достигает
условного максимума на пространстве Ек+1. Таким обра-
образом, получаем такие последовательности:
§1 #2 ■■■ ёк
Ех Е2 ... Ек
Х$ Ху Х% ... Ха-
По индукции легко показывается, что гиперпростран-
гиперпространство Ек может рассматриваться как множество векторов
вида
к
У = х0 -Г 21л Агбгт
г=1
ГДе 8г — градиенты функции Р в точках х0, . . .
..., 1ц, а ~кк принимают любые действительные значения.
Отсюда, очевидно, следует, что Ег (Ц Е}- при I ^ /.
2. Из анализа известно, что если гладкая функция
достигает условного экстремума на некотором гиперпро-
гиперпространстве в точке х, то градиент функции в этой точке
ортогонален гиперпространству. Применительно к наше-
нашему построению отсюда следует, что §к+1 ортогонален вся-
всякому вектору вида х — у, где х и у принадлежат Ек, т. е.
(#ь+1, (х - у)) = 0 при х, у е Ек. A6.2)
В частности, векторы х0 и х0 -\- §1 при г ^ к принадле-
принадлежат Ек в силу A6.1), откуда
(ёк+ь §1) = 0 (I < к),
§ 1. ИДЕЯ МЕТОДА 375
а следовательно, и вообще
(§1, В]) = 0 при I ф /. A6.й)
Отсюда следует, что если §к+1 Ф О, то вектор §к+1 невыра-
невыразим линейно через §г, . . ., §к и поэтому пространство Ек+1
имеет размерность на 1 большую, чем Ек.
Таким образом, размерность пространства Ек последо-
последовательно нарастает с ростом к до тех пор, пока §к+1 не
обратится в нуль. Ио последнее означает, что в точке хк
достигнут уже абсолютный максимум Р (х). Действитель-
Действительно, поскольку Р (х) — выпуклая гладкая функция, то
обращение в нуль ее градиента является необходимым и
достаточным условием максимума.
После обращения в нуль §к+1 процесс зацикливается,
потому что при этом Ек+1 совпадает с Ек, соответственно
хк+1 — с хк и т. д. Поэтому в дальнейшем будем
считать, что процесс обрывается, как только 8к+х °б~
ратится в нуль, и тем самым будет установлено, что
точка хк, найденная на предыдущем шаге, доставляет
абсолютный максимум Р (х) во всем пространстве Еп.
В то же время это обязательно должно произойти при
к ^ п, так как если при к < п градиент §к не обращается
в нуль, то размерность гиперпространства Ек, увеличи-
увеличиваясь каждый раз на 1, на п-м шаге достигнет размерно-
размерности всего пространства Еп, т. е. Ек совпадает с Еп, и тем
самым условный максимум на Ек, естественно, совпадет
с абсолютным.
Рассмотренный процесс, конечно, не является удоб-
удобным алгоритмом, для нахождения максимума, так как
формально на каждом шаге требуется находить условный
максимум Р (х) в пространствах последовательно нара-
нарастающей размерности вплоть до полной размерности всего
пространства. Однако оказывается, что в действительно-
действительности можно искать условный максимум на каждом шаге
в гиперпространстве размерности 2, т. е. на обыкновенных
двумерных гиперплоскостях, или даже в гиперпростран-
гиперпространстве размерности 1, т. е. на прямой.
3. Для обоснования этого положения установим сле-
следующие факты. Обозначим через ук (к ^ 1) вектор
хк — Хк-ъ т- е- смещение от условного максимума в Ек^,
к условному максимуму в Ек.
а) ук ф 0. A6.4)
376 ГЛ. XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
В самом деле, процесс продолжается лишь до тех нор,
пока §к не обратится в нуль. Поэтому достаточно показать
что при §к ф О хк Ф хк_х. Поскольку градиент функции
Р (х) в точке не равен нулю, функция возрастает при дви-
движении вдоль прямой хк^х -\- Х§к из точки хк.л по крайней
мере при малых Х^>0. Следовательно, на этой прямой есть
точки, в которых Р (х) больше, чем Р (хк^х). Но эта прямая
принадлежит Ек и, следовательно, тах Р (х) и подавно
хек,.
больше, чем Р (хк_г), т. е.
Р(х,)УР(х^1). A6.5)
Отсюда ясно, что хк ф хк_х и A6.4) верно. Из A6.5) также
следует, что хк ф Ек_х.
б) Векторы уг и у, при I ф / ортогональны относитель-
относительно матрицы А, т. е.
(уг, Ау3) = О при I ф ] A6.6)
Поскольку матрица А симметрична,
(Уг, АУз) = (У1, аУг)-
Поэтому для определенности будем считать, что / ^> г.
По определению
(Уг, АУ]) = (Уг, а (х1 — Х]-х))-
После очевидного преобразования получим
(Уг, аУз) = (Уг, (а%1 — ъ)) — (Уи (Ах1-х — Ь)),
но для любого к
Ъ — Ахк,
поэтому
(Уи АУз) = (Уг, 8}) — (Уг, ёи-д-
Далее, вектор уг = хг — хг_г есть разность двух векторов
из Еи и так как при г < / Ег (Ц Е-3_х, можно применить
соотношение A6.2)
(Уи 81) = ((XI — *1-х), 8]) = О
и
(У1, Вид = ((ъ — х1-х), 8^х) = 0.
Окончательно,
(■/I, Ау3) =--- 0 при г ^= /.
§ 1. ИДЕЯ МЕТОДА 377
в) Система векторов ух, • . ., ук линейно назависи-
ла, т. е. не существует чисел Я,х, . . ., Я,й, не все из которых
равны нулю, таких, что
(с
г=1
В самом деле, предположим противное, и пусть, например,
К} Ф 0. Тлгда
У] = 2 ЪУи
где положено
11" V
Умножая справа и слева это равенство на Ау;, получим
в силу A6.6)
(//;, Ау3) = 0,
но это невозможно, поскольку У] Ф 0 (утверждение а)) и
квадратичная форма положительно определена.
г) Утверждения б) и в) устанавливают, что векторы
Ух, • • •, У и образуют 4-ортогональный базис. В силу
известных теорем линейной алгебры отсюда следует, что
всякий вектор пространства Ек представим в виде
Это утверждение можно доказать и непосредственно по
индукции. Для Ех утверждение очевидно, так как всякая
точка прямой х0 -\- Х§х может быть представлена и в виде
х0 -\- X (х0 — хх), если учесть, что хх, так же как и х0,
лежит на этой прямой и х0 — хх ф 0. В общем случае
предположим, что A6.7) верно для Ек^г, т. е. всякий вектор
х вида
представим и в виде
^ = 2 Тгг/1
378 ГЛ. XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
Положим поэтому
к-Х
хк-х = 2 агУг + хо,
г=1
к к-х
хк = 2 ^ + Х0 = 2 &гУг + ^#* + Х0'
Здесь Хь ф. О, потому что хь ^ ■Ё'ь-г- Вычитая первое
равенство из второго, получим
к-х
У к = 2 Фь — ад Уг +
г=Х
откуда
Наконец, каждый вектор х из Ек представим в виде
к
Х
= 2
г=1
а следовательно, и в виде
х — 2л агУг ""Ь ^кёк + х0-
Подставляя сюда выражение A6.8) для §к, получим пред-
представление произвольного вектора из Ек в виде A6.7).
д) Найдем теперь, как выражается вектор ук+г через
й Ли 8к+х- Для точки хк е Ек в силу A6.7) су-
существует представление вида
к
Хк = 2 п1Уг + Х0,
для хк+х — представление вида
к
г=1
§ 1. ИДЕЯ МЕТОДА 379
Следовательно,
/с
Ук+1 = 2 С\У\ + ^/с+1- С16-9)
г=1
Убедимся теперь, что в этом разложении отлично от нуля
только одно с, а именно ск. Умножим скалярно выражение
A6.9) на вектор Ау}<
(г/т, ^г/г) ^ 2 сг (г/г, ^г/0 + я,
При /Х/св силу A6.6) отсюда следует
Ч (у}, АУ1) + X (§к+1, Ау,) = 0. A6.10)
Далее возможны преобразования
Ау} = А (х, — х^х) = (Ах} — Ъ) — Dх;_г — Ъ) =
откуда при / < /с в силу A6.3) справедливо
(#ь+г, ^г/;) = ^ь+1 {81 - ёнд = 0, A6.11)
а при / = к имеет место
{8к+ъ Ауп) = 8к+1 (8к - §и+1) = —\8*+1? A6.12)
Возвращаясь к A6.10), получим, что при / < к коэффици-
коэффициенты С} = 0, в то время как при / = к
1, лУк)
/С+11
поскольку (ук, Аук) Ф 0.
Окончательно A6.9) примет вид
A6-13)
Тем самым устанавливаем, что
380 ГЛ. XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
или, иначе,
Таким образом, точка хк+х заведомо лежит на двумерной
плоскости
х = хк + Х§к+Х + сук A6.14)
(X и с — параметры) и даже на одномерной прямой вида
(к — параметр), и поиск максимума в пространстве размер-
размерности к может быть заменен поиском максимума на плос-
плоскости или на прямой.
§ 2. Метод сопряженных градиентов
Метод сопряженных градиентов для нахождения макси-
максимума квадратичной формы имеет несколько модификаций.
1. Одна из них получается непосредственно из рас-
рассмотренного выше процесса, если заменить максимизацию
функции Р (х) на гиперпространстве Ек отысканием макси-
максимума на прямой вида A6.15). Как было показано в преды-
предыдущем пункте результат от этого не изменится, так как
эти максимумы совпадают.
Алгоритм получается таким (модификация I):
А. Начальный шаг.
1) Находится градиент §х функции Р (х) в произволь-
произвольной точке х0;
2) полагается гх = §х;
3) находится точка хх, доставляющая максимум функ-
функции Р (х) на прямой х = х0 + Хгх (К — параметр).
Б. Общий шаг. Пусть уже найдены точки х0, хх,. . .
• • -1 хк-ъ хк-
1) находится градиент §к+х функции Р (х) в точке хк\
2) полагается
2Ь+1 = ёк+1 4" ак+1 (хк — хк-\}-1
где
§ 2. МЕТОД СОПРЯЖЕННЫХ ГРАДИЕНТОВ 381
3) находится точка хклъ доставляющая условный мак-
максимум Р (х) на прямой
В. Останов алгоритма. Процесс обрывается в тот мо-
момент, когда градиент §к+1 обратится в нуль, т. е. достига-
достигается максимум Р (х) на всем пространстве Еп.
При абсолютно точном вычислении алгоритм должен
привести к максимуму не более чем за «шагов, так как при
этом точки х0, . . ., хк, вычисляемые методом сопряжен-
сопряженных градиентов, совпадают с точками х0, . . ., хк, полу-
получающимися в процессе, описанном в предыдущем пункте:
как было показано, этот процесс выводит на абсоютный
максимум не более чем за п шагов.
В реальных условиях, при ограниченной точности вы-
вычислений, процесс поиска максимума следует остановить
не при точном обращении в нуль градиента, а в тот момент,
когда градиент станет достаточно мал. При этом на самом
деле может потребоваться более п шагов. Более подробно
эти вопросы будут рассмотрены ниже.
Чтобы придать алгоритму более «конструктивную»
форму, найдем формулу, определяющую точку максимума
квадратичной формы на прямой х = х* -\- А,2.
Подставляя уравнение прямой в выражение функции
Р (х), получим
Р (х) = - -у- X2 (г, Аг) + X B, § (ж*)) + Р (ж*),
где § (х*) — градиент Р (х) в точке х*. Максимизируя по
%, получим
\ \2' ;
Лппт — ~Г~
^опт ~ B, Аг)
и соответственно
A6.16)
Таким образом, вычисление в пункте 3) алгоритма мо-
может быть осуществлено по формуле
382 ГЛ. Ху1. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
2. Более известна модификация метода, при которой
для вычисления очередного направления т,к+1 используют-
используются векторы #й+1 и т,к вместо #й+1 и ук.
Рассмотрим систему векторов 2г,. . ., гк,. . ., кол-
линеарных соответственно векторам ух,. . ., ук (т. е.
ги — бйуй при некоторых действительных 6& Ф- 0). Для
векторов 2,- и 2/ сохраняется условие 4-ортогональности
(гг, Аг}) = 0 при г ^ у. A6.17)
Кроме того, из A6.11) следует, что
(гк+1, Лй) = 0 при I < й. A6.18)
Наконец, остается в силе соотношение типа A6.9)
A5.19)
1=1
Умножая правую и левую части A6.19) на Аг% и учиты-
учитывая A6.17) и A6.18), получим при I < /с
сг- (гь 4гг) = 0,
откуда сг = 0 при I < /с. При I = к получим
0 = (гй+1, Лгг) = ск (гк Агк) + X (§к+1, Агк),
откуда
(%а±^) A6.20)
Соотношение A6.20) определяет 2ь+1с точностью до произ-
произвольного множителя через §к+х и гк. При выводе A6.20)
использовались лишь соотношения A6.17), A6.18), A6.19).
Поэтому процесс построения векторов гк может рассмат-
рассматриваться как процесс 4-ортогонализации векторов §к.
Полагая в A6.20) "к = 1 и гг = §х, получим конкрет-
конкретную систему векторов гк, коллинеарных ук. Каждый век-
вектор т.к задает направление прямой, исходящей из хк+1, на
которой лежит хк. Алгоритм, таким образом, примет сле-
следующий вид (модификация II).
А. Начальный шаг, такой же как и в модификации I.
Б. Пусть уже найдены точка хк и направление гк.
1) Находится градиент §к+1 функции Р (х) в точке хк;
§ 2. МЕТОД СОПРЯЖЕННЫХ ГРАДИЕНТОВ 383
2) полагается
3) находится точка хк+1, доставляющая условный мак-
максимум Р (х) на прямой
X = Хк -\- ^2^-+1
по формуле
Формулы A6.21) и A6.22) могут быть преобразованы.
Так, полагая
имеем из A6.22)
У л = (хк — яь-х) =
откуда получаем, применяя A6.12),
,г,
A6.23)
Чг 1к
С другой стороны, поскольку
( 0 1 7/1 ^ (&1 7, \ О
\Ьк1 Ук—1/ Уьку ^к~\) — *-Л
из A6.21) имеем
и, таким образом,
Т.* =-[-11. A6.24)
Наконец, из A6.21), A6.23) и A6.24) получаем
384 ГЛ. XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
Таким образом, формулы A6.21) и A6.22) могут быть за-
записаны в виде
где
и
Совпадение результатов действия по формулам A6.21)
и A6.22), с одной стороны, и A6.25), A6.26), с другой,
может служить критерием правильности вычислений.
3. Метод сопряженных градиентов может быть приме-
применен и для максимизации функций Р (х), не являющихся
квадратичными. Известно, однако, что вблизи максимума
достаточно гладкие функции, как правило, хорошо аппрок-
аппроксимируются квадратичной функцией, например, с по-
помощью разложения в ряд Тейлора. При этом обычно пред-
предполагается, что коэффициенты аппроксимирующей квад-
квадратичной функции неизвестны, но для любой точки мож-
можно найти градиент § (х) функции Р (а;).
При этом пункт 1) алгоритма может быть выполнен
без изменений, пункт 2) должен выполняться по формуле
A6.25), поскольку в эту формулу не входит явно матрица
А, а пункт 3), нахождение условного максимума на пря-
прямой, может быть выполнен одним из известных способов,
например, методом Фибоначчи. Применение метода со-
сопряженных градиентов дает обычно значительно более
быструю сходимость к максимуму по сравнению с метода-
методами наискорейшего спуска, Гаусса — Зайделя и др.
4. Что будет, если применить метод сопряженных гра-
градиентов для максимизации квадратичной формы с поло-
положительно полуопределенной формой (х, АхI
Если квадратичная форма (х, Ах) положительно полу-
полуопределена, то, как известно из линейной алгебры, в со-
соответствующей системе координат функция Р {х) примет
вид
п
Р (X) -= 2~2 сгх\ + 2 Мг + Й>
1=1
§ 2. МЕТОД СОПРЯЖЕННЫХ ГРАДИЕНТОВ 385
где все с,- ^ 0 и некоторые из с,- = 0. При этом функция
имеет максимум, если выполнено условие: когда с,- = 0,
то и Ъг = 0. Легко видеть, что максимум в этом случае
достигается на целом гидерпространстве. А именно, пусть,
например, при I, меняющемся от 1 до к, с{ Ф 0, а при I,
меняющемся от к -\- 1 до н, с, = 0 и Ъг = 0. Тогда макси-
Ъ.
мум достигается в точках с координатами хг = -1- при
1 ^ г <С ^ и с произвольными значениями X; при г~^> к.
Они образуют гиперпространство размерности гс — к.
Если же при некоторых I с, = 0, а 6; =/= 0, то функция
не имеет максимума и возрастает неограниченно. В самом
деле, пусть, например, Ък ~^> 0 и ск = 0; тогда, если поло-
положить XI = 0 при 1^ьк я устремить хь к + оо, то, очевидно,
и -?1 (х) будет возрастать до бесконечности.
Оказывается, что метод сопряженных градиентов (при
точном счете) позволяет в первом случае достигнуть мак-
максимума не более чем за к шагов, где к — число с, не рав-
равных нулю, а во втором случае не более чем через к шагов
выводит на направление, по которому функция Р (х) воз-
возрастает неограниченно.
В исходной системе координат функция Р (х) имеет
вид
Р (х) = - -|- (х, Ах) +Ъх + с,
причем матрица А вырождена и имеет ранг к < п. При
этом, как и раньше, обращение градиента в нуль есть
критерий достижения максимума, а ортогональность гра-
градиента гиперпространству — критерий условного экстре-
экстремума на гиперпространстве.
Рассмотрим применение метода сопряженных гради-
градиентов в форме II в этом случае. Здесь приходится изме-
изменить условие остановки, т. е. теперь возможно, что при
вычислении длины шага
1к (**, А*к) (**, АЧ)
знаменатель (гк, А%к) может обратиться в нуль (при вычис-
вычислении значения ак+1 величина (гк, Агк) также входит в зна-
знаменатель, но если она равна нулю, то уже предыдущий
шаг невозможен).
386 ГЛ. XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
Таким образом, условие останова будет таким.. Про-
Процесс останавливается, если:
на очередном шаге #ь+1 = О
или
на очередном шаге оказывается, что
АЧ+д = 0.
В первом случае алгоритм, естественно, приводит в-
точку максимума. Во втором случае направление 2ь+1
будет направлением неограниченного возрастания функ-
функции Р (х). В самом деле, на прямой
х = хк + Хгк+1
при (гй+1, Агк^) = 0 функция Р (х) имеет вид
X2
Р(х) = Р (хк) — -у
причем
(Вт §пп) > 0,
так как при &к+х = 0 останов произошел бы по пункту
а). Но теперь очевидно, что при Х-уоо функция Р (х)
возрастает неограниченно. Можно показать, что при этом
из всех направлений, по которым функция бесконечно
возрастает, она растет быстрее всего в направлении 2ь+1.
Нам остается убедиться, что останов произойдет не
более чем через к шагов, где к — ранг матрицы А. В самом
деле пусть при I ^ т выполнено условие (гг, Агг) ^> 0.
Тогда остаются в силе соотношения
(гг, Аг3) = 0 при 1ф] (г, у < т)
2г) = 0
(при выводе этих соотношений положительно-определен-
ность не использовалась).
Отсюда следует, что векторы гг A ^ 1 <^ т) образуют
4-ортогональный базис, а градиент §т в точке хт орто-
ортогонален гиперпространству Ет размерности т, состоя-
состоящему из векторов вида
х = хо +
| 3. МЕТОД ПАРАЛЛЕЛЬНЫХ КАСАТЕЛЬНЫХ (ПАРТАН) 387
причем
так что в точке хт достигается условный максимум функ-
функции Р (х) на Ет. Далее, на гиперпространстве Ет функ-
функция Р (х) имеет вид
п
Р(х)^Р (х0) + 2 № B4, Аг) + 2 ^ь
1=1
где
Л1 = г-г (Ъ — Ах0),
и так как (т,г, Агг) ^> 0, то квадратичная часть Р (х) поло-
положительно определена. Но, как известно из линейной ал-
алгебры, это возможно только в том случае, когда размер-
размерность пространства Ет меньше или равна рангу к матри-
матрицы А.
Следовательно, останов обязательно произойдет при
т ^ к.
§ 3. Метод параллельных касательных (партан)
Выше было показано, как процесс, описанный в § 1,
приводит к методу сопряженных градиентов, если отыска-
отыскание условного максимума в пространстве Ек заменить
равноценным поиском максимума на прямой. Там же по-
показано, что равноценным будет также поиск на двумерной
плоскости, проходящей через точку хк и два исходящих
из нее вектора ук и #&+1, т. е. точка хй+1 может быть пред-
представлена в виде
или, иначе,
Для нахождения максимума квадратичной функции
на плоскости можно использовать различные методы.
Метод, известный под названием «партан» или «метод па-
параллельных касательных», основан на простом геометри-
геометрическом принципе.
На рис. 28 изображены линии уровня функции Р (х),
представляющие собой подобные концентрические эллип-
эллипсы. Пусть х0 — произвольная точка, Ао — линия уровня
388 ГЛ. XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
(эллипс), проходящая через х0, 1Х — касательная к эллип-
эллипсу в точке х0, §х — градиент функции Р (х) в точке х0.
Очевидно, что градиент §х нормален к линии уровня, т. е.
перпендикулярен касательной 1Х.
Точка хх определяется как точка максимума функции
Р (х) на прямой г, проходящей через х0 в направлении
градиента §х. В точке хх эта прямая касается некоторой
линии уровня. Поэтому градиент #2В точке хх перпендику-
перпендикулярен вектору §х и, сле-
следовательно, прямая 12, про-
проходящая через хх в направ-
направлении §21 параллельна 1Х.
Далее, точка х2 находится
как точка максимума Р (х)
на прямой 12, где она ка-
касается эллипса А2. Оче-
Очевидно, что подобным ежа-
Рис. 28. тием можно перевести од-
одновременно прямую 1хж эл-
эллипс Ах в прямую 12 и эллипс А2. При этом точка х0перей-
х0перейдет в х2. Но при подобном сжатии к центру точка х0 переме-
перемещается по прямой, проходящей через центр эллипсов.
Поэтому прямая (х0, х2) проходит через центр эллипсов,
т. е. точку максимума функции на плоскости. Таким об-
образом, приходим к следующему способу:
1) из произвольной точки х0 провести прямую г в на-
направлении градиента функции §х в точке х0;
2) на этой прямой найти точку условного максиму-
максимума хх;
3) через хх провести прямую в направлении градиента
и на этой прямой найти точку х2, доставляющую услов-
условный максимум;
4) соединить точки х0 и х2 прямой и найти точку мак-
максимума на этой прямой. Найденная точка есть точка, до-
доставляющая максимум функции на всей плоскости.
Вернемся теперь к задаче о нахождении максимума
Р (х) в «-мерном пространстве Еп. В соответствии со ска-
сказанным выше, процесс, описанный в § 1, может быть при-
приведен к следующему виду.
А. Начальный шаг.
1) В произвольной точке х0 пространства Еп находит-
находится градиент §х функции Р (х);
§ 3. МЕТОД ПАРАЛЛЕЛЬНЫХ КАСАТЕЛЬНЫХ (ПАРТАН) 389
2) на прямой х = х0 + \§х ищется точка хх, достав-
доставляющая максимум функции Р (х).
Б. Общий шаг. Пусть уже найдены точки х0, хх, . . .,
хЧ-\1 хк •
1) В точке хк находится градиент §Ы1 функции Р (х);
2) на плоскости, проходящей через точки хк_ъ хк
и параллельной направлению 8ъ+1, т. е. на плоскости
X = ХЦ-! -\- Аг (хк — хк-д ~Ь ^2§к+1,
ищется точка хк+1, доставляющая условный максимум
функции Р (х).
В. Останов алгоритма. Процесс прекращается, когда
на очередном шаге окажется, что §т+х = 0. Тогда хт —
точка максимума Р (х) во всем пространстве Еп.
Для осуществления пункта 2) общего шага применим
метод параллельных касательных. Обозначим А.к двумер-
двумерную плоскость вида
X = Хк_г -\- "кг (Хк —
/г-г) "Т
(\ и Х2 — параметры) и, начиная с точки х = гц, будем
действовать по методу «партан». Прежде всего необходимо
найти в точке хк_х условный градиент функции Р (х) на
плоскости Лй. Известно, что условный градиент на ги-
гиперпространстве Л есть проекция полного градиента на
это гиперпространство. Таким образом, нам нужно спроек-
спроектировать вектор §к = \Р (хь_г) на плоскость Ак. Но
в соответствии с A6.2) и A6.3) вектор §к ортогонален
8к+1, а векторы (хк — хк-т) и §к+1 ортогональны между со-
собой. Поэтому проекция §к на плоскость Л.к коллинеарна
вектору (хк — 1И).
Прямая, проходящая через точку хк^1 в направлении
условного градиента на плоскости, имеет, таким образом
вид
х = хк„х + X (хк — хк-у),
а точка максимума на этой прямой есть хк, так как эта
прямая принадлежит пространству Ек и хк доставляет
максимум Р (х) на всем Ек.
Итак, оказывается, что первый шаг двумерного «пар-
тана» фактически уже выполнен и точка хх этого алгорит-
алгоритма совпадает с хк.
390 ГЛ. ХДП. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
Далее, нужно взять условный градиент Р (х) в точке
хк. Но направление полного градиента %к+1 в точке хк при-
принадлежит гиперплоскости Л.к. Поэтому условный гради-
градиент совпадает с полным. Теперь через точку хк нужно про-
провести прямую
X = Хк + ^#й+1
и найти на этой прямой точку хй+1, доставляющую усло-
условный максимум Р (х). Наконец, точку хк_х необходимо
соединить с х^+1 прямой и на этой прямой найти точку, в ко-
которой достигается условный максимум Р (х). Эта точка
и есть хк+х.
Таким образом, общий шаг алгоритма приобретает
следующий вид:
1) в точке хк находится градиент ёп+ъ
2) на прямой х = хк + ^#ь+1 определяется точка хй+1,
в которой функция Р (х) достигает условного экстремума
по формуле
4+1 = К
где
3) на прямой х = Х&-! + % (а?й+1 — хп-г) ищется точка
доставляющая условный экстремум Р (х), по фор-
формуле
Хк+1 = %к-1 + К
где
Эти формулы получены в соответствии с общей формулой
A6.16), выведенной в § 2. Отметим, что при точном счете
процесс должен закончиться не более чем через п шагов.
Метод параллельных касательных может быть приме-
применен и в случае неквадратичной функции, при этом поиск
условного экстремума на прямой должен производиться
одним из известных методов одномерного поиска. Однако
при этом нет никаких гарантий, что процесс закончится
через п шагов. Экспериментально же установлено, что
этот метод поиска сходится значительно лучше, чем ме-
методы наискорейшего спуска или Гаусса-Зайделя.
§ 4. АНАЛИЗ ПОГРЕШНОСТЕЙ МЕТОДА 391
§ 4. Анализ погрешностей метода
В § 1 был рассмотрен процесс, в котором строились
последовательность вложенных гиперпространств Ех, . . .
..., Ек возрастающей размерности и последовательность то-
точек хх, . . ., хк, доставляющих условный максимум функции
Р (х), соответственно, на гиперпространствах Еъ . . .Ек.
При этом оказалось, что векторы (хк+х — хк) являются
4-ортогональными.
Покажем сейчас, что справедливо в некотором смысле
и обратное утверждение.
Если:
1) векторы ъх, . . ., гк 4-ортогональны, т. е.
г1Ат,1 = 0 при I ф ],
2) точки х0, хх, . . ., хк получены из рекуррентного ус-
условия: хк+1 доставляет условный максимум функции
Р (х) на прямой
х = хк-\- ЪгК!
при произвольной фиксированной точке х0,
то точка хк доставляет условный максимум Р (х) на ги-
гиперпространстве Ек, определяемом как совокупность век-
векторов вида
к
ж = жо + 2 С1*1- A6.27)
1=1
В самом деле, подставляя формулу A6.26) в выраже-
выражение для Р(х), получим
к
Р = Р (х0) 2" 2 С1сз (гь Ац) + 2 сг Bг, (Ъ — Ах0)).
1,1 г=1
Положим
йг = Bь (Ъ — А%о)) и щ = ъхАъ%.
Тогда, учитывая 4-ортогональность г{ и %] при I ф у,
получим
к к
Р = Р (х0) ~4 <$Щ + 2 сЛ- A6.28)
1=1 г=1
Чтобы найти вектор Хопт, доставляющий максимум Р (х)
на Ек, продифференцируем Р по с{ и приравняем частные
392 ГЛ. XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
производные к нулю. Тогда
(здесь а-г ф. О из-за положительной определенности фор-
формы), откуда
Хопт(й)=ж0 + 2 «г-г-. A6.29)
1=1
Сопоставляя выражения A6.27) для хот (к) и хоат (к + 1),
имеем
Я'опт A) = 3^0 Ч" 21 "^~ I
ЖОПТ (& + 1) = Х0ПТ {к) + 2к+1 ~ .
ак+1
Таким образом, точка хопт (к + 1) лежит на прямой
вида
х = хош (к) + Хгь+1
и, очевидно, доставляет функции Р (х) условный макси-
максимум на этой прямой, поскольку в этой точке достигается
условный максимум на всем гиперпространстве Ек+1,
включающем прямую.
Поэтому при точном счете последовательности х0, хъ. . .
. . ., Хъ и х0, х A), . . ., х (к) совпадут. Если же при вы-
вычислении допускаются ошибки, то ошибки на каждом
шаге будут просто складываться (векторно). В самом деле,
пусть в результате первых к шагов процесс приводит в не-
некоторую точку х%, отличную от хопт (к). Положим
2* = а;опт (к) + Ахк.
Будем считать, что х*к е= Ек. Тогда коэффициенты сг для
х1 при 1^> кв представлении A6.27) равны нулю. Поиск
максимума на прямой
X = X*; + ^2Ь+1
равносилен поиску максимума выражения A6.28) по пе-
переменной сй+1 при фиксированных остальных перемен-
переменных сг. Осуществляя эту операцию, убеждаемся, чтоск+10Щ,
§ 4. АНАЛИЗ ПОГРЕШНОСТЕЙ МЕТОДА 393
как и раньше, равно -^ . Таким образом, (к -\- 1)-й шаг
возмущенного процесса совпадает с соответствующим
шагом невозмущенного, откуда следует, что ошибки про-
просто складываются. Если суммарная накопившаяся ошиб-
ошибка после п шагов заведомо мала по сравнению с переме-
перемещением от начальной точки к точке оптимума (это усло-
условие выполняется при работе на ЭВМ), то во всяком слу-
случае после двух-трех повторных применений алгоритма
максимум будет найден с очень высокой точностью.
Все эти рассуждения верны в предположении, что си-
система 4-ортогональных векторов т,г получена заранее и
с достаточно высокой точностью. Но в действительности
метод сопряженных градиентов строит эти векторы, ис-
используя рекурсивную процедуру. Оказывается, что при
этом дело может обстоять значительно хуже, а именно:
однажды возникшая малая ошибка может привести к ла-
лавинообразному нарастанию ошибок в ходе дальнейших
вычислений.
В самом деле, рассмотрим метод сопряженных гради-
градиентов в форме II: х0 — произвольно и при к > 1
1) 8иг =ёк-А[хк- хк^), A6.30')
2) гй+1=**+1 + ак+12й1 A6.30")
3) хк+1 = хк + Ук+1гк+1, A6.30"')
где
к+1 ~~ С 37Т"'
A6.31)
Выведем рекуррентные соотношения для величин (#й, 2;)
и {гк, А%г). Из A6.30") имеем
хк — хк_! = укгк.
Подставляя это выражение в A6.30') и умножая скалярно
обе части равенства на ги получим
(ёк"+1, Ч) = (8к, гг) — ук {гк, А^)
394 ГЛ. XVI. МЕТОД СОПРЯЖЁННЫХ НАПРАВЛЕНИЙ
(в последнем члене использовано равенство (Агк, гг) =
= (гк, Аг{)). Далее, чтобы получить рекуррентное выра-
выражение для (гй+1, 42;), заменим гк+1 по формуле A6.30");
получим
Bй+1, Аг^ = ак+1 (гк, Аг() + (^.+1, Ац). A6.32)
Теперь воспользуемся снова соотношением, вытекающим
из A6.30') и A6.30"),
Ч
и подставив его в A6.32) получим
Ац) — — ((&+1 — §4
ч
Наконец, из формулы A6.30")
и окончательно рекуррентное соотношение примет вид
, 4г{) — — [B|+
ч
Перепишем рекуррентные соотношения в новых обозна-
обозначениях, полагая (§к, гг) = ай_;, (гй, Аг>) = сй,{. При I > 1
получаем
1, г = «я, г — Ть ся, г A6.33)
При ^ = 1 получаем
[а^+1,2 A +
Нетрудно убедиться, что коэффициенты ук и ак подоб-
подобраны в алгоритме именно так, чтобы ак+1, к и сь+1;ь обра-
обратились точно в нуль. Поэтому можно рассматривать си-
систему A6.33) при к ;> I + 1 с граничным условием
аь,ь_г = 0, ск,к^ = 0. Так как система A6.31) является
линейной и однородной, то при этих начальных условиях
она имеет единственное решение
«М ^ ° ' СМ = ° при А > I.
§ 4. АНАЛИЗ ПОГРЕШНОСТЕЙ МЕТОДА
395
Заметим, что этот вывод является другим доказательством
того, что метод сопряженных градиентов на к-м шаге до-
достигает условного максимума в Ек, так как для этого
достаточно, чтобы (#ь+1, гг) = 0 при I ^ к.
Но система A6.31) может быть неустойчивой. Этого
нельзя утверждать в общем случае, ибо оказывается, что
всегда можно подобрать функцию Р (х) и начальную точку
так, чтобы а1 и у* приняли любые наперед заданные поло-
положительные значения, а последние можно подобрать и так,
чтобы система оказалась устойчивой. Но во многих случа-
случаях она все-таки оказывается неустойчивой. Покажем это
на примере, положив
Уг = 0,5, у3 = 1 при I ф /, аь = 1
для всех I.
Допустим, что при некотором к ^> I происходит еди-
единичное возмущение величины ак^, т. е. Аак<1 = 1, причем
Аай, 1 = 0 при / ф I, Аск_Ъ1 = 0 при всех {.
Легко видеть, что решение выглядит следующим
образом:
Ааы
г—2
1—1
1
1 + 1
1 + 2
к
1
к + 1
1
з
1
к + 2
1
—3
9
—3
1
1
—3
9
—27
9
—3
1
1 — 1
г
г + 1
к
—1
4
-1
к + 1
—1
4
12
4
-1
(г + 2
4
—12
36
—12
4
396 ГЛ. XVI. МЕТОД СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ
Аналитическое решение таково:
_ Г(-1)8-' З8-' при 8 - / > О,
1 \ О при 8 — у < О,
_ |4 (—I)8'3' З8-^1 при 8 — / + 1 > О,
с"+«' *+'" ~ { 0 при 8 — / + 1 < О,
т. е. величины аг& и С;Ь возрастают примерно как Зк и
имеет место лавинообразное накопление ошибки. Тем не
менее, конечно, функция Р (х) будет на каждом шаге
убывать и процесс будет сходиться, но не за п шагов.
Такого рода явления можно устранить, если на каж-
каждом шаге проводить полную 4-ортогонализацию очередно-
очередного вектора т,к+1 относительно всех предшествующих т,и а
не только т,к, но это требует большего числа действий на
каждом шагз.
КОММЕНТАРИИ *)
К главе I
Считается, что первой работой, положившей начало исследо-
исследованию в области обучения распознаванию образов, была работа
Ф. Розенблатта [90]. Американский физиолог ф. Розенблатт рас-
рассмотрел модель восприятия, которая, вообще говоря, не являлась
новой в физиологии. Однако в отличие от других физиологов Ф. Ро-
Розенблатт построил эту модель не умозрительно, а в виде техниче-
технического устройства, которое он назвал персептроном. Первопачально
алгоритм построения весов Д-элементов персептрона (алгоритм по-
поощрения в терминологии Ф. Розенблатта) отличался от того алго-
алгоритма построения разделяющей гиперплоскости, который был опи-
описан в главе I. Сразу же после публикации сообщения о персептроне
появилось множество различных исследований законов поощрения.
Все они, как правило, обосновывались ссылками на физиологиче-
физиологические феномены. И только с появлением теоремы американского ма-
математика А. Новикова [87] алгоритм построения весов Д-элементов
получил геометрическую интерпретацию. В свое время теорема
А. Новикова произвела чрезвычайно сильное впечатление на иссле-
исследователей. Достаточно сказать, что она была передоказана не менее
чем десятью авторами.
Теорема Новикова явилась поворотным пунктом в исследовании
феномена восприятия. Она продемонстрировала, что исследования
можно вести на языке математики, и это во многом определило
стиль и уровень последующих работ.
Что касается дальнейших построений моделей восприятия, то
они пошли по пути усложнения конструкции персептрона. Ф. Ро-
Розенблатт строил и многослойные персептроны, и персептроны с пере-
перекрестными связями [54]. Однако эти модели, как правило, не оп-
оправдывали возложенных на них надежд — на них не удалось проде-
продемонстрировать ни новых свойств восприятия, ни получить новых
теоретических результатов. Подробно исследование возможных
и невозможных путей обобщения с помощью персептрона рассмотре-
рассмотрено в книге М. Минского, С. Пейперта «Персептроны» [46].
В дальнейшем исследование феномена восприятия пошло по пути
моделирования на ЭВМ. Однако после появления персептропа в тех-
технике возник интерес к адаптирующимся элементам. Так были
*) Эти комментарии отражают точку зрения авторов на разви-
развитие идей в области распознавания образов и никак] не претендует
на библиографическую полноту.
398 КОММЕНТАРИИ
построены на фотохимическом принципе обучающаяся матрица
К. Штейнбуха [92], адалины Б. Уидроу [94, 95]. Эти элементы нахо-
находят применение в различных технических конструкциях.
Что касается закона поощрения Д-элементов персептрона, то,
как теперь выясняется, он фактически реализует релаксационные
методы решения линейных неравенств, рассмотренные еще в 1954 г.
Т. Моцкиным и И. Шенбергом [86].
К главе II
Сейчас, вероятно, трудно определить, кто первый предложил
рассматривать задачу обучения распознаванию образов как задачу
минимизации среднего риска. Такие работы постановочного харак-
характера появились в начале 60-х годов почти одновременно. При этом
уже с самого начала обнаруживалась «специализация» в постановке.
Одни авторы [53, 72, 73, 74] примыкали к классическим работам
дискриминантного анализа и рассматривали задачу обучения рас-
распознаванию образов как задачу параметрической статистики, дру-
другие [1, 67, 68, 70, 71] предпочитали видеть проблему обучения в соз-
создании алгоритмов постепенного улучшения качества решающего
правила (рекуррентных алгоритмов), третьи связывали алгоритмы
обучения распознаванию образов с методом минимизации эмпири-
эмпирического риска [9—19, 24, 41, 81].
Иначе говоря, при постановке задачи методы обучения распоз-
распознаванию образов оказались связанными со всеми тремя путями ми-
минимизации риска.
Интересно отметить, что содержательная постановка задачи
обучения распознаванию образов появилась в 1957—1958 годах, а
формальная постановка — только в 1962—1966 годах. Эти пять —
восемь лет от содержательной до формальной постановки были
чрезвычайно яркими годами — годами «распознавательной роман-
романтики». В те времена казалось, что задача обучения распознаванию
образов несет в себе начало какой-то новой, никак не основанной на
системе старых понятий, идеи, хотелось найти новые постановки, а
не сводить задачу к уже известным математическим схемам. В этом
смысле сведение задачи обучения распознаванию образов к схе-
схеме минимизации среднего риска вызывает некоторое разочарование.
Правда, существуют попытки понять задачу в более сложной поста-
постановке [32]. Однако таких работ пока чрезвычайно мало.
Сейчас, через много лет после периода «распознавательной ро-
романтики», трудно оценить, что принесла формализация задачи. Не
оказалось ли так, что из стремления найти строгую постановку при-
пришлось сузить ту содержательную задачу, которую пытались ре-
решать в начале 60-х годов.
К главе III
Вероятно, трудно различить, где кончаются классические мето-
методы дискриминантного анализа и начинается задача обучения распоз-
распознаванию образов, решаемая методами параметрической статистики.
По определению задача дискриминантного анализа состоит в отне-
отнесении объекта к одному из К классов, заданных функциями распре-
Комментарии 399
ДеЯёния. На Практике почти все исследования проводятся для слу-
случая, когда плотности распределения вероятностей векторов каждого
класса заданы нормальным законом. Проблемы, которые подыма-
подымались дискриминантным анализом, в основном концентрировались
вокруг построения линейной дискриминантной функции. Поста-
Постановка такой задачи впервые была дана Р. Фишером [77], который
для решения ее предложил минимизировать некоторую функцию
(функцию Фишера). В 1962 году задача построении линейной ди-
дискриминантной функции для нормальных распределений была
решена Т. В. Андерсоном и Р. Р. Бахадуром [74, 2].
Другие исследования связаны с попыткой сформулировать
функционал, минимизация которого приводила бы к построению
линейной дискриминантной функции (не только для нормальных
распределений). Сначала в качестве такого функционала использо-
использовали функцию Фишера, а затем рассматривались и другие функции
[62]. Подробный обзор литературы по дискриминантному анализу
приведен в [63].
Случай независимо распределенных дискретных признаков так-
также известен в дискриминантном анализе. В 1952 году А. М. Аттли
[93] построил на этом принципе веротностный дискримйнантный
автомат, алгоритм которого, по существу, мало чем отличается от сов-
совместных алгоритмов, использующих гипотезу о независимости дис-
дискретных признаков.
В общем, различая работы по классическому дискриминантно-
дискриминантному анализу и параметрическим методам обучения распознаванию
образов, вероятно, можно указать на то, что в последних как-то
больше акцентируется внимание на восстановлении параметров
распределения с учетом ограниченности объема выборки.
К главе IV
Идея метода стохастической аппроксимации возникла, по-види-
по-видимому, давно, но в четкой форме была сформулирована в 1951 году
Г. Роббинсом и С. Монро [89]. Они указали итеративную процедуру,
позволяющую определять корень уравнения регрессии. В 1952 году
Е. Кифер и Дж. Вольфовиц применили этот метод для поиска
минимума функционала [82]. Начиная с этого времени ведутся рабо-
работы по определению условий сходимости метода. Подробно с библио-
библиографией метода стохастической аппроксимации можно ознако-
ознакомиться в обзоре [42]. В 1965 году Я. 3. Цыпкин указал на связь
метода стохастической аппроксимации с рекуррентными алгоритма-
алгоритмами обучения распознаванию образов [67, 68]. Эти работы стимули-
стимулировали исследования по теории метода стохастической аппрокси-
аппроксимации.
С 1964 года М. А. Айзерман, Э. М. Браверман, Л. И. Розоноэр
разрабатывали теорию метода потенциальных функций, которая
оказалась чрезвычайно близкой теории стохастической аппрокси-
аппроксимации. Этими учеными получены достаточно тонкие условия сходи-
морти процедур стохастической аппроксимации [1]. Дальнейшие
обобщения были получены недавно Б. Т. Поляком и Я. 3. Цыпки-
ным [52].
Конечно-сходящиеся рекуррентные алгоритмы исследовал
В. А. Якубович [70, 71]. Ему же принадлежит и сам термин.
400 КОММЕНТАРИИ
К главе V
Построение алгоритмов обучения распознаванию образов на
основе методов минимизации эмпирического риска началось сразу
же с появлением первых работ Ф. Розепблатта. За границей —
это работы О. Селфриджа [91], система программ Г. С. Себастиана
[58], в СССР работы [9—19]. Однако наиболее четко идеология
минимизации эмпирического риска проявились у В. Хайлимена
[81]. Хайлимен предлагал различные алгоритмы построения линей-
линейного решающего правила, минимизирующего число ошибок. Он
оценивал вероятность ошибок на экзамене по частоте ошибок
на обучении и применял сглаживание функции штрафа для по-
построения эффективного алгоритма минимизации. Обобщение этой
постановки на произвольные классы решающих правил было дано
в работе [41].
В первые идея о связи равномерной близости частот к вероят-
вероятностям по классу событий с оценкой качества алгоритма, миними-
минимизирующего эмпирический риск, была высказана в работе [16]. Од-
Однако в этой работе был исследован лишь случай конечного числа
событий. Затем удалось получить условие равномерной сходимости
для случая, когда частоты равны нулю [17]. И, наконец, были по-
получены исчерпывающие необходимые и достаточные условия равно-
равномерной сходимости частот появления событий к их вероятностям [18].
Несмотря на то, что условия равномерной сходимости частот
к вероятностям не были известны, многие авторы понимали, что ем-
емкость класса решающих правил влияет на экстраполяционную
способность алгоритма. Такие идеи можно проследить у М. М.
Бонгарда [4]. Н. Нильсон в своей монографии [49] приводит оценку
числа линейных решающих правил, разделяющих в ге-мерном про-
пространстве / векторов.
Что же касается конструктивных идей построения алгоритмов
обучения распознаванию образов, реализующих метод минимизации
эмпирического риска, то они много разнообразней идей, основанных
на реализации других методов минимизации среднего риска. Во
всяком случае методы минимизации эмпирического риска позволяют
эффективно искать решающие правила не только в классе линейных
или кусочно-линейных правил, но и в иных классах решающих
правил, например в классе логических функций определенного
вида [4, 9, 10].
К главе VI
Одной из наиболее важных особенностей в исследованиях обуче-
обучения распознаванию образов является стремление строить конструк-
конструктивные методы обучения более эффективные, чем те, которые выте-
вытекают из стандартных приемов минимизации риска, принятых в мате-
математической статистике. Здесь существует два возможных направле-
направления исследования, идя по которым можно надеяться достигнуть
успеха.
Первое направление связано с определением класса решающих
правил, внутри которого ищется нужное. Классическая статистика
игнорирует такую проблему, отмечая, что априори нет никаких
формальных способов определить, какой класс решающих правил
окажется предпочтительнее, и поэтому определение класса решаю-
КОММЕНТАРИИ 401
щих правил считается внешним моментом в постановке задачи.
В теории же обучения распознаванию образов допускаются нефор-
неформальные методологические соображения.
Второе направление связано с созданием конструктивных
квазибайесовых процедур, использующих некоторые априорные
гипотезы о характере тех задач, которые предстоит решать.
Первые работы по теории обучения распознаванию образов во
многом были посвящены исследованию этих двух особенностей за-
задачи. Именно поэтому период «распознавательной романтики» так
богат гипотезами о структуре «разумных» задач. В этом отношении,
вероятно, наиболее интересной работой остается монография
М. М. Бонгарда [4]. Гипотеза о структуре «разумных» задач, по су-
существу, содержится и в алгоритмах Браиловского — Лунца [5],
[6], ив идеях раздвигающей метрики Себастиана — Неймарка [48],
[58], и во многих других алгоритмах. Наконец, следует отметить
работу Н. В. Загоруйко [30], который явно высказал гипотезу о
структуре «разумных» задач в терминах сложности. Во всех этих ра-
работах гипотеза о структуре «разумных» задач нужна была для того,
чтобы ввести априорное упорядочение возможных задач и искать
решение не в классе всех возможных задач, а в некотором подклассе,
т. е., по существу, для того, чтобы провести идею упорядочения
минимизации риска.
Следует отметить, что идея упорядоченной минимизации риска
не является новой в математике. Она появлялась каждый раз,
когда метод минимизации эмпирического риска приводил к абсурд-
абсурдным результатам. Впервые, вероятно, эта идея возникла при иссле-
исследовании задачи об определении степени полиномиальной регрессии.
Известно, что если априори задана степень полиномиальной регрес-
регрессии, то метод наименьших квадратов является, вообще говоря, эф-
эффективным средством построения регрессии [43]. Другое дело, если
заранее степень регрессии неизвестна и предлагается, используя
выборку фиксированной длины, определить и степень регрессии и
значение ее параметров. В этом случае заранее известно, что мини-
минимум эмпирического риска будет достигнут, если степень полинома
равна длине выборки. Однако такое решение является абсурдным.
Поэтому в свое время К. Ф. Гаусс предложил минимизировать не
величину эмпирического риска Дэмп (ос), а величину Дэмп(а),
где / — объем выборки, а п — степень полинома. По существу, эта
процедура поиска полиномиальной регрессии является двухуровне-
двухуровневой процедурой. На первом уровне методом наименьших квадратов
строится / — 1 оценка регрессии различной степени, а на втором
уровне выбирается то решение, которое минимизирует приведен-
приведенную оценку.
С тех пор предлагалось много идей поиска полиномиальной ре-
регрессии, однако все они касались лишь критерия выбора второго
уровня, оставляя неизменной двухуровневую схему упорядоченной
минимизации риска.
Идея упорядоченной минимизации появилась и в связи с реше-
решением некорректных задач математической физики. Согласно
А. Н. Тихонову [60], решение уравнения
Ах = у
402 Комментарии
называется корректным, если оно существует, единственно и если
малой вариации у соответствует малое изменение х. Однако уже
для простейших задач (таких как решение некоторых типов линей-
линейных интегральных уравнений) последнее условие не имеет места:
достаточно малому изменению у может соответствовать большое
изменение х. Такая неустойчивость решения делает организацию
поиска решения невозможной. Поэтому А. Н. Тихонов предложил
искать решение не путем минимизации
/ = || у - Ах ||2, (•)
а минимизируя функционал
Л = || у - Ах ||2 + а || х ||2, (••)
где а — есть некоторая константа.
Последний метод носит название метода регуляризации Тихо-
Тихонова [61]. Заметим, что регуляризация по Тихонову есть тоже про-
проявление метода упорядоченной минимизации. В самом деле, вве-
введем сначала априорный порядок в классе возможных решений
|| ж ||< с1; . . ., || х ||< сп (сг < с2 < . . . < сп),
на первом уровне в каждом классе найдем решение х, доставляющее
условный минимум /, а затем из найденных решений отберем то,
которое удовлетворит критерию выбора второго уровня. Такая про-
процедура поиска решения эквивалентна минимизации функционала
/ь причем значение а определяет правило выбора второго уровня.
В самом деле, минимизация (*) при условии!ж || ^ с\ эквивалентна
минимизации (**), где а — множитель Лагранжа.
Таким образом, оказывается, что идея упорядоченной минимиза-
минимизации риска уже встречалась в математике. Однако ни для одной из
проблем, к решению которой она привлекалась, так и не удалось
до конца ответить на вопросы: как вводить априорное упорядочение
и каков должен быть критерий выбора второго уровня.
В задаче обучения распознаванию образов были рассмот-
рассмотрены две процедуры выбора второго уровня: процедура метода
скользящего контроля [45] и процедуры выбора правила
с наилучшим гарантированным качеством. Что же касается спо-
способов введения порядка, то, как оказалось, в задаче обучения
распознаванию образов они далеко не безразличны даже с фор-
формальной точки зрения.
К главе VII
Применение методов обучения распознаванию образов началось
одновременно с появлением первых работ по теории обучения. В на-
настоящее время установилась хорошая традиция, согласно которой
каждый вновь предложенный алгоритм обучения немедленно опро-
бывается на решении тех или иных задач практики. Установились
и свои традиционные сферы приложения методов обучения к реше-
решению задач практики.
КОММЕНТАРИИ 403
Это прежде всего — геология, метеорология, контроль каче-
качества, медицина, криминалистика. Большие работы ведутся по соз-
созданию буквочитающих автоматов, автоматов воспринимающих
речь.
В главе VII приведены результаты практического применения
алгоритмов метода обобщенного портрета. Эти результаты могли
быть получены только благодаря работам больших коллективов уче-
ученых. Так, задача о различении водоносных и нефтеносных пластов
в скважине была поставлена в Московском институте нефтехимиче-
нефтехимической и газовой промышленности под руководством III. А. Губерма-
на [25] и была успешно решена также группой М. М. Бонгарда, ра-
работы по криминалистике поставлены в Институте судебных экспер-
экспертиз под руководством Л. Г. Эджубова [28], работы по контролю
качества электронных приборов были поставлены В. С. Морозовым
[47], работы по применению методов обучения распознаванию обра-
образов в метеорологии ведутся в Гидрометцентре СССР под руковод-
руководством А. И. Снитковского [3] и в ВЦСО АН СССР под руководством
Л. Н. Романова [56]; наконец, работы по применению методов обуче-
обучения в медицине ведутся в Институте экспериментальной и клиниче-
клинической онкологии под руководством Т. Г. Глазковой и К. Н. Гурария
[23] и в I Московском медицинском институте под руководством
Л. Д. Линденбратена. Благодаря этим коллективам была отрабо-
отработана стандартная методика использования алгоритмов метода обоб-
обобщенного портрета, найдены оптимальные параметры алгоритмов,
словом, сделано все, что необходимо для того, чтобы алгоритмы
превратить в рабочий инструмент для решения практических
задач.
Кроме названных, существует большое количество других кол-
коллективов, которые успешно применяют современные методы обуче-
обучения распознавания образов для решения задач практики. В Москве
это — группы С. Н. Брайнеса, П. Е. Кунина, которые применяют
методы распознавания в медицине [7, 38]; коллектив, возглавляемый
Ю. И. Журавлевым, который ведет большие работы по применению
распознавания в геологии [29]. В Ленинграде коллектив сотрудни-
сотрудников, возглавляемый В. А. Якубовичем, провел значительные исслег
дования в криминалистике [35]. В Горьком большая группа сотруд-
сотрудников под руководством Ю. И. Неймарка весьма успешно применя-
применяет методы обучения распознаванию образов в медицине [48]. В Ново-
Новосибирске коллектив, возглавляемый Н. Г. Загоруйко [30], применяет
методы распознавания в социологии и другие. В настоящее время
идея применения методов обучения распознаванию образов весьма
популярна и эти методы привлекаются для решения самых различ-
различных задач практики.
Особое место в практическом применении методов обучения рас-
распознаванию образов занимают работы по созданию читающих ав-
автоматов и автоматов, воспринимающих речь. Эти задачи явились
первыми объектами приложения методов обучения распознаванию
образов.
Однако, несмотря на это, проблема создания читающих
автоматов и автоматов, воспринимающих речь, до сих пор далека
от завершения. Эти две задачи сейчас составляют самостоятельные
направления исследований [30, 31].
404 КОММЕНТАРИИ
К главе VIII
Применение методов обучения распознаванию образов для
решения задач практики принесло свои неожиданности: прежде
всего, оказалось, что результаты, полученные при использовании
различных алгоритмов обучения распознаванию образов для реше-
решения одной и той же задачи, не слишком сильно различаются между
собой (конечно, речь идет об алгоритмах обучения, имеющих разум-
разумное статистическое обоснование). Неожиданным оказался тот факт,
что метод минимизации эмпирического риска в, казалось бы, раз-
разных классах решающих правил позволяет отыскивать решающие
правила, обладающие примерно одинаковыми качествами.
Такое утверждение с формальной точки зрения не выдерживает
никакой критики: нетрудно представить себе два различных класса
решающих правил таких, что для одних задач в первом классе есть
удовлетворительные решающие правила и нет удовлетворительных
правил во втором классе, а для других задач, напротив, предпочти-
предпочтительней второй класс.
Создатели алгоритмов обучения распознаванию образов рассчи-
рассчитывали именно на такую ситуацию. Однако оказалось, что классы
задач, которые приходится решать, и классы конструктивных решаю-
решающих правил, которыми пользуются, таковы, что если некоторую за-
задачу решает один алгоритм, то близкое качество решения может
быть получено и с помощью другого.
Этому факту не может быть дано объяснения, если не привлечь
гипотезу о семиотической структуре мира, который мы пытаемся
познать. Такая гипотеза пока не сформулирована, хотя на необхо-
необходимость ее указывали представители самых разных отраслей знаний,
цель исследования которых состоит в познании законов природы.
Так, свое понимание семиотической структуры мира И.Ньютон
высказал в «Правилах умозаключения в физике», изложенных
в третьей части знаменитой книги «Математические начала нату-
натуральной философии». И первое правило таково: «Не должно прини-
принимать в природе иных причин, сверх тех, которые истинны и доста-
достаточны для объяснения явлений. По этому поводу философы утверж-
утверждают, что природа ничего не делает напрасно, а было бы напрасным
совершать многим то, что может быть сделано меньшим.
Природа проста и не роскошествует излишними причинами ве-
вещей». Этот принцип был сформулирован около трехсот лет назад.
С тех пор было предложено много различных гипотез о структуре
мира. И все они как-то оказывались связанными с понятием «слож-
«сложность».
В последнее время (особенно в связи с появлением вычислитель-
вычислительной техники) понятие сложность стало предметом исследования ма-
математиков: по разным причинам хотелось бы иметь возможность
оценить меру сложности различных математических объектов и в
частности функций. Оказалось, что понятие простоты или сложности
функций вовсе не так просто, как могло показаться с первого взгля-
взгляда. Во всяком случае, до сих пор не удалось построить критерий слож-
сложности функции, который удовлетворил бы всех исследователей. Для
тех же объектов, для которых удается ввести естественный критерий
сложности, неожиданно обнаруживаются любопытные факты. Так.
если ввести понятие сложности для классификации логических
КОММЕНТАРИИ 405
функций п переменных в зависимости от того, с помощью какого
числа базисных (например, пороговых) элементов эти функции мо-
могут быть реализованы, то окажется, что из всех 22 возможных функ-
функций подавляющее большинство составляют наиболее сложные,
т. е. те, которые могут быть реализованы лишь с помощью — 2П
элементов, и лишь ничтожная часть функций имеет малую слож-
сложность (число функций, реализуемых одним пороговым элементом,
меньше 2™*). Но самое интересное заключается в том, что, хотя поч-
почти все функции сложные, построить (просто выписать в виде табли-
таблицы значения во всех 2П точках) сложную функцию чрезвычайно
трудно. Во всяком случае, уже для п = 7 нет примеров сложной
функции.
Еще пример. Можно ввести естественное определение сложно-
сложности числа такое, что алгебраические числа будут проще трансцендент-
трансцендентных. И опять здесь оказывается, что трансцендентных чисел на чис-
числовой оси подавляющее большинство, и, несмотря на это, нам из-
известно чрезвычайно мало трансцендентных чисел, а известные
способы конструирования трансцендентных чисел позволяют по-
получить лишь ничтожное меньшинство всех имеющихся трансцендент-
трансцендентных чисел.
Если при любом «разумном» определении сложности окажется,
что сложные функции составляют подавляющее большинство всех
функций, то гипотеза «мир прост» становится чрезвычайно содержа-
содержательной. Вопросы исследования сложности математических объек-
объектов в настоящее время являются чрезвычайно актуальными [20, 37].
К главе IX
В настоящее время существуют достаточно тонкие критерии,
позволяющие судить о сходимости процессов, полученных с по-
помощью процедуры стохастической аппроксимации. В этой главе
хгаложены условия, при которых'процедура стохастической аппрок-
аппроксимации применена для минимизации функционала
Я (а) = ^ <? (*, а) ЛР (*)
с выпуклыми по а при любом фиксированном я функциями потерь
(? (г, а). Результаты для этого частного случая могут быть полу-
получены из общих теорем о сходимости процессов процедуры стохасти-
стохастической аппроксимации. Однако здесь приведены доказатель-
доказательства сходимости для этого частного процесса процедуры стохасти-
стохастической аппроксимации непосредственно в том виде, в каком
они были получены Б. М. Литваковым [44]. Аналогичные резуль-
результаты получены и Ю. М. Ермольевым [27]. Вообще же для рас-
рассмотренного случая известно [26], что если (? (г, а) — одноэкстре-
мальная функция, то при определенных условиях процедура стоха-
стохастической аппроксимации приведет к глобальному минимуму,
если же (? (я, а) — многоэкстремальная функция," то процедура
стохастической аппроксимации гарантирует достижение лишь ло-
локального минимума.
406 КОММЕНТАРИИ
К главам X, XI, XII
Задача восстановления вероятностной меры по эмпирическим
данным является одной из основных задач статистики. Известные
методы решения этой задачи распадаются на два типа: параметри-
параметрические и непараметрические методы.
Параметрические методы основаны на том, что предполагается
вид распределения, зависящий от конечного числа параметров.
В этом случае восстановление распределения эквивалентно оценке
этих параметров по эмпирическим данным.
Непараметрические методы не связаны с предположением о виде
функции распределения. Они основаны на реализации одной из
двух идей:
1) восстановление плотности распределения вероятностей
(в этом случае достаточна гипотеза о гладкости функции плотности
распределения вероятностей);
2) восстановление вероятностей определенного множества со-
событий.
Методы восстановления функции плотности распределения ве-
вероятностей предлагались Е. Парзеном [88], Н. Н. Ченцовым [69],
М. А. Айзерманом, Э. М. Браверманом, Л. И. Розоноэром [1]. По-
Последние авторы рассматривали эту задачу в связи с проблемой обу-
обучения распознаванию образов в вероятностной постановке. Однако
восстановление плотности распределения вероятностей требует зна-
значительного объема выборки. Это особенно существенно в многомер-
многомерном случае, когда для восстановления плотности распределения
часто необходима длина выборки во много раз большая, чем 2П,
где п — размерность пространства.
Вторая идея связана с восстановлением вероятностей класса
событий. Вероятностная мера будет восстановлена, если восстано-
восстановить сразу вероятности всех событий полной о-алгебры. Однако,
как показано в книге, вообще говоря, это сделать невозможно.
Этот метод применим в том случае, когда требуется определить ве-
вероятности определенного, сравнительно узкого класса событий.
Если класс состоит всего из одного события, то вопрос стоит
о сходимости частоты к вероятности для одного фиксированного со-
события. Ответ на этот вопрос был получен еще в XVIII веке Яковом
Бернулли (сходимость почти наверное установлена Э. Борелем одно-
одновременно с введением этого понятия).
Случай конечного числа событий принципиального интереса не
представляет, так как равномерная сходимость частот к вероятностям
здесь легко следует из закона Бернулли.
В 30-е годы особое внимание уделялось равномерной сходимости
эмпирических кривых распределения к функциям распределения.
В 1933 году В. И. Гливенко доказал [79], что имеет место равномер-
равномерная сходимость эмпирических кривых к функциям распределения
для произвольной функции распределения. В том же году А. Н. Кол-
Колмогоров для непрерывной функции распределения Р(х) установил
следующую асимптотическую оценку [83]:
Р {/7-зир | Р (х) - Р (х) |< е} —-> К (е),
КОММЕНТАРИИ 407
где Р1 (х) = V1 {| : | < х} — эмпирическая кривая распределения,
Дальнейшие уточнения были получены Н. В. Смирновым [59].
Он исследовал также уклонение эмпирических кривых, построен-
построенных по двум независимым выборкам, при неизменном распределе-
распределении [59]. Как сказано в основном тексте, исследование близости
эмпирических кривых к функциям распределения равносильно
исследованию равномерной близости частот к вероятностям по
классу событий вида
Разумеется, из равномерной близости эмпирических кривых к
функциям распределения следует равномерная близость частот к
вероятностям и в более широких классах событий (но не для всех
событий!).
Таким образом, интерес исследований 30—40-х годов к равно-
равномерной сходимости ограничивался одномерным случаем, что, види-
видимо, связано с ограниченностью вычислительных возможностей того
времени. После появления быстродействующих вычислительных
машин стали возможными новые методы обработки статистических
данных, например, такие, которые применяются в задачах обучения
распознаванию. В связи с этим возникла необходимость предельно
обобщить теорему Гливенко и выяснить, насколько широк может
быть класс событий, чтобы еще имела место равномерная сходимость
частот к вероятностям, и как изменяется скорость такой сходимо-
сходимости с расширением класса. Ответы на эти вопросы получены нами
в работах [18, 19] и составляют предмет изложения глав X, XI и
XII. Полученные оценки не так точны, как оценки Колмогоро-
Колмогорова — Смирнова для близости эмпирических кривых к функциям
распределения. Вопрос получения асимптотически точных оце-
оценок остается пока открытым.
Отметим, что необходимые и достаточные условия равномерной
сходимости частот к вероятностям оказались связанными с опреде-
определенным образом введенной энтропией класса событий относительно
выборок конечной длины. Эта энтропия во многом аналогична
шенноновской энтропии, рассматриваемой в теории информации.
К главе XIII
Начиная с первых работ по распознаванию указывалось, что
эффективное обучение возможно только в том случае, когда на класс
задач наложено заранее достаточно жесткое ограничение (априор-
(априорная гипотеза). Однако оценки достаточной длины обучающей после-
последовательности в зависимости от той или иной гипотезы были полу-
получены не сразу. К числу первых, безусловно, относится оценка Нови-
Новикова для персептрона, хотя в первоначальном варианте она оцени-
оценивала число исправлений, а не длину обучения. Длину обучения легко
оценить, если теорему Новикова дополнить условием останова.
408 КОММЕНТАРИИ
В ряде работ оценивается достаточная длипа выборки в случае
гипотезы о нормальном распределении классов [55].
В работе [16] мы исходим из предположения, что классы заведо-
заведомо безошибочно разделимы одним из N заданных решающих правил.
При этом оказалось, что достаточная длина обучающей выборки оце-
оценивается сверху:
1п N — 1п ц
дост < — 1п A — е)'
где е — точность, 1 — т] — надежность выбора решающего правила.
Этот результат немедленно прилагается к задаче нахождения линей-
линейного решающего правила для дискретных ограниченных множеств.
Случай, когда разделяемые множества могут быть заключены
в параллелепипед с гранями, параллельными осям координат, рас-
рассматривал Б. М. Курилов [39].
У. Хайлимен [81] предлагал для оценки достаточной длины
обучения в классе линейных решающих правил вспользоваться
обычным биномиальным распределением. Этот путь является лож-
ложным, так как при этом не учитывается требование равномерной бли-
близости оценок риска к их истинному значению по всему классу решаю-
решающих правил. Этим путем можно вывести конечные оценки длины
обучения для сколь угодно емких классов решающих правил, что
неверно.
В работе [17] мы ввели в рассмотрение функцию роста и получи-
получили оценки достаточной длины в детерминированной постановке зада-
задачи обучения распознаванию, а в статье [18], уже опираясь на общие
результаты по равномерной сходимости частот событий к их вероят-
вероятностям, получили оценки и в общем случае. В этой кпиге оценки
несколько уточнены.
Отметим, что приводимые оценки достаточной длины обучения
завышены, во-первых, потому, что они рассчитаны на наихудший
случай, и, во-вторых, поскольку при их выводе был сделан ряд
огрублений. Но существенно, что они позволяют увидеть качествен-
качественную зависимость требуемой длины обучения от параметров класса
решающих правил и устанавливают, что существуют не слишком
«страшные» оценки, не зависящие от распределения.
Вопрос о равномерной по параметру сходимости средних к ма-
математическим ожиданиям возник в связи с исследованием эффектив-
эффективности оценок максимального правдоподобия. Упомянутый резуль-
результат Л. Ле-Кама [85] получен им на основе идей А. Вальда [96]. Ре-
Результат, основанный на сведении к равномерной сходимости частот
к вероятностям, получен в [19]. Оба условия являются лишь доста-
достаточными и не перекрывают друг друга. Необходимых и достаточных
условий равномерной сходимости средних к математическим ожида-
ожиданиям пока нет.
К главе XIV
Метод обобщенного портрета был предложен в 1963 году в ра-
работах [13, 15]. Позже [17] было показано, что построение обобщенно-
обобщенного портрета эквивалентно отысканию максимума неположительно
определенной квадратичной формы в положительном квадранте, а
КОММЕНТАРИИ 409
известные алгоритмы построения разделяющей гиперплоскости раз-
различаются так, как различаются методы минимизации квадратичной
формы в положительном квадранте. В этой же работе и было пред-
предложено использовать метод сопряженных направлений.
К главе XV
Библиотека программ метода обобщенного портрета была созда-
создана А. А. Журавель и Т. Г. Глазковой. Подробное описание библо-
теки дано в статьях [12, 11].
Предлагаемые здесь программы несколько отличаются от тех,
которые были изложены в этих работах.
К главе XVI
Метод сопряженных направлений был предложен в 1952 году
для решения системы линейных алгебраических уравнений [80].
Этот метод позволяет находить решение алгебраических уравнений
(или, что то же самое, точку минимума квадратичного функционала
в конечномерном пространстве) за конечное число шагов. Позже
метод был обобщен для случая неквадратичных функционалов [75].
В 1969 году Б. Т. Поляк предложил обобщение метода сопряжен-
сопряженных градиентов для решения задач с ограничениями [51]. На много-
многочисленных примерах неоднократно демонстрировалась эффектив-
эффективность этого метода для решения различных задач.
ЛИТЕРАТУРА
1. Айзерман М. А., Браверман Э. М., Р о з о н о-
э р Л. И., Метод потенциальных функций в теории обучения
машин. М., «Наука», 1970.
2. А н д е р с о н Т. Введение в многомерный статистический ана-
анализ. М., Физматгиз, 1963.
3. Багров А. Н.,Вапник В.Н.,СнитковскийА.И.
К прогнозу опасных явлений погоды. Метеорология и гидро-
гидрология, № 3, 1974
4. Бонгард М. М., Проблема узнавания. М., «Наука», 1967.
5. Браиловский В. Л., Л у н ц А. Л., Формулировка за-
задачи распознавания объектов со многими параметрами и методы
ее решения. Известия АН СССР, Техническая кибернетика,
№ 1, 1969.
6. Браиловский В. Л., Л у н ц А. Л., Программа класси-
классификации многопараметрических объектов, основанная на отборе
статистически полезных признаков. Сб. под ред. В. Н. Вапника
«Алгоритмы обучения распознаванию образов». М., «Советское
радио», 1973.
7. Браннее С. Н., Биологическая и медицинская кибер-
кибернетика. М., «Медицина», 1971.
8. Бпэкуэлл Д., Г р и ш и к М. Л., Теория игр и статисти-
статистических решений. М., ИЛ, 1958.
9. Вайнцвайг М. Н., Алгоритм обучения распознаванию
образов «Кора». В сб. под ред. В. Н. Вапника «Алгоритмы
обучения распознаванию образов». М., «Советское радио»,
1973.
10. Вайнцвайг М. Н., Об одном алгоритме распознавания
двоичных кодов. Проблемы передачи информации, т. 2, вып. 3,
1966.
И. Вапник В. Н., Глазкова Т. Г., Червонен-
к и с А. Я. Алгоритмы обучения распознаванию образов, ис-
использующие метод обобщенных портретов. Алгоритмы ОП-4,
ОП-5, ОП-6, ОП-7. Сб. под ред. В. Н. Вапника «Алгорит-
«Алгоритмы обучения распознаванию образов». М., «Советское радио»,
1973.
12. Вапник В. Н., Журавель А. А., Червонен-
к и с А. Я., Алгоритмы обучения распознаванию образов, ис-
использующие метод обобщенных портретов. Алгоритмы ОП-1,
ОП-2, ОП-3. Сб. под ред. В. Н. Вапника «Алгоритмы обучения
распознаванию образов». М., «Советское радио», 1973.
ЛИТЕРАТУРА 411
13. В а п н и к В. Н., Л ернер А. Я., Узнавание образов при
помощи обобщенных портретов. Автоматика и телемеханика,
т. 24, № 6, 1963.
14. В а п н и к В. Н-, Л е р н е р А. Я., ЧервоненкисА. Я.
Системы обучения распознаванию образов при помощи обоб-
обобщенных портретов. Известия АН СССР, Техническая киберне-
кибернетика, № 1, 1965.
15. В а п н и к В. Н., Червоненкис А. Я., Об одном клас-
классе персептронов. Автоматика и телемеханика, т. 25, № 1, 1964.
16. В а п н и к В. Н., Червоненкис А. Я., Об одном клас-
классе алгоритмов обучения распознаванию образов. Автоматика и
телемеханика, т. 25, № 6, 1964.
17. Вапник В. Н., Червоненкис А. Я., Алгоритмы
с полной памятью и рекуррентные алгоритмы обучения рас-
распознаванию образов. Автоматика и телемеханика, т. 29, №4,
1968.
18. Вапник В. Н., Червоненкис А. Я., О равномерной
сходимости частот появления событий к их вероятностям. Теория
вероятностей и ее применения, т. XVI, № 2, 1971.
19. Вапник В. Н., Червоненкис А. Я., Теория равно-
равномерной сходимости частот появления событий к их вероятно-
вероятностям и задача поиска оптимального решения по эмпирическим
данным. Автоматика и телемеханика, № 2, 1971.
20. Витушкии А. Г., Оценка сложности задачи табулирова-
табулирования. М., Физматгиз, 1959.
21. Гнеденко Б. В. Курс теории вероятностей. М., Физматгиз,
1961.
22. Гладышев Е. Г., О стохастической аппроксимации. Тео-
Теория вероятностей и ое применения, т. 10, № 2, 1965.
23. Г л а з к о в а Т. Г., Г у р а р и й К. Н., Д а н и л е н-
к о С. И., и др., Возможности применения ЭВМ для клинико-
рентгенологической дифференциальной диагностики рака и
доброкачественного поражения пищевода. Вестник радиологии
и рентгенологии, № 2, 1971.
24. Головкин Б. А., Машинное распознавание и линейное
программирование. М. «Советское радио», 1972.
25. Г у б е р м а н Ш. А., И з в е к о в а М. Л., X у р г и н Я. И.
Применение методов распознавания образов при интерпретации
геофизических данных. Сб. «Самообучающиеся автоматические
системы». М., «Наука», 1966.
26. Д е в я т е р и к о в И. П., Пропой А. И., Ц ы п-
к ин Я. 3., О рекуррентных алгоритмах обучения распозна-
распознаванию образов. Автоматика и телемеханика, № 1, 1967.
27. Ермольев Ю. М., О методе обобщенных стохастических
градиентов о стохастических квазифейеровских последователь-
последовательностях. Кибернетика, № 2, 1969.
28. Журавель А. А., Трошко Н. В., Э д ж у б о в Л. Г.,
Использование алгоритма обобщенного портрета для опознания
образов в судебном почерковедении. В кн.: Правовая кибер-
кибернетика. М-, «Наука», 1970.
29. Журавлев Ю. И., Дмитриев А. Н., К р е н д е-
п е в Ф. Н., О математических принципах классификации
412 ЛИТЕРАТУРА
предметов и явлений. Дискретный анализ. Сб. трудов ИМ
СО АН СССР. Новосибирск, № 7, 1966.
30. Загоруйко Н. Г., Методы распознавания и их примене-
применения. М., «Советское радио»., 1972.
31. Ковалевский В. А. (редактор), Сб. «Читающие авто-
автоматы». Киев, «Наукова думка», 1965.
32. Ковалевский В. А., Современное состояние проблемы
распознавания образов. Кибернетика, № 5, 1967.
33. Козинец Б.Н-, Об одном алгоритме обучения линейного
персептрона. Сб. «Вычислительная техника и вопросы програм-
программирования». ЛГУ, 1964.
34. Козинец Б. Н., Рекуррентный алгоритм разделения двух
множеств. В сб. под ред. В. Н. Вапника «Алгоритмы обучения
распознавания образов». М., «Советское радио», 1973.
35. Козинец Б. Н., Л а н ц м а н Р. М-, С о к о л о в Б. Ы.,
Якубович В. А., Опознание и дифференциация почерков
при помощи электронно-вычислительных машин. Сб. «Само-
«Самообучающиеся автоматические системы». М., «Наука», 1966.
36. Колмогоров А. Н., Три подхода к определению понятия
«количество информации». Проблемы передачи информации,
т. 1, вып. 1, 1965.
37. Колмогоров А. Н., Фомин СВ., Элементы теории
функций и функционального анализа. М., «Наука», 1968.
38. К у н и н П. Е., Б о я д ж а н В. А., и др., Распознавание
образов и дифференциальная диагностика. Вестник АМН
СССР, № 5, 1968.
39. К у р и л о в Б. М., Получение достаточных характеристик
при; распознавании образов. Вычислительные системы. Сб. тру-
трудов ИМ СО АН СССР, вып. 22 Н, 1966.
40. Л е К а м Л., О некоторых асимптотических свойствах оценок
максимума правдоподобия. Сб. Математика, М-, 1960.
41. Логинов В. И., Хургин Я. И., Общий подход к проб-
проблеме распознавания образов. Сб. тр. МИНХ и ГП, «Недра», вып.
62. М., 1966.
42. Логинов Н.В., Метод стохастической аппроксимации.
Автоматика и телемеханика, № 4, 1966.
43. Л и н н и к Ю. В., Метод наименьших квадратов. М., Физмат-
гиз, 1962.
44. Л и т в а к о в Б. М., О сходимости рекуррентных алгорит-
алгоритмов обучения распознаванию образов. Автоматика и телемеха"
ника, № 1, 1968.
45. Лунц А. Л., Браиловский В. Л., Об оценке призна-
признаков, полученных в статистических процедурах распознавания.
Известия АН СССР, Техническая кибернетика, № 3, 1969.
46. Минский М., Пейперт С, Персептроны. М., «Мир»,
1971.
47. Морозов В. С..Морозова В. А., и др., Прогнозирова-
Прогнозирование индивидуального срока службы электронных приборов
с помощью метода обобщенных портретов. Электронная техника,
серия 1. Электроника С. В. Ч., выпуск 9, 1969.
48. Неймарк Ю. И., Баталова 3. С. и др. Распознавание
образов и медицинская диагностика. М., «Наука», 1972.
ЛИТЕРАТУРА 413
49. Н и л ь с о н Н., Обучающиеся машины. Ы-, «Мир», 1967.
50. П е р в о з в а н с к и й А. А., Распознавание абстрактных
образов, как задача линейного программирования. Известия
АН СССР, Техническая кибернетика, № 4, 1965.
51. П о л я к Б. Т., Метод сопряженных градиентов в задачах на
экстремум. Журнал вычислительной математики и математиче-
математической физики, т. 9, № 4, 1969.
52. Поляк Б. Т., Ц ы п к и н Я. 3. Псевдоградиентные алгорит-
алгоритмы адаптации и обучения. Автоматика и телемеханика, № 1,
1973.
53. Пугачев В. С, Статистические проблемы теории распозна-
распознавания образов. Тр. III всесоюзного совещания по автоматиче-
автоматическому управлению. М., «Наука», 1967.
54. Розенблатт Ф., Принципы нейродинамики. Персептрон
и теория механизмов мозга. М., «Мир», 1965.
55. Р а у д и с III. Ю., Об определении объема обучающей выборки
линейного классификатора. Сб. тр. ИМ СО АН СССР, вып. 28.
Новосибирск, 1965.
56. Р о м а н о в Л. Н., Д ы м н и к о в а Т. Р., Построение ли-
иейных разделяющих функций для классификации синоптиче-
синоптических ситуаций. В кн.: Статистические методы в метеорологии,
ч. I, Новосибирск, 1969.
57. Р ы ж и к И. М., Г р а д ш т е й н И. С, Таблицы интегралов,
сумм, рядов и произведений. М., ГИТТЛ, 1951.
58. Себастиан Г. С, Процессы принятия решений при рас-
распознавании образов. «Техника», 1965.
59. Смирнов Н. В., Теория вероятностей и математическая
статистика (Избранные труды). М., «Наука», 1970.
60. Т и х о н о в А. Н., О регуляризации некорректно поставлен-
поставленных задач. ДАН СССР, 153, 1, 1963.
61. Т и х о н о в А. Н., О решении некорректно поставленных за-
задач и методе регуляризации. ДАН СССР, 181, 3, 1963.
62. У и л к с С, Математическая статистика. М., «Наука», 14N7.
63. У р б а х В. Ю., Дискриминантный анализ: основные идеи и
приложения. Сб. Статистические методы классификации, вып. 1.
МГУ, 1969.
64. Ф е л л е р В., Введение в теорию вероятностей и ее приложе-
приложения. М., «Мир», 1964.
65. Француз А. Г., Некоторые вопросы статистической теории
опознания образов. Сб. Бионика. М., «Наука», 1966.
66. X и н ч и н А. Я., Об основных теоремах теории информации.
Успехи математических наук, т. XI, вып. 1 F7), 1956.
67. Ц ы п к и н Я. 3., Адаптация и обучение в автоматических си-
системах. М., «Наука», 1968.
68. Цыпкин Я. 3., Основы теории обучающихся систем. М.,
«Наука», 1970.
69. Чепцов Н.Н., Оценка неизвестной плотности распределе-
распределения по наблюдениям. ДАН СССР, т. 147, № 1, 1962.
70. Якубович В. А., Некоторые общие теоретические прин-
принципы построения обучаемых опознающих систем. Сб. Вы-
Вычислительная техника и вопросы программирования. ЛГУ,
1965.
414 ЛИТЕРАТУРА
71. Якубович В. А., Рекуррентные конечносходящиеся алго-
алгоритмы решения системы неравенств. ДАН СССР, т. 166, № 6,
1966.
72. АЬгатзоп N.. Вгауегтап Б., Ьеагшпд 1о Несо§шге
Раиегз т а Капйот Епушттеп1. Тгапз. 1КЕ 1Т-8, № 5, 1962.
73. АЬгатзоп N.. Вгатегтап Б,, ЗеЬазНап О.,
РаЦегп Кесо§пШоп апй МасЫпе Ьеагт§. ШЕЕ Тгапз. оп
Ыогтайоп ТЬеогу V. 1—9, № 4, 1963.
74. Апйегзоп Т. \\г., ВаЬайиг К. К., С1а55ШсаЫ.оп т1о
Ыо тиШуапа1е погта1 йЫпЬиЬшпз ш1Ь с!Шегеп1 соуапапсе
та1псз. ТЬе аппа1з о! МаШета11са1 з1а11зЦсз, .Типе., у. 133,
№ 2, 1962.
75. Б а п 1 е 1 .Г. \У., ТЬе соп]и§а1е §гасПеп1 теШой 1ог Нпеаг
апй попНпеаг орега1ог ееиайоп. 81АМ Nитег. Апа1. 4, № 1,
1967.
76. В уоге 1з ку А. , Оп з1осЬаз11с арргох1таЦоп. Ргосеес11п§з
о! Ше III ВегкеПу 8утроз1ит оп Ма1ЬетаЦса1 ЗЬаИзЫсз апй
РгоЬаЫШу, V. 1, 1956.
77. ПзЬег Н. А., СопЬпЬиНопз 1о Ма1ЬетаИса1 81а11зисз.
Кеда-Уогк, 1952.
78. Г 1 х I. Е., Н о A § е з 3. Ь., БхзтттаЬогу апа1уз1з; поп-
рагате1г1с Й1зспт1па11оп: сопз1з1епзу ргорегйез. Нерог1 4 о!
№е С8АГ 8сЬоо1 о{ Аухайоп МесНсте, Напс1о1рЬ ПеЫ, Техаз,
1952.
79. ОНуепко V. I., 8и11а Йе1егт1па11опе етртса Й1 ргоЬаЫ-
Н1а, О1огпа1е йе1Г 1зй1и1е НаНапо йе§Н АЦиаг1, 4, 1933.
80. Н е з I е п е з М. Н., 8 I 1 е I е 1 Е., МеШой о!соп]и§а1е §гасИ-
еп1'з {ог зо1у1пв Нпеаг зуз1етз. ^., Нез. Ка1. Виг. 81апс1агс1з, 49,
№ 6, 1952.
81. Н1§Ь1еутап \У. Н., Ыпеаг Йес131оп 1ипс11опз ш№ аррН-
сайопз 1о раНет гесо§пШоп. Ргос. ШЕ, № 6, 1962.
82. К 1 е { е г Е., 1оПо111г |., 81осЬазис езЦтаНоп о! №е
тах1тит оГ а гестезз1оп {ипс11оп. Апп. МаШ. 81а1. V. 123,
№ 3, 1952.
83. Ко1то§огоН А. N.. 8и11а йе1егт1раЦопе етр1пса сИ ипа
1姧е сИ Й1з1пЬииопе, О1огпа1е Йе11' 1зЦ1и1е ИаНапо йе§Н А1-
1иап, 4, 1933.
84. Ь е Кат Ь., Оп зоте азутр1о11с ргорег11ез о! тах1тит Нке-
Ьоой ез11та1ез апй ге1а1ес! Вауез' езЦта1ез. СаН1*. РиЬИо.
81аиз1. И, 1953.
85. Ь е Кат Ь., Оп азутрЬоЦс 1Ьеогу о{ езИтаЦоп апй 1ез11п§
Ьуро1езез. Ргос. III ВегИеу 8утроз1ит оп МаШ. 81а1. апЗ
РгоЬаЫШу, V. 1, 1956.
86. М о I 2 к 1 п Т., 8сЬоепЬсг§ I., ТЬе ге1аха11оп те1Ьос!
Ьг Нпеаг 1пестиа1Шез. СапасНап ^. Ма№., 6, № 3, 1954.
87. Р4оу1ко{1 А., Оп сопУег§епсе ргооГз 1ог регсер1гопз. Ргосе-
ес11п§з о! 8утроз1ит оп Ма№ета11са1 ТЬеогу о! Аи1ота1а.
Ро1у1есЬтс 1пз111и1е о{ ВгооЫуп, V. XII, 1963.
88. Р а г 2 е п Е., Оп сопз1з1еп1 езЦтаЬез о! Ше зрес1гит о! з1а11опа-
гу Цте зепез. Апп. МаШ. 81а1., уо1. 28, 1957.
89. НоЬЬ1пз Н., Мопго 8., А з1осЬаз11с арргох1та11оп
теШой. Аппа1з о! МаШ. 81а1., V. 22, № 1, 1951.
ЛИТЕРАТУРА 415
90. Н о зепЫаИ Г., ТЬе регзер1гоп, а ргоЪаЫШу тойе1 Гог
тГогтаЦоп з1ога§е апй ог§аШ2а11оп т Ше Ьгат. РзусЪо1.
Неу., 65, 1958.
91. 8е11г1с1§е'О., РаЦегп гесо§пШоп апй 1еагп1п§. Ргосеес1т§
о{ Ше ТЫгй Ьопйоп 8утроз1ит оп 1пГогтаЦоп ТЬеогу. К
Уогк, 1956.
92. 8 I е 1 п Ь и с Ь К., Р 1 з к е II. А. \У., Ьеагшп§ таЬпсз
Ше1г аррИсаЦоп. ШЕЕ ТгапзасЦоп о! Е1ес1гоШс Сотри1егз,
V. ЕС—12, № 6. Бес. 1963.
93. II I I 1 е у А. М., А 1Ьеогу оГ №е тесЬашзт о! 1еагп1п§ оп 1Ье
сотриЬаНоп о{ сопс1111опа1 ргоЬаЬПШез, Ргос. 1 з1. 1п1. Соп-
&Г658 СуЬегпеИсз. Катиг, 1956.
94. ^ 1 с! г о да В., ОепегаНгаЦоп аш! тГогтаЦоп з1ога§е 1п пе1-
даогкз оГ айаНпе пеигопз. 8е1Г-Ог§аШ2Ш§ 8уз1етз, 1962. \УазЫад-
(;оп, 1962.
95. \У 1 с! г о да В., <(Воо1зЬагр 1еагт§» 1п 1ЬезЬоЫ 1о§1з. Ргос. оГ
№е III Соп^гезз о{ №е 1ГАС. Ьопйоп, 1966.
96. \У а 1 с! А., Р4о1е оп сопз1з1епсу о{ №е тоз1е НкеЬоой езЦща1е.
Апп. МаШ. 81а1. 20, 1949.
Владимир Наумович Вапник
Алексей Яковлевич Червопенкис
ТЕОРИЯ РАСПОЗНАВАНИЯ ОБРАЗОВ
(статистические проблемы обучения)
М., 1974 г., 416 стр. с илл.
Редактор О. Н. Киселев
Техн. редактор К. Ф. Брудно
Корректор А. Л. Ипатоеа
Сдано в набор 3/ХИ 1973 г. Подписано^ печати
7/Ш 1974 г. Бумага 84X108/32. Фиэ. печ. л. 13
Условн. печ. л. 21,84. Уч.-изд. л. 19,76.
Тираж 8700 экз. Т-05530. Цена книги 1 р. 48 к.
Заказ № 3253
Издательство «Наука»
Главная редакция физико-математической
литературы
117071, Москва, В-71, Ленинский проспект, 15
2-я типография издательства «Наука».
Москва, Шубинский пер., 10