КЛАССИКА МИРОВОЙ ПЕДАГОГИКИВ.Ф. ШаталовИЗУСТНАЯ
АЛГЕБРА2.	а>1 эограгт.2< ^ -^г/л ^'г.ыв&гт
5 Чш	Ь''й:-гг?й*4- Прг а>1 1'лУ>1, гглущУ!'5''ягг<С5 4<'('
В.Ф. ШаталовИЗУСТНАЯАЛГЕБРАМосква - 2009
УДК 371.32
ББК74. 202.4
Ш28Шаталов В.Ф.Ш 28 Изустная алгебра. Учебное пособие. М.: «Школа Шаталова», 2009. - 36 с.
18ВМ 978-5-933-234-6Методические материалы предназначены для школьников, учителей и родителей,
а также студентов педагогических вузов.УД К 371.32
ББК74. 202.418ВМ 978-5-933-234-6© Шаталов В.Ф., 2009.© «Школа Шаталова», 2009.
кто СТАНЕТ АВТОРОМ СОТОЙ?Это происходило многократно. После семинаров по математике, а они проводились
ежемесячно на протяжении 30 лет, в Донецк приходило, как минимум, одно письмо со странной
просьбой о приглашении ещё раз на этот же семинар. Зачем? Мотивация была предельно
откровенной и убедительной. «После двух месяцев работы в новом методическом режиме мне
стало до боли сердечной понятно, что я НЕ УМЕЮ ГОВОРИТЬ».Три четверти писем, и это понятно, шли от молодых учителей, но ещё более понятно, что на
обнажённую откровенность возрастному учителю решиться безмерно трудно — письма такого
содержания приходили от них много реже.Причин лекционного несовершенства среди учителей математики много, и одна из них
ввдится в том, что на курсовых экзаменах по математике в высшей школе редкий экзаменатор —
дефицит времени! — обращает внимание на лексическую ущербность речи студента. Написано
правильно и устные дополнения к записям воспринимаются фрагментарно: всё восполняет
визуальная проверка математических преобразований в экзаменационных черновиках. Для
оценки в зачётке большего и не требуется. Волна за волной уходят из студенческих аудиторий
выпускники, лексическая составляющая которых, мягко говоря, далека от совершенства.Кульминацией такого небрежения стал случай, о котором нам, студентам-заочникам
Владивостокского педагогического института, рассказал заведующий районо, преподававший по
совместительству педагогику на заочном отделении.Рассказ этот относился ко времени, когда только-только на дальние окраины страны стали
приезжать выпускники университетов с академическими значками, украшенными гербом
страны. У всех прочих на голубом фоне красовалась открытая книга.Школа приняла универсала с затаённым ожиданием поучиться у столичного профессионала.А у внешне уверенного в себе и несколько амбициозного учителя математики первые же уроки
пошли вразнос: не понимали его дети!Двойки, скандалы, жалобы родителей и — обилие детских слёз. При посещении его уроков
коллегами и администраторами школы вдруг вьыснилось, что выпускник университета не
учитель, а лектор. Лектор, какими были его преподаватели. Математических ошибок у него не
было, но и живыми, участливыми, шутливо-располагающими интонациями при объяснении
нового материала пользоваться его не научили. О возрастной детской психологии он и знать
ничего не знал — не содержалась эта самая психология в университетских программах тех лет.
К концу третьей недели всё стабилизировалось: дети перестали его слушать.
Азачем, если всё равно «ничего не поймёшь»?Попытки районного отдела народного образования чем-то помочь молодому учителю
несколько припозднились, и, дабы не потерять начинающего учителя с университетским
дипломом, с его согласия был подписан приказ о переводе его в окраинную школу в районе
Первой Речки.Наивные помощники! Едва только новый учитель появился в школьном коридоре, как по
классам прошла волна дестабилизации: "это тот, у которого ничего не поймёшь".Первый урок, обволакивающая тишина — дети приготовились его
НЕ ПОНИМАТЬ.Через две недели — новая школа, новые нервные терзания, бесплодные попытки следовать
многочисленным советам, увольнение.
—	Весной, — закончил свой грустный рассказ преподаватель, — я случайно встретил его в городе.
Он стал имбициликом и тихо разговаривал сам с собой.Реакция отдельных представителей науки на первые листы с опорными сигналами по
математике была воинственной. Новым методическим пособиям они приписывали нелепые, ими
же самими придуманные недостатки. А дети работали с упоением, от родителей одни только
восторги, от участников семинаров—десятки тысяч благодарственных писем.Первопричиной же глубокого проникновения практиков в существо новой системы являлось
ИЗУСТНОЕ восприятие учебного материала, которое получали и участники семинаров, и
школьники, но которого сторонились, более того — избегали кабинетные критики. О родителях и
говорить нечего: они видели радость детского труда, в результате которого выпускники школы без
посторонней помощи поступали в самые престижные институты, а по прошествии десяти лет один
за другим стали защищать научные диссертации, и общее количество таких диссертаций учеников
автора приближается к первой сотне. Кто защитит СОТУЮ научную работу? Не дано было понять
некоторым кабинетным учёным, что двуединая система УЧИТЕЛЬ-УЧЕБНИК вдруг
превратилась в ТРИЕДИНУЮ, дополнившись ЛИСТАМИ С ОПОРНЫМИ СИГНАЛАМИ,
беспромедлительно укрепившимися на второй позиции, потеснив учебник. Не отработав в новых
условиях хотя бы один семинарский цикл, уяснить смысл и значение листов практически
невозможно. Если, тем более, для такой работы нет ни желания, ни внутреннего долга чести.
Именно это и стало трагедией для уже ушедших из жизни и доживающих свой век
критиканствующих кабинетчиков.А новая система ширится, укрепляется, живёт, проясняя всем, что из ТРИЕДИНОЙ связи по
прошествии некоторого времени сначала отходит УЧИТЕЛЬ, во многом теряет свою давнюю
значимость УЧЕБНИК, а каналы долговременного хранилища памяти заполняются чертежами,
контрольными связями и логическими взаимопереходами листов с опорными сигналами.
Непродолжительный взгляд на страницу, мысленное проговаривание уже закрытого текста и
ШКОЛЬНИКИ, СТУДЕНТЫ, ПРЕПОДАВАТЕЛИ готовы вести обстоятельные ИЗУСТНЫЕ
воспроизведения самых сложных разделов, десятилетиями казавшихся недоступными
ВСЕОБЩЕМУ сознанию.В последний день работы над рукописью книги пришло сообщение из
Испании о том, что 88-ю диссертацию защитил ученик автора Алексей Тарасов.
В июле он вместе с женой-испанкой возвращается в Донецк, и в новом издании
«Изустной алгебры» можно будет увидеть его фотографию.
Арифметическая прогрессияа,	п аразностьа <с1 ~ О паст.X “ X “Ь 41 «Простое» число
Щь&счлен. Эйл^1.	а^2.	а^+ Н3.	Я|+ 2с4.	а^+319. а л « с!	- -		Проверим подмеченную нами за-П • а«+(1]г~1)с1 Ц кономерность при П = 1.2. Предположим, что эта законо¬
мерность верна для П>го члена,
и докажем, что она справедлива
для (п+1) -го члена.“ а,+Н(п—1)+Н == а,+/^бфл ^[1и^1шх Тсщсс1+2+3+	+99+100 = 5050 И
= +а^а -ап+7«-= вы + в,Я4-/Любой удвоенный член арифметической прогрессии
равен сумме равноотстоящих от негочленов.
Арифметическая прогрессия -это числовая последовательность, в которой каждый член, начиная со второго, равен
предыдущему, сложенному с постоянным для этой последовательности числом.СИМВ0ЛИ1СА: — первый член;П —рассматриваемых членов;Яд — произвольный член;Л —разность прогрессии;1§ —сумма рассматриваемых членов;	условный знак арифметической прогрессии.Прогрессия ВОЗРАСТАЮЩАЯ, еслиУБЫВАЮЩАЯ, если (1<0,ПОСТОЯННАЯ, если (1=0.Запишем столбиком несколько первых членов прогрессии и заметим, что порядковый номер
каждого члена на ЕДИНИЧКУ больше коэффициента при Д. Если это свойство сохранится идалее, то формула ДЕВЯТОГО члена будет такой: С1^ ~	8 А, а формула И-го(произвольного) члена запишется просто:а„= а,+(п-1)11В суш;ности, это она и есть, но способ её нахождения — Метод Неполной Математической
Индукит. ОПАСНЫЙ МЕТОД!! Подметив любопытную закономерность, мы предположили, что
она всесильна.Исторический Факт. Великий русский математик Леонард Эйлер, рассматривая трёхчленX-Х + 41 , нашёл, что при X = 1 образуется простое число 41, а при X = 2 получаем
очередное простое число - 43. Далее пойдут: 47, 53... Прямо-таки, если довериться
неполной математической индукции, КОПИЛКА простых чисел! Увы, копилки не было:
далее одно за другим стали образовываться составные числа.Стало быть, заниматься НМИ — пустая трата времени? Ничуть не бывало: этот метод позволяет
высказать ГИПОТЕЗУ, завершать которую следует методом Полной Математической Индукции.Суть его в том, что подмеченную закономерность проверяют сначала при П= 1, предполагают,что она верна для П-го члена и доказывают её справедливость для (п+1) -го члена.Математический КАПКАН! Если она окажется верной для (П+1) -го члена, то она будет вернойдпя(П+2)-го члена, затем для (П+3)-го и т.д. до бесконечности.Используем этот метод для вывода формулы ЛЮБОГО члена арифметической прогрессии. Дляпервого члена сомнений нет: = Я}	. Теперь предположим, что она верна для П-гочлена: Я„ = Я1 + (п-1)й и определим по ней следующий член:я„+1= я„+ (1 = Я, + й (п—1) + й = я, + йп —^
Конструкция та же: Коэффициент при Д на единичку меньше порядкового номера!Не совсем документально, но интересно: ученик начальной школы, будущий «корольматематиков» Клрл Фридрих Гаусс без труда назвал сумму всех чисел от 1 до 100: 5050 , пояснив,
что сначала сложил два крайних числа и результат умножил на 50, так как каждая новая пара
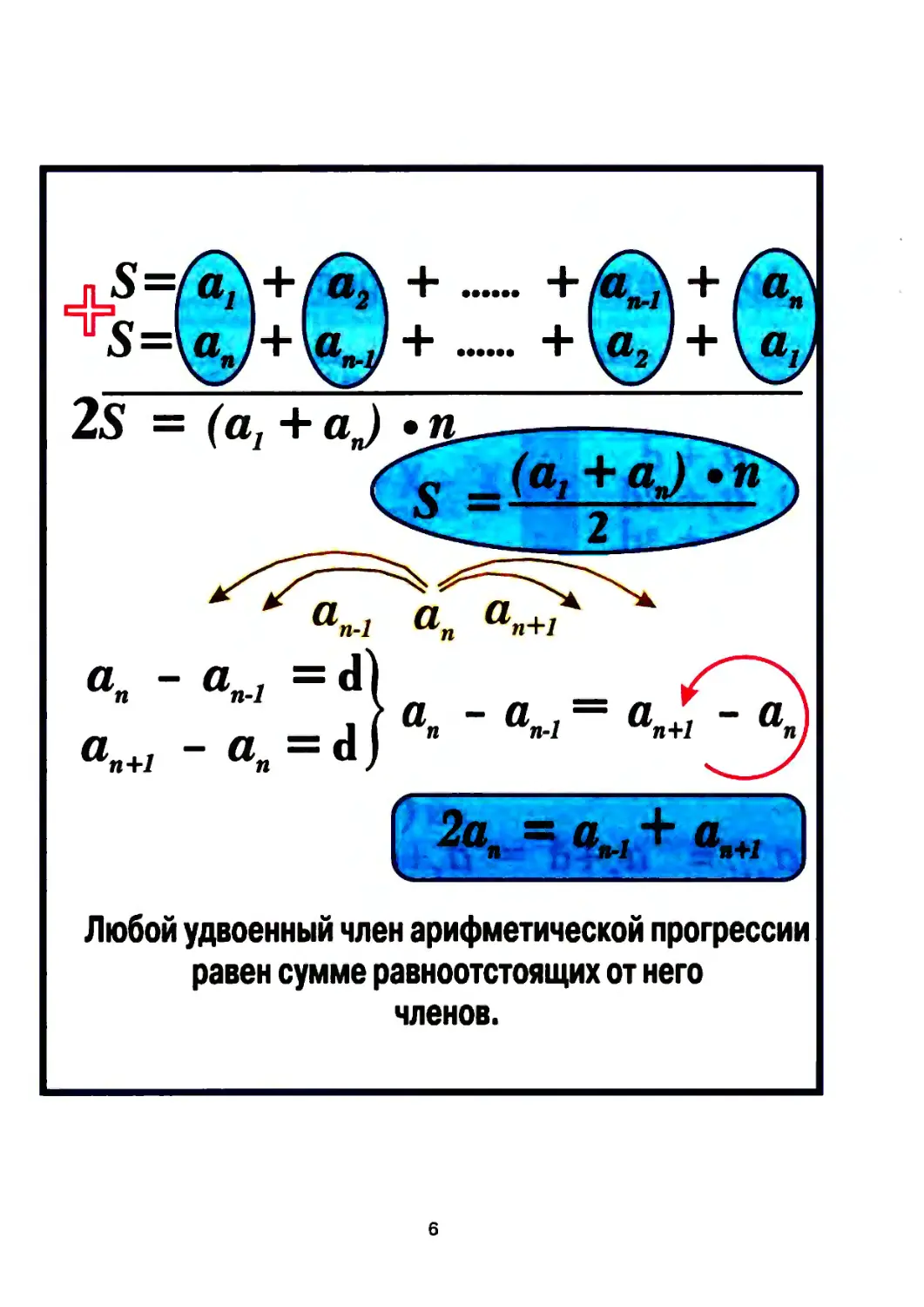
крайних снова дает в сумме 101.Не вдаваясь в историческую подлинность этого рассказа, запишем одной строкой суммуП членов арифметической прогрессии, а под ней сумму этих же членов, но записанных в обратном
порядке. В каждой новой вертикальной паре один член становится на (1 больше, другой на
Д меньше, а сумма их остается неизменной: Я| + а„ . Таких пар П, и все вместе они дают удвоенную
сумму членов прогрессии. А сама сумма оказывается равной:^ (а. + а^пИз трех соседних членов арифметической прогрессии СРЕДЙИЙ на с1 больше ПЕРВОГО и на
Й меньше ТРЕТЬЕГО, откуда следует равенство:К-1 ~ К+1 ~ КИ вывод: УДВОЕННЫЙ СРЕДНИЙ РАВЕН СУММЕ КРАЙНИХ: 2я„ = Я^+1 + а„.,.Если же заметить, что в каждой новой паре сумма остаётся неизменной, то всё завершается
чрезвычайно важным выводом:ЛЮБОЙ УДВОЕННЫЙ ЧЛЕН АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ РАВЕН СУММЕРАВНООТСТОЯЩИХ ОТ НЕГО ЧЛЕНОВ.8
ЗнаменательГеометрическая прогрессия>^1 п.у
11.й п-1123нмизнакоперем.Л	м иР Р о п-л Е "
5 =^ + ‘^ + ^+... +^	^	 п	п (Все члены ((мнйжим на^	^ ^ ^ ^««;/(ййл исхо^ш^юа9^10()
5 =1V1^-1 ^ ^1ьхКвадрат любого члена геометрической
прогрессии равен произведению
равноотстоящих от него членов.Л^ + Г + 3’‘ + ... + п’^-^ _п(п+1Н2п+1)V - -	 -	-	О 	Пмип(п+1).(2п+1) .	п{п+1).(2п+1)+6(п+1)1.	6	■ 6	_(п+1){2п*+п+6п+6) (п-И)(2пЧЗп+4п-Ь6) (п+1)(п+2)(2п+3)666П.П. 17.18.19.10
Геометрическая прогрессияПоследовательность, в которой каждый член, начиная со второго, равен предыдущему,
умноженному на постоянное для этой последовательности число, называется геометрической
прогрессией.СИМВОЛИКА:	— первый член;П — количество членов;I — произвольный член;—	сумма члечов прогрессии;-	знаменатель прогрессии;условный знак геометрической прогрессии.Прогрессия ВОЗРАСТАЮЩАЯ, если
УБЫВАЮЩАЯ, если
ПОСТОЯННАЯ, если ^=1,ЗНАКОПЕРЕМЕННАЯ (колеблющаяся), если ^ 0.Запишем столбиком несколько первых членов прогрессии и заметим, что порядковый номеркаждого члена на ЕДИНИЦУ больше показателя у	Но это снова-таки неполнаяматематическая индукция. Поэтому на основании метода ПМИ проверим справедливость нашегопредположения для первого члена, предположим, что оно верно для П-го члена, и докажем еговерность для (П"1“ 1)-го члена.Конструкция результата, как видим, сохранилась; порядковый номер члена на единицу более
показателя у знаменателя. Итак, окончательно:Члены возрастающей геометрической прогрессии увеличиваются несопоставимо быстрее, чем
члены арифметической прогрессии. Тому несколько иллюстраций.Общеизвестная легенда об изобретателе шахмат. Дополним её русским сказом о крестьянине,
который после долгих торгов продал жадному боярину лошадь при условии оплаты: копейка за
первый гвоздик в подкове лошади, а за каждый следующий в два раза больше. При
16 гвоздях боярину пришлось выложить более 700 рублей, хотя лошадь стоила 50.И ещё один пример. Французская графиня Элизабет-Анжелика де Буотвиль овдовела в 20 лет.
Её супруг, губернатор Сенлиса, по завещанию велел выплатить ей после первого года одиночества
ОДНУ золотую монету, и за каждый следующий год вдвое больше, если она не выйдет замуж.
Графиня прожила одинокой 69 лет и получила право на 147 573 952 314 798 306 112 золотых монет,
что равнозначно сегодняшним 737 квинтиллионам долларов. Правда, умерла графиня
320 лет назад и достоверность этого документа вызывает сомнения.Для вывода формулы суммы членов геометрической прогрессии, запишем их одной строкой иумножим каждый член на Вторую строку запишем над первой, сместив все члены правой части
на одну позицию вправо. Очевидно, что — это второй член, — третий член. Послевьиитаниянижнейстрокиизверхней,слеваостанутся5^ --5,асправа	—11
Отсюда конечная формула:	П	п1в ней можно заменить ^ на	, вынести за скобки и получить ещё одну формулу,незаменимую в последующих разделах.^ (9" -1)1Рассмотрим три последовательных члена геометрической прогрессии.Разделив средний на первый и третий на средний получим ^ и приравняем левые части:Отсюда следует, что квадрат среднего равен произведению крайних. И снова-таки, это свойство
можно расширить. ЬСаждый предыдущий в ^ раз меньше последующего, а каждый последующийв ^ раз больше предыдущего. Потому КВАДРАТ ЛЮБОЮ ЧЛЕНА ГЕОМЕТРИЧЕСКОЙ
ПЮГРЕССИИ РАВЕН ПЮИЗВЕДЕНИЮ РАВНООТСТОЯЩИХ ОТ НЕЮ ЧЛЕНОВ.Заметим, что эти свойства двух прогрессий обратимы: они определяют наличие прогрессий.Практически важная формула СУММЫ КВАДРАТОВ ЧИСЕЛ НАТУРАЛЬНОГО РЯДА.
Доказывается методом полной математической индукции.При11= 1 онаверна.Предположим, что она вернадля II членов, и докажем, что она верна для (П+1) членов.
Прибавим к ней квадрат следующего члена. Приведём к общему знаменателю и, разложив на
множитель числрггель, получим формулу той же конструкции:(п+1)(п+2)(2п+3)612
в-642<к
оШаг!^5 Ь 1; I'"_Н1-Ф"]_»10ПБЕСКОНЕЧНЫЕ ПРОГРЕССИИ8..,= 2-(1)"8... - 21\“(I)-^=2-ф’п-оо (1)"-о
< 8 8„.. - 2Если переменная величина изменяется так, что абсолютная
величина разности между нею и данной постоянной величиной
может стать и остаться меньше сколь угодно малой наперёдзаданной 8, то тогда эта постоянная величина называется
пределом этой переменной величиныСет = 2ОсновныеП—00П л—Ок1-»Отеоремы о пределах13
Бесконечные прогрессиив сущности, каждая прогрессия, если не ограничивать количество её членов, бесконечна, и это
хорошо видно на четырех графиках. На розовом при первом члене 2 каждый следующий на
единицу больше и — в бесконечность. Это БЕСКОНЕЧНО ВОЗРАСТАЮЩАЯ
АРИФМЕТР1ЧЕСКАЯ ПРОГРЕССИЯ. Её разность равна 1 и именуют её иногда ШАГ.На зелёном графике - члены БЕСКОНЕЧНО УБЫВАЮЩЕЙ АРИФМЕТИЧЕСКОЙ
ПРОГРЕССИИ с тем же первым членом, но с отрицательным шагом — 1.Уже четвёртым своим членом она проникает в область отрицательных чисел и далее - бездна.
Оранжевйй график иллюстрирует быстрый рост членов БЕСКОНЕЧНО ВОЗРАСТАЮЩЕЙ
ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ с первым членом 1 и знаменателем 2.Это снова шахматы, подковы и завещание.Совсем иное дело — красный график. На нём — члены БЕСКОНЕЧНО УБЫВАЮЩЕЙ
ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ с первым членом 1 и знаменателем 1/2.По формуле суммы членов найдём сумму первых 10 членов.1-ф"_ , ,1^,1-, ■ Щ	1 - ^-^2>2 . ;Легко видеть, что для (П+1) членов конструкция результата останется такой же, но из неё
Следует, что при бесконечно большом П дробь станет мало отличимой от О, а сама сумма станет
практически равной 2.Следовательно модуль разности (без учёта знака) станет и в дальнейшем останется меньшесколь угодно малой наперёд заданной величины 8.Отсюда—определение ПРЕДЕЛА ПЕРЕМЕННОЙ,
б/ ^Поскольку у * * в сущности своей - это та же геометрическая прогрессия, то в формуле её
суммы разделим почленно	и ^ на знаменатель дроби. ВИДИМ: в уменьшаемом всеэлементы — постоянные величины, а в вычитаемом при бесконечно большом П его числитель, а
вместе с ним и вся дробь, станут практически равными НУЛЮ. Формула же суммы членов
БЕСКОНЕЧНО УБЫВАЮЩЕЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ оказывается предельно
простой, удобной при решении задач и числовых расчётах.ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ мож;но оставить для самостоятельного
ЛОГР1ЧЕСКОГОАНАЛИЗА.14
у = а2.	При а>1 ^(х) возраст.а< 1 Г(х) убывает3.	Чем больше а, быстрее рост4.	При а> 1 Г(х)> 1, если х>0Г(х)<1, если х<05.	При а<1 - наоборот6.	Г(0)=115
Показательная функция
7=3*Определимся: .)Я^0, иначе появятся корни чётной степени изотрицательных чисел...) Я^Г, т.к. при Я~ 1 ничего другого, кроме
ЕДИНИЦЫ получить невозможно.число.Как ни антинаучно, но сегодня почти все авторы рассматривают свойства показательной
функции по внешнему виду нескольких графиков.Опустимся и мы на время к уровню этого математического примитива, рассматривая графики
функций.у = У у = (^Г у=10’‘1.ЕСЛИ	Г(х)^0.При всяком положительном основании функция всегда положительна.2.приа>1	Г(х) —возраст.Приа^1 Г(х)—убыв.При основании больше ЕДИНИЦЫ функция —ВОЗРАСТАЮЩАЯ.При основании меньше ЕДИНИЦЫ функция —УБЫВАЮЩАЯ.З.Чем больше основание, тем быстрее рост.4.	При основании, большем единицы, функция от X тоже больше!, если х>0
функция от X меньше ЕДИНИЦЫ, если Х"^ О5.	При основании, меньшем единицы, всё наоборот.6.Р(0)	= 1 Узелок!16
у = а* а>0V— ариф.1.	При »>0 Их) > Оа)X	- целое (М)а*= а • а • а...б)	(дробь) а^=л/^ =....в)	X = -д (отриц.) а"*=1/а'‘ ^	 > О „„«биг)	X = а (иррац.)	^«2 > 02.Еслиа>Ьто Г(х» 1 (х>0)
Р(х) < 1 (х<0)Дано: а> 1а)	X — целое а*> ГШ	т «б)Х=	п (дробь) а >1в)	X = а (иррац.) ^ а“^
а“'>1 а“^>1дробиг)X	= —р (отриц.)&’’= ^ а'’>1 =>-^<1З.Приа>1 !(х) возрастаета)Х|>Х2(целое) а*'>а**17
Показательная функцияИсходные условия те же: а>0,аэб1 . Корни арифметические.0 При а>0 1(х)>0.) ЕслиXнатуральное,тоЯ*= Я • а • &... - сомножители ©
Р	-г..) ЕслиХ="5'(дробь), тоу д т.к. корни арифметические....) Если Х=—(1 (отрицательное) а^= 1/а**Числитель и знаменатель положительные....) Если Х= (X (иррациональное).Можно показатель взять с НЕДОСТАТКОМ или ИЗБЫТКОМ.Оба дробные и с ними функция положительна.
Истинная - между ними и потому тоже положительна.0	При а>1,то Г(х)> 1 (х>0) .Если х<0,то Г(х)< 1.
Дано: а>1..) X - целое. Возводим обе части встепеньХ: Е *>гш..) Х= П (дробь). Сначала возводим обе части в степень Ш, а затем извлекаем из обеих частей
корни П-ой степени:.	^ ^1"...) Если Х== (X (иррациональное).
Приближённые значения показателей взятые и с
НЕДОСТАТКОМ и с ИЗБЫТКОМ, дроби!
С ними результаты БОЛЕЕ ЕДИНИЦЫ. Истинный - между
ними и потомуон тоже более ЕДИНИЦЫ.....)ЕслиХ= -р (отрицательное). Тогда а а’’У этой дроби знаменатель БОЛЕЕ ЕДИНИЦЫ, а**^!а сама дробь МЕНЕЕ ЕДИНИЦЫ.)Х,>Х2 —(целые). Я ' Влевой части сомножителей больше...) П > V (дроби). Приводим их к Н 03: пцр > рпОбе части - числа ЦЕЛ Ы Е.01в 1^11
Для них: а > аИзвлекаем из обеих частей корни степени18
_х = 33’‘ = 81X = 3.3.3.3 х'* = 81 X =	1Возвел, в степень х ="'/^=3 Нахожд. логарифмаИзвлечение корняЛогарифм - показательу = вод^у = йод.оХу = вод^Х19
Из предельно простого равенства 3^ = 81 можно составить три уравнения, разместив
неизвестное на месте одного из трёх его членов.В самом деле: X = 3“*. Это действие мы давно уже назвали действием ВОЗВЕДЕНИЯ В
СТЕПЕНЬ, и для нахождения неизвестного необходимо ТРОЙКУ умножить саму на себя четыре
раза. Что в этом сложного?Если же рассмотреть второе уравнение = 81, то и здесь всё привычно: для нахождения
неизвестного достаточно извлечь корень четвёртой степени из 81.Но вот третье уравнение: 3* = 81. Неизвестное разместилось на позиции показателя степени.
Эка беда?! Назовём это действие нахождением показателя степени при известном основании
степени и самой степени.Только ПОКАЗАТЕЛЬ СТЕПЕНИ будем называть его международным именем ЛОГАРИФМ.
Вот и пришли мы к действию НАХОЖДЕНИЯ ЛОГАРИФМА.В третьем уравнении, как видим, этот логарифм равен 4. В дальнейшем же мы установим
строгие законы его нахождения и правила обращения с ним, как раньше установили правила
действий со степенями и правила действий с радикалами.Для начала построим графики трёх функций. Первая;В ней у = в,од^ - это показатель, в который нужно возвести ДВОЙКУ, чтобы получить X.А более строго: ИГРЕК — это логарифм X при основании 2.Ничего сложного, но к этому некоторое время придётся привыкать.Атеперь начнём неторопливо наносить точю1 на график..) Чтобы получить ЕДИНИЦУ, щжно ДВОЙКУ возвести в нулевую степень...) Чтобы получить ДВОЙКУ, нужно ДВОЙКУ возвести в первую степень....) Чтобы получить 4, нужно двойку возвести в квадрат.....) Для получения ВОСЬМЁРКИ двойку надо возвести в куб.	) Можно получать и Т, и Т, и "в , возводя ДВОЙКУ в минус первую, в минус вторую и в минустретью степени.Полученные точки принадлежат графику функции у = €.од^.Также неторопливо отметим точки зелёного графика у =	и ограничимся тремяточкамирозовогографикау = йодГюХ.	^20
свойства логарифмов1.	При всяком + основании отрицательные числа
не имеют логарифмов.а) У = ^од^Х X = > О б) точки справа.2.	Логарифм самого основания = 1.а* = а3.	Логарифм ЕДИНИЦЫ = 0.а) узелок	б) Сод^^ =0^ а^ = 14.	При основании > 1 логарифмы чисел > 1 положительны.логарифмы чисел < 1 отрицательны.5.	При а < 1 логарифмы чисел < 1 полояа1т^ыш.логарифмы чисел > 1 отрицательны.При а > 1 у БОЛЬШЕГО ЧИСЛА БОЛЬШИЙ ЛОГАРИФМ.6.	При а < 1 у БОЛЬШЕГО числа МЕНЬШИЙ логарифм.N. > N2 йод^,N, > Сод^^г
N. < N, 	^21
СВОЙСТВА ЛОГАРИФМОВ зеркально перекликаются со свойствами показательной
функции и потому воспринимаются наглядно просто.1.	у = €.од^ X = > 0. При всяком положительном основании функция всегда
положительна.Для наглядности; все 1'очки графиков находятся в правой полуплоскости.2.	= 1 => а' = а. И это справедливо, т.к. любое число, будучи возведённым в ПЕРВУЮ
степень, остаётся неизменным.3.	= О => а" = 1. На координатной плоскости все кривые проходят через общую точку
(1;0), образуя УЗЕЛОК.4.	Получать числа, БОЛЬШИЕ единицы, при основании, БОЛЬШЕМ единицы, можно только
при положительных показателях степени, и это иллюстрирует РОЗОВЫЙ участок координатной
плоскости.ЗЕЛЁНЫЙ участок - для самостоятельного анализа.5.	При основании, МЕНЬШЕМ единицы, это свойство зеркально преображается.6,7. Приа>1мыимеемделосВОЗРАСТАЮШ^ЕЙфункцией,аПриа<1	-сУБЫВАЮЩЕЙ.Если N1>N2, то	йод^^N2.Если N^<N2, то...22
ЕслнN,=а’‘' =>x,*йод^,N,N2=8’“	=^Xг=бодI.N2N..N,= 8’“-*» ^x.^-x,=€од.(N..N^еод,(N ,•N2)=^од,N,+йод,Кг(Т^огарифм ПРОИЗВЕДЕНИЯ=суммелогарифмов сомножителей.€од,(N,:N^)=€о0,N, - ^д^^г^Логарифм ЧАСТНОГО = разности логарифмовделимого и делителя.№ = (аТ=а^“^ пх=Сод^Кбод,N"= п•йод,N(^Логарифм СТЕПЕНИ=произведению
показателя степени на логарифмоснования.V^=N‘(^УТогарифм КОРНЯ=частному отделения логарифма подкоренного
выражения на показатель корпя23
Самый ПРОСТОЙ и самый АКТИВНЫЙ листЛогарифмированиеПеремножим два числаN, = а*‘ и N2 = 8**.Получим: N,•N2=8*'***.НоX,-это€од,N,, Х2- это^од,N2,а x,+X2-это^од,(N,•N2).Стало быть, йодI,(N,•N2) = ^од,N,+Отсюда первое правилологарифмирования:ЛОГАРИФМ произведения равен СУММЕлогарифмовсомножителей.Теперь разделим эти же числа; N,:N2= а*' ** ^ х, - х,= Г ^ ^Значит:бод.(N,:N2)=	^ ‘И сразу же ВТОРОЕ правило:ЛОГАРИФМ частного равен РАЗНОСТИ логарифмов делимого и делителя
Возведём первое число в П-ю степень: № = (а*)"=а“=>ПХ =Новая связка: ^од,N"= п•йод,N и ТРЕТИЙ вывод:ЛОГАРИФМ степени равен произведению показателя степени
на логарифм основания.Извлечём корень П-й степени из первого числа:Логарифмируем это выражение, уже зная, чему равен
ЛОГАРИФМ СТЕПЕНИ: Сод VN * 1	.ЧЕТВЁРТОЕ правило: логарифм КОРНЯ равен частному от деления ЛОГАРИФМА
подкоренного выражения на ПОКАЗАТЕЛЬ КОРНЯ.С каким восторгом мы, курсанты школы военных разведчиков, впервые осмыслили эти правила
в первом послевоенном году и с каким вдохновением решали самые разные упражнения!Сегодня, спустя более 60 лет, это остается так же захватывающе интересно и останется им
навсегда. Успехов вам, молодым!24
ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВОЛогически: закроем в и ^
р	Читаем!—	Логарифм при основании — это показатель, в который надо возвести В(открываем 3^), чтобы получить ^ (открываемАналитически: логарифмируем при основании В.:логарифмируем при основанииФормула обратной связилогарифмируем при новом основании С:= Сод^1Логарифм данного числа по СТАРОМУ основанию равен логарифму этого же числа по
НОВОМУ основанию, делённому на логарифм СТАРОГО основания по НОВОМУ.вод^а. — модуль перехода25
ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВОИ его несколько необычное доказательство.Закроем указательными пальцами крупно написанные Э и и вслух прочитаем оставшееся:«Показатель, в который нужно возвести 3, чтобы получить^».Неторопливо прочитаем этоещё раз, и, называя Э, откроем Э, а называя откроем
Всё красиво и просто становится само собой разумеющимся.После этого проведём доказательство со всеми, так сказать, математическими строгостями.
Логарифмируем обе части равенства при основании В.В левой части - логарифм степени. Он равен произведению показателя степени на логарифм
основания. В правой части получаем 0.0^^Но	и теперь в бывшем равенстве можно поставить третью КРАСНУЮ чёрточку:ТОЖДЕСТВО!Логарифмируем наше тождество при основании заменив после этого правую часть
ЕДИНИЦЕЙ: еод,1*вод,а =Получаем чрезвычайно активную при решении упражнений формулу обратной связи:В завершение снова логарифмируем тождество, но уже при новом основании С:Из него найдём	2.Полученную формулу иногда называют «модулем перехода», хотя МОДУЛЕМ ПЕРЕХОДА к
новому основаниюслужитЛОГАРИФМ СТАРОГО ОСНОВАНИЯ ПО НОВОМУ-еод^аОтсюда окончательно:Логарифм данного числа по СТАРОМУ основанию равен логарифму этого
же числа по НОВОМУ основанию, делённому на логарифм СТАРОГО
основания по НОВОМУ.26
Десятичные логарифмы|)^дЮ =1	)^^100 =2	V йдЮ" = пйд10 = п^1000 =_3,_	)2)вдОЛ =1	Л
Сд0,0\ =2	} йдЮ" = -пйдг10 = -п^д0,001=3	)	_	.
	 ... Включая и ноль целых/3)	1 < Йд56,1 < 2
Йд56,1 = 1,...(трансцендентное)4)	-2<йд0,08<-1
СдО,ОЕ = 2,...... Включая и ноль целых!г5)	й^40 = Й5г(4«10) = СдА + СдЮ = + 1Мантисса не изменяется.Следствиеед852 =2,..1е
^^0,0852 = 2,..-1-27
Десятичные логарифмыЗа основание логарифма, в принципе, можно принять любое число, и одним из них является
число 10.1.	В этих случаях в записях основание не обозначается, а вместо С.од пишут Так, к
примеру, ^^10 = 1. И это понятно: показатель, в который нужно возвести число 10, чтобы
получить 10, равен ЕДИНИЦЕ.Точнотакже:^дг100 = 2,а ^д^1000 = 3.И вообще: Сд 10" = Х\Сд 10 = П.Отсюда: «Десятичный логарифм числа, выраженного единицей с последующими нулями,
содержит столько единиц, сколько нулей в изображении этого числа».2.	Так же просто определить десятичный логарифм десятичной дроби, выраженной единицейс предшествующими нулями. _	_&ф,\ =1; €д0,02 =2; ед0,001=3.Ивообшс: ^др!0’"=—П^10= ПЭтот логарифм содержит столько отрицательных единиц, сколько нулей в записи этого числа,
ВК.ПЮЧАЯИНОЛЬ ЦЕЛЫХВажная особенность: для упрощения дальнейших вычислений минус записывается НАД
ЛОГАРИФМОМ и зачитывается «единица под минусом», «двойка под минусом» и так далее.3.Вспомним	ещёраз:^10= 1,а^д[100 = 2.Сталобыть, 1 <^^56, К 2, то есть ^356,1 = 1....Целая часть этого логарифма называется ХАРАКТЕРИСТИКОЙ, и она содержит столько
положительных единиц, СКОЛЬКО ЦИФР В	ЧАСТИ этого числа БЕЗ ОДНОЙ.Дробная часть десятичного логарифма — МАНТИССА. Это бесконечная непериодическая
дробь из области ТРАНСЦЕНДЕНТНЫХ ЧИСЕЛ.Точнотакже -2 < ^^0,08 < — 1, и,значит, 6^0,08 = 2,...4.	ХАРАКТЕРИСТИКА десятичного логарифма десятичной дроби, содержащей НОЛЬ
ЦЕЛЫХ, имеет столько ОТРИЦАТЕЛЬНЫХ ЕДИНИЦ, сколько нулей предшествуе! первой
значащей цифре, ВКЛЮЧАЯ И НОЛЬ ЦЕЛЫХ.Вот только теперь становится понятным, почему МИНУС ставится над
ХАРАКТЕРИСТИКОЙ; он относится только к ней. Мантисса же всегда положительна и минус
не имеет к ней никакого отношения.В вычислениях с десятичными логарифмами отдельно производят действия с
ХАРАКТЕРИСТИКАМИ и отдельное МАНТИССАМИ. Потом результаты суммируют.Как видим, приписывание нулей к числу не изменяет МАНТИССЫ его десятичного
логарифма. Изменяется только ХАРАКТЕРИСТИ КА.СЛЕДСТВИЕ:	^38,52 =0,...*-^852
^,0852 = 2,Перенос запятой в числе изменяет только ХАРАКТЕРИСТИКУ его
десятичного логарифма.МАНТИССА остаётся неизменной.28
ПЕРВЫЙ лист ГРУППОВОГО КОНТРОЛЯ1.	Арифметическая прогрессия.2.	Символика арифметической прогрессии. Возрастание, убывание.3.	Вывод формулы любого члена (неполная математическая индукция).4.	Трёхчлен Эйлера. Полная математическая индукция.5.	Вывод формулы любого члена (полная математическая индукция).6.	Вывод формулы суммы членов арифметической прогрессии.7.	Свойство любого члена арифметической прогрессии (доказательство).8.	Геометрическая прогрессия.9.	Символика геометрической прогрессии. Возрастание, убывание.10.	Вывод формулы любого члена (неполная математическая индукция).11.	Вывод формулылюбогочлена(полнаяматематическаяиндукция).12.	Вывод формулы суммы членов геометрической прогрессии.13.	Свойство любого члена геометрической прогрессии (доказательство).14.	Сумма квадратов чисел натурального ряда (доказателытао).15.	Бесконечные прогрессии.16.	Предел переменной (доказательство).17.	Формула суммы членов бесконечно убывающей геометрической прогрессии (доказа¬
тельство).18.	Основные теоремы о пределах.19.	Графикипоказательных функций.20.	Графическая интерпретация свойств показательной функции.21.	Первое свойство показательной функции (доказательство).22.	Второе свойство показательной функции (доказательство).23.	Третье свойство показателщойфункции (доказательство).29
ВТОРОЙ лист ГРУППОВОГО КОНТРОЛЯ1.	Возникновение логарифма.2.	Графики логарифмических функций.3.	Первое свойство логарифмов, графическая интерпретация.4.	Логарифм основания. Почему?5.	Логарифм единицы. Почему? Графическая интерпретация.6.	Четвёртое свойство логарифмов. Графическая интерпретация.7.	Пятое свойство логарифмов. Графическая интерпретация.8.	Возрастающие изнывающие логарифмические функции.9.	Логарифм произведенрм. Доказательство.	^10.	Логарифм частного (дроби). Доказательство.11.	Логарифм степени. Доказательство.12.	Логарифм корня. Доказательство.13.	Логарифмическое тождество. Логическое доказательство.14.	Логарифмическое тождество. Доказательство.15.	Формула обратной связи. Вывод.16.	Формула перехода к новому основанию. Вывод. Модуль перехода.17.	Десятичный логарифм числа, выраженного единицей с последующими нулями.18.	Десятичный логарифм дроби, выраженной единицей с предшествующими нулями.19.	Характеристика десятичного логарифма произвольного числа.20.	Мантисса.21.	Характеристика десятичного логарифма десятичной дроби, не содержащей целых единиц.22.	Случаи неизменности мантиссы.23.	Следствие.30
МЕТОДИКАПодведём первые итоги.На 30 страницах изложен огромный материал повышенной сложности, не случайно
отнесенный к изучению в ДЕВЯТОМ и ДЕСЯТОМ классах. Ещё более сложна его практическая
часть, составляющая основу оценки знаний учащихся на вступительных экзаменах в высших
учебных заведениях. По времени этот материал охватывает более двух учебных четвертей, а его
практическая значимость пронизывает все учебники физико-математических и технических
факультетов.В условиях же семинарских занятий при работе не только с учителями,
но и с учениками ему отводится шесть дней, последний из которых—завершающий экзамен.Детализируем. За пять дней учащиеся воспроизводят по памяти все 12 листов с опорными
сигналами и озвучивают их ИЗУСТНО по 4-5 человек с опорой на собственные записи, как это
обычно делается на вступительных экзаменах, или на плакаты, позволяющие включать в ответы
всю группу учащихся. Сам по себе этот вид контроля включает более 50 человек в устные ответы по
всему материалу, но он не идёт ни в какое сравнение с работой по листам группового контроля,
когда небольшие группы по 5-6 человек без предварительной подготовки дают развёрнутые ответы
по всему л^атериалу, сопровождая свои ответы чертежами и выкладками на доске перед всеми
учащимися группы. Объём живой речи в этих условиях в несколько раз превосходит всё то, что
происходит в школах на обычных уроках: идёт одновременный рассказ по всем ДВЕНАДЦАТИ
листам, сложность и математическое содержание которых уже оценил читатель. Иными словами,
проводится экзамен, на котором ребята излагают не отдельные темы, а ВЕСЬ ИЗУЧЕННЫЙ
КУРС МАТЕМАТИКИ. Новизна этой работы требует от читателя глубокого проникновения в
методику работы, и до конца разобраться в ней может только участник семинара. Не стоит только
думать, что преимущественно теория составляет основу работы.Параллельно с опросом по листам группового контроля идёт решение самых разнообразных
упражнений, среди которых лишь малую часть составляют ознакомительные задания. Они в
тексте опущены.Уже в ходе первого занятия группа переходит к решению конкурсных задач, составляющих
реквизит письменных и устных экзаменов в высших учебных заведениях. Благо, разделы
«Арифметическая и Геометрическая прогрессии» позволяют использовать РАСЧЕТНЫЙ
МАТЕРИАЛ, доступныйдлявсехучащихся.На следующих страницах представлены все задачи и примеры, которые были решены на
одном из последних семинаров, и, если процесс работы над теоретическим материалом вызвал у
некоторых читателей вполне извинительные сомнения, то какими же они станут после
ознакомления с тремя страницами упражнений! Вот оно — непроходимое препятствие на путях
рассуждения кабинетных мудрецов! Без семинара осмыслить это невозможно!Упредим ещё одно возможное заблуждение. Кому-то может показаться, что в решении этих
упражнений у доски могут бьггь задействованы только 24 человека. Нелепость!Обратимся к примеру № 15. Быстро сменяя друг друга, к доске попеременно выходят
ПЯТНАДЦАТЬ человек, выполняя подготовительные и завершающие действия над его
изолированными одна от другой частями. Нетрудно представить себе уровень внимания ребят на
этом участке урока. Ежесекундно к доске может быть приглашён КАЖДЫЙ, и 1САЖДОМУ
прививается заряд уверенности в своих способностях.И снова необычное: уравнение образца № 16 решают одновременно от начала до конца ТРИ
ЧЕЛОВЕЬСА, и вместе с ними эти же упражнения самостоятельно решает КАЖДЫЙ ученик.
Процесс: все три записывают на большой доске условия примеров и создают паузу в 20-30 секунд,
предоставляя возможность тем, кто сидит за партами, уйти вперёд. Гандикап! В работе весь класс!
Приступили кработе ребята у доски, и теперь сидящие в классе могут сравнивать свои результаты с
неторопливыми выкладками на доске. Но с кем сравнивать, если эти трое вдруг разбредутся в
своих преобразованиях?Так на уроке происходргг игра, финал которой — исправление ошибок.Теперь уже не вызовет сомнения простой расчёт: при решении всех упражнений у доски
побывают 150 человек! Суммируйте читатель!Вполне естественно, что при работе в таком ритме в тетрадях ребят не исключаются описки и
ошибки, и потому ежедневным домашним напутствием является разъяснение: необходимо
беловое переписывание всех решений в специальные тетрадки-решебники. Разъяснения нужны
только на первых двух уроках, уже на третьем в обилии решённых задач и примеров каждому
становится понятна многолетняя значимость таких тетрадей, беловые записи становятся
психологическими убеждённостями каждого.31
1.	+ 3’‘^' = 7 • + 19 • 3*^'X	2 + лйс + хI	1 + •'йс /1 ■'■2.\3.3	.(I) =813_ 2X^-1 _ЗХ^ = 3x2-1 _2х2«4.2,5 ^ *0,4 ~ ' =5'®.0,1'5.	Сумма первого и пятого членов арифметической прогрессии равна 5/3, а произведение третьего и
четвёртого её членов равно 65/72. Найти сумму первых 17 членов этой прогрессии.6.	При делении девятого члена арифметической прогрессии на второй член в частном получается 5,
а при делении тринадцатого члена на шестой в частном получается 2, а в остатке 5. Найти первый
член и разность прогрессии.7.	Найти третий член бесконечной геометрической прогрессии со знаменателем |о| < 1, сумма
которойравняется 8/5, второйчленравен—1,2.Сод.58.	\25	+49 =9.	+27^»’“ +3^’’10.€.од^ + Сод^х + Сод^х =11X11Содз(3 - 8) = 2 - X12.	Сумма трёх первых членов геометрической прогрессии равна 21, а сумма их квадратов равна 189.
Найти первый член и знаменатель этой прогрессии.13.	Найти четыре числа, образующие геометрическую прогрессию, у которой сумма крайних
членов равна -49, а сумма среднихчленов равна 14.14.	Найти три первых члена бесконечной геометрической прогрессии со знаменателем |я| < 1, сумма
которой равняется 6, а сумма первых пяти членов равна 93/16.16.3 •5^’-'-2 •5’“'-0,217.	9^’“’ - 27 = 6 • 3^’“’X	418.5 .0,2 =125’“"* 0,0432
19.	Найти первый член и знаменатель геометрической прогрессии, если известно, что
а,-а2= -45/32, а а,-а,= -45/512.20.	Три числа, из которых третье равно 12, образуют геометрическую прогрессию. Если вместо
12 взять 9, то три числа составят арифметическую прогрессию. Найти эти числа.21.	Найти трёхзначное число, цифры которого образуют геом^ическую прогрессию. Если из
этого числа вычесть 792, то получится число, записанное теми же числами, но в обратном порядке.
Если из цифры, выражающей число сотен, вычесть 4, а остальные цифры искомого числа оставить
без изменения, то получится число, цифры которого образуют арифметическую прогрессию.22.	Знаменатель геометрической прогрессии равен 1/3, четвёртый член этой прогрессии равен 1,54,
а сумма всех её членов равна 121/162. Найти число членов прогрессии.23. ^д8 - вд^х + 6 =вдХ6- ^д{х - 2)Сборник задач для поступающих во ВТУЗы. М., 1988.33
Несколько перефразируя Данте Алигьери,
настоятельно посоветуем:
ОСТАВЬ СОМНЕНЬЯ ВСЯК СЮДА ВХОДЯЩИЙНа следующей странице представлен полный список учащихся последней группы,
и каждая фамилия — реальный ученик со всеми его родственниками. В ближайщие дни
ребята получат эту книгу, так как работать на семинаре им довелось по первым
издательским версткам, содержавшим значительное количество типографских ошибок.
Списка в вёрстках, естественно, не было, а теперь читатель видит перед собой группу из
35 мальчиков и девочек, 21 из которых до начала занятий не имели ни малейшего
представления о прогрессиях, показательных и логарифмических функциях —
возрастом не приспели.Из 14 оставшихся более половины, как выяснилось, вообще имели смутное
представление о МАТЕМАТИКЕ, с трудом определяя, как найти неизвестный делитель
или неизвестное уменьшаемое, не говоря уже о действиях с алгебраическими дробями
или о решении квадратных уравнений. Но кто из учителей-практиков ежедневно не
сталкивается с такими фактами, ни в малой степени не представляя, что все эти трудности
остались в давно прошедшем времени у С.С. Богоявленской, и Э.С. Ламакиной,
Г.А. Псахье, В.Д. Корнеева, Л.Э. Глок и у тысяч учителей, прошедших школу Донецких
семинаров.34
АЛГЕБРА - 2007№п/пФамилия,
имя3I'8Астахов А.Ахтарнп М._й.БакшеевМ.Белхииа Е.Бобром А.Боидаренко В.ВидюомЮ.8Величко Л-рей.Величко Ал._5:510Гвозденко П.И11ригорьп А.121>бииаА.13Зайцева И.14Зу<!1И1ЛИнА.15Колесников С.16КорочкинД.17Лалияа Е.18Мазурин Э.19Оснпоаа М.20Петренко А.21Петрова А.22Рогожин п.23Смирно* А.24Солаапсикова л.25Соловьёва И.26Тронмна А.27Чемакииа А.282930~зГЖ3334^5_Чумарнкова И.
Шитов А.
Шагов М.
Шепелев А.
Яковлева К.Тюрин Е.
Кондратьева В.
Голубкова О.3._а.35
В.Ф. ШаталовИЗУСТНАЯ
АЛГЕБРАУчебное пособиеКомпьютерная верстка — В.П. Давыдов
Корректорская читка — НА. РостовскаяПодписано в печать 05.01.2009 г.Бумага офсетная 80 г/м*
ГарнитураНе\у1опС. Печать офсетная.Печатных листов 2,25. Тираж 1000 экз. Заказ № 22/4Отпечатано в типографии
«Школа Шаталова»107078, г. Москва, 1-й Басманный пер., д. 3, стр. 1, ком. 202
(495)772-47-34, 767-47-3436
КЛАССИКА МИРОВОЙ ПЕДАГОГИКИВИДЕОЗАПИСИ УРОКОВ-	ПЕДАГОГИЧЕСКОЕ
МАСТЕРСТВО
(семинар с учителями
в МПГУ 2006 г.)-	АЛГЕБРА-	ГЕОМЕТРИЯ•	ФИЗИКА•	АСТРОНОМИЯ-	ТРИГОНОМЕТРИЯ•	с 1969 по 1990 голы к* ■ыпускиикм «га классе*
поступали а ауаы.■ Сагадия ом проаоцит итпиа а дни каникул и
лает гоАоаон курс аа 10 часе*.•	По ■иаоозаписям этих уроков учатся а Еаропс
и Америка.-	Видеозаписи доступны любой семье
(4 кассеты, 8 часоа записи,от 750 руб. вместе с учебником).Жарой Е. учтет математики жвпы №к, г. Пуштио
Иоскоеской области: «Самый пучшм псюарск сдапал пн
01«4. каш Л0А1РИ110ЫЛПОТ мдмпяия 1и»кло*<>Т<р>мм Р„ Иосш- Учмласк 4 дня ■ март» 20М г,
дипломант дауж кмшурсоа молодых испотителм а Прага •
2вО!г. •Я>«мл)мпммга1к1»яу1П1«|ымалинахп Уроки
гвоиетрм! лро«заеп> сх|хм«>в перечень в шом Учителымцэ
б|М потрасм ыоиш мнмм. Поем ткул т «мфспмж и
ииостштиок юлучп и *&•Далкоаа С Н. Учипаск у Шагааоаа • 19в«-«9 году. Иммт
СМИ (юнас. Еа фир*« участвовала а строителкстк Храма
Христа Спасшем. В 2009 пмцг шиоичия Прааослаамый
Саато-Ттомоаскм) Богдсжмспм Лктггут, -м™ Шгалова
рлтиат '^агто уаармсан • себе '«тостъ и ашурап«сть
цщгиим оякалку •«алгоианаосп. Его учм«и иогуг ншт
оаВя ■ повок облает По Шаталааг а изучала и гумаии<арнйе
самлратапиала*Горелик Л-, США, Аяасжа: >Лолучила уроки Шаталоаа по
гммагрмл » Финк» яа ОУО Опюмое спасибо Вышгига,
по1ил^кп|.тркгонаие1р«о алгеСруивое. что есп»ПРОВОДИТ АВТОР самой эффективной в мире методики обучения,
НАРОДНЫЙ учитель СССР, почетный президент
итальянской ассоциации 'ДАНТЕ АЛИГЬЕРИ", КАВАЛЕР ОРДЕНА
НИКОЛАЯ ЧУДОТВОРЦА ЗА ПРИУМНОЖЕНИЕ ДОБРА НА ЗЕМЛЕШАТАЛОВ В.Ф.Тел.:(495)772-47-34.\ллллл/. 5Ьа1а1оУ5сИоо15. ш