Текст
основы ТЕОРИИ ЦЕПЕЙ
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
А — параметр четырехполюсника; обозначение фазы трехфазной цепи;
а — собственное затухание четырехполюсника; фазовый оператор ei 1200.
В — параметр четырехполюсника; обозначение фазы трехфазной цепи; магнитная индукция;
Ь — реактивная проводимость; коэффициент фазы четырехполюсника;
Ьс — емкостная проводимость;
bL — индуктивная проводимость;
С — емкость; обозначение фазы трехфазиой цепи;
с — скорость света в пустоте (примерно 3 • 10s м/сек); действительная часть комплексной частоты;
Е — постоянная э.д.с.; действующее значение переменной э.д.с.;
Е — комплексная э. д. с.;
е — мгновенное значение э.д.с.; основание натуральных логарифмов (примерно 2,718);
F(j<o) — спектральная характеристика; Ё(р) — изображение функции по Лапласу; функция комплексной частоты;
f — частота периодической функции;
G — параметр четырехполюсника;
g — активная проводимость; параметр четырехполюсника (мера или коэффициент передачи);
Н — параметр четырехполюсника;
/ — постоянный ток; действующее значение переменного тока;
1 —комплексный ток;
i — мгновенное значение тока;
, /=/-1;
К/ —коэффициент передачи по току;
Ки —коэффициент передачи по напряжению;
k — коэффициент связи, постоянная фильтра;
L — индуктивность;
— индуктивность рассеяния;
М — взаимная индуктивность;
т — постоянная фильтра; индекс, обозначающий амплитуду переменной величины;
п — коэффициент трансформации; коэффициент отражения;
Р — активная (средняя) мощность; р — мгновенная мощность: комплексная частота;
Q — реактивная мощность; добротность катушки, конденсатора, контура;
q — электрический заряд; г — активное сопротивление;
S — полная мощность; площадь поперечного сечения;
Т — период;
t — время;
U — постоянное напряжение; действующее значение переменного напряжения;
1) —комплексное напряжение;
и — мгновенное значение напряжения;
W —энергия (постоянная);
w — число витков; мгновенное значение энергии;
ш£’шс —энергия, запасенная в индуктивности н емкости;
х — реактивное сопротивление;
хс — емкостное сопротивление;
xL — индуктивное сопротивление;
2^1 — комплексное сопротивление взаимной индукции;
Y — комплексная проводимость; параметр четырехполюсника;
Yи —входная проводимость i-ro контура (ветви) или узла;
Ykt — передаточная проводимость контуров (ветвей) или узлов;
Y(U)—собственная проводимость ветвей, сходящихся в узле;
— общая проводимость между узлами i и k;
Y(p)—обобщенная (операторная) проводимость;
у — полная проводимость (модуль комплексной проводимости);
Z — комплексное сопротивление; параметр четырехполюсника;
ZB — комплексное волновое сопротивление линии;
Zc — характеристическое сопротивление;
Zu — входное сопротивление i-ro узла нли контура (ветви);
Z^i — передаточное сопротивление узлов или контуров (ветвей) i и А:
Z^zz j — собственное сопротивление контура ij
5
Z^ky — общее сопротивление контуров i и k;
Z(p) — обобщенное (операторное) сопротивление?
z — полное сопротивление (модуль комплексного сопротивления);
« — коэффициент затухания линии; р — коэффициент фазы линии;
у — коэффициент распространения линии;
й — угол потерь; относительная расстройка частоты;
А —определитель системы уравнений;
А,* — алгебраическое дополнение элемента i-й строки fe-ro столбца; еа — абсолютная диэлектрическая проницаемость;
О — температура;
Л — магнитная проводимость;
Л, — длина волны;
Приставки для дольных и кратных единиц
На именование единиц Измерения Обозначение Отношение к основной единице
Пико п 10—12
Нано н 1О-*
Микро МК 10-е
Милли м 10-8
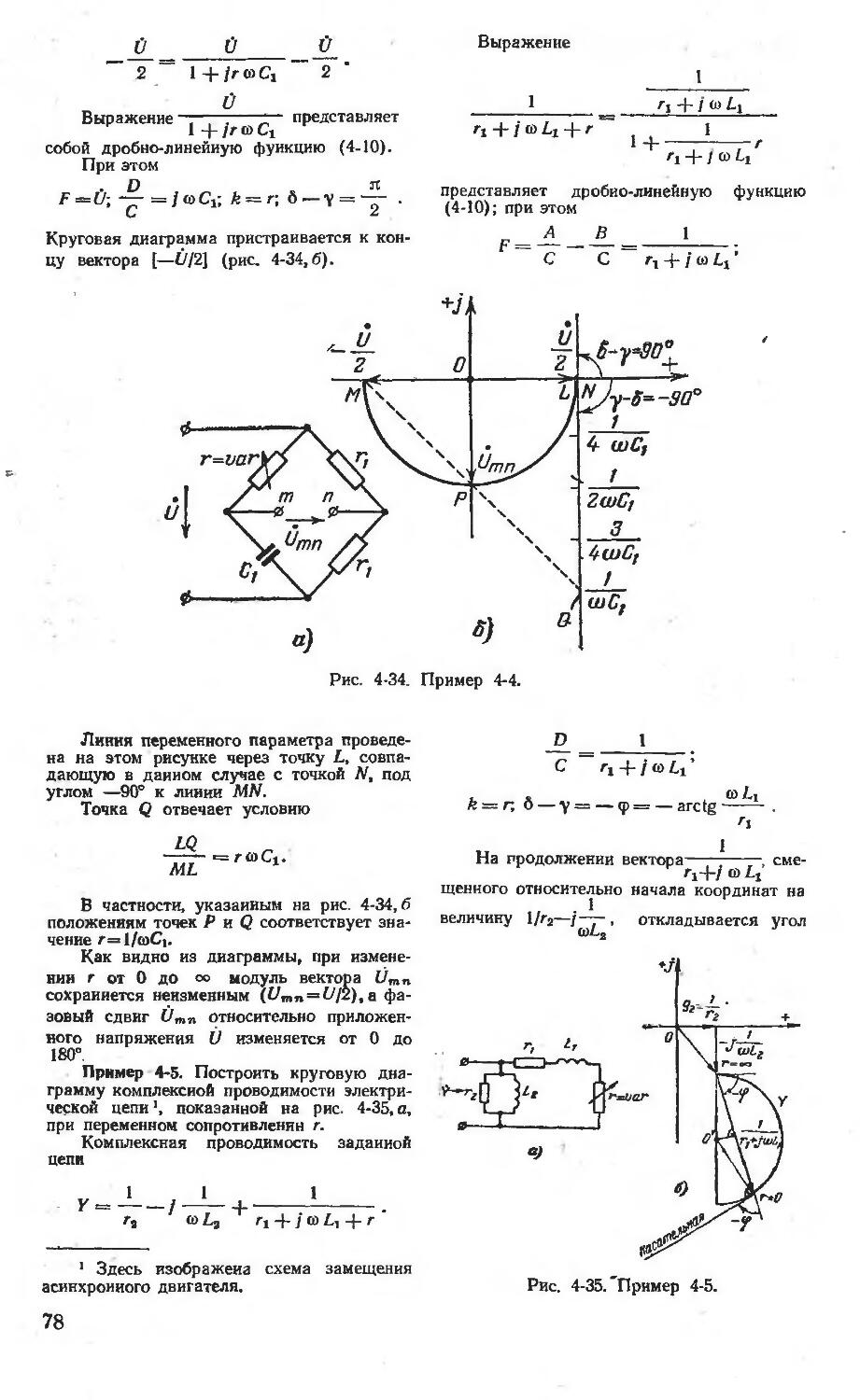
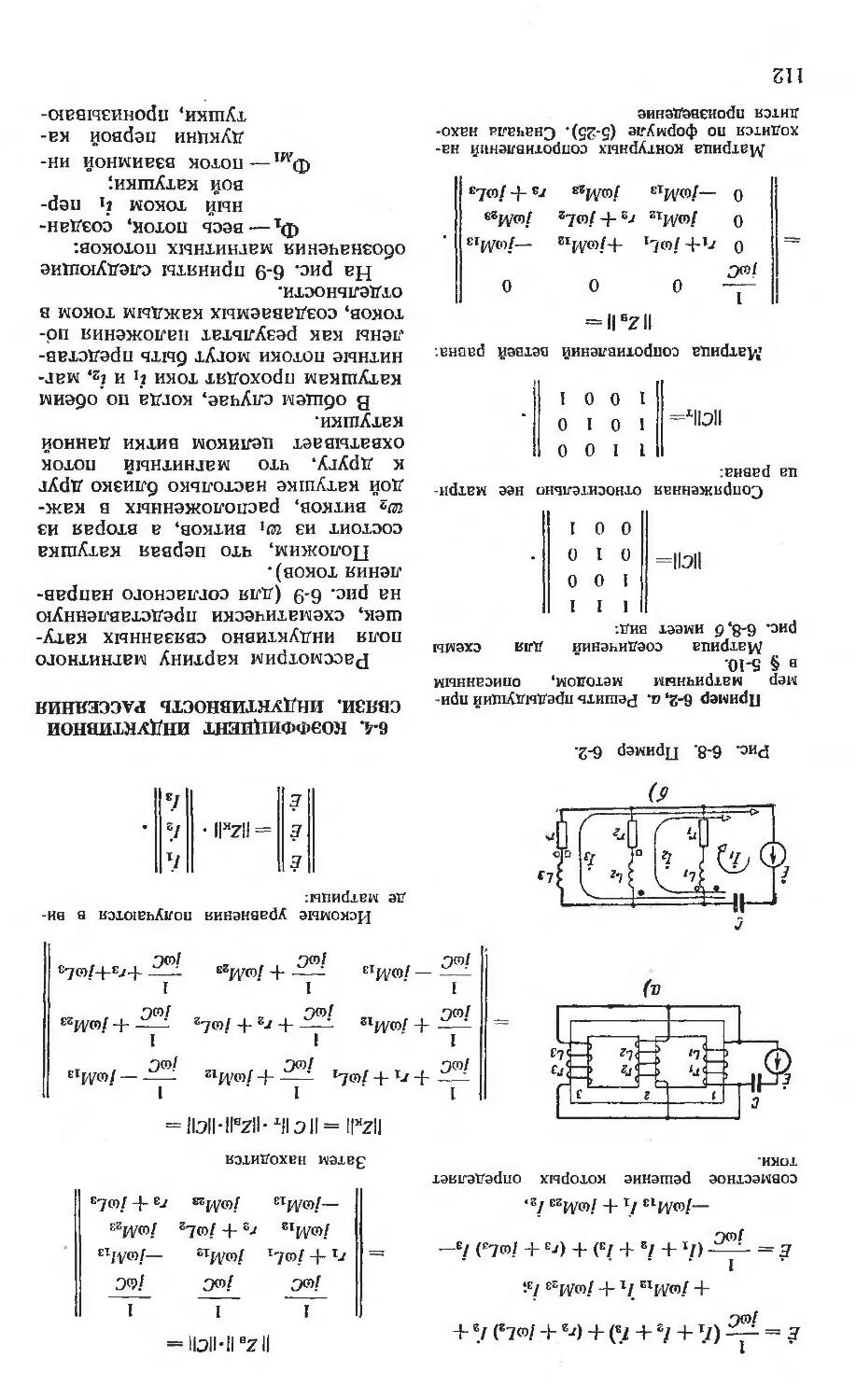
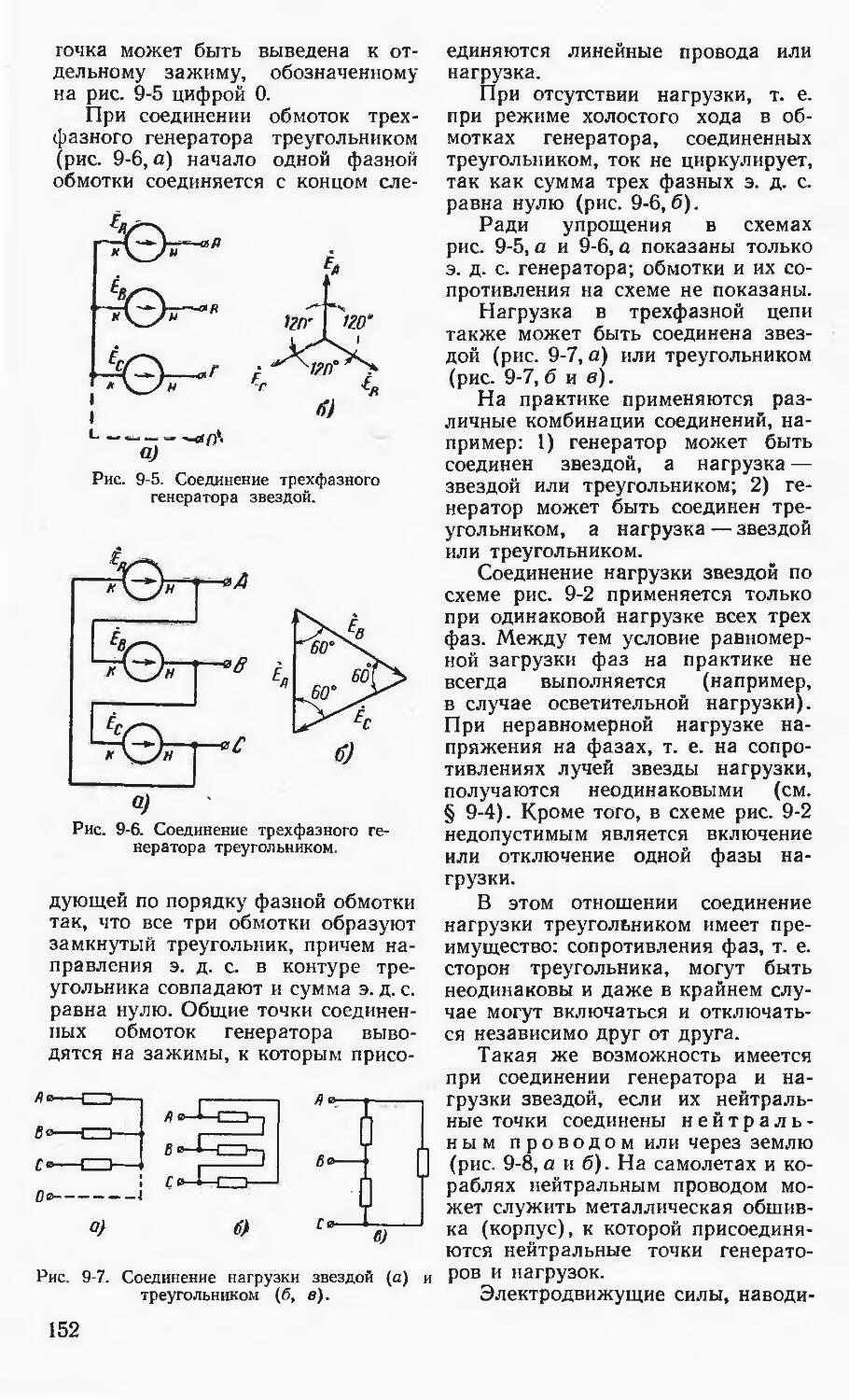
Санти с 10-2
Гекто г 108
Кило к 103
Мега м 108
Ра — абсолютная магнитная проницаемость;
р — удельное электрическое сопротивление; волновое сопротивление контура;
т — время; постоянная времени;
Ф — магнитный поток;
<р — фазовый сдвиг;
Ф — потокосцепление;
ф — начальная фаза:
© — угловая частота.
Основные электрические и магнитные единицы измерения в системе СИ
Единица измерения
Величина наименование обо-зн ячейке
Ток ампер а
Заряд . кулон к
Потенциал, напряжение, э. д. с вольт в
Напряженность электрического поля .... вольт в!м
Сопротивление .... на метр ом ОМ
Емкость ....... фарада ф
Магнитный поток . . . вебер вб
Магнитная индукция . . тесла тл
Индуктивность .... генри гн
Магнитодвижущая сила . ампер а
Напряженность магнитного поля ..... ампер а'/м
Энергия ....... на метр джоуль дж
Мощность ватт вт
ВВЕДЕНИЕ
Электротехника и радиотехника — родственные науки, изучающие электромагнитные процессы и возможности использования энергии электромагнитного поля для практических целей.
Основными задачами электротехники являются генерирование, передача на расстояние и преобразование электрической энергии в механическую, световую, тепловую, химическую и другие формы энергии.
Передача электрической энергии от источников к потребителям осуществляется с помощью проводов. Носитель энергии — электромагнитное поле — концентрируется в диэлектрике, окружающем провода, и поэтому рассеивание энергии при низкой частоте весьма мало; энергия передается на расстояние с высоким к. п. д., и только незначительная доля ее расходуется на нагрев проводов.
Основной задачей радиотехники является передача на расстояние без применения соединительных проводов, различных сигналов, несущих ту или иную информацию. С этой целью создается электромагнитное поле излучения, которое распространяется в свободном пространстве. Хотя значительная часть ее и рассеивается, но даже та малая доля энергии, которая достигает чувствительного приемного устройства, достаточна для воспроизведения сигнала — звука, изображения k или команды.
Роль и значение электрической энергии в развитии народного хозяйства общеизвестны. Электричество стало основой развития всех отраслей техники, базой для развития промышленности, транспорта, сельского хозяйства, электросвязи; оно стало основой комплексной механизации и автоматизации производственных процессов. Электричество и
радио прочно вошли в быт. Исключительно важное значение они заняли и в современной авиации; установленная мощность источников электрической энергии на самолетах, исчислявшаяся долями киловатта в начальный период развития авиации, в настоящее время достигает сотен киловатт на крупных самолетах. Продвижение науки по пути освоения космического пространства и изучения планет солнечной системы было бы невозможным без применения электричества и радио.
Столь широкому распространению электрической энергии во всех областях народного хозяйства и во всех отраслях техники способствовало удобство передачи электромагнитной энергии на расстояние и удобство преобразования ее в другие формы энергии.
Классики марксизма-ленинизма с первых же шагов развития науки об электричестве предсказали ей великое будущее. Известно, с каким пристальным вниманием следили К. Маркс и Ф. Энгельс за опытами по передаче электроэнергии на расстояние, предсказав огромное революционное значение применения электричества в промышленности.
В течение XIX и XX вв. учение об электричестве непрерывно развивалось, причем электротехника на ранних ступенях развития являлась разделом физики.
Исследования Эрстеда, Ампера, Фарадея, Петрова, Ленца, Джоуля и других физиков XIX в. положили начало систематическому изучению электрических явлений.
На основании теоретического обобщения экспериментальных данных по электричеству и магнетизму во второй половине XIX в. Максвелл выдвинул гипотезу существования электромагнитиого поля излучения. Разработанная им теория электромагнитного поля изложена в
7
его труде «Трактат об электричестве и магнетизме» (1873 г.).
В 1888 г. Генрих Герц опубликовал свои работы, в которых экспериментально доказал существование поля излучения. Однако Герц и современные ему физики, занимавшиеся исследованием электромагнитного поля, не считали возможным выйти за пределы своих лабораторий и применить электромагнитные волны для беспроволочной связи.
Такую задачу впервые поставил и блестяще разрешил' выдающийся русский ученый Александр Степанович Попов, практически осуществивший в 1895 г. первую радиосвязь. Изобретение радио открыло новую эру в истории человечества.
В дореволюционной России электротехника и радиотехника развивались слабо. Энергетическая база была крайне слаба. Радиопромышленность не развивалась, радиоаппаратура заказывалась иностранным фирмам.
С первых дней существования советской власти коммунистическая партия придавала решающее значение делу электрификации страны и радиовещанию. Всем памятны слова В. И. Ленина «Коммунизм — это есть Советская власть плюс электрификация всей страны». В. И. Ленин придавал большое значение использованию радио как средства связи и политической пропаганды.
В настоящее время СССР является страной с высокоразвитой электротехнической и радиотехнической промышленностью. По производству электроэнергии наша страна занимает первое место в Европе и второе в мире.
Ведущая роль электротехники и радиоэлектроники в развитии всех отраслей народного хозяйства, в осуществлении всего современного технического прогресса раскрыта в Программе КПСС, принятой XXII съездом КПСС.
В электротехнике и радиотехнике применяются два способа описания электромагнитных явлений: при помощи понятий теории поля и теории цепей. Выбор того или другого способа диктуется условиями постановки задачи.
Теория поля изучает изменение электрических и магнитных величин от точки к точке в пространстве и во времени. Она исследует напряженности электрического и магнитного полей и с их помощью такие явления, как излучение электромагнитной энергии, распределение объемных зарядов, плотностей токов и т. д.
Теория цепей исходит из приближенной замены реального электротехнического или радиотехнического устройства идеализированной моделью — схемой замещения. Эта схема содержит участки цепи, на которых определяются искомые напряжения и токи. ,
Теория цепей позволяет с достаточной для инженерной практики точностью определять непосредственно токи, не прибегая к вычислению их плотностей в различных точках сечения проводника. Напряжение между концами рассматриваемого участка цепи также находится непосредственно, без вычисления его между промежуточными точками.
Разграничения областей применения теории поля и теории цепей являются условными. Например, процессы распространения электрических сигналов в линиях электропроводной связи исследуются как методами теории поля, так и методами теории цепей.
Здесь сочетаются такие понятия, как скорость распространения электромагнитной энергии, характерная для теории поля, и напряжение и ток, характерные для теории цепей.
Предметом курса «Основы теории цепей» является изучение как с качественной, так и с количественной стороны установившихся и переходных процессов в электрических цепях. Этот курс, базирующийся на курсах физики и высшей математики, содержит общую теорию цепей и инженерные методы их расчета, анализа и синтеза. Он имеет исключительно важное значение для формирования научного кругозора специалистов по радиотехнике, и на нем основываются все радиотехнические дисциплины.
8
Глава первая
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ЗАКОНЫ, ЭЛЕМЕНТЫ И ПАРАМЕТРЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
1-1. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ
Электрической цепью называется совокупность устройств, предназначаемых для прохождения электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий напряжения и тока. В общем случае электрическая цепь состоит из источников и приемников электрической энергии и промежуточных звеньев (проводов, аппаратов), связывающих источники с приемниками.
Источниками электрической энергии являются гальванические элементы, аккумуляторы, термоэлементы, генераторы и другие устройства, в которых происходит процесс преобразования химической, молекулярно-кинетической, тепловой, механической или другого вида энергии в электрическую. К источникам можно отнести и приемные антенны, в которых в отличие от перечисленных выше устройств не происходит изменение вида энергии.
Приемниками электрической энергии, или так называемой нагрузкой, служат электрические лампы, электронагревательные приборы, электрические двигатели и другие устройства, в которых электрическая энергия превращается в световую, тепловую, механическуй) и т. п. К нагрузкам относятся и передающие антенны, излучающие
электромагнитную энергию в пространство.
Расчеты электрических цепей и исследования процессов, происходящих в них, основываются на различных допущениях и некоторой идеализации реальных объектов электрических цепей. Под элементами в теории электрических цепей подразумеваются обычно не физически существующие составные части электротехнических и радиотехнических устройств, а их идеализированные модели, которым теоретически приписываются определенные электрические и магнитные свойства так, что они в совокупности приближенно отображают явления, происходящие в реальных устройствах.
В теории электрических цепей различают активные и пассивные элементы. Активными элементами считаются источники электрической энергии: источники напряжения и источники тока. К п а с -сивным элементам электрических цепей относятся сопротивления, индуктивности и емкости. Соответственно различают активные и пассивные цепи; активные цепи содержат источники электрической энергии, пассивные же цепи состоят только из пассивных элементов.
Эти важные понятия, лежащие в основе теоретической электротехники, подробно рассмотрены ниже.
9
1-2. ПОЛОЖИТЕЛЬНЫЕ НАПРАВЛЕНИЯ ТОКА И НАПРЯЖЕНИЯ
Электрический ток в проводящей среде есть упорядоченное движение электрических зарядов. Известно, что электрический ток проводимости в металлах, так же как и ток переноса в электровакуумных приборах, представляет собой перемещение отрицательно заряженных частиц (электронов), а ток проводимости в электролитах и газах — перемещение как положительно, так и отрицательно заряженных частиц (ионов).
Электрическому току приписывается направление. Хотя в общем случае ток представляет движение электрических зарядов того и другого знака в разные стороны, однако за направление тока принимают направление перемещения положительных зарядов; это направление противоположно направлению движения отрицательных зарядов.
Численно ток определяется как предел сггношення количества электричества, переносимого заряженными частицами сквозь рассматриваемое поперечное сечение проводника за некоторый промежуток времени, к этому промежутку времени, когда последний стремится к нулю. Следовательно, если обозначить через q количество электричества, прошедшего через рассматриваемое сечение проводника за время t, то мгновенное значение тока, т. е. значение его в любой момент времени t, определится как производная q по t: i=dqldt. Здесь q=q++q_, где q+ и q_ — положительный и отрицательный заряды, переместившиеся в противоположные стороны за время t.
В Международной системе единиц i измеряется в амперах1 (а), q — в кулонах (к) или ампер-секундах (а-сек), t—в секундах (сек).
1 Ампер — величина неизменяюшегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу, равную 2-10-7 единиц силы Международной системы на каждый метр длины (ГОСТ 9867-61).
Электрический ток может быть постоянным (неизменяющимся) или переменным, т. е. изменяющимся в зависимости от времени.
Направление тока характеризуется знаком тока. Понятия положительный ток или отрицательный ток имеют смысл, только если сравнивать направление тока в проводнике
Рис. 1-1. Участок электрической цепи с выбранными положительными направлениями тока и напряжения.
с некоторым заранее выбранным ориентиром — так называемым п о-ложителышм нагьравл-е-н и е-м.
Положительное направление тока выбирается произвольно; оно обычно указывается стрелкой. Если в результате расчета тока, выполненного с учетом выбранного положительного направления, ток имеет знак плюс (t'>0), то это означает, что его направление совпадает с выбранным положительным направлением. В противном случае, когда ток отрицателен (i<0), он направлен противоположно.
Таким образом, выбранное для тока положительное направление само по себе не означает направления, в котором перемещаются электрические заряды; оно только придает определенный смысл знаку тока.
Изобразим некоторый участок электрической цепи, через который проходит ток i, в виде прямоугольника и обозначим концы (зажимы) этого участка цифрами 1 и 2 (рис. 1-1). Разность электрических потенциалов точек 1 и 2 представляет напряжение на данном участке цепи. Напомним, что разность электрических потенциалов — скалярная величина, которая определяется работой, затрачиваемой на перенос единичного положительного заряда из точки 1 в точку 2.
10
Значение напряжения в любой текущий момент времени обозначается через и; оно может быть постоянным или переменным. В системе СИ напряжение и измеряется в вольтах (в).
Для придания определенного смысла знаку напряжения на рассматриваемом участке цепи для напряжения, так же как и для тока, произвольно выбирается положительное направление. Чаще всего его выбирают совпадающим с/положительным направлением тока и указывают стрелкой.
В выбранном положительном направлении и отсчитывается напряжение. Пусть на рис. 1-1 отсчет напряжения ведется от точки 1 к точке 2. Когда потенциал точки 1 выше потенциала точки 2, напряжение положительно, в противном цлучае оно отрицательно.
Для уяснения выбранного направления отсчета напряжения можно вместо стрелки пользоваться обозначением с помощью индексов, при котором порядок расположения индексов, соответствующих точкам цепи, отвечает положительному направлению, выбранному для напряжения. Так, применительно к рис. 1-1 напряжение, отсчитываемое в положительном направлении тока, равно «и- Напряжение, отсчитываемое в обратном направлении, имеет противоположный знак: «21 = —«12-
Двойное индексное обозначение возможно и для тока. Например, йг обозначает ток, который имеет положительное направление на участке цепи от точки 1 к точке 2. Однако на практике большее распространение нашло обозначение с помощью стрелок.
Положительными направлениями токов и напряжений пользуются при исследовании процессов, происходящих в электротехнических устройствах, и при расчете электрических цепей. Для краткости положительное направление будем называть просто направлением.
Отчетливое уяснение этих важных понятий совершенно обязательно для усвоения всего, последующего материала.
1-3. МГНОВЕННАЯ МОЩНОСТЬ И ЭНЕРГИЯ
Положим, что через участок электрической цепи (приемник энергии) под воздействием приложенного напряжения и проходит электрический заряд q. Совершаемая при этом элементарная работа или, что то же, поступающая в приемник элементарная энергия равна:
dw—udq=uidt.
Производная энергии по времени, т. е. скорость поступления в цепь электрической энергии в данный момент времени, представляет собой мгновенную мощность. Следовательно, мгновенная мощность, поступающая в приемник, равна произведению мгновенных значений напряжения и тока:
dw do
р— — = и — = ut. dt dt
Мгновенная мощность р— величина алгебраическая; она положительна при одинаковых знаках и й i и отрицательна при разных знаках и и I.
Если положительные направления для напряжения и тока приняты совпадающими, то при jtf>0 энергия поступает в приемник, а при р<0 энергия возвращается из рассматриваемого участка цепи обратно к источнику.
Энергия, поступившая в приемник за промежуток времени от й до t2, выражается интегралом
t,
U7 — §pdt.
t,
В отличие от мгновенной мощности р, которая может иметь отрицательный или положительный знак, энергия, поступившая в приемник, всегда имеет положительный знак.
В системе СИ работа и энергия измеряются в джоулях (дж), мощность р — в ваттах (ет).
1-4. СОПРОТИВЛЕНИЕ
Сопротивлением называется-идеализированный элемент цепи, характеризующий потери энергии на нагрев, механическую работу или
11
излучение -электромагнитной энергии.
Следует заметить, что термин «сопротивление» и соответствующее ему условное обозначение г применяются в электротехнике и радиотехнике для обозначения как само
го элемента, в котором происходит необратимый процесс поглощения электромагнитной энергии, так и для количественной оценки величины, равной отношению напряжения
Рис. 1-2. Условное обозначение сопротивления.
на данном элементе цепи к проходящему через него:
току,
(Ы)
поло-и на-
Здесь предполагается, что жительные направления тока пряжения совпадают; при этом знаки и и I одинаковы и /'>0.
Величина g=\fr, обратная сопротивлению, называется проводимостью. В системе СИ сопротивление г измеряется в омах (ол<), а проводимость g — в сименсах (сим).
Формула (1-1) выражает закон Ома, экспериментально установленный Омом в 1826 г.
Условное графическое изображение сопротивления с указанием выбранных положительных направлений тока и напряжения приведено на рис. 1-2.
Мгновенная мощность, поступающая в сопротивление, равна произведению мгновенных значений напряжения и тока:
pr=ui=ri2 =gu\
Следовательно, параметр г может быть численно определен как отношение мгновенной мощности к квадрату мгновенного значения тока, проходящего через сопротивление:
r = -₽t.
Электрическая энергия, поступившая в сопротивление и превращенная в тепло, начиная с некоторого момента времени, например
/=0, до рассматриваемого момента t, равна:
В случае постоянного тока (i— =7=const), wT=rl2t.
Превращение всей электрической энергии wr в тепловую впервые было доказано опытным путем Джоулем и Ленцем.
Рис. 1-3. Вольт-амперная характеристика сопротивления.
а — нелинейная; б — линейная.
Выделение током теплоты было впервые использовано для целей освещения А. Н. Лодыгиным, создавшим в 1873 г. лампу накаливания *. Оно целесообразно используется в технике — электронагревательных приборах и т. п. К вредным последствиям теплового действия тока относятся потери электрической энергии в проводах, машинах, аппаратах, порча изоляции проводов от нагрева и т. д.
Параметр г в общем случае зависит от тока i (например, вследствие нагрева сопротивления током). Зависимость напряжения на сопротивлении от тока, проходящего через данное сопротивление, называется вольт-амперной характеристикой, которая в общем случае нелинейна.
Если сопротивление г не зависит от величины и направления тока, то имеет место прямая пропорциональность между напряжением и током, выражающая закон Ома. В этом случае сопротивление называется линейным. На рис. 1-3
1 Эдисон изобрел лампу накаливания в 1879 г., после Лодыгина.
12
Показаны вольт-амперные характеристики сопротивления — нелинейная (кривая а) и линейная (прямая б). В этой книге рассматриваются линейные сопротивления.
Очевидно, величина линейного сопротивления г пропорциональна тангенсу угла наклона прямолинейной вольт-амперной характеристики к оси тока:
и т„ АВ т„ х
г. = — = -2— = — tga, i mj OB mi
где mu и mt— масштабы напряжения (в/мм) и тока (а[мм) на чертеже.
1-5. ИНДУКТИВНОСТЬ
Индуктивностью называется идеализированный элемент электрической цепи, приближающийся по свойствам к индуктивной катушке, в которой накапливается энергия магнитного поля. При этом .термин «индуктивность» и . соответствующее ему условное обозначение L применяются для обозначения как самого элемента цепи, способного накапливать энергию магнитного поля, так и для количественной
Рис. 1-4. Зависимость потокосцепления от тока. а — нелинейная; б — линейная.
оценки отношения потокосцепления самоиндукции к току в данном эле-менте *:
* Термином «индуктивность» заменен ранее применявшийся в литературе и ныне не рекомендуемый термин «коэффициент самоиндукции».
Потокосцеплением самоиндукции цепи называется сумма произведений магнитных потоков, обусловленных только током в этой цепи, на числа витков, с которыми они сцеплены. Если все витки пронизываются одним и тем же магнитным потоком, то потокосцепление равно произведению магнитного потока на число витков.
В Международной системе единиц Y измеряется в веберах (вб), L — в генри (гн). При этом всегда потокосцепление и ток имеют одинаковый знак, так что £>0.
Зависимость потокосцепления от тока в общем случае нелинейная, и параметр L зависит от тока. В случае, когда характеристика 4f(i) прямолинейна, индуктивность L постоянна (линейная индуктивность). На рис. 1-4 показаны нелинейная и линейная зависимости потокосцепления от тока. В этой книге во всех главах, кроме гл. 12, рассматриваются линейные индуктивности.
На основании закона электромагнитной индукции Фарадея — Максвелла изменение потокосцепления самоиндукции вызывает электродвижущую силу (э. д. с.) самоиндукции, которая выражается формулой
= ——. (Ь2)
L dt v ’
По закону Ленца, выражающему принцип электромагнитной инерции, эта э. д. с. противодействует изменению потокосцепления, что и учитывается знаком минус в (1-2), поскольку положительное направление для eL выбрано совпадающим с положительным направлением i.
Ввиду совпадения положительных направлений eL и i положительные направления магнитного потока вдоль оси витков и наводимой им э. д. с. самоиндукции, точно так же как и положительные направления тока и создаваемого им магнитного потока, связаны правилом правоходового винта.
Условное графическое изображение индуктивности с указанием выбранных положительных направлений тока и э. д. с. самоиндукции приведено на рис. 1-5.
13
Если L не зависит от I, то предыдущая формула принимает вид:
eL = ~^. (1-3)
Величина
= (1-4)
называется падением напряжения в индуктивности, или, что то же, напряжением на индуктивности. Положительное направление
Рис. 1-5. Условное обозначение индуктивности и положительные направления тока, э. д. с. самоиндукции и напряжения.
uL совпадает с положительным направлением i (рис. 1-5). Итак, напряжение на индуктивности пропорционально производной тока по. времени. Например, если ток изменяется по закону, изображенному на рис. 1-6,а, то напряжение на индуктивности представится в виде рис. 1-6,6 (здесь принято L=3 мгн).
На основании (1-4) ток в индуктивности
i — — (* и. dt
L J L или t
1 С л i = — I и, dt.
L J L
—со
Нижний предел интеграла принят равным —сю, так как до рассматриваемого момента времени t процесс мог длиться сколь угодно долго.
При t=0 ток в индуктивности равен:
о
«(0>=у J uLdi-, —со
следовательно,
t
i=i(O)+ --^‘uLdt, о
т. е. в интервале времени от нуля до t ток в индуктивности изменяется t
1 С м
на величину — I uLdt, определяе-
0
мую площадью, ограниченной в этом интервале кривой напряжения uL.
Рис. 1-6. Ток (а) и напряжение (б) в индуктивности.
Мгновенная мощность, поступающая в индуктивность, равна произведению мгновенных значений напряжения и тока:
. т . dl
Pl = ul T-
L L dt
Она связана с процессом нарастания или убывания энергии магнитного поля. Энергия магнитного поля в произвольный момент времени t определяется по формуле
t i
wL = J pL dt = J Li di = —oo о
Li* V* Z1 . v
s= — = —. (l-4a)
2 2L v '
Здесь учтено, что при /= — сю ток в индуктивности i(—сю)=О.
Если часть магнитного потока, связанного с индуктивным элементом, связана одновременно и с другим индуктивным элементом, то эти два элемента, кроме параметров L\ и L2, обладают параметром М, называемым взаимной индуктивностью. Взаимная индуктивность представляет собой отношение потокосцепления взаимной индукции одного из элементов к току в другом^ элементе:
14
t Af==^»=bL; (1-5)
здесь 4fi2 — потокосцепление первого элемента, обусловленное током второго элемента; 4*21 — потокосцепление второго элемента, обусловленное током первого элемента.
В этом случае в первом и во втором элементах наводятся э. д. с. взаимной индукции, равные соответственно:
е1М = — — =— М~ •
1A1 dt dt ’
(1-6)
е =_____________________м dil
Выражения (1-6) получены в предположении, что М не зависит от i’i и i2, так как здесь рассматриваются линейные цепи.
М измеряется, так же как и L, в генри. Однако в отличие от параметра L взаимная индуктивность М обозначает не какой-либо самостоятельный элемент электрической цепи, а лишь магнитную связь между индуктивными элементами.
Вопрос взаимной индуктивности подробнее рассмотрен в гл. 6.
1-6. ЕМКОСТЬ
Емкостью называется идеализированный элемент электрической цепи, приближенно заменяющий конденсатор, в котором накапливается энергия электрического поля. При этом термин «емкость» и соответствующее ему буквенное обозначение С применяются для обозначения как самого элемента цепи, способного накапливать энергию электрического поля, так и для количественной оценки отношения заряда к напряжению на этом элементе:
С = (1-7)
«с
Если q и ис измеряются в кулонах (к) и вольтах (в), то С измеряется в фарадах (ф). При этом всегда заряд и напряжение имеют одинаковый знак, так что С>0.
Зависимость заряда от напряжения в общем случае нелинейна, и, следовательно, параметр С зависит от напряжения.
В случае, когда характеристика q(u) прямолинейна, емкость С постоянна (линейная емкость). На рис. 1-7 показаны нелинейная и линейная зависимости заряда от напряжения. В этой книге рассматриваются линейные емкости.
Предположим, что емкость образована двумя пластинами, разделенными диэлектриком. Под влиянием приложенного напряжения на
Рис. 1-7. Зависимость электрического заряда от напряжения.
а — нелинейная; б — линейная
пластинах сосредоточатся равные количества электричества противоположных знаков; пластина с более высоким потенциалом зарядится положительным электричеством, а пластина с более низким потенциалом — отрицательным электричеством.
При изменении напряжения, приложенного к пластинам, изменится в соответствии с (1-7) электрический заряд: к пластине, потенциал которой возрастет, поступит дополнительный положительный заряд, а к пластине, потенциал которой снизится, поступит такой же отрицательный заряд.
Ток равен производной электрического заряда по времени. Поэтому с изменением напряжения на емкости в присоединенной к ней последовательно электрической цепи создается ток, величина которого определяется скоростью изменения заряда на емкости:
dg __q duc
dt ~~ dt'
(1-8)
Здесь знак заряда q соответствует знаку пластины, к которой направлен ток L.
15
Этот ток рассматривается как ток проводимости в проводниках, присоединенных к емкостному элементу (ток, обусловленный движением заряженных частиц под действием электрического поля в веществе, обладающем электропроводностью), переходящий вток смещения в диэлектрике емкостного элемента. Последнее понятие, введенное Максвеллом и применяемое в теории поля, означает скалярную величину, прямо пропорциональную скорости изменения напряженности электрического поля (в случае однородного поля и е=const).
Напомним, что напряженность электрического поля численно определяется силой, действующей на электрический заряд, равный единице.
Благодаря введению понятия тока смещения ток в цепи с емкостью представляется замкнутым через диэлектрик.
Согласно (1-8) ток положителен, когда заряд q и соответственно напряжение ис возрастают.
На основании (1-8) напряжение на емкости
1 С • иг — — I t at с с J
или
t
Злясь, как и в предыдущем параграфе, предполагается, что до рассматриваемого момента времени t процесс мог длиться сколь угодно долго и поэтому нижний предел интеграла принят равным —оо.
При /=0 напряжение на емкости равно:
о
—оа
Следовательно,
т. е. в интервале времени от нуля до t напряжение на емкости изме-у t
1 няется на величину —
J i dt, опре-о
деляемую площадью, ограниченной в указанном интервале кривой тока i.
Условное графическое изображение емкости с указанием положительных направлений тока и на-
Рис. 1-8. Условное обозначение емкости и положительные направления тока и напряжения.
пряжения приведено на рис. 1-8. Полярность емкости, указанная на рис. 1-8 знаками «+» и «—», соответствует положительному напряжению ис, т. е. положительному заряду на пластине «+».
Мгновенная мощность, поступающая в емкость, равна: pc=uci= =Сис—^~.Она связана с процессом накопления или убыли электрического заряда в емкости.
Когда заряд положителен и возрастает, то ток положителен, и в емкость поступает электрическая энергия из внешней цепи.
Когда заряд положителен, но убывает, т. е. ток отрицателен, то энергия, ранее накопленная в электрическом поле емкости, возвращается во внешнюю цепь.
Допустим, что к емкости С приложено некоторое напряжение ис. Энергия электрического поля в произвольный момент времени t определится по формуле
__ д*
2 “ 2С *
(1-8а)
Здесь учтено, что при /=— оо напряжение на емкости ис(—оо) = = 0.
16
1-7. ЗАМЕЩЕНИЕ ФИЗИЧЕСКИХ УСТРОЙСТВ ИДЕАЛИЗИРОВАННЫМИ
ЭЛЕМЕНТАМИ ЦЕПИ
Представление о сопротивлении, индуктивности и емкости как идеализированных элементах электрической цепи основано на предположении, что потери энергии, магнит-нитное поле и электрическое поле сосредоточиваются в отдельных, не зависящих друг от друга элементах цепн. Раздельное рассмотрение сопротивления, индуктивности и емкости представляет приближенный метод исследования цепи. В действительности потери энергии, магнитные и электрические поля сопутствуют друг другу.
Электропроводность всякого изотропного вещества характеризуется так называемой удельной электрической проводимостью, равной отношению величины плотности тока проводимости к величине напряженности электрического поля. Величина, обратная удельной электрической проводимости, называется удельным электрическим сопротивлением.
Электрическое сопротивление проводника при постоянном токе, равное отношению постоянного напряжения на рассматриваемом проводнике к постоянному току в нем, зависит от длины проводника I (м), площади поперечного сечения S (ти2) и удельного сопротивления р (ом-м):
В широких пределах изменения температуры зависимость удельного сопротивления проводника от температуры практически прямолинейна, причем в случае металлических проводников кривая p=f(6) с повышением температуры возрастает, а в случае неметаллических материалов (например, угля) и электролитов — падает.
Если обозначить через pi и ра удельные сопротивления при температурах 61 и 6г, а через 6о— температуру, соответствующую точке пересечения спрямленной характеристики р=/(6) с осью (рис. 1-9), то получится пропорция
Ра 6р — Р1 0О — 0!
Эта пропорция служит для вычисления pa, если известно рь
Значения р! (при 01=20° С) и Оо для некоторых проводников приведены ниже: алюминий: pi=2,83 • 10-8 ом • м\
0о=—236° С;
медь: pi = 1,724 • 10-8 ом • м\
0о=---234° С;
уголь: pi=3 500 ом-м\
0о=-{-1 825° С.
Как было пояснено выше, понятие сопротивление непосредственно обязано с потерей энергии, т. е. с необратимым процессом поглощения электромагнитной энергии.
Рис. 1-9. Спрямленная характеристика p=f(0o).
Количество тепла, выделяемого при прохождении тока через какой-либо проводник, зависит от целого ряда факторов, в том числе от частоты тока. При невысоких частотах сопротивление проводника мало отличается от сопротивления при постоянном токе. С повышением же частоты ток распределяется по сечению проводника неравномерно: внутри проводника плотность тока уменьшается, ток вытесняется к поверхности проводника, что вызывает как бы уменьшение сечения проводника, а значит увеличение сопротивления. Последнее приводит к увеличению тепловых потерь в проводнике. Это явление носит название поверхностного эффекта.
Неравномерность распределения тока по сечению проводника и возрастание вследствие этого тепловых потерь происходят также под влиянием тока, проходящего
2—1118
17
по соседнему проводнику. Это явление носит название эффекта близости.
Кроме того, переменное магнитное поле наводит в окружающей проводник проводящей среде вихревые токи, что вызывает дополнительную потерю энергии на нагрев.
К этому можно еще добавить излучение в пространство электромагнитной энергии, наблюдаемое при высоких частотах и вызывающее дополнительное увеличение сопротивления.
Вследствие наличия магнитного и электрического полей проводник наряду с сопротивлением имеет некоторую индуктивность и емкость.
Вычисление сопротивления, индуктивности и емкости проводника с учетом указанных выше факторов относится к задачам теории поля.
Теперь представим себе простейшую индуктивную катушку в виде нескольких круговых витков проводника, по которому проходит ток.
При постоянном токе напряжение на зажимах катушки определится величиной падения напряжения на ее сопротивлении в соответствии с (1-1), и ток во всех точках витков будет одинаковым.
При переменном же токе изменяющееся магнитное поле будет наводить в витке э. д. с. самоиндукции. Между витками, так же как и между отдельными точками смежных витков, электрическое поле станет переменным. В связи с этим ток в различных витках будет неодинаковым, так как появится ток смещения между витками. Чем выше частота переменного тока, тем больше будут э. д. с. самоиндукции и ток смещения. При низких частотах током смещения можно пренебречь; при высоких же частотах ток смещения, обусловленный изменением напряженности электрического поля, может быть соизмерим по величине с током в витках или даже может превышать его. Таким образом, в зависимости от выбранного диапазона частот индуктивная катушка может быть
представлена либо как сопротивление г (при постоянном токе — рис. 1-10, с), либо как индуктивность L с последовательно включенным сопротивлением г (при низких частотах— рис. 1-10,6), либо как индуктивность L и сопротивление г, соединенные параллельно с емкостью С (при высоких частотах — рис. 1-10, в).
Рис. 1-10. Электрические схемы замещения индуктивной катушки.
а — при постоянном токе; б — прн низких частотах; в — при высоких частотах.
Если катушка имеет много витков, то проходящий через нее ток создает магнитный поток, пропорциональный числу витков. Считая, что этот магнитный поток сцеплен со всеми витками катушки, приходим к выводу, что потокосцепление самоиндукции и соответственно индуктивность катушки пропорциональны квадрату числа витков.
Положим, например, что катушка, состоящая из w витков, насажена на тороид, или достаточно длинный прямолинейный сердечник, длина которого I, м, и площадь поперечного сечения S, м2. Обозначим через ра абсолютную магнитную проницаемость 1 сердечника (равную произведению относительной магнитной проницаемости р на магнитную постоянную р0=4л- 10-7 гн/м).
Магнитный поток в сердечнике определяется отношением намагничивающей силы (н. с.) всей катушки iw к магнитному сопротивлению I магнитопровода Гы~ — / Ца О
1 Абсолютная магнитная проницаемость для изотропного вещества — скалярная величина, характеризующая магнитные свойства вещества; она равна отношению величины магнитной индукции к величине напряженности магнитного поля.
18
' Поэтому индуктивность катушки согласно определению
I ________к>2ца5
Л-* —— " 1 — ель,
i I
Она определяется геометрическими размерами катушки, магнитной проницаемостью сердечника и квадратом числа витков.
Перейдем теперь К рассмотрению плоского конденсате р а, состоящего из двух параллельных пластин, разделенных диэлектриком. При постоянном напряже-
Рис. 1-11. Электрическая схема замещения конденсатора.
нии и идеальном диэлектрике тока в цепи не будет. Если напряжение переменно, то в процессе изменения электрического заряда возникает переменный ток, создающий переменное магнитное поле. Эффект, вызываемый магнитным полем, может быть учтен в электрической схеме замещения с помощью некоторой индуктивности, включенной последовательно^ с емкостью конденсатора. Обычно этой индуктивностью пренебрегают из-за ее относительной малости. Наконец, в диэлектрике благодаря некоторой проводимости возникают тепловые потери, которые возрастают с частотой. Потери на нагрев учитываются в схеме замещения конденсатора посредством сопротивления г, включенного параллельно емкости С (рис. 1-11).
Емкость конденсатора определяется размерами пластин, расстоянием между ними и диэлектрическими свойствами среды, заполняющей пространство между пластинами.
Если расстояние между пластинами конденсатора (толщина диэлектрика) достаточно мало по сравнению с размерами пластин, то емкость конденсатора вычисляется по формуле
С = ф
где еа — абсолютная диэлектрическая проницаемость изоляции между пластинами1 (равная произведению относительной диэлектрической проницаемости е на электрическую постоянную ео=8,855 • 10-12 Ф1м)\
S—площадь поверхности каждой пластины, м2;
d—расстояние между пластинами, м.
Чем выше частота и чем больше линейные размеры самих устройств, тем в большей мере проявляется взаимосвязь электрических и магнитных параметров и неотделимость друг от друга электрического и магнитного полей, являющихся лишь двумя сторонами единого электромагнитного поля.
Строго разграничить области частот, прн которых справедлива та или иная схема замещения, не представляется возможным, так как это зависит от множества факторов.
1-8. ИСТОЧНИК э. д. С.
И ИСТОЧНИК ТОКА
В теории электрических цепей пользуются идеализированными источниками электрической энергии: источником э. д. с. и источником тока. Им приписываются следующие свойства.
Источник э. д. с. (или идеальный источник напряжения) представляет собой активный элемент
Рис. 1-12. Источники напряжения: идеальные (а, б) и конечной мощности (в).
1 А бе о л ю-ти-а-я д и э л е к т ри ч е с -кая проницаемость для изотропного вещества — скалярная величина, характеризующая электрические свойства диэлектрика; она равна отношению величины электрического смещения к величине напряженности электрического поля.
о*
19
с двумя зажимами, напряжение на которых не зависит от тока, проходящего через источник. Предполагается, что внутри такого идеального источника пассивные элементы (г, L, С) отсутствуют, и поэтому прохождение через него тока не вызывает в нем падения напряжения.
Упорядоченное перемещение положительных зарядов в источнике от меньшего потенциала к болыпе-
Рис. 1-13. Источники тока: идеальные (а,, б) и конечной мощности (в).
му возможно за счет присущих источнику сторонних сил. Величина работы, затрачиваемой сторонними силами на перемещение единицы положительного заряда от зажима «—» к зажиму «+», называется электродвижущей силой (э. д. с.) источника и обозначается е(().
В соответствии со сказанным выше напряжение на зажимах рассматриваемого источника равно его э.д.с., т. е. u(t)=e(t).
Условные обозначения идеального источника напряжения приведены на рис. 1-12, а и б. Здесь стрелкой или знаками «+» и «—» указано положительное направление э. д. с., или полярность источника, т. е. направление возрастания потенциала в источнике для тех моментов времени, в которые функция e\t) положительна.
Величина тока в пассивной электрической цепи, подключенной к источнику напряжения, зависит от параметров этой цепи и э. д. с. e(t). Если зажимы идеального источника напряжения замкнуть накоротко, то ток теоретически должен быть бесконечно велик. Поэтому такой источник рассматривают как источник бесконечней мощности (теоретическое понятие). В дейст
вительности при замыкании зажимов реального источника электрической энергии — гальванического элемента, аккумулятора, генератора и т. д. — ток может иметь только конечное значение, так как э. д. с. источника уравновешивается падением напряжения от тока внутри источника (например, в сопротивлении г, индуктивности L).
Источник напряжения конечной мощности изображается в виде источника э. д. с. с подключенным к нему последовательно пассивным элементом, который характеризует внутренние параметры источника и ограничивает мощность, отдаваемую во внешнюю электрическую цепь (рис. 1-12, в). Обычно внутренние параметры источника конечной мощности незначительны по сравнению с параметрами внешней цепи; они могут быть отнесены к последней или в некоторых случаях могут вовсе не учитываться (в зависимости от соотношения величин и требуемой точности расчета).
Идеальный источнм тока представляет собой активный элемент, ток которого не зависит от напряжения на его зажимах. Предполагается, что внутреннее сопротивление идеального источника тока бесконечно велико, и поэтому параметры внешней электрической цепи, от которых зависит напряжение на зажимах источника, не влияют на ток источника.
Условные обозначения идеального источника тока приведены на рис. 1-13, с и б. Стрелка в источнике тока или знаки «+» и «—» указывают положительное направление тока t(() или полярность источника, т. е. направление перемещения положительных зарядов, или, что то же, направление, противоположное направлению движения отрицательных зарядов, для тех моментов времени, когда функция i(t) положительна.
По мере неограниченного увеличения сопротивления внешней электрической цепи, присоединенной к идеальному источнику тока, напряжение на его зажимах и соответственно мощность, развиваемая им, неограниченно возрастают. По
20
этому идеальный источник тока, так же как и идеальный источник напряжения, рассматривается как источник бесконечной мощности.
Источник тока конечной мощности изображается в виде идеального источника тока с подключенным к его зажимам пассивным элементом, который характеризует внутренние параметры источника и
Рис. 1-14. Вольт-амперное характеристики источников напряжения и тока.
а — идеальные источники; б — генератор постоянного тока с независимым возбуждением; в — ге« нератор постоянного тока с последовательным возбуждением.
ограничивает мощность, отдаваемую во внешнюю электрическую цепь (рис. 1-13,в).
Представляя собой теоретическое понятие, источник тока, как будет показано ниже (гл. 4 и 5), применяется в ряде случаев для расчета электрических цепей.
Некоторым подобием источника тока может служить устройство, состоящее из аккумулятора, соединенного последовательно с дополнительным большим сопротивлением. Другим примером источника тока может являться пятиэлектродная усилительная электронная лампа (пентод). Имея внутреннее сопротивление, несоизмеримо большее, чем сопротивление внешней электрической цепи, эти устройства отдают ток, почти не зависящий от изменения внешней нагрузки в широких пределах, и именно в этом отношении они аналогичны источнику тока.
Вольт-амперные характеристики идеальных источников напряжения и тока представляются прямыми, параллельными осям i и и (рис. 1-14,а). Реальные источники электрической энергии по своим вольт-амперным характеристикам могут приближаться к идеальным источникам напряжения или тока. Так, например, в значительной части ха
рактеристики и=f(i) напряжение на зажимах генератора постоянного тока с независимым возбуждением *, а также ток i генератора постоянного тока с последовательным возбуждением2 изменяются незначительно. На рис. 1-14,6 и в соответствующая часть характеристики показана сплошной линией.
1-9. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Как уже указывалось выше, настоящая книга посвящена в основном рассмотрению электрических цепей, в которых сопротивления, индуктивности и емкости не зависят от величин и направлений токов и напряжений. Такие электрические цепи, как и сами элементы, из которых они состоят, называются линейными, так как напряжение и ток в каждом элементе связаны между собой линейным уравнением — алгебраическим или дифференциальным.
Действительно, в случае, если параметр г не зависит от и и I, то закон Ома (1-1) выражает линейную зависимость между напряжением и током.
Если L и С не зависят от и и i, то напряжение и ток связаны линейными дифференциальными уравнениями (1-4) в случае индуктивности и (1-8) в случае емкости.
Что касается активных элементов линейных электрических цепей, то условием линейности идеального источника напряжения является независимость величины э. д. с. от тока, проходящего через источник, а условием линейности идеального источника тока является независимость тока от напряжения на его зажимах.
Реальные электротехнические и радиотехнические устройства, строго говоря, не подчиняются линейному закону. При прохождении тока через проводник выделяется тепло, проводник нагревается и его сопротивление изменяется. С изменением тока в индуктивной катушке с ферромагнитным сердечником со
\ 1 Обмотка возбуждения питается от по-
стороннего источника.
г Обмотка возбуждения соединена последовательно с цепью якоря.
21
отношение между потокосцеплением и током, т. е. параметр L, не остается постоянным. В зависимости от диэлектрика в большей или меньшей степени изменяется и емкость конденсатора в функции от заряда (или приложенного напря-^ жения). К нелинейным устройствам относятся, кроме того, электронные, ионные и полупроводниковые приборы, параметры которых зависят от тока и напряжения.
Если в рабочем диапазоне, на который рассчитывается то или иное устройство, т. е. при заданных ограниченных пределах изменений напряжения, тока и т. п., закон линейности с достаточной для практики степенью точности сохраняется, то такое устройство рассматривается как линейное.
Исследование и расчет линейных цепей сопряжены, как правило, с меньшими трудностями, чем исследование и расчет нелинейных цепей. Поэтому в тех случаях, когда линейный закон достаточно близко отражает физическую действительность, цепь рассматривается как линейная.
В радиоэлектронике и автоматике напряжение н ток, подводимые к цепи, принято называть воздействующей функцией илн входным сигналом, а напряжение и ток, возникающие при этом в какой-либо интересующей нас части цепи, называют реакцией 1 цепи или выходным сигналом. Сигналы можно рассматривать как функции времени.
В линейной электрической цепи соблюдаются принципы наложения и пропорциональности сигналов.
Принцип наложения заключается в том, что если входным сигналам И /2вх(/), порознь подводимым к цепи, соответствуют выходные сигналы £1вых(0 и faВЫХ (О> то суммарному входному сигналу Ьвх(0+Г2вх(0' будет соответствовать выходной сигнал Авых(0+--f-flBUX (О-
Принцип пропорциональности состоит в том, что входному сигналу А/вх(О соответствует выходной
1 В литературе встречается также термин «отклик» (от- английского- response}.
22
сигнал AfВЫХ (/), где А — постоянный множитель.
Если с течением времени параметры и схема цепи сохраняются неизменными, то цепь называется инвариантной во времени.
Допустим, что заданная линейная цепь до момента t=0 пассивна. Условие инвариантности цепи во времени означает, что если входному сигналу соответствует выходной сигнал /вых(/)♦ то входному сигналу /вх(^+т), запаздывающему по сравнению с первым на время т, будет соответствовать выходной сигнал /вых(^+т).
Отсюда можно заключить, что для линейных электрических цепей, инвариантных во времени, выполняется следующее условие: дифференцирование или интегрирование входного сигнала влечет за собой дифференцирование или соответственно интегрирование выходного сигнала. Действительно, пусть по условию инвариантности входному сигналу fBx(i + At) соответствует вы-ХОДНОИ /вых (/+Af). Если за входной сигнал принять ^~^8Х , то по условию линейности и инвариантности цепи выходной сигнал будет равен:
/вых U + АО — /вых (Q д*
Устремив А/ к нулю, в пределе получим входной и выходной сигналы
Й/вх(О „ d/вых (О ---- И -------. dt di
Аналогично можно рассмотреть и операцию интегрирования.
1-10. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ОТНОСЯЩИЕСЯ К ЭЛЕКТРИЧЕСКОЙ
СХЕМЕ
Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов рассматриваемой электрической цепи.
«Электрическими» элементами схемы служат активные и пассивные элементы цепи. «Геометрическими» элементами схемы являются ветви-иузлы.
Ветвь образуется одним или несколькими последовательно соединенными элементами цепи (рис. 1-15). При этом под последовательным соединением элементов цепи понимается такое их соединение, при котором через все эти элементы проходит один и тот же ток.
В общем случае, если состав ветвн не известен, последняя изображается прямоугольником.
Рис. 1-15. Изображение ветвей-электрической схемы.
Рис. 1-16,-Изображение узла электрической схемы.
Узел — место соединения трех1 или большего числа ветвей (рис. 1-16}. Линии, связывающие ветви в схеме, представляют соединения без сопротивлений. Поэтому, например, схемы рис. 1-16, с и б в электрическом смысле одинаковы: они содержат один узел.
Ветви, присоединенные к одной паре узлов (рис. 1-17), называются параллельными.
Рисунок 1-18 в виде примера иллюстрирует электрическую схему, содержащую пять ветвей и три узла.
Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром. Нарис. 1-18 указано стрелкой направление обхода одного из контуров, образованных в данной электрической схеме.
В зависимости от числа контуров, имеющихся в схеме, различа
1 Место соединения двух ветвей рассматривается как «устранимый узел».
ют одноконтурные н многоконтурные схемы. Одноконтурная схема является простейшей. Если пользоваться правилами преобразования схем (гл. 4), в ряде случаев удобно заменить многоконтурную схему одноконтурной, что упрощает расчеты.
Рис. 1-17. Параллельное соединение двух ветвей.
Если ток в электрической цепи постоянен, т. е. его значение ие изменяется во времени, то отсутствует явление самоиндукции: производная потокосцепления по времени равна нулю и напряжение, например, на индуктивной катушке определяется только величиной падения напряжения от тока в сопро
Лаея
Рис. 1-18. Схема электрической , цепи.
»Г'
тивлении катушки. Схема замещения индуктивной катушки Для этого случая приводилась на -рис. 1-10, а.
В свою очередь если не учитывать проводимости диэлектрика конденсатора, т. е. рассматривать конденсатор как идеальную емкость, то ветвь с такой емкостью представится в электрической схеме цепи постоянного тока разомкнутой: постоянный ток через емкость не проходит.
Таким образом, при рассмотрении электрической цепи постоянного тока в установившемся режиме, при котором напряжения и токи в цепи являются постоянными, пас-
23
сивнымн элементами схемы являются сопротивления, а активными— источники постоянной э. д. с. или постоянного тока.
Индуктивности и емкости учитываются в схемах цепей переменного тока и при переходных (не-установившихся) процессах, возникающих в электрических цепях при переходе от одного режима к другому (гл. 13).
1-11. ВОЛЬТ-АМПЕРНАЯ < ХАРАКТЕРИСТИКА УЧАСТКА ЦЕПИ С ИСТОЧНИКОМ
Закон Ома может быть применен к участку цепи с источниками, и для такого участка может быть построена вольт-амперная характеристика.
Разность потенциалов, взятая в направлении от зажима 2 к зажиму 1 (рис. 1-19,а), обратна по знаку выражению (1-9), т. е. равна э.д.с. источника за вычетом падения напряжения от тока i в сопротивлении г:
«ах=—«12=Е — ri. Следовательно, напряжение на зажимах ветви равно:
и—иа=Е— ri. (1-Ю)
Характеристика, построенная по этому уравнению, называемая внешней характеристикой, приведена на рис. 1-19, в.
Тангенс угла а пропорционален сопротивлению г.
При отрицательном знаке тока i напряжение на сопротивлении г
а)
Рис. 1-19. Последовательное
соединение сопротивления и источника постоянной э. д. с.
а — схема; бив — вольт-амперные характеристики.
На рис. 1-19,а показана ветвь с последовательно соединенными источником постоянной э. д. с. Е и сопротивлением г. Через ветвь проходит ток i, величина и направление которого в общем случае зависят не только от данного источника э. д. с., но и от источников остальной части электрической цепи, присоединенной к зажимам / и 2.
При указанных на рис. 1-19, с направлениях э. д. с. и тока потенциал зажима 1 ниже потенциала зажима 2 на величину э. д. с. за вычетом падения напряжения от тока i в сопротивлении г.
Следовательно, напряжение на зажимах ветви составляет:
им=— Е+П. (1-9)
Вольт-амперная характеристика для этого случая показана на рис. 1-19,6.
складывается с э.д.с. Е, и в этом случае и>Е.
На рис. 1-20, с показан участок цепи, состоящий из источника постоянного тока / с параллельным сопротивлением г. Т ак же как и в предыдущем случае, направление и величина тока i, проходящего через зажимы 1 и 2, зависит не только от данного источника, но и от источников остальной части цепи, присоединенной к зажимам 1 и 2.
При указанных на рис. 1-20, а направлениях токов через сопротивление г от зажима 2 к зажиму 1 проходит ток /—i, создающий напряжение
и12=п —ri.
По этому уравнению строится вольт-амперная характеристика (рис. 1-20,6).
24
Разность потенциалов, взятая в направлении от зажима 2 к зажиму 1, составляет:
uai=г! — ri.
Соответствующая вольт-амперная характеристика дана на рис. 1-20, в.
Таким образом, вольт-амперные характеристики участков цепи, состоящих из линейного сопротивления, соединенного последовательно с источником э.д.с. или параллель-
где Ши и тт — масштабы, в которых отложены на рис. 1-21 напряжения и сопротивления.
При переходе через источник э.д.с. по направлению, совпадающему с направлением действия э.д.с., потенциал возрастает скачкообразно на величину Е, затем при прохождении через сопротивление гх (по направлению тока) убывает прямолинейно на величину падения напряжения гх1. Если не выделять сопротивление г, а рассматривать
Рис. -1-20. Параллельное соединение сопротивления и источника постоянного тока.
а — схема; б и в — вольт-амперные характеристики.
но с источником тока, прямоли-нейны.
Из сопоставления вольт-амперных характеристик рис. 1-19,6, в и 1-20, б, в видно, что источник напряжения эквивалентен источнику тока при условии Е=г1, и потому они могут быть взаимно заменяемы.
1-12. РАСПРЕДЕЛЕНИЕ ПОТЕНЦИАЛА ВДОЛЬ ЦЕПИ С СОПРОТИВЛЕНИЯМИ
И ИСТОЧНИКАМИ НАПРЯЖЕНИЯ
Допустим, что на участке цепи, изображенном на рис. 1-19, а, величина тока i=I задана. Обозначив через гх и их некоторую часть сопротивления г и соответствующее напряжение относительно зажима 1, получим по аналогии с (1-10) =Е—гх1. Следовательно, зависимость их(гх) представляется прямой линией (рис. 1-21), причем тангенс угла наклона прямой к оси абсцисс пропорционален /:
tg₽= = А . _L =
АВ ти тг ти
его как сопротивление источника напряжения, равномерно,распределенное внутри самого источника, то график изменения потенциала внутри источника представится в виде прямой линии О А (рис. 1-21).
Рис. 1-21. Зависимость напряжения от сопротивления (при заданном токе).
Теперь рассмотрим какую-нибудь неразветвленную электрическую цепь постоянного тока, содержащую сопротивления и источники э.д.с. (рис. 1-22,а), и построим для нее график изменения потенциала. Приравняем нулю потенциал одной точки этого контура. Начав обход контура с этой точки, придем к исходному потенциалу. Примерный график распределения потенциала
25
в этом случае показан на рис. 1-22,6. Следует обратить внимание на то, что при переходе через источник э.д.с. в направлении, противоположном э.д.с., потенциал снижается на величину этой э.д.с.
На графике наклон прямых линий одинаков, так как ток во всех сопротивлениях один и тот же (одноконтурная цепь). В случае раз-
Рис. 1-22. Распределение потенциала вдоль цепи постоянного тока.
а — схема; б — график Потенциала.
ветвленной цепи, где токи в ветвях различны, наклон прямых линий графика потенциала неодинаков.
1-13. ЗАКОНЫ КИРХГОФА
Основными законами теории цепей наряду с законом Ома являются законы баланса токов в разветвлениях (первый закон Кирхгофа) и баланса напряжений на замкнутых участках цепи (второй закон Кирхгофа).
Распределение токов и напряжений в электрических цепях подчиняется законам Кирхгофа, которые должны быть основательно усвоены для отчетливого понимания всех последующих разделов курса.
Первый закон Кирхгофа
Алгебраическая сумма токов в узле равна нулю:
2i=0. (1-11)
Суммирование распространяется на токи в ветвях, сходящихся в рас
сматриваемом узле. При этом знаки токов берутся с учетом выбранных положительных направлений токов: всем токам, направленным от узла, в уравнении (1-11) приписывается одинаковый знак, например положительный, и соответственно все токи, направленные к узлу, входят в уравнение (1-11) с противоположным знаком. Иначе говоря, всякий ток, направленный от узла, может рассматриваться как ток, направленный к узлу, но имеющий противоположный знак.
На рис. 1-23, а в качестве примера показан узел, в котором схо-
Рис. 1-23. Иллюстрация к первому закону Кирхгофа.
дятся четыре ветви. Уравнение (1-11) имеет в этом случае вид:
— h —
Первый закон Кирхгофа выражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.
Первый закон Кирхгофа применим не только к узлу, но и к любому контуру или замкнутой поверхности, охватывающей часть электрической цепи, так как ни в каком элементе цепи, ни в каком режиме электричество одного знака не может накапливаться.
Так, например, для схемы рйс. 1-23,6 имеем;
—’ ti+t'a+ia=O-
Второй закон Кирхгофа
Алгебраическая сумма э.д.с. в любом контуре цепи равна алгебраической сумме падений напряжения на элементах этого контура:
26
2e-2u. (1-12)
Обход контура совершается в произвольно выбранном направлении, например по ходу часовой стрелки. При этом соблюдается следующее правило знаков для э.д.с. и падений напряжения, входящих в (1-12): э.д.с. и падения напряжения, совпадающие по направлению с направлением обхода, берутся с одинаковыми знаками.
Рис. 1-24. Иллюстрация ко второму закону Кирхгофа.
Например, для схемы рис. 1-24 имеем:
— e2=Ui+ua+us — u4.
Уравнение (1-12) можно переписать так:
2 (и — е)=0. (1-13)
Здесь и—е — напряжение на ветви.
Следовательно, алгебраическая сумма напряжений на ветвях в любом замкнутом контуре равна нулю.
Формулы (1-11) и (1-12) написаны в общем виде для мгновенных значений токов, напряжений и э.д.с.; они справедливы для цепей как переменного, так и постоянного тока.
График изменения потенциала, рассмотренный в предыдущем параграфе, служит графической иллюстрацией второго закона Кирхгофа.
1-14. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1-1. Определить сопротивление медного провода при 10° С, если при 60° С оно равно 5 ом.
Ответ: 4,15 ом.
1-2. Показать, что величины rC, Lfr и -jf LC имеют размерность времени.
1-3. Показать, что гЧ? имеет размерность индуктивности, уАL/C — размерность
сопротивления, Lfr2 — размерность емкости.
1-4. Ток i=e~at проходит через ветвь, состоящую из последовательно соединенных сопротивления г и индуктивности L.
Определить напряжения на сопротивлении, индуктивности и на всей ветви, приняв a=r/L-, объяснить физически полученный результат.
1-5. Начиная с момента 1=0, через сопротивление 1 ом проходит ток 1= 1—е~‘, а. Какое количество энергии выделится в виде тепла к моменту времени, когда ток достигнет значения 0,632 а?
Ответ: 0,169 дж.
1-6. Начиная с момента 1=0, через индуктивность L=l гн проходит ток 1= = 1—е~а. Определить напряжение иа индуктивности и энергию магнитного поля в момент времени, когда ток достигнет значения 0,632 а.
Ответ: 0,37 в; 0,2 дж.
1-7. Емкость С—1 ф, имеющая электрический заряд </= 1 к, в момент 1=0 начинает разряжаться через сопротивление г= = 1 ом. Ток изменяется по закону i=e~,а. Определить напряжение на емкости и энергию электрического поля в момент, когда ток достигнет значения 0,37 а.
Ответ: 0,37 в; 0,068 дж.
1-8. Сохранив условия предыдущей задачи, определить, какое количество энергии выделится в виде тепла к моменту времени, когда ток достигнет значения 0,37 а?
Ответ: 0,432 дж.
1-9. Сохранив условия задачи 1-7, убедиться в том, что энергия, выделенная в виде тепла за бесконечно большое время, равна энергии электрического поля до начала разряда. Определить эту энергию.
Ответ: 0,5 дж.
1-10. Плоский конденсатор состоит из двух листов фольги, каждый площадью 40 см3, разделенных парафииированиой бумагой толщиной 0,05 мм. Вычислить емкость конденсатора, приняв относительную диэлектрическую проницаемость парафинированной бумаги равной 1,8.
Ответ: 1,275 • 10-3 мкф.
1-11. Плоский конденсатор, диэлектриком которого служит слюда толщиной 3 лои, имеет емкость С=0,0443 10-3 мкф. Площадь каждой пластины конденсатора равна 25 см3. Чему равна относительная диэлектрическая проницаемость слюды?
Ответ: 6.
1-12. Вычислить приближенно индуктивность катушки без ферромагнитного сердечника, имеющей 300 витков, длину 10 см и сечение 1 см3.
Ответ: 0,113 мгн.
1-13. Тороидальная катушка состоит из w витков, насаженных на сердечник, поперечное сечение которого — прямоугольник; d\ и d2 — внутренний и внешний диаметры тороида; h — толщина тороида. Доказать, что индуктивность катушки
2л dr
Указание. Следует составить выражение для кольцевого магнитного пото
27
ка бесконечно малого сечения и провести интегрирование по сечению тороида.
1-14. Что такое положительное направление тока?
1-15. Зависит ли выбор положительного направления напряжения от положительного направления тока?
1-16. Что понимается под полярностью источника напряжения и источника тока?
1-17. Почему результат расчета элект
рической цепи не зависит от выбора положительных направлений токов?
1-18. Как выбрано положительное направление э. д. с. самоиндукции в формулах (1-2) н (1-3)? Пояснить связь с законом Ленца.
1-19. Пояснить процесс прохождения переменного тока через конденсатор.
1-20- Исходя из выражений энергии, показать, что сопротивление, индуктивность и емкость всегда положительны.
28
Глава вторая
ЦЕПИ ГАРМОНИЧЕСКОГО ТОКА
2-1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
тельного значения аргумента t спра-
Электромагнитный процесс в электрической цепи, при котором мгновенные значения напряжений и токов повторяются через равные промежутки времени, называется периодическим. Наименьший промежуток времени, по истечении которого наблюдаются повторения мгновенных значений периодических величин, называется перио-д о м. Если величину, являющуюся периодической функцией времени t, обозначить через F (t), то для любого положительного или отрица-
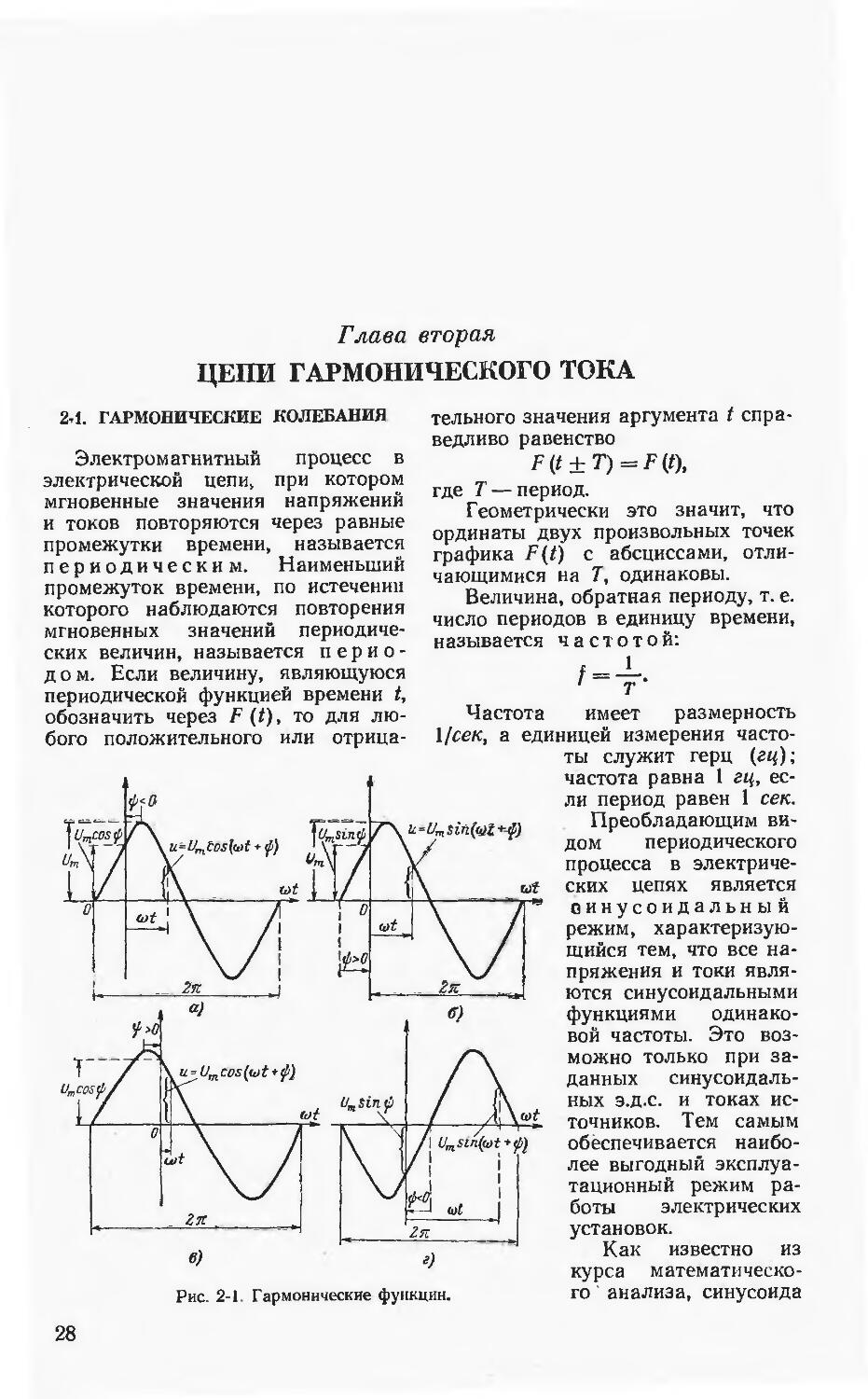
Рис. 2-1. Гармонические функции.
ведливо равенство
F(t±T) = F (О, где Т — период.
Геометрически это значит, что ординаты двух произвольных точек графика F(t) с абсциссами, отличающимися на Т, одинаковы.
Величина, обратная периоду, т. е. число периодов в единицу времени, называется частотой:
Частота имеет размерность \[сек, а единицей измерения частоты служит герц (гц);
частота равна 1 гц, если период равен 1 сек.
Преобладающим видом периодического процесса в электрических цепях является синусоидальный режим, характеризующийся тем, что все напряжения и токи являются синусоидальными функциями одинаковой частоты. Это возможно только при заданных синусоидальных э.д.с. и токах источников. Тем самым обеспечивается наиболее выгодный эксплуатационный режим работы электрических установок.
Как известно из курса математическо-
го анализа, синусоида
28
является простейшей периодической функцией; всякие другие несинусоидальные периодические функции могут быть разложены в бесконечный ряд синусоид, имеющих кратные частоты (гл. 10). Поэтому для исследования процессов в цепях переменного тока в первую очередь необходимо изучить особенности цепей синусоидального тока. Так как косинусоида может рассматриваться как сдвинутая синусоида, то условимся к синусоидальным функциям причислять и косинусоидальные. Колебания, выражаемые этими функциями, будем называть гармоническими.
На рис. 2-1 изображены функции
Ц=С/тсо5(<о<+ф) (2-1)
и
u=Um sin (erf+ф); (2-2)
здесь Um— максимальное значение или амплитуда;
<о— скорость изменения
аргумента (угла), называемая угловой частотой; она равна произведению частоты на 2л:
со=2л/, padjceK-, (2-3) ф—начальная фаза,
определяемая величиной смещения гармонической функции относительно начала координат; при записи (2-1) она измеряется абсциссой положительного максимума, а при (2-2) — абсциссой точки перехода отрицательной полуволны в положительную.
Начальная фаза ф представляет алгебраическую величину. На рис. 2-1, а и г угол ф отрицателен. На рис. 2-1, бив угол ф положителен. В дальнейшем будем пользоваться преимущественно записью (2-1).
За аргумент функций (2-1) и (2-2) может быть принято время t или соответственно угол at. Аргу
менту t соответствует период Т, а аргументу at — период аТ=2л. Следует иметь в виду, что аргумент at измеряется в радианах, причем в тех же единицах измеряется и начальная фаза.
Если угол ф вычисляется в градусах, то аргумент at также переводится в градусы *, в этом случае период составляет 360°.
Величина <о/+ф, определяющая стадию изменения функций (2-1) и (2-2), называется фазовым углом или фазой. С течением времени фаза возрастает, причем после увеличения фазы на 2л цикл изменения синусоидальной величины повторяется.
Рассмотренные в данном параграфе понятия, характеризующие гармонические колебания, являются исходными при изучении электрических процессов в цепях переменного тока.
2-2. ГЕНЕРИРОВАНИЕ СИНУСОИДАЛЬНОЙ Э. Д. С.
Наиболее распространенным в промышленности способом получения синусоидального тока является применение электромагнитных машин, так называемых синхронных генераторов, приводимых во вращение тепловыми, газовыми, гидравлическими или другими двигателями.
Генератор переменного тока состоит из двух частей — неподвижного статора и вращающегося ротора. На одном из них (чаще на роторе) располагаются полюсы, т. е. электромагниты, обмотка которых питается от источника постоянного тока, или постоянные магниты. На другом (обычно на статоре) располагается главная обмотка, в которой наводится переменная э.д.с.
Генератор может иметь одну или несколько пар полюсов. На рис. 2-2, а упрощенно показан явнополюсный генератор с двумя парами полюсов, размещенных на роторе. Указанному на рис. 2-2,а положению ротора относительно
1 Напомним, что 1 рад=57,3°.
29
статора соответствует на рис. 2-2,0 развернутая на плоскость схема расположения обмотки и полюсов.
В каждом проводе обмотки, находящемся в пазу статора, при вращении ротора наводится по закону Фарадея э.д.с. e=Blv, где В — магнитная индукция поля под проводом; I — длина провода; v — линейная скорость перемещения магнитного поля. В Международной
Рис. 2-2. Принцип устройства синхронного генератора.
системе В измеряется в теслах (гл), т. е. вб/мг.
При постоянных значениях I и v закон изменения э.д.с. e(t) определяется законом распределения магнитной индукции В в воздушном зазоре машины. Благодаря специальной форме полюсных наконечников закон изменения магнитной индукции делается приблизительно синусоидальным вдоль всей окружности зазора между ротором и статором; магнитная индукция максимальна против середин и постепенно убывает к краям полюсных наконечников.
В момент времени, которому соответствует указанное на рис. 2-2 положение ротора, магнитная индукция под проводом равна нулю и поэтому э.д.с. е также равна нулю.
После поворота ротора на одну восьмую часть полного оборота (половина полюсного шага) э.д.с. достигнет максимума и будет направлена от зажима 1 к зажиму 2 (по правилу правой руки) *. Когда ро-
1 Это правило заключается в следующем: если вектор магнитной индукции входит в ладонь, а отогнутый большой палец совпадает с направлением движения проводника относительно поля, то остальные четыре пальца указывают направление наводимой 9. д. с.
Аналогично по правилу левой руки большой палец определяет направление силы, действующей на проводник с током.
тор повернется еще на половину полюсного шага, э.д.с. вновь обратится в нуль. При последующем вращении ротора еще на одну восьмую часть оборота э.д.с. достигнет максимума, но будет противоположно направлена — от зажима 2 к зажиму 1, и т. д. Таким образом, на зажимах генератора возникнет практически синусоидальная э.д.с.
При числе пар полюсов р и числе оборотов ротора в минуту п частота наводимой переменной э.д.с. равна:
7 = (2-4)
В энергосистемах СССР и большинства других стран частота промышленного тока равна 50 гц. В США принята частота 60 гц.
В авиации с целью уменьшения веса оборудования применяются машины с повышенной скоростью вращения. Частота f при этом получается повышенной (400—800 гц). Например, генератор, имеющий р=2 и п=12000 об]мин, ^генерирует синусоидальную э.д.с. с частотой , 2-12000
f —-------= 400 гц.
60
При большой скорости вращения (о>50 м!сек) крепление полюсов затруднено, и для обеспечения механической прочности применяются неявнополюсные машины, у которых обмотка возбуждения укладывается в пазы цилиндрического ротора неравномерно, так чтобы форма поля была по возможности-синусоидальной.
Проводная электросвязь использует широкий диапазон частот: от f=0 (постоянный ток) до /=104н--j- 105 гц, а радиотехника — еще более высокие частоты.
Радиоволны, т. е. электромагнитные поля, с помощью которых осуществляется передача информации радиотехническими методами, распространяются в воздухе со скоростью v~3’ 108 м/сек. За период Т радиоволна распространяется на расстояние, равное длине волны:
Х = пТ = у- = 3-108//, м, где f — в герцах.
30
В связи с этим в радиотехнике принято количественно характеризовать периодичность процесса не только частотой f, но и длиной волны X, обратно пропорциональной частоте.
Ниже приведена примерная классификация частот и соответствующих им длин волн.
Классификация радиочастот (радиоволн)
Наименование волн Параметр
частота длина волны
Длинные .... 30—300 кгц 10000— 1000 м
Средние .... 300—3000 кгц 1000— 100 м
Короткие.... 3—30 Мгц 100— 10 м
Ультракороткие Выше 30 Мгц Меньше 10 м
Генерирование токов высокой частоты осуществляется с помощью электронных или полупроводниковых устройств.
На рис. 2-3 в виде примера показана одна из схем электронного генератора высокой частоты. Анод
Рис. 2-3. Упрощенная схема электронного генератора.
трехэлектродной лампы (триода) присоединен через контур L—С к положительному полюсу источника постоянного напряжения, например аккумуляторной батареи. В контуре L—С, называемом резонансным, возникают незатухающие гармонические колебания тока, частота которых зависит от выбора параметров L и С. Электрическая энергия, необходимая для поддержания этих колебаний, поступает от аккумуляторной батареи.
Работа электронных генераторов здесь не рассматривается. Про
цессам, происходящим в резонансных цепях, будет посвящена гл. 7. Принципы действия и работы электронных и полупроводниковых генераторов будут разобраны в последующих специальных курсах. Приведенная выше схема электронного генератора служит примером получения гармонических колебаний высокой частоты.
Начало практического внедрения переменного тока относится ко второй половине XIX в., когда выдающийся русский электротехник Павел Николаевич Яблочков (1847— 1894 гг.) стал применять на практике изобретенные им электрические свечи.
2-3. СРЕДНЕЕ И ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЯ ФУНКЦИИ
Среднее значение периодической функции f(t) за период Т определяется по формуле
т
fc₽=y-J/(0dt (2-5)
Отсюда видно, что среднее значение за период равно высоте прямоугольника с основанием Т, площадь которого равна площади, ограниченной функцией f(t) и осью абсцисс за один период.
В случае гармонического колебания среднее значение за период равно нулю, так как площадь положительной полуволны компенси-
Рнс. 2-4. Среднее полупе-рнодное значение гармонической функции.
руется площадью отрицательной полуволны гармонической функции. Поэтому здесь пользуются понятием среднего значения функции, взятой по абсолютной величине, или, что то же, среднего полу-периодного значения, соответствующего положительной по
31
луволне гармонической функции (рис. 2-4).
В соответствии с этим среднее значение тока i=Im cos at с амплитудой А=1т будет:
т
/ср= j cosat dt =
_ "т_ 4
Т
= [sincod' = —/^0,637/ аТ | LZ л m m
4 (2-6)
Аналогично среднее значение гармонического напряжения о f7cp=—^«0,637f/m. (2-7) л
Тепловое действие тока, а также механическая сила взаимодействия двух проводников, по которым проходит один и тот же ток, пропорциональны квадрату тока. Поэтому о величине тока судят обычно по так называемому действующе-м у 1 (среднеквадратичному) значению за период.
Действующее значение периодической функции f(t) вычисляется по формуле
Р==у/Г-f J [/(О]2^- (2-8)
Из этой формулы следует, что величина F2 представляет собой среднее значение функции [/(/)]2 за период Т, т. е. равна высоте прямоугольника с основанием Т, площадь которого равна площади, ограниченной функцией [f(0]2 и осью абсцисс за один период (рис. 2-5).
В соответствии с (2-8) действующее значение периодического тока
Возведя (2-9) в квадрат и умножив обе части полученного выражения на гТ, найдем:
т г FT = [лМ
Это равенство показывает, что действующее значение периодического тока равно по величине такому постоянному току, который, проходя
Рис. 2-5. Действующее значение гармонической функции.
через неизменное сопротивление г, за период времени Т выделяет то же количество тепла, что и данный ток I.
Аналогично действующее значение периодического напряжения
При токе i=Im cos at т т
J i2 dt = J cos2 at dt=
о 0
T
fl C fl
= _TL (1 4- cos 2<n/) dt = lUL T
2 J 2
о
Следовательно, согласно (2-9)
/=-^^0,7077т. (2-9a)
/2
1 Этим термином заменен применявшийся ргшее в литературе и ныне не рекомендуемый термин «эффективное» значение.
Аналогично действующее значение гармонического напряжения
U = ^0,707Um. (2-1 Оа)
V?
Номинальные токи и напряжения электротехнических устройств определяются, как правило, действую-
32
щими значениями; поэтому действующие значения представляют наиболее распространенный электрический параметр.
Для измерения действующих значений применяются системы приборов: тепловая, электромагнитная, электродинамическая и др.
2-4. ПРЕДСТАВЛЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ В ВИДЕ ПРОЕКЦИЙ
ВРАЩАЮЩИХСЯ ВЕКТОРОВ
Мгновенные значения функции U—UmCOS (<о/+ф) можно получить как проекцию на горизонтальную ось отрезка длиной Um, вращающе-
гося относительно начала угольной системы координат с угловой скоростью <о=2л/ в положительном направлении (т. е. против хода часовой стрелки). Вращающийся отрезок условимся называть вектором *.
В момент f=0 вектор образует с горизонтальной осью угол ф и его проекция на горизонтальную ось равна Um cos ф, т. е. мгновенному значению заданной функции при t—О (рис. 2-6, а).
За время /=Л вектор повернется на угол ati и окажется повернутым относительно горизонтальной оси на угол шЛ+ф; его проекция на эту ось будет равна Um cos (соЛ+ф) И т. д.
Таким образом, рассмотрение гармонических колебаний можно заменить рассмотрением вращающихся векторов.
Для получения мгновенных значений в соответствии
с вышесказанным условим-
ся проектировать векторы на горизонтальную ось. Рассмотрим теперь функцию
Um sin (со/ 4- ф) =Um cos^cof + ф —. Она представится проекцией вращающегося вектора, имеющего начальную фазу ф— — (Рис- 2-6,6).
Следовательно, векторы, изображающие косинусоидальную и синусоидальную функцию, взаимно перпендикулярны.
Если гармонические колебания имеют одну и ту же частоту, то соответствующие этим колебаниям векторы вращаются с одинаковой угловой скоростью и поэтому углы между ними сохраняются неизмен-
прямо- ными.
Рнс. 2-6. Представление гармонических функций в виде вращающихся векторов.
На рнс. 2-7 показаны две гармонические функции
«1 = и 1т COS (at фх) и
иг = U2mcos(at — ф2),
1 Этот вектор, вращающийся в плоскости прямоугольной системы координат, не следует смешивать с вектором в трехмерном пространстве из области механики или теории электромагнитного поля.
имеющие одинаковую угловую частоту ш и начальные фазы ф, и —ф2. Кривая щ, смещенная влево относительно «2> возрастает от нуля
3—1118
33
до своего положительного максимума раньше, чем кривая и2. Поэтому говорят, что Ui опережает по фазе и2, или, что то же. и2 отстает по фа зе от Разность начальных фаз д>=е-ф]—(—фг)=ф1+ф2 называется фазовым сдвигом или углом сдвига П| относительно и2. Этот угол и образуют между собой векторы, показанные на рис. 2-7 (вверху).
При равенстве начальных фаз, т. е. при фазовом сдвиге, равном ну-
Рис. 2-7. Фазовый сдвиг.
Вверху — между векторами; внизу — между косинусоидами.
лю, векторы направлены в одну и ту же сторону (совпадают по фазе).
При фазовом сдвиге 180° векторы направлены в диаметрально противоположные стороны (находятся в противофазе).
Диаграмма, изображающая совокупность векторов, построенных с соблюдением их взаимной ориентации по фазе, называется векторной диаграммой.
Векторное представление гармонических функций, частота которых одинакова, облегчает операции сложения и вычитания этих функций. Ввиду того, что сумма проекций двух векторов равна проекции геометрической суммы этих векторов, амплитуда и начальная фаза результирующей кривой легко нахо
дятся из векторной диаграммы геометрическим сложением векторов. Например, пусть требуется сложить функции щ — t/lmcos ((,)/+ф1) и и2— U2mcos(fi)t -Ьфг).
Из графического построения рис. 2-8,а следует:
(2-11)
ter ,h — Ulm Sin + U™ sitl Ф8 (9 191 g'1’ Ulm COS Ф, + l)2m COS Ф, ( '
Здесь угол ф находится с учетом знаков числителя и знаменателя, определяющих знаки синуса и косинуса.
Рис. 2 8. Сложение (а) и вычитание (б) векторов.
В случае, когда функция и2 вычитается из Uj (рис. 2-8,6), угол фг в (2-11) и (2-12) заменяется на фг+л или, что то же, на фг—л.
Амплитуда Um и угол ф могут быть также получены непосредственно из векторной диаграммы.
При пользовании векторной диаграммой с целью установления фазовых сдвигов или амплитудных значений гармонических величин,
34
имеющих одинаковую частоту, векторная диаграмма может считаться неподвижной (при равенстве частот углы между векторами не зависят от времени).
Построение векторных диаграмм обычно не связано с определением мгновенных значений гармонических функций; в таких случаях векторные диаграммы строятся не для амплитуд, а для действующих значений. т. е. модули векторов уменьшаются по сравнению с амплитудами в V 2 раз. При этом векторная диаграмма мыслится неподвижной.
В отличие от векторных диаграмм кривые мгновенных значений называются временными диаграммами.
2-5. ГАРМОНИЧЕСКИИ ТОК В СОПРОТИВЛЕНИИ
Если напряжение t7mcos(oj/+ +фи) подвести к сопротивлению г, то через сопротивление пройдет гармонический ток
i= -у- = cos (и/ +• ф„) =
= Im cos (at + фД
Следовательно, напряжение на зажимах сопротивления и ток, проходящий через это сопротивление, имеют одинаковую начальную фазу, или, как говорят, совпадают по фазе: они одновременно достигают своих амплитудных значений Um и 1т и соответственно одновременно проходят через нуль (рис. 2-9).
В данном случае фазовый сдвиг между напряжением и и током i (и соответственно между векторами напряжения U и тока /) равен нулю:
Ф = —% = 0.
При прохождении гармонического тока через сопротивление г не только мгновенные значения напряжения на сопротивлении и тока в нем, но и амплитуды и соответственно действующие значения напряжения и тока связаны законом Ома:
Um = rlm- U — rl.
Пользуясь величиной проводимости получаем:
l = gU.
Мгновенная мощность, поступающая в сопротивление,
pr — ui = Um Im cos* (to/ + ф) =
= Ш |1 cos 2 (со/ + ф)] (2-13) изменяется с угловой частотой, удвоенной по сравнению с частотой напряжений и тока и колеблется в пределах 0—2 UI (рис. 2-10).
Рис. 2-9. Гармонический ток в сопротивлении.
Как видно из (2-13), кривая рТ состоит из двух слагающих: постоянной слагающей UI и косинусоидальной функции, имеющей амплитуду UI и угловую частоту 2со.
Ввиду того, что в рассматриваемом случае напряжение и ток совпадают по фазе, т. е. всегда имеют одинаковый знак (плюс или минус), их произведение всегда положительно.
Среднее значение мощности за т
период Р— ~^prdt называется и
‘ р
ZU1 Рг
Ы мд .
о ♦
Z ш ш
Рис. 2-10. Мгновенные значения мощности, поступающей в сопротивление (ф=0).
3*
35
средней или активной мощностью и измеряется в ваттах.
В рассматриваемом случае, как это видно из выражения (2-13) и рис. 2-10, средняя мощность = UI—rl2. Это следует также и из определений, данных в предыдущем параграфе. Сопротивление г в свою очередь может быть определено как отношение средней мощности к квадрату действующего значения тока
В § 1-7 отмечалось, что сопротивление проводника при переменном токе больше, чем при постоянном токе, вследствие явлений поверхностного эффекта, эффекта близости, возникновения вихревых токов и излучения электромагнитной энергии в пространство. В отличие от сопротивления при постоянном токе, которое называют омическим, сопротивление проводника при переменном токе называется активным сопротивлением.
В теории электромагнитного поля доказывается, что вследствие поверхностного эффекта сопротивление rt провода круглого сечения диаметром d при частоте / связано с сопротивлением того же провода Го при постоянном токе формулой: г/=г0.0,0385 d y~f, т. е. сопротивление растет пропорционально корню квадратному из частоты.
, Излучаемая в пространство мощность
Р = Л/2/2 72 = гиз/2 пропорциональна второй степени частоты, длины провода и действующего значения тока. Следовательно, при I X сопротивление излучения
Л = ^(-2-)’ зависит от соотношения длины провода .-и длины электромагнитной волны. При" низких частотах оно ничтожно мало, а при высоких частотах может быть соизмеримо с /у или даже больше него.
2-6. ГАРМОНИЧЕСКИЙ ТОК В ИНДУКТИВНОСТИ
Пусть через индуктивность L проходит ток
36
i = 7mcos(tof+ ф).
Электродвижущая сила самоиндукции определяется по формуле (ЬЗ):
eL = = (oLImsin(at + ф) =
= — Um cos + ф 4—— j.
Значит, напряжение на индуктивности
uL = —eL = Umcos(tot + Ф 4- -у) -
Полученное выражение показывает, что напряжение на индуктив-
Рис. 2-11. Гармонический ток в индуктивности.
ности опережает ток на угол л/2: максимум напряжения смещен влево относительно максимума тока на л/2 (рис. 2-11); когда ток проходит через нуль, напряжение достигает положительного или отрицательного максимума, так как оно пропорционально скорости 'изменения тока (di/dt), которая в момент прохождения тока через нуль максимальна (косинусоида тока в этот момент имеет наибольшую крутизну). Когда ток достигает максимума, скорость его изменения, а следовательно, и напряжение на индуктивности обращаются в нуль.
Под фазовым сдвигом ф тока относительно напряжения понимается разность начальных фаз напряжения и тока (§ 2-4). Следовательно, в данном случае
<p = if„—= •
На_ векторной диаграмме вектор тока_/ отстает от вектора напряжения U на угол л/2 (рис. 2-11,в).
Амплитуды, так же как и действующие значения напряжения и тока, связаны соотношением, подобным закону Ома:
U = <лЫ = х,1• U = х, /. т т L m ’ L
Величина xL = aL, имеющая размерность сопротивления, называется индуктивным сопротивлением; обратная ей величина Ьъ= ==--- называется индуктивной
a>L
проводимостью.
Итак,
lm = bLUm; I = bLU.
Индуктивное сопротивление представляет расчетную величину, с помощью которой учитывается явление самоиндукции.
Мгновенная мощность, поступающая в индуктивность, будет:
Рь = An cos(“< +Ф + -у)х
х cos (со/ -|- if) =— —• 2 sin (<O/+
+if) cos (co/ + if) = = — Ul sin 2 (co/ 4- tf).
Она колеблется по синусоидальному закону с угловой частотой 2<о, имея амплитуду UI. Мгновенная мощность в данном случае равна скорости изменения энергии магнитного поля индуктивности (§ 1-3).
Энергия магнитного поля индуктивности согласно формуле (1-4а)
WL=~ = "^-COS2 (И/ + if) =
= -^-[l + cos2(o/ + if)]
изменяется периодически с угловой частотой 2со в пределах от 0 до ^/а=-^-(рис. 2-12).
Поступая от источника, энергия временно запасается в магнитном поле индуктивности, затем возвра
щается источнику при исчезновении магнитного поля. Энергия магнитного поля достигает максимума в момент перехода тока в индуктивности через амплитудное значение, затем она убывает и обращается в нуль при токе, равном нулю.
Рис. 2-12. Мгновенные значения мощности, поступающей в индуктивность, и энергия магнитного поля.
Таким образом, происходит колебание энергии между источником и индуктивностью, причем средняя мощность, поступающая в индуктивность, равна нулю.
Так как максимальное значение энергии, запасаемой в магнитном поле, равно wLttaKC = Ll2, то индуктивное сопротивление xL=taL может
акс быть определено как =— •
2-7. ГАРМОНИЧЕСКИЙ ТОК В ЕМКОСТИ
Пусть напряжение на емкости и —Um cos (tut + if).
На основании (1-8)
i = С = — uCUm sin (to/ + if) =
= 7mcos(<o/ + Tf + ^-). (2-14)
Изменение электрического заряда происходит по косинусоидальному закону в соответствии с приложенным напряжением и. При этом попеременное накапливание положительных и отрицательных' электрических зарядов на пластинах емкости обусловливает прохождение в цепи гармонического тока i.
37
Его величина определяется скоростью изменения заряда на емкости (dq/dt).
Выражение (2-14) показывает, что ток I опережает приложенное напряжение и на угол л/2 (рис. 2-13). Нулевым значениям тока соответствуют максимальные (положительные или отрицатель-
Рис.
2-13. Гармонический ток в емкости.
ные) значения напряжения и. Физически это объясняется тем, что, когда электрический заряд q и соответственно напряжение u = q!C достигают максимального значения (положительного или отрицательного), ток t равен нулю.
Под фазовым сдвигом тока относительно напряжения здесь, как и раньше, подразумевается разность начальных фаз напряжения и тока, т. е.
Ф = фо —
Таким образом, в отличие от цепи с индуктивностью, где <р=л/2, фазовый сдвиг тока относительно напряжения в случае емкости отрицателен (ф=—л/2).
На векторной диаграмме вектор тока 1 опережает вектор напряжения U на угол л/2 (рис. 2-13,в).
Амплитуды и соответственно действующие значения напряжения
38
и тока связаны соотношением, подобным закону Ома
£/т = —— lm ~.хс I ; U — хГ1. m х .z-» ш с m ’ С
Величина хс=1/соС, имеющая размерность сопротивления, называется емкостным сопротивлением. Обратная ей величина Ьс — аС называется емкостной проводимостью. Следовательно,
lm = bCUm', f = bcu.
Мгновенная мощность, посту: пающая в емкость,
Рс = ui = Um lm cos (<о/ + ф) X
х cos I at 4- ф 4- —) = \ 2 /
= — UI sm 2 (at 4- ф) колеблется синусоидально с угловой частотой 2<о, имея амплитуду, равную W; выражение рс в рассматриваемом случае аналогично выражению для pL в § 2-6.
Мгновенная мощность, поступающая в емкость, равна скорости изменения энергии электрического поля емкости.
Энергия электрического поля емкости согласно (1-8а)
Си 2 CU'*
= cos2M4-4) =
= [ 1 4- cos 2 (at 4- ф)]
изменяется периодически с угловой частотой 2(о в пределах от 0 до
ClA
CU2 = ~- (рис. 2-14).
Поступая от источника, энергия временно запасается в электрическом поле емкости, затем возвращается к источнику при исчезновении электрического поля. Энергия электрического поля достигает максимума при максимальном значении напряжения на емкости. Затем
1 Следует заметить, что только в случае сопротивления г закон Ома применим к мгновенным значениям напряжения и тока; в остальных случаях отношение мгновенных величин и и t, имеющее размерность сопротивления, представляет некоторую функцию времени, не имеющую физического смысла и практического применения.
она убывает и обращается в нуль при напряжении, равном нулю.
Таким образом, так же как в случае индуктивности, происходит колебание энергии между источником и емкостью, причем средняя мощность Р=0.
Так как максимальное значение энергии, запасаемой в электриче-
Рис. 2-14. Мгновенные значения мощности, поступающей в емкость, и энергии электрического поля.
ском поле, равно и>смакс = С172, то U емкостное сопротивление хс=— —
1 й
= —— может быть определено как
_ с макс
~ /2 •
2-8. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ г, L. С
При прохождении гармонического тока i=lm cos tut через электрическую цепь, состоящую из последовательно соединенных элементов г, L, С (рис. 2-15), на зажимах этой
Рис. 2-15. Последовательное соединение сопротивления, индуктивности и емкости.
цепи создается гармоническое напряжение, равное алгебраической сумме гармонических напряжений на отдельных элементах (второй закон Кирхгофа):
и = 11 г + UL + «с -
Напряжение «т на сопротивлении г совпадает по фазе с током i, напряжение uL на индуктивности L опережает, а напряжение ис на емкости С отстает от i на л/2 (рис. 2-16). Следовательно, напряжение и на зажимах всей цепи равно:
и = Um cos (со/ + ср) = rlm cos и/ + u)LJ m cos ^со/ Н—-f-
. If / . я \
= rlm cos to/ + ftoL-—'i X
\ coC /
x/mcosfco/+ yV (2-15)
Рис. 2-16. Напряжения иа сопротивлении, индуктивности и емкости (соединенных последовательно) при гармоническом токе.
Уравнение (2-15) представляет тригонометрическую форму записи второго закона Кирхгофа для мгновенных значений напряжений. Входящая в него величина x=xL—хс= —u)L----— называется реактив-
ным сопротивлением цепи, которое в зависимости от знака может иметь индуктивный (х>0) или емкостный (х<0) характер. В отличие от реактивного сопротивления х активное сопротивление г всегда положительно.
Для нахождения U и ср воспользуемся векторной диаграммой, соответствующей уравнению (2-15). На рис. 2-17,а показан случай, когда х>0, и на рис. 2-17,6 случай, когда х<0.
39
Падение напряжения от тока в активном и реактивном сопротивлениях изображается катетами прямоугольного треугольника напряжения ОаЬ, гипотенуза которого изображает напряжение на зажимах цепи. Отсюда
или
Рис. 2-17. Векторные диаграммы дли последовательной цепи г, L, С при х>0 (а) и х<0 (б).
Полученное выражение показывает, что действующие значения (так же, как и амплитуды) напряжения иа зажимах цепи и тока, проходящего через данную цепь, связаны соотношением, аналогичным закону Ома:
называется полным сопротивлением рассматриваемой цепи.
Активное, реактивное и полное сопротивления относятся к числу основных понятий, применяемых в теории электрических цепей. Из векторных диаграмм следует, что угол фазового сдвига тока i относительно напряжения и равен:
1
<о£ — ——
Ф = arctg — = arctg------—. (2-17)
г г
Если задано напряжение и= = Um cos (со/+ф) на зажимах цепи с последовательно соединенными г, L и С, то ток определяется по формуле
i= cos (at 4- ф — ф).
Угол ср, равный разности начальных фаз напряжения и тока, отсчитывается по оси at в направлении от напряжения к току и является углом острым; прямым или равным нулю:
1ФК-7-
Угол ф положителен при индуктивном характере цепи, т. е. при х>0; при этом ток отстает по фазе от напряжения, и ф отсчитывается в положительном направлении: на временной диаграмме вправо от напряжения к току (рис. 2-18,п), а на векторной диаграмме против хода часовой стрелки от тока / к напряжению О (рис. 2-17,а).
Угол <р отрицателен при емкостном характере цепи, т. е. при х<0; при этом ток опережает по фазе напряжение, и ф отсчитывается в отрицательном направлении: на временной диаграмме влево от напряжения к току (рис. 2-18,6), а на векторной диаграмме — по ходу часовой стрелки от тока I к напряжению U (рис. 2-17,6).
Итак, следует всегда помнить, что угол ф положителен при отстающем и отрицателен при опережающем токе. На временной диаграмме угол отсчитывается от напряжения к току, а на векторной
40
диаграмме — от тока к напряжению.
Ток совпадает с. напряжением по фазе при x=xL—хс=0, т. е. при равенстве индуктивного и емкостного сопротивлений. Такой режим работы электрической цепи называется резонансом напряжений (гл. 7).
Рис. 2-18. Временные диаграммы для последовательной цепи г, L, С.
а — чък отстает от напряжения; б — ток опережает напряжение.
Из выражений (2-16) и (2-17) следует, что активное и реактивное сопротивления цепи связаны с полным сопротивлением формулами:
r = zcoscp; x = zsin<p. (2-18)
Умножив правые и левые части выражений (2-18) на действующее значение тока /, получим действующие значения напряжений на активном и реактивном сопротивлениях, изображаемые катетами треугольника напряжений и называемые активной и реактивной составляющими напряжения:
UB = rl = гсоэф/ = С/соэф; L2-19) Uv — xl — z sin tpl — U sin ф. I
Мгновенные значения напряжений на активном и реактивном сопротивлениях, суммирующиеся алгебраически в соответствии с (2-15),
имеют фазовый сдвиг л/2. Поэтому непосредственное сложение действующих значений этих функций не дает действующего значения напряжения на всей цепи; как видно из треугольника напряжений и уравнений (2-19), активная и реактивная составляющие напряжения связаны с действующим значением суммарного напряжения формулой
г/= +
Если все стороны треугольника напряжений разделить на /, то получится прямоугольный треугольник сопротивлений, подобный треугольнику напряжений (рис. 2-19,а, б).
Треугольник сопротивлений представляет геометрическую интерпретацию уравнений (2-16) и (2-17). Его положение не зависит от начальных фаз напряжения и и тока i: сопротивление г откладывается по горизонтальной оси вправо (в положительном направлении), а реактивное сопротивление х в зависимости от его знака откладывается вверх (х>0) или вниз (х<0). Угол ф в треугольнике сопротивлений отсчитывается от катета гкги-
потенузе г, что соответствует отсчету ф в треугольнике напряжений от ий=г! к U=zl.
Для характеристики индуктивных катушек, представляемых цепью с последовательным соединением активного и индуктивного сопротивлений, пользуются понятием добротности катушки Qi=XiJr, ко
Рис. 2-19. Треугольник сопротивлений при х>0 (а) и х<0 (б).
торое равнозначно тангенсу угла сдвига фаз ф для катушки. Чем меньше сопротивление г, тем выше при прочих равных условиях добротность катушки.
Добротность индуктивных катушек, применяемых в диапазоне ча
41
стот от 1 кгц до 100 Мгц, обычно составляет Ql = 50-^500.
2-9. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ г, L, С
Если к зажимам электрической цепи, состоящей из параллельно соединенных элементов г, L, С (рис. 2-20), приложено гармоническое напряжение u = Umcosrnt, то гармонический ток, проходящий через эту цепь, равен алгебраичес-
Рис. 2-20. Параллельное соединение сопротивления, индуктивности и емкости.
кой сумме гармонических токов в параллельных ветвях (первый закон Кирхгофа):
4 = С + 4г + 4с •
Ток ir в сопротивлении г совпадает по фазе с напряжением и, ток
hit
Рис. 2-21. Токи в сопротивлении, индуктивности и емкости (соединенных параллельно) при гармоническом напряжении.
it, в индуктивности L отстает, а ток ic в емкости С опережает напряжение на л/2 (рис. 2-21).
Следовательно, суммарный ток i в цепи равен:
i = lm cos (<о/ — <р) = у- Vm cos
+ Ц- Um COS (со/----------+
coZ. 1 2 /
+ coC(/m cos {bit -I- ~ j =
— — Um cos mt + {—-------------
r \ coL
cos
mt ——V (2-20) , 2 /
Уравнение (2-20) представляет собой тригонометрическую форму записи первого закона Кирхгофа для мгновенных значений токов. Входящая в него величина Ь = = Ьь—Ьс=-----тС называется ре-
coL
активной проводимостью цепи, которая в зависимости от знака может иметь индуктивный (Ь>0) или емкостный (Ь<0) характер. В отличие от реактивной проводимости b активная проводимость g=l/r всегда положительна.
Для нахождения 1п и ср воспользуемся векторной диаграммой, соответствующей уравнению (2-20) (рис. 2-22, а и б). Прямоугольный треугольник с катетами 1Г и [7д+/с] и гипотенузой / называется треугольником токов. Треугольник токов построен на рис. 2-22, а для б>0, а на рис. 2-22,6 — для б<0.
Из треугольника токов следует, что
У \ /
ИЛИ Г^уи- —
Здесь
y = Vg2 + b2 =
(2-21)
— полная проводимость рассматриваемой параллельной цепи.
Активная, реактивная и полная проводимости относятся к числу основных понятий, применяемых в теории электрических цепей.
42
Угол фазового сдвига тока х относительно напряжения и равен:
1
---— <йС
<р = arctg — = arctg ---------,(2-22)
g 1
г
Если задано напряжение и= — Umcos (со/+ф) на зажимах цепи с параллельно соединенными г, L и С, то ток определяется по формуле
i = yUm cos (coif + ф — ср).
Угол ср, как и в предыдущем случае, отсчитывается на временной диаграмме @ от напряжения к току, а на векторной диаграмме — от тока к напряжению; он является острым или прямым углом:
Угол ср положителен при тивном характере цепи, т. е. при Ь>0; при этом ток отстает по фазе от напряжения. Угол ср отрицателен при емкостном характере цепи, т. е. при 6<0; при этом ток опережает по фазе напряжение. Ток совпадает с напряжением по фазе при Ь — — bL—bc=0, т. е. при равенстве индуктивной и емкостной проводимостей. Такой режим работы электрической цепи называется резонансом токов (гл. 7).
Из (2-21) и (2-22) следует, что активная и реактивная проводимости цепи связаны с полной проводимостью формулами:
g=z/coscp; b = у sin ср. (2-23)
Умножив правые и левые части выражений (2-23) на действующее значение напряжения U, получим действующие значения токов в ветвях с активной и реактивной проводимостями, изображаемые катетами треугольника токов и называемые активной и реактивной составляющими тока:
I& = gU = у cos <p£Z == / cos ср; | /р — bU = у sin cpU = 1 sin ср. I
Как видно из треугольников токов и уравнений (2-24), активная и реактивная составляющие тока связаны с действующим значением суммарного тока формулой
I-V 11+1-
Разделив стороны треугольника токов на U, получим прямоугольный треугольник проводимостей, подоб-
Рис. 2-22. Векторные диаграммы для параллельной цепи г, L, С при Ь>0 (а) и Ь<0 (б).
индук- ный треугольнику напряжений (рис. 2-23, щ б).
Треугольник проводимостей служит геометрической интерпретацией уравнений (2-21) и (2-22); активная проводимость g откладывается по
Рис. 2-23. Треугольник проводимостей при Ь>0 (а) и б<0 (б).
горизонтальной оси вправо, а реактивная проводимость b в зависимости от ее знака откладывается вниз (б>0) или вверх (Ь<0). Угол ср в треугольнике проводимостей отсчитывается от гипотенузы у к катету g, что соответствует отсчету ср в треугольнике токов от 1—yU к !a=gU.
Для характеристики конденсаторов, представляемых цепью с емкостной и активной проводимостями, применяется понятие добротность
43
конденсатора Qc=blg=(aCr, которое равнозначно тангенсу угла |<р| конденсатора. Обратная величина называется тангенсом угла диэлектрических потерь конденсатора tg 6=1/QC (угол диэлектрических потерь б дополняет угол |<р| до 90°).
Чем больше сопротивление г, тем больше (при прочих равных условиях) добротность конденсатора и тем меньше угол потерь.
Добротность конденсаторов для разных частот и диэлектриков колеблется в широких пределах, примерно от 100 до 5 000. Слюдяные конденсаторы обладают большей добротностью, чем керамические.
Добротность конденсаторов, применяемых в высокочастотной технике, примерно в 10 раз превышает добротность индуктивных катушек.
2-10. МОЩНОСТЬ В ЦЕПИ ГАРМОНИЧЕСКОГО ТОКА
В § 2-5—2-7 рассматривались энергетические соотношения в отдельных элементах г, L и С при гармоническом токе.
Разберем теперь более общий случай участка электрической цепи, напряжение на котором равно и— = Um cos со/, а ток
i - lm cos (со/ — ср).
Мгновенная мощность, поступающая в цепь,
Р ~ Um Im COS COS (w^ — <р) =
—UI (cos ср -|- cos (2со/ — ф)] (2-25)
состоит из двух слагающих: постоянной величины /17 cos ф и гармонической, имеющей удвоенную частоту по сравнению с частотой напряжения и тока.
Среднее значение второй слагающей за время Т, в течение которого она совершает два цикла изменения, равно нулю. Поэтому средняя мощность, поступающая в рассматриваемый участок цепи, г
Р = -у- uidt — IU cos ф. (2-26)
Множитель cos ф носит название коэффициента мощности.
44
Как видно из (2-26), активная мощность равна произведению действующих значений напряжения и тока, умноженному на коэффициент мощности.
Чем ближе угол ф к нулю, тем ближе cos ф к единице и, следовательно, тем меньше требуется величина тока /, при которой заданная средняя мощность Р при данном напряжении U будет передана от источника к приемнику.
Повышение коэффициента мощности промышленных электроустановок представляет важную технико-экономическую задачу.
Выражение средней мощности может быть преобразовано с учетом (2-18) и (2-23):
Р = zP cos ф = г/2;
Р = yU2 cos ф = gU2.
Активная мощность может быть также выражена через активную составляющую напряжения (U&= = t/cos ф) или тока (/а=/со5ф):
P=UJ-, l=Ula.
Приведенные общие выражения мгновенной и средней мощности применимы к частным случаям, разобранным выше, когда ф=0 (§ 2-5), Ф=л/2 (§ 2-6) и ф=—-л/2 (§ 2-7); мы не будем здесь повторять полученные ранее результаты.
Рассмотрим более общий случай активно-реактивной цепи, например цепи, содержащей сопротивление и индуктивность; при этом
0 < ф < -у и 0 < cos ф < 1.
Согласно (2-25) мгновенная мощность колеблется с удвоенной угловой частотой 2м относительно линии, отстоящей от оси времени на P=UIcosф (рис. 2-24).
В промежутки времени, когда и и л имеют одинаковые знаки, мгновенная мощность положительна; энергия поступает от источника в приемник, преобразуясь в сопротивлении в тепло и запасаясь в магнитном поле индуктивности.
В промежутки времени, когда и и i имеют разные знаки, мгновенная мощность отрицательна и энергия частично возвращается приемником
источнику. Как видно из рис. 2-24, в течение большей части периода мгновенная мощность положительна и соответственно положительная (расположенная над осью времени) площадь кривой р преобладает над отрицательной площадью кривой р. В результате активная мощность Р>0.
Аналогичная картина получается и в случае активно-емкостной цепи.
Рис. 2-24. Мощность, поступающая в активно-индуктивную цепь-
В электрических системах, в которых источниками электрической энергии являются генераторы переменного тока, мощность получается от первичных двигателей, приводящих генераторы во вращение. В радиотехнике и электронике, где гармонические колебания создаются с помощью электронных или полупроводниковых приборов, мощность получается от источников постоянного тока, питающих электронные генераторы или другого рода устройства.
Величина, равная произведению действующих значений тока и напряжения на зажимах цепи
S=UI, (2-27) называется полной мощностью цепи и измеряется в вольт-амперах (ва). Следует заметить, что амплитуда гармонической составляющей мгновенной мощности (2-25) численно равна полной мощности.
На основании (2-26) и (2-27) коэффициент мощности равен отношению активной мощности к полной:
Р cos<p = —.
При расчетах электрических цепей и на практике в эксплуатации пользуются также понятием реактивная мощность, которая вычисляется по формуле
Q—UI sin<p
и является мерой потребления (или выработки) реактивного тока.
Эта мощность измеряется в реактивных вольт-амперах (вар).
Очевидно,
sin<p= — ;
tgq> = y-.
Выражение реактивной мощности может быть преобразовано с учетом (2-18) и (2-23):
Q=z/2sin <р=хР;
Q=yU2 sin <p=bU*.
Реактивная мощность может быть также выражена через реактивную составляющую тока (7Р= = /sin<p) или напряжения (Up— = U sin ср):
Q=WP;
В соответствии с принятым ранее правилом знаков для угла q> реактивная мощность положительна при отстающем токе (индуктивная нагрузка) и отрицательна при опережающем токе (емкостная нагрузка).
Понятия активная (средняя), реактивная и полная мощности являются удобными определениями мощностей, которые прочно укоренились на практике.
Реактивная мощность, подводимая к индуктивности, может быть представлена в следующем виде:
Q=UI sin -у - UI =
—<i)LP — a —— ы^Лмакг.» 2
где W, — максимальное зна-чение энергии, периодически запасаемой индуктивностью.
45
Реактивная мощность, подводимая к емкости, равна:
Q=W sin у-] = — 67=—aCU2 =
= -а»^ = -^Сиакс,
где —максимальное зна-
чение энергии, периодически запасаемой емкостью.
Реактивная мощность на зажимах цепи, содержащей индуктивность и емкость, пропорциональна разности максимальных значений
энергии, запасаемой в магнитном и электрическом полях:
(2-28)
В табл. 2-1 дана сводка уравнений основных элементов цепи в общей форме (дифференциальной, интегральной) и при гармоническом режиме — для мгновенных и действующих значений.
В табл. 2-2 приведены выражения полных сопротивлений и проводимостей цепи для различных сочетаний элементов г, L, С и соответствующие им значения tg<p.
Уравнения элементов цепи
Таблица 2-1
Элемент Общая форма Гармонический режим
мгновенные значения действующие значения
Сопротивление и = ri и = rlm COS (СО/ + т|>) U = rl
—1 i = gu i = gUm cos (со/ + if) I~gU
г di и = L~— и ~ v>Llm cos (со/ -J- чр) и =a>U
Индуктивность t 1 с 1 ! 31 \ 1 ,,
i—— I udt i — — Um cos со/ 4- яр —— / = —и
L J соД т \ т 2 ) соД
L Емкость —co t « = J it}t « = -77 >т cos (со/ + чр) 7= —/
HI— С —co du dt ! п \ i = ыСит cos f со/ + яр -}- — 1 / = соС7
Выражения г, у и tg <р
Таблица 2-2
Цепь Последовательное соединение Параллельное соединение
Z 1g ч> У tg<p
v>L ./ 1 1 г
г, L У С2 + (ю£)2 Г 1 у г* + (соД)2 (&L
г. С 1 / [ 1 \2 I/ /’2+ у [v>cj <лС г 1 У 7? + (“О2 —го>С г(~ -сое) \ соД )
r,L,C |/ + \ юС / св£ — —— соС , / 1 /1 V ]/ ^ + Ьт-“С)
46
Для указанных в табл. 2-2 случаев предлагается читателям в виде упражнения:
1) построить временные и векторные диаграммы;
2) построить треугольник сопротивлений и проводимостей;
3) при заданном напряжении U на зажимах цепи написать выражения для тока I, средней мощности Р, реактивной мощности Q и полной мощности S.
2-11. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
2-1. Вычесть напряжение 5 sin to t нз напряжения 10 cos to t.
Ответ: 11,2 sin(cot+116D30').
2-2. Ток изменяется по закону i= =20 cos <в t, а-, частота f=50 гц. Определить наибольшую скорость изменения тока и соответствующее этому моменту значение тока.
Ответ: 6 280 а/сек; 0.
2-3. На зажимах цепи, состоящей из последовательно соединенных сопротивлений г=50 ом и индуктивности £=0,1 гн, задано напряжение и=ул 2-100 cos cot. Частота f=50 гц. Вычислить полное сопротивление цепи и действующие значения напряжения на г и £; вывести выражение для гармонического тока i(t); построить кривые i(t), «(/) и напряжений на г н L.
О_твет: 59 ом; 85 в; 53,4 в; I— = V2-\,7 cos(cot—32°10')а.
2-4. На зажимах цепи, состоящей из последовательно включенных сопротивления г=30 ом и емкости С=6 мкф, задано напряжение u= F2 • 120 cos cot, в; частота f= =400 гц. Вычислить полное сопротивление цепи и действующие значения напряжений на г и С; вывести выражение для гармонического тока /(/); построить кривые u(t), i(t) и напряжений на г и С.
Ответ: 72,8 олс; 49,5 в; 109,5 в; i— =у/Г 2-1,65 cos(cot+65°40,)a.
2-5. Напряжение на зажимах сопротивления г=3,63 ом и индуктивности L— =0,02 гн, соединенных параллельно, и—
.— I л \
=У 2 • 120 sin 314t+— , в. Вычислить пол-\ 6 /
ную проводимость цепи и действующие значения токов в г и L; вывести выражение для суммарного гармонического тока в цепи; построить кривые u(t), i(t) и токов в г и L.
Ответ: 0,318 сим; 33,1 а; 19,1 a; 1= =У 2-38,2 sin 314t, а.
2-6. Напряжение на зажимах сопротивления г=1 000 ом и емкости С=1 мкф, соединенных параллельно, и= V 2 • 120 cosX Х2 512 t, в. Вычислить полную проводимость и действующие значения токов в г и С; вывести выражение для суммарного гармонического тока i(t); построить кривые w(t), i(t) и токов в г и С.
Ответ: 0,00269 сим; 0,12 а; 0,301 а; i =у'~2“-0,323 cos (2 512 t-|-68°20')a.
2-7. Вычислить действующее значение
напряжения иа зажимах цепн, имеющей активную проводимость 0,07 сим и реактивную проводимость 0,044 сим, если действующее значение гармонического тока, проходящего через цепь, равно 10 а.
Ответ: 121 в.
2-8. К цепи, состоящей из последовательно соединенных сопротивления г=1 ом, индуктивности £=0,1 гн и емкости С= = 101,4 мкф, приложено напряжение 33,8Х Xcos 314/, в. Найти ток; построить кривые тока и напряжений на сопротивлении, индуктивности и емкости.
Ответ: 33,8 cos 314 t, а.
2-9. Определить напряжение на зажимах цепи, состоящей из г, L и С, соединенных последовательно, если напряжение на С равно l/msincot.
О г в ет:
Um V (1—а>2 £С)а + (г со С)» sin (со/ -J- а);
г со С
a = arctgT3^F-
2-10. Напряжение на г, L и С, соединенных параллельно, равно Un cos cot. Определить суммарный ток.
Ответ:
VmV (т/ + (^“шС/СО5(ю/“<р);
Ф = arctg г (—-— — со С V \ со L )
2-11. Через цепь, состоящую из параллельно соединенных сопротивления (г= =8,33 ом) и индуктивности (£=6,36 мгн), проходит ток 0,141 cos cot, а; частота равна 500 гц. Определить напряжение иа параллельных ветвях.
Ответ: 1,1 cos (со/+22<’36')е.
2-12. Цепь состоит из источника э. д. с. 100 sin 400 /, в, сопротивления г=50 ом и индуктивности £=0,1 гн, соединенных последовательно. Считая ток синусоидальным, найти для момента /=л/200 сек мгновенные значении тока, напряжений на элементах и мощностей, подводимых к ним; определить действующие значения тока и напряжений на элементах.
Ответ: —0,975 а; —48,8 в; 48,8 в; 47,5 ат; —47,5 ет; 1,1 а; 55 в; 44 в.
2-13. Сохранив условия задачи 2-12, заменить индуктивность емкостью 100 мкф.
Ответ: 0,8 а; 40 в; —40 а; 32 ет; —32 ет; 1,26 а; 63 е; 31,5 а.
2-14. Цепь состоит из источника э. д. с. 100 sin 300 t, а, сопротивления г=40 ал и индуктивности £=0,1 гн, соединенных последовательно. Считая ток синусоидальным, найти мгновенные значения тока н напряжений на элементах при /=0,01 сек; вычислить энергию, поступающую от источника, с момента /=0 до £=0,01 сек.
Ответ: —1,42 а; 56,8 а; —42,4 е; 0,833 дж.
2-15. Цепь состоит из источника э. д. с. 100 sin 400 t, а, сопротивления г и индуктивности £=0,025 гн. Найти г, если при t = n/800 сек мгновенное значение напряжения иа £ равно 35,35 в; получить выраже
47
ние для синусоидального тока; вычислять для /=л/800 сек энергию, запасенную в магнитном поле, и мгновенную мощность, поступающую от источника.
Ответ: 13,55 ом; 5,95 sin (400/— —36°30')а; 0,284 дж; 478 вт.
2-16. Цепь состоит из источника э. д. с. 100 cos I 0001, в, сопротивления г и емкости С, соединенных последовательно. Ток в цепи равен 10 cos(l 000/+л/3)а. Найти г и С; вычислить для /=л/1 000 сек мгновенные значения напряжений на г и С н мощностей, поступающих в них.
Ответ: 5 ом; 115 мкф; —25 в; —75 в; 125 вт; 375 вт.
2-17. Что такое положительное направление гармонического тока?
2-18. Что понимается под полярностью источника гармонической э. д. с. или источника гармонического тока?
2-19. Что такое фазовый сдвиг тока от
носительно напряжения? Чем вызван фазовый сдвиг?
2-20. Какова разница между активной, реактивной и полной мощностью? В каких единицах они измеряются?
2-21. Для чего стремятся повысить коэффициент мощности электрической установки?
2-22. Цепь, состоящая нз г, L и С, соединенных последовательно, питается от источника э. д. с. ПО в переменной частоты. Определить коэффициент мощности цепи при 60 гц, если известно, что при частоте 45 гц напряжение на емкости, так же как и на индуктивности, составляет 200,8 в.
Указание. При 45 гц имеет место резонанс напряжений, т. е.
Ответ: 0,69.
48
* Глава третья
ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ К РАСЧЕТУ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ (МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД)
3-1. ПРЕДСТАВЛЕНИЕ ГАРМОНИЧЕСКИХ ФУНКЦИИ С ПОМОЩЬЮ
КОМПЛЕКСНЫХ ВЕЛИЧИН
Расчеты электрических цепей гармонического тока в тригонометрической форме или графически с помощью векторных диаграмм применяются на практике только в случае простых схем, подобных тем. которые рассмотрены в предыдущей главе.
С усложнением электрических цепей, с увеличением числа контуров, источников, добавлением взаимных индуктивностей и т. д. тригонометрические или графические расчеты становятся крайне затруднительными. Требуется метод, позволяющий рассчитывать электрические цепи переменного тока алгебраически, аналогично цепям постоянного тока. Таким удобным расчетным методом служит метод комплексных амплитуд (комплексный метод), введенный в электротехнику А. Е. Кеннеди и П. Ч. Штейнметцом в 1893— 1894 гг. Этот метод, как и векторные диаграммы, основан на представле
нии гармонических функций в виде проекций вращающихся векторов, причем вращающиеся векторы выражаются аналитически, в комплексной форме. Алгебраически интерпретируя векторные диаграммы, этот метод удобно сочетает аналитические расчеты с геометрическими представления ми.
Все последующее изложение данного курса и радиотехнических дисциплин базируется на этом методе.
Известно, что каждая точка на комплексной плоскости определяется радиусом — вектором этой точки, т. е. вектором, начало которого совпадает с началом координат, а конец находится в точке, соответствующей заданному комплексному числу (рис. 3-1).
Пользуясь показательной или полярной формой записи комплексного числа, имеем
1 В этой книге обозначения комплексных величин даны в соответствии с ГОСТ 1494-61, введенным в СССР в 1962 г.
В зарубежной литературе и в ряде отечественных книг для комплексных величин применяется жирный шрифт в отлнчне от модулей, обозначаемых светлыми буквами.
48
A=Aefa=Al_a;
здесь A — модуль; a — a pry -мент или фаза; /=1^—1
(в электротехнике не пользуются обозначением i= ]/ —1, так как буква i обозначает ток).
Применив формулу Эйлера, можно получить тригонометрическую форму записи комплексного числа
А=A cos а+/А sin а
Рис. 3-1. Вектор, изображающий комплексное число.
или соответственно алгебраи ческу ю форму
А=А1+/А1,
где
Aj=Acosa; A1=Asina. Очевидно,
А3=А*+А%; a=arctg-^-.
Вектор, вращающийся в положительном направлении, т. е. против хода часовой стрелки, с угловой скоростью to, может быть выражен следующим образом:
Aa/(m/+a> = А е/0*, (3-1)
где А=Ае’“ =А|_а — комплексная амплитуда, представляющая данный вектор в момент /=0 (рис. 3-2). Иначе говоря, это комплексная величина, не зависящая от времени, модуль и аргумент которой равны соответственно амплитуде и начальной фазе заданной гармонической функции.
Множитель является оператором вращения; умножение комплексной амплитуды А на
е1** означает поворот вектора А на угол a>t в положительном направлении.
Записывая комплексную функцию (3-1) в тригонометрической форме
Ае/(“'+“>=A cos(<of-f-a) + +/Asin (соН-а), заключаем, что гармоническая функция A cos +а) может рассматриваться как действительная часть
Рис. 3-2. Вращающийся вектор.
комплексной функции (3-1), или, что то же, как проекция вращающегося вектора на действительную ось.
Условно это записывается так:
A cos (<jrf4-a)=Re(Ae,“,|-
Символ Re обозначает, что берется действительная часть комплексной функции.
Например, 10 cos ^2 512< + =
=Re (10е Те'26,:а), где 10е 4 — комплексная амплитуда.
Аналогично функция A sin (art+ +ф) может быть в случае необходимости представлена как мнимая часть комплексной функции (3-1), взятая без множителя ], или как проекция вращающегося вектора на мнимую ось. Условно это записывается так:
Asin(<i)f+a)=Im (Ae/“,)« где символ 1m обозначает, что берется мнимая часть комплексной функции. Например,
10 sin (2512/ + =
= Im(10e ^ыи).
4—1118
49
Другой способ представления гармонической функции с помощью комплексных величин основан на применении формул
Лсо5(^+ф) = у е/1и‘+ф> +
4-
+ 2 е ’
A sin (at 4* ф) == = — g/(wt+4>)
_ 1 / Л ^at — A e-jat j \ 2 2
(3-2)
Согласно (3-2) можно заключить, что функция A cos (со/+ф) равна геометрической сумме двух комплексно-сопряженных векторов, имеющих модуль А/2 и вращающихся в противоположные стороны с одинаковой угловой скоростью со.
В результате сложения таких двух векторов получается вектор, расположенный на действительной оси, т. е. для любого момента времени t получается действительная величина (рис. 3-3,а).
Аналогично из (3-3) видно, что функция A sin (<о^+ф) равна геометрической разности тех же двух
Рис. 3-3. Представление гармонической функции вращающимися комплексносопряженными векторами.
вращающихся векторов, деленной на /. Разность этих векторов для любого момента времени t представляет мнимую величину (рис. 3-3,6), и поэтому ее делят на / для получения действительной функции.
Вращение вектора в отрицательном направлении (по ходу часовой стрелки) связано с понятием отрицательной круговой частоты (—со), которое является чисто математическим понятием, вытекающим из вышеприведенных формул. Введение этого понятия в ряде случаев удобно для исследования процессов в электрических цепях, и мы встретимся с ним в гл. 10, 15 и в последующих радиотехнических дисциплинах. Из сравнения построения на рис. 3-3, а и б видно, что представление гармонических функций с помощью двух векторов, вращающихся в противоположные стороны, для функции вида A cos (ы/+ф) проще, чем для функции A sin (со/-Ьф).
3-2. ЗАКОНЫ ОМА И КИРХГОФА В КОМПЛЕКСНОЙ ФОРМЕ
Рассмотрим применение метода комплексных амплитуд в случае последовательного и параллельного соединений элементов г, L, С.
Последовательное соединение г, L, С. Положим, что в уравнении Кирхгофа
u=ri+L^- + -L\idt (3-4) ш С J
заданными являются параметры г, L, С и гармоническое напряжение u=Um cos (со/+ф) на зажимах цепи, а искомой величиной является ток i. Ввиду того, что здесь рассматривается установившийся режим цепи гармонического тока, решение этого дифференциального уравнения должно дать гармоническую функцию вида
t=lm cos (cot+ф — q>), где 1т и (ф—ф) — пока неизвестные амплитуда и начальная фаза тока.
Пусть в соответствии с предыдущим параграфом заданное гармоническое напряжение символизируется комплексной функцией 0те1Ш, а искомый гармонический ток — комп
50
лексной функцией imei,u', комплексные амплитуды напряжения и тока равны соответственно:
U —U d*- I — I
Сложение, дифференцирование и интегрирование гармонических функций в уравнении (3-4) заменяются теми же математическими операциями над действительными частями комплексных функций:
Re (^^9 =rRe(/me'“/) +
+ L^-Re(/m^) +
+ -ljRe(/m^)^. (3-5)
Операции над действительными частями комплексных функций могут быть заменены операциями над самими комплексными функциями с последующим выделением действительной части полученного результата. Объясняется это коммутативностью операций сложения, дифференцирования и интегрирования относительно символической операции Re. Итак, (3-5) преобразуется следующим образом:
Re _Re/r/,c'" +
Полученное уравнение удовлетворяется для любого момента времени. Поэтому заключенные в скобки комплексные выражения, от которых берется действительная часть, должны быть равны друг другу. Производя дифференцирование и интегрирование, получаем:
И^-‘ = г1^ + 1ши^“ +
(3-«)
/(ОС
Здесь следует обратить внимание на то, что при интегрировании функции e’at постоянная интегрирования опущена, так как в рассматриваемом установившемся режиме цепи гармонического тока электрические заряды или напряжения на емкостях представляют гармонические функции, не содержащие постоянных слагающих.
В результате сокращения всех частей уравнения (3-6) на множитель ei<at получается алгебраическое комплексное уравнение
= + + (3-7)
/соС
Ток im может быть вынесен за скобки. При этом вводится условное обозначение для комплексного сопротивления рассматриваемой электрической цепи:
Z = г 4- / [toL — = г 4- jx. (3-8)
Таким образом, получается уравнение
um = zim, (3-9) выражающее закон Ома для комплексных амплитуд.
Разделив обе части уравнения (3-9) на У~2, получим закон Ома для комплексных действующих значений1:
U = ZL (3-10)
Следовательно, комплексное сопротивление электрической цепи равно отношению комплексного напряжения на зажимах данной цепи к комплексному току в этой цепи.
Комплексное сопротивление Z представлено в выражении (3-8) в алгебраической форме. Та же величина в тригонометрической и показательной (полярной) формах имеет вид:
Z = z cos го 4- iz sin ф; 1
7 /Ф I (З-П)
Z = zew — z/ф. J
Здесь z=|Z|—модуль комплексного числа Z — представляет полное сопротивление цепи, а ф— аргумент комплексного числа Z-.
г =рлг2 4- х2 ; ф — arctg— .
На основании (3-9) комплексная амплитуда тока
/т == = -^-/(ф —д>),
1 Комплексное действующее значение
гармонического тока (комплексный ток) — комплексная величина, не зависящая от времени, модуль и аргумент которой равны соответственно действующему значению н начальной фазе данного гармонического тока.
4*
51
где ф ф — начальная фаза тока. Следовательно, искомый ток в тригонометрической форме
* = Re (7me/tDf) — ~ cos (<of + ф — q>),
что совпадает с результатом, полученным ранее (§ 2-8).
На рис. 3-4 дана геометрическая интерпретация на комплексной плоскости уравнения (3-10). Рисунок
Рис. 3-4. Векторные диаграммы для последовательной цепи г, L, С при х>0 (а) и х<0 (б).
Рис. 3-5. Треугольник сопротивлений при х>0 (а) и х<0 (б).
3-4, а относится к случаю, когда реактивное сопротивление цепи имеет индуктивный характер (х>0) и соответственно ток отстает по фазе от напряжения (ф>0). Рисунок 3-4,6
относится к случаю, когда реактивное сопротивление цепи имеет емкостный характер (х<0), и поэтому ток опережает по фазе напряжение (ф<0).
В случае чисто реактивной цепи (г=0) ток отстает от напряжения по фазе на л/2, если сопротивление цепи индуктивное, и опережает напряжение на л/2 при емкостном сопротивлении цепи.
Как видно из векторных диаграмм, приведенных на рис. 3-4, йт=г1 — напряжение на сопротивлении г (совпадает по фазе с током /), 0L=j со L1 — напряжение на
индуктивности L (опережает ток / на угол л/2) и Uc=—j— 1 — напря-соС
жение на емкости С (отстает от тока / на угол л/2).
Геометрическая сумма векторов UT, UL и йс дает вектор приложенного к цепи напряжения:
U = йг + (JL + йс.
Активная слагающая напряжения йл=йг, реактивная слагающая 0p=UL+0c и суммарное напряжение U образуют треугольник напряжений.
Т реугольник сопротивлений, подобный треугольнику напряжений и повернутый относительно него на угол ф—ф (рис. 3-5), представляет геометрическую интерпретацию уравнений (3-11). Его положение не зависит от начальных фаз U и /; сопротивление г откладывается на комплексной плоскости в положительном направлении действительной оси, а реактивное сопротивление х в зависимости от его знака откладывается в положительном (х>0) или отрицательном (х<0) направлении мнимой оси (рис. 3-5, а и б).
Параллельное соединение г, L, С. Пользуясь рассужде-
ниями, аналогичными приведенными выше, можно прийти к комплексной форме законов Ома и Кирхгофа для электрической цепи, состоящей из элементов г, L и С,
соединенных параллельно.
Ограничиваясь записью для комплексных действующих значений, пропорциональных комплексным амплитудам, имеем- в соответствии с первым законом Кирхгофа:
/ = ^ + -L-f/ + /<nCt7 = i<oL
(3-12)
здесь lr = ёй — ток в сопротивлении г (совпадает по фазе с напряжением U);
52
IL = — /—(J — ток в индуктивности (отстает от напряжения на л/2);
/с = / аСй — ток в емкости (опережает напряжение нал/2). Выражение
У = g-i(-1r =g-/&(3-!3)
представляет собой комплексную проводимость рассматриваемой цепи; g и Ь — активная и реактивная проводимости цепи.
Уравнение
I^YU - (3-14)
выражает закон Ома в комплексной форме. Следовательно, комплексная проводимость электрической цепи равна отношению комплексного тока в данной цепи к комплексному напряжению на ее зажимах.
Тригонометрическая и показательная (полярная) формы комплексной проводимости имеют следующий вид:
У = ycos<p —/ysincp;
У = уе~/ф = у/—<p;
здесь у= |У| — модуль комплексного числа У— представляет полную проводимость цепи, а (—<р) — аргумент комплексного числа У:
y=Vg2 + bs-, q> = arctg—.
8
На основании (3-14) комплексное действующее значение тока равно:
I = = yU /(ф-Ф),
что соответствует гармоническому току
i = Re (ZmeM) = yUm cos(<of -f- ф —ф).
На рис. 3-6 дана геометрическая интерпретация на комплексной плоскости уравнения (3-12). Рисунок 3-6, а относится к случаю, когда реактивная проводимость цепи имеет
индуктивный характер (&>0) и соответственно ток отстает по фазе от напряжения (ф>0). Рисунок 3-6,6 относится к случаю, когда реактивная проводимость цепи имеет емкостный характер (&<0) и соответственно ток опережает по фазе напряжение (ф<0).
Активная слагающая тока 1Л=1Г, реактивная слагающая
и суммарный ток / образуют треугольник токов.
Рис. 3-6. Векторные диаграммы для параллельной цепи г, L, С при Ь>0 (а) и Ь<0 (б).
Треугольник проводимостей, подобный треугольнику токов и повернутый относительно последнего на угол ф по ходу часовой стрелки (рнс. 3-7), служит геометрической интерпретацией выражения (3-13): активная проводимость g откладывается на комплексной плоскости в положительном направлении действительной оси, а реактивная проводимость b в зависимости от ее знака откладывается в отрицательном (б>0) или положительном (&<0) направлении мнимой оси (рис. 3-7,а и б).
В табл. 3-1 дана сводка уравнений элементов цепи в комплексной форме.
Следует обратить внимание на то, что комплексное сопротивление индуктивного элемента равно j <о L,
53
Таблица 3-1
Комплексная запись уравнений элементов цепи
Элемент Напряжение Ток
Сопротивление i~gu
Индуктивность й = joLi 1 . /=-/ — и
Емкость ' <оС )=ju>CO
1
а емкостного элемента равно------=
/шс
. 1
=—/------; комплексная проводи-
те
мость составляет соответственно:
1 .1 . п
----— — j-----и
ja>L <о£
Рнс. 3-7. Треугольник проводимостей прн о>0 (а) и 6<0 (б).
При последовательном соединении г, L и С складываются в комплексной форме сопротивления, а при параллельном соединении — проводимости.
В табл. 3-2 приведены выражения комплексных сопротивлений и проводимостей цепи для различных сочетаний элементов г, L, С.
Таблица 3-2 Выражения комплексных сопротивлений я проводимостей
Цепь
Z при последовательном соединении
Y при параллельном соединении
I, L
г, С
Г, L.C
г + /сиД 1
( • \
г -4- <( (ul. — ——
Л «С /
1 . 1
г wL
3-3. ЗАВИСИМОСТЬ МЕЖДУ СОПРОТИВЛЕНИЯМИ И ПРОВОДИМОСТЯМИ УЧАСТКА ЦЕПИ
Пользуясь комплексной формой записи, при заданном комплексном сопротивлении Z=r+jx некоторого участка цепи находим для того же участка цепи комплексную проводимость 1
У = А = 1 = г _
Z Г + jx ~
(3-15)
В свою очередь если задана комплексная проводимость некоторого участка цепи Y=g—jb, то комплексное сопротивление того же участка цепи
Z = ™ = 1 = е I
Г g-jb g*+&
+/^=r+/x- (3-16)
Выражения (3-15) и (3-16) показывают, что реактивное сопротивление х и реактивная проводимость b одного и того же участка цепи имеют одинаковый знак.
Кроме того, каждая слагающая проводимости (g и Ь) зависит как от активного, так и от реактивного сопротивлений, т. е. от г и х. Соответственно каждая слагающая сопротивлений г и х является функцией активной и реактивной проводимостей g и Ь.
Соотношения g—1/r и Ь=\1х справедливы только в частном случае, когда элемент г, L или С рассматривается в отдельности, например;
Ь,
— ; Ьс = — =соС.
ti>L с хс
Предлагается учащимся в виде упражнения написать выражения для активного и реактивного сопротивлений, активной и реактивной проводимостей цепей, указанных в табл. 3-2.
1 В зарубежной литературе под реактивной проводимостью обычно понимается
&=-
соответственно
величина
комплексная проводимость записывается в виде Y^g+jb.
54
3-4. КОМПЛЕКСНАЯ ФОРМА ЗАПИСИ МОЩНОСТИ
Допустим, что через электрическую цепь проходит гармонический ток, причем положительные направления тока и напряжения на зажимах цепи приняты совпадающими (рис. 3-8).
Рис. 3-8. Положительные направления (а) н комплексные напряжение н ток (б).
Комплексные действующие значения тока и напряжения равны соответственно:
/ = ifa и й =. и fa.
Фазовый сдвиг тока относительно напряжения равен разности начальных фаз:
<Р = —Ф1-
Умножим U на комплексное лей-
*
ствующее значение 7=7 /—iplt сопряженное с 7:
ui^ui/fa-^uifa
Отсюда следует, что
S == UI = Ul cos <р 4- fUI sin <р = - Р + /Q.
Так как напряжение U может рассматриваться как сумма активной и реактивной слагающих 1/= = 0л+ир (§ 3-2), то почленное умножение этих слагающих на 7 дает активную и реактивную мощности:
U.J + Upi = U cos ср //СГ +
+ U sin ср/ Z п/2 = 7* + jQ.
Аналогично мощность может быть выражена через активный и реактивный ток.
Таким образом, комплексная величина S определяет действительной частью активную мощность, а мнимой частью реактивную мощность, поступающую в цепь.
Модуль X равен полной мощности. X носит название мощности в комплексной форме, или комплексной мощности.
На комплексной плоскости X изображает гипотенузу прямоугольного треугольника, катетами которого служат Р и Q (рис. 3-9).
Рис. 3-9. Треугольник мощностей на комплексной плоскости.
Треугольник мощностей, изображенный на рис. 3-9, подобен треугольнику сопротивлений:
Q/P = x/r = tgq>.
Если комплексно-сопряженное
*
напряжение U умножить на комплексный ток 7, то получится:
U/ = U1 cos ф — jUl sin ф = Р — jQ.
Поэтому мощности Р и Q на зажимах цепи могут быть записаны в следующем виде:
Р = (UI + (77); Q = -1- (Ui—U'l)
Комплексное сопротивление цепи легко вычислить, если известны комплексная мощность X и действующее значение тока 7:
s = ui = zii = zp, откуда
Воспользовавшись выражением (2-28), получим:
р <d(W', маке — W. , к) у * у • ' L, Mt-JKC G М JKCZ
~ 7 ~ •
55
Эта формула справедлива при любой схеме соединений индуктивности, емкости и сопротивлений.
Энергетический метод определения комплексного сопротивления применим и к комплексной проводимости:
S--=UI = О UY U2Y,
откуда Y=S/U2, где У — комплексная проводимость, сопряженная с У. Следовательно,
у=Л_/А = Л +
U* 1 и» у» 1
. мвкс ~иакс)
+'-------а-------•
Итак, активные сопротивление и проводимость цепи зависят от поглощаемой цепью активной мощности, а реактивные сопротивление и проводимость — от разности максимальных значений энергии, запасаемых в магнитном и электрическом полях (§ 2-5—2-7).
3-5. УСЛОВИЕ ПЕРЕДАЧИ МАКСИМУМА СРЕДНЕЙ МОЩНОСТИ ОТ ИСТОЧНИКА К ПРИЕМНИКУ
Пусть требуется подобрать комплексное сопротивление нагрузки таким образом, чтобы при заданном комплексном сопротивлении источника обеспечивалась переда-
Рис. 3-10. Передача энергии от источника к приемнику.
ча максимума активной мощности от источника к приемнику. Обозначим комплексные сопротивления источника напряжения и нагрузки соответственно через
Zo—ro + jxo и Z=r+jx (рис. 3-10).
Средняя мощность, потребляемая нагрузкой, равна:
Р = г/2 = - =
IZo + ZI2 =__________гЕг_______
('о + И2 + (*0 + *)а
Будем сначала изменять реактивное сопротивление х. Очевидно, при любом значении г ток и соответственно средняя мощность достигают наибольшей величины при х=—х0.
При этом
('o + ')2 •
Найдем теперь условие максимума полученной функции в предположении, что г — переменная величина, т. е. из условия, что dP!dr=G\ это даст
(го + rf- 2г (г0 + г) = 0. откуда
г = г0.
На основании найденных равенств заключаем, что условием передачи максимума активной мощности от источника к приемнику является равенство
Z = Z0, (3-17)
*
где Zo — комплексное сопротивление, сопряженное с Zo.
При соблюдении этого условия приемник потребляет мощность
и к.п.д., определяемый как отношение средней мощности, потребляемой приемником, к суммарной мощности, поглощаемой активными сопротивлениями цепи, равен 0,5.
В том случае, когда комплексное сопротивление источника имеет индуктивный характер, комплексное сопротивление приемника на основании (3-17) должно быть емкостного характера. Такая компенсация реактивного сопротивления цепи осуществляется на практике с помощью конденсаторов, включаемых последовательно или параллельно нагрузке.
Если условие (3-17) не выполняется, то относительное отклонение передаваемой
56
средней мощности от максимальной составляет:
Рмакс — Р (го — <)* + (х0 4~ *)*
Р макс (Го + ')*+(*Ь + *)а‘
В тех случаях, когда реактивное сопротивление источника относительно невелико по сравнению с его активным сопротивлением, условия, близкие к оптимальным, получаются прн активной нагрузке, если сопротивление приемника принято равным активному или полному сопротивлению источника.
Например, прн ZO=618 /—14° и 2-=618 / 0° поступающая в приемник средняя мощность отличается от максимально возможной только на 1,5%, в этом случае компенсация реактивного сопротивления источника практически не требуется.
3-6. УСЛОВИЕ ПЕРЕДАЧИ ИСТОЧНИКОМ МАКСИМУМА МОЩНОСТИ ПРИ ЗАДАННОМ КОЭФФИЦИЕНТЕ МОЩНОСТИ ПРИЕМНИКА
На практике часто возникает необходимость подбора комплексного сопротивления нагрузки таким образом, чтобы при заданных комплексном сопротивлении источника и коэффициенте мощности приемника обеспечивалась передача максимума полной и соответственно средней мощности от источника приемнику.
Пользуясь условными обозначениями, принятыми в предыдущем параграфе, находим полную мощность на зажимах нагрузки:
=_________г£Д_________
9 I г II . I2 *
го Р+— /(<р —<ро)|
I га I
где <р и ф0 — углы комплексных сопротивлений Z и Zo-После преобразования получим:
-------------------------—— . (3-18)
г / г \2
1 + 2 — cos (<р — фо) + — I го \ 2о /
Приняв величину г за переменную, записываем условие максимума функции S: dSldz—Qt откуда
1 + 2 —соэ(ф —ф0)+(—j —
•’о \ го /
— z[2 — соз(ф —фо)+ 2-^-1 =0 L го J
или
Следовательно,
(3-19)
Е*
Подстановка (3-19) в (3-18) дает;
5 _
2г0 [1 +соз(ф—фоН
Таким образом, передача максимума мощности в нагрузку при заданном cos ф достигается при равенстве полных сопротивлений нагрузки и источника. При этом передаваемая мощность тем больше, чем больше разность углов сопротивлений нагрузки и источника |ф—Фо1
Если условие (3-19) ие соблюдается, то относительное отклонение передаваемой полной мощности от максимальной составляет:
®макс — S -------- =Я 5макс
(•--)
=--------------^2----------- . (3.20)
z / г \2
1+2 — соз(ф —ф0) + ( — гО \ z0 /
Практически допустимы отклонения от условия (3-19), при которых величина (3-20) не превышает заданного предела.
Формулы, приведенные выше, справедливы и для цепей постоянного тока; при этом комплексные величины заменяются действительными.
Условия передачи максимума мощности широко используются в радиотехнике, электропроводной связи, автоматике и приборостроении. В энергетических же системах, генерирующих и потребляющих большие мощности, стремятся обеспечить высокий к.п.д. генераторов; поэтому сопротивления нагрузок значительно превышают сопротивления генераторов.
3-7. БАЛАНС МОЩНОСТЕЙ *
Из закона сохранения энергии следует, что для любой электрической цепи соблюдается закон ба
57
ланса средних мощностей: средняя мощность, генерируемая источниками, равна средней мощности, потребляемой всеми приемниками.
В свою очередь можно показать, что сумма отдаваемых реактивных мощностей равна сумме потребляемых реактивных мощностей.
Если воспользоваться комплексной формой записи токов, напряжений и мощностей, то высказанные положения будут вытекать из следующих рассуждений.
Для электрической цепи, содержащей q узлов, можно написать по первому закону Кирхгофа q—1 уравнений вида
41 + ’ + 4,-1 + 4» = °.
где положительные направления всех токов приняты от узла k к узлам 1, 2,..., q.
Умножим каждое из этих уравнений на комплексное напряжение, отсчитываемое от соответствующего узла к узлу q, и просуммируем эти произведения:
Ц? ( Аг + Аз +---Ь A J + 0^ ( 41 +
+ 4з Н-----1" ^2?) —ь
+ UQ-i,Q ( 4-1.1 + 4-1.2 -j—Ь
+4-1. J=°.
откуда с учетом того, что
—й = йь kq mq km
И
^mk ~ I km’ получим:
^12 Аг + <Аз Аз +' ’ ’ “Ь
+ 4,-1., 4-1.С = °-
Итак, сумма комплексных мощностей, потребляемых всеми ветвями электрической цепи, равна нулю; следовательно, также равны нулю в отдельности алгебраические суммы действительных и мнимых частей мощностей.
Иначе говоря, равна нулю как алгебраическая сумма потребляемых всеми ветвями цепи средних
мощностей, так и алгебраическая сумма потребляемых реактивных мощностей.
Поскольку отрицательные потребляемые мощности представляют собой мощности отдаваемые, то отсюда следует закон баланса как средних, так и реактивных мощностей.
В случае цепи постоянного тока сумма мощностей источников равна сумме мощностей, расходуемых в сопротивлениях, причем знаки мощностей источников определяются по указанному выше правилу: мощность положительна при совпадении направлений э.д.с. Е и тока /, проходящего через источник, и отрицательна при встречном направлении э.д.с. и тока. В последнем случае, если источником энергии служит аккумулятор, то мощность Е1 расходуется на его зарядку; если же источником служит генератор, то мощность Е1 расходуется на механическую работу (генератор работает в режиме двигателя).
3-8. ПОТЕНЦИАЛЬНАЯ (ТОПОГРАФИЧЕСКАЯ) ДИАГРАММА
В § 1-12 рассматривался график распределения потенциала для простейшей цепи постоянного тока. В случае цепи гармонического тока аналогично строится другой график, который называется потенциальной или топографической диаграммой напряжений. Эта диаграмма представляет собой векторную диаграмму, на которой отложены комплексные потенциалы отдельных точек заданной цепи по отношению к одной точке, потенциал которой принят за нуль. Таким образом, порядок расположения векторов падения напряжения на диаграмме строго соответствует порядку расположения элементов цепи на схеме. Конец вектора напряжения на каждом последующем элементе примыкает к началу вектора напряжения предыдущего элемента. При таком построении векторной диаграммы напряжений каждой точке электрической цепи соответствует определенная точка на потенциальной диаграмме.
58
Потенциальная диаграмма позволяет весьма просто находить напряжения между любыми точками цепи: действующее значение и фаза искомого напряжения определяются прямой, соединяющей соответствующие точки потенциальной диаграммы.
Рис. 3-11. Схема (а) и потенциальная диаграмма (6).
На рис. 3-11 изображена схема неразветвленной электрической цепи и для нее построена потенциальная диаграмма напряжений. Направления векторов напряжений на потенциальной диаграмме увязаны с произвольно выбранным направлением вектора тока I.
Обход схемы ведется навстречу положительному направлению тока I. В соответствии с порядком расположения в схеме элементов С, r2, L, ri на диаграмме изображены -векторы напряжений
^4Б = —/-^-Л^34 = Г2А
^23 ~ 1 ® ' ^12 = G
Начала и концы векторов (рис. 3-11,6) пронумерованы в соответствии с нумерацией точек, принятой на схеме (рис. 3-11,а).
Напряжение между какими-либо двумя точками схемы, например напряжение на участке 2—4 схемы, взятое в положительном направлении тока 7, определяется по потенциальной диаграмме вектором Uu,
соединяющим точки 2 и 4 диаграммы и направленным на диаграмме от точки 4 к точке 2. Это соответствует известному правилу вычитания векторов, согласно которому какой-либо вектор Vmn, представляющий разность напряжений (или потенциалов) Um—направлен от конца вектора Un к концу вектора Um. Итак, вектор напряжения на диаграмме направлен к точке высшего (уменьшаемого) потенциала, а то же напряжение на схеме указывается стрелкой, направленной от высшего потенциала к низшему.
Если при построении потенциальной диаграммы обход схемы совершался бы в положительном направлении тока /, то изменялась бы нумерация начала и конца каждого вектора напряжения на потенциальной диаграмме, что противоречило бы принятому правилу расстановки индексов при вычитании векторов.
3-9. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
3-1. Произвести вычисления
а) 10 /30° 4-5 /60°.
Ответ: 14,53 /40°.
б) 10 /3(Г—5 /60°.
О т в е т: 6,2 /6°,12'.
в) (8,664-/5) • (3,534-/3,53).
О т в е т: 50 /752-
г) (8,664-/5) : (2,54-/4,33).
О т в е т: 2 / —30°.
Д) (54-/5)®.
Ответ: —2504- /250.
v-----------
е) / 54-/8,66.
Ответ: 1,78 / 15°; 105°; —75° или
—165°.
/70°
ж) 1п (50 е‘ ).
Ответ: 3,914-/1,22.
3-2. Решить в комплексной форме следующие задачи:
а) Сложить напряжения ui =
(л \ / л \
сон «2=5 sin I со /-1
о / \ 12/"
б) Сложить токи й=10 sin со/ и t2= = 10 соз(со/4-л/4).
Ответ: u=14 sin (со/-|-45°30'); *= =7,65 sin (со/4-67°30').
3-3. К цепи, состоящей из г=7 ом и £=63,7 мгн, соединенных последовательно, приложено напряжение 250 sin 377 t, в. Найти тригонометрическое н комплексное выражения тока, комплексные напряжение
59
и сопротивление; построить векторную диаграмму.
Ответ: 10 sin (со/—73°40') в;
10 250
------/— 73° 40' а; 1& в; 25 /73°40' ом.
W У 2
3-4. К цепи, состоящей из г ”20 ом, £”100 мгн и С—50 мкф, соединенных последовательно, приложено напряжение и— =14,14 sin Snt, в.
Вычислить комплексные ток и напряжения на г, L и С; построить векторную диаграмму.
Ответ: 0,396 /37°25' о; 7,92 737°25' в;
14,95 / 127°25' в; 21,15 /—52°35' в.
3-5. Сохранив условия предыдущей задачи, вычислить мгновенные значения тока и напряжений на г, L и С при /”0,01 сек.
Ответ: —0,538 а; —10,76 в; —6,22 в; 8,52 в.
3-6. Комплексное сопротивление равно 3+/5 ом. Вычислить активную и реактивную проводимости.
Ответ: 0,0882 сим; 0,147 сим.
3-7. Комплексная проводимость равна 0,2—/0,2 сим. Вычислить активное и реактивное сопротивлении.
Ответ: 2,5 ом; 2,5 ом.
3-8. Заданы в комплексном виде напряжение на ветви (7=30 в и ток 7— =6-f-/0,9 а, проходящий через эту ветвь. Определить комплексное сопротивление и комплексную проводимость цепи; построить векторную диаграмму.
Ответ: 4,95 /—8°30' ом; 0,202/8°30' сим.
3-S. Через ветвь, комплексное сопротивление которой равно 5 / 30° ом, проходит
ток 7=10 / 30° а. Определить напряжение на ветви в комплексной и тригонометрической форме; построить векторную диаграмму.
Ответ: 50 / л/3 в; У 2 50 sin(co/+ +л/3) в.
3-10. К г и L, соединенным последовательно, подведено напряжение U— ”100 / 30° а; г—30 ом; <о£=4О ом. Написать выражение для мощности в комплексной форме.
Ответ: 120+/160 во.
3-11. Доказать, что
-----7 + U'l);Q = ~~ [й I - Ul').
3-12. Напряжение иа индуктивной катушке г, £ равно 120 а при прохождении через катушку как постоянного тока 20 а, так и сниусондального тока 6 а, частотой 50 гц.
Определить емкость, которую следует включить последовательно с катушкой, чтобы ток возрос до 12 а, а напряжение на зажимах цепи было равно 120 а.
Рассмотреть два случая, удовлетворяющих этому требованию, найти напряжение на катушке и построить векторные диаграммы.
Ответ: 118, 289 мкф.
3-13. Как переходят от мгновенных значений токов к комплексным?
3-14. На какую ось проектируют вращающийся вектор при переходе от комплексных выражений к тригонометрическим?
3-15. В чем заключается удобство комплексной формы расчета электрической цепи?
60
Глава четвертая
ПРЕОБРАЗОВАНИЕ СХЕМ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ. МЕТОД ГЕОМЕТРИЧЕСКИХ
МЕСТ
4-1. ПОСЛЕДОВАТЕЛЬНОЕ
И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ
При расчете электрических цепей часто возникает целесообразность преобразования схем этих цепей в более простые и удобные для расчета. Так, например, при одном или нескольких источниках электрической энергии в ряде случаев удается преобразовать электрическую схему в одноконтурную или в схему с двумя узлами, что весьма упрощает последующий расчет.
60
Описываемые ниже приемы преобразования схем электрических цепей применимы для цепей постоянного и переменного тока; ради общности изложения они приводятся в комплексной записи.
Одним из основных видов преобразования электрических схем, часто применяемых на практике, является преобразование схемы со смешанным соединением элементов. Смешанное соединение элементов представляет собой сочетание более простых соединений — последовательного и параллельного, рассмот
рению которых и посвящен данный параграф. Смешанное соединение рассматривается в § 4-2.
Последовательное соединение. На рис. 4-1 изображена ветвь электрической цепи, в которой последовательно включены комплексные сопротивления Zlt Z2,.... Zn- Через
Рис. 4-1. Последовательное соединение.
все участки цепи, соединенные последовательно, проходит один и тот же ток I.
Напряжения на отдельных участках цепи обозначены через Ui, йп.
По второму закону Кирхгофа
# = 01 + 0з+...+<7я
или, что то же,
u = zll + z2l+--- + zni.
Сумма комплексных сопротивлений всех последовательно соеди
ненных участков цепи
z-Sz, называется эквивалентным
комплексным сопротивлением.
Если
представляют сопротивления одинакового характера — индуктивного или емкостного (рис. 4-2), то эквивалентное комплексное сопротивление находится в результате арифметического сложения в отдельности сопротивлений rk, индуктивностей
Рис. 4-2. Последовательное соединение однородных звеньев.
Lk или величин 1/Ск, обратных ем костям:
Z — г + / to L
или
где п п
г. = rk; L = S
п
—=У—
с Ск‘
Л=1
Ток в цепи равен:
Напряжения на участках цепи, соединенных последовательно, относятся как комплексные сопротивления этих участков: напряжение на й-м участке равно произведению суммарного напряжения U на отношение комплексного сопротивления £-го участка к эквивалентному комплексному сопротивлению цепи:
й„ = и-^.
11 Z
Приведенные выше формулы справедливы при любых значениях Zk.
Параллельное соединение. На рис. 4-3 изображена схема электри-
Рис. 4-3. Параллельное соединение.
ческой цепи с двумя узлами. Между этими узлами параллельно соединены ветви с комплексными проводимостями Уь Ys,.... Yn. Напряжение на всех ветвях одинаковое, равное U.
Токи в ветвях обозначены через 12, • • In-
По первому закону Кирхгофа
= Л т --------
61
или, что то же,
I = Yfi+Y2U++¥£
Сумма комплексных проводимостей всех ветвей, соединенных параллельно,
п
называется эквивалентной комплексной проводимостью.
Рис. 4-4. Параллельное соединение однородных звеньев.
Если Ул=£л—jbk представляют проводимости одинакового характера — емкостного или индуктивного (рис. 4-4), то эквивалентная комплексная проводимость находится в результате арифметического сложения отдельных активных проводимостей gk, емкостей Ск или величин l/Lk, обратных индуктивностям:
Y =g + jwC или
y = g—i-~r, ш L
где п П
«=2fo:c-Sc^
Л=1 п - = У—. £ ^Lk *=1
Суммарный ток в цепи
/ = YU.
Токи в ветвях относятся как их комплексные проводимости: ток в k-й ветви равен произведению
суммарного тока всех ветвей на отношение комплексной проводимости k-й ветви к эквивалентной комплексной проводимости:
i
* Y Zk
Данным выражением особенно удобно пользоваться при п>2. При этом значения Yh могут быть любыми.
В случае параллельного соединения двух ветвей (п=2) обычно пользуются выражениями, в которые входят сопротивления Z^l/Yi и Zz= 1/У2 ветвей; эквивалентное комплексное сопротивление
1 = 1 =
Yi + Ya 1 1 Zx -|- Za
zx + za
Токи в параллельных ветвях:
= * ------ 1
Zi + za zx + z2
т. e. ток одной из двух параллельных ветвей равен суммарному току, умноженному на сопротивление другой ветви и деленному на сумму сопротивлений обеих ветвей.
4-2. СМЕШАННОЕ СОЕДИНЕНИЕ
Электрические схемы, имеющие смешанное соединение, могут быть преобразованы в более простую
Рис. 4-5. Смешанное соединение.
электрическую схему путем замены параллельных ветвей одной ветвью и соответственно последовательно соединенные участков цепи — одним участком.
На рис. 4-5 показан пример электрической цепи со смешанным соединением. Эта схема легко приводится к одноконтурной. Первоначально вычисляется эквивалентная комплексная проводимость парал-
62
дельных ветвей; затем находится величина, обратная проводимости, т. е. общее комплексное сопротивление параллельных ветвей; найденное комплексное сопротивление суммируется с комплексным сопротивлением последовательно включенного участка. Полученное суммарное комплексное сопротивление эквивалентно сопротивлению исходной цепи со смешанным соединением.
Расчетные выражения для рассматриваемого случая будут следующие:
Суммарное комплексное сопротивление всей цепи равно:
Z = Z1 + ~ =Z,+---------------
Уg Z%Ze “I- Z^Ze
а суммарный ток
Токи в ветвях относятся как комплексные проводимости ветвей:
Л= ; / = / 2k; /4 =/; 21.
1у9 • з 1Гэ . 4
Таким образом, многоконтурная электрическая схема со смешанным
Рнс. 4-6. Цепная схема.
соединением приводится к одноконтурной, имеющей суммарное комплексное сопротивление Z или соответственно суммарную комплексную проводимость У. Распределение токов и напряжений в смешанной цепи подчиняется правилам, указанным в предыдущем параграфе.
Описанный выше порядок преобразования схемы и нахождения распределения токов принципиально применим и для так называемой цепной схемы, показанной на рис. 4-6. Просуммировав комплексные сопротивления Zj и Z6 в послед
ней ветви, найдем комплексную проводимость ветви, которую алгебраически сложим с 1/Z6 и получим суммарную комплексную проводимость двух последних ветвей; вычислив обратную величину, т. е. комплексное сопротивление, прибавим к ней Z6. Продолжая таким образом и дальше, получим в итоге результирующее комплексное сопротивление цепи и соответственно суммарный ток Л, который может быть путем последовательных вычислений распределен между всеми ветвями сложной цепи.
Однако такой способ расчета цепной схемы является достаточно трудоемким и утомительным. Более целесообразно в этом случае воспользоваться другим методом, который известен под названием метода подобия или единичного тока.
Задавшись током в последней ветви, равным единице (/j =1), находим напряжение на комплексном сопротивлении Z6, равное (Z7+ +Z8) 1. При этом ток/g =
Ze Следовательно,
/'=/;+/; = + 1.
DO1/ 7 1
Прибавив к напряжению на Z8 падение напряжения от тока /'5 в комплексном сопротивлении Z5, получим напряжение на Z4. Продолжая таким образом дальше, найдем в конечном итоге ток /1 и напряжение U'. Ввиду того, что ток /7 был произвольно выбран равным единице, полученное напряжение не будет равно заданному напряжению U на зажимах цепи. Для нахождения действительного распределения токов в схеме необходимо все вычисленные значения токов умножить на отношение U/U'.
4-3. ЭКВИВАЛЕНТНЫЕ УЧАСТКИ ЦЕПИ С ПОСЛЕДОВАТЕЛЬНЫМ
И ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЯМИ
Обозначим комплексное сопротивление участка цепи, состоящего из двух последовательно соединен-
63
них элементов, через Z=r+jx. Комплексная проводимость данного участка цепи равна Y=l/Z= =g—jb, причем активная и реактивная проводимости равны:
Если два элемента с проводимостями g и Ь, вычисленными по этим формулам, соединить парал-
Рнс. 4-7. Активно-индуктивные цепи, эквивалентные при определенной частоте.
лельно, то суммарная комплексная проводимость будет равна Y и соответственно комплексное сопротивление будет равно Z.
Такие две цепи с последовательным и паралелльным соединением, имеющие одинаковые сопротивления на зажимах, называются эквивалентными.
Ввиду того, что реактивное сопротивление х, входящее в расчетные формулы, в общем случае зависит от частоты, условие эквивалентности этих цепей выполняется только при той частоте, для которой вычислено х.
Пусть, например, задана схема с последовательным соединением сопротивления и и индуктивности Lt (рис. 4-7,а). Преобразуем ее в схему с параллельным соединением элементов (рис. 4-7,6).
Активная и реактивная проводимости исходной цепи:
g =-----—-----; Ь =----—-----
Из условия эквивалентности цепей следует, что параметры новой цепи будут:
1 г. . f&Li VI
'•«= —= fi 1 + -г ••
g L \ ri / J
coLt = -j- = asL1 Г1 + 1-
b L \<o£i / J
Вычислив по этим формулам г2 и £2, получим схему цепи, эквивалентной исходной при данной ча
стоте ф. При других значениях частоты ф параметры г2 и L2 будут иметь другие значения, следовательно, эквивалентность цепей нарушится. В области высоких частот
1, и поэтому r2sa£O2L®/rlt
и L2~Li.
Если исходной является схема рис. 4-7, б и заданными параметрами являются r2, L2 и ш, то параметры эквивалентной цепи (рис. 4-7,а) определяются из выражений
Из полученных выражений видно, что численные значения ri и L\ эквивалентной цепи зависят от частоты £0.
Рис. 4-8. Активно-емкостные цепи, эквивалентные при определенной частоте.
Условия эквивалентности для цепей с последовательным и параллельным соединением сопротивления и емкости (рис. 4-8) имеют вид:
а=Г1[1 4-------------1
;
1
Г,—Г--------------;
а1+ (<oC,r2)=’ , . 1
и
Ч
В области высоких частот (£»ада»1 тогда
----!-----, г»(<»С«)а
64
4-4. ПРЕОБРАЗОВАНИЕ ТРЕУГОЛЬНИКА В ЭКВИВАЛЕНТНУЮ ЗВЕЗДУ
Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольника, цепью, соединенной по схеме звезды, при
Рнс. 4-9. Упрощение схемы преобразованием треугольника в звезду.
которой токи и напряжения в остальной части цепи сохраняются неизменными. Иначе говоря, эквивалентность треугольника и звезды понимается в том смысле, что при одинаковых напряжениях между
Рис. 4-10. Соединения треугольником (а) и звездой (б).
одноименными зажимами токи, входящие в одноименные зажимы, одинаковы. Это равносильно тому, что мощности в этих цепях одинаковы.
На рис. 4-9 показан случай, когда преобразование треугольника в эквивалентную звезду дает возможность преобразовать многоконтурную схему в одноконтурную.
Для вывода расчетных выражений, служащих для преобразования треугольника в эквивалентную звезду, ниже приняты следующие обозначения (рис. 4-10):
Z12, ^м, Z81—сопротивления сторон треугольника;
Zlf Z2, Zs — сопротивления лучей звезды;
Л» 4» 4— токи, приходящие к зажимам 1, 2, 3;
4в» 4з» 41 — ТОКИ в ветвях треугольника.
Выразим токи в ветвях треугольника через приходящие токи.
По второму закону Кирхгофа сумма напряжений в контуре треугольника равна нулю:
^is 4з"1-^аз 4s~b^si 41==0.
По первому закону Кирхгофа для узлов 2 и 1:
4з= 4» 4; 4i= 4s 4-
Решение этих уравнений относительно /12 дает:
у %31 h — 2аз la 2ia + 2аз + 2ji
Напряжение между зажимами 1 и 2 схемы рис. 4-10, а будет:
f] у 1 2si 212 1г — Zis Za3 /а
12- 12 IS- Zla_|_ZM_|.Zsi ’
а в схеме рис. 4-10,6 оно равно:
L/i2=Zj 4 z2 4.
Для эквивалентности необходимо равенство напряжений Ut2 при любых токах /1 и 4, т. е.
2ц Zia j 21д Zas j
2ia + 2аз + 2si 2аа + Zaa 4- 2Si
— Zi 4 ^2 4-
Это возможно при условии:
2 ___ 2з1 Z^
1 Zia + Zas + Zsi
z -------^12,3----. (44)
212 + 2аз -f- Zsi
z________2аз Zgi
S 212 + Za3 4- 2ц i
Третье выражение получается в результате круговой замены индексов.
Итак, комплексное сопротивление луча звезды равно произведению комплексных сопротивлений прилегающих сторон треугольника, деленному на сумму комплексных сопротивлений трех сторон треугольника.
Б—1118
65
Выше было получено выражение для тока в стороне 1—2 треугольника в зависимости от токов !\ и /2. Круговой заменой индексов можно получить токи в двух других сторонах треугольника:
г ___ 21а/а— 2зг/3 г
/яо - «1 -*51 -------------
2ia + Zas + Z31
__ 2аз /з — 212 Л
2ia + 2аа -f- Z31
Пользуясь условиями (4-1), так же легко выразить токи в сторонах треугольника через токи эквивалентной звезды. Например,
21 71 — Za 7а Zsi 71 z23/а
212 Zig-j-Zgs-f-Zai
4-5. ПРЕОБРАЗОВАНИЕ ЗВЕЗДЫ В ЭКВИВАЛЕНТНЫЙ ТРЕУГОЛЬНИК
В расчетах также возникает необходимость замены звезды эквивалентным треугольником. На рис. 4-11 показан, например, случай.
Рис. 4-11. Упрощение схемы преобразованием звезды в треугольник.
При переходе от звезды к треугольнику заданными являются сопротивления звезды Zb Z2, Z3. Выражения для искомых сопротивлений треугольника находятся в результате совместного решения трех уравнений (4-1).
Деление третьего уравнения на первое, а затем на второе дает:
23 - Z^s Z3 ____Z31
2i Zi2 Za Zu
Выражая отсюда Z23 и Z3l через Z]2 и подставляя их в первое уравнение (4-1), получаем:
7 Г/ -4-7 ^31__71
I ^12 । ^12 т |~^12 7 ’
откуда
Z12=Z1+Za+^-a. (4-2)
Аналогично круговой заменой индексов получим:
z„=zt+z,+^ (4-2а)
и
ZS1=ZS+Z1 + ^. (4-26)
Следовательно, комплексное сопротивление стороны треугольника равно сумме комплексных сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.
Токи в лучах звезды легко выражаются через токи в сторонах треугольника. С учетом положительных направлений рис. 4-10
А = Аг — An А = Аз — 11а!
А=А1 — ^аз-
Пример 4-1. Пользуясь правилами преобразования звезды в треугольник и треугольника в звезду, вычислить сопротивление на зажимах мостовой схемы рис. 4-12,а.
когда такая замена позволяет преобразовать сложную электрическую схему в одноконтурную.
Рис. 4-12. Пример 4-1.
66
Возможны 2 варианта решения.
1) Звезда с лучами 5, 10 и 10 ом преобразуется по формулам (4-2) в эквивалентный треугольник (рис. 4-12,6), после чего получается схема с параллельными и последовательными ветвями, преобразуемая к сопротивлению 10 ом.
2) На рнс. 4-12, а треугольник со сторонами 10, 10 и 5 ом преобразуется в эквивалентную звезду с лучами 4, 2 и 2 ом (рнс. 4-12,в); после дальнейшего преобразования получим 10 OJH.
4-6. ЭКВИВАЛЕНТНЫЕ ИСТОЧНИКИ НАПРЯЖЕНИЯ И ТОКА
Два разнородных источника электрической энергии — источник напряжения и источник тока — считаются эквивалентными, если при замене одного источника другим
°)
Рис. 4-13. Эквивалентные источники напряжения (а) и тока (6)-
токи и напряжения во внешней электрической цепи, с которой эти источники соединяются, остаются неизменными.
На рис. 4-13 изображены эквивалентные источники напряжения и тока, посылающие во внешнюю цепь ток Ii, и поддерживающие на своих зажимах одинаковое напряжение U.
Условием эквивалентности источников, именуемым в дальнейшем правилом об эквивалентных источниках напряжения и тока, служит следующее соотношение между э. д. с. Ё источника напряжения и током 7 источника тока:
£=ZI, (4-3)
где Z— внутреннее комплексное сопротивление как источника напряжения, так и источника тока.
Действительно, напряжение U на зажимах источника напряжения получается в результате вычитания из
э. д. с. Ё падения напряжения от тока 71 в комплексном сопротивлении Z источника (рис. 4-13,о).
Соответственно напряжение U иа зажимах источника тока при той же величине тока 71, посылаемого во внешнюю цепь, равно падению напряжения от тока /—71, в комплексном сопротивлении Z источника (рис. 4-13,6).
В обоих случаях напряжения на зажимах источника одинаковы:
U = Ё — Zi^Z (I — I,) =Z/- Ztlf т. е. получается условие (4-3).
При отсоединении эквивалентных источников напряжения и тока от внешней цепи (/1=0) напряжение на зажимах обоих источников равно Ё. Именно это обстоятельство и равенство внутренних комплексных сопротивлений обоих источников и обеспечивают их эквивалентность при любом режиме работы (§ 5-9).
Следует заметить, что мощности, расходуемые во внутренних сопротивлениях эквивалентных источников напряжения и тока, неодинаковы. В первом случае полная мощность, расходуемая в источнике, равна z7i2, во втором случае z\l—Л|2. Например, при отсоединении источников от внешней цепи в первом случае мощность в источнике не расходуется, а во втором случае она составляет z/2.
Поэтому эквивалентность источников следует понимать только в смысле неизменности токов, напряжений и мощностей во внешней электрической цепи, присоединенной к источникам.
Если внутреннее сопротивление источника напряжения равно нулю, то непосредственное применение формулы (4-3) для нахождения эквивалентного источника тока по заданной величине э. д. с. источника не представляется возможным. В таких случаях сопротивление внешней цепи, включенной последовательно с э. д. с., можно рассматривать в качестве внутреннего сопротивления источника, что позволит применить формулу (4-3).
5*
67
В случае сложной электрической цепи замена источника напряжения эквивалентным источником тока или обратно может иногда упростить расчет.
Целесообразность такой замены иллюстрирована, в частности, в следующем параграфе. -
4-7. ПРЕОБРАЗОВАНИЕ СХЕМ С ДВУМЯ УЗЛАМИ
Применим правило об эквивалентных источниках напряжения и тока к преобразованию схемы с параллельным соединением вет-
Таким образом, п параллельных ветвей с источниками напряжения между двумя узлами могут быть за
менены одним источником тока (рис. 4-14, в) или источником напряжения (рис. 4-14,г).
Ток во внешней цепи (в ветви с сопротивлением Zri+i) равен:
/ =/______z. - Ё
n+* z + zn+1 z + z„+1-
Напряжение между двумя узлами находится по формуле
(К/ Г—-Z"+1 -
z + zn+l
Рис. 4-14. Преобразование параллельного
соединения ветвей с источниками напряжения.
, 1
Л+1
s Yk 4=1
2 YkEk
4=1_____
л+1
S^4
4=1
(4-4)
Выведенные здесь выражения широко используются для расчета электрических цепей с двумя узлами, а также для расчета более сложных цепей, приводящих-
ся к двум узлам.
4-8. ПЕРЕНОС ИСТОЧНИКОВ В СХЕМЕ
вей, содержащих источники напряжения (рис. 4-14,а).
Заменяя заданные источники напряжения источниками тока, получаем схему рис. 4-14,6. Источники тока в совокупности образуют один эквивалентный источник тока I (рис. 4-14,в), причем
п
Е Yk
4=1
Пользуясь этим соотношением, можно в конечном итоге перейти от схемы в к схеме г, являющейся эквивалентом исходной схемы а. Здесь
I YkEk E=Z'I=—-----
п
Е Yk 4=1
Расчет электрической цепи облегчается в ряде случаев в результате переноса в схеме источников э. д. с. или тока. Как это видно из уравнений Кирхгофа, токи в схеме определяются заданными величинами суммарных э. д. с. в контурах независимо от того, из каких отдельных слагающих они состоят. Поэтому изменение расположения в схеме источников э. д. с., при котором суммарные э. д. с. во всех контурах сохраняются неизменными, не влияет на токи в ветвях. Аналогично напряжения на ветвях определяются заданными величинами суммарных токов источников тока в узлах, и поэтому изменение расположения в схеме источников тока, при котором их суммарные токи во всех узлах сохраняются неизменными, не влияет на напряжения в схеме.
Если, например, требуется исключить источник э. д. с. из какой-либо ветви, то в данную ветвь вводится компенсирующая э. д. с., причем точно такая же э. д. с. вводится одновременно во все остальные вет
68
ви, сходящиеся в одном из узлов данной ветви. Компенсирующая и дополнительные э. д. с. имеют одинаковое направление по отношению к рассматриваемому узлу. В результате этого источник э. д. с. из ветви исключается и появляются источники э. д. с. в других ветвях схемы. Суммарные э. д. с. во всех контурах и соответственно токи в ветвях остаются прежними.
Итак, источник э. д. с. может быть перенесен из какой-либо ветви схемы во все другие ветви, присоединенные к узлу данной ветви, без изменения токов в схеме.
Справедливо и обратное положение: если во всех ветвях, кроме од
Рнс. 4-15. Перенос источников э. д. с. в схеме.
ной, сходящихся в узле, имеются одинаковые источники э. д. с. (рис. 4-15,а), направленные все к одному узлу или все от узла, то они могут быть заменены одним источнико.м э. д. с. в ветви, в которой источник отсутствовал (рис. 4-15,6).
Это положение подтверждается тем, что суммарные э. д. с. в контурах схем на рис. 4-15, а и б одинаковы.
Имеется и другое доказательство данного положения: ввиду равенства э. д. с. всех источников вторые зажимы их могут быть объединены как имеющие одинаковый потенциал. В результате такого объединения, показанного на рис. 4-15, а пунктиром, получается схема рис. 4-15,6.
В случае переноса источников тока последние присоединяются к узлам схемы так, чтобы оставались неизменными их суммарные токи в узлах. Так, например, несмотря на то, что источники тока размещены в схемах на рис. 4-16, а и б различно, суммарные токи источников в узлах обеих схем одинаковы. По-
Рис. 4-16. Перенос источника тока в схеме.
этому и напряжения между узлами не изменились.
а)
б)
Рис. 4-17. Пример 4-2.
Итак, источник тока может быть заменен источниками тока, подключенными параллельно всем ветвям, которые составляли контур с рассматриваемым источником.
Перенос источников в схеме успешно сочетается на практике с различными методами преобразований и расчетов (пример 4-2).
Пример 4-2. Вычислить ток в диагональной ветви Гв мостовой схемы рис. 4-17, а.
Дано: /=10 а; г, = 1 ом; га=2 ом; гэ=3 ом; г< = 4 ом; г$—5 ом.
Заданный источник тока может быть, заменен двумя источниками, подключенными параллельно сопротивлениям п и (рис. 4-17,6). Пользуясь условием эквивалентности источников напряжения и тока, получаем схему рнс. 4-17, в с двумя узлами. По формуле (4-4) напряжение на ветви ге равно:
69
40 10
ill’
7 + 3 + 5
Искомый TOK
3,52 /s= —--=0,704 a.
5
4-9. ПРЕОБРАЗОВАНИЕ СИММЕТРИЧНЫХ СХЕМ
Схема электрической цепи, в которой имеется ось симметрии, называется симметричной. Например, схема рис. 4-18, а симметрична относительно вертикальной оси. В сим
Рис. 4-18. Симметричная цепь (а, б) и ее отсеченная половина (в).
метричных схемах легко выявляются точки или узлы с одинаковым потенциалом. В ветвях, присоединенных к таким узлам, токи равны нулю. Поэтому эти ветви можно разрезать, не нарушая распределения токов и напряжений в схеме. Точки, имеющие одинаковый потенциал, могут быть объединены. Рассечение ветвей, по которым не проходит ток, и объединение точек равного потенциала упрощает схему и облегчает расчет.
Так, в симметричной схеме рис. 4-18,6 токи в соединениях, пересекающих ось симметрии, отсутствуют. Разрезав схему по оси симметрии, получим с обеих сторон одноконтурную схему рис. 4-18, в, которая легко рассчитывается.
Допустим теперь, что полярность источников в симметричной схеме неодинакова (рис. 4-19, tz). В этом случае (равенство э. д. с. источников и различие в их полярности) токи в симметричных ветвях (например, Л и /2) и напряжения между соответствующими парами зажимов, симметрично расположенными относительно оси, равны по величине и противоположны по знаку. Отсюда следует, что напряжения между всеми точками, лежащими на оси симметрии, равны нулю ({7=—U, т. е. 17=0). Поэтому все точки схемы на оси симметрии могут быть замкнуты накоротко (рис. 4-19,6).
Таким образом, расчет сложных симметричных схем приводится к расчету более простых схем.
На рис. 4-20, а и б показана симметричная мостовая схема, имеющая две оси симметрии—вертикальную и горизонтальную. В продольных ветвях ток отсутствует; потенциалы средних точек поперечных (перекрещенных) ветвей одинаковы.
Поэтому продольные ветви могут быть рассечены, а средние точки по-
Рис. 4-19. Симметричная цепь с неодинаковой полярностью источников (а) и ее закороченная половина (б).
Рис 4-20. Симметричная мостовая схема (а, б) и ее преобразованная часть (в).
70
перечных ветвей — объединены. В результате с обеих сторон получится одноконтурная схема (рис. 4-20,в), расчет которой крайне прост.
Если изменить полярность одного из источников (рис. 4-21,а), то роли продольных и поперечных ветвей поменяются и преобразованная часть схемы примет вид рис. 4-21,6.
В разобранных выше примерах э. д. с. источников были равны. В случае неравенства э. д. с. источников преобразование симметричной схемы удобно сочетается с методом наложения (см. пример 5-5 в гл. 5).
Рис. 4-21. Симметричная мостовая схема (а) и ее преобразованная часть (б).
4-10. ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ЗАВИСИМОСТЕЙ КОМПЛЕКСНЫХ
ВЕЛИЧИН ОТ ПАРАМЕТРА
Исследование зависимости какой-либо комплексной величины (или отношения комплексных величин) от переменного параметра сводится к нахождению зависимостей модуля и угла от параметра.
При пользовании прямоугольной системой координат строятся кривые модуля и угла, которые в совокупности и характеризуют изменение исследуемой величины. Вместо зависимостей модуля и угла в прямоугольной системе координат могут быть построены зависимости от параметра действительной и мнимой частей исследуемой комплексной величины.
Таким образом, графическое изображение исследуемой зависимости в прямоугольной системе координат осуществляется с помощью двух кривых: модуля и угла или соответственно действительной и мнимой частей.
При комплексной форме записи полное представление о зависимости исследуемой величины от пара
метра может быть достигнуто с помощью одной кривой, изображаемой на комплексной плоскости. Сущность такого графического изображения заключается в том, что исследуемое комплексное выражение представляется на комплексной плоскости вектором, геометрическое место конца которого при изменении входящего в это выражение параметра изображается кривой. Эта кривая, называемая также годографом, наглядно показывает изменение модуля и фазы рассматриваемой комплексной величины в зависимости от параметра.
Такой графический метод применим к комплексным величинам — напряжениям, токам, мощностям и к отношениям комплексных величин — сопротивлениям, проводимостям, передаточным функциям и т. д.
Переменным параметром электрической цепи может служить какая-либо из величин, характеризующих источник электрической энергии или пассивный элемент: величина или фаза э. д. с. (или тока) источника, частота ш, сопротивление г, индуктивность L, взаимная индуктивность М, емкость С или соответственно реактивная составляющая сопротивления или проводимости и т. д.
В качестве переменного параметра может рассматриваться полное сопротивление z при неизменном значении аргумента <р или, наоборот, переменным параметром может служить угол <р при постоянном Z.
Изменение каждого из этих параметров может быть графически представлено на комплексной плоскости. Например, изменение активного или реактивного сопротивления изображается прямой, параллельной соответственно действительной или мнимой оси. Изменение полного сопротивления при постоянном угле <р изображается прямой линией, образующей с действительной осью угол <р. В свою очередь изменение угла <р при неизменном z изображается окружностью радиуса z.
71
4-11. ПРЕОБРАЗОВАНИЕ ВИДА У = — Z
Положим, что вектор Z при изменении соответствующего параметра описывает на комплексной плоскости окружность или прямую. Требуется построить геометрическое место конца вектора Y — \/Z.
Пусть точка Zo на комплексной плоскости Z служит центром окружности, радиус которой равен R. Комплексная форма уравнения такой окружности может быть представлена так:
(Z-Z0)(Z-Z*0)=fl2
или
ZZ - ZZ0 - zzo+zo Zo=R2. <4'5)
Подстановка Z=l/Y дает:
уу y_______%0________Y Zp___
Z0Z0—R* Z0Z0 — R3
+ —J----- =0
zozo — r?
или, что то же,
Yy__у Y Zq|
20Z0 — R* ZoZo — R»
4----------s —22------. (4-6)
(Z0Z0~R2)2 (Z0Z0 — R2)2
Из сопоставления (4-5) с (4-6) следует, что вектор У описывает ок-R ружность радиуса р= —---------- с
Рис. 4-22. Преобразование окружности Z в окружность У,
центров в точке z« комплекс-
Z0Z0 —R2 ной плоскости У.
Наиболее удаленной от начала координат точке b окружности Z соответствует наиболее близко расположенная к началу координат точка Ь' окружности У, и наоборот. Диаметры соответствующих окружностей, проходящие через начало координат, образуют с действительной осью одинаковые углы, отсчитываемые в противоположных направлениях (рис. 4-22).
Следует заметить, что координаты центров окружностей векторов Z и У не подчиняются условию y=l/Z; иначе говоря,
* 1/20.
В случае, когда окружность проходит через начало координат, ZqZ0=R2 и на основанйи (4-5)
ZZ —ZZ0—-ZZo=0. (4-7)
Рис. 4-23. Преобразование окружности Z в прямую У,
Вектор У описывает при этом прямую, находящуюся на расстоянии 1/2R от начала координат (рис. 4-23). Диаметр окружности Z, проходящий через начало координат, и перпендикуляр, опущенный из начала координат на прямую У, образуют с действительной осью одинаковые углы (отсчитываемые в противоположные стороны).
Уравнение прямой У получается, если обе части уравнения (4-6) умножить на ZZ0—R2 и затем перейти к пределу ZZ0—R2 -> 0. Тот же результат может быть получен непо
72
средственно из (4-7) заменой Z= = 1/У:
YZo+YZo-l=O. (4-8)
В свою очередь уравнение прямой линии в плоскости Z, не проходящей через начало координат, записывается по аналогии с (4-8):
ZY0 + ZY — 1 = 0.
При этом уравнение окружности, описываемой вектором Y, имеет вид:
YY — YY0 — УУо=О.
стом комплексного сопротивления Z=r+jx служит прямая, параллельная действительной оси (рис. 4-25,6). Геометрическим местом комплексной проводимости Y = — является полуокружность, проходящая через начало координат комплексной плоскости Y, диаметр которой равен 1/|х| (рис. 4-25,в).
Вторая половина окружности, соответствующая отрицательным значениям г, из рассмотрения исключается.
Рис. 4-24. Преобразование прямой Z в прямую У.
Рис. 4-25. Переменное активное сопротивление при последовательном соединении.
а—схема; б—-диаграмма Z; в — диаграмма Y.
Если геометрическим местом вектора Z служит прямая, проходящая через начало координат под углом <р к действительной оси, то геометрическое место вектора Y представляет прямую, также проходящую через начало координат и образующую с действительной осью угол —<₽ (рис. 4-24).
Преобразования прямой в окружность и окружности в окружность иллюстрированы ниже на примерах простейших электрических цепей.
4-12. ДИАГРАММЫ СОПРОТИВЛЕНИЙ И ПРОВОДИМОСТЕЙ ПРОСТЕЙШИХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Рассмотрим диаграммы сопротивления и проводимости цепи с последовательным, параллельным и смешанным соединением при изменении одного параметра.
Последовательное соединение. При изменении сопротивления г (рис. 4-25, а) геометрическим ме-
Значению г=0 соответствует наиболее удаленная точка окружности Y, а значению г=со — точка 0 в плоскости У.
При х>0 геометрическое место конца вектора Z располагается в первой четверти, а при х<0 — в четвертой четверти комплексной плоскости.
Рис. 4-26. Переменное реактивное сопротивление при последовательном соединении.
а — схема; б — диаграмма 2; в — диаграмма Y.
73
Соответственно полуокружность У при х>0 располагается в четвертой четверти, а при х<0— в первой четверти. '
При изменении реактивного сопротивления х (рис. 4-26, а) геометрическим местом конца вектора Z служит прямая, параллельная мни-
ца вектора Y=\/r—j \/х служит прямая, параллельная действительной оси (рис. 4-27,6). Геометрическим местом конца вектора Z=l/y является полуокружность (рис. 4-27,в), верхняя при х>0 и нижняя при х<0; диаметр окружности равен |х|. Значению г=0 .соответству-
Рис. 4-27. Переменное активное сопротивление при параллельном соедииеиии.
а — схема; б — диаграмма У; в — диаграмма Z.
Рис. 4-28. Переменное реактивное сопротивление при параллельном соединении.
а — схема; б — диаграмма У; в — диаграмма Z.
мой оси (рис. 4-26,6). Геометрическим местом конца вектора y=l/Z является окружность, проходящая через начало координат комплексной плоскости; диаметр окружности равен 1/г (рис. 4-26, в).
Значениям х>0 соответствует Нижняя, а х<0— верхняя полуокружность.
При х=0 цепь имеет только активное сопротивление и соответственно активную проводимость. При х** ±оо проводимость цепи равна нулю.
- Параллельное соединение. При изменении сопротивления г (рис. 4-27, а) геометрическим местом кон-
ет начало координат, а значению г— оо — диаметрально противоположная точка окружности.
При изменении реактивного сопротивления х (рис. 4-28, а) геометрическим местом конца вектора У служит прямая, параллельная мнимой оси (рис. 4-28,6), а геометрическим местом конца вектора Z= = 1/У — окружность диаметром г, проходящая через начало координат (рис. 4-28,в). Значениям х>0 соответствует верхняя, а х<0 — нижняя полуокружность. При х=0 полное сопротивление пепи равно нулю, а полная \ проводимость бесконечно велика.
74
При х=в±ао сопротивление и проводимость цепи являются активными.
Смешанное соединение. Рассмотрим в качестве примеров две схемы цепи со смешанным соединением элементов.
На рис. 4-29, а показана схема цепи, в которой переменным параметром является реактивное сопротивление х. Диаграмма Z такой цепи (рис. 4-29,6) отличается от диаграммы Z (рис. 4-28, в) тем, что окружность смещена относительно начала координат на величину сопротивления Гь Изменение х может
Рис 4-29. Переменное реактивное сопротивление при смешанном соединении. а — схема; б — диаграмма.
вектора У служит прямая, параллельная мнимой оси (рис. 4-30,6), а геометрическим местом конца вектора Z — окружность, проходящая через начало координат; диаметр окружности равен г+ -—— (рнс.
4-30,в). Часть окружности, начерченная тонкой линией, исключается из рассмотрения, так как она соответствует отрицательным значениям С.
Рассмотренные здесь диаграммы сопротивлений и проводимостей изображают в определенном масштабе: 1) ток i=YU — при заданном напряжении U на зажимах цепи; 2) напряжение U=Z1 — при заданном токе I, проходящем через цепь; 3) комплексную мощность S = = U2Y=1ZZ—при заданных U или /.
Если начальная фаза заданного напряжения (или тока) отлична от нуля, то диаграмма тока (или напряжения) поворачивается на соответствующий угол (пример 4-3).
+Jm
Рис. 4-30. Переменная емкость при смешанном соединении. а — схема; б — диаграмма У; в — диаграмма Z.
быть обусловлено изменением частоты или изменением параметра L или С.
На рис. 4-30,0 показана схема цепи, в которой переменным параметром является емкость С. Проводимость ветви г, L равна:
1______г — j&L
r+jwL га+(<в£)2 ’
проводимость ветви с емкостью равна /(оС.
Геометрическим местом конца
Пример 4-3. Напряжение На зажимах участка цепи, состоящего из последовательно соединенных сопротивления г и емкости С, задано: U=*UI_^ (рис. 4-31, а). Построить круговые диаграммы тока и напряжения на сопротивлении при иамеиеиии г от нуля до бесконечности.
Круговая диаграмма тока по-
вернута относительно диаграммы проводимости, изображенной на рис. 4-2S, е (для случая х<0), на угол ф, равный начальной фазе приложенного напряжения.
Диаметр круговой диаграммы тока равен току UI—jxc, соответствующему зна
75
чению г=0 и опережающему U на л/2 (рнс. 4-31,6).
Напряжение на сопротивлении совпадает по фазе с током. В силу равенства г!—]хс1=й конец вектора ri описывает окружность, диаметром которой служит U.
Рис. 4-31. Пример 4-3.
4-13. ПРЕОБРАЗОВАНИЕ ВИДА
_ А -р — C + Dk
Если в сложной линейной электрической цепи переменным параметром служит какая-либо одна из величин: г, L, С, х, г или у, то исследуемая функция может в общем случае представлять дробно-линейную функцию
= (4-9)
C + Dk ’ v '
где
Л = |Л|/а; B = |B|/g;
С = |С|/у; £> = |О|/б
— комплексные числа; k — переменный вещественный параметр.
Согласно круговому свойству дробно-линейной функции при изменении параметра k конец вектора W описывает окружность. Центр и радиус этой окружности могут быть найдены аналитически или графически.
Следует заметить, что в том случае, когда переменным параметром служит частота, характер исследуемой функции и кривой, выражаемый ею, зависит от степени о. Если <о входит в (4-9) в первой степени, то круговое свойство функции сохраняется. При более высоких степенях о получаются кривые высшего порядка.
Уравнение (4-9) может быть
преобразовано путем деления числителя на знаменатель:
_А__ _В_
IV/ В , С D
'+-s
Первое слагаемое, не зависящее от параметра k, представляет вектор, через конец которого проходит искомая окружность. На основании (4-10) BID равно значению W при fe=oo; B/D=Wh=ae.
Второе слагаемое (4-10) является уравнением окружности. В самом деле,
А __В_
V = -£ ~ D = ~ f
тогда
V + V — k = F. С
Это равенство показывает, что постоянный вектор F получается в результате геометрического сложения вектора V с вектором Vk\D/C\l (б—у), опережающим его на постоянный угол б—у; постоянство этого угла означает, что конец вектора V описывает дугу окружности, опирающуюся на хорду F.
На основании (4-10) А/С равно значению W при Л=0;
А/С = Н7а=0.
Следовательно,
F = Wb_n — W. .
Л=0 Л=оо*
На рис. 4-32 показан способ графического построения окружности 1Г по заданным значениям А/С, BID и угла б—у. У конца вектора F (служащего хордой искомой окружности) от его продолжения откладывается угол б—у, положительный — против хода часовой стрелки, отрицательный — по ходу часовой стрелки. Полученная прямая касательна к искомой окружности. Центр этой окружности находится в точке О' пересечения перпендикуляров, восстановленных к касательной (в конце вектора AID) и к хорде в середине вектора F. Из построения следует, что положительным значениям
76
параметра k соответствует дуга окружности, заключенная между хордой и касательной.
Каждая точка полученной окружности соответствует определенному численному значению параметра k. Для нахождения точки круговой диаграммы, соответствующей задан-
угольников MPN и MLQ следует, что
LQ _ PN
ML “ МР’
откуда
Рис. 4-32. Построение круговой диаграммы по уравнению (4-9). а — при 6 — у < 0; б — прн 6 — у > 0.
ному значению параметра А, пользуются следующим графическим приемом (рис. 4-33).
Выбирается точка L на хорде MN так, чтобы выполнялось условие mML=|C/D|, т. е. чтобы отрезок
Рис. 4-33. Построение линии переменного параметра.
ML в удобном масштабе т (например т=1) изображал величину |C/D|. Далее проводится прямая из точки L под углом у—б к хорде MN. Продолжение любого текущего вектора V до этой прямой (точка Q) дает отрезок LQ, который равен k/m. В самом деле, из подобия тре-
Таким образом, полученная точка Р на круговой диаграмме соответствует заданному значению параметра А.
По мере удаления точки Q точка Р перемещается в сторону точки М, которая соответствует значению А= со (линия МР становится параллельной линии LQ).
Вспомогательная прямая LQ носит название линии переменного параметра.
Построение круговой диаграммы с помощью дробно-линейной функции W иллюстрировано ниже примерами, относящимися к разветвленной электрической цепи.
Пример 4-4. На рис. 4-34, а показана схема так называемого фазовращателя. В плечи мостовой схемы включены два равных сопротивления и, емкость С] и переменное сопротивление г.
Пользуясь графическим методом, описанным выше, направив вектор U по действительной оси, начертим круговую диаграмму напряжения йтп между зажимами тип при изменении г от 0 до со.
Напряжение 1/тп находится как разность напряжений На емкости и на сопротивлении г:
0^ = 0
1
j ® Ci
1
/ <в Ci
77
и_________С __й
2 1 -J- jf a Сх 2
й
Выражение j р. ш £ представляет собой дробно-линейиую функцию (4-10).
При этом . D л
F—U-, ~ =i<£>Ci, k = r, б —у = — .
Круговая диаграмма пристраивается к концу вектора [—U/2] (рис. 4-34,6).
Выражение 1 _____J_____ ri 4- / © £i Г1 + /<в£1 + г“ , , 1
1 +--------г
ri +1 ©
представляет дробио-линейную функцию (4-10); при этом
F==A_A =_________
С С + / и £х ’
Рис. 4-34. Пример 4-4.
Линия переменного параметра проведена на этом рисунке через точку L, совпадающую в данном случае с точкой N, под углом —90° к линии MN.
Точка Q отвечает условию
D 1
С + /©£.! ’
, х , и £i
k = г, о — у = — <Р = — arctg----.
П
LQ
ML
rtoCi.
В частности, указанным на рис. 4-34,6 положениям точек Р и Q соответствует значение г= 1/соС).
Как видно из диаграммы, при изменении г от 0 до °° модуль вектора l/mn сохраняется неизменным (UТПП-- £7/2), а фа-
зовый сдвиг йтп относительно приложенного напряжения I) изменяется от 0 до 180°
Пример 4-5. Построить круговую диаграмму комплексной проводимости электрической цепи *, показанной на рис. 4-35, а, при переменном сопротивлении г.
Комплексная проводимость заданной цепи
Y = — — } —*— +---------; ’------ .
© £д гj -)- ] © £, г
1 Здесь изображена схема замещения асинхронного двигателя.
На продолжении вектора------, сме-
r ri+jaLi
78
6—у=—<p по ходу часовой стрелки. Полученная прямая касательиа к искомой окружности, центр которой находится в точке О'.
Рабочая часть диаграммы показана на рис. 4-35, б жирной линией.
4-14. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
4-1. Сопротивление 2 ом и емкость 0,191 мкф соединены параллельно. Найти эквивалентиую схему с 'последовательным соединением г и С прн частоте [=1; 1,5; 2 мгц.
Ответ: г=0,296; 0,143; 0,083 ом; С= =0,224; 0,206; 0,199 мкф.
4-2. Параллельно соединены ветви, одна из которых состоит из С=10 мкф, а вторая — нз последовательно соединенных г= = 10 ом и £= 100 мгн. Вычислить комплексное сопротивление цепи при ш=377 рад!сек.
Ответ: 13,5+/43,4 ом.
4-3. Добавив в схеме, взятой из предыдущей задачи, последовательно г =10 ом и подводя к цепи £7=100/ 0е в, вычислить токи в ветвях и суммарный ток; построить векторную диаграмму.
Ответ: 0,347 /101°6'; 2,36 /—64°:
2,02 / —бГЗО'.
4-4. Индуктивная катушка, имеющая г=8 ом и L=0,05 гн, соединена параллельно с емкостью С=1 мкф. Найти частоту, при которой напряжение на зажимах данной цепи в фазе с суммарным током; определить сопротивление цепи.
Ответ: 713 г^; 6 250 ом.
4-Б. Параллельно соединены две ветви: первая ветвь состоит из последовательно соединенных и и £ и ее сопротивление равно 40+/30 ом; вторая состоит из последовательно соединенных гг и С, и ее сопротивление равно 80—/ 150 ом. Определить сопротивление и проводимость всей пепи, если частота возрастает в 1,5 раза; начертить на комплексной плоскости сопротивления и проводимости ветвей н всей цепи.
Ответ: 58,4 /21°35' ом;
1,71 • 10-» /—21^35' сим.
4-6. Параллельно соединены три ветви: первая состоит из л =25 ом, вторая — из С=50 мкф, третья — из индуктивной катушки, имеющей г2=10 ом и £,=50 мгн. Напряжение иа ветвях равно 100 cos 400 t, в. Вычислить действующее значение суммарного тока и активную мощность цепи.
Ответ: 4,47 а; 330 вт.
4-7. Индуктивная катушка, имеющая г и L, соединена параллельно с емкостью С. Найти L и С, при которых сопротивление всей цепи равно 500 / 0° ом, если г= = 100 ом и угловая частота ш=105 рад)сек.
Ответ: £=2 мгн; С=0,04 мкф.
4-8. Последовательно с емкостью С подключена цепь, состоящая из г=500 ом и
L, соединенных параллельно. Приняв <о= = 105 рад/сек, найти L и С, при которых общее сопротивление равио 100 / 0° ом.
Ответ: 2,5 мгн, 0,05 мкф.
4-9. Доказать, что полное сопротивление цепи, состоящей из параллельно соединенных индуктивной катушки (г, £) и
I
емкости (С), при частоте ц>= • 11 ~ не за-V 2LC
висит от г.
4-10. Сопротивления 50—/ 20, 100+/ 0 и 40+/ 60 ом соединены треугольником. Преобразовать данный треугольник в эквивалентиую звезду.
Ответ: 18,5+/ 7,7; 23,1—/ 15,4;
26,5+/ 26 ом.
катушка, имеющая
4-11. Индуктивная сопротивление 15+/ 20 ом, последовательно подключена к участку цепи, состоящему из параллельно соединенных г=10 ом и
С= —----Ф- Определить действующее зна-
30 со
чение тока в индуктивной катушке и напряжения на г и С, если к зажимам всей цепи приложено напряжение 100 / 0° е.
Ответ: 2,76—/ 1,96 а; 19—/ 26 в.
4-12. Два генератора, имеющих одинаковую частоту, работают параллельно иа общую нагрузку. Заданы: комплексные э. д. с. генераторов Et и Ег, комплексные сопротивления генераторов Z\ и Z2, комплексное сопротивление нагрузки Zs.
Определить ток в нагрузке.
Ответ:
Z3£i +
ZjZ2 -р Z2Zs + Z,Zt
4-13. Показать с помощью круговой диаграммы, как изменяются напряжения на элементах г и L, включенных последовательно, если г изменяется от нуля до бесконечности, при неизменном напряжении 200 в на зажимах цепи. Построить линию переменного параметра г и найти графически напряжение на £ и фазовый сдвиг тока относительно приложенного напряжения при /=400 гц, £,=31,8 мгн и г=60 ом.
Ответ: 160 в; 53°.
4-14. В чем заключается удобство расчета схемы с двумя узлами?
4-15. В каких случаях целесообразно применять метод единичного тока?
4-16. Привести пример, в котором требуется преобразовать звезду в треугольник (или треугольник в звезду).
4-17. Пояснить ход построения круговой диаграммы по заданному комплексному выражению.
4-18. Пояснить ход построения лииин переменного параметра.
4-19. Как определяется рабочая часть круговой диаграммы?
4-20. В чем заключается преимущество метода геометрических мест перед аналитическими методами?
79
Глава пятая
МЕТОДЫ РАСЧЕТА СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
5-1. ПРИМЕНЕНИЕ ЗАКОНОВ КИРХГОФА ДЛЯ РАСЧЕТА СЛОЖНЫХ ЦЕПЕЙ
В предыдущих главах рассматривались простейшие схемы электрических цепей — одноконтурные схемы, цепная схема с одним источником электрической энергии и схемы с двумя узлами. Были описаны методы преобразования схем, с помощью которых в ряде случаев удается упростить расчет разветвленной электрической цепи. При этом под расчетом цепи подразумевается вычисление электрических величин или их отношений при заданных схеме и параметрах цепи.
В случае, когда схема электрической цепи достаточно сложна и не приводится к схеме одноконтурной цепи или цепи с двумя узлами, пользуются более общими методами расчета.
Описываемые ниже методы и теоремы применимы для цепей постоянного и переменного тока; ради общности изложения они приводятся в комплексной форме.
В общем случае искомые электрические величины и их соотношения могут быть найдены в результате совместного решения системы уравнений, выражающих первый и второй законы Кирхгофа для заданной электрической цепи.
Положим, что в схеме, содержащей р ветвей и q узлов, заданными являются источники э. д. с., а искомыми — токи в ветвях. Следовательно, число неизвестных равно числу ветвей.
По первому закону Кирхгофа, выражающему равенство нулю алгебраической суммы токов в узле, может быть записано q—1 независимых уравнений; уравнение для последнего, 9-го, узла является следствием предыдущих q—1 уравнений. Действительно, ввиду того, что каждая ветвь связывает между собой два узла, ток каждой ветви входит дважды с различными знаками в уравнения, записанные для
q узлов. Поэтому, если просуммировать q уравнений, то получится тождество вида 0=0. Следовательно, одно из этих уравнений является зависимым, т. е. вытекающим из всех остальных уравнений.
Узлы, для которых записываются независимые уравнения по первому закону Кирхгофа, можно назвать независимыми узлами. Из сказанного следует, что из общего числа q узлов любые q—1 узлов являются независимыми, а оставшийся последний узел является зависимым.
По второму закону Кирхгофа, выражающему равенство алгебраической суммы э. д. с. в контуре алгебраической сумме падений напряжения в нем, может быть записано р—q+1 независимых уравнений. В самом деле, если ко всем ветвям применить закон Ома, то получатся р уравнений вида
(5-1)
здесь Ulk—комплексное Напряжение между узлами i и k;
Ёп, 1п— комплексные э. д. с. источника и ток в п-й ветви, направленные от узла i к узлу k;
Zn — комплексное сопротивление той же ветви.
В систему уравнений вида (5-1) входят р неизвестных токов и q—1 неизвестных потенциалов Uu Uk и т. Д. (потенциал одного из узлов принимается равным нулю). Если из имеющейся системы уравнений исключить эти неизвестные потенциалы, останутся р—^+1 уравнений, связывающих комплексные э. д. с. источников с напряжениями на комплексных сопротивлениях; полученные таким путем уравнения выражают второй закон Кирхгофа.
Итак, расчет электрической цепи с помощью первого и второго законов Кирхгофа сводится к решению (q—1) + (р—9+1)=р уравнений — по числу ветвей.
80
Контуры, для которых уравнения, записанные по второму закону Кирхгофа, являются независимыми, называются независимыми контурами.
На рис. 5-1 в виде примера показана электрическая схема с числом ветвей р=9 и числом узлов q=6. Соответственно число уравнений по
Рис. 5-1. Электрическая схема с четырьмя независимыми контурами.
первому закону Кирхгофа равно 6—1=5 и по второму закону Кирхгофа 9—6+1=4. В схеме рис. 5-1 независимыми являются четыре контура.
На рис. 5-1 показан один из многих возможных вариантов выбора независимых контуров.
Для того чтобы уравнения по второму закону Кирхгофа, а следовательно, и сами контуры были независимыми, достаточно, чтобы каждый последующий контур отличался от предыдущих хотя бы одной новой ветвью. Например, если в схеме рис. 5-1 обходить контур 4 не в последнюю очередь, то каждый последующий контур будет содержать новую ветвь.
Независимый контур в отдельных случаях может не содержать новой ветви схемы, например контур 4 в схеме рис. 5-1, если обходить контуры в порядке их нумерации.
Всегда можно выбрать такой порядок обхода независимых контуров, чтобы каждый последующий контур содержал новую ветвь схемы.
При выборе независимых контуров заданную схему цепи удобно изображать в виде графа, в котором ветви представляются отрез
ками линий; идеальный источник напряжения учитывается как короткозамкнутая ветвь, а идеальный источник тока — как разомкнутая ветвь. На рис. 5-2, а показан граф схемы рис. 5-1.
Граф содержит всю информацию, относящуюся к геометрической структуре соединения ветвей. Часть
Рис. 5-2. Граф схемы на рнс. 5-1 (а) и одно из его возможных деревьев (б).
графа, содержащая все узлы, но не содержащая ни одного замкнутого контура, называется деревом. Легко показать, что число ветвей дерева на единицу меньше числа узлов схемы, т. е. равно q—1.
Ветви графа, не входящие в состав дерева, называются главными ветвями дерева, или хордами. Подключений к дереву каждой из главных ветвей создает по одному независимому контуру. Совокупность главных ветвей дерева называется дополнением дерева.
Так как граф содержит р ветвей, а дерево q—1, то число главных ветвей дерева равно р—(q—1) =р—q+ + 1, т. е. равно числу независимых контуров.
На рис. 5-2, б сплошными линиями показано одно из возможных деревьев графа, а пунктиром — главные ветви дерева.
Из сказанного следует способ выбора независимых контуров; чертится дерево схемы и затем поочередно добавляются главные ветви. Любой контур, образуемый добавлением новой ветви, является независимым, так как он отличается от предыдущих контуров новой ветвью.
В итоге, когда к дереву добавляются все главные ветви, получится граф схемы и число независимых контуров будет достаточным для расчета цепи.
6—1118
81
Предлагаем читателям выбрать таким способом независимые контуры в схеме рис. 5-1.
Для получения независимых контуров, достаточных для расчета цепи, можно начать и не с построения дерева, а с самого графа схемы, а затем поочередным размыканием главных ветвей дойти до дерева. В этом случае руководствуются следующим правилом: в заданной схеме выбирается какой-либо контур; размыкается одна из ветвей этого контура и в оставшейся части схемы выбирается новый контур; затем размыкается одна ветвь этого нового контура и т. д. до тех пор, пока в схеме не останется ни одного контура. Предлагаем читателям применить для выбора независимых контуров и это правило.
Пример 5-1 [Л. 10]. В мостовой схеме, представленной на рис. 5-3, заданы все комплексные сопротивления н э. д. с. Е. Тре-
Рис. 5-3. Пример 5-1.
буется определить ток /5 в ветви Zs (ток в диагонали мостовой схемы).
Схема содержит четыре узла и шесть ветвей. Следовательно, могут быть составлены три уравнения по первому закону Кирхгофа и три уравнения по второму закону Кирхгофа:
для узла А
-Д—Zs + /e = 0;
для узла В
Za — + Z5 = 0;
для узла С
Zs + Ц — ze = 0;
для контура ABDA
—24 А Ч- 22 z2 — =
для контура BCD В
ZJа — ZJ4 Ч~ 2В Z6 = 0;
для контура АВСЛ
2а^гЧ“2згз+2в/в — Ё.
В полученной системе шести уравнений неизвестными являются токи в вет
вях. Решая систему уравнений относительно искомого тока, находим:
Ё
т
где М = Ze [(Zx + Z4) (Z2 + Z3) +
4—Ze (Zi + Zs + Za -|- Z4)] + ZiZ4 X
X (Z2 + Za) -f- ZjZa (Zi + Z4) -f-+ 2a (Zi + Z2) (Za + Z4)'.
Полученное выражение показывает, что ток в диагонали равен нулю, если выполнено условие Z,Z3=Z2Z4 (условие равновесия мостовой схемы).
5-2. МЕТОД КОНТУРНЫХ ТОКОВ
Метод контурных токов является одним из основных методов расчета сложных электрических цепей, которым широко пользуются на практи-
Рис. 5-4. Иллюстрация к методу контурных токов.
ке. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так называемые контурные токи, замыкающиеся в контурах.
На рис. 5-4 в виде примера показана двухконтурная электрическая цепь, в которой Л и Аг— контурные токи. Токи в сопротивлениях Zx и Z2 равны соответствующим контурным токам; ток в сопротивлении Z3, являющемся общим для обоих контуров, равен разности контурных токов Л и /г, так как эти токи направлены в ветви Z3 встречно ’. При этом если положительное направление искомого тока в ветви Z3 принять совпадающим с направлением контурпого тока Л, то ток в ветви будет равен Ц—12. В противном случае он будет равен /2—Л-
1 Следует отметить, что если положительное. направление одного из контурных токов (/i нли Z2) изменить на обратное, то ток в ветви Z3 будет равен сумме этих токов.
82
Число уравнений, записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, т. е. для электрической схемы с числом узлов q и числом ветвей р задача нахождения контурных токов сведется к решению системы р—<7+1 уравнений. Так, в схеме рис. 5-4 <7=2, р=3; следовательно, число уравнений равно 3—2+1=2 (числу независимых контуров) .
Условимся сумму комплексных сопротивлений, входящих в контур, называть собственным сопротивлением контура, а комплексное сопротивление, принадлежащее одновременно двум или нескольким контурам,— общим сопротивлением этих контуров.
Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от данного контурного тока в собственном сопротивлении контура берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис. 5-4, где направление обоих контурных токов выбрано по ходу часовой стрелки.
Для заданной электрической схемы с двумя независимыми контурами (рис. 5-4) могут быть записаны два уравнения по второму закону Кирхгофа, а именно:
Ё1— (21+Z3) Ii — Zs /я;
— Ёа~ —Z3 A+(Za+Z3)/a;
здесь Zj+Zg и Z2+Z3 — собственные сопротивления контуров 1 и 2;
Z3— общее сопротивление
контуров 1 и 2 (знак минус в уравнениях обусловлен выбором положительных направлений контурных токов).
Если заданная электрическая схема содержит п независимых контуров, то на основании второго закона Кирхгофа получается система из п уравнений:
£i=Z(ii) А+^в) А"1 "
"Ь Л1п> А*
Д2==2(21) A”b^(22) А-^' ’ ’ “Ь
"1" ^(2п) А»
(5-2)
2(п1) А+Z(n2) /2+ • • • +
п<
здесь Et— контурная э. д. с. в контуре 1(1=1, 2, .... п), т.е. алгебраическая сумма э. д. с., действующих в данном контуре; э. д. с., совпадающие по направлению с направлением обхода, берутся со знаком плюс, а направленные встречно — со знаком минус;
2(п) — собственное сопротивление контура i;
Z(Zft)— общее сопротивление — контуров1 i и k.
В соответствии со сказанным ранее собственные сопротивления Z(il) войдут со знаком плюс, поскольку обход контура принимается совпадающим с положительным направлением контурного тока А- Общие сопротивления Zift войдут со знаком минус, когда токи А и А направлены в них встречно.
Решение уравнений (5-2) относительно искомых контурных токов может быть найдено с помощью определителей:
F 7 ...7 ^1^(12) (1п)
L = — ^2^(22) ^<2п) •
1
F 7 .. .7
^,+(«2) (пл)
1 Индексы собственных и общих сопротивлений контуров заключены в скобки для отличия нх от входных и передаточных сопротивлений, приводимых в последующих разделах книги.
6*
83
^<11)^1 ' ‘ ’Z(ln)
/# = —— ^(21)^2’ ' '^(2n)
ДЛ................
7 P .. .7 ь(п1)1'л (nn)
и t. д.< где определитель системы 1
7 7 .. .7
^(11^(12) ^(In)
7 7 • -Z
^(21)^(22) (2n)
7 7 ...7
^(nl)^(n2) ^(nn)
Согласно правилу разложения определителя по элементам столбца определитель равен сумме произведений элементов столбца на их алгебраические дополнения. Поэтому решение уравнений запишется в виде 2 *
/1 = ёА1 + £2^- + --- + дг дг
। Р Дд1 .
+ Е"“5Г-
/,-£141 + £Л'!+-" +
Дг Дг
I Р Дд2 .
+ " Дг ’
(5-3)
Д(А — алгебраическое дополнение элемента определителя системы, т. е. умноженный на (—l)/+ft минор элемента Z(th) (минор образуется из определителя системы исключением из него i-й строки и А-го столбца).
• Сокращенно система уравнений (5-3) записывается в виде
п
<5'4)
f=l
Первый индекс алгебраического дополнения i, обозначающий номер
1 Определитель снабжен индексом г, так как его элементами являются комплексные сопротивления.
2 На практике во многих случаях реше-
ние системы уравнений (5-2) может быть
выполнено более просто последовательным
исключением неизвестных.
строки, вычеркиваемой в определителе системы, соответствует номеру контура, контурная э. д. с. которого умножается на данное алгебраическое дополнение. Второй индекс k, обозначающий номер столбца, вычеркиваемого в определителе системы, соответствует номеру контура, для которого вычисляется контурный ток.
Уравнения (5-2), выражающие второй закон Кирхгофа, записаны в предположении, что источниками электрической энергии служат источники напряжения. При наличии в электрической схеме источников тока последние могут быть заменены эквивалентными источниками напряжения. Если проводимости источников тока равны нулю, то целесообразно в этом случае выбрать заданные токи в качестве контурных; тогда число неизвестных контурных токов и соответственно число уравнений сократится на число заданных токов.
Если в заданной электрической схеме имеются параллельные ветви, то замена их эквивалентным комплексным сопротивлением сокращает число контуров (за счет тех, которые образованы параллельными ветвями).
Электрические цепи могут быть планарными или непланарными.
Планарная, или плоская, электрическая цепь может быть вычерчена на плоскости в виде схемы с неперекрещивающимися ветвями. В некоторых случаях пересечение ветвей в электрической схеме, являющееся результатом принятого способа начертания схемы, устраняется при другом способе изображения данной планарной электрической цепи, как это, например, представлено на рис. 5-5.
Электрическая цепь, приведенная на рис. 5-5, а, планарная, так как имеющееся пересечение ветвей устранимо в соответствии с рис. 5-5,6.
Непланарная электрическая цепь не может быть вычерчена на плоскости в виде схемы с неперекрещивающимися ветвями. Примером такой электрической цепи служит приведенная на рис. 5-5, в непланар
84
ная цепь, пересечение ветвей в которой не может быть устранено.
Если направление контурных токов во всех контурах планарной электрической цепи одинаково, например совпадает с ходом часовой стрелки, то общие сопротивления смежных контуров входят в систему
£
/2 = — [Zs Za + Za (Zi + 22 + Zs)], м
где M имеет то же значение, что и в примере 5-1.
Искомый ток в диагонали мостовой схемы равен разности контурных токов
h — f 2 — h— "ГГ (ZsZi — Zi Za),
Рис. 5-5. Планарные (а и б) и непланарная (в) электрические цепи.
уравнений (5-2) со знаком минус, так как контурные токи смежных контуров направлены в общих ветвях встречно. Направление контурных токов по ходу часовой стрелки принимается во всех контурах, кроме внешнего контура, охватывающего всю схему. В последнем контурный ток направляется против часовой стрелки (см. пример 5-2). Это правило, однако, не является обязательным.
В случае непланарной электрической цепи не представляется возможным иметь в общих ветвях только разности контурных токов, как это, например, видно из схемы рис. 5-5, в.
Пример 5-2 [Л. 10]. Пользуясь методом контурных токов, определить ток в диагонали мостовой схемы рис. 5-6.
Выбранные положительные направления контурных токов Ii, /2, /», указаны на схеме стрелками. Число уравнений, записываемых по второму закону Кирхгофа, равно трем (по числу независимых контуров):
0 = (Zj Z2 -f-Z6) — Zs 72 — Z2 /a;
0 = — Zs /1 -f- (Zs + Z4 -f- Zs) /2 — Zs I»,
—Ё — — z2it—zsis-t- (Z2 + Zs + ze) 7S-
Решение полученной системы уравнений относительно контурных Токов ZI и /2 дает:
К — “ [2а Za + Z2 (Za + Z4 Ze)];
что совпадает с полученным в примере 5-1 ответом.
Следует заметить, что если в заданной схеме контуры выбрать так, чтобы через
Рис. 5-6. Пример 5-2.
ветвь Ze проходил только один контурный ток, то искомый ток в ветви Z5 будет равен именно этому контурному току, т. е. задача сведется к нахождению только одного контурного тока (вместо двух).
5-3. МЕТОД УЗЛОВЫХ НАПРЯЖЕНИИ
Метод узловых напряжений заключается в том, что на основании первого закона Кирхгофа определяются напряжения в узлах электрической цепи относительно некоторого базисного узла. Эти искомые напряжения называются узловыми напряжениями, причем положительное направление их указывается стрелкой от рассматриваемого узла к базисному.
Напряжение на какой-либо ветви равно, очевидно, разности узло
85
вых напряжений концов данной ветви, произведение же этого напряжения на комплексную проводимость данной ветви равно току в этой ветви. Таким образом, зная узловые напряжения в электрической цепи, можно найти токи в ветвях.
Если принять потенциал базисного узла равным нулю, то напряжения между остальными узлами
Рис. 5-7. Иллюстрация к методу узловых напряжений.
и базисным узлом будут равны также потенциалам этих узлов. Поэтому данный метод называется также методом узловых потенциалов.
На рис. 5-7 в виде примера изображена электрическая схема с двумя источниками тока, имеющая три узла 1, 2 и 3. Выберем в данной схеме в качестве базиса узел 3 и обозначим напряжения узлов 1 и 2 через Ui и Uz- Согласно принятым на рис. 5-7 обозначениям комплексные проводимости ветвей равны соответственно:
Для заданной электрической цепи с тремя узлами могут быть записаны два уравнения по первому закону Кирхгофа, а именно:
для узла 1
4 = m+T3A-i72) =
= (Yl + Y3)Ul-YJU3,
для узла 2
/2 = У2С72 + У3 А-^) =
= -УД + (Гг + ^1/8.
Величина У + ^з, представляющая сумму комплексных проводимо
86
стей ветвей, сходящихся в узле I, называется собственной проводимостью узла /; величина У3, равная комплексной проводимости ветви между узлами 1 и 2, входящая в уравнения со знаком минус, называется общей проводимостью между узлами 1 и 2.
Если заданы токи источников тока и комплексные проводимости ветвей, то узловые напряжения находятся совместным решением уравнений.
В общем случае, если электрическая схема содержит q узлов, на основании первого закона Кирхгофа получается система из q—1 уравнений (узел q принят за базисный):
'1= Wi+y(i2A+--+
+у й • (5-5)
К—1 ~ ^(<7—1.2)^2"*“
i 4-У(?_1, ?_1 А-г
Здесь ток источника тока, приходящий к узлу, берется со знаком плюс, а отходящий от узла — со знаком минус; У(Ц) — собственная проводимость всех ветвей, сходящихся в данном узле i; У«А) — общая проводимость между узлами i и k, входящая со знаком минус при выбранном направлении всех узловых напряжений к базису, независимо от того, является ли данная электрическая цепь планарной или непланарной.
Решив систему уравнений (5-5) при помощи определителей *, получим формулу для напряжения k-ro узла относительно базиса:
«7-1
и 7=1
(5-6)
где Ду — определитель системы2:
1 См. сноску 2 на стр. 84.
2 Определитель снабжен индексом у, так как его элементами являются комплексные проводимости.
V Y . -Y
r (11/ (12) ' (l.<7—1>
Y Y • • -Y
1 (21/ (22) 1 (2,?-l)
Y Y • -Y
1 (<7-1.1/ (0—1,2) 1 (<7-l. 0-1)
Ait— алгебраическое дополнение элемента y(ift) данного определителя.
Первый индекс i алгебраического дополнения, обозначающий номер строки, вычеркиваемой в определителе системы, соответствует номеру узла, заданный ток источника тока которого умножается на данное алгебраическое дополнение. Второй индекс k, обозначающий номер столбца, вычеркиваемого в определителе системы, соответствует номеру узла, для которого вычисляется узловое напряжение.
Уравнения (5-5), выражающие первый закон Кирхгофа, записаны в предположении, что в качестве источников электрической энергии служат источники тока. При наличии в электрической схеме источников напряжения последние должны быть заменены эквивалентными источниками тока.
Если в схеме имеются ветви, содержащие только э. д. с. (проводимости таких ветвей бесконечно велики), то эти ветви следует рассматривать как источники неизвестных токов, которые затем исключаются при сложении соответствующих уравнений. Дополнительными связями между неизвестными узловыми напряжениями будут являться известные напряжения между узлами, равные заданным э. д. с.
При наличии только одной ветви с э. д. с. и бесконечной проводимостью целесообразно принять за базисный узел один из узлов, к которым примыкает данная ветвь; тогда напряжение другого узла становится известным и число неизвестных сокращается на одно.
Метод узловых напряжений имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа. Если за
данная электрическая схема имеет q узлов и р ветвей, то в соответствии с вышесказанным метод узловых напряжений представляет преимущество при q—1<р—q+1 или, что то же, при 2(<у—1)<р.
Здесь имеется в виду общий случай, когда число уравнений не сокращается за счет известных контурных токов или узловых напряжений.
Пример 5-3 [Л. 10]. Пользуясь методом узловых напряжений, определить ток в диагонали мостовой схемы (рнс. 5-6).
Рнс. 5-8. Пример 5-3.
В результате замены заданного источника напряжений эквивалентным источником тока получается схема (рис. 5-8), содержащая четыре узла. Для этой схемы по первому закону Кирхгофа записывают 4—1=3 уравнения (по числу независимых узлов). Если выбрать в данной схеме в качестве базиса узел 4 н направить узловые напряжения к базису, то уравнения примут вид:
для узла 1
УеЁ = (У, + Уг + Yt) -Y2U2- У, 03;
для узла 2
0 = — Y2Ui +(Уг + У« + Уе) — YgUg;
для узла 3
-YtE = -YeU1-Y3U2 +
+ (Y3 + Yt+Ye)Ua.
Решение полученной системы уравнений относительно даст:
Ё
Us = — Ув(У2У4-У1Уз), где
N = Уб [(Уг + У2) (Y3 + У4) +
+ Ув (Ki + У2 + У„ + У4)] +
+ У1 У4(У2 + И>) + У* У3 (У, +У*) +
+ Ув (Ут +''л) (У3 + Уз).
Умиожив найденное узловое напряжение й2 на проводимость Уб диагональной ветви мостовой схемы и изменив знак в соответ
87
ствии с выбранным ранее направлением тока Ig (рис. 5-3), найдем искомый ток:
Л=-^-^^(Г1Уз-Г1!Г4).
5-4. МЕТОД НАЛОЖЕНИЯ
В линейной электрической цепи, содержащей источники напряжения, контурные токи (и соответственно токи в ветвях) представляют линейные функции контурных э. д. с. Математически они' выражаются формулой (5-4):
4=1
Физический смысл этой формулы заключается в том, что ток в любом контуре линейной электрической цепи может быть получен как алгебраическая сумма токов, вызываемых в этом контуре каждой из э. д. с. в отдельности.
Метод расчета токов, основанный на определении токов в одном и том же контуре (или в ветви) при поочередном воздействии э. д. с. и последующем алгебраическом сложении этих токов, называется методом наложения.
При определении частичных слагающих токов по методу наложения необходимо считать включенными внутренние сопротивления тех источников напряжения, которые принимаются отсутствующими при вычислении слагающих токов. Если в цепи заданы источники э. д. с., т. е. внутренние сопротивления источников равны нулю, то при определении токов, вызываемых какой-либо э. д. с., все остальные источники э. д. с. закорачиваются.
В свою очередь в линейной электрической цепи, содержащей источники тока, узловые напряжения (и соответственно напряжения на ветвях) представляют линейные функции от задающих токов источников. Математически они выражаются формулой (5-6):
я—1
Физический смысл этой формулы заключается в том, что узловое напряжение любого узла линейной электрической цепи может быть получено как алгебраическая сумма напряжений, вызываемых в этом узле каждым из задающих токов в отдельности. Таким образом, формула (5-6), так же как и (5-4), представляет собой математическую запись метода наложения, справедливого для линейных электрических цепей.
При определении частичных слагающих узловых напряжений по методу наложения необходимо считать включенными внутренние проводимости тех источников тока, которые принимаются отсутствующими при вычислении слагающих напряжений. Если источники тока заданы без внутренних проводимостей, т. е. проводимости их равны нулю, то при пользовании методом наложения ветви с неучтенными источниками тока разрываются.
Если в линейной электрической цепи заданными являются одновременно источники напряжения и источники тока, то метод наложения применим и в этом случае. Например, ток в каком-либо контуре данной цепи может быть получен в результате алгебраического сложения токов, вызываемых в этом контуре поочередным действием источников напряжения и тока. При этом внутренние сопротивления отсутствующих источников напряжения и внутренние проводимости отсутствующих источников тока сохраняются в схеме.
Пример 5-4. Пользуясь методом наложения, определить ток в ветви Z3 схемы рис. 5-4.
Искомый ток /3 определяется как сумма токов /3 и /3 , проходящих через ветвь Z3 под воздействием источников э. д. с. Еу (рнс. 5-9, а) и Е3 (рнс. 5-9,6), взятых порознь.
Токи 73 и /3 суммируются, а не вычитаются, так как положительные направления их выбраны совпадающими:
т z* Ё1
3 ^2 + ^8 7 I ^3
1 + zs+z8
88
_____Z, £t____
^2 + ^2 ^3 4“ Z3
r _ _A__ _
3 Zv+Z3 2 ZiZs
z2 T 7 . _
каждой из которых э. д. с. источников равны. В первой схеме источники имеют э. д. с.
— (£!-1-£2) =10 в и полярность их одинакова, во второй схеме источники имеют э. д. с. — (£i—£2) =2 в и полярность раз-
следовательно,
21£г
2а + Z8 Zx
лична.
Пользуясь методикой, описанной в § 4-9, произведем соответствующие рассе-
•г Z2£1-|-Z1£2
'3 ~ 'з + ‘з —
Z1 Z2 + Z2 ~л~ Z3Zi
Пример 5-5. Задана симметричная схема с неравными э. д. с. £j = 12 в и £2=8 в
чения и замыкания накоротко по оси симметрии (рис. 5-10,6 и в).
Искомые токи найдутся методом наложения:
Рис. 5-9. Пример 5-4.
10 2
/1 = — + — = 2,83 а;
1 4 6
10 2
/2 =---------— =2,17 а.
2 4 6 ’
5-5. ВХОДНЫЕ'И ПЕРЕДАТОЧНЫЕ
ПРОВОДИМОСТИ И СОПРОТИВЛЕНИЯ
Условимся называть источник э. д. с. независимым или автономным (самостоятельным), если э. д. с. источника не зависит от на-
Рис. 5-10. Пример 5-5.
(рис. 5-10, а). Значения сопротивлений (в омах) указаны на схеме. Вычислить токи h и /2. Заметив, что £i =—(£(+£2) + +-^-(£,-£,) и E2=-^-(£i + £2)— 1 .
— ~(Е^—£2), можно вместо заданной схемы рассмотреть две симметричные схемы, в
Рис. 5-11. Определение понятий входных и передаточных проводимостей и сопротивлений.
пряжений и токов в цепи (с понятием «зависимый» источник мы встретимся в § 5-7).
Пусть в какую-либо ветвь контура электрической цепи включен независимый источник э. д. с. Et (рис. 5-11,а), причем данная ветвь не является общей, а принадлежит только контуру i. Если вся остальная часть электрической цепи не содержит независимых источников электрической энергии, то в соответствии с формулой (5-4) заданная э. д. с. Ef вызовет в данном контуре i и в каком-либо другом контуре k токи
/,“^1 (5-7)
И
Ц = (5-8)
Аг
89
На рис. 5-11, а показаны контуры ink заданной электрической цепи.
Отношение контурного тока к э. д. с., действующей в том же контуре, при отсутствии независимых источников во всех остальных контурах называется входной проводимостью электрической цепи:
4==4 = У«- (5-9)
В свою очередь отношение контурного тока к э. д. с., действующей в другом контуре, при отсутствии независимых источников во всех остальных контурах называется передаточной (или взаимной) Проводимостью контуров:
4 = —= (5-Ю)
Элементами определителя системы и алгебраических дополнений в выражениях (5-9) и (5-10) служат собственные и общие сопротивления контуров заданной электрической цепи. Определитель Д2 имеет размерность сопротивления в степени п, где п — порядок определителя (равный числу независимых контуров данной цепи); алгебраические дополнения Дн и Д^ имеют размерность сопротивления в степени п—1. В результате деления алгебраического дополнения на определитель системы получается величина, имеющая размерность проводимости.
На основании (5-9) и (5-10) заключаем, что входная и передаточная проводимости численно равны токам в контурах i и k, когда в контуре i действует э. д. с., равная 1 в.
С учетом обозначений (5-9) и (5-10) выражения для токов (5-4) принимают вид:
Л- (5-11)
/=1
Аналогичные рассуждения могут быть проведены и в отношении узлов i и k электрической цепи в предположении, что к узлу i приключен независимый источник тока1 Ц, а
1 Источник тока называется независимым, нли автономным, если ток источника не зависит от напряжений и токов в цепи.
вся остальная часть цепи не содержит независимых источников (рис. 5-11,6). В соответствии с (5-6) заданный ток Ц обусловит появление узловых напряжений в узлах i и k:
= (5-12)
и
= (5-13)
Отношение напряжения в узле к току, заданному в том же узле, при отсутствии в схеме других источников называется входным сопротивлением электрической цепи
4 = £-'=£„, (5-14)
и соответственно отношение напряжения в узле к току, заданному в другом узле, при отсутствии в схеме других источников называется передаточным (или взаимным) сопротивлением узлов:
= '(5-15)
Элементами определителя системы и алгебраических дополнений в (5-14) и (5-15) служат собственные и общие проводимости узлов заданной электрической цепи. Определитель Др имеет размерность проводимости в степени т, где т — порядок определителя (на единицу меньший числа узлов в заданной схеме); алгебраические дополнения Дн и Дгь имеют размерность проводимости в степени т—1. В результате деления алгебраического дополнения на определитель системы получается величина, имеющая размерность сопротивления.
На основании (5-14) и (5-15) заключаем, что входное и передаточное сопротивления узлов численно равны напряжениям в узлах i и k (относительно базисного узла), когда в узле i задан ток, равный 1 а.
С учетом обозначений (5-14) и (5-15) выражения для напряжений (5-6) принимают вид:
Uk=^Zkilt. (5-16)
90
Следует иметь в виду, что входным сопротивлением может также называться величина, обратная выражению (5-9), а входной проводимостью — величина, обратная выражению (.5-14).
Очевидно, что для одной и той же пары зажимов электрической цепи, не содержащей источников,
Рис. 5-12. Отношение токов (а) и напряжений (б).
величины Уц и Zu, определяемые из (5-9) и (5-14), взаимно обратны, т. е.
Отношение двух контурных то-ijob Ik и Ik+i, вызываемых в контурах k и &+1 источником э. д. с. £{, включенным в контур i (рис. 5-12,а), определяется на основании (5-10) отношением соответствующих передаточных проводимостей, а именно:
h = YkiEj Ук1
Д+i Yk+i.iEi yk+i,i
Аналогично отношение двух узловых напряжений йь и Uk+i, обусловливаемых в узлах k и Л+1 источником тока заданным в узле i (рнс. 5-12,6), определяется на основании (5-15) отношением соответствующих передаточных сопротивлений:
Vk Zklh = Zkt
Ek+i zk+i,i h 2k+i.i
Входные и передаточные сопротивления и проводимости, а также отношения одноименных электрических величин (токов, напряжений) подробнее рассмотрены в гл. 18.
5-6. ТЕОРЕМА ОБРАТИМОСТИ (ИЛИ ВЗАИМНОСТИ)
Пассивные линейные электрические' цепи обладают важным свойством, известным под названием обратимости. Основанная на этом свойстве теорема обратимости (илй4 взаимности) может быть
сформулирована в двух вариантах — применительно к источникам э. д. с. и источникам тока. Ограничимся рассмотрением первого варианта.
Вариант с источником э. д. с. На рис. 5-13 условно показана электрическая цепь с выделенными контурами i и k. Электродвижущая сила в контуре i (рис. 5-13, а) вызывает ток в контуре k, который согласно (5-10) равен:
Ik-YkiEt.
Соответственно э. д. с. Eh в контуре k (рис. 5-13,6) вызывает ток в контуре i
It=YikEk.
Рис. 5-13. Теорема обратимости (вариант с источником э. д. с.).
Отсюда следует, что lk УЫ Et Ц Ytk Ё/;
Алгебраические дополнения Д,ь и Ды, входящие в выражения У кг и Yik, отличаются только тем, что в них строки заменены столбцами с учетом того, что их элементы — общие сопротивления контуров заданной цепи — не изменяются от перестановки индексов.
Поэтому Дгь=Ды, и, следовательно,
Yki=Ytk. (5-17)
Электрические цепи, для которых выполняется условие (5-17), называются обратимыми цепями. Для таких цепей имеем:
h _ Ej h Ek
ЕСЛИ ПРИНЯТЬ £j = £fe, ТО А = /«.
Таким образом, для обратимых цепей справедливо следующее положение: если некоторая э. д. с., находящаяся в каком-либо контуре электрической цепи, вызывает ток
91
в другом контуре данной цепи, то та же э. д. с., будучи перенесенной во второй контур, вызовет в первом контурный ток той же величины и фазы.
При соответствующем выборе контурных токов ток в ветви равен контурному току. Поэтому данная теорема справедлива также для токов в ветвях.
Использование свойства обратимости пассивных линейных электрических цепей в ряде случаев упрощает расчеты. С этим важным свойством пассивных линейных цепей нам придется неоднократно встречаться далее, особенно в гл. 18.
Практическое применение теоремы обратимости иллюстрировано в примерах 5-6 и 5-7.
Пример 5-6. Воспользовавшись теоремой обратимости, вычислить ток f в схеме рис. 5-14, а прн любом конечном значении сопротивления Z.
Дано: £=10 / 0 в.
Рис. 5-14. Пример 5-6.
Применение теоремы обратимости облегчает в данном случае расчет тем, что и после переноса э. д. с. в ветвь Z (рис. 5-14,6) получается схема, в которой ток источника равен нулю; поэтому искомый ток, равный току в емкости схемы рис. 5-14, б, находится как отношение э. д. с. к сопротивлению емкостной ветви:
10/0
?==ТГ='2а-
5-7. ТЕОРЕМА КОМПЕНСАЦИИ
Токи в электрической цепи не изменятся, если любой участок цепи заменить э. д. с., равной по величине напряжению на данном участке и направленной навстречу току, проходящему по данному участку.
Справедливость этого положения, носящего название теоремы
компенсации, вытекает из того, что любое из слагающих падения напряжений, входящих в уравнение по второму закону Кирхгофа, может быть перенесено в другую сторону уравнения с противоположным знаком, т. е. может рассматривать-
Рис. 5-15. Теорема компенсации.
Рис. 5-16. Замена пассивной ветви (а) зависимым источником э. д. с. (б) или зависимым источником тока (в).
ся как дополнительная э. д. с., направленная навстречу току.
Иллюстрацией вышесказанного служит рис. 5-15: уравнение по второму закону Кирхгофа, записанное для схемы рис. 5-15, а как E=ZVI+ +ZI\ может быть представлено в виде Е—ZI—Z\t.
Последней записи уравнения соответствует схема рис. 5-15,6, в которой вместо сопротивления Z включена э. д. с. ZI, направленная противоположно току /.
Данная теорема справедлива и для разветвленных электрических цепей. Рисунок 5-16,6/ и б иллюстрирует возможность замены комплексного сопротивления Z источником э. д. с. £=Z(/i—/2), действующим навстречу току Ц—/2, проходящему через сопротивление Z.
Вместо источника э. д. с. может быть включен источник тока (рис. 5-16,в), обусловливающий протекание между узлами 1 и 2 того же тока, что и в схеме рис. 5-16, а; токи и напряжения в остальной части цепи при этом не меняются.
Следует заметить, что э. д. с. или ток источника, заменяющего собой участок цепи, определяется в зависимости от тока, проходящего че
92
рез данный участок. При изменении параметров остальной части цепи ток на данном участке в общем случае изменяется, и поэтому вышеуказанный источник не является самостоятельным источником, а представляет собой так называемый з а-в и с и м ы й или неавтономный источник.
t Применение теоремы компенсации облегчает изучение свойств линейных электрических цепей. Так, заменяя какой-либо участок цепи неавтономным источником э. д. с. или тока и пользуясь методом наложения, легко убедиться в том, что напряжения и токи в остальной части цепи являются линейными функциями напряжения на данном участке или тока, проходящего через него. Например, если при изменении комплексного сопротивления Z в какой-либо ветви изменяется ток Ц в этой ветви, то ток 4 в какой-либо другой ветви связан с линейной функциональной зависимостью:
4~4(2=оо) "Ь
здесь 4(z=oo)—значение тока 4 при Z = 00, т. е. при разомкнутой первой ветви.
Комплексный коэффициент К находится из условия, что при Z = 0
4(2=0) = 4(2=00) + ^^1(2=0) »
поэтому
/ / , ^2(2=0) _/2(Z=oo) i
'2 — /2(2=оо)-Г . '1-
Л(2=0)
5-8. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ТОКОВ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
ПРИ ИЗМЕНЕНИИ СОПРОТИВЛЕНИЯ В ОДНОЙ ВЕТВИ
На основании методов наложения и теоремы компенсации вытекает следующая теорема об изменении токов в электрической цепи, вызываемом изменением параметра в одной ветви данной цепи.
Если комплексное сопротивление какой-либо ветви электрической цепи изменится на величину ±Z', то изменение токов в цепи будет таким же, какое вызывается действием в
ветви Z±Z' э. д. с., направленной противоположно первоначальному току I в данной ветви и равной по величине и знаку ±Z'I.
Сказанное поясняется рис. 5-17.
Положим, что в ветви, комплексное сопротивление которой равно Z,
Рис. 5-17. Изменение сопротивления ветви.
проходит ток I (рис. 5-17,а). Спрашивается, как изменится ток, если сопротивление ветви изменится на величину +Z', т. е. станет равным Z+Z'.
На рис. 5-17,6 показана ветвь с измененным сопротивлением; предполагается, что в результате изменения сопротивления Z на величину Z' первоначальный ток I изменился на величину I', т. е. стал равным /+/'.
Включим в данную ветвь две противоположно направленные э. д. с. El и Ё2, равные Z7 каждая (ток в цепи при этом не изменится), и, пользуясь методом наложения, рассмотрим действие этих э. д. с. поочередно. При отсутствии Е2 получаются условия, тождественные первоначальным, так как схемы рис. 5-17, я и в эквивалентны: падение напряжения от тока I в Z' компенсируется на основании теоремы компенсации дополнительной э. д. с. El=Z'I. Следовательно, изменение тока в цепи обусловливается действием э. д. с. E2=Z'I, направленной навстречу I (рис. 5-17,г), что и требовалось доказать.
Применение данной теоремы бывает целесообразно в тех случаях.
93
когда известны токи в цепи до изменения параметров ветви.
Кроме того, измерив ток в электрической цепи с помощью амперметра, сопротивление которого известно, можно, основываясь на этой теореме, уточнить значение тока в цепи, т. е. исключить погрешность,
°)
Рис. 5-18. Размыкание ветви.
а — варианты с источником тока; б — вариант С источником э. д. с.
вызванную сопротивлением прибора. Дополнительный ток, обусловленный сопротивлением прибора, согласно теореме равен:
? _ _ -iz'
1 ~ z3 ~ гэ •
где 7—истинный ток (без ам-
перметра) ;
Z' — сопротивление ампер-
метра;
Z3—эквивалентное сопротивление пассивной цепи (с амперметром).
Через амперметр проходит ток
Следовательно, имея показание амперметра /а, можно вычислить искомый ток по формуле
Следует заметить, что размыкание какой-либо ветви заданной электрической цепи соответствует предельному случаю Z'=oo, когда решение по вышеприведенной теореме становится неопределенным. В этом случае применим любой из следующих приемов.
1. Включим между разомкнутыми точками два источника тока 1,
соединенных параллельно. При принятом на рис. 5-18, а направлении этих источников ток в данной ветви в соответствии с первым законом Кирхгофа равен нулю. Применяя метод наложения и считая, что ток 7 выбран равным по величине току в ветви до ее размыкания, приходим к выводу, что размыкание ветви равносильно добавлению к токам предшествующего режима новой системы токов, обусловленных действием в данной ветви пассивной электрической цепи источника тока, равного току, протекавшему в той же ветви перед ее размыканием.
2. Обозначим через напряжение между разомкнутыми зажимами электрической цепи (н а п р я ж е-ниехолостого хода) и присоединим к ним источник э. д. с. £•= = t/x; токи и напряжения в цепи при этом не изменятся. Применив метод наложения, получим, что распределение токов и напряжений в исходной цепи слагается из соответствующих электрических величин двух схем (рис. 5-18,6): активной цепи с замкнутыми зажимами и пассивной цепи с источником э. д. с.
присоединенным к указанным зажимам.
На рис. 5-18 буквой А обозначена заданная цепь, содержащая источники электрической энергии (активная цепь), а буквой П—та же цепь в предположении, что на месте источников оставлены только комплексные сопротивления или проводимости (пассивная цепь). Знаки сложения и равенства на рис. 5-18 относятся к токораспределе-ниям.
Практическое применение теоремы об изменении токов в электрической цепи иллюстрировано ниже на примере расчета несбалансированной мостовой схемы.
Пример 5-7. Найти ток в диагональной ветви мостовой схемы рис. 5-19, а, если сопротивления в трех плечах моста равны 10 ом каждое и сопротивление в четвертом плече равно 10,1 ом; сопротивление диагональной ветви 1 ом.
При равенстве сопротивлений всех плеч (10 ом) ток в диагональной ветвн отсутствовал бы и через каждое плечо проходил бы ток, равный 10/20=0,5 а. Увеличение сопротивления одного плеча на 0,1 ом
94
равносильно на основании вышеуказанной теоремы введению в измененное плечо дополнительной э. д. с. 0,1-0,5=0,05 в (рис. 5-19,6). Последняя вызывает в диагональной ветви ток,. который может быть вычислен по теореме .об эквивалентном источнике напряжения (см.'§ 5-9).
Искомый ток равен 0,00225 а.
Для вычисления этого тока можно также воспользоваться теоремой обратимости (вариант с э. д. с.), согласно которой искомый ток равен тому току, который про-
4JJ 6) Ч
Рис. 5-19. Пример 5-7.
ходил бы через плечо с сопротивлением 10,1 ол4, если бы источник э. д. с. 0,05 в был перенесен в диагональную ветвь (рис. 5-19, в).
В этом случае расчет может быть упрощен, если пренебречь разницей в сопротивлениях плеч мостовой схемы: приближенное значение искомого тока получается равным 0,05/2,11=0,00227 а.
5-9. ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОМ ИСТОЧНИКЕ
Теорема об эквивалентном источнике часто применяется в расчетах электрических цепей. С помощью этой важной теоремы сложная электрическая схема с произвольным числом источников электрической энергии приводится к схеме с одним источником, благодаря чему расчет электрической цепи упрощается.
Существуют два варианта теоремы об эквивалентном источнике: вариант с источником напряжения и вариант с источником тока.
Теорема об эквивалентном источнике напряжения. Ток в любой ветви тп линейной электрической цепи не изменяется, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником напряжения; э. д. с. этого источника должна быть равна напряжению на зажимах разомкнутой ветви тп, а внутреннее сопротивление источника должно равняться входному сопротивлению пассивной
электрической цепи со стороны зажимов m и п при разомкнутой ветви тп.
Данная теорема доказывается следующим образом: в ветвь тп вводятся две равные по величине и противоположно направленные э. д. с. Umn при условии, что 0тп равно напряжению между зажимами т и п при разомкнутой ветви тп, т. е. напряжению холостого хода (рис. 5-20).
Рис. 5-20. Теорема об эквивалентном источнике напряжения
Применение метода наложения в соответствии с рис. 5-20 приводит к выводу, что ток в ветви Z равен:
(5-18)
где Zo— комплексное сопротивление пассивной цепи П. Таким образом, ток в ветви Z получается в предположении, что данная ветвь приключена к источнику напряжения, э. д. с. которого равна а внутреннее сопротивление равно Zo. Следует заметить, что в соответствии с рис. 5-20 ток в какой-либо другой ветви заданной электрической цепи может быть получен в результате алгебраического сложения тока, проходящего через эту ветвь при разомкнутых зажимах тп, с током, возникающим в ней под воздействием э. д. с. Umn в ветви Z (когда остальная цепь пассивна). Поэтому, если известно распределение токов в электрической цепи при разомкнутой ветви Z, то последующее распределение токов при включенной ветви находится весьма легко наложением на предыдущий режим тех токов, которые обусловливаются
95
воздействием на пассивную цепь Э. Д. С. Umn в ветви Z.
Как уже указывалось выше, метод наложения применим не только к токам, но и к напряжениям. Поэтому, пользуясь описанным приемом, можно (гаходить также и распределение напряжений.
При наличии в электрической цепи нескольких источников э. д. с. и тока одинаковой частоты напряжение холостого хода является линейной функцией от заданных э. д. с. и токов источников.
нок 5-21 иллюстрирует случай размыкания ветви Za.
Напряжение холостого хода йтп находится в этом случае как разность э. д. с. л £, — Ёг
Ei и падения напряжения от тока ----—
комплексном сопротивлении Zt (рис.
Umn =£1 ~ 8 = + .
Z1 + Za Z,+Z2
Под воздействием э. д. с. Umn в схеме рис. 5-21, б через комплексное сопротивление Z3 идет ток
Рис. 5-21. Пример 5-8.
_____Umn
7 I ^*^2
£i ~Ь Zi £2
Z'2 + Z2 Zj -J- Za Z2 который разветвляется в Z] и Z2: через Zt проходит ток
_Ь_ J ^+Z2 /а*
Для доказательства теоремы об эквивалентном источнике в ветвь вводились две противоположно направленные э. д. с., равные напряжению холостого хода на этой ветви. Такой же прием может быть применен одновременно и к двум ветвям любой сложной активной цепи. Тогда действительное токорас-пределение в цепи получится как сумма токораспределений в двух схемах:
1) в активной схеме при разомкнутых ветвях;
2) в пассивной схеме при питании ее из двух ветвей источниками э. д. с., равными напряжениям холостого хода на этих ветвях и направленными так же, как и токи, т. е. как напряжения холостого хода.
Указанный прием бывает удобен, когда известно токораспределение при режиме холостого хода для обеих ветвей. Тогда при замыкании этих ветвей достаточно лишь наложить токи, полученные из второй схемы с двумя э. д. с.
Пример 5-8. Пользуясь теоремой об эквивалентном источнике напряжения, определить токн в ветвях схемы рис. 5-4.
Размыкание ветви и соответственно нахождение напряжения холостого хода может быть произведено в любой из трех ветвей заданной электрической цепи. Рису-
а через Z2 ток
j zt + zta'
Искомые токи в ветвях Zi и Z2 определяются в результате сложения токов, протекающих в схемах 5-21, а и б, т. е.
Z2 ZsEl + Z1E2
Z1-i-Z2 Z2 Z2 -f- Z2 Zs -f- Zj Zj
__ (Z2 -|- Zs) £i — Zs£2 _
Z±Z2 -f- Z2 Zs -f- Z3 Zj
>___ £t — £g____
2“ Z,+Z2
Zi Z2 £a
Zi + Z2 Zi Z2 -) Z2 Za -f- Zs Zi
__— (Zi + Zs) Ё2 + Z3
Z2 Z2 + Z2 Zs + Zs Zi
Данный пример иллюстрирует применение теоремы об эквивалентном источнике для вычисления токов в разных ветвях, причем здесь не ставится цель получить решение кратчайшим путем.
Пример 5-9. Пользуясь теоремой об эквивалентном источнике напряжения, определить ток в диагональной ветви мостовой схемы рис. 5-22,о.
Разомкнув ветвь ZB, находим напряжение холостого хода limn как разность
96
напряжений на участках Z4 и Z3 (рис. 5-22,6):
£ £
Ётп — Z4 —— Zs -
Zi + Zi Z2 + Z3
____Zj Zb — Zt Zs
(Zi + Z4) (Z2 -j- Z3)
Сопротивление между зажимами m и n
при £=0 и разомкнутой ветви Zs равно:
2 ___ %* , Z3 Zg
Zi -|- Zb Z2 + Zs
4 6)
V
Рис. 5-22. Пример 5-9.
ZQ (рнс. 5-23, а), может быть заменен источником тока (рис. 5-23,6)
‘тп — Zo
Последнее выражение есть не что иное, как ток, проходящий между зажимами т и п, замкнутыми накоротко (ток короткого замыкания). Искомый ток в це
пи равен:
Z„ . У
1 = zo + z ,тп Уо + У tmn'
(5-19)
где У = IfZ.
Если известно распределение токов в электрической цепи при закороченных зажимах тп, то распределение токов в цепи при включенной ветви Z может быть найдено посредством наложения на предыдущий режим тех токов, которые получаются в результате присоединения источника тока /тп к ветви Z (когда остальная часть цепи пассивна).
При наличии в электрической цепи нескольких источников э. д. с. и тока одинаковой частоты ток короткого замыкания является линейной функцией от заданных э. д. с. и токов источников.
Пример 5-10. Пользуясь теоремой об эквивалентном источнике тока, определить ток /3 в ветви Z3 схемы рис. 5-4.
На основании (5-18) i °™ 5 Zo +Zs-
Теорема об эквивалентном источнике тока. Ток в любой ветви тп (рис. 5-20) линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником тока; ток этого источника должен быть равен току, протекающему между зажимами тип, замкнутыми на-
Рнс. 5-23. Теорема об эквивалентном источнике тока.
Рис. 5-24. Пример 5-10.
Ток эквивалентного источника равен току короткого замыкания (Z3=0, рис. 5-24, а):
£, £2
lmn = 1k -= -Г" + -Л = У1Ет + У2Ег-
Z1 £-2
Комплексная проводимость эквивалентного источника равна У0=У1+^2- Следовательно, на основании (5-19) искомый ток равен:
/ - Ys i = Y* 1
’ И.4-Уз k У1 + У2 + Уз * =
Zg£i 4~ Z^Es
ZtZ2 + Z2Z3 -|- Z3Zj
коротко, а внутренняя проводимость источника должна равняться входной проводимости пассивной электрической цепи со стороны зажимов тип при разомкнутой ветви тп.
Данное положение вытекает из условия эквивалентности источников напряжения и тока, а именно: источник напряжения, э. д. с. которого равна напряжению холостого хода
а внутреннее сопротивление равно
5-10. ПРИМЕНЕНИЕ МАТРИЦ К РАСЧЕТУ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Математическая символика и правила матричной алгебры позволяют упростить запись систем уравнений, получающихся при расчете сложных электрических цепей. В этом отношении матричную алгебру мож-
7—UM
97
ио сравнить со стенографией, которая облегчает н ускоряет запись.
Напомним, что матрица представляет совокупность величин, называемых ее элементами и расположенных в виде прямоугольной таблицы *. Если число строк равно числу столбцов, то матрица называется квадратной. Матрица, содержащая один столбец, называется столбцовой или матрицей-столбцом.
Приведенная в § 5-2 система уравнений, записанных по второму закону Кирхгофа для контурных э.д.с. и контурных токов, может быть представлена в виде произведений квадратной матрицы собственных н общих сопротивлений контуров на столбцовую матрицу контурных токов. При этом следует помнить, что произведением двух матриц называется матрица, элементы которой равны сумме произведений элементов соответствующей строки первой матрицы на элементы соответствующего столбца второй матрицы. Итак, уравнения (5-2) в матричной форме имеют вид:
Ё1
Ё»
Z(1I) ^(12) • ^(21) ^(22) •
^(nl) Z(„2) -
• • Z(ln)
• • Z(2«)
X
нлн сокращенно
ll£|| = l!z|| • Ц/Ц-
Данное матричное уравнение может быть решено относительно матрицы ||/||.
Для этого обе стороны уравнения должны быть умножены на матрицу, обратную Матрице ||Z||;
IIZ||£|| = l|z 1Г1-||zII - il'zll.
Как известно, для получения обратной матрицы необходимо заменить в исходной матрице каждый элемент его алгебраическим дополнением, затем заменить строки соответствующими столбцами2 3 и полученную таким образом матрицу разделить на определитель исходной матрицы. Напомним, что алгебраическим дополнением элемента квадратной матрицы называется умноженный на (—1)4* определитель, получающийся из элементов матрицы после
1 Матрицу не следует смешивать с
определителем. Определитель может быть вычислен, матрица же не может быть приравнена числу, а может равняться только матрице. Две матрицы считаются равными, если они содержат одинаковое число строк и столбцов и если равны все нх соответственные элементы.
3 Матрица, получающаяся в результате замены строк соответствующими столбцами, называется сопряженной или транспонированной относительно исходной матрицы.
исключения i-й строки и fe-ro столбца. В свою очередь определителем матрицы называется определитель, составленный из элементов квадратной матрицы, расположенных в том же порядке, как и в матрице. Итак, обратная матрица имеет вид:
। Au Ай ... ДЯ1
II Z ||—1 = —— Д12 Д22 • • • Ап2 ..........
Ащ А2п • . . Апя здесь Д2— тот же определитель системы, что и в §5-2.
Произведение обратной матрицы на исходную матрицу равно единичной матрице, т. е. квадратной матрице, у которой все элементы главной диагонали, идущей от левого верхнего угла к правому нижнему, равны единице, а остальные элементы равны нулю.
Следовательно,
IIZII-1 • ||2|| = || 1 ||
И
1ИГ1-1|£|| = 1|1|1-1)/||.
где ||1|| — единичная матрица.
Произведение единичной матрицы на матрицу ||/|| равно матрице Ц/||, поэтому
Il/|| = ll2 |Г' -||£||
или в развернутой форме
/1 ^2
Л;
1
Аг
Ан А21. . . Дщ
Ай Ам . . . Дп2
Ащ А2п . . . Дяп
Ё1
£2
Ёл
В результате умножения матриц получаются выражения для контурных токов вида (5-4).
Аналогично решается матричное урав* нение для узловых Напряжений
II/II = 11 Г II-III? II.
где ||/|| н |Ц7||—столбцовые матрицы токов, заданных в узлах, и искомых узловых напряжений;
||У|| — квадратная матрица собственных и общих проводимостей узлов:
11ПГ* • II / II = II HI-1 • II у II • lit? II.
откуда
lit? II = 11ГII-1 .||/|].
В результате умножения матрицы |У||—1 иа матрицу ||/|'| получаются выражения для узловых напряжений вида (5-6).
Матричная алгебра широко применяется для расчета сложных четырехполюсников (гл. 18)
В случае относительно простой электрической схемы без взаимной индукции матрица контурных сопротивлений легко запи-сывается непосредственно по заданной схе*
98
ме. В более сложных случаях матрица контурных сопротивлений может быть получена с Помощью матрицы сопротивлений ветвей. Ниже показана связь, существующая между матрицами контурных сопротивлений и сопротивлений ветвей *. Вывод, сделанный в общей форме, иллюстрирован на примере простой схемы рис. 5-25, легко решаемой обычным способом.
Рис. 5-25. Схема к расчету матричным методом.
Обозначим гоки, напряжения э.д.с. н сопротивления ветвей индексом «в», а соответствующие контурные величины индексом «к». Связь между токами в ветвях И контурными токвмн выражается зависимостью
II4II = 11С ||-ЦМ- (5-20)
Здесь ||С|| —матрица соединений (иннИденний). Число ее строк равно числу ветвей, а число столбцов — числу контурных токов. Элементами матрицы соединений служат числа +1, —1 и 0. + 1 означает, что выбранные на схеме положительные направления тока в ветвн и контурного ТОка совпадают; —1 берется тогда, когда Их направления различны; наконец, 0 означает, что данная ветвь не входит в рассматриваемый контур.
Например, для схемы рис. 5-25 имеем.
4 1 0 0
ib 1 —1 0 /1
ie = 0 1 0 > •
h 0 1 1 la
>е 0 0 1
Уравнения по второму закону Кирхгофа в матричной форме записываются так:
IIС ||т-116411 = 110 ||, (5-21)
где ||С||т — матрица, транспонированная относительно матрицы соединений ||С|| к отличается от последней тем, что строки заменены столбцами.
Строка ЦС||т, так же как и столбец ||С[|, содержит, кроме нулей, единицы на местах, соответствующих ветвям данного контура; поэтому произведение ее на 1| U* II даст алгебраическую сумму напря
1 Существует также н зависимость между матрицами проводимости ветвей и узловых проводимостей [Л. 18 и 19].
жений ветвей этого контура. Согласно второму закону Кирхгофа алгебраическая сумма напряжений Ни ветвях в любом контуре равна нулю, т. е произведение любой строки ||С||Т на || 67а|1 должно равняться нулю, что И выражает (5-21).
Например, для схемы рис. 5-25 имеем:
1 10 0 0
0—11 10
0 0 0 —1 1
йа Ub 0с
йс
о о о
Считая, что направления э.д.с. и токов в ветвях совпадают, получаем матрицу напряжений на ветьях в виде
II II = II 2В || - IIZ.II- ||£в||- (5-22)
Подстановка (5-20) в (5-22) дает:
|ZB||-||C||.|| ZK ||-||Ё.|| = ||б7в ||,(5-23) а подстановкой (5-23) в (5-21) получаем;
1|С||Т.||2В||.||С||.||?К||-
—IIС ||т • || £„ || = || 01[, откуда
IIС ||т- II2В II -II С II- II /к || = 11С ||т-||£в||.
Сопоставив это уравнение с уравнением для контурных токов Ц2К|| • ||/к|| = = ||£к||, приходим к выводу, что э.д.с. в ветвях и контурные э.д.с. связаны матричным уравнением
IIС Цт - || £в|| «||£кП . (5-24)
а матрица контурных сопротивлений получается по формуле
||ZK|| = ||C||T-||ZB|I-||С|| (5-25)
Для схемы рис. 5-25 матрица сопротив-
лений ветвей записывается в виде
г-i 0 0 0 0
0 /со£1 0 0 0
«*.»- ° ° 00
0 0 0 /со£2 0
0 0 0 0 г2
Матрица контурных сопротивлений согласно (5-25) равна:
1 10 0 0
0—11 10
II ZK || =
0 0 0 —1 1
Г1 0 0 0 0 1 0 0
0 /Ы/.! 0 1 0 0 1 —1 0
0 0 1 0 0 0 1 0
А /шС 0 1 —1
0 0 0 /ы£2 0 0 0 1
0 0 0 0 г2
7*
99
r\ + i&Li — jaLi О
— /<°^1 /® (^-1 + ^-з)+ . п — /а>£2 /<оС
О — /<о£2 г2 + /ш£2
Пример для цепи с взаимной индукцией приведен в § 6-3.
5-11. НЕКОТОРЫЕ ОСОБЕННОСТИ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ С ЕМКОСТЯМИ
В гл. 4 было показано, что при параллельном соединении емкостей Сь С2,Сп эквивалентная емкость равна:
п
С=Сг4-С24------f-Cn= IjCfe-
При последовательном соединении емкостей эквивалентная емкость находится из уравнения
Например, для двух последовательно соединенных емкостей Ct и С2 эквивалентная емкость составляет:
Распределение напряжений на этих емкостях находится решением уравнений
и1+ы2=ы и ?=С1и1=С8иа,
откуда
Ci
Сх + С»
т. е. напряжения распределяются обратно пропорционально емкостям.
Данное правило распространяется на мгновенные, амплитудные и действующие значения напряжений в цепи гармонического тока, а также на постоянные напряжения в цепи постоянного тока.
Здесь, так же как раньше и под емкостями подразумеваются идеальные конденсаторы, активная проводимость которых равна нулю.
В случае соединения трех емкостей звездой или треугольником возможно преобразование звезды емкостей в эквивалентный треугольник
Рис. 5-26. Соединение емкостей звездой (а) и треугольником (б).
емкостей или обратно (рис. 5-26, а и б) по формулам:
q________С2С2 . q_________С2С8___
Сх + С2 + Сз 23 + С2 + Сз ’
Сх=С12+С81+^5
^a=^2s+^'ia
Сз, ’
C8=CSi+Cae +
СзхСзз ^хз
Эти соотношения, вытекающие из выражений (4-1) и (4-2), справедливы для всех частот, включая и нулевую частоту (т. е. при постоянных токах и напряжениях).
Если напряжения в электрической цепи постоянны, то электрические заряды емкостей сохраняют постоянную величину, находясь в статическом равновесии.
Для нахождения распределения электрических зарядов емкостей и соответственно напряжений на емкостях при статическом равновесии зарядов пользуются законом сохранения количества электричества и вторым законом Кирхгофа.
По закону сохранения количества электричества алгебраическая сумма зарядов на обкладках емкостей, соединенных в узел и не приключенных к источнику электрической энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения.
В самом деле, положим, что несколько отдельных емкостей, предварительно заряженных (некоторые
100
из них могли и не иметь заряда), соединяются в узел и включаются своими другими концами в какую-либо электрическую цепь. Если обкладки емкостей, соединенных в узел, отделены от остальной части цепи идеальным диэлектриком, то сосредоточенные на них начальные электрические заряды не могут перейти из рассматриваемого узла в другую часть цепи; по этой же причине не может быть притока заряда к узлу извне.
Из сказанного следует, что если на обкладках, соединяемых в узел, первоначально имелись заряды q\, Чч., —. ц'п (каждый из этих зарядов в зависимости от полярности обкладок мог соответственно иметь положительный или отрицательный знак), то после перераспределения зарядов между обкладками, соединенными в узел, алгебраическая сумма зарядов в узле должна остаться неизменной, т. е. если
-----Ь-Чп = 90-
то 2<7=?о- (5-26)
Если емкости не были предварительно заряжены, то после их включения в электрическую цепь на их обкладках появятся заряды, алгебраическая сумма которых в узлах, не присоединенных к источникам электрической энергии, равна нулю:
2?=0.
По второму закону Кирхгофа алгебраическая сумма э. д. с. в контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него емкостях. В цепях с емкостями и источниками э. д. с.
2е=2-^-. (5-27)
Формулы (5-26) и (5-27) справедливы как для переменных, так и для постоянных зарядов.
Следует заметить, что для расчета цепей с емкостями с учетом первоначальных зарядов емкостей и при наличии в схеме источников постоянных или гармонических э. д. с. применим метод наложения.
5-12. ДУАЛЬНЫЕ ЦЕПИ
Под условней дуальности понимается такое соответствие электрических цепей, прн котором заксн изменения контурных токов в одной цепи подобен закону изменения узловых напряжений в другой цепи.
Для элементов электрической цепи, изображенных на рнс. 5-27 (слева и спра
Рис. 5-27. Дуальные элементы.
ва), зависимости между напряжениями
и токами имеют вид:
(5-28)
иг — пг;
di, u,~L—p-L dt
duc ic = C' ~ ; c dt
(5-29)
Следует иметь в виду, что входящие в уравнения (5-28) и (5-29) напряжения н токн, имеющие одинаковые буквенные обозначения, не равны друг другу.
Из сравнения уравнений (5-28) и (5-29) видно, что условию дуальности удовлетворяют следующие элементы: 1) сопротивление н проводимость; 2) индуктивность и емкость; 3) источник э.д.с. и источник тока.
Элементы цепи, удовлетворяющие условию дуальности, называются аналогами нли дуальными элементами.
При последовательном соединении элементов цепи суммируются напряжения, при параллельном соединении элементов цепи суммируются токн. Поэтому последовательному соединению элементов соответствует параллельное соединение нх аналогов, а параллельному соединению элементов — последовательное соединение их аналогов.
ЮГ
Например, при замене последовательно соединенных элементов г, L, С (рнс. 5-28, а) их аналогами g', С, L', соединенными параллельно (рис. 5-28,6), получаем дуальные цепи.
Рис. 5-28. Дуальные цепи.
Уравнение напряжений для исходной цепи
di
e(t) = ri + L — at
t
подобно уравнению токов для второй цепи
du 1
40 = g'«+cz—+ — dt L
и di. (5-31)
Контурному току i в (5-30) соответствует узловое напряжение и Допустим, что э.д.с. и подчинены одному и тому пример, косинусоидальны и вую начальную фазу, т. е. k — коэффициент пропорциональности, имеющий размерность сопротивления. Тогда законы изменения контурного тока в схеме рнс. 5-28, а и узлового напряжения в схеме рис. 5-28, б совпадают, т. е. условии, что
в (5-31).
ток источников же закону, найм еют одинако-где
u=ki, прн
г L L'
— = — = — = k\ g' С С
Иначе говоря, при одинаковом законе изменения дуальных источников отношения напряжений и токов дуальных элементов равны k.
В случае сложной электрической цепи каждой ее области, ограниченной независимым контуром, с учетом также области, внешней по отношению ко всякой цепи, соответствует узел дуальной цепи. Следонательно, число областей заданной цепи равно числу узлон дуальной цепи.
При построении дуальной цепи по отношению к заданной планарной цепи удобно
пользоваться графическим приемом (рнс. 5-28). В каждой области, ограниченной независимым контуром заданной цепи, наносится точка, рассматриваемая в качестве будущего узла дуальной цепи. Узлы, соответствующие каждой паре смежных областей, соединяются между собой параллельными ветвями, число которых равно числу элементов, последовательно включенных в цепь, граничащую с указанными областями. Элементами параллельных ветвей являются аналоги элементов заданной цепи, удовлетворяющие условию (5-32).
Графический способ построения дуальной цепи иллюстрирован ниже на примере рис. 5-29.
Исходная цепь (рнс. 5-29, а) содержит три независимых контура, внутри этих контуров фиксируем три точки (/, 2, 3), соответствующие узлам искомой дуальной цепи. Четвертую точку, соответствующую узлу 4, фиксируем в области, внешней по отношению к заданной цепи. Проводим между этими точками пунктирные линии, пересе-
дуальных источников руководст-следующим правилом: если э.д.с.
кающие элементы цепи и представляющие ветви дуальной цепи: пересекаемые элементы заменяются их аналогами, включенными между соответствующими узлами дуальной цепи.
При согласовании направлений эл.с. и токов вуются источника действует в положительном направлении контура (по ходу часовой стрелки), то ток источника тока в дуальной цепи направлен к узлу, соответствующему данному контуру исходной схемы.
Следует заметить, что если графический способ построения дуальной цепи повторно применить к схеме рис. 5-29,6, то получится исходная схема рнс. 5-29, а.
Существуют дуальные электрические цепи, имеющие одинаковую схему, например мостового типа (так называемые автодуальные схемы).
При соблюдении пропорции (5-32) комплексное сопротивление цепи, общей для двух смежных контуров схемы, пропорционально комплексной проводимости цепи, соединяющей два соответствующих узла дуальной цепи. Например, в схеме рис. 5-28,а комплексное сопротивление цепи равно:
ш£ — —— <оС
(5-32)
d
у
Рис. 5-29. Графический прием построения дуальных цепей.
102
а в схеме рис. 5-28,5 комплексная проводимость цепи
¥' = ₽' — /(— — <оС'^ . \®Ь /
С учетом (5-32) получаем: Z*=k2Y'.
Аналогичная пропорциональность получается между входным сопротивлением и проводимостью более сложных дуальных цепей. Это свойство используется, в частности, в теории электрических фильтров (гл. 19).
5-13. ЭЛЕКТРОМЕХАНИЧЕСКИЕ
АНАЛОГИИ
Явления, исследуемые на основе законов физики, описываются математически при помощи систем уравнений. Исходя из единства уравнений, соответствующих некоторым двум явлениям, происходящим в различных областях, например в электрической цепи и механической системе, можно установить аналогию между этими явлениями. «Единство природы обнаруживается в «поразительной аналогичности» дифференциальных уравнений, относящихся к разным областям явлений» 1.
Благодаря единству уравнений электрических и механических систем исследование явлений в механической системе может быть заменено исследованием процессов в электрической цепн.
Выполнение электрических цепей обычно сопряжено с меньшими трудностями, чем выполнение механических систем; они более компактны, и, что особенно важно, измерения в них более точны и удобны. Процессы в электромеханических системах, представляющих совокупность электрических и механических устройств, также могут с успехом исследоваться с помощью электромеханических аналогий.
Механические системы с сосредоточенными параметрами, которые по аналогии с электрическими цепями будем называть механическими цепями, состоят из активных элементов (источников энергии) и пассивных элементов.
Рассмотрим идеализированные элементы простейших линейных механических цепей, совершающих поступательное или вращательное движение (комбияированное поступательно-вращательное движение опустим).
В случае поступательного движения заданная внешняя сила, приложенная к цепи, рассматривается как источник силы, а заданная скорость какой-либо точки цепи — как источник скорости.
В случае вращательного движения заданный вращающий момент, приложенный к цепи, рассматривается как источник момента, а заданная угловая скорость какой-либо точки — как источник угловой скорости.
1 В. И. Ленин. Материализм и эмпириокритицизм. Соч., нзд. 4-е, т. 14, стр. 276.
Роль пассивных элементов в механических цепях выполняют массы, моменты инерции, пружины и механические (демпфирующие) сопротивления.
Массой называется идеализированный элемент механической цепи, обладающий инерцией. В нем накапливается кинетическая энергия. При этом термин «масса» н соответствующее ему условное обозначение т применяются для обозначения как самого инерционного элемента, так и для его количественной характеристики. Сила F (иьютон, н), приложенная к центру тяжести свободного твердого тела, сообщает ему линейную скорость v (м/сек) и линейное ускорение dv/dt (м/сек2), совпадающие по направлению с силой. Если масса неизменна, то
dv
F = т-----, (5-33)
dt
т. е. масса т (кг) представляет коэффициент пропорциональности между силой и ускорением.
На вращение тела влияет не только масса, но и ее распределение относительно оси вращения. Поэтому вращающийся инерционный элемент характеризуется моментом инерции J=mr2, где г—радиус инерции тела относительно осн вращения. Это пассивный элемент, в котором накапливается кинетическая энергия вращения.
Момент М(н-м). приложенный к свободному твердому телу, сообщает ему угловую скорость <о (рад/сек) и угловое ускорение du/dt (рад/сек2). Если момент инерции постоянен, то
dto
М = J — , (6-34)
dt
т. е. момент инерции J (кг • м2) представляет коэффициент пропорциональности между моментом и угловым ускорением.
Кинетическая энергия поступательного движения равна — mv2, а кинетическая энергия вращательного движения-^" 7ы2 (дж).
Пружина играет роль пассивного элемента, в котором накапливается потенциальная энергия Сила натяжения нли давления F, развиваемая соответственно растянутой или сжатой пружиной при данном относительном перемещении х, м, ее концов, пропорциональна ее жесткости Л, н/м (1 н/м = \ кг/сек2).
Сила F, необходимая для относительного перемещения х конца пружины, действует вдоль оси х и равна по закону Гука:
F=Kx = /(fvdt.
Продифференцировав обе части уравнения, получим:
<5'35)
at
Величина, обратная К, называется податливостью пружины.
103
Момент, необходимый для создания углового перемещения <р концов пружины, подвергающейся скручиванию, пропорционален жесткости К (я • м/рад):
Л4 = К<р =
Мощность, расходуемая на трение, равна прн поступательном движении fv2, а при вращательном |ш2(вт).
Сопоставление уравнений (5-33)—(5-38) с уравнениями элементов электрических цепей
откуда
.1 dM dt
(5-36)
В этом случае коэффициент пропорциональности К~* 1 называется податливостью при кручении.
Потенциальная энергия при растяжении или сжатии пружины равна — Кхг, а потенциальная энергия при скручивании — Лдр2(йж).
Демпфирующее механическое сопротивление создается вязким трением. Вследствие механического сопротивления происходит необратимый процесс преобразования кинетической энергии в тепло.
В линейной механической цепи с поступательным движением сила трения пропорциональна первой степени относительной скорости точек, принадлежащих трущимся поверхностям:
F = (5-37)
где f, к • сек]м, — коэффициент трения (1 я • сек/м=1 кг! сек).
При вращательном движении момент силы трения пропорционален первой степени относительной угловой скорости:
М = (5-38)
at
В этом случае коэффициент треиия f измеряется в я-л- сек!рад (1 я-м- сек/рад= = 1 кг • л2/сек • рад).
и~ L
di
~dt~ ’
du
i — С------; и = ri
dt
показывает, что механическая сила и вращающий момент соответствуют напряжению, линейная и угловая скорость — току, масса и момент инерции — индуктивности, податливость пружины — емкости, механическое сопротивление — сопротивлению.
. в; v*Ldt
С
Л dt
Рис. 5-30. Пассивные элементы механической цепи с поступательным движением и их электрические аналоги.
u^ri
На рис. 5-30 приведены условные изображения пассивных элементов механической цепи с поступательным движением1 и показаны их электрические аналоги.
Рассмотренная система электромеханических аналогий, сведенная в табл. 5-1, не является единственной. Взяв дуальную электрическую цепь, можно заключить, что механическая сила и вращающий момент
1 Механическое сопротивление изображается в виде демпфера.
Таблица 5-1
Электромеханические аналогии
Механическая цепь
Электрическая цепь
Сила F (я) или вращающий момент М (н-м) Перемещение линейное х (л) или угловое <р(рад)
Скорость линейная v (м/сек) или угловая
<о (рад/сек)
Масса т (кг) или момент инерции / (кг • л2)
Податливость К ~1 при поступательном движении
(м/н) или кручении (рад/н-м)
Коэффициент трения f прн поступательном движении (кг/сек) или вращении (кг- м2!сек-рад)
Кинетическая энергия (дж)
1 1
Потенциальная энергия “^“Кх2 или-^-Кф2 (дж)
Мощность от треиия )о2 или f®2 (вг)
Мощность Fv или М ш (вг)
Напряжение и (в)
Заряд q (к)
Ток I (а)
Индуктивность L (гн) Емкость С (ф)
Сопротивление г (ом)
1
Магнитная энергия-^- L? (дж)
1
Электрическая энергия Си2 (дж)
Мощность в сопротивлении ri2 (вг) Мгновенная мощность ui (вг)
104
соответствуют току, линейная и угловая скорость — напряжению, масса и момент инерции — емкости, податливость пружины — индуктивности, механическое сопротивление — проводимости.
Дифференциальные уравнения движения механической цепи могут быть выведены на основе второго закона Ньютона, который для поступательного движения гласит: если на тело действует несколько сил, то его ускорение совпадает по направлению с рае-
и
Рис. 5-31. Механическая цепь (а, б) и ее электрические аналоги (в, г).
недействующей этих сил и пропорционально отношению последней к массе тела.
Для вращательного движения применяется следующая формулировка второго закона Ньютона: если относительно оси вращения тела действует несколько моментов, то его угловое ускорение относительно той же оси пропорционально отношению результирующего момента к моменту инерции тела.
Дифференциальные уравнения движения механической цепи могут быть также получены на основании принципа Да-ламбера: при движении тела действующие на него силы и сила инерции удовлетворяют уравнению равновесия сил.
Уравнения такого же типа, получаемые для электрических цепей1 на основании законов Кирхгофа, могут быть либо уравнениями напряжений, либо уравнениями токов.
В качестве примера рассмотрим простейшую механическую систему: масса m находится под воздействием силы F и опирается на пружину (рис. 5-31,а). Тело движется между неподвижными направляющими; между телом и направляющими возникает вязкое трение. Массой пружины пренебрегаем.
На рис. 5-31, б изображена схема данной механической цепи. По второму закону Ньютона
do р
m —— = F — fv —К ( v di dt J
или
do С
F ~ fv + m -f- К 1 vdt. dt J
Пользуясь первой системой электромеханических аналогий (сила — напряжение,
табл. 5-1), шяучаем уравнение электрической цепи рис 5-31, в:
di 1 Г
в“"+г-“ЗГ+т)“"-
В свою очередь, применив вторую систему аналогий (сила — ток), получим уравнение электрической цепи рис. 5-31, г:
du If,
i-= g' и + С — + — \ udt.
dt L J
Таким образом, можно пользоваться двумя системами электромеханических аналогий: в одной из них напряжение, а в другой ток являются аналогом силы. Обе электрические цепи, аналогичные одной и той же механической цепи, являются дуальными цепями, так как контурные токи одной цепи служат аналогами узловых напряжений другой.
Электромеханические аналогии находят практическое применение в электрических моделях. Вопросы, затронутые в этом параграфе, подробно рассмотрены в [Л. 5].
5-14. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
5-1. Методом контурных токов определить ток в ветви Z3 рис. 5-4.
Ответ: см. в тексте (пример 5-4).
5-2. Методом узловых напряжений определить напряжение на ветви Z3 рис. 5-7.
Ответ:
УхУг + ^а^з + УзУх
5-3. Решить задачу 5-2 методом наложения.
5-4. Решить задачу 5-1 по теореме об изменении токов в электрической цепи, зная ток в ветви при Z3=0.
5-5. В схеме рис. 5-4 принять Е,= =230 /30° в. £*2 = 230 / 0в, Zt=Z2=j 1 ом-, Z3——/10 ом. Используя решение задачи 5-1 в общем виде, вычислить активные мощности и построить векторные диаграммы.
Ответ: £> =—Р2=13,9квг.
5-6. В схеме рис. 5-4 Е\ = 100 /Он; Zi=Z2=/10om; Z3=20 /0 ом.
Найти Е2, если мощность первого источника активная, а второго — реактивная.
Ответ: 212 /—45°в.
5-7. В схеме рис. 5-4 £> = 120 /0 в; £2=110 /0в; Z, =0,4+/0,6 ом; Z2=0,3+ +/ 1,2 ом; Z3=10 ом.
По теореме об эквивалентном источнике вычислить напряжение иа сопротивлении Z3.
Ответ: 113,9 /—2°в.
5-8. Вычислить ток в диагональной ветви мостовой схемы рис. 5-22, если £=10 в; Zj=20+/10oM; Z2=—jiOoM; Z3=20 ом; Z4——j 20 ом; Z3=10 ом.
Ответ: 0,351 а.
5-9. Доказать, что при наличии комплексного сопротивления Z в одной ветви
105
электрической цепи ток в какой-либо другой ветви равен:
7 7 , '(Z=0)~
' - '(Z=“) Г- 7 . -Г *0
Z + Zo
где ^(z=oo) » ^(Z=0)—токи во второй ветви при соответственно разомкнутой и замкнутой первой ветви;
Zo — комплексное сопротивление цепи, к которой приключено сопротивление Z, при отсутствии источников.
5-10. Вычислить ток в индуктивности Lt схемы рис. 5-29, а, если
ех = 10 sin со/, в; ег = 20 cos си/, в;
Г1 = гг — гз = 1 ел; = Лг = 0,1 мгн',
Ci — Сг = 1 мкф-, f ~ 400 гц.
Применить: а) метод контурных токов; б) метод узловых напряжений; в) теорему об эквивалентном источнике.
5-11. На примере рис. 5-28 показать, что если отношение комплексных э.д.с. и тока источников дуальных цепей равно k, то активные мощности на их зажимах равны, а реактивные — отличаются только по знаку (смысл коэффициента пояснен в §5-12).
5-12. Пояснить целесообразность применения различных методов расчета электрических цепей к схемам разной конфигурации.
5-13. Иллюстрировать на примере практическую целесообразность применения теоремы об изменении токов в электрической цепи.
5-14. В чем заключается различие между общим и передаточным (взаимным) сопротивлениями?.
106
Глава шестая
ИНДУКТИВНО СВЯЗАННЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
6-1. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ОПРЕДЕЛЕНИЯ
При изменении магнитного поля, связанного с каким-либо витком, в последнем наводится э. д. с., которая в соответствии с законом электромагнитной индукции определяется скоростью изменения магнитного потока независимо от того, чем вызвано изменение потока. В катушке, состоящей из большого числа витков, наводится э. д. с., пропорциональная скорости изменения потокосцепления, т. е. скорости изменения суммы магнитных потоков, сцепленных с отдельными витками данной катушки. Если все витки катушки пронизываются одним и тем же магнитным потоком, то, как указывалось в § 1-5, потокосцепление равно произведению магнитного потока на число витков.
При рассмотрении цепей гармонического тока до сих пор учитывалось явление самоиндукции, т. е. наведение э. д. с. в электрической цепи при изменении потокосцепления самоиндукции, обусловленного током в этой цепи. Отношение потокосцепления самоиндукции к току
характеризовалось скалярной величиной — индуктивностью L.
Теперь нам предстоит заняться рассмотрением явлений взаимной индукции, т. е. наведения э.д.с. в электрической цепи при изменении потокосцепления взаимной индукции, обусловленного током в другой электрической цепи. Цепи, в которых наводятся э. д. с. взаимной индукции, называются индуктивно связанными цепями.
Связь потокосцепления взаимной индукции одной электрической цепи с током в другой цепи, равная отношению потокосцепления взаимной индукции в одной цепи к току в другой цепи, характеризуется взаимной индуктивностью1 М, которая, так же как и индуктивность, представляет скалярную величину.
Если потокосцепление к^Фмг первой цепи обусловлено током 1’2 второй цепи, то взаимная индуктивность цепей определяется как
М = ^2-. (6-1)
f2
1 Этим термином заменен применявшийся ранее в литературе и ныне не рекомендуемый термин «коэффициент взаимной индукции».
106
Соответственно если потокосцепление и>2Фдп второй цепи обусловлено током й первой цепи, то
Л421==^_. (6-2)
Для линейных электрических цепей всегда выполняется равенство
M12=M2i;
и поэтому индексы у параметра взаимной индуктивности могут быть опущены.
Справедливость последнего равенства можно доказать, если выразить потоки взаимной индукции Фдп и Фм2 через соответствующие и. с. iiWj и i2w2 и магнитную проводимость путей, по которым замыкаются эти потоки
Лд.= 2-Н^-; м I •
м _ 'М’лМ _
/и12 — ———- —
*2
лл.
«1 = ^1^2^-
Отсюда также видно, что величина М пропорциональна произведению чисел витков катушек и магнитной проводимости пути общего потока, которая зависит от магнитной проницаемости среды и взаимного расположения катушек.
На основании сказанного формулируется свойство взаимности для индуктивно связанных цепей: если ток, проходящий в первой цепи, обусловливает во второй цепи потокосцепление взаимной индукции ^гФмь то такой же ток, проходящий во второй цепи, обусловит в первой цепи потокосцепление взаимной индукции о»1Фм2 той же величины.
* Картина распределения магнитных силовых трубок потоков Фм1 и Фл/2 не зависит от величии токов ц и i2, т. е. при любых токах оиа одинаковая; поэтому проводимость Лм для каждого нз этих потоков одна и та же.
6-2. ПОЛЯРНОСТИ ИНДУКТИВНО СВЯЗАННЫХ КАТУШЕК; Э. Д. С. ВЗАИМНОЙ ИНДУКЦИИ
Напомним, что положительные направления тока и создаваемого им магнитного потока согласуются всякий раз по правилу правоходового винта. Условимся положитель-
Рис. 6-1. Согласное направление токов в индуктивно-связанных катушках.
ные направления токов h и i2 в двух индуктивно связанных катушках считать согласными, если положительные направления создаваемых ими магнитных потоков самоиндукции и взаимной индукции совпадают.
На рис. 6-1, а и б показаны индуктивно связанные катушки, насаженные на общий сердечник; здесь в зависимости от направления намотки витков выбраны такие положительные направления для токов It и i2, при которых магнитные потоки самоиндукции и взаимной индукции в каждой катушке совпадают. Таким образом, рис. 6-1, а и б иллюстрируют согласное направление токов.
При согласном направлении токов ц и i2 в двух индуктивно связанных катушках зажимы этих катушек, относительно которых токи h и i2 направлены одинаково, называются одноименными или однополярными.
На рис. 6-1, а, где витки обеих катушек намотаны в одном направлении, одноименными зажимами являются зажимы, отмеченные точками (два других зажима на рис. 6-1, а составляют вторую пару одноименных зажимов).
Аналогичным образом на рис. 6-1,6, где витки катушек намотаны в противоположных направлениях, одноименные зажимы также отмечены точками.
107
Таким образом, одноименные зажимы индуктивно связанных катушек характерны тем, что при одинаковом направлении токов i\ и относительно этих зажимов магнитные потоки самоиндукции и взаимной индукции в каждой катушке складываются.
В связи с введением понятия об одноименных зажимах при вычер
Рис. 6-2. Схематическое изображение индуктивио-связаниых катушек с обозначением одноименных зажимов и выбранных положительных направлений токов.
а — согласное направление токов; б — встречное направление токов.
чивании электрических схем нет не-обходимости показывать намотку витков индуктивно связанных катушек, а достаточно разметить на схеме их одноименные зажимы. На рис. 6-2 показано схематическое Изображение двух индуктивно связанных катушек с указанием одноименных зажимов и выбранных положительных направлений токов ц и 1'2. Как это следует из вышесказанного, токи ij и I2 направлены согласно на рис. 6-2, а и встречно на рис. 6-2,6.
В § 1-5 отмечалось, что положительное направление э. д. с. самоиндукции выбирается совпадающим с положительным направлением тока; поэтому положительные направления магнитного потока и наводимой им э. д. с. самоиндукции связаны правилом правоходового винта. Так же и положительное направление э. д. с. взаимной индукции в\м, наводимой в катушке / током 1’2, принимается совпадающим с положительным направлением тока ij. Аналогично положительное направление э. д. с. взаимной индукции е2М-, наводимой в катушке 2 током i'i, совпадает с положительным направлением 1'2. При таких условиях и при согласном направлении токов it и i2 в формуле э. д. с. взаимной
индукции имеется знак «минус», так же как в формуле э. д. с. самоиндукции (1-2), причем положительное направление магнитного потока и наводимой э. д. с. взаимной индукции связаны правилом правоходового винта:
еш
е2М
dt ~ iV1 dt ;
dt ~ 1 dt '
(6-4)
Рассмотрим случай, когда через катушку 1 проходит ток ib причем di\ldi>G. На основании (6-4) в катушке 2 наводится э. д. с. взаимной индукции
е —_____л
2« dt < °’
В этом случае потенциал зажима катушки 2, одноименный с тем,
Рис. 6-3. Экспериментальное определение одноименных зажимов.
в который входит ток ii, оказывается выше потенциала второго зажима катушки 2.
Отсюда можно заключить, что одноименные зажимы двух индуктивно связанных катушек обладают той особенностью, что подведение к одной из них тока, возрастающего по величине, вызывает повышение потенциала на одноименном зажиме второй катушки.
На указанном свойстве основано экспериментальное нахождение одноименных зажимов индуктивно связанных катушек. Одна из них включается в цепь источника постоянного напряжения, а к другой присоединяется вольтметр постоянного тока (рис. 6-3).
Если в момент замыкания цепи источника стрелка измерительного прибора отклоняется в сторону положительных показаний, то зажимы индуктивно связанных катушек, подключенные к положительному полюсу источника электрической энергии и к положительному зажи
108
му измерительного прибора, являются одноименными.
Теперь рассмотрим случай встречного направления токов А и iz, схематически изображенный на рис. 6-2,6, где токи it и 1ц направлены различно относительно одноименных зажимов.
Рис. 6-4. Согласное (а) и встречное (6) направления токов в индуктивно-связанных катушках, соединенных последовательно.
Ввиду того, что положительные направления магнитных потоков самоиндукции и взаимной индукции в этом случае противоположны, э. д. с. взаимной индукции при встречном направлении токов вычисляются по формулам, содержащим знак «плюс»:
W1d<Dm dia
e'M~ dt~—m~dt'
Рассмотрим последовательное соединение двух индуктивно связанных катушек (рис. 6-4,а и б).
При согласном направлении токов (рис. 6-4,а) э. д. с. взаимной индукции е1Д1= -М и =
=—Л4 совпадающие по направлению с токами, могут быть при обходе контура в том же направлении заменены падениями напряжения от взаимной индукции uiM =—еш и «2м=—&2М- Поэтому суммарное напряжение на обеих катушках с учетом того, что равно:
цсог=Г1А+ М +г2£2 +
dt dt
at at
+ (L1+La+2M)^~. (6-6)
dt
Полученное выражение показывает, что две индуктивно связанные катушки, соединенные последовательно, при согласном направлении токов эквивалентны катушке, имеющей активное сопротивление Г1+г2 и индуктивность Lf|-L2+2M.
Таким образом, как и следовало ожидать, наличие взаимной индукции при согласном направлении токов в катушках, соединенных последовательно, увеличивает индуктивность цепи.
При встречном направлении токов (рис. 6-4,6) падение напряжения от взаимной индукции при обходе контура в направлении тока получается со знаком «минус»:
«ВСТ — Г1£1+^1 + Г212’Г
at at
at at
+ (L1+L2~2M)^-. (6-7)
Данное выражение показывает, что две индуктивно связанные катушки, соединенные последовательно, при встречном направлении токов эквивалентны катушке, имеющей активное сопротивление Г14-г2 и индуктивность Lj + Аг—2Л4.
Следовательно, наличие взаимной индукции при встречном направлении токов в катушках, соединенных последовательно, уменьшает индуктивность цепи.
На основании сказанного можно сделать следующий вывод: при согласном направлении токов падение напряжения от взаимной индукции имеет знак «плюс», а при встречном — знак «минус» (обход цепи в обоих случаях совершается в положительном направлении тока).
6-3. КОМПЛЕКСНАЯ ФОРМА РАСЧЕТА ЦЕПИ С ВЗАИМНОЙ ИНДУКЦИЕИ
Представив ток в комплексной форме, получим выражение э. д. с. взаимной индукции для случая согласного направления токов в комплексной форме:
-М imeiat = -at
109
откуда комплексное действующее значение э. д. с, взаимной индукции
и соответственно падение напряжения от взаимной индукции
где — комплексное сопротивление взаимной индукции, которое в радиотехнике принято называть сопротивлением связи.
Рис. 6-5. Векторные диаграммы при согласном (а) и встречном (б) направлениях токов.
Комплексные напряжения, соответствующие (6-6) и (6-7), запишутся так:
^ЕСТ— [rl+rs+jCD — 2М)J /.
Отсюда, между прочим, вытекает следующий способ нахождения вааимной индуктивности М: если через Хоог обозначить индуктивное сопротивление цепи при согласном направлении токов последовательно соединенных элементов, а через Хвст —то же прн встречном направлении, т. е. положить
(6-8)
X„CT=?6J (£j-££2—2М), j то в результате вычитания второго равенства из первого получим:
— *сог *врт 4ш
На рис. 6-5 изображены векторные диаграммы для случаев согласного и встречного направлений то
ков двух индуктивно связанных катушек, соединенных последовательно. При построении векторных диаграмм принято, что L]>M и La>M.
При этом как при согласном, так и при встречном направлениях токов ток / отстает по фазе от результирующего напряжения U. Если принять то и в этом случае
ток получится отстающим, так как всегда £]+£2—2М>0 (§ 6-4). Условия £]<Л1 и £в<Л4 одновременно существовать не могут.
Порядок расчета разветвленных электрических цепей при наличии взаимной индуктивности иллюстрирован ниже на примере схемы рис. 6-6. Предполагается, что элементы
Рис. 6-6. Разветвленная электрическая цепь с взаимной индукцией.
£t, £2 и L3, входящие в схему, связаны друг с другом индуктивно.
Заданными являются э. д. с. £i и Ец и все параметры цепи. Искомыми ЯВЛЯЮТСЯ ТОКИ /1, /г И /д.
Если бы в каждом контуре был только один индуктивно связанный элемент, то запись уравнений для контурных токов не вызвала бы затруднений. В данном же случае удобнее записать уравнения непосредственно для токов в ветвях по первому и второму законам Кирхгофа. Совершая обход контуров по направлению токов /| и /2, будем составлять уравнения напряжений по второму закону Кирхгофа С учетом падений напряжения в сопротивлениях связи. При согласном направлении токов падение напряжения в сопротивлении связи входит со знаком плюс (1Ли=/<йЛ!/), а при встречном—со знаком минус (йм =
£1==(Z14-/w£i) Л~Ь/Ю^12 Д
ПО
— -J- й3~
/CoAljj /]
— 1<йМф13-^-из,
/о)Л4 2S/2;
A+4’B4^;
здесь Uz — напряжение между узлами схемы. Решение уравнений дает токн.
Отметим, что слагаемые с одинаковыми взаимными индуктивностями входят в уравнение с одинаковыми знаками, что может служить проверкой правильности записи уравнений.
Таким образом, расчет разветвленной электрической цепи при наличии взаимной индуктивности может быть проведен одним из описанных ранее методов с учетом падений напряжений в сопротивлениях связи.
Метод узловых напряжений в данном случае непосредственно неприменим, так как токи в ветвях зависят не только от напряжений между узлами, к которым присоединены эти ветви, но и от токов других ветвей, с которыми они связаны через взаимную индукцию.
В разобранном выше примере одноименные зажимы всех трех индуктивно связанных элементов были обозначены одинаково (точками), так как предполагалось, что эти элементы имеют общий нераз-ветвленный сердечник.
В том случае, когда три или большее число элементов располагаются на сложном, разветвленном сердечнике, необходимо одноименные зажимы каждой из пар индуктивно связанных элементов обозначать разными условными знаками (пример 6-2).
Пример 6-1. Определить комплексное сопротивление на входе электрической цепи, состоящей из двух параллельно соединенных катушек, связанных индуктивно при согласном направлении токов (рис. 6-7).
Приняв положительные направления контурных токов согласно рис. 6-7, составляем контурные уравнения:
Ё = (а + /coLi) )1 4- }(£>М1ъ
Ё = (г2 + /<о£2) /2 -b/coAf/i.
Обозначим:
= гг + 2, = г2 +
ZM =ч jwM, тогда
E = Zt 7t + ZM f%;
Ё — + z2 f2-
Рис. 6-7. Пример 6-1.
Решив уравнения относительно Е и /г. найдем общий ток:
' — ' 1 Т ' J “п
Zj Z2 — ZM
Искомое сопротивление всей цепи по отношению к зажимам источника
£
7 _---_---------------в
7 Zy_ + Z^2ZM
При переключении концов одной из катушек получается параллельное соединение катушек с встречным направлением токов, В этом случае в уравиевиях и конечном выражении для Z следует принять Zm со знаком «минус», что приведет к изменению знака при 2ZM в знаменателе упомянутого выражения.
При отсутствии индуктивной связи ZM=0 и конечное выражение совпадает с известной формулой для сопротивления двух параллельных ветвей.
Пример 6-2. Составить уравнения контурных токов для электрической цепи, состоящей из источника э.д.с. £, емкости С и трех индуктивно связанных катушек, насаженных на трехстержневой сердечник (рис, 6-8, л), Взаимная индуктивность катушек: Мц, Mis, Л42з. Цепь рассматривается как линейная (Af=const).
Рисунок 6-8,6 изображает электрическую схему заданной цепи. Точками, кружками и квадратиками обозначены одноименные зажимы, соответствующие каждой паре катушек.
Выбрав направления коитуриых токов, указанные на схеме рис. 6-8,6, составляем контурные уравнения:
Ё — ~~ (/i + Е + fs) + 4- ftol-i) Z'i +
/<±>С
+ )<йЛ412 /2 — /С0Л11з 73;
111
Ё = ~ (А + 4 + А) + (га + /wl2) 4+ /ИС
+ /&>Л41а 71 + /®м23 А;
Ё = -4т- (/1 + А + 7з) + (Гз + i<oL3) А~ /COG
—ja>M33 /j + /<оЛ123 4.
совместное решение которых определяет токи.
||ZBIHIC|| =
1 1 1
/<оС j(£>C jd>C
гг + /coLi ]ыМ12 —/<оЛ113
/<оЛ412 г2 + /со£2 ]<оМ23 —/<о7И1з /<оЛ42з г3 + /<о£3
Затем находится
«7
IIZkII =I|C||t-||Zb||-||C|| =
1
— + /®M12 /coC
. ~ + r2 + jfolv ]<i}C
— + п + /®4
+ /соЛ112 i -iaM"
i
— — /<oM13
/<оС
1
— + juM23
1<аС
1
. „ +rз+уш^-з /соС
Рис. 6-8. Пример 6-2.
Искомые уравнения получаются в виде матрицы:
Пример 6-2, а. Решить предыдущий пример матричным методом, описанным в § 5-10.
Матрица соединений для схемы рис. 6-8,6 имеет вид:
||С||= I 1 1 1 0 0 0 1 0 0 0 1
Сопряженная относительно нее матрица равна:
||СЦТ=
110 0
10 10
10 0 1
Матрица сопротивлений ветвей равна:
1|2В|| =
— 0 0 0
/соС
0 Г1+ /(of.! +/<оЛ413 —/о)Л41з .
0 je>M12 r2 + jb>L2 ММ23
О — jaM13 jwM23 г3 + ja>L3
Матрица контурных сопротивлений находится по формуле (5-25). Сначала находится произведение
6-4. КОЭФФИЦИЕНТ ИНДУКТИВНОЙ СВЯЗИ. ИНДУКТИВНОСТЬ РАССЕЯНИЯ
Рассмотрим картину магнитного поля индуктивно связанных катушек, схематически представленную на рис. 6-9 (для согласного направления токов).
Положим, что первая катушка состоит из витков, а вторая из W2 витков, расположенных в каждой катушке настолько близко друг к другу, что магнитный поток охватывает целиком витки данной катушки.
В общем случае, когда по обеим катушкам проходят токи ц и 4, магнитные потоки могут быть представлены как результат наложения потоков, создаваемых каждым током в отдельности.
На рис. 6-9 приняты следующие обозначения магнитных потоков:
Фх—весь поток, созданный током ц первой катушки;
Ф^! — поток взаимной индукции первой катушки, пронизываю
Н2
щий витки второй катушки;
Ф51 — поток рассеяния
первой катушки,
пронизывающий только витки этой катушки;
Ф2, Ф,И2, ®s2 — аналогичные потоки, созданные током »2 второй катушки; Фм — общий поток взаимной индукции, пронизывающий витки обеих катушек.
Рис. 6-9. Магнитные потоки двух индуктивно связанных катушек.
Из сказанного следует, что Ф] = = Ф81+Фмь Ф2=Фв2 + ФлГ2; Флг = = ФлГ1+ФлГ2-
Чем меньше потоки рассеяния Фв1 и Ф82, тем больше приближаются Фм1 к Ф1 и соответственно Фм2 к Ф2.
При изменении токов ij и i2 во времени изменяются также и потоки, создаваемые этими токами. Индуктивность каждой катушки, как известно, определяется отношением потокосцепления самоиндукции к току данной катушки:
Первые слагаемые этих выражений
®1®S1 и,
LS1 = —;-----; LS2=-------;--(6- !0)
•1
называются индуктивностями рассеяния катушек.
Магнитные потоки могут быть выражены через произведения и. с. на магнитные проводимости путей, по которым замыкаются эти потоки:
= ^)S2==t2U,2^S2>
®M2 = t'2al2^M-
Следовательно,
Li=“’?(Asi+Am); ^2 = aJ2 (AS2~I"Am)-
(6-И)
Таким образом, индуктивность катушки пропорциональна квадрату числа витков и сумме магнитных проводимостей путей потоков рассеяния и взаимной индукции (см. § 1-7)-
Магнитная проводимость в свою очередь зависит от формы и размеров катушек, их взаимного расположения и магнитной проницаемости среды (§ 6-1). На основании (6-1), (6-2), (6-9) и (6-10) индуктивности рассеяния LSi и LSi можно выразить через L2 и М следующими формулами:
LS2 = L2— — М-
(6-12)
Эти выражения нам понадобятся в следующем параграфе при рассмотрении схемы замещения трансформатора.
Степень индуктивной связи двух катушек характеризуется коэффициентом связи k, определяемым как среднее геометрическое из отношений потока взаимной индукции ко всему потоку катушки, т. е. ___________
, 1 / ФЛП ФМ2 ,г
k= у -ФГ’-ФГ- (613)
Если выразить потоки через параметры L|, L2 и М по формулам (6-1), (6-2) и (6-9), то получим:
_ 1 / Mt'1^1 Mi2w2
V w2L1i1 tc'j L2i2 или
k= -M (6-14)
8—1118
113
Из формулы (6'13) видно, что коэффициент связи всегда меньше единицы (так как Флп/Ф1<1 и Фм2/Фа<1). Коэффициент связи возрастает с уменьшением потоков рассеяния Фа: И Феа.
С учетом (6'3) и (6-11) коэффициент связи может быть выражен через магнитные проводимости:
*= Лм
(Asi + Лм)(Лз2+ лм)
Повышение коэффициента связи достигается бифилярным способом
Рис. 6-10. Катушки с коэффициентом связи, близким к единице (а) и к нулю (б).
намотки катушек (рис. 6-10, а) и применением ферромагнитного сердечника, так как с увеличением магнитной проницаемости и соответственно магнитной проводимости сердечника доля потоков рассеяния снижается.
При перпендикулярном расположении осей катушек (рис, 6-10.6) коэффициент связи обращается в нуль. Поэтому, перемещая одну катушку относительно другой, можно плавно изменять коэффициент связи в широких пределах, а при последовательном соединении этих катушек— плавно изменять их результирующую индуктивность. Такое устройство называется вариометром (§ 7-6).
При наличии ферромагнитного сердечника цепь теряет свойство линейности. Однако в тех случаях, когда по условиям работы магнитная индукция в ферромагнитном сердечнике не выходит за пределы прямолинейного участка кривой намагничивания и его магнитная проницаемость может быть принята постоянной, данная цепь рассматривается как линейная, и вышеизложенная теория сохраняет силу.
Как уже указывалось, схематическая картина магнитного поля иа рис. 6-9 соответствует согласному направлению токов. Если изменить на рис. 6-9 положительное направление тока 12> то изменится направление магнитных потоков Фаг и Фмг, что будет соответствовать встречному направлению токов.
В этом случае в уравнениях, приведенных выше, должен быть изменен знак перед Фзг, Фмг и Фг. При этом, как видно из предыдущих формул, величины Lb L2, М, k, LBl, LS2 сохраняются неизменными.
В предыдущем параграфе было показано, что прн встречном направлении токов в двух катушках, соединенных последовательно, результирующая индуктивность равна L\ + + L2—2М.
Докажем теперь, что величина L}+L2—2М всегда положительна.
Для этого воспользуемся двумя неравенствами:
(ПТ-ГаГ)’ = l1 + l2-
Заменив в первом неравенстве К LiL2 меньшей величиной (М), получим:
Li+L2 — 2Л4 > 0.
Пример 8-3. Индуктивная катушка состоит из w витков, соединенных последовательно, согласно.
Индуктивность каждого витка раина 4-Приняв коэффициент связи витков ранным единице, определить результирующую индуктивность катушки.
Прн отсутствии рассеяния взаимная индуктивность каждой пары витков равна L. По аналогии с (6-6) результирующая индуктивность катушки определится суммой индуктивностей всех витков и взаимной индуктивности, умноженной на число размещений из w витков по два:
ipe3’=“’L + ^L-
Так как
.1
то Lpe3 = wL-\-(w—\)wL = w2L.
Как и следовало ожидать ча основании выражения (6-11), результирующая индуктивность катушки пропорциональна квадрату числа витков.
114
6-5. УРАВНЕНИЯ И СХЕМЫ ЗАМЕЩЕНИЯ ТРАНСФОРМАТОРА БЕЗ ФЕРРОМАГНИТНОГО СЕРДЕЧНИКА
Трансформатор представляет собой аппарат, передающий энергию из одной цепи в другую посредством электромагнитной индукции. Он применяется для различных целей, но чаще всего пред-
Рис. 6-11. Трансформатор без ферромагнитного сердечника.
назначается для преобразования величин переменных напряжений и токов *. Трансформатор состоит из двух или нескольких индуктивно связанных обмоток, насаженных на общий сердечник. В настоящем параграфе рассматривается двухобмо-точный трансформатор на одном неферромагнитном сердечнике. Такой трансформатор может служить составной частью линейной электрической цепи в устройствах электроавтоматики, измерительной техники или связи.
Если пренебречь емкостями, существующими как между витками каждой из обмоток трансформатора, так и между самими обмотками и обмотками и землей, то трансформатор может быть представлен схемой рис. 6-11, в которой активные сопротивления обмоток условно вынесены и изображены отдельно.
Обмотка трансформатора, присоединяемая к источнику питания, называется первичной, а обмотка, к которой подключается нагрузка, вторичной. Соответственно напряжения и токи на зажимах этих обмоток называются первичными и вторичными. Следует заметить, что такое наименование в некоторых случаях является условным, если в зависимости от режима энергия может передаваться как в одну, так и в другую сторону.
1 Отсюда происходит само название «трансформатор», т. е. преобразователь.
При заданной полярности зажимов обмоток трансформатора на схеме рис. 6-11 токи направлены встречно, что не имеет принципиального значения-
уравнения трансформаторе в дифференциальной форме при встречном направлении токов имеют вид:
u^r^+L^ — М , 1 1 1 1 dt dt ’
Если напряжения и токи — гармонические функции, то уравнения трансформатора в комплексной форме запишутся следующим образом:
—- C/g-^Cra-f-fcoEg) /g ’ А,-
Эти уравнения равносильны следующим:
i71=[Г14-/со (LjЛ4) +/й)Л1] /j —
— t/g= [r8 4- /и (E2 — Л4)+/®Л1] /8 —
Последние уравнения являются контурными уравнениями, которые соответствуют схеме рис. 6-12.
Рис. 6-12. Схема замещения трансфор-матора без ферромагнитного сердечника.
Следовательно, эта схема может рассматриваться в качестве схемы замещения трансформатора без ферромагнитного сердечника. В отличие от рис. 6-11 в схеме замещения первичная и вторичная цепи трансформатора связаны не индуктивно, а электрически1 (кондук-тивно).
1 Такая схема замещения дает возможность, например, применить метод узловых напряжений в цепи с взаимной индукцией.
115
Если Li = L2, то Li—М>0 и L2—Л1>0, так____как коэффициент
связи k = M/ ]/rL1L2<l. При неравных значениях Lx и L2 одна из разностей (Lr—М или —Л4) может оказаться отрицательной. Например, если Wx ш2, то на основании (6-12) £t>M и £2<Л1. В этом случае схема замещения рис. 6-12 может быть практически осуществлена
Рис. 6-13. Схема замещения, приведенная к первичной обмотке.
только при фиксированной частоте, когда отрицательная индуктивность может быть замещена емкостным элементом: в общем же случае схема с линейным элементом, имеющим отрицательную индуктивность, практически нереализуема.
Входящие в схему рис. 6-12 разности Lj—М и L2—М имеют физический смысл только при одинаковом числе витков первичной и вторичной обмоток (W1 = W2)- в этом случае, как видно из (6-12), они представляют собой индуктивности рассеяния Z-S1 и Ls2 первичной и вторичной обмоток трансформатора.
При неодинаковом числе витков первичной и вторичной обмоток (гг>1 =^= w2) на практике часто пользуются так называемой приведенной схемой замещения трансформатора, показанной на рис. 6-13. Приведение заключается в том, что напряжение U2 и ток /г заменяются величинами, приведенными к первичной обмотке: напряжение U2 умножается на п, а ток /2 делится на п. Здесь n=Wifw2 — отношение чисел витков, которое называется коэффициентом трансформации.
Придав уравнениям (6-15) следующий вид:
Ui^iri+faLi) k — fanM ;
— nfja—пг (ra-f- j(»L2) -junMIi,
можно преобразовать их следующим образом:
^i=[ri+/w(A1 — пТИ)] /j-r-
4- — jatn М ;
— nL/a=na [г2 + /ю (la — -^- +
+jtitnM ---
Полученные уравнения являются контурными уравнениями для приведенной схемы замещения трансформатора (рис. 6-13).
Схема замещения трансформатора, приведенная к первичной обмотке, содержит: сопротивление и индуктивность рассеяния LSi первичной обмотки трансформатора; индуктивность — М в поперечной ветви (эта ветвь называется ветвью намагничивания); сопротивление г2 и индуктивность рассеяния LS2 вторичной обмотки, приведенные к первичной обмотке трансформатора, т. е. умноженные на п^= (Wi/w2)2 (квадрат отношения чисел витков).
Индуктивные сопротивления ®£Si и a>LS2 представляют собой сопротивления рассеяния первичной и вторичной обмоток трансформатора, а индуктивное сопротивление пыМ— сопротивление ветви намагничивания. Намагничивающая сила, определяющая общий магнитный поток, который пронизывает первичную и вторичную обмотки, при встречном направлении токов равна:
Й®1 — (й — — ) —
\ wl)
— (й----—
\ п /
Ток i’i-— и соответствующий ему
п
комплексный ток й— 2зи, который в га
схеме замещения трансформатора, приведенной к первичной обмотке, проходит через ветвь намагничивания, принято называть намагничивающим током трансформатора.
116
Схеме рис. 6-13 соответствует векторная диаграмма, показанная на рис. 6-14. При построении векторной диаграммы в качестве исходных могут быть приняты приведенные вторичные напряжение и ток.
Падения напряжения от приведенного вторичного тока /2/п в приведенных активном сопротивлении
Рис. 6-14. Векторная диаграмма к схеме рис. 6-13.
г2п2 и индуктивном сопротивлении рассеяния ы£е2п2 вторичной обмотки геометрически складываются с приведенным вторичным напряжением nU2. Полученное напряжение равно падению напряжения от намагничивающего тока в индуктивном сопротивлении ветви намагничивания
—-^-j, причем намагничивающий ток отстает от полученного напряжения на 90°. Первичный ток находится как геометрическая сумма намагничивающего тока и приведенного вторичного тока:
форматора. Для того чтобы схема замещения стала эквивалентной заданной схеме трансформатора, можно воспользоваться так называемым идеальным трансформатором, которому будем приписывать следующее свойство: при любых условиях отношение первичного напряжения к вторичному на зажимах идеального трансформатора равно отношению вторичного тока к первичному и определяется коэффициентом трансформации п. Идеальный трансформатор не имеет потерь энергии, и при разомкнутой вторичной обмотке через его первичную обмотку ток не проходит. В действительности такого трансформатора не существует, однако по своим свойствам к нему приближается трансформатор с коэффициентом связи, близким к единице, и со столь большим числом витков, что сопротивление его ветви намагничивания /щиЛ4 = /щш2 Лм практически равно бесконечности.
Дополнив схему рис. 6-13 идеальным трансформатором с коэффициентом трансформации п, получим эквивалентную схему трансформатора (рис. 6-15).
Рис. 6-15. Схема замещения с идеальным трансформатором (n=WilWi).
\ и / п 1
Падение напряжения от тока Ц в активном сопротивлении и индуктивном сопротивлении рассеяния первичной обмотки геометрически складывается с напряжением на ветви намагничивания, образуя первичное напряжение.
Ввиду того, что вторичные электрические величины — напряжение U2 и ток /2 — в схеме рис. 6-13 приведены к первичной обмотке, т. е. изменены пропорционально отношению числа витков, то данная схема приведенного трансформатора не эквивалентна исходной схеме транс-
Рисунки 6-12—6-15 соответствуют встречному направлению токов, принятому в исходной схеме рис. 6-11.
Схемы замещения с измененным положительным направлением вторичного тока соответствовали бы согласному направлению токов в исходной схеме.
Пример 6-4. Решить пример 6-1 с помощью схемы замещения трансформатора (рнс. 6-12).
Рассматривая индуктивво связанные элементы схемы рис. 6-16, а в качестве трансформатора с попарно соединенными первичными и вторичными зажимами и пользуясь схемой замещения рис. 6-12 (с изменением направления тока Л), полу
117
чаем эквивалентную схему рис. 6-16,6 без индуктивных связей.
Комплексное сопротивление всей цепи равно;
Ё — iaM 4-
[г, + /со (Li - Af)] [га + /со (L2 - Л4)]
ri + га + (Li + Z-2 — 2Л4)
Применяя сокращенную запись
Zi “= ri + Za = r3 +
ZM « /<оЛ1,
Рис. 6-16. Пример 6-4. находим:
^za-z^
Zi+Zs-2ZM'
Как и следовало ожидать, мгновенная мощность, подводимая к трансформатору с первичных зажимов, равна сумме мгновенных значений мощностей, расходуемых иа нагрев обмоток, скорости изменения энергии и>м, накопленной в магнитном поле, и мощности, передаваемой нагрузке.
Первое слагаемое энергии магнитного поля равно энергии поля первой обмотки при ij*0; второе слагаемое равно энергии поля второй обмотки при й=0; третье слагаемое представляет энергию, связанную с взаимным расположением обеих обмоток.
Пря согласном направлении токов третье слагаемое в выражении энергии будет иметь знак плюс.
Первое и второе слагаемые положительны, третье же в зависимости от зна-______ ков мгновенных токов i| и
[/; i2 может иметь положи-
-'’'''''—CZD—'v тельный или отрицатель-
ный знак. Поэтому энергия системы, состоящей из двух индуктивно связанных обмоток, может быть больше или меньше суммы энергий обеих обмоток, взятых отдельно.
Пример 6-5. Две индуктивно связанные катушки имеют индуктивности £1=4 гн и ба= =25 ен; коэффициент связи А:=0,5.
Определить энергию поля, создаваемую этими катушками при токах и = 10 a и jj=20 а.
Взаимная индуктивность катушек
М k = 0,5 VT25 = 5ан.
6-6. ЭНЕРГИЯ ИНДУКТИВНО СВЯЗАННЫХ ОБМОТОК
Рассмотрим вопрос об энергии индуктивно связанных обмоток.
Дифференциальные уравнения двух индуктивно связанных обмоток при встречном направлении токов (рис. 6-11) имеют вид:
«г ='•ih + bi-т- — м ;
at at
din dii
0 = u3 4- r3l3 + L3 — M —— ,
Умножив первое уравнение на й, а второе на jj, сложив и сгруппировав слагаемые, получим:
Pj = Д1 «2 *2 + Г1 Г1 + г2 *2 4"
di, di» / di» di, \
+ GG “77 + “77 — M ( Ц — + it — I
at at \ at at j
или
.» л dm
Pi ri h 4- ri l2 4" -г. • 4-
где шм—энергия магнитного поля:
- .9 . .2
Z-j if б2 i‘>
Юм = -у- + -у— - Л41?а.
Энергия каждой катушки, взятой отдельно, составляет:
4-108 2
= 200 Эж;
2
Ь2 »2 25-20*
2 ~ 2
= БОООбж.
Энергия взаимного расположения
Л4УЯ = 5-10-20 = 1 000 дж.
Энергия поля всей системы при согласном направлении токов
wM = 200 4- 5 000 + 1 000 = 6 200 дж, а при встречном направлении токов
,= 2004-5000—1000 = 4200 дж.
6-7. ВХОДНОЕ СОПРОТИВЛЕНИЕ ТРАНСФОРМАТОРА
Если нагрузка Z„ присоединена к источнику электроэнергии не непосредственно, а через трансформатор (рис. 6-17), то согласно (6-15)
0= + /шЛ4/14-(га4- jcoLa4-2H) /а.
118
Следовательно,
/ _ йр jaMfi
откуда сопротивление на входных зажимах трансформатора
—ri+faLj -|-
+-------. (6-16)
ri + + ZB
Третье слагаемое в правой части выражения (6-16) представляет со-
Рис. 6-17. Присоединение нагрузки к источнику через трансформатор.
Рис. 6-18. Схема для определения входного сопротивления нагруженного трансформатора.
бой комплексное сопротивление, вносимое из вторичной цепи в первичную; схема рис. 6-18 эквивалентна схеме рис. 6-17.
В зависимости от характера ZB мнимая часть вносимого сопротивления может быть положительной или отрицательной.
Допустим теперь, что нагрузка ZB присоединена к идеальному трансформатору. Учитывая условия U, I, — = — = п, которыми характери-h
зуется идеальный трансформатор, получим входное сопротивление
Z1BX= =n2ZH. (6-17)
п '2
Следовательно, идеальный трансформатор, включенный между нагрузкой и источником электроэнергии, изменяет сопротивление нагрузки пропорционально квадрату коэффициента трансформации без изменения его угла.
Это свойство практически используется в различных областях электротехники, связи, радио, приборостроения, автоматики для уравнивания сопротивлений источника и нагрузки (с целью повышения отдаваемой источником мощности) .
Поэтому в том случае, когда требуется изменить величину сопротивления какой-либо нагрузки без изменения самой нагрузки, включается промежуточный трансформатор, по свойствам приближающийся к идеальному трансформатору с коэффициентом трансформации, определяемым на основании (6-17):
где г1вх — требуемая величина сопротивления.
Формула (6-17) непосредственно вытекает также из приведенной схемы замещения трансформатора (рис. 6-13), поскольку идеальный трансформатор не имеет активных сопротивлений и индуктивностей рассеяния (ri = r2=“0; Zei=^s2=0) и его взаимная индуктивность равна бесконечности.
Входное сопротивление идеального трансформатора при замкнутых выходных зажимах равно нулю, а при разомкнутых — бесконечности.
Пример 6-6. Определить входное сопротивление цепи, показанной на рис, 6-19,а.
Пользуясь схемой замещения, представленной на рис. 6-19,6, находим:
Z = /у + /<о (Li — Л1) +
[га + /<о (La — Л1)1 1/аЛ1 + Z°1 + jcoLj Zo
119
Рис. 6-19. Пример 6-6. а — исходная схема; б — схема замещения.
шего напряжения (рис. 6-21,а).Так же как и трансформатор, он может быть понижающим или повышающим.
Уравнения автотрансформатора в комплексной форме для указанных на рис. 6-21, а положительных направлений токов и напряжений записываются так:
[ri+7® (£14-А1)] /j-j-
+ [ra+/® (ji—
[r2+/G>(^2+Af)]/i — (''г+М^-гУг-
Пример 6-7. Определить входное сопро-тивление цепи, состоящей из двух трансформаторов, включенных каскадно, с нагрузкой гя на выходе (рис. 6-20, а). Активные сопротивления обмоток трансформаторов не учитываются.
Рис. 6-20. Пример 6-7.
а исходная схема; б — схема замещения.
Рис. 6-21. Автотрансформатор без ферромагнитного сердечника (а) и его схемы замещения (б и в).
В соответствии с (6-16) входное сопротивление второго трансформатора будет:
Za ~ jaLa
(<о/И8)а /wZ-a+rи
Рассматривая Za в качестве нагрузки первого трансформатора, определяем входное сопротивление цепи по той же формуле
(6-16):
Z = /«’Ll +
(<oMi)2
-|- Zg
После преобразований находим:
2 __ ЮГн ( ~ ^1) +
со ( L, L> + Ll — Ml) —
+/со2 ( Z2 L2 + Z.j Z2— Zj M2 — L2 Mi )
~1гн + A?)
К тому же результату можно прийти на основе схемы замещения, показанной на рис. 6-20, б.
6-8. АВТОТРАНСФОРМАТОР
Автотрансформатор отличается от трансформатора тем, что его обмотка низшего напряжения является частью обмотки выс-
Эти уравнения соответствуют схеме замещения, показанной на рис. 6-21,6. Правая ветвь схемы состоит из практически неосуществимого линейного элемента — отрицательной индуктивности (—М). Поэтому полученная схема замещения рис. 6-21,6 может быть использована только для расчета. Практически осуществить ее можно только для фиксированной частоты, когда элемент —М замещается емкостью. Однако если индуктивность нагрузки, подключенной к выходным зажимам, компенсирует отрицательную индуктивность, то схема замещения автотрансформатора в сочетании с нагрузкой практически осуществима.
Итак, схема замещения автотрансформатора представляет трехлучевую звезду. Сопротивления лучей этой звезды могут быть найдены и другим способом, если по
120
очередно приравнять суммы сопротивлений двух лучей сопротивлениям между соответствующими зажимами автотрансформатора» (приразомкнутом третьем зажиме).
Обозначим: индуктивность каждого витка L, общее число витков w, число витков обмотки низшего напряжения to2; приняв коэффициент связи равным единице, т. е. пренебрегая рассеянием, получим в этом случае схему замещения автотрансформатора, показанную на рис. 6-21, в.
В режиме холостого хода автотрансформатора (т. е. при разомкнутых выходных зажимах), если не учитывать рассеяния, отношение первичного напряжения Ut ко вторичному равно отношению суммарного числа витков обмотки к числу витков обмотки низшего напряжения:
где п — коэффициент трансформации автотрансформатора.
При нагрузке подводимая к автотрансформатору мощность передается на вторичную сторону как посредством электромагнитной индукции (через магнитное поле), так и непосредственно через электрическую связь.
Применение автотрансформатора вместо обычного трансформатора той же мощности и с таким же коэффициентом трансформации дает экономию в меди, затрачиваемой на обмотку. Экономия достигается за счет сокращения общего числа витков и уменьшения толщины провода вторичной обмотки, через которую проходит ток, равный разности первичного и вторичного токов.
Экономия в меди тем больше, чем ближе к единице коэффициент трансформации, так как при этом уменьшается разность |?i—/а|.
6-9. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
6-1. Перекрестив в схеме рис. 6-7 концы одной нз индуктивно связанных катушек, определить сопротивление параллельно соединенных катушек без учета активных сопротивлений.
Ответ:
Li + Lt-i-2M
6-2. В ветвь первой катушки схемы рис. 6-7 последовательно включена емкость 50 мкф-, Г1=20 ом; г2=10 ом; Li=0,2 гн; £2=0,1- гн; коэффициент связи равен 0,4. Вычислить напряжение иа емкости, если напряжение на параллельных ветвях равно 100Z0°e; со =400 рад!сек.
Ответ: 83,6 Z—143'в.
6-3. Заданы параметры трансформатора: сопротивление 40 ом и индуктивность 0,05 гн — для первичной обмотки, сопротивление 50 ом и индуктивность 0,05 гн — для вторичной обмотки; коэффициент связи 0,6. Первичная обмотка присоединена к источнику э.д.с. 100Z0°e, вторичная обмотка — к источнику э.д.с. 150 Z—30° в, угловая частота равна 400 рад! сек. Электродвижущие силы источников направлены к одноименным зажимам трансформатора. Вычислить активные мощности, поступающие от обоих источников и идущие иа потери внутри трансформатора.
Ответ: 128 вт; 360 от.
6-4. Две индуктивно связанные одинаковые катушки с сопротивлением 10+/ 10 ом каждая соединены последовательно и согласно; сопротивление взаимной индукции равно / 4 ом. К общему зажиму катушек подключена емкость — /20 ом. К свободным зажимам катушек подключены источники э.д.с. 10Z0°e и 10Z30°e, вторые зажимы которых присоединены к свободному зажиму емкости.
Найти напряжение на емкости.
Ответ: 10,95 Z—1°18'в.
6-5. Трансформатор, имеющий две обмотки на общем сердечнике, характеризуется следующими данными: Г] = 100 ом, Lg= = 1 гн, общее сопротивление вторичной обмотки и нагрузки 10000 ом, отношение чисел витков ай|/аи2=10, коэффициент связи й=0,5. Вычислить параметры схемы рис. 6-12.
Ответ: Lt—М——0,04 гн; Lt—Af= =0,95 гн; М—0,05 гн.
6-6. Вывести формулу (6-17) на основании выражения (6-16), положив, что Li и Ls стремятся к бесконечности, ЛР=£1£г, П=г2=0
6-7. Какие зажимы называются однополярными?
6-8. Что называется током намагничивания?
6-9. Пояснить понятие «идеальный трансформатор».
6-10. В чем заключается приведение схемы трансформатора к первичной цепи?
6-11. Построить векторную диаграмму токов и напряжений для цепи, показанной иа рис. 6-7.
6-12. Как применить трансформатор в качестве согласующего устройства?
6-13. Почему в случае двух индуктивно связанных катушек не могут одновременно выполняться" условия Li<M и L2<А4?
121
Глава седьмая
ОДИНОЧНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР
7-1. КОЛЕБАТЕЛЬНЫЕ (РЕЗОНАНСНЫЕ) ЦЕПИ
Колебательными или резонансными цепями называются электрические цепи, в которых могут возникать явления резонанса напряжений или токов.
Резонанс представляет собой такой режим электрической цепи, содержащей индуктивности и емкости, при котором реактивное сопротивление или реактивная проводимость цепи равны нулю; соответственно равна нулю реактивная мощность на зажимах цепи.
Резонанс напряжений наблюдается в электрической цепи с последовательным соединением участков, содержащих индуктивности и емкости. Неразветвленная цепь, состоящая из последовательно соединенных г, L, С, рассмотренная в § 2-8, представляет один из простейших случаев такой цепи. В радиотехнике ее называют колебательным контуром последовательного питания или сокращенно последовательным колебательным контуром.
При резонансе напряжений индуктивное сопротивление одной части цепи компенсируется емкостным сопротивлением другой части цепи, последовательно с ней соединенной. В результате реактивное сопротивление и реактивная мощность на зажимах цепи равны нулю.
В свою очередь резонанс токов наблюдается в электрической цепи с параллельным соединением участков, содержащих индуктивности и емкости. Один из простейших примеров такой цепи, состоящей из параллельно соединенных элементов г, L, С, был рассмотрен в §2-9. В радиотехнике такую цепь называют колебательным контуром параллельного питания или сокращенно параллельным колебательным контуром.
При резонансе токов индуктивная проводимость одной части цепи компенсируется емкостной прово-152
димостью другой части цепи, параллельно с ней соединенной. В результате реактивная проводимость и реактивная мощность на зажимах цепи равны нулю.
Частоты, при которых наблюдается явление резонанса, называются резонансными частотами.
Исследование резонансных режимов в электрических цепях заключается в нахождении резонансных частот, зависимостей различных величин от частоты1 или параметров L и С, а также в рассмотрении энергетических соотношений при резонансе.
Колебательные цепи — неотъемлемая часть всякого радиотехнического устройства. Изучению явления резонанса, свойств и частотных характеристик последовательных и параллельных колебательных контуров посвящена данная глава. Более сложные колебательные системы, составленные из колебательных контуров, связанных друг с другом, рассмотрены в гл. 8.
7-2. ПОСЛЕДОВАТЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР. РЕЗОНАНС НАПРЯЖЕНИЙ
Колебательная цепь с последовательным соединением г, L, С (рис. 7-1) является простейшей
Рис. 7-1. Последовательный колебательный контур.
цепью для изучения явления резонанса напряжений и подробно рассматривается ниже.
1 Такие зависимости, называемые частотными характеристиками, рассмотрены в § 7-3 и далее.
Комплексное сопротивление такой цепи зависит от частоты:
Z=r+jx=r+j^wL—(7-1)
Резонанс напряжений наступает при частоте «о. когда х= г 1 п
=u>qL----=0, откуда
<ооС
«0=-^. (7-2)
V LC
При резонансе напряжений максимумы энергии магнитного поля индуктивности и электрического поля емкости равны. В этом легко убедиться, вспомнив, что реактивное сопротивление цепи, содержащей индуктивность и емкость, пропорционально разности максимальных значений энергии, запасаемой в магнитном и электрическом полях (§ 3-4):
^^(^м-кс-^Сиакс)-
Условию резонанса х=0 соответствует равенство
П7 =IF
Гмакс Смаке*
Если принять, что при резонансе ток в контуре i=Im cos toOt то напряжение на емкости ис= *=Ucm sin io0t В этом случае мгновенные значения энергии магнитного и электрического полей
L Р о .
W, = ----- =-----COS2 to04 и
L 2 2 0
Ci£ сиг.т
wc=-------=------— sin2to0t
c 2 2 °
Кривые зависимостей wL и wc от времени показаны на рис. 7-2. В моменты t=0, Т/2,... энергия магнитного поля достигает максимума WL макс = L/^/2, а энергия электрического поля равна нулю; в момен-
Т 3
ты t=— , —Т,..., наоборот, энергия 4 4
электрического поля достигает максимума Wc макс =» СU*m /2, а энергия магнитного поля обращается в нуль.
Как уже отмечалось выше, максимальные значения энергии магнитного и электрического полей равны:
= А (М2 = ЕЕ?
2 2 \ы0Г / 2 ’
где Um— амплитуда напряжения на реактивных элементах при резонансе;
Рис. 7-2 Кривые wL и шс.
wL и wc колеблются с удвоенной частотой около среднего значения
4 т 4 т
Таким образом, при резонансе происходит непрерывное перераспределение энергии магнитного и электрического полей, причем суммарная энергия остается неизменной:
LI2
wL+wc = [cos2to0Z-hsin2to0/] =
7/2 ГТ/2 — L w ’ 2 ~ 2
Иначе говоря, энергия, первоначально запасенная в контуре при подключении его к источнику, «колеблется» в режиме резонанса между L и С без участия в этом процессе источника. Именно поэтому контур называется колебательным.
Если бы колебательный контур не содержал сопротивления г, то при резонансе энергия не поступала бы в контур от источника. При наличии же в последовательном колебательном контуре сопротивления г вся электрическая энергия, которая при резонансе поступает в контур от источника, расходуется в сопротивлении. За один период она равна
wr=PT,
где Р— средняя мощность на зажимах контура при резонансе;
123
Т — период.
Эта энергия обычно во много раз меньше той, которая запасена в колебательном контуре.
Мы уже встречались с понятием добротности индуктивной катушки QL=xfr=&Llr (§ 2 8) и конденсатора Qc = b/g = aCr (§ 2 9).
Умножив и разделив выражение
для Ql на получим:
2
=2л
Ql — и
£макс
РТ ’
здесь Р — средняя мощность, расходуемая в последовательном сопротивлении г при амплитуде тока /т.
Аналогично рассуждая, т. е. умножив и разделив выражение Qc на ~ , получим:
* 9
— С1А П7
гу 2 о “'Смаке
Qc = co----— -2л
1 Um
РТ
2 г
где Р— средняя мощность, расходуемая в параллельном сопротивлении г при амплитуде напряжения на емкости Um-
Следовательно, добротность определяется в зависимости от отношения максимума энергии реактивного элемента к энергии, поглощаемой сопротивлением за период. В обоих случаях добротность равна отношению реактивной мощности (взятой с положительным знаком) к средней мощности.
В случае колебательной пепи также пользуются понятием добротности контура
<2 = <00-^. (7-3)
Следует обратить внимание на то, что все величины, входящие в (7-3), соответствуют условию резонанса.
Для последовательного колебательного контура (рис. 7-1) на основании (7-3) получаем:
q_<V- _ 1 ]/ с
г ы0Сг г
_ (7-4)
где р= ~ называется характеристическим (или волновым) сопротивлением колебательного контура.
Характеристическое сопротивление составляет в среднем несколько сотен ом, а сопротивление г — несколько ом; поэтому добротность колебательных контуров, применяемых в радиотехнике, достигает Q== ===100-:-300.
Величина, обратная добротности контура, называется затухани-е м контура и обозначается
d-~^- (7‘5)
Это наименование связано с тем, что при отключении колебательного контура от источника, когда контур
Рис, 7-3. Нагруженный колебательный контур.
замыкается накоротко, колебательный процесс затухает тем интенсивнее, чем больше величина d.
В радиотехнических устройствах к одному из реактивных элементов колебательного контура, например к емкости, подключается нагрузка в виде сопротивления гн (рис. 7-3,а). Вследствие этого возрастают потери в цепи и соответственно уменьшается добротность.
Для определения добротности нагруженного контура параллель
124
ное соединение С и гя можно заменить эквивалентным при резонансной частоте последовательным соединением емкости и «вносимого» сопротивления гвв (рис. 7-3,6). Переписывая соотношения, рассмотренные в конце §4-3, в виде <йоСг„»1, гвнл?—-Ц—- и учиты-ги (<о0С)«
вая, что 1/©оС=р, получаем:
Как отмечалось в § 4-3, при высоких частотах емкости эквивалентных схем (рис. 7-3, а и б) могут быть практически приравнены друг Другу.
Таким образом, в схеме рис. 7-3,6 содержатся те же реактивные элементы, что и в схеме рис. 7-3, а, а сопротивление равно: г+гвн.
Добротность нагруженного контура равна:
Qa = -P-=—, ' + 'вн Г + Ра/»н
(7-6)
а затухание увеличивается на величину «вносимого» затухания dBB= =рАн!
= — +—=^+^вн- (7-7)
Р
Если вносимое сопротивление гвн значительно превышает сопротивление г, то
(7-8) Р 'и
При резонансе входное сопротивление последовательного контура минимально, а ток в контуре достигает максимальной величины. Поэтому в условиях, близких к резонансу, напряжения на индуктивности и емкости могут быть значительно больше приложенного к цепи напряжения.
На рис. 7-4 показана векторная диаграмма тока и напряжений при резонансе. Напряжения на реактивных элементах при резонансе определяются из выражения
<7'9)
При Q>1 эти напряжения превышают по величине напряжение
U=E, приложенное к колебательному контуру. Поэтому резонанс в последовательном колебательном контуре и называют резонансом напряжений.
о
исо J шос
Рис. 7-4. Векторная диаграмма при резонансе напряжений.
Из (7-9) следует, что
Q = (7-10)
т. е. добротность рассматриваемой цепи определяется отношением напряжения на L или С при резонансе к величине приложенного к контуру напряжения.
Из выражения (7-2) следует, что резонанс напряжений может быть достигнут изменением параметров L и С (при фиксированной частоте <п источника напряжения) или частоты источника со (при фиксированных параметрах L и С).
Рис 7-5. Настроечные кривые I(L) и /(С).
Зависимости тока в контуре и напряжений на индуктивности и емкости от L или С при заданной частоте называются настроечными кривыми.
На рис. 7-5 показаны кривые тока в зависимости от L и С (рис.
125
7-5,а и б). Они построены по формуле
При L=0 ток равен
Е
. При L=l/w2C ток
достигает максимального значения Е/r, и по мере увеличения L ток спадает, стремясь к нулю при L->-eo.
При С=0 ток отсутствует. При C—\/a>zL ток достигает максимума, а затем с увеличением С стремится в пределе к — Е --------.
V г*+(ыЕУ
Значения ULo и Uco, получаемые на основании (7-9), не являются экстремальными: максимум напряжения UL наступает при частоте выше резонансной, а максимум {Л?— при частоте ниже резонансной. Более подробно этот вопрос рассмотрен в конце § 7-3.
7-3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ПОСЛЕДОВАТЕЛЬНОГО РЕЗОНАНСНОГО КОНТУРА
При построении частотных характеристик удобно пользоваться относительными единицами, так как при этом сокращается число параметров и становится возможным пользоваться стандартными кривыми. Например, в качестве аргумента вместо частоты ш может быть взята относительная частота со/шо, т. е. отношение текущей частоты к резонансной. Кроме того, применяется также относительная расстройка частоты, о которой будет сказано ниже.
Рассмотрение частотных характеристик последовательного контура начнем с зависимостей от относительной частоты комплексного сопротивления контура, отнесенного к сопротивлению г, его модуля и угла. Согласно (7-1) с учетом (7-2) и (7-4)
Соответственно модуль равен:
а угол
<p=arctgQ(——(7-13)
Рис. 7-6 Частотные зависимости относительного сопротивления (в) и угла (б).
На рис. 7-6 показаны зависимости zjr и <р от относительной частоты со/соо.
Каждая из этих зависимостей представляет семейство кривых параметра Q. Семейство кривых г/г проходит через точку с координатами <о/<оо— 1, которая соот-
ветствует условию резонанса. Семейство кривых ф проходит через точку о/соо= 1, <р=0, которая также соответствует резонансу.
Ток в цепи, отнесенный к току /0 при резонансе, равен:
1 Ё Ё г
г г \ <оо сосйоДС/
-1+/С(——(7-11)
<7-14) 'о
126
Частотную зависимость модуля
принято называть амплитудно-частотной характеристикой или резонансной кривой тока.
Частотная зависимость угла фазового сдвига тока относительно приложенного напряжения называется фазо-частотной или просто фазовой характеристикой тока; она выражается зависимостью (7-13). Положительные значения фазовой характеристики соответствуют отстающему, а отрицательные —- опережающему по фазе току.
Как и следовало ожидать, при частотах ниже резонансной, когда емкостное сопротивление преобладает над индуктивным, сопротивление последовательного контура имеет активно-емкостный характер. При частотах выше резонансной сопротивление контура становится активно-индуктивным, причем с дальнейшим ростом частоты <р стремится к 90е.
На рис. 7-7, а показано семейство резонансных кривых тока в относительных единицах. Так же как и зависимость z/r, кривые Z//o для
Рис. 7-7. Частотные зависимости тока.
разных Q проходят при резонансе через точку с координатами (1,1).
Если по оси ординат откладывать ток / (вместо отношения //Zo), то максимумы резонансных кривых тока, построенных для разных значений г, не совпадут в одной точке (рис. 7-7,6).
Величина 1 = Q(—------—), вхо-
\ о>о о / дящая в выражения (7-11)—-(7-15), может быть названа обобщенной расстройкой контура: она учитывает отклонение частоты от резонансной и добротность Q. Из (7-11) следует, что обобщенная расстройка £ в случае последовательного контура равна отношению реактивного сопротивления контура к г.
£ = —. (7-16)
Г
Если по оси абсцисс откладывать не относительную частоту ы/соо, а обобщенную расстройку Ё, то каждая из зависимостей z/r, ///о и <р .вместо семейства кривых пред-
Рис. 7-8. Нормированные характеристики сопротивления (а), тока (б) и угла (в).
127
ставится одной «нормированной кривой» (рис. 7-8):
— == '-----------------------;
г 1о /1+Е2
<p=arctg£. (7-17)
Наибольший интерес в частотной характеристике представляет ее часть вблизи точки резбнанса. В этой области частот
со ш0 02— то __
<о0 со со0 со
(со—<ос) (соЧ-сор) ~ 2Дсо 1 g)
СОрСО СОр ’
так как вблизи точки резонанса со 4- <0р ~ 2<в0.
В выражении (7-18) величина Дсо = со—соо называется расстройкой контура (абсолютной). Она положительна при со>соо и отрицательна при со<соо- Условимся называть относительной расстройкой величину 6=Дсо/соо-Тогда вблизи точки резонанса
— — -^^26. (7-18а)
СОр со
С учетом (7-18а) выражения (7-12), (7-13) и (7-15) упрощаются и принимают вид, более удобный для практических расчетов: -£-^/l+(2Q6)2; 4-^ z -:
r у 1+(2Q6)2
<p=arctg2Q6. (7-19)
Выражения (7-19) достаточно точны при |6| <0,1. При ]5| =0,2 погрешность в сопротивлении z меньше 10%.
Чем выше добротность контура Q, тем острее резонансные кривые. Таким образом, величина Q характеризует остроту резонансной кривой («остроту настройки)»; согласно (7-3) чем больше отношение энергии, запасенной в колебательном контуре, к энергии, рассеиваемой в контуре за один период, тем острее резонансная кривая.
Полосу частот вблизи резонанса, на границах которой ток снижается до 1/ 1^2=0,707 максимального (резонансного) значения /о, принято называть полосой про-
пускания колебательного контура. При токе V2 мощность,
расходуемая в сопротивлении г, равна:
т. е. составляет половину мощности, расходуемой при резонансе. Поэтому полосу пропускания характеризуют как полосу, границы которой соответствуют половине максимальной мощности. На границах полосы пропускания колебательного контура активное и реактивное сопротивления равны по величине: г= |х|.
Е2
Это следует из условия г-----==
I £2
= — г — что дает г2+х2=2г2.
2 г2
Соответственно и фазовый сдвиг между напряжением на зажимах цепи и током составляет 45°: на нижней границе комплексное сопротивление цепи имеет емкостный характер (ток опережает напряжение) и <р=—45°; на верхней границе комплексное сопротивление цепи имеет индуктивный характер (ток отстает от напряжения) и <р=45°.
На основании (7-17) условие для границы полосы пропускания записывается в следующем виде:
1-Н2 = /V
или
1=±1. (7-20)
Итак, на границах полосы пропускания обобщенная расстройка по абсолютной величине равна единице. Вблизи резонанса g«2Q6. Поэтому можно записать 2Q6»±1, откуда относительная расстройка частоты на границах полосы про-
пускания равна ~ и
~ 1
~2Q'
Следовательно, при высокой добротности контура полоса пропускания практически симметрична относительно резонансной частоты и находится из условия
128
или
e J_ = d. (7-21)
<£>0 Q
Для контуров с невысокой добротностью решение уравнения (7-20) дает:
6i,2 = - 1 + 2Q + ]/ 1 + ^. причем условие (7-21) остается в силе.
Если задана резонансная кривая тока, то для нахождения добротности контура удобно пользоваться формулой
Q= —-°—. (7-22)
<в2 — <!>!
Предыдущие расчетные формулы и частотные характеристики относились к колебательному контуру, питаемому источником э.д.с. Е (рис. 7-1). Если колебательный контур подключен к источнику напряжения с внутренним сопротивлением rt-, то последнее, добавляясь к сопротивлению г, влияет на добротность и полосу пропускания контура: чем больше г«, тем ниже «эквивалентная добротность»
и тем шире полоса пропускания d3=l/Q3.
Поэтому для получения по возможности более узкой полосы пропускания последовательного колебательного контура выгоден источник напряжения с малым внутренним сопротивлением.
В радиотехнических устройствах напряжение на реактивном элементе (L или С) последовательного колебательного контура используется как выходное напряжение. Поэтому представляют практический интерес частотные характеристики напряжений на индуктивности и емкости, отнесенных к напряжению на зажимах контура.
Возвращаясь к схеме рис. 7-1, записываем так называемые коэффициенты передачи или усиления напряжения:
_^с_ 1 с Ё iwCZ
Амплитудно-частотные и фазовые характеристики находятся в этом случае по формулам:
Здесь, как и в (7-14), знак фазовой характеристики противоположен знаку аргумента (угла) комплексного коэффициента передачи. Положительные значения фазовой характеристики соответствуют отставанию по фазе напряжения на реактивном элементе от приложенного к контуру напряжения, а отрицательные значения соответствуют опережению.
Частотные характеристики | Kl I, [Кс I, <рь и <рс представлены на рис. 7-9.
Напряжение на индуктивности Ul=(£>LI при (о=О равно нулю; поэтому кривая | Ль| начинается с нуля. С увеличением со/соо кривая | Ль | растет до тех пор, пока ток не начнет снижаться быстрее, чем возрастает со/соо. После этого | Ль | спадает, стремясь в пределе к 1.
129
9—1118
или
Напряжение на емкости Uc=
1 I а
= — / равно при со=О приложен-соС
ному к контуру напряжению; поэто-му кривая |лс|, начиная с 1, возрастает до тех пор, пока ток растет быстрее, чем ш; затем | Кс I спадает, стремясь В пределе к нулю.
Рис. 7-9. Частотные характеристики коэффициентов передачи (а, б) и фазовые (в).
Кривые | K.L | и | Кс | пересекаются при резонансе, причем ордината точки пересечения в соответствии с (7-10) равна Q.
Это также вытекает из анализа выражений (7-23) и (7-24). При фиксированных параметрах колебательного контура максимум | Кь | соответствует условию минимума подкоренного выражения (7-25):
откуда
Решение этого уравнения относительно искомой относительной частоты со/соо дает:
со 1
(7-29)
Аналогично максимум |Лс| наступает при
— = 1Z1---------------- . (7-30)
а>0 V 2QS
Итак, в тех случаях, когда величиной 1/2Q2 нельзя пренебречь по сравнению с 1, т. е. при невысокой добротности контура, максимум I Kl] (и UL) располагается несколько выше, а максимум | Кс | (и Uc) — ниже резонансной частоты.
Из выражений (7-29) и (7-30) следует, что при Q= 1/1^2 максимум | Kl | наступает при а/ао— °о, т. е. в этом случае UL с ростом частоты непрерывно стремится к зна-
чению приложенного к контуру напряжения. Максимум же функции Кс в этом случае имеет место при нулевой частоте (<й=0), когда UC=E.
Вблизи резонанса можно принять ы/соо» 1 и —------— »2б.
(Do со
В этом случае предыдущие выражения упрощаются:
К---;
с l+PQb
4>L =~ ~ +arctg2Q6;
(7-31)
4>c = ^- + arctg2Q6.
При резонансе
^ = -*с = /<2; Фь = -фс=—7
В заключение обратим внимание на наклон фазовых характеристик: кривые <р, ф£ и <рс возрастают, т. е. производные по относительней частоте положительны и безразмерны.
130
На основании (7-13), (7-27) и (7-28)
dtp ^Фс
Добротность рассматриваемого контура на основании (7-3) равна: nfl
Q*== С00 ~~~~ “ ш0 Сг, яа —-, (7-33) 2-- ₽
г
т. е. обратна по величине добротности последовательного контура г, А, С.
При резонансе наклон фазовой характеристики равен удвоенной добротности контура
9
V
Рис. 7-10. Параллельный колебательный контур.
причем в пределах полосы пропускания фазовая характеристика близка к прямой линии.
Если производная берется по частоте а (а не по относительной частоте со/гоо), то при резонансе наклон
Гдф1 _ 2Q _ 2£ |дй> г
имеет размерность времени. Как будет показано в гл. 13, это так называемая постоянная времени колебательного контура.
7-4. ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР. РЕЗОНАНС ТОКОВ
Явление резонанса токов проще всего изучать в электрической цепи с параллельно соединенными г, L, С (рис. 7 10), так как при этом можно непосредственно воспользоваться результатами предыдущего параграфа.
Действительно, комплексная проводимость параллельного колебательного контура рис. 7-10
Y=g - jb = g - / (-L - <оС) (7-32)
по своей структуре аналогична выражению комплексного сопротивления последовательного колебательного контура, а резонансная частота, как и в предыдущем случае, равна:
1
V LC
По аналогии с предыдущим вы- , ражение (7-32) приводится к виду
21 = 1 +/q /2'L _ (7.34)
g \®0 ® /
Ток, идущий от источника в цепь, отнесенный к току в неразветвлеы-ной цепи при резонансе, равен:
— = YE: gE = — = ~ ё~\ (7-35)
I, g
Сравнивая полученный результат с (7-11), убеждаемся в том, что выражение Уlg=tlta для рассматриваемого параллельного колебательного контура имеет тот же вид, что и выражение Z/r для последовательного контура *. Воспользовавшись обобщенной расстройкой параллельного контура g=a= п/ co <Dn \ b
=Q------- — =------, получим Нор-
\ю0 co ) g
мированную характеристику Y/g=a = 1 +/§. Поэтому кривые рис. 7-6 и 7-8 применимы и в данном случае: кривые рис. 7-6, а и 7-8, а выражают зависимость от со/соо и от £ отношения ylg= — t а кривые рис. 7-6,6
Л>
и 7-8, в выражают зависимость ф от ю/соо и от
При частотах ниже резонансной проводимость индуктивной ветви больше проводимости емкостной ветви, и поэтому входная проводимость параллельного контура имеет активно-индуктивный характер.
1 Последовательный н параллельный контуры г, L, С можно рассматривать как дуальные.
9*
131
При частотах выше резонансной емкостная проводимость больше индуктивной и входная проводимость контура имеет активно-емкостный характер.
При резонансе токов полная проводимость параллельного колебательного контура рис. 7-10 минимальна, т. е. входное сопротивление достигает максимума. При этом ток, идущий от источника, минимален и равен Io=gE, а токи в индуктивном и емкостном элементах равны по величине и противоположны по знаку:
А?о = lo=E=i i0Q.
Полученное выражение показывает, что добротность рассматриваемого параллельного колебательного контура определяется как кратность токов в L и С по отношению к суммарному току /о.
При Q>1 эти токи превышают по величине /о- Поэтому резонанс в параллельном колебательном контуре и называется резонансом токов.
При определении полосы пропускания параллельного колебательного контура исходят из предположения, что контур питается источником тока (не зависящим от частоты), причем границы полосы пропускания соответствуют уменьшению напряжения на контуре по сравнению с напряжением при резонансе в р42 раз.
В случае идеального источника тока (с бесконечно большим внутренним сопротивлением) полоса пропускания параллельного контура вычисляется как d=l/Q.
Если источник тока имеет внутреннее сопротивление г,-, то чем меньше будет сопротивление г,-, тем ниже будет эквивалентная добротность Q, = /р = —и тем '+" 14-Л-
г
шире полоса пропускания контура d3=l/Q3. Поэтому в отличие от последовательного колебательного контура с точки зрения сокращения полосы пропускания параллельного колебательного контура выгоден источник тока с большим внутренним сопротивлением.
При резонансе токов, как и при резонансе напряжений, происходит непрерывный обмен энергией между индуктивным и емкостным элементами. Если бы параллельный колебательный контур состоял только из L и С, соединенных параллельно, то его входное сопротивление при резонансе было бы бесконечно велико и ток от источника в контур не поступал бы. Энергия, первоначально сообщенная контуру, не расходовалась бы, а периодически перераспределялась бы между магнитным и электрическим полями, источник можно было бы отключить, и колебания продолжались бы неограниченное время.
Такой колебательный контур, как и на рис. 7-10, является идеализированным. так как не учитывает потерь энергии в параллельных ветвях L и' С контура.
В следующем параграфе рассматриваются другие схемы, с сопротивлениями в параллельных ветвях контура.
7-5. РАЗНОВИДНОСТИ ПАРАЛЛЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА
Допустим, что параллельный колебательный контур состоит из двух ветвей с комплексными сопротивле-
Рис. 7-11. Резонансная цепь с двумя параллельными ветвями.
НИЯМИ Z1 = r1+/Xi И Z2=r2-|-/X2 (рис. 7-11).
В зависимости от характера реактивных сопротивлений xt и х2 различают три основных вида параллельного колебательного контура.
Контур I вида содержит индуктивность L в одной ветви и емкость С в другой ветви (рис. 7-12, а); в этом случае х^—аЬ,
Контур II вида содержит индуктивность Li в одной ветви и индуктивность L2 и емкость С в дру
132
гой ветви (рис. 7-12,6); в этом случае
Х1 = ы£-1, x2=(bL8--—.
Согласно (7-36)
1 ______5L—
Контур III вида содержит ин-
дуктивность L и емкость С\ в одной и> следовательно, ветви и емкость С2 в другой ветви
(рис. 7-12,в); в этом случае г
Рис. 7-12. Варианты схем параллельного колебательного контура.
Входная проводимость параллельного контура (рис. 7-11) равна: у _ 1 } 1 1 । 1 -
Zj Z2 Tj -|- /X) г2 -|- /х2
= — + = e — jb
' Л , „2 ₽
Т *1 '2 Т *2
Здесь эквивалентная активная проводимость
а эквивалентная реактивная проводимость
b = —-----1---—.
Условием резонанса является Ь=0, т. е.
(г22+х%)+*2 ('?+*?) = °- (7-36>
При резонансе входная проводимость параллельного контура вещественна:
у = п = Г1 -L г*
° ё0 rUZ
' 1 । Х1 г2 ' *2
Условимся называть ее в дальнейшем резонансной проводимостью контура. Обратную величину будем называть резонансным сопротивлением1.
1 В радиотехнической литературе применяется также термин «эквивалентное сопротивление» параллельного контура прн резонансе. Это сопротивление иногда обоз-
начается Ro».
При частотах, близких к резонансной, обычно
/-! «С |хг| и г2 < |х2|.
Поэтому условие резонанса (7-36) приближенно записывается так:
Xj Xj+Jt2 xi ~ 0 (7-38)
или
х^ — х2.
Следовательно, в параллельном колебательном контуре с малыми потерями резонанс токов наступает в том случае, когда реактивные сопротивления ветвей равны друг другу по абсолютной величине и противоположны по знаку.
В этом случае резонансная проводимость параллельного контура приближенно приравнивается величине
Г1 + г2 Г1 + Гд
X2 X* '
(7-39)
Ниже наиболее подробно рассмотрен контур I вида.
Контур I вида (рис. 7-12, а). Резонансная частота находится из уравнения (7-36)
a0L
1____
«в2 С»
^(4+^*)-о.
133
откуда
Пренебрегая сопротивлениями О и гг, получаем на основании (7-38) или (7-40) приближенную формулу резонансной частоты параллельного колебательного контура
т. е. такую же, как и в случае последовательного колебательного контура.
Резонансная проводимость параллельного контура согласно (7-37) равна:
(М2) 'l+(%i)a
или приближенно с учетом (7-39) и (7-41)
go—-2-= ~; (7-43)
(<оо£)2 Р2
здесь
Если сопротивлениями г\ и ъ нельзя пренебречь, пользуются выражениями (7-40) и (7-42). При этом явление резонанса возможно только в том случае, если подкоренное выражение в (7-40) имеет положительный знак или, что то же, величины р2—Г; и р2—гj имеют одинаковый знак. В противном случае резонанс в параллельном контуре невозможен.
Когда г!=га=г, радикал в (7-40) обращается в единицу и резонансная частота получается не зависящей от г:
®о*= LC •
В этом случае g0 -------.
Наконец, при г1=гг=р выражение (7-40) становится неопределен
ным: цепь резонирует на любой частоте (так называемый безразличный резонанс).
На рис. 7-13 показана векторная диаграмма при резонансе токов в параллельном контуре. Токи в ин-
Рис. 7-13. Векторная диаграмма прн резонансе токов.
дуктивной и емкостной ветвях слагаются из активных (/га, /са) и реактивных (Уьр, /Ср) составляющих, причем
^Lp~ ^Ср’ Кв "Ь 4;» “ 4-
Когда r<g; |xi| и Г2«:|Х2|, ток /ьо в индуктивной ветви отстает почти на 90°, а ток в емкостной ветви опережает почти на 90° приложенное к параллельному контуру напряжение U. Иначе говоря, токи в параллельных ветвях сдвинуты по фазе относительно друг друга на угол, близкий к 180°, а по величине практически одинаковы, т. е. они образуют как бы один контурный ток /к~ замыкающийся в контуре.
Добротность контура I вида на основании (7-3) равна:
^Ьмакс Ыо L
Q—®0 „ — о ---------7, •
Р z{g0
Согласно (7-42)
-f- *2 COg LC ёо ~ п >
*1
откуда
Q --------, (7-44)
Г1 “Ь
где резонансная частота соо опреде-ляется по (7-40).
На рис. 7-14' показан частный случай контура I вида, когда г^—г и г2=0.
134
Резонансная частота такого контура согласно (7-40)
соо - -А— 1/ )а, (7-45)
if LC * ' ₽ '
а добротность контура на основании (7-44)
Q = ^ = А (7-46) г г
Из сопоставления (7-45) с (7-2) видно, что при одних и тех же па-
Рнс. 7-14. Частный случай параллельного •колебательного контура I вида.
раметрах г. L и С резонансные частоты для схем рис. 7-1 и 7-14-отличаются множителем У 1—(г/р)а .
При г/р<0,1 разность резонансных частот не превышает 1 % • Кроме того, выражение (7-45) показывает, что резонанс токов в контуре рис. 7-14 возможен только при r!p<z
Входное сопротивление такого контура
(г + /<в£)
£___ /<оС
г + / со£-----
V <ос/
£ . J_
________rC ~ZaC_________
. . Ш0£7(й 1 \’
1 -|_ у I ---- I
г \о0 gxo0 LC /
При высокой добротности контура с учетом (7-41), (7-46) и соотношений
<оо
-—i—^rQ2-, —
rC аС toa>o£C со
— —
<i)0 CO
получается приближенное выражение для входного сопротивления параллельного контура рис. 7-14:
2^—. (7-47)
1 + /2Q6 4 ’
При этом токи в ветвях
4 = -?-^
L г -{- /со£ 1 -|- /2QS
lc = jaCZlxi—.
G ' 1 + /2 QS
Здесь 7 — ток в неразветвленной части схемы.
Коэффициенты передачи (или усиления) тока и Kc—Idl
приближенно выражаются так:
KL^-KC^
(7-48)
1+/2Q6
т. е. аналогично выражению (7-31) в § 7-3 для последовательного колебательного контура. Поэтому кривые рис. 7-9 применимы и в данном случае.
В случае питания параллельного контура от идеального источника тока (с бесконечно большим внутренним сопротивлением) напряжение на контуре U=ZI, отнесенное к напряжению при резонансе токов tJo=ilgo, равно:
1+/2(2S’
что совпадает с выражением (7-14) для ///0 при резонансе напряжения. Следовательно, резонансные кривые напряжения VIU0 для параллельного контура совпадают с кривыми 7//0 последовательного колебательного контура (рис. 7-7, а и рис. 7-8,6).
Если параллельный контур питается источником напряжения с э. д. с. Ё и внутренним сопротивлением п (что равносильно пита'нию контура источником тока Ё’/г,- с тем же внутренним сопротивлением), то возможны следующие крайние случаи:
1) п^>го (го — резонансное сопротивление параллельного контура).
Ток в неразветвленной части схемы
• F F
I =-----------~.— = const,
г,- + Z Г/
При этом резонансная кривая напряжения на контуре U=zl в известном масштабе представляется
135
или
частотной характеристикой полного сопротивления z параллельного контура.
2) n<t;ro- В области частот, близкой к резонансу,
1 = —и U-.Ё. ri + Z Z
При этом резонансная кривая тока 1 в известном масштабе представляется частотной характеристикой полной проводимости у параллельного контура.
В предыдущем параграфе было показано, что полная проводимость параллельного колебательного контура рис. 7-10 имеет минимум при резонансной частоте.
Для схемы рис. 7-14 можно показать [Л.1], что при изменении частоты (о или индуктивности L минимум полной проводимости контура, а также минимум тока в неразвет-вленной части схемы наступает не при резонансной частоте. В том же случае, когда переменным параметром является емкость С, проводимость и суммарный ток достигают минимума при резонансе токов.
На основании л (7-43) и (7-46) или подстановкой \6=0 в (7-47) находится приближенное значение резонансного сопротивления контура
r0^rQ’.
(7-49)
7-12, б).
Контур II вида (рис.
Для нахождения резонансной частоты и резонансного сопротивления контура II вида воспользуемся приближенными формулами (7-38) и (7-39); подставив в них x^woZi и г 1
= <ооЬ2-----, получим:
<оо С
^1+®0 (-2----~ 0,
W0C
рткуда
ин-
.Здесь L=Li+L2 — су арная дуктивность контура при последовательном его обходе.
Обозначим p=Li!L. Тогда
Х1=<о0£1=рй)0£~ро и
r0^p2rQ2. (7-50)
Здесь г=Г! + г2.
Коэффициент р называется коэффициентом включения контура; он может изменяться в пределах O^p^l. Значение р—1
Рис. 7-15. Параллельный колебательный контур II вида с регулировкой коэффициента включения р.
соответствует контуру I вида, а значение р=0— случаю £|=0.
На рис. 7-15 показан контур II вида с регулировкой коэффициента р. При перемещении скользящего контакта резонансная частота практически не изменяется, так как сумма L=Li + L2 почти сохраняется неизменной.
Если Li и L2 — индуктивности двух частей одной катушки, а М — взаимная индуктивность этих частей, то коэффициент р определяется по формуле
p==__A±L
Lt + Ц + 2Л-1
В контуре II вида после резонанса токов возможен резонанр напряжений в ветви r2L2C. При этом входное сопротивление контура it соответственно напряжение на нем (при питании от источника с большим, внутренним сопротивлением) резко снизятся.
На рис. 7-16 показана резонансная кривая напряжения.
.В области частот значительно нике резонансной ветвь nZ-i имеет малое сопротивление, которое практически и определяет входное сопротивление контура. При резонансе токов сопротивление контура и напряжение на нем велики. Нако-нец, при угловой частоте tl^ L2C, большей резонансной, сопротивление ветви r2L2C снижается до мини-
136
мального своего значения г2, определяющего входное сопротивление контура. С дальнейшим ростом частоты сопротивления обеих ветвей, имеющие индуктивный характер, растут и напряжение на контуре повышается.
Примерная резонансная кривая напряжения показана на рис. 7-17.
Сопоставляя выражения резонансных сопротивлений контуров I, II и III видов, приходим к выводу, что формула го«р2р2/г является для них общей.
Рис. 7-16. Резонансная кривая напряжения для параллельного колебательного контура II вида.
пая напряжения для параллельного колебательного контура III вида.
Следовательно, контур II вида обладает способностью выделения напряжения резонансной частоты и подавления напряжения частоты 1/К£2с.
Контур III вида (рис. 7-12, в). Подставив в (7-38) и (7-39) xi =
1 1 1
= to0L-------— и х2=--------, по-
C0e Cj
лучим:
tooL----?— -----?— ^0,
СОд С] С2
откуда резонансная частота
__ . 1 п п С,С2
со0 ~, где С = —!—Ц
1/ LC С1Ч-С2
а резонансная проводимость контура
£о ~ = г (<оо С2)2 V откуда
*2 L \ С )
r0^p2pzlr, где коэффициент включения р=С/С2.
В контуре III вида при частоте 1/Г£С,<<оо в ветви t\LC\ наступает резонанс напряжений и сопротивление этой Ъетви снижается до минимального своего значения н, определяющего в основном входное сопротивление всего контура. С повышением частоты сопротивление растет, достигая резонансного значения, а затем по мере уменьшения сопротивления ветви г2С2 снижается.
Для контура I вида р=1, для контура II вида p—LJL, для контура III вида р=С1Сг.
Во всех этих случаях параллельный колебательный контур можно рассматривать как «согласующий трансформатор», преобразующий низкоомное сопротивление г в высокоомное р2р2/г, необходимое для получения выгодного режима работы устройства. Например, если г — сопротивление нагрузки, а г< — внутреннее сопротивление источника питания, то для передачи максимума мощности в нагрузку при резонансе должно выполняться условие z0=r, (§ 3-5), т. е. р2р2/г=г,.
Отсюда находится оптимальное значение коэффициента включения контура: р0Пт= К гп/р=Уг</гомакс. где Гомакс — резонансное сопротивление контура при р=1.
Мощность, подводимая к контуру при резонансе, поглощается низкоомным сопротивлением г.
Она равна P=z0I^.
Следует обратить внимание на то, что в отличие от схемы рис. 7-10, где мгновенная мощность на за?ки-мах контура при резонансе равна мощности, поглощаемой сопротивлением г, в схемах с двумя параллельными ветвями (контуры I, II и III видов) мгновенная мощность на зажимах контура отлична от мгновенной мощности, поглощаемой сопротивлениями ветвей. Например, в тот момент, когда ток в неразвет-
137
вленной части схемы проходит через нулевое значение, мгновенная мощность на зажимах контура равна нулю; в этот момент токи в ветвях, сдвинутые по фазе относительно суммарного тока, отличны от нуля, и поэтому мгновенная мощность, поглощаемая сопротивлениями ветвей, также не равна нулю.
Объясняется это тем, что в контурах I, II и III видов энергия, накапливаемая реактивными элементами, периодически расходуется частично в сопротивлениях ветвей, а затем пополняется за счет энергии источника.
Наряду с возможностью согласования нагрузки с внутренним сопротивлением источника важнейшим свойством контура является его частотная избирательность, т. е. наличие полосы пропускания, определяемой остротой настройки (добротностью) контура.
7-6. ЭЛЕМЕНТЫ КОЛЕБАТЕЛЬНОГО КОНТУРА
В § 1-7 указывалось, что схемы замещения индуктивной катушки и конденсатора зависят от выбранного диапазона частот.
При прохождении тока через индуктивную катушку наряду с магнитным полем возникает электрическое поле, обусловленное разностью потенциалов между соседними витками. Если один конец катушки заземлен, то создается электрическое поле и между витками и землей. Вследствие этого появляются токи смещения как между витками, так и между обмоткой и землей (корпусом). Это явление учитывается в схеме замещения индуктивной катушки с помощью емкостей, распределенных между витками, а также между витками и корпусом (рис. 7-18, а).
Междувитковые емкости и емкости относительно корпуса заменяются одной эквиьалентной емкостью Сэ, показанной на рис. 7-18,6. При некоторой частоте и0£.~ 1/]/^-Сэ индуктивность L и собственная емкость катушки Сэ резонируют, а при более высоких частотах индуктив
ная катушка ведет себя как емкость. Следовательно, индуктивная катушка при достаточно высокой частоте сама по себе является параллельным колебательным контуром, и ее роль как индуктивности ограничивается верхней предельной частотой сооь-
Рис. 7-18. Схема замещения индуктивной катушки.
В параллельном резонансном контуре к собственной емкости катушки добавляется емкость, которая обычно превышает собственную емкость катушки и поэтому для резонанса токов является определяющей.
Равномерно распределенное сопротивление обмотки катушки учитывается в схеме замещения сосредоточенным сопротивлением г (рис. 7-18,6).
Что касается конденсатора, то наряду с электрическим полем в нем проявляется при высоких частотах и магнитное поле, создаваемое током смещения. При этом проводники, соединяющие зажимы конденсатора с его пластинами, так же как и сами пластины конденсатора, обладают некоторой индуктивностью. В эквивалентной схеме замещения конденсатора это учитывается последовательной эквивалентной индуктивностью La. Потери энергии в конденсаторе учитываются сопротивлением, соединенным параллельно с ветвью С, La (рис. 7-19).
Ч С
Рис. 7-19. Схема замещения конденсатора.
138
При достаточно высокой частоте соос=1/ V LgC наступает резонанс напряжений, а при еще более высоких частотах конденсатор ведет себя как индуктивная цепь.
Таким образом, при сверхвысоких частотах конденсатор сам по себе является последовательным колебательным контуром, и его роль
сматривается автоматическое закорачивание неработающих катушек или витков.
Плавное изменение индуктивности достигается различными способами. Одним из способов является применение вариометра (рис. 7-21), состоящего из двух последовательно включенных катушек, взаимная ин-
а)
Рис. 7-20. Скачкообразное изменение индуктивности (а, в) и емкости (б).
е)
как конденсатора ограничивается верхней предельной частотой мое.
Следует напомнить, что с ростом частоты сопротивления проводников возрастают пропорционально корню квадратному из частоты (§ 2-5). Кроме того, увеличиваются потери электрической энергии в окружающих диэлектриках и проводниках, и возрастает энергия, излучаемая проводниками в пространство. Это приводит к увеличению результирующего активного сопротивления колебательного контура и к уменьшению его добротности
Колебательные контуры, состоящие из индуктивных катушек и конденсаторов, оказываются непригодными при сверхвысоких частотах (выше 30 Мгц, что соответствует длине волн меньше 10 м). В этом случае применяются колебательные системы с распределенными параметрами (гл. 16).
Для изменения резонансной частоты колебательного контура применяются катушки переменной индуктивности и конденсаторы переменной емкости, которые выполняются со скачкообразным или плавным изменением параметров.
Скачкообразное изменение параметров осуществляется с помощью переключателей, которые либо переключают индуктивные катушки или конденсаторы (рис. 7-20, а, б), либо изменяют рабочее число витков катушки (рис. 7-20, в). Иногда преду-
дуктивность которых изменяется поворотом оси одной катушки относительно другой. Индуктивность вариометра изменяется в пределах от LMHKI-= L< + La+2М (при согласном
Рис. 7-21. Вариометр.
направлении магнитных потоков катушек) до Lmhh=L14-L2—2М (при встречном направлении магнитных потоков катушек)
Рис. 7-22. Плавное изменение емкости.
Плавное изменение емкости можно получить изменением расстояния между пластинами конденсатора. Однако на практике распространен другой способ — изменение
139
рабочей площади пластин. Группа неподвижных плоских параллельных пластин конденсатора присоединяется к одному из его зажимов, а группа подвижных пластин — к другому зажиму (рис. 7-22). Закон изменения емкости в зависимости от угла поворота пластин зависит от их формы.
Конденсатор, емкость которого изменяется линейно в зависимости от угла поворота (C=a<p+Cf), называется прямоемкостным.
Если форма пластин конденсатора рассчитана так, что резонансная частота колебательного контура, в который включен конденсатор, линейно зависит от угла поворота пластин (<оо=^ф+ю1), то конденсатор называется прямочасто т-н ы м.
7-7. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
7-1. В цепи с последовательно соединенными г, L н С наступает резонанс напряжений при угловой частоте 500 рад! сек; г=34 ол<; £=400 мгн; напряжение на зажимах цепи 17=120 Z0° в. Определить емкость С и мгновенные значения тока и напряжений на элементах цепи; построить векторную диаграмму.
Ответ: 10 мкф-, 5 sin 500 t, а; 170 sin 500/, в; 1000 sin (500/±л/2), в.
7-2. Цепь состоит из индуктивной катушки (г, L) н емкости, соединенных последовательно. Напряжение на зажимах цепи равно 120 в. Определить напряжение на катушке при резонансе, если при этом напряжение на емкости равно 208 в.
Ответ: 240 в.
7-3. Вычислить резонансную частоту и частоты, при которых напряжения на L и С максимальны в цепи с последовательно соединенными г=50 ом-, £=10 мен и С= = 1 мкф.
Ответ: 10 000 рад/сек; 10 700 рад/сек-, 9350 рад!сек.
7-4. Вычислить резонансную частоту и добротность контура, состоящего из последовательно соединенных г = 5,1 ом; £=65-10-6 ен; С= 1,56 • 10~® ф. Определить сопротивление цепи при частоте, превышающей резонансную иа 1%.
Ответ: 5 • 105 гц; 40; 5,63 Z38,6O35' ом.
7-5. Резонанс напряжений в контуре
г, L, С наступает при частоте 1 Мгц. Полоса пропускания резонансного контура равна 5000 гц: сопротивление цепи при резонансе 50 ол4. Найти г, £ и С.
Ответ: 50 ом: 1,59 мгн; 15,9 пф.
7-6. Резонанс напряжений в контуре г, L, С наступает при 1,5 Мгц; добротность контура равна 250. Вычислить частоты, соответствующие половинной мощности.
Ответ: 1,497 и 1,503 Мгц.
7-7. Последовательно с £ включен участок цепи, состоящий из параллельно соединенных г и С. При частоте 1 000 гц индуктивное и емкостное сопротивления элементов £ и С равны каждое 100 ом; г= =200 ом. Вычислить резонансную частоту и проводимость цепи при резонансе, пояснить явление резонанса в заданной цепи.
Ответ: 866 гц; 0,02 сим.
7-8. Если в цепи рис. 7-14 сопротивление г превысит определенное значение, то резонанс токов будет невозможен. Пояснить это физически и привести условие, при котором резонанс невозможен.
Ответ: г L/C.
7-9. Индуктивная катушка и последовательно соединенная с ней емкость питаются от источника гармонической э.д.с.; частота равна 1 кгц. Максимальное значение тока в цепи 1,1 а достигается при С=10,4 мкф; при этом напряжение на емкости в 11,1 раза превышает приложенное к цепи напряжение. Вычислить сопротивление и индуктивность катушки и напряжение иа емкости прн токе 1,1 а.
Ответ: 1,38 ом; 2,43 мгн; 16,9 в.
7-10. Контур, состоящий из г=100 ом; L= 10 мгн и С= 1 мкф, питается от источника переменной частоты. Найти наибольшее отношение напряжения на £ (или С) к приложенному к контуру напряжению.
Ответ: 1,155.
7-11. Цепь состоит из г=100 ом, L= = 10 мгн и С, соединенных последовательно; угловая частота равна 104 рад!сек. Прн каком значении С напряжение на С максимально; во сколько раз оно превышает приложенное к цепи напряжение?
Ответ: 0,5 мкф; 1,41.
7-12. Найти минимальное значение С, при котором наступит резонанс в цепи рнс. 7-12,о, если п = 10 ом, £=50 мгн, г2=5 ом, /=50 гц; определить сопротивление цепи при резонансе.
Ответ: 152 мкф; 25,2 ом.
7-13. Резонанс напряжений в контуре г, L, С наступает при 500 кгц. При этом сопротивление контура равно 75 ом; полоса пропускания равна 3 кгц. Найти £ и С.
Ответ: 3,98 мгн; 25,4 пф.
140
Глава восьмая
СВЯЗАННЫЕ КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ
8-1. ВИДЫ СВЯЗИ х
более четкого разделения колебании
Для повышения крутизны резо- разных частот или, как принято го-нансных кривых, необходимой для ворить, для повышения избира-140
тельйости колебательных систем, в радиотехнике наряду <с одиночными колебательными контурами широко применяются связанные контуры. Связанными называются контуры, взаимно влияющие друг на друга.
лексные сопротивления Zi и Z2 пер
Один из видов связи — при помощи взаимной индукции — был описан в гл. 6. Такая связь колебательных контуров, наиболее распространенная в радиотехнике, называется гИ н д у к т и в н о й, или трансформаторной (рис. 8-1, а).
Кроме того, применяется и электрическая связь — концу ктивная, или емкостная.
Пользуясь, схемой замещения трансформатора, рассмотренной в гл. 6 (рис. 6-12), можно от схемы рис. 8-1, а перейти к эквивалентной схеме рис. 8-1, б, в которой индуктивная связь заменена электрической (кондуктивной).
Другая разновидность электрической связи, а именно емкостная связь, показана на рис. 8-1, в, где емкостный элемент С12 составляет общую ветвь двух колебательных контуров. Пользуясь правилом замены звезды эквивалентным треугольником (§ 4-5), можно последовательную («внутреннюю») емкостную связь, показанную на рис. 8-1, в, заменить параллельной («внешней») емкостной связью, как это изображено на рис. 8-1, а.
Применяется также комбинированная, индуктивно-емкостная связь (рис. 8-1, д).
8-2. СОПРОТИВЛЕНИЕ СВЯЗИ
И ВНОСИМЫЕ СОПРОТИВЛЕНИЯ
Все указанные выше виды связи можно проанализировать с помощью обобщенной двухконтурной схемы рис. 8-2, содержащей комп-
вичного и вторичного контуров и «сопротивление связи» Zi2 общей
Рис. 8-2. Два связанных контура.
ветви. Уравнения для этой схемы запишутся так:
£ = Zlx7! Z12/2;
О — —Z12/j +Z22/2,
(8-1)
где собственные сопротивления контуров Zii=Zi+Zi2 и Z22=Z2+Zi2.
Решение системы уравнений дает:
-
Z12
zu — — Z23
f __ /’ Z18
2— '1 7 • z22
(8-2)
(8-3)
141
Следовательно, при рассмотрении первичного контура можно влияние вторичного контура учесть некоторым «вносимым» сопротивле-^2
нием ZiBn—-------, добавляемым к
2 22
собственному сопротивлению первичного контура, как это показано в схеме замещения для первичного
контур с сопротивлением Z22 (рис. 8-3, в).
Рассмотрим случаи реактивных сопротивлений связи, когда Za= =jxi2 (здесь Х12 может быть любого знака).
Сопротивление, вносимое из вторичного контура в первичный,
—(8'5)
Рис. 8-3. Схемы
замещения для первичного (а) и вторичного (б, в) контуров.
контура рис. 8-3,а. Частным случаем этой схемы была схема рис. 6-18, рассмотренная в гл. 6.
Подставив (8-2) в (8-3) и умножив числитель и знаменатель на Z22/Z11. получим:
-----Ц-. (8-4) 2^ 2»а— _
Это выражение может быть выведено и по теореме об эквивалентном источнике (предлагается читателю сделать вывод самостоятельно).
Числитель выражения (8-4) есть напряжение на сопротивлении связи при разомкнутом вторичном контуре, а знаменатель — эквивалентное сопротивление вторичного контура, в котором влияние первичного контура учтено сопротивлением /гвн= 72 4.J2
—------, вносимым из первичного
2ц
контура во вторичный контур. Схема замещения для вторичного контура показана на рис. 8-3, б.
На основании (8-3) влияние первичного контура на второй может быть учтено и другим способом — с помощью зависимого источника э. д. с. Z12/1, включенного в
а сопротивление, вносимое из первичного контура во вторичный,
7_________(Мда)2 *12 ,я ~
л2вн — —-— — —•. (8-Ь)
ZU Z11
Здесь ' 2ц=г1-}-/(х1-}-х12) =Г14-/хц;
/22=^2+7x22.
Поэтому
*12
^1вн = г1вн + /Х1вн =:— =
r2 + JX22
^2вн ^2зп + /Х2вн = ——:---
'I + 1Хи
Следовательно, согласно (8-2) и (8-4)
£ jXlt
_____________rl + JXll___________
I /*12'/ . [ /*12 V 1
r2 + I I‘ri+1 lx22~ I I *ti vu / L vii / 1
• (8-10)
142
В\случае индуктивной связи
а в случае последовательной емкостной связи
(8-12)
Таким образом, активные составляющие вносимых сопротивлений Г1вн и г2вн всегда положительны, а знаки реактивных составляющих *1вн и х2вв противоположны знакам реактивных сопротивлений х22 и Хц вторичного и первичного контуров соответственно. При частотах выше резонансной частоты вторичного контура х22>0 и Хщн<0, а при частоте ниже резонансной ХггСО и *1вн>0. Аналогично при хц>0 Х2вв<0, а при Хц<0, х2ви>0.
Как Пон и г2вн, так и XiBH и х2вн зависят от частоты (или от относительной частоты расстройки).
По мере приближения частоты источника к резонансной частоте вторичного контура г1ъв возрастает, стремясь к максимальному значению Пвн.макс=х?2/г2, а х1вн стремится к нулю. В свою очередь если частота будет приближаться к резонансной частоте первичного контура, то г2ен будет расти, стремясь к ^гвн.макс==lri, а х2вв будет стремиться к нулю.
Следует обратить внимание на то, что
^IbhA”1вн == "“^-22/^2 ^йви/®2вн
т. е. углы комплексных сопротивлений ZiBB и Z2BH соответственно равны и противоположны по знаку углам комплексных сопротивлений Z22 и Z«.
В случае индуктивной связи уравнения (8-1) записываются так:
а в случае последовательной емкостной связи
(8-14)
8-3. ВЕКТОРНЫЕ ДИАГРАММЫ
Для построения векторных диаграмм токов и напряжений удобно пользоваться схемой замещения рис. 8-3, а.
На рис. 8-4, а показана векторная диаграмма для индуктивной связи в предположении, что ХиХ) и, следовательно, Х1Вн'<0. Так как углы комплексных сопротивлений ‘ гг+/ --------тг*) и г1вн+/х1вн рав-
\ © ^2 /
ны по абсолютной величине, то треугольники напряжений на этих сопротивлениях подобны.
Сопоставив первое уравнение (8-13) с (8-9), заключаем, что напряжение (Г1вн+/Х1вн)/1 на сопро-, тнвлении, вносимом из вторичного ^внтурд в первичный, равно —/с)Л1/2. Отсюда легко находятся напряжения г2/2 и ------------
\ to С*2 /
//И' / -
143
Рис. 8-4. Векторные диаграммы токов и напряжений при Хвк<0-
а — индуктивная связь; б — последовательная емкостная связь.
Векторные диаграммы можно строить и непосредственно по уравнениям (8-13) и (8-14) или аналогично рис. 6-14.
8-4. КОЭФФИЦИЕНТ СВЯЗИ
Ограничиваясь случаями реактивных сопротивлений связи, введем для количественной оценки взаимного влияния связанных контуров обобщенной схемы рис. 8-2 понятие коэффициента связи, подразумевая под этим абсолютное значение отношения сопротивления связи к среднему геометрическому реактивных сопротивлений обоих контуров, без учета элементов, характер сопротивлений которых отличен от характера реактивного сопротивления связи.
Коэффициент связи для эквивалентных схем рис. 8-1,а и б равен:
k = ———.......- = -7=- > <S'15)
У со L, со L3 У LjL3
что совпадает с ранее полученным выражением (6-14).
^м1г r,i,
лг)
Рис. 8-5. Векторные диаграммы токов и напряжений при настройке обоих контуров иа частоту источника.
а— индуктивная связь; о — емкостная связь.
На рис. 8-4, б показана векторная диаграмма для последовательной емкостной связи (при хг2>0).
В случае настройки первичного и вторичного контуров на частоту источника ток It совпадает по фазе с э.д. с. Ё, а ток /2 опережает 7\ (при индуктивной связи) или отстает от него (при емкостной связи) на 90°, как это показано на рис. 8-5.
В случае последовательной емкостной связи (рис. 8-1, в)
1
144
Если Ci и С2 весьма малы по сравнению с С12, то
С12
В случае параллельной емкостной связи (рис. 8-1, г) заменой треугольника эквивалентной звездой на основании (8-16) получим:
= — С12 --------------.
(ct + с12) (с2 + с12)
Если CJ и С2 значительно больше, чем С'2, то
В случае комбинированной связи (рис. 8-1, д), если катушки включены так, что падения напряжений от взаимной индукции находятся в противофазе с напряжением на конденсаторе С|2, то при соЛ4> 1/соС12 связь может рассматриваться как индуктивная:
1
40 М-------
£ toCia
со V LXL2
а при соЛ1<:1/соС12 — как емкостная:
Следовательно, при комбинированной связи коэффициент связи зависит от частоты.
Если связанные колебательные контуры настроены на одинаковую частоту, совпадающую с частотой генератора, то индуктивное и емкостное сопротивления каждого контура приблизительно равны волновому сопротивлению контура и коэффициент связи приближенно равен:
fa,__ 1*св| .
1Л>1Рг
(8-17)
здесь pi и р2 — волновые сопротивления первичного и вторичного контуров.
8-5. НАСТРОЙКА СВЯЗАННЫХ КОНТУРОВ. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
На практике часто стремятся к получению максимальной величины тока /2 (или максимальной мощности Р2) во вторичном контуре. Это достигается соответствующей настройкой связанных контуров. Существуют различные способы настройки, а именно: 1) изменение параметров первичного контура (например, емкости Ci); резонанс, который при этом возникает, называется первым частным резонансом; 2) изменение параметров вторичного контура (например, емкости С2); в этом случае возникает второй частный резонанс; 3) изменение параметров одного из контуров и сопротивления связи; резонанс в этом случае называется сложным; 4) изменение параметров обоих контуров и сопротивления связи; в этом случае резонанс называется полным.
Первый частный резонанс. Согласно (8-3) вторичный ток прямо пропорционален первичному. Поэтому максимуму тока 1\ соответствует и максимум 1г-
Первый частный резонанс на основании (8-9) имеет место при
v X 2
*ц-(—) *22 = 0. (8-18)
\ г22 1
В
этом случае
^2макс
Е f-Kjal
Е l-Kjal
, (*п)2
+---------г2
И
(8-19)
г1г22
Второй частный резонанс. Второй частный резонанс согласно (8-10) имеет место при
/у \2
*ii = 0. (8-20)
\ ги /
10—1118
145
При этом
^гмакс
«11
Е |х12|
Е |Xi2|
,г + «
*«*п т-------
*и
(8-21)
Сложный резонанс. При настройке первичного контура оптимальное сопротивление связи найдется, если приравнять нулю первую производную выражения (8-19) ПО |х12|
^ймакс
4 |Х12|
г. Г . (’Чг)2 о I х121 "|
Е I Г 1*22 4" *2 * Г2 I
_ L*22*22 I ______________ /\
отсюда V \2 га. (8-22) *22 /
Следовательно, оптимальное сопротивление связи
l-^ialonr = ^22 V*i/*2 • (8-23)
В этом случае получается максимум максиморум вторичного тока. На основании (8-19) и (8-23)
т. е. и в этом случае выполняется условие передачи максимума средней мощности от источника к приемнику.
При этом согласно (8-21) и (8-25)
(8-26)
Следовательно, при сложном резонансе максимум максиморум вторичного тока не зависит'от того, какой из контуров настраивается на резонанс.
Полный резонанс. При настройке на полный резонанс сначала настраивают первичный контур при разомкнутом вторичном, т. е. добиваются выполнения условия хи =0. Затем настраивают вторичный контур, добиваясь условия х22=0. Наконец, подбирают оптимальное сопротивление связи.
На основании (8-10) при хц= = Х22=0
j _____ Е |Х12|
«Знаке , । is •
*1*2 + 1*1г12
(8-27)
Оптимальное сопротивление связи находится из условия
амакс _ Е (гггг — |*ц|2) __ q
|Xia| (*1*а + |Xial2)a
откуда
Условия (8-18) и (8-22), которые при этом выполняются, означают, что собственное сопротивление первичного контура равно сопротивлению, комплексно сопряженному с сопротивлением, вносимым из вторичного контура в первичный, т. е.
Z11 = Двн •
Из § 3-5 [формула (3-17)] известно, что это и есть условие передачи максимума средней мощности от источника к приемнику.
Аналогично при настройке вторичного контура оптимальное сопротивление связи равно:
1^1а1опт= zn • (8-25)
причем условия (8-20) и (8-25) в совокупности означают, что
7.-1 «-22 — «-2вн»
l-^ialonr
(8-28)
При этом вторичный ток
2мако.макв —
(8-29)
Хотя максимум максиморум вторичного тока при настройке на полный резонанс получается таким же, как при настройке на сложный резонанс, настройка на полный резонанс имеет то преимущество, что абсолютная величина сопротивления связи получается меньшей, чем при настройке на сложный резонанс; она, как и активные сопротивления ri и г2, исчисляется единицами ом.
Если два идентичных колебательных контура связаны индуктивно, то оптимальный коэффициент связи при настройке на полный ре-
146
зонйнс с учетом (8-28) примерно равей затуханию контура:
ь _ ~ г
геОПТ----- , —~
,со0 L a0L
(8-30)
Например, для радиотехнических контуров с добротностью Q= = 100 оптимальный коэффициент связи составит йопт~0,01.
Эффективность передачи энергии из первичного контура во вторичный оценивается коэффициентом полезного действия двухконтурной системы, равным отношению мощности, расходуемой в сопротивлении г2. к сумме мощностей, расходуемых в сопротивлениях Г1 и г2:
₽1 + Р.‘
Очевидно, Р1=г1/2, Р2=г2Г^ =г1ъп11 (здесь Л и 12 — действующие значения первичного и вторичного токов). Поэтому
т] = - Лнн
Г1 + Г1ВН
Когда вторичный контур настроен на частоту источника.
Г® Г1 г2 + *12
При настройке на полный резонанс |Х12| = V Г1Г2 и г] = 0,5.
8-6, РЕЗОНАНСНЫЕ КРИВЫЕ СВЯЗАННЫХ КОНТУРОВ. ПОЛОСА ПРОПУСКАНИЯ
Ограничимся рассмотрением случая, когда связанные контуры имеют одинаковую резонансную ча-стоту <ао= 1/ V LtCi— 1/ У L2C2.
Добротность контуров может быть различной (Qi и Q2).
Для построения резонансных кривых вторичного тока воспользуемся выражением (8-4)
f______________
Z22 — (Zj2)®
Выразив Zu и Z22 через обобщенную расстройку Zn = n (l+/gi) и Z22= =г2(1 +/Ъ)>
где
“о \ _ Q2 е
<в ) Qt
найдем:
(1 +/Ъ)(1 +
При частотах, близких к резонансной, с учетом (8-17)
^kVQtQ2,
Кроме того, согласно (8-29)
Следовательно, приближенно 1г = 2kVQAQ2
I амакс.макс 1(1+/£1)(1-№)+*2<21<2г1 '
или
—h— =
^гмакс-макс
____ .______Qi Q2_______________ _ У(1 + k* Qt Q2 - & g2)® 4- + g2)2
____________2feV _______________
(1+fQA-J й)’+(ч-^)’й
(8-31)
Беря производную no от подкоренного выражения и приравняв ее .нулю, получим:
Это уравнение имеет три решения.
Первое из них gi=0 соответствует частоте со=соо-
Два других решения получаются из уравнения
Ю*
147
1 + ^QiQ--тг B?-VI
Qi
2Qj
= 0,
откуда
= (8-32)
где kitp — критический коэффициент связи:
Очевидно, если коэффициент связи k меньше критического коэффициента связи, то выражение (8-32) лишено физического смысла и в этом случае имеется только одна частота <й=соо, при которой вторичный ток максимален. Итак, при k<Z <Лкр резонансная кривая /2 получается одногорбой.
В случае резонансная
кривая /г двугорбая. Максимумы /2 наступают при £i=±Qi । #2—/гкР, а решение g] = 0 соответствует впадине двугорбой кривой.
Так как Qi(—--------—V то ча-
\ <в0 <0 /
стоты, при которых наступают максимумы вторичного тока, находятся из уравнения
= ± / fe2 —
Шо со ' кр
которое приводится к квадратному:
или
При
Расчетные выражения и их анализ упрощаются, если наряду с одинаковой резонансной частотой связанные колебательные контуры имеют одинаковую добротность: Qi= — Qz=Q. В этом случае согласно (8-31) и (8-32)
----4-------------- - - 2Л(? (8.35) ^гмаксгмакс-----------------------([ -J-Q2^2 g2)2 -}-4g2
И
|1Л1 = ± V(Qfe)? — 1-
Если контуры настроены на частоту источника, то и
/за 2Qk
I Знаке.макс 1 Q2 Л2
Критический коэффициент связи согласно (8-33) равен:
— d,
кр q ,
т. е. совпадает с оптимальным коэффициентом связи двух идентичных контуров, настроенных на полный резонанс [сравните с (8-30)].
При QZs<l резонансная кривая имеет только один максимум, меньший единицы, так как при |=0 вторичный ток не достигает значения максимума максиморум: ^2 о/^2 макс.макс 1 •
При Qk=l, т. е. при коэффициенте связи, равном критическому, получается предельная одногорбая резонансная кривая, и при |=0 вторичный ток достигает значения максимума максиморум: I 2 о/^2 макс.макс — 1 •
Наконец, при Qk> 1 резонансная кривая двугорбая, причем при gi и |п, определяемым по (8-35), вторичный ток достигает значения максимума максиморум: /2//2макс.макс= 1. Сказанное иллюстрировано рис. 8-6.
148
Полосой пропускания связанных колебательных контуров, как и в случае одиночного колебательного контура, условно считается область частот, на границах которой резонансная кривая снижается
1 _ 2Qk
у- ~ 1+Q2£2 ’
откуда Qk=2,4l.
Подставив это значение Qk в (8-36), найдем:
Рис. 8-6. Резонансные кривые связанных колебательных контуров.
не более чем в у2 раз по сравнению с максимумом.
Так как — = —— =
Q ш0 ш
9 2
CD —<DJ
(Do CD
со — соо со + соп ,
= -------- --------- , то, приняв вбли-
С00 (й
- и (О -1“ (Dz\
зи резонансной частоты —*—- «2,
. °
можно считать, что — «2161 оп-Q
ределяет полосу пропускания связанных контуров при Qk > 1 (здесь 6 — относительная расстройка частоты, см. § 7-2).
Решением уравнения
1 _______________2Qk_____________
К2 ' К(1 + Q2 k* — £2)2 4- 4£2
служит
£ = + VrQ2k2 + 2Qk — l . (8-36)
Это выражение справедливо до тех пор, пока впадина резонансной кривой выше или равна 1/У"2. В предельном случае
т. е. при Qk—2,4l полоса пропускания в 3,1 раза больше, чем у одиночного колебательного контура.
Если Qk=l, то ||| =|//2 и ||| /Q— 2 d, т. е. при Qfc=l поло-
са пропускания в 1,41 раза больше, чем у одиночного контура.
При QZs=0,68 полоса пропускания связанных контуров равна полосе пропускания одиночного контура, а при Qfc<0,68 она меньше полосы пропускания одиночного контура.
Величина Qk .называется параметром связи.
8-7. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
8-1. В схеме рис. 8-1, г с параллельной емкостной связью Cj = 100 пф, С2 = 10 пф и С12 =50 пф заменить данную схему эквивалентной последовательной емкостной связью (рис. 8-1, в).
Ответ: С|=650 пф; С2=65 пф; С12=130 пф.
8-2. Два индуктивно связанных колебательных контура имеют следующие параметры: Li=100 мкгн; £2=250 мкгн; г2= =80 ом; М=50 мкгн; /=800 кгц и С2= = 1 000 пф.
Вычислить емкость Ct первого контура при первом частном резонансе.
Ответ: Ci=440-10-12, ф=440 пф.
8-3. Как определяется полоса пропускания индуктивно связанных колебательных контуров?
8-4. Показать, что максимумы двугорбой кривой рнс. 8-6 соответствуют ц ==р2,19.
8-5. Как зависит глубина впадины двугорбой резонансной кривой от параметра связи Qk?
149
Глава девятая
ЦЕПИ ТРЕХФАЗНОГО ТОКА
9-1. ТРЕХФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Трехфазная электрическая __пь может быть представлена как совокупность трех однофазных це
пей (цепей однофазного тока), в которых действуют э. д. с. одной и той же частоты, сдвинутые относительно друг друга на одну треть периода или, что то же, на угол 2л/3.
Эти три составные части трех-
149
фазной цепи называются фазами *, и им ниже будут приписываться буквенные обозначения А, В, С.
На рис. 9-1 схематично показана трехфазная цепь, фазы которой электрически не связаны друг с дру-
Рис. 9-1. Несвязанная трехфазная цепь.
гом. Такая трехфазная цепь называется несвязанной (в настоящее время не применяется).
На рис. 9-1 для простоты обмотки трехфазного генератора не показаны. Сопротивлениями обмоток и шести соединительных проводов ввиду их малости по сравнению с сопротивлениями .нагрузки можно для начала пренебречь.
Фазы А, В, С изображены на рис. 9-1 под углом 120°, для того чтобы подчеркнуть, что э. д. с. Ел, Ёв, Ёс сдвинуты относительно друг друга на одну треть периода. При равенстве амплитуд э. д. с. и одинаковых сопротивлениях в фазах токи /а, 1р и /с также равны по величине и сдвинуты относительно друг друга на одну треть периода, образуя так называемый трехфазный ток,
Сумма этих токов в любой момент времени равна нулю; поэтому если три провода, по которым токи возвращаются к источникам, объединить в один провод, то ток в этом проводе будет равен нулю. При отсутствии в проводе тока излишним в данном случае является и сам провод; от него можно отказаться, перейдя, таким образом, к схеме рис. 9-2. В результате этого
1 Таким образом, термином фаза в электротехнике обозначаются два понятия: угол, определяющий стадию периодического процесса, н составная часть многофазной цепи
достигается экономия материала проводов; кроме того, по сравнению с несвязанной трехфазной цепью исключаются потери мощности от токов /а, 1р и 1С в обратных проводах.
Рис. 9-2, Связанная трехфазная цепь.
Трехфазная цепь на рис. 9-2, фазы которой соединены электрически, представляет одну из разновидностей связанных трехфазных цепей.
OCbfi
Рис. 9-3. Принцип выполнения трехфазного синхронного генератора.
Благодаря технико-экономическим преимуществам связанных трехфазных цепей они получили широкое распространение.'
Для получения связанной трехфазной цепи не требуются отдельные однофазные генераторы, а используется трехфазный генератор, схематически показанный на рис. 9-3. Обмотки, в которых наводятся э. д. с., помещаются в пазах статора1 2. Обмотки фаз сдвинуты
2 Следует отметить, что на практике применяются также трехфазные генераторы, в которых полюсы неподвижны, а обмотки вращаются.
150
относительно друг друга на угол 1207р, где р — число пар полюсов. В случае двухполюсного генератора (рис. 9-3) р—1 и угол равен 120° (подробнее см. § 9-6).
При. вращении ротора в силу идентичности трех обмоток генератора в них наводятся э. д. с., имеющие одинаковую амплитуду и ча
Рис. 9-4. Мгновенные значения (а) и векторная диагоамма э. д. с. (б) трехфаз-иого генератора.
стоту, причем эти э. д. с. сдвинуты по фазе по отношению друг к другу на одну треть периода. Векторы, изображающие эти э.д.с., равны по величине и составляют между собой угол 120° (рис. 9-4,6).
Мгновенные значения э. д. с. трехфазного генератора, показанные на рис. 9-4, а, выражаются аналитически следующим образом:
еА = Ет sin“Z;
= F sinfrof--—j ;
в т \ 3 /
f * I л. । 2л> \
С- = sin (cot Я----I.
с 1 з /
Мгновенные значения э. д. с. равны соответствующим проекциям трех векторов ЕтА, ЁтВ, ЁтС (рис. 9-4,6), образующих симметричную звезду и вращающихся в положительном направлении с угловой скоростью го (на рис. 9-3 положение ротора соответствует моменту t—0).
Положительные направления э. д. с. в обмотках указаны на рис. 9-3 точками и крестиками; точка означает острие, а крестик — конец стрелки, совпадающей с положительным направлением э. д. с. (положительное направление э. ц. с. не следует смешивать с действи
тельным направлением э. д. с. в произвольный момент времени).
Создание в 1889 г. связанной трехфазной цепи переменного тока явилось важным событием в истории электротехники.
Впервые такую цепь осуществил выдающийся русский инженер и ученый Михаил Осипович Доливо-Добровольский (1862-1919 гг.). Им были разработаны основные звенья генерирования, передачи, распределения и преобразования электроэнергии трехфазного тока, а именно: трехфазные генератор, трансформатор и асинхронный двигатель. Изобретение М. О. Доливо-Доброволь-ским асинхронного двигателя, являющегося простейшим и самым дешевым двигателем переменного тока, существенно способствовало широкому промышленному внедрению трехфазного тока.
Технические и экономические преимущества трехфазного тока обеспечили ему ведущую роль в современной электротехнике.
Неуклонно возрастает также роль трехфазного переменного тока в авиации.
9-2. СОЕДИНЕНИЕ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ
Каждая фазная обмотка имеет две крайние точки или два вывода, которые условно называются началом и концом обмотки. За начало обмотки генератора обычно принимается тот вывод, к которому направлена положительная э. д. с. На рис. 9-2 одноименные выводы фазных обмоток генератора обозначены буквами н (начало) и к (конец).
Показанное на схеме рис. 9-2 соединение обмоток трехфазного генератора называется звездой: все концы фазных обмоток генератора соединены в одну общую точку. В дальнейшем для простоты мы не будем располагать фазы генератора под углом 120°, а будем изображать их параллельно (рис. 9-5).
Общая точка фазных обмоток генератора называется нейтрал fail о й или нулевой точкой. В зависимости от требований нейтральная
151
точка может быть выведена к отдельному зажиму, обозначенному на рис. 9-5 цифрой 0.
При соединении обмоток трехфазного генератора треугольником (рис. 9-6, а) начало одной фазной обмотки соединяется с концом сле-
Рис. 9-5. Соединение трехфазного генератора звездой.
Рис. 9-6. Соединение трехфазного генератора треугольником.
дующей по порядку фазной обмотки так, что все три обмотки образуют замкнутый треугольник, причем направления э. д. с. в контуре треугольника совпадают и сумма э. д. с. равна нулю. Общие точки соединенных обмоток генератора выводятся на зажимы, к которым присо
Рис. 9-7. Соединение нагрузки звездой (а) и треугольником (б, в).
единяются линейные провода или нагрузка.
При отсутствии нагрузки, т. е. при режиме холостого хода в обмотках генератора, соединенных треугольником, ток не циркулирует, так как сумма трех фазных э. д. с. равна нулю (рис. 9-6,6).
Ради упрощения в схемах рис. 9-5, а и 9-6, а показаны только э. д. с. генератора; обмотки и их сопротивления на схеме не показаны.
Нагрузка в трехфазной цепи также может быть соединена звездой (рис. 9-7, а) или треугольником (рис. 9-7,6 и в).
На практике применяются различные комбинации соединений, например: 1) генератор может быть соединен звездой, а нагрузка — звездой или треугольником; 2) генератор может быть соединен треугольником, а нагрузка — звездой или треугольником.
Соединение нагрузки звездой по схеме рис. 9-2 применяется только при одинаковой нагрузке всех трех фаз. Между тем условие равномерной загрузки фаз на практике не всегда выполняется (например, в случае осветительной нагрузки). При неравномерной нагрузке напряжения на фазах, т. е. на сопротивлениях лучей звезды нагрузки, получаются неодинаковыми (см. § 9-4). Кроме того, в схеме рис. 9-2 недопустимым является включение или отключение одной фазы нагрузки.
В этом отношении соединение нагрузки треугольником имеет преимущество: сопротивления фаз, т. е. сторон треугольника, могут быть неодинаковы и даже в крайнем случае могут включаться и отключаться независимо друг от друга.
Такая же возможность имеется при соединении генератора и нагрузки звездой, если их нейтральные точки соединены нейтральным проводом или через землю (рис. 9-8, а и 6). На самолетах и кораблях нейтральным проводом может служить металлическая обшивка (корпус), к которой присоединяются нейтральные точки генераторов и нагрузок.
Электродвижущие силы, наводи-
152
мне в фазных обмотках генератора, напряжения на их зажимах, напряжения на фазах нагрузки и токи в них называются соответственно
а = е' 120° = cos 120° + / sin 120° = ---------------------
2 2
Рис. 9-8. Соединение звезда — звезда с нейтральным проводом (а) и заземленными нейтральными точками (б).
фазными э. д. с., напряжениями и токами и обозначаются:
Еф, ^ф и /ф.
Напряжения между линейными проводами и токи в них называются линейными напряжениями и токами и обозначаются:
U. и /„.
При соединении фаз звездой фазные токи равны линейным токам: /ф=/л- При соединении фаз треугольником фазное напряжение равно соответствующему линейному напряжению (7ф=[/л*.
Различают симметричный и несимметричный режимы работы трехфазной цепи. При симметричном режиме сопротивления всех трех фаз одинаковы и э. д. с. образуют симметричную систему; в противном случае имеет место несимметричный режим.
9-3. СИММЕТРИЧНЫЙ режим работы ТРЕХФАЗНОИ ЦЕПИ
Расчет трехфазной цепи, так же как и расчет всякой сложной цепи, ведется обычно в комплексной форме. Ввиду того, что фазные э. д. с. генератора сдвинуты относительно друг друга на 120°, для краткости математической записи применяется фазовый оператор — комплексная величина:
* Кроме того, применяется понятие «фазное напряжение в данном сечении» трехфазной цепи по отношению к какой-либо точке, принимаемой за нуль, например земле, нулевой точке генератора или искусственной нулевой точке.
Умножение вектора на оператор а означает поворот вектора на 120° в положительном направлении (против хода часовой стрелки).
Соответственно умножение вектора на множитель а2 означает поворот вектора на 240° в положитель
Рис. 9-9. Симметричный режим работы трехфазной цепи.
а — трехфазная цепь; б — векторная диаграмма.
ном направлении или, что то же, поворот его на 120° в отрицательном направлении.
Очевидно,
2 / 240° —1 120°
а = е =е =
=____1___ Уз
2 1 2 ‘
Если э. д. с. фазы А равна ЁА, то э. д. с. фаз В и С равны соответственно:
Ёв = а2 Ёд; Ёс = аЁА.
В простейшем случае симметричного режима работы трехфазной цепи, когда генератор и нагрузка соединены звездой (рис. 9-9,а), векторная диаграмма э.д.с. и токов имеет вид, показанный на рис. 9-9, б.
Ток в каждой фазе отстает от э. д. с. той же фазы на угол <р= = arctg —• где г и х — активное и г реактивное сопротивления фаз.
Ток в фазе А находят так же, как в однофазной цепи, потому что нейтральные точки генератора и нагрузки в симметричном режиме могут быть соединены как имеющие одинаковые потенциалы:
153
Соответственно токи в фазах В и С выражаются через ток 1а'.
1^1 а) 4 = Чг
Наличие нейтрального провода не вносит при симметричном режиме никаких изменений, так как сумма токов трех фаз равна нулю и ток в нем отсутствует:
+/с=(1+ав+а)/д=0-
Таким образом, при симметричном режиме работы трехфазной цепи задача сводится к расчету одной из фаз аналогично расчету однофазной цепи. При этом сопротивление обратного (нейтрального) провода не учитывается, так как ток в нем и соответственно падение напряжения на нем отсутствуют.
По мере удаления от генератора фазные напряжения, определяемые падениями напряжения до нейтральной точки нагрузки, изменяются по величине (обычно убывают) и по фазе. Линейные напряжения определяются как разности соответствующих фазных напряжений, например: Uab=Ua—UB. В любом месте трехфазной линии при симметричном режиме соблюдается следующее соотношение между модулями линейных и фазных напряжений:
ил = у~зиф.
Действительно,
^ав = 0A(l-a*) = V~3UA^ 30°, т. е. Uав опережает по фазе UA на 30°, причем модуль UAb в У 3 раз превышает UA.
В случае соединения треугольником линейные токи определяются в соответствии с первым законом Кирхгофа как разности фазных токов, и при симметричном режиме соблюдается соотношение /л = = УТ /ф.
Соединение фаз генератора или нагрузки треугольником должно быть для расчета заменено эквивалентным соединением фаз звездой; вследствие этого расчет трехфазной цепи с соединением фаз треугольни
ком приводится в конечном итоге к расчету эквивалентной трехфазной цепи с соединением фаз звездой.
Между сопротивлениями сторон треугольника (Za ) и лучей звезды (Zz) имеет место соотношение Zz — , вытекающее из формул
преобразования треугольника сопротивлений в эквивалентную звезду (§ 4-4).
Это соотношение справедливо как для сопротивлений симметричной трехфазной нагрузки, так и для сопротивлений симметричного трехфазного генератора. При этом фазные э. д. с. эквивалентного генератора, соединенного звездой, берутся в У~3 раз меньшими фазных э.д.с. заданного генератора, соединенного треугольником (кроме того, они должны быть сдвинуты на угол 30°). Это легко усмотреть из векторной потенциальной диаграммы напряжений генератора.
Активная мощность симметричной трехфазной нагрузки равна:
Р==3(/ф/фСозф.
Ввиду того, что при соединении нагрузки звездой Уз иф=и„ и /ф= =/л, а при соединении нагрузки треугольником иф=11л и]/3 /ф=7л, активная мощность трехфазной цепи независимо от вида соединения выражается через линейные напряжения и ток следующим образом:
Р=]Лз'[/л/лсо8ф, здесь ф — угол сдвига фазного тока относительно одноименного фазного напряжения.
Аналогичным образом для реактивной и полной мощностей симметричной трехфазной нагрузки имеем:
<2-ил 1Л sin ф; S= УТ ил 1Л.
Приведенные выражения не означают, что при пересоединеиии нагрузки со звезды на треугольник (или наоборот) активная и реактивная мощности не изменяются. При пересоединеиии нагрузки со звезды на треугольник при заданном линейном напряжении фазные токи возрастут в У~~3 раз, а линейный ток—в 3 раза, и поэтому мощность возрастет в 3 раза.
154
Если нейтральная точка симметричной трехфазной нагрузки выведена, то измерение активной мощности может быть осуществлено одним ваттметром, включенным по схеме рис. 9-10, а (одноименные или так называемые генераторные за-
Рис. 9-10. Измерение активной мощности при симметричном режиме.
жимы последовательной и параллельной цепей ваттметра отмечены на рис. 9-10,а звездочками). Утроенное показание ваттметра равно суммарной активной мощности трех фаз.
Если нейтральная точка не выведена или нагрузка соединена треугольником, то можно воспользоваться схемой рис. 9-10,6, где параллельная цепь ваттметра и два добавочных активных сопротивления Гдоб, равные по величине сопротивлению параллельной цепи ваттметра, образуют искусственную нейтральную точку 0*.
Для получения суммарной мощности, как и в предыдущем случае, показание ваттметра утраивается.
На рис. 9-11 показан способ измерения реактивной мощности в
* Следует заметить, что здесь применим только электродинамический и ер-родниамический ваттметр, сопротив-.-ние параллельной цепи которого является чисто активным. Индукционный ваттметр неприменим по той причине, что параллельная цепь индукционного ваттметра имеет реактивное сопротивление; для создания искусственной нейтральной точки в этом случае потребовались бы реактивные добавочные сопротивления.
симметричной трехфазной цепи при помощи одного ваттметра: последовательная цепь ваттметра включена в фазу А, а параллельная — между фазами В и С, причем генераторные зажимы ваттметра присоединены к фазам Л и В.
Показание ваттметра в этом случае равно:
U вс a cos (ф 90 ва a s'n Ф*
Для получения суммарной реактивной мощности показание умножается на
Разделив активную мощность на полную мощность, получим:
Р COS <Р = -.
F S
Рис. 9-11. Измерение реактивной мощности при симметричном режиме
Пример 9-1. Определить ток в генераторе при симметричном режиме работы трехфазной цепи, представлеииой на рис. 9-12, а.
Сопротивления соединенные треугольником, заменяются эквивалентной
звездой из сопротивлений-~ Z*.
О
При симметричном режиме нейтральные точки генератора и нагрузки, как было указано выше, могут быть объединены. Тогда режим работы каждой фазы, например фазы А, может быть рассмотрен в однофазной расчетной схеме (рис. 9-12,6).
Результирующее сопротивление цепи одной фазы равно:
Za(Zs + Tz*)
Zt 4- Zb+ “Z" Z4 о
Z = Z, +
6)
Рис. 9-12. Пример 9-1.
155
Искомый ток в фазе А
1а Z
9-4. НЕСИММЕТРИЧНЫЙ РЕЖИМ РАБОТЫ ТРЕХФАЗНОИ ЦЕПИ
Несимметрия в трехфазной цепи может быть вызвана различными причинами: 1) неодинаковым сопротивлением фаз (несимметричная нагрузка); 2) несимметричным коротким замыканием (например, ме-
Рис. 9-13. Несимметричная трехфазная цепь, соединенная звездой (с нейтральным проводом).
жду двумя фазами или фазой и нейтралью); 3) размыканием фазы; 4) неравенством величин э. д. с. и т. п.
Расчет токов и напряжений в трехфазной цепи при несимметричном режиме может производиться теми же методами, которые применяются для расчета однофазных цепей.
Рассмотрим несколько простейших вариантов (без взаимной индукции между фазами).
1. Несимметричная трехфазная цепь, соединенная звездой, с нейтральным проводом (рис. 9-13). Несимметричная трехфазная цепь, показанная на рис. 9-13, может рассматриваться как трехконтурная цепь с тремя э.д.с. Такая цепь может быть рассчитана методом контурных токов, узловых напряжений и другими методами. Поскольку в схеме имеются только два узла, наиболее целесообразно в данном слу
чае определить узловое напряжение (напряжение смещения) между нейтральными точками 0' и О по формуле, аналогичной (4-4):
yaea + ybeb+ycec
YA + YB + Тс + Y„
(9-1)
где YA, Yb, Yc и Yn — проводимости соответствующих ветвей.
После этого найдем токи:
Ia=YA(EA-U^
~ Yc (4 ^n) •
В симметричной трехфазной цепи Уа=Ув = Тс, и поэтому при ЕА-\-+Ёв+£с=0 узловое напряжение UN равно нулю.
Случаю размыкания какой-либо фазы или нейтрального провода соответствует равенство нулю проводимости данной фазы или нейтрального провода.
При отсутствии нейтрального провода, полагая в (9-1) У«=0, имеем:
_ya^a~Y УвЁв + УсЁ0 ya+yB + y0 '
2. Несимметричная трехфазная нагрузка, соединенная звездой (без нейтрального провода), с заданными линейными напряжениями иа зажимах (рис. 9-14).
Рис. 9-14. Несимметричная трехфазная нагрузка, соединенная звездой (без нейтрального провода).
Если заданы линейные напряжения Uab, Uвс и Uca на зажимах нагрузки, соединенной звездой, то то
156
ки в фазах звезды определяются следующим образом.
Обозначив фазные напряжения на зажимах нагрузки через йА, Ub и йс (рис. 9-14), получим:
где Ya, Yb и Yc — проводимости фаз нагрузки.
Равенство нулю суммы токов трех фаз записывается в виде
YA^A + yBOB+YcUc = Q. (9-2)
Фазные напряжения йв и йс могут быть выражены через йА и заданные линейные напряжения:
= (9-3)
Подстановка (9-3) в (9-2) дает:
- YBUAR — YrUr, и,=— Ав------(9-4)
А Ya+Yb+Yc
Круговой заменой индексов (с порядком следования АВСА и т. д.) находятся:
У yc йвс — ya йАВ В~ Ya + YB+Yc ' (9-4а)
jy Y А^СА YBUBC
С“ Ya + Yb+Yc '
По фазным напряжениям нагрузки находятся фазные токи.
В случае симметричной нагрузки (Ка= Ув= Ус) вектор фазного напряжения равен одной трети диагонали параллелограмма, построенного на соответствующих линейных напряжениях. Фазные напряжения в этом случае определяются векторами, соединяющими центр тяжести треугольника напряжений (точка пересечения медиан) с вершинами треугольника.
На рис. 9-15 построение сделано для фазы А по формуле (9-4):
= 3
В качестве примера рассмотрим схему фазоуказателя, используемую для определения чередования фаз по времени, состоящую из конденса
тора и двух одинаковых электрических ламп, соединенных звездой.
Положим, что конденсатор присоединен к фазе А, а лампы к фазам
В и С; емкостное конденсатора берется равным по величине сопротивлению лампы, т. е. ZA= — jxc; ZB=Z(:^~r, причем Хс = Г.
Неравенство напряжений на лампах проявится в том, что накал ламп будет разным. Отношение напряжений согласно выведенным
сопротивление
Рис. 9-15. Нахождение фазных напряжений.
выше выраже-
ниям (9-4) равно при симметрии линейных напряжений:
Uв а? — а— / (1 — а2)
Uc j (а— 1) — (в2—а)
__ ! 3,23 + j 0,866 | 3 73
| 0,23+ /0,866 |
Следовательно, лампа, присоединенная к фазе В (т. е. к фазе, опережающей ту, к которой присоединена вторая лампа), будет светить ярко, а лампа, присоединенная к отстающей фазе, — тускло.
Вместо конденсатора можно при-
менить индуктивную катушку, подобрав ее индуктивное сопротивление приблизительно равным по величине сопротивлению лампы. В этом случае ярче будет светить лампа, присоединенная к отстающей фазе.
Эти соотношения также весьма просто могут быть получены непосредственно из векторной диаграм
мы.
3. Несимметричная трехфазная нагрузка, соединенная треугольником, с заданными напряжениями на зажимах (рис. 9-16).
Если на зажимах несимметричной трехфазной нагрузки, соединенной треугольником, заданы линейные напряжения йАВ, йвс и йсл (рис. 9-16), то токи-в сопротивлениях нагрузки равны: йАВ^АВ, UBc/ZBc и Vca/Zca-
Токи в линии определяются как
разности соответствующих токов на-
157
грузки, например: / = —— — А ZAB
— 9са и т. д.
ZCA
Если на зажимах несимметричной трехфазной нагрузки, соединенной треугольником, заданы фазные напряжения UA, (Jb и Uc источника, соединенного в звезду, то линей-
Рис. 9-16. Несимметричная трех-фаз'ная нагрузка, соединенная треугольником.
ные напряжения на зажимах нагрузки находятся как разности соответствующих фазных напряжений, в результате чего задача сводится к только что рассмотренному случаю (рис. 9-16).
Пример 9-2. Сопротивления фаз нагрузки, соединенной звездой:
ZA = 40 + /30 = 50 36°54';
ZB = 30 + /40 = 50 53°6';
Zc = 20 0° ом
Сопротивление нейтрального провода ZN = з + /4 = 5 -г: 53°6' ОМ
Напряжение на зажимах цепи представляет собой симметричную звезду;
0А = 100 0°;
Ов = 100 -< — 120° = — 50 — /86,6;
0о = 100 120° = — 50 + /86,6 в.
Требуется определить фазные напряжения нагрузки.
Проводимости фаз нагрузки и нейтрального-провода:
Y. = = 0,02 — 36°54' =
= 0,016 — /0,012сим;
У» = -9- = 0,02 — 53°6' = в ZB
= 0,012 — /0,016 сим;
Уг = —9~ — 0,05 0° сим; с zc
Уд, = -у— = 0,2 — 53°6' = ^N
= 0,12 — /0,16 сим.
На основании формулы (9-1)
___0,02^— 36°54'+ 0,02^ —
О., = 100—--------------1-----------
N 0,016-/0,012 + 0,012 —
— 173°6' + 0,05 120°
* —/0,016 + 0,05 + 0,12 — /0,16 ~
= — 14,9 + /0,39в
Искомые фазные напряжения нагрузки: UA—l)N= 100+ 14,9 — /0,39 = = 114,9 —/0,39= 114,9^ —0°12'в;
0B '-Un = -50-/86,6+ 14,9 —/0,39 = = — 35,1 — /87,0 = 93,5 — 112° в;
1)в — 0N = — 50+ /86,6+ 14,9 — /0,39 = = — 35,1 + /86,2 = 93,0 112°50' в.
9-5. МОЩНОСТЬ НЕСИММЕТРИЧНОЙ ТРЕХФАЗНОЙ ЦЕПИ
Пользуясь комплексной формой записи мощности, можно написать общее выражение для мощности трехфазной цепи:
S-Pj^ + l^+Vc- (9-5)
Действительная часть этого выражения представляет собой активную мощность
Р =UA lA C0S Фд+^В, lB COS Фв+ +Ц? Л?С°5фв"
, Суммарная активная мощность, потребляемая несимметричной трехфазной цепью, может быть в соответствии с этим измерена при помощи трех ваттметров, включенных на подведенные к данной цепи фазные напряжения относительно нейтрали и одноименные с ними токи. Активная мощность равна сумме показаний трех ваттметров. Такой метод измерения применяется при наличии нейтрального провода (рис. 9-17) или искусственно созданной нейтральной точки.
В случае отсутствия нейтрального провода измерение может быть произведено с помощью двух ватт
158
метров (рис. 9-18). В этом случае выражение (9-5) преобразуется следующим образом: исключая ток 1С
Рис. 9-17. Измерение мощности при наличии нейтрального провода.
из условия
К = Л — получаем:
или
напряжения или тока, подводимого к данному ваттметру, записывают полученное показание со знаком * минус. При симметричном режиме фч работы трехфазной цепи такое положение имеет место при
|Ф|>60°,
что видно непосредственно из векторной диаграммы (рис. 9-18,6).
При симметричном режиме показания двух ваттметров в схеме рис. 9-18, а будут следующие:
/дСО8(ф —30°) =
=UI cos(<p — 30°);
Р*=ик1в cos (q>+30°) =
=UI cos(<p4-30°).
Сумма и разность показаний ваттметров соответственно равны:
(9-6)
В соответствии с (9-6) при измерении активной мощности двумя
P1+P2=C//-2cos<pcos30° =
= 3 UI cos<p;
Рг — Р2=Ш • 2 sin ф sin 30°=W sin ф.
Рис. 9-18. Измерение мощности двумя ваттметрами (при отсутствии нейтрального провода).
ваттметрами к одному из них подводится напряжение 0АС и ток 1А, а ко второму — напряжение UBc и ток /в (рис. 9-18,а). Показания ваттметра складываются алгебраически.
Круговой заменой А, В и С в выражении (9-6) можно получить выражения для других равноценных вариантов включения двух ваттметров.
Следует иметь в виду, что если стрелка одного ваттметра отклоняется по шкале в противоположную сторону, то, изменив направление
Следовательно, при симметричном режиме работы трехфазной цепи тангенс угла сдвига фаз может быть вычислен по формуле
1/ о Р1
9-6. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ
Пусть через катушку проходит ток i=/msin(cof+ip). На рис. 9-19,0 катушка условно изображена в виде витка, причем точка и крестик указывают положительное направление тока; точкой обозначено ост
159
рие, а крестиком — конец стрелки, совпадающей по направлению с током. Принятому положительному направлению тока соответствует по правилу буравчика положительное направление вектора магнитной индукции1 B = Bmsin(co/+ip), указанное стрелкой вдоль оси катушки
зультат наложения двух круговых полей, вращающихся в противоположные стороны с угловой скоростью, равной угловой частоте переменного тока, и имеющих максимальную индукцию на вращающейся оси, вдвое меньшую амплитуды индукции пульсирующего поля
6)
Рис. 9-19. Разложение пульсирующего магнитного поля катушки на два вращающихся при синусоидальном и косинусоидальном токе (в момент 1=0).
Рис- 9-20. Образование кругового вращающегося магнитного поля из двух пульсирующих.
(Вт — максимальное значение магнитной индукции в центре катушки); когда ток отрицателен, вектор магнитной индукции имеет противоположное направление, показанное на рис. 9-19, а пунктиром.
Таким образом, магнитное поле изменяется (пульсирует) вдоль оси катушки; такое магнитное поле называется пульсирующим.
Условимся круговым вращающимся магнитным полем называть магнитное поле, ось которого равномерно вращается, причем значение магнитной индукции на этой оси неизменно. Легко убедиться в том, что магнитное поле, пульсирующее по гармоническому закону, может рассматриваться как ре-
1 Предполагается линейная зависимость индукции от тока.
,160
(рис. 9-19,6 и в). Это следует из формул:
sin со/ = — —
2j и
cosco/ = А- -Ье-'™).
Положения векторов на рис. 9-19,6 и в соответствуют моменту /=0.
Допустим теперь, что через две катушки, расположенные взаимно перпендикулярно, проходят токи одной и той же амплитуды и частоты, сдвинутые по фазе относительно друг друга на четверть периода. На рис. 9-20, а катушки обозначены цифрами 1 и 2. Принятым положительным направлениям токов it = = /msinci)/ и t2=/msin (со/ + л/2) = — Imfiosat соответствуют взаимно
перпендикулярные пульсирующие магнитные потоки с индукциями в точке пересечения осей катушек fii=Smsinw/ и Bz=Bmcoswf, направленными по действительной и мнимой осям.
Заменив каждое из пульсирующих полей двумя вращающимися (рис. 9-20, бив), убеждаемся в том, что векторы магнитной индукции — j^e™ (рис 9-20,6) и j~eiait (рис. 9-20,в), вращающиеся в положительном направлении, взаимно компенсируются (их сумма равна нулю). Два других вектора образуют в сумме вектор магнитной индукции вра-
щающийся в отрицательном направлении (по часовой стрелке).
К тому же выводу приходим и на основании выражения, получаемого для результирующего вектора магнитной индукции:
Bl+jBst=Bm (sin at 4-
4- / cos at)=jBm e~iat.
Это выражение показывает, что ось результирующего магнитного поля равномерно вращается с угловой скоростью со, причем значение индукции на оси неизменно равно Вт, т. е. получается круговое вращающееся магнитное поле.
Направление вращения магнитного поля зависит от положительных направлений магнитных индукций и от того, какая из индукций является отстающей. В рассматриваемом здесь случае индукция отстает по фазе на л/2 от индукции В2 и магнитное поле вращается в отрицательном направлении. Если изменить направление тока в одной из катушек, например в катушке 1, что равносильно изменению фазы тока ii на л, магнитное поле будет вращаться в положительном направлении. В этом можно убедиться, повернув векторную диаграмму рис. 9-20,6 на 180е или воспользовавшись выражением
В—Вт (— sin tirf-E / cos at)—
Таким образом, от сложения двух взаимно перпендикулярных пульсирующих магнитных полей, сдвинутых по фазе на четверть периода, получается круговое магнитное поле, вращающееся с угловой скоростью <в в сторону отстающего по фазе вектора индукции.
Описанный способ получения кругового вращающегося магнитного поля с помощью двухфазной
Рис. 9-21. Получение вращающегося магнитного поля при помощи трехфазной системы токов.
системы токов широко используется в приборостроении и электромашиностроении.
Большое удобство с точки зрения возможности получения кругового вращающегося поля представляет трехфазный ток.
Расположим три одинаковые катушки таким образом, чтобы их оси были сдвинуты относительно друг друга в пространстве на угол 120° (рис. 9-21), и подключим эти катушки к симметричной трехфазной цепи. Тогда через катушки будут протекать токи:
С=/ sin (at — —У
B m \ 3 /
. - I . , 2л \
\ *3 /
Положительным направлениям токов, обозначенным на рис. 9-21 с помощью точек и крестиков, соответствуют по правилу буравчика указанные стрелками положительные направления магнитных потоков (векторов индукций), создаваемых токами Ia, Ib, ic.
11—1118
161
При пропорциональной зависимости индукций от токов мгновенные значения индукций фаз выразятся следующим образом:
В .=^В„ sin и/; Ат ’
Вв=Вт sin а/
Вс=Вт sin
С т I 1 з I
(9-7)
где Вт — амплитуда индукции на оси каждой из катушек.
При выбранном на рис. 9-21 направлении осей + и + j результирующий вектор индукщш находится сложением векторов ВА, Вв и Вс-
B^f(BA+azBB+aBc). (9-8)
Подстановка (9-7) в (9-8) дает:
В = /В„, (sin ы t + a2 sin <в t cos 120° —
—а2 cos ш/sin 120° +
-h a sin co t cos 120° +
+ a cos co t sin 120° =
=/ l,5Bm(sinco/ + /cosco/)
или
B = —l,5Bme“/mi-
Полученное выражение показывает, что результирующий вектор магнитного поля имеет постоянный модуль, равный 1,5 Вт, и равномерно вращается с угловой скоростью со от оси фазы А по направлению к оси фазы Й и т.д. (на рис. 9-21 по ходу часовой стрелки), т. е. получается круговое вращающееся поле.
Для изменения направления вращения поля достаточно поменять местами токи в каких-нибудь двух катушках, например токи iB и ic-
При нёсимметрии токов в катушках, например, если концы одной катушки поменять местами, или при несимметрии питающих напряже-. ний вместо кругового вращающегося поля получится эллиптическое вращающееся поле, результирующий вектор индукции которого описывает эллипс и имеет переменную угловую скорость.
В электрических машинах вращающееся магнитное поле создает
ся совместным действием н. с. статора и ротора.
Линии магнитной индукции замыкаются по телу статора, воздушному зазору и телу ротора. Место выхода линий индукции из статора можно рассматривать как северный полюс, а место входа их в статор — как южный полюс магнитного поля обмотки статора.
Кривая распределения индукции В вдоль воздушного зазора имеет ступенчатую форму, которая при большом числе пазов статора близка к трапеции с углом наклона боковой стороны 60° и может быть приближенно заменена синусоидой.
Синусоидальный ток частоты f, проходя через фазную обмотку статора, создает поле, пульсирующее с той же частотой. Таким образом, магнитное поле одной фазы изменяется синусоидально как во времени, так и в пространстве (по окружности зазора).
Обмотки трех фаз расположены на статоре так, что их оси, а следовательно, и оси трех пульсирующих магнитных полей сдвинуты в пространстве на 120°. Поэтому при прохождении через обмотки трехфазного тока пульсирующие поля образуют в сумме Двухполюсное вращающееся в зазоре синусоидальное поле, амплитуда индукции которого постоянна и равна 3/г амплитуды слагающих фазных полей.
За один период Переменного тока такое магнитное поле совершит один оборот, а за 1 мин 60 f оборотов.
Если обмотку статора выполнить многополюсной, т. е. с полюсным шагом 180°/р, то три пульсирующих поля будут сдвинуты в пространстве на 120°/р, и в результате получится 2р-полюсное вращающееся поле, имеющее скорость вращения, равную 60 f/p, об/мин.
9-1. ПРИНЦИП ДЕЙСТВИЯ АСИНХРОННОГО И СИНХРОННОГО
ДВИГАТЕЛЕЙ
Простейшим по устройству и наиболее распространенным в промышленности типом двигателя пере
162
менного тока является трехфазный асинхронный двигатель, изобретенный в 1888 г. М. О. Доливо-Добро-вольским. Его ротор выполняется в виде стального цилиндра, собранного из стальных листов, с обмоткой, размещенной в пазах по его поверхности. Вращающееся магнитное поле, созданное обмотками статора, наводит в замкнутой обмотке ротора токи. Механическое взаимодействие этих токов с вращающимся полем приводит ротор во вращение в том же Направлении, в котором вращается поле.
Ротор вращается асинхронно, т. е. его скорость вращения (и, об/мин) меньше скорости вращения магнитного пбля (пь об/мин).
Разность скоростей вращения поля и ротора, отнесенная к скорости поля, называется скольжением:
Скольжение не может быть равным нулю, так как при одинаковых скоростях поля й ротора прекратилось бы наведение токов в роторе и, следовательно, отсутствовал бы вращающий момент.
В рабочем режиме асинхронный двигатель Находится в динамическом равновесии, когда создаваемый благодаря скольжению вращающий момент уравновешивает тормозящий момент нагрузки на его валу. С увеличением механической нагрузки тормозящий момент становится больше вращающего и скольжение увеличивается. Вследствие этого возрастают индуктированные в обмотке ротора э. Д. с. и токи, что вызывает увеличение вращающего момента до нового состояния динамического равновесия (при большем скольжении).
Однако вращающий момент может расти с увеличением скольжения только до определенного предела, так называемого критического значения при критическом скольжении, после чего он падает.
При нормальной нагрузке скольжение асинхронных двигателей в среднем составляет 2—4%.
Трехфазный генератор (рис. 9-3), как и многие другие типы электри
11*
ческих машин, обладает свойством обратимости: он может работать как синхронный двигатель. Поэтому конструктивно синхронный двигатель мало отличается от генератора.
Если присоединить обмотку статора к источнику (сети) трехфазного тока, а обмотку ротора (обмотку возбуждения) — к источнику постоянного тока, то вращающееся магнитное поле статора будет периодически создавать на валу моменты разных знаков. Поэтому ротор не сможет прийти во вращение, он будет вибрировать.
Для пуска двигателя необходимо сначала (при разомкнутой обмотке возбуждения) привести ротор во вращение до скорости, близкой к синхронной. Если после этого включить обмотку возбуждения, то двигатель «втянется в синхронизм». Ротор будет вращаться синхронно с полем статора.
Для пуска синхронного двигателя может быть использована специальная пусковая обмотка ротора, действующая так же, как в асинхронном двигателе.
При строго синхронном вращении ротора имеется угловой сдвиг между осями полей статора и ротора, зависящий от нагрузки (от момента сопротивления на валу). С увеличением нагрузки этот угол увеличивается, благодаря чему момент вращения также увеличивается. Максимальный вращающий момент получается при угле между э.д.с. двигателя и напряжением сети, равном 90°, после чего дальнейшее увеличение нагрузки приводит к остановке двигателя и «выпадению» его из синхронизма.
Если изменять постоянный ток в цепи возбуждения ротора, то можно в широких пределах регулировать coscp двигателя. Так, при «недовоз-буждении» двигателя угол <р положителен, т. е. ток отстает от напряжения, а при «перевозбуждении» угол <р отрицателен: ток опережает напряжение. Это свойство синхронных двигателей весьма ценно и широко используется в промышленности для повышения cos ф электроустановок.
163
Синхронные двигатели выполняются обычно для номинальных режимов работы при СОЭф=1 ИСОЭф — =0,8 (опережающем).
Более подробное изучение конструкций, электрических процессов и режимов работы асинхронных и синхронных двигателей относится к курсу электрических машин.
9-8. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
9-1. В симметричной трехфазной цепи нагрузка Z=10+/5 ом (на фазу) соединена звездой; линейные напряжения на нагрузке равны 230 в. Вычислить ток.
Ответ: 11,9 а.
9-2. В симметричной трехфазной цепи нагрузка ZaB=Zbc=Zca = 10 Z30° ом соединена треугольником; линейные напряжения на нагрузке равны 100 в. Определить активную и реактивную мощность нагрузки.
Ответ: 2600 вт; 1500 вар.
9-3. В симметричной трехфазной цепи нагрузка Z = 10—j 14 ом (на фазу) соединена звездой; комплексное сопротивление линии от генератора до нагрузки равно 1+/2 ом (на фазу). Линейные напряжения на зажимах генератора равны 100 в. Вычислить фазное напряженке на нагрузке.
Ответ: 61,2 в.
9-4. Несимметричная трехфазная нагрузка соединена треугольником: ZAB = = 100 Z0°; ZBC = 100Z—90°; Zca =
= 141 Z45° ом. Линейные напряжения на нагрузке симметричны и равны 200 в. Вычислить линейные токи и активную мощность нагрузки, приняв С/АВ=200 Z0° в.
Ответ: 2,13 Z— 40°а; 1,04 Z—105°а; 2,73 Z120° а; 600 вт.
9-5. Решить ту же задачу при тех же напряжениях, но при обратном чередовании фаз.
Ответ: 3,39 Z6° а; 3,86 Z—165°а; 0,735 Z60“ а; 600 вт.
9-6. Несимметричная трехфазная нагрузка соединена звездой: Za = 100 Z—90° ом; ZB = 100Z0° ом; Zc = 141 Z45° ом. Линейные напряжения на нагрузке симметричны и равны 200 в. Вычислить линейные токи и активную мощность нагрузки.
Ответ: 1,34 Z32°а; 1,72 Z—138° а; 0,463 Z 72° а; 317,4 вт.
9-7. Несимметричная трехфазная нагрузка соединена треугольником: Zab = =8,66+/ 5 ом; Zbc = 3+j 4 ом; Zca — =5—j 5 ojh; линейные напряжения на нагрузке симметричны и равны 100 в каждое. Определить активную, реактивную и пол
ную мощности нагрузки при прямом и обратном чередовании подведенных напряжений.
Ответ: 3066 вт; 1100 вар;
3260 ва.
9-8. На зажимах несимметричной трехфазной нагрузки, соединенной треугольником, ZAB=/3 ом; ZBc=3 ом; Zca =—]3ом, активная мощность измеряется двумя ваттметрами (схема рис. 9-18). Напряжения на нагрузке симметричны и равны 100 в каждое. Определить показания ваттметров.
Ответ: 2 885 вт; 448 вт.
9-9. Вычислить линейные токи, реактивную и полную мощности в симметричной трехфазной цепи по показаниям двух ваттметров, включенных по схеме рис. 9-18,а: 1 986 вт и 2517 вт. Линейное напряжение равно 208 в.
Ответ: 12,8 а; — 919 вар; 4600 ва.
9-10. К трехфазному генератору, соединенному звездой и имеющему фазные э.д.с. 100 в, подключена с помощью четырехпроводной линии несимметричная нагрузка: между фазой А и нейтральным проводом 50 ом, между фазой В и нейтральным проводом — /50 ом, между фазами В и С40+/20 ом. Комплексные сопротивления линейных проводов и нейтрального провода одинаковы и равны 1+/2 ом. Вычислить линейные токи и активную мощность на зажимах генератора, приняв сопротивление его равным нулю.
Ответ: 1а = 1,92 а; 388 вт.
9-11. Трехфазный генератор, соединенный звездой, имеет фазные э. д. с. 135 в; —67,5—/117 в и —67,5+/117 в и внутреннее сопротивление 0,1+/1,5 ом (на фазу). От генератора отходит линия, имеющая комплексное сопротивление 0,9+/0,5 ом; в конце линии несимметричная нагрузка соединена в треугольник: zab=40+j60 ом; ZBC = 100 ом; Zca =50—/20 ом.
Вычислить линейные токи.
Ответ: 7,06 Z—20°24' а; 2,85
Z—161°42'а: 5,15 Z139°24'a.
9-12. Пользуясь решением предыдущей задачи, вычислить фазные токи, напряжения и активную мощность нагрузки.
Ответ: 2,97 Z—28,7° а, 2,33 Z—92,4° а; 4,15 Z 165,4° а; 214,5 Z27,6° в; 232,8 Z—92,4* в; 224 Z 143,6° в; 1 760 вт.
9-13. В чем заключается преимущество трехфазного тока перед однофазным?
9-14. Как определяется чередование фаз опытным путем?
9-15. В какую сторону вращается магнитное поле, созданное двумя пульсирующими полями, оси которых сдвинуты на угол 90°, а токи в обмотке сдвинуты по фазе на четверть периода?
9-10. Пользуясь правилами правой и левой руки, показать, что короткозамкнутый ротор, выполненный в виде беличьей клетки, приходит во вращение в том же направлении, в котором вращается магнитное поле.
9-17. Как изменить направление вращения поля?
164
Глава десятая
ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ПРОЦЕССЫ
10-1. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА РЯДА ФУРЬЕ
До сих пор изучались линейные электрические цепи однофазного и трехфазного токов, в которых все э.д.с., токи и напряжения изменялись гармонически с одинаковой частотой.
При разборе принципа генерирования синусоидальной э. д .с. (§ 2-2) отмечалось, что для получения синусоидальной э.д.с. в обмотке как явнополюсного, так и неявнополюсного генератора стремятся получить синусоидальную форму распределения магнитной индукции в воздушном зазоре между статором и ротором. В действительности, однако, распределение магнитной индукции может отступать от синусоиды, вследствие чего э. д. с., наводимая генератором, может быть не точно синусоидальной. Электронные генераторы, применяемые в технике высоких частот, генерируют токи, которые в зависимости от режима работы электровакуумных и полупроводниковых приборов также могут в большей или меньшей степени отличаться от синусоидальных. По этим причинам, а также если источники синусоидальных э. д .с., присоединенные к цепи, имеют разные частоты, напряжения и токи в цепи оказываются несинусоидальными.
Во многих электротехнических и радиотехнических устройствах несинусоидальный режим работы цепи является нормальным режимом. Особенно характерен такой режим для нелинейных цепей. Даже при синусоидальной э.д.с. форма кривой тока может резко отличаться от синусоиды при наличии в цепи нелинейного элемента (электрической дуги, индукционной катушки с насыщенным ферромагнитным сердечником, полупроводникового прибора и т. д.).
Настоящая глава посвящена исследованию периодических процес
сов в линейных электрических цепях, находящихся под воздействием несинусоидальных э. д. с. Электрические и магнитные величины в таких цепях представляют собой периодические несинусоидальные функции.
Рис. 10-1. Периодическая несинусоидалыгая функция времени.
Явления, происходящие в линейной электрической цепи с периодической несинусоидальной э. д. с., проще всего поддаются исследованию, если эту э. д. с. разложить на сумму постоянной слагающей и синусоидальных слагающих (называемых гармониками), затем на основе уже изученных методов расчета линейных электрических цепей определить токи и напряжения, вызванные каждой слагающей э.д.с. в отдельности, н, наконец, просуммировать соответствующие величины. Полученные таким образом токи и напряжения будут представлять собой периодические несинусоидальные функции времени, причем их период будет равен периоду заданной несинусоидальной э. д. с.
Кроме вычисления токов и напряжений в электрической цепи по заданной несинусоидальной э.д. с. источника (или по заданному току источника тока), на практике может возникнуть необходимость выявления гармонического состава или степени отклонения от синусоиды той или иной периодической функции времени, полученной, например, экспериментально в результате осциллографирования.
На рис. 10-1 в виде примера показана периодическая несинусои-
165
дальняя функция времени с периодом Т:
№) = № + Т).
Вид разложения такой функции зависит от выбора начала отсчета (§ Ю-З).
В пределах интервала времени Т функция f(t) может быть либо непрерывна, либо иметь точки разрыва непрерывности. Будем считать, что все эти точки разрыва непрерывности обладают следующим свойством: если функция f(t) претерпевает разрыв непрерывности в точке (рис. 10-1), то существуют конечные пределы функции f(t) при приближении к точке разрыва как справа (т. е. от значений так и слева (т. е. от значений Эти пределы условно обозначаются f(/i+0) и f(ti—0) или, что то же, f(h+) и га,-).
Как известно, такие точки разрыва непрерывности называются точками разрыва первого рода.
Будем также считать, что в пределах времени Т число разрывов первого рода, а также число максимумов и минимумов функции f(t) конечны.
Таким образом, будем рассматривать функции, удовлетворяющие условиям Дирихле; следует заметить, что э.д.с., токи и напряжения в реальных электрических цепях удовлетворяют этим условиям.
Известно, что периодическая несинусоидальная функция, удовлетворяющая условиям Дирихле, может быть представлена в виде бесконечного гармонического ряда — ряда Фурье. Сумма этого ряда совпадает со значениями f(t) для всех точек непрерывности этой функции, а в точках разрыва дает среднее арифметическое левого и правого предельных значений f(t), т. е.
у [/(*“) + №+)]-
Обозначим ®=2л/Т и будем называть со основной угловой частотой. Косинусоидальная и синусоидальная слагающие с угловой частотой а образуют основную гармонику.
Слагающие с более высокими угловыми частотами представляют высшие гармоники.
Гармонический ряд в тригонометрической форме имеет вид:
f(0 = -^ +
ею
+ (an cos п® Z + Ьо sin и ®i), (10-1)
Ф=1
где
2
а„= — I /(Ocosncof dt\ (10-2)
^0
м-r
ftn = -£ J f (t) sin n a tdt-, (10-3) t.
здесь a0/2 — постоянная слагающая;
ae и bo — амплитуда косинусоидальных и синусоидальных членов ряда.
Постоянная слагающая ао/2, определяемая на основании (Ю-2) при
Рис. 10-2. Несинусоидальиая функция, среднее значение которой за период равно нулю.
п=0, представляет собой среднее значение функции f(t) за период. Она равна нулю, когда площади положительных и отрицательных значений f(t) одинаковы (рис. 10-2).
Коэффициенты ряда Фурье On и Ьп не зависят от 4; поэтому значение t0 может быть выбрано произвольно. В этом легко убедиться, если учесть, что подынтегральные функции в (10-2) и в (10-3) имеют период Т. Обозначив подынтегральную функцию через g(t), получим:
t<s+T о т
fg(O^= fg(O<ft+ fg(ty# +
t, t, 0
166
M-r +
Так как g(t)=g(t—T), то
M-r i.+r
f g(t)dt = f g(t-T)dt. т т
Заменой переменной x=t—T находим: to+т t0 r0
J g(t)dt = [ g (x)dx = § g(t)dt. т о 0
Следовательно, t.+T т
J g(t)dt^\g(fydt. to 0
Положив /о=О и введя новую переменную a—at, находим (с учетом того, что соГ=2л и da=(od/)j
/(a)=-J + оо
+ S (ап cos и a + b„ sin п а), (10-4) П=1
где *
2тс
ап — — ^/(ajcosna da- (10-5) о
ьп = -^- J f (a) sin па da. (10-6) о
Если принять t0=s-----, то пре-
делы интегрирования будут равны соответственно —л и +л.
Сумма косинусоид и синусоид, выражаемая формулой (10 1) или (10-4), может быть представлена в виде суммы только одних косинусоид с соответствующими начальными фазами.
Так, если принять: ancosn a + fr„sinna =
— Fn cos (n a — ipj, (Ю-7)
гдеЛ, ; Ф« = arctg
°n то ряд получит вид:
/(a) = 4. j? pn cos(na — ф„). <I0'8)
z
/2=1
Напомним, что угол фп находится с учетом знаков ап и Ьп, определяющих знаки косинуса и синуса.
Форма (10-8) удобна в том случае, когда требуется знать процентное содержание каждой гармоники; она обычно применяется Для расчета несинусоидальных токов и напряжений в электрических цепях (§ Ю-5).
Сходящийся ряд Фурье может выражать заданную функцию с любой требуемой степенью точности; если он сходится быстро, то практически достаточно взять небольшое число гармоник.
Встречающиеся на практике периодические несинусоидальные функции могут быть разбиты на две группы. Первая группа включает в себя кривые геометрически правильной формы. Вторая группа включает в себя кривые более сложной формы; разложение их в ряд Фурье производится графо-аналитически.
Графо-аналитический метод разложения в ряд Фурье представляет приближенный метод численного интегрирования, при котором вычисление определенного интеграла заменяется нахождением суммы конечного числа слагаемых. С этой целью период функции f(a), равный 2л, разбивается на tn равных интервалов Аа, так, что тДа=2л.
Расстояние от начала координат до середины А-го интервала состав-/, 1 \ 2л _
ляет угол а= (к----)---, рад.
\ 2 ) tn
Пусть Д(а) есть значение периодической несинусоидальной функции в середине А-го интервала.
Интегралы, входящие в (10-5) и (10-6), заменяются суммами:
2п
aa^ — ^f(a) cos п аДа ~
о
m
— J}f*(a)cosn (k-------М — ;
tn \ 2 ) m
fi=i 2к
sin n aAa ~
Jl 0
167
Если в пределах периода имеются точки разрыва, то при указанном графическом методе разложения целесообразно делать разбивку на интервалы так, чтобы точки разрыва не были в серединах интервалов.
В описанной выше технике выполнения графо-аналитического разложения в ряд Фурье брались значения функции в середине интервалов; если вместо этого брать значения в конце или в начале интервалов, то в случае четной функции наряду с косинусоидами в разложении появятся и синусоиды, которых четная функция не содержит. ь
10-2. СЛУЧАИ СИММЕТРИИ
Периодические несинусоидальные функции, изображающие электрические и магнитные величины, обладают обычно каким-либо видом симметрии, и это облегчает их разложение в ряд Фурье.
Рассмотрим следующие случаи симметрии.
1. Функция f(a) симметрична относительно оси ординат (рис. 10-3),
Рис. 10-3. Функция, симметричная от-
носительно оси ординат.
т е. f(a)=f(—а). Такие функции называются четными. Поскольку синусоиды любых частот являются нечетными функциями, они не входят в состав ряда.
Поэтому при данном виде симметрии со
f(a) = + £a„cos«a,
Я=1
т. е. четная функция может содержать только косинусоиды и постоянную составляющую.
Важным свойством четных функций является также то, что для определения коэффициентов ап дос
таточно пользоваться кривой f(a) за половину периода, т. е.
к
ап = J f (a) cos п a da. (10-9)
о
Это следует из равенства
it о
j f(a)cosnada= Jf (a)cosnada+
Я
+ ) /(a)cosnada.
Замена в первом интеграле а на —а приводит к (10-9).
2. Функция f(a) симметрична относительно начала координат (рис. Ю-4), т. е. f(a) = —f(—а). Такие функции называются нечет-
Рис. 10-4. Функция, симметричная относительно начала координат.
н ы м и. Поскольку постоянная слагающая и косинусоиды этому условию не удовлетворяют, то при данном виде симметрии ряд примет вид
со
f(a) = S&„sinna,
т. е. нечетная функция может содер жать только синусоиды.
В этом случае, так же как и в предыдущем, для определения коэффициентов Ьп достаточно пользо ваться кривой f(a) за половину периода, т. е.
Ьо = jf (a) sin п a d а. (10-10) о
3. Функция f (а) симметрична относительно оси абсцисс при совмещении двух полупериодов во време
168
ни (рис. 10-5), т. е. На) = —ffa+л).
Заменяя f(a) в соответствии с (10-4), получаем:
со
-J- + V [ao cos п a 4- ba sin п а] =>
со
— — ~ — S ia«cos п (a +я)+
Л==1
4- bosinn(a + л)],
Рис. 10-5. Функция, симметричная относительно оси абсцисс при совмещении двух полупернодов во времени.
откуда для четных п
со
ae4-2 S \ап cos п а 4-л=2.4.6...
4-&п sin па] =0.
Это условие удовлетворяется при произвольных значениях а только в том случае, если Оо=0 и ап = =6„=0 при четных п.
Поэтому при данном виде симметрии
со
f (а) *= S |an cos п a 4-n=l,3.6-
4- 6„sinna|,
т. e. функция, симметричная относительно оси абсцисс при совмещении двух полупериодов во времени, содержит только нечетные гармоники.
Коэффициенты an и Ьп могут вычисляться в этом случае по формулам (10-9) и (10-10).
Раскладывая периодическую несинусоидальную функцию в ряд Фурье, следует предварительно выяснить, не обладает ли заданная функция каким-либо видом симметрии. Наличие симметрии позволяет заранее предсказать, какие гармони
ки следует ожидать в разложении.
Если одновременно выполняются условия симметрии по пп. 1 и 3, то в разложении содержатся только нечетные косинусоиды, если — по пп. 2 и 3, то содержатся только нечетные синусоиды.
Допустим, что функция, содержащая только нечетные косинусоиды, удовлетворяет, кроме того, условию /(а)"=—/(л—а). Так как при нечетных п cos па = —cos п(л—а), то в этом случае для определения коэффициента ап достаточно пользоваться кривой f(a) за четверть периода:
Л
2
ап — — f f (a) cosn a da. (10-9a)
Я J и
В свою очередь, если функция, содержащая только нечетные синусоиды, удовлетворяет условию f(a)=f(n—а), то ввиду того, что при нечетных п sin na=sinn(n—a), то и в этом случае для определения коэффициентов Ьп достаточно пользоваться кривой f (а) за четверть периода:
п 2
bn = J/(a) sin п a da. (10-10а)
о
Виды симметрии зависят от выбора начала отсчета. Если начало отсчета может быть выбрано произвольно, то целесообразно выбрать его так, чтобы получить наибольшую симметрию.
Данные о коэффициентах ряда Фурье, относящиеся к разобранным выше случаям симметрии, сведены в табл. 10-1.
Пример 10-1. Требуется разложить в ряд Фурье пилообразную функцию, показанную на рис. 10-6. Эта функция удовлетворяет условию
a
f (a) = 1 -— — при 0 < a < 2л. л
Заданная функция является нечетной, поэтому в разложении в ряд отсутствуют постоянная составляющая и косинусоиды; на основании (10-10)
л
169
Условия симметрии и коэффициенты ряда Фурье
Таблица 10-1
Симметрия относительно Математическое условие Коэффициенты
ап Ьп
Осн ординат (четная функция) Начала координат (нечетная функция) Оси абсцисс прн совмещении двух полупериодов Случаи 1 и 3 одновременно Случаи 2 и 3 одновременно /(а) = Я—а) Да) = — f(—а) f(a) = — f(a -J-л) Да) =Д—а) =—Да-J- л) f(a)=—f( — а)= — Да -J- л) Есть1 Нуль Нуль Нуль Нуль Есть Нули Есть только нечетные Есть только нечетные Нули Нули Есть Есть только нечетные Нули Есть только нечетные
1 В частном случае, когда среднее значение функции Пи) за период равно нулю. До—0.
Следовательно,
2 rsina sin 2а
/(а)= — Я
sin a sin За
1 + з'
sin3a
В точках а=0, 2л, 4л... сумма ряда равна нулю, т. е. среднему арнфметическо-
Рнс. 10-6. Пример 10-1.
му левого н правого предельных значений функции /(a).
Пример 10-2. Требуется разложить в ряд Фурье знакопеременную прямоугольную функцию, показанную на рис. 10-7. Эта функция удовлетворяет условиям
{1 при 0 < a < л:
—1 прн л < a < 2л.
Заданная функция нечетна и, кроме того, симметрична относительно оси абсцисс прн совмещении полупериодов. Поэтому в разложеини в ряд отсутствуют постоянная составляющая, все косинусоиды и четные синусоиды. Кроме того, выполняется условие f(a)=f(n—а). Поэтому для определения коэффициентов Ьп воспользуемся формулой (10-10а):
л 2
4 f . 4
Ьп — — I sin ла аа= — , nJ пл
о
где п — нечетное, Отсюда
10-3. ПЕРЕНОС НАЧАЛА ОТСЧЕТА
Положим, что для некоторой периодической несинусоидальной функции f (а) коэффициенты ап и Ьп являются заданными, т. е. известно разложение данной функции в ряд Фурье:
t (a) = -у + S Ia« cos " a +
+ bosin/ia|.
Если сместить начало отсчета на некоторую величину р вправо или влево относительно исходного начала координат, то разложение в ряд Фурье относительно новой координатной системы будет получено заменой а на сц+Р, где щ — абсцисса в новой системе координат; положительное значение р соответствует смещению нового начала отсчета вправо, а отрицательное — влево.
170
Итак,
7(a1 + P) = fi(a1)=-^ +
+ J} [a„cosn(ai + P) +
+ bn sin n (a, + ₽)]. (10-11)
Эта формула позволяет быстро находить разложение в ряд Фурье функции, если известны коэффициенты ряда Фурье для другой функции, получаемой в результате смещения первой по оси абсцисс на постоянную величину.
Пример 10-3. Требуется найти разложение в ряд Фурье функции, изображенной
Рнс. 10-8. Пример 10-3.
Функция (рис. 10-8) получается прн переносе начала координат на рис. 10-7 (точ-п
ка О) вправо иа отрезок 0=—. Следовательно, в соответствии с (10-11)
10-4. КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ
Тригонометрическая форма ряда Фурье может быть преобразована в комплексную следующим образом.
Исходя из того, что cos na = Те------s
2 ’
/««
sinna = -----------,
2/
выражение, заключенное в скобки в формуле (10-4), приводится к виду: ап cos па -f- ba sin па =
_ ап — fin cina Од ~Т fan с~1па
ряд (10-4) записывается следую-
и
щим образом:
| + fan
+ 2
На основании (10-5) и (10-6) ап четная, а Ьп нечетная функции относительно п, т. е. ап сохраняет свой знак при отрицательных значениях п, а Ьп меняет его:
а = а ; b — — b л —л’ п —п*
Поэтому е учетом того, что
Др _ / ап ~ №п ~ 'сА 2 \ 2 /л==о ’
। уЧ an — fan е1па _ ап — jbn cjna
n=—1 —"
Таким образом, ряд Фурье в комплексной форме имеет вид:
оо
/(а) = 4-Х^е/"“> (1012>
—со
где комплексный коэффициент (комплексная амплитуда) 1 согласно (10-5) и (10-6)
1 Применявшаяся ранее для представления синусоидальной функции комплексная амплитуда, например 0т, связана с введенным здесь одноименным понятием соотношением
Im [l?m е** ] = -у [F^ + F1 ,
откуда следует:
Re [ -/ Um е** ] = Re [Ё^] н Um = jFt
171
2тс
Л = а„ —jbn = р(а) e~'"ada о
(и = О, ± 1, + 2---). (10-13)
Как указывалось выше, a=coi;
следовательно, ряд (10-12) содержит
Здесь индексом т обозначены амплитуды гармоник.
Если цепь линейна, т. е. параметры г, L, М, С неизменны, то ток в цепи находится методом наложения, путем суммирования токов, создаваемых каждой из слагающих э. д. с. в отдельности:
Рнс. 10-9. Синусоидальная функция как сумма двух сопряженных векторов, вращающихся в противоположных направлениях.
1 (0 = 4 + S tnm S’n (ntof 4-ip„ — ф„), n=l
(10-14)
где
I _ ^0 T _________ Enm
0 г(0) ’ Пт г(пы) '
Под z (0) подразумевается сопротивление цепи при частоте, равной нулю, т. е. сопротивление постоянному току; z(nco)—полное сопротивление при частоте гги.
Угол срп определяется как арктангенс отношения реактивного сопротивления цепи к ее активному сопротивлению при частоте по.
В случае, когда цепь состоит из последовательно соединенных элементов г, L и С,
два бесконечных ряда сопряженных относительно оси действительных величин векторов, вращающихся в противоположные стороны с угловыми скоростями пм. Геометрическая сумма каждой пары сопряженных векторов дает только действительное значение (рис. 10-9). В результате суммирования двух бесконечных рядов сопряженных векторов получается действительная функция f(«/).
10-5. ПРИМЕНЕНИЕ РЯДА ФУРЬЕ К РАСЧЕТУ ПЕРИОДИЧЕСКОГО НЕСИНУСОИДАЛЬНОГО ПРОЦЕССА
Пусть требуется найти ток в электрической цепи под воздействием периодической несинусоидальной э. д. с.
e(t) =Е0 + £ Епт sin (ncrf + ф„). /i=i
г(пи) =
2 + (ncoL-----— У;
\ паС /
1 naiL — — , пыС
Фл = arctg-------------.
При этом г(0) =оо, так как цепь для постоянного тока разомкнута.
По мере повышения номера гармоники, т. е. с увеличением частоты па>, индуктивное сопротивление naL растет по закону прямой линии,
1 а емкостное сопротивление --------
паС убывает по закону гиперболы. Поэтому в цепи, состоящей из последовательно соединенных г и L, гармоники тока выражены слабее, чем в э. д. с. источника. В отличие от этого высшие гармоники тока в цепи, состоящей из г и С, могут достигать больших значений.
В смешанной индуктивно-емкостной цепи при ncoL------— =0 на-
лах?
172
ступает явление резонанса для п-й гармоники.
В общем случае цепи, состоящей из элементов г, L, С, как реактив-
-----zrr—-----
Для!-й гармоники
Рис. 10-10. Соотношение масштабов углов для разных гармоник.
ное, так и активное сопротивления являются функциями частоты пш (см., например, § 3-3).
Периоды различных гармоник обратно пропорциональны номеру гармоники. Поэтому, если по оси абсцисс откладывается не время t, а угол ая=псо/=па, то углу а основной гармоники соответствует на той же абсциссе угол па для п-й гармоники (рис. 10-10).
Расчет периодических несинусоидальных токов и напряжений в разветвленных электрических цепях ведется, как правило, в комплексной форме.
Если периодическая несинусоидальная э.д.с. задана в тригонометрической форме ряда Фурье вида (10-8), то э.д.с. и ток могут быть представлены так:
e(O = £o + Slm(E„m^);
72=1
iW^/o + flnK/^),
Л—1 где
Л / = I
пт ^пт ♦ * пт 1 пт^ *
Следовательно, комплексная
форма расчета периодического несинусоидального тока заключается в нахождении комплексных амплитуд
токов i-nm, соответствующих заданным комплексным амплитудам э.д.с. Ёпт для разных значений и. При этом ввиду того, что отдельные слагающие имеют неодинаковые частоты, комплексные амплитуды не складываются непосредственно, а суммируются проекции векторов, вращающихся с разными угловыми скоростями псп, т. е. суммируются мгновенные значения отдельных гармоник.
Пример 10-4. Вычислить суммарный ток в схеме рис. 10-11. Заданы:
е (/) = 30 + 15 sin <о/ + 20 sin 3<irf, в;
гг = 1 ом;
&L - 1 ом;
rs = 0,5 ом;
Рис. 10-11. Пример 10-4.
30 _
Г5 = 20й‘
Ев
Искомый ток находится методом наложения, т. е, поочередным вычислением постоянной слагающей и гармоник тока с последующим их суммированием.
Сопротивление z(0)==rj+r2=l,5 ом. щая тока
/о“г(0)
Комплексное сопротивление пепн для основной частоты:
Z (/со) = 1,63 +71 ,09 ом.
Комплексная амплитуда тока основной частоты
постоянному току
Постоянная слагаю-
15
11т =----------:---=7,65 — 33’36' а.
т 1,63 4-/1,09
Комплексное сопротивление цепи для утроенной частоты:
Z (/Зсо) = г± +
(г3 + /Зсо£) (— /
\ ЗсоС
4
= 19— /Зол.
1
ЗсоС
Комплексная амплитуда тока третьей гармоники:
20
= Ъ----^ = 1»04^8°36'а.
Jo
173
Мгновенное значение суммарного тока;
i (/) = 20 + 7,65 sin (col — 33°36') 4-
+ 1,04 sin (3at + 8°54').
В заключение следует отметить, что в простых случаях установившийся периодический ток может быть получен не только в виде суммы гармоник, но и в более удобной форме аналитического выражения, справедливого для определенного интервала времени (например, полупернода). Для этого интервала записывается дифференциальное уравнение для тока, которое решается так называемым классическим методом (гл. 13) или с помощью преобразования Лапласа (гл. 14). Полученное решение включает в себя неизвестное начальное значение тока, которое затем находят из условия периодичности.
Рассмотрим простой пример. Пусть в цепи последовательно соединенных г и L действует периодическая знакопеременная э.д.с. вида рис. 10-7. Тогда для первого полупернода справедливо уравнение ri+ di
4- L ~^~=Е, решение которого имеет вид
»>=-----)- Ае ь . При 1=0 i=i(0), следо-
г
Е тельно, A=i(0)——. Кривая тока, так же как и кривая э. д. с., будет симметрична относительно осн времени н не будет иметь скачков благодаря индуктивному характе-/ Т \
ру .цепи. Поэтому Эт° Дает;
гт
е 2L = —i (0)
Отсюда находится 7(0):
гТ
таеа~й
»(0)=
Eje^-V) г(е-а+\) '
Подставляя это в выражение для
ка, получим окончательно для первого
то-по-
лупернода
0
Е
Во втором полупериоде кривая тока будет иметь тот же вид, но противоположного знака.
Итак, периодическая несинусондальная функция представляется не только в виде ряда Фурье, но и в замкнутой форме, т. е. в виде аналитического выражения с конечным числом слагаемых, справедливого для выбранного интервала времени. Другой метод решения в замкнутой форме описан в § 14-12.
10-6. ДЕЙСТВУЮЩЕЕ И СРЕДНЕЕ ЗНАЧЕНИЯ ПЕРИОДИЧЕСКОЙ
НЕСИНУСОИДАЛЬНОЙ ФУНКЦИИ
Действующее ’ значение периодической несинусоидальной функции определяется по формуле (см. §2-3).
Если функция задана в виде (10-8), то после возведения ее в квадрат интеграл под знаком корня разложится на ряд интегралов, дающих в результате сумму квадрата постоянной слагающей (а0/2)2, и средних значений квадратов отдельных гармоник (которые согласно § 2-3 равны F„/2), средние же значения удвоенных произведений, гармоник разных порядков или произведений постоянной слагающей на отдельные гармоники будут равны нулю.
Следовательно, действующее значение периодической несинусоидальной функции выражается формулой
Поскольку Fn — амплитуда п-й гармоники, то Еп/]^2— действующее значение гармоники. Таким образом, полученное выражение показывает, что действующее значение периодической несинусоидальной функции равно корню квадратному из суммы квадратов действующих значений гармоник и квадрата постоянной слагающей.
Отсюда следует, что действующее значение функции, представляющей сумму гармоник разных частот, не зависит от начальных фаз этих гармоник, а всецело определяется их действующими значениями.
Например, если несинусоидальный ток выражается формулой (10-14), то действующее значение тока равно:
i^il + ri + P2 + ....
174
Действующее значение периодической несинусоидальной функции может быть измерено, так же как и при гармонических токах, с помощью электроизмерительного прибора электромагнитной, электродинамической, тепловой и других систем.
Наряду с понятием действующего значения периодической несинусоидальной функции в электротехнике и радиотехнике пользуются понятием среднего значения функции, взятой по абсолютной величине; последнее в соответствии с § 2-3 выражается интегралом вида
т
у о
Этот интеграл равен среднему значению функции /(7) за положительный полупериод, если f(t) имеет одинаковые положительную и отрицательную волны:
т т т
FcP = -y о о
Среднее значение функции за полупериод измеряется с помощью магнитоэлектрического прибора с выпрямителем (магнитоэлектрический прибор без выпрямителя измеряет постоянную слагающую).
10-7. МОЩНОСТЬ В ЦЕПИ ПЕРИОДИЧЕСКОГО
НЕСИНУСОИДАЛЬНОГО ТОКА
В соответствии с (2-26) активная мощность равна среднему значению мощности т
P = ±§Uldt.
о
Если вместо и и i подставить их выражения через тригонометрический ряд вида (10-8), то интеграл разложится на ряд интегралов, дающих в результате сумму произведения постоянных слагающих напряжения и тока и средних значений произведений гармоник напряжения и тока одного и того же порядка. Остальные интегралы будут
равны нулю, так как они представляют собой средние значения произведений гармоник разных порядков или произведений постоянной слагающей на отдельные гармоники.
Итак,
©о
Р = и</о + 2*44cos<p„, (10-15)
т. е. активная мощность периодического несинусоидального тока равна сумме активных мощностей отдельных гармоник плюс мощность постоянных слагающих.
Иначе говоря, активная мощность от взаимодействия разноименных гармоник напряжений и токов или от взаимодействия гармоник с постоянными слагающими равна нулю.
По аналогии с понятием реактивной мощности для гармонических функций может быть введено понятие реактивной мощности в цепи с периодическими несинусоидальными величинами. Последняя определяется как сумма реактивных мощностей отдельных гармоник.
Содержание в одной из кривых (напряжения или тока) гармоник, отсутствующих в- другой кривой, не отражается на величинах активной и реактивной мощностей, но повышает действующее значение той функции, которая содержит эти гармоники. Поэтому, если полную мощность в рассматриваемой цепи определить как произведение действующих значений напряжения и тока S=UI, то на основании сказанного можно заключить, что в отличие от гармонического режима сумма квадратов активной и реактивной мощностей в цепи с периодическими несинусоидальными величинами не равна квадрату полной мощности:
Р2 + Q2 = S2 — Т2.
Величина Т носит название мощности искажения; она характеризует степень различия в формах кривых напряжения и и тока i. Если сопротивление цепи активное, то кривые напряжения и тока подобны; при этом Q=0 и 7=0.
175
Пример 10-5. Вычислить активную мощность, поступающую в цепь, в примере 10-4.
е (0 = 30 -|- 15 sin at 4- 20 sin 3orf;
1 (О = 20 + 7,65 sin (orf — 33°36') +
+ 1,04 sin (3orf + 8°54').
На основании (10-15)
„ 15-7,65
P = 30-20 4-----------cos 33°36' 4-
2
= 600 4-47,9 4- 10 = 657,9 em.
10-8. КОЭФФИЦИЕНТЫ, ХАРАКТЕРИЗУЮЩИЕ ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ФУНКЦИИ
По аналогии с гармоническими функциями отношение активной мощности при несинусоидальных токах к полной мощности называется коэффициентом мощности и обозначается х-
т [ ui dt
= —- (1(И6> 1/2 / у. j,
1/ f tfl di [ i» dt ’ 0 b
Отношение в правой части (10-16) обращается в единицу только при наличии прямой пропорциональности между и и i.
Положим, что напряжение синусоидально, а ток несинусоидален. В этом случае активная мощность в соответствии с (10-15) определяется мощностью первой гармоники
Р = cos <рх = Ucos <рх.
При этом действующее значение тока ___________________
/ = /Jg + 7?4-Z|+... >7Х.
Следовательно, коэффициент мощности
UI-. cos те. Z. ,
X = Ь1 = -у cos фг = ktt COS фх.
Множитель ^и=-у-<1 называется коэффициентом искажения.
В радиотехнике и электротехнике пользуются также коэффициентами формы кривой (&$) и амплитуды (ka).
Коэффициент формы кривой определяется как отношение действующего значения функции к среднему значению функции, взятой по абсолютной величине:
V
ьг °________________
кф — т
у- f 1/(01* о
Для гармонической функции
2 V2
Коэффициент амплитуды определяется как отношение максимального значения функции к действующему значению:
&а =---- lm
Г т
Л "г f dt г «
Для гармонической функции kz = 1,41.
Несинусоидальные кривые напряжения и тока заменяются в ряде случаев эквивалентными синусоидами. Замена производится таким образом, что действующие значения синусоидальных функций принимаются равными действующим значениям несинусоидальных функций, а угол сдвига фаз между эквивалентными синусоидами принимается равным углу arccosx, где X определяется из (10-16).
10-9. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
10-1. Разложить в тригонометрический ряд Фурье периодическую функцию, получаемую прн однополупериодном выпрямлении косинусоиды:
л
/ю = cos at при —। —
Ответ:
1
п
эт 2
1 4- — cos at 4- — cos 2erf —
Z о
2 \
------ cos 4at 4-... I.
15 j
10-2. Разложить в тригонометрический ряд Фурье периодическую функцию, получаемую при двухполупериодном выпрямлении косинусоиды.
176
Ответ:
2/3 2
—11+ — cos 2ю/ — — cos 4го/ +
2
+ ~COs6w/----).
10-3. В цепи, состоящей нз индуктивности £=5 гн н емкости С=10 мкф, соединенных последовательно, действует э. д. с., полученная в результате двухполупернод-ного выпрямления косинусоидальной э. д. с. Параллельно емкости присоединено сопротивление г=2000 ом. Найти напряжение на сопротивлении, приняв (о=377 рад/сек.
Ответ:
2
— Ет [1 + 0,0242 cos (2(о/ — 176°) —
sin го/------sin 3<о/ +
1 \
— 0,0012 cos (4го/ — 178°) +•.•], в.
10-4. Индуктивность L присоединена к источнику, э. д. с. которого задана кривой прямоугольной формы вида рис. 10-8. Найти ток.
Ответ:
4
го£.л
+ — sin 5(0/ —* *' j •
10-5. Разложить в тригонометрический ряд Фурье функцию треугольной формы:
2 я я
f (0 =----о/ при---— < ГО/ < —;
п 2 2
, 2 я Зя
/ (/) =- (я — со/) при — < со/ < — .
я 2 2
Ответ:
8 л*
-(sinсо/—-±- sin Зю/ +
' 1 \
+ — sin 5ю/------I .
10-6. Сопоставив результаты
предыдущих задач, пояснить, какова ма кривой тока в задаче 10-4.
Ответ:
двух фор-
1
L 1
я. л
при--------< (0/ < — .
2 2
10-7. Вычислить действующее значение функции в задаче 10-2.
Ответ: 0,707.
10-8. Вычислить амплитуду п-й гармоники периодической функции, заданной в виде равнобочной трапеции, симметричной относительно начала координат. Наклонная часть трапеции на участке от а= =0 до a=ai выражается уравнением а
г (а) =А —, где А — высота трапеции. Со-а1
поставить результаты вычислений по формулам (10-6) н (10-10а).
Ответ:
2Д
Ьп =------sin па, (1 — cos пл);
nn*at 11 ’
при четных я Ьп—0; при нечетных п
Ьп=> —-—sinnai.
nn®ctj
10-9. Вычислить мощности: активную, реактивную, полную и мощность искажения, если
и = 141 sin (о/ + 11 sin (Зго/ + 30°), в;
1= 10,19 sin ((о/ — 11°18') + 2 cos Зю/ + + sin 5(о/, а.
Ответ:
Р = 709,5 вт-, Q = 123,8 вар (инд);
S = 738 ест, Т= 160,5ва.
10-10. Найти эквивалентные синусоиды напряжения и тока, если
и — 156 sin (со/ + л/6) + 50 sin (Зсо/—я/3) +
+ 2 sin (5(о/ + я/4);
/=31,1 sin (го/ + 25°) -|- 5 sin 5«/.
Ответ: 164 sin (го/+30°);
31,55 sin (ro/+9°12').
10-11. Вычислить действующее значение несннусондального тока i=5+ + 10 sin го/—10 cos го/, а;
Ответ: 11,2 а.
10-12. Вычислить действующее значение несннусондального напряжения и= = 10 sin 400 /+5 sin 800 /+cos 1200 /, в.
Ответ: 7,95 в.
10-13. Вычислить действующее значение разности двух несинусоидальиых токов:
ii = 5+4 cos (го/ — л/3)+2 cos (2го/+л/6), а
и /а = 3 — 5 cos го/— 3cos (2го/ + л/4), а
Ответ: 6,85 а.
10-14. Сопротивление 50 тн н емкость 50 мкф, соединенные параллельно, приключены к источнику напряжения, имеющему э.д.с. 50+100 sin (400 /+я/6) + +50 sin (1 200 /—л/4), в, и внутреннее сопротивление 30Z.00 ом. Определить действующие значения напряжения на параллельных ветвях н суммарного тока.
Ответ: 54,1 в; 1,62 а.
10-15. Сохранив условия предыдущей задачи, вычислить активную мощность, расходуемую в обоих сопротивлениях, н энергию, запасенную в емкости при /=0.
Ответ: 95,5 вт; 0,01 дж.
10-16. Вычислить напряжение и(/) в схеме рис. 10-11 (пример 10-4).
Ответ: 10+9,64 sin (ы/+26°12/) + + 18,97 sin (Зго/—4°48'), в.
10-17. Входное напряжение трансформатора (см. рнс. 6-11) П|=20+
+ 100 sin 1 000 /+40 sin 3000/, в; выходные зажимы замкнуты; и=20 ом\ 2-1 = 15 мгн\ г2=40 ол; 2.2=30 мгн; /И=20 мгн. Определить токи /1 и /2.
Ответ: ij = l +3,54 sin (1 000/—2Г10') + + 1,09 sin (3 000 / — 18°5'), с; /2 = = 1,42 sin(1 000 /+32°)+0,665 sin(3 000 /+ +6°), а.
10-18. Зависит ли действующее значение несннусоидальной функции от начальных фаз и от частот отдельных гармоник?
177
12—1118
Глава одиннадцатая
ЦЕПИ С ФЕРРОМАГНИТНЫМИ СЕРДЕЧНИКАМИ ПРИ ПОСТОЯННОМ МАГНИТНОМ ПОТОКЕ
11-1. НАЗНАЧЕНИЕ И ТИПЫ МАГНИТНЫХ ЦЕПЕЙ
Магнитной цепью называется совокупность устройств, содержащих ферромагнитные тела, служащих для сосредоточения магнитного потока в определенной части пространства. Магнитные цепи вклю-
Рнс. 11-1. Магнитная цепь.
а — магнитоэлектрический прибор; б — электромагнитное реле; в — электромагнит; а — электрическая машина.
чают в себя участки из ферромагнитных материалов с высокой магнитной проницаемостью ц. В силу непостоянства ц магнитные цепи нелинейны.
Различают цепи с постоянными магнитами и цепи, в которых магнитный поток создается током в обмотке, насаженной на ферромагнитный сердечник.
Если вся магнитная цепь выполнена из какого-либо одного ферромагнитного материала, ее называют однородной. При включении в магнитную цепь материалов с различными магнитными свойствами ее называют неоднородной.
Магнитная цепь, во всех сечениях которой магнитный поток одинаков (§ 11-2), называется нераз-
ветвленной. В разветвленной магнитной цепи потоки на различных участках неодинаковы.
На рис. 11-1, с—в показаны примеры неразветвленных магнитных цепей, а на рис. 11-1, г — пример разветвленной магнитной цепи. Все эти примеры даны в упрощенном виде без обмоток.
Для магнитных цепей характерна соизмеримость продольных и поперечных размеров. Поэтому при расчете магнитных цепей приходится в большей мере привлекать понятия теории поля, учитывая изменение магнитных величин в пространстве от точки к точке.
Так же как и электрические цепи, магнитные цепи в частных случаях могут приниматься за линейные; при этом расчеты носят приближенный характер и справедливы лишь для определенных режимов работы.
11-2. ОСНОВНЫЕ ЗАКОНЫ МАГНИТНОЙ ЦЕПИ И СВОЙСТВА ФЕРРОМАГНИТНЫХ
МАТЕРИАЛОВ
Одним из основных законов, используемых при расчете магнитной цепи, является закон полного тока
jHdl= ZI-, он формулируется следующим образом: циркуляция вектора напряженности магнитного поля Н по замкнутому контуру равна алгебраической сумме токов S/, охватываемых этим контуром; знак тока определяется по правилу правоходового винта. Если длина I измеряется в метрах, ток I — в амперах, то напряженность Н имеет размерность ампер на метр. В случае, когда контур интегрирования охватывает w витков катушки, через которую проходит ток 1, закон полного тока принимает вид:
§HdI = Iw=F, (Н-1)
178
где F— намагничивающая сила1 (н. с.) или магнитодвижущая сила (м.д.с.), измеряемая в амперах или ампер-витках.
С вектором напряженности магнитного поля Н связан вектор магнитной индукции В, модуль которого измеряется в теслах (тл) или вб/м2-.
В = рр0Я = [iaH, где р,— относительная магнитная проницаемость (безразмерная величина);
р0—магнитная постоянная,
равная 4л • 10~7 гн1м\
ра — абсолютная магнитная
проницаемость, гн[м.
Векторы В и Н необязательно совпадают друг с другом по направлению. Несовпадение может быть в материалах, анизотропных в магнитном отношении, т. е. в материалах, у которых величина р зависит от направления вектора Н. Большинство практических расчетов производят в предположении совпадения 2 по направлению векторов В и Н.
Контур интегрирования обычно выбирают таким образом, чтобы он совпадал с линией_вектора напряженности3 Н, что позволяет заменить подынтегральное выражение в (11-1) произведением скалярных величин Hdl.
Для практических расчетов интеграл заменяют суммой произведений Hhlk, индекс k указывает участок, вдоль которого Н и р при
1 Намагничивающая сила — скалярная величина, характеризующая намагничивающее действие электрического тока, равная линейному интегралу напряжен-
ности магнитного поля вдоль рассматриваемого замкнутого контура (ТТЭ).
3 В цепях с постоянными магнитами направления В и Н могут быть взаимно противоположны [Л. 12].
’Линия вектора напряженности магнитного поля — линия, в каждой точке которой касательная к ней совпадает с направлением вектора напряженности магнитного поля (ТТЭ). На границе сред с разными магнитными прони-цаемостями напряженность магнитного паля изменяется скачкообразно.
нимаются неизменными. В результате формула (11-1) записывается в виде закона магни тн ой цепи:
k=ri k=n
^Hklk = ^-^-lk=F, (11-2) На*
где n— число участков.
Произведение при отсутствии обмотки с током на k-м участке носит название разности скалярных магнитных потенциалов двух точек4 или падения магнитного напряжения вдоль участка пути и обозначается VMmn, где т и п — начало и конец участка.
Для воздушных зазоров магнитная проницаемость может быть принята равной магнитной постоянной По, и связь между В и Н приобретает вид:
Н = — ==-----^0,8- 106В. (11-3)
р0 4л. Iff-7 ’ v ’
Если принять размерности: Н, a/см; В, гс, получается соотношение
Н, а/см - 0,8 В, гс.
Так как линии магнитной индукции5 непрерывны и замкнуты, то поток вектора магнитной индукции сквозь замкнутую поверхность равен нулю:
<D=$BdS = 0. (11-4)
Из уравнения (П-4) вытекает следующее важное положение: в нераэветвленной магнитной цепи поток на всех ее участках одинаков, а в разветвленной цепи поток на участке,' подходящем к месту разветвления, равен сумме магнитных потоков на участках, отходящих от
4 Разкость скалярных магнитных потенциалов двух точек— скалярная величина, равная линейному интегралу напряженности магнитного поля вдоль выбранного участка пути между двумя точками при условии, что путь интегрирования расположен в области, где плотность электрического тока равна нулю
(ТТЭ).
’Линия магнитной индукции — всегда замкнутая линия, в каждой точке которой касательная к ней совпадает с направлением вектора магнитной индук-
ции (ТТЭ).
12*
179
места разветвления В этом отношении поток Ф в магнитной цепи подобен току в электрической цепи, и именно в данном смысле можно говорить о том, что в разветвленной магнитной цепи поток ф подчиняется первому закону Кирхгофа. При этом, однако, необходимо помнить, что прохождение тока в электрической цепи физически совершенно отличается от появления магнитного потока в магнитной цепи. Речь может идти только об аналогии двух принципиально различных явлений.
Если принять, что вектор индукции В одинаков во всех точках поперечного сечения S неразветвленной магнитной цепи и направлен перпендикулярно этому сечению, то его поток Ф= \BdS можно записать s
как
<b=BkSk, (11-5) где индекс k указывает участок, вдоль которого В и S могут быть приняты неизменными.
В результате подстановки в (11-2) Вь = Ф/5ь получается зависимость между магнитным потоком и н. с., которую называют законом Ома для магнитной цепи:
ф= Г .. = _L_ = -L,
У 1к гы ’
Р-аЛ1
где гм— магнитное сопротивление цепи, имеющее размерность 1/генри.
При неизменных поперечном сечении S и магнитной проницаемости Ца
г __ А:р
“ HaS ’
где /Ср — длина средней линии магнитной индукции2. В случаях,когда
1 В данном случае предполагается, что магнитный поток рассеяния либо отсутствует, либо путь магнитного потока рассеяния является ветвью магнитной цепи (11-5).
2 Обычно предполагают, что средняя линия магнитной индукции проходит через центры тяжести поперечных сечений магнитной цепи. В материалах, изотропных в магнитном отношении, с этой линией совпадает средняя линия вектора напряженности
магнитного поля.
магнитная цепь состоит из участков с различной магнитной проницаемостью, говорят о магнитных сопротивлениях участков3. Величина, обратная магнитному сопротивлению,
Рис. 11-2. Петли гистерезиса.
называется магнитной проводимостью
Лм=— (см. гл. 6). гм
Закон Ома для магнитной цепи в большинстве случаев не может
быть применен для расчета вследствие того, что связь между В и Н нелинейна Примерная графическая зависимость B=f(H) для ферромагнитных материалов показана на рис. 11-2; такая двузначная зависимость называется петлей гистерезиса. При возрастании Н индукция В изменяется (возрастает) по нижней части петли гистерезиса, а при убывании Н индукция В изменяется (уменьшается) по верхней части петли. При Вмакс = —Вмин получается симметричная петля гистерезиса. Индукция Вг при //=0 называется остаточной. Ширина петли в основном зависит от свойств материала, в некоторой степени от максимальной напряженности Н и от скорости
’Магнитное сопротивление участка магнитной цепи — скалярная величина, равная отношению м. д. с. вдоль рассматриваемого участка магнитной цепи к магнитному потоку в этом участке (ТТЭ).
180
dH/dt, с которой происходит изменение Н.
Чтобы практически исключить влияние dHfdt, снимают статическую петлю гистерезиса при достаточно медленном перемагничивании образца. Ширина петли
ние ферромагнитных материалов на эти две категории условно, так как имеются материалы с характеристиками, отличными от упомянутых.
Если построить для большого числа постепенно возрастающих максимальных напряженностей
Рис. 11-3. Кривые намагничивания.
1— листовая сталь Э-31; 2— литая сталь.
равна удвоенному значению коэр-цитивной силы1 Нс.
Ферромагнитные материалы с широкой петлей гистерезиса (Яс> >4 000 a/м) называются магнитно-твердыми2; их применяют для постоянных магнитов. Ферромагнитные материалы с узкой петлей гистерезиса (Яс<200 а/м) называются магнитно-мягкими; их применяют в переменных магнитных полях, а также в постоянных магнитных полях, когда желательна возможность регулирования В посредством изменения Н. Деле-
11 Коэрцитивная сила — напряженность магнитного поля, необходимая для того, чтобы довести магнитную индукцию в предварительно намагниченном веществе до нуля (ТТЭ).
s В литературе применяется также термин магнитно-жесткне материалы.
Дмакс какого-либо магнитно-мягко-го материала семейство статических петель гистерезиса, то вершины петель расположатся на кривой, называемой основной кривой намагничивания3 данного материала. Эти кривые часто называются просто кривыми намагничивания и приводятся в справочниках. В качестве примера на рис. 11-3 приведены такие кривые намагничивания.
Зависимость между В и Н при непрерывном увеличении их от нуля, т. е. при постепенном намагничивании предварительно размагни-
’Основная кривая намагничивания — кривая, представляющая собой геометрическое место вершин симметричных петель гистерезиса, получающихся при различных максимальных значениях напряженности магнитного поля (ТТЭ).
181
ченного образца материала, называется кривой первоначального намагничивания. Обычно эта кривая располагается несколько выше основной кривой намагничивания того же образца материала.
Впервые нелинейность зависимости B=f(H) установил выдающийся русский физик А. Г. Столетов, описавший эту зависимость в 1871 г. А. Г. Столетов также впервые указал на большой эффект, получаемый в результате применения замкнутых ферромагнитных сердечников.
11-3. НЕРАЗВЕТВЛЕННАЯ МАГНИТНАЯ ЦЕПЬ
Простейшей неразветвленной магнитной цепью является замкнутый магнитопровод с одинаковым поперечным сечением и одинаковой
Рис. 11-4. Тороидальный магнитопровод.
магнитной проницаемостью по всей длине, например тороидальный магнитопровод (рис. 11-4) при /в=0.
В силу соотношения (11-5) магнитная индукция В во всех точках такой цепи одинакова Напряженность магнитного поля Н также одинакова. Выражение (11-2) в этом случае принимает вид
Hlcp=F, где /q>—длина средней линии напряженности магнитного поля.
Часто в состав неразветвленной магнитной цепи входят участки из
1 Здесь предполагается, что магнитные потоки рассеяния отсутствуют. Методы расчета цепи с .учетом потоков рассеяния см. в [Л. 3].
различных материалов с неодинаковыми поперечными сечениями. Вследствие того, что магнитный поток во всей цепи одинаков, значения магнитной индукции2 Bh на различных участках неодинаковы и в соответствии с (11-5) определяются выражением
Расчет неразветвленной цепи сравнительно прост, если задан магнитный поток Ф и требуется определить н. с. F; это так называемая прямая задача расчета магнитной цепи, которая заключается в определении Нь по значениям Bh и суммировании произведений Нъ1к. Решение прямой задачи иллюстрировано в примере 11-1.
Сложнее обратная задача расчета магнитной цепи, когда по заданному значению н. с. требуется определить магнитный поток3.Расчет для такой задачи может быть выполнен с помощью магнитной характеристики цепи F=f(d>).
Для построения такой характеристики необходимо задаться несколькими значениями Ф и найти соответствующие значения F, решая, таким образом, несколько прямых задач, причем необходимо, чтобы какие-то значения F были больше и меньше заданного. С помощью магнитной характеристики по заданной н. с. определяется Ф.
Для сокращения вычислений желательно ограничиться возможно меньшим числом точек характеристики, для чего необходимо задаться первым (исходным) значением Ф, по возможности близким К ИС-тинному. Если имеется воздушный зазор, представляющий основную часть магнитного сопротивления цепи, первое значение магнитного потока находится из выражения
ф' = — = ~— (11-6)
гм.в 0,8.10»ZB’ k '
2 Допускается, что равномерность распределения индукции при изменении сечения ие нарушается.
8 Соотношения разностей скалярных магнитных потенциалов различных участков в этом случае неизвестны.
182
где гм.в— магнитное сопротивле- т
ние воздушного зазора; “
SB — поперечное сечение маг- «
нитного потока, прохо- s
дящего через воздуш- *
ный зазор; я
1В—толщина воздушного за- t_l зора.
Магнитный поток Ф' в этом случае заведомо больше действительного, поскольку в выражении (11-6) магнитное сопротивление цепи определяется только воздушным зазором, а магнитное сопротивление стали не учитывается.
Решение обратной задачи показано в примере 11-2.
Пример 11-1. Магнитная цепь, изображенная на рис. 11-5, представляет собой сердечник из листовой электротехнической стали с обмоткой из kj=300 витков. Тре-
Рис. 11-5. Пример 11-1. ’с
F-
X буется иайти ток в обмотке, создающий Е в сердечнике магнитный поток Ф= S
= 1,3-10~4вб. н
Цепь может быть разбита на четыре «
участка (1—4) с длинами отрезков сред- о ней линии магнитной индукции li =0,025 м; а. <г=0,12 м; 1э=0,025 м; <4=0,5-10-3 Jfi и поперечными сечениями
S1 = Ss = S4 = 210 4jk^, Sa= 1-10-4m3.
Значения индукции в поперечных сечениях:
-= Вз = Вл =
= 1,3-10—4/2-10-4 =0,65 тл;
Bs = 1,3-10—4/1 • 10-4 = 1,3 тл.
Напряженности магнитного поля в стали в соответствии с кривой намагничивания, изображенной на рис. 11-3, равны:
Hi — Н3 = 100 а/м; Нг = 650 а!м.
Напряженность магнитного поля в воздушном зазоре согласно выражению (11-3) Нц = 0,8- 10»В4=0,8-10«-0,65=520-103 а/м.
Намагничивающая сила обмотки
F —- 2-Hk Ik — Hjli -)- На<2 + H3I3 + HJ-з = = 100-0,025 + 650-0,12 -j- 100-0,025 4-+ 520-103-0,5-10-3 = 343 a.
10*8 2,81 1,55 1.14
СМ
Я ° О S о ж#4 со
СМ
LO о О о
fo й СП см £
<3
in со % о ПО
4 вч
it Tf СО со см
0 0 CD ш 03 ю
0 LQ CD S
it CM
e
lO ОО
со со О ю
*
£ со СО см
co"
1 ю ю UO ю
О Ч о о* О* сГ
* LO (М ш см LD СМ а
о о О о
о о о о
Яс см СМ см см
V—.4 е—Ч
ж в. в. в,
о о о о
ю Ю ю LD
Я; СМ см см СМ
0 о о о
в. в.
о о о о
750 о <D 580 520
S3
ж
’и О а О см S
a:
о О о о
о о о со
<3 см со CD
з:
ш 0 О
СП со см О
*• S3 •-Ч
(М 1Л
СП со CD
в.
03 о о о О
ч LQ
СМ Ш
ст> 00 CD
п
03 о о О О
ТЛ со со СО
0? •—1
ю
1-4 см ш
СП 00 о
СЗ о о 0 о
ш
00 <D Tf со
6 —
0—9 »Ч< •—ч
•
183
Ток в обмотке . F 343 , / = — — — = 1.14 а. w 300
Пример 11-2. В магнитной цепи, рассмотренной в примере 11-1, требуется найти магнитный поток Ф в сердечнике, если ток в обмотке /=1,25 а.
Цепь разбивается на такие же участки, как и в примере 11-1. Первое прибли
женное значение магнитного потока в соот-
ветствии с (11-6);
1,25-300.2.10-*
ф' =------------------
0,8-10«.0,5.10-з
1,87.10-*вб.
Расчет для удобства сведен в табл. 11-1. По данным расчета строится магнитная характеристика цепи, показанная на рис. 11-6.
При помощи этой характеристики по заданной и. с. F= 1,25 - 300= 375 а определяется искомый магнитный поток Ф= = 1,36-10-* вб.
Намагничивающие силы в этом случае аналогичны э. д. с. электрической цепи, а разность скалярных магнитных потенциалов между концами участков аналогична напряжениям между концами ветвей электрической цепи.
На рис. 11-7 показаны разветв-
ленная магнитная цепь и аналогичная ей электрическая цепь. В разветвленной цепи действуют первый и второй законы Кирхгофа.
Первый закон Кирхгофа: алгебраическая сумма магнитных потоков в узле равна нулю:
2Ф*=0. (11-7)
При этом магнитным потокам, направленным к узлу, приписывается один знак (например, положительный), а магнитным потокам, направленным от узла, противоположный знак.
Второй закон Кирхгофа: алгебраическая сумма н. с. в любом
контуре равна алгебраической сумме произведений потоков на соответствующие магнитные сопротивления данного контура.
При этом необходимо задаться положительным направлением обхода контура.
11-4. РАЗВЕТВЛЕННАЯ МАГНИТНАЯ ЦЕПЬ
В разветвленной магнитной цепи может существовать несколько магнитных потоков, которые складываются или вычитаются на некоторых участках.
По аналогии с разветвленной электрической цепью такая цепь может быть разбита на ветви и узлы *.
1 Под узлом разветвленной магнитной цепи здесь подразумевается точка, в которой сходятся три или большее число средних линий магнитной индукции. Это понятие является условным, так как размеры поперечных сечений ветвей магнитной цепи соизмеримы с длинами ветвей. При этом под длинами ветвей магнитной цепи понимаются расстояния между соседними узлами вдоль средней линии магнитной индукции.
Рис. 11-7. Разветвленная магнитная цепь и аналогичная ей электрическая цепь.
184
Разветвленные магнитные цепи, так же как и неразветвленные, обычно являются нелинейными, и расчет их приходится производить с помощью магнитных характеристик подобно расчету нелинейных электрических цепей [Л. 3].
Рис. 11-8. Разветвленная магнитная цепь, для которой можно произвести однократный расчет.
В некоторых случаях можно произвести однократный расчет без применения магнитных характеристик, например для цепи, изображенной
напряженность магнитного поля на участке /8, Н6=УЫвг/1&.
Далее по кривой намагничивания находится индукция В8, по которой определяется Ф8=В8Х8, что дает возможность вычислить потоки Ф4 = Ф5 = Ф1 + Фв и индукции В4 = = Ф4/54 и В5=Ф6/£5. По кривой намагничивания находятся Hi и Н5, что позволяет вычислить разность скалярных магнитных потенциалов
Аналогичным образом определяется На1в и в итоге н. с.
В разветвленной магнитной цепи с двумя узлами (рис. 11-9, а), для которой заданы н. с. и магнитные характеристики (рис. 11-9,6), магнитные потоки могут быть определены графически.
Рис. Ц-9. Разветвленная трехстержневая магнитная цепь с двумя узлами (а), магнитные характеристики (б) и (в).
на рис. 11-8. Здесь на участке /4 предполагается заданным магнитный поток Ф1 и требуется определить н. с., создаваемую обмоткой.
Каждый из участков имеет одинаковое сечение и одинаковую магнитную проницаемость по всей своей длине. Расчетные величины в этом случае определяются в следующем порядке: разность скалярных магнитных потенциалов между точками в и г:
*=з
С этой целью строятся магнитные характеристики
Ф1(71ш1-771/1)^Ф1(^мсб);
Ф8 (72^2 Н212) = Ф2 (V мад);
Ф3(773/3) = Ф3(1/мсб),
(П-8)
где а и б в индексах означают граничные точки средней линии вектора магнитной индукции среднего стержня (аналогичные точки показаны на рис. 11-8).
185
Если положительные направления магнитных потоков, выбранные одинаково относительно узлов, совпадают с заданными направлениями н. с., то магнитные характеристики получаются смещением соответствующих характеристик ветвей магнитной цепи (рис. 11-9,6) на величину заданных н. с. влево от начала координат (рис. 11-9,в).
Далее строится результирующая характеристика (Ф1+Фг+Фз) X
X ( Емаб)-
Для этого суммируются ординаты кривых Ф1(Умаб)> Фг(Емаб) И Фз(Умаб) для одних и тех же значений магнитного напряжения Умаб.
Пересечение результирующей характеристики с осью абсцисс и дает решение задачи, поскольку при этом удовлетворяется выражение (П-7). Ординаты характеристик, соответствующие точке пересечения, дают искомые потоки.
11-5. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
11-1. Сердечник, изображенный на рнс. П-4, изготовлен из ленты, свитой в спираль. Размеры сердечника следующие: наружный диаметр dH=10 см, внутренний диаметр dEH=6 см, зазор /Е=0, толщина (ширина ленты) Ь=2 см. Коэффициент заполнения поперечного сечения сталью feci =0,9. На сердечник намотана обмотка, число витков которой 250. По обмотке пропускался постоянный ток / и измерялся соответствующий магнитный поток Ф. Данные этих измерений для нескольких токов приведены ни^ке:
а-.-. 0,1005 0,805 2,01
Ф, вб... 2,16-1,0-4 4,5. io-4 5,15-10~4
Рис. 11-10. Задача 11-2.
Построить кривую намагничивания В — 4(H)-
Указание. Считать, что магнитная индукция В распределяется по сечению равномерно.
11-2. Сердечник, изображенный на рис. 11-10, изготовлен из листовой электротехнической стали Э-31 с коэффициентом заполнения йСт=0,9; размеры его даны в миллиметрах. Число витков обмотки w= = 1 000, индукция магнитного поля в воздушном зазоре fiB = l,2 тл. Определить ток в обмотке.
Указание. Поперечное сечение магнитного потока, проходящего через воздушный зазор, считать равным сечению стали правого стержня сердечника без учета коэффициента йот.
Ответ: 0,63 а.
11-3. В обмотке сердечника, рассмотренного в задаче 11-2, проходит ток, равный 1 а. Определить магнитную индукцию в воздушном зазоре.
Ответ: 1,33 тл.
П-4. При каком токе в обмотке сердечника, рассмотренного в задаче 11-2, индукция в воздушном зазоре будет Вв = = 1,2 тл, если воздушный зазор уменьшится по величине до /в=0,05 мм!
Ответ: 0,41 а.
11-5. Сердечник, изображенный на рис. 11-11, изготовлен из литой стали. Стержни сердечника имеют круглое сече-
Рис. 11-11. Задача Ц-5.
ние, а основание — прямоугольное сечение. Ярмо изготовлено из листовой электротехнической стали с коэффициентом заполнения fee т =0,9. Размеры указаны в миллиметрах. Воздушные зазоры /в=0,2 мм. На стержни насажена обмотка с числом витков 2 000. Определить ток в обмотке, при котором магнитный поток в сердечнике равен 4,5 • 10-4 вб.
Ответ: 0,66 а.
11-6. Определить ток в обмотке сердечника, рассмотренного в задаче 11-5, если магнитный поток в сердечнике равен 2,25 • 10-* вб.
Ответ: 0,17 а.
11-7. Чему будет равен магнитный поток в сердечнике, рассмотренном в зада
186
че 11-5, если воздушные зазоры возрастут до величины /в = 1 мм, а ток в обмотке будет равен 0,635 а?
Ответ: 2,28 • 10~4 вб.
11-8. Сердечник, изображенный на
Рис. 11-12. Задача 11-8,
рис. 11-12, собран из листовой электротехнической стали. Размеры даны в миллиметрах Коэффициент заполнения стали feCT=0,9. Обмотка, навитая иа левый стержень 1, состоит ИЗ' 800 витков, а на правый стержень 2 — из 1 000 витков. Ток в обмотке 2 /2=0. Определить ток /ц если магнитный поток в среднем стержне Фэ = =5,2- 10~4 вб.
Ответ: 5 а.
11-9. В обмотках сердечника, рассмотренного в задаче 11-8, токи Л=0,5 а и /в= =0,4 а. Определить значения магнитных потоков в стержнях.
Ответ: Ф1=<Т>2=4,9-10~4 вб;
Фэ=9,8 • 10-‘ вб.
11-10. В обмотках сердечника, рассмотренного в задаче 11-8, токи Л=5 а и Zj= =—4 а. Определить значения магнитных потоков в стержнях.
Ответ: Ф1=Фа=6,48 • 10~4 вб', Фа=“0.
11-11. В обмотках сердечника, рассмотренного в задаче 11-8, токи Л=0,52 а и /2=4,25 а. Определить значения магнитной индукции в стержнях.
Ответ: 1,2; 1,8; 1,5 тл.
187
Глава двенадцатая
ЦЕПИ ПЕРЕМЕННОГО ТОКА С ФЕРРОМАГНИТНЫМИ ЭЛЕМЕНТАМИ
12-1. НЕКОТОРЫЕ ОСОБЕННОСТИ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА С ФЕРРОМАГНИТНЫМИ ЭЛЕМЕНТАМИ
Основной частью всякой цепи переменного тока с ферромагнитным элементом является обмотка, насаженная на ферромагнитный сердечник. Наиболее простой пример такой цепи — это катушка со стальным сердечником. Развитие современной техники обусловило появление большого числа весьма сложных устройств в некоторых случаях с сердечниками специальной формы или с включением в цепь обмотки емкостей.
В качестве материала для сердечников наряду со сталью применяются и другие специальные ферромагнитные материалы с различными зависимостями В =
Отличительной особенностью электрических цепей с ферромагнитными элементами при переменном токе является то, что токи в обмотках и магнитные потоки в сердечниках взаимосвязаны. С одной стороны, магнитный поток зависит от то
ков в обмотках, и поэтому при исследовании приходится в значительной мере пользоваться методами, разработанными для магнитных цепей при постоянном магнитном потоке (см. гл. 11). С другой стороны, токи в обмотках зависят от характера изменения магнитного потока. Такая взаимосвязь весьма усложняет исследования. Поэтому при расчетах вводят ряд допущений, упрощающих рассмотрение явлений, и определяют основные величины, характеризующие данную цепь, пренебрегая теми величинами, которые не оказывают существенного влияния на процесс в рассматриваемом режиме. Например, в некоторых случаях предполагают связь между В и Н линейной, но учитывают потери в стали; в других случаях пренебрегают потерями в стали, но предполагают связь между В и Н нелинейной. Такие упрощения неизбежно вносят погрешности в расчет, но на практике с этим приходится мириться, довольствуясь в ряде случаев приближенными результатами.
187
При расчетах цепей со сталью в большинстве случаев нельзя принимать индуктивность L и взаимную индуктивность М постоянными, и поэтому приходится пользоваться непосредственно зависимостями между э. д. с. и магнитным потоком или потокосцеплением.
Для гармонического магнитного потока Ф=Фтсоз<о/ эта связь имеет вид (при отсутствии рассеяния):
е = — = £ок»Фт sin о$=Ет sin cot
dt
откуда действующее значение э. д. с.
Е = /шФт ж 4,44ДуФт.
/Т Z 2
Следует обратить внимание на то, что э. д. с. е отстает по фазе от потока ф на п(2.
В цепях со сталью возникают несинусоидальные напряжения и токи (см. § 12-3). Иногда такие напряжения и токи удобно заменять эквивалентными синусоидами (§ 10-8).
Амплитуда эквивалентной синусоиды равна действующему значению соответствующей несинусоидальной величины, умноженному на У 2, а сдвиг фаз между эквивалентными синусоидами напряжения и тока определяется по формуле
Р <p=arccos —, * U1 '
где U — действующее значение напряжения и;
1 — действующее значение тока i;
Р—активная мощность несинусоидального тока.
Если одна из величин (и или i) синусоидальна, то эквивалентная синусоида, полученная для второй величины, ориентируется по фазе относительно первой’. В случае, если несинусоидальны как и, так и I, за начальную фазу эквивалентной синусоиды напряжения может быть выбрана начальная фаза основной гармоники напряжения и.
Представление несинусоидальных величин в виде эквивалентных синусоид позволяет производить анализ их с помощью векторных диаграмм.
188
12-2. ОСНОВНЫЕ СВОЙСТВА ФЕРРОМАГНИТНЫХ МАТЕРИАЛОВ
ПРИ ПЕРЕМЕННЫХ ПОЛЯХ
При изменении магнитного поля в ферромагнитном материале часть энергии магнитного поля преобразуется в тепло. Мощность, соответствующая этой части энергии, называется потерями в сталии обозначается РСт; в расчетах обычно пользуются удельными потерями в стали рст, измеряемыми в ваттах на килограмм.
Потери в стали состоят из потерь от гистерезиса (потерь от перемагничивания) и динамических потерь. Удельные потери от гистерезиса, обозначаемые рг, вызываются необратимыми процессами в стали при перемене ориентации областей самопроизвольного намагничивания и пропорциональны частоте. Для вычисления удельных потерь от гистерезиса применяется приближенная формула
(12-1)
где ог1 и ог2 — коэффициенты, зависящие от сорта материала;
f — частота;
Вт — амплитуда магнитной индукции.
Динамические потери вызываются вихревыми токами, индуктированными в массе магнитного материала, и отчасти зависят от магнитной вязкости, которая особенно заметно проявляется на крутых участках петли гистерезиса (вблизи Н—Нс) при малых изменениях поля. В большом числе практических случаев динамические потери можно отождествлять с потерями от вихревых токов.
Точное исследование вихревых токов и потерь, связанных с ними, проводится методами теории электромагнитного поля Ниже приводится приближенный вывод формулы потерь от вихревых токов. В итоге вывода показано, что одним из способов уменьшения потерь от вихревых токов является разделение магиитопровода на листы, располагаемые вдоль линий магнитной индукции. На рис. 12-1 показана в упрощенном виде часть такого магнитопровода с навитыми витками обмотки, обтекаемой током Л Вихревые токи вызываются вихревыми э. д. с.
<!Ф ен = — —, в dt
наводимыми в соответствии с законом электромагнитной индукции изменяющимся магнитным потоком Ф, распределенным по сечению магиитопровода.
Элементарный вихревой ток циркулирует в слое толщиной dx. Длина контура (показанного пунктиром), по которому циркулирует элементарный вихревой ток, приближенно рввиа 4 х+2 h; так как х значительно меньше h, можно принять
Рис. 12-1. Часть магинтопро-вода, разделенного иа листы.
длину контура равной 2 h. Поперечное сечение пути элементарного вихревого тока равно Idx. Активное сопротивление этого пути
2й
'в=Р7Г. Idx
где р — удельное сопротивление материала магннтопровода. При частотах порядка нескольких сотен герц можно принять гв не зависящим от частоты.
Если допустить, что индукции распределена равномерно по сечению листа и равна В=*ВШ sin со/, то э. д. с. в контуре
dB
ев — —h-2x-— = —h-2xa)Bmcosa>t = в dt т
= — EBmcosat,
где EBm=4hjcxfBm.
Действующее значение вихревой э. д. с.
Ев=2 У 2 nhxfBm.
Мощность, расходуемая на элементарном пути вихревого тока,
£в (гУ~2~ nhx fBmVldx _
гв р-2Л
4n*pB^hlx?dx
Р
Мощность, расходуемая во всем листе, а/2
п С 4л2 О I Xs |°/2 где а — толщина листа.
Удельные потери от вихревых токов Р = ~ ~ а*РЕ£, = о РВ2, (12-2)
Рв hlay бру т т
где у—плотность стали;
ов — коэффициент, зависящий от сорта стали и толщины листа.
Из выражения (12-2) видно, что рв пропорционально квадрату частоты и квадрату толщины листа. Следовательно, одним из способов уменьшения ръ является уменьшение толщины листа. Однако листы нельзя изготовлять чрезмерно тонкими. В частности, уменьшению толщины листов препятствует то обстоятельство, что при этом увеличиваются удельные потери от гистерезиса рТ. Для различных частот существуют различные оптимальные толщины листов. Например, при частоте 400 гц применяют листы толщиной 0,1—0,35 мм, а при частоте 50 гц листы толщиной 0,35—0,5 мм.
При гармоническом магнитном потоке вихревые токи можно считать отстающими от магнитного потока на четверть периода.
Намагничивающая сила, создаваемая вихревыми токами, должна компенсироваться частью н. с. обмотки. Поэтому ток в обмотке должен иметь составляющую, находящуюся в противофазе с вихревыми токами, т. е. опережающую магнитный поток на четверть периода.
При частотах порядка тысяч герц и выше сказывается поверхностный эффект, в результате которого магнитная индукция не одинаково распределяется по сечению магнитопровода (она больше на периферии и меньше в центре сечения).
Из-за поверхностного эффекта и увеличения потерь в стали применение сердечников, собранных из стальных листов, при высоких частотах нецелесообразно. При высо
189
ких частотах применяют сердечники из ферритов *, обладающих большим удельным электрическим сопротивлением.
Различие в зависимостях рг и от частоты [выражения (12-1) и (12-2)] позволяет определить, какая
1 — при частоте 60 гщ 2 — при частоте I 000 гц.
именно часть потерь в сердечнике затрачивается на гистерезис и какая на вихревые токи, или, как говорят, разделить потери.
Для разделения потерь достаточно знать суммарные потери в сердечнике для двух частот при неизменной Вт (пример 12-2).
Потери в стали обусловливают несовпадение по фазе индукции В и напряженности поля И, характеризуемое углом потерь 6. Если В и Н — несинусоидальные функции времени, то 6 является сдвигом фаз между соответствующими эквивалентными синусоидами. Подробнее об угле потерь сказано в § 12-3.
Если представить индукцию и напряженность поля в виде комплексных амплитуд
Вт=Вт^°
то магнитная проницаемость может
1 Ферритами называются магнитные материалы полупроводникового типа. Ферритовые сердечники изготовляются из порошков прессованием с последующим отжигом. Подобно другим полупроводниковым ма-териалаЫ они чувствительны к изменениям температуры, сохраняя свой магнитные свойства примерно до 70 -5-120* С.
быть представлена в комплексной форме
/Im с
Wo= Т- =РРо^— 0 =
=g0 (р cos fi — /р sin 6) --= fAo(Hi —/Нг).
где ро = 4л • Ю-7 гн}м— магнитная постоянная;
pi и р2 — действительная и мнимая части относительной комплексной магнитной проницаемости (квази-
упругая и поглощающая проницаемости) . Понятие о комплексной магнитной проницаемости было введено В. К. Аркадьевым в 1913 г.
Зависимость между амплитудными значениями индукции Вт и напряженности Нт при определенной частоте в предположении, что эти величины синусоидальны, называется динамической кривой намагничивания.
При одном и том же материале сердечника с увеличением частоты динамические кривые намагничивания располагаются ниже и становятся более пологими, как показано на рис. 12-2. Этй кривые приближенно характеризуют зависимость B=f(H) и не отображают ее неоднозначность. Неоднозначная зависимость B=f(H) характеризуется динамической петлей гистерезиса. Ширина петли возрастает с увеличением частоты магнитного поля. Расширение петли гистерезиса вызывается увеличением составляющей, компенсирующей вихревые токи (динамические потери). При этом учитываются одновременно не только гистерезис,
190
но и вихревые токи, что в ряде случаев весьма удобно.
Листовые ферромагнитные материалы с целью улучшения магнитных свойств подвергаются особой обработке, в результате которой материалы приобретают магнитную анизотропию, т. е. зависимость магнитной проницаемости р, от направ-
электрических машин, трансформаторов, реле и т. п. механические напряжения, обычно появляющиеся в магнитопроводах, практически не оказывают влияния на их работу.
При расчете любого устройства, содержащего магнитную цепь с переменным магнитным полем, необходимо учитывать явления, обуслов-
Рис. 12-3. Схема для приближенного определения параметров катушки с ферромагнитным сердечником при переменном токе в обмотке.
ления магнитного поля. Сердечники при этом конструируют таким образом, чтобы направление магнитного поля соответствовало наибольшим значениям р. Такая конструкция сердечников дает возможность производить расчет магнитной цепи так же, как и И случае изотропных материалов. Магнитные свойства некоторых типов материалов резко ухудшаются при появлении в них механических напряжений. Сердечники из таких материалов приходится помещать в специальные кожухи из диэлектрика, На который наматывается обмотка, для предотвращения механического сжатия сердечника витками обмотки1.
Свойством изменения р в зависимости от механических напряжений обладают по существу все ферромагнитные материалы. На этом, например, основано определение механических напряжений в стальных конструкциях посредством измерения переменных магнитных полей, создаваемых в отдельных небольших участках этих конструкций. Однако для большого количества
1 Здесь имеются- в виду кольцевые сердечники устройств автоматики.
ленные главным образом гистерезисом и вихревыми токами. Для учета этих явлений используются такие величины, как потери в стали, угол потерь, комплексная магнитная проницаемость и т. д., а также динамическая кривая намагничивания и динамическая петля гистерезиса.
Указанные величины и характеристики можно принимать в качестве основных свойств ферромагнитных материалов при переменных магнитных полях. Они не описывают полностью всех процессов, происходящих в материале магнитопровода, но дают возможность достаточно точно рассчитать число витков обмоток и размеры магнитопровода.
12-3. КАТУШКА С ФЕРРОМАГНИТНЫМ СЕРДЕЧНИКОМ
Основные свойства ферромагнитного материала определяют в результате экспериментального исследования катушки с сердечником из однородного ферромагнитного материала, одинакового поперечного сечения, без воздушного зазора. Для такого исследования предпочтительна тороидальная форма сердечника, так как при этом обеспечиваются наиболее точные измерения.
191
Схема, показанная на рис. 12-3, позволяет определить основные характеристики материала сердечника.
При исследовании обычно известны число витков обмотки w, активное сопротивление г, сечение магнитопровода 5Ст, длина средней линии напряженности /Ср и частота f. По показаниям электроизмерительных приборов определяются ток /, напряжение U на зажимах обмотки и потребляемая мощность Р (при определении Р из показания ваттметра необходимо вычесть мощность потерь в амперметре и вольтметре).
Действующее значение напряженности Н магнитного поля определяется по формуле
При гармоническом напряжении амплитуда магнитного потока, замыкающегося по сердечнику катушки, согласно § 12-1
Е
ФИ=Ш ..
(ми 4,44fw
(12-3)
где Е—действующее значение э.д.с., наводимой в обмотке вышеуказанным магнитным потоком.
Кроме магнитного потока Ф, замыкающегося по сердечнику катушки, имеется еще магнитный поток рассеяния Ф8, замыкающийся через воздух и показанный на рис. 12-3 условно (поток рассеяния может быть сцеплен лишь с частью витков обмотки). Ввиду того, что магнитное сопротивление воздуха значительно больше магнитного сопротивления сердечника, поток Ф8 можно считать совпадающим по фазе с током и прямо пропорциональным ему. Это дает возможность учитывать э. д. с., наводимую потоком рассеяния, с помощью сопротивления рассеяния ха.
Так как положительные направления тока и наведенной потоком Ф э.д.с. совпадают, то сумма приложенного напряжения и наведенной э. д. с. равна падению напряжения в активном сопротивлении и сопротивлении рассеяния:
U+E=(r+jxs)i,
откуда
— E+(r+jxs) 1.
В большинстве случаев Е мало отличается от U. Амплитуда магнитной индукции
Разность между мощностью, потребляемой катушкой, и мощностью, затрачиваемой на нагрев обмотки, равна потерям мощности в стали сердечника:
Р —/72=РСТ.
Удельные потери в стали
Уст Icp SCT где Уст— удельный вес материала сердечника.
Для катушки с ферромагнитным сердечником рассматриваются два режима работы: 1) напряжение на зажимах обмотки синусоидально, а ток в обмотке несинусоидален; 2) ток в обмотке синусоидален, а напряжение на зажимах несинусоидально.
В первом случае при г «О можно принять магнитный поток синусоидальным и построить кривую тока i(t). Порядок построения кривой i(i) показан на рис. 12-4. На кривой магнитного потока Ф(1) произвольно выбирается точка 1 и посредством горизонтальной линии 1—2, пересекающей кривую Ф(0, и вертикальной линии 2—3 определяется значение тока i, равное абсциссе 0—3, соответствующее значению (ординате) потока в точке 1; это значение тока откладывается в виде ординаты 0—4 и переносится в координатную систему i(t) посредством проведения горизонтальной линии 4—5 до пересечения с вертикальной прямой 1—^5. При выборе исходных точек на нисходящей части кривой abc значение тока i определяется также по нисходящей ветви abc петли Ф(1).
Изображенная на рис. 12-4 кривая 1(0 симметрична относительно оси абсцисс, что означает отсутствие четных гармоник (см. § 10-2). Эквивалентная синусоида тока ia
192
сдвинута по фазе относительно магнитного потока Ф на угол 6, поэтому 1 —
При синусоидальном приложенном напряжении э.д.с., наводимая в обмотке, несинусоидальна вследствие появления высших гармонических составляющих в токе. Однако искажение э. д. с. обычно незначительно, и, представляя ее в виде эк-
Иногда в расчетах применяется комплексное сопротивление ветвей намагничивания и потерь в стали
Zo = 77- = го + /*о-‘ о
Ток в обмотке представляется в виде двух составляющих: намагничивающего тока 1ф=ЬоОф и тока потерь в стали /п=ёоЙф. Если при-
Рис. 12-4. Графическое определение тока в катушке при синусоидальном магнитном потоке.
Бивалентной синусоиды, можно при-
нять — Е = t/ф = t/фб , где составляющая приложенного напряжения U, затрачиваемая на преодоление э. д ,с. Е.
Отношение — —Уй=уп —
/ Л „ \
— I — о!—комплексная проводимость ветвей намагничивания и потерь в стали; у0 — полная проводимость ветвей намагничивания и потерь в стали (напоминаем, что угол между Ё и Фщ равен л/2);
У0=у0 cos(-y —6)~
— й/о sin ---б) =
= у0 sin d — jy0 cos б = g0 — jb0, где go — проводимость ветви потерь в стали;
Ьо— проводимость ветви намагничивания.
нять, что Фт совпадает с действительной осью комплексной плоскости, то ток
/=/ф+/7п=/^б.
В соответствии со сказанным изображаются схема замещения (рис. 12-5) и векторная диаграмма (рис. 12-6) катушки с ферромагнитным сердечником.
На рис. 12-6 показаны вектор магнитной индукции Вт=-~ — = и вектор напряженности
*ср
Активная мощность, поглощаемая катушкой, ^=^обм+/’ст=г/2+^ф /n==7t/cos<p.
Определение по показаниям приборов напряженности магнитного поля, магнитной индукции, потерь в сердечнике и построение векторной
13—1118
193
диаграммы катушки с ферромагнитным сердечником иллюстрированы примерами 12-1—12-3.
тивление обмотки принимается равным нулю.
Магнитный поток сердечника согласно (12-3)
Рис. 12-5. Схема замещения катушки с ферромагнитным сердечником.
Фи = _£_ =
4,44 fw 4,44-400-200 = 3,38-10“4 вб.
Активное сечеиие стали сердечника с _ ^вя о, SC1 =- о —
83,5 — 56 й .
--------20-0,9-10“ь = 2,4-10“4 л».
тушки с ферромагнитным сердечни-
ком.
Амплитуда иидукиин в сердечнике
Вт =
Фт 3,38-10“4
=-------— = 1,41
“ст 2,4-10“4
тл.
Длина средней линии напряженности магнитного поля
4р —
83,5 + 56
2
IO-3 л = 0,219 м.
Амплитуда напряженности магнитного поля в сердечнике
Нт
0,3-200~И 2
0,219
-= 387 а/м.
Пример 12-2. Для сердечника, рассмотренного в примере 12-1, определить удельные потери в стали, если при частоте fi= =400 гц, напряжении U=120 в и токе /1 = =0,3 а мощность, измеряемая ваттметром (рис. 12-3), равна Pi = 10 вг.
Произвести разделение потерь, если при уменьшении частоты до 4= 100 гц, напряжения до 64=30 в и тока до 4=0,28 а показание ваттметра равно /4=3 вг. Сопротивление обмоткн сердечника, измеренное при постоянном токе, равно г—20 oju. Потери в измерительных приборах принимаются равными нулю.
Вес сердечника
Ост = Уст £ст 4р = 7,8-0,24-0,219=0,41 ®з.
Так как э.д.с. £=4,44 BmSOtf прямо пропорциональна частоте, то приближенно имеем:
От = 120 £, = 4,44filn,SCT4 =
17а 30 £в 4,44BsmScsfi
Пример 12-1. Определить значения В» Н Нт в стали сердечника катушки по результатам измерений в схеме (рис. 12-3), если приложенное напряжение Л7=12О в, ток /=0,3 а, частота (=400 гц. Сердечник катушки изготовлен из листовой стали (рис. 12-4) и имеет размеры dBH=56 мм, аж*83,5 мм, 5=20 мм, 1в—0, коэффициент заполнения поперечного сечеиия сталью (коэффициент заполнения стали) йСт=0,9; обмотка сердечника состоит из 200 витков. Для упрощения расчета активное сопро
откуда В1т=Д2т- Применяя методику, указанную в § 12-3, производны разделение потерь.
Удельные потери в стали при частоте fi =400 гц
Pl-rtf 10—20(0,3)»
Реп = —----------------------= 20 вт(кг.
Ост
194
Удельные потери в стали при частоте ,Г2=100 гц
P2 — r/f 3 — 20(0.28)2
Рстг ——-------~~~ 0 41 =3,5в/л/кг.
В соответствии с выражениями (12-1) и (12-2) можно принять, что
₽ст1 = 20 = Аг Л + Ав fl = Аг.400+А>в-4002;
Рст2 = 3.5=ЛГ /2+*в f|=fer.100+AB.1008, где kr и kB — коэффициенты пропорциональности:
kr = 2,98-10~ 2 вт-сек/кг
и kB — 5,04-10—5 вт-сек2/кг.
При частоте fi=400 гц удельные потери от гистерезиса
Рп = Mi = 2,98-10~2-400 = 11,9 вт/кг и от вихревых токов
₽в1=Л fl = 5.04-10~5 (400)2 = 8д вт/кг-
при частоте /2=100 гц
Ргг = Ма = 2,98-10~2.100 = 2,98 вт/кг;
Рв2 = Л»ft = 5,04-IO"5 -1002 = 0,504 вт/кг.
Пример 12-3. Построить векторную диаграмму катушки, рассмотренной в примерах 12-1 и 12-2, при частоте /=400 гц, если индуктивность рассеяния катушки L,~5 мгн.
Индуктивное сопротивление обмотки или, что то же, сопротивление рассеяния xs = 2n/£s = 2-3,14-400.5.10~3= 12,6 ом.
Сдвиг фаз между эквивалентной синусоидой тока и напряжением
Р 10
q> = arccos — = arccos Q g = 73=50'.
Комплексное сопротивление катушки
U 120
г=т^ф_-^73.50- =
= 400 73°50' = 111 -j-/384 сш.
Комплексное сопротивление ветвей намагничивания и потерь в стали
Z0 = Z —г —/х5= 111 +/384 — 20 — — / 12,6 = 91 +/371,3 = 382 ^76°13' ом.
Комплексная проводимость ветвей намагничивания и потерь в стали
ток потерь в стали
7п
go
Уо
= 0,3
6,23-IO-4
26,2-10—4
Намагничивающий ток
, , Ь<> 1л = 1 Уо
= 0,3
25,4-Ю-4
26,2.10-“
0,071 в.
= 0,291
а.
Угол потерь
в = arctg-y- = arctg-^T^T = 13°47'.
/ф o.zUl
Электродвижущая сила обмотки
Е = z0 I = 382-0,3 = 114,5 в.
Магнитный поток ражению (12-3):
в сердечнике по вы-
114,5 4,44.400-200
3,24-10—Чб.
По значениям фт, Е, 1$, в, /п, /, <₽, г, х,, U строится векторная диаграмма.
= б,23 IC— /25.4-10-4 сим;
проводимость ветви потерь в стали gD = 6,23-10_4 сим;
проводимость ветви намагничивания Ьо = 25,4-10~4 сим;
12-4. ТРАНСФОРМАТОР
С ФЕРРОМАГНИТНЫМ СЕРДЕЧНИКОМ
В гл. 6 дано определение понятия «трансформатор» и рассмотрен трансформатор без ферромагнитного сердечника. Наличие ферромагнитного сердечника дает возможность значительно увеличить магнитный поток и благодаря этому увеличить мощность, передаваемую из одной цепи в другую. Однако при этом трансформатор становится нелинейным элементом цепи и в сердечнике появляются потери.
В большинстве случаев стремятся сконструировать трансформатор таким образом, чтобы нелинейность по возможности мало влияла на его работу. При анализе работы трансформатора часто пренебрегают его нелинейностью и представляют напряжения, токи и магнитный поток в вице эквивалентных синусоид.
В зависимости от назначения трансформаторы подразделяются: а) на силовые; б) измерительные; г) специального назначения (разделительные, пик-трансформаторы и др.). Процессы, определяющие работу трансформаторов различных типов, по существу одни и те же и могут быть изучены на примере работы двухобмоточного силового трансформатора, схема включения которого показана на рис. 12-7. На схеме принято встречное направле-
131
195
ние токов (точками отмечены одноименные зажимы обмоток).
Для изучения работы такого трансформатора пользуются приведенной схемой замещения, показанной на рис. 12-8. Основное отличие
Рис. 12-7. Двухобмоточиый трансформатор.
схема замещения трансформатора.
Рис. 12-8. Приведенная
этой схемы от аналогичной схемы, рассмотренной в гл. 6 (см. рис. 6-13), заключается в наличии ветви потерь в стали g0, включенной параллельно ветви намагничивания Ьо, как это показано в § 12-3 для катушки со стальным сердечником. Этой схеме замещения соответствует векторная диаграмма рис. 12-9, а при сопротивлении нагрузки Zu=zHZ(pH, где <ри>0.
Намагничивающий ток /ф создает магнитный поток Ф, замыкающийся по сердечнику Этот поток наводит э.д.с. £t=£2, которая отстает на 90° ог вектора Ф,п.
Напряжение на ветви намагничивания, положительное направление которого совпадает с поло-
жительными направлениями тока 7ф и э. д. с. Еь равно С/ф= —£i. Напря-равно геометрической сум-
жение Ui
ме падений напряжений в активных и индуктивных сопротивлениях обмоток и напряжения t/2 на нагруз-
Рис. 12-9. Векторные диаграммы трансформатора для встречного (а) и согласного (б) направлений токов.
196
ке. В свою очередь первичный ток равен /1 = / > + /о, откуда н. с. fawi = =fawi—faw2 (составляющую /2^2 иногда называют размагничивающей). Здесь штрихами обозначены величины, приведенные к первичной обмотке.
Векторная диаграмма рис. 12-9,а соответствует встречному направлению токов Ji и fa. Если токи направлены согласно, то векторная диаграмма трансформатора может быть получена поворотом на 180° векторов, в которые входит ток /•>, в том числе и вектора Lfa, равного падению напряжения от тока fa в сопротивлении Z'H. Векторная диаграмма, показанная на рис. 22-4.6 для согласного направления токов, дана не для приведенных величин. При этом Н. С. f0Wi=faWi+t2W2.
Режим при ZH=0 называют режимом короткого замыкания. Для силовых трансформаторов этот режим при нормальном напряжении может существовать лишь весьма кратковременно как аварийный: выделение большого количества тепла в сопротивлениях обмоток rt и г2 может вызвать разрушение трансформатора.
На практике производят так называемый опыт короткого замыкания трансформатора. При этом опыте напряжение Ui — UiK подбирают таким образом, чтобы ток fa=faK был равен номинальному (нормальному) вторичному току. Обычно при этом L'ik в несколько раз меньше нормального напряжения Ui. Соответственно уменьшаются Eit Ez и Фт. Ток /о при этом уменьшается в значительно большее число раз вследствие работы сердечника в ненасыщенном режиме.
По результатам опыта короткого замыкания определяют сопротивления гр xs, r'2, x's2, для чего полагают, что go~O, &0 «0, г,^г2и xsl~<2. Получаемая при этом точность вполне приемлема для большинства практических случаев.
Режим при ZH= 00 называют режимом холостого хода или просто холостым ходом трансформатора. При этом /2=0 и /1=7о. Поэтому ток
/е называют током холостого хода. В действительности ток /0 при холостом ходе несколько больше тока /о при нормальном значении Zh, так как вследствие уменьшения падения напряжения в первичной обмотке увеличивается Ei, что в свою очередь вызывает увеличение Фт, а значит, и /о- Измерения lfa, fa и Pi, произведенные при холостом ходе, который в этом случае называют опытом холостого хода, позволяют легко определить go и Ьо, если известны (из опыта короткого замыкания) Г1 И Xsi.
Пример 12-4. На сердечнике катушки, рассмотренной в примерах 12-1—12-3, кроме первой обмоткн с числом витков =200, дополнительно намотана вторая обмотка с числом витков и>2=100. Таким образом, получается трансформатор с коэффициентом трансформации
ш, 200 п= — = -— = 2. и>2 100
При замкнутой накоротко вторичной обмотке этого трансформатора, напряжении 17) = 12 в и при частоте f=400 гц ток /1=0,249 а, мощность /’1=2,47 вг.
Определить показания приборов (рис. 12-7) при напряжении 1/1 = 120 в, сопротивлении нагрузки Zu = 25 Z 45° ом и построить векторную диаграмму.
Угол между векторами первичного напряжения и тока
Р 2 47
<рк = arccos = arccos-y^^^ 36°5'
Входное сопротивление (сопротивление короткого замыкания трансформатора)
12^36°5'
ZK =---------= 47^36°5'=38+/ 27,7 ом.
0,249
Из примера 12-1 известно, что при 1/| = = 120 в и разомкнутой вторичной обмотке индукция в сердечнике Бт~ 1,41 гл.
При 1/1 = 12 в и замкнутой вторичной обмотке индукция уменьшится более чем в 10 раз, а напряженность поля уменьшится в несколько десятков раз вследствие нелинейной связи Поэтому про-
водимость уо уменьшится по сравнению с вычисленной в примере 12-3 в несколько десятков раз.
Если принять //0=0, то сопротивление вторичной обмотки, приведенное к первичной обмотке,
Z2 = ZK — г, — /X, = 38+/ 27,7 — 20 — — / 12,7 « 18 + / 15 ом.
Сопротивление нагрузки, приведенное к первичной обмотке,
ZH = n2ZH = 22-25 45’ = 100 45' =
= 70,7 + / 70,7 ом.
При напряжении 171 = 120 в .необходимо учитывать проводимость Уо, которая
197
может быть принята такой же, как в примере 12-3. Схема замещения трансформатора при нагрузке изображена на рис. 12-10, а.
На рис. 12-10, б схема замещения преобразована для расчета, в результате которого получается *:
= 120 86°12' в; 4 = 1,01 38°12' щ
7в = 0,256 13°47' с; 4 = 0,782 226° а.
Рис. 12-10. Пример 12-4.
Остальные величины, необходимые для построения векторной диаграммы, получаются в результате следующих вычислений:
— £1 = ZCT = (382 76°13') X
X 0,256 13°47' = 97,8 90° в;
А £t —97,8^90°
£1 = ~ =-------------= 48,9 — 90° в;
£,^90° 97,8
4,44 fWi 4,44-400.200
= 2,76-10~J1 ^0° вб;
I2 = п1'2 == 2-0,782 226° = 1,56^ 226° а;
С12 = ZB /2 = (25 45°) -1,56^: 226'- =
= 39 271° в;
Pi = 14 Л cos <рх = 120-1,01 cos 48° = 90 вт;
Рц = Ua ia cos <р2 — 39-1,56 cos 45°= 48,8 вт
Начальная Лаза вектора /0 равна углу потерь вычисленному в приме-
ре 12-3.
Векторные диаграммы иа рис. 12-9 построены по полученным в данном примере значениям напряжений и токов.
12-5. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
12-1. Потери на гистерезис в ферромагнитном материале pri = l вт/кг при частоте fi = 100 гц. Определить потери на гистерезис рп при частоте fs=400 гц, если индукция изменяется по гармоническому
1 Здесь принято согласное направление токов.
закону и амплитуда ее сохраняется неизменной.
Ответ: 4 вт/кг.
12-2. Потери на вихревые токи в ферромагнитном материале рщ=0,5 вт/кг при частоте 4=100 гц. Определить потери иа вихревые токн рв2 при частоте f2=400 гц, если индукция изменяется по гармоническому закону н амплитуда ее сохраняется неизменной.
Ответ: 8 вт/кг.
12-3. В результате испытаний образца стали из листов толщиной Д1=0,1 мм и Д2=0,35 мм были определены потери иа гистерезис рг и потери на вихревые токи Ръ.
ДЛЯ ЛИСТОВ ТОЛЩИНОЙ Д1=0,1 мм
Рг=1,1 вт/кг; рв=0,1 вт/кг;
для листов толщиной Д2=О,35 мм рг=0,5 вт/кг-, рв=0,3 вт/кг.
Испытания производились при частоте f=50 гц.
Определить потери рСт в этих сортах стали при частотах 50, 150 и 400 гц, если индукция во всех случаях синусоидальна и ее амплитуда неизменна.
Ответ: для Д! 1,2; 4,23; 15,2 вт/кг; для Д2 0,8; 4,24; 23,2 вт/кг.
12-4. При частоте 4 = 100 гц потери в стали рСт1=2 вт/кг, при частоте f2« =200 гц потери в стали рСт2=7 вт/кг.
Определить потери в стали рСтв прн частоте fs=400 гц, если индукция изменяется по гармоническому закону и амплитуда ее сохраняется неизменной.
Ответ: 26 вт/кг.
12-5. Сердечник, изображенный на рис. 12-4, изготовлен из стальной ленты и имеет размеры dBa=45 леи, dH=60 мм, 5 = 15 мм, 1в=0. Коэффициент заполнения поперечного сечения сердечника сталью feCT=0,85. Магнитное поле в сердечнике характеризуется магнитной индукцией, изменяющейся по гармоническому закону с частотой /=1000 гц и амплитудой Вт =0,8 тл. Материал сердечника характеризуется динамической кривой намагничивания рис. 12-2. На сердечник намотана обмотка, состоящая из и =1000 витков. Определить наводимую э. д. с. и ток в обмотке. ч
Ответ: 340 е; 0,175 а.
12-6. Потери в материале сердечника из задачи 12-5 рг=20 вт/кг и рв=40 вт/кг. Определить угол потерь.
Ответ: 7°5'.
12-7. Последовательно с обмоткой сердечника из задачи 12-5 соединена емкость С=0,1 мкф. Определить напряжение на зажимах цепи, если сопротивление обмотки г =100 ом и индуктивность рассеяния L.=0
Ответ: 64 в.
12-8. Определить э.д.с и ток в обмотке сердечника из задачи 12-5 при частоте f=50 гц и амплитуде индукции Вт=0,8 тл.
Ответ: 17 в; 0,035 а.
12-9. Определить угол потерь б дм сердечника из задачи 12-5 при f=50 гц н Вт =0,8 тл, если учесть, что потери в материале сердечника при частоте 1000 гц приведены в задаче 12-6.
Ответ: 13°.
198
12-10. Определить напряжение на за-‘ =.чах обмотки сердечника из задачи 12-5 :?и /=50 гц, Вт=0,8 тл, г—100 ом и £а=0.
Ответ: 17,3 е.
12-11. В цепь катушки включены приборы, как показано на рис. 12-3. Напряжение на зажимах цепи </=120 в. При налипни стального сердечника ток в обмотке 7=0,69 а и мошность Р=32,2 вт. Прн отсутствии стального сердечника ток в обмотке /=2,23 а и мощность Р=100 вг. Определить параметры схемы замещения катушки со стальным сердечником в соответствии с рис. 12-6 и построить векторную
диаграмму, если сопротивление рассеяния ха=23 ом.
Ответ: г=20 ом; go=0,00227 сим;
t>o=O,OO65 сим. <
12-12. Как влияет изменение частЪты иа форму динамической кривой намагничивания?
12-13. В чем заключается отличие динамической кривой намагничивания от основной кривой намагничивания?
12-14. Чему равно напряжение на разомкнутых вторичных зажимах трансформатора и как оно связано с магнитным потоком?
199
Глава тринадцатая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ
В ЛИНЕЙНЫХ ЦЕПЯХ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ (КЛАССИЧЕСКИЙ МЕТОД)
13-1. ВОЗНИКНОВЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
В предыдущих главах рассматривались установившиеся процессы в линейных электрических цепях, т. е. такие процессы, при которых напряжения и токи либо неизменны во времени (цепи постоянного тока), либо представляют периодические функции времени (цепи переменного тока).
I Наступлению устанлвияшегяря процесса, отличного пт первоначального” режима работы цепи, предшествует', как'пра'вйло, переходиььй процесс, при котором напряжения и токи изменяются непериодически.
Переход от одного режима работы цепи к другому режиму может быть вызван изменением параметров или схемы цепи, называемым в общем случае в электротехнике коммутацией.
Можно теоретически считать, что коммутация цепи производится мгновенно, т. е. на включение, выключение или переключение цепи время не расходуется. Тем не менее переход от исходного режима работы цепи к последующему установившемуся процессу происходит не мгновенно, а в течение некоторого времени.
Объясняется это тем, что каждому состоянию цепи соответствует оп
ределенный запас энергии электрических и магнитных полей. Переход к новому режиму связан с нарастанием или убыванием энергии этих полей. Энергия wL=Li?L/2, запасаемая в магнитном поле индуктивности L, и энергия Wc — Cuj. /2, запасаемая в электрическом поле емкости С, не могут изменяться мгновенно: энергия может изменяться непрерывно, без скачков, так как в противном случае мощность, равная производной энергии по времени, достигала бы бесконечных значений, что физически невозможно. Именно поэтому, например в случае размыкания ветви с индуктивной катушкой, в месте размыкания неизбежно возникает искра, в сопротивлении которой расходуется энергия, накопленная в магнитном поле индуктивной катушки. Аналогично, если замкнуть накоротко зажимы конденсатора, который был предварительно заряжен, то запасенная в нем электрическая энергия рассеется в сопротивлении соединяющего провода и между контактами.
Если исключить случаи размыкания индуктивности и замыкания накоротко емкости и рассматривать цепи, в которых энергия, накапливаемая в магнитном или электрическом поле, может рассеиваться в виде тепла в сопротивлениях, то, считая, что коммутация происходит
199
мгновенно, можно искрообразование не учитывать.
Для завершения переходного и наступления установившегося процесса теоретически требуется бесконечно большое время. Практически, однако, время переходного процесса определяется малым интервалом, по истечении которого токи и напряжения настолько приближаются к установившимся значениям, что разница оказывается практически неощутимой. Чем интенсивнее происходит рассеивание энергии в сопротивлениях, тем быстрее протекает переходный процесс.
Если бы электрическая цепь состояла только из сопротивлений и не содержала индуктивностей и емкостей, то переход от одного установившегося состояния к другому совершался бы мгновенно, без затраты времени. В реальных электротехнических устройствах тепловые потери, обусловленные током, магнитные и электрические поля сопутствуют друг др'угу. Применяя специальные схемы и подбирая соответствующие параметры цепи, можно ускорить или замедлить переходный процесс.
В одних случаях переходные процессы в электрических цепях нежелательны и опасны (например, при коротких замыканиях в энергетических системах). В других случаях переходный процесс представляет естественный, нормальный режим работы цепи, как это, например, имеет место в радиопередающих и радиоприемных устройствах, системах автоматического регулирования и других цепях.
Существуют различные методы расчета переходных процессов в линейных электрических цепях. Настоящая глава посвящена классическому методу решения дифференциальных уравнений, описывающих переходные процессы.
13-2. ЗАКОНЫ КОММУТАЦИИ И НАЧАЛЬНЫЕ УСЛОВИЯ
Высказанные выше положения о том, что запас энергии магнитного или электрического поля может изменяться только плавно, без скачков, выражают принцип непрерыв
ности во времени потокосцепления индуктивности и электрического заряда емкости и называются законами коммутации.
Невозможность скачкообразного изменения потокосцепления следует из того, что в противном случае на индуктивности появилось бы бесконечно большое напряжение uL —
dW
— — =оо, что лишено физического смысла. Ввиду равенства 4r = Li принцип непрерывности потокосцепления означает, что при неизменном L ток i не может изменяться скачком. Итак, в начальный момент после коммутации ток в индуктивности остается таким же, каким он был непосредственно перед коммутацией, а затем плавно изменяется.
Аналогично невозможность скачкообразного изменения электрического заряда q следует из того, что в противном случае через емкость проходил бы бесконечно большой dij
ток 1С=— =оо, что также лишено Л
физического смысла. Ввиду равенства q—Cuc принцип непрерывности электрического заряда означает, что при неизменном С напряжение ис не может изменяться скачком. Итак, в начальный момент после коммутации напряжение на емкости остается таким же, каким оно было непосредственно перед коммутацией, а затем плавно изменяется.
При этом следует отметить, что в цепях с идеализированными сосредоточенными параметрами скачкообразно могут изменяться: I) токи в сопротивлениях и емкостях; 2) напряжения на сопротивлениях и индуктивностях.
Значения тока в индуктивности и напряжения на емкости в момент коммутации называются независимыми начальными условиями.
Обычно принимают, что коммутация происходит в момент времени t—О; тогда ток в индуктивности и напряжение на емкости в момент времени непосредственно перед коммутацией обозначаются через 1ь(0—) и ис(0—), а в начальный момент переходного процесса после коммутации — через it(0) и ис(0).
200
На основании законов коммутации
М°-)=М0);
ис(0-)=«с(0). (13-1)
Эти равенства выражают начальные условия цепи, в которых происходит коммутация.
При нулевых начальных условиях, т. е. когда it (0—)=0 и “с(0—)=0» индуктивность в начальный момент после коммутации равносильна разрыву цепи, а емкость равносильна короткому замыканию.
В случае ненулевых начальных условий, т. е. когда 1’ь(0)#=0 и ис(0)=#=0, индуктивность в первый момент t=0 равносильна источнику тока 1‘ь(0), а емкость равносильна источнику э.д.с. Цс(0).
Независимые начальные условия характеризуют энергию магнитного и электрического полей, запасенную к моменту коммутации, и для расчета переходного процесса обязательно требуется знание этих начальных условий, причем совершенно безразлично, каким образом эти условия в цепи были созданы.
При расчете переходных процессов в разветвленных электрических цепях наряду с независимыми начальными условиями используются так называемые зависимые начальные условия, а именно значения токов, напряжений и их производных в начальный момент времени (/=0). Методика вычисления зависимых начальных условий и их использование в расчете описаны в § 13-7.
До сих пор нами исключались из рассмотрения случаи коммутации, при которых неизбежно возникает между контактами искра или дуга. Один из таких случаев иллюстрирован на рис. 13-1, а. До коммутации ток проходит через индуктивность Li и контакт, шунтирующий индуктивность L2; ток в L2 равен нулю. В момент t—О контакт размыкается и индуктивности Lt и L2 оказываются включенными последовательно; ток в них принудительно становится одинаковым. Поскольку в момент
коммутации ток в Li не изменяется, а ток в L2 равен нулю, то в силу первого закона Кирхгофа ток должен замкнуться через дугу, образовавшуюся между контактами. Кроме того, если под L2 подразумевать реальную индуктивную катушку, то
Рис. 13-1. Случаи размыкания (а) или замыкания (б> при частичной потере энергии.
ток может частично замкнуться и через межвитковую емкость. После быстрого погасания дуги токи в Т-i и L2 уравниваются. Эта начальная стадия переходного процесса протекает столь быстро, что ею практически можно пренебречь, считая, что токи в Li и L2 уравниваются мгновенно. Именно в этом смысле можно условно говорить о скачкообразном изменении токов в индуктивностях, которое предшествует исследуемому переходному процессу в це-пи. При этом для расчета переходного процесса используется принцип непрерывности суммарного потокосцепления при коммутации, т. е. £(1‘(0—) = (Li + L2)t(0). Скачкообразное изменение токов и соответствующих им потоков в L\ и L2 в момент коммутации не сопряжено в данном случае с наведением бесконечно большой суммарной э. д. с. са-. моиндукции, поскольку суммарное потокосцепление не претерпевает скачкообразного изменения. При новых значениях токов в Lt и L2 магнитная энергия, запасенная в катушках, будет меньше энергии, запасенной в первой катушке до коммутации. Часть энергии превратится в тепло в искре, а также излучится.
Найденный таким образом ток
201
1(0) в Li и Z-г может рассматриваться как независимое начальное условие для расчета переходного пронесся во всей цепи рис. 13-1,а после разрыва дуги.
При коммутациях в цепях с емкостями при отсутствии сопротивлений также возможны весьма быстрые перераспределения зарядов, условно рассматриваемые как мгновенные. В этом случае применим принцип постоянства суммарного заряда. Полученные при этом значения зарядов и напряжений на отдельных емкостях используются в расчете последующего переходного процесса как независимые начальные условия.
1 Например, в случае схемы рис. 13-1,6 принцип постоянства суммарного заряда до и после коммутации выражается равенством
(0-) + «. (0-) = Л(0) + <*(0)-= “с(О)(С, + С2).
При сделанном допущении в остальной электрической цепи, соединенной с емкостями, не возникает бесконечно большого тока, так как суммарный заряд не изменяется скачкообразно при /=0.
В процессе рассматриваемой коммутации энергия электрического поля уменьшится, так как часть ее превратится в тепло в очень малом сопротивлении проводника при очень большом токе, а также может выделиться в искре и излучиться.
13-3. ПРИНУЖДЕННЫЙ и свободный режимы
В общем случае анализ переходного процесса в линейной цепи с сосредоточенными параметрами г, L, С, М сводится к решению обыкновенных линейных неоднородных дифференциальных уравнений, выражающих законы Кирхгофа. Эти уравнения представляют линейную комбинацию напряжений, токов, их первых производных и интегралов по времени.
Например, если какая-нибудь э.д.с. e(t) включается в цепь, состоящую из последовательно соединенных г, L и С, то интегро-диффе
ренциальное уравнение имеет вид:
ri+ L ~ f i dt = е (0. (13-2)
Это уравнение после дифференцирования приводится к неоднородному-дифференциальному уравнению вто-. рого порядка
+ г —+ —= —• <13-3> Л2 dt С dt
Как известно, общий интеграл такого уравнения равен сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Частное решение выражает. принужденный режим, задаваемый источником. Если воздействующая функция, стоящая в правой части уравнения, постоянна или является периодической функцией времени, то принужденный ток будет одновременно и установившимся. Расчеты установившихся токов рассмотрены в предыдущих главах Нахождение частного решения в других, более сложных случаях будет изложено в § 13-7, а также в § 14-12.
Общее решение физически определяет поведение цепи при отсутствии внешних источников электрической энергии и при заданных начальных условиях. Функции, определяемые общим решением, называются свободными составляющими (токов, напряжений и др.)-
В случае, рассмотренном выше, однородное уравнение имеет вид:
+ пз'4)
и соответствующее ему характеристическое уравнение
Lp*+rp+ = 0. (13-5)
Если корни характеристического уравнения обозначить через и рг, то общее решение запишется в виде
МО =4^ 4-Д^', (13-6) где 4 и Д— постоянные интегрирования, которые определяются из начальных условий (§ 13-7).
202
Полный переходный ток в цепи равен сумме принужденного и свободного токов:
*(0=M*)+M0. (13-7)
Аналогично напряжение, заряд, магнитный поток и другие функции на любом участке цепи в переходном режиме состоят из принужденной и свободной составляющих.
На основании законов коммутации (§ 13-2) можно найти начальные независимые условия it(0) и ис(0). После этого можно написать согласно (13-7):
^(O)=fLnp(O)+fLcB(O); UC(°) = UCnp(0)+UCcB(0). откуда
_ _ Ml оо)
«CcE(0) = «c(0)-uCnp(0).f
Итак, начальные значения свободных ФУНКЦИЙ 1ьсв(0) и Uccb(O) определяются изменениями в момент коммутации соответствующих принужденных функций.
В частном случае при нулевых начальных условиях
^св(0) = -‘7пр(0);
«Ссв(0) = -«Спр(0).
В зависимости от порядка дифференциальных уравнений, описывающих исследуемые переходные процессы, различают цепи первого, второго и более высокого порядка.
В цепях первого порядка накопление энергии происходит только в' в одном элементе, L или С, в форме магнитной энергии (в цепи с индуктивностью— § 13-4) или электрической энергии (в цепи с емкостью— § 13-5). Одноконтурная цепь, содержащая элементы, в которых накапливается энергия обоих видов — магнитная и электрическая, представляет цепь второго порядка (цепь г, L, С — § 13-6). Разветвленные, цепи могут быть более высокого порядка (§ 13-7).
13-4. ПЕРЕХОДНЫЙ ПРОЦЕСС В ЦЕПИ г, L
Положим, что в момент t—0 цепь, состоящая из сопротивления г
и индуктивности L, включенных Последовательно, присоединяется к источнику э.д.с. e(t) (рис. 13-2).
Рис. 13-2. Включение цепи г, L.
Дифференциальное уравнение для времени записывается в виде
, . , di e=ri+L —.
dt
Характеристическое уравнение имеет вид r-f-pL=O и соответственно г корень уравнения pt =--— .
Отсюда свободный ток
1№=А(?'‘^Ае L .
Переходный ток в цепи определится суммой принужденного и свободного токов:
i=inp+Ae“T'. (13-9)
Принужденный ток может быть найден, если задана э.д.с. e(t).
Рассмотрим три случая:
1) включение в цепь г, L постоянной э. д. с. Е;
2) короткое замыкание Цепи г, L;
3) включение в цепь г, L гармонической э.д.с.
Ет cos(cof-l-ip).
I. Включение в цепь г, L постоянной э. д. с. При включении в цепь г, L постоянной э. д. с. Е принужденный ток равен Е/r. Поэтому согласно (13-9)
i= —+Ае~~1. (13-10)
Г
Постоянная интегрирования А находится по начальному условию i(0) = i(0—) = 0.
Согласно уравнению (13-10) при /=0
0 = — + А, Г
203
откуда
4=--*. Г Следовательно,
1—е~Т= / f i_e-T У г \ / \ /
о / Е
Здесь /=------предельное зна-
г
чение, к которому стремится ток
Рис. 13-3. Принужденный, свободный и переходный токи при включении в цепь г, L постоянной э. д. с.
i(/) по мере неограниченного возрастания t, называемое установившимся током.
В начальный момент/=0 э. д. с. самоиндукции eL~—L— (0) = ® —Е и полностью компенсируется э.д.с. источника, так как ток 1(0) равен нулю.
С течением времени э. д. с. самоиндукции убывает, а ток в цепи возрастает, асимптотически приближаясь к установившемуся значению.
На рис. 13-3 показаны кривые принужденного, свободного и переходного токов; на том же рисунке изображена кривая напряжения на индуктивности ,
о, = = Ее~.
L dt
Из курса математического анализа известно, что если y—f(t), то
D подкасательная равна — . о 1«/' I данном случае при любом значении t
Величина т= — носит название Г
постоянной времени. Постоянная времени измеряется в секундах:
[L 1 гн ом-сек
— = — =---------= сек.
г J ом ом
Выражение (13-11) показывает, что постоянная времени графически определяется длиной подкасательной к кривой или uL при любом значении t.
Нарастание тока происходит тем быстрее, чем меньше постоянная времени и соответственно чем быстрее убывает э. д. с. самоиндукции. Для различных моментов времени ток в цепи, выраженный в процентах конечного (установившегося) значения, составляет:
t ~ т 2т Зт 4т 5т со
у 100% = 63,2 86,5 95,0 98,2 99,3 100
Следовательно, постоянная времени цепи г, L равна промежутку времени, в течение которого свободная составляющая тока убывает в е=2,718 раза, и соответственно ток в этой цепи, включенной на постоянное напряжение, достигает 63,2% своего установившегося значения.
Как видно из рис. 13-3 и приведенных значений t и i/l, переходный процесс теоретически длится бесконечно долго. Практически же можно считать, что он заканчивается спустя t= (4 -ь 5)т.
2. Короткое замыкание цепи г, L. Положим, что цепь г, L, присоединенная к источнику постоянного или переменного напряжения, замыкается при t—О накоротко (рис. 13-4, а). В образовавшемся при этом контуре г, L благодаря наличию магнитного поля индуктивной катушки ток исчезает не мгновенно: э.д.с. самоиндукции, обусловленная убыванием магнитного потока, стремится поддержать ток в контуре за счет энергии исчезающего магнитного поля. По мере того как энергия магнитного поля постепенно рассеивается, превращаясь в сопротивлении г в тепло, ток в контуре приближается к нулю.
204
Процесс, происходящий в короткозамкнутом контуре г, L, является свободным; принужденный ток в данном случае равен нулю.
Положив в (13-9) 1Пр=0, имеем:
i=Ae
Постоянная интегрирования А находится из начального условия
i(0) = ‘(0-),
Рис. 13-4. Короткое замыкание цепи г, L.
а — расчетная схема; 6 — кривые тока I и напряжения
откуда
-L-t __L
i(f) = i(O)e L = i(0)e z ;
здесь i(0—) —значение тока в индуктивности в момент, непосредственно предшествовавший короткому замыканию; оно может быть положительным или отрицательным.
На рис. 13-4,6 изображены кривые спада тока в короткозамкнутом контуре и кривая напряжения на индуктивности
uL = L ~ = —ri(0)e~~
в предположении, что i(0)>0.
Постоянная времени контура т== — может быть найдена графически как подкасательная к кривой i(f) (например, в момент i=0).
Переходный процесс в короткозамкнутом контуре заканчивается теоретически при t—co. За это время в сопротивлении г выделяется в виде тепла энергия
СО ОО
j' гр dt—r [i(0)]2J е L dt — о о
= Z.R (0)Р
2 ’
т. е. вся энергия, запасенная в магнитном поле катушки до коммутации.
Так же как и в предыдущем случае, переходный процесс в коротко-
замкнутом контуре можно практически считать законченным спустя (= = (4ч-5)т.
3. Включение в цепь г, L гармонической э. д.с. При включении в цепь г, L гармонической э.д.с. e=ETncos(coi+ip) принужденный ток
будет:
I’np=^m COS (с^+Ф — ф). где
На основании (13-9) i = lm cos (mi + Ф —
t
— ф) + Ае т ,
где
Постоянная интегрирования определяется по начальному условию i(0)=i(0—)=0.
Следовательно,
0=/m cos (ф — ф) 4- А, откуда
А = — Im cos (ф — ф).
Поэтому искомый ток будет:
i = lm [cos (ш/ 4- ф — ф) — — cos (ф — ф) е х ].
На рис. 13-5, а изображены кривые inp, iCB и i. Начальные ординаты inp(0), iCB(0) одинаковы по абсолютной величине и противоположны по знаку; поэтому ток в начальный момент равен нулю. Свободный ток убывает по показательному закону. По истечении времени t— =т свободный ток уменьшается в е=2,718 раза по сравнению с начальным значением iCB(0). Постоянная времени прямо пропорцио
205
нальна добротности контура Q и обратно пропорциональна частоте со:
т _ vL Q аг а
Если в момент коммутации (/ = = 0) ток 1Пр проходит через нуль, т. е. выполняется условие ф—<р = = ± —, то свободный ток не возни-2
можно рассматривать как интегрирующее звено.
В свою очередь при достаточно малой постоянной времени, пренебрегая вторым слагаемым уравнения, приближенно получаем;
откуда
, di L de
uL = L ~ •----------,
L dt r dt
Рис. 13-5. Принужденный, свободный и переходный токн при включении в пгпь г, L гармонической э. д. с.
кает, и в цепи сразу наступает принужденный, установившийся режим без переходного процесса.
Если же коммутация происходит при ф=<р или ф—<р= ±л, то начальный свободный ток максимален (рис. 13-5,6), а именно iCB(0) = =F/m, и ток переходного режима достигает экстремального значения (положительного или отрицательного) в конце первого полупериода. Однако даже в предельном случае, когда г=0 и, следовательно, т= — =оо, г
ток не может превышать амплитуду установившегося режима более чем вдвое.
При достаточно большой постоянной L
времени т«=—первым слагаемым в правой части дифференциального уравнения
di e^ri+L~
можно пренебречь по сравнению со вторым ai слагаемым, приняв приближенно e-L.—', t
откуда е dt и соответственно иг~
I ari*a — j* е dt. о
Следовательно, цепь с последовательно соединенными сопротивлением и индуктивностью при большой постоянной времени
т. е. цепь с последовательно соединенными сопротивлением и индуктивностью при ма лой постоянной времени представляет дифференцирующее звено.
В обоих случаях функция е(/) может быть произвольной.
Интегрирующие и дифференцирующие звенья входят в качестве элементов в системы автоматического управления и регулирования.
13-5. ПЕРЕХОДНЫЙ процесс в цепи г, С
Положим, что в момент f=0 цепь, состоящая из сопротивления г и емкости С, включенных последовательно, присоединяется к источнику э.д.с. e(t) (рис. 13-6).
На основании второго закона Кирхгофа уравнение для времени t^O имеет вид:
e=rt-buc, где ис — напряжение на емкости.
С учетом того, что i=C , получаем:
л dur е=гСтг+и^
здесь искомой величиной является напряжение на емкости.
Характеристическое уравнение имеет вид 1 + гСр=0 и соответственно корень уравнения pi~------.
206
Следовательно, свободная слагающая напряжения на емкости
иСсв = Ае”гС = Ае т, где х=гС — постоянная времени контура г, С( измеряется в секун-дах: [гС]—оМ'ф=ом------= сек].
Рис. 13-6. Включение цепн г, С.
Переходное напряжение на емкости равно сумме принужденного и свободного напряжения:
__t_
«с=«с„Р+^ т. (13-12)
В свою очередь ток в контуре
_ dur ~ dur„n л _ _L
t=C —=С-^2 — — е т . (13-13) dt dt f
Рассмотрим три случая:
1) включение в цепь г, С постоянной э. д. с. Е;
2) короткое замыкание цепи г, С;
3) включение в цепь г, С гармонической э.д.с.
Ет cos (®Z+ip).
1. Включение в цепь г, С постоянной э.д.с. Включим постоянную э. д. с. Е в цепь с сопротивлением г и предварительно заряженной емкостью С (полярность заряженной ем--кости указана на рис. 13-6 знаками «+» и «—»); начальное напряжение на емкости ис (0) обозначим для простоты через U.
Принужденное напряжение на емкости равно э. д. с. источника. Поэтому согласно (13-12)
ис = Е+Ае т. (13-14)
Постоянная интегрирования А, входящая в (13-14), находится по начальному условию:
при 1=0 имеет С/=£+А, откуда A = U—E.
Сл едов ательно, _t_
ис= E — (E — U)e т. (13-15)
Согласно (13-13) ток в контуре
(13-16)
Если E>U, то с течением времени напряжение на емкости возра-
Рис. 13-7. Ток и напряжение при включении в цепь г, С постоянной э. д. с.
стает, стремясь к установившемуся значению Е. а ток убывает, стремясь в пределе к нулю; на рис. 13-7, а изображены кривые нарастания «с и спада 1. Чем больше постоянная времени, тем медленнее происходят нарастание ис и спад L
Если £<17, то кривые tic и 1 имеют вид, показанный на рис. 13-7,6.
Постоянная времени т=гС может быть найдена так же, как раньше, графически как подкасательная к кривой i в любой точке (например, при 1=0).
’— Закон изменения напряжения иа емкости и тока в данной цепи ана-
207
логичен закону изменения тока и напряжения в контуре г, L, рассмотренном ранее. Поэтому все сказанное о постоянной времени в предыдущем случае сохраняет силу для данного случая.
2. Короткое замыкание цепи г, С. Замыкание накоротко цепи, состоящей из последовательно соединенных г и С, равносильно принятию в предыдущем случае э. д. с., равной нулю. Предполагается, что емкость С заряжена, т. е. в момент включения на ее зажимах имеется напряжение U.
Положив в (13-15) и (13-16) э. д. с. Е равной нулю, получим:
Uc = ие х ;
где
При коротком замыкании цепи г, С электрический ток идет от зажи-
Рис. 13-8. Ток и напряжение ври коротком замыкании цепи г, С.
мах«+» к зажиму «—». Следовательно, при выбранной на рис. 13-6 полярности емкости ток проходит через сопротивление г в направлении, противоположном тому, которое принято на рис. 13-6 за положительное. Поэтому в выражении для тока стоит\знак «минус». На рис. 13-8 изображены кривые спада tzc и i.
В отличие от напряжения на ем«— кости, которое изменяется непре
рывно, ток в контуре г, С, пропорциональный скорости изменения ис, совершает при t=0 скачок.
Энергия, рассеиваемая в сопротивлении г в течение всего переходного процесса, равна энергии, запасенной в электрическом поле до коммутации:
Р Р
\ a2dt= — | е rC dt = — .
J r J 2
0 0
Так же как и для цепи г, L, переходный процесс может считаться законченным спустя ^=(44-5)т, так как к этому времени емкость разрядится на 98,2—99,3% и напряжение на емкости снизится до 1,8— 0,7% первоначального значения (см. § 13-4, случай 1).
3. Включение в цепь г, С гар-
монической э.д.с. При включении в цепь г, С гармонической э. д. с. Emcos (<oZ-|-tp) принужденное напряжение на емкости
на основании (13-12)
Если предполагать, что конденсатор не был заряжен, то постоянная интегрирования определяется • по начальному условию uc(0)=0:‘
0 = Ль cos (гь — <р—— 'j-j- А, аС V 2 J
откуда
А=- cos (v =
= -^-sin(<p — if).
208
V
Тогда искомое напряжение на емкости будет:
ur = -^-[cos fcoi 4- ib— го-—4-
c aC L \ 2/
+ sin
а ток б цепи
i = C~-=— lm Jsin [at 4~ф —<p —
n \ 1 ---1
----1 4--sm (<p — ib) e T .
2 j arC J
Из написанных выражений видно, что если включение цепи г, С происходит в момент, когда принужденный ток должен достигать максимума — положительного или отрицательного (т. е. <р—ф = 0), а принужденное напряжение на емкости должно быть равно нулю, то свободная слагающая напряжения на емкости не возникает и в цепи сразу без переходного процесса наступает принужденный установившийся режим.
Так как цепь г, С по протеканию переходного процесса подобна цепи г, L, то при соответствующем подборе параметров г и С она также может служить дифференцирующим или интегрирующим звеном.
13-6. ПЕРЕХОДНЫЙ ПРОЦЕСС В ЦЕПИ г, L. С
При включении в цепь г, L, С э.д.с. e(t) (рис. 13-9) переходный процесс исследуется с помощью дифференциального уравнения (13-3)
rd2» . di . i de \
dt* dt C ~ dt
Соответствующее ему характеристическое уравнение (13-5)
Ер2 -4- гр+ -£- = О
имеет корни __________________
Р1'2 ~ 2L ~ У ( 2L ) LC ~~
„fi+j/fi2 —(13-17)
где 6 =4" > “о ~ — Рез0‘
2L Vlc нансная частота.
Свободный ток согласно (13-6) равен:
i\,== Л^Ч А.^.
Ток в цепи определяется суммой принужденного и свободного токов:
.^-М/ЧлА (13-18)
Рис. 13-9. Включение цепи г, L, С.
Принужденный ток находится в соответствии с заданной э. д. с. e(t). Что касается свободного тока, то его характер зависит от знака подкоренного выражения (13-17).
1. Включение в цепь г, L, С постоянной э.д.с. Рассмотрим сначала случай, когда э. д. с. источника постоянна: е=Е и емкость имеет начальное напряжение
uc(0) =U.
Ввиду наличия индуктивности начальное значение тока
i(0) = 0.
Исходное уравнение
Е — ri + L-^~ 4- иг dt с
для начального момента записывается в виде
E = L-^-(0)4-uc(0), откуда находится начальное значение производной (0), которое является зависимым начальным условием, необходимым для вычисления Л1 и Аг:
= (13-19)
dt L
При установившемся режиме ток будет равен нулю, что следует как из физического смысла, так и из вида правой части дифференциального уравнения (13-3). Продифференци
14—1118
209
ровав (13-18), с учетом того, что i'np=0, получим:
+ (13-20)
at
Подставляя в (13-18) и (13-20) t—Q и используя (13-19), получаем:
0 = Д1 4- Д;
—“— = A Pi + А2 Pz~
незначительно, и кривая тока близка к кривой тока в цепи г, С (рис. 13-7).
Выражение (13-21) может быть преобразовано в гиперболическую форму:
Z-/62-w2
X sh/’б2 — со2/. (13-22)
Рис. 13-10. Расположение корней характеристического уравнения на комплексной плоскости.
Из этих уравнений следует:
1 t(Pi-p2)
E—U
2L б2 —wg
Поэтому
i =----£~и (g^— g**). (13-21)
2l]/" б2 —о2
Рассмотрим возможные три случая.
Случай 1. б>соо, т. е. г>2 (апериодический процесс).
Согласно (13-17) корни характеристического уравнения pt и р2— Отрицательные, действительные чис-ла (рис. 13-10,7z). Если индекс 1 соответствует верхнему знаку перед корнем, то |pi|<|p2f, и поэтому кривая ep,t спадает медленнее, чем ep,t . На рис. 13-11 показана кривая
i, построенная по выражению (13-21).
При больших значениях С влияние емкости мало и кривая тока приближается к кривой тока в цепи г, L (рис. 13-3); при малых значениях L влияние индуктивности
Следует заметить, что при коротком замыкании цепи г, L, С, т. е. при Е=0, ток в цепи обусловливается разрядом емкости.
Случай 2. б = юо, т. е. г—2 (критический случай).
Согласно (13-17) корни характе-
ристического уравнения одинаковы: Р1—Р2—------- = —6 (рис. 13-10,6).
Выражение (13-21) приводит в этом случае к неопределенности ви-
210
Раскрывая неопределенность по правилу Лопиталя дифференцированием числителя и знаменателя по pi, получаем:
i = lim _£z^_(e₽.'_^)== р,-р2 L (pi—р2)
То же выражение получится, если воспользоваться общим решением однородного дифференциального уравнения с кратными корнями:
ice = (B1+B2/)e“\
В рассматриваемом случае ^св (0) ==-Si = 0 и
— = В2 е~и — В2 Н)е~ы.
dt 2 2
Следовательно,
А-(0) = В2= dt ' ’ 2 L
Кривая тока аналогична кривой i на рис. 13-11.
Случай 3. б<соо, т. е. л<2 -ф-
(колебательный ^процесс).
'Корни характеристического уравнения комплексные и сопряженные:
(13-23)
Pi,2 = — 6 ± /“св’
где _______
“св = V “о - 62 •
Согласно (13-24)
(13-24)
Корни характеристического уравнения располагаются симметрично относительно действительной оси в левой полуплоскости, на полуокружности, центр которой совпадает с началом координат, а радиус равен:
“о = —~— (рис. 13-10, в). V LC
Сопоставление рис. 13-10, а—в показывает, что о характере переходного процесса в цепи г, L, С можно судить по расположению корней характеристического уравнения, т. е. нулей функции Z(p) на комплексной плоскости.
Если расположенные в левой полуплоскости нули функции Z(p) ле
жат на действительной оси, то имеет место апериодический процесс: совмещению нулей в одной точке отвечает критический случай; наконец, если нули функции Z(p) являются комплексно-сопряженными, то имеет место колебательный процесс.
Величина ысв (рис. 13-10, в) называется угловой частотой свободных или собственных колебаний в цепи г, L, С, а ^св= —-------периодом колебаний.
®св
Ток в цепи согласно (13-22)
• Е — U —Gt • • л 1=------е sh /сосв I =
/Исв Е
= ё~и sin Юсв t*. (13-25)
СОсв Е
Полученное выражение показывает, что при включении цепи г, L, С на постоянное напряжение, когда б<«св, в цепи возникают затухающие гармонические колебания, причем огибающими кривой тока слу-
, Е — U —и , жат кривые ±-----------е (рис.
сосв Е
13-12). Колебания возникают вследствие периодического преобразования энергии электрического поля в энергию магнитного и обратно; причем колебания сопровождаются потерей энергии в сопротивлении.
При t= 1/6 ордината огибающей в е=2,718 раза меньше начального значения огибающей. Поэтому величину \l6=2Llr называют постоянной времени колебательного контура.
На рис. 13-12 показана также кривая напряжения ис на емкости, которая в другом масштабе выражает также зависимость электрического заряда q от времени. Функции ис и i имеют одинаковый множитель затухания. При нулевых начальных условиях (£7=0) кривая ис начинается с нуля.
* Тот же результат получится, если исходить из общего решения однородного дифференциального уравнеиня с комплексно-сопряженными корнями:
—ы
‘св = (М cos wCB f-j- N sin wCB 0 e
14*
211
Как видно из (13-23) и рис. 13-10, в. угловая частота этих колебаний гоСв определяется абсолютной величиной ординаты корня характеристического уравнения, которая при б=#=0 всегда меньше резонансной частоты <оо.
О быстроте затухания колебательного процесса судят по величи-8Г не е св, называемой декрементом колебания, или по величине In е8Гсв = бТ'св, называемой логарифмическим декрементом колебания.
На рис. 13-13 в виде примера последовательно показано изменение характера переходного процесса с уменьшением величины 6.
Приведенные выше величины шСв и 0 связаны с параметрами последовательного резонансного контура — добротностью Q=-2— и затуханием d=l/Q, введенными в гл. 7:
Рис. 13-12. Колебательный процесс при При достаточно высокой доброт-включеиии в цепь г, L, С постоянной э. д. с. НОСТИ юСв соо-
Рис. 13-13. Изменение характера переходного процесса с уменьшением Л.
Чем меньше б по сравнению с ы0, тем медленнее затухает колебательный процесс и тем больше частота собственных колебаний цепи г, L, С приближается к резонансной частоте.
В пределе при 6 = 0 <оев = а>о колебания не затухают и корни характеристического уравнения располагаются в этом случае на мнимой оси (рис. 13-10,в).
этом случае 0=----, от-
“св С
куда . Для контура сред-
Я
него качества d«0,01 и логарифмический декремент 8 «0,03.
2. Включение в цепь г, L, С гармонической э.д. с. Если цепь г, L, С присоединяется к источнику гармо
212
нической э. д. с. Ет cos (со/ + ф —
то принужденный ток равен:
l'np = lm cos ----ф j
и переходный ток согласно (13-18) равен:
/ — I т COS Q) t —|— ф — ф -|-
+ Ai -р- А2 .
Кривые принужденного, свободного и переходного токов при апериодическим и колебательном процессах показаны в виде примера на рис. 13-14.
Частота принужденного тока равна частоте источника гармонического напряжения; свободный же ток при 6<Со)о изменяется с собственной частотой цепи соСв- Частота «св может быть в зависимости от параметров г, L и С меньше, больше или равна частоте со.
Свободные колебания тока накладываются на принужденный ток И затухают пропорционально множителю е~ъ>. По мере затухания свободного тока кривая переходного тока приближается к кривой принужденного тока.
Та из двух слагающих тока i, частота которой меньше, служит как бы криволинейной осью для другой
слагающей, колеблющейся относительно нее (рис. 13-14,6). При близком совпадении частот со и соСв в цепи возникают биения. Этот вопрос подробнее рассмотрен в [Л. 9 и 16].
13-7. РАСЧЕТ ПЕРЕХОДНОГО ПРОЦЕССА В РАЗВЕТВЛЕННОЙ ЦЕПИ
Переходный процесс в разветвленной электрической цепи описывается системой линейных дифференциальных уравнений с постоянными коэффициентами, общее решение которых находится как сумма принужденной и свободной составляющих.
Рассмотрим сначала методику расчета принужденного режима.
Во многих случаях воздействующая функция, например э. д. с. источника, может быть представлена в обобщенной форме Ете& ept, где p=c+jta — комплексное число. В зависимости от значений буквенных величин, входящих в приведенное выражение, получается тот или иной закон изменения э.д.с., причем мгновенные значения э. д с. определяются мнимой или действительной частью выражения.
Условие со=/=О соответствует гармонической э. д. с. с возрастающей (с>0), убывающей (с<0) или неизменной (с=0) амплитудой (рис. 13-15).
Условие ю=0 соответствует возрастающей (0-0) или убывающей (с<0) показательной функции; при с=0 э.д.с. постоянна (рис. 13-16).
Задавшись э. д. с. Ете>^ ищем принужденный ток в виде /me'“epf. Данная функция при дифференцировании (по переменной t) умножается на р, а при интегрировании делится на р. Поэтому подстановка выражения 1те'а ерг в исходное дифференциальное (или интегро-дифференциальное) уравнение приводит к алгебраическому уравнению, которое отличается от уравнения для установившегося режима, записанного в комплексной форме, только тем, что /ш заменяется на р. Таким образом, принужденный ток получается равным.
р .pt р
/ /А ___ с___к___________
apU~ Z{p) ~ Z(c + )to)
213
В зависимости от схемы и постановки задачи Z(p) означает обобщенное входное сопротивление или величину, обратную обобщенной пе-
(в) амплитудами.
Рис. 13-16. Возрастающая (с>0), убывающая (с<0) показательная функция и постоянная (с=0).
редаточной проводимости; Z(p) получается из соответствующего комплексного сопротивления заменой . , , 1 1 iwL на pL и ----- на ----.
1 1'а>С рС .
Мгновенные значения тока определяются мнимой или действительной частью /np(f).
В случае гармонической э.д.с. (с=0, p=ja) принужденный ток равен установившемуся гармоническому току
/уст (/) = —---------
у 7 Z(/<o)
Если э.д.с. есть показательная функция (ф = 0. р—с, Ет=Е), то принужденный ток изменяется также по показательному закону
F&t
где
Z(c)=[Z(p)]p^.
При постоянной э. д. с. (ф=0, /7=0, Ет=Е) принужденный ток равен установившемуся постоянному току
/=Л-, 2(0)’
где z (0) — сопротивление при постоянном токе.
Перейдем теперь к рассмотрению свободного режима.
Свободные составляющие представляют собой общее решение системы однородных линейных дифференциальных уравнений. Для заданной цепи степень характеристического уравнения ие зависит от выбора контуров, для которых составляются уравнения по второму закону Кирхгофа. Однако если выбрать контуры так, чтобы порядок дифференциальных уравнений был наименьшим, то степень характеристического уравнения не будет превышать суммы порядков исходных дифференциальных уравнений системы. При этом, как будет показано ниже, для получения характеристического уравнения отнюдь не обязательно приводить систему дифференциальных уравнений к одному уравнению относительно одной неизвестной функции.
Корни характеристического уравнения могут быть действительными и комплексными. Если корни комплексные, то' они всегда образуют комплексно-сопряженные пары. В связи с этим характеристическое уравнение нечетной степени всегда имеет хотя бы один действительный корень, остальные же корни могут
214
быть действительными или комплексно-сопряженными; характеристическое уравнение четной степени имеет четное число действительных или комплексно-сопряженных корней. Действительные части всех корней характеристического уравнения всегда отрицательны, что физически обусловлено затуханием свободных составляющих в пассивных цепях с течением времени. При этом все коэффициенты характеристического уравнения должны быть действительными и положительными.
Корни единого характеристического уравнения используются для нахождения в данной цепи свободных составляющих как токов, так и напряжений.
Допустим, что характеристическое уравнение имеет п корней. Тогда свободный ток в любой ветви
йв(0 = £Д/6<; (13-26)
здесь pk— корни характеристического уравнения;
Ак—постоянные интегрирования.
Аналогичная структура решения получается и для свободных составляющих напряжений
В случае, когда рь =—бь является действительным корнем m-й кратности, решение для этого корня записывается в виде
т
z=i
Если имеются сопряженные комплексные корни, например ph, ?<+i= = —6fe±/cofe, то выражение Аье р,г‘ 4* +Ak+le Pfl+lt преобразуется в
= (М cos со^ / 4“ sin t).
Для т-кратных сопряженных комплексных корней решение принимает вид:
е-5** У] t‘~1 (М, cos / 4- W, sin akf). z=i
Методика получения характеристического уравнения иллюстриро
вана ниже на примере двухконтурной схемы, изображенной на рис. 13-17.
Первый контур содержит сопротивления п и г3 и индуктивность L, второй контур содержит сопротивле-
ние. 13-17. Пример двухконтурной схемы.
ния г2 и г3 и емкость С; поэтому порядок дифференциального уравнения для каждого из этих контуров равен единице:
гз (й 4- й) + ri й Ч~ £ = е;
at
fs (й ~Ь й) й *1 У й dt —
Соответственно степень характеристического уравнения равна двум.
Для получения характеристического уравнения применяется следующий прием. Система однородных дифференциальных уравнений для свободных слагающих токов
гз (йсв + йсв) 4- fi йен + L. - j- =0; at
гз(йсв + ^*2св) “Ь ^2 Ajcb 4-
+ ~ f йсв dt = О
записывается в символической алгебраической форме, при которой символ р заменяет операцию дифференцирования, а символ 1/р— операцию интегрирования:
(ri 4~ гз + pL) йсв 4- rs йсв — 0;
Г3 Йсв + р2 + Г3 н-~?)йсв = 0-
\ рс /
Данная система уравнений имеет решение, отличное от нулевого, если определитель системы равен нулю, т. е.
G 4- Гз 4- PL Гз
215
или
(G+'a + pL){ Г2 + r3 + -M - rl =
= -L {(r2 + r3) LCp2 4- [(r, rz+ pt.
+ riz’s~l_r2rs)^ + ^]p + ri + ra}=:0-
Таким образом, получается характеристическое уравнение второй степени:
(г2 4- г3) LCp2 4- [(г l г2 4-г1г34-
4- rzr3)C 4- L| р 4- Tj 4- гя = 0.
Ввиду прямой пропорциональности, существующей между входным сопротивлением цепи Z(p) и определителем системы Д(р) [(5-9) в § 5-5], то же характеристическое уравнение получается и по формуле Z(p)=0.
Обобщенное сопротивление Z(p) получается из комплексного сопротивления Z(/co) заменой /со на р. При этом, разомкнув любую ветвь в пассивной цепи, находим в месте размыкания входное сопротивление Z(p) *.
Если характеристическое уравнение имеет степень п, то искомыми являются п постоянных интегрирования (Л1, Л2, .... Л„), входящих в выражение (13-26) **. Постоянные интегрирования находятся в результате решения системы п уравнений, соответствующих моменту времени #=0. Эта система уравнений получается путем (п—1)-кратного дифференцирования уравнения (13-26):
«с8(0) = Ч0)-1-пр(0)=1;Л,:
*==1
4=1 _ } (13-27)
(0) = t"_1(0)-i<"-1>(0) =
= S р1~' Аь • fe=l
* Предыдущие рассуждения основывались иа уравнениях контурных токов. Аналогично, исходя из метода узловых напряжений, можно показать, что У(р)=0 также является характеристическим уравнением, если под У(р) подразумевать обобщенную проводимость между любыми двумя узлами заданной схемы пассивной цепи.
** Методика вычисления постоянных интегрирования остается такой же и в случае кратных или комплексных корней характеристического уравнения.
Значения свободного тока и его производных при f=0, входящие в (13-27), находятся предварительно на основании законов коммутации (§ 13-2) и уравнений Кирхгофа.
Для определения начальных значений токов и напряжений в цепи можно для наглядности воспользоваться схемой замещения, которая составляется из исходной схемы после коммутации, если заменить индуктивности идеальными источниками токов с токами, равными оДО), а емкости — идеальными источниками напряжений с э. д. с., равными цс(0). Эта схема замещения справедлива только для /=0.
При нулевых начальных условиях индуктивность равносильна разрыву ветви, а емкость — короткому замыканию.
По этой схеме замещения можно найти другие токи и напряжения в момент t—О, если воспользоваться уравнениями Кирхгофа или правилами преобразования схем.
Итак, в соответствии со сказанным выше расчет переходного процесса классическим методом проводится в следующем порядке:
1. Производится расчет режима до коммутации, из которого определяются конечные значения (т. е. при t=0—) функций, не изменяющихся скачком (токов в индуктивностях, напряжений на емкостях). Далее с использованием законов коммутации находятся независимые начальные условия, т. е. Д(0), ис(0).
2. Составляется система дифференциальных уравнений Кирхгофа, описывающая процесс в цепи после коммутации.
3. Находится общее решение системы однородных дифференциальных уравнений.
4. Находится тем или иным методом частное решение системы неоднородных дифференциальных уравнений, указанных в п. 2, соответствующее принужденному режиму цепи.
5. Определяются зависимые начальные условия для искомых функций на основании найденных в п. 1 независимых начальных условий и уравнений Кирхгофа из п. 2, примененных для /=0.
216
6. По начальным условиям определяются постоянные интегрирования, содержащиеся в общем решении.
7. Найденные принужденные и свободные токи и напряжения складываются
Приведенный ниже пример 13-1 иллюстрирует нахождение начальных условий; в примере 13-2 дан численный расчет переходного процесса в цепи (рис. 13-17).
Пример 13-1. В цепи, изображенной на рис. 13-18, моменту /=0 предшествовал установившийся режим постоянного тока. При t=0 замкнулся контакт К. Найти начальные значения тока в индуктивности
и напряжений на емкостях и их первых производных.
Независимыми начальными условиями будут ток в индуктивности i4(0) =/4(0—) =
Е
= г и напряжения иа емкостях их (0) = =п1(0—) и щ>(0) =и2(0—).
Напряжения на емкостях до коммутации находятся из условий равенства их зарядов (так как емкости соединены последовательно) и равенства суммарного напряжения на емкостях напряжению на сопротивлении гц
Ci«i(0—) = С2и2 (0 —);
«1 (0 -) + «2 (0 -) = ГХ 43 (0- )=г, U (0-), откуда
И1 (0 —) = г14 (0—) — ~~—;
'-‘i + t-г
и2 (0-)=ПЧ(0-)—.
G1 Т С-г
1 В случае, когда э. д. с. изменяется в виде импульса, имеющего кусочно-аналитическую форму, представляется часто целесообразным применять интеграл Дюамеля (§ 14-11).
Требуемые зависимые начальные условия определятся из уравнений
du, „
Ci -/(О) = 4(0) at
и
с2 (0) = z2 (0)
токи же й(0) и »2 (0) — из уравнений Кирхгофа после коммутации:
Е = r2 4 + Uj + u2: иг = 4 is,
4 4- 4 = 4 + 4 = 4-
Подстановка в эти уравнения найденных значений i4(0), щ(0) и «г(0) дает:
. £_U1(0)-U2(0)
4 (0) =-----------------;
г2
4 (0) = i5 (0) — is (0);
4 (0) = 4 (0) — 4 (0) и далее
at Ci
^?(0)= dt С2
Начальное значение производной тока в индуктивности определяется также из уравнения Кирхгофа:
dit
£ = г2 4 4~ О 4 4~ £ ,
откуда при t=0
dit = £ — 4 4 (0) — 4 4 (0)
dt ( ' L
Пример 13-2. Определить ток i в цепи (рис. 13-17), если известно, что е=Е= 100 в; 4=5 ом; г2—3 ом; 4=100 ом; £=0,1 гн; С=100 мкф; «с(0)=0.
Подстановка заданных величин в приведенное выше характеристическое уравнение дает:
1,03-Ю^р2 4-0,1815 р+ 105 = 0 или
р2 4- 176 р 4- 1,02- 10s = 0;
корни характеристического уравнения — комплексные:
р12 = —88*:/307.
Искомый ток
4 = Чпр 4- 4св-
Принужденный ток
100
'1ПР 105 °’952
217
Свободный ток
11св = e~№t(A1el3077 + Л2₽-'‘307') =
= е-88 '(М cos 307 1 4- N sin 307t).
В начальный момент li(0)=0; следовательно, 0=0,952+44, откуда М =—0,952.
Производная тока по времени
= е~88' (— 307 М sin 307 t + dt
+ 307 N cos 307t) — 88 e-887 (Л4 cos 3071 + + N sin 307 C- -
В начальный момент flc(0)=0;
100
i1(0)=0 и i2(0) = — = 0,971 й.
Следовательно, в начальный момент напряжение на ветви г2С (и на параллельной ей ветви п£) равно 3-0,971=2,913 в. Начальное значение производной diJdt(O) опреде-dit Л ляется из уравиеиня 2,913=0,1 (0), от-
di’i
куда ^-(0) =29,13.
Следовательно, подставлия значение dij
— (0) в выражение для производной при dt
1=0, получаем:
29,13 = 307IV — 88Л4 = 307 N + 83,8,
откуда
N = — 0,178
Итак,
11 = 0,952 — е-88' (0,952 cos 3071 + + 0,178 sin 3071), а.
13-8. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
13-1. Сопротивление г=1000 ом и незаряженная емкость С=1 мкф, соединенные последовательно, подключаются при 1=0 к источнику постоянной э.д.с. £=100 в. Вычислить ток и первую производную тока по времени для 1=0, не находя функциональной зависимости 1(1).
Ответ: 1(0) =0,1 с;
di
—— (0) — — 100 а!сек.
dt
13-2. Сопротивление г=10 ом и индуктивность L=I гн, соединенные последовательно, приключаются при 1=0 к источнику э.д.с. £=100 в. Вычислить ток и первую производную тока по времени для 1=0, не находя функциональной зависимости 1(1).
dt
Ответ: 1 (0) = 0; —— (0) = 100 а/сек. dt
13-3. Сопротивление г=10 ом и незаряженная емкость С=10 мкф, соединенные
218
последовательно, приключаются при 1=0 к источнику э. д. с. 10 е~‘ sin 1, в. Определи гь 1(1).
Ответ:
1 = 10—4 е~* (cos 1 — sin 1) — I0-4 е~10<7, а.
13-4. Цепь, состоящая из последовательно соединенных сопротивлений г=75ож, индуктивности L=3-10~4 гн и незаряженной емкости С = 12-10~10 ф, подключается при 1=0 к источнику постоянной Э.Д.С. £=100 в. Определить 1(1).
Ответ: i = 0,2 e~12's l0‘zsin (1,66-10«1),о.
13-5. Сопротивление г=20 ом и емкость С=5 мкф, соединенные последовательно, подключаются при 1=0 к источнику постоянной э.д.с. £=25 в. Определить 1(1), если начальное напряжение иа емкости равно 50 в.
От в е т: i = 3,75 е~10<7 ,а, или i = — 1,25 е~т, а.
13-6. Сопротивление г=50 ом и незаряженная емкость С=3,75 мкф, соединенные последовательно, подключаются при 1=0 к источнику э.д.с. £=20 в. Определить 1(1).
Ответ: 1 = 0,4 е~53337 ,а.
13-7. В цепи (рис. 13-17) г2=0 и е=Е. Определить: 1) напряжения иа rt и на L для 1=0 и 1= со;
2) первые производные напряжений на Г] и на £ по времени для 1=0.
Ответ: flri(0) =иь(0) =0;
«п (°°) = Е —: uL (со) = 0; Г1+т8
dfln dt
(0) = 0;
du, dt
E rs/C
13-8. Заряженная емкость С! = 10 мкф с начальным напряжением 1000 в присоединяется при 1=0 к двум параллельным вет-> вям. Первая ветвь состоит из одного сопротивления Г1 = 10с ом, вторая ветвь состоит из сопротивления г2=2-10с ом и незаряженной емкости С2=20 мкф, соединенных последовательно. Вычислить вторую производную тока вс второй ветви для 1=0, не находя функциональной зависимости от времени.
Ответ: 1,41 • 10-6 а/сек2.
13-9. Сопротивление г=100 ом и заряженная емкость С=100 мкф, соединенные последовательно, приключаются к источнику э.д.с. е =141 sin (3771+л/б) в при 1=0. Определить i(t), если начальное напряжение иа емкости равно 50 в.
Ответ: 1 = 1,37 sin (3771 + 44°48') + + 0,241с-1007, а,
или 1 = 1,37 sin (3771 + 44° 48') —
— 0,759e~ltx)7,fl.
13-10. Возможно ли включение на переменное гармоническое напряжение контуров г, L; г, С н г, L, С, не сопровождаемое переходным процессом (пояснить физическую сторону явления).
13-11. Может ли частота колебательного разряда в контуре г, L, С быть равной или больше резонансной частоты этого контура?
13-12. Пояснить физический смысл постоянных времени цепей г, L и г, С. Почему с увеличением г-постоянная времени для
первого контура уменьшается, а для второго контура увеличивается?
13-13. Цепь г, L подключается при 1=0 к источнику гармонической э.д.с. Выбрать начало отсчета времени так, чтобы свободный ток отсутствовал.
13-14. Изменив в схеме рис. 13-6 полярность заряженной емкости, начертить кривые тока и напряжения при включении в цепь г, С постоянной э.д.с.
13-15. Зависит ли характеристическое уравнение (и соответственно порядок цепи) от воздействующей функции?
2’9
Глава четырнадцатая
ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА К РАСЧЕТУ ПЕРЕХОДНЫХ ПРОЦЕССОВ
14-1. ОБЩИЕ СВЕДЕНИЯ
Необходимость определения постоянных интегрирования из начальных условий в ряде случаев сильно осложняет расчет переходных процессов классическим методом решения линейных дифференциальных уравнений, обыкновенных или с частными производными, описывающих исследуемые процессы. По мере усложнения электрических схем и возрастания порядка дифференциальных уравнений трудности, связанные с нахождением постоянных интегрирования, увеличиваются.
Для инженерной практики более удобным является метод решения линейных дифференциальных уравнений, при котором заданные начальные условия включаются в исходные уравнения и для нахождения искомых функций не требуется дополнительно определять постоянные интегрирования.
В прошлом столетии в математике развивалось так называемое символическое исчисление, построенное на системе формальных операций над символом р: производная df(t)/dt представлялась как результат действия на функцию f(t) символа р; операция интегрирования рассматривалась как применение символа 1/р и т. д. В числе работ, посвященных этому вопросу, большого внимания заслуживает моно
графия М. Е. Ващенко-Захарченко «Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений» (Киев, 1862).
В конце XIX в английский инженер-электрик О. Хевисайд успешно применил и развил символический метод решения линейных дифференциальных уравнений для расчета переходных процессов в электрических цепях с сосредоточенными и распределенными параметрами. Строгое обоснование символического или, как его стали называть, операционного исчисления было дано лишь в 20-х годах нашего столетия на базе общей теории функциональных (интегральных) преобразований.
В настоящее время формальнооперационное исчисление Хевисайда полностью вытеснено более общим и строгим методом—преобразованием Лапласа, нашедшим широкое применение в технике.
Идея этого метода заключается в том, что из области функций действительного переменного решение переносится в область функций комплексного переменного1 р=с+/<п, где операции принимают более простой вид, а именно: вместо исходных
1 В современной литературе наряду с обозначением комплексного переменного р широко распространено также обозначение s.
2’9
дифференциальных или интегродиф-ференциальных уравнений получаются алгебраические уравнения; затем полученный решением алгебраических уравнений результат «интерпретируется», т. е. производится обратный переход в область функций действительного переменного. Этот переход осуществляется с помощью формул или таблиц.
В этом отношении преобразование Лапласа можно сравнить с логарифмированием, когда от чисел переходят к логарифмам, над логарифмами производят действия, соответствующие действиям над числами, причем умножению чисел соответствует более простая операция сложения логарифмов и т. д.; наконец, по найденному логарифму определяют искомое число (пользуясь таблицами).
14-2. ПРЯМОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ОРИГИНАЛ
И ИЗОБРАЖЕНИЕ
Пусть f(t)—функция действительного переменного t, заданная в области />0 и равная нулю при /<0, возрастает не быстрее показательной функции, т. е. |/(01 < <Мес°‘ при 1>0; здесь М и с0 — постоянные (положительные и действительные); t — переменное (время). Постоянная с0 называется показателем роста функции f(t). Говорят, что функция имеет ограниченный рост, если показатель роста конечен.
Из курса матам этического анализа известно, что если /(/) имеет ограниченный рост, то интеграл
оо
F(p)^f(t)e~p‘dt (14-1) о
сходится абсолютно и является аналитической функцией комплексного переменного p = c-rju> в полуплоскости Re р = с>с0 (рис 14-1).
Интегральное уравнение вида (14-1) представляет собой прямое преобразование Лапласа. Функция f(t) называется оригиналом, а функция F(p) — изображением по Лапласу. Следовательно, оригинал и изображение представляют
собой пару функций действительного переменного t и комплексного переменного р, связанных преобразованием Лапласа.
Из определения изображения следует, что каждый оригинал име-
Рис. 14-1. Комплексная плоскость.
ет единственное изображение. В свою очередь оригинал вполне определяется своим изображением с точностью до значений в точках разрыва оригинала.
Фразу «оригинал f(t) имеет своим изображением F(p)» будем записывать символически (с помощью знака соответствия = ):
/(О=Г(р) или F(p) = f(O-
Такая сокращенная запись равносильна интегральному уравнению (14-1). В литературе применяется также и другая условная форма записи прямого преобразования Лапласа, а именно:
L[f(O] = F (р).
Для обоснования операционного исчисления Хевисайда в свое время использовалось изображение по Карсону1
F(p) = p отличающееся от изображения по Лапласу множителем р.
В настоящее время в теории автоматического регулирования и в радиотехнике применяется преобразование Лапласа, имеющее прямую связь со спектральным преобразованием Фурье (гл. 15). Поэтому все последующие рассуждения будут относиться к изображениям по Лапласу, а не по Карсону.
1 Изображение по Карсоиу имеет ту же размерность, что и оригинал, однако эта особенность ие имеет для практики существенного значения.
220
14-3. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ ПРОСТЕЙШИХ ФУНКЦИИ
При исследовании переходных процессов в электрических цепях часто предполагается что в некоторый момент времени, принимаемый за начальный (1=0), в электричес-
О
Рис. 14-2. Единичная функция.
кую цепь включается источник постоянной, гармонической или какой-либо другой э. д. с., выражаемой функцией f(t). Для всех значений ^<0 функция f(t) принимается равной нулю; это означает, что данная э.д.с. не воздействует на рассматриваемую электрическую цепь до момента ее включения.
Если функция f(t) имеет ограниченный рост, то на основании § 14-2 она рассматривается как оригинал.
Простейшими оригиналами являются единичная и показательная функции.
Единичная функция (рис. 14-2), заданная условием
f(ft = ( 1 * * при z>°; ( 0 при t < 0, соответствует случаю включения постоянной э. д. с., равной 1 в.
Единичная функция имеет условное обозначение 1(1). Однако для простоты записи в дальнейшем будем условно писать [(/) = !, помня, что всякий оригинал (в том числе и единичная функция) по определению равен нулю при 1<0.
Изображение единичной функции согласно (14-1) имеет вид:
Следовательно, 1=— При Rep>01. (14-2) ___________Р
1 При Re р < 0 интеграл расходится.
Умножение единичной функции на любую функцию времени оставляет последнюю без изменения при 1>0 и дает нуль при 1<0.
Поэтому, умножив, например, единичную функцию на показательную функцию е’4, получим функцию-оригинал
e4t при 1 > 0;
Г() I 0 при /< 0,
для которой, применяя в дальнейшем сокращенную запись
условно сохраним название показательной функции1.
Найдем изображение этого оригинала, полагая, что q — произвольное комплексное число:
F (р) = e~pt е”1 dt =
О
со
I _ 1
p — q Г p — q о
при Re(p—q)>0, т. е. при Rep> >Re#. Итак,
еч‘ = —!— при Re р > Re#. (14-3) р —<7
Полученное выражение справедливо также для действительных или мнимых значений #.
14-4. ОСНОВНЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Математическим операциям над оригиналами соответствуют определенные операции над изображениями, и наоборот
Знание этих операций или. как их называют, свойств преобразования Лапласа облегчает нахождение изображений: оно позволяет переходить от дифференциальных (или интегро-дифференциальных) уравнений. записанных для функций-оригиналов к «операторным» уравнениям, записываемым для изображений. и облегчает последующее нахождение искомого оригинала по вычисленному изображению.
1 Данная условность распространяется
и на другие функции времени, косинусои-
дальные, синусоидальные и т. д.
221
Основные свойства преобразования Лапласа, известные из курса математического анализа, приведены в табл. 14-1. Во всех соотношениях предполагается, что f(t) == f(p)-
Пользуясь соответствием (14-3) и свойством линейности преобразования Лапласа (изображение линейной комбинации есть линейная комбинация изображения), легко найти изображения следующих функций-оригиналов, часто встречающихся в задачах по электротехнике:
е/(ю,Н-Ф) е'ф _ (14-4)
sin (оц t + ф) = [ е/(“‘/+ф)—
+ W]
р sin ф + <и, cos ф . (14-5)
р2 + о>2
COS(оч t + ф)^ Рсозф-^вф^ (14.fi) р2 + со2
Такие изображения соответствуют, например, э. д. с., включаемым в электрическую цепь, если эти э.д.с. задаются в комплексной (показательной), косинусоидальной или синусоидальной форме (амплитуда равна единице).
Ниже приводятся дополнительные разъяснения к табл. 14-1 и применение некоторых свойств преобразования Лапласа иллюстрируется на примерах.
Особого внимания заслуживают преобразования, связанные с дифференцированием и интегрированием оригиналов (теоремы дифференцирования и интегрирования).
По теореме дифференцирования
Г (t)~pF(p)-f(G). (14-7)
Здесь под f(0) подразумевается предел /(0+), к которому стремится f(t), когда t неограниченно убывает, оставаясь положительным. В случае, когда оригинал в начальной точке непрерывен, т е. f (0) = =f(0—)=0, его дифференцированию соответствует операция умножения изображения нар:
f(t)-FpF(p). (14-8)
Повторным применением операции, выражаемой формулой (14-7), можно распространить теорему о дифференцировании на производные высших порядков:
/"(() = р[рР(р)_/(0)]-Г(0) = = P2F(p)-pf(0)-f(0)
и т. д.» откуда
п
fw (0 = рп F (р) - S (0) p(n~k\
k=l
где f(h~^(0)—правое предельное значение, т. е.
lim (0.
Если, в частности, f(O)=f'(O) = = ... =f(n-D(0)=0, то
f(0=pnF(p)
и, следовательно, п-кратному дифференцированию оригинала соответствует n-кратное умножение на р (если все производные при t=0 равны нулю).
По теореме интегрирования
t
f/(()d/=-L(PL. (14.9)
Повторное применение операции, выраженной этой формулой, дает:
t t
(14-10)
о о
Теоремы дифференцирования и интегрирования показывают, что комплексное переменное р можно рассматривать как оператор (отсюда и наименование «операторный метод»).
По теореме запаздывания
f(t-t0)^e~^F(p). (14-11)
Формула (14-11) показывает, что умножение изображения на е~ ро сдвигает график оригинала вправо на t0 (рис. 14-3).
Пример 14-1. Найти изображение функции (рис. 14-4, а)
f (t) = I е~°* при 0 < * < ta’ (0 при t > t0
(а—положительное действительное число).
222
Таблица 14-1
Основные свойства одностороннего преобразования Лапласа
Наименование Формула
Свойство линейности (р) 1=1 1=1
Свойство коммутативности преобразований Лапласа и операций Re и Im Re / (Z) == Re F (р) Im f (t) = Im F (p)
Дифференцирование оригинала (теорема дифференцирования) r(O~₽F(p)-/(O)
Интегрирование оригинала (теорема интегрирования) t C f (t) dt = F(p) f J ' p 1 °
Дифференцирование изображения 1 d" F (p) d pn
Интегрированна изображения co I 1 F (p) dp V ( ' J
Дифференцирование по параметру d d ——f (t, x) =F (p, x) dx dx
Интегрирование По параметру X X J f (t, x) dx== J F (p, x) dx *0 Xo
Изменение масштаба независимого переменного (теорема подобия) 1 / p \ /(a 0 = — F — a \ a /
Смещение в области действительного переменного (теорема запаздывания) /(r-f0)==e-₽/"F(p)
Смещение в области комплексного переменного (теорема смещения) e±k/f(O=F(p=i=*)
Предельные соотношения: начальное значение оригинала конечное значение оригинала lim/ (/) = lim pF (p) t~+0 P-*-GO lim / (t) — lim pF (p) /-*00 p-»0
Умножение изображений (теорема свертывания) f fl (T) f2 (t — T) d т = F! (p) F2 (p)
Следствие теоремы свертывания t d f — I /i (т) /2 (< — r) d т = p f! (p) F2 (p) di j
Интеграл Дюамеля t fi (0) f2 (П + г h (T) f2 (t — t) d T = h (t) f2 (0)4-b i +| fi (т) fi (t — t) d т pFi (p) Fа (p)
223
Продолжение табл. 14-1
Наименование Формула
Умножение оригинала на косинус или синус / (Г) cos t == — F(p —/coj 4-F(p + /a>i) 2 / (Г) sin сох t = | f (р — j <ох) — F (p -f- /соО 1 2/ L J
Согласно (14-1)
F (р) = j e~at e~pt dt=
О
= —!— 11 — e- <₽+a)fol, p + a '
Рис. 14-3. Смещение в области действительного переменного.
Тот же результат получится, если рассматривать j(t) как сумму двух функций, показанных на рис. 14-4,6: f(O=fi(O+f»(O-
Функция ti(t) имеет изображение—;— .
Поэтому в соответствии с (14-11) функция fa(t) имеет изображение
е~е—Pt>
Р + а
Искомое изображение функции f(t) в силу линейности преобразования Лапласа равно:
-1— р + «
Рис. 14-4. Пример 14-1.
Пример 14-2. Найти изображение полупериода синусоиды (рис. 14-5, а) с амплитудой, равной единице, н с основанием, равным Т/2.
Такой импульс можно получить сложе-
нием двух синусоид, сдвинутых на полпериода (рис 14-5,6). По теореме запазды-
вания
f(p) =
Ь>1 -Р-2
P2+(£>1 P2+Wt
—Р—
Пример 14-3. Найти изображение «выпрямленной» синусоиды, т. е. функции f(t) =sin|<i>i<| (рис. 14-6).
Заданная кривая получается периодическим повторением полуволи синусоиды, для которой в предыдущем примере найдено изображение F>(p). По теореме запаздывания изображение «выпрямленной» синусоиды будет:
( — —
F(P)= (Р)П + е Р'2 +е~рт+...
Рис. 14-5. Пример 14-2.
Fi (р)
Следовательно,
224
Ц>1
р2 + “>?
р л cth—-
2(0!
Пример 14-4. Найти изображение пилообразной функции (рис. 14-7, а).
Заданная пилообразная кривая получается периодическим повторением кривой (рис. 14-7,6). Последняя слагается из трех
г
Рис. 14-6. Пример 14-3.
Рис. 14-7. Пример 14-4.
функций: прямолинейных 1 н 2 и единичной 3. Тангенсы углов наклона прямых равны соответственно 1/Т н —1/7".
По таблице приложения IV и теореме запаздывания рассматриваемая кусочная функция fi (0 имеет изображение
„ 1 е РТ е~рТ
1{P^~Tpi р ~ Тр*
То же получится, если применить непосредственно формулу (14-1) н вычислить интеграл F1(p) = f-y e~ptdt.
Изображение заданной функции f(t) находится сложением изображений одинаковых треугольников с учетом сдвига:
f (Р) = Л (Р)(1 + е~рТ + е~2рТ +-•) =
= = 1 _ е~РГ 1_е-₽т р(1_е-рту
Теорема смещения
e**f(t)^F(p + Л) (14-12) показывает, как изменяется изображение при умножении оригинала на показательную функцию. При этом следует иметь в виду, что число X может быть как действительным, так и комплексным. Если F(p) определено при Re р> Со, то изображение
(14-12) определено при Re р>с0± ±ReA.
Предельные соотношения. Первое предельное соотношение согласно табл. 14-1
lim f (f) = lim pF (p) (14-13) /-*0 p-+oo
дает возможность найти начальное значение функции f(t) при f=0 непосредственно по изображению. Эта формула устанавливает существование равенства между двумя частными значениями: значением функции f(t) в начале координат (при подходе справа) и значением функции F (р) в бесконечно удаленной точке (в предположении, что р стремится к бесконечности внутри угла |argp|<n/2, т. е. в правой полуплоскости).
Второе предельное соотношение lim f (f) = lim pF (p) (14-14)
t-*co
дает возможность найти предел функции f(t) при t->~oo по значению функции F(p) в начале координат.
Эта формула имеет смысл только в том случае, когда предел функции f(t) при f—>-оо существует.
Предельные соотношения (14-13) и (14-14) полезны для проверки вычислений с помощью преобразования Лапласа.
Теорема умножения изображений (теорема свертывания)
t
Pi (Р) Fа (Р) = f fi (т) f2 (t—r)dx (14-15) 6
устанавливает, что умножению в области комплексного переменного соответствует свертывание в области действительного переменного.
Если произведение представляет собой произведение более чем двух сомножителей, то теорема свертывания может быть применена к попарно сгруппированным сомножителям (в любом порядке).
Применение интеграла Дюамеля pF1(p)F2(p)=/1(0)/2(f) +
+J f;(t)f2a-T)dT=/](o/2(O) +
+ f (14-16)
15—1118
225
облегчает вычисления по сравнению с формулой
РЛ (Р) (Р) =
t
”™П1(т)/2а-т)Л (14-17) ar J
о
в тех случаях, когда после дифференцирования функции Л(т) или /2(/—т) подынтегральное выражение упрощается и вычисление интеграла в результате этого облегчается. Следует иметь в виду, что функция
—т) в (14-16) дифференцируется по переменной t.
В § 14-11 будет специально рассмотрен метод расчета переходных процессов в электрических цепях с помощью интеграла Дюамеля.
14-5. НАХОЖДЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ С ПОМОЩЬЮ ОБРАТНОГО ПРЕОБРАЗОВАНИЯ
ЛАПЛАСА
Из теории функции комплексного переменного известно, что если функция F(p) аналитична в полуплоскости Rep > Со, стремится к нулю при | р | ->оо в любой полуплоскости Rep=c>c0 равномерно относительно аргумента р и интеграл с-н°°
J F(p)dp абсолютно сходится, C—joQ то F(p) является изображением функции
с+/“
f F(p)^dp. (14-18)
С—joe
Эта формула, носящая название обратного преобразования Лапласа, представляет собой решение интегрального уравнения (14-1) относительно функции f(t).
В литературе применяется также условная форма записи обратного преобразования Лапласа:
L ’’ [F(p)] =/(0-
За путь интегрирования в (14-18) может быть принята любая бесконечная прямая, параллельная мнимой оси, расположенная на расстоянии с>с0 от последней (рис. 14-1), так чтобы все особые точки функции F(p) оставались левее пути интегрирования. Интеграл в (14-18)
принимается в смысле главного значения *.
При практическом применении обратного преобразования Лапласа путь интегрирования вдоль прямой, параллельной оси мнимых величин, заменяется замкнутым контуром1 2, что дает возможность применить теорему о вычетах, согласно которой оригиналом F(p) служит функция /(0 = 2 ResF (р) d* (t > 0), (14-19)
Pk
где сумма вычетов берется по всем особым точкам ph функции F(p).
При f<0 функция f(t) равна нулю.
Формула (14-19) позволяет вывести теорему разложения (§ 14-6) применительно к мероморфной функции F(p), т. е. когда особенности интегральной функции в конечной области — только полюсы.
14-6. ТЕОРЕМА РАЗЛОЖЕНИЯ
Пусть изображение задано в виде правильной дроби F(p)= ,
FAp) причем числитель и знаменатель не имеют общих корней. Положение полюсов функции F(p) определяется корнями уравнения
Га(р) = 0. (14-20)
Обозначим п корней уравнения (14-20) через plt р2, .... рп- При этом возможны два случая: а) все корни простые; б) некоторые или все корни кратные.
Рассмотрим эти случаи в отдельности.
а) Случай простых корней. Из теории функций комплексного переменного известно, что вычет функции <р(р)/ф(р) по полюсу первого порядка р=Рь равен:
ResJ₽w_ = Г(р_ =
pk ф(р) L 'Ф(р)1р=рд,
= Ф(РЛ1. (14-21)
Ф' (Pk)
1 То есть как предел интеграла вдоль отрезка (с — /ы, с+/ш) при ы-»оо.
2 Возможность такой замены основывается на лемме Жордана.
226
Если, как в формуле (14-18), функция комплексного переменного
FilP)
р имеет вид причем все
F8 (р) г
корни уравнения (14-20) простые (полюсы первого порядка), то на основании (14-19) и (14-21)
Л(р) ...
f2(p) ‘
2^ rf2(p> 1
*=1 LP— P*JP=Pfc п
_ V fi (pa)ePft< (14-22) F? ( Pk)
k=i
Это — общая форма теоремы разложения для случая простых корней. Выражение в квадратных скобках в знаменателе сначала надо сократить на множитель (р—рь), после чего произвести подстановку Р=Рь-
В случае комплексных корней получаются два сопряженных слагаемых, сумма которых равна удвоенному значению действительной части (пример 14-11).
Пример 14-5. Пользуясь теоремой разложения (14-22), найтн оригинал по изображению
________1________
Р (Р + а) (Р + Ь)
В данном случае Fi (р) = 1;
fa (Р) = Р (Р + о) (Р + Ъ).
Кории уравнения F2(p)=0 равны соответственно
Р1 = °; Ра = — «J Рз = — ь. Следовательно, на основании (14-22)
__________1
Р (Р + а) (р + Ь)
ё~^ е~ы
<_«)(— а 4-5) + (-Ь)(-Ь + а)
1 ae-bt — be-at ab ab(b-~a)
б) Случай кратных корней. До-
пустим, что корень рк повторяется
m раз. Из теории функций ком-
плексного переменного известно,
что если функция имеет в
fa (р)
точке pk полюс порядка пг, то вычет функции в этой точке равен:
Pk Ft(p) (m— 1)!
d"1-1 FAP) dpm~l Ft (p)
(р-РкГ^\
]p~Pk
х
Как и в предыдущем случае, все операции производятся после сокращения множителя (р—Ра)”1-Обозначив 4(р) = -г^ (р—ph)m, Ft(p) продифференцируем А(р)е?‘ по р пг—1 раз:
-^A(p)ept = ept[iA(p) + A'(p)];
~A(p)eP‘ = eP‘[t2A(p) +
+ 2tA'(p) + A"(p)];
^-±A(p)epi = epl[tm~IA(p)^ + (пг-1)Г-2Л'(р) +
+ (т ~ ~ 2) /т_3 А" (р) +
+ • • • + Л^’р]*. Следовательно,
ResfdeLe*-^ Г-^~_2.<р) +
Ph Ft(p) [ (m —1)1
, tm~2A-(p) , ^-3Л"(Р) ,
(m —2)! (m — 3)!21
(m—1)! _p=pk
m
epkt у tm-б) * * * lAll-r, (Pk) .
Xj (m-i)!(i-l)! i=i
(14-23)
Формула (14-23) универсальна; она справедлива для любого корня. Здесь предполагается, что 0! = 1. По
• То же получается непосредственно по формуле Лейбница
(ио)(я) = uv^ + пи' о<п—9 +
+ П и(2) и(»-2)+ ... + „(»)
15*
227
этому если в (14-23) принять zn=l, то получится выражение
A* t°A°(Pk) _ Fijpk)^
О! О! ГРв(р) 1
IP—PfcJ₽=₽fc
соответствующее случаю простого корня Pk.
Это в равной мере относится и к приведенной выше исходной формуле вычета функции в полюсе порядка т, которая при т=1 переходит в формулу (14-21).
Если уравнение (14-20) содержит несколько кратных корней, то формула (14-23) применяется поочередно для каждого корня, после чего полученные результаты суммируются.
Если имеются одновременно простые и кратные корни, то формулы (14-22) и (14-23) применяются раздельно соответственно для простых и кратных корней; затем производится суммирование.
Пример 14-6. Найти оригинал по изображению
Fi(p) __ р + 2
Fa(p) (р-1)»Р”
Заданная функция имеет полюс второго порядка pi=l и полюс третьего порядка Рг=О. Применив формулу (14-23) поочередно для случаев т=2 и т=3, получим:
tp + 2 Ра
d Р +21
dp р* Jp=i
= (3t — 8)е‘;
р + 2 i.f d р + 2
. 2 (р-1)» dp (р-1)» +
Id’ р + 2 1
Следовательно,
•^Ь^<з'-«)е'+',+а+8-
Другой способ нахождения оригинала при наличии кратных корней, не требующий дифференцирования, заключается в том, что заданное дробное рациональное выражение раскладывается на простые дроби: для перехода от простых дробей к оригиналу используется соответствие
---!—- = —!— tl~l & .
(Р-Р*У (*-1)1
Разложение на простые дроби может быть произведено известным в математике методом неопределенных коэффициентов, который, однако, связан с решением системы уравнений, что практически не всегда удобно.
Если заданная рациональная дробь имеет m-кратный полюс pk, то разложение на простые дроби может быть осуществлено непосредственным делением полиномов, расположенных по восходящим степеням р. Например, в рассмотренном выше примере в результате деления полиномов получаем:
Flip) = 2 + Р _ 2
Г2(р) р»-2р4 + р» р3 '
+ -L+JL 1 Пр8 —8р4
Р2 р “И рЗ — 2р4 + р®
Остаточный член в данном случае разлагается весьма просто:
8(рЗ_р«) + 3рв _ 8 з
(р-1)2рз р-1 (р-1)»'
Если имеется m-кратный полюс рь, отличный от нуля, то после замены р—pk=z производится деление полиномов, расположенных по восходящим степеням г.
Пусть, например,
Flip) = ря
Flip) (Р + 2)4(р + 1)*
Здесь ph=—2 полюс кратности 4.
Обозначив р+2—z и соответственно р=г—2; р + 1=z—1, получим:
(г — 2)3 —8+12г —6г» + г» _
г*(г—1) “ —г4 + г® “
___£ _2_ J 1
г4 г» г» г г — 1
Следовательно,
Flip) 8 4
Flip) (Р + 2)4 (р+2)3
+ ^-+-»-------------
(Р + 2)» Р + 2 р + 1
В заключение отметим, что для разложения Pi(p)/f2(p) на простые дроби при наличии /n-кратного полюса р* можно пользоваться формулой
Fi(P) Kt
Flip) —
228
где
KL =-----------A(m~n (pft).
(m —I)!
Данное разложение приводит к формуле (14-23).
14-7. ТАБЛИЦЫ ОРИГИНАЛОВ И ИЗОБРАЖЕНИИ
Теорема разложения для случаев простых и кратных корней (§ 14-6) в сочетании с другими свойствами преобразования Лапласа (§ 14-4) дает возможность составить таблицы оригиналов и изображений, сильно облегчающие и уско.-ряющие расчеты переходных процессов. Такие таблицы широко применяются на практике.
Наиболее полные таблицы приводятся в справочниках по операционному исчислению и в специальных трудах, посвященных преобразованию Лапласа. При практическом пользовании той или иной таблицей во избежание возможных недоразумений надлежит в первую очередь проверить форму записи изображения: дается ли изображение по Лапласу или по Карсону. Если изображение дается по Карсону, то в соответствии с § 14-2 его надлежит разделить на р для получения изображения по Лапласу.
В ряде типовых примеров, разобранных в предыдущих параграфах, были приведены оригиналы и изображения по Лапласу. Эти пары функций, а также некоторые другие, встречающиеся на практике, помещены в сводной таблице в приложении IV.
Возможность пользования таблицами оригиналов и изображений наряду с теоремами и различными свойствами преобразования Лапласа представляет большое удобство. Поэтому преобразование Лапласа широко применяется на практике для расчета переходных процессов в линейных электрических цепях. К этому следует добавить, что изображения по Лапласу, приводимые в таблицах, непосредственно связаны с гармоническим анализом непериодических функций (гл. 15), что делает этот метод еще более универсальным.
14-8. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА К РЕШЕНИЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Рассмотрим цепь с ненулевыми начальными условиями, показанную на рис. 14-8. Допустим, что в момент времени (=0 участок г, L, С подключается к источнику э.д.с.
Рис. 14-8. Включение источника э. д. с. в цепь с нулевыми начальными условиями.
e(t). Требуется найти изображение тока на этом участке.
По второму закону Кирхгофа для />0 имеем:
/
e=ri+L^~ + JLfidt+uc(Oy, (14-24) fll С J
О
здесь uc(0)—начальное напряжение на емкости, обусловленное электрическим зарядом емкости в момент коммутации.
Будем рассматривать e(t), ис(0) и i(t) как функции-оригиналы, имеющие изображения Е(р), ис(0)/р и /(р).
На основании свойств линейности преобразования Лапласа и теорем дифференцирования и интегрирования исходному уравнению (14-24) соответствует следующее уравнение для изображений:
Е (p)=r 1 (р)+рЫ (р) —
—+ + (14-25)
рС р
здесь i(0)—начальный ток в индуктивности.
Благодаря тому, что операциям дифференцирования и интегрирования оригинала соответствуют операции умножения и деления изображения на р, уравнение для изображений получается алгебраическим, т. е. более простым, чем ис
229
ходное интегро-дифференциальное уравнение. Его решение относительно 1(р) дает:
«о (°)
Е(Р)~ —— + П(0)
/(р) =---------Р----------. (14-26)
r+pL + -^ рС
Далее после преобразований получим:
"+т,’+й
Рис. 14-9. Включение ветви в цепь с источником тока.
Искомая функция l(t) (оригинал) находится по изображению (14-26а) одним из указанных выше способов, а именно: с помощью теоремы разложения (или других правил) или по готовым таблицам.
Для схемы, показанной на рис. 14-9, уравнение записывается по первому закону Кирхгофа (при t> >0, т. е. после подключения сопротивления г):
о
где i — ток источника тока;
и(/) — напряжение между узлами;
it (0) — ток в индуктивности при 7=0.
Полагая 1(1) =•!{#) и
находим:
/Со) = £М + рш(Р)-
— С«(0)+ + (14-27)
pL р
здесь и (0) — начальное напряжение между узлами, равное напряжению на емкости.
После преобразований получается изображение искомого напряжения
. 1 рГ (P) + рСи (0) — iL(0)
U(P) = —
1 1
Рг +р „ + rC LL, указанными выше
находится оригинал
для которого способами и (7).
При нулевых начальных условиях, т. е. при включении источников в пассивные цепи, выражения (14-26) и (14-27) упрощаются, а именно:
/ (о) = £<р) = £(Р)
w 1 Z (р)
r + pL+— рС
и
= + ± + pC\U(p)~
\ Г pL )
= Y(p)U(p);
здесь Z (р) и Y (р) представляют собой сопротивление и проводимость соответствующих цепей при комплексной частоте p=c+ja. Это те же сопротивление и проводимость, которые уже встречались ранее в гл. 13. Они называются обобщенными или операторны-м и сопротивлением и проводимостью.
В общем случае порядок решения задачи следующий:
1) записываются интегро-дифференциальные уравнения Кирхгофа для цепи, в которой исследуется переходный процесс;
2) записываются те же уравнения для изображений с учетом независимых начальных условий;
3) уравнения для изображений решаются алгебраически относительно изображения искомой функции;
4) на основе полученного изображения находится оригинал искомой функции.
При достаточном навыке или если схемы относительно просты, уравнения для изображений записываются непосредственно, без предварительного составления интегро-дифференциальных уравнений (примеры 14-8, 14-11 и др.).
В случае сложной схемы можно также обойтись без записи интегро-дифференциальных уравнений, если предварительно нарисовать эквива
23Q
лентную схему для изображений. Как видно из предыдущих рассуждений, такая схема отличается от схемы цепи для установившегося гармонического режима тем, что комплексные величины jwL и /соС заменяются соответственно на pL и рС и вместо комплексных функций времени вводятся их лапласовы изображения. Кроме того, при ненулевых начальных условиях в схе-
ния Кирхгофа непосредственно для изображения; структура этих уравнений аналогична структуре уравнений для установившегося гармонического режима. Сказанное проиллюстрировано в примере 14-7.
Если воздействующая функция, например э. д. с. источника, гармоническая функция, то переходный процесс можно рассчитывать в действительной или комплексной фор-
Рис. 14-10. Схемы замещения элементов для изображений.
му для изображений последовательно с индуктивностью включается дополнительный источник с э. д. с., равной 7.1д(0) (рис. 14-10, с), а последовательно с емкостью — дополнительный источник с э. д. с., равной uc(tylp (рис. 14-10,6).
В случае индуктивной связи между двумя элементами соответствующая схема замещения представлена на рис. 14-10,в. При коэффициенте связи £=1 имеют место соотношения:
L1 = ^l М; L2 = ^-М
И
ii(0)a>1=i2(0)a>2;
поэтому в этом случае в схеме замещения э. д. с. дополнительных источников взаимно уничтожаются.
После введения дополнительных источников записываются уравне-
ме. При комплексной форме расчета начальные значения токов в индуктивностях и напряжений на емкостях учитываются в виде комплексных амплитуд и уравнения записываются для изображений комплексных функций токов и напряжений. Искомые функции времени определяются действительной частью найденных комплексных оригиналов (пример 14-10). Любая из указанных здесь форм решения уравнений для изображений приводит в конечном итоге к необходимости нахождения оригинала по теореме разложения или по таблице; оригинал получается в виде суммы принужденной и свободной составляющих.
Вычисления во многих случаях могут быть облегчены, если предварительно рассчитать принужденный режим и определить по формулам (14-8) начальные значения свободных ТОКОВ В ИНДУКТИВНОСТЯХ I'lcb(O)
231
и свободных напряжений на емкостях пссв(О). Используя эти значения как начальные условия в уравнениях для свободного режима или в соответствующих эквивалентных схемах замещения с дополнительными источниками, но без основных источников, можно получить изображение свободного тока. Оно будет иметь более простой вид, чем изображение полного тока. Соответственно облегчится и нахождение оригинала по изображению. Полный ток определится как сумма принужденного тока, найденного отдельно, и оригинала свободного тока (пример 14-11).
Такой метод расчета целесообразен в том случае, когда принужден-
Соответствующие уравнения для изображений. если обозначить
li (Р) = 11^ «1 (0 и /8 (р) = /2 = i2 (0,
примут вид:
р COS if — <£>! sin if Ет '
р2 + <о?
1 \ j 1 ’ ’ РсГ1~Гэ + рС, “с (°)
+------£Л(0);
Р
О = (Гг Тгз+р£г + рС )
Рис. 14-11. Пример 14-7.
ный ток, входящий в состав полного тока, значительно усложняет лапласово изображение для полного тока и тем затрудняет нахождение оригинала.
Пример 14-7. Составить уравнения для изображений контурных токов схемы рис. 14-11, а после замыкания контакта. Начальные значения тока в индуктивности L и напряжения иа емкости С обозначим через й(0) и пс(0), приняв положительное направление напряжения иа емкости в направлении тока й. Уравнения по второму закону Кирхгофа для t > О запишутся так: dtt , е = Ет cos (ejj t + if) = rtit + Lt — +
III
Те же самые уравнения получаются и иа основании эквивалентной схемы рис. 14-11,6, составленной для изображений.
Пример 14-8. Найти токи в схеме рис. 14-12 после замыкания контакта.
Начальные значения тока в индуктив- • иости и напряжения иа емкости равны соответственно:
г»
и „с (0) = -1 Е.
Г1 + г3
На основании расчетной схемы можно иепосредствеиио написать уравнения по второму закону Кирхгофа для изображений:
у + UL(0) = (rs + pI)74;
t
+ r.(G-W+4- f -Ц)dt +«C(0);
G J
0 — r3it + Lt + rt (is —ii) + at
t
G J
Е иа (°) I , 1 \ , = I г3 + _ ) Is-
Р Р \ РС /
Отсюда
E+LIl (0)р Р (га + PL}
~ +iL(P)P
232
Переходя к оригиналам по формуле (14-22), находим:
Рис. 14-12. Пример 14-8.
По формуле (14-22) найдем оригинал
Рис. 14-13. Пример 14-9.
Пример 14-9. Определить ток в контуре цепи рис. 14-13 после размыкания контакта, если до размыкания в цепи был установившийся постоянный ток.
В задаче пренебрегают временем горения дуги на контакте; считается, что токи в индуктивностях Li и Lt уравниваются мгновенно. В § 13-2 указывалось, что решение такого рода задач основано на принципе непрерывности суммарного потокосцепления до и после коммутации.
Дифференциальное уравнение для данной цепи запишется так:
При /=0 токи в индуктивностях были д
«|(0—)=0 и ii(0—)=—. Начальным условием для переходного процесса после разрыва дуги будет:
L,la(0-) = (Ll + LI)i(0), откуда
Пример 14-10. В момент 1=0 цепь, состоящая из последовательно соединенных г и L, присоединяется к источнику гармонической э-д.с. e(/)=£'tncos (<0|/+ф).
Определить ток i(t), пользуясь комплексной формой расчета переходного процесса.
При t > 0
£те«“.<+Ф) = ri (f) + L .
Переходя к изображениям, приняв J(t)=I(p), получаем:
£те№----------= П (р) + pLl (р),
Р — 1ОЦ
откуда
Г ~ (р — / “i) (г + pL)
Оригинал находим по формуле (14-22):
/(/) =
г + jaiiL
Е — t
е--£ •
r + i^iL
I' (О— ) ЦО) =-^--------’-=±
И •+ l2
Переходя к изображениям, напишем:
— = г/ (р) + (Li + Li) р! (р) — Р
- (Li + 1(0),
Искомый ток определяется действительной частью этого выражения, т. е.
I w = £тС05(<М + Ф —Ф) _ +(<»!£)’
Emcos(H> —ф) е--£ < //* + (<0,/.)’
откуда
+ Lfjz (0 —) г » + Р (ii -f- Lf)
где
ф = arctg----.
Пример 14-11. Найти методом отделения свободного тока от принужденного ток
233
в цепи рис. 14-14 после замыкания контакта.
Дано:
Ет = 10 в; <»! = 400 рад) сек\ ft — 10 ом;
гг — 5 ом; L = 0,1 ая; С — 100 мкф.
Обычным методом расчета установившегося гармонического режима легко найти до коммутации ток и напряжение «с. Оии будут:
t = 0,472 sin (4001 — л/4) а;
ис — — 11,8 cos (4001 л/4), в.
Отсюда находятся начальные условия:
((0) = i (0 —) = — 0,332 а;
ис (°) = иС (° —) = — 8.34 в.
Аналогичным расчетом после коммутации находятся те же принужденные функции: tnp (/) =* 0,633 sin (4001 — 71е 30'), а,
и
кСпр Ю = — 15>8 cos (400/ — 71*30'), в, что для (=0 дает:
*пр (0) = 0,6 а и ксПр (0) = — 5 в.
Согласно (13-8) начальные независимые значения свободных составляющих будут:
iCB (0) = — 0,332 -f- 0,6 = 0,268 а;
«ссв (0) = — 8,34-|-б == — 3,34 в.
Изображение свободного тока для такой цепи имеет вид:
£гсе(0)-Лсв(0)
^СВ (р) | —
гв + pL 4---——
0,1-0,268---—
________ Р
10е
5+₽°’1+мБо
0,268р 4- 33,4 р« 4- 50р4-106
0,268 р 4-33,4
(Р —Pi)(P —Ps)
здесь pi,2=—25+/315.
По формуле (14-22) иаходим оригинал:
0,268 (— 25 4- / 315) 4-33,4
‘св (0------------------------------
2-/ 315
0,268 (—25 — / 315) 4- 33,4 р>( — 2./315
= 2 Re [0.141 е-П7°30' е-25/ е/315< ] = = 0,282 e~25t cos [315/- 17»30'[ а.
Как видно, оригинал свободного тока достаточно просто нашелся.
Пример 14-12. Найти ток в контуре гС в случае включения в него источника э.д.с. треугольной формы (рис. 14-15). Начальные условия нулевые.
Функцию e(i) можно представить в виде суммы трех прямолинейных функций, изображенных на рис. 14-15,а. Тангенсы углов наклона Первой и третьей прямой равны
1 „ / 2 \
—, а второй прямой ( — I . Используя теорему запаздывания для функции е(/), получаем изображение
= е~рт е~2рТ
1 р’ ip2 ip*
Тот же результат получится, если применить непосредственно формулу (14-1) и произвести интегрирование.
Рис. 14-15. Пример 14-12.
Изображение искомого тока будет:
первое слагаемое э. д. с. даст:
Второе и третье слагаемые имеют тот же вид, но запаздывают относительно первого соответственно на Т и на 27 (второе слагаемое учитывается при Г>Т, третье — при 1>2Т). Поэтому
((/) = (t) - 2», (t - 7) 4- (t - 27).
234
14-9. УЧЕТ НЕНУЛЕВЫХ НАЧАЛЬНЫХ УСЛОВИЙ МЕТОДОМ ЭКВИВАЛЕНТНОГО ИСТОЧНИКА
Если в электрической цепи при ненулевых начальных условиях (т. е. при наличии токов в индуктивностях или напряжений на емкостях) происходит замыкание или размыкание какой-либо ветви, то переходный процесс, вызываемый изменением схемы, может быть рас-
Рис. 14-16. Замыкание ветви электрической цепи.
считан методом эквивалентного источника. В случае замыкания ветви удобно применять теорему об эквивалентном источнике э. д. с., а в случае размыкания — теорему об эквивалентном источнике тока (гл. 5).
На рис. 14-16 показан случай замыкания ветви электрической цепи в момент 2=0. Так же как в § 5-9, буква А означает активную цепь, а буква П — пассивную цепь; ux(t) — напряжение, существовавшее до момента замыкания ветви, условно продолженное на время t> >0.
Режим электрической цепи при i>0 мог быть как установившимся, так и переходным. Ход рассуждений в обоих случаях остается одним и тем же. Включив в замкнувшуюся ветвь две э. д. с., равные по величине ux(t) и противоположно направленные (рис. 14-16,6), и пользуясь методом наложения, приходим к двум схемам рис. 14-16, в иг, в первой из которых токи те же, что и в первоначальной схеме.
Таким образом, переходный процесс при замыкании ветви находится в результате наложения токов предшествующего режима (при разомкнутой ветви), условно продолженного на время />0, на токи, получаемые в результате включения в пассивную цепь источника э. д. с.
ux(t). При этом если при f<0 режим был установившимся, то напряжение ux(t) может быть как постоянным, так и переменным (гармоническим).
При ux(t) =U—const в расчет вводится изображение Ux(p) — l)lp, а при гармоническом напряжении их(1), записанном в комплексной форме итеКш'*+м в расчет вводится изображение Ume^ -------.
р —/oh
Ток в замыкаемой ветви находится по изображению
/(Р)=^, (М-28)
2(р)
где Z (р) — операторное сопротивление всей пассивной цепи, рассматриваемой со стороны места замыкания. Применительно к схеме рис. 14-16 оно равно входному операторному сопротивлению пассивного двухполюсника.
Рассмотрим для иллюстрации изложенного метода один простейший пример.
Пример 14-13. Найти ток t(f) в ветви с сопротивлением га, замыкаемой при />=0 (рис. 14-17).
Рис. 14-17. Пример 14-13.
Напряжение на разомкнутых контактах равио Е. Следовательно, изображение
Ux (р) равно —. Входное операторное со-Р
противление пассивной цепи, рассматриваемой со стороны замыкающего контакта пр/, Z(p) = ra + —.
Следовательно, иа основании (14-28)
ripL \ ri + pL )
Е (fi + pL)
Р [<Л + (П + га) pL]
Переходим к оригиналу:
1 (П = — —----------—-------е (г'+г*>1- 1 .
rz ri(ri + гг)
235
На рис. 14-18 показан случай размыкания ветви электрической цепи в момент t=0. Здесь ik(t) — ток, существовавший до момента размыкания ветви, условно продолженный на время />0.
Включив параллельно в месте размыкания два источника тока действующие в противоположных направлениях — рис. 14-18(6), и пользуясь принципом наложения, приходим к двум схемам (в и г). В
Рис. 14-18. Размыкание ветви электрической цепи.
первой схеме токи те же, что и в первоначальной схеме а.
Таким образом, переходный процесс при размыкании ветви находится в результате наложения токов предшествующего режима (при замкнутой ветви), условно продолженного на время t>0, на распределение токов, получаемое в результате включения в пассивную цепь источника тока ik(t).
Напряжения в исследуемом переходном режиме также находятся методом наложения, т. е. алгебраическим сложением напряжений на одинаковых участках цепи рис. 14-18, аиг.
Ток ik(t) заменяется изображением 1ь(р), и напряжение в месте размыкания определяется по изображению
l7(p)=Z(p)Mp); (14-29)
здесь Z(p) — входное опер аторное сопротивление пассивного двухполюсника (схема г).
Если исследуемый переходный процесс вызывается изменением схемы электрической цепи не при 1 = 0, а при /=/ь то заменой переменной t'=t—1\ начало отсчета времени переносится в t\ (примеры 14-14 и 14-15).
Пример 14-14 [Л. 5]. В схеме иа рис. 14-19 при 1=0 замыкается контакт Къ
в при 1=6 — контакт К2. Требуется определить ток в цепи контакта К2 методом эквивалентного источиика.
При t<ti, т. е. до замыкания контакта Ка, напряжение иа нем определяется напряжением на сопротивлении г2:
(1-е-*), 'it's
где
Искомый ток вызывается этим напряжением, уничтожаемым в момент Ц вследствие замыкания контакта К2. Начнем отсчет времени снова, приняв момент замыкания контакта К2 за 1=0.
Рис. 14-19. Пример 14-14.
Произведем замену переменной: 1= =fi+l'. Следовательно.
«х (Л =
Егг (ri + гз)
(1 _ e-°tr е-^)-
Пусть ux(t')==Ux(p), т. е.
1/х(Р) =
Егъ f 1 _ e~atl \ + г2 \ р р + а /
e Er2[a + p(l-e-atQ] (ft + гг) р(р + а)
Изображение искомого тока находится по формуле (14-28):
__ Ух (р)
~ 2(Р) ’
1(Р)
где
Z(p) =
гг (Г1 4~ рО
Г1 + г2 + рЕ
Подставляя выражения Ux(p) и Z(p) в выражение для 1{р), получаем:
I (р) = £[a + p(l-e-°G)l (Г1 + ^г) (Р + Р
здесь
Переходя к оригиналу, находим:
236
Пример 14-16 [Л. 5]. В схеме рис. 14-20 при 1=0 замыкается контакт Къ а при t—ti размыкается контакт Кг. Требуется определить методом эквивалентного источника напряжение на зажимах Кз после его размыкания.
При <=<i, т. е. до размыкания контакта Кз, проходящий через вего ток равен:
14-10. ФОРМУЛЫ ВКЛЮЧЕНИЯ
Как было показано выше, включение источника э.д.с. в пассивную (без энергии) электрическую цепь вызывает ток
где
Операторное сопротивление Z(p) может представлять собой либо входное сопротивление (в этом случае 1(р) является входным током), либо величину, обратную передаточной проводимости.
Если включаемая э.д.с. задана в виде показательной функции Ее&, то
и соответственно
, Производим замену переменной: t— Следовательно,
Е
ik (t') = — e~at' ё~°-1 . Г1
Полагая ii(f) == 1ь(р), имеем:
F
ri
р + а
Обозначим через Z(p) входное операторное сопротивление пассивной цепи, рассматриваемой со стороны зажимов контакта Кг:
Уг Р + а Г1 + >г Р+Ь’
где
(ri + г г)С
Изображение искомого напряжения на зажимах Кз находится по формуле (14-33):
a(P) = z(p)/ft(p) =
__ £гя (р + а) е~°*' (ri + гз)(р + а)(р + Ь) ~
__ Erse-^'
(''i + г2)(р 4- Ь)
Оригинал искомой функции
и (!') = —— e-{at'+u">(t'>0).
ri + г3
(p — q)Z (р)
Применяя теорему разложения (14-22), получаем формулу включения для показательной э.д.с.1
Etfl1
+ S, т- (|4'30’
(Pk — <dz (Pk)
Первое слагаемое представляет собой принужденный ток, сумма остальных слагаемых образует свободный ток.
Наиболее распространенными на практике случаями являются случаи включения источников постоянной или гармонической э.д.с.
При включении источника постоянной э.д.с. q=0 формула (14-30) принимает вид:
t(/)=_£_ + y..ggf*L . (14-31)
2(0) т ^PkZ'(Pk)
*=i
В случае включения источника гармонической э. д. с. (в комплексной форме) q—jat, причем вместо
1 Здесь по аналогии с § 13-7 предполагается, что уравнение Z (р) =0 имеет п корней.
237
Е должна быть введена комплексная амплитуда Ете® *•
/(0 =
Z
4. V Ете^еРк‘ (Pk — /А) Z' (pk) fe=i
Нетрудно убедиться в том, что формулы включения (14-30) — (14-32) остаются справедливыми и в том случае, когда Z(p) представляет собой дробную функцию вида Z (/?) = , однако при этом
удобнее пользоваться теоремой разложения (14-22) и (14-23).
14-11. РАСЧЕТ ПЕРЕХОДНОГО ПРОЦЕССА С ПОМОЩЬЮ ФОРМУЛ НАЛОЖЕНИЯ
Если пассивную электрическую цепь (без запаса энергии), имеющую операторное сопротивление Z(p), присоединить к источнику э.д.с. e(f) == Е(р), то возникает ток iff) == /(р) = Р ^3°бражение искомого тока равно произведению двух функций: 1/Z(p) и Е(р).
Рассматривая функцию l/Z(p) как изображение, соответствующее некоторому оригиналу у& (/), можно воспользоваться формулой (14-15) умножения изображений (теоремой свертывания). В результате получим:
t
i J e (т) у6 (t — x)dx =
e(t — x) y6(x) dx. (14-33)
Выражение, 1/Z(p) может трактоваться как изображение тока, возникающего в данной цепи под воздействием э. д. с., изображение которой равно единице. Функция, изображение которой равно единице, представляет собой предел прямоугольного импульса длительностью т и высотой 1/т при т->-0. Действительно, прямоугольный импульс на рис. 14-21, а, заштрихованная площадь которого равна единице,
может быть представлен как разность двух единичных функций (рис. 14-21,6 ив), имеющих изображения 1/тр и /тр. Следова-
тельно, изображение прямоугольно-го импульса равно—• (1—е J. хр
При т->-0 данное выражение прини-„ 0 г-.
мает неопределенный вид —. Рас
крывая неопределенность по правилу Лопиталя, находим:
импульс как разность двух единичных функций.
lim — (1 —е ₽t) — lim-е = 1.
Х-.0 гр т-»0 р
Хотя физически этот предел нереализуем, однако на основании сказанного выше условно считается, что функция, изображение которой равно единице, означает бесконечно большой импульс бесконечно малой продолжительности; площадь, ограниченная импульсом, равна единице. Такая функция называется импульсной функцией и обозначается 6(f)-
Итак, оригинал у& (f) представляет не что иное, как реакцию цепи па импульсную функцию. Если функция у» (/) известна, то переходный процесс в той же цепи под воздействием произвольной э. д. с. e(t) рассчитывается по формуле (14-33), представляющей собой одну из разновидностей формул наложения.
Другие разновидности формул наложения основаны на том, что первоначально исследуется переходный процесс под воздействием единичной функции, т. е. в предположении, что заданная цепь присоединя
238
ется к источнику постоянной э.д.с., равной 1 в. ,
Ток, возникающий под воздействием единичной функции, имеет изображение l/pZ(p). Функция
----- носит в литературе pZ (р)
название переходной проводимости.
Ток i(t), возникающий под воздействием э.д.с. e(t), имеет изображение
= = (14-34)
Z(p) pZ(p)
Следовательно, задача сводится к нахождению оригинала по изображению, сомножителями которого являются
Р, E(p) = e(t) и —
PZ (Р)
В данном случае можно воспользоваться следствием теоремы свертывания, т. е. одной из формул интеграла Дюамеля (14-16):
i (0=е (0) У1 (t)+^ е' (т) У1 (t—T)dr =
(0 У1(р)+ [ е(т)у ;<о(*-т) dr. (14-35)
Таким образом, зная реакцию электрической цепи на импУльснУю или на единичнУю фУнкцию, можно найти реакцию той же цепи на про-извольную фУнкцию с помощью одной из интегральных формул (14-33) и (14-35). Эти формулы могут быть также выведены на основе метода наложения.
Заданную кривую э.д.с. e(t) можно приближенно заменить ступенчатой кривой в виде серии прямоугольных импульсов длительностью Ат (рис. 14-22, а). При достаточно малом Ат реакция цепи на первый прямоугольный импульс приближенно равна реакции цепи на .импульсную функцию, помноженную на площадь первого прямоугольного импульса е(0)Атг/б (0-Реакция цепи на второй прямоугольный импульс приближенно равна е(Лт)Лту8 (t—Ат), где е(Дт)Ат — площадь второго прямоугольного импульса, Уь (t—Дт) — реакция цепи на импульсную функ
цию, соответствующую моменту времени Ат.
Следовательно, для рассматриваемого момента времени t=rAr реакция цепи приближенно выражается так:
i (0 S е (Л Ат) Дтуб (i — kАт).
4=0
Когда Ат-*0, н—>ос.
В этом случае
п
i (/)=lim Л е (йАт) Атуй (t — &Ат).
ДХ-*° 4- 0
Рис. 14-22. Иллюстрация к выводу формул наложения.
По мере приближения Ат к нулю изменение АДт вместо скачкообразного (дискретного) становится непрерывным; операция суммирования превращается в операцию интегрирования по переменной т= =ААт:
t
i(0 = [е(т)у6(/ — г} dr.
*)
На рис. 14-22,6 кривая e(t) приближенно заменена серией ступенчатых функций, запаздывающих относительно друг друга на Дт. Реакция цепи на первую ступень равна реакции цепи на единичную функцию, помноженную на высоту первой ступени: e(O)yi(f)- Реакция цепи на вторую ступень равна &eiyi(t—Ат), где Де4 — высота второй ступени; yi(t—Дт)—реакция цепи на единичную функцию, смещенную в сторону запаздывания на Дт.
Следовательно, для рассматриваемого момента времени t=n&.r реакция цепи приближенно равна:
п
i (0 « е (0) У1 (0 + У Де* ух (I — ЛДт).
ь=1
239
При Дт-»-0 и п->-<ю
( (О=е(О)^(О+Нт f ^ydt~ дт-о . , Дт п—» fe=1
— Ш) Дт=е (0) У! (0 + t
+ J е' (т) у i(t — T)dT.
и
Метод интеграла Дюамеля це--лесообразно применять в тех случаях, когда известна или легко находится реакция на единичную функцию, а воздействующая функция имеет кусочно-аналитическую форму.
Если воздействующая функция является разрывной при (>0, то удобнее пользоваться той формой интеграла Дюамеля, которая не содержит производной от этой функции. В противном случае должна быть учтена дополнительно реакция цепи на соответствующий скачок функции.
Пример 14-16. Сопротивление г и емкость С, соединенные последовательно, подключаются при t =0 к источнику э. д. с. в виде треугольного импульса (рис. 14-15,а). Определить ток при f>27".
Реакция цепи на единичную функцию равна У1(р) =--------——.Следовательно,
мо-у'*-75’-
Воспользуемся первой формулой
(14-35)
t
= e (0) yj (0 -Ь f е' (т) ух (t — т) dr;
о
Проинтегрировав, получим ток после окончания действия импульса, т. е. для t>2T:
1(0 =
Нетрудно убедиться, что полученный результат совпадает с результатом примера 14-12, найденным с помощью преобразования Лапласа. В данном случае интеграл Дюамеля дал очень легкое решение.
Пример 14-17. Сопротивление г и индуктивность L, соединенные последовательно, подключаются при t—0 к источнику ступенчатой э. д. с., показанной на рис. 14-23. Определить ток при и t>t3.
Решение находится проше всего методом наложения. Суммируются реакции цепи на две единичные ступени напряжения, одна из которых запаздывает на Л; при
к(У
Рнс. 14-23. Пример 14-17.
О/s вычитается реакция цепи на удвоенную ступень напряжения, смешенную в сторону запаздывания на ts.
Итак, при ts>t>ti
t(0 = -y^l — е t'+l — e L(/ «•’
Для сравнения приведем решения по формулам (14-33) и (14-35). По первой формуле (14-33)
t
И0 = Je(T) уб (t — x)dx. о
Изображение реакции цепи на импульсную функцию равно:
г + pL
Следовательно,
1 “Г"'
У(> (0 = ~ е L ; ye (f — т) =
240
При
По второй формуле (14-35)
i (/) = е (0 j/i (0) + J е (т) (t — т) dt
Реакция цепи на единичную функцию равна:
У1 (в = ~
Г
Следовательно,
, 1 ----------------------
j/i(0) = 0; j/j (t — т)= — е L
т. е. получаются те же интегралы, которые были вычислены выше.
14-12. НАХОЖДЕНИЕ В ЗАМКНУТОЙ ФОРМЕ УСТАНОВИВШЕЙСЯ РЕАКЦИИ
ЦЕПИ НА ПЕРИОДИЧЕСКУЮ НЕСИНУСОИДАЛЬНУЮ ВОЗДЕЙСТВУЮЩУЮ ФУНКЦИЮ
В § 10-5 было показано, что в случае периодической несинусоидальной воздействующей функции установившаяся реакция цепи может быть получена не только как сумма гармоник, но и в замкнутой форме с, конечным, относительно малым числом слагаемых. Решение основывалось на интегрировании дифференциального уравнения в определенном интервале времени и нахождении постоянной интегрирования из условия периодичности процесса.
Другой метод решения этой задачи основан на применении преобразования Лапласа. Допустим, что первый период воздействующей периодической функции (равной нулю при (<0) имеет изображение Fi(p). Тогда изображением периодической функции-оригинала будет:
F(Р)=Л(Р) (1+г-₽г+г-2рЧ--) =
Л(р)
1 — е~рт ’
где Т — период.
Обозначив передаточную функцию цепи1 через К(р), получим реакцию цепи на периодическую функцию-оригинал как сумму вычетов функции:
1 — е р‘
Установившаяся реакция цепи равна сумме вычетов относительно полюсов воздействующей функции } F1 > а свободная реакция — сумме вычетов относительно полюсов передаточной функции К(р)-
Число полюсов воздействующей функции бесконечно велико, так как уравнению 1—е_рТ = 0 соответствует бесчисленное множество корней: 2л
ph=jk— (k — целые числа).
Поэтому находить установившуюся реакцию цепи непосредственно по изображению —f 1 ^L.- X
ХК(р) нецелесообразно (получится ряд Фурье).
Свободная же реакция цепи определяется суммой конечного числа слагаемых, так как число полюсов передаточной функции К(р) ограничено (здесь рассматривается цепь с сосредоточенными параметрами).
Если из полной реакции цепи вычесть свободную реакцию, то получится установившаяся реакция цепи. При этом для первого периода полная реакция цепи на функцию F(p) не отличается от реакции на функцию Ft(p) и поэтому находится по изображению Fl(p)K(p')-
1 Ход рассуждений останется тем же, если вместо передаточной функции воспользоваться сопротивлением нли проводимостью цепи.
16—1118
241
Поясним сказанное на примере, разобранном в конце § 10-5. Периодическая знакопеременная э. д. с. прямоугольной формы, равная нулю при /<0, имеет изображение
Ех(р)
р
е~р
Р2
и всей пилообразной функции (рис. 14-7,а):
£(₽)==
Е
Р
1— 2е ₽2 +2е~рТ----
£j(P)
1 — е~р
Сопротивление цепи Z (р) = г+pL. Изображение тока в цепи
Передаточная функция равна:
г 2 р
1 = Г”= Г” ‘
/’+_sr 2 + "~ р+т
рС р 2
Изображение реакции цепи на пилообразную функцию
17(р) =
Цр)=— Р
1 — е р — ре~р р[р + ^-)(1-е-₽)
(r±pL)
Свободный ток
^са= Res —
' Р
(1-е р 2Г)еР< — -г \
1 + е Р 2 )(<+₽£.)
1 е~р
р(р+у) (₽+т)(‘-в-₽)
Свободное напряжение на сопротивлении
Г
«св = Res —--------— —
1 / , 1 \ ₽=-2- +
где с=—.
2L
Переходный ток в течение первого полупернода
Следовательно, искомый установившийся ток
что совпадает с результатом, полученным в § 10-5.
Ниже приводятся два типовых примера для цепей первого и второго порядков.
Пример 14-18 [Л. 19]. Сопротивление г=2 ом и емкость С=1 ф, соединенные последовательно, подключены к источнику пилообразной э. д. с. вида, изображенного на рис. 14-7, а; период Г=1 сек. Найти установившееся напряжение на сопротивлении.
Из примера 14-4 известно изображение первого периода (рис. 14-7,6):
Переходное напряжение на сопротивлении в течение первого периода (т. е, реакция цепи на первый «зубец»)
Ui = Res ₽=-|-
ер‘
₽(₽ + 1“)
(0 < t < 1).
Здесь принято во внимание только первое слагаемое изображения «зубца», так как два вторых слагаемых не относятся ко времени 1<1.
Установившееся напряжение на сопротивлении в течение первого периода
_ I
«уст — «1 ~ «св —— 2 ——- 2е —
Г" t П
.+.4
242
_ JL
2
= 2----------— (0<l < 1).
Правильность ответа может быть проверена по условию непрерывности установившегося напряжения на емкости:
— 1 2е 2
Пример 14-19 [Л. 19]. Сопротивление г=3 ом, индуктивность L—1 гн и емкость С=*/а ф, соединенные последовательно, подключены к источнику периодической э. д. с. треугольной формы-
... ft
е (1) = {
12 — 1 1 <1<2 и т. д.
Найти установившееся напряжение на емкости.
Из примера 14-12 известно изображение треугольника (рис. 14-15,о):
(Р) = (1 - 2е-р+ е~2^ =
Р2 \ 1
Периодическая э. д. с. треугольной формы, равная нулю прн 1<0, имеет изображение
2(1 — 2а~’~р4 е~~2р) р"(р+1)р + 2)
имеет простые полюсы pi =—1 и ps=—2 и полюс второго порядка рз=О.
В интервале 0<К1 принимается во внимание только первое слагаемое числителя, так как второе и третье слагаемые относятся к последующим интервалам времени.
На основании (14-22) и (14-23) переходное напряжение на емкости
«1 (0 = -j- (21 - з + 4е-« - е~2‘)
(О < t < 1);
Ui (1) = U1 (1) — 2иг (t — 1) (1<1<2).
Искомое установившееся напряженке на емкости
3 4в-<<-1>
«ует-f- 2 + 1+е - 1+е2
(О < t < 1);
3
иуст — (t 2) 4 2
^-«-2) е-2 (t-2)
14-е + 14-ез
(1 <1<2).
Проверка:
—3 + 5е — 5е» + Зез «уст(0) = «уст(2)= 2(1+е)(1+е2)
£(р) =
£i(p)
1 — е“2₽
1 — ё~р p2(l+fl-P)
Передаточная функция равна:
1
рС 1
1 ~ 1 3
r + pL + Рс ТР’ + 2 p+l
_________2
~ (р + 1)(р + 2)
14-13. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Изображение реакции цепи на периодическую э. д. с.
2(1 —е~Р)
Щр) =
Р2(1 + е-Р)(р + 1) (р + 2)
Свободное напряжение на емкости 2(1-е~Р)^
исв = Res ——---------4
р=-1р2(1+е-Р)(р41)(р4 2)
+ к ..2С-«-0^-------------
2 р('+«-,(р + ооч-э
Изображение напряжения на емкости в первом периоде
14-1. Сопротивление г=2 ом и индуктивность L—1 гн, соединенные последова тельно, подключаются при 1=0 к источнику э.д.с. е(1)=1, в. Определить 1(1).
1 1 , 1 -2/
Ответ;—-1 — • а-
2 4 4
14-2. Применить обратное преобразование Лапласа к изображениям:
Зр. Р Ч~ 1 ф (р® 4 >)(Р2 4 4) ’ Ра4-2р ’
1 1
(р 4- 1 )(Р 4 2)2 Р (Р2 + 2р 4- 5)
Р2
(Р24-1)2 ‘
Ответ: cos 1—cos 21;
в-'-е-2'(1+1);
— Г14 — ё~* (—2 cos 21 — sin 21)1;
5 12 I
^1(р) = £1(р)
2
(Р 4 О (Р + 2)
16*
243
14-3. Применив преобразование Лапласа, решить задачи предыдущей главы: 13-3, 13-4, 13-5, 13-6 и 13-9.
14-4. Цепь, состоящая из последовательно соединенных сопротивления г=2 ом, индуктивности £=1 ен и незаряженной емкости С=0,5 ф, подключена при 1=0 к источнику э.д.с. e(l)=sin 1, в. Определить 1 (1).
Ответ:
0,2(cos 1 + 2sin 1 — ё~'cos 1 —Зе-' sin t), а.
14-5. Два одинаковых индуктивных контура г, L, С связаны взаимной индуктивностью М. В один из них при 1=0 включена постоянная э. д. с. Е.
Найти ток в другом контуре.
Ответ:
Е е81' sin <ог 1 е8*' sin <ogl
Т <0i(£ + М) —
б1-2 2 (L Л1) ’
®?-8=С(1а:Л0“в?-2-
14-6. Сопротивление г =10 ом и индуктивность £=0,1 гн, соединенные последовательно, подключаются при 1=0 к источнику э.д.с. 10 е-41, в. Определить 1(1).
Ответ: 1,О4(е-4<—е~100<). а-
14-7. Сопротивление r= 1000 ом и незаряженная емкость С=10 мкф, соединенные последовательно, подключаются при 1=0 к источнику э. д. с. 2,5-Wfl—e~4f), в. Найти 1(1).
Ответ: l,04(e-4f—e-WOi), а.
14-8. Найти оригинал по изображению р1_р+Ю
(р + ОЧр’ + ’ОО) '
О т н е т:
0,1191е-' — 0,027г-' 4-0,027 cos 1014-
4-0,086 sin 101.
14-11. Решить предыдущую задачу, если э. д. с. равна Ete~ai.
Ответ:
Е г — aL
EL ( -т'
+--------\ е
('- а£)2
14-12. Источник тока, посылающий ток 1=1 а в виде прямоугольного импульса длительностью 0,001 сек, подключен при 1=0 к сопротивлению г=100 ом и емкости С=10 мкф, соединенным параллельно. Начальные условия нулевые. Определить напряжение на зажимах цепи.
Ответ:
100(1—е-10*')-.
— 100[1—е~10’('-0,00,) ] 1(1 — 0,001), в.
14-13. Пользуясь решением примера 14-12 (рис. 14-15), найти установившийся ток в г н С, соединенных последовательно и подключенных к источнику периодической э. д. с. треугольной формы.
Ответ:
(0 < 1 < Г);
14-9. В контуре, состоящем из сопротивления 40 ом и индуктивности 0,1 гн, при установившемся режиме действует э. д. с. е= 100 cos 400 1, в.
Найти 1(1) при 1>0, если, начиная с момента 1=0, амплитуда э. д. с. становится равной 40 в.
Ответ: 0,707 cos (400 1—л/4) +
+0,75 е~4°°‘, в.
14-10. Прн нулевых начальных условиях в контур г, L включается источник э. д. с. Ee~at. Определить токи при а r/L и a—rIL.
Ответ:
Е г—aL
I —at L \е —е
— &
14-14. Доказать применимость теоремы об эквивалентном источнике напряжения к изображениям.
14-15. Как учитывается энергия магнитного и электрического полей, имеющаяся к началу исследуемого переходного процесса?
14-16. На каком основании прн обратном преобразовании Лапласа применяется теория вычетов?
14-17. Что такое импульсная функция?
Показать, что J d(f)dt—l.
о
14-18. Найти изображение импульса произвольной формы, если известно изображение функции, получаемой периодическим повторением данного импульса.
244
Глава пятнадцатая
СПЕКТРАЛЬНЫЙ метод
15-1. ВРЕМЕННОЕ И СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
Сигналы можно представлять двояко: в виде функций времени и в виде частотных спектров. Например, гармоника, выражаемая функцией Дсоз(ю<-|-ф) (рис. 15-1,с) полностью характеризуется положением на шкале частот заданной ам-
« «9
Рис. 15-1. Временное (а) н спектральное (б, в) представление гармоники.
плитуды А и начальной фазы ф. Так как гармоника — простейшая периодическая функция, то ее амплитудный и фазовый спектры изображаются наиболее просто, в виде одиночных ординат А и ф, соответствующих заданной угловой частоте о (рис. 15-1, б).
При комплексной форме записи косинусоиды
A cos И + ф) = -А [ <№+*> +
вводится чисто математическое понятие отрицательной угловой частоты. В этом случае шкала частот дополняется отрицательной полуосью: амплитудный и фазовый спектры изображаются парами ординат (рис. 15-1, в), соответствующих положительному и отрицательному значениям угловой частоты (о и —со). По шкале частот компоненты амплитудного спектра располагаются симметрично относительно оси ординат, а компоненты фазового спектра — симметрично относительно нулевой точки.
Если периодический сигнал несинусоидален, то, как известно (гл. 10), он может быть разложен в ряд Фурье, т. е. представлен в виде дискретного ряда гармоник (здесь предполагается, что сигнал удовлетворяет условиям Дирихле).
При тригонометрической форме записи ряда Фурье
сю
. f (0=-у + S Ап соз^-ф») (15-1)
амплитуды Ап и начальные фазы фп вычисляются по формулам:
-t„ = arctgi.(15.2) ап
Здесь коэффициенты разложения г
ап = (t) cos по! t di; (15-3)
о т
bn = -A j f (t) sin noii dt. (15-4) о
Основная угловая частота toi = =2л/Г.
От каждой точки nwi(n= = 0, 1, 2 ...) перпендикулярно оси частот могут быть отложены амплитуды Ап и начальные фазы ф„ соответствующих гармоник. Совокупности построенных таким образом ординат Ап и фп и образуют линейчатые (дискретные) амплитудный и фазовый спектры данного несинусоидального периодического сигнала.
245
При комплексной форме записи ряда Фурье
= Y £ Aneine>it (15-5)
П=—~ оо
комплексные амплитуды вычисляются по формуле
— А„ = — А„ e~,itn =
2 2
1 , ...
•= — (а„ — М ==
т
= Y di’ (15-6)
причем формулы (15-2)—(15*4) остаются в силе.
Частоты пен при п=0, ±1, ±2 ... образуют на оси частот ряд равноотстоящих точек. Совокупность амплитуд соответствующих
1 . 1 .
гармоник—Лп =—Л_п,т. е- модулей комплексных коэффициентов ряда Фурье, отложенных против соответствующих положительных и отрицательных частот, представляет симметричный относительно оси ординат линейчатый амплитудный спектр. В свою очередь совокупность ординат, равных аргументам фп =—ф-n комплексных коэффициентов ряда Фурье, отложенных против соответствующих частот, образует линейчатый фазовый спектр несинусоидального периодического сигнала, симметричный относительно начала отсчета.
Четность коэффициентов ап и нечетность коэффициентов Ьп относительно частоты ио [согласно (15-3) и (15-4)] подтверждает то, что
— Д = — А _ и ф_ =—ф
2 я 2 —п 'я '—п
Таким образом, в зависимости от формы записи ряда Фурье (тригонометрической или комплексной), так же как и в случае одиночной гармоники, получаются спектры двух видов: на положительной полуоси или на обеих полуосях частот. Следует заметить, что шкала
частот может быть проградуирована по номерам гармоник. Что касается шкалы времени сигнала, то она может быть заменена шкалой фазовых углов (Dll.
Ниже рассмотрены спектры некоторых типовых несинусоидальных периодических сигналов.
Пример 16-1. Периодическая последовательность прямоугольных импульсов задана условием 1 (рис. 15-2, а):
Здесь период 7=21ь Согласно (15-6)
Ап = — f dt = — (1 — е-'™1).
4 J inn
о
Для п четных е ,Я1 = 1 и Яп=0.
Для п нечетных е—/пп =—1, так что при
„ / 2
п=±1,±3... Ап — -—. /пп t t, Прн п=0 До= —Jdl = l.
1 о
Следовательно,
СО
сю
= —+ У е,пш* * (п—нечетные).
Г£з=~сс
Амплитудный и фазовый спектры на обеих полуосях частот показаны на рис. 15-2,6 н в. Для удобства на шкале частот указаны номера гармоник.
Применительно к формуле (15-1)
ОО /(04+7^7sin№lf = Паа!
СО
п— (нечетные)
спектр будет ограничен положительной полуосью, причем Ад сохранит свое значение, а остальные ординаты амплитудного спект-
1 Если по оси абсцисс вместо t откладывать oil, то прямоугольные импульсы будут следовать в интервалах от 0 до л, от 2л до Зл и т. д.
246
ра уДнойтся. Фазовый спектр останется таким же, как на положительной полуоси (рис. 15-2, в).
Пример 15-2. Сигнал, рассмотренный в Предыдущем примере, смещен по шкале времени в сторону опережения на Л/2. В итоге получена периодическая последовательность прямоугольных импульсов, симметричных относительно оси ординат (рис. 15-3, а):
/(0 =
пл
sin---
о
----------- pjnOit пл
2
= — + 7 . (^1) — в'"'6*'
2 ^J |п|л
—ОО
(в последней сумме п— нечетные).
Полученное выражение можно запн сать н так:
Рис. 15-2. Пример 15-1.
/(о—^-+2 (-о 2
М-1
J— gjnaj
или по формуле (15-1)
О» пл
12 2
/(/) = — + — —----COS ПШ1 t,
2 л п
На основании (15-6) t, 2
е-/««мЛ =
/ПО1Л
по», Л пл
in —-— sin----
____L_ =_______
по!Л пл
2~~ ~~2~
Для п четных Лп=0. Для п нечетных
. 2
Ап = ±——. Знак плюс относится к л ]л|
|п|=1, 5, 9..., а знак минус к |л| =3, 7,11...
При п—0 «4о=1. Следовательно,
Ввиду того, что функция [(f) симметрична относительно оси ординат, коэффициенты Ап действительные; когда они положительны, начальные фазы равны нулю, а когда отрицательны, то грп = ±л. Амплитуды убывают пропорционально первой степени номера гармоник.
Так как в данном случае коэффициенты Лп действительные, можно не рисовать в отдельности амплитудный и фазовый спектры, а ограничиться только изображением по шкале частот коэффициентов ~ с учетом их знаков (рис. 15-3, б).
А
Из сравнения рис. 15-2, б и 15-3, б видно, что сигналы рис. 15-2,о и 15-3,о имеют одинаковые амплитудные спектры. Следовательно, сдвиг сигнала во времени не влияет на амплитудный спектр, а изменяет только фазовый спектр.
247
В этом легко убедиться, заменив в (15-6) t на t±t0. Коэффициент Ап умножится при этом на е±/п“1'0 , т. е. его модуль не изменится, а к аргументу прибавится угол ±nWo. Это свойство является общим для всех сигналов, в том числе и непериодических (§ 15-7).
ваться типовой кривой y=sin х/х (рис. 1Б-5), которая в масштабе N изображает огибающую коэффициентов — Ля. Огибающая
пересекает ось абсцисс при—~——як или
n=Nk(k=±.l, ±2 ...).
Отсюда можно заключить, что число спектральных линий между на-
Рис. 15-3. Пример 15-2.
Пример 15-3. Последовательность прямоугольных импульсов, симметричных относительно оси ординат, с периодом, значительно превышающим длительность им_-пульса (рис. 15-4,а):
Величина N=Tltt получила название скважности импульсов. В радиотехнических устройствах она может достигать сотен или даже тысяч. Согласно (15-6)
£«_ 2
/n = yJ e-/WA =
2 no, t, rm
„ sin —-— „ sin —-
= ________?__= —--------5L (15-7)
T ncoj tt N rm
2 ~N~
2
При n=0 A>=— N
Следовательно, no-
a0 1
стоянная составляющая —— = — обратно 2 N
пропорциональна скважности импульсов. Итак,
На осиоваиии выражения (15-7) можно построить спектр. При этом удобно пользо-
чалом отсчета по шкале частот и первым нулем огибающей, равное числу спектральных линий между соседними нулями, составляет N—1. Чем больше скважность импульсов, тем гуще линейчатый спектр.
На рис. 15-4, б показан спектр для частного случая N=5.
Пример 15-4. Последовательность треугольных импульсов (рис. 15-6, а) отвечает условиям:
1 — 0 < <о11 < л;
л
1 _j_ — л < <й t < 0.
л
На основании (15-6)
—л
х dM+
1 Г 4 4 / е/«л_______е— inn
л* [пл2 лп2 У,11П 2j
е/л«+е-/»л\ 2 einn_e-jnn-
-------2------) + V-------2/------.
4 /
=------11 — пп sin пп —
п2п2 \
, 2 . \
— COS ПЛ-4----sin пл).
пл }
248
Рис. 15-4. Пример 15-3.
Для всех целых значений п sin пл—О, т. е.
Ап = —(1 —cos/иг). " nW
Для п четных cos пл= + 1 и 4п=0.
8
Для п нечетных cos пл=—1 и Ап —--------.
П2Л2
При п=0 и До=О.
Итак, в силу симметрии f(t) относительно оси ординат коэффициенты ряда получились действительными; они убывают пропорционально квадрату номера гармоники:
f(t)= — У — е^па,< (л-нечетные).
я2 п2
72=—оо
Рис. 15-5. Типовой график у—
Спектр изображен на рис. 15-6, б. Более быстрое убывание коэффициентоа ряда по сравнению с предыдущими примерами объясняется отсутствием разрывов функции.
Спектры линейно связаны с сигналами. Это свойство, непосредственно вытекающее из уравнения (15-6), означает применимость к спектрам метода наложения. Поскольку коэффициенты — Ап представляют комплексные амплитуды напряжения или тока, то к спектрам сигналов применимы общие правила расчета цепей по частотным характеристикам — комплексным сопротивлениям, проводимостям или передаточным функциям цепей. С подобными расчетами несинусоидальных периодических процессов мы уже встречались в гл. 10.
Как будет показано в следующем параграфе, непериодический сигнал, выражаемый интегралом Фурье, получается в результате суммирования гармонических коле
Рис, 15-6. Пример 15-4.
249
баний бесконечного спектра частот, причем амплитуды этих колебаний бесконечно малы.
Частотный подход к исследованию процессов в электрических цепях удобен тем, что он позволяет учитывать частотные свойства цепей при прохождении сигналов, судить о распределении энергии в спектре (§ 15-5) и оценивать значимость отдельных участков спектра. В сочетании с методом наложения он дает возможность исследовать переходные процессы в линейных электрических цепях. Именно поэтому спектры играют роль важнейшей математической и физической характеристики исследуемых процессов.
Временное и спектральное представления сигналов равноправны и взаимозаменяемы. Они успешно применяются в радиотехнике, причем в зависимости от постановки задачи и характера рассматриваемого процесса предпочтение отдается тому подходу, который в данном конкретном случае оказывается наиболее удобным.
Нахождение спектра сигнала, заданного в виде функции времени, составляет задачу гармонического анализа, а обратная процедура нахождения функции времени по заданному спектру — задачу гармонического синтеза.
Настоящая глава посвящена рассмотрению взаимосвязи между временными и частотными характеристиками, ознакомлению со свойствами спектров и применению спектрального метода к расчету переходных процессов в линейных электрических системах.
Чтобы применить гармонический анализ к заданной непериодической функции, превратим ее в периодическую путем повторения ее с произвольным периодом T>t2—t\ (рис. 15-7). В интервале времени (~ у- у) кривая f (0 (рис. 15-7,а) совпадает с периодической функцией (рис. 15-7, б), и поэтому может быть представлена рядом Фурье. За пределами этого интервала времени заданная непериодическая функция не описывается рядом Фурье.
Рис. 15-7. Непериодическая (о) и периодическая (6) функции времени.
Для того чтобы функция f(t) В возможно большем интервале времени определялась рядом Фурье, необходимо неограниченно увеличивать период Т.
Перепишем (15-5) в следующем виде:
15-2. НЕПЕРИОДИЧЕСКИЕ СИГНАЛЫ. ИНТЕГРАЛ ФУРЬЕ
КАК ПРЕДЕЛЬНЫЙ СЛУЧАИ РЯДА ФУРЬЕ
Пусть сигнал задан в виде непериодической функции времени f(t), удовлетворяющей условиям Дирихле и абсолютно интегрируемой в бесконечных пределах, т. е. интегралу | f (t) | dt имеет конеч'ное значе-—со ние.
X — (П— 1)с>1] =
СО
Здесь Д (поп) =/1Ш1—(п—1)ац— частотный интервал между состав-
2л (jj /2=-------СО
250
ляющими ряда Фурье, равный частоте повторения wi=2n/7’. Так как т 2
Ап = -у J f (0 ® М, то f(t) =
Jт_
2 7/2
1 VI А / \ Г £/_t\ ~/Л®1*
= ЯО® di-
п——<х> —Т/2
По мере возрастания периода Т интервал Д(пац) сокращается и линейчатый спектр все более сгущается, а модули Ап комплексных амплитуд — уменьшаются. При Т*-оо п<В1 -* <о (т. е. спектр из дискретного превращается в сплошной), а Д(пш1) -> dtoj. Интеграл, стоящий под знаком суммы при Т -> со, дает функцию, называемую спектральной плотностью, спектральной характеристикой или просто спектром непериодической функции и обозначается F(/co):
F(jco)= j* f(t)e~la* dt. (15-8)
—co
При неограниченном увеличении периода Т операция суммирования превращается в операцию интегрирования по переменной to в бесконечных пределах:
оо
Z(0=dr f F^e'atda>- с15-9) ---------OQ
Преобразование, выражаемое формулой (15-8), называется двусторонним преобразованием Фурье функции f(t), а преобразование (15-9)—обратным преобразованием Фурье функции F(ja>). Обе формулы представляют взаимно связанные интегралы уравнения, каждое из которых служит решением другого. Они позволяют преобразовать функцию времени в функцию частоты и обратно. Для выражения связи между F(ju) и f(t), накладываемой преобразованием Фурье на эти функции, может быть применен тот же знак соответствия =, которым мы пользовались в предыдущей главе. Итак, сокращенная условная запись F(j(o) ~[(t) обозначает, что
F(jto) и f(0 связаны уравнениями (15-8) и (15-9), т. е. функция времени [(f) имеет спектр F(/to).
Согласно (15-9) заданная непериодическая функция f(t) представляет совокупность бесконечной суммы гармоник с бесконечно малыми амплитудами — F (j<£>)d(a во 2л
всем диапазоне частот от - <ю до + °°-Иначе говоря, представление непериодической функции в виде интеграла Фурье подразумевает бесконечное суммирование незатухающих и бесконечно близких по частоте гармонических колебаний сплошного спектра частот с бесконечно малыми амплитудами.
Такой метод представления непериодических функций несколько сходен с методом разложения периодических функций в ряд Фурье. При этом интеграл Фурье обладает тем ценным свойством, что, правильно описывая заданную функцию во всем интервале времени (—оо, + оо), он тождественно обращается в нуль в тех промежутках времени, в которых заданная непериодическая функция равна нулю.
Формулы (15-8) и (15-9) могут быть переписаны так:
—©О
X р(0е-мЛ = —оо
—оо —оо
со со
= — f dco f /(t)cos<o(Z — т)б1т +
2л J J
—• OO -DO
oo co
+ / J da) J [(f) sin to (t — t) dr. —oo —co
Второй интеграл равен нулю, так как подынтегральная функция нечетна относительно <о.
Следовательно,
[(f) j" da> j* f (т) cos to (t — t) dt
251
или ввиду четности подынтегральной функции относительно со
СО СО
f(t)= — J da J / (т) cos со (I — т) dr.
О —со
(15-10)
Полученная формула представляет интеграл Фурье в тригонометрической форме.
Так же как и при разложении периодической функции в ряд Фурье, значение функции в точке разрыва, получаемое на основании интеграла Фурье, разно среднему арифметическому предельных значений слева и справа от точки разрыва, т. е.
f(0 = ± + (15-11)
Представление непериодической функции в виде совокупности незатухающих гармонических колебаний позволяет исследовать переходный процесс в линейной электрической цепи, применяя к спектру непериодической функции общие методы расчета установившихся гар
монических процессов (§ 15-12). При этом формулы (15-8) и (15-9) позволяют вести расчет в комплексной форме.
Большим преимуществом интеграла Фурье является возможность получения выражений в замкнутой форме, а не в виде медленно сходящихся рядов.
15-3. СВЯЗЬ МЕЖДУ ДИСКРЕТНЫМ И СПЛОШНЫМ СПЕКТРАМИ
При пользовании комплексной формой записи коэффициенты ряда Фурье и спектральная плотность могут быть действительными и комплексными. Обозначив в общем случае Ап=Апе^п
и F(j«>) = |JF(/a>)|e«’t<a>, будем иметь амплитудные спектры — А, и 1^?(/ш)| и фазовые спектры фп И ф(со).
Для сравнения в табл. 15-1 приведены формулы гармонического анализа периодических и непериодических функций.
Основные формулы
Таблица 15-1
Ряд Фурье (периодическая функция)
Интеграл Фурье (непериодическая функция)
F (/со) e'at da>
n=s—со
An=Y J _____т_ 2
F (До) = j f (t) e~,at dt
—co
F (До) = |F (/co)) e1^
Как уже отмечалось выше, всякая периодическая функция имеет линейчатый (дискретный) спектр. По мере увеличения периода линейчатый спектр сгущается.
На рис. 15-8 показано изменение коэффициентов ряда Фурье в зависимости от периода, причем взята рассмотренная в примере 15-3 периодическая последовательность пря
252
моугольных импульсов, расположенных симметрично относительно оси ординат.
Увеличение периода равносильно увеличению скважности импульсов N=Tjti.
В примере 15-3 отмечалось, что огибающая линейчатого спектра пересекает ось абсцисс при ПЫ1=—/г G (й—±1, ±2, ...). Положение нулей огибающей на шкале частот не за-
характеристика превратится в пределе в сплошную спектральную плотность F (/со) непериодического одиночного прямоугольного импуль-
са, заданного в интервале от —
до --(Рис- 15-9).
Иначе говоря, огибающая коэффициентов ~Ап не зависит от Т и точно совпадает со спектром непе-
Рис. 15-8. Изменение спектра с увеличением скважности импульсов.
висит от выбора Т, а всецело определяется длительностью импульсов. При этом, как видно из формулы (15-7) и рис. 15-8, коэффициенты ряда заданного периодического сигнала обратно пропорциональны периоду Т (или скважности импульсов), т. е. с ростом Т огибающая снижается, стремясь при Г->оо совпасть с осью абсцисс.
Если коэффициенты ряда Фурье -i- Ап умножить на период Т и уст-
ремить Т к бесконечности, то частотный интервал между линиями т дискретной характеристики — А„ устремится к нулю и линейчатая
риодического сигнала, вычисленным по формуле (15-8)з
6
2 £(/©)= J e~,aidt =
2
<0 sin— h
= h-----=—. (15-12)
2
Сказанное справедливо не только для рассмотренного здесь частного примера прямоугольного импульса, но и для любой непериодической функции /(/), заданной в конечных пределах.
253
В этом случае всегда можно подобрать такое Т, чтобы выполнялось равенство
F(/to) = =
V
г
2
= С f (t)e~,e“ dt. (15-13) _*L
2
Соответствующая этому случаю периодическая функция, совпадаю-
Т Т щая с f(t) в пределах от — - до — и имеющая период Т, характеризуется линейчатым спектром
т 2
7^"=7 У (15-14)
2
Из сопоставления (15-13) с (15-14) видно, что спектральная плотность F(/co) заданной в конечных пределах функции f(t) в мас
штабе 1/7 представляет огибающую дискретного спектра-^- Ап разложения, соответствующего периодическому повторению заданной функции:
Y4»lF(/<o)]a^. (15-15)
На основании (15-14) можно заключить, что
Ф„=[ф(ы)]и=„Ш1.
Как и в случае периодической функции, амплитудный спектр 17(/со) | — четная, а фазовый спектр ф(со) — нечетная функция to:
If (j<o)| = |F (—/со)|; ф (ы)=*—ф (—<о).
Размерность дискретного амплитудного спектра периодической функции определяется размерностью самой функции. Между тем амплитудный спектр непериодической функции имеет размерность этой функции, умноженную на размерность времени.
15-4. СЛУЧАИ СИММЕТРИИ НЕПЕРИОДИЧЕСКОЙ функции
На основании (15-8) и (15-9)
I 00
(0= ( F(До) cosa>tda +
J F (/©) sin at da; (15-16)
J уА
0
Рис. 15-9. Переход от дискретной характеристики Т А
— Ап периодической последовательности прямоугольных импульсов к сплошному спектру F(/co) одиночного импульса.
F (/co) = Fj (to) — /Fs (co);
Л (®)= J f (0 cos tot dt;
—oo
F2 (to) = J f (t) sin at dt.
— CO
(15-17)
Входящие в (15-16) и (15-17) интегралы с бесконечными пределами — несобственные.
Если подынтегральная функция нечетная, то главное значение несобственного интеграла равно нулю.
Формулы (15-17) показывают, что Fi (со) — четная, а
254
F2(w)—нечетная функция частоты со.
Рассмотрим три случая.
1. Функция f(t) четная. Ввиду того что косинус и синус являются соответственно четной и нечетной функцией t, то в данном случае f(t) cos (at — четная, a f(t) sin со/ — нечетная функция t, и поэтому на основании (15-17)
F2(co)=O и
F (/со) = Fx (со) == 2 J f (/) cos со/ dt, о
(15-18) т. е. F(j(a) —действительно и четно относительно со (примеры 15-2, 15-3, 15-4). В этом случае функция F(jco) sin со/ нечетна относительно со, и поэтому второй интеграл в формуле (15-16) обращается в нуль:
оо
/(/) = Fj (со) cos со/ dco. (15-19)
о
Сопоставив формулы (15-18) и (15-19), можно заключить, что переменные со и / взаимно заменимы: если рассматривать F (jt) = = — F(—jt) как функцию време-2л
ни, то ее спектром будет f (со) = =Н-и).
На рис. 15-10, а в виде примера показаны прямоугольный импульс /(/) и его спектр F(j(a), а на рис. 15-10,6 изображены спектр f (со) и функция времени — F(jt).
2. Функция f(f) нечетная. В этом случае функция f(/) cos со/ — нечетная, a f(t) sin со/ — четная функция /, и поэтому на основании (15-17) А (со) =0 и
F(/co) = —/F2(co) -
= — /2 J/(/)sinco/d/, (15-20)
т. e. F(/co) — мнимо и нечетно относительно со.
Функция F (/со) cos со/ — нечетная относительно со, и поэтому первый интеграл в формуле (15-16) обращается в нуль: оо
/(/)= — f F2(co)sinco/dco. (15-21)
л J
Рис. 15-10. Взаимозаменяемость сигнала и спектра.
Предыдущий вывод относительно взаимной заменимости переменных со и / применим и в этом случае, а именно, если рассматривать
F (—№=— ~~ F(jt) как функ-2л 2л
цию времени, то ее спектром будет f(w).
3. Функция /(/) не обладает симметрией. Любая несимметричная функция /(/) может быть представлена как сумма двух функций — четной и нечетной. Действительно, четная функция
К (0 + /(-<)],
а нечетная
Отсюда
/1(П + /я(0=/(0.
В этом случае F(jca) — комплексная функция, действительная часть которой четная, а мнимая часть — нечетная функция со.
Как уже отмечалось в § 15-3, амплитудный спектр |F(/co) |—четная, а фазовый спектр ф(со) =
Г —F, (<») ] = arctg --------— нечетная
I Fi(®) J функция со.
15-5. РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ В СПЕКТРЕ
Если напряжение или ток выражается периодической функцией времени /(/), то величина
255
т
у J пропорциональна сред-
о
ней за период мощности.
На основании § 10-7 средняя мощность несинусоидального периодического тока равна сумме средних мощностей одноименных гармоник плюс мощность постоянной составляющей. Поэтому
1р(/)]ч<=||)! + о
со оо
+тЕЛ!.- S (т)‘- (15-22)
Л—1 7=—ОО
Отсюда следует, что средняя мощность сигнала может определяться как сумма мощностей отдельных компонент амплитудного спектра сигнала.
Чтобы перейти от периодической функции к непериодической, следует умножить (15-22) на Т, заменить в (15-22) Д„/2 через у |F(/®)|b>=nai и устремить Т к бесконечности.
При Т ->оо выражение
ад-
со
= S у 1/7 (/“)!«=»<«, стремится
Лг=—со
к величине, пропорциональной энер-гии сигнала f(t) за все время его действия. Приняв, как и в § 15-2, при Т -> оо пш. —>• со и — = — =
н 1 Т 2л
Д (nwi) 1 ,
— —--------»• — аы и заменив опе-
2л 2л
рацию суммирования операцией интегрирования, получим:
J™ S y^G’^IUroy
/2=—оо
оо
= 2^ f I^Gfi>)|2d© =
—оо
со
= у | о
Итак, оо оо
J и (0]3 dt = -j- j* |F (Ml2 du. (15-23) -OO 0
Это — теорема Релея (или равенство Парсеваля), устанавливающая связь между энергией непериодического сигнала и его спектром. Она показывает, что энергия может быть вычислена двояким способом: интегрированием квадрата функции времени или интегрированием квадрата амплитудного спектра.
В соответствии с этой теоремой можно каждому участку амплитудного спектра непериодического сигнала приписать плотность энергии, пропорциональную |F(/w)|2. Следовательно, по виду функции |F(/w) | можно судить о распределении энергии в спектре непериодического сигнала. Например, в случае единичного прямоугольного импульса около 90% полной энергии сигнала сосредоточено в полосе частот от 0 до ш = 2л/0- Чем короче прямоугольный импульс, тем шире полоса частот, в которой сосредоточена основная доля энергии сигнала. Именно в этом смысле и понимается обычно термин «ширина спектра» (в данном случае полоса частот обратно пропорциональна длительности импульса).
15-6. СВЯЗЬ МЕЖДУ ПРЕОБРАЗОВАНИЕМ ФУРЬЕ И ПРЕОБРАЗОВАНИЕМ ЛАПЛАСА
До сих пор на непериодическую функцию f(t) не накладывались ограничения при /<0. Допустим теперь, что задана функция f(t), равная нулю при /<0, преобразуемая по Лапласу, причем показатель роста Со отрицателен, т. е. для всех/>0
|/(0| <Me~w. (15-24)
Это означает, что функция не превосходит некоторой затухающей экспоненты; следовательно, интеграл | |f(0 \dt сходится. В таком случае лапласово изображение F(p) =f(t) является аналитической функцией в полуплоскости Res>co,
256
а следовательно, и на мнимой оси (так как здесь принято с0<0). Ввиду этого в формулах преобразования Лапласа
F(p) = f dt о
и
с+/оо
/(0=^. f F(p)^dp 2л/ J
С—/со
можно положить с=0 и p=ja, т. е. за путь интегрирования в формуле обратного преобразования Лапласа выбрать мнимую ось.
Тогда будем иметь:
F(j(o) = J f (t) e~'at dt; (15-25) О
оо
/(0=Л f (15-26)
Первая формула выражает одностороннее1 преобразование Фурье функции f(t), т. е. нахождение спектра непериодической функции, заданной при />0 и равной нулю при /<0. Вторая формула не отличается от (15-9) и представляет обратное преобразование Фурье функции F(ja)-
Преобразование Фурье имеет более узкую область применения, чем преобразование Лапласа. Это связано с тем, что для сходимости несобственного интеграла (15-25) на функцию f(t) наложено ограничение (15-24), которое является более жестким, чем условие |/(0|< <ZMeiCcit , предъявляемое к функциям-оригиналам (§ 14-2).
Например, такие функции2, как единичная, возрастающая показательная, периодические и некоторые другие функции-оригиналы, имеющие лапласовы изображения, не могут быть непосредственно представлены в виде интеграла Фурье (15-26).
1 Этот термин указывает на то, что функция f(t) определена при />0 и равна нулю при /<0.
2 Здесь имеются в виду функции, равные нулю при «О.
Если заданная функция, преобразуемая по Лапласу, удовлетворяет условию (15-24), то свойства преобразования Лапласа сохраняют силу при р=/со. Соответственно свойства преобразования Фурье получаются на основании свойств преобразования Лапласа заменой р на /со. В этом смысле можно говорить, что преобразование Фурье является частным случаем преобразования Лаплас?..
Из вышесказанного следует, что всякая функция, для которой применимо одностороннее преобразование Фурье, всегда может быть преобразована по Лапласу.
Если для такой функции известно лапласово изображение, то замена комплексного переменного р мнимой величиной /и дает искомую спектральную характеристику
F [F(p)]ps=le>. (15-27)
Такой способ нахождения спектров является наиболее простым и удобным, так как он позволяет использовать таблицы оригиналов и изображений (§ 14-7 и 15-9).
Родственная связь, существующая между преобразованиями Лапласа и Фурье, вносит, таким образом, физическое содержание в понятие «изображение» как обобщенную форму спектральной характеристики. Она распространяется и на основные свойства преобразований Фурье и Лапласа.
15-7. СВОЙСТВА преобразования ФУРЬЕ
В табл. 15-2 приведены основные свойства преобразования Фурье, которые в ряде случаев облегчают нахождение функций времени или их спектров. Если над некоторой функцией времени, спектр которой известен, производится одна из операций, указанных в табл. 15-2, то спектр, отвечающий новой функции времени, находится по соответствующему правилу из первоначального спектра.
В свою очередь, если спектр претерпевает какую-либо операцию, то функция времени, соответствующая новому спектру, также находится по известным правилам. ,
17—1118
257
Таблица 15-2
Основные свойства преобразования Фурье
Ноимеиованйе Формула
Линейность , п X at ft (I) = S a. Ft (jiO) 1=1 i=i
Взаимозаменяемость независимых переменных f(co)=^-F(-/O
Диффепенцирование функции времени Двустороннее преобразование d — f (0 = (/*») at Одностороннее преобразование d — j(uF (/co) — / (0) at
Интегрирование функции времени t C F (/GJ) J /<*> —oo
Дифференцирование спектральной характеристики F (/co) = (—/7) / (Z) ggj
-Интегрирование спектральной характеристики (D J F (/u>)do)T=~ —co
Изменение масштаба независимого переменного r , , 1 / CO \ /(o0 =— Fit — a \ a
Смещение функции времени flt + t^e^FUw)
Смещение спектральной характеристики = f [/(co 4=oih)J
Умножение спектральных характеристик Fi (/co) F2 (/co) = J A (t) ;2 (t — t) dT = J f2 (t) h (t — t) dt —co —oo
Умножение функции времени на косинус или синус f (/) cos coj t =- -L {F [j (co — oij)] + F [j (co + coj]} f (t) sin C0j t = ,2- {F [/• (<0 — (Oj)] _ F [/ (co 4- cOi)]} 2/
Теорема Релея co co J lf(0l2<tt =“ f ff(/co)Pcto ^-oo —co
258
Ниже приводятся дополнительные разъяснения к табл. 15-2.
В § 15-4 при рассмотрении случаев симметрии непериодической функции f(t) было выяснено свойство взаимозаменяемости независимых переменных t и со, которое в общем виде записывается так:
{15’28)
Данное соответствие, справедливое при любой функции f(t) —четной, нечетной или не обладающей симметрией, в общем случае легко выводится, исходя из (15-8) и (15-9).
Для доказательства внесем множитель 1/2л под знак интеграла (15-9) и, заменив знак и, получим:
e-^d(-(D) =
J 2л
= f -F(—,<й)- e-'^da. (15-29)
J 2л v '
Далее, умножив обе части уравнения (15-8) на 1/2л и также заменив знак со, получим:
оо
±F(~j^=/- f f(f)e'atdt. (15-30)
2л 2л J
—со
Меняя в (15-29) и (15-30) местами t и со, находим:
[ (со) = ( ——— e~>at dt;
J 2л —оо оо
Полученные выражения доказывают соответствие (15-28).
Теперь рассмотрим дифференцирование функции времени. При двустороннем преобразовании Фурье производной функции f(t) соответствует спектр
—оо = jaF (/со), так как функция f(t), представляемая интегралом Фурье, обращается в нуль при t= ±ос. Таким образом, спектр производной получается из спектра функции умножением на /со.
При одностороннем преобразова нии Фурье нижним пределом явля ется нуль, а не —оо, поэтому спект; производной равен /со£(/со)—f(0+)
Это непосредственно вытекает и из одностороннего преобразования Лапласа по теореме дифференцирования оригинала с заменой р=]ы.
В случае интегрирования функции времени f(t) ее спектр F(/co) делится на /со, причем в табл. 15-2 ради общности нижний предел интеграла равен —со.
Для доказательства теоремы интегрирования обозначим через i
yV(j<iy) спектр функции f f(t)dt. На основании теоремы дифференцирования находим, чго функции / (/) = t
— — J f(t)dt соответствует спектр
F(/co) =/соЧг(/со), откуда 1Р(/со) = =F (/со)//со.
При одностороннем преобразовании Фурье интеграл от —ею до 0 обратится в нуль и поэтому нижним пределом интегрирования будет 0.
Теорема умножения спектральных характеристик доказывается так: перемножив спектры оо
Л (!<*)= J fi (t)e-imdr
И
Fa(/co)= pa(0>“/<eed6,
—со
находим:
Fi(/co)f2(M) =
СО e~‘ai dt = J e~'atdf(t). —со
Интегрируя по частям, получаем:
= J J Л(т)/а(6)е-,и(х+0)с2тс2е,
где т и 0 — независимые переменные.
17*
259
Замена переменной G = t—т,
dQ — dt дает:
?1 (/<») ^2 (М) =
= J J KWfAt-rje-^drdt, следовательно, произведение Fi (/а>) F2(/g>) есть не что иное, как
оо
спектр функции J fi(x)fa(<—x)dx.
При одностороннем преобразовании Фурье нижним пределом интеграла будет нуль, а верхним пределом будет t, так как fz(t—т) =0 при
Важный физический смысл имеет теорема об изменении масштабов: при изменении масштаба времени в а раз масштаб частот изменяется в 1/а раз. Это означает, что ширина спектра увеличивается при сжатии сигнала во времени и сокращается при растягивании сигнала (без изменения самого характера спектра). С таким явлением мы уже познакомились в конце § 15-5, рассматривая прямоугольный импульс. При этом под шириной спектра сигнала понимается область частот, в пределах которой заключена основная доля его энергии.
Бесконечно короткий импульс должен иметь бесконечно широкий спектр (§ 15-8). Этим объясняется, например, то, что разряд молнии создает помехи радиоприему на всех частотах.
15-8. СПЕКТРЫ НЕКОТОРЫХ ТИПОВЫХ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
Спектры сигналов в общем случае определяются по формуле (15-8). Однако, как уже отмечалось выше, в ряде случаев нахождение сигналов облегчается использованием свойств преобразования Фурье (табл. 15-2) и при одностороннем преобразовании—применением таблиц лапласовых изображений с учетом (15-27).
Сигналы условно разделяются на видеосигналы и радиосигналы. К первым относятся сигналы, сохраняющие знак неизменным. Вторые характеризуются колебательным процессом. Очевидно, огибающей коле
баний «высокочастотного заполнения» является видеосигнал.
Если /(/) обозначает функцию, изображающую видеосигнал, то f(/)cos<uif или f (^)sincoi^ представляет аналитическое выражение радиосигнала. Поэтому, зная спектр видеосигнала, можно по теореме умножения функции времени на косинус или синус (табл. 15-2) найти спектр радиосигнала.
Ниже рассмотрены спектры некоторых типовых непериодических сигналов, причем там, где это целесообразно, использованы свойства преобразования Фурье и изображения по Лапласу. Первые пять примеров относятся к видеосигналам, остальные пять — к радиосигналам.
Пример 15-5. Убывающая экспонента (рис. 15-11, а):
Л0 =
Гв-0' if >0;
(о <<0.
Согласно (15-8)
F (/to) = j о
—at „—jot 1
е е dt ------------------;
а + /со
|Е (/со)| = -_________
]/ в2 +
260
ф (cd) = — arctg —. a
Кривые |F(jco) | и ф(со) изображены на рис. 15-11,6 и в.
Пример 15-6. Колоколообразный1 импульс (рис. 15-12)
= *==0;
здесь а — действительная величина, определяющая «ширину» импульса. Согласно (15-8)
F (/«) = J e~<aly dt.
Рис. 15-12. Пример 15-6.
Для вычисления интеграла показатель степени преобразуется:
Произведя замену переменной at+/ — — х; dt = — dx, 2а а
получим:
е'31" dx.
Этот интеграл известен. Он равен К л. Следовательно,
Г®’.
Ввиду четности функции f(t) спектр получился действительным, причем, как и сам импульс, он имеет колоколообразную форму. В соответствии с теоремой об изменении масштаба коэффициент а, определяющий ширину импульса, входит в знаменатель показателя степени в
1 В литературе применяется также термин «колокольный импульс».
выражении для спектра. Поэтому, как и следовало ожидать, чем больше а (т. е. чем уже сигнал), тем шире спектр, и наоборот.
Пример 15-7. Прямоугольный импульс (рис. 15-13, а)
' 10 0>/>/.;
F(/co) = j e-ie“di = ± (1-е-'™‘) = о
е 2
Тот же результат может быть получен на основании (15-27), если в изображении по Лапласу
Рис. 15-13. Пример 15-7.
F (р) = — (1 — e~pt'} р
заменить р через /со.
Амплитудный спектр равен: №)1 = |-^-ах
нули функции К(/(й) соответствуют значениям
261
=Лл(/г=1,2...). Прн =
= -у (2Л+1)
№)| = ~ М
~(‘2/г + ))
— . <0/, ,
С учетом знака sin фазо
вый спектр ф(<о) определяется следующим образом:
, , . «о/i п . .2л
ф (со) = —1 при 0 < о < —;
2 tx
ф (<о) = — — л при — < со <
2 /1
4л
— И Т. д. h
го рода функциям непосредственно не применим. Чтобы обойти ограничения, накладываемые условием абсолютной интегрируемости, применяют искусственный прием (§ 15-9).
Пример 15-8. Спектры импульсных функций. Наиболее наглядное представление о спектрах импульсных функций получается при рассмотрении предельных переходов от спектров импульсов конечной продолжительности.
На рис. 15-14, а показан прямоугольный импульс величиной 1/т, имеющий продолжительность т. На основании предыдущего примера спектр единичной импульсной функции
kf(t)
0 v а)
Кривые |F(/w)| и ф(о>) изображены на рис. 15-13,6 и в.
Амплитудный спектр совпал в данном случае со спектром симметричного прямоугольного импульса (рис. 15-9), так как согласно теореме смещения функции времени (табл. 15-2) перемещение импульса вдоль оси времени при сохранении длительности импульса не влияет на амплитудный спектр, а только изменяет фазовый спектр.
С увеличением длительности импульса Ц. амплитудный спектр группируется все в более узкой области частот вблизи нулевой частоты, причем значение амплитудного спектра при нулевой частоте, равное ti, возрастает, стремясь в пределе к бесконечности. Это физически означает, что при Л —*-оо энергия сигнала стремится к бесконечности, сосредоточиваясь около частоты ы = 0. Функции, определяющие сигнал с бесконечной энергией, не удовлетворяют условию абсолютной интегрируемости, и интеграл (15-8) к тако-
sin£7 -'F
F (/а>) = lim-— е = 1.
т—о <»т/2
На рис. 15-14,6 представлены три графика |/?(/о)|, соответствующие разным т. Так как с уменьшением т интервал между нулями амплитудного спектра возрастает, при г, значительно меньшем ть график приобретает вид наклонной линии. Наконец, при т-*0 величина |F(/o>) | стремится к единице.
К тому же выводу приходим, исходя из лапласова изображения единичной импульсной функции первого порядка 6(0- Для которой F(p) = l. Согласно (15-27) F(/co) = l.
Это означает, что единичная импульсная функция, приложенная в момент (=0, обладает сплошным спектром, простирающимся неограниченно по шкале частот с постоянной спектральной плотностью.
Если импульсная функция приложена в момент времени то ее лапласово изображение равно
262
г-”*" и соответственно F (/ю) = откуда я|э(со) = —utto- Следовательно, фазовый спектр в этом случае изобразится прямой, образующей с осью абсцисс угол, равный —arctgmfo (рис. 15-14,в), где т — масштабный коэффициент. При to= =0 фазовый спектр совпадает с осью абсцисс, амплитудный же спектр не зависит от выбора t0.
Импульсная функция второго порядка имеет изображение F(p)=p.
Рис. 15-15. Амплитудный (а) и фазовый (б) спектры импульсной функции второго порядка.
_ J е-/ю(п-1)Г е-/юг
п<оГ
j _ e—jna>T sin 2 — j<u(n—1) -i-
----------- = ---------e
I __e—/шГ “Г
sin — 2
Итак,
Полученное выражение справедливо для импульсов любой формы.
Соответственно спектр F(jg))=/g>= . к 1 — 2
=(ое . Следовательно, в данном случае амплитудный спектр |F(/co)| = | со |, а фазовый спектр ф(ш)=п/2 (рис. 15-15).
Пример 15-9. Спектр серии им-' пульсов. Допустим, что сигнал состоит из конечного числа периодически повторяющихся импульсов. По теоремам линейности и смещения функции времени (табл. 15-2) спектр сигнала
F (fa)=Fr (fa) [ 1 +е-/иг+ • • + j-
где FjQ'co) — спектр первого импульса;
п— число импульсов;
Т — период.
2Л »Л БЛ 8л Т Т г т
Рис. 15-16. Пример 15-9.
В скобках — геометрическая прогрессия, знаменатель которой
Сумма геометрической прогрессии с» — tin Q •»
где и ап — первый и
1 q последний члены прогрессии. Следовательно,
В качестве примера рассмотрим амплитудный спектр серии прямоугольных импульсов при «=»=5 и скважности импульсов Л7==3 (рис. 15-16,а). С учетом (15-12) спектр
263
Fr} первого импульса F1(/cd) = ii-----
cu/j ~2
Следовательно,
tOti sin — 2
<0/1
2
. n<oT sin----
2
<oT sin у
Мы уже неоднократно встречались с кривой y = sinx/x, и поэтому график первой дроби нам знаком.
Что касается второй дроби, то
числитель и знаменатель ее одновременно обращаются в нуль при — =лЛ(Л = 0, 1, 2 ...). Раскрывая
неопределенность, находим, этих случаях дробь равна:
что в
В интервале от 0 до чис-
литель второй дроби, а следовательно, и вся дробь п—1 раз принимают нулевое значение. На рис. 15-16,6 изображен график второй дроби, а на рис. 15-16,в — амплитудный спектр заданной серии прямоугольных импульсов.
Пример 15-10. Затухающая синусоида (рис. 15-17, а)
/<0;
—at
е Sin Од/
<01
(а + /<о)2 -Ь <01
|FM =
<£i
(а2+<о2 — <о2)2 + 4а2 со2
ф (со) = —arctg
2а<о
а2 + <о2 — ш2
Кривые |F(/a>) | и ф(а») показаны на рис. 15-17,6 и в.
Пример 15-11. Отрезок синусоиды (прямоугольный радиоимпульс — рис. 15-18, а)
(sin coj/ Ю
где т=пТ ~n—;
<01 n — целое число
мя т.
0</<т, О > / > т,
Т — период;
периодов за вре-
Изображение по Лапласу отрезка синусоиды, заданного в интерва-
ff(t)
а)
О)
Рис. 15-17. Пример 15-10.
0ХП до п — , имеет вид: (01
_J21_ (i-e-^). Р2 + «о?
На основании (15-27)
Г/- \ <“1 I 1 —'7Гп2я
F(/co) = - у И —g
<01—а> \
Тот же результат получится, если воспользоваться спектром прямоугольного видеоимпульса —!— (1 — ё~, вычисленным в /<о
примере 15-7, и применить формулу умножения функции времени на синус (табл. 15-2):
/(<0 —а
е—Дш-Н»,)! ‘
1 —________________
/ (СО + <01)
264
При со1т=п-2л, где п — целое число,
F(M-
<0j—<0
Отсюда получается амплитудный спектр
<0, о • { ® '
-2 sin — пл со? — аг \<°i ,
При (й = а>1 эта функция равна предельному значению, которое находится по правилу Лопиталя:
'f(t)
<01
со? — со2
— /— и-2л
1 — е
ПЗС
Рис. 15-18. Пример 15-11.
|Г (/й)| = Пт
СО—(Dj
при— n=k(k=0,1,2...) |F(/g»)|=0. wi
Кривые |F(jg>) | и ф(со) изображены на рис. 15-18,6 и в. По мере увеличения п амплитудный спектр группируется все в более узкой области частот вблизи он. При п—оо составлящая амплитудного спектра, соответствующая о = соь стремится к бесконечности, что соответствует дискретному спектру, имеющему ко
нечное значение амплитуды на этой
частоте.
Пример 15-12. Отрезок косинусоиды (рис. 15-19, а)
,... _ fcoscojZ 0 < t < т;
Z ' (О 0 > t > т, 2я где т=пТ=п — ; Т — период;
п — целое число периодов за время т.
Ввиду того, что COS С01#=
Id/- /X
= — —(sinotiO, для нахождения dt
спектра отрезка косинусоиды воспользуемся формулой дифференцирования функции времени. В предыдущем примере для отрезка синусоиды был получен спектр
Так как sin 0=0, то
_ ;^-п-2п 1 _ е
COS (Й11 = /И------------
со/— аг
со „ . сопл -------- 2 sin----- I? — a? <°i
пл—я
Амплитудный спектр равен:
<о п . / со ------2 sm — пп со? — а? \ Ш1 -
Кривые |/7(/а>) | и ф(со) изображены на рис. 15-19, б и в.
Пример 15-13. Колоколообразный радиоимпульс (рис. 15-20, а) f (/) =е~(а02 cos
Для нахождения спектра воспользуемся формулой умножения функции на косинус (табл. 15-2), имея в виду, что спектр огибающей колебаний высокой частоты coi был рассмотрен в примере 15-6.
Спектр видеосигнала с ростом частоты убывает. Поэтому если ограничиться областью частот, близких к Ы1, то при /(f) = Ft (/со) можно приближенно считать, что
f (О COS <0! t = у Fx [/ (со—<01)1.
С учетом выражения, полученного в примере 15-6, искомый спектр примет вид:
265
Построенный по этому выражению график приведен на рис. 15-20, б.
Ш
Зы °-"п
Зш,
в)
Рис. 15-19. Пример 15-12.
Рассматривая, как и в предыдущем примере, область высоких частот йь находим амплитудный спектр с учетом спектра видеосигнала, полученного в примере 15-9:
sin
Соответствующий график представлен на рис. 15-21,6.
15-9. ОБОБЩЕННАЯ ФОРМА ИНТЕГРАЛА ФУРЬЕ
В § 15-6 указывалось, что непериодическая функция f(t), равная нулю при ?<0, имеет спектр и представима в виде интеграла Фурье, если она не превосходит некоторой убывающей показательной функции, т. е. имеет показатель роста с0, меньший нуля. Для напряжений, токов,
^f(t)
---у ——
б)
Рис. 15-20. Пример 15-13.
Рис. 15-21. Пример 15-14.
Пример 15-14. Серия прямоугольных радиоимпульсов (рис. 15-21,а).
зарядов и других функций времени, наблюдаемых в реальных электрических цепях, данное условие удов
266
летворяется. Однако при теоретических исследованиях переходных процессов иногда пользуются функциями-оригиналами f(t) с показателем роста, равным нулю (со=О). Сюда относятся, например, единичная ступенчатая функция 1(0. синусоида 1(0 sin®if и др. К таким функциям интеграл Фурье непосредственно неприменим.
Умножив f(t) на множитель e~ci(c>0), «гасящий» f(t) при больших значениях аргумента, можно для новой функции е-^ f(t) вычислить спектр
F (с, ju) = е~1с+1'а) * dt (15-31)
и можно представить новую функцию в виде интеграла Фурье:
©о
2Л J —со
Xelatda. (15-32)
Заданная функция f(t) рассматривается как предел выражения (15-32) при с->0, т. е. при стремлении гасящего множителя к единице:
f(0 = lime-£7(0 =
С-0
.. 1
=lim — с-»о2Л
(15-33)
Полученное выражение представляет одну из обобщенных форм интеграла Фурье.
В свою очередь спектр заданной непериодической функции находится как предел функции F(c, /а) при с-->0:
F (/co)=lim Е(с, /и). (15-34)
с—0
Для нахождения спектра функции, имеющей показатель роста, равный нулю, вместо умножения функции на гасящий множитель e~ct с последующим переходом к пределу при с=0 можно воспользоваться лапласовым изображением функции и, заменив р на /о>, сразу получить спектр заданной функции.
Для функций с положительным показателем роста спектры не вычисляются.
Рассмотрим несколько типовых примеров.
1. Единичная ступенчатая функция (рис. 15-22, с).
Для этой функции изображение по Лапласу равно F(p)=—. Сле-Р довательно, спектр единичной ступенчатой функции определится как
F(/(o) = А /<о
Единичную ступенчатую функцию можно рассматривать как сум
fW
Рис. 15-22. Единичная ступенчатая функция и ее амплитудный и фазовый спектры.
му постоянной составляющей, равной 1/2 (рис. 15-22,6) и разрывной функции (рис. 15-22,в).
Известно, что
Csincctf ,
I ------НО)
J ш
О
„ 1 Г sin ot ,
Поэтому — | -------- асо есть не что
л J и> о
иное, как аналитическое выражение разрывной функции рис. 15-22,6. Итак,
267
... 1 , I fsinof .
1(0=-----1---I ------aco=
2 я J co о
= P />0; (15-35)
[0 t < 0.
К этой интегральной форме единичной ступенчатой функции можно прийти на основании (15-33), если вместо заданной функции сначала рассмотреть затухающую экспоненту e~ct • 1 (0, для которой в примере 15-5 предыдущего параграфа был найден спектр
F(C, /G>) =--~r-
е + /со
Согласно (15-32)
1
2л
do
cos a>t , , . с sin tot ——-
c + /to J c -f- /to
—oo
sin tot , ------паз . C-kjto
Устремив под знаком интеграла с к нулю, получим (15-35).
Амплитудный и фазовый спектры
|F(/®)| = ^- и ф(о)=--^-|со| 2
показаны на рис. 15-22, г и д.
Скачок при t—О заданной функции времени есть результат суммирования бесконечно большого числа синусоид с бесконечно малыми амплитудами.
Спектр содержит колебания всех частот, но энергия низкочастотных колебаний преобладает.
При и->0 амплитудный спектр стремится к бесконечности. К тому же выводу мы пришли и в § 15-8 (пример 15-7), рассматривая предельный переход прямоугольного импульса к видеосигналу неограниченной длительности.
Вообще, всякий непериодический сигнал с показателем роста, равным нулю, обладает бесконечной энергией, и его амплитудный спектр |F(/g>) | хотя бы на одной из частот равен бесконечности.
Внезапные броски постоянного тока или тока промышленной частоты, происходящие в электрических установках (например, при пуске двигателей или коротких замыканиях в электросети), близки по характеру к ступенчатой функции, энергия которой распределена в спектре неравномерно и преобладает на низких частотах. Это служит причиной того, что промышленные помехи радиоприему больше всего ощущаются в диапазоне длинных волн, (т. е. в области низких частот) и почти незаметны на коротких волнах.
2. Незатухающая синусоида sin (Do/ - 1 (/).
Для этой функции изображение по Лапласу равно F(p) = -—5—.
Р2 + «о Поэтому спектр синусоиды, равный нулю при /<0, определяется как
CDq— со2
На рис. 15-23,а и б показаны амплитудный и фазовый спектр синусоидального сигнала.
___|_________________
U
б)
Рис 15-23. Амплитудный (а) и фазовый (б) спектры синусоидального сигнала.
Угол ф(ы) равен нулю при ы<
<(Do и равен — л при о)>а>о-
Из § 15-8 (пример 15-10) известно, что затухающая синусоида e-'f sincuo/- l(t) имеет спектр
F(G/o)) =-------
(с + Ito)11 +
268
Применяя преобразование (15-33), получаем:
sin<DoM(O =
IS 1 (* “о J
= lim— 1 -------5------da=
£-►0 2л (c _|_ j^yz ш2
откуда
cos со,/• 1 (/) =
Р со sin coi , I —-------—da—
J co| — co2 о
== lim
c->0
1
4л/
ле4*-'01’' —
{cos aQt 0
/ > 0; t<Q.
(15-37)
-лй-(е+М)/ + 2/
(c + /co)2 + COq ]
Эту интегральную форму косинусоидального сигнала можно получить,
Переходя к пределу под знаком интеграла, получаем интегральную форму синусоидального сигнала
• j « f Sit! СОл/ .
sin со,/ • !(/) = —-f-
со0 cos (at tog— со2
da
sin aot 0
(15-36)
3. Незатухающая косинусоида
COS (Dob 1(0-
Для этой функции изображение
по Лапласу равно F(p) ——-------.
Р2+ “о
Поэтому спектр косинусоиды, равный нулю при 1<0, определяется как
F(/co) = /
со
9 е
cog — СО'
На рис. 15-24,а и б показаны амплитудный и фазовый спектр косинусоидального сигнала.
Затухающая косинусоида e~ct cos <оо/ • 1 (0 имеет спектр
F (с, /со) = J cos aote~lc+,a)t dt — о
_ c + jco (с + /со)2 -|- СО2 ’
Поэтому согласно (15-33) cos со,/•1 (0 =
= Гda,
2л J -j- (Од
Рис. 15-24. Амплитудный (а) и фазовый (б) спектры косинусоидального сигнала.
продифференцировав (15-36) с учетом того, что
, id., cos aot =-----sin <o0r.
coo at
По теореме дифференцирования функции времени спектр косинусоиды равен спектру синусоиды, умно-. со женному на /— .
15-10. ОСОБЫЕ СЛУЧАИ
Из математики известно, что оригинал f(t) вполне определяется своим лапласовым изображением F(p) с точностью до значений в точках разрыва f(t). Это положение распространяется и на частный случай преобразования Лапласа — на преобразование Фурье. Две кусочно-непрерывные функции, имеющие одинаковый спектр, могут отличаться только в точках разрыва. Если из
269
вестей спектр F(/(o) функции f(t), представимой в виде интеграла Фурье, то эта функция определяется единственным образом во всех точках непрерывности по формуле обратного преобразования Фурье (15-26), где интеграл понимается в главном значении.
В § 15-9 было введено понятие о спектре функций, не удовлетворяющих условию абсолютной интегри-
руемости в бесконечных пределах, а именно имеющих показатель роста, равный нулю. Естественно возникает вопрос: не могут ли в этом случае несколько разных функций иметь одинаковый спектр Е(/ю) = =limF(c, /о). Оказывается это воз-с—-о
МОЖНО.
На рис. 15-25, а показана разрывная функция, не удовлетворяющая условию абсолютной интегрируемости в бесконечных пределах. Заменив ее функцией, представленной на рис. 15-25,6, где с>0, найдем:
о
F(c,/<о)= J necte~!'a! dt-\-—со
4- те^ e~iat dt = б
__ п [ т (т—n)jio—(m-j-n)c
С—/<1> с-)-/<о (/<о)2— с2
Если положить т—п= 1, где т и п — алгебраические величины, то, перейдя к пределу, получим:
=-L.
с-о (/со)2 —с2 /о
Таким образом, варьируя значениями тип, можно получить бесчисленное множество разрывных функций вида, показанного на рис. 15-25, б, имеющих одинаковый спектр F (/со) = 1 /ja. Все эти функции разнятся постоянной составляющей, к которой преобразование Фурье не применимо.
Единичная ступенчатая функция, а также разрывная функция на рис. 15-22,в являются частными случаями функции на рис. 15-25, а, и поэтому для них спектр определен тоже как 1//<о.
Решая в подобных случаях обратную задачу, т. е. находя f(t) по спектру, следует пользоваться обобщенной формой интеграла Фурье
оа
f (/) = lim — f F (с, ja)eia>i da, с-о2п J
—сю
переходя к пределу лишь на последней стадии интегрирования, как это делалось в примерах § 15-9.
Если же сразу перейти к пределу с=0 под знаком интеграла, т. е. пытаться вычислить /(/) по спектру Е(/со)
/(0=т-2л J
—ев
то в случае F(ja) = 1//<о получим:
/(/)= - = 2л J
—оо
__ 1 Г COS (Of ____L f S*n
2л J /<о 2л J a
—co —oo
Так как lim f —s— da = 0, to fl-»-oo J /CO
—a
oo
Z(0==_Lf!HL^do)==
mJ co
о
— «>0;
2
----- t<fi-
2
270
Как и следовало ожидать, получилась функция вида,- показанного на рис. 15-22,в без постоянной составляющей, так как интеграл Фурье постоянную составляющую не учитывает.
Действительно, если к постоянной составляющей применить прием, описанный в § 15-9, а именно рассмотреть сначала функцию e-c<f) при б>0 (рис. 15-26), удовлетворяю-
Рис. 15-26. Экспоненциально убывающая функция.
щую условию абсолютной интегрируемости в бесконечных пределах, то получим:
о
F(c,;w)= J
—со
оо
1 _ 2с
С + /со са — (/о)2'
Устремив с к нулю, получим F(/о)) = = 0. Следовательно, обобщенная форма спектра не дала возможности обнаружить присутствие постоянной составляющей.
Между тем постоянная составляющая имеет спектр в виде дискретной линии при ю=0, и поэтому спектральная плотность при о=0 должна быть бесконечно велика. В этом можно убедиться, исследуя график F(jo) для симметричного прямоугольного импульса, изображенный на рис. 15-9.
Расстояния от начала отсчета (о=0) до пересечений оси абсцисс спектральной характеристикой обратно пропорциональны длительности импульса tit а спектральная плотность при о = 0 равна Zt.
При любом значении Ц площадь, ограниченная спектральной харак
теристикой и осью абсцисс, равна 2л. Действительно, с учетом (15-12)
со
= 2 J-^dr=2n. —со
Если устремить ti к бесконечности, то спектральная плотность, группируясь у оси ординат, в пределе выродится в единичную импульсную функцию, умноженную на 2л:
F (уо) — 2 л -б (о).
К этому же можно прийти и на основании формального применения свойства взаимозаменяемости независимых переменных: так как единичной импульсной функции 8(t) соответствует спектральная плотность F(/co) = l (пример 15-8), то постоянной составляющей, равной единице, должна соответствовать спектральная плотность в виде единичной импульсной функции, умноженной на 2л.
Аналогично в случае незатухающего косинусоидального колебания j(0=coscoif, заданного от t——оо до /=оо, спектр содержит дискретные линии при cot и —mi и поэтому спектральная плотность при этих частотах бесконечно велика, а в остальных точках — равна нулю.
Если к произведению 1 • cos <щ£ применить теорему об умножении на косинус, то получится спектральная плотность
-у- [2л • б (со — сох) 4- 2л • б (со + coi)] в виде двух единичных импульсных функций, умноженных на л, в точках <01 и —<01-
Здесь уместно предостеречь читателей от формального пользования некоторыми приемами, описанными ранее. Например, возможность нахождения спектра по лапласову изображению F(j<o) =[Е(р)]р=/и сохраняется только до тех пор, пока показатель роста функции f(t) или, что то же, абсцисса абсолютной
271
сходимости не превышает нуля. Для функций с положительной абсциссой абсолютной сходимости преобразование Фурье неприменимо и нахождение F(/co) как предела обобщенного спектра F(c, fa) при с-»-0 лишено смысла. Нанример, возрастающая показательная функция
I о /<0
имеет изображение по Лапласу
. 1 1
F (р) =----=------------•
р — а с + /со — а
В этом случае абсцисса абсолютной сходимости равна а>0 и должно выполняться условие с>а. Поэтому нельзя устремить с к нулю. При с—0 получится спектр не заданной, а совершенно другой функции, равной нулю при />0 и —eat при /<0. Если же положить с=а, то получится спектр 1//со единичной ступенчатой функции.
Таким образом, спектральный метод неприменим в случаях, когда абсцисса абсолютной сходимости больше нуля. Сюда относятся случаи возрастающих экспонент, колебаний с неограниченным ростом амплитуды, гиперболических функций и т. д.
15-11. НАХОЖДЕНИЕ СИГНАЛА ПО ЗАДАННЫМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ ДЕЙСТВИТЕЛЬНОЙ И МНИМОИ СОСТАВЛЯЮЩИХ СПЕКТРА
Рассмотрим задачу гармонического синтеза, когда по частотным характеристикам действительной и мнимой составляющих комплексного спектра требуется получить временную функцию.
Воспользуемся условными обозначениями, принятыми в § 15-4, уравнения (15-17): F(fa) =Ft (а) — —jFzfa), где Л (со)—четная, а Fz(co) —нечетная функция со.
Отсюда
оо f(0=-^jF(/to)e/“fdco = ----------СО
оо
= J [У7! (со) cosco/ +
4* /Fx (со) sin со/ — ?F2 (со) cos со/ 4-4-F2 (со) sin со/] dco.
Ввиду нечетности функций Ft(co)X X sin со/ и F2(co) cosco/ интегралы от них в бесконечных пределах приравнены нулю. Поэтому
/ (/)= -^- J [Fx (со) cos со/ 4-о
4- F2 (со) sin со/] dco. (15-38)
Если Fi(co) и F2(co), т. е. действительная и мнимая части комплексного спектра, заданы в виде графиков, то можно воспользоваться методом приближенного вычисления интеграла (15-38).
В ряде случаев заведомо известно. что f(t)=O при /<0 (например, когда процесс начинается с момента /=0 при нулевых начальных условиях). Это равносильно тому, что f(—i) =0 при />0, г. е.
со
0=—С fFx(co)cosco/—
Л J о
— F2 (со) sin со/] dco (/ > 0). (15-39)
Произведя поочередно сложение (15-38) с (15-39) и вычитание (15-39) из (15-38), получим:
оо
f (/)= — f Fi (со) cosco/ dco=
Л J о
co
= — C F2 (co) sin co/ dco (/ > 0). (15-40) л j о
Следовательно, в этом случае для нахождения функции времени достаточно воспользоваться частотной зависимостью только действительной или только мнимой частей спектра.
Читателя не должно смущать то обстоятельство, что выражение (15-40) отличается множителем 2 от формул (15-19) и (15-21), так как последние относились к случаям четной или нечетной функции /(/), т. е. когда функция f(t) не приравнивалась нулю при /<0.
272
Вытекающее из (15-40) равенство
(" Fj (со) cos at da —
оа
J F2 (<o) sin at da
(/>0)
устанавливает связь между действительной и мнимой частями любого спектра.
Это равенство распространяется и на действительные и мнимые части передаточных функций линейных электрических систем (§ 15-14).
15-12. ПРИМЕНЕНИЕ СПЕКТРАЛЬНОГО МЕТОДА ДЛЯ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Представление непериодической функции в виде бесконечной суммы незатухающих гармонических колебаний бесконечно малой амплитуды дает возможность применять к бесконечно малым гармоническим составляющим напряжений и токов, а следовательно, и к самим спектрам обычные методы расчета установившихся синусоидальных процессов в линейных электрических цепях и затем, пользуясь методом наложения, определять результирующие напряжения и токи.
Положим, что линейная цепь, имеющая комплексное сопротивление Z(ja), присоединена к источнику э.д.с. e(t). Спектр э.д.с. обозначим через E(ja). Тогда спектр тока найдется по формуле
I (ja) — Y (ja) Е (ja); (15-41)
здесь У(ja) = —-------комплексная
2 (/а)
проводимость цепи.
Переходный ток в цепи находится по формуле
со
ф)=-^- J — со со
= — f Y (ja) Е (ja) da. (15-42)
2л J
—со
Если процесс начинается с момента t=0, то вычисление i(t) непосредственно по формуле (15-42)
не имеет преимуществ по сравнению с вычислением при помощи обратного преобразования Лапласа. При этом для вычисления 1(f) можно пользоваться одним из правил нахождения функции времени по спектру, которые аналогичны правилам нахождения оригинала по изображению Лапласа (с заменой р на /со).
Формула (15-42) может иметь преимущество перед другими методами расчета в тех случаях, когда спектр E(ja) задан графически или когда процесс длится с t=—оо. Возможен и другой ход рассуждений. Так как спектр единичной импульсной функции 6(t) равен единице, то У(/со) = l/Z(/co) можно рассматривать как спектр реакции цепи на 6(t), т. е. спектр импульсной характеристики Lt(f). Имея в виду, что спектр воздействующей э.д.с. e(t) равен E(ja), воспользуемся формулой умножения спектров (табл. 15-2):
i(0= (е(т)Е6(< — r)dr.
—со
Реакция цепи на единичную импульсную функцию, приложенную в момент t=0, равна нулю при t< <0. Соответственно и Lt (t—т) =0 при I—т<0, вследствие чего подынтегральная функция обращается в нуль при r>t. Поэтому верхним пределом интеграла будет t-.
t
i(f)= J e (т) (t — t) dr. (15-43) —oo
Во второй формуле умножения спектров
со
1(0= J e(t — T)L6(r)dr —со
с учетом того, что Lt (т) =0 при т<0, нижним пределом интегрирования будет нуль:
i(0= —т)Е6(т)г/т. (15-44)
6
В случае одностороннего преобразования Фурье е(т)=0 при т<0 и e(t—т)=0 при t—т<0; поэтому нижним пределом интеграла
18—1118
273
(15-43) будет нуль, а верхним пределом интеграла (15-44) будет t и полученные формулы полностью совпадут с формулами свертывания предыдущей главы.
Пример 15-15. Последовательно с г и L включена э.д.с. eat, действующая в бесконечном интервале от t——оо до / = 0. Найти ток при />0.
С учетом примера 15-5 спектру Y (йо) = —5-- соответствует функ-
r ja>L
1 '
ция времени Lh(t)——e L . Так как э. д. с. действует только при /<0, то согласно (15-43)
Тот же результат получается и по формуле (15-44) с учетом того, что е{1—т)=0 при t—т>0:
г —|— gL»
В случае, когда э.д.с. задана в виде единичной ступенчатой функции, незатухающей синусоиды или косинусоиды, причем известна частотная характеристика активной или реактивной проводимости двухполюсника, удобно пользоваться интегральной формой воздействующей функции.
Допустим, например, что в момент t = 0 к источнику постоянной э.д.с. Е подключается цепь, комплексная проводимость которой равна:
У(/<о) = г(<о)—
С помощью интегральной формулы (15-35) единичной ступенчатой функции со
1(0 = — + -L f s-^-d&
4 ' 2 л J со
О
находим ток в контуре:
*(0=
Е
2Z(0)
Е Г sin (со/ — ср) _ nJ со | Z (/со) |
о
СО
Е . Е (‘ cos ф sin со/ 2 Z(0) + л J со |Z (/со)1 о
da—
Е f sin Ф cos со/ , ------1------~------da>.
я J со IZ (/со) I о
Вводя в подынтегральные выражения активную и реактивную проводимости
, ч COS ф , , . sin ф g(co) = :---Л- и Ь(а) = -—— ,
|Z(/co)| |Z(/<o)|
получаем:
оо
1 /л Eg (0) Е . . sin со/ j
1 (/)= -Ш. + £(ш)-------dco—
2 nJ со
о
— — fb(co)^^-dco. (15-45) я J со
о
Это выражение, справедливое для любого момента времени, должно обращаться в нуль при /<0. Следовательно, при />0 i(—1)=0 или, что то же,
о = f g(to)^dG)_
2 л J со
— — (b (со) dco. (15-46)
л J со
о
Поочередно складывая (15-45) с (15-46) и вычитая (15-46) из (15-45), находим для />0:
/(0 + » (-0 = ^(0)-
nJ со
О i (f) = i (t) — i (—t) = . (15-47)
со
2£ С , . sin со/ , - ------ ёГ(со)------------da).
л J со
о
По последней формуле вычисляется переходный ток в электрической цепи, если известна частотная характеристика только его активной проводимости g(co). Знание частот
ной характеристики реактивной проводимости b (со) в этом случае не требуется, потому что последняя функционально связана с первой (гл. 17).
Пример 15-16. Цепь, заданная идеализированной частотной характеристикой активной проводимости
Е (и) =
g = const
О
О и <оо; со > со0,
подключается к источнику постоянной э.д.с. Е. Определить время t, в течение которого ток в двухполюснике достигнет 90% установившегося значения.
Пользуясь формулой (15-47), имеем:
“л
((()_
Я J О) о
= ^-Si(co00, л
т. е. ток в цепи нарастает по закону интегрального синуса.
Установившийся ток равен iycT = =gE. Следовательно, согласно заданию
— Si (ц>о 0 = 0,9, откуда t — 1,63 . л ©0
Рассмотрим теперь подключение цепи в момент 1=0 к источнику синусоидальной или косинусоидальной э. д. с.
Пользуясь интегральным выражением (15-36) для синусоиды
• j 1 /j.\ sin . sina)oM(0 = —р-+
co
©0 cos tof
©0— to2
da,
находим ток в цепи:
i za= £m sin(coo/ —фп) 2 |Z(/©0)|
j Em Г ©o cos (mZ — tp) fa _ я J (©2- <o2)|Z(/co)| “
0
= -~r-g(<oo)sin<oot —
— £> (coo) cos coo /+
. Em Г ©0g(©)cos©Z fa, " J ©2-©2
0
©0 b (to) sin at
2 ‘
% — ©
da.
Рассуждая аналогично предыдущему, можно получить расчетные формулы для t>0, а именно:
i(0 = i(0 + »(—П =
= —Emb (©0) cos ©0 / +
0
2Em Г ©og(©)cos©( d[|].
31 J co2 — co2 о
i(0 = i(0-i(-0 =
= Emg (©0) sin ©o t +
©ofe(a) sintof fa 4 о
©y—©
/
(15-48)
В случае подключения цепи к источнику косинусоидальной э.д.с., пользуясь выражением (15-37) для косинусоиды
cos©,/-1 (0
cos to„ t 2
оо
1 C © sin со t , -----I----------аа,
31 J ©у — ©2
находим ток:
- /а = E” cos _
U 2 |Z(/©O)I
_ Em f to sln(mZ-cp)
11 J (“o~“2) | Z(/©)|
= у gW COS©01 + b (©0) X
Em C cog (to) sin to/ , x smffljf-----— I —-—d© +
Л J to2-©2
oo
И Ъ (и) COS И t ©fl — ©2
18*
275
По аналогии с предыдущим получаем расчетные формулы для />0:
i (0 = i (/) + £(— 0 =
= Enig (а0) cos wot +
C to b (to) cos co t d n J cog — to2
1(0 = i(t) — =
= £m&(coo)sincoof—
_ (* <o g (to) sin co f £
n J cog — co2
0 0
(15-49)
Следовательно, для расчета переходного процесса достаточно иметь частотную характеристику активной проводимости g(co) и знать величину Ь(соо) или иметь частотную характеристику реактивной проводимости b (со) и знать величину g(coo). Это возможно в силу того, что активная и реактивная проводимости электрической цепи являются взаимозависимыми (гл. 17).
Применение расчетных формул (15-47), (15-48) и (15-49) целесообразно в тех случаях, когда заданы частотные характеристики активной или реактивной проводимости цепи. В этих случаях спектральный метод имеет преимущество перед преобразованием Лапласа и классическим
методом расчета переходных процессов.
Частотные свойства электрической цепи при установившемся режиме, выражаемые комплексной проводимостью У (/со) или ее компонентами, однозначно определяют переходный процесс в цепи. В свою очередь по реакции цепи можно определить частотные свойства цепи.
Пример 15-17. Цепь, заданная идеализированной характеристикой активной проводимости
£(«) =
g — const coj -С со со2;
О COj > со > и2,
подключается при t=0 к источнику синусоидальной э. д. с.
e(t) = £msincoo/.
Найти закон нарастания тока в цепи, если частота источника соо=
= V союза удовлетворяет условию 6(со0) =0.
На основании (15-48)
i(t) = coscotdco =•
11 J cog — со2 СП- u
CDS
COS со t cos co t \ J ----------------------------I fl Cl) =
CO + coo co — Wo /
CO4
<DS
gEmT C cos (w-}-Wp) t cos w0 t
я [J <0 + w0 CDj
<O8
sin (co -|- w0) t sin coo t j ---------------------------— u co — w + w0
CD,
f cos (w — w0) t cos Wo t J
i -----d co -4-
J co — co0
W1
। C sin (co — co0)fsinco0f 1 _
J co — coo ]
(Dj
(o)2-f-cn0) t
= ^Mcosco0t f -^-dx-\-n L J x
t
(“1+“о) t , • , f sin x ,
+ sin coo t I --------------dx —
(ш,—m0) t
„ „ j C COS X , .
— cos co01 | --------dx-\-
J X
(U),—CD,) f
(U)j--W#) t
. л C sinx i 1
+ sin coo t I ----------------dx .
((Dj— Wt) t
Итак,
i (/) = {cos Шо t [Ci (co2 + Ио) t —
—Ci (cdj-J-coq) i] -(-sin <oo t X
X [Si (ti)24-<Oo) t—Si (ci^-j-coo) /J —
—cos coo t [Ci (o)2—coo) t—
—Ci (coj— coo) /] 4-sin coo * [Si (co2—
—coo) t—Si (coj—coo) /]}.
Если g>i и co2 достаточно велики, приближенно можно считать, что
со3—со0^со0—С01 — (со2—COJ;
й)34-С00 ~ COi-f-COo-
276
Ввиду того, что Ci(coi—<oo)f= = Ci(co0—coi)/, a Si((oi—ы0)^= =—Si (coo—со1)Л полученное выше выражение для тока упрощается и приобретает следующий вид:
i(f) = Si гс»-0* tsinю /
' л 2 0
15-13. УСЛОВИЕ НЕИСКАЖЕННОЙ ПЕРЕДАЧИ СИГНАЛА
ЧЕРЕЗ ЛИНЕЙНУЮ СИСТЕМУ
Как уже указывалось в начале § 15-12, в случае линейной электрической цепи общие методы и теоремы, относящиеся к установившемуся гармоническому процессу, применимы и к спектральным характеристикам непериодических функций. Это позволяет распространить на переходный режим многие понятия и свойства цепей, рассмотренные ранее для установившегося режима.
Например, ввиду равенства У12(/со) и Уа(/со), которое свойственно обратимым цепям, теорема обратимости или взаимности (§ 5-6) сохраняет силу и в переходном режиме.
То же можно сказать и о теореме об эквивалентном источнике, применимой к спектрам напряжений и токов при расчете переходных процессов с помощью преобразования Фурье.
Подобных примеров, иллюстрирующих применимость к спектрам общих методов расчета гармонических процессов, можно привести большое множество.
Переходный процесс в любой линейной электрической цепи зависит от частотных характеристик цепи. Если две линейные системы, имеющие разные структуры, обладают одинаковыми частотными характеристиками, то они одинаково влияют на прохождение через них сигнала (реакция систем на подводимый сигнал одинакова).
Справедливо и обратное положение, а именно: для того чтобы переходный процесс протекал определенным образом, система должна обладать вполне определенными частотными свойствами.
Рассмотрим условия, которым должны удовлетворять частотные характеристики системы, чтобы сигнал, проходя через систему, не претерпевал искажений.
В линейной системе, состоящей из сопротивлений и накопителей
Рис. 15-27. Смещение функции времени (а), амплитудно-частотная (б) и фазо-частотная (в) характеристики неискажающей системы.
энергии, выходной сигнал отличается от входного по величине и запаздывает относительно него во времени.
Если форма сигнала сохраняется неизменной, то передача называется неискаженной, а сама система — неискажающей. Очевидно, условием неискаженной передачи сигнала является
где k—постоянной множитель;
t3—время запаздывания (рис. 15-27, а).
Переходя отсюда к уравнению для спектров входного и выходного сигналов, с учетом теоремы смеще-
ния функции времени имеем:
FВЫХ (/ со) =^вх (/ “) e~'al3 = =k (i со) FBX а а), где А>(/со) —комплекс-
ная передаточная функция.
277
Итак, при неискаженной передаче амплитудно-частотная характеристика системы
lfe(7 <o)|=ft=const, (15-50)
а фазо-частотная характеристика ф(со)=—at3. (15-51)
Это означает, что во всем диапазоне частот колебания на выходе прямо пропорциональны колебаниям на входе, причем все гармонические колебания запаздывают на одно и то же время.
На рис. 15-27,6 и в показаны амплитудно-частотная и фазо-частотная характеристики неискажающей системы.
Время запаздывания равно t3— __ |ip(<o) I
I и Г
В реальных цепях с сосредоточенными параметрами реакция цепи на выходе возникает мгновенно, однако она практически не ощутима в некотором интервале, определяемом как время запаздывания t3.
Осуществить линейную электрическую цепь с идеальными характеристиками (15-50) и (15-51) в диапазоне частот от 0 до сю не представляется возможным. Однако на практике это и не требуется, так как реальные сигналы обладают некоторой конечной шириной спектра и поэтому достаточно, чтобы электрическая цепь имела характеристики, близкие к идеальным, только в полосе частот, соответствующей заданной ширине спектра.
Чем короче импульс, тем шире его спектр и соответственно шире полоса частот, в которой должны соблюдаться условия неискаженной передачи. Импульсные функции имеют бесконечно широкий спектр; поэтому неискаженная передача таких сигналов практически невозможна.
Для объяснения причин искажения формы короткого импульса при прохождении его через линейную систему можно воспользоваться не только спектральным, но и временным подходом к анализу явлений: под воздействием короткого импульса возникает переходный про
цесс, продолжительность которого соизмерима с длительностью самого импульса, в результате чего форма сигнала искажается.
15-14. ПРОХОЖДЕНИЕ СИГНАЛА ЧЕРЕЗ ЛИНЕЙНУЮ СИСТЕМУ С ОГРАНИЧЕННОЙ ПОЛОСОЙ ПРОПУСКАНИЯ
Допустим, что линейная электрическая система имеет передаточную функцию, которая удовлетворяет идеальным условиям только в конечном диапазоне частот от 0 до too (рис. 15-28), причем вне этой поло-
1 \к(юН
Рис. 15-28. Передаточная функция, удовлетворяющая идеальным условиям в конечном диапазоне частот.
сы частот гармонические колебания задерживаются системой:
А (/ со) =
е /ш<3со<со0—полоса пропускания;
0 <о><оо—полоса
задерживания.
Здесь принято, что в полосе пропускания |ft(7<o) | =А= 1.
Рассмотрим случаи воздействия на эту линейную систему трех типовых функций: 1) единичной импульсной функции (дельта-функции), 2) единичной ступенчатой функции и 3) прямоугольного импульса.
Воздействие единичной импульсной функции. Применяя условные обозначения, принятые в предыдущем параграфе, имеем;
со
/вых(0 = J ^вх (7 <о) k (i со) X
—оо
xe^'do^ f FBX(7<o) X
2п J —“о
278
В данном случае спектр воздействующей функции Fnx(/co) = l и, следовательно,
/вых (О = f COS [со (/—4)] dco —
2л J —
(ОО
—/'4г [sin И*—U]rfw-
—“о
Второй интеграл равен нулю. Поэтому сигнал на выходе выражается функцией
/вых (0 = . (15-52)
л соо (/—/3)
График этой функции дан в первой строке табл. 15-3.
При t~ta эта функция достигает максимума, равного соо/л. После этого она проходит через нуль при соо(»—13) =л или t=— + t3. Следовало тельно, ширина основной частоты выходного сигнала составляет 2(t— —tg) — 2л/сОо-
Интервал времени, в течение которого нарастает основная часть сигнала от нуля до максимума (длительность нарастания фронта сигнала), равен л/соо.
С увеличением граничной частоты соо> т. е. по мере расширения полосы пропускания, искажение сигнала уменьшается, максимум выходного сигнала и крутизна фронта возрастают, «размазанный» сигнал постепенно приближается по своему виду к входной единичной импульсной функции. В пределе для системы с идеальными характеристиками в неограниченном диапазоне частот сигнал на выходе представляет единичную импульсную функцию 6(/—13), запаздывающую относительно входного сигнала на время t3.
На основании (15-52) можно предположить, что реакция цепи возникает при /<0, т. е. до момента воздействия на систему единичной импульсной функции. Этот парадокс является следствием того, что была выбрана передаточная функция с бесконечно большой ’крутизной характеристики |A’(/w)| при частоте соо (рис. 15-28), которая в действительности не реализуема.
Воздействие единичной ступенчатой функции. В этом случае целесообразно воспользоваться интегральной формой единичной ступенчатой функции (15-35), на основании которой
/вых (0 = 4- + — fSinff0(/~<s)l dco = 2 Л J £0
о
=4-+vs, ^«(/~Z3)i- (15’53)
Г рафик полученной функции представлен во второй строке табл. 15-3. Значение функции при t — t3 равно l/i. Длительность нарастания фронта сигнала в этом случае определяется ориентировочно как величина Т, обратная производной функции в точке (i3,
dfsbix 0). = L j Si с
dt n dt 1
-4)]^3
<0<)
it ’
откуда T=jt/coo.
Следовательно, как и в предыдущем случае, длительность нарастания фронта сигнала обратно пропорциональна граничной частоте too-
Сказанное выше о нереальности выбранных характеристик передаточной функции и об уменьшении искажения сигнала с ростом граничной частоты соо относится и к данному случаю.
Воздействие прямоугольного импульса. Если прямоугольный импульс симметричен относительно оси ординат, то, рассматривая его как разность
/вх(0=1(<+4’)-1(^-т)
двух единичных ступенчатых функций, получаем на основании (15-53):
/BHx(0 = “{Si[con((/-Z3+
4-4)l-SiL0(/-/3-4'j]. (15-54)
А / I I \ All
279
Таблица 15-3
Прохождение сигналов через линейную систему
Воздействующая функция fBX (О Сигнал на выходе ?вых (f)
Аналитическое выражение График Аналитическое выражение График
Единичная импульсная функция (дельта-импульс) ««>-(" 1 оо (=0 й (0 = ~ при т-* 0 2_ % Ht) t
0 <с
Единичная ступенчатая функция fit)
/(0 = О о V Л о —. т
0
Прямоугольный импульс о _2l>z>2l 2 2 П0= t t 2^2 . fd) 1 _ t
1,0 t, 'г г
График этой функции показан в третьей строке табл. 15-3. При /'= = t3 ~ и t"=ta + функция достигает значения Si((o0/i), а разность абсцисс равна длительности прямоугольного импульса: t"—t'=ti.
Так как спектр дельта-функции равен единице, то передаточную функцию k (/со) линейной электрической системы можно рассматривать как спектр сигнала на выходе этой системы, когда на вход системы подана дельта-функция.
В § 15-11 было установлено, что действительная и мнимая части любого спектра связаны условием (15-40). Очевидно, это условие распространяется и на действительную и мнимую части передаточной функции. Приняв
k (/ со)=(<о)—jk2 (со) можно утверждать, что любая физически осуществимая или, как говорят, физически реализуемая линейная электрическая система должна удовлетворять условию
(со) cos со i dot —
= (со) sin со/ dco (/>0).
Так как L& (t) =k(jco), то
©о
fe(j®) = J Ls(t)e~ia>tdt.
—oo
Воспользовавшись зависимостью между импульсной и переходной характеристиками
^(0 = f/(0)6(/) +
получим:
*(/«)- (0)6(/) сЙ +
— СО л
со
+ (й(0 -й(0)1(0]е“;“'л =
--ОО
©о
____t_
Например, если y(t)=e гС ’ то , то со __ t
= 1 _ _L 'с e~!w,dt = о
= 1 _ 1 1___ _ 7<ocC
rC 1 1 -j- i co rC
+/w
rC
15-15. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
15-1. Сопротивление г, индуктивность L н емкость С, соединенные параллельно, подключены при / = 0 к источнику постоянного тока 1. Найти напряжение на зажимах цепи при нулевых начальных условиях спектральным методом.
15-2. Доказать, что пилообразная функция с высотой зубцов, равной 1, и шириной каждого зубца равной а, имеет спектральную характеристику:
1_________е~'см
“(М2 / со (1 — е-'°“) ’
15-3. Сравнить спектральные характеристики затухающих синусоид вида sin 314/ при а=50 и а= = 500.
15-4. Какая связь существует между спектральной характеристикой и коэффициентами ряда Фурье?
15-5. В чем заключается родственность преобразований Фурье и Лапласа?
15-6. О чем можно судить на основании спектральной характеристики электрического сигнала?
15-7. Доказать применимость теоремы обратимости (взаимности) в переходном режиме линейной цепи при нулевых начальных условиях.
15-8. Доказать применимость теоремы об эквивалентном источ-
281
нике к расчету переходных процессов с помощью преобразования Фурье.
15-9. Пользуясь теоремой об эквивалентном источнике, вывести общее условие эквивалентности источников напряжения и тока:
E(joj) = Z (j со) I (j co),
где E(/co) и 1 (/co)—спектры э.д.с. и соответственно тока эквивалентных источников; Z(jco)—их внутреннее комплексное сопротивление (т. е. сопротивление последовательной ветви источника напряжения, равное сопротивлению параллельной ветви источника тока).
282
Глава шестнадцатая
ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
1G-1. ПЕРВИЧНЫЕ ПАРАМЕТРЫ ОДНОРОДНОЙ ЛИНИИ
До сих пор рассматривались электрические цепи с сосредоточенными параметрами, т. е. предполагалось, что электрическая цепь представляет совокупность некоторых самостоятельно существующих элементов г, L и С, сосредоточенных в различных ее точках. Напряжение и ток в этих элементах связываются соотношениями ur=ri;
г di » dur
ub=L----; t=C___, основанными
dt dt
на предположении, что ток, входящий в каждый из этих элементов цепи, равен току, выходящему из него. Решение этих уравнений дает закон изменения исследуемой электрической величины в зависимости от времени, но не от координаты длины, которая в эти уравнения не входит.
Однако представление электротехнических устройств в виде цепей с сосредоточенными параметрами не всегда возможно. Например, рассматривая электромагнитные процессы, происходящие в электрических линиях, при помощи которых электрическая энергия или сигналы передаются на расстояние, необходимо иметь в виду, что магнитное и электрическое поля распределены по всей длине линии и превращение электромагнитной энергии в тепло также происходит по всей длине линии. Таким образом, линия явля
ется цепью с распределенными параметрами.
Если мысленно выделить какой-либо конечный участок этой линии, то токи на концах этого участка окажутся неодинаковыми вследствие наличия токов смещения, обусловленных емкостью между токоведущими проводниками, и токов утечки через изоляцию. Только при бесконечном уменьшении участков линии токи на концах их можно считать равными друг другу.
Следовательно, приведенные выше уравнения непосредственно не применимы ко всей линии в целом или к конечным ее участкам; строго говоря, они могут быть применимы только к участкам бесконечно малой длины.
Величина магнитного потока, который сцепляется с контуром тока, образуемым токоведущими проводниками, определяет индуктивность цепи.
Емкость между проводами, а также емкости этих проводов по отношению к земле (или соответственно к корпусу машины, самолета, корабля и т. д.) и к другим соседним проводам определяют емкость цепи.
Тепловые потери в проводах с учетом поверхностного эффекта и эффекта близости обусловливают продольное активное сопротивление цепи.
Наконец, несовершенство изоляции (проводимость изоляции и диэлектрические потери, возникающие
282
в ней) определяет поперечную активную проводимость цепи.
В качестве цепи с распределенными параметрами ниже рассматривается однородная двухпроводная линия, т. е. такая линия, индуктивность, емкость, активное сопротивление и проводи-
Рис. 16-1. Двухпроводные линии. а — воздушная; б — коаксиальный кабель.
мость которой равномерно распределены вдоль всей длины линии. Эти электрические параметры, отнесенные к единице длины линии, называются первичными параметрами линии; они обозначаются через L, С, г и g*.
Однородная двухпроводная линия является распространенным типом линии; она используется в электропроводной связи и в радиотехнике и выполняется в виде параллельных проводников (рис. 16-1, а) или коаксиального кабеля (рис. 16-1, б).
Уравнения для напряжений и токов такой линии в принципе применимы и к другим типам линий — трехфазным и многопроводным.
Первичные параметры линии зависят от ее конструкции и от частоты. Вычисление первичных параметров линии относится к задачам теории электромагнитного поля.
В области радиочастот первичные параметры однородной двухпроводной линии с медными проводами вычисляются по следующим формулам.
Воздушная линия (параллельные провода) (рис. 16-1,а):
8,ЗЗУ/ в . . .
г.^-----— iq-8 ojw/ju (линии);
* Следует обратить внимание на то, что здесь г =# l/g, так как параметры линии г и g ие связаны друг с другом; параметр г — продольный (активное сопротивление провода), параметр g — поперечный (активная проводимость изоляции).
L ^0,9211g— КгЪм/Ж; а
12,07 12 г,
С х10 ф/м.
Коаксиальный кабель (рис. 16-1,6):
г » 4,16 (— + — УТ- 10'8 ом/м-, \ а b }
g=mC\g§, сим)м
(б— угол диэлектрических потерь);
L ж 0,461g— 10—6 гн/л1; а
0,241 е ю—ю
—ю ф!м
(е — диэлектрическая проницаемость изоляции).
С повышением частоты угол потерь б уменьшается. Изоляция, применяемая w для коаксиальных кабелей, обычно имеет tg б порядка 10-3—10-4.
Активная проводимость g между параллельными проводами, зависящая от метеорологических условий, состояния изоляторов, к которым подвешены провода, и Других факторов, определяется экспериментально.
Практически во многих случаях можно считать, что g ~ 0.
На высоких частотах ввиду значительного преобладания индуктивного сопротивления токоведущего проводника над его активным сопротивлением последним можно во многих случаях пренебречь.
Следует заметить, что на низких частотах и при малой длине линии, когда емкостная и активная проводимости незначительны, токи в начале и конце линии практически одинаковы и в этом случае линия с достаточной точностью может рассматриваться как цепь с сосредоточенными параметрами. Разграничение понятий «короткая» и «длинная» линия связано с частотой, на которой работает рассматриваемая линия; этот вопрос освещен в § 16-3.
283
16-2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ОДНОРОДНОЙ ЛИНИИ
Напряжение и ток в линии являются функциями двух независимых переменных: пространственной координаты х, определяющей место наблюдения, и времени t, определяющего момент наблюдения. Здесь
Рис. 16-2. Элементарный участок цепи с равномерно распределенными параметрами.
предполагается, что направление координатной оси х совпадает с направлением оси линии.
Нашей ближайшей задачей является нахождение пространственно-временного распределения величин тока в линии i(x, t) и напряжения между проводами и(х, t). При этом в общем случае может рассматриваться передача электромагнитной энергии по линии, когда источник и приемник имеются на обоих концах линии.
Выберем положительное направление тока'в линии слева направо (рис. 16-2) и условимся называть «началом» линии левый конец. Расстояние до произвольной точки линии от начала обозначим через х, а от конца — через х'. Таким образом, вся длина линии 1=х+х'.
Выделим элементарный участок линии длиной Дх, находящийся на расстоянии х от начала. Пользуясь первичными параметрами г, g, L и С, отнесенными к единице длины линии, приближенно представим рассматриваемый элементарный участок линии в виде последовательно включенных сопротивления гДх и индуктивности £Дх, и параллельно включенных активной проводимости £Дх и емкости СДх.
Обозначим:
и — напряжение между верхним и нижним проводами в точке х;
Ди — приращение напряжения на участке Дх;
I— ток в точке х;
Ai — приращение тока на участке Дх.
Уравнения для приращений напряжений и тока на элементе длины Дх запишутся следующим образом:
— &и— (ri + L Д х-
\ dt )
— Лл =|g(u +Ди) +
+ Са(ц + Аы)]дх. dt J
Ввиду наличия двух мых переменных (х и t) записываются в частных
(16-1)
независи-уравнения производ-
ных.
По мере стремления Дх к нулю степень точности этих уравнений повышается, причем величина второго порядка малости [^Ди + + С——Дх в правой части нижие-dt -J
го уравнения (16-1) может быть опущена.
Итак, линия рассматривается как цепная схема с бесконечно большим числом звеньев, электрические параметры которых бесконеч
но малы.
Разделив обе части уравнений (16-1) на Дх и перейдя к пределу Дх=0, получим дифференциальные
уравнения линии:
ди . , di
— = П 4- L — :
дх dt
(16-2)
di дх
r>du
-«“+са-
Эти уравнения известны в литературе под названием телеграфных уравнений.
Если за начало отсчета принять
конец линии, т. е. ввести координату х', то уравнения примут вид:
ди . , . di ----= п 4- L — ; дх'-dt
di , ди
—. = gu + C — . дх dt
(16-3)
Уравнения (16-2) или (16-3) могут быть решены однозначно при использовании начальных и гранитных условий. Начальными ус
284
ловиями будут значения напряжения и тока в начале или в конце линии в момент времени, принятый за нуль. Г раничные условия определяются связями между напряжением и током в начале или в конце линии, зависящими от заданного режима работы линии.
Решение указанных выше уравнений дает функциональные зависимости напряжения и тока в линии от переменных х (или х') и t.
16-3. ПЕРИОДИЧЕСКИЙ режим в однородной линии
При периодическом режиме под воздействием приложенного к линии гармонического напряжения в любой точке линии напряжение и ток изменяются гармонически с частотой источникаОбозначим комплексные действующие значения напряжения и тока на расстоянии х от начала линии через U=lJ(x) и /=/(*) •
Применяя комплексную форму записи, получаем на основании (16-2):
tdU . ,
ГТГ’ = (г + j <в L) 1;
' . (16-4)
ах
Ввиду того что комплексные величины U и / не зависят от t и являются только функциями х, при переходе от уравнений (16-2) к (16-4) частные производные по х заменены обыкновенными.
Исключая из системы (16-4) ток /, получаем уравнение относительно U:
~=(r + jaL)(g + iaC)U. (16-5) dx2
Аналогично, исключая из (16-4) напряжение U, получаем уравнение относительно /:
= (г. 4- jo>L)(g + jaC) 1. (16-6) dx2
1 Обоснованием высказанного положения является линейность уравнений (16-2) и (16-3), так как только в таких уравнениях сохраняется гармонический закон изменения всех функций.
Обозначим квадратный корень из комплексного множителя при 0 или j через
Т= K(r + /aL)(g + /(dC) =а+/р
(16-7) и назовем эту величину коэффициентом распространения. Смысл такого названия выяснится позже. Итак, уравнения (16-5) и (16-6) записываются в виде
d2(7 dx2 ‘
(16-8)
Получились одинаковые однородные линейные дифференциальные уравнения второго порядка. Решение первого из них имеет вид:
= (16 9)
Ток / проще всего находится подстановкой (16-9) в первое уравнение (16-4)
' = 7^(А‘^~"-А‘^ =
или
/=-L(Ae-^-A2^), (16-10)
где
(16-11)
называется вол новый сопротивлением линии.
Подставив (16-7) в (16-9), получим:
(7 = А^е-’^ + А^е^,
Мгновенное значение напряжения в точке х равно мнимой части выражения Vr2Ue"s,t.
и(х, t) = Im \V2~Ate~ax e~i?x eimt +
+ А#™e';,t= /2 |А|х
х e~ax sin (и t 4- — ₽ х) +
-f- J' 2 )А>| е" sin (toj- фа -J- |3х);
(16-12)
285
здесь ipi и ярг — аргументы комплексных величин Ai и Аг.
Таким образом, мгновенное значение напряжения в любой точке линии слагается из двух функций.
Рассмотрим вначале первую из этих слагающих функций.
Если считать точку х фиксированной и рассматривать изменение напряжения в данной точке в зависимости от времени, то первая слагающая выражения (16-12) представит собой гармоническую функцию с постоянной амплитудой.
Если же считать момент времени t фиксированным и рассматривать изменение мгновенного напряжения вдоль линии (т. е. в зависимости от х), то получим затухающую гармоническую волну напряжения, амплитуда которой ^2|Л1|е~“х убывает с ростом х, т. е. по мере удаления от начала линии к концу.
Величина а, характеризующая изменение амплитуды волны на единицу длины линии, называется коэффициентом затухания, а величина р, характеризующая изменение фазы на единицу длины линии, называется коэффициентом фазы.
Убывание амплитуды волны вдоль линии обусловливается потерями в линии, а изменение фазы — конечной скоростью распространения электромагнитных колебаний.
Оба эти коэффициента а и р входят в комплексный параметр у= = а+/р, который, следовательно, характеризует распространение волны напряжения и тока по линии.
На рис. 16-3, а буквой % обозначена длина волны напряжения, равная расстоянию между двумя точками линии, в которых фазы рассматриваемой слагающей напряжения различаются на 2л. Следовательно,
[со t + — Р х[ — [со t 4- ф1 — р (х -|-
4- %)] = 2л, откуда
(16-13)
Полученная формула выражает зависимость, существующую между
286
длиной волны и коэффициентом фазы линии.
На рис. 16-3, а изображены волны напряжения, соответствующие двум следующим друг за другом моментам времени: 4 и t%.
Рис. 16-3. Прямая (падающая) (а) и обратная (отраженная) (б) волны.
С течением времени волна перемещается от начала линии к ее концу; она носит название прямой или падающей волны.
Скорость перемещения падающей волны вдоль линии, называемая фазовой скоростью волны *, определяется как скорость перемещения точки, фаза колебания в которой остается постоянной. Это условие записывается для прямой волны в виде
+ — Р х = const,
откуда
4(соН-Ф1-Рх) = 0 at
и, следовательно, dx /1 г 1 л \
- = «ф = у. (16-14)
Аналогичное исследование второго слагаемого выражения (16-12) показывает, что для произвольного момента времени она представляет синусоидальную волну, амплитуда которой ]/г2|А2| авозрастает с увеличением х, т. е. по мере удаления от начала линии к ее концу. С течением времени волна перемещается от конца линии к ее началу (рис. 16-3,6); она называется обратной или отраженной волной.
1 Скорость распространения группы смежных по частоте волн характеризуется понятием групповой скорости.
Фазовая скорость обратной волны получается равной Оф=—со/р; знак минус указывает, что обратная волна движется в направлении, противоположном прямой волне.
Итак, мгновенное напряжение
можно рассматривать как сумму двух волн, движущихся в противоположных направлениях, причем каждая из этих волн затухает в направлении движения.
На основании (16-13) и (16-14) „________<о__2л f
Оф «ф
= J “ °ФТ>
(16-15)
т. е. за время, равное одному периоду, как падающая, так и отраженная волны перемещаются на расстояние, равное длине волны.
Линии, физическая длина которых соизмерима с длиной волны, считаются Длинными линиями. При достаточно высоких частотах практически любая протяженная электрическая цепь становится «длинной» по отношению к длине волны.
Как будет показано ниже, фазовая скорость в воздушной линии близка к скорости света (примерно 3-108 м/сек) и поэтому частоте 50 гц соответствует длина волны 6 000 км, а частоте 3 • 109 гц — длина волны 10 см. Следовательно, в первом случае длинной линией является линия, протяженностью в сотни или тысячи километров, а во втором случае —щепь, протяженностью в несколько сантиметров.
Возвращаясь к уравнениям (16-9) и (16-10) и записывая прямую и обратную волны в комплексной форме, имеем:
U^Un+Uo-,
Это соотношение объясняет смысл названия ZB — волновое сопротивление.
Постоянные интегрирования Aj и Аг, входящие в (16-9) и (16-10), находятся в зависимости от напряжения и тока в начале линии (граничные условия), если они заданы. При х=0
(7(0) = (71 = А1+Аг;
(0) ~ 2B/i = Ах — Аг,
откуда
Ai
2 ’ 2 2
Введем понятие коэффициента отражения волны в начале линии:
ио(Р) = А = -Zb Л я
4(0) '
(16-16)
Zi+ZB’
где Zi=Ui/li—входное сопротивление линии.
Подстановка выражения для At и А2 в (16-9) и (16-10) с учетом (16-16) дает:
(7=‘^+АА (e-vx+nie^; / = A+Z°A (e-v*-nigv*).
(16-17)
Если заданы граничные условия на конце линии, то удобнее отсчитывать расстояние от конца, приняв координату х'.
Заменяя в уравнениях (16-9) и (16-10) х на (/—х') и используя заданные граничные условия U (/) = = (72; /(/) =/2, получаем для Ai и А2 следующие выражения:
где
(7П = А,^'; Оо = А^х.
Напряжение и ток прямой и соответственно обратной волн связаны законом Ома:
йп __ 4 ___у
in
Л __ О-2 + ZB /2 evl .
1 2
д = 4 %в ~ 2
Подставив их в (16-9) и (16-10),
267
получим окончательные выражения для U и 1:
0=
/= (evx'_n e-v'*)
2ZB v 2
(16-18)
где аналогично предыдущему п2— коэффициент отражения в конце линии:
„ _ ^о(0 __ ,
(7П(/) Zxe-v»
= и? — z° = (16-16а)
tfa + zB/a z» + zB
— выходное сопротивление на конце линии или в случае приемника входное сопротивление его.
Если сопротивление приемника равно волновому сопротивлению линии (Z2=ZB), то коэффициент отражения равен нулю (п2=0). При этом в линии имеется только одна прямая волна; обратная волна отсутствует.
Это важное свойство реализуется в линиях связи, отражения в которых нежелательны по ряду причин.
Во-первых, если затухание в линии невелико, то отраженная волна создает эффект эха в начале линии.
Во-вторых, отражения связаны с потерей энергии. Часть энергии, достигшая приемного конца, не поступает Bi приемник, а возвращается по линии обратно в виде энергии отраженной волны. При этом возникают дополнительные потери энергии в сопротивлении г и проводимости g линии. Если сопротивление источника, питающего линию, не равно волновому сопротивлению линии, то отраженная волна, достигнув начала линии, претерпевает повторное отражение и т. д.
Происходящая вследствие этого потеря энергии в линии понижает общий к. п. д. передачи.
В-третьих, в случае отражений может иметь место нежелательное увеличение напряжения или тока в линии (§ 16-6).
Вследствие указанных причин
на практике стремятся согласовать сопротивление приемника с волновым сопротивлением линии. При согласовании нагрузки с линией выражения (16-18) упрощаются: с учетом того, что ZB/2=t/2, находим:
[)=t/eevx'; / =/2evx . (16-19)
Эти выражения показывают, что при перемещении точки наблюдения вдоль линии, нагруженной согласованно на конце в направлении от конца к началу линии, модуль напряжения возрастает в еах' раз, а фаза — на £х' рад.
Выражения (16-19) показывают, что при согласованной нагрузке (Z2=ZB) геометрическим местом конца вектора напряжения U является логарифмическая спираль. На рис. 16-4, иллюстрирующем сказанное, принято {72=^2Ь0о (вектор й2 направлен по действительной оси).
Большой интерес представляет также рассмотрение двух частных случаев нагрузки линии, а именно случаев, когда линия на конце разомкнута (режим холостого хода) или замкнута (режим короткого замыкания). В первом случае Z2=oo и соответственно коэффициент отражения п=1; во втором случае Z2=0 и п2=—1.
К рассмотрению этих двух случаев мы еще вернемся несколько позже.
Система уравнений (16-18) может быть переписана в следующем виде:
~ ZB 2
(16-20)
ev*'+e-v*'
Уравнения (16-18) и (16-20) представляют собой уравнения линии в показательной (или волновой) форме при отсчете рас
288
стояния от конца линии. Они преобразуются с помощью гиперболических функций:
U = (72 ch yx'+ZB /2 sh ух’-, 1 = /2 ch ух' sh Ух'-
2В
(16-21)
Положив в этих уравнениях х'= =1, получим уравнения линии в гиперболической форме, вы-
Рис. 16-4. Геометрическое место конца вектора напряжения при согласованной нагрузке.
16-4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ОДНОРОДНОЙ ЛИНИИ
Вторичными или характеристическими параметрами линии являются коэффициент затухания а, коэффициент фазы р и волновое сопротивление ZB, которые в свою очередь выражаются через первичные параметры линии и частоту.
Из выражения
у = V(r (g =
= Vrg — a2LC+ja(Lg-}-Cr) =
=a4-/p (16-23)
следует, что
a2+/2ap — ₽2=rg-
— co2 (Lg-^-Cr),
откуда
a2 — p2=rg — to2 LC;
2cd3—toLg+coCr.
Совместное решение этих уравнений дает:
ражающие напряжение и ток в начале через напряжение и ток в конце линии:
Uj = йя ch yl+ZB /2 sh yl; Л = /2chy/ + -^-i72shy/.
(16-22)
+W+«)212)(g2+co2С2) ]; (16-24)
Показательная и гиперболическая формы записи уравнений линии (16-18) и (16-21) взаимно дополняют друг друга и применяются в зависимости от условий задачи.
Преимущество показательной формы записи уравнений заключается в большей наглядности рассмотрения физических процессов в линии с помощью прямых и обратных волн и в удобстве построения геометрических мест на комплексной плоскости. Поэтому уравнения (16-18) широко использованы в последующих параграфах данной главы.
Гиперболическая форма записи уравнений также представляет в ряде случаев известные удобства с точки зрения исследования и расчета электрических величин в линии и их фазовых соотношений.
+K(r2+co2 L2) (g2+co2 С2) J. (16-25)
Полученные выражения показывают, что а и р в общем случае зависят от частоты. Однако, как показывает исследование, в отличие от коэффициента затухания, который изменяется в сравнительно ограниченных пределах, коэффициент фазы неограниченно растет с частотой.
Формула (16-25) позволяет выразить фазовую скорость распространения электромагнитной волны через первичные параметры линии и частоту по формуле (16-14).
Выражения (16-24) и (16-25) неудобны для практического использования ввиду их громоздкости. Существует ряд приближенных расчетных формул для вычисления вторичных параметров линии, учитывающих, что в области высоких частот (порядка 1 Мгц и выше) со
19—1118
289
противление г весьма мало по сравнению с a>L, а проводимость g ничтожно мала по сравнению с соС. Первое допущение (w£3>r) обусловлено тем, что индуктивное сопротивление прямо пропорционально частоте, между тем как сопротивление проводов г пропорционально квадратному корню из частоты вследствие поверхностного эффекта (см. § 16-1). Второе допущение справедливо для высокочастотных фидеров, которые, будучи «длинными» по сравнению с длиной волны, имеют весьма малую физическую длину и поэтому могут иметь надежную изоляцию между проводами. Особенно ничтожно мала проводимость g кабельных линий.
Используя для выражения
1
Т=М<£С(1-/^’ X
k 2
/-£ соС,
(16-26)
бином Ньютона, ограничиваясь первыми двумя членами разложения
|16'27) и пренебрегая ввиду малости сла-rg
гаемым —/ -------—, получаем
4<о КЕс
окончательно:
Я^саУЕС. (16-29)
Эти формулы представляют собой пределы, к которым стремятся коэффициент затухания и коэффициент фазы с ростом частоты.
Выражение (16-28) не следует понимать в том смысле, что а не зависит от Частоты; входящие в него параметры г и g сами являются функциями частоты (см. § 16-1).
Первое слагаемое в правой части выражения (16-28) определяет ту долю затухания, которая обусловливается продольным активным сопротивлением линии. Второе слагаемое
определяет долю затухания, которая вносится в передачу вследствие наличия поперечной активной проводимости линии.
Для уменьшения потерь при передаче электромагнитной энергии по линии стремятся к тому, чтобы сопротивление линйи г и проводи-
Рис. 16-5. Частотные характеристики аир.
мость изоляции g были по возможности малы.
Фазовая скорость согласно (16-14) и (16-29) равна:
»Ф = Т~ <16'30’ р Уис
Это — предельная фазовая скорость распространения волны вдоль линии при бесконечно большой частоте. При постоянном токе (со=О) понятия «коэффициент фазы» и «фазовая скорость» теряют физический смысл; на основании Выведенной ранее формулы для у (16-7) Ври й) = 0
a=Vrg\ ₽=0.
На рис. 16-5 показан характер изменения а и 0 в зависимости от частоты; коэффициент 0 с ростом частоты асимптотически приближается к Прямой, образующей с осЫО to угол
arctg (УУС т), где т — масштабный коэффициент.
Для кабельных линий характерна резко выраженная емкостная проводимость соС, по сравнению с которой проводимость изоляции g ничтожно мала. Кроме того, если частота не очень велика, то индуктивное сопротивление со£ мало по сравнению с активным сопротивлением г из-за малого расстояния ме
290
жду жилами. Поэтому в случае кабельной линии, пренебрегая параметрами g й L по сравнению с г и С, получаем упрощенные расчетные формулы:
у as ]Лjr ohC = гк>С 45° или
у — у raiC — -----Ь / —— j.
Следовательно,
В случае воздушной линии ба? 1 й р~1, поэтому фазовая скорость в пределе стремится к скорости света в пустоте.
В случае кабельной линии е= =44-5, и поэтому предельная фаговая скорость примерно вдвое меньше скорости света в пустоте.
Рисунок 16-6 иллюстрирует зависимость фазовой скорости волны от частоты и типа линии.
Волновое сопротивление линии
Соответственно фазовая скорость распространения волны в кабельной линии равна:
<1М2>
т. е. прямо пропорциональна корню квадратному из частоты.
В теории электромагнитного поля доказывается, что произведение удельных значений индуктивности и емкости в линии
LC = -J, (16-33)
где с— скорость света в пус-
тоте (примерно 3-108 м/сек};
е и р,— диэлектрическая и магнитная проницаемости среды, окружающей токоведущие проводники.
Предел, к которому с ростом частоты стремится фазовая скорость волны, равен на основании (16-30) и (16-33):
с
УФ =
Рис 16-6 Зависимость фазовой скорости распространения волны от частоты и типа линии.
при постоянном токе (со=О) и при частоте и = оо имеет действительные значения:
(и=0);
(й)=оо).
В остальной части диапазона частот волновое сопротивление линии имеет емкостный характер, так как л с L г обычно —>— [аргумент знаме-g f нателя в правой части (16-34) больше аргумента числителя].
На рис. 16-7 показаны кривые изменения модуля ZB и угла <р волнового сопротивления линии в зависимости от частоты.
Подставив выражения L и С из § 16-1 в формулу zB= L/C, получим приближенные расчетные формулы для высоких частот в зависимости от размеров:
zB=276 lg —, ом (воздуШ-а
ная линия);
138 . Ь .
га = —— 1g —, ом (коак-
V в
сиальный кабель).
(16-35)
J9*
291
Средние значения zB для воздушных линий 400—500 ом, для кабелей— 50—70 ом.
Рисунок 16-8 иллюстрирует графические зависимости zB от d/a и b/а для воздушных и кабельных ли-
Рис. 16-7. Зависимость модуля и угла волнового сопротивления лннни от частоты.
ний, построенные по формулам (16-35).
16-5. ЛИНИЯ БЕЗ ИСКАЖЕНИЙ
Сигналы, передаваемые по линии связи, представляют собой совокупность множества различных
или тока в конце линии прямо пропорциональны соответствующим ординатам кривой в начале линии.
Такое явление имеет место в том случае, когда коэффициент затухания линии и соответственно фазовая скорость на всех частотах одинаковы.
Неодинаковое затухание на разных частотах создает так называемые амплитудные искажения, а неодинаковая скорость волн на разных частотах — фазовые искажения.
Согласно (16-31) и (16-32) коэффициент затухания и фазовая скорость в случае кабельных линий пропорциональны квадратному корню частоты. В случае воздушных линий также существует зависимость а и Уф от частоты. В результате этого получаются амплитудные и фазовые искажения.
Итак, для неискаженной передачи требуется, чтобы коэффициент затухания а не зависел от частоты, а коэффициент фазы р был прямо пропорционален частоте; в послед-
. Рис. 16-8. Волновое сопротивление линии. а — воздушной; б — кабельной.
частот: дискретных — в случае периодических несинусоидальных сигналов и образующих непрерывный спектр — в случае непериодических сигналов (гл. 15).
Неискаженной передачей сигнала называется такая передача, при которой форма сигнала в начале и конце линии одинакова, т. е. все ординаты кривой напряжения
нем случае фазовая скорость рф= = о)/р получается не зависящей от частоты.
Такое положение имеет место при условии, что
— = —. (16-36)
r g
В этом случае коэффициент распространения равен:
292
y=/(r+/<oL)(^+jtoC) =
l+jto—;
S /
с учетом (16-36)
y = /rg -[-/toyTg — r
ИЛИ
T = Vrg + jtoVLC .
•
Если считать, что первичные параметры линии не зависят от частоты, то коэффициент затухания в данном случае будет постоянен:
а « УП, (16-37) а коэффициент фазы —прямо пропорционален частоте:
Р=ю VLC. (16-38)
Линия, параметры которой удовлетворяют условию (16-36), называется линией без искажений, поскольку любые сигналы распространяются по ней с сохранением их формы. Линия без искажений является одновременно и линией с минимальным затуханием, которое только и возможно при заданных параметрах г и g.
Волновое сопротивление линии без искажений — действительное число, что равносильно активному сопротивлению, не зависящему от частоты; в соответствии с (16-34) оно выражается простой формулой
(16-39)
Фазовая скорость в линии без искажений постоянна и совпадает с полученным ранее выражением (16-30) для предельной скорости распространения волны вдоль линии при бесконечно высокой частоте:
V LC
Для устранения искажений, вызываемых несогласованностью сопротивления приемника с сопротивлением линии, т. е. во избежание i возникновения отражений на приемном конце, сопротивление приемника должно быть равно zB.
Коэффициент полезного действия линии имеет в этом случае наибольшее возможное значение, равное е~2о“, как в линии при согласованной нагрузке.
Ввиду того что волновое сопротивление линии без искажений является активным, при согласованной нагрузке напряжение и ток в любой точке линии совпадают по фазе.
Отношение мгновенных значений напряжения и тока в любой точке такой линии равно:
откуда
Li2 Си2
2 ~ 2
(16-40)
Следовательно, на любом отрезке линии без искажений, нагружен ной согласованно, энергия магнитного поля в каждый момент времени равна энергии электрического поля.
Следует заметить, что на практике условие (16-36), как правило, не выполняется; отношение £/г обычно значительно меньше отношения C/g. Вследствие этого затухание линии всегда превышает минимальное. Наименее соответствуют условию (16-3f>) кабельные линии.
Чтобы линия более соответствовала условию (16-36), следует изменить какой-либо первичный параметр, например уменьшить г или С либо увеличить g или L.
Уменьшение активного сопротивления г возможно за счет применения проводов большего диаметра, что, однако, значительно удорожало бы линию. Увеличение проводимости изоляции g невыгодно, так как при этом возросло бы затухание линии.
Наилучшим средством для приближения первичных электрических параметров к оптимальному соотношению (16-36) является искусственное увеличение индуктивности включением в линию через определенное расстояние индуктивных катушек или применением кабеля, проводящие жилы которого обмотаны тонкой лентой из материала с высокой магнитной проницаемостью.
293
16-6. ЛИНИЯ БЕЗ ПОТЕРЬ
Независимо от того, соблюдается ли оптимальное соотношение первичных параметров (16-36) или не соблюдается, во всех случаях желательно, чтобы активное сопротивление г и проводимость изоляции g были по возможности малы (для уменьшения потерь энергии). В воздушных линиях обычно индуктивное сопротивление линии превышает активное сопротивление г, а емкостная проводимость соС превышает активную проводимость g. С ростом частоты разница между указанными величинами становится еще более значительной.
В ряде случаев оказывается полезным в первом приближении рассматривать линию, не имеющую потерь, т. е. пренебрегать активными сопротивлением и проводимостью по сравнению с соответствующими реактивными составляющими. Такая идеализация допускается для приближенной качественной и количественной оценки исследуемых явлений. При этом сильно упрощаются расчетные выражения, и гиперболические уравнения линии переходят в тригонометрические.
Итак, основным исходным предположением, которое делают при рассмотрении линии без потерь, является приближенное условие, что г «О и g~0. В этом случае вторичные параметры линии принимают весьма простой вид, а именно:
LC; а=0; =
Следовательно, в линии без потерь затухание отсутствует. Ввиду постоянства фазовой скорости
отсутствуют также и фазовые искажения.
Выражения для коэффициента фазы, фазовой скорости и волнового сопротивления линии без потерь совпадают с выражениями, полученными для линии без искажений. Следовательно, все сказанное о линии без
искажений полностью относится и к линии без потерь.
Ввиду того что гиперболические функции с мнимым аргументом преобразуются в тригонометрические функции, гиперболические уравнения линии (16-21) принимают тригонометрическую форму:
cos px'+/zn /2 sin fix';
/=/2 cos Ц- / — sin ZB
(16-41)
Эти уравнения используются ниже при рассмотрении стоячих волн в линии без потерь (§ 16-7).
Энергия, передаваемая по линии, складывается из энергии электрического и магнитного полей.
В том случае, когда к концу линии без потерь присоединено сопротивление, равное волновому, на любом отрезке линии соблюдается условие (16-40), полученное для динци без искажений. При этом вся энергия, доставляемая падающей волной, поглощается в сопротивлении нагрузки.
Если сопротивление нагрузки отлично от волнового, то в месте присоединения нагрузки энергия перераспределяется между полями, в результате чего возникают отражения.
В предельном случае, когдр линия на конце разомкнута, падающая волна встречает бесконечно большое сопротивление, ток в конце линии обращается в нуль и соответственно энергия магнитного поля переходит в энергию электрического поля. Напряжение на разомкнутом конце линии удваивается, и возникает отраженная волна того же зндка, что и падающая [п2=1; (16-16а)].
В другом предельном случае, когда линия на конце замкнута накоротко, падающая волна встречает сопротивление, равное нулю, напряжение в конце линии обращается в нуль и соответственно энергия электрического поля переходит в энергию магнитного поля. Ток на короткозамкнутом конце линии удваивается, и возникает отраженная волна, знак которой противоположен знаку падающей волны (п2=—1).
При Гй>£в коэффициент отражения «2>0; п2<0 при r2<ZzB. Поэто
294
му в первом случае возрастает напряжение и убывает ток, а во втором случае, наоборот, убывает напряжение и возрастает ток по сравнению с режимом согласования нагрузки (п2=0).
16-7. РЕЖИМЫ РАБОТЫ ЛИНИИ БЕЗ ПОТЕРЬ. СТОЯЧИЕ ВОЛНЫ
Исследуем закон распределения действующих значений напряжения и тока вдоль линии без потерь. С этой целью воспользуемся уравнениями линии (16-18) и (16-41) в комплексной и гиперболической формах.
Приняв в (16-18) мнимый коэффициент распространения у=/Р= =/2л/Х, получим для любой точки линии на расстоянии д/ от конца:
(16-42)
Входящий в эти уравнения коэффициент отражения
« _ ^2 гв
“2 - ~ ,
?2 + 2В
представляет собой в общем случае комплексную величину.
Выражения (16-42) наглядно свидетельствуют о том, что комплексное напряжение в любой точке х' слагается из падающей и отраженной волн напряжения, амплитуды которых находятся в соотношении 1 : |п2|; в свою очередь комплексный ток равен разности падающей и отраженной волн тока с тем же соотношением амплитуд.
Точкам x'+k— (k — целое чис-2
ло), удовлетворяющим условию
, 2л ,
—I — х + п2е к
2п , — х X
I е
= 1 +14
(16-43>
соответствует максимальное действующее значение U, так как при этом фазы падающей и отраженной волн напряжения совпадают. На расстоянии Л/4 от этих точек падающая и отраженная волны оказываются в противофазе и действующее значение напряжения имеет минимум. При этом удовлетворяется условие
е к —п2е 1 =
= 1-1^1. (16-44)
Координаты максимумов и минимумов U, являющиеся многозначными функциями п2 и Л, не зависят от времени, они остаются на одном и том же месте; минимум U располагается посередине между двумя соседними максимумами U, причем расстояние между ближайшими максимумами (или минимумами) составляет Х/2-
Таким образом, кривая действующих значений напряжения вдоль линии без потерь представляет волнообразную кривую, максимумы и минимумы которой чередуются (см. дальше рис. 16-10,6 и г).
Аналогичные рассуждения приводят к выводу, что и кривая действующих значений тока вдоль линии без потерь представляет волнообразную кривую, смещенную относительно кривой действующих значений напряжения на четверть длины волны. Места максимумов напряжения совпадают с местами минимумов тока, и, наоборот, минимумы 17 совпадают с максимумами /.
При отсутствии отраженной волны (п2=0) действующие значения U и 1 вдоль линии без потерь не изменяются.
Чем больше приближается коэффициент отражения |я2| к единице, тем больше разнятся максимумы и минимумы U (или /).
При [п2[ = 1, т. е. при равенстве амплитуд прямой и обратной волн, в линии устанавливаются стоячие волны напряжения и тока. Кривые действующих значений U и / вдоль линии представляют собой в этом случае «выпрямленные» синусоиды; на линии образуются узлы, т. е. точки, в которых Uni равны нулю,
295
и пучности, т. е. точки, в которых U или I максимальны.
Из сказанного выше следует, что узлы напряжения совпадают с пучностями тока и, наоборот, узлы тока совпадают с пучностями напряжения. Соответственно узлы (или пуч-
ности) напряжения и тока сдвинуты на четверть длины волны относительно друг друга.
На рис. 16-9 в виде примера показано сложение прямой и обратной волн напряжения, имеющих одинаковые амплитуды, для трех моментов времени: Л, t2 и t3. Сумма бегущих в противоположные стороны волн образует стоячую волну, показанную на рис. 16-9 в виде мгновенных значений для моментов времени ti, ^2 и t3.
Из этого рисунка видно, что на протяжении всего участка между двумя соседними узлами стоячей волны гармоническое изменение напряжения во времени происходит с одинаковой начальной фазой: при прохождении узла начальная фаза гармонических колебаний изменяется скачкообразно на величину л. Сказанное в равной мере относится и к стоячей волне тока.
На основании приведенного выше выражения для коэффициента отражения п2 можно заключить, что условие |п2| = 1 выполнимо в трех
396
случаях: при Z2=ca (холостой ход), Z2=0 (короткое замыкание) и Z2 = —jx (реактивная нагрузка). Этим условиям соответствуют стоячие волны, возникающие в линии без потерь.
Рис. 16-10. Действующие значения напряжения и тока вдоль линии без потерь.
Распределение действующих значений напряжения и тока вдоль линии для холостого хода и короткого замыкания иллюстрируется на рис. 16-10, а и д.
Для сравнения на рис. 16-10 показано распределение напряжения и тока для других режимов работы линии.
При активной нагрузке Z2=r2= =3zB, п2=0,5 (случай б) максимумы и минимумы U тл I совпадают по своему местоположению с аналогичными значениями для режима холостого хода; при активной нагрузке Z2=r2=4-zB, п2=—0,5 (случай г) О
максимумы и минимумы расположены так же, как при коротком замыкании; при согласованной нагрузке Za=ra=zB, п2=0 (случай в) кривые
U Vi I изображаются прямыми, параллельными оси абсцисс.
Стоячие волны легко исследуются с помощью уравнений (16-41) линий без потерь.
При холостом ходе (/а=0)
U=Ut cos— х';
г к ’
f = / sin ?£- х'.
1 г. А
(16-45)
Узлы напряжения находятся в точках,
для которых
2л , „
cos—х = 0 к
или
2п , п . , — X =---------hfat,
к 2
откуда
хуз-—7~Л-
Пучности напряжения находятся в точках, для которых
2л , ,
cos — х = 4-1 А
или
откуда
Хпуч=
Разомкнутый конец линии совпа
дает с узлом тока и пучностью напряжения (рис. 16-10, а).
Как видно из (16-45), ток опережает по фазе напряжение на 90°, 2л . 2л ,
когда sin — хи cos — х имеют А к
одинаковый знак fo<x <—;
\ 4
А 3 , \
— <х < —л и т. д. ), и отстает на
90° от напряжения, когда знаки
2л , 2л ,
sin — х и cos — х различны Л Л
— ; —А.<Гх <ГА. и т. д. |.
\ 4 2 4 “ /
При коротком замыкании, положив в (16-41) t/2=0, получим:
. »• . 2л . t4=/z„/2s,n К
Г г 2л .
/=/2cos---X .
к
(16-46)
На замкнутом конце линии х'=0 и в точках, удаленных от него на целое число полуволн x'=kkl^ находятся узлы напряжения и пучности тока, а в точках, удаленных от конца на нечетное число четвертей волн Гх'= (2k+1) —1, находятся пучно-L 4 J
сти напряжения и узлы тока (рис. 16-10, д).
Как видно из (16-46), ток отстает по фазе от напряжения на 90°, ког-2л , 2л , да sin — хи cos— х имеют оди-к к
наковые знаки (О^.х'^. — ; — <
\ 4 2
3 , \
— л и т. д. |, и опережает на 4 /
напряжение, когда знаки , 2л ,
х и cos — х различны
90°
. 2л
£1П т
/ А А 3 ... \
— <х <—; —к<х < А, и т. д. .
4 2’4 )
Следует заметить, что наличие хотя бы самых малых потерь в различных линиях приводит к тому, что действующие значения U и / не снижаются до нуля, а достигают некоторых минимальных значений в точках, соответствующих узлам.
В случае стоячих волн мощность в узлах напряжения и тока равна нулю. В остальных точках линии имеет место только реактивная мощность, так как напряжение и ток сдвинуты по фазе на 90°.
В этом случае энергия не передается вдоль линии, а происходит лишь обмен энергией между электрическим и магнитным полями на участках линии, ограниченных узлами напряжения и тока.
Если в линии имеются потери или приемник потребляет активную мощность, то узлы исчезают; амплитуда падающей волны превышает амплитуду отраженной волны и за счет разности амплитуд происходит процесс передачи энергии вдоль линии.
Для количественной оценки степени согласования линии с нагруз
297
кой в радиотехнике используется коэффициент бегущей волны, под которым понимается отношение минимума в кривой распределения U или 1 к максимуму той же величины:
Кв= . (16-47)
^макс 'макс
С учетом (16-43) и (16-44) имеем:
(16-48) * + 1пг1
откуда
|л,| = . (16-49)
1 + Лб 1А<акс + ^Мнн
В случае активной нагрузки выражение (16-48) упрощается.
При rg>zB |па| = Гг~~гв согласно г2 + гВ
(16-48)
Кб=—; (16-50)
Г2
при Г2< 2В |п2| = гв~Гг И, гв + г2
следовательно,
Кб=-^-. (16-51)
гв
В реальных условиях коэффициент’бегущей волны обычно не ниже 0,5—0,6.
Кривую распределения действующих значений напряжения вдоль линии используют на практике для измерения длины волны или частоты. Длина волны определяется удвоенным расстоянием между соседними максимумами или минимумами кривой распределения, а частота вычисляется по длине волны на основании (16-15).
16-8. ВХОДНОЕ СОПРОТИВЛЕНИЕ ЛИНИИ
Входное сопротивление линии, измеренное в произвольной точке иа расстоянии х' от конца, определяется отношением Z=U/I и может быть представлено в комплексной или гиперболической форме. Ради общности рассмотрения вопроса будем считать, что линия нагружена
на конце некоторым сопротивлением Z2, которое в зависимости от условий может быть любым.
Комплексная форма выражения для входного сопротивления линии получается на основании (16-18):
U 7 еух' + п2е^',х’ ——
I ё'/х —пге^
или
I , . «—2ах' л—/26*'
Z = ZB . (16-52)
Данное выражение показывает, что с изменением координаты х' модуль входного сопротивления линии колеблется между некоторыми максимумами и минимумами (которые в общем случае отличаются друг от Друга).
Допустим, что модуль Z достигает некоторого максимума в точке x'ext- Тогда максимумы будут также в точках, соответствующих изменению аргумента 20х' на величину 2kn, что даст:
2|3^+2&г=2₽
Г“'+‘т) =
Следовательно, максимумы чередуются через каждые полволны. Посередине между максимумами будут минимумы, которые также чередуются через каждые полволны.
Если вместо координаты х' варьировать коэффициентом фазы Р=2л/Х, меняя частоту источника, то получится аналогичная волнообразная кривая, причем максимумы и соответственно минимумы будут отстоять друг от друга на я/х' (здесь x'=const). Исследуя изменение входного сопротивления линии при плавном изменении частоты источника, можно зафиксировать два следующих друг за другом максимума (илн минимума) г, соответствующих частотам ft и fz-
В этом случае
<0! 2nft ai2 2nfa
pi — — • P2 — —
Oi Oj O2 O,
и, следовательно,
откуда
,_________t>iP2
2 (vifs — °ifi)
298
При малом расхождении частот ft н fa фазовые скорости почти одинаковы: t>i~ *=и2«Оф.
При этом
, V*
X « --—----- .
2(fa-fi)
Данная формула позволяет определить расстояние от точки наблюдения до ближайшей точки линии, в которой имеет место отражение (например, при коротком замыкании на линии), производя измерение только н одной точке.
Волнообразный характер кривой z подчиняется в общем случае закону изменения модуля гиперболического тангенса с комплексным аргументом, что видно из следующего вывода.
Непосредственно из (16-21) следует:
2 а Vх' —
7Я ch ух' + sh ух'
= _g* + z»thY*' . (] 6-53)
1 4--^ th ух'
Обозначив Z2/ZB=thM имеем:
2__ 2 th Л1 + th ух' _
в 1 +thMthvx' ~
= ZBth(Tx'4-M). (16-54)
При холостом ходе (Z2=°o) входное сопротивление линии согласно (16-53) равно:
Z^=ZB cth ух, (16-55)
а при коротком замыкании (Z2=0)
ZK=ZBthTx'. (16-56)
С учетом (16-55) и (16-56) входное сопротивление Z легко выразить через Zx и ZK:
2 = 2 %к
Этой формулой пользуются в том случае, когда из опытов холостого хода и короткого замыкания известны ZK и Zjf.
Данные опытов холостого хода и короткого замыкания используются также для вычисления характеристических параметров линии.
На основании (16-55) и (16-56)
ZB = /ZX;
thTx'= ]/. (16-57)
У Zx
Ввиду того что коэффициент фазы 0 определяется по (16-57) неоднозначно, при вычислении производится проверка на основании (16-14), причем первоначально фазовая скорость Пф выбирается ориентировочно. Вычисление характе-
Рис. 16-11. Входные сопротивления линии при холостом ходе и коротком замыкании.
ристических параметров по формулам (16-57) иллюстрировано ниже примером 16-1.
На рис. 16-11 показаны кривые изменения модулей Zx и ZK в зави симости от координаты х'. В пределе, т. е. при х'-*-оо, максимумы и минимумы кривой стремятся к значению zB.
Входные сопротивления линии без потерь при холостом ходе и коротком замыкании могут быть получены из (16-55) и (16-56) заменой у=/0=/2л/Х:
Zx=—/zBctg^-x';
Л
•у • . 2л , 2K=/zB tg — х .
Л
Эти реактивные входные сопротивления с учетом их знака изображаются котангенсоидами и тангенсоидами (рис. 16-12). Аргументом может служить также величина 0, если изменять частоту при постоянной длине х'.
Входное сопротивление линии без потерь при х'^Х/4 индуктивно в случае короткого замыкания и емкостно в случае холостого хода. При х'=Х/4 в первом случае наступает резонанс токов (z = oo), во втором случае — резонанс напряжений (z— = 0)..
299
Входное сопротивление линии
без потерь, нагруженной произвольным сопротивлением Za, согласно (16-52)
1+1П2|е/(ф-^'>
2=гв
(16-58)
где Ф — аргумент комплексного коэффициента отражения:
пг=|п2! А
Рис. 16-12. Входные сопротивления линии без потерь, а—холостой ход; б — короткое замыкание.
Входное сопротивление линии достигает максимума при
Ф — 20*'4-2&л;=:О
или =
при этом с учетом (16-48)
Z=rMaKC=2B = Лг.. (16-59) в 1—|пя| Кб
Минимум входного сопротивления наступает при
2g 4 ’
при этом
2=rMBB=zB-^j-=K6aB. (16-60) 1 + 1пг1
На основании (16-59) и (16-60) волновое сопротивление линии без
300
потерь может быть определено как среднее геометрическое максимального и минимального значений входного сопротивления линии
?в Р^макс^мин- (16-61)
Следует заметить, что в реальных условиях вследствие наличия потерь входное сопротивление линии никогда не снижается до нуля и никогда не достигает бесконечного значения.
При этом короткозамкнутая линия при х'=Х/4 имеет большее входное сопротивление, чем разомкнутая линия при х'=Х/2, а разомкнутая линия при x.f = ’k]b имеет меньшее входное сопротивление, чем короткозамкнутая при х'=Х/2.
Пример 16-1. Даны результаты измерения входных сопротивлений линии длиной 160 км на частоте 1 000 гц при холостом ходе и коротком замыкании: Zx = =887Z_—35° ом; Z„=540Z21° ом. Требуется вычислить первичные и вторичные параметры линии.
Расчет начинается с вычисления волнового сопротивления и коэффициента распространения:
ZB - VZKZK = V (887 35n)(540 -=21°) =
= 692 ^—7°,
thyl =
540 ^21°
887 ^—35°
= 0,78 ^28° = 0,688 + /0,366;
1 4- thy' 1,688 +/0,366
1 — thy/ = 0,312-/0,366
1,726 ^12°15'
0,480 49°35'
= 3,6^61°50' =
= 3,6 (1,08 + 2nfe)
Целое число k находится на основании ориентировочного расчета величины 2 р/; если исходить из приближенного значения фазовой скорости =300 000 км/сек (если линия воздушная), то
, , и 6 280
Следовательно, надо принять k = 1 и 2 р/= 1,08+6,28=7,36 рад. Итак, = = е1,28ея,зб1 откуда 2 al—1,28 неп. Коэффициент затухания
1.28
а = —-— = 0,004 неп/км, 2460
коэффициент фазы
7,36
Р = „ — = 0,023 рад/км;
2‘loU
коэффициент распространения
V = a + /р=,0,004 + /0,023 =0,0233^80°8'; фаговая скорость
® 6 280
оф = — = = 273 044 км/сек,
.едина волны
, 2л 6,28
К =----= j* = 273,04 км
р 0,023
Первичные параметры линии находятся иа основании выражений
у
у/в = о + /и1 и — = g + jaC;
' 4- /со! = /0,0233 --80о8')(692 ^—7°) = = 16,12 ^73°8' = 4,887 + /15,426;
. „ 0,0233 ^80°8'
р -|— /соС — - ~
* 692 ^—7°
= 10~6-33,6 ^87°8' = (1,68 + /33,6)-10-®
Таким образом.
, 15,426
г = 4,887 ол !км-. L =-------=
6280
= 0,00245 гн'км;
g = 1,68-Ю-6 сим 1км;
33.6-1O-6
С —— --------— 0,00535 мкф!км
6280 *
16-9. МОЩНОСТЬ В ЛИНИИ БЕЗ ПОТЕРЬ
При наличии стоячих волн с узлами, когда амплитуды падающей и отраженной волн одинаковы, а именно при холостом ходе, коротком замыкании или чисто реактивной нагрузке, мощность в узлах напряжения и тока равна нулю. В остальных точках линии мощность реактивна. так как напряжение и ток сдвинуты по фазе на 90°.
В этом случае энергия не передается вдоль линии, а происходит лишь обмен энергией между электрическим и магнитным полями на участках линий, ограниченных узлами напряжения и тока.
Если в линии имеются потери или приемник потребляет активную мощность, то узлы исчезают, амплитуда падающей волны превышает амплитуду отраженной волны и за счет разности амплитуд происходит процесс передачи энергии вдоль линии.
В § 16-7 было показано, что максимум действующего значения на
пряжения получается при совпадении по фазе падающей и отраженной волн напряжения, а минимум — при фазовом сдвиге между ними в 180°; в соответствии с (16-42)
(7макс = —^1 1 + — I (1 +|Л8|); * I ^2 I
^мнн= — V |1 + —1(1— |п.|).
МИН g I 1 2 Р >
(16-62)
Максимум тока получается тогда, когда падающая и отраженная волны тока находятся в противофазе, а минимум — при совпадении их по фазе
2гв I Z2I
2гв | Zt |
(16-63)
На основании (16-62) и (16-63) можно заключить, что
1/макс t/мин г
/макс /мин
U макс __1 ~i~ 1»г1
/МИн “ В 1 - W
/"макс*
(16-64)
//мин „ 1 I я? I г
I гв . , | , * МИН'
/ макс 1 + I я2 I
Если потери в линии отсутствуют, то вся активная мощность поступает в приемник, следовательно,
Р = Гиакс Iмин = 6МНН /макс
ИЛИ
ра — г г (J 1 )2 откуда с учетом (16-61)
Р = 2В /.маке /мин- (16-65)
Аналогично можно доказать, что
= —С/максС/мвн. (16-66)
гв
С помощью выражений (16-65) и (16-66) легко вычисляется активная мощность в линии без потерь.
Вместе с тем эти выражения показывают, что при предельно допустимом (с точки зрения диэлектрической прочности изоляции) напряжении Г7Макс передаваемая активная мощность тем больше, чем выше коэффициент бегущей волны, т. е. чем меньше отражений. Максимум передаваемой мощности наступает при
301
согласованной нагрузке (Z2=zB), КОГДа t/макс = ^мин ИЛИ Хб= 1-
При несогласованно подобранной нагрузке в линии часть энергии затрачивается на отражения. Поскольку действующие значения напряжений падающей и отраженной волн и Uo для всех точек линии без потерь неизменны, то, очевидно, ^мякс — ^мви = t/0,
откуда
Д’ — — .Чп—-^0- . (16-67)
^макс */п+Ц>
На основании (16-66)
Р = -?-((/„ + (/0)([/п-С/0) =
2В
“Т-И-Ч). гв
Отсюда видно, что мощность падающей волны {PB=UB!zB) слагается из полезной мощности, потребляемой приемником (Р), и мощности отраженной волны (Ро = Ц/2в).
Отношение полезной мощности к мощности падающей волны равно:
Р ^РП~РО .
Pn Рп и2п
или с учетом (16-49)
Ра U+Кб/
4/<б
(1 + Яб)2'
(16-68)
16-10. ЛИНИЯ КАК СОГЛАСУЮЩИЙ ТРАНСФОРМАТОР
В § 6-7 было показано, что трансформатор с коэффициентом трансформации n = wl/w2, нагруженный сопротивлением ZB, имеет входное сопротивление ZiBX=n2ZH. Поэтому он может использоваться в качестве согласующего устройства между источником и приемником. Ту же роль может выполнять линия без потерь, имеющая длину Х/8 или Л/4-
Линия без потерь, нагруженная сопротивлением Z2, при х=7/8 имеет входное сопротивление
л
Zg + /гв 1g ~Г~
7 4
2 = ZB------;---— =
2в + 1%г tg -Г" 4
= (16-69)
гВ + /^2
В случае активной нагрузки (Z2=r2) модули числителя и знаменателя (16-69) равны, и поэтому модуль входного сопротивления линии равен волновому сопротивлению |Z| =zB.
Таким образом, с помощью линии длиной Х/8 можно согласовать по. модулю произвольную активную нагрузку с источником, имеющим внутреннее сопротивление zB.
При х=7/4 входное сопротивление линии без потерь, нагруженной сопротивлением Z2, равно:
Построенная по этому выражению графическая зависимость Р/Рв от 5=1/Кб показана на рис. 16-13.
tgT
z = Zb‘V--------= (16'70)
Рис. 16-13. Зависимость Р/Рв от S=l/Ke
Если сопротивление Z2 активно, то входное сопротивление линии также активно. Следовательно, четвертьволновая линия играет роль согласующего трансформатора, причем волновое сопротивление, линии выбирается равным среднему геометрическому двух согласуемых сопротивлений — приемника (Z2) и источника (Z):
zB = /ZZT. (16-71)
302
Как видно из (16-70), четвертьволновая лиция способна трансформировать большое сопротивление в малое и наоборот.
Предельными случаями для Z2 является короткое замыкание и холостой ход, при которых входное сопротивление четвертьволновой линии без потерь обращается в бесконечность (при Zj=0) и в нуль (при ^=00).
Практическое применение четвертьволновая линия находит, например, в качестве согласующего устройства между антенной и высокочастотным фидером. В этом случае врлповоё сопротивление zB четвертьволновой линии выбирается в соответствии с формулой (16-71), в которой Zz означает активное сопротивление антенны, a Z — волновое сопротивление высокочастотного фидера.
Предельное соотношение между согласуемыми сопротивлениями, практически допускающее применение четвертьволновой линии в качестве согласующего устройства, равно ориентировочно десяти.
Входное сопротивление полуволновой линии без потерь (х= =А/2) равно сопротивлению приемника
гв + /Z2 tg Я
Поэтому такая линия равносильна идеальному трансформатору с коэффициентом трансформации п= = 1. Каскадное включение полуволновой и четвертьволновой линий (А. А з \
х— — Ч-----= —X ]не меняет сог-
2 4 4 /
ласующих свойств последней. Поэтому сказанное выше в отношении чтетвертьволновой линии сохраняет силу для линий, имеющих длину, кратную нечетному числу Х/4.
Для согласования сопротивлений источника и приемника на практике применяются также «экспоненциальные» линии, индуктивность и емкость которых изменяется вдоль линии пр закону показательной функции.
16-11. СОГЛАСОВАНИЕ СОПРОТИВЛЕНИЙ ПОСРЕДСТВОМ ПАРАЛЛЕЛЬНОГО ПРИСОЕДИНЕНИЯ ОТРЕЗКОВ ЛИНИИ
В том случае, когда высокочастотная линия, длина которой в несколько раз превышает длину волны, питает смешанную, активно-реактивную нагрузку Zz, например ненастроенную антенну, согласование нагрузки с линией может быть выполнено посредством параллельного присоединения к линии одного или двух отрезков такой же линии. Познакомимся с методикой присоединения одного такого отрезка, замкнутого на конце. Короткозамкнутый отрезок имеет преимущество перед разомкнутым с точки зрения уменьшения потерь на излучение и более прост в конструктивном отношении.
Отрезок линии присоединяется вблизи нагрузки в такой точке, где комплексная проводимость цепи в сторону нагрузки равна г —------jb.
Подобрав длину отрезка так, чтобы его проводимость была равна jb, получим суммарную проводимость в месте присоединения отрезка, равную l/zB, т. е. входное сопротивление в этой точке будет равно волновому сопротивлению основной линии.
При таком условии не будет отражений и стоячих волн на основном участке линии — между источником и местом присоединения отрезка — и, следовательно, сократятся потери.
До того как отрезок был включен, входная проводимость линии в произвольной точке х' согласно (16-58)
у 1 1 -
Zb 1 + |п21е'<Ф-2₽Х’»'
Опуская в дальнейшем ради упрощения записи индекс 2 при коэффициенте отражения, имеем:
Y__ 1 1 — I я | cos (Ф — 2flx') —
ев 1 + | я | cos (Ф — 20х') +
— /1 я | sin (Ф —
+ / | я | sin (Ф — 2₽х'j ’
303
или
у_ 1 I — |л|а — /2 |л| sin (Ф — 2flx') zB 1 + I л I2 + 2 I л I cos (Ф — 2fix')
Полагая Y—g—jb, находим:
gzB=----------; (16-72)
1 +|л|* + 2|л|со8(Ф — 2₽x')
te = ----21 n | sin (Ф — 2fix')-- (16-73)
1-Нл|2 + 2|л|со5(Ф—2PZ)
Рис. 16-14. Согласование сопротивления посредством параллельного присоединения отрезка линии.
На основании (16-72) и (16-73) на рис. 16-14 построены графики (для |и|=0,5).
Величина gzB достигает максимума при Ф—2р%!2= —л, откуда
, Ф4-л Х9 = --!.
2 2р
(16-74)
В точке х' b = 0 и
е== 1 t + l«l 1
zB 1 — IЛ | Лб zB "
Следовательно, в этой точке в соответствии с (16-64) Z=rMmi= = Лб?в, т. е. имеет место минимум напряжения.
Точка х' (рис. 16-14), в которой g=l/zB, находится на основании (16-72)
j = 1-И12________
1 +1Л|2 + 2 !л| cos (Ф— 2$х\) ’ откуда соз(Ф—2₽х^) = — |и|. Ввиду того что arccos(— |п|) = —л + -t-arccos|n|, получаем:
Х1 = .P + "^rccosJn|, (16 ?5)
Подставив (16-75) в (16-73), находим реактивную проводимость в точке х, из выражения
2 |л| sin (л -j- arccos | л |) _ ® 1-|-|л|24-2 |n|cos(n-|-arccos |л|)
Рис. 16-15. Круговые диаграммы линии без потерь в осях («1, т2).
В точке х[ присоединяется отрезок линии, входная проводимость которого согласно (16-46)
^P = ~/^ctg-^-Z (16-77)
гв л
удовлетворяет условию
= (16-78)
В результате подстановки (16-76) и (16-77) в (16-78) получаем уравнение
, 2л , 2 |л|
Ctg --I— ----- 1 1 ,
Х ]/ 1 — |л|2
откуда
X
2л
arctg
/
= — arctg . (16-79) 2л 1 — Кб
304
Полученное выражение позволяет найти длину отрезка линии, присоединяемого параллельно основной линии в точце xj,T. е. на расстоянии
v . ZMXVS. |П|
2
= —— arccos1 —
4л 1 + Кб
от точки минимального напряжения.
Благодаря присоединению отрезка линии результирующее сопротивление цепи в точке х\ (в сторону нагрузки) равно волновому сопротивлению гв, и поэтому на линии между источником и точкой х{ энергия передается без отражений.
16-12. Круговые диаграммы для линии без потерь.
Согласно (16-58)
Z = 1 + | П | е/ (Ф-2РХ') _
г„ 1_|П|е/(ф-2₽х') “
= + jtn2.
или с учетом (16-49)
(1 4 т1 + ?(ф-2^’ =
1 4- Кб
= т1 — 1 + /т2. (16-80)
В результате преобразований получаем:
1 -I к2
т? — т.--------— + = — 1,
1 1 Кб 2
что можно записать в виде уравнения окружности
т 1 + ^1
т,----------
1 2Кб
2
I + т\=
\ ЧКб / ’
представляющей геометрическое место конца вектора Z/zB при постоянном Кб- Центр этой окружности лежит на оси абсцисс в точке
1 + /Сб
2Яб
а
радиус равен:
1-Kg _ 1
2Яб 2
Как и следовало ожидать, координата центра окружности определяется полусуммой, а величина радиуса — полуразностью максимального и минимального значений ZfzB, согласно (16-59) и (16-60) гмакс _ 1 _ гмин _______ „ _ 1
гЕ “ Кб ’ гв ~ б~ S '
гв
Для различных значений 5 может быть построено семейство окружностей, показанное на рис. 16-15 (сплошные линии).
Придав исходному уравнению (16-80) вид
S—1 С/(Ф—2Рх') __ /Их — 1 +
S 4~ 1 Wlx -}- 1 -р l^n.2
и освободившись от мнимой части в знаменателе, получим:
5^1 е/(ф-2₽*’)= S+1
— 1 + + /2/п2
(1 + mi)24-m2
(16-81)
Положив Ф—0, будем отсчитывать угол рх' от оси абсцисс. Согласно (16-81)
tg(-2px') = -r^—-— 1 4-
и aR - 1 + /д2 + = 0.
1 2 tg 20х
ИЛИ
m2+
1__V
tg2₽xj
tg2 20х' sin2 2fix'
Следовательно, геометрическое место точек Z/zB при постоянном значении рх' представляет окружность радиуса 1/sin 2рх'. Центр этой окружности лежит на оси ординат в точке l/tg2px'.
Для различных значений рх' может быть построено семейство окружностей, изображенных на рис. 16-15 (пунктирные линии). Все эти окружности проходят через точку 1; 0, причем для удобства отсчета численные значения углов даны на рис. 16-15 для рх'.
Круговые диаграммы, изображенные на рис. 16-15, могут быть использованы и для величины, обратной Z/zB, а именно zBY; в этом случае mi и т2 будут соответствовать действительной и мнимой частям zBY. Вверх от оси абсцисс будет откладываться положительная (емкостная) проводимость, а вниз — отрицательная (индуктивная) проводимость.
20—1118
305
С помощью круговых диаграмм ряс. 1б-Й> можно решать различные за/щчи. 'Гак, если из трех величин: сопротивления нагрузки Za, аргумента ex' и входного сопротивления линии Z — известны какие-либо две величины, то третья величина легко находится по диаграмме рис. 16-15.
Применение круговой диаграммы иллюстрировано ниже на примере. '
Пример 16-2. К концу линии без потерь, имеющей zB=500 ом и Рх/=120°, присоединено сопротивление Zs= 1000+/500. Требуется найти входное сопротивление линии.
Сопротивление нагрузки, отнесенное Z2 к волновому сопротивлению, равно --=
=2+/1. Следовательно, н данном случае Д?1=2, Точка 24-/1 в верхней полуплоскости соответствует концу линии (*'= =0). Она лежит на окружности 5=2,63. От этой точки по окружности S=2,63 должен быть отложен в сторону отрицательных углов, т. е. по ходу часовой стрелки, угол ₽х,= 120р.
Таким образом, будет получена точка Z
—=0,41 + /0,25. Следовательно, искомое 2В
входное сопротивление линии равно Z= =205+/ 125=240е^зг>24 . При аналитическом расчете по формуле (16-53) получается Z=208+/123 ом.
Следует заметить, что при отсутствии стоячей волны (Кб=1), зна-чедню оч= — =1 соответствует Аб
окружность нулевого радиуса, т. е. точка 1 на оси абсцисс. Окружности для всех других значений S охватывают эту точку, и предельному значению S=oo соответствует на диаграмме рис. 16-15 окружность бесконечного радиуса, совпадающая с осью ординат. Окружности S и рх' неконцентрические и соответственно шкалы для отсчета S и fix' неравномерны? Это вносит неточности при интерполировании. Кроме того, ограниченные размеры диаграммы затрудняют расчеты с большими сопротивлениями.
На практике получила распространение модификация круговой диаграммы линии без потерь, предложенная в 1939 г. Ф. Смитом. В этой диаграмме любые значения сопротивлений охватываются кругом единичного радиуса.
306
Диаграмма строится, исход? и» (16-8Ц, в координатах (р, д):
m2 — 1 + п? (т1 + 1)2 +
, . _____2т^______
(znl + 1)2 + m2 ’ откуда
т? — 1 + п&
Р — —-------------;
(«l + l)’ + «2
<7 = .
(«I + 1)2 + ml
Исключая поочередно двух уравнений и Щг, \ «г+* /
1 .
“fai + lj* ’
(р-1)2 + (<7--Ц2=
\ та /
ИЗ ЭТИХ находим:
(16-82)
1
т2 ’ т2
Первое уравнение (16-82) выражает семейство окружностей для постоянных значении тс, центры их т, расположены в точках —— на
й 1 оси абсцисс, а радиусы равцы-----.
Л11+1
Второе уравнение (16-82) выражает семейство окружностей для постоянных тс, центры их расположены в точках 1-}-/ —, а радиусы равны 1/тг. Эти два семейства qk-. ружностей изображены ца рис. 16-16.
Рис, 16-16. ма линии
Круговая диаграм-без потерь в осях (?. .
16-13. ЛИНИЯ КАК ЭЛЕМЕНТ РЕЗОНАНСНОЙ ЦЕПИ
Четвертьволновая линия с малыми потерями, разомкнутая на конце, обладает свойствами резонансной цепи, состоящей из последовательно соединенных г, L и С. При частоте, при которой на линии укладывается четверть волны (такую частоту условимся называть резонансной), входное сопротивление линии будет активным и притом минимальным.
При малом отклонении частоты от резонансной модуль входного сопротивления линии резко возрастает; входное сопротивление приобретает емкостный характер при понижении частоты и индуктивный характер при повышении.
Входное сопротивление линии с малыми потерями, разомкнутой на конце, мо^но получить из (16-21), разлагая shyx' и chyx' по формулам тригонометрии и принимая ввиду малости a, chax'~l,ashax'~ ~axJ.
Выражение примет вид:
g C9S fix' + lax'sin Р*, 8 ах' cos рх' -|- / sin fix'
Вблизи резонансной частоты рх'дал/г и sinpx'» 1, a cospx'-cl.
Поэтому
Zx 5» zB (ax' — / cos рх') =
\ ax }
Если через Po обозначить коэффициент фазы при резонансной частоте, т. ё. принять Рох'=л/2 и
<0 On
учесть еооггцснцение f*= — ~ ~> Р Ро то cos рх можно преобразовать следующим образом:
cos рх' cos р0 — х' =
(Ор
== CQS(PoX' + pox'fi) =
= ?os(-y +М'б) =
= — sin PqX'6 — рх'б.
Здесь, так же как и в гл. 7, 9 =-----и — расстройка частоты по
отношению к резонансной.
Следовательно,
Zx^zBax'(l+/-^)- (16-83)
При частоте, близкой к резонансной, когда величина б значительно меньше единицы, комплексное сопротивление резонансной цепи приблизительно равно:
Z^r(l+j2Q&). (16-84)
Рассматривая четвертьволновую ЛИНИЮ, как резонансную цепь, можно в сцлу одинаковой структуры выражений (16-83) и (16-84) считать, что добротность линии равна:
При этом резонансные характеристики, приведенные в гл. 7, останутся применимыми и к рассматриваемой линии.
Соответственно полоса пропускания, представляющая величину, обратную добротности (§ 7-2), равна:
Здесь под полосой пропускания, так же как и в § 7-2, подразумевается отнесенная к резонансной частоте ширина резонансной кривой между точками, соответствующими половине максимальной мощности (когда г— 'xj.
При малых значениях коэффициента а добротность получается высокой, достигая примерно 1 000— 4000, что намного превышает добротность контуров г, L, С. В связи с этим возрастает и острота настройки.
16-14. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Переходные процессы в цепях с распределенными параметрами (в линиях, обмотках электрических машин и т. п.) возникают при коммутациях, при передаче непериодических сигналов или под влиянием внешнего электромагнитного поля (например, при гррзовых разрядах). Для исследования переходных процессов в однородных цепях с рас
20*
307
пределенными параметрами пользуются дифференциальными уравнениями (16-2) в частных производных
ди , , , di
----—rlA-L—;
дх dt
di . г- du
dx s dt
где r, Lt g и C— параметры цепи на единицу длины;
х— координата рассматриваемой точки, отсчитываемая от начала цепи.
В общем виде решение этих дифференциальных уравнений достаточно сложно. Решение упрощается, если пренебречь потерями, т. е. считать, что г и g равны нулю. В этом случае
(16-85) дх dt
_di_=C — . (16-86)
dx dt
Дифференцируя (16-85) по х:
5au _ L & (\_________L д ( di }
dx2 dx \dt / dt \dx J
и используя (16-86), получаем:
дги ___ f р SPu
дх2 ~ dtP '
(16-87)
Дифференциальное уравнение (16-87) известно в математической физике под названием уравнения колебаний струны. Его решение дано Даламбером и имеет вид: u=/i(x — vt) 4- /а(х + vt), (16-88)
где
Р =
Первая слагающая представляет собой одиночную прямую волну напряжения, которая без изменения перемещается в сторону возрастающих х, т. е. от начала к концу цепи. Для всех значений х, при которых х—vt—const, эта слагающая имеет одно и то же значение, т. е. волна движется со скоростью v= —dxldt.
Вторая слагающая представляет собой одиночную обратную в о л-н у напряжения, которая без изме
нения перемешается в противоположном направлении.
Для нахождения тока произведем замену переменных, обозначив |=х—vt и T]=x-j-vt. На оснований (16-86) и (16-88)
_ с ( dfi <% л .
\ д^ dt ch] dt)
=Cv
\ dg dri)
HO
dx Д- dx dg
И
df2 = df2 dt] .
dx dr) dx dx\ *
Следовательно,
di _(jv / dfi df2 \
dt. \ dx dx J
Интегрирование последнего уравнения дает *:
» = l/y- [Zi(* — vt) —
-fz(x + vt)]. (16-89)
Выражения (16-88) и (16-89) записываются сокращенно
U=Un4-Uo; (16-90)
i = —(un —uo) = i„ —to; (16-91)
здесь i„ и io—прямая и обрат-______________ ная волны тока;
zB = £/С — волновое сопротивление.
Следовательно, напряжение и ток прямой и соответственно обратной волн связаны с законом Ома:
Аналогичный результат был получен в § 16-3 для установившихся прямой и обратной волн при рассмотрении гармонического режима в однородной линии. Физически установившиеся волны представляют собой бесконечные суммы прямых
1 Постоянная интегрирования может быть отнесена к функциям fi и f2.
308
(16-94)
и обратных одиночных волн, отраженных от обоих концов линии.
Итак, при отсутствии потерь в однородной цепи с распределенными параметрами напряжение и ток могут быть представлены как сумма и как разность двух волн, движущихся ^одинаковой скоростью v= = 1/У^ЬС в противоположных направлениях, без изменения их формы. При этом в любой точке однородной цепи отношение напряжения и тока для прямой и обратной волн равно волновому сопротивлению zD.
Если на пути распространения волны встречается неоднородность, например воздушная линия переходит в кабельную или волна достигает конца линии (разомкнутого или замкнутого через сопротивление или накоротко), происходит отражение волны. В зависимости от характера неоднородности отражение может быть частичным или полным. В первом случае наряду с отраженной волной возникает преломленная волна, распространяющаяся за место нарушения однородности; во втором случае преломленная волна отсутствует.
Обозначим:
ц, и ix—напряжение и ток в месте отражения;
uin и iln—напряжение и ток падающей (прямой) волны;
uio и ilo-4r напряжение и ток отраженной (обратной) волны;
«2 и i2—напряжение и ток преломленной (прямой) волны;
и z2— волновые сопротивле-
ния для прямой и обратной волн (21) и преломленной волны (2г).
В месте неоднородности выполняется условие равенства напряжений и токов:
Ui п2;
Следовательно,
“in+«io=«a; (16-92)
i’in (16-93)
Подстановка в (16-93) значений
i — tlD t — “lo .. / — Us
Iln I llo — И la —
г1 г1 гг
дает:
ц1п — цю _ “я
Z] гг
В результате совместного решения уравнений (16-92) и (16-94) находятся отраженная («ю) и преломленная (п2) волны:
ulo=nuln;
u2=(l+n)Uin,
где и= ——— — коэффициент от-г3 + г1
ражения.
Соответственно ток отраженной волны
j (16-95)
а ток преломленной волны
i = = (! + п> = 2“1П
г2 Z2 Zi + Za
Последнее выражение показывает, что ток в конце линии после отражения можно найти как ток в эквивалентной цепи, в которую включается напряжение, равное двойному напряжению падающей волны, и которая состоит из волнового сопротивления первой линии 2t и последовательно соединенного с ним сопротивления нагрузки (в которое входит вторая линия своим волновым сопротивлением гг).
Опишем процесс включения однородной линии без потерь. После присоединения линии к источнику э. д. с. по линии начнет распространяться зарядная волна, создающая напряжение и ток. Если в конце линии присоединена нагрузка, равная волновому сопротивлению линии, то падающая волна, достигнув ее, не отразится и в линии сразу наступит установившийся режим. Если же нагрузка с линией не согласована, то падающая зарядная волна, достигнув конца линии, претерпит отражения. Распространяясь в обратную сторону, отраженная волна сложится с падающей, причем напряжения волн суммируются, а токи вычитаются (алгебраически). Достигнув начала линии, обратная волна снова отразится от источника э. д. с. как от короткозамкнутого конца; появится новая прямая вол-
309
на напряжения и тока, которая также отразится от конца, и т. д. Процесс будет продолжаться до наступления установившегося режима. Теоретически в идеальной линии без потерь при чисто реактивной нагрузке процесс колебаний будет продолжаться бесконечно долго. В реальной линии при наличии потерь волны напряжения и тока будут постепенно затухать в направлении распространения.
Напряжение и ток в линии в произвольный момент времени определятся как алгебраические суммы и соответственно разности напряжений и токов прямых и обратных волн.
Пользуясь формулами и схемой замещения, описанной выше, можно найти напряжение и ток, возникающие в месте присоединения сосредоточенной нагрузки или в месте перехода одной линии в другую (пример 16-3).
Следует отметить, что индуктивность, включенная последовательно в линию, или емкость, включенная параллельно проводам линии, сглаживают фронт преломленных волн; активное сопротивление, включенное в линию параллельно, уменьшает преломленную волну.
Различные случаи отражения и преломления волн рассмотрены в [Л. 9, 15 и 16].
Пример 16-3. К концу линии, имеющей
и
u2 = 3U~ zBi2 =--------Ir + z^e т
гв + Г \
L
здесь г= г 2|_ г ’ ^“0 соответствует момен-
ту падения волны на катушку.
16-15. ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
В § 16-2 были выведены дифференциальные уравнения однородной двухпроводной линии; ввиду наличия двух независимых переменных (/ и х) дифференциальные уравне-
ния получились в частных водных
di
дх
— gu-j-C — .
6 dt
произ-
(16-96)
Минусы в левой частя уравнений (16-96) соответствуют случаю, когда расстояние х отсчитывается от начала линии или, точнее, в положи-
волновое сопротивление zB, присоединена индуктивная катушка г, L. Определить ток в катушке и напряжение иа иен' под воздействием прямоугольной волны U.
На рйс. 16-17 показаны расчетная схема и эквивалентная схема замещения. Диф-
тельном направлении тока.
Формула дифференцирования по параметру (см. табл. 14-1) позволяет применить преобразование Лапласа к уравнениям (16-96), в которых х является параметром.
Если изображения искомых функций обозначить через
и (х, 0 т=- и (х> р)=и\ i(x, 0=г= Цх. р)=1, системе
дифференциальных
и
%
«4
о)
Рис. 16-17. Пример 16-3.
то
уравнений в частных производных (16-96) будет соответствовать система уравнений
~ = (r+PL)l~Li(x,G)-
dx
~ = (g+pC)U—Cu{x, 0); ах
фереициальное уравнение Кирхгофа для такой цепи запишется так:
отсюда
du
= ia(*B + r) + L ,
(16-98)
здесь Цх, 0) и u(x, 0)—начальные (по времени) значения тока и напряжения в точке х.
Ввиду того что р не зависит от х и в уравнениях (16-98) производные по р отсутствуют, при переходе от уравнений (16-96) к (16-98) частные
310
производные по х заменены обыкновенными.
Исключая из системы (16-98) I, получаем уравнение относительно U-.
— (rA-pL) (g+pC) U 4-
4- L di<^ _ с (r+pLMx, 0). (16-99) dx
Аналогично, исключая из (16-98) U, получаем уравнение относительно /:
— =(r-|-pL) (g-{-pC) 1
+СL(g+pC)i(x,0). (16-100)
ах
Эти уравнения решаются как обычные дифференциальные уравнения второго порядка.
Обозначим ____________
Т (Р)=К(r+pL) (g+pC)
и назовем это выражение операторным коэффициентом
распространения.
При нулевых начальных значениях уравнения (16-99) и (16-100)
упростятся:
— = y2t7; dx* r
d*J
(16-101)
Обращает на себя внимание сходство полученных операторных уравнений (16-101) при нулевых начальных условиях с дифференциальными уравнениями однородной линии при установившемся режиме.
Соответственно остаются в силе для (16-101) решения, полученные в § 16-3, если под U и I подразумевать изображения напряжения и тока, а под ______
^р) = 1/
V g+pc
операторное волновое сопротивление линии1.
В общем случае переход от изображений U(x, р) и 1(х,р), являющихся трансцендентными функци
1 Если в выражениях У(р) и ZB(p) за-
менить р на /со, то получатся известные
выражения для параметров линии при гар-
моническом режиме.
ями от р, к искомым оригиналам и(х, t) ni(x,t) представляет значительные трудности. При решении задач обычно делаются какие-либо упрощающие предположения [Л. 1 и 9].
16-16. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
16-1. Вычислить при частоте 1000 гц волновое сопротивление однородной линии, коэффициент распространения и фазовую скорость по заданным первичным параметрам: г=6,5 ом/км; L=2,29-10-3 гн/км; С— =5,22-10-s мкф/км; £=0,5-10~6 сим/км.
Ответ: Z„=692Z—12° ом; у= (49,2т -4-/222)10—* 1/км; Оф =283 000 км/сек.
16-2. К линии, указанной в предыдущей задаче, присоединена активная нагрузка 200 ом. Вычислить коэффициент отражения.
Ответ: 0,558 Z173°.
16-3. Входное сопротивление линии длиной 200 км при частоте 800 гц равно: при холостом ходе 747—26°30' ом, при коротком замыкании 516Z0°30' ом. Вычислить вторичные и первичные параметры линии.
Ответ: ZB=620Z—13° ом; у = (47,5+ +;180)10-4 l/км; г=5,4 ом/км; L= = 2,04-10-а гн/км; С=6-10-9 ф/км; g=> = 8,7 • 10~7 сим/км.
16-4. Входное сопротивление линии длиной 50 км при частоте 800 гц равно: при холостом ходе 328Z—29°12' ом, при коротком замыкании 1 548Z6°48' ом. Вычислить вторичные и первичные параметры.
Ответ: ZB=712 Z—11°12' ом; у= = (91,6+/280) • 10-4 l/км; г=10,25 ом/км; £=3,66-10-з гн/км; С=8,22-10-9 ф/км; g=5- 10-е сим/км.
16-5. Однородная линия имеет параметры: г=5 ом/км; С=5-10_з мкф/км; g= = 10-з сим/км.
При какой индуктивности в линии отсутствовали бы искажения?
Ответ: 25 мгн/км.
16-6. Вычислить входное сопротивление линии без потерь при коротком замыкании. Длина линии 35 м, длина волны 50 м, волновое сопротивление линии 505 ом.
Ответ: 1554Z900 ом.
16-7. Условия и требование предыдущей задачи, ио принять длину линии равной 23 м.
Ответ: 129Z—90° ом.
16-8. Волновое сопротивление линии без потерь равно ZB=500 ом. Определить амплитуду тока на расстоянии 1 м от разомкнутого конца линии при частоте f= = 108 гц, если действующее значение напряжения иа разомкнутом конце равно 10 в.
Ответ: 0,0245 а.
16-9. Однородная линия с первичными параметрами г= 10.4 ом/км; £=3,67 мгн/км; С =0,00835 мкф/км и g=0,8-10_® сим/км, длиной 100 км подключена к источнику э. д. с. 100 в; частота равна 1 000 гц; линия нагружена активным сопротивлением 200 ом. Вычислить: токи в начале и в кон
311
це линии; напряжение в койне линии; активную мощность в начале и в койне линии.
Ответ: 0,167Z0°30' а; 0,113Z—200°30' а;
22,6Z—200°30' в; 16,7 ет; 2,55 ет.
16-10. Чем отличаются цепи с распределенными параметрами от цепей с сосредоточенными параметрами?
16-11. В каких линиях и при каких условиях возникают стоячие волны?
16-12. Будет ли передаваться энергия по линии без потерь, замкнутой на реактивное сопротивление?
16-13. Каковы первичные и вторичные параметры линии без потерь?
16-14. Как определяются напряжение и ток в начале (или в конце) линии в зависимости от напряжения и тока в конце (или в начале) линии?
312
Глава семнадцатая
ДВУХПОЛЮСНИКИ
17-1. ОПРЕДЕЛЕНИЕ И КЛАССИФИКАЦИЯ ДВУХПОЛЮСНИКОВ
Любая электрическая цепь, рас
сматриваемая относительно каких-
либо двух ее зажимов, называется двухполюсником. Двухполюсник может быть сколь угодно сложной конфигурации.
тивные и пассивные.
Активным называется двухполюсник, содержащий источники электрической энергии, которые не
Рис, 17-2. Пример пассивного двухполюсника, содержащего
источники э. д. с.
Рис. 17-1. Условное изображение двухполюсника.
В общем случае, когда внутренняя схема соединений двухполюсника неизвестна или раскрытие ее не требуется, двухполюсник изображается в виде прямоугольника с двумя зажимами (рис. 17-1).
Двухполюсники могут классифицироваться по различным признакам. По признаку линейности элементов, входящих в двухполюсник, различают линейный и нелинейный двухполюсники. По числу элементов, входящих в двухполюсник, различают одноэлементный, двухэлементный и многоэлементный двухполюсники.
По характеру элементов двухполюсники разделяются на реактивные, т. е. состоящие из индуктивностей и емкостей, и двухполюсники с потерями, содержащие активные сопротивления1 . Реактивные двухполюсники
1 Цепи с потерями называкнся диссипативными цепями.
представляют собой идеализированные электрические системы, приближающиеся по своим свойствам к фи-
зически реализуемым цепям с малыми потерями.
Различают двухполюсники ак-
компенсируются взаимно внутри двухполюсника.
Пассивным называется двухполюсник, не содержащий источников электрической энергии; в случае линейного двухполюсника он может содержать источники электрической энергии, взаимно компенсирующиеся таким образом, что напряжение на его разомкнутых зажимах равно нулю. Такой линейный двухполюсник относится к категории пассивных; его сопротивление, измеренное на зажимах, не изменится, евли источники электрической энергии внутри него заменить пассивными элементами — внутренними сопротивлениями источников напряжения или соответственно внутренними проводимостями источников тока. Пример пассивного двухполюсника, содержащего скомпенсированные источники, показан на рис. 17-2.
Два двухполюсника, имеющие разную структуру, эквивалентны в электрическом смысле, если
312
их сопротивления или соответственно проводимости равны друг другу во всем спектре частот. Замена в электрической цепи какого-либо двухполюсника эквивалентным ему двухполюсником не влияет на токи или напряжения в остальной части электрической цепи. Это положение справедливо как для установившегося, так и для переходного режима.
Зависимости сопротивлений или проводимостей двухполюсников от частоты называются частотными характеристиками.
Частотные характеристики двухполюсников, образующих электрическую цепь, предопределяют частотные свойства данной цепи, т. е. зависимости амплитуд и фаз токов или напряжений от частоты.
Нижеследующие параграфы посвящены изучению частотных характеристик линейных двухполюсников.
Существенным отличием их от более сложных двухполюсников является то, что знак комплексного сопротивления и комплексной проводимости каждого из этих двухполюсников не изменяется при изменении частоты.
Комплексное сопротивление индуктивного элемента во всем спектре частот имеет положительный знак, а комплексная проводимость — отрицательный знак:
ZL = jxL = jaL-t
Yb—ibL— !±.
Емкостный элемент во всем спектре частот имеет отрицательное комплексное сопротивление и положительную комплексную проводимость:
Zc = -ixc = ~}^
Yc = jbc = faC. (17-2)
(17-1)
17-2. ОДНОЭЛЕМЕНТНЫЕ РЕАКТИВНЫЕ ДВУХПОЛЮСНИКИ
Индуктивность и емкость представляют собой одноэлементные реактивные двухполюсники (рис. 17-3).
L
0----------------0
а)
£ Рис. 17-3. Одиоэле-
0-----II---------& ментные реактив
g, ные двухполюсни-
’ ки.
Рис. 17-4. Частотные характеристики одноэлементных двухполюсников.
а — сопротивления; б — проводимости.
Частотные характеристики Zt и Ус, построенные в прямоугольной системе координат, представляют собой прямые линии, а частотные характеристики Zc и YL— гиперболы (рис. 17-4). Таким образом, кривые ZL и Zc аналогичны соответственно кривым Ус и YL.
Следует заметать, что как сопротивления, так и проводимости рассматриваемых здесь одноэлементных реактивных двухполюсников возрастают (с учетом знака) по мере повышения частоты, т. е.
JL>0. ^L>o.
jd<o jda
Как будет показано ниже, это является общим свойством всех реактивных двухполюсников, а не только одноэлементных.
Двухполюсник, состоящий из последовательно или параллельно соединенных однородных элементов (индуктивностей или емкостей), относится к числу одноэлементных двухполюсников, так как последовательно или параллельно соединенные однородные элементы мо
313
гут быть заменены одним эквивалентным реактивным элементом того же характера.
В результате сведения числа элементов двухполюсника до минимума путем замены их эквивалентными получается приведенный двухполюсник.
17-3. ДВУХЭЛЕМЕНТНЫЕ РЕАКТИВНЫЕ ДВУХПОЛЮСНИКИ
Двухэлементный реактивный двухполюсник получается в результате последовательного или параллельного соединения индуктивности и емкости (рис. 17-5, а и
При последовательном соединении индуктивности и емкости алгебраически складываются реактивные сопротивления. На рис. 17-5, б жирной линией показана частотная характеристика двухполюсника, полученная в результате графического сложения кривых ZL и Zc.
Эта характеристика пересекает ось абсцисс при резонансной частоте ©1 = 1/рг£С (резонанс напряжений).
Здесь и ниже частоты резонанса напряжений обозначаются нечетным индексом.
Частотная характеристика проводимости двухэлементного реактивного двухполюсника представляет собой функцию, обратную сопротивлению Y—1/Z. Кривая У показана на рис. 17-5, в.
Частотные характеристики Z и У, построенные на рис. 17-5, соответствуют уравнениям:
Z==/x==/(xL —хс) =
₽=/ 1<вь---1 ~ IL и-------)
\ адС/ * \ wLC/
и
или с учетом, что coi= \!^LC,
г <в2 —<0? x=L----------;
ш
t =-------------
L (со2 — со2)
(17-3)
На основании рис. 17-Б и уравнений (17-3) следует, что в области частот ниже резонансной (co<coi) сопротивление емкостного элемента превышает по абсолютной величине сопротивление индуктивного элемента; при этом результирующее сопротивление двухполюсника име-
Рис. 17-5. Частотные характеристики двухэлементного реактивного двухполюсника L, С.
а — схема двухполюсника; б — со* противление; в — проводимость.
ет емкостный характер. В области частот выше резонансной (q>>qh) абсолютная величина емкостного сопротивления меньше величины индуктивного, поэтому результирующее сопротивление двухполюсника имеет индуктивный характер.
При параллельном соединении индуктивности и емкости алгебраически складываются их комплексные проводимости. На рис. 17-6, б жирной линией показана частотная характеристика двухполюсника, полученная в результате графического сложения У г, и Ус.
При резонансной частоте сз2= = \lY~LC эта характеристика пересекает ось абсцисс (резонацс токов).
314
Здесь и ниже частоты резонанса токов обозначаются четным индексом.
Частотная характеристика сопротивления того же двухполюсника представляет собой функцию, об-
Рис. 17-6. Частотные характеристики двухэлементного реактивного двухполюсника L, С.
а — схема двухполюсника; б — проводимость; в —сопротивление.
ратную проводимости: Z— 1/У. Кривая Z показана на рис. 17-6, в.
Частотные характеристики Z и Y, построенные на рис. 17-6, соответствуют уравнениям:
г = ^/ь = -/(^-ьс) =
и
Z=/x=/
1
ИЛИ С учетом, ЧТО С02=1/У^С,
(17-4)
6=С
2 2
COJ— (О
CU ’
(О
На основании рис. 17-6 и уравнений (17-4) следует, что в области частот ниже резонансной абсолютная величина проводимости индуктивного элемента больше величины проводимости емкостного элемента и сопротивление двухполюсника имеет индуктивный характер. В области частот выше резонансной наблюдается обратное явление: сопротивление двухполюсника имеет емкостный характер.
Таким образом, в зависимости от частоты двухэлементный реактивный двухполюсник может иметь либо индуктивное, либо емкостное сопротивление.
При этом, так же как и в случае одноэлементного реактивного двухполюсника, Z и У возрастают по мере повышения частоты, т. е. производные от Zjj и Y/j по частоте положительны.
В отличие от сопротивлений одноэлементных двухполюсников, которые выражаются только через текущую частоту, сопротивления двухэлементных реактивных двухполюсников зависят также и от разности квадратов резонансной и текущей частот в соответствии с (17-3) и (17-4).
17-4. МНОГОЭЛЕМЕНТНЫЕ РЕАКТИВНЫЕ ДВУХПОЛЮСНИКИ
Трехэлементный реактивный двухполюсник может быть составлен из двух индуктивностей и одной емкости (рис. 17-7, а и 17-9, а) или из двух емкостей и одной индуктивности (рис. 17-8, а и 17-10,а).
Общее число возможных схем трехэлементных реактивных двухполюсников равно четырем.
Пользуясь частотными характеристиками одноэлементных и двухэлементных реактивных двухполюсников, приведенными выше, можно легко построить частотные характеристики для трехэлементных двухполюсников.
315
При последовательном соединении одноэлементного и двухэлементного реактивных двухполюсников, образующих в совокупности трехэлементный двухполюсник (рис. 17-7,а и 17-8,а), суммиру-
получаются обращением соответствующих характеристик проводимостей (рис. 17-9,0 и 17-10,0).
Из сопоставлений частотных характеристик трехэлементных двухполюсников следует, что двухпо-
Рис. 17-7. Частотные характеристики трехэлементиого реактивного двухполюсника.
а — схема двухполюсника; б — сопротивление; в—проводимость.
Рис. 17-8. Частотные характеристики трехэлементного реактивного двухполюсника.
а — схема двухполюсника; б — сопротивление; в — проводимость.
ются характеристики сопротивлений составных двухполюсни-ков (рис. 17-7,6 и 17-8,6). Характеристики проводимостей трехэлементных двухполюсников получаются обращением соответствующих характеристик сопротивлений (рис. 17-7,0 и 17-8,в).
При параллельном соединении одноэлементного и двухэлементного реактивных двухполюсников, образующих трехэлементный двухполюсник (рис. 17-9, а и 17-10, а), суммируются характеристики проводимостей составных двухполюсников (рис. 17-9, б и 17-10, 6). Характеристики сопротивлений трехэлементных двухполюсников
люсники, состоящие из двух индуктивностей и одной емкости (рис. 17-7,а и 17-9,а), имеют однотипные частотные характеристики. Параметры этих двухполюсников могут быть подобраны так, что характеристики сопротивлений и соответственно проводимостей обоих двухполюсников совпадут, т. е. эти двухполюсники будут в электрическом смысле эквивалентными.
То же следует сказать и в отношении трехэлементных двухполюсников, состоящих из двух емкостей и одной индуктивности (рис. 17-8, а и 17-10, а). При соответствующем
316
Рис. 17-9. Частотные характеристики трехэлементного реактивного двухполюсника.
а — схема двухполюсника; б — проводимость; в — сопротивление.
Рис. 17-10. Частотные характеристики трехэлементного реактивного двухполюсника.
а — схема двухполюсника; б — проводимость; в — сопротивление.
подборе параметров эти двухполюсники могут быть эквивалентны.
Частотная характеристика Z, построенная на рис. 17-7,6 соответствует выражению
С учетом (17-6) получается
со3 =
£-0 £g
(17-7)
Z—/ю^-о+/
со
(П-5)
1 где = ——
У' £g Cg
(17-6)
— частота резонанса токов контура L2C2.
При частотах со>Ю2 сопротивление контура Lz, С2 имеет емкостный характер, и при некоторой частоте <оз>со2 наступает резонанс напряжений.
Частота резонанса напряжений определяется из уравнения
£-0 £2 Cg
С помощью (17-7) выражение (17-5) может быть преобразовано в следующее:
2 2
СО,— СО Z=/(oLo4------ (17-8)
со2— со
Аналогично могут быть получены выражения для сопротивлений и резонансных частот других типов трехэлементных двухполюсников. По схеме рис. 17-8, с 7 2
z C0+Cg со,-^ /со Со С2 <о2 — со2 1
WgT-o +
со3
С2(<°2 “з)
= 0.
«1 = —:
1/ Lg (Co + Cg)
1
•
Cg
(17-9)
.317
По схеме рис. 17-9, а
2 2
Z=/w -----------3----.
Li + £3 (о| — ц>2
1 и2= —_____l ;
V С3 (£, +£з)
1 W3 — ~. V L3CS По схеме рис. 17-10, а
9 2
z _____1 ^3—м .
/® С1 <1)2— Сй2'
(17-10)
(17-11)
Таким образом, сопротивления трехэлементных реактивных двухполюсников содержат разности квадратов резонансной и текущей частот в числителе и знаменателе; при этом частота резонанса напряжений входит в числитель, а частота резонанса токов — в знаменатель выражения Z.
Условия эквивалентности трехэлементных двухполюсников по схемам рис. 17-7, а и 17-9, а и соответственно рис. 17-8, а и 17-10, с получаются в результате приравнивания друг другу выражений для сопро
тивлений и соответственно для резонансных частот.
На основании (17-6) — (17-8) и (17-10) двухполюсники по схемам рис. 17-7, а и 17-9, с эквивалентны, если
т __ 4i Lg _
° Z-i+4.’
LzC2=(L1+Ls)C3- ^s±h. e ' 4-0 х-g C<2 4-3 C3
откуда
[ __ Lj Ls _ » ___ 41
° L^Lg’ 2 Ц + Lg
Cg=C3^ + L?>a; (17-12)
4
Lr i т . r Lo (Lo + Lg) _ 1—l0Tl2> b3 — r •
В свою очередь в соответствии с (17-9) и (17-11) двухполюсники по схеме рис. 17-8, а и 17-10, а эквивалентны, если
^-= A-- L2(C04-C2) = LsCs;
со с2 С1
т с __ Lg С3 Ca
2 2“ Ci + Сз
Таблица 17-1
318
откуда
Cq---Cj-j-CgJ С2
^(Ct + Сз). Сз
/-2
С3
Lz Ls (Q + C3F’
(17-14)
Частотные характеристики сопротивлений всех четйрёхэлемёнт-ных реактивных дйухйолюсййков сводятся в конечном итоге к двум типовым характеристикам, Изображенным на рис. 17-11,6 й 17-12,6.
_ л /">2
£ __ Ср Cg . q _ ь0
1 ~ Со + С2 8 ~ Со + с2’
£s=ZJ.Q±£?)2 0745)
Формулы (17-12) — (17-15) сведены в табл. 17-1.
Приведенные формулы служат для перехода от одного трехэлементного реактивного двухполюсника к другому экйивйй'ентйбму ему двухполюсййку.
В отличие от двухэлементных реактивных двухполюсников, имеющих одну резонансную частоту, трехэлСМентййе реактивные двух-пблкоснйкй характеризуются наличием двух резонансных частот, причем в зависимости от схемы двухйолюсцика первоначально на-стуйает либо резонанс напряжений, либо резонанс токов. Если первым наступает резонанс напряжений, то множитель /и Входит в знаменатель выражения для сопротивления двухполюсника; если же первым наступает резонанс токов, то множитель /to Входит в числитель.
В общем случае число резонансов на единицу меньше числа элементов приведенного реактивного двухполюсника, причем резонансы напряжений и токов чередуются.
Если при 0=0 сопротивление двухполюсника равно нулю, т. е. имеется путь постоянному току, то первым наступает резонанс токов, за ним следует резонанс напряжений.
В противном случае порядок расположения резонансов обратный: первым наступает резонанс напряжений, вторым — резонанс токов.
Четырехэлементные реактивные двухполюсники состоят из двух индуктивностей и двух емкостей. Общее число возможных схем четырехэлементных реактивных двухполюсников равно восьми.
Рис. 17-11. Частотные характеристики четырехэлементного реактивного двухполюсника.
а — схема двухполюсника; б — сопрОтнЖлейие.
Рнс. 17-12. Частотные характеристики четырехэлементного реактивного двухполюсника. а — схема двухполюсника; б — сопротивление
319
(ш2-со2)(со2-со2)
Последние получаются в результате суммирования частотных характеристик сопротивлений составных двухполюсников, которые в схемах рис. 17-11, а и 17-12, а соединены последовательно.
Можно показать, что сопротивления четырехэлементных -двухполюсников выражаются следующими формулами:
для схемы рис. 17-11, а
£ (<£>?— СО2) (<0?— (О2)
Z = А U(17-16) /“ со2—со2
для схемы рис. 17-12, а
2 2
7_. СО С03— СО /17 1*74
~7 C2ct ^-2 +
Таким образом, сопротивления четырехэлементных двухполюсников содержат две разности квадратов резонансной и текущей частот в числителе и одну разность квадратов резонансной и текущей частот в знаменателе, или наоборот.
Резонансные частоты, входящие в числитель выражений (17-16) и (17-17), являются частотами резонансов напряжений, а входящие в знаменатель — частотами резонансов токов.
Если первым наступает резонанс напряжений, то множитель /со входит в знаменатель выражения для сопротивления; если же первым наступает резонанс токов, то множитель /со входит в числитель.
17-5. ОБЩЕЕ ВЫРАЖЕНИЕ СОПРОТИВЛЕНИЯ ПАССИВНОГО МНОГОЭЛЕМЕНТНОГО РЕАКТИВНОГО ДВУХПОЛЮСНИКА
Положим, что к входным зажимам пассивного двухполюсника, представляющего сколь угодно сложную электрическую цепь, присоединен источник э. д. с. (рис. 17-13). Эта э.д.с. может рассматриваться как контурная действующая во входном контуре двухполюсника. Соответственно и ток на входе двухполюсника может рассматриваться в качестве контурного тока.
Обозначив входной контур двухполюсника цифрой /, найдем вход
ное сопротивление Z двухполюсника как отношение контурной э. д. с. к контурному току /ц
Z = |i-=At (17-18) где Д— определитель системы, элементами которого служат собствен-
Рис. 17-13. Пассивный многоэлементный двухполюсник с присоединенным к нему источником э. д. с.
ные сопротивления Zu и общие сопротивления Zik контуров; Ди — алгебраическое дополнение (равное в данном случае минору) элемента ZH определителя системы (5-2).
Число строк, а также столбцов в определителе системы равно числу независимых контуров (п) в двухполюснике.
Умножим числитель и знаменатель правой части (17-18) на (/со)"
Z = А (/<в)пДц ’
Умножение определителя Д на /со равносильно умножению всех элементов одного ряда (строки или столбца) на /со. Соответственно умножение Ди на (/со) 71-1 равносильно умножению всех элементов определителя Дц на /со.
Положим, что двухполюсник состоит из реактивных элементов, причем собственное сопротивление контура i
Zlt=-iwLtt -j- * , /соСп
а общее сопротивление контуров i и k
Отсюда
/coZH=(/(o)2 Lu + и /(oZ/ft =
L Q* J
Вводя обозначение
p=/co, (17-19)
320
получаем:
pZrt—р'Ьц 4* ~; С-п
P^-ik— — (р* L(lr + ~r—1 \ Ctk!
(17-20)
Определитель рпД, состоящий из элементов вида (17-20) и имеющий порядок п, является полиномом степени 2п относительно р или, что то же, полиномом степени и относительно р2. Соответственно определитель рп-,Дц, состоящий из аналогичных элементов и имеющий порядок п—1, представляет Полином степени 2п—2 относительно р или, что то же, полином степени п—1 относительно р2.
Итак,
а2я Р2Л + 2 Р2Л 2 +
₽ ( ^2л—1 Р2Л 2 + ^2л—3 Р2"-4 +
+ “'4~агР2 4~Яо -(17-'
Полином степени п относительно р2 в числителе (17-21) имеет п корней
(17-22) обращающих его в нуль (число k принимает значения от 1 до и). Как видно из выражения (17-22), эти корни отрицательные действительные, в то время как
p2fe_i=± /<о2/г_1—мнимые числа.
Полином степени п—1 относительно р2 в знаменателе (17-21) имеет п—1 корней
---------------------<&, <17-23) где число k принимает значения от 1 до п—1.
Разлагая эти полиномы на множители, переписываем (17-21) в следующем виде:
Z = -Р?) (р2 — Рз)--‘
Р^л-i (р? — Рг) (р2—Р2) • • •
—- ~p2"-i) Л 7-241
-(Р2-
Обозначив
Н = (17-25)
b2n—1
и умножив числитель и знаменатель (17-24) на р, получаем на основании (17-19), (17-22) — (17-24)
z_ /<оЯ (со2 — со2) (<о2 — <й|) « (со2 — Wq) (со2 — со|) (со2 — со2) • • •
...(аА—м* .1
где соо=О.
Частоты с нечетными индексами, обращающие числитель в нуль, называются нулями функции Z, а частоты с четными индексами, обращающие знаменатель в нуль,— полюсами функции Z.
Формула (17-26) известна под названием теоремы Фостера.
В приведенном выше выводе предполагалось, что корни уравнений, т. е. нули и полюсы функции Z, простые (однократные).
Степень числителя относительно со выше степени знаменателя на единицу. Функция Z имеет два внешних полюса: в бесконечности (со2п=оо), в начале координат (CDO = 0).
Это объясняется тем, что как собственные, так и общие сопротивления контуров двухполюсника были приняты индуктивно-емкостного типа (L и С, соединенные последовательно). Двухполюсник, составленный из таких контуров, не пропускает постоянного тока и тока бесконечно высокой частоты.
Для построения частотной характеристики сопротивления двухполюсника на основании (17-26) достаточно знать расположение внутренних нулей и полюсов и коэффициент Н. Последний легко определяется, если в дополнение к сведениям о расположении нулей и полюсов известно сопротивление двухполюсника при какой-либо промежуточной частоте (не совпадающей с нулем или полюсом).
На рис. 17-14 изображена частотная характеристика сопротивления двухполюсника, отвечающая формуле (17-26).
Нули и полюсы функции чередуются, и соответственно производная от Z/j по частоте положительна:
0=(Оо < COj < соа < • • •
• • * й>2п_2 Ю2л—1 < 00
21—1118
321
и
---> 0 при О со < со jdv>
При каждом переходе через нуль или полюс изменяется знак сопротивления Z.
При некоторой частоте со, расположенной достаточно близко от полюса, по левую сторону от него, сопротивление Z положительно. Если
Рис. 17-14. Частотная характеристика со-
противления двухполюсника, не пропускающего постоянный ток.
Рис. 17-15. Четыре вида частотной характеристики реактивного двухполюсника
л — внешние полюсы; б — внешние нули; в — внешние нуль и полюс; г — внешние полюс и нуль.
же частота со расположена по пра-
вую сторону от полюса, то сопротивление Z отрицательно. В соответствии с (17-26) это возможно только при положительных значениях Н. Таким образом, множитель Н, входящий в состав (17-26), всегда положителен.
В зависимости от расположения нулей и полюсов возможны четыре вида частотной характеристики сопротивления многоэлементного реактивного двухполюсника.
Частотная характеристика с двумя внешними полюсами (рис. 17-15,а); при соо=0 и ы2„ = оо сопротивление
двухполюсника равно бесконечности, т. е. путь для постоянного тока
и тока бесконечно высокой частоты
отсутствует.
Двухполюсник с характеристикой такого вида рассматривался выше (рис. 17-14).
Частотная характеристика с двумя внешними нулями (рис. 17-15,6): при Ш| = 0 и cosn-i = оо сопротивление двухполюсника равно нулю, т. е. имеется путь для постоянного тока и тока бесконечно высокой частоты.
Частотная характеристика с внешним нулем при 0)1=0 и внешним пол юсом при о)2„ = оо (рис. 17-15, в): имеется путь для постоянного тока и отсутствует путь для тока бесконечно высокой частоты.
Частотная характеристика свнешним ПОЛЮСОМ При (Оо = 0 и внешним нулем при «2п-1 = 00 (рис. 17-15,г): путь для постоянного тока отсутствует, путь для тока бесконечно высокой частоты имеется.
Здесь, так же как и в предыдущем параграфе, частоты, соответствующие нулям функции Z, обозначены нечетными, а частоты, соответ-
322
“вующие полюсам ^функции Z, четными индексами.
Если условиться нули функции отмечать кружками, а полюсы — крестиками, то указанную выше по-
-«с 17-16. Последовательности нулей и полюсов.
-—внешние полюсы; б —внешние нули; в — внешние нуль и полюс; г —внешние полюс и нуль.
.оедовательность чередования ну-*ей и полюсов можно изобразить г помощью рис. 17-16.
17-6. КАНОНИЧЕСКИЕ СХЕМЫ
РЕАКТИВНЫХ ДВУХПОЛЮСНИКОВ
Дробно-рациональная функция 17-26) может быть разложена следующим образом:
-= (1 + S -2-°-*7 ) • <17-27)
\ *=1 “ - “^«-2 )
Единица в разложении получается в результате выделения целой *асти дробно-рациональной функции (17-26).
Для определения коэффициента а^-г умножим обе части равенств 17-26) и (17-27) на со2—<о^_2 и перейдем к пределу w=co2h-2. Тогда
Сумма двух первых слагаемых в ю а вой части (17-27) выражает сопротивление двухэлементного реак--»вного двухполюсника
/ ря— 1 =
I со!—---I
L \ о0н) J
= / ,-7-).
состоящего из индуктивности L2n = H>0, соединенной после-
Рис. 17-17. Двухэлементные
реактивные двухполюсники.
довательно с емкостью Со= ——1/а0Н (рис. 17-17,а).
В соответствии с (17-28) а0<0 и, следовательно, Со> >0.
Остальные слагаемые в правой части (17-27) имеют вид:
Z2k-2=*> \ • (17-29)
“ W2ft—2
Данное выражение соответствует сопротивлению двухэлементного реактивного двухполюсника по схеме рис. 17-17,6:
у _ /т^2Л—2______
2*—2 1 г.12 / С
I — № L.2k_2
1 где ю2/,_2 = --- — часто-
V ^-2*—2 C2ft—2
та резонанса токов контура Егь-г, Czh-z-
Приравнивая (17-29) к (17-30), находим:
с>« = -жЬ>0- (17-31)
323
Подстановку (17-28) в (17-31) дает:
^2*—2~
/м 1
Z (<о2 — 2
(17-32)
При заданной резонансной частоте (02Л-2 индуктивность L2fc-2 находится по формуле
----• (17-33)
®2Л—2 С24—2
Рнс. 17-18. Схема обобщенного реактивного двухполюсника, состоящего из последовательно соединенных двухэлементных двухполюсников.
На рис. 17-18 представлена схема обобщенного реактивногр двухполюсника, сопротивление которого выражается формулой (17-26).
Такая схема двухполюсника именуется канонической (приведенной) схемой. Ей соответствует частотная характеристика, изображенная на рис. 17-14.
Следует заметить, что схема рис. 17-18 не является единственной формой канонической схемы двухполюсника. Вместо последовательного соединения двухэлементных реактивных двухполюсников схема обобщенного двухполюсника может содержать параллельно соединенные двухэлементные двухполюсники (рис. 17-19).
Действительно, на основании (17-26) проводимость двухполюсника
у = <ог(<о2 —<oj) (<в2-со2)-..
/<1)Я (о2 — (О2) (<В2 — СО3) • •.
(17-34)
Данная дробно-рациональная
функция может быть представлена в виде суммы дробей
.. (17-35)
*=i <о2
Умножив обе части равенств (17-34) и (17-35) на со2—«2*—i и
устремив to к <02л-ь находим:
. (17-36)
|“=<в24—1
Рис. 17-19. Схема обобщенного реактивного двухполюсника,
состоящего из параллельно соединенных двухэлементных
двухполюсников.
Каждое слагаемое в первой части (17-35) выражает проводимость двухэлементного реактивного двухполюсника
9 9 9 9*
состоящего из индуктивности L2ft_i=///p2ft-i и емкости C2ft_i =
1 = —---------, соединенных последо-
Ш2*—1 ^2А—1
вательно.
С учетом (17-36)
Д. , = — ----1 . (17-37)
1 I 2 2 I ' f
— ®2fe—1 1
Проводимость реактивного двухполюсника, представленного на рис. 17-19, выражается формулой (17-34), а его сопротивление — соответственно формулой (17-26). Следовательно, двухполюсники по схемам рис. 17-18 и 17-19 эквивалентны.
Выше рассматривались две схемы обобщенного реактивного двухполюсника, имеющего характери
324
стику сопротивления вида рис. 17-15, а. Такой двухполюсник состоит из 2п элементов (рис. 17-20,а). За вычетом внешних полюсов частотной функции число резонансных частот такого двухполюсника равно 2л—1.
Частоты ыо=О и Ы2п=‘х>, соответствующие внешним полюсам функции Z, могут рассматриваться
рассматриваться как двухполюсник, у которого Ш1=0 и Ю2п-1=оо; при
этом
Т-2л—1
ш2л—1 ^2л—1
(рис. 17-20, б — справа) и элементы
Рис. 17-20. Канонические схемы реактивного двухполюсника.
а — внешние полюсы; б—внешние нули; в — внешние нуль и полюс; г — внешние полюс и нуль.
как частоты резонансов токов двух-полюсников L0C0 и L2nC2n, имеющих элементы
Т-о = =оо и =—--------------=0
®0 С0 а2п ^2п
(рис. 17-20,а).
Таким образом, внешние полюсы функции Z можно условно причислить к резонансам токов двухполюсника.
Остановимся на других частных случаях канонической схемы реактивного двухполюсника (рис. 17-20).
Двухполюсник с двумя внешними нулями (рис. 17-15,6) может
Lo, Со, Ь2п, С2п отсутствуют (рис. 17-20,6 — слева).
Сопротивление такого двухполюсника по аналогии с (17-26) выражается формулой
jH (<£>2 — <0j) (<02 — (£>|) • •' ш (ш2 — (ш2 — <£>2) • • •
... (<02-<^п_2)
(17-38)
Двухполюсник с внешними нулем и полюсом (рис. 17-15, в) может рассматриваться как двухпо
21а—1118
325
ЛЮСНИК, у которого (£>1 — О И (02я = оо; при этом Ci=oo, Сгп=0 и элементы Lo и Со отсутствуют (рис. 17-20,в).
Сопротивление такого двухполюсника выражается формулой
Согласно (17-38) с ростом частоты Z -* j На основании рис. 17-20,6 при возрастании о
/юЯ(со2—ь>|).. • (<о2—<oln_i) (<о2—
(17-39)
Наконец, двухполюсник с внешними полюсом и нулем (рис. 17-15, г) может рассматриваться как двухполюсник, у которого ыо=0 и Ю2п-1=оо; при этом
Г 1
Со = —— = <»;
WqCo
, ( 1 1 IV-1
I r + г +•••+<? )
\ ъ2п—2 /
ИЛИ
Z-> 1
1
откуда
и элементы LZn и Сгп отсутствуют (рис. 17-20,г).
Сопротивление такого двухполюсника выражается формулой
Согласно (17-39) по мере увеличения частоты а на основа-
нии рис. 17-20,в при возрастании со
(<°2-М1) * »• (<°2—Ш2п-3) ш(<02—со2)...(ш2—
Z или Z -►
(17-40)
откуда
В формулах (17-38) — (17-40), так же как и в формуле (17-26), число двучленов с разностями квадратов текущей и резонансной частот в числителе и знаменателе одинаково. Разделив каждый двучлен в числителе и знаменателе на
(О2 о2, получим двучлены вида 1— —,
(О* которые при ы—оо стремятся к единице. Это позволяет найти множитель Н, входящий в формулы (17-26), (17-38) — (17-40).
Согласно (17-26) с ростом частоты Z-> /сйН, а на основании рис. 17-20, а при возрастании ы Z -^j^Lzn или
Согласно (17-40) по мере увели-ZH
-> / —, а на осно-
Сй
вании рис. 17,20, г при возрастании а)
или
1__\-i
^2п—1 /
откуда
7> ___' _
№-2п-1 '
(17-41)
Результаты определения множителя Н сведены в табл. 17-2.
326
Таблица 17-2
Двустороннее преобразование Одностороннее преобразование
подучаем:
J^ = ^_ + L2n +
lda> со2 Со
>2k — <о2) — и (— 2ы) = 1
у1 “2 + <o2fe
17-7. ЗНАК ПРОИЗВОДНОЙ ПО ЧАСТОТЕ ОТ СОПРОТИВЛЕНИЯ
ИЛИ ПРОВОДИМОСТИ РЕАКТИВНОГО ДВУХПОЛЮСНИКА
Комплексное сопротивление обобщенного реактивного двухполюсника, состоящего из последовательно соединенных двухэлементных Двухполюсников (рис. 17-18), определяется суммой комплексных сопротивлений составляющих двухполюсников
п-1 + /<оГ2п 4- У Z2k, 1<»с0 *=i
где у________________/со
С2ИЮ2*-“)
Беря производную от Z/j по ш,
А==1
(17-45)
Все слагаемые в правой части (17-45) положительны. Следовательно, производная от комплексного сопротивления двухполюсника по частоте в общем случае имеет положительный знак.
Аналогично можно показать, что и производная от комплексной проводимости двухполюсника по частоте в общем случае положительна.
21а*
327
Действительно, на основании схемы рис. 17-20,о (справа)
<0
~ /£ (со2 - со2^)
(17-46)
Отсюда
Согласно (17-43) H=Lt-, следовательно, £в=5 гн.
Пользуясь формулами (17-32) и (17-33), находим:
(4 — 16) (4 — 36)-10—*
(4 — 9) (4 — 25) (4 — 49) “
= 1,625-Ю-6 ф
С2 —
^•2*—1
*4-1) + со (2м) (со2-^)2
£2
^2*—1
0.
\2
~ Ш2*—1)
*=1
Из свойства положительности производной dZ/jd^ следует, что нули и полюсы функции Z должны чередоваться, так как при наличии двух последовательных нулей, не разделенных полюсом, имелся бы участок характеристики с отрицательной производной. То же относится к функции Y.
Пример 17-1. Требуется построить каноническую схему многоэлементного реактивного двухполюсника по заданным значениям нулей со3=300, 11)6=500, <07== =700 рад!сек, полюсов со2=200, со4=400, 106=600 рад!сек (рис. 17-21, а) и сопротивления двухполюсника Z=/1250 ом при ю=50 рад/сек.
На основании (17-39)
4-104-1,625-10-» 15.38г«.
Аналогично находятся остальные параметры схемы рис 17-21, б:
С, = 2,31- 10-е ф.
Св = 3,315-10—вфг, Согласно (17-37) , с 9-25-49
4-16-36
, „ 9(9 - 25)(9 - 49)
L3 = о ----------------------“30.5 гн:
(9 —4) (9—16) (9 —25) ’ ’
1
Сз=т-1О:.-зо,5
/шЯ (со2—со|) (со2—со|) (со2—со2)
(со2—со|
£4 = 2,704 гн;
£« = 0,838 гн.
= 23,92 гм;
Аналогично определяются остальные параметры схемы рис.
С6 = 0,173-10-• ф,
С7 = 167-10-«$б;
17-21, в:
£е = 23,1 гн;
£7 = 12,18гн.
Правильность решения может быть проверена по формуле (17-43)
/11 1
1<23,92 + 30,5 + 23,1
5,
т. е. решение правильно.
dY _ у jda ~
л
<02 + «!*!
и
£ 5
1
Канонические схемы двухполюсника в соответстани с рис. 17-20, в (табл. 17-2) показаны иа рис. 17-21,6 и в.
При io=5O рад!сек
250=50Н (0’25~9) (°-25~25) (0.25-49)
Н (0,25—4) (0,25—16) (0,25—36) ’ откуда Я=5.
о гоо зоо
£« св
1F
Сг
£
400 500 500 700
а)
Св
—IH
б)
£j 9
-х
17-8. ЦЕПНЫЕ СХЕМЫ РЕАКТИВНЫХ ДВУХПОЛЮСНИКОВ
Наряду с рассмотренными выше схемами обобщенного двухполюсника, отвечающими выражениям для Z, существуют канонические цепные схемы типа рис. 17-22, которые могут быть получены, если сопротивление двухполюсника выразить непрерывной дробью
Z-Z.+—L—
*'• +-i
+ v
j
1
г
в)
Рис. 17-21. Пример 17-1.
(17-47)
328
Дробно-рациональная функция Z, выраженная формулой (17-21), раскладывается в виде непрерывной дроби одним из двух способов.
1) Пусть Z=M)N, где
М = а2п Р2П+а2п-2 P2n-Q+" • ---------f-oap24-ac
И
N=b2n-1 Р^+Ь^п-З Р2"~3+ ” ---------№Р8+61Р.
т. е. степень М превышает степень N на единицу.
г,
z
1
L2 ’р *+ • • •
. (17-50)
Из (17-50)
0
Рис. 17-22. Цепная схема обобщенного двухполюсника.
Частное от деления числителя М на знаменатель N по положительным степеням р представляется в виде двух слагаемых, в первое из которых р входит в первой степени; второе слагаемое является остатком:
M'
N' здесь М' полином степени 2п—2. Степень N превышает степень М' на единицу; поэтому, представив оста-1
ток в виде ----, можно продол-
NIM'
жить деление:
Z-L1P +------
' . N'
CiP М' М
где N' — полином степени 2п—3, т. е. на единицу ниже степени М'.
Продолжая таким образом, получаем:
Z=L1P+------—
CiP + —
Lip + c ...+ !___ t-nP + Г СпР
Сопоставляя выражение (17-47) сопротивления цепной схемы с разложением функции Z в виде беско
(17-48)
нечной дроби (17-48), находим с учетом того, что p—ja:
Zk=joiLk; 1 a+i=/<oCa. (17-49)
Соответствующая этому случаю цепная схема с индуктивностями Ln и емкостями представлена на рис. 17-23, а — слева.
2) Если деление М на N выполнить по отношению к величине р~1, т. е. по отрицательным степеням р, то это приведет к разложению вида г—1 , •
=Ci р Н------—-
—1Л—’ 1 р
Ln'P сопоставления (17-47) с следует, что
——; Y... -—.(17-51) juCf, *+’ jvLk
Цепная схема с элементами Сл и Lft, соответствующая этому случаю, показана на рис. 17-23, а — справа.
Схемы рис. 17-23, о, эквивалентные схемам рис. 17-20, а, отвечают этому случаю, когда функция Z имеет два внешних полюса.
Если функция Z имеет два внешних нуля, то из левой схемы рис. 17-23,о исключаются элементы Lt и Сп, а из правой схемы — Ct и Ln. Этому случаю соответствуют схемы рис. 17-23, б.
Если функция Z имеет внешние нуль и полюс, то в левой схеме рис. 17-23, в отсутствует емкость Сп, а в правой — емкость Ci.
Наконец, если функция Z имеет внешние полюс и нуль, то в левой схеме рис. 17-23, г отсутствует индуктивность Lb а в правой — индуктивность Ln.
Пример 17-2. Требуется построить цепные схемы многоэлементного реактивного двухполюсника, эквивалентного рассмотренному в примере 17-1.
По условию
](йН (со2—со2) (со2—со?) (со2—со2)
—to:
(W2-C02) (ю2_ю|)
5р7 + 4,15-10eps -f-р9 + б.б-Ю’р4 +
329
+ 9,45-10» р34-5,51-1018р
4-7,84- 10“>р2 + 2,3-1018 ’
Данная дробно-рациональная• функция разлагается а виде бесконечной дроби
1 — 5/Н------------------—
0,74-10—»p-f------------
Эр -I--------------
1,087-10-вр-Ь----
23,9-* р-‘+ — ™------------
(0,706- 10—6)—Jp—14- • - • -
10,2—1 р—14---------------------
(0,227 • 10-«)-1 р-1 4-...
1
б,5р 4- ----------------—
2,68-10-«р 4-------
3,43р
18,9-1 р-»4---------------------
(0,0212-10-в)-1р-‘4- —
в)
г)
Рис. 17-23. Цепные схемы реактивного двухполюсника.
а — внешние полюсы; б — внешние нули; в — внешние нуль н полюс; г — внешние нолюс и нуль.
Соответствующая полюсника показана
цепная схема двух-на рис. 17-24, а, где
1
139—‘р—1 ‘
Lt = 5 гн;
L^ — Qzh;
La = 6,5 гн.
Сг = 0,74-10-в ф;
Cs= 1,087-10-«4б;
Са = 2,68-10-«д5.
£« = 3,43 гн;
Разложение функции Z в бесконечную дробь по отношению к величине р~* имеет вид:
Соответствующая цепная схема двухполюсника показана на рис. 17-24,6, где
Li = 23,9 гн;
Lt = 10,2 гн,
Ls — 18,9 гн;
Lt = 139 г/с
Gj » 0,706-IO-*#
Св = 0,227.10-»#
С< = 0,212.10—
330
17-9. ПОТЕНЦИАЛЬНОЭКВИВАЛЕНТНЫЕ ДВУХПОЛЮСНИКИ И УСЛОВИЯ ИХ ЭКВИВАЛЕНТНОСТИ
В предыдущих параграфах рассматривались различные канонические схемы (рис. 17-20 и 17-23) эквивалентных реактивных двухполюсников. Условием их эквивалентности являлось совпадение нулей и полюсов и равенство множителей Н. Только при этом условии обеспечивались равенства комплексных сопротивлений двухполюсников во всем спектре частот, т. е. двухполюсники являлись эквивалентными.
Численное изменение резонансных частот одного из двухполюсников при сохранении последовательности чередования нулей и полюсов или численное изменение множителя Н, входящего в выражение для Z, нарушает эквивалентность: комплексные сопротивления двухполюсников, бывшие до этого эквивалентными, оказываются неравными.
Такие два двухполюсника именуются потенциально-эквивалентным и; это означает, что они могут быть эквивалентны при соблюдении соответствующих условий.
Потенциально - эквивалентными могут являться не только реактивные двухполюсники, но и двухполюсники с потерями.
Рассмотрим в виде примера схемы на рис. 17-^5, о и б.
Комплексные сопротивления их выражаются следующим образом: для схемы рис. 17-25, а:
Z = dZY +
bZ1 + cZ|
— Z?+(fc + d)Z1Z2
_£__________________; (17-52)
Zi + zt c
Рис. 17-25. Потенциально-эквива-
лентные двухполюсники.
для схемы рис. 17-25, б:
(в + 1) Z± Z2
= cZ! + flZiZ2.j (17-53) (a+l)Zl + Zi
Выражения (17-52) и (17-53) равны друг другу во всем спектре частот, если выполняются условия bd. > . , । b
а — — ; а = b -р а : а + 1 = — с с
или
, а2 / а \2 j а
Ь =-----; с = I----- ; а =----- .
а + 1 \а -J- 1 / a -f- 1
Таковы условия эквивалентности двухполюсников, изображенных на рис. 17-25, а и б.
Рассмотрим еще один пример, показанный на рис. 17-26.
Комплексное сопротивление двухполюсников на рис. 17-26, о:
2 — + r)(Z2 + г)
21 + 2а + 2г
(Zr + Z^r + Z^ + r^ гг + г2+2г
При соблюдении условия Z\Z2— = г2 получается Z=r, т. е. двухполюсник на рис. 17-26, а становится
331
Таблица 17-3
Схемы потенциально-эквивалентных _______Ввух тлюониквв
aZ, bZ
Условия эквивалентности
Z,
CL Zj
' -0j2r
гг
с Zf
(а-Ь)г
b=a(a*Qc=(a*i)\ d=a+l
Z1 Z,
гГ~~н h f nd U* 1 “> СЭ
izZy bi ' dZz' LczriJ
Zt
CZf в-Zz
jZ, bZt
енссэссз
Zz
eZ, fZj
—H H
C Z-f c= eZt > CZ?
0” <ZZz 4=3 » > >-0 fZz H 4=±jJ
fz3
_____________(a-b)2 (а+1)(Ь*1)г__(а+1)г(Ь*1)
e a+1 '
Ъ+1
B(ahR) , a=_2№_ A+B~2b ’ A*B~2b
B(A-B) 2bB
S B-A-2b ,f B-A+2b где A =a +b+t, b=Va2-bab
r(2b-A_ 2b-A +8 c---ЪГв Л=~гв~
(А *В-2Ы(А -В) A *6- 2b
MB ~2i
гдеА=а+Ъ+1, В=УАг~иаЬ
Z2
e=
ZtZ2=r2
Cti b Z9
cZ,
bZz
ZtZz=^2
<ZZ,
c=a+i <z=b*i
(a-b)Z e_ Ь(а+'!)г(Ъ+-1) ~ (a-b)Z
332
эквивалентным простейшему одноэлементному двухполюснику, состоящему из активного сопротивления г (рис. 17-26, б).
Схемы некоторых потенциально-эквивалентных двухполюсников и
Рис. 17-26. Потенциально-эквивалентные двухполюсники.
условия их эквивалентности приведены в табл. 17-3.
17-10. ПОТЕНЦИАЛЬНО-ОБРАТНЫЕ ДВУХПОЛЮСНИКИ И УСЛОВИЯ
ИХ ВЗАИМНОЙ ОБРАТНОСТИ
Два двухполюсника называются обратными, если произведение их сопротивлений Z, и ZH равно постоянной величине, не зависящей от частоты
%=*«; (17-54)
здесь k — постоянная величина, имеющая размерность сопротивления.
Если два двухполюсника при соблюдении определенных условий могут быть обратными, то такие двухполюсники называются п о -тенциально - обратными.
Обратные двухполюсники представляют собой дуальные цепи (§ 5-12), сопротивления которых удовлетворяют условию (17-54). Такие двухполюсники широко применяются в качестве составных элементов электрических фильтров (гл. 19).
На рис. 17-27 в качестве примера показаны обратные двухполюсники, выполненные в виде ценных схем. Частотная характеристика
сопротивления одного из этих двухполюсников аналогична частотной характеристике проводимости второго из них.
Рис. 17-27. Обратные двухполюсники.
Рассматривая типовые частотные характеристики сопротивления реактивного двухполюсника, изображенные на рис. 17-15, легко убедиться в том, что двухполюсники с характеристиками а и б являются потенциально-обратными. То же следует и в отношении двухполюсников, имеющих характеристики в и г (рис. 17-15). Условием взаимной обратимости их служит совпадение нулей и соответственно полюсов функции Z и У двухполюсников на всей шкале частот.
Пусть в соответствии с (17-26)
2 _ МЛ (м2 ~ (ы2 — ”>з) • • •
1 (со2 — со2)( <й2 — COj) ...
(17-55)
Обратный двухполюсник имеет сопротивление1
11 0)2 — wi)( 0)2 — ®з) •
...(и2- т2п 2)
1 Здесь в отличие от предыдущего частоты резонансов напряжений обозначены четными, а частоты резонансов токов — не-
четными индексами.
333
Произведение (17-55) на (17-56) удовлетворяет уравнению (17-54)
Z,Zn = — = const.
Если в соответствии (17-39)
z = (17 57)
' (<о2-^)...(ш2-4,_2)
то обратный двухполюсник имеет сопротивление
(со2—ай)...(со2—айя 2)
Z.. = (17-58)
П /соН2(со2-а>2)..,(со2-ш2л_2)
Произведение сопротивлений Z, и ZH согласно (17-57) и (17-58) удовлетворяет уравнению (17-54)
Z.Z., = — = const.
1 11 Ht
17-И. МНОГОЭЛЕМЕНТНЫЕ ДВУХПОЛЮСНИКИ С ПОТЕРЯМИ, СОДЕРЖАЩИЕ ЭЛЕМЕНТЫ ДВУХ ТИПОВ
Ниже рассмотрены два типа многоэлементных двухполюсников с потерями: двухполюсник, содержащий элементы г, L, и двухполюсник, содержащий элементы г, С.
Двухполюсник типа г, L. Если двухполюсник состоит из элементов г и L, т. е. Zu=ru+pLii и Zift= =—(rik+pLik), причем число независимых контуров равно п, то определитель системы Д в (17-18) содержит степени р от 0 до п, а алгебраическое дополнение Дп — от 0 до п—1. Следовательно, степень полинома знаменателя на единицу ниже степени полинома числителя
z _ gnPn + g<1,iPn~1+--_____
^1рл-1 + ьп_2Р,,-2+-"’
— 4- Д1Р + Др
... + btf ь0
(17-59)
Дробь (17-59) неправильная, поэтому функция Z имеет в бесконечности полюс1. Нули и остальные по-
1 Ввиду того что разность степеней числителя и знаменателя равна единице, полюс в бесконечности простой — полюс первого порядка [Л. 1],
люсы функции Z действительны и отрицательны; обозначим их соответственно через pi, р3,.... p2n-i и-р2> Pi,—, Р2п-2-
На действительной отрицательной полуоси они чередуются
°° Ср2п_1<р2л_2<С...<р2</,1^0-
Числитель и знаменатель (17-59) могут быть разложены на линейные множители, т. е. представлены в виде произведений разностей р—pk.
7 Я(р-Р1) (р-р3) .. (p-P2n_i)
(Р-Р2) (Р-Р4) - - (р-Р2п-2)
(17-60)
От деления числителя на знаменатель дроби (17-59) имеем:
Z = ^ + -^_p + Ьо Ъп_х
+ дп-1 р""1 + дп-2 Р"~2 + • • • + Д1Р bn-lPn l + bn—2Pn~2 + -"+fy)
где a'n_It а[—новые коэффициенты, получаемые в результате деления. Последнее выражение может быть представлено в следующем виде:
+ У gM~2P . (17-61)
Р Р24—2 *=2
Первое постоянное слагаемое выражает сопротивление
г = —, (17-62)
ьо
показанное на схеме рис. 17-28.
Второму слагаемому1 соответствует индуктивный элемент, показанный на схеме рис. 17-28, т. е.
Ь8в = -^=//. (17-63)
/2—1
а2*—2 Р „
Слагаемое ----------- по своей
Р ~P2k—2
структуре
1 Второе? слагаемое в выражении (17-61) представляет единственное слагаемое в так называемой бесконечной части функции в полюсе р=оо.
334
соответствует двухполюснику, состоящему из параллельно соединенных сопротивления Ггь-г и индуктивности Lik-2,
7 _ r2*—2₽^2S—2 r2k—lP
2А-2 ~ ~г + 1Гг г
r2k—2 Т РЬ2Й_2 Л2й—2
rlJ— ' —-
Если исходить из выражения проводимости двухполюсника
у (Р- Pj(P -Pt) - (Р - Р2П-2}
Н(Р ~ Р1Х₽ ~ РЯ) • ’ (Р - Р2П-1) и разложить его на элементарные дроби
Рис. 17-28. Двухполюсники типа г, L, соответствующие выражению (17-61).
то каждое слагаемое
a2ft—1
---------может рассмат-
Р ~ PZk—l
В данном случае
Г2к—2 a2k—2»
риваться как проводимость двухполюсника, состоящего из последовательно соединенных со-
r2fe—2
L2k-2
(17-64)
Итак, задача свелась к определению (12k—2-
Умножив обе части (17-61) на Р--P2k-2 и устремив р к Р2Й-2. по-
лучим1:
Рис. 17-29. Двухполюсник типа г, L, соответствующий выражению (17-67).
“гл-г —
f (Р — Р2А-2) — Lna • (17‘65)
L' к ' р ]Р=₽2*-2
Как и следовало ожидать, агд-г имеет размерность сопротивления.
Индуктивность Lzk-z находится из выражения (17-64) как
противления Ггл-i и индуктивности Lik-Г-
<17'66)
P2k—2
Таким образом, выражению (17-61) соответствует двухпол юс-ник, показанный на рис. 17-28, причем элементы его определяются на основании (17-62) — (17-66).
r2k—( + pLik—1
1
Lik— I
Следовательно, в данном случае
1 Слагаемое ---------можно рассмат-
Р ~ P2k—2
рнвать как первый член с отрицательной степенью в разложении функции Z/p в ряд Лорана в окрестности полюса Рж-г. Поэтому a2h-2 есть вычет функции Z/p относительно точки psh-2. Если сопротивление Z выразить через проводимость У, то вычет может быть найден по формуле
1
IpdYX
\ dp JP=P2k—2
(17-68)
Коэффициент a2fc-i находится по формуле1
1 Коэффициент Ozk-i равен вычету функции У относительно Ргл-i.
335
®2А—1 [(^ P^k— 1) ^]р=Р24—I
_ _______1_______
/ dZ \
\ dp /р=Пь—1 (k = 1, 2....и).
(17-69)
Двухполюсник типа г, С. Если двухполюсник состоит из элементов г и С, т. е.
= гн + —— и Zik => рСц
Таким образом, выражению (17-67) соответствует двухполюсник, показанный на рис. 17-29, при-
Рис. 17-30. Цепные схемы двухполюсника типа г, L.
чем элементы его определяются на основании (17-68) и (17-69).
Многоэлементный двухполюсник типа г, L может быть также выполнен в виде цепных схем (рис. 17-30, а и б).
Схема рис. 17-30, а соответствует разложению Z в непрерывную дробь
----!—-
'Г'+----------,
£,р+^+....
-...+----- (17-70)
^лР+ —Г г„
Схема рис. 17-30, б соответствует разложению Z в непрерывную дробь
(17-71)
причем число независимых контуров равно п, то сопротивление двухполюсника
2___ Л ___ р” Д
Ли рп Лц
представляет отношение полиномов степени п без постоянного члена в знаменателе
дяР"+дп 1Рп 1+---+д1р + с0
Ьп рп I рп’~| -|----Ffyj Р2+^1 Р
(17-72)
Нули и полюсы функции Z действительны и отрицательны (17-11); обозначим их соответственно через Р1» Рз.. Р2п—1 и Р2. Pi,—, Р2п-2-
На действительной отрицательной полуоси они чередуются:
-°°<Р2П_1<Р2П_2<
— <Ps<Pi<Po = O.
Числитель и знаменатель (17-72) могут быть разложены на линейные множители
z Н(Р -Р,)(Р -Р3) • • (Р-P2n-i)
Р(Р-Р^{Р — Рл) " (Р-Р1П-2) ' (17-73)
Выделяя постоянную часть и раскладывая оставшуюся правильную дробь на элементарные дроби, находим:
п
z = gg- 4- У “2>-2 . (17-74)
Ьп р — P2S—2
А=1
Первое слагаемое разложения (17-74) выражает сопротивление
r2„ = limZ = ^, (17-75)
Р-“ ЬП
показанное на схеме рис. 17-31.
СХрь 2
Слагаемое----------- соответству-
Р — ₽2*—2
ет сопротивлению двухполюсника, состоящего из параллельно соеди
336
ненны^ сопротивления г2ь-2 и емкости С2Ь^:
7 ' Г2*-2^7
Л2А—2 ————j- — —
r2k-2+ pC^h^,
1
Рис. 17-31. Двухполюсник типа г, С, соответствующий выражению (17-74).
то каждое слагаемое -----------
Р — P2k—1
может рассматриваться как проводимость двухполюсника, состоящего из последовательно соединенных сопротивления r2k-i и емкости C2h-i:
Следовательно, здесь
Следовательно, в данном случае
1
С ~ а2Ь—2»
С24—2
1
r — p^k-2;
г2*—2 '•'24—2
“24-2 — [ (Р P2k-2 ) Z] P=Pik-2 ~
(17-76)
(fe = 1,2, ...,n).
При k= 1 а0= (^2)^0=
и
Со = —; r0 = oo. (17-77) Co
Таким образом, выражению (17-74) соответствует двухполюсник, показанный на рнс. 17-31, причем элементы его определяются на основании (17-75) —(17-77).
Если исходить из выражения проводимости двухполюсника
у= р(р~ (p-pJ-(p- Р2П-2)
Н(Р- Рг)(р -ра)...(р- р2п_})
и представить его в виде суммы дробей
п
У= У- а^-|Р , (17-78)
Р — P2k—\
(17-79)
' ^'Р=Ряк-.1
(k = 1,2, ...,п),
Схема двухполюсника, отвечающая выражениям (17-78) и (17-79), показана на рис. 17-32.
Рис. 17-32. Двухполюсник типа г, С, соответствующий выражению (17-78).
Многоэлементный двухполюсник типа г. С может быть также выполнен в виде цепных схем (рис. 17-33, а и б).
337
Схема рис. 17-33, а соответствует разложению Z в непрерывную дробь вида
По заданию
2м* 4- 14ма со» 4- 20(0* 4- 64cos
откуда
14 32
W—= 1 и Н — — 64 7
(17-80)
Для построения цепи по схеме рис. 17-31 воспользуемся расчетными выражениями (17-75) и (17-76).
В рассматриваемом случае Z (р) — правильная дробь; следовательно.
Рис. 17-33. Цепные схемы двухполюсника типа г, С.
Схема рис. 17-33,6 соответствует разложению Z в непрерывную дробь вида
Пример 17-3. Требуется построить схемы двухполюсника типа г, С (рис. 17-31— 17-33) по заданным значениям нулей и полюсов функции Z(p): нули в точках pi = =—1, Рз=—3; полюсы в точках ро=О; р2=—2; р4—4. Задано, что при со=О Re Z (/со) = 1 ом.
На основании выражения (17-73)
г!п = lim Z (р) = 0.
При k=1 3 12
a0 = (pZ)p=0 = ^Y = Т:
при k = 2
1 8
«а = Кр 4- 2) Z]^_2 = Я— = —;
при k = 3
3 12
а4 = 1(Р 4- 4)) Z]p=_4 =Я — = — -
Следовательно,
7 7 , 7
со— „ С2— ф, Ct— ф,
О 1Z
8 4 12 3
Г2=7Г2 = Тол; г^^ГГ~Том-
Для построения цепи по схеме рис. 17-32 воспользуемся расчетными выражениями (17-79). Если проводимость двухполюсника
р (р 4- 2) (Р4- 4)
Я(р4-1)(Р4-3) ’
то
Г VI 3 21
а, = (р 4- 1) — = — = 77;
L р J р=— 1 Н-2 64
Г VI 17
«з = (Р 4-3) I = — “
|_ р Jp=—з Н-2 64
Следовательно,
64 64 21
ri = —- ом; г3^ — ом; Сх= —- ф, 21 7 64
Н(р+1)(р + 3)
Р (Р + 2) (р 4- 4) г Рг + 4р + 3 р8 6р8 -|- 8р
Полюсу в бесконечности емкость С3; при р -» oo Y — откуда
соответствует Р
Н ’
При p—jtss
Z(ja}=H
(2<о*4- 14а8) — /(<о8+1 Зо>3+24со)
<о» 4- 20ш* 4- 64а2
= ~Ф-
32
При этом г6=0.
338
Ц^пиой схеме рис. 17-33, а соответствует разложение
32 Р' + 16 1_____
' 17 + 28 1
96 Р+ 48 1
т+—’
— Р 96
На основании выражения (17-80): П=0;
16 48
гг=-уом; га = —ом-,
7 7 7
Сг = — ф; С, = — <£; С3 = — ф.
32 2 24 96
Цепной схеме рис. 17-33,6 соответствует разложение
На основании выражения (17-81)
С1~12*: С«~иЛ =
. 12 ri = 1 ол; г» = — ом; га = 0.
121
17-12. ЧЕТНОСТЬ АКТИВНОЙ И НЕЧЕТНОСТЬ РЕАКТИВНОЙ СОСТАВЛЯЮЩИХ СОПРОТИВЛЕНИЯ ОТНОСИТЕЛЬНО ЧАСТОТЫ. ЗНАК АКТИВНОГО СОПРОТИВЛЕНИЯ И АКТИВНОЙ ПРОВОДИМОСТИ
В выражении для сопротивления двухполюсника Z(/co) = = Д(/со)/Ди(/со) определитель системы в случае цепи с потерями состоит из элементов
“ ги + j -----------.
и
%ik ~ и» + / („—
Он может быть разложен по элементам строки
Д = Zu Ди 4- Zu Д12 4- - - • 4~ Zln Д1п,
где Д<ь — алгебраическое дополнение элемента Z,fe. Продолжая разложение по элементам, получаем сумму различных произведений элементов определителя системы. Для выяснения структуры Д достаточно ограничиться рассмотрением произведений элементов главной диагонали определителя:
Следовательно,
Д= (с0+а2 со2+а_2со~2 +а4<о4 4-+а_4<о-4 4-----) 4- / (0)0) 4- 4-
4- а3 со3 4- п_3со-3 4-).
Действительная часть полученного выражения содержит четные, а мнимая часть — нечетные степени со.
Итак, в общем виде
Д = Л(«2)4-/а>Га(со2), где Fj (ю2)—четная, a <oF2(<d2)— нечетная функция от со.
Аналогично
Д11 = /=,3(<о2)4-/а>Г4((о7
Легко убедиться в том, что и отношение Д/Дп обладает свойством четности действительной и нечетности мнимой составляющих относительно частоты со:
= (Fi + lvFJiFt-ivFi) =
= F, Г3 4-<о2 Гг f 4 ।
F3 4- шз F4
+ = г(®) + IхИ-
Ез+Ш Fj
Как функции Fb F3, F3, Fit так и их парные произведения F\F3, FzF^ F?F3, F\Ft — четные относительно со. Следовательно, активное сопротивление г (со), представляющее действительную часть выражения Z(ja),
339
является четной функцией относительно со, а реактивное сопротивление х (а), представляющее мнимую часть Z (ja>), — нечетной функцией.
Аналогичная зависимость от частоты имеет место и для активной и реактивной проводимостей двухполюсника:
ления по частоте: dr/das стремится к нулю или к бесконечности по мере того, как со стремится к одному из этих пределов.
Активная мощность, потребляемая пассивной цепью, не может быть отрицательна
iaRe [Z(/co)] >0.
Следовательно, поскольку i2>0, то
Re [Z (/и)] > 0.
Итак, активное сопротивление
Г (<£>) + /х(со) г2-|-х2
—/7^- = гМ-пи-
Следовательно, активная проводимость (со) является четной, а реактивная проводимость b (со) — нечетной функцией от со.
На основании свойства нечетности реактивных составляющих сопротивления и проводимости относительно частоты следует, что как реактивное сопротивление, так и реактивная проводимость двухполюсника не могут быть равны постоянным величинам (отличным от нуля), не зависимым от частоты со.
Если со устремить к нулю или к бесконечности, то активное сопротивление г (со) будет стремиться к величине, пропорциональной со2” (которая постоянна при п=0), а реактивное сопротивление х(со) — к величине, пропорциональной со2л+а, где п — целое число, положительное, отрицательное или нуль.
Следовательно, в отличие от активного сопротивления х(со) может стремиться только к нулю или бесконечности по мере того, как частота стремится к одному нз предельных значений (0 или оо).
Тем же свойством обладает и производная от активного сопротив-
340
пассивной цепи г (со) положительно или равно нулю.
Отсюда
Re (/со)] = Re Г—4—1 = [Z (/со) J
= Re f-Z(~/t0)1 > 0,
т. е. активная проводимость пассивной цепи g(a) также положительна или равна нулю.
Пример 17-4. Для заданного двухполюсника, показанного на рис. 17-34, а, построить на комплексной плоскости зависимости сопротивления и проводимости от частоты.
Комплексное сопротивление
........1
г-|- /со/,
1 — со2ДС-|-/гсоС'
г =____________/<йС _
г-Ь/соД + т-^-/соС
Комплексная проводимость
у 1 — <i?LC -I- /гсоС г + /соД
При со=О 2=т и У=1/г. С изменением со от 0 до оо Z и У описывают кривые, изображенные на рис. 17-34,6.
Как видно нз рнс. 17-34, б, обе кривые 2 и У располагаются в правой полуплос-
костя, бни пересекают действительную ось
ветствующей явлению резонанса токов. При ю-Л» Z-t-О и У-»/оо.
17-13. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ АКТИВНОЙ
И РЕАКТИВНОЙ СОСТАВЛЯЮЩИХ СОПРОТИВЛЕНИЯ
ИЛИ ПРОВОДИМОСТИ ДВУХПОЛЮСНИКА
Действительная и мнимая части сопротивления или проводимости физически реализуемого пассивного двухполюсника, являются в займ-
Рис. 17-35. Интегрирование вдоль контура.
но зависимыми функциями частоты. Здесь рассматриваются такие двухполюсники, для которых Z(/co) или У (/со) не имеют полюсов на мнимой оси, т. е. на осн частот со.
Сопротивления таких двухполюсников представляют функции м и-нимального реактивного сопротивления, а проводимости — функции минимальной реактивной проводимости (гл. 20).
Для установления аналитической зависимости, существующей между частотными характеристиками активного и реактивного сопротивлений двухполюсника, рассмотрим контурный интеграл &^-dp, JP- /®0
взятый в плоскости комплексного переменного р = с+/со по пути, ука
22—1118
занному на рис. 17-35. Здесь Z(p) — положительная действительная функция, не имеющая особых точек на мнимой оси и в правой полуплоскости; е>о — произвольная действительная частота.
Точка р=/'соо является единственным полюсом подынтегральной функции. В непосредственной близости от этого полюса совершаем обход по полуокружности радиуса г, оставляя полюс вне замкнутой области. Поэтому интеграл по замкнутому контуру в соответствии с теоремой Коши равен нулю
г J = Q
J Р — /“о
ИЛИ
/(<»•—г) IR
М i + j +f+ II-’-
(17-82)
Будем считать, что при р -> оо
~ ---->0. Следовательно, послед-
Р — 1&0 ний интеграл в (17-82) при р^-оо стремится к нулю.
Предпоследний интеграл можно вычислить с точностью до величины порядка г с учетом того, что
р — ja>o = re<<t и dp = /ге/ф с?<р;
lim f_lW_dp = z(/(Do)x г-0 J р— /<00
(г) п 2 !*
—:= jnZ (ja0). (17-83)
re19
_ л_ 2
При R -> оо сумма первых двух интегралов представляет главное значение интеграла в пределах от —оо до 4- оо с исключением точки (Dq.
На основании (17-82) и (17-83)
+/«
f Z(p) dp=z _ inZ
J Р — /“о —
Рассматривая Z(/<o) как предел, к которому стремится Z (р) при р -> ->/’со, получаем:
оо
f Z den — — jnZ (/cd0),
J <>j—ш0
341 '
откуда
I W—Wq J W—Wo
* 0
dco-C 2(~^dto= w — w0 J w + w0
Рис. 17-36. Интегрирование вдоль контура.
__ Р w [Z (jw) — Z (—/ю)1 + _ _
~J w2 * *-
6
___ + coo [Z (jw) + Z (—/w)] =
— ®o
= —/nZ(/<oo).
Пусть
Z (/co) = r (to) + jX ((£>).
Ввиду четности активной и нечетности реактивной составляющих
Z(/co) + Z(—М = 2г(<о);
Z (/со) — Z (—/со) = /2х (со).
Следовательно,
2wor (w) + j'2wx (w) _
W2 --- Wg
= —/л ]r(coo) + /x(coo)].
Разделяя действительные и мнимые части, находим:
2
Л
f^dco;
J W2—Wg
о
(17-84)
X(to0)-=
Г-'И-dp, 31 J 0)2—“о
Полученные формулы выражают связь между частотными характеристиками активного и реактивного сопротивлений пассивного двухполюсника, удовлетворяющего принятым выше условиям. При этом следует помнить, что интегралы (17-84) берутся в смысле главного значения, с исключением точки со= = соо- Активное и реактивное сопротивления согласно (17-84) вычисляются для любой частоты соо.
Учитывая, что In Z=In ze/ф = =lnz+/cp, можно распространить зависимости вида (17-84) на частотные характеристики натурального логарифма модуля и соответственно угла комплексного сопротивления двухполюсника.
Наряду с (17-84) существуют и другие аналитические зависимости, связывающие действительную и мнимую составляющие сопротивления двухполюсника.
К числу таких зависимостей относятся интегралы активного и реактивного сопротивлений.
Пусть Z(p)—функция, аналитичная в правой полуплоскости, включая точки р=0 и р = со. Разложим Z(p) в ряд Тейлора в окрестности р=0:
Z (р) = Ао-}-Вор Ахр2 +
+ В1Р84-.-. (17-85)
и в окрестности р=оо
Z(p)=AM--—+ ^-~ р ₽*
В,’
----г + (17-86) рЗ
Вдоль мнимой оси, т. е при р=» ==/<1), имеем:
Z (/со) = г (со) + jx (со), (17-87) где г (со) и х(со) —активное и реактивное сопротивления двухполюсника.
Из сравнения (17-86) с (17-87) видно, что
В'^ = lim [сох (to)]. (17-88)
Ci)-*-сю
Проинтегрируем функцию Z(p)— —А вдоль замкнутого контура, составленного из мнимой оси и полу
ч342
окружности бесконечного радиуса в правой полуплоскости (рис. 17-36).
Ввиду отсутствия особенностей в замкнутой области интеграл равен нулю
(f |Z(p) —Л„] dp = 0, откуда с учетом (17-86) и (17-87) +/°°
j [г (®)+/* (со) — d (/со)+
L
—+••• dp = 0. (17-89) р» j
Функция х(со) нечетна относительно со. Кроме того, вдоль полуокружности p=Rei'p и dp=jRei(‘> dcp, где R-*-co. Следовательно,
и
1.
На основании (17-89)
Рис. 17-37 Пример 17-5.
Y [г(со) - Л„] dco-b^ZT =0. (17-90)
Функция г (со) четна относительно со; следовательно,
J [г (со) — Лю] dco = — со
= 2 [°[г(со)-Лм] dco. (17-91) о
Итак, на основании (17-88), (17-90) и (17-91) ео
J [Г (<о) - dco = - -у В'„. (17-92) в
Этот интеграл, носящий название интеграла активного сопротивления, устанавливает связь между г (со) и предельным значением В'^ =lim[cox(co)] и пока-зывает, что площадь, ограниченная кривой г (со), зависит только от величины В'т и не зависит от промежуточных значений реактивного сопротивления двухполюсника.
Пример 17-5. Показать справедливость формулы (17-92) на примере схемы двухполюсника, изображенного на рис. 17-37, с.
Комплексное сопротивление заданного двухполюсника
| _ >+,„t
/соС
или
2=-------------------------4.
(1— со2 £С)2 4-(гшС)2
. <о£ (1 — со2 £С) — г2 соС
+ / (1 — <о»£С)2-|-(/-соС)2
Следовательно,
г (со)= -----------------------
(1 — СО2£С)2_|_ (Г(ОС)2
, . шЬ (1 — со2 LC) — г2 соС (Со) = ---------------.
(1 — со2 £С)2 + («оС)2
Отсюда
Л„ = 0; В^ =
iJm со2 £ (1 — ш2 £С) —г2 со2 С _
(1 — со2 £С)2 + (гсоС)2
1
С '
На основании (17-92) ОО г л
----- Дев = . (1— со2 LC)2-j-(rcoC)2---------2С
Это может быть подтверждено вычислением интеграла. Разбив подынтегральное выражение иа простые дроби, получим:
---------—-------------= ——-----------— + (1 — со2 £С)2 -|- (rcoCj2 a —b 1 -j-czco2
b г + b — a 1 + Ьсо2 ’
22»
343
где
а = -у (/« С2 — 2LC + гС )/>С2—4£с) ; 6= -i- (лС2- 2LC — rC ]А2 С2 — 4£С) .
Интегрируя приведенное выше выражение почленно, находим:
а С г da Ь С г da
а — b J I-f-affl Ъ — a J 1 Ьа* о о
тура с обходом полюса в начале координат (рис. 17-38).
На основании (17-93)
о
ггы
J /<0 J р
—]оа Li
+Т +
J /ш о
L,
(17-94)
В силу четности г (со) и нечетности х(со) относительно со
так как (уЛа+y^b)2=a+2ab+6—r2C2.
На рис. 17-37,6 изображены типичные характеристики г (со) двухполюсников, вы-
х (со) da а
г (со) со
Рис. 17-38. Интегрирование с обходом начала координат.
Далее
В соответствии с этим уравнение (17-94) преобразуется следующим образом:
2/ С dco-HApt _ jAm л = О о
или
полненных по схеме рис. 17-37, а с одинаковыми емкостями С. Площади, ограниченные характеристиками г (со), одинаковы.
Интеграл реактивного сопротивления выводится из условия
dp=O (17-93) р
в предположении, что интегрирование ведется вдоль замкнутого кон-
(|7‘96) о
Этот интеграл носит название интеграла реактивного сопротивления.
Положив u = In со, найдем du = •^dw/a, откуда на основании (17-95)
со
Jx(U)=-|-(Ao-4). (17-96) -»СО
344
Полученная формула аналогична (17-95) с той разницей, что интегрирование ведется по логарифмической шкале частот. Эта формула устанавливает, что площадь, ограниченная кривой реактивного сопротивления, построенной по логарифмической шкале частот, зависит только от разности значений активных составляющих сопротивления цри нулевой и бесконечной частотах и не зависит от промежуточных значений активной составляющей.
Пример 17-6. Показать справедливость формулы (17-95) для схемы двухполюсника, приведенной в примере 17-5.
Пользуясь выражениями, полученными выше, имеем:
<i>L (1 — со2 LC) — г2 шС х (а>) =---------------------•
(I — <о2 LC)2 -f- (гыС)2 А0 = г, 4оо=0.
Следовательно, на основании (17-95) f Z,(l—to2 LC)—г2 С я
I -------------------- __---- -- г
J (1 — <o2LC)2+(ra€)2 2
о
Это может быть подтверждено вычислением интеграла.
Рисунок 17-39 иллюстрирует равенство площадей кривых реактивного сопротивления, построенных в логарифмическом масштабе при одинаковых значениях г.
Рис. 17-39. Пример 17-6-
Наряду с формулами, выведенными выше, существуют также и другие зависимости между частотными характеристиками г(ю) и х(со) физически реализуемых двухполюсников. Эти зависимости позволяют находить характеристику г (со) по характеристике х(со), заданной во всем спектре частот, и, наоборот, находить х(со) по характеристике г(со). Кроме того, имеется возмож
ность найти г (со) и х(со) для всего спектра частот, если г (со) задана для одной части, а х(со)—для остальной части спектра.
По аналогии с приведенными выше формулами, связывающими г (со) и х(со), можно вывести зависимости между частотными характеристиками активной и реактивной проводимостей двухполюсника.
Кроме методики, примененной выше, для установления связи между активной и реактивной составляющими сопротивления или проводимости можно также использовать тот факт, что до момента подачи напряжений ток в реальном двухполюснике отсутствует.
Полученные выше формулы показывают, что активная и реактивная проводимости физически реализуемого двухполюсника взаимосвязаны и не могут выбираться независимо друг от друга.
Для практических расчетов удобен алгебраический способ вычисления коэффициентов полиномов, выражающих частотную зависимость реактивной составляющей сопротивления или проводимости двухполюсника, по заданной активной составляющей. Этот способ основан на следующем.
Представив функцию сопротивления в виде отношения двух полиномов
Z(p) -^- = ' В(Р) а» 4- с2р2 +• •/
(17-97)
Ъо 4- + &2Р2
можно выделить час/и числителя и знаменателя с четными и нечетными степенями р:
Ач (Р) = ао 4- ад2 + одР4 Н—;
Лн (р) ~ Qi р + а3 р3 + as р6 4----;
Вч (Р) = Ьо + Ь2рг + Ь^р* 4- • • • ;
BK(p} = b1p + bsp3 + b5p&-]--------.
Преобразуем выражение для Z(p):
Z(p) = Л(р)В(-р) д
В(р)В(-₽)
_ [Лч (р) 4- »в (р)] [Вч (—р) 4- Вн (—Р)1 В(р)В(-р)
345
откуда с учетом равенств Вч(—р) = =Вч(р), Вн(—р)=— В„(р)
g / [Д _. (Р) Вч (Р) (р) (р) I
В(р)В(—р)
I (р) Вч (р) — Ач (р) Д, (р) В(р)В(—р)
При p—jw первое слагаемое, четное относительно частоты со, выражает активное сопротивление двухполюсника, а второе слагаемое, нечетное относительно частоты, выражает реактивное сопротивление.
Итак,
ReZ(/a)= —Л(р)Д.(р)]
’ L в(р)-в(-р) !₽=/<»*
(17-98)
Будем считать заданным
Re 2(/<о)= Гс° + с2Р2 + с«Р,+ -" ' |/4> + ^2 Р2 + ^4 Р4+ ’ " • Jp=/<4 (17-99)
Приравнивая выражения в числителе (17-98) и (17-99), получаем уравнение:
Со+^+СарЧ-------=
==(ао4'а2Р2+ ‘ ) (^<Н"^2Р2+ ' ' ‘ )-
—(aip+азРЧ------)Х
X(6ip-W+ • • •), (17-100)
в котором коэффициенты с в левой части известны. Коэффициенты b находятся в зависимости от полюсов функции Z(p). При этом следует иметь в виду, что из числа полюсов функции
с0+ с8Ра + с4 ₽*+•
^0 + ^2 р2 + <4 Р* + • • *
только полюсы, расположенные в левой полуплоскости, принадлежат Z(p).
Искомые коэффициенты а находятся в результате приравнивания коэффициентов при одинаковых степенях р правой и левой частей уравнения (17-100).
Описанный способ применим только для функций, не имеющих полюса в бесконечности. На рис. 17-40 изображен двухполюсник с последовательным реактивным сопротивлением jx' (рис. 17-40, а) или с параллельной реактивной проводимостью —jb' (рис. 17-40,6). По
ложим, что Z—r+jx и Y=g—jb. Очевидно, входные сопротивление и проводимость равны соответственно:
2ВХ = г. + / (х + х')-
YBx = g — j(b+b').
Ввиду того что слагаемые х' и Ь' не влияют на величину активных со-
Рис. 17-40. Иллюстрация к функциям, имеющим полюс в бесконечности.
а — сопротивления; б — проводимости.
ставляющих rug, описанный метод не учитывает этих внешних слагаемых: предполагается, что х'=0 и 6'=0, т. е. имеются в виду цепи минимального реактивного сопротивления и минимальной реактивной проводимости.
Пример 17-7. Определить функцию Z (р) и изобразить схему двухполюсника, если частотная характеристика активного сопротивления подчиняется закону
Подстановка p^ja дает:
1_________________1____________
1 4- р* • •
(Р—Pi) (Р—Pi) (Р—Ра)(Р—Рг)
где рг=—pi, pt к pi — сопряженные комплексные величины;
* 1 . . I
Р1,Р1 =-----
У2 У2
• 1 . 1
Рг> Рг— ____ -*! __ •
У2 Уг
Функции Z(p) принадлежат только полюсы с отрицательными действительными »
частями, а именно рх и pi- Поскольку полюс в бесконечности отсутствует, число нулей равно числу полюсов, т. е. двум. Итак,
Z (р) = д° Р + Р2 (Р — Pi) (Р — Pi) ____ Др ~Ь Д1 р р2 р* + УГ р +1
346
Следовательно, 60=62=1, 61= V 2. По заданию Со=1; С2=Сч=0. На основании (17-100)
1 = («о + аара)(1 +Р2)— ахрУ^р
или, что то же,
I = а0 + аг рг + а0 р3 + аа р« — У 2 at ра.
Отсюда
0,= !; ао-{-аг — У2а1 = 0; а2 = 0и,
следовательно.
Окончательно получаем:
2(Р) =
ра + /2р+1
1 р + У2
У2 р* + У2р+1
Этому выражению отвечает двухполюсник, изображенный на рис. 17-41.
Рис. 17-41. Пример 17-7.
17-14. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
17-1. Какие двухполюсники называются реактивными?
17-2. Что такое приведенный реактивный двухполюсник?
17-3. Чем определяется число нулей и полюсов приведенного реактивного двухполюсника, а также их последовательность на характеристике?
17-4. Что такое эквивалентные двухполюсники?
17-5. Почему нули и полюсы функции Z должны чередоваться?
17-6. Как определяется нулями и полюсами сопротивление Z?
347
Глава восемнадцатая
ЧЕТЫРЕХПОЛЮСНИКИ
18-1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И КЛАССИФИКАЦИЯ ЧЕТЫРЕХПОЛЮСНИКОВ
Часть электрической цепи, рассматриваемая по отношению к любым двум парам ее зажимов, называется четырехполюсником (рис. 18-1). Понятием «четырехполюсник» пользуются тогда, когда интересуются величинами токов и напряжений только в двух ветвях или двух парах узлов электрической цепи. Так, в качестве четырехполюсника могут быть представлены длинная линия, электрический фильтр, трансформатор, усилитель, корректирующее и всякое другое устройство с двумя парами зажимов, включенное между источником и приемником электрической энергии, когда предметом исследования
являются токи и напряжения на этих зажимах, а не токи и напряжения внутри самого четырехполюсника.
Рис. 18-1. Четырехполюсник.
Зажимы четырехполюсника, к которым присоединяется источник электрической энергии, называются входными, а зажимы, к которым присоединяется нагрузка, — выходными. Ради краткости применяются также термины «вход» и «выход» четырехполюсника.
347
На практике возможны случаи, когда обе пары зажимов четырехполюсника являются входными (случай двустороннего питания четырехполюсника) или выходными (случай четырехполюсника, содержащего независимые источники
Рис 18-2. Разновидности четырехполюсников.
электрической энергии и нагруженного с обеих сторон).
Четырехполюсники могут быть классифицированы по различным признакам.
По признаку линейности элементов, входящих в них, четырехполюсники разделяются на линейные и нелинейные. Ниже рассматриваются линейные четырехполюсники.
По схеме внутренних соединений четырехполюсников различают Г-об-разный (рис. 18-2, а), Т-образный (рис. 18-2,6), П-образный (рис. 18-2, в), мостовой (рис. 18-2, г), Т-образный мостовой (рис. 18-2, д) и др.
Четырехполюсники делятся на активные и пассивные.
Четырехполюсник называется активным, если он содержит внутри источники электрической энергии. При этом если эти источники являются независимыми, то в случае линейного четырехполюсника обязательным дополнительным условием активности четырехполюс
ника является наличие на одной или обеих парах его разомкнутых зажимов напряжения, обусловленного источниками электрической энергии, находящимися внутри него, т. е. необходимо, чтобы действия этих источников не компенсировались взаимно внутри четырехполюсника. Такой активный четырехполюсник называется автономным.
В случае, когда источники внутри четырехполюсника являются зависимыми, как это, например, имеет место в схемах замещения электронных ламп и полупроводниковых триодов, после отсоединения четырехполюсника от остальной части цепи напряжение на разомкнутых зажимах его не обнаруживается. Такой активный четырехполюсник называется неавтономным.
Четырехполюсник называется п а с с и в н ы.м, если он не содержит источников электрической энергии; линейный четырехполюсник может содержать источники электрической энергии, взаимно компенсирующиеся таким образом, что напряжения на обеих парах разомкнутых зажимов четырехполюсника равны нулю. Так, например, четырехполюсник на рис. 18-3, а пассивен, так как любые две э.д.с. четырехполюсника взаимно компенсируются в контуре (в уравнениях Кирхгофа эти э.д.с. взаимно уничтожаются); четырехполюсник, изображенный на рис. 18-3,6, пассивен вследствие того, что напряжение на зажимах ветви с источниками всегда равно нулю.
Если все э.д.с. в схемах рис. 18-3 приравнять нулю, то получатся четырехполюсники, эквивалентные в электрическом смысле исходным. Под эквивалентностью двух четырехполюсников понимается возможность взаимной замены их в электрической цепи без изменения токов и напряжений в остальной ее части.
Различают четырехполюсники симметричные и несимметричные. Четырехполюсник является симметричным в том случае, когда перемена местами его входных и выходных зажимов не изменяет токов и напряжений в цепи, с кото
348
рой он соединен. В противном случае четырехполюсник является н е-симметричным.
Четырехполюсник называется обратимым, если выполняется теорема обратимости, т. е. отношение напряжения йа входе к току на
Рис. 18-3. Четырехполюсники, внутри которых действия источников электрической энергии скомпенсированы.
выходе или, что то же, передаточное сопротивление входного и выходного контуров не зависит от того, какая из двух пар зажимов является входной и какая выходной. В противном случае четырехполюсник называется необратимым.
Пассивные линейные четырехполюсники являются обратимыми, несимметричные же активные (автономные и неавтономные) четырехполюсники — необратимы. Симметричные четырехполюсники всегда обратимы.
Основной смысл теории четырехполюсника заключается в том, что, пользуясь некоторыми обобщенными параметрами четырехполюсника, можно находить токи и напряжения на входе и выходе четырехполюсника.
Сложная электрическая цепь (например, канал связи), имеющая входные и выходные зажимы, мо
жет рассматриваться как совокупность составных четырехполюсников, соединенных по определенной схеме.
Теория четырехполюсника позволяет вычислить параметры такого сложного четырехполюсника по параметрам составных четырехполюсников и, таким образом, получить аналитическую зависимость между токами и напряжениями на входе и выходе результирующего сложного четырехполюсника, не производя расчетов токов и напряжений внутри заданной схемы.
Получаемые таким путем электрические величины на входе и выходе позволяют оценить режим работы передачи в целом. При этом пользование обобщенными параметрами четырехполюсника дает возможность сопоставлять и правильно оценивать передающие свойства электрических цепей, различных по своему типу и структуре.
Теория четырехполюсника позволяет также решать задачи синтеза, т. е. находить структуру и элементы четырехполюсника по заданным характеристикам (гл. 20).
Основы теории пассивного четырехполюсника разрабатывались многими советскими и зарубежными учеными. Понятие четырехполюсник может быть применено и к механизму, служащему для передачи силы и скорости от источника механической энергии к приемнику. Т акой «механический четырехполюсник», имеющий два полюса (вход и выход), может быть описан линейными уравнениями, связывающими силы и скорости на полюсах [Л.5].
Механическому четырехполюснику соответствует электрический четырехполюсник, построенный по одному из двух принципов электромеханических аналогий, указанных в § 5-13; силы заменяются напряжениями, скорости — токами либо силы заменяются токами, а скорости — напряжениями.
В настоящей главе рассматриваются активные (неавтономные) и пассивные четырехполюсники, имеющие одну пару входных и одну пару выходных зажимов. Рассмот
349
рение общей теории многополюсника не входит в рамки данного курса.
18-2. СИСТЕМЫ УРАВНЕНИЙ ЧЕТЫРЕХПОЛЮСНИКА
Положим, что имеется четырехполюсник, не содержащий независимых источников электрической энергии. Обозначим левую пару зажимов четырехполюсника цифрами
Рис. 18-4. Положительные направления токов и напряжений четырехполюсника.
1—Г, а правую пару зажимов — 2—2'. Этого условного обозначения будем придерживаться во всем последующем изложении, приписывая индексы 1 и 2 токам и напряжениям, относящимся соответственно к левой и правой парам зажимов четырехполюсника. Теми же индексами 1 и 2 будут обозначаться входной и выходной контуры четырехполюсника.
На рис. 18-4 обозначены принятые положительные направления для токов и напряжений на зажимах четырехполюсника. Вариант с токами 7Х и /2 принято называть прямой передачей (см.уравнения по форме ||Л||), вариант с токами /1 и 7г — обратной передачей (см. уравнения по форме ||В||). Используется также вариант с токами /] и72, который будем называть третьим вариантом (см. уравнения по формам ||У||, ||Z||, ||Я||, ||GII). Во всех случаях каждое из напряжений t?i и t/2 понимается как разность потенциалов верхнего (/ или 2) и нижнего (Г или 2') зажимов четырехполюсника.
Напряжения и токи на зажимах четырехполюсника обусловливаются присоединением активных цепей к обеим парам зажимов либо при
соединением активной цепи к одной паре и пассивной цепи к другой паре зажимов четырехполюсника.
Электрические цёпи, присоединенные к зажимам 1—Г и 2—2', могут быть на основании теоремы компенсации в любом режиме замещены источниками э.д.с. Ё} = йх и E2=U2, которые могут рассматриваться как контурные э.д.с., включенные в два независимых контура четырехполюсника, а токи /1=—/1 и 72=—h —как контурные токи.
Соотношения между напряжениями и токами на входе и выходе четырехполюсника могут быть записаны в виде следующих ниже шести форм уравнений:
1. Форма ||У||:/1 и /2 выражаются в зависимости от Ut и U2:
А — ¥ 11^1+ Уia^a', 1 /jg
/;=у2д + у^2. J
2. Форма |)Z||: Ut и U2 выражаются в зависимости от Ц и /2:
= Ziili + Z1272; (182)
G2 = ZqjIi + z22/2.
3. Форма МН: t?i и 7i выражаются в зависимости от U2 и /2:
4. ются
5. ются
— ЛА -|- ДХ2/2;
А = ДА + А2я/2.
Форма ||В||: U2 и /2 выража-в зависимости от Ui и h:
(18-3)
^ = ^4-ад; А ~ 4* ЛгЛ-
(18-4)
Форма ||Я||: Ut и /2 выража-в зависимости от Ц и (]2:
— Ни1 х -|- АА1
А = А1А 4" АА"
Форма ||G||:/i и U2 выража-
(18-5)
6. <
ются в зависимости от Ut и /2:
A @ifii 4* ЦзА’ t72 — -ь g22/2.
Из перечисленных выше форм уравнений рассмотрим подробно формы ||У|| и ||Л||.
(18-6)
шести более
350
Коэффициенты и определители каждой системы- уравнений четырехполюсника могут быть выражены через коэффициенты и определители любой другой системы (см. приложения II и III). Таблицы облегчают переход от одной формы записи уравнений четырехполюсника к другой.
Контурные токи Ц и h связаны с контурными э.д.с. Ёг — Ui и Ё2=С/2 (рис. 18-4) линейными уравнениями (18-1), которые непосредственно следуют из (5-11) (см. § 5-5), поскольку рассматриваемый четырехполюсник не содержит независимых источников электрической энергии.
Коэффициенты У представляют собой входные и передаточные проводимости контуров 1 и 2. В общем случае — это комплексные величины, зависящие от частоты; они определяются следующим образом: у ___ ( А А
1 п — I | — входная прово-
\1/1 /<4=0
димость со стороны зажимов 1 при закороченных зажимах 2;
V (ГЛ
Y га — I I — входная прово-\l/2 /U,=0
димость со стороны зажимов 2 при закороченных зажимах У;
V (ГЛ
г el — I тг- I — передаточная
\с/1 /и^=о
проводимость при закороченных зажимах 2;
у ___f А
1 и — I— передаточная \l/a /и,=о
проводимость при закороченных зажимах 1.
В случае обратимого четырехполюсника
^12 = ^21,
(18-7)
т. е. только три коэффициента в уравнениях (18-1) являются независимыми.
Если четырехполюсник симметричен, то наряду с (18-7) выполняется условие
Л1=У22. (18-8)
В этом случае число независимых коэффициентов равно двум (например,. Уп и У12).
Коэффициенты Z221 Z2I, Z12 в' общем случае комплексные и зависят от частоты. Онн имеют размерность сопротивления н могут быть определены следующим образом:
Z = | — ] — входное сопротивление
\ А / 4“°
со стороны зажимов 1 при разомкнутых зажимах 2;
7 №
Z22 = I "у" I — входное сопротивление \ А //,=о
со стороны зажимов 2 при разомкнутых зажимах Г,
Z21 = I —7 I —передаточное сопротивле-\ А / 1'^=0
ние при разомкнутых зажимах 2;
Z12 == I ~гг — передаточное сопротивление \ А ) А=о
при разомкнутых зажимах 1.
В случае обратимого четырехполюсника
Z12 = Zal, (18-9)
т. е. только три коэффициента в уравнениях (18-2) являются независимыми.
Если четырехполюсник симметричен, то наряду с (18-9) выполняется условие
ZU = ZM. (18-10)
В этом случае остаются только два независимых коэффициента (например, Zu н Z12)*.
18-3. УРАВНЕНИЯ
ЧЕТЫРЕХПОЛЮСНИКА В ФОРМЕ ||А||
Как уже отмечалось в § 18-2, при записи уравнений в форме ||Д|| положительное направление токов /, и /2 выбирается согласно рис. 18-4. Удобство выбора именно такого положительного направления тока /2 связано в данном случае с тем, что форма ||Л|| применяется обычно при передаче электрической энергии от входных зажимов к выходным, причем четырехполюсник, включенный между источником и приемником, может состоять из нескольких четырехполюсников, сое
* Коэффициенты четырехполюсников по форме ||Z|| не являются обратными величинами по отношению к коэффициентам по форме || УII, так, что, например,
У21 ¥ -7— или Уи .
Z21 4ц
351
диненных каскадно; вход каждого последующего четырехполюсника совпадает с выходом предыдущего четырехполюсника.
Выведем форму ||4|| из формы ||У||. Для этого в уравнениях (18-1), заменив 12 через —12, получим:
Из второго уравнения (18-11) следует:
671=_^с/2-^-/2. (18-12)
*21 T 21
Подстановка этого выражения в первое уравнение (18-11) дает:
+ ГиО. = —£14 (18-13)
*И ‘ 21
где
1П = Л1 У^-У12Уг1.
Положив в (18-12) и (18-13):
Д_______Уза . д 1
1 21 У 21
A __Л. А_____Zu.
Л21 — v - Л22 — v
*21 *21
(18-14)
получим систему уравнений четырехполюсника1 * (18-3).
Коэффициенты 4ц, 412, A2i, А22 в общем случае комплексные и зависят от частоты; 4ц и А22— безразмерные, 412 имеет размерность сопротивлений, 421 имеет размерность проводимости. Эти коэффициенты могут быть определены аналогично предыдущему следующим образом:
А
Ли — . I — отношение на-\и2 //,==о
пряжений при разомкнутых выходных зажимах;
А \
— I . I — отношение токов \ /2 /и,=о
при закороченных выходных зажимах;
А Л 4
— ( . I — величина, обрат-\ /2 * и,=о
ная передаточной проводимости при
1 Коэффициенты Д1ь Д12, Д21 и Л22 ча-
сто также обозначаются через А, В, С и D.
закороченных выходных зажимах;
А — (4 л
Л21 — I ~ I — величина, обратка //,=0
ная передаточному сопротивлению при разомкнутых выходных зажимах.
Определитель, составленный из коэффициентов А, равен:
ИI = А1А. - . (18-15)
* 21
В случае обратимого четырехполюсника У12=У21 и поэтому
141 = 4И4И - 412421 = 1, (18-16) т. е. только три любых коэффициента в уравнениях (18-3) являются независимыми; четвертый коэффициент связан с остальными условиями (18-16).
Если четырехполюсник симметричен, то на основании (18-14) с учетом (18-8)
= 422, (18-17)
т. е. число независимых коэффициентов равно двум (например, 4И и 4j2).
В случае перемены направления передачи электрической энергии, а именно при передаче энергии от зажимов 2 к зажимам 1, в уравнениях четырехполюсника связывают напряжения и токи U2, /2 и Ui, [уравнения (18-4) по форме ||В||]. Если заменить в (18-3) токи Ц на —и 12 на —Г2 и решить уравнения относительно 02 и Г2, то получим уравнения четырехполюсника в форме ||В||, выраженные через коэффициенты формы ||4||. Для обратимого четырехполюсника:
6^2 422 (71-}-4127i, | (jg-18) 4 =421t714-41171. J
Сопоставляя уравнение (18-18) с уравнениями (18-3), соответствующими направлению передачи энергии от зажимов 1 к зажимам 2, заключаем, что с переменой направления передачи энергии коэффициенты 4ц и 422, входящие в системы уравнений, меняются местами.
352
18-4. ПАРАМЕТРЫ ХОЛОСТОГО ХОДА И КОРОТКОГО ЗАМЫКАНИЯ
В § 18-3 было показано, что коэффициенты Гц и У22 представляют собой входные проводимости четырехполюсника рис. 18-4, измеренные слева и справа при закороченных противоположных зажимах; соответственно Z\\ и Z22 представляют собой входные сопротивления четырехполюсника при разомкнутых зажимах.
Введя индексы «к» и «х» для обозначения режимов короткого замыкания (зажимы замкнуты) и холостого хода (зажимы разомкнуты), получим параметры холостого хода и короткого замыкания:
2 _ J_. 7__________L
v , л2к —
1 И 7 33
(18-19)
Этих параметров достаточно для составления уравнений обратимого четырехполюсника. Для записи уравнений необратимого четырехполюсника недостаточно параметров холостого хода и короткого замыкания, так как из них только три являются независимыми.
Действительно, на основании (18-19) и таблицы приложения II
Лк;. 1 _ |У|
%1х У и Уи Узз
и
___ |У|
^2Х У23 ^22 Уц У 32
откуда
& (18-20)
%1х. ^зх
Таким образом, параметры холостого хода и короткого замыкания, выражаемые формулами (18-19), принудительно связаны уравнением (18-20).
В случае симметричного четырехполюсника
7 — 7 7 —7 /-1К— *-2к» —^ахг
т. е. симметричный четырехполюсник характеризуется только двумя параметрами.
Параметры холостого хода и короткого замыкания могут быть вы
ражены через любую систему коэффициентов, например через коэффициенты А:
7 ^12.
1К~А-’ /122
7 __^12.
ZK~A ’ Я11
7 __^11.
z'i>!—Т-» Ал
7 ___^22
2Х —А ’ Л21
(18-21)
В
свою очередь любая система коэффициентов обратимого четырехполюсника может быть выражена через параметры холостого хода и короткого замыкания. Например, для коэффициентов А получаем1:
А1 = 1/ (18-22)
г ^2Х ^2К
и, используя (18-21), выражаем все остальные коэффициенты через Дп:
А —А 7 А — zlx
А2 = Л„^.
^1Х
(18-22а)
18-5. СХЕМЫ ЗАМЕЩЕНИЯ ЧЕТЫРЕХПОЛЮСНИКА
На основании уравнений четырехполюсника могут быть построены различные схемы замещения, которые охватывают исследование общих свойств рассматриваемой цепи. Ниже показаны некоторые схемы замещения четырехполюсника, параметры которых выражаются через коэффициенты У, Z и Д.
На практике чаще всего пользуются П-образной и Т-образной схемами ника.
На рис. 18-5, а показана П-об-разная полюсника, в которой проводимости ветвей выражены через коэффициенты У. При этом зависимый источник тока (У21—У 12)^1 сохраняется в эквивалентной схеме только в случае необратимого четырехполюсника; в схеме обратимого четырехполюсника (У12=Уг1) источник тока отсутствует (рис. 18-6,а).
замещения четырехполюс-
схема замещения четырех-
1 Эта формула дает двузначное решение, так как входящие в нее параметры не изменяются от перекрещивания любой пары зажимов.
353
Схема рис. 18-5, а соответствует системе уравнений (18-1). Действительно, по первому закону Кирхгофа ток 71 равен сумме токов, входящих в ветви с проводимостями У11+У12 И —У|2- Ток, ВХОДЯЩИЙ В
Рис. 18-5. Схемы замещения необратимого четырехполюсника.
а — с параметрами У; б — с параметрами Z; в — с параметрами Л.
первую ветвь, равен (Уц + У12)01, а ток, входящий во вторую ветвь, равен —У12(01—йг)-
Рис. 18-6. Эквивалентные схемы пассивного четырехполюсника.
Итак,
4 = (Уи+Уи) 01 - У12 (#1 - 02) = =У1101+У120а.
В свою очередь ток Г2 равен сумме токов, входящих в ветви с проводимостями У22+У12 и —У12, и
тока источника (У21—Yl2)Ui. Следовательно,
4 = ^22+^2)02-^12(02-01) + +041 - Ум) 01=-УИ 01+^22 02-На рис. 18-5,6 показана Т-образная схема замещения, в которой сопротивления ветвей выражены через коэффициенты Z четырехполюсника. Применив второй закон Кирхгофа, легко убедиться в том, что данная схема соответствует уравнениям (18-2).
Схема замещения четырехполюсника содержит зависимый источник э. д. с. или тока в случае, когда четырехполюсник необратим. В схеме обратимого четырехполюсника (Z12=Z21) зависимый источник отсутствует (рис. 18-6,6).
Параметры схемы замещения четырехполюсника могут быть выражены также через коэффициенты А. Так, например, пользуясь табли-цией приложения II, можно в П-об-разной схеме (рис. 18-5, а) проводимости ветвей выразить через коэффициенты 4; при этом получится схема рис. 18-5, в; в случае обратимого четырехполюсника будем иметь схему рис. 18-6, в, которая часто применяется для расчета энергетических систем.
Пассивный П-образный четырехполюсник может быть преобразован в Т-образный (или наоборот) по правилу преобразования треугольника в эквивалентную звезду (§ 4-5).
Следует заметить, что П-образ-ная и Т-образная схемы замещения четырехполюсника не всегда физически реализуемы ’.
Под физически реализуемой пассивной схемой понимается такая схема, в которой параметры г, L и С положительны (гл. 20). Если в какой-либо ветви схемы данное условие не выполнено, то схема физически нереализуема. Например, схема рис. 18-6,6 нереализуема при отрицательном знаке действительной части Z\2, т. е. если
Re Z12 < 0.
1 Это не относится к четырехполюсникам, не содержащим реактивных элементов.
354
Схемой замещения четырехполюсника может служить и мостовая схема (§ 18-15). Мостовая схема является физически реализуемым эквивалентом для любого реально осуществимого симметричного пассивного четырехполюсника.
Схемы замещения необратимых четырехполюсников, описанные выше, применяются для анализа и расчета электрических цепей, содержащих электронные лампы и полупроводниковые триоды.
Пример 18-1. Рассматривая автотрансформатор (рис. 6-21, а) как четырехполюсник, построить для него Т-образиую схему замещения.
Выбрав положительные направления токов по третьему варианту и воспользовавшись параметрами Z, найдем:
2ц = *1 + + /<° (Li + L2 + 2Л4);
222 = гя + jtoLz’
/ (7, \
Zu — Z21 = I . , I — r2 -|- /co(La М). \ l2 Jh=O
На осиоваиии рис. 18-6, б получаются следующие сопротивления ветвей Т-образ-иой схемы:
— Zu — ri + (7-1 + ТИ);
Z22 — Zj2 = •—
Z12 = r3 -}- /со (Lj -J-ТИ).
Полученный результат совпадает сданными § 6-8 (рис. 6-21,6).
18-6. ВХОДНОЕ СОПРОТИВЛЕНИЕ
ЧЕТЫРЕХПОЛЮСНИКА
ПРИ ПРОИЗВОЛЬНОЙ НАГРУЗКЕ
Обозначим через Z1BX входное сопротивление четырехполюсника со стороны зажимов 1, когда к за
жимам 2 присоединено произвольное комплексное сопротивление Z2 (рис. 18-7,о); соответственно через Z2BX обозначим входное сопротивление четырехполюсника со стороны зажимов 2, когда к зажимам 1 присоединено произвольное комплексное сопротивление Zi (рис. 18-7,6).
Следовательно, входное сопротивление Zibx равно отношению напряжения (71 к току 71 при прямой передаче энергии:
7 ^iBX - . >
/1
a Z2BX равно отношению напряжения U2 к току /2 при обратной передаче энергии:
Z —
^гвх — }< •
'2
Входные сопротивления четырехполюсника могут быть выражены через любую систему коэффициентов четырехполюсника и комплексные сопротивления нагрузок Zi и Z2.
Например, если воспользоваться системой уравнений (18-3), то, разделив первое из уравнений на второе, получим:
7 ^11 "Ь -^12 А
л1вх —-----;--------
^21 (72 + А22 /2
_ Al Z2 Аз -^21 ^2 + ^22
(18-23)
Аналогично при обратной передаче на основании (18-18)
Рис. 18-7. Несимметричный четырехполюсник при прямой и обратной передаче.
а и б — произвольная нагрузка; вне — согласованная нагрузка.
а22 + Aj2 ^2вх — . .,
^21 О\ + /;
— Лгз 21 + Лц. (18-24)
Tki + Ai
Если воспользоваться таблицами приложений II и III, то можно выразить ZiBX и Z2bx через другие коэффициенты четырехполюсника.
На практике применяются и другие выражения для Z]BX и Z2BX. Например, в тех случаях, когда известны параметры холостого хода (Z[x и Z2x) и короткого за-
355
мыкания (Z1K и Zjk). удобно пользоваться зависимостями Z1BI и Z2bx от этих параметров. С этой целью выражениям (18-23) и (18-24) с учетом (18-21) придается следующий вид:
получим:
Ас
Ас
__Ац Zgc -f- ^12.
А2ХZ2C -f- A22
__ A22 Zjc ^12
A2i Ac + Ац
7 __ А22
^2bx — ~
Л21
jo
7111___
Лоо / + Z2 Л21
Лчл
/ + Д
Л22____
Au т-+л A2i
Z^tK ~Ь Z2 _ lx -----*»
Zjx + zB
_ 7 Zik ~Ь Zi ~ 2xzlx + z1
Рассмотренные выше функциональные зависимости Z1BX=F](Z2) и Z2Bjx —E2(Zi) представляют собой дробно-линейные преобразования, связывающие величины сопротивлений на зажимах четырехполюсника; они иллюстрируют одно из свойств четырехполюсника — способность преобразовывать сопротивления.
18-7. ХАРАКТЕРИСТИЧЕСКИЕ ПАРАМЕТРЫ ЧЕТЫРЕХПОЛЮСНИКА
Положим, что сопротивления Z] и Z2 в схемах рис. 18-7, а и б подобраны таким образом, что Z1BX=Z] и Z2bx=Z2. Иначе говоря, будем считать, что существуют два сопротивления: Z]=Z1C и Z2=Z2C, которые удовлетворяют следующему условию: входное сопротивление Z1BX четырехполюсника, нагруженного сопротивлением Z2C, равно Z1C (рис. 18-7, в); входное сопротивление Z2Bx четырехполюсника, нагруженного сопротивлением Zlc, равно Z2C (рис. 18-7, г).
Такие два сопротивления называются характеристическими сопротивлениями несимметричного четырехполюсника.
Условие, когда четырехполюсник нагружен соответствующим характеристическим сопротивлением, называется условием согласованной нагрузки или согласованного включения.
Положив в (18-23) и (18-24)
Авх = А = Ас и
Авх = Z^2 — Ас>
Совместное решение этих уравнений относительно величин Ас и Z2c дает:
Ас =
7 — ‘-гс —
Ац А12
A2i А22
А22 Ада
A2i А1х
(18-25)
Введем для рассматриваемого обратимого четырехполюсника новый параметр g, удовлетворяющий условиям:
chg = jA4n Л22;
shg = V Л21.
(18-26)
Эти условия всегда осуществимы, так как параметр g может быть комплексным. Кроме того, эти условия взаимно дополняют друг друга, так как имеющая место связь между коэффициентами (18-16) соответствует тригонометрической формуле
chag — sh2g=l.
Параметр g в общем случае комплексный; g=a+jb называется мерой передачи1 четырехполюсника. Это третий характеристический параметр обратимого четырехполюсника. Его действительная часть а называется собственным затуханием четырехполюсника, а мнимая часть b — коэффициентом фазы.
Физический смысл этих коэффициентов будет пояснен ниже. Выразим коэффициенты четырехполюсника формы ЦЛЦ через характеристические параметры.
На основании (18-25):
1 Иногда этот параметр называется коэффициентом передачи, его ие следует смешивать с терминами «коэффициент передачи по напряжению» и «коэффициент передачи по току». В литературе ранее применялось обозначение g=b+ja.
356
и
(18-28) V
Если воспользоваться известным математическим соотношением
ch g+sh g—e*,
Умножение (18-26) на (18-27) и (18-28) дает:
то уравнения (18-33) упростятся:
Ai=l/f^ chg;
Г
(18-29)
A^VZ^shg. (18-30)
(18-34)
Деление (18-26) на (18-27) и (18-28) дает:
21 —
ch (18-31)
В результате подстановки (18-29) — (18-32) в (18-3) получаются уравнения несимметричного обратимого четырехполюсника в гиперболической форме, соответствующие положительным направлениям токов /] и /г, указанным на рис. 18-4:
V1=]/^(U2chg + Т ^зс
+ Z2c/ashg-);
4= тЛ* (4chg +
Г ^1с \
+ ^-(7ash Д
(18-33)
Обращает на себя внимание сходство полученных уравнений с уравнениями (16-22) однородной линии (§ 16-3).
Эти уравнения показывают, что однородная линия представляет собой симметричный четырехполюсник с характеристическими параметрами:
g=yl и ZC=ZB.
При согласованно подобранной нагрузке (Z2=Z2c) имеет место равенство
Z^ /а = Us или — (7а = /а.
Отсюда следует, что при согласованно подобранной нагрузке модули напряжений и соответственно токов на входе и выходе четырехполюсника связаны уравнениями:
shg. (18-32)
Множитель ]^Zic/z2c еа равен отношению амплитуд или действующих значений напряжений на входе
и выходе четырехполюсника при согласованной нагрузке. В свою очередь множитель i^zzc/zice0 равен отношению амплитуд или действующих значений токов прн той же нагрузке.
Если аргументы (углы) комплексных характеристических сопротивлений Z]C и Z2c обозначить через Ф1С и ф2С, то фазовый сдвиг напря
жения на входе относительно напряжения на выходе определится величиной Ь+ (<р1с—фгс), а фазовый
сдвиг тока на входе относительно тока на выходе — величиной Ь + + — (фгс—ф1с)-
В общем случае коэффициент фазы b может быть определен как полусумма фазовых сдвигов между напряжениями и соответственно между токами на входе и выходе четырехполюсника, нагруженного согласованно. При равенстве углов Ф1с и ф2с и согласованно подобранной нагрузке фазовые сдвиги между напряжениями и соответственно между токами четырехполюсника одинаковы и равны Ь.
Характеристические параметры Zic, Z2c и g могут быть выражены через параметры холостого хода и короткого замыкания, а именно на
357
основании (18-21), (18-25) и
(18-26):
(18-35)
Подстановка (18-26) в формулу chg-l-shg=e^ приводит к выражению, связывающему характеристический параметр g с коэффициентом четырехполюсника формы ЦЛ||:
eg=eae>b=V А^^ +
+ (18-36)
По этой формуле величина g вычисляется однозначно, если подставлять под радикалы коэффициенты А в показательной форме с последующим сложением углов и делением их суммы на 2. По формуле (J8-35) для тангенса принципиально невозможно получить однозначное решение, так как входные сопротивления под радикалом не изменяются от перекрещивания зажимов четырехполюсника. Поэтому формула (18-36) предпочтительнее формулы (18-35) для th £.
Вычисление g по формуле для thg ведется в следующем порядке:
thg =
eg — e~g eg -f-e—g
откуда-
e2* = J+_thg = M <p;
1-thg
в результате логарифмирования
g=a+jb
In TH , q>
2 + !~2'
Следует отметить, что параметр g может быть также получен как половина натурального логарифма отношения произведений комплексных напряжения и тока на входе и выходе четырехполюсника при согласованной нагрузке.
Действительно, на основании (18-34)
откуда
В случае симметричного четырехполюсника (Лц=Л22) характеристические сопротивления Zie и Z2c равны друг другу:
---7 __7 -- 1 / ^12 1С_________^2С-_ I/ ~ -
Г
Следовательно, входное сопротивление симметричного, четырехполюсника, нагруженного характеристическим сопротивлением Zc, равно Zc. Это означает, что всякому симметричному четырехполюснику соответствует некоторое характеристическое сопротивление Zc, обладающее следующим свойством: если нагрузить данный четырехполюсник сопротивлением Zc, то отношения напряжения к току на входе и выходе четырехполюсника будут одинаковыми, т. е.
На основании (18-33) уравнения симметричного четырехполюсника при произвольной нагрузке записываются в гиперболической форме (для положительных направлений рис. 18-4) так:
(>i= 02 ch g 4- Zc/S sh g-, Л=4сЬ§+ ^^shg. zc
Если нагрузка подобрана согласованно, т. е. Zciz=L)2t то
(18-38)
В этом случае амплитудные изменения напряжения и тока определяются множителем е“, а фазовый сдвиг между напряжениями или токами — углом Ь. Собственное затухание а будет:
а= In
(Ui\ \Uj
(18-39)
358
Величины g, а и Ь — безразмерные. Угол Ь вычисляется в радианах (рад)-, собственное затухание а, входящее в (18-39), вычисляется в неперах (неп).
Затуханию 1 неп соответствует уменьшение амплитуды и действующего значения напряжения или тока в е—2,718 раза (так как при In —=
= 1 имеем -77=2,718).
о2
В радиотехнике принято затухание вычислять в белах (б) или децибелах (дб), которые определяются следующим образом.
Если полная мощность на выходе четырехполюсника в 10 раз меньше мощности на его входе, то затухание составляет 1 б\ если мощность уменьшается в 100 раз, то затухание оценивается в 2 б и т. д. Поэтому
О2 и 2* 2
В случае согласованно нагруженного симметричного четырехполюсника
Si = ММ1 = /Л.?
S2 w! / \ /2 /
и, следовательно, °б=21g ~ = 21g.
Децибел — единица затухания, в 10 раз меньшая бела.
Затухание 1 дб соответствует уменьшению полной мощности в 1,26 раза или уменьшению величин напряжения и тока в 1,12 раза.
Таблица 18-1
Затухание а, дб.
при различных отношениях * S2
S, А. S1
а s, а $3 а
0,1 1,02 4 2,51 8 6,31
1 1,26 5 3,16 9 7,94
2 1,58 6 3,98 10 io
3 1,99 7 5,01 10 п 10п
Таблица 18-1 иллюстрирует зависимость затухания в децибелах от отношений полных мощностей S1/S2
на входе и выходе четырехполюсника; соответствующие им отношения величин напряжений или токов симметричного четырехполюсника,, нагруженного согласованно, составляют ySj/Sa.
Для перехода от неперов к децибелам или обратно можно воспользоваться приведенным выше условием:
Рис. 18-8. Питанце приемника непосредственно от источника (а) и через четырехполюсник (б).
ad6=20 1g^-=201gea«- = =20аяел 1g с=20•0,4343акеп= = 8,686a„n,
т. е.
1 неп = 8,686 дб или
1 дб — 0,115 wen.
18-8. ВНОСИМОЕ ЗАТУХАНИЕ ЧЕТЫРЕХПОЛЮСНИКА
Вносимое затухание (или усиление) является мерой оценки изменения условий передачи при включении четырехполюсника между источником и приемником.
Положим, что между источником напряжения, имеющим внутреннее сопротивление Zi, и приемником Z2 включен четырехполюсник.
Под вносимым затуханием четырехполюсника подразумевается половина натурального логарифма или десятикратное значение десятичного логарифма отношения пол- -ной мощности 51, которую непосредственно отдавал бы источник сопротивлению Z2 (рис. 18-8,а), к полной мощности S2 на выходе четырехполюсника, нагруженного сопротивлением Z2 (рис. 18-8,6):
aBB= — In —, неп (18-40) 2 So
359
или
cBI!=101g-|-,66. (18-41)
ZtZi
Zk 7
ztc 1
2
Мощности S1 и Sa выражаются следующим образом:
= ;
|Z1+Z2|2’
S2=z2/2
Согласно (18-40)
После ряда алгебраических преобразований получается:
й _ ^yi^(Z1 + zlc)
— -• ~г1~ ' А.
z2
^ВВ = 2 'п
U*
|А+ 22|2z1
X
sVZxZic
(Za 4- Ztc) (1 — ПхПдй—*^)
(18-42)
где
Отношение Uli* входящее в -(18-42), может быть выражено че--рез характеристические параметры четырехполюсника и сопротивления Zi и Z2.
Пользуясь обозначениями рис. 18-8,6 и уравнениями четырехполюсника, записанными в форме ||Л||, находим:
«1 =
Zi — Zlc _ ____ za — zac
' ' И lie - — .
Zi 4- zlc Z2 -}- ZK
называемые коэффици-отражения на входе и четы рехпол юсника. связи с этим
— так енты выходе
В связи с этим выражение
(18-42) принимает следующий вид: Zi 4- -Zu I 1
Овв
1С
(7=£z1+z1/1=X11 (7а+Лм/.+
=(/4uZ24-/4114->421Z1Z24->4a2Z1) /2,
-}- In
Z^ 4~ Zte
’2С
— In
4- In 11 —п^ет*^ —
Zt 4~ Zt
.откуда
-г- =A11Zi+Ali+ I,
,____ I. (18-42а)
чуZiZs I
-}-AalZ1-Zt+Ass^1. (18-43) На основании (18-29) — (18-32):
(18-44)
Подстановка (18-44) в (18-43) дает:
Следовательно, вносимое затухание состоит из пяти слагаемых. Первое слагаемое — собственное затухание четырехполюсника, второе — затухание вследствие несогласованности сопротивлений на входе четырехполюсника, третье — затухание вследствие несогласованности сопротивлений на выходе, четвертое — затухание вследствие взаимодействия несогласованностей на входе и выходе и пятое со знаком минус — затухание вследствие несогласованности сопротивлений источника и приемника.
В случае согласованного включения сопротивлений на входе и выходе четырехполюсника, т. е. при 2i=Zic и Z2=«=Z2c, вносимое затухание равно собственному - затуханию четырехполюсника.
Если вносимое затухание равно нулю, то это означает, что мощности на входе и выходе четырехполюсника равны между собой.
Когда четырехполюсник является усилителем мощности (например, в случае лампового или полупровод-
360
пикового триода), выражения (18-40) и (18-41) дают отрицательные значения авн, это указывает на то, что вместо затухания в данном случае имеет место усиление (измеряемое в неперах или децибелах).
В случае, когда сопротивление приемника Z2 равно внутреннему сопротивлению источника Zlt затухание называется рабочим. На основании (18-42а) рабочее затухание
аРаб=а+1п I Z1,+ Zlc
I 2 И Z±Z1C
^2 "Ь ^2С
2/z2Z2c
+ In | 1—
+ In
18-9. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
Передаточной функцией, коэффициентом передачи или амплитудно-фазовой характеристикой четырехполюсника называется отношение комплексных амплитуд или комплексных действующих значений электрических величин на выходе и входе четырехполюсника при заданном режиме передачи. Необходимо помнить, что именно выходная электрическая величина делится на входную, а не обратно.
Отношения одноименных электрических величин — коэффициент передачи по напряжению К.и— — IJ^IUa и коэффициент передачи по току — — представляют со-
бой безразмерные, в общем случае комплексные и зависящие от частоты величины. Применительно к усилительным устройствам они носят название коэффициентов усиления по напряжению и току.
Отношения разноименных электрических величин — передаточное сопротивление Z = и передаточная проводимость —
имеют соответственно размерности
сопротивления и проводимости и также являются в общем случае комплексными величинами, зависящими от частоты.
Модули этих комплексных отношений представляют собой а м п -литудно-частотные, а их аргументы — фазо-частотные характеристики четырехполюсника. Эти характеристики имеют важное значение для работы устройств автоматики и радиотехники.
В общем случае четырехполюсника, нагруженного произвольным сопротивлением Z2, передаточные функции могут быть выражены через любую систему коэффициентов четырехполюсника и сопротивление Z2.
Через коэффициенты формы |]Л|] они выразятся следующим образом (положительные направления для токов соответствуют прямой пере-
При холостом ходе и коротком замыкании эти коэффициенты примут вид:
- £' i
/1ц /122
В случае обратной передачи, очевидно, можно написать (при |/4j = = 1):
= 7-
/122 Л11
Отсюда видно, что для обратимого четырехполюсника коэффициент передачи по напряжению при
Рис. 18-9. Согласованное каскадное соединение четырехполюсников.
23—1118
361
холостом ходе и прямом направлении передачи энергии равен коэффициенту передачи по току при коротком замыкании и обратном, направлении передачи энергии. В свою очередь коэффициент передачи по току -при коротком замыкании и прямом направлении передачи равен коэффициенту передачи по напряжению при холостом ходе и обратном направлении передачи.
18-10. КАСКАДНОЕ СОЕДИНЕНИЕ ЧЕТЫРЕХПОЛЮСНИКОВ, ОСНОВАННОЕ НА СОГЛАСОВАНИИ ХАРАКТЕРИСТИЧЕСКИХ СОПРОТИВЛЕНИИ
На практике широко распространено каскадное или цепочечное соединение четырехполюсников, при котором входные зажимы каждого последующего четырехполюсника присоединяются к выходным зажимам предыдущего четырехполюсника; цепи, служащие для передачи электрической энергии, обычно состоят из отдельных звеньев, следующих друг за другом.
Каскадное соединение четырехполюсников, выполненное по принципу согласования характеристических сопротивлений, заключается в том, что входное сопротивление на зажимах любого четырехполюсника равно характеристическому.
Рисунок 18-9 иллюстрирует каскадное соединение двух четырехполюсников. Ввиду того что комплексное сопротивление нагрузки согласовано с выходным характеристическим сопротивлением Z3c второго четырехполюсника, входное сопротивление этого четырехполюсника равно характеристическому (Z2c); при этом оно служит согласованной нагрузкой для первого четырехполюсника. Поэтому входное сопротивление первого четырехполюсника равно характеристическому (Z1C).
Отсюда следует, что каскадно соединенные четырехполюсники с согласованными характеристическими сопротивлениями могут быть замещены одним четырехполюсником, имеющим характеристические сопротивления, равные входному характеристическому сопротивлению
первого и выходному характеристическому сопротивлению последнего четырехполюсников (рис. 18-9). Мера передачи g результирующего четырехполюсника определяется алгебраической суммой мер передачи । составных четырехполюсников.
В самом деле, применительно к схеме рис. 18-9 в соответствии с "(18-34)
откуда
Ul= 1/ — Uaes“+e6; г ^зс
Ц = /аее“+еб.
Полученные выражения подтверждают сказанное выше: результирующий четырехполюсник имеет характеристические сопротивления Zic и Z3c и меру передачи g=ga+ +йб- Соответственно собственное затухание результирующего четырехполюсника а=аа+Об, а фазовый коэффициент Ь=Ьа+Ьа.
В гл. 3 (§ 3-5) было показано, что передача максимума активной мощности обеспечивается тогда, когда комплексные сопротивления источника и нагрузки являются сопряженными. Это условие не выполняется в случае согласования характеристических сопротивлений каскада в прямом и обратном направлениях, если характеристические сопротивления комплексные. Однако если они активные (включая сопротивление источника), как это нередко имеет место на практике, то обеспечивается оптимальное условие передачи мощности.
Согласование характеристических сопротивлений широко применяется в автоматике, приборостроении и электронике.
362
18-11. УРАВНЕНИЯ СЛОЖНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ
В МАТРИЧНОЙ ФОРМЕ
Для получения параметров результирующего четырехполюсника, составленного из более простых четырехполюсников, параметры которых известны, удобно пользоваться матричной записью (§ 5-10).
Рис. 18-10. Каскадное соединение четырехполюсников.
В зависимости от схемы соеди
нения сложного четырехполюсника применяется та или иная форма уравнений, а именно:
1) при каскадном соединении (рис. 18-10)—форма ||Л|| или ||В||;
2) при последовательном соединении (рис. 18-11)—форма ||Z||;
3) при параллельном соединении (рис. 18-12)—форма ||У||.
Каскадное соединение четырехполюсников (рис. 18-10). Уравнения составных четырехполюсников в матричной форме ||Л|| имеют вид:
Здесь индексом а отмечены величины, относящиеся к первому четырехполюснику, а индексом б — величины, относящиеся ко второму четырехполюснику.
При каскадном соединении: z ^А — й1аг А — ilat
^2 — ^26’ А = ^2б'г й%а = й1б;
^2а ~ Аб-
Следовательно,
Таким образом, матрица ЦЛ|| результирующего четырехполюсника равна произведению матриц составных четырехполюсников:
Это правило распространяется на случай каскадного соединения любого числа четырехполюсников. При этом матрицы, подлежащие перемножению, записываются в порядке следования соответствующих четырехполюсников, так как умножение матриц не подчиняется переместительному закону.
Последовательное соединение четырехполюсников (рис. 18-11). Уравнения составных четырехполюсников в матричной форме ||Z|| имеют вид:
Г1 Ik
Здесь
= ^Аа 4- Ul6‘, ^2 — ^2в+^2б-Если при этом
А — Аа=Аб И А ~ Аа = Аб>
Рис. 18-11. Последовательное соединение четырехполюсников.
Таким образом, матрица ||Z|| результирующего четырехполюсника равна сумме матриц составных четырехполюсников:
23*
363
||Z||=||Ze||+||Z6||.
Параллельное соединение четырехполюсников (рис. 18-12).
Уравнения составных четырехполюсников в матричной форме | У|| имеют вид:
|Ы ;
|Л|О К a
= и2 = и2а = и^ К ~ la + Лб • Л = Ла Лб‘
Следовательно,
Таким образом, матрица ||У|| результирующего четырехполюсника равна сумме матриц составных четырехполюсников:
Рис. 18-12. Параллельное соединение четырехполюсников.
При параллельном- соединении четырехполюсников:
11П = 11М + Пб11.
Правила нахождения матриц сложных четырехполюсников сведены в табл. 18-2. Они справедливы при любом числе составных четырехполюсников. Однако правила сложения матриц применимы только при равенстве токов входящего и выходящего в каждой паре зажимов составных четырехполюсников, которое должно быть обеспечено тем или иным способом.
Соединение четырехполюсников, удовлетворяющее этому условию, называется регулярным [Л. 1 и 10].
Таблица 18-2
Матричные уравнения сложных четырехполюсников
Соединение
Схема
Матричное уравнение
Каскадное
Последовательное
Параллельное
Последовательно-параллельное
Параллельно-последовательное
18-12. ОДНОЭЛЕМЕНТНЫЕ ЧЕТЫРЕХПОЛЮСНИКИ
Простейшими четырехполюсниками являются одноэлементные четырехполюсники, состоящие из пос
ледовательного (рис. 18-13, а) или параллельного (рис. 18-13,6) двухполюсника.
Уравнения первого из них в форме ||Л1| записываются следующим
364
образом:
ul = u2 + zi2-t
/>о + 4
или, что то же, С7Х|| 111 z|| |t/2||
/.Но il'l/J-
Уравнения одноэлементного четырехполюсника с параллельной ветвью (рис. 18-13,6) в форме ||Л|| записываются следующим образом:
0 " —а
б)
Рис. 18-13. Одноэлементные четырехполюсники с последовательной (о) н параллельной (б) ветвями.
*4 = ^+0; 4 = у*4+4
или, что то же,
<4
4
<4
1 о
А 1 z
Поэтому при перекрещивании входных или выходных зажимов любого четырехполюсника его матрица ||Л[[ умножается на II—1 °Н
О __j > что равносильно пере-
мене знаков коэффициентов А.
Рис. 18-14. Соединения: прямое (а) и перекрещенное (б).
18-13. Г-ОБРАЗНЫЙ ЧЕТЫРЕХПОЛЮСНИК
Коэффициенты Г-образного четырехполюсника (рис. 18-15) могут быть получены непосредственно по формулам, приведенным в § 18-2 и 18-3. Например, для схемы рис. 18-15,а коэффициенты формы ||Л|| согласно формулам § 18-3 будут:
Если в первом четырехполюснике (рис. 18-13, а) положить Z=0
или, что то же, во втором четырехполюснике (рис. 18-13, б) принять Z=oo, то получится уравнение в форме ЦАЦ:
К
1 0
0 1
02
1
Za ’
^21 —
соответствующее
непосредственному
прямому соединению, показанному на рис. 18-14,а.
Легко убедиться, что перекрещенному соединению (рис. 18-14,6) соответствует уравнение в форме 1И11 :
и*
4
Аналогично могут быть вычислены и другие коэффициенты.
Характеристические параметры Г-образного четырехполюсника могут быть вычислены по формулам (18-25) и (18-26).
Для схемы рис. 18-15, а:
(18-45)
г
365
Для схемы рис. 18'15,6:
(18-46)
18-14. Т-ОБРАЗНЫИ
И П-ОБРАЗНЫИ ЧЕТЫРЕХПОЛЮСНИКИ
В § 18-5 рассматривались схемы замещения четырехполюсника и приводились схемы Т-образного и П-образного четырехполюсников. Коэффициенты таких четырехполюсников вычисляются по общей мето-
Рис. 18-15. Г-образный четырехполюсник.
При расчете электрических фильтров (гл. 19) и в ряде других случаев за исходные схемы Г-об-разных четырехполюсников принимаются схемы рис. 18-15, в и г, причем мера передачи Г-образного четырехполюсника обозначается через g/2, для того чтобы при согласованном каскадном соединении двух таких четырехполюсников получался Т- или П-образный четырехполюсник с мерой передачи g (§ 18-14). При этом характеристическое сопротивление со стороны параллельной ветви обозначается через Zn, а со стороны последовательной ветви — через Zj .
На основании (18-45) или (18-46):
дике, описанной в § 18-2, 18-3 и 18-4.
Так, для Т-образной схемы рис. 18-16 получим:
’ । Zb Zc с' Z ‘•а
1 + ^ 2ь +
Характеристические параметры находятся ио формулам (18-25) и (18-26).
Симметричные Т- и П-образные четырехполюсники можно получить согласованным каскадным соединением двух одинаковых Г-образных четырехполюсников (рис. 18-17, а и б). Результирующие четырехполюсники имеют характеристические сопротивления Zt и Zn, определяе-
(18-47)
Рис. 18-16. Т-образный четырехполюсник.
(18-48)
Эти выражения используются в теории электрических фильтров.
мые согласно (18-47), и меры передачи g, вдвое превышающие меру передачи Г-образного четырехполюсника.
366
С учетом (18-48) имеем: chg=l+2sha-&- =1 1 + &. (18-49) 2 2Za
Тот же результат получается на основании (18-26),
(18-50)
Рис. 18-17. Разложение симметричных Т-образного (с) и П-образного (б) четырехполюсников на Г-образные.
Рис. 18-18. Мостовой четы-
рехполюсник.
|8-15. симметричный мостовой ЧЕТЫРЕХПОЛЮСНИК
Для симметричного мостового четырехполюсника (рис. 18-18) в соответствии с § 18-3 можно получить коэффициенты формы ||Л||:
ЦД||«
Zi + Za
Za — Zi
2
Z2 — Zi
2ZjZg Zz-Zi Zi + z% Zi — Zi
‘ Характеристические параметры симметричного мостового четырехполюсника находятся по формулам:
сЬ₽=Ли =
Zi -j-Zj
Zj — Z1
(18-50)
sh § — Л^ ^4ji — = 2 У ZtZ, .
Zs — Zj
Как уже отмечалось в § 18-5, мостовой четырехполюсник является физически реализуемым эквивалентом для любого реально осуществимого симметричного пассивного четырехполюсника [Л. 1 и 19].
18-16. идеальный трансформатор КАК ЧЕТЫРЕХПОЛЮСНИК
С понятием «идеальный трансформатор» мы уже встречались в гл. 6 (§ 6-5).
Матрица ||Л|| такого трансформатора, изображенного на рис. 18-19, а, имеет вид:
1И1| =
п
0
о
1 •
п
(18-51)
где п — коэффициент трансформации.
Следовательно, присоединение идеального трансформатора на входе или выходе заданного четырехполюсника преобразует матрицу последнего по формуле
367
/гЛи
Т Л1
/гЛ12
(18-52)
Перекрещивание одной из пар зажимов трансформатора равносильно изменению полярности обмоток (рис. 18-19,6). При этом изме-
или соответственно
^11 ^12
^21 ^22
п О II
О —
няется знак элементов в матрице (18-51) и матрица ЦАЦ принимает вид:
иАп А]2
п
п.А*1 А22
п
(18-53)
О
1
п
(18-56)
Соответственно в матрицах (18-52)—(18-55) изменяется знак элементов, содержащих множитель п или Мп.
Рис. 18-19. Трансформатор как четырехполюсник.
Полагая, что матрицы проводимостей и сопротивлений четырехполюсника до включения идеального трансформатора были соответственно равны [Л. 1]:
^11
22i
^12
222
11
12
21
22
при
находим матрицы ||Z|| и ||У|| включении идеального трансформатора на входе четырехполюсника:
II21|= f12
HZ21 ^22
— У Г 12 П
— Y
ПУ81
и при включении рехполюсника:
на
22
(18-54)
выходе четы-
^11
— Z
^21 п
— Z
*-12 П
— Z
Уи иУ12 лУ 21 П2У22
(18-55)
Идеальный трансформатор с коэффициентом трансформации, равным единице, имеет единичную матрицу ||А|| = ||q ? |.
Включение такого трансформатора на входе или выходе заданного четырехполюсника и соответственно перемножение единичной матрицы в любой последовательности с матрицей ||А|| заданного четырехполюсника не преобразует последнюю.
Прип = —1 H =
18-17. ОБРАТНАЯ СВЯЗЬ
Последовательно-параллельное соединение двух четырехполюсников представляет собой один из основных видов цепи с обратной связью, в которой напряжение на выходе воздействует на входные напряжения системы. Пусть некоторое устройство, которое назовем основным, представляет собой четырехполюсник с передаточной функцией К' (/®) = уЙ- (рис. 18-19). Если и1
выходное напряжение й2 подвести
368
к зажимам другого четырехполюсника, называемого устройством обратной связи, и включить его противоположные зажимы последовательно с входными зажимами основного устройства, то получится система с обратной связью по напряжению.
Это выражение показывает, что передаточная функция системы зависит от передаточной функции устройства обратной связи. Регулируя последнюю, можно воздействовать на передаточную функцию всей системы.
Рис. 18-20. Цепь с обратной
связью.
18-18. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
18-1. Доказать, что в случае симметричного четырехполюсника, нагруженного согласованно, коэффициент передачи по напряжению равен:
1
Ajj — 1
18-2. Доказать, что
Обозначим передаточную функцию устройства обратной связи
О'
через К" (/со) = -г-. Очевидно, = t7a
Следовательно, передаточная функция всей системы
или, если разделить числитель и знаменатель на U[,
К = ——. (18-57)
1 — К'К"
Если поменять полярность одной из пар зажимов устройства обратной связи, то в знаменателе (18-57) вместо знака минус получится знак плюс. .
Обратная связь, при которой напряжение, пропорциональное выходному напряжению, добавляется к вводному напряжению системы так, что | К | > | К' | называется положительной; если же |/(|<|/С|, то обратная связь называется отрицательной.
Выражение (18-57) может быть переписано так:
K = J_.
К’ 1 — К'К"
Если 1, то
К
^21 — ±V22X(Z1X— Z1K) ,
где Zlx, Z2I, Zik — параметры холостого хода и короткого замыкания.
18-3. Доказать, что
—•2а Zlc Z1K
е « =------------—
Zic + Zu
Zsc %2К
2гс -J- Z2K
18-4. Доказать, что коэффициент передачи по напряжению четырехполюсника, нагруженного произвольным сопротивлением Z2, равен коэффициенту передачи по на-
пряжению прн холостом ходе, деленному
1 %SK на 1+ ~.
z2
18-5. Доказать, что коэффициент передачи по току четырехполюсника, нагруженного произвольным сопротивлением Z2, равен коэффициенту передачи по току прн коротком замыкании, деленному на
^2Х
18-6. Определить коэффициент передачи по напряжению прн холостом ходе и коэффициент передачи по току при коротком замыкании для П-образного четырехполюсника, продольная ветвь которого состоит из L, а поперечные ветви — из С (каждая).
1
Ответ: --------
1 — (iPLC
18-7. В схеме рис. 18-16 заданы: Zo = =30—/40ол; Zb=Zc=12+/16 ом. Определить а и Ь.
Ответ: 0,562 неп; 0,703 рад.
18-8. Определить коэффициенты А трансформатора (рис. 6-11). Дано: п = = 15 ом; 7., =20 мгн; г2=45 ом; £2=60 мгн;
мгн; о = 1000 рад/сек.
Ответ: 1Z—36°50'; 72.3Z— 3°20' ом; 0,04 Z —90° сим; 3Z —36°50'.
18-9. Определить характеристическое сопротивление и меру передачи симметричного мостового четырехполюсника.
369
18*10. Доказать для симметричного мостового четырехполюсника, что
Z-ц = (Zi + Za); Zi2 = (Z2 — Zi);
18-11. Вывести условия эквивалентности симметричных Т-образиого н мостового четырехполюсников.
18-12. Несимметричный четырехполюсник нагружен сопротивлением Z2. Пользуясь формой ||Z||, доказать, что коэффициент Z21
передачи по току равен Ki =———, 7 ^22 “Г ‘^3
а коэффициент передачи по напряжению
д- __ Zal Z2________
ZiiZaa — ^igZgi+ZiiZj f
18-13. Опыт холостого хода со стороны входных зажимов и опыты холостого хода и короткого замыкания со стороны выходных зажимов четырехполюсника дали следующие результаты: /|Х=0,24 а; Рц = 13 ет; 12х= 1,11 д; Рак«92,3 вт; /2к = = 1,04 а; Р2К“89,2 вт.
Напряжение источника питания при всех опытах было равно 100 в, и все три тока отставали по фазе от напряжения.
Определить коэффициенты А.
Ответ: 7,44Z120°30'; 715Z151°30'ojk; 17,9 • 10-2Z63°25' сим; 1,59Z97°.
370
Глава девятнадцатая
ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
19-1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И КЛАССИФИКАЦИЯ ЭЛЕКТРИЧЕСКИХ
ФИЛЬТРОВ
Электрическим фильтром называется устройство, при помощи которого электрические колебания разных частот отделяются друг от друга. Он представляет собой пассивный четырехполюсник, пропускающий некоторую определенную полосу частот с малым затуханием. Вне этой полосы частот затухание велико.
Полоса частот, при которых затухание мало, называется полосой пропускания фильтра. Остальная область частот называется полосой задерживания фильтра.
Практическое применение электрических фильтров весьма широко и разнообразно. Они применяются в радиотехнике, проводной связи, автоматике, приборостроении и во многих других областях современной техники, использующих принцип разделения-частот.
Система одновременного телеграфирования и телефонирования по одному и тому же проводу с использованием индуктивностей и емкостей для устранения влияния одного вида связи на другой была применена в России впервые в 1880 г. военным инженер-капитаном
Г. Г. Игнатьевым, осуществившим разделение двух каналов связи (телефона и телеграфа) с помощью индуктивных катушек и конденсаторов.
Эти элементы, примененные в целях отделения полосы нижних частот от полосы верхних частот, являлись простейшим видом фильтрующих устройств.
Совершенствование электрических фильтров неразрывно связано с последующим развитием высокочастотной техники и электроники. Создание многоканальной проводной связи и радиосвязи сопровождалось разработкой теории электрических фильтров и методов их расчета и непрерывным совершенствованием самих фильтров.
Теория электрических фильтров базируется на общей теории четырехполюсников.
Электрические фильтры могут быть классифицированы различным образом.
Классификация по пропускаемым частотам. В зависимости от пропускаемого спектра частот фильтры разделяются на фильтры: а) нижних частот (низкочастотные); б) верхних частот (высокочастотные); в) полосовые; г) заграждающие (режекторные).
370
Классификация по схемам звеньев. Фильтры могут СОСТОЯТЬ из звеньев Г-, Т-, П-образных, мостовых и др. В зависимости от числа звеньев фильтр может быть однозвенным или многозвенным.
Классификация фильтров по характеристикам. В отличие от простейших фильтров типа k различают фильтры более высокого класса — производные фильтры типа т и др.
Классификация фильтров по типам элементов. Различают фильтры: а) реактивные (состоящие из элементов L и С); б) пьезоэлектрические (состоящие преимущественно из кварцевых пластин); в) безындукционные (состоящие из элементов г и С) и др.
19-2. УСЛОВИЕ ПРОПУСКАНИЯ РЕАКТИВНОГО ФИЛЬТРА
Наименьшее число элементов, из которых может состоять фильтр, равно двум (Г-образное звено). Фильтры, содержащие Т- и П-об-разные звенья, могут рассматриваться в качестве комбинаций, составленных из Г-образных звеньев.
В случае симметричного Т- или П-образного фильтра (рис. 19-1, а и б) параметры Ли и g вычисляются по формуле (18-49):
Ai = chg=l+^-. (19-1)
Мера передачи g симметричного Т- или П-образного фильтра может быть определена как удвоенная мера передачи g/2 Г-образного фильтра. Согласно (18-48)
sh -£- = 1ZА- . (19-2)
2 у 4Za
Полосой пропускания реактивного фильтра является область частот, при которых собственное затухание реактивного фильтра равно нулю (а«=0). Покажем, что четырехполюсник, состоящий из одних индуктивностей или одних емкостей (знаки Zi и Za одинаковы), не может иметь полосы пропускания. Иначе говоря, такой четырехполюсник не является фильтром.
Действительно, пусть Г-образ-
ный или симметричный Т- или П-об-разный четырехполюсник состоит из чисто реактивных элементов, т. е.
= i jx^, Zt == + /ха; (19-3) здесь Xi и Хг — абсолютные значения реактивных сопротивлений; положительные знаки относятся к индуктивным, отрицательные — к емкостным элемента м(
it
Рис. 19-1. Симметричные Т-и П-образные фильтры.
Согласно (19-2)
sh — sh /— + / —1 = 2 \2 2 )
, с б , » , в • б
= sh — cos---Н ch —sin — =
2 2 2 2
4х3
откуда, разделяя вещественные и мнимые части, получаем:
ch — sin == 0. (19-4)
Ввиду того что гиперболический косинус действительного аргумента не может быть равен нулю (ch ~ > >1), то на основании (19-4)
sin— = 0 и cos — = ± 1.
2 2
Таким образом, при одинаковом характере сопротивлений Z( и Z2 затухание фильтра определяется по формуле
371
т. е. а>0 (четырехполюсник не имеет полосы пропускания).
Четырехполюсник обладает свойствами фильтра только в том случае, когда сопротивления Zj и Z2 имеют разные знаки, т. е.
Z, = + jxi, Z2 =+ jxz. (19-5) При этом
и, следовательно, sh—cos—= 0; (19-6)
2 2
ch—sin—=+1/^-^-.(19-7) 2 2 _ k 4x2
Уравнение (19-6) удовлетворяется при
sh-5-=O (19-8)
или
cos-^- = 0. (19-9)
Условие (19-8) соответствует полосе пропускания (п=0). В этом случае ch-^- = l и согласно (19-7)
По такому закону изменяется коэффициент фазы фильтра в полосе пропускания (xi и х2 зависят от частоты).
В свою очередь условие (19-9) соответствует полосе задерживания. В этом случае b = ±n\ sin-^-= = ±1 и на Основании (19-7)
(19-11)
По такому закону изменяется затухание фильтра в полосе задерживания. Формулы (19-10) и (19-11) справедливы для Г-образных и симметричных Т- и П-образных фильтров. При этом под а/2 и Ь/2 подразумеваются собственное затухание и коэффициент фазы каждого Г-образного звена. Т- или П-образный фильтр состоит из двух Г-образных
звеньев, и поэтому его собственное затухание и коэффициент фазы равны соответственно а и Ь.
Для любого симметричного реактивного фильтра в полосе пропускания, т. е. при а=0, выполняется условие
AiM=chg = ch (а + jb) = = ch jb — cos b.
Поскольку косинус изменяется от —1 до +1,
— 1 < Al (и) < 1-
Это условие в случае Т- или П-образного фильтра принимает вид:
— 1 <1 1
2Z2
или
2,
_ 2 < -А- < 0.
2Z2
Разделив все части неравенства на два, получим:
— 1 0. (19-12)
4Z2
Таким образом, предельные частоты, лежащие на границе полосы пропускания (так называемые ч а -стоты среза), удовлетворяют условиям:
Z1== — 4Z2;
2г = 0.
Неравенство (19-12) носит название условия- пропускания реактивного фильтра (Г-, Т- или П-образного).
Частоты среза находятся из уравнений (19-13) аналитически (если заданы функциональные выражения Zi и Zs в зависимости от частоты) или графически (если заданы частотные характеристики Zx и Z2).
На рис. 19-2,6 в виде примера показаны частотные характеристики Zi и Z2 фильтра, изображенного на рис. 19-2, а; полоса пропускания графически найдена на рис. 19-2, в.
Частоты среза могут быть также получены из рассмотрения частотной характеристики входного сопротивления фильтра, нагруженного согласованно, т. е. при помощи
(19-13)
372
Рис. 19-2. Графическое определение полосы пропускания на основании условий (19-13).
характеристического сопротивления фильтра.
В случае Т-образного фильтра характеристическое сопротивление
ZT=1/ + (19-14)
в случае П-образного фильтра
V 1+ 4Z?
Как было доказано выше, условие а=0 может быть получено только при разных знаках Zi и Z2. В этом случае
-^-<0, (19-16)
42g
а произведение ZXZ2 — действительное число.
Выражения (19-14) и (19-15) получаются действительными при
т. е. при
(19-17)
Сопоставление (19-16) и (19-17) с (19-12) показывает, что условие, при котором характеристическое сопротивление рассматриваемого фильтра имеет действительное значение, совпадает с условием пропускания фильтра. Поэтому предельные частоты полосы, соответствующей действительным значениям характеристического сопротивления, являются частотами среза.
Физически это объясняется следующим образом. В полосе частот,
при которых характеристическое сопротивление фильтра действительно, фильтр нагружен активным сопротивлением г, равным характеристическому по условиям согласованного включения.
Рассматриваемая здесь теория фильтров предполагает нагрузку фильтра согласованной, хотя в действительности согласовать нагрузку на всех частотах невозможно.
Мощность, потребляемая этой нагрузкой, является активной мощностью. Она равна:
f/2
Р2=г/^ = -А, (19-18)
Г
где 12 и U2 — действующие значения тока и напряжения на выходе фильтра.
Входное сопротивление симметричного фильтра, нагруженного согласованно, в зоне пропускания также равно г, и поэтому мощность на в!ходе фильтра равна:
P1==rZ? = _L; (19-19)
Г
здесь и Ui — действующие значения тока и напряжения на входе фильтра.
Поскольку рассматривается идеальный фильтр, т. е. фильтр, состоящий из чисто реактивных элементов, активная мощность внутри фильтра не расходуется, и поэтому Pl=P2.
На основании (19-18) и (19-19) следует, что
4 = 4; £4 = *4,
т. е. затухание равно нулю.
373
Итак, в полосе пропускания фильтр имеет активное характеристическое сопротивление. В полосе задерживания характеристическое сопротивление фильтра является реактивным.
Отсюда вытекает простой способ графического нахождения частот среза по частотным характеристикам входных сопротивлений холо-
19-3. ФИЛЬТРЫ ТИПА k
Пусть составные элементы Г-об-разного звена являются взаимно обратными двухполюсниками. Это означает, что произведение их комплексных сопротивлений во всем диапазоне частот постоянно, т. е. не зависит от частоты:
-l~Zj2Z2 = Z,Z2 = ft2, (19-21)
Рис. 19-3. Графическое определение полосы пропускания на основании условия (19-20).
стого хода (Zx) и короткого замыкания (ZK).
Характеристическое сопротивление Zc фильтра связано с Zx и ZK формулой
Ze = УГ?Х’. (19-20)
Очевидно, что Zc будет действительным числом при разных знаках Zx и ZK.
На рис. 19-3,6 показаны кривые Zx и ZK для фильтра рис. 19-3, о. После умножения Zx на ZH и извлечения корня получается кривая на рис. 19-3, в; полоса частот, в пределах которой Zc имеет действительное значение, т. е. представляет активное сопротивление, соответствует полосе пропускания фильтра.
Очевидно, что эта полоса ограничена частотами сщ и сог (рис. 19-3,6); в пределах этой полосы Zx и ZK имеют разные знаки. Вне этой полосы Zx и ZK имеют одинаковый знак и, следовательно, характеристическое сопротивление в соответствии с (19-20) имеет мнимое значение (реактивное сопротивление), показанное на рис. 19-3, в пунктиром.
Данное положение является общим для фильтров без потерь всех типов.
где k — действительное число.
Можно показать, что и произведение характеристических сопротивлений Zt и Zn того же Г-образного звена также равно k2.
Действительно, умножая (19-14) на (19-15), получаем:
^Т^П = ^1^2 =
Фильтры, удовлетворяющие условию (19-21), получили название фильтров типа k.
С учетом (19-5) и (19-21) выражения (19-10)—(19-12), (19-14) и (19-15) принимают вид:
h b v
sin—=± —=+-£-; (19-10а)
2 2х8 2Л
ch-^-= —=-^-; (19-Па)
2 2xs 2* '
1:>' 5Г>0- <1912а)
374
Рис. 19-4. Фильтр нижних частот типа k.
2С
0--II—|--0
2а
о—- Г----0
а)
Рис. 19-5. Фильтр верхних частот типа k.
Таким образом, при заданном значении k достаточно воспользоваться только одной из частотных функций Xi или х2 (представленной аналитически или графически) для определения всех прочих характеристик фильтра типа k *.
Приведенные выше формулы справедливы для Г-, Т- и П-образ-ных звеньев. Иначе говоря, при одних и тех же значениях k и xt (или х2) ширина полосы пропускания и характеристические сопротивления Г-образного фильтра получаются такими же, как и в случае Т- и П-образных фильтров.
’ В расчетах коэффициент k выбирается из условии согласования сопротивления нагрузки с характеристическим сопротивлением фильтра при определенной частоте.
Разница заключается лишь в собственном затухании и коэффициенте фазы, которые при переходе от Г-образного звена к Т- или П-об-разному звену удваиваются.
На рис. 19-4—19-7 показаны схемы фильтров нижних частот, верхних частот, полосовых и заграждающих (для Г-, Т- и П-образных звеньев).
Физическое действие таких фильтров легко объяснить тем, что на низких частотах индуктивные сопротивления малы, а емкостные велики; на высоких же частотах имеет место обратное явление — индуктивные сопротивления велики, а емкостные малы.
Поэтому, например, в фильтре нижних частот (рис. 19-4) токи ниж-
Рис. 19-7. Заграждающий фильтр типа k.
375
Таблица (9-1
Основные характеристики фильтров
Характеристика Фильтр нижних частот Фильтр верхних частот Полосовой фильтр Заграждающий фильтр
Полоса пропускания b sin — 2 при a — 0 f fc fc f F 1 “ F
Полоса задерживания . a chT b f fc Л fc f — Л IH 1 1Л
V'O! н/ 1+ ’
2Т feki + (/Fp
V + (iF)’
Zn k k k k
V'-Ш V'+Ш ]/’+— V (/O3
V 1 + (/F)2
k i/T VT 1 / — — 1 / ~ V c2 ~ у C,
f '__1_т
f
Примечание. F = ——-----------.
/ Im
гм
Таблица 19-2
Расчетные параметры фильтров
Фильтр нижних частот Фильтр верхних частот Полосовой фильтр Заграждающий фильтр
k L = Я/с k L = 4л/с k L ЬУг-Ы 4я/х/а , /=(/2-/1) 1 nfifz k 4n(/a-/j)
1 С = л/с k С = 4л/сй С - f*~fl 1 1 Са~ лй (/,-/,) 1 C1 ~ 4лй (/2 - A) r /2 /1 Co ЛЙ/1/з
/1,2 —
/1,2 —
я V LC
них частот проходят через индуктивность в нагрузку, лишь в малой степени ответвляясь в емкость.
В области же верхних частот индуктивность представляет большое сопротивление и, кроме того, ток высокой частоты, прошедший через индуктивность, замыкается в основном через емкость, представляющую для него малое сопротивление.
Аналогичные рассуждения применимы и к фильтрам верхних частот (рис. 19-5), которые благодаря емкостному характеру сопротивления продольной ветви и индуктивному характеру сопротивления поперечной ветви обусловливают большое затухание на нижних частотах и малое затухание на верхних частотах.
В свою очередь в полосовых и заграждающих фильтрах (рис. 19-6 и 19-7) проявляются частотные зависимости сопротивлений двухполюсников, состоящих из последовательно и параллельно соединенных индуктивностей и емкостей.
Частотные характеристики а, Ь, ZT и Zn рассматриваемых фильтров типа k изображены на рис. 19-8—19-11, а расчетные выражения основных характеристик и параметров фильтров сведены в табл. 19-1 и 19-2.
Как видно из расчетных выражений и характеристик (рис. 19-8 и 19-9), в пределах полосы пропускания напряжение на входе симметричного фильтра, нагруженного согласованно, опережает напряжение на выходе (Ь>0 — фильтр нижних частот) или отстает от него (6<0— фильтр верхних частот); в случае полосового фильтра (рис. 19-10) знак Ь изменяется в пределах полосы пропускания с минуса на плюс. В полосе задерживания симметричного фильтра коэффициент фазы b равен л (фильтр нижних частот) или —л (фильтр верхних частот); в случае симметричного полосового фильтра коэффициент
24—1118
377
фазы ниже полосы пропускания равен —л, а выше полосы пропускания равен л.
Выше отмечалось, что коэффициент фазы Г-образного фильтра равен Ь/2, и поэтому в полосе задерживания он равен л/2 или —л/2 в зависимости от типа фильтра.
Рис. 19-8. Частотные характеристики фильтра нижних частот типа k.
Если Г-образный фильтр нагружен согласованно, то угол фазового сдвига между напряжениями на входе и выходе составляет ~^-(Ь + + ф!с—ф2с), где Ф1С И ф2с—углы характеристических сопротивлений рассматриваемого Г-образного фильтра (§ 18-7).
В полосе задерживания характеристические ‘ сопротивления мнимые разного знака и соответственно разность углов фю—фгс составляет л или —л. В этом случае угол между входным и выходным напряжениями Г-образного фильтра, нагруженного согласованно, с учетом того, что в полосе затухания Ь/2= = ±л/2, получается равным ±л. Это соответствует физическим представлениям о фазовых сдвигах в реактивных цепях, поскольку в полосе задерживания нагрузка фильтра предполагается также реактивной.
Следует заметить, что если, например, Г-образный фильтр нижних частот согласованно нагружен со стороны выхода, имеющего характеристическое сопротивление Zn, то в полосе пропускания нагрузка фильтра, равная Zn, активна.
Можно показать, что в результате параллельного соединения ак-
Рис. 19-9. Частотные характеристики фильтра верхних частот типа k.
тивного сопротивления нагрузки (Zn) с емкостным сопротивлением поперечной ветви Г-образного звена (2Z2) получится активно-емкостное сопротивление, емкостная составляющая которого компенсирует индуктивное сопротивление продольной ветви (‘/2 Zi). В результате останется только активная составляющая, равная характеристическому сопротивлению ZT при данной частоте f.
Для определения знака характеристического сопротивления фильтра в полосе задерживания (+/ или —/) удобно пользоваться формулами табл. 19-1, в которых под корнем
378
сохранен множитель /. В полосе задерживания слагаемое, содержащее множитель /, больше единицы; поэтому при отбрасывании слагаемого 1 под корнем остается выражение с множителем / в числителе или знаменателе в зависимости от типа фильтра и от того, рассматривается ли ZT или Zn.
Преимуществом фильтров типа k является их простота, а также то, что в полосе задерживания затуха-
?Г • %л Индуктивное Активное
/%П
Емкостное
i'Zt Емкостное
Рис. 19-10. Частотные характеристики полосового фильтра типа k.
ние по мере удаления частоты от частоты среза неуклонно возрастает.
Что касается недостатков фильтров типа k, то они в основном заключаются в следующем:
1. Характеристические сопротивления ZT и Zn в полосе пропускания фильтра очень резко изменяются в зависимости от частоты, вследствие чего согласовать нагрузку с фильтром удается только в ограниченной части полосы пропускания.
2. Кривая затухания вблизи частоты среза имеет недостаточную
крутизну, вследствие чего не обеспечивается четкое разделение частот.
Для увеличения крутизны кривой затухания приходится применять многозвенный фильтр.
Рис. 19-11. Частотные характеристики заграждающего фильтра типа k.
19-4. ФИЛЬТРЫ ТИПА т
В целях наилучшего согласования нагрузки с фильтром необходимо, чтобы характеристическое сопротивление фильтра было по возможности постоянным в полосе пропускаемых частот. В связи с этим попытаемся изменить продольную или поперечную ветвь Г-образного звена типа k таким образом, чтобы получилось новое Г-образное звено с характеристическим сопротивлением, мало изменяющимся в зависимости от частоты в полосе пропускания. Второе характеристическое сопротивление этого звена должно быть равно характеристическому сопротивлению исходного звена типа k (именуемого «прототипом»).
24*
379
Равенство характеристических сопротивлений нового фильтра (так называемого фильтра типа т) и
причем
1 > m > 0.
(19-24)
прототипа позволяет включать их согласованно и образовывать, таким образом, комбинированные фильтры, сочетающие в себе преимущества фильтров обоих типов.
Подстановка (19-23) в (19-22) и
решение полученного уравнения относительно 2Z2m дают:
2Zto = —2 + A (19.25)
т 2 т
эис. 19-12 Образование последовательно-производного звена типа т.
mZf
Рис. 19-13. Образование параллельно-производного звена типа т.
Из этого выражения видно, что поперечное плечо последовательно - производного Г-образ-ного звена типа т состоит из двух последовательно включенных сопротивлений и -* ~ Z1 2тг (рис. 19-12, в).
Рассмотрим теперь второй вариант. Исходя из условия равенства характеристических сопротивлений применительно к рис. 19-13, а и б, имеем:
Ввиду того что Г-образный прототип ^имеет два характеристических сопротивления, в данном случае возможны два варианта.
1. Одинаковыми остаются характеристические сопротивления ZT (рис. 19-12). Полученное при этом звено т носит название последовательно-производного.
2. Одинаковыми остаются характеристические сопротивления Zn (рис. 19-13). В этом случае звено т носит название параллельнопроизводного.
Рассмотрим первый вариант. Из условия равенства характеристических сопротивлений ZT звеньев, изображенных на рис. 19-12, а и б, следует:
+!“-)• <19'22)
Пусть
Zlm=mZ1, (19-23)
Пусть
(19-27) m
причем сохраняется условие (19-24).
После подстановки (19-27) в (19-26) решение уравнения относительно 2/Zim дает:
— = — + — ~~ т2. (19-28) Zirn mZi Zz 2т
Следовательно, продольное плечо параллельно-производного Г-об-разного звена типа т состоит из „ mZ, 2mZ„ сопротивлении —— и-------^.соеди-
ненных параллельно (рис. 19-13,в).
В соответствии с (19-25) и (19-28) могут быть найдены выра
380
(19-34)
жения характеристических сопротивлений ZTnj (рис. 19-13) и Znm (рис. 19-12):
Z_ = Z-------1----; (19-29)
1 7 9
1 + (1-т2)Й
2Пт=2п[’+(1-^)Д]. (19-30)
Очевидным является соотношение
^m2nm = ZTZn=^. (19-31)
Полосы пропускания фильтров типа k и полученных из них фильтров типа т совпадают. Действительно, на основании (19-23) и (19-25) можно получить:
Zjm __ ____mZi________
42г« 4 / Zz Z1 1 — m2\
\ т 4 mJ
(19-32)
__ /п2
~ 4Z, '
—Ц-1-И2
то же самое выражение получается на основании (19-27) и (19-28) для другого варианта фильтра типа т.
Подставляя в (19-32) условия (19-13), отвечающие предельным частотам фильтра типа k, получаем при Zi — О и Z\ ——4 Z2:
А*. = 0;= — 1. (19-33) 4Zam 4Zam
Эти условия соответствуют предельным частотам фильтра типа т (имеющего последовательно- или параллельно-производное звено). Следовательно, частоты среза для обоих типов фильтров совпадают.
О совпадении полос пропускания прототипа и производных от него звеньев можно также судить на основании равенства характеристических сопротивлений (в полосе пропускания характеристические сопротивления имеют действительные значения).
В полосе задерживания в
соответствии с общей формулой (19-11)
Затухание обращается в бесконечность при частоте , при которой — +1—zn2=0, или, что то же, Zi
Z±==------!—. (19-35)
4Za 1—m3
При этом условии Z2m, выражае-мое формулой (19-25), обращается в нуль. Это означает, что при
наступает резонанс напряжений в поперечной ветви (в случае последовательно-производного звена). При этом же условии Zlm, выражаемое формулой (19-28), обращается в бесконечность, что означает резонанс токов в продольной ветви (в случае параллельно-производно-
го звена). Частота называется частотой бесконечно большого затухания.
При переходе частоты через значение , т. е. в области частот f>L ?когда >fc) или /<L (когда <fc), сопротивления обоих плеч фильтра Zim и Z2m имеют одинаковый знак. В этом случае в соответствии с § 19-2 в левой части формулы (19-34) гиперболический косинус должен быть заменен ги
Рис. 19-14. Кривые затухания фильтра типа т.
При 4Z2/Z(, стремящемся к ну-
лю,
sh — т (19-36) 2 V\ — т2
381
На рис. 19-14 показано семейство
(^Зля филыпраич или-^ для фи литра вч)
Рис. 19-15. Характеристическое сопротивление фильтра типа т.
Рис. 19-16. Фильтр нижних частот типа т.
При т=1 кривая затухания обращается Бихарактеристику фильтра типа k.
Чем меньше коэффициент т, тем меньше значение fm , т. е. тем круче кривая затухания а. Однако, как 382
видно иа рис. 19-14, предельное зна- _
Z1
чение а при — со уменьшается 4Za
по мере снижения т.
Наряду с большой крутизной кривой затухания фильтры типа т отличаются от фильтров типа k от-
Рис. 19-17. Фильтр верхних частот типа т.
носительно большим постоянством характеристических сопротивлений ^тт или ^пт (по сравнению с частотными характеристиками ZT и Zn)-
На рис. 19-15 изображены кривые Z^lk и соответственно --------
Znm
в зависимости от величины 1 / 1^11
И l4Za|* равной fife для фильтров нижних частот и fdf для фильтров верхних частот.
В спектре частот, соответствующем 1/ |.?l| = 0-j-0,9, характе-
V |4Za|
ристические сопротивления ZTm и Znm отклоняются от величины k на ±5% при т=0,59 и на ±10% при zn=0,54.
Типовые схемы Г-образных звеньев фильтров нижних частот, верхних частот и полосовых фильтров типа k и т приведены на рис. 19-16—19-18. Частотные характеристики фильтров типа т показаны на рис. 19-19—19-21.
Как видно из частотных характеристик, фильтры типа т имеют более постоянную величину характеристического сопротивления в полосе пропускания, чем фильтры типа k. Кроме того, они обладают большей крутизной кривой затухания.
Недостатком фильтров типа т является снижение затухания при f<fx (фильтры верхних частот и полосовые) и при f>f„ (фильтры нижних частот и полосовые).
Соединяя последовательно звенья фильтров типов k и т, мож-
Lr
Рис. 19-18. Полосовой фильтр типа т.
же или выше частоты бесконечно большого затухания. На рис. 19-22,а в виде примера показан полосовой фильтр, состоящий из Т-образного фильтра типа k (в середине) и двух Г-образных звеньев типа т (по концам). На рис. 19-22,6 изображена характеристика затухания такого фильтра.
Пример 19-1. Требуется рассчитать фильтр иижинх частот, составленный из звеньев типа k и т. Дано: Л=500 ом, частота среза (о = 1000 гц, частоты бесконечного затухания f« = = 1 065 и I 250 гц.
Параметры прототипа (фильтра типа k) k 50° nfc n-1 000 = 0,159 гн;
C= nfck = n-1 000-500 = = 0,636 мкф.
Рис. 19-19. Частотные характеристики фильтра нижннх частот типа т.
На рис. 19-23,а показано Т-образиое звено типа k с индуктивностями L/2 в продольных плечах. Постоянная т фильтра, имеющего частоту бесконечного затухания 1065 гц. находится иа основании (19-35). С учетом того, что
уравнение (19-35) приобретает вид:
Рис. 19-20. Частотные характеристики фильтра верхних частот типа т.
откуда
= "И1 —0,882 = 0,343.
Параметры Т-образного фильтра типа т:
mL 0,343-0,159
2 ~ 2
0,0273 гк
1 — т2
4т
1 —0,118
1,372
•0,159 = 0,102 гн;
но достигнуть некоторого постоянства характеристических сопротивлений и крутизны кривой затухания при одновременном сохранении необходимой величины затухания ни-
тС ~ 0,343-0,636 = 0,218 мкф.
Г-образиые звенья типа т с частотой бесконечного затухания 1 250 гц, включав-
383
мые по концам фильтра, имеют параметры:
тС
2
0,6-0,636
2
= 0,191 мкф.
Суммируя индуктивности, соединенные на рис. 19-Й, а последовательно, получим окончательную схему на рис. 19-Й, б.
На рнс. 19-23, в изображена частотная характеристика данного фильтра, снятая
ь
Рис. 19-21. Частотные
h
О
I\f1 »./_ f I/
Л
экспериментально (при добротности индуктивных катушек Q=40).
19-5. ИНДУКТИВНО СВЯЗАННЫЕ
КОНТУРЫ КАК ФИЛЬТРУЮЩАЯ СИСТЕМА
Индуктивно связанные контуры при соответствующем подборе пара-
I метРов представляют полосовой fz । < фильтр, пропускающий заданную if по-
а-
0-
Zna;-*-
II
характеристики лосового фильтра типа т.
0
%Пт
полосу частот. Положим, что в первичную и вторичную цепи трансформатора включены емкости С (рис. 19-24, а).
Индуктивности обмоток трансформатора примем равными L; коэффициент индуктивной связи обозначим через k0.
Трансформатор с емкостями С представляет собой симметричный
Рис. 19-22. Комбинированный фильтр.
° — схема; б — характеристика затухания.
четырехполюсник, эквивалентная схема которого показана на рис. 19-24, б. Выше мы уже встречались с аналогичной схемой полосового фильтра (рис. 19-2). Исследуем теперь более подробно фильтрующие свойства рассматриваемого четырехполюсника в предположении, что он нагружен согласованно. Его ха-
рактеристическое сопротивление может быть вычислено по формуле
0,079гн 0}027?н0,027гн 0,(№7гн
Q126fff 0,106?» 0,074гн
Рис. 19-23. Пример 19-1.
о. б — схема фильтра; в — кри« вая затухания (эксперимент тальная).
6}
384
(19-14), куда следуетподставить:
Zx=/2 [<o(L —(И)—Ц; I соС J
Z2=ja>M.
После преобразования получим:
Zc = -ly-^QL+A^-llx"
X [юаС (L — ТИ) — 1] .
Приняв Юо = 1/LC и введя коэффициент индуктивной связи k0— =M/L, получим окончательно:
2с = 41/ -[(—yaw-i]x соС У [\<оо )
хГ(—Га-Ло)-1].
1\“в / j
Характеристическое сопротивление Zc действительно при условии, что выражения в квадратных скобках имеют разные знаки, а именно: p_y(l+fto)_l>0;
\ ^0 /
£)2(1-feo)~1<0’ откуда
<0р < и < M°
Vl + Ao Kl -Ао ’
COq G>o
®i — ___> <i)2_____ >
Vl+Ao Vl-Ao
g>i и <o2 представляют собой частоты среза полосового фильтра.
t-м с
С L-M
0—II
б)
Рис. 19-24. Фильтрующая систе-
ма.
а — индуктивно связанные резонансные контуры; б — схема замещения.
В области частот ниже он характеристическое сопротивление фильтра емкостное и с уменьшением частоты приближается к — / .
В области частот выше со2 характеристическое сопротивление фильтра индуктивное и с увеличением ча-стоты приближается к jaL]/^ 1
—^о-
1 7 —
При частоте <о—<оо— —
У LC
= — /2(оо М
и
Zc=(oflAl=
knL
На рис. 19-25 показаны частотные характеристики фильтра.
Рис. 19-25. Частотные характеристики индуктивно связанных резонансных контуров.
19-6. МОСТОВЫЕ ФИЛЬТРЫ, ПЬЕЗОЭЛЕКТРИЧЕСКИЕ РЕЗОНАТОРЫ
Согласно § 18-15 (18-50) характеристическое сопротивление и мера передачи симметричного мостового фильтра (рис. 19-26) находятся по формулам:
ZM ~ ;
Полоса пропускания фильтра (а=0) имеет место при мнимых
385
значениях корня V Zi/Z2 и дейст-вительных значениях корня КZjZj. При этом Zi и Zj имеют разные знаки.
Коэффициент фазы определяется в этом случае по формуле
(19-38)
Рис. 19-26. Мостовой фильтр.
В полосе задерживания Zi и Z2 имеют одинаковые знаки. В этой полосе возможны два случая:
Ь=0 или Ь= + л.
На рис. 19-27 показаны простейшие схемы мостовых фильтров нижних частот (а), верхних частот (б), полосового фильтра (в) и заграждающего фильтра (г).
Основываясь на том, что в полосе пропускания Zt и Z2 имеют разные знаки, а в точке пересечения кривых Zi и Z2, т. е. при Zj = Z2, а = <х>, можно легко найти частоты среза и бесконечно большого затухания. В виде примера это показано применительно к фильтру нижних частот на рис. 19-28. При отсутствии пересечения Zi с Z2 частота бесконечно большого затухания отсутствует или удалена в бесконечность (при асимптотическом приближении Zi к Z2).
На практике применяются также мостовые схемы с дифференциальным трансформатором (дифференциально-мостовые схемы), эквивалентные по своим электрическим
Рис. 19-27, Мостовой фильтр нижних частот (а), верхних частот (б), полосовой (в), заграждающий (а).
В первом случае
Это решение соответствует условию |Z1|<|Z2|, так как гиперболический тангенс не может превышать единицы. Во втором случае
th -£- == cth -£- «= 2 2
Данное решение соответствует условию | Zj | > | Z21, так как гипер-
болический котангенс не может
быть меньше единицы.
При Zi = Z2 затухание а=со, так как при этом th — = 1 и напряжение
на выходе мостовой схемы равно нулю. Физически это объясняется тем, что мост уравновешен.
качествам мостовым схемам, но имеющие меньшее число элементов (рис. 19-29).
Рис. 19-28. Нахождение частоты среза и частоты бесконечно большого затухания мостового фильтра.
Следует заметить, что в соответствии с (19-37) ZM зависит от произведения, a g — от отношения сопротивлений плеч мостового фильтра. Поэтому характеристические па
386
раметры Zu и g мостового фильтра не связаны друг с другом в той мере, как это, например, имеет место в Т- и П-образных фильтрах (задача 19-16), и, следовательно,
г,л'/г
гл
0 0.
гг,
2г/г
Рис. 19-29. Диффереициально-мостовые схемы.
Рис. 19-30 Пьезометрический резонатор.
а — эквивалентная схема; б — частотная характеристика реактивного элемента.
ZM и g могут выбираться независимо друг от друга. Это свойство является одним из преимуществ мостовых фильтров по сравнению с другими.
Мостовые фильтры часто выполняются с помощью пьезоэлектрических резонаторов. Последние представляют собой электромеханическую систему, состоящую из пьезоэлектрической пластинки *, электродов и держателя. Пьезоэлектрическая пластинка под воздействием переменного электрического поля совершает механические колебания с частотой приложенного напряжения. При этом на ее поверхностях возникают электрические заряды. При совпадении частоты поля с частотой собственных колебаний пластинки наступает резонанс: амп-
1 В технике связи применяются преимущественно кварцевые пластинки.
литуда колебаний и соответственно величина зарядов на пластинке достигают максимума.
Эквивалентная электрическая схема пьезоэлектрического резонатора представляет собой двухполюсник (рис. 19-30,а). Частотная характеристика реактивного сопро-0 тивления резонатора изображена на рис. 19-30,6.
В отличие от индуктивных катушек, добротность которых в лучшем я случае измеряется сотнями единиц, добротность пьезоэлектрических резонаторов достигает десятков ты-
сяч.
С помощью таких резонаторов удается получить полосовые фильтры с весьма узкой полосой пропускания и высокой крутизной кривой затухания вблизи частот среза (кварцевые мостовые фильтры допускают полосу пропускания порядка 20—50 периодов при частоте 500 кгц).
Емкость С2, входящая в схему замещения пьезоэлектрического резонатора (рис. 19-30,а), значительно превышает емкость С\\ поэтому частоты ст и о>2 (рис. 19-30,6) располагаются весьма близко друг к другу.
19-7. БЕЗЫНДУКЦИОННЫЕ ФИЛЬТРЫ
Изготовление индукционных катушек для фильтров, работающих в области низких частот, сопряжено с трудностями, особенно когда катушки должны иметь большую индуктивность при высоком коэффициенте добротности. Увеличение сечения обмотки повышает вес, размеры и стоимость катушки, применение же ферромагнитного сердечника создает зависимость индуктивности от величины тока, проходящего по обмотке.
Применение пьезокварцевых резонаторов для фильтров низких частот также не всегда возможно, так как самая низкая частота, на которую изготовляется кварц, составляет несколько сотен герц.
Во избежание получения громоздких фильтров с низкой добротностью катушек применяют безындукционные фильтры
387
(rC-фильтры), состоящие из активных сопротивлений и емкостей.
На рис. 19-31 показан гС-фильтр нижних частот. При низких частотах, когда емкостное сопротивление велико, напряжение на выходе
Итак, в отличие от реактивных фильтров, рассмотренных в предыдущих параграфах, гС-фильтр не имеет области частот, в пределах которой собственное затухание а равно нулю.
Рис. 19-31. гС-фильтр иижиих частот.
Рис. 19-32. гС-фильтр верхних частот.
фильтра немногим меньше напряжения на его входе и, следовательно, затухание мало. С повышением частоты емкостное сопротивление убывает, напряжение на выходе уменьшается и, следовательно, затухание возрастает.
На рис. 19-31, в показана частотная характеристика собственного затухания такого фильтра. Ввиду малой крутизны кривой затухания однозвенного rC-фильтра применяют двух- или трехзвенный фильтр, однако при этом увеличивается затухание и в полосе пропускания.
На основании (19-1)
ch g=ch (aj- jb)=ch a cos b-f-
-f-/she sin 6=1+/ откуда
chacos6=l; sh asin6=^4 (19-39) 2
При постоянном токе (co = 0)
ch a cos 6=1; sh a sin 6=0. (19-40) Эти равенства удовлетворяются при <2 = 0 и b = 0 одновременно.
При значениях ш>0 >0 и
sin6>0, так как sha>0.
388
Частотные характеристики гС-фильтра нижних частот могут быть построены по выражениям для а и Ь, которые получаются в результате совместного решения уравнений (19-39), первое из которых можно представить в следующем виде:
(1+sh2 а)(1 — sin26)= 1.
Подставляя сюда выражение для sin b, получаемое из второго уравнения (19-39), приходим к биквадратному уравнению
, . /<огС\2 ,, /<огС\2 „
sh4a— -----1 sh2a — l----] = 0,
\ 2 / V 2 }
откуда
(19-41)
При значениях со, при которых __________________________
, 1 / (йгС
sh а ~ а ~ 1 / --- .
V 2
За частоту среза гС-фильтра нижних частот условно принимается
частота, при которой равны активное и емкостное сопротивления ветвей Г-образного звена, т. е.
При значениях со, при которых
—!—< 1,
2согС
т
2
2
--- ИЛИ сос С
а>сгС
4~
shtz^tz
1
2а> rC
В этом случае выражение (19-41) дает sha=2,2, откуда а =1,53 неп.
На рис. 19-32 представлен гС-фильтр верхних частот с примерной частотной характеристикой затухания.
При низких частотах, когда емкостное сопротивление велико, напряжение на выходе фильтра мало, т. е. получается большое затухание (при постоянном токе — бесконечно большое). С увеличени- .__>|
ем частоты емкостное сопро-тивление уменьшается и напряжение на выходе возрастает, т. е. затухание убывает. Ча- 0— стотная характеристика собственного затухания такого фильтра показана на рис. 19-32, в.
Если за частоту среза условно принять частоту, при которой сопротивления ветвей Г-образного звена равны друг другу
„ 1 1 ,
2г. —---- или ------= 1,
2сос С 4®с гС
то на основании (19-43) будем иметь:
sha=2,2; а 1,53 неп.
Рис. 19-33. Полосовой rC-фильтр.
Для повышения крутизны кривой затухания применяют несколько звеньев, однако при этом неизбежно увеличивается затухание и в полосе пропускания.
Пользуясь формулой (19-1), получаем в рассматриваемом случае: ch a cos 6=1;
sh a sin b ----. (19-42)
2rcoC
При бесконечно большой частоте (<о— оо) получаются условия (19-40), которые, как было установлено выше, выполняются, если одновременно а и b равны нулю.
При значениях 0<ш< оо shasin6<0; поскольку а>0, то 6<0.
Совместное решение уравнений (19-42) приводит к биквадратному уравнению
Простейшие схемы полосового и заграждающего rC-фильтров и примерные частотные характеристики затухания приведены на рис. 19-33 и 19-34.
Рис. 19-34. Заграждающий гС-фильтр.
sh4a—
--------sh’a (2<orC)2
(2<orC)2
откуда
sh а=
_L_ + _L_
8(игС)2 2<огС
1
--------. (19-43)
(4<1>гС)2 '
Полосовой rC-фильтр основан на том, что емкость первого звена обусловливает затухание более низких частот, а емкость второго звена — затухание более высоких частот.
389
Средняя частота полосы пропускания, при которой собственное затухание фильтра минимально (рис. 19-33, б), ориентировочно равна:
f0as--
2 л г С £
При Г1«=Г2“Г И С|"“С2“»С f ~ 1 '° 2л гС
Как видно из рис. 19-34, а, заграждающий rC-фильтр состоит из двух параллельно соединенных Т-образных rC-фильтров верхних и нижних частот. Соответствующим подбором параметров элементов можно добиться того, что при определенной частоте токи на выходе обеих Т-образных схем будут равны по величине и противоположны по знаку, вследствие чего ток в нагрузке будет равен нулю. Следовательно, затухание на этой частоте будет бесконечно большим (рис. 19-34,6).
rC-фильтры часто применяются в сочетании с усилителем. В этом случае в полосе пропускания не только отсутствует затухание, но, наоборот, имеет место усиление.
19-8. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
19-1. Рассчитать фильтр нижних частот с частотой среза 1 000 гц и характеристическим сопротивлением 100 ом при нулевой частоте.
Ответ: 4=31,8 мгн-, С=3,18 мкф.
19-2. Задан Т-образный фильтр инжних частот, состоящий из двух индуктивностей, каждая из которых равна 0,1 мгн, и емкости 2 мкф. Определить частоту среза и построить график характеристического сопротивления. ___________
Ответ: е>0 = 105; /1 = 10^ 1—со2 -10~10.
19-3. Задай П-образиый фильтр нижних частот, состоящий из индуктивности 0,2 мгн и двух емкостей по 1 мкф каждая. Определить частоту среза и построить график характеристического сопротивления.
10
Ответ; <ас = 105; Zn ——. ~~ ~ .
- <->’• Ю-10
19-4. Пользуясь результатом решения задачи 18-1, доказать, что в случае Т- или П-образного фильтра нижних частот (рис. 19-4), нагруженного согласованно, пе-
редаточная функция по напряжению имеет вид:
19-5. Основываясь на предыдущей задаче, показать, что в полосе пропускания коэффициент передачи по напряжению равен единице.
19-6. Два Г-образных фильтра верхних частот, каждый из которых состоит из емкости 1 мкф и индуктивности 10 мгн, образуют Т-образиый фильтр. Вычислить для Т-образного фильтра частоту среза fD, характеристическое сопротивление и собственное затухание при 2fo; характеристическое сопротивление и коэффициент фазы при 0,5 fо.
19-7. Два Г-образных фильтра верхних частот, указанные в предыдущей задаче, образуют П-образный фильтр. Вычислить для П-образного фильтра то же, что в задаче 19-6.
19-8. Пояснить, исследуя формулы для симметричного фильтра без потерь, почему в полосе пропускания фильтра его характеристическое сопротивление — активное, а в полосе задерживания — реактивное.
19-9. Как определить характеристические сопротивления несимметричного фильтра по данным опытов холостого хода и короткого замыкания?
19-10. Как иайти полосу пропускания фильтра по заданной частотной зависимости его характеристического сопротивления?
19-11. Пояснить физическую сущность коэффициента фазы фильтра.
19-12. Как определяется в полосе пропускания и в полосе задерживания угол фазового сдвига между напряжениями на входе и выходе Г-образиого фильтра, нагруженного согласованно?
19-13. Начертить схему последовательно-производного и параллельно-производного звеньев заграждающего фильтра_типа т.
19-14. На примерах схем реактивных мостовых фильтров, показанных иа рис. 19-26, убедиться в том, что при разных знаках Z\ и Z2 появляются полосы пропускания.
19-15. Доказать, что в полосе пропускания реактивного мостового фильтра вы-
Zi
полняется условие —1 < —------— <0, что
Z2*-Zi
Zi
равносильно условию—оо< —<0. Пояс-Z2
нить физический смысл последнего условия.
19-16. Вывести для фильтров типа k зависимости
ZT=fcch-^- и 2П—------
2 rh-£-
-cbT
19-17. Пояснить с помощью табл. 19-1 построение частотных характеристик фильтров типа k (рнс. 19-8—19-11).
390
Глава двадцатая
СИНТЕЗ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
20-1. ХАРАКТЕРИСТИКА ЗАДАЧ СИНТЕЗА
При проектировании различного рода устройств автоматического управления, каналов электропроводной и радиосвязи и т. п. возникает необходимость подбора схем и параметров электрических цепей, отвечающих определенным требованиям. Нахождение схемы и элементов цепи, удовлетворяющих заданным условиям, составляет задачу синтеза электрической цепи.
Ввиду того что установившийся и переходный процессы во всякой линейной электрической цепи зависят от частотных свойств цепи, задача синтеза обычно сводится к нахождению цепи по заданной частотной характеристике. Искомым может быть двухполюсник с заданной зависимостью сопротивления (или проводимости) от частоты либо четырехполюсник с заданной передаточной функцией или частотной зависимостью его параметров. Построение схемы пассивной цепи по заданной частотной функции принято называть реализацией или осуществлением функции.
В отличие от задачи анализа, в которой искомая величина — реакция цепи на приложенное воздействие получается однозначно, задача синтеза может иметь несколько решений (или вовсе не иметь решения)- Заданная частотная функция считается реализуемой или осуществимой, если соответствующая ей электрическая цепь может быть составлена из сопротивлений, индуктивностей и емкостей (возможно также применение трансформаторов).
Поскольку задача синтеза может иметь несколько решений, возникает необходимость сопоставления полученных вариантов и выбора оптимального решения.
В этом вопросе не имеется впол
не определенного критерия, так как приходится сравнивать схемы с разнородными элементами. При этом обычно руководствуются следующими соображениями. Желательны схемы с наименьшим количеством элементов, имеющих практически приемлемые параметры, причем предпочтение следует отдавать схемам, содержащим простейшие элементы — сопротивления и емкости.
Индуктивность — менее желательный элемент цепи. Если в схеме последовательно включены индуктивность и сопротивление, то оии могут быть практически выполнены в виде индуктивной катушки. Однако при этом приходится считаться с витковой емкостью, которая может внести в работу цепи искажения при высоких частотах.
Еще менее желательным элементом схемы является трансформатор, практическое осуществление которого сопряжено с появлением тепловых потерь и межвитковых емкостей. Кроме того, коэффициент связи может не совпадать с расчетным.
В задачах синтеза частотные характеристики сопротивлений, проводимостей или передаточных функций могут быть заданы графически или аналитически. Если характеристика задана графически или не является рациональной функцией, то она приближенно аппроксимируется рациональной функцией, т. е. отношением двух полиномов, которое по определенным правилам синтеза реализуется в виде двухполюсника или четырехполюсника.
Таким образом, первым этапом в задаче синтеза является аппроксимация заданной частотной характеристики рациональной функцией; этот этап, относящийся к области математики, здесь не рассматривается. Второй этап заключается в реализации рациональной функции, что и составляет основное содержание данной главы.
391
20-2. ИССЛЕДОВАНИЕ ДВУХПОЛЮСНИКА ПРИ КОМПЛЕКСНОЙ частоте
При исследовании переходных процессов в линейных электрических цепях мы пользовались понятиями комплексной частоты p=c-j-+/W и обобщенного сопротивления Z(p). Если Z(/®) представляет собой комплексное сопротивление цепи, то обобщенное сопротивление получается заменой /со через р-
Расположение нулей и полюсов Z(p) на комплексной плоскости характеризует частотные свойства линейной электрической цепи, от которых в свою очередь зависят установившийся и переходный процессы в данной цепи.
Нули функции Z(p) двухполюсника являются корнями характеристического уравнения (гл. 13). Они могут быть любыми числами, но обязательно с отрицательной действительной частью, так как эта часть физически определяет затухание свободных токов в данной цепи. Это условие распространяется также на нули функции Z (р) дуального двухполюсника, которая равна функции У (р) исходного двухполюсника, где У(р) = 1/Z(p). Но нули функции У (р) есть в то же время полюсы функции Z(p). Поэтому полюсы Z(p), так же как и нули, располагаются в левой части комплексной плоскости.
В общем случае, пользуясь комплексной частотой р, можно представить обобщенное сопротивление Z(p), как отношение двух полиномов, которые не имеют общих корней:
Z(p) = fl" р"+а"-г РП~‘+- ‘ -+а1Р+ао bm Pm+bm-l Pm~I-l-------Ь\р+6о
(20-1)
Таким образом Z(p) является рациональной функцией р. Обозначив через pi, рз, .... Ргп~1 корни числителя (число их равно степени полинома п) и через рг, р^ .... Ргш корни знаменателя (число их равно степени полинома т), разложим числитель и знаменатель на множители:
ZW= (20.2)
(Р — Ра) (Р — Р«)- ”(Р — Рат)’
здесь Н=ап1Ьт—постоянный множитель (действительное число);
Р2й—1— нули функции
2(р);
р2А — полюсы функции Z(P).
Коэффициенты полиномов в числителе и знаменателе (20-1) должны быть положительными и действительными, так как только в этом случае корни этих полиномов, соответствующие нулям и полюсам функции Z(p), как уже было отмечено выше, располагаются в левой полуплоскости. Следует заметить, что если некоторые нули полинома расположены на мнимой оси, то в полиноме могут отсутствовать некоторые степени р. Когда все нули лежат на мнимой оси, полином имеет только четные или только нечетные степени р-
В § 20-3 будет показано, что кратные нули и полюсы Z(p) могут быть в левой полуплоскости, исключая мнимую ось; нули и полюсы на мнимой оси могут быть только простыми, т. е. однократными.
Степени полиномов в числителе и знаменателе (20-1) различаются не более чем на единицу. Только при таком условии нуль и полюс в бесконечности простые.
В случае реактивных, двухполюсников полиномы могут содержать только четные или только нечетные степени р, при этом Z(p) представляется в виде отношения полиномов, один из которых содержит четные, а другой — нечетные степени р. Это положение доказано ниже в § 20-4.
В общем случае при наличии потерь полиномы содержат как четные, так и нечетные степени р.
Выражение (20-2) может быть переписано в показательной форме. Обозначив через и azh-i модуль и аргумент бинома (р—Ргй-i), а через Л42й и агь модуль и аргумент бинома (р—р2й), получим:
Z(p) = ' *^2п—1^а2и—1
392
или
^мгм3-..м2п-1 _
Л12 Mf • -мгт
, , , , х (20-3)
а~~ (®1+аз+ * ' ’ ~Ьа2п—l)
—(о2+а4+ ••+а2т).
Следовательно, для выбранного значения р модуль функции Z(p), определяется отношением произведения модулей (р—P2h-i) к произведению модулей (р—р2й); аргумент функции Z(p') определяется разностью двух сумм: суммы аргументов (р—P2k-i) и суммы аргументов (P—P2k).
При исследовании частотных свойств двухполюсника в установившемся режиме текущая переменная р берется на мнимой оси (р=/ш).
Если у двухполюсников, имеющих разные структуры, нули и соответственно полюсы функции Z(p) совпадают, а множители Н одинаковы, то такие двухполюсники эквивалентны: их частотные характеристики одинаковы.
По расположению нулей функции Z(p) можно судить о наличии или отсутствии потерь электрической энергии в двухполюснике. Чем ближе расположены комплексные нули функции к мнимой оси, тем меньше при прочих равных условиях потери.
В случае, когда двухполюсник состоит только из реактивных элементов, т. е. если потери электрической энергии в нем отсутствуют, аргумент сопротивления составляет ±90° В соответствии с (20-3) прямой угол возможен только при том условии, что все нули и полюсы лежат на мнимой оси. При этом общее число нулей и полюсов нечетно (числа нулей и полюсов разнятся на единицу); следовательно, в начале координат (т. е. в точке р=0) должен находиться нуль или полюс.
Нули или полюсы должны обязательно чередоваться. Если бы за нулем следовал нуль или за полюсом — полюс, то в соответствии с (20-3) при некоторых частотах угол был бы равен ±180°, что противоречило бы исходному условию, что на заАимах реактивного двухполюсника фазовый угол между напря-
жением и током не превышает 90°.
Таким образом, для реактивных двухполюсников характерным является расположение нулей и полюсов, показанное на рис. 20-1.
Рис 20-1. Расположение нулей и полюсов Z(p) в случае реактивного двухполюсника.
В случае, когда двухполюсник состоит из элементов г, L или г. С, нули и полюсы Z(p) располагаются по действительной оси (в левой полуплоскости) . Аргумент комплексного сопротивления такого двухполюсника не достигает ±90°; поэтому нули и полюсы должны быть простыми и должны чередоваться. Числа нулей и полюсов могут разниться не более чем на единицу.
При частоте, равной нулю, сопротивление двухполюсника типа г, L в зависимости от его структуры равно нулю или имеет действительное значение. Поэтому нуль Z(p)
25—1118
393
такого двухполюсника либо совпадает с началом координат (рис. 20-2, а), либо смещен влево по действительной оси (рис. 20-2,6); при этом ближайшим к началу координат является нуль, а не полюс. При бесконечной частоте сопротивление
Рис. 20-2. Расположение нулей и полюсов Z(p) в случае двухполюсников г, L (а, б) и г, С (в, г).
двухполюсника типа г, L действительно или бесконечно велико.
Что касается сопротивления двухполюсника типа г, С, то при частоте, равной нулю, оно имеет действительное значение (рис. 20-2, в) или бесконечно велико (рис- 20-2,а).
Ближайшим к началу координат является полюс, а не нуль. При бесконечной частоте сопротивление обращается в нуль или действительное число.
Поменяв местами нули и полюсы Z(p), получим картину расположения нулей и полюсов У(р).
Следует заметить, что при наличии потерь, когда нули и полюсы функции являются действительными или комплексными величинами, сопротивление и проводимость не могут принимать нулевые или бесконечно большие значения при частотах, лежащих на мнимой оси. Однако при частоте, соответствую
щей проекции полюса ри на мнимую ось, т. е. при частоте, соответствующей мнимой части полюса, когда модуль разности /ш—р* снижается до минимума, абсолютное значение исследуемой функции проходит через максимум, а при частоте, соответствующей проекции нуля на мнимую ось, оно проходит через минимум. Чем меньше действительные части полюсов и нулей, тем резче выражаются максимумы и минимумы функции.
Симметричное расположение нулей и полюсов относительно действительной оси, обязательное для всех линейных двухполюсников, свидетельствует на основании (20-3) о том, что модули функции 2(/ы) и Y(jco) четны относительно ш, так как все модули в (20-3) для и —одинаковы, а аргументы их нечетны относительно ш.
Итак, по расположению на комплексной плоскости нулей и полюсов обобщенного сопротивления Z (р) можно судить как о характере самой цепи, так и о ее частотных свойствах.
20-3. СОПРОТИВЛЕНИЕ И ПРОВОДИМОСТЬ КАК ПОЛОЖИТЕЛЬНАЯ ДЕЙСТВИТЕЛЬНАЯ функция
Функция Z(p) комплексного переменного р называется положительной действительной функцией, если она удовлетворяет двум требованиям:
1) комплексным числам р в правой полуплоскости соответствуют значения Z(p), расположенные также в правой полуплоскости, т. е. действительная часть функции Z(p) при положительных действительных частях р положительна (отсюда название «положительная» функция);
2) функция Z(p) действительна при действительных значениях р (отсюда название «действительная» функция).
Убедимся теперь в том, что обобщенное сопротивление двухполюсника Z(p), представляющее собой рациональную функцию вида (20-1), удовлетворяет указанным .двум условиям.
394
В самом деле, поскольку полюсы Z(p) могут находиться лишь в левой полуплоскости или на мнимой оси, Z(p) аналитична в правой полуплоскости. Кроме того, при любой частоте ю средняя мощность, поступающая в пассивную цепь, не отрицательна:
P=Re [Z(/<o)] /2>0.
Так как /2>0, то действительная часть комплексного сопротивления не отрицательна:
Re > 0. (20-4)
На основании принципа максимума и минимума модуля следует, что наибольшие и наименьшие значения действительной части функции Z(p), аналитичной в правой полуплоскости, достигаются только в граничных точках области. В данном случае границей области является мнимая ось, где Z (р) принимает значения Z(jcd).
Следовательно, с учетом (20-4)
Re [Z(p)] >0 при Rep>0. (20-5)
Если на мнимой оси расположены полюсы, то они могут быть обойдены дугами окружностей сколь угодно малого радиуса и предыдущие рассуждения могут быть отнесены к оставшейся части.
Итак, согласно (20-5) для Z(p) выполняется первое условие: Z (р) — положительная функция.
Ввиду того чго все коэффициенты полиномов в (20-1) действительны, функция Z(p) принимает действительные значения при действительном аргументе. Следовательно, выполняется и второе условие: Z (р) — действительная функция.
Таким образом, обобщенное сопротивление любого пассивного двухполюсника представляет собой положительную действительную функцию.
Обобщенная проводимость пассивного двухполюсника также является положительной действительной функцией. В этом легко убедиться, приняв Z(p) —r(c, tt>)-f-. J-/x(c, w), где p—c-\-jo).
Очевидно,
Y (р) = -1- = —1— = ~
Z(p) r+jx
В правой полуплоскости г>0 и —-— >0; при этом действитель-r2-J-x2
ным значениям р соответствуют действительные значения У(д).
Таким образом, У(р) удовлетворяет требованиям,, предъявляемым к положительным действительным функциям.
Если обобщенное сопротивление (или проводимость) двухполюсника задано в виде рациональной дроби (20-1), то построение соответствующей схемы двухполюсника может быть выполнено по определенным правилам, основанным на общих свойствах положительных действительных функций.
Рассмотрим некоторые из этих свойств.
1. Если на мнимой оси имеются полюсы или нули, то все они простые, причем вычеты в полюсах и производные в нулях действительны и положительны.
Допустим, что функция Z (р) имеет m-кратный полюс в точке р=/<оО- Разложение Лорана в окрестности полюса записывается в виде
m с—(m—1) _ _
(р — !<й0)т~1
ck(p—
Р — /И0 2-J
л=о
В достаточно малой окрестности точки р=/о>о поведение функции Z(p) определяется первым членом разложения
с—т
Z[.P) (Р-Ыт
Пусть с_т=Де?8 и р—/о>о=ре^ф, где р>0 — сколько угодно малая величина (рнс. 20-3).
Для действительной части функции Z (р) получается выражение
ReZ(p)«Re-4- е^т^ Р
А
==-^-соз(тф —0). р
При обходе вокруг /о>о по окружности радиусом р угол ф изменяется от 0 до 2л, значение же 0 сохраняется неизменным.
Знак действительной части функции определяется в этом случае знаком cos (тф—0), который при обходе т-крат-ного полюса изменяется 2т раз.
Если Z(p)— положительная функция, то действительная часть ее в правой полуплоскости положительна и не меняет знака. Следовательно, полюс, расположенный
25*
395
на мнимой осн, должен быть простым (т=1), причем угол 0 должен быть равен нулю, а величина A = C-t должна быть положительной; только при этих условиях
с.
Re Z (р) ----- cos гр сохраняет положнтель-
Р
ный знак в правой полуплоскости р, где —л/2<гр<л/2; здесь с_[ — вычет функции Z (р) в точке p=jioo.
?ис. 20-3. Полюс на мнимой оси.
Y (р) = 1/Z (р) — положн-
Поскольку тельная действительная функция, то указанное выше свойство распространяется и на У(р), а именно если иа мнимой оси имеются полюсы функции У(р), то они простые и вычеты в этих полюсах действительны и положительны. Но простой полюс функции У(р) есть простой нуль функции Z(p), а вычет функции У(р) в простом полюсе обратен производной dZ(pj/dp в нуле функции Z(p).
Следовательно, на мнимой осн нули могут быть только простыми, причем производные в них действительны и положи
тельны.
2. Нули и соответственно полюсы рациональной положительной действительной функции могут быть действительными или сопряженно-комплексными.
Данное положение следует нз того, что рациональная функция (20-1) является положительной действительной функцией только в том случае, если все коэффициенты полиномов в числителе и знаменателе действительны и одинакового знака. Замена комплексного аргумента р сопряженной величиной р дает прн таком условии сопряженную функцию Z(p)=Z(p). Поэтому если Ро—комплексный нуль функции Z(p), то наряду с равенством Z(po)=O обязательно должно выполняться равенство Z(Po)=-Z(po)=O; иначе говоря, р0 также является нулем функции Z(p).
То же положение распространяется на нули функции У (р) = 1/Z (р), т. е. на полюсы функции Z(p).
На основании сказанного комплексные нули и соответственно полюсы Z (р) и У(р) располагаются симметрично относительно действительной осн, т. е. образуют сопряженные пары.
3. Наибольшие и соответственно наименьшие показатели степеней р в числителе и знаменателе рациональной положительной действительной функции не могут различаться более чем на единицу.
С ростом (р) функция (20-1) или, что то же, (20-2) стремится к Нрп~т.
Ввиду того что бесконечно удаленную точку можно считать лежащей на мнимой осн, на основании свойства 1 соответствующий нуль или полюс функции должен быть простым.
Если р—оо есть простой нуль или полюс, то степень числителя на единицу ниже или выше степени знаменателя. Возможны три случая при р-> <х>;
1) Z (р) -» Нр, когда и — т = 1;
2) Z (р) -» Hip, когда п — т = — 1;
3) Z (р) -» Н > 0, когда п — т = 0.
Поскольку точка р=0 (начало координат) принадлежит мнимой осн, на основании свойства 1 нуль или полюс в точке р=0 должен быть простым. Следовательно, наименьшие показатели степеней в числителе и знаменателе положительной действительной функции (20-1) не могут различаться более чем на единицу. Возможны трн случая при р-» 0:
1) Z (р) — а0/Ь0, когда
Сд 0, Ьо 0;
2) Z (р) —• ajbip, когда
Ла =#0, Ьо = 0;
3) Z (р) Qj р/Ь0, когда а0 == 0, bo=f=0.
20-4. УСЛОВИЯ ФИЗИЧЕСКОЙ РЕАЛИЗУЕМОСТИ ФУНКЦИИ
В задачах синтеза функция Z(p) может быть задана непосредственно или получена из частотной характеристики Z (/ш) с помощью подстановки j(O = p.
Функция считается физически реализуемой, если соответствующая ей электрическая цепь может быть составлена из элементов (сопротивлений, индуктивности, емкостей) с положительными действительными параметрами.
Для всякой положительной действительной функции может быть построен двухполюсник, для которого она является обобщенным сопротивлением (или проводимостью). Поэтому условие положительности и действительности функции является достаточным для ее реализуемости. В связи с этим, если требуется построить двухполюсник по заданной рациональной функции, предварительно выясняют, является ли она положительной и действительной.
В соответствии с тем, что было сказано в предыдущем параграфе, рациональная функция является положительной и действительной, ес
396
ли одновременно выполняются следующие условия:
1) все коэффициенты полиномов действительны (условие действительности функции);
2) в правой полуплоскости полюсы отсутствуют (условие аналитичности функции);
3) в бесконечно удаленной точке функция ведет себя, как Нр, Н или — (свойство 3);
Р
4) полюсы на мнимой оси могут быть только простыми с действительными и положительными вычетами (свойство 1);
5) действительная часть функции на мнимой оси не отрицательна [условие (20-4)].
Перечисленные условия являются необходимыми и достаточными, чтобы заданная рациональная функция была положительной и действительной. Если хотя бы одно из этих условий не выполнено, то заданная функция не есть положительная действительная функция.
Действительная часть функции на мнимой осн [ReZ(j(o)J сравнительно просто находится, если полиномы А(р) и В(р) в числителе и знаменателе (20-1) представить как суммы полиномов с четными и нечетными степенями р;
Л (р) = Лч(р) + Лн(р); В (p)=B4(p)+Btl(p).
При этом
Z(p) =
Л(Р)В(-Р)
В(р)В(-р)
__ [Лч (р) + А,. (р)][(Вч (-Р) + Вн (—р)] В(Р)В(-Р)
откуда с учетом равенства Вч(—р)=В.,(р) н Вн(—р) =—Вп(р)
, Лч (р) Вч (р) — Л„ (р) Вн (р)
Z IDI —---------------------—------4-
Лн (р) Вч (р) — Лч (р) Вн (р)
В(р)В(-р)
При р=](й первое слагаемое, четное относительно частоты (о, выражает активное сопротивление двухполюсника, а второе слагаемое, нечетное относительно частоты, выражает реактивное сопротивление.
Итак,
Re Z —
Г Лч (р) Вч (р) — А„ (р) Ви(р) ] "L 5Й-В(-Р)--------------U.- 120 6)
В случае реактивного двухполюсника выражение (20-6) обращается в нуль, т. е. выполняется условие (при р=/ы)
Лч (р) Вч (Р) = Лн (р) Вн (р).
При этом
. = Лч (р) + Л, (р) = W Вч (р) + В„ (р)
, . , ,ЛЧ (р) Вч (р)
а.(р)+Д.<р>
Ач (р) Лн (р)
Ва (р) Вч (р)
Следовательно, в случае реактивного двухполюсника полином в числителе (20-1) содержит только четные, а в знаменателе — только нечетные степени или наоборот.
Пример 20-1. Проверить положительность и действительность функции
F(P)
1) коэффициенты полиномов действительны;
2) в правой полуплоскости полюсы отсутствуют;
3) в бесконечности функция ведет себя, как р;
4) на мнимой оси полюсов нет;
2
5) ReZ (jW)'= — > °.
Проверка показывает, что заданная функция является положительной действительной.
20-5. МЕТОДЫ ПОСТРОЕНИЯ ДВУХПОЛЮСНИКА ПО ЗАДАННОЙ
ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
Для построения двухполюсника по заданной положительной действительной функции применяются различные методы синтеза.
Ниже рассмотрены два метода:
I) метод последовательного выделения нулей и полюсов и 2) метод разложения в непрерывную дробь.
Метод последовательного выделения нулей и полюсов. Если Z(p) есть рациональная положительная действительная функция (20-1), причем степень числителя на единицу превосходит степень знаменателя, то, выполнив деление, получим:
Z(p)=acop+Z0(p); (20-7) здесь аоо=Н — действительная положительная величина.
Действительная часть п^.р на мнимой оси равна нулю; поэтому
Re Zo (j(o)=Re Z (jcd) > 0.
397
Ввиду того что функция 2о(р), получившаяся из Z(p) после выделения аоор, не отрицательна на мнимой оси, Z0(p)—положительная действительная функция.
Если Z(p) и соответственно Z0(p) имеет полюсы ±/сой и 0 на мнимой оси с вычетами щ и ао, причем на основании свойства I (§ 20-3) эти полюсы простые, a ah и ао — действительные положительные числа, то разложение Zo{p) на простейшие дроби дает *:
С <7
Чр) = — + £ ~~+ S -^-+
Р р + i’’ip — p*k Л=1 *=1
Q +Z1(p)=““+2-2^+Zl(p). (20-8) Р +
На мнимой оси выражения ао/р 2aiip
и ’ 2 2 принимают мнимые зна-
чения. Поэтому
ReZj (/®)=ReZo(/<o)=ReZ(/<o) > 0 и, следовательно, Zt (р) — положительная действительная функция.
Функция Zi(p), получившаяся из Z0(p) после выделения всех полюсов, лежащих на мнимой оси, может иметь полюсы в левой полуплоскости. Если все полюсы Z0(p) лежат на мнимой оси, то Zt(p) не имеет особых точек и поэтому на основании теоремы Лиувилля Zt(p) есть постоянная.
Подстановка (20-8) в (20-7) дает:
z(p)=a„ Р+ ~ +
Р а
+ г + 2 *НД>- (20'9)
р +“*
Полученному выражению соответствует схема, изображенная на рис. 20-4.
Полюс р=оо обусловлен наличием в схеме индуктивности а<», а полюс р—0 — наличием емкости 1/ао. Если Zi(p)—постоянная, то она реализуется как активное сопротивление.
1 Вычеты а* в сопряженных мнимых
полюсах равны в силу того, что они дей-
ствительны.
Аналогично можно доказать, что если Zt(p)—рациональная положительная функция, имеющая ну-ли±/(Ол и оо, причем степень числи-
Рис. 20-4. Двухполюсник, соответствующий выражению (20-9).
теля на единицу меньше степени знаменателя, то
Г(р) = 7^-=а„р + ^ + Z(p) р
+ у 2ак.Р +Г2 (р)> (20-10)
—' р- + *4 fc=l
где аь и ао — вычеты Y(р) в ±/сол и 0; Уг(р) — рациональная положительная действительная функция.
Если все нули функции Z(p) лежат на мнимой оси, то Уг(р) есть постоянная (реализуемая как активная проводимость).
Выражению (20-10) соответствует схема, показанная на рис. 20-5.
Когда все нули и полюсы заданной рациональной функции Z(p) лежат на отрицательной действительной полуоси, в соответствии с (20-9)
2(p) = a„p + Z1(p),
398
где Zi(p)—положительная действительная функция, нули и полюсы которой расположены в левой полуплоскости.
Функция Zt (р) аналитична в бесконечности, так как степень числителя не превышает степени знаменателя.
Рис. 20-6. Двухполюсник, соответствующий выражению (20-11).
Если постоянное слагаемое в числителе Zi(p) равно нулю, то р= =0 является нулем функции Zi(p). В этом случае Zi{p) раскладывается на сумму дробей:
(20-п)
где Ра принимает действительные положительные значения.
При ро=О разложение (20-11) содержит постоянное слагаемое сц,.
Функция (20-11) может быть осуществлена по схеме рис. 20-6.
Если постоянное слагаемое в числителе Zi(p) не равно нулю, то Zi(p) раскладывается на простые дроби:
<7
z‘W = S-rr + ». <2СМ2> Г.'-'-
где а — положительная постоянная.
Условие ро=О отвечает наличию полюса в точке р—0 при равенстве нулю постоянного слагаемого в знаменателе выражения для Zt(p).
Функция (20-12) осуществима по схеме на рис. 20-7.
В общем случае полюсы и нули заданной положительной действительной функции могут лежать на мнимой оси в левой полуплоскости.
Такая функция осуществляется шаг за шагом путем выделения непосредственно реализуемых элементов.
Первоначально могут быть выделены все полюсы функции Z(p), лежащие на мнимой оси. При этом в соответствии с (20-9) получится новая, более простая функция Zi(p), которая уже не будет им^ть noj госов на мнимой оси; такая функция называется функцией минимального реактивного сопротивления.
Таким образом, после выделения полюсов, лежащих на мнимой оси, задача сводится к осуществлению
p+/s, p+fl4
Рис. 20-7. Двухполюсник, соответствующий выражению (20-12).
функции минимального реактивного сопротивления Zi(p).
Если нули и полюсы Zi(p) лежат на отрицательной действительной полуоси, то Zi(p) реализуется с помощью двухполюсника типа rL или гС в соответствии с (20-11) и (20-12)-
В случае, если Z4(p) имеет нули на мнимой оси, они выделяются на основании (20-10), в результате чего получается обобщенная проводимость Уг(р), которая не имеет полюсов на мнимой оси; такая функция называется функцией минимальной реактивной проводимости. Следовательно, после выделения пулей Zt(p), лежащих на мнимой оси, задача сводится к осуществлению функции минимальной реактивной проводимости У2(Р).
Выделение полюсов и нулей продолжается до тех пор, пока не получатся непосредственно реализуемые элементы.
В предыдущих рассуждениях реализация заданной функции начиналась с выделения полюсов, лежащих на мнимой оси. Однако реализация той же функции может быть начата с выделения нулей, лежащих на мнимой оси. В этом случае получится схема двухполюсника, отличная от предыдущей, при
399
чем в зависимости от конкретных условий и требований может быть выбрана та или иная схема.
Пример 20-2. Требуется осуществить положительную действительную функцию
2ра + р +
|3 + р8 + р+ 1
Заданная функция имеет на мнимой оси полюсы в точках ±/ 1. Вычет функции Z (р) относительно полюса / 1 (или —j 1)
равен:
Kes Z (р)
Г2р* + р4-1 ] |3р2 -}- 2р -|- 1 Jp=jl
-2+/+1 _ 1
—3 + 2/ 4- 1 2
Следовательно, согласно (20-9)
2(р)=-г^-;+21(р), Ра + 1
где Zi (р) — функция минимального реактивного сопротивления:
2ра + р + р3 + р2 + р +
Р 1
Ра4-1~Р4-1
„ , Р
Дробь ----;— реализуется с помощью
ps-j-l
индуктивности L=1 и емкости С=1, вклю-
1 ченных параллельно, а дробь----;—с по-
Р + 1
мощью сопротивления г=1 и емкости С=1, включенных параллельно.
Таким образом, функция Z(p) реализуется в виде двухполюсника, показанного на рис. 20-8.
Пример 20-3. Требуется осуществить положительную действительную функцию
ч р» + 5р4 + 9рз+18р2 + 8р + 4
Z(p) =----------------------------.
(Ра+1)(р34-2р2 + 4р + 2)
Заданная функция имеет на мнимой оси полюсы в точках ±/ 1. Вычет функции Z(p) относительно полюса /1 (или —j 1) равен:
3
Res Z (р) = lim (р — /1) Z (р) = — .
p->jl 2
Следовательно, на основании (20-9) Зр 2(р) = тГП + 2х(р), ра +1
т. е. Z (р) реализуется по схеме рнс. 20-9, а, где Z, (р) — функции минимального реактивного сопротивления:
Зр
Л (Р) = 2 (р) — — =
р2 +1
_ р« + 2р2 + 2р + 4
Р3 + 2р2 + 4р + 2 (р2 + 2) (р + 2) рз + 2р«+4р-|-2 '
Z,(p) имеет на мнимой оси нули в точках ±/^ 2. Вычет функции Vj (р) = -—— относительно полюса / у^ 2 (нли — j yf 2) равен:
Resrx(p)= Iim_ (р — j’V?) Y1(p)=~ .
P---/T2 2
Рис. 20-8. Пример 20-2.
Следовательно, на основании (20-10)
р
т. е. У|(р) реализуется по схеме рис. 20-9,6, где Кг(р)—функция минимальной реактивной проводимости:
У2(Р) = Л(Р)
Р+1
Р + 2
Первое слагаемое в знаменателе выражения для ¥г(р) означает сопротивление, а второе — параллельное соединение емко
Рнс. 20-9. Пример 20-3.
400
сти и сопротивления; эти элементы включаются последовательно.
Итак, функция Z(p) реализуется в виде двухполюсника, показанного на рнс. 20-9, в.
Метод разложения в непрерывную дробь. Наряду с рассмотренными выше схемами двухполюсника, отвечающими функции (20-1),
Рис. 20-10. Цепная схема.
существуют цепные схемы типа изображенных на рис. 20-10, сопротивления которых могут быть выражены непрерывной дробью (в схеме на рис. 20-10 последовательные ветви обозначены сопротивлениями, а параллельные — проводимостями):
z=z1+—!—-
Уа+-------Г
Z3 + f4+...-i-—_
* п
Разложение заданной дробно-рациональной функции Z(p) в непрерывную дробь осуществляется делением числителя на знаменатель, причем оно продолжается до тех пор, пока получаемое в остатке выражение не представит собой сопротивления или проводимости некоторого известного двухполюсника. Этот двухполюсник является конечным звеном цепной схемы, соответствующей полученному разложению в непрерывную дробь.
Следует заметить, что непрерывные дроби и соответствующие им цепные схемы различны в зависимости от того, располагаются ли полиномы в числителе и знаменателе заданной дробно-рациональной функции по восходящим или нисходящим степеням р. Кроме того, вместо функции Z(p) в непрерывную дробь может быть разложена функция У (р) —---, числитель и знамена-
' ' z (р)
тель которой также могут располагаться по восходящим или нисходящим степеням р. В результате этого могут быть получены дополнительные разновидности цепных схем.
Наконец, возможно разложение в непрерывную дробь, при котором в процессе деления сначала соблюдается один, а затем другой порядок расположения степеней р.
В отдельных случаях некоторые или даже все полученные варианты разложения в непрерывную дробь не допускают физической реализации двухполюсника.
Построение двухполюсника методом разложения Z(p) в непрерывную дробь проиллюстрировано ниже примерами 20-4 и 20-5.
Пример 20-4. Требуется осуществить положительную действительную функцию
р2 + р+1
Z (п) =-------------- .
р3 + р24-2р + 1
Заданная функция разлагается в непрерывную дробь:
Z(P) =-------Ц----- •
Этому выражению соответствует цепная схема, изображенная на рис. 20-11.
Рис. 20-11. Пример 20-4.
Пример 20-5. Требуется осуществить положительную действительную функцию
Z(p)
__ 2р3 + Зр2 + 2р + 1
2р2 + 2р + 1
Степень числителя выше степени знаменателя, следовательно, функция имеет полюс в бесконечности, что указывает иа наличие последовательной индуктивности.
Начиная с расположения полиномов по возрастающим степеням р и изменяя в процессе деления порядок расположения степеней р, можно заданную функцию представить в следующем виде:
1
2 (р) = р -4----------==
' н 1 + 2р + 2р2
1+р + р2
401
1 + р + Р8 р + р2
Полученной непрерывной дроби соответствует схема двухполюсника, показанная на рис. 20-12.
Рис. 20-12. Пример 20-5.
20-6. ИССЛЕДОВАНИЕ ЧЕТЫРЕХПОЛЮСНИКА ПРИ КОМПЛЕКСНОЙ ЧАСТОТЕ
Так же как и в случае двухполюсников, введение комплексной частоты p=c-f-/to расширяет возможности исследования общих свойств четырехполюсников.
Передаточная функция четырехполюсника может быть выражена отношением полиномов вида (20-1). При этом в отличие от сопротивления или проводимости двухполюсника степени передаточной функции четырехполюсника могут разниться более чем на единицу.
Передаточная функция четырехполюсника, представляющая собой отношение электрических величин в двух разных контурах или узлах, свободна от некоторых ограничений, свойственных сопротивлению и проводимости двухполюсника. Так, на
пример, передаточные сопротивления и проводимость четырехполюсника могут иметь действительную X отрицательную часть.
, Что касается полюсов передаточной функции, представляющей собой отношение электрических величин на выходе и входе линейного четырехполюсника, то, так же как и в случае двухполюсника, полюсы не могут иметь положительной действительной части: они располагаются в левой полуплоскости, так как совпадают с полюсами входного сопротивления или входной проводимости четырехполюсника.
Однако подобное ограничение не распространяется на нули передаточной функции четырехполюсника: нули могут находиться как в левой, так и в правой полуплоскости.
Передаточная функция, не имеющая нулей в правой полуплоскости, называется функцией м и -нимальнойфазы, а передаточная функция, нули которой располагаются в правой полуплоскости, называется функцией неминимальной фазы. Соответственно различают и цепи минимальной и неминимальной фаз.
На рис. 20-13 в виде примера показано размещение нулей и полюсов передаточных функций минимальной (рис. 20-13, а) и неминимальной (рис. 20-13,6) фаз.
Амплитудная и фазовая характеристики могут быть построены на основе (20-3). В рассматриваемом случае отношения М^М2 равны друг другу и поэтому при равенстве множителей Н амплитудные характеристики совпадают. Фазовые же характеристики неодинаковы: передаточная функция минимальной фазы характеризуется всегда мень
Рис. 20-13. Размещение нулей и полюсов передаточных функций минимальной (а) и неминимальной
(б) фаз.
402
шим в алгебраическом смысле фазовым сдвигом, чем функция неминимальной фазы при той же амплитудной характеристике. Это видно из рис. 20-13, где угол сц меньше угла, дополняющего его до 180°
Существенной особенностью функций минимальной фазы является то, что амплитудная и фазовая характеристики однозначно определяют друг друга: имея одну из этих характеристик, можно найти другую характеристику.
В цепных схемах ток в нагрузке может быть равен нулю в том случае, когда какое-либо из сопротивлений продольных ветвей бесконечно велико или какое-либо из сопротивлений поперечных ветвей равно нулю. Поэтому передаточная функция для цепной схемы всегда является функцией минимальной фазы: ее нули обусловливаются полюсами сопротивлений продольных и нулями сопротивлений поперечных ветвей цепной схемы, которые всегда располагаются в левой полуплоскости.
Интересной разновидностью передаточных функций неминимальной фазы служит функция, нули которой располагаются в правой полуплоскости в виде зеркальных изображений полюсов (полюсы и нули располагаются по окружности). Четырехполюсник, обладающий такой передаточной функцией, отличается той особенностью, что он пропускает все частоты с одинаковым затуханием. Действительно, для всех точек мнимой оси модуль выражения (20-3) сохраняется постоянным. Аргумент выражения (20-3), т. е. фазовый сдвиг между электрическими величинами на выходе и входе четырехполюсника, прн этом зависит от частоты. Характеристика передаточной функции на комплексной плоскости представляет собой окружность.
Такое изменение фазы прн постоянной амплитуде свойственно, например, симметричному мостовому четырехполюснику, нагруженному согласованно. Четырехполюсники подобного типа применяются в технике связи в качестве устройств, корректирующих фазу.
Построение четырехполюсника по заданным частотным характеристикам представляет в общем случае задачу более сложную, чем построение двухполюсников [Л. 1 и 6]. В зависимости от условий задачи в основу построения четырехполюсника в ряде случаев могут быть положены общие методы синтеза двухполюсников.
20-7. ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
20-1. Показать, что
р2 + р + 4
Р2 + Р + 1
рз + зр2 + 2р + 2 р (Ра + 2)
рЗ + Зр2 + Зр + 1’ (р2+1)(р2 + 4)
— положительные действительные функции. 20-2. Показать, что
р(раЧ-5) .
(р2+02 ’
р3 + 2р + 1 Р3+7рЗ+ 15р + 9
р2 ’ р4 + 6р2 + 9
не являются положительными действительными функциями.
20-3. Осуществить
,, , (р + П<1> + 3>.
ZM~—р(р + 2>'--
Р4 + 4р« + 3.
Z(p)=—— .
р3 + 2р
р4 + 4ра + 3
^(р) =и 7? —
разложением на простейшие дроби.
20-4. Решить задачу 20-3 разложением в непрерывную дробь.
20-5. Осуществить
Z(p) =
(Р2+ 1)(р2 + 9) р (р2 + 4)
последовательным выделением полюсов и нулей.
20-6. Решить задачу 20-5 разложением в непрерывную дробь.
20-7. В каких случаях полином, все корни которого расположены на мнимой оси, содержит только нечетные степени р?
20-8. Основываясь на формуле (20-3), показать для реактивного двухполюсника, что нули и полюсы чередуются.
20-9. Почему полюсы передаточной функции не могут находиться в правой полуплоскости, между тем как иа нули передаточной функции это ограничение ие распространяется?
20-10. Почему обобщенные сопротивления н проводимости двухполюсников представляют собой положительные действительные функции?
403
ПРИЛОЖЕНИЕ 1
МЕТОД СИГНАЛЬНЫХ ГРАФОВ1
В гл. 5 при выборе независимых контуров для записи уравнений по второму закону Кирхгофа использовалось понятие графов. Однако графы применяются не только для выбора контуров, но и для решения систем уравнений, записанных для электрической цепи. Для этой
пели используются сигнальные графы.
Возьмем, например, систему уравнений, полученных для схемы рис. 5-6 в примере 5-2. Для построения сигнального графа необходимо
сначала разрешить каждое уравнение относительно одной переменной (разной для разных уравнений). Разрешим, например, первое уравнение относительно А, второе — относительно 72 и третье — относительно /з:
А=^12^2“Ь- Дз^з!
г—АгЛ+АзЛ»;
(I-D
А — ^3171Ч-Аз2^2-1~
Здесь коэффициенты передачи:
I ____ ^5 . j __ ^2
+ ^2 + ^5 -|- Zj Zs ’
_ _____Zj____ . j, __ ____Z3____ .
^3 + ^4-f-Zs 2 Z3+Z4 + Zs
f ___ ^2 . 4 ___ Z3 ,
31 Z2 + Z3 + Ze’ ® z2 + z3 + ze’
^2 + Z3 +
Полученной системе уравнений соответствует сигнальный граф, изображенный на рис. 1-1, а.
Сигнальный граф обладает следующими свойствами:
1. Сигнальный граф состоит из узлов и ветвей. Ветвь изображается
1 Написано инж. Ш. Н. Хусаиновым.
направленным отрезком, соединяющим два узла сигнального графа. Направление ветви указывается стрелкой.
2. Каждая ветвь графа характеризуется коэффициентом передачи
Рис. 1-1.
ветви tn,. Первый индекс (i) соответствует номеру узла, в который входит ветвь, а второй (А) — номеру узла, из которого она выходит.
3. В каждом узле графа имеется сигнал, который передается от узла по всем ветвям, выходящим из него. При решении уравнений электрических цепей под сигналами понимаются токи, напряжения и т. д.
4. При прохождении по ветви сигнал умножается на коэффициент передачи ветви.
5. Результирующий сигнал в узле равен сумме всех сигналов, приходящих в данный узел по ветвям, входящим в этот узел.
В соответствии с вышесказанным ток It представляет сигнал в вершине графа 1 на рис. 1-1, а, ток /2 — сигнал в вершине 2, ток /3 —
404
сигнал в вершине 5 и э. д. с. Е — сигнал в вершине 4. Согласно первому уравнению системы (1-1) в вершину 1 должны входить ветвь с коэффициентом передачи tn, выходящая из вершины 2, и ветвь с коэффициентом передачи Лз, выходящая из вершины 3 (рис. 1-1, а). В вершину 1 по этим ветвям согласно четвертому свойству приходят сигналы taIz и tl3i3 соответственно, так что результирующий сигнал It в вершине 1 удовлетворяет первому уравнению системы (1-1). Аналогичные рассуждения относятся и к остальным ветвям графа, изображенного на рис. 1-1, а.
Выше отмечалось, что для построения сигнального графа следует каждое уравнение разрешить относительно одной переменной. Очевидно, это можно сделать по-разному. Например, первое уравнение рассмотренной выше системы уравнений можно разрешить относительно /г, а не Д, второе уравнение — относительно /3, третье — относительно /г. В результате получится система уравнений, отличная по форме от системы (1-1), и соответственно сигнальный граф для такой системы будет отличен от графа на рис. 1-1, а.
Таким образом, для данной системы уравнений можно построить различные графы, но данному графу соответствует совершенно определенная система уравнений.
После построения сигнального графа для данной системы уравнений решение ее сводится к вычислению коэффициентов передач графа.
Коэффициентом передачи сигнального графа от источника, откуда только выходят ветви графа, к стоку, куда только входят ветви графа, называется отношение сигнала в стоке к сигналу в источнике.
Узел 4 графа на рис. 1-1, а является источником. Узел 1 не является стоком, но можно добавить узел 1' с сигналом Л и соединить его с узлом 1 ветвью с единичным коэффициентом передачи, что соответствует уравнению Д —Д. Узел 1' являет
ся стоком, тогда коэффициент передачи от узла 4 к узлу Г
К д т — — — — 14 Ё Ё ’
откуда Ц = Тг4Е, т. е., зная передачу графа от узла 4 к узлу 1', можно определить ток /1.
Ниже рассмотрены два метода нахождения коэффициента передачи сигнального графа: 1) последовательным упрощением графа и 2) вычислением коэффициента передачи графа по формуле Мейсона.
Метод упрощения сигнального графа основан на следующих правилах.
1. Параллельно соединенные ветви, направленные в одну сторону, заменяются одной ветвью, коэффициент передачи которой равен сумме коэффициентов передачи параллельно соединенных ветвей (рис. 1-2, а).
2. Последовательно соединенные ветви, направленные в одну сторону, заменяются одной ветвью, коэффициент передачи которой равен произведению коэффициентов передачи ветвей (рис. 1-2,6).
3. Если в точке соединения двух ветвей с коэффициентами передачи Д2 и /23 имеется петля с коэффициентом передачи Да (петля — это ветвь, выходящая из того же узла, куда она входит), то все эти три ветви заменяются одной ветвью с коэффициентом передачи Д3= -*18 -га
I — <22 (рис. 1-2, в).
Указанные выше правила являются частными случаями общего правила устранения вершин. При устранении вершины графа устраняется и сигнал, соответствующий этой вершине, т. е. устранение вершины равносильно исключению переменной из системы уравнений. Вообще всякому преобразованию графа соответствует определенное преобразование системы уравнений.
При устранении некоторой вершины (рис. 1-2, а) удаляются все ветви, входящие или выходящие из этой вершины. Коэффициенты передачи оставшихся ветвей (вблизи удаленного узла) соответствующим
405
образом меняются. Если в исходном графе имеется ветвь, идущая из узла k в узел s с коэффициентом передачи tSh, и ветвь, идущая из узла s
t) '
Рис. 1-2.
в узел i с коэффициентом передачи ttK (рис. 1-2, г), то новый коэффициент передачи ветви между узлами k и 1 вычисляется по формуле
И’2) 1к IR 1 1 л » '
1 lSS
где tss — коэффициент передачи петли в вершине s.
Если в исходном графе отсутствует ветвь между узлами k и I, то в формуле (1-2) следует положить tik—0. Аналогично при отсутствии петли в вершине s ^.<==0. В частном случае вершины i и k могут совпадать, что приведет к появлению петли в новом графе. Коэффициенты передач t'/m, t'lm и t'lk находятся по формуле, аналогичной формуле (Ь2).
В качестве примера применения формулы (1-2) устраним вершину 2 из графа на рис. 1-1, а. В результате получится граф, изображенный на рис. 1-1,6. Выражения для коэф
фициентов передач ветвей указаны на рисунке.
Далее можно удалить узел 3 из графа на рис. 1-1, б; получится граф, содержащий узлы 1 и 4, причем в узле 1 будет петля. Для удаления этой петли можно добавить ветвь с единичным коэффициентом передачи, как указано было ранее (пунктирная линия на рис. 1-1, а), и устранить узел 1. Окончательно получится граф, содержащий единственную ветвь с коэффициентом передачи Тш—ЩЁ. Указанные преобразования предлагается выполнить читателю в качестве упражнения и результат сравнить с (1-5).
Описанный выше метод является громоздким. Более удобно вычислять коэффициент передачи сигнального графа по формуле Мейсона.
Коэффициент передачи графа от источника к стоку равен:
S Pk &k
Т= , (1-3)
где А — определитель графа; Pk — величина k-ro пути в графе от источника до стока; Ah — алгебраическое дополнение пути. Суммирование выполняется по всем возможным путям.
Путь в графе берется с учетом направления ветвей, т. е. идя от источника до стока необходимо все время идти в направлении стрелок. Величина пути равна произведению коэффициентов передач всех ветвей пути.
Определитель графа
А= 1 — S L, + S* L, Lk — i i.k
-S* L,LkLm + ..., (1-4)
i,k,m
где Lt — величина i-го контура, равная произведению коэффициентов передач всех ветвей контура. Контуры выбираются так, чтобы все ветви в контуре были направлены в одну сторону. Звездочки у знака сумм означают, что следует брать произведения величин двух, трех и т. п. некасающихся контуров.
Алгебраическое дополнение Ай вычисляется по той же формуле
406
(1-4), но при этом следует учитывать во всех суммах лишь контуры, не касающиеся пути Ръ.-
В качестве примера вычислим коэффициент передачи графа на рис. 1-1, а от узла 4 к узлу 1. Определитель графа
1 — (W32+W8i+Wsi+ ^13 (12^32+^23^12^31) -
Все контуры касаются друг друга, поэтому в выражении определителя нет произведений контуров:
—^зЛз^ха; = 1»
так как все контуры касаются пути Рг, Pa=Wi3, Дг= 1 — по той же причине.
Теперь остается подставить выражения определителя, величины путей и их алгебраические дополнения в выражение (1-3):
У ___ Pl^l ~Ь ^2^2
что дает:
Л ____ ^34^23^12~1-^34^»
Ё 1 — (^23?32-М12^21-Н13^31 +
---------------------------. (1-5)
+ ^13^12^32 + W12^31)
ПРИЛОЖЕНИЕ П
Соотношения между коэффициентами четырехполюсника
г Y H G A В
Z •я м Н W N N Я о» П2 ~УТ2 Ml H12 1 —G12 Al Ml to stojsto й° 2° | ~
Ml Ml Al tl Ml Ml Hn H22 -Hu 1 H22 /72г ©*i Ai ^u 1 л22
G11 On z2i Ai Ai в21
У ^22 ^12 Al У12 Al A2 ;?|- - 1 |ro 1G | Cj2 Л22 —| A | Вц -1
Ml |Z| Zg Zu Ml Ml C> I 1 c *2 Cb ю “°l- “° “1 “ Л12 Л12 -I Лц ЛХ2 Л13 | 04 С4| СЧ из 0Q £Ц Я 031 я оз оз
Hu Hu
н N 1 J N I to Nj to CN to Ito to | N N N to . to t- to to to 1 -r12 Hu Htt Hu H22 G22 —G12 Л12 | Л | ев 11 „to I to a |_to а » to jjS» [JO | -
Yu Yn Ai mi Ai rU |G| |G| G21 gu ^22 ^22 —1 Ai
|G| |G| ^22 -^22
G 1 N nL ro l-k l-k n s’li Im Ml n2 H22 Hu Ml Ml -Я21 Hu C Q to £> иР to Ы Ai Ml >411 >411 1 л12 B21 -I ®22 B22 1 В 1 Z?12 ®22 B22
Y 22 Y22 -Г21 1
Al Al Y 22 Y 22 Ml Ml >4и Ai
А „ N N to In nIt? M to M to — 1 _ -y2S -1 Ai r21 -Ml -Yu -Ml -Hu H2i H2l -H22 -1 1 G22 ^11 ^12 ^21 ^22 to Ls° to kJ0 »-* (to *|Bto
®|os <3* <5*1 ©
Al Al Y2i Y21 H2i H21
В a2 _mi_ Z12 a2 1 Ai A2 Z12 Определит -Yu -1 Аг Yu -Ml -Yn 1 Hu |G | —G22 G12 G12 -G„ -1 Л22 л12 Bu Bu B21 B22 . ЖЕНИЕ HI в
^12 ^12 H22 \H\ IA |Л| Ai Ац Ml Ml ПРИЛО лрехполюсиико
Yls Yu ели, выражешп H12 Hls м через коэф( 6?12 жциенты четь
z Y н G А В
Ml A1A2— —A2A1 1 Ml Hn G22 >412 Bu B21
Hu Gu Л21
mi 1 Ml А1Аг~ -A2A1 sc I ас — to "* jto I M |Hk » II-k Ai to I-*
>412
1 и | N N to |-k to м Y 22 1 и « a: 1 1 |G| Ац B22 Bu
Ai А22
IGI A2 Yu TST ^11^22““ —g12g21 а22 At В11
Al y22 B22
Ml si 5 N N Yl2 _ Hu H21 Gu А1А2— —>412Л21 1 Ml
Yu Gu
Ml N N M to to l-k Ya Hu Gu 1 Ml BuBt2— —BuB2i
Yu Hu G12
408
ПРИЛОЖЕНИЕ ГУ
Оригиналы и изображения по Лапласу
F (р)
1
1
Р
1
Р2
1
Р"
1
Р + °
1
Р(р + а)
1
Р2 (Р + а) 1 (р + аУ Р (Р + °У
1
(Р + а)3
Р
(Р + а)3 1
Ср + а)"
1 р (р + а)п
Рп (р + а)п+'
__________1_________
(Р + а) (Р + Ь)
__________1_________
Р (Р + а) (Р + Ь)
__________Р_________
(Р + а) (р + 6)
1
р2 + cfl
1
р (р* + а2)
Р р’ + а2
б(Г) =
f (0
1
lim — при 0 < t < т
т->0 т
О при 0 > t > т
t
tn-l
-—, —; n — целое положительное число (я — 1)!
e-at
— (1-е-а<)
а
4 (e-^ + af-l)
te-11*
(1 — дО е-о/
У tk
— k)\ (Л)!2
n — целое положительное число
1
— sin at а
1
--- (1—cos at) а2
cos at
26—1118
409
Продолжение приложения TV
I ! — shai
р2 — а2 а
Р ch ai
р2-—а2 р cos Ь — a sin Ь
cos (ai 4- b)
p' + cfl
р sin Ь + a cos Ь sin (at 4- 6)
р2 + а?
1 sin at t cos al
(р2 + а2)2 2а» 2а»
Р 1 — t sin at
(р2 Ч- а2)2 2a
Р2 1 —— (sin at 4- at cos at)
(р2 + а2)2
2a
р2 — а2 t cos ai
(Р2Ч~°2)2 -
1 t ch ai sh at
(р2 — а2)2 2a2 2a3
Р 1 — ish at 2a
(р2 — а2)2
1 sinW
(Р + а)2 +*2 b
р + д е—°* cos Ы
(р + о)2 +&2
(р + a) cos ф — Ь sin ф e—o/cos (ЫЧ-Ф)
(р + а)2 +
(р -}- Д) sin Ф + Ь cos Ф e—a<sin (ИЧ~Ф)
(р + а)2 +&2
1
(рЧ-а)2—Ь2 e b
Р Ч-а e—01 chM ♦
(рЧ-«)2-Ь2
1 1
р 2 /^7
3 _ r~r~
„ 2 2 1/ —
р Ч Я
ЛИТЕРАТУРА
1. Атабеков Г. И., Теория линейных электрических цепей, изд-во «Советское радио», 1960.
2. Атабеков Г, И., Теоретические основы электротехники, ч. 1, изд-во «Энергия», 1966.
3. А т а б е к о в Г. И., К у п а л я и С. Д., Тимофеев А. Б., Хухриков С. С., Теоретические основы электротехники, ч. 2 и 3, изд-во «Энергия», 1966.
4. Б а л а б а и я и Н., Синтез электрических цепей, Госэнергоиздат, 1961.
5. Гарднер М. Ф., Бэрнс Дж. Л., Переходные процессы в линейных системах, Физматгиз, 1961.
6. Г о и о р о в с к и й И. С., Радиотехнические цепи и сигналы, изд-во «Советское радио», 1963 и 1966.
7. Г р и н б е р г Е. Г., Колобков Д. С., Макаровский А. А., Т и м о ф е е в В. А., Штнтельман Б. И., Теория электро-радиотехнических цепей, ч. III, изд-во «Советское радио», 1964.
8. Жуховицкий Б. Я., Негне-в и ц к и й И. Б., Теоретические основы электротехники, ч. 2, изд-во «Энергии», 1965.
9. 3 е в е к е Г. В., И о н к н и П. А., Нетушнл А. В., Страхов С. В., Основы теории цепей, Госэиергонздат, 1963.
10. 3 е л я х Э. В., Основы общей теории линейных электрических схем, изд-во АН СССР, 1951.
11. Зернов Н. В., Карпов В. Г., Теория радиотехнических цепей, изд-во «Энергия», 1965.
12. Нонкин П. А., Мельников Н. А., Д а р е в с к и й А. И., Кухаркин Е. С., Теоретические основы электротехники, ч. 1, изд-во «Высшая школа», 1965.
13. Каплянский А. Е., Лысенко А. П., П о л о т о в с к и й Л. С., Теоретические основы электротехники, Госэнергоиздат, 1961.
14. Котельников В. А., Николаев А. М., Основы радиотехники, ч. 1 и 2, Связьиздат, 1950 и 1954.
. 15. К р у г К. А., Основы электротехники, ч. ! и 2, Госэнергоиздат. 1946.
16. Н е й м а н Л. Р., Демирчян К. С., Теоретические основы электротехники, ч. 1 и 2, изд-во «Энергия», 1966.
17. П о л и в а и о в К. М., Теоретические основы электротехники, ч. 1, изд-во «Энергия», 1965.
18. Реза Ф., Сили С.. Современный анализ электрических цепей, изд-во «Энергия», 1964.
19. СешуС., БалабанянН., Анализ линейных электрических цепей, Госэнергоиздат, 1963.
20. X а р к е в и ч А. А., Основы радиотехники, Связьиздат, 1963.
26“
411
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
А
Абсолютная диэлектрическая проницаемость 19
— интегрируемость 262
— магнитная проницаемость 18
— сходимость 272
Автономный источник 89, 90
— четырехполюсник 348
Автотрансформатор 120
Активная мощность 36, 44, 175, 193
— проводимость 42, 340
— составляющая напряжения 41
--- тока 43
— цепь 9
Активно-емкостные эквивалентные цепи 64
Активно-индуктивные эквивалентные цепи 64
Активное сопротивление 36, 40, 339
Активный двухполюсник 312
— четырехполюсник 348
— элемент цепи 9
Алгебраическая форма комплексного числа 49
Ампер 10
Амплитуда 29
— искажения 292
— комплексная 49, 249
Амплитудная характеристика 402
Амплитудно-частотные характеристики 127,
361
Амплитудный спектр 245, 263, 265, 269
Аналогии электромеханические 103
Анизотропия магнитная 191
Анизотропные материалы 179
Апериодический процесс 210, 213
Аргумент (фаза) 49
Асинхронный двигатель 162
Б
Базисный узел 85
Баланс мощностей 57
Бегущей волны коэффициент 298
Безындукционный фильтр 387
Бел 359
Бесконечно короткий импульс 260
Биения колебаний 213
В
Вариометр 114
Ватт 11
Вебер 13
Вектор вращающийся 33
Векторная диаграмма 34
— — катушки с ферромагнитным сердечником 194
Векторные диаграммы связанных контуров
143
412
Ветвь 23, 184
— намагничивания 116, 193
Взаимная индуктивность 106
— (передаточная) проводимость 90
Взаимное (передаточное) сопротивление 90
Взаимности (обратимости) теорема 91
Взаимозаменяемость сигнала и спектра 255
Видеоимпульс прямоугольный 264
Вихревые токи 18, 188
Включение в цепь с источником тока 230
— • гармонической э. д. с. 213
— на э. д. с. треугольной формы 234
— цепи г, С 207
---г, L 203
---г, L, С 209
Включения формулы 237
Внешняя связь 141
— характеристика 24
Вносимое затухание четырехполюсника 359
— сопротивление 119, 125, 142
Внутренняя связь 141
Воздействующая функция 213
Волна обратная 286, 308
Волна отраженная 286
— падающая 286
— прямая 286
— стоячая 295
Волновое сопротивление линии 285
—--- операторное 311
— (характеристическое) сопротивление контура 70
Вольт 11
Вольт-амперная характеристика 21, 24
Вращающееся магнитное поле 159
-------круговое 160
-------эллиптическое 162
Вращающийся вектор 33
Временные диаграммы 35
Встречное направление токов 109, 197
Вторичная обмотка трансформатора 115
Вторичные параметры линии 289
Второй закон Кирхгофа 26
Входная проводимость цепи 90
---четырехполюсника 351
Входное сопротивление линии 298
—— трансформатора 118
--- цепи 90
---четырехполюсника 351, 355
Высшие гармоники 166
Вязкость магнитная 188
Г
Гармоники 165
Гармонические колебания (функции) 29, 33
Гармонический ряд 166
— ток 35, 36, 37
Гасящий множитель 267
Генератор 30, 31
Генерирование синусоидальной э. д. с. 29
Генри 13
Геометрические элементы схемы 22
Герц 28
Гиперболическая форма уравнений линии 289
Гистерезис 181
Главные ветвн 81
Г-образный четырехполюсник 348, 365
Годограф 71
Граннчные условия 283
Граф 81
График распределения потенциала 26
Графическое изображение зависимостей комплексных величин от параметра (круговые диаграммы) 71
Графо-аналитическое разложение в ряд
Фурье 167
Групповая скорость 286
Д
Двигатель асинхронный 163
— синхронный 163
Двустороннее преобразование Фурье 251
Двухполюсник 312
— активный 312
— двухэлементный 312
— многоэлементный реактивный 312, 315
— обобщенный 329
— одноэлементный 312, 313
— пассивный 312
— реактивный
— с потерями 334
— трехэлементный 315
Двухполюсники взаимно-обратные 333
— эквивалентные 331
Двухполюсников классификация 312
Действительная положительная функпия 394
Действующее значение комплексное 51
--- Функции несинусоидальной 174
------ синусоидальной 32
Декремент колебаний 212
Дерево 81
Децибел 359
Джоуля — Ленца закон 12
Джоуль И
Диаграмма векторная 34
— круговая 71, 75, 77
— потенциальная 58
— проводимостей 73
— Смита 306
— сопротивлений 73
— топографическая 58
Динамическая петля гистериза 190
Динамические кривые намагничивания 190
— потери в стали 188
Дирихле условия 166
Дифференциальное уравнение линии 284
---трансформатора 115
Дифференцирование изображения 223
— оригинала (теорема дифференцирования) 223 *
— по параметру 223, 310 *"
Дифференцирующее звено 206, 209
Диэлектрическая проницаемость 19
Длина волны 31
Добротность катушки 41
— конденсатора 44
— контура цепи 124
Дробь непрерывная (цепная) 401
Дюамеля интеграл 225, 239
— интеграла выбор формы 240
Е
Единичная функция 221, 267, 278
Емкостная проводимость 38
— связь 141
Емкостное сопротивление 38
Емкостные цепи 100
Емкость 15, 37, 46
— кабеля 283
— конденсатора 19
— линии 283
3
Зависимые начальные условия 201, 209
Зависимый (неавтономный) источник 93, 142, 354
Заграждающий (режекторный) фильтр 370, 375, 377
Закон Джоуля — Ленца 12
— Ленца 13
— магнитной цепи 179
Закон Ома 12
---для магнитной цепи 180
---при переменном токе 37, 38, 40, 51
— полного тока 178
Закон сохранении количества электричества 100
— Фарадея — Максвелла (электромагнитной индукции) 13
Законы Кирхгофа 26
—--для магнитной цепи 180, 174
— коммутации 200
Замкнутая форма периодической несинусоидальной функции 174, 241
Замыкание ветви 235
Заряд электрический 10, 15, 26
Затухание вносимое 359
— контура 124
— собственное четырехполюсника 356
Звено дифференцирующее, интегрирующее 206, 209
И
Идеализация элементов цепи 9, 17
Идеальный источник напряжения 19
--- тока 20
— трансформатор 117, 119, 367
Избирательность колебательных систем 140,
141
Изображение выпрямленной синусоиды 224
— пилообразной функции 225
— по Карсону 220, 229
— по Лапласу 220, 229, 409
Изображений умножение 225
Импульсная функпия 238
Инвариантность цепи во времени 22
Инвариантные во времени цепи 22
Индуктивнаи катушка 18, 41
— проводимость 37
— связь 141
Индуктивное сопротивление 37
Индуктивио-связаиные цепи 106
-------как фильтры 384
Индуктивность 13, 36, 46
— взаимнаи 15, 106
— кабеля 283
— катушки 19, 27
— линии 283
413
Индуктивность рассеяния 112, 116, 119
Индукция 179
— остаточная 180
Интеграл Дюамеля 225, 239
— Фурье 250
Интегралы активного и реактивного сопротивлений 342
Интегрирование изображения 223
— оригинала (теорема интегрирования) 223
Интегрирующее звено 206, 209
Искажение амплитудное 292
— фазовое 292
Искажения мощность 175
Искусственная нейтральная точка 155
Источник зависимый (неавтономный) 93, 142, 354
— напряжения 19
— независимый (автономный) 89, 90
— тока 19, 25, 230
— э. д. с. 19, 24, 229
— электрической энергии 9
Источники эквивалентные 67
К
Канонические схемы реактивных двухполюсников 323
Каскадное соединение четырехполюсников 362
Катушка с ферромагнитным сердечником 191
Квадратная матрица 98
Кирхгофа законы 26
---для магнитной цепи 180, 184
Классификация двухполюсников 312
— фильтров 370
— четырехполюсников 348
Классический метод расчета переходных процессов 199
Колебания затухающие 211
— незатухающие 212
— энергии 37, 39, 123
Колебательная цепь 122
Колебательный контур 122
— процесс 211
Колоколообразный (колокольный) импульс 261, 265
Комбинированная связь 141
Коммутация 199
Компенсации теорема 92
Комплексная амплитуда 49
— магнитная проницаемость 190
— мощность 55
— передаточная функция 277
— проводимость 53
— форма расчета 48
---ряда Фурье 171
— частота 230, 392, 402
Комплексное действующее значение 51
— сопротивление 51
---двухполюсника 334, 343
--- намагничивания и потерь в стали 193
Комплексные действующие значения 51
— потенциалы 58
Комплексный расчет переходных процессов 231
— ток 51 - «
Конденсатор 15
Коидуктивная связь 141
Контур 23
— независимый 81
— параллельный колебательный 131
— последовательный колебательный 122
Контурный ток 82
Короткое замыкание 97, 353
----однородной линии 296, 297
----трансформатора 197
•---Цепи г, С 208
-------г, L 204
----четырехполюсника 353
Коэрцитивная сила 181
Коэффициент амплитуды 176
— бегущей волны 298
— включения контура 136
— затухания линии 286
— искажения 176
— мощности 44, 176
— отражения 360
— передачи 129, 361
---- сигнального графа 405
— полезного действия двухкоитурной системы 147
“ распространения 285
----операторный 311
— связи 113
---- критический 148
----оптимальный 148
— трансформации 116, 121
— усиления 129, 361
— фазы линии 286
— формы кривой 176
— четырехполюсника 356
Коэффициенты ряда Фурье 166
— четырехполюсника 351, 408
Кривая первоначального намагничивания 182
Кривые намагничивания 181
Критический коэффициент связи 148
Круговая диаграмма 71, 75, 77
----линии 304
Круговое вращающееся магнитное поле 160
Кулон 15
Кусочно-аналитическая форма 240
Л
Лапласа преобразование 219
Ленца закон 13
Линейная электрическая пепь 22
Линейное напряжение 153
Линейные электрические дели 21
Линейный ток 153
— элемент цёпи 2|
Линейчатый (дискретный) спектр 245
Линия без искажений 292
---- потерь 294
Лииня вектора напряженности магнитного поли 179
•=- как элемент резонансной цепи
— магнитной индукции 179
— однородная 283
Линия переменного параметра 77
Логарифмический декремент колебаний 212
М
Магнитная анизотропия 191
— вязкость 188
— индукция 30, 160, 179
— постоянная 18, 179
— проводимость 180
— проницаемость 18, 179, 190
— характеристика 182, 185
— цепь 178
Магнитное поле 159, 199
----вращающееся 159
----пульсирующее 160
414
Магнитное сопротивление 180
Магнитно-мягкий материал 181
Магнитио-твердый материал 181
Магнитный поток ИЗ, 179
---рассеяния 113, 192
Магнитопровод 182
Максвелла — Фарадея закон 13
Масштабы напряжения и тока 13
Матрица 98
— соединений (иициденций) 99
Матричные уравнения 98
---четырехполюсников 363
Мгновенная мощность 11
Международная система единиц (СИ) 6
Мейсоиа формула 405
Мера передачи 356
Метод выделения нулей н полюсов 397
— двух узлов 68
— единичного тока (метод подобия) 63
— комплексных амплитуд 48
— контурных tcjkob 82
— наложения 88
— отделения свободного тока от принужденного 233
— подобия (метод единичного тока) 63
— разложения в непрерывную дробь 401
— узловых напряжений 85, 111
Методы синтеза цепей 391
Механическая цепь 103
Механический четырехполюсник 349
Многоэлементиый двухполюсник 215
Модуль 49
Мостовая схема 69, 70, 82, 85, 348, 355
Мостовой фильтр 385
— четырехполюсник 348, 367, 403
Мощность активная (средняя) 44, 55, 175
— искажения 175
— комплексная 55
— мгновенная 11, 44
— полная 45, 55, 175
— реактивная 45, 55, 175
— средняя (активная) 44, 55, 175
— трехфазной цепи 154, 158
Н
Наложения метод 88
Намагничивания ветвь 116, 193
Намагничивающая сила 18, 116, 179
Намагничивающий ток 116, 193
Направление тока 10
— токов встречное 109, 197
---согласное 107, 109
Напряжение 10
— активное 41
— комплексное 51
— линейное 153
— реактивное 41
— смещения нейтрали 156
— узловое 85
— фазное 153
— холостого хода 95
Напряженность магнитного поля 178
— электрического поля 16
Настроечные кривые 125
Настройка иа полный резонанс 146
Нахождение сигнала по частотным характеристикам 272
Начальная фаза 29
Начальные условия 200, 284, 235
. Независимые начальные условия 200
Независимый (автономный) источник 89
Независимый контур 268
Незатухающие косинусоиды, спектры 269
— синусоиды, спектры 268
Неискажающая система 277
Неискаженная передача 292
Нейтральная точка 151, 155
Нейтральный провод 152
Ненулевые начальные условия 201, 229, 235
Необратимый четырехполюсник 349
Неоднородная магнитная цепь 178
Непер 359
Непланарная цепь 84
Непрерывная дробь 401
Неразветвлеииая магнитная цепь 179
Несвязанная трехфазиая цепь 150
Несимметричная трехфазная цепь 156
Несинусоидальный периодический процесс 165
— ток в замкнутой форме 174, 241
Неустановившийся пропесс 199
Нормированные характеристики 127
Нулевая точка 151
Нулевые начальные условия 201
Нули функции 392
О
Обмотки вторичная, первичная 115
Обобщенная воздействующая функция 213
— расстройка контура 127
— форма интеграла Фурье 266
Обобщенное сопротивление двухполюсника 395
Обобщенные (операторные) проводимость, сопротивления 230
Обратимости (взаимности) теорема 91
Обратимые цепи 91
Обратимый четырехполюсник 349
Обратная волна 286, 308
— задача расчета магнитной цепи 182
— матрица 98
— передача 350
— связь 368
Обратное преобразование Лапласа 226
---Фурье 251
Обратные двухполюсники 333
Обращение в комплексной плоскости 71
Общая проводимость узлов 86
— форма теоремы разложения 227
Общее сопротивление контуров 83
Одногорбая резонансная кривая 148
Одноименные (однополярные) зажимы 107
Одноконтурная схема 23
Однородная линия 283
— магнитная цепь 178
Одностороннее (прямо) преобразование
Лапласа 220
— преобразование Фурье 257
Одноэлементные двухполюсники 313
— четырехполюсники 364
Ом 12
Омическое сопротивление 36
Оператор вращения (поворота) 49
Операторное волновое сопротивление линии 311
Операторные (обобщенные) проводимость, сопротивление 214, 216, 235, 392
Операторный коэффициент распространения
311
Опережение по фазе 40
Определители, выраженные через коэффициенты четырехполюсника 408
415
Определитель графа 406
Оптимальный коэффициент связи 148
Опыт короткого замыкания 197
— холостого хода 197
Оригинал 220, 409
Основная кривая намагничивания 181
— частота 166
Остаточная индукции 180
Отклик цепи 22
Относительная диэлектрическая проницаемость 19
— магнитная проницаемость 18, 179
— расстройка 128
— частота 126
Отражение волн 286, 308
Отставание по фазе 40
П
Падающая (прямая) волна 286, 308
Падение магнитного напряжения 179
Параллельная (внешняя) емкостная связь
141
Параллельное соединение 23, 46, 61
----емкостей 100
----четырехполюсников 364
Параллельно-последовательное соединение четырехполюсников 364
Параллельный колебательный контур 122
Параметры однородной линии вторичные 289
-------первичные 283
— четырехполюсника 353
---- характеристические 356
----холостого хода и короткого замыкания 353
Парсеваля равенство 256
Пассивная цепь 9
Пассивный двухполюсник 312, 320
— четырехполюсник 348, 349
— элемент цепи 9
Первичные параметры линии 283
Первоначального намагничивания кривая 182
Первый закон Кирхгофа 26
Передаточная (взаимная) проводимость 90, 351
— функция четырехполюсника 361
Передаточное сопротивление 90, 351
Передача максимума мощности 50
— неискаженная 292
Переменный ток 10
Перенос источников в схеме 69
Переходная проводимость 239
Переходный процесс 199
----в разветвленной цепи 213
-------цепи с распределенными параметрами 307, 310
—---------сосредоточенными параметра-
ми 199
Период 28, 166
Периодический процесс 28
— режим в линии 283
Петля гистерезиса 180
Пилообразная функция 169, 281
Планарная (плоская) цепь 84
Плотность спектральная 253, 254
П-образный четырехполюсник 348, 353, 366
Поверхностный эффект 17, 36, 189
Подобии теорема 223
Показательная (полярная) форма записи комплексного числа 48
— форма уравнений линии 288
416
Поле магнитное 18
---вращающееся 159
---пульсирующее 160
— электрическое 16
Полная мощность 45, 175
— проводимость 42
Полное сопротивление 40
Полный резонанс 146
Положительная действительная функция 354
Положительные направления тока и напряжения 10, 14, 16
Полоса задерживания (затухания) 370
— пропускания 128, 147, 149, 370
Полосовой фильтр 370, 376—383, 389
Полюсы функции 392
Последовательная (внутренняя) емкостная связь 141
Последовательное соединение 23, 46, 61
---емкостей 100
---четырехполюсников 363
Последовательно-параллельное соединение четырехполюсников 364
Последовательный колебательный контур 122
Постоянная времени 204
— магнитная 18, 179
— электрическая 19
Постоянные интегрирования 202, 215
Постоянный ток 10, 23, 25
Потенциалы комплексные 58
— скалярные магнитные 179, 184
— электрические 10
Потенциальная диаграмма 58
Потенциально-обратные двухполюсники 333
Потенциально-эквивалентные двухполюсники 331
Поток магнитный ИЗ, 179
— рассеяния ИЗ, 192
Потокосцепление 106, 201
— самоиндукции 13, 113
Правило левой руки 30
— правой руки 30
— правоходового винта 13
Предельные соотношения 225
Преимущество спектрального метода 276
Преобразование дробно-линей ное 76
— звезды в треугольник 66
— Лапласа 219
— симметричных схем 70 .
— схем с двумя узлами 68
---с источниками 68
---'Со смешанным соединением 62
— треугольника в звезду 65
— Фурье 251
Приведенная схема замещения 116, 196
Принужденный режим 202
Принцип непрерывности потокосцепления 201
— постоянства суммарного заряда 202
Проводимость 12
— активная 42, 340
— взаимная (передаточная) 90, 351
— входная 90, 351
— емкостная 38
— индуктивная 37
— комплексная 53
— магнитная 180
— обобщенная (операторная) 392
— общая узлов 86
— передаточная (взаимная) 90, 351
— переходная 239
— полная 42
— реактивная 42
собственная узла 86
Проводимость электрическая удельная 17
Проницаемость диэлектрическая 19
— магнитная 18
Прохождение сигнала через линейную систему 280
------- систему с ограниченной полосой пропускания 278
Процесс непериодический (переходный) 199
— периодический 28, 165
Прямая волна 286, 308
— передача 350
Прямое преобразование Лапласа 220
Прямоугольные импульсы 246, 248, 263, 279
Пульсирующее магнитное поле 160
Пучности стоячих волн 296
Пьезоэлектрический резонатор 387
Р
Рабочее затухание 361
Радиан 29
Радиоимпульс прямоугольный 264, 266
Разветвленная магнитная цепь 184
— цепь с взаимной индукцией ПО
Разделение потерь в стали 190
Размыкание ветви 236
Разновидности четырехполюсников 348
Разность скалярных магнитных потенциалов 179, 184
— электрических потенциалов 10
— фаз 40
Разряд конденсатора апериодический 210
Расположение нулей и полюсов 211, 392—400
Распределение потенциала вдоль цепи 25
— энергии в спектре 255
Рассеяние 112, 113, 192
Рассеяния индуктивность 112
— магнитный поток 113, 192
— сопротивление 117, 195
Расстройка контура (абсолютная) 128
--- относительная 128
Реактивная мощность 45, 175
— проводимость 42
—> составляющая напряжения 41
--- тока 42
Реактивное сопротивление 39
Реактивный двухполюсник 312
— фильтр 371
Реакция цепи 22
— — на периодическую несинусоидальную функцию 241
Реализация функции 391
Реализуемость двухполюсников 396, 401
— функции 396
— четырехполюсников 354
Регулярность соединения четырехполюсников 364
Режим короткого замыкания трансформатора 197
-------четырехполюсника 353
— неустановившийся (переходный) 199
— принужденный 202
— свободный 202, 214
— установившийся 202
— холостого хода трансформатора 197
— — — четырехполюсника 353
Резонанс напряжений 41, 123
— полный 146
— > сложный 146
— токов 43
• — частный 145
Резонансная кривая 127
---двугорбая 148, 149
--- одногорбая 148
— цепь 122, 140, 307
— частота 122
Резонатор пьезоэлектрический 385
Релея теорема 256
Ряд гармонический (Фурье) 166
С
Свободные колебания 211
— составляющие 202
Свойства преобразования Лапласа 221, 223
---Фурье 258
Свойство коммутативности 223
— линейности 223
Связанная трехфазная цепь 150
Связанные колебательные контуры 140
Связь емкостная 141
— индуктивная 141
—' индуктивно-емкостная 141
— обратная 368
Сдвиг фаз 34
СИ (Международная система единиц) 6
Сигнальные графы 404
Сименс 12
Симметричная петля гистерезиса 180
— трехфазная цепь 153
Симметричный четырехполюсник 348
Симметрия непериодической функции 254 — периодической несинусоидальной функции 168
Симметрия схемы 70
Синтез электрических цепей 391
Синусоида эквивалентная 176, 188
Синхронный генератор 30
— двигатель 163
Скважность импульсов 363
Скольжение 163
Скорость групповая 286
— фазовая 286
Сложный резонанс 146
Случаи неприменимости спектрального метода 272
— симметрии непериодических функций 255
Смешанное соединение 62
Смещение нейтрали 156
Смита диаграмма 306
Собственная проводимость узла 86
— частота контура 211
Собственное затухание четырехполюсника 356
—» сопротивление контура 83
Согласное направление токов ’07
Согласование сопротивлений 119, 357
— характеристических сопротивлений 262
Соединение звездой 151
— параллельное 61
— последовательное 61
— смешанное 62
— треугольником 152
Соединения четырехполюсников 363
Сопротивление 11
— активное 36
— ветви намагничивания 116, 193
— взаимное (передаточное) 90
— вносимое 119, 125, 142
— волновое 285
— входное 90, 118,298. 351
— двухполюсника 313
— емкостное 38
417
Сопротивление индуктивное 37
— комплексное 51
— линии волновое 265
— магнитное 180
— обобщенное (операторное) 214, 216, 235, 392
— общее контуров 83
— омическое 36
— передаточное (взаимное) 90
— полное 40
— приведенное к первичной обмотке 116
— проводника 17
— рассеяния 117, 195
— реактивное 39
— связи 141
Сопротивление собственного контура 83
— характеристическое 124, 356
— электрическое удельное 17
Спектр (спектральная характеристика) 245
— амплитудный 245
— прямоугольных импульсов 263
— фазовый 245
Спектральная плотность 253, 254
Среднее значение периодической функции 31
--------- несииусоидальиой 175
Средняя (активная) мощность 44, 175
Столбцевая матрица 98
Стоячая волна 194
Схема замещения автотрансформатора 120
---асинхронного двигателя 78
--- вторичного контура 142
---индуктивной катушки 18
---катушки с ферромагнитным сердечником 194
--- конденсатора 19
--- первичного контура 142
---приведенная трансформатора 116, 196
—'— трансформатора 115, 196
---четырехполюсника 353
Схема мостовая 69, 70, 82, 85, 348, 355
— симметричная 70
— цепная 63, 328, 401
— электрическая 22
Схемы замещений для изображений 231
Т
Таблица изображений и оригиналов 231
Телеграфные уравнения 284
Теорема взаимности (обратимости) 91
— дифференцирования 222
— запаздывания 222
— интегрирования 222, 223, 259
— компенсации 92
— об изменении токов при изменении сопротивлений 93
---эквивалентном источнике напряжения 95
।--------тока 97
►— подобия 223
— разложения 226
— свертывания 223, 225
— смещения 223, 225
Фостера 321
Тепловые потерн в диэлектрике 19
Тесла 30, 179
Т-образный четырехполюсник 348, 353, 366
Ток 10
— активный 43
>— апериодический 210
1— гармонический 28
•— комплексный 51
Ток контурный 82
— короткого замыкания 97
— линейный 153
— намагничивающий 116, 193
— несинусоидальный 165, 174, 241
— однофазный 149, 165
— переменный 10, 29
— переноса 10
— переходный 203
— постоянный 10, 23, 25
— потерь в стали 193
— принужденный 202, 213
— проводимости 10, 16
— реактивный 43
.— свободный 202
— синусоидальный 28
> — смещения 16
— трехфазный 149
— установившийся 50, 202
— фазный 153
Тока источник 19, 25, 90, 230
Токи вихревые 188
Топографическая диаграмма 58
Тороидальный магнитопровод 182
Точка нейтральная 151, 155
— нулевая 151
Транспонированная матрица 99
Трансформатор 115
— идеальный 117
— с ферромагнитным сердечником 195
Треугольник мощностей 55
— напряжений 52
— проводимостей 53, 54
— сопротивлений 52
— токов 53
Трехфазная цепь 149
---несимметричная 156
---симметричная 153
Трехфазный генератор 150
— ток 149, 151
Тригонометрическая форма комплексного числа 49
---ряда Фурье 165
У
Угловая частота 29
---свободных колебаний 211
Угол диэлектрических потерь 44
— магнитных потерь 190
— сдвига фаз 34
Удельное сопротивление проводника 17
Удельные потери от вихревых токов 189
------- гистерезиса 180
Узел 22, 184
Узловое напряжение 85
Узлы стоячих волн 295
Умножение изображений (теорема сверты-
вания) 223, 225
Уравнение характеристическое 202
Уравнения колебаний Даламбера 308
контурных токов 83
— линий в гиперболической форме 289
— линии в показательной форме 288
---дифференциальные 284
— матричные 98
— механических цепей 103
— трансформатора 115
— узловых напряжений
— четырехполюсника 351
• — элементов цепи 46
Условие инвариантности 22
— неискаженной передачи сигнала 277
418
Условие пропускания 371
— физической реализуемости 396
Условное обозначение емкости 16
--- индуктивности 14
--- сопротивления 12
Установившийся режим 202
— ток 50, 202
Устранимый узел 22
Учет ненулевых начальных условий 235
Ф
Фаза 29, 150
— начальная 29
Фазиое напряжение 153
Фазный ток 153
Фазовая скорость распространения 286
Фазовращатель 77
Фазовый сдвиг 34, 36
— спектр 245
Фазоуказатель 157
Фазо-частотная характеристика 127
Фарада 15
Фарадея — Максвелла закон 13
Ферриты 190
Ферромагнитный сердечник 195
Ферромагнитных материалов свойства 180, 188
Физическая реализуемость двухполюсников 396, 401
Физически реализуемая система 281
Фильтр 370
— безындукционный 387
— верхних частот 370, 375—378, 382, 388, 390
—• заграждающий (режекторный) 370,
376—378
— мостовой 371, 385
— иижних частот 370
— полосовой 370
— реактивный (идеальный) 371
— типа К 375
---Т 371
Фильтров классификация 370
Формулы включения 237
Фостера теорема 321
Функция воздействующая 213
— единичная 221, 267, 278
— нмпульснаи 238
— минимального реактивного сопротивлении 341
— минимальной реактивной проводимости 341
---фазы 402
— неминимальной фазы 402
— передаточная 361
— периодическая 28
--- несинусоидальная 165
— положительная действительная 354
— синусоидальная 28
X
Характеристика амплитудно-фазовая 361
— внешняя 24
— вольт-ампериая 21, 24
— магнитная 182
— спектральная (спектр) 245
Характеристики частотные 122, 126
Характеристические параметры линии 289
— сопротивления (параметры) четырехполюсника 356
Характеристическое (волновое) сопротивление контура 124
— уравнение 202
Холостого хода напряжение 95
Холостой ход 95, 353
---однородной линии 288
1--трансформатора 197
четырехполюсника 353
Ц
Цепи гармонического тока 28
— дуальные 101
— эквивалентные 63—68
Цепная схема 63, 328, 401
Цепь активная 9
— емкостная 100
— линейная 22
— механическая 103
— непланарная 84
— однофазная 149, 165
— пассивная 9
— планарная (плоская) 84
— резонансная (колебательная) 122, 140
307
— с обратной связью 368
---распределенными параметрами 282
— — сосредоточенными параметрами 17
— трехфазная 149
— электрическая 9
Ч
Частота 28
— комплексная 230
— основнаи 166
— резонансная 122
— собственных (свободных) колебаний 211
— среза 372
— угловая 29
Частотные зависимости тока 127
Частотные характеристики 122, 126
---реактивного двухполюсника 322
Чередование (последовательность) фаз 157
Четырехполюсник активный 348
— Г-образный 348, 365
— механический 349
— мостовой 348, 367, 403
— необратимый 349
— несимметричный 348
— обратимый 349, 351
— одноэлементный 364
— пассивный 348, 349
— П-образиый 348, 353, 366
— при комплексной частоте 402
— симметричный 348
— Т-образный 348, 353, 366
Четырехполюсники эквивалентные 348
Четырехполюсников классификация 348
Э
Эквивалентная проводимость 62
— синусоида 176, 193
Эквивалентное сопротивление 61
Эквивалентного источника метод 95, 235
Эквивалентность четырехполюсников 348
Эквивалентные звезда и треугольник 65
— двухполюсники 331
— источники напряжения и тока 67
— участки цепи 63
— четырехполюсники 348
Экспериментальное определение одноименных зажимов 108
419
Электрическая постоянная 19
— схема 22
— цепь 9
---- инвариантная во времени 22
----линейная 21
Электрический заряд 10, 15, 26
Электрическое поле 15, 199
Электродвижущая сила 19 ----взаимной индукции 106 ----самоиндукции 13, 106
Элементов цепи уравнения 46
Элементы механической цепи 103
— схемы геометрические 22
— электрической цепи 9, 22
Эллиптическое вращающееся поле 162
Энергия магнитного поля 13
— электрического поля 16
Эффект близости 18, 36
— поверхностный 17, 36, 189
Эффективность передачи 147
СОДЕРЖАНИЕ
Предисловие ........................ 3
Условные обозначения ............ 5
Введение .....-..................... 7
Глава первая. Основные определения, законы, элементы и параметры электрических цепей ..• 9
1-1. Электрическая цепь ......... 9
1-2. Положительные направления тока и напряжения .......... 10
1-3. Мгновенная мощность и энергия ................. И
1-4. Сопротивление .............. П
1-5. Индуктивность ............. 13
1-6. Емкость ................... 15
1-7. Замещение физических уст-
ройств идеализированными элементами цепи ............ 17
1-8. Источник э. д. с. и источник тока ...................... 19
1-9. Линейные электрические цепи 21 1-10. Основные определения, относящиеся к электрической схеме ........................... 22
1-1L Вольт-амперная характеристика участка цепи с источником .......................... 24
1-12. Распределение потенциала вдоль цепи с сопротивлениями и источниками напряжения ............................ 25
1-13. Законы Кирхгофа............ 26
1-14. Задачи и вопросы для са-
• мопроверки .............. 27
Глава вторая. Цепи гармонического тока ................... 28
2-1. Гармонические колебания .. 28
2-2. Генерирование синусоидальной э. д. с................. 29
2-3. Среднее и действующее значения функции .............. 31
2-4. Представление гармонических
колебаний в виде проекций вращающихся векторов .... 33
2-5. Гармонический ток в сопротивлении ................... 35
2-6. Гармонический ток в индуктивности ................... 36
2-7. Гармонический ток в емкости 37
2-8. Последовательное соединение
г, L, С................... 39
2-9. Параллельное соединение г, L, С .................... 42
2-10. Мощность в цепи гармонического тока ............... 44
2-11. Задачи и вопросы для самопроверки ................... 47
Главатретья. Применение комплексных чисел к расчету элект-
рических цепей (метод комплексных амплитуд) ................... 48
3-1. Представление гармонических функций с помощью комплексных величин ........... 48
3-2. Законы Ома и Кирхгофа в комплексной форме .......... 50
3-3. Зависимость между сопротивлениями и проводимостями участка цепи ............... 54
3-4. Комплексная форма записи мощности ................... 55
3-5. Условие передачи максимума средней мощности от источника к приемнику............ 56
3-6. Условие передачи источником максимума мощности при заданном коэффициенте мощности приемника ................ 57
3-7. Баланс мощностей .......... 57
3-8. Потенциальная (топографическая) диаграмма .......... 58
3-9. Задачи и вопросы для самопроверки 59
Глава четвертая. Преобразование схем электрических цепей. Метод геометрических мест ......... 60
4-1. Последовательное и парал-
лельное соединения ......... 60
4-2. Смешанное соединение .... 62
4-3. Эквивалентные участки цепи с последовательным и параллельным соединениями • • 63
4-4. Преобразование треугольника в эквивалентную звезду.. 65
4-5. Преобразование звезды в эквивалентный треугольник.. 66
4-6. Эквивалентные источники напряжения и тока ............ 67
4-7. Преобразование схем с двумя узлами................... 68
4-8. Перенос источников в схеме 68
4-9. Преобразование симметричных схем ................... 70
4-10. Графическое изображение зависимостей комплексных величин от параметра ....... 71
4-11. Преобразование вида ?2
4-12. Диаграммы сопротивлений и проводимостей простейших электрических цепей ... 73
4-13. Преобразование вида
А + ™ 76
C + Dk................
4-14. Задачи и вопросы для самопроверки ................... 79
Глава пятая. Методы расчета сложных электрических цепей .... 80
421
5-1. Применение законов Кирхгофа для расчета сложных цепей ......................... 80
5-2. Метод контурных токов . — 82
5-3. Метод узловых напряжений 85
5-4. Метод наложения............. 88
5-5. Входные и передаточные проводимости и сопротивления.. 89
5-6. Теорема обратимости (нли
взаимности) ............... 91
5-7. Теорема компенсации....... 92
5-8. Теорема об изменении токов
в электрической цепи при изменении сопротивления в одной ветви.................... 93
5-9. Теорема об эквивалентном источнике ................... 95
5-10. Применение матриц к расчету электрических цепей .... 97
5-11. Некоторые особенности расчета электрических цепей с емкостями .................. 100
5-12. Дуальные цепи ............. 101
5-13. Электромеханические аналогии ........................ 103
5-14. Задачи и вопросы для самопроверки ................... 105
Глава шеста и. Индуктивно связанные электрические цепи......... 106
6-1. Основные положения и оп-
ределения .................. 106
6-2. Полярности индуктивно связанных катушек; э. д. с. взаимной индукции.............. 107
6-3. Комплексная форма расчета цепи с взаимной индукцией 109
6-4. Коэффициент индуктивной связя. Индуктивность рассеяния ........................ 112
6-5. Уравнения и схемы замещения трансформатора -без ферромагнитного сердечника . - 115
6-6. Энергия индуктивно связанных обмоток ................ 118
6-7. Входное сопротиаление
трансформатора ............. 118
6-8. Автотрансформатор ......... 120
6-9. Задачи и вопросы для самопроверки ................... 121
Глава седьмая. Одиночный колебательный контур ............... 122
7-1. Колебательвые (резонансные) цепи................... 122
7-2. Последовательный колебательный контур. Резонанс напряжений .................. 122
7-3. Частотные характеристики последовательного резонансного контура .............. 126
7-4. Параллельный колебатель-
ный контур. Резонанс токов 131
7-5. Разновидности параллельного колебательного контура. - 132
7-6. Элементы колебательного
контура .................. 138
7-7. Задачи и вопросы для самопроверки ................... 140
Глава восьмая. Связанные ко-
лебательные контуры ............. 140
8-1. Виды связи................. 140
8-2. Сопротивление связи и вно-
симые сопротивлении ........ 141
8-3. Векторные диаграммы...... 143
8-4. Коэффициент связи ......... 144
8-5. Настройка связанных конту-
ров. Энергетические соотношения ...................... 145
8-6. Резонансные кривые связанных контуров. Полоса пропускания .................. 147
8-7. Задачи и вопросы для самопроверки ................. 149
Глава девятая. Цепи трехфазного тока ..................... 149
9-1. Трехфазные электрические цепи ...................... 149
9-2. Соединение звездой и треугольником ................ 151
9-3. Симметричный режим работы трехфазной цепн............ 153
9-4. Несимметричный режим ра-
боты трехфазной цепи...... 156
9-5. Мощность несимметричной трехфазиой цепи ........... 158
9-6. Вращающееся магнитное поле ........................ 159
9-7. Принцип действия асинхронного и синхронного двигателей ....................... 162
9-8. Задачи и вопросы для самопроверки .................. 164
Глава десятая. Периодические иесннусоидальные процессы........ 165
10-1. Тригонометрическая форма ряда Фурье................. 165
10-2. Случаи симметрии ......... 168
10-3. Перенос начала отсчета .. 170
10-4. Комплексная форма ряда
Фурье ..................... 171
10-5. Применение ряда Фурье к
расчету периодического ие-синусоидальиого процесса .. 172
10-6. Действующее и среднее зна-
чения периодической иеси-иусоидальной функции .... 174
10-7. Мощность в цепн периоди-
ческого несннусондального тока ...................... 175
10-8. Коэффициенты, характеризующие периодические неси-нусоидальиые функции .... 176
10-9. Задачи и вопросы для самопроверки ................ 176
Глава одиннадцатая. Цепи с ферромагнитными сердечниками при постоянном магнитном потоке 178 11-1. Назначение и типы магнит-
ных цепей ................. >78
11-2. Основные законы магнитной цепи и свойства ферромаг-
нитных материалов .......... 178
11-3. Неразветвлениая магнитная
цепь .................... 182
11-4. Разветвленная магнитная цепь ...................... 184
11-5. Задачи и вопросы для самопроверки ................ 186
Глава двенадпатая. Цепн переменного тока с ферромагнитными элементами ................... 187
12-1. Некоторые особенности це-
422
пей переменного тока с ферромагнитными элементами . 187
12-2. Основные свойства ферромагнитных материалов при переменных полях ......... 188
12-3. Катушка с ферромагнитным сердечником .............. 191
12-4. Трансформатор с ферромагнитным сердечником ....... 195
12-5. Задачи и вопросы для самопроверки ............... 198
Глава тринадцатая. Переходные процессы в линейных цепях с сосредоточенными параметрами (классический метод) ............ 199
13-1. Возникновение переходных процессов ................ 199
13-2. Законы коммутации и начальные условия .......... 200
13-3. Принужденный и свободный режимы ............... 202
13-4. Переходный процесс в це-
пи г, L .................... 203
13-5. Переходный процесс в це-
пи г, С .................. 206
13-6. Переходный процесс в цепи
г. L. С .................. 209
13-7. Расчет переходного процес-
са в разветвленной цепи . 213
13-8. Задачи и вопросы для самопроверки ............... 218
Глава четырнадцатая. Применение преобразования Лапласа к расчету переходных прШессов.. 219 14-1. Общие сведения ............. 219
14-2. Прямое преобразование
Лапласа. Оригинал и изображение ................. 220
14-3. Изображения некоторых простейших функций .... 221
14-4. Основные свойства преобразования Лапласа.......... 221
14-5. Нахождение оригинала по изображению с помощью обратного преобразования Лапласа ........................ 226
14-6. Теорема разложения ....... 226
14-7. Таблицы оригиналов и изо-
бражений .................. 229
14-8. Применение преобразования
Лапласа к решению дифференциальных уравнений электрических цепей ..... 229
14-9. Учет ненулевых начальных условий методом эквивалентного источника............ 235
14-10. Формулы включения ..... 237
14-11. Расчет переходного процесса с помощью формул наложения .. .=................. 238
14-12. Нахождение в замкнутой форме установившейся реакции цепи иа периодическую иесинусоидальную воздействующую функцию .............. 241
14-13. Задачи и вопросы для самопроверки .................. 243
Глава пятнадцатая. Спектральный метод .................... 245
15-1. Временное и спектральное представление сигналов ....
15-2. Непериодические сигналы. Интеграл Фурье как предельный случай ряда Фурье
15-3. Связь между дискретным и сплошным спектрами ............
15-4. Случаи симметрия непериодической функции ..............
15-5. Распределение энергии в спектре .......................
15-6. Связь между преобразованием Фурье н преобразованием Лапласа ..................
15-7. Свойства преобразования Фурье..........................
15-8. Спектры некоторых типовых непериодических сигналов ..
15-9. Обобщенная форма интеграла Фурье ...................
15-10. Особые случаи............
15-11. Нахождение сигнала по заданным частотным характеристикам действительной и мнимой составляющих спектра .......................
15-12. Применение спектрального метода для расчета переходных процессов .................
15-13. Условие неискаженной передачи сигнала через линейную систему ...................
15-14. Прохождение сигнала через линейную систему с ограниченной полосой пропускания 15-15. Задачи и вопросы для самопроверки ....................
245
250
252
254
255
256
257
260
266
269
272
273
277
278
281
Глава шестнадцатая. Цепи с распределенными параметрами .. 282
16-1. Первичные параметры од-
нородной линии ........... 282
16-2. Дифференциальные уравнения однородиой линии.... 284
16-3. Периодический режим в од-
нородной линии ........... 285
16-4. Вторичные параметры однородной линии ............. 289
16-5. Линия без искажений .... 292
16-6. Линия без потерь ........ 294
16-7. Режимы работы линии без
потерь. Стоячие волны .... 295
16-8. Входное сопротивление линии ...................... 298
16-9. Мощность в линии без потерь ..................... 301
16-10. Линия как согласующий трансформатор ............ 302
16-11. Согласование сопротивлений посредством параллельного присоединения отрезков линии ........................... 303
16-12. Круговые диаграммы для линии без потерь.......... 305
16-13. Линия как элемент резонансной цепи ............. 307
16-14. Переходные процессы в цепях с распределенными параметрами ................ 307
16-15. Исследование переходных процессов в цепях с распре-
423
деленными параметрами с помощью преобразования Лапласа ................ 310
16-16. Задачи и вопросы для самопроверки ............... 311
Глава семнадцатая. Двухполюсники ...................... 312
17-1. Определение и классификация двухполюсников ..... 312
17-2. Одноэлементные реактивные двухполюсники .......... 313
17-3. Двухэлементные реактивные двухполюсники .......... 314
17-4. Многоэлемеитные реактивные двухполюсники ...... 315
17-5. Общее выражение сопротивления пассивного многоэлементного реактивного двухполюсника ............... 320
17-6. Канонические схемы реак-
тивных двухполюсников .. 323
17-7. Знак производной по часто-
те от сопротивления или проводимости реактивного двухполюсника .......... 327
17-8. Цепные схемы реактивных двухполюсников ............ 328
17-9. Потенциально - эквивалент-
ные двухполюсники и условия их эквивалентности .. 331
17-10. Потенциально - обратные двухполюсники и условия их взаимной обратиости........... 333
17-11. Многоэлемеитные двухполюсники с потерями, содержащие элементы двух типов 334
17-12. Четность активной и нечетность реактивной составляющих сопротивления относительно частоты. Знак активного сопротивления и активной проводимости .... 339
17-13. Связь между частотными характеристиками активной и реактивной составляющих сопротивления или прово-
димости двухполюсника .. 341
17-14. Задачи и вопросы для самопроверки .............. 347
Глава восемнадцатая. Четырехполюсники .................. 347
18-1. Основные определения и классификация четырехполюсников ................ 347
18-2. Системы уравнений четырехполюсника ............ 350
18-3, Уравнения четырехполюсника в форме 1ИП........... 351
18-4. Параметры холостого хода и короткого замыкания .... 353
18-5. Схемы замещения четырехполюсника ............... 353
18-6. Входное сопротивление четырехполюсника при произвольной нагрузке......... 355
18-7. Характеристические параметры четырехполюсника .. 356
18-8. Вносимое затухание четырехполюсника ............ 359
18-9. Передаточная функция ___ 361
18-10. Каскадное соединение четырехполюсников, основанное на согласовании характеристических сопротивлений ..........-.. 362
18-11. Уравнения сложных четырехполюсников в матричной форме ......................... 363
18-12. Одноэлементные четырехполюсники .................... 364
18-13. Г-образный четырехполюсник ...................... 365
18-14. Т-образиый н П-образиый четырехполюсники ......... 366
18-15. Симметричный мостовой четырехполюсник ............ 367
18-16. Идеальный трансформатор как четырехполюсник........... 367
18-17. Обратная связь ......... 368
18-18. Задачи и вопросы для са-
мопроверки ............... 369
Глава девятнадцатая. Электрические фильтры .............. 370
19-1. Основные определения и классификация электрических фильтров ............ 370
19-2. Условие пропускания реактивного фильтра .......... 371
19-3. Фильтры типа k........... 374
19-4. Фильтры типа т........... 379
19-5. Индуктивно связанные кои-
туры как фильтрующая система .................... 384
19-6. Мостовые фильтры, пьезоэлектрические резонаторы .. 385
19-7. Безындукционные фильтры 387
19-8. Задачи и вопросы для самопроверки ................. 390
Глава двадцатая. Синтез линейных электрических цепей .... 391
20-1. Характеристика задач синтеза ..................... 391
20-2. Исследование двухполюсника при комплексной частоте 392 20-3. Сопротивление и проводимость как положительная действительная функция .. 394
20-4. Условия физической реализуемости функции ......... 396
20-5. Методы построения двухполюсника по заданной частотной характеристике .... 397
20-6. Исследование четырехполюсника при комплексной частоте .................. 402
20-7. Задачи и вопросы для самопроверки ............... 403
Приложения:
I. Метод сигнальных графов.... 404 II. Соотношения между коэффициентами четырехполюсника.. III. Определители, выраженные через коэффициенты четырехполюсника ..................... 408
IV. Оригиналы и изображения по Лапласу .................... 409
Литература ....................... 411
Алфавитный указатель.............. 412
424