А. Н. КР Ы Л О В
О НЕКОТОРЫХ
ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЯХ
МАТЕМАТИЧЕСКОЙ
Физики
А. И. КРЫЛОВ
О НЕКОТОРЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ,
ИМЕЮЩИХ ПРИЛОЖЕНИЕ
В ТЕХНИЧЕСКИХ ВОПРОСАХ
ПЯТОЕ ИЗДАНИЕ
Допущено Министерством высшего образования СССР
в качестве учебного пособия для высших учебных заведений
>ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1 9 5 0 ЛЕНИНГРАД
11-5-2
Редактор Б. И, Цукерман,
Техн, редактор М. Д, Суховцева.
Подписано к печати 4/Х1 1950 г. Бумага 70х108/ц 11 >5 бум. л. 31,51 печ. л. 29,53 уч.-изд. л.
37547 тип. зн. в печ. л. Т- 07974. Тираж. 10 000 экз. Цена книги 10 р. 35 к. Переплет 2 р.
Заказ № 595
16-я типография Главполиграфиздата при Совете Министров СССР.
Москва» Трехпрудный пер., 9.
СОДЕРЖАНИЕ
Предисловие к пятому изданию........................................... 6
Предисловие к первому изданию.......................................... 8
Предисловие ко второму изданию........................................ 11
Глава I
Обыкновенные линейные уравнения с постоянными коэффициентами
1. Уравнение второго порядка с последним членом. Общий интеграл его ...	13
2. Составление частного решения данного вида, применяя способ неопределен-
ных коэффициентов................................................. 15
3—5. Случай, когда последний член выражается суммою, составленной из
синусов или косинусов разных кратностей переменной независимой.
Амплитуда, разность фаз, декремент................................ 17
6.	Резонанс........................................................	21
7.	Биения.......................................................  _	24
8.	Действие сил малой продолжительности.............................. 27
9.	Линейные уравнения высших порядков. Символический способ интегриро-
вания их...........................................................   31
10.	Малые колебания системы с несколькими степенями свободы........... 36
11.	Случай равных корней характеристического уравнения. Численный пример. 42
12.	Нормальные координаты и основные колебания системы...............  45
13.	Малые колебания системы в сопротивляющейся среде. Функция рассеяния. 47
14,	15. Вынужденные колебания системы. Резонанс....................... 50
16—20. Приведение векового уравнения к виду, удобному для численного реше-
ния его. Пример. Особенные случаи.................................. 55
21.	Колебания при постоянном трении................................... 73
22.	Общие замечания об устройстве регистрирующих приборов. Прибор для
записи вибрации корабля. Индикатор Уатта. Прибор Фрама................ 76
23.	Поперечные колебания вращающегося вала............................ 83
Глава II
Линейные уравнения с частными производными высших порядков
и с постоянными коэффициентами
24.	Метод Даламбера и Эйлера интегрирования уравнений, где во всех чле-
нах порядок производных один и тот же................................. 86
25.	Общий вид линейного уравнения с постоянными коэффициентами и его самого
общего решения........................................................ 88
26.	Пример—уравнение распространения тепла............................ 90
27.	Случай равных корней характеристического	уравнения.................92
28.	Обобщение формул § 25............................................. 92
29.	Начальные условия и нахождение решения,	им	удовлетворяющего... 93
30.	Формулы Фурье..................................................... 94
31.	Доказательство теоремы Фурье.....................................  95
32.	Метод Коши....................................................... 99-
33.	Случай уравнения с последним членом ..........................	.	101
34—37. Пример 1-й: колебания неограниченной упругой среды............ 102
38, 39. Пример 2-й: уравнение движения неограниченной пластинки...... 107
Глава III
Интегрирование линейных* уравнений с частными производными при условиях
на границах ограниченной среды. Первый метод Пуассона
40.	Замечание об истории вопроса..................................... 111
41.	Изложение метода на примере уравнения колебания струны. .......	112
42.	Свойства колебательного движения струны............	. . . ж . . .	120
1*
Z4
ОГЛАВЛЕНИЕ
43.	Задачи 1-я и 2-я относительно интегрирования уравнения движения струны
при разных граничных условиях......................................... 124
44,	45. Задача 3-я: уравнение распространения тепла в пруте........... 131
Глава IV
Интегрирование линейных уравнений с частными производными при условиях
на границах ограниченной среды. Второй метод Пуассона
46.	Изложение метода на примере уравнения движения струны. Сравнение
полученного решения с даламберовым.................................... 138
47.	Пример приложения метода к уравнению распространения тепла в пруте. 145
48.	Поперечные колебания упругого стержня . <,........................ 149
49.	Замечания о вычислении корней трансцендентных уравнений........... 157
Глава V
Приложения теории функции мнимого перемёййоГО и свойств интегральных
вычетов к интегрированию линейных уравнений обыкновенных и с частными
производными. Метод Коши
50.	Понятие о функции мнимой переменной............................... 161
51.	Понятие об интеграле от функции мнимой переменной................. 163
52.	Теорема Коши. Интегральный вычет..............................  .	166
53.	Две основные теоремы об интегральных вычетах.....................  170
54.	Приложение интегральных вычетов к нахождению определенных интегралов.
Примеры........................................................... 171
55,	56. Приложение интегральных вычетов к разложению функций в ряды...	174
57,	58. Приложение интегральных вычетов к интегрированию обыкновенных
линейных уравнений.................................................... 185
59. Определение постоянных произвольных по данным начальным значениям
неизвестной и ее производных...................................... 189
60,	61. Интегрирование систем линейных уравнений...................... 194
62.	Теорема Гурвица................................................... 198
63, 64. Приложение интегральных вычетов к интегрированию линейных уравне-
ний с частными производными.....................................   199
Глава VI
Некоторые замечания о сходимости рядов Фурье и им подобных
и о суммировании сих рядов
65.	Теорема Абеля....................................................    206
66.	Приложение теоремы Абеля к определению условий сходимости рядов
Фурье............................•...............................   207
67.	Порядок коэффициентов ряда Фурье относительно при разложении разного
рода функций........................................................... 209
*68, 69. Места разрывов и величины скачков функции и ее производной и их
связь с коэффициентами ее разложения в ряд Фурье. Применение этих
формул к усилению быстроты сходимости рядов Фурье.................  211
70. Нахождение производных функций, представленных рядами Фурье, когда
: ; почленное дифференцирование недопустимо.....................  ...	224
71; Ряды, подобные рядам Фурье.......................................... 227
Г л а в а VII
Решение линейных дифференциальных уравнений с частными производными
и постоянными коэффициентами, имеющих последний член. Вынужденные коле-
бания струн и стержней и другие практические приложения общей теории
72.	Изложение общего метода на примере определения вынужденных колебаний
струны..............................................L	• • *............ ^29
73.	Случай, когда колебания происходят в сопротивляющейся среде......... 237
74.	Вынужденные поперечные колебания стержня	.	239
7,5	. Поперечные колебания стержня, вызываемые равномерно движущейся на-
грузкой .........................................v...................... 242
76.	Действие на балку малой массы равномерно движущейся нагрузки. Уравнение
Стокса, интегрирование его........................................ .	.	259
ОГЛАВЛЕНИЕ
5
77.	' Поперечные колебания балки под действием периодически изменяющейся
нагрузки................................................................ 251
78,	79. Колебания тяжелого груза, подвешенного на упругой нити. Технические
вопросы, приводимые к этой задаче....................................... 257
80.	Приложение выводов предыдущего параграфа к теории индикатора Уатта. 263
81.	Частные случаи пре дыдущей задачи................................... 263
82.	Действие внезапно приложенной силы................................•	270
83—85. Анализ записи давления в цилиндре компрессора, полученной индика-
тором Виккерса...................................................... 275
86. Крутильные колебания вала........................................... 283
87. Колебания струны, вызываемые заданным колебательным движением данной
ее точки ................,.......................................... 284
88—94. Распространение тока по кабелю . .	............................. 283
95—100. Продольные колебания ствола орудия при выстреле................. 303
101—103. Графическое представление полученного решения................. 3201
104—106. Вибрация судов. Общий метод расчета ........................... 323
107, 108. Метод численного интегрирования............................... 329
109, 110. Определение постоянных произвольных.........................   332
111. Влияние местной жесткости на общую выбрацию........................ 333
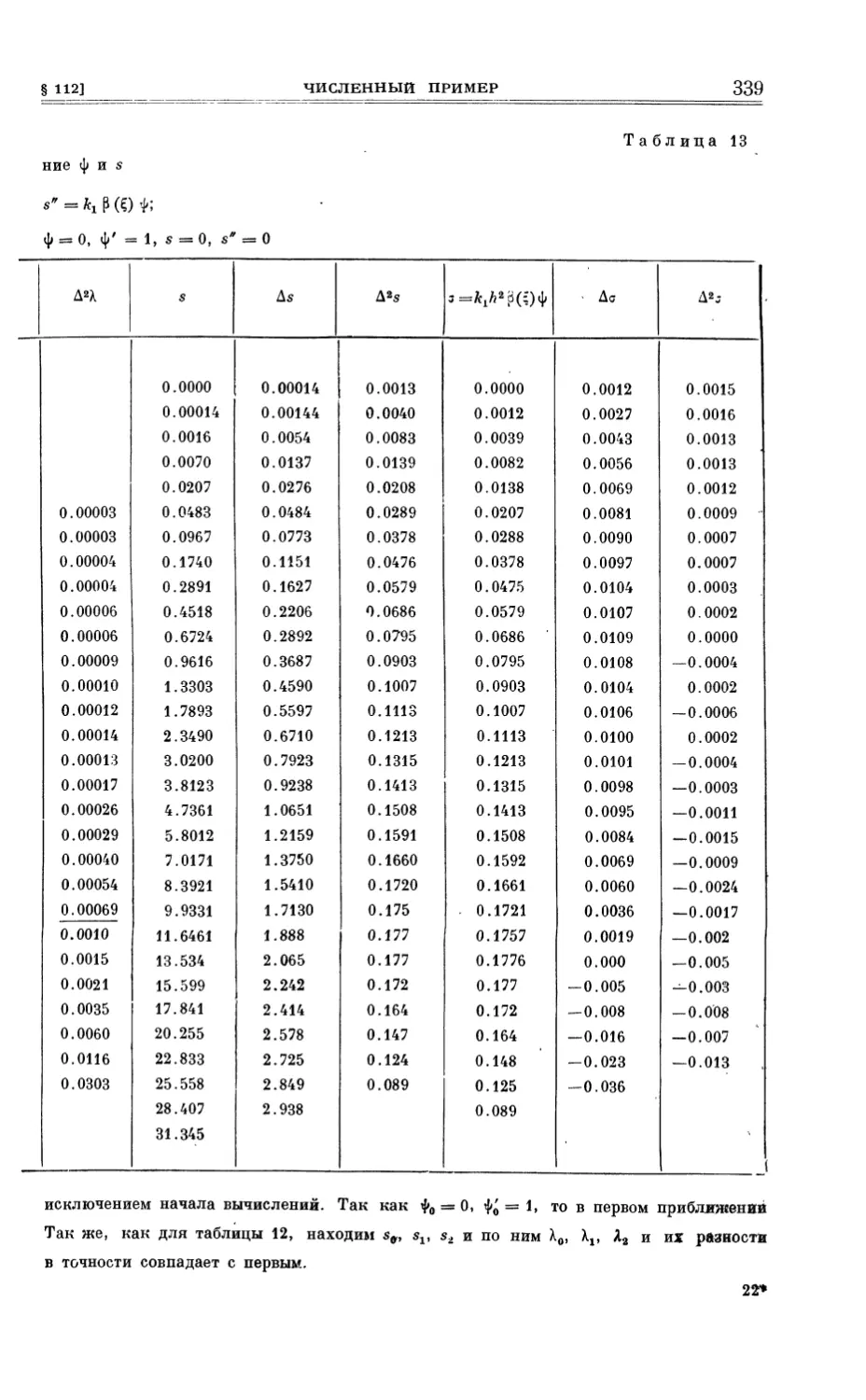
112, ИЗ. Численный пример..............................................  334
114.	Метод вычисления фундаментальных функций и характеристических чисел
численным интегрированием . ............................................ 343
Глава VIII
Радиальные колебания полого цилиндра
115.	Уравнения, к которым приводит вопрос о радиальных колебаниях полого
цилиндра. Случай действия переменного давления на внутреннюю по-
верхность .............................................................. 352
116,	117. Определение свободных колебаний..............................  354
118,	119. Основные свойства функций Бесселя............................. 358
120.	Трансцендентное уравнение, определяющее основные тона.............. 363
121,	122. Определение вынужденных колебаний при действии переменного
давления на внутреннюю поверхность.....................................  363
123. Численный пример—радиальные колебания 12-дюймовой пушки............ 365
ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
Книга покойного академика Алексея Николаевича Крылова «О некото-
рых дифференциальных уравнениях математической физики, имеющих
приложение в технических вопросах» в первом издании вышла в 1913 году
в Известиях Морской Академии. Как пишет А. Н. Крылов в предисловии
к этому изданию, содержание книги составлено из лекций, которые он
читал в 1912 году слушателям Академии. Второе и третье издания появи-
лись в 1931—1933 годах в серии научно-технической литературы Академии
Наук СССР. По сравнению с первым изданием они были дополнены изложе-
н нем работы А. Н. Крылова о численном решении векового уравнения и рядом
технических примеров. Четвертое издание было опубликовано в 1948 году,
уже после смерти автора, в Собрании его трудов, которые и по сие время
издаются Академией Наук СССР. В этом издании в отдельных местах, относя-
щихся к теоретическим вопросам, были сделаны несущественные изменения,
а также проверены таблицы.
Настоящее пятое издание воспроизводит предыдущее.
Книга А. Н. Крылова представляла собою в 1913 году и представляет
до настоящего времени единственное большое руководство по математиче-
ской физике, в котором, с одной стороны, весьма полно изложены класси-
ческие работы по математической физике первой половины XIX века,
а с другой стороны-*-большое внимание уделено приложениям методов
математической физики к конкретным, практически важным техническим
задачам. Среди этих задач центральное место занимают вынужденные коле-
бания упругих систем и, в частности, явление резонанса.
Основным метрдом исследования является здесь применение метода
Фурье или, как его называл А. Н. Крылов, «второго метода Пуассона»,
обобщенного А. Н. Крыловым на случай вынужденных колебаний. Основным
в этом отношении является мемуар А. Н. Крылова о вынужденных колеба-
ниях стержней постоянного сечения, опубликованный в 1905 году. Содержа-
ние этой работы с некоторыми дополнениями изложено в VII главе книги.
Тот же метод црименен в VIII главе к исследованию вынужденных радиаль-
ных колебаний полого цилиндра. Во всех случаях проводится глубокое
качественное исследование характера воздействия вынуждающей силы на
упругую систему.
В первой главе подробно исследуются вынужденные колебания, описы-
ваемые линейными обыкновенными дифференциальными уравнениями вто-
рого порядка, в связи с вопросом об устройстве различных регистрирующих
приборов.
Еще в работе 1905 года А. Н. Крылов приметил тот факт, что вынуж
дающая сила может не удовлетворять предельным условиям собственных
колебаний, в связи с чем в результате применения того метода, о котором
мы говорили выше, ответ на задачу выражается медленно сходящимся рядом-
особенно вблизи концов основного промежутка. Таким образом, естественно
возникает задача улучшения сходимости рядов Фурье и им подобных рядов.
А. Н. Крылов указал чрезвычайно простой и остроумный прием для реше-
ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ	7
ния этой задачи—прием, основанный на выделении из суммы ряда элемен-
тарных функций так, чтобы уничтожались те части коэффициентов ряда
Фурье, которые медленно убывают при возрастании значка. Этот прием
изложен в VI главе настоящей книги.
Отметим еще, что в первой главе А. Н. Крылов дает новый простой
метод вычисления корней векового уравнения. Сначала излагается история
вопроса, связанная с именами Лагранжа, Лапласа, Леверрье и Якоби.
Основная трудность развертывания векового уравнения состоит в том, что
неизвестное (искомая частота) входит в диагональные члены определителя,
равенство нулю которого и дает вековое уравнение. А. Н. Крылов указы-
вает прием, при помощи которого это неизвестное можно сосредоточить
в одном столбце определителя—прием, основанный на вычислениях, ана-
логичных тем, при помощи которых система дифференциальных уравнений,
породивших вековое уравнение, приводится к одному уравнению высшего
порядка. В связи с этим исследованием А. Н. Крылова у нас появился целый
ряд работ, посвященный этому же вопросу. В работах Н. Н. Лузина,
И. Н. Хлодовского и Ф. Р. Гантмахера дан алгебраический анализ метода
А. Н. Крылова и в работе А. Данилевского дан новый алгебраический метод
развертывания векового уравнения.
В предисловии к изданным им лекциям П. Л. Чебышева А. Н. Крылов
рекомендует эти лекции инженерам, ибо, как он пишет, Чебышев не зада-
вался целью сделать свой курс безукоризненно строгим, а довольствовался
«той разумной строгостью, которая, предохраняя от ошибок, сообщает
непреложность выводам». Эти слова достаточно характеризуют и стиль
предлагаемой книги.
Акад, Вл, Смирнов
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
По уставу 1909 г. продолжительность курса для технических отделов
Морской Академии увеличена до трех лет, причем в учебный план третьего
года включены необязательные для слушателей лекции по математике.
Чтение этого необязательного курса было поручено Конференцией
Академии мне, и предметом его избрано изложение способов интегриро-
вания дифференциальных уравнений математической физики, встречающихся
в технических вопросах.
Прочитанный мною в продолжение осеннего полугодия 1912 г. при
трех часовых лекциях в неделю курс и составляет содержание
этой книги.
В главе I я напоминаю слушателям известную уже им из общего курса
теорию интегрирования обыкновенных линейных дифференциальных урав-
нений с постоянными коэффициентами, подробно останавливаясь на уравне-
нии второго порядка и разборе его решений в разных случаях; здесь же
выясняются столь важные для всех технических приложений явления
резонанса. Затем я перехожу к уравнениям высших порядков и показываю
символический способ нахождения их решений. Этот способ вошел во все-
общее употребление в английских руководствах и вообще в английскую
литературу, с которою особенно часто и придется иметь дело морским инже-
нерам. Рассмотрев общую теорию малых колебаний системы с несколькими
степенями свободы, я даю, в заключение главы, несколько примеров техни-
ческого характера, в которых приходится иметь дело с уравнениями разо-
бранного в главе вида и с явлениями резонанса.
В главе II я даю изложение метода Коши интегрирования линейных
дифференциальных уравнений с постоянными коэффициентами и с част-
ными производными высших порядков при начальных условиях, относя-
щихся к среде неограниченной. Эта глава составлена мною по лекциям
покойного проф. А. Н. Коркина, прочитанным им в 1891 г. группе своих
учеников, собиравшихся на квартире проф. А. И. Садовского. Эти лекции
были мною тогда же тщательно записаны и проредактированы, и в этой
главе воспроизведено с возможною точностью образцовое изложение
моего незабвенного учителя, столь многие годы трудившегося на пользу
нашей Морской Академии.
Изложенные в этой главе вопросы находят ряд применений при иссле-
дованиях, относящихся к распространению электрических колебаний и бес-
проволочной телеграфии. Этих приложений я не касаюсь, так как в Акаде-
мии читается специальный по этому делу курс.
В главе III я рассматриваю первый метод Пуассона для интегрирова-
ния линейных дифференциальных уравнений с частными производными
и постоянными коэффициентами при условиях, относящихся к среде огра-
ниченной. Здесь я также сперва воспроизвожу сообщенное мне А. Н. Кор-
киным изложение этого метода, затем проделываю ряд примеров, взятых
главным образом из мему ара Пуассона, помещенного в XIX тетради жур-
нала «Ёсо1е poly technique».
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
9
В главе IV я излагаю метод Фурье, или второй метод Пуассона, инте-
грирования тех же уравнений для ограниченной среды и поясняю этот метод
рассмотрением классических примеров, относящихся к определению сво-
бодных колебаний струн и стержней,
В главе V я даю краткое изложение теории интегральных вычетов
и показываю, следуя мемуарам Коши, приложения этой теории к интегри-
рованию уравнений обыкновенных и в частных производных, а также к раз-
ложению функций в ряды, подобные рядам Фурье, которые встречались
в главе IV и где условия их сходимости не могли быть обоснованы. Метод
Коши дает как эти условия, так и общий способ для нахождения коэффи-
циентов при разложении в ряды по функциям, зависящим от корней транс-
цендентных уравнений. Таким образом, эта глава составляет естественное
теоретическое дополнение предыдущей.
В главе VI я рассматриваю сперва, независимо от теории Коши, усло-
вия сходимости рядов Фурье и им подобных, и показываю затем прием
усиления быстроты сходимости таких рядов, приложимый во многих довольно
общих случаях. Этот прием не только дает практическую возможность
с удобством пользоваться такими рядами в приложениях, получая желае-
мую степень точности, взяв самое ограниченное число (3—5) членов пре-
образованного ряда, но часто приводит к представлению суммы предложен-
ного ряда в замкнутой форме под видом разрывной функции. Этот же прием
дает возможность находить производные от функций,, представленных
такими рядами Фурье, почленное дифференцирование которых недопустимо.
Этого приема я не встречал ни в руководствах, ни в литературе, хотя, по его
простоте и очевидности, я не смею утверждать, что он является
новым.
В главе VII я излагаю общий способ интегрирования линейных диф-
ференциальных уравнений с частными производными и постоянными коэф-
фициентами с последним членом, придерживаясь того метода, который
дан мною в статье «Ueber die erzwungenen Schwingungen von gleichformigen
elastischen Staben», напечатанной в «Mathematische Annalen» за 1905 г.
Я прилагаю этот метод к рассмотрению вынужденных колебаний струн,
стержней и балок, к теории индикатора, колебаний вала и тому подобным
вопросам практического характера, выясняю при этом явление резонанса
и разбираю случаи действия сил «малой продолжительности», причем реше-
ния всех этих вопросов даются как в виде рядов, так и в виде разрывных
функций, представляющих суммы этих рядов.
В главе VIII я рассматриваю вынужденные, радиальные колебания
полого упругого цилиндра, чтобы дать пример уравнения с переменными
коэффициентами и ознакомить слушателей Академии с простейшими свой-
ствами функций Бесселя. Вопрос же этот мною избран потому, что он имеет
практическое значение при проектировании орудий и был мне предложен
таким знатоком этого дела, как ген.-лейт. А. Ф. Бринк.
Из этого общего обзора содержания предлагаемого курса видно, что
я придерживался главным образом способов изложения «старых авторов»,
Фурье, Пуассона, Коши, для которых главная цель состояла в нахожде-
нии решения, а не в безукоризненно строгом его обосновании и не в доказа-
тельстве его существования в общем случае или при установленных необ-
ходимых ограничениях. Эта часть мне представлялась имеющей лишь спе-
циально математический интерес; вместе с тем желающие ознакомиться
с этими вопросами найдут их изложение в сочинениях акад. В. А. Стеклова,
напечатанных частью на русском, частью на французском языках.
Для технических же приложений поверка полученного решения может
быть сделана при помощи приемов, показанных мною в главе VI и пояснен-
ных на ряде примеров в главе VII.
10
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Я не касался в своем курсе уравнения Лапласа ни для двух, ни для
трех переменных, ибо это уравнение рассматривается в курсе электричества
и в курсе теории земного магнетизма, читаемых в Академии; что же касается
приложения этого уравнения к изучению струйного течения жидкостей,
то мне просто пришлось бы воспроизвести труды проф. Н. Е. Жуковского,
и я предпочел отослать слушателей к изучению их в подлиннике.
Наконец, в новейшее время, для решения вопросов математической
физики, проф. Д. Гильберт в Геттингене развил особый метод «интеграль-
ных уравнений». Этого метода я также не касаюсь в своем курсе, так как
его можно найти в изложении проф. Кнезера—«Die Integralgleichungen»,
вполне приспособленном для учебных целей.
Само собою разумеется, что такой обширный предмет, как интегри-
рование уравнений математической физики, не может быть изложен с исчер-
пывающей полнотой ни в каком курсе. Но не в этом состояла моя задача:
я имел целью дать слушателям, ознакомив их с трудами великих авторов,
образцы решения могущих встретиться ц их практике вопросов и выяснить
важность и всеобщность тех явлений, которые известны под общим назва-
нием «резонанса».
Составление такого курса для высших учебных заведений вообще
является настоятельно необходимым при современном развитии техники;
но если не считать имеющей более элементарный характер прекрасной книги
Hort’a «Die technische Schwingungslehre», то мне такого курса неизвестно.
Ввиду того, что предлагаемый курс является, таким образом, первою попыт-
кой в достижении намеченной цели, он, с разрешения начальника Академии
и согласно постановлению Конференции Академии, печатается в ее «Изве-
стиях».
В заключение считаю своим долгом выразить глубочайшую благодар-
ность Типографии Академии Наук, сделавшей из этой книги образец книго-
печатного искусства, в особенности же—штатному корректору типогра-
фии Н. А. Виташе.вскому, который не только тщательно держал коррек-
туру, но не раз обращал мое внимание на погрешности и неясности в самом
оригинале.
А. Крылов
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Первое издание этой книги составляло 2-й выпуск «Известий Морской
Академии» и вышло в составе 500 экз. в 1913 г. Этот выпуск «Известий»
очень быстро разошелся и составил затем библиографическую редкость.
Ввиду того, что вопросы, рассматриваемые в этой книге, имеют непо-
средственное приложение к технике в широком смысле этого слова и соот
ветствуют нуждам нашего строительства и многочисленных высших учебных
заведений, особенно технических, Редакционно-издательский совет Академии
Наук постановил выпустить второе издание, предложив мне сделать в книге
надлежащие дополнения.
Эти дополнения составили около одной трети первоначального объема
книги и заключают: §§ 16—20. Численное решение уравнения, которым
определяются частоты малых колебаний материальной системы, §§ 83—85.
Анализ одной замечательной индикаторной диаграммы; §§ 88—94. Распро-
странение тока по кабелю; §§ 95—103. Продольные колебания орудия при
выстреле; §§ 104—114. Вибрация судов. В остальном первоначальный текст
оставлен без изменения, но тщательно пересмотрен и где нужно исправлен.
Целый ряд необходимых исправлений был мне указан проф. В. С. Игнатов-
ским, который при чтении первого издания этой книги проверил все выкладки
и результаты, исправил все замеченные им опечатки и ошибки и, узнав
о готовящемся новом издании книги, сообщил мне о них.
Считаю своим долгом принести проф. В. С. Игнатовскому свою особен-
ную благодарность.
При издании этой книги Издательством и Типографией Академии Наук
проявлены в полной мере их обычная заботливость и тщательность.
Чтобы сделать книгу более компактной, принят сравнительно мелкий
шрифт, а чтобы иметь его четким и отчетливым,* шрифт был взят вновь
отлитый, не бывший еще в употреблении. Набор сложных математических
формул этим мелким шрифтом представлял большие технические трудности,
и надо было все необыкновенное искусство тт. наборщиков Типографии
Академии Наук, чтобы эти трудности преодолеть с таким успехом, что
внешность этой книги нисколько не уступает математическим изданиям
знаменитой типографии Готье-Вилляра в Париже.
Корректуру правил ученый корректор Академии Наук С. А. Шабуневич,
следивший с одинаковою тщательностью как за верностью текста, так и за
внешностью его, испещряя поля гранок множеством чисто технических
типографских указаний.
Выражая свою искреннюю признательность Издательству и Типогра-
фии Академии Наук, я прошу тт. наборщиков и С. А. Шабуневича принять
выражения моей особенной благодарности за их труд, исполненный не
только с величайшею заботливостью, тщательностью и искусством, но и с той
истинной любовью к делу, которая служит вернейшим залогом его успеха.
Декабрь 3931 г.
А. Крылов
ГЛАВА» I
ОБЫКНОВЕННЫЕ ЛИНЕЙНЫЕ УРАВНЕНИЯ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
§ 1. Уравнение второго порядка с последним членом. Общий интеграл
его. Мы начнем наш курс с рассмотрения обыкновенного линейного урав-
нения второго порядка
^ + 2A-J + ^ = /(Z),	(1)
которое, обозначая производные значками, мы будем писать так:
у”+ 2hy' + №y = f(t).	(lz)
В этом уравнении коэффициенты h и к мы будем считать заданными
постоянными, / (t) — заданною функцией переменной независимой Z.
Уравнения такого вида встречаются во множестве технических вопро-
сов, из которых некоторые мы разберем подробнее, вместе с тем к инте-
грированию этого уравнения приводится интегрирование большей части
и других уравнений, с которыми нам придется иметь дело.
Соответствующее уравнению (1) уравнение без последнего члена есть
и” + 2W + №и = 0.	(2)
Подстановкою и = e~htv это уравнение приводится к такому:
v" + (k2-h2)v = 0.	(3)
Уравнение же (1) такою же подстановкою
приводится к виду
z" + (k*-h*)z==ehtf(t).	(4)
В том случае, когда А2 —/г2 > 0, полагаем
к2 — h2 = nf
и можем написать общий интеграл уравнения (3) под видом
v = Сг cos п^ + С2 sin	(5)
следовательно, общий интеграл уравнения (2) будет
и = е~м [Сг cos nxt + С2 sin прф	(6)
Полагая для краткости письма
’	eMf(t)=F(t)
и применяя для нахождения частного решения Z уравнения
z" + n%z = F (t)	(4)
14 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕЙТАМИ [Гл. I
способ изменения произвольных постоянных, получим, положив
Z = A cos nrt + В sin nrt,	(7)
следующие два уравнения для нахождения А' и В', рассматриваемых как
функции от /:
A' cos nTt + В' sin = О,
— nxAr sin nxt + cos nxt = F (£),
откуда следует
A' _ F (t) sin пг£ и В' = — F (t) cos
значит,
t	t
A——— F(t)sin Yiitdt',	(t)cosnit dt,
1 a	a
где а есть какая угодно заданная постоянная, которой впоследствии можно
будет распоряжаться так, чтобы выкладки становились проще.
Написав, во избежание неясностей, под знаком интеграла вместо
буквы t букву $, получим:
t	t
1 Г -	1	с
Z — — sinn^t \ F(i) cosrajS di —cosn^ \ F(i)sinned?, (7')
a	a
что можно написать иначе так:
Z = 1	(7")
а
и, следовательно, общий интеграл уравнения (4) будет
t
т с
z = Сг cos nJ + С2 sin nJ Н— \ F (£) sin п± (t — (•)	(8)
а
откуда следует общий интеграл уравнения (1)
t
у =^е~м (Сг cos nJ + C2sinn1Z) + ^- e~ht eh*f(s) sin nx (Z — c) di, (9)
a
причем
= k2 — h2
и
*2-^2 >0.
В том случае, когда величина к2 — h2 < 0, полагаем
А2 „ ^2 __ _ п2 или /^2 — £2 _ д2
и получим общий интеграл уравнения (3) в виде
у = С'1еп2# + С'2е“п2#	(10)
и, значит, для уравнения (2) будет
и = е~ы (Сгеп^ + С^е-П2*) =	t + С2е“<п2+л)	(Ц *
Вместо уравнения (7) будет
Z = Аеп* + Ве~п^
СПОСОБ НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ
15
§ 2]
и вместо системы (*)—такая:
А'е”^ + В'е~п^ = О,
п2А'еп<^ — п2В’е-п^ = F (Z),
откуда следует
А' = ^~ e-^F (/), В' = -Л-е^Р (t) dt,
t	t
A-^\e~nitF{t}dt' B=-^\enitF^dt
a	a
II
Z==i Я eni<'-5)F(?)d;-^- $ e-n^-5)F(c)d?,	(12)
a	a
после чего сейчас же напишется и общий интеграл уравнения (1).
Наконец, в том случае, когда
№ — h* = 0,
то уравнение (3) примет вид
v" = О
его общий интеграл есть
I' — С jt -f“ С 2 >
значит, для уравнения (2) будет
u = e~ht ((\t+ С2).
Затем, будет
t
z = (z-£)F(S)d£,	: *
а
и общий интеграл уравнения (1) напишется в таком виде:
t
y = e-w(C1« + C2) + e-w e^(z-£)/(£)</;.	(14)
а
§ 2. Составление частного решения данного вида, применяя способ
неопределенных коэффициентов. В формулах (7'), (8), (9), (12), (14) функ-
ции /(5)hF(c) могут быть какие угодно, формулы эти остаются справедли-
выми, но во многих случаях частное решение уравнений (4) и (1) может
быть получено и не пользуясь этими общими формулами, а применяя способ
неопределенных коэффициентов; именно это будет во всех тех случаях, когда
функции f(t) или F (t) имеют вид суммы, составленной из членов вида
(a+bt + ct*+.. . + pt1),
причем может быть как вещественною, так и мнимою постоянною, так
что к рассматриваемым случаям относятся и те, когда во второй части
наших уравнений находятся члены вида
(а + bt 4- ... + pt1) sin aZ; (a2 + b^ + ... + p^1) cos aZ;
или
(a + bt + ... + pt1) sin aZ;	+ bTt + ... + p±tl) cos aZ;
или для случая p. = 0 вида
a + bt + ct2 + ... + pt1.
16
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Во всех этих случаях надо искать частное решение того же вида, как
И вторая часть уравнения, т. е. под видом суммы, составленной из членов
(А + Bt + Ctz + ... + Pt1),
причем А, В, С, Р суть неопределенные коэффициенты, которые и най-
дутся, когда подставим решение написанного вида в уравнение и отож-
дествим левую часть правой.
При этом надо иметь в виду, что в том случае, когда в каком-либо
члене показатель [х есть корень «характеристического» уравнения для дан-
ного линейного, т. е. уравнения
у2 + 2Лу + Л2 = 0,
то вместо функции А 4- Bt 4- ... + Pt1 надо брать такую же функцию,
умноженную на г, т. е.
t (А Bt -j- . •. 4" Pt^)
д, значит, частное решение, соответствующее этому члену, искать под видом
[At + Bt2+ ... + Рг1*1];
если же характеристическое уравнение имело бы равные корни, и у. рав-
нялось бы этому корню, то надо искать решение под видом
[At2 + Bt2 + ... + ZV+2],
В том случае, когда во второй части будет член вида
(а + bt + ... 4- pl1) sin аг,
то, помня, что по формулам Эйлера
at	-at	at	, -at
sin at = --------------- и cos at = --------V-------->
2/-1	2
т. е. присутствие члена sin аг равносильно наличию обеих показательных
функций	и	значит, надо искать частное решение вида
[(Л + Bt + ... + Pt1) eat У~1 + (Ax + В it + ... + Pit1) e~at
или, заменив мнимые показательные функции тригонометрическими, реше-
ние вида
(А 4- Bt 4- ... 4- Pt1) sin аг 4- (А 4~ Bit 4- • • • + Pit1) cos at
хотя бы, повторяем, во второй части предложенного уравнения (1) был
только член, содержащий sin аг, или только член, содержащий cos at.
Так, например, для уравнения
у" 4- 0.2у' 4- 5у = 0.7 sin г
частное решение надо искать под видом
Y == A sin г -ь A cos г
и для определения коэффициентов А и Аг получатся уравнения
44-0.24,-0.7,
0.24 4- 44, = 0,
так что
л=та=ол75’	-0.009
$ 3]	СЛУЧАЙ, КОГДА ПОСЛЕДНИЙ ЧЛЕН—ВИДА S Н sin (pf+r)17
и, следовательно, искомое частное решение будет
Y = 0.175 sin t — 0.009 cosZ.
§ 3. Случай, когда последний член выражается суммою, составлен-
ной из синусов или косинусов разных кратностей переменной незави-
симой. Амплитуда, разность фаз, декремент. В тех приложениях, которые
мы будем рассматривать, вторая часть уравнения (1) будет по большей части
представлять сумму членов вида
Asin pt 4- В cos pt;
каждую пару таких членов, соответствующих тому же аргументу pt, можно
соединить в один член, делая
А = 7/cos у, В = 77 sin у,	(1)
так что
Н = угА2 + В2 и tgy = ~	(1')
и вышеупомянутый двучлен примет вид
Я sin {pt + у).
Итак, в нашем случае уравнение (1) примет вид
У" + 2/г/ + №у “2я sin + т)»	(2)
где под знаком 2 надо разуметь сумму конечного числа членов того вида,
как под этим знаком написано.
Общий интеграл этого уравнения будет вида
у -e~ht [Сх cos nxt 4- C2sin тг^] 4-У,
причем пг — k2 — h2, ибо в наших приложениях будет к2 — Л2 > 0.
Частное решение Y мы будем искать под видом
У=> 2	+ ? + ?)’	(3)
где N и 8—неизвестные постоянные; для определения этих постоянных
возьмем как в сумме (2), так и (3), лишь по одному члену, и что проде-
лаем по отношению к ним, то будет относиться и до всех остальных членов.
Подстановка величины Y = N sin {pt -г у 4- 8) в уравнение
у" 4- 2hy' + к2у — Н sin {pt 4- у)
приводит к равенству
Лт {к2 — р2) sin {pt 4- у + 8) 4- 2hp N cos {pt 4- у 4- 8) = H sin {pt + у),
или иначе
[TV {к2 — р2) cos 8 — 2hpN sin 8] sin {pt 4- у) 4-
4- [TV {к2 — p2) sin 8 4- 2hp N cos 8] cos {pt 4- y) = 77 sin {pt 4- y),
откуда, отождествляя, получаем для определения N и 8 уравнения
7V(A2 — jD2) cos 8 — 2/?/? TV sin 8 = H,	.
2hр N cos 8 4- N {к2 — p2) sin 8 = 0.
Из этих уравнений получаем:
AT	Н
N =---...........—	,	(М
+ /(/с2 —/>2)2 + 4/>2 р2	' '
,	(/с2-/>2)Н	. пГ . а -ЫрН
N COS 0 - (/с2_р2)2 + ^2 р2 > TV SU1 0	__	+ kh2p2
2 А. Н. Крылов
18
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (1л- I
или иначе
к2 — р2	. л	— 2hp	zrv
. cos о =-- г ъ_г-._	; sin 6 =----===£====..	(5)
+ И (*2 — Р2)2 + 4Л2 р2	+	(к2 —р2)2-\-Ь№ р2
Формулы (4) и (5) определяют вполне как величину N, так и угол о, при-
чем для последнего знаки cos и sin укажут и надлежащую четверть.
В случае, когда Л —О, т. е. когда предложенное уравнение имеет вид
у" + к2у = Н sin {pt + у),
то частное его решение Y будет
y = *2?72Sin(^ +Т)-	(6)
Этот вид решения не имеет более места, когда к — р, в каковом слу-
чае надо искать решение вида
Y — Nt cos (Az + у),	(7)
причем окажется
(’’>
§ 4. Уравнение
у" -f- 2hy’ 4- №у = У, Н sin (pt 4- у)
можно рассматривать как уравнение движения маятника, совершающего
малые колебания в среде, сопротивление которой пропорционально первой
степени скорости, причем на этот маятник действуют возмущающие силы,
изменяющиеся периодически с течением времени.
В таком случае входящие в состав общего интеграла члены
e~ht (Cj cos пх t + С2 sin пг Z),	(1)
в которых произвольные постоянные Сг и С2 определятся по начальным
условиям, представляют так называемые свободные колебания, т. е. такие,
которые происходят единственно только вследствие первоначального откло-
нения маятника от положения равновесия (г/ = 0) под действием «восста-
новляющей» силы ( — к2у), стремящейся возвращать маятник в положение
равновесия, и под действием сопротивления среды.
Член же
У-2 Arsin(^4-Y4-o)	(2)
представляет так называемые вынужденные колебания, происходящие от
действия внешних возмущающих сил.
Полагая
С2 = A sin а, С2 — 4 cos а,	(3)
мы	выражение свободных колебаний напишем так: Ae~ht sin (nJ + а)	(4)
или	иначе, положив 2 те — =Я1>
так:	Ae~ht sin	.	(4')
В таком случае, т есть период свободных колебаний маятника, Л —на-
чальная их амплитуда и а —начальная фаза.
§ 5]	СЛУЧАЙ, КОГДА ПОСЛЕДНИЙ ЧЛЕН—ВИДА S Иsin (pt+r) 19
Иногда формулу (4') пишут так:
4<rwsin-(#4-p),	(4")
так что 3 —	~ представляет начальную фазу, выраженную в долях не-
риода.
Множитель e~ht характеризует быстроту погашения свободных колеба-
ний, именно, за время каждого полного размаха, или период ампли-
туда убывает в отношении к 1, т. е* с течением времени амплитуды
убывают в геометрической прогрессии с знаменателем e~h^, тогда как
время возрастает через промежутки, равные Ясно, что если вместо
амплитуд взять их логарифмы, то получится также убывающая арифме-
тическая прогрессия с разностью з = — hxlf называемою «логарифмиче-
ским декрементом», определив который из наблюдений, получим и «коэффи-
циент сопротивления» h.
Во многих случаях коэффициент сопротивления Среды небольшой по
т т	1	2тс 2те
сравнению с коэффицгентом «восстановления» к; тогда период = — — ~ у2
колебаний маятника в сопротивляющейся среде разнится весьма мало от
2тс	’
периода х=у колебании в пустоте, т. е. если не Принимать в расчет со-
противления.
В практических применениях этим обстоятельством пользуются весьма
часто: обыкновенно точное определение, коэффициента сопротивления h по
расчету, имея лишь чертежи какого-либо механизма или составляя его
проект, затруднительно, а то и просто невозможно, величина же к полу-
чается По расчету или чертежу непосредственно; тогда достаточно убедиться,
что отношение- ~ вообще небольшое, и период свободных колебаний мо-
жет быть принят равным и рассчитан по формуле
2к
§ 5. Величина Н, входящая в состав члена вида #sin(p£ + v), опре-
деляет напряжение той возмущающей силы, период Изменяемости которой
Т и начальная фаза у. Эта величина может быть охарактеризована ве-
личиною, или амплитудою, того «статического» отклонения г/0, которое про-
извела бы постоянная сила той же величины Н.
Это отклонение определится из уравнения (1) § 1, делая в нём
y = Jo = constM т. е- из уравнения
значит,
, (1)
между тем формула (4) § 3 показывает, что амплитуда N колебания, произ-
водимого силою #sin(/rt + Y), выражается так:
N = H • —1  - =
К(*2 — р2)2 + 4Л2р2
и, значит, отношение N : г/0, которое обозначим буквою к, выражается фор-
мулою
Л2	1
/ (Zt2 — р2)2 + 4А2 р2	Л/"Г. P*\z Ы* р* '	'
V к1 ь*) +КТ2
2*
20 ОБЫКНОВЕННЫЕ УРАВИёНйЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Из формулы видно, что это отношение есть функция только двух пе-
ременных
Р	2h
= q и -г = а,
к * к
а не трех: р, h, к, ибо первые две входят в состав формулы (2) лишь
ph
в комбинациях и .
Л К
Но величина q =	, т. е. равна отношению периода свободных
колебаний системы без сопротивления к периоду возмущающей силы.
Таким образом, изучение величины возмущения, производимого данною
силою,, сводится к изучению величины
/(I - <72)2 + я2
(2)
где-
период свободы, колеб.
период, возм. силы
(3)
q
§ 6]
РЕЗОНАНС
21
Нетрудно видеть, что при малых значениях а и при величине q, чув-
1
ствительно отличающейся от величина X будет близка к	’ где
|1 —<?2| означает абсолютную величину разности 1— q2.
Чтобы с, наглядностью судить о ходе изменения величины X, которую
можно считать как бы мерою динамической восприимчивости колебаний,
составлена таблица 1 (стр. 22)'и по ней график (фиг. 1).
Кроме величины к, необходимо еще обратить внимание, на величину о,
представляющую опаздывание > в фазе, или разность фаз между возмущением
и силою, его производящею.
что будут вхо-
Формулу (5) § 3 также можно написать в таком виде,
дить только величины q и а, именно будет
COS о —
1	?2	= (1 - £2) • А,
У (1 _ 92)2 + а2^2 Х
sin о —
________
]Л(1 — q2)2 4- а2^2
— — %q • X.
(4)
В той же таблице 1 показаны значения ( — с) с теми же аргументами
а и q, как и для к: на фиг. 2 представлен графически ход изменения ве-
личины ( — о).
§ 6. Резонанс. Рассмотрение таблицы 1 и графика, ей соответствующего,
покажет, что величина возмущения, производимого данною периодиче-
скою силою, по мере приближения периода силы и периода свободных
колебаний системы к равенству весьма быстро возрастает и при ра-
венстве обоих периодов достигает значения, равного которое при
22
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Таблица 1
Величины Л ® "	------—- и — d = arc tg—~—
j/(l—?2)a+aV	1 —92
<1	А = 0.0	а= 0.1		= 0.1 5		а==0.2		а = 0.3		a = 0.4		a = 0.5	
	Л	Л	— 5	Л	-а	Л	-а	Л	-5	Л		Л	
0.00	1.00	1.00	о 0.0	1.00	О 0.0	1.00	о 0.0	1.00	о 0.0	1.00	о 0.0	1.00	о 0.0
0.10	1.01	1.01	0.6	1.01	0.9	1.01	1.3	1.01	1.9	1.01	2.5	1.01	2.9
0.20	1.04	1.04	1.2	1.04	1.8	1.04	2.4	.1.04	3.6	1.04	4.7	1.04	5.9
0.30	1.10	1.10	1.9	1.10	2.8	1.10	3.7	1.10	5.6	4.09	7.5	1.09	9.4
0.40	1.19	1.19	2.8	1.19	4.1	1.18	5.4	1.18	8.1	1.17	10.8	1.16	13.4
0.50	1.33	1.33	3.8	1.33	5.8	1.32	7.6	1.30	11.3	1.29	15.0	1.26	18.5
0.60	1.56	1.55	,5.3	1.55	8.1	1.54	10.6	1.50	1:5.7	1.46	20.6	1.41	25.2
0.70	1.96	1.94	7.8	1.92	11.7	1.89	15.4	1.82	22.4	1.72	28.8	1.62	34.5
0.75	2.28	2.25	9.7	2.22	14.4	2.16	18.9	2.03	27.2	1.88	34.4	1.72	40.6
0.80,	2.78	2.71	12.5	2.64	18.4	2.53	23.9	2.31	33.7	2.08	41.7	1.86	48.0
0.85	3.60	3.44	1,7.0	3.26	24.6	3.07	31.4	2.65	42.5	2.28	50.8	1.98	56.8
0.90	5.26	4.76	25.3	4.29	35.4	3.82	43.5	3.03	55.0	2—46	62.2	2.05	67.2
0.925	6.95	5.85	32.7	5.00	43.9	4.27	52.2	3.20	62.5	2.52 1	68.7	2.07	72.7
0.95	10.26	7.33	44.1	5.76	55.5	4.67	62.7	3.30*	71.0	2.55	75.5	2.06	78.3
0.975	20.50	9.16	63.4	6.45	71.5	4.98	75.9	3.36	80.5	2.55	82.9	2.04	84.2
1.00	оо	10.00	90.0	6.67	90.0	5.00	90.0	3.33	90.0	2.50	90.0	2.00	90.0
1.025	1,9.76	8.73	116.5	6.17	108.3	4.73	104.0	3.20	99.4	2.42	97.1	1.94	95.6
1.05	9.76	6.80	134.8	5.30	123.0	4.28	116.5	3.02	100.3	2.31	103.9	1.87	101.1
1.075	6.45	5.31	145.3	4.47	134.0	3.77	125.8	2.80	115.7	2.10	109.8	1.79	106.2
1.10	4.76	4.22	152.3	3.75	141.8	3.29	133.7	2.55	122.3	2.05	115.5	1.70	110.8
1.15	3.11	2.94	160.3	2.74	151.8	2.53	144.8	2.17	133.0	1.78	125.4	1.52	119.3
1.20	2.27	2.19	164.8	2.10	157.8	1.99	151.4	1.76	140.6	1.54	132.5	0.36	126.3
1.25	1.78	1.74	167.4	1.69	161.5	1.63	156.0	1.48	146.3	1.33	138.2	1.19	132.0
I 1.30	1.45	1.42	169.3	1.40	164.2	1.36	159.4	1.26	150.5	1.16	143.0	1.06	136.7
: 1.40	1.04	1.03	171.8	1.02	167.7	1.00	163.9	0,96	156.4	0.90	149.7	0.84	143.8
1.50	0.80	0.80	173.2	0.79	168.8	0.77	166.5	0.75	160.2	0.72	154.3	0.69	149.0
1.75	0.49	0.48	175.1	0.48	172.8	0.48	171.5	0.47	166.7	0.45	161.3	0.45	157.0
I 2.00	0.33	0.33	176.2	0.33	174.3	0.33	172.4	0.33	168.7	0.32	165.0	0.32	161.6
! 2.50	0.19	0.19	177.2	0.19	175.9	0.19	174.5	0.19	171.9	0.19	169.2	0.18	166.6
3.00	•0.125	0.125	177.8	0.125	176.8	0.125	175.7	0.123	173.5	0.123	171.5	0.123	169.5
1 4.00	0.067	0.067	178.5	0.067	177.6	0.067	177.0	0.066	475*5	0.066	174.0	0.066	172.3
; 5.оо	0.042	0.042	178.9	.0.042	178.1	0.042	177.6	0.042	176.4	0.042	175 3	0 012	174.0
§6]
РЕЗОНАНС
23
малой величине а весьма велико; для системы же без сопротивления эта ам-
плитуда даже возрастает беспредельно со временем.
Вместе с тем, в этом случае разность фаз равна — у.
Чтобы найти наибольшее значение величины X, стоит только взять
сперва	= (1 — q2)2 + a2 q2 и заметить, что минимум этой величины имеет
место при q2 — 1 — — и равен а2 —- , и значит, будет
)	- 1	1	-1 Л±а24- Л
V ‘-4
при
* С 1	2 Л
Обыкновенно величина а небольшая ( около -------_ J , и т0ГДа видно,
что как только q стклбнится от 1, т. е. период свободных колебаний и пе-
риод силы от равенства, на сравнительно небольшую величину, хотя бы
около 10%, то X становится гораздо меньше своего максимума, причем по
мере приближения q к 0 величина X приближается к 1, по мере же воз-
растания q сверх 1 величина X быстро убывает и, например, при со-
1
ставляет уже всего около .
Отсюда видно, что если при действии на какую угодно систему (будь
то маятник, гальванометр, корабль, локомотив и т. д.), уравнение движе-
ния которой имеет вид
у" + 2hy' +к2у = Н sin (pt + у),
мы будем изменять только период возмущающей силы ^т. е. величину
р — то заметим следующее явление: при приближении периода Т или
частоты р колебаний силы к некоторому определенному значению, колеба-
ния системы, произкодимые силою, начинают быстро возрастать, достигают
некоторого максимума, и затем, при дальнейшем увеличении частоты, ве-
личина производимого возмущения также быстро падает, уменьшаясь по-
степенно до нуля.
В этом и состоит явление так называемого «резонанса», с которым мы
постоянно будем встречаться в нашем курсе.
Точно так же, когда на нашу систему действует совокупность различ-
ных. периодических сил, так что уравнение движения нашей системы есть
у" + 2*г/' + к2у = ЦЯ {sin(pf£ 4- у.),
i
то если мы в нашей системе начнем изменять величину к2, иными словами,
период свободных колебаний нашей системы, например, постепенно умень-
шая его от весьма большого значения, то обнаружится следующее явление:
сперва система совершает лишь ничтожно малые колебания, затем, при
приближении периода свободных колебаний к некоторому определенному
значению Tv а частоты их кх к значению рг, амплитуда колебаний быстро
возрастает, достигает максимума, затем быстро падает и остается сравни-
тельно малою, пока период т не начнет приближаться к некоторому значе-
нию Т2, по мере приближения к которому амплитуда быстро возрастает^
достигает максимума, затем быстро падает и т. д.
24 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. Г
Таким образом, если бы изббразить графически ход явления, отклады-
вая по оси абсцисс период свободных колебаний* системы т, а по оси орди-
нат амплитуду колебаний yQ при этом периоде, то получилась бы кривая
такого вида, как показано на фиг. 3, с несколькими весьма резкими ма-
ксимумами.
I Jl£a' L.
7$	?3	7/
Фиг. 3.
Эти максимумы соответствуют тем значениям периода т, которые рав-
ны периоду одной из слагающих возмущающей силы*, и таким образом имеет-
ся возможность выделять отдельные ее составляющие, а заметив, что по
формуле
ЛГ .	_ Н> _ __ Hi
2pih
найти и напряжение силы Нj, ибо в этом случае вместо всей суммы
у = 3 sin + 7.4-8.)
можно взять лишь один главный ее член, именно тот, при котором Л7= pj*
На этом свойстве и основано пользование резонаторами при анализе звуков.
§ 7. Биения. Иногда, при производстве подобного рода наблюдений,
замечается следующее явление: амплитуда колебаний при каком-либо и&
Фиг. 4 и 5.
максимумов, скажем, для простоты речи, при х = Т1У не остается постоян-
ной, а, несмотря на то, что величина т сохраняется и в системе никаких
перемен не происходит, эта амплитуда то возрастает до значительной вели-
БИЕНИЯ
I
25
чины, то постепенно убывает почти до нуля, чтобы после того опять возра-
сти до своего наибольшего значения, и т. д., при этом возрастания и убы-
вания идут периодически, но их период обыкновенно во много раз (50 — 100)
более периода 7\.
Таким образом, если бы величину у изобразить графически в зависи-
мости от времени Z, то мы не получили бы правильной синусоиды с пери-
одом = как в прочих случаях, и которая изображена на фиг. 4,
а получили бы кривую такого характера,; как изображенная на фиг. 5, где
самая амплитуда тех колебаний, которые представлены сплошною чер-
тою, периодически меняется по тому закону, который представлен пунк-
тирною кривою.
Объяснение этого явления, называемого биением, состоит в следующем:
положим, что в состав возмущающих сил входят две такие, которых периоды
мало разнятся между собою, например на 1 — 2%; пусть эти периоды будут
и Г2> ясно, что соответствующие им частоты рг и /?2 также будут раз-
ниться между собой на ту же процентную величину, и, значит, когда
система будет настроена так, что ее период свободных колебаний т будет
близок к Тг, то он окажется близок и к Т2, й в сумме
2^tsin(Pi« + Yi + «i)
у	I
не один член будет большой и преобладающий над всеми прочими, а таких:
членов будет два, именно*.
A\sin(p1Z + Yi + oj) и N2 sin (p2t + y2 + 8a)
и когда свободные колебания погасятся, то останутся* вынужденные, пред-
ставляемые приблизительно формулою
Y = A\sin(/>1£ +Yi + Sj) 1-TV2 sin (p2£ + Ys + M»	(1>
ибо все прочие члены нашей суммы будут малы по сравнению с этими двумя..
Очевидно, будет
N N^N, N^N2
/V2-------------~
и пусть
Yl + ^l = sl и Y2 4“ c2 = 32>
значит,
Y = tSin + Sl) + Sin № + £2)] +
+ ~~2 — [sin	+ sj — sin (p2t + a2)] =
= (Nt + N2) cos t + sin t +	+
+ (^i - TV2) sin t + cos t 4-	.
Делая на время
(Л\ 4- N2) cos t +	= A
И
26
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ,С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
мы предыдущую формулу напишем так:
Y = A sin	+
или иначе
У = |/Л2 + ^3 sin z +	+ Q) 	(2)
причем
(3)
и
/= У N\ + Af + 2NtN2 cos [(A -p2)t + - s2)].	(4)
Эти формулы показывают, что когда разность р^ — р2 —величина малая
ио сравнению с суммою рг + р2, то в течение промежутка времени, равного
—, величина 12 изменится весьма мало, аргумент
Pl±P* t 4- Q
изменится на 2к, амплитуда же У А2 + В2 также сохранит почти пос оян-
ное значение, значит, в течение каждого такого промежутка колебание (2)
представится простым синусоидальным. Между тем, в течение промежутка
азремени ——— аргумент (Pi—Рг) * + (г1““32) изменяется на 2к, и, значит,
Pi — Pz
cos этого аргумента пройдет через все свои значения от —1 до + 1, и ве-
личина У А2 + В* пройдет через все значения от — Лг2 до Ni + N2, и если
и разности TV2 <яала по сравнению с Л\Н-7У2> то колебания и будут
представлять биения, по временам совершенно затухая, по временам же
достигая значительной силы.
Так как частота биений выражается формулою
период же биения
* 2те
- а — :------
Pl - Pi
(5)
(6)
благодаря его сравнительной медленности легко наблюдается, то этим
явлением часто пользуются, чтобы точно определить, скажем, период Ту,
тогда вводят возмущающую силу, период которой Т2 точно известен, полу-
чают биения, определяют их период о и, зная Т2 из формул (5) и (6), нахо-
дят и неизвестное Тг.
Характерные биения получаются на двухвинтовых судах при критиче-
ском числе оборотов,, при котором происходит вибрация корабля. Так как
числа оборотов машин всегда, хотя и незначительно, но разнятся между
♦собою, амплитуды же вибраций, производимых каждою машиною в отдель-
ности, между собою равны, то биения и происходят от полного затухания
до наибольшей резкости.
Иногда можно получить биения, воспользовавшись свободными коле-
баниями системы, именно в том/случае, когда сопротивление весьма мало,
-так что погашение совершается весьма медленно; для этого поступают так:
настроив систему так, чтобы получился резонанс, т. е. чтобы вынужденные ко-
лебания достигли своего максимума, дают системе или толчок,или вообще возбуж-
дают в ней свободные колебания, они вместе с вынужденными и дадут бие-
ния, которые, поскольку период свободных колебаний системы известен, и по-
служат для точного определения периода возмущающей силы или наоборот.
§ 8]	действие сил малой продолжительности	27
§ 8. Действие сил малой продолжительности. В предыдущих пара-
графах рассмотрен характер колебаний системы с одной степенью свободы,
например маятника под действием внешних возмущающих сил, периодиче-
ских или состоящих из суммы таковых. При этом оказалось, что амплитуда
производимого силою возмущения лишь в том случае близка к статической
и разность фаз близка к нулю, когда отношение периода свободных коле-
баний системы к периоду действующей силы весьма мало.
В случае равенства периодов происходит, вследствие резонанса, весьма
сильное возмущение, когда же период свободных колебаний системы весьма
велик по сравнению с периодом возмущающей силы, то производимое этою
силою возмущение весьма мало.
Кроме сил повторных и периодических, в практике приходится часто
иметь дело с силами, которые действуют в течение небольшого промежутка
времени, сперва быстро нарастая, затем несколько медленнее убывая, подоб-
но, например, тому, как действует давление пара в цилиндре паровой машины,
давление газов в двигателе внутреннего сгорания, давление пороховых газов
в канале орудия, давление жидкости в компрессоре его и т. п.
Может случиться, что силы подобного рода воспринимаются системою,
могущею совершать колебательное движение с одной степенью свободы,
обусловленное не только действием этой силы, но и «силою восстановил-
ющею», стремящеюся вернуть систему в положение равновесия и притом
пропорциоцальнрй отклонению» системы от этого положения.
В подобных условиях находятся, например, поршень индикатора, кото-
рым снимают диаграмму работы пара или газа, столбик крешера, сдавли-
ваемого пороховыми газами, стрелка баллистического гальванометрабалка,
стойка или иное устройство, воспринимающее* на корабле действие выстрела
или входящее в самое устройство орудийной установки, участок рельса
между двумя шпалами при проходе поезда и т. п.
Спрашивается, что во всех таких случаях разуметь под силою «малой
продолжительности» и какое такая сила будет оказывать «действие» на систему?
Мы увидим при дальнейшем раз:итии нашего курса, что решение
поставленного вопроса сводится к исследованию уравнения
у" + 2hy' + k2y = f(t),	(1)
которое получается для маятника или для подвешенного на пружине груза
(не принимая в расчет массы пружины), т. е. для простейших из рассмат-
риваемых систем.
В § 1 дан общий интеграл этого уравнения:
t	~	’
^==e-**(C1cosn1£-hC'2sinn1Z) + — e~ht \ eh'- / (?) sin n± (t — £) di, (2)
a
где 12^ = к2 — h2 для нашего случая есть величина положительная.
Нам придется иметь дело с решением этого уравнения, удовлетворя-
ющим начальным условиям: при Z —О должно быть
У—О и г/' = 0,	(3)
т. е. сила начинает действовать на систему, находившуюся в равновесии
и покое.
Если только взять п = 0, то постоянные произвольные Сг и С2, опре-
деляемые по начальным условиям (3), окажутся равными нулю, и искомое
решение будет
t
У = -^е~м S е"’:/(?)sinrei(г—
а
28
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Как сказано, функция /(Z) имеет вид, показанный на фиг. 6, т. е. она
сперва возрастает от нуля до некоторой наибольшей величины, затем убы-
вает до нуля.
Обозначим продолжительность нарастания функции / (0 через Т19 пол-
ную же продолжительность действия силы—-через Т и соответственные
участки функции — через Л(£) и /2 (Z), таким образом, наша функция
такова:
для*значений t\ от 0 до 7\ функция = и /J (t) > 0, 4
»	»	»	» Тх » Т	»	/ (z) = /2 (0	» /2 (Z) < О,
»	»	»	» t > Т	»	/(£) = ().
При выполнении показываемого формулою (4) интегрирования надо сообра-
зоваться с этим общим ходом функции / (Z).
Обозначая попрежнему ehi/(5) через F(;), имеем:
F (£) sin пг (t — Г) di = ~ £F(?) cos пх (t — ?) j — ~ Ff (;) cos nr (t — i)di =
0	00
t
= “ eht f (0 - P' 0: cos nx (t - 6)
0
ибо /(0) = 0.
Подставив в формулу (4),,„ получаем:
у=/ (0 - е~м (ehif ®)'cos (г -V <к.
(5>
Мы уже упоминали, что «статическое» отклонение от положения равно-
весия, производимое данною силою, вы-
ражается формулою
Разность
1	1	1	1 __ А2 1
nf Л2 "“Л2-Л2 к2 ”” к2 ’ к2~№
составляет при малой величине отноше-
h	1
ния лишь весьма малую долю от ,
и, значит, первый член формулы (5)
представляет «статическое» отклонение, производимое силою / (Z). Второй же
член этой формулы есть та поправка, которую надо к «статическому» откло-
нению присовокупить, чтобы получить «динамическое».
К исследованию этой-то поправки и перейдем.
Покажем прежде всего, что эта поправка малая в том случае, когда
период свободных колебаний системы мал по сравнению с продолжительно-
стью нарастания силы.
В амом деле, пусть будет

§ S]
ДЕЙСТВИЕ СИЛ МАЛОЙ ПРОДОЛЖИТЕЛЬНОСТИ
29
где I есть некоторое целое число и.0<а<|; тогда, обозначая через
сказанную поправку, имеем:
п\ = cos F' (?) cos dZ + sin n1t1 Ff (£}sin n£ dz. (6)
о	о
Положим сперва, что tr < Tlf так что мы находимся на восходящей ветви
кривой /(£), и найдем наибольшее значение, которого превзойти не
может.
Пусть будет
h	н
Ai = Ff (:) cos d: и Bj = F' (?) sin dz,
b	b
очевидно, что будет
'*1
Чтобы найти пределы для величины разобьем промежуток от О до tx
на такие частные промежутки, в которых cos сохраняет постоянный знак»
так что будет
т	Зт	5^	2Z-F-1	2Z+1 ,
4	Т	Т	“Т-^ — т+°
= С Ff (:) cos TZi?	+ +	4~	0) cos л^? (??.
о	т Зт	21— 1	21+1
Т 4	4 Т 4 т
Ясно, что в первом интеграле cosn£ все время положительный, во втором
♦отрицательный, в третьем положительный, и т. д.; функция F'(?) =
= heh*f(z) + e^f (?) знака своего не меняет и все время положительная,
поэтому, применив для каждого из интегралов первую теорему о средней,
получим:
т	т
4	4
^F'(;)cosW1U;==F'(ei) $ cosn1’:^ = ^-F'(SJ) = ^F'(51)	(в<Ь<|)'
о	о 1
Зт	Зт
4	4
{ F’ (?) cos dS =F' (?2) ( cos nJ dz=—-^-F' (?2) = - ±F' (?2) (1- < $2 < 3c)
T	T
4	4
.5т	5t
T	4
^'Ocos^US-^' (;3) $ cosn15d; = ^-F'(e8) = ^F'(;s) (J < $3 <
3т	3t
4	4
И T. Д.
Таким образом, будет
[ 4 F' (?!) - F’ (?2) + F' ($3) - F' ($4) +
± Gz+г) ] ,
(7)
i где 0 есть положительная правильная дробь, и
2Z + 1
4
< ^Л-2 <
2Z + 1
4
Т + 3.
30 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Функция F(q) обыкновенно такова, что на протяжении от 0 до 7\,
при котором она имеет максимум, величина ее производной
= + /'($)]
не только остается все время положительной, но и имеет не более одного
максимума; пусть этот максимум будет F' (?0); тогда, как легко видеть»
будет
Совершенно так же увидим, что по абсолютной величине будет и
1*11 (со)
и, значит,
и
(8>
Эта формула получает особенно простой вид и простое истолкование»
когда Л = 0, ибо тогда F' (с) = /' (»•),	= А2, и у нас получится
• у/'(«о)-	,.(9)
Величина • /' (с0) есть изменение усилия, действовавшего на систему,
происходящее в промежуток времени, равный у, т. е. полупериоду свобод-
ных колебаний, и величина, стоящая в правой части (9), — статическое
отклонение, производимое таким усилием*
Следовательно, если период свободных колебаний системы настолько
мал по сравнению с продолжительностью нарастания силы, действующей
на систему, что наибольшей величиной изменения действующего усилия
за промежуток времени, равный полуиериоду свободных колебаний системы,
/ (О
можно пренебречь по отношению к , то отклонение системы может быть
расчисляемо «статически», и погрешность не превосходит той величины,
которая соответствует сказанному изменению давления.
В общем случае при h, не равном нулю, заключение о величине пре-
дела погрешности несколько сложнее. Формула (8) дает, конечно, и в этом
случае оценку второго слагаемого формулы (5).
Другой крайний случай есть тот, когда период свободных колебаний
системы весьма велик по сравнению с продолжительностью действия силы.
В этом случае для t > Т формула (4) напишется так:
т
у = — е-м С (£) sin щ (t — ?) dl	(10)
ni J
о
или иначе
т	т
y — -^-e~ht sin И]/	(?) cos n/; dz — cos nxt eh*f (?) sin n£ d• ] .
1	о	о
тт	T	~
Но пг — — , и по предположению отношение — есть весьма малая дробь,
§ 9]
ЛИНЕЙНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
31
функция /(В) все время положительная, и 40 теореме о средней имеем:
т	т
ehZf (q) cos di = e'hT cos п^Т f(z)di,
г	° т	(И)
eh7 (£) sin zip di -- e lhT sin n^T / (;) di,
о	0
где 6 и Oi — положительные правильные дроби.
Если отношение — настолько мало, что величиною sm — можно пре-
небречь по сравнению с единицею, то второй из этих интегралов будет
весьма мал по сравнению с первым, величина hT будет также малая, ибо
обыкновенно декремент Лт выражается десятыми и сотыми долями, значит,
e4hT можно полагать равным 1, и у нас получится
У~-±- e~ht Isinn^,	(12)
где
т
о
есть величина, пропорциональная импульсу силы, действовавшей на систему.
Таким образом, в этом случае, когда продолжительность действия силы
«мала» по сравнению с периодом свободных колебаний системы, то отклоне-
ние и дальнейшее колебание системы около положения равновесия опреде-
ляется величиною импульса силы за полное время ее действия и не зависит
от наибольшего значения силы или продолжительности ее действия. Фор-
мулы (11) показывают, в каком смысле здесь надо понимать Слово «малое».
§ 9. Линейные уравнения высших порядков. Символический способ
интегрирования их. НаМ понадобятся и некоторые свойства линейных урав-
нений высших порядков с постоянными коэффициентами.
Положим, что дано уравнение
J/(n).+ а^п~х} 4- а2У(п-2) + ... + апу = / (Z),	(1)
в котором коэффициенты аг, а2, ...,ап суть заданные постоянные, /(г) —
данная функция переменной независимой t.
Общий интеграл этого уравнения состоит, как известно, из суммы
общего интеграла и уравнения
+	... + ап^--0	(2)
без последнего члена, соответствующего уравнению (1), и частного решения
уравнения (1).
Разыскание общего интеграла уравнения (2) сводится к нахождению
корней а «характеристического» уравнения
+ а^-1 + а2%п-2 + ... +ап-=0	(3)
и после того как этот общий интеграл и найден, то частное решение Y
всегда может быть найдено способом изменения постоянных произвольных.
Можно составить частное решение У и не прибегая к этому способу,
а пользуясь следующим символическим приемом.
Условимся обозначать знаком D дифференцирование (нахождение про-
изводной) по букве t, так что

32
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Тогда действие D сочетается между собою и с постоянными по таким же
правилам, как будто это был множитель, стоящий перед буквою у или
вообще перед знаком той функции, которая за ним следует.
Так, например,
Р + 5)У = РУ + 5у = 4Н5^
(Р + 3) (D + l)y = (P + 3) (Dy + y) = D[Dy+y] + 3{Dy + y) =
= D>y+^j + 3y = (D*+bD + 3)y = &+b% + 3y
и т. д. Понятно, что при таком условном обозначении первая часть уравне-
ния (1) напишется так: ф(Р)у, первая часть уравнения (2) —так: ср(Р)м,
и самые эти уравнения —так:
<р(Р) ?/ = /(*),	(Г)
,?(Р)И=0,	(2')
и если ах, а2, а3, . . ., ап суть корни характеристического уравнения, то
уравнения (!') и (2') можно написать, в силу вышесказанного условия
и свойств символа D, так:
(Р - ах) (Р - а2) ... (Р - ап) у = / (Z),	(1")
(Р-а^Р-Яг) ...(Р-хп)и = 0.	(2")
Условимся, кроме символа Р, ввести символ Р-1, ему обратный,
т?» е. такой, что
D[D-^y)] = y.
Ясно, что символ D^1 равносилен неопределенному интегралу от функ-
ции, стоящей под его знаком, так что	•
t
P-4F(Z)]= \F(t)dt + C= ^F®d; + C,
a
где С произвольная постоянная и а — какая-нибудь заданная постоянная.
Введем и более общие символы обратных действий, как-то (D — а)-1
и [Н^)]-1-
Под действием, обозначаемым символом (Р — а)”1, будем разуметь такое
.действие, что
(Р-а)[(Р.-а)-1^]=/Л
иными словами действие (Р — а)-1 / (t) = у равносильно решению дифференци-
ального уравнения
(P-a)y = /(0
или
Dy — a.y = f(t), т. е. у'- ay =
В самом деле, пусть будет
у = (Р-а)-Ч(0	(4)
неизвестный нам пока результат действия (Р—а)-1, примененного к функ-
ции /(О-
Проделаем над обеими частями равенства (4) действие (Р —а); тогда
.получим равенство
(Р - а) у = (Р а) [(Р - а)~1 /(£)] = /(#),
§9] ЛИНЕЙНЫЕ УРАВНЕНИЯ. СИМВОЛИЧЕСКИЙ СПОСОБ ИНТЕГРИРОВАНИЯ 33
т. е. у есть такая величина, которая удовлетворяет равенству
Dy— =
иначе равенству
у'-ay^f(t).
Это уравнение можно писать в виде
иначе
D (e~at у) = е-0*} (t),
откуда
e-^y^D-1 [e^f (Z)],
или
y = e*tD-1[e-*tf(l)].
Сличая эту формулу с (4), мы видим, что
t
(D —а)”1/(£)== еЧР-1 [е~а7 (Z)] = eat J di + Сё*.
а
Так как нас интересует главным образом разыскание частных решений,
то мы будем полагать постоянные произвольные, вводимые обратным дей-
ствием Z)-1, равносильным интегрированию, равными нулю и писать
t
(D — а)-1 / (z) = e^D-1 [e~atf (г)] = ел* e~^f (t) d*.	(5)
a
Положим теперь, что надо найти величину
у— (D — a.)~1[(D — ^')~1f (t)],
иными словами, у удовлетворяет уравнению
(/)-₽) (P-a)y = /(Z),
т. е.
[Z>2 — (a + р) D + сф] у = у" — (а + р) / + сф = / (t).
На основании формулы (5) имеем:
t
(D _ p)-i / (t) = е& J e~^f (?) di = ф (Z)
a
и затем
Г	t	7)
y = (D—a)-17 (t) = eat e_CC73cp (iq) d*f\ = eat e(₽-ah dy e~^f (i) dit
a	a	a
ибо очевидно, что
•n
(p (•/)) =	(?) di.
a
Таким образом, искомое частное решение нашего уравнения представ-
лено в виде двухкратного интеграла
/	7]
у =	dy J (?) di.	(6)
а	а
3 А. Н. Крылов
34
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Стоит только выполнить одно интегрирование по частям, чтобы при-
вести наш кратный интеграл к простым. В самом деле, имеем:
t	7)
e~rxty=^ еСЗ-*)7) d't] e“p’/(5)rf; =
а	а
г	~ а)т> ?	1 t 1 Г
= [	\ е"37 (?) <*? ] а ~ р-а W dr‘ =
а	а
= у_я е-₽'/ (5) б?е + —е-лу (у) dvj,
а	а
откуда следует
t	t
У == рг-а е₽* e~*f (5) dl + а-Т-в \ e-aV Ol) d'n,	(7)
а	* а
и мы получили частное решение нашего уравнения с последним членом,
не применяя способа изменения постоянных произвольных.
Но эта выкладка может быть проделана и проще: символы (£>-—а),
(Z> — В), (D — а)”"1, (D — р)-1 комбинируются между собою совершенно подобно
умножению алгебраических количеств, но величина
(О——И”1 —' и _	' п —<х~
следовательно, действие (Z> —a)-1 (D — р)-1, производимое над какой угодно
функцией / (£), можно заменить действием
("-«>-’
и, таким образом, для уравнения
у" — (a + P) y'+ap?/ = [Z>2 —(a + P)D4-aP]^ = /(Z)
у нас будет
у = (D -a)”1 (-D- р)-1	=	Р)-1 / (#) + (Л- «н / (0>
т. е. в силу формулы (5)
У = р4-а е₽‘ $ ^’7 (5) + гЬ	(?)d?-	(7)
а	а
Вог это-то разложение сложного символического действия
[p2_(a+P)P + ap]-l
на простейшие элементарные, выполняемое совершенно подобно тому, как
разлагается на частные дроби алгебраическая дробь
1 ___ 1
DD 4- 4 “ (и - a) (D - 0)
и вноси то обобщение и то упрощение, которое мы имели в виду достигнуть.
В самом деле, когда предложено уравнение
?СО)у=/(0,
§ 9] ЛИНЕЙНЫЕ УРАВНЕНИЯ. СИМВОЛИЧЕСКИЙ СПОСОБ ИНТЕГРИРОВАНИЯ 35;
то символически его решение напишется так:
причем символы ср (D) и ср-*1 (D) комбинируются совершенно подобно алге-
браическим количествам.
Но дробь
f© (D)]-i = —1 —_________________________
разлагается на сумму следующих частных дробей:
1	I	I	I
(b) D — <хх * D — а2‘ * ’ * * D — ап
и при том тождественно, и произведение
поэтому будет
Y = ?-1 (Р) / (Z) = A (D - «о-1 / (t) +
+ A2{D— а2)-1/(#) + ... + ЛП(Р —an)-J7(i), -i
или иначе
t	t
Y =	\ e~^ / (c) d; + A2e°* \ e~^ f (ft dl + ... +
(8)
a
a
+ Апеа^е-^
a
Это и есть искомое частное решение предложенного уравнения,
дело свелось к разложению дроби на частные.
Мы предполагали, написав предыдущую формулу, что все
и все
корни
ax, a2, ... , an между собою различны.
Случай кратных корней не представляет никаких затруднений. В самом
деле, положим сперва, что ах = а2 = а; тогда в ряду частных дробей,
на которые разложится дробь , будет такая	; ей будет соот-
ветствовать символическое действие
(Р-И1)-2/(?);
обозначим результат этого действия через тогда можем написать
(D — ax) z = (D — aj)-1 / (t) = eat D-1 [e~a< / (Z)] — <o (z),
значит,
z — (D— ax)-1 & (t) = e04 D~T [e~a/ ш (Z)],
подставляя теперь вместо a> (Z) его величину, получим:
z = е*4 D-1 [D-1 e-u f (Z] = e*4	/ (Z)]
или иначе
t '  •?/> -
a a
3*
36 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Выполняя интегрирование по частям, приведем этот двойной интеграл
к простому, а именно:
t	ч	\	*
е~^ / (?) di = £ т]	/ (?) de J а — у т)с~а7} / (tj) dy =
а	а	а	а
t	t	t
= t e-^' /(?)<£-$ ?e~aE / (?) di = (t - ?) e_“5 / (0 di,
a	a	a
что можно было написать и сразу на основании известной формулы при-
ведения повторного интегрирования к простому.
Совершенно так же увидим, что
t	7)	5
(D — а)~3 / (Z) = ел/Л~3 [e~at f (£)] = dy di е-аш / (со) dco =
а	а	а
t
1 * A J
а
я вообще
t
1 с
(D - а)-" / (0 = e^D~n [e-*»f (0] = е*‘ 12	(п_{) (Z -	/ (?) di.
а
Таким образом, решение уравнения
? (-D) У = У(п) £	+ • • • + апу = / (0
сводится к нахождению корней характеристического уравнения
<р (а) = ап + «! ап-1 + ... +ап-1« + «п = 0
и к разложению дроби —на простейшие; когда эти операции выполнены,
то общий интеграл уравнения без последнего члена пишется сразу, нахож-
дение же частного решения сводится к квадратурам, причем к способу
изменения постоянных произвольных прибегать не придется.
В том случае, когда корни уравнения —мнимые сопряженные, следует,
воспользовавшись формулами Эйлера, мнимые показательные заменить
тригонометрическими функциями, и тогда мнимые знаки пропадут.
§ 10. Малые колебания системы с несколькими степенями свободы.
К линейным уравнениям с постоянными коэффициентами приводит изучение
малых колебаний системы около устойчивого положения равновесия. Вместе
с тем оказывается, что с совершенно подобными же уравнениями приходится
иметь дело и во множестве других вопросов, относящихся к самым разно-
образным областям техники.
Итак, положим, что имеется какая-нибудь материальная система,
обладающая к степенями свободы, все связи которой выражаются конеч-
ными уравнениями между координатами ее точек и не содержат времени
явным образом. Положение и конфигурация такой системы могут быть
вполне определены к независимыми координатными параметрами
?1>	» ?/с<
(1)
Мы будем предполагать, что на систему действуют двоякого рода
силы: 1) силы, которые мы будем называть восстановляющими и которые
§ 10] МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ 37
имеют потенциал и под действием которых система может занимать опре-
деленное положение равновесия, предполагаемого нами устойчивым, так
что если систему из этого положения вывести, сообщив достаточно малые
отклонения и скорости ее точкам, то под действием сил восстановления система
стремится вернуться к своему положению равновесия и совершает около нею
«малые» колебания; 2) силы возмущающие — такие, которые выражаются
явными функциями времени, значит, для которых определенного постоянного
положения равновесия нет и под действием которых система, даже нахо-
дившаяся вначале в равновесии и покое, придет в движение.
Разобрав сперва этот простейший случай, мы перейдем к более слож-
ному, присовокупив к числу действующих на систему сил еще и 3) силы
сопротивления среды, зависящие от скоростей точек системы.
Параметры gx, q2, ... , qk можно всегда выбрать таким образом, чтобы
в положении равновесия системы было
= ^2 = 9з == • • • — 9к = 0;
тогда под словом «малые» колебания мы будем разуметь такие, что во все
время движения каждый из этих параметров qi получает лишь «малые»
значения, выражаясь, в зависимости от времени, функцией вида a>ifi(t),
где а£ есть постоянный множитель, который может быть сделан сколь
угодно малым, если взять начальные отклонения и начальные скорости
системы достаточно малыми, функция же /£ (t) при всяком значении t
остается конечною, как, например, sinn£ или cos nt.
Таким образом, мы будем предполагать, что параметры выражаются
формулами вида
9i = ai/j (t); q2=а2/2 (?);...;£* = а*/* (?)	(2)
и все величины ах, а2, ... , ал будем считать одного и того же порядка
малости, скажем, первого, так что величины aj, axa2, a2a3 и т. п. будем
считать величинами второго порядка и т. д. Производные по времени
от функций fift), /2ft), ...	будем предполагать так же конечными,
как и самые функции, и, следовательно, величины ^х, q'2, ... , q'k будем
считать малыми величинами первого порядка, как и самые q.
Итак, положим, что имеется какая угодно система, обладающая
к степенями свободы и находящаяся под действием заданных сил, имеющих
потенциал; тогда избираем какую угодно совокупность к независимых
координатных параметров
Pv Ръ> • • • > Рк,
при которых уравнения связей системы тождественно удовлетворяются -
Составляем уравнения равновесия системы, т. е. уравнения
21 = 0; f-0;...;21 = 0,	(3)
<?Р1	' др2	дрк	' 7
где 2V (р19 р2, ... , рк) есть потенциальная функция, и, решив эти урав-
нения, находим значения	••• > Рк^ параметров р для положения
равновесия*
Сделав затем
Pi=	+ 9ъ Р2 — Р2^ + 02J • • • ; Pk = Pk^+qk,	(*)
получим параметры qlf q2, . . . , qk, которые также будут между собою
независимы и будут тождественно удовлетворять уравнениям связей, но их
' ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Особенность будет еще та, что при положении равновесия системы
«1 = ?2 = ?3= •••'.= ?* = О
«. i I r V 1 .	,	. 4	z
1 назначит, если система «мало» отклоняется от своего положения равно-
весия, jto все величины q остаются малыми.
Сделав такой выбор параметров, составляем выражение живой силы
Н2Т системы и потенциальной функции 2V.	ч
• иЭтеь выражения будут вида	, .
= Ахдх2 + A2q'22 4- . .. + Akqk2 + 2S12^2 + • • • + 2Blkq{qk +
•	-	+ • • • + %Вк_^к__^к
и
!	== К 4- jDi^2 4t D2Q2 + • • • +	4“ 22? 12Q1Q2 -+-•••.+ 22?/c_i, к
ибо по предположению связи не содержат времени явно, значит, 27 будет
однородною функциею второй степени v от q2, . .. , qk. Выражение же
потенциала мы разложим в ряд по степеням qu q2, ... , qk, тогда в силу
равёйства (3) и (*)’ членов, содержащих первые степени q19 не будет, и если
ограничиться членами второго порядка, То V и будет вышенаписанного
вида, причем К и 7>х, D2, . . . , Dk, 2?12, jE13, .. . , Ek-t, к суть величины
постоянные.
Величины А1? ... , Bk_if к будут вообще функциями от qlf q2, .. . , qk,
их также можно разложить в ряды по степеням этих величин, и пусть,
например, разложение Ах будет
Ах = «1 + 61^1 + &2?2 + • • • + bkqk + С]/7? + • • • + 2б?Х2^1?2 4 ...
При составлении уравнений движения системы по схеме Лагранжа,
т. е. в виде
№=1,2,з.......я
dt Xdqj dqi dqi
первое уравнение будет такое:
__ dT__&V
dt ydql) dq1~dq1"
HO
^7 = Ац?1 + 512<?2 + 513^ + . .. + B\kqk,
затем
Jt =	+ B^ + • • • +	+	+	+
Член
Arf’! = <hq'i + Я1 (Mi + М2 4- • • • 4- M*) 4- q] (crff
будет состоять из членов разных порядков малости, именно: первого
члена который первого порядка, и остальных членов, коих порядки
выше первого; совершенно то же можно сказать и о членах 512^2 •..
и. т. д.; как видно, члены первого порядка получатся, если ограничиться
в разложениях Аь А2, . .. , Ак, Въ В2, .. . , Bk_iik лишь их достоянною,
т. е. не содержащею величин qx, q2i . .. , qk частью, иными словами зна-
чением их при qr — q2 ~ . .. = qk = 0.
Точно так же все величины произведений q[ и т. д. будут второго
чквысшцх порядков, если в выражениях Аг, А2, ... , Вк_х,к брать какие бы
'нй было члены, кроме постоянных.
§ 10] МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ 39
Так как при составлении уравнений движения мы хотим ограничи-
ваться только членами первого порядка, то надо в выражении живой
силы сохранить лишь члены, не содержащие величин q19 q2, ... , qk,
и в выражении потенциала У —только члены второй степени относительно
тех же букв.
Таким образом, исследование малых колебаний системы около поло-
жения равновесия приводится к изучению движения такой системы, для
которой живая сила Т и потенциальная функция V выражаются однород-
ными функциями второй степени — первая от производных gj, q2, ... , qk,
вторая от самих параметров q^ q2, .. ., qk с постоянными коэффициентами,
т. е. будет
271 — А^2 + А^2 + • • • + Akq'k + 2-В12^#2 + • • • + ZBk-^k qk-iQk>	/т\
2V =	+ D2q% + . . о + D^q^ -J- ^E^2q^q2 + • • • + 22?/c_qk—\qk>
причем все коэффициенты Alf ... ,Ek-i,k постоянные.
Если на систему никаких «возмущающих» сил не действует, то ее
колебания называются свободными и происходят только вследствие началь-
ного отклонения системы от положения равновесия и сообщенных ее точкам
скоростей по инерции и под действием сил восстановления.
Колебания же системы, производимые «возмущающими» силами, назы-
ваются вынужденными.
Мы начнем с рассмотрения свободных колебаний.
Уравнения движения нашей системы будут
—B1q1 + 512^2 —El2q2 + B12q2—E12q2-\~ .. . A~Blkq"k — E^q^-G,
B12Q1 — ^12^1 + ^2^2	-^2^2 + ^23?3 —^23?3 + • • • 4- B2kq'k — E2kQk = 0,
W— ^13^1 + ^23^2 —E23q2 + ^3^3 —D3q3 + • • • + Взкф'к — E3kqk — G, (II)
BikQi — Elkqi + B2kq" — E* + B3kq3 — -®за?з + • • • + Ak.qk — Dkqk — 0,
т. e. это будет система k линейных уравнений второго порядка с постоян-
ными коэффициентами и без последних членов. Вместе с тем в этой системе
не содержится членов с производными первого порядка от неизвестных
функций q.
Для интегрирования такой системы уравнений будем искать частные
решения следующего вида:
g1 = a1sin(kz +з); g2 = a2sin(k£ + s); ... ; ^ = a/£sin(kz+ г),	(4)
где ах, а2, ... , а/с суть некоторые постоянные, так же, как и к и е.
Подставляя величины (4) в уравнения (II), получим следующую
систему уравнений первой степени для определения постоянных аг, а2,..., а*:
(АД2 -j-DJa,! +(512к2 + 1?12) ^2 4’(-®13^2 + -^1з)аз+•••4~(^l/ck24"-E'l/c)^7c = 0,
‘(^12к2 + ^12) «1 + (А2к2 + Z>2) а2 +(^23^2 + -^2з)аз + •••+(^2к^2+-^2й) <*к ”
<ВхД2 + Е1Л) Л1 + (52/с^2 + -Е'2А)а2 4’(^зЛ^2 + ^,3/с)аз4“”* + (^/Д2 + -О/с)<*/с = 0«
Как видно, в этих уравнениях вторые части —нули, следовательно,
эти уравнения только тогда имеют решения, отличные от
... = а* = 0, когда определитель системы равен нулю.
Значит, величина к должна быть взята таким образом, чтобы было
АД2 + Dr В12\2-[-Е12 ... J?i/c^2 + -®ia
В12к2-\-Е12 АД2 + D2 ... В2кк2 + Е2к
В1к^2 Е^к B2kk2 + Е2к • • • АД2 -|- Dk
40
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. I
Если этот определитель раскрыть, то в левой части предыдущего
равенства получится целая функция от К степени 2Л, содержащая только
четные степени к, почему мы ее и обозначили через А (к2).
Полагая в уравнении А (к2) = 0, к2 — у., мы получим уравнение степени Л:
А(н) = О.	(IV')
Пусть корни этого уравнения различны и суть
Рч, 1*2...Нс-
Каждому из этих корней соответствуют два равных, по абсолютной величине,
но противоположных по знаку значения к, которые мы обозначим так:
± ± • • • ±
Возьмем, например, корень + кх и подставим его величину в систему урав-
нений (III), тогда эти уравнения станут совместными и допускающими
решения, отличные от нуля, ибо тогда одно из уравнений будет следствием
остальных.
Пусть это уравнение есть первое; тогда, отбросив это уравнение и раз-
делив остальные на ах, мы получим систему к — 1 уравнений первой сте-
пени с неизвестными
<4	“к
ах ’ «j ’ “ ‘ ’ (Xj
Определителем этой системы будет так называемый минор, соответству-
ющий элементу Лхк2-^/)! главного определителя А, т. е. такой опреде-
литель, который получается, если отбросить в определителе А первый столбец
и первую строку1). Обозначим этот минор через Дх, точно так же через
Д2, Д3, ... , Ад миноры, соответствующие второму, третьему, ... , А-му
элементам первой строки определителя А, тогда, если вместо к будет под-
ставлено его значение кх, решение нашей системы будет
.	а2 _А2 (kj) а8__Д8 (кх) ад______Ад (kj)
«х “Ах (кх) ’ ах “ Дх (кх) ’ • • • ’ «х Дх (ко ’
или иначе
п __А2 (к0	_Д3 (Ах)	___Ад (kQ	/у\
2 — ДГ(М ъ 3— Д1(*1) ........... к~	Ai(xi)ap	™
причем 04 остается произвольным, и Ах(кх) мы считаем отличным от нуля.
Таким образом, корню кх уравнения (IV), называемого характеристи-
ческим для данной системы, соответствует решение
g1 = a1sin(k1Z4-ei); ?2 = ^la1sin(k1Z + e1); ... ; gft = A1a1sin(k1Z -f-Sj), (VI)
где ax и sx суть произвольные постоянные,
даются формулами
а _Аа(кО. р_А3(кО.
1 Ах(кх)’ С1"Дх(кх)’ ’
величины же 6Х, с19 ... , hx
h _Ад(ЛО
‘“Ах (к0‘
(VII)
Если мы вместо корня + кх
61, сх, ..., hx отношений
возьмем корень — kj= —	то величины
Оа Оз	ад
ах а1 ’	9 а1
х) Минором для элемента, стоящего в пересечении i-й строки и /г-го столбца,
условимся называть определитель, получаемый из главного, отбрасывая этот столбец
и эту строку, и умноженный на (— 1)*+Л. На это последнее условие надо обращать
внимание, чтобы не было ошибки в знаке.
§ 10] МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ 41
сохранят свои значения; поэтому, написав вместо буквы ах букву Сг
и вместо ех букву 8Х, мы получили бы решение
9i = ^i sin (— kx£ + 8Х); q2 = biCxsin (— kxt + 8X); ... ; qk = h1C1 sin (— kxZ 4~ 8X).
Но это решение не есть независимое, а получается из (VI), соответ-
ствующего корню кх, сделав Сх = ах и зх —тг — 8Х. Следовательно, чтобы
получать независимые решения, надо брать лишь корни
4- кх, 4» к2, • • • > +
и для каждого из этих корней сделать ту же выкладку, которую мы про-
делали для кх.
Для каждого корня получится решение, подобное (VI), содержащее две
произвольные постоянные.
По известному свойству линейных уравнений без последнего члена сумма
решений есть также решение, следовательно, общим интегралом системы
будет
9i=	я sin (kxZ -f- si) + Р sin (k2£ 4" £г) 4* • • • 4" 0 sin fykt 4" £&) >
q2 =	sin (kxZ 4- гх) 4- 62р sin (k2£ 4- s2) 4- • • • 4- bk<s sin (\kt 4- £J,
?з “	sin (kx£ 4~ £i) 4" 'c2p sin (k2tf 4" £2) 4~ • • • 4~ sin 0<kt 4- £a)	(VIII)
9k = &iasin(V 4- £1) 4- M sin (k2Z 4- £2) 4- • • • + hks sin (\kt 4-
причем a, ₽, y, ... , a, sx, e2, • • • > sk суть произвольные постоянные,
kx, k2, .. . , k/c —корни уравнения (IV), bv b2, ... , hk — определенные постоян-
ные, даваемые формулами
bi~ мм ’ Ci ~ rai ’ • • • ’hi ~ га> >	(1Х)
соответственно значению каждого корня.
При этом выводе сделано два предположения: во-первых, что все вели-
чины кх, к2, . .. , kfc вещественные, и во-вторых, что все эти величины между
собою неравные. Кроме того, мы считаем, что минор Дх(к) отличен от нуля
при к — кх, к2, ... , Хк.
Допустим, что уравнение (IV) имеет и мнимые корни. Это будет в том
случае, когда уравнение (IV') имеет или отрицательные, или мнимые корни.
Отрицательному корню уравнения (IV') будут соответствовать чисто
мнимые значения к, мнимому или комплексному значению будут соот-
ветствовать комплексные значения к.
Положим, для общности, что уравнение (IV') имеет пару комплексных,
сопряженных корней; тогда для к получится две пары также сопряженных
комплексных значений и притом противоположных по знакам. Пусть пара
таких значений будет
^• = £4-/1^ — 1 ,
x/+l =£-//—1,
соответственно этим корням в выражениях для qх получились бы члены вида
asin[(g + /|/"=7T)« + s] и р sin [(g — / |/ — 1) i4-vj]
и тогда, заменив по формулам Эйлера тригонометрические функции мнимого
аргумента через показательные и считая т) .= е, а аир — комплексными сопря-
женными, мы получили бы вещественное решение вида
Mei* sin (gt 4- з) 4- Ne~^ sin (gt 4- s) 4- Pe^ cos (gt 4- e) 4- Qe~^ cos (gt 4- г),
где M. N, P и Q выразились бы через a, р.
42
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Присутствие членов вида МёР sin (gt + г) и РеР cos (gt 4- е) в выражении
для qr дало бы подобного же вида члены и в остальных величинах q2, g8, ...
... , qka Эти члены с течением времени t неопределенно возрастают, значит,
величины q не оставались бы постоянно малыми, и система, будучи сколь
угодно мало отклонена от положения равновесия, колебалась бы около него,
так что эти колебания все более и более бы возрастали, т. е. положение
равновесия было бы неустойчивое.
Мы же предполагали равновесие устойчивым, и значит, аналитическим
критерием такой устойчивости служит условие, чтобы все корни уравнения
Д(н)=о
были бы положительные, и это уравнение не имело бы ни отрицательных,
ни мнимых корней.
§ 11. Случай равных корней характеристического уравнения. Числен-
ный пример. Случай равенства двух или нескольких корней характеристи-
ческого уравнения между собою требует более подробного рассмотрения.
Лагранж, которому принадлежит вышеизложенная теория малых колебаний
системы, в своей Аналитической механике» высказался следующим обра-
зом: «... изложенное выше решение основано на предположении, что вели-
чины qt, q2, ... , qk весьма малые; чтобы это предположение имело место,
необходимо, чтобы корни р2, .. • , были все вещественные, положи-
тельные и неравные, дабы время t, которое может возрастать неопределенно,
содержалось бы лишь под знаками синуса или косинуса.
Когда же некоторые из этих корней становятся отрицательными или
мнимыми, то при сказанных синусах появятся показательные множители
(это и пояснено выше)... когда же некоторые корни станут просто рав-
ными между собою, то появятся члены, содержащие целые степени вре-
мени t вне знаков синуса и косинуса», т. е. в случае равенства двух корней
(Xi = Х2) будет решение вида
(а + ₽Z) sin \xt + (аг + (3^) cos Х^;
в случае равенства трех корней Х1 = Х2 = Х3 будет решение вида
(а + + у£2) sin	+ (aj + PjZ +	cos "kjt
и т. д., как видно, при возрастании t, и эти множители (a + ^), (a-h^ + yZ2),
и т. д. могут возрастать неопределенно, и колебания, в противность пред-
положению, не остались бы малыми.
Затем Лагранж продолжает: «... но так как развитие [подробное иссле-
дование] этого случая [равных корней] бесполезно для предмета нашего
изложения, то мы не будем на нем останавливаться».
«Аналитическая механика» появилась первым изданием в 1788 г., вто-
рым—еще при жизни ее ав ора в 1812 г., третьим —в 1853 г. под редакцией
знаменитого Жозефа Бертрана, и вышеприведенная выписка сдёлана из этого
третьего издания. Это утверждение Лагранжа относительно равных корней
оставалось общепринятым до 1858 г., когда германский математик Вейер-
штрасс обратил внимание на ошибочность этого утверждения Лагранжа
и разъяснил, в чем эта ошибочность состоит.
Дело вот в чем: мы видели, что уравнение (IV), коим определяются
корни X, выражает то условие, чтобы в системе (III) одно из уравнений
было следствием остальных, и весь наш дальнейший вывод и был основан
на том, что таких уравнений, действительно, только одно.
Так оно и есть, когда X есть простой корень характеристического урав-
нения. Но если это уравнение имеет кратные корни и, например, Х! = Х2,
то если в системе (III) вместо X подставить его величину Хп то в этой
системе не одно, а два уравнения сделаются следствиями остальных, если же Хх
S 11]
СЛУЧАЙ РАВНЫХ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ
43
есть тройной корень, т. е. ^=^2 — к3, то три уравнения сделаются след-
ствиями остальных, и т. д., иными словами, в первом случае надо брать
произвольно, не одну величину а! = а, но надо взять произвольно две вели-
чины, например и <х2= Р, и, откинув два уравнения, определить из
остальных величины а3, а4, .. . , а/с через а и [3. Таким образом, в случае равен-
ства двух корней, например кх = к2, соответствующее частное решение было бы
вида
51 = а sin (kxZ -f- 8Х); q2 •== р sin (k^ + з2); q3 = сха sin (k^ + sj 4-
4- c23 sin (k^ 4- з2); . .. ; qk = sin (k^ 4- S1) 4- h2$ sin (k^ 4- з2)
и, значит, общий интеграл системы был бы вида
51 a sin (V 4~ ei) + Y sin (k3Z + £3) 4- • • - + <? sin (kJ 4- ej,
5г = ? sin (k^ 4- e2) 4- 63 у sin (kJ 4- з3) + • • • + M sin (kftZ 4- ek),
53 = cia sin(k1^4-e1)4- sin (k^4- s2) 4-s3y sin (k3Z 4-s3) 4- ... 4- c^csin (kJ -f-ej,
4k = h joe sin (kJ 4- e x) 4- sin (kJ 4- e2) 4- h3^ sin (k3Z + s3) 4-... 4- hkG sin (kJ 4- e/c),
причем попрежнему: a, p, у, • • • >	3i> ®2> • • • > суть произвольные посто-
янные, величины же 63, ... , 6ft, cv с2, ..., ск, ... , hk будут вполне определен-
ными числами, которые найдутся, как показано ниже на примере.
Точно так же в случае равенства трех корней k1=k2=k3 можно три
величины взять по произволу, например ах —а, а2 = р и а3 = у> откинуть
в системе (III) три уравнения и найти остальные величины a4, а5, ... , ak
через а, £ и у, так что соответствующее корню кх частное решение будет
51 == sin (kxZ 4" ®i), 52= Р sin (к^ 4- з2); 5з~У®1п(к1^4"£з)»
54 = djx. sin (kJ 4- sj 4- d2p sin (kJ 4- e2) 4- d3y sin (kx£ 4- e3),
qk = Aja sin (kJ 4- s3) + Л2р sin (k^ 4- £2) + A3y sin (kJ 4- s3),
сообразно чему общий интеграл примет вид
5i - asin (kJ -f- sx)	4-8 sin (kJ 4- £4) 4- ... 4-
4-a sin (M4-®k),
8 sin (kJ 4~ ®г)	4“ ^48 sin (kJ 4~ ®<) 4- • • • 4~
4-Msin(k^4-£/t),
53 =	Y sin (W + ез) + ^48 sin (kJ 4-e4)4-...4-
4-^sin(k^4-eJ,
5k — hjx. sin (kJ 4~ 3|) 4- h2ft sin-(kx£ 4~ £г) 4* ^3Y sin (kJ 4" ®3) 4~ ^48 sin (kJ 4~	4*
4- ... 4-Afcasin(V+£k)-
Мы не будем входить в подробности вывода и общего доказательства
этих результатов1), ибо в каждом численном примере они обнаружатся сами
собою, для пояснения же выкладок проделаем такой численный пример.
х) Желающих с ними ознакомиться отсылаем к т. Ш лекций по математической
физике Гельмгольца (Vorlesungen uber theoretis.che Physik von Н. v. Helmholtz, Bd. III.
Die mathematische Principien der Akustik), где эти доказательства изложены с удиви-
тельною простотою, основываясь непосредственно на свойствах определителя. При
своем доказательстве Гельмгольц берет выражение живой силы в виде 2Т = т1Е{24-
+ ^2С22 + - • •+7Пк£д:2» к каковому его весьма легко привести простою заменою пере-
менных, представив сперва Т в виде суммы квадратов линейных функций qlt q2t.. . , q^
из коих первая содержала бы все к переменных д, вторая к — 1 и т. д.

ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Положим, что имеем систему с тремя степенями свободы, и Живая сила
и потенциал для этой системы выражаются так:
2 т=б?;2 + и??+22?;2 +12?;?; + 22?;?; 4-28?;?;,
— 2V = 9?2 4* 38?| 4* 49?| 4* 30?i?2 4- 40?j?3 -f- 82?2?3,
тогда уравнения движения будут
6?i + 9?1 + 6?/2 + 15?2 4- И?з + 20?3 = О,
6?^4-15?1 + 11?; + 38?2 + 14?^ + 41?з =0,	(5>
ll?i + 20?1 4- 14?2 + 41?2 + 22?з + 49?з = 0;
полагая
?х= a1sin(ki + s1); ?2 = a2sin (XZ + ej), ?3 = а38М1(к£4-ег),
получаем для определения постоянных ax, a2, а3 уравнения
(6k2- 9)ax + ( 6k® —15)a24-(Hk2 —20)a3 = 0,
(6k2—15) аг 4-(ilk2 —38)a2 4-(14k2—41) a3 = 0,	'6>
(Ilk2 -20) 04 4- (14k2 -41) a2 4- (22k® -49) a3 = 0.
Определитель этой системы есть
Д(к2) =
6k* - 9
6k®-15
Ilk2-20
6k2-15 Ilk2-20
Ilk2 —38 14k2—41
14k2-41 22k2-49
Чтобы развить этот определитель, поступаем так: сперва первую строку
вычитаем из второй и удвоенную первую строку — из третьей, в полученном
определителе первый столбец вычитаем из второго и удвоенный первый стол-
бец—из третьего; тогда наш определитель примет вид
Д(к2) =
6k2-9	- 6
-6 5k2-17.
-к2 — 2 Зк2 — 9
-к®-2
Зк® —9
2к®-5
В этом определителе вычтем вторую строку из третьей; тогда все члены
нижней строки будут иметь общего множителя — к2 4- 4, взяв которого
за черту, получим:
Д(к®) = ( —к24-4)
6к®-9	—6
-6 ^к2—17
1	2
-к2-2
Зк2 —9
1
В этом последнем определителе вычитаем удвоенный первый столбец,
из второго и первый столбец—из третьего; по упрощении получаем:
Д(к®) = ( —к®4-4)	-12к®4-12 — 7к24-7 5к2— 5	3к®-3	—
	= (4 —к2) (1 — к®)2 _	12	7 5 _3 = (к2-4)(к2-1)2.
Следовательно, корни уравнения Д(к2) = 0 суть
к? = к2 = 1 и к| = 4.
Таким образом,
х1 = х2=1 и к3=2.
S12]
НОРМАЛЬНЫЕ КООРДИНАТЫ И ОСНОВНЫЕ КОЛЕБАНИЯ
45
Берем сперва к = кх = 1 и подставляем в уравнения (6), которые тогдаг
переменив знак, принимают вид
Зах4- 9a2+ 9a3 = 0,
9осх + 27a2 4~ 27a3 = 0,
9otx + 27a2 4~ 27a3 = 0;
как видно эти три уравнения не суть независимые, а в них два суть след-
ствия третьего, так что между тремя неизвестными ax, а2 и а3 имеет место*
только одно уравнение, именно:
ах 4- За2 4~ За3 = О
и, взяв произвольно ах = а и а2 = р, мы должны взять
1 1 □
а3= — yai-a2 = — у а —р,
сообразно чему соответствующее двойному корню Хх = Х2=1 частное реше-
ние будет
q± — a sin (г 4- ах),
?2 = Psin(«4-s2),	(7y
q3= —-j- asin^ + ej —psin(« + 82),
причем a, £, ex и а2 суть произвольные постоянные.
Взяв корень Х = Х3 = 2 и подставив в систему уравнений (6), получаем
15ах4- 9а2 +24а3 = 0,
9o&i 6я2 + 15а3 = О,
24ах 4- 15а24~ З9а3 = 0.
Здесь одно уравнение есть следствие двух других, поэтому берем ах
произвольно: ах~у, и, отбросив первое уравнение, пишем
2ос2 4" 5а3 = —Зу,
5а24- 13а3= — 8у,
откуда
а2 = Х; аз“ “X
и частное решение, соответствующее корню Х2, есть
£1= У sin (2г 4-е3),
?2 — у sin (2г 4-£3),
q3 = — у sin (2г4-з3)о
Соединяя группу (7) и (8), получим интеграл нашей системы:
q± = a sin (г 4- ех) 4- у sin (2г 4- е3),
= ₽ Sin (г 4- е2) 4- у Sin (2г 4- а3),
?3 = — у asin (г 4- гх) — рsin (г + г2) — у sin (2г 4- г3)>
причем а, £, у, ах, е2 и s3 суть постоянные произвольные.
§ 12. Нормальные координаты и основные колебания системы. Возь-
мем формулы (III) § 10, дающие выражения переменных q в функции вре-
мени г, и сделаем в этих выражениях
asin(X^ + ex) = gx, psin(M4-s2)==52, ..., a sin (kkt 4- г*) =	(1)
46 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. t
тогда уравнения (VIII) напишутся так:
#2 =	+ Ь^2 + • • • + W/c,
Яз ~ С1^1 + С2’2 + • • • + C/cS/c,	(2)
Цк = ^1^1 +	+	•	•	•	+ hkikt
причем fer, 62, .. ., hlf ..., hk суть вполне определенные для данной систе-
мы числа, даваемые формулами (IX) § 10.
Из уравнений (1) следует, что переменные $2, •••>£* удовлетво-
ряют таким дифференциальным уравнениям:
%' + k^2==0,	/Q.
Отсюда следует, что если бы мы вместо переменных qt ввели бы новые
переменные связанные с ними уравнениями (2), то система совокупных
уравнений (И) преобразовалась бы в систему уравнений (3), в которых
каждое уравнение заключает только одну неизвестную функцию.
Но вместо того, чтобы преобразовать систему (II), можно бы было пре-
образовать к новым переменным выражение живой силы и потенциала,
и тогда по схеме Лагранжа мы получили бы уравнения (3).
Ясно, что при таком преобразовании живая сила Т обратилась бы
в однородную функцию второй степени от переменных 5$ с постоянными
коэффициентами, V —в таковую же функцию самих величин 5/. Посмотрим,
каков будет вид этих функций.
Уравнения движения в новых переменных написались бы по схеме
(i=1, 2,	(4)
а1\д^у dc.i 4	п	х '
дТ
ибо величина = 0, так как Т самих переменных не содержит, а лишь
их производные £z, точно так же V не содержит производных St- Считая,
что уравнения (3) суть уравнения Лагранжа, и сличая уравнения (4)
с уравнениями (3), видим, что должно быть
ЭТ „ dV . 2 .
Значит, будет
27^^;2 + ^2 + ...+^'2,
- 2V =	+ ... +	( '
т. е. что в новых переменных удвоенная живая сила выразится суммою
квадратов их производных, удвоенная потенциальная функция — суммою
квадратов самих переменных, умноженных на постоянные множители.
Очевидно, что без ущерба общности можно положить ах — а2 = •.. = ak — 1,
так что будет
27 = ^ + ^+...+^
и
-27--k^ + ki?i+ ... + х?п,
§ 13]
МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
47
т. е. живая сила равна сумме квадратов производных переменных потец-
циальная функция — сумме квадратов самих переменных, умноженных
на постоянные множители.
Действительно, всегда можно такие новые координаты найти, и когда
они найдены, то вопрос можно считать решенным, ибо решения уравне-
ний (3) пишутся сразу в форме (1).
Отсюда видно, что координатные параметры будут таковы, что движе-
ние системы, представляемое изменением каждого из них, есть простое
гармоническое, независимое от прочих и совершающееся со своим периодом
и со своею амплитудою и фазою.
Такие колебания для системы называются основными, координатные же
параметры — нормальными.
Из формулы (VIII) следует, что в каких бы координатных параметрах
мы движение системы ни выражали, это движение будет состоять из наложе-
ния простых основных кол баний, совершающихся каждое со своим перио-
дом, амплитудою и фазою.
Равенство корней характеристического уравнения укажет лишь на то,
что некоторые из периодов основных колебаний между собою равны, но оно
не имеет отношения к устойчивости или неустойчивости равновесия системы,
т. е. к увеличению амплитуды с течением времени; такой случай будет
только, если в выражении —V будут члены отрицательные.
Таким образом, вопрос об интегрировании уравнений движения (II) § 10,
относящихся к малым колебаниям системы, сводится к разысканию формул
преобразования (2), которыми бы одновременно две квадратичные формы Т
и V приводились к виду (5), именно, такая постановка вопроса и указала
Вейерштрассу на ошибочность утверждения Лагранжа, но мы не будем
входить в теорию этих «линейных преобразований», так как все выкладки
остаются те же самые, которые в нашем изложении служили бы сперва для
нахождения переменных qt по уравнениям движения, а по ним перемен-
ных Si, если бы мы желали найти и нормальные координаты.
§ 13. Малые колебания системы в сопротивляющейся среде. Функция
рассеяния. Случай, когда малые колебания совершаются в сопротивляющейся
среде, отличается от рассмотренного выше тем, что к силам «восстановле-
ния», имеющим потенциал V, присовокупляются силы сопротивления среды,
зависящие от скоростей точек или элементов системы. Эти силы мы будем
считать пропорциональными первой степени скорости и, значит, выража-
ющимися линейными функциями от производных q't.
Обыкновенно по условиям задачи весьма нетрудно составить выражения
этих сил сопротивления в прямоугольных и прямолинейных координатах,
пусть эти силы будут
/?2, ..., 7?п>
их составляющие: Х19 Yv Zx, Хг, Y2, Z2, ..., Xn, Yn, Zn и координаты
точек приложения: х19 у19 zlf ..., xn, yn, zn.
При составлении уравнений движения системы в параметрах q по схеме
Лагранжа
d fdT\ dTi п / • л о 1 х
стоящая в правой части величина Qi получается преобразованием выраже-
ния элементарной работы cU = Z(Xbx + Yty + Zbz), будь оно полный диф-
ференциал или нет, к виду
ь17 = Qi oqi + Q2 Zq2 + . . . + Qk tqk.
48 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Тогда те силы, которые имеют потенциал, дадут в составе выражения Qt
dV
величину , прочие же дадут выражения вида
07/

(1)
причем суммирование распространяется на все значения значка А.
Отбросив в этих выражениях члены высших порядков, мы и получим
в составе величин Qi члены, представляющие линейные функции величин q'i9
и уравнения (II) будут вида
Ai9l —^i9i + J^i9i	— -^12^2~l“-E]2^2 + • •• +
+ Blkqk — Fr qk + Elkqk = 0,
^12^ — F21q{ + E12Q1 + Л2^2 —^2^2 + ^2^2 4-• • • 4-
4“ BzkQk F2kqk + E2kqk = 0, (2)
&ki9i 4" Flkqr 4- B2kq2 — Fk2q2 + E2kq2 + • • • +
Aktfk —СкЯ'к + ^k9k = 0-
Так как в первые части этих уравнений входят и члены с первыми
производными, то решение надо искать вида
^ = 04^; q2 =	9з=*зеЫ', •	9к=- <4^
и тогда, повторив то же рассуждение, как и выше*, увидим что Х1? ..., Ха
определяются уравнением
ЛД2 —Сг\ 4- Dx В12\2 —F12\ 4- Е12 ... В1к\2— F3k\+Elk
В12Х2 ^гД + Е12 Л2Х2 —С2\ 4“ D2 ... В2кк2—F2k^A~E2k
В±$? Fk^k-]-Eik В2к\2 Fk2k + E2k ... ЛД2 Скк -\-Dk
которое доставит 2п значений X; каждому из этих значений, например Хь
будет соответствовать система решений вида
qi=KeW9 q2 = b1ae2‘ltf q^c^e^, ..., qk--hjUeW	(3)
и b19 c19 hi суть вполне определенные числа, находимые через реше-
ние уравнений первой степени, а — постоянная произвольная; так как различ-
ных корней уравнения (3) вообще 2к, то общий интеграл системы будет вида
qr = aeA1* 4~	+ . .. +	,
q2 -=z b2 + b2fie'^ 4- ... 4- b2k<se*2kt,
=	4-А28еА2/ -f- . . . +h2k^2kt.
Чтобы колебания оставались малыми, надо, чтобы все корни X были
с отрицательною вещественною частью; тогда соответствующие паре сопряжен-
ных корней члены в формуле (4) по замене мнимых показательных вещест-
венными примут вид
(a cos ft 4- b sin ft)
и, значит, система (4) представит колебания, затухающие с течением времени.
§ 13] МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ	49
Во многих случаях уравнения (2) имеют ту особенность,- что коэффи-
циенты при членах, представляющих силы сопротивления, не все различны
между собою, а связаны соотношениями
т. е. F12=F21, F13 = F31 и т. д.; тогда, составив функцию
2W =	+ С2^22 + • • • +	+“
+	4- ... + 2F/£_1э /с ,	(5)
мы увидим, что члены, содержащие в уравнениях движения производные
первого порядка q'v q'2, q'k, представляют соответственно частные произ-
водные от функции W, так что уравнения движения напишутся:
d { дТ \ , dW dV n z. „ о M
dt V dq\ J oqt	dqi '	'	x 7
Умножив первое из этих уравнений на q\, второе —на q2 и т. д., сложив
и заметив, что по теореме Эйлера об однородных функциях будет
,dW , ,dW ,	, ,dW ОТЯ7
?1	#2	• • • “Ь Як л—, — 2Ж»
получим:
'[Г-П--2».
Величина Е = — V есть потенциальная энергия системы, Т — кинетиче-
ская энергия, и предыдущее равенство можно писать так:
£[T + E]=-2W.	(7)
В том случае, когда сил сопротивления не было бы, т. е. W = 0,
имел бы место закон сохранения энергии, выражаемый равенством
1,[7+В]=0,
уравнение же (7) показывает, что при сопротивлении энергия системы
не остается постоянной, а все время убывает и тем быстрее, чем больше
абсолютное значение функции W. Эту функцию, показывающую таким обра-
зом меру быстроты убывания энергии, лорд Рэлей и назвал «функцией рас-
сеяния» (dissipation function) и, представив уравнения движения в форме (7),
исследовал некоторые их общие свойства, на которых мы останавливаться
не будем.
В самом общем случае, кроме сил «восстановления», происходящих
от потенциала V, сил «сопротивления», коим соответствует «функция рас-
сеяния», могут *быть приложены внешние «возмущающие» силы, не имеющие
потенциала, а также и силы, зависящие от скорости, но не входящие в состав
предыдущих.
В самом деле, если равенства
Flt = Ftf,...
не имеют места, то не будет и равенства
Qi =	+ Fnq[ + Fi2q2 4- .., Ц- Fikq'k =	.
4 А. Н. Крылов
50 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Но очевидно, что можно писать, каковы бы ни были Fz/- и Fj{:
Pii =----— +-------2---
и	...
F.. A- F.. F.. — F-.
р — о к о н
н 2	2
Сделаем
так что будет,	.
Fij = GijНGji = Gij и Hji=^ — Нij
и, следовательно,
, Qi — CiQi + (£fi + ^ii) *?i + (^/2 +	q'2 + • • • -j- (Gij +Hij) q'j + .. .
Силы, входящие в состав Q4 и Qf с коэффициентами Gzy при производ-
ных, можно рассматривать как происходящие от «функции рассеяния» и, зна-
чит, как сопротивления, силы же с коэффициентами Нц называются силами
«гироскопическими», ибо подобного рода силы появляются, когда в состав
системы входит быстро вращающееся с ' постоянною угловою скоростью
тело—гироскоп, как, например, на корабле с успокоителем качки Шлика.
Нетрудно видеть, что присутствие таких гироскопических сил не нару-
шает закона сохранения энергии и формула (7) будет попрежнему иметь
место, если взять за W функцию
2W ~ Crf']2 + C2qf22 -г • • • + Ckq^ + 2<?12#^ + • • - + 2Ga-i,
Если на систему действуют и возмущающие силы, коих «обобщенные
составляющие», т. е. входящие в правые части второй формы лагранжевых
уравнений, мы назовем через R19 R2, . .., R^t то вместо уравнения (7)
мы получили бы такое:
\Т + Е} = Riq'i +7?2^2 +,-•• + Ekqk — 2И',	(8)
которое и показывало бы, как распределяется производимая возмущающими
силами работа и какая ее часть идет на увеличение энергии, и какая «рас-
сеивается», затрачиваясь на преодоление сопротивлений движению.
Этим уравнением, например, пользуются в теории корабля при изложении
успокоения качки прибором Шлика, где это уравнение является основным
и объясняющим сущность дела.
§ 14. Вынужденные колебания системы. Резонанс. Начнем с рассмотре-
ния простейшего случая, именно, положим, что система не включает ни сопро-
тивлений, ни гироскопических сил; тогда уравнения движения ее будут отли-
чаться от уравнений (II) § 10, представляющих свободные колебания, тем, что
в правых частях вместо нуля будут находиться величины R19 R2, ..., Rk
обобщенных составляющих возмущающих сил.
Эти величины будут вообще заданными функциями времени; особенно
прост и часто встречается тот случай, когда эти функции составлены из перио-
дических членов, т. е. членов вида
Li sin \p,t + 3,).	(1)
В этом случае надо искать частное решение того же вида, как и вторые
части уравнений/т. е. для всякого члена второй части брать в выражении
§ 14]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ. РЕЗОНАНС
5
для q^ q2, ..., qk член с тем же самым тригонометрическим множителем,
но коэффициент при нем в каждом из этих выражений оставлять неопреде-
ленным. Подставив Затем эти выражения в предложенные уравнения и ото-
ждествив полученные равенства, будем иметь для определения неизвестных
коэффициентов столько уравнений первой степени, сколько у нас этих
неизвестных, и притом для каждого sin {ptf -|- 5г) получится своя система
уравнений.	,
Таким образом, что мы скажем об одном члене, то будет относиться
к каждому из них.
Итак, пусть вторые части наших уравнений суть
L1sin(p^. 4-о), L’2sin {pt + о), ..., LK sin {pt 4- о);
тогда мы ищем частное решение вида
^1 = 7V1sin(/?Z+ ^),	— /V2sin {pt 4-Л), ..., qk — A/\sin {pt + g).	(2)
Подстановка этих величин в систему (II) доставит для определения
неизвестных Nu N2, ..., Nk систему уравнений первой степени, только
тем оличающихся от уравнений (III) § 10, что вместо буквы к будет стоять
буква р и вместо букв ах, а2, ..., а* — буквы Nu TV2, • •, Nk, и во вторых
частях вместо нуля —буквы Zx, L2, ...»
Очевидно, что определитель этой системы есть А(/?2).
Если р таково, что оно не равно ни одному из корней характеристического
уравнения А(Х2) — 0, то для A7X, TV2, .. ., Nk получатся конечные и определен-
ные значения.
Отсюда видно, что если р будет весьма близко к одному из корней
характеристического уравнения, то определитель А (/>2) будет иметь значение,
близкое к нулю, и, значит, величины коэффициентов Ny, N2, ... , Nk при
тех же значениях £2, ..., Lk будут весьма велики, т. е. когда период
возмущающей силы близок к периоду одного из основных колебаний системы»
то амплитуда этого колебания становится весьма большой по сравнению
с прочими, и проявляются явления резонанса.
В том случае, когда величина р окажется в точности равной одному
из корней X ~ Xf уравнения A (X2) =0, определитель системы обращается в нуль,
уравнения становятся несовместными, если только величины Llf L2, ..., Lk
не заданы так, что одно из уравнений есть следствие остальных.
В этом случае, чтобы не исследовать разных исключительных обстоя-
тельств, а применять общий метод, следует вместо координатных параметров
•••> У* ввести нормальные координаты	как о том
сказано в § 12. Система (II) распадается на ряд уравнений вида
е; + х2;1==Ех,-
•	•	о *
т *1 2£2   О
। f'-hSk l-Jk>
причем Sx, S2, ..., S/c будут вообще вида Mj sin {pt + £), и по предполо-
жению /? = Х/. В частном случае некоторые из величин могут быть
и равны нулю.
Решение уравнений (3) затруднений никаких не представит, и, найдя
нормальные колебания $х, ?2, ..., найдем и наши координатные пара-
метры q19 q2, ..., qk в функции времени:
Как видно, для того из уравнений (3), которое содержит решение
будет
t COS {\(t	о),
4*
52 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
т. е. амплитуда соответствующего нормального колебания возрастает неопре-
деленно с течением времени.
Поясним вышеизложенное примером. Возьмем уравнения § 11 и положим,
что вторые части этих уравнений будут не нули, а следующие:
Qi = sin t + sin 2t + sin 3z,
Q2 = 2 sin t + sin 2t — sin 3z,
Q3 = — 2 sin t — sin 2t 4- 2 sin 3z,
так что наши уравнения суть
6g'{ + 9?i + 6g'' + 15g2 + HgJ 4- 20g3 = sin t 4- sin 2t 4- sin 3z,
6g i + 15дг + llg'2 r 38g3 + 14g3 + 41g2 = 2 sin 14- sin 2t — sin 3t,	(4)
llgj 4- 20gi 4- 14g" 4- 41g2 4- 22g£ 4- 40g3 = — 2 sin t —- sin 2t + 2 sin 3z.
Мы видели, что общий интеграл соответствующей (4) системы без последних
членов есть
gi = a sin (t +	+ у sin (2t + s3),
g2 = P sin (t 4- 32) + Y sin (2t 4- з3)>	(5)
g3 = — | a sin (t + ®i) — ? sin (? + з2) — у sin (2t 4- з3),
поэтому для разыскания нормальных координат полагаем
02 = »! + С,	(6)
так что
В= asin(Z +si), IQ = рsin (Z-+ г2), С = ysin(2Z + г3)
и, следовательно, эти переменные удовлетворяют уравнениям
5»+е=о, ^+-»i=o, c'+4q=o.	(7)
Подставив выражение (6) в выражение живой силы 2Т и потенциала —
2V, получим [см. стр. 44, формулы (*)]:
.... 27’ = 1q°.'2 + 571'2 + C3-v!V>
10	14	(8)
-2V = ^c2 + 57)2 + 4!;2 -Jh?)
У	о
к уравнения
ли
dt \д^) dt
будут следующие:
,	?0" + ?)-з-«+’)) = 0,
5 (71"+ 7))-2 (? + $)= о,	<10>
О	- , -
£"4-4£ = 0;
очевидно, что эта система равносильна системе (7), хотя выражения Т и V
и содержат произведения и
§ 15]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ. РЕЗОНАНС
53
Чтобы составить уравнения, соответствующие (9), для того случая, когда
есть и возмущающие силы Ql9 Q2, Q3, надо взять выражение элементарной
работы
8t7 = Qityi +
и подставить вместо bqlt cq2, §q3 их величины
S?i = 8>+^;	=	cg3= — ^8$—8tj —8С,
о
следующие из уравнений (6), и тогда будем иметь:
и = (<?1 - |<2з) 85 + (<?2 - <2з) 8-п + (<21+<?2 - Сз) ас=
= Q sin t +sin 2г 4-1 sin Зг^ 8; + (4 sin t + 2 sin 2г — 3 sin 3г) to; +
+ (5 sin t + 3 sin 2г + 2 sin Зг) 3C;
уравнения движения будут
тт (?" + $) — в Of + i»))=-|sinz + |sin 2г + ^зп13г,
У	о	Ооо
+ 5) + 5(т)" + = 4 sin 14- 2 sin 2г — 3 sin Зг,
о
7' + 4С = 5 sin г + 3 sin 2г + 2 sin Зг
и интегрирование их не представляет никаких затруднений, если предвари-
тельно первые два разрешить относительно £" + 5 и т/' + tj, так что они
примут вид
+ $ = a sin г + b sin 2г + с sin Зг,
т)" + т) = a,i sin г + Ьг sin 2г + Ci sin Зг.
После того как 6, щ, С будут найдены, по формуле (6) найдем и qlr q2, q3-
§ 15. В том случае, когда система включает или сопротивления, или
гироскопические силы, т. е. когда ее уравнения имеют вид (2) § 13, и если
на нее действуют и возмущающие силы, то уравнения будут того же вида,
только во второй части будут стоять не нули, а обобщенные составляющие
этих сил.
Если эти возмущающие силы будут состоять из суммы периодических
членов вида Lt sin {pt + 8) или, что то же, вида Кi sin pt + cos pt, то надо
для каждого члена брать в составе величин qv q2, ..., qi9 ..., qk по паре
членов вида
Ni sin pt + Pi cos pt.
Подставив и отождествив, получим для определения 2к неизвестных Nt
и Pi столько же уравнений, причем определитель их нулем не будет, когда
уравнение Д(к) = О имеет только комплексные корни.
Другой способ нахождения частного решения есть способ изменения
постоянных произвольных, излагать которыц мы здесь не будем, предполагая
его достаточно известным.
Наконец, третий способ состоит в применении символического приема,
изложенного в § 9.
Чтобы применить его к нашему случаю, поступают так: заменив диф-
ференцирования символом 8, рассматриваем этот символ как буквенный
54 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
множитель, и тогда система (2) § 13, предполагая ее уравнения с последними
членами, примет вид
(А3о2 — Cfi f- Dx) + (^i2^2 — F 12° —^12) #2 + • • • +
+ (-^i^2 — Flkb + Etk) qk — Qi,
{Bl2Z2 — F218 + Et2) Qi + GM2 ~ С2Ъ + D2) q2 + • . • +
+ (В2кЬ2 — F2$ + E2k) Qk ~ (?2,	(H)
(Si/cS2 — Fk1<j + Eik) Qi + (B2kb2 — Fk2^ + F2k) ?2 + • • • +
+ (A$2 — СкЪ + Dk) qk ~ Qk-
Если эту систему решить относительно q2i • •, qk> то получатся
решения вида
Д(е).9г-Аа(б)^ + А1-2(3)^24-...+Д1Н^)<?/с (/ = 1,2,3, ...,Л),	(12)
где Д(о) есть определитель системы (11) и Дп, Д/2, ...—его миноры, соот-
ветствующие г-му столбцу.
Во второй части этого равенства, развив определители по степеням
буквы 8, выполняем соответствующие им дифференцирования над заданными
функциями Qi, Q2t . . ., QK\ тогда вторая часть обратится в известную функ-
цию переменной Z; обозначим ее через Тогда уравнения (12) напи-
шутся так:
Д(о)^ =<fi(0 (i = l, 2, ..., к).	(13)
По предположению, уравнение
Д(Х) = О
имеет только комплексные корни с отрицательною вещественною частью,
значит, величина Д (к) разлагается на произведение множителей вида
	)2+2^Д + /у,
причем	//-§!> о.
1
Дробь разложится на сумму дробей вида
	йуХ + &у X2 + 2g + f j ’
так что	к 1 _ VI	+ bj A(X)~Zj,X2 + 2^X + /7.’. 7 = 1	'
причем будет тождественно
-	‘	к	Л , ш  а : Л Ь ! А(>-) • 2 k» + 2gk + /-^1- /=1
Из уравнения множитель,	(13) следует для о, рассматриваемого как буквенный =	=	(14)
или иначе	к	. >	d: 8 -р Ъ : — 2 «2 + 2g а + / •ср'1 /=1 1 .
S-16]
ПРИВЕДЕНИЕ ВЕКОВОГО УРАВЙЁНИЯ
55
будем теперь о рассматривать как символ объясненного в § 9 действия и
в каждом члене суммы (15) выполним над функцией действие а7$ + д7;
получим:	(а;о 4- bj) (t) = ау <fi (z) + bj-ft (Z) =	(Z);
тогда будет ;	~ Ъ $2 + 2gj$ + fj V' (0>	, i Z=i	'
1
обозначим результат действия (р“Т”9—> . у над функцией (Z), через ;7Г-, так
ЧТО	^ = (^ + 2gy3+//)-4F(Z),
или иначе	(S2 + 2g’y8 + //):/i = ’]>1-(Z),
или иначе	с12Е,ц J +2g/	= ^(Z), ,	-	(16)
т. е. величина определится через решение дифференциального уравнения
второго порядка, нами уже подробно исследованного.;
Мы привели систему (II) к уравнениям для каждого qi9 причем левые
части этих уравнений одинаковы для различных Дальнейшее сводится
к решению уравнений (12). Если для каждого qt написать общий интеграл,
-то, подставляя в систему (11), получим необходимые связи для произвольных
постоянных, входящих в упомянутые общие интегралы
§ 16. Приведение векового уравнения к виду, удобному для числен-
ного решения его. Пример. Особенные случаи. В предыдущих параграфах
изложена в главных чертах теория малых колебаний систем. Как видно,
в том случае, когда требуется найти не только вынужденные, но и свобод-
ные колебания, то вопрос приводится к решению так называемого «веко-
вого» уравнения (IV) для систем без сопротивления и уравнения (X) § 13
для систем с сопротивлением.
Решение этих уравнений требует сперва развития соответствующих
определителей, что при написанной их форме при сколь-нибудь значительном
числе строк и столбцов практически почти невыполнимо или требует громадной
работы.
В моей статье «О численном решении уравнения, которым в технических
вопросах определяются частоты малых колебаний материальных систем»г)
изложены методы Лапласа, Леверрье и Якоби для этого решения, разобраны
критически, и в заключение приведен метод, развитый мною, который всего
проще и с наименьшею затратою труда ведет к цели. Отсылая к указанной
•статье, я приведу лишь ее заключительнуюг практическую часть.
Положим, что первоначально введенные лагранжевы координатные пара-
метры суть
$1, $2, ♦ •	sk;	(1)
тогда живая сила выразится квадратичною формою
27 = 3	(2)
и элементарная работа «обобщённых сил»
W =	+ S£s2 + ... + S£sk,	(3)
х) Изв. Академии Наук, № 4, 1931.	е
56 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
причем Mik суть заданные постоянные, ^—-заданные линейные функции
переменных.
Прежде всего, для упрощения выкладок, надо привести живую силу
к виду
27 —	+ С2^2 + . . . + CkSk)2 + (с?252	^3S3 + • • • + dkSR)2 + ...
... + (gk-iSk-1 + gkSk)2 + (hks'k)2,	(4>
что всегда возможно, ибо живая сила есть «определенная» квадратичная
форма.
Это приведение совершается весьма просто и не требует решения каких:
бы то ни было уравнений. Поясним его примером. Пусть будет
2Т = 6s'2 + 11s;2 + 22s'2 + 12$Х + 22s's' + 28#'
Умножив, чтобы избежать иррациональностей, обе части этого равен-
ства на 6, дополняем члены, содержащие переменную до полного квад-
рата суммы всех трех переменных, умноженных на постоянные множители;
получаем:
2. бт = (6s; + 6s; + iis;)2 + 30s;2 + iis;2 + 36s;s;.
Это равенство множим на 30 и дополняем до полного квадрата члены,
содержащие t'2, имеем:
2 • 6 • 307 = зо (6s; + 6s; +1is')2 + (30s; + i8s;)2 + 6s;2.
За новые переменные берем, чтобы избежать дробей,
S з === 30^3,
30s2 + 18s3 = 6 • 30 • х2,
6sx + 6s2 + lls3 =
Таким образом, будет
27 = 6# + 180а:;2 + 30#;
положив затем
|/ вхг = qv )/ 180я2 = q2, ЗОх3 = q3,
получаем:
27-# + # + #.
Совершенно подобно надо поступать и при 'любом числе переменных-
Таким образом, в общем случае, положив
hksk = q^f
gk-lsk-l + gk$k = Qk-ii
...................... .....	(5>
ctSi + c2s2 + ... + cksk = qlt
вместо параметров s£ вводим параметры Очевидно, что из уравнения (5}
непосредственно находятся выражения переменных st через переменные q^
Эти выражения будут вида
Sk = h'kfyt*
S/c-i =£а-1£л-1 +gL?;.>
(6>
Sl = <^<11 + ^2^2 + • • • +
где все коэффициенты h'k, ...,с'к постоянные.
§ 16]
ПРИВЕДЕНИЕ ВЕКОВОГО УРАВНЕНИЯ
57
Очевидно, что, заменив переменные при помощи выражений (6),.
мы получим:
27’ = g? + g23 + ??4-(7>
= Q^q\ + Q2f+ • • • +	(8)'
причем величины Q19 Q2, ..»,Qk будут известными линейными функциями
переменных дг, q^, ..., qk и мы их обозначим так:
Ql = allQl + а12?2 + «13?з + • • • + UlkQkt
Qz = ^21?I + а22Ч2 + ^23?3 + » • • + ^27<?Ь
Q3 = «31^1 + ^32?2 + #33?3 + • • • + ^ЗА?/с,	(9)
Qk ~ ак1$1 + ^2^2 + ^АЗ^З + • • • + ЯккЦк’
Заметим здесь же, что в том случае, когда интеграл живых сил имеет
место, то выражение (8) будет представлять полный дифференциал, и между
коэффициентами aik будут иметь место соотношения
fh = 1, 2, ... , к— 1,
Oih-ам	кг = 1, 2, ... ,к — 1,к) ’
пока же мы этого предполагать не будем.
На основании выражений (7), (8), (9) уравнения движения нашей
системы будут
~ аи?1 + ^12?2 + «13^3 + • • • +
^2 ~ а21?1 + ^22^2 + а2з#з + . . . + U^qki
?3 = Л31?1 + а32?2 + %3?3 + • • • + aSkqk)	(11)
q'k.= akiqi + ^2^2 + й>кзЯз +•.•? + akkqk* ,
Для системы (11) характеристическое уравнение будет
	«11-х2	«12	«13	• • й±к
	«21	«22— X2	«23	. • «2А
Д(Х) =	«31	«32	^зз	•	• • ®3к
(12)
67/cjL	Uk2	Uk%	• • . Ukk k2
Хотя это уравнение проще (IV), но ввиду того, что неизвестная к
находится в диагональных элементах, развитие этого определителя сложно;
поэтому применим к интегрированию системы (11) тот метод, который
в любом курсе анализа, начиная с Лакруа, изданного 120 лет тому назад,
пользуются для приведения системы совокупных уравнений к одному урав-
нению соответствующего порядка или, лучше сказать, для доказательства
возможности такого приведения, причем будем придерживаться того свое-
образного изложения, которым на своих лекциях пользовался А. Н. Коркин.
Положим
x = qlt	(*)
где х есть вспомогательная переменная (можно полагать в общем случае и
« = aqx + bq2 + cq3 + ... + fqk,
причем а, Ь, с, ... / — любые заданные постоянные).
58 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Продифференцируем равенство (*) дважды по времени t и в полученном
равенстве
х" = q”
заменим q[ его величиною
q'l = #ntfi + #12^2 + • • • + амДк
из предложенной системы (11), так что будет
Х" = #ц^1 + #12^2 + . . • + aikqk*
Дифференцируем это равенство дважды по времени и в полученном
^равенстве
£IV = au<7j' + #12^2 + • • • + aikq'i
заменяем
qnv qf2> ---9ql
их величинами из предложенной системы; получим уравнение вида
#IV = 621<?1 + ^22^2 + • • • + ЬъкЦк)
и продолжаем поступать таким образом при составлении производных
XNI> ^VIII,
Таким образом, вместо предложенной системы получим ей эквива-
лентную:
X* — #11?! + #12^2 + #13?3 + • • • +
£IV = 62i^i + ^22^2 4" &2з*7з + • • • + b2kqK,
xN1 = c3i9i + ^3202 + с3з£з + • • • + C3kqk,	(13)
х2к = hiqi + /к2^2 + Аз?з + • • • + fkkqk,
исключая переменные q, мы получим одно обыкновенное дифференциальное
уравнение порядка 2к:		
	-х 1	0	0 ... 0	
	—	#11 #12	#13 * * *	
	Х^	Ь<2,2 ^23 * * * Ь%к	= 0.	(14)
	— хУ^ С31 С32 ^зз • • • ^3/с	
	— Х^^ //с1 /л2 f кз * * ‘ fkk	
Ищем его решение вида
причем Сj— произвольная постоянная; получаем для определения к урав-
нение
-1	1	0	0 ..	. 0		
-к2	а11	#12	#13 • •	• #1/с		
— к4	b2i	^22	623 /.	• Ь^к	= 0;	(15)
— к6 ।	С31	С32	сзз • •.	• Сзк		
1	• 		} 2к	/	/		/		
	Ml	/А2	/-3 • •	• /Хл		
§ 16]
ПРИВЕДЕНИЕ ВЕКОВОГО УРАВНЕНИЯ
59
придав затем первый столбец ко второму, приводим это уравнение к виду
Л(Х) =
$11	$]2	&13	а1к
^21 —	^22	^23	• • •	^2й
С31 к6 С32	С33	. . .	С3к
j ki	/ А2	/йЗ	•••	f кк
(16)
Это и есть «вековое» или характеристическое уравнение для нашей
системы (11), написанное^в том виде, в котором оно получится, если при-
менить общий метод, интегрирования, излагаемый во.всех курсах анализа,
и довести его до конца.
Пусть будет
$11	$12 • • • а1к
&21	&22 • • • ^2й
~ о ^31	с32 • • • СЗЙ ’
/й! /й2 • • • fkk
обозначим через
. , .	Ар А2, Д3, • • <, Д/с.
миноры определителя До, относящиеся к первому столбцу, так что
До = alt Дх -|- 621^2 4* сзхАз + • • • +
тогда уравнение (16) напишется, положив к2 —а, так:
(17)
(18)
Д/^а^ + Ай-!^"1 + ... + А1а — Ао = О
или, разделяя на Д/с и полагая
^ = 5,;	-£ = Bt	(19)
придаем ему вид
а* 4- •Bja*-'1 + В2^к~2 4~ • • • + iа + В& = О,
после чего и решаем его по обычным способам.
Как видно, миноры (18) все численные порядка (Л —1); их вычисление
совершается весьма просто, эта простота получилась потому, что неизве-
стная а и ее степени находятся в одном первом столбце, а не в диагональ-
ных элементах определителя, цри каковом ихрасположении развитие такого
определителя, как (19), при сколь-нибудь значительном к практически
непосредственно не выполнимо и требует тех особенных приемов, которые
и были даны Лапласом, Якоби и Леверрье. , _
Покажем теперь, каким образом по заданным коэффициентам
‘	‘	‘ $11> • • • > ®кк
последовательно составляются коэффициенты
^21> ^22>	, ^2Й>
СЗР С32> • • • > СЗЙ> •	“
/й1, /й2> • • • , tkk* ‘
60 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Стоит только выполнить всякий раз указанную выше замену, и мы
увидим, что будет
621 =	+ 012^21 + • • • + #1^1»
622 ~ Яц&12 + ^12^22 4“ • • • 4" Я1А#А2>
.................................................... (20)
&2к = ^ца1к "Ь ®12®2fc "I" • • • 4" а^к^кк'
Затем,
е31= 621йх1 + ^22^21 Ь ^23^31 + • • • + ^2к^кЦ
С32 = ^21а12 4" ^22^22 + ^23^32 + • • • 4” 1>2как2’
^Зк — bzi^ik 4~ ^22^2/с + ^23а3к 4“ • • • 4" ^2какк\
коэффициенты c?4i получатся, заменив в схеме для вычисления c3i вели-
чины d2f через c3i и т. д., как то. показано на численном примере ниже.
§ 17» Положим теперь, что нам дана система уравнений, соответству-
ющая колебаниям с гироскопическими членами и сопротивлением, так что
уравнения движения будут вида
9] =	+	^12^2	+ • ♦ • + alkQk +	+ ^12<?2 4" • • • 4"
?2 ~ ^21*71 4- a22^2 + • • • 4“ CfokQk 4“ ^2i^4 + ^22?2 -p . . . 4"	(22)
9 k ~ &ki91 4“ ak2^2 + • • ‘ 4“ akkQk 4" ^Tcl71‘4“ ^A2#2 4" • • • 4~ hfrkQkt
причем равенств
fl// = «/i и hij = hjt
может в общем случае и не быть.
В таком случае, если бы положить
Qi = С1еЛ*> 92 — С2еи, ..., 9к = Скеи9
то для определения к получилось бы уравнение
Д(к) =	aii4- hrl\— X2 ^21 4“ ^21^	^12 4“ ki2)< ^22 4” k22\ — k2	... alk 4- • • • ^2k 4" ^2/ck	= 0,
	aki 4-	^/c2 4- kk2\	• • • akk 4- Ла/Д — X2	
развитие которого даже для случая к = 4 потребовало бы весьма длинных
и громоздких выкладок.
Для такой системы надо поступать следующим образом:
1) Прежде всего привести введением добавочных неизвестных все
уравнения системы к первому порядку, для чего положить
91~ 9к+1> 92~9к+2, • • • , 9к~ 9zk\
тогда предложенная система примет вид
g; = 0	+0	+ •	..+0	+	4*		0	+ .		0,
?2 = °	+0	+ 	• • +o	+	0	+	9k+2 4“ 0.			0,
?* = 0	+0	+ •	.. 4- 0	 +	0	4~	0	+ •		92k
9k+i = ^h9l 4" ^12?2 4“ • •	• 4“ aik9k 4- 4“ ^12?л+2 +	•	• •	4" hlkq2k>	(23)
9к+2 = ^21^1 4" а2292 + • •	• + <^2к9к + ^213/c+l 4" ^22?/с+2 4"	•	• •	4“ Ь>2к92к,
9к+з — a3i9i 4- ^32^2 4- • •	• -+ а>зк9к 4" ^зх^л+i 4* Ьзъ9к+2 4~	•	• •	4- k3kq2k9
9^к — ак191 + ^А2^2 4- • • • 4- Ukkqk +	4- ^A2<?/c+2 4“ • • • 4" hkk92k*
§ 17]
ПРИВЕДЕНИЕ ВЕКОВОГО УРАВНЕНИЯ
61
2) Положить
^ = 91
и последовательно дифференцировать это равенство 2к раз, заменяя после
всякого дифференцирования производные переменных qlt q2, ..., ?2/с их
выражениями (23); тогда предложенная система заменится следующей ей
эквивалентной:
х =q19
xf =0	4-0	4"..............4* ?/c+i	4".......4-0,
X" =	4- ^12?2 4" • • • 4-	4-^ll<?/c+l	4" • • • 4" ^1W2/c,	(24)
= b1q1 4” b2q2 4- • • • 4- bkqk	4- 6/c+i?k+i	4- • • • 4* &2k?2/6
^(2A) —/i?l 4”/2?2 4~ • • • 4“/к?Л	4“//c+l?k+l	4- • • • +/2/c?2/c,
при понятном обозначении и понятном	последовательном составлении коэффи-
циентов, которые, очевидно, все будут постоянные.
Исключая из этой системы все величины
?1> ?2, • • • , ?2к>
получим обыкновенное дифференциальное уравнение
— X	1	0 ..	. 0	0	0	. 0	
—х'	0	0 ..	. 0	1	0	. 0	
— X"	а11	^12 • .	• ^1к	^ii	Л12	• Ь1к	
— х'"	Ь,	ь2 ..	. Ьк	^+i	6/с+2 • •	• b2k	= 0.	(25)
-х™	С1	с2 . ..	. Ск	сМ-1	Ск+2 • •	• С2к	
—	/2 . . ’ fk fk+1 fk+2 • • • /2А
Ищем	решение вида		ж_еЛ(;	тогда	ДЛЯ	определения		к получим урав-
пение								
		-1	1 0 .	... 0	0	0	... 0	
		-к	0 0 .	... 0	1 :	0 <	... 0	
		— к2	а11 а12	.. . а^к	Ьц	^12	.. . h^k	
	Д(л) =	-к3	Ьг ь2	• • Ьк	Ьк+1	Ьк+2	. .. b2k	= 0.	(26)
		-к4	ci с2	 - • Ск	ск+1	С к+2	. . . С2к	
		— к2*	fl /2	 • fk	fk+i	fk+2	• • • /2k	
Приложив первый столбец ко второму, получаем:
~—	к	0	0 .	.. 0	1	0	.. 0	
Яц	к2	«12	а13 •	• • aik	Ли	Л12	• • hlk	
Ьг-	к3	&2	63	• • ь^	Ьк+1	fr/c-}-2 • *	• • b2k	= 0.
С1	к4	с2	с3 ..	• Ск	С к+1	^Л4*2 • *	• • С2к	
/1	^2/С /2/3 • • • fk fk+1 fk+2 ••• /2А
Это уравнение может быть написано и в другом Ниде, который полу-
чится, если умножить столбец к 4-1 на X, придать , его к первому и вычерк-
62 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
путь затем верхнюю строку и столбец Л 4-1. Тогда будет
А(Х) =
аи 4- Лц X К2 * (112 ui3
^l+^k+l X—X3 62 63
^1 + ^+1 X —X* с2 с3
<hk ^12	•	•	•
Ьк ^Л+2 • • • ^2к
Ск ^/<+2 • • • ^2й
-0.	(27)
/i + А+1 х х2/с /2 /3 ... /л /ус+2 ... f2k
Определитель этот будет порядка 27с— 1, развитие его по элементам
первого столбца затруднений не представляет, и, обозначая соответствующие
этим элементам миноры через
Др ^2, • • • > Д2Л—1>	(27')
приведем «вековое» уравнение в этом случае сперва к виду
(ап + ЛиХ — X2) Aj + (bi бк+i '< — X3) Д2 4- . • • 4" (Л + А<+1 X — Х2к) Д-27С-1 = 0,
а затем к окончательному виду
Х2/С + Вхк2*-1 + В2Х2Л-2 + . . . + В2Л_1Х + В2к - о,
причем нам потребуется лишь вычислять численные определители (27'),
каждый из которых будет порядка 2к — 2.
§ 18. Чтобы пояснить наш метод примером, возьмем этот пример из
«Recherches astronomiques» Леверрье (Ann. de I’Observ. de Paris, t. II,
p. 128), а именно — систему в наших обозначениях:
^=-5.509882^4- 1.870086 q2 4- 0.422908 q3 4- 0.008814 q^
q'z = 0.28786591-11.811654?2 4- 5.711900?3 + 0.058717^,
q£ = 0.049099^4- 4.308033 q2 - 12.970687 q3 4- 0.229326 q^
q"= 0.006235^4- 0.269851^4- 1.397369 g3 -17.596207 g4.
Округляя коэффициенты на пять знаков и приискав соответствующие
им пятизначные логарифмы, пишем эту систему с логарифмическими коэф-
фициентами, после чего вычисляем по приведенным схемам числа
&2f> C3i>	(^ = 1> 2, 3, 4)
и по ним коэффициенты
51, В2, В3, В±
«векового» уравнения, вычисление корней которого, как не представляющее
никаких трудностей и не требующее пояснений, опускаем.
Вычисление коэффициентов приведено в таблице 2 со всею подробностью
в том именно виде, как оно на самом деле произведено, чтобы дать пол-
ный пример и образец подобной работы.
Контрольное вычисление обнаруживает вполне удовлетворительное при
вычислении по пятизначным логарифмам согласие, а именно:
Bi = 47.886 и 47.8884
12311 и 12 297.
Так как контрольные числа получены по непосредственному вычислению,
то им надо отдать предпочтение; таким образом, при наших обозначениях
«вековое» уравнение для написанной системы есть
а4 4- 47.8884 а3 4- 797.24 а2 4- 5350.0 а 4-12 297 = 0.	(*)
§ 18]
ПРИВЕДЕНИЕ ВЕКОВОГО УРАВНЕНИЯ
63
Таблица 2
Численное решение векового уравнения
Схемы вычисления
Заданная система
// <1г	Я1	?2	#3	?4
41	а11	«12	а1з	«14
4.2	«21	«22	«23	«24
4з	«31	«32	азз	а34
4'1	«41	«42	«43	«44
Схема вычисления b2i
1	«ц —	- а12 —	«13 —	«14 —	Ъц
1	«ц«ц	«12а21	«13«31	«14«41	Ъц
2	«ц«12	«12«22	^13^32 •	а14а42	^22
3	«11«13	«12^23	«13^33	«14«43	^23
4	«ц«14	«1’^2*	а13а34	«14«44	&24
Схем1а вычисления с31-
i	Ь21 =		^23 —	^24 =	С31
1 /	^21а11	1	^22а21	^23а31	^24^41	,	С31	।
2	&21а12	^21^21	^23а32	^24а42	С3 2
3	&21а13	^22а23	^23а33	^24а43	сзз
4	, .	^21а14	bi2a2i	&23#34	&24а44	С34
Заданная система (коэфф, логар.)
4i"	Qi	<h	Чз	?4
41"	0.74114 (—)	0.27186	1.62625	3.94517
41"	1.45919	1.07231 (—)	0.75678	2.76876
4з"	2.69107	0.63428	1.11296 (—)	Г.36045
4l"	3.79484	1.43112	0.14531	1.24542 (—)
64 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Вычисление &21-
i						1g hi
1	1.48228 +30.358	1.73105 0.53833	2.31732 0.020764	5.74001 0.00006	30,8985	1.48994
2	1.01300 (-) —10.304	1.34417 (—) —22.089	0.26053 1.8219	3.37269 0.00238	-30.569	1.48528 (-)
3	0.36739 (-) —2.3303	1.10264 10.6817	0.73921 (—) —5.4854	2.09048 0.012316	2.8783	0.45914
4	2.68631 —0.048563	1.04062 0.109805	2.98670 0.096984	1.19059 (-) -0.15509	0.003139	3.49679
Вычисление с31-
i				*	c3i	lg Csi
1	2.23108 (—) —170.25	0.94447 (-) —8.7998	1.15021 0.1413	5.29163 0.0000	-178.91	2.25264 (-)
2	1.76180 57.783	2.55759 361.07	1.09342 12.400	4.92791 0.0008	431.25	2.63473
3	1.11619 1 .0675	2.24206 (-) -174.61	1.57210 (—) -37.334	3.64210 .0.004	—198.87	2.29857
4	1.43511 0.27234	0.25404 (—) —1.7949	1.81959 0.66007	2.74221 (-) —0.055235	-0.9177	1.96270 (—)
Вычисление
•	i				-	dit	
r	1 2 3 4 A(0) =	2.99383 985.90 2.52450„ —334.58 (—) 1.87889 (-) -75.664 0.19.781.(—) — 1.5769 0.74114 J. 48994 2.25265 3.04158	2.09392 124.14 3.70704 (-) -5093.8 3.39151 2463.3 .1.40.349 25.322 On (-)	0 1 (-)	2 3	0.98964 (—) —9.764 2.93285 (—) —856.74 3.41153 2579.5 1.65902 (—) -45.606 ргделитель L .27186 .48528 (—) .63473 .79833 (-)	3.75754 (—) —0.006 1.39332 (—) —0.25 0.10801 (—) —1.28 1.20812 16.148 L(0) T. 62625 0.45914 2.29857( 3.69599	1100.27 —6285.37 4965.86 -5.713 3. 3. J- 0.	3.04150 3.79833 (—) 3.69599 0.75686 (-) 94517 49679 96270 (-) 75686 (-)
§ 18]
ПРИВЕДЕНИЕ ВЕКОВОГО УРАВНЕНИЯ
65
					!g dit
Вычислена 1.48528 (-) 2.29857 (-) 0.75686п(—)	е миноров Дх, 2.63473 3.69599 3.49679	Д2, Д3, Д4, отн 3.79833 (—) 0.45914 1.96270 (—)	ОСЯЩИХСЯ К 3.79833 (-) 2.29857 (-) 3.49679	гемонтам 1 сто 1.48528 (—) 3.69599 1.96270 (—)	лбца Д (0) 2.63473 0.45914 0.75686 (-)
4.54071 (-) -34730 0.27186 2.29857 (-) 0.75686 (—)	3.82751 6722.2 2.63473 3.69599 3.94517	4.22017 16602.5 Д1 = - 3.79838 (-) 1.62625 1.96270 (—)	3,59369 3923.6 147.541 3.79833 (-) 2.29857 (-) 3.94517	5.14397 139.305 0.27186 3.69599 1.96270 (-)	3.85083 (—) —7093.0 2.63473 1.62625 0.75686 (-)
3.32729 2124.7 0.27186 0.45914 0.75686 (-)	4.27589 18.875 1.48528 (-) 3.69599 3.94517	3.38733 2439.7 а2 = - 3.79833 (-) 1.62625 3.49679	4.04207 11017.2 -21.986 0.79833 (-) 0.45914 3.94517	3.93055 (—) -8522.2 1 0.27186 3.69599 3.49679	3.01784 (-) —1041.9 1.48528 (-) 1.62625 0.75686 (-)
1.48786 (—) —30.751 0.27186 0.45914 1.96270 (-)	3.12644 (—) —1337.95 1,48528 (-) 2.29857 (—) 3.94517	0.92137 (—) -8.34 д8 = - 2.63473 1.62625 3.49679	2.20264 (—) -159.455 1320.59 2.63473 0.45914 3.94517	1.46464 29.150 0.27186 2.29857 (—) 3.49679	1.86839 73.857 1.48528 (-) 1.62625 1.96270 (-)
0.69370 (-) -4.9397 Прим бы избежать точности.	1.79202 53.582 е ч а н и е. Ми малых разнос	1.75777 0.5725 До- норы вычислен тей больших	1.03904 10.9405 -27.578 [Ы по этому б( чисел и прог	0:06722 (—) —1.1674 злее длинному гсходящей от	1.07423 11.8640 приему, что- этого утраты
5 Н» А. Крылов
66 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Вычисление коэффициентов Bi
1	lg А*	lg Bt	Bi	1j ЛГ«11	
0	5.53085 (-)	4.09029	12.311		
1	5.16891 (—)	3.72835	5350.0	5.91005	812 930
2	4.34215 (—)	2.90159	797.24	5.83209 (-)	—679 350
3	3.12077 (—)	1.68021	47.886	5.37341	236 270
4	1.44056 (-)			4.48206 (-)	— 30 343
					339 507
Контроль
Д(0) = — 625.1; 2.7959' 4.9031	2.79597 (-) —625.13 0.69043 4.9026 1.33062 0.21410 4.54942 (—) —0.00035434 J	212J 7(-)	2.32( )	—201.		2.32669 212.17 2.30355 (-) -201.165 1.27383 18.786 2.18570 (-) —0.015336 185 )71 .150		1.68108 47.982 1.98802 97.279 1.75251 (-) —56.560 2.89989 (—) —0.079413 48.061 1.68179 97.358		3.94517 (—) 2.76876 1.36045 1.24542		lg ап 0.74114 (-) 1.07231 (—) 1.11296 (-) 1.24542 (-)		аи 5.5099 11.8115 12.9705 17.5965
									Вг =47.8884 888 258 = 6.76999 (—) 3.31980 (—)		
							3.31980 (—) 1g 5				
и.оуичо 0.21445 1.33133 2.79597 (-) 2.30352 (—) 1.75190 (-)		18.801 1.27418 0.69046 1.27418 1.68179		—)	1.уоой — 56.48: 1.75191 1.33133 2.32671 1.98837		/ • 1 К-) 1.381 2.303 1.681	1 33 52 (-) 79	4 В4 = Д( 2.79597 (—) 1.27418 (-) 1.98837		.08979 0)- 12 297 0.69046 2.32671 1.75190 (-)	
6.85139 (-) — 7 102 200 1		3.64643 4430.3		3.6’1641 4430.1 — 5 88		3.31664 (—) —2073.2 1 >8 258		6.05852 (—) — 1 144 250		4.76907 (-) -58 759 		
§ 19]
ПРИВЕДЕНИЕ ВЕКОВОГО УРАВНЕНИЯ
67.
По вычислениям Леверрье, произведенным по семизначным* а может
быть и десятизначным, логарифмам, это уравнение есть
а4+ 47.888430 а3+797.2789 а2+5349.457 а+ 12296.555=0. .
Все корни этого уравнения вещественные и отрицательные. Вычисление
по логарифмической линейке покажет, что один корень лежит между
— 5 и —6, второй —между — 7 и —8. Вычисление этих двух корней вы-
полняется весьма просто, после чего остальные два найдутся решением
квадратного уравнения. Корни нашего уравнения будут отличаться лишь
в 5-ом знаке от корней, вычисленных Леверрье, которые суть
а1= — 5.29870, а3= -17.15266,
а2=-7.57404, а4 =-17.86303.
§ 19. В предыдущем примере все миноры вычислены независимо и От-
дельно, ибо они третьего порядка, а вычисление такого определителя про-
изводится весьма просто, но если бы порядок был не 4, а, скажем, 8, то
такое раздельное вычисление потребовало бы много излишней работы, ко-
торой можно избежать, поступая следующим образом.
Обозначим двучлены или трехчлены первого столбца через
Л, В, С, D, t..,F .
и поставим этот столбец на последнее место, так что наш определитель
будет вида
@2	*•• ^к—1	А.
&1 &2	. . •	В
^2	• • • 1	С
/1 /2 •	• • //с-1	F
разделяем каждую строку соответственно на первый член ее и затем вычи-
таем первую строку пз всех остальных; тогда, отбросив первый столбец
и верхнюю строку, приводим наш определитель к виду
&2 Ъ3, ...	1
Cg С3 . . ,. С/с—1
/2 /з ’ * • А-1
А =	. ../j
bi1B—ai1A
с~гС — а^А
а'1 А
С этим определителем поступаем так же
определитель порядка к — 2 такого вида:
Д —
• • • fl ^2 С2 ’ * * /2
й, по упрощении, получим
< ^ ...
61 з 6Z4 ... dk—1
(vC + р^ + аЛ)
(З^ + рЯ'+а-Л)
(v,F 4- $В + аЛ)
fl К ♦.. /^1
и продолжаем таким образом, пока не дойдем до определителя четвертого?
порядка, миноры которого будут третьего порядка и вычисляются непосред-
ственно, как показано выше, после чего определитель Д развивается по эле-
ментам своею последнего столбца и представляется в виде	1
Д = nA + тВ*'+ рС + ... + rF.
"68 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Очевидно, что п, т, />,.. ., г и будут искомые миноры, относящиеся
к числам первого столбца первоначально предложенного определителя, а так
как достаточно знать лишь числа, им пропорциональные, то нет надобности
производить умножение на величину
• • • /1^2с2 • • • /2 • • •
Особенно просто это вычисление произвести, пользуясь логарифмиче-
ской линейкой, что для технических вопросов вполне достаточно, так же
просто выполняется оно и по логарифмам, на подробностях чего останав-
ливаться не будем.
§ 20» В предыдущих параграфах мы рассмотрели тот случай, когда
все корни характеристического уравнения, соответствующего данной системе,
не равны между собой.
Первоначально я имел в виду ограничиться этим общим случаем, как
наиболее часто встречающимся в технических вопросах, но акад. Л. И. Ман-
дельштам, ознакомясь с этою статьею в рукописи, любезно обратил мое
внимание на то, что случай равных корней представляет такие особенности,
что с первого взгляда может показаться, что изложенный метод к этому
случаю не применим, поэтому для практиков представляющееся затрудне-
ние желательно разъяснить.
Здесь приходится особенно вспомнить слова Ньютона: «три изучении
наук примеры не менее поучительны, нежели правила», а также Эйлера,
который, излагая какой-либо вопрос, всегда начинал с разбора простейших
частных случаев, на которых наглядно выясняется сущность дела. Лагранж
как раз в данном случае, следуя своему обычаю рассматривать всякий во-
прос в самом общего виде, впал в свою знаменитую ошибку, вовлек в нее
Лапласа, и эта ошибка удержалась в науке в течение 70 лет, пока почти
одновременно ее не разъяснили К. Вейерштрасс (в 1858 г.) и наш акаде-
мик О. И. Сомов (в 1859 г.).
Начнем с того примера, который мне сообщил акад. Л. И. Мандель-
штам:
=2#! + q2 +
Q2 — <7i + 2?2 +	(28)
?з “ <71 + ?2 + 2^3.
Характеристическое уравнение для этой системы, написанное в виде

2-Х2 Г
1	• 2-Х2
1 1
1
1
2-Х2
(29)
очевидно, имеет корень
Х2 = 1,
а так как при этом значении не только
(30)
но и все миноры второго порядка этого определителя равны нулю, то ко-
рень X2 = 1 есть двойной. Второй корень, как легко проверить, есть X2 = 4,
таким образом:
Д(Х2) = (Х2- 1)2р~4).
§ 20]
ПРИВЕДЕНИЕ ВЕКОВОГО УРАВНЕНИЯ
69
Обращаясь к системе (28) и применяя метод § 16, получим последов
вательно:
ж" = 2дх+ ?2 +
6^+ 5^2 + 5?3,	(31)
= 22^fx -}- 21^2 -|- 21^3о	1
По исключении, следуя буквально правилу § 16, переменных qlf q2, q-3,
мы написали бы уравнение
— X	1	0	0	
— Х"	2	1	1	
-х™	6	5	5	= 0;
-х™	22	'21	21	
(32)
соответствующее ему характеристическое
	-1 *1 2	1 9	0 А	0 А		2 —X2	1	1	
А(Х) =	— к* -Xе	6 22	1 5 21	1 5 21	=	6-Х4 22-Xе	5 21	5 21	= 0.
(33)
Развивая этот определитель по элементам первого столбца, получим
(2-Х2)
5
21
(34)
Очевидно, что все написанные миноры равны нулю, и вместо уравне-
ния мы получим тождество
0 = 0»
Очевидно также, что если бы мы стали развивать уравнение (32), то
получили бы то же самое тождество.
В чем же дело и в чем причина этого кажущегося противоречия?
Дело в том, что когда мы составляем систему (31), чтобы затем исклю-
чить переменные qit q2, q3, в этом частном случае нет надобности составлять
четвертое уравнение, а достаточно только первых трех уравнений, ибо>
переменные q2 и q3 входят лишь в виде суммы q2 + q3 и исключаются обе
сразу, а не каждая порознь; в самом деле положив на время в уравне-
нии (31)
+ 9з = 5»
мы напишем систему (31) так:.
ж =?1,
х" =2?1 + е,	(35)
*IV=6?1 + 5?,
и результат исключения будет
— х 1
-ж" 2
-х™ 6
0
1 =0,
5
70 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
или в развитом виде
xlN — Ъх" -}- 4# = 0,
(36)
-1 1 0
-X2 2 1
-к* 6 5
и характеристическое уравнение
5k2 4-4=0,	(37)
откуда корни
Ц=1; )! = 4,
соответственно чему
q^A^+B^ + C^1 +Die-2t,	(38)
причем Av Blt Сг и Dx — произвольные постоянные.
Совершенно так же, если бы, положив	. *
У = 02,
мы исключили бы затем переменные qx и <?3, то получили бы уравнение
z/iv — 5г/'г 4-5 = 0
и из него имели бы общее решение:
q2 = А2е* -j- B2e~t + С2е^ + D2e~^,	(ЗУ)
а если бы, положив
?з = 2,
исключили q± и q2i то имели бы
9з - А3е* + В3е~* + C3e2t ± D3e~*.	(40)
Но постоянные произвольные Alf ..., D3 не суть независимые меж-
ду собою, а связаны теми соотношениями, которые следуют из уравнений
системы.
Так, возьмем частное решение
q^A^e*, q2 = A2e*, q3 = A3el;
подставляя, получим
Л-i = 2Аг 4- А2 4- А3,
А2 = Л14-2А24- Ап	(41)
А3 = А14" А2 4“ 2А3;
очевидно, эти три уравнения заменяются одним:
Ах 4~ А2 4" А — 0,
откуда
А3=—(А^А).	(42)
Совершенно так же, рассматривая частное решение:
=	92 = £2е~*>	=
§ 20]
ПРИВЕДЕНИЕ ВЕКОВОГО УРАВНЕНИЯ
71
соответствующее второй паре равных корней, получим
53 = — (5Х + В2).	(43)
Наконец, для частного решения:
21	q2=C2e2t, q3 = C3e2t,
получим
4(7^ =	4" ^2 4~ С3,
4{72 = С,1 4-2С'24-С'3,	(44)
4С3=(71 + С2 4~ 2С3,
или иначе
— 2С'14- С2 4- С3—0,
G-2G4- С3 = 0,	(45)
Сг+ С2-2С3=0.
Очевидно, что сумма первых частей этих уравнений тождественно равна
нулю, значит, одно из этих уравнений (скажем, третье) есть следствие пер-
вых двух, и, отбросив его, мы получим
— 2С14” С2-\-С3—0,
C*i — 2С2 4- С3 — О’,
принимая Сг произвольным, имеем
Совершенно так же будет
Z>2 —
В3 = Dp
*
Таким образом, общий интеграл системы будет
qi = Аге* 4-	+ Cre2t + D^1,
q2 == Л26* 4- B2e-t 4-	4- D^-21,
?з — (Д1 + ^2) et —	4- В2) е~* 4- С^2' 4- Вге~21,
причем А19 В19 А2, В2, (\, Dr — произвольные постоянные.
Возьмем еще пример:
Qi=5qt 4“30у2 — 48^3,
?2 = 3?i4-14g2-24g3,
q"3 = 3q± 4- 15qr2 — 25q3.
Отсюда следует:
?Г= - 2991 -150^2 + 240?3.
Таким образом, имеем
« =	91,
х" —	5?х+ 30^-48^,
xw = - 2991 - 5 (30?2 - 48?2).
(46)
(47)
(48)
(49)
(50)
72 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Ясно, что Переменные q2 и qs исключатся одновременно, и мы получим
— X
—х”
-х™
1 О
5.1
-29 '— 5
соответствующее характеристическое уравнение будет
-1	1 О
-к2	5	1
-V -29 -5
= V + 5к2 + 4 = (к2 + 1) (к2 + 4) = 0.
Взяв определитель
5-к2	30 -48
Д(к2) =
14 - к2 -24
15 -25-к2
(52)
3
положив в нем к2 — —1, имеем
1
6
Д(-1)= 3
3
30 -48
15 -24 = —6-15-24 1
15 -24
1
1 1
1 1
1 1
= 0
и так как все три строки одинаковы, то и все миноры равны нулю, т. е.
к2=—1 есть двойной корень уравнения Д (к2) = 0; зная это, доканчиваем
интегрирование, как обыкновенно.
Возьмем!в заключение систему:
д4 — 12g! + 27g2 + 135g3 — 231g4,
g" = 10gi + 15g2 + 90g3 — 154g4,
g3 = 5gx+ 9g2+ 42g3— 77g4,
?4= 5gi+ 9g3+ 45g3— 80g4,
(53)
и, положив
x = qi,
составляем по схеме § 16 коэффициенты 626 получаем таблицу:
Таблица 3
1	@11 —12 ’	а12=27	—135	а14= —231	Ьл
1	144	270	675	— 1155	— 66
2	324	405	1215	— 2079	— 135
3	1620	2430	5670	— 10395	— 675
4	—2772	—4158	— 10395	18480	1155
Значит, будет
я . =	91»
хя ==	4“ 27^2 ~Ь — 231^,
tfiv = __ 66^ - 135^2 - 675^3 + 1155^4.
§ 21]
КОЛЕБАНИЯ ПРИ ПРОСТОЯННОМ ТРЕНИИ
73
Очевидно, что, положив
27?1 + 135д2-231?4-5,
напишем эту систему так:
s =	?i,
х" = 12ух+
х^ = -66^-55,
откуда следует:					
	— X	1	0!		
	— х"	12	1	= 0.	(54)’
	-х™	-66	-5		
Значит, характеристическое уравнение будет
А(^) =	•L1 I 'to	1 12 -66	0 1 -5	=	12 —к2 1 -66-к4 -5	= к4 +5к2+6 = 0,
т. е.						
’(к* + 2)(\2 {-3)=0.
Обращаясь к основному определителю для нашёй системы, находим, что
при К2 — — 3 все миноры равны нулю, так что этот корень тройной, корень
же к2 ——2 есть простой, после чего интегрирование заканчивается, как
обыкновенно.
Эти примеры с ясностью показывают, что если по вычислению по изло-
женным правилам окажется, что уравнение
Д(к2) =	«И—к2 «12 &21 —	^22 C3i к6 С32 tki-vkik2	«13	.	. &23 * * сзз • • /аз • •	• а1к • ^2А • С3к • fkk	= 0	(55)
обращается в тождество	0 = 0,			•	
т. е. все миноры, соответствующие первому столбцу, равны нулю, то это
будет указывать, что исключение неизвестных
01, 02, • • •, Чк	(56)
может быть выполнено не из полного числа &+1 уравнений (13) стр. 77,
а из меньшего их числа, тогда вычеркиваем в этой системе уравнения, по-
следовательно начиная с нижнего, и определяем то наименьшее их число,,
при котором все переменные (56) исключаются; пишем соответствующее'
обыкновенное уравнение с неизвестной х и для него характеристическое,—
степень его будет ниже 2к, находим его корни и, обратившись к основному
определителю (55), находим кратность корней, после чего и заканчиваем
интегрирование, как показано выше.
§ 21. Колебания при постоянном трении. Во многих случаях в число
сил, действующих на элементы системы, входит и сила трения, которая,
находясь лишь в зависимости от величины нормального давления, а не от
скорости движения, сохраняет постоянную величину. Но необходимо иметь
74 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
в виду, что направление силы трения изменяется одновременно с измене-
нием скорости, и эта сила всегда направлена в сторону, противоположную
движению. Это обстоятельство заставляет, при рассмотрении колебательного
движения с трением, поступать подобно тому, как в следующем примере.
Пусть тело, масса коего т, скользит по горизонтальной плоскости CD
и находится под действием пружин АЕ и FB, концы коих А и В укреплены
неподвижно (фиг. 7). Положение равновесия тела есть то, когда центр
тяжести G тела находится посредине между А и В. Пусть мера жесткости
пружин есть к, коэффициент трения — /, требуется найти движение тела,
предполагая, что в начальный момент точка G находилась в расстоянии
xQ = а справа от среднего положения и ско-
рости телу сообщено не было.
Пусть в рассматриваемый момент центр
тяжести тела находится в расстоянии х от
середины и движется в сторону отрицателъ-
Фиг. 7.	ных х; тогда на него действуют следующие
силы: 1) натяжение пружины Q — кх, направ-
ленное в сторону отрицательных х; 2) трение F = fmg, направленное обратно
скорости движения, т. е. для первого размаха в сторону положительных х.
Таким образом, уравнение движения будет
тх" = — кхfmg,
(1)
или, полагая
к 2
— = п2
т
откуда
X" + п2х fg,
х — С± cos nt + С2 sin nt + ~ .
В начальный момент t = 0 должно быть х — а и х' = 0, что дает
a = cl + 4,
О = пС2,
и, следовательно, будет
х = (а — ^cosnt + ^-	(2)
Уравнение (1), а значит, и его интеграл (2), имеет место, лишь пека
проекция на ось х скорости движения отрицательная, а так как
х' = — п (а — sin nt,
то предполагается, что а > 2 (если бы это условие не было выполнено, то
начальное натяжение пружины было бы меньше силы трения,, и тело не
•сгвинулось бы с места, а осталось бы в покое), и будет х' < 0, пока
sin nt > 0, т. е. пока 0 < nt < я.
Когда nt сделается равным к, то скорость х’ обратится в нуль, и тело
достигнет своего крайнего размаха влево, именно, будет

— av
§ 21]
КОЛЕБАНИЯ ПРИ ПОСТОЯННОМ ТРЕНИИ
75
Если величина удовлетворяет неравенству
«1>
№
п2 ’
т« е.
а > зЦ,
п2 ’
то натяжение пружины будет больше силы трения, и тело пойдет в сто-
рону положительных х. Уравнение его движения будет
тх" = — кх — /gm, 9	(3)
или
X" + п2х = — /g,
при начальном условии: при t = tl = ~ должно быть х = — alf х' = 0.
Общий интеграл
х = Сл cos nt + С2 sin nt — .
Начальные условия дают
значит,
(4)
Уравнения (3) и (4) имеют место с момента Z = Z1 = -^- все время, пока
. 2л
скорость положительная, т. е. до момента t = —, когда
2/?	4/g
б = а2.
Если окажется, что а2 >	, то натяжение пружины превысит трение,
и тело не останется в покое, а начнет размах влево и дойдет до амплитуды
/	2/?\	/	6/?\
я3 = —а3=—Г а2—\ = — ( а— \ и т, д., и тело остановится после
г-го размаха, когда по абсолютной величине будет
la_2p-p</f.
I	/г2 | лг3
Представим это движение графически. *Сделаем для сокращения = 6,
тогда для первого размаха
х = (а — 6) cos nt + 6,
или
х — b = (а — b) cos nt9
т. е. величина х — b представляется простою синусоидой, симметрично рас-
положенной относительно прямой х = Ь.
Точно так же для второго размаха
х = (а — 36) cos nt — 6,
или иначе
х-\-Ь= (а— ЗЬ) qqs nt,
1Q ОБЫКНОВЕННЫЕ УРАВНЕНЦЯ с ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
массою и жесткостью
виднр, что х 4- b представляется простою синусоидой, симметричной относи-
тельно прямой х = — Ь, и т. д.
Проведем параллельно оси Ot прямые х = Ь и ж — 6, отложим О А - а
и строим, приняв длину ОК = ~ синусоиду АС В так, что АН = ВС^а — Ь
(фиг. 8).
Затем, начиная с В, строим сйнусоиду BDE с тем же периодом, но ам-
плитудою ВНг ~ « 36.
Затем, начав от точки Е, строим синусоиду EFG с амплитудою ЕН% —
—56, и так как точка G упадет между прямыми х~Ь и х— — 6, то,
после третьего размаха при х =
— NG, телр остановится, и дви-
жение прекратится
Подобные колебания совер-
шает, например, картушка ком-
паса при трении его топки о
шпильку. Величина 6 представ-
ляет «застой» компаса. Как
видно, эта величина обратно
пропорциональна величине А,
которая для компаса пропор-
циональна направляющей силе-
Вот почему при определении
застоя и надо уменьшать на-
правляющую силу в 3 — 5 раз,
чтобы получить во столько же
раз увеличенную величину за-
стоя для более точного его опре-
деления.
Обратим
связь0 между
пружины.
еще внимание на
периодом колеба-
ния тела, его
Период
п2 = — ,
т
Т — И
п
значит.
Пусть вес тела есть р — mg, тогда под действием нагрузки, равной
весу тела, удлинение пружины составит К = у , и, значит, предыдущая
формула может быть написана так:
" =	(5)
т. е. период колебания тела, находящегося под действием пружины, равен
периоду такого простого маятника, коего длина равна удлинению пружины
под действием нагрузки, равной весу тела.
Это свойство дает возможность весьма просто подсчитать вперед период
колебания тела, что бывает нужно при построении разного рода приборов,
служащих для записи различных явлений.
§ 22. Общие замечания об устройстве регистрирующих приборов.
Свойствами колебательного движения тела, подвешенного на пружине или
вообще так, что оно имеет определенное положение устойчивого равновесия
§ 22]'
УСТРОЙСТВО РЕГИСТРИРУЮЩИХ ПРИБОРОВ
77
и при выводе из него подвергается действию «восстановляющих» сил, поль-
зуются для устройства разного рода самопишущих приборов.
Здесь приходится встречаться с тремя главными типами приборов,
сообразно их назначению:
1)	приборами, которые не должны отзываться на действие возмущающих
сил, как, например, кренометры, сейсмографы (приборы для записи земле-
трясений), палографы (приборы для записи вибраций судов, мостов и т. п.),
мареграфы (приборы для записи приливов) й т. п.;
2)	приборами, которые предназначены именно для записи «возмуща-
ющей» силы, как-то: индикаторы, гальванометры, крешеры и т. п.;
3)	приборами, предназначенными для записи импульса силы, как,
например, баллистический гальвайометр:
Из изложенного в предыдущих параграфах видны те общие соображе-
ния, коими при устройстве таких приборов надо руководствоваться, а именно:
1)	Надо прежде всего, хотя бы приближенно, дать себе отчет о харак-
тере действия возмущающих сил: периодические они или нет, если перио-
дические,—каков период, если не периодические, — то как нарастают.
2)	Если прибор не должен отзываться на действие возмущающей силы,
то период его свободных колебаний (а если прибор имеет несколько степе-
ней свободы, то наименьший из периодов его основных колебаний) должен
быть велик по сравнению с периодом возмущающей силы.
3)	Если прибор предназначен для записи силы и, значит, желательно,
чтобы он как бы следил за нею статически, то период свободных колебаний
прибора должен быть мал по сравнению с периодом силы или с продолжи-
тельностью ее нарастания.
4)	Если прибор должен показывать импульс силы, то его период
должен быть велик по сравнению с продолжительностью действия силы.
Значение слов «велик» и «мал» видно из изложенного в предыдущих
параграфах, где даны выражения возмущений, производимых силою, при-
ложенной к данной системе. Для всякой величины отношения периодов эти
возмущения можно учесть и, сообразуясь с требуемою от показаний прибора
степенью точности, избрать такую величину этого отношения, осуществле-
ние которой на практике не вызывает слишком больших затруднений.
Пр	имер 1. Прибор для записи вибраций корабля. Поясним эти общие
соображения примером: положим, что надо записать вибрацию корабля, кото-
рая появляется, когда машина этого корабля делает 120 оборотов в минуту.
Здесь, как видно, надо устроить такой прибор, в котором подвешен-
ная часть не колебалась бы при вибрации корабля, а так как период этой
вибрации есть = сек., то подвес должен быть таков, чтобы собствен-
1
ный период был велик по сравнению с у сек. Пусть при записи мы до-
вольствуемся точностью в 10%, значит, возмущение не должно превосхо-
дить — статического, а это отношение выражается формулою (2) § 5, и при
а =0 будет
где
__ т __период свободных колебаний
~~ Т период возмущающей силы
•Значит, должно быть
I 1 I < 1
|1- q2 1^10’
g2 — 1 > 10,
78 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
или
?>/П = 3.3.
Следовательно, т —З.ЗТ = 1.7 сек.
Таким образом, период свободных колебаний подвешенного на пружине
тела должен быть не менее 1.7 сек.
Чтобы выбрать пружину, имеем соотношение
откуда
-2
х = S = 0.7m,
т. е. удлинение пружины под действием груза, на ней висящего, должно
составлять не менее 0,7 м.
Таким образом, получаем следующую простейшую схему прибора:
в точке А палубы закреплен конец пружины, на другом конце которой
висит груз Р. Пружина подобрана
1	______А	так, что ее удлинение X под дейст-
вием груза Р составляет не менее
0.7 м. Штифт, укрепленный на грузе
Р, чертит его колебания на барабане
В (фиг. 9).
Фиг. 9.
Фиг. 10.
Барабан В, точка подвеса. А и все прочие части корабля совершают
периодические вертикальные колебания, период коих у сек., грузу же Р
эти колебания точки его подвеса А передаются пружиною уменьшенными
в 2-— , т. е. приблизительно в 10 раз, и, значит, груз Р можно считать
неподвижным в пространстве.
Чтобы получить более компактный переносный прибор, Шлик поступил
таким образом: он закрепил пружину не непосредственно за груз Р, а за
точку В рычага, вращающегося около точки О (фиг. 10), и этим увеличил
период колебаний груза при той же жесткости пружины.
В самом деле, пусть ОВ = а, ОР = 1, положим, что рычаг наклонен
на малый угол ср от прямого своего положения равновесия, тогда появится
добавочная сила F = ka'^, приложенная в точке В и направленная вверх,
и уравнение движения груза, пренебрегая массою рычага, будет
1^" = — ка2^,
где I есть момент инерции груза относительно точки О. Приближенно
Р
можно принять I — —Ь2, и наше уравнение движения есть
-у + ка2^ = 0,
§ 22]
УСТРОЙСТВО РЕГИСТРИРУЮЩИХ ПРИБОРОВ
2?
или
ср" + п2ср = О,
причем
kg
Р
2 а*
р
где /. = т>
т. е. период увеличивается в отношении
с тем, что было бы при непосредственной подвеске груза
Пример 2. Индикатор Уатта, Как другой при-
мер, возьмем индикатор паровой машины. В идеально
простом виде он сводится к цилиндру С, в котором
ходит притертый поршень Р, опирающийся на пру-
жину, этот поршень воспринимает давление пара и
сжимает пружину; смещения поршня относительно ци-
линдра автоматически записываются, величина их
пропорциональна сжатию пружины и должна слу-
жить мерою действовавшего в каждый момент на
поршень давления (фиг. 11).
Пусть площадь поршня есть s, действующее на
него в момент t давление р = f (/), значит, усилие,
действующее на поршень, есть
F=--sp = sffi).
Смещение поршня пусть есть х, жесткость пру-
жины — к, тогда со стороны пружины действует усилие
Т=—кх;
Ъ
— сравнительно
обозначая через т массу поршня и пренебрегая массою прочих движущихся
частей прибора и массою самой пружины, получим уравнение движения:
тх" — — kx + sf(t),
или
/(Z),
где
2 к
п2 = — ,
т
s sn2
а так как — = у, то наше уравнение будет
X" + П2Х = -у / (Z).
Статическое сжатие было бы xQ = j-f (О == af (О» и> значит, наше урав-
нение можно писать так:
>	х"-^n2x = n2af (I).
(1)
На основании сказанного в § 8, формула (5), общий интеграл этого
уравнения есть
t
х — af(t)— а, /' (£) cos n(t — l) di,	(2)
о
и желательно, чтобы смещение# было как можно ближе к af (t), т. е. чтобы
второй член ‘формулы (2), представляющий погрешность прибора, был воз-
можно меньше.
80 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
Из сказанного в § 8 втддно, что для этого надо, чтобы период свобод-
ных колебаний поршня на пружине его был мал по сравнению с продол-
жительностью нарастания силы.
Так, например, положим, ч:о машина делает 240 оборотов в минуту
1
л что давление нарастает на протяжении — доли хода поршня ее.
Если длина хода поршня машины есть L, то смещению его на
соответствует угол поворота мотыля а, определяемый приближенным равен-
ством
4(1-cosa) = 25L’
или
• о 1	1
siir — a — — .
2	10’
откуда
a—36°,
и, значит, продолжительность нарастания давления составляет
60	36	1
480 ° 180 “40 СеК*
и, следовательно, период свободных колебаний поршня индикатора на пру-
I
жине его должен быть мал по сравнению с сек.
Положим, что желательно, чтобы погрешность не превышала 2%,
тогда т определится из неравенства
[см. формулу (9) § 8]. За величину /' (?) можно принять среднюю быстроту
нарастания давления, т. е.
40/(0,
40
таким образом будет
4х40/()<1/О,
*откуда
т 1^осек‘
Сообразно этому периоду можно найти жесткость пружины, задавшись
. весом поршня.
Пусть, например, вес поршня Р—50 а = 0.05 /га; из равенства
* = 2*1/2
У s
• имеем
"'2 •	1	1	1
= 1000 • 1000 ’ 4^9£0° ЖЛг = 40д0
Положим, что площадь поршня $ = 3 кв. см\ тогда при давлении в 1 кг
на квадратный сантиметр, полное давление на поршень было бы 3000 г,
и, значит, сжатие пружины
з°оо . I _ 2. мм
50	4000	66 М ’
§ 22]
УСТРОЙСТВО РЕГИСТРИРУЮЩИХ ПРИБОРОВ
81
Ясно, что с такою жесткою пружиною индикатор был бы неприменим,
и, чтобы иметь практически применимый прибор, надо иметь более мягкую
пружину, а такой пружине соответствует больший период т, а большему
периоду — и большая погрешность, которую и найдем по приведенным в § 8
общим формулам.
В этом очерке мы пренебрегали массою пружины, но, как видно, она
сравнима с массою поршня, почему мы еще вернемся к вопросу о колеба-
ниях индикатора, принимая в расчет массу пружины.
Пример 3. Прибор Фрама. Как третий пример, возьмем схему при-
способления Фрама для уменьшения вибраций корабля, применимую и во
многих других случаях.
Положим, что имеем массу М, подвешенную к неподвижной точке А
на упругой связи. К массе М подвешена на пружине
сравнению с М, и прикреплен цилиндр катаракта, пор-
шень которого прикреплен к массе т (фиг. 12).
Предполагая катаракт устроенным так, что сопро-
тивление его на поршень пропорционально первой
степени относительной скорости цилиндра и поршня,
требуется исследовать вынужденные колебания си-
стемы, когда возмущающая сила действует на массу М
и выражается формулою. Н sin pt.
Пусть О есть положение массы М при равно-
весии и покое всей системы, Ог — положение массы
т относительно Л/, когда натяжение пружины, под-
держивающей т, равно весу ее, так что тогда длина
этой пружины есть 6.
Положим, что в момент t ОМ = х1,О1т = х2; тогда
на массу М действуют следующие силы:
1)	вес ее = P —вниз;
2)	натяжение нижней пружины Т2— вниз;
3)	натяжение верхней пружины Т1 — вверх;
4)	реакция жидкости, действующая на дно цилиндра катаракта R^
5)	возмущающая сила F=Hsinpt\
6)	сопротивление среды, пропорциональное скорости х{ и равное —Nxi.
На массу m действует:
1)	ее вес р, направленный вниз;
2)	натяжение пружины Т2, направленное вверх;
3)	реакция на поршень катаракта Rr.
Значит, уравнения движения будут:
для массы М\
Мх\ — Mg--T1 + T2 + R1-\ Hsinpt — Nx'v
для массы тп ускорение есть (хг + х2 + 6)" = х" + х2 и, значит, уравне-
ние движения:
m + х") ^mg — T2 — R±.
Надо теперь выразить силы Т19 Т2, R± в функции и х2.
Сила Тi равнялась Р + р, когда точка М была в О\ следовательно,
если жесткость верхней пружины есть к19 то
Т1 == Р + Р + к^х-^
Сила Т2 равнялась р, когда Мт — Ь, в рассматриваемом же положении
будет Т2— р + где /<2 есть жесткость нижней пружины.
Сила Rt по условию пропорциональна скорости поршня в отношении
цилиндра, т. е. ж', причем если х'2 возрастает, то поршень испытывает
6 А. Н. Крылов
82 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
давление снизу вверх, дно же цилиндра — сверху вниз. Итак,
Д1= — hx2.
Таким образом, уравнения движения будут
Мх\ 4 Nx\ + kiX± — к2х2 — hx2 = Н sin pt,
т (х'[ + х'£) + к2х2 + hx2 = О,
или, разделив первое уравнение на М, второе на т и полагая
2V г» Л"! a МЪ	к‘2,	9 h Г)	Н л
--- — 2g,, ~ — тг2 -^г=а, — — п?, —— 2g2 и -,’Г = п12а,
М 61 М 1 М	т 2 т 62 М 1
мы получим уравнения движения в таком виде:
х'[ 4-	+ ri^X! — 2fig2x2 — an|^2 — an2 sin pt,
+ ^2 + 2&2^2 + nlx2 = 0.
Если бы массы m не было, то масса М совершала бы колебания, опре-
деляемые уравнением
5" + 2g+ тг2; = an2 sin pt,
и тогда амплитуда вынужденных колебаний установилась бы, согласно фор-
муле 4 § 3, такая:
ЧП - ,---------------,
/ ("1 —• р2)2 + 4^2
и при р близком к пх эта амплитуда стала бы наибольшей, достигая вели-
чины
anx _ л
2/1	’
Величина g± мала по сравнению с п1, и амплитуда А при синхронизме
велика по сравнению со статическою амплитудою а.
Посмотрим теперь, каковы же будут вынужденные колебания, когда
к массе М присоединен «успокоитель», т. е. масса т с катарактом.
Ищем частное решение уравнений (3) под видом:
хг = В sin pt + С cos pt,
x2 — D sin pt-Y E cos pt,
тогда получим для определения неизвестных В, С, D и Е уравнения
(п| — р2) В — ZgypC + 2zg2pE — an|Z> = anj,
ZgipB + (Pi—P2)C —	—	2a.g2pD = 0,
2g2 pE + (n2-^p2)D^0,
-P2C + (n22-p2)E	4	2g2pD = 0.
Чтобы выяснить без длинных выкладок сущность дела, возьмем тот случай,
когда возмущающая сила синхронна с колебанием массы М, т. е. п^ — р,
и положим, что мы настроили и успокоитель так, что щ-п^-р, тогда
наши уравнения будут
— 2g гС -н 2&g2 Е — &pD =ар,
^giB —ярЕ — 2g2aD = 0,	ф
рВ +2g2E	=0,	1 '
— рС	+ 2g2B = 0.
§ 23]	ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ ВРАЩАЮЩЕГОСЯ ВАЛА	83
Определив из последних двух уравнений D и Е и подставляя их вели-
чины в первые два, получаем
лрВ +	С = — ар,
(2g1 + g)B-aJPC = 0,
откуда находим, что амплитуда вынужденных колебаний массы М в этом
случае будет
v ------------------- 1 ---------
2s,y>4-|D2+<
и, значит,
ува+с2_1
А ~ 1/<1 J- Y ।	'
Успокоителю можно дозволять гораздо большие амплитуды колебаний,
нежели главной массе М. Так, из последних двух уравнений (*) видно, что
/z>2 + #2 р
]/ £2 _|_ ^2 ~2g3
и, например, если взять a = —— 50 и —- = 100, то будет
г	1000 ’	2g2	2gx
т. е. успокоитель уменьшит амплитуду колебаний массы М в 6 раз, хотя
его собственная масса составит всего 77— от массы М. но зато амплиту-
1000	J
да его колебаний будет в 50 раз	«
больше амплитуды колебаний	п
массы М.	/	_________
Подобного рода приспособив- (
ние было применено Фрамом для	S
успокоения вибрации судов: на
корме парохода, где колебания	 ....... *	-_
наибольшие, был поставлен при- - - ----- --- — ------- —— —
бор, подобный большому пало-	—	—
графу, т. е. состоящий из рычага	Фиг. 13.
ОР (фиг. 13), вращающегося около
точки О, с тяжелым грузом Р на конце, рычаг удерживается пружиною
S и снабжен катарактом С.
В данном случае упругие колебания (вибрации) корабля аналогичны
колебаниям массы М на ее подвесе, прибор и успокаивает их, энергия же,
происходящая от возмущающей силы (для корабля силы инерции неуравно-
вешенных частей машины), поглощается катарактом и «рассеивается», пре-
вращаясь в теплоту.
§ 23. Поперечные колебания вращающегося вала. Рассмотрим еще»
как пример особого вида резонанса, поперечные колебания упругого вала-
Опыт показывает, что на сравнительно тонких, длинных и быстро вра-
щающихся валах, как, например, передаточные валики от электромоторов;
к водоотливным турбинам на некоторых судах, замечается такое явление:
если постепенно увеличивать скорость вращения вала <о, то при некотором
значении o) = oj1 вал не сохраняет прямолинейной формы и начинает бить;
6*
84 ОБЫКНОВЕННЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. I
если скорость о> еще увеличить, то биение прекращается, но при некоторой
скорости о) = о)2 начинается вновь, и т. д.
Требуется объяснить это явление и рассчитать по заданным размерам
вала «критические» скорости вращения о>х, ф2, и т. д.
Мы ограничимся простейшим случаем, чтобы показать сущность дела.
Положим, что имеется цилиндрический вал АВ, вращающийся в шаровых
подшипниках, так что концы его А и В можно считать подпертыми (фиг. 14),
и рассмотрим, при каких условиях вал может вращаться равномерно, приняв
и сохраняя не прямолинейную, а изогнутую форму своего динамического
Предполагая эту форму плоской, обозначим через z ординату CD, соот-
ветствующую абсциссе х точки D той кривой, в которую первоначально
прямая, ось вала АВ изогнулась; пусть р есть вес одной погонной единицы
длины вала, тогда, при угловой скорости вращения <о, на элемент
DD1^CC1 = dx действует, вследствие центробежной силы, нагрузка, равная
&2zdx, следовательно, вал может принять, и сохранять такую форму дина-
мического равновесия, которая соответствует этой нагрузке, т. е. по -у
на погрнную ’^единицу длины в каждой точке вала.
Отсюда "следует, что форма равновесия определится из уравнения
EI^,=P^	(1)
dx* g ’	’
где E — модуль упругости материала вала и I — момент инерции площади
его сечения относительно диаметра ее.
Это уравнение вытекает из известного дифференциального уравнения,
выражающего условие равновесия изогнутого однородною стержня при дей-
ствии заданной нагрузки F (х}, именно:
El^=F(x\
dx* v f ’
в нашем же случае
Для полного определения z надо к уравнению (1) присовокупить гра-
ничные условия, выражающие условия закрепления концов вала, которые
в нашем случае будут:
Для конца А, соответствующего абсциссе я = 0, должно быть
= “ и (£-)„. = 0-	(2)
< . Точно так же для конца В, соответствующего абсциссе х = 1, должно
быть
W.-.-0 и (£О„, = 0.	(2')
ибо оба конца предположены подпертыми.
§ 23]
ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ ВРАЩАЮЩЕГОСЯ ВАЛА
85
Сделаем
gEI
тогда уравнение (1) напишется так:
d*z
dx*
a4z = 0.
(!')
Его общий интеграл есть
z = Аелх + Ве~~°-Х + С cos ах + D sin ах,
примем постоянные произвольные А, В, С, D определяются по условиям (2)
и (2'), именно:
А + В + С = 0,
а + в-с = о9
Аел1 + Ве~^1 + С cos al + D sin al — 0,
Ae*1 + Be~°l — C cos al — D sin al — 0.
Из этих уравнений следует, что если определитель системы не равен нулю,
то A — B = C = D = 0, т. е. тогда z = 0, и вал будет сохранять прямолиней-
ную форму. Если же величина угловой скорости со такова, что при соот-
ветствующем ему значении а сказанный определитель есть нуль, то выше-
приведенной системе могут удовлет орять и значения постоянных, отлич-
ные от нуля, а тогда z не будет равно нулю, и вал будет бить.
В нашем случае вышеприведенные уравнения дают
А = 0,	5 = 0, С = 0,
5 sin al = 0,
т. е. определитель системы есть sin а/, и, значит, «критические» значения
доставляются равенством
sin al = 0,
откуда
чему соответствует
л
2п
I
Это и суть значения «критических» скоростей вращения, при коих вал
теряет «устойчивость» своей прямолинейной формы.
Мы не будем разбирать более сложных случаев, например, когда на
вал насажены один или несколько шкивов, отсылая к статье проф. Dunker-
ley, напечатанной в «Philosophical Transactions» за 1894 г., сер. А, а также
к статье Dr. Chree в «Philosophical Magazine» (май 1904 г.), где этот вопрос
разобран подробно и где даются приближенные способы его решения, когда
точное решение чрезмерно сложно.
ГЛАВА II
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
ВЫСШИХ ПОРЯДКОВ И с постоянными
КОЭФФИЦИЕНТАМИ
Эта глава составлена без всяких перемен по лекциям, которые прочел
покойный А. Н. Коркин некоторым из своих учеников в 1891 г. совершенно
частным образом на квартире проф. Садовского.
Эти лекции были мною тогда же тщательно записаны и редактированы,
и я думаю, что в этих страницах ученики Александра Николаевича узнают
ясность и сжатость изложения своего незабвенного учителя.
§ 24. Метод Даламбера и Эйлера интегрирования уравнений, где во
всех членах порядок один и тот же. Многие вопросы математической
физики приводят к линейным уравнениям с частными производными и с
постоянными коэффициентами; поэтому изложение способов их интегриро-
вания составляет как бы введение к курсу математической физики.
Даламбер в 1747 г. дал общий интеграл уравнения колебания струны
Ж =	(*)
dt2 дх2	' 7
Если взять переменные
£ = х — at,
~f] = x + at,
то уравнение (1) примет вид
откуда заключаем, в силу того,
д2и _	__
д%дч\ с?
что ~ есть функция только переменной тр Полагая
01),
имеем
М=?(7)) + <!»($),
так что
и = <р (x-\-at) + <J> (ж— at),	(2)
-^==0.
ЧТО
где ср и ф — произвольные функции.
Эйлер обобщил соображения Даламбера на уравнения высших порядков.
Возьмем уравнение линейное с постоянными коэффициентами, во всех членах
которого производные одного>и того же порядка п. Общий вид такого урав-
нения будет, при переменных независимых х и у,
дпи , дпи	дпи	/ № _
а дхп + ° дхп-'ду + С	+	1 дуп
(3)
так что
§ 241
МЕТОД ДАЛАМБЕРА И ЭЙЛЕРА
87
Эйлер поступает так: он ищет и под видом
где к не зависит ни от х, ни от у.
О ЭПи
Взяв n , получим
дхУдуп~д ’ J
Сделав g = n, п — 1, п — 2,...,1, 0, выведем все входящие в уравнение (3)
производные; будем иметь
(а + Ьк 4- ск2 + ... + Zkn) «р<п> (х + ку) = 0.	(4)
Чтобы удовлетворить этому уравнению, делаем
а + Ь\ + ск2 + ... + /к" = 0
и решаем это алгебраическое уравнение относительно к. Пу ть корни его
суть
^2, ^3» * • ’ >
обыкновенно они бывают неравные. Подставив их в нашу формулу, имеем
w = (я + б^у),
И = ?2
и = 7n (% + апу);
все это будут решения уравнения (3).
Сумма решений всякого линейного однородного уравнения есть также
решение этого уравнения, и.мы можем написать решение нашего уравне-
ния с п произвольными функциями:
^ = ?i(^+«iy) + ?2(^ + «2?/) + •• • + ъЛх+апУ)-	(5)
Это и есть общий интеграл уравнения (3).
Если бы два корня были равны, например, аг — то первые два члена
соединились бы в один. В этом случае вместо первых двух членов можно
взять такие:
?i (я + «1У) + УЪ (я + «ij/);
при трех равных корнях
<Р1 (х +«!?/) + У?2 (я + а>1У) + У2?з (я + «1У)>
и т. д.
После Даламбера и Эйлера над этим вопросом работал Лаплас. Его
исследования1) помещены в «Memoires de I’Academie» за 1773 г. и последу-
ющие; так, в 1779 г. он интегрирует линейные уравнения второго порядка
при помощи определенных интегралов, но не в самом общем виде.
Фурье дал теорему, доставляющую возможность решать вопрос о линей-
ных уравнениях в самом общем виде. Первая его работа была напечатана
в 1811 г. в томах IV и V «Annales de Physique et de Chimie», затем
появился ряд других его работ, которые все сведены в одно целое — «Theorie
analytique de la chaleur», изданное в 1822 г.
Пуассон занимался также этим вопросом; его работы помещены в
«Journal de FEcole polytechnique» в 1823 г. В его же «Theorie mathematique
х) Эти исследования вошли в тт. IX и X полного собрания сочинений Лапласа,
изданные в 1890 и 1893 гг.
88 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ	[Гл. II
de la chaleur», изданной в 1835 г., встречаются уравнения не только
с постоянными, но и с переменными коэффициентами.
§ 25. Общий вид линейного уравнения с постоянными коэффициен-
тами и его самого общего решения. Самый общий вид уравнения линей-
ного с частными производными высших порядков и с постоянными коэффи-
циентами есть такой:
~ * dA+M-v+...+'с
—т = /(#, у, я, ..., t)-	(6)
" dxkdy^dzy..,dtx ' v	V 7
Относительно этого уравнения можно высказать такие теоремы:
1)	Если известно некоторое частное решение, например w, уравнения
(6), так что
^Л+ji+v+...+t w
то, сделав u — v-[-w, получим для v такое же уравнение, как и (6), только
без последнего члена.
Будем поэтому говорить пока об уравнениях без последнего члена,
чтобы показать, почему тут приходится прибегать к теореме Фурье. Но
сперва припомним еще две теоремы относительно линейных уравнений без
последнего члена.
2)	Всякое решение линейного уравнения без последнего члена можно
умножить на постоянное произвольное, — произведение будет также
решением.
3)	Сумма нескольких решений уравнения без последнего члена есть
также решение его.
Возьмем уравнение без последнего члена;
dxkdy^dz\..dt?
Припомним способ интегрирования обыкновенных линейных уравнений
с постоянными коэффициентами, будем поступать и для уравнения (7)
подобным же образом.
Для обыкновенного уравнения, например
У[п> +	. •.+ рпу = О,
мы ищем какое-нибудь решение, полагая у = еЛХ\ тогда имеем
(ап + ^п-1 + ... +/?п) = 0
и выбираем а так, чтобы было
ап +	. + рп = 0.
Подобным же образом для уравнения (7) полагаем
н =	(8)
где под а, р, у» ..., «> разумеем произвольные постоянные. Заметив, что
каждое дифференцирование по букве х вводит множитель а, так что диф-
ференцирование к раз по х введет множитель аА, дифференцирование по у
вводит множитель р и т. д., таким образом будет
пЛ+и + v+... + T ..	Л	л
____________- =аЛ В** Yv (|)Tea«+₽y+Yz+...+u)t<
dxi-dyv-dz't...df- г I • • •
Подставив в уравнение (7) и взяв показательную функцию за знак
суммы, получим
еах+₽у+...+ш( 2аал уЛ. .аЛ = 0.
§ 25]
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
89
Сократив на показательную функцию, получим между а, р, . ..,ф такое
алгебраическое уравнение:
2ааА yv.. .сот=:0.	(9)
Понятно, что одна зависимость между переменными й, р, у, ... , ш
дозволяет принять одну из них, например за неизвестную, а остальные
оставить произвольными. Если высшая степень ф есть р, то это уравнение
дает р корней:
“1, о>2, ... , V
все эти корни будут функции от й, р, у, ... Предполагая в выражении (8) <о
равным (Oj, затем <о2, ..., а)р, мы получим р решений; умножив каждое
пз них на постоянное произвольное и сложив все решения, будем иметь
и = 24eaa?+₽»+rz+...+<0it	_|_ . . . -J_	. (ДО)
В этом решении величины &, р, у, ..., А, В, К суть совершенно
произвольные, но независимые от х, у, z, для каждой из них мы
можем вообразить ряд значений, который она проходит; все эти значения
можно комбинировать между собой, причем для каждой комбинации по-
лучится член такого же вида, как написанный в формуле (10), с тою
только разницей, что й, р, у, ..., А, В, ... , К будут иметь определенные
частные значения, им приписанные.
Сложив все таким образом полученные члены, мы найдем решение
уравнения (7) в таком виде:
и = +u>lf + +Ш2* + ... + (11)
Если число членов в каждой сумме конечное, то формула (И) дает
совершенно определенную величину для и, удовлетворяющую уравнению (7).
То же самое будет, если каждая из сумм состоит из бесконечного
числа членов, но остается конечною и определенною.
Можно предположить, что а, р, ..., у, ..., Л, В, ..., К изменяются
непрерывно и что ряд значений для каждой из этих переменных составляют
все величины, заключенные между какими-нибудь определенными границами.
В этом случае а, р, у, ... надо принять за переменные, независимые друг
от друга; что касается А, В
функциями от а, р,
не зависящих от х, у,
При этом суммы
у,	С, ...
Таким образом, в
., К, то их можно считать произвольными
у, ... и еще от некоторых величин 5, 4, С,...,
z, . .., t и, следовательно, таких же как а, р, у, ...
(11) заменяются интегралами по переменным а, р,
предположении, что наши произвольные постоянные
а, р, у, ..., 5,
изменяются непрерывно, формулу (11) можно заменить такою:
и =	ср (а, р, у, ..., В, т),	••.) da dp dy.. .d; dr^dl
... 4-	ф (#, p, y, . •., 5,4, C, • ••) d& dp dy.. .d? ...dvjd^ (12)
Кратность интегралов равна числу переменных
а, р, у, ..., 5, 4, С, ...,
90
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
[Гл. II
т. е. удвоенному числу переменных, входящих в уравнение (7), кроме пере-
менной t\ что же касается их пределов, которые считаются, конечно,
не зависящими от х, у, ..., t, то они обусловлены только тем, чтобы
кратные интегралы оставались конечными и определенными; тогда фор-
мула (12) дает решение уравнения (7) с р произвольными функциями.
Изложенное в этих параграфах и заключает самое общее решение
линейных уравнений с частными производными и с постоянными коэф-
фициентами.
Подстановка	принадлежит Эйлеру.
§ 26. Пример—уравнение распространения тепла. Прежде чем войти
в дальнейшие подробности, поясним изложенную теорию примером.
Возьмем уравнение распространения тепла в неограниченной среде, где
предполагаются теплопроводность и теплоемкость постоянными.
Это уравнение такое:
ди о।	। д2и\	/л\
+ (1)
коэффициент а зависит от теплопроводности и теплоемкости и предполагает-
ся постоянным; и есть тогда температура в точке (х, у, z) в момент t.
Подставив вместо и величину
и = Ae^x+^y+yz+liyt,
получим
(а2
по сокращении будет
со = а2 (а2 + р2 + у2),
что дает такое решение:
ц — 21важ+£У’’Ь,12+а2(а2 + £2 + Т2У.
Заметим, что пока а, £, у действительные, до тех пор наше решение
не годится, ибо тогда црп возрастании t неопределенно возрастает и и, что
не соответствует действительности,
Поэтому делаем
а = 'ку~1,	р =	y = v}/"=4,
тогда будет
U == 24e(Aa;+Iiy + vz) К-1 е-а2(Л2 + Н2+ V2)*.
Величину А возьмем таким образом:
А =  1 з- е-яеК-i e-wV"-i
и, подставив в формулу (12), берем шестикратный интеграл.
Получим
4-00
и = _1_	e~a2?2t еА(ж-пГ=1	ехг-г,)/=1х
X ? (5, V), С) сГк dp dv dl drt\dZ, (2)
где
P2 = k2 4- p,2 -f- v2.
Интегралы по переменным k, ji, v можно взять на самом деле, так как
е~/<2у2 cos Zu rfi; ~е 12 и e~x2dx — |/*тг,
— оо	—со
§ 26]	ПРИМЕР—УРАВНЕНИЯ РАСПРОСТРАНЕНИЯ ТЕПЛА	91
и уравнение (2) можно написать так:
И= -Ь 5 5 И	е~а2Л2‘d), J	e~a2^t (fax
—CD —CO	—00
+ 0°
X eX*-OK-i e-a2y2t fly j	q	(3)
—co
Замечая, что в первом интеграле
ея(о;-0 К-1 — COS X (х — £) + |/ — 1 sin X (х —5)
и при интегрировании по X величина х — 5 есть постоянная, получим
е-а2/л2 еЛ(ж-е)К“1йХ = Га2™ cos \	ц,
—со	—ср
___+JO	/--	(X-z)2	G-*)2
+ V-1 { e~a2t*2 sink(«-^)dk = 2JL е iaSt =J-Le ia2t ,
K '	4	’ аУt	aVt
—co
ибо второй интеграл равен нулю, как интеграл от нечетной функции.
Во втором интеграле, входящем в выражение и, вместо разности ж —$
будет стоять у — ?), в третьем  z — С. Произведение этих трех интегралов
будет
fl/—\3	(с-Я)2	(Tj-y)2	V-Z)2
М7 е 4a2t е 4a2t е 4a2f
а* (/ г)3
Подставив в формулу (3), получим
+°°	(£ —ft)2 (т,—у)2 (£—z)2
/П8ИЬ ia2t е 4a t е 4a%(UQW:-
8 (/*) а3(/*) J • J
—оо
Это и есть решение уравнения (1). Его легко преобразовать в лапла-
совское, для чего надо положить
$ — х = 2d\Tixx,
т] — y = 2ayrty1,
ч — z = 2aj/zzx;
пределы будут попрежнему + оо и — оо, ибо > 0. Тогда будет
+ОО
и =-7-Т=\з Ц \ e-<-xi+vi+*b <? (х + 2a]/Fx1( у + 2a\/rTy1, z +
\ V j ”
—оо
+ 2a)/rFz1) dx± dyx dzv (4)
Это и есть лапласов интеграл уравнения (1).
Если бы и не содержало переменной то уравнение (1) было бы
dt а \дх^^ду^)	k )
и тогда
+оо
и = ~	e“(xi+^><p (х+ 2a]/rtxlf у+ 20^^^ dxrdyv	(4')
— 00
92
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
|Тл. II
Наконец, если бы уравнение было
ди 9 д2и
~дГ==а д^’
4-оо
w ——\ е~х*у (х + 2а dxr.
у л
—со
(4")
При t = 0 формула (4) дает такую величину:

4-оо	4-со	4-со
? (я, у> z) e~xi dx! dy1 е~т* dzx
—со	—со	—со
и будет
Но = т(я, У> Z).
Таким образом, формула (4) дает решение, обращающееся при 1 = 0
в произвольную функцию <р(я, yf z).
Это есть начальное тепловое состояние пространства.
§ 27.	Случай равных корней характеристического уравнения. Мы
предполагали корни уравнения (9) неравными между собою. Это уравнение
есть следующее:
2	... (от == 0,	(9)
где X, и, ..., т — целые и положительные числа.
Величина еаас+₽»+—или, что то же, еах+№+'-- • eWit служит решением
обыкновенного линейного уравнения с постоянными коэффициентами
(*)
где Т есть неизвестная функция. Поэтому, не исследуя равных корней
уравнения (9), мы можем сказать, что когда есть Л-кратный корень
уравнения (9), то показательная ему соответствующая, может множиться
на величины
Z, Z2, .. ., г*-1,
и произведения будут также решениями уравнения (*).
Таким образом, для ^-кратного корня можем написать такие к ре-
шений:
gax4-₽y4-...	garc4-Py4-...	,,,	garc4-§y4-...	1
тогда в формуле (11) первые к сумм будут
Подобным образом в формуле (12) первые к интегралов заменятся дру-
гими, где под интегральными знаками будут множители
te^, t2e^f, ..., tk~1e^t
и в каждом интеграле произвольная функция будет особенная.
§ 28.	Обобщение формул § 25. Формулы (11) и (12) можно написать
в более общем виде: обозначим через
Т2, ..., Тp-lf Тр
какие угодно р частных решений уравнения (*), независимых между собою,
§ 29]
НАЧАЛЬНЫЕ УСЛОВИЯ
93
(«> ₽> ..с, г), ...) da d$ ... dsdy ... + ...
т. е. таких, между которыми нет линейных связей; тогда мы можем их
подставить в формулах (11) и (12) вместо решений
Что касается величин T19T2t ...9Тр9 то все они выводятся из общей
величины
7=	+ С2е^ + о.. + Сре<*Р*9	(**)
где С19 С2, .. .9 Ср — постоянные произвольные. Величины Т19 Г2, .... Тр
получаются при частных значениях этих постоянных.
Понятно, что формула (**) относится к случаю неравных корней;
нетрудно ее распространить и на случай равных. Тогда формулы (11) и (12)
можно написать так:
к =	^A2eix^v+-T2 + ... + S Ape*x+to+-Tp (13)
и
e«x+fa+...
• • • +	еа®+₽»+— Трур (а, р, ..., 5, т], ...) da. d$ ... dldy ... (14)
§ 29. Начальные условия и нахождение решения, им удовлетворяю-
щего. До сих пор мы решили задачу только о том, чтобы и удовлетворяло
заданному уравнению (7). Но при интегрировании уравнений существуют
две задачи:
1) удовлетворить заданному уравнению,
2) найти произвольные величины, входящие в общее выражение неиз-
вестной по заданным наперед условиям.
Для уравнения (7) можно поставить р условий по наибольшему чис-
лу дифференцирований относительно Z, а именно, можно требовать, чтобы
при t — О
и обращалось в (х, у, z, ...),
ди	. /	\
—	»	» /2(ж, у, Z, ...),
д2и	/	\
•7ТГ	»	» /з(«» У> 2,
Ur	t t	V
-^=F	»	» fp(x, y, z, ...),
где /х, /2, ..., fp — заданные функции от переменных х9 у9 z9 ..., не содер-
жащие буквы t. Решение этого вопроса выполняется при помощи так назы-
ваемой теоремы Фурье.
Но сначала мы видоизменим формулу (14), полагая в ней
?1(«, р, ...Д, т), С,	. ф1 (?, у, с, ...),
<Рр (а, «...., т), С) = е-»еК-1 . е-^Г-1 . е-тсГ-1 ... фр (5, т;, С, ...),
и, кроме того, переменные а, р, у, ... в показательных елх9 е&9 ... изменим
на а ]/" — 1, 3	— 1, ... Затем интегрирование по всем переменным возьмем
от — оо до + оо, число же переменных 5, С, ... возьмем равным п — числу
переменных х9 у9 z9 ..., а также и а, р, у, ...
94
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
[Гл. П
Таким образом, получим
+ оо
и —	... Т 1ег(х-^Уг-'1 e₽(9-’j)Kzi х
—СО
X	Г; ...) dadpdy... d’i di\ dZ ... + ...
4-oQ
• • • + 5 \ \ • • • \ Трв^-^У-^ е^У-^У-^ У
X е^-'УУ-1 ... фр(£, 7), С, • • .)<Zarf?d/ ... didy d",- (15)
Теперь уравнение (9) примет вид
S «(а/^Т)л0/^1)Ч7/^1Г...«^ = 0,	(9')
а уравнение (*) —вид
§1=о-	(*)
Теорему Фурье можно было бы вывести, проводя аналогию между
уравнениями с частными производными и уравнениями обыкновенными
линейными и с постоянными коэффициентами. В самом деле, Лагранж
в «Mecanique analytique» рассматривает движение п точек, связанных негиб-
кими и нерастяжимыми стержнями, и приходит к системе п совокупных
уравнений с постоянными коэффициентами. Удовлетворить этим уравнениям
оказалось весьма нетрудно, но определить постоянные произвольные по началь-
ным условиям составляло некоторую трудность. Лагранж дал особенную
формулу интерполирования, от которой, при бесконечно большом и, после
перехода к пределу получается один из рядов Фурье, именно — ряд по сину-
сам кратных дуг. От рядов Фурье можно перейти и к интегралу Фурье.
Таким образом, ясно, что и второй вопрос может также быть выведен
из аналогии с обыкновенными уравнениями.
Короче будет, однако, оставив аналогию, привести прямо теорему Фурье.
§ 30. Формулы Фурье. В томе III «Annales de Physique et de Ghimie»
Фурье дал две формулы, из которых следует его теорема и которые заключа-
ются в последней.
Пусть будет (ж)—четная функция х и ф (х) — нечетная функция, опре-
деленные на промежутке (—оо, + со); тогда формулы Фурье следующие:
СО 4-00
(я) = -А- da cos ах cos а? (?) di,
О —оо
оо 4-оо
ф (х) = А- da \ sin az sin а?ф (?) di-
О	—оо
Вместе с этими возьмем очевидные формулы:
оо 4-оо
ICC
— \ da \ cos ах cos а? ф (?) di = О
О	—оо
оо 4-оо
1 с л
— da у sin ах sin а? (?) di = 0.
О —оо
§ 311
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ФУРЬЕ
95
Сложив две формулы Фурье с этими двумя уравнениями и между собою,
получим
ср (ж) + ф (ж) = X da cos а (ж — с) [<р(?) + ф(£)] di.
0	— оо
Если функция j(x) состоит из суммы четной функции с нечетною, то,
полагая
/(ж) = <р(ж) + ф(ж),
получим теорему Фуръе в таком виде:
/(a;) = ^-^da cosa(#-—£)/(£) cR==^ da \ cos a (х — с) / (с) di.
О	—оо	—оо	—оо
§ 31. Доказательство теоремы Фурье. Доказательство теоремы Фурье
дал Лежен-Дирихле в томе IV журнала Crelle, но потом он это доказатель-
ство переделал и дал другое в «Doves Repertorium der Physik». В томе XVII
журнала Crelle Дирихле прилагает тот же принцип к доказательству сходи-
мости рядов, расположенных по функциям Лапласа, т. е. рядов, встречаю-
щихся в теории приливов и отливов и почти во всех задачах математиче-
ской физики, относящихся к случаю сферы.
Ввиду важности теоремы Фурье для всего дальнейшего изложения,
приводим здесь доказательство ее, которое А. Н. Коркин предполагал
известным своим слушателям.
Введем предварительно некоторое новые понятия. Положим, что функ-
ция /(х) терпит разрыв непрерывности при х = с, но обладает тем свойством,
что / (с + Л) и — при стремлении положительного переменною h к нулю
имеют определенные конечные пределы. Мы будем обозначать эти пределы
следующим образом:
/(c + 0) = lim/(c + A), /(с — 0) = lim/(c— h)	(h>0).
h-+0	h-*Q
При этом говорят, что / (х) имеет при х — с разрыв непрерывности
первого рода. Если бы /(с + 0) и / (с — 0) совпадали, то никакого разрыва
непрерывности при х = с не было бы. Далее говорят, что функция / (ж)
удовлетворяет на конечном промежутке от а до Ь условиям Дирихле, если
она или непрерывна в этом промежутке или имеет конечноэ число разры-
вов первого рода и если, кроме того, она имеет конечное число максимумов
и минимумов в этом промежутке. На концах промежутка предполагается
существование конечных предельных значений /(« + 0) и / (Ь — 0). В силу
сказанного выше относительно максимумов и минимумов, весь промежуток
от а до b можно разбить на конечное число таких частичных промежутков,
в каждом из которых /(х) меняется монотонно.
Для доказательства теоремы Фурье предположим, что функция f(x),
определенная внутри промежутка (— оо, + оо), подчиняется следующим
► требованиям: 1) в любом конечном промежутке она удовлетворяет условиям
Дирихле; 2) она абсолютно интегрируема по всему бесконечному промежутку,
т. е. интегралы
0	оо
| / (ж) | dx и | / (ж) | dx
—оо	0
имеют конечные значения. Мы будем доказывать теорему Фурье при ука-
занных выше условиях. При этом в местах разрыва надо брать полусумму
96
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
[Гл. II
соответствующих пределов слева и справа, т. е. теорема Фурье выражается
следующей формулой:
y[/(*-0) + /(* + 0)] = ^-\da	/ (5) cos в (5-ж) d?.
О	— оо
Если х есть точка непрерывности /(ж), то
7[/(^-0) + /(^ + 0)]=/(а;)
и предыдущая формула будет:
/ (я) = da cos а (с — ж) ds.
О	—оо
В основе лежит следующая формула Дирихле, доказанная им при рассмо-
трении предела суммы членов тригонометрического ряда:
ъ
lim - \ F (z) dz = ~F (+ 0),
р.->0°-ТС о	2	2
причем считается, что F {z) удовлетворяет условиям Дирихле на конечном
промежутке от 0 до b и
F( + 0) = limF(A) (Л>0).
h->0
Для доказательства теоремы Фурье надо показать, что J
/(?)cosa(? — x)dz = 4-[/(# —0] +[/(^ + 0)].	(*)
о Л	.
В силу абсолютной интегрируемости /(#)> интеграл
+оо
/(;)cosa(;—»)d?J
—ОО
сходится равномерно при всех вещественных а. Действительно, интегралы
N'	-NI
/(;)cosa(c — x)dz и у / (?) cos a (? — х) d; (0<7V<2V')	(**)
N	-N'J
по абсолютной величине не превосходят интегралов
N'	-N'
N	-N
которые не зависят от а, и для любого заданного положительного з суще-
ствует такое 7V0, что при всех N и N' > 0 интегралы (**) будут < г.
Равномерная сходимость указанного интеграла позволяет менять порядок
интегрирования в повторном интеграле основной- формулы (*), и мы можем
написать, вводя специальное обозначение V (р, х) для этого интеграла:
V (н х) = da / (?) cos а (5 — х) dz = ~	/ (?) cos a (? — х) da.
0	— оо	—со 0
Выполняя интегрирование по а во внутреннем интеграле правой части,
получим:
4-оо
§
доказательство ТЕОРЕМЫ ФУРЬЕ
97
Разбив промежуток интегрирования (— оо, -f-оо) на два промежутка,
(—оо, х) и (ж, + оо) и вводя вместо $—х переменную —z в первом
и 2 во втором промежутке, получим:
V (р., «)=1 f (x~z>)3~? dz + f(x+ z'j’^^dz.
•	о
Оба написанных интеграла суть интегралы того же вида, что интеграл,
входящий в формулу Дирихле, причем для первого из них F1(z)==f(x — z)
и для второго F2(z) = /(4» + z). Осложнением является тот факт, что проме-
жуток интегрирования для них бесконечен» Пользуясь указанными выше
условиями, которым удовлетворяет /(ж), нетрудно показать, что, несмотря
на бесконечность промежутка интегрирования, для обоих интегралов имеет
место обычная формула Дирихле, причем F1( + 0) = /(^ —0) и Р%( + 0)==
=/(я + 0), т. е.
Lim — / (х — z)	dz = -1 / (х—0),
«	Г**)
llml f/(x + 2)^^=4/(x + 0).
lwco * J	3	2
Из этих формул и написанного выше выражения (Урь, х) и следует непо-
средственно основная формула (*)» При z > 1 функция —при любом ве-
щественном z по абсолютной величине <1, а функция f(x — z) по условию
абсолютно интегрируема, по промежутку от 0 до оо. Поэтому при любом
заданном положительном в существует такое число N большее единицы, что
при всяком р
со	оо
|157 !/(« —г)Иг <«•
N	N
Интеграл Дирихле:
N
л;/(x_2)s^d2i
те J	з
о
на конечном промежутке стремится к j f(x — 0) при беспредельном возра-
стании р., и, следовательно, при всех достаточно больших р мы будем иметь:
N
|| J/(®~ ?)8—^2-1/(а:-0)| <е.
о
Далее мы можем, очевидно, написать:
4 $/(3;-2)1М<й-1/(з-0) =
о
оо	- ' -	' N ' '
N	0
7 А. Н. Крылов
98 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ[Гл. П
Принимая во внимание предыдущие неравенства, получим при всех доста-
точно больших ji:
|1	< 1-1 |$/(г-2)^*| +
О	N
N
+ ll\f(X-Z)s-^dZ-jf(x-0)l<e + s = 2s,
о
откуда, в силу произвольности а, и следует первая из формул (***). Вторая
доказывается совершенно так же.
Напишем теорему Фурье в более удобной форме, которую получим,
присоединив уравнение
4-00.-к» ,
О =	— 1 sin а (х - - $) / (?) dl da.,
—оо —оо
которое следует из того, что подинтегральная функция есть нечетная функ-
ция^, и предполагается, что написанный интеграл имеет смысл.
Складывая последнее равенство с формулой, выражающей теорему Фурье,
и считая / (х) непрерывной, получим
4-оа -f-оо
/ (ж) =	ел <*-’>	/ (5) ей da.
-ОО —оо
Теорему Фурье можно распространить на функции со сколькими угодно
переменными. Например, пусть задана функция / (х, у); тогда, считая в ней
у за постоянную произвольную, получим
4-оо 4-оо
=	еа(ж-5)1ГГТ/(^, y)dUa.
— ОО -00
С другой стороны, по той же теореме Фурье, считая $ за постоянную
произвольную, пишем:
4-оо 4-оо
/(«» У^ = ^\	еНу-и) V=i / ($, 7j)rf7]dp;
— ОО -ОО
подставив в предыдущую формулу, получим
4 оо
—оо
Совершенно так же для функции с п переменными имеем
4-ор
/(х, у, Z, =	•••	X
— ОО
Хе^Г^	7), ...)dadp ...dcdijd;, ....
причем кратность интеграла есть 2п и переменные т), ч, ... должны
переходить от — оо до + °° через действительные, а не мнимые значения.
§32]
МЕТОД КОШИ
9$
§ 32» Метод Коши. Обращаясь теперь к формуле (15) для величины и,
удовлетворяющей уравнению (7), мы в ней положим
Ф1(?; 7], с ,...) = (^n/i(^ 7), С, ...),
Mt ъс, ...),
С, ...) = (-±.fp0, С, ...),
тогда формула (15) примет вид
+оо
—оо
7>iga (®-5) К-1 е? (»->)) К-1 X
ХеН«-оК-1	Ti, С, . ..)dad^d^ ...dld-^dr
-Foo
* • • + (W" И ’ * • й Tp^ (“-5) ГГТ (*-Ч)	(г"С) ГГГ • • •
—ОО
• ../Р(5»’Ч> С, ...) darfpdy о..	.
(16)
Каковы бы ни были функции /п f2,	/р, эта формула удовлетворяет
уравнению (7), лишь бы интегралы оставались конечными и определенными.
Заметим еще раз, что п означает число переменных х, у, z, ..., а значит
и 5, т],С, ••• и a, f, у, ...
Остается выполнить так называемые начальные условия, т. е. чтобы при
t = 0 само и обращалось в fL(x, у, z, ...), ^ —в /2 (х, у, z, ...) и т. д.
и <э^-в/р(а:> У' z' •••)•
Этого мы достигнем немедленно, если подберем решения Тъ Т2, .. .,Тр
так, чтобы при 2 = 0 величина Тг обращалась в 1, остальные —в 0, чтобы
при £ = 0 величина ^-2 обращалась в 1, остальные первые производные —
в 0, вообще, чтобы при t — О производная обращалась в 1, производ-
ные же того же порядка от остальных функций Т обращались в нуль.
В самом деле, если, сделав £ = мы получим T1=i, а остальные Т
равные 0, то формула (16) будет состоять из одного первого члена, и в нем
Т\ заменено 1; и тогда этот член по теореме Фурье равен Л (£, у, z, . ..).
Так как производная порядка к от и есть
Ч-оо
St* '	+ (2я)п J J J dt* е	Х
— ОО
хвК»-ч)Г=1	7], ...)(Zad?...^tZ7)... + ...
и в силу условий относительно Т при t == 0 все производные порядка к
dkTfa.!	дки	.
равны нулю, кроме - d~~ , то в выражении — останется только член /к+1
(?, т] и в нем будет = 1, и, значит, при Z = 0 будет
^7 = Л+1(^» У, ...).
Итак, остается подобрать наши решения Т19 Т2) ..., Тр сообразна
высказанным условиям.
100
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
[Гл. II
Решение уравнения
есть
Т = Сх	+ С2 е^ + ... + Ср e^v*,
следовательно, будет
= 4 Сг eWlt + 4 С2 е“2' +	о>* Ср ешр'
и, значит, при £ = 0 будет
(<У0о = ш1 + «5^2 + . . . + 0>р Ср.
Таким образом, для. функции , Тк, , для определения
Су С2, Ср, получим уравнения
Ci+ С2 + о о. +	Ср==0,
(01(714-	<tt2^,2+ •••+ Шр^р = 0,
Ш1 1 ^1 + ш2 1 ^2 + » » • 4" шкр 1 Ср~1,
...	°)f 1 Сг 4- о>2 1 С*2 + * о • 4" шр Ср — О.
постоянных
(17)
Как известно, если wj, ш2, .<ор не равны между собою, то ати урав-
нения допускают одно определенное решение относительно неизвестных
(71, (72, ..., Ср, следовательно, мы для, Тк получим величину в Виде совершен-
но определенной функции от а, р, у, ..., которые заключаются в выражениях
(Ор (02, ..., (0р.
Итак, получаем следующую теорему, данную Коши в его статье, поме-
щенной в 19-й тетради «Journal de 1’Ecole Polytechnique»»
Теорема. Чтобы удовлетворить уравнению
^+М^-Ь..+*ии
дхх ду^ ... dt^
(I)
и начальным условиям, что при £ —О должно быть
u = fi(x, у, z,	= h{x, у, z, ...)	= у, Z, ...), (II)
следует поступать так*.
1)	В каждом члене предложенного дифференциального уравнения заме-
нить число К дифференцирований по х множителем,	, чцсло р. диф-
ференцирований по у множителем (^]/ — 1)и и т. д., .но этого не де-
лать относительно главной переменной t и число дифференцирований, по t
d^T - '
. Таким образом, составится
заменить множителем
обыкновенное диф-
ференциальное уравнение порядка р с переменною независимою t и неизвестною
функцией Т, где р есть наивысшее число дифференцирований по t. Это
уравнение будет
3a(«y^i)4fU/~^i)‘...g = o.	(in;
2)	Найти его общий интеграл по известным правилам.
3)	Взять р частных решений этого уравнения
Ту Т2, ..., тр
§ 33]	СЛУЧАЙ УРАВНЕНИЯ С ПОСЛЕДНИМ ЧЛЕНОМ 101
— таких, что производная порядка k— 1 от решения Тк при t = 0 есть 1,
производные же остальных порядков от нулевого до (р — 1)-го суть нули.
4)	Подставить эти величины Ти Т2, ..., Тр в формулу
4-°°
и=(tH V • • й71 е‘(ж-5) Г~1 е₽ (9-г,)	•
... /i (£, к), С, ...) dot. d$ ... dzdy	.
• • • +(W” 5 V • •	... (IV)
• • • /₽(£> 'Л, С, •. •) dadfi .. . did^i;
тогда получится величина и, удовлетворяющая как предложенному уравне-
нию, так и начальным условиям.
В том случае, когда корни уравнения (9) «),, о>2, ;.., не равны между
собою, общая величина Т определяется формулою
Т = С1 е^ + С2 е^ + ... +Ср е^,
а величины постоянных для решения Тк—системою уравнений (17).
Заметим еще раз, что предыдущая формула выражает искомую величину
и только в том случае, если определенные интегралы, в нее входящие, конечны
и определенны, функции же /1? /2, ..., fp удовлетворяют ограничениям,
вытекающим из «условий Дирихле», при которых теорема Фурье имеет место.
§ 33.	Случай уравнения с последним членом. Обратимся теперь к
уравнениям с последним членом.
Возьмем уравнение
У а ----------^-= /(#., у, 2, ..., t).	(А)
дх* ду»-... dtz 4 и	'
Относительно него можно повторить замечания, относящиеся к обыкно-
венным линейным уравнениям; так, мы видели, что для того, чтобы освобо-
диться от последнего члена, достаточно знать какое-нибудь частное реше-
ние уравнения (А). Оно весьма легко находится, если функция / будет вида
/(ж, у, z, ..., t) = ekx+ly+---+mt<f>(x, у, z, ..., t),
где <р есть заданная целая функция от букв, в нее входящих, некоторой
степени q, а к, I, ..., m — заданные постоянные; тогда мы можем искать
частное решение V такого же вида, как функция /, и положить
V = екх+1у+—+mt Ф (х, у, 2, ..., Z),
где Ф есть общая целая функция с п + 1 переменными и с неопределен-
ными коэффициентами той же степени q.
Подставив эту величину У в уравнение (А) и сократив общий множи-
тель e/cx+Zy+-*+mf, получим в левой части целую функцию степени q, коэф-
фициенты которой составлены линейно из коэффициентов функции Ф, в пра-
вой же части будет вполне определенная функция той же степени q.
Сравнивая коэффициенты подобных членов, мы получим столько уравнений
первой степени, сколько неизвестных коэффициентов в функции Ф.
Понятно, что и тут будут исключения, когда величины
а = А, p.= Z, ..., о) = тп
удовлетворяют уравнению (9). В этом случае, смотря по кратности корней
этого уравнения, надо модифицировать форму функции V.
102 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ	[Гл. II
Понятно также, что если / (х, у, 2, ..., Z) есть сумма таких величин,
как рассмотрено выше, то и V надо положить равным таковой же сумме.
§ 34.	Пример 1-й; колебания неограниченной упругой среды. При-
ложим теперь общую теорию, изложенную в предыдущих параграфах, к клас-
сическим примерам.
Пример 1. Колебания неограниченной упругой среды.
Уравнение этих колебаний есть следующее:
д2и	о / д2и д2и д2и\
di* ~~Л \д& +
Оно исследовано Пуассоном в 1823 г. в статье, напечатанной в «Memoi-
res de I’Academie».
Применяя к этому уравнению общую теорему, приходим к уравнению
такого вида:
= а2 [(а К =й)2 + (? /“I)2 + (у /~1)2] Т,
т. е.
+	=	(2)
где
р2 == а2 + £2 + у2.
Общий интеграл этого уравнения:
Т = Сг cos apt + С2 sin apt.	(3)
Найдем теперь ТА и Т2-
dT
Чтобы найти Tj, надо, чтобы при Z = 0 было 7\ = 1 и -^=0, е.
Сх = 1 и С2 = 0.
dT
Для Т2 надо, чтобы при £ = 0 было T2 = Q и -^ = 1, т. е.
Ct =0 и арС2= 1,
1
откуда С2 = —; следовательно,
7’1 = cosapZ и jT2 = — sin др/.
Подставляя в формулу (IV) общей теоремы, имеем интеграл уравне-
ния (1) в таком виде:
+ оо
11=S S S Scos a?t е% (ж"')	е₽ (у-1|) х
X /1 (5,	0 da d$ dy di dt[ dZ 4-
+ OO
+ M M	г’ x
X /2 (£, tq, 0 d% dfi dy d; dr\ dZ- (4)
Пуассон показал, что эти шестерные интегралы могут быть приведены
к двойным. Для этой цели он доказал одну весьма важную теорему о при-
ведении некоторых двойных интегралов .к простым.
Положим, что дан интеграл
тс
JV = du / (a sin и cos v + [3 sin и sin о + у cos и) sin и dvt
б о
§ 34]
ПРИМЕР 1-Й: КОЛЕБАНИЯ НЕОГРАНИЧЕННОЙ УПРУГОЙ СРЕДЫ
103
где а, р, у — постоянные. Пусть
а2+£2 + 72
И
a = psin9coscp р = рsin 0 sin ср и у = р cos9,
где 9 и <р—также постоянные, легко получаемые через а, у, тогда
a sin и cos v + р sin и sin г + у cos и = р [sin и cos и sin 6 cos ср +
+ sin и sin и sin 6 sin ср Н- cos и cos 6] — р [cos и cos 6 + sin и sin 6 (cos г cos ср +
+ sin v sin ср)] = p [cos и cos 6 + sin и sin 6 cos (v — <p)].
Эта формула имеет простой геометрический смысл. Возьмем на сфере
радиуса 1 две точки М и N, коих полярные координаты соответственно
<р, 9 и и, и; тогда
cos МN — cos a — cos и cos 9 + sin и sin 9 cos (v — cp).
Значит,
a sin и cos v + p sin и sin v + у cos и == p cos a;
Следовательно,
7L 2те	те 2те
W =	/ (p cos a) sin и du.dv •=	/ (p cos a) ds. (5)
0 0	0 0
где ds есть элемент поверхности сферы радиуса,
равного 1.
Так как полюс С на шаре совершенно произ-
вольный, то можно взять полюс в точке М (фиг. 15)	Фиг. 15.
и от него определять положение точки N\ тогда
будет: MN = з — дополнение широты, CMN — ф — долгота от меридиана СМ
и, значит, ds = sin айас?ф, и можно написать
те 2те
W == da / (р cos a) sin а йф.
о о
Долгота ф не входит под знак функции /, а потому, интегрируя по ф,
получим
те
W = 2к / (р ccs a) sin a da.
о
Таким образом, мы имеем следующую формулу Пуассона:
те 2те
du / (a sin и cos v + В sin и sin d + у cos и) sin и dv —
о о
= 2к / (]/"а2 + р2 + у2 cos a) sin a da
о
или, взяв cos с за переменную, т. е. полагая cosa = z, получим
те 2те
du / (a sin и cos v + р sin и sin v + у cos и) sin и dv =
о о
+i
= 2к / (/aT-H2 + y2z) dz. (6)
-i
104
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
ГГл. TI
Чтобы обратить шестерные интегралы формулы (4) в двойные, восполь-
зуемся формулой Пуассона. Если обозначить через ш в формуле Пуассона
величину
ш = a sin а cos v 4- Р sin и sin v 4- у cos и
и за функцию / взять / (ад) = eatii> то получим
тс 2тс	4-1
еа««1>У-1 gjjj и da _ 2л еа(м Vе-1 dz =
00	-1
_ 2я________	=	. sinafP .
atf> Y -1 '	t ар
г.	sin ato
Отсюда можно вывести ~~р в виде двойного интеграла» именно:
тс 2тс
sin atp
Г аР
(*)

о о
Дифференцируя по t, получим
тс 2тс
cos atp =	\ \ eaft3i^~^t sin и du do.
г 4л dt j J
о о
Заменяя cos apt и —этими величинами под знаками интеграла в фор-
муле (4), мы получим, вместо шестерных, восьмерные интегралы, и у нас
будет
тс 2тс	-f-oo
2-Й член формулы (4) = А	e^(x+at sin и cos
0 0	—оо
X (&+at sin и sin о—gT (z+at cos u—
X /2 (£> 4, C) da d3 dy dz di\ d\ j t sin и du. do.
Но по теореме Фурье величина, стоящая , в [ ], как раз равна функ-
ции /2, гДе вместо 5, т), С подставлено
х + at sin и cos и, у 4- at sin и sin и, z 4-a£cos и.
образом, эта формула напишется проще:
тс 2тс
ICC
формулы (4)= — \ \ /2 (х 4-a/sin u cost?, у 4- at sin и sin и, z 4-
, о о
Таким
2-й член
4- at cos u) t sin и du do.
получить первый член той же формулы, заменим cos apt его вели-
Чтобы
чиною (**); тогда получим
тс 2тс
1-й член формулы (4) = ^ \ $ [-^
о о
5 s<n и cos и
X fi (ЦС) da сф dy dz d*t\ dt, t sin и
тс 2тс
5	S^n K 008 У + at s*n u s*n z + at cos a) t sin и du do.
о 0
$36]
ПРИМЕР 1-Й: КОЛЕБАНИЯ НЕОГРАНИЧЕННОЙ УПРУГОЙ СРЕДЫ
105
Складывая эти два выражения, мы получим величину и:
it 2к
в X /2 (х + at sin и cos d, у + a^sin и sin u, z + at cos u} t sin и du dv +
0 0
it 2/c
4- X fl fx (x 4. at sin и cos y, y + at sin и sin e, z + at cos u) t sin и du dv, (7)
oo	<
причем интегрирование по и от 0 до к и по v от 0 до 2тс.
Это и есть знаменитый пуассонов интеграл уравнения (1).
Очевидно, что и при Z = 0 обращается в /i(^, у, z) и — в /2 (ж, у, z).
Предлагается в виде задачи проверить, что величина (7) удовлетворяет
уравнению (1).
§ 35. Если величина и, удовлетворяющая уравнению (1}, не зависела бы
от х, то она удовлетворяла бы уравнению
№	2/ д2и , д2и\	..
Мы эту величину получим, предположив, что функции и /2 не содер-
жат величины z 4-яг sin и cos о под своим знаком.
Переменив в последнем уравнении буквы у на х и z на у, мы получим
уравнение (1'):
№	2/' Э*и 1	,л'\
dt2 \ дх2 1 ду2 J	' '
Формула же (7) дает для этого уравнения следующий интеграл:
тс 2 тс
и =	/2 (х 4- at sin и sin v, у + at cos и) t sin и du do 4-
0 0
it 2it
+,— J; \ \fi(x 4-at sin н sin v, y + at cos a)< sin и du do. (8)
Ч7С ОС Л ( J	'
о 0
§ 36. Наконец, предположим в уравнении (!'), что и не зависит
тогда оно обратится в такое:
д2и 9 д2и
dt2 ду2 9
от х;
(1")
а если мы переменим здесь у на х, то получим уравнение движение струны:
д2и 9 д2и
^Т2=а Т •	Л )
dt2 дх2	к	7
Следовательно, сделав указанные замены в формуле ^), мы получим
интеграл уравнения (1"') в таком виде:
« =	/2 (X -I- at cos и) t sin и du de +	\ /1 (x + at cos “)z sin u du
00	bo
Интегрирование no v можно выполнить, и получим
м /2 (^ + cos u) t sin udu-f-^- ( Д (x 4- at cos u) t sin и du. (9)
a	o'
Нетрудно отсюда получить известный даламберов интеграл.
106
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
[Гл. II
В самом деле, пусть будет
$/2(^)^ = F2(S) и f1(^)dl = F1(^)>
*
тогда, делая в формуле (9)
x-^at cosw = £,
мы получим
1
— t sin и du = — d;,
а
кроме того,
при tz = O l = x + at,
при и = к Z=x — att
и уравнение (9) дает
«—at	х—at
5 /Ж =
x+at	x^-at
1	1/9
= ^[F2(x + at) — F2 (x — at)] + ^^[F1(x + at) — Fl (x — at)] =
= ^[рг(х + а*) —(x~a0] +4 (A (ж + aO + A(s —af)]-
Ясно, что и при 2 = 0 обращается в h(x)t а его производная
=4 f/г <ж+az)+a (^—«*)]+4 ш +at>) ~fdx- «01
Оъ А	й
обращается в /2(я).
Если бы мы сделали, для сокращения письма,
A F2 (x + at) + у A (« + a0 = ?(® + «0
И
—^F2 (х -а1) + ± fr (x - aZ) = ф (ж — at),
то наша величина и приняла бы вид
a = <р (х + at) + ф (х — at},
в котором Даламбер и дал общий интеграл уравнения колебания струны.
§ 37» Если	бы, вместо того, чтобы в уравнении (1)	предполагать, что
и	не зависит от	х, а только от	у и z, мы предположили	бы прямо, что оно
не зависит от 2, то функции /х и /2 не зависели бы от последней величины,
стоящей под их	знаком, вместо	того, чтобы не зависеть	от первой; тогда
в	интеграле (8)	уравнения (Г)	к х было бы прибавлено	a^sinwcosv, ку —
величина aZsinwsinv. Вообще, сделаем, для сокращения письма,
рг = at sin и cos и, р2 = at sin и sin и, р3 ~ at cos и,
тогда формулу (7) можно написать в более общем виде следующим образом:
-тс 2-Я
и = А ^f2(x + ph, у + рк, Z + Pl)t sin и du dv +
о о
•те 2ti
+	fi(x + Pi> У + Pb z + pjtsinududv,
о о
§ 38] ПРИМЕР 2-Й: УРАВНЕНИЕ ДВИЖЕНИЯ НЕОГРАНИЧЕННОЙ ПЛАСТИНКИ Ю7
где А, А, I представляют значки 1, 2, 3 в каком угодно порядке, точно
так же Z, /, т — те же значки в каком угодно порядке.
Мемуар Пуассона, заключающий эти результаты, читан Академии
в 1819 г. и озаглавлен: «Sur Integration de quelques equations lineaires
aux differences partielles et particulierement de I’equation generale dumouve-
ment des fluides elastiques».
§ 38. Пример 2. Уравнение движения неограниченной пластинки.
Уравнение это следующее:
o»t2 + b С дх* + 2 дх* ду* "* ду* ) ~~	t1)
Применяя общий метод, составляем сперва обыкновенное уравнение
с неизвестною Т. Оно будет
5 + 62 [(a	+ 2 (а (Р /^)2 + (Р /	= О,
иначе
или
^ + ^(а< + 2^ + р<)Т = О,
-^ + &Ч«2 + Р2)аГ=0.
Общий интеграл его есть
Т = Сг cos Ь (а2 + Р2) t + С2 sin Ь (а2 + р2) t,
отсюда получим Т\ и Т2. Замечая, что при £ = 0 должно быть
7\ = 1 и ^- = 0, Та = 0 и -^ = 1,
1	at	at
окажется
Л = cos b (а2 + t, Т2 = Sin/(^~/^))‘ = 5 COS b + 1 dt'
Зная и T2, пишем общий интеграл нашего уравнения с двумя
произвольными функциями в таком виде:
и = C°S & (а2 "I”	X
—со
X /1 (£> Ч) di dy da d$ +
t	+00
4-	П cos6(a2 + P2)ifea(a:_5)rZTe₽^-’i)Vri’
0	—00
X /2 (S, >]) di di\ da d$ j dt.
Здесь четверные интегралы по переменным a, р, 5, щ могут быть све-
дены к двойным. Для этой цели удобнее показательные функции заменить
косинусами и синусами и написать формулу (2) в таком виде:
4-оо
W==(2^)2 $ cos 6 (а2 + Р2) cos а (д;—-$) cos р (г/ —т))/i (£, tj) di d^dad^
—00
t	+°°
+ (А*5 ^[5^5 5cosHa2 + P^c°sa(.-5)c°sP(?/ —i))/2(e, т)) di d-ц d<i .
0	—00	*
(2')
108
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
[Гл. II
Займемся сперва первым членом, ибо после его преобразования прямо
напишем второй, заменив /х на /2.
Для этого преобразования нам нужны следующие интегралы:
cos hx2 cos lx dx
sin hx2 cos lx dx = sin
причем предполагается h > 0.
Для вывода этих интегралов можно поступать различно.
Во-первых, можно взять известный интеграл
Н-ОО
С e-/cz2 cos lz dz __ e 4/c
'	V к
в котором к или действительная и положительная величина, или мнимая,
у которой действительная часть положительная.
Сделав поэтому k = g + А }/ — 1, где* g и h — положительные действи-
тельные величины, подставив в предыдущие интегралы и отделив в правой
и левой частях действительные от мнимых и уравняв действительные
и мнимые, получим два определенных интеграла, более общих, нежели (*)•
Из них найдем (*), предполагая g бесконечно малым и переходя к пределу•
Другой способ следующий.
Известны интегралы
cos£2d# =
+со
sin#2d#
—оо
Подставим здесь х = у — Z, так что
rr2 = y2 —2Zy4-Z2;
тогда
cos х2 = cos (у2 + Z2) cos 2ly + sin (г/2 + Z2) sin 2Zy,
sin x2 = sin (y2 + Z2) cos 2ly — cos (y2 + Z2) sin 2ly.
Ho cos и sin дуг y2-\-l2 сведутся на cos и sin дуг у2 и Z2. Сделав
это и подставив в выражения cos £2 и sin ж2 их величины под знаками
интеграла, мы получим два уравнения, из которых найдем, как неизвест-
ные, интегралы
4-оо	4-со
cos у2 cos 2ly dy и sin y2bbs2lydy,	(*')
—оо	—со
ибо очевидно, что интегралы, содержащие sin2Zy, как интегралы нечетной
функции, равны нулю. От интегралов (*') переходим к интегралам (*)г
полагая y2 — hx2 или у=.#]/А и заменяя постоянную 21 }/” А через Z.
Приняв, следовательно, уравнения (*), разберем первый член фор-
мулы (2').
Так как
cos bt (а2 + р2) == cos bt а2 cos bt р2 — sin bt a2 sin bt p2,
то, подставив эту величину в первый член формулы (2'), мы его можем
$ 38] ПРИМЕР 2-Й: УРАВНЕНИЕ ДВИЖЕНИЯ НЕОГРАНИЧЕННОЙ ПЛАСТИНКИ 109
написать в таком виде:
1-й член формулы (2') =
+оо 4-оо
(i^n[H(cosfcza2cos^2~
—оо —СО
— sin bt a2 sin bt p2) cos a (x — J) cos
(у — •n) ? da d$ ] /x (;, 7]) dl dy.
Интеграл в [ ] распадается на произведение интеграла, взятого по а,
на интеграл, взятый по р, и будет
1-й член формулы (2') =
4-оо 4-оо	4- 00
= (2я)«^[ S cos“а003 (ж — acos bt Р2 cos (у — х\) $d3 —
—оо —со	—оо
4-00	4-оо
— sin bt a2 cos (х — 5) a da sin bt р2 cos (у — »]) р d$ ] /х (5, ц) dt\.
—оо	—оо
Сделав в формуле (*)ft = 6z, а затем последовательно l = x — $, потом
у— 7}, получим
1-й член формулы (2х) =	$ $ £ [С03 (т~(^ьГ^ cos
—оо
— оо
4-ео 4-оо
—со —со
Положим
£ — X	V — у
г_ =хг	и	—= у19
°2tfbt	21/bt *
тогда будет
$ = « + 2]Zbtxx, т\ = г/ + 2]Лб/у!, dZd^^^btdx^dy^
и, по подстановке и сокращении,
1-й член формулы (2') =
4-ео 4-ео
= v sin и + У?) /1 (ж + 2 |/	У + 2 Кbt У1) ^1 Луг
—со —оо
, На основании этой формулы пишем интеграл нашего уравнения в таком
преобразованном виде:
4-ео
u = А sin (х2 + yl) /1 (х -ь 2 У bt Хр у + 2 У bt yt) dxx dy! +
-^OO
t	+oo	(2)
+ dt sin (x2 + yl) f2 (x -f- 2 У btxu у + 2)/ bt г/г) dXi dyv
0	—oo
110 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ[Гл. П
§ 39.	Пуассон приходит к интегралу этого уравнения иначе. Мы видел»
(§ 26), что интеграл уравнения
(Л)
dt \dx2 dy2J	'
выражается формулою
4-оо
ср = е-(а?+ур / (х + 2 ]/* at х1У у + 2 at ух) dxx dyr. (В)
—оо
Из уравнения (А) находим
И»,
dt* L "г ду2 J ’
подставляя снова во вторую часть вместо его величину из уравнения (А),
получим
Гр (	+ р (^t + Y1
д*Ч> _ 2	\дха	ду* ) | Ч <?*а ду* ) _ 2 Г -L- 2 д4? , д4? 1
Л2 L дх* "г ду* . J— L дх* дх* ду* ду* J '
• **
Сравнивая это уравнение с (1), видим, что ср обратится в и, если
а2 = —Ь2, т. е. когда а= +6}/— 1 или —	— 1. Мы получим, следова-
тельно, и в виде суммы двух двойных интегралов, из которых первый
получится из формулы (В), подставляя туда вместо а величину +6}/ — 1,
а другой — из той же формулы (В), подставив в нее — 6]/—1 вместо а
и переменив функцию / на другую F от тех же величин. Таким образом,
получается общий интеграл уравнения (1) с двумя произвольными Функ-
циями j и F, но не отвечающими начальным условиям.
Из них Пуассон выводит наши формулы, выражающие эти условия,
но не строго.
Задачи. Интегрировать следующие уравнения:
д*и I А2	9	№ _1_ д*и\ _ С\
dt* V*4 + 2 dx2 dy2	dy*) О*
d*u   , 2 Zd*u ? d*u d*u\
dt* \dx* dx2 dy2 *" dy*/ *
Примечание. Можно применить показанный в предыдущем параграфе метод
Пуассона, ибо мы знаем интеграл уравнения
д2ср __ / d2© ’	d2? \
dt2 а dx2 dy2 / ‘
Дифференцируя два раза по t, получим после замены:
4-2-^2 -
dt* \ dx* dx2 dy* dy*J *
Следует также применить и общий метод и, для преобразования интегралов,
воспользоваться формулою Пуассона, показанной в § 34.
Проф. А. Н. Коркин ограничился лишь этою чисто математическою стороною
дела, причем все приведенное в этой главе было им изложено со всеми выкладками
в течение трех вечеров!
ГЛАВА ш
ИНТЕГРИРОВАНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ
ПРОИЗВОДНЫМИ ПРИ УСЛОВИЯХ НА ГРАНИЦАХ
ОГРАНИЧЕННОЙ СРЕДЫ
ПЕРВЫЙ МЕТОД ПУАССОНА
Большая часть заключающегося в этой главе составляет также изло-
жение этого предмета А. Н. Коркиным. Дело было так.
В 1901 г. я попросил Александра Николаевича объяснить мне непо-
нятое мною место в одном из мемуаров Пуассона, помещенных в 19-й тетради
журнала Политехнической школы. Александр Николаевич не только
в нескольких словах разъяснил то, что мне представлялось непонятным*
но еще и прочел мне целую лекцию, в которой дал свое изложение метода
Пуассона. В какой мере он владел этим предметом,—читатель может судить
по тому, что эта лекция, составляющая §§ 40, 41 и 43 этой главы, была им
прочитана в ответ на мой вопрос, для Александра Николаевича неожиданный,
немедленно, без всякой подготовки, причем Александр Николаевич почти
не пользовался карандашом, который держал в руке, а лишь следя глазами
за моею записью, продиктовал мне все изложенное ниже со всеми выклад-
ками и формулами.
§ 40.	Замечание об истории вопроса. Первоначально Лагранж, рас-
сматривая движение многоугольника, стороны которого суть негибкие и
нерастяжимые стержни, соединенные в углах бесконечно малыми шарни-
рами, концы же многоугольника закреплены, дал решение этого вопроса
при помощи особенной формулы интерполирования, зависящей от сину-
сов различных дуг1.
Если мы предположим стороны многоугольника бесконечно малыми,—
следовательно, число их бесконечно большим,—то из лагранжевых формул
получим новую, относящуюся к движению струны, когда перейдем
к пределу.
Для движения многоугольника приходится интегрировать некоторую
систему линейных совокупных уравнений; если же поставить вопрос о струне
прямо и решать его непосредственно, то придется интегрировать уравнение
с частными производными второго порядка, которое было дано еще
Даламбером.
Из этого примера видно, что система бесконечно большого числа сово-
купных уравнений заменяется уравнением с частными производными.
Нужно заметить, что Даламбер дал общий интеграл для уравнения
движения струны, но Даниил Бернулли заметил, что это решение, по край-
ней мере непосредственно, не показывает обстоятельств движения и что
нужно рассматривать ряды, расположенные по синусам кратных дуг, чтобы
эти обстоятельства обнаружить, тогда и будет видно, что звучащая струна
издает бесчисленное множество звуков, из коих каждый соответствует одному
члену ряда.
1 Аналитическая механика, т. 1. отд. VI, § 30 и след.
112
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИЯХ НА ГРАНИЦАХ [Гл. до
Вопросы об удовлетворении условиям на границах движущихся тел,
а также те условия, которые дает для этих границ теория тепла, оставались
совершенно неисследованными до появления мему ара Фурье в начале
1812 г. Затем, в 1815 г., Пуассон, зная уже работы Фурье, представил
в Институт мемуар о распространении тепла в твердых телах, а затем напе-
чатал два мемуара об этом предмете в 19-й тетради журнала Политехниче-
ской школы.
Метод, который он здесь дает, относится только к уравнениям, содер-
жащим, кроме времени, одну переменную независимую.
Затем появились сначала «ТЬёоне analytique de la chaleur» Фурье,
затем «Theorie mathematique de la chaleur» Пуассона.
В последнем сочинении Пуассон уже не употребляет того метода, кото-
рый он изложил в 19-й тетради журнала Политехнической школы, но при-
меняет другой метод, при котором вычисление несколько проще, но у ко-
торого зато есть и свои недостатки х.
При изучении методов, относящихся к интегрированию при задан-
ных условиях на границах, приходится ограничиться поэтому теми част-
ными случаями, которые до сих пор рассмотрены, и самые эти методы
рассматривать как средство для нахождения требуемого решения, которое
в каждом случае следует строго доказать.
Мы начнем изложение этих методов с классического примера, именно,
с уравнения колебания струны или продольных колебаний прута.
§ 41.	Колебания струны. Уравнение колебания струны следующее:
д*и о д*и
--- -=.0“— .
dt\
(1)
При этом условия для концов струны будут различны, смотря по тому,
концы эти (я=0 и х=1) свободны или нет.
Рассмотрим сначала случай, когда перемещение
\	а и Равно НУЛЮ при концах во все время движения,
_Tbs.—Z-+- т. е. когда должно быть
Р X
_	...	и —О при ж = 0 1
Фиг-	> при всяком значении I. (*)
и = 0 при я = / J
Общий интеграл уравнения (1) был дан Даламбером и, как известно,
следующий:
и = ср (х 4- at) + ф (х — at),
где ср и ф — совершенно произвольные функции.
Предположим, что в начале движения каждую точку струны ОА
поместили произвольно, но достаточно близко к прямой О А, так что кри-
вая ОМА — произвольная; нужно только, чтобы она проходила ,через точки О
и А. Ордината ее РМ — и, соответствующая абсциссе х = ОР, будет, следо-
вательно, произвольно заданная функция от х (фиг. 16). Затем, каждой
точке струны сообщается произвольная скорость или толчок, вследствие
ди	-
чего при начале движения будет также другая произвольно заданная
функция от х.
Пусть при £ = 0 будет
и = /(х),
тогда эти функции заданы для всех ж от ж = 0 до и=/.
1 Этот метод изложен в гл. IV этого курса.
41] ИЗЛОЖЕНИЕ МЕТОДА НА ПРИМЕРЕ УРАВНЕНИЯ КОЛЕБАНИЯ СТРУНЫ ИЗ
Таким образом, необходимо, чтобы:
1)	при Z —О было
« = /(«) и J = F(a:),
где f(x) и F (х) должны быть заданы так, чтобы при ж = 0 и х — 1 они
были равны нулю;
2)	при ж = 0 было w = 0 при всяком t;
3)	при х = 1 было а = 0 при всяком t.
По этим условиям можно определить функции ср (ж + at) и ф (х — at)
для всех величин аргументов x-j-at и х — at от —оо до + оо.
Мы применим для решения этого вопроса метод Пуассона, изложен-
ный им в 19-й тетради журнала Политехнической школы, и будем намечать
те главные операции, из коих он состоит.
Положим, что надо интегрировать какое ни есть линейное уравнение
L = 0 с частными производными по х и f, какого угодно, например вто-
рого, порядка, с постоянными коэффициентами и без последнего члена.
Мы будем предполагать, называя через и неизвестную функцию, что
входит в уравнение £ = 0; тогда мы знаем из главы II, что при помощи
теоремы Фурье мы всегда можем найти такое решение и, что оно удовле-
творит уравнению L == 0, и при Z = 0 само и обратится в /(ж), а ~ — ъР(х),
причем предполагается, что определенные интегралы, которые вводит теорема
Фурье, имеют смысл и будут величинами конечными и что функции /(ж)
и F (х) известны для всех величин х от —оо до + оо.
Первая операция в методе Пуассона и состоит в том, что по пра-
вилам главы II составляется общее выражение и, удовлетворяющее предло-
женному уравнению и такое, что при £ = 0 само и обратится в f(x)
Bg-BF(x), когда эти функции будут заданы оАя= —со до +оо.
Применим это к нашему уравнению (1).
По правилу § 32 мы должны напирать:
4-со 4-со	4-об 4-ео
—оо —оо	—оо —оо
при этом как Т19 так и Т2 будут частными решениями уравнения
dt2
Общая величина Т будет
Т = (\ cos a at + С2 sin a at
и надо, чтобы при f = 0 было
Т1 = 1,	^=0,
?’2=о.	dt —
так что мы получаем
7\ = cosaotf, 7,2 = -—sinaa£
*	. аа
8 А. Н. Крылов
114 ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ
(Гл. Ill
и, значит, у нас будет
Ч-оо Ц-оо
и =	cosaa^/(с)	+
—ОО —со
4-оо 4-со
+ « С С
Zitd J J а
—оо —оо
Но мы не знаем величин /($) и F (?) вне пределов Е = 0 и 5 — /, ибо
эти функции заданы лишь между этими пределами.
Вторая операция состоит в том, что, пользуясь условиями, отно-
сящимися к значениям и при ж = Оиж=/, и заданными значениями функ-
ций f (х) и F (х) для промежутка от я = 0 до х = 1, составляются условия,
дающие возможность найти эти функции для любого значения аргумента.
Чтобы вывести эти условия для функций /($) и F (£), сделаем
£ — x = z,	dz — dz,
пределы по z будут те же, что и по $, т. е. — оо и + оо.
Мы делаем эту подстановку для того, чтобы’ величина ж, для которой
поставлены условия на границах, вощла в наши функции / и F.
Мы получим
4-со 4-оо
u =	cos aat e~^z f (х + z) dz da +
—CO —00
4-oo 4-oo
+ Д- \ sin g-az У“-1 P (ж_|_ z)dzd^-
J J a	\	*
—CO —00
Соединим теперь элементы интеграла по z, относящиеся к величинам
z и —z; тогда и напишется так:
4-оо 4-оо
ICC	*
a =	\ \ cosaaf cosaz[/(x-|-z)-[-/(£—-z)]dzda +
<йТС J J
—оо О
4-со Ч-оэ
+ 2^ sin^aat cog [F (ж z) 4- -F (я — 2)] dz dy,
—оо 0
ибо члены, содержащие под знаком интеграла sin az, пропадут, так как
интегрирование по а производится от — оо до + оо и подинтегральная
функция относительно а будет нечетная»
Совершенно подобным же образом мы трактовали бы и уравнение
L = 0, если бы для границ х = 0 и х=-1 были заданы какие-нибудь диффе-
ренциальные уравнения линейные с постоянными коэффициентами без по-
следнего члена. Понятно, что под интегралы входили бы, кроме функций /
и F от аргументов x + z и x — z еще и их производные по z. Затем инте-
грированием по частям (по переменной z) можно дифференцирования, сде-
ланные по этой переменной, перевести на другие множители, после этого
выражение и под знаком интеграла будет содержать только функции / и F.
В нашем случае, для того, чтобы при х = 0 было а~0, нужно, чтобы
каждый элемент того и другого интеграла в отдельности уничтожался
особо; значит, должно быть
(*)
/(z) + /(-z) = O,
F(z) + F( —z) = 0.
§ 41] ИЗЛОЖЕНИЕ МЕТОДА НА ПРИМЕРЕ УРАВНЕНИЯ КОЛЕБАНИЯ СТРУНЫ 115
Зададим функцию /(z) для всех значений z от 0 до I совершенно
про-
ИЗБОЛЕНО.
Пусть длины (фиг. 17)
АО=^АА1^А1А2 = ... = ОВ = ВВ1 = ... = Z;
тогда у нас будет известен кусок ОМА.
В силу условия, / (z) + / (— z) = б, нам сделается известен кусок ON В
от О до В.
Сделаем теперь х = Тогда должно быть и = 0, и будут
/ (/ + z) + / (Z — 2) = О,
F (I + z) + F (I — z) = О.
Если мы теперь возьмем нашу функцию, уже известную от А до В,
то для всякой абсциссы АР — 1—z будем знать ординату PN—u\ но и по
Фиг. 17.
условию f(l+ z)= — f(l — z) мы будем знать ординату PjN} — PN, соответ-
ствующую абсциссе	Таким образом, это условие дает нам вели-
чины нашей функции до точки А2, а тогда, вследствие условия
/(z)	= 0, будем знать нашу функцию и до точки В2 и т. д.
Легко видеть, что* эти два условия определяют наши функции /(£)
и F (В) для всех величин 5 от — оо до +оо.
Теперь мы могли бы довольствоваться величиною и, полученной по
правилу главы II, так как под знаком определенных интегралов функции
вполне известны.
Но собственно метод Пуассона состоит в преобразовании интегралов,
заключающихся в и, в ряды так, что в этих последних остаются только
значения /($) и F (5), заданные от 0 до Z, и не будут совсем входить в фор-
мулы те величины этих функций, которые мы показали как вывести из
заданных.
Третья операция состоит в нахождении интегралов
+оо	4-оо
е_аЕ у и $ е~<* 1Г=1 F (?) di,
— ОО	—00
которые, будучи потом умножены на
еах V-i cosaatdtx
сс
и проинтегрированы от —оо до + оо по а, и доставят величину
Величина этих интегралов вообще неопределенная, и их надо рассмат-
ривать как предел, к которому стремятся другие интегралы, имеющие
116 ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ (Гл. III
определенную величину. С этой целью Пуассон вводит интегралы
СО	—ОО
p(h)= e~hzf(z)dz, q(h) = ehzj(z)dz,
• о	*.	о
и
Р(Л)= e~hzF{z) dz, Q(h)= ehzF(z)dz,
Ос
где h есть некоторая величина, не зависящая от z и положительная, если
она действительная, и с положительной действительной частью, если она
мнимая.	,	___
< ^Возьмем Л==з-|-а]Л—1 в интеграле р(К) и Л = з—	—1 в ийте-
£рале q(h), причем г есть бесконечно малая положительная величина; тогда
предел разности этих двух интегралов, т. е.
lim[p (г + а К— 1) - 9(s — а jA7!)] =
оо	—со	4-со
 = е~лг f (z) dz —	e-®2/ (z) dz =	e-®2^-1/(z)(Zz,
О	0	—co
и есть первый из тех двух интегралов, которые надо найти; очевидно, что
второй выразится совершенно подобным же образом через Р (h) и Q(h).
Чтобы найти величины p(h) и q(h), возьмем наши условия, относя-
щиеся к функции f (z), так как относительно функции F (z) будет то же
самое, чГои для первой,
к / v Итак, имеем
с. i	г <	/(z) + /(-z)=O,
'	'	/(Z + z)-{-/(Z —z) = 0.
Умножим оба эти уравнения на e~h2dz и интегрируем от 0 до оо;
получим
!	' e~h2f(z) dz+ e-h*/( — z) dz = O,
о	о	/<л
	«о	<»	' '
$ e~hz f (Г+ z) dz + ,e-h7 (Z - z) dz = 0.
О :	0
Мы имеем непосредственно
e~hz f (z) dz = p (Л).
о	*
Затем
£ e~ftz/(—z)dz= —	ehz f (z)dz = — q(h).
о	о
Следовательно, первое уравнение (2) дает
(	<	p(h) — q(h) = O.	(3)
$ 41] ИЗЛОЖЕНИЕ МЕТОДА НА ПРИМЕРЕ УРАВНЕНИЯ КОЛЕБАНИЯ СТРУНЫ 117
Деваем Z«J-z = y, dz = dy; пределы по у будут: I и со\ \	?
Тогда	;',	’ f
+©о	•	оо	оо
e~hz f(l + z)dz—\e~h(v~l)f(y)dy==ehl ( e~hv / (у) dy —
о	i	i	<	1	.	:
= eftz e~hz f(z)dz — e-hz/(z)dzl = ehl Гр(Л) — \ e~hzf(z) dzj.
L о	о	о	J ‘
Подобным же образом, если положить l — z = y,dz =—dy, пределы
для у будут: у = 1 и у = со, и м,ы получим
\ e~hzf (lr-z) dz =— e-h(l-v)f (y)dy= — erhl \ ehvf(y)dy =
о	i
= — e~hl [ ebvf(y)dy— eh»f(y)dy~^ = —e~hl
0	0
Таким образом, уравнения (2') будут
p(h)-q(h) = O,
i
[?(*)- 5 ^f(y)dy^ .
ehlp(h) —e~hlq (Л) = ehl у e~hzf (z) dz — е“Л* ehzf (z) d£.
о	о
Отсюда найдем
i	г
ehl e~hz f (z) dz — <?”ftz e hzf (z) dz
p{h) = q (Л) = —5-------enr_e-ra ° ------—
Сделаем для сокращения
i	1
X (Л) = ehl e~hzj (z) dz — e~~hl ehzf (z) dz
o	o
и
p. (/?) — ehl — e~hl,
тогда
(4)
Остается выполнить переход к пределу. Пусть г есть бесконечно малая
положительная величина; тогда, как мы видели, интеграл
4-оо	_____ ___________________
е-аг]Л=1у dz — lim [р (г + а ]/— 1)— (г — а — 1)] =
_ Пт Г	.
L |1 (з 4- а — 1) J1 (з — а у — 1) J
• Но функции X и р. нечетные; следовательно, p(h) и q(h) будут четные
и, следовательно, при 8 = 0 упомянутый предел равен нулю, исключая те
величины а, для которых у-(а j/" — 1) = 0.
118
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ
(Гл. 1П
Но у (a jZ 1) =±= 2• 1 sin aZ; значит, наш предел может быть не-
равен нулю только для тех величин а, для которых
sin aZ = О,	•	(5)
значит, для которых
Za = кя,
где к — какое угодно целое число: положительное, отрицательное или нуль.
Сделаем = и, кроме того, положим
а = рй + а'.
Тогда, при интегрировании по а от — оо до +оо, надо брать вели-
чины а, только бесконечно мало разнящиеся от всякого корня, т. е. брать
а' от —у* до +Sft, где у* и 6/с —положительные бесконечно малые вели-
чины.
Заметим теперь, что
X (з + a }/" — 1) == X [г + (3* + а') ]/" — 1] = X — 1) -f- беек. мал. величина,
fi(e+a У — 1) = р. [s +РаУ — 1+<х'У - 1] =
= (е + а' ]/ — 1) р/ У — 1) + беек. мал. вел. выс. пор.
Значит,
и (з + a _ 1) (з + a' /— 1)/ (рлУ— 1)
Переменив знак при У — 1, получим
Х(з-ауГ1) _ _х^уГл)
ц(з —«У—1) (з — а' / - 1) / (pfc У-1)
Подставляя эти величины в предельное уравнение, мы получим
4-оо	___
С e-az У-1 f (z)	/
s 4- a' — 1 s — a' Z “ 1 J
lim ‘(ЬУД
/ (^Z- 0
2з
s24-a'2 °
Умножим теперь это уравнение на елх Z-i cos a at da и интегрируем по
а от — оо до +оо; причем не забудем, что надо брать величины Л, беско-
нечно близкие к корням $к; следовательно, в множителе cos aat е*х
можно положить a = {В*, так как мы этим изменим элемент интеграла беско-
нечно мало. Переходим к пределу и получаем
4-со +оо
cos a aZ (*-•> К-i / (?) dl da =
—ОО —00
4-со
~ 2 I™ cos
&=— 00
ибо dx = da'.
X (fi/, У—1) ( 2s da'
p'Uy~i) ? 72+ a'2
~ • к
$41] ИЗЛОЖЕНИЕ МЕТОДА ЦА ПРИМЕРЕ УРАВНЕНИЯ КОЛЕБАНИЯ СТРУНЫ 119
Ясно теперь, что
2
-г*
zda*
s2 _}_ а'2
, +8#
tg(j) ] =2 (arctg^ + arctg^)
-тл
и, следовательно,
o , ,
C 2s da o
J s* 4- a'2 "" TC*
Значит,
£
2к
'Г'"
( cos aat V"”1 / (?) dz da == У cos a%teB*x K-i . —yfe z—<
J J	.. „	h' Wk V - 1)
Но мы имеем
e№ cos $kX	]/* __ 1 sin 3/cZ = cos + V — 1 sin ,
X(^/-l) = kgV-1) =
I	I
= ekn K—i	e“₽*z K—i f ^z) dz — e^kv> J'4"”*1	/ (z) dz,
о	0
а так как
eAn r=i==(— i)k9
TO
I
x (?* |/"2П) = (-1)* 5/(2)[e-₽^>r=I-e₽*»K=T]dz =
0
I
= — (— 1)* 2 }/^l sin -p- / (z) dz.
о
Вместе с тем,
p.’(h) = I (ehl + e-M).
Значит,
(3, ]f~l) = I (e‘^	4- e~ г₽* 1^) = 21 cos ^kl = 21 cos b = 21 (- 1)*
Следовательно,
2<fe»5Ei>
v будет
-i t cos actt еа(ж-£) f (J) dz da =
2k j J
—GO —OO
4-00	«__ I
= — 2 C0S	(cos fax + V — 1 sin fikx) - / (z) sin -p" ^z-
k»—oo	0
.120 ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ
[Гл. *Ц1
Соединяя соответствующие члены для + & и — к вместе, получим
4-со 4-со
—со —оо	,
оо	t
2 Vi akitt • kitx С . kitz , z х ,
=t2j cos ~sin ~ ysm ~т' (z)	1
к=0	О
Совершенно так же мы найдем
4-со 4-оо
* С С «inert е.(х-5) r=i F (?) dtdi =
2ait j J a	x '
—op —op
,	-	«л e knot	»
°° sin_______	1
2 vi I • kitx f . kitz 7? ✓ \ 7
—p >. ------j----sin -y- \ sin — г (z) dz =
al	kit	I J I v '
A = 0	T	0
co	I
'	2 VI 1 • kit at . kitx Г n , 4 . kr.z .
= — 5 -j- sm sm -r- \ F (z) sin -p dz-
an Zj к I	I j v f I
A=1	Q
Отсюда будет
co	I
2' vi kit at . kitx C , / \ • kizz , .
й -y 2j cos ~t~ sin ~ \ / w sln т dz +
A=0	0
co	I
. 2 vi 1 • kit at . kitx С z? / \ • kitz ,
4-----Л т sin —r- sin ~T- \ F (z) sm -p dz.
ait к I I j	I
k=Q	0
Эта величина и удовлетворяет всем условиям:
во-первых — уравнению (1);
во-вторых, при Z = 0 величина и обращается в /(я), ибо она так со-
ставлена по теореме Фурье, и функция /(ж) остается совершенно произволь-
ной от х = 0 до х = 1;
в-третьих, производная при t — 0 обращается подобным же обра-
зом в F (х)у которое также задано от х = 0 до х = 1\
в четвертых, при я = 0 и при ж = / будет н = 0 при всяком t.
Mt>i видим отсюда следующее представление произвольной функции f(x)
между х — 0 и х = Z:
со	I
/ (я) = 2 sin / (z) sin dz>
a=i	о
т. е. известный ряд Фурье.
§ 42. Свойства колебательного движения струны. Скажем несколько
слов о различных свойствах колеблющейся струны.
Во-первых, предположим, что первоначальное положение струны есть
прямая ОА (фиг. 18) и что концы ее О и А закреплены.
Вначале каждая точка М струны О А выводится из первоначального
положения произвольно, так что ее перемещение как по величине, так и
по направлению задается совершенно произвольным образом. Возьмем ОР = х\
тогда можно перемещение МР разложить на три: PR = v, PQ = w, PN = и\
понятно, что uf и, w будут наперед заданы как функции ОР = х, если
только РМ задано по величине и направлению. Каждое из трех составляю-
$ 42]
СВОЙСТВА КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ СТРУНЫ
12Г
щих перемещений удовлетворяет дифференциальному уравнению того же*
вида, именно:
д2и 9 д2и
--- — /7“ ---
dt* дхг ’
д2иг_ 2
dfi~a дх*'
dt* дх* ’
где
Р
причем Z — длина струны О А, 72 — вес ее, ш—натяжение в прямом состоя-
нии О А, и 62=~^, где q = sE> причем s есть площадь сечения струны
и Е — модуль упругости ее материала»
Мы рассматривали только первое из этих уравнений, предполагая, что*
точке М сообщена также произвольная по величине и направлению ско-
рость, которую мы разлагаем по тем же осям, так что движение точки М
определяется совокупным движением
точек N9 Q и R.
Мы, следовательно, будем иметь
заданными наперед
PN = u — f(x)
и скорость точки N, которая пусть
будет F(x).
Возьмем простейший случай, к(
ж = /, иначе говоря, что точка N двг
Фиг. 18.
F (#)==() для всех х от я —0 до*
я, не получив вначале никакого
толчка.
Тогда, делая в нашем решении F(z) = 0flnn всякого 2, мы получим для
и такую формулу:
оо
kit at . kitx
Ак COS -j— SIH — ,
k=l
где
i
Ak = 5- f(z) sin dz-
4 J	4
0
Возьмем один член этого ряда
. kit at . kitx
ик = Ак cos -j— sin — ,
так что
U = Uy + U2 + И3 + •. • + uk + .. .
Член uk дает свой звук, выражающийся известным тоном, которому
соответствует определенное число колебаний в единицу времени»
Заметим, что все аргументы синусов и косинусов в наших формулах
выражены отвлеченными числами. За единицу времени можно принять
1 сек., при перемене же единицы времени t умножилось бы на некоторый
постоянный множитель, который отнесем к а.
Пусть есть время полного колебания, т. е. такое, что, придав его
к i, мы получим ту же самую величину uk и ее производной, какие имели
до этой прибавки. Очевидно, что для этого должно быть
klW	О гттгтх	2*
—	= или тл=-^.
122 ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ (Тл. HI
Обозначим через пк число колебаний в 1 сек., так что
1
Это число и определяет тон (высоту звука).
Заметим теперь, что если бы мы взяли длину струны
Ч’о дле нее получили бы член
D T^at . та?
= //j COS sin jr »
где
I'
= 2 /(z)sin ™dz.
e
Понятно, что Di можно представить так:
о кп al . kitx
и, -== cos -у— sm —,
и, следовательно, число колебаний, которое дает звук vx, будет одинаково
•с тем, которое дает звук ик для струны I.
Таким образом, тон ик и тон —один и тот же.
Тон
.	2кп at . 2кпх
U2k = OOS —  81П —j—
называют октавою тона, соответствующего члену в*, причем струна делает
вдвое больше колебаний, нежели пк.
Тон, число колебаний которого вчетверо больше против пк, называют
двойною октавою. 1 акже звук, которому соответствует число колебаний
в 8 раз больше соответствующего ик9 на-
зывается тройною октавою.
1^^^^	Звук, число колебаний которого бу-
~ дет 2 пк9 называют терцией тона ик. Тон
О	з
фиг 19	число колебаний которого есть пк9 на-
зывается квинтою тона ик. Этот послед-
ний со своей терцией, квинтой и октавой составляет так называемый ма-
жорный аккорд.
Возьмем пример, который иллюстрировал бы наш вопрос о сотрясении
струны.
Пусть первоначальное отклонение нашей струны составляет ломаную
ОСА (фиг. 19), где СВ есть произвольное перемещение середины В нашей
струны ОА = 19 и она не получила никаких толчков.
Составим f(x) и сделаем СВ = $-9 тогда
f(x)=^X ОТ Х = 0 ДО X = Y
н, напротив,
28	I
f(x) — 2$—тх от	ДР х~1.
4	Л
§42]
СВОЙСТВА КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ СТРУНЫ
123
Чтобы вычислить Аь составляем сперва интегралы
1 Г I . 7mz
= т- j—sm-7----z cos
г l . kit I kit
— 19 a Sin "7Г ~zCi cos ~ a
о k2it2 2 2kit 2 ’
I
C z . kitz j I ,	, I . kit . I kit
- } T Sin T dz = 008	+ W Sin 2 “ 2/S C08^
L
2
I
C . kitz j	l Г kitz 11	I	kit
^Sin-Td2=-^|_COS-Tj г =-^C08^+^cOS 2
Г
Умножив эти величины на ~ и сложив, получим
А 83 kit
Л*=1^81П2 *
Сделаем к = 2/ (т. е* Л —число четное); тогда
Л2/- = 0.
Если же к = 2/ + 1 (т. е. к — нечетное), то
^2/+1 = (2/+ 1)2 к2 (“
Таким образом, будет
88 Г	• ях 1 3ratt . Эта , 1 5n<zt . 5тс 1
И = -Г COS -j- Sin -j- — 55 COS -7— Sin -j- + -J COS -7— sin -7-...	.
It*	I	l О	I	I I)	I	I	J
Тон, соответствующий первому члену, называется основным, тогда со-
ответствующий второму будет октава квинты, третьему — двойная октава
терции и т. д.
Можно выбрать функцию f(x) так, что в ряде и останется только один
член, например и*. Для этого достаточно положить
/ (х) — A sin ,
тогда ясно, что
о
все же члены где i не равно к, будут 0.
Дав вышеприведенное изложение первого метода Пуассона интегриро-
вания линейных дифференциальных уравнений с частными производными
при граничных условиях, А. Н. Коркин рекомендовал применить этот ме-
тод к ряду примеров, решенных Пуассоном частью этим методом и отно-
сящихся к теории распространения тепла в пруте, частью —его вторым
124 ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВЙИ НА ГРАНИЦАХ
[Гл. Ht
методом, который мы изложим в главе V нашего курса, и относящихся к ко- ,
лебанию струны.
Мы дадим здесь некоторые из этих примеров, чтобы на них еще
подробнее выяснился первый метод Пуассона. .
§43. Задача 1. Интегрировать уравнение
d2u____ 2 d2u
<№"~а dtf
(1)
при условиях: 1) чтобы при Z = 0
и обращалось в f(x),
ъ >
и 2) чтобы обращалось в 0 при « = 0 и при х — 1 при всяком t.
Функции f (х) и F (х) заданы на протяжении от ж = 0 до x = Z.
Решение. Будем следовать вполне изложенному методу Пуассона:
1) Составляем решение и, удовлетворяющее уравнению (1) и началь-
ным (t = 0) условиям; оно попрежнему будет
со оо
а—-^- \ { cos(Kxtea<x~i'>y-1f(i)dida +
J J
—со —оо
4-оо 4-оо
&TZCL J J	®
—oo —oo	♦
(2)
2) Полагаем x — $ = z и соединяем члены, относящиеся к +z и -г; по-
прежнему имеем
4-°о ©о
1 С	с
и = — \ da \ cos ait cos az [/ (ж + z) 4- / (z — z)] dz 4-
—oo	0
4-00 oo
+ Д; \ da sin а at cos az [F (ж 4- z) 4- F (ж — z)]dz.
1	J	Gt
—co	о
3)	Составляем граничные условия (z = 0 и x = l).
Имеем
4-со со
du 1 С С , л Г д/ (я + z) , <9/ (ж — г) 1 , , ,
-з- = -з- \ \ cos aaZ cos az	—<- 4-	dz da 4-
dx 2k J j	L	dx J 1
—oo 0
sin ant
------cos az
—oo 0
dx 1 dx J
и, заметив, что
df (x 4- z) = df (x + z)
dx	dz
dF (x + z)_dF (x 4- z)
dx	dz
df (x — z)_ df (x — z)
dx	dz	’
dF (x — z)__ dF (x — z)
dx	dz
ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ СТРУНЫ
125
$43]
имеем
du 1 С С	Г д/ (я + z) df (х — z) 1 , л ,
— = \ \ cos aat cos az	----—- I dz da 4-
dx 2я J J	L dz	dz J	1
—oo Q
4-oo oo
, 1 С Г sin aat	Г dF (x + z) dF (x — z) 1 д j
+ s— \ \-------cos az —\	’-------dz da;
2ra J J a.	, L dz	dz J *
—oo 0
полагаем x = 0; получаем условие
d/(z)	d/(-z) n
dz • dz v
и
dF (z) dF (—z) n
dz	dx ’
откуда следует
/(z)-/(-z) = C1 и F(z)-F(-z) = C2,
где и C2 —произвольные постоянные. Эти постоянные могут быть только О,
ибо, переменив z на — z, имеем
— (7i = (7i и —С*2 == 6/2»
Иштак,
/(z) —/( —z)=0.	(3)
’ Совершенно так же получим
/(Z + z)-/(Z-z) = O.	(4)
4)	Вычисляем функции p(h) и q(k):
СО
р(Л) = e~hzf(z)dz
о
п
q (h) = ehzf (z) dz.
о
Из уравнения (3), совершенно так же, как и в § 41, имеем
Р (й) — ^hzf ( — z)dz = Qt
о
или иначе
р(Л) + ?(Л) = О.	(3')
Затем из уравнения (4) выводим
e~hzf(l + z) dz —• е" fe/ (I — z)dz = О,
о	6
или
i	i
^ыр (Л)	(Л) = ehl e~hzf (z) dz + e^hl ehzf (z) dz, (4')
о	о
126
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ
(Гл.Ш
отсюда следует
i	t
ehl e~hzf (z) dz 4- e~hl ehzf(z)dz
P(h) = —q (ty =	— eftl _ e_hl 	=
(5)
при само собою понятном обозначении.
Таким образом,
/1Л х W
* ' ’ И W
(6)
5)	Чтобы найти интеграл
+»
—оо
ищем предел разности
lim [р (г + а )/ — 1) — q (в — а	=
е->0
оо	—оо
=	(z) dz --	(2) dz —
о	о
— lim Г х(£ + а . х (в —• а К^Т)
причем замечаем, что X (Л) есть функция четная, р. (Л) — нечетная; следова-
тельно, разыскиваемый предел равен нулю для всех тех значений а, при
которых рь (а |/ — 1) не равно нулю.
Таким образом, получаем уравнение
На К771) = 0,
но
[1(а	— 1) = е1лУ~~^—	= 2 ]/~ — IsinZa,
значит,
sin la —О или 1а — кк,
причем Л: —любое целое, положительное или отрицательное Число или нуль»
Полагаем попрежнему Р/с = ~ и, поступая совершенно так же, как
в § 41, и заметив, что (i'(Л) — функция нечетная, найдем, что интеграл
4-00
—оо
вообще равен нулю, и лишь в сопредельности с р* будет
С е-а5.Г-1 / ($) di = lim	’
J	е->0 ц' (З/г V — 1)
‘_______+___________1
I/ 1 s — а' 1

2е
в2 4-а'2*
J? 431
ИНТЕГРИРОВАНИЕУРАВНЕНИЯ ДВИЖЕНИЯ СТРУНЫ
127
Умножаем на cosaaZ •	интегрируем от —со до + оо; полу-
чаем
-f-оо 4-оо
с os алл	(?) di da =
—ОО —00
и, заметив, что
= lim V cos a?*Z e$k
*->0
*(fo У72!) С 2s dz'
h2 + “'2
“5a
+'к
lim 5 £4^ = 2к,
-«л
получим
cos aaZ	у (J) dt == 2
—oo	k=— oo
cos afikt	.
/ (fc /-1)
Мы, имеем
X (pfc/ -1) = e1^-1	/(z) dz +	£ e^kV^f (z) dz =
0	0
I
= (cos l$k + V— 1 Sin Z3A) (cos z?/c —	— 1 sin / (2) dz +
0
1
+ (cos ZP/c — jZ — 1 sin ZpA)	(cos z3k + ]/ — 1 sin z$k) f (2) dz,
0
HO
Z[3a = Atc,
так что
cos lfik = (— 1)Л, sin l^k = 0,
и мы получим
___________________	i	1
X (?k У ^1) == (- l)fc 2 cos z3k / (z) dz = (- l)fc 2 / (z) cos dz.
0	0
Вместе с тем,
р/ (Л) — Z (ehl + е~П1),
значит,
p' (^k y~i) = I (e'₽*r=T +	= 21 cos /?* = (- l)fc 21
и, следовательно, будет
4-со 4-oo
M ( cosaaf	f(i)dida —
J J
—eo —oo
j	кт^У — 1	I
KTtat ------- 1 r kitz , z 4 ,
cos —j~ e	1	-j-\ cos — f (z) dz =2
k^—oo	0
*“	I	oo	I
1 С ил л-	<	2	vi	Ariw;	Г	kitz	ttxl
\ f\z)dz	+	у	Zi cos — cos —	\ cos —	f (z) dz*
о	A=1	0
128
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ (Гл. III
Точно так же будет
4-оо 4-оо
1 г	г
2ra J	J	а	' '
— 00 —00
. knot , _г—_
sin —-— кпху 1
-тг-е 1
кп
Г
C0S"-pF(z) dz =
•	. fatal	>
с	о© sin  	*
= ^f(z)dz + /я2 —cos — \F(z)cos^dz.
О	/с=1	О
Таким образом, окончательно имеем
« = У [/(z) + tF(z)]dz + 2 4*cos^cos^ +
0	k«l
. 2 XI 1 D • ®Zc7Ut fatx
+^2jTBfcSln—COS"T’
/c«l
причем
i
Ak = 7-^ / (z) cos	dz,
о
i
Bk = ^F(z) cos^dz..
Так как при t = 0 величина и обращается в /(ж), то полученная фор-
мула дает такое представление произвольной функции:
I	ео	I
f (х) = j / (х) dx 4- y 2 cos	/ (z) cos	dz.
О	А=1	О
Это есть известный тригонометрический ряд косинусов»
Задача 2» В § 495 своей «Механики» Пуассон приводит еще одно
решение того же уравнения:
д*и 9 д2и
а дх*>
мхри следующих условиях:
при Г = 0 и должно обращаться в /(ж),
>	7 = 0 g >	>	>Р(ж),
>	х = 0 и должно быть равно 0
, ди	л > при всяком t.
>	я = zz >	>	> О
от	)
Требуется интегрировать предложенное уравнение.
§ 43]ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ СТРУНЫ 129
Взяв и, как и раньше, положив х— С = 2, имеем
v	4-оо оо
1 С С 1
и =	\ \ — cos ааЛ cos az [/ (х + z) + f (х — z)j dz da 4-
—oo 0	'
+ <^	cos az [F (®-f-z) + F(x—z)]dzda',
—oo 0-
полагаем я = 0 и получаем первые условия:
/(2) + f(-z)~0 й F(2)+F(-z) = O.	(1)
Взяв производную по х, т. е. , и заменив дифференцирование по х
дифференцированием по z, получим
df(l + z) W-z) А
dz . dz v
и	• : ч . /
dF (14- z) dF (I z) ~
dz	dz
f(l + z)~f(l-z) = C1 и F(l + z)-F(l-t)=C2.
Заменив z на — z, видим что C± = C2 =0, и вторые условия будут
/(Z + z)-/(Z-z) = O и, F(l + z)~-F(l-z) = r).	(2)
Берем сперва условия, относящиеся к f(z), и составляем функции
p(h) и q(h):
ОО
р (Л) = e~hzf (z) dz,
0
—00
q (Л) = ehzf (z) dz.
0	.	?
На основании условий (1) и (2), получаем, подобно предыдущему, урав-
нения
Р(Л)-?(Л) = о,
1	1
ehlp (h) + e~hlq (Л) = ehl< e~h7f (z) dz + e~~hl ehzf (2) dz,
. о	0
откуда
е^г
P(h) = q(h) = —
I ,	I
e~h3f(z)dz 4- eh*f(z)dz
0 *_______ 0_____X (7г)
е^гу. (7г)
Как видно, обе функции к (Л) и р. (Л) четные.
Уравнение р. (а У — 1) -= 0 будет
gZ<x/-i	__ 2~ с os Za 4
9 А.Н. Крылов
130 ИНТЕГРИРОВАНИЕ УРАВНЕНИИ ПРИ УСЛОВИИНАГРАНИЦАХ (Гл. IH
откуда	,	 г .
a = (2* + !^ = ₽fc.	(3)
Далее, совершенно подобно предыдущему, получим
'* A	/СО <Оа = 2 ^os a$kt
—оо	А=—оо	11 Vp/cV-’-l/
и, подставляя в выражения л (Л):и и/ (Л) вместо h его величину
•г ₽*У^Л/—1-;;:
получим . .	'	/	Л г	'
k(₽ft/ZZl) = e^r^^-^rr7Wdz + e-'₽^ ^e^^fiz)dz = -
О	о
= -/Зй (-1)* $ (ЛгК=Т - е-^2^) / (2) dz =
О
= (- 1)к 2 sin (2*+/)ТС? / («) dz>
О
< (Л) = I (е™ - е~ *9, [X' (Р* У ^Т) = 2Z У ^31 sin <!Ц1>2 = 21У =7 (-1)*,
и, следовательно,
X(pfc/=1) _	1 С . (2fe + l)K3 ,	,
Hfe/3-i)-(/=irin 2/ f^dz
и, значит, интеграл
+ со
1 cos aat	f(^dHda =
(2fc + l)<uct <2А-Ц>»жК~Т	1	(2Л + 1)лз,
- 3 cosL—2Г—е	Г7^13/( ) ^r~dz-
к= -^оо	О
Соединяя члены, которые соответствуют значениям к, равным
О и —Г,
1 и -2,
’ ' -	•	' 2 и -3,
i — 1 и — i,
получим
+ оо
1 cos a« e4*-vV^ f (5) dzdi =
^co
-1 2 cos (2t-^J sin J f (z) sin dz.
i=l	0
8 441 - ЗАДАЧА З^Я:. УРАВНЕНИЯ РАСПРОСТРАНЕНИЯ ТЕПЛА В ПРУТЕ 13j,
Совершенно так же найдем
_1_ с с sjE^ea(x-nr=iF(5)^da=-
2л« J J а
. (2$ — 1) лад	— г /
С in -__- 	1
1 -О	2/	2 .24 — 1 СпМ • 2« —1	,
= 7 2 —(2Z-1T— • 7 sm-2/-	J F <2) SW ~ИГ™ dz
21	*
и, следовательно, окончательно будет
ос.	I
2 VI 24 — 1	, . 21 — 1 С , , . . (24 — 1)	, .
U —-j- 7, COS —2f— Sln 2~ кх \ / Vs) 8Щ .21 nz °'z +
1«»1	О
оо	Г
, 4 х? 1	24 — 1	, . 24 — 1 С . 24 — 1	,
+ ^S2'4^1COS“2T’taZSin ~2T™}F <Z>Sln ~2Г ^ZdZ‘
#	'	i«=l	О
Это есть формула Пуассона, приведенная в его «Механике».
§ 44. Задача 3. Уравнение, представляющее распространение тепла
в пруте, есть следующее:
du	2.	/А\
^ = а TTz — bu,	(1}
dt	dx2	' 1
где а и ft —некоторые постоянные.
Начальное условие такое: при Z = 0 должно быть
м = /(х).	(2)
Граничные же условия суть
при всяком Z,	(3)
где Pj ‘и 32 —также некоторые постоянные. :
Требуется интегрировать это уравнение при вышеприведенных началь-
ном и граничных условиях.
Мы приводим это уравнение не~ столько ради тех приложений, кото-
рые оно имеет, сколько ввиду замечательной формулы для цредставления
произвольной функции в виде ряда, к которой оно приводит и которая
имеет важное значение и понадобится нам в вопросах, имеющих чисто
прикладное значение.	. .
Поступая по общему правилу, составляем сперва обыкновенное урав-
нение
~х + pitt = 0	при я = +Z
—	= 0	ЙРИ — Z
^ + (а2а2 + 6)Г = 0	(4)
и, найдя его общий интеграл
определяем постоянную Сг так, чтобы Т при t = 0 обращалось в 1, что дает
Сг = 1, так что
Тх —	— €-bt е-а 2*2t
9*
132
ИНТЕГРИРОВАНИЕ УРАВНЕНИИ ПРИ УСЛОВИИ НА ГРАНИЦАХ [Гл. III
и, таким образом, будет
и == “• e~bt e-a2a2f cog a у (£) & (fa*	(6)
—оо О
Полагаем попрежнему (5 — x) = z; тогда
u=^e~bl e-“2a2< cos az f (х + z) dz da.	(6')
— oo 0
Составляем теперь количества
ди । о
и
ди о
di
чтобы воспользоваться граничными условиями:
-f-OO 00
£ + М = V 5 5 e<,2a2< cos az [ ~/(аг+г) + Vif (ж + з) ] dz d*>
—оо О
4-со оо
g _ р2н = J	е-“2»2' cos az [	— ₽2/ (* + z) ] dz da.
—со О-
Соединив элементы, относящиеся к и —z, получим
^ + Р1Й = £±? Fe-aWzcosa2[^±£)+2H^) +
тс J J	[ дх 1 дх 1
О О
+ ?i/(3;+2) + ?i/(3: — г)] dzda, (7)
дх г й	тс J J	L ох	ох
О О
-* ₽г/ (я + я) — М (# — 2) J dz da. (8)
Полагая в уравнении (7) х = +1 и в уравнении (8) х = — I на основа-
нии граничных условий, заменив предварительно дифференцирование по
х дифференцированием по z, получим
£^H)^(^ + Pi/(Z + 2) + pi/(/_2) = Oi	{9)
J	UZ	Utt
df (^z-— - ~-(gF~- - Рг/ (- ^ + Z) - рг/ (- / -. z) = 0.	(10)
(73	(73
Множим первое уравнение на	интегрируем от z = 0 до z—оо
и вводим рбозначения
00	--СО
p(h) — 5 е‘тйг f(z)dz, q (h) = ehz f (z) dz.
.	о	о
$ 441
ЗАДАЧА 3-Я: УРАВНЕНИЯ РАСПРОСТРАНЕНИЯ ТЕПЛА В ПРУТЕ
133
Тогда замечаем, что
e~hz^dz~ &z == [/ (^ + 2)	e-hz / (/ + z) dz.~
о	’	9
оо	' I
= —f(t)+h^ehl e~hv f(y)dy = — f(l) + hehl p(h)^—hehl ^e~hzf(z)dt,
i	...	о
J e-ftz	dz = [f(l- z) е-лг]“ + h e~^ f(l-z)dz =
0	0
oo	I
= — f{l) — he~hl ehv f(y)dy= —f(J) —he~hl q(h) + he ~hl ehz f (z) dz,
о	о
co	oo	'	I
e~hz f(l + z)dz=^	f (y) dy = ehl p(h) — ehl e~h2 f (z) dz,
oi	о
co	—oo	—oo
e~hz f(/ — z)dz= —	/ (y) dy—— e~hl ehz f (z) dz —
о	i	i
i
— — e-hl q (h)+e~hl ^ehzf(z)dz.
о
Таким образом, из уравнения (9) получаем
i
(А + РО ehl р (А) + (А - £х) e~hl q (h) = (h + PO e*1 e~hz / (z) dz +
о
i
+ (A — px) e~hl ehz / (z) dz.
о
Уравнение (10) дает подобное же уравнение, которое получится при
перемене / на — I и pt на — р2, и будет
(А -р2) е-м р (А) + (А + р2) е** q (А) =
-I	-I
= (h — р2) e~hl e~hz / (z) dz + (А + р2) ehl ^hz f (^) dz.
о	о
Решая эти уравнения относительно p(h) и #(А), получим
4 7	И (А)
а '	Н(-А)
(И)
причем
). (А) = (h + РО (Л + р2)	$ е-*2 f (z) dz - (Л - pj (h - p2) e~^\ e»2 f (z) dz -|-
0	0
+<
+ (A + p2)(A-p1) ^2f{z)dz,
И (A) = (Л + Pi) (Л + p2)	‘-{h- px) (h - p2) e-2A«.
134 ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ [Гл. Ш
Таким образом, будет
+С«г-1 /(2)</г=НЮ г	1
3	.-»0 L|»(a)<—1 + s) n(a}<—1—s)J
—co
йбо этот интеграл равен
lim [/> (з + a — 1) — q (з — a]/' — 1)].
е->0
Составляем уравнение
И(а/~1) = О;
оно будет
ft (а/^1) = (а/“1 + ₽i) (а/^Т+ р2)
— (aj/ — 1 —р1)(а|/г — 1 —р2) е—2a-zV-~5 =
e (₽j₽2 — а® + (a₽i +	— 1) (cos 2aZ + |/ — 1 sin 2aZ) —
—-(?iPa — a2 — («pj + a[32) j/" — 1) (cos 2al — У — lsin2aZ) =
= 2 У — 1 [a (fSj + p2) cos 2aZ + (ргр2 — a2) sin 2aZ].
Следовательно, уравнение
^У~=л)=о
будет
(Pi + р2) a cos 2aZ + (PiB2 — a2) sin 2aZ = 0.	(12)
Это уравнение имеет очевидный корень a = 0, который мы обозначим
через (о0. Обозначим его положительные корни через
шх, (о2, *.юд, ..
тогда легко видеть, что и
-О)п — со2, . .. , — о)д, ...
будут также корни уравнения (12). Обозначим их через
О)-!, О)-2, «о»,	....
Мы видели, что интеграл
e- azV~-i J (z) dz
-со
вообще равен нулю и лишь в сопредельности с-<»* будет
С е-мУ-1 j dz —	]jm Г 1
J	Н' (<»k/- 1) е->0 Ls +“ J
—со
где а'— бесконечно малая величина, и при интегрировании по а надо брать
лишь элементы интеграла, смежные с каждым из корней мд, и считать
* 44] ЗАДАЧА 3-Я: УРАВНЕНИЯ РАСПРОСТРАНЕНИЯ ТЕПЛА В ПРУТЕ 135
da = da'; таким образом будет
и = ~ e~bt e-a2a2f еа(я-8)1<-1 f	=
— ОО—ОО
С +°°	г—-	^к
= *г« у е-а^еш^Г^.И<->*У-£) lim f 2^
2тс	у/ —1) J e2-f-a 2
k=-oo	н к лг >	-Yjfe
Но мы видели, что •
"...	.^к	,
£ 2з
—	lim \ »-, 7g da.' = 2тс<
J в2.4- а'8
Следовательно, будет	, .
и = е-м у е~а2*4'. х (‘“ft/— о	(13)
При этом ? '	. ,
.	-vi
К (а*А]/^ — 1)=[(₽1р2 — <“*) cos 2a>*Z—(^ 7 р2) 0)* sin 2ш*Z] g-^zK^i / (z) dz —
-I
+ 1
 -[№+«>a2) + (Pl — ₽2> <»* /-1] $ e-^^f(z)dz,
-I
H-' («/Д/ —1)= 2 (Pi +	— 2Za>^jcos2(»feZ —
— 4(0^ (1 ~|“ /pi -£• /рг) sin 2a)jfcZ =. 2iRk<> (14)
Выражение и может быть представлено в ином виде, для чего надо
заметить, что
<1>ь о>0 = 0, ц' (—	— 1) =р' (o>fcj/—1),
и соединить члены, соответствующие +Д и —Л; тогда будет
u = e~bt У е_а2<ок'• ---— X-
. Л=о . ..
X [Х(«к|<'=Л)е“*а!1<^1 + Х(_Юк)/''=Г1)е-шьхГ^].	(15)
Выражение -. •	.
вещественное; преобразовав выражение в [ ], увидим, что оно также веще-
ственное и равно следующей величине:
[... ] = 2 | [(Р1Рг— <»|) cos 2шк1 —	+ ₽2) to*sin 2<»*Z — РхРа-to«] х
+i	+z
X ^/(z)cOSa)*Z.<Zz + (Pi -i-P2)<ofc^ /(2)sin4»*zdzj COSa)*® +
-?	-z
+ 2 {[(PiPe—<“^cos2e>*Z —(p1 + p2)e>*sinHa>*/4-Pip24-e>|]x	(16)
X ^/^sinZOfcZZZz-fr^! —p2)x»* ^/(zJCOStofcZzZzlsin®*®^! e ;
— I	—I
~ J =^2Pkcoswkx + 2Qksinwkx.
136
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ’ [Гл. 111^
^cosm^rrsin ,	(17)
Подставляя в формулу (15), получим тот результат, который дает
Пуассон в своем мему ape «Sur la distribution de la chaleur dans les corps
solides», а именно:
и == e~bt e_<x2<0«f
причем Pkt Qk и ftk имеют вышеприведенные значения. z	*
Предлагается в виде задачи проверить, что найденная величина • и
удовлетворяет как уравнению (1)\ так и условиям (3). Что же касается
условия (2), т. е. что при Z = 0 имеет место равенство
м = /(ж),	.	•
иначе
/(ж)= У fs^costBfca:+b-sino>fcxV	(18)
' \ £1к	Лк	у
/с=0
причем есть положительный корень уравнения
(Pi + р2)ш cos 2Zo> + (Pi Р2 — w2) sin 2Z<o = 0
и
^A = [(P1P2 —o)2)cos2Za)/c—(p1+p2)0)/cSin2Za)/£ — p1p2 — (0i]X	• .
x $ / (y) cos (О* у dy + (p! — p2) <oA / (y) sin 0)A у dy,
—I	-i
Qk == [(Pi P2 — °*2) cos 2Zo)jt — (Pi + p2) &k sin 2Z<i)fc + Pj p2 + X
-H '	-h
X /(yJsin wft^tZy + p! —p2)«)A f(y) cos^kydy
—i	—i
и
Rk = [(Pl + p2) + 2Z (Pi p2 — 0)2)] cos 2Zo)fc — [2 + 21 (Pl + p2)] 0)ft sin 2Za)Zo
то по поводу этого равенства Пуассон говорит: «... так как формула (18)
есть необходимое следствие нашего анализа, то не может быть сомнения
в ее справедливости, но было бы затруднительно получить эту формулу
непосредственно или проверить ее во. всей ее. общности».
Необходимо при этом заметить, что функция f(x) представляется этою
формулою лишь между пределами х =’ — Z до х = + Л Чтобы формула имела
место и при пределах, необходимо, чтобы функция f (х) удовлетворяла
уравнениям
^У^ + М(я)—о при. X=+1,
’	;	ПрИ Х=— I. .
§ 45. Мы остановимся на замечательнейшем случае предыдущей задачи.
Именно» положим, что р2 = оо. Тогда второе из уравнений (3) будет
и = 0 при х = — L
§ 45] ЗАДАЧА 3-Я: УРАВНЕНИЯ РАСПРОСТРАНЕНИЯ ТЕПЛА В ПРУТЕ 137
Уравнение, определяющее корни о, по разделении на р2 и положении
₽2 = оо, будет
pj sin 2Zu) + со cos 2Zu) == О	(19)
и затем будет
+ i	+z
(₽i cos 21<»к — <лх sin 21<лк - fJJ / (у) cos у dy — f (у) sin ci>fc у dy
Rk	(1 4- 2ZpJ cos 2Z<d£ — 2Zo)fc sin 21&к	’ ffl))
+i л -  7	+I
(Pi cos 2Z(0fe — xbk sin2l<s>k — p2) f (y) siKuk ydy ък ?' / (у) cos ^ydy
:__________-«...........: z2n
Rk	(Ц-2/pj cos2Zo>fc — -2/u)fc sin 2/u>fc	*
Эти величины и надо бы подставить как в выражение для и, так
и в формулу (18). Но результат примет более простой вид, если перенести
начало в ту точку, где fz = O, т. е. надо написать хх— I вместо х и уА — 1
вместо у, вместо же функции / (у) = / (j/i — 0 будем просто писать /(yj.
Тогда выражение
Рк cos а? 4- Q/c gin х__
Rk
. (Рк cos ^kl — Qk sin 0>fc Z) cos <О^Х 4- (Pk sin <ofc I 4-	cos a>k I) sin <ak
на основании уравнения (19) может быть упрощено, именно, будет
Рк cos b&k — Qk sin Ao* = 0,
и после простых преобразований получим
PkS<n.kl + Qkc^ = 2(Й + 4)	С у (у) Sinу dy,
Rk	₽, + 21 (Р? + <»Ь J,w кУ У'
так что величина и будет
оо 2	2	—a2u>2f
а = 2е-ы 2	sin a>fc х / (у) sin <»к у dy,	(22)
kcl	0
а, соответственно ей, формула (18) примет вид
о°	2	2	21
/ (л:) = 2 2 ,	' sin w* х V (У')sin ^У dy. (23)
Формулы (18) и (23), представляющие произвольную функцию в виде
ряда, расположенного по синусам и косинусам дуг, зависящих от корней
трансцендентного уравнения, составляют как бы обобщения тригонометри-
ческих рядов Фурье, и с подобными рядами нам не раз еще придется иметь
дело.
ГЛАВА IV
ИНТЕГРИРОВАНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ
С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПРИ УСЛОВИЯХ
НА ГРАНИЦАХ ОГРАНИЧЕННОЙ СРЕДЫ
ВТОРОЙ МЕТОД ПУАССОНА
§ 46.	Изложение метода на примере уравнения движения струны.
В своей «Механике» Пуассон применяет другой метод интегрирования
уравнений с частными производными. Этим же методом пользовался Фурье
в своей «Theorie analytique de la chaleur» и даже Эйлер, и единственно для
краткости речи будем этот метод называть «вторым методом Пуассона».
Мы изложим Этот метод йа ряде примеров, начав с простейшего,
за каковой возьмем уравнение движения струны.
Итак, положим^ что надо интегрировать уравнение
д*и___
dt* ~а
(1)
при начальных условиях: при £ = 0 должно быть
. .	и g =	,	(2)
и при граничных условиях: ,
при х = 0 должно быть и = 0 1
> ж-Z »	» ' „_Л при всякой/,	(3)
функции же / (ж) и F (х) заданы От ж=0 до х = 1.
В главе II было указано, что для всякого линейного уравнения без
последнего члена всякое решение, будучи умножено на постоянную про-
извольную, дает также решение этого уравнения, и сумма нескольких
решений есть также его решение.
Будем искать решение уравнения (1) под видом суммы, составленной
из частных решений этого уравнения и притом таких: 1) что каждое
из них в отдельности удовлетворяет граничным условиям и 2) что каждое
из них имеет вид Т • X, где Т есть функция только буквы t и X —функ-
ция только буквы х.
Итак, полагаем
	 ‘	‘ Й =.(4)
причем каждый член этой суммы, как уже сказано, удовлетворяет урав-
нению (1)...........................-	-	.
д2(ГХ)
дхг
ТХ",
§46) ИЗЛОЖЕНИЕ МЕТОДА НА ПРИМЕРЕ УРАВНЕНИЯ ДВИЖЕНИЯ СТРУНЫ 139
где значками обозначено дифференцирование каждой. из функций Т и X
по той переменной, от которой она зависит; подставляем эти величины
в уравнение (1), тогда получим равенство
Т'Х^&ТХ*.
Это равенство не иначе может иметь место, как только при условии
х Т" X”
сХт У = cons^*
Эту постоянную для удобства дальнейших выкладок обозначим через — А2;
тогда имеем-уравнения	‘
T№+a4?T = Q
И	.
Х" + Л2Х = 0,
откуда
Т = A cos akt + В sin akt	- ' >	(5)
и
X =% С cos кх + D sin кх.	(6)
Если подставить величины (5) и (6) в формулу (4), то, какие бы
ни взять значения постоянных произвольных А, В, \С\ © и к,/ сумма (4)
будет удовлетворять уравнению (1), ибо каждый ее член в отдельности
этому уравнению удовлетворяет. .
Но второе наше требование состоит в том, чтобы каждый член в от-
дельности удовлетворял граничным условиям, т. е. чтобы при всяком
значении I было
Т(г)Х(0) = 0 и T(0X(Z) = 0,
т. е.
-	Х(0)^0 и X(Z) = 0.
vДелая х=0ия = / в выражении Х> получаем
С = 0, .
D sin kl» О.
Так как мы ищем решения, отличные от 0, то D не равно нулю;
значит, величина к не может быть взята произвольно, а лишь в ряду
корней уравнения
sin kl = 0,	(7)
иначе	с
kl nn,
где п —любое целое число» Итак, будет
/ к = п~ (л =1,2,3,.. .).
Отрицательных значений к брать нет надобности, ибо решения, им
соответствующие, не суть независимые от уже найденных; и, значит,
Xn = Dnsin^t	(8)
~ An cos	sin	(9)
140
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ	|Тл.'Ill
и наша сумма будет	’
оо	,	оо
amzt . ппх , vi п г, • annt • пкх
AnDnCQS — sin — + 2j BnDn3in— sin — ,
n=l	* "	n=l
где An, Bn. Dn — какие угоДнй постоянные. Так как произведения AnDn
и BnDn суть такие же постоянные произвольные, как и АпВп, то, не нару-
шая общности, можно брать f)n = l и писать:
- -  ’	- оо	:	.	оо
j	ЛПТсЬ • CLTZX .	1 "г\ • (ZTlIZt • IbTZX	/л f\\
и= >| Ancos -j- sin — + >, BnSm -j- sin у .	(10)
H — 1	.n=l"
Эта величина и удовлетворяет уравнению (1) и условиям (3).
Остается удовлетворить начальным условиям.
Делая в уравнении (10)/—0» мы должны в левой части получить / ($)
[ибо и при £ = 0 должно обратиться в /(#)]> Р правой же будет сумма
со
2Л . nizx
Ап sin -у .
П = 1
Итак, получим равенство
оо
/(«) = 2 A.sin^,	(11)
п = |
из которого и надо определить коэффициент Ап.
Чтобы этого достигнуть, поступаем так: напишем равенство
/(ж) = Altsin у + A2sin-y + 4-AAsin у- + ...	(12)
и для определения коэффициента Ап множим обе части на sin *— dx
и интегрируем в пределах от 0 до /. Тогда, в силу того, что
i
\ sin y-sm — = 0, если / п,
о
11 ’ ’
sin2 у^ dx = у ^1 — cos dx = у ,
о	-о4
получим	-
I
. .. . . Лп = 4	(13)
О
Совершенна так же, взяв производную положив £ = 0 и уравняв
полученный результат F(x), будем иметь равенство
00
Z7 /	»->	• flTZX	.
Р(Ж)= 2) —^«siny ,
П = 1
§ 46} ИЗЛОЖЕНИЕ МЕТОДА НА ПРИМЕРЕ УРАВНЕНИЯ ДВИЖЕНИЯ СТРУНЫ 141
из которого, подобно предыдущему, найдем
. .' 1 •
п	Вп = — \ F (z)sin^dz.	(14)
amt j	I	' 7
0
Переменив, во избежание путаницы, под знаками ийтегралов (13) и (14)
букву х на другую, например 5, получим:
со -	/
2 VI amtt . mtx f J . птсЕ :
cos ~~T sin ~ \ I sm aE +
n-1	о
t	n«=oo '	I
*	, 2 VI 1 • an7zt «5 nra? f
+ 2 7sin — sin~ V (?)sln7
t “	n««j[	0 t
— формулу, которую мы уже имели.
u Как видно этот прием решения быстро й без сложных выкладок привел
к цели.
Но необходимо обратить внимание на следующие обстоятельства:
1) сумма ЪТХ удовлетворяет уравнению (1) без всяких оговорок, когда
каждый ее член этому уравнению удовлетворяет, если она состоит
из конечного числа членов; когдаь же число этих членов бесконечно, то диф-
ференцирование ряда почленно допустимо лишь с известными ограниче-
ниями: надо, чтобы полученный после дифференцирования ряд был равно-
мерно сходящийся; 2) определение постоянных Ап и Вп в рассматриваемом
примере оказалось возможным произвести весьма просто, — опять-таки
предполагая, что написанное разложение возможно, что оно единственное
и что интегрирование ряда почленно допустимо.
В самом деле, если бы мы взяли, например, вместо п = 1, 2, 3, .
только четные значения п = 2,4,6, ... , то полученная сумма удовлетво-
ряла бы уравнению (1), удовлетворяла бы и граничным условиям; равен-
ство (11) написалось бы так:
, z ч л . 2га: , А . 4га; ,
f (х) = Л2 sin — + 4а $т — + .. к ,
и из него мы получили бы те же самые значения коэффициентов; между
тем равенство
/ (х) = 2 A* sin 2-^? = 4 2 sin V(s) Sin
!-=1	1-=1	О
было бы неверное, как то известно из теории тригонометрических рядов.
Необходимо брать члены, соответствующие всем положительным корням
уравнения sinA/ = O.
Необходимо заметить, что как тот, так и другой метод Пуассона
приводят к суммам, зависящим от корней того же самого трансцендент-
ного уравнения, и из первого метода было ясно видно, что непременно
надо брать члены, соответствующие всем корням, а не некоторым из них.
Это замечание необходимо иметь в виду, применяя второй метод Пуас-
сона к какой бы то ни было задаче, и от корней какого бы трансцендентного
уравнения ни зависели функции, по которым приходится разлагать задан-
ную функцию —надо брать все корни подряд.
В практических вопросах, где требуется лишь ограниченная точность,
большая часть этих затруднений теоретического характера отпадает, ибо
142
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ [Гл. ИГ.
вместо бесконечных сумм придется брать 9лишь небольшое чисдо их первых
членов, и главное затруднение будет в определении коэффициентов Ап и Bnt
если только оно не выполнится подобно вышеизложенному.
Полученное решение -> оказалось совершенно того же вида, как то,
которое дается первым методом Пуассона; между тем в главе II показан
найденный Даламбером общий интеграл предложенного уравнения в виде
п = «)	+	+ at). ;	•
Покажем связь между обоими решениями.
Так как	-	' >	-	,	>
 » >
2 cqs у at sin у ж = sin у (ж + ai) + sin — (х — at),
то первая сумма, входящая в состав .величины и, может быть написана так:
оо	со	<• 	со
' У. ЛП cos Y e/:&iB ~ Х== у У Ап sin Т (* + at) + у 5 sin (х — at),
n —1	n = l	л®1	:
причем
e
4n = у /(5)sin
а так как формула
co
2.	. nnx
Asm у-
И“1
представляет функцию / (х) в промежутке от х = 0 др х = 1 и функ-
цию — f(x) в промежутке от ж —0 до ж = — Z, для остальных же. значений
аргументов х значения функции следуют из того, что ее период есть 2Z
(фиг. 20), то, обозначив эту функцию вообще через g(x), видим, что.
оо
2’А sin У (х + at) = g (х + at).
n=l
Совершенно так же
ео
2 Ansi^{x — at)=.g{x — at)
n=l
и, значит, первый член в выражении и есть
Lg(x + at) + ±g(x-af).'
второй член в выражении и обозначим на время через v, так что
‘	 > -	е	:	ОО	>
•		2 I Вп • аптс . . niix
•	. •	—sin -f t sin -j- ,
an 2 4-J n:	L Z
n=l
причем
z?n = 45F(5)sinTd?-
0
< 46] ИЗЛОЖЕНИЕ МЕТОДА ЙА ПРИМЕРЕ УРАВНЕНИЯ ДВИЖЕНИЯ СТРУНЫ 143
Тогда» очевидно, будет
. . СО , .
n	dv VI г> nit л . nit
-лт- = >| />п cose-r at sib -г- х*
dt *	I	I ‘	......
п=1
В силу показанного выше, стоящая в правой части этого равенства
сумма может быть преобразована совершенно подобным же образом»
А так как сумма	' ‘
со .	,
. Ппх'
Вп sin -у
п®1......
представляет заданную функцию F (х) на протяжении от я = 0 до х = 1,
на протяжении же от я = 0 до х= — I функцию — F(x)t для дальнейших
же значений аргументов величины представляемой этою суммою функции
следуют из того, что ее период есть 2/, то, обозначая эту функцию вообще
через G(x), видим, что
-g- = lG(a: + a0 + |G(x-^),
снедовагельно, если обозначить вообще
ф®=НС(5)<й’
о
то будея
v = 4 Ф (х + at) — ~ Ф (х — at) + С,
2.	л
где С есть произвольная постоянная или даже произвольная функция
буквы х, а так как при Z — 0 величина и = 0, то (7 = 0 и, следовательно,
v = 4 Ф (х + at) — 4 ф (ж "" at)'
2	Л
Таким образом, имеем
« = 4 [<(« + «0 4-Ф(« + ««)] + y[g(«— а«)—-Ф(ж —	(15)
что с очевидностью показывает, что полученное решение заключается в общем,
данном Даламбером.
Эта формула решения может ’быть”с большею" наглядностью представлена
графически.	о
В самом деле, на чертеже (фиг. 20) показано графическое представление
функции g(x), когда задана на протяжении от ж = 0 до х = 1 функция
/ (х) — начальная форма струны. Ясно, что стоит только построить по данной
F(x) соответствующую ей функцию G(x) (фиг. 21) и затем по этой послед-
ней функцию Ф(я), которая пусть представится чертежом на фиг. 22,
то функции
®(®) = у[?<®) + Ф(«)]>
?(«) = т[ё'(а:) — ф(ж)]
Ал
144	. ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ
[Гл. III
сейчас же строятся, как полусумма и полуразность ординат предыдущих
кривых при той же абсциссе х.
Пусть о) (х) и ф (х) представляются чертежами на фиг» 23а и б; тогда
если c = at для рассматриваемого значения t, то, чтобы получить функцию
о (х + at) = (о (х + с),
стоит только всю кривую о) (х) продвинуть влево (в сторону отрицательных х)
на величину с, как показано пунктиром на чертеже (фиг. 24а и б); точно
так же, чтобы получить 9 (х— at) = y (x— с), стоит только продвинуть кри-
вую ср (х) на величину с вправо, как показано пунктиром.
Фиг. 20
Фиг. 21
Фиг 22
Фиг. 23а
Фиг. 236
Величина и, определяющая форму струны в момент t=—, получится,
если возьмеде сумму соответствующих ордйнат обеих, пунктирных кривых
на протяжении от х = 0 до х = Z, как изображено толстой сплошною кривой.
Предполагается в виде задачи вычертить ц для моментов
1-0, t=i, ...............< =	'
о	о	о
2/
где т = — •
а
Вышеуказанное построение принимает особенно простой вид, когда
функция F(x)=0 и функция / (х) состоят из прямолинейных участков; так,
например, если взять случай, рассмотренный в § 37, то функция g(x) пред-
ставится чертежом фиг. 25, и у нас будет
« = 4 te aZ)];
полагая последовательно aZ = O, — > у и т’ будем получать серию черте-
жей (фиг. 25а, 256).
$47] ПРИЛОЖЕНИЕ МЕТОДА К УРАВНЕНИЮ РАСПРОСТРАНЕНИЯ ТЕПЛА 145
Все эти чертежи можно свести к одной весьма простой диаграмме, кото-
рая указана в лекциях Гельмгольца. Именно: строится параллелограмм,
коего стороны параллельны и равны соответствующим частям струны в началь-
ном ее положении, проводим диагональ АВ этого параллелограмма — она
будет параллельна оси ж, откладываем по ней в обе стороны от точки б?,
Физ. 25
Фиг. 25а
Фиг. 25 б
Фиг.25—26.
оси х, величины ~, 2 •	, 3 • ~ ит. д., и через полученные точки 1, 2, 3,...
проводим вертикальные прямые (фиг. 26), до их пересечения со сторонами
параллелограмма, и эти точки помечаем теми же нумерами 1.1, 2.2, 3.3 и т. д.;
тогда последовательные формы струны будут АСВ, Al IB, А22В, АЗЗВ и т. д.
Предлагается в виде задачи построить диаграмму скоростей точек
струны в те же моменты.
§ 47. Пример приложения метода к уравнению распространения
тепла в пруте. Как второй пример для пояснений излоЖёйного метода,
возьмем последний частный случай задачи о распространении тепла в пруте,
т. е. где надо интегрировать уравнение
ди
2д2и к
= а2—-2 — ои
дх2
(1)
to А. Н. Крылов
146
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ
[Гл. III
при граничных условиях: при всяком t должно быть
и — 0 при х = О,
g + M = Q при х — 21,	(2)
и при начальном условии: при 2=0 должно быть
u = f(x).	(3>
Ищем и в виде суммы:
и = %ТХ.	(4>
Каждый член этой суммы должен удовлетворять как предложенному
уравнению (1), так и граничным условиям (2).
Подстановка величины ТХ вместо и в уравнение (1) дает равенство
Т'Х = а*ТХ"-~ЬТХ,
или
(Г +ЪТ)Х = а?ТХ".
что не иначе возможно, как взяв
Т'±ът х№ .	/2
—_e- = conSt.= -AS
откуда следует
Т' + (аЧ2 + 6)Г = 0,	(5)
к*Х = О.	(6)
Отсюда получаем
Т == Ае^ь+а2к^ = Ae~bt e~a2k2tt
X = С cos кх + D sin кх.
Обращаясь к граничным условиям, которым должен удовлетворять,
по предположению, каждый член нашей суммы, по сокращении на Т по-
лучаем
Х(0) = 0,
+	=о,
\ dx ri </rc=2l
ИЛИ
С = 0,
D (к cos 2kl + рх sin 2kl) = 0;
значит, величина к должна удовлетворять уравнению
к cos 2kl + sin 2kl = 0-	,	(7)
Пусть корни этого уравнения суть
... — (Оп,	<»2, — 0)1, 0,	«2, . .	®п, , . .
Каждому из этих корней o)f соответствует своя функция Х( и своя
функция Т if а именно:
Xi—Dt sino)f£,
Ti = Ate-bt е-“М',
$ 47]
ПРИЛОЖЕНИЕ МЕТОДА К УРАВНЕНИЮ РАСПРОСТРАНЕНИЯ ТЕПЛА
147
а так как произведение постоянных произвольных DtAt есть тоже постоян-
ная произвольная, то, не нарушая общности, можно положить Dt = 1, и тогда,
в силу того, что величины = и Xt~ — Xif члены, соответствующие
корням о)£ и — о)£, соединятся в один; обозначая сумму постоянных произ-
вольных Л£ —	= Bif получим равенство
u = e~bt В,-е~а2“$* sin ц^х.	'	(8)
j=1
Остается удовлетворить начальному условию» Делая в формуле (8)
£ = 0 и u = f(x)t получаем равенство
t (я) = 3 Bi sin	(9)
из которого и надо найти коэффициенты Bt. Обозначая, попрежнему, sino>^
через Xi9 напишем предыдущее равенство так:
/ (Ж) =	+ ^2^2 + • • • + В^Х^ + о..,	(10)
причем мы, в силу граничных условий и уравнения (7), знаем, что каждая
из функций Xt удовлетворяет равенствам
Хг(0) = 0’	(И)
x;(2Z) + ₽1xf(2Z)=o	(11)
и уравнению
Xl + ^Xi^O.	(12)
Покажем, что для этих функций интеграл
21
XiXk dx — 0, если i Ф к.	(13)
о
В самом деле, заменим под знаком интеграла его величиною из
уравнения (12); тогда наш интеграл будет
21	21	21
— О)? XkXt dx = ХкХ” dx = [XкХ^X'JXj dx»
оо	о
Совершенно так же будет
21	21	21
- О) Д XkXi dx = ХгХпк dx = [ХДЛо* - J X'iX‘k dx,
о	о	о
откуда следует
И -	$ XkXt dz = [XkX't - XtX']2o' =
0
= Xk (2Z) X’ (21) - Xt (21) X'k (21).
Но из уравнений (И), второе из коих можно писать так:
_й Xi(2l)_Xk (21)
Xi(2l)^Xk(2l)
следует, что
х; (21) Хк (21) - X, (21) Хк (21) = о,
значит, и
21
(о>2 —(о|)	XtXkdx^0.
; О
148
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ
[Гл. III
А так как o)f не равно <ок, то и будет
21
Xdx == 0, если
о
иначе
sin* югя sin <оrX dx = 0, если i =/= к.
На основании этого свойства, для определения коэффициента В сто-
ят толйко умножить обе части равенства (10) на Xt и проинтегрировать
ет 21.
Получим при замене под знаком интеграла буквы х буквою £:
21
/ (5) sin (o/gdE
о_________________
21
Sin2(o/£di-
О
Величина интеграла, входящего в знаменатель этой формулы, в данном
случай легко находится непосредственно; а именно, будет
21	21
•	О
Но так как, в силу равенства (7),
............ '	ctg2d)iZ=—
1 sin 4<ot4
4	о>/
sin 2<о/51 21
2(о/ J о
следовательно,
sin 2o>iZ =
cos 2o)/Z =

то будет
Bt
ж получится
8in4<0(/=-7^|
С . , . » P1 + 2Z («“ + ??)
------20^й)-
О ,	*
2 <о>» + В»)	р'
₽1 +2/(<>“+ й) 81П di
'	о
21
е”а2ш? sin <s>iX / (5) sin со/В cfc.
о
Нойшо было бы для нахождения интеграла
21
Xldx
а = 2е^’2
я
о
§ 481
ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ УПРУГОГО СТЕРЖНЯ
149
применить и другой прием, к которому приходится прибегать, когда непо-
средственное вычисление этого интеграла требовало бы слишком длинных
выкладок»
Мы имели равенство
21
(«4 - ш?) XtXk dx - Хк (21) X't (21) - Xi (21) Х'к (21). .
о	.	1
Составим функцию Х(<о, х) совершенно так же, как Хк составлено из
и х\ тогда можно написать равенство
ХС (2/) X (а>, 2Z) - Xi (21) X' (а>, (21)) .
0)2 - СО2	’
i
. ~ о
вторая часть этого равенства при о> = (of принимает неопределенный вид ;
обозначая числитель этой дроби через F (ш) и переходя к пределу по извест-
ному правилу, получим
21	21	F(<Oi)
lim ( XtXdx — \ Xjdx — lim =	-----
1	i 1	a»2 — ей2	2о>;
21
XiXdx
так, в нашем случае
F (w) = o)f cos 2Zo)f sin 2Za) — sin 21^ cos 2Zco,
A F (w) — 2Zo)/ cos 2Za), cos 2Zw — sin 2Z<of cos 2Z<d + 2Zio sin 21<зц sin 2Z»,
д<л '
— F (a),) = 2lwt—sin 4Zo>i,
(70)	4	2
и формула (*) дает
21
( Xafdx = l-^^1,
J	4
0
как и раньше.	*
Этот прием, как видно, сводит нахождение интеграла
21
^X2idx
о
к дифференцированиям.
Как видно, и в этом примере определение коэффициентов Bj оказалось
возможно произвести весьма просто благодаря свойству функции X, выражаемо-
му равенством
21
XiXk dx = O, если i #= к.
о
В остальном остаются в силе сделанные в § 46 замечания.
§ 48. Поперечные колебания упругого стержня. Чтобы дать еще
пример на приложение второго метода Пуассона, рассмотрим задачу о попе-
речных колебаниях упругого стержня или прута постоянного поперечного
сечения и однородного материала.
Мы увидим, что эта задача приводится к интегрированию уравнения
^Д-62^=0
dt2 + дх* U
150
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ ГГл. II
при’ начальных условиях: при t = 0 должно быть
« = /(*) И ^ = 7?(ж),
и граничных условиях, относящихся к концам стержня я = 0 и #==/, выра-
жающихся различным образом, а именно:
1)	для конца закрепленного должно быть при всяком t
и = 0 и и- = 0;
дх
2)	для конца подпертого должно быть при всяком t
3)	для конца свободного должно быть при всяком t
Ясно, что возможных комбинаций этих граничных условий может быть
шесть, а именно: 1) оба конца закреплены, 2) оба конца подперты, 3) оба
конца свободные, 4) один конец закреплен, другой подперт, 5) один конец
закреплен, другой свободен и 6) один конец подперт, другой свободен.
Возьмем сперва простейший случай и употребительнейший в строитель-
ном деле — оба конца стержня или балки подперты.
В этом случае граничные условия будут
и = 0 и |~=0, при я = 0 1
„2	У при всяком t.	(3)
ю = 0 и ^ = 0, при х —Z |
дх2	r	J
Согласно общему правилу, ищем решение вида
’ u-SZX,
причем каждый член суммы удовлетворяет уравнению (1) и граничным ус-
ловиям, или, как их называют для балки, условиям закрепления концов.
Имеем
^X + 62TXiv = o,	(4)
или иначе
Г* X1V	«	7 4
--™ = —vt" = постоянной = я4
—“ ОЛ1 А
и, значит, уравнение (4) равносильно следующим двум:
Г' + 62А47 = 0,
Х1У-Л4Х = 0.
Отсюда следует
Т = A cos ЬкЧ + В sin ЬкЧ,
X = С ch кх + D sh кх + Е cos kx + F sin кх,
где Л, В, С, D, Е9 F суть произвольные постоянные так же, как и к9
£
суть так называемые гиперболические косинус и синус.
§ 48]	ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ УПРУГОГО СТЕРЖНЯ 151
Составляем теперь граничные условия, которым величина X должна
удовлетворять, а именно:
при х — 0 должно быть X = 0 и X" = О,
» х — I »	» X = 0 и X" ~ 0;
таким образом, получаем
(7 + ^ = 0,
С ch kl + D sh kl + E cos kl + F sin kl = 0,	' '
C ch kl + D sh kl — E cos kl — F sin kl = 0.
Отсюда следует
C = 0, jE = O,
после чего последние два уравнения принимают вид
D sh kl + F sin kl = 0,
DshW-FsinM = 0.	™
Эти два уравнения будут совместны, только когда
shAZsin£Z = O,
т. е. или shAZ = O или sinAZ = O.
Первое уравнение имеет, кроме Л = 0, только мнимые корни; поэтому,
чтобы иметь дело с вещественными величинами, берем
sinW = 0,	(8)
т. е.
kl = nn (п = 1, 2, 3, ...);
тогда
Z> = 0,
причем мы ограничиваемся лишь положительными значениями к, так как
решения, соответствующие отрицательным к, не будут независимы от первых.
Корень к = 0 не представляет интереса, так как дает Х = 0.
Точно так же, если бы мы взяли уравнение sh&Z = O и затем освободи-
лись от мнимых знаков, то пришли бы к тем же результатам.
Итак, функция Хп будет
Xn = Fnsinn^,	(9)
оо	оо
2 я гд . ПТЪХ , П2Л2 , , ХП п • ПКХ .	> 7l27U2
AnFn sin -j- cos b -p-1 + 2 BnFn sin у sin 6 у t,
n=l	n-1
причем, ввиду произвольности An и Bn, можно брать Fn = l, так что будет
со	оо
2 л . ПКХ П27С2Ь . , VI П • итог • п2тс2Ь л
Ап sm — cos -у— t + >, Вп sin у- sin —-р-1.	(10)
n=l	n=l
Начальные условия дают
/ (*) = 2 Ап sin Т" ’
п:‘ 	(И)
р XI п2к2Ь г. . ппх t
F w = 2j Т2~ sin — ’
n = l
152 ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ [Гл. III
откуда находим, как уже не раз делали,
г
* t	(12)
О
Возьмем теперь какое-нибудь другое сочетание условий закрепления,
например то, которое имеет место при изучении вибраций корабля, т. е. что
оба конца свободны.
В этом случае функция X должна удовлетворять таким условиям:
Х"=^0 и Х"' = 0, при х = 0,	.ох
Х" = 0 и Х"' = 0, при х = 1.	( '
Составив эти производные, имеем
X" = к2 [С ch кх + D sh кх — Е cos kx — F sin кх],
X*ff = A3 [C sh кх + D ch кх + E sin kx — F cos kx]
и, значит, наши условия будут
С-Е = О,
D-F = O,
C ch kl + D sh kl — E cos kl — F sin kl — 0,	* '
C sh kl + D ch kl + E sin kl — F cos kl = 0,
причем предполагается пока, что к не равно нулю.
Из первых двух уравнений следует
Е = С, F = D,
после чего последние два уравнения напишутся так:
С (ch kl — cos kl) + D (sh kl — sin kl) = 0,
C (sh kl + sin kl) + D (ch kl — cos kl) = 0.	' '
Эти два уравнения, однородные относительно С и D, только тогда допу-
скают решения, отличные от нуля, когда определитель равен нулю, т. е. когда
(ch kl — cos kl)2 — (sh2 kl — sin2 kl) = 0,
или
ch2 kl — 2 ch kl cos kl + cos2 kl — sh2 kl + sin2 kl = 0.
Замечая, что
ch2 kl — sh2 kl = 1,
получим
2 — 2 ch kl cos kl = 0,
или окончательно
ф (к) = ch kl cos kl — 1 = 0»	(16)
Это трансцендентное уравнение определяет значения Л, при которых
функции X удовлетворяют условиям закрепления концов стержня.
Пусть положительные корни этого уравнения будут
*i, й2, *з> •••> кп,	(*)
тогда это уравнение будет иметь и отрицательные корни
— *1 = ^!, —/с2 = А_2,	=	(**>
§ 48]ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ УПРУГОГО СТЕРЖНЯ 153
каждому корню соответствует своя функция X, которую обозначим тем же
значком, как и соответствующий корень.
Когда мы возьмем к равным одному из значений (*) или (*♦), то из
уравнений (15) одно станет следствием другого, и, обозначая через Н про-
извольную постоянную, можно брать
-С	Р	н
sh kl — sin kl ch kl — cos kl
и, значит, будет
Xi — Hi [(ch fciX + cos к\х) (sin kil — sh k\l) +
+ (sh ktx + sin hx) (ch kil — cos &;/)],	(17)’
причем, как уже не раз замечено, без ущерба для общности можно
полагать Hi — i.
Нетрудно видеть, что
XLi=-Xi
и, значит, нет надобности рассматривать функции X с отрицательными»
значками, ибо члены, им соответствующие, сложатся с членами с положитель-
ными значками.
Итак, получим
со	со
и = 3 АпХп cos k*nbt + 2 ВпХп sin knbt,
П = 1	n«=l
ибо соответствующая корню kn функция T есть
Тп = Ап cos knbt + Вп sin k^bt,
где Ап и Вп суть произвольные постоянные.
Замечание. Указанная выше формула для и не является, строго говоря,
обшей, ибо мы не рассмотрели случай к — 0. При этом уравнения для X и Т прини-
мают вид: JT1V = O и Т” = 0. Первое из них допускает решение X (x)*=c + dx, удов-
летворяющее граничным условиям (13), где с и d — произвольные постоянные. Мы*
имеем таким образом два линейно независимых решения для X Выберем их следу-
ющим образом:	и Х{] — х — I. При таком выборе они удовлетворяют условию'
21
X^1Xodx = 0,
о
Решения Х~г и Х9 надо умножить еще на общий интеграл уравнения 7^ = 0, т. е.
на полином первой степени от г с произвольными постоянными. Таким образом,
к приведенному выше выражению для и мы должны добавить выражение вида.
(«-1 + 6_1<) + (а0 + 60«)	— у),
где а_15	а0, &0 — произвольные постоянные. Эти члены в выражении и будут4
отсутствовать, если функции f(x) и F (х) удовлетворяют условиям:
21	21	21	21
/ (х) Х^ dx = / (х) Хо dx—	F (х) Хж1 dx = F (х) XQ dx = 0,
о	о,о	о
что равносильно условиям:
21	21	21	21
/ (х) dx =	/ (х) х dx — F (x)dx— F (х) xdx — Q.
оо	0	0
Все дальнейшие вычисления мы будем проводить, считая, что дополни-
тельные слагаемые, соответствующие к = 0, отсутствуют.
154
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ [Гл. III
Прежде чем итти дальше, уже можем сделать общее замечание,
а именно: мы видим, что вид функций X определяется условиями закреп-
ления. Во всех случаях эти условия приведут к четырем уравнениям первой
степени между четырьмя постоянными произвольными, входящими в функ-
цию X, и вторые части этих уравнений будут нули, а чтобы эти уравнения
допускали решения, отличные от нуля, необходимо, чтобы определитель их
был равен нулю.
Равенство нулю этого определителя доставит трансцендентное уравне-
ние относительно буквы к и послужит для определения тех значений, кото-
рые эта величина может принимать» Значений этих будет бесчисленное
множество, и каждому корню будет соответствовать своя функция X, зави-
сящая от этого корня и содержащая произвольный постоянный множитель,
который, без ущерба общности, может быть взят равным 1.
Начальные условия приводят к равенствам
f(x)=^AnXn,
(18)
F(x) = S к%ЬВпХп,
п = 1
из которых и надо будет определить коэффициенты Ап и Вп.
Это определение производится на основании следующего общего свой-
ства функции X для всякой комбинации условий закрепления концов:
i
XtXj dx — О, если i у.	(19)
о
Чтобы доказать это свойство, припомним, что функции Xt и X; опре-
деляются уравнениями
= O и Х^-к^Х^Ъ	(20)
и сочетанием граничных условий:
а)	для заделанного конца (я = 0 или х = 1)
А\=0 и Х=о,
а также
и Х;=0;
б)	для подпертого конца
Х£ = 0 и Xj = O,
а также
Xf = () и Xj = O;
в)	для свободного конца
х;=о и х"'=о,
•а также
х;=о и Х/"=0.
Очевидно, будет, в силу уравнений (20) *и интегрирования по частям,
А4 XtXfdx= J ХГХ}<1х =
о	о
I
= [X-'Xf-X’iX'i + XiX’i-xtx';’]l0 + J xtx^dx-,
0
§ 48]ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ УПРУГОГО СТЕРЖНЯ	155
заменяя в последнем интеграле X/V его величиною ЛуХ;, получим
i
(к} - kj) J XtXj dx = [X'^Xj - X‘Xt + X'iX'j - XtX'" ;	(21)
0
в силу же условий закрепления, величина, стоящая в [ ], обращается
в нуль как при х = 1, так и при ж = 0, каковы бы эти условия закрепления
ни были*, значит, будет
i
(kl-k}) XtXjdx = 0,
О
а так как, по предположению, и kj между собою не равны, то будет
i
XiXj dx = 0, если i Ф j.
о
На основании этого свойства получаем, как уже не раз показано:
_ _ 9
“	(22)
j F(0Xn(0dg
1 о
Непосредственное вычисление интеграла
L
\xzn®dt,
о
входящего в знаменатель этих формул, может потребовать длинных выкла-
док; поэтому здесь удобнее воспользоваться тем приемом, который был
показан в § 47, именно, составить функцию X [кх] совершенно так же, как
функция Xj составлена из kj х, и рассматривать интеграл
i
Xjdx
О
как предел, к которому приближается интеграл
i
Xj(kx)Xjdxt
о
когда к приближается к пределу kj*, тогда, обозначая через 2 (к) функцию
2 (Л) = [ X”'Xf - Х"Х + Х'Х, - XX'j" ]',	(23)
б^дем иметь
f	dfi (к)
\x2dx = -^.	(23')
156	ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ (Гл. Ш
ь——-—ч.г-аяяавг    ,    	------— " 	- -	’
Это вычисление может быть произведено в общем виде
Заметим, во-первых, что в выражении 2 значками обозначены диффе-
ренцирования, произведенные по букве но надо помнить, что аргументом
функции X служит кх, так что, если положить кх — у, то будет
Х' = ^^ = АХ'(у), Х’ = -^^-=А2Х'(г/), X'" (кх) = к3Х'" (у),
йх	сьзс
причем в правых частях этих равенств значком обозначено дифференцирова-
ние по букве у.
Точно так же, если обозначить kjX~z, то будет
X'i = kiX'j (z), X’j = k^x’i (z), X'i" = к3Х'" (z).
Отсюда ясно, что при таком обозначении
Х™(у) = Х(у)
Xf(z) = X/(z),
в силу того уравнения, которому функции X удовлетворяют»
Таким образом, будет
Й(Л) =
= [ к3Хк (у) Xi (z) - №kjX" (у) X'i (z) + кк* X' (у) X‘i (z) -k3jX (у) X'i" (z) ]'.
Дифференцируя по к, надо помнить, что у = кх и, значит, = х,
величина же z от к не зависит.
Выполнив дифференцирование и полагая затем к — kj, откуда X (у) =*
= Xj(z)9 получим
= [ ЗА2 X'i' Xi + А^Х2,. -2,х!х,-2k3xX’j"X'i + к3х(Xj)2 J q , (24)
причем у всех функций аргумент есть z.
Заметим теперь, что условия закрепления суть,
конец заделан
Х/==0, Х~0,
конец подперт
Х7-0, < = 0,
конец свободен
=	Х'" = 0.
Отсюда видно, что при всяком условии закрепления конца величины
XjX*” и X'jX”i равны нулю при подстановке соответствующего значения х,
значит, эти члены можно из предыдущей формулы опустить. Остальные
члены содержат множитель х и, значит, равны нулю при нижнем пределе,
и у нас останется
= ikf [X2i (к,1) - 2Х'" (kil) X'i (kil) + (X’i (kil))*]
и, значит, будет
i
\ X? dz = | / [Xf - 2X'i'X'i + (X;')2]x=z.	(25)
$49]	О ВЫЧИСЛЕНИИ КОРНЕЙ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ	f57
Отсюда 'составляем следующую таблицу значений нашего интеграла:
Таблица 4
Род закрепления конца х = 1	Род закрепления конца ж —0	Значение интеграла 1 ^Xfdx 0
Заделан . . . .	f заделан У < подперт >. . 1 свободен]	(ktiy
Подперт ....	Г заделан 1 < подперт 1. 1 свободен J	A
Свободен • • • •	Г заделан А < подперт > . . 1 свободен J	^l(X (kil))*
При этом значками обозначена производная функция Х\ так, например,
для случая, когда оба конца подперты, будет
X = sin кх = sin z, X' = cosz, X"'— — cosz, А =
X'X*a = — cos2 z = — cos2 kx
и
- 4 IX"' (kl) X’ (kl) = 11 cos2 kn = 11.
Подобным же образом надо пользоваться этою таблицею и в остальных
случаях, беря самое функцию X сообразно условиям закрепления обоих
концов»
§ 49. Замечания о вычислении корней трансцендентных уравнений»
Эти примеры в достаточной степени поясняют метод и доказывают, насколь-
ко просто он ведет к цели, когда особые свойства функций X, входя-
щих в решение задачи, позволяют находить коэффициенты в разложении
произвольной функции по ним.
Если такого свойства, подобного, например,
I
XtXj dx = 0, если i Ф ],
о
подметить не удается, то следует прибегнуть к первому методу Пуассона,
хотя по выкладкам он оказывается гораздо сложнее.
Вместе с тем, первый метод, вытекающий непосредственно из тео-
ремы Фурье, укажет и те ограничения, которым должна быть подчинена
разлагаемая функция (условие Дирихле), а также и то, что в местах раз-
рыва получается полусумма значений функций, соответствующих месту
разрыва.
Необходимо сделать еще одно замечание. Как первый, так и второй
метод приводят к необходимости решать, некоторое трансцендентное урав-
нение. Вычисление и исследование корней этого уравнения может также
представить затруднения; работа облегчается, если при решении таких урав-
нений руководствоваться , теми приемами, которые мы также поясним на
примерах.
158 ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦАХ [Гл. III
Пример 1. Положим, например, что надо решать уравнение
к cos 2kl 4- pi sin 2kl — 0
относительно неизвестной к при заданных Pi и L
Тогда, для краткости, полагаем
2к1 = \
и., делая 2рк/ = аэ напишем наше уравнение так:
этого уравнения, что делается
с большою наглядностью путем
построения кривой
z/ = tgk
и прямой
абсциссы X точек пересечения
которых и дают требуемые
корйи, из коих нам нужны
только положительные.
Этот чертеж (фиг. 27) сей-
час же покажет, что искомые
корни будут, при а > 0, вида
^1==~2~ + Р'1> Х2=у + Н2>Х3 —
5« ,	.	21 — 1	.
= -2 +**3’ ° °	=—2“* +
причем р4, рь2, .. о, jtf, ... суть положительные величины, меньшие — и быстро
убывающие по мере возрастания значка i.
Вычислить цг, |ла,.. . с любой степенью точности уже не представляет никаких
затруднений, когда численная величина а задана.
Пусть, например, а = 2, так что наше уравнение будет
tgA=-lA;
чтобы найти I*!, делаем Х = после чего предыдущее уравнение примет вид
а
4.	Я . 1
ctgHi= +Т И1;
само собой разумеется, что здесь щ выражено отвлеченным числом; умножив обе части
этого уравнения на 57.3, получим равенство
57.3ctg|*xe = 45 + ±|4e,
где 1*1° означает угол щ, выраженный в градусах.
Тогда обозначим через (Р4°) величину
t (Н1о) - 57.3 ctg |4Э - 45 - 11Н»,
§ 49]
О ВЫЧИСЛЕНИИ КОРНЕЙ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
159
и, пользуясь логарифмической линейкой, вычисляем значения	получим
<	р (40°)	= 68.2 — 45 — 20 = 3.2,
<	р (41°)	= 65.9 — 45 — 20.5 = 0.4,
<	р(41°15/) = 65.3 — 45 — 20.6= —0.3;
если требуется бблыпая точность, то надо обратиться к таблицам тригонометрических
величин (натуральных) и вычислить значения функции
л 1
ctglh — -4— у 1*1
в смежности со значением
14 = 41° 15' = 0.71995.
Когда корень найден с приближением до Г, но почему-либо требовалась боль-
шая точность (в технических вопросах этого потребоваться не может), то стоит только»
прибегнуть к известному методу Ньютона, применяемому совершенно подобно тому,
как для уравнения алгебраических, — и корень получится с желаемой степенью
точности.
Для больших значений значка I можно воспользоваться разложением корн»
нашего уравнения в ряд.
2/__j
В самом деле, сделаем ———гс = п; тогда наше уравнение будет:
Ctg +
но
111
ctgw=-- 3 M-4vS
и предыдущее уравнение напишется так:
откуда
1/1 IV. 2а 1	(1	8а3	1
п + зЛ3’Ь’“’”2г -1 ’ к V + 3/ (2г — I)3 ‘ гсз + ,,в
Пример 2. Как другой пример, возьмем уравнение
ch kl cos kl — 1,
или, делая опять kl — \, уравнение
ch k cos k = 1.
Написав это уравнение так:
ch k = seck,
построим кривые
y=chk=-^-4^-
и
у — sec к.
Нетрудно показать, что в промежутке от 0 до корня нашего уравнения
нет, остальные же корни, как показывает схематический чертеж (фиг. 28),
выражаются так:
kx==j + pi, k2 = y —р2, Xs = 7y+fi3........>ч = -^у-- •« + (— i)'+1 •!*{»
причем pi, р2) ... , (л, положительные и меньше и по мере возрастания
значка быстро убывают.
460 ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ УСЛОВИИ НА ГРАНИЦА^
[Гл. Ш
В самом деле, напишем наше уравнение так:
.	1	2
cos к = -T-т = —;---г- •
chX ^л е л
Делая Х1 = ^г+Рп имеем
£
sin U.J = ---------------
‘ х - отс
е* |>i
Значит, Uj приблизительно равно
2	1
зк — 55 ’
Л
ч?. е. около 1°, и, значит, приближенное значение есть
у + 0.0176 = 4.73...
Точно так же будет
sin р-2 —	---------— O.OOO77
Л (^4-г-5т+-^)
и, значит,
= 0.00077 =0°2'40"
и
х2 = 5?-0.00077 = 7 8542
и т. д; как видно, корень Х3 уже
разнится на весьма малую величину
7л
от у , и, следовательно, можно при-
.	2< + 1
нимать hi = —£— тс	для всякого
i > 3.
Не входя в большие подробности по этому поводу, обратим внимание
на статью Коши «Sur la nature des racines de quelques equations trans-
cendantes» в томе II 2-й серии полного собрания его сочинений, где можно
найти исследование корней многих уравнений, встречающихся при решении
вопросов математической физики.
г
ГЛАВА V
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
И СВОЙСТВ ИНТЕГРАЛЬНЫХ ВЫЧЕТОВ К ИНТЕГРИРОВАНИЮ
ЛИНЕЙНЫХ УРАВНЕНИЙ ОБЫКНОВЕННЫХ
И С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
МЕТОД КОШИ
§ 50. Понятие о функции мнимой переменной. Исследования Коши,
которыми он как установил основания теории функций мнимого переменного,
так и указал важнейшие ее применения, считаются одним
из главнейших вкладов, сделанных в науку этим знаме-
нитейшим автором. В этой главе мы постараемся дать
очерк той части этих работ, которая имеет непосред-
ственное отношение к излагаемому нами предмету*
Как известно, комплексное количество
условно изображается вектором ОМ, соединяющим
начало координат О с точкою М, прямоугольные и прямолинейные коорди*:
наты которой суть х и у (фиг. 29)*
Длина
ОМ = + \/х2 + У2 = Р
называется модулем количества z, угол хОМ, считаемый по направлению
от положительной оси Ох в сторону к положительной оси Оу> называется
аргументом z.
Величина z может быть написана:
z = р (cos 0 + i sin 6) = р •
где через i обозначено для краткости письма — 1, и равенства
a? = pcos0, г/= psin 0
определяют вполне угол 0О, заключенный в пределах
0<60<2к,
для которого
cos0o = — и sin0o±=—;
Р	Р
тогда общая величина 6 есть
0 = % “h Якя^
где к есть любое целое, положительное или отрицательное^ число или Пуль*
11 А. Н. Крылов
162
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
[Гл. V
Известно также из элементарного курса, что сумма величин
И
z2 = a2 + 2/2j/ — 1»
т. е.
21 + z2 = (ж, + «г) + (г/i + г/2) V — 1,
представляется диагональю ON параллелограмма, построенного на векто-
рах OMx = zY и OJ/2 = 22 как сторонах, или, как говорят, «геометрическою
суммою» векторов ОМХ и ОМ2 (фиг. 30).
Точно так же разность
21	22
этих величин изображается вектором ОР, кото-
рый представит вторую сторону такого парал-
лелограмма, у коего ОМ± есть диагональ и
ОМ 2—сторона.
Перейдем теперь к установлению понятия
о функции от мнимого переменного.
С первого взгляда может показаться, что
стоит взять любое выражение вида
?(*, у) + Ф(X, у)У— i,
в котором ср (х, у) и ф(ж, у)—две какие угодно дифференцируемые функции
от переменных х и у, то это выражение можно рассматривать как диф-
ференцируемую функцию от х + y\f — 1, ибо когда величине х + у |/ — 1
будет приписано какое-либо частное значение a + byf—1, то найдется
и соответствующее ему частное значение ср (а, д) + ф(а, b) — 1 выражения
<Р (я, у) + * (X, у) У^Т
Но если бы такое определение сделать, то оно не удовлетворяло бы тому
понятию о функции от х + у У — 1, которое мы составляем в дифферен-
циальном исчислении. Положим, что мы имеем комплексную функцию
Г = <р(ж, y} + *t(x, г/)У —1
(1)
мнимого независимого переменного z — x + уУ —1. Придадим z некоторое
приращение Az == Дж + Ду j/*,—Г, при этом функция V получит приращение
Д7 = [ср (х + Дж, г/+ Дг/) +<р(ж+ Дж, у + Дг/) У — 1] —
— [? (я, + $ У) У —Т].
Составим отношение Ду: Az приращений:
_ =	+Дж, у4-Ду)—<р (ж, у)] + [(Ф (ж + Дж, у + Ду)—Ф(ж, у)]	2)
*	Да; + Ду — 1
и потребуем, чтобы оно имело определенный конечный предел, когда Дж
и Ду произвольным образом, независимо друг от друга, стремятся к нулю.
Упомянутый предел мы обозначим через V' и назовем производной от V
по 2. Будем сначала считать, что в формуле (2)Ду = 0, а Дж отлично
от нуля и стремится к нулю. При этом в пределе получим
г=|?+|4ут^1;	(3)
дх дх, r	v '
Если мы теперь будем считать, что Дж = 0, а Ду отлично от нуля и стре-
§ 51]
ПОНЯТИЕ ОБ ИНТЕГРАЛЕ ОТ ФУНКЦИИ МНИМОЙ ПЕРЕМЕННОЙ
163
мится к нулю,, то в пределе получим
V' =	4- д— .	1
ду~ау У—1’
ИЛИ
(4)
ду ду у	'
Сравнивая выражения (3) и (4) для У', мы приходим к следующим двум
равенствам, связывающим <?(х,у) и ф (я, г/):
д?__дф
дх~ду’
<9? _<Эф
ду дх *
Таким образом эти равенства являются необходимым условием сущест-
вования производной от V по z. Нетрудно показать, что, наоборот, если
ф и ф имеют непрерывные частные производные первого порядка, которые
удовлетворяют равенствам (5), то существует определенная производная от V
по z. Действительно,
dV = dx + dy + dx +dy\ — 1
дх ду * \дх 1 ду J Y
И
dx + ^dy у/ — 1 4- (^dx~ ^-dy У —	j/— 1
dV______дх ду * г_________\J)x ду а 7
dx + dy^— 1	dx + dy^—1
Пользуясь (5), получим
dP _ dy	+	_ Л? cty i/~T
dz	dx-\-dy^ — 1	dx -h dy ]/ — 1	dx dx
На основании изложенного Коши и сделал такое определение:
Выражение
у = ^(х, у) + Ц(х, у)У — 1	(6)
называется моногенной функцией или просто функцией мнимого переменного
Z = x+y |/ — 1, если входящие в его состав функции <р(ж, у) и ф (я, у)
удовлетворяют условиям (5).
В этом случае пишут обычно
V = F(z) = F(x + y/“l)	.	(7)
И
f =	(8)
Отметим, что из уравнений (5) следует, что
<?!? 4._ о
<^2±^2 ’	(9)
^ф , ^ф„ n	v f
dx*+ ду2 “ и° ‘	•
§ 51. Понятие об интеграле от функции мнимой переменной. Понятие
об интеграле обобщено в применении к функции мнимого переменного
следующим образом.
Положим, что на плоскости хОу дана какая-нибудь кривая АВ, урав-
нения которой суть (фиг. 31)
я = Л(0> У = /2(0,
164
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
[Гл. V
и пусть точка А соответствует значению t = tQ и точка В — значению t~T.
Разделим промежуток Г — tQ на п частей,— для простоты рассуждения, ска-
жем, равных между собою, — и отметим точки кривой: Аи Л2, ...,ЛП_1,
соответствующие значениям
^2> • • • > tn—I)
где
tk = t0 + k • Т я ” ? •
Каждой из этих точек соответствует свое значение переменной z, рав-
ной ^+г/|Л —1; так например, для точ-
ки Л* будет
Пусть будет задана какая-нибудь не-
прерывная функция F (z)\ составим сумму
Р (z0) fa — ZO) + F fa) fa — zt) + . . .
• •• 4~F(zn—i)(Z zn_j)
и положим, что число делений п воз-
растает неопределенно; тогда эта сумма
будет приближаться к определенному пределу, который и называют ин-
тегралом от функции F (z) dz, взятым по пути АВ от точки А до точ-
ки В. Условившись его обозначать знаком
АВ
получим по определению равенство
F (2) dz = lim [F (z0) (z2 — z0) + F (zj) (z2 — zx) + • •
AB
...+F(zn_1)(Z-zn_1)]. (10)
Нетрудно видеть, каким образом величина этого интеграла может быть вы-
числена. В самом деле, пусть
F(z) = ^(», г/) + К~ИС*» ’/) = ?[/i(*)> /а(О] + К —1Ф[Л(О> А(0] =
= F1(Z) + F2(Z)/^1,
тогда, очевидно, будет
АВ
т
$ [Л (t)+f2 (0 / -1] [/; (t) + У' (z) / -1] dt =
*0
- F2 (Z) /' (Z)]dZ + / - Ц [Fx (Z) /' (Z) + F2 (z) /; (Z)] dt. (11)
to
to
Если положить
$ [**: (О Л (0 - W Г2 («)] dt = 2 (Т) - 2 (tQ)
to
§ 51]
ПОНЯТИЕ ОБ ИНТЕГРАЛЕ ОТ ФУНКЦИИ МНИМОЙ ПЕРЕМЕННОЙ
165
И
т
5 [л (о /; ю+ю /;«] л=ф (Т) - ф (z0),
«о
то будет
[F(z)dz\ = Q(T)-Q(t0) + ]/~~i [Ф(П-Ф(М] =
АВ	___ ___________________
= [2(П + Ф(П/-1]-[2('о)4-Ф(М/-1].
Можно это вычисление произвести и иначе, написав равенство
F (z) dz =	[? (х, у) + У — 1 ф (х, г/)] (dx + dy j/ — 1) =
АВ	АВ
= 5 М®’ y)dx — i>(x, г/)й] + К—y)dx + <f(x, у) dy].
АВ	АВ
Но, в силу равенств (7),
ду   дф
ду	дх
И
<9ф __д?
ду дх*
количества
у(х, y)dx — <b(x, y)dy
И
ф(я, y)dx + v(x, y)dy
суть полные дифференциалы} обозначая их соответственно через dP(x> у)
в dQ(x, у) и координаты точек Л и В—-через гг0, г/0 и X, Y, получим
[? (х> У) dx - Ф (х> У) dy] = P(X9 Y) — P (ж0, у0),
АВ
\ [Ф(я, y)dx + <t'(x9 y)dy] = Q(X, Y)-Q(x0, yQ)
AB
и, значит, будет
\F(z)dz = [P(X, У) + /ТЛ<2(Х, y)]-[/>(*o, Уо) + /“К?(хо, г/о)Ь (12)
АВ
Нетрудно видеть, что Р(Х, У) + |/ — 1@(Х, У) есть моногенная функ-
ция величины X + У “р4 — 1; обозначая ее через Z и считая, что X и У —-
переменные, равно как и Z, ж0 yQ — заданные постоянные, можем предыдущее
равенство написать так:
j F(z)dz = Q(Z)-Q(z0),	(13)
АВ
причем величина Z соответствует точке В, величина и0—точке А.
Формула (13) показывает, что в рассматриваемом случае величина инте-
грала
J F(z)dz
АВ
166
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
[Гл. V
не зависит от пути АВ, а лишь от положения начальной его точки А и ко-
нечной точки В, совершенно подобно тому, как, например, работа силы,
коей составляющие были бы 9(х, у) и — Ф(я, у) или ty(x, у) и ф(х, у), ибо
эти силы имели бы соответственно потенциалы Р(х, у) и Q(x, у).
Проведем между точками А и В кривые АСВ и ADB, обе «простые»;
они ограничат площадь ACBDA (фиг. 32). Положим, что как на контуре,
так и внутри этой площади, функция F (z) остается моногенной.
В силу доказанного выше будет для всякой функции F (z) конечной
и однозначной:
F(z)dz= F(z)dz,
АСВ	ADB
пли иначе
F(z)dz—	F(z)dz = 0.
АСВ	ADB
Но так как
-	F(z)dz=	F(z)dz,
ADB	BDA
то предыдущая формула напишется так:
F(z)dz+ F(z)dz — F (z)dz = O\
АСВ	BDA ,	ACBDA
таким образом, мы получаем следующую основную теорему Коши: Интеграл,
взятый по произвольному простому замкнутому контуру от всякой функ-
ции мнимого переменного, моногенной как для всех точек плоскости внутри
контура, так и на нем самом, равен нулю,
§ 52. Теорема Коши. Интегральный вычет. Рассмотрим теперь
тот случай, когда функция F(z), при некотором z — а, обращается в
бесконечность, причем точка M(z = a) лежит внутри контура ACBDA, и
lim (2 — a) F (z) = К (фиг. 33).
Опишем около точки М (z = а) круг EGF радиуса р, возьмем на этом
круге две произвольные точки G и F и соединим их произвольными про-
стыми линиями, например прямыми, с точками А в В нашего контура;
тогда получится два простых контура ACBFEGA и AGHFBDA, обойденных,
как указано, в положительном направлении, т. е. так, что ограничиваемая
площадь остается слева. Для каждого из таких контуров интеграл
F (2) dz
§ 52]
ТЕОРЕМА КОШИ. ИНТЕГРАЛЬНЫЙ ВЫЧЕТ
167
равен нулю, ибо та точка М, где функция F (z) обращается в бесконечность,
лежит вне обходимых площадей.
Таким образом, имеем
F(z)dz + F (z) dz — O.
ACBFEGA	AGHFBDA
Но нетрудно видеть, что в состав двух вышенаписанных интегралов
вошли интегралы от А до G и от G до А и от F до В и от В до F: так
как функция F (z) однозначна, то эти интегралы равны между собою и раз-
ных знаков, — значит, в сумме пропадают,—затем, из остальных частей об-
разуется контур ACBDA, обойденный в положительном направлении,
и контур GHFEG\ таким образом, предыдущее равенство равносильно
такому:
F(z)dz+ F(z) dz=Q,
ACBDA	GHFEG
или иначе
F (z) dz=* F (2) dz.
ACBDA	GEFHG
Остается найти интеграл
F(z)dz,
GEFHG
когда радиус круга p неопределенно убывает, ибо величина этого интеграла
не зависит от величины р.
По сделанному предположению
lim(z—a) F (z) = К,
z-+a
где К есть конечная и определенная величина; пользуясь этим, можно по-
казать, что
F(z) = 7=7+<I>(z)>
причем функция Ф(з) моногенна и в точке z = a уже остается конечной;
следовательно,
£ F(z)dz = K	$ Ф(г)</2.
GEFHG	GEFHG	GEFHG
Последний из этих интегралов равен нулю, — остается найти
С dz
J z — а
Для контура GEFHG будет z = а + ре'1'; значит, dz =ipe111 df), и наш ин-
теграл будет
С	- С	_9„,’_ 9-1/----4
\	----- = 1г \ ----- —	-- tejTC I/	lo
} z—a	J	Off10	r
GEFHG	u0
Таким образом,
J F(z)dz = 2vy~lK,	(1)
GEFHG
168
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
[Гл. V
где
К = lim (z — a) F (z).
z-*a
(2)
Коши назвал вообще интеграл, взятый по бесконечно малому круго-
вому контуру, описанному как из центра из той точки, где подинтеграль-
ная функция обращается в бесконечность, и разделенный на	— 1,—*
«residu», что принято по-русски переводить термином «интегральный вычет»,
Фиг. 34.
и предложил обозначать его знаком
причем знак £ есть начальная буква
в слове «extraction» — извлечение или
нахождение вычета, буква же о указы-
вает, к какому значению переменной z
вычет относится.
В более общем случае функция
F (z) внутри заданного контура может
обращаться в бесконечность не для
одного значения zt а для нескольких,
например:
z = a, z = 6, z = c.
Кроме того, может оказаться, что к
конечному пределу приближаются не произведение (z — a)F(z) или(2—-6)
F(z)..., а произведения (z —a)*F(z), (z — b)lF(z), (z—c)nF(z), причем A,
Z, n —заданные целые положительные числа.
Опишем около точек z = a, z = b, z = c (фиг. 34) круги бесконечно ма-
лого радиуса р, и, взяв на каждом из них по две произвольные точки,
проведем, как показано, прямые АЕ, FG, HJ, КВ; тогда наша площадь
разобьется на две,-ограниченные простыми контурами ACBKQJНNGFМЕЛ
и AESFGTНJUKBDA, и внутри этих контуров и на границе их функция
F (z) в бесконечность не обращается и повсюду однозначна. Применяя тео-
рему Коши и обозначая, для краткости письма, первый контур через Сг9
второй—через С2, получим
F (z) dz + F (z) dz = 0.
Cl	C2
Обратим затем внимание, что, при обходе этих контуров, участ-
ки АЕ, FG9 HJ> КВ пройдем дважды, и, значит, части интегралов, к ним
относящиеся, пропадают, и затем остальные слагаемые образуют: во-первых,
интеграл
F (z) dz,
взятый по контуру ACBDA, обойденному в положительном направлении, и,
во-вторых, сумму интегралов
F (z) dz + F (z) dz + F (z) dz,
E3FME	GTHNG	JVKQJ
или, что то же,
— F (z) dz
EMFSE
F(z)dz — F(z)dz.
GNH7G	JQKUJ
§52]
ТЕОРЕМА КОШИ. ИНТЕГРАЛЬНЫЙ ВЫЧЕТ
169
Таким образом, получим равенство
F(z)dz = F(z)dz+ F(z)dz+ F(z)dz.
ACBDA	EMFSE	GNHTG	JQKUJ
Стоящие в правой части этого равенства интегралы суть, по определе-
нию Ноши, не что иное, как вычеты, умноженные на 2к]/ — 1и относящие-
ся к значениям
z = a, z — bt z = c.
По указанному выше обозначению получим
\ F(Z)dZ=gaF(z) + $bF(Z) + geF(z)+...	(3)
1 ACBDA
Сумму всех вычетов, заключенных внутри данного контура, Кошл
называет «полным вычетом» (residu integral) и обозначает тем же знаком g,
но без значка, так что предыдущее равенство напишется так:
, J—i	\ ' F{z)dZ = ^F(z).	(4)
1 ACBDA
Чтобы исчислить величину вычета, относящегося к точке z = a, для
которой
lim (z — а)к F (z) == Л,	(5)
поступим подобно предыдущему.
Пользуясь равенством (5), можно показать, что функция F (z} будет
^^ = (z-a)fc+ (2—а)*'-’ + ”• + z — а -* ф
причем В, С, .о., К — некоторые постоянные, Ф (я)—такая функция, кото-
рая при z — a в бесконечность не обращается.
Делая опять
z — а = ре01
и замечая, что при обходе по кругу 6 изменяется от какого-либо значения
60 Д° бо + 27Г> получим
°о+2те
F^dk-A $ **
EMFSE	b0 Р
С
J Л-1 е(Л-1)9/ •••
Ьо
Оо+2эт .
t..+K	--g МС <t>(z)dz.
J	ре	_ J
9о	г	BMFSE
Последний интеграл правой части равен нулю, предпоследний, оче-
видно, равен 2к'|/г — 1.
Все остальные интегралы равны нулю.
В самом деле, возьмем, например, первый:
6о+2я	9о<4-2л
С .Р/е __________L— С е-(*-!)«</7А =1
j	- р*-‘	ао
9q 	Но
0о+2л
= -^=г	[cos (А —1)0 —	— 1 sin(fc— l)0]<f6=O,
9о
170
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
[Гл. V
ибо
0о+2те	Оо+2тъ
cos (к— Г 0 с/0 =0 и sin (А— 1)0 с?0=О
Go	Оо
и притом тождественно относительно 0О.
Таким образом, будет
gaF(z) = ^,
где К есть коэффициент при первой степени в разложении функции F (z)
1
по степеням & в сопредельности со значением z = а.
§ 53. Коши дал множество различных приложений теории интеграль-
ных вычетов. Те из них, которые нам понадобятся, вытекают из предыду-
щей основной теоремы и из следующих двух:
Теорема 1. Вычет функции , где f(z) есть однозначная функ-
ция переменной z, не обращающаяся ни в нуль, ни в бесконечность при
z — c, равен /(с).
В самом деле, полагая
видим, что по условию, высказанному в теореме, будет
lim F (z) (z — c) = lim f (z) = / (c).
z->c	z->c
Итак, имеем равенство
l^Ldz = gc^- = f(c),	(1)
2тс 1 Js“c	2~c	V
причем интеграл берется по такому контуру, внутри коего никаких других
«критических» точек, кроме.z = с, не заключается.
/ (z)
Теорема 2. Вычет функции	, где п есть целое и положи-
тельное число, большее единицы, и f(z) есть однозначная функция, не обра-
щающаяся в бесконечность при z~c, равен
1	/ (с)
4 • 2 • 3 . . . (п — 1) dcn~l •
В самом деле,- так как параметр с не входит в пределы интеграла
формулы (1), то, дифференцируя и—1 раз кряду по этому параметру
формулы (1), получим
1-2.3...(к-1) Г f(z)	2
Но, по определению, взятый по любому контуру, не заключающему
внутри никаких других критических точек, кроме точки z — c, интеграл
1 С Я*) dz-P
и, значит, предыдущее равенство дает
1 С / (z)	_<&	f (z)  	1______cP-1/ (с)
2к J (2 - <0п	“ ес (Z - с)п “ 1 . 2 . 3 .. . (п - 1) dc“-i •
Обратим еще внимание на следующую теорему.
s 54] ПРИЛОЖЕНИЕ ВЫЧЕТОВ К НАХОЖДЕНИЮ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 174
Если /(z) есть функция с конечным числом критических точек на всей
плоскости, для которой модуль произведения zf (z) имеет своим пределом
нуль, когда модуль z неопределенно возрастает, то полный вычет равен
нулю, т. е. будет
£/(*) = 0.
В самом деле,
с
причем С есть окружность круга, описанного из начала координат, как
из центра, достаточно большим радиусом, ибо такой круг будет заключать
все те значения z, для коих f (z) может обращаться в бесконечность, значит,
взятый по контуру этого круга интеграл и будет равен сумме всех вычетов
функции f(z)>
Обозначим этот радиус через R; тогда сделаем z-Re"*, откуда
dz = Rie^dft — izdft, и наш интеграл будет
0о + 2те
f(z)dz = \f — 1 zf(z)dfh
с	Оо
Интеграл второй части, при неопределенном возрастании R, имеет
своим пределом нуль, что’и доказывает теорему.
§ 54. Приложение интегральных вычетов к нахождению определен-
ных интегралов. Из приложений теории интегральных вычетов мы рассмотрим
следующие:
1)	к нахождению определенных интегралов,
2)	к разложению функций в ряды Фурье и им подобные,
3)	к интегрированию обыкновенных линейных дифференциальных урав-
нений с постоянными коэффициентами,
4)	к интегрированию линейных дифференциальных уравнений с частными
производными и с постоянными коэффициентами.
Формула
---F(z)dz = £F(z)
прилагается особенно удобно к нахождению интегралов с бесконечными
пределами.
Пусть, например,
_Р(х)
где Р(х) и О(х) — целые функции х и степень Q(x), по крайней мере, на
две единицы выше степени Р(х).
Тогда интеграл
будет иметь конечное значение,
Возьмем функцию
если все корни знаменателя мнимые.
F(Z) =

Для всех точек оси х она будет равна F (ж), для точек же, для которых
Р (z)
модуль Z 'бесконечно велик, модуль дроби будет бесконечно малый, и
172
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
ГГл. V
Z P (z) g,	~
модуль произведения будет иметь своим пределом нуль, ибо степень
Q(z), как сказано, по крайней мере, на две единицы выше степени P(z).
Если из начала координат, как из центра, радиусом R описать полу-!
круг, то интеграл, взятый по контуру AOBDA (фиг. 35), будет
( F (z) dz = F dz+ F (z) dz = F (x) dx 4- F (z) dz.
AOBDA	AOB	BDA	-R	BDA
При неопределенном возрастании R, интеграл

будет иметь
интеграл
в пределе обратится в нуль,
-R
своим пределом
\P^Ux,
J Q (*)
у нас будет
BDA
и
Пред. ( F(z)dz=\ dx = $F (z) 2к
v	J	\*^Z
AOBDA	—oo
(1)
где вычеты надо взять для всех корней, лежащих внутри полукруга
AOBDA, т. е. для всех тех, у коих коэффициент при ]/’ — 1 положительный.
Пусть а, р, у, ...,Х суть такие корни уравнения	0; тогда
предыдущая формула равносильна такой:
1 Т, ^p(z) 	1 * *(*)
2ЙЛ=Т 3 W)aX~$*Q(z) + ^Q(z)
—00
Если а есть простой корень уравнения Q(z) = 0, то будет
<?(*) = (*-*)&(*)> (*)
причем Qi (z) при z — а в нуль не обращается, и тогда
*»/>(*)_*»	1	Р(*) _ Р(«)
Qi(z) ” Qi(a)
по 1-й теореме § 53.
Но, в силу равенства (*), будет (?i (а) = ()'(<х); значит,
ф Р (z)_________________________ Р (а)	/р\
^Q(z)“ Q'(a)
для простого корня а.
Если же который-нибудь из корней кратный, скажем р —Л-кратный
корень, то будет
<?(z) = (z-^<?2(z)t
причем Са(2) в нуль при z = p не обращается; тогда
~ Р(2)_г	1	Р(«)_ t	d^1 /Р(Р)\ /ок
Q2(z)	1.2.3...(*-1)	W
$ 54] ПРИЛОЖЕНИЕ ВЫЧЕТОВ К НАХОЖДЕНИЮ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 173
Пример 1. Найдем интеграл
+оо
5 T^^dx (т<п),
—оо
причем тип— целые и положительные числа и т < п.
По предыдущей формуле будет
1	q__ до Я2ш	ф2ш	а;2т
2к /Z7J	° ~1 + гс2П	Тба2 J + Ж2п+	••• + 6ай ! + Х2П	>
trie
тс ,	--7 .л	Зк , т/---л . Зте
a1 = c°s^ + y-lsin2-, a2 = cos2-+y-lsm2-, ...
ибо лишь эти корни знаменателя имеют положительный коэффициент
при ]/ — 1.
Обозначим осг просто через а; тогда будет
а1==а, а2 = а3, Л3 — а5, ».», ап —а2п-1.
Вместе с тем,
Р(аЛ) = а2т = а2т (2*-О,
О' (аЛ) = 2па2п~1 = 2па2пат1 = — 2паг1= — 2па“<2*“1\
следовательно,
S? ?	—____1 а<2т+1)(2Л“1)
Ga*Q(2) 2п
и, значит,
п
4	1 х-л	.	1 a2W+l_a2W + l а2П
____1— 5= —-V a(2m+D(2*-i)= __L _?-------------?----_ =
2п .	2п 1_а(2и>+1)2
г	/с==1
1	а2т+1
“ “ 7Г 1— (а2,Л + »)2 •
Подставляя вместо a2m+1 его величину
cos	+ у—[sin	,
2я 1 r	2n ’
после простых преобразований, получим
о	гс
. (2m + l)7t ‘
nsin *—-——
2п
очевидно, будет
со
f dx 	7U
\ j Х2П ~	 (2иг+ l)7t •
К	2n sin
2n
Положив
x2n = a
и
2m + 1
2n a’
получим
00
~rv— du =	—	(0 < a < 1)
J 1 + и sin ait	\	/
0
— известный интеграл, найденный Эйлером.
174 ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
[Гл. V
Пример 2. Найдем интеграл
Ч-оо
о С COS ах ,
\	—»dx.
J р2 4- х2
—оо
Взяв функцию
= («>°)
и проинтегрировав ее по такому же контуру, как и в предыдущей задаче»
увидим, что при интегрировании по АВ будет
Г	у-,	/	\	у	С	cos ах ?	, -в /“ л Г	sin ах	»
\	F(z)dz	= \	+	\	^~T^dx’
J	J	р	I"	J	р I
АВ	—R	-R
второй из этих интегралов, очевидно, равен нулю, и останется
F(z)dz = { ™~dx.
J v '	j p24-x2
AB	—R
При интегрировании по полукругу, при неопределенном возрастании
его радиуса, интеграл приближается к нулю, и, значит, по теореме Коши,
будет
4-OG
5 F(z)dz= F(z)dz = 5 -^^dx = ^V~l^F(z).
AOBDA	AB	-“oo
Но внутри рассматриваемого полукруга лежит лишь один корень
уравнения
/?2 4-22 — О,
именно z = + р]/~ — 1; и у нас будет
а?К-1	Г	1	л
%F (z) = g-----------------= —----------=	_ = —е - аР
(з — руГ—1) (з + /> Y—1) L з + руГ—1 Jz=pK-I ^р/~ 1
и, следовательно,
4-с°
I cos ах у тс	у /л\
\-рГ^Лх = -е-Р	(а > 0),
— ОО
откуда следует
оо
I cos ах у _ тс	.	~.
\p^-^dx=rpe~ap- («>°)-
о
Мы не будем останавливаться на дальнейших примерах, отсылая или
к обычным руководствам анализа, или к мемуарам Коши в томе VI 2-й
серии его «Oeuvres completes».
§ 55. Те ряды, которыми нам приходилось и придется и дальше поль-
зоваться в нашем курсе, вытекают из приложения формулы Коши
2тс/-1 J <? О)	?(2)	v '
причем сумма вычетов берется для всех корней функции ср (z), лежащих
внутри контура С.
§ 56. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯДЫ
175
Мы будем рассматривать лишь такие функции <р (z) и f (z), которые
однозначны и при конечных значениях z конечны.
Вычет, соответствующий каждому корню 9(z), имеет конечное и вполне
определенное значение.
Обозначим эти вычеты, соответствующие корням, лежащим внутри С,
через
^2, • • •, Ак>
тогда предыдущая формула напишется так:
(2)
Положим теперь, что j (z) и <p(z) или, по крайней мере, одна из этих
функций содержит под своим знаком, кроме переменной z, еще перемен-
ный параметр а, не зависящий от z; тогда все вычеты будут вообще функ-
циями этой величины а, и наша формула напишется так:
^=t	* - А («) + Л («) +   • + Л, («).
(3)
Положим теперь, что мы за контур С возьмем круг, описанный из
начала координат, как из центра, радиус которого будем неопределенно
увеличивать, тогда число корней функции cp(z), заключающихся внутри
этого круга, может также неопределенно возрастать; значит, в правой
части предыдущего равенства получится бесконечный ряд, члены которого
будут некоторые определенные функции буквы а.
В левой части нашего равенства будет стоять интеграл
('-Ж
.1 'f (г,«)
с
причем, как сказано, круговой контур С неопределенно возрастает; при
этом величина интеграла также будет приближаться к некоторому пре-
делу, который будет вообще функцией от а. Если мы сумеем найти эту функ-
цию, которую обозначим через ш(а), то получим разложение
ш (а) =	(а) + А2 (а) + ... + Ак (а) + ...
этой функции в ряд, расположенный по функциям ЛДа).
Выполнение этого вычисления в общем виде и доставит как требуе-
мые разложения, так и те условия, при которых они имеют место.
§ 56. Положим, что подинтегральная функция имеет вид

и уравнение к (z) = 0 имеет лишь «простые» корни
Xi, Х2, • • •, ^п, • • •
Тогда формула (3) предыдущего параграфа напишется так:
lim^hi^/(z’a)dz==	(О
r С	п=1
и все сведется к вычислению предела, стоящего в левой части интеграла,
когда радиус круга С неопределенно возрастает.
Сделаем
z =	,	([z = yr —
176
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
[Гя. V
тогда предыдущий интеграл будет
s = sV S	С)
этот интеграл будет приближаться к конечному и определенному пределу,
если выражение	₽ ' г...
при возрастании величины г по некоторому определенному закону будет*
приближаться к таковому, независимо от величины 6 и равномерно.
Интеграл (*), если сделать в нем 0О =s — у и обозначить jZ — 1 через
i, можно написать так:
ТС	ЗТС
^*2*	•	2~
ж .) it(re ‘)	ZTC J тс (ге )
тс	тс
“Г	~2
или, полагая в последнем из этих интегралов
— тс + О = 0г
и написав под знаком интеграла опять 6 вместо 0Ь получим
4
5=^4^/(re1i’a)e0‘d9-£	с2')
J тс (ге	)	J тс(—ге	)
тс	тс
2	~2
Это показывает, что 5 будет иметь конечный и определенный предел,
если величина
r-	v32?/ (-ге>1’«)]
L тс (ге ‘)	тс (—re )	J
при неопределенном возрастании г по некоторому определенному закону
приближается к пределу независимо от величины 0.
S будет также иметь конечный и определенный предел, когда
Ф (rffQi) -t f Bi \	Ф (—и Bi \
гН—ок/(ге ’a) и r
тс (ге )	тс (—ге )
будут приближаться и к различным пределам, лишь бы эти пределы были
конечные и определенные.
Точно так же, если для некоторого ограниченного числа частных зна-
чений 6 — 0/ вышеприведенные величины не будут стремиться ни к какому
определенному пределу, но если при этом
г J (...)d0
имеет порядок а при упомянутом возрастании г, то 5 будет иметь конеч*
ный и определенный предед,
§ 56]
РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯДЫ
177
Если сделать опять re4i'=z, то видно, что когда 6 изменяется от
те , те
— у до + у , то z есть такая комплексная величина, у которой веще-
ственная часть положительная или, в крайнем случае, нуль, и видно,
что условие существования предела для 5 состоит в том, чтобы или про-
изведение
стремилось равномерно к конечному и определенному пределу, или чтобы
количества
^/(*) и (-г)4£!/(-0
стремились к таковому, когда модуль z неопределенно возрастает по неко-
торому закону и вещественная часть z не есть отрицательная.
Коши, чтобы получить те ряды, которые он потом прилагает к реше-
нию задач математической физики, берет за функцию f(z, а) следующую:
а
/ (z, а) = е^л-*> F (ft) dp (а > а0),
ао
где F (р) есть функция буквы р., удовлетворяющая условиям Дирихле.
Таким образом, надо будет исследовать предел выражения
а	а
ао	а0
при неопределенном возрастании модуля z и условии, что вещественная
часть z не есть отрицательная.
Первый член этого выражения может быть написан так:
Z ez(a~ао)	Р-) Р (р.) йр. = Z	gZ(a—а0) е—z(H—a-о) Р (р.) dpf
ао	ао
и если величина
Ш е2(а-ао)
« (з)
имеет своим пределом 0, то этот член также стремится к нулю, ибо величина
a
z e~z^~a°'>F (р.) t/p.
*0
конечна для функции F(p), удовлетворяющей условиям Дирихле.
В самом деле, в этом случае промежуток от а0 до а можно разбить
на такие частные промежутки:
от а0 до аь от до а2, от до а,
в каждом из которых функция F (р.) изменяется в одну сторону, т. е. или
все время возрастая, или все время убывая, и, значит, для каждого из
этих промежутков приложима вторая теорема о средней. Число таких про-
межуткова к будет конечное (условие Дирихле).
42 А. Н. Крылов
17R
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
[Гл. V
Итак, возьмем первый промежуток, и пусть будет
Zg-Z(tl-o.0) = /> + ()/ -1,
тогда нам надо будет исследовать интегралы
PF (р) dpt и QF (р.) dp..
а-0	*0
Возьмем первый; по второй теореме о средней будет
«•1	01	Л)
РР W = Р (Ло) Р dp. 4- Р (<Xj) Р dp (а, < ?!<«!).
,	<	«о	*0
Но величина интеграла
^Pdp
*0
есть вещественная часть интеграла
Pi
ze~z(FX“ao> dp. = 1 —-
«•о
т. е. величина конечная, ибо вещественная часть z или нуль, или поло-
жительная, и Pi > а0.
Точно так же увидим, что и второй из этих интегралов конечный.
Совершенно так же убедимся, что и интеграл
«-1
QF (ft) dp
a0
конечный, а следовательно, конечный и интеграл
a
зе-Хн—•) F (рь) dp.
«0
и, следовательно, когда предел выражения
ez(a-a.)
K(z)
есть нуль, то и предел выражения
Z 4^ g«(a-a0) f е-г(ц-ав) F (u.) df
n(z)	J	?
а0
равен нулю, если функция F (р.) удовлетворяет условиям Дирихле.
Перейдем теперь ко второму члену формулы (3) и найдем сперва предел
a
z \ е“2(а-^) F (р.) dp..
J	•
a>0
§ 56]	РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯДЫ f 179
Очевидно, что если вещественная часть z, оставаясь положительней^
так же неопределенно возрастает, как и модуль. 2, то предел ze~z* есть
нуль, и, значит, предел интеграла
2	F (р.) dp	1	‘
ао
есть нуль, лишь бы вещественная часть произведения za неопределенно
возрастала.
Таким образом, остается найти предел выражения
а	л	л
z e~z^~^F (р) dp = F (a) e~~z^~^zdp +	[F(p)--F(at)]dp^
а-8	• e	* а —e
Первый член второй части есть F (а) (1 — c-ze).
Во втором члене разность F(p) — F(a) будет изменяться при доста-
точно малом а в одну сторону, ибо функция F(p)’• по условию Дирихле
имеет ограниченное число максимумов и минимумов, разделенных конеч-
ными промежутками между собою, и, значит, можно воспользоваться второй
теоремою о средней, чтобы исчислить вещественную и мнимую часть этого
интеграла.
Полагая попрежнему,
ze-z(a-H) =
можем написать равенство
е-я(»-Ю [F (р.) — F(a)]zdfi =
<х	a
= $ С[С(и)-F(a)]dF+ $ C[C({*)-F(a)]dpx
или, в силу второй теоремы о средней,
e-z(»-P’) [F (р.)—F(a)]zdp =
а—в
= [F(a — г) — F(a)] | Pd? + V~ 1	,
a—s	a—e
где	‘
я — e < p < a
и
a — a < у < qc.
Но интеграл
P dp
a—a
есть вещественная часть интеграла
е	' 1 '
С g-z(a-ii)	— е—z(a— Р) — e~z9
12*
180 ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО [Гл. V
и так как вещественная часть z или положительная, или в крайне^ случае
нуль, то этот интеграл —конечный или нуль; а так как, при бесконечно
малом е, разность F(a — е)— F(a) имеет своим пределом нуль, то, значит,
предел нашего интеграла есть нуль.
Таким образом, видим, что
a
lim z e~z F (у.) dp = F (a)	(4)
a0
и лишь для случая, когда аргумент z равен + у или —у, этот предел
может и не равняться величине F (а); но, повторив вышеприведенное рас-
суждение и применив теорему о средней, увидим, что этот интеграл остается
копенным при возрастании модуля z.
Таким образом, мы видим, что
★I.
lim----ех^~^Р ([*) с/р. dz = —	dO =
2тс /— 1 J к(г) J	r	J 2л п (- г)
С «о	__тс
2
2 v 7 тс (— z)
Поэтому, если функции ф (z) и я (z) таковы, что
то, на основании формул (1) и (4), будет
оо	л
=	5 еЯп	F	W ф (а > а0),
п = 1	а0
где величины Хх, Х2> • • • > Хп, ... суть корни уравнения
к (z) = 0
и функция 9 С2) такова, что
lim z —у = с и lim e2(a-ao) = O,
ТС (- Z)	К (z)
когда
lim|z] = oo.
Необходимо при этом еще заметить, что если бы функция F (а) не была
непрерывна при х = а, то вместо F (а) надо брать
limF(a — e) = F(a — 0).
е->0
Если мы вместо функции ф (z) возьмем функцию х (z) такою, чтобы
было
lim^-7^ = C и lim * ez = 0
тс (z)	тс (— Z)
ж вместо интеграла
a
a0
§56]
РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯДЫ
181
возьмем
а1
F (р) dp,
а
то получим, совершенно подобно предыдущему,
со	ai
4-CF(a) = 2	рп<«-н)Р(р)ф	(Я1>а),	(6)
п=1	а
причем, если при z = a функция F (а) имеет разрыв, то надо брать
limF (a +1\) = F (a 4- 0).
7)->0
Формулы (5), (6) не представляют непосредственно простых разложений
функции F(a). Чтобы получить таковые, Коши поступает следующим обра-
зом: он берет функции ф (z) и Z (z) так, чтобы было
Ф(2) + х(г)=«(г),	(7)
и выбирает эти функции так, чтобы было
lim^-^ = l,	)
It (z)	те(— Z)	’ I
lim 5^ = 0,	lim = 1, f	(8)
те (z)	’	n (— z)	’I	4 '
lim ez (a-ao) = 0, lim -Ц^2? ez (*!-») = 0,1
те (z)	к (— z)	’ 7
причем вторая строчка написанных условий есть очевидное следствие пер-
вой строчки»
Значит, в формулах (5), (6) будет: С = 1ис=1, и эти формулы на-
пишутся так:
со	a
- 4F («) = 2	5 ^~^F О) Ф.	(5')
П=« 1
СО	«1
4 F («)=2 йг! \eAn {^F	<6')
n = l	a
причем попрежнему > a > а0.
Заметив, что
Ф(Хп)+х(Хп) = 1г(Хп) = 0,	(7')
получим, вычитая первое из вышенаписанных равенств из второго,
СО	<*1
7?(а)= -2 ^«Ana $ e-^F^dy.^
п=1	«о
co	ai
= 2 еЛпл 5е-АпИ F	(9>
л = 1	ад
причем для мест разрыва вместо величины F (а) надо брать
|[F(a-0)+F(a + 0)].
182
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
ГГл. V
Это и есть то разложение, данное Коши, которое заключает в себе
множество разложений, зависящих от корней трансцендентных уравнений»
Так, например, пусть будет
к (z) = eaz — 1
(а > 0),
так что
z .(z) = еа\ (z) = — 1.
Корни уравнения я (z) = 0 суть
* 1 1
z =	----- (к — целое положительное или отрицательное число или нуль);
у (чА	г
—___---- при неопределенном возрастании модуля z будет иметь своим
чс (г) в 1
пределом 1,
= go7~f имеет своим пределом 0,
у г_z\ е“^л
— _____ при неопределенном возрастании модуля z имеет своим пре-
делом 0,
Ф (— z)	— 1 '	л
-Ц—г = —_ имеет своим пределом 1. <
л (— z) е~а* — 1
Затем	,	‘
2\	g-azgz (»!—а)<	g-z(a—<п+а)
м—е2	__.—__—— — —_—— будет иметь пределом 0,
ти (—z)	—1	в 1
если
О или «j — а < а,
gZ(o—в0) =
*,(*)
Z(a—а0)	gz(a-a0—«)
—г = “7^5—Г~ бУДет йметь пределом О,
С ' —‘ 1'	с — л
если
а — а0 — а < 0, иначе а < а0 + а. ,
Таким образом, если а1-— а < а < а0 + а, то всё условия соблюдены,
и формула Коши

П = 1
*1
Q-lnV-F (ft) C?pL
а0
имеет место и дает

к=—оо
i2*« у—л	V-; с - —ц У“г
F-1 . „ ,Г-Ц е а
а0
е2лк
ИЛИ

+°° 2ктеа  «1	2кяц.  _
2 ?	а
=—ОО	ад
при а! — а < а < а0 + а-
$56]РАЗЛОЖЕНИЕ ФУНКТТИЙ В РЯДЫ 183
Выделяя член, соответствующий /£ = 0, и соединяя попарно остальные,
-соответствующие к = — п и А = + п, получим
'(«) = Т\	d>* + 7 2 \ 008 <а — >*)Fd?>
(Ц)	П1==1 ао
ВЗЯВ
а = 21, а, ==/, а0=—Z,
получим
(а) = Z7(р.) rffi +-у-2 § cos Т"(а—	(4Q>
—z	.	n-i —i
— известное разложение в тригонометрический ряд Фурье.
Возьмем как второй пример
it(z) = z (ев2 + e~az) + h (eaz — е_<и)	(а > 0 и h > 0).
Делаем
1 (z) = eaz (z + h), ф (z) = e~az (z — h).	.
Тогда будет
lim ^7^ = 0,
л (z)	к (z)
lim 414=0, am 4=4=i,
Tty— Z)	7C(- z)
liffi +Д2 ez (.-«,) _ Um ^(x-a»-a)(2-/0	= 0
nm7c(z)e , lim^(z + 4+^3(2-h) u’
если
a — a0—2a < 0, t. e. a <, a0 + 2a,
lim LlzilL #	2 +	= о
,	Umit(-z)^ “ш z+ *)-(z +A) e"’
если	:	,
aj — a — 2a < 0 или a > a2 — 2a.
Остается рассмотреть корни уравнения k(z) = 0.
Это уравнение будет . 	.
z(e«2 + e-flZ) + ^(ea2—e~az)=0.	(И)
Это уравнение может иметь лишь чисто мнимые корни, кроме корня z = 0.
В самом деле, если сделать az=^x-^-iy и в полученном уравнении
•отделить вещественную часть от мнимой, то это уравнение распадется
на два
	^l(1!,_e-«) + (e. + e-)(i+±sx)=o.	; ;
При х9 не равном нулю, будет
1 t ' ,хех+е-."'  1
ah. е^^-егх •
,	1 У _	Ж gX — е~Х	,	-	,	5 .. ’
ah tg у * ah 4- е^х
184
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
[Гл. V
Первое из этих количеств всегда положительное, второе — отрицатель-
ное, между тем ytgy и должно быть одного и того же знака; следе-
вательно, х может быть только равно нулю, и тогда первое уравнение (*)
удовлетворяется тождественно, второе же обращается в такое:
которое у нас уже было.
Таким образом, делая z = X	1, видим, что уравнение тс(з) = 0
обратится в такое:
X cos al + h sin аХ = 0.	(12)
Затем
те' (z) = (1 + ah) (eaz + e~az) + az (e0* — e~az),
«' (X / ^1) = 2 (1 + ah) cos aX — 2aX'sin aX =	— ,	(* *)
и формула Коши дает разложение
«•О
(<%! — 2a < a < a0 + 2a),
и суммирование распространено на все корни уравнения (12).
Выделив член, соответс вующий X —0, который обратится в
2 (1+аЛ)	d?
»о
на основании равенства (**'), и соединив остальные попарно соответственно
значениям Хи —X, получим
0.1	СО	0>1
=	2^j?in2aXn J ^)c°8Ma-H^,
a-o	Zl —1	aq
причем должно быть
0Ci — 2a < a < a0 + 2a.
Взяв
aj = a, a0= —a,
получим
"(•>“5173)5	(14>
—a	n=l	—«
где Xn суть положительные корни уравнения
X cos aX 4- h sin aX = 0.	(12)
Это и есть общее разложение по синусам и косинусам дуг, зависящих
от корней уравнения (12).
§ 57]
ИНТЕГРИРОВАНИЕ ОБЫКНОВЕННЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ
185
Из этого разложения, совершенно подобно тому, как для разложений,
по синусам и косинусам кратных дуг получаются разложения только по си-
нусам или только по косинусам для функции, заданной от 0 до а.
В самом деле, положим, что F (— р.) = —F (р) в пределах от — а < р < а;:
тогда будет
(°<’<»> <15>
п = 1	О
Если же F( —p) = F(p), то будет
Л	оо	а
'	(16)'
О	П = 1	О
§ 57. Приложение интегральных вычетов к интегрированию обык-
новенных линейных уравнений. Покажем теперь, каким образом Коши
применил теорию вычетов к интегрированию линейных уравнений, и начнем
с уравнений обыкновенных.
Положим, что требуется найти общий интеграл уравнения
г/(п) + «1^п_,)+ •• • + ап-!у' + апу = 0	(1).
с постоянными коэффициентами.
Составляем характеристическое уравнение:
F (к) = кп 4- fljk71”1 + . . 4- ап—Д + ап = 0.	(2)‘
Простому корню к2 этого уравнения соответствует частное решение-
вида еА1Х, А-кратному корню kj соответствует к частных решений:
еАг‘х xe*iX ...
или иначе
Я	d2	ЯЫ
е“х’ ж;'"'1 хе"‘.......
Чтобы получить общий интеграл, каждое частное решение множится
на произвольную постоянную, и берется сумма полученных произведений. ч
Коши замечает, что, если взять выражение
где ф (к) есть какая угодно функция от к — моногенная на всей плоскости к,
то полный вычет
у___$ ?(*)gAag
F(X)	•
и будет как раз требуемым общим интегралом предложенного уравнения.
В самом деле, заметив, что
F(X) К ’
видим, что результат подстановки этой величины у в предложенное уравне-
ние есть
«(1)	= о,
ибо, по предположению, функция <р(к) в бесконечность не обращается»
186
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКИИЙ МНИМОГО ПЕРЕМЕННОГО
ГГл. V
Значит, величина (4) удовлетворяет уравнению (1).
Надо теперь показать, что эта величина содержит и требуемое число п
постоянных произвольных.
Если, например, Хх есть простой корень уравнения F (Х)=0, то вычет,
ему соответствующий, есть
pZiX
а так как <р (X) есть произвольная функция от буквы X, то величина ср (XJ
есть произвольная постоянная; такова же и величина • Значит, каж-
дому простому корню соответствует в сумме (4) одна произвольная по-
стоянная.	•
Вычет, соответствующий Zc-кратному корню Х£, найдется по формуле
g yft)	1
U F (Ь)	1 . 2 • 3 ... (fc—1)<9Х*-1 Fi&i) ’
где
Л (К) (k —=
Так как функция ср (X) произвольная, то ее производным
?'(М, ф".(Х), ...»
можно приписывать любые постоянные значения и, значит, предыдущее выра-
жение равносильно такому:
(Сг + С2х + С3х2 + ... + Скхк~1) ел*х,
т. е. представляет как раз сумму тех к частных решений, которые соответ-
ствуют Zr-кратному корню характеристического уравнения.
Следовательно, величина
„ — S? ’ (*) еЛХ	/еа
у ~ * F (X) .
есть, действительно, общий интеграл уравнения (1).
§ 58. Положим теперь, что предложено уравнение
У(п)+а1У(п-1)+ . •. +an-i у' + апу = f(x)	(1)
с последним членом, и будем искать его решение под видом
И
причем вычеты берутся по корням уравнения F (X) = 0.
Подчиним функций) Ф (X, х), подобно тому, как это делается при спо-
собе изменения постоянных произвольных, тем п— 1 условиям, которые
выражают, чтобы производные от 1-го до (п — 1)-го порядка, от у при ф (X, ж),
зависящем от х, выражались так же, как и при ф(Х, х), не содержащем
буквы х.
Итак, имеем
У —F (X)	® дх F (А)
и, значит, первое из сказанных условий есть
(3)
,	•	ОХ Г {К)	' '
3 58) ИНТЕГРИРОВАНИЕ ОБЫКНОВЕННЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ 187
При соблюдении этого условия будет
У ke F(k)	 F(X)
и, значит, второе условие будет
^Ф х л	их
При соблюдении этих двух условий (3) и (4) будет
У ~6* 6 F(K) +®е	№ F(X) ’ 
и третье условие будет
Продолжая таким образом, видим, что сказанные п — 1 условий можно
выразить формулою
AL. =0 если 0 < к < п~ 1.	(6)
дх Ъ (к)	' '
При соблюдении этих условий будет	t
y(n) _ <е\п елх Ф_^2_£) л_ яелх дФФ» ж) ALL •
У	е р(ж)	дх F(X)»
подставляя величины
У> У'> •••» ^п)
в предложенное уравнение, получим
Но так как
FQC>^(k. Х)е^х А
® F(X) —U’
то последнее условие, которому должна удовлетворять функция ф(Х,х), есть
gel,?+^,^=/(J).	(7)
Таким образом, надо найти такую функцию ф(Х,гг), которая удовле-
творяла бы условиям (6) и (7).
Но так как при всяком к < п — 1
s? AL-__о
® F (к) ~ U’
ибо в этом случае
1 С xkdx = o
9
когда контур С есть круг, радиус коего неопределенно возрастает, jr
® F(X) .  ’
188	" ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
[Гл. V
ТО СТОИТ ТОЛЬКО взять
дф (X, X)
е дх
(8)

и условия (6) и (7) будут удовлетворены»
Из уравнения же следует
ф (X, я) = <р (X) + е“А5 /(?) (К,
а
(9)
где ф(Х) есть произвольная функция от X, моногенная на всей плоскости X,
и, следовательно, искомая величина у есть
у _	| gpAx V р-А f (О
У-^е F(X) + ®e V F (X) •
а
(10)
Припомнив ту связь, которая существует между нахождением вычетов
и разложением рациональных дробей на простейшие, увидим полную анало-
гию этой формулы с формулами (8) § 9.
Для пояснения метода возьмем уравнение
+2hy' +n*y=f(x),
предполагая, что
п2 —Л2 = nl > 0.
Уравнение
F(X) = 0
будет
Х2 + 2ЛХ + и2 = 0;
его корни:
11= —h + n^—l,
12 = — h — пх У — 1.
Формула (11) дает
у — ¥е2.х	I S? Г ел (х-5)	/(€)^
У 6 Х2 + 2ЛХ +«* J е	Х2 + 2ЛХ + га2’
а
Затем имеем	•
X2 Лм4-п2 = еЛ1Ж 2Й2Л + еЛ2Х 2гал = С1еА1* + С*Л2Х =
Л -f- 2ЛЛ -f- Пл	-f- Zfl
— e~hx [A cos nyc + В sin пух},
X	X
6 Je Л24-2ЛХ + П2"- 2 J*'*'
a	a
eAi (x-S)
Xi + A
еЛз (x~S)
X s ~r h
Но
X1 + A = n1j/r —1, 12 + Л= — nt jZ — 1,
и предыдущее выражение будет
e~h / (?) sin пх (х — ?) гй,
а
S 59,
ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ПРОИЗВОЛЬНЫХ
189
‘и, значит, общий интеграл нашего уравнения
х
у = е-Лж (Л cos пгх + В sin п^х) +	e_hac е71’ / (?) sin пх (ж—?) di,
а
что мы имели и раньше.
§ 59. Определение постоянных произвольных по данным начальным
значениям неизвестной и ее производных. Коши, изложив этот способ
в своем мемуаре «Application du calcul des residus 4 Fintegration des
equations differentielles lineaires aux coefficients constants» (Oeuvres, II serie,
t. VI, p. 252), этим не ограничился, и в мемуаре «Sur la determination des
Constantes arbitraires renfermees dans les integrates des equations differentielles
lineaires» (Oeuvres, II serie, t. VII, p. 40) прилагает интегральные вычеты
к определению постоянных произвольных, входящих в общий интеграл
линейного уравнения по заданным начальным условиям.
Итак, положим, что надо интегрировать уравнение
/") +	+ а2у(п-2) + ... + ап_! у' + апу = 0	(1)
при условии, чтобы при x = xQ было
У = 'По,	У" = Ъ, •••>	(2)
Прежде чем решить этот общий воирос, Коши решает частный, именно,
вместо условий (2) он ставит такие: при х = х0 должно быть
у = ^°, у’^1, уг = Г12, ...» г/(п-1) = 7]п-‘,	(3)
т. е. берет все эти величины в геометрической прогрессии.
Мы видели, что общий интеграл уравнения (1) есть
t fi)
F(X) ’
У=8
где <p(k)—произвольная функция к.
Ввиду того, что
y(ft) — %	еЛХ
у ° F(k) е ’
то надо, значит, выбрать функцию <р (К) так, чтобы были выполнены
условия
£	[* = 0,1,2......(n-1)].	(4)
Но величина сама может быть представлена как вычет, именно:
следовательно, предыдущее условие напишется так:
Sp-W2--^]-0	[А=0, 1. 2...(„_!)],
или иначе
gk*?(Х)(\у F(Х) = ° [* = 0’	2..(»-!)]=0. (V)
190 ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО[Гл. V
Знаменатель, по корням коего вычеты берутся, есть целая, функция*
степени п+1; значит, условие (4') будет выполнено, если выбрать функ-
цию <р (к) так, чтобы числитель был также целой функцией, но степени
не выше n—1; а так как первый множитель уже при к = п — 1 будет
степени n—1, то, значит, надо, чтобы было
ср (к) еЛх° (к — у) — F (к) = С = const.
Отсюда следует
Если желательно, чтобы 9 (к) было конечное при к = т), то стоит только
взять С так, чтобы
F (71) + С = О,
или
-F(T])
и тогда будет
<р (X) = F ft> 2	e~ixo
и, следовательно,	.
J =	<---•>•	©
Выражение
Fa)-F(Ti)
А —
есть целый полином степени п—1 относительно как к, так и т). Располо-
жим его по степеням ?), и пусть будет
F(X) F (iq)  j j j । j 2 i	i A	1
----- ^0 T T Л2 T • ‘ • T ^Л-l q >
где
Aq,	• • • J -^n — l
будут известными функциями k. Подставив эту величину в формулу (5)г
получим для у выражение подобного же вида, т. е. в виде полинома сте-
пени n—I относительно т\. Пусть оно будет
У = Р0 + Р1Ч + РгТ?+ ...+Рп-1Щп~\	(6>
причём
Л),	• • • » ^П-1
будут известными функциями буквы X.
Величина (6) для у должна удовлетворять уравнению (1) при всяком
значении буквы iq; значит, каждая из величин
• • •» ^п—1
в отдельности этому уравнению удовлетворяет, а так как эта величина у
удовлетворяет и условиям (3), то, значит, функции
^2» • • • 9 Рп-1
S 591
ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ПРОИЗВОЛЬНЫХ
191
таковы, что, при x = xQi PQ обращается в 1, остальные —в нули, обращается
в 1, а все остальные производные первого порядка, т« е.
Р' Р' Р’
z О» L 2» • • •♦ Zn — 1
— в нули, и т. д., как показывает следующая схема:
Ро = 1,	Л = 0,	Р2 = о...... Рп-1 = 0,
-	Р'=о,	р\ = 1,	Р' = о,
/>"=о,	Р';=о,	р;	= 1......... Л31=о,	(7>
Р(ап~1> = о, Р("- ° = 0, Р%~ ° = О..P^Zf = 1.
Отсюда видно, что, представив у в виде
У = Ро 7)° + Pi # + р2^ + • • • + рп~1 т-1
и написав вместо показателей при букве у значки, т. е. заменив соответ-
ственно:	черев т}0; т}1 через iqf, т)2 через у2; ,.. т^-1 через мы по-
лучим величину
г/= Л, ^0 +	+• . • . + Л,-1 Tln-i,	(8>
которая, удовлетворяя уравнению (1), вместе с тем, в силу условий (7)^
такова, что при х = х0 будет
г/ = 71о’ У' =Ъ> У" = Ъ...= -Пп-i,
т. е. что эта величина у удовлетворяет и начальным условиям.
Таким образом, имеем следующее правило:
Чтобы найти такое решение уравнения
г/(п) +	+ а2у<п-^ + ... + апу = О,
которое при x = xQ удовлетворяет условиям
г/ = т1о> У' =7li...У(п_1) = •»)«-1»
надо, составив выражение
•	г/ = Ж	ел (х~жо)	(ду
представить его в виде
у=/>о’1° + Л’11'+Л^а+ • •• + Л1-1?)П_1	(10)
и заменить показатели при букве у соответствующими значками*
Так, например, положим, что надо интегрировать уравнение
у" + «2у = 0
при условии, чтобы при х = 0 было у = 1 и у' = 0.
Сперва ищем такое решение, чтобы при х=0 было у = и
и затем полагаем т]0=1, тц —0.
По правилу составляем
F(X) = X2 + a2,	. .
A — 7]	Л — 7]	-	11	‘	‘	1
192 ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО[Гл. V
Значит,
у=г (ч»+-11) еХх=I еаУ^х+4 е~а}Г^х cos аж;
как видно, этот способ Коши избавляет от необходимости решать для
нахождения значений постоянных произвольных, удовлетворяющих началь-
йым условиям, систему уравнений первой степени, к которой приходим,
пользуясь обычным способом.
Положим теперь, что предложено уравнение с последним членом
/п) +	+ а2г/<п-2> + • • • + an-iy’ + any = f (ж)
и что надо найти такое решение, которое удовлетворяло бы условиям:
при ж =	должно быть
У = -)0» / = -11» • "» /П-1)=-1п-1»	(*)
где 7)0, Щр ,,. , vin-i — заданные величины.
Мы видели, что общий интеграл нашего уравнения есть
Xq
Обозначим, для краткости письма, первый член через и> второй—
через и, так что
y = u + v.
Покажем теперь, что при x = xQ будет
и==0, и' =0, vff = 0, ... ,и(п“О = 0.
В самом деле,
vW=g w [)к 5 (ж-г) f ®	+ *к~2 /'(*)+••• + Л*-‘> (*) ]»
ХО
и при х = х0 эта величина обращается в нуль, если к = 0, 1, ... , п — 1.
Значит, присутствие члена и в формуле (12) не оказывает влияния
на условия (*), и их можно заменить такими: при x — xQ должно быть
га следовательно,
где, после разложения по степеням буквы tj, надо показатели степени >
.заменить соответствующими им значками.
Пример 1. Интегрировать уравнение
/ + а2У = /(®)
лри условии, чтобы при х — 0 было
2/ =-1о И /=7)!.
§5»]	ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ПРОИЗВОЛЬНЫХ	193
Применяя правило, имеем
F(k) = k2 + a2, .
gcir-gfo) = к+i = W + 7i1’
значит,	•	-	.	,	,
Но
к1 = Л|/"—1, к2=—а]/ —1,
значит,
и =Г £ 7) (eaV^lx _р e-a^~ix) + 1 -(gaV'-ix _ e-aV^lx\ =
2 а У —1
= 7)0 cos dx + sin ах.
Затем найдем у:
««'-’‘’/(ЭЙ	,
°=» ‘	>.+«.—
о.	. о
= 2-aV±T S f ® [еаГГТ(*-0 -di = | $ / (;) sin а (х -?) di,
а * о	о
и, значит, искомая величина у есть
х
у = tj0 cos ах + sin ах + -1 / (?) sin а (х—;) </;.
а
Пример 2. Интегрировать уравнение
у" — 2у' + y = f(x')
при условии, чтобы при х — 0 было	и
y = flo и у' =T)V
Имеем
F(>.) = X2-2k + l = (X- I)2,
мл=(>. _! >+(,-, ).<-,_ 2),»+
значит, будет
И = S [(к - 2) 7)0 + 71J (Т^	[(к - 2) 7)0 + 7)J	] А-1 =
= К + (711— '»1о)ж]е“-
Затем	:	‘	"1
*" (>_.)—-а[j= J
О.	\ о
13 A. H. Крылов
1$4 ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО[Гл. V
следовательно, искомая величина у есть
х
У = К+ 011 — ‘П0)я]ех+
о
§ 60» Интегрирование систем линейных уравнений. Метод Коши рас-
пространяется и на интегрирование систем линейных дифференциальных урав-
нений с постоянными коэффициентами:
= #11^1 4" #12^2 + #13^3 4~ • • • 4“ #1л^л>
dx2	।	,	.1
— #21^1	#22^2 4“ #23^3 4“ • • • 4- #2л^л»
. (1)
— — #31*£1 + Я32^2 4“ #33^3 4“ • • • Т ^зпХп»
0>п1хп 4~ &п2х2 4" ^пзХ3 4” • • • 4“ &ппхп*
На основании изложенного в главе I, решения этой системы будут
вообще вида
%! = АгеЫ 4- A2e*2t 4~ • • • ,
где кь к2, • • * СУТЬ корни «характеристического» уравнения
	#П — к	#12	#13	• • • #1л	1	
	#21	#22 — к	#23	• • • G>2n	
F(k) =	#31	#32	#зз к	. .. азп	— 0,	(2)
	#Л1	#п2	#ЛЗ	••• #ЛЛ к	
следовательно, можно положить
^=«5®'"................................................................ (3)
причем <Pi (к), ?2 (к), <рп (к) — некоторые пока неизвестные функции к.
Подставив эти выражения в систему (1), мы увидим, что эти функции
должны быть выбраны так, чтобы имели место равенства:
# (к — ®п) ?i (к)	а12 р2 (к)	... а1П ъп (к) , t_zx
е -и,
<g> - Л21 ?1 (к) 4- (к #22) ?2 (к)	• • • а2П ?П (к) 2,t О
ё	Р(Х)	е -и,
Чтобы удовлетворить этим уравнениям, стоит только взять
(к — ап) ср! (к) — «12?2 (к)	• • •	(к) =	(к),
— #21? (к) 4~ (к Л22) ?2 (к)	• • •	#2л?л (к) = <х27^ (к),
где ах, а2, ... суть постоянные произвольные.
Нетрудно видеть, что решения этой системы уравнений будут вида
?i (к) = ai 6ц (к) 4" а2612 (к) 4” • • • 4“ ап^1л (к),
?2 (к) = 02i (к) 4~ а2е22 (к) 4- • • • 4- ап®2п (к),
?л (к) =	(к)	4"	а2®п2	(к)	4~	•	•	•	4"	an^nn	(к)>
gf)O|	ИНТЕГРИРОВАНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ	196
где Оц, 012, • . • , ЬПп суть целые функции буквы к, и притом
0ц, O22, б33, • • • , ^пп
будут степени n—1, все же остальные функций б^, у которых значки i
и к между собою не равны, будут степени п — 2.
Таким образом, каково бы ни было характеристическое уравнение
F (к), формулы (3) и (4) доставят решения нашей системы, содержащие п
постоянных произвольных ап а2, а3, .. . , ап.
Более того: эти решения будут таковы, что при Z = O величина хг
обратится в ап х2 обратится в а2, хп обратится в ап, и т. д.
В самом деле, подставив, например, в первую из формул (3) вместо.
Фх(к) его величину (4), получим
# а1бц + a20i2 (к) + ... 4- an6in (к)
х^с	рг^	е .
При £ —О эта величина обратится в такую:
\ а1^И W + а^12 (к) + ’ ‘ * +'aZiOin (к)
(^i)o -- £	•
Но, как уже сказано, 012, б13, ... , б1п суть целые функции степени
п — 2; следовательно,
<£> 012 (к)   /ч	013 (к)   р.	61П (к)   гх
F(K) V’ Ь F(k) v,	V
п остается
/~ \ __ <£ а10ц (к) _ 0ц (к)
VMo—®	,
а так как функция 6u(k) степени (n —1) относительно к, функция же F(к)
степени п, то вычет
равен отношению коэффициентов при высших членах числителя и зна-
менателя, которое равно единице; значит, будет
-	(^])0 = а1.
Совершенно так же увидим, что будет
(^2)0 = а2» (Я'з)о = а3> • • • , (^п)о ап*
Этот метод приложим и к интегрированию систем, содержащих урав-
нения порядка выше первого, без их предварительного, приведения
к виду (1).
Так, например, положим, что дана система
— А2х + В2у -j- C2z,
d^ = A^ + B3y + C3z,
для которой характеристическое уравнение есть
	Л— к2	Вг		
	Л2	В2->*	^2	= 0;
	Аз	в3	Ca-'iA	
13*
196 ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО ГГл-JV
положив попрежнему
X~®F(k)e ’ У-е ?(к)е ’ Z~CF(K)e 9
видим, что эти величины будут удовлетворять предложенной системе, если
функции Фг, <р2 и ?з определить таким образом, чтобы было
~ С2 - A) h (V - а) - С1Ъ С) pAZ _ 0
д	е - и,
(X) + С2 - В2) ?3 (X) - С/ч (X) ,f _ п
F(X)	6 -U’
<£>	^з'С1 (X)	-^3?2 О + (X2 Сз) (X)	 л
®	е — и.
Этим уравнениям можно удовлетворить, взяв
()? - Л3.) Т1 (к) — В1 ?2 (к) - Сг ?3 (к) = (ад + РО F (к),
- А?! (X) + (к2 - Ъ (к) - С2?3 (к) = (а2к + р2) F (к),
- Л3?2 (к) - В3*2 (к) + (к2 — С3) ?3 (к) = (а3к + р8)F (к),
где «1, Р1,а2, р2> аз и ?з СУТЬ произвольные постоянные.
Следующие из этих уравнений величины epi, <р2, ?з будут вида
?х (X) = (аА + Pi) 6ц (X) + (а2Х + р2) 6и (X) + (а3Х + р3) б13 (X),
?2 (X) = (ахХ+ рх) 623 (X) -4- (а2Х + р2) 022 (X) + (а3Х + |33) 02з (X),
(М = (а1Х + Pi) 631 (X) + (а2Х + р2) ^32 (X) + («3Х + рз) 033 (X),
причем 6ц(Х), 022 (Х), 033 (X) будут целыми функциями от X четвертой сте-
пени, остальные же bik — второй степени относительно X.
Таким образом, величины ж, г/, z приведутся к следующим:
т__<&	4- fti) 6n (X)
F{\) е ’
„__<£ («2Х 4- р2) 622 (X) Af
F(k)	е 9
„ _<£ (азХ 4- $8) Овз (X)	•
F(k)	е 
При t = Q величина х обратится в такую:
г __£ (аЛ 4- Pi) 0ц (X)
F(Xj 9
и так как F(X)—шестой степени относительно X и коэффициент при X6
есть 1, функция Оц(Х)—четвертой степени относительно X и коэффициент
при X4 есть 1, то этот вычет равен ах.
Взяв производную по букве t, имеем
dx _ х(а1Х* + ргХ)Оп (X) t
dt~~c F (X) е
и при t = 0 будет
(аЛ24-31Х)0п(Х)
F(K)
Функция (X) — вида аХ4 + ЬХ2 + с, и коэффициент а = 1; поэтому
предыдущий вычет равен следовательно, найденное решение таково,
что при £ = 0 сама величина х обращается в 04
Совершенно то же докажем и относительно у и z.
§ 61]
ИНТЕГРИРОВАНИЕ СИСТЕМ С ПОСЛЕДНИМИ ЧЛЕНАМИ
197
§ 6L Интегрирование систем с последними членами* Метод Коши
приложим и к интегрированию систем уравнений с последними членами. >
Пусть будет дана система
= Л11#1 + #12^2 + • • • + а1п%п + /1 ft),
— ^21^1 + #22^2 + • • • + О'Чп^п + /2 ft),
— ап\%1 + ап2%2 + • • • + аппхп + fn
В том случае, когда
/iW = /2^.-=/n(O=o>
решение, как мы видели, дается формулами	«	/
х __ g аАт ft) + аа6п ft) 4- ... 4- Mu (X) 4- ... 4- gnQtn ft) ем ft = 1 2 3,	, n),
в которых аА, а2, • ••, ап суть произвольные постоянные, 0 ik (к) --целые функ-
ции от к степени (п — 2) при i Ф к и степени (n — 1) при i — k.
Будем искать решения того же вида, но считая а2, ..., ап за функ-
ции от t.
Эти функции тогда определяются уравнениями	'	'
g ajQ*i ft) 4- ft) 4- ... + a;0fi ft) 4- ... 4-	?- fi) eu _ f ft = 1 2 3 n)
как то следует из подстановки в данную систему.
Этим уравнениям мы удовлетворим, взяв
(Г=1, 2, 3, ..., n),
ибо тогда в стоящих в левых частях предыдущих равенств вычетах придется
удержать лишь по одному члену, именно —содержащему 0l7(k), так как
вычеты от всех прочих будут нули.	!
Таким образом, после подстановки предыдущие равенства примут вид
(* = 1,2,3,
а так как
& в** ft) ______________________________4
° F(X)
то эти равенства имеют место тождественно, и, следовательно, взятые вели-
чины удовлетворяют системе (*).
Таким образом, будет	. '	*
^ = ^•7/ft),
откуда следует
Я( = С( + $ e-^fi ($)	(г = 1,2,3....п),
а * ' /
где Cj —постоянные произвольные, а — заданное постоянное число.
198
ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО
[Гл. V
Если Желательно иметь такие частные решения, которые при Z = 0
обращались бы в 0, то надо взять Cf = 0 и а = 0, т. е. бр&ть
t
«/ = 5 e~K'fi (?)
О
и, следовательно, будет
х. = J /1 W + А (х) + • • • + (?) Qin (*) di
(/ = 1,2, 3, ...,тг).
Стоит только к этим величинам придать найденные выше, соответ-
ствующие уравнениям без последних членов и обращающиеся при Z = 0
в ап а2, . . ., ап, — и мы получим такие решения для хх, х2, . .., хп, которые
удовлетворяют заданной системе дифференциальных уравнений с последними
членами и при 2 = 0 принимают наперед назначенные значения.
§ 62. Теорема Гурвица. Коши показал также ряд приложений своей
теории к решению алгебраических уравнений высших степеней, именно —к
определению числа корней данного уравнения, заключающихся внутри задан-
ного контура. Не излагая этой теории, приведем без доказательства один
результат, полученный Гурвицем, имеющий прямое отношение к нашему
предмету. Исследование малых колебаний материальной системы приводится,
как показано в главе I, к интегрированию системы линейных уравнений
с постоянными коэффициентами, а это последнее —к решению характеристи-
ческого уравнения. Колебания будут «затухающие», если все корни харак-
теристического уравнения будут иметь отрицательную вещественную часть.
Необходимые и достаточные для этого условия даются следующей теоре-
мой Гурвица:
Необходимое и достаточное условие для того, чтобы уравнение
aQxn +	+ а2хп~2 4- ... + ап 0
при а$ > 0 имело все корни с отрицательною вещественною частью, состоит
в том, чтобы все определители числом п
Д2» А3, ...,
составленные по ниже показанной схеме, были положительные.
Эти определители составляются так:

«1	а3	«5 ’•	• 1
Оо	Я2	а& . .	. a2k—2
0		а3 . .	. а2к—з
0	«о	(22 • •	. a2k-4
		• •	. . ak
так что будет
•		Л j -^3	,	^3 —	«1	«3	«5	
Aj — a19	Д2 =				a2	«4	r
		Uq a4		0	«1	fl3	
	H* a co a СЯ ft	
д4 =	aQ a2 a^ aG	, . . . II T. Д
	0	6i3 a5	
	0 а^ a 2 a±	
§ 63]
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
199
Затем все коэффициенты, указатели коих больше и, заменяются нулями;
так, например, условия при тг = 4 будут
«1 >
О,
Л1 «3	>0,	ax a3 0 ^0 ^2 ^4	>0
б?2		0	a5	
Ci J 6Z«	s 0 0		
	> $4 0	> 0,	
0	i a3 0		
0 fl/Q 6Z2 ^4			
последнее условие можно писать так: а4>0.
Доказательство этой теоремы, которое можно найти в превосходном
курсе акад. Д. Л. Граве «Элементы высшей алгебры», слишком сложно,
чтобы его давать в нашем курсе, самая же теорема и пользование ею,
как видно, весьма просты.
§ 63. Приложение интегральных вычетов к интегрированию линей-
ных уравнений с частными производными. В мемуаре, озаглавленном:
«Memoire sur Implication du calcul des residus a la solution des problemes
de physique mathematique», изданном в 1827 г., Коши прилагает теорию
вычетов к решению уравнений с частными производными линейных и с по-
стоянными коэффициентами.
При изучении этого метода необходимо постоянно иметь в виду фор-
мулы §§ 57, 58 и 59, дающие решения обыкновенных уравнений, й фор-
мулу § 56, которую Коши пишет так:
х
' (1)
Хо
В этой формуле вычеты берутся для всех корней уравнения
и вместе с тем:
Я (л) = О
		
lim = 1,	lim z-->co	Z_(=£> = 0, z(-2)
lim —= 0,	lim z-x»	?( —\ It ( — 2)
lim	== 0, 2-»«я<2)	lim Ц z->oo r’( z)	ez(X-x)_0,
(2)
(3)
причем вторая строчка написанных условий есть очевидное следствие пер-
вой строчки.
Мы уже имели примеры разложений, получаемых на оснований фор-
мул (1), (2) и (3). Коши обращает еще внимание на следующие, которые
получаются, если сделать
у (2) = F (z) еа*
и
Ф (2) — — F(b — z) ea^b~z\
причем 6 —какая угодно постоянная, а — положительная величина, большая
Х , и F (2)— целая функция 2.	'
1:200 ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО [Гл.’У
;. е Вт этом тслучае будет	t :
lim = Hm	_ j,
”(*) F(z)eaz — F(b-z)ea<-b~z^
lim*(-a) = lim__________F( — z)e~az________
я ( — z)  F ( - z) e-a2 — F (b + z) e"(5t2) ~ ’
11 m n (z)	l mF(z)en2 —F(b —г)ея‘6-2>' U’
'	F(b‘+z)e^
n( —z)	F(—z)e“a2 —F(7> + z)e">b2)	’
lim	= lim	=
K(~~z)	F^ — z)e~az-F(b + z)ea<-b+z)
, .................................. ’	Г(-г)вг(х-л:12а>
‘		= liin-------£--------1---— .
: ,	•		F(b + z)eai-F(-z)e~2*z
Этот предел будет 0, если X — х— 2а < 0, т. е. когда
X — 2а < х,
.	’ V уЮл-^'г F(a-.z)ea<b-zKz<x-x>>>
lm я fzj е ° llm Р (z) е«о — F(b — z) е"**-2)—
/	r F (b - z) е^-^о-2»)
Ш F (2) <?-«* - F (6 -V- z) e'2ttZ
Этот* предел будет 0, если х — я0 — 2a < 0, т, е. когда
я < #о + 2а»
Таким образом, для величины х, удовлетворяющей неравенствам
X — 2a < х < х0 + 2a,
будет иметь место формула
х
х	F(K)eaK V (н)
/ w ° g j	1 fr> * ° g 2 F (Ь_.	 С)
причем вычеты берутся для всех корней уравнений*
z (л) F (k) e<*-F(b - к) еа^ = 0.
§ 64. При изложении метода Коши мы не будем следовать буквально
за его автором, а будем согласовывать обозначения со сделанными в преды-
дущих параграфах, и самое изложение будем вести так, чтобы яснее высту-
пала как связь этого метода со вторым методом Пуассона, так и их различие-
Пусть дано уравнение:
№ I t	, к dz f	/4\
— =al-^-r + br — + ciz9	(1)
dt2 dt 1 dx2 ‘ 1	1	'
и требуется его интегрировать так, чтобы было соблюдено условие:
|| + Az =0 при
^ + к^ = 0 .при
ж = 0
х = I
при всяком значении t.
(2)
§ 64J
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
201
Затем, чтобы при Z = 0 было	в
Z==/O(x)
и
’	• •	> =	’	(3>
причем функции fQ(x) и /х (х) заданы для промежутка от а —0 до х~1~
По второму методу Пуассона ищем решение вида
2=^X7,
причем каждый член этой суммы в отдельности должен удовлетворять как
уравнению (1), так и граничным условиям (2).
Совершенно так же поступает и Коши, и, значит, для определения
функций X и Т имеем уравнение
(аТ" + ЬТ') X - («1Х" + ЬУХ' + схХ) Т,
которое распадается на два:
аТ" + ЬТ’ 	4- сгХ
Т	X
где а есть какая угодно произвольная постоянная величина.
Написав уравнение (4) так:
= а,	(4)
аТ"+ЬТ' =	(5)
a tX" + Ь^Х' +	- а) X = 0,	(6)
получаем соответствующие (5) и (6) характеристические уравнения:
ар.2 + 6р. = а,	(7)
аДа + 6jk+ Ci = a,	(8)
где, как уже сказано, Л —какая угодно постоянная.
Далее следовало бы решить уравнение (8), и если обозначить его корни
через /4 и л2, то будет г'
X = АеЛ1Х + Ве^х,
причем А и В — какие угодно постоянные.
Корни и Х2 выразились бы через а.
Коши, для упрощения вычислений, поступает иначе. Так как я—вели-
чина произвольная и, в силу уравнения (8),
Xj=?i(*) и ^2 = ?2(а),
то, значит, будет .	.
т. е. вместо того, чтобы оба корня выражать через произвольную а, можно
один из них принять произвольно и выразить другой или, в общем случае,
все остальные через него. Итак, пусть будет
>ч = Р>
тогда
* =	-|- Cj
202	ПРИЛОЖЕНИЯ ТЕОРИЙ ФУНКЦИИ МНИМОГО ПЕРЕМЕННОГО	[Гл. V
и уравнение (8) напишется так:
«хк2 -Ь bjK + С] = ajp2 + 6гр + Ср
ИЛИ
«1 О-2 - г2) + Ьг (к - р) = (к - Р) [а, (к + Р) + 6J = 0,
н, значит, будет
ki = p, Z2= —h.—р = /с—р,	(9)
и, следовательно, функция X будет
X = Ае?х +
Надо теперь выбрать постоянные А и В так, чтобы удовлетворить
граничным условиям^ по составлении которых имем
Л(р + Л)+5(А:-р + Л) = 0,
Л (р + kJ е"1 +В(к-? + hj) <£к~М = 0.	UVJ
Эти два уравнения лишь тогда допускают решения, отличные от нуля,
когда определитель равен нулю, т. е. когда
A(H) = (p + M(A-p+A)^-(p+A)(A-p + A1)e<*-f)' = O • (И)
и вместо Л и В можно взять
Л = (А--р+/г)С
£=-(р + Л)С,
где С —любая постоянная величина. Мы уже видели, что без ущерба
общности эту постоянную можно принять paBHOIf 1.
Таким образом будет
Х= — (? + h) е^к^х + (/< — р + й)еРж.	(12)
Уравнение (7) напишется так:
ар2 + 6р — fljp2 + btf + cv	(13)
Пусть его корни суть: = о и р2= со, причем а и со будут известными
функциями р; тогда решение уравнения (5) будет
T = Dezt + Ее*',
и, следовательно, величина z, удовлетворяющая уравнению (1) и граничным
условиям, будет
z=^{De^ + Ee^)Xy	(14)
причем суммирование распространяется на все значения р, удовлетворяющие
уравнению (И), D и Е— произвольные постоянные.
Коши пишет формулу (14) иначе, а именно:
Z =	' ф (P?IX) W 1 ’	(Ь)
где через Ф (р, р) обозначена функция
Ф (р, р) -= ар2 + 6р — ахо2 — 6хр — сд	(13?)
и сперва надо взять вычет по букве и, функция же <р(р, р) какая угодно.
64] ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 203
Остается теперь выбрать эту функцию так, чтобы были удовлетворены
и начальные условия (3). Коши для этой цели поступает так: он берет
функцию ф (|л, р) равной
? (р, р) = (р + АО \	Z)
•	r /
0
причем, после выполнения деления
Ф (р, н) - - Ф (?, /)
1А -1
в полученном полиноме степени буквы /, т. е.
/° и Р -
заменяются функциями
/о(а) И /1(я)-
В самом деле, в этом случае величины z и — , следующие из выра-
жения
___« g е*1'? (?> Ю *
Д(?)’
при Z — 0 будут, на основании сказанного в § 59,
i
Лг-а)/0(х)^
2о=^?------------о-------------,	(16)
<1?>
О
Действительно, по извлечении вычетов относительно буквы и, величина
s	г *<? f>-»<b/)eX,_.)dl
1 ф(ь :0 J н — /
о
при t — 0 обратится в
e?(i-*)/0(a)da,
6
и ее производная по t обратится в
i
о
ибо при всяком р величина
*!Х* Ф(о, и) — Ф(?, /)
^Ф(р, н) я-/
удовлетворяет уравнению
Ф(Д,?)Т = 0
204 ф ПРИЛОЖЕНИЯ ТЕОРИИ ФУНКЦИЙ МНИМОГО ПЕРЕМЕННОГО [Гл. V
и при £ = 0 обращается: само Т в /а и в У1, а так как мы условились после
взятия вычетов по заменять /° через /0(а) й у1 через /Да), то формулы (16)
и (17) и будут иметь место.
Остается еще показать, что величина z, даваемая формулой (16),
и даваемая формулой (17), действительно, равны /0(ж) и /Дж). Для
этого поставим вместо X его величину (12), вместо Д (?)—- его величину
(11); тогда формула (16) примет вид
z = £	(? + Ч) 1^ ~ ? + /0 (р + /I) е(Л'~р)Ж ]
°	(? + А,) (А - Р + h) е?г - (? + h) (к - ? + Ах) е<-к~Ъ1
I
(Р + Ах) (к — р + A) е?' е? <*-*"> f0 (л) di
“ (р + Ai) (А - р + ft) ef/ (р +h)(k- Р.+ Ах) «<*"?>'
z
\ ef(z-’)/0(a)da =
0
(? + Ax) (P + Л) *?Z ekx e-K«+»)/0 (a)da
_________________________0________________________
(? + (k - p. + h) e?1 - (p 4- h) (k - p + h.)
В силу формулы (*) § 63, первый член равен /0(ж): чтобы убедиться
в этом, стоит только в формуле (?) положить F(X) = (Z+ ЛХ) (А— /.4- /г)
и заменить букву к буквою р, букву а буквою I и букву Ъ буквою k
и пределы у интеграла взять яо = 0 и X == I; второй же член этой формулы
при всяком х > 0 равен нулю, что мы видели при доказательстве теоремы
Кощи, из коей получилась формула (*) (см. § 53).
Совершенно так же поступим и для
чина равна /Дх).
(Ю.
и убедимся, что эта вели-
Таким образом, получаем следующую теорему:
Чтобы найти такое решение уравнения
d2z / dz d*z j dz .
U д#2 "Ь * л 13“2 4"	5—И
dt2 dt 1 dx2 ldx 1
которое удовлетворяло бы граничным условиям".
при я = 0 должно быть —
> х = 1	»	»
dx 1
при всяком значении t
и начальным условиям: при t=^0 должно быть
z = f0(x) и g^/Дя;),
надлежит:	.
во-первых, составить уравнение
axk2 л-	4-Ci = ah>2 4-	+ ci
и выразить его корни черев р, при этом всегда один из корней будет — р;
во-вторых, составить функцшд
X = Ае?х 4- Ве^х
§ 64] ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 205
и определить отношение между величинами А и В так, чтобы эта функ-
ция удовлетворяла граничным условиям*, тогда величина р будет корнем
некоторого трансцендентного уравнения
Д(р) = О,
именно*.
Д G) = 0 + Л1) (* - Р + Л) - (р + h) {k- р + Лх)
произвольный же постоянный множитель, входящий в состав функции X,
можно взять равным 1;
в-третьих, составить функцию
Ф(р, р.) =г «|л24-да—«ip2 —dip—Сп
тогда искомая величина z будет выражаться формулою
, _ •£ Я ?(!* ?)еМ Х
Ф(р>ю д(Р) >
причем
<р(н р) = (р + Л1)
С Ф(Р, |х)-Ф(Р,/)е?(г_а)(га
J н-/
о
и, по выполнении стоящего под знаком интеграла деления, надо величину
заменить через /0(а) и У1 заменить через /2(а), при извлечении же вычетов
сперва найти вычеты, относящиеся к букве а, а затем к букве р.
Как видно, этот метод дополняет второй метод Пуассона как раз в том
пункте, который составлял его слабое место, т. е. в удовлетворении началь-
ным условиям, когда заданную функцию приходилось представлять в виде
бесконечного ряда, расположенного по известным функциям, зависящим от
корней трансцендентного уравнения.
Коши дает в вышеупомянутом мемуаре и ряд других способов для
определения функции <р(р, jx), ъ также и ряд примеров, прилагая выведен-
ные формулы к решению задачи о колебании струны, распространению
тепла в пруте и пр.; но мы на этом останавливаться не будем, так как
главная наша цель при изложении этого метода состояла в том, чтобы
показать, что есть общий способ для доказательства сходимости получаемых
по второму методу Пуассона разложений, а также и нахождения тех условий,
при которых эти разложения имеют место.
В практике же следует пользоваться вторым методом Пуассона, как
приводящим простейшими выкладками к цели, и лишь если определение
коэффициентов в разложениях представит затруднения, то йадо восполь-
зоваться или методом Коши, или же первым методом Пуассона; что же
касается доказательства сходимости полученных рядов, а также применения
пх для численных вычислений и изучения функций, ими представляемых,
то в следующей главе мы даем простой способ, приложимый во многих
случаях.
ГЛАВА VI
НЕКОТОРЫЕ ЗАМЕЧАНИЯ О СХОДИМОСТИ РЯДОВ ФУРЬЕ
И ИМ ПОДОБНЫХ И О СУММИРОВАНИИ СИХ РЯДОВ
§ 65. Теорема Абеля. Из предыдущих параграфов видно, что решения
рассмотренных нами задач математической физики представляются в виде
бесконечных рядов, подобных рядам Фурье; поэтому исследование сходимости
таких рядов и величины остаточных членов может дать указания на то,
сколько членов брать в ряде для получения той, по большей части весьма
грубой, степени точности, которая требуется в технических вопросах.
Приведем сперва те замечания, которые по этому поводу делает в своих
лекциях о распространении тепла умерший в 1912 г. знаменитый математик
А. Пуанкаре.
Основанием для своих рассуждений он берет следующую теорему
Абеля:
Дан ряд
<5 = иг + ^2 4: U3 + . . . + U.n -f“ . . . ,	(1)
сходящийся или колеблющийся (т. е. коего суммы первых п слагаемых
ограничены, но не имеют определенного предела,, например 1 — 1 + 1 — 1 + ...)
и совокупность положительных чисел
f	«1, «2. а3....«П, • • • ,	(2)
неопределенно убывающих с возрастанием значка п и стремящихся к нулю,
тогда ряд
5 ==	+ a2w2 + • • • + *nUn +•••
сходящийся.
В самом деле, если ряд (1) сходящийся, то, каково бы ни было
число р, при достаточно большом п будет
I Зп+р —5П | <	(3)
где рп — сколь угодно малая величина. Если же ряд (1) колеблющийся,
то в неравенстве (3) рп будет величиною конечною.
Составим теперь верхний предел остатка ряда S-
Имеем
Sn+p Sn — an-H Un.± 1 4~ an+2 ^п + 2 4“ • • • + an+p ^п+р’
Вторую часть этого равенства можно писать так:
an+1 (^n+l	$п) 4" an+2 (<3п+2	1) 4~ • • • 4~ an+p (°л+р ^п+р —1) —
— an-pl (^л+1 — Зп) + Яп + 2 [(^п+2	3n) (an+ 1 an)] 4“ • • •
. • • + an + p [(“л + р &п) (^n+p—1	^n)] —
= (an+i — sn) (an+1 ~ an+2) 4- (sn+2 — sn) (»n+2— ап+з)+ • • •
... 4" (~n + p — 1	(^n-f-p-1	an + p) 4” i^n+p	~n) 3>n+p*
§ 66]	ОПРЕДЕЛЕНИЕ УСЛОВИЙ СХОДИМОСТИ РЯДОВ ФУРЬЕ	207
Так как числа а все убывающие, то все разности . (ап4.л.— ап+&-1)
положительные, и так как по абсолютной величине
| $п + р	&п I
то по абсолютной величине предыдущая сумма будет меньше
Рп [(ал + 1	ал) + (ал+2 ап-м) + • • • + (ал+р + 1 ал+р) + йПтр]>
т. е-
!^л + /)	I рл ап+р+1 •	(4)
При неопределенном возрастании значка п эта величина стремится
к нулю; значит, ряд (2) сходящийся, лишь бы рл было конечное, и формула
(4) дает верхний предел остатка этого ряда.
§ 66. Приложение теоремы Абеля к определению условий сходи-
мости рядов Фурье. Покажем теперь, следуя Пуанкаре, приложения этой
теоремы.
Пусть будет
пх)/* —1
ип = е ,
тогда
sn+p — On = епхУ~^ [ехУ~~1 + е2хУ^ + ... +	=
__	_e(p+i)V-ix	___i_~ePxV-^
__епхУ — 1 е_______________— е(п+ *) XV~ ~ 1____rzrr- =
1 - 1 -
= е(п+1)хГ-1
. X	% г---1	• Я
Sin— COS——У — 1 sin —
z z	z
следовательно, модуль величины an+p — ап равен модулю величины
. х ’
sm-
т. е. меньше
1
. х ’
sm-
следовательно, можно брать
Эта величина конечная для всех значений х, кроме как для х% равных
четному кратному числа тс и х = 0.
Следовательно, если взять ряд
„ хУ"i ,	2яУ-1 	। „ _пх’К-1 ।	/~\
ОС^е "Г" 0&2в	-j- ... “7"	j* • • • *
где числа аь а2, ..., ап, ... положительные и бесконечно убывающие, то
этот ряд будет сходящийся, кроме значений х, равных четному кратному
числа к и х ~ 0.
Ясно, что то же заключение относится и к рядам
cos х 4- а2 cos 2х + . . . + ап cos пх + ...,
ах sin х + а2 sin 2х + .. + ап sin пх + ...,
208
О СХОДИМОСТИ И СУММИРОВАНИИ РЯДОВ ФУРЬЕ
[Гл. VI
представляющим вещественную часть и коэффициент при -1 в мнимой
части предыдущего ряда.
Если взять числа xQ и xt так, чтобы было
то всегда найдется такое число М, не зависящее от ж, что будет
1
м
И,
и,
их можно интегрировать почленно.
значит, в пределах от я0 до хх ряды (6) будут равномерно сходящиеся
значит,
Если, например, взять
1
ап == —,
п п 9
то
получатся ряды
с х? sinn-r
и
cos пх
п
сходящиеся для промежутка 0 < х < 2тг, но не абсолютно.
Взяв
__ 1 1
Лп ~ пг ’	п3’ "
получим ряды
sin пх гр _______ cos пх
с sin пх т _______________5Л cos пх
Эти ряды равномерно и абсолютно сходящиеся, ибо абсолютные вели-
чины их членов соответственно меньше членов сходящихся рядов
ill	1
Т + 22 + 32 + • • • + ^2 + • • • ’
111	1
т + у8 + зз+ ... +^.+ ••• >
которые буквы х не содержат.
Если взять производную от ряда S2 почленно, то получится
dS2  ’’О cos пх  гр
dx 21 п 1
и так как ряд Тг равномерно сходящийся при условии (7), то сумма 7\
представляет производную функции S2 для всех значений буквы х, кроме
х = 0 и х> равного четному кратному числа те»
Формула -^-=Т12 имеет место без всяких ограничений; но имеет
разрыв непрерывности при я = 2Ъг, и т. д.
Возьмем теперь ряд вида ..............
S — 2 Рп cos пх,
§ 66] ПОРЯДОК КОЭФФИЦИЕНТОВ РЯДА ФУРЬЕ ОТНОСИТЕЛЬНО -	209
л 
в котором Рп есть целый полином относительно :
Р — Д_ Xp+1	_L Xp+Q
^71 — пр I njp+1 -Г » » • -h np + q ,
где Хр, Хр+1,	, Хр+g—постоянные числа, не зависящие от п. Тогда, оче-
видно, будет
S — ^рТр + Xp_j.iTp+i + ... + Xp+gTp+g,
и, значит, исследование ряда S привелось к уже рассмотренным рядам
Тр, ... , Tp-l Q.
Положим теперь, что в ряде
S = 2 ап cos пх
• * 1
коэффициенты ап могут быть разложены в ряд по степеням —, так что
_ j ^P+l f
П пР '	+ i '
^p+q.
flP*q
д^+ff+l "Г
и пусть будет
р	I ^р+1 1 д_
п пР^ пР*1 “Г • • • “Г np+q >
’ _^p+^+1 .
п	п? + ?+1 "Г • • • •
Тогда наш ряд напишется так:
S == 2 рп cos пх + 2 Rn cos пх.
Первый из этих рядов представляет, как мы видели, непрерывную функцию
вместе со своими /? —2 первыми производными, производная же (/? —1)-го
порядка имеет разрывы.
Что же касается ряда 2 Нп cos пх9 то по абсолютной величине будет
।	। < дР+0 + 1 >
где к есть некоторое постоянное число. Ряд
2п-р4и-со8пж
равномерно сходящийся вместе со своими (p + q— 1)-ми производными, то же
будет и по отношению ряда 2^ncosn#; значит, ряд 2ancosn# имеет не-
прерывные производные до порядка (р — 2) и вообще может быть уподобляем
рядам Sp и Тр в отношении условий сходимости и дифференцирования.
§ 67. Порядок коэффициентов ряда Фурье относительно — при раз-
ложении разного рода функций. Рассмотрим теперь, каков будет порядок
относительно ~ коэффициентов ряда Фурье при разложении разного рода
функций.
Мы знаем, что если
со
/ (ж) = у aQ + 2 (ап cos пх + bn sin пх),
п=1
то коэффициенты ап и Ьп выражаются формулами
2те	’	2к
cos nidi и Ьл —	/ (В) sin ni di,
о	о
14 А. Н Крылов
210	О СХОДИМОСТИ И СУММИРОВАНИИ РЯДОВ ФУРЬЕ[Гл. VI
Положим, что промежуток от 0 до 2тс может быть подразделен на
конечное число /?+1 таких частных промежутков, именно:
от 0 до къ от кг до к2, от к2 до к3, ... , от кр до 2тс,
в каждом из которых функция f(x) и ее производные непрерывны вплоть
до концов этих промежутков; тогда мы можем, написав равенство
ап =	/ (?) cos riz dz +	/ (В) cos rii + .. * +	/ (£) cos пс ей,
0	А1	кр
выполнить интегрирование по частям, после чего имеем
/ci	Аг	2 те
—f (?) sin nidi —- \ /' (?) sin ni di — ... —- /' (?) sin ni di
тог j ' '7	КП j ' ' ’	mt j ' ''
0	Ai	kp
и, пользуясь обозначением
limf(*+e) = /(fc + 0)
6->0
и	(s > 0)
lim/(A—s) = /(& — ()),
e—>0
получим
где
тгЛ = sin nkx [/ (&J — 0) — / (A'x + 0)] +
+ sin nk2 [/ {k2 — 0) — / (*2 + 0)] + ... + sin nkp [/ (kp — 0) — / (kp + 0)],
величина же b'n есть коэффициент при sin/гж в разложении функции, соста-
вленной из производных /'(ж) так же, как сама функция f(x) составлена
из значений f(x), заданных в вышеупомянутых промежутках.
Совершенно так же получим
где
— кВ = —f (+ 0) + cos nA’i [/ (Л-j — 0) — / (Алх 4- 0)] +
+ COS пк2 [f (к2 — 0) — /(/г2 + 0)] + . .. +/(2тг —0),
величина же а'п есть коэффициент при cos пх в вышеупомянутом разложении
функции, составленной из /' (я).
Совершенно так же будем иметь
,	Л'	Ъп '
а' =-------- ,
п	п	п
где •••Д' суть место разрыва /'(я):
«Л' = sin пкг [/' (к[ 0) — (&£ + 0)] +
+ sin пк’г [/' (А' — 0) — (А' + 0)] 4-... + sin пк’р [/ (А' — 0) — / (А' + 0)]
и Ь'п есть коэффициент при sin/г^.в разложении функции, составленной из
значений /" (ж) для каждого из вышеуказанных промежутков.
§ 67]
УСИЛЕНИЕ БЫСТРОТЫ СХОДИМОСТИ РЯДОВ ФУРЬЕ
211
Точно так же
где
— кВ' = — /' (4- 0) + cos пк[ [/' (к{ — 0) — /'	+ 0)] + ... + /' (2тс - 0)
/С	v	«
и ап есть коэффициент при cosn# в разложении функции, составленной из
значений /" (х).
Таким образом, будет
^4 В
п п2	П2 ’
, __ в , Л'	Ь"
+ 7?“2>
следовательно, чтобы полученный ряд Фурье был абсолютно сходящимся,
достаточно, чтобы при всяком п было
Л=0 и В = 0,
ибо при этом условии полученный ряд будет иметь коэффициенты второго
порядка относительно и может быть уподобляем рядам S2 и Т2, коих
члены, по абсолютной величине, меньше членов ряда
ill	1
1 + 2-. + ^+..
а тогда этот ряд будет и равномерно сходящимся.
Но чтобы было Л = 0 и 2? = 0, необходимо, чтобы было
/(*1-0) = /(А1 + 0),
/(*2-0) = /(^ + 0),
/(*р-0) = /(Лр + 0),
/(2тс —0) = /( + 0).
Таким образом, видим, что при указанных выше условиях ряд Фурье,
представляющий непрерывную функцию в промежутке от 0 до 2тс, итакую,
что / (0) = / (2тг), будет абсолютно и равномерно сходящийся.
Отсюда следует, что если функция, представляемая рядом Фурье, или
имеет разрывы непрерывности в промежутке от 0 до 2тс, или значения ее,
соответствующие 0 и 2тг, между собою не равны, то коэффициенты в раз-
~ 1
ложении будут первого порядка относительно — .
§ 68. Места разрывов и величины скачков функции и ее производной
и их связь с коэффициентами ее разложения в ряд Фурье. Применение
этих формул к усилению быстроты сходимости рядов Фурье. Полученные
в предыдущем параграфе выражения показывают, что коэффициенты при —
в составе величин ап и Ьп зависят только от величины скачков в значениях
функции f(x) в местах разрывов; поэтому если функцию f(x) представить
в виде
/(ж)«Г(ж) + ?(ж)
и выбрать функцию F (х) так, чтобы она имела те же скачки, как и f(x)9
то разность ср (х) = / (х) — F (я) представится таким рядом Фурье, порядок
коэффициентов которого будет не ниже второго.
Наоборот, если дано разложение некоторой функции в ряд Фурье,
то ясно, что при нахождении суммы этого ряда или при приближенном
14*
212
О СХОДИМОСТИ И СУММИРОВАНИИ РЯДОВ ФУРЬЕ
[Гл. VI
представлении этой функции первыми членами ряда, вообще говоря, можно
взять для достижения одной и той же степени точности тем меныпее число
1
членов, чем их порядок относительно выше.
Оказывается, что такое выделение функции F (ж) возможно всегда выпол-
нить таким образом, что остаток представится рядом Фурье, коэф-
фициенты КОТОРОГО будут склл^ угпдно ВЫСОКОГО НОРЯДКН относительно о
Покажем теперь общий прием такого выделения.
Мы видели, что в разложении функции /(ж), заданной от 0 до 2к
в ряд вида	<	(
со
/ (ж) = у а0 + У, (an cos пх 4- bn sin пх)
п=1
коэффициенты ап и Ьп выражаются так:
кап ~ / (с) cos to; (К и = ^ / (5) sin n; dl.
о	о .
Воспользовавшись общею формулою интегрирования по частям:
ис№ dx =	— и'*/*-*2) +	.
< ... i	v(k~p) -|- ц(р) p)
1
получим, останавливаясь для краткости письма на членах ,
/ (;) cos nt dt=_1 f (с) sin n; 4- 4 /' (?) cos nt — y3 /" (?) sin nt —
1	fl	fl	fl
- i	(?) cos nt +1 /<IV> (t) cos nt dt,
\ / (;) sin nt dt = — у / (c) cos nt 4- 4 /' (?)sin «? + 4 f" (?) cos nt —
1	fl	fl	fl
-±f'№ (?) sin «-? + „Ц /(1V) (?) sin rit dt.
Обозначая затем через kl9 /г2, k39 ...9kp места разрывов функции f(x)
между пределами 0 и 2»т, через к'г, к'29 .. места разрывов функции f (х)9
т. е. места разрывов производных тех функций, из совокупности коих для
отдельных промежутков функция f (х) составлена, через к[9 к29 ...,к*> тоже
для функции /"(ж), и т. д., получим
п~ап = А 4—1----------
11	1 И	И®
п3 * п4 п4
п~Ьп = — В -г 4
__ ^3
П2 713
(1)
А 4-^2
п4 ' п4 9
где
Л =[f (fcr — 0) — / (+ 0)] sin пкх + [/ (к2 — 0) — / (Л2 4- 0)] sin пк2 + ..
•••+[/ (кр — 0)-/(*р + 0)] sin пкр,
Ai = f (2к—0)	( + 0) + [/' (^ — 0) — /' (Аг^ 4-0)] cosпк' + ...
• • • + [/' (&' — 0) - /' (к’я + 0)] cos nk'q,
As = [/" (к’{ - 0) - /" (AJ + 0)] sin пк" + .... + [j" (к'' - 0) -(k"r + 0)] sin k"r
B.= /,(2я -0) -/ (+ 0) + [/ (At -0)] - / (Aj + 0)] cos nkt 4- ..,
.. •. 4- If 0)—f (kp 4- 0)] cos nkp,
5 68]
усиление быстроты сходимости рядов фурье
213
В1 = [/' (К — 0) — /' (К + 0)] sin пк' + .. • + [/' (А' - 0) — f (А' + 0)] sin nA',
В2 =± [Г (2« - 0) - Г (+ 0)] + [f (К - 0) - Г + 0)] cos пк" + ...
•••+[/" (к" -0)-f" (к"т + 0)} cos nA-;,
W и Ь<?> обозначают коэффициенты в разложении /V)(«) по. косинусам
и синусам.
Полагая
/(2тс-О)-/( + О) = ^о>	/'(2к-0)-/'( + 0) = ^,
/(А1-О)-/(А1 + О) = ^1,	Г(к'1-0)-Г(к'1 + 0) = К,1, п
f(kp-0)-Hkp+o)^K^  7(^-0)!/'(а;+0)=^'/’
/"(2гс_0)-/"( + 0) + ^,
/"(а;-о)—/"(а; + о) = к;,
f" (Л-; _ 0) - /’ (А; + 0) = К",
и т. д., мы можем предыдущие формулы написать так:
А =Кг sin пкг 4- К2 sin nk2 + ... + Кр sin nkp,
Аг = К'ц + К [cos nk[-j- Kf2C0S nk'2+ . . . + Kq COS nkq9
A2 = K" sin nk'i + K2 sin nk 2 + ... 4- K" sin nk",
В = /Со + Кг cos пкг 4- K2 cos nk2 + ... 4- Kp cos nkp,
B1 = K'1sinnk'1 + K2sinnk2 + ... 4- KqSinnkq,
B2 = Kq 4- К г cos nk'{ 4- K2 cos nk2 + ..4- K"r cos nk",
Формулы (1) и (2) показывают, что в разложении коэффициентов ап и Ьп
в ряды, расположенные по степеням , коэффициенты А и В при первой
1
степени — зависят только от мест разрывов и величины скачков самой функ-
ции /(ж), коэффициенты и В± при — зависят только от мест разрывов и
величины скачков первой производной /' (х) той функции, которая данным ря-
дом Фурье представляется, коэффициенты А2 и В2 при зависят только
от мест разрывов и величины скачков второй производной /" (х) и т. д.
Отсюда видно, что если желательно, например, выделить функцию F (х)
в выражении
f(x) = F +	(3)
так, чтобы ряд Фурье, представляющий функцию у(х)9 имел бы коэффи-
циент порядка ] относительно —, то надо, определив места разрывов функ-
ции f(x) и первых ее (/ — 1) производных, составить функцию F (х) из от-
дельных кусков прямых линий и параболических кривых, уравнения коих
г/ = а1«»+р1я: + у1,
г/= а2гс3 +	4- у2® + 8, 
у = а;_2а?/-1 + P/-2«/-2 + . • • + X.
214
О СХОДИМОСТИ И СУММИРОВАНИИ РЯДОВ ФУРЬЕ
[Гл. VI
оцределенных так, чтобы величины скачков и места разрывов функции /1(ж)
и первых ее j-^-1 производных были как раз те же самые, как и найден-
ные для заданной рядом функции f(x).
Самый процесс такого нахождения функции F (х) выполняется в сле-
дующей . постепенности: прежде всего находим места разрывов и величины
скачков самой функции f(x), т. е. величины
&i, ^2, • о., кр и Kq9 К29 •••^Kpt
воспользовавшись для этого формулами (2) и (1), которые должны иметь место
тождественно, т. е. при всяком значении п. Сделав затем в предложенном
ряде х равным 0, к19 к21 ...,кр, вычисляем соответствующие значения сум-
мы этого ряда» На основании теоремы Дирихле, эти значения будут
4-[/(2*-0)+/(+0)]>
!-[/(*!-°)+/(*1 + °)],
|[Ж-0) + ж + 0)],
-Н/(*р-0)+/(*р + 0)],
а так как
/(2л-0)-/(4-0) = 2Го,
/(*i~0)-(*14-0) = Jff1>
/(V-o)-/(*p+o)=^p.
и величины j£0, К19 .. ., Кр уже найдены, то найдутся и значения
/(4-0) и /(2л —0), /(fcx-О) и /(^4-0), ...,/(*р-0)
и /(Лр + О)-
Наносим эти значения на график, проводим через соответствующие
точки прямые линии; тогда функция Рг(х)9 составленная из этих прямо-
линейных участков, и будет такою, которая имеет те же разрывы, те же
скачки и те же самые значения в местах разрывов и при х — 0 и при я = 2к,
как и предложенная /(ж). Иными словами, функция F^x) определяется
так:
^(ж>7(4-0)4--^[Ж-0)-/( + 0)]	для 0<x<klt
Fi (*) = /(*14- 0) 4-	[/ (kz -0) -/ (k. 4- 0)] для k,<x < kz, .
Fl (s) =7 (*2 4- 0) 4-grr* [/ (*3 - o) - / (*2 4- 0)] для k2 <x < ks, (4)
••••»»•••• ...................................
Fi (x) = f(kp + O) +	[/(2«-0) -/(kp 4-0)] для kp<x < 2л.
Если взять
F{x) + F1(x),
т. e. положить
/(a:)=Fi(a;)4-?i(a;),
то функция
<Fi (ж) = /(»)-Л (ж)
§ 681	УСИЛЕНИЕ БЫСТРОТЫ СХОДИМОСТИ РЯДОВ ФУРЬЕ 215
будет непрерывна на всем протяжении от я = 0 до х = 2щ и вместе с тем
будет
?х (0) = 0 и (2к) = 0;
следовательно, при разложении в ряд Фурье функции срх (ж), коэффициенты
1
получаются по меньшей мере второго порядка относительно —.
Отсюда видно, что стоит только разложить функцию F± (х) в ряд Фурье
и полученное разложение вычесть из заданного, остаток и будет функцией <р (х).
Пусть полученный таким образом ряд для
?1(ж) = /(ж)—^1(«)
будет
ОО	GO
<Pi (ж) = с0 4- 3 сп cos пх + 3 dn sin пх,	(5)
П = 1	Л = 1
коэффициенты сп и dn будут, вообще говоря, второго порядка относитель-
но — . Выполнив дифференцирование ряда, получим разложение <?!(#)>
♦
в коем коэффициенты будут первого порядка относительно — .
Совершенно подобно предыдущему представляем <р'(я) в виде
<?i (®)=*1 (®)+®1 (ж)	(6)
так, чтобы функция ф1(я) состояла из прямолинейных отрезков и имела
те же самые скачки и те же места разрывов, как (ж); тогда функция (х)
будет представляться рядом, коего коэффициенты второго порядка относи-
1
тельно — о
п
Интегрируя равенство (6), получим функцию
(ж) = ф1 (х) dx + coj (ж) dx.
При вычислении
(х) dx
обнаруживается, что вместо прямолинейного отрезка ax^-d получится со-
ответствующая ему парабола
4- ах2 + Ьх+С.
Постоянные произвольные (7, вводимые таким интегрированием, определят-
ся из того условия, что функция непрерывна и частные ее значения,
соответствующие местам разрывов функции ф1(я), найдутся по формуле (5).
Интеграл же
(х) dx
будет представлен рядом, коего коэффициенты трэтьего порядка относи-
1
тельно —.
п	•	.
Полагая
\ Ф1 (я) dx = F2 (х) и \ о)х (х) dx ср2 (я),
получим равенство
/ (ж) = Л (?) + ^2 (®) + <?2 (*)•
216
О СХОДИМОСТИ И СУММИРОВАНИИ РЯДОВ ФУРЬЕ
ГГл. VI
Очевидно, что если взять
F^F^+F^x),
то в равенстве
/ (ж) = F (х) 4- <р2 (ж)
ряд, представляющий функцию <Рг (ж), будет иметь коэффициенты третьего
порядка относительно — , разрывная же функция F(x), заданная чертежом
или аналитически, для отдельных промежутков будет состоять из прямоли-
нейных отрезков и отрезков парабол.
Функцию <?2(ж) продифференцируем дважды; тогда ряд, представляю-
щий <р£(я), будет иметь коэффициенты первого порядка; определив места
разрывов и величины скачков функции <р2(ж) и составив функцию Ф2(я)
из прямолинейных отрезков так, чтобы она имела те же места разрывов:
и те же скачки, как и у£(х), делаем
Фа (ж) == Фа (®) Ч-<»2 (ж).
Это равенство интегрируем два раза подряд почленно, причем постоян-
ные произвольные определяем по частным значениям функции <?2(я) и ее
производной; получим выражение вида
?2(«) = ^3(ж) + ф3(ж),
в котором <р3(я) будет представлена рядом с коэффициентами четвертого
1
порядка относительно —.
Продолжая таким образом, можем, очевидно, дойти до любого порядка.
Заметим, что из тех же выражений следует, что если функция /(ж)
составлена из отдельных частей, каждая из которых есть целая функция
относительно х, то коэффициенты ап и Ьп будут целыми функциями от —,
степени коих не более так единицею выше, нежели наивысшая степень х-
Так, например, если бы / (ж)	была	задана	условиями
/ (ж) = ах + b	ДЛЯ	х от	л 0 до -4-
/ (ж) = ж2	Для	х от	7Г	К Г до Г
/(ж) = 0	Для	х от	у До 2л
то коэффициенты ап и Ьп были бы вида
Применяя вышеописанный процесс, мы получили бы ф3(я) = 0 на всем
протяжении от х = 0 до я = 2тс и, значит, по данному разложению нашли бы
и саму функцию j(x).
Возьмем, например, ряд
с sin х sm 2х sin 3#
>1 = —+ -^- + -Г“
sin пх
п
который, как мы видели, сходящийся для всех значений х между 0 и 2к.
Так как и при ж = 0и при ж = 2тс величина 52 = 0, то эта функция конечна
на всем протяжении от я = 0 до я = 2тг, включая эти пределы, и наши форму-
лы применимы.
§ 69]
УСИЛЕНИЕ БЫСТРОТЫ СХОДИМОСТИ РЯДОВ ФУРЬЕ
217
Имеем
птсап = 0 = Кг sin nkx + К2 sin иА2 + ...,
7гкдп = к= — [АГ0 + A’1cosn&1+ • • •],
Из второго уравнения следует
2Г0 = /(2тг — 0) —/( 4-0) = — ти,	... =0»
Следовательно, функция / (я?) в промежутке от я = 0 до я = 2тс мест
разрыва не имеет, но разность значений / (2тг — 0) — / ( Н- 0) = —тс.
Так как, при х = к, /(ж) = 0, то если мы возьмем за функцию Fi(x)
участок прямой, проходящий через точки Д, В и С, то функция (фиг. 36)*
т (*)=/(*)-Л (*)
<р (0) = <р (2тс), то разложение <р(я)*
не будет иметь разрывов, и так к
может иметь только коэффициенты
1
второго порядка относительно - - .
Итак, функция
F1(x)=^:^- для 0<я<2тс;
составив ее разложение, увидим,
что
F1(x) = f(x) для 0<ж<2к
и что <р (х) — 0.
Необходимо иметь в виду, что
гается, что сама функция / (х) и ее
во всех этих рассуждениях предпола-
производные до рассматриваемого по-
рядка (/--1) остаются конечными для всех значений х между 0 и 2тс вклю-
чая и эти пределы, поэтому, если бы мы взяли ряд
, , ч cos х cos 2х ,	, cos пх ,
/(*) = — + -3-+...
2
то для это о ряда наши рассуждения были бы неприменимы, ибо при я = 0
и х - 2к, / (х) == оо, и, значит> формулы, коими мы пользовались, непри-
менимы.
§ 69. В приложениях гораздо чаще встречаются ряды, расположённые
Ttx
или только по синусам, или только по косинусам аргументов кратных у ,
предполагая, что функция f (х) задана от х=0 до х = 1.
В этом случае коэффициенты разложений
со	...
f (x) = a0+ 2 ап cos^p
п—1
И
f(x)=^bnSYa~
п = 1
выражаются формулами^
о
218	О СХОДИМОСТИ И СУММИРОВАНИИ РЯДОВ ФУРЬЕ[Гл. VI
и
ап = 4 V (5) cos d;, Ья = | $ / (;) sin Я.
о	о
Поступая совершенно подобно предыдущему, получим
nitiiji	л t / -A-i ^4-2	/2 Л3 .
~2	"" г,ж п к2п2 к3п3
Р » f t j2	/3 В8
2	"Т* к п ‘ тс2 п2	л3 п3	* * * ’
л = [/ (^ - 0) - / (Ля + 0)] sin ^ + ... + [/ (Ар - 0) - / (кр + 0)] sin	,
Лх = /'(Z-O)cosпк — /'(4-0) 4-[/' (^-0)-/' (^4-0)]cos^4- ...
••• + [/'(*;-0)-/(^ + 0)]cos^,
Л = [/" (k'i - 0) - Г (Л; 4- 0)] sin 4- • • •
•••+[/(^-0)-/(A;4-0)]sin^,
B = /(Z-0)cosnrt-/(4-0)4-[/(Ai-0)-/(A1 + 0)]cos^4- ...
••+[/(^-0)-/(^ + 0)]sin^,
= [/' (К - 0) - Г (к[ 4- 0)] sin	+ [/' (к'2 - 0) -(к'2 4- 0)] sin2^ + ...,
В2 = f(l-0) cos пк - /(4- 0) 4- [/" (*: - 0) - Г {К + 0)] cos	+ ,.. ,
Полагая, подобно тому как в § 68,
K0 — f{l — 0) cos пк — /(4- 0),	Ко =/'(Z — 0) cos п~ —/'(4-0),
2^=/(*x—0) —/(Лгг + О),	^=/'(л;-0)-/'(^4-0),
^р=7(4-°)-/(*р + 0)/ ’ ’ ’ Ч=/;(^-О)-?(4+’о) ”
ж т. д., мы предыдущие формулы напишем таким образом:
A = К, sin ~l + K2 sin 2^? 4-... + Kpsinn-^£ ,
A^K'o + Ki cos2^4-...+K:cos^,
(8)
т» жг I ту* riTtk-t .	HTck-i <	। yy Ti/Ttkn
В ^К0 + Кг cos -у-1 + K2 cos -j - + • • • + cos -y2 ,
l	t
d iz/ • nnk j * Trf * i^Tzka .	, r/i • TlTtkg^
Br = K± sin -y-i + K2 sin -y-2 + ... + Kq sin -y- ,
В остальном надо поступать совершенно так, как сказано выше.
Так, положим, что дан ряд, представляющий функцию /(ж):
/(ж)= 2 sin 22? ,
п=1
§ 69]
УСИЛЕНИЕ БЫСТРОТЫ СХОДИМОСТИ РЯДОВ ФУРЬТЕ
219
заданную в пределах от я = 0 до я = /. Пусть эта функция изображается
чертежом (фиг. 37).
Так как в пределах между 0 и Z эта функция имеет разрывы при
х = к19 х — к29 х = к3, соответственно равные: — А‘1 = Л5 = /(А1 + 0) —
— / (*х —0), -К2 = СР = /(*24-0)-/(£2-0), -^3=-^£ = /(Л3 + 0)-
—/(*з — 0), то составим, определив величину и места этих разрывов,
функцию Fx(x), которая была бы такова:
Fi(x) = /( + 0) +J[/(^^0)~/( + 0)]	для 0 < х < к19
Pl(s) = / (&1 + 0) + zj/ [/(*2 — 0) — /(^1 + 0)1 для кг<х<к2,
ед = /(Л2+0) + ^=^-[/(^з-0)-/(Л2 + 0)] ДЛЯ к2<х<ка,
Р1(ж) = /(Л8 + 0) + -^^[/(г-0)-/(А:з+0)] для ка < х < I,
т. е. F1(rc) представляется изображенной на чертеже линией, составленной
из прямолинейных участков так, чтобы скачки были как раз равны и на
тех же местах, как у заданной функции.
Составленную таким образом функцию F^x) разлагаем в ряд Фурье
КХ
по синусам аргументов, кратных у , и вычитаем этот ряд из предложен-
ного; останется такой ряд, в котором коэффициенты — второго порядка
<1
относительно—; обозначим эту функцию через <?(#)• Составляем произ-
водную ф' (х)\ дифференцируя этот ряд почленно, получим ряд, подобный
предложенному. Находим его места разрывов и величину скачков и, по-
добно предыдущему, составляем функцию <Pi(#)> которая имела бы те же
места разрывов, как и <р(я) и состояла бы из прямолинейных участков.
Тогда будет
= (ж) + ф (ж),
причем ф (х) будет представлять функцию, разложение которой по коси-
нусам имеет коэффициенты не ниже второго порядка относительно — .
Разлагаем ^(х) в ряд Фурье и определяем разложение ф(я), взяв
разность рядов
220
О СХОДИМОСТИ И СУММИРОВАНИИ РЯДОВ ФУРЬЕ
[Гл. VI
Интегрируя, имеем >
? (я)	(ж) dx + ф (ж) дх.
Интеграл
фх(я) dx
будет состоять из соответствующего прямолинейного участка вида ах + $
для участков, где срДя) изображается прямою, царадлельною оси х\
где же <рх (х) изображалось прямой ах 4-6, будет ^- + Ьх + у; постоянные
произвольные определим по значениям функции ср (х) в местах разрывов
ее цроизводной. Таким образом, выделим из нашего разложения функцию
Pi (х) + <Pi (х) dx,
такую, что остаток будет представлять ряд с коэффициентами третьего
порядка относительно —. Таким образом, можно продолжать до тех пор,
пока получится такой ряд, вычисление суммы которого с требу мой сте-
пенью точности уже не представит затруднений, ибо он будет достаточно
быстро сходящимся.
Пример 1. Возьмем ряд
•	/(a:) = ^L^sinT-^sin-r+psm-T----J ’
который мы имели в § 42 и для которого коэффициент Ьп выражается
формулою
, 8р 1 . пп
^п = ^-а81Пт,
и положим, что мы хотим найти ту функцию, которая этим рядом пред-
ставляется.
Так как коэффициент Ьп второго порядка относительно — t то самая
функция /(х) от х~0 до х = 1 непрерывна.
Составляем производную
// z \	88 1 Г 1 пх 1 Зпх ,
f (ж) = Тт1тС087-ТС08-г +
П = 1
ппх
COS у .
По формуле (7) имеем
= sin = {[/' (^-0)-/'(/-1 + 0)] sin п-^+ ...] ;
так как это равенство должно иметь место тождественно, то будет
ппкл пп	7 I
~Г = 2> Т. е.
/'(*1-0)-/' (*1 + 0)Ц?.
По теореме Дирихле, для места разрыва кг=^~ имеем
Л
QO sin -
4 I/' (*. - 0) + Г Л + 0)] - '4 2	“г = 0-
п=1
f 69]	УСИЛЕНИЕ БЫСТРОТЫ СХОДИМОСТИ РЯДОВ ФУРЬЕ 221
Отсюда следует
/'(*1-0) = 2/, № + 0)=^.
Значит, за F[(x) следует взять функцию
F'i tx) = у для 0 < х < у ,
Fi(x)=— 7 Для 4<ж<^
т. е. /^(ж) изображается графически чертежом (фиг. 38).
И в'самом деле, разлагая F'1(x) в ряд Фурье, получаем
.	717С
о 00 sin —
1	ти / \ р VI 2 nitx
Рг (х) = —7 У----- cos -7- ,
1X ' Ttl	П	I
п=1
т. е.
/'(ж)=г;(ж).
Значит,
/(ж) =Рг(х) + С.
Но, интегрируя величину F'^x), видим, что для участка от ж —О
I
ДО X = -5- получится
^х(ж) = уж для 0 < ж < у ,
так как при я = 0 должно быть —0.
Для участка от до I получится
Fi (ж) = — х~ЬС19
и так как при х ^1 должно быть Fl(a:) = 0, то
G = 2?
и, значит,
(ж) = у (I — ж) для у < ж < I.
Таким образом, будет
/ (ж) = Pi (®) = 7 ® Для 0 < ж < у ,
/(ж = )Р(ж) = ^(7 —ж) для ~<х<1г
так что графически /(ж) изображается ломаною АВС (фиг. 39), причем
стрелка BD=$ и AD = DC = -^ .
222
О СХОДИМОСТИ И СУММИРОВАНИИ РЯДОВ ФУРЬЕ
Гл. VI
Нетрудно видеть, что когда коэффициенты в ряде Фурье выражаются
целыми функциями от , то, поступая подобным образом, мы составим
функцию, им представляемую, и она на отдельных участках будет выра-
жаться кривыми, уравнения коих будут вида
у = ахк 4- Ьхк-1 + ... + Л,
где Ж —целое и положительное число.
Пример 2. Возьмцм теперь ряд, у которого коэффициенты не суть
целые функции от . Пусть будет
, z к ( 1 . itx 2 Vi П C°S 2	• nizx I
/ (x) = a ~ sin T - - 2 “^l2 Sln — )
n=2
и желательно усилить быстроту сходимости этого ряда.
Разлагаем коэффициент Ьп по степеням и остановимся на члене
1
с , тогда имеем
п 1	1	_ 1 И , 1 , 1 ,	1-1
п2 — I2 п 1 п ' п2^ п*' л 1	’
1	— —.	1 — -г
следовательно, предложенный ряд можно написать так:
nit
п cos —
2	• nitX о । о i
12 81П	+^3 + S.
п=2

причем
n=2
nit
COS yr
2	. nitx
-------sm -r ,
n------I

nit
COS —
2 . nitx
—a— sm -y-
n3 I
Q = ~ 2
‘	n=2
nit
c°sT
n5
Обозначим функцию,
ряда имеем
ТПС 7	71TZ
у ьч = — a COS У =
= - [ Fx (I - 0) cos - Fj (+ 0) + [Л (kj. - 0) - Fj (кг + 0)] cos
откуда следует
1	. nitx
Sln __.
представляемую рядом S19 через F1(x)] тогда для
F^Z —0) = 0, Fj(+0) = 0
nit nitfi^
T = ~ ’
т. е.
— у >
F 1 (^i — 0) — F1 (^i + 0) = а
§ 69]
УСИЛЕНИЕ БЫСТРОТЫ СХОДИМОСТИ РЯДОВ ФУРЬЕ
223
т. е. что функция при х = к1 = -^- делает скачок, величина коего
есть а.
Подставляя	ряд Si и пользуясь теоремой Дирихле,.
£
получим
Таким образом, имеем уравнения
Р 1 (^i — 0) — Pi (^i + 0) = а,
откуда следует
Л(*1-0) = | и 7^ + 0)=
а так как
^( + 0) = 0 и ^X(Z —0) = 0,
то за Fr{x} берем функцию
F\ =	для 0 < х < у ,
®)==у (ж —Z) для у < ж < Z
и представляем ее в виде ряда Фурье, расположенного, как и предложен-
ный, по синусам аргументов, кратных от у •
Будем иметь
j_
2	I
bl, п = р \ р 5 sm -р de + — \ р (£ — Z) sin -р d£ =
0	_±
2
i	i
2а С f.	. пт£	2а Г	. пт£	1f. 2а	mz
= -^ \ $ sin -г- dl-г \ sm -г- d; —-cos ;
/2 J l	I J l	mz	2
0 1
2
следовательно,
~	niz
00 COS -jr
17 /м\ о 2a xi	2	mzx
3 slnT.
n=l
Таким образом, будет
Сумма
niz
о 00 cos —
n 2а ул 2	. nizx
О3 =---->.----Sin -у-
П=1
представляет функцию, непрерывную вместе с первою своею производною;
поэтому, дифференцируя эту функцию дважды, получим
о 00 cos —
$3= +-fS -^sinn-^ = F"(x),
n=l
1224
О СХОДИМОСТИ И СУММИРОВАНИИ РЯДОВ ФУРЬЕ
[Гл. VI
..а эта функция, на основании сказанного о функции F^x), определяется
^равенствами
^з(Ж) = ~^х ДЛЯ 0<Ж<у,
рз(а:)= — 7?^ —О Для 4
Значит,
Ра{х) = — 75- 4“ + cix + с* для 0<ж<4’
Рз(х)=+ С8(ж —Z) + C4 для 4<ж<^
„Для определения постоянных Сг, <?2, С3, Ct имеем условия
F8(0) = 0,	F3(/) = 0,
Q_^^+cix + c3y г=(_^^+сз(ж-/) + с4). t,
У Х =  4	S х= 
2	2
, = (-^^ + с.(^А+с.)' ,,
44	а;®— v	х=—
2	2
’ибо функция Fz(x} сама и первая ее производная непрерывны для 0 < х < I
и вместе с тем F3(0) = F3(Z) = 0..
Таким образом, будет
G = G=o, G=C8 = g
и, значит, функция F3 (х) такова:
^з(я)= — ^xS + ^x	для 0<ж<4»
Рз(х)= — 77* (х~ l)s +^(ж — 0 для -^<х<1,
так что F3(x) представляется графически чертежом (фиг. 40). Полагая
/ (*)=тsin т++ 7<’3 <*) + Q’
И^-------1------> у- где F1(x)i F3{x) суть найденные выше функ-
0	I	ции, мы сведем вычисление значений функ-
2	ции / (х) к вычислению значений функций
фиг. 40.	F3(x}, которое весьма просто, и к
вычислению суммы 2, представляемой рядом,
1
коего коэффициенты — пятого порядка относительно — , тогда как в пред-
ложенном ряду они были первого порядка.
§ 70. Нахождение производных функций, представленных рядами
Фурье, когда почленное дифференцирование недопустимо. К такому приему
выделения из данного ряда тех его членов, которые дают разрывы или
в самой функции, или в ее производных, приходится по необходимости при-
бегать в том случае, когда надо вычислить или представить в виде ряда произ-
водную первого или высшего порядка данной функции и когда непосредственно
этой производной дифференцированием предложенного ряда найти нельзя.
Поясним это на примере.
Пусть функция /(я), например, задана так:
/ (х) = a sin у для 0<я<у,
/(ж) = 0 для < х < I.
§ 70]
ПРОИЗВОДНЫЕ ФУНКЦИЙ, ПРЕДСТАВЛЕННЫХ РЯДАМИ ФУРЬЕ
225
Очевидно, что такая функция лишь в месте разрыва, т. е. при. я==у:,
не имеет производной, для всех же остальных значений х существует
производная любого порядка.
Так, например, для предложенной функции производная второго
порядка была бы
—JF sm т для 0 < X < — ,
/" (ж) — 0	ДЛЯ у < X < I,	.	;
между тем, ряд Фурье, представляющий данную функцию, имел бы свои
коэффициенты первого порядка относительно —; если бы его дважды про-
дифференцировать почленно, то получился бы ряд, коего коэффициенты
были бы первого порядка относительно тг, т. е. коего члены неопределенно
возрастали бы,—такой ряд, как расходящийся, не имел бы смысла.
Между тем, если представить эту функцию так:
/ (ж) = Pl (я) + F2 (х) 4- <р (х),
где Fr(x) и F2(x) были бы те функции, которые имеют те же разрывы,
как f(x) и /' (х), и, значит, а? (я) имело бы разложение, коего коэффициенты
были бы третьего порядка относительно , тогда можно бы написать
/" (х) = F'{ (х) + F^ (х) + ср" (х),
^причем F'{(x) и ,F''(x) определялись бы, пользуясь заданием функций
Fx(x) и Р2 (х), а не дифференцированием тех рядов, коими, они представля-
ются, /р" (х)—дифференцированием соответствующего ему, ряда почленно.
Так, возьмем наш пример, т. е.
/ (х) ~ a sin у для 0 < х <	, •	‘	- -
f(x) = O для у<я</,	*	1	‘ ”
тогда ряд для f(x) такой:	*	.....*.... 4
пп	n7Z > •
к	_	00 ZICOS—-
г / ч а . itx 2а уд	2 nitx
/(z)=ysinT -t -^ZTsin —:	'	
n=2
он рассмотрен в предыдущем параграфе, и мы имели равенство' *	- *
7 (х) = у sin у + 7?! (ж) 4- Sg +'2i
 •• Но • •• '		.	 -
00 COS	‘	‘	' ** ‘
е । гл 2а XI 2 v. nitx
^з + 2 = --2^ТЛ>^т’’
п=2
функция же F х(х) состоит из прямолинейных участков, и, следовательно,
производная второго порядка от нее равна нулю, кроме места разрыва,
где этой производной нет.	о
Таким образом, имеем	. z
со
/	COS-_- <	’
t < x a . itx . ri > x 2a	 2 ' / t: :-'nitx J J : 
- / W==T-sin -г + Fi lx)---->1—7-0—rxSin .^--
' v z 1 2 I 1	1 v ' it n (n2--rl) I
'...................... ...	H«2	-	....... ... 7 Ji .7 J. Г/f
15 A. H. Крылов
226
О СХОДИМОСТИ И СУММИРОВАНИИ РЯДОВ ФУРЬЕ
[Гл. у Г
и двукратное дифференцирование дает
пк
тъ cos_
... , ч а к2 . itx , 2а л2 vi 2 mzx
=	2^т81Пт =
п=2
а . itx
TsinT
П2 — 1
mt
п cos ~
. mtx	, z \ к2
sm~ J =
и, значит,
/"(*) = —р- sin J ДЛЯ 0 < X < у ,
/" (х) = 0	для 4 < я: < /,
Л
при х = -^ функция/"(я) имеет разрыв.
Если бы функции f(x) нам была неизвестна, то полученное уравнение
Г (®)+^/М=о
послужило бы для ее определения.
В самом деле, из этого уравнения следует
f(x) = C, sin ~ + C2cos™,
причем и С2 еуть произвольные постоянные, которые для разных участ-
ков функции /(ж) могут иметь и различные значения, ибо функция f(x}
при изменении х от 0 до I имеет разрывы.
Значения постоянных Су и С2 должны быть определены по значениям
функции для начала и конца каждого участка.
Так, мы нашли в § 69, что функция / (х) имеет разрыв при х = -^ ,
следовательно, первый ее участок простирается от х = 0 лох = ^. Для
этого промежутка мы видели, что
f(0) = 0 и /(1-о) = а,
следовательно,
}	С^а и С2 = 0
и, значит, будет
— a sm — для 0 < х <	•
Второй участок нашей ^функции — от х — до х = I. [В этом проме-
жутке, как мы видели,
/(4+°)=° и до=о,
следовательно,
С1 = 0 и С2 = 0*
т. е*
/(^«0 для
Таким образом, функция f(x) определена вполне.
При пользовании рядами Фурье для решения вопросов теории упру-
гости и сопротивления материалов, необходимо всегда иметь в виду сказан-
§ 71
РЯДЫ, ПОДОБНЫЕ РЯДАМ ФУРЬЕ.
227
ное в этом параграфе о вычислении производных функций, представленных
такими рядами.
Заметим также, что изложенный прием усиления быстроты сходимости
рядов Фурье и нахождения производных от функций, ими представляемых^
может служить для доказательства или для проверки того» что представляе-
мая рядом функция действительно удовлетворяет тому дифференциальному
уравнению, как решение коего она найдена, хотя бы самый ряд и нельзя
было дифференцировать почленно требуемое число раз.
Предлагается в виде задачи сделать такую поверку для величины и,
данной на стр. 170 и представляющей решение задачи о колебании струны.
§ 7L Ряды, подобные рядам Фурье. Обратив внимание на вывод
формул (7), нетрудно убедиться, что все сказанное в §§ 67 — 70 относится
вообще к рядам вида	’
f (#) = aQ + cos + а2 cos + а3 cos -у + ...
и
х	F(a:) = 61sin^p+&2 sin^ + &3 sin^y+..
в которых
(«I, о)2, - . . , О)п, . < • , Р1, р2> • * • > рп, • • •
суть корни трансцендентных уравнений
?(*) = 0	(1)
Ф(и) = 0,	(2).
причем имеют место равенства
i
cos о>£ у cos ф, у dx = 0, если i #= /,	(3)*
о
i
sin pf у sin р; у dx = 0, если i Ф j,	(4)
о
так что коэффициенты ап и Ьп определяются равенствами
i
/ (х) cos ур dx
«п =	-------------= jKn / (х) cosу^ dx,	(5>
$cos8^ , Ь
о
I
F (х) sin £у dx	z
bn =	-- Ln F (х) sin ^у dx,	f6>
sin8 2yd#	0
6
где Kn и Ln будут некоторые определенные функции, первая —от шп,.
вторая — от рп.	;*'
Посмотрим теперь, каков должен быть вид уравнений (ю) = 0 и ф (J = 0,.
чтобы формулы (3) и (4) и их следствия (5) и (6) имели' место.
Имеем
i	i
г> Г	<О:Х J	С f Шл — Ш; . (Ол 4- (0; \ _
2 \ cos—у cos у—ах = \ ( cos—-y-^-rc + cos ~у j- x}dx=s
о	о
— I s*n — шл) | I sin vwi +
~~ O>i —
455*
-^28—	О СХОДЙМОСТИ И СУММИРОВАНИИ РЯДОВ ФУРЬЕ[Гл. VI
Чтобы эта величина равнялась нулю, когда <of Ф , необходимо и доста-
точно, чтобы было
((0{ 4- (Dy) sin ((Df — (Dy) + ((Df — (Dy) sin ((Df + (Dy) = ()•
Это уравнение можно написать так:
[sin	— (Dy) + sin (<d£ + (Dy)] 4- (Dy [sin (o)£ — (Dy) —sin (<of 4- a>y)] = 0,
или
(»>i COS (Dy sin (Df — (Dy sin (Dy COS (Dj — 0,
откуда следует
со/ sin <0/	<0/ sin <0/
—------- — ----- = a,
COS (Of	COS toy
где a есть любая постоянная величина.
Таким образом, уравнение ср (ш) = О есть такое:
(DsincD — acos(D = 0,	(!')
или иначе
(Dtg<D = a.	(Г')
Совершенно так же из условия (4) подучим
2 sin sin dx = ^cos	— cos	dx =
о	о
__ sin (р/— рО	у sin (р/4- pfc) q
Pi ““Р/с	Pi + Р/с
откуда следует уравнение.
(Pi + Pfc) sin (pt - p*) - (р( — pfc) sin (Pr + pfc) = 0,
ИЛИ
Pi [sin (рг — pfc) — sin (р{ — р*)] + pfc [sin (pf — pk) 4- sin (?i + p*)] = 0,
иначе
— sin pk cos pf 4- p& sin pf cos p* •= 0,.
Pf COS pi _pk COS p?r ' q
sin pi sin p/c P’
где p — произвольная постоянная
, ' Таким образом, уравнение ф(р) = О есть следующее:
pctgp = p,
или
Р cos р — р sin р — 0.	(2')
В некоторых случаях удается распространить выводы этой главы /
на функции, зависящие от корней трансцендентных' уравнений, подобные,
например, встречающимся в задаче о колебаниях стержня, которых основное
свойство, выражаемое равенством
i
^XkXidx = 0, если i-=f=k,
о
и служит для нахождения коэффициентов ряда при разложении по этим
функциям. В развитие этого вопроса мы, однако, входить не будем, ибо
сущность дела видна из изложенного выше простейшего и наиболее часто
встречающегося случая рядов Фурье.
ГЛАВА VII
РЕШЕНИЕ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С ЧАСТНЫМИ ПРОИЗВОДНЫМИ И ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН.
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТРУН И СТЕРЖНЕЙ
И ДРУГИЕ ПРАКТИЧЕСКИЕ ПРИЛОЖЕНИЯ
ОБЩЕЙ ТЕОРИИ
§ 72. Изложение общего метода на примере определения вынужден-
ных колебаний струны. В предыдущих главах показаны различные методы
интегрирования уравнений без последнего члена; в этой главе мы покажем
общий прием интегрирования таких уравнений, имеющих последний член,
причем будем придерживаться того же способа изложения, т. е. развивать
метод на классических частных примерах.
Положим, что дано уравнение, представляющее колебание струны под
действием внешней возмущающей силы, которую, подобно нагрузке на балку,
отнесем на единицу длины струны. Тогда наше уравнение будет вида
(1)
где f(x, t) есть заданная функция переменных х и I, именно:
Ж	*)>
Г	v
причем р. есть масса единицы длины струны, F (х, ^ — вышеупомянутая на-
грузка, действующая в момент t в точке, абсцисса коей х, и отнесенная
на единицу длины струны.
Кроме уравнения (1), должны быть заданы граничные и начальные
условия. Пусть они будут:
при х = 0 должно быть и — 0|
,	> при всяком t	(2)
ъ х = 1	>	» и - О J
и при А—0 должно быть
« = ?(«)» ^ = Ф(Ж).
причем функции <р (х) и ф (х) заданы на протяжении от
х = 0 до ж =
Для решения этого вопроса будем поступать совершенно подобно тому,
как мы поступали для уравнений обыкновенных, т. е. полагаем
И ==	-|- 1^2
распоряжаемся величинами иг и и2 так, чтобы иг представляло свободные
олебания струны и и2 •— вынужденные'.
230	РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН	[Гл. VII
Под словом «свободные» колебания разумеют те, которые при данных
граничных условиях происходят без действия внешней силы, а лишь вслед-
ствие начального отклонения струны от формы равновесия и вследствие
сообщенных ее частям начальных скоростей.
«Вынужденными» колебаниями называются те, которые производятся
и поддерживаются действием внешней возмущающей силы.
Отсюда видно, что величина должна удовлетворять:
во-первых, дифференциальному уравнению
во-вторых, граничным условиям:
При X = 0 ДОЛЖНО быть = 01
,	У при всяком t,	(5)
» x — l »	»	= 0J	v '
в-третьих, начальным условиям: при должно быть
и	(6)
Что касается н2, то так как сумма
h = Ui + w2
Должна удовлетворяв уравнению (1) и условиям (2) и (3), а величина иг
удовлетворяет уравнению (4) и условиям (5) и (6), то ясно, что и2 должно
удовлет! орять:
во-первых, дифференциальному уравнению
™
во-вторых, граничным условиям:
при я = 0 должно быть н2 —01
т	1 при всяком t,	(8)
» х = 1	»	» и2 —0J.
t
в-третьих, начальным условиям: при / = 0 должно быть
и2 = 0 и ^ = 0.	(9)
С первого взгляда может представиться, что такое подразделение вели-
чины и на составляющие их и и2 не вносит никакого упрощения в решение
вопроса, так как все равно величина и2 должна удовлетворять уравнению (7),
не отличающемуся ничем от предложенного уравнения (1).
Но надо помнить, что при решении вопросов, зависящих от уравнений
в частных производных, одна из главных трудностей состоит в удовлетворе-
нии не только уравнению, но и граничным и начальным условиям, а отсюда
и видно, что для величины и2 начальные условия весьма просты.
Решение начинаем с разыскания величины иг, причем будем пользо-
ваться вторым методом Пуассона, т. е. полагаем
и^^ХТ	(10)’
и, как объясн но в § 46. получим для определения функций Т и X урав-
нения
Г' + а2Л271 = 0,
Х" + А2Х = 0,	(Н)
§ 72]
ОПРЕДЕЛЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ СТРУНЫ
231
откуда
Т = A cos akt + В sin akt,
Х = С cos кх + D sin кх.	(12)
Функции X определяем так, чтобы они удовлетворяли граничным усло-
виям; это приводит к трансцендентному уравнению, служащему для опре-
деления постоянной к.
В нашем случае это уравнение есть
sin kl = 0,	(13)
так что
к = ™ (п = 1,2,3,...)
и тогда
ТГГ	• МТСХ	у Л
Xn = sin —,	(14)
Та — Ап cos ——и 2»n sm —j- .	(15)
Таким образом, будет
GO	ОО
2Л an nt . ппх ,	. an nt . ппх	z,n4
An cos -j- sm —j-~ + 2j t>n sm —y- sm — ,	(16)
n = l	71 = 1
причем An и Bn ~ постоянные произвольные, которые определяются по
начальным условиям; именно будет
i
Аа==7 ®($)sin^^,
%	(17)
О
и, значит, иг найдется.
Чтобы найти н2, поступаем так: будем искать эту величину в виде
суммы
оо
«2=3 XnSn,	(18)
71 = 1
где Хп суть те же самые функции, зависящие от корней трансцендентного
уравнения (13), которые вошли в состав величины их и по которым эта
величина разложена в ряд.
Мы видели, что эти функции Хп удовлетворяют граничным условиям;
значит, и величина и%, определяемая рядом (18), будет удовлетворять гра-
ничным условиям.
Остается выбрать функции Sn переменной t так, чтобы были удовле-
творены уравнение (7) и начальные условия (9).
Чтобы этого достигнуть, подставляем величину (18) в уравнение (7),
оно примет тогда вид
2 (S'nXK-a*SnX’n) = f(x, t).
71 = 1
Но функция Хп удовлетворяет уравнению
X'iV—Xn^
232 РЕШЕНИЕ УРАВНЕНИИ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН	[Гл. VII
и, значит, предыдущее уравнение напишется так:
'	2 ^ + a^~Sn)Xn = f(x,t).	(19)
71 = 1
Но, с другой стороны, функцию /(ж, t), если рассматривать в ней t как
переменный параметр, независимый от буквы х9 можно представить в виде
ряда
f(x, i) = 2 нпХп,	(20)
71 = 1
причем коэффициент Нп определяется совершенно подобно тому, как Ап
или Вп при представлении функций ф(я) и 9 (х) в виде ряда, расположен-
ного по функциям ХП9 зависящим от корней трансцендентного уравнения (13).
Так, в нашем случае, когда
•\тг	• nitX
Хп = sm — ,
будет
=	t)sinn^di,	(21)
О
так что Нп получится в виде вполне определенной функции буквы I, ко-
торую мы и обозначим для краткости Нп (г).
Уравнение (19) примет вид
2 (S”n+a^Sn-Hn(t)\Xn = Q,
п = 1 4	7
ему мы удовлетворим, взяв 8п так, чтобы при всяком п было
^ + ^5п = Яп(г) (и = 1, 2, 3, ...).	(22)
Чтобы величина
^2 = 2 Хп	(*)
л = 1
удовлетворяла и начальным условиям: при £ = 0 должно быть и2 = 0
и ^ = 0, надо взять Sn так, чтобы при всяком п при 2 = 0 было
^(0)-0и Уп(0) = 0,	(22')
а тогда уравнение (22) дает, на основании формулы (4) § 8,
t
Sn = ~^Hn(a)sinn^(t-a)da,	(23)
О
или, подставляя вместо Нп его величину (21),
£n= ^Jrfap(e,a)sin^(«-a)sin^d;	(24)
о о
и величина и2 будет
оо
2 о . nitx
Snsm-j- .
n=l
§ 72]
ОПРЕДЕЛЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ СТРУНЫ
233
Во многих частных случаях нет надобности пользоваться общею фор-
мулою (23) для нахождения величины Sn, а проще применять приемы,
изложенные в главе I, т. е., найдя общий интеграл уравнения (22), опре-
делить содержащиеся в нем две постоянные произвольные так, чтобы при
t ~0 было
5п(0) = 0 и S'n(p) = O,
и найденную величину Sn подставить в формулу (*).
Обратим, между прочим, внимание на тот случай, когда внешняя сила
сосредоючена в одной точке х = с, и величина этой силы есть P = F(t).
Этот случай надо рассматривать как предельный, предполагая, что сила
распределена как бы то ни было на участке от х —с до х — с + 'к и что»
полная величина силы есть Р, сколько бы мало к ни было, так что
с+л
С
Тогда в формуле (24) одно интегрирование может быть выполнено,
именно, будет
i	с+л	с+л
/ (;, о) sin dz =	/(£, o)sin^d; —sin/ (с, di = sin ”^F (а)
Ос	с
и, следовательно, Sn будет:
2sin~- *
Sn =------ \Р(з
апк j v
о
Отсюда видно, что если есть такое целое значение п = п1, что
пхс = Z,
) sin (Z — з) б/з.	(25)
то sin^ = 0 и, значит, 6'п = 0, и в выражении и2 члена, соответствующего
n — nlt не будет, т. е. будет отсутствовать тот тон, для которого точка приложе-
ния силы совпадает с одним из узлов.
Пусть, например,
P = 2fsin/rt;
тогда по формуле (25) будет, если сделать для краткости письма
ЛТС71 э .
Т =л’
t
Sn = sin ^у К sin рз sin к (t — з) dz =
о
t
-—-sin {cos [kt — (к + р) з]— cos [kt — (к — р) з]} с?з ==
6
= Цк*"-~р*) sin — sin pt - Ik sm — SU1 ht
и, значит, будет
m . mtc	__	. mtc
n r_ 00 л sm -г-	„	00 sm —
2pK v] 1 I • mtx . nitat . 2a •	. xn I • nizx
U,a  ---— >,---------------Sin -г- Sin -г- + -y- sin pt >.  2 й-х-- sin —
2 ал ^-1 n а2л2п2 e I I I	ZJ а2к2п2 o I
пм —p--------P2	7Г—P
1'234
РЕШЕНИЕ УРАВНЕНИИ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
причем, предполагается, что нет такого целого числа п, при котором было бы
Если же такое целое число есть, например п = тгх, то соответствующий
*ему член должен, быть заменен таким:
в первой сумме:
1	. rnitc	л . mitx
—г sin ~~ К sin pt sin -Jy- ,
p2 I	r I ’
во второй сумме:
1	. mite	л . mitx
----Sin -7— Kt COS pt Sin .
p l	J	l
Эти формулы обнаруживают и здесь явления резонанса, именно, когда
«частота» р перемен возмущающей силы будет приближаться к частоте
одного из тонов струны, то соответствующая этому тону амплитуда коле-
бания будет быстро возрастать, и это колебание получит преобладающее
значение, если же было бы полное совпадение частот, то амплитуда, при
отсутствии сопротивления колебаниям, неопределенно возрастала бы про-
порционально времени.
Понятно, что можно было бы не прибегать для решения нашего при-
мера к общей формуле (24), а, найдя по формуле (21) величину Нп, кото-
рая в нашем случае будет
С+Л	C-f-Л
тт 2 I г,v • mtfc -ft, 2 • mtc ( » ry. v	2 rr . Tiicc •	,
Hn=— \ f(z, г) sin — dz = у sm -y \ f(z,.t) az = у К sin — sin pt,
c	c
подставить эту величину в уравнение (21), которое тогда будет
, а2п2к2 о 2	. плс .
ОпЧ—у 5п = -J К sm — sin/rt.
Общий интеграл этого уравнения есть
<Sn = j4ncos -7- t + BnSin-j-t + тК sin-p-т^--------- sm pf,
I	I	>	1 u a 7t	_
-рГ-Рг
постоянные произвольные An и Bn надо определить так, чтобы было при
7 = 0: 5п(0) = 0 и Sn (0) = 0, откуда следует
*	. mtc
Z2
и по подстановке в формулу
со
. mtx
Sn sm -р
n=l
мы получим тот же результат, как и раньше.
Заметим еще по поводу этих формул, что первая сумма, входящая
в состав величины и2, именно:
со
2рК у j_
ait п
п=1
. mtc
sin -у
а2л2л2 _
-р--?
. mtx .
sm — sm
amtt
T ’
приложится к свободным колебаниям струны, и эту сумму можно рас-
сматривать как те свободные колебания, которые произойдут, если на струну,
I ^2] .
ОПРЕДЕЛЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ СТРУНЫ
235
находившуюся вначале в равновесии и покое, начнет в момент t ~ 0 дей-
ствовать заданная внешняя сила; тогда, кроме «вынужденных» колебаний,
имеющих тот же период, как и период возмущающей силы, образуются
и эти свободные-
Сумма
2К .	, v z
z = — Sin/tf / I ТГй---------
I г а2п2п2 о
П=1 —/2-----/>2
Sin —у
представляющая собственно «чистые» вынужденные колебания, может быть
найдена при помощи изложенного в главе VI приема.
Для этого напишем эту сумму так:
2К1 .	, v	1	• riitx
z = ^-sin pt 2 —Y——p-sin — ,
n=1 n
полагая затем
p4* _
a2-2 —
имеем
GO
22fa2 . л vi • nite . nitx 1
sin^ 2>n-sin — ^
' n= t
nite
co	oo SID.____
2jKa2 .	. Vl 1	• nite . nitx , 2Ka* л vi 1 I . nitx
= -pq-smpt 2-^sin^sin _ + —Smp< 2	sm —
n=l	n—1
Сумма
co
c VI 1	. nitx
5»= 2j7^sin ~sin-T
n=l
представляет непрерывную функцию от x — Q до х = 19 составленную из
прямолинейных отрезков, и, следовательно, вторая производная от этой
функции равна нулю на всем протяжении, кроме места разрыва первой
производной; поэтому, дифференцируя предыдущее равенство дважды
по букве х, получим
°° Ч]П ___
„	2К^ it2 .	.	/	. nitx
/" = - sm 2	~ ’
П=1
откуда следует
Следовательно,
z = С sin (ж + Р),
причем для отдельных участков значения постоянных произвольных Сир
могут быть и различные.
Нетрудно видеть, даже не прибегая к общему способу, что место разрыва
первой производной от функции z есть х = с9 сама же функция z непрерывна.
При х = 0 и при х = 1 величина z = 0>
236 РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН[Гл. VII
Значит, на участке от я = 0 до х — с надо брать
z = Asin “ГГ,
а
на участке же от х — с до х = I должно быть
z = J5sin^- (Z — х).
При х — с значение 2, даваемое и тою и другою формулою, должно»
быть одно и то же; значит,
A sin — с — В sin ~ (I — с),
поэтому можно брать
sin — с	sin — (I — с)
а	а '
где Н пока неизвестная величина, не зависящая от х.
Таким образом, будет
. Р
sm — х
z — Н-------— для 0 < х < с
р
sm — с
а
z^H
sin в —
sin — (Z — c)
a
ДЛЯ C < X < I.
Значение постоянной H можно определить, или разложив функцию,
определяемую вышеприведенными равенствами, в ряд Фурье и сличив
с заданным ее разложением, или определив величину скачка первой про-
изводной, или же непосредственно из механических соображений.
Так как параллельная оси z сила
= sin pt,
приложенная в точке х = с, должна уравновешиваться натяжением струны Г,
то будет
т (2Z)c-0 + Р (2')с+о = рР•
Отсюда следует
Н £-
а
НО
Р
cos — с
а
• Р
sin
а
cos — (I — с)
р а
а . р z. ч
sin ~ (Z — с)
= у К sin pt
следовательно, будет
н	1
Т	а2 ’
р	р
. sin — с sin — с)
__ 1	а	а 4	7
~~~ар_____________________. pl
sm —
а
Таким образом, будет
. sin — (I — с)
1 тг	Л	- « р .
z = — К-----------------sin — х sm pt
ар	. pl	а г
sin —
а
• Р
sin — с
z = —К---------sin — (Z — х) sin pt
ар . pl	а '	/ л'
Sin —
а
К sin pt-
для С < X < I.
для 0 < х < сг
§ 73]	СЛУЧАЙ КОЛЕБАНИЙ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ -	237
§ 73» Случай, когда колебания происходят в сопротивляющейся
среде» В том случае, когда струна колеблется в воздухе и встречает сопро-
тивление своим движениям, и если это сопротивление принять пропорцио-
нальным первой степени скорости, уравнение движения струны будет
где через функцию f(x,t) обозначена возмущающая сила, действующая
на струну.
Поступая совершенно подобно предыдущему, полагаем
и — и±-\- и2,
причем Kj удовлетворяет уравнению
+ (1)
граничным условиям при ВСЯКОМ Г. при X — О ДОЛЖНО быть &! = () и при
х — 1 должно быть ^ = 0, и начальным условиям: при t = 0 должно быть
«i = <P(s) и =	(2)
величина же и2 удовлетворяет уравнению
^? + 2/г5г-а2^ = /(ж, Z),	(3)
at* at дхг х 7	х '
тем же граничным условиям, как и иъ и начальным условиям: при £ = 0
должно быть
н2 = 0 и ^ = 0.	(4)
Прежде всего ищем иъ полагая
иг=^ТХ	(5)
и определяя функции Т и X, так, чтобы каждый член суммы удовлетворял
уравнению (1) и граничным условиям.
Тогда для определения Т и X имеем уравнение
Т"Х.+ 2hT'X - а2ТХ" = 0,
или
T"+2hT' _Х" __
X ~ К >
так что величины Т и X удовлетворяют уравнениям
Т"+ 2hT' + а2к2Т ==0,
X" + *2X = 0.	W
Отсюда видно, что так как граничные условия остались прежние,
то функции X и то трансцендентное уравнение, коим определяется вели- *
чина А, останутся без изменения, так что
V	•	/ j о
An = sm —	(п = 1, 2, ..., п„.. .),
и разница будет лишь в том, что Тп определяется уравнением
rn + 2hTn + a^T =0,	(7)
а не уравнением
как то было при Л = 0.
238
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
Общий интеграл уравнения (7) есть
Тп = е~м { An cos qnt + Вп sin qnt j,
где	________
Vn = y°^-h*
и, значит, будет
w1 = e~ftZ 2 Asinn-^cos?nI + e-« 2 Вп sin^y sin qnt\
n=l	n==l
коэффициенты An и Bn определятся из начальных условий, именно:
попрежнему будет
Ап = -у (5) sin ^у dz,
о
для определения же Вп послужит равенство
ОО	ОО
’<*> " “h 2 л"sin "у + 2’л sin	•
n=l	n=l	.
из которого следует
i
'НО sin ^у di = — hAn + qnBn.
О
Присутствие множителя e~ht в выражении показывает, что свобод-
ные колебания в этом случае «затухают» совершенно подобно тому, как для
маятника, колеблющегося в среде, коей сопротивление пропорционально-
первой степени скорости.
Вынужденные колебания и2 будем искать попрежнему под видом
со
^2 :== 2
П = 1
где Sn есть функция только t, Хп —та самая функция Xn = sin
по которой разложено и которая определяется уравнением (6) и гранич-
ными условиями.
Повторив выкладку предыдущего параграфа, видим, что Sn будет
удовлетворять уравнению
Sn + 2hSn + ^-Sn^Hn,	(8)
где попрежнему
i
#nW=4$/(?,0sin™M.
о
Начальные же условия для Sn таковы: при t = 0 должно быть Sn = 0
я S'n — 0, вследствие чего будет
t
Sn = e~ht eho Нп (<з) sin qn (t — a) ds,
п	о
т. е*
t	i
Sn = ^- e"ht S de \ eh° S*n "Г S*n °)
п о о
§74]
ВЫНУЖДЕННЫЕ ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
23Ф)
и все,-сказанное в главе I относительно вида и свойств решения уравне-
ния (8), будет приложимо и здесь и будет относиться к тем членам, из;
коих составляется сумма почему мы не будем на этом подробно оста-
навливаться.
§ 74. Вынужденные поперечные колебания стержня. Как второй при-
мер рассмотрим вынужденные поперечные колебания упругого стержня,
или балки.
Это движение определяется уравнением
5 + *ag=/(*> О,	(D-
где z есть стрелка прогиба балки в точке, коей абсцисса есть х в момент,
времени t\	где £ —модуль упругости балки, J —момент инерции:
площади ее сечения s относительно центральной оси, перпендикулярной,
к плоскости колебания, р —плотность материала балки (масса единицы
объема), f(x9 t) = — F (ж, t) и F (х9 t) — внешняя нагрузка, отнесенная на
единицу длины, действующая в момент t в той точке, коей абсцисса есть х*.
Фиг. 41.
Кроме уравнения (1) величина z должна удовлетворять условиям «гра-
ничным», иначе условиям закрепления концов балки, и условиям «началь-
ным», как о том сказано в § 48.
Это уравнение и условия могут быть выведены следующим образом.
Положим, что имеется балка АВ (фиг. 41), коей конец А соответствует'
абсциссе я = 0, а конец В— абсциссе я = /, и что на нее действует нагрузка Р9
отнесенная к единице длины балки, причем Р есть заданная функция,
абсциссы х. Возьмем сечение балки, соответствующее абсциссе х\ тогда»
условие равновесия балки выражается уравнением
(*>•
где М есть изгибающий момент в рассматриваемом сечении, так что вообще *
будет
i
.	(£— ж).Р (Г) + «Ж + 6,
ибо элементарная нагрузка Р(;)^В на элемент балки DD19 лежащий между
абсциссами 5 и £ + d;, дает момент изгиба в точке С, равный -г (с - х) Р (с) di9
и, значит, полный момент в этом сечении от нагрузци Р($) будет
г
+ $ ($-х)/>(;)<£.
Знак + взят потому, что при избранном направлении осей положительная
нагрузка Р дает момент, стремящийся сообщить балке кривизну, вогнутость,
коей направлена в сторону положительной оси z. Кроме момента от
нагрузки Р(5), может быть еще момент от пары закрепления в конце В*
240
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
ГГЛ. VJI
и от реакции опоры В\ этот момент выражается линейною функциею
-абсциссы х.
Итак, будет
i
X
Дифференцируя это уравнение по х дважды, получим
i
EJd^=-\P®& + a	(2)
’И	,	X
EJ^ = P(x).	(3)
Уравнение (3) представляет уравнение равновесия упругой балки
постоянной площади сечения.
В том случае, когда нагрузка Р зависит не только от абсциссы но
и от времени Z, т. е. изменяетсяг с течением времени, балка-будет совершать
колебательное движение, для получения уравнения которого стоит только
по принципу Даламбера написать уравнение равновесия, присовокупив
и силы инерции к числу действующих на систему сил.
В нашем случае, значит, надо взять силу инерции, отнесенную к едп-
нице длины балки. Она будет равна —	, и, значит, уравнение (3)
заменится таким:
	...	(4)
. 4 е	.	*
:причем вместо Р (х) написано F (х, t)*— выражение переменной нагрузки.
EJ	1
Полагая — = 62 и f (х, .1) = — F (х, t), получим вместо уравнения (4)
уравнение
Что касается условий закрепления концов, то очевидно, что для конца
f заделанного должно быть ’
...	Z.=*Q И /g = o, '<   :	<
т. е. прогиб z равен нулю, и направление центральной фибры должно быть
касательно к оси х, т.«е.»^ = 0.
дх
Для конца подпертого должно быть z = 0, т. е. прогиб равен нулю,
и, кроме того, изгибающий момент должен быть нуль, а значит, в силу
уравнения (*), ц ^| = 0.	...
Для конца свободного должен быть изгибающий момент равен нулю,
m л дЧ л .	.	'
т* е’ = и сРезывающее условие равно нулю, т. е., в силу уравне-
ния (2), должно быть ^Д — 0.
. . . - . .	Эх*	.
Чтобы выяснить сущность метода и не иметь дела со сложными выклад-
ками, возьмем случай балки, подпертой в обоих концах, так что наша
задача ставится таким? образом:
§ 74] ВЫНУЖДЕННЫЕ ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ 241
Определить функцию z, удовлетворяющую уравнению
граничным условиям', при z = 0 должно быть
z = 0 и р2=0,
при х = 1 должно быть
2 = 0 и р2=0,
дх2
и начальным условиям: при 1 = 0 должно быть
* = ?(*), д~=^(х).
По общему правилу, делаем
2 = “f" ^2
и распоряжаемся так, чтобы zr представляло свободные, z2 — вынужденные
колебания нашей балки, т. е. чтобы удовлетворяло уравнению без
последнего члена:
^fl = 0
dt2 дх* v’
граничным условиям: при х = 0 должно быть
Z1 = 0 и §з = 0,
при X = I должно быть
21=0 И 7ГТ = 0,
•*	дх2
и начальным условиям: при t = 0 должно быть
«! = ?(«) и д-^=Ь(х),	(**)
величина же z2 должна удовлетворять уравнению с последним членом:
(п
граничным условиям: при £ = 0 должно быть
z2 = 0 и § = 0,
что следуют из условий (**).
Решение задачи начинаем с разыскания zt; поступая, как показано
в § 48, получим
^1=3 ГХ,
где Т и X определяются уравнениями
Т" + Ь2А4Т==0,
Xiv-A4X = 0,
причем функция X должна удовлетворять и граничным условиям, и тогда
получается, что постоянная к есть корень трансцендентного уравнения
sinAZ=O
и
хт- . nitx
Хп = sm — ,
т Л Ьп2тгН , D . bn2it2t
Тп = Ап cos ---h Bn sin ,
46 A. H. Крылов
242
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
(Гл. VII
после чего постоянные произвольные Ап и Вп определяются по начальным
условиям.
Чтобы найти z, полагаем
со
z2=^SnXn,	(5)
П = 1
где Sn — функция только переменной Z, функции же Хп — те самые, по кото-
рым разложена величина иг в рассматриваемой задаче.
Представляем функцию / (ж, Z) в виде ряда
со
f(x, t)^Hn(t)Xn	(6)
n=l
и, подставив в уравнение (!') вместо z2 величину (5) и вместо f(x9 t) вели-
чину (6), получаем уравнение
'	^(Sn + b-^S^)Xn^Hn{t)Xn,
л = 1	П = 1
что дает для определения Sn уравнение
Sn + -i^-Sn = Hn(t),	.
а так как при t = 0 должно быть
2s = 0 и §-0,
то для Sn должно быть
5п(0)=0 и ^(0) = 0,
так что
t
(8)
О
а так как в нашем случае
i
о
то будет
5n='W \ Лз c)sin^sin-^-(f-a)d5,	(9)
О о
Z2=2^sin7-	(«я
n = l
Эти формулы и дают общее решение вопроса о вынужденных колеба-
ниях подпертой балки.
Совершенно подобным же образом мы получили бы решение и для
всякого другого из шести случаев различных способов закрепления концов.
§ 75. Поперечные колебания стержня, вызываемые равномерно дви-
жущейся нагрузкой. Рассмотрим некоторые замечательнейшие случаи ко-
лебания подпертой балки под действием переменной нагрузки.
Как первый пример возьмем случай постоянной нагрузки р на еди-
ницу длины, перемещающейся равномерно со скоростью с по балке.
Чтобы выяснить сущность дела, не усложняя выкладок, возьмем про-
стейший случай, когда протяжение нагрузки к настолько мало по сравне-
нию с длиною балки Z, что можно пренебречь временем пробега нагрузки
§75]
ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
243
над опорами балки по сравнению с полным временем пробега всей длины
балки.
В этом случае функцию f(x, I) можно взять так:
/ (ж, I) = 0 для
/(ж, t) = fi Для
/ (х, t) = Q для
О < х < ct — у,
ci —у <ж<с?+у ,
ct + | <а?</.
Следовательно, будет
Значит,
Я4р 1 . пкХ . mtct	. птс ct
п = ~ — S1H -грSin —7—= AnSlH	,
ps птс 21 I п I ’
и уравнение (7) § 74 будет
Sn +
&2П4ГС4 о	. mt ct
—I*- Sn = Kn sin —г
откуда
Sn — Ап COS
bn27t2t
I2
-j- Bn sin
bit2n2t
I
r_ . mtct
Kn sin ~
&2n4K4 n2tt2c2 *
/4	p
причем An и Bn определяются из условий
Sn(0) = A = 0,
it /л\ Ьк2м2 jrj t К nmt_c_
n “ “F“ Пп^—Г bW riW
t. e.
B _Knlc I*
n bn?itz b2n2it2-c2l2 ’
и, следовательно, будет
«» Sin —
4p clb 1	2/	. mtx . bn2n2t
Z2 — — ps	— c2/2 sin ~T Sln ~P~~
n = l
. tlTtk
co sin_________
. 4p /4 vi 1	2/	. mtx . mtct
+ — -Г У Vo --------------77» sm -7- sm -p .
ps к3 nz b2n2Tt2 — C2l2 I	I
n=l
В случае сосредоточенной нагрузки надо считать, что длина К бесконечно
малая, но что полная нагрузка, т. е. произведение имеет заданную вели-
чину Р. Переходя к пределу, видим, что в этом случае будет
4р Z4 . mt\	2Р13 п
- -т sm -г- =----------г ,
os к3 2i ps к’
«6*
244
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН	[Гл. VII
и предыдущая формула будет
2Р/4с VI 1	1	• ппх . bn2n2t
Zo =-------г~г	~ч zT~9~9-----575 S1H ~7~	—г*
* psfrrc4 п3 b£Ti2n2 — с2!3 I	I2
п=1
go
2P/3 vi 11^. mix t . nnct
+ psit2 2j bhW — c2Z2 sin ~T bln I 
n = l
Необходимо помнить, что эта формула имеет место, лишь пока ct^l,
т. е. пока нагрузка движется по балке, в момент же ct = I нагрузка достига-
ет конца балки, второй член в предыдущей формуле обращается в нуль, и
остается
оо
:	___ 2PZ4c 1	1	• Ъп2ъ2 . ппх
Zz ~ psbir4 2j b2it*ns — c42 Sin cl 8m ~T 
n=l
Взяв производную и делая в ней t =l-, получим
оо
<Zz2__	%Р1*с чо 1 bn2it2 1	. mix о bn2n2
~dt ^sbnl~ 2j ~li~ о2п2л2 — e2Z2 Sln ~T COS ~l
n==l
oo
2PZ8 vi 1 nTCC 1	• tvkx
~~ p^S 2j ~T b*nW — c2Z2 sin ~T 008
n = l
что и представит начальное состояние балки для дальнейшего движения,
функция /(ж, Z) = 0, т. е. колебания будут свободные, и, следовательно, z
будет выражаться формулою, если время считать с момента схода нагрузки
с балки,
2PZ4c v? 1	1	• bn2n2 , mix bn2Ti2t.
Z —*	—l Г s i "TT iT5 5 5	575 SIH rz Sin ~~z COS —»a~" ' —
ps&it4 ZJ n3 b2Ti2n2 — c2l2	cl2 I	I2
n=l
v? 1	1	bn2Ti2 . mix . &n2i:2Z1
^b^ 2j b2Ti2n2— c2l2 cos "7Г sin— sin —2
n=l
2PZ4c 1	(— l)n •	• ЬпРпЧ^
“ ^sbiib 2j b2n2n2 — c2Z2 Sin ~T Sin “Z2 ’
n = l
Заметив, что
^4+g,
мы можем в предыдущей формуле соединить первые две суммы в одну и на-
писать равенство
со
___ 2PZ4c у 1	1	. mix bn2n2t
Qsbn* 211 п3 b2Ti2n2 — c2Z2 Z Z
n=l
__ ЪРРс Vi 1	(— l)n • flux . Ьп2к2 S' c\
” psb45 Z) bWn* — c2Z2 81П ~T Sin
n = i
Все эти формулы предполагают, что нет такого целого числа п, при котором
62nM-c2/2 = 0.
§ 75]
ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
245
Само собою понятно, что в этом случае, если п —есть такое целое
число, то соответствующие ему члены в суммах заменятся другими, где время t
будет вне знака sin иди cos. Выписывать эти формулы не будем.
Обратим еще внимание на следующий случай:
1) если нагрузка движется по балке весьма медленно, то ясно, что.
во всякий момент балка будет иметь соответствующую
равновесия; надо посмотреть, вытекает ли это свойство
формул и что значат тогда слова «весьма медленно».
Напишем формулу (*) так:
форму статического
из вышеполученных
2PZ4 c	1	• nizx •
Z2 =---г >. -------;----777-r sm -7—sin
psdW ZJ ъ( сЧ* \ I
71=1 V &Mn27
bn^itH
~1
1
I	V
ps&2 it4 Zj
n = l
nitx . nitct
sin — Sin —у ,
___c2/2 \
62it2n2 )
и положим, что в рассматриваемый момент = так что в первой сумме
ЬпЧьЧ	bn4t2a	»	nitct ~ anit
вместо аргументов —у- надо писать ^2 ,, во второй вместо -у будет -у .
Движение нагрузки вдоль по балке мы будем считать медленным, когда
с2/2
величиною &2^-2 можно пренебречь по сраврению с 1, а так как отношение
«,	1 cl
множителей* 1, стоящих перед знаками сумм, есть то, значит, первою
суммою можно пренебречь по сравнению со второю, и, заметив, что b\s — EJr
где Е есть модуль упругости и J —момент инерции площади сечения балки,
получим
. anit
Sin —y—
l . nitx
-----— sm -y- .
n4	I
(**)
22 rSEJ
n — i
Чтобы представить сумму, входящую в эту формулу, в ином виде, положим
~	. anit
°0 sm —
I . nitx
— sm -7- ;
n4	/ ’
?(*)=2
П = 1
cl
1 Отношение у может быть представлено в другом виде, из которого сразу будет
видно, какие скорости движения с приходится считать малыми. Мы видели, что
ь
Величина I/ — зависит только от материала балки и представляет скорость V
распространения звука по этому материалу. Эта скорость для металлов весьма велика,
так, например, для стали будет
2200000 • 980 • 1000	,
= 522000 см]сек = 5220 м/сек.
7.9
Величина j/*— представляет радиус инерции площади сечения балки; обозначим
его через г; тогда будет — . Отношение — для балки, обладающей достаточной
о у г	г
1с
жесткостью, составляет 10—20, и, значит, даже при скорости с = 30 м/сек, -& составит
1	с2/2	1
около То и bw около 1000
246
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
тогда, дифференцируя эту функцию три раза, получим
оо
z ч к3 Vi 1 апп mzx
?•’(») = -? 2й81П-гСО£5т--
п=1
• По формулам § 69 имеем
- sin = [<?"' (к. - 0) (Лх + 0)] sin ,
следовательно,
Ах = а и T"'(fti~0) —<p"'(^i + 0)=—
а так как
EJz2 = ^<f(x),
то функция (Z?Jz2)"' имеет при точке а скачок, равный Р, т. е. графически
представится чертежом (фиг. 42).
Чтобы определить величину Q, надо заметить, что в разложении 9"' (ж)
постоянного члена а0 нет; значит,
. i
ср"' (х) dx = 0,
о
но
I
ср"' (х) dx = (P + Q) (I -a)-\-Qa=z О,
о
откуда следует
Р(1-а)
Упомянутый чертеж представляет эпюру срезывающих усилий, действу-
ющих на балку, коей центральная фибра представляется уравнением (**).
Как видно, эта эпюра такова, как при статическом действии сосредото-
ченной в точке (х = а) нагрузки Р.
Из этого графического представления
Фиг. 42.
Из
Следует, после интегрирования один раз,
EJz"2 —
EJz" = р“(1-а) + (а -ж) =
для 0 < х < а
ДЛЯ
и так как, в силу формулы (**), z\ равно нулю как при х — О,
х — Z, то к предыдущим величинам постоянных произвольных
нет надобности.
Из предыдущих формул следует
jEJ2' = ^(Z —х)2 + С1	для a<x<Z,
г» т / Р (I — й)ж2 , /1	А .
EJz2 =----—J—- J-+ ^2 для 0 < х < а.
а < х < Z,
I х
так и при
прибавлять
Постоянные С\ и Cg определятся из условий:
1) при х = а величины z'2, следующие как из первой, так и из второй
формулы, должны быть между собою равны;
§ 751
ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
247
2) так как в разложении z2 постоянного члена нет, то интеграл
i
z'2dx
о
равен нулю.
Таким образом, для определения и С2 имеем
J“(Z_a)2 + <71== -^=±>^ + Са
и
а	0
откуда следует
С1=-4т(^-«)(/+«),
C2 = |^(Z-a)(2Z-a).
О Ъ
Наконец,
EJz2~Cyx —	— х)3 + С3 для а < х < Z,
of
EJz2 = C2x—	+ С4. Для 0 < х < а.
Постоянные С4 и С3 определяются условиями: z2 = 0 при ж=0 и при
х = I, так что
С4 = 0, С3 ^-Сх1.
Таким образом, получаем
1 Р а(1 — а) Г. (I - х)3 1	_
22 = T£J z”L(Z + a)(Z-a;)'4^-J ДЛЯ а<*<А
1 Р а(1 — я) f /о?	\	х31	г\
^ = -6EJ~4- 1^-а)х~^ \	ДЛЯ °<ж<«-
Это и показывает, что формула (**) представляет, действительно, ста-
тическую форму равновесия балки под действием сосредоточенной в точке
х = а нагрузки, равной Р, и что из этой формулы вытекают все те следствия
относительно величины срезывающего усилия и изгибающего момента, как
и из представления этих величин разрывными функциями или эпюрой.
Входящая в состав величины z2 сумма
со
«	2Р13 у-i	1	. mtct . mzx
С = Ml 2J	sin “Г Sm У ’
П=1 П Ql-62lc2„aJ
представляющая «чистые» вынужденные колебания балки, может быть найдена,
если поступить подобно тому, как это было показано для струны.
В самом деле, так как в этой сумме коэффициенты — четвертого порядка
1 у
относительно — , то функция, ею представляемая, непрерывна вместе с своими
двумя первыми производными, третья же производная имеет разрыв непре-
рывности.
Но, делая
^=а»
248
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VIT
имеем
~~nEJ
. nitct
sin —J—
n
co
™tx .	9	1
COS—+ a2 2 „
n— 1
. nitct
sm —
n2 — a2
nitx
COS —
Обозначим всю величину, стоящую в скобках, через <р (я), первую сумму
через вторую —через со (ж), так что будет
—	У" = <? (ж) = <Р1 (ж)1 + a2d) (ж).
Для функции срх(ж) по формулам § 69 имеем
у sin	(Ах - 0)-Т1 (Ах + 0)] sin + ...,
откуда следует
?i (^i — 0) — (Ад + 0) = у ,
kA — ct.
Так как в нашей сумме коэффициент ао = О и функция состоит
из двух прямолинейных участков, параллельных оси х, то должно быть
(^i—• 0) + (I— Ад) ©j (Ад + 0) = 0,
следовательно, будет
?1(^-0)=	?1(А1 + 0)=—
и функция <рх(ж) определяется равенствами
1$.	•	।	<рх (х) — — <~1 ~ для 0 < ж < к1. — ct,
С 1	|	2	4	(***)
*'* fe К, ] 4	<Р1(«)=-ут Для к1<х<1
Г27 ।
1—1-----J и представляется чертежом (фиг. 43).
Фиг. 43.	Функция со (ж) имеет как первую, так и
вторую производные, которые получаются диф-
ференцированием почленно ряда, эту функцию представляющего, произ-
водная же функция <рх (х) равна нулю для всех значений х;, следовательно,,
будет
<р" (х) =а2 со" (х).
Но
..	я2 n nitct nitx те2 f .
°) (ж)= -р 2j— cos —=
Л = 1
а так как
2 ТС2 С2
ГУ -- - -
Z2 &2 ’
то предыдущее уравнение будет
Т*(®) + ^?(ж) = о,
откуда следует
<р(ж)= Ясов у(ж + у),
§ 75)
ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
249
?J'(Z) = 0.
где H и у—постоянные произвольные, имеющие различные значения для
участков и от х = 0 до х — кг = ct и от х — кх до х — 1.
Обратив внимание на то, что первая производная функции <Р1(я), на
основании равенства (***), равна нулю, имеем
ф' (0) = 0 и
Следовательно, можно брать
ср (х) = Нх cos ~ х
ср (х) — Н2 COS у (Z — х)
^1,
для кг < х < Z.
Так как

то по трехкратном интегрировании получаем
— ^^t, = ^1(x) = A1x2 + B1x + C1 — b^ HiSin ^x для
«а 1г	О	U
-^^-t = ^(x) = A2(l-xy + B2(l-x) + C2 +
Л Jr
+ H2 sin ~ (I — x) для
Постоянные произвольные Ви Clt Hlt А2, В2, С2,
I.
Н2 определяют-
ся из условий, непосредственно вытекающих из представления функции С
рядом
1
— n*EJ .
n=l«4
mtct . nitx
__^sin__sin— ,
Ь2К2П2 )
а именно, должно быть
<МО) = о, <|»;(О) = о,
<MZ)=o, <!>;(/)=о,
Ф1 (^1) = ^2 (^i)> Ф1 (^i) = <?2 (^1)> Ф1 (^1) ~ Фг (^1)>
ФГ(*1)^Ф^(*1) = 7-
Из этих уравнений получится:
Ai = Ci — А2 = С2 = О,
о __ я М / — кг о _ я Ь2 кг
Т? “7““ ’	2"^ Т >
sin~ (Z — ki)	sin— Л,
тг п Ь V ' гт	я b
7/2=1-у—77’
sin-г I
о
ct,
• с t
Sin-г- I
b
и, следовательно, будет, при замене кг его величиной
, t	,	sin	4-	(I	— ct)
I — ct	b	b	'
— X------
I	c
r_ __ 21 Ь2
EJc2
г _____
EJc*
. ex
sm -г-
b
. cl
sm -T-
0
sin £ ct
—— sin 4 {I — s)
. c . b '	'
sm-v-1
b
для О
(I)
для. ct. О
ct f »	,
г(/-ж)-7
1250
ДЕЙСТВИЕ НА БАЛКУ МАЛОЙ МАССЫ
[Гл. VII
Стоит только предположить, что отношение у бесконечно малое,
удержать в разложениях синусов первые два члена, затем перейти к пре-
делу, тогда получатся формулы (**).
Само собою понятно, что исследование чисто вынужденных колебаний
и всех обстоятельств изгиба балки при помощи формул (1) гораздо проще,
нежели при помощи ряда.
§ 76. Действие на балку малой массы равномерно движущейся на-
грузки. Уравнение Стокса, интегрирование его. В предыдущем параграфе
рассмотрен случай действия на балку подвижной нагрузки, которую мы
приняли за некоторую силу, точка приложения которой перемещается
вдоль по балке. В том же случае, когда нагрузка материальная, она
обладает инерцией и, участвуя в движении самой балки, давит на балку
с переменным усилием, равным
Р / __д*2 \
g V dt2 у x—ct'
Предыдущий случай можно рассматривать, следовательно, как пре-
: дельный, когда можно пренебречь ускорениями колебательного движения
сравнительно с ускорением силы тяжести.
Если бы расчет показал, что величиною	пренебречь нельзя,
то можно прибегнуть к способу последовательных приближений: решить
сперва задачу, пренебрегая силою инерции нагрузки, полученное реше-
ние принять за первое приближение и, просуммировав найденный ряд,
выразить ускорение ( t в функции времени t, после чего заменить Р
вышенаписанной величиною, — получится второе приближение и т. д.
Другой предельный случай есть тот, когда масса самой балки весьма
мала но сравнению с массою движущегося по ней груза, и, значит, можно
q	бы пренебрегать инерцией самой балки.
____________----—Понятно, что к этому случаю выше-
----------------приведенные формулы (I) не относятся.
О\	Пусть (фиг. 44) движущийся груз Р в
W	рассматриваемый момент t находится в точке С.
Фиг. 44.	Обозначим через у прогиб CD балки в
месте приложения груза.
Под действием усилия Q, приложенного в точке С, балка принимает
изогнутую форму, определяемую равенствами
z==iSjaJLT^[(2l-a^x-T] для 0<а:<а’
при х = а стрелка прогиба
= «2)2-
Следовательно, на груз Р со стороны балки при величине прогиба у
действует вверх сила
ЪЕЛу
(al — а2)2 ’
а так как
a = ct,
8 77|
ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ ВАЛКИ
251
то уравнение движения груза Р будет
Р__р_ ЗЕЦУ
g dt2	(lct-сЧ2)2
Положив
g ЗЕ Tig
&--=р>	и ct=x>
мы приведем предыдущее уравнение к виду
= р — (lx -я2)2 у’	С1)
Это уравнение было получено в сороковых годах прошлого столетия
знаменитым английским математиком и физиком Стоксом, участвовавшим
в трудах английской мостовой комиссии, исследовавшей причины обрушения
какого-то железнодорожного моста и устанавливавшей нормы для постройки
металлических мостов.
Стокс сперва проинтегрировал это уравнение при помощи разложения
в ряды и составил таблицы, но вскоре затем В. Томсон (лорд Кэльвин)
показал, что это уравнение может быть проинтегрировано в квадратурах.
Не проделывая подробно этой выкладки, сообщим лишь результат.
/2
Если, считая — > а, положить
4
л
X
У == -----------------R V
(1-х)*
и взять а и р так, чтобы было
И
то уравнение (1) приведется к такому, у коего правая часть—полный диф-
ференциал.
По интегрировании получится
dx * lx-x2 J ж
Это уравнение линейное, и его общий интеграл есть
Мы не будем вдаваться в дальнейшие подробности по этому вопросу
и упомянули о нем лишь для того, чтобы привести замечательный при-
мер интегрирования.
§ 77о Поперечные колебания балки под действием периодически из-
меняющейся нагрузки. Положим теперь, что на балку в смежности с* точ-
кою С, абсцисса которой есть х = а, действует переменная нагрузка, выража-
ющаяся формулою
р sin kt,
равномерно распределенная на участке от
X	. х
до ж = а + у.
252
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
для и < х <; а—>
. X	, к
для а — у<ж<а + у,
, к ;
ДЛЯ «+ J < X < Z.
Требуется определить колебания балки и рассмотреть также случаи
сосредоточенной нагрузки.
В рассматриваемом случае фунцкия f(x, t) такова:
/ (ж, t) = О
fix, Z) = ^sinz7
/(«, О = о
Значит,
i
Нп=\ / (£, Z)sin^ = — jpsinAz sin^c?$ =
Следовательно,
тт	4»	. nizk	. aim	- .	1
Нп—	sin--r-sm-^smл/ = — GnSinkt
а	psnn 21 I	n	n
и, значит, уравнение (7) § 74 будет
Sn 4--ji— Sn = ~ Gn sm kt
и
'	o A bn2Tt2 . D . Zm2rc2£ . 1 Gn/4 . 7
Sn — An cos p t + Bn sm	F — 62ra4jt4 _ sm kt\
начальные для Sn условия, именно: при t = 0 должно быть
Sn — 0 и Sn —0,
дают
А ________________________Л „ D ________к_ 1	^П^8____
п	п п3 bn2 Ъ2п№ -
и, значит, будет
со	оо
kl9	Gn 1 . mzx . bn2it2t , 1Л . 7 л vi Gn 1 . пкх
Zi — Ьгё5 2	- кЧ* n5 Sln ~Г Sin ~Р~ + Z sm 2 b^nW—кЧ1 п 81П ~Т *
п=1	п=1
В случае сосредоточенной нагрузки будет
lim рк = Р
х«о
. пкк	nitk
и sin-^- заменится через так что
Я2Р . апп *	7 л
= --sin-5-smto
I
§ 77]
ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ БАЛКИ
253
и, следовательно,
1	„	2Р . anit
		  7	Sin —Z	,
п------------------psZ I
и предыдущая формула даст
со	• ап7Г
_	2кР I5	81П I	• nitx . Ъп2пЧ
Zi —	PS 2j И2 (&2га«Л* — W‘) sin т~sin ~Р~ +
П = 1
_	. «ПК
ПП73	Sin-j-
, 2PZ3 . 7 л VI	I • nitx
+ ~— sm kt >, 19 л -г—Гт?! sm -т- ,
ps	&2к4п4 •— кЧ* I
П = 1
предполагая, что нет такого целого числа тг, при котором было бы
62414д4_Д2/4_0.
Если же при п = п1 будет
то члены в суммах, соответствующие значению п = пг, должны быть заме-
нены такими:
1 Р 1 л . n.ita 7	. щпх
------г т sm A— cos kt sm -
ps I к • I	I
И
1 P 1 . плтш .	. n^itx
— -y т-z sm -S— sm kt sm -y- ,
ps l к2 I	I
что ясно обнаруживает явление резонанса. Необходимо, однако, обратить
внимание на то, что эти члены пропадают, если точка приложения силы
•совпадает с одним из узлов, соответствующих числу пх, т. е. если а таково,
что
у- = целое число,
ибо тогда множитель
. плъа ~
Sin -у— == 0.
Нетрудно видеть, сто в случае, если стержень колеблется в среде,
коей сопротивление пропорционально первой степени скорости, то сво-
бодные колебания будут заключать множитель e~ht и с течением времени
пропадут, для вынужденных — все выкладки останутся без всяких изменений,
только величина Sn будет определяться уравнением вида
Sn + 2hS’n+^^-Sn^Hn(t)=^sin^sinkt	(*)
Ь	pot	t
и, значит, первая сумма, входящая в состав z2, будет заключать множитель
и с течением времени пропадет, вторая же — составится по формулам
§§ 5 и 6, и сказанное в этих параграфах будет относиться к каждому из
членов этой суммы, а именно, будет, отбросив сумму, умноженную на e~hi,
оо
2PZ3 V А •	/7^ .	\ • ИКХ
^2 = — >1 Ап sin (kt + 3П) sm -у- ,
П = 1
причём
. anit
sm -у—
^4	__________*_________
п	~ кЧ‘)* + чн?кЧ» ’
_ 2hk
bg «П — Ь2П4Я4 _	’
254
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
Гл. V€
Отсюда нетрудно видеть, каков будет характер движения балки, если
при данном а, т. е. сохраняя неизменной точку приложения, сила Р меняет
частоту колебания к.
При к весьма малом по сравнению с ~ величина z2 будет весьма близка
к сумме
2Р/3
ps62K4
00 sin —
SI . nitx . » .
—7- sm -r- sm kt,
n* I
n = l
которая представляет форму статического равновесия нашей балки, как то»
показано в предыдущем параграфе, под действием сосредоточенной в точке С
нагрузки Psin- t.
Если мы обозначим
и
bit2_________________________________________2it
Ч2'~~Т1 9
то Т\ есть период, соответствующий наименьшему секундному числу коле-
баний балки, т. е. период основного её тДна, т есть период изменяемости
силы, и, значит, если основной период балки мал по сравнению с периодом
изменяемости силы, то сила действует статически.
По мере увеличения к или, что то же, уменьшения т, коэффициенты АЛ
будут изменяться, как сказано в § 5, и наконец, когда к приблизится
к акому значению к19 при котором будет
или когда
=
Л = с,
тогда коэффициент Аг будет весьма быстро возрастать и будет близок
к величине
. ait
sm у
2hkLl*
и первый член суммы будет гораздо больше всех прочих, так что z2 прак-
тически сведется к этому первому члену
Р . ait cos кл . itx
—.SID -у- .	1 81ПТ ,
psZ I krh I
kth
ибо ап близко к — и, значит, балка будет совершать весьма большие
колебания с периодом = т-
Л1
форма же ее во всякий момент есть синусоида
, . itx
вида /sin z .
Когда величина к, при дальнейшем своем увеличении, перейдет значе-
ние /гг ==	• , соответствующее совпадению с основным тоном балки, то ко-
лебания весьма быстро уменьшатся и будут оставаться малыми до тех пор,,
пока 4 не будет приближаться к такому значению к~к2, при котором
имеет место равенство
22лг462 = 7 |Z4, т. е. Л2 = 2А-х,
т. е. когда период изменяемости силы приблизится к совпадению с перво-
гг,	2 2 ТС	„	g>
дом /2 = — — первого ооертона балки, тогда второй член суммы будет
§ 77]
ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ БАЛКИ
255 >
получать преобладающее значение, и величина z2 будет приближенно равна .
Р . 2ал cos 2кЛ
—у Sin -7---?
psZ I 2krh
. 2пх
sin —
И т. д.
Нетрудно видеть, что описанное явление резонанса будет иметь место <
и при всякой другой комбинации закрепления концов балки, а не только’
когда она подперта. Форма кривой изгиба будет другая, будут также дру-
гие периоды; но явление резонанса сохранится, ибо уравнение (*), опреде-
ляющее 8п, сохранит свой вид.
Сумма
-	2Р13	• VI	I • ппх
^=-^8inkt 1 ~	F/~sin~r ’
n==1 п	bW
представляющая «чистые» вынужденные колебания балки в рассматриваемом’
случае, может быть найдена, если воспользоваться
приемом.
Сделаем попрежнему
изложенным в § 69 ’
4	№
а* —---.
Ь2п* 9
„	. апп
00 sin —
/ \ Vi / ппх
?(ж)=2-^^81П-г *
Л=1
тогда функция ср(х) и две первые ее производные непрерывны на всем»
протяжении от х = 0 до х = Z, третья же производная имеет разрыв непре-
рывности, которая окажется при я = Именно, будет
п3
... , ч к8	п* . апп ппх
?’(«)=-72т^7’тТС(в- =
п3 XI 1 • апп	ппх
---7Г >| — Sin -т-COS-7-
/3 ZJ n I I
л-1
„ апп
sin
I ппх
7 Z л\ COS ”7
л (л4—а4) I

Первая из этих сумм уже была i айдена в § 75, и функция, ею пред-
ставляемая, есть
<?1 (я) = —р- 2 ~т~ ДЛЯ о < х < а,
?1(ж) = 7з- 2 7 Для в<ж<Г
Дифференцируя равенство
_	. опте
.	00	sm -7-
(х) = у; (х) = -тт а4 У	—jr cos
' ' 7	1J ' Is	п(п4~ а*) I
Л = 1
и замечая, что производная ср£ (я) = 0, получим уравнение
<PIV(a:) = -7r
или, заменив а4 его величиною,
fIV—£-?=о.	(**)’
.256
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Функция <р(я) состоит из двух участков:
от х == 0 до х — а пусть будет (ж) = (х)
и
от х = а до х — 1 пусть будет — Ф2(я).
Обе функции ф1 и Ф2 удовлетворяют уравнению (**), и, делая
можно писать
«pi = Аг ch {ta: 4-7?! sh p# + Ci cos + Dx sin рж,
<p2 = A2 ch p (I — x) + B2 sh p (Z — x) + C2 cos p (I — x) + D2 sin p (I — x).
Постоянные произвольные Aj9 Blf ..., B2 определяются из следующих
условий:
Ч>1(0)= о, Ф1(О) = О,
ф2(0 = 0, О) = о>
• Ф1(а) = Ыа)> ФИ«) = Ф2(«)> Фх («) = («)»
К' («)-К(«)=-$•
Отсюда получается
Ai — Ci — А2 — С2 = О,
о   я4 sh р (I — а)	к4 sin р (I — а)
1—	shjz ’	171 “"27^ sinpZ
о______тс4 sh ра	_ л4 sin Р«
2~	2/Z3 sh pZ ’	2“ 2p3Z3 sin pZ ’
и функции (х) и ф2 (х) определяются вполне.
К тем же результатам можно было бы притти и из других соображе-
ний, а именно: величина С, как видно, представляется в виде
£ —ср (я) sin kt,
причем <р(я) есть функция непрерывная вместе со своими первыми двумя
производными, третья же ее производная при х — а делает скачок, рав-
ный Р, представляющий срезывающую силу, которая и уравновешивает
сосредоточенную в этой точке нагрузку. На всем протяжении от ^0
до х = I величина С должна удовлетворять дифференциальному уравнению
Ж ,	А
^+6^=0’
которое принимает вид
[ — Л2ф (х) + 62?1 v (#)] sin kt = 0.
Следовательно, функция у(х) должна удовлетворять уравнению
которое мы уже имели. Условие же закрепления концов балки и непре-
рывность ее формы и кривизны и величина скачка в срезывающем усилии
доставят те же самые восемь начальных условий, которые и послужат для
определения восьми постоянных произвольных, входящих в выражения
функций и ^2, коими Z представляется на участках от я = 0 до х — а
и от х — а до х=
Совершенно подобным же образом можно трактовать и тот случай,
когда балка колеблется в сопротивляющейся среде; надо только сперва
заменить выражение
Ап sin (kt + en)
§ 78]
колебания груза, подвешенного на упругой нити
257
через
Лп cos en sin kt + Ап sin n sin kt
и cos sn и sin зп—их значениями, следующими из tg гп.
Эту выкладку предлагается выполнить в виде задачи»
§ 78. Колебания тяжелого груза, подвешенного на упругой нити.
В мемуаре, помещенном в 18-й тетради журнала Политехнической
школы и озаглавленном: «Memoire sur la maniere d’exprimer les fonc-
tions en series de ouantites periodiques et sur 1’usage de cette transforma-
tion dans la resolution de differents problemes», Пуассон решает, между
прочим, задачу о прямолинейном движении тяжелого тела, подвешенного
к концу растяжимой нити.
Пуассон рассматривает лишь свободные колебания тела, мы же рас-
смотрим вынужденные и покажем, что к этой задаче сводится теория инди-
катора паровой машины, что эта же задача является основною в исследо-
вании крешеров, служащих для изучения действия взрыва или для измере-
ния давления газов в канале орудия. К этой же задаче сводится изучение
крутильных колебаний вала с маховиком на конце, изучение разного рода
«дрожащих» клапанов и т. д.
Составим сперва уравнения движения тела и нити или струнй в задаче
Пуассона.
Примем точку закрепления струны за начало координат и направим
ось х по оси струны вертикально вниз.
Обозначим через и перемещение точки струны, соответствующей абс-
циссе ж; тогда перемещение точки, соответствующей абсциссе x + dx, будет
। ди
и + дхХ* относительное удлинение струны в рассматриваемом месте есть
и натяжение ее есть где k — Es, причем Е есть модуль упруго-
сти, $ — площадь сечения струны.
Таким образом, на рассматриваемый элемент, масса коего есть qdx,
причем через q обозначена масса погонной единицы длины струны, дей-
ствуют силы:
7 ди
Вверх -kJx,
вниз + /. f т- + dx \ ;
\дх ‘ дт2 J 1
д2и
ускорение этого элемента есть , и, значит, уравнение движения струны
есть
д2и __ / д2и
qat*~ та?
или, полагая
имеем
5^ - „2^
dt2 и дх2
(1)
предполагая, что на струну никаких сил не действует.
Если же на струну действует внешняя сила, то, отнеся ее величину
к погонной единице длины струны и обозначая через F (х, £), мы вместо
уравнения (1) получим уравнение
д2и 9 д2и , 1 n z
= я2 Р (#> О-
dt2 дх2 1 q ' ’ 1
17 А. Н. Крылов
(2)
258 РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН[Гл. УП
К этому уравнению необходимо еще присовокупить граничные и началь-
ные условия.
Чтобы составить граничные условия, замечаем:
1) что конец струны, соответствующий абсциссе я = 0, остается непо-
движным; следовательно, при я = 0 должно быть
и = 0	(3)
при всяком t,
2) на конце, соответствующем абсциссе я = 7, висит груз Р, с которым
этот конец связан неизменно, так что движение груза Р должно быть
такое же, как и этого конца.
Если на этот груз Р действуют какие бы то ни было внешние силы,
в том числе и сила тяжести, то их должно отнести к функции F (х, t)
и рассматривать приложенными как бы к последнему элементу струны,
а не к грузу.
Так следует поступать для того, чтобы получить по возможности
простое граничное условие, не зависимое от внешних сил и одинаковое как
для свободных, так и для вынужденных колебаний, ибо наши общие формулы
выведены для таких граничных условий.
ТТ	х	7 &и	Р
Натяжение струны выражается формулою к , масса груза есть у ;
Следовательно, при отнесении, как сказано, всех внешних сил к функции
F (х, t) уравнение движения груза, а значит, и второе граничное условие
будет: при х — 1 должно быть
—	= — /г	при всяком t	(4)
gf dt2	дх 1	'
или, делая
получим
Начальные условия, т. е. те, которые относятся к моменту времени
Z==0, выразим уравнениями: при Z = 0 должно быть
“ = ?(*) и ^ = ф(я:),	(5)
причем у(х) и Ф (х) — заданные на протяжении от х = 0 до х = 1 функции.
Итак, рассматриваемая задача о колебании струны с грузом на конце
сводится к следующей математической: найти функцию u(x,t), удовле-
творяющую*.
во-первых, дифференциальному уравнению
д2и о д2и , 1 то ,
~^г = а + -F(x, t),
dt2 дх2 q х '
во-вторых, граничным условиям:
при х = 0 должно быть u — Q	1
,	д2и о ди f при вСЯКОМ t,
>	Х—1 .	>	»	--	— с2 —-
dt2	дх '
в-третьих, начальным условиям: при Z = 0 должно быть
«=?(«) м
§78] колебания груза, ПОДВЕШЕННОГО НА УПРУГОЙ нити ;2Ш&
Прежде чем решать эту математическую задачу, покажем, что<юнёй же
приводятся и упомянутые технические вопросы об индикаторе и о кру-
тильных колебаниях вала.
Относительно индикатора сама собою понятна полная аналогия: вместо
слова струна надо говорить слова пружина индикатора, тогда величина к
есть «жесткость» пружины, т. е. тот множитель, на который надо ^умножить-
ее относительное удлинение, чтобы получить натяжение. Связь между вели-
чиною к и величиною «цены» одного миллиметра удлинения или сжатия пру-
жины очевидна. Вместо массы груза у надо брать массу поршня и приве-
денную массу всех частей прибора, с поршнем связанных и участвующих
в движении его.	' ' । - *
Чтобы получить «приведенную массу» подвижных частей индикатора,
можно поступить так: вообразить, что в рассматриваемый момент скорость
поршня есть о, скорости всех прочих частей прибора будут пропорцио-
нальны о, причем, коэффициенты пропорциональности определяются кине-
матическими связями между поршнем и рассматриваемыми частями* ,
Составив живую силу всей системы, представляем ее в виде
7 = 4	+	;
Мг и будет «приведенною массою».
Полагая
£+М^М,	,	:
надо граничное условие (3) писать: при х = 1 должно быть
мд*и____к~
т dt*~~ к дх	Рл
или, делая
получим
д*и 9 ди
dt* L дх *
(3")
как для случая струны с грузом.
Давление же пара на поршень относим, в силу сказанного выше,
к .функции F (х, t), т. е. к внешней нагрузке, действующей на пружину.
Для случая вала с маховиком М на конце В, соответствующем абсцис-’
се х = I, составим уравнение движения следующим образом.
Начало координат возьмем в точке Л —свободном конце вала, ось х
направим по оси вала, обозначим через и угол закручивания вала в сече-
нии, соответствующем абсциссе х; тогда приходящееся на единицу длины
ди
закручивание у этого сечения есть , значит, скручивающий момент бу-
дет где = причем G есть «модуль сдвига», J — момент инерции
площади сечения вала. Пусть будет К — момент инерции единицы длины
вала, тогда, рассматривая элементарную часть вала, заключенную между
абсциссами х и x+dx, имеем:
момент инерции
скручивающий момент в сечении х
»	»	»	» х + dx
Kdx,
7 ди
дх
17*’
260
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
Угловое ускорение будет
д2и
"dt2
значит, если на вал
его движения будет
никаких внешних сил не действует, то уравнение
к — I.
dt* дх*
или, полагая
получим
к 2
к ~а
д2и __ g д2и
'dt2 ~~й дх2 ’
(1)
Если же на вал действует внешний скручивающий момент, величину
которого, отнесенную к единице длины вала, обозначим через F (ж, Z), то
вместо уравнения (1") будет
K^-^k-~+F(x,
dt2 дх2 х '
к вместо (1) будет
^=«’5+1^*	м
Что же касается граничных и начальных условий, то легко видеть,
Что попрежнему будет:
1) при я = 0 должно быть н = 0 при всяком I?
2) при х = I имеем насаженный неизменно на вал маховик; если момент
инерции этого маховика обозначим через К1Г то наше граничное условие
будет: при х — 1 должно быть
тг д2и , ди
Kl~d^~ дх9
к
или, обозначая через с2 =	, получим
д2и « ди
________ — — р® —
dt2_дх 9
как и раньше. Если к маховику приложено еще внешнее усилие, напри-
мер, происходящее от приводного ремня, то, в силу сказанного выше,
момент этого усилия относим к внешней нагрузке, действующей на вал,
г» е. к функции F (х, Z).
Само собою понятно, что начальные условия будут попрежнему: при
должно быть
и 5 -</(х).
Таким? образом, математически и эга задача равносильна задаче о коле-
бании струны с грузом на конце.
§ 79. Для решения поставленной в предыдущем параграфе матема-
тической задачи применим наш общий прием, а именно, полагаем
и = иг 4-и2
и выбираем; ut так, чтобы оно представляло свободные колебания, и2—
вынужденные колебания, т. е. иг должно удовлетворять;
1)	уравнению
, 79]	КОЛЕБАНИЯ ГРУЗА, ПОДВЕШЕННОГО НА УПРУГОЙ НИТИ 261
2)	граничным условиям:
при х = 0 должно быть и1 — 0	)
,	д*и. , ди, 1 при всяком I,	(2)
> x=l > >
3)	начальным условиям: при Z = 0 должно быть
«! = ?(«) И ^ = i>{x).	(3)
Величина же н2 должна удовлетворять:
1)	уравнению
_ аа = ± р (х, 0;	(4)
dt2 дх2 q v '	* 7
2)	тем же граничным условиям, как и и^
3)	начальным условиям: при t = 0 должно быть
«2=° и Ь_ = 0.	(5)
Подобно тому, как и раньше, начинаем решение с разыскания юх;
чтобы составить соответствующие задаче «нормальные» функции X и транс-
цендентное уравнение, от корней коего они зависят, делаем
щ^ТХ.
Для определения Т и X получаем уравнения
Значит,
Т == A cos amt + В sin amt,
X = С cos тпх + D sin mx.
Обращаемся к граничным условиям.
На основании первого из них будет
С = 0,
значит,
X = Z>sin mx,
или просто
X = sin mx,
ибо, не теряя общности, можно брать D=A, и, значит, будет
иг = 2 (Л cos amt + В sin amt) sin mx.
Чтобы эта величина удовлетворяла второму граничному условию, т. е.
чтобы при х — 1 было при всяком t
т. е. чтобы было
2 (а2тп2 sin ml — me2 cos ml) (Л cos amt 4- В sin amt) = 0,
при всяком t достаточно, чтобы имело место равенство
a2msinmZ —c2cosmZ= 0,	(7)
РЕШЕНИЕ УРАВНЕНИИ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
или, полагая	<
ml —у.
делая •	'
сЧ	gig _Q
а?	Р Р	1’
где Q есть вес струны или пружины, имеем уравнение
HtgH== Y-	(8)
Пусть корни этого уравнения суть	’ - z ’
И1> иг» р3» • • •, Pn, • • •;	(9)
д.4я каждого корня получаются соответствующие функции X и Т, именно:
yn = sin^,	......
7’n = ^ncos^ + B„sin!^ ,
и, значит, будет
;	ui— S Д1 sincos-^-у- + 2 5n sin i-y-sin ^-у- .
n—1 •	n=l ,	.
Чтобы определить коэффициенты Ап и Вп, надо обратиться к началь-
ным условиям, которые дают
, ,	?(ж)=*2 ^nSiny—,
п=»1
П = 1
Чтобы получить коэффициенты Ап и Вп, надо воспользоваться доказан-
ным в § 71 равенством
i
cos у cos рп у dx = 0, если i Ф к\
о
когда же
1 = к, т. е. р< = р/с,
то интеграл
5 cos2 dx = *- J (1 + cos 2-^) dx = 1 ; + -L sin 2р) =
0	0
Z, Г! .	=тА-(2p.fc4-sin2p.ft).		' (10)
^г/с
Таким образом, нахождение коэффициентов в ряду
<“(*)= 2 GjCos^
П«1
производите^'по формуле
/ j" .:_-U(;)cost^^ ; ‘ '' ’
» I	£, 2рп + s,in 2pn J	/
' 5	*	о А
§80]
ПРИЛОЖЕНИЕ К ТЕОРИИ ИНДИКАТОРА УАТТА
263
Чтобы привести к этому наш случай, стоит только положить
ш (ж) = <р'(ж) = 2 GiCos-"-,
П=1
тогда будет
со
<р(я) = 2 ^nsin^,
П = 1
причем
А. = — = 9	4 9— \ ?' (?) cos (К.
Р-n 2р.п 4- sm 2р.п 3 г 7 I
о
Точно так же будет
о
(11)
(12)
(12')
Само собою разумеется, что, выполнив в этих двух формулах инте-
грирование по частям, заменим их другими двумя, в которых под знаком
интеграла будут входить только сами заданные функции ср (я) и 9(ж)»
а не их производные.
Перейдем теперь к нахождению величины и2»
По общему правилу полагаем
«2=2 Sn sin ’
71 = 1
где Sn зависит только от времени I.
1 *
Представив функцию — F (х, t) в виде ряда
If (ж, г) = 2	,
71=1
определяем коэффициенты Нп (t) по формулам
нп (0 - у * ££Ip)Cos^ (Z«;
v 7 И 2|лп 4-sin 2|лп J	I '
0
тогда^функция Sn будет определяться уравнением
Sn + ^-Sn = Hn(t)
ж условиями: при £ = 0 должно быть 5л = 0 и 5А —0, так что
i
5п = -Цнп (о) sin а-р (t-a) ds.
0
(13)
(*)
Таким образом, задача решается вполне.
§ 80. Приложение выводов предыдущего параграфа к теории инди-
катора Уатта. Чтобы применить формулы предыдущего параграфа к теории
индикатора, стоит только предположить, что внешняя сила F (х, t) представ-
ляет действующее на поршень индикатора давление пара, которое, если счи-
тать время от момента впуска, будет некоторой функцией /(£)•’
264
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
Уже было упомянуто, что давление следует рассматривать как усилие»
сосредоточенное на последнем элементе пружины, иначе, как предельный
случай усилия, распределенного на протяжении от с до с + Х, причем в пре-
деле с должно приближаться к Z, и X должно приближаться к нулю, пол-
ная же величина нагрузки к Af(t), где А есть площадь поршня индика-
тора, причем мы считаем /(0) = 0.
Отсюда следует, что функцию F (х, t) надо взять так:
F (х9 Z) = 0 для промежутка от я —0 до я =
F (ж, I) = а) (х) f (t) >	»	> х=с » я = с + Х,
F(x, t) = 0	»	»	> я—с + k» x = Z,
причем
<Н-А
со (х) dx = А
с
независимо от величины 1.
При таком выборе функции F (х, I) будет
I	с+Д
\ ®'(5)eos^-5<R,
•	е
с+Д	с4»Д	«+А
ш' (5)cos^у dl = £<» (с)cos ^у | + у ш (5) sin^y <й.
0	с	с
Будем брать функцию <о (с) так, чтобы было
(0 (с + X) = (0 (с) = О,
тогда будет
с+д	с+д
( о)' (?) cos^— = ~ ( <о (5) sin ^~-di.
J	V	l J	I
e	c
Затем имеем
с+д	e	c+A 6
о 0) sin^~d? = | [ J °) (a) ] sin—|*+Л	\ ш (^) cos
c	c	c	c
В пределе при бесконечно малом X величина, стоящая в { }, обра-
щается в
A sin ,
ибо, по предположению,
с+А
lim \ a)(a)da = Ao
А—►О
С
Величина жо
с+л е
,	o>(a)d% j cos-"-d 5
с с
имеет своим пределом 0.
§80] •	ПРИЛОЖЕНИЕ К ТЕОРИИ ИНДИКАТОРА УАТТА	26&’
В самом деле, функция <о(а) между пределами с и с + к, по самой су-
ти дела, положительная; значит, таковою ее и надо воображать, а тогда
$	с+л
to (a) da < о (а) da == А,
с	с
т. е.
a) (a) da < А;
с
значит,
с+Л 5
w(a)daj d; < Ак,
С с
а так как по абсолютной величине рассматриваемый иитеграл меньше этого,
то и будет
с+л е
lim <» (a) di J cos	di = О;
таким образом, будет
с+А
lim С о' (?) cos = l*n sin-&1 Л = у- Л cos рп
с-н J	*	1	1
Л-,0 с
и, следовательно,
Нп (t) = Ц	Af\t)	(14)
и на основании формулы (♦) стр. 263.
Sn =	s-г Д / (a) sin (t - a) da
aq j*n(2ця + sin2jxn> J/K/	’
О
и попрежнему
со
«2= 3 ‘S’nsin
n=l
Так как при начале движения
ср (х) = 0 и ф (х) = О,
то
йг = 0
и остается
со
о • Ил	*
и = и2 =	о л sm — .
п-1
Для теории индикатора представляет интерес единственно движение*
поршня, а не какой-либо промежуточной точки пружины. Чтобы его по-
лучить, стоит только положить в предыдущей формуле # = тогда она*
обратится в следующую:
со	i
cos |ал sin |лп Г г / \ Л • л|1п z х ♦
И2 = 2 = -1- V —/о-	\ \ / (°) sm (* - б)
£ aq pn (2pn + sin 2pn) J • ' ' I '	’
n~l	0
266
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
В силу уравнения
•будет

7 cos н
J----- = sin u,
я предыдущую формулу можно написать так:
z 2 —ё-2?"   ( j (a) Sin (t - a) da.
«7 2|J.n4-sin 2|in .1 J 4 7 I v 7
п=1	о
Величина, пропорциональная смещению поршня индикатора zt и записы-
вается на барабане его.
Применив к каждому члену суммы преобразование, показанное в § 8,
мы из предыдущей формулы найдем те условия, при которых запись на бара-
бане действительно представляет изменяемость давления на поршень, а также
м величину погрешности показаний прибора.
В самом деле, имеем
t
i
sin^(i_e)d3==±./(0_l_ /'(a)cos^-a)da;
*n	n о
О
ятодставляя, получаем
sin2 Цп
Z a*q t 3 nn (2|»n + sin 2цп)
л = 1
kAl 4 sin2'|xn
a2q
Сумму
Zl —та—, . 9—г / (о) cos (Z — a) da..
" Hn(2Hn + sin2Hn) ' 7 к 7 I v 7
Л = 1	О
• sin2 ни
Ид (2р.п 4- sin 2рп)
п=1
^нетрудно найти, стоит только представить величину х в виде ряда, распо-
• Нп#
ложенного по sin-y- ; тогда получится
I
^1 у Sin Ип . Нп*
Нп (2Нп + 5’П 2,1п) I ’
п=1
жак то следует из формулы (12) § 79. ;
Делая в этой формуле x = lt получим
оо
Ssin8n„ _ 1
Рп (2[лп + sin 2^п)	4
п=1
^а так как a2q = kf где к есть мера жесткости пружины, то получится
Z =4? А (0 - 4 Т "S 	9—А	/' (°) С0^ V5 С - 9)
Л	А к Нп (2Нп + sin 2нп) .) 7 \ 7 I 7
п=1	о *
§ 80]
ПРИЛОЖЕНИЕ К ТЕОРИИ ИНДИКАТОРА УАТТА
267
Величина

представляет то смещение поршня, которое должно бы быть, если бы давление
действовало «статически», и значит, величина
n = l	О
sin2
представляет погрешность показаний прибора.
Величина верхнего предела этой погрешности может быть представлена
в более наглядной форме, для чего стоит только воспользоваться формулами
§ 8, в силу которых, положив
а^п___ч
можно написать ряд неравенств:
t
/' (g) cos Xг (£ — a) da < ^ /' (Ц),
о	I
t
/' (ojcosk2(«— a) da
о	8
t
/' (а) cos — a)d<3
о
где /' (ti) есть наибольшее значение производной от функции Д(г) за время
нарастания ее и с—постоянная. Считается, что /' (с) положительна и имеет
единственный максимум.
Значит, будет по абсолютной величине:
оо
। МЫс ,, , . vi 1 sin8 |in
к а 7 W ДМп(*2п +8Й12Ип)’
Л = 1
(15)
Так как корни уравнения p	идут, возрастая, приблизительно
как ряд натуральных чисел, то
1 <Г —
Р-n Pi
и, следовательно,
оо	ОС
V 1	• sin2 Нп А. V siina Нп
Нп Нп (2цп + Sin 2|1п) Hi Нп (2рп + sin 2|in) ’
п=1	л = 1
1 1
т. e. рассматриваемая сумма меньше у —
Таким образом, имеем
Величина
с -----------/ (ti).
к ар-! ' х 1/
(16)
268
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
есть наибольший из периодов колебаний пружины вместе с поршнем,
т. е. период «основного» колебания ее; поэтому предыдущую формулу можно
написать так:
. । А1 /2 ,,,, .
Is!<т—/
Отсюда следует, что для правильности показаний индикатора необходимо,
чтобы период основного колебания его пружины вместе с поршнем был мал
по сравнению с продолжительностью нарастания давления.
Повторив рассуждения § 8, увидим, что когда период весьма велик
по сравнению с продолжительностью действия давления, то индикатор пока-
зывает импульс давления, и будет
Al ajK Т
^ах = Т-гЛ
причем pi есть наименьший из корней уравнения
{itg(x = v,
___Q___вес пружины
У Р вес поршня *
Нахождение корней уравнения p.tgu. = y производится по приему,
объясненному в § 49; здесь же приведем таблицу значений наименьшего корня
для разных величин у
Таблица 5
Значения наименьшего корня уравнения и tg ц = ?
7	Iх!	7	1*1	7	Hi
0.01	0.10	1.0	0.86	10.0	1.417
0.05	0.22	1.5	0.98	15.0	1.473
0.1	0.32	2.0	1.13	20.0	1.523
0.2	0.43	3.0	1.20	100.0	1.568
0.3	0.52	4.0	1.27	оо	1.571
0.4	0.59	5.0	1.32		
0.5	0.65	6.0	1.37		
0.6	0.70	7.0	1.39		
0.7	0.75	8.0	1.40		
0.8	0.79	9.0	1.41		
0.9	0.82				
§ 81. Частные случаи предыдущей задачи. Понятно, что в рассмот-
ренном общем случае, когда отношение массы пружины к массе поршня ко-
нечное, должны заключаться и два простейших частных случая, именно,
когда это отношение весьма велико и когда оно весьма мало.
Если предположить, что масса поршня ничтожно мала, то в уравнении (8)
надо сделать у= и оно обратится в такое:
cos р. = О,
и его корни будут
я Зя 5л 2п — 1
у» у» у» • • •» 2 п> -
6 81] ЧАСТНЫЕ СЛУЧАИ ПРЕДЫДУЩЕЙ ЗАДАЧИ 269
и соответствующие функции будут
Xe = 8in^zJ? (п = 1, 2, 3, ...).
*• с
В силу уравнения jxtgp. = у, будет -с°8- =sinp, и, следовательно,
т COS Нп 8in Нп__sin* Нп______1
Рп (2нп + sin 2нп) ~ 2нп + sin 2нп ~ (2п — 1) я
и величина z обратится в такую|
аап ^1 2п -1 J п '	I '	'
п=1	о
которую нетрудно получить и непосредственно.
Другой случай, когда масса пружины ничтожно мала по сравнению
с массой поршня, приводит к трансцендентному уравнению
ptgfi = O,
и его корнй суть
|i = 0, к, 2тс, 3irt n&t 4..;
вое коэффициенты
sin2 нл
2|in + 8in2|An
обратятся в нуль, кроме первого, принимающего неопределенный вид, и вели-
чина z будет
2 = S [ S? 2-^aU] V <’>si" т <' - “) d,‘
При разыскании этого предела необходимо иметь в виду следующие
соотношения:	/
а2 = 7» Q=8ql>
= =
Из последнего уравнения следует, что при бесконечно малом q наимень-
ший корень р. выражается так:
значит, lim- Затем .. 4Л sin2 |л 1 aq 2^ -f- sin 2<л и, полагая мы видим, что lim ~ — Z	*_!;« 1 iZ к	_ 1/к? 1 ~lun 1 V q Г Р ~ V IP* -4Л11ттд|-л11т7^/^--л» le а? = ~ «	ip> ' а и величина |/*, и у нас по t = у- а / (а) sin а (t — з) dа 0
270	РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН[Гл. VII
в согласии с формулами § 8, представляющими колебание грузам висящего-
на пружине, массою коей пренебрегают, и подверженного действию пере-
менной силы.
При пользовании индикатором или крешерами необходимо сообразоваться
с изложенным в этих параграфах, ибо если период основного колебания
системы не мал по сравнению с продолжительностью действия силы, то пока-
зания прибора не дают нарастания и вообще хода давления в зависимости
от времени, и даже в том случае, когда этот период велик по сравнению со
сказанной продолжительностью, то, например, обжатие крешера может
быть пропорционально импульсу
давления, & не наибольшей вели-
чине давления.
Чтобы дать наглядное пред-
ставление о величине и характере
погрешности в записи, даваемой
индикатором при разной величине
отношения периода колебаний его
поршня к продолжительности на-
растания давления, приведу пример,
рассмотренный в моей статье «Не-
которые замечания о крешерах и
фиг-	индикаторах» (Иав. ими. Акад.
Наук, 1909).
Этот пример составлен так: за функцию /(£)> представляющую измени->
емость давления, взята следующая:
/(Z) = asin^- для 0<Z<7\,
+	для t>Tlt
причем h — настолько большая величина, что с принятою для расчета сте-'
пенью точности величиною е~л(1 + Л) можно пренебречь.
Такая функция изображается чертежом (фиг. 45), и, изменяя величины
Ti и Т2, можно придавать этой кривой разный вид.
Взяв затем различные величины отношения
Ti 1
и — р.
и положив для примера К = р-, рассчитываем по выведенным выше формулам
величину z, т. е. запись, даваемую индикатором, и на основании этих рас-
четов составляем чертежи (фиг. 46 — 51), на которых эта запись и показана
пунктирною чертою, а истинный закон нарастания давления — сплошною.
Для простоты все предыдущие расчеты сделаны в предположении, что масса
пружины мала, но сущность дела остается без перемены и во всех осталь-
ных случаях.
§ 82. Действие внезапно приложенной силы. По поводу предыдущей
задачи рассмотрим также действие силы, внезапно приложенной, причем
ограничимся тем лишь случаем, когда масса поршня ничтожно мала.
Мы видели, что в общем случае величина и2 дается формулою
оо	t
4Л Xi т cos	. Рп * С j. / \	\ 7
=г? s Р„(2;„+,1»2,л)J / <=) ™Т - °)
п = 1	О
В силу уравнения
p,tgp.= у,
§ 82]
ДЕЙСТВИЕ ВНЕЗАПНО ПРИЛОЖЕННОЙ СИЛЫ
271
значит,
sm|in=sin—« = ( — 1) S
и предыдущая формула принимает вид
<ю	t
4Л Vi (— I)""1 . In — 1 тся С , f \ . 2п — 1 arc , v ,	/ j к
=™g S sin ~ T v <’>sin — 7 - °^3-	(1>
n = l	0
272
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Рассмотрим подробнее тот частный случай, когда сила прилагается вне-
запно. Для этого стоит только сделать
и у нас получится
8А1	(-l)71"1 . 2п —	2п —1атс 1
и2 = —— р у )-—sin—г--------г 1 — cos—к—т Z -	(2)
л к2а2^ г (2п — I)2	2 I L	2 I J
л=1
Чтобы получить полное сжатие пружины, т. е. колебание конца ее В,
-стоит только сделать х = 1; тогда будет
со
8 Apl VI 1 л . л 2п — 1 атсг
tt*=z=^S
л = 1
2/
Очевидно, что z достигает наибольшего значения при t == у, и будет
__ 16 Apl yi 1
Zmax ” r№q Zj (2n - I)2 °
л = 1
Но известно, что
Oo
El__________
(2n — 1)« — 8 ’
n = l
-так что
_ 2Apl _ n Apl
т. e. вдвое больше статистического сжатия, соответствующего давлению р.
Этот результат относится к любой упругой системе: наибольшая дефор-
мация, производимая усилием, внезапно приложенным, вдвое больше дефор-
мации, соответствующей равновесию под действием того же усилия.
Любопытно, вместе с тем, проследить за самым процессом, каким обра-
; зом после приложения внезапного усилия нарастает деформация пружины
не только в ее конце, но и в промежуточных точках, т. е. исследовать вид
. функции, представляемой уравнением (2).
Для этого применим тот прием суммирования рядов Фурье, который
показан в § 69.
Пусть будет
Л = 1
Ясно, что эта функция имеет своим периодом 4Z, равна нулю при х = 0
и при х = +21 и х — — 21; при х = I будет (Z) = у ; при х = — Z будет
. Fx( — Z) =——•; вместе с тем, эта функция имеет производную, которая
выражается равенством
Л = 1
i и так как период этой функции есть 4Z, функция эта четная и интеграл
21
С 2л — 1 тсж 2к — 1 тсж 7 л	,
\ cos —г--т- cos —-— -г- ах = 0, если п Ф к;
J	Z I
о
$ 82]
ДЕЙСТВИЕ ВНЕЗАПНО ПРИЛОЖЕННОЙ СИЛЫ
полагая, что F[(x)==<p(x)f составляем выражение коэффициента ап в раз-
ложении ср (я):
21
2 С /Ч 2п — 1 пх у
Л } ? (х) cos----2---Tdx = an
0
и, предполагая, что функция (х) имеет разрывы в точках с19 с2, ...,
1
получим, что члены первого порядка относительно	в выражении ап
будут
(2п~—1)й {(? (С1 “°)-? (С1 + 0)]	у1 +
+ [?(c2-0)-?(C2 + 0)]sin^^+... } .
Значит, будет
_те (- i)«-i
21 2п — 1
= (2^	-0) - ? (Сх + 0)] Sin	,
То е.
Ф(с1-О)-ф(с1 + О) =
Из первого из этих равенств следует
сх = /,
а так как
=	0) + у ? (ci + °) = °,
?(сх — 0) = + и ?(cj + 0) = - ,
и у нас будет
F{(х) = <р (х) = + ~ для 0 < х < Z,
(ж) = ср (х) = для I < х < 2Z,
т. е. функция F\(x) представляется графически чертежом (фиг. 52, а), сле-
довательно, функция
представляется графически чертежом (фиг. 52, б), и наибольшая ордината
,__8Л/рте2__Alp
n2a2q 8 a2q
В состав величины «2 входит еще член
р (г\_____6AlP V Ц”'1 еоч 2ге~ 1 агЛ «in 2га-1 ™
*г\Х>~	п1агя 2j (2n-l)2COS 2 I Sin 2 I ’
n = l
но так как
o 2n — 1 ant . 2n — 1 пх . 2n — 1 те r , n . 2n — 1 те r ,
2 cos —Z r sin —T r = sm —  r [x + at] + sm —r г [ж - at],
Zf	Al	Al	Al
то, положив
x-^at = Z и x — at = ri,
18 A. H4 Крылов
274 РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
мы напишем предыдущее равенство так:
Wg [ 2 (2п — 1) SU1 2 I +21 (2п — l)’Sin 2 I J ’
П = 1	П — 1
откуда следует
Pi (®) = — 4 [/i («) + fi (’))] = — 4 [A (x+at) + fi {x - aZ)];
графическое же представление функции fi(x) дано ниже.
Будем теперь придавать времени t последовательно значения:
причем
4/
и строить величину и2, даваемую формулою
«2 = /1 (х) — 2 [fl (х 4- al) + fi(x- at)},
пользуясь графическим представлением функции
§ 83]
АНАЛИЗ ЗАПИСИ ДАВЛЕНИЯ В ЦИЛИНДРЕ КОМПРЕССОРА
275
т	I
Очевидно, что при t = 0 будет н2==0; когда £ —	, то , и зна-
чит, будет
f1(x + at) = f1(x + -^ и f1(x-at)=f1
Графически функцию	получим, продвинув ломаную,
изображающую—у/i (я), влево на , функцию же —у ^получим >
продвинув ту же ломаную вправо на ; тогда получится чертеж (фиг. 52, в)\
Беря затем на протяжении от х = 0 до х = 1 алгебраическую сумму
ординат всех трех ломаных, получим и2.
Совершенно так же поступаем для дальнейших значений t и полу-
чаем тот ряд ломаных, который показан на чертежах фиг. 52, г, д.
Отметим, что деформация бежит равномерно по длине пружины; вместе
с тем и колебание конца пружины совершается не синусоидальное гармони-
ческое, а прерывистое —сперва равномерно возрастающее до наибольшей
величины, затем сразу меняющее скорость на обратную, равномерно убывая
до нуля, достигнув которого скорость вновь сразу меняет знак и т. д.
Нетрудно видеть, что движение промежуточных точек происходит
с остановками. Предлагается, например, в виде задачи построить график,
изображающий скорость и закон движения середины пружины.
§ 83. Анализ записи давления в цилиндре компрессора, полученной
индикатором Виккерса. С правильностью показаний индикатора и в осо-
бенности с правильным их истолкованием часто связаны весьма большие
интересы, как то можно видеть по следующему примеру.
--- Наблюденная кривая
Фиг. 53.
В январе 1914 г., при испытании стрельбою на полигоне пробной
установки 12-дюймовых орудий 52 калибров длиною, предназначенных
для линейных кораблей, снимались специальным индикатором Виккерса
диаграммы давления в цилиндре компрессора; получалась кривая, пред-
ставленная на чертеже (фиг. 53, а).
18*
276
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Эта диаграмма показывает, что по записи индикатора наибольшее
давление достигает 450 ат. По контракту с Металлическим заводом, построив-
шим эту установку, испытание цилиндров компрессоров должно было про-
изводиться двойным давлением, т. е. до 900 ат, между тем все 48 компрессо-
ров были уже готовы, рассчитаны они были на нормальное давление 250 ат,
т. е. на пробное 500 ат. Замена их новыми повлекла бы расход около
2 500000 руб. и значительно отдалила бы срок готовности кораблей. Произ-
веденное мною исследование этого вопроса показало, что индикатор работал
в условиях, соответствующих фиг. 51, и записал давление, в два раза
большее действительно имевшего место. Так как подобное обстоятельтво может
представиться и в других случаях, то привожу сущность упомянутого иссле-
дования.
§ 84. В § 80 показано [формула (16)], что период колебаний поршня
индикатора на пружине его выражается формулою
в которой Р4 есть наименьший положительный корень уравнения
=	(2)
где Q есть вес пружины, Р — вес поршня, t — длина пружины в ненагру-
женном ее состоянии,
Р)
причем к есть мера жесткости пружины, т. е. множитель, на который надо
умножить относительное сжатие пружины ~ , чтобы получить действующее
усилие F:
F = k±.	(4)
В рассматриваемом Случае было: (7 = 0.817 кг9Р = 0.092 кг, длина пру-
жины 1= 12 см, жесткость пружины к = 1165 кг. Таким образом,
Q_o.8n on
0.092
Наименьший корень уравнения
I* tg р. = 8.9
есть
14 = 1.41,
следовательно, период основного колебания
^ = f^o = °-O13ceK-
' По записанной кривой видно, что расстояние между двумя последо-
вательными вершинами волн записи составляет около 11 см, что при ско-
рости отката в этот момент около 8.5 м/сек и будет соответствовать продол-
жительности 0.013 сек.
% 84]
АНАЛИЗ ЗАПИСИ ДАВЛЕНИЯ В ЦИЛИНДРЕ КОМПРЕССОРА
277
При снятии диаграммы не было произведено велосимметрической записи
отката, но при другом выстреле наибольшая скорость составляла 22 фута (7 м)
в секунду. Расчетная же величина наибольшей скорости отката составляла
до 9 м/сек.
Таким образом, видно, что если бы принять даваемую индикатором
запись за истинную кривую давления, то надо бы допустить, что это давле-
ние претерпевало показанное волнообразное изменение в течение времени
около 0.013 сек., которое или в точности равно, или весьма близко к периоду
свободных колебаний поршня индикатора.
Именно, в этих условиях, как следует из теории прибора, его показания
совершенно не согласуются с истинной кривой давления, а представляют
наложение свободных колебаний поршня, вследствие инерции его и пружины,
на вынужденные, которые пропорциональны действующему давлению.
Примером такой разницы показаний прибора и истинной кривой дав-
ления могут служить фиг. 46 — 51, на которых сплошною чертою пока-
зана истинная кривая давления, пунктиром —та запись, которую доставил бы
йндикатор при различном отношении периода его свободных колебаний
к продолжительности нарастания давления.
Уже сказанного в предыдущем параграфе достаточно, чтобы убедиться,
что в рассматриваемом случае прибор Виккерса может служить для нахожде-
ния среднего давления за время отката, но не может давать закона быстро
происходящих (по сравнению с 0.013 сек.) изменений* давления с течением
времени.
Нетрудно подтвердить это обстоятельство и математическим анализом,
причем даже достаточно воспользоваться упрощенной 1еорией индикатора,
в которой рассматривается лишь главное его колебание, соответствующее
основному тону.
Форма колебания, соответствующая основному тону, есть
и = A cos	sin ,
колебание же поршня получится, положив х = 1, т. е. будет
z = A cos (sin р j,
следовательно, величину и, т. е. смещение точки пружины, соответствующей
абсциссе х, можно писать так:
.	|4«
sm -|-
и =
sin |4
Живая сила всей системы, состоящей из поршня и пружины, будет
2Г = — я'2 + —- {.u'^dx — — z'2 + ~~	sin2 ~dx,
g lg J	2	1 lg sin214 }	/	’
о	0
т. e. будет
причем а есть «коэффициент приведения» массы пружины:
i	i	i
а ""	sin2 -~Г	= 'о7~т"2— [	cos dxl =
I sin214 J I 21 sin214 L	' I J
0	0	0
__	1 Г 1_____sin 2j4 “I
sin2 и, L 2	4 J
278	РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
В нашем случае ^=1.41 = 81°, и будет
а = 0.465.
Обозначая через М «приведенную» массу системы
Л/ = 1(Р + а0,	(7')
видим, что живая сила системы будет
T=±Mz?.	(8)
Когда пружина сжата на величину z, то противодействие, ею оказы-
ваемое,
F = ^-
и, значит, элементарная работа при перемещении 82 будет
W--= -^lz,
следовательно, уравнение движения истемы будет
Mz"+~z = Q,	(9)
когда на нее никаких сил не действует. Если же на поршень действует
какая-нибудь внешняя сила G, то уравнение движения будет
Mz" + ^z = G.	(10)
В нашем случае G есть внешнее давление на поршень индикатора
жидкости, находящейся в компрессоре, оно зависит только от времени, если
же поршень испытывает трение или иные сопротивления, то их надо также
присовокупить к силе G.
Из уравнения (10) следует, что период свободных колебаний поршня
равен:
в нашем случае это составит
о 1/0.092 + 0.465 • 0.817 л лл оп
т = 2гсУ-----НббТ981-----12 = 0.0137 сек.,
т. е. величина, близкая к рассчитанной выше.
§ 85. Когда выражение G известно, то по уравнению (10) найдется
смещение поршня z. В нашем же случае мы встречаемся с обратною
задачею — известна величина z, надо найти G. При этом z задано графи-
чески и не в функции времени Z, а в функции $ длины пути, пройденного
от начала отката.
Так как нам приходится рассматривать лишь небольшой участок, соот-
ветствующий значениям $: от $—10 до $ = 28 еж, то можно считать, что
на этом протяжении, или, точнее, на протяжении каждой полуволны, ве-
личина $ изменяется пропорционально времени, т. е. скорость отката по-
стоянная.
Чтобы воспользоваться уравнением (10) для определения G, пришлось
бы величину z, заданную графически, дважды дифференцировать. Такой
85]
АНАЛИЗ ЗАПИСИ ДАВЛЕНИЯ В ЦИЛИНДРЕ КОМПРЕССОРА
279
процесс чрезвычайно ненадежен, и, чтобы его избежать, следует в подобных
вопросах представить самую величину такою функцией времени t> которою
эта величина изображалась бы достаточно точно на всем ее протяжении,
и уже эту функцию подставлять в уравнение (10).
Для выбора такой функции надо сообразоваться с самым характером
явления.
Так, в нашем случае мы, очевидно, имеем дело с затухающими коле-
баниями. Простейший случай таких затухающих колебаний есть тот, когда
сопротивление состоит из постоянного трения.
В этом случае последовательные амплитуды размахов уменьшаются
в арифметической прогрессии. Случай этот разобран в § 21, и на основании
выводов этого параграфа, допустив на время, что давление на поршень
постоянно равно АГ, так что
G==N±F,
где F —сила трения и знак + надо брать, когда z' < 0, и знак —, когда
zr > 0, мы увидали бы, что z должно представляться формулами такого
вида:
~ (а — Ь) ^1 — cos ,	(11)
z2 = (a + 6) + (a-36)cos^J,	(12)
23 = (а-6)-(а-5б)сой^,	(13)
причем первая формула относится к первому полуразмаху (zf > 0), вто-
рая—ко второму (У < 0), третья —к третьему (z' > 0), и время Z, t2
считается всякий раз от начала этого полуразмаха.
Чтобы найти величины а и Ь9 надо взять последовательные ординаты,
соответствующие вершинам и подошвам волн нашей записи. Эти последова-
тельные ординаты суть в миллиметрах на чертеже: 0. 30, 10, 20; таким
образом, делая
t=^ в формуле (11),
«Х = у >	>	(12),
<8=1 »	»	(13),
получим
30 = 2а-26,
10 = 46,
20 = 2а-66.
Все эти три уравнения оказываются совместными и дают
а = 17.5,	6 = 2.5.
Подставляя эти величины в формулы (11), (12) и (13) и вычисляя вели-
чины zlt z2, z3 для значений t, и t2 через т, получим таблицу 6.
Вынося эти величины на график и сопоставляя их с действительно наблю-
денною кривою, видим систематическое уклонение на первой и второй
280
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
полуволне, при этом уклонение это имеет также периодический характер
с периодом (фиг. 53, а).
Таблица 6
Время от нача- ла движения поршня	Время от подошвы ка- ждой полу- волны	Первая полуволна	Вторая полуволна	Третья полуволна
^/12	Т/12	мм	мм	мм
0	0	0.0				
4	1	2.0	—.	—
2	2	0.5	—		
3	3	15.0	—		
4	4	22.5	—		
5	5	28.0	—	—
6	6.0	30.0	30.0	—
7	1	—	28.7	—
8	2	—	25.0	—
9	3	, —	20.0	—
10	4	—	15.0	—
11	5	—	11.3	—
12	6.0	—	10.0	10.0
13	1	—	—	10.7
14	2	—	—	12.5
15	3	—	—	15.0
16	4	—>	—	17.5
17	5	—	—	19.3
18	6.0	—	—	20.0
По ходу кривой, представляющей это уклонение, видно, что его сле-
дует представлять формулою
£ =	—cos y),	(14)
и, действительно, взяв с —2.5 мм и присовокупляя величину вычислен-
ную по формуле (14), к величинам и z2, получим следующую таблицу,
которая показывает, что на своем протяжении величина z, рассчитанная
по формулам
Z = Z1 + ^	для	t	от	0	ДО	6 12’
Z = z2 + С	ДЛЯ	t	от	6т 12	ДО	12Г2’
z = z3	ДЛЯ	t	от	12- 12	до	18Г2’
практически совпадает с наблюденною кривой, так как показанные в таблице 7
разности ординат, вычисленные по формулам и снятые с чертежа, выражаясь
десятыми долями миллиметра, не выходят за пределы ширины карандаш-
ной линии на подлинной записи индикатора.
Таким образом, получив аналитическое представление функции z, мы
можем воспользоваться уравнением (10) для нахождения величины 6, и мы
получим:
§ *5]
АНАЛИЗ ЗАПИСИ ДАВЛЕНИЯ В ЦИЛИНДРЕ КОМПРЕССОРА
281
Таблица 7
Время от начала движения	Вычисленные ординаты	Ординаты с чертежа	Разности выч.—снят.
Т/12	мм	мм	мм
0	0	0	0
1	0.7	1	-0.3
2	3.8	3	0.8
3	10.0	9	1.0
4	17.7	18	—0.3
5	26.7	26	0.7
6	30.0	30	0.0
7	26.7	26	0.7
8	21.2 •	21	0.2
9	15.0	16.5	—1.5
10	11.2	12.5	— 1.3
И	10.0	9.8	0.2
12	10.0	9.8	0.2
13	10.7	11.0	-0.3
14	12.5	13	-0.5
15	15.0	15	0.0
16	17.5	17	0.5
17	19.3	19.5	-0.2
18	20.0	20	0.0
а)	Для первой полуволны:
z = (а — b) (1 — cos nt) — с (1 — cos 2nt),
где
а = 17.5 л€лс = 1.75 см,
Ь= 2.5мм = 0.25 см,
с = 2.5 мм = 0.25 см,
п — 450,
п* = 202 000 = -А,
1М
М = (0.092 + 0.465 • 0.817) А = £_”? = 4.8 . 10-4.
Vox Vol
Из уравнения (10) следует
^=z" + n2z,
или, по подстановке,
= п2 [а — b — с] — Зп2 с cos 2nt.	(15)
б)	Для второй полуволны:
z = (а + Ь) + (а — 36) cos nt — с (1 — cos 2nt),
~ = п2 (а + Ь + с) — Зп2 с cos 2nt.
(16)
в)	Для третьей полуволны:
z = а — b — (а — 56) cos nt,
G 2 ( М	(I7)
— ^(а-б)..
В формулах (15), (16), (17) надо величины а, b и с выражать в санти-
метрах, тогда сила G получится в килограммах.
282
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Присутствие в этих формулах члена 3n2c cos 2nt с периодом колебания
системы заставляет искать причину появления этого члена не в изменении
давления в цилиндре компрессора, а в особенностях конструкции самого
прибора.
Написав равенство
cos 2nt = 1 — 2 sin2 nt,
видим, что член
— 3n2c cos 2nt = Зп2с + 6n2c sin2 nt
и, значит, например, для первой полуволны будет
= и2 {а — Ь — 4с) + 6n2c sin2 nt,
но при
а=1.75, 6 = 0.25, с = 0.25
будет
а —6 —4с = 0.5
и остается
6п2 с sin2 nt + 0.5n2;	(15')
точно так же для второй полуволны будет
jj- = (а + Ь — ic)n2-^ 6n2 с sin2 nt.	(16')
В выражениях для z главный член есть первый, и тогда для первой
полуволны будет приближенно •	;
z' = z\ = п (а — b) sin nt,
для второй:
dz	•
dj = z' = z'2 = — п (a—-3b) sin nt,
следовательно, член 6п2с sin2 nt будет приближенно пропорционален z'2,
т. е. второй степени скорости движения поршня, и значит, его надо искать
в тех гидравлических сопротивлениях, которые поршень индикатора
встречает.
Обращаясь к конструкции прибора, мы заметим, что завинтованный
отросток, которым индикатор ввинчивается в трубку, соединяющую его
с цилиндром компрессора, прикрыт ввернутой в него особой втулкой, кото-
рая снабжена лишь двумя маленькими дырочками диаметром в 0.05 дюйма,
и лишь через эти две маленькие дырочки находящаяся под поршнем индикатора
полость сообщается с цилиндром.
Очевидно, что это приспособление сделано, чтобы гасить колебания
поршня, не влияя на установившиеся показания прибора.
Обратив внимание на это устройство, мы сейчас же видим, откуда
берется член — Зп2 ccos2nt в формуле (16).
Для. второй полуволны поршень движется в сторону к нулевому своему
положению и, значит, он должен выталкивать из полости под ним
жидкость через две вышеупомянутые дырочки; ясно, что он будет встре-
чать сопротивление, пропорциональное квадрату скорости своего движения.
Необходимо обратить внимание, что скорость тока жидкости через
сказанные дырочки будет весьма велика.
В самом деле, наибольшая скорость поршня будет
п (а —За) = 450 • 1.00 = 450 см/сек.
86]
КРУТИЛЬНЫЕ КОЛЕБАНИЯ ВАЛА
283
1
Площадь поршня 5 —~кв. дюйма.
те Z 1 \2	1
Площадь дырочки s = ( %)) = 500 КВ‘ Дюима> значит, отношение
— — 25
а принимая во внимание сжатие струи, будем иметь, что отношение ско-
ростей протока жидкости и поршня составит не 25, а около 40.
Значит, наибольшая скорость протока составит около 180 м/сек, чему
соответствует давление до 300 ат.
Сопоставляя все вышеизложенное, мы можем притти к заключению,
что по самому своему устройству прибор Виккерса может давать запись
лишь установившегося и сравнительно медленно изменяющегося давления,
показываемые же им колебания в рассматриваемом случае не служат
признаком изменяемости давления, и если бы давление, например, на-
растало так, как показано на фиг. 53, б ломаной О АВ , то прибор зачер-
тил бы кривую OCDE, полученную при испытаниях.
Вообще этот прибор пригоден для определения по его записи сред-
него давления, а не быстрой изменяемости давления с течением времени.
§ 86. Крутильные колебания вала. Чтобы показать, каким образом
выводы предыдущих параграфов прилагаются к рассмотрению крутильных
колебаний вала, возьмем следующий пример.
На вал, несущий на своем конце маховик, в точке А действует пере-
менный момент
М — MQ + т sin pt = Af0 + т sin	,
на маховик же действует постоянное усилие, равное —Л/о; требуется
найти крутильные колебания вала, происходящие вследствие такой изме-
няемости движущего момента.
Ясно, что это колебательное движение не будет зависеть от вели-
чины Jf0, которая производит лишь равномерное закручивание вала на про-
тяжении от А до В, и значит, для нашей задачи можно взять и Л/а = 0,
от которого установившееся колебательное движение не зависит, если
только не рассматривать того колебательного движения, которое про-
изойдет от внезапного приложения усилий Л/о в точке А и усилия — MQ
в точке В.
Итак, в нашем случае надо сперва вообразить, что движущий момент
приложен в смежности с точкою А, абсцисса которой равна 6, и распре-
делен как бы то ни было на протяжении от b до б + Х, однако так,
что полная величина этого момента есть msin/tf, т. е. взять функцию
F (х, t) так:
F (х, t) = 0 для промежутка от ж = 0 до х = Ь,
F (х, t) = (z)sin/tf	»	»	>	x—b	» x=zb + \9
F(x, t) = 0	»	»	»	x = b+\	» x — I,
причем
ь+л
^{x)dx = m,
ъ
независимо от k, и рассмотреть предельный случай, когда Х = 0; ясно,
что эта задача ничем не отличается от предыдущей, только вместо
функции f(t) надо брать sin pt, и абсцисса с неравна I, а равна 6.
284
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Вместе с тем из формул § 80 видно, что величина Hn(t) не зависит
от вида функции о> (ж); поэтому можно в формуле
Ь+А
A (2pn + sin 2pn) Нп	=	(t) $ ш (0 sin di
ъ
брать
<»(£) = £
при условии, что
lim (Ск) = т
Л—>0
и
/(Z)-=sinpi;
тогда будет
4 (2рп + sin 2[*п) Нп (t) = — sin pt Г cos 1 *+Л =
'х	A	I	I J О
ъ
= 2 sin/rt sin у (б + 4')sin^T
A	I	& у	л>1
и, значит, в пределе при Х = 0 будет
, |лл sm -7-
у г z .\	I	.
Нп (Ч = Б------i--• ~~п" ~ sin pt*
КI 2	-j- s 1 п 2 pi д
Следовательно,
. Нп Ь
„	1>п81п~ р . t
Kl 2р„ + sin 2|1п «Vn - «*/>* Sln pt
и
U2 — У, ^nSiniy? .
п = 1
Случай резонанса очевиден, и так как он был уже не раз рассмотрен,
то пояснений не требует.
§ 87. Колебания струны, вызываемые заданным колебательным
движением данной ее точки. Необходимо еще пояснить, каким образом
решать те задачи о вынужденных колебаниях струн или стержней, когда
задается не внешняя сила, действующая на струну или стержень, а движе-
ние одной из точек струны или стержня.
Такой случай будет, например, когда какая-либо точка струны связы-
вается неизменно с ножкою камертона; в аналогичном условии находится,
например, дрожащий пружинный клапан, управляемый каким-либо приво-
дом, и т. п.
В практике движение, сообщаемое точке, обыкновенно периодическое,
т. е. ее перемещение представляется выражением
uQ == Ь sin pt
или же состоит из наложения нескольких таких колебаний, т. е. пред-
ставляется формулою
uQ = sin prt 4- b2 sin p2t + 63 sin p3t + ... + bh sin ph t.
Эта задача может быть сведена к предыдущей.
§ 87]
КОЛЕБАНИЯ СТРУНЫ
285
В самом деле, чтобы сообщать рассматриваемой точке струны какое-
либо движение, необходимо соединить эту точку с каким-либо телом, дви-
жущимся заданным образом, а это равносильно тому, что к рассматри-
ваемой точке прилагается некоторое внешнее усилие; следовательно, вопрос
сводится к нахождению этого усилия, после чего решение докончится
по формулам предыдущих параграфов.
Чтобы пояснить это рассуждение, возьмем для примера струну, одну
из точек которой, соответствующую абсциссе	заставляем двигаться
заданным образом.
Математически задача ставится, следовательно, так: требуется найти
функцию и, удовлетворяющую:
1)	дифференциальному уравнению
д2и
ы2
2 д*и Л
я2т-ч = О
дх2
2)	граничным условиям:
при х = 0 должно быть и = 0 1
г	I при всяком t,
» х = 1	»	> и = 0 J
3)	начальным условиям: при f = 0 должйо быть
« = ?(«) и
причем функции
?(«) и ф(ж)
таковы, что
ср(с) = О и ф(с) = 6р,
4)	условию, что функция и должна быть такова, чтобы при х = с было
M==6sin/rt.
В § 72 показано, что при действии в точке х — с сосредоточенной силы
переменного напряжения
F — ^P sin pt	= ps)
вынужденные колебания выражаются формулою
H2 = Psin pt 2 Gisin^p ,	(*)
n= 1	t
причем
. nnc	ainnitc
sin -r-	Sin —
zi __ *	*	_97	*
"	l а2п2п2 “ а2к2п2 — p2l2.
—---------P2
Кроме того, эта сила производит и свободнее колебания, сопутствующие
этим вынужденным. В случае сопротивления среды эти свободные колеба-
ния пропадают, в остальных же их можно отнести к тем, которые образу-
ются вследствие начальных условий.
286
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Отсюда видно, что стоит только в формуле (*) положить я = с
и уравнять полученный результат величине fesinpZ, и мы найдем неизве-
стную Р:
ь
р =
. nite
Cn sin —
n»l
а значит, и величину и2.
Итак, будет
и2= b sin pt
. nitx
n=l \
(1)
. nite
Cn sin —
n=l
где, как уже сказано,
. nite
sin —
Г __9/ _________
n aW — p42 ’
Входящие в выражение u2 суммы были уже найдены’ в] § 72, где
показано, что сумма
sin — для 0 < x < c,
a
2^7	. nite
On sm -j-
n=l
представляет такую функцию <р(я):
sin 7 (Z - с)
ср (х) —-------------
т' 7 ар	. pl
г	sin —
. ре
sin ~
?(«)= ——Дет ^(Z-x) для с<®</.
F sin —
а
Сумма же
~*^pl
sin —
р
00	4 sin — csin — (I — c)
. nite f x 1 a a v
Cnsm —= ?(c)=-
n=l
следовательно, будет
, . рх
sin— '
7 а
и2 = о----sm pt
sin —
а
. р (I — х)
sm—------
г	П
Ui~b . P(l-c) S
sin —-----------
а
Вместе сЛгем видно, что величина
(2)
реакции
. pl
sin —
а
F = pP = pbap
sin— csin — (Z—с)
а а
§ 87]
колебания струны
287
Эти результаты могут быть получены и иначе, не переходя через ряды,
а разыскивая величину и2 в виде
и2 = ср (х) sin pt	(3)
и выбирая, подобно тому как показано в § 77, функцию ср (х) так, чтобы
были удовлетворены: уравнение
dt* а дх*	4'
условия граничные и условие: при я = с должно быть H2 = 6sin/tf, иначе
ф (с) = Ь.
Подставляя величину и2 в дифференциальное уравнение, увидим, что
функция ф должна удовлетворять уравнению
а2ср" (х) + р2р (х) = О,
(4)
причем на участке от я = 0 до х = с функция <р (х) представляется одним
выражением: ?(ж)=ср1(ж), hq участке от х — с до х — 1 другим:
? СО = ?2 («)•
Условия, которым удовлетворяют функции <?]_(#) и <р2(я), СУТЬ
<Р1(0) = 0,	¥1(с) = 6,
<р2 (Z) = 0,	<р2 (с) = Ъ.
На основании ура] ничных условий берем	внения (4), коим функция ср (я) определяется, и гра- (#) = sin х,
тогда условие	ср2 (я) = Л2 sin (Z — х), ?1(С) = ?2 (с) = &
даст	л	Ь	л	b А. =	 и Л2 =	; ' -	р	р sin —с	sin— (1—с) а	а
таким образом, будет	• Р	• sin — X
и2 = ср, (я	y) = b	sin pt для 0 < X < С, sin — с а sin—(Г-ж)
«2 = ®2 (я	:) = b —		sin pt для с < х < 1. sin-~ (1 — с)
Совершенно подобным же образом поступим и в том случае, когда
величина и при х — с должна по условиям задачи представляться в виде
суммы нескольких заданных периодических членов разных периодов,
а также и тогда, когда задается движение одного из концов стержня или
струны»
288	РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
§ 88» Распространение тока по кабелю. Рассмотрим еще один знаме-
нитый пример, именно распространение тока по кабелю, которое приводится
к интегрированию системы уравнений
-f = RI + Ld±,
дх	dt	/л\
91 CV^CdV
-^=GV+C di ’
в которой V и I обозначают потенциал и силу тока в момент времени t9
в точке кабеля, коей абсцисса есть х\ R — омическое сопротивление, L —
самоиндукция, С —емкость, G — проводимость изоляции на единицу длины
кабеля; все эти величины предполагаются постоянными.
Граничные и начальные условия будут приведены ниже.
Эта система уравнений составляла предмет весьма многочисленных
работ, из которых упомянем лишь основной мемуар Кирхгофа, двухтомное
исследование В. И. Коваленкова и превосходное по краткости и ясности
изложения исследование К. А. Поссе, помещенное в «Известиях Электро-
технического института» за 1904 г., но надо заметить, что результаты
этого исследования уже находились в руководстве Ваши (V a s с h у, Traite
d’electricite et de magnetisme, Ь II, Paris, 1890).
Приведем сперва решение в том виде, как оно дано Ваши и Побсе,
в котором оно вошло во множество руководств, отметив при этом неко-
торый недостаток его.
Исключив из уравнения (1) неизвестную функцию 19 получаем для
определения V уравнение
Z-LC&^ + (CK + LG)^ + RGV,	(2)
которое, положив в нем
LC = a*,
CR + LG = 2h,	(3)
ЯС = 62,
принимает вид	•
<4>
при следующих граничных и начальных условиях:
граничные условия*.
при х = 0 должно быть V = Е1 при всяком значении
» х = 1	»	» Р = о] времени t,
начальные условия: при 2 = 0 должно быть
V = 0, J = 0	(6)
для всех значений х в промежутке 0 < х < Z.
Ваши и Поссе полагают
V^v + F(x)	(7)
и определяют функцию F (х) так, чтобы она удовлетворяла уравнению (4)
и следующим граничным условиям:
при х — 0 должно быть F(Q)—E9
» x — l »	» F(Z)=O;	( }
тогда функция и будет определяться:
§ 88]
РАСПРОСТРАНЕНИЕ ТОКА ПО КАБЕЛЮ
289
1)	уравнением	d*v дх2 а	2^1 —9h- dt‘l	dt	- Ъ2о = 0,	(9)
2)	граничными	условиями: при х = »	X —	0 ДОЛЖНО 1	>	быть V — 0, » и — 0,	(10)
3)	начальными	условиями:	при t = 0 ,	должно быть	
^0.	(11)
Это показывает, что указанною заменою «неоднородные» граничные
условия (5) для функции V приводятся к «однородным» (10) для функ-
ции дифференциальное же уравнение, определяющее эти функции,
остается без перемены.
Как видно, обозначая производные значками, для определения функ-
цим F имеем уравнение
F"-b2F^0,	(12)
из которого на основании условий (8) следует
eb(l-x) _ e-b(l-x)
F(x) = E
£ sh — %)
sh bl
(13)
ebl - e~bl
Функция у, удовлетворяющая однородному дифференциальному урав-
нению (9) и однородным граничным условиям (10), находится по обычному
способу, применяемому в решении задачи о колебаниях струны.
Следуя этому способу, функцию v ищем под видом суммы
v = %XT,	(14)
в ко юрой X зависит только от переменной х, Т — только от' переменной Z,
и каждый член суммы в отдельности удовлетворяет граничным усло-
виям (10), а вся сумма сверх того и начальным условиям (11).
Таким образом, получаем
Х"Т (а2Т" -Ь 2hT' + b2T) X == 0;
отсюда
X" +2hT'+ Ь*Т 9
Х~~ Т — m ,
где т2 — какая угодно постоянная. Затем,
Х" + т2Х = 0<
следовательно, ’будет
л— С cos mx + D sin mx,	r
T = Ae^ + Be^,	’’
причем а и p —корни уравнения
a2\2 + 2h\ + b2 + m2 = 0,
t. e.
a = _ A + А.(62 + m2),
₽ == - ~ ± VМ-аЦЬ* + т*.
19 A. H. Крылов
290 РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Граничные условия дают
С = 0,
Z)sin7wZ = 0,
откуда следует
т=у	(*=1,2,3.......п).
Таким образом, будет
хт ГА ’ kltX
Xk = Dksm —,
Тк = Акеч* + В,.е*1*,
причем
лк = - 4 +	/ hW-a*(b4* + kW) = - «л + пА,
h t r______________________ (17)
аЦЪЧ* + кЧ?) = -н-п*.
Так как произведения AkDk и —такие же произвольные постоян-
ные, как Ак и В к, то без ущерба общности можно положить D=l, так
что будет
v = 2 (Ake^t + BkeW) sin .
k — i
Затем начальные условия дают
— F (х) =2	+ вк) sin ~ ,
к-1
0=2 (a*^* + M*)sin-^.
к = 1
Отсюда следует
Л + ВА=-| ^F($)sin^d?,
6
^кАк "I" $КВ к = 0.
Заметив, что при
„	еЪ(1~х) _е-Ъ(1-х)
= -------------------
интеграл
i
2 С Z7/t\ •	2/сТС	Z7
I ^-F(£)sin z di —	+	E.
о
получим окончательно
r = p Y 2*д	- aKP*( • kmc
Ь E 21 b4* + uw	a-c— pA	sin I
и, заменив аЛ и их значениями (17), на основании формулы (7), имеем
г = вЛли'> -	2 WTIw [ Л + .7 sb "*' ] si“  <18')
к=1
§ 89]
РАСПРОСТРАНЕНИЕ ТОКА ПО КАБЕЛЮ
291
Из формулы (17) и последней формулы видно, что нри неопределенном
возрастании времени t функция и стремится к нулю, и «установившееся^
состояние провода определяется равенством
у __ sh 6 (7 —
~~ sh bl
Е----~ы_-^ьт^
§ 89. После того как потенциал V найден, надо найти силу тока L
Для этого Поссе пользуется первым из уравнений (1), т. е. уравнением
L-^- + RI= --f-,	•	(19)
dt	дх	х 9
которое является по отношению к неизвестной функции I уравнением обык-
новенным и, будучи написано так:
at
дУ
дх ’
дает
/_ - >
L .) дх
О
(20)
причем положено
и принято, что при Z = 0 должно быть 7=0.
Вот относительно этой формулы (20) и возникает сомнение, ибо стоя-
х	дУ	о
щая под знаком интеграла функция — представляется рядом расходящимся,
и результат интегрирования такого ряда, в особенности интегрирования
почленного, может оказаться и неверным.
Если написать формулу (20) так:
t
/=--^ e~nlепхУ (х, т)dt,	(20')
О
рассматривая х как параметр, то этим сказанное затруднение как будто бы
формально устраняется в том смысле, что при такой последовательности
действий не приходится иметь дела с расходящимися рядами, но сомнение
в верности формулы (20').тем не менее остается.
Это затруднение имеет место и в случае пользования уравнением
д!
дх
GV+C^,
ибо и здесь величина — представляется расходящимся рядом. Написав
формулу
X	X
I =	— G V($, t)dl-C^ V(?, f)dt,	(21)
мы формально сказанное затруднение обходим, но сомнение в верности
формулы (21) остается, ибо нельзя утверждать, что равенство

имеет место.
19*
292
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ИЛЕЙ [Гл. УЙ
Тем не менее доведем выкладку до конца, и так как пользование
формулой (21) проще, нежели (20), то ее и применим. Тогда получим
СО
I -«(0+“ chx*)-- 2аЕ^г' 2 О+ £shтйт+
/С=1
ккх
00 cos—	„2-1
+ 2СЕ1е~^ У т¥,-.-4-2-	sh nkt,
1	b2l2 + k2K2 L nk J
•	A=f
HO
2	9 b2l2 + kW
V-2-n«——a
и тогда, заметив, что a?—LC, получим
оо
Г п/л ,	ch&(/-x)	VI < К . , и 1 Л cos I
+ b shbl	2 (ch nkt + nk sh nktJ) b4i + k^ +
A=1
OO
, 2E vi 1 i , knx
+ 77 e * Zi	cos ~T *
jLjL	Ь
k=i
Произвольная функция H (t) определяется по условию
LH' (t)+RH(t) = Q,
следующему из уравнения
и из начального условия, что при t — О должно быть /(ж, 0) = 0 при вся-
ком х в промежутке 0 < х < Z.
Отсюда получаем
f _л г
г •
Таким образом, окончательно имеем
* - Е	2	+£ »ь »-' ] si" Т
А = 1
, GE ch Ь (I - х)	RL -4- 1
1	b shbl	Е
«>	cos —
- 2GIE^' J [cb nj + £ ,b„i( ]	iS- 2 1 sh cos .
k— i	/c=l
§ 90.	По поводу предыдущего решения сделаем еще одно замечание:
когда от предложенной системы уравнений (1)
дУ
дх
RI + L^>
di
дх
= GV + C%
§ 90]
РАСПРОСТРАНЕНИЕ ТОКА ПО КАБЕЛЮ	293
мы переходим к дифференциальному уравнению
dx2 adt2 dt v	v z
или к уравнению
a2'S-2h ~ь*1=°«
dx2 dt2	dt
то этим самым мы налагаем некоторые ограничения на функции V и I,
а именно, что на всем протяжении от х= Одо х = 1 и при всяком значе-
чении t существуют вторые производные этих функций, и тем самым
производные первого порядка непрерывны, тогда как для предложенных
уравнений этого ограничения нет, поэтому правильнее рассматривать урав-
нения задачи в том самом виде, как они предложены. Это же относится
и до граничных и начальных условий.
Итак, будем определять искомые функции V и Г.
1)	системою дифференциальных уравнений
дх * (1)
2)	непосредственно заданными граничными условиями:
при х — 0 должно быть V (О, Z) — Е | при всяком значении
» х — 1	»	» V(M) = 0 j времени t > О,
3)	что же’касается начальных условий, то можно сказать, что по усло-
виям задачи должно быть
V(x, 0) = 0
для всех значений х в данном промежутке, кроме значения х = 0, при
котором по условию V (О, I) — Е, т. е. надо бы писать, пользуясь обычным
обозначением
У(я + 0, 0) = 0.
Относительно производной	ничего не задано, и условие, принятое
гг SdV(x,tY\ л	°
Поссе: ( ——- )	= 0, основано лишь на допущении, что до момента £ = 0
на всей длине кабеля потенциал V (х, 0) равен нулю. Но, очевидно, это
условие не относится до точки х=0, в которой при 1—0 потенциал V
мгновенно становится равным Е, — в этой точке производная при t = 0
не существует.
Можно рассуждать и так: пока Z<0 и к концу ж = 0 напряжения не
приложено, то очевидно,’ Что для всего кабеля 7 = 0 и 1-0. В момент
= 0 значение V ( + 0, 0) = Е, но для остальных значений х величина
V (х, 0) = 0, то же и величина 7 (х, 0) = 0.
Таким образом, естественно, ничего не предполагая о начальном значе-
« dV
нии производной , принять следующие начальные условия: при t = 0
должно быть
V(xf0) = 0 для 0<я</,
I (х, 0) = 0 для 0 < х < I.
294
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Если к системе (1) применить способ решения Ваши или Поссе, то
надо поступить так: полагаем
I = У + 9
и определяем функции ср (я) л ф (х) так, чтобы они удовлетворяли систе-
ме (1) и граничным условиям
ср (О) — /?, © (Z) = 0.
Тогда имеем
— ср' ==/?(!),
— ф' = G<p.
Отсюда следует
ср"— 62<р = 0,
причем попрежнему 62 =:/?(?, и следовательно,
<р = A ch b (I — х) + В sh Ь (I — х).
Условия (5) дают
4 = 0, 5=^-.
’ shdZ
Таким образом,
ch 6 (Z - х)
R shbl
Для функций о и у имеем:
1)	уравнения
-% = Ry + L^-,
дх v 1 dt
-% = G0 + C%,
дх	dt
2)	граничные условия
при ж = 0 должно быть v=0 )	~
} при всяком t > 0.
» х ^=1	»	» у = 0 J
3)	начальные условия: при £ = 0 должно быть
»=—?(*), у=— ф(ж).
Соответственно граничным условиям полагаем
со
2 т • кпХ
2\sin — ,
к=1
№<Уо(0 + 2 ^cos-^r>
причем Тк и 5/с —функции только переменной t.
§ 90]
РАСПРОСТРАНЕНИЕ ТОКА ПО КАБЕЛЮ
295
2	62	/С2К2
а2 а2/2
На основании уравнений (1) имеем для определения этих функций
уравнения
— ^Тк —BSk +LS'k,
^Sk = GTk+CT’k,
исключив неизвестную Sk, получаем уравнение
CLT"k + (CR + LG) Т'к + (GR + тк = 0,
в котором, положив попрежнему
т 2 d L2 CR-^LG	h
CL = a\ GR = bs, WL =
имеем
Tk = е~^ [ Ак ch nkt + Вк sh nkt],
Sk — e~^ [C/c ch nKt + Dk sh nkt],
причем
h
— a2 > П* —
и между постоянными
Л/с, Вк, Ск, Dk
имеют место соотношения
^Ck = (G-pC)Ak + nkCBk,	(22)
у Dk = (G —	Вк 4- пкСАк,
причем
г r г CR + LG LG — CR
G — v.C = G---=
Кроме того, для определения 50 имеем уравнение
RS0 + LSq = о,
откуда
—R- t
5*0 — Сое L .
Начальные условия дают уравнения
— <р (я) = 2 Л* sin ,
л=1
-ф(х) = С0+2 Скcos.
А = 1
Отсюда следует:
i
о
I
Ск=-^- ^(5)cos^d:,
о
Л= —у 5 4>(5)sin^-:d;,
о
после чего коэффициенты Вк и Dk находятся из соотношений (22).
296
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Чтобы найти вышенаписанные интегралы, воспользуемся следующими
известными разложениями, которые нам понадобятся ниже:
= — Г ~2 cos х + 7 7~"г cos 2я ~ cos Зя + ... 1 ,	(23)
sh ^тс тс L . 14- 72	4 4- 72	9 + }2	’ J ’	' '
(—тс<ж< +тс)
sh ух 2 Г sinx 2	. п 3	. о	1	/о,ч
— — __2——8т2я+ 77---O 81пЗ$—— ... .	(24)
sh^TC .тс [_1+72	+	9 + ч2	J	х“*'
Из этих разложений, положив
Ы . тс (I — z)
Y —-- И X = —,
* тс	I ’
следует
ch Ь (I — z) __ 1	9, , Г 1 tcz 1	2tcz .	"1
ShbZ ~	[ W2 + Л2 C0S Т + W + 4л2 C0S “Г + • ’ • J ’
sh Ъ (I — z) „ Г 1	. лг 2	. 2лг .	1	(2а)
shbl ~ 2” [ ЪЧг + л2 81П Т + j2/2 + 4TC2sln -/“+ • •• J •
На основании этих разложений имеем
b°~ Ш'
Ск = — 2EGI w + w ,
Ак= — 2Е b4i + Ача к
Эдесь на основании соотношения (22)
Bk=^Akt
Пк
ji2 — п2 С r u r 2Е t
-----п—“ТтЬк ——	>
71 j;	Сг	71 ,	JLt.1 Пк
 Dk=£ck
ибо
„	,	Ь«/« + Л«я« ЪЧг + к^
•	а212	CLt2
Следовательно, будет
оо
У - В -Ч&Г1 -2^-2 ЖЙГ +
А=1
Eb ch&(*-0	д	I 2ge~'H V 1 еЬ/игсо?та
1 ~7i shbl	HI	+ LI 2-, Пк й kt 08 I
k==l
~	kitx
•	co	COS __
- 2EGle~^3  [ ch nkt + ± sh nkt ]	, (26)
т. e. те самые формулы, которые мы имеем в § 89.
§ 91. Мы видели, что
пк — у р- а2 - аЧг ,
, b* fLG- СЛУ*
- 2LC-/»
§ 91J
РАСПРОСТРАНЕНИЕ ТОКА ПО КАБЕЛЮ
297
следовательно, какова бы ни была величина	, всегда найдется такое
целое к, начиная с которого п* станет мнимым. Очевидно, чгто товдщ гипер-
болические функции заменятся тригонометрическими.
Особенно прост тот случай, когда
иначе, когда	
и в этом случае	=	—1	(#= 1, 2, ..., п)
Значит, будет	ch nkt — cos , sh nut al . kitt 	= j- sm	, n/£	kit	al R G V"- L ~ G
и, следовательно,
V Е %)
~~ sh Ы
х>
пп	7* Лтсг 1	. kitx
ZEe-v* У ,Й7Й ,	( cos —г + у— sin — 1 sm -у- ,
ЬЧ* 4- Л2ла \ \al * кк al J I
к—l
Ebchbtl — x) E . 2E a V 1 • kitt kitx
е~^,л + -f------------------e~^ > -y- sm —r cos ----
R sh bl Rl	L к	I к al I
(27)
kitx
cos ~
- 2EGle-^ У (cossin ) ,2,2 , ,2 a
\ al kn al J b42 + k№
/c = l
Все суммы, входящие в эти формулы, находятся в конечном виде,
пользуясь формулами
о kitt . kitx . Лк / t t \	. kit / t \
2 cos —г sin -г- = sm -г ( х 4—	+ sm т х------------),
al I	I \ a J I < a J
о . kitt .kitx .kit/' ,	.kit/' t\
2 sm —г cos -т- = sm -т- ( я 4— ) — sin ~ ( x------------------),
al	I	I \	'	a J	I	\	a J
о .	kitt	.	kitx	kit /	t \	kit	f	,	t \
2 sin —г sm —r- = cos т x-----------------— cos v x 4— ),
al	I	I \	a J	I	\	a	J
o	kitt	kitx	kit f	, t \
Z COS —r COS -T' = cos -r ( X 4---------)
.	al I	I \ a J
+ cos
и разложениями (23) и (24).
Мы не будем приводить графиков всех этих функций и их разрывов,
так как вопрос этот подробно разобран в сочинении В. И. КоваленковЬ,
а ограничимся лишь немногими примерами, чтобы показать сущность дела-
Возьмем формулу для V.
Сумма
оо
2о XI къ f kitt . kitx . uaZ . kitt . kitx\
= 22j -b44WQcos^-sin-T + Ksin аГ8Ш-Г> •
A=1
входящая в состав функции V, разлагается на следующие четыре суммы г
У] = 51 + *У2 +	(*^ з —	»
298
РЕШЕНИЕ УРАВНЕНИИ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VU
причем
СО
Vi кк • ^тс Л , £ Л
= 2 ЬЧ* 4- Л2я2 31П7 V а / ’
*=1
ОО
о хз Ал	. Ал / t \
^2=2 ЬЧ* + *’5С* Sln Т V _ ~а) ’
к=1
^3=2 ЬЧ* + к»п* С08Т (Ж “) ’
*=1
Si = 2 ьч* + kW C0S Т СЖ + «О ’
к=1
Мы имеем разложение
1 shb(l-x) _ z ч	51 кк -  кпх
2 sh&Z — ?W 2j ЪЧ* + кЧ? 81 I ’
/с=1
Это разложение имеет место для промежутка 0 < х < Z, вне же этого
промежутка для значений — Z<#<0 ряд представляет функцию —ср(ж).
Все прочие значения находятся на основании периодичности, т. е.
равенства
ср (21 + х) = <р (х).
Таким образом, функция, представляемая рядом, изображается графи-
чески чертежом (фиг. 54), причем в местах разрыва сумма ряда есть нуль.
Положим, что
О < ct < Z,
причем	тогда ряд представит функцию cp(#+cZ), т. е. надо всю
^ступенчатую кривую ср (х) подвинуть параллельно самой себе влево на вели-
чину ct, тогда в промежутке от 0 до I ляжет участок кривой, обозначен-
ной на фиг. 56 через <р(#4-сг).
Ряд 52 представит функцию <р(х — ct), т. е. надо всю кривую продви-
нуть вправо на величину ct, и в промежутке от 0 до Z лягут части кривых,
помеченные ф(ж— ct), причем на протяжении 0 < х < ct значение функции
будет отрицательное, равное y(ct — x), как это и видно по чертежу.
Совершенно так же для сумм 53 и 54 мы будем исходить из разложения
chb(Z — х)_	1
2Ы sh bl "W
1	kitx . z ч
PTM^cos — =ф(х).
S 91]
РАСПРОСТРАНЕНИЕ ТОКА ПО КАБЕЛЮ
299
Функция ф(я) изображена на фиг. 55.
Как видно, сама эта функция непрерывна, но в местах
я = 0, 2Z, 4Z, ...; — 2Z, -4Z, ...
она имеет угловые точки, т. е. разрывы первой своей производной.
Совершенно подобно предыдущему видим, что ряды £3 и предста-
1 1
вляют функции ф (х — ct) — и ф {х -Ь ct) —	, и части соответствующих
1очА
кривых, лежащие в промежутке от 0 до Z,
помечены на фиг. 56 соответствующими
значениями.
Из этого чертежа видно, что сумма
S на участке 0 < х < d и на участке
ct < х < I выражается различно, а именно:
Для промежутка 0 < х < ct будет
2i=?(^ + ^) — <p(cz—-ж) +
+ fiaZ [ф {х — ct) — ф (cZ + ж)]
и для промежутка ct < х < Z будет
? (Ct + х) + ф (х — ct) +
+ paZ [ф(я — ct) — ф (х -h cZ)],
но мы имеем
2 sh Ы ср {ct + х) = sh b {I — х — ct),
2 sh bl {ct — х) — sh b{l — ct x).
Следовательно,
sh bl [9 {ct + x) — cp {ct —• ж)] =
= — sh bx ch b {I — ct).
Совершенно так же получим
bl sh bl [ф {x — ct) — ^ {ct 4- ж)]
следовательно, принимая во внимание, что
- sh 6# sh b {Ict),
p? — 4 •
b “
но мы имели
i=8Ь8ьь7ж) -e-ii<	=shi (sh b (J -*)+sh bxe~bll=e~bx‘
Итак, для промежутка 0 < х < ct будет
V = Ee~bx.
300
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
Для промежутка ct < х < I
2 sh Ы (х — ct) — sh b (I — х + ct).
2 sh Ы (х + ct) — sh b (I — x — ct),
следовательно,
sh bl [<p (x — ct) + (x + cZ)] = sh b (I — x) ch be.
Совершенно так же получим
pal [ф (х — ct) — ф (х + cZ)] = -h	sh bet,
следовательно, будет
у ___ sh&(Z -х) bct _ t shb(l- x)
^2 sh&Z	sh&Z
и
7 = 0.
Таким образом, V определяется такою разрывною функцией:
для 0 < х < ct V = Ее~Ъх,
» ct <х<1	7 = 0,
представленной на фиг.. (57).
Из уравнения
Kfe'6®	1 П	i 1	1 .	1	1	дх	dt следует, что для промежутка 0 х < ct
о ct	х Фиг. 57.	будет 1=Не~^1 + b4e~bx^He-^ + b-f е~Ьх} л	к
причем Н есть произвольная функция от х, которая определяется из усло-
вия, что при t — О должна быть
Цх, 0) = 0, ’
следовательно,
Н=-^е~Ьх.
Таким образом, будет
Для промежутка же
ct < х < I'	' '
будет
/ = 0,
следовательно, I(x, t) представляется такою разрывною функцией: з
для 0 < х < ct I ,~bx[i — e~vt],
» ct < х ,< I I ~0.
14	.. „ , ... - -	.. -	41	
Заметим здесь же, что скорость, с которою бежит место разрыва, есть
_ — 1 ' ’
с 7 » Zc ’
J
§ 92]
РАСПРОСТРАНЕНИЕ ТОКА ЙО КАбЁЛК)
301
Совершенно подобным образом найдутся выражения V и I для значе-
ний Z, при которых
I < а < 2Z.
Затем —для значений Z, при которых
21 < ct < 3Z,
й т. д. На этих подробностях останавливаться не будем, отсылая к сочи-
нению проф. В. И. Коваленкова.
§ 92. Полученные в §§ 90 и 91 результаты показывают наглядно, что,
несмотря на разрывность функций V (ж, Z) и I(x, Z), система уравнений (1)
и следующее из нее дифференциальное уравнение (4) равносильны, поэтому
вместо сказанной системы можно пользоваться этим уравнением и соответ-
ствующими граничными и начальными условиями.
Является еще один вопрос: Ваши и Поссе, чтобы привести граничные
условия к однородным, положив
определяют функцию ф(я) так, чтобы она удовлетворяла дифференциальному
уравнению (4).
В том частном случае, когда при х 0 должно быть V — Е, эта замена
выгодна и в смысле простоты выкладок, но не следует думать, что она
единственная и что условие, чтобы функция <р(я) удовлетворяла уравне-
нию (4), есть необходимое.
Функцию ф(.£) можно брать как угодно, важно лишь, чтобы при x~Q
было ф(0) = ^ и при х — 1 было <р (Z) — 0, — разница будет только в том,
что уравнение, коим определяется о, не будет однородным, но это обстоя-
тельство не представляет никаких существенных затруднений.
На рассмотренном примере все это выясняется весьма просто.
Очевидно, что простейшая функция, принимающая при я = 0 и х — 1
вышеуказанные значения, есть
поэтому полагаем
И-о + £(1-Л);	'
тогда функция у будет определяться дифференциальным уравнением
f28’
и условиями:
граничными:
при х = 0 должно быть о = 0,
» х = 1	»	>	с —0,	( '
начальными: при / = 0 должно быть
2-=°'	w
применяя общий способ разыскания «вынужденных» колебаний, полагаем
v - + v2
и определяем этим функции так, чтобы представляло свободные коле-
302 РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН[Гл. VII
бания, вынужденные. Для этого необходимо, чтобы эти функции опре-
делялись следующим образом:
Функция
1} дифференциальным уравнением без последнего члена, т. е. урав-
нением
^-^д!-2Л§-№г = 0;	(31)
2) граничными условиями:
при	х~0	должно	быть	1^ = 0,
»	х = 1	>	>	и1 = 0;	'
3) начальными условиями: при должно быть
5‘-0.	' <з:->
Функция г2 определяется:
1)	дифференциальным уравнением с последним членом:
Z ~	<34>
2)	граничными условиями:
при x — Q должно быть r2 = 0,	q
» х = 1	»	>	у2=0;	?
3)	начальными условиями: при Z = 0 должно быть
о2 = 0, ^- = 0.	(36)
Поступая подобно тому, как указано в §§ 88 и 89, ищем сперва под
видом суммы
оо
Ет . кпх
тк sin —
/с = 1
и получаем
оо
— е~^ 2 (Ак chnkt + Bkshnkt) sin^p
при прежних обозначениях, т. е.
__ h __CR + LG
а2 ~ WL ’
Затем для определения коэффициентов Ак, Вк по начальным условиям
имеем равенства
/с = 1
о - 2 (— м* + Вкпк) sin ,
к~1
§ 92]
РАСПРОСТРАНЕНИЕ ТОКА ПО КАБЕЛЮ
303>
которые дают
i
л 2Е С f А	х \ . kitx , 2Е
Ак^ ~~Г\v-T)sin — dx= --ы. ’
о
о _ А А
к kitnk'
Таким образом, будет
оо	•
°°	sin 
2(chnAf + ^shn^—-2- .
Функцию У2 ищем под видом суммы
оо
«2=2 ^*(0sin 7^;
л=1
тогда, представив вторую часть уравнения (36) под видом суммы
А=1
видим, что функции Sk определяются уравнениями
-^-Sk-azSak-2hS'k-bzSk = ^Е (к = 1, 2, 3,...>
и условиями: при £ = 0 должно быть
Sk = 09 Srk = 0.
Отсюда следует
Sk = (Мк ch nkt + Nk sh nkt) -	,
причем
м 2E b42
1Vlk~ kit b*l2 + W ’
Nk = ^Mk.
nk
Таким образом, будет
9P >	1 sin	__ .	sin
Vi = ~ V S к ЪЧг + W -J' V Ц< S nkt + nk sh nkt>)kK ЬЧг + Л2я«
A-=l	fc=l
Но мы имели
У = ^(1-|)+Г1 + „2
получим
™	, kitx
7.	z	fat sin —
V = 2E b2r + w sm у — 2Ee-' 2j (e11 nkt + sh nkt^ ьгр + к^2
304	РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. Vll
а так как мы имели разложение
оо
nV) кк ' • кпх sh Ъ (I — х)
' ' Л Ъ ЪЧ2 /с2тс2 Sin ~ “ sh bl ’
то будет
„	г . к~х
Т..Г/1 X	08 Х	fat SIH —
v - Е - 2Е‘~Г' 2 О11 ь£ sh«) иг+да •
* = 1
т. е. та самая формула (18), которую мы имели в §§ 89 и 90.
Отсюда ясно, что при решении этой задачи за функцию ф(я) можно
'брать просто линейную функцию х, выбирая ее так, чтобы граничные усло-
вия стали однородными. Таким образом, во многих случаях выкладки зна-
чительно упрощаются.
Мы нарочно остановились столь подробно на рассмотрении простейшего
случая нашей задачи, ибо на нем с полной ясностью обнаруживаются все
особенности ее решения, из которых наиболее существенные следующие две:
1)	предложенную систему двух уравнений первого порядка, несмотря
на разрывность решений, можно заменять одним уравнением второго порядка;
2)	чтобы сделать граничные условия однородными, нет надобности брать
функции переменной х, удовлетворяющие дифференциальным уравнениям
задачи, можно брать любую функцию, делающую граничные условия одно-
родными, проще всего линейную.
§	93. Более общий случай тот, когда граничными условиями служат:
при х = 0 должно быть V (0, t) = ЕеЫ1,
»	x — l »	»	V (Z, г) = 0м
начальные же условия попрежнему: при t — 0 должно быть
У(«,0) = 0.
Исключив из предложенной системы (1) неизвестную функцию /, полу-
чаем для определения V уравнение
dx2 dt2	dt	х '
Чтобы сделать граничные условия однородными, полагаем
(38)
тогда для определения неизвестной функции v служат:
1)	дифференциальное уравнение
-2h~-b*v = E( l-^W-a2o2^2W)eiu)',	(39)
дх2 at2 dt	\ L у
2)	граничные условия'.
при	х = 0	должно	быть	г; = 0,
ъ	х — 1	»	»	1=0,	'
3)	начальные условия', при Z = 0 должно быть
<41>
Полагаем по общему правилу:
§ 93]	РАСПРОСТРАНЕНИЕ ТОКА ПО КАБЕЛЮ	305
и определяем функции и v2 так, чтобы представляла свободные колеба-
ния функции, и2 —вынужденные; тогда эти функции определяются:
а)	Функция
1)	дифференциальным уравнением без последнего члена, т„ е.
">-а2^-2л>-^=°> <42)
2)	граничными условиями:
при	х — §	должно	быть	V! = 0,
»	х — 1	»	»	^'1 = 0,	'	'
3)	начальными условиями: при t — О должно быть
(44)
б)	Функция и2 определяется:
1)	дифференциальным уравнением с последним членом*,
^_a^ — 2h^-b^z = E(l~Vb*-a№ + 2hiv)eM,	(45)
иХ2	otf	ot	I J
2)	граничными условиями:
при x = Q должно быть ?;2 = 0,
»	х — I »	»	v2 = 0,
3)	начальными условиями: при / = 0 должно быть
р2 = 0 и ^ = 0.	(47)
Если ограничиваться только вещественною частью наших функций, как
это и следует по смыслу физической задачи, то, как видно, функция г,
определяется тем же самым уравнением и теми же самыми условиями, как
в § 92, следовательно, будет
= - те-м 2 (ch +nVh ”А01sin kJr •
к~1
Для нахождения функции v2 полагаем
оо
VI о , кхх
у2 = 2)Sk sin "Т ’
А=1
и, представив сперва вторую часть уравнения (45) под видом
Е - аЕ 2®2 + 2hU) (1 - у) = 2	& sin ’
А = 1
так что
Нк W =	(Ь2 — а2<о2 + 2/г/а))	,
имеем для определения Sr уравнение
-Sk-a*S'k-2hS'K- b*Sk = Hk(f)
и условия: при t — 0 должно быть
5/с(0) = 0,	5Ц0) = 0.
20 А. Н. Крылов
306
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
Отсюда следует
$к = е~^ (Мк ch nkt + Nk sh nkt) + Pk cos u>t + Qk sin <dZ,
причемf. на основании начальных условий, будет
Мк = — Рк>
Nk±-±(Pk + «>Qk),
Г1к
и величины Рк и Qk будут
2£ (&2-а2<
Рк = - ЪГ 77~
Л2л2\ ’
w
Л2Л2\2
а2(о2 4- -р- J 4- 4А2(о2
1
Q -= Aio&rc
х I2
к2п2 2
а2(о2 4-	 j 4- 4Л2(о2
Таким образом, будет
cos *4“ ^2»
причем и у2 определяются приведенными выше формулами. Не выписы-
вая результата подстановки вместо ох и и2 их значений, заметим, что в выра-
жении V можно будет произвести упрощение, подобное тому, как в § 92.
После того как V найдено, функции I (х, I) находятся совершенно
подобно тому, как в § 92.
Мы остановились так подробно на этой задаче потому, что уравнение,
к которому она приводится, наиболее общее из рассмотренных нами и заклю-
чает, как частные случаи, уравнение распространения тепла и уравнение
колебаний струны.
§ 94» Уравнение
^дя2 dt2 dt
введением новой неизвестной функции и новых переменных независимых
приводится к более простому виду, в котором оно часто и рассматривается.
Наиболее обычное приведение такое.
Полагают
V — ektU
и выбирают к так, чтобы в преобразованном уравнении
^-a^-2^k + ‘h)ft-^ + a^ + 2hk)U = 0	(1)
. ди	.. Т7
пропал или член, содержащий . или член, содержащий с/.
В первом случае надо взять
тогда будет
Ь2а2к2-\-2hk-b2 —	,
НО
ti> = RG, h = CR^~~~ , a2 = LC,
S 94]
РАСПРОСТРАНЕНИЕ ТОКА ПО КАБЕЛЮ
307
так что
А2 л2 (CR —LG)2
Ь а2 ~ kLC
есть, очевидно, величина отрицательная, которую мы обозначим через
тогда рассматриваемое уравнение принимает вид
d2U	2d2U ,2ТТ А
дх2 dt2 1
Разделив на 62 и полагая затем
»	byt
и • -i- =zn
получим уравнение
д2и о2и п
dt* dx2^~Ui
или, опуская значки,
dt* ~ дх* U'
Это есть первый вид, в котором часто пишется основное уравнение
рассмотренной задачи.
Другой вид получается, если выбрать к так, чтобы было
а2Л2 + 2ЛЛ+62 = 0,
иначе
a2 a Y cfi
Но мы видели, что
А2 , 2 (CR - LG)2
а2 “ 4LC
поэтому будет
CR + LG	CR — LG
2LC ± 2LC ’
т. е.
И 2(а2А1Ч- h)^CR-LG,
и 2(a2kl +h) —LG — CR;	
это показывает, что всегда можно взять то значение к, при котором
а2к + h > 0;
обозначая эту величину через 2hu получим уравнение
дх2 ’-~а dt2+2Л1 dt ’
разделив на кг и полагая
л	л а2	!
 х~п^х^
получим
dU ' ‘
дх* dt*+^ dh ’
или, опуская значки,
д*и _	, 9
дх* dt* dt ’	W
20*
308	РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. УП
а это уравнение есть уравнение колебательного движения струны в среде,
оказывающей сопротивление, пропорциональное первой степени скорости,
когда же это уравнение относится к распространению электричества, то его
обыкновенно называют «уравнением телеграфистов».
Таким образом, для перехода от уравнения (4) к уравнению (2) или (3)
служит подстановка
V = ekiU.
Очевидно, что если для неизвестной функции V было граничное усло-
вие: при x—Q должно быть V — E, то для функции U оно будет
U^Ee~kt,
а если бы оно было Ее^л, то для U получилось бы
U = Ее^к+^.
Это показывает, что существенной разницы между задачею, рассмотрен-
ной Поссе, и более общею задачею § 93 нет, и если бы при решении первой
задачи сперва привести основное уравнение к одному из простейших видов
его, то решение второй могло бы быть получено простою заменою буквы к
на — А + До и отделением вещественной части от мнимой. Мы ограничимся
этим замечанием, соответствующих же выкладок производить не будем,
так как после изложенного выше они очевидны.
§ 95. Продольные колебания ствола орудия при выстреле. Хорошим
примером является также изучение продольных колебаний орудия при выстреле
или, точнее говоря, его цилиндрической внутренней трубы или. ствола.
Рассмотрение поставленного вопроса начнем с установления тех сил,
которыми в стволе вызываются продольные напряжения, независимые
от тех, которыми сопровождаются поперечные напряжения и которые
вызываются этими последними.
Те продольные напряжения, которые мы имеем в виду изучить, вызы-
ваются: 1) силами инерции, развивающимися при откате орудия, 2) про-
дольными упругими колебаниями ствола орудия, происходящими от изме-
няемости усилия, действующего на дно канала.
Пусть имеется орудие, ось канала которого примем за ось х, про-
извольную неподвижную на ней точку О — за начало координат (фиг. 58).
В момент времени t положение орудия определяется абсциссою xt его
центра тяжести G, положение снаряда-—абсциссою х2 его центра тяжести Л,
положение заряда, которой мы предположим уже вполне сгоревшим, —
абсписсою х3 центра тяжести В объема, занимаемого газами. Если канал
цилиндрический (без каморы), что мы и будем предполагать для простоты
выкладки, то точка В лежит посредине между дном снаряда и дном канала.
§ 96] ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТВОЛА ОРУДИЯ ПРИ ВЫСТРЕЛЕ	809
Обозначим через Мт массу орудия, через т2 —массу снаряда, через
и?з — массу заряда, пренебрежем трением снаряда о нарезы и давлением
на поршень компрессора (оно в большей части случаев не поспевает
и развиться ранее вылета); тогда будем иметь уравнение
М±х± + т2х2 + т3х3 == const.,	(1)
ибо при сделанных предположениях центр тяжести всей системы остается
неподвижным.
Дифференцируя уравнение (1) два раза по времени, получим
+ т2х" + m3xl — 0,	(2)
но, очевидно,
x3=±(x2-b)+	— «) — у (Ж1 + жз) — у (« + Ь),
причем а и b имеют показанные на чертеже значения, следовательно,
1 1
/у.» _ 1	/у." I 1 /г"
•^з — 2	2	9
й уравнение (2) принимает вид
+	+ (лг2+ у»г3^4 = 0.	(3)
Обозначив через р давление в канале в момент t и через s площадь
сечения канала, имеем
m2x”t= ps ~F(t),	(4)
причем F{t) есть некоторая заданная функция времени Г.
Отсюда, на основании (3), следует
(5)
Положив для краткости письма
14-1™»
____2 т2 _ 2т2 + тя 1
Jf1+lm» "2Л/1 + т.т2
имеем
x'[=—kF(t).	(7)
§ 96. Определяемое уравнением (7) движение всего орудия, как твер-
дого тела, вызывает в каждом его поперечном сечении натяжение, вели-
чина которого равна произведению из расположенной впереди этого сече-
ния массы ствола на ускорение ж].
Пусть х есть абсцисса рассматриваемого сечения и — длина дульной
части впереди центра тяжести G орудия, тогда сказанная масса рДя) будет
р.(ж) = р <•>(?)«£,	(8)
X
где w (?) есть площадь сечения тела орудия, р — плотность металла.
Таким образом, в рассматриваемом сечении в момент t будет действо-
вать продольное усилие
=	=	’ (9)
310
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл VII
Отсюда видно, что если бы это действие было статическое > то соот-
ветствующее напряжение металла определилось бы по уравнению
Так как масса т3 заряда не превышает массы орудия, то вместо
точной величины к, даваемой уравнением (6), можно брать приближенно
А =	+	±	(И)
и писать
a =	+	(12)
2 mJ v 7	\ i
Само собою разумеется, что вычисление величины |л(я) сейчас же
сводится к вычислению продольного распределения массы орудия, считая,
например, абсциссы от дна канала или, лучше, от дульного среза. В этом
последнем случае будет
Zi+^i	xi+h-x	z
р-(я) = р	<*>i($)cR = р о)1(£)<К = p.1(z),	(13)
х	оо
и, следовательно, натяжение в момент времени t в сечении, отстоящем
на z от дульного среза, будет
х 7 О) (z) <	2 w2/	f	x '
Вычисление интеграла (13)
z
(13')
0
имея чертежи орудия, не представляет никаких затруднений и не требует
пояснений.
При статическом действии усилий нет надобности знать изменяемость
силы ps с течением времени, д. е. нет надобности знать функцию F(Z),—
достаточно знать наибольшее ее значение, соответствующее наибольшему
давлению в канале, причем безразлично, при каком положении снаряда
по длине канала оно имеет место. Обозначая это наибольшее значение
функции F (t) через ^шах, будем иметь для наибольшего напряжения
в данном сечении формулу
г (?\ ____________________	‘1 (1 I	Н (z) р __
"max \%) —1 » V J — ^max —
°>(z) \	2 mJ Jktj
- * <1 4_ 1	P	‘ 1 ?
“ ш (z) V T mJ	^max’
где Pmax Ость наибольшее давление газов в канале.
Эта формула и решает поставленный вопрос о распределении продоль-
ных напряжений, при предположении, что действие усилий, вызывающих
этц напряжения, статическое.
Чтобы при действии на какую угодно упругую систему усилия, изме-
няющегося с течением времени, можно было это действие, в смысле вызы-
ваемых им деформаций и напряжений, считать статическим, необходимо,
чтобы период свободных колебаний системы, а если таких периодов много,
то наибольший из них, был мал по сравнению с продолжительностью
нарастания усилия от начального нулевого его значения до наибольшего.
I 97]
ПРОДОЛЬНЫЕ колебания ствола орудия при выстреле
311
Между тем, по отношению к стволу орудия это предположение вообще
не имеет места. Возьмем, например, морскую 4-дюймовую пушку 60 калиб-
ров длиною. Давление достигает в ней наибольшего своего значения при-
близительно через 0.003 сек., продолжительность движения снаряда
по каналу около 0.01 сек. Длина этого орудия 6 м, период основного тона
продольных колебаний приблизительно равен продолжительности пробега
звуковой волной, бегущей по стали, двойной длины орудия, а это составит
12
около 5200	0-0024 сек., т. е. величину, близкую или во всяком случае
того же порядка, как продолжительность нарастания давления. В этом
случае действие «статическое» и «динамическое» может разниться весьма
значительно, ибо в стволе возбудятся продольные колебания, напряжения
от которых и заменят собою статические.
§ 97. Определение продольных колебаний ствола орудия, если стре-
миться принять в расчет все особенности его конструкции, представляет
задачу чрезмерно сложную и едва ли в общем виде разрешимую, поэтому
необходимо разобрать сперва вопрос при разного рода упрощающих дело
допущениях, чтобы по анализу этих частных случаев судить хотя бы пред-
положительно об общем.
Простейшим из этих частных случаев является тот, когда ствол состоит
из простой цилиндрической трубы одинаковой повсюду толщины стенок.
С этого случая и начнем, чтобы на нем пояснить метод решения.
Очевидно, что в этом случае площадь сечения о> ($) есть величина
постоянная, которую обозначим через ш; тогда, если пренебречь массою
затвора по сравнению с массою тела орудия, будем иметь такую задачу.
-------------Ъо
-.......*---------1—
О Ft А
Фиг. 59.
К концу А свободного однородного стержня (фиг. 59), длина коего Z,
приложена переменная сила F-^Fty)', требуется определить движение
стержня, принимая во внимание и упругие колебания его.
Пусть G есть центр тяжести стержня. Если бы стержень был телом
неизменяемым, то перемещение uQ как центра тяжести, так и всех прочих
точек стержня, определялось бы уравнением
причем сила F, действующая на дно снаряда, увеличена в отношении
чтобы получить такое же движение центра тяжести, как и в случае орудия.
Начальные условия'. при/ = 0 должно быть
"•-° “ СЮ.-0-
Пусть сечение Н± отвечает абсциссе x1=^GH1, считаемой от центра
тяжести, и абсциссе 5i = S0+#i, считаемой от неподвижного начала О, но
= с -f- Uq,
312 РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
где с есть начальная абсцисса центра тяжести; таким образом для сече-
ния Н2, соответствующего х2==х1 + dxlt будет
= + и di1 = dx1.
Обозначим через v~u0 + u перемещение сечения тогда перемеще-
ние сечения Н2 в тот же момент будет
dV j	, .ди 7
v -t ч— dxt = и + и 4- — dxv
дхг 1	0	‘ дхг 1
Отсюда видно, что натяжение в сечении Нг будет
Еи^Е^
и в сечении. Н2 оно будет
£» Г* +Р<),
Vd#! dxl
значит, на элемент	масса которого есть	действуют силы
о । р (ди 1 д2и , \	>7 д2и л
-Ею-—у Ею ( т—F	= dxx,
дхх 1 \дхх дх2	дх2
и мы получаем уравнение движения
/	7	\ d2v гт д2и у
(pcod^i) ы^Ем — dx^
м 17 dt2 dxl 1
но
dV2__д2и% д2и__ 1 p , v d2u
dt2 ~~ dt2 + di*~Mi 1 v/ ’ dt2 ’
подставляя, получаем уравнение
d2u	n d2u	1	/ л
зтг —,	(17)
dt2 dx2	Mr 1 x 7	'
причем положено
7= «2-	(18)
К уравнению (17) необходимо присоединить условия граничные и началь-
ные: первые относятся к концам стержня А и В, отвечающим значениям
я = =Ь у , вторые — к моменту времени t — 0.
В конце 4 ^!= —у) действует сила FT (£), конец В (хх = + у)
свободен от всякого напряжения, следовательно, для величины и будут
условия:
граничные:
при хг = — ~ должно быть Ею == F± (Z) ] при всяком
}	значении	(19)
, I	ди А I	.	v 7
»	#1= +у >	>	дх'==® I времени tr
начальные же условия суть: при £ = 0 должно быть
w==g(®l) И =	(20)
где g(#i) и / (%]) — заданные функции переменной хг для значений этой
переменной от xt = — у до хг = + у .
В нашем частном случае обе эти функции равны нулю для упомяну-
того участка.
§ 98] ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТВОЛА ОРУДИЯ ПРИ ВЫСТРЕЛЕ	313
решение представляет
физически равносиль-
I
хг = —2* > возьмем также
каждую погонную единицу
и затем определим предел,
и, кс>гда Ь приближается
§ 98. Если ставить задачу в такой форме, то ее
излишние трудности, но можно взять другую задачу,
ную этой и гораздо более простую для решения.
Уравнение (17) представляет вынужденные колебания стержня под.
действием равномерно распределенной по его длине нагрузки, рав-
ной —	на каждую погонную единицу длины стержня.
Вместо силы	приложенной к концу
Fj (г)
равномерно распределенную нагрузку - у-7 на
длины на протяжении от хх = b до xr = b + к
к которому приближается искомая функция
к — у и л к нулю.
Для выкладок удобнее, если перенести начало счета абсцисс в конец Л;
эти абсциссы будем обозначать просто через ж, а вышеупомянутую
нагрузку, распределенную на участке от b до Ь 4- к, обозначим через
(х, t)\ тогда наша задача приведется к такой математической:
Требуется определить функцию и, удовлетворяющую:
1) дифференциальному уравнению
а2 ^4 =	~ ? (я, £)
dt2 дх2 Мг 1 х 7 (ли • '	7
2) граничным условиям:
при я = 0 должно
(21)'
при всяком
значении t,
(22).
» Х = 1	»
быть ~ = О
дх
ди р.
> Ч- =0
дх
3) начальным условиям: при t — 0 должно
« = ?(*) И
быть
(23)
причем g(x) и /(х) — заданные функции в промежутке от x—Q до х = 1\
в нашем частном случае обе эти функции равны нулю на всем этом про-
тяжении.
Поставленная задача решается по общему способу определения выну-
жденных колебаний, положив
и = и1’\-и2	(24)
и определяя функции иг и и2 так, чтобы иг представляло свободные коле-
бания, «2— вынужденные. Для этого необходимо подчинить функцию иг:
1)	дифференциальному уравнению того же вида, как (21), но без
последнего члена, т. е.
(25)
dt2 дх2	4	7
2)	граничным условиям тем же, которые относятся к функции а, т. е.
в нашем случае:
при х = 0 должно быть ^ = 0,
*	(26))
>	ди* л
»	х — 1	>	>	-^ = 0,
их
3)	начальным условиям тем же, которые относятся к функции и.
314	РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН (Гл. VII
Что касается функции представляющей вынужденные колебания,
то она должна удовлетворять:
1)	дифференциальному уравнению (21), т. е.
д2ца а2— фГж О	(27)
dt2 дх2 Мг	'
2)	граничным условиям:
при х == 0 должно быть = 0,
* (28)
»	Х=1	»	>	-^- = 0,
дх
3)	начальным условиям: при t = 0 должно быть
и2 = 0 и -^=0.	(29)
Решение надо начинать с нахождения функции их под видом
и^^ХТ,	(30)
>тде X есть функция одной только переменной х и Г —функция только t,
причем каждый член этой суммы должен удовлетворять дифференциальному
уравнению (25), граничным условиям (26), а вся сумма должна удовлетво-
рять начальным условиям.
Таким образом, имеем
Г"Х-а2Х'Т==0.	(31)
Этому уравнению нельзя удовлетворить иначе, как положив
T"=-aVTt	(32)
X"=-m2X,	(33)
• где m —постоянная величина, пока произвольная.
Отсюда следует
Т = A cos mat + В sin mat,
(34)
X = С cos mx + D sin mx.
Граничные условия дают
X'(0) = wZ> = 0,	ZQca
X' (I) = mC sin ml = 0.
Отсюда следует
m = ™	(n = 0,1,2,	...).	(36)
Таким образом, будет
Xn = cos^ (n = 0, 1,2,	(37)
Tn = -4n cos n + Bn sin n ,	(38)
4	4
^ибо без нарушения общности все постоянные произвольные С можно брать
равными 1. ч
Необходимо еще заметить, что при и = 0 будет
Х,= 1 И Го = 4> + Вог.	(39)
§ 99]
ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТВОЛА ОРУДИЯ ПРИ’ВЫСТРЕЛЕ
315
Таким образом, получится
со
иг — Ло + Bot + 2 cos ~j~ (A cos п + Вп sin п ,	(40)
П = 1
где Ао, 50, Ап, Вп—произвольные постоянные, которые определяются по
начальным условиям, именно, будет
i
А = 4	(41)
о
I
А = 4 5g(g)cos^de,	(42)
о
I
B0 = ±\f(i)dl,	(43)
о
I
5П = — С/(£)cos	(44)
итса J v ' t	'	'
О
Как видно в нашем частном случае, когда на всем протяжении от
ж —0 до х — 1 функции g(x) = f(x) = O, то будет и
•	(^ = 0.
§ 99» Вынужденные колебания ищем под видом
«2=2 cosT5nW’	<45>
п=0
где Sn (0 — неизвестные функции t.
Для этого представляем сперва вторую часть уравнения (27) под видом
суммы
2 нп(0cos7 = -	Fi(0 + Д Т (*, t),	(46)
п«1
тогда будет
i
о
г	(47)
ад=4 $ 4t(£,°cos?^’
о
и величина Sn(t) будет определяться уравнением
S'k + ^Sn = Hn(t) (п = 1, 2, ...,«),	(48)
S№0 = H0(t)	(49)
и начальными условиями: при £ = 0 должно быть
5п(0) = 0,	5А(0) = 0,
А(0)=0,	А(0)=0.	' 7
316 РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл> VII
В нашем случае функция t) такова:
при

>	6 < $ < 6 4- X
»	(6 + М<£<1
<?(£, 0 = 0,
?(«» 0 = уЛ(0,
<?(Е, /) = 0
и, следовательно, будет		
^о(О =	_^1(0+ 1 С Л/1	pZ<o J X 1 * * 4 * ' 7 * * * ь ь+л Л i */у(г)С08^	= /рш з х 1X7	i ъ 2 1 I Г . тис(Ь + А) . nitb‘ Zp<o Л mt L	I	I	^[^(О-Л(О]=о,
п (^)		]Л(0 =
4 I . пкк	+
= М^ Sin IT C0S-------------1-------& = G"7' 1 W’
причем
к l	ПлХ
Сти — лт V SIH yry* COS
mtk	21
Таким образом, для определения S9 и Sn имеем уравнения
5’0 = Я0 = 0,
1	/»2„2«р2
^+^-5n = GnFI (?),
решения коих, удовлетворяющие условиям (50), суть
^0 = 0,
I
О
Но величина
I r U I . mA Л”(6 + ТХ)
amt п amtM1 mtXSin 2Х C0S I
в пределе при 6 = 0, Х = 0 будет
lim	= il- .
, Л -> 0 VanTC у аг™ М1
Следовательно, предельное значение Sn(t) будет
t
5n(z) = -2L_ (/умsin^(z-о«К
4 f amt Мг j 1 v 7 I '	7	’
0
и искомая функция и2 есть
оо
«2 = 5 Sn(t)cos^,
Л«1
(51)
(52)
(53)
причем суммирование взято от п=1 до п = оо, ибо 5о = О.
Выражение (53) для и решает поставленную задачу.
§ 100] ПРОДОЛЬНЫЕ колебания ствола ОРУДИЯ ПРИ ВЫСТРЕЛЕ 317
§ 100. Хотя входящая в состав выражения и2 сумма и может быть
найдена в простой замкнутой форме (способ нахождения этой суммы совер-
шенно подобен тому, который изложен ниже), но мы на этом останавли-
ваться не будем, ибо нас не столько интересуют величины перемещений
различных точек стержня при его продольных упругих колебаниях, сколько
происходящие от них напряжения, выражаемые формулою
На основании формулы (53) имеем
	со ди ди*	VI mt а /л\ • n7ZX 7г =	” 21 V W S1H -г = дх дх	1	' '	1 п=1 со	t 2 Ж	• mtX С Е» / \ • ЛМ7С z	v 7 = аМ12	sin i	Hi(T)sin	i п = 1	0
полагая	a (t — т) = $,
получим	со	at ди	2	• mtx С у-,	• 717С$ =- —	===- > Sin -5- \ F, ( t	) Sin -J- di. дх	а2Мг	JJ	k «J	I n=l	0
но	a2 — y-,	— pa)Z,
поэтому будет	a = E^=	Ф(ж, t),	(54) dx	<0	'	7	7
причем	oo	at ф (x, o=42sin T	(? ~ 1)sin njTdv	(55> n= 1	0
Функция Ф (х, t) может быть найдена в простой замкнутой форме на
основании свойств рядов Фурье и функций, ими представляемых.
В самом деле, известно, что сумма
оо • I
2=42 sinT 5 /^sin	<56>
и = 1	О
представляет такую функцию 2 (ж), которая в промежутке от я = 0 до х~1
равна f(x), в промежутке от х — Ь до х~ — /эта функция равна —/( — ж),
вне же этого основного участка, т. е. от х= — I до х— -\-1, функция 2
определяется условием периодичности 2 (я+ 2/) = 2 (я). В местах разрыва
ряд представляет значение
l[2(e + 0) + Q(C-0)].
Нам величина нужна только для участка от х = 0 до х = Z, поэтому
мы ограничимся ее составлением для этого участка.
318	РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
1) Положим, что частное значение tr переменной t таково, что
О < а1х < Z,
тогда, если взять функцию /($) так, чтобы было
для 0<$<агх	=
>	/($) = 0,
то очевидно, что интеграл
I	ati
$ /($)sin^d5= $ Л £)sin^U
О	о
и, следовательно, сумма 21 Представляет такую функцию Ф(я, t), которая
такова:
для	Ф(я, t1) = F1Q1— ~
> atx^x<il Ф(ж, z1) = 0.
(57>
2)	Пусть частное значение t2 переменной t таково, что
I 62^2 2Z,
тогда положим
2Z “ бх^2 — h,
величина h будет меньше Z.
Очевидно, будет
al%	I	at%
О	О I
т. е.
а*2	I	at2
5 F* (?2 -1) sin ~Г -1) sin х di + i F*	- 4) sin nT di~
0	0	I
Сделаем в последнем интеграле
2z-e==e1,
тогда будет
а<2	I
CF162-r)sin^=-	(
J \. ay I	J* \ а /	•
I	21—atz
Следовательно, рассматриваемая сумма разложится на две и будет:
n=I	О
оо	I
2 хч • nizx С г? 2Z — 5
“7 2j SinT J -----------------7-JsinT~db
n=l	2Z—at 2
Первая сумма представляет такую функцию Фх (ж, t2), которая в про-
межутке от х = 0 до х = 1 равна
§ 100]	ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТВОЛА ОРУДИЯ ПРИ ВЫСТРЕЛЕ	319М
вторая сумма представляет функцию Ф2(я, t2), которая такова:
для 0<z<2Z — at2 Ф2(я. £2) = 0,
>	2Z—a£2<#<Z	Ф2(я, h)=Pi(j2 — 2Z"7>
следовательно, функция Ф (ж, t2) определяется условиями:
для 0<#<2Z — at2 Ф(^> Z2) = Z?,1^2 —,
» 2Z —aZ2<x<Z	Ф(я, tz) = Fi(t2—— ^1(^2— -Z ~х
3)	Пусть
21 < at3 < 3Z,
тогда будет
at8	I	21	ats
$ = \ ’
.0	О	I	21
соответственно этому и сумма 31 разобьется на три суммы, и нетрудно*
видеть, что первая сумма представляет такую функцию Фх(ж, /3), которая
в промежутке от х = 0 до х = I равна
Ч’~Ч
вторая сумма, послэ преобразования интеграла к такому виду, чтобы в нем.
верхний предел равнялся Z, будет со знаком — и представляет собою йа про-
тяжении от я = 0 до х — 1 функцию Ф2(я, 12), которая равна
Ч--ЧЧ
и, наконец, третья сумма представляет функцию Ф3(я, t3), которая в про-
межутке от ж = 0 до x = at3 — 2l равна
Ч'--^)
и в промежутке от x = at3 — 2l до х — 1 равна нулю.
Таким образом, будет:
для 0<ж<аг3 — 21:
Ф (х.	 л	- f) - F, (t„ - 2-^) + л
и для at3 — 21 < х < Z:
Ф (X, «8) = Fl (t3 -^-F. (t3 - 2-^) .
4)	Совершенно так же увидим, что если
3Z < at& < 4Z,
то функция Ф (х, £4) будет:
для 0<#<4Z— at±:
Ф (х,	= F, ) - Г,(<.-	+	('• -	
и для 4Z —
ф [х,	(<. -	+F. (<. - Ft у-уу.
и т. д.
320	РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Как видно, этими формулами вопрос решается вполне, ибо функция
F х(^) предполагается заданной для всего времени движения снаряда
по каналу, причем это задание может быть и графическое.
§ 101. Графическое представление полученного решения. Понятно,
что когда функция F± (t) задана графически, то и функцию Ф (х, t) надо строить
графически же. Это построение, на основании выведенных выше формул,
выполняется весьма просто.
Для наглядности сделаем сперва сводку формул, определяющих функ-
цию Ф(я, t) для различных значений времени Г.
1)	0<a^<Z,
0<a:<aZi, Ф(ж, G) = Fi(ti — 0,
at! < х < I, Ф (х, tj) — 0;
2)	Z<aZ2<2Z,
0<®<2Z —a<2, Ф(®, М =	—	>
21 -at2<х<I,	Ф (х, t2) = Fi(t2-^-F!(t2-	,
3)	2Z<aZ3<3Z,
0<x<aZ3-2Z,	=	+
aZg 2Z << a: < Z; Ф (x, t3) = Fx (ts — Fx (ts — - ) ,
и т. д.
Для составления графика следует принять определенное соответствие
масштабов для времени t и абсцисс я, именно, следует эти масштабы избрать
так, чтобы на чертеже промежуток времени
в течение которого звуковая волна, бегущая по металлу со скоростью а,
проходит путь, равный длине I орудия (стержня), изображался бы такою же
длиною, как и Z.
Затем напряжения
дх
которые пропорциональны Ф(я, t) или F1(t), изображать тою же кривою
Fr(t), но только читать ее ординаты в соответственном масштабе.
Пусть кривая (?Л1Л2Л3... (фиг. 60а) изображает в принятом мас-
штабе функцию jF\(Z). Помечаем на оси времен точки 7, 27, 37 и т. д.
Проводим на отдельном чертеже прямую Ох, откладываем по ней длину
АВ ~1~ОТ с первого чертежа и проводим концевые ординаты.
Положим, что надо построить функцию F (х, tr)\ тогда на первом чер-
теже (фиг. 60а) откладываем длину Ot±, изображающую промежуток вре-
мени Z, и на втором чертеже (фиг. 606) откладываем длину АОг~Ot±. С кри-
вой Fx(t) снимаем шаблон и, повернув этот шаблон точкою О вправо, при-
кладываем его так, чтобы точка О легла в и ось t совмещалась бы с осью х,
тогда точка tx ляжет в Л и ордината	ляжет по оси ЛФ; по шаблону
очерчиваем кривую САОА — эта кривая и представит функцию
которой равна Ф(я, £г) для значений х от я = 0 до я — atx = AO1. Для даль-
нейшего протяжения ОгВ эта функция равна нулю — напряжение еще не
поспело распространиться до конца В орудия (стержня).
§ 101]-
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПОЛУЧЕННОГО РЕШЕНИЯ
321
Положим теперь, что промежуток времени Z2 такой, что I < at2 < 21.
Выносим на первый чертеж (фиг. 60а) точку t2 по оси Ot, на втором
чертеже (фиг. 60в) проводим ось Ах и концевые ординаты через точки А и В;
Прикладываем шаблон кривой, изображающей Fx(£), так, чтобы ординаты
Z2C2 легли на оси А 1> и точка О легла на оси Ах в точку О2, такую, что
AO2 = Ot2,, и прочерчиваем пунктирно часть C2D кривой между осью О2Е
и концевою ординатою, —этот участок представит функцию
щаем на шаблоне ординату, проходящую через точку D и оборачиваем
шаблон так. чтобы точка О легла в О' и точка D легла бы в D'9 и обчер-
чиваем пунктирно кривую O'2D' —эта кривая представит функцию
По пунктирным кривым C2D и O'2D’ строим сплошную кривую С2ЕВ,
ординаты которой представляют алгебраическую сумму ординат кривых C2D
и O'2D'. Полученная кривая С2ЕВ и представляет функцию Ф(жх, Z2) для
рассматриваемого значения t2 времени t.
Физический смысл этого построения таков: распространяющееся по стволу
напряжение, достигнув дульного среза (свободный конец стержнд), отра-
жается, изменившись на противоположное, и распространяется с тою же
21 А. Н. Крылов
322
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
скоростью в обратную сторону, причем к рассматриваемому моменту t3 эта
отраженная волна достигнет точки 0'2> симметричной с точкой О2, в которую
она пришла бы, если бы стержень был неограниченным.
Совершенно так же для значения t3 времени такого, что 21 < at3 < 31?
наносим на первом чертеже (60а) точку t3, помечаем на шаблоне ординату
t3C3, накладываем шаблон на второй чертеж (фиг. 60г) так, чтобы эта орди-
ната шла по ЛФ, а начальная точка О шаблона лежала в точке О3 на оси
Ох. Прочерчиваем пунктирно часть C3D кривой между осью А и концевою
ординатою, помечаем на шаблоне ординату, проходящую через точку D,
оборачиваем шаблон так, чтобы точка О3 легла в О3 и точка D легла бы
в D', прочерчиваем пунктирно кривую CXD'. Между осью ОФ! и концевою
ординатою намечаем ординату, проходящую через точку С19 оборачиваем
шаблон так, чтобы точка О3 легла в О3 и точка О± в прочерчиваем кри-
вую С^Оз пунктирно. По ординатам пунктирных кривых C'Og, C3D,
строим сплошную кривую ЕНВ, ординаты которой равны алгебраической
сумме ординат трех предыдущих кривых, кривая ЕН В и представит функ-
цию Ф(я, t3). Как уже сказано, оборот шаблона соответствует отражению
волны от конца стержня; построение, как видно, состоит в том, чтобы волну,
которая в неограниченном стержне заняла бы положение C3DO3, собрать
отражениями с переменой при всяком отражении знака на участок между
концами стержня, иначе, между дульным и казенным срезом орудия.
Отсюда ясно, каким образом выполнять построения для любого момента
времени.
§ 102. Физическое истолкование полученного решения делает его почти
очевидным a priori: приложенная к концу х = 0 сила (Z) возбуждает в этом
конце натяжение, ей соответствующее, этому натяжению отвечает определен-
ное относительное удлинение материала (расширение), это расширение (волна
расширения) бежит по длине стержня со скоростью распространения звука
по металлу, достигает свободного конца, от него. отражается, превращаясь
в волну сжатия, и бежит обратно к первому концу, достигнув которого
вновь отражается, обратившись вновь в волну расширения и т. д., причем
действие силы служит постоянным источником все новых и новых волн. Все
эти волны не выходят из стержня, отражаясь от концов его, образуют,
§ 105]
ВИБРАЦИЯ СУДОВ. ОБЩИЙ МЕТОД РАСЧЕТА
323
накладываясь друг на друга, сложную систему равнодействующей волны
напряжений.
§ 103. Если бы встретилась надобность построить не только величины
напряжений, но и самих перемещений, то для каждого данного момента вре-
мени мы имеем соотношение
х
С ди ,
и= \ — ах.
J дх
0
Но вместо того, чтобы интегрировать всякий раз кривую^, проще
сперва по заданной кривой Fi(Z) построить ее интегральную крив)ю
t
о
а затем с этой кривою поступить совершенно так же, как мы поступали
с кривою Fr (Z^, — получится распределение упругих перемещений по длине
ствола, в масштабе, определяемом величиною
Если бы потребовались и абсолютные положения каждого сечения
по отношению к неподвижному началу, то к исчисленным величинам и надо
присовокупить величину uQ перемещения всего стержня, как неизменяемого
тела, рассчитав и0 по формуле
с г
1 о о
Таким образом, случай колебаний однородного упругого стержня, воз-
буждаемых действием переменной силы, приложенной к одному из его кон-
цов, а значит, и простейший случай продольных колебаний ствола орудия,
получает полное решение, весьма наглядное, простое и удобное для практи-
ческого пользования им.
§ 104. О вибрации судов. На многих судах, снабженных поршневыми
машинами, замечается следующее явление: при некотором определенном
числе оборотов корпус корабля испытывает сильные сотрясения (вибрации),
которые пропадают почти совершенно, как только число оборотов будет
изменено в ту или другую сторону на 4 — 5% от вышеупомянутого «крити-
ческого».
На судах с весьма быстроходными машинами иногда замечается два
критических числа оборотов, значительно отличающихся друг от друга..
Уже самый характер явления показывает, что мы имеем здесь случай
резонанса: корабль представляет собою громадную упругую балку перемен-
ного сечения. Такая балка, подобно балке постоянного сечения, имеет вполне
определенные частоты свободных колебаний; если в машине силы инерции
движущихся частей не вполне уравновешены, то при работе этой машины
происходят периодические усилия, воспринимаемые фундаментом ее; перет
даваясь корпусу корабля, они и вызывают его вибрацию.
Таким образом, вибрация корабля представляет собою вынужденные
колебания. Наша задача состоит в вычислении их.
Таким образом, мы имеем такую задачу: даны возмущающие силы
и пары, происходящие от неуравновешенных сил инерции движущихся частей
машины, требуется вычислить вибрацию, которая будет происходить на дан-
ном корабле при работе на нем этой машины.
§ 105. Положим сперва, что все неуравновешенные силы инерции
машины приводятся к одной вертикальной силе, лежащей в диаметральной
21*
324	РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН (Гл. Vlj
плоскости корабля, тогда можно принять, что на корабль действует внешняя
сила
R = — Q sin kt,
приложенная в некоторой точке, лежащей в машинном отделении; пусть
с есть абсцисса этой 1очки, считаемая от кормового перпендикуляра.
Сила R производит двоякого рода действие: 1) колебательное движение
всего корабля, рассматриваемого как неизменяемое твердое тело, и 2) упру-
гие колебания корабля, составляющие его вибрацию*
Колебания первого рода состоят из килевых качаний корабля и верти-
кальных колебаний его; В общем случае и те и другие слагаются из коле-
баний свободных и вынужденных, но, вследствие сопротивления воды, сво-
бодные колебания весьма быстро погашаются и остаются одни вынужденные.
Так как период силы весьма мал по сравнению с периодами упомяну-
тых свободных колебаний корабля и сопротивление сравнительно не велико,
то вынужденные колебания определятся из уравнений
Со — Qp Sin kt,
(1)
0" + j = _	) sin kt,
т. е. из уравнений вертикальных и килевых качаний корабля, пренебрегая
сопротивлением воды, где
причем Р есть вес корабля, S — площадь его грузовой ватерлинии, q — вес
кубического метра воды (пресной 1000 кг, соленой 1025 кг), К—мылвт
инерции корабля около поперечной оси, — а) — возвышение продольного
метацентра над центром тяжести корабля.
Из уравнений (1) следует
г -	1 -in kt
^0— р п*— £2Sin/df>
n Q I — 2c 1	. , .
9=£-2-Z=nr*sinA/-
Величины n2 и p2 весьма мал л по сравнению с к2 ^меньше поэто-
му можно писать
Со = a sin kt,
a sin kt,	(2)
причем
Положение продольной недеформированной оси корабля, совершающего
вышеприведенные колебания, очевидно, будет
С = чо -I- & (я —	= (b+ ах) sin kt,
положив
b — a—
al
T
§ 106]
ВИБРАЦИЯ СУДОВ. ОБЩИЙ МЕТОД РАСЧЕТА
325
Для численных примеров, приводимых ниже, взято:
	Q 1 . 1 ЛАЛ .	1 7 1 7	1 >. 7 TtJV тг7б
Р ~ 100 ’	Л> с — 2	3 Z и 6^’	— 30 - 30 ’
/,- 63.25;	=
тогда по вышеприведенным формулам имеем:
при с = - I а — 0.155 ел/, а =	0$	b =* 0.155 см,
» с = ^1 а = 0.155 см, (I—— 0.000051, 6 = 0.410 см,
О
» с = -^-1 а = 0.155 см, а =—0.000102, 6 = 0.665 см.
О
По этим данным положение продольной оси корабля, в недеформиро-
ванном состоянии, легко наносится для любого момента времени Z.
Заметим, что формулу (2) можно получить сразу из уравнений
у — Qsin kt и Kh" = — Q^c — y^sinAtf,
представляющих колебания не плавающего, а свободного тела.
Так как паша задача состоит в определении вибраций корабля (коле-
бательное его движение исключается из окончательного результата), то можно
принимать корабль, плавающий на тихой воде, за свободное тело, находя-
щееся в равновесии. Это допущение равносильно отбрасыванию влияния:
1) изменений пловучести, происходящих от вышеуказанного колебательного
движения, и 2) сопротивления воды.
Легко видеть, что влияние изменений пловучести на вибрацию ничтожно
мало, сопротивление же воды погашает свободные упругие колебания, почти
не влияя на вынужденные, за исключением случаев почти полного син-
хронизма.
§ . 106. При вычислении статических прогибов корабля и напряжений, про-
исходящих от данного изгибающего момента, корабль принимается за упру-
гую балку, поперечными размерами которой пренебрегают по сравнению
с ее длиною Z; при тех же предложениях будем вычислять и вибрацию.
Пусть «жесткость», т. е. произведение момента инерции J площади
поперечного сечения корпуса корабля на модуль упругости Е материала
(стали), есть заданная функция
EJ~f(x),
и отнесенная на один погонный метр приведенная масса есть также задан-
ная функция
абсциссы х рассматриваемого сечения, w (х) есть вес корабля вместе с весом
увлекаемой воды (стр. 330) на один погонный метр, g—ускорение силы
тяжести.
При указанных предположениях и обозначениях очевидно, что опреде-
ление вибрации г корабля равносильно задаче об определении вынужденных
упругих колебаний балки, оба конца которой свободны под действием силы
/?= — ()sinZtf,
приложенной в точке х — с.
326
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Эта же последняя задача выражается математически следующим
образом:
Требуется найти такую функцию v переменных независимых х и t,
которая удовлетворяет:
во-первых, дифференциальному уравнению
<?2 Г 4	\ ll / \ Т? /	#\
во-вторых, граничным условиям:
А	-	д2У А	д3У А при х = 0 должно оыть — = 0 и ^-§ = 0, 0QC	(УХ
7	d2v А д3у А >	Х=^1	>	>	и п“з=0, дх2	дх3
(3)
(4)
в-третьих, условиям сопряжения, которые состоят в том, что при х ~ с»
где действует сосредоточенная внешняя сила, значения
dv
V* дх * дх2
d3v
остаются непрерывными, значение же претерпевает разрыв непрерывно-
сти, так что
= 77-r^sin kt.	(5)
6_>0	V**3A+e /(С) Y	V 7
Начальные условия нет надобности рассматривать, ибо ищется вынуж-
денное синусоидальное колебание того же периода, что и вынуждающая
сила.
Функция F (х, t) в правой части уравнения (3) представляет отнесен-
ную на один погонный метр «внешнюю» нагрузку, действующую на балку
в момент времени t в точке, абсцисса коей есть х\ в нашем случае она сво-
дится к силе инерции колебательного движения корабля, рассматриваемого
как неизменяемое твердое тело, и следовательно, будет
ж:
F(x, t)=-q(x)d^,	(6)
причем
С = Со + (х — б = (6 + ах) sin kt
И
• , I
Ь — а — а-^.
По подстановке в уравнение (3) получаем
£[/(*)£] +?(ж)|^=А:2(б+аа:)?(ж)sin^’ <3')
и, положив
v — и — (Ь + ад) sin kt,	(7)
имеем
£.[/w£]+’W$=°-	<8>
Условия граничные и условия сопряжения будут:
при я —О должно быть — = 0 и ^ = 0,
§ 106]
ВИБРАЦИЯ СУДОВ. ОБЩИЙ МЕТОД РАСЧЕТА
327
Величины и, — , при х = с непрерывны:
lim f@sin Atf.	(5')
е_>о	8A-s e^o<^ /c+8 /(c)Y	4
Таким образом, наша задача приведена к определению функции и,
представляющей «чистые» упругие колебания или вибрацию корабля. Для
определения этой функции подразделим полную длину I корабля сечением
= с на две части, из которых первая заключается между значениями
# = 0 и х = с,
вторая — между значениями
я = с и Х = 1)
причем абсцисса х считается от кормового перпендикуляра.
Для первой части полагаем
и = (?!(#) sin kt4	(9)
для второй части удобнее считать абсциссы от носового перпендикуляра,
поэтому, положив
берем
и = ф2 (хг) sin kt\	(10)
наша задача сводится к определению функций «рДя) и <р2(жх).
Положив
и подставив выражения (9) и (10) в уравнение (8), получим для определе-
ния функций <рх и <р2 обыкновенные дифференциальные уравнения
(*)££] -^(х)?1 = 0,	(И)
(12)
Оба эти уравнения — линейные, четвертого порядка, следовательно, их
общие интегралы содержат по четыре произвольных постоянных и притом
линейно. Значения этих постоянных определяются условиями граничными
и условиями сопряжения.
Мы примем, что функция / (х) не равна нулю ни при х = 0, ни при
xc = Z; тогда граничные условия выражаются уравнениями
?i(0) = 0, ф'1"(0) = 0,
ч4(0) = 0, ?Г(0) = 0;
условия сопряжения суть
<Р1 (с) = 9а (I — с)> ф 1 (с) = — ?2 (I — с),	(с) =	— с),
?Г(с)= -Ф2"(г-с)+т^<?.	(14)
причем, как обыкновенно, производные обозначены штрихами. Знак минус
при производных нечетного порядка функции <р2 приписан потому, что про-
изводные надо брать по переменной х, аргумент же функции <р2 есть
x^l — х, поэтому будет, например,
328
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
ГГл. VII
Прежде чем переходить к численным расчетам, необходимо сделать
«приведение» нагрузки, учитывая добавочную массу воды, увлекаемую
кораблем при вибрации.
Для производства этого учета, в статье I. Lookwood Taylor «Vibration
of ships» (Tr. Inst. N. A.,. 1930) указан следующий способ: объем воды,
увлекаемый каждым сечением корабля, отнесенный к единице длины, про-
порционален погруженной площади этого сечения А(х), отношению b : 2d
ширины сечения при грузовой к его удвоенному углублению 2d, причем
коэффициент пропорциональности С есть произведение чисел Сг и С2, пока-
занных в ниже приводимых таблицах.
Коэффициент С] показан для сечений трех видов:
I.......прямоугольник,
II......треугольник,
III.....две дуги круга.
В таблице 9 L есть длина корабля, В—наибольшая ширина его.
Таблица 8
Коэффициенты Сг
Форма сечения I		Форма сечения II		Форма сечения III	
b/d	С.	b/d	С,	b/d	Сг
4	1.07	2	1.19	2	1.00
3	1.12	1.5	1.23	1.5	1.03;
2.5	1.15	1	1.06	1	1.04
2	1.19	0.5	0.98	0.5	1.01
Коэффициенты
Таблица 9
Отношение: L : В	6	7	8	9	10
С2 (две узловые, точки) . . .	0.674	0.724	0.764	0.797	0.825
С2 (три узловые точки) . . .	0.564	0.633	0.682	0.723	0.760
Таким образом, для сечения, абсцисса коего есть х19 будет
j, (I) = С | Л (г),
б
где у есть масса единицы объема воды, q2 (х) — добавочная масса. Обозна-
чая через (я) массу, рассчитанную по кривой полной нагрузки корабля,
получим «приведенную массу», для сечения, коего абсцисса есть х, па
формуле
?(®) = 91(я) + &(ж).
Эта приведенная масса и вводится в расчет вибрации.
§ 1071
МЕТОД ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
329*
§ 107. Метод численного интегрирования. Наметив общий ход расчета,
необходимо показать, каким образом он на самом деле выполняется. Это
может быть сделано лишь на численном примере, применяя для интегри-
рования уравнений (11) и (12) метод приближенного численного интегри-
рования, в данном случае метод Штермера, подробное изложение которого
можно найти во многих статьях моих по этому предмету, а также в моем
курсе «Лекции о приближенных вычислениях». Здесь же дл. ясности приведем
его сущность.
Метод Штермера развит его автором в применении к уравнениям вида
g = /(«.	(15)
и начальных условий: когда x = xQ, то должно быть
У = Уо * (Юо = ^’	(15,)'
причем у0 и у' задаются численно.
Проинтегрировать уравнение (15) численно—значит составить таблицу
значений искомой функции у, удовлетворяющей уравнению (15) и усло-
виям (15'), для ряда последовательных, обыкновенно равноотстоящих значе-
ний аргумента х, начиная с x = xQ.
Пусть эти значения аргумента будут
xQ, x1 = xQ + hy x2 = xQ + 2h, ..., xn = xQ-\-nh
и соответствующие им значения функции у:
Уо> Ух» У2, •• •> Уп-
Метод Штермера состоит в применении следующего процесса к про-
должению таблицы этих значений.
Пусть будет
^л = Л2/(^п,^п),	(16)
и положим, что составляются следующие две таблицы:
п	хп	Уп	Д?/п	Д22/п
п—к	ХП-4	Уп-1	ДУл-4	
п—3	^П-З	Уп-ь	ДУп—з	Д22/л-4
п—2	ХП—2	 Уп-2	Дул-2	Д23/л-з
п—-1	ХП-1	Уп-i	Дул-1	Д2Уп-2
п	хп	Уп	Дул	Д2Ул-1
п + 1	ХП+1	Уп+1		
Таблица 10	Таблица И
Чп		Д2Чп	Д*1л	Д4Чп !
Т)п-4 ’In-S Чп-2 ’In-i Тт	Д^П-З ^ln-i	Д‘Чп-4 Д’Чп-З	Д’Чл-4 Д’Чп-3	Д4Чл-4 (
и что при составлении их мы дошли до значения уп, соответствующего*
значению х~хп. Чтобы продолжить таблицы, надо составить значение,
соответствующее я = яп+1, причем табличный промежуток h выбранг
настолько малым, чтобы разности четвертого порядка величины т) можно
I
330 РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
было считать постоянными, с тою степенью точности, с которою вычисле-
ние производится. Тогда по данной проф. Штермером формуле:
&Уп-1 = + ^ [ ДЧ.-2 + Д^п-З + Д4,»)п-4 — ДЧ.-4 ] .	(17)
•вычисляем величину Д2уп__1, пользуясь, как видно, числами, стоящими
в нижней косой строке таблицы И, и вписываем эту величину в свое место
таблицы 10, как показано прямым шрифтом; затем имеем
Д?/п= Аг/п-1+ Д2?/п-1,
Уп+1 = Уп + Дг/П>
причем эти величины сразу вписываются в свои места; таким образом
таблица 10 будет заполнена до указателя п + 1.
После того как yn-i-i вычислено, вычисляем 7)n+i по формуле
7)п+1 = Л2/(жп+1, г/п+1),
выписываем в свое место таблицы 11 и, составив разности, заполняем косую
^строку, начиная с 7)n+j, й продолжаем таким образом далее, пока не дойдем
до того крайнего значения аргумента, на котором таблица заканчивается.
Если взять промежуток h настолько малым, что можно пренебрегать
третьими или четвертыми разностями величины tj, то формула (17) прини-
мает весьма простой вид
Д2Уп-1 = т1П +	(18)
и вычисление идет весьма быстро.
Чтобы начать вычисление, стоит только взять h настолько малым,
чтобы в формуле (18) можно было ограничиться одним первым ее чле-
ном, т. е.
Д2г/п-1 = ^п.	(18')
Тогда будем иметь
п = 0:	Уп~~Уо (задано),
п = 1:	=	= +
V)! = А2 / (л?!, г/х),
и таблицу можно будет продолжать как объяснено выше, увеличив про-
межуток h так, чтобы пользоваться формулой (18) или (17).
§ 108.	Чтобы применить этот метод к нашему случаю, надо прежде
всего привести уравнения и начальные условия к соответствующему для
применения метода Штермера виду.
Возьмем сперва уравнение (11) и полагаем
(19)
тогда уравнение (11) принимает вид
Л2 ?(*)?!•	(20)
Таким образом, уравнение (11) заменяется эквивалентною ему системою
(1Г)
§ 108]	МЕТОД ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ	331
к которой метод Штермера непосредственно был бы применим, если бы
были заданы начальные значения
(21)о. «)о» (?1)о и (<р;)0,
соответствующие значению х — 0 аргумента.
В предположении, что / (0) не равно нулю, имеем, на основании урав-
нения (13), при ж = 0
z1 = (z1)o = O и z[ — (zx)o = O,	(21)
но величины <рх (0) и <рх (0) остаются произвольными, поэтому полагаем
?1(0) = А, = <	(22
и принимаем Лх и Вг за произвольные постоянные.
Так как уравнения (11') линейные, то будет
?i («)=(») + Bi Ф1 (®) + G	(«)+Л Xi. (^),
причем А19 В19 С19 Z)x — произвольные постоянные, <оА(ж), фх(я), ах (х)
и /х (х) — независимые частные решения системы (11'). Линейно независимые
частные решения всегда можно выбрать таким образом, чтобы произволь-
ные постоянные А19 В19 Cl9 представляли начальные значения фун.ций
z1 и срх и их первой производной z'± и ср'; поэтому можно положить
^1==(21)о> -®1 = (21)о>	(21')
а тогда, на основании равенств (21), будет
C1^=D1 = 0
и остается
?i (х) = Лхо)х (ж) + Вг фх (ж).	(23)
Величина z± содержит те же произвольные постоянные Аи В19 С19 D1
и также линейно, поэтому полагаем
zi~ А1У1 +	,	(24)
причем г/х и $х — также два независимых между собою частных решения
системы (11').
Таким образом, вместо двух неизвестных функций zx и <рх мы будем
искать четыре функции «)х, фх, уг и $х, удовлетворяющие той же системе (11'),
и для этих функций мы можем выбирать начальные значения по произволу,
надо лишь брать их так, чтобы выполнялись условия (21') и (22), т. е.
чтобы было
-41 (У1)о + Вг ($Х)0 — 0,
АШ + ях(*;)0 = о,	(21)
Лхо)х(0) + 5хф1(0) = Alf	zoom
лхш;(0) + вхф;(0) = £х.	( 2)
Очевидно, эти условия будут удовлетворены, если взять
(У1)о = 0. (У1)о = 0> ш1(0) = 1, ю'(0) = 0,
(*i)o=o, W)o=o, <мо)=о,	( }
332
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. УГГ
причем неизвестные функции	определяются уравнениями
У1 = k2q (х) «h,
„ 1
®1 = ~ГГ\ У1>
1	/(я)»1’
S'i = A2 g(«)<j>x,
(26>
(26')
к численному интегрированию которых метод Штермера теперь непосред-
ственно применим.
Совершенно таким же образом надо поступать и для определения
функции <p2(#i)> относящейся к промежутку от х=с до х = 1 или от хг= О
до — с. У нас будут совершенно те же начальные условия, только
вместо независимой переменной х будем иметь переменную х19 поэтому
мы представим функцию <р2 формулой
(%) = Л о>2 (хг) + В2 ф2 (а^),	(23'}
причем А2 и В2 — произвольные постоянные, введем вспомогательные
функции у2 и ^2* так что наши четыре неизвестные функции
г/2(жх), ^2{хх) s^xj и
будут определяться уравнениями

Й, _ ,	<26'>
/1 (xj ^2’
j.;, ,	(26л >
dxi f1(x1) 82
и начальными условиями: при хг = 0 должно быть
(z/2)o = o> (^2)0 = 0, ш2(0) = 1, о>;(0) = 0,
(82)о = О, (s')o = O, ф2(0) = 0, Ф'(0)=1.
§ 109. Определение постоянных произвольных. Прежде чем перехо-
дить к численному примеру, надо показать, каким образом определяются
произвольные постоянные Въ А2, В2 по условиям сопряжения..
При сделанных обозначениях эти условия будут
+-®1Ф1(С) =	А2ю2(1 — с) + В2$2(1 — с),
А<“1'(с) +5^1 (с) = — [A<d'(^~c) +Sz^2(l-c)],
A®l(c) +5!^(c) =	Л2<0"(/ —с) +В2Щ(1 — с),	(27))
А ®1" (с) + Bi ’J’i" (с) = — [Л w2" (1 —с) -И в2 ¥2" (1 -с)] +•	<?>
Прежде всего необходимо заметить по поводу этих уравнений, что»
мы не будем иметь аналитических выражений функций о^, со2г ф2>,
а лишь таблицу значений этих функций и их вторых производных, нам же?
надо, кроме того, иметь первую и третью производные. Для нахождения1
их значений надо будет воспользоваться, как для всяких табличных
функций, формулою Стирлинга, которая будет приведена ниже, и при-
менение ее пояснено на численном примере.
В общем случае определитель системы уравнений (27) не будет равен
нулю (он обращается в нуль в трэд случае, когда число оборотов машины
§111] влияние местной жесткости на оБщуй) вибрАцйв^	333
равно частоте одного из основных «свободных» уп^у^их
корабля), поэтому уравнения (27) доставят вполне определенные
постоянных Blf А2, В2> причем все эти значения будут.
1
Множитель т* е- будут вида
^2 =/"(3) Са2> ^2==Дё)^2’
где а,, а2, blt b2 будут известные числа, таким образом будет
и =	[<?!«>! (ж) + £>!<!>! (я)] sin для 0<ж<с,
7 \с)
и = [аг о>2 (®i) + Ь2 Ф2 (жг)] pin kt для с<ж</,
7
колебаний
значения
содержать
(28)
(29)
причем жх = Z—ж; по уравнению (7) полное движение корабля, состоящее
из его упругих колебаний (вибрации) и качаний как неизменяемого
плавающего тела, будет
v = и— (Ь 4- аж) sin kt-	(20)
Эти формулы и заключают полное решение поставленного вопроса.
§ ПО. Мы предположили, что определитель системы (27) не равен
нулю. Значение этого определителя зависит от величины к9 т. е. от числа
оборотов машины, представляющего «частоту» изменяемости возмущающей
силы. При «критическом» числе оборотов имеет место резонанс, и опре-
делитель системы обращается в нуль, и, значит, решение стало бы беско-
нечным, как и вообще при резонансе и отсутствии погашения.
На практике амплитуда вибрации в этом случае зависит от сопро-
тивления воды этим колебаниям; вычислить эту зависимость невозможно,
если не сделать каких-либо более или менее произвольных допущений,
входить в рассмотрение которых не будем, заметив лишь, что при таком
резонансе и неуравновешенной машине вибрация становится настолько
значительной, что такого числа оборотов держать нельзя и надо, его изме-
нить на 4 — 5%, увеличив или уменьшив.
Таким образом, если бы при расчете оказалось, что определитель
системы (27) равен нулю, то это служило бы признаком резонанса и кри-
тического числа оборотов, но может быть, что определитель не равен
нулю, между тем число оборотов близко к критическому, и вибрация
значительна, спрашивается, по какому признаку можно об этом судить.
Для этого стоит только, имея кривую «жесткости» корабля El = j(x)y
рассчитать по заданной нагрузке Q статическую деформацию или наиболь-
шую стрелку прогиба, этою нагрузкою вызываемую, и сличить величину
это о прогиба с наибольшею амплитудою вибрации. Это сличение и даст
ответ на поставленный вопрос»
§ 111. Влияние местной жесткости на общую вибрацию. Присутствие
1
множителя -7-г-т в
/ (с)
выражении и приводит к замечанию, имеющему непосред-
ственное практическое значение, не только в случае корабля, но во всех
аналогичных вопросах. Формулы (29) представляют чистую вибрацию корабля,
т. е. ту, которая замечалась бы наблюдателем, находящимся на корабле,
причем эта вибрация считается от принимаемой за неизменную продольной
оси корабля; мы получим более ясное представление об этой вибрации,
и притом подлежащее непосредственному наблюдению, если мы отнесем
334
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
вибрацию не к оси корабля, а к другой прямой, которую мы получим,,
соединяя в любой момент t точки
(я = 0, z — (0)) и (rc = Z, £ = <Р2(О))>
т. е. его оконечности в деформированном состоянии. Отступления от этой
прямой и будут представлять, так сказать, «искривление» корабля при
вибрации.
Пусть будет
z — ух + 8
— уравнение сказанной прямой, очевидно, что у и 3 будут также содержать
1
множитель ; составляем разности
Fz (Хх) = ъ (х.) - [у {I - Ж1) + 8]	(31>
и получаем
w = (х) sin kt для 0<ж<с,
w = F2(z)sin kt »	c<#<Z.	^2)
Тогда функция о (я), равная ±^1(ж) в промежутке от 0 до с и равная
в промежутке от с до Z, представит крайние величины искривления
корабля при вибрации. Очевидно, что оно будет также пропорцио-
нально , как и амплитуды вибрации.
Присутствие делителя /(с), представляющего «жесткость» в месте
приложения силы R, показывает, что с увеличением этой местной жест-
кости уменьшается общая вибрация корабля.
Мы показали, как рассчитывается действие одной сосредоточенной
силы, но практически на корабль будут действовать несколько сил, точки
приложения которых расположены в районе машинного отделения; отсюда
ясно, что для уменьшения вибрации надо увеличивать жесткость корабля
в районе машинного его отделения как устройством фундаментов под
машину, так и взаимною связью палуб, надлежащим устройством кожуха
машинного люка и пр. Практика вполне подтверждает этот теоретический
вывод. Вот почему на судах «Нефтесиндикат СССР» и «Советская Нефть»
по моему проекту выполнена весьма солидная арочная связь в машинном
отделении. Подобная связь начинает теперь входить в практику загранич-
ного судостроения.
§ 112. Численный пример. Перейдем теперь к пояснению самих
численных расчетов и способа их производства. Мы будем предполагать,
что для данного корабля составлены кривые «жесткости» и «нагрузки».
По этой последней, разделив ординаты на ускорение силы тяжести g, полу-
чаем и кривую q(x) «распределения приведенных масс».
Меры, для простоты рассуждений, будем предполагать метрическими.
Произведение EJ при обычных единицах (тонны и сантиметры) обыкно-
венно выражается громадными числами, с которыми, даже при упрощенном
начертании их (например 2.573 • 109), оперировать неудобно; при счете
логарифмической линейкой надо следить за показателями 10, причем легко
ошибиться, а ошибка в показателе влечет весьма крупную ошибку
в результате; поэтому удобнее распорядиться так, чтобы с такими боль-
шими числами дела не иметь. Мы этого достигнем, если будем вести весь
расчет в величинах относительных, и лишь окончательный результат
переведем в абсолютные.
§ 112]
ЧИСЛЕННЫЙ ПРИМЕР
335-
Обозначим через /0» Qo значения / (у) и ? (у) * т> е* ПРИ миДеле‘>
обыкновенно это будут и наибольшие значения этих величин; тогда можно*
писать
/о	Уо
Сделаем х = Ц и положим
ф=№	(33>
тогда уравнение (11) напишется так:
jf, [»(?)^] — Ar1p(g)Ti = °,	(34}
^ = 42^/4.	(35)
Соответственно этому уравнения (26) будут
(36>
и условие (15'), при $ = 0, должно быть
2/1=0,	ю1=1’ 7?=0-	(36')
Точно так же уравнения (26'") будут
^=aT")S2’ ё =	(37)
U-C.^ (А
и условие (25'), при ^ = 0 (где 1 —?), должно быть
S2 = °, ^=0, ф2 = 0, g^ = l.	(37')
Как видно, здесь Е будет отвлеченное число, изменяющееся от 0 до 1;’
функции а(;) и [3(c) будут также отвлеченными числами, независимыми от
принятых единиц мер.
Чтобы избежать грубых ошибок, полезно составить приближенную
величину постоянной кх для корабля обычного типа.
Величина момента инерции площади связей Zo определяется из равенства
т -мн
*0 ф >
где М — изгибающий момент, Н — удаление от нейтральной оси до опасней-
шей фибры, Т — допускаемое напряжение.
Приближенно можно положить, обозначая через Р вес корабля,
»=»'•
Тогда будет
Т 1
7°““ 400 Т
и, значит,
336
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
Е
Отношение — не зависит от принятых единиц мер и составляет для
встали около 2000; значит, будет приближенно
/о = 5Р^.
Вычисление Вели-
са" у,
а(<0
при £ = 0 должно быть: у = 0,
п 30 с 30 £х	»(С)	?(?)	л» «(<)		со	До>	Д2О)
0	0.1045	0.0523	0.01063	0.01195	1.0000	0.00000	0.00006
1	0.20,79	0.1564	0.00535	0.03570	1.0000	0.00006	0.00021
2	0.3090	0.2588	0.00360	0.05920	1.00006	0.00027	0.00045
3	0.406,7	0.3584	0.00273	0.08200	1.00033	0.00072	0.00078
4	0.5000	0.4540	0.00222	0.1039	1.00105	0.0015	0.00122
5	0.5878	0.5446	0.00189	0.1245	1.0026	0.0027	0.00176
6	0.6691	0.6293	0.00166	0.14 8	1.0053	0.0045	0.00242
7	0.7431	0.7071	0.001495	0.1615	1.0098	0.0069	0.00322
8	0.8090	0.7772	0.001373	0.1775	1.0167	0.0101	0.00417
9	0.8660 г	0.8387	0.001283	0.1918	1.0268	0.0143	0.00528
10	0.9136 ।	0.8910	0.001215	0.2035	1.0411	0.0196	0.00662
И	0.9511 (	0.9336	0.001169	0.2135	1.0607	0.0262	0.00819
12	0.9782	0.9659	0.001136	0.2205	1.0869	0.0344	0.01005
13	0.9945	0.9877	0.001119	0.2254	1.1213	0.0444	0.01225
14	1.0000	0.9986	O.OOlllj	0.2280	1.1657	0.0567	0.01482
15	1.0000	1.0000	O.OOllli	0.2285	1.2224	0.0715	0.01767
16	> 1.0000	0.9986	O.OOlllx	0.2280	1.2939	0.0892	0.02102
17	0.9945	0.9877	0.001119	0.2254	1.3831	0.1103	0.02495
18	0.9782	0.9659	0.001136	0.2205	1.4933	0.1352	0.02982
19	0.9511	0.9336	0.001169	0.2135	1.6285	0.1650	0.03574
20	0.9136	0.8910	0.001215	0.2035	1.7935	0.2007	0.04317
21	0.8660	0.8387	0.00128g	0.1918	1.9942	0.2439	0.05256
22	0.8090	0.7772	0.001373	0.1775	2.2381	0.2965	0.06473
23	0.7431	0.7071	0.001495	0.1615	2.5346	0.3612	0.08104
24	0.6691	0.6293	0.00166	0.1438	2.8958	0.4422	0.1033
25	0.5878	0.5446	0.00189	0.1245	3.3380	0.5455	0.1355
26	0.5000	0.4540	0.00222	0.1039	3.8835	0.6810	0.1852
27	0.4067	0.3584	0.00273	0.08200	4.5645	0.866	0.270
28	0.3090	0.2588	0.00360	0.05920	5.431	1.136	0.444
29	0.2079	0.1564	0.00535	0.03570	6.567	1.580	
30	0.1045	0.0523	0.01063	0.01195	8.147		
Примечание. Эги же таблицы служат для определения величины
=» 1.0411, а>2 = 1.7935. Для вычисления служат формулы
A2a)n-i == ^п. +	А2^п-а>
Вычисления начинаются следующим образом: так как <d0 — 1 и <о' = о, то в пер
аа, а также Доо, Дах, Д%. По формулам
Д*/о == у№ + °0 + 4 Дао “ д2°0’
находим Ду0, Д2у0 и по ним определяем yY и у2. По неизвестным у0, yLt находим
Эти разности вместе с <о0 = 1.00 дают исправленные значения а>х и о>2. Исправления
Д*у, по ним определяем а>3, у3 и т. д.
§ 112]
ЧИСЛЕННЫЙ ПРИМЕР
337
Чтобы получить приближенную величину д0, вообразим, что кривая
нагрузки совпадает со строевою по шпангоутам (кривая площадей погружен-
ной части шпангоутов), эту же последнюю примем за синусоиду, так что будет
q (х) — q (Zc) = 90 sin у = ?0 sin
Таблица 12
чин <о и у
у' = 0, о> = 1, <о' = О
^==0.2285,
£n = nh
	> h2 Л==	ДХ	Д2А.	У	• Ду	Д*У		Да	Да а
	0.0000	0.00005	0.00010	0.0000	0.0100	0.0357	0.01195	0.02375	-0.00025
	0.00005	0.00015	0.00009	0.0100	0.0457	0.0592	0.03570	0.02350	—0.00067
	0.00020	0.00024	0.00009	0.0557	0.1049	0.0820	0.05920	0.02283	—0.0008
	0.00044	0.00033	0.. 00011	0.1606	0.1869	0.1039	0.08203	0.0220	—0.0012
	0.00077	0.00044	0.00010	0.3475	0.2908	0.1247	0.1040	0.0208	—0.0010
	0.00121	0.00054	0.00012	0.6383	0.4155	0.1445	0.1248	0.0198	—0.0013
	0.00175	0.00066	0.00014	1.0538	0.5600	0.1629	0.1446	0.0185	—0.0010
	0.00241	0.00080	0.00015	1.6138	0.7229	0.1804	0.1630	0.0175	-0.0010
	0-00321	0.00095	0.00016	2.3367	0.9033	0.1969	0.1805	0.0165	-0.0015
	0.00416	0.00111	0.00022	3.2400	1.1002	0.2119	0.1970	.0.0150	-0.005
	0.00527	0.00133	0.00024	4.3402	1.3121	0.2265	0.2120	0.0145	— 0.0013
	0.00660	0.00157	0.00029	5.6523	1.5386	0.240	0.2265	0.0132	0.0000
	0.00817	0.00186	0.00033	7.1909	1.779	0.253	0.2397	0.0132	0.0000
	0.01003	0.00219	0.00038	8.970	2.032	0.266	0.2529	0.0131	0.0005
	0.01222	0.00257	0.00029	11.002	2.298	0.280	0.2660	0.0136	0.0021
	0.01479	0.00286	0.00047	13.300	2.578	0.295	0.2796	0.0157	0.0010
	0.01765	0.00333	0.00059	15.878	2.873	0.312	0.2953	0.0167	0.0010
	0.02098	0.00392	0.00093	18.751	3.185	0.330	0.3120	0.0177	0.0005
	0.02490	0.00485	0.00105	21.936	3.515	0.348	0.3298	0.0182	-0.0011
	0.02975	0.00590	0.00150	25.451	3.863	0.366	0.3480	0.0174	—0.0005
	0.03565	0.00740	0.00195	29.314	4.229	0.383	0.3657	0.0169	—0.0025
	0.04305	0.00935	0.00275	33.543	4.612	0.397	0.3826	0.0144	-0.0016
	0.05240	0.01210	0.00410	38.155	5.009	0.410	0.3970	0.0128	—0.0066
	0.06450	0.01620	0.0059	43.164	5.419	0.415	0.4098	0.062	—0.0073
	0.08070	0.0221	0.0098	48.583	5.834	0.414	0.4160	-0.100	-0.0105
	0.10280	0.0319	0.0172	54.417	6.248	0.403	0.4150	-0.115	—0.0180
	0.1347	0.0491	0.0347	60.665	6.651	0.372	0.4035	—0.295	-0.0230
	0.1838	0.0838	0.0856	67.316	7.02	0.320	0.3740	-0.525	—0.0350
	0.2676	0.1694		74.34	7.34	0.231	0.3215	-0.875	
	0.4370			81.68	7.65		0.2340		
				89.33					
При этом надо иметь в виду, что = 1 — £. Например, для £ будет £х « — , так что
ои	oU
^Уп-1 =	+ Л Д2ОП-2-	(1)
вом приближении полагаем <о0 = и>1 = <о2 = 1, что дает возможность определить а0, clf
Д2Уо = «о + Д°о + ^2 Л*9°	(2)
Ло, Хь Х2 и разность ДХ0, ДХх, Д2Х0, что дает Д<о0, Д2соо по формулам, аналогичным (2),
незначительны, и а0, сх, а^ не меняются. Далее пользуемся формулами (1) для Д2и-,.
22 А. Н. Крылов
338
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. VII
Вычисле

при £ = 0 должно быть:
п 30 ; зо	/г2 *(С)	М2 3 (О	ф	Дф	 Д2ф	Л = —-j- 6- “(5)	ДХ	
0	0.01063	0.01195	0.0000	0.0333	0.0000	0.0000		
1	0.00535	0.03570	0.0333	0.0334	0.0000	0.0000		
2	0.00360	0.05920	0.0667	0.0333	0.0000	0.0000		
3	0.00273	0.08200	0.1000	3.0333	0.0000	0.0000		
4	0.00222	0.1039	0.1333	0.0333	0.0001	0.00005	0.00004	
5	0.00189	0.1245	0.1666	0.0334	0.0002	0.00009	0.00007	
6	0.00166	0.1438	0.2000	0.0336	0.0003	0.00016	0.00010	
7	0.001495	0.1615	0.2336	0,0339	0.0004	0.00026	0.00014	
8	0.001373	0.1775	0.2675	0.0343	0.0006	0.00040	0.00018	
9	0.001283	0.1918	0.3018	0.03*9	0.0008	0.00058	0.00024	
10	0.001215	0.2035	0.3367	0.0357	0.0011	0.00082	0.00030	
И	0.001169	0.2135	0.3724	0.0368	0.0015	0.00112	0.00039	
12	0.001136	0.2205	0.4092	0.0383	0.0020	0.00151	0.00049	
13	0.001119	0.2254	0.4475	0.0403	0.0026	0.00200	0.00061	
14	0.00111!	0.2280	0.4878	0.0429	0.0034	0.00261	0.00075	
15	0.00111!	0.2285	0.5307	0.0463	0.0042	0.00336	0.00088	
16	0.001111	0.2280	0.5770	0.0505	0.0053	0.00424	0.00105	
17	0.00111g	0.2254	0.6275	0.0558	0.0066	0.00529	0.00131	
18	0.001136	0.2205	0.6833	0.0624	0.0082	0.00660	0.00160	
19	0.00116g	0.2135	0.7457	0.-0706	0.0102	0.00820	0.00200	
20	0.001215	0.2035	0.8163	0.0808	0.0128	0.01020	0.00254	
21	0.001283	0.1918	0.8971	0.0936	0.0160	0.01274	0.00323	
22	0.001373	0.1775	0.9907	0.1096	0.0203	0.01597	0.0042	
23	0.001495	0.1615	1.1003	0.1299	0.0260	0.0202	0.0057	
24	0.00166	0.1438	1.2302	0.1559	0.0339	0.0259	0.0078	
25	0.00189	0.1245	• 1.3861	0.1898	0.0453	0.0337	0.0113	
26	0.00222	0.1039	1.5759	0.2351	0.0628	0.0450	0.0173	
27	0.00273	0.08200	1.8110	0.2979	0.0930	0.0623	0.0297	
28	0.00360	0.05920	2.1089	0.3909	0.1545*	0.0920	0.0600	
29	0.00535	0.03570	2.4998	0.5454		0.1520		
30	0.01063	0.01195	3.0452					
Примечание. Все, сказанное для таблицы 12, верно и для таблицы 13, за
полагаем фх = h = 0.0333,	= 2h = 0.0667 и находим о0,	с2.
и по последним Д%, Д2^. Второе приближение для уг,
§ 112]
ЧИСЛЕННЫЙ ПРИМЕР
339
Таблица 13
ние ф и s

ф = 0, ф' = 1, s = О, s" = О
	Д2Х	S	As	Д2$	3=V2pGH	Да	дч-
		0.0000	0.00014	0.0013	0.0000	0.0012	0.0015
		0.00014	0.00144	0.0040	0.0012	0.0027	0.0016
		0.0016	0.0054	0.0083	0.0039	0.0043	0.0013
		0.0070	0.0137	0.0139	0.0082	0.0056	0.0013
		0.0207	0.0276	0.0208	0.0138	0.0069	0.0012
	0.00003	0.0483	0.0484	0.0289	0.0207	0.0081	0.0009
	0.00003	0.0967	0.0773	0.0378	0.0288	0.0090	0.0007
	0.00004	0.1740	0.1151	0.0476	0.0378	0.0097	0.0007
	0.00004	0.2891	0.1627	0.0579	0.0475	0.0104	0.0003
	0.00006	0.4518	0.2206	0.0686	0.0579	0.0107	0.0002
	0.00006	0.6724	0.2892	0.0795	0.0686	0.0109	0.0000
	0.00009	0.9616	0.3687	0.0903	0.0795	0.0108	—0.0004
	0.00010	1.3303	0.4590	0.1007	0.0903	0.0104	0.0002
	0.00012	1.7893	0.5597	0.1113	0.1007	0.0106	-0.0006
	0.00014	2.3490	0.6710	0.1213	0.1113	0.0100	0.0002
	0.00013	3.0200	0.7923	0.1315	0.1213	0.0101	-0.0004
	0.00017	3.8123	0.9238	0.1413	0.1315	0.0098	—0.0003
	0.00026	4.7361	1.0651	0.1508	0.1413	0.0095	—0.0011
	0.00029	5.8012	1.2159	0.1591	0.1508	0.0084	—0.0015
	0.00040	7.0171	1.3750	0.1660	0.1592	0.0069	—0.0009
	0.00054	8.3921	1.5410	0.1720	0.1661	0.0060	—0.0024
	0.00069	9.9331	1.7130	0.175	0.1721	0.0036	—0.0017
	0.0010	11.6461	1.888	0.177	0.1757	0.0019	—0.002
	0.0015	13.534	2.065	0.177	0.1776	0.000	—0.005
	0.0021	15.599	2.242	0.172	0.177	-0.005	—0.003
	0.0035	17.841	2.414	0.164	0.172	—0.008	— 0.008
	0.0060	20.255	2.578	0.147	0.164	—0.016	—0.007
	0.0116	22.833	2.725	0.124	0.148	-0.023	—0.013
	0.0303	25.558	2.849	0.089	0.125	-0.036	
		28.407	2.938		0.089		
		31.345						 1
исключением начала вычислений. Так как ф0 = О, = 1, то в первом приближений
Так же, как для таблицы 12, находим s2 и по ним Хо, Х„ и их разности
в точности совпадает с первым.
22*
340
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
а так как
то
о
л D
где g есть ускорение силы тяжести.
Следовательно, будет
Чо 14._
/о 10 g ’
Обозначим через п минутное число оборотов машины, когда А =
и, следовательно,
к — А>2	74 __ ГС8 пЧ _ 1 пЧ	/ОС\
к 1 " 9000 у “285 g •
Нетрудно видеть, что, какая бы величина (метр, фут) ни была принята
за единицу длины, величина кх останется без перемены.
Обратимся теперь к численному примеру, для которого вычисления
выполнены в прилагаемых таблицах 12 и 13.
Для простоты расчетов предположено, что как кривая нагрузки, так
и кривая жесткости симметричны относительно миделя; иными словами.
а (?) = а($1) = «(!-?),₽(с) = ₽ (Bi) = Р (1 - 5).
В этом случае очевидно, что со2 и у % будут такими же функциями
как и от £, и, значит, для вычисления этих функций может служить
та же самая таблица и схема. Аналогичное будет иметь место и для фх и
В нашем численном примере предположено
/ = 100л€,
п = 76 (оборотов в минуту),
c~Ll.
3
Для величин £ табличный промежуток h взят равным , иными сло-
вами, длина корабля подразделена на 30 равных частей; тогда будет
= 0,2285,	(39)
и вычисление расположится, как показано в таблицах 12 и 13, которые не тре-
буют дальнейших пояснений, кроме сказанного выше.
Таблицы 12 и 13, в которых вычисление значений функций сох (?) и о>2 (;х),
Фх($) и «fa ($i) произведено для всех значений аргументов ? и ?х от 0 до 1,
дают возможность найти производимую силою Р вибрацию при любом
месте приложения этой силы, стоит только составить «условия сопряжения»
для этого места.
Так, в нашем случае	следовательно, соответствующие значе-
ния суть
значит, надо «сопрягать» величины, соответствующие этим значениям,
т. е. отвечающие значениям указателя п —10 и п = 20. г
Чтобы выполнить это сопряжение, нам потребуются значения производ-
ных со' (е), со* (с), со/'(с) и аналогично для других функций.
§ 112]
ЧИСЛЕННЫЙ ПРИМЕР
341
В таблицах же имеются лишь значения о)х и Л2а>£. Для нахождения
производных мы будем пользоваться следующим/ методом.
Пусть z есть какая-нибудь функция z = F(x) переменной x — nh, задан-
ная таблично, так что
zn = F (хп) = F (nh)..
Надо найти z'n = F'(хп). Для этого берем ряд значений функции z
так, чтобы zn занимало в нем среднее место, и составляем таблицу разно-
стей, как обыкновенно; таким образом получим:
Таблица 14
п	zn	Azn,	&2zn	Д»2„
п-2	Zn-2	^2П-2		
п—1		Д2П-1	A22n-2	A3zn_a
п	zn	Azn	Д22П-1	Д’гП_1
п -F1	Zn + 1	&zn-i	A2zn	
п-|-2	Zrt+2			
Берем затем
= j (Azn + Azn_i), 5П= у (Д32п-1 + A3z„_2), ...,
т. е. полусуммы разностей нечетного порядка, прилегающих к строке,
соответствующей значению п; тогда по формуле, данной еще ’ Стирлингом
в 1730 г., будет
hzn — Ап—(40)
В нашем случае по большей части достаточно будет довольствоваться
первым членом, в крайнем случае — первыми двумя. Так, по данным
таблицы 12 будем иметь для величин cdj и = (табл. 15):
Таблица 15
30 5	о>1	До)!	Д2сох		Ai	ДАХ	Д»Лг	Д3А1
8	1.0167	0.0101			0.00321	.0.00095		
9	1.0268	0.0143	0.0042	0.0011	0.00416	/ 0.00111	0.00016	0.00006
10	1.0411	0.0196	0.0053	0.0013	0.00527	0.00133	0.00022	0.00002
И	1.0607	0.0262	0.0066		0.00660	0.00157	0.00024	
12	1.0869				0.00817			
Лл=0.01695,	#п=0.0012,	А,, -0.00122,	#п=0.00004,
о)/^=0.01695-0.0002=0.01675,	A[A = U)i"A3=0.00121.
-0.1828, Вп= -0.0067, Ап = -0.00665, Вп = -0.00045,
ф'Л = — 0.1828 + 0.0011 = -0.1817,	=	-0.00658.
342
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VU
Так как для величины <+2 нам надо производную то располагаем
таблицу 15 по возрастающим аргументам 6, а не ?х, как они расположены
в таблице 12; будем иметь:
Таблица 16
30 Сл	30 ?	СО ,	До)2	Д2<о2	Д3<оа	Л*.	дл2	ДгЛ2	дзлл
22 1	8	2.2381	-0.2439		1	0 05240	—0.00935		
21	9	1.9942		-0.0432	<	0.04305		0.00195	
			—0.2007		-0.0075		—0.00740		-0.00045
20	10	1.7935	-0.1650	—0.0357	—0.0059	0.03565	—0.00590	0.00150	—0.00045
19	И	1.6285	-0.1352	—0.0298		0.02975	—0.00485	0.00105	
18	12	1.4933				0.02490			
Совершенно так же поступим и относительно фх и Ф2 и получим следу ю-
«.	10 с
щие результаты при Е = — = — :
ov I
toj = 1.4011,	’h =	0.3367,
ш2= 1.7935,	ф2 =	0.8107,
= 0.01675,		0.0353,
Лад'= -0.1817,	Ж =	-0.0753,
hW' = 0.00527,	Л^' =	0.00082,
hW' =	0.03565,	Л2ф2' =	0.01020,
h^’= 0.00121,	/г3фх" =	0.00027,
/г3<'= -0.00658,	лзф;" =	— 0.00225.
На основании вышеприведенных значений, условия сопряжения будут,
если принять для удобства вычислений №Р = 0.001:
1.0411 А+ 0.3367 Bj-1.7935 А-0.8163 В2 = 0,
0.01675 А+ 0-0353 А+ 0.1817 А+ 0.0753 В2 = 0,
0.00527 А+ 0.00082 Вх-0.03565 А-0.01020 В2 = 0,
0.00121 А+ 0.00027 А+ 0-00658 А+ 0.00225 В2 = 0.001.
.Из этих уравнений, производя вычисление логарифмической линейкой,
имеем
А = 0.613, Вг= -1.174, А=-0.0597, В2 = 0.430.
Таким образом, будет
Т1(5)= 0.613 ю, (?)- 1.174 АО),	0<$<|,
Т2($)=-0.0597ш20)+0.430 ф2(5),	|<5<1,
причем значения функций (ох ($),	(5), со2 (?), ^2 (?) даются в таблицах 12 и 13.
§ 113]	ЧИСЛЕННЫЙ ПРИМЕР 343
§ ИЗ. Остается еще показать, каким образом перейти от величин
относительных, в которых произведен расчет, к абсолютным.
Для этого стоит найти только ту величину Р, которая взята в урав-
нениях «сопряжения», и выразить ее в желаемых единицах.
Последнее из уравнений (27), если бы его написать в общем виде,
было бы
Настоящее же уравнение должно бы быть
=_1_а
По уравнению (25) имеем ^Ь=1.
Когда мы ввели вместо переменной х переменную то мы, попреж-
нему, сохранили обозначения функций и ф1? хотя их следовало бы обо-
значить для ясности другими буквами, например и
Вместо условия (25) мы взяли условие
^=1,	(42)
ас,
но # = /£, поэтому, чтобы условие (42) совпадало с (25), очевидно, надо •
брать	и, следовательно, писать
и = /[АД(5) + ВЛ(?)]
или, сохраняя прежнее обозначение,
ъ = 1	(») + ^1Ф1 (’)]>
иными словами, прогиб, рассчитанный по формуле
<Pi =	($) +	(с),
выражается в долях длины корабля, принятой за единицу.
Таким образом, уравнение (**) равносильно такому:
Г — 1	— L3 Г 1	—
иначе
^2ГЙ] -А3/2[Й1 =F’
l_a^3jc-o	Jc+o r
Сличая его с уравнением (*), видим, что
ft = 4т Ph3l2 = -4т y-h3l2.
г /(с)	“(с) /о
В наШем численном примере Л = (отвлеченное число), у. = 0.001,
а (с) = 0.9136, /0 —5PZ3, значит, будет
<? = р/о«(с) д^^О.001 • 5Р!3 • 0.9136	= 123.5А
где Р —вес корабля.
344 РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. УП
При таком значении Q и силы Z? = (JsinZtf прогиб и выражался бы
формулою
и = /[0.613 ШХ(О —1.1744»!0)],
и = I [ -0.0597 ш2 (gj + 0.430 Ф2 ($,)],	| <5 < 1,
причем Ei —1 — Е, где Z — длина корабля, множители же в скобках суть
отвлеченные числа, даваемые таблицей 17, составленной по таблицам 12 и 13.
Ясно, что вышеприведенные величины имеют чисто условный смысл,
но от них легко перейти к любым мерам.
Так, если (7 = 0.01 Р и / = 100 м, и мы хотели бы получить и в санти-
метрах, то вышеприведенные величины стоило бы умножить на
100 • 100 А о,
100-12X5 = 0-81’
а так как наибольшая стрелка прогиба в относительных мерах при у. = 0.001
составляла 0.087, то ее величина в сантиметрах, при ^ = 0.01Z), будет
0.147 • 0.81 = 0.119 см = 1.19 мм,
как то и показано в последнем столбце таблицы 17.
Сравним эту величину с приближенным значением статического прогиба
балки такой же длины, как наш корабль, и такой же средней жесткости.
Предполагая, что для этой балки распределение добавочной силы
поддержания, уравновешивающей нагрузку Р, есть равномерное, получим,
1	Р1
что наибольший изгибающий момент будет М = у QI, т. е. — .
Стрелка прогиба будет
1 I МЧ
s~ 3 El Q ’
а так как, по предположению, EI — ЬР12, то будет
_	1 рчг «ООО _ 20 _ 1 _ п
S"3.5PZ2 0.01Р 9002 ”243 “ 12 "" СМ'
При вышеприведенном расчете было положено с = -~/, т. е. что сере-
дина машины расположена на одной трети длины судна, считая от кормо-
вого перпендикуляра.
Совершенно подобным же образом производится расчет и при всяком
другом положении машины, стоит только сопряжение делать для соответ-
ствующего значения абсциссы.
Для сравнения приведем результаты, относящиеся к значениям с =I
1 ,
и к С=у/.
При с ~ у I получаем
?1 (?) = 0.461 coi (0 - 0.700О1 (Е),
?2(с1)--0.369ш2(;1) + 1.14Ф2(;1);
выбирая значения tyi(c), w2(?i)> Фг(-1) из таблиц 12 и 13; получаем
таблицу 18.
Совершенно так же, при с=у/, имеем
?1 (Е) = 0.292 о), (Е) - 0.417Фг (Е),
?2 (Ех) = 0.292 ш2 (?х) - 0.417ф2 (EJ.
§ 113]
ЧИСЛЕННЫЙ ПРИМЕР
345
Таблица 17
30 <			?i=A<°1+ +^1Ф1	Ординаты прямой Z	2—?1	3 —<Р1 (б мм)
	' V»		<р2==Л2о>2-В		2	?2	з—<р2 (в мм)
0	0.613	—0.000	0.613	0.613	0.000	0.00
1	0.613	-0.039	0.574	0.591	0.017	0.14
2	0.613	—0.078	0.535	0.568	0.033	0.27
3	0.613	—0.117	0.496	0.546	0.052	0.42
4	0.614	—0.156	0.458	0.523	0.065	0.53
5	0.614	—0.196	0.418	0.501	0.083	0.67
6	0.616	—0.235	0.381	0.478	0.097	0.78
7	0.619	-0.274	0.345	0.456	0.111	0.90
8	0.623	—0.314	0.309	0.433	0.124	1.01
9	0.630	-0.355	0.275	0.411	0.136	1.10
10	0.633	—0.396	0.242	| 0.389	| 0.147	| 1.19
10	—0.107	0.351	0.241			
И	—0.097	0.321	0.224	0.367	0.143	1.16
12	-0.089	0.294	0.205	0.344	0.139	1.13
13	-0.083	0.270	0.187	0.322	0.135	1.09
14	-0.077	0.248	0.171	0.299	0.128	1.04
15	—0.073	0.228	0.155	0.277	0.122	0.99
16	—0.070	0.2Ю	0.140	0.254	0.114	0.92
17	-0.067	0.192	0.125	0.232	0.107	0.87
18	—0.065	0.176	0.111	0.209	0.098	0.79
19	-0.063	0.160	0.097	0.187	0.090	0.73
20	-0.062	0.145	0.083	0.164	0.081	0.66
21	-0.061	0.130	0.069	0.142	0.073	0.59
22	-0.061	0.115	0.054	0.119	0.065	0.53,
23	-0.060	0.100	0.040	0.097 	0.057	0.46
24	-0.060	0.086	0.026	0.074	0.048	0.39
25	—0.060	0.072	0.012	0.052	0.040	0.32
26	-0.060	0.057	—0.003	0.029	0.032	0.26
27	—0,060	0.043	—0.017	0.007	0.024	0.19
28	-0,060	0.029	-0.031	—0.016	0.015	0.12
•29	—0.060	0.014	-0.046	—0.038	0.008	0.06
30	-0.060	0.000	-0.06.0	—0.060	0.000	0.00
Л^О.613,
Вх=—1.174,
Л2=-0.0597,
Я2=0.43.
346
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
Таблица 18
30 §	30		Я1Ф1	?1	Ординаты прямой z	cpi-z
						
0	30	0.461	0.000	0.461	0.461	0.000
1	29	0.461	-0.023	0.438	0.433	0.005
2	28	0.461	—0.047	0.414	0.405	0.009
3	27	0.461	-0.070	0.391	0.378	0.013
4	26	0.461	—0.093	0.368	0.350	0.018
5	25	0.462	—0.117	| 0.345	| 0.322	| 0.023
5	25	—1.233	1.578			
6	24	—1.070	1.402	0.332	.0.295	0.037
7	23	—0.935	1.253	0.318	0.267	0.051
8	22	-0.825	1.130	0.305	0.239	0.066
9	21	—0.736	1.023	0.287	0.212	0.075
10	20	—0.662	0.930	0.268	0.184	0.084
И	19	—0.601	0.850	0.249	0.156	0.093
12	18	-0.551	0.777	0.226	0.129	0.097
13	17	-0.510	0.715	0.205	0.101	0.104
14	16	—0.478	0.658	0.180	0.073	0.107
15	15	-0.452	0.605	0.153	0.046	0.107
16	14	—0.430	0.555	0.125	0.018	0.107
17	13	-0.414	0.510	0.096	—0.010	0.106
18	12	—0.400	0.466	0.066	-0.037	0.103
19	И	—0.392	0.424	0.032	-0.065	0.097
20	10	—0.384	0.384	0.000	—0.093	0.093
21	9	-0.379	0.344	—0.035	—0.120	0.085
 22	8	—0.375	0.305	—0.070	-0.148	0.078
23	7	—0.372	0.266	-0.106	—0.176	0.070
24	6	—0.371	0.228	—0.143	-0.203	0.060
25	5	—0.370	0.190	—0.180	—0.231	0.051
26	4	-0.369	0.152	—0.217	-0.259	0.042
27	3	—0.369	0.114	—0.255	-0.286	0.031
28	2	—0.369	0.076	—0.293	—0.314	0.021
29	1	-0.369	0.038	—0.331	—0.342	0.011
30	0	—0.369	0.000	—0.369	—0.369	0.000
Л1=0.461,
Л2=—0.369,
В1=—0.700,
Ва=1.140.
§ 113]
ЧИСЛЕННЫЙ ПРИМЕР
347
Это показывает, что форма вибрации симметрична относительно миделя.
Форма эта дается таблицей:
Таблица 19
30;	л1">1	2М1	<Pi	20~
		^2%	?2	
0	0.292	0.000	0.292	0.000
1	0.292	—0.014	0.278	0.014
2	0.292	-0.028	0.264	0.028
3	0.292	 —0.042	0.250	0.042
4	0.292	-0.055	0.237	0.055
5	0.293	—0.069	0.224	0.068
6	0.293	—0.083	0.210	0.082
7	0.294	—0.097	0.197	0.095
8	0.297	—0.112	0.185	0.107
9	0.300	—0.126	0.174	0.118
10	0.304	—0.140	0.164	0.128
И	0.310	-0.155	0.155	0.137
12	0.317	-0.171	0.146	0.146
13	0.327	—0.187	0.140	0.152
14	0.340	—0.203	0.137	0.155
15	'	0.357	-0.222	0.135	0.157
16	0.340	-0.203	0.137	0.155
17	0.327	—0.187	0.140	0.152
18	0.317	—0.171	0.146	0.146
0.292, В^- 0.417.
Мы рассмотрели тот случай, когда неуравновешенные силы инерции
машины сводятся к одной силе. Если бы они привелись к одной паре,
то решение задачи отличалось бы от изложенного только тем, что в усло-
виях сопряжения разрыв был бы в выражении производной второго порядка,
т. е. было бы
е_>о <dx Ус~г s->o ^dx 6 / (с)
где М sin kt есть возмущающая пара.
Наконец, если бы силы инерции привелись к одной силе Q~Psinkt
с точкой приложения х = с и к паре N = 71/sin (Л/ 4- у), то, на основании
«принципа наложения малых колебаний», следовало бы рассчитать в отдель-
348
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН [Гл. VII
ности вибрацию, производимую силою, и вибрацию, производимую парой,
и взять их алгебраическую сумму.
Совершенно подобным образом может быть рассчитана вибрация любого
сооружения, например моста, фундамента под. машиною и т. п., надо лишь
иметь кривые жесткости, распределения масс и действующую периоди-
ческую силу или пару.
§ 114. Метод вычисления фундаментальных функций и характери-
стических чисел численным интегрированием. В §§ 104—113 показано,
каким образом вычисляются «вынужденные» упругие колебания балки
переменного сечения под действием периодически изменяющейся силы или
пары. Для большей части практических вопросов только это и требуется,,
но подобный же метод может быть применен для вычисления самих фунда-
ментальных функций и характеристических чисел.
Поясним это на примере балки, оба конца которой свободны.
Свободные колебания нашей балки как раз представлялись бы урав-
нением
д2 Г и \	, ч д2и А	...
совершенно подобным уравнению (8) § 106.
Повторяя рассуждения § 106, увидим, что фундаментальные функции X
будут определяться уравнением вида
(2)
подобным уравнениям (11) и (12), и граничными условиями:
при	ж = 0	должно	быть	Х" = 0	и	X"' =0,
»	х—1	»	»	Х" = 0	и	Х"'=--0.
Так как функция X определяется уравнением линейным, то она будет
вида
X —AY + BZ+ CU + DV,
причем Л, jB, С, D— произвольные постоянные, У, Z, U, V —четыре неза-
висимых частных решения уравнения (2). Очевидно, что эти решения будут
зависеть и от параметра К, значение которого пока неизвестно.
Граничные условия, обозначая значками производные по х, будут
ЛУ" (0,	k) + SZ" (0,	\) + CU" (0,	k)4-.DV" (0,	k)=0,
AY'" (0,	k) + BZ'" (0,	k) + CU'" (0,	k) + DV" (0,	k) = 0,
AY" (I,	).)+BZ" (Z,	k) + CtZ" (Z,	k) + Z)7" (Z,	k) = 0,	(4>
ЛУ'"^,	k) + BZ"'(l,	\)+CUr"(l,	k) + DV"(1,	k) = 0.
Чтобы эти уравнения допускали для Л, В, С, D решения, отличные
от нуля, необходимо, чтобы определитель
Д(к) = |У"(О, k), Z'" (0, к), С7"(/, к), V"'(Z, к)| —0.	(5)
Это и есть то трансцендентное уравнение, которым определяются
характеристические числа к.
Но ясно, что лишь для весьма немногих частных видов функций f(x)
и q(x) этот определитель может быть составлен аналитически, в большей же
части случаев это недостижимо, а когда функции f(x) и q(x) заданы гра-
фически, как это бывает в практических вопросах, и совсем невозможно.
Но для того чтобы вычислить приближенные значения к, нет надобно-
сти иметь этот определитель в аналитическом, развернутом виде; доста-
§ 114] ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ И ХАРАКТЕРИСТИЧЕСКИЕ ЧИСЛА
349
точно, если мы будем иметь возможность вычислять частное его значение
Д(А), когда величине К будет приписано какое-либо частное значение а = Л.
В самом деле, если на основании каких-либо соображений, изложение
которых здесь опускаем, было бы известно, что одно из приближенных
значений некоторого корня К, скажем первого, есть к, то, вычислив Д(А),
положили бы затем \ = k + h и вычислили бы Д(/г если эти величины
окажутся разных знаков, то искомое значение к лежит между к и k + h,
после чего обычным приемом последовательных приближений оно и най-
дется с любою степенью точности»
Таким образом, все дело свелось к тому, чтобы показать, каким обра-
зом можно вычислить частное значение Д(Л).
Постоянные произвольные можно выбрать так, чтобы они представляли
частные значения функции X и первых трех ее производных при я = 0,
для этого стоит только взять такие частные решения У, Z, U, V, которые,
как говорят, обладали бы «единичною матрицею», т. е. чтобы при х — 0 было
У = 1,	Y' = 0,	У" = 0,	У"'=0,
Z = 0,	Z'= 1,	Z"-0,	Z"'=0,
[7 = 0,	[7'=x0,	[7"=1,	[7"' = 0,	W
V = 0,	V'-O,	7" = 0,	7"' = b
Так как функция
X — AY + BZ + CU + DV
удовлетворяет граничным условиям (3), то, очевидно, будет
С = 0 и =
так что остается только найти функцию У и Z, чего мы и достигнем совер-
шенно подобно тому, как указано в § 107, введя вспомогательные неизве-
стные у и $, так что У и у будут определяться системою
d2Y  1
/ПЧ
/72,,	7
и начальными значениями: при я = 0 должно быть
у = 0, / = 0,
У —1, У' = 0,
которые следуют из уравнений первой строки матрицы (6).
Применяя к этой системе метод Штермера, составим таблицу значений
У и у от я = 0 до ж = 7, причем попутно получится и таблица значений
их вторых производных.
Совершенно так же, положив
d*Z_____________________________1_
dж2“/(л?)Z,	/7*\
/?2т	'
^^—kq(x)Z,
dx2 * '
и взяв за начальные условия: при х = 0 должно быть
z = 0 и	'z' = 0,	zq\
Z = 0 и Z' = l,	(8)
составим таблицу значений функции Z и попутно с нею и значений Z'.
Таким образом, будет
Х = AY + BZ,
350
РЕШЕНИЕ УРАВНЕНИЙ, ИМЕЮЩИХ ПОСЛЕДНИЙ ЧЛЕН
[Гл. УП
причем постоянные произвольные определяются уравнениями
АУ"(Л M + ^Z" (Z, к) = 0,
ЛУ"(/, k) + BZ"'(Z, к)^0,	w
причем значения У " и Z'" при х = 1 найдем в том случае, когда функции
t{x) и q(x) заданы аналитически, из уравнений (7) и (7'), продифферен-
цировав их, когда же j(x) и q(x) заданы таблично или графически, то —
ио формулам интерполяции, подобным формуле Стирлинга; таким образом,
уравнения (9) примут вид
причем Р, Q, М и N будут известные числа, и, значит, частное значение
определителя будет
&(k) = PN — QM.
Если бы оно оказалось равным нулю, то значение к = к и было бы
характеристическим числом, если же к(к) нулю не равно, то, положив
надо повторить процесс, найдем значение Д(&4-Л) и, как ска-
зано выше, будем последовательными приближениями искать значение X.
Таким образом, имеется возможность действительно найти значения
характеристических чисел, но, как видно, вычисление было бы весьма
продолжительно, в особенности, если исходное значение к взято недостаточно
близко к истинному.
Чтобы избежать длинных вычислений, поступают так: принимают за X
какую-нибудь функцию, удовлетворяющую условиям (9), например для
балки постоянного сечения и соответствующего веса, или берут целый поли-
ном; пусть эта функция будет F(x), так что
X = F(x),
причем в нашем случае будет
F'(0) = 0, F"(0) = 0,
F"(Z) = O, F"'(Z) = 0.	' ’
Если бы уравнение (2) было бы точное, то мы имели бы
Л 2
(12)
Умножим обе части этого равенства на F(x)dx и проинтегрируем
в пределах от 0 до Z, тогда будет
i	i
К $ q (х) [F (ж)]2 dx =	(х)	[/ (х) F" (ж)] dx.
о	о
Затем, интегрируя по частям, получим на основании условий (11)
i
Г	/72
3 F^& [f (х) F" (х)] dx =
о
I I
= (*) i U W F" } - SF' W £ f/ Ю F" dx=
0	0
I	I	I
= - | F' (x) / (x) F" (z)} + / (®) [F" (ж)]2 dx = / (ж) [7?" (ж)]2 dx.
0	0	0
§ 114] ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ И ХАРАКТЕРИСТИЧЕСКИЕ ЧИСЛА
351
Значит, на основании уравнения (12), будет
j /(х)1?" (*)]*<&
к==4--------------
Вычисленное по этой формуле значение к, даже при грубом приближе-
нии функции F (х), обыкновенно оказывается весьма близким к истинному.
Приняв это значение за первое приближение к, вычисляем, как объяснено
выше, X и X", определяя отношение В : А из уравнения
A(P + M) + B(Q + N) = 0,
представляющего сумму уравнений (10), после чего, положив, например,
Л==1, вычисляем по формуле (13) величину к, которую и принимаем
за k + h, и продолжаем таким образом, пока не получим величину к с тре-
буемой степенью точности.
При этом вычислении необходимо обращать внимание, чтобы не только
разность
PN - QM
была достаточно близка к нулю, но и чтобы отношение QM.: PN было
близко к единице, в той мере точно, как производится вычисление и как
то в поставленном вопросе требуется.
Совершенно подобным же образом надо поступать с другими типами
уравнений, нами рассмотренных, когда вместо постоянных коэффициентов
в них будут коэффициенты переменные, например в уравнении струны,
когда оно относится или к продольным колебаниям стержня переменного
сечения, или к вычислению сейш (приливов) в озерах или в замкнутых
морях.
ГЛАВА VIII
РАДИАЛЬНЫЕ КОЛЕБАНИЯ ПОЛОГО ЦИЛИНДРА
§ 115. Уравнения, к которым приводит вопрос о радиальных колеба-
ниях полого цилиндра. Чтобы дать пример уравнений с переменными коэф-
фициентами, интегрирование которых совершается подобно тому, как интегриро-
вание уравнений с постоянными коэффициентами, т. е. приводится к функциям
хорошо исследованным, для которых существуют таблицы, рассмотрим
радиальные колебания полого цилиндра, задача о которых имеет прило-
жение при проектировании орудий.
Радиальные колебания полого цилиндра, внутренний радиус коего
есть а, внешний 6, определяются уравнением
в котором и есть радиальное перемещение слоя, отстоящего на величину г
от оси цилиндра, р есть плотность (масса единицы объема) материала
цилиндра, F(r, t) — внешнее усилие, действующее в момент t на единицу
массы в слое, отстоящем на г от оси, к и ^ — коэффициенты упругости
материала, а именно: р. —модуль сдвига и
k (X + 2|1)
X р.
(2)
где ^ — модуль упругости (модуль Юнга).
К уравнению (1) необходимо еще присовокупить граничные и началь-
ные условия. В том случае, когда обе поверхности цилиндра «свободны»,
граничные условия выражаются так:
при г = а должно быть г + угу и = 0 ) при всяком
/	. **	? значении
» г=Ь »	» гv + i . » и —О времени^.
дг Х-р2р • / г
(3)
Начальные условия относятся к моменту t — 0 и выражаются так:
при t == 0 должно быть и = ср (г),
»	£ = 0	»	»	^ = ф(г),
сп 1 ' '
причем <р(г) и <J(r)—две функции переменной г, произвольно заданные
от г^а до г — Ь.
По общему способу решения вопроса о вынужденных колебаниях,
полагаем
и — иг + и2
и подчиняем эти функции таким уравнениям и условиям, чтобы их пред-
ставляло свободные колебания и и2 — вынужденные.
§ 115]
УРАВНЕНИЯ РАДИАЛЬНЫХ КОЛЕБАНИЙ ПОЛОГО ЦИЛИНДРА
353
Для этого необходимо, чтобы величина удовлетворяла:
во-первых, уравнению, соответствующему (1), но без последнего
члена, т. е.
d2ut 2 Z<?2w1	1 ди}
dt2 С \дг2 ' г дг
(4)
где
+ 2И *
Р ’
во-вторых, граничным условиям:
при г = а должно быть г + hu1 — О
» г + hux = 0
дг 1
при всяком
(5)
где
1 Х .
1 ~ \ + 2р. ’
в-третьих, начальным условиям:
при Z = 0 должно быть
» t — о »	»
ZZJ = <?(г),
Что касается величины то она должна удовлетворять:
во-первых, уравнению с последним членом:
_ С2 (	+ 1	_ “Л =Р(Г> /),
dt2 \ дг2 1 г дг т2 J '	7
(6)
(7)
> г = b »

во-вторых, граничным условиям:
при г = а должно быть г + hu2 = 0
» г = b »	»	+ hu2 = 0
дг *
при всяком Z,
(8)
в-третьих, начальным условиям: при t = 0 должно быть
и2 = 0 и -^2 = 0.	(9)
Необходимо теперь же сделать следующее замечание. С первого взгляда
может представиться, что решаемая задача не относится к тому случаю,
когда цилиндр подвержен давлению, действующему на внутреннюю . его
поверхность и изменяющемуся с течением времени, ибо граничные условия
получены так, что приравнена нулю, при г = а и при г = Ь, нормальная
слагающая напряжения, которая выражается формулой
(). + 2И) J + X -,
\	1 f cfr 1 г
и можно думать, что следовало бы эту величину уравнять величине
внутреннего давления.
Но можно поступать иначе: граничные условия должно составлять
для свободных колебаний тела, все же внешние условия относить
к «нагрузке» pF (г, t), выбирая подобающим образом вид функции F (г, t),
т. е. когда действует давление на внутреннюю поверхность, то надо его
вообразить замененным нагрузкою, сосредоточенной на бесконечно тонком
слое, прилегающем к внутренней поверхности, и перейти к пределу, беря
толщину слоя равной нулю.
А. Н. Крылов	,
354 РАДИАЛЬНЫЕ КОЛЕБАНИЯ ПОЛОГО ЦИЛИНДРА	[Гл. VI
Такая замена приводит к однородным граничным условиям и дает
возможность решить вопрос о вынужденных колебаниях, подобно тому как
это показано в главе VII этого курса.
§ 116. Определение свободных колебаний. Решение необходимо начи-
нать с разыскания свободных колебаний, хотя бы при £ = 0 система была
в равновесии и покое, т. е. когда <р(г) = О и 6(г) —0, и свободных колеба-
ний не было бы, так как тогда а^О.
Строим выражение
TR,	(10)
где функция Т зависит только от переменной t, функция R — только от
переменной г, и определяем функции Т и R так, чтобы оно удовлетворяло
как уравнению (4), так и граничным условиям (5).
По подстановке величины (10) в уравнение (4), оно примет вид
T"R-^(R" + ^R'-^T = Q,	(*)
где значками обозначены производные по той переменной, от коей функция
зависит.
Следовательно, функции Т и R должны быть взяты так, чтобы выпол-
нить уравнение (*), что не иначе может быть, как если будет
где — /?2 есть какое угодно число, не зависящее ни от /, ни от г.
Таким образом, для нахождения функций Т и R имеем уравнения
Т" =	(12)
Д'+1ДЧ(>--Г)Я = 0.	(13)
Первое из этих уравнений дает
Т — С cos cpt -р D sin cpt,
где С и D — постоянные произвольные.
Уравнение (13), как видно, также линейное, но с переменными коэф-
фициентами. Функции, этому уравнению удовлетворяющие, хорошо
исследованы, и для них составлены таблицы; эти функции называются
бесселевыми или цилиндрическими и встречаются во множестве вопросов
математической физики, когда приходится иметь дело с цилиндром или
шаром.
Ниже мы приведем те свойства этих функций, которые нам понадо-
бятся, чтобы воспользоваться их готовыми таблицами.
Сделав в уравнении (13) ‘
рг = х,
мы получим уравнение
£?+-‘!л+(1--2')я=о,	(13')
ах* х ах ' \ ху *	'	'
которое показывает, что величина R есть функция только буквы х9 т. е.
произведения рг, а не переменных р и г в отдельности.
Общий интеграл уравнения (13') будет вида
R^AI^ + BY^x),
§ 116]	ОПРЕДЕЛЕНИЕ СВОБОДНЫХ КОЛЕБАНИИ	355
где А и В —произвольные постоянные, Щх) и Yl(x) — два независимых,
частных решения уравнения (13'); следовательно, будет
7? = AI1(pr) + BY1 (рг).
Составляя граничные условия, которым должна удовлетворять
ция R, получаем
aRf (а) + hR (а) = О,
bR'(b) +hR(b) = O,
причем
(14)
функ-
(15)
(16)
необ-
(17)
может
Развив условия (15) на основании формулы (14), имеем
A [apl{ (ар) + hl,, (ар)] + В [ар У] (ар) + kYх (ар)] = О,
Л [6pz; (bp) +hh (bp)] + в [bpY{ (bp) + hYx (bp)] = 0.
Чтобы уравнения (16) допускали решения, отличные от нуля,
ходимо, чтобы было
[ар (ар) + hh (ар)] [bpY] (bp) + hYг (ftp)] —
— [bp (bp) + hh (6p)] [apY[ (ap) + hY y (ар)] = 0.
Это трансцендентное уравнение определит те значения, которые
принимать оставшееся пока произвольным число р.
Пусть Эти значения будут:
Pi> Рг, Рз> -•-> Рк, • • •>
каждому из этих значений будет соответствовать своя функция R и своя
функция Т\ мы их обозначим соответственно
л, т2, т3,..., тк.......
^1> ^2>	Rfc, • • • >
так что
Тк^=Ск cos cpkt 4- D/csin cpkt,
Rk-Hk{ [ар^ (apk) + hY x (а/?*)] Ц (pk r) — [apk I[ (apk) + A/x (a^)l Y x (pk r)],
где Ck, Dk и Hk — произвольные постоянные, причем эта последняя заме-
няет постоянные Ак и Вк, связанные первым уравнением (16), ибо, в силу
(17), второе есть следствие первого, так что надо фрать
Ак = Нк [арк У; (арк) + ЛУХ (а/^)],
— Нк[арк I^ap^ + hl^ap^].
В виду того, что в выражение ггх входят лишь произведения ТkRk,
можно без ущерба общности брать Нк^=1, ибо СкНк и DkHk суть
такие же произвольные, как Ск и Dk-
Таким образом, за функцию Rk берем
Rk = [apk Y^apkj + hY! (арк)] /х (рк г) -
— [арк Гх (арк) + Л/х («/?*)] Ух (рк г) (18)
и скажем здесь же, что для функций 7Х и Ух и их производных имеются
готовые таблицы.
2а*
356	 РАДИАЛЬНЫЕ КОЛЕБАНИЯ ПОЛОГО ЦИЛИНДРА	Г Гл. VII
Ищем и± в виде суммы построенных выше выражений (10)
оо	ОО
иг= ^CkRkcoscpkt + DkRksincpkt	(19)
А —1	/с==1
и постоянные произвольные Ск и Dk определяются по начальным условиям.
§ 117. Определение постоянных произвольных по начальным условиям
приводит к равенствам
оо
?(г)= 2
оо
й (г) = У срк Dk Rk,
требующим разложения заданных функций <р(г) и Ф(г) по функциям Rk,
определяемым дифференциальным уравнением (13) в связи с уравне-
нием (17).
Это определение выполняется на основании следующего свойства
функции Rk:
ъ
Rtn Rn rdr == 0, если т Ф п.
а
В самом деле, функции R)n и Rn удовлетворяют дифференциальным
уравнениям, которые получаются после замены в (13) для первой р
через рт и для второй через рп, т. е.
я; + 7«п + (^-г4-)лп=о.
Эти уравнения можно написать так:
=0,
	(гЯ'п)' + (р?1-^)ЯпГ = О.
Умножая первое уравнение на /?п, второе на Rm и вычитая его из пер-
вого, получим равенство
(рт Рп) Rm Rn Г = Rm (rRn)f Rn (pRm) •
Умножив это уравнение на dr и интегрируя в пределах от г = а до
г — Ь, получим
b	b	ь
( Рт — Рп) Rm Rn rdr = Rm d [гЯ'п] —	Rn d [r7?m];
a	a	a
выполнив во второй части интегрирование по частям, получим
b	ь
(Pin Рп) RmRnrdr — rRm Rn  rRn Rm —
= [bR'n (b) Rm (b) — bRm (b) Rn (6)] — [a/?; (a) Rm (a) — aR’m (a) Rn (a)].
1171	ОПРЕДЕЛЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ	357
Но, в силу уравнений (15), будет
айт(«)= — hRm(a), aR'n(a) = — hRn(a),
bR'm (b) = - hRm (b), bR'n (b) = - hRn (fc);
следовательно, вторая часть предыдущего равенства есть нуль, а так как
по предположению рт не равно рп, то будет
ь
Rm Rn rdr = 0, если пг Ф п.	(20)
а
На основании этого свойства произвольные постоянные С к и Dk
определяется совершенно подобно тому, как и для рядов Фурье, и, зна-
чит, будет
ь	ъ
y(r)r^dr
с»=Ц-----------•	---------	<21>
\ «Irdr	( Л» rdr
а	а
Входящий в знаменатель этих выражений интеграл
ь
R2k rdr
а
может быть найден по обыкновенному примеру, подобно тому как в задаче
об упругих колебаниях стержня.
Действительно, мы имеем вообще
ь
ь	£ rRniR't rRnRfm J
Rm Rn rdr =-------2---------- ;
.)	Pl - Pn
a
когда т становится равным n, то выражение во второй части принимает
неопределенный вид . Чтобы раскртдть эту неопределенность, заменим р,а
через р и обозначим соответствующую ^ункцию через Я; тогда вторая часть
предыдущего равенства обратится в дробь вида
F(p)
Р*-Рп ’
причем
F (рп) - 0.
Истинное значение этой дроби есть
Г ™ (р) -1
др____
_ 2р Jp-Pn
Но
ь	ь
F(p) [rRR’n—rBnR']= [rRR'n-rRn£ ] ;
3£8	РАДИАЛЬНЫЕ КОЛЕБАНИЯ ПОЛОГО ЦИЛИНДРА[Гл. VH
величины Rn и R'n буквы р не содержат, величина же R есть функция про-
изведения рг, как то указывает формула (14); следовательно, будет
Л— d*R — d2R —4 dR r d*R
dp p dr И dp dr	dr dp p dr ' p ~dr2
И; Значит;	>
.	Ь V ! ‘
dF Г n, dR n d*R "I _ Г r* R, dR r R dR r* „ <PR 1
dp - L n dp ~rtin dpdr J ~Lt> " pn~fr~~pn dr* J •
! a . °
При p — pn функция R обращается в Rn и, в силу уравнения
будет
и, следовательно,
<*2ЯП	1 dR	f
dr* + r dr
,2 d*Rn _
dr2
r^ + (p*r-l)Rn
dF(p)
dp____
%P
1 b
= ^[r4V* + R^p*r?-l)].
(22)
Таким образом, задача о нахождении свободных колебаний сводится
к составлению функции Rk.
§ 118. Основые свойства функций Бесселя. Приведем теперь без до-
казательства те главнейшие формулы, относящиеся к бесселевым функциям,
которые нам понадобятся.
Уравнение (13')
d2R , 1 dR ,
есть частный случай уравнения
+	+ --2У = 0-	(23)
dx2 х dx \ х2у	v '
соответствующий п = 1.
Когда в уравнении (23) п есть целое и положительное число, то его
общий интеграл будет вида
R —AIn(x) + BYn(x),
причем 1п (я) называется бесселевой функцией первого рода и n-го порядка,
Yn (#) — бесселевой функцией второго рода и n-го порядка.
Эти функции определяются следующими рядами:
/п (^) 2Н • 1 • 2 • 3 . . . п L 1	2 (2п + 2)	2 • 4 (2п + 2) (2п + 4)	•
/	4 \А
' • • + ( —	2 • 4 . . . 2Л (2п + 2) (2п + 4) . . . (2п + 2к) Зг
Yn (х) = In (х) In х — [ 2П“1 (п — 1)! х~п + ——х~п ¥2 +

ХП~2 *1 Хп 50 1
2"-1 (п— lj! J ~ 2п+1пГ ~к +
1
оо
I X1 (	1   Л	хп + 2к
,	+ Zj 2'1+2- А! (п + к)! nt k
к= 1
§ 118]	ОСНОВНЫЕ СВОЙСТВА ФА'НКЦИЙ БЕССЕЛЯ	359
причем
[ 2Л + 2 (п 4- /г) ] ““ 3 2/г ;	^2^
Л=1	Л = 1
По поводу этих двух рядов сделаем следующее замечание.
Чтобы найти общий интеграл уравнения
у"+~у'+(1-J-)^=0’	(23')
надо найти два каких бы то ни было линейно независимых его решения;
будем искать частные решения вида
оо
у — хл (aQ + а±х + а2х2 + а3х3 4- ...)== ^ акх*+к.
А = 0
Подставляя эту величину у в данное уравнение, получим
(а2 — п2) aQxa + [(а 4- I)2 — и2] а^^1 4- 2 {[(а + к)2 — и2] ак 4- ак_2} хл+л=0.
А=2
Чтобы это равенство могло иметь место при всяком значении перемен-
ной х, необходимо взять показатель а и коэффициенты а0, alf а2, ... так,
чтобы'каждая степень х в отдельности пропадала, т. е., чтобы было
а2 — п2 = 0 и aQ =4 0.
Следовательно, можно взять
а = 4 п и а = — п.
Возьмем сперва а = + п\ тогда величина (а 4-1)2 — п2 — 2п + 1 нулю .
не равна ^мы предполагаем, что п не равно , и, значит, должно быть
ах-= 0.
Дальнейшие коэффициенты определяются системою уравнений
[(7. ]-/02~лг2]^.4-^_2-0	(А = 2, 3, 4,...),
т. е. при а = п системою
Л’(2п4-А‘)^ + аА-2 = 0	(& = 2, 3, 4, ...). ‘	(*)
Так как аА =0, то из этой системы видно, что. будет и
а3 — а5 — а^ . = ^2/+1 — ••• =—- 0•
Затем, для четных значений к получим
л _________________ао
"2	2 (2/г + 2) '
4"(2А~+4У =2-- 4 (2п+2)(2п + 4) ’
п ________а1 __________________ ао____;_____
6 “	6 (2/Г+ 6)	2 . 4 . 6 (2п + 2) (2п + 4) (2п + 6) ’
и т. д., причем закон составления коэффициентов очевиден; такйм образом,
одно частное решение уравнения (23) будет
, _ п Г1 г2	xi
У1 -а^х 1 — 2^7+2) + 2 • 4 (2,1 + 2) (2п + 4) ~
____________________________________________’ । 1
2 • 4 • 6.(2п + 2)(2п+4) (2п + 6)	J’
360	РАДИАЛЬНЫЕ КОЛЕБАНИЯ ПОЛОГО ЦИЛИНДРА
Гл. VIII
причем а0 остается произвольным, и так как при составлении общего инте-
грала множится на произвольную постоянную А, то а0 можно брать как
угодно. По соображениям, которые излагать не будем, принято брать1)
_	1
—2#Т (п +1)
и соответствующую величину обозначать знаком /п(ж), так что
/п W=2nr (п +1) • [ 1 ~2 (2п + 2)+ 2 • 4(2п + 2)(2п + 4) “ * * * J ’	>
Если п не есть целое положительное число, то, взяв
а— —п,
мы получили бы второе решение у % вида
г , х*	_1_	1
у2 — а0Х 1	2 (2 — 2п) + 2 • 4 (2 - 2«) (4 — 2п) ' ' ' J ’
которое было бы независимо от первого, и, взяв по аналогии
_ 1
^0— 2-'Т(— П+ 1) *
обозначили бы функцию, ему соответствующую, через 1_п(х), так что
/_п (х) = 2_„г (_ n + ,) [ 1 — 2 (2 — 2п) + 2 • 4 (2 — 2п) (4 — 2п) ~~ ' ' ' ]
и общий интеграл уравнения (23) был бы
у = А1п (х) + В1_п (х).	(25)
Но если п есть цело? и положительное число, то значение а — — п не дает
решения независимого от первого.
В самом деле, в этом случае система уравнений (*) будет
«1 = 0,
А (А — 2п) + аА_2 = 0 (к = 2, 3, 4, 5,...);
попрежнему получится
aQ '= а5 ==	. = 0.
Но если взять а0 не равным нулю, то коэффициент л2п и все за ним
следующие заключали бы в знаменателе множитель 2п—2п, равный 0, т. е.
были бы бесконечны; следовательно, надо брать
CLq =	— ^4 = . . . = ^2п—2 ~
Тогда уравнение, соответствующее значению к = 2п в системе (*) будет
2п (2п — 2п) а2п = 0.
Значит, а2п можно брать произвольно, последующие уравнения будут
(2п + 2) (2п + 2 — 2п) а2п+2 + #2п = 0>
{2п + 4) (2п + 4 — 2п) ^2п+4 + а2п + 2 — 0>
х) Функция Г(п + 1) есть эйлеров интеграл второго рода
4 оо
Г (п. + 1) = Хпе-хdx.
б
При п целом и положительном Г (n + 1) = 1 • 2 • 3 . .. п. При п = 0 значение функции
Г (п + 1) есть 1.
| 118]	ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ БЕССЕЛЯ	361
и т. д., и получится
«2п+2	(2п"+ 2)2" ’
_______ 	 <*2П+2	_ ________а2.П______
U2n + it—_____________________________(2л + 4)4 (2л + 4) (2л + 2) 4 • 2*
и т. д.; величина у2 будет
У2 = Х~П [«2пЯ2" + «2п+2^2п+2 +•••] =
п Г . х2	ж4	1
= Я2пх [ 1 — 2 (2п + 2) + 2 • 4 (2л + 2) (2л + 4)	' J ’
т. е. у2 отличалось бы от уг постоянным множителем и не было бы незави-
симым интегралом уравнения (23).
Чтобы найти этот второй независимый интеграл, можно поступать
следующим образом: искать непосредственно решение вида
у2 = ж-п (а0 + b0 In х) + х~п+1 (аг + 6, In х) + ...,
То е.
со
у2 = х~п (ак +• bk In х) хк>
к=0
и, подставив эту величину в уравнение (23), собрать в нем члены с одина-
ковыми степенями буквы х и уравнять нулю коэффициенты при них, причем
получится некоторая система уравнений, из которой все коэффициенты ак
четного порядка выразятся через а2п, которое само остается произвольным,
все коэффициенты Ьк четного порядка .выразятся через Ь2п, которое само
остается произвольным, все же коэффициенты ак и Ьк нечетного порядка
равны нулю.
Оказывается, что величина у2 будет
У2 = ^2пУ1 4“ Ь2п%п>
где
2 (2п +2) + 2.4(2/14-2) (2п + 4)
и
zn	2(2л + 2) + 2 • 4 (2л + 2) (2ге + 4)
- 2*-* • п! (п - 1)! (х- +	+ 2 . 4	2) (2„ _ 4) + 
хп~2	\	хп+2 / 1	14
+ (2 • 4 • б ... 2л -- 2)2)	0	’	+ 2 (2л+ 2) + 2л+ 2	) ~
________/	1	, 1	 • 1 , 1 л ,
2 • 4 (2л + 2) (2л + 4) \	2	'г 4	"г 2л + 2 2л + 4 >
...+(_ 1)*-1_____________________________(к + л +
~	>	2 • 4 ... 2Л(2л + 2)(2л + 4) ... (2Л + 2А-Д2
11	1	1 X
й + 2л + 2 +2л + 4 + • ‘ ’ + 2л + 2Л ) + ' ’ ’
При п = 0 величина zn не заключает отрицательных степеней буквы х9
и будет
+ \1 ’’’ 2 + 3 ) 22 • 42 • ба
362
РАДИАЛЬНЫЕ КОЛЕБАНИЯ ПОЛОГО ЦИЛИНДРА
Гл. VIII
Но вместо этой функции у2 рассматривают другую, которая полу-
чается, если приписать а2п и Ь2п некоторые определенные частные зна-
чения, выбранные так, что соответствующая им величина у2 обладает
свойствами, вполне аналогичными свойствам функций	Такая функ-
ция и обозначается знаком Yn(x), и выражение ее приведено выше; она
называется бесселевой функцией второго рода п-го порядка.
§ 119.	Для бесселевых функций составлены следующие таблицы:
1)	Значения функций /0 (х) и Щх) для аргументов: от х = 0 до
х = 15.50 через 0.01.
2)	Значения функций 1п(х) для целых значений значков п и аргу-
ментов х через 1, пока величина функции остается больше .
3)	Значения первых 50 корней уравнения 1± (х) = 0 и соответствующих
им значений Zo (х\.
4)	Значения функций Уо (х) и Ух (х) для аргументов от х = 0
до х — 10.2; до х = 1 через 0.01 и затем через 0.1.
Первые три таблицы имеются в руководстве Gray and Mathews —
«Treatise on Bessel functions», последняя— в томах XXVI журнала
«Messenger of Mathematics», а также в сборнике таблиц: Янке и
Эмде, Таблицы функций. Все эти таблицы, сокращенные до пяти знаков,
находятся также в изданном Академией Наук «Сборнике математических
и астрономических таблиц» проф. С. П. Глазенапа.
Как видно, чтобы пользоваться этими таблицами, необходимо порядок
функций привести к нулю или единице. Для всех функций целого порядка
это достигается при помощи следующих формул приведения, доказывать
которые не будем, отсылая к руководствам по бесселевым функциям.
Для краткости письма мы опускаем аргумент (х), так что вместо 1п (х)
будем просто писать 1п и вместо Yn (х) просто Уп.
Эти формулы следующие:
Z„_1-Jzn + Zn+1 = O,
Fn_x-5rn + yn+1 = 0.
(I)
Эти две формулы дают возможность выразить функции Бесселя любого
целого порядка через функции нулевого и первого порядков, для коих
составлены таблицы.
При пользовании функциями Бесселя встречаются обыкновенно, как
и в нашей задаче, не только сами функции, но и их производные.
Понятно само собою, что, пользуясь дифференциальным уравне-
нием (23), можно производную второго и всех высших порядков выразить
через самую функцию и ее производную первого порядка.
Что же касается первой пройзводной, то оказывается, что эти производ-
ные выражаются следующим образом:
v' ~ lv	v ______v	п v
1 ч — х 1 И 1 п+1 — 1 п-1	х 1 п’
(И)
а в частном случае
Гй=-ц,
(Ш)
Формулы (I), (II) и (III) и дают возможность приводить всякое выра-
жение, содержащее бесселевы функции любого целого порядка и их произ-
водные любого порядка, к такому виду, в который входили бы только функ-
§ 121J
ОПРЕДЕЛЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
 363
ции нулевого и первого порядка, и, значит, при вычислениях пользоваться
готовыми таблицами, а не теми рядами, коими функции определяются.
Выше приведены те значения аргументов, для коих таблицы составлены;
как видно, эти значения невелики, и следовательно, если бы встретилась
надобность найти значение функции для аргумента, лежащего вне таблич-
ной границы, то пришлось бы обратиться к рядам, —а так как для боль-
ших значений х эти ряды медленно сходятся, то пришлось бы брать в них
много членов.
Чтобы этого избежать, составлены для больших значений х следующие
две приближенные формулы:
In (х) =	[р cos	к - z) + Q sin (^±2 я ] ,
Yn (х) = )/1 [In 2 - С] 1п (х) +	(26)
+ /2^[<?cos(?4jTC-a;)“Psin(^’r“a:)]*
где
р (4п2 — 1) (4п2 — 9)	(4п2 — 1) (4п2 — 9) (4п2 — 25) (4па — 49) __
1	2! (8х)2	+	4! (80*
4„2 _ J (4„2 __	(4п2 __ 9) (4п2 __ 25)
" ~ Хх	3! (8х)*	•
Здесь С есть эйлерова постоянная ((7 = 0.57721566 ...), так что
In 2 —(7 = 0.115931516 ...
Очевидно, что ряды для Р и (2 —расходящиеся, и при пользовании пре-
дыдущими формулами надо брать лишь немногие первые их члены, пока
эти члены идут убывая, подобно тому как п ри пользовании рядом Стирлинга.
§ 120.	Трансцендентное уравнение, определяющее основные 'гона.
Мы имели формулу
Rk = [apkY'i (арк) + hY1 (арк)] I. (pkr) — [аркГ. (ap^+hl. (арк)] Y. (ркг)>
причем рк есть А-ый корень уравнения
[apl'i (ар) + hl. (ар)] [bpY] (bp) + hY. (bp)] - (bpl'. (bp) +
+ hl. (bp)] [apY’. (ap) + hYx (ap)] = 0.
Чтобы при вычислениях пользоваться таблицами, надо в этих формулах
заменить I'1(ap)t Y^ap), li(bp) и Y'^bp) их выражениями
I'.(ap) = I0(ap)-^I.(ap) и Y'.(ap) = Y0(ap) — ±Y.(ap),
I'.(bp):-I0(bp)-^Ii(bp) и =
после чего в эти формулы будут входить только функции, значения коих
непосредственно даются таблицами.
§ 121.	Определение вынужденных колебаний при действии перемен-
ного давления на внутреннюю поверхность. Прежде чем приступать
к численным вычислениям, покажем, каким образом найти вынужденные
колебания н2.
Следуя общему методу, поступаем так?
1)	представляем функцию F (г, t), стоящую во второй части уравнения
Л2 С V<?r2 + г дг гг) Г \Г’ 1>'
364
РАДИАЛЬНЫЕ КОЛЕБАНИЯ ПОЛОГО ЦИЛИНДРА
[Гл. VIII
в виде ряда, расположенного по «фундаментальным» функциям Rk, коими
определяются свободные колебания нашего цилиндра, т. е. полагаем
F(r, t)=%Nk(t)Rk,	(27)
k=l	*
тогда величина коэффициента Nk(t) определится равенством
ь
J’ F (г, г) Rk г dr
Nk(t) = —i--------•	(28)
J* rR\dr
a
2)	Величину м2 ищем под видом суммы
W2= S Sk(t)Rk,	(29}
/c= 1
расположенной по тем же функциям Rk.
3)	Подставляем величину (29) в уравнение (7) и получаем равенство
к = 1
но, в силу уравнения (10),
Rk +^R'K-~Rk=-PlR
и предыдущее равенство примет вид
S W + c*p*Sk-Nk(t)]Rk = 0,	(30}
7<-=1
которое не иначе может иметь место, как если брать
Sk + c*p*Sk = Nk(t).	(31 >
Это уравнение и послужит для определения $к.
Так как при t = 0 должно быть
м2 = 0 и ^ = 0,
то необходимо и величины Sk подчинить условиям, чтобы при £ = 0 было
S* = 0 и 5* = 0	(32}
и, значит, величина Sk будет
t
Sk = ~\N(Z)sincPk(t-i)di,	(33)
сРк J	i
О
причем
ь
f F(£, r)Rkrdr
A4i)=5L-b---------•	(33')
j* Rkr dr
a
Формулы (29) и (33) и решают поставленный вопрос о вынужденных
колебаниях цилиндра.
§ 122.	В § 115 был отмечен тот частный случай, когда внешнее усилие
приложено не в виде объемной силы pF (г, Z), а сосредоточено на внутрен-
ней поверхности и представляет некоторое давление, изменяющееся с тече-
нием времени t. Там же указан и способ решения в этом случае.
§ 123]
РАДИАЛЬНЫЕ КОЛЕБАНИЯ 12-ДЮЙМОВОЙ ПУШКИ
365
Итак, пусть сказанное давление, отнесенное на единицу площади вну-
тренней поверхности цилиндра, есть
тогда будем сперва брать функцию [>F (г, t) так, чтобы было
[>F(g, Z) = ^- = -|-/(Z) для a<r<a + X,
F(r, t)~0	для a+X<r<6,
причем X предполагается весьма малою величиною.
Ясно, что при таком выборе нагрузки [>F (г, Z) вся сила сосредоточена
на слое, прилегающем к внутренней поверхности цилиндра и имеющем тол-
щину X, причем на элементарную призму, коей основание есть 1 и высота
X, действует усилие, равное Р. Стоит только перейти к пределу X — 0, и мы
получим решение, относящееся к случаю давления Р, сосредоточенного на
внутренней поверхности.
При вышеуказанном выборе функции pF (г, Z) будет
Ь	Ъ	а+л
Nkty^rR*dr=^F$;ti)Rkrdr==^ f ft Rkr dr,
a	a	a
а так как X весьма малая величина, то последний интеграл равен
V/№(«)>
значит,
2vfc(e) = £_«H^L/(x)
J г^кdr
а
и, следовательно,
t
~	\ / (5) sin срк (t -n di.	(35)
J rRkdr 0
а
Это выражение совершенно подобно тому, которое встречается вообще
при изучении колебательных движений, и его свойства по отношению
к «статическому» или «динамическому» характеру действия силы в зави-
симости от быстроты ее нарастания по сравнению с периодом основного
«тона» (соответствует значению к — 1) системы, изложенные в главах I и VII,
целиком применимы и к настоящему случаю.
На этом мы закончим теоретическую часть рассмотрения вопроса
и перейдем к численному примеру, соответствующему случаю колебания
•стенок камеры 12-дюймовой пушки.
§ 123.	Численный пример — радиальные колебания 12-дюймовой
пушки. Для наших орудий толщина стенок приблизительно равна калибру;
следовательно, будет
Ь — За.
Вместе с тем, в виду плотного прилегания сильным натяжением колец и
кожуха к трубе и между собою, можно для радиальных колебаний, в осо-
бенности при растяжении, считать стенку как бы сплошною, а не слойчатою.
Величина
h =	-г-
К -J- 2*jl
j
может быть принята равной — , т. е. Х = и; тогда, полагая
о
ар = а,
366
РАДИАЛЬНЫЕ КОЛЕБАНИЯ ПОЛОГО ЦИЛИНДРА
[Гд. VIII
Решение*
FW = [3aZ0(a)-2Z1(a)] [9аУ0 (За)-21\ (3x)J
I	II	III	IV	V i	VI	1 VII 1	VIII	IX	X
		1	' )	4		! I 1	g 1		1 rS 1
							•		
0.0	—	—	—	—	—	—	—	—	—
0.5	0.94	-0.48	-0.59	4.56	1.5	0.51	— 1.12	0.66	1.17
1.0	0.76	—0.88	0.23	2.35	3.0	—0.26	—0.68	0.56	-1.10
1.5	0.51	— 1.12	0.66	1.17	4.5	—0.32	0.46	—0.34	-0.89
2.0	0.22	— 1.15	0.83	0.20	6.0	0.15	0.55	—0.44	0 ’б!
2.5	—0.05	—1.00	0.78	-0.57	7.5	. 0.26	-0.27	0.22	0.78
3.0	—0.26	—0.68	0.56	— 1.10	9.0	—0.09	-0.49	0.38	—0.: 8
3.5	—0.38	—0.27	0.25	— 1.32	10.5	—0.24	0.03	—0.139	—0.72
Вычисление наименьшего;
0.5	0.938	-0.484	-0.590	+4.567	1.5	0.512	—1.116	0.660	1.166
0.6	0.912	-0.573	—0.379	+3.893	1.8	0.340	—1.163	0.789	0.568
Приближенная величина корням
В промежутках, отмеченных в'столбце XXI
S_123j|
РЛ'Д1ГАЛЬНЫЕ;КОЛЕБАНИЯ 12-дюймовой пушки
36/
Таблица 20
уравнения
-[ЗаГ0(*)-2У,(*)] [9*Ze(3*)-21,(3*)] =0
	XI	XII	1 XIII	XIV	XV	XVI	XVII	XVIII	XIX	XX	XXI
	'""о СО	со о	'"’о ч	5^ со о 1X1 о	ся а о СО	фя со о о	оя "Я4 со	фя 1 ч"© а	(XV) . (XVI)	(шлх) • (плх)	II * *
		—	—		1	—	—	—	—			—	-10.67
	1.41	2.30	-0.88	3.00	0.93	4.17	3.68	1.18	3.89	4.34	- 0.45
	2.28	— 2.28	0.69	5.04	1.40	3.94	3.04	— 2.96	5.52	— 9.00	14.52
	2.30	—4.32	3.00	-4.59	1.18	-5.48	4.17	-3.86	- 6.47	—16.12	9.65
	1.32	2.70	5.00	-7.92	0.17	-7.31	5.20	3.25	— 1.24	16.80	— 18.04
	—0.38	5.85	5.85	4.95	-1.38	5.73	5.28	5.58	— 7.90	29.50	—37.40
	—2.34	—2.43	5.04	10.30	—3.02	9.92	4.94	—2.92	—30.00	— 14.50	— 15.50
	4.00	-7.56	2.62	-4.38	—4.27	— 5.10	1.30	-7.48	21.8	- 9.73	31.53
	корня	0.5<аг<1.00:									
1	1.406	2.302	—0.885	2.970	0.922	4.136	3.682	1.186	3.820	4.37 1	-0.550
	1.642	1.835	—0.682	4.260	1.069	4.828	3.211	0.673	5.160	2.160	3.000
0 SSO 1
°-50+?^ • <-п = 0.50 + 0.016 = 0.516
о • <ЭЭи 1U
толстою чертою, лежат корни
368
РАДИАЛЬНЫЕ КОЛЕБАНИЯ ПОЛОГО ЦИЛИНДРА
[Гл. VH
будем иметь
Ьр = За
и уравнение (17) примет вид
[За/; (а) + 1г (а)] [9а У; (За) + 7! (За)] -
- [За У;(х) + Yt (а)] [9x7] (За) + 7, (За)] = 0.
Но по формулам (II) § 119 будет
/;(«) = /,(«)-р1(а) И /; (За) = 70 (За) — — 7Х (За),
У;(а) = У0(а)-^У1(а) и У[ (За) = У0 (За) —± У, (За).
Подставляя эти величины в предыдущее уравнение, получим.
[За/0 (а) — 2Z\ (а)] [9аУ0 (За) - 2УХ (За)] -
-[ЗаУ0(а)-2У1(а)] [9а/0 (За) - 2Д (За)] =0.	'
Таким образом, вычисление корней уравнения (17) приведено к вычис-
лению корней уравнения (36) (см. табл. 20, стр. 366 — 367), в которое
входят лишь такие величины, которые непосредственно даются таблицами.
Заметим, что, в силу формул (24), при а = 0 первая часть уравне-
ния (36) равна — 10-— — —10.66...
Для решения уравнения (36) вычисляем значения первой его части
при а = 0, 0.5, 1, 1.5,..., затем сближаем пределы там, где происходит
перемена знака.
Оказывается, что наименьший корень
= 0.516.
Выражая все длины в сантиметрах и веса в килограммах, имеем
л - or	> /г пг 0.008
а = 1о.25,	0 = 45.75, р= hcM .
Уо 1
Тогда
с = 550 000 см[сек,
так что период соответствующий низшему тону, будет
2л __ 2л*15.25	__ 1
0.516*550000	~ 2960 СеК’
Следовательно, продолжительность действия силы надо сравнивать
с величиною *4, приблизительно равной сек., и малой продолжи-
тельности надо считать те силы, коих время
нпю с сек., а так как продолжительность
1
орудии при выстреле составляет не менее
нарастания мало ио сравне-
нарастания давления в этом
сек., то действие выстрела
можно рассчитывать «статически», ибо оно «медленное» по сравнению
с периодом радиальных колебаний стенок пушки.
Этим примером мы и закончим наш курс.