Автор: Соловейчик Ю.Г. Рояк М.Э. Персова М.Г.
Теги: математика естественные науки
ISBN: 978-5-7782-0749-9
Год: 2007
Текст
УЧЕБНИКИ Н Г Т У
Я>| »| —Ь 4МВПЯ Ш nrn r wr—i r Т - Г—Пипд г У-т - - г -1
Ю.Г. СОЛОВЕЙЧИК, М.Э. ВСЯК,
М.Г. ПЕРСОВ А
РЕДАКЦИОННАЯ КОЛЛЕГИЯ
СЕРИИ «УЧЕБНИКИ НГТУ»
д-р техн, наук, проф. (председатель) НВ. Пустповой
д-р техн, наук, проф. (зам. председателя) Г. И. Расторгуев
д-р техн, наук, проф. А. Г. Вострецов
д-р техн, наук, проф. В. В. Губарев
д-р техн, наук, проф. В.А. Гридчин
д-р техн, наук, проф. В. И Денисов
д-р экон, наук, проф. К Т Джурабаев
д-р филос. наук, проф. В.И. Игнатьев
д-р техн, наук, проф. КП. Кадомская
д-р филос. наук, проф. В. В. Крюков
д-р физ.-мат. наук, проф. А.К. Дмитриев
д-р физ.-мат. наук, проф. Х.М. Рахимянов
д-р техн, наук, проф. Ю. Г. Соловейчик
д-р техн, наук, проф. А.А. Спектор
д-р экон, наук, проф. В.А. Титова
д-р техн, наук, проф. А.И. Шанин
д-р техн, наук, проф. А.Ф. Шевченко
д-р техн, паук, проф. Г.М. Шумский
Ю.Г. СОЛОВЕЙЧИК, М.Э. РОЯК,
М.Г. ПЕРСОВА
МЕТОД КОНЕЧНЫХ
ЭЛЕМЕНТОВ
ДЛЯ РЕШЕНИЯ СКАЛЯРНЫХ
И ВЕКТОРНЫХ ЗАДАЧ
Библиотека
Новосибирского
государственного
технического университета
НОВОСИБИРСК
2 0 0 7
УДК 5 17.962.1/(075.8)
С 602
Рецензент:
д-р физ.-мат. наук, проф. В.П. Ильин
Соловейчик, Ю.Г.
Метод конечных элементов для решения скалярных и векторных
задач : учеб, пособие / Ю.Г. Соловейчик, М.Э. Рояк, М.Г. Персова -
Новосибирск: Изд-во НГТУ, 2007. - 896 с. («Учебники НГТУ»)
ISBN 978-5-7782-0749-9
Рассматриваются вопросы теории и практики МКЭ и его воз-
можности при использовании узловых и век горных базисных функций
для решения различных классов задач. Много внимания уделяется
технологическим аспектам при реализации МКЭ, методам тестирова-
ния и способам оценки точности получаемых конечноэлементных ре-
шений, а также специальным постановкам, позволяющим с высокой
точностью решать сложные трёхмерные задачи. Особый интерес эта
книга может представлять для тех. кто хочет освойть самые современ-
ные методы решения наиболее сложных задач шектромагметизма -
трёхмерных, векторных, нелинейных.
ISBN 978-5-7782 0749-9
УДК 517.962.1/(075.8)
© Ю.Г. Соловейчик, М.'). Рояк,
М.Г. Персова. 2007
© Новосибирский государственный
технический университет, 2007
Оглавление
5
ОГЛАВЛЕНИЕ
Предисловие........................................................14
Введение...........................................................16
1. Математические модели физических процессов в виде
краевых и начально-краевых задач...................................24
1.1. Краевые задачи для уравнения эллиптического типа............24
1.2. Начально-краевые задачи для уравнений параболического и
гиперболического типа.............................................25
1 3. Краевые и начально-краевые задачи, используемые для
моделирования электромагнитных полей........................26
1.3.1. Задачи электростатики...................................27
1.3.2. Стационарные электрические ноля в проводящих средах.....28
1.3.3. Задачи магнитостатики...................................29
1.3.3.1. Описание стационарных магниз ных полей с использованием вектор-
потенциала....................................................30
1.3.3.2. Описание стационарных магнитных полей с использованием скалярного
магнитного потенциала.........................................34
1.3.4. Модель нестационарного электромагнитного поля в виде одного
векторного уравнения.....................................36
1.3.5. Модель в виде уравнений для всктор-потенциала
электромагнитного поля и скалярного потенциала электрического
поля.....................................................38
1.3.6. Модель с совместным использованием всктор-потенциала и
скалярного потенциала магнитного поля....................41
2. Основные идеи и принципы МКЭ...................................47
2.1. Вариационные постановки на основе МНК Аппроксимация на
конечномерном подпространстве, определяемом набором
базисных функций.................................................47
2.2. Вариационные постановки, используемые в методах Ритца и
Галёркина........................................................54
2.2.1. Построение эквивалентных вариационных формулировок с
уменьшенными требованиями к гладкости решения...................54
2.2.2. Построение дискретных аналогов..........................61
2.2.3. Учёт главных краевых условий............................65
2.3. Применение финитных кусочно-линейных функций для
построения конечноэлементных решений одномерных краевых
задач............................................................68
2.4. Технологии сборки глобальных матриц и векторов в МКЭ........73
2.5. О методе коллокации.........................................81
3. Вариационные формулировки и конечномерные
подпространства для узлового МКЭ...................................84
3.1. Теоретические аспекты МКЭ. Вариационная постановка в
форме минимизации функционала.....................................84
3.2. Вариационная постановка в форме уравнения Галёркина.........97
3.3. Аппроксимации на конечномерных подпространствах.............101
3.4. Конечноэлементные СЛАУ.....................................104
3.5. Основные принципы построения базисных функций
конечномерных подпространств................................108
3.6. Сходимость и точность конечноэлементных решений.............I 10
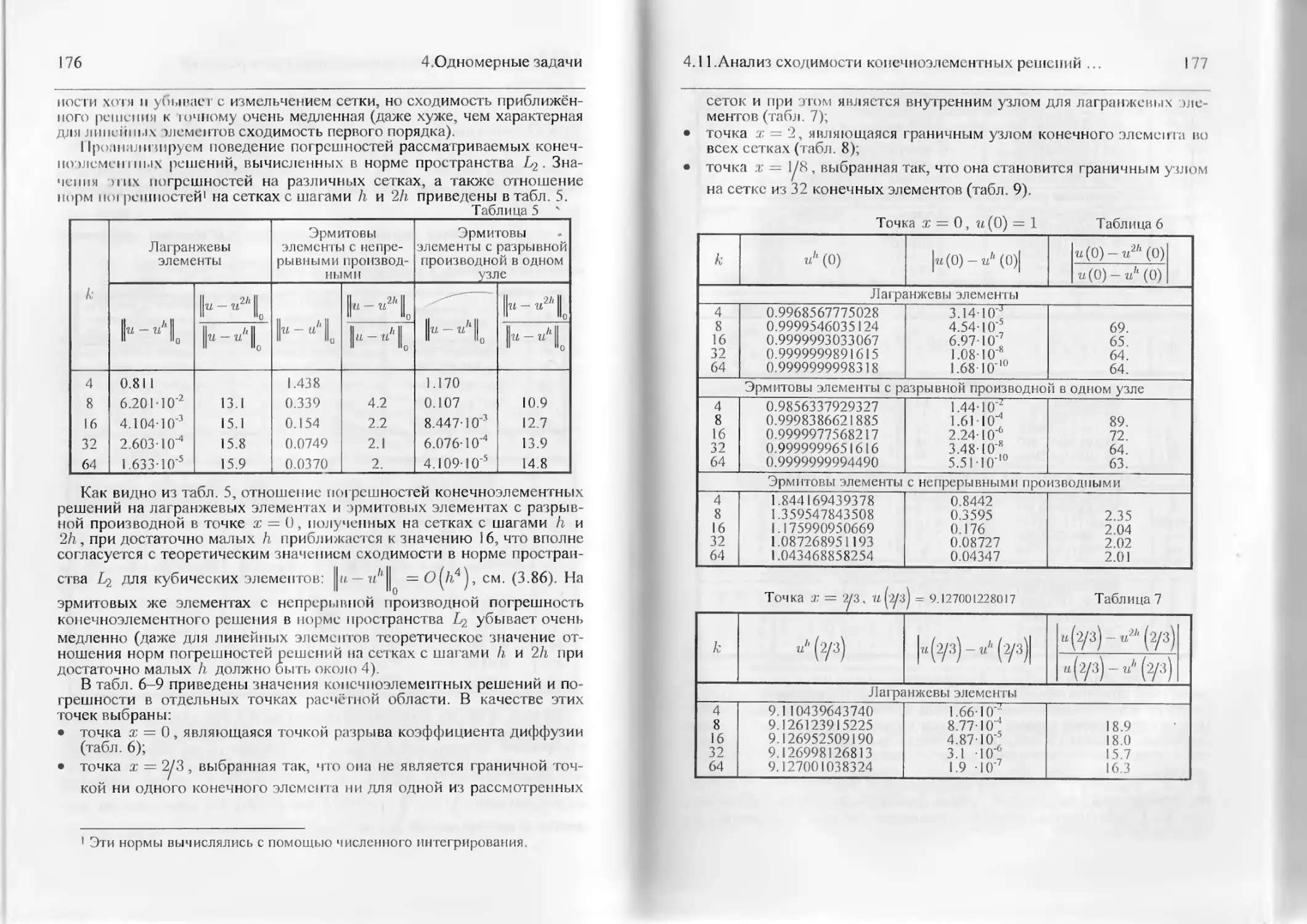
6
3.7. О сравнении погрешностей конечноэлементных решений,
полученных на различных сетках...........................117
3.8. Способы представления параметров краевых задач в
эквивалентных вариационных постановках...................123
3.9. Погрешности МКЭ при решении задач в областях с
искривлёнными границами..................................125
4. Одномерные задачи.........................................
4.1. Особенности вариационных постановок для одномерных задач
4.1.1. Одномерная !адача в декартовых координатах.........
4.1.2. Одномерная задача в цилиндрических координатах.....
4.1.3. Одномерная задача в сферических координатах........
4.2. Одномерные элементы первого порядка...................
4.3. Использование шаблонных базисных функций при решении
одномерных задач...........................................
4.4. Одномерные элементы второго порядка...................
4.4.1. Базисные функции и локальные матрицы одномерных
128
128
128
129
130
131
135
136
квадратичных элементов................................
4.4.2. Пример использования квадратичных элементов для решения
одномерной эллиптической задачи..............................
4.4.3. Сравнение погрешности конечноэлементны,х решений,
полученных на линейных и квадратичных элементах..............
4.5. Одномерные лагранжевы элементы третьего порядка...........
4.6. Одномерные эрмитовы элементы третьего порядка.............
4.7. Сопоставление лагранжевых и эрмитовых кубических
элементов по точности и вычислительным затратам................
4.8. Сравнение по точности линейных, квадратичных и кубических
элементов на примерах решения эллиптических задач на
равномерных сетках.............................................
4.8.1. Сравнение лагранжевых и эрмитовых кубических элементов.
4.8.2. Сравнение линейных и квадратичных элементов для задачи без
краевых условий первого рода.................................
4.8.3. Сравнение линейных и квадратичных элементов для задачи с
4.9.
4.10.
4.1 I.
4.12.
4.13.
краевыми условиями первого рода
О возможности использования э
решения задач с разрывным коэффициентом диффузии.......
Пример использования комбинированного эрмитова базиса для
решения задач с разрывным коэффициентом диффузии.......
Анализ сходимости конечиоэлементных решений на примере
решения задачи с разрывным коэффициентом диффузии......
О возможности учёта второго краевого условия как главного
для эрмитовых элементов................................
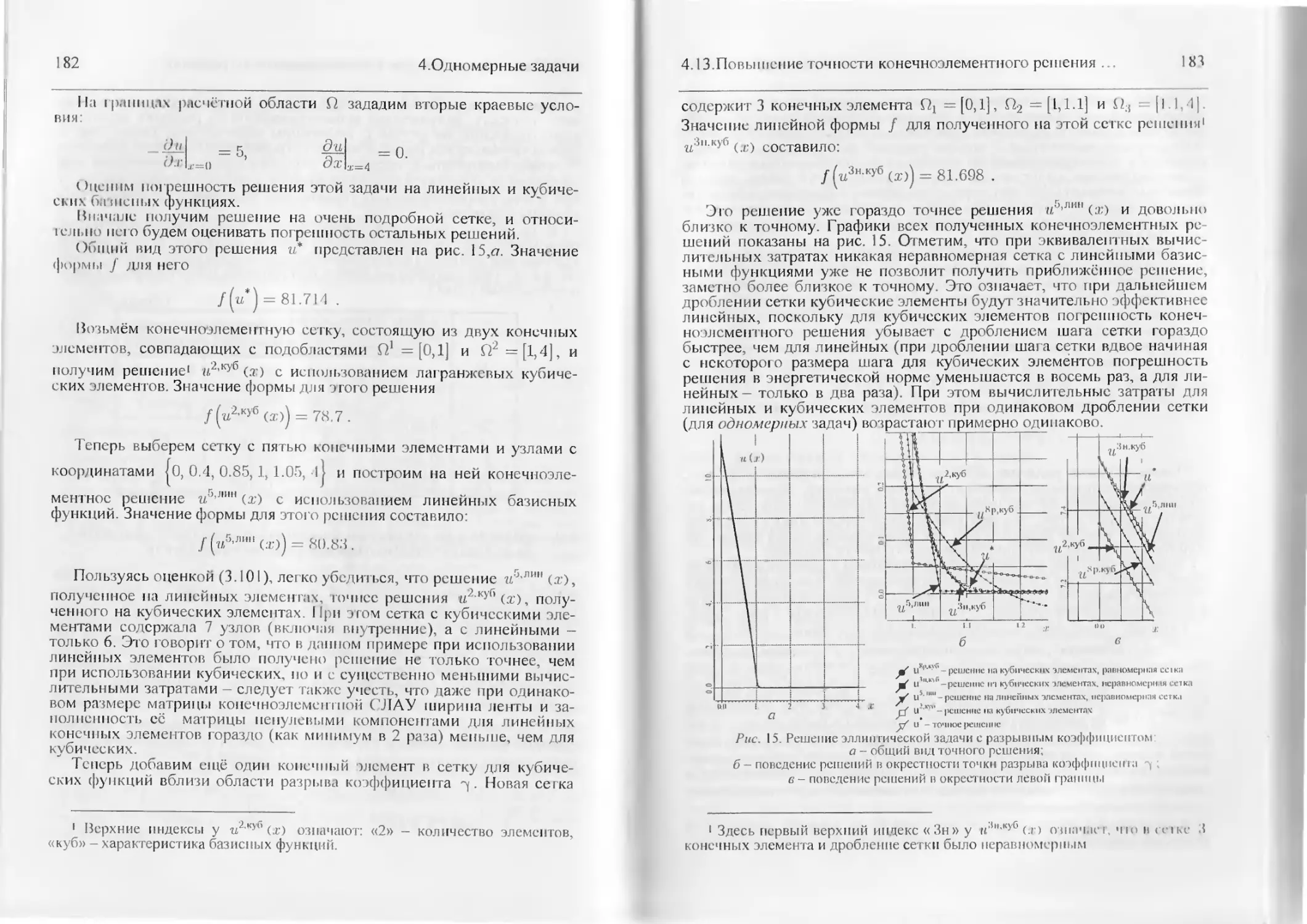
Повышение точности конечноэлементного решения за счёт
?митовых элементов для
использования неравномерных сеток......................
4.14. Тестирование процедур построения конечноэлементных
решений......................................................
4.14.1. Тестирование одномерных кубических эрмитовых элементов....
I 14.2. Тестирование одномерных кубических лагранжевых элементов
1.14.3. Тестирование одномерных эрмитовых элементов с разрывной
производной для решения задач с разрывным коэффициентом
диффузии....................................................
1.15. Одномерные конечные элементы в цилиндрических
координатах...............................................
1 15.1. Локальные матрицы жёсткости и массы для линейных элементов
1 15.2. Локальные матрицы жёсткости и массы для квадратичных
элементов.....................................................
136
140
143
135
149
154
158
159
163
164
167
168
174
180
181
185
186
188
190
192
192
194
Оглавление
7
4.15.3. Вычисление локальной матрицы массы для задачи с — 1/г2 .....195
4.15.4. Пример решения эллиптической задачи с использованием
квадратичных элементов............................................. 196
4.15.5. Пример решения тестовой эллиптической задачи для случая с
7 - 1/г2 .................................................198
4.16. Одномерные конечные элементы в сферических координатах.........201
4.16.1. Локальные матрицы жёсткости и массы для линейных элементов.201
4.16.2. Пример решения одномерной эллиптической задачи в
сферических координатах..........................................202
4.17. Использование кубических эрмитовых элементов для
построения интерполяционных и сглаживающих сплайнов.................204
4.17.1. Построение кубического интерполяционного сплайна.........204
4.17.2. Кубические сглаживающие сплайны..........................208
4.17.3. Примеры носгросния одномерных кубических сплайнов..........213
4.18. Согласованные результанты....................................218
4.18.1. Технология построения согласованного результанта.........218
4.18.2. Пример построения согласованного результанта...............221
5. Двумерные скалярные задачи..........................................
5.1. Основные особенности технологии построения МКЭ-
аппроксимаций при решении двумерных задач........................
5.1.1. Локальные матрицы для двумерной задачи в декартовой системе
координат......................................................
5.1.2. Локальные матрицы для двумерной задачи в полярной системе
координат......................................................
5.1.3. Локальные матрицы для осесимметричной задачи................
5.1.4. О вычислении локальных векторов правых частей...............
5.2. Построение МКЭ-аппроксимаций на прямоугольных сетках ....
5.2.1. Билинейные базисные функции.................................
5.2.2. Об учёте краевых условий первого рода.......................
5.2.3. Пример использования билинейных элементов...................
5.2.4. Биквадратичные базисные функции.............................
5.2.5. Бикубические лагранжевы базисные функции....................
5.2.6. Бикубические эрмитовы базисные функции......................
5.2.7. Использование бикубических эрмитовых элементов при решении
задач с разрывным коэффициентом диффузии.......................
5.2.8. Учёт краевых условий для бикубических эрмитовых элементов ....
5.2.9. Примеры решения эллиптических задач с использованием
бикубических эрмитовых элементов...............................
5.2.9.1. Тестовый пример..........................................
5.2.9.2. Пример решения задачи с разрывным коэффициентом диффузии.
5.3. Применение МКЭ для решения двумерных краевых задач на
треугольных сетках...............................................
5.3.1. £ -координаты на треугольнике...............................
5.3.2. Линейные треугольные элементы...............................
5.3.3. Примеры решения эллиптических задач с использованием
линейных треугольных конечных элементов........................
5.3.4. Треугольные элементы с квадратичными базисными функциями ..
5.3.5. Треугольные элементы с кубическими лагранжевыми базисными
функциями .....................................................
5.3.6. Треугольные элементы с кубическими эрмитовыми базисными
функциями .................................................
5.4. Четырёхугольные элементы.......................................
5.4.1. Базисные функции на четырёхугольных элементах.......
5.4.2. О сходимости аппроксимаций на четырёхугольных конечных
элементах .................................................
225
.225
.226
.226
.227
.227
.229
250
253
256
258
.258
.265
274
.275
.278
.282
.289
295
2Р6
297
297
’о*;
8
5.4.3. Локальные матрицы четырёхугольных,конечных элементов
первого порядка..................................................300
5.4.4. Вычисление значения конечноэлементного решения в
произвольной точке расчетной области для сетки с ячейками в
виде четырёхугольников...........................................304
5.4.5. Об очном общем способе вычисления значений и производных
консчпоэлсментного решения, полученного на нерегулярной сетке,
с использованием переинтерполяции.................................306
5.4.6. Четырёхугольные элементы высоких порядков.................309
5.5. Двумерные конечные элементы с криволинейными границами........310
5.6. Вычисление локальных матриц массы и жёсткости при
преобразовании системы координат. Инвариантность
локальных матриц массы и жёсткости к повороту и
параллельному переносу декартовой системы координат................315
5.7. Тестирование процедур конечноэлементного решения
двумерных задач....................................................319
6. Трёхмерные скалярные задачи....................................328
6.1 11ос троение МКЭ-аппроксимаций па сетках из прямоугольных
параллелепипедов............................................330
6.1.1. Трилинейные базисные функции............................331
6.1.2. Лагранжевы базисные функции высоких порядков на
прямоугольных паралслепипедах...................................334
6.1.3. Трикубические эрмитовы базисные функции.................335
6.2. Тетраэдральные конечные элементы............................337
6.2.1 Тетраэдральные сетки....................................337
6.2.2. £ -координаты на тетраэдре..............................338
6.2.3. Линейные тетраэдральные элементы......................... 341
6.2.4 Тетраэдральные элементы с базисными функциями высоких
поря дков ......................................................344
6.3. Конечные элементы на треугольных призмах....................345
6 3 1. Об использовании призм в качестве ячеек сетки...........345
6.3.2. )лемспты первого порядка на треугольных призмах.........346
6.3.3. Элементы высоких порядков на треугольных призмах........348
6.4. Шссгигранные элементы.......................................349
6.5. Гссчпрование процедур конечноэлементного решения
трёхмерных задач..................................................352
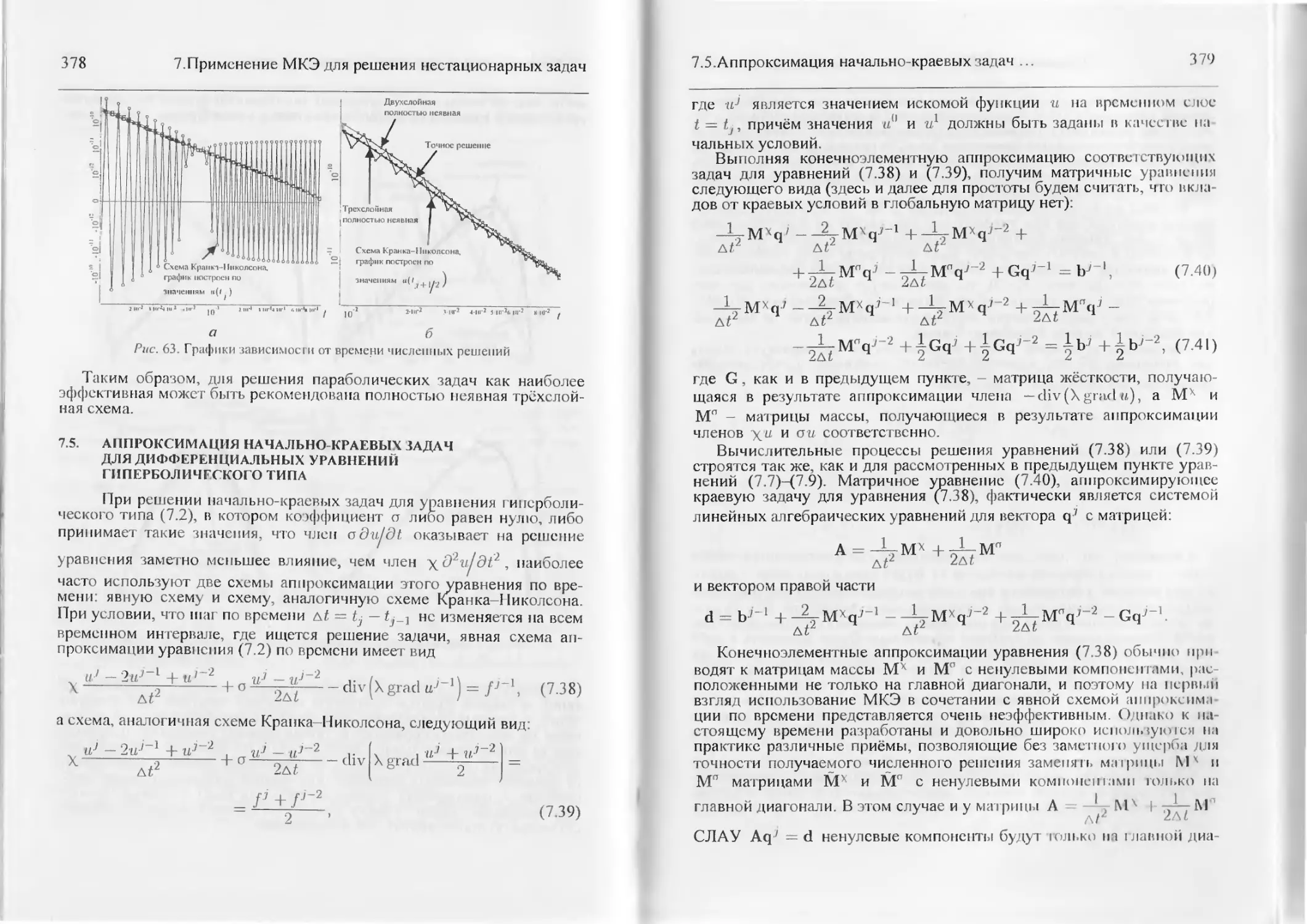
7. Применение МКЭ для решения нестационарных задач................364
7.1. О дискретизации по времени..................................364
7.2. Аппроксимация начально-краевых задач для
дифференциальных уравнений параболического типа..................365
7.3. Гесгпрованнс процедур решения начально-краевых задач для
уравнений параболического тина...................................371
7.4. примеры решения начально-краевых задач для уравнений
параболического тина.............................................373
7.5. Аппроксимация начально-краевых задач для
дифференциальных уравнений гиперболического типа.................378
7.6. Об очередности выполнения аппроксимации по времени и
пространству при решении нестационарных задач....................382
7.7. Решение задач с гармоническими по времени источниками.......384
7.7.1 Постановка задачи.......................................384
7.7.2. Построение копечноэлементной анпрокепмацп...............385
7.7.3. 11| имср решения одномерной гармонической задачи........388
7.7.4. Об ошибке аппроксимации конечноэлсмен гных решений
гармонических задач......................................392
Оглавление
9
8. Сосредоточенные источники в скалярных задачах............401
8 1. Типы сосредоточенных источников..................... 401
8.2. Конечноэлементные аппроксимации трёхмерных задач с
сосредоточенными источниками ...............................404
8.3. Сосредоточенные источники в двумерных и одномерных
задачах.....................................................414
9. Конечноэлементные процедуры решения краевых задач с
выделением части поля...........................................418
9.1. Примеры решения задач с выделением части поля............418
9.2. Общая схема построения конечноэлементных процедур
решения задач с выделением части поля........................428
9.3. Применение технологии выделения основного поля для
решения задач с сосредоточенными источниками.................435
9.4. Многоэтапная технология выделения поля...................438
9.5. Вычисление полей влияния.................................442
9.5.1. Основные типы задач, требующих вычисления полей влияния .442
9.5.2. Операторная форма задачи, определяющей поле влияния......443
9.5.3. Построение копечноэлементной СЛАУ, аппроксимирующей поле
влияния....................................................443
9.6. О различных способах вычисления полей влияния и их
эффективности.................................................444
10. Структуры данных, сетки и алгоритмы работы с ними в
МКЭ.................................................................448
10 1, Основные методы описания расчётной области...................448
10.2. Структуры данных для описания двумерных задач Двумерные
сетки. . .............................................449
10.2.1 Описание двумерных расчётных областей с прямоугольными
подобластями. .................................. 149
10.2.2. Общие принципы построения структур данных для храпения
конечноэлементпых сеток..........................................452
10.2.3. Хранение регулярных прямоугольных сеток.................452
10.2.4. Описание двумерных областей с криволинейными границами..457
10.2.5. Регулярные сетки с четырёхугольными ячейками............462
10.2.6. Хранение нерегулярных сеток.............................468
10.2.7. Построение нерегулярных треугольных сеток...............472
10.3. Структуры данных для описания трехмерных задач.
Трёхмерные сетки..................................................480
10.3.1. Описание трёхмерных областей и принципы построения
трёхмерных сеток с ячейками в вице параллелепипедов и
шестигранников.................................................. 180
10.3.2. Метод тиражирования сечений.............................487
10.3.3. Построение тетраэдральных сеток методом тиражирования
сечений.........................................................489
10.4. Ст^ктуры данных для хранения матриц конечноэлементных
10.4.1 . Особенности матриц конечноэлементпых СЛАУ............. 191
10.4.2 . Профильный формат хранения матрицы СЛАУ................ 192
10.4.3 . Ленточный формат хранения матрицы СЛАУ.................. 191
10.4.4 Разреженные форматы хранения матриц СЛАУ................. 195
10.4.5 . Алгоритмы занесения локальных матриц в глобальную матриц},
хранящуюся в разреженном формате................................ 198
10.4.6 . Диагональный формат хранения матрицы СЛАУ...............501
10.4.7 . Блочные форматы храпения. Разреженный блочный формат. 502
10.4.8 . Процедура сборки глобальной матрицы, хранящейся в
разреженном блочном формате......................................506
10
10.5. Построение портрета конечноэлементной матрицы.............. 508
10.6. Алгоритмы нумерации базисных функций, граней и рёбер
конечных элементов.................................................512
10.6.1. 1(умерация глобальных базисных функций.....................512
10.6.2. Построение списков граней трёхмерных конечных элементов.
Использование упорядоченного списка граней для ускорения
процедуры нумерации базисных функций.............................514
10.6.3. 11остроение списка рёбер конечных элементов и их нумерация.519
10.7. Алгоритмы работы с конечноэлементными решениями..............521
10.7.1. Поиск конечного элемента в нерегулярной сетке..............521
10.7.2. Построение производных конечноэлементного решения........523
11. Комбинированные и несогласованные сетки......................528
11.1. Согласованные и несогласованные сетки и конечные элементы......528
I 1,2. Комбинированные согласованные сетки из треугольников и
прямоугольников с базисными функциями одного порядка.......530
11.3. об использовании несогласованных сеток в мкэ...................532
11.4. 1 {ссогласоваппые сетки с прямоугольными ячейками..............532
11.5. 11ример несогласованной стыковки элементов на
несогласованной прямоугольной сетке............................534
11.6. Построение согласованных конечных элементов с
несогласованными локальными базисными функциями ................536
I 1.6.1. Демонстрация рассматриваемого способа согласования на
простейшей прямоугольной сетке................................536
11.6.2 . Общая схема построения конечноэлсментпой СЛАУ при
согласовании элементов на несогласованных сетках с
использованием матрицы перехода...............................539
11.6.3 . Алгоритм сборки матрицы конечноэлементной СЛАУ из
локальных матриц элементов с несогласованными локальными
базисными функциями...........................................542
11 6.4. Способы хранения матрицы перехода и алгоритм её построения.544
11.6.5 . 11ример сборки глобальной матрицы СЛАУ с использованием
матрицы перехода..............................................552
11.7. Согласование конечных элементов на несогласованной сетке с
использованием переходных элементов............................554
11.8. Несогласованные i рёхмерные сетки........................567
11.9. Комбинированные трёхмерные сетки.........................572
сетках с элемен «ами разных порядков. Иерархические
базисы..........................................................579
12.1 . Использование технологии Т-преобразования для
согласования элементов разных порядков............................579
12.2 . Иерархические базисы Согласование конечных элементов
разных порядков ..................................................583
12.2.1 . Иерархические базисы одномерных элементов..............583
12.2.2 . Иерархические базисы па прямоугольниках................586
12.2.3 . Иерархические базисы на прямоугольных параллелепипедах.588
12.2.4 . Согласование иерархических элементов разных порядков на
прямоугольниках и параллелепипедах...............................590
12.2.5 . Иерархические базисы на симплексах. Согласование треугольных
и тетраэдральных иерархических элементов различных порядков......594
12.2.6 . Иерархические базисы на прямых призм*х.................599
12.3 . Согласование иерархических конечных элементов на
несогласованных сетках............................................601
12.4 . Сравнение лагранжевых и иерархических элементов............614
Оглавление
I 1
13. Основные способы уменьшения погрешности
конечноэлементных решений дву- и трёхмерных задач............616
13.1. О некоторых стратегиях повышения точности
конечноэлементных решений..................................616
13.2. Соотношения, позволяющие проводить сравнения
погрешностей конечноэлементных решений.....................617
13.3. р -технологии, h-технологии и р-h-технологии уточнения
решений. Адаптивные сетки..................................622
14. Применение узлового МКЭ для решения векторных
задач........................................................631
14.1. Математическая модель и вариационная постановка.....632
14.2. Построение конечпоэлементной аппроксимации задачи,
описываемой системой вариационных уравнений...............634
14.3. Хранение и сборка глобальной матрицы................639
14.4. Применение процедуры выделения поля при решении
векторных задач............................................641
14.5. Тестирование конечпоэлементных процедур решения
векторных задач............................................643
15. Векторный МКЭ для решения задач электромагнетизма..........647
15.1. Векторные дифференциальные уравнения второго порядка с
разрывными решениями........................................647
15.2. Вариационная постановка...............................650
15.3. Приближение решения на подпространствах...............653
15.4. Учёт неоднородных главных краевых условий.............656
15.5. Энергетическое скалярное произведение и погрешность
приближённого решения в энергетической норме................660
15.6. Принципы построения базисных вектор-функций из
пространства Нгс1 на двумерных сетках.......................667
15.6.1. Оощие принципы.....................................667
15.6.2. Базисные всктор-с >ункции па прямоугольнике.................668
15.6..3. Базисные вектор-пункция па треугольнике.....................674
15.6.4. Базисные вектор-*' )ункции на четырёхугольнике..............681
15.7. О некоторых возможностях построения на прямоугольных
edge-элементах базисных вектор-функций (из Н ,f) с
непрерывными нормальными составляющими............................689
15.8. Конечноэлементные матрицы и векторы, получаемые при
решении двумерных векторных задач с использованием
базисных вектор-функций из пространства 7/|и’ ....................693
15.8.1 Особенности вариационной постановки для двумерной векторной
задачи...........................................................693
15.8.2. Локальные матрицы и векторы прямоугольных edge-элементов...697
15.8.3. Локальные матрицы и векторы треугольных edge-элементов.....700
15.8.4. Локальные матрицы и векторы четырёхугольных edge-элементов.703
15.9. Пример сборки глобальной матрицы и вектора правой части
СЛАУ и учёта краевых условий в векторном МКЭ......................710
15.10. 0 ранге глобальной матрицы жёсткости в векторном МКЭ и
связанных с этим трудностях решения стационарных и
некоторых нестационарных электромагнитных задач..................718
15.1 1.Базисные вектор-функции из пространства Н" 1 на
трёхмерных сетках................................................ 720
15.111. Базисные вектор-фупкцпн на параллелепипеде..................720
12
15 11.2. Базисные вектор-оункции на тетраэдре..................
15.11.3. Базисные векторч >ункции на треугольной призме........
15 11.4. Базисные вектор-оункции на шестиграннике..............
15.12 Генерация конечноэлементной СЛАУ в векторном МКЭ при
решении трёхмерных задач..........................................
15.12.1 Основные соотношения, определяющие конечноэлементные
матрицы и векторы..............................................
15.12.2. Локальные матрицы параллелепипеда с векторными базисными
функциями .....................................................
15.12.3. Локальные матрицы тетраэдра с векторными базисными
функциями .....................................................
15.12.4. Локальные матрицы треугольной призмы с векторными
базисными функциями............................................
15.12.5. Локальные матрицы шестигранника с векторными базисными
функциями......................................................
15.12.6. Генерация вкладов от конечных элементов в вектор правой части
15.12.7. Учёт краевых условий................................
15.13 .Построение конечноэлементных аппроксимаций при
совместном использовании скалярного и векторного
730
735
738
743
744
744
746
748
потенциалов магнитного поля................................
15.13.1. Постановка задачи....................................
15.13.2. Построение конемпоэлементных аппроксимаций при совместном
использовании векторных и узловых базисных функций.............
15 13.3. Построение конечноэлементных аппроксимаций для задач с
разрывным скалярным потенциалом................................
15.14.06 очерёдности выполнения в векторном МКЭ аппроксимации
нестационарных задач по пространству и времени..................
15.15.Ос обенности применения различных технологий МКЭ при
использовании векторных базисных функций........................
15 15.1. Об оценке точности конечноэлементных решений в векторном
МКЭ............................................................
15.15.2. Технологии уменьшения погрешности приближённых решений в
век горном МКЭ.................................................
15.15.3. Тестирование процедур построения конечно элементных
аппроксимаций..................................................
15.15.4. Сосредоточенные источники в векторных задачах........
15.15.5. О выделении поля в векторном МКЭ.....................
15.15.6. Использование сеток с несогласованными ячейками в векторном
МКЭ
15.16.Другие возможности векторного МКЭ для решения
нестационарных задач электромагнетизма..........................
15.16.1. О постановках с совместным решением уравнений для
напряжённости магнитного поля и для скалярного магнитного
потенциала.....................................................
15.16.2. Об исполыованпи базисных вектор-функций из пространства
H,liv..........................................................
782
782
785
788
792
794
794
796
800
.804
805
.811
821
.821
.824
16. Решение нелинейных задач.......................................829
16.1. Нелинейные эллиптические краевые задачи....................829
16.2. Метод простой итерации......................................831
16.2.1. Схема метола ...831
16.2.2. Останов итерационного процесса.........................832
16.2.3. Использование релаксации ..............................832
16.3. Метод Нью гопа ....................................... 833
16.4. Пример решения одномерной нелинейной >адачи с
коэффициентом диффузии, зависящим oi решения......................838
16.5. О сходимости конечно элементных решений нелинейных
краевых задач.....................................................844
Оглавление
13
16.6. Вычислительные схемы решения нелинейных задач
магнитостатики...................................................847
16.6.1. Применение метода НьютонИ для решения двумерных
нелинейных задач магнитостатики................................847
16.6.2. Решение трёхмерных задач магнитостатики с использованием
неполного скалярного потенциала................................857
16.6.3. Решение трёхмерных нелинейных задач магнитостатики с
использованием двух скалярных потенциалов......................859
16.6.4. Задание кривых намагничивания и вычисление производных
(1 (l/p) JdB2 и t/р/dH2 ................................868
17. Методы решения СЛАУ, применяемые в МКЭ........................871
17.1. Прямые методы решения СЛАУ................................871
17.1.1. LU -разложение........................................872
17.1.2. LLT -разложение..................................... 874
17.1.3. LDLT -разложение.................................... 874
17.2. Неполные разложения матриц................................874
17.3. Итерационные методы решения СЛАУ с разреженными
матрицами........................................................877
17.3.1. Метол сопряжённых градиентов..........................877
17.3.2. Локально-оптимальная схема............................880
17.3.3. GMRES.................................................882
17.3.4. Другие методы.........................................885
Библиографический список..........................................888
Предметный указатель..............................................890
14
Предисловие
ПРЕДИСЛОВИЕ
Метод конечных элементов (МКЭ) стал основным инструментом
большинства исследователей, работающих с математическими моде-
лями в виде краевых и начально-краевых задач для дифференциальных
уравнений с частными производными. Несмотря на это, найти подхо-
дящую учебную литературу по этому методу совсем не просто. Наша
цель заключается в том, чтобы не только ознакомить с основами МКЭ
и дать первоначальные навыки работы с ним (для тех, кто только на-
чинает работать с этим методом), но и научить применять МКЭ для
решения сложных практических задач. При этом довольно много вни-
мания будет уделено технологическим аспектам реализации ключевых
алгоритмов метода, наиболее существенно влияющих на его вычисли-
тельную эффективность.
Предлагаемая вашему вниманию киша в первую очередь предна-
значена для тех, кто хочет научиться самостоятельно разрабатывать
алгоритмы и программы (а возможно, и даже методы) для решения
сложных задач с помощью МКЭ. Однако она может быть очень полез-
на и тем, кто хочет научиться грамотно пользоваться сложными ко-
нечноэлементными пакетами и лучше понимать трудности, которые
могут возникнуть (или, наоборот, не должны возникать) при использо-
вании МКЭ.
Эта книга, в общем-то, не рассчитана на строго поступательное её
прочтение (или тем более прочтение её «залпом»). Мы считаем, что
она будет особенно полезна тем, кто после первого (возможно, даже
выборочного и не слишком тщательного) прочтения будет использо-
вать её как некоторое руководство для написания собственных про-
грамм или для решения задач с помощью готовых конечноэлементных
пакетов. Для этого мы постарались изложить материал в книге так.
чтобы можно было более или менее независимо читан> различные её
разделы, и там. где для понимания одного раздела требуется (или по-
лезно) знать ма1ериал другого, даны соответствующие ссылки.
При изложении теоретических аспектов МКЭ мы будем пользо-
ваться в основном стандартным аппаратом линейной алгебры и мате-
матического анализа. Естественно, при формулировке задач нам пона-
добятся соответствующие разделы уравнений математической физики.
Всё это должно входить в стандартные учебные программы высшего
образования, ориентированные на подготовку специалистов техниче-
ского профиля. Ио поскольку приближённые решения в МКЭ строятся
как некоторые кусочно-гладкие функции, определённым образом ап-
проксимирующие (приближающие) искомое решение, его теоретиче-
15
ская база соприкасается с некоторыми разделами функционального
анализа (гильбертовы пространства, скалярные произведения и нормы
в них). Поэтому знать соответствующие разделы функционального
анализа очень полезно для более глубокого понимания теоретических
основ МКЭ. Тем не менее основное содержание этой книги должно
быть понятно и тем, кто не изучал функциональный анализ, а некото-
рые наиболее необходимые сведения из функционального анализа
будут приведены нами при изложении соответствующего материала.
Конечно, в одной книге невозможно рассмотреть все возможности
МКЭ. все его тонкости при использовании для решения сложных задач
и нюансы создания различных программных реализаций. Но мы наде-
емся, что читатель сможет получить наиболее важные знания теории и
практики метода и научится наиболее эффективно использовать его
для решения своих задач. Мы также надеемся, что после тщательного
ознакомления с этой книгой читателю станут гораздо понятнее воз-
можности МКЭ и перспективы его развития.
Путь, который необходимо пройти для достаточно глубокого пони-
мания МКЭ и овладения им как инструментом решения различных
научных и практических задач, может показаться слишком длинным.
Но когда вы почувствуете всю красоту и мощь этого метода, его ог-
ромные возможности для решения самых сложных задач, вы не пожа-
леете о потраченном времени и силах. Все эти затраты полностью оку-
пятся теми колоссальными преимуществами, которые дадут вам зна-
ние МКЭ и умение его применять для решения наиболее актуальных
задач, так необходимых для развития многих современных наукоёмких
технологий.
16
Введение
ВВЕДЕНИЕ
Эту книгу мы стремились написать так, чтобы читатель мог изу-
чить метод конечных элементов, начиная с самых его азов и не обра-
щаясь при этом к каким-либо дополнительным источникам. Поэтому в
ней относительно мало ссылок на работы других авторов, а некоторые
из книг, приведённых в списке литературы, включены в него в основ-
ном как дань уважения к тому вкладу, который их авторы внесли в
теорию и практику МКЭ.
Довольно много внимания будет уделено нами технологическим
аспектам МКЭ. Будут довольно детально рассмотрены структуры дан-
ных, используемые для описания сеток и обработки конечных элемен-
тов, а также некоторые наиболее важные алгоритмы работы с ними.
Наряду с желанием систематически и с самого начала изложить ос-
новы МКЭ, нашей целью было также стремление познакомить читате-
ля и с самыми последними его достижениями, позволяющими решать
наиболее сложные задачи (трёхмерные, векторные, нелинейные). Не-
которые из соответствующих подходов, которые будут нами рассмот-
рены достаточно подробно, вы не найдёте ни в отечественной, ни в
зарубежной литературе (они разработаны авторами этой книги, и в
научных статьях изложены лишь их основные идеи).
Таким образом, первая половина книги имеет в основном учебный
характер, а во второй довольно много внимания будет уделено гораздо
более глубоким и тонким аспектам МКЭ, связанным с последними его
достижениями при решении наиболее сложных задач. В соответствии с
этим в первой половине книги приведено довольно много примеров
учебного плана, а во второй её половине будет преобладать более на-
учный стиль изложения.
А теперь кратко прокомментируем, какой материал мы предлагаем чи-
тателю для изучения и как он будет распределен по основным разделам.
В первом разделе мы рассмотрим некоторые классы задач, для ре-
шения которых МКЭ применяется чаще всего (исключение здесь со-
ставят лишь задачи теории упругости, хотя излагаемые в книге методы
более чем успешно могут быть применены и для решения задач этого
тина1). Наибольший интерес этот раздел может представлять для тех,
кого интересуют задачи электромагнетизма, — в нём рассматривается
широкий спектр математических моделей, наиболее подходящих для
описания тех или иных электромагнитных полей. Практически для
1 При этом заметим, что изначально МКЭ был предложен как метод реше-
ния именно задач теории упругости.
17
всех приведённых в первом разделе моделей в дальнейшем будут рас-
смотрены наиболее эффективные методы построения соответствую-
щих конечноэлементных аппроксимаций. Непосредственно к самому
МКЭ этот раздел прямого отношения не имеет, и те, кого, например,
интересуют в основном технологии метода конечных элементов и осо-
бенности реализации соответствующих алгоритмов, могут без особого
ущерба его пропустить.
Во втором разделе на примере решения простейшей одномерной
краевой задачи продемонстрированы основные идеи и принципы МКЭ.
Здесь вводится понятие эквивалентной вариационной формулировки,
аппроксимации решения на конечномерном функциональном про-
странстве. сравниваются различные методы построения эквивалентных
вариационных постановок, даётся представление о финитных базис-
ных функциях, локальных матрицах и векторах конечных элементов и
о технологии сборки глобальной матрицы и вектора конечноэлемент-
ной системы линейных алгебраических уравнений (СЛАУ) из локаль-
ных матриц и векторов конечных элементов.
В третьем разделе изложены теоретические основы МКЭ. В самом
его начале очень кратко приведены некоторые сведения из функцио-
нального анализа, на которых базируется теория МКЭ. В довольно
общей форме для эллиптической краевой задачи в этом разделе сфор-
мулированы эквивалентные вариационные постановки в форме Ритца
и Галёркина и приведено доказательство эквивалентности этих поста-
новок дифференциально-краевой задаче. Здесь же рассмотрены основ-
ные принципы построения базисных функций в МКЭ, определяющих
конечномерные функциональные пространства, на которых ищутся
приближённые решения, а также затронуты вопросы построения ап-
проксимаций функций на конечномерных пространствах и приведены
соотношения, в самом общем виде определяющие компоненты матриц
и векторов конечноэлементных СЛАУ.
Довольно много внимания в третьем разделе уделено проблеме
точности конечноэлементных решений. Будет показано, что для эл-
липтической краевой задачи получаемые методом конечных элементов
приближённые решения (которые часто называют МКЭ-решениями)
являются ближайшими в энергетической норме к точному среди всех
функций конечномерного пространства, где ищется это конечноэле-
ментное решение. Кроме того, будет показано, как можно сравнивать
по точности МКЭ-решения, получаемые в различных конечномерных
пространствах (т.е. с использованием различных сеток или элементов
различных порядков), и делать это даже в тех случаях, когда точное
решение задачи не известно.
Некоторое внимание в третьем разделе будет уделено вопросам ап-
проксимации параметров дифференциального уравнения и краевых
условий на конечных элементах и участках их границ, а также по-
грешностям конечноэлементных решений, возникающих из-за неточ-
ностей аппроксимации искривлённых границ.
В целом третий раздел включает в себя почти все основные теоре-
шчсские аспекты, на которые мы будем опираться при изложении
ос тального материала книги. И поэтому после первого (быть может, не
Библиотека
Новосибирского
I государственного I
I технического университета
18
Введение
слишком тщательного) ознакомления мы рекомендовали бы возвра-
щаться к нему по ходу изучения материала других разделов - теорети-
ческие обоснования многих рассматриваемых в этой книге вопросов
изложены именно в этом разделе.
В четвёртом разделе для одномерных задач эллиптического типа
детально рассмотрены все основные вопросы, связанные с использова-
нием конечных элементов различных порядков. Здесь также будет
продемонстрировано, как можно сравнивать по точности и по вычис-
лительным затратам элементы различных порядков и различных типов
(с лагранжевыми и эрмитовыми базисными функциями), проводить
анализ сходимости конечноэлементных решений, а также повышать
точность и уменьшать вычислительные затраты за счёт использования
неравномерных сеток.
На примере кубических эрмитовым элементов в четвёртом разделе
будут рассмотрены довольно тонкие вопросы, связанные с построени-
ем специальных базисов при решении задач с разрывным коэффициен-
том диффузии и позволяющие значительно глубже понять суть и воз-
можности конечноэлементных аппроксимаций. Много внимания здесь
ещё уделено очень важным для практики МКЭ вопросам тестирования
процедур построения МКЭ-решений, а также особенностям построе-
ния конечноэлементных аппроксимаций задач в криволинейных коор-
динатах (цилиндрических и сферических).
В конце четвёртого раздела довольно подробно рассмотрены тех-
нологии построения кубических сплайнов (включая сглаживающие)
через эрмитовы элементы, а также методы вычисления производных
решения через согласованные результанты, которые без особого труда
переносятся и на многомерный случай.
Пятый и шестой разделы посвящены вопросам построения базис-
ных функций на двумерных и трёхмерных элементах различных типов
и вычисления соответствующих им локальных матриц и векторов. В
пятом разделе на примерах решения эллиптических задач достаточно
подробно проиллюстрирована процедура сборки глобальной матрицы
и вектора конечноэлементной СЛАУ для конечных элементов различ-
ных типов. При изучении двумерных элементов немало внимания бу-
дет уделено особенностям конечноэлементной аппроксимации задач,
заданных в цилиндрической системе координат. На примере бикубиче-
ских эрмитовых прямоугольных элементов будет показано, как можно
строить специальные базисы (из более гладких функций) для решения
задач с разрывным коэффициентом диффузии в многомерных случаях.
В конце каждого из этих двух разделов рассмотрены очень важные для
практического использования МКЭ вопросы тестирования процедур
построения конечноэлементных аппроксимаций решения эллиптиче-
ских задач в двумерном и трёхмерном случаях.
Седьмой раздел посвящён вопросам использования МКЭ для реше-
ния нестационарных задач. Здесь рассматриваются методы решения
начально-краевых задач для дифференциальных уравнений параболи-
ческого и гиперболического типов и даётся представление о явных и
неявных схемах аппроксимации неешционарных задач по времени.
Определённое внимание уделяется вопросам тестирования процедур
19
построения решения начально-краевых задач и рассматриваются при-
меры решения нестационарных задач с использованием МКЭ. Хоро-
шим дополнением к материалу этого раздела может служить раз-
дел 15.14, в котором обсуждается вопрос об очерёдности выполнения
аппроксимации по пространству и времени для нестационарных век-
торных задач.
Отдельно в седьмом разделе рассмотрены так называемые гармо-
нические задачи, в которых источниками поля являются функции, из-
меняющиеся во времени по синусоидальному или косинусоидальному
закону. Для этих задач рассмотрены вопросы построения конечноэле-
ментных аппроксимации и обсуждены вопросы точности получаемых
МКЭ-решений. На примерах гармонических задач проиллюстрирован
разреженный блочный формат хранения матриц конечноэлементных
СЛАУ, являющийся одним из наиболее экономичных.
В восьмом разделе обсуждаются вопросы, связанные с использова-
нием МКЭ для решения задач с так называемыми сосредоточенными
источниками. Рассматриваются разные типы сосредоточенных источ-
ников - точечные, сосредоточенные на линии и поверхностные. Для
сосредоточенных источников каждого типа обсуждаются схемы по-
строения соответствующих конечноэлементных аппроксимаций. До-
вольно много внимания уделяется проблемам сходимости МКЭ-
решений для задач с сосредоточенными источниками.
Поскольку из-за большой ресурсоёмкости трёхмерных задач при их
решении очень актуально создание специальных методов, существенно
снижающих вычислительные затраты для получения численного решения
требуемой точности, мы хотели оы обратить особое внимание читателя на
девятый раздел, где рассматривается конечноэлементная технология ре-
шения краевых задач с выделением части искомого поля. Эта технология
особенно эффективна тогда, когда решаемая задача довольно близка к
некоторой гораздо более простой задаче (решение которой может быть
найдено с высокой точностью при значительно меньших вычислительных
затратах), но исследователя интересует влияние именно тех аспектов,
которые и составляют отличие исходной сложной задачи от близкой к ней
простой. Такая ситуация совсем нередко возникает на практике, так как
многие вычислительно сложные трёхмерные задачи имеют довольно хо-
рошее двумерное или осесимметричное приближение. При этом вычис-
лительные затраты, необходимые для достижения нужной точности при
использовании стандартной технологии повышения точности конечно-
элементных решений (т.е. за счёт дробления сетки или повышения поряд-
ка конечных элементов), могут на несколько порядков превосходить вы-
числительные затраты на получение численного решения той же точности
при использовании изложенной в девятом разделе технологии выделения
поля. Довольно подробно в этом разделе рассмотрены особенности при-
менения -ехнологии выделения основной части поля для задач с сосредо-
точенными источниками и возможности ещё большего повышения её
эффективности в многоэтапном варианте, а также вопросы использования
этой технологии дпя вычисления полей влияния отдельных конструктив-
ных элементов или объектов при решении соответствующих полевых
задач в сложных конструкциях или средах.
20
Введение
Десятый раздел в значительной мере можно охарактеризовать как ин-
струкцию по практической реализации МКЭ. Здесь довольно детально
рассмотрены основные технологические аспекты МКЭ, связанные с гене-
рацией конечноэлементных сеток, с описанием соответствующие струк-
тур данных (включая и различные форматы хранения конечноэлементных
матриц), с нумерацией неизвестных, с формированием портретов конеч-
ноэлементных матриц и со сборкой матриц, хранящихся в различных
форматах. Конечно, в первую очередь это. материал ориентирован на тех,
кто хочет научиться самостоятельно реализовывать алгоритмы построе-
ния конечноэлементных решений. Но он может быть очень полезен и тем,
кто хотел бы стать высококвалифицированным пользователем готовых
конечноэлементных пакетов, поскольку квалификация пользователей
таких пакетов во многом определяется тем, насколько хорошо они пред-
ставляют всю специфику вычислительной работы, которую необходимо
выполнить для получения численного решения.
В одиннадцатом разделе рассматриваются вопросы, связанные с ис-
пользованием комбинированных и несогласованных сеток. Комбиниро-
ванные сетки (т.е. сетки, в которых одновременно присутствуют ячейки
разных типов — прямоугольники и треугольники, призмы и тетраэдры и
т.д.) удобны тем, что позволяют при решении задачи использовать пре-
имущества сразу нескольких типов конечных элементов, одни из которых
могут быть более точными, другие - вычислительно менее затратными
или более удобными для описания геометрии расчётной области. Оче-
видно. это придаёт МКЭ дополнительную гибкость. Но основное внима-
ние в этом разделе будет уделено МКЭ-технологиям, позволяющим ис-
пользовать так называемые несогласованные сетки, для которых стан-
дартные схемы сборки глобальной матрицы и глобального вектора ко-
псчноэлсментной СЛАУ из локальных не работают. Эти технологии по-
зволяют использова i ь такие конечноэлемсн гные сетки, в которых к одной
стороне ячейки могут примыкать сразу несколько сторон других ячеек и
при этом вершины некоторых ячеек могут лежать па рёбрах или внутри
граней других. В результате появляется возможнос ть очень эффективно
(практически без появления так называемы «лишних» узлов) выполнять
локальные дробления двух- и трёхмерных сеток с ячейками в виде четы-
рёхугольников (включая прямоугольники) или шестигранников (включая
прямоугольные параллелепипеды). Это позволяет значительно увеличить
привлекательность таких сеток (с четырехугольными и шестигранными
ячейками), поскольку к их преимуществам, связанным с хорошими ап-
проксимационными свойствами и относительной простотой построения,
добавляются возможности выполнять локальюые дробления ничуть не
менее эффективно, чем для сеток с ячейками в виде симплексов (тре-
угольников в двумерном случае или тетра щра в i рёхмерном).
В двенадцатом разделе рассматриваются конечноэлементные тех-
нологии, позволяющие в одной сетке использовать элементы разных
порядков. Здесь вводится ещё один тип базисных функций - так назы-
ваемые иерархические базисные функции, с помощью которых проще
всего осуществляется согласованная стыковка элементов разных по-
рядков па согласованных сетках. Обсуждаются возможные пути согла-
сования элементов различных порядков на несогласованных сетках и
21
связанные с этим преимущества и недостатки лагранжевых и иерархи-
ческих базисов, а также возможные вычислительные преимущества
иерархических базисов по сравнению с лагранжевыми даже при ис-
пользовании сеток с элементами одного и того же порядка.
Тринадцатый раздел посвящён проблеме уменьшения погрешности
конечноэлементных решений. В связи с этим рассматриваются некоторые
стратегии, позволяющие наиболее эффективно приближать конечноэле-
ментные решения к точному и основанные как на дроблениях ячеек сетки
(/г-технологии), так и на повышении порядка конечных элементов (р-
технологии), а также технологии уточнения конечноэлементных реше-
ний, в которых одновременно используются и дробления ячеек сетки, и
повышение порядка конечных элементов ( р - h -технологии).
В четырнадцатом разделе мы покажем, как с использованием МКЭ
можно решать краевые задачи для системы дифференциальных уравне-
ний, в которых искомыми могут быть как несколько скалярных функций,
так и компоненты вектор-функций. В этом разделе на примере решения
одной векторной задачи электромагнетизма будет продемонстрирован
подход с раздельной аппроксимацией уравнений решаемой системы (но,
естественно, с сохранением их взаимосвязи, определяемой вхождением
нескольких искомых функций в одно уравнение). При этом в качестве
базисных функций, через линейные комбинации которых ищутся функ-
ции-решения (т.е. каждая искомая скалярная функция или компонента
вектор-функции), используются скалярные (узловые) функции. Довольно
характерной особенностью задач такого рода является специфичная блоч-
ная структура матрицы конечноэлементной СЛАУ. В связи с этим рас-
смотрены структуры данных, позволяющие очень экономично хранить
такие блочные матрицы, и продемонстрирована сборка глобальной мат-
рицы, хранящейся в блочном формате.
Несмотря на то, что рассмотренный в четырнадцатом разделе подход к
решению векторных задач (т.е. задач в виде системы дифференциальных
уравнений в частных производных для нескольких неизвестных функций)
проиллюстрирован на примере одного класса трёхмерных нестационар-
ных электромагнитных задач, он вполне (и очень эффективно) может
быть использован для решения, например, многомерных задач теории
упругости, а также задач других типов, описываемых системами диффе-
ренциальных уравнений в частных производных.
Пятнадцатый раздел посвящён так называемому векторному МКЭ,
т.е. построению таких конечноэлсментных аппроксимации, в которых
используются определяемые специальным образом векторные базис-
ные функции. В первую очередь этот раздел адресован тем, кого инте-
ресуют современные возможности численных методов при решении
наиболее сложных задач электромагнетизма. Однако он может ока-
заться весьма полезным и тем читателям, которые хотели бы глубже
познакомиться с методологией МКЭ, его возможностями построения
решений для задач, описываемых векторными дифференциальными
уравнениями в частных производных.
В шестнадцатом разделе рассматриваются методы решения нели-
нейных краевых задач с использованием МКЭ. Вопросы сходимости
МКЭ-решений нелинейных задач обсуждаются в контексте выбора
22
Введение
оптимальных стратегий, дробления конечноэлементных сеток или по-
вышения порядка элементов.
Довольно много внимания в шестнадцатом разделе будет уделено спе-
циальным постановкам, применяемым при решении нелинейных задач
магнитостатики и учитывающим специфику зависимости параметров
уравнений от решений, характерную именно для этого класса задач.
Последний, семнадцатый, раздел имеет в основном вспомогатель-
ный характер. В нём очень кратко рассмотрены методы решения
СЛАУ (точнее, их вычислительные схемы), наиболее часто используе-
мые при решении конечноэлементных СЛАУ с симметричными и не-
симметричными матрицами. Здесь будут также приведены фрагменты
программ, реализующих соответствующие алгоритмы решения СЛАУ
для тех форматов хранения матриц, которые чаще всего используются
в МКЭ и учитывают структуру матриц конечпоэлементных СЛАУ (их
слабую заполненность ненулевыми элементами).
И в заключение скажем несколько слов об обозначениях. Мы постара-
лись использовать примерно одну и ту же систему обозначений на протя-
жении всей книги. Так, для обозначения матриц мы будем использовать
прописные полужирные латинские буквы, а и\ компоненты обозначать
соответствующей прописной наклонной буквой с двумя нижними индек-
сами (например, компоненты матрицы А будем обозначать Д). Анало-
гично векторы неизвестных и правых частей СЛАУ будем обозначать
полужирными строчными латинскими буквами, а их компоненты - соот-
ветствующей строчной наклонной буквой с одним нижним индексом
(например, компоненты вектора b будем обозначать Ь,).
Почти везде локальные матрицы и векторы мы будем обозначать со-
ответствующими символами со знаком «л» над ними. Например, А -
локальная матрица, b - локальный вектор. Также знак «Л» мы будем
использовать для обозначения локальных узлов (а иногда и номеров).
Например, x.L — это .г-координата г-го узла в глобальной нумерации, а
.г, - это х -координата г-го узла в локальной нумерации. В некоторых
же особых случаях, когда сопоставляются локальная и глобальная нуме-
рации, для лучшего понимания через i мы будем обозначать локальный
помер узла с глобальным номером i (т.с. тот же индекс без знака «Л»
будет означать соответствующий глобальный номер узла).
Иногда у локальной матрицы или локального вектора, для того что-
бы конкретизировать, какому именно конечному элементу соответст-
вует эта матрица или вектор, на месте верхнего индекса мы будем ста-
вить обозначение этого конечного элемента (например, А и b
это локальная матрица и локальный вектор конечною элемента П2)- В
некоторых случаях верхний индекс локальных матриц и векторов бу-
дет обошачать то, что они построены не для обычного (объёмного)
элемента, а для поверхностного элемента, являющегося частью грани-
цы расчетной области (например, А -локальная матрица поверхно-
стного элемента, являющегося частью границы S$ с заданным на ней
23
краевым условием третьего рода, а b - локальный вектор поверхно-
стного элемента, являющегося частью границы S-2 с заданным на ней
краевым условием второго рода).
Знак «Л» над базисной функцией (например, ф-) везде будет обо-
значать, что эта функция является локальной (т е она определена толь-
ко на одном конечном элементе) и нижний индекс у неё определяет её
локальный номер (т.е. номер в локальной нумерации базисных функ-
ций конечного элемента).
Через полужирные прописные буквы со знаком «“*» сверху (на-
пример. А, В и т.д.) мы будем обозначать вектор-функции (например,
А (х, у, z) = (А1:(х, у, z), А;/(х, у, z), Az(x, у, г)) , т.е. вектор-функция
А (ж, у, z) имеет три компоненты, являющиеся функциями трёх пере-
менных х , у и z ).
Запись [7|q будет означать, что рассматриваются значения функции
U на множестве точек S (как правило, через S будет обозначаться
поверхность).
Запись V : К|5 = 0, как обычно, будет означать, что рассматрива-
ются такие функции V, для которых выполняется условие, записанное
после двоеточия (т.е. в данном случае это такие функции, которые рав-
ны нулю на поверхности S ).
Довольно часто будет использоваться квантор V , означающий «для
любых» (или «для всех»). Так, например, запись W: V|s. = 0 будет
означать следующее: «для любых функций V таких, что К|5, = О».
Мы будем пользоваться в основном двумя уже введёнными нами
аббре в и ату рам и:
СЛАУ - система линейных алгебраических уравнений,
МКЭ — метод конечных элементов (также МкЭ-решение — решение,
полученное методом конечных элементов, МКЭ-аппроксимация — ап-
проксимация на основе метода конечных элементов и т.д.).
И, наконец, в тех местах, где будут вводиться новые понятия, они
будут выделяться полужирным шрифтом, а там, где мы захотим об-
ратить ваше особое внимание на какие-либо слова или выражения, они
будут выделены курсивом.
24
1 Математические модели физических процессов ...
1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ФИЗИЧЕСКИХ
ПРОЦЕССОВ В ВИДЕ КРАЕВЫХ И НАЧАЛЬНО-КРАЕВЫХ
ЗАДАЧ
В данном разделе будут рассмотрены основные краевые задачи,
с помощью которых описываются различные физические процессы.
Особое внимание будет уделено математическим моделям электромаг-
нитных полей, сформулированным в виде как скалярных, так и век-
торных задач.
1.1. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
Эллиптическая краевая задача для функции и определяется
дифференциальным уравнением
—div (X grad w) 4- = f, (1.1)
заданным в некоторой области Q с границей S = S1 U S2 U S3, и крае-
выми условиями u\Si=u^ (12) х^ =е, (13) дп S-2
\ дн_ дп S3+₽(“ls3-^) = 0> С1-4)
в которых u\s — значение искомой функции и на границе S.t, а
Цр- - значение на «S'./ производной функции и по направлению
внешней нормали к поверхности S;. Коэффициент X в уравнении (1.1)
часто называют коэффициентом диффузии.
Краевая задача (I 1у—(1.4) может описывать стационарное (т.е не за-
висящее от времени) распределение температуры и в области Q, если
X - коэффициент теплопроводности, а (/ — уи) — плотность объёмных
источников тепла. При этом краевое условие первого рода (1.2) соответ-
ствует заданию на температуры ид краевое условие второго рода
1.2.Начально-краевые задачи ...
25
(1.3)- заданию на плотности теплового потока, равного 0, а краевое
условие третьего рода (1.4) — заданию на S3 плотности теплового потока,
пропорциональной разности температуры и на границе 53 и температу-
ры окружающей среды (коэффициент пропорциональности |3 > 0 в
этом случае называется коэффициентом теплоотдачи}.
Если принять область Q за поперечное сечение канала, X — за ко-
эффициент вязкости, и — за скорость течения жидкости вдоль оси ка-
нала, a f - за плотность силы, то при однородном краевом условии
и |5- = 0 и отсутствии вторичных течений решение уравнения (1.1)
даёт профиль продольной скорости течения вязкой жидкости в канале
с постоянным поперечным сечением (краевое условие и |5 = 0 задаёт
условие прилипания частиц жидкости к стенкам канала).
Уравнение (1.1) с краевыми условиями первого и второго рода, ха-
рактеризующими проницаемые и непроницаемые участки границы
области Q, описывает процесс фильтрации, если и — напор, а X -
коэффициент фильтрации. Краевая задача для уравнения (1 1) может
быть использована для описания установившегося безвихревого тече-
ния идеальной жидкости, причём и в этом случае является потенциа-
лом вектора скорости V (т.е. V — — grad и).
1.2. НАЧАЛЬНО-КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЙ
ПАРАБОЛИЧЕСКОГО И ГИПЕРБОЛИЧЕСКОГО ТИПА
Многие нестационарные физические процессы описываются на-
чально-краевыми задачами для уравнений следующего вида:
— div^Xgradwj + ци + о= f , (1-5)
причем коэффициенты о, X, и f могут быть функциями не только
пространственных координат, но и времени t. Начально-краевая задача
включает в себя кроме уравнения параболического типа (1.5) краевые
условия вида (1.2)-( 1.4) и начальное условие вида
и = uQ, (1.6)
г ic п() - функция пространственных координат, заданная в расчётной
полисiи Q.
(Ji мстим, что начально-краевые задачи параболического типа опи-
с.ывлют процессы с бесконечной скоростью распространения. Это оз-
н 1ч:к г, что при изменении в какой-либо момент времени t источника
по 1я в одной части пространства реакция на него будет ненулевой в
побои сколь угодно олизкий момент времени в любой сколь угодно
bi г'кои о| источника точке пространства. На первый взгляд, это про-
М11ю|н'4111 основным законам физики, но на самом деле для многих
np.ik 1ИЧССКИ важных задач решение параболического уравнения очень
26
1 Математические модели физических процессов ...
точно описывает реальный физический процесс. К таким процессам
можно отнести, например, почти все тепловые и очень многие элек-
тромагнитные процессы, изучаемые на временных интервалах, не со-
поставимых по величине с временными интервалами, на которых мо-
жет оказаться существенной конечная скорость распространения ре-
ального процесса.
Для описания физических процессов, в которых необходимо учи-
тывать конечную скорость распространения возмущений, используют-
ся уравнения гиперболического типа
- div (Xgradiz) + уи + о + Х~^г = f- (1-7)
Кроме самого уравнения (1.7), краевых условий вида (1.2)-(1.4) и на-
чального условия вида (1.6), гиперболическая начально-краевая задача
включает в себя ещё и начальное условие для производной искомого
решения и по времени:
ди
dt
— >
(1.8)
t=ii}
где u('j — функция пространственных координат, заданная в расчётной
области Q.
Отметим, что после проведения аппроксимации по времени уравне-
ний параболического или гиперболического типа процедуры проведения
их конечноэлементной аппроксимации по пространственным перемен-
ным практически не отличаются от аналогичных процедур для соответ-
ствующих уравнений эллиптического типа. Поэтому все основные ас-
пекты техники проведения конечноэлементной аппроксимации по про-
странственным переменным для задач всех типов будут рассмотрены
нами в основном при решении эллиптических краевых задач, а в седь-
мом разделе, посвящённом решению нлчнлыю-краевых задач, основное
внимание будет уделено изучению различных процедур их аппроксима-
ции по времени и связанным с ними особенностям построения вычисли-
тельных процессов решения нестационарных задач.
1.3. КРАЕВЫЕ И НАЧАЛЬНО-КРАЕВЫЕ ЗАДАЧИ, ИСПОЛЬЗУЕМЫЕ
ДЛЯ МОДЕЛИРОВАНИЯ ЭЛЕКТРОМАГНИТНЫХ ГЮЛЕЙ
Фундаментальной математической моделью, используемой для
моделирования практически всех макроскопических электромагнитных
явлений, является система уравнений Максвелла, устанавливающая
связь между компонентами электрического и магнитного полей, пара-
метрами среды (электропроводимостью, магнитной и диэлектрической
проницаемостью) и сторонними источниками электромагнитного поля в
форме системы векторных дифференциальных уравнений [8]:
rotH = Г’
4-оЕЧ—‘ —
(1.9)
1.3.Краевые и начально-краевые задачи ...
27
rotE = -4£, (1.10)
dt
divB = 0, (1 11)
diveE = p, (1.12)
где H - напряжённость магнитного поля, JCT - вектор плотностей
сторонних токов (возбуждающих электромагнитное поле), Е - напря-
жённость электрического поля, о - удельная электрическая проводи-
мость среды, е - диэлектрическая проницаемость среды, В — индук-
ция магнитного поля (связанная с напряжённостью Н соотношением
В = pH, р, - коэффициент магнитной проницаемости).
Как правило, при численном моделировании электромагнитных по-
лей дискретные аналоги нс строятся напрямую для системы уравнений
(1.9)-(1.12). Численные аппроксимации строятся для несколько иных
дифференциальных уравнений, полученных в результате преобразова-
нии этой системы с учётом характера исследуемого электромагнитного
поля. Чаще всего такие преобразования проводятся путём введения
новых искомых функций, называемых потенциалами. Ниже мы рас-
смотрим именно такие математические модели электромагнитных
процессов.
1.3.1. ЗАДАЧИ ЭЛЕКТРОСТАТИКИ
Под задачами электростатики мы будем понимать задачи, в
которых требуется найти распределение напряжённости электрическо-
го поля Е в непроводящей среде при условии неизменности во време-
ни электромагнитного поля (хотя иногда задачами электростатики на-
зывают любые задачи моделирования неизменного во времени элек-
трического поля, в том числе и в проводящей среде).
Очевидно, что при неизменности электромагнитного поля во вре-
мени в среде с нулевой проводимостью напряжённость электрического
поля можно искать независимо от магнитного поля.
Действительно, при о = 0 и <ЭЁ dt = 0 только два уравнения
(1.10) и (1.12) из системы (1.9)-(1 12) включают в себя неизвестную
вектор-функцию Ё, причём с учётом того, что дВ/dt = 0 , уравнение
(1.10) принимает вид
rotE = 0. (1.13)
В этом случае вектор-функцию Е, удовлетворяющую уравнениям
(1 12) и (1.13), удобно искать в виде градиента некоторой скалярной
функции V, называемой электрическим потенциалом, причём
обычно знак Е считается противоположным знаку градиента V :
Ё = —gradV. (1.14)
28
1 .Математические модели физических процессов ...
При таком представлении Ё уравнение (1.13) выполняется автома-
тически (поскольку rot (grad Iz) = 0 для любой функции V ), и поэто-
му математическая модель электростатического поля включает в себя
единственное уравнение
— div(еgrad V) = р, (1-15)
получаемое из (1.12) с уче i ом (1.14).
Таким обра юм, электрическое поле в задачах электростатики опи-
сывается эллиптическим уравнением (сравните с (1.1)) с коэффициен-
том диффузии е, являющимся диэлектрической проницаемостью сре-
дой и правой чашыо р , являющейся функцией распределения зарядов в
пространстве.
Обратим внимание на следующую особенность большинства задач
электростатики Несмотря на то, что источниками поля в этих задачах
являются элс1 । ричсские зтряды, чаще всего в них потенциал И требу-
ется найти именно в гои области, где р = 0. Как правило, в такого
рода задачах плотность зарядов р в расчетной области задаётся равной
нулю и поле описывается однородным уравнением
— div (е grad 1 i 0. (1-16)
В этом случае в качестве исходных данных для моделирования
электрического поля используют значения потенциала V на тех гра-
ницах области, которые являются границами некоторых проводящих
тел (т.е. проводников, которые обычно называют электрооами) Эти
значения потенциалов на электродах задаются на границах расчётной
области как правые части краевого условия первого рода вида (1.2).
1.3.2. СТАЦИОНАРНЫЕ ЭЛЕКТРИЧЕСКИЕ ПОЛЯ В ПРОВОДЯЩИХ СРЕДАХ
Электромагнитные процессы такого инн характеризуются наличи-
ем стационарного (постоянного) гока в проводящих телах. Исходными
данными для их моделирования могу г быть гак заданные па отдельных
частях границы расчётной области значения шсктрического потенциа-
ла. так и плотности втекающих (или вытекающих) с некоторых частей
границ расчётной области токов. Математическая модель такого рода
процессов получается из системы уравнений Максвелла следующим
образом.
Как и в рассмотренных чуть выше задачах электростатики, напря-
жённость электрического поля Е представляется в виде (1.14), что
обеспечивает (как и в задачах электростатики) автоматическое выпол-
нение уравнения (1.10) (имеющее и в этих задачах вид (1.13)). Однако
в отличие от задач нахождения электрического поля в непроводящих
средах уравнение (1.9) не может быть исключено из рассмотрения,
поскольку теперь о 0 и правая часть (1.9) содержит Ё. Поэтому
основное уравнение для моделирования таких процессов получается
как следствие из этого уравнения системы Максвелла.
1 3 Краевые и начально-краевые задачи ...
29
Воздействуем оператором div на левую и правую части уравнения
(1.9). Учитывая, что для любой вектор-функции W справедливо тож-
дество div (rot W) = 0, получим
div(jCT+oE) = 0. (1.17)
Заметим, что в рассматриваемых здесь задачах под Jc понимаются
только токи вне расчётной области (которые в задаче могут быть учте-
ны как краевые условия) и поэтому внутри расчётной области
JCT = 0, (1.18)
и тогда из уравнения (1.17) с учётом (1.14) получаем:
— div (о grad V) = 0. (1.19)
Осталось проанализировать ситуацию с уравнением (1.12) системы
уравнений Максвелла. Это уравнение связывает напряжённость элек-
трического поля Е с распределением зарядов р Однако в проводящих
телах распределение зарядов, как правило, априорно неизвестно, по-
скольку заряды в них могут перераспределяться под воздействием
электрического поля. Поэтому в областях с о 0 именно р является
неизвестной функцией, которая может быть получена по известному
распределению Ё (или V ) как р = div(eE (или р = — div (е grad V)).
В результате математической моделью рассматриваемого электромаг-
нитного процесса является однородное уравнение эллиптического типа
(1 19) (в котором коэффициент диффузии - это электропроводимость
среды) с краевыми условиями первого и второго рода. Краевые условия
первого рода задаются на тех границах расчётной области, где известны
значения потенциала V , а вторые краевые условия - на тех границах, где
известна плотность стекающего стороннего тока Заметим, что постоян-
ный ток не может перетекать из проводника в изолятор и поэтому на гра-
нице между проводником и изолятором плотность стекающего в провод-
ник тока задаётся нулевой (и изолятор не включается в расчётную об-
ласть).
1.3.3. ЗАДАЧИ МАГНИТОСТАТИКИ
Задачами магнитостатики называют задачи моделирования
магнитного поля, создаваемого стационарным (постоянным) электри-
ческим током с известной плотностью распределения J . Очевидно,
что такие поля описываются системой из двух уравнений полной сис-
темы Максвелла:
rot Н = J ,
div В = 0 .
(1-20)
(1.21)
30
1 .Математические модели физических процессов ...
Для численного анализа стационарных магнитных полей в зависи-
мости от их особенностей используются различные виды математиче-
ских моделей, к которым может быть преобразована система (1.20)-
(1.21). Мы рассмотрим наиболее часто используемые модели, полу-
чаемые с применением либо векторного потенциала, либо скалярного
магнитного потенциала.
1.3.3.1. ОПИСАНИЕ СТАЦИОНАРНЫХ МАГНИТНЫХ ПОЛЕЙ
С ИСПОЛЬЗОВАНИЕМ ВЕКТОР-ПОТЕНЦИАЛА
Представим В в виде ротора некоторой вектор-функции А, на-
зываемой вектор-потенциалом: В = rot А.
При таком представлении поля В уравнение (1.21) превращается в
тождество div (rot Aj = 0, и вектор-потенциал А может быть найден
из уравнения (1.20), в котором Н = — В = — rot А, т.е. А должен
удовлетворять уравнению:
rot i rot A j = J . (1.22)
Наиболее просто вычислить потенциал А в случае, когда
р = const, т.е. среда однородна по магнитной проницаемости (для
определённости будем считать, что р = р(), где р() - магнитная про-
ницаемость вакуума). В этом случае уравнению
rot (rot А) = р0 J (1-23)
удовлетворяет вектор-функция А, компоненты которой являются ре-
шениями трёх независимых дифференциальных уравнений:
рО*Л/.ч ~ M’O'Zz, (1.24)
где оператор Лапласа А для любой достаточно гладкой скалярной
функции F определяется соотношением
AF = div (grad F). (1-25)
Покажем, что вектор-потенциал А, удовлетворяющий системе
(1.24), является и решением векторного уравнения (1.23).
Поскольку div J = 0 (что является следствием уравнения (1.20)), то
из уравнений (1.24) их дифференцированием и сложением получим
+ div
- by- div (grad Аг) +
\ox v ' dy
(grad Д)
1.3.Краевые и начально-краевые задачи ...
31
= —div(p,oj). (1J26)
Меняя порядок дифференцирования в слагаемых левой части урав-
нения (1.26) (можно показать, что гладкость решений Ал., Д и Az
уравнений (1.24) является для этого достаточной) и учитывая, что
div (p,0J^ = pg div J — 0 , получаем
— div (grad (div A j j = 0 . (1.27)
Таким образом, для функции w = divA справедливо уравнение
Лапласа
-Aw = 0, (1.28)
и, с учётом условия div А —> 0 при стремлении координат к бесконеч-
ности (или при выполнении условия w = div А = 0 на всех внешних
границах расчётной области), единственным решением уравнения
(1.28) является тривиальная функция w = 0.
Таким образом, вектор-функция А, являющаяся решением системы
(1.24) (для правой части p0J которой справедливо div (р,0 = 0 ),
удовлетворяет условию
divA = 0. (1.29)
Воспользуемся тождеством
rot (rot 4 | — — div (grad A j 4- grad (div A.j, (1-30)
в котором выражение div (grad A j означает вектор-функцию с компо-
нентами АД, АД и АД .
Тогда из справедливости для А уравнений (1.24) и с учётом того,
что в этом случае для него справедливо условие (1.29), получим, что
вектор-потенциал А удовлетворяет и векторному уравнению (1.23),
что и требовалось доказать.
Известно, что решением уравнения Пуассона
-А^ = / (1.31)
в бесконечном пространстве (если г (г) —> 0 при г—>оо, где
г = (х,у, г) и г = ||г|| = у]х2 + у2 -Ь 22 ) является функция
32
1 .Математические модели физических процессов ...
dx'dy'dz'. (1-32)
Поэтому компоненты вектор-потенциала А, удовлетворяющего
системе (1.24) (а значит и векторному уравнению (1.23) и условию
(1.29)), могут быть вычислены как соответствующие интегралы от
компонент вектора плотности тока J . В векторном виде эта формула
может быть записана следующим образом:
(1.33)
Из формулы (1.33) соответствующим дифференцированием легко
получить известный закон Био-Савара [8], описывающий магнитное
поле токов в вакууме:
В*' (г) = rot А (г) =
(1.34)
Таким образом, в однородном по магнитной проницаемости про-
странстве не только компоненты вектора-потенциала, но и компоненты
индукции магнитного поля В могут быть вычислены довольно просто
в виде соответствующих интегралов от J
Вектор-потенциал А довольно часто используется для решения
двумерных задач магнитостатики в неоднородных по магнитной про-
ницаемости средах. Двумерными называют задачи, в которых реше-
ние зависит только от двух пространственных координат (заметим, что
если в цилиндрических координатах г} решение задачи не зави-
сит от угловой координаты tp, то такую задачу часто называют осе-
симметричной). В этом случае векторное уравнение (1-22) чаще всего
оказывается эквивалентным одному скалярному уравнению для одной
из компонент вектор-потенциала А. Рассмотрим два наиболее часто
встречающихся случаях двумерных задач магнитостатики.
В первом случае предполагается, что в декартовых координатах
вектор плотности токов имеет только одну ненулевую компоненту Jz ,
зависящую только от координат х и у, и при этом магнитная прони-
цаемость р, зависит также только от координат ж и у. В этом случае
магнитное поле может быть полностью определено только через одну
компоненту Az = Az (ж, у) вектор- потенциала А, удовлетворяющую
двумерному уравнению:
1.3.Краевые и начально-краевые задачи ...
33
— div — grad Az = Jz.
(1.35)
Действительно, если взять вектор А = < О, О, Az (х, у)), в котором
Az = Az (х, у) удовлетворяет уравнению (1.35), то легко убедиться, что
такой вектор удовлетворяет уравнению (1.22). Таким образом, двумер-
ное магнитное поле в декартовых координатах может быть описано
эллиптическим уравнением (см. (1.1)) с коэффициентом диффузии
X = 1/р и правой частью f = Jz. При этом, как правило, в соответст-
вующей краевой задаче задаются однородные краевые условия первого
или второго рода.
Второй случай соответствует осесимметричной задаче, в которой
век гор плотности тока J в цилиндрической системе координат
{r,ip,z} имеет только одну ненулевую компоненту J^, причём и
и магнитная проницаемость р не зависят от координаты ф:
J — J; (г, z), р = р (г, z). В этом случае магнитное поле также может
быть полностью определено только через одну компоненту
Др = Др (г, г) вектор-потенциала А, удовлетворяющую двумерному
уравнению
г (1 т л d
-div —gradДр -|----?------
(k рГ2 г дт
(1.36)
Это уравнение довольно просто можно получить из (1.22) с учётом
того, что в цилиндрической системе координат для вектор-потенциала
А = (0, Др (г,г),О) справедливы следующие соотношения:
rot.p
— rot А = -
.И )
1А Г
г dr р dr
А
дг ( ЦТ
d 1
dz^р dz
div —
1 д г । д 1
г дг р 5г dz Ip dz
(1-37)
(1-38)
Обратим внимание на то, что в задачах магнитостатики производная
коэффициента 1/р по координате г, как правило, отлична от нуля внутри
магнитных материалов, а на их границах эта производная в уравнении
(1.36) определяет поверхностный источник (поскольку она является про-
изводной разрывной по г функции). Поэтому уравнение (1.36) можно
переписать в виде, близком к виду эллиптического уравнения (1.1):
- div(X grad Др)+ ^Др+/5 (Др) = (1-39)
34
1.Математические модели физических процессов ...
внутри подобластей с
где коэффициент диффузии X = 1/р, коэффициент внутри
подобластей с ц - - const и = -Дг — — —
рг2 гдт[р,
изменяющейся по г магнитной проницаемостью. Функция же fs (Др)
определяет поверхностный источник на границах, где магнитная про-
ницаемость терпит разрыв. Плотность этого источника определяется
пг, где пг - г -компонента вектора нормали п
выражением-----— —
г 1Н$
к границе S , - скачок функции 1Дх
в соответствии с направлением нормали п (более подробно поверхно-
стные источники будут рассмотрены в восьмом разделе).
Заметим, что при построении конечноэлементных аппроксимаций
осесимметричных задач в некоторых случаях лучше использовать ис-
— rot А J = (подробнее об этом будет сказа-
ли )
на границе S , посчитанный
ходное уравнение rot^
но в разделе 16.6.1).
1.З.З.2. ОПИСАНИЕ СТАЦИОНАРНЫХ МАГНИТНЫХ ПОЛЕЙ
С ИСПОЛЬЗОВАНИЕМ СКАЛЯРНОГО МАГНИТНОГО ПОТЕНЦИАЛА
При решении трёхмерных задач магнитостатики рассмотренная
выше векторная постановка (для всктор-потенциала А ) приводит, как
правило, к гораздо более трудоёмким вычислительным схемам, нежели
любая эквивалентная ей по смыслу скалярная постановка. Действи-
тельно, если использовать уравнение (1.22) для описания трёхмерного
поля, то при решении задачи нужно либо искать три неизвестные
функции А,, (х, у, z), А,, (х, у, z} и Az (х, у, z), удовлетворяющие систе-
ме из трёх скалярных уравнений, либо решать задачу как векторную с
использованием специальной технологии представления вектор-
потенциала А. И в том, и в другом случае вычислительные затраты
гораздо (на порядок и более) выше, чем при решении одного скалярно-
го уравнения для достижения той же точности вычисления характери-
стик магнитного поля. Дополнительной (и довольно существенной)
трудностью является неоднозначность определения вектор-потенциала
А из уравнения (1.22): если уравнению (1.22) удовлетворяет вектор-
функция А , то ему удовлетворяет и вектор-функция А 4- grad 17, где
IV — произвольная скалярная функция. В результате гораздо более
эффективным является использование скалярного магнитного потен-
циала для решения трёхмерных задач магнитостатики.
Будем искать напряжённость магнитного поля Н в виде
Н = Н‘ - grad U ,
(1.40)
1.3.Краевые и начально-краевые задачи ...
35
где Нг — магнитное поле токов J в вакууме, U — некоторая скалярная
функция, называемая скалярным магнитным потенциалом. При этом
rot Н' = J по определению Нс, и тогда, учитывая, что rot grad U = 0,
убеждаемся, что Н автоматически удовлетворяет уравнению (1.20):
rot Н = rot И' — rot grad U = J.
Поэтому для нахождения поля И достаточно решить одно скаляр-
ное уравнение с одной неизвестной скалярной функцией U :
div(pHf j — div (u grad 17) = 0, (1.41)
которое при представлении Н в виде (1.40) полностью эквивалентно
уравнению (1.11).
Уравнение (1.41) удобнее переписать в виде
— div (р grad 17) = — div (pH' j. (1.42)
Таким образом, функция 17 может быть найдена как решение эл-
липтического уравнения вида (1.1) с коэффициентом диффузии X = р
и правой частью / = — div(pHf ). Вектор-функция же Нс в соответст-
вии с (1.34) может быть вычислена по формуле
Н,:(г) = 3-В'(г) = -Р f J(r)x(r~r )(I 43)
Но 4it J ||r_r'||
Заметим, что при использовании для численного анализа модели
(1.42) могут возникать значительные трудности при решении нели-
нейных задач магнитостатики, т.е. при наличии в расчётной области
подобластей, где магнитная проницаемость р зависит от напряжённо-
сти магнитного поля: р = р Нj. Эти трудности могут быть преодоле-
ны введением так называемого полного потенциала Ur в тех подобла-
стях, где р = р (Н и J = 0). Потенциал Uv в этих подобластях (на-
зываемых подобластями полного потенциала') определяет поле Н
через соотношение
H = -gradi7p. (1.44)
В остальных подобластях (называемых подобластями неполного
потенциала) задаётся неполный потенциал U, определяемый соотно-
шением (1.40). На границах же подобластей полного и неполного по-
тенциала задаются специальные условия связи потенциалов. Подробно
36
1 .Математические модели физических процессов
решение задач магнитостатики с использованием полного и неполного
потенциалов будет рассмотрено в разделе 16.6.3.
1.3.4. МОДЕЛЬ НЕСТАЦИОНАРНОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
В ВИДЕ ОДНОГО ВЕКТОРНОГО УРАВНЕНИЯ
Для описания нестационарных электромагнитных полей система
уравнений (1.9)-(1.12) при условии независимости р от времени мо-
жет быть преобразована к векторному уравнению вида
rot[lrotE] + ^ + ^ = -^l. (1.45)
U»' ) dt dt1 ot v 7
Это уравнение может быть легко получено из уравнения (1.10) де-
лением его на |i и применением операции rot к его левой и правой
частям. При этом используются соотношение В — pH (В/p заменяет-
ся на Н) и уравнение (1.9) (rotH заменяется на правую часть (1.9)), а
также меняется порядок дифференцирования по времени и по про-
странственным координатам. После этого слагаемые с Е переносятся
в левую часть уравнения.
Уравнение (1-45) при моделировании нестационарных электромаг-
нитных полей без учёта токов смещения в средах с однородной маг-
нитной проницаемостью (р = р(), р0 - магнитная проницаемость ва-
куума) преобразуется к виду
rot(rotE) + = -ро . (1.46)
Уравнение такого вида очень часто используется при вычислении
электромагнитных полей методом интегральных уравнений (МИУ) [1,2].
При этом обратим внимание на то, что искомая вектор-функция Е может
быть разрывной на границах разрыва коэффициента о, т.е. на границах
сред с различной проводимостью. Действительно, если применить опера-
цию div к обеим частям уравнения (1.9), то в областях, где нет сторонних
токов Лсл (и при пренебрежении токами смещения), получим
div(oE) = 0. (1.47)
Это означает, что непрерывной является нормальная составляющая
произведения стЕ, и поэтому нормальная составляющая Еп вектор-
функции Е должна иметь соответствующий разрыв на границе разры-
ва коэффициента ст (если, конечно, Еу 0 на этой границе). Разрыв-
ность Ен никак нс усложняет вычислительные схемы МИУ, но создаёт
определённые трудности при применении МКЭ (не векторного).
1.3.Краевые и начально-краевые задачи ...
37
В случае, когда решается нелинейная по р нестационарная задача
(т.е. ц является функцией зависящей от времени напряженности маг-
нитного поля Н и, следовательно, тоже зависит от времени), система
уравнений (1.9>-(1.11) может быть преобразована к виду, аналогично-
му (1.45):
rot [— rot а] + о + е = JCT, (1.48)
(Ц ) dt dt2
где A - вектор-потенциал, через который определяются индукция В
магнитного поля и напряжённость Е электрического поля в виде
В = rot А, (1.49)
Ё = -^. (1.50)
Нетрудно убедиться, что В и Е, вычисленные по вектор-потенциалу
А с помощью соотношений (1.49) и (1.50), удовлетворяют всем уравне-
ниям системы Максвелла (1.9)-(1 11), если А является решением уравне-
ния (1.48) (напомним, что уравнение (1.12) в данном случае фактически
определяет распределение зарядов р по известному полю Е). Действи-
тельно, уравнение (1.11) с учётом (1.49) является тождеством. Уравнение
(1.10) также становится тождеством после подстановки в его левую часть
соотношения (1.49), в правую - соотношения (1.50) и изменения порядка
дифференцирования по пространственным и временной переменным в
любой из его частей. А после подстановки (1.49) и (1.50) в уравнение (1.9)
(с учётом того, что Н = В/| i) оно превращается в уравнение (1.48) (если
с не зависит от времени, что справедливо практически всегда), т.е. В и
Е, определённые из (1.49) и (1.50), удовлетворяют и уравнению (1.9) (так
как А определяется как решение уравнения (1.48)).
Очевидно, что в случае, когда уравнение (1.45) справедливо (т.е. ко-
эффициент р, не зависит от времени), оно может быть легко получено из
уравнения (1.48) дифференцированием его по t (и заменой dA.!dt на
—Е согласно соотношению (1.50)), т.е. уравнение (1.45) фактически яв-
ляется следствием уравнения (1.48). По своему виду уравнения (1.45) и
(1.48) практически совпадают и поэтому процедуры их численного реше-
ния также одинаковы. Таким образом, можно было бы рассматривать
только более общее уравнение (1.48), но в некоторых случаях уравнение
(1.45) оказывается более удобным.
Например, если исследуются компоненты напряжённости Е элек-
трического поля или производные по времени компонент индукции В
38
1 .Математические модели физических процессов ...
магнитного поля, то в этом случае при использовании уравнения (1.45)
нет необходимости выполнять дифференцирование по времени полу-
ченного численного решения.
Обратим внимание еще и на то, что вектор-потенциал А , удовлетво-
ряющий уравнению (1.48), так же, как и напряженность электрического
поля Е, может быть разрывен (например, на границах разрыва коэффи-
циента о или е, т.е. на границах сред с различной проводимостью или
диэлектрической проницаемостью). Причиной этого является связь А и
Е в виде соотношения (1 50) (ниже будет показано, что при другом спо-
собе определения вектор-потенциала А он может быть непрерывным во
всей области определения и при разрывном коэффициенте о).
Отметим также, что модель (1.48) в принципе может описывать и
стационарные (не изменяющиеся во времени) поля, о чём уже говори-
лось в разделе 1 3.3 (см. соотношение (1.22)). Однако уравнение (1.22)
имеет не единственное решение, т.е. вектор А определяется с точно-
стью до градиента некоторой скалярной функции (см. раздел 1.3.3.2,
с. 34). Это может создавать дополнительные трудности при использо-
вании модели (1.48) для расчёта электромагнитных полей, выходящих
на стационарный режим. Модель же (1.45) в принципе непригодна
для расчётов полей, выходящих на стационарный режим, поскольку
при edd/dt —* 0 она позволяет определить неизвестную функцию Ё
лишь с точностью до градиента некоторой скалярной функции (в то
время как в стационарном режиме, как было показано в разделах 1.3.1
и 1.3 2, напряжённость электрического поля Е определяется именно в
виде градиента скалярной функции И )
Похожая ситуация возникает и в случае, когда в нестационарном
электромагнитном поле токи смещения являются пренебрежимо ма-
лыми, т.е. можно считать, что = 0 . Тогда уравнение (1.48)
принимает вид
rot[— rotA Ta4^ = JCr. (1-51)
(р dt v '
Как правило, проводимость о не во всей расчётной области отлична от
нуля (например, во всех практических задачах о = 0 в воздухе и лю-
бых других изоляторах). Тогда в этих подобластях (где коэффициент о
равен нулю) потенциал А также не может быть однозначно опреде-
лён, что создаёт дополнительные трудности при применении МКЭ.
1.3.5 МОДЕЛЬ В ВИДЕ УРАВНЕНИЙ ДЛЯ ВЕКТОР-ПОТЕНЦИАЛА
ЭЛЕКТРОМАГНИТНОГО ПОЛЯ И СКАЛЯРНОГО ПОТЕНЦИАЛА
ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Рассмотрим довольно часто встречающуюся на практике ситуа-
цию. когда токами смещения можно пренебречь, коэффициент магнит-
1.3.Краевые и начально-краевые задачи ...
39
ной проницаемости р = ц() (р0 — магнитная проницаемость вакуума), а
проводимость о равна нулю в некоторых подобластях расчётной облас-
ти. Исключение токов смещения из уравнения (1.9) приводит его к виду
rotH = Зст + оЁ . (1.52)
При р = Цо соотношение (1.52) принимает вид
— rot В = Л^+стЁ. (1.53)
Ро
Введение вектор-потенциала А и скалярного потенциала У с по-
мощью соотношений
В = rot А , (1.54)
Ё = - дА _ dt - grad V (1.55)
позволяет преобразовать систему (1.53), (1.10), (1.11) к виду
—— ДА + ст Ро дА dt к grad У J = JCT, (1.56)
— div (ст grad У) - - div dt -div Г, (1-57)
где под ДА понимается вектор функция, в общем случае (т е. не толь-
ко в декартовой, но и в цилиндрической и сферической системах коор-
динат) определяемая соотношением
ДА = grad (div а) — rot (rot а). (1-58)
Отметим, что в декартовой системе координат векторное уравнение
(1.56) фактически является системой трёх скалярных уравнений:
—-— ДА. И о Ро 'дА,: dt дх = J? (1.59)
-— ДА + о Ио ' Ж/ dt \ । дУ ду гст - Jy (1.60)
-— ДА 4~ о Ио dAz dt эу dz t JCT J z (1-61)
Система (1.56)-(1.57) (или (1.57), (1.59)—(1.61)) решается, как пра-
вило, в области большого объёма, на внешней границе S которой на-
пряжённости электрического и магнитного поля должны быть очень
малы. Соответственно и краевые условия для скалярного потенциала
40
1 .Математические модели физических процессов ...
V и компонент вектор-потенциал а А нужно задавать таким образом,
чтобы выполнялись условия rot А « 0 и gradK^O. Эти условия
можно выполнить, если на границах области большого объёма задать в
качестве краевых условий для А и V однородные краевые условия
первого рода:
a|s = o,v|s=o.
(1.62)
Действительно, решение ^А, Vl системы (1.56)—(1.57) обладает сле-
дующим свойством: при удалении границы S от подобластей с нену-
левыми сторонними токами пространственные производные функции
V и компонент вектор-функции А на S довольно быстро стремятся к
нулю. Поэтому границу S можно удалить настолько, что пространст-
венные производные V и компонент А на S станут сколь угодно
малыми. Это обеспечит выполнение не только условий rotA « 0 и
grad V ps 0, но и условия div А ~ 0.
Покажем теперь, что если потенциалы удовлетворяют сис-
теме уравнений (1.56)-(1.57) в области Q, на внешней границе кото-
рой выполняется условие
= 0,
s
(1.63)
то определяемые через потенциалы ^A.Vj с помощью соотношений
(1.54) и (1.55) вектор-функции В и Ё внутри Q удовлетворяют сис-
теме уравнений (1.53), (1.10), (1.11).
Легко убедиться, что справедливость уравнений (1.10) и (1.11) сра-
зу же следует из соотношений (1.54) и (1 55) (как и из соотношений
(1.49) и (1.50), обоснование этого приведено в разделе 1.3.4). Остаётся
показать справедливость соотношения (1.53).
Для этого применим к левой и правой частям уравнения (1 56) опе-
рацию div:
——div (ДА
Но \
+ div ст
> + gradV
= div JvT .
(1.64)
Учитывая соотношение (1.57) и соотношения (1.58) и (1.25), опре-
деляющие воздействие оператора Д на вектор-функцию и скалярную
функцию соответственно, получим
—— д(сИуА) = 0. (1.65)
Но ' '
1.3.Краевые и начально-краевые задачи ...
41
В результате мы получили, что функция W = chvA (где А удов-
летворяет системе (1.56)—(1.57)) является решением первой краевой
задачи для уравнения Лапласа (1.65) с однородным краевым условием
(1,63). Отсюда следует, что во всей области Q выполняется условие
divA = 0 (1.66)
Тогда с учётом соотношений (1.58) и (1.66) получим, что потенциалы
А,У"), удовлетворяющие системе уравнений (1.56)—(1.57), удовлетворя-
ют и уравнению
— rot
Но
<9 А
dt
1тг тст
+- grad V = J .
(1.67)
Заменяя в (1 67) rot А на В (см. (1.54)) и ^y + gradV на —Ё
(см. (1.55)), убеждаемся в справедливости и уравнения (1.53).
Использование системы уравнений (1.56)-(1.57) при выполнении ус-
ловий её применимости (т.е несущественности токов смещения и по-
стоянстве коэффициента магнитной проницаемости) оказывается до-
вольно выгодным при конечноэлементном моделировании нестацио-
нарных электромагнитных полей в расчётных областях, содержащих
значительные подобласти с ст = 0. Уравнения системы (1.56)-(1.57)
естественным образом учитывают разрывность коэффициента о (при
сохранении непрерывности вектор-потенциала А во всей расчётной
области Q), а их конечноэлементная аппроксимация приводит к СЛАУ
с достаточно сильно разреженной и хорошо обусловленной матрицей.
Однако при необходимости учёта токов смещения или включении в
расчётную область объектов с ц Цо система (1.56)—(1.57) не может
быть использована для описания электромагнитного поля. Определён-
ные трудности её использования могут возникать и в случае необхо-
димости расчёта электромагнитных процессов в средах, содержащих
объекты с проводимостями, которые на много порядков превышают
проводимость вмещающей среды. Для решения задач с отдельными
проводящими объектами, окружёнными непроводящей средой, а также
с объектами, магнитная проницаемость которых отличается от магнит-
ной проницаемости вакуума, могут быть использованы подходы, осно-
ванные на другом представлении характеристик поля через скалярный
и векторный потенциалы.
1.3.6. МОДЕЛЬ С СОВМЕС ГНЫМ ИСПОЛЬЗОВАНИЕМ ВЕКТОР-ПОТЕНЦИАЛА
И СКАЛЯРНОГО ПОТЕНЦИАЛА МАГНИТНОГО ПОЛЯ
Существует довольно большой класс нестационарных задач
электромагнетизма, в которых электромагнитное поле формируется в
основном за счёт вихревых токов, циркулирующих в отдельных объек-
тах с высокой проводимостью, окружённых непроводящей или очень
слабо проводя щей средой. Это, например, задачи моделирования не-
42 1.Математические модели физических процессов ...
стационарных электромагнитных полей в средах с металлическими
объектами и в высокоомных средах (например, в вечной мерзлоте) с
рудными месторождениями. При этом металлы и руды могут иметь
магнитную проницаемость среды, существенно отличающуюся от маг-
нитной проницаемости вакуума (т.е. могут быть ферромагнетиками). В
данном разделе рассматривается модель, позволяющая достаточно
эффективно решать задачи такого типа с использованием метода ко-
нечных элементов [21].
Будем считать, что среда, в которой изучается электромагнитное
поле, состоит из двух (возможно, неодносвязных) подобластей Qn и
Q°, причём в подобласти Qn удельная проводимость о отлична от
нуля, а в подобласти Q” проводимость равна нулю. Магнитная прони-
цаемость р, в обеих подобластях может быть произвольной функцией
координат (в том числе и зависеть от напряжённости магнитного по-
ля). Будем также считать, что в подобласти П() отсутствуют сторонние
токи. Если же в задаче есть изолированные обмотки с заданными (сто-
ронними) токами, то такие обмотки не входят в расчётную область и
их влияние учитывается специальным образом (например, как в зада-
чах магнитостатики, выделением из Н поля Нс, см. с. 35, или введе-
нием специальных разрывов скалярного магнитного потенциала, о чём
будет сказано в разделе 15.13.3, см. с. 788).
Таким образом, в подобласти Q для напряжённости и индукции
магнитного поля должны выполняться уравнения
rotH" =0, (1.68)
divB“=0. (1.69)
Уравнение же (1.10) можно не принимать во внимание, поскольку оно
служит для определения напряжённости Е электрического поля (через
изменение магнитного поля во времени), а для задач рассматриваемого
типа значения Е в подобласти Q’’, как правило, вычислять не нужно.
Поэтому в подобласти Q1 (как и в задачах магнитостатики) напря-
жённость магнитного поля Й'1 можно представить в виде
Н° =-gradt/, (1.70)
где U — полный скалярный магнитный потенциал. Соответственно
индукция магнитного поля В° в подобласти Q() представляется в виде
В =— р grad С/. (1-71)
Очевидно, что соотношение (1.70) автоматически обеспечивает вы-
полнение уравнения (1.68) (так как оно превращает это уравнение в
тождество rot (grad U) = 0). Поэтому в подобласти Q() нам остаётся
добиться выполнения уравнения (1 69), т.е. нужно, чтобы скалярный
потенциал U в Qu удовлетворял уравнению
1.3.Краевые и начально-краевые задачи ...
43
— div (р, grad U) = 0 .
(1.72)
В подобласти Q° индукцию магнитного поля В1 представим через
вектор-потенциал А с помощью соотношения
B°=rotA. (1.73)
Полагая, что напряжённость электрического поля Е в подобласти
Qn определяется через вектор-потенциал А с помощью соотношения
jgn <9 А
dt ’
(1-74)
убеждаемся, что при таком представлении В и Ё в автоматически
выполняются уравнения (110) и (111) из системы уравнений Мак-
свелла. Уравнение же (1.52) (полученное из уравнения (1.9) пои пре-
небрежимо малых токах смещения) с учётом соотношений (1.73) и
(1.74) преобразуется к виду:
rot [— rot А.] + — JCT - (1-75)
(р ) ot
Таким образом, в подобласти Q0 с нулевой проводимостью индук-
ция магнитного поля В" определяется через скалярный потенциал U
и магнитное поле описывается уравнением (1.72)? а в подобласти Q' с
проводимостью о, отличной от нуля, индукция Вп определяется через
вектор-потенциал А и электромагнитное поле описывается уравнени-
ем (1.75). Чтобы индукция В, определяемая соотношением
В1’ в Q0,
В° в
(1.76)
удовлетворяла системе (1.52), (1.10), (1.11) во всей расчётной области
Q = U Qn , на границе 5П между подобластями Ql) и должны
выполняться следующие соотношения (обеспечивающие непрерывность
нормальной составляющей В и тангенциальных составляющих Н [17]):
В?,=В", (1.77)
Й“ =Н", (1.78)
где п - любая (например, внешняя по отношению к Пп) нормаль к
рассматриваемой границе 5П, т - произвольный касательный к гра-
нице S' (т.е. ортогональный к её нормали п ) вектор.
44
1 Математические модели физических процессов ...
Особенностью рассмотренной модели является то, что во многих
случаях для сохранения её корректности требуется либо вводить по-
верхности разрыва скалярного магнитного потенциала внутри Q”,
либо изменять способ разделения расчётной области на подобласти Q11
и Q° . Это необходимо делать в случае, когда внутри Q1 можно про-
вести такой замкнутый контур L, что интеграл от всех токов, пересе-
кающих натянутую на этот контур поверхность , не равен нулю.
Простейший пример такой ситуации приве-
дён на рис. 1. Здесь по полому цилиндру с не-
нулевой проводимостью циркулирует ток, и
поэтому мы будем считать этот цилиндр по-
добластью . Вне этого цилиндра (включая
его полость) проводимость равна нулю и токов
нет, и поэтому, казалось бы, везде вне полого
цилиндра (включая полость) можно определить
поле Н в виде градиента скалярного потенциа-
ла £7, считая это пространство подобластью
Q(). Однако получить правильные значения
характеристик электромагнитного поля по та-
кой модели нельзя.
Действительно, если мы проинтегрируем
левую и правую части уравнения (1.52) по поверхности Г^, натянутой
на контур L , и воспользуемся формулой Стокса ] rotHdS = ф HdZ ,
Г/ L
то получим
(f)Hdi = f (JCT + oEjrfS. (1.79)
L VL
Учитывая, что L полностью лежит в подобласти Q“ и Н в Q°
представляется в виде — gradt/ (см. (1.70)), получаем, что
(j) Hdl = —(j)grad Udi =0. (1.80)
L L
Поскольку контур L выбирался так, чтобы правая часть (1.79) (т.е.
сумма протекающих токов) была ненулевой, фактически мы получили,
что нарушена справедливость уравнения (1.52). Нетрудно убедиться,
что основной причиной, приводящей к нарушению интегрального эк-
вивалента дифференциального уравнения (1.52), является не представ-
ление индукции магнитного поля в непроводящей подобласти Q() с
помощью соотношения (1.71), а только взаиморасположение подобла-
стей Q° и Q(j) * l).
Проанализируем возможные пути разрешения связанных с этим
проблем. Одним из способов устранения возможности обхода ненуле-
1.3.Краевые и начально-краевые задачи ...
45
вого тока по контуру, целиком лежащему в Q , является введение
внутри Q° поверхности S1’ разрыва скалярного магнитного потенциа-
ла. Эта поверхность должна быть построена так, чтобы все замкнутые
контуры L, по которым можно обойти ненулевой ток, пересекали её
нечётное число раз.
Будем считать, что по некоторой обмотке течёт ненулевой суммар-
ный ток I (J = Р J<TdS, Pjr - любая поверхность, натянутая на лю-
бой из контуров if, окружающих обмотку). В этом случае во всех точ-
ках поверхности S1’ нужно задать скачок скалярного потенциала, рав-
ный I, т.е. значение U\s1, функции U с одной стороны от поверхно-
сти S1' должно отличаться от значения U\sp функции U с другой
стороны S1' на величину I:
U\s1, = u\sp +/- <L8l>
Кроме того, наложим на U дополнительное ограничение:
ди s4
+ ди
дп ’
(1.82)
где и - значения нормальных производных U с разных
дп Is? дп sp
сторон поверхности S1’ (п — нормаль к S1’), а р4 и р,“ - значения ко-
эффициента р с разных сторон поверхности S1’ (нормальная состав-
ляющая Н на поверхности Sp равна
с одной стороны и с
дп sp
другой).
Выполнение условия (1.82) обеспечивает непрерывность нормаль-
ных составляющих индукции В на Sp (непрерывность касательных
составляющих Н на Sp сразу следует из (1.81) с учётом того, что
I = const).
В результате циркуляция Н по контуру L, пересекающему по-
верхность Sl> , должна вычисляться следующим образом:
(])HdT = -
L
Z,
(1.83)
где q - точка пересечения контуром L поверхности Sv. Таким обра-
зом, уравнение (1.79) (и, следовательно, (1.52)) оказывается справед-
ливым.
46
1 .Математические модели физических процессов ...
Более сложной является ситуация, когда ток, обходимый по конту-
ру L С Ql), не является сторонним, т.е. должен быть вычислен в ходе
решения задачи. В этом случае для предотвращения возможности об-
хода ненулевых токов J'oEdS (Г/- поверхность, натянутая на L) в
П
подобласть Qa следует включить часть расчётной области, в которой
коэффициент о равен нулю, так, чтобы все контуры L, по которым
можно обойти ненулевой ток, пересекали подобласть Q° . Заметим, что
в этом случае в той части подобласти QCT , где о = 0 , решение А урав-
нения (1.75) перестаёт быть единственным, что заметно усложняет
численный анализ электромагнитного поля с использованием рассмот-
ренной в данном разделе модели. Тем не менее разработанные на ос-
нове именно этой модели в последнее время вычислительные схемы
МКЭ являются наиболее эффективными для численного анализа элек-
тромагнитных полей в задачах с существенным влиянием вихревых
токов (и при пренебрежимо малых токах смещения).
2.1.Вариационные постановки на основе МНК...
47
2. ОСНОВНЫЕ ИДЕИ И ПРИНЦИПЫ МКЭ
Прежде чем приступить к изучению математического аппарата
МКЭ, позволяющего решать наиболее сложные задачи математиче-
ской физики, продемонстрируем основные идеи этого метода на при-
мере решения простейшей краевой задачи для обыкновенного диффе-
ренциального уравнения второго порядка
= (21)
dx
определённого на интервале (а, с). На этом примере мы познакомимся
с основными принципами, на которых базируется МКЭ:
• эквивалентные вариационные постановки;
• построение подпространств функций, на которых ищется прибли-
жённое решение;
• технологические особенности построения аппроксимирующих за-
дачу систем линейных алгебраических уравнений (СЛАУ), осно-
ванные на вычислении вкладов от отдельных ячеек сетки и внесе-
нии их в конечноэлементную СЛАУ.
2.1. ВАРИАЦИОННЫЕ ПОСТАНОВКИ НА ОСНОВЕ МНК.
АППРОКСИМАЦИЯ НА КОНЕЧНОМЕРНОМ ПОДПРОСТРАНСТВЕ,
ОПРЕДЕЛЯЕМОМ НАБОРОМ БАЗИСНЫХ ФУНКЦИЙ
Одним из наиболее простых и наглядных (но отнюдь не самых эф-
фективных при решении краевых задач) является вариационный прин-
цип, основанный на методе наименьших квадратов (МНК). Суть его
состоит в следующем.
Вместо того, чтобы решать уравнение (2.1), мы будем искать минимум
функционала, определённого через среднеквадратичное значение невязки1
1 Под среднеквадратичным значением функции R, заданной в области Q,
мы понимаем квадрат её нормы в функциональном пространстве L2(Q), где
L2(O) - пространство суммируемых с квадратом на Q функций (т.е. таких
функций w , для которых значение fwi/Q конечно).
п
48
2.Основные идеи и принципы МКЭ
уравнения (2.1) при подстановке в него произвольной (пробной) функ-
ции v:
с ( (ft V
Линк = I - —у - / dx —> min
J I dx ) v
a
(2.2)
При этом подразумевается, что чем меньше значение Линк W) > тем
ближе функция v к и (что кажется естественным, хотя вовсе не оче-
видно и требует доказательства, но в данный момент мы обратим своё
внимание на другие вопросы).
Рассмотрим следующий метод минимизации функционала (2.2).
Пробную функцию v представим в виде линейной комбинации п не-
которых известных линейно-независимых функций ф,- (х) (которые
обычно называют базисными функциями):
№) = ^2<7/ф, (я), (2.3)
г = 1
причём веса в разложении будем искать из условия минимальности
Линк <v) • Подставляя (2.3) в (2.2), получаем (индекс суммирования г при
вычислении произведения двух сумм в одной из них заменяем на j ):
Линк —
d2^j (ж)
dx2
d2^.j (х)
-----у-----да;) dx =
drft
Md2^ (х) d2^ (х) г <£2ф, , j
dx2 dx2 dx + jT,4i-^-fWdx +
a t~1 J-1 a » —1
рфЦ Д2ф,(а;) p
+ / —f(x)dx + I f2(x)dx.
J dxz J
a J ~1 a
(2-4)
Учитывая, что коэффициенты q, в разложении (2.3) не зависят от
переменной х , из (2.4) получим выражение для функционала Линк (V)
в виде квадратичной формы
Линк ft С, (2.5)
г-1
в которой коэффициенты Д,, и С определяются соотношениями
г d2ft.t (.г-) с/2ф, (Ж) ,
I -----------------—dx
J dx dxz
a
(2-6)
2.1.Вариационные постановки на основе МНК...
49
. г d2^ U) _ z ч
bj = — I —— f (x)dx, (2.7)
J dx1
a
c
C = J f\x)dx. (2.8)
a
Нетрудно убедиться, что минимум квадратичной по q, функции (2.5)
достигается на векторе q = (tfi, , <7„ У , являющемся решением СЛАУ
Aq = b, (2.9)
где А — матрица, а b — вектор, компоненты которых определяются
соотношениями (2.6) и (2.7) соответственно. Для доказательства этого
утверждения достаточно продифференцировать правую часть соотно-
шения (2 5) по qL и приравнять полученные производные к нулю. То,
что полученная стационарная точка будет точкой минимума функцио-
нала (2.2), гарантируется неотрицательной определённостью матрицы
А : действительно, для любого вектора q квадратичная форма
d2^j
dx2 dx2
п п
У? У? AijQiQj
г=1 7=1
и и.
J ЕЕ ад
а ’=17=1
d2tyj
dx2
dx =
dx =
где v(.t) — некоторая функция, определяемая соотношением (2.3).
Итак, на основе вариационного принципа (2.2) и представления ис-
комой функции в виде (2.3) мы можем найти некоторое {приближён-
ное) решение ипр уравнения (2.1) в виде
ипр(я) =
2 = 1
(2.Ю)
где q* — вектор решения СЛАУ (2.9) с матрицей А и вектором правой
части Ь, компоненты которых определяются соотношениями (2.6) и
(2.7). При этом функция ипр(.'с) является приближением точного ре-
шения уравнения (2.1) в том смысле, что она обеспечивает для вы-
бранного набора функций фг (ж) минимум среднеквадратичного зна-
чения функции-невязки г — f + d2vjdx2 этого уравнения среди всех
функции и, представимых в виде (2.3).
Рассмотрим вопрос о выборе функций (ж), с помощью которых
ищется приближённое решение (2.10). В качестве одного из возмож-
ных вариантов можно взять
50
2.Основные идеи и принципы МКЭ
Яр,; (X) = X1 \ (211)
т.е. искать приближённое решение в виде полинома степени п — 1:
(2.12)
1=1
Из соотношений (2.6) и (2.7) видно, что в этом случае первая и вто-
рая строка и первый и второй столбец СЛАУ (2.9) нулевые, и поэтому
коэффициенты q} и q2 в разложении (2.12) не могут быть найдены из
СЛАУ (2.9). Этого и следовало ожидать, поскольку ни исходное диффе-
ренциальное уравнение (2.1), ни соответствующий ему функционал (2.2)
никак не реагируют на линейную часть q^ + q2x функций и или v : при
добавлении к и или к v любой линейной функции q} 4- q2x не меняют-
ся ни уравнение (2.1), ни значение функционала /мнк т.е. решение
уравнения (2.1) или вариационной задачи (2.2) может быть найдено с
точностью до произвольной линейной функции Qj + q2x . Для того что-
бы выделить одно из решений дифференциального уравнения (2.1), не-
обходимо привлечь дополнительную информацию об искомой функции.
В краевой задаче такой информацией являются краевые условия, задан-
ные на границах а и с области определения уравнения (2.1). Очевидно,
что и для нахождения единственного решения сформулированной нами
вариационной задачи (2.2) также необходимо привлечь заданные на
границах интервала (а, с) краевые условия В этом смысле сформулиро-
ванная вариационная задача эквивалентна лишь дифференциальному
уравнению, а не краевой задаче, поскольку в ней никак не учитывается
информация о краевых условиях.
Таким образом, процедура нахождения приближённого решения
(2.10) краевой задачи для дифференциального уравнения (2.1) на осно-
ве минимизации функционала (2.2) выглядит следующим образом.
С помощью соотношений (2.6) и (2.7) вычисляются компоненты
Ач и Ь, матрицы и вектора правой части СЛАУ (2.9), из невырожден-
ной части которой (г > 3, j' > 3) находятся компоненты 93, <74,...,5*
разложения приближённого решения ипр по базисным функциям
(2.10). Компоненты же q{ и q2 определяются из краевых условий.
Например, если на левой границе интервала (а, с) задано краевое
условие первого рода
u(a) = ufl, (2.13)
а на правой - второго
2.1 .Вариационные постановки на основе МНК...
51
то при использовании базисных функций (2.11) коэффициенты q* и q*>
могут быть выражены через д*, <74,..., д7* следующим образом.
Подставив приближённое решение (2.12) в краевое условие (2.14),
получим
52 =0-£9*(г-1)с-2, (2.15)
г=3
а из (2.12) и первого краевого условия (2.13) можем легко найти значе-
ние qi :
<71 = иа 1 (2.16)
i=2
Заметим, что для рассмотренной процедуры вычисления приближён-
ного решения wnp (ж) в виде полинома (2.12) точность представления
решения it (ж) исходной задачи зависит от числа п слагаемых в этом
полиноме. Это значит, что для повышения точности приближённого
решения мы должны соответствующим образом увеличить п . Но тогда
пропорционально п возрастёт размер СЛАУ (2.9), которую необходимо
решать для нахождения весов q, в разложении (2.12). При этом матрица
А этой СЛАУ является плотной и затраты на вычисление решения
СЛАУ (2.9) с ростом п растут очень быстро (пропорционально п3).
Не менее важным для реализации рассмотренной вычислительной
процедуры является и то, что с ростом п очень быстро ухудшается
обусловленность матрицы А (имеется в виду, естественно, её невы-
рожденная часть - подматрица i > 3, j > 3). В результате даже при
относительно небольших значениях п мы получим слишком высоко-
затратный вычислительный процесс, да ещё и численно очень неус-
тойчивый. Отсюда можно сделать вывод, что простой и удобный на
первый взгляд базис (2.11) на самом деле обладает очень серьёзными
недостатками: для построения приемлемого по точности решения чис-
ло слагаемых в представлении (2.12) должно быть достаточно велико,
а это приводит к тому, что нужно решать СЛАУ с плотной матрицей
довольно большой размерности, причём вычислять решение этой
СЛАУ очень сложно (чаще всего просто невозможно) из-за крайне
плохой обусловленности её матрицы.
Возможной альтернативой полиномиальному базису (2.11) может
служить так называемый тригонометрический базис. Для рассматри-
ваемой нами задачи с краевыми условиями (2.13), (2.14) этот базис
может быть записан в виде
ф,- (ж) = sin (——(/tv - § И ,
\ с — а \ 2 / /
i = 1... л ,
(2.17)
причём приближённое решение i/,np (ж) представляется в виде
52
2 Основные идеи и принципы МКЭ
апр (ж) = ид — 0а + 0т 4- q*^ (х). (2.18)
г=1
Очевидно, что функции *фг (а?) удовлетворяют однородным первому и
второму краевым условиям соответственно на левой и правой границах
интервала (а, с), и линейная часть и,7 — Оа 4- 6х добавлена к линейной
комбинации функций (2.17) для того, чтобы ипр (т) удовлетворяла тре-
буемым неоднородным краевым условиям (2.13) и (2.14). Добавление
этой линейной части к пробной функции v никак не влияет на значение
функционала /мнк > и поэтому для задачи (2.2) минимизации функ-
ционала Тмнк <^) совершенно безразлично, на каких функциях v искать
п
его минимум — на функциях и (х) = гд ф( (т), удовлетворяющих одно-
i= 1
родным краевым условиям, или на функциях
и
v(x) = и;/ — 0а + Qx 4- У^^гФг (т), удовлетворяющих требуемым неод-
z=i
нородным краевым условиям (2.13) и (2.14). Поэтому можно минимизи-
ровать функционал /мнк на функциях v(x), представленных в виде
линейной комбинации функций (2 17), а фиксированную линейную часть
п
ид — 0 а 4-0т добавлять только к результату минимизации qt ф, (т)
для формирования приближённого решения (2 18), удовлетворяющего
требуемым неоднородным краевым условиям (2.13) и (2.14).
Вообще говоря, то же самое справедливо и для случая рассмотрен-
ного выше полиномиального базиса (2.1 1) - в нем значимыми для ми-
нимизации функционала Тмнк W) являлись функции .т’-1 при i > 3, и
поэтому функции (х) = х1) = 1 и ф-2 (.с) = х также вполне могли
бы быть исключены из базиса (2.11) и привлечены в выражение для
адпр (ж) только для того, чтобы обеспечить выполнение для него тре-
буемых краевых условий1. Очевидно, что причина этого заключается
только в том, как была сформулирована вариационная задача (2.2) - в
ней никак не были учтены краевые условия, позволяющие выделить
единственное решение из множества решений дифференциального
уравнения (2.1). Поэтому при использовании такой вариационной фор-
мулировки мы должны были искать минимум функционала /МН|< (V)
либо на множестве функций v, удовлетворяющих требуемым краевым
условиям, либо на множестве функций, не удовлетворяющих требуе-
мым краевым условиям, а затем корректировать полученное решение с
1 Фактически, это и делалось при исключении первых двух полностью ну-
левых строк и столбцов СЛАУ (2.9) и вычислении и q-2 по формулам
(2.15) и (2.16).
2 1 .Вариационные постановки на основе МНК... 53
помощью линейной функции (являющейся решением однородного
уравнения — d2uldx2 =0) таким образом, чтобы выполнились нужные
нам краевые условия (так мы и поступили при использовании полино-
миального базиса (2.11)).
Возможны и другие варианты учёта краевых условий, когда, напри-
мер. минимум функционала ищется на множестве функций,
удовлетворяющих однородным краевым условиям (т.е. ищется решение
дифференциального уравнения (2.1), удовлетворяющее однородным
краевым условиям), а затем к полученному решению добавляется ли-
нейная функция, удовлетворяющая однородному дифференциальному
уравнению и требуемым неоднородным краевым условиям - так мы
поступили при использовании тригонометрического базиса (2.17).
По существу, последний вариант является некоторой модификаци-
ей самого первого из рассмотренных вариантов учёта краевых усло-
вий. Действительно, в нём мы фактически переформулировали исход-
ную краевую задачу с неоднородными краевыми условиями в краевую
задачу с соответствующими однородными краевыми условиями и за-
тем для полученной задачи применили вариант, в котором минимум
функционала ищется на функциях, удовлетворяющих нужным нам
(после преобразования задачи - однородным) краевым условиям. При
этом для перевода неоднородных краевых условий в однородные вовсе
не обязательно было использовать функцию, являющуюся решением
соответствующего однородного дифференциального уравнения. Это
могла бы быть любая функция vfl>0 («), удовлетворяющая неоднород-
ным краевым условиям (2 13) и (2.14) и имеющая вторую производ-
ную, — тогда в задаче с однородными краевыми условиями нужно было
бы соответствующим образом скорректировать правую часть, т.е. вме-
Л 0(а;)
сто взять функцию f = f Ч-----Ч,— .
dx
Вернёмся к анализу достоинств и недостатков рассмотренных нами
базисных функций. Прежде всего, тригонометрический базис (2.17) по-
зволяет с любой точностью аппроксимировать (приближать) решение
дифференциального уравнения (2.1) с однородными краевыми условиями
за счёт выбора подходящего числа п базисных функций. При этом глав-
ным достоинством этого базиса является ортогональность его функций
(2.17) в том смысле, что все внедиагональные элементы матрицы А, вы-
числяемые из соотношения (2.6), оказываются равными нулю, т.е. матри-
ца А является диагональной. Таким образом, для нахождения весов q,
очень просто решить СЛАУ (2.9): для этого достаточно лишь поделить
компоненты сё правой части на диагональные элементы матрицы А .
Но тригонометрический базис обладает и слишком серьёзными не-
достатками: его практически невозможно использовать при решении
дву- и трёхмерных краевых задач в областях со сложной геометрией, а
также при наличии разрывов в коэффициентах дифференциального
уравнения Поэтому тригонометрический базис малоприсмлсм для
решения абсолютного большинства практических задач.
54
2.Основные идеи и принципы МКЭ
Таким образом, нам хотелось бы построить такой базис, чтобы в
нём были достоинства рассмотренных нами выше базисных функций и
отсутствовали их наиболее существенные недостатки:
• структура базисных функций должна быть такова, чтобы можно
было с необходимой точностью представить в виде линейной ком-
бинации базисных функций решение интересующей нас краевой
задачи; при этом желательно, чтобы с ростом количества п базис-
ных функций погрешность представления решения в виде их ли-
нейной комбинации достаточно быстро стремилась к нулю;
• процедура вычисления коэффициентов д,- разложения приближён-
ного решения по базисным функциям ф7; должна быть численно
устойчивой при любых, даже достаточно больших п, и вычисли-
тельные затраты на получение этих коэффициентов не должны
быть слишком высокими;
• базисные функции должны быть такими, чтобы их можно было
использовать при решении задач, определённых в расчётных облас-
тях со сложной дву- и трёхмерной геометрией.
В дальнейшем мы убедимся, что всем этим требованиям удовлетво-
ряют так называемые кусочно-полиномиальные функции. Эти функ-
ции строятся как полиномы пространственных координат в каждой из
мелких подобластей1 Q/., на которые разбивается расчётная область
Q. На границах подобластей Q/. полиномы стыкуются таким образом,
чтобы полученные из них базисные функции (или пробные функции,
являющиеся произвольными линейными комбинациями базисных)
были допустимы для вариационной формулировки, т.е. для них имела
смысл подстановка в минимизируемый функционал.
Очевидно, что для функционала (2.2), сформулированного на осно-
ве МНК, такие функции должны иметь, по меньшей мере, суммируе-
мые с квадратом вторые производные Это серьёзно усложняет всю
вычислительную процедуру построения приближённого решения с
использованием кусочно-полиномиального оазиса — в этом случае для
решения соответствующей вариационной задачи в виде оазисных
функций необходимо использовать как минимум сплайны с непрерыв-
ной первой производной.
2.2. ВАРИАЦИОННЫЕ ПОСТАНОВКИ, ИСПОЛЬЗУЕМЫЕ
В МЕТОДАХ РИТЦА И ГАЛЁРКИ НА
2.2.1. ПОСТРОЕНИЕ ЭКВИВАЛЕНТНЫХ ВАРИАЦИОННЫХ ФОРМУЛИРОВОК
С УМЕНЬШЕННЫМИ ТРЕБОВАНИЯМИ К ГЛАДКОСТИ РЕШЕНИЯ
Итак, сложность вычислительной процедуры построения при-
ближённого решения на основе эквивалентной вариационной поста-
новки при использовании кусочно-полиномиального базиса сущест-
венно зависит от того, каков максимальный порядок входящих в ми-
нимизируемый функционал производных. Поэтому нам хотелось бы
1 Эти подобласти называют конечными элементами.
2.2.Вариационные постановки, используемые в методах ...
55
использовать функционалы такого типа, чтобы их подынтегральные
выражения содержали производные меньшего порядка, нежели исход-
ное дифференциальное уравнение. Примером такого функционала
может служить функционал следующего вида:
/(v) =
(х) v(x) dx — 20w (с).
(2-19)
Минимизацию этого функционала необходимо проводить на мно-
жестве функций удовлетворяющих только первому краевому
условию, второе же краевое условие (2.14) будет автоматически вы-
полняться для функции и , доставляющей минимум I Си).
Рассмотрим очень схематичное доказательство эквивалентности за-
дачи минимизации функционала (2.19) решению краевой задачи для
дифференциального уравнения (2.1) с краевыми условиями (2.13) и
(2.14). Строгое доказательство эквивалентности минимизации соответ-
ствующего функционала решению краевой задачи для п -мерного
дифференциального уравнения эллиптического типа будет дано ниже,
в третьем разделе. Здесь же мы обратим внимание в основном на саму
возможность использования для поиска решения функционала, содер-
жащего производные функций v только первого порядка, в то время
как исходная дифференциальная задача содержит производные второ-
го порядка.
Покажем, что стационарная точка1 и, доставляющая минимум функ-
ционалу (2.19), является решением краевой задачи (2.1), (2.13), (2.14).
Для функции и, доставляющей минимум I (v), справедливо:
1 (и) < Ци +х^о)> (2.20)
где v = и + хч» - некоторый элемент функционального пространства
пробных функций, полученный смещением из точки и на величину
ХЧ), причём х ~ произвольный коэффициент, а Ч) _ произвольная
функция, удовлетворяющая однородному первому краевому условию
на границе х = а (так как и\х-а — и(/ и г/|ж=„ = ug, и значит,
„I = = о ).
uh;=tr л/ V
Л-
Вычислим значение I (и + X4j)
I (и + ХЧ)) =
1 В данном случае под словом «точка» понимается элемент некоторого
функционального пространства - функция и(х).
56
2.Основные иДеи и принципы МКЭ
где
- 26 (н(с) + ХЧ) (О) = f (^7)
= I (и) + 2x7? + Х2^2>
26и (с) +
(2.21)
Р = f ^^dx~ J fvudx ~ °7,d (c) ’
a a
(2.22)
(2.23)
Нетрудно убедиться, что условие (2.20) для произвольных х и Ч)
выполняется тогда и только тогда, когда справедливо уравнение
f ~^~r^dx ~ f fvodx ~ (Ц> — о
J ах dx J
(2-24)
для любой функции Ц) (такой, что vl} (а) — 0 ). Действительно, если
предположить, что найдётся какая-то функция > Для которой вели-
чина р, определяемая соотношением (2.22), отлична от нуля, то, взяв
X = — -Д-, из (2.21) получим
d
/(u + ХЧ)) = + </(w),
а d d
что противоречит неравенству (2.20), т.е. выполнение уравнения (2.24)
является необходимым условием выполнения неравенства (2.20) (мы
учитывали, что для любой непрерывной функции д(), удовлетворяю-
щей условию ??()(«) = 0, неотрицательная величина г/2, определённая
соотношением (2.23), равна нулю тогда и только тогда, когда v[} = 0, и
поэтому могли взять число х как результат деления (—р) на d2).
Очевидно, что выполнение уравнения (2.24) является и достаточ-
ным условием выполнения неравенства (2.20) - если р = 0, то из
(2.21) сразу же следует (2.20).
Итак, мы доказали, что выполнение условия (2.20) полностью эквива-
лентно выполнению уравнения (2.24). В дальнейшем уравнения вида
(2.24) мы будем называть вариационными и задачу нахождения его ре-
2.2.Вариационные постановки, используемые в методах ...
57
шения и так же, как и задачу нахождения минимума функционала, будем
называть вариационной задачей или вариационной постановкой.
Вообще говоря, в классическом вариационном исчислении под ва-
риационными понимают задачи нахождения стационарных точек неко-
торых функционалов (в которых обращаются в нуль вариации этих
функционалов), в то время как уравнения вида (2.24) называют урав-
нениями в слабой форме. Однако мы, обращая внимание на сходство
уравнений вида (2.24) с задачами минимизации функционалов именно
по наличию принципа варьирования функций в тех и других1, а также
ещё и на то, что стационарная точка функционала является, как прави-
ло, и решением соответствующего уравнения в слабой форме, будем
называть вариационными постановками (или вариационными задача-
ми) как задачи минимизации функционалов, так и задачи нахождения
решений уравнений в слабой форме (вида (2.24)).
Продолжим доказательство эквивалентности вариационной поста-
новки (теперь уже в виде вариационного уравнения (2.24)) решению
краевой задачи (2.1), (2.13), (2.14).
Применим формулу интегрирования по частям для преобразования
первого слагаемого левой части уравнения (2.24):
du dvu
dx dx
(2.25)
Подставляя это выражение в уравнение (2.24) и учитывая, что
(«) = 0 , получаем
vi)dx + (4^1 ~ Ч) (с) — О
dx2 ) \dx\x=c I
Vv0 : v0 (ft) — 0 .
(2-26)
Поскольку t'() - произвольные функции, выберем из них только такие
г>(), которые обращаются в нуль при х — с. Тогда из (2.26) получим
v()dx = О
Уч> : Д) (а) = £0 (с) = 0,
откуда и следует, что на интервале (ft, с) невязка R (а:) = —
d2u
dx2
- f диф-
1 Действительно, как в задаче минимизации функционала I Си) решением
считается функция и, доставляющая минимум I (го среди всех функций и
некоторого функционального пространства, так и при решении уравнения в
слабой форме (вида (2.24)) ищется функция и, удовлетворяющая этому урав-
нению для любых функций д() из некоторого функционального пространства.
58
2.Основные идеи и принципы МКЭ
ференциального уравнения (2.1) почти всюду равна нулю1, т.е. для и
почти всюду на (а, с) выполняется дифференциальное уравнение2 * (2.1).
Учитывая это, из уравнения (2.26) получаем 1^ — G) г?0 (с) = О
и, выбирая такую v(), что и0 (с) 0, убеждаемся и в справедливости
краевого условия (2.14).
Первому же краевому условию функция и удовлетворяет в силу
выбора пространства пробных функций v, которому принадлежит и
функция и.
1 Мы в дальнейшем (при выводе и обосновании эквивалентных вариаци-
онных постановок) будем ещё не раз использовать тот факт, что функция R
равна нулю почти всюду в области Q, если для любой функции v выполня-
ется равенство J RvdQ, — 0 . Заметим, что эго утверждение из функциональ-
о
него анализа, в общем-то, допускает и простое «интуитивное» понимание
(полезное для тех, кто не изучал функциональный анализ). Действительно,
если бы функция R была отлична от нуля в некоторой подобласти 6Q, мера
(объём) которой не равен нулю, то, выделив из этой подобласти Ю ту её
часть (также с ненулевым объёмом), где R > 0 (или ту часть , где
/? < 0 ) и взяв в качестве пробной функцию v такую, что v > 0 на Ю+ (или
на 6ГГ ) и v = 0 на Q \ Ю+ (или на Q \ 6Q- ) мы получим, что j RvdQ, pa-
52
вен интегралу по 6Q4 (или ) от строго положительной на 6Q+ (или стро-
го отрицательной на №“ ) функции и поэтому он не может быть равен нулю.
2 На самом деле, условие, что дифференциальное уравнение справедливо
не в каждой точке расчётной области, а именно почти всюду в ней, гораздо
больше соответствует ситуациям, возникающим при решении практических
задач. Даже при решении простейшей краевой задачи для дифференциального
уравнения (2.1), если его правая часть f, например, разрывна, то в точках
разрыва f значение второй производной решения и не определено (хотя
само решение существует и единственно). Иллюстрацией этого может слу-
жить задача для дифференциального уравнения (2.1) с правой частью (2.52),
которую мы рассмотрим чуть ниже, — в точках х = 2 и х — 3 значение вто-
рой производной функции и, определяемой соотношением (2.57) и являю-
щейся решением рассматриваемой задачи, не определено. В многомерном
случае аналогичная ситуация возникает на всех поверхностях, где разрывны
параметры f или (да, в общем-то, и X ) дифференциального уравнения
(1.1). Но это нисколько не мешает находить решения таких задач, в которых,
фактически, дифференциальное уравнение не определено на множествах точек
расчётной области, имеющих объёмную меру нуль, а значит, уравнение для
невязки R исходного дифференциального уравнения в виде J RvdQ = 0 Vv
(которое часто называют уравнением в слабой форме) является даже более
естественным, чем само дифференциальное уравнение (которое через невязку
R может быть записано в виде: R = 0 на Q).
2.2.Вариационные постановки, используемые в методах ...
59
В результате функция и, являющаяся решением вапиационной за-
дачи (т.е. доставляющая минимум функционалу (2.19) и удовлетво-
ряющая вариационному уравнению (2.24)) является и решением крае-
вой задачи (2.1), (2.13), (2.14).
Обратное утверждение доказывается совершенно элементарно - ес-
ли функция и является решением краевой задачи (2.1), (2 13), (2.14),
то для неё справедливо уравнение (2.26), а значит, с учётом равенства
(2.25), полученного на основании формулы интегрирования по частям,
для ?/. справедливо и вариационное уравнение (2.24).
Таким образом, минимизация функционала (2.19) на множестве
функций v, удовлетворяющих первым краевым условиям (v(a) = и(/),
эквивалентна и решению вариационного уравнения (2.24), и решению
краевой задачи (2.1), (2.13), (2.14).
Сделаем несколько замечании о вариационных задачах в виде ми-
нимизации функционала (2.19) или решения уравнения (2.24).
Во-первых, эти вариационные задачи включают в себя информацию
о втором краевом условии на границе х = с (в виде слагаемого
—20 и (с) в функционале или слагаемого —Ov()(c) в вариационном
уравнении), и поэтому при их решении не нужно дополнительно забо-
титься о выполнении второго краевого условия — оно выполняется
автоматически в результате минимизации функционала (2.19) или ре-
шения вариационного уравнения (2.24) (но при этом нужно помнить,
что функции и в функционале (2.19) и функция и в уравнении (2.24)
должны удовлетворять первому краевому условию).
Во-вторых (и это самое главное), функции, на которых нужно ис-
кать минимум функционала (2.19) (или для которых нужно решать
уравнение (2.24)), не обязаны иметь вторые производные — вполне
достаточно, чтобы они имели суммируемые с квадратом первые про-
изводные. Этот факт имеет чрезвычайно большое значение в МКЭ,
поскольку позволяет для построения приближённого решения краевых
задач для дифференциальных уравнений второго порядка использовать
кусочно-полиномиальные функции, являющиеся лишь непрерывными
(а не непрерывно дифференцируемыми, как это было бы необходимо
для существования суммируемой с квадратом второй производной) в
точках сшивки кусочных полиномов.
Прежде чем приступить к изучению техники МКЭ, обсудим ещё
один вопрос, связанный с построением эквивалентных краевым вариа-
ционных задач в виде уравнений в слабой форме (типа уравнения
(2 24)) Уравнение (2 24) было получено нами как необходимое и дос-
таточное условие минимальности функционала (2.19) в точке и. Од-
нако это уравнение можно получить и исходя из несколько иных сооб-
ражений.
Пусть нам необходимо найти решение и краевой задачи (2.1),
(2.13), (2.14) на интервале (а, с). Это решение и будем искать из усло-
вия, что невязка — — f уравнения (2.1) должна быть ортогональна
(far
в смысле скалярного произведения пространства (а, с) всем функ-
60
2.Основные идеи и принципы МКЭ
циям ц, из пространства* Н\ функций, определенных на интервале
(а, с), имеющих суммируемые с квадратом первые производные и рав-
ных нулю на границе х = а, т.е.
С , 2 X
J |-^-Ж()^ = 0 (2.27)
а
для любых Ц) G 77(1. Как уже отмечалось выше (см. сноску на с. 58),
выполнение уравнения (2.27) для любых элементов v() определённого
функционального пространства обеспечивает выполнение исходного
дифференциального уравнения (2.1) на (а, с) («почти всюду»).
Преобразуем уравнение (2.27) с использованием соотношения
(2.25):
1Г^1^Иг1х_Ш _ 'ffv dx = 0 VvueHf,.
J dx dx \dx ) (l J
и a
(2.28)
Учитывая, что каждая функция w(1 из пространства Я(* должна
удовлетворять условию и0 (а) = 0, а на границе х = с задано краевое
условие (2.14), из (2.28) получаем следующее вариационное уравнение
f _ 0 ц (с) _ f fv{}dx = 0
J dx dx J
Vu(): -yo(a) = O.
(2.29)
Сравнивая уравнение (2.29) с полученным ранее уравнением (2.24),
являющимся необходимым и достаточным условием минимальности
функционала (2.19) в точке и, убеждаемся в их полной идентичности.
Таким образом, мы показали, что уравнение в слабой форме (2.24)
может быть получено не только из условия минимальности некоторого
функционала, но и из условия ортогональности невязки рассматривае-
мого дифференциального уравнения определённому функциональному
пространству.
Обратим внимание на то, что элементы этого функционального про-
странства должны обращаться в ноль на границах, где в исходной крае-
вой задаче заданы краевые условия первого рода (т.е. удовлетворять од-
нородный первым краевым условиям), даже если в исходной краевой
1 Это функциональное пространство является гильбертовым (т.е. линей-
ным полным пространством со скалярным произведением), и поэтому для его
обозначения использована латинская буква Н (от английского Hilbert}', верх-
ний индекс «1» у //(> обозначает, что это пространство включает в себя функ-
ции, имеющие суммируемые с квадратом первые производные, а нижний
индекс «0» — что все входящие в него функции удовлетворяют однородному
первому краевому условию на той границе, где первое краевое условие (воз-
можно, и неоднородное) задано в исходной краевой задачи.
2.2.Вариационные постановки, используемые в методах ...
61
задаче краевые условия первого рода являются неоднородными. Именно
благодаря этому в полученной нами (после интегрирования по частям)
вариационной задаче не появляются члены с производной искомого ре-
шения (вида на границах, где краевым условием определяется
лишь значение самой функции и, а значения её производной могут быть
найдены только в результате решения всей краевой задачи. На тех же
границах, где в краевое условие входит производная решения, значение
пробной функции не фиксируется — там производная решения заменя-
ется соответствующим выражением из краевого условия, что и обеспечи-
вает выполнение этого краевого условия естественным образом из реше-
ния вариационной задачи (более подробно об этом будет сказано ниже).
Итак, в данном пункте мы рассмотрели два типа вариационных за-
дач: вариационные задачи, основанные на минимизации функционала
вида (2.19), и вариационные задачи в виде уравнения в слабой форме
(2.29) (или (2.24)). У этих задач есть очень важная общая черта (кото-
рой, например, не обладает рассмотренная в разделе 2.1 вариационная
задача (2.2)): и функционал, и вариационное уравнение не содержат
вторых производных искомых функций, хотя в исходное дифференци-
альное уравнение вторые производные решения входят.
2.2.2. ПОСТРОЕНИЕ ДИСКРЕТНЫХ АНАЛОГОВ
Для решения вариационных задач в виде минимизации функционала
(2.19) или в виде уравнения в слабой форме (2.29) мы можем воспользо-
ваться тем же приёмом, который был продемонстрирован при решении
вариационной задачи (2.2). Так, при минимизации функционала (2.19}
мы можем представить функцию v в виде линейной комбинации (2.3)
базисных функций ф,; (.?;). Подставляя это выражение для v в функцио-
нал (2.19), получаем его представление в следующем виде:
г, ч ГV''V"' (%) j
(I
- 2 f /52 Q^^dx - 2052 (2.30)
a ' = 1
Функционал (2.30) может быть записан в виде квадратичной формы
/ ао = 52 52 ~ 252’ (2 31)
i=l >1 г=1
коэффициенты квадратичной и Ь, линейной части которой опреде-
ляются соотношениями
с ch\). (ж) (х)
1 —----------5-----dx,
J dx dx
(2.32)
62
2.Основные идеи и принципы МКЭ
= j (^) + ®Фг (с) •
а
(2.33)
Дифференцируя квадратичную форму (2.31) по неизвестным и
приравнивая эги производные к нулю, получаем СЛАУ для определе-
ния весов q.j, доставляющих минимум функционалу (2.31):
7=1
или в матричной форме
Aq = b,
(2.34)
где компоненты матрицы А и вектора b определяются соотношения-
ми (2.32) и (2.33).
Функция и где q ~ вектор решения СЛАУ (2.34) с
4=1
матрицей (2.32) и вектором правой части (2.33), является приближён-
ным решением вариационной задачи для функционала (2.19). Рассмот-
ренный же метод построения этого решения, основанный на представ-
лении функций v в виде линейной комбинации выбранного набора
базисных функций ф,: и поиске минимума функционала (вида (2.19))
на конечномерном подпространстве V, натянутом на функции ф£,
называется методом Ритца.
Аналогично может быть построена процедура решения вариацион-
ного уравнения
f 4^ — 9^ (с) — f fvdx — 0 .
J dx dx J
a a
(2.35)
Будем считать, что функции и и v в вариационном уравнении
(2.35) являются элементами конечномерного функционального про-
странства, натянутого на базисные функции фу, j = 1... п, т.е.
» = W = (2-36)
./=1 7=1
где q'j — веса в разложении функции и по базисным функциям ф7-, а
q" - веса в разложении произвольных функций v по тем же базисным
функциям
Нетрудно убедиться, что с учётом разложения (2.36) вариационное
уравнение (2.35) эквивалентно системе уравнений
2.2.Вариационные постановки, используемые в методах ...
63
п
d
J=1 J d^ (t)
dx
dx
dx — 0ф,: (c) —
i - 1 ...n .
(2.37)
Действительно, уравнения (2.37) сразу получаются из уравнения (2.35)
при подстановке в него функции и в виде (2.36) и функций v = ф7 (для
г = 1... п ). Из уравнения (2.37) так же легко можно получить уравнение
(2.35), если умножить каждое г-е уравнение системы (2.37) на коэффици-
ент д‘‘, просуммировать их все и учесть представление (2.36) функций и
и v в виде их разложения по базисным функциям ф,-.
Система уравнений (2.37) может быть переписана в виде
d^i (т) di\),Лх)
dx dx dX
г = l...n,
или в матричной форме
Aq" = b,
(2.38)
(2.39)
где компоненты матрицы А и вектора b определяются соотношения-
ми (2.32) и (2.33).
Рассмотренный метод решения уравнения в слабой форме (2.35),
основанный на представлении функций и и v в виде линейной ком-
бинации базисных функций, называют методом Галёркина.
Вариант этого метода, когда функции и и v представляются в виде
линейной комбинации одних и тех же базисных функций, как это было
сделано нами в соотношениях (2.36)-(2.38), часто называют методом
Бубнова-Галёркина. В принципе же, возможны варианты метода
Галёркина, когда функции и и v являются элементами различных
функциональных пространств и соответственно представляются в виде
линейных комбинаций оазисных функций разных пространств.
Обратим внимание на то, что дискретные аналоги в виде СЛАУ
(2.34) и (2.39), полученные как методом Ритца (в результате минимиза-
ции функционала на конечномерном функциональном пространстве),
так и методом Галёркина (в варианте Бубнова-Галёркина, когда функ-
ции и и v разлагаются по одному и тому же базису), абсолютно иден-
тичны — и матрицы, и векторы правой части этих СЛАУ определяются
одними и теми же формулами (2.32) и (2.33). Этого, вообще говоря, и
следовало ожидать - ведь нами было доказано, что минимизация фупк-
64
2.Основные идеи и принципы МКЭ
ционала (2.19) полностью эквивалентна решению уравнения в слабой
форме (2.24). Поэтому тогда, когда для дифференциальной краевой за-
дачи удастся сформулировать эквивалентную вариационную задачу в
виде минимизации функционала типа (2.19), оба рассмотренных в дан-
ном разделе метода построения приближённого решения - и метод Рит-
ца. и метод Галёркина (в варианте Бубнова-Галёркина) - приводят к
одной и той же СЛАУ, из которой определяются веса разложения при-
ближенного решения по базисным функциям ф?.
Но в принципе метод Галёркина обладает заметно большими воз-
можностями построения дискретных аналогов эквивалентных краевым
вариационных задач. Действительно, метод Ритца может быть приме-
нён, как правило, лишь для решения дифференциальных уравнений с
самосопряжённым линейным оператором, так как доказать эквива-
лентность минимизации соответствующего функционала решению
исходной краевой задачи удаётся при выполнении именно этих огра-
ничений на вид оператора дифференциального уравнения (более под-
робно этот вопрос будет рассмотрен в следующих разделах). Метод же
Галёркина может быть применён для решения вариационного уравне-
ния (уравнения в слабой форме), полученного из условия ортогональ-
ности невязки дифференциального уравнения исходной краевой задачи
всем функциям из некоторого функционального пространства, и в том
случае, когда оператор исходного дифференциального уравнения явля-
ется и несамосопряжённым, и даже нелинейным.
Важной особенностью и метода Ритца, и метода Галёркина являет-
ся то, что в соответствующих вариационных постановках участвуют
производные решения и или пробных функций v меныинх порядков,
нежели в дифференциальном уравнении исходной краевой задачи, т.е.
в методе Галёркина для решения эллиптической краевой задачи при
выводе эквивалентной вариационной постановки предполагается обя-
зательное выполнение процедуры интегрирования по частям для сни-
жения порядка входящих в получающееся вариационное уравнение
производных решения. В связи с этим некоторые авторы (напри-
мер, [91) называют и сами вариационные уравнения вида (2.29) или
(2.35) уравнениями Галёркина (или уравнениями в форме Галёрки-
на), подразумевая, что в этой (галёркинской) форме требования к
гладкости решения снижены в результате применения процедуры ин-
тегрирования по частям. Иногда галёркинской формой называют не
только соответствующую форму вариационного уравнения, но и вхо-
дящую в него билинейную форму (см., например, [9], с. 61)
а (?/,, v) = J" grad и grad udQ.,
Я
которая в рассматриваемом нами одномерном случае имеет вид
Г
а (и, v) = f ~~~^dx .
4 ’ z J dx dx
(I
2.2.Вариационные постановки, используемые в методах ...
65
Сделаем ещё одно замечание об учёте краевых условий первого ро-
да при построении дискретных аналогов методами Ритца и Галёркина.
Строго говоря, функция и = фг (ж), где q — вектор решения
4=1
СЛАУ (2.34) (или (2.39)) с матрицей (2.32) и вектором правой части
(2.33), может быть очень далека отточного решения и исходной крае-
вой задачи (2.1), (2.13), (2.14), если конечноэлементное решение
п
и = qi ф2 (я) не удовлетворяет первому краевому условию1 (2.13).
Дело в том, что минимизацию функционала (2.19) нужно было выпол-
и.
нять на множестве функций v = <7уф7 (аг), удовлетворяющих пер-
7=1
вому краевому условию, т.е. минимум функционала (2.30) или соот-
ветствующей ему квадратичной формы (2.31) следует искать с учётом
ограничения на компоненты вектора q, вытекающего из краевого ус-
ловия (2.13):
52^Ф>(а) = • (2.40)
Это означает, что свободными в квадратичной форме (2.31) явля-
ются не п компонент вектора q, а лишь (п — 1) его компонента. Одна
же из компонент вектора q должна быть выражена2 через остальные
(п — 1) его компоненте помощью соотношения (2.40).
2.2.3. УЧЁТ Г ЛАВНЫХ КРАЕВЫХ УСЛОВИЙ
Будем считать, что базисные функции ф? (х) удовлетворяют со-
отношениям
ф[(а)^0, ф,(а) = 0, i = 2...п . (2.41)
Условия (2.41) позволят существенно упростить последующие рас-
суждения и при этом нисколько не влияют на их общность.
1 Однородное краевое условие первого рода может выполняться как бы
«автоматически», если все базисные функции ф/ж) удовлетворяют ему: т.е.,
например, если в задаче задано краевое условие и (а) = ufl = 0 и
ф^ (о) = 0, г = 1...71.
2 Чаще всего, как мы увидим в дальнейшем, краевое условие первого рода
просто фиксирует некоторые веса qt. Например, если базисные функции
ф7(т) таковы, что ф,(о) = 0 V? 1, то условие (2.40) фактически фиксиру-
ет вес qi (т.е. ft = и^/фДа)).
66
2.Основные идеи и принципы МКЭ
Действительно, если конечномерное пространство, на котором мы
собираемся минимизировать функционал (2.19), имеет базис ф7(ж), не
удовлетворяющий условиям (2.41), то с помощью элементарных преоб-
разований фг (ж) = фг (ж) — ф7 (ад (i = 2...n) мы получим нужный
нам базис, удовлетворяющий условиям (2.41) (при этом, естественно,
подразумевается, что рассматриваемое пространство пробных функций
содержит функции-константы гЦ.т) = С ). Функция же ф1 (ж) должна
быть такой, что (а) 0 , и именно её вес в разложении пробных
функций v (ж) по базису ф7 (ж) будет определять значение v в точке
х — а (т.е. если (а) 0, то (ж) = ф1 (ж), а если фт (а) = 0 , то
ф] (ж) = фт (ж) 4- С , где С - любая константа, отличная от нуля).
Аналогичным образом можно преобразовать базис и в том случае,
когда первое краевое условие задано на обеих границах х = а и
х = с - в этом случае для преобразования базиса можно вместо кон-
станты использовать линейную на (а, Ь) функцию.
Заметим, что большинство базисов, используемых в МКЭ, построе-
ны таким образом, что условия (2.41) выполняются естественным об-
разом.
Итак, мы должны искать минимум функционала (2.30) (или соот-
ветствующей ему квадратичной формы (2.31)) на множестве функций
7/
v = (ж), удовлетворяющих первому краевому условию
7=1
v(<i) = . С учётом (2.41) это краевое условие принимает вид
?1Ф1 (а) = и,,, (2.42)
т.е. компонента q} оказывается фиксированной и минимизация (2.31)
должна проводиться лишь по весам Поэтому квадратичная
форма (2.31) не должна дифференцироваться по весу и в СЛАУ
и
(2.34) не появится уравнение (с коэффициентами А] и
, 7=1
Oj, определяемыми соотношениями (2.32)-(2.33)), но вместо него в
СЛАУ должно быть включено уравнение (2.42).
Таким образом, учёт первого краевого условия в методе Ритца сво-
дится фактически к замене некоторых уравнений аппроксимирующей
СЛАУ (полученной в результате минимизации функционала без учёта
ограничений, определяемых краевыми условиями первого рода} уравне-
ниями вида (2.42) (обеспечивающими выполнение краевых условий пер-
вого рода для приближённого решения и ).
Аналогично и при использовании метода Галёркина СЛАУ (2.39) с
матрицей (2.32) и правой частью (2.33) может дать вектор решения qu
2.2.Вариационные постановки, используемые в методах ...
67
71.
такой, что приближённое решение У^фуф, не будет удовлетворять
первому краевому условию (2.13). Йричииа этого также заключается в
том, что при формировании аппроксимирующей СЛАУ (2.39) не было
никак учтено ограничение на пробные функции v в виде ц(а) = 0
(обратим внимание на то, что, вообще-то, исходной краевой задаче
эквивалентно вариационное уравнение (2.29) с ограничениями на
пробные функции (а) = 0, а не уравнение (2.35), по которому
строилась СЛАУ (2.38)). Если же считать, что базисные функции
ф, (х) удовлетворяют соотношениям (2.41), то условие v(a) — 0 экви-
валентно фиксации веса q{' = 0 в разложении (2.36). Это означает, что
из системы уравнений (2.37) должно быть исключено первое уравне-
ние. Действительно, чтобы получить уравнение (2.29), нужно, учиты-
вая (2.36) и (2.41), умножить соответствующие уравнения (2.37) на q-
и просуммировать их только для i = 2... п.
С другой стороны, из уравнения (2.29) при условии выполнения со-
отношений (2.41) невозможно получить уравнение (2.37) для I = 1 (так
как мы не можем взять в качестве ц, (х) функцию ipj (.г), поскольку
(а) = 0 , а тр! (а) 0 ). Таким образом, требование равенства нулю
пробной функции на границе с первым краевым условием фактиче-
ски исключает из системы (2.37) первое уравнение. Вместо него нам
нужно включить в конечноэлементную СЛАУ уравнение (см. (2.40))
Ла) = и;/, (2.43)
7=1
которое и обеспечит выполнение первого краевого условия для Функ-
ции и . Уравнение (2.43) при условии выполнения соотношений (2.41)
примет вид, абсолютно аналогичный (2.42):
д"Ф1 (а) = ид. (2.44)
Таким образом, как и следовало ожидать, учет краевых условий
первого рода абсолютно одинаков при построении дискретных анало-
гов и по методу Ритца, и по методу Галёркина. Фактически он сводит-
ся к замене в соответствующих СЛАУ так называемых фиктивных
уравнений1 уравнениями типа (2.42) и (2.44), обеспечивающими на
границе с первым краевым условием равенство приближённого реше-
ния заданным значениям ид.
Проведённые рассуждения об учёте краевых условий первого рода
справедливы и в многомерном случае. Применяемые при построении
конечноэлементных приближений базисные функции, как правило,
1 Под фиктивными мы, очевидно, понимаем уравнения, которые не могут
быть получены из соответствующей вариационной формулировки и были
записаны без учёта ограничений на пробные функции.
68
2.Основные идеи и принципы МКЭ
строятся таким образом, что для выполнения краевых условий первою
рода оказывается достаточным задать веса некоторых базисных функ-
ций равными значениям функции и{) (из правой части краевого усло-
вия первого рода г/, = uf/ ) в определённых точках границы . Неко-
IS]
торым исключением является процедура учёта краевых условий перво-
го рода для так называемых эрмитовых элементов - её особенности
будут рассмотрены ниже, в соответствующем разделе этой книги.
2.3. ПРИМЕНЕНИЕ ФИНИТНЫХ КУСОЧНО-ЛИНЕЙНЫХ
ФУНКЦИЙ ДЛЯ ПОСТРОЕНИЯ КОНЕЧНОЭЛЕМЕНТНЫХ
РЕШЕНИЙ ОДНОМЕРНЫХ КРАЕВЫХ ЗАДАЧ
Приступим к рассмотрению вопросов, связанных с практическим по-
строением приближённого решения краевой задачи методом конечных
элементов. Приближённое решение ипр будем искать в виде кусочно-
линейной функции, представленной в виде линейной комбинации так
называемых финитных кусочно-линейных базисных функций ф£ (а;).
Построим конечноэлементное решение краевой задачи (2.1), (2.13),
(2.14). Для этого разобьём расчётную область Q = [«., с] узлами
.Т],..., хн на подобласти QA. = [а,>, а;/-+1 ], k = 1... n — 1, называемые
конечны ми элементами. Обозначим через hk = xkx — xk длину эле-
мента Q/.. Поставим в соответствие каждому внутреннему узлу .г,
кусочно-линейную функцию ф, (а;), определяемую соотношениями
(2-45)
а граничным узлам и хп - функции ф1 (а;) и фп (а;), определяемые
соотношениями
Ф1 (а:) = • (xi-xVhi, хЛ<х<хъ п > (2-46) 0, х > з;2, 0, х < ,
ф„(ж)= , . (2.47)
Вид этих функций показан на рис. 2. Нетрудно убедиться, что лю-
бая непрерывная кусочно-линейная на Q = UQa функция и1' (линей-
2.3.Применение финитных кусочно-линейных функций ...
69
ная на каждом конечном элементе QA.) может быть представлена в
виде линейной комбинации определяемых соотношениями (2.45)-
(2.47) функций ф,:
= 52$’^ •
г=1
(248)
При этом веса ф- в соотношении (2.48) - это значения функции vh в
узлах х.,.
внутренним и граничным узлам конечноэлементной сетки
Таким образом, функции фг являются базисными функциями ко-
нечномерного пространства Vh кусочно-линейных на Q (линейных
на каждом элементе ) функций vh и размерность этого пространст-
ва совпадает с числом узлов в копечноэлементной сетке.
Вычислим компоненты Ач матрицы А конечноэлементной СЛАУ
(2.38) (или (2.39)), определяемые соотношениями (2.32). Обратим вни-
мание на то, что для каждого значения г = 2...п — 1 подынтегральное
выражение в (2.32) отлично от нуля только для трёх значений j, рав-
70
2.Основные идеи и принципы МКЭ
ных i — 1, г или t + 1. Действительно, функция ф2 (а;), определяемая
соотношением (2.45), отлична от нуля лишь на двух подобластях
=[я7_1,^] и Q2 =[a;j,x,+1] (в этом случае также говорят, что
носителем ф, является подобласть U £1,). Поэтому у функций
ф.2 (ж) и ф7 (ж) для j < i — 2 или j > i + 2 носители (т.е. области, где
они отличны от нуля) не пересекаются, и поэтому произведение
с?ф- <7ф.
Равно нулю на всей расчётной области Q. Это означает, что
AtJ = 0 для j < i — 2 и для j > i + 2 .
Получим выражения для компонент Д 2-1, Д2 и Д i+i. Носители
функций ф,_л (®) и ф, (х) пересекаются лишь по подобласти
П2_1 = , и поэтому с учётом (2.45)
(2.49)
Носителем функции ф2 (ж)
Пд-i U П2 = .т2] U [а;г,£,+1], и поэтому
является
подобласть
(2-50)
Носители функций ф2 (.т) и ф2+1 (7?) пересекаются по подобласти
Q, = [.7-t,.T,+1], и поэтому
^+* j dx h?h‘~ k' (2'5I)
•I -J-i '
Таким образом, использование финитных кусочно-линейных базис-
ных функций приводит к конечноэлементной СЛАУ с матрицей,
имеющей трёхдиагоналъную структуру.
Чтобы вычислить по формуле (2.33) компоненты вектора правой
части Ь, необходимо конкретизировать вид функции /(ж) из правой
части уравнения (2.1). Вместе с этим конкретизируем всю краевую
2.3.Применение финитных кусочно-линейных функций ...
71
задачу и сетку, на которой ищется приближённое решение
uh = СО.
_)=1
Будем считать, что область Q, на которой решается краевая задача,
является отрезком [0,7]. Будем также считать, что источник в краевой
задаче является распределённым (см. раздел 8.1) и его плотность f (гг)
определяется соотношениями1
/(гс) =
0,
1,
0.25,
(2.52)
Зададим параметр 0 в краевом условии (2.14) равным —1. При-
ближённое решение будем искать на сетке с узлами .г-j = 0, гс2 = 2,
гс3 — 3, гс4 = 7 (т.е расчётная область Q разбита на три конечных
элемента = [0,2], П2 — [2,3] и Q3 = [3,7]). Тогда
7 з
b2 = / f (а-‘) ф2 Ог*) dx. + 0ф2 W = fl Т ~ dx Т 0 • 0 = ,
J IZ JL
0 2
7
Ьз = J* f (х) фз (х) dx + 0ф3 (6) =
о
3 7
= f + f 0.25-^-^da; + e-0 = | + | = l,
2 3
7
b4 = J f GO ф4 (rr) dx + 0ф2 (b) =
0
7
= /o.25-^<fc + (-l)l = l-l = -|. (2.53)
3
Первое уравнение формируемой конечноэлементной СЛАУ соот-
ветствует узлу, в котором задано краевое первого рода, и поэтому в
соответствии с проведёнными в предыдущем разделе рассуждениями
1 Обратим ваше внимание на то, что мы (в общем-то, намеренно) не задали
значения функции / в точках её разрыва х = 2 и х = 3. Тем самым мы хо-
тели подчеркнуть, что решение рассматриваемой задачи не зависит от этих
значений (естественно, при условии, что в задаче не заданы сосредоточенные
в этих точках источники - см. раздел 8).
72
2.Основные идеи и принципы МКЭ
об учёте краевых условий первого рода оно должно быть сгенерирова-
но в виде (2.44), т.е.
А1 =1, : = 0(7 1), = ид =1. (2.54)
В результате соотношения (2.49)-(2.54) дают нам вид матрицы и
вектора правой части конечноэлементной СЛАУ:
1 0 0 0 1
3 -1 0 1
А = 2 п 2 1 5. , ь = 2 (2.55)
и — 1 4 4 1
0 1 0 _1 4 1 4J 2)
Решая СЛАУ Aq = b, получаем вектор весов q в разложении при-
ближённого решения и1' по базисным функциям ф,- (х):
q = (1,3,3.5,1. б)т. (2.56)
Заметим, что веса q, фактически определяют значения приближён-
ного решения и' в узлах хг (поскольку базисные функции ф, (х) по-
строены так, что ф,: (х,) = 1 и ф7 (х,) = 0 для j i).
На рис. 3 представлены графики точного решения рассмотренной
краевой задачи, определяемого соотношениями
и(х) =
х Т1, о < X < 2
-0.5 (х-3)2 +3.5, 2 < X <3,
-1(х--3)2+З.Г>, X <7,
(2-57)
4
и конечноэлементного решения и1' (х) = (/;ф у (х), полученного на
.7=1
сетке из трех конечных элементов с узлами Xj — 0, х% = 2, х3 = 3,
х4 = 7 и определяемого вектором весов (2.56) и базисными функция-
ми (2.45)—(2.47).
Конечноэлементное решение и!' (х) является кусочно-линейной
функцией, причём в узлах сетки функция и1' (х) оказалась точно сов-
падающей с искомой функцией w(x). Тем не менее нельзя говорить,
что мы получили в качестве конечноэлементного решения точное ре-
шение задачи. Действительно, и1 (х) определена во всей расчётной
области Q = [0,7], а не только в узлах сетки, и, например, в точке
2.4.Технологии сборки глобальных матриц и векторов в МКЭ
73
а; = 2.5 функция иВ * * 11 (т) принимает значение 3.25 , а точное решение
и(х) равно 3.375. Кроме того, и краевому условию (2 14) и'1 (х)
удовлетворяет со значительной погрешностью:
duh
dx
= -0.5,
в то
время как ЭД = —1. Однако полученная функция и1' (х) всё-таки
иЗ?|3-=7
довольно хорошо аппроксимирует искомое решсйие. Более того, в
следующих разделах будет показано, что конечноэлементное решение
uh (я) является в так называемой энергетической норме ближайшей
функцией к точному решению иСх) среди всех функций, представи-
мых в виде линейной комбинации базисных функций т.е.
функция и11 (х) является ближайшей к и (з;) среди всех кусочно-
линейных функций, определённых на выбранной нами конечноэлемент-
ной сетке.
Рис. 3. Графики точного решения и и конечноэлементного решения uh
2.4. ТЕХНОЛОГИИ СБОРКИ ГЛОБАЛЬНЫХ МАТРИЦ
И ВЕКТОРОВ В МКЭ
В предыдущем разделе компоненты матрицы А конечноэле-
ментной СЛАУ вычислялись по формулам (2.49)-(2.51), полученным
из соотношений (2.38) при некотором фиксированном значении индек-
са i. Каждому же значению индекса г соответствуют базисная функ-
ция (х) и узел .т7, в котором функция ф7 (ж) равна единице. Факти-
чески г-е уравнение СЛАУ (2.38) получается в результате подстановки
в вариационное уравнение (2.29) вместо пробной функции ц, базис-
ной функции 'фДя), т.е. можно сказать, что г-е уравнение конечно-
74
2.Основные идеи и принципы МКЭ
элементной СЛАУ является результатом обработки i -го узпа конеч-
ноэлементнои сетки. Поэтому рассмотренная в предыдущем разделе
технология генерации конечноэлементной СЛАУ часто называется
поузловой — в этом случае уравнения СЛАУ генерируются последова-
тельно и целиком для каждого узла сетки по формулам вида (2 49)—
(2.51).
Поузловая технология сборки глобальной матрицы конечноэлемент-
ной СЛАУ представляется довольно простой и наглядной лишь при
решении одномерных задач. В случае же решения двух- и трёхмерных
задач такая технология становится гораздо более вычислительно трудо-
ёмкой и алгоритмически труднореализуемой, чем так называемая по-
элементная сборка, основанная на внесении в генерируемую конечно-
элементную СЛАУ вкладов от отдельных конечных элементов.
Чтобы проиллюстрировать идею поэлементной сборки конечноэле-
ментной СЛАУ, представим компоненты СЛАУ (2.38) следующим
образом. В соотношениях (2.32), определяющих компоненты AtJ гло-
бальной матрицы А конечноэлсментной СЛАУ (2.38), интеграл по
расчётной области Q = [а, с] представим в виде суммы интегралов по
конечным элементам О/<: = [хд.,х^.+1]:
Г (х) ^Ф> (х) _ 'k'r difa (х) (х)
~ J dx dx J dx dx r
(2.58)
Полученное соотношение показывает, что элементы Д, глобальной
матрицы А конечноэлементной СЛАУ могут быть представлены в
виде суммы вкладов от отдельных конечных элементов Qk. При этом
конечный элемент = [хл.,х/.+1] бает вклады в элементы Akl.,
А-,А:+1» Ач-1,А: и А-+1Л+1 матрицы А конечноэлементной СЛАУ. Для
описания же процедуры формирования вкладов в матрицу конечно-
элементной СЛАУ от конечного элемента QA. удобно ввести на нём так
называемую локальную нумерацию глобальных базисных функций
Рис. 4. Локальные базисные функции
Фк (Я) И фл+1 (х) .
Введём такую локальную нуме-
рацию следующим образом. Функ-
ции фд. (х) дадим локальный но-
мер 1, а функции ф/;+1 (х) - локаль-
ный номер 2 Соответственно на
элементе обозначим через ло-
кальную функцию 'фх (х) глобаль-
ную функцию фд. (х), а через ло-
кальную функцию ф2 (х) - глобаль-
ную функцию фл+1 (х). Вид этих
2.4.Технологии сборки глобальных матриц и векторов в МКЭ
75
локальных функций, определённых только на конечном элементе
= [zjt,zjt+1], показан на рис. 4, т.е. на элементе Пк они определя-
ются соотношениями:
О Хк+1 ~ Х 7 Х — Хк 7
= , ф2 (z) = , , hk=xk+l-xk. (2.59)
щ- пк
Тогда вклады от О.к в элементы глобальной матрицы А конечно-
элементной СЛАУ можно записать в виде:
ДЛЯ JX’+1 7 1 7 -Hi + l , " , 'J д . д _ f . Г - 1 п 60-> Аа: • Al - J dx - J dx dx dx. - , (2.60) •4
ДЛЯ 2 Г d^k Gh|4-+i , chpi с?ф2 i . Aji+i:A2= 1 7- - тг"—dz = I =-y-, (2.61) AA+i iz j dx dx J dx dx hk
ДЛЯ л л V* d'^’A+i di\)k ZfL d^ d'fh . 1 A+ia. :Ai= / —Lr±J--r£-dz= 1 =-у1--, (2.62) J dx dx J dx dx hk 4 :l:l- Л:к
ДЛЯ Д .2 -ЧГ ^k+i ^t+1 , J f‘ rf'b _ 1 P fiTI 4+1Л-+1 • 42 - J dx dx dx-J dx dx dx - hk ,(2.63)
где Ast — компоненты локальной матрицы А размера 2x2 (т.е.
s = 1,2 и t = 1,2 — индексы, являющиеся локальными номерами гло-
бальных базисных функций фд. (z) и (ж) на элементе О.к).
Таким образом, локальная матрица А конечного элемента О/,. для
рассматриваемой нами задачи имеет следующий вид:
' _1_____1_'
hk hk
_1_
. hk hk,
или в более простой форме записи:
- 1 ( 1 -11
hk -1 1 •
(2-64)
(2-65)
A = -г-
Очевидно, что занесение компонент Дч/ локальной матрицы А в
глобальную должно проводиться по соответствию локальных номе-
ров базисных функций г|д и ф2 глобальным номерам базисных функ-
76
2.Основные идеи и принципы МКЭ
ций фд и фд+1, т.е. компонента локальной матрицы А должна
быть занесена (добавлена) в компоненту Дд. глобальной матрицы А,
компонента Д2 - в компоненту Дд.+1, компонента А21 - в компонен-
ту Д+1,д- и компонента А22 - в компоненту Д+1А:+1. Действительно,
согласно соотношениям (2.60)-(2.63) компоненты Ast локальной мат-
рицы А вычислялись с использованием локальных функций фЛ. и ф,,
которые фактически на $Д являются глобальными функциями ф, и
ф j, причём локальному индексу s = 1 соответствует глобальный ин-
декс i — к , a s = 2 соответствует i = к + 1; аналогично значению
индекса t = 1 соответствует j = к, a t = 2 соответствует j = к + 1.
Исходя из проведённых рассуждений, мы можем представить про-
цедуру генерации глобальной матрицы конечноэлементной СЛАУ
следующим образом. Для каждого конечного элемента Од. на основе
соотношений (2.60)-(2.63) вычисляется локальная матрица вида (2.65).
В цикле проходом по всем конечным элементам компоненты As]t ло-
кальных матриц (2.65) добавляются как вклады в компоненты Д. гло-
бальной матрицы по соответствию локальных номеров базисных
функций рассматриваемого конечного элемента Од. глобальным номе-
рам этих функций.
Аналогично может быть сгенерирован и глобальный вектор b ко-
нечноэлементной СЛАУ, компоненты 6, которого определяются соот-
ношениями (2.33). В этих соотношениях интеграл по расчётной облас-
ти Q = [а, с] также может быть представлен в виде суммы интегралов
по конечным элементам Од. = [жд,Жд+1]:
'' я—1^+1
I f(x)^j;(x)dx = Ф/ (X)dx ,
a жд
и компоненты Ъь глобального вектора b конечноэлементной СЛАУ
могут собираться из вкладов от отдельных конечных элементов Од.
Аналогично локальной матрице А (определяющей вклады в компо-
ненты глобальной матрицы А от одного конечного элемента) удобно
ввести локальный вектор Ь, определяющий вклады в компоненты гло-
бального вектора b от одного конечного элемента . Очевидно, что
от конечного элемента Од = [жд^’д-ц] ненулевыми в рассматриваемой
нами ситуации будут только вклады в две компоненты глобального
вектора b:
2.4.Технологии сборки глобальных матриц и векторов в МКЭ
77
4+1
j f (ж) фд (x)dx —> bk (т.е. это вклад в компоненту Ьк )
4:
И
4 + 1
У f (х) фЛ+1 Сх) dx —+ bk+i (т.е. это вклад в компоненту Ьк+1)
4
Если учесть, что на &к глобальные базисные функции фА. (а?) и
фд.+1 (х) совпадают соответственно с локальными базисными функ-
циями фх и ф2 > определяемыми соотношениями (2.59), то локальный
вектор конечного элемента £1к будет иметь вид
'4 + 1
J* /(а?)'ф1(гг)
4
4+1
J f (х) ф2 (X)
< J:k
(2.66)
В принципе, соотношение (2.66) можно привести к такому виду,
чтобы компоненты локального вектора b вычислялись через значения
функции f (х) в некоторых точках элемента О.к. Этого можно добить-
ся, если, например, на элементе £1к заменить (в смысле аппроксимиро-
вать) функцию f(x) её линейным интерполянтом
f (ж) ~ fk (хк) фх (т) + fk (хк+1) ф2 (.т),
(2-67)
где f1' 1 (.г\.) - значение f (х) в точке хк,а fk {хк+1) - значение f (х) в
точке Жд.+1 на-элементе Пк (заметим, что слова на элементе здесь
принципиальны, так как функция f (ж) может быть разрывной, и если
хк - точка разрыва, то fk (хк) - значение f (т) в точке хк в пределе
справа, т.е. значение на элементе Q/., что и обозначает верхний индекс
k У fk М и fk (^.+1)).
С учётом (2.67) локальный вектор (2.66) принимает вид:
78
2.Основные идеи и принципы МКЭ
ь =
•'А
(2.68)
1ч.
3
так как
6
а-
*ан ]
И J
гк
Занесение локальных векторов b в глобальный вектор b конечно-
элементной СЛАУ должно выполняться аналогично сборке глобальной
матрицы — по соответствию локальных номеров базисных функций фч
глобальным номерам базисных функций ф?-, т.е. компонента Ь[ ло-
кального вектора b должна быть занесена в компоненту bk глобально-
го вектора b, а компонента Ь2 - в компоненту Ьк+Х.
Таким образом, процедура сборки глобального вектора b конечно-
элементной СЛАУ полностью аналогична процедуре сборки глобаль-
ной матрицы А: для каждого конечного элемента на основе соотно-
шений (2 66) (или (2.68)) вычисляется локальный вектор b, и в цикле
проходом по всем конечным элементам компоненты bs локальных
векторов b добавляются как вклады в компоненты Ьг глобального
вектора по соответствию локальных номеров базисных функций рас-
сматриваемого конечного элемента Пд. глобальным номерам этих
функций. Заметим, что обычно сборка глобальной матрицы А и гло-
бального вектора b выполняется одновременно, в одном проходе по
конечным элементам.
Завершается генерация конечноэлементной СЛАУ учётом краевых
условии. При этом сначала осуществляется учёт естественных крае-
вых условий, т.е. краевых условий второго и третьего рода. Для одно-
мерной задачи краевые условия второго рода учитываются добавлени-
ем в соответствующую компоненту вектора b вклада от второго крае-
вого условия, равного значению 6 из этого краевого условия (см.
(2.33)). В нашем случае краевое условие (2.14) учитывается добавлени-
ем 6 к Ь.п , поскольку только базисная функция ф„ (а;) отлична от нуля
в точке х = с (если бы краевое условие второго рода было задано в
точке х = а, то 6 нужно было бы добавить к bY, поскольку в точке
2.4.Технологии сборки глобальных матриц и векторов в МКЭ 79
х = а лишь ipj отлична от нуля и равна единице, а остальные базис-
ные функции ф2(а) =...= ф„(а) = 0). Заметим, что естественными
называют те краевые условия, которые не накладываются на искомое
решение и или пробные функции v в виде ограничений, а выполня-
ются в результате минимизации функционала или решения вариаци-
онного уравнения (т.е. можно сказать, что они выполняются естествен-
ным образом, без ограничений на поведение функции и или v в соот-
ветствующих точках границы). В принципе, вклады от естественных
краевых условий можно заносить в конечноэлементную СЛАУ как
перед циклом, в котором выполняется проход по конечным элементам
Qjl, так и во время выполнения этого цикла, однако обычно это дела-
ется после внесения в глобальную матрицу и вектор вкладов от всех
конечных элементов.
Учёт краевого условия первого рода всегда завершает процедуру
генерации конечноэлементной СЛАУ При этом следует обратить вни-
мание на то, что в процессе обработки конечных элементов обычно
формируются так называемые фиктивные уравнения. Например, для
рассматриваемой нами задачи после обработки конечного элемента Qi
в глобальную матрицу могут быть занесены элементы первой строки
локальной матрицы этого конечного элемента (это делается для того,
чтобы не нарушать однородности процесса сборки), и тем самым будет
сформировано уравнение, не предусмотренное вариационной поста-
новкой (об этом говорилось более подробно на с 65 -68). Вместо него в
аппроксимирующую краевую задачу СЛАУ должно быть включено
уравнение типа (2.44):
Ф1=и!г (2.69)
Поэтому учёт краевого условия первого рода осуществляется сле-
дующим образом. В строке, соответствующей узлу с первым краевым
условием, обнуляются все внедиагональные элементы, на главную
диагональ заносится единица, а в правую часть — значение и,, (см.
(2.69)). Тем самым из конечноэлементной СЛАУ исключается фиктив-
ное уравнение и формируется уравнение, обеспечивающее выполнение
главного краевого условия.
Продемонстрируем технологию поэлементной сборки конечноэле-
ментной СЛАУ на примере решения краевой задачи (2.1), (2.13), (2.14).
Определим параметры этой краевой задачи и конечноэлементную сет-
ку так же, как это было сделано на с. 71: функцию /(ж) зададим соот-
ношением (2.52), параметрам краевых условий дадим значения 0 = — 1
и uq = 1, а расчётную область разобьём узлами хх = 0, х2 = 2,
xs = 3 , х4 = 7 на три конечных элемента Q] = 10,2|, Q2 — [2,3] и
П3 =[3,7].
Процесс сборки глобальных матрицы и вектора выглядит следую-
щим образом Сначала обнуляются все элементы глобальных матрицы
А и вектора b. Затем запускается цикл формирования локальных мат-
80
2.Основные идеи и принципы МКЭ
риц и векторов конечных элементов с занесением их в глобальные
матрицу и вектор.
Локальные матрица и вектор конечного элемента = [0,2] имеют
вид (см. соотношения (2.65) и (2.66) или (2.68))
и после занесения их в глобальные матрицу и вектор последние при-
мут вид
' 0.5 -0.5 0 О' го
-0.5 0.5 0 0 0
А = > ь =
0 0 0 0 0
0 0 0 0 к > 0
Локальные матрица и вектор конечного элемента Q2 = [2,3] имеют
вид
-1
-1
0.5
0.5
и после занесения их в глобальные матрицу и вектор получим
' 0.5 -0.5 0 О' О'
-0.5 1.5 -1 0 0.5
А = , Ь =
0 -110 0.5
0 0 0 0 0
7
Локальные матрица и вектор конечного элемента Q3 = [3,7] имеют
вид
1 1 -1
4 -1 1
0.5
0.5
и после занесения их в глобальные матрицу и вектор получим
0.5 -0.5 0 0
-0.5 1.5 -1 0
А = 0 -1 1.25 -0.25
0 0 -0.25 0.25
о
0.5
1
0.5
I i
( 1
А = 4
Для учёта краевого условия второго рода, заданного на правой гра-
нице Q, добавим 6 = — 1 к компоненте 64 . Для учёта же первого крае-
вого условия, заданного на левой границе, вместо первой строки (оп-
2.5.0 методе коллокации
81
ределяющей фиктивное уравнение, которое не могло быть получено из
вариационной постановки) формируется строка, обеспечивающая вы-
полнение уравнения (2.69).
В результате глобальные матрица и вектор конечноэлементной
СЛАУ принимают окончательный вид:
1 0 0 0 1
-0.5 1.5 -1 0 0.5
А = 0 -1 1.25 -0.25 , ь = 1 (2.70)
0 к 0 -0.25 0.25 > -0.5
Итак, поэлементная сборка конечноэлементной СЛАУ привела к
тем же матрице А и вектору Ь, что и поузловая (сравните (2.70) с
(2.55)). Однако поэлементная сборка гораздо удобнее для программи-
рования процесса генерации СЛАУ, и это её преимущество становится
особенно очевидным при решении многомерных краевых задач.
2.5. О МЕТОДЕ КОЛЛОКАЦИИ
При построении конечноэлементных аппроксимаций кроме рас-
смотренных выше вариационных методов (метода наименьших квад-
ратов, метода Ритца и метода Галёркина1) иногда используют и другие
подходы. В качестве одного из таких подходов мы рассмотрим и про-
анализируем так называемый метод коллокации (который называют
также и методом совпадений). Суть его заключается в следующем.
Пусть нам требуется решить краевую задачу (2.1), (2.13), (2.14).
Приближённое решение этой задачи и1, будем искать в виде линейной
комбинации базисных функций ф7- (а):
и
и1' = ф0 (ГС) + q.^j (ж),
>=1
(2.71)
причём функция фо (ж) должна удовлетворять краевым условиям (2.13) и
(2.14) решаемой краевой задачи, а функции (я;),...,фп (ж) - соответ-
ствующим (2.13) и (2.14) однородным краевым условиям (т.е. ф7- (а) = О
f/'ф. (.г"
И dx
и:
-ф0 (X) , ф[ (X)
= 0 для j = 1... п ). Отметим, что функции
=с
,..., ф.п (т) строятся относительно независимо от решаемо-
го дифференциального уравнения (2.1) (они являются как бы базисными
функциями подпространства, в котором мы будем искать приближённое
решение), а само приближённое решение определяется значениями весов
<7/, j = п. Такой подход к построению приближённого решения
1 Метод Галёркина также относят и к классу проекционных методов - но
об этом чуть позже.
82
2.Основные идеи и принципы МКЭ
применяется, как мы уже видели, не только в методе коллокации. Отли-
чительной же особенностью метода коллокации является способ вычис-
ления коэффициентов qf в представлении (2.71) приближённого решения
uh, который основан на следующих соображениях.
В расчётной области Q выбирается и узлов х, (называемых узла-
ми коллокации). Для этих узлов формируются п уравнений путём
подстановки приближённого решения и1, представленного в виде
(2.71). в исходное дифференциальное уравнение:
d2
dx2
п
ф() (ГЕ) + 52 77Ф7 <%)
.7=1
= fM,
(2.72)
i = 1... п .
Систему уравнений (2.72) можно записать в матричном виде
Aq = b, (2.73)
где матрица А и вектор b определяются соотношениями
. <7.2ф.(х?)
А,=-------i = j = (2.74)
dx
i = l...n. (2.75)
dx
Решив СЛАУ (2.73), мы с помощью полученных значений q опре-
делим приближённое решение (2.71).
Из рассмотренной выше схемы метода коллокации видно, что этот
метод базируется на двух основных положениях: представлении при-
ближённого решения в виде линейной комбинации (2.71) выбранного
набора базисных функции (что характерно и для рассмотренных нами
методов наименьших квадратов, Ритца и Галёркина) и формировании
СЛАУ (2.73)-(2.75) для определения коэффициентов разложения q,
приближённого решения и' по базису {ф,} из условия точного вы-
полнения исходного дифференциального уравнения в фиксированных
точках х,, называемых узлами коллокации (и это является главной
отличительной особенностью метода коллокации).
Несмотря на кажущуюся простоту и наглядность, метод коллока-
ции обладает рядом серьёзных недостатков, делающих затруднитель-
ным его применение при решении сложных задач. Одним из наиболее
существенных является требование повышенной (по сравнению, на-
пример, с методами Ритца и Галёркина) гладкости базисных функций -
для решения дифференциального уравнения с производными второго
порядка нужно использовать дважды дифференцируемые базисные
функции. Это требование становится особенно обременительным при
построении конечноэлементных аппроксимаций на основе метода кол-
локации
2.5 ,0 методе коллокации
83
Очевидно, что если носители базисных функций фу (я) совпадают
со всей расчётной областью Q, то матрица А, определяемая соотно-
шением (2.74), будет плотной (полностью заполненной ненулевыми
компонентами) и вычислительные затраты на получение приближён-
ного решения и1' будут расти катастрофически быстро с увеличением
числа п базисных функций и узлов коллокации (причём это справед-
ливо не только для полиномиальных, но и для тригонометрических
базисов).
Чтобы избежать этого, необходимо использовать характерные для
МКЭ базисные функции с финитными (локальными) носителями, т.е.
функции, отличные от нуля на небольших подобластях расчётной об-
ласти (в этом случае матрица СЛАУ будет слабо заполнена ненулевы-
ми элементами). Но если при решении одномерной задачи построить
дважды дифференцируемые базисные функции не столь уж сложно, то
при решении многомерных задач (т.е. краевых задач в дву- и трёхмер-
ных областях) необходимость использования дважды дифференцируе-
мых базисных функций может существенно усложнить процедуру чис-
ленного решения задачи (особенно в тех случаях, когда расчётная об-
ласть имеет сложную геометрию).
Ещё более серьёзные проблемы при выборе базисных функций в
методе коллокации возникают тогда, когда необходимо решать задачи
с разрывными коэффициентами диффузии (т.е. если, например, в урав-
нении (1.1) коэффициент X принимает различные значения в разных
подобластях расчётной области) — в этом случае базисные функции
должны быть такими, чтобы можно было корректно вычислять значе-
ния div (X grad ф*). В методах же Ритца и Галёркина как в случае
сложной геометрии расчётной области, так и в случае разрывных ко-
эффициентов задачи столь серьёзных проблем с построением базисных
функций с финитными носителями не возникает (во многом из-за того,
что соответствующие им вариационные постановки содержат произ-
водные меньшего порядка, чем исходные дифференциальные уравне-
ния). По точности же они как минимум нисколько не уступают методу
коллокации. Поэтому в дальнейшем мы всё внимание сосредоточим на
построении конечноэлементных аппроксимаций, базирующихся имен-
но на этих методах
84
3.Вариационные формулировки ...
3. ВАРИАЦИОННЫЕ ФОРМУЛИРОВКИ
И КОНЕЧНОМЕРНЫЕ ПОДПРОСТРАНСТВА
ДЛЯ УЗЛОВОГО МКЭ
В этой и нескольких следующих разделах мы будем рассматри-
вать методы построения конечноэлементпых аппроксимаций эллипти-
ческой краевой задачи вида (I. I)-(I I) Эту задачу можно считать фун-
даментальной для большинства задач, в которых искомой является
скалярная функция, поскольку на разработанных для её решения мето-
дах построения конечноэлеменгных аппроксимаций базируются вы-
числительных процедуры решения не только соответствующих ста-
ционарных задач, но и начально-краевых задач для уравнений парабо-
лического и гиперболического типов.
В данном разделе кроме некоторых теоретических аспектов по-
строения вариационных формулировок будут также рассмотрены во-
просы приближения искомых решении функциями из конечномерных
подпространств и оценки точности МКЭ-аппроксимаций.
3.1. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ МКЭ. ВАРИАЦИОННАЯ ПОСТАНОВКА
В ФОРМЕ МИНИМИЗАЦИИ ФУНКЦИОНАЛА
Как уже было показано в разделе 2, МКЭ базируется на так на-
зываемых вариационных постановках, в которых решение краевых
задач заменяется либо минимизацией некоторого функционала, либо
решением некоторого вариационного уравнения. При этом функцио-
нал или вариационное уравнение определяются на множестве функ-
ций, которые являются гильбертовым пространством, содержащим в
качестве одного из своих элементов и решение и интересующей нас
краевой задачи. Прежде чем выяснить, каким пространствам должны
принадлежать функции f и и, дадим несколько определений.
Будем называть пространством 1Г" множество функций v, кото-
рые вместе со всеми своими производными до т-го порядка включи-
тельно суммируемы с квадратом на Q (см. также сноску на с. 60). Оче-
видно, что Н{} ЭЛ1 D Н2 D ...
Под записью grad v • grad w мы будем понимать скалярное произ-
ведение вектора gradv на вектор grad ш, а под записью (gradи)2
будем понимать grad и grad v.
3.1.Теоретические аспекты МКЭ. ...
85
Определим, какому пространству должно принадлежать решение
краевой задачи (1.1)-(1.4), если правая часть f уравнения (1.1) являс г-
ся интегрируемой с квадратом функцией, т.е. f Е Н1}.
Если X - достаточно гладкая функция, то решение и будет при-
надлежать пространству Н , так как вторые производные и должны
быть суммируемы с квадратом (это сразу следует из уравнения (1.1)).
Однако если считать пространством решений все пространство Н2, то
некоторой f Е II может соответствовать не единственная функция
и , удовлетворяющая уравнению (1.1).
Действительно, если = 0 и для некоторой f Е Н{} функция и
удовлетворяет уравнению (1.1), то этому уравнению удовлетворяет и
функция «| = и + с, где с - некоторая константа, отличная от нуля,
т.е U] и и единственность нарушена.
Итак, чтобы поставить в соответствие f единственное и, недоста-
точно, чтобы и удовлетворяло только уравнению (1.1). Необходимо
также, чтобы и удовлетворяло и краевым условиям (1.2)—(1.4), задан-
ным на границе S области Q. Таким образом, решение и нужно ис-
кать не во всём пространстве Н2, а в его сужении — пространстве
функций, имеющих суммируемые с квадратом вторые производные и
удовлетворяющих краевым условиям на границе о области Q, кото-
рое мы будем обозначать Ilj . В этом случае дифференциальный опе-
ратор уравнения (1.1) устанавливает взаимно однозначное отображе-
ние из Н2 в //”, т.е. для всякой функции f Е Н{] дифференциальное
уравнение (1.1) имеет единственное решение и Е Hg . Таким образом,
краевую задачу можно представить в виде
Lu = f, <3.1)
где оператор L есть взаимно однозначное отображение Н2 в Н1}, и
вид оператора L можно получить из сравнения уравнений (1.1) и (3.1):
Л = [-div (X grad*) 4-^*]. (3.2)
Очевидно, что оператор L , в общем-то, не связан с краевыми усло-
виями - их выполнение обеспечивается выбором пространства II g
вместо Н2.
Однако заметим, что рассмотренные нами требования к гладкости
решения и соответствуют именно дифференцисшьно-кръеъоп задаче В
принципе же для этой задачи могут быть построены эквивалентные
постановки с более низкими требованиями к гладкости элементов
функционального пространства, где должно искаться решение. Поста-
новки именно такого типа используются в МКЭ.
86
3.Вариационные формулировки ...
Мы рассмотрим эквивалентные вариационные формулировки двух
видов: в виде задачи минимизации некоторого функционала (исполь-
зуемой в методе Ритца) и в виде вариационного уравнения (исполь-
зуемого в методе Галёркина).
Сначала мы рассмотрим эквивалентную вариационную формули-
ровку рассматриваемой краевой задачи в виде задачи минимизации
функционала. Она формулируется в виде следующего утверждения.
Решение краевой задачи для уравнения (1.1) с краевыми условиями
первого, второго и третьего рода (1.2) (I 4), заданными соответст-
венно на границах , S? и области Q, при условии неотрица-
тельности коэффициентов X, и 0 эквивалентно минимизации
функционала
I (v) = f (х (grad u)2 + yti I j $v2dS —
Q ,S';j
- 2J'fvdQ - 2 ГОш/S - 2 f' (Цуш/S
Г2 5'2
(3.3)
на множестве допустимых функции i>, удовлетворяющих краевым
условиям первого рода v |5j = иД.
Прежде чем приступить к доказательству этого утверждения, опре-
делим, на каком классе функций и необходимо минимизировать функ-
ционал I(и) (т.е. какие функции являкнея допустимыми для мини-
мизации / (О ).
Как уже было сказано выше, для достаточно гладкого X решение
краевой задачи и лежит в Я;.. Значит, класс функций, на котором
минимизируется I (v), должен содержат! пространство Н . Заметим,
однако, что выражение для 1 (?;) не содержит вторых производных.
Это значит, что I (v) можно определи н, и па функциях и, у которых
только первые производные (а нс вторые) суммируемы с квадратом.
Следовательно, класс функций, на которых задача минимизации имеет
смысл, шире, чем прсстрансню //’, и для минимизации функционала
допустимыми являются элементы пространства Я1 .
Однако пространством функций, допустимых для минимизации
функционала I (г), будет нс все пространство Я1, а лишь его под-
множество НД - множество всех функций v, имеющих суммируемые
с квадратом первые производные (па что указывает верхний индекс) и
удовлетворяющих только первым краевым условиям на границе Sj (на
3 1.Теоретические аспекты МКЭ. ...
87
что указывает нижний индекс д). Отметим, что пространство1 * * * * * //,’
является полным в метрике, определяемой так называемым энергети-
ческим скалярным произведением:
(у, = у X grad v • grad wdQ + J*yuwdft + J fivwdS, (3.4)
о Q 5-3
в то время как предельные элементы последовательностей из Я| при
использовании метрики на основе скалярного произведения (3.4) могут
не принадлежать Н$, и поэтому пространство Hg в этой метрике яв-
ляется неполным. Кроме того, после замены Hz на Ну у нас появи-
лось ещё одно большое (и для МКЭ очень принципиальное) преиму-
щество: минимум функционала 7(д) разрешается искать на функци-
ях v, у которых только первые производные суммируемы с квадратом.
Обратим внимание, что Н\ является пространством функций,
удовлетворяющих только первому краевому условию (т.е произволь-
ная функция v Е Н* может не удовлетворять краевым условиям вто-
рого и третьего рода). Однако чуть ниже мы убедимся, что функция и ,
минимизирующая /(д) на Ну , будет удовлетворять как вторым, так и
третьим краевым условиям на границах S2 и соответственно.
Для доказательства эквивалентности минимизации функционала
(3.3) краевой задаче (1.1)-(1.4) нам понадобится ещё один класс функ-
ций - пространство Hq . Будем называть пространством H{\ множест-
во функций v Е Н[, которые на границе удовлетворяют нулевым
(на что указывает нижний индекс ноль у Я() ) первым краевым услови-
ям (а не первым краевым условиям исходной задачи, которым допжны
удовлетворять функции v Е Н\ )
Приступим теперь непосредственно к доказательству эквивалент-
ности минимизации функционала (3.3) краевой задаче (!.!)-(1.4).
Пусть функционал 1(д) принимает минимальное значение на
функции и Е Н]. Покажем, что в этом случае и является решением
рассматриваемой краевой задачи.
1 Отметим, что термин «пространство» мы будем использовать нс только
для обозначения множества функций, образующих линейное (в том числе и
гильбертово) пространство, но и для обозначения его подмножества даже в
тех случаях, когда эго подмножество само по себе не является линейным про-
странством, - это касается как только что рассмотренных бесконечномерных
пространств П$ и //,*, так и конечномерного пространства I7,,', когорос бу-
дет введено чуть ниже
88
3.Вариационные формулировки ...
Выберем произвольное число е и произвольную функцию v() G .
Очевидно, что функция v = и + ед() - элемент множества Н},: v G Н1,
гак как и G С 771 и v{} G С 771, и v удовлетворяет первым
краевым условиям исходной краевой задачи (так как
v Is-, ~ 11 Lsj = и Isj , поскольку и(||5 == 0 по определению
класса 77(* ). А так как и минимизирует 7 (v) на Г1*, то I (и) < I (w),
или
I(li) < l(u -I Е1»о).
(3-5)
Вычислим значение 7 (и + ел()), воспользовавшись определением
(3.3) функционала 7(0:
7(«, + еЦ)) = j Xgrad(?z + grad (?/+ Ea())tZQ+
+f + ЕЦ))2 <7Q + J (3(u 4 ew0)2 dS -2f f(u 4- Ep(l)dQ -
n S3 Q
— 2 J ft(u + EV[})dS — 2 J (Зар (?/ 4- EW()) dS —
S2 ‘4»
/ X grad 7i • grad udQ 4- I ^i?(7Q 4- Г flu2dS —
Ц ’$2 S'3
-2 J /ш1^-2^ QudS
s2
2e J X grad u • grad 4 J yuvydQ 4-
J $uv(}dS —
П S3
Выражение в первой квадратной скобке даёт 7 (и). Выражение в
третьей квадратной скобке, которое умножается на е2, нс может быть
3.1.Теоретические аспекты МКЭ. ...
89
отрицательным: под интегралами стоят произведения неотрицатель-
ных функций X, ч и |3 на квадраты функции г>0 и её производных.
Поэтому обозначим эту скобку с2. Скобку, которая умножается на 2е ,
обозначим cl, т.е.
(3-7)
Тогда
I(и + ед0) — 7(и) + 2еб/ + е2с2 . (3.8)
Подставляя это значение в (3.5), получаем
I (и) < I (w) 4- 2е</ + е2с2
или
2ес? + е2с2 > 0 .
(3-9)
Покажем, что d = 0 . Предположим противное: d 0 . В силу про-
извольности выбора е мы можем взять е = — ~, тогда
ст
‘ted + ^c2 = -^±^с2 =-^-<0 (3.10)
cz с4 с
при d 5* 0 . Ио (3.9) противоречит (3.10), следовательно, d = 0 .
Мы доказали, что d = 0 , если с 0 . Если же с — 0 , то равенство
нулю d следует сразу из (3.9), если в нём взять е = — d (хотя, вообще
говоря, с2 0 для любой функции г'о 0, если г/0 € II).
Таким образом, d = 0 , т.е. (см. (3.7))
= 0
(З.Н)
V^o Е Hq.
Воспользуемся формулой Грина, которая является обобщением
формулы интегрирования по частям для многомерного случая, в виде
90
3.Вариационные формулировки ...
J X grad и. grad r/odQ = — J*div (X grad u) r()dQ + J"X VydS . (3.12)
12 12 S
Подставим это соотношение в (3,11) и объединим интегралы по по-
верхности й'з:
12 S 12
+ — wp) V()dS — J 0(\}dS — J fvadQ, = 0 .
S3 Sj n
Учитывая, что S = U S2 U S3, получаем
f (— div (X grad u) + yu — f) und\H f X vl}dS +
J J (JTL
n s}
+/(xB“e)4,rfS, + J(xft7 1 =
S-2 S3
Поскольку Vq 6 H\ (т.е. v0 на Л’| равна нулю), поверхностный ин-
теграл от по $1 обращается в ноль, и тогда
J* (- div (X grad и) + уи. - f) vl}di i I р X — oj v(}dS +
12 s2 П
+J(xf^ + P(«->'11))’^’ = °- (3.13)
S:l
Последнее равенство справедливо для любых y() 6 Hq . Но класс
И] содержит в себе пространство бесконечно дифференцируемых в
области Q функций -ф таких, что ip|s, = 0. Обозначим это простран-
ство . Тогда из (3.13) получим
У* (— div (X grad n) + — f) фгК? = 0 V-ф € .
3.1.Теоретические аспекты МКЭ. ...
91
Но равенство J FtydQ = 0 справедливо для любых *ф 6 только
о
тогда, когда F = 0 почти всюду1 на Q, т.е.
— div(X grad и) + уи - f = 0 почти всюду на Q, (3.14)
а значит для функции и выполняется (в некотором обобщённом смыс-
ле) уравнение (1.1} исходной краевой задачи.
Учитывая (3.14), из (3.13) получаем
f[x^-0\v„dS + /(Xf^ + f3 *(!i“Un))4>rf5=0- <315>
s2 V 11 S2
Выбирая из класса Иц множество Gs.2 функций таких что
Я = 0, получим из (3.15)
У(х|^--е)Е.<!5 = 0 v^€G,2. (3.16)
«2
Пусть S-2 — односвязная гладкая граница. Рассмотрим пространст-
во DS1 бесконечно дифференцируемых на 8% функций г]. Для каждой
функции q, заданной на , найдётся функция £ е Gs.2 С Н\ (задан-
ная на Q ) такая, что Ы = т] (чтобы получить такую Е,, достаточно
ls2
определённым образом продолжить т| на всю область Q), поэтому
J(xB“e)’1<B = f(xtHeM = 0 v'"e£V
s2 S2
Но равенство J Qv\dS = 0 для любых т] G Ds.2 справедливо только
S2
тогда, когда Q = 0 почти всюду2 на S2 :
1 Напомним, что фраза « F = 0 почти всюду на Q» означает, что функция
F = 0 на П везде за исключением, быть может, множества точек из £ I объ-
ёмной меры нуль (объёмная мера определяется, естественно, в соответствии с
размерностью рассматриваемой задачи - в декартовых координатах элемен-
тарный объём для одномерной задачи dCl = dx, для двумерной - rZQ = dxdy ,
для трёхмерной - d£l = dxdydz ).
2 Здесь выражение « Q = 0 почти всюду на S2 » означает, что функция Q
равна нулю на поверхности S2 везде за исключением, быть может, множества
точек поверхностной меры нуль.
3.Вариационные формулировки
X — 0 = 0 почти всюду на S2, (3.17)
। .с функция и удовлетворяет второму краевому условию на границе S-2
Абсолютно аналогично доказывается, что функция и удовлетворя-
ем! третьему краевому условию на границе :
X + |3 — «ц) = 0 почти всюду на S3 . (3.18)
При доказательстве (3.17) мы потребовали, чтобы S2 была одно-
связной гладкой границей. Если S2 - многосвязная или кусочно-
гладкая (т.е. S2 =^52 , где S2 - одпосвязные гладкие границы), то
г
приведённые рассуждения справедливы для каждой из S2 > т е- равен-
ство x|j^- — 6 = 0 справедливо на каждой S2 , а значит, и на всей гра-
нице S2 (аналогично и для S3).
Таким образом, нами доказано, что если минимум функционала I
достигается на функции и , то и является решением исходной краевой
задачи: удовлетворяет уравнению (1.1) и вторым и третьим краевым
условиям (первым краевым условиям и удовлетворяет в силу выбора
допустимого для минимизации пространства Н\).
Обратное утверждение доказывается снизу вверх. Действительно,
если и - решение исходной краевой задачи, то справедливо равенство
(3.13), из которого следует, что входящее в (3.8) и определяемое соот-
ношением (3 7) выражение d равно пулю. I огда из (3.8) получаем для
любого е и произвольной 6
I (и -ь Е ) = I (и) + е2с2 (3.19)
или I (и + ЕЦ)) > I (и), а так как любой элемент v Е может быть
представлен в виде и = и + ег() (для этого достаточно взять
= (f - ЮД ), то I (v) > Ни) для любого v Е Ну, т.е. решение и
краевой задачи (1.1)-(1.4) доставляет минимум функционалу 1(т),
определяемому соотношением (3.3). Таким образом, утверждение об
эквивалентности задачи минимизации функционала (3.3) решению
краевой задачи (!.!)-(1.4) полностью докатано.
Функционал I (v) можно записать в виде
I (v) = L(y,v}- 2f (и), (3.20)
3.1 .Теоретические аспекты МКЭ. ...
93
где £(ц ш) и f(v) - билинейная1 и линейная формы, заданные на
функциях v,w € Я1. Вид этих форм можно определить из сравнения
записей (3.3) и (3.20) одного и того же функционала I (д):
и grad wdQ +
vdS.
/(?;) = J' fvdQ + J QvdS + J |3up
(3.21)
(3.22)
S;(
n
Очевидно, что форма2 f(v) является линейным ограниченным функ-
ционалом, заданным на элементах v 6 Н', а форма L(u,w) удовле-
творяет следующим соотношениям для любых v,w,p 6 Н и любых
вещественных к и р,:
L (ц и) = L (ш, v),
(3.23)
1 В научной и учебной литературе по МКЭ билинейная форма L(d,w) ча-
ще всего обозначается как a(w,w). Мы будем использовать обозначение
L(v,w), в основном, для напоминания того, что эта билинейная форма полу-
чается после умножения Lv (L - оператор уравнения) на функцию w и ин-
тегрирования по расчётной области. Однако в разделе 7.7 4 нам понадобится
билинейная форма J X grad v • grad wdQ, которая для рассматриваемой там
о _
задачи не совпадает с билинейной формой, получаемой после умножения Lv
на функцию w и интегрирования по расчётной области, и поэтому мы обо-
значим её через a(v,w) (очевидно, обозначать её через L(v,w) в этом случае
будет не вполне корректно).
2 В дальнейшем мы будем использовать одну и ту же букву f (или /())
для обозначения как функции, стоящей в правой части решаемого дифферен-
циального уравнения, так и формы вида (3.22). Очевидно, что при однород-
ных естественных краевых условиях или при их отсутствии форма f (v) пол-
ностью определяется правой частью f дифференциального уравнения. В этом
случае вместо f (О можно записать (f,v), понимая под этим обычное скаляр-
ное произведение пространства Я° = L2 (Q) - некоторые авторы используют
именно такую форму записи правой части в уравнении Галёркина вида (3.26).
Но в общем случае форма f (гО зависит не только от правой части дифферен-
циального уравнения, но и от правых частей краевых условий, поэтому мы нс
будем использовать для неё форму записи в виде скалярного произведения.
Отличить же, когда через f обозначена форма вида (3.22), а когда функция,
являющаяся правой частью дифференциального уравнения решаемой ыдачи,
можно будет по контексту (очевидно, что запись f (•), где под точкой пони-
мается некоторая функция, всегда будет означать форму вида (3.22); при не-
обходимости же мы будем добавлять слово «форма» или «функция»).
94
3.Вариационные формулировки
L(v,k/w + Ц7?) = к/Дн, id) -р \i,L(y,p), (3.24)
Z(y, ?;)>() (3.25)
Установить справедливость свойств (3.23)-(3.25) очень легко непо-
средственной проверкой их для (3.21) Свойства (3.23)-(3.25) являются
свойствами скалярного произведения (т.е. свойствами симметричности,
линейности и неотрицательности), и для того, чтобы L(i?,w) стало
скалярным произведением, к свойствам (3.23)-(3.25) достаточно доба-
вить лишь одно: L(t>,v) = 0 тогда и только тогда, когда v = 0 [24].
При определённых условиях (обеспечивающих единственность реше-
ния исходной эллиптической краевой задачи (1.1)—< 1.4)) и это свойство
выполняется и форма Z(v, w) становится скалярным произведением,
которое называют энергетическим скалярным произведением и обо-
значают (v,w)3 (см. (3.4)).
При записи функционала 1 (v) в виде (3.20) нетрудно убедиться,
что минимизация этого функционала эквивалентна решению некоторо-
го вариационного уравнения, т.е. справедливо следующее утвержде-
ние.
Минимизация функционала (3.20) на множестве функций Н* экви-
валентна решению уравнения
L (и, vl}) = f (yl}) (3.26)
Докажем это.
Если функция и минимизирус! /(») на Я/,, то для произвольных
G и числа е
I (и) < 1(и + ЕЦ)) = L(u + ev(), и I ЕЦ))-2/(и 4-е^0). (3.27)
Используя свойства (3.23) (3.24) симметричности и линейности
формы L(v, и свойство линейноеги функционала f (и), получаем
L(w4-e^(),w,+ ev()) = L(u + E7>(),f/) I еЛ(«+ ei/(),v0) =
= L (u, U + EV()) 4- eL (vn, U, -I Е?»,) ) =
= L(u,u) + eL(u, р()) + еЛ(цьм) f еЧ(цьг>0) =
= Z (u, iz)+ 2e£ (zz,?4)) 4-e:’/ (<>(),?>()). (3.28)
f(u -| EBtl) = fill.) ( e/(v()). (3.29)
Подставим эти значения в (3.27):
I(u)<[L (и,u) — 2f(и)] + 2е [L (и, vl}) - f (ц,)] + e2L (ць v{}) =
3.1.Теоретические аспекты МКЭ. ...
95
= /(и) + 2е[Т(^/ц))-/(ц))] + е21(г/и,ц)), (3.30)
откуда
2e[L(?z,v0) - /(v0)] + £2L(v0,V0) > О . (3.31)
По свойству (3.25) неотрицательности L(v,v) можно положить
с2 = Z(v(),i/()) > 0, и в этом случае нетрудно показать, что сомножи-
тель при 2е в (3.31) должен быть нулевой1, т.е.
L(u,v0)-/(v0) = 0 \/Ц)€Я(),
а это и есть уравнение (3.26).
Обратное утверждение (т.е. то, что из (3.26) следует, что функция
и доставляет минимум функционалу (3.20)) доказывается совсем про-
сто (из (3.26) сразу следует (3.30)).
Таким образом, утверждение об эквивалентности минимизации
функционала (3.20) решению вариационного уравнения (3.26) полно-
стью доказано.
Рассмотренное только что доказательство фактически является аб-
страктным доказательством основной части утверждения об эквива-
лентности минимизации функционала (3.3) исходной краевой задаче.
Но оно короче и потому более наглядно, чем доказательство для функ-
ционала I (v) вида (3.3). Однако запись функционала / (v) в виде
(3.20) не позволяет определить его конкретный вид для краевой задачи
со вторыми и третьими краевыми условиями и показать, что эти крае-
вые условия будут выполняться автоматически при минимизации
функционала 7 (г) (как это было показано для функционала I (v) вида
(3.3)). Этим определяется полезность первого доказательства с полны-
ми выкладками.
Обратим внимание на то, что при записи билинейной формы (3.21)
мы намеренно использовали символ L, чтобы показать, что она поро-
ждена дифференциальным оператором (3.2) исходной краевой задачи
(1.1)—(1.4). Тем не менее не следует забывать, что эта билинейная Фор-
ма содержит в себе информацию и о третьих краевых условиях. Ана-
логично и линейная форма (3.22) порождается не только функцией /
из правой части уравнения (1.1), а содержит в себе информацию и о
краевых условиях второго и третьего рооа.
Будем называть краевые условия первого рода главными, а крае-
вые условия второго и третьего рода - естественными. Такие назва-
ния краевых условий определяются ролью, которую они играют в вы-
боре пространства решений : все функции пространства решений
должны удовлетворять первым краевым условиям (поэтому они и на-
• Доказательство этого абсолютно аналогично тому, как при доказательст-
ве утверждения об эквивалентности задачи минимизации функционала (3 3)
исходной краевой задаче (1.1)-(1.4)) было показано, что из справедливости
неравенства (3.9) сразу следует равенство нулю величины d.
96
3.Вариационные формулировки ...
зываются главными), но не должны удовлетворять вторым и третьим
краевым условиям, поскольку их выполнение обеспечится автоматиче-
ски (естественным образом) в процессе минимизации функционала
I Си). Требовать выполнения вторых и третьих краевых условий для
всех функций v, на которых минимизируется функционал I Cv), в
таком случае даже нецелесообразно, поскольку при минимизации I (ц)
на некотором подпространстве пространства можно в результате
этого отсечь более близкие к точному решению функции1 (это под-
тверждает и пример решения простейшей одномерной задачи, рас-
смотренный во втором разделе на с. 71-73).
Сделаем одно замечание о виде пространств Н* и Hq , когда
mesS’] = 0, т.е. когда первого краевого условия в исходной краевой
задаче нет. В этом случае допустимым для минимизации функционала
/ Си) множеством функций становится все пространство Н1, поэтому
мы формально будем считать, что при mess'] = 0 Н\ — Н1. Анало-
гично и с пространством : при отсутствии первого краевого усло-
вия (mess'] =0) будем понимать под Нц все пространство Я1, т.е.
Я,, = Я‘ . Очевидно, что все результаты, полученные ранее для клас-
сов Я* и Я(], остаются справедливыми, если учесть это замечание.
Например, в уравнении (3.26) или (3.11) при mesS] = 0 функции
должны принадлежать всему пространству Я1, но в этом случае
Я/, = Я1, и поэтому никаких недоразумений не возникает. Аналогич-
но, минимизация функционала I Си) при mes S'] = 0 должна прово-
диться на всем пространстве Я1 , но в этом случае Я^ = Н и резуль-
1 Да и вообще, последовательность функций, удовлетворяющих вторым и
третьим краевым условиям, может сходиться в норме пространства Я1 к
функции, нс удовлетворяющей этим краевым условиям (примеры таких по-
следовательностей приведены, например, в [7], с. 16-28, или в [22], с.35-36).
Поэтому мы можем получить для минимизации функционала I (д) множество
функций и , нс содержащее своих предельных точек, т.е. незамкнутое множе-
ство (или неполное пространство) функций. В )том случае появляется сле-
дующая проблема: если функция и предельная, то она может не лежать в
определённом таким образом классе функций, а значит, может и не удовле-
творять естественным краевым условиям. Нели же минимизировать I (д) на
пространстве функций //’ (т.е. не учитывать при определении допустимого
для минимизации пространства в торые и третьи краевые условия), то функция
и, доставляющая минимум /(в), будет удовлетворять краевым условиям
второго и третьего рода, и в силу замкнутости Я* и при ограниченности I (д)
снизу эта функция и существует и лежит в чго обеспечит выполнение и
краевых условий первого рода.
3.2.Вариационная постановка в форме уравнения Галёркина
97
тат также не меняется. Далее мы не будем специально оговаривать, что
при mes S} = О = П[ и Hl = Н1.
3.2. ВАРИАЦИОННАЯ ПОСТАНОВКА В ФОРМЕ УРАВНЕНИЯ
ГАЛЁРКИНА
Полученное в предыдущем разделе уравнение (3.11) (или в со-
кращённой форме (3.26)), являющееся эквивалентным вариационной
задаче минимизации функционала (3.3) (или (3.20)), называется урав-
нением Галёркина1 (сравните с (2.24), с. 56). Один из основных ре-
зультатов доказанных в предыдущем разделе утверждений заключает-
ся в том, что если для порождаемой оператором L билинейной формы
выполняется свойство (3.23) (являющееся фактически свойством само-
сопряжённости £), то минимизация функционала (3.20) (для нашей
задачи функционал принимает вид (3.3)) эквивалентна решению урав-
нения Галёркина (3.26) (для нашей задачи решению уравнения (3.11)).
Однако вариационную постановку в виде уравнения Галёркина
можно получить и более общим способом, который применим не толь-
ко для уравнений с линейными самосопряжёнными операторами (при-
мером которого является оператор уравнения (1.1)). Рассмотрим этот
способ на примере решения той же краевой задачи (1.1)—(1.4).
Уравнение (1.1) можно записать в виде
Я(«) = 0, (3.32)
где выражение
RCn) = — div (X grad it) + уи, — f (3.33)
является невязкой уравнения (1.1).
Потребуем, чтобы невязка R(u) дифференциального уравнения
(1.1) была ортогональна (в смысле скалярного произведения про-
странства2 № ) некоторому пространству Ф функций v, которое мы
будем называть пространством пробных функций, т.е.
У (— div(Xgradtz) + уи — /)vdQ, = 0 Vr G Ф . (3-34)
1 Это уравнение называется также уравнением в слабой форме. Заметим
однако, чго понятие «уравнение в слабой форме» является более широким,
чем понятие «уравнение Галёркина». Так, уравнение J RvdQ = 0 V//, где
о
R - невязка некоторого дифференциального уравнения, также называется
уравнением в слабой форме, но при этом его уже не называют уравнением
Галёркина.
2 Напомним, чго Я° - это пространство суммируемых с квадраюм на Q
функций, которое довольно часто обозначают как Ь2 (.Q).
98
3.Вариационные формулировки ...
11рсобр.нусм слагаемое J (— div (X grad и)) vd£l в (3.34) с исполь-
Q
зеванием формулы Грина (3.12):
J X grad и grad vdQ, — J X vdS +
о s
+ f (1й ~ f)— 0 Vv G Ф , (3.35)
Q
i де S = S1 U S2 U S3, как и ранее, граница Q .
Интегралы по границам 52 и S3 можно преобразовать, воспользо-
вавшись краевыми условиями (1.3) и (1.4):
f X grad и grad vdQ — Г X vdS — f QvdS —
J J on J
Q S] S2
-J 0(u — Wp) vdS + f Ы “ f) vdtt = 0 Vv G Ф . (3.36)
S3 Q
Поскольку на границе краевыми условиями не определяется
значение (задаётся лишь значение самого и), слагаемое
on
J X vdS следует исключить из уравнения (3.36), потребовав, чтобы
•51
пространство пробных функций Ф содержало только функции, кото-
рые принимали бы нулевые значения на границе Sx (напомним, что
ранее такие функции мы обозначали уп ).
Обратим внимание также на то, что в уравнение (3.36) входят про-
изводные пробных функций и. Поэтому в качестве Ф мы можем вы-
брать Яд (напомним, что Н{\ — пространство функций, имеющих сум-
мируемые с квадратом производные и равных нулю на границе 6\).
Таким образом, получаем вариационное уравнение вида
J X grad и grad + J yuul}dQ + J* fl uvQdS =
n П s3
— J* fv()d£l -I- J' QvadS + J' PttpHodiS Vvq G Hq- (3.37)
Q S2 S3
Сравнивая (3.37) c (3.11), убеждаемся в их полной идентичности.
Очевидно, что приведённые в данном разделе рассуждения (связан-
ные с выводом уравнения (3.37)) доказывают только то, что если функ-
ция и является решением исходной краевой задачи (1.1)—(1.4), то она
3.2.Вариационная постановка в форме уравнения Галёркина
99
будет удовлетворять и вариационному уравнению (3.37). Для доказа-
тельства же полной эквивалентности полученной вариационной поста-
новки (в виде уравнения (3.37)) исходной краевой задаче необходимо
доказать и обратное, т.е. что решение вариационного уравнения (3.37)
удовлетворяет краевой задаче (1.1)-(1.4). Это доказательство уже было
проведено в предыдущем разделе1 на с. 89-92, поэтому здесь мы его
повторять нс будем.
Очевидно, что рассмотренный выше метод построения эквивалент-
ной вариационной формулировки в виде уравнения Галёркина может
быть использован для решения нелинейных краевых задач, т.е. за-
дач, в которых либо коэффициенты уравнения и краевых условий ( X,
или ч, или 0 ) зависят от решения и, либо их правые части ( f , или 6,
или Up) нелинейно2 зависят от и. Действительно, при выводе уравне-
ния (3.37) мы нигде не использовали свойство линейности исходной
краевой задачи.
Заметим, что при доказательстве эквивалентности вариационной
формулировки в виде минимизации функционала (3.3) решению ис-
ходной краевой задачи (или даже уравнению Галёркина) свойство ли-
нейности было необходимо для выполнения соотношений (3.6), (3.8) и
(3.19) (при доказательстве в операторной форме свойства линейности
форм (3.21) и (3.22) использовались в соотношениях (3.28) и (3.29)).
Точно так же при выводе вариационной формулировки (3.37), во-
обще говоря, не требовалась и положительная определённость опера-
тора (3.2), которая используется в доказательстве того, что минимум
функционала (3.3) достигается на решении исходной краевой задачи.
Действительно, неотрицательность
L("Уо, Ц)) = J X(gracli'o)2 dQ + JT J fiv^dS (3.38)
была необходима, чтобы показать, что для функции, доставляющей
минимум функционалу (3.3) (или в операторной форме (3.20)), спра-
ведливо уравнение (3.11) (или в операторной форме (3.31)). Свойство
же неотрицательности (3.38) может нарушаться, например, в случае,
если ч < 0 на некоторой подобласти Q с ненулевой мерой.
Аналогично, для вывода уравнения Галёркина не требовалось и
свойство самосопряжённости оператора уравнения (1.1) исходной
краевой задачи. Поэтому такой подход применим также и для уравне-
ний с несамосопряжёнными операторами. Например, если необходимо
решить краевую задачу для уравнения
р • grad и — div (X grad и) + уи = f, (3.39)
1 Оно было приведено для уравнения (3.11), полностью идентичного (3.37)
2 Заметим, что под нелинейной зависимостью f от и понимается ситуа-
ция, когда /(ск^ + a2?i2) + а2/(мг)» гДе Щ и - функции, <ч( и
с\-2 - константы; аналогично и для 6 и .
100
3.Вариационные формулировки ...
с краевыми условиями (1.2)-(1.4), то соответствующее вариационное
уравнение Галёркина примет вид:
J(P' grad w) VydQ, + J X grad и grad + f yuv{}dQ 4
Q Q Q
+ Jfiu-UudS = j'fvodQ-}- J* 0undS 4 fVu() G (3.40)
S3 Q S'2 S3
Таким образом, общая схема построения вариационной формули-
ровки в форме уравнения Галёркина выглядит следующим образом.
I ели нам нужно решать краевую задачу для дифференциального урав-
нения
Lu = f, (3.41)
то следует левую и правую части этот о уравнения домножить на функ-
цию v из пространства пробных функций Ф и проинтегрировать по
Q. Фактически это соответствует скалярному умножению Lu и f на
v в пространстве L2 (Q):
(Lu,v) = (f,v) VoG<l>. (3.42)
Очевидно, что уравнение (3.42) можно записать в виде
{Lu -f,v) = 0 VpGT, (3.43)
что означает ортогональность невязки Lu — f дифференциального
уравнения (3.41) пространству Ф пробных функций v .
Далее в уравнении (3.42) необходимо (и это принщтиалъно для по-
строения уравнения Галёркина) преобразовать его левую часть с ис-
пользованием формулы Грина (интегрирования по частям) для пони-
жения порядка дифференцирования функции и и затем некоторые
полученные (после интегрирования но частям) поверхностные инте-
гралы преобразовать с использованием краевых условий.
В результате (после переноса вправо некоторых слагаемых) в левой
части должна получиться форма, аналогичная (3.21) (но не обязательно
билинейная и не обязательно симметричная, как, например, в уравне-
нии (3.40)), а в правой части — форма, аналогичная (3.22) (также не
обязательно линейная), т.е. в опера горной форме должно получиться
уравнение
L (и, v) = f (v) \/и С Ф .
После этого не мешает убедиться, что полученная вариационная
формулировка действительно являс!ся жвивалентной исходной крае-
вой задаче (аналогично тому, как это было сделано нами на с. 89-92
при доказательстве эквивалентности вариационного уравнения (3.11)
эллиптической краевой задаче (1.1)- (1.4)).
Таким образом, эквивалентные вариационные постановки в форме
Галёркина чаще всего строятся на основе принципа ортогональности
3.3.Аппроксимации на конечномерных подпространствах
101
невязки дифференциального уравнения решаемой краевой задачи не-
которому функциональному пространству1. При этом окончательный
вид вариационного уравнения получается после применения формулы
Грина (интегрирования по частям) и замены потоков в появившихся
повер.хнос гных интегралах на соответствующие значения из краевых
условий (а в некоторых случаях и из условий сопряжения). Именно
таким способом будут построены эквивалентные вариационные фор-
мулировки практически для всех рассмотренных ниже задач.
3.3. АППРОКСИМАЦИИ НА КОНЕЧНОМЕРНЫХ ПОДПРОСТРАНСТВАХ
Итак, для получения решения и краевой задачи (1.1)—(1.4) мы
можем либо минимизировать функционал /(ц) на бесконечномерном
пространстве , либо искать решение вариационного уравнения Га-
лёркина как элемент бесконечномерного пространства Н\, причём
пробные функции должны браться из бесконечномерного пространства
Й-
Как мы уже упоминали во втором разделе, при построении числен-
ного решения по методу Ритца минимум функционала ищется не на
всём пространстве а на подмножестве Vj' конечномерного под-
пространства Vh пространства II . При этом конечномерное про-
странство I ' мы всегда будем определять как линейное пространст-
во, натянутое на базисные функции гр,, i = 1... п .
Функции из пространства2 Vj’ должны в некотором смысле удовле-
1ворять главным краевым условиям исходной задачи. Слова «в неко-
тором смысле» мы вставили потому, что в конечномерном пространст-
ве V1' вообще может не оказаться функций, точно удовлетворяющих
главным краевым условиям. Это может случиться при решении дву-
или трёхмерных задач, если функция ufl на Sy не является полиномом
(кусочным полиномом) нужной степени (соответствующей степени
используемых базисных функций). Тогда и(/ на Sj заменяется функ-
1 При решении задачи для системы дифференциальных уравнений в част-
ных производных эквивалентная вариационная формулировка может вклю-
•кгть в себя несколько вариационных уравнений, построенных на основе того
ке принципа ортогональности невязок каждого из дифференциальных урав-
нении соответствующим функциональным пространствам.
Отметим, что пространства и являются подмножествами про-
странств 1Г п Ул, но при этом они не являются линейными прострит тви\ш
при неоднородных главных краевых условиях. Напомним, что словосочс! нше
«пространство функций» у нас может обозначать и линейное (в том числе и
। итьосрюво) пространство, и некоторое подмножество линейного (шльоср-
1ова) пространства, которое сами по себе может не быть линейным нро-
етраш вом ( е. пространством, которому принадлежит любая линейная ком-
оннапня сто wicmchtob).
102
3.Вариационные формулировки ...
цией такой, что, во-первых, достаточно близка к и и, во-
вторых, в V есть функции, которые па границе SA принимают значе-
ния и\}. В этом случае пространство 1 , строго говоря, может и не
быть подмножеством пространства Я,' (но при этом Vjl, естественно,
остаётся подмножеством пространства Vft).
Если же в I есть функции, точно удовлетворяющие главным
краевым условиям, то I'// будет нс только подмножеством конечно-
мерного подпространства I по и подмножеством пространства Н\.
В методе Ритца точным решением будем называть функцию и,
доставляющую минимум функционалу I Си) на всем допустимом про-
странстве II},, а приближённым решением - функцию и1', достав-
ляющую минимум функционалу 1(и> па множестве функций V, (яв-
ляющегося подмножеством конечномерного пространства V и, воз-
можно, подмножеством пространства /Г1).
Как правило, в МКЭ базисом пространства является набор фи-
нитных кусочно-полиномиальных функций ф;. При этом приближённое
решение и1' € У('', полученное как линейная комбинация таких финит-
ных кусочно-полиномиальных функций ф,, называют МКЭ-решением
(т.е. решением, полученным но методу конечных элементов).
Таким образом, аппроксимации Ритца-это функция и1', миними-
зирующая I Си) на множестве функций 1 'CV1:
/(?? )< /(/) V//' ev/;.
Как уже отмечалось во в юром разделе, в классическом методе Рит-
ца базисные функции пространства I выбирались в виде полиномов,
тригонометрических или других функций, ненулевых почти на всей
расчётной области Q. Такой выбор пространства приводил либо к
большой заполненности и плохо!! обусловленности матрицы СЛАУ,
получаемой в результате минимизации / и1') на Vg (в случае полино-
миального базиса), либо к непреодолимым трудностям в вычислениях
при решении задач в областях Q со сложной геометрией (в случае
тригонометрического базиса).
Главным отличием МКЭ от классического метода Ритца является
то, что в нём в качестве базисных функций фг берутся именно финит-
ные функции (или функции с локальным носителем), т.е. такие функ-
ции, каждая из которых отлична от пуля лишь на нескольких малых
подобластях расчётной области Q. Эти подобласти Ц, на которые
3.3 Аппроксимации па конечномерных подпространствах
103
разбивается расчётная область Q, в совокупности с ненулевыми на
базисными функциями называются конечными элементами.
На каждой подобласти базисная функция ф£ является полино-
мом заданной степени. Таким образом, пространство является про-
странством кусочно-полиномиальных функций. Такой выбор про-
странства V1' позволяет объединить в МКЭ все преимущества вариа-
ционных и конечно-разностных методов: получать приближённые ре-
шения, ближайшие к точному в энергетической норме, и при этом ре-
шать задачи в областях с геометрией любой сложности и работать со
СЛАУ, имеющими хорошо обусловленные и слабо заполненные (не-
нулевыми элементами) матрицы.
При построении конечноэлементных аппроксимаций по методу Га-
лёркипа пространства и так же, как и в методе Ритца, заменя-
ются конечномерными пространствами V'.' и . При этом чаще всего
в МКЭ функции из пространств Vj' и И, являются элементами одного
и того же конечномерного пространства V'1 с базисом {ф,} (т.е. ис-
пользуется вариант Бубнова-Галёркина).
Таким образом, при построении МКЭ-решения основную роль бу-
дет играть конечномерное пространство Vh, аппроксимирующее гиль-
бертово пространство Н (V ' С Н ) и имеющее баше {ф7} из фи-
нитных кусочно-полиномиальных функций фх, г = 1...п (т.е. базис-
ные функции ф7 в прямом смысле образуют базис именно пространст-
ва Vй \ При этом мы будем считать, что конечномерные пространства
Кг/Л и KJ1, аппроксимирующие соответственно пространства Н\ и Н{\,
строятся на основе пространства V1' следующим образом. Элементами
пространств V и Ц? являются такие линейные комбинации базис-
ных функций ф7; пространства V1, в которых зафиксированы значе-
ния коэффициентов перед базисными функциями, не равными нулю на
границе Sx (с заданным па ней краевым условием первого рода)
Обычно коэффициенты фиксируются так, чтобы для любой функции
£ Vg в узлах сетки на границе St выполнялось условие Vg — и;/
(см. (1-4)), а для любой функции Vy Е в узлах сетки на границе .S)
выполнялось условие vft = 0 .
Таким образом, если mesS] =0, то Vg и совпадают с Г
(i очно так же, как в этом случае совпадают с Н пространен^ //1 и
).
Г,ели же mcsSj 0, то Vg и являются подпространствами
пространства I 1, причём размерность и К()/£ меньше размерное гп
104
3.Вариационные формулировки ...
I на число базисных функций, веса которых в разложениях произ-
вольных элементов € VJ' и щ'} € Г((1 по базисным функциям ф,;
пространства 0' были зафиксированы для обеспечения выполнения
условий = и„ и г#|5 = 0.
В дальнейшем через мы будем обозначать размерность про-
странств V^' и , а через /У() - множество индексов г таких, что ба-
зисные функции ф; пространства I ' являются и базисными функ-
циями пространств и Ц, (т.е. при mes/?] = 0 т?() = п и
М) = {1...п] ).
При практической реализации МКЭ мы будем опираться на тот
факт, что минимизация функционала (3.20) эквивалентна решению
уравнения Галёркина (3.26), которое фактически является операторной
формой записи уравнения Галёркина (3.11). Кроме того что метод
Галёркина (по сравнению с методом Ритца) может быть применён для
решения гораздо более широкого класса задач, вычислительные схемы
на его основе строятся заметно проще. Поэтому, если при анализе точ-
ности и сходимости МКЭ мы ещё будем иногда проводить параллели
между обеими вариационными (формулировками (для метода Ритца и
метода Галёркина), то построение всех аппроксимаций и вычислитель-
ных схем МКЭ будет выполни н.ся памп уже только доя уравнения
Галёркина.
3.4. КОНЕЧНОЭЛЕМЕНТНЫЕ СЛАУ
Получим аппроксимацию уравнения I алёркина (3.11) па конеч-
номерных подпространствах Vj' и Г,, , аппроксимирующих исходные
пространства Н\ и Н\. Для этого заменим в (3.11) функцию Е Н*
аппроксимирующей её функцией , а функцию Ц) € Hq —
функцией Vq Е I'll’:
J X grad и1' • grad i^dQ. 4- j J ^ullv^dS =
П О Л’з
= J fv^dQ+P QvftdS + I [iuyi^dS
Q S2 Л’з
G Ию
(3-44)
Поскольку любая функция vfo G Ц, может быть представлена в ви-
де линейной комбинации
»еМ)
(3-45)
3.4.Конечноэлементпые СЛАУ
105
вариационное уравнение (3.44) эквивалентно следующей системе урав-
нений:
J Xgrad и,1' • grad + j" + J* (Su^fadS =
П Q S;<
= J" /ф/ZQ + J ftyjdS 4- J pwp'ipjdS’,
Q S-2 S;j
(3-46)
i e 7V0 •
Убедиться в эквивалентности (3.46) и (3.44) очень просто. Действи-
тельно, с одной стороны, каждое из уравнений (3.46) фактически явля-
ется уравнением (3.44) для vfj = фг Е Vjl; с другой же стороны, для
того чтобы показать, что справедливость уравнения (3.44) для любой
функции е V()‘ следует из справедливости системы (3.46), доста-
точно просуммировать уравнения системы (3.46) с весами </•', опреде-
ляющими эту функцию Е Ц/1 в линейной комбинации (3.45).
Таким образом, МКЭ-решение и1' удовлетворяет системе уравне-
ний (3.46). Поскольку и'1 Е , оно может быть представлено в виде
линейной комбинации базисных функций пространства V":
j=i
(3-47)
причём п — компонент вектора весов q = (<?i,..., qn )т должны быть
фиксированы и могут быть определены из условия
(3.48)
1.5!
Подставляя (3.47) в (3.46), получаем СЛАУ для компонент q, век-
тора весов q с индексами 3 С No:
i Е Nl} .
7/
52 J х &rad чк/ •
y=1 Q
(3.49)
Обратим ещё раз внимание на то, что система (3.49) содержи! п()
уравнений (л0 - размерность пространств Ц,' и Ц>'), в то время как
вектор q имеет п компонент. Недостающие п — л() уравнений (при
mess'! * 0) для компонент q, с индексами /’ 0 Nn могу! бы и. полу-
чены из условия (3.48):
106
3 Вариационные формулировки ...
(3.50)
Соотношение (3.50) чаще всего преобразуется в п — п() уравнений
вида q, = ufl (х7), где i — номера узлов сетки х7-, лежащих на границе
(исключение составляет, например, гот случай, когда в качестве
базисных функций используются кусочные полиномы, равные нулю во
всех узлах сетки, причём веса этих полиномов определяются значе-
ниями производных функций и в узлах копечноэлементной сетки -
позже этот случай будет рассмотрен более подробно).
Итак, при решении краевой задачи (!.])—(1.4) с использованием ба-
зисных функций, принимающих нулевые значения во всех узлах сетки,
кроме одного, конечноэлементная СЛАУ (3.49) для вектора весов q
может быть записана в матричном виде:
Aq = b, (3.51)
где компоненты матрицы А и вектора b определяются соотношениями
J Xgradipy-grad^pjdQ+J J |Зф7ф//5', i G Nlh
а Ц s:i (3.52)
6,г $ А(),
+ J QtyjdS 4- J* i G AIb
Q S? S3
U<)
(3.53)
в которых bt/ - символ Кронексра (b77 = 1 и6,; --0 при i j).
Аналогично может быть получена аппроксимация уравнения Га-
лёркина (3.10) в случае решения краевой задачи для уравнения (3.39) с
песамосонряжспным оператором. В этом случае компоненты матрицы
А конечно uicMciiiiioii СЛАУ будут определяться соотношениями:
J ip-grad ф,)ф//П | I X grad ф/• grad ф7б/Г2+
S2 \l
+ I чФ/Ф,(/и + I [1ф/ф^5') i G
n Si
b,7, i. ф TVjj
(3-54)
(компоненты же вектора правой части Ъ для этой задачи определяют-
ся, как и в предыдущей задаче, соотношениями (3.53)).
3.4.Конечноэлсмснтныс СЛАУ
107
Как уже неоднократно отмечалось, используемые в МКЭ базисные
функции являются финитными, т.е. каждая функция ф, не равна нулю
только на нескольких примыкающих к определяющему её узлу х,
подобластях (конечных элементах) Следовательно, для фиксиро-
ванной функции ф1 только небольшое число функций фу отличны от
нуля в подобласти, где ф., ^ О. Тогда из соотношений (3.52) (или
(3.54)) очевидно, что в каждой строке матрицы А содержится очень
мало ненулевых элементов, т.е. матрица А является сильно разрежен-
ной. Поэтому для хранения и обработки матриц в МКЭ чаще всего
применяются специальные форматы {структуры данных), позволяю-
щие существенно экономить вычислительные ресурсы.
Кроме того, значения компонент Д глобальной матрицы А не
очень удобно вычислять напрямую по формулам вида (3 52) (особенно
для многомерных краевых задач). Базисные функции являются кусоч-
но-полиномиальными (некоторыми заданными полиномами координат
на каждом конечном элементе), и поэтому фактически интегралы в
(3.52) вычисляются как суммы интегралов по конечным элементам ,
на которые разбита расчётная область (аналогично и для поверхност-
ных интегралов):
G,j=f X grac^ygrac^dQ =У Xgrac^ygrac^dQ, (3.55)
о k ilk
= f = 52 ГтФ/ФЛ (3.56)
Q ilk
= f p^.ds = Е/Wj*- »e • (3-57)
S-A ' S-j
Традиционно матрицу G с компонентами (3.55) называют матрицей
жёсткости, а матрицу М с компонентами (3.56) - матрицей массы1.
Очевидно, что формулы (3.55)-(3.56) можно записать в виде
^::ЕЕ- = о-58)
к к
где и Му - соответствующие вклады в компоненты матриц жёст-
кости и массы от элемента £1^. Заметим, что алгоритмически вычис-
лять компоненты G., и М , можно по-разному.
11срвый вариант (и, как мы убедимся, не самый удачный) состоит в
гом, что переход к вычислению следующей ненулевой компонен1ы ма>
рицы осуществляется только после того, как полностью будет вычис-
лена предыдущая компонента суммированием вкладов ио всей копеч-
1 Эти названия пришли из задач теории упругости, для решения коюрых и
был впервые применён МКЭ.
108
3.Вариационные формулировки ...
ным элементам (т.е. в формулах (3.58) как бы фиксируются индексы г и
j номера компоненты матрицы и для неё выполняется суммирование
вкладов от всех конечных элементов) I акой способ вычисления матриц
называется поузловой сборкой. Недостатком этого варианта является
необходимость выполнения довольно большого количества повторных
вычислений для одного и того же конечного элемента.
Гораздо более эффективным является вариант поэлементной сбор-
ки конечноэлементных матриц. Суп. его заключается в том, что от
одного конечного элемента QA. вычисляются сразу все необходимые
вклады в соответствующие компоненты глобальной матрицы. Очевид-
но, что эти вклады от одного конечного элемента можно рассмат-
ривать как матрицы жёсткости Gz и массы Мх этого элемента. При
этом удобно уменьшить размер этих матриц так, чтобы избавиться от
заведомо нулевых компонент (т.е. таких, которые вычисляются по ба-
зисным функциям, равным нулю на конечном элементе Q/.. )•
Фактически все ненулевые компоненты матриц GA и М/; (размера
п х п ) можно разместить в матрицах G и М? размера Ц. х 1к , где 4 -
количество базисных функций, отличных от нуля на конечном элемен-
те Q/.. Эти матрицы G1' и М' называют локальными матрицами
жёсткости и массы конечного элемента П/.. -Ясно, что соответствие
между компонентами матриц Gz и М (размера 4 х 4 ) и матриц Gz
и МА: (размера n х п ) легко установи i ь. Для одномерного случая при-
мер установления такого соответствия и поэлементной сборки гло-
бальной матрицы был приведён во втором разделе на с. 75. Соответст-
вующие примеры для многомерных краевых задач будут приведены
позже.
Заметим, что сборку глобального вектора правой части с компонен-
тами (3.53) так же, как и сборку глобальной матрицы, удобно прово-
дить поэлементно.
3.5. ОСНОВНЫЕ ПРИНЦИПЫ ГИК ТРОЕНИЯ БАЗИСНЫХ ФУНКЦИЙ
КОНЕЧНОМЕРНЫХ ПОДПРОСТРАНСТВ
Итак, при построении конечноэлементного решения на основе
минимизации функционала (3.3) или решения уравнения Галёркина
(3.11) прежде всего необходимо выполнить разбиение области Q на
подобласти (конечные элементы) $4 и определить конечномерное
подпространство V1' С Н1 (и соответствующие подпространства V!}1 и
И1‘).
Пространство в МКЭ, как мы уже говорили, определяется как
линейное пространство, натянутое па финитные кусочно-
полиномиальные функции ф,, т.е. все сю элементы vh являются ли-
3.5.Основные принципы построения базисных функций ...
109
нейными комбинациями базисных функций: rZt = У^7/Ф? • Полому
i
для определения пространства Vй необходимо построить базисные
функции ф7.
В МКЭ принято строить базисные функции, задавая их поведение
на отдельных конечных элементах. Для этого на каждом конечном
элементе строятся так называемые локальные базисные функции* ф„ .
Их вид определяется требуемым видом полинома, который должен
быть точно представим с помощью этих функций на каждом конечном
элементе, а также требуемой гладкостью глобальных базисных функ-
ций ф7 на границах конечных элементов £lk (т.е. их непрерывностью,
возможно, вместе с некоторыми производными). Затем из локальных
базисных функций ф„ , заданных на своих элементах , путём склеи-
вания и доопределения нулём получают глобальные финитные базис-
ные функции ф,, определённые уже на всей расчётной области Q (но
ненулевые только на небольшом количестве конечных элементов Q/..).
Таким образом, требуемая гладкость функций ф7 (а значит, и функ-
ций и1 ) обеспечивается специальным подбором локальных базисных
функций ф„ (определением поведения их самих и, если это необходи-
мо для увеличения гладкости ф7, их производных на границах конеч-
ных элементов) и способом склеивания. Фактически от того, как из
локальных базисных функций ф„ склеиваются глобальные базисные
функции ф,, зависит, будут ли конечные элементы обладать очень
важным свойством согласованности, а также то, как будет соответст-
вовать локальная нумерация узлов (и соответственно оазисных функ-
ций) глобальной.
Для рассматриваемого класса задач (т.е. при решении скалярных
дифференциальных уравнений второго порядка) конечные элементы
Qz. с определёнными на них функциями vh из пространства Vh назы-
ваются согласованными, если при переходе через границу конечного
элемента любая функция г? является непрерывной. При использова-
нии согласованных конечных элементов все входящие в функционал
(3.3) (или уравнение Галёркина (3.11)) объёмные и поверхностные
интегралы могут быть представлены в виде суммы интегралов по ко-
нечным элементам Q/.. (для объёмных интегралов) и в виде суммы
интегралов по границам конечных элементов Q/. (для поверхностных
интегралов), т.е. для всех объёмных интегралов, входящих в функцио-
нал I Си) (или уравнение Галёркина), будут выполняться равенства
1 Локальные базисные функции иногда называют ещё и функциями фор-
мы.
по
3.Вариационные формулировки ...
J »dQ, = у j (П°Д символом «•» понимается соответствующее
Q k О/.
подынтегральное выражение); аналогичные равенства будут выпол-
няться для поверхностных интегралов.
Заметим, что при использовании метода Ритца свойство согласо-
ванности конечных элементов является необходимым условием до-
пустимости функций v'1 для минимизации функционала (3.3).
Иногда при решении задач для уравнении высокого порядка при-
меняют несогласованные элементы. В этом случае существует опас-
ность того, что приближённое решение не будет сходиться к точному
решению. Поэтому необходимо проверять применимость несогласо-
ванных элементов для решения той или иной задачи. Одним из таких
способов является кусочное тестирование |9, 22]. Однако все проце-
дуры такого рода не вполне тривиальны, в то время как использование
согласованных элементов обычно обеспечивает гарантированную схо-
димость и хорошую точность приближенного решения. Поэтому мы
будем рассматривать только согласованные конечные элементы.
3.6. СХОДИМОСТЬ И ТОЧНОСТЬ KOHI ЧНОЭЛЕМЕНТНЫХ РЕШЕНИЙ
Коротко остановимся на проблемах точности МКЭ-решения uh.
Исследование точности конечноэлсмситного решения обычно заклю-
чается в оценке величины его отклонения от истинного решения и
(т.е. погрешности и —и'1 приближённого решения и1' ) и оценке зави-
симости этой погрешности от дроблении конечноэлементной сетки и
от порядка полиномов, используемых при построении базисных функ-
ций. При этом под сходимостью понимают стремление погрешности
приближённого решения и1' к нулю при дроблении сетки, а под по-
рядком сходимости (или порядком точности) - степень к в оценке
зависимости погрешности приближённого решения и1 вида
||u-i?||< rV, (3.59)
где к — некоторый характерный размер элементов в конечноэлемент-
ной сетке, С — константа, не зависящая от сетки.
Введём понятие энергетической нормы — нормы, порождённой в
пространстве Н1 энергетическим скачярным произведением (3.4):
Ik Пэ = • (3-6°)
Напомним, что энергетическое скалярное произведение (и,?;)э по-
строено на основе оператора решаемой дифференциально-краевой
задачи и краевого условия третьего рода.
Сформулируем и докажем одно из важнейших положений теории
МКЭ.
Для энергетической нормы разности между конечноэлементным
З.б.Сходимость и точноеть конечноэлементных решений
111
решением uh и точным решением и краевой задачи Л)-(] А) спра-
ведливо неравенство
Чек,", (3.61)
где V^1 — конечномерное пространство, на котором искалось МКЭ-
решение и1'.
Сначала покажем, что выполняется соотношение
-0 . (3.62)
\ /э
Действительно, для функций и и и1' справедливы уравнения Га-
лёркина (3.26) и (3.44) (последнее в аналогичной (3.26) операторной
форме может быть записано в виде L(uh= f (vq )), которые в тер-
минах энергетического скалярного произведения имеют вид:
(“,Ч|)э = /(”<>) V4) € ЯД, (3.63)
= (3.64)
Учитывая, что Ц{1 С , для произвольной функции 6 И!‘ по-
лучаем, что
(^Л,4)э = У ('4) = (3-65)
откуда сразу следует (3.62).
Теперь вычислим квадрат энергетической нормы отклонения про-
извольной функции 6 от точного решения и :
||л — v#|| = (и — Vy, и — vfy = (и — uh + uh — v!‘, и — uh + uh — =
= (u — uh,и — uh j + ^{u — uh, uh — + (uh — V^u1' — Vgj . (3.66)
Заметим, что для любой функции G Vj’ разность uh — v\lt факти-
чески является элементом v[\ функционального пространства Vq' (так
как (л/' — г^)|^ = ull\$ — =u,l—uf/ =0)1. Поэтому второе сла-
1 Это справедливо даже в случае, когда V’’ не является подмножеством
ll'i , т.е. когда ufl не может быть представлена точно через значения функций
из V1' на .9]. В этом случае ufl фактически заменяется некоторым споим при-
ближением <Zf/.
112
3.Вариационные формулировки ...
гаемое последнего выражения в (3.66) равно нулю в соответствии с
(3.62). Тогда
откуда (напомним, чн’ с' - прои. шальная функция из V7,/)
<3-67>
Из (3 67) сразу следует неравенство (3.61).
Cooiношения (3.61) и (3.67) показывают, что в энергетической нор-
ме koi 1счпоэлементное решение является самым точным приближени-
ем искомой функции и на конечномерном пространстве V/', т.е. МКЭ
даёт наилучшее по точное ги решение в энергетической норме. Это
свойство конечпоэлементного решения позволяет довольно просто
получить оценки его погрешности через характерный размер h ко-
нечных элементов.
Под характерным размером конечного элемента в одномерном
случае понимается, естественно, ei о длина. В двумерном и трёхмерном
случаях характерным размером темен га может быть либо диаметр
шара минимального размера, в который целиком включается этот ко-
нечный элемент, либо длина максимального ребра элемента А вот,
например, корень из объема двумерного или трёхмерного элемента
(квадратный в двумерном случае или кубический в трёхмерном) нельзя
использовать в качестве характерно! о размера, поскольку возможно
устремить объём к нулю без изменения длин некоторых рёбер.
Для получения оценки погрспшосги конечноэлементного решения
достаточно оценить погрешность представления функции и на каж-
дом конечном элементе её полиномиа зьным интерполянтом и1', по-
скольку в силу (3.61) выполняется
||<1-и"||э<||«-г||). (3.68)
Основным для оценки ошибки интерполяции произвольной функ-
ции v её кусочно-полиномиальным шнерполянтом v’ степени т
является соотношение1
(3 69)
где полунорма |у|5 функции v определяется соотношением
1 Оно приведено, например, в [22] на с. 173 (соотношение (10а)).
З.б.Сходимость и точность конечноэлементных решений
113
(3.70)
Очевидным следствием соотношения (3 69) является неравенство
(3.71)
где ||д || — Соболевская норма:
При s = 0 и s = l норма (3.72), очевидно, принимает вид
При s > 2 в соотношениях (3.69) и (3.71) (и далее) под |д|ч и ||г ||
понимаются аналогичные (3.70) и (3.72) выражения, в которых инте-
гралы от производных второго порядка и выше берутся не по всей рас-
чётной области сразу, а как сумма интегралов по ее подобластям (ко-
нечным элементам Q/.), и при этом на границах эти производные
могут не существовать (при s = 0 и s = 1 интегралы в рассматривае-
мых нормах и полунормах для любых функций v Е Н' просто совпа-
дают с суммой интегралов по подобластям1 * * *).
Из (3.71) сразу следует оценка ошибки интерполяции решения и
кусочным полиномом степени т :
||«-й‘|( <С„Л"'+1"\ (3.75)
1 В принципе, основное соотношение (3.69) правильнее было бы записать
в виде | v — V1' |sQa < Chm+1~s | v |,„+1S2a. , где под | v Q/. понимается полу пор-
мг! вида (3.70). в которой интеграл берётся не по всей расчётной области 12, а
по подобласти О2.. Отсюда естественным образом следует определение ||а ||м
при s>2 в виде ||и ||л = (|ц|цдд + • • + j - нужные производные
।очного решения и должны быть суммируемы с квадратом только на но<)оо-
частях (конечных элементах) 12^.
114
3.Вариационные формулировки ...
где Сп — константа, зависящая только от и (точнее, от ||« || _) и не
зависящая от //,.
Поскольку энергетическая норма (3.60) и норма (3.74) эквивалент-
ны [24], из (3.68) и (3.75) сразу следуют оценки погрешности конечно-
элементного решения в этих нормах:
(3.76)
<("«>>'" (3.77)
Теперь получим оценку погрешности u — uh в норме (3.73) про-
странства Н ' (которое фактически является пространством
суммируемых с квадратом на 42 функций).
Для этого сформулируем дополнительную задачу для функции
in € Я,1) в виде вариационного уравнения1
(w, v)3 = (и - и'\ (3.78)
т.е. правая часть этого уравнения является обычным скалярным произ-
ведением (пространства ^(Q)) изучаемой погрешности и —и1' на
пробную функцию v. Очевидно, вариационная задача (3.78) эквива-
лентна дифференциально-краевой за ыче для уравнения
Lw = u-uh (3.79)
с однородными краевыми условиями (L - это дифференциальный
оператор —divXgrad + ^ ).
Из теории дифференциальных уравнений с частными производны-
ми известно, что при достаточной гладкости коэффициента X для ре-
шения w краевой задачи для уравнения (3.79) с однородными краевы-
ми условиями справедливо неравенство
||™||2<Ci||"-u''|(i. (3.80)
где константа CL зависит лишь oi оператора задачи и расчётной об-
ласти (т.е. не зависит от правой части уравнения (3.79)).
Обозначим через иг кусочно-полиномиальный интерполянт функ-
ции w. С учётом эквивалентное) и шергетической нормы и нормы
(3.74), а также неравенства
1 Такой приём известен как приём Нитше [22].
При этом достаточно кусочной непрерывности X — в этом случае под
квадратом нормы j|w|| понимается сумма интегралов от квадратов соответст-
вующих производных w , взятых по участкам непрерывности параметра X .
З.б.Сходимость и точность конечноэлементных решений
115
|w-w^i<Oft||w||2, (3.81)
сразу следующего1 из (3.71) при s = 1 и т = 1, получим оценку от-
клонения иг от w в энергетической норме:
||w - й'‘|э < С, ||w - < С2Л ||w ||2,
и окончательно с учётом (3.80)
(3.82)
Вернёмся к уравнению (3.78). Подставив в него вместо произволь-
ной функции v разность и — и'1, получим
(г/. — и!', и — и'1) = (ш, и — tz? j = (и — и1', wj . (3.83)
В левой части (3.83), очевидно, стоит квадрат интересующей нас
(«нулевой») нормы погрешности и — г//1. Преобразуем правую часть
(3.83). Добавим к ней нулевое слагаемое2 в виде — (и — ull,wll\ :
Подставляя (3.84) в (3.83), получим
||w — = (и — и1' ,w — why . (3.85)
Воспользуемся неравенством Коши-Буняковского
(« - «',№- й'*)э < ||« - ||ш - ЮЛ||э .
Подставим его в (3.85) и воспользуемся неравенством (3.82):
о гкуда
1 Для этого достаточно, чтобы конечномерное пространство V1', в кото-
ром было найдено конечноэлементное решение и'1, содержало все кусочные
полиномы первой степени (что выполняется всегда для рассматриваемых
нами краевых задач и методов построения их конечноэлементных аппрокси-
мации).
2 Оно равно нулю потому, что uh является конечноэлеменгпым решением
и для пего справедливо (и — uh,vh j = 0 W' G Vj' (cm. (3.62)), а кусочный
П1нсрнолян1 wh лежит в Ц,', поскольку w должна удовлетвори и. однород-
ным главным краевым условиям.
116
3.Вариационные формулировки ...
и с учётом (3.76)
<О",+‘. (3.86)
Итак, соотношения (3 6), (3.77) и (3.86) гарантируют, что ошибка
копсчноэлемситной аппроксимации будет стремиться к нулю как к'1"
для энергетической нормы (3.60) и для нормы (3.74) и как 1-1 для
нормы (3.73), но только при условии, что на каждом конечном элемен-
те может быть точно представлен новой полином степени т. Этот
факт очень важен и должен обязательно учитываться при построении
базисных функций. Таким образом, конечноэлементное решение и1'
будет сходиться к точному решению и (со скоростью О (к"'} в нор-
мах (3.60) и (3.74) и со скоростью <>(//."'1 *) в норме (3.73)), если сис-
тема базисных функции выбрана гак, что на каждом конечном элемен-
те представим любой полином степени до т включительно. А по-
скольку под аппроксимацией вМК ) (в отличие от конечно-разностной
аппроксимации) понимается приближение решения элементами опре-
делённого конечномерного функционального пространства (кусочно-
полиномиальных функций), порядок аппроксимации и порядок сходи-
мости становятся в МКЭ эквивалентными понятиями.
Тот факт, что конечпоэлементпое решение является в энергетиче-
ской норме самым точным приближением искомой функции и, позво-
ляет лучше понимать, в каких местах необходимо сгущать сетку. Так
при использовании кусочно-полиномиальных базисных функций из-
мельчать следует те элементы, на которых предполагаемое решение
плохо описывается соответствующими полиномами. Например, для
кусочно-линейных базисных функции сетку следует сгущать в местах
существенного изменения градиента решения
Можно также отметить довольно важный и удобный для построе-
ния тестовых задач факт, который легко получить из соотношения
(3.67): если точным решением задачи является какой-либо полином,
представимый в виде разложения по базисным функциям, то конечно-
элементное решение совпадёт с точным без всякой погрешности. При
этом, естественно, из-за вычислительных iioi рсшностей (таких, как
погрешность округления или погрешность решения СЛАУ) численное
решение может незначительно отличаться от конечноэлементного, но
в дальнейшем мы чаще всего не будем обращать внимания на эту раз-
ницу между конечноэлементным и численным решениями.
Обратим внимание еще на один очень важный результат, который
был получен в ходе доказательства справедливости неравенства (3.62).
Соотношение (3.62) фактически означает, что разность между конеч-
ноэлементным и точным решениями ортогональна (в смысле энергети-
ческого скалярного произведения) конечномерному пространству VJ'.
3.7.0 сравнении погрешностей конечноэлементных решении I 17
При этом заметим (см. с. 103-104), что пространство Vj' можно рас-
сматривать как аффинное пространство функций vg вида = д 4- t/j,
где д - некоторая фиксированная функция, удовлетворяющая краево-
му условию первого рода = ид и имеющая вид д = g^j
1 ‘ jeN\N(}
(^ = {1- .n} - множество индексов j всех базисных функций
пространства v", N„ — множество индексов j таких, что базисные
функции ф.- пространства Vй являются и базисными функциями про-
странства Ц)1, д, - фиксированные веса).
• Поэтому из (3.62) следует, что конечноэлементное решение являет-
ся ортогональной проекцией точного решения на конечномерное про-
странство Vg . Соотношение же (3.67) можно рассматривать как неко-
торый аналог теоремы Пифагора. На основании этого свойства конеч-
ноэлементного решения и учитывая, что соотношение (3.62) (как было
показано чуть выше, см. с. Ill) фактически является прямым следст-
вием уравнений Галёркина L(u,Vq^ = и t/Q — f (*4), мы
имеем все основания отнести метод Галёркина к классу проекционных
методов1, поскольку методы, в которых используется принцип орто-
гональности некоторому функциональному пространству, называются
проекционными.
3.7. О СРАВНЕНИИ ПОГРЕШНОСТЕЙ КОНЕЧНОЭЛЕМЕНТНЫХ
РЕШЕНИЙ, ПОЛУЧЕННЫХ НА РАЗЛИЧНЫХ СЕТКАХ
В данном разделе мы приведём соотношения, которые могут
быть использованы при сравнении погрешностей конечноэлементных
решений, полученных как на различных сетках, так и с использовани-
ем элементов различных типов.
Сначала мы рассмотрим случай, когда в задаче либо нет главных
краевых условии, либо заданы только однородные главные краевые
условия.
1 Некоторые авторы строго разделяют вариационные и проекционные ме-
тоды, оставляя за первыми наличие в эквивалентной постановке минимизи-
руемого функционала, а за вторыми - ортогональность погрешности и — и'
всем функциям некоторого функционального пространства. В этом случае
и уравнения вида (3.26) не называют вариационными, а называют либо урав-
нениями в слабой форме, либо уравнениями Галёркина. Мы же будем тол ко
вать термин «вариационный» расширительно и использовать его для уравне
ний вида (3.26), основываясь не только на том, что эти уравнения получаются
в процессе нахождения стационарных точек функционалов, по и па иллинии
принципа вариативности в самих уравнениях вида (3.26) в том смысле, чю
пробные функции v в них должны варьироваться (перебираться в некотором
фун к ц но । пл ь ном 11 ространстве).
118
3.Вариационные формулировки ...
Покажем, что в этом случае выполняется соотношение
(3.87)
где /(v) - линейная форма, являющаяся правой частью уравнения
Галёркина (3.11) (или линейной частью функционала Ритца (3.3)) и
определяемая соотношением (3.22).
Для этого представим левую часть соотношения (3.87), являющую-
ся квадратом энергетической нормы погрешности конечноэлементного
решения uh, в следующем виде:
Используя соотношение (3.62) и го г факт, что при сформулирован-
ных выше ограничениях на главные краевые условия (т.е. в случае их
однородности ИЛИ отсутствия) вместо произвольной функции Vg в
соотношение (3.62) может быть подставлена и1', получим, что
[и-и\ и'1} =0. (3.88)
Тогда
= (и, и) —(и!\и\ .
Так как (w, v) = L(u, v) (см. (3 4) и (3.21)) и учитывая соотноше-
ния (и,и) = /(v) и которые могут быть получены
из уравнения Галёркина (3.26) при подстановке в него вместо пробной
функции v() точного решения и и конем поэлементного решения и'1
соответственно, убеждаемся в справедливости (3.87).
В случае, когда в задаче заданы неоднородные главные краевые ус-
ловия, соотношение (3.87) не выполняется, поскольку не выполняется
соотношение (3.88). Действительно, в этом случае в соотношение
(3.62) вместо функции Vq нельзя подставить функцию uh, поскольку
ик не удовлетворяет однородным главным краевым условиям.
Однако и в случае неоднородных главных краевых условий можно
получить аналогичные (3.87) выражения для погрешности приближён-
ного решения Для этого выберем некоторую (известную) функцию
ш!1 такую, чтобы она удовлетворяла главным краевым условиям. Эту
функцию вычтем из точного решения и исходной задачи, в результате
чего получим функцию
иг — и — w",
(3.89)
3.7.0 сравнении погрешностей конечноэлементных решений... I 19
которая является решением уравнения Галёркина для задачи с одно-
родными краевыми условиями:
Г(<д°) = /°(д1)). (3.90)
Очевидно, что для функции w() будет справедливо доказанное нами
соотношение (3.87), но при этом линейная форма /() в задаче для
и? может не совпадать1 * * * с формой (3.22) задачи для и .
Форма /(| может быть записан в виде, аналогичном (3.22):
/’(«) = J*fudQ + JQ(]udS + f Qu°udS , (3.91)
в которой функция /°, являющаяся правой частью дифференциально-
го уравнения для и{], и параметры 0f и краевых условий соответ-
ствующей краевой задачи определяются через параметры исходной
краевой задачи (для и) и функцию следующим образом:
= f + div (X grad w'7) — уш!1,
е° = е-хД^-, «'! = (3.92)
дп i5 p p on
С другой стороны, с учётом того, что
/(*/’) =. L(u, v°) — L(u° + wa, v°) = L(u[\v(}^ + L(w!I,
а также с учётом вида уравнения Галёркина (3.90) для задачи с одно-
родным главным краевым условием, форма /° может быть выражена
также и через линейную форму (3.22) исходной задачи и её билиней-
ную форму (3.21) следующим образом:
= (3.93)
Выберем функцию w-'7 такую, чтобы она не только удовлетворяла
исходным (неоднородным) главным краевым условиям, но и была
1 В некоторых случаях форма J может и совпасть с формой f. Ilinpn-
мср, когда в исходной задаче = 0 , и(/ = const и отсутствуют краевые усло-
вия третьего рода - тогда во всей расчётной области Q можно ичяп»
ш'1 const = ufj и форма /(1 совпадете /.
120
3.Вариационные формулировки ...
точно представима в базисе конечномерного подпространства1 * * * * * Vh, в
котором ищется решение и11, т.е.
w!l — = 0, ф£ - базисные
функции V]‘, q'“’ - коэффициенты разложения wq по базису {фг}.
Тогда нетрудно убедиться, что конечноэлементное решение u0,/t зада-
чи с однородным главным краевым условием связано с конечноэле-
мснтным решением uh задачи с неоднородным главным краевым ус-
ловием так же, как и точные решения (см. (3.89)):
u[}'h = и'1 — w!l. (3.94)
Равенство (3.94) можно легко доказать исходя из того, что для эл-
липтической краевой задачи с самосопряжённым оператором метод
конечных элементов, основанный на минимизации функционала Ритца
или на решении уравнения Галёркина, в качестве приближённого ре-
шения даёт ближайшую в энергетической норме к точному решению
функцию из конечномерного подпространства, натянутого на базисные
функции (см. (3 61)). Действительно, если функция u0,h доставляет
минимум норме |k° —, то функция
uh = ui},h + У2 Qi'^i — u^'h + w’v
I.
доставляет минимум и норме k — tr , так как
и — vh = и(} 4- w!l — vh = — (vh — w!l j
и, следовательно, ||u —v,l|| — |p — (vk — w'7)|| , а значит, энергетиче-
ская норма разности функций и и v'1 принимает минимальное значе-
ние только тогда, когда vl — w!l совпадает с и0,“ (т.е. при
vh = и0,1' 4- w!l), откуда следует, что функция и0'1' + wfl доставляет
минимум норме ||tz — i/'j| и, значит, эта функция совпадает с функцией
и'1.
Аналогично доказывается, что если и'1 доставляет минимум норме
II11 — vl> Пэ ’ Т° фуНКЦИЯ U°h = U>1 ~ W>' Д°ставляет минимум норме
1 Конечно, далеко не всегда существует такая функция wf', для которой вы-
полнимы сразу два этих условия (т.е. то, что wfl удовлетворяет исходным не-
однородным главным краевым условиям и при этом она точно представима в
базисе пространства V1'). Однако при решении практических задач чаще всего
икос возможно (или почти возможно), и поэтому проведённый ниже анализ
мо.кс! представлять не только теоретический, но и практический интерес.
3.7.0 сравнении погрешностей конечноэлементных решений... 121
||гл° — v°’/l|| и, следовательно, функция uh — w° является конечноэлс-
ментным решением задачи с однородными главными краевыми усло-
виями.
В результате мы можем получить выражение для оценки энергети-
ческой нормы погрешности конечноэлементного решения uh исход-
ной задачи через норму погрешности конечноэлементного решения
7/0,л задачи (3.90) с однородным главным краевым условием:
|u_4=|u''+^-(^+w»(=P-u».'< =
= /° (w°) — (^(,’л)- <3-95)
С учётом соотношений (3.89) и (3.94) и линейности формы /° вы-
ражение (3.95) может быть преобразовано к виду:
||и — г?‘||2 = — f(} = /п (и — w'7) — /° (uh — w!) j =
= f (w) - /° (w!l) - /° (uh) + /° (w,;) ,
т.е.
11“С = /" <«’-/’ (“'') <3-96)
Соотношение (3.96) позволяет вычислять норму погрешности ко-
нечноэлементного решения и11 задачи с неоднородным главным крае-
вым условием через линейную форму /° соответствующей задачи с
однородными главными краевыми условиями (с решением
и1} = и — w!l ).
В принципе, из соотношения (3.95) нетрудно получить выражения
для вычисления погрешности решения задач с неоднородным главным
краевым условием через линейную форму и конечноэлементное реше-
ние этой же задачи. Для этого сначала преобразуем (3.95) с помощью
соотношения (3.93) (с учётом подстановки в (3.93) в качестве функции
v() точного и{ и приближённого и0,А решений задачи с однородным
главным краевым условием):
||и-и^ = /“(«»)-/«(»»") =
= /(«")-/ ) - (b(ш9,«°) - £ (w9, и0'")). (3.97)
Воспользовавшись соотношениями
f («) = / («° + w!l) = f (w°) + f (w!l) ,
122
3.Вариационные формулировки ...
/' (+ w!l) = f (д0,Л ) + f (w!l) ,
L (w!l,u) = L (w!l, ) -b L (wg, w!l),
L (wfl, ull>) = L (w!l, ul}'h j 4- L (w!l, w-7),
окончательно получим:
|p — uh |£ = f (u) — f (uh) — (b (w!l, u) — L (w!l, uh)). (3.98)
Непосредственно для оценки погрешности конечноэлементного
решения uh соотношения (3.96) и (3.98) можно использовать лишь в
случае, когда известно точное решение и, (так как только тогда можно
вычислить значение или значения f (и) и L(w!l, и)). Однако
из этих соотношений очень легко можно получить выражения для
сравнения погрешностей конечноэлементных решений на различных
сетках.
Обозначим через и1’’1 - решение на сетке 1, и!1'2 - решение на сет-
ке 2. Тогда из соотношения (3.96) получаем:
|р — г?1’11| — |р — дЛ'2||2 = (иЛ’2) — /°
или
(3.99)
(заметим, что если в задаче нет главных краевых условий или заданы
только однородные главные краевые условия, то линейные формы f и
j тождественно совпадают).
Таким образом, вычислив значения /() и /1) (uh,2>j, по знаку
их разности можно легко определи гь, какая из погрешностей
|р — w/tJ|| или |р — д/',2|| меньше и соответственно какое из решений
и1' или и!' является более точным 11римеры, показывающие, как на
практике можно применять соотношение (3 99), будут приведены в
последующих разделах при изучении погрешности решений на раз-
личных сетках и с использованием элементов различных порядков.
В случае неоднородных главных краевых условий мы можем полу-
чить формулу для сравнения погрешностей двух конечноэлементных
решений г?*’1 и uh'2 также и из соотношения (3.98):
3.8. Способы представления параметров краевых задач в
— f (uh'2) — f (и11'1 'j — L(wff, uh'2) + £ (u)!l, ) •
123
(3.100)
При отсутствии в задаче неоднородных главных краевых условий
соотношение (3.99) (с учётом того, что линейные формы f и /( в
этом случае тождественно совпадают) можно записать в следующем
виде:
Цгг-гЛ1]^-|р-^’2||2 = /(гЛ2) - f (1Л1) (3.101)
(это соотношение также сразу следует и из (3.100) при подстановке в
него w9 = 0)
Заметим, что в соотношении (3.100) билинейные формы L(w!lj
и L [w!l >uh’2'} можно достаточно легко вычислить с помощью матрицы
конечноэлементной СЛАУ. Соответствующие соотношения будут при-
ведены чуть позже, в разделе 4.8 3 (см. (4.51)) При этом необходимо
помнить об ограничении, о котором мы говорили выше - функция w!l
должна быть точно представима в базисах {ф* { и |ф2} пространств,
соответствующих сравниваемым конечноэлементным решениям иьл и
ull,i (т.е.
Е О и w9 - 52
= 0).
3.8. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ПАРАМЕТРОВ КРАЕВЫХ ЗАДАЧ
В ЭКВИВАЛЕНТНЫХ ВАРИАЦИОННЫХ ПОСТАНОВКАХ
Рассмотрим проблему представления параметров X, , f , |3,
и 0 исходной краевой задачи (1.1)—(1 4) в функционале (3 3) или
уравнении Гёлеркина (3.11). Все перечисленные параметры могут быть
некоторыми функциями координат, и поэтому необходимо определить
способ представления этих параметров на конечных элементах .
Очевидно, что пока способ представления этих параметров не оп-
ределён (или все параметры решаемой краевой задачи не заданы в яв-
ном виде), интегралы по конечным элементам в соотношениях (3.55)-
(3.57) и в аналогичных соотношениях для локальных векторов правых
частей аналитически вычислить невозможно.
I ели же зафиксировать какой-либо способ представления парамет-
ров решаемой задачи, то становится возможным довольно технологич-
ное решение: можно получить аналитические выражения для локаль-
ных матриц и векторов, пригодные для использования при решении
побои краевой задачи заданного типа.
Рассмотрим некоторые наиболее часто применяемые на практике
. нособы представления параметров решаемой краевой задачи, позво-
i тощие получить достаточно унифицированные формулы расчёта
пн ta iob в локальные матрицы и векторы конечных элемен тов.
124
3.Вариационные формулировки ...
Самый простой способ заключается в том, что функции X, и f,
заданные в области Q, заменяются параметрами X, и / , которые
постоянны на каждом конечном элементе Ql:. Аналогично функции р,
Ufj и 0, заданные на границе S области Q, заменяются функциями (3 ,
и 0 , постоянными на каждой из частей границы S, являющихся
границами конечных элементов. В этом случае производится миними-
зация не функционала (3.3), а функционала
/ (v) = J (X (grad п)2 + чг/ ) dQ + J4 fiv2dS —
- 2^ fvdCl — zj fivdS —2J fiu^vdS ,
Q St
или вместо уравнения Галёркина (3.11) решается аналогично изменён-
ное вариационное уравнение.
Другой способ заключается в юм, что параметры краевой задачи
X, ч и f на каждом конечном элементе Qk заменяются своими ин-
терполянтами X'7', ^'1> и f4> (аналогично и функции |3, г/р и G, задан-
ные на границе S, заменяются интерполянтами РФ, и$' и 6г/'). На-
пример, под интерполянтом X параметра X на двумерном конечном
элементе мы понимаем функцию
Х^’(.г-,у) = ^2 Жм//v) у) . (3.102)
где {тр,^р} — узлы конечного элемент , а — его локальные ба-
зисные функции. Аналогично определяются , f'1', Р'7', и,'}1 и О'7'.
Заметим, что для построения иширполянтов, в принципе, нс обяза-
тельно использовать те же базисные функции, через которые представ-
ляется конечноэлементное решение При этом чем сложнее полиномы,
из которых построены базисные функции для интерполянтов, тем
сложнее считаются интегралы в формулах для соответствующих вкла-
дов в локальные матрицы и век юры и гем более громоздкими получа-
ются арифметические выражения для них после вычисления интегра-
лов. Поэтому чаще всего каждый из параметров X, , f, Р, up и 0 в
зависимости от типа решаемой задачи заменяется на интерполянт сво-
его вида, включая и кусочно-постоянную аппроксимацию (при кото-
рой значение рассматриваемого параметра принимается равным кон-
станте на каждом конечном элементе П/ ).
Заметим, что интерполирование типа (3.102) производится на ко-
нечных элементах локально, поэтому разрывные на границах элемен-
3.9.Погрешности МКЭ при решении задач в областях с ...
125
тов функции X, f, Р, «р и 0 в результате такой интерполяции
останутся разрывными на границах Од..
Нередко при вычислении локальных матриц и векторов используют
формулы численного интегрирования. В этом случае достаточно иметь
процедуры, выдающие значения параметров задачи в отдельных точ-
ках.
Но применение численного интегрирования при вычислении ло-
кальных матриц и векторов, как правило, приводит к значительному
увеличению числа арифметических операции при генерации конечно-
элементной СЛАУ. Поэтому оно используется, в основном, тогда, ко-
гда базисные функции на конечных элементах определяются через
полиномы на так называемых шаблонных элементах, что приводит к
появлению дополнительных сомножителей в подынтегральных выра-
жениях, возникающих из-за отображения шаблонного элемента в ко-
нечный элемент Од.. В результате нс удаётся получить достаточно
простые арифметические выражения для вычисления значений этих
интегралов. Такие ситуации характерны, например, для конечных эле-
ментов в виде четырехугольников, шестигранников или элементов с
искривлёнными границами.
3.9. ПОГРЕШНОСТИ МКЭ ПРИ РЕШЕНИИ ЗАДАЧ В ОБЛАСТЯХ
С ИСКРИВЛЁННЫМИ ГРАНИЦАМИ
До сих пор мы считали, что расчётная область О точно пред-
ставляется набором конечных элементов Од. (т.е. О = U Од. ). Однако
для многих практических задач это условие может не выполняться.
11оэтому важно знать величину погрешности, появляющейся в конеч-
ноэлементном решении из-за неточности аппроксимации расчётной
области совокупностью конечных элементов.
Обозначим через О7' объединение всех конечных элементов, т.е.
О7' = иОд. Аналогично и границы области O7i, на которых вместо
А:
соответствующих искривлённых границ S2 и заданы краевые ус-
ювия второго и третьего рода, обозначим соответственно через Sy и
.S',. Тогда методом конечных элементов будет искаться решение не
исходного уравнения Галёркина (3.11), а вариационного уравнения
j X grad • grad ul}dQ, + J* vi}dQ + J* v^dS —
o'* s!{
- / QvndS - Jfiupi\}dS = 0 Vv0 € H' ,
ll1, S2 S!i
(3 1(H)
i • iniici рирование в этом вариационном уравнении производится пи
пи области О, а по объединению всех конечных элементов О7,, и нс по
126
3.Вариационные формулировки ...
искрив icinii.iM границам Sj и S3, а по границам S2 и S3 конечных
мсмсшов (пли, что то же самое, по границам ), аппроксимирую-
щим искривленные границы исходной области О. Под //' понима-
емся еоо । вс ги гвующее пространство функций, заданных на Q/! (а не на
И) и удовлетворяющих однородному главному краевому условию на
5',' , (ответственно и решение вариационного уравнения (3.103)
является элементом пространства функций Н‘
заданных на
QZi
h ’
и
удовлетворяющих главному краевому условию1 на Sf, а конечноэле-
мепшое решение uh будет ближайшим в энергетической норме не к
цл
и , а именно к а .
Очевидно, что при измельчении шага сетки (т.е. при разбиении Q
па все более мелкие конечные элементы Q/ ) область О и её искрив-
лённые границы будут все лучше аппроксимироваться объединением
всех конечных элементов О.1' и сю границами, и функция будет
приближаться к и. Изучение погрешности этой аппроксимации явля-
ется специальной задачей численного анализа. Мы приведём соответ-
ствующие результаты только для тех случаев, когда двумерная область
О аппроксимируется объединением треугольных или прямоугольных
конечных элементов [22].
Погрешность, появляющаяся только за счёт изменения искривлён-
ной границы области и переноса краевых условий на соответствующие
границы треугольных конечных элементов, оценивается следующим
образом (h , как обычно, характерный размер конечного элемента):
(3.104)
При использовании же прямоугольных конечных элементов эта по-
грешность оценивается как
1 Фактически главное краевое условие переносится на границу S{‘, яв-
ляющуюся объединением аппроксимирующих границ конечных элементов
3 9.Погрешности МКЭ при решении задач в областях с ...
127
(3.105)
Последнее соотношение показывает, насколько медленно может
убывать с уменьшением размеров ячеек сетки та часть погрешности
кусочно-полиномиальной аппроксимации любой функции из Н1, ко-
торая вызвана лишь неточностью представления геометрии расчёт-
ной области Q. Однако МКЭ в этом смысле предоставляет самые ши-
рокие возможности использования ячеек подходящей для решаемой
задачи формы. В качестве конечных элементов в МКЭ могут быть взя-
ты не только треугольники, четырёхугольники, тетраэдры, призмы и
шестигранники, но и фигуры и тела с искривлёнными границами,
очень точно описывающие соответствующие границы расчётной об-
ласти Q.
128
4. Одно мерные задачи
4. ОДНОМЕРНЫЕ ЗАДАЧИ
Во втором разделе были рассмотрены одномерные кусочно-
линейные базисные функции. Обычно конечные элементы с опреде-
ленными на них линейными базисными функциями называют элемен-
тами первого порядка (но степени полиномов, определяющих базис-
ные функции). Аналогично, конечные элементы с квадратичными
базисными функциями называются элементами второго порядка, с
кубическими — третьего и т.д.
В данном разделе мы рассмотрим основные этаны построения ко-
нечноэлементных решении одномерных эллиптических краевых задач
при аппроксимации пространства // конечномерными подпростран-
ствами \г1 кусочно-линейных, кусочно-квадратичных и кусочно-
кубических функций, а также вопросы, связанные со сходимостью
конечноэлементных решений при равномерных и неравномерных
дроблениях конемпоэлементной сетки, и вопросы тестирования конеч-
ноэлементных процедур решения краевых задач.
4.1. ОСОБЕННОСТИ ВАРИАЦИОННЫХ ПОСТАНОВОК
ДЛЯ ОДНОМЕРНЫХ 1АДАЧ
Рассмотренные в предыдущем раз челе вариационные постановки
с функционалом (3.3) или уравнением I алеркипа (3.11) справедливы для
задач любой размерности и для различных систем координат. Однако
для решения конкретной задачи (т.е конкретной размерности в кон-
кретной системе координат) необходимо конкретизировать вид входя-
щих в вариационную постановку объемных и поверхностных интегра-
лов. Для одномерных задач мы рассмотрим наиболее часто используе-
мые системы координат: декартову, цнлип щическую и сферическую.
4.1.1. ОДНОМЕРНАЯ JA.IA4A В ДЕКАР ТОВЫХ KOOP ЦИ1АТ\Х
В декартовых координатах дифференциальное уравнение эллип-
тического типа (1.1) для одномерно! о случая принимает вид:
Расчётная область Q в одномерном случае является отрезком [а,с].
На его границах (левой т = а и правой .г = с) заданы краевые усло-
вия одного из трех типов: слева
4.1 .Особенности вариационных постановок ...
129
(/.<«) — Ua , ИЛИ — 6(1 >
или -Х^-1 _ 4- - //1bi I О
и справа
и(с) = и(., или Ху7 = 0Г, или Х^Ы 4-Рг(^с) — = 0,
где tza, uc, 0,t, 0r, j3„, 3r, и tzp( - задаваемые при постановке крае-
вой задачи константы.
Для определённости будем считать, что на левой границе задано
краевое условие третьего рода, а на правой - первого. Тогда функцио-
нал (3.3) примет вид:
I (и) =
4- уи2 dx 4- (и (аУ)2 —Zf fodx - 2|3„upn v (a),
а уравнение Галёркина (3.11) - вид
du dvo
dx dx
u(a)vl} (a) =
v4) 6 я,‘>,
(4.2)
причем минимизация функционала должна проводиться на функциях
удовлетворяющих краевому условию и(с) = иг, а входящие в
уравнение Галёркина функции и(т') и v0 (ж) должны удовлетворять
краевым условиям и (О = и,, и v() (с) = 0 . Аналогично выписываются
вариационные постановки для любой другой комбинации краевых
условий.
Обратим внимание на то, что границы Slt S2 и S3 в одномерных
ыдачах вырождаются в граничные узлы и интегралы по S2 и S3 в
функционале (3.3) или уравнении Галёркина (3.11) - это значения по-
।интегральных выражений в соответствующих граничных узлах.
I 1.2. ОДНОМЕРНАЯ ЗАДАЧА В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
В цилиндрических координатах (r,ip,z) под одномерной задачей
обычно понимают случай, когда решение и краевой задачи зависит
ю п.ко от координаты г. Тогда дифференциальное уравнение эллин
1НЧССКОЮ типа (1.1) принимает вид
--(rJr¥} + ^u = f- с-3’
т dr \ dr I
130
4.Одномерные задачи
Расчётная область Q = [rrt,rc] в этом случае является частью цилин-
дра и по тому элементарный объём dQ, равен rdr, а границы S2 и
Л’з это цилиндрические поверхности, и поэтому интегралы по ним
равны шипениям подынтегральных выражений, умноженным на якоби-
ан г.
Дня этой задачи будем считать, что на левой границе задано крае-
вое ус повис третьего рода — Х^Ч +13 [v(r(l) — иЛ — 0, а на правой -
'Г=Ги
второго
= О,.. Тогда функционал (3.3) примет вид
- 2 J fvrdr - 2fiuftv (rn) г„ - 26f.v (гг) гс,
'а
а уравнение Галёркина (3.11) — вид1
ri: !}
J xdr^rdr + f ^uvrdr + 3 u )v &>) =
ra ra
+ I fvrdr + fiupv(ra)ra.+ 0( v(rr.)/;. Vv € Hl .
(4.4)
4.1.3. ОДНОМЕРНАЯ ЗАДАЧА В СФЕРИЧЕСКИХ КООРДИНАТАХ
В сферических координатах под одномерной задачей обычно
также понимают случай, когда решение и краевой задачи зависит
только от координаты г. Тогда дифференциальное уравнение эллип-
тического типа (1.1) принимает вид
-Д--^-(Хг2 + = / (4.5)
(1т \ dr /
Расчётная область Q = [r«5rfc] в этом случае является частью шара,
и поэтому элементарный объём dO равен r2dr, а границы S2 и S3 -
это сферические поверхности, и поэтому интегралы по ним равны зна-
чениям подынтегральных выражений, умноженным на якобиан г2 .
1 Обратим внимание на то, что в рассматриваемой краевой задаче нет глав-
ных краевых условий, и поэтому Я,1, = Я1, а значит пробные функции v и
решение и лежат в одном и том же функциональном пространстве.
4.2.Одномерные элементы первого порядка
131
Для этой задачи будем считать, что на левой границе задано крае-
вое условие второго рода , а на правой - первого
'г=:7а
и(г() = и(.. Тогда функционал (3.3) примет вид
I (.V) =
+ yv2 r2dr —
Гс
2 J fvr2dr - 2Q(lv (ru) г2 ,
Га
а уравнение Галёркина (3.11) - вид
Г . ^0. r'2^r Г or2dr —
J dr dr J '
= f far2 dr + Vn (r„) r2
Vv() 6 Я?) ,
(4-6)
причём минимизация функционала должна проводиться на функциях
v(r), удовлетворяющих краевому условию v(rc) = и(:, а входящие в
уравнение Галёркина функции и (г) и v0 (г) должны удовлетворять
краевым условиям и(гс) = и(. и Ц) (fa) = 0 .
4.2. ОДНОМЕРНЫЕ ЭЛЕМЕНТЫ ПЕРВОГО ПОРЯДКА
В втором разделе была рассмотрена схема конечноэлементной
аппроксимации простейшей одномерной краевой задачи для эллипти-
ческого уравнения (2.1). Там же были введены одномерные кусочно-
линейные базисные функции. Теперь мы рассмотрим вычислительную
схему МКЭ для решения одномерного эллиптического уравнения, за-
писанного в более общем виде (4.1), с использованием тех же кусочно-
линейных базисных функций. При этом глобальную матрицу и вектор
правой части конечноэлементнои СЛАУ будем собирать из локальных
матриц и векторов, как это описано в разделе 3.4.
Будем считать, что расчётная область Q — [а, с] разбита узлами
.7хп на конечные элементы Ц,; = [^,^+1], к = 1...П — 1. Обо-
значим через hk = xk+1 — xk длину элемента . Введём на конечном
элементе flk локальную нумерацию узлов: = xf., х2 = .тАч] . Па
этом конечном элементе ненулевыми являются только две бапиные
функции фл и фл+1, которые в соответствии с локальной ну mi рацией
узлов обозначим через и ф2- Эти функции на элементе опреде-
ляются соотношениями
132
4.Одномерные задачи
J 2 7 z л *7 \
^=~V- (4-7)
Получим выражения для вычисления компонент локальных матриц
жёсткости (3.55) и массы (3.56) и локального вектора правой части.
При этом будем считать, что коэффициент диффузии X и правая часть
f на элементе С1к аппроксимируются своими линейными интерполян-
гамп X'7' = ХА (ж^ф! + Xfc (ж2)ф2 и Г7' = fk (£1)ф1 + (®2)ф2 (где
X1 i Г| и X (х2) - значения параметра X в узлах х\ и х2 конечного
элемента Q.k, a и fk(x-2) - соответствующие значения / ). Ко-
)ффициент же будем считать на О/, постоянным и равным .
Тогда компоненты Grj локальной матрицы жёсткости G конечного
элемента QA. будут вычисляться следующим образом (см (3.55)):
Gtj =f X'7'grad ф, grad ф,сЮ = j (хА: (.Tt) + ХА’ (х2) ф2) •
^А: »Т
,, d'i’i 1 </ф2 1 Г с ьк
Учитывая, что ~ = -±- и I w^dx = получим
dx hk ах - hk J 2
•'•А:
X1 (Д-!) + Хл (.ё-г)f 1 -J
(4.8)
Чтобы получить выражения для компонент локальной матрицы М,
П- 4-1
необходимо вычислить интегралы вида J ф7ф7т/т (см. (3.56)). Ко-
>к
нечно, такого рода интегралы для линейных на базисных функций
можно легко вычислить напрямую, подставляя в них значения базис-
ных функций ф, и фу из соотношения (4.7). По при использовании в
качестве базисных функций полиномов более высоких порядков по-
дынтегральные выражения станут более громоздкими, и поэтому для
вычисления соответствующих интегралов (в том числе и для компо-
.с т ।
f <7ф,- ^ф7 ,
иент I X —- ах матрицы жесткости) становится целесообраз-
•'А
ным использование следующего технического приёма, позволяющего
значительно упростить выкладки при вычислении компонент локаль-
ных матриц жёсткости и массы. Этот приём мы продемонстрируем на
4.2.Одномерные элементы первого порядка
133
ч+1
J ф^ф^т для линейных ба-
ч
примере вычисления интегралов вида
зисных функций на Од = [жд:,.г>+1]. Заключается он в следующем.
. .. X — Хк
Проведем замену переменной х на переменную с, = —т——, т.е
Лд-
ФгФ/з; = J ф?. (я (У) Ф,j (х (У) hkd^ .
о
(4.9)
Но тогда функция *ф1 СТ(У) будет линейной функцией переменной £
и может быть обозначена через ф! (У, причём эта функция фд (£,)
определена на интервале (0,1) и равна единице при £. = 0 и нулю при
£ = 1, т.е. Ф1 (У = 1 — У Аналогично Ф2 (л;(У) может быть обозна-
чена через ф2 (У и ф2 (Q = £ на интервале (0,1). Тогда из (4 9)
Ч+1 1 1 .
f фД^з; = J Ф1 (У Ф1 (У = hk J (1 - у2 .
;,к 0 I)
Аналогично вычисляются все остальные интегралы типа (4.9). В ре-
зультате получим
М = ^12. (4.10)
Во втором разделе мы уже вычисляли локальный вектор правой
части Ь при условии, что функция f на заменялась своим линей-
ным ин терполя! ином fk (з?])ф1 + f1' (з?2)ф2 (см (2 67)):
6 /(•«!)+ 2/4*2)
(4.Н)
Мы хотим продемонстрировать здесь несколько иной способ вы-
числения локального вектора Ь, который применим во всех случаях,
когда f на Ид. заменяется своим приближением в виде разложения
по базисным функциям ф/. Для этого введём локальную
I
матрицу массы С, соответствующую единичному коэффициент) :
134
4 Одномерные задачи
Го гд а
(4-12)
= J 12 = 52 pi f 'Mhdft = 52 Pi^i >
'иД I I llk i
или н матричном виде
b = (Jp; .
(4-13)
Для рассмотренных нами линейных базисных функций
и
— 6
к 2 1
1 2
£ hk
ь — —
и 6
2Р1: + Р2
Pl + 2/4
(4.14)
Учитывая, что для построения на Q;- линейного интерполянта
функции fk (ж) коэффициенты р1 нужно задать равными значениям
этой функции в узлах х} (т.е. =/A’(fz)), убеждаемся в полной
идентичности (4.14) и (4.11) для этого случая
Обратим внимание на то, что индекс к у и рА означает сле-
дующее: функция fk определяется только на элементе Од. (равной на
нём правой части f дифференциального уравнения (4.1)) и значения
весов рк разложения функции f по локальным базисным функциям
ф/ тоже должны вычисляться именно на элементе . Это особенно
важно в ситуациях, когда функция f (т) разрывна на границах элемен-
тов - тогда значение fk (£/) определяется как значение f в граничной
для элемента Q,. точке xt в пределе со стороны именно элемента
Заметим, что если на элементе коэффициент считается рав-
ным константе Д', то матрица массы М связана с матрицей С про-
стым соотношением
М = .
Обратим внимание также на то, что из соотношения (4 8) следует,
что если бы мы заменили X его средним значением
4.3.Использование шаблонных базисных функций при ...
135
Г“Д А } -j- Л ^2/ о
X = — —- на элементе Пд., то локальная матрица жестко-
сти осталась бы прежней (см. (4.8)), в то время как локальный вектор
правой части при кусочно-постоянной аппроксимации f имел бы вид,
не совпадающий с (4.14). Это свойство матрицы жёсткости сохраняет-
ся и в двумерном и трёхмерном случаях, но только при использовании
кусочно-линейных базисных функций. Если же используются базис-
ные функции более высокого порядка (или система координат не де-
картова), то это свойство может не выполняться.
4.3. ИСПОЛЬЗОВАНИЕ ШАБЛОННЫХ БАЗИСНЫХ ФУНКЦИЙ
ПРИ РЕШЕНИИ ОДНОМЕРНЫХ ЗАДАЧ
Отметим, что рассмотренный в разделе 4.2 приём позволяет ис-
пользовать для построения локальных матриц и векторов локальные
базисные функции, определённые на шаблонном интервале (0,1). По-
кажем, как с помощью шаблонных базисных функций можно вычис-
лять локальные матрицы одномерных конечных элементов произволь-
ного порядка.
Будем считать, что параметры X и заменяются на конечном эле-
менте Од. константами X и . Тогда компоненты локальных матриц
жёсткости G и массы М конечного элемента Од. любого порядка мо-
гут быть вычислены через заданные на интервале (0,1) шаблонные
базисные функции ф7 (Е,) по следующим формулам (Лд. - длина Од):
fyi- dtyj СО
J dx dx
ih
(Ц dt, (E,) dt,
dt, dx dt, dx 'k
_ Г (2Ф/ 1 ^7 1 t, лс - X* f d(pj dCpj
J dt, hk dt, hk hk J dt, dt, ’
1
My = J V Ф* (2-0 'Ф , (x) dx = J Ф-i (О Ф j (0 dt,.
oZ: о
(4-15)
(4.16)
Аналогично могут быть получены формулы для вычисления ком-
понент локально! о вектора b через интегралы по интервалу (0,1) oi
шаблонных базисных функций фг (Е,).
Соотношения (4.15)-(4 16) применимы при использовании базис-
ных функций любого вида - квадратичных, кубических и г.д. 11о пому
кусочно-полиномиальные базисные функции высоких порядков проще
136
4.Одномерные задачи
определить сразу на шаблонном элементе' (0,1) и для вычисления
компонент локальных матриц использовать формулы (4.15) и (4.16).
4.4. ОДНОМЕРНЫЕ ЭЛЕМЕНТЫ ВТОРОГО ПОРЯДКА
Рис. 5. Вид квадратичных базисных
функций на шаблонном элементе
4.4.1. БАЗИСНЫЕ ФУНКЦИИ И ДОК \ЛЫ1Ы1 МАТРИЦЫ ОДНОМЕРНЫХ
КВАДРАТИЧНЫХ ЭЛЕМЕНТОВ
В одномерных элементах второго порядка базисные функции,
естественно, являются кусочно-квадратичными. Для построения ко-
нечноэлементных аппроксимации с использованием этих элементов
применим технику шаблонных базисных функций, описанную в пре-
дыдущем разделе.
Поскольку квадратичные полиномы
одной переменной полностью опреде-
ляются своими значениями в трёх точ-
ках, поставим на шаблонном конечном
элементе (0,1) три узла с координатами
6,1 = 0, 6,2 = 0.5 и 6,3 =1 - Каждому из
этих узлов поставим в соответствие
квадратичную базисную функцию
фр (6,), равную единице в этом узле и
нулю в двух остальных. Вид этих квад-
ратичных функций показан на рис. 5.
Поскольку квадратичный полином
ф| (6,) имеет в качестве своих корней
точки 6, - 0.5 и 6, = 1, он может быть
представлен в виде ф] (6.) = Л (6, — 0.5) (6, — 1), а коэффициент d может
быть легко найден из условия ф, (0) 1, т.е. 1 = d(0 — 0.5)(0 — 1),
откуда d — 2 и
Ф1(Е.) = 2(^-П5)(Г,-|) . (4.17)
Так же легко может быть получен аналитический вид двух других
квадратичных полиномов:
Фг (У = -<£,(£. -I). (4.18)
Ч’.зИ = 2^(Е,-О.г>). (4.19)
Заметим, что построенные нами функции Ф1 (6.), Ф2 (6,) и фз (6.)
фактически являются базисными полиномами Лагранжа, поэтому и
конечные элементы с базисными функциями такого вида называют
элементами с лагранжевой интерполяцией или просто лагранже-
1 Иногда вместо термина «шаблонный элемент» используют термин «эле-
мент-прот от ип »
4.4.Одномерные элементы второго порядка
137
выми элементами. В принципе, они могут быть построены по стан-
дартным формулам, определяющим базисные полиномы Лагранжа /ф'
71 -го порядка, равные единице в одном из узлов и нулю в осталь-
ных узлах конечного элемента1:
pi (с \ _ £»!.)•••(£» £»г —1 ) (£> £>/-Ц )••(£» ^>7/.+1)
Очевидно, что любой квадратичный полином может быть пред-
ставлен в виде линейной комбинации определённых выше квадратич-
ных полиномов ф>! (£,), ф2 (£,) и ф3 (£,) - для этого достаточно взять в
качестве коэффициентов этой линейной комбинации значения исход-
ного квадратичного полинома в узлах шаблонного конечного элемента.
Из сказанного выше ясно, что каждый конечный элемент с кусочно-
квадратичными базисными функциями должен иметь по три узла - два
граничных и один внутренний. Поэтому при использовании кусочно-
квадратичных базисных функций конечноэлементная сетка строится,
как правило, следующим образом. Сначала задаются границы конеч-
ных элементов узлами £j,£3,...,x2»i+i, т.е. &-й конечный элемент име-
ет вид Q/, = (a>2fc_i,a>2fc+l)j k = ]...n . Затем вычисляются координаты
х-21- = (а?2А.-1 + узлов, являющихся центрами конечных эле-
ментов Пд..
Вид глобальных кусочно-квадратичных базисных функций приведён
на рис. 6. Эти функции строятся из шаблонных квадратичных базисных
функций Ф1(О, Ф>2 (U и Фз (Q с помощью замены переменной
6, = (ж — .T2A:-i (где Л/. = а:2/.+1 — .t2a--i - длина конечного элемента
(ф). При этом функции ф2д. (ж) отличны от нуля только на одном конеч-
ном элементе Гф и их прототипом является шаблонная функция ф2 (Q .
То же самое можно сказать о глобальных функциях (ж) и
ф2„+1 > соответствующих граничным узлам расчётной области Q, -
они отличны ог нуля только на одном из конечных элементов Qj или
и их прототипами являются шаблонные базисные функции (£)
и ф3 (^) соответственно.
Функции же фгл+1 Для & = — 1, соответствующие граничным
у злам .т2А:+1 двух конечных элементов и ^А +1, получаются в ре-
зультате сшивки в узлах ж2А.+1 локальной базисной функции ф3(ж)
1 Нетрудно убедиться, что соотношения (4.17)-(4.19) могут быи. сразу по-
1УЧСНЫ in coo l ношения (4.20) при п = 2 (т.е. фу (£,) = />' ((,)).
138
4.Одномерные задачи
конечного wicMcina .0/, с локальной базисной функции (гг) конеч-
ного элемента (прототипами которых являются соответственно
шаблонные базисные функции ф3 (У и ф] (У ), и поэтому каждая из
функций ф2А-| 1 бт) (А; = 1...П — 1) отлична от нуля на двух примы-
кающих к узлу конечных элементах Гф и .
Рис. 6. Вид глобальных кусочно-квадратичных базисных функций
Элементы локальных матриц жесткости G и массы М конечных
элементов Q.k = (x-2k-i, x2k+i) с квадратичными базисными функция-
ми могут быть легко вычислены по формулам (4.15)-(4.16) через инте-
гралы от шаблонных квадратичных базисных функций Ф1 (У , Ф-2 (У И
Фз (У и их производных
f \ А: Ф,: (Ж) dx = xfc (
hk J
Ф,: (У 4>j (У
... „
3;2A--1 0
J’2A-l+/lA 1
j чЧг (-T) "i’j U) dx = ^hk J* фг (У Ф7 (У d^ .
’••2k-l ' О
dx dx
(4.21)
(4.22)
Подставляя выражения (4.17)—(4.19) в соотношения (4.21) и (4.22),
получаем
1
8
7
м = ус = ^
4
2
-1
2 -1
16 2
2 4
/
(4-23)
(4-24)
4.4.Одномерные элементы второго порядка
139
где локальная матрица С определяется соотношением (4.12)
Столь же просто вычисляются компоненты локального вектора b
конечного элемента Qfc = (a^-b^A+i)- Заменяя на Q/, функцию f её
квадратичным интерполянтом + Л V2 + /з^Фз (гДе — f СФ) и
т1 = + 0, 3’2 — x-2k, -7"з = — 0 - это узлы элемента в
локальной нумерации), так же. как и в (4.13), получаем
b = Cf =
30
2
16
2
3(1
2 /2‘
' 4^+2^-//
2/il + 16// + 2/3‘
-Пк+2fi +4f3k
(4.25)
Рассмотренный выше базис пространства кусочно-квадратичных
функций является очень удобным (поскольку искомые веса — это
фактически значения приближённого решения в узлах сетки), но, оче-
видно. не единственно возможным. Среди остальных базисов стоит
упомянуть так называемый иерархический базис [4], Этот базис в од-
номерном случае строится путём добавления одной квадратичной
функции к двум линейным. Для шаблонного элемента базисные функ-
ции этого базиса имеют вид:
ФГ (У = 1 - е., Ф" (0 = -4ЦЕ. -1), Фз" (0 = У (4.26)
Нетрудно убедиться, что базисы (4.26) и (4.17)—(4.19) являются бази-
сами одного и того же пространства, поскольку они легко выражаются
один из другого:
Ф1(У = Ф1(У-|ФНУ.
Ф2 (О = Ф" (У,
Фз(У = ФЗ(У-|ф2(У-
Заметим, что для иерархического базиса (4.26) веса ф и <?3 в раз-
ложении приближённого решения на одном конечном элементе
+ фФ'" + <7зФз совпадают со значениями uh (tj) и и" (.г3),
а вот uh (т2) = <72 + •
Очевидно, что при использовании любого из двух рассмотренных
базисов (лагранжева и иерархического) мы получим одно и то же ко-
нем поэлементное решение (поскольку базисы определяют одно и то тс
функциональное пространство), но соответствующие конечно темен г*
пыс СЛАУ будут разными (и различаться будут как векторы пспзвео
пых. гак и матрицы и векторы правой части). Это cootbcictbciiiio mo-
140
4.Од номерные задачи
жет привести к различию в обусловленности конечноэлементной
СЛАУ и, как следствие, может повлиять на скорость сходимости ите-
рационных методов её решения. Более подробно иерархические бази-
сы, их достоинства и недостатки будут рассмотрены нами ниже, в двс-
над нагом разделе.
4.4.2. ПРИМЕР ИСПОЛЬЗОВАНИЯ КВАДРАТИЧНЫХ ЭЛЕМЕНТОВ ДЛЯ РЕШЕНИЯ
О (НОМЕРНОЙ ЭЛЛИП ГИЧЕСКОЙ ЗАДАЧИ
Проиллюстрируем процедуру построения копечиоэлементно! о
решения эллиптической задачи с использованием квадратичных эле-
ментов на примере решения задачи, рассмотренной во втором разделе
(там эта задача решена с использованием линейных элементов, см.
с. 71-73). В этой задаче ищется функция, удовлетворяющая в области
Q = [0,7] эллиптическому уравнению (4.1) с коэффициентами X = 1,
4 = 0 и правой частью /(.г*), определяемой соотношением (2.52). На
левой границе расчётной области задано первое краевое условие
«lj =o = 1, а на правой — второе 4^-1 = — 1.
«г|4.=7
Как и в рассмотренном во втором разделе случае с линейными эле-
ментами, будем считать, что расчётная область разбита на три конеч-
ных элемента Q] =[0,2], Q2 — [2,3| и Q3 = [3,7]. Тогда при исполь-
зовании квадратичных элементов конечноэлементная сетка содержит
четыре граничных (относительно конечных элементов) узла хл =0,
.т3 = 2, з;5 = 3, х7 = 7 и три внутренних - = 1, а;4 = 2.5, xG =5,
а конечноэлеменгное решение а1' (.г) может быть найдено как линей-
ная комбинация семи глобальных базисных функций ф (т) с веса-
ми q .
Приведём локальные матрицы и локальные векторы правых частей,
получаемые на каждом конечном «пементе. и продемонстрируем про-
цедуру занесения этих локальных мат риц и векторов в глобальные (эту
процедуру называют также генерацией или сборкой глобальных мат-
риц и векторов).
Учитывая соотношения (4.23) (4.25), получаем, что локальная мат-
рица и вектор правой части первого конечного элемента имеют вид:
о
о
о
к >
По соответствию локальных номеров базисных функций этого эле-
мента глобальным занесем локальную матрицу и вектор первого ко-
нечного элемента в глобальную матрицу и вектор (отметим, что для
этого элемента глобальные номера его базисных функций совпадают с
локальными):
4.4.Одномерные элементы второго порядка
141
7 _4 1 0 0 0 0
6 3 6
_4 3 8 3 _4 3 0 0 0 D
1 _4 7 0 0 0 0
А = 6 0 3 0 6 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 к 0 0 0 0 0 0
о
о
о
о
о
о
Локальная матрица и
вид:
вектор второго конечного элемента имеют
7.
з
8
3
1
_8
3
1G
3
_8
3
1'
3
8
3
7
ЗУ
Для этого конечного элемента локальная базисная функция с номе-
ром 1 является частью глобальной базисной функции с номером 3,
локальная базисная функция с номером 2 - частью глобальной базис-
ной функции с номером 4, а локальная базисная функция с номером
3 - частью глобальной базисной функции с номером 5. Поэтому после
занесения локальной матрицы и вектора второго элемента глобальная
матрица и вектор примут следующий вид (Д}2 добавляется к
Д£ - к Л34 , Д32 - к и т.д.):
2- -4 4 о ООО 0
6 3 б
-4 4-4 о ооо 0
3 3 3
- -4 3.5 —у 4 0 0 1
6 3 3 3 6
А = о 0 4 4 0 0 , ь - 2
3 3 3 3
о о 4-4 4 ° ° 1
3 3 3 6
0 0 0 0 000 0
0 0 0 0 000 1 0
Аналогично для третьего конечного элемента локальная матрица и
вектор имеют вид:
142
4.Одномерные задачи
и после занесения их в глобальную матрицу и вектор получаем
4
3
1
6
О
о
о
-4 | о о о и
3 6
| о о о и
3.5 1 о О
° "з “з ° 0
о 1 _8 35 2 X
3 3 12 3 12
° и ° “3 3 "3
1
3
2
3
1
Теперь учтём краевые условия. Вначале нужно внести вклады от
естественных краевых условий - в нашем случае это второе краевое
условие = —1. Оно учитывается как добавка 0ф7 (7) к компо-
«.т|,;=7
ненте Ь7 вектора правой части (т.е. добавкой к Ь7 значения «-1», так
как 0 = — 1, *ф7 (7) = 1).
На заключительном этапе обрабатываются главные краевые усло-
вия - в рассматриваемом примере это первое краевое условие
и|.к=о = 1. Оно учитывается путём замены первого уравнения системы
(которое, вообще говоря, является фикчпвным, см. с. 65-68), уравнени-
ем = 1 .
После учёта краевых условий получаем окончательный вид гло-
бальной матрицы и вектора правой части конечноэлементной СЛАУ:
1 0 0 0 0 0 0
_1
з
1
6
о
о
о
о
4-4 ° и ° °
о 3
4 35 4 j 11 11
° ~3 ±3 “з ° 0
n 1 _8 35 _2 X
3 3 12 3 12
° ° ° ~3 3 “3
±
6
1
3
2
3
(4.27)
4.4.Одномерные элементы второго порядка
143
В результате решения системы с матрицей и вектором правой части
(4.27) получаем вектор q с компонентами
q = (1,2,3,3.375,3.5,3,1.5) .
(4-28)
Заметим, что значения полученного конечноэлементного решения в
узлах сетки (в виде весов ), как и для линейных конечных элементов
(см. с. 71-73), совпадает со значениями в этих узлах точного решения
и (т) =
х + 1, 0 < х < 2 ,
-0.5(т-3)2 4-3.5, 2<т<3 ,
-|(.т-3)2 4-3.5, 3<т<7 .
(4-29)
Однако полученное конечноэлементное решение на квадратичных
элементах u - R полностью совпадает с точным (в то время как ко-
нечноэлементное решение на линейных элементах Л|11’ не совпадает
с точным внутри конечных элементов Q2 и ^з )•
Вообще говоря, при оценке точности конечноэлементного решения
важна его близость к точному не только в отдельных точках (будь то
узлы сетки или какие-то другие точки), а в целом во всей расчётной
области. Ведь конечноэлементное решение - это функция, и поэтому
оценивать его погрешность имеет смысл с использованием норм соот-
ветствующих функциональных пространств. Одной из таких норм яв-
ляется энергетическая норма, рассмотренная нами в разделе 3.7. В сле-
дующем разделе мы продемонстрируем, как можно вычислить энерге-
гическую норму погрешности конечноэлсменшых решений п/'>л,1н и
<ЛКО.
1.4.3. ( РАВНЕНИЕ ПОГРЕШНОСТИ КОНЕЧНОЭЛЕМЕНТНЫХ РЕШЕНИИ,
ПОЛУЧЕННЫХ НА ЛИНЕЙНЫХ И КВАДРАТИЧНЫХ ЭЛЕМЕНТАХ
Сначала покажем, как можно использовать для сравнения по-
грешностей конечноэлементных решений и/'’1""1 и ил,кв соотношение
(3 99). Напомним, что это соотношение справедливо в случае, когда в
шдаче либо нет главных краевых условий, либо они однородные. По-
ному, чтобы воспользоваться соотношением (3.99), рассмотрим функ-
цию //." (.?;) = и(.г) — 1. Очевидно, чго функция д°(.г) удовлетворяет
юм) же эллиптическому уравнению (4.1), что и и(х), и тому же вто-
рому краевому условию на правой границе
du[}
dx
= — 1, а на левой
7
iраиице для л"(т) справедливо однородное первое краевое условие.
I яким образом, линейная форма /’ совпадает с формой f (гак как в
144
4.Одномерные задачи
соотношениях (3.92) добавка div (X grad w!l) — yiv!! к правой части
уравнения н добавка
dw-1
дп
к краевому условию равны нулю, по-
скольку w1' = L).
Сравним энергетические нормы погрешностей конечноэлементных
peiiicHiiii н/',л1И1 и tz/l,KB, полученных на описанной выше сетке, с ис-
полыовапием соотношения (3.99).
В результате копечноэлементной аппроксимации эллиптической
краевой задачи для и(.г) на сетке из трёх линейных элементов
(?) = |0,2], Q2=[2,3] и Q3 = [3,7] мы получим вектор весов
q = (1, 3, 3.5, 1.б) , при этом глобальный вектор правой части
соответствующей конечноэлементной СЛАУ имеет вид
Ь,,п" = (о, 0.5, 1, -0.5]Т.
Обратим внимание на то, что при вычислении значения формы
J (иЛ) = q Ъ должен быть взят глобальный вектор правой части b
не результирующей конечноэлементной СЛАУ, а полученный до учё-
та первых краевых условий, поскольку
= J + f е£</,'‘Ф,<к + f
О и=1 s2 ?:=1 S3 ’:==1
= £<?'' f f^,dO + f &ф,<И + J'fluydS ,
1=1 U s2 S3
т.е. скалярное произведение1 qZl - b содержит в качестве слагаемых и
произведения q'1 j* fd/dQ , соответствующие узлам с первыми краевы-
п
ми условиями.
При использовании квадратичных базисных функций на той же сет-
ке из трёх конечных элементов Qj =[0,2], Q2 = [2,3] и Q3 =[3,7]
вектор весов был вычислен нами чуть выше (см. выражение (4.28)).
Глобальный же вектор правой части, полученный до учёта первых
краевых условий, имеет вид
1 Иногда скалярное произведение двух векторов мы будем записывать в
матричной форме как произведение сiроки на столбец (например, скалярное
произведение qz' • ф может быть записано как (qz')T ф
4.4.Одномерные элементы второго порядка
145
ЬКВ = (0,0,77,4,4,4,- i )
\ ’ ’6’3 3’3 о J
(сравните с вектором правой части результирующей конечноэлсмент-
ной СЛАУ (4.27)).
Вычислим значения форм /(u/lJ1HH) и f (гЛкв):
Из (3.99) получаем, что квадрат энергетической нормы погрешно-
сти решения на квадратичных элементах меньше квадрата энергетиче-
ской нормы погрешности решения на линейных элементах на
/(иЛ’кв) — /(u/l’J1,,,,j = . Поскольку точное решение ?д(.т) точно
представимо в базисе квадратичных элементов, конечноэлементное
решение гЛкв(я) должно полностью совпадать с л (.т). В этом также
можно убедиться, вычислив значение формы f (u):
2 з
f (.и) = о-(х + i)dx + J 1 • (-0.5(2 - з)2 + 3.5) dx +
о 2
7
+ f 0.25 • (—0.125 (.т - З)2 + 3.5) dz — 1 1.5 = 0 + ™ + 44 ~ 15 = >
3
и тогда из (3.95)
||и _ и"к" £ = / (U) - / ) = и _ м = 0 ,
т.е. и(.т) = п/,,кв (ж).
Покажем, как можно проанализировать сходимость конечноэле-
ментного решения к точному при дроблении сетки на примере реше-
ния рассматриваемой задачи на линейных элементах. Для этого вычис-
лим значения формы / ещё для двух последовательно вложенных
(руг в друга сеток:
J 4,лин] 73 4,11,1,1 9Q7
f д2 = тг, f иА =¥г-
j 16 ’ J 64
/ \
С учётом соотношения (3.95), энергетическая норма погрешности
/. пин 4,ЛИН 4.ЛИН
миючноэлементных решении и’ , и2 и w 4 равна
146
4.Одномерные задачи
4, ЛИН
'll, — и 2
4, ЛИН
и. - и 4
_ г 4,ЛИН
7 (и)-/ U 2
< J
„ г| 4,лип
/(«) — / и 4
Мы видим, что с каждым дроблением сетки энергетическая норма
погрешности конечноэлементною решения уменьшается вдвое - на-
помним, что в энергетической норме линейные элементы должны
иметь первый порядок аппроксимации, т.е. с каждым дроблением шага
сетки вдвое погрешность конечноэлементного решения должна умень-
шаться примерно в два раза (в нашем случае погрешность при каждом
дроблении уменьшается точно вдвое потому, что решение является
кусочно-квадратичной функцией).
Итак, мы рассмотрели ситуацию, когда в качестве функции w9 бы-
ла использована константа: ы9 = 1.11риведём пример оценки нормы
погрешности в случае выбора дру| их функций w9 . Такая ситуация
может возникнуть в случае, когда в задаче на нескольких границах
заданы разные главные краевые условия.
Возьмём в качестве функции и>9 функцию вида w9 (х) — 1 — хр,
о < х < 7 .
Используя соотношения (3.92), получим значения правых частей
дифференциального уравнения и в юрою краевого условия
fnw = f(xy, e(, = e + xi^’- = -i+| = _6.
Нетрудно убедиться, что в этом случае векторы правых частей
Ь0,л,,и и ^о,кв (определяющие формы у0 и У° (uA,KB)) имеют
следующий вид:
Ь°-™н = (o,o.s,i,-i)T,
Вычисляя значения форм /'
| 0. КН
\ ’ ’б’З’З’З’ 42/
получаем:
./(.лип 1 .Олин 125
° “ "2S" ’
/|,кп i О,кв _____ 205
Ч ~ 42 •
’ й.,лин
Таким образом, энергетическая норма погрешности решения, полу-
ченного на линейных функциях (поскольку квадратичное решение
совпадает с точным), определяется как
4.5.Одномерные лагранжевы элементы третьего порядка
147
и совпадает с нормой погрешности, полученной в предыдущем приме-
ре (с функцией w-1 = 1).
Рассмотрим ещё один пример, в котором продемонстрируем воз-
можность использования в качестве w'J финитной функции, отличной
от нуля лишь в небольшой окрестности границы с неоднородными
краевыми условиями первого рода.
Выберем ш!1 следующим образом:
1-ж
2 ’
О,
О < х < 2,
2<я<7.
Воспользовавшись соотношениями (3.92), получим, что при таком
выборе w-1 функция /° (х) и параметр 6" примут вид
/°(й = /<.т)-16(2), е"=е,
где 6(р) - дельта-функция Дирака, описывающая сосредоточенный в
х = р источник (подробнее о сосредоточенных источниках и 6-
функциях см. в восьмом разделе).
Вычислив соответствующие векторы правых частей .для линейных
и квадратичных элементов (Ь0,лин и bD,KB). получим следующие зна-
чения линейных форм
/° (тЛлин) = ч/1-лин Ь°’Л,1Н = g, /° = qZi’KB • ь°’кв = .
В результате энергетическая норма разности конечноэлементных
решений на линейных и квадратичных элементах будет равна:
II Д,кв _ uh,nW
'иМин
т.е., как и следовало ожидать, она полностью совпадает с погрешно-
стями, вычисленными с помощью двух других рассмотренных в дан-
ном разделе функций w!l.
4.5. ОДНОМЕРНЫЕ ЛАГРАНЖЕВЫ ЭЛЕМЕНТЫ ТРЕТЬЕГО ПОРЯДКА
Для построения конечноэлементных аппроксимаций с использо-
ванием одномерных лагранжевых элементов третьего порядка также
применим технику шаблонных базисных функций, описанную чуть
выше. Для построения кубического лагранжева интерполянта необхо-
димо, чтобы одномерный конечный элемент содержал четыре узла
Обычно эти узлы располагаются равномерно на конечном элементе,
г.е. есть на шаблонном кубическом лагранжевом элементе узлами ян
ляются точки =0, f > 6.3 — | и ^4 = 1- Соответственно шаб-
юнные базисные функции, являющиеся базисными полиномами Ла-
гранжа, имеют вид
148
4.Одномерные задачи
Ф1(Ю = -!(£.-DCi-Dte-i). Ф-2(У = <£.(£,
Фз(О = -^^(t-Dfc-1), Ф|(У = ^(Е.-|)(^-Ю- (4.30)
Графики этих базисных функций показаны на рис. 7.
Итак, каждый конечный элемент с кусочно-кубическими лагранже-
выми базисными функциями должен иметь по четыре узла - два гра-
ничных и два внутренних. Поэтому при использовании таких базисных
функций конечноэлементная сетка с i роится, как правило, следующим
образом. Сначала задаются границы конечных элементов узлами
.Xi, ж4,..., а?3п+1, т.е. /с-й конечный элемент имеет вид
С/, — (хЗк-2>хЗк+1 , к = 1...п. Затем вычисляются внутренние узлы
Рис. 7. Вид кубических базисных функций
на четырёхузловом шаблонном конечном элементе
Компоненты локальных матриц жесткости G и массы М и локаль-
ный вектор правой части b легко вычисляются с помощью соотноше-
ний (4.15}-(4 16) В результате получаются следующие выражения:
148 -189 54 -13'
-189 432 -297 54
“ 4Qhk 54 -297 132 - 189
-13 54 -189 148
128 99 -36 19'
-кЛ -k hk 99 618 -81 -36
’ ’ 1680 -36 -81 648 99
19 -36 99 128
4.6.Одномерные эрмитовы элементы третьего порядка
149
' 128// + 99// - Зб//; + 19//
b = Cf =
hk
1680
99// + MSf2k - Sl/f - 36//
-36// - 81// 4- 648// 4- 99//
19// - 36// 4- 99//’ 4- 128//
при условии, что параметры X и заменены на QA. своими средними
значениями X и , а функция / заменена на Q*. своим кубическим
интерполянтом //ч^ 4- //ф2 + //Фз + //Ф4 (где Ф/ - локальные ба-
зисные функции конечного элемента Q/., определяемые из (4 30) как
Ф< = fy3fc~2]’ а flk=f(£l) И i'l = T3fc-2+0, Х2 = хзк_ъ
.т3 = xsk, х4 = Жзд +1—0 — это узлы элемента О/, в локальной нумера-
ции).
4.6. ' ОДНОМЕРНЫЕ ЭРМИТОВЫ ЭЛЕМЕНТЫ ТРЕТЬЕГО ПОРЯДКА
Кроме рассмотренного в предыдущем разделе, возможен и дру-
гой способ задания кусочно-кубических функций на конечных элемен-
тах Qfc. Четыре коэффициента кубического полинома на конечном
элементе Qk могут быть определены по двум его значениям в гранич-
ных узлах Qk и двум значениям его первой производной в тех же гра-
ничных узлах. В результате на конечном элементе Qk не будет внут-
ренних узлов (т.е. Qfc = (хк,хк+1)) и поэтому такие конечные элемен-
ты с кубическими базисными функциями называют двухузловыми. В
отличие от конечных элементов, у которых локальные базисные функ-
ции являются полиномами Лагранжа (т.е. строятся только по значени-
ям в узлах сетки), конечные элементы, у которых локальные базисные
функции строятся не только по их значениям в узлах сетки, но и по
значениям их производных (т.е. являются эрмитовыми полиномами),
называют эрмитовыми.
Заметим, что с помощью двухузловых кубических локальных базис-
ных функций могут быть определены глобальные базисные функции как
того же пространства кусочно-кубических функций, что и при исполь-
зовании четырёхузловых локальных базисных функций, так и его под
пространства кусочно-кубических функций с непрерывной прои {водной.,
т.е. из двухузловых локальных базисных функций можно построй п.
глобальные базисные функции так, что натянутое на них пространство
не будет содержать функции с разрывной производной. Ниже мы на
примерах продемонстрируем, как из одних и тех же локальных базис-
ных функций можно строить базисы разных пространств
150
4.Одномерные задачи
При использовании двухузловых конечных элементов с кубически-
ми базисными функциями также удобно воспользоваться техникой
вычисления локальных матриц конечных элементов по шаблонным
базисным функциям. В этом случае вводятся четыре шаблонных ба-
зисных функции ф1 (У, ф2(У, Фз (У и Ф4 (У > причём функция
фз (У равна единице при £ = 0 и нулю при £ = 1 и имеет нулевые
производные при £, = 0 и 6, = I , функция ф2 (У имеет производную
ф>2 (0) = 1 и ф2 (П = 0 и нулевые шипения при £ = 0 и £, =Д, функ-
ция ф3 (6, ’ равна нулю при £, 0 и единице при ^ = 1 и имеет нуле-
вые производные при £, = 0 и £, 1, а функция ф4 (У имеет произ-
водную ф'] (0) = 0 и ф.1 (1) 1 и нулевые значения при £ = 0 и
Е, = 1 Вид этих шаблонных функций показан на рис. 8.
Рис. 8. Вид кубических базисных функций
на двухузловом шаблонном конечном элементе
Коэффициенты оф каждого из таких кубических полиномов
ф7 (У = а1/ 4- о •£, + сфС, + оф У могут быть легко получены по их
значениям и значениям их производных в узлах шаблонного конечного
элемента. Так, для функции фз (У (точнее, для её коэффициентов оф)
эта система примет вид
1 — фз (0) = ОД + CYj 0 + (Y.J • 0 + ОД • 0 ,
0 — фз (0) — 0 Т 0-3 Т од • U Т cy'i^ • 0 ,
О = фз (1) = CK.J + Од ’ 1 + ОД • 1 + (АД • 1 ,
0 = ф,1(1) = 0 + а1+of-2 + о?-3 • (4.31)
Аналогичные системы могу| быть получены для коэффициентов
оставшихся трёх кубических полиномов, причём матрицы у всех этих
систем одинаковые и совпадают с матрицей системы (4.3 1). Поэтому
все четыре системы для коэффициентов а’’ четырёх кубических поли-
номов ф, (У можно объединить в одно матричное уравнение
4.6.Одномерные эрмитовы элементы третьего порядка
151
Г1 0 0 О' а? а2 а3 а4 1 0 0 О'
0 1 0 0 а} а2 а3 Ot4 (I 1 0 0
1 1 1 1 а? а2 а3 а4 0 0 1 0
0 1 2 3 „ 3 „ 3 „ 3 з 0 0 0 1
CYj а2 а3 cy4 1
(4.32)
Из матричного уравнения (4.32) сразу следует, что матрица коэф-
фициентов а'/ полиномов ф,- (Q может быть вычислена как обратная к
матрице, являющейся первым сомножителем в левой части матричного
уравнения (4.32):
а? а2 а3 а4' 1 0 0 О' -1 ' 1 0 0 О'
aj а2 а3 а4 И 1 0 0 0 1 0 0
а? а2 а3 а4 1 1 1 1 -3 -2 3 -1
Л з 3 Л 3 г 3 0 1 2 3 2 1 —2 1
«1 а2 а3 а4 к
т.е.
Ф1Ю = 1-3«.2+2е, Ф2 (0 = ^-2^+^,
Фз(О = зе,2-2^. ф4(£.) = Ч2 + ^-
(4.33)
Обратим внимание на очень важную деталь, связанную с построе-
нием локальных базисных функций ф2 (т) и ф4 Ст). Чтобы локальная
базисная функция ф2 (я) имела равную единице производную в левом
узле конечного элемента, она должна быть не просто получена из шаб-
лонной функции ф2 (^) заменой переменной 6, на (ж — , а иметь
вид ф2 (т) = (^ - длина конечного элемента QA., на кото-
ром определяется ф2(т), X/. — координата его левой границы.
£/.г) = (,т — x^/h/. ). Действительно,
б/ф2Сг) ,
~dl— = hk----Тх--~hk
&
(в то время как
#2 ).
152
4.Одномерные задачи
Аналогично и ф4 (т) должна быть построена из ф4 (GJ в виде
ф4 Ст) = hkv4 (G, Ст)).
Поэтому при вычислении локальных матриц жёсткости и массы и
вектора правой части через шаблонные функции ф1 (У , ф2 (У, фз (У и
ф4 (У мы должны учесть »ту особенность построения базисных функ-
ций с чётными номерами, заменив в формулах (4.15J—<4.16) функции
Ф2 (У и ф4 (У на ЛА.ф? (У и /д.ф4 (У. Г аким образом,
о„ = F cl2 = XL
hk J dG, dG, lz hk J dG, dG,
A _ XA f </ф1 t/фз a _ X* f </ф1 , </ф4
1314"vJ~d^hk^:d^
G.a^\hk^hk^.dki
hk J K dG, dG, s h.k J K dG, dG,
и т.д. Вычисляя интегралы в этих выражениях с учётом того, что функ-
ции фг (У определяются соотношениями (4.33), получаем
' .36 злА - 36 ЗЫ
с.-з ЗОЛк 3/lA; -36 А1,к -^hk -ЗАа 36 -3hk (4.34)
з/ч- -1‘к - з/м Mil
Аналогично вычисляются и компоненты локальной матрицы массы
' 156 2‘lhk 54 — 13ЛА.
22Ла. 54 4//f 13ЛА. l3At -ЗЛ(2 156 -22Ла. (4-35)
-13Л, -з/?А2 -22hk ^hl
Для вычисления компонент локального вектора правой части ко-
нечного элемента QA- = (хк,хк+1) заменим на нём правую часть f
дифференциального уравнения сё кубическим интерполянтом
Ц'Х'1 , где pf = /(«,), pl = X(i|), Рз = f(x2), pj- = ^-(£2) И
4.6.Одномерные эрмитовы элементы третьего порядка
153
х1 = xk+Q, х2 = .77+1 — 0 - это узлы1 элемента Q/. в локальной нуме-
рации. Тогда (см. (4.13)):
166pf + 22^ + 54pJ - 13hkp$'
22/it-Pi + + 13/1ьрз - З/i^P4
54pf + + 156p| -22htp^
- 3li^p2 -22hkpl + 4/i^p^
Построим теперь глобальные кусочно-кубические базисные функ-
ции на двухузловых конечных элементах таким образом, чтобы они
имели непрерывные производные dtyjldx на всей расчётной области
Q (и поэтому порождали бы конечномерное пространство Vh кусоч-
но-кубических функций с непрерывной производной), т.е. чтобы V'
фактически являлось подпространством гильбертова пространства Н'
(Н2 - гильбертово пространство функций, имеющих суммируемые с
квадратом производные до второго порядка включительно).
Для этого в каждом узле x.k конечноэлементной сетки определим
две глобальные базисные функции ф2Л-1 и “ФгА- (узлы xk раз-
бивают в этом случае область на конечные элементы (Д = (х^, 27.4.1),
и внутри конечных элементов узлов нет). Вид локальных и гло-
бальных кусочно-кубических базисных функций на двухузловых ко-
нечных элементах показан на рис. 9. Эти функции строятся из шаблон-
ных локальных базисных функций (4.33) с помощью стандартной за-
мены переменной = (х — )//?.;. (с учётом домножения функций с
чётными номерами на hk) и сшивки локальных базисных функций
граничащих друг с другом конечных элементов.
Так, глобальная базисная функция тр2А._1 (т) (А; = 2...П — 1), соот-
ветствующая узлу хк. (являющемуся внутренним узлом сетки и гра-
ничным узлом конечных элементов ) и
QA. — (хк>хк+1)) и равная единице в этом узле, получается в результате
сшивки локальной базисной функции "ф3 (т) конечного элемента ।
с локальной базисной функцией (х) конечного элемента Q/.. Фупк-
1 Ещё раз обратим внимание на то, что в случае разрывной функции f или
её производной значения f и df/dx в узлах конечного элемента Пд должны
браться внутри элемента, т.е. в пределе справа для левого узла и в пределе
слева для правою узла, о чём и говорят записи .77 = -I 0 и ,г? .17 ( ( О .
154
4.Одномерные задачи
ция же ф2/,- > соответствующая тому же узлу хк и имеющая равную
единице производную при х = хк (сама трзл равна нулю при
х = хк ), получается в результате сшивки локальной базисной функции
ф4 (х) конечного элемента Clk-i с локальной базисной функцией
ф2 Ст) конечного элемента .
Очевидно, что в гаком случае нечетные компоненты вектора q, яв-
ляющегося решением консчноэлсмснгпой СЛАУ, будут давать значения
конечноэлементного решения и’1 в узлах сетки, а чётные компоненты
q - значения производных du /dx этого решения в узлах сетки.
Рис. 9. Вид локальных (а) и глобальных (б) кусочно-кубических базисных функций
для двухузловых конечных элементов
4.7. СОПОСТАВЛЕНИЕ ЛАГРАНЖЕВЫХ И ЭРМИТОВЫХ КУБИЧЕСКИХ
ЭЛЕМЕНТОВ ПО ТОЧНОСТИ И ВЫЧИСЛИТЕЛЬНЫМ ЗАТРАТАМ
Покажем теперь, что с помощью рассмотренных в предыдущем
разделе двухузловых локальных базисных функций можно построить
базис того же пространства кусочно-кубических функций, которое
получается при использовании четырёхузловых локальных базисных
функций. Для этого сформируем глобальные функции следующим
образом.
4.7.Сопоставление лагранжевых и эрмитовых кубических ...
155
В каждом внутреннем узле хк (к = 2...rz — 1) конечноэлсментной
сетки определим три глобальные функции Фз£'"3, Ф3™2 и Ф3Г i » как
показано на рис. 10.
Как видно из этого рисунка, глобальная функция ф3™3 строится
следующим образом: она не равна нулю только на одном элементе
= (ж/с_1,ж/1;') и, в отличие от рассмотренных чуть выше кусочно-
кубических базисных функций ф2;- (х) с непрерывной производной,
продолжается нулём на элемент = (ж^,ж^+1) (на остальных эле-
ментах она, естественно, равна нулю).
Глобальная базисная функция ф3^2 строится точно так же, как
строилась функция ф2д-1 (х) с непрерывной производной (т.е. сшив-
кой локальных базисных функций ф3 (ж) конечного элемента и
ф?! (ж) конечного элемента Q/i;).
Глобальная функция ф3£Лр в отличие от функции ф2д. Сж) с непре-
рывной производной, не равна нулю только на одном конечном эле-
менте Од, а на Од-_] (так же, как и на всех остальных элементах) она
равна нулю.
В крайних узлах tj и ж„ функции фт, ф2 и Фзп-з > Фзп-2 опреде-
ляются так же, как были определены в случае с непрерывными произ-
водными функции фп ф2 и ф2п, ф2„_ 1 соответственно, см. рис. 9,6
Все эти функции не равны нулю только на одном конечном элементе и
ф”м" определяется локальной базисной функцией Ф1 (ж) конечного
элемента а ф2™’ - локальной базисной функцией ф2 (ж) элемента
. Аналогично ф3п"3 (как и ф2„ в случае с непрерывной производ-
ной) определяется локальной базисной функцией ф4 (ж) элемента
, а Фз£-2 (как и ф2„-1 в случае с непрерывной производной) -
локальной базисной функцией ф3 (ж) элемента .
Рис. 10. Вил глобальных кусочно-кубических базисных функций
для специальных двухузловых конечных элементов
156
4.Одномерные задачи
Нетрудно убедиться, что пространство, натянутое на определённые
таким образом функции ф”си’, ф3,7-2 > полностью совпадает с про-
странством, натянутым на кубические базисные функции
Ф1, ..., Фзп_2, построенные на основе полиномов Лагранжа. Эти ба-
зисные функции имеют следующий вид (который легко получить из
вида шаблонных базисных функций (4.30)):
o,
Ф-2 =
'Фз =
g I т — 11Г х — .zj
2^2-3:!
2 I [ x-xx
3J[t2 -Ti
27 s - p - хг 2 |[ х-т.4
2 x2 - xi (x2 - xY 3 I [ x2 - .iq
0,
27 x-Xj
2 x2 — хг
X — Хч
x2 - xx
-1
x e Qi,
x
(4-36)
(4.37)
(4.38)
0,
ф' =
x G Qj,
x
x G
x g Qb
9 х-хч ( х-хч _ 1V х-хч 2) c o
2 x2 - хч (x2 - a?! 3 Д r2 - jq 3 J
xefl2i
2{x3-x2 3){x3-x2 ЗД.т3-.т2 )’
0, x fi] (J Q2 j
(4.39)
27 x - x2 ( x - x2 _ 2 И x - x2 _ i
2 x3 -x2[x3-x2 3 Д .r3 - x2
0,
x G Q2
x Q2
(4.40)
ит.д.
Действительно, любая из функций ф* может быть выражена как
линейная комбинация функций ф'"'"' и наоборот. Коэффициенты раз-
ложения ф{ по базису из функций ф’"'"' могут быть легко вычислены,
например, следующим способом.
В линейной комбинации 52<72Ф^И’ = w вес базисной функции
j
ф^’" фактически равен значению w(aq), вес базисной функции ф3‘”"4
(А; = 2...п) - значению производной w в точке хк_ч справа, вес ба-
4.7.Сопоставление лагранжевых и эрмитовых кубических ... 157
зисной функции Фзд.-3 “ значению производной w в точке .17. слева,
вес базисной функции Фз^-2 ~ значению ш(жд). Тогда, поскольку
_ 11
„ 2 (х2 — ж,) ’
XI+0 \ z 1/
^Фт
7--------V и
(.г-2 -Ху)
ф5 (т2) — 0, функция ф{ в базисе {ф"*’’"} представляется как
dx
^2-0
Ф'1(х1)=1.
Ф'1 = ФГ" - 11 \ ФГ" - , 1 X ФГ"• (4-41)
Аналогично:
Ф2 = t ФГ" + 7/,^—х ФГ", (4 -42)
(•'г2 2-’]) 2(а>2 ^1)
Фз = 2--гФГ1-, —-'ФГ'"- (4.43)
2(.Т2-Х1) (Я2-Я1)
Функция же гр4 имеет в качестве носителя два элемента, и П2,
и поэтому коэффициенты разложения нужно искать на этих двух эле-
ментах. Мы приведём общий вид функций такого типа:
„I.Z ___ 1 „i.new । 11___„(.new I „i.new
- (хк - ) 'а'^4 + 2(хЛ. - гц) Ф“~3 ^“~2
---7—11-----'Фм"|~7------1----гф'м", к = 2...п. (4.44)
2(^+1-.rt) “-1 (®4+1"М
Остальные функции (ФзЛ._4 и Фзд._3, (Л = 3...п)) определяются
формулами, аналогичными (4.42) и (4.43).
Очевидно, что проверить справедливость полученных соотношений
(4.41)-(4.44) можно также подстановкой в них явных выражений для
функций ф”е’" и ф£.
Получение же представления функций ф”' “ в виде линейной ком-
бинации функций ф- оставляем читателю в качестве упражнения (для
угого мы рекомендуем воспользоваться тем, что в линейной комбина-
ции q/ф, = w вес базисной функции совпадает со значением функ-
I
ции //; в соответствующем узле сетки, в том числе и во внутренних
узлах .гА;+1 = хк 4-1 hk и хк+з_ = хк +| hk , где hk = хк н - тК,
А- = 1...71-1).
Заметим, что используемая нами здесь нумерация узлов отличается
oi введенной в разделе 4.5 - мы ввели дробные индексы при нумера
ции внутренних узлов, и поэтому номера узлов нс совпадаю! с нбме-
рлми базисных функций (как и у эрмитовых элементов). Однако при
158
4.Од номерные задачи
программной реализации нет никакой необходимости хранить коорди-
наты внутренних узлов, и нумерация с дробными индексами, вообще
говоря, является более естественной при хранении в памяти компью-
тера только граничных узлов конечных элементов (так как в этом слу-
чае номер узла совпадает с номером ячейки массива, в которой хра-
нится координата соответствующего узла).
Очевидно, что такой способ нумерации узлов можно, в принципе,
использовать и для квадратичных элементов - при этом внутренний
узел на элементе будет иметь номер к +|, и узлам с целочисленным
индексом k будет соответствовать базисная функция > а для У3-
лов с дробным индексом к + | - базисная функция ф2А. •
Вернёмся к вопросу сопоставления лагранжевых и эрмитовых ку-
бических элементов. В качестве упражнения читатель может доказать,
что в случае одинакового разбиения расчётной области на конечные
элементы пространство, натянутое на базисные функции эрмитовых
элементов с непрерывной производной, является подпространством
пространства, натянутого на базисные функции лагранжевых элемен-
тов. Для этого достаточно показать, что любая из базисных функций
эрмитовых элементов с непрерывной производной (см. рис. 9,о) может
быть представлена в виде линейной комбинации базисных функций ф-
(см. (4.36}-(4.40)); обратное же, очевидно, невозможно (ни одна из
базисных функций ф, не имеет непрерывной производной и поэтому
не может быть представлена в виде линейной комбинации базисных
функций эрмитовых элементов с непрерывной производной).
Заметим также, что при одинаковом разбиении расчётной области
на конечные элементы размерность пространства решении Гт.е. число
неизвестных весов в разложении решения по базисным функциям,
которое часто называют числом степеней свободы) у эрмитовых эле-
ментов порядка 2N (где N - число конечных элементов), а у лагран-
жевых- порядка 3N . Таким образом, размер СЛАУ для лагранжевых
элементов в 1.5 раза больше, чем для эрмитовых, при использовании
одного и того же разбиения расчётной области на конечные элементы.
Но если оценивать общие вычислиюльпые затраты на получение ко-
нечноэлементного решения, следует учитывать ещё и заполненность
матрицы СЛАУ. В результате выигрыш но вычислительным затратам у
одномерных эрмитовых элементов при использовании одной и той же
сетки сокращается примерно до 15%.
4.8. СРАВНЕНИЕ ПО ТОЧНОСТИ ЛИНЕЙНЫХ, КВАДРАТИЧНЫХ
И КУБИЧЕСКИХ ЭЛЕМЕНТОВ НА ПРИМЕРАХ РЕШЕНИЯ
ЭЛЛИПТИЧЕСКИХ ЗАДАЧ НА РАВНОМЕРНЫХ СЕТКАХ
В данном разделе мы проведём сравнение по точности конечных
элементов различных типов с использованием рассмотренного в разде-
ле 3.7 подхода к вычислению энергетической нормы погрешности,
4.8.Сравнение по точности ...
159
основанному на вычислении значений линейной формы /(и) (см. со-
отношения (3.87), (3.96), (3.98), (3.99) и (3.101)).
4.8.1. СРАВНЕНИЕ ЛАГРАНЖЕВЫХ И ЭРМИТОВЫХ КУБИЧЕСКИХ ЭЛЕМЕНТОВ
Рассмотрим следующую краевую задачу для дифференциального
уравнения (4.1), определённого в области Q = [0,3]. Параметры урав-
нения определим следующим образом:
Х = 0.5, ч = 2, = (4.45)
а на границах расчётной области зададим краевые условия третьего и
второго рода:
-Хф-| + ti(0) + 0.5 = 0, Х^| = ес+0.5. (4.46)
^1.г=0 ^11=3
Нетрудно убедиться, что точным решением этой задачи является
функция:
и(:г) = е2х +т. (4.47)
На рис. 11 показан вид точного решения (4.47) рассматриваемой за-
дачи и его конечноэлементных приближений, полученных на сетках из
одного и двух эрмитовых элементов.
Таблица 1
Количество конечных элементов Лагранжевы элементы Эрмитовы элементы
1 160957.503 160957.503
164940.372 164857.435
3 165161 Г78- 165145.652
165187.740 165183.560
5 165192.827 165191.390
6 165194 Г47 165193.564
I65194.57T" 165194.304
Г“ 165194.730 165194.596
165194.797 165194.725
10 165194.828 165194.787
Проведём сравнение по точности конечноэлементных решений, по-
лучаемых с использованием лагранжевых и эрмитовых кубических
элементов на различных сетках. В данном случае для сравнения по-
грешностей двух конечноэлементных решений мы можем воспользо-
ваться соотношением (3.101), поскольку в рассматриваемой задаче на
неоднородных краевых условий первого рода.
В табл. 1 приведены значения формы f(uh f (т.е фактически квад-
рата энергетической нормы соответствующего консчноэлсмсн1пого
решения) для лагранжевых и эрмитовых элементов при различном
количестве конечных элементов в равномерной сегке.
Вычислим значение формы f для точного решения (147)
160
4.Одномерные задачи
3
f(u) = J f(x)u(jc)dx + 0upu(O)-F-
о
iz(3) =
,2т
О
О
С
1.т=3
О
Д'численное решение in сетке из одного элемента
численное решение на сетке из двух элементов
У точное решение
Рис. 11. Вид точного решения и двух
эрмитовых копечноэлементных
приближений
В табл. 2 приведены значения
погрешностей конечноэлементных
решений для лагранжевых и эрми-
товых элементов в энергетической
норме (т.е. вычисленные по фор-
муле ||и - и1' ||э = ,
см. соотношение (3.87)) и в норме
пространства 1% (вычисленные по
\2
) dQ с ис-
и — и
формуле И*
N Я
пользованием численного интег-
рирования).
Как видно из приведённых в
габл. 2 данных, при одинаковом
разбиении расчётной области ла-
гранжевы элементы дают более
точное решение по сравнению с
эрмитовыми. Однако следует пом-
нить, что при одинаковом разбие-
нии лагранжевы элементы по
сравнению с эрмитовыми требуют
и больших вычислительных за-
трат.
этих элементов при условии пример-
ного равенства вычислительных затрат, то легко убедиться, что эрми-
товы элементы имеют некоторое преимущество перед лагранжевыми.
Действительно, вычислительные затраты для эрмитовых элементов на
сетке с шестью элементами примерно равны вычислительным затратам
для лагранжевых элементов с пятью элементами, а погрешность ко-
нечноэлементных решений в энергетической норме для эрмитовых
элементов на 20 % ниже
||и — и1' || = 1.43 для лагранжевых).
Если же проводить сравнение
иА || =114 для эрмитовых против
4.8.Сравнение поточности ...
161
Нормы погрешности___________Таблица 2
Количество конечных элементов Энергетическая норма Норма пространства L2
Лагранжевы элементы Эрмитовы элементы Лагранжевы элементы Эрмитовы элементы
65.1 65.1 19.52 19.52
Т~ 15.95 18.4 3.12 ТП
Т~ “Г8 7.02 0.811 1.17
~г~ 2.67 3.36 0.287 0.445
5 1.43 1.86 0.125 0.205
6 0.847 1.14 " 0.06201 0.107
7 ~О.ЗТГ ~Т748 0 0341 0.0615
8 0.37 0.518 0.0203 0.03'78
' 9 0.26 0.373 00128 0.0246
10 " 0.19 0.28 0.0084 0.0166
Для сетки же из семи эрмитовых элементов вычислительные затра-
ты даже меньше, чем для сетки из шести лагранжевых, а погрешность
приближенных решений в энергетической норме для эрмитовых эле-
ментов на 11 % меньше (0.748 против 0.847). На сетке же из десяти
эрмитовых элементов, которая по вычислительным затратам практиче-
ски соответствует сетке из восьми лагранжевых элементов, погреш-
ность конечноэлементного решения в энергетической норме (рав-
ная 0 28) на 25 % меньше, чем для лагранжевых элементов на сетке из
восьми элементов (для нее noiгрешность равна 0 3 7).
Аналогичная ситуация наблюдается и для погрешности конечно-
элементных решений в норме пространства Z-2
Таким образом, при примерном равенстве вычислительных затрат
эрмитовы элементы оказываются несколько точнее лагранжевых, т.е.
для рассмотренного примера эрмитовы элементы являются чуть более
эффективными по сравнению с лагранжевыми элементами Отметим,
что такая ситуация характерна для большинства эллиптических крае-
вых задач.
Обратим внимание ещё на одну немаловажную деталь, связанную с
поведением производной численного решения, полученного с помо-
щью кубических лагранжевых и эрмитовых элементов. Кроме того что
у эрмитовых элементов производная непрерывна во всей расчётной
области, она, как правило, более равномерно приближает производную
dujdx точного решения. У лагранжевых же элементов на одних участ-
ках расчётной области производная численного решения может быть
довольно близкой к точной, но зато на других - существенно откло-
няться от нее. Это проиллюстрировано на рис. 12.
На рис 12,а показано поведение производной dujdx точного реше-
ния (4.47) рассмотренной в данном разделе задачи и производных двух
162
4.Одномерные задачи
численных решений (на кубических лш ранжевых и эрмитовых эле-
ментах) для сетки из двух конечных элементов1. Видно, что в окрест-
ности точки х = 1.5 производная на лагранжевых элементах терпит
разрыв и справа от точки х = 1.5 довольно существенно отклоняется
от точного решения (хотя слева от этой точки она проходит заметно
ближе, чем у эрмитовых). На рис. 12,6 показано (в более крупном мас-
штабе) поведение du^lx и производных двух численных решений для
сетки из восьми конечных элементов в окрестности одного из узлов
сетки (хц; = 1.875). Здесь мы видим, что, хотя погрешности производ-
ных численных решений, полученных на лагранжевых и эрмитовых
элементах, довольно близки, производная на эрмитовых элементах
ведёт себя более гладко, что больше соответствует поведению произ-
водной точного решения. Такое поведение производных рассматри-
ваемых нами конечноэлементпых решений характерно и для окрестно-
стей других узлов, являющихся I раницами конечных элементов.
Рис. 12. Графики производной точного и численных решений на сетке:
а - из двух конечных элементов; б — из восьми конечных элементов
Обратим также внимание на то, что мы сравнивали поведение про-
изводных для лагранжевых и эрмитовых элементов на одинаковых
1 Графики производных построены по набору их значений в отдельных
точках расчётной области, поставленных с шагом 0.001:
Д </ч|> i(».)| „ .
= Е Заметим, что фактически при вычислении про-
изводной в точке х^ нужно использовать только те базисные функции, кото-
рые нс равны нулю на конечном элементе, содержащем точку жд.. Довольно
подробно соответствующая процедура для эрмитовых элементов будет рас-
смотрена в разделе 4.17 (при вычислении значений и производных сплайна в
произвольной точке).
4.8.Сравнение по точности ...
163
сетках, и следует учесть, что кубические эрмитовы элементы на одном
и той же сегкс требуют меньших вычислительных затрат по сравнению
с лагранжевыми
4.8.2. СРАВНЕНИЕ ЛИНЕЙНЫХ И КВАДРАТИЧНЫХ ЭЛЕМЕН IОВ
ДЛЯ ЗАДАЧИ БЕЗ КРАЕВЫХ УСЛОВИЙ ПЕРВОГО РОДА
Для рассмотренного в предыдущем разделе примера (краевой за-
дачи для дифференциального уравнения (4.1) с параметрами (4.45),
краевыми условиями (4.46) и решением (4.47)) проведём сравнение по
точности конечноэлементных решений, полученных с использованием
линейных и квадратичных элементов на сетках с одинаковым количе-
ством узлов, т.е. в сетке с квадратичными элементами число конечных
элементов будет вдвое меньше.
Для линейных элементов возьмём равномерную сегку с шестью ко-
нечными элементами, а для квадратичных соответственно с гремя.
Векторы правых частей и векторы весов для линейных и квадра-
тичных элементов выглядят следующим образом:
Ь/,’ЛИ11 = (-А, 0.5,1,1.5, 2, 2.5, jj-106) ,
q/; Лин _ 74, 2 57( 6 S8j 18 д 49 д 139> 391jT ,
Ь,/ КВ = (-0.5, 2, |, 1.5-106 )Т ,
q '’кв = (1.08, 3.33, 8.73, 21.9, 57.6,149. 403^ ,
(компоненты векторов весов приводятся с точностью до трёх значащих
цифр).
Для сравнения приведём также значения в у шах точного решения
q7i = (1., 3.22 ,8.39 ,21.6, 56.6, 151, 40б)Т .
Поскольку в задаче отсутствуют неоднородные главные краевые
условия, мы можем воспользоваться соотношением (3.101) для сравне-
ния погрешностей конечноэлементных решений. Вычислим значения
формы f для конечноэлементпых решений и1 ,лин (на линейных эле-
ментах) и t?' KB (на квадратичных элементах):
f = Ьл’л,,н • чм,,и = 158810 ,
/(ii/t,Kn) = Ьл,кв • qft,KB =163918.
Используя эти значения, с помощью соотношения (3.101) можно
сравнить соответствующие погрешности:
-L-uM|2 = = 5108. (14Х)
164
4,Одномерные задачи
Таким образом, квадратичные элементы оказались точнее линей-
ных при одинаковом количестве узлов. Правда, и вычислительные
затраты для них несколько выше, поскольку даже при одинаковой раз-
мерности конечноэлементной СЛАУ её матрица для квадратичных
элементов заполнена ненулевыми компонентами почти в 1.5 раза
больше, чем для линейных.
В принципе, полученная разность погрешностей (4.48) хотя и пока-
зывает, что квадратичные шеменгы дают меньшую погрешность в
решении, но по сё значению нс совсем ясно, насколько эта разность
велика по сравнению с самими погрешностями. Представление об этом
может дать, например, сравнение мой разности с разностью погреш-
ности на линейных или кв трагичных элементов на двух разных сет-
ках - рассматриваемой и вложенной к ней (т.е. на сетках с шагом h и
h!2). Так для линейных элементов разность решений на двух таких
сетках равна 4716 (для них f и
А.,лип
= 163525.55), а для квадратич-
Д КП
ных она равна 1174 (для них f и 2
= 165092.21). Таким образом,
разность между погрешностями на линейных и квадратичных элемен-
тах при одинаковом количестве узлов оказалась даже больше, чем ме-
жду решениями на двух вложенных сетках.
Заметим, что погрешность решения на квадратичных элементах
оказалась меньше, чем на линейных шементах даже для сетки с удво-
енным количеством узлов. Дальнейшее дробление сетки приведёт к
ещё большему преимуществу квадратичных элементов по критерию
точности при примерно равных вычислительных затратах. Это харак-
терно для ситуации, когда решение задачи является достаточно глад-
кой функцией. Однако ниже будет рассмотрен пример, показывающий,
что увеличение порядка элемента может не быть столь эффективным
способом повышения точности решения, если задача решается в об-
ласти с сильно различающимися по её подобластям параметрами диф-
ференциального уравнения.
4.8.3. СРАВНЕНИЕ ЛИНЕЙНЫХ И КВАДРАТИЧНЫХ ЭЛЕМЕНТОВ
ДЛЯ ЗАДАЧИ С КРАЕВЫМИ УСЛОВИЯМИ ПЕРВОГО РОДА
Вообще говоря, как вычислять норму разности погрешностей
двух конечноэлементных решений для задачи с неоднородными крае-
выми условиями первого рода, мы уже рассматривали выше в разделе
4.4.3. Но в приведённом там примере погрешность вычислялась только
через значения формы . В данном разделе мы хотим показать, как
можно вычислять норму разности погрешностей решений не только с
помощью соотношения (3.99), в котором используются значения изме-
нённой линейной формы но и с помощью соотношения
(3.100 ), в котором линейная форма берётся из исходной задачи, но
4.8.Сравнение поточности ...
165
необходимо вычислять значения билинейной формы L(w!,,uh ). В по-
следнем случае мы продемонстрируем, как можно вычислять значение
L[w!,,uh^ с помощью матрицы конечноэлементной СЛАУ.
Рассмотрим краевую задачу для дифференциального уравнения
(4.1) с параметрами (4.45). Краевые условия зададим в виде
-Х^-\ 4-и(0) + 0.5 = 0, w(x)|T=3 =eG+3, (4.49)
dx lx=o
т.е. на правой границе вместо второго краевого условия, определённо-
го в (4.46), зададим главное краевое условие. Очевидно, что точным
решением полученной краевой задачи (4.1), (4.45), (4.49) является
функция (4.47).
Поскольку рассматриваемая краевая задача содержит неоднородное
краевое условие первого рода, для оценки разности погрешностей двух
конечноэлементных решений можно использовать либо соотношение
(3.99), либо соотношение (3.100). Рассмотрим эти ситуации. В качестве
функции w<J выберем константу, равную значению главного краевого
условия:
w!l = eG + 3 .
С помощью соотношений (3.92) получим, что при таком выборе w!l
функция /°(х) и параметр и^, определяющие форму /° (и1'j, примут
вид:
/° (х) = f(x) — уш!/ = 2.т — 2 (е6 + 3),
и° = - w!l = -0.5 - (eG + 3) = -3.5 - eG .
Нетрудно убедиться, что в этом случае форма /() на функциях
гЛлин и ин,кв примет следующие значения:
/О (?ЛЛИН) =-173242,
f(u,l'KR] = -167883.
Используя соотношение (3.99), получаем, что разность квадратов
норм погрешности конечноэлементного решения гГ,лин, полученною
на линейных элементах, и погрешности конечноэлементного решения
мА,кв, полученного на квадратичных элементах, равна
||и - !Л™Н||2 - ||u - w/‘'K,‘||2 = /° («''“) - /° (и''-1"") = 5359, (4.50)
г.е. квадратичные элементы, как и в задаче со вторым краевым услови-
ем на правой границе, оказались точнее (сравните с (4.48)).
166
4.Одномерные задачи
С другой стороны, поскольку функция wfl точно представима в ба-
зисах обоих подпространств (подпространств линейных и квадратич-
ных базисных функций), для оценки погрешности можно воспользо-
ваться соотношением (3.100). Для этого вычислим значения билиней-
ных форм L(w9,uh'mn>j и L(w//,u/,’kb) , а также линейных форм
/(•<ЛЖИ) и /(1ЛЮ).
В данном случае векторы правых частей (до учёта главного краево-
го условия) и векторы весов решении на линейных и квадратичных
элементах выглядят следующим образом:
Ь'1'™» =(-А 0.5,1. 2.2 5, Ы)Т,
д/1.лин _ (о.77, 2.85, 7.13,1S.9. 51.7 144, 40б) ,
b*’“ =(-ол,у.2.| Л!,1)Т,
ql'.l'B = (1.09. 3.36,8.8. 22. 58.1 150, 406J .
Исходя из этого, получим значения линейной формы
/(<ЛЛИН) = Ю76 , /(7/Л’к") = 1036 .
Учитывая представления и>!1 = = (ч™)Т,Ф и
г=1
п
и1' = гр = гртцд (гр — вектор, составленный из базис-
г=1 ___
ных функций фь г = 1, п , qw - вектор весов разложения функции w!l
по базису {ipi} ), значение билинейной формы L(w!1 ,и>1 можно вы-
числить следующим образом:
L (w!l, uh^ = J X grad w!) • grad uhdil 1 J yu)!,uhdQ. +
+ J&w!,ulldS = j X (q"’)Tgrad ф grad 3pTqz dQ +
S3 $ i
+ f '1(ч,")Ч-фГЧ/‘Ж + [0(q"’)4ibTq'‘dS = (q“)T Aq'“. (4.51)
Поэтому
= (q"’)T A,mnq'M. = 174318 ,
4.9.0 возможности использования эрмитовых элементов ...
167
L(w!l,ull'KB) = (q1")T AKBq/l’KB = 168919,
где матрицы Ал,,н и Акв — это матрицы конечноэлементных СЛАУ,
полученных в результате конечноэлементной аппроксимации с помо-
щью линейных и квадратичных базисных функций соответственно
Обратим внимание на то, что при вычислении значения билинейной
формы
L(wfl,u/t) = (q’")TAq/' (4.52)
глобальная матрица А конечноэлементной СЛАУ должна быть взята
до учёта первых краевых условий (так же. как и вектор b при вычис-
лении значений формы f — (q/l) • b)
Теперь с помощью соотношения (3.100) вычисляем значение разно-
сти квадратов норм погрешности конечноэлементного решения «л>лин ,
полученного на линейных функциях, и погрешности конечноэлемент-
ного решения гЛкв, полученного на квадратичных функциях:
= = 5359,
и, как и следовало ожидать, это значение точно совпадает со значени-
ем разности норм погрешностей, полученных другим способом (см.
соотношение (4.50)).
4.9. О ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ЭРМИТОВЫХ ЭЛЕМЕНТОВ
ДЛЯ РЕШЕНИЯ ЗАДАЧ С РАЗРЫВНЫМ КОЭФФИЦИЕНТОМ
ДИФФУЗИИ
Как уже говорилось выше, из двухузловых кусочно-кубических
локальных базисных функций можно построить глобальные базисные
с непрерывной производной (см. рис 9,6). Это даёт возможность при-
менять эрмитовы элементы с такими базисными функциями (в отличие
от лагранжевых элементов) при решении краевых задач с бигармони-
чсским оператором (т.е. краевых задач для уравнения четвёртого по-
рядка вида —А (А^) 4- уи = f, А - оператор Лапласа ). Кроме того,
>рмитовы элементы удобно использовать при решении задач сглажи-
вания и при построении сплайн-аппроксимаций - эти вопросы мы под-
робно рассмотрим в разделе 4.17.
При решении же эллиптических краевых задач эрмитовы элементы
с непрерывными производными, хотя и не могут дать более точного по
сравнению с лагранжевыми элементами решения при одном и к>м же
разбиении расчётной области на конечные элементы (поскольку про-
странство, натянутое на базисные функции эрмитовых элементов, в
случае одинакового разбиения является подпространством просгран-
168
4.Одномерные задачи
ства, натянутого на базисные функции ла!ранжевых элементов), но
при этом они требуют (как было ска кто чуть выше) немного меньших
вычислительных затрат и удобны для решения задач, в которых иссле-
дователя интересуют значения ие только самой искомой функции, но и
её производных.
На практике значительный интерес представляют задачи с разрыв-
ным (довольно часто кусочно-постоянным) коэффициентом диффузии.
Если при этом интерес представляет не только решение, но и его произ-
водная (в областях непрерывности коэффициента диффузии), то возни-
кает желание использовать возможности построения более гладкого
приближённого решения, предоставляемые эрмитовыми элементами.
Однако использовать только функции с непрерывной производной в
этом случае совершенно нецелесообразно, поскольку точное решение
имеет в точках разрыва коэффициента диффузии разрывную производ-
ную, и аппроксимация точного решения в окрестности этих точек на
эрмитовых элементах с непрерывной производной будет плохой.
Поэтому для решения эллиптических задач с разрывным коэффи-
циентом диффузии можно использовать специальным образом постро-
енные базисы, обеспечивающие непрерывность производной прибли-
жённого решения в областях непрерывности коэффициента диффузии
и её разрывность в точках разрыва коэффициента диффузии.
В следующем разделе мы продемонстрируем возможность использо-
вания комбинированного эрмитова базиса с непрерывной производной в
одних узлах и разрывной в дру| их па примере решения эллиптической
задачи с разрывным коэффициентом диффузии. При этом попутно будет
продемонстрирована сборка копечноэлсментной СЛАУ для несколько
нестандартного базиса {ф^} - мы надеемся, что это позволит читателю
чуть-чуть с другой стороны взглянуть на процедуру сборки конечноэле-
ментных матриц и векторов и глубже понять её основные принципы.
4.10. ПРИМЕР ИСПОЛЬЗОВАНИЯ КОМБИНИРОВАННОГО ЭРМИТОВА
БАЗИСА ДЛЯ РЕШЕНИЯ ЗАДАЧ С РАЗРЫВНЫМ КОЭФФИЦИЕНТОМ
ДИФФУЗИИ
Рассмотрим эллиптическую краевую задачу для уравнения (4.1),
определенного в области Q = [ 1 з], со следующими параметрами:
10, — 1 < J' < 0,
х = 1.0<.Г<.1, <4-53> 0, - 1 < ./ < 0,
4. «<«<., <4-54> 0. -)<.Г<0,
/(т) = •иг о < г < з <4'55>
4.Ю.Пример использования ...
169
Эти параметры были подобраны нами таким образом, чтобы диффе-
ренциальному уравнению (4.1) удовлетворяла функция:
а (ж) =
1 + ж, — 1 < х < о ,
е2а + 8ж, о < х < 3 .
(4-56)
На границах расчётной области Q = [—1,3] зададим краевые усло-
вия третьего и второго рода, параметры которых определим в соответ-
ствии с видом функции (4.56):
хДа| +(ul .+10) = 0, =2(ес + 4), (4.57)
' и—I / ст|5;=з ' '
т.е. в третьем краевом условии (3 = 1, = —10, а во втором краевом
условии 0 = 2 (eQ + 4).
Покажем, как можно построить конечноэлементное решение этой
краевой задачи с использованием эрмитовых элементов с комбиниро-
ванным базисом на сетке из четырёх конечных элементов:
Qi =[-1,0], Q2 =[0,1], Q3 =[1,2], Q4 =[2,3].
В узлах х = — 1, ж = 1, ж = 2, ж = 3 определим стандартным об-
разом по две глобальные базисные функции, отвечающие за значения
конечноэлементного решения и его производную (при этом во внут-
ренних узлах ж = 1 и ж = 2 глобальные базисные функции строятся
стандартной сшивкой соответствующих базисных функций прилегаю-
щих к ним конечных элементов, см. раздел 4.6, с. 149).
В узле же ж = 0, где терпит разрыв коэффициент диффузии X
(см. (4.53)), определим три глобальные базисные функции. Одна отве-
чает за значение производной слева и на конечном элементе
Qj = [—1,0] определяется как локальная функция ф4, а на остальных
элементах доопределяется нулём - в глобальной нумерации это будет
функция ф3. Вторая отвечает за значение решения и определяется
сшивкой локальной функции ф3 конечного элемента =[—1,0] и
локальной функции % конечного элемента Q2 = [ОД] ~ в глобальной
нумерации это будет функция ф4 . Третья отвечает за значение произ-
водной справа и на конечном элементе Q2 = [0,1] определяется как
локальная функция ф2, а на остальных элементах доопределяется ну-
лём - в глобальной нумерации это будет функция ф5.
Вид первых семи глобальных базисных функций приведён на
рис. 13.
Продемонстрируем процедуру сборки глобальной матрицы для та-
кого базиса. С помощью соотношений (4.34}-(4.35) вычислим локаль-
170
4.Одномерные задачи
ные матрицы и векторы правых частей всех четырёх конечных элемен-
тов:
Рис. 13. Вид первых семи глобальных базисных функций
Сборку будем проводить, как обычно, по соответствию локальной и
глобальной нумерации базисных функций. После занесения локальной
матрицы и вектора первого элемента получим (обратим внимание, что
третья локальная базисная функция соответствует четвёртой глобаль-
ной, а четвёртая локальная — третьей глобальной):
4.10.Пример использования ...
171
12 1 1 -12 0 0 0 0 0 0 0 О'
1 4 3 _1 3 -1 0 0 0 0 0 0 0 0
1 -12 _1 3 -1 4 3 -1 -1 12 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
А”1 = 0 0 0 0 0 0 0 0 0 0 0 , bQ| = 0
0 0 0 0 0 0 0 0 D 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
Рассмотрим занесение в глобальную матрицу локальной матрицы
второго элемента Здесь локальный номер 1 соответствует глобально-
му номеру 4, локальный номер 2 - глобальному номеру 5 и т.д. Поэто-
му элемент А^2 заносится в Л44 , Д**2 - в Л45, А^2 - в Д1С и т.д. Ана-
логично (по соответствию локальных и глобальных номеров) заносятся
элементы локального вектора в глобальный. Таким образом, после
занесения локальной матрицы и вектора второго элемента получаем:
12 1 1 -12 0 0 0 0 0 0 о' 0
1 4 3 _1 3 -1 0 0 0 0 0 0 0 0
1 _1 •5 4 1 -1 0 0 0 0 0 0 0 0
-12 J -1 о -1 514 13 _24 L 0 0 0 0 24 5
35 42 35 42
0 0 0 13 6 1 13 0 0 0 0 16 15
Д«1+»2 = 0 0 0 42 _24 35 1 42 94 210 _13 0 0 0 0 56 5
35 42 35 42
0 0 0 1_ __13 _13 6 0 0 0 0 5
42 210 42 35
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
После занесения локальных матриц и векторов третьего и uciBcpio-
ю конечных элементов глобальная матрица и вектор примут вид
172
4.Одномерные задачи
12 1 1 -12 0 0 0 0 0 0 0
1 4 3 1 3 -1 0 0 0 0 0 0 0
1 3 4 3 - 1 0 0 0 0 0 0 0
12 -1 -1 514 3,5 13 42 _24 35 _х 42 0 0 0 0
0 0 0 13 12 6 3.5 _1 42 13 210 0 0 О' 0
"ЬПз +^4 0 0 0 24 3.5 1 42 188 35 0 _24 35 L 42 0 о-
0 0 0 1 42 13 210 0 12 35 1 42 13 210 0 0
0 0 0 0 0 _24 35 1 42 188 _ 0 _ 24 35 L 42
0 0 0 0 0 1_ 42 13 / 21(У 0 12 35 1 42 13 210
0 0 0 0 0 0 0 _24 35 1 42 94 35 __13 42
к 0 0 0 0 0 0 0 L 42 13 210 _13 42 6 351
+0-2 +^3 +^4 _ о, о, 5 16 15 3'2, Я 1.5’ ы- в 216 5 ’ 104 15 Г-
После учёта краевых условий получаем окончательный вид гло-
бальной матрицы А и вектора правой части b конечноэлементной
СЛАУ;
13 1 1 -12 0 0 0 0 0 0 0 ’
1 4 3 _1 3 -1 0 0 0 0 0 0 0
1 _1 3 4 3 -1 0 0 о 0 0 0 0
-12 - 1 -1 514 35 13 42 _24 35 _1_ 12 0 0 0 0
0 0 0 13 42 6 35 1 42 13 210 0 0 0 0
А = 0 0 0 _24 35 1 42 188 35 0 _84 35 1_ 42 0 0
0 0 0 _х 42 13 210 0 12 35 1 42 13 210 0 0
0 0 0 0 0 24 35 •12 188 35 0 _24 35 1 42
0 0 0 0 0 __1_ 42 13 210 0 12 35 1 42 13 210
0 0 0 0 0 0 0 _24 35 1 42 94 35 13 42
0 0 0 0 0 0 0 1_ 42 13 210 13 42 6 35
Н -10, о, о, 24 5 16 15’ 32, £ “ 32 15’ 216-1-2 5 сС+4^ 104 ’ 15 Г-
Решением полученной конечноэлементной СЛАУ является вектор
(с точностью до четырёх знаков)
4.10.Пример использования ...
173
q — ^—0.0131, 0.9087, 0.9987, 0.9856,11.58,15 75, 25.82, 71.85,124.2, 427.3, 785.9) .
При этом вес q} = —0.0131 фактически является значением копсчно-
11
элементного решения uh (х) = 7?;ф, в первом узле ж = —1, вес
г=1
q2 = 0.9987 - значением в нём au!l/dx, q% = 0.9987 - значением
du!1'/dx слева во втором узле х = 0, 74 = 0.9856 — значением и1' в
этом узле, qrj — 11.58 - значением в нём duh'/dx справа, qc = 15.75 -
значением uh в третьем узле х = 1, ([,’ = 25.82 — значением в нём
duh/dx, 78—71.85— значением uh в четвёртом узле х — 2,
7э = 124.2 — значением в нём du!'/dx, qw = 427.3 - значением uh в
пятом узле х = 3 и 7ц = 785.9 — значением в нём du!1/dx . Графики
точного решения и(х) и конечноэлементного решения и1' (х) в окре-
стности точки разрыва коэффициента X приведены на рис. 14.
Рис. 14. Поведение точного и (т) и коиечноэлсмснтного Л г) решений
в окрестности точки разрыва коэффициента X
174
4.Одномерные задачи
Обратим внимание на то, что разрыв производной конечноэлемент-
ного решения во втором у шс *duh jdx = q3 = 0.9987 слева и
duMdx = q-t = 11.58 справа) практически соответствует разрыву в
ко тффициепте X (т.е.
= 1-11.58).
Ж?
dr
= 10 -0.9987 « |Х^-|
О |-()
4.11. АНАЛИЗ СХОДИМОСТИ КОПЬ ЧИО ЭЛЕМЕНТНЫХ РЕШЕНИЙ
НА ПРИМЕРЕ РЕШЕНИЯ ЗАДАЧИ ( РАЗРЫВНЫМ
КОЭФФИЦИЕНТОМ ДИФФУ И1П
В данном разделе мы проанализируем сходимость конечноэле-
ментных решении, построенных с исполт юванием кубических лагран-
жевых и эрмитовых элементов (с непрерывными производными и с ком-
бинированным базисом), на примере решения рассмотренной в преды-
дущем пункте эллиптической краевой тдачи, определяемой уравнением
(4.1) с параметрами (4.53)-(4.55) и краевыми условиями (4.57).
Построим конечпоэлемепгиые решения на последовательно вло-
женных сетках с использованием кубических элементов следующих
типов: лагранжевых, эрмитовых с непрерывной производной и эрми-
товых с разрывной производной в гом узле, где терпит разрыв коэф-
фициент X (т.е. в узле с координатой х = 0). В последнем случае до-
бавляется дополнительная неизвестная, позволяющая строить решение
с разрывной производной в узле ./ 0 (т.е. в этом узле определяется
три глобальные базисные функции, две из которых отвечают за произ-
водную слева и производную справа соответственно).
Погрешность решения будем оценивать в энергетической норме,
норме пространства L - а также но отклонению приближённого реше-
ния отточного в некоторых узлах расчётной области.
Вычислим значение формы (3.22) для точного решения (4.56):
з
f (w) f (х) и (х) dx +13и, (— 1) I X
-1
u(3) = 366742.747013.
з
В табл. 3 приведены значения формы / для численных решений
uh, полученных с использованием кубических лагранжевых элемен-
тов, эрмитовых элементов с непрерывной производной и эрмитовых
элементов с разрывной производной в точке х = 0, в зависимости от
количества к конечных элементов в равномерной сетке.
В табл. 4 приведены энергетические нормы погрешности, вычис-
ленные по формуле (см. (3.87))
||« - «"II =7/(и’-/(“'')>
4.11.Анализ сходимости конечноэлсмснгных решений ...
175
Нй|
а также величина —---г-2- (где и - решение, полученное на ссгке
с удвоенным шагом, т.е. на сетке с количеством конечных элементов
вдвое меньшим, чем при вычислении и'1). Фактически величина
-------: — является показателем скорости сходимости численного
lh-«"II.,
решения к точному в энергетической норме.
__________Таблица 3
к Лагранжевы элементы Эрмитовы элементы с непрерывными производными Эрмитовы элементы с разрывной произ- водной в одном узле
4 366675.375067 366631.239199 366644.323547
8 366741.313321 366735.583156 366740.146517
16 366742.722546 366740.484324 366742.691436
32 366742.746622 366741.652983 366742.745964
64 366742.747007 366742.202673 366742.746995
Таблица 4
Лагранжевы элементы Эрмитовы элементы с непре- рывными производ- ными Эрмитовы элементы с разрывной производной в одном узле
к 2/i „ 2Л
и — и и — и J и — и э
|Ь — и1' || II. и/'II |-д — и1' || 1.. о,/‘II IIм — U>1 II II,, „л||
II II э IIм ||э Г U Из Г”и ||э
4 8.208 10.56 9.921
8 1.197 6.9 2.677 3.9 1.613 6.2
16 0.156 7.7 1.504 1.8 0.236 6.8
32 0.0198 7.9 1.046 1.4 0.0324 7.3
64 0.0025 7.9 0.738 1.4 0.0042 7.7
Из табл. 4 видно, что с измельчением шага сетки вдвое погрешность
чис пенного решения на лагранжевых элементах и эрмитовых элемен тах
с разрывной производной в точке х = 0 убывает на достаточно подроб-
ных ссгках приблизительно в 8 раз, т.е. эти численные решения в jiicp-
югичсской норме сходятся к точному решению с третьим поря псом
аппроксимации (||t/. — ?//'|| = см. (3.76)). На эрмитовых же эле-
ментах с непрерывными производными энергетическая норма погрет-
176
4 Одномерные задачи
пости хотя п убывает с измельчением сетки, но сходимость приближён-
ного решения к 1 очному очень медленная (даже хуже, чем характерная
для линиипых элементов сходимость первого порядка).
Прознали шрусм поведение погрешностей рассматриваемых конеч-
ноэлеменгных решений, вычисленных в норме пространства L). Зна-
чения них погрешностей на различных сетках, а также отношение
норм hoi ровностей1 на сетках с шагами h и 2h приведены в табл. 5.
______________________________________Таблица 5 4
k Лагранжевы элементы Эрмитовы элементы с непре- рывными производ- ными Эрмитовы элементы с разрывной производной в одном узле
11“ -ч IIй-Л. 11“-“‘II. ||“-л. 11“-л.
11“-“"11. 11“-“"II.
4 0.811 1.438 1.170
8 6.201-10’2 13.1 0.339 4.2 0.107 10.9
16 4.104-10’3 15.1 0.154 2.2 8.447-10'3 12.7
32 2.603-10’4 15.8 0.0749 2.1 6.076-10’4 13.9
64 1.633 10’5 15.9 0.0370 2. 4.109-10’5 14.8
Как видно из табл. 5, отношение погрешностей конечноэлементных
решений на лагранжевых элементах и эрмитовых элементах с разрыв-
ной производной в точке х = 0, полученных на сетках с шагами h и
2/z, при достаточно малых h приближается к значению 16, что вполне
согласуется с теоретическим значением сходимости в норме простран-
ства L} для кубических элементов: ||д — г/'Ц = o(h4^, см. (3.86). На
эрмитовых же элементах с непрерывной производной погрешность
конечноэлементного решения в норме пространства Lq убывает очень
медленно (даже для линейных элементов теоретическое значение от-
ношения норм погрешностей решений на сетках с шагами /?, и 2h при
достаточно малых h должно быть около 4).
В табл. 6-9 приведены значения конечноэлементных решений и по-
грешности в отдельных точках расчётной области. В качестве этих
точек выбраны:
• точка х = 0, являющаяся точкой разрыва коэффициента диффузии
(табл. 6);
• точка х = 2/3, выбранная так, что опа не является граничной точ-
кой ни одного конечного элемента ни для одной из рассмотренных
1 Эти нормы вычислялись с помощью численного интегрирования.
4.11.Анализ сходимости конечноэлементных решений ...
177
сеток и при этом является внутренним узлом для лагранжевых )ле-
ментов (табл 7);
• точка а; = 2, являющаяся граничным узлом конечного элемента во
всех сетках (табл 8);
• точка а; = 1/8 , выбранная так, что она становится граничным узлом
на сетке из 32 конечных элементов (табл. 9).
Точка .т = 0 , «(0) = 1 Таблица 6
к иЛ(0) |«(0)-И''(0)| и(0)-?а2/‘ (0)
и(0)-г?(0)
Лагранжевы элементы
4 8 16 32 64 0.9968567775028 0.9999546035124 0.9999993033067 0.9999999891615 0.9999999998318 3.14 1(Г 4.54-1О'5 6.9710’7 1.08-10'8 1.68 1010 69. 65. 64. 64.
Эрмитовы элементы с разрывной производной в одном узле
4 8 16 32 64 0.9856337929327 0.9998386621885 0.9999977568217 0 9999999651616 0.9999999994490 1.44-10’2 1.61 Ю"'1 2.24-10'6 3.48-10‘8 5.51 10’ 0 89. 72. 64. 63.
Эрмитовы элементы с непрерывными производными
4 8 16 32 64 1.844169439378 1.359547843508 1.175990950669 1.087268951193 1.043468858254 0.8442 0.3595 0.176 0.08727 0.04347 2.35 2.04 2.02 2.01
Точка а; = 2/3. и (уз) = 9.127001228017 Таблица 7
к и"(2/3) |и(73)-“"(73)| а(2/3! -«2Л(2/3)
“(2/3 - (2/3)
Лагранжевы элементы
4 8 16 32 64 9.1 10439643740 9.126123915225 9.126952509190 9.126998126813 9.127001038324 1.66-10'2 8.7710'1 4.87 10’1 3.1 -10’6 1.9 -10'7 18.9 18.0 15 7 16.3
178
4.Одномерные задачи
Эрмитовы элементы с разрывной производной в одном узле
4 8.958089626174 0.169
8 9.124600352823 2.401-10'3 70.4
16 9.126801323004 1.999-10'4 12.0
32 9.126991835572 9.392-10* 21.3
64 9.127000582241 6.458-10‘7 14.5
Эрмитовы элементы с непрерывными производными
4 8.849242545851 0.278 „
8 9.055096252254 7.190-10'7 3.86
16 9.108371806601 1 863-1О'7 3.86
32 9.117977105943 9.024-1О’3 2.06
64 9.122516137282 4.485-10'3 2.01
Точка х = 2, и (2) = 70.59815003314 Таблица 8.
к uh (2) и (2)- u2h (2)
u{2}-uh(2}
Лагранжевы элементы
4 8 16 32 64 70.54708936191 70.59734857835 70.59813738895 70.59814983497 70.59815003006 5.11 ю; 8.01 10‘4 1.26-10’5 1.98-10’7 3.08-10-9 63.7 63.4 63.8 64.3
Эрмитовы элементы с разрывной производной в одном узле
4 8 16 32 64 71.8450851743 70.68853960047 70.60331036775 70.59845283064 70.59816864734 1 246 9.04 I02 5.1610'3 3.03-1О’4 1.8610’5 13.8 17.5 17.0 16.3
Эрмитовы элементы с непрерывными производными
4 8 16 32 64 71.87110061960 70.68620772960 70.60201878871 70.59781550065 70.59785137347 1 273 _ 8.81 I0'7 3.87-1О’3 3.35-10"4 2.99-10'4 14.5 22.8 1 1.6 1.1
Из приведённых в табл. 6 9 результатов видно, что в разных точках
расчётной области наблюдается различная и часто неравномерная схо-
димость конечноэлементных решений к точному. В точках, являю-
щихся граничными узлами элементов (точки ж —0 и х = 2),у ла-
гранжевых элементов наблюдается очень высокая скорость сходимо-
сти (отношение погрешностей на двух соседних сетках около 64, т.е.
- иногда это свойство называют суперсходимостью). В точках,
не являющихся граничными узлами конечных элементов (например,
х — 2/3), наблюдается скорость сходимости, близкая к скорости схо-
4.11 .Анализ сходимости конечноэлементных решений ...
179
димости в норме пространства £2 . Особый интерес представляс! точка
х = 1/8 - в пей наблюдается очень неравномерная сходимость. Одна
ко следует обратить внимание на то, что на сетке из 32 конечных эле-
ментов эта точка становится граничным узлом конечного элемента (в
этот момент погрешность уменьшается очень резко), и при дальней
шем дроблении сетки погрешность начинает убывать со скоростью
характерной для других рассмотренных нами точек, являю-
щихся граничными узлами конечных элементов
Точка х = 1/8, — 2.284025416688 Таблица 9.
к и1' (1/8) | и (1/8) - г? (1/8)| и 1 V8) - u2h И
U (1/8 1 - uh (1/8)
Лагранжевы элементы
4 8 16 32 64 2.299430315712 2.2841826823 1 2.283983000417 2.284025404350 2.284025416496 1.54 10^ 1.573 10"* 4.242 10'5 1.234 10'8 1.915-10'10 98 3.7„ 34 4-102 64.4
Эрмитовы элементы с разрывной производной в одном узле
4 8 16 32 64 2.375253745065 2.284929619187 2.283946303147 2.284031558227 2.284025844011 9.12 10'2 9.04-10’1 7.91-10'5 6.14-10'6 4.27-10'7 00.9 11.4 12.9 14.4
Эрмитовы элементы с непрерывными производными
4 8 16 32 64 2.327170451747 2.050916091712 2.159130114464 2.278274344669 2.272558737308 4.315-10'- 0.233 0.125 5.751-IO’’ 1.14710’2 0.19 1.9 21.72 0.501
Эрмитовы элементы с разрывной производной в точке х — 0 в точ
кс разрыва ведут себя аналогично лагранжевым (скорость сходимости
(’(^ь)), а в остальных точках скорость сходимости близка к O(h ]
(как в норме пространстве L2).
,/(ля эрмитовых же элементов с непрерывной производной наблюла
С1ся крайне медленная и неравномерная сходимость - в точках г I) и
I 2/3 скорость сходимости соответствует сходимос ти в норме / 2 , а в
iочках .г = 1/8 и х = 2 погрешность ведёт себя очень нсс1аоилыю (в
180
4.Одномерные задачи
точке х = у8 она даже возрастает при переходе от сегки с 4 к сетке с 8
элементами и при переходе от се тки с 32 к сетке с 64 элементами).
Заметим, что результаты проведённых исследований практически
нс изменились бы, если вместо точного решения было бы использова-
но решение на более подробной сетке (например, на сетке из 128 ко-
нечных элементов), т.е анализ сходимости конечноэлементных реше-
ний можно проводить, в принципе, и без знания точного решения.
В заключение проведённого анализа отметим, что конечноэлементное
решение — это всё же функция, а не набор значений в узлах. и поэтому его
погрешность всё-таки корректней оценивать в какой либо норме функ-
ционального пространства (наиболее естественной здесь является энер-
1 егическая), а нс по значениям в отдельных точках расчётной области.
4.12. О ВОЗМОЖНОСТИ УЧЁТА В ТОРОГО КРАЕВОГО УСЛОВИЯ
КАК ГЛАВНОГО ДЛЯ ЭРМИТОВЫХ ЭЛЕМЕНТОВ
Поскольку у эрмитовых элементов в качестве весов разложения
конечноэлсменгного решения но базисным функциям используются
значения не только самого решения, но н его производных, может воз-
никнуть желание (якобы) для более точного учёта второго краевого ус-
ловия зафиксировать вес базисной функции, отвечающей за соответст-
вующую производную конечноэлсменгного решения (т.е учесть второе
краевое условие как главное) Однако с теоретической точки зрения
такая процедура не должна привести к улучшению точности конечно-
элементного решения в целом Действительно, жёсткая фиксация одного
(или нескольких) весов фактически умети,шает размерность подпро-
странства, в котором ищется приближённое решение, а с учётом того,
что МКЭ ищет на выбранном подпространстве функцию, ближайшую в
энергетической норме к точному решению, с уменьшением размерности
этого подпространства точность может только ухудшиться.
Проиллюстрируем это на решении задачи (4.1), (4.53)-(4.55), (4.57)
рассмотренной в предыдущих разделах. Оба решения будем искать с
использованием эрмитовых элементов с разрывной производной (см.
раздел 4.10), но в первом случае второе краевое условие (из (4.57))
будем учитывать как естественное, а во втором - как главное, то есть
заданием уравнения Фн+t 1 ' (гДе п ~ количество узлов в
сетке) вместо последнего уравнения конечноэлементной СЛАУ. При
этом следует помнить, что линейная форма /(и) и во втором случае
должна иметь добавки от второго краевого условия, иначе решение
будет абсолютно неверным (из-за неэквивалентности вариационной
постановки исходной краевой задаче).
В табл. 10 приведены энергетические нормы погрешности и величи-
на ||u — Дд —uz'|| , определяющая скорость сходимости для ре-
шений, полученных на различных сетках (эта таблица построена ана-
логично табл. 4).
4.13.Повышение точности конечноэлсментного решения ... 181
Как видно из табл. 10, при учёте второго краевого условия как глав-
ного точность получаемого конечноэлементного решения несколько
хуже (особенно на сетках с небольшим количеством элементов). <
измельчением сетки разница между погрешностями в обоих решениях
начинает уменьшаться, поскольку, с одной стороны, размерности под-
пространств становятся более близкими, а с другой стороны, вес q-2lt. i
при учёте второго краевого условия как естественного стремится к
точному шачению.
В целом же -проведённые рассуждения и рассмотренный пример
показывают, что не имеет никакого смысла учитывать второе краевое
условие как главное (фиксированием соответствующего веса). Т очно
так же это нецелесообразно делать при решении и многомерных (двух-
и трёхмерных) задач.
_____ ____________Таблица 10
к с учётом второго крае- вого условия как есте- ственного с учётом второго краево- го условия как главного
“‘II и — и21' 1 и — и2'1 э
и — и'1 и — и1'
4 8 16 32 64 9.921 1.613 0.236 0.0324 0.0042 6.2 6.8 7.3 7.7 14.2 2.099 0.28 0.0359 0.0045 6.8 7.5 7.8 7.9
4.13. ПОВЫШЕНИЕ ТОЧНОСТИ КОНЕЧНОЭЛЕМЕНТНОГО РЕШЕНИЯ
ЗА СЧЁТ ИСПОЛЬЗОВАНИЯ НЕРАВНОМЕРНЫХ СЕТОК
До сих пор для повышения точности приближённого решения мы
использовали самый очевидный и простой способ - равномерное
уменьшение размеров всех элементов сетки. Однако во многих случаях
(особенно при решении двух- и трехмерных задач) гораздо более эффек-
тивным является другой способ, заключающийся в использовании не-
равномерных сеток со сгущениями узлов в тех местах расчётной облас-
ти, где погрешность приближённого решения особенно велика. Проил-
люстрируем это на примере решения следующей эллиптической задачи
Пусть расчётная область Р = [0,4] состоит из двух подобластей
Q1 =[0,1] и Q2 =[1,4]. При этом коэффициент диффузии X равен
единице во всей области П, а коэффициент и правая часть /(./)
уравнения (4.1) определяются соотношениями:
Ч(-'Г) =
1, х Е Q1,
1000, х Е Q2,
/(.т) =
10, .гЕР1,
0, .г Е Р2.
182
4.Одномерные задачи
На границах расчетной области Q зададим вторые краевые усло-
вия:
— — Ч <9и| _ г,
°’ 5.а,=4
Оценим погрешность решения этой задачи на линейных и кубиче-
ских базисных функциях.
Вначале получим решение на очень подробной сетке, и относи-
гельмо iici о будем оценивать погрешность остальных решений.
Общий вид этого решения д* представлен на рис. 15,а. Значение
формы J для него
/(и’) = 81.70 .
Возьмём конечиоэлеменгную сетку, состоящую из двух конечных
элементов, совпадающих с подобластями Q1 = [0,1] и Q2 =[1,4], и
получим решение1 л,2,куб (.т) с использованием лагранжевых кубиче-
ских элементов Значение формы для этого решения
/(u2’Ky6U)} = 78.7.
Теперь выберем сетку с пятью конечными элементами и узлами с
координатами {0, 0.4, 0.85,1,1.05, 41 и построим на ней конечноэле-
менч нос решение (а?) с использованием линейных базисных
функций. Значение формы для этого решения составило:
./' (7/Лл,,н (.г)) = 80.83 .
Пользуясь оценкой (3.101), легко убедиться, что решение и5-ли" (х),
полученное па линейных элементах, точнее решения и.2 куб (х), полу-
ченного на кубических элементах. При этом сетка с кубическими эле-
ментами содержала 7 узлов (включая внутренние), а с линейными -
только 6. Это говорит о том, что в данном примере при использовании
линейных элементов было получено решение нс только точнее, чем
при использовании кубических, по и с существенно меньшими вычис-
лительными затратами — следует также учесть, что даже при одинако-
вом размере матрицы конечноэлементиой СЛАУ ширина ленты и за-
полненность се матрицы ненулевыми компонентами для линейных
конечных элементов гораздо (как минимум в 2 раза) меньше, чем для
кубических.
Теперь добавим ещё один конечный элемент в сетку для кубиче-
ских функций вблизи области разрыва коэффициента Новая сегка
1 Верхние индексы у w2,Kyb (.г) означают: «2» - количество элементов,
«куб» - характеристика базисных функций.
4.13.Повышение точности конечноэлементного решения ...
183
содержит 3 конечных элемента =[0,1], Q2 = М-1] и =[| 1,4|.
Значение линейной формы / для полученного на этой сетке решения1 *
^Зн.куб составило;
/(д3н кУби)) = 81.698 .
Эго решение уже гораздо точнее решения (а:) и довольно
близко к точному. Графики всех полученных конечноэлементных ре-
шений показаны на рис. 15. Отметим, что при эквивалентных вычис-
лительных затратах никакая неравномерная сетка с линейными базис-
ными функциями уже не позволит получить приближенное решение,
заметно более близкое к точному. Это означает, что при дальнейшем
дроблении сетки кубические элементы будут значительно эффективнее
линейных, поскольку для кубических элементов погрешность конеч-
ноэлсментного решения убывает с дроблением шага сетки гораздо
быстрее, чем для линейных (при дроблении шага сетки вдвое начиная
с некоторого размера шага для кубических элементов погрешность
решения в энергетической норме уменьшается в восемь раз, а для ли-
нейных- только в два раза). При этом вычислительные затраты для
линейных и кубических элементов при одинаковом дроблении сетки
(для одномерных задач) возрастают примерно одинаково.
Рис. 15. Решение эллиптической задачи с разрывным коэффициентом
а - общий вид точного решения;
б — поведение решений в окрестности точки разрыва коэффициента ;
в - поведение решений в окрестности левой границы
1 Здесь первый верхний индекс «Зн» у н’'"'куб(.г) озпачас!, то и ccikc J
конечных элемента и дробление сетки было неравномерным
184
4.Одномерные задачи
Тем не менее рассмотренный пример показывает, что в существен-
но неоднородных областях (т.е. в областях, состоящих из подобластей,
в которых параметры решаемого дифференциального уравнения могут
очень сильно различаться и точное решение не является достаточно
гладким) вполне приемлемое по точности конечноэлементное решение
с минимальными вычислительными загратами могут давать именно
линейные элементы. Но при этом существенным фактором, обеспечи-
вающим хорошую точность при малых вычислительных затратах, яв-
ляется то, что разбиение подобластей и i элементы делается с неравно-
мерным шагом дискретизации.
Отметим, что стандартное дробление ccikh вдвое даже на кубиче-
ских элементах совсем не скоро привело бы к приемлемому по точно-
сти решению. Продемонстрируем ио, решая рассматриваемую задачу
па сетках, полученных последов не п.ными равномерными дробления-
ми исходной сетки (содержащей два > 1смсита, совпадающих с подоб-
ластями Q1 и Q2).
После двух равномерных дроблении эта сетка состоит из восьми
конечных элементов £^ = [0,0.25], , [0.25,0.5], Q3 — [0.6,0.75],
= [0.75,1], Q5 =[1,1.75], Ц, =[1.75,2.5], Q7 =[2.5,3.25],
= [3.25,4]. Значение формы I для мои сетки составляет1:
/(г?р’куб (.-/•)) ВО 15 .
Таким образом, решение u8p,Mt (.») даже хуже решения и5’;,т| (ж),
полученного с помощью линейных ч.нпсных функций. Причём вычис-
лительные затраты на его получение уже намного больше. Этот ре-
зультат говорит о том, что при равномерных дроблениях сетки с из-
мельчением каждой ячейки вдвое для определённых задач можно до-
вольно долго нс получать приемлемое по точности решение.
Отметим ещё один интересный факт, связанный с особенностью дроб-
ления сетки. Для этого более по ipoGiio рассмотрим поведение конечно-
элементных решений в окрестности точки ; = 1 разрыва коэффициентов
и в окрестности левой границы .г 0 расчетной области (см. рис. 15,б,«).
Сравним поведение конечно шементных решений гС’Л|,,‘(.т) и
^ьр.куо Очевидно, что в окрестное in точки х = 0 конечноэлемент-
ная сетка, на которой было получено решение и8р,куб, гораздо подроб-
нее сетки, на которое получено решение у/лЛ,,н (и, кроме того, был на-
много выше и порядок полиномов, использованных при вычислении
д8р,куб). Тем нс менее функция ur,,IU111 в окрестности точки х = 0 го-
раздо ближе к точному решению, чем функция «8р,куо, т.е. дробление
сетки в окрестности точки / 0 не привело к существенному умень-
шению погрешности в этой подобласти. Причина этого заключается в
том, что для а р,куб слишком велика погрешность в окрестности точки
1 Здесь первый верхний индекс «8р» у и'1’,куб (.с) означает, что в сетке 8
конечных элементов и дробление сетки было равномерным.
4.14.Тестирование процедур построения ... 185
х = 1 (где из-за большого скачка в значении коэффициента очень
сильно меняется поведение точного решения), и это определяет поведе-
ние конечноэлементного решения даже в удалённых от нее подоблас тях
расчётной области. Это означает, что для снижения погрешности конеч-
ноэлементного решения в некоторой (интересующей исследователя)
подобласти часто бывает совершенно недостаточно измельчать сетку
только в её окрестности - более существенное влияние на точность по-
лучаемого конечноэлсментного решения может оказать сетка в местах
резкого изменения поведения точного решения (определяемых резкими
изменениями в значениях параметров решаемой задачи).
Таким образом, рассмотренная в данном разделе модельная задача
показывает, что использование сеток с неравномерным шагом дискре-
тизации может быть очень эффективным средством существенного
повышения точности конечноэлементыого решения при минимальном
увеличении вычислительных затрат.
Особенно большой эффект от использования неравномерных сеток
достигается при решении двух- и трёхмерных задач в неоднородных
областях. Такая ситуация довольно характерна для многих практиче-
ских задач, и этим объясняется тог факт, что при решении практиче-
ских задач обычно используются конечные элементы с базисными
функциями невысокого порядка (чаще всего это линейные элементы).
4.14. ТЕС ТИРОВАНИЕ ПРОЦЕДУР ПОСТРОЕНИЯ
КОНЕЧНОЭЛЕМЕНТНЫХ РЕШЕНИЙ
Как уже говорилось в разделе 3.6, для проверки правильности
процедур построения конечноэлементных решений удобно использо-
вать тестовые задачи, решениями которых являются полиномы или
кусочные полиномы, точно представимые в виде линейной комбина-
ции базисных функций. Так, при тестировании конечных элементов с
линейными базисными функциями используются линейные (или ку-
сочно-линейные) полиномы, квадратичных — линейные и квадратич-
ные (а также кусочпо-линеипые или кусочно-квадратичные функции),
кубических - полиномы (или кусочные полиномы) до третьей степени
включительно. При тестировании процедур, использующих эрмитовы
конечные элементы с непрерывными производными, необходимо пом-
нить, что тест нужно строить таким образом, чтобы искомая функция
была непрерывна вместе со своей первой производной. Для тестирова-
ния же процедур, использующих эрмитов базис с разрывными коэф-
фициентами, нужно рассматривать и такие тестовые задачи, решения
ми которых являются функции с разрывной производной.
В принципе, можно предложить довольно стандартную схему но
строения тестовой задачи. Расчётная область разбивается на шсколько
подобластей (обычно на 2-3), в них определяются коэффициенты X и
(как правило, принимающие постоянные значения па Э1н\ подобла-
стях) и внутри каждой подобласти задаётся функция в вп ic полинома,
степень которого не выше порядка базисных функций ic< шруемых
элементов. При этом полиномы должны быть шданы i ik, чтобы на
186
4.Одномерные задачи
границах подобластей сшитая из них функция и (определяемая нами
как решение тестовой задачи) была непрерывна и имела такие скачки в
производных dufdx (для тестирования с разрывным X), чтобы непре-
рывной была величина Xdu/dx . После этого вычисляется правая часть
| X 4- и выбираются такие параметры краевых усло-
вий, чтобы им удовлетворяла функция и .
В качестве одного из примеров тестовых задач для квадратичных
элементов вполне может быть использована задача, описанная в разде-
ле 4.4.2 (её решением является кусочно-полиномиальная функция,
являющаяся линейным полиномом па отрезке [0,2] и квадратичным -
па отрезке [2,7]).
Построение тестовых задач для одномерных линейных элементов
является слишком уже простой задачей, поэтому здесь мы рассмотрим
несколько примеров тестирования процедур построения конечноэле-
ментных решений для случая, когда в этих конечноэлемепгных проце-
дурах используются кубические элементы.
4.14.1. ТЕС ТИРОВАНИЕ ОДНОМЕРНЫХ КУБИЧЕСКИХ ЭРМИТОВЫХ ЭЛЕМЕНТОВ
13 качестве первого примера продемонстрируем, как может быть
построена тестовая задача для проверки процедур вычисления конеч-
ноэлементных решений эллиптических задач с использованием эрми-
товых кубических элементов. Будем считать, что задача решается в
области Q = [0,7], состоящей из двух подобластей Q] — [0, .1 ] и
=[1,7].
В качестве искомого решения выберем такую функцию, чтобы в
точке х = 1, являющейся границей между подобластями QI и Q2, она
была непрерывна вместе со своей производной. Для этого в подобла-
сти П| = [0,1] выберем (произвольным образом) полиномиальную
функцию степени не выше 3 и определим её значение и производную в
узле х = 1. В подобласти Q2 = [1, ?] также возьмём некоторую поли-
номиальную функцию степени не выше 3 с учётом того, что значение
и производная в левом узле у нее известны. Указанным выше требова-
ниям удовлетворяет, например, функция вида
ц(:г) =
л ! 4- З.г,
б.т — 2,
0 < х < 1 ,
I < х < 7.
(4.58)
Поскольку искомая функция должна обладать непрерывной произ-
водной, коэффициент X должен быть непрерывной функцией во всей
области Q . Мы выберем его постоянным во всей области:
Х = 1. (4.59)
Коэффициент ч выберем следующим образом:
4.14.Тестирование процедур построения ...
187
1, 0<.т<1 ,
О, 1 < х < 7 .
(I 60)
Тогда после подстановки искомой функции (4.58) и коэффициентов
(4.59), (4.60) в уравнение (4.1) получим, что правая часть будет опре-
деляться следующими соотношениями:
/ Ст) =
-3;и + а;3, О < х < 1 ,
0, 1 < х < 7 .
(4.61)
Итак, функция (4.58) удовлетворяет" дифференциальному уравне-
нию (4.1) с параметрами (4.59)—(4.61). Для того чтобы она стала реше-
нием краевой задачи, на границах расчётной области можно задать
следующие краевые условия:
4=0= °- ^L=7+4'“L=7-4=°- <4-62)
Напомним, что при использовании эрмитова базиса обычно исполь-
зуется следующая нумерация базисных функций и соответственно
неизвестных - весов в разложении приближённого решения по этим
базисным функциям. Всего таких весов '2п, где п - количество узлов
в конечноэлсмент ной сетке, при этом компонента (k — 1-п)
вектора весов q является значением приближённого решения и1' в к-
м узле, а компонента _ производной приближённого решения в к-
м узле.
Будем считать, что расчетная область разбита на два конечных эле-
мента, совпадающих с подобластями Qj = [0,1] и — ЦД]> и содер-
жит гри узла а?! = 0, т2 = 1, = 7 . Очевидно, что решение (4.58)
эллиптической задачи с параметрами (4.59)-(4.61) дифференциального
уравнения (4.1) и краевыми условиями (4.62) представляет собой функ-
цию, точно представимую в базисе рассматриваемых эрмитовых эле-
ментов, и поэтому приближенное решение должно полностью совпаст ь
с точным решением (т.е. компоненты вектора q должны точно сов-
пасть со значениями функции (4.58) и её производными в узлах сетки).
Приведём вид глобальной матрицы и вектора правой части конеч-
ноэлементной СЛАУ после её сборки из двух локальных матриц и век-
торов и учёта всех краевых условий:
188
4.Одномерные задачи
1 О О ООО
19
210
351
420
53
420
86
16
105
15
14
29
420
О
15
10.5
29
420
17
420
О
29_____17
420 420
186_____11
105 210
11 99
210 10.5
_1_______1_
.5 10
1 _1
10 5
О О
_1 1
•5 10
1 _1
10 5
11 _J_
5 10
1 4.
10 5J
О О
Результатом решения этой системы является вектор весов:
q = (о. 3,4.6.40. б)Т . (4 63)
Итак, вектор (4.63) определяет конечноэлементное решение
G
и1' , полностью совпадающее с точным (определяемым со-
г=1
отношением (4.58)). При этом q1 — 0, q:i = 4 и q§ — 40 — это значе-
ния решения в узлах расчётной области = 0, т2 = 1 и х3 = 7, а
веса q2 = 3, = G и дс = 6 — это значения производных решения в
этих узлах.
4.14.2. ГЕ( ГИРОВАНН! ОДНОМЕРНЫХ КУБИЧЕСКИХ ЛАГРАНЖЕВЫХ
ЭЛЕМЕНТОВ
В качестве второго примера продемонстрируем, как можно по-
строить тестовую задачу для проверки процедуры вычисления конеч-
ноэлеменiного решения эллиптической задачи с использованием ла-
гранжевых кубических элементов. При этом тестовую задачу построим
так, чтобы у сё решения производная была разрывна.
Будем считан,, что задача решается в той же области Q = [0,7], со-
стоящей из двух подобластей Qj = [0, J ] и Q2 =[1,7]. На каждом ин-
тервале выберем некоторую полиномиальную функцию, представи-
мую в рассматриваемом базисе, при этом полиномы на и Q2 по“
строим таким образом, чтобы в точке х = 1 стыковки подобластей Г?!
и Q2 было непрерывно только значение функции. Например, в качест-
ве решения тестовой задачи может быть выбрана функция:
.г3 -I- 7т, 0 < х < 1,
Коэффициенты дифференциального уравнения (4.1) будем считать
постоянными в каждой из подобластей, при этом коэффициент диффу-
зии X должен быть выбран таким, чтобы выполнялось условие непре-
4.14.Тестированис процедур построения ...
189
рывности потока х4^-| = X . Этому условию удовле-
творяет, например, коэффициент X, определяемый соотношением
0 < х < 1,
1 < х < 7 .
10,
(4 65)
Коэффициент определим с помощью соотношения
2, 0 < а; < 1 ,
1, 1 < х < 7
(4.66)
После подстановки функции (4 64) и коэффициентов (4.65)—(4.66) в
уравнение (4 I) получим, что его правая часть будет определяться сле-
дующими соотношениями:
f № =
—6х 4- 2(х3 + 7 т),
-20 + (х2 - х + 8),
0 < х < 1,
1 < х < 7 .
На краях расчётной области можно задать следующие краевые ус-
ловия (которым должна удовлетворять функция (4.64)):
<;=1) = 0, 10 4^1 + 0.1 (?/,|./;=7 — 1350) = 0.
(IX К=7
Будем считать, что расчётная область разбита на два конечных эле-
мента, совпадающих с подобластями = [0,1] и П2 — [С?], и содер-
жит гри граничных (относительно конечных элементов) узла Т] = 0,
х2 = 1, x:i = 7 и 4 внутренних - Ej х = -j, а;1+э = j, z2+i = 3 и
М = 5 '
Поскольку точное решение (4.64) является кусочным полиномом с
максимальной степенью 3, оно представимо в используемом базисе, и
поэтому конечноэлементное решение должно полностью совпасть с
точным.
Приведём вид глобальной матрицы и вектора правой части коисч-
ноэлсмеитной СЛАУ после её сборки из двух локальных матриц и век-
торов и учёта всех краевых условий:
190
4 Одномерные задачи
1 0 0 0 0 0 0 0
129 81 1053 183 0 о о 39
28 7 140 140 70
183 1053 81 129 Q о о 96
140 110 7 28 35
А = 127 183 129 220 1053 297 199 Ъ = 233
420 140 28 21 140 140 420 ' 42
0 0 0 105.3 140 711 35 1773 140 297 140 243 10
0 0 0 297 _J773 Ш 1053 162
110 1 10 35 110 5
0 0 0 199 420 1 10 1053 1 10 706 105 303 2
В результате решения этой системы получим следующий вектор
весов:
q = (о, «. и. •«. so) .
(4-67)
Очевидно, что определяемое вектором весов (4.67) конечноэле-
ментное решение совпадает с точным, причём значения являются
не только весами в разложении копечноэлементного решения
7
по базису {гр,} кусочно-кубических базисных функций
i= ।
лагранжева типа (см. раздел 4.5), но и значениями в узлах сетки:
7t = 0 - значение и в узле Ti = 0, <72 — тт ~ в узле .t.,i = 4,
Z । 1 "Г ,j м
7з = - в узле .т1+2 = |, <7.1 = 8 - в узле х2 = 1 и т.д.
Отмстим, что рассмотренную здесь задачу не имеет смысла приме-
нять для тестирования процедуры, использующей эрмитовы элементы с
непрерывными производными, гак как производная решения этой зада-
чи имеет разрыв в точке .г = 1 . Для решения такого рода задач кроме
лагранжевых могут быть использованы и эрмитовы элементы с разрыв-
ной производной (см. с. 155 и разделы 1.9 и 4.10). В следующем разделе
будет приведён ещё один пример использования эрмитовых базисных
функций с разрывной производной для задачи с разрывным коэффици-
ентом диффузии для си туации, когда такой эрми тов базис порождает то
же самое конечномерное проса рапс изо, что и базис из полиномов ла-
гранжева типа.
4.14.3. ТЕСТИРОВАНИЕ ОДНОМЕРНЫХ Н’МП ГОВЫХ ЭЛЕМЕНТОВ С РАЗРЫВНОЙ
ПРОИЗВОДНОЙ ДЛЯ PI 1111 ННЯ 3k I VI ( РАЗРЫВНЫМ КОЭФФИЦИЕНТОМ
ДИФФУЗИИ
При использовании эрмитова базиса с разрывной производной
количество неизвестных (весов в разложении приближенного решения
по базисным функциям) равно Зл 4-1, п - количество элементов в
копечноэлементной сетке, при этом каждая ‘3k — 2 (А; = 1...п) неиз-
вестная является значением искомой функции в k-м узле, а неизвест-
4.14.Тестирование процедур построения ...
191
ные с номерами Зк — 1 и Зк (к = l...n — 1) - соответственно произ-
водными искомой функции в к-м узле справа и слева (напомним, чго
натянутое на такой базис подпространство полностью совпадает с про-
странством, натянутым на кусочно-кубические функции лагранжева
типа, но у лагранжевых базисных функций веса соответствуют зна-
чениям приближённого решения в узлах сетки, число которых, вклю-
чая внутренние узлы £fe+i и яЛ,2, равно Зп 4-1, где п — количество
элементов в копечноэлементной сегке).
Рассмотрим конечноэлементную аппроксимацию краевой задачи
(4 1) на конечномерном подпространстве с базисом {ф^} из эрмитовых
кусочно-кубических функции с разрывной производной (аналогичные
базисные функции были рассмотрены в разделе 4.7 и изображены на
рис. 10). Глобальная матрица и вектор правой части имеют в этом слу-
чае следующий вид:
1 0 0 0 0 0 0 0
43 16 _д_ 4 0 0 0 2
210 105 21 105 7
4 16 13 о о 0 47
105 21 105 210 105
А — 33 4 43 216 101 __4_ _43 ь = 454
1TL 35 105 210 35 35 35 35 35
о о 0 101 352 _124 4 35 _36
35 35 35 5
0 0 0 __4_ 124 352 101 -18
35 35 35 35
о Q 0 _43 4 101 303 846
1 35 35 35 70 . 5 ,
В результате решения этой системы получим следующий вектор
весов q3:
q = (о, 7,10, 8,1,13, 5о)Т .
(4.68)
Нетрудно убедиться, что этот вектор весов так же, как и в преды-
дущем примере, определяет конечноэлементное решение
7
uh , полностью совпадающее с точным (см. (4.64)). При
/=1
этом веса </L = 0, = 8 и q7 = 50 - это значения решения в узлах
расчётной области .14 = 0, = 1 и ж3 =7 ; q2 = 7 и qG = 13 про-
изводные решения в узлах 34 = 0 и т3 = 7, а д3 = 10 и = I - про-
изводные решения в узле х-2 — 1 соответственно слева и справа.
Таким образом, несмотря на то, что в этом и предыдущем примере
мы получили различающиеся друг ог друга конечноэлемеш ные ( IIAV
и векторы решений (4.67) и (4.68), конечноэлсменгпые решения н них
примерах полностью совпадают (и равны точному решению ia мчи)
192
4.Одномерные задачи
просто векторы (4.67) и (4.68) являются весами в разложении точного
решения по разным базисам одного и того же функционального про-
странства. Тем не менее в вычислительном плане мы получили все-
таки разные задачи - их конечпоэлсмснтные матрицы обладают раз-
ными свойствами, которые Moiyi повлиять на вычислительный про-
цесс решения соответствующих СЛАУ.
4.15. ОДНОМЕРНЫЕ КОНЕЧНЫЕ )Л1 МЕНТЫ В ЦИЛИНДРИЧЕСКИХ
КООРДИНАТАХ
4.15.1. ЛОКАЛЬНЫЕ МАТРИЦЫ ЖЁ( 1 КОС ГН П МАССЫ
ДЛЯ ЛИНЕЙНЫХ ЭЛЕМЕНТОВ
Сначала рассмотрим конечные шементы с линейными базисны-
ми функциями. Будем считан,, что расчётная область Q = [ra,rr] раз-
бита узлами па конечные элементы Q/. = (г/., ?).+1),
к = 1.. .71 — ] (при этом, очевидно, 7) =, т?п — ?;.). Представим все
параметры X, д и / уравнения (4,3) на каждом конечном элементе
Qz.. в виде разложения по локальным базисным функциям
-Ф1 (?) = (rfc+J - r)/hk и ф2 (г) = (/• - :
уч> = X| ф] (/) X.' Ф2 (?'), (4.69)
= %Ф] (70 1 Д?Ф2 (г), (4.70)
Г = /гФ1 (?) 1 _/2Ф2(Г), (4.71)
где h,k = 7),+1 - rk, X] = X (rk -|- 0), Х2 = X - 0), = ^(гк + 0),
5-2 = л(Д:+1 - °), 71 = Ж + ./? = /(д+1 - °) как всегда, аргу-
мент 7)ь. +0 означает, что значения соответствующих функций вычис-
ляются справа от узла гк ,а 7/. |.| О слева от узла 7/.+1 (т.е. парамет-
ры задачи X, и f разлагаются но локальным базисным функциям
независимо на каждом элементе - это позволяет естественным образом
учитывать наличие разрывов у этих параметров).
Исходя из вариационной иостанов! и (4.4), вычислим локальную
матрицу жёсткости элемента QZi :
J X'1’ grad фу grad фд/П =
Щ.
'J-+1 л .к > Т
-^-^-rdr.
dr dr
4.15.Одномерные конечные элементы в цилиндрических ...
193
Учитывая, что d\\\/dr = — l]hk , d^/dr = \Jhk ,
г = rk + ^hk
i
= f Ф1 (e,) (rk + ea)me, =
о
i 1 l
= f + = f + f (1-У^Е,=
0 () 0
и
r = rk + £Jlk
1
= f Ф-2 (0 (n- + Vh; ) fh-dk =
()
1 1 1
= f Un.- + = hkrk f + hk f E,2dE, =
= | | (rZ; 4- j/i/.),
где фт (^) и ф2 (E.) ~ шаблонные функции на элементе (см. раздел 4.3),
получим
2Ла.
-1
1 "
(4-72)
В случае же, когда параметр X является на элементе константой X,
матрица жёсткости примет вид
(4.73)
Компоненты локальной матрицы массы элемента при замене
параметра его линейным интерполянтом определяются форму-
лой
Д+1
\ читывая, что
194
4.Одномерные задачи
Д+1
f ф? (г) rdr = rkhk -J- i ,
ч
Ч+l
J ф? (г) ф2 (Г) rdr = --L гА./ч + hi,
д
Д+1
J Ф1 (?’) Фг ( f) = -[7) ПЛ + ,
д
Д+1
У Ф-2 (г) rdr = “ rkhk ч-1 h'l,
д
получим
M = I№
12
nA- p1 +5'2
5i + 5-2
5i + 52 л/ P5i +25г
i -
5i + З42 G() 25j + 352
/
25i + 352 ’
351 +12^2
Очевидно, что при замене па Ц. параметра константой 5 (в
этом случае можно также счинпъ, что 51 —5г = 5) матрица массы
примет вид
" 'S/ii И hi । П
М = -V- гк | % . (4.74)
6 к [ 2 1 1 3 v '
Напомним, что когда правая час и» / на конечном элементе QA.
представляется в виде интерполян га локальный вектор пра-
[
вой части можно вычислить по формуле b = Cf' (в нашем случае
fZ = (// >У2А ) , гДе .// = У(г/. I 0), у/' = У('//.+1 - 0)) с использовани-
ем локальной матрицы массы С, компоненты которой определяются
соотношением (4.12). Л поскольку М =^С, из (4.74) для рассматри-
ваемой нами задачи получаем
С
‘I
I з
(4.75)
4.15.2. ЛОКАЛЬНЫЕ МАГР1ЩЫ ЖТ ( 1 К()( I Н II МАССЫ ДЛЯ КВАДРАТИЧНЫХ
ЭЛЕМЕНТОВ
Здесь мы приведём (без вывода) матрицы жёсткости и массы для
квадратичных элементов также при условии, что параметры X и
4.15.Одномерные конечные элементы в цилиндрических .
195
заменяются своими средними значениями X = const и = const пл
конечном элементе Qfc.
7 —8 1 3 -4
-8 16 -8 +4 -4 16
1 -8 7 1 к -12
М = —
iV1 30
4 2 -1 1 0
2 16 2 + "Т 0 16
-1 к 2 4 -1 4 к
(4.76)
(4.77)
4.15.3. ВЫЧИСЛЕНИЕ ЛОКАЛЬНО!! МАТРИЦЫ МАССЫ
ДЛЯ ЗАДАЧИ С Ч = 1Л’2
Здесь мы отдельно рассмотрим случай, когда коэффициент в
уравнении (4.3) имеет вид ^ = — . Эта ситуация представляет опредс-
г"
ленный практический интерес, когда с использованием цилиндриче-
ских координат моделируются осесимметричные электромагнитные
ноля (см. уравнение (1.3б), раздел 1). В этом случае компоненты ло-
кальной матрицы массы элемента Q/, =(/):,?х+]) определяются соот-
ношением (с учетом того, что d£l = rdr ):
Д + 1
Г 1 /‘ 1 -
Му ~ J 2 Ф/Ф/.^ — J .'ФдФ^7'-
1 Ч
(4-78)
Вообще говоря, сомножитель в подынтегральном выражении со-
отношения (4.78) можно заменить его средним значением на элементе
либо представить в виде линейного интсрполяпта — ф] -I----— тф-2 (в
7 А- 7/.: + 1
принципе можно заменить — и интерполянтом более высокого поряд-
ка - квадратичным или кубическим), но это приводит к существенным
ошибкам в аппроксимации и во многих случаях к неоправданно мел-
кому шагу сетки для получения решения с нужной точностью. По ло-
му лучше вычислять интеграл в выражении (4.78) точно. Отмстим, что
то же самое справедливо и при решении двумерных краевых задач для
\равнения (1.36) (при использовании прямоугольных элементов мат-
рица массы может быть сформирована с помощью соотвстс тву ющнх
одномерных матриц, аналогично тому, как это сделано в разделе 5.2 1 )
В качестве примера покажем, как можно вычислил» одну компо-
ненту матрицы М :
196
4.Одномерные задачи
Д+1
^ц= j 'Ф1'Ф1с/г =
чч (ЮФ1 (Ю
(л + ел)
(i-Ю2
(ц- +
Воспользуемся табличными интегралами:
•^(ь + к«)^=
, с2 ,
т; , с- ч = з о (6 + ^й)2 “ 26 (^ + ^а) +1)2111 (6 + &
(О -Г ) о. \
В результате получим:
(4.79)
/чА =
Если этот элемент вычислял, без замены переменных, то выраже-
ние для компоненты Мп можс! получиться более громоздким.
Остальные элементы вычисляются аналогичным способом. В ре-
зультате локальная матрица массы примет вид:
М = In
М)
(1 I "О'
—(1
1
т , (4-80)
где d = у-.
hk
4.15.4. ПРИМЕР РЕШЕНИЯ ЭЛЛИН I ИЧЕСКОЙ 1ЛДАЧИ С ИСПОЛЬЗОВАНИЕМ
КВАДРАТИЧНЫХ ЭЛЕМЕНТОВ
Рассмотрим краевую задачу для уравнения (4.3). Определим рас-
чётную область, параметры X, ч и I дифференциального уравнения
и краевые условия.
Пусть расчётная область имссз вид Q = [0.5,10], а параметры X,
и f являются следующими константами:
Х = 1, -у = 0, / = 0. (4.81)
Краевые условия определим следующим образом:
4.15.Одномерные конечные элементы в цилиндрических ...
197
ХМ=,Г~2' “Ь» = °- (,Х2)
Нетрудно убедиться, что решением задачи1 (4.3), (4.81), (4.82) миля
ется функция
и (?) — In г — In 10 .
(4.83)
Разобьём расчётную область на три конечных элемента
= [0.5,2], Q2 =[2,5], Q3 =[5,10].
Получим решение с использованием квадратичных базисных функ-
ций. Подробное описание сборки локальных матриц в глобальную
было приведено в разделе 4.4.2, поэтому здесь мы приведём лишь вид
локальных матриц AQ1 , А4*2, Ai2:‘ (все локальные векторы в этой за-
даче нулевые), а также глобальную матрицу А и векгор правой части
b конечноэлементной СЛАУ после учёта всех краевых условий:
23 _14 5 37
18 9 18 18
А01 = 14 40 26 Аа‘2 — _22
9 9 9 9
5 _26 47 7
к 18 9 18 J 1 18
23 _14 _5 о 0 0
18 9 18
_Т4 40 -26 о о 0
9 9 9
5 -26 1 4 —22 7 g
18 9 3 9 18
А = 0 0 —22 56 _34 0
9 9 9
0 0 7 _34 56 _10
18 9 9 3
0 0 0 0 _10 3 8
0 0 0 0 0 0
_22 9 56 9 7 18 _34 9 , А°3 = 17 10 0.5 _14 3
6 _10 3 3 8
_34_ 9 61 18) 0.5 1 _14 3 25 6 J
0 -1
0 0
0 0
0 5 Ь = 0
0.5 0
_14 3 0
1 0
Результатом решения полученной конечноэлементной СЛАУ явля-
ется следующий вектор (решение приводится с округлением до четы-
рёх значащих цифр):
(\Т
-2.969, -2.083, -1.605. -1.051, -0.6923, -0.2SS5. 0.1 . (4 84)
Размерность конечноэлементной СЛАУ и вектора весов q равна 7,
поскольку использовались квадратичные базисные функции и в цешр
каждого элемента добавлялся дополнительный узел (сравни ic пол)
ценное численное решение в виде вектора (4.84), компонен ты которою
1 Заметим, что рассматриваемая задача описывает магниптс ноле, соиы
васмое током в бесконечном проводе.
198
4.Одномерные задачи
фактически являются значениями конечноэлементного решения
7
г?' = ф,- в узлах сетки, со значениями точного решения (4.83) в
4=1.
этих узлах).
Для оценки энергетической нормы погрешности полученного ко-
нечноэлементного решения вычислим значение линейной формы f
для аналитического решения (4.83) и для полученного решения и.1'.
Поскольку в задаче нет неоднородных главных краевых условий,
значение формы f (и) для аналитического решения может быть полу-
чено следующим образом:
10
/(«) = J и - f • rdr + 0- ( </. г) |,._()5 =
0.5
10
= J (In г - In 10) • 0 • rdr - 2 • (In 0.5 - In 10) • 0.5 = 2.9957.
0.5
Нетрудно убедиться, что значение формы f (uh j = q ' b для числен-
ного решения равно 2.969.
Таким образом, энергетическая норма погрешности полученного
конечноэлементного решения равна:
|« - « 0.163,
а относительная погрешность решения (с учётом того, что
||и ||э = ^(и,д)э = у[Т^) = V2T957 « 1.731)
= 0-163
0.1
0.094,
т.е. относительная погрешность полученного конечноэлементного ре-
шения составляет примерно 9.4 %.
4.15.5. ПРИМЕР РЕШЕНИЯ ТЕСТОВОЙ У ЛЛИПТИЧЕСКОЙ ЗАДАЧИ
ДЛЯ СЛУЧАЯ С Ч = 1Д’2
Рассмотрим конечноэлемепгную аппроксимацию краевой задачи
для дифференциального уравнения:
+ = f. (4.85)
г dr \ dr} г1 7
4.15.Одномерные конечные элементы в цилиндрических ...
199
Заметим, что уравнение (4.85) описывает поле кругового тока с
плотностью f.
Будем считать, что расчётная область Q является отрезком
[10-5,10], а правая часть f уравнения (4.85) определяется соотноше-
нием
г < Д),
г > Дг
(4.86)
Аналитическим решением
правой частью (4.86) является
дифференциального уравнения (4.85) с
функция
-у г (а - г),
О
С
. г ’
г < Дь
Г > Д>.
Зафиксируем значения параметров Д> и р — возьмём 7?(1 = 2 и
р = 3. Параметры а и С найдем из условий непрерывности решения
и. и его производной в точке г = Д} = 2 :
2(«-2) = е,
а —2-2 = -%
I 4
т.е. а = 3, С = 4 и решение и примет вид:
г (3 — г), г < 2,
(4.87)
«= 310--',
Па левой границе области Q зададим краевое условие первого ро-
да, а на правой - второго таким образом, чтобы этим краевым услови-
ям удовлетворяла функция (4.87):
X&I =-0.04. (4.88)
Построим конечноэлементное решение краевой задачи (4.85),
(4.86), (4.88). Для этого разобьём область Q на два конечных элемента
= [1СГ5,2] и — [ДЮ] и в качестве базисных возьмём линейные
функции.
Глобальная матрица и вектор правой части после занесения в них
вкладов от обоих конечных элементов и учёта краевых условии при
мут следующий вид:
200
4.Одномерные задачи
А = 1 -6.1-10-5 0 0 ' 2.515 -0.503 , Ь — ЗЮ-5 4 (4.89)
0 -0.503 1.1006 —0.4
Заметим, что в эквивалентной вариационной формулировке (4.4)
вклад от второго краевого условия определяет слагаемое Gf.u(rr)rr, т.е.
при учёте второго краевого условия на границе г = т(. = 10 поток
с) и I
0 — Х-ттЧ = —0.04 должен быть умножен на якобиан г = г, — 10 .
Решением конечноэлементной СЛАУ с матрицей А и вектором
правой части Ь, определяемыми соотношением (4.89), является вектор
весов
Рис. 16 Графики точного и двух конечноэлементных решений
4.16.Одномерные конечные элементы в сферических ...
201
Очевидно, что на столь грубой сетке полученное консчноэлсмсн i
3
ное решение гЛ1 — q-ф,1 (ф) — глобальные базисные функции для
7 — 1
сетки из двух конечных элементов) довольно далеко от точного.
Добавим дополнительные узлы и построим конечноэлементнос ре-
шение u/l2 на сетке (ю-5,1,1.5,2,3.4.6, io) Вектор весов для этого реше-
ния будет выглядеть следующим образом:
q2 = (3 10~5, 2.01. 2.24, 1.98, J.32. 0.986. 0.658. Од) .
8
Решение г?'-2 = У^ </2ф2 (ф2 - глобальные базисные функции для
«=1
сегки из семи конечных элементов) уже гораздо точнее аппроксимиру-
ет точное решение (4.87).
Графики решений л/'1 и и1'2 в сравнении с точным решением и
показаны на рис. 16.
4.16. ОДНОМЕРНЫЕ КОНЕЧНЫЕ ЭЛЕМЕНТЫ В СФЕРИЧЕСКИХ
КООРДИНАТАХ
4.16.1. ЛОКАЛЬНЫЕ МАТРИЦЫ ЖЁСТКОСТИ II МАССЫ
ДЛЯ ЛИНЕЙНЫХ элементов
Как и в случае цилиндрических координат, для аппроксимации
одномерного эллиптического уравнения (4.5) в сферических координа-
тах рассмотрим конечные элементы с линейными базисными функ-
циями.
При условии, что параметр X па конечном элементе Q/v. заменяется
своим средним значением X = const, компоненты матрицы жёсткости
вычисляются следующим образом:
^4*1 1 I
G,j = j X grad ф;/ • grad ф/ZQ = J X^--^r2dr =
Од il
= J >'2dr = ф(-1)'+7 (^/3 + Л(г(. + rf).
,c Ц
Аналогично в случае, когда параметр на Q, заменяется своим
средним значением 5’ компоненты матрицы массы М могу« бын.
вычислены по формуле
202
4.Одно мерные задачи
Для вычисления значений компонент матрицы М удобно восполь-
зоваться заменой переменных, переводящей интервал в ин-
тервал (0,1):
'k+i
Л7Н — ‘Ч J 'ФгФ1г2^г —
'к
Г = П: + ЦЧ;
1 1
= чJФ1 (У Ф1 (У С'Ь + У^-)2 = lf (1 - У2 (n- + №)2
о о
1
М12 = М21 = (1 - ^(rk + thk)2 hkd^,
о
1
М-12 = ДЧ2 (’i+
о
В результате локальные матрицы жёсткости и массы примут сле-
дующий вид:
ю ю'
ю зо
/
+ /чл
г2
3
з V
12
4.16.2. ПРИМЕР РЕШЕНИЯ ОДНОМЕРНОЙ ЭЛЛИПТИЧЕСКОЙ ЗАДАЧИ
В СФЕРИЧЕСКИХ КООРДИНАТАХ
Рассмотрим краевую задачу для уравнения (4.5), определённого
в области Q = [0.1,1]. Значение коэффициента X выберем постоянным
во всей расчётной области и равным единице, а коэффициент и пра-
вую часть f дифференциального уравнения (4.5) - равными нулю.
Аналитическим решением такой задачи является функция вида
/у
гь =--F С1, описывающая поле заряженного шара.
На левой границе (в точке г = 0.1) зададим краевое условие второ-
го рода, а на правой границе (в точке г — 1) -краевое условие первого
рода:
4.16.Одномерные конечные элементы в сферических ...
203
Х^| =100,
on !/.=().1
Точным решением поставленной задачи является функция и = 1/г.
Разобьём область на четыре конечных элемента и получим конеч-
ноэлементное решение и1' с использованием линейных базисных
функций на сетке (од, 0.2,0.4, 0.7,1.).
Глобальная матрица и вектор правой части конечноэлементпой
СЛАУ после учёта всех краевых условий примут следующий вид:
7 30 __7_ 30 0 0 0 1
__7_ 30 0.7 __L 15 0 0 0
А = 0 _7_ 15 1.5 -31 30 0 , ь = 0
о о _31 52 _73 0
30 15 30 1
0 к 0 0 0 1
Заметим, что в эквивалентной вариационной формулировке (4.6)
вклад от второго краевого условия определяет слагаемое 6аЦ](га)т^,
т.е. при учёте второго краевого условия на левой границе г = га = 0.1
поток 0 = Х-Фд =100 должен быть умножен на якобиан
cml,=().i
г2 = 0.01 .
Результатом решения полученной конечноэлементной СЛАУ явля-
ется вектор:
q = (s.807, 4.522. 2 379, 1.411. 1.) .
Поскольку, как и в примерах из предыдущего раздела, искомое ре-
шение точно не представимо в используемом базисе, полученное ко-
5
нечноэлементное решение и1' = (/,4^ не совпадает с аналитическим
«=1
и = A-jr (сравните, например, компоненты вектора q, являющиеся
значениями приближённого решения и1' в узлах сетки, со значениями
в этих узлах точного решения 1Д). Однако с уменьшением шага сетки
численное решение будет довольно быстро приближаться к точном}
При этом, учитывая характер искомого решения, дробление сетки луч
ше выполнять неравномерно, с некоторым сгущением к левой границе
области.
204
4.Одномерные задачи
4.17. ИСПОЛЬЗОВАНИЕ КУБИЧ1 ( КПХ ЭРМИТОВЫХ ЭЛЕМЕНТОВ
ДЛЯ ПОСТРОЕНИЯ ИНТЕРПОЛЯЦИОННЫХ И СГЛАЖИВАЮЩИХ
СПЛАЙНОВ
Очень часто при решении различного рода задач бывает необхо-
димо построить гладкую функцию по сё значениям в некотором набо-
ре точек. В качестве такой функции обычно используют кубический
сплайн - непрерывную кусочно кубическую функцию с непрерывны-
ми первыми (а в некоторых случаях и в торыми) производными.
Для построения кубических сплайнов очень удобно использовать
эрмитовы кубические базисные функции. В данном разделе мы проде-
монстрируем, как можно стропи, интерполяционные и сглаживающие
сплайны на основе техники одномерных эрмитовых кубических эле-
ментов, рассмотренных в разделе I 6.
4.17.1. ПОСТРОЕНИЕ КУБИЧЕСКОГО НН 11 РИО ЛЯЦНОННОГО СПЛАЙН \
Задача интерполяции coctoiii в построении достаточно гладкой
функции F(:r) по набору значений J, некоторой функции / в точках
х, (т.е. /(.?:,) = i = 1... п )таким образом, что ~ fi .
Интерполяционным кубическим сплайном, построенным по зна-
чениям таблично заданной функции i = будем назы-
вать кусочно-кубическую функцию /'(.г) такую, что P(xl') = ft и на
всём интервале (.г-ь.т„) Р(х) имесл непрерывные производные перво-
го или первого и второго порядка.
Очевидно, что интерполяционный кубический сплайн может быть
представлен в виде линейной комбинации рассмотренных в разделе 4.6
глобальных эрмитовых базисных функций ф,:
/’<« = <->•> । £//ф2л«, «ад)
1=1 » I
где f' — значения производной интерполируемой функции в точках
Таким образом, для определения сплайна (4.90) нам нужно каким-
либо образом задать значения производных // (т.е., вообще говоря,
интерполяционных сплайнов, значения которых в узлах х, совпадают
с fz, может быть много, и конкретный вид сплайна определяется спо-
собом построения значений ft ). Рассмотрим некоторые способы зада-
ния значений f .
Довольно распространенным является следующий способ. В каче-
стве // берутся значения производных квадратичного интерполяцион-
4.17.Использование кубических эрмитовых элемитов...
205
ного полинома Лагранжа, вычисляемого потрём ближайшим к .г, гон-
кам. Так если точка т,; - внутренняя, т.е. i = 2,п — 1, то полином Ла-
гранжа имеет следующий вид:
Продифференцировав Pf (я) по т и подставив х = х,, получаем ис-
комое значение производной сплайна в точке хг:
/ _ dP,L (гс) ________. h-j - h,-i
'' — dx _ ~ /?,,_! (/г,-!-M,У'-1 K-ih,
+ MVi
(4.91)
где i > *4+1 4 •
Аналогично через производные полиномов Лагранжа, построенные
по трем первым точкам и трем последним точкам, могут быть получе-
ны значения // и f' соответственно (т.е. фактически для вычисления
// будет использован полином P^tx), а для вычисления — поли-
ном P,^i (ж)):
/ _ dP2J (х) _ 21\ + h2 - hy + г
~ dx ~ h{ (fy + h2)'1 hxh2
_______h\____ r
(hi+h2)h2 3’
г t (Д') __________hn_j________ „ _
j" ~ <1* r_ + /«,,_.)J"-2
J.—
_ (^n-2 + hH-i) 2hv_i + Д„_2
^71-1^7-2 " 1 hn-} (h„_2 + hn^i)
(4.92)
(4.93)
Значения J\ и f' могут быть найдены и другим способом, напри
мер. как среднее между производной, вычисленной с иснольюваписм
полинома Лагранжа, и производной линейной функции пос г роенной
по значениям /j и J'2 либо /„_1 и fn соответственно:
206
4.Одномерные задачи
, = J dP2L (ж) 1 Л ~ fi
2 dx 2 х2 — .Tj
x=:q
1
2
3/i] -}- 2/ъ^
(/?<! + /?2)-i
+ 2h2 .Д1
^1^2 J (^1 + ^2) ^'2
(4.94)
Г I = 1 &Pn-\ . 1 fn ~fi 1
" 2 dx _ ±2хн-х„Г
.1, — J,n
_ 1 ____________^11- 1__________ Г
2 /i„_2 (ha_2 + "
3/^-! 4~ 2hu^2
hn-l (jhi-2 + ^11.-1) ‘ )
(‘2l>n-2 + ^rt-1)
^</.-1^71—2
(<95)
Очевидно, что в соотношениях (И .94) и (4.95) веса производной,
вычисленной с помощью полинома Лагранжа, и производной линей-
ной функции можно взять и другими (в общем случае о. и 1 — а ).
В принципе, возможны и другие варианты нахождения производ-
ных fi1. Довольно распространенным является способ, основанный на
обеспечении требования непрерывности второй производной сплайна
в точках х,. Покажем, как это можно сделать с использованием куби-
ческих эрмитовых элементов.
Вычислим значение второй производной сплайна (4.90) в точке хг
слева и справа от нее.
d2P(x)
dx2
^4’2,.-3 ^2ф2/.-2
T~2 ‘ Л-1 T~2
dx dx
:к= .1, 0
о
dx2
j.fd2^.2l U)
(4.96)
Так как 3p2/-3 на интервале (a;,_j,.rz) является локальной базисной
функцией Ф1 <^) = Ф1 (^>^9) = 1 - 3(6,(т))2 + 2(^(з;))3 (см. (4.33)) и
X — X I
связана с х соотношением F =-----------—го
I
(/2Ф2д-зС?9 ^Ч2/.-3 W = 6
d'^ dx2 ,;=u;._() Л2-] ’
Аналогично вычисляются производные остальных функций. В ре-
зультате
4.17.Использование кубических эрмитовых элементов...
207
d2P(x)
dx2
6
2
А
Лл£1+/Ч-,'
Точно так же может быть получено значение второй производной
сплайна Р (х) справа от ж,:
^2z-l
d2P(rr)
dx2
dx2
>1 +о
d2^2i+i (ж)
I’i + 0
dx2
+<)
+/;+1
d2^2i+2 W
dx2
'.Г. — +1)
f/ 4 । / 6 fi 2
Л? +/,+1/i? Л+Ч’
Приравнивая (4.96) и (4.97^ для всех внутренних узлов ж;, получа-
ем п — 2 уравнения:
Z:-i ту— + //-1 ту----л ту~ т л у— --
Л(-_] <Ч-\ hi_x Щ-1
= flff + Л+1 4 - i = 2-п - 1 •
6 г/ 4
:3.‘j +0
(4.9 7)
(4.98)
Поскольку количество неизвестных ft' в представлении (4.90) рав-
но п, для их нахождения нужно к системе (4.98) добавить ещё два
уравнения. Эти уравнения обычно записываются для // и f,' в виде
(4.92) и (4.93) (или (4.94) и (4.95)).
Таким образом, для нахождения f нужно решить систему с трёх-
диагональной матрицей А и вектором правой части b:
f 1 0 0 0 0 0 0
°21 Go;! 0 0 0 0 1>2
0 «32 а33 а34 0 0 0
(4.99)
0 0 0 ... 0 a,,_iiTI_2
0 0 0 ... 0 0 0 1 1>-
/ v z
। де компоненты матрицы определяются формулами
208
4.Одномерные задачи
9 111 9
= й~7’ a" 4V7+ М’ ,tM+l=V =
а компоненты вектора правой части определяются соотношением
для i — 2...?! — 1 и соотношениями
l _ _ 2/z.j + /22 г . hi + /^ ._hx
h[ (hy 4- h^) h\h^ 2 (/4 +/ь2) Д2
l _hn-x _ (/?„ 2 + />7t-i) .
" ^-2(^-21^.-2
।_^hn _ [ + h-ц 2
htl-\ (hn_-2 + h„ .J
или
З/4+2/22
1 2[ /ц(/4+Д2)
/4 + 2/i2 r h\
hilfy (h[ + Д2) /4?
________hn—i________
Jhi—2 (hn—2, 3 -1)
( 2/l7t 2 +/+ — 1)
hu-\hyi-2
^^-1+2/4, .2 r
hn-i (hn_-2 + /4,-1) " t
в зависимости от выбранного способа аппроксимации производных
сплайна на концах интервала (xi,t„ ).
Заметим, что сплайны с непрерывными вторыми производными,
хотя и являются более гладкими функциями (в смысле числа непре-
рывных производных), далеко нс всегда лучше интерполируют таб-
лично заданные функции по сравнению со сплайнами, производные
которых вычисляются через полиномы Лагранжа по формулам (4.91) и
(4.92Н4.93) (или (4.94)-(4.95)).
4.17.2. КУБИЧЕСКИЕ СГЛАЖИВАЮЩИЕ СИЛ МШЫ
Пусть задан некоторый набор значений »'Де - значе-
ния (возможно, с некоторой погрешностью) функции /(.т) в точке aij
(j = l...А:). Под задачей сглаживания понимают построение доста-
точно гладкой функции, значения которой в точках .ту максимально
близки к значениям (..
4.17.Использование кубических эрмитовых элементов...
209
Задачу сглаживания чаще всего решают на основе метода паи
меньших квадратов. В этом случае функцию Р(х), аппроксимирую-
щую f, находят из условия минимальности суммы квадратов откло-
нений значений P(Xj) от fj:
52(р(ж/)-л)2 -*rain-
.7=1
При этом в качестве функции Р(х) довольно часто используют куби-
ческий сплайн (4.90). Отметим, что узлы а;г- этого сплайна могут не
совпадать с точками x.t, в которых заданы значения .
Получим соотношения для вычисления коэффициентов и оп-
ределяющих сглаживающий сплайн в виде соотношения (4.90). В дан-
ном случае сплайн Р(х) удобней записать в виде
2и
Р&) = 52 7,/Фг <а;) ’
/=1
(4.100)
где ф, (х) - глобальные эрмитовы базисные функции, a q.t = /(»+1)/2
для нечётных г и qL = //у2 для чётных г.
Коэффициенты дг (г = 1...2п) будем находить из условия миними-
зации функционала
к ' 2п
j=l Vt—1
(4.101)
где и.- - некоторые известные веса, с помощью которых можно регу-
лировать близость сплайна Р(х) в точке х} к значению /:) (за счёт
увеличения значения параметра можно приблизить значение Р(х
к fj)-
Учитывая, что
2 и.
52 = ЧТФ бт) = *фт (х) q,
7=1
где *фСт) = (фт (T),...,3p2n ^’>)т и q = (Qi,...,Q2nГ» преобразуем функ-
ционал F(q):
210
4.Одномерные задачи
А:
Обозначив матрицу ^ио/ф(1 , I Ф'('о) через А, вектор
7=1
А _ А __ 2
через Ь, а число ( Г Л через с, получаем:
7=1 /-1
F(q) = q'Aq- <1'Ь I с. (4.102)
Для нахождения значений qiy доставляющих минимум функциона-
лу F(q), продифференцируем квадратичную форму (4 102) по каждо-
му из q, и, приравняв эти производные к нулю, получим следующую
СЛАУ, определяющую коэффициенты сплайна (4.100):
Aq = b, (4.103)
где матрица А и вектор правой часш b (размерности 2п) определя-
ются соотношениями:
А = у;ш/|>(.г,)ф'(.г,),
>1
ь = 12ш/',т(г/)А’
7=1
или покомпонентно
А-
А.||. — У2 Ш7 ) Ф|1 (*,/ ) •>
7=1
А-
7 = 1
(4.104)
(4.105)
(4.106)
4.17.Использование кубических эрмитовых элементов...
211
Заметим, что матрица (4.104) может оказаться вырожденной, если,
например, к < 2п или в некоторые интервалы (хг,хг+^ попадает не-
достаточное количество точек хГ Вырожденность матрицы А означа-
ет, что существует не единственный сплайн с минимальной суммой
квадратов отклонений его значений в точках . В этом случае опре-
делить единственный сплайн, делающий взвешенную сумму квадратов
отклонений (4.101) «почти минимальной», можно путём введения до-
полнительных (регуляризирующих) слагаемых в функционал F(q),
например:
F (q) = 12 (2Ъ ) - f:i Г + J а W dx +
7=1 и
(4.107)
При с\ > 0 и Р > 0 минимизация функционала (4.107) определяет
единственный сплайн (4.100). Второе слагаемое в функционале (4.107)
влияет на первые производные сплайна (делая их меньше при увели-
чении cy ), а третье - на его вторые производные (также уменьшая их
при увеличении |3). При этом следует помнить, что с увеличением
значений а или [3 для сплайнов (4.100), параметры которых qt опре-
деляются из условия минимизации функционала (4.107), может увели-
чиваться первое слагаемое (определяющее взвешенную сумму квадра-
тов отклонений значений сплайна Р(х) в точках xt от значений /;),
т.е. с увеличением параметров с\ или 3 сплайн Р (х) может начать
всё сильнее отклоняться от значений .
Предлагаем читателю убедиться, что функционал (4.107) при под-
становке в него вместо Р(х) разложения (4.100) может быть записан в
виде квадратичного функционала (4.102) и его минимизация эквива-
лентна решению СЛАУ (4.103) с матрицей А и вектором правой части
b следующего вида (сравните с (4.104) и (4.105)):
a V-'' . /~ \ |Т/~ \ Г tZ'tp (х) б/"фт (т) .
А = См + j а——7h~dx +
7=1 .1.4
+ 7(3^?') (4.108)
J dxz dxz
'1
А-
ь = Л • (4 109)
/=1
212
4.Одномерные задачи
Второе слагаемое в правой части (4.108) фактически определяет
матрицу жёсткости. Её так же, как и при решении соответствующих
краевых задач с использованием )рмитовых элементов, удобно соби-
рать из локальных матриц жёсткости, вид которых приведён в разде-
ле 4.6, см. с. 152.
Матрица, определяемая третьим слагаемым, также может быть соб-
рана из локальных матриц отдельных элементов. Эти локальные мат-
рицы имеют вид:
60 30 60 30)
л3 II2 /7 л2
30 16 _ 30 11
л2 II h2 II
_ 60 _30 60 _30
/? h2 //’ h2
30 14 30 16
/12 h b2 /1
(4.110)
где h, —длина конечного элемент.
В принципе и матрицу, определяемую первым слагаемым, можно
собирать из локальных матриц отдельных элементов. Компоненты
этих локальных матриц можно вычислить по формуле:
4„ = (£,)• м,н=1-4,
j
где ф„ — локальные базисные функции соответствующего элемента
(.г7,.?7+1) и суммирование ведётся только по гем j, для которых точки
5ij принадлежат текущему элементу (отметим, что точки совпа-
дающие с граничными точками элементов .77, могут быть учтены в
любом из элементов или (//,./7 н), но только один раз).
До сих пор мы рассматривали, как можно построить сглаживающие
кубические сплайны, у которых непрерывна только первая производ-
ная. Не представляет особого труда построить процедуру, позволяю-
щую получить сглаживающий сплайн с непрерывной второй произ-
водной. Для этого мы должны иснольювать п — 2 уравнения вида
(4.98), а минимизацию функционала (4.101) или (4.107) проводить
только по тем 7,, которые отвечают за значения сплайна в узлах (т.е.
это qt с нечётными номерами г), и по 7-> и Q-in • Обратим внимание па
то, что в рассматриваемой нами силиции в уравнениях вида (4.98)
неизвестными являются не только // (в нашем случае qt с четными
номерами), но и / (в нашем случае 7, с нечётными номерами) и по-
4.17.Использование кубических эрмитовых элементов...
213
этому соответствующие слагаемые с / должны быть Перенесены в
левую часть.
4.17.3. ПРИМЕРЫ ПОСТРОЕНИЯ ОДНОМЕРНЫХ КУБИЧЕСКИХ СПЛАЙНОВ
Рассмотрим примеры построения сглаживающего и различных
интерполяционных сплайнов по набору значений {а;,,./-}, представ
ленных в табл.11.
Таблица 11
i 1 2 3 4 5 6 7 8 9 10 11
0 0.5 1.1 1.5 2 2.5 3. 4. 4.5 4.8 S
2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.3 1.2 0.8 0
Для построения интерполяционного сплайна вычислим значения
производных с помощью квадратичных полиномов Лагранжа по фор-
мулам (4.91), (4.92) и (4.93). В этом случае вектор значений производ-
ных имеет вид:
г = (о. 0,0.0, о, о. -Х_а (4.111)
По тому же набору значений {.г\,/•} построим интерполяционный
сплайн с непрерывными вторыми производными. Для этого производ-
ные сплайна (4.90) будем искать с помощью решения СЛАУ (4.99).
Для рассматриваемого примера матрица и вектор правой части систе-
мы (4.99) имеют вид:
1 0 0 0 0 0 0 0 0 0 0
4 44 3 10 3 0 0 0 0 0 0 0 0
0 10 3 50 3 5 0 0 0 0 0 0 0
0 0 5 18 4 0 0 0 0 0 0
0 0 0 4 16 4 0 0 0 0 0
A = 0 0 0 0 4 16 4 0 0 0 0
0 0 0 0 0 4 12 2 0 0 0
0 0 0 0 0 0 2 12 4 0 0
0 0 0 0 0 0 0 4 64 3 20 3 0
0 0 0 0 0 0 0 0 20 3 100 3 10
0 0 0 0 0 0 0 0 0 0 1
о
о
о
о
о
-1.2
-276
796
15
-140
3
_76
15 .
(4.112)
Решением СЛАУ с матрицей А и вектором правой час ги Ь бу ь i
век юр Г', определяющий значения производных онлайна ( I 90)
214
4.Одномерные задачи
f' = |о, -3 10”1 , 1.3-10-3, -4.1-10-3,1.7 10-?, -6.4-10-’, 0.24. -1.9, -1.31, -2.62, -5.067j
Теперь по набору значений {.г,,/,}, представленных в табл. 11, по-
строим сглаживающий сплайн. В качестве конечноэлементной сетки, в
узлах которой будем определять коэффициенты сглаживающего
сплайна, выберем сетку, состоящую из двух конечных элементов:
Qj =[Q,2], Q2 =[2,5].
Как уже говорилось в предыдущем разделе, найти коэффициенты
сглаживающего сплайна можно в результате минимизации функцио-
нала (4.107) путём решения СЛАУ (4.103) с матрицей (4.108) и векто-
ром правой части (4.109). Коэффициенты Юу, а и 0 функционала
(4.107) определим следующим образом:
со, = 1, а = 0., 0 = 0.001.
Используя соотношения (4.1081 (4.110), получим, что матрица А и
вектор правой части b СЛАУ (4.103) имеют следующий вид:
’ 1.9247 0.3542 0 5006 -0.2313 0 0 6.0631
0.3542 0.1455 0.2436 —0.1064 0 0 1.1914
0.5006 0.2436 3.5553 0.301 0.5316 -0.3687 J 1.299
А = ъ =
-0.2313 -0.1064 0.301 0.5478 0.3788 -0.2433 0.9654
0 0 0.5316 0.3788 3.4556 - 0.8888 4.438
0 0 -0.3687 -0.2433 -0.SSS8 0 408 —2 3074
Векгор решения СЛАУ, определяющий коэффициенты сглажи-
вающего сплайна (4.100), выглядит следующим образом (с округлени-
ем до третьего знака):
q = (-2.5, -0.0117, 2.48. -0 0673. 0.0488, -3.35^ .
На рис. 17 представлены графики всех трёх построенных нами
сплайнов: интерполяционного сплайна с производными, полученными
с помощью квадратичных полиномов Лагранжа, интерполяционного
сплайна с непрерывными вторыми производными и сглаживающего
сплайна.
Как видно из рис. 17, интерполяционный сплайн с непрерывными
вторыми производными имеет больше колебаний, чем интерполяцион-
ный сплайн, построенный с помощью полиномов Лагранжа (см. окре-
стность точки .г = 3.5), т.е. увеличение гладкости сплайна в этом при-
мере нс улучшило, а даже несколько ухудшило результат. Наиболее
плавно изменяется сглаживающий сплайн - он не только имеет наи-
меньшие колебания в окрестности точки т = 3.5, но и совершенно
алатил колебания в окрестности точки х = 4.6. Однако следует пом-
нить, ню при использовании сглаживающего сплайна всегда сущсст-
4.17.Использование кубических эрмитовых элементов...
215
вует опасность сглаживания «истинных» колебаний аппроксимируй-
Как уже говорилось, сглаживающие сплайны наиболее часто ис-
пользуются для аппроксимации функций по их значениям, содержа-
щим случайную ошибку. В следующем примере мы покажем, как
можно построить сглаживающий сплайн для набора значений {т,| /J,
в котором f содержат некоторую случайную ошибку. Эти значения
представлены в табл. 12.
Таблица 12
1 2 3 4 5 6 7 8 9 10 1 1 12 13
0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. 1.1 1.2
10.1 9.4 11.2 8.7 10.6 9.2 10.8 8.5 9.5 9.2 7.4 7.2 5.5
i 14 15 16 17 18 19 20 21 22 23 24 25 26
11 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2. 2.1 2.2 2.3 2.4 2,5
J. 5.5 4.1 3.7 2.2 1.9 1.4 1.3 1.15 0.85 1.2 1.02 0 8 1.
В качестве конечноэлементной сетки, в узлах которой будем онре-
IC I гь коэффициенты сглаживающего сплайна, выоерсм сетку, со-
и ящую из пяти конечных элементов: Q] =[0,0.5], Ч ) 5.1 ],
216
4.Одномерные задачи
Q3 =[1,1.5], Q4 =[1.5,2], =[2,2.5]. Коэффициенты л и |3
функционала (4.107) определим так же, как и в предыдущем примере,
т.е. Wj = 1, ot = 0., (3 = 0.001.
Коэффициенты сглаживающего сплайна (4.100) для данного приме-
ра будут определяться вектором q , который имеет следующий вид:
q = (1(1.(Н,-0.228. 9.88.5.- 0.085, 7.8! 1,-8.826, 3 318,-8.923, 1.076,-0.4:14, 0.939.-0.12!)) . (4.113)
Вид сглаживающего сплайна (4.100), определённого базисными
функциями описанных выше пяти конечных элементов и вектором
весов (4.1 13), приведён па рис. 18
Очевидно, что в данном случае построение интерполяционного
сплайна бессмысленно, поскольку он пройдет через все значения Д ,
содержащие случайную ошибку, п мы просто получим сильно колеб-
лющуюся функцию. Чита!ель можс! в этом убедиться самостоятельно.
Приведём пример вычисления в точке х = 0.8 значения и произ-
водной сглаживающего сплайна, iiociроенного по набору {.г,,/}
(табл. 12) и определяемого вектором весов (4 113) (этот сплайн изо-
бражён на рис. 18).
Рис. 18. Табличные значения (точки) и график сглаживающего сплайна
Для этого вначале определим, в какой из конечных элементов попа-
дает эта точка. В данном случае точка т = 0.8 попадает в элемент
«2 =[0.5,1].
Вычислим значения и производные базисных функций, принимаю-
щих ненулевые значения па этом конечном элементе. Очевидно, что
это будут базисные функции с номерами 3, 4, 5 и 6 (локальные номера
4.17.Использование кубических эрмитовых элементов...
217
этих функций на втором конечном элементе соответственно равны I, 2,
3 и 4). Поэтому, воспользовавшись соотношениями (4.33), получим.
ф4 (0.8) = 0.048 , .^(9.-8) = _0 32 ,
ф5 (0.8) = 0.648 , = 2 88 ’
фс (0.8) = -0.072 , ^М0-8) = _0 12
Воспользовавшись значениями коэффициентов сплайна, опреде-
ляемыми вектором (4.113), получим значение Р(х) в точке х = 0.8 :
с
Р(0.8) = 52 7,Ф, (°-8) = 9-885 • 0 352 + (-0-085) 0.048 +
7 = 3
+ 7.811-0.648+ (-8.826)-(-0.072) = 9.173.
Используя значения производных базисных функций, можно вы-
числить значение производной сплайна Р(.'г) в точке х = 0.8 :
М = +дгМ8)=_4.885.
dx
Таким образом, для вычисления значений (или производных)
сплайна (как сглаживающего, так и интерполяционного) в произволь-
ной точке необходимо определить конечный элемент, в который эта
точка попала, вычислить значения в ней базисных функций (или их
производных) и просуммировать произведения значений базисных
функций (или их производных) в этой точке на соответствующие ком-
поненты вектора весов q.
В заключение этого раздела обратим особое внимание на то, что
рассмотренная нами техника построения одномерных (т.е. зависящих
от одной неизвестной х) интерполяционных и сглаживающих сплай-
нов легко может быть распространена на многомерный случай. Мно-
гомерные сплайны, аппроксимирующие функции по их значениям в
отдельных точках, могут быть получены с использованием бикубиче-
ских эрмитовых элементов для двумерного случая (см. раздел 5.2.6),
грнкуоичсских эрмитовых элементов для трёхмерного (см раз-
дел 6.1.3) и т.д.
218
4.Одномерные задачи
4.18. СОГЛАСОВАННЫЕ РЕЗУЛЬТАНТЫ
4.18.1. 11 XIIO. IOI ИЯ ПОСТРОЕНИЯ СОГЛАСОВАННОГО РЕЗУЛЬТАНТА
Рассмотренные нами методы решения краевых задач с использо-
ванием МКЭ дают приближённое решение и.1' в виде кусочно-
полиномиальной функции. Довольно часто исследователей интересует
поведение не только самой функции и, являющейся решением крае-
вой задачи, но и её производной. Очевидно, что только при использо-
вании эрмитовых элементов производная приближённого решения
является непрерывной функцией. Если же для решения задачи были
использованы лагранжевы элементы, то производная du1'Jdx будет
иметь разрывы на их границах. Существует довольно простой способ
получения непрерывной производной, близкой к duh jdxэтот способ
основан на использовании так называемых согласованных результан-
тов.
Согласованным результантом будем называть функцию wh , ко-
торая является линейной комбинацией базисных функций ф,, с помо-
щью которых было построено конечноэлементное решение, и миними-
зирующая следующий функционал:
(4.114)
Представив и1, и w1' в виде линейных комбинаций и1' = и
*=1
II
wh = (<?/ — известные значения, a q'" - искомые), получим,
г=1
что функционал (4.1 14) примет вид
(4.115)
Учитывая, что
= (q")‘4>a) = фт(.т)д" и = (q"')T3p(.'E) = -фт(.т)д"\
г=1 i=l
преобразуем (4.115) к виду
F (<!"’) = f |Ё -?“ - Ё 1 ® =
Ц U=1 ' 7=1 J
4.18.Согласованныс результанты
219
T fZTp(.t )
dx
r - (q"')T t|h./;)V/P =
dx 4 ' /
— 2(q’")T
Q
- M xt <2*ф(д;) j dty (x)
' dx
dx
с/ф(т)
dx
q" +
Из последнего соотношения видно, что функционал F(q'") являет-
ся квадратичной формой
F(q"') = (q"')T Aq'" - 2(q,")T b + с, (4.116)
в которой матрица А, вектор b и число с определяются соотноше-
ниями:
А = I 'фЧту/О,
о
(4.Н7)
(4.118)
(4.1 19)
Минимизация квадратичной формы (4.116) эквивалентна решению
СЛАУ с матрицей А и вектором правой части Ъ (в чем можно убе-
диться путём её дифференцирования по q"' и приравнивания этих про-
изводных к нулю):
Aq"'=b. (4.120)
Таким образом, для нахождения весов q\" разложения функции wb
но базису {ф;} необходимо решить СЛАУ (4.120) со стандартной мат-
рицей массы с компонентами (см. (4.117))
А;/ = / 'ФтФ/^,
(4.121)
I также вектором правой части, компоненты Ь, которого определяю гея
следующим соотношением (см (4 1 18)):
220
4.Одномерные задачи
ах
(4.122)
В принципе вектор b может быть вычислен в виде b = Dq", где
компоненты несимметричной матрицы D имеют вид:
D = f
' J ах
12
Очевидно, что при решении задачи построения согласованного рс-
п
гультанта w1' = q}для генерации матрицы и вектора СЛАУ
4=1
(4.120) наиболее удобна та же технология, которая используется при
решении краевых задач: сборку матрицы А и вектора b следует осу-
ществлять через локальные матрицы конечных элементов
Полученные нами соотношения вполне пригодны для построения
согласованных результантов и в многомерном случае. Например, если
необходимо построить согласованный результант wh для частной нро-
~ ди1'
ИЗВОДНОИ
(где и1' = q" i|\
•4=1
конечноэлементное решение
двух- или трёхмерной задачи, а под £ можно понимать любую из пе-
ременных х, у или г), то для нахождения весов q"' в разложении
п
w1' = нужно решить СЛАУ (4.120) с матрицей массы А (см.
г— I
(4 117) и (4.! 1)) и вектором правой части Ь с компонентами вида
(сравните с (4.122)):
" Г 'Ж
;=1 о 4
В принципе, можно пытаться строигь и вторую производную ко-
печноэлементного решения и'1 с помощью согласованного результанта
для dw * где wh _ согласованный результант для ~~ . Однако на
ах J ах
практике это далеко не всегда приводит к успеху, особенно если ко-
нечноэлсментное решение иВ * * 11 получено с недостаточной точностью.
Заметим, что иногда согласованные результанты строятся не во всей
расчётной области, а лишь в некоторой сё подобласти. Это делается,
например, в тех случаях, когда решается задача с разрывным коэффици-
ентом диффузии и производная точного решения имеет разрывы.
Обратим внимание па то, что рассмотренная здесь технология по-
строения производных фактически является некоторой технологией
4.1 8.Согласованные результанты
221
сглаживания и сё, в принципе, можно модифицировать, используя раз
личные базисы для разложения и’1 и wh .
4.18.2. ПРИМЕР ПОС I РОЕНИЯ COI ЛЛСОВАННО! О РЕЗУ ЛЬТЛИ ГЛ
В качестве примера построим согласованный результант wh для
производной duMdx конечноэлементного решения и1' краевой задачи
для уравнения (4.1), определённого в области Q = [0,3].
Будем считать, что параметры уравнения определяются соотноше-
ниями
Х = 1, ^ = 4, / = 4«,
на левой границе расчётной области Q задано второе краевое условие
du I _ _ о
dn.\:r={}
а на правой - третье:
44 + ?ДЗ)-Зес+4 = 0.
Нетрудно убедиться, что аналитическим решением этой задачи яв-
ляется функция и — е2с + х, а производной решения - функция
ф = 2с2;/ + 1. (4.123)
dx
Получим конечноэлементное решение и1 с использованием линей-
ных базисных функций на сетке из пяти конечных элементов:
Q) =[0,1.25], Q2 = [1.25,2.1], Q3 = [2.1,2.6], Q4 = [2.6,2.9],
Q5 = [2.9,3]. Вектор весов (разложения решения uh по базисным
функциям) в этом случае будет иметь вид (с округлением)
qM = (-0.9134,8.8438.61.531, 177.27. 328.07, 401.83J1 . (4.124)
du1'
Для построения согласованного результанта для необходимо
решить СЛАУ (4.120) с матрицей, компоненты которой определяю гея
соотношением (4.121), и вектором правой части, компоненты которого
определяются соотношением (4.122). Используя значения вектора ве-
сов (4 124), получим, что матрица А и вектор правой части b hmcioi
следующий вид:
тп
4.Одномерные задачи
_5_ 12 5 24 0 0 0
5 24 0.7 17 120 0 0
0 17 120 0.45 1 12 0
0 0 1 12 4 15 0.05
0 0 0 0.05 2 15
0 0 0 0 1 60
0 0 '4.8786' 31.222
0 0 b = 84.216 133.27
1 112.28
G0 1 36.88
30,
Решением этой СЛАУ является вектор (с округлением)
q'" — fl.3462, 20.725, 116.01 344 92,611 13,800.83
определяющий веса разложения согласованного результанта wh по
базису {ф,;},где ф, - это кусочно-линейные базисные функции
На рис 19,t/ показаны графики производной аналитического реше-
ния d.ujdx (см. (4.123)), производной du1' idx (кусочно постоянной
функции, полученной дифференцированием конечноэлементного ре-
6 6
шения и1' --У^<7гфг(^)) и согласованною результанта д/'-ф/х).
>=1 z=i
Сравним значение согласованного результанта ш1 и производной
duh[dx с производной аналитического решения в произвольно вы-
бранной точке х = 2.7. Нетрудно убедиться, что «/‘(2.7) = 430.33,
du1' (2.7)fdx = 502.65, а производная аналитического решения, опре-
деляемая соотношением (4.123), равна //u(2.7)/(Zx = 443.81.
Используя ту же процедуру, получим согласованный результант uIl
для производной dwh/dx (который фактически аппроксимирует уже
вторую производную решения и ).
На рис. 19,6 приведены графики второй производной аналитиче-
ского решения (I2u]dx2 — 1г2' и второй производной конечноэле-
ментного решения и1', построенной с помощью согласованного ре-
зультанта vh для d-wh[dx.
Таким образом, построение согласованного результанта позволяет
получать значение производной консчпоэлсмент ного решения с доста-
точно высокой точностью и даст возможность пользоваться линейными
элементами даже в тех случаях, когда в качестве результата необходимо
получить не только значения искомой функции, по и её производные.
4.18.Согласованные результанты
223
Рис. 19. Графики производных и согласованных результантов
В рассмотренном примере конечноэлементное решение и.1 было
построено с достаточно высокой точностью, и поэтому даже его вторая
производная, полученная с помощью согласованного результанта для
dwh'ldx, довольно близка ко второй производной аналитического ре-
шения (см. рис. 19,6).
Рассмотрим ещё один пример построения первой и второй произ-
водной конечпоэлементного решения с помощью согласованного ре-
зультанта.
Расчётную область Q выберем в виде: Q = [l,2|. Коэффициенты
уравнения (4.1) определим следующими соотношениями:
Х = 1. 7 = 0, / = -2/.г3.
На левой границе расчётной области Q зададим первое краевое ус-
. ювие, а на правой — третье:
„| =1 xk| +и(2)- 0.25 = 0.
/:=1 du[i:=2
Нетрудно убедиться, что аналитическим решением этой задачи яв-
ляется функция и — 1/х , а производной решения - функция
dujdx =
(4.125)
Конечноэлсментное решение ?//' получим с использованием линейных
и гшеных функций на равномерной сетке из пяти конечных элементов
Как и в предыдущем примере, с помощью согласованного pciyjn.
1.ЧНП1 построим первую и вторую производные конечношеменinoi о
решения На рис.16// приведены графики производной аналитически-
224
4.Одномерные задачи
го решения (4.125), производной du!'/dx (кусочно-постоянной функ-
ции, полученной дифференцированием конечноэлементного решения
и* ) и согласованного результанта wh .
Рис. 20. Графики производных и согласованных результантов
для случая относительно грубой сетки
На рис 20.6 показаны график второй производной аналитического
решения d2u/dx2 = 2/хл и график второй производной конечноэле-
ментного решения и11, построенной с помощью согласованного ре-
зультанта vh для dw>l/dx.
Как видно из рис. 20,а, для данного примера значения согласован-
ного результанта, построенного для первой производной и, в окрест-
ности точки х = 1 несколько отклоняются от значений производной
аналитического решения, по тем не менее эго расхождение является, в
общем-то, приемлемым. Значения же второй производной, построен-
ной с помощью согласованного результанта (см рис 20,6), уже суще-
ственно отличаются от значений второй производной аналитического
решения, особенно в той подобласш, где была значительной погреш-
ность у •«/' Читатель может самостоятельно убедиться, что с дробле-
нием сетки (особенно в окрестноети .г = 1 ) функция w1' будет быстро
приближаться к (lu/dx, а вслед за этим и функция v1' начнет намного
точнее аппроксимировать d2u/dx2 .
5.1 Основные особенности технологии построения М1< )
2?5
5. ДВУМЕРНЫЕ СКАЛЯРНЫЕ ЗАДАЧИ
5.1. ОСНОВНЫЕ ОСОБЕННОСТИ ТЕХНОЛОГИИ ПОСТРОЕНИЯ
МКЭ-АППРОКСИМАЦИЙ ПРИ РЕШЕНИИ ДВУМЕРНЫХ ЗАДАЧ
Как уже было показано выше, для вычисления компонент гло-
бальной матрицы конечноэлементной СЛАУ, в принципе, нет необхо-
димости в явном виде строить глобальные кусочно-полиномиальные
базисные функции ф, конечномерного пространства V1', на котором
ищется МКЭ-решение uh в виде uh = (/гф7 . Как правило, бывает
вполне достаточно определить эти базисные функции ф, на отдельных
конечных элементах, т.е. построить локальные базисные функции фр
в виде полиномов пространственных координат определенной степени.
Глобальные же базисные функции получаются естественным образом
сшивкой локальных базисных функций соседних конечных элемен-
тов При этом сшиваются те локальные базисные функции (из разных
конечных элементов), которые соответствуют одному и тому же узлу в
глобальной нумерации.
Таким образом, для лагранжевых элементов иод сшивкой факт иче-
ски понимается объединение локальных функций нескольких примы-
кающих к одному узлу конечных элементов, и это должно быть сдела-
но так, чтобы глобальная функция была как минимум непрерывна во
всей расчётной области (очевидно, что вне примыкающих к опреде-
ляющему глобальную функцию узлу конечных элементов эта функция
должна быть равна нулю).
При использовании эрмитовых конечных элементов чигываегся так-
же и то, какое значение соответствует рассматриваемой базисном функ-
ции: значение в узле самого решения и или значение какой-либо из его
производных (в двумерном случае это может быть первая пром людная по
х , первая производная по у, смешанная производная по х и у и т.д )
)(ля проверки корректности задания локальных базисных функции ил
конечном элементе необходимо убедиться лишь в том, что глобаньныс
базисные функции, полученные в результате сшивки из локальных функ
ций, обеспечивают согласованность всех конечных элсмснгов (при ре
шении эллиптических краевых задач для дифференциально! о уравнения
второго порядка для согласованности конечных элементов доенпочно
226
5. Двумерные скалярные задачи
непрерывности глобальных кусочно-полиномиальных базисных функций
на границах конечных элементов, ч то и обеспечивает допустимость этих
функций для вариационной формулировки), а также в том, что их линей-
ные комбинации представляют любые кусочно-полиномиальные функ-
ции требуемого вида (это свойство часто называют свойством полноты).
В дальнейшем мы будем использован, именно такой способ проведения
конечноэлементной аппроксимации решаемой задачи.
В связи с тем, что при таком способе построения конечноэлемент-
ной аппроксимации глобальную матрицу удобней всего собирать из
соответствующих локальных матриц, конкретизируем выражения
(3.55)-(3.56) для компонент локальных матриц в наиболее часто ис-
пользуемых системах координш (с учётом двумерности расчётной
области).
5.1.1. ЛОКАЛЬНЫЕ МАТРИЦЫ ДЛЯ (ВУ Ml ГНОЙ 1АДАЧИ В ДЕКАРТОВОЙ
СИСТЕМЕ КООРДИНАТ
Дифференциальное уравнение (1.1) для двумерной эллиптиче-
ской краевой задачи в декартовой системе координат {х,у} может
быть записано в виде
дх\ дх! ду[ <)ц)1Г J- ( ’
Компоненты локальных матриц, определяемые выражениями
(3.55)-(3.56), в этом случае имеют вид:
Г (сМ) chb ^Ф,'! - с ' -
= J Х + М'-> = J ^jdxdy. (5.2)
5.1.2. ЛОКАЛЬНЫЕ МАТРИЦЫ ДЛЯ ДЮ Ml ГНОЙ ЗАДАЧИ В ПОЛЯРНОЙ
СИСТЕМЕ КООРДИНАТ
Дифференциальное уравнение (1.1) для двумерной эллиптиче-
ской краевой задачи в полярной системе координат {г, ф) может быть
записано в виде
X д ( \ ди\__1_ с)
г дг\ дт) г2 dtp
+ уи = f .
Компоненты локальных матриц, определяемые
(3.55)-(3.56), в этом случае имени вид;
, = Г
'' J дг д г
1 дф,
г2 dtp dtp
Мг) -J -уф^фуп/гг/ф.
&
rdrdtp;
(5.3)
выражениями
(5.4)
(5.5)
5.1.Основные особенности технологии построения МКЭ...
227
5.1.3. ЛОКАЛЬНЫЕ МАТРИЦЫ ДЛЯ ОСЕСИММЕТРИЧНОЙ ЗАДАЧИ
Дифференциальное уравнение (1.1) для эллиптической осесим-
метричной краевой задачи (т.е. для двумерной задачи в цилиндричс
ской системе координат {г, z) ) может быть записано в виде
_! <9 I х &и\_д I\ ди\
г dr \ dr) dz\ dz)
+ уи = f
Компоненты локальных матриц,
(3.55)—(3.56), в этом случае имеют вид:
(5 6)
определяемые выражениями
ЙА
dr dr dz dz
rdrdz_
М, = J ^^rdrdz . (5.7)
ЙА
5.1.4. О ВЫЧИСЛЕНИИ ЛОКАЛЬНЫХ ВЕКТ ОРОВ ПРАВЫХ ЧАСТЕЙ
Компоненты локального вектора правой части b конечного эле-
мента определяются следующими выражениями:
• в декартовой системе координат
ь. = ff^dxdy ; (5.8)
ЙА.
• в полярной системе координат
bt = J" f^\rdrd<p ; (5.9)
йа
• в цилиндрической системе координат
l)t = f f^rdrdz . (5.10)
йа
В выражениях (5.8)-(5.10) функция f - правая часть соответствующе-
го дифференциального уравнения (5.1), (5.3) или (5.6).
Интегралы в выражениях (5.8)—(5.10) могут быть вычислены раз-
личными способами. Иногда (для аналитически заданных функций /')
их вычисляют аналитически. Однако этот способ является очень не-
технологичным и используется крайне редко. Довольно часто ннтсгра
лы в выражениях (5.8)—(5.10) вычисляют методами численного интег-
рирования, например, с помощью квадратурных формул Гаусса.
Мы же в основном будем использовать рассмотренный нами и оч
номерном случае способ (фактически являющийся некоторым енецн-
альным способом численного интегрирования), который заключат юя в
следующем.
Локальный вектор правой части Ь будем вычислять с \ чётом юго.
что функция f на конечном элементе представлена в виде райю-
228
5.Двумерные скалярные задачи
f
(, V=1 1
и
жения по базисным функциям , где п - число локальных
v=l
базисных функций конечного элемента . Тогда (см. рассуждения,
приведённые на с. 133) локальный вектор b может быть вычислен
через матрицу С, фактически являющуюся матрицей массы элемента
Qa. при 5 = 1:
Ь = Ср. (5.11)
В принципе, значения компонент вектора р можно было бы нахо-
дить из условия максимальной близости к f линейной комбинации
п
У2 Рр'Фр в норме пространства Л2 , г.с. из условия минимизации по Д,
V = 1
функционала
dil. (5.12)
Однако в этом случае пришлось бы каким-либо способом считать ин-
тегралы вида
(5.13)
Мк
(например, численно). На самом деле, можно показать, что получаемые
при использовании такой процедуры значения компонент Ь, локально-
го вектора правой части фактически являются самими значениями ин-
тегралов (5.13), которые нужно вычислять при минимизации функцио-
нала (5.12), и поэтому вычисление компонент вектора р является со-
вершенно излишним. Мы же хотели здесь лишь обратить внимание
читателя на то, что замена функции ' ближайшей к ней в норме про-
странства Ь2 линейной комбинацией локальных базисных функций
п
РмФм в рассматриваемых нами схемах МКЭ полностью эквива-
v=l
лентна прямому вычислению компонент Ь, в виде интегралов (5.13)
(естественно, при вычислении интегралов (5.13) одним и тем же спо-
собом в обеих процедурах).
В дальнейшем мы так же, как и в одномерном случае, в двумерных
задачах будем заменять правую часть /’ на элементе её полиноми-
альными интерполянтамн. Очевидно, что тогда для лагранжевых эле-
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках 229
ментов веса р1? нужно задавать как значения fv правой части f диф-
ференциального уравнения в соответствующих узлах ху элемента .
5.2. ПОСТРОЕНИЕ МКЭ-АППРОКСИМАЦИЙ
НА ПРЯМОУГОЛЬНЫХ СЕТКАХ
Пусть требуется решить
краевую задачу для дифференци-
ального уравнения (5.1) в дву-
мерной области Q, состоящей из
прямоугольных фрагментов. В
качестве примера такой области
рассмотрим расчётную область
Q, структура которой показана
на рис. 21. Эта область состоит
из трёх прямоугольных фрагмен-
тов - Q1, Q2 и Q3. В каждом из
этих фрагментов заданы свои
значения параметров X, -у и f
дифференциального уравнения
(5.1), которые могут быть либо
константами, либо некоторыми
функциями координат (а в случае
нелинейной эллиптической зада-
Рис. 21. Пример двумерной расчётной
области Q
чи - и функциями решения и). Будем также считать, что на границе
S) (в примере на рис. 21 S) = S'* U S'2, где Sj = {.т = 2; 1 < у < 2},
S'2 = {2 < х < (у у = 2} ) задано краевое условие первого рода (1.2), на
границе S'2 (в рассматриваемом примере S’2=S2US2, где
S2 = {.? = 6; 2 < у < 5} , Sf = {1 < х < 2\у ~ 1}) - краевое условие
второго рода (1.3), на границе S3 (в нашем примере
S3=SjU5jU533, S'1={1<J.<2;S = 5}, = {2 < х < 6-,у = 5},
5$ = {х = 1; 1 < у < 5} ) - краевое условие третьего рода (1.4)
Рассмотрим аппроксимацию этой краевой задачи на прямоугольной
сетке. При этом ячейками дискретизации являются прямоугольники
П/;л. = [.тр, др+1 ] х [v/.s-, 2/.s+i ]> те- ячейки этой сетки строятся в виде при
мого (декартова) произведения независимых друг от друга одномср
1 На регулярных прямоугольных сетках конечные элементы довольно ч.ь
то нумеруют с использованием нескольких индексов. В двумерном случае
один индекс указывает на положение конечного элемента по осп г, а ню
рой- на положение по оси у. При использовании же nepciулярпых сток
(включая и прямоугольные с «дырами») номер конечного HicMeiiia определи
ется, как правило, одним индексом.
230
5.Двумерные скалярные задачи
ных сеток [tj,...,тп} и - Тогда выражения для вычисления
компонен! локальных матриц (5.2) принимают вид:
(5-14)
(5.15)
5.2.1. БИЛИНЕЙНЫЕ БАЗИСНЫЕ ФУНКЦИИ
Наиболее просто на прямоугольнике Q ,Л. строятся так называе-
мые билинейные базисные функции. Э1и функции определяются сле-
дующим образом. На отрезке ; | задаются две одномерные ли-
нейные функции
V, (.г> = ''''ф \ U) = h., =xt,+l -хр. (5.16)
Аналогично на интервале (ys, уЛ.+1) задаются линейные функции
= = h,=V,»-V.- (5.17)
ЬУ у
Локальные базисные функции на конечном элементе
— |ж/п тр+1 j x [y/A,;t/.s+i ] представляются в виде произведения функ-
ций (5.16) и (5.17):
Ф| (т,//) = Х| О;)У1 (//),
Фз ( н.'/) = Azi (ж) Y-2 (у),
ф-2 (^ у) = ^2 и-) У1 Су) ,
Ф’4 (з\ У) = Х2 (X) Y2 ((/) .
(5.18)
Поскольку функции ф, (т,у) линейны но каждой из переменных х и
у, и\ называют билинейными функциями.
Очевидно, что функция фт (ж, у) равна единице в узле (xp,ys) и
нулю во всех остальных узлах конечного элемента Q/;s; аналогично
функция ф2 (ж, у) равна единице в узле (т/;+1 и нулю во всех ос-
тальных узлах Q/w, Фз (.г, у) - единице в узле (ж/)7 t/s.+1 ) и нулю во
всех остальных узлах Q//s., ф4 (.т, //) - единице в узле (з;р+1) т/ч+1) и
нулю во всех остальных узлах Q?,s.. Па рис. 22 показана локальная ну-
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках 23 I
мерация узлов прямоугольника Qps., соответствующая локальном ну-
мерации определённых нами локальных базисных функций ф, (./, //)
При использовании билинейных
базисных функций (5.18) компоненты
локальных матриц жёсткости (5.14) и
массы (5.15) легко вычисляются через
компоненты матриц жёсткости и мас-
сы линейных одномерных элементов.
Действительно, учитывая представ-
ление базисных функций (5.18), для
вычисления интегралов (5.14) и (5.15)
достаточно предварительно вычис-
лить одномерные интегралы
Jp+h-r J'p+1'я:
с clX dX.. г
/ ^-^dx и / XyrX..dx (и
J dx dx J 1
J:i> Ti>
такие же интегралы от произведении
Рис. 22. Расположение узлов
на прямоугольном конечном элементе
с билинейными базисными функциями
функций (у) и их производных), которые фактически и являются
компонентами локальных матриц жёсткости и массы для одномерных
конечных элементов с линейными базисными функциями (см. соотно-
шения (4.8) и (4.10)). Тогда, если параметр X на конечном элементе
Qps. заменить его осреднённым значением X и учесть, что
р +^ir
' г dXidX-2 ! 1
J dx dx h, ’
Xp
•'/>+/'.r
r (V <& = •&
о
Ip
(аналогичный вид имеют и интегралы от произведений функций (</)
и их производных), получим
Xp+l'ti l/.i+l'n
!ls
ш2
дх
Wi
< ду .
2)
dxdy =
232
5 Двумерные скалярные задачи
Аналогично вычисляются остальные компоненты локальной мат-
рицы жёсткости G.
11с менее просто вычисляются компоненты локальной матрицы массы
(параметр также заменим на П/(Л. его осрсднённым значением ^):
•/;р+/':<• Ux+1'fi . j
Мц=чГ A? (Yj)2 dxdy = ч j X'fdx J Y?dy =
т.р ys
''p+^j: !/s+hy
ЛЛ2=7 f XlX2Yl2dn = ^ f XtX2dx Г y2dy = ^^-
•f J J 1.0
51 pS tr.p t)N
и т.д. В результате получим
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках 233
' 2 -2 1
Г /1„ -2 2 -1
r~i _ Л ___У
6 h:i: 1 -1 2
-1 1 -2
М = ^С =
-1'
-2
1
2
/
(5.19)
4 2 2 f
_ ll j h y 2 4 12
36 2 1 4 2
12 2 1
/
(5.20)
Локальный вектор правой части b конечного элемента Q//s вычис-
лим, представив на правую часть f дифференциального уравне-
4
ния (5.1) в виде билинейного интерполянта ^2.А,Фр так, как это было
V— 1
описано в разделе 5.1.4. Локальный вектор b в этом случае легко вы-
числяется через матрицу С, фактически являющуюся матрицей массы
при = 1 (см. соотношение (5.20)):
b = C-f =
h.rhy
~36'
4/1 +2/2+2/3+1
271+4/2+./3+2Л
2/1+/2+4/3+2Л
/1+2/2+2/з-|-4/4
(5.21)
Когда используются элементы более высокого порядка (с биквадра-
тичными или бикубическими базисными функциями), вычисления
компонент локальных матриц становятся гораздо более громоздкими.
Поэтому мы хотим продемонстрировать другой (гораздо легче алго-
ритмизируемый) способ вычисления компонент локальных матриц
жёсткости и массы для прямоугольников через компоненты матриц
жёсткости и массы одномерных элементов.
Получим таким способом локальные матрицы билинейных элемен-
тов. Обозначим матрицы жёсткости и массы соответствующих одно-
мерных линейных элементов следующим образом:
М2 f
6 1 2
/
(5.22)
(5.23)
234
5 .Двумерные скалярные задачи
Тогда элементы верхнего треугольника матрицы жёсткости можно
представить в виде:
(7n = X(Gfl<l+WiG»),
Gu^Gf^ + M^),
G22=X(GhMfl + A^2G;'I),
G24 = \(G}2M?2 + M^G{'.2),
с12 = х(сг2м»+m(2g»),
GH = X(G1W“ +лДс*)
G23 = x(G?1Mi’2 + M^1qQ,
G33 = X(GF1M|2 + Mf,G|2),
GM = X (GiW& + , И = X (G^M^ + M$2G“2) (5.24)
(остальные элементы матрицы G нс приводятся, поскольку она сим-
метричная).
Элементы матрицы массы (также с учётом её симметричности) мо-
1утбыть представлены в виде:
Мп=^М[\, M12=WiW?i,
Л/]4 = W1W12,
л/2, = W22M", м23 = ^м^м[>2 ,
Л = Wii Л^2, Щ Ч-?м->2,
м13 =
м24 =
(5.25)
Очевидно, что соотношения (5.24) и (5.25) (с учётом (5.22)-(5.23))
фактически являются другой записью соотношений (5.19) и (5.20).
Вклады в глобальную матрицу и вектор правой части конечноэле-
ментной СЛАУ от краевых условий третьего и второго рода также
могут быть представлены в виде локальных матриц и векторов ребер,
па которых заданы эти краевые условия. При этом на каждом ребре
(которое в случае прямоугольной сетки ориентировано вдоль одной из
осей координат) ненулевыми являются только две базисные функции
т]1! и ф2, причём они линейны па этом ребре. Тогда локальная матри-
ца ребра Г длины h с заданным на нём краевым условием третьего
рода фактически является матрицей массы одномерного конечного
элемента с линейными базисными функциями (считаем, что 3 = const
па Г)
fp(^)\/r
Г г
f Рф2Фг7Г J
/г г
И2 г
6 12
(5-26)
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках 235
а локальный вектор bS:! этого ребра Г при представлении на 1 в
виде разложения по базисным функциям фх и (ч с
г/р = «i'ih + Uji2Ф2 ) имеет вид
f Р(^1Ф1 +
Г
+ 'W
6 + 2й|Г2^
(5-27)
Локальный вектор Ь5’2 ребра Г длины h с заданным на нём крае-
вым условием второго рода при представлении параметра 9 на г в
виде буф] + 6-2'Ф2 вычисляется аналогично Ь3:! и имеет вид
Ь5'2 = —
6
20! 4-02'
01 + 202
)
(5.28)
Сборка глобальной матрицы и вектора правой части конечноэле-
ментнои СЛАУ из локальных матриц и векторов конечных элементов
так же, как и в случае одномерных элементов, выполняется по соответ-
ствию локальной и глобальной нумерации базисных функций. На за-
ключительном этане должны быть учтены краевые условия первого
рода. Возможные процедуры учёта первых краевых условий будут
рассмотрены в следующем разделе.
5.2.2. ОБ УЧЁТЕ КРАЕВЫХ УСЛОВИЙ ПЕРВОГО РОДА
Учёт первых краевых условий (которые в рассматриваемых ва-
риационных постановках являются главными), как было сказано выше,
проводится после полной сборки глобальной матрицы и правой части
(включая учёт естественных краевых условий - условии второго и
третьего рода) путём фиксации соответствующих весов qt при реше-
нии СЛАУ. Таким образом, фактически из сгенерированной СЛАУ
должны быть исключены уравнения с теми номерами, которые явля-
ются номерами узлов, лежащих на границе с краевыми условиями пер-
вого рода, а весам с этими номерами присвоены значения перво» о
краевого условия в соответствующих узлах сетки. Заметим, что проце-
дура учёта первого краевого условия может быть реализована по-
разному.
Например, можно на место исключенных уравнений iiociaBiiii.
уравнения вида qt = (где (ж,,у/) — координаты у era с i 10
бальным номером /, который лежит на границе с краевым ус ювисм
первого рода), т.е. в матрице СЛАУ в г-й строке (строке ш ключпемою
уравнения) на место диагонального элемента ставится единица, все
236
5.Двумерные скалярные задачи
остальные элементы этой строки матрицы обнуляются, а г-й компо-
ненте вектора правой части присваивается значение uf/ .
Вообще говоря, если узел сетки лежит на границе с краевым усло-
вием первого рода, то в конечноэлементной СЛАУ не должно было бы
генерироваться соответствующее уравнение (поскольку при переходе
от вариационной формулировки к конечноэлементной аппроксимации
вместо пробной функции нс должны подставляться базисные функции
прос транства V", которые не входят в базис пространства Ц,’,
см. с. 103). Это означает, что после прохода по всем конечным элемен-
там некоторые из сгенерированных нами уравнений конечноэлемент-
ной СЛАУ (соответствующих узлам с первыми краевыми условиями)
являются фиктивными. Поэтому фактически мы должны были бы
получить прямоугольную матрицу (размера х п , где - размер-
ность пространства Vj1, а и — размерность пространства V1'), причём
и — /?.() весов — это известные значения, определяемые из первых крае-
вых условий.
Очевидно, что можно было бы получить СЛАУ с квадратной мат-
рицей п(1 х п(), но для этого нужно было бы во всех уравнениях, куда
входят переменные фиксируемые через первые краевые условия,
перенести произведения а,,//., в правую часть СЛАУ (это можно, на-
пример, реализовать умножением j-io столбца матрицы на число qt и
вычитанием полученного вектора из вектора правой части). Сущест-
венным недостатком такого способа является то, что в этом случае
нумерация неизвестных в копечноэлементной СЛАУ не совпадает с
нумерацией узлов сетки (точнее, весов в разложении решения по бази-
су пространства V1'). В результате возникает необходимость запомн-
или. соответствие между нумерацией весов и нумерацией неизвест-
ных. Кроме того, при хранении матриц конечноэлементпых СЛАУ в
упакованных форматах появляются дополнительные сложности реали-
зации исключения соответствующего столбца матрицы.
Рассмотренный же нами первым способ учета главных краевых ус-
ловий с обнулением соответствующей строки матрицы и занесением
на сё диагональ единицы и значения фДт,,//,) в соответствующую
компоненту вектора правой части, хотя и сохраняет соответствие ну-
мерации неизвестных в копечноэлементной СЛАУ и весов (базисных
функции), но всегда нарушает симметричность матрицы. В результате
для решения конечноэлементной СЛАУ не могут быть без определен-
ных модификаций использованы методы, учитывающие симметрич-
ность сё матрицы.
Однако не представляет особого груда сохранить как симметрич-
ность матрицы, так и полное совпадение нумерации неизвестных
СЛАУ с нумерацией весов базисных функций. Для этого достаточно
провести исключение определяемых первыми краевыми условиями
значений д, с обнулением внедиагональных элементов г-й строки и
г-го столбца матрицы (путём их Гауссова исключения с помощью г-й
5.2.Построение МКЭ-аппроксимаций па прямоугольных сетках 237
строки), оставив эти строки и столбцы в матрице, и это снимае! как все
проблемы при использовании методов решения СЛАУ для симметрии-
ных матриц, так и проблему соответствия нумерации неизвестных
СЛАУ нумерации весов базисных функций.
На практике довольно часто применяют ещё один довольно про-
стой в реализации способ учёта первых краевых условий. Вместо того
чтобы на место фиктивного г-го уравнения ставить уравнение
q, = и,! диагональный элемент а.и в матрице заменяется неко-
торым очень большим числом С, а г'-я компонента вектора правой
части заменяется значением Czz(/(.г,,?/.,). Число С выбирается так,
чтобы < еС, 1де е фактически определяет точность, с которой
мы хотим выполнения требуемого уравнения q, — (естест-
венно, при выборе числа С следует помнить о представлении вещест-
венных чисел в компьютере и о возможности переполнения). Заметим,
что и в этом способе есть проблемы при использовании некоторых
итерационных методов решения СЛАУ, связанные с создаваемой при
такой обработке первых краевых условий разномасштабностью урав-
нений СЛАУ, которая порождает разномасштабность соответствую-
щих компонент вектора невязки. Поэтому пользоваться таким методом
нужно с определенной осторожностью.
5.2.3. ПРИМЕР ИСПОЛЬЗОВАНИЯ БИЛИНЕЙНЫХ ЭЛЕМЕНТОВ
Проиллюстрируем всю процедуру генерации глобальной матри-
цы и вектора правой части на следующем примере. Пусть эллиптиче-
ская краевая задача для уравнения (5.1) решается в области, описанной
в начале раздела 5.2 и изображённой на рис. 21. Будем считать, что
коэффициенты уравнения (5.1) принимают значения
1 в Q1 2 в Q1 2.т в Q1
X = 10 в Q2 , 7 = 1 в Q2 , f = 1.8 +0.1а; в Q2 . (5.29)
10 вО3 0 в Q3 0 в Q3
Будем также считать, что краевые условия па границах области за-
даны следующим образом:
2, uL = 0.1а;+ 1.8, Х^
ди
dll S1
Л ,=0’
<772
!=0’
ди
дп
0.5(12 + 1))
\ дп 4 7
= 0.
(5.30)
238
5 Двумерные скалярные задачи
Зададим в расчётной области Q — Q1 U U максимально гру-
бую конечноэлементную сетку, для которой нумерация конечных эле-
ментов и глобальная нумерация узлов показана на рис. 23.
Рис. 23 Грубая конечпоэлемептпая сетка в расчётной области Q
Используя соотношения (5.22)Д5.25), вычислим значения компо-
нент локальной матрицы и вектора правой части первого конечного
элемента.
А01
' 8
9
18
_JL
18
__5_
I 18
_1____1_____5_'
18 18 18
8 __5_ _J_
9 18 18
5 8 _JL
18 9 18
_1_____1_ 8
18 18 9 J
A'
3
5‘
6
2
3
5
По со01ветствию локальной нумерации узлов прямоугольного ко-
нечною элемента (см. рис. 22) их глобальной нумерации на Q,
(рис. 23) заносим компоненты локальной матрицы AQ1 и вектора bQ1
в глобальные матрицу А и вектор Ъ. На этом элементе локальные
номера узлов совпадают с глобальными, и поэтому А-;21 просто пере-
носится в Л(/ и 6 s21 в Ь, :
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках 239
- те I -те -те 0 ° ° ° ° 0 0
- те -те I -те 0 0 0 0 0 ° °
- те -А -те | “
О 0 0 00000000
0 0 0 00000000
О 0 0 00000000
О 0 0 00000000
О 0 0 00000000
О 0 0 00000000
О 0 0 00000000
о
о
о
о
о
J
Теперь вычислим
го элемента:
компоненты локальной матрицы и вектора второ-
' 23 _13
18 36
_13 23
36 18
1____И
18 36
__11 7
I 36 18
7 _lf
18 36
11 7
36 18
23 _13
18 36
13 23
36 18j
м
3
5.
3
4
3
5
Ы
Для этого конечного элемента локальный номер 1 соответствует гло-
бальному номеру 3, локальный номер 2 — глобальному номеру 4, ло-
кальный номер 3 - глобальному номеру 6, локальный номер 4 — гло-
бальному номеру 7. Поэтому компонента заносится в Д33, компо-
нента Ау2 в Л34, в 4ЗС, Л^2 в Д37, Л^2 в Л43, Л22 в Л44, Дгз2 в
и т.д. (аналогично bf1'2 заносится в Ь3 , Ь^2 в и т.д.):
240
5 Двумерные скалярные задачи
' 8 9 J:i_ 18 1 18 __5_ 18 0 0 0 0 0 0 0 o' 3
18 8 9 __5_ 18 L 18 0 0 0 0 0 0 0 5 6
L IS __5_ 18 13 6 __5_ 12 0 _7 18 _ 1] 36 0 0 0 0 2
5 18 L 18 5 12 13 6 0 _11 36 7 18 0 0 0 0 I 5 2
0 0 0 0 0 0 0 0 0 0 0 0
А = 0 0 7 18 _ u 36 0 23 18 _13 36 0 0 0 0 b 4 3
0 0 _11 36 7 18 0 _13 36 23 18 0 0 0 0 5 6
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
Локальные матрицы и векторы остальных конечных элементов
формируются и заносятся в глобальные аналогично:
A^ = 8 9 __1_ 18 18 __5_ 18 18 8 9 __5_ 18 18 Я. 18 5 18 8 9 __1_ 18 18 _J_ 18 L 18 8 9 J b“:{ = 2' 3 5 6 2 3 5 gJ >
' 8 9 L 18 __1_ 18 __5_ 18 0 0 0 0 0 ‘ c 0 3
__1_ 18 8 £ 5_ 18 1_ 18 0 0 0 0 0 c 0 5 6
L 18 __5 18 13 6 __5_ 12 0 7 IS H 36 0 9 c 0 2
__5_ 18 L 18 5 12 13 6 0 - 11 36 7 IS 0 0 c 0 5 2
0 0 0 0 0 0 0 0 0 c 0 0
A = 0 0 7 18 _JJ_ 36 0 13 6 "12 0 L 18 __5 18 0 , ь 2
0 0 _11 36 7 IS 0 - 5 12 13 6 0 "Is L IS 0 •5 2
0 c 0 0 0 0 0 0 0 c 0 0
0 ( 0 0 0 - 1 18 __5_ 18 0 8 9 L 18 0 2 3
0 ( 0 0 0 - 5 IS 18 0 1_ 18 8 9 0 5 6
0 k c 0 0 0 0 0 0 0 1 0 - 0
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках 241
Л
А$1'«
83 19 _97 _71_ 64
9 9 18 18 15
19 S3 _71 _97 68
9 9 18 18 Ьи« = 15
_97 _71 83 19 64
18 1S 9 9 15
_71 _97 19 83 68
18 18 9 9 115
' 8 9 1 18 L 18 __5_ 18
1 Я 5 1
18 9 18 18
1 5 13 5
18 18 6 12
5 1 5 905
18 18 12 18
0 0 0 19 9
0 0 7 18 _Н_ 36
0 0 36 -5
0 0 0 _71 18
0 0 0 0
0 0 0 0
0 0 0 0
ь = /2 1*. 203
\3’ 30 ’
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 7 _11 0 0 0 0
18 36
19 _11_ -5 _71 0 0 0
9 36 18
83 0 _71 — 97. 0 0 0
9 18 18
0 13 5 0 __1_ __5_ 0
6 12 18 18
_71 5 205 19 5
Q
18 12 18 9 18 18
_97 0 19 83 0 0 0
18 9 9
0 __5_ 0 8 _ _L о
18 18 9 18
0 5 __1_ 0 _ 1 8 о
18 18 18 9
0 0 0 0 0 0 0
68 203 68 2 5
15’ ’ 30’ 15’ 3’ 6’ ) ’
Aslft
85 35
6 6
35 85
6 6
155 _85
12 12
_85 155
12 12
155 _85'
12 12
85 155
12 12
85 35
6 6
35 85
6 6
bUr>
'О’
о
о
о
242
5 Двумерные скалярные задачи
8 9 L 18 1 18 5 18 0 0
1 8 5 1 о 0
18 9 18 18
1 5 13 5 7
18 18 6 12 18
5 1 5 205 19 11
18 18 12 18 9 36
0 0 0 19 83 0
9 9
Л = 0 0 7 18 36 0 13 6
0 0 11 -5 71 5
36 18 12
0 0 0 _71 _97 0
18 18
0 0 0 0 0 __1_
18
0 0 0 0 0 5_
18
0 к 0 0 0 0 0
0 0 0 0 0 ' 2 '
3
0 0 0 0 0 5
11 36 0 0 0 0 6 2
-5 _71 18 0 0 0 203 30
_71 _97 0 о о 68
18 18 15
э 0 __1_ __5_ о 1 Ь “ 2
12 18 18
230 143 __5_ _467 _85 203
9 18 18 36 12 30
143 421 о _85 155 68
18 1S 12 12 15
__5_ 0 8 L 0 2
18 9 18 3
167 _85 L 271 35 5
36 12 18 18 6 6
_85 155 о 35 85 0
12 12 6 6 J
Для учёта естественных краевых условий воспользуемся описанной
в разделе 5.2.1 технологией, когда вклады в глобальную матрицу и
вектор правой части конечноэлементной СЛАУ от краевых условий
третьего и второго рода представляются в виде локальных матриц и
векторов рёбер, на которых заданы эти краевые условия.
Рассмотрим учёт второго краевою условия, заданного на границе
S']. Эта граница включает в себя два ребра Г5 8 (ребро между верши-
нами с номерами 5 и 8) и Г811 (ребро между вершинами с номерами 5
и 8). С помощью соотношения (5.28) вычислим локальные вектора
„ £ Гг>Л £ГМ1
правых частей b и b второго краевого условия, заданного на
границе S). Учитывая то, что параметр 0 2 (у), определяющий второе
краевое условие на границе S? (см (5.30)), является константной на
этой границе, и, следовательно, веса б['г,’к, 0/',к и б' ' , of8,11 ею раз-
ложения по линейному базису на обоих рёбрах границы Sj равны 1,
получим:
5.2.Построение МКЭ-аппроксимации на прямоугольных сетках 243
где Д5.8 = 2 и Л81ц = 1 длины рёбер Г5>8 и Г8 п соответственно.
„ Гг,.к - гх,п
Занесение локальных векторов b и b в глобальный выпол-
няется по соответствию локальной и глобальной нумерации Так, ком-
- Гл.х - Ггцк - Гид 1
понента ' добавляется к 65, компоненты 65 и ~ к &8 и
Гкл 1
компонента Ь2 - к ои .
Таким образом, после учёта вторых краевых условий глобальный
вектор правой части примет вид:
ь — (2 5 о 203 S3 -> 203 181 2 5 0 АТ
\3’ 6’ ’ 30' 15’ 30 1 30’ 3’ 6’ / ’
Правая часть второго краевого условия, заданного на 1ранице S2 ,
равна нулю, и поэтому учёт этого краевого условия никаких измене-
ний в глобальный вектор правой части (и, естественно, в конечноэле-
ментную СЛАУ в целом) не вносит.
Рассмотрим учёт третьего краевого условия, заданного на границе
»$з. Эта граница состоит из одного ребра Гд1(), длина которого hg1()
равна 1. С помощью соотношений (5 26) и (5.27) вычислим локальную
матрицу А1"9-11’ и локальный вектор ЬГ°’10 этого ребра. Учитывая то,
cjl
что параметр (Г3 этого краевого условия на Гд]() равен 1, а веса раз-
51
ложения параметра w t 1 (т) по локальным линейным базисным функ-
s) si
циям этого ребра принимают значения = 1, й^-2 — 2 , - получаем:
Г‘).1о
0*4,ю Р
6 1
I6
2Й^‘ +
Далее по соответствию локальной и глобальной нумерации локаль-
ная матрица А1910 и локальный вектор ЬГ911’ заносятся в глобальные,
компонента Д1}1,11’ добавляется к компоненте Ajg, Д1^'10 - к Ljjo,
А ?и’ - к Додо, Ьр’10 - к by и &J9,10 -к &10• Аналог ично выполняется
учёт третьих краевых условий, заданных на границах и S'*/ (см
(5.30)).
244
5.Двумерные скалярные задачи
После учёта всех заданных третьих краевых условий глобальная
матрица А и глобальный вектор правой части b примут вид:
' 19 18 __1_ 18 1 36 5_ 18 0 0 0 0 0 0 0
L 18 8 9 5_ 18 __1_ 18 0 0 0 0 0 0 0
1 36 __5_ 18 8 3 __5_ 12 0 5 9 _П 36 0 0 0 0
5 18 1 18 __5_ 12 205 18 19 9 _11 36 -5 71 18 0 0 0
0 0 0 19 9 S3 9 0 _71 18 _97 18 0 0 0
А 0 0 5 9 _Ц 36 0 8 3 5 12 0 1 36 5 18 0
0 0 _Ц 36 -5 _ 71 18 __5_ 12 230 9 143 18 5 18 467 36 _85 J2
0 0 0 _71 18 _97 18 0 143 18 421 18 0 _85 12 155 12
0 0 0 0 0 1 36 5 18 0 25 18 1 9 0
0 0 0 0 0 __5_ 18 167 36 _85 12 1 9 645 36 43 6
0 0 0 0 0 0 _85 12 155 12 0 43 6 101 6 J
Ь = ( 5 5 Г2’ 6 5. 4‘ 203 30 ’ 83 5 15' 4 203 30 181 30 ’ 12 51 13' 5 287 30 \Т
Как было сказано в разделе 5.2.2, при учёте первых краевых усло-
вии в конечноэлементной СЛАУ изменяются уравнения с номерами,
совпадающими с номерами узлов, лежащих на границах с первыми
краевыми условиями. В рассматриваемом примере это узлы с номера-
ми 2, 4 и 5. В строках матрицы А с этими номерами на диагональ ста-
вится значение 1, а остальные компоненты этих строк обнуляются. В
соответствующие же компоненты вектора правой части заносится зна-
чение функции и;) (из первого краевого условия) в соотвстствующем
узле
Таким образом, после учёта первых краевых условий матрица А и
вектор правой части b конечноэлементной СЛАУ примут окончатель-
ный вид:
5.2.Построение МКЭ-аппроксимаций на прямоугольных ссгках 245
f 19 1 5 0 0 0 0 0 0 0 5.)
18 18 36 18 1 ’
0 I 0 0 0 0 0 0 0 0 0 2
1 5 8 5 0 5 _11 0 0 0 0 5
36 18 3 12 9 36 1
0 0 0 1 0 0 0 0 0 0 0 2
0 0 0 0 1 0 0 0 0 0 0 2.4
А = 0 0 5 9 11 36 0 8 3 _|Ъ_ 12 0 1 36 __5_ 18 0 Ь = 5 4
11 -5 71 5 230 143 5 467 85 203
36 L8 12 9 18 18 36 12 30
о 0 0 - 71 97 0 143 121 0 85 155 181
18 18 18 18 12 12 30
о 0 0 0 0 1 5 0 25 1 0 12
36 18 18 9 13
о о 0 0 0 5 467 85 1 645 43 51
18 36 12 9 36 6 5
о о 0 0 0 0 _85 155 0 43 101 287
1 12 12 6 6 ( 30
Вектор решения полученной конечноэлементной СЛАУ, являю-
щийся вектором весов разложения искомой функции и1' по билиней-
ному базису, имеет следующий вид:
q = (1, 2, 1, 2, 2.4, 1. 2, 2.4, 1, 2, 2.4^.
Заметим, что рассмотренный пример построен как тестовая краевая
задача, поскольку её точное решение является функцией
х в Q1
1.8 + 0.1т в Q2 UQ3 ’
(5.31)
принадлежащей соответствующему конечномерному пространству
кусочно-билинейных функций (натянутому на базисные функции, оп-
ределяемые в соответствии с изображённой на рис. 23 конечноэле-
ментной сеткой). Нетрудно убедиться, что компоненты вектора реше-
ния полученной СЛАУ действительно являются весами разложения
точного решения по базисным функциям этого пространства (и, кроме
того, значениями точного решения в соответствующих узлах сетки).
5.2.4. БИКВАДРАТ! 1ЧНЫЕ Ь \<ИСИЫЕ ПКЦИИ
Кроме билинейных базисных функций на прямоугольных» копеч
пых элементах довольно часто используются полиномиальные функ-
ции более высоких порядков - биквадратичные и бикубические.
Биквадратичной называется функция вида
Ф (х, у) = «О + а[х + + аЗл'У + «42'2 + +
+ асх2у + а7ху2 4- а8.г2?;2 . (5.32)
246
5.Двумерные скалярные задачи
Очевидно, что каждая би квадратичная функция фактически опре-
деляется значениями девяти коэффициентов. Поэтому на конечном
элементе = j.rp,.T?+1 jx [z/s, z/s.+]] мы можем представить любую
биквадратичную функцию в виде линейной комбинации некоторых
девяти линейно-независимых биквадратичных функций. В качестве
таких функций (фактически являющихся локальными базисными
функциями элемента £l,s) удобно взять биквадратичные функции,
равные единице в одном из узлов элемента и нулю во всех остальных
сто узлах. Таким образом, биквадратичный элемент должен содержать
9 узлов. Обычно в качестве таких определяющих биквадратичные ба-
зисные функции узлов на прямоугольнике задают четыре его вершины,
четыре точки в серединах сторон и ещё одну точку в центре прямо-
уюльпика. Па рис. 24 представлен биквадратичный элементе одним из
возможных вариантов локальной нумерации его узлов.
Рассмотрим наиболее часто ис-
пользуемый (и наиболее удобный)
способ определения явного вида этих
биквадратичных базисных функций на
прямоугольном конечном элементе.
Представим каждую базисную функ-
цию в виде произведений одномерных
квадратичных базисных функций ко-
ординат X и у.
Обозначим через X] (ж) квадра-
тичную функцию, равную единице
при х = хр и нулю при х = Xp+L и
квадратичную
единице при
при х = х., и
!/
Гис. 24. Расположение узлов
на прямоугольном конечном элементе
с бнкнядратичными базисными
функциями
а? — ;e7H.i ,
функцию,
X - Ж ,1
/'*2
квадратичную
X — X
равную
и нулю
функцию, равную единице
и х — х £. Аналогично введём
г = j />+ j , а через Х3 (ж) -
при .г = .г/Н1 и нулю при ,
функции /Ду), Y2(y) и У3 (</) (Yt(y) равна единице при у — ys и
нулю при у — у £ и у = уч. £ и т.д.). Тогда локальные базисные
Л + 2
функции ф, (х,у) на конечном элементе = [эф,-гр+1] х г/л.+1] с
показанной па рис. 24 локальной нумерацией его узлов имеют сле-
дующий вид
Фз (*,у) = Л'з (.Т) Vj (г/),
Фз &,у) = %2 ЮЪ (у),
4’2 у) = ^2 (я) ?i (у),
4м &у) = Xi (x)Y2 (</),
Фе &у) = X3(x)Y2 (</),
5.2.Построение МК')-аппроксимаций на прямоугольных сслк i\
217
Ф7 (?, у) = ^-) Уз (у), Ф8 у) = хл ю У-л (//),
Фо (-А2/) = Лз (ж)У3 (?/).
(5.33)
Выражения для вычисления компонент локальных матриц жёстко-
сти и массы и вектора правой части прямоугольного конечного эле-
мента с биквадратичными базисными функциями наиболее удобно
получить через компоненты локальных матриц одномерных квадра
тичных элементов (так же, как это было показано на с. 234 для били-
нейных элементов):
G, = x(G". .М'> . . +МГ , Gr' J, (5.34)
Mrj , ,М" ,-А, (5.35)
где Gt j, G'1^ , Л7 и Л/''} - компоненты локальных матриц жёсткости
и массы соответствующих одномерных конечных элеменюв с квадра-
тичными базисными функциями (см. соотношения (4.23)-(4.24)):
7 -8 1
G= -о-^- -8 16 -8
3/1...
1-8 7
4 2 -1'
2 16 2 ,
-1 2 4
мт
Ь:1:
30
( -8 1
G1' = 4- -8 16 -8
3/1(.
И 1 —8 7
(
-1 2 -1
М!> = 2 16 2
30
-1 1 2 4
(5.36)
(5-37)
В соотношениях (5.34) и (5.35) индексы а = р(г) и |3 = p(j) для
и МФ$, а также cv = н(г) и Р = v(j) для G'^ и вычисляют-
ся через целочисленные функции р, и и, задающие соответствие меж-
ду номерами одномерных и двумерных базисных функций. Для нуме-
рации, определённой соотношениями (5.33), эти функции могут быть
записаны в следующем виде:
ц (г) = ((г — 1) mod 3) + 1,
vW = [±i_i]+1’
(5.3S)
где a mod b — остаток отделения числа а на число b, [а] - целая часть а .
Локальный вектор правой части b с учётом того, чго функция J
(являющаяся правой частью уравнения (5.1)) на конечном элементе
9
представлена в виде биквадратичного интерполянта } Фм , может
v I
быть вычислен (см. раздел 5.1.4) с помощью соотношения
248
5.Двумерные скалярные задачи
b = Cf,
(5.39)
где f = -вектор, составленный из значений правой части /
дифференциального уравнения в узлах элемента, С — матрица массы
(5.35) при = 1, т.е.
С„ = М* . ЛГ' , , v (5.40)
Для краевых условий третьего и второго рода локальные матрицы и
векторы рёбер, на которых заданы эти краевые условия, фактически
являются локальными матрицами массы и локальными векторами од-
номерных конечных элементов с квадратичными базисными функция-
ми (аналогично билинейным элементам, см. с. 234). Так, локальная
матрица ребра Г длины h с заданным на нем краевым условием
третьего рода имеет вид (считаем, что Р = const на Г)
(5.41)
а локальный вектор Ь5;{ этого ребра Г при представлении и,, на Г в
виде разложения по одномерным квадратичным локальным базисным
функциям -ф1? ф-2 и Фз (т е- — «р1Ф1 +'йИ211,2 + +}3ф3) имеет вид
Ь’9:» = AS;l
= 3 —
1 30
^03
4'Ut}J + 2й[)2 — '/фз
2?z(J1 + 16й[)2 + 2W(j3
—й(И + 2'^)2 + 4il|j3 ,
(5-42)
Локальный вектор Ь5г ребра Г длины h с заданным на нём крае-
вым условием второго рода при представлении параметра 0 на Г в
видсб^ф, Ь 62Ф2 + вз'Фз вычисляется аналогично bA;1 и имеет вид
46, + 262 - Оз
Ь5’2 _ _L
30
20, +160-2 +203
-б, +262+463
(5-43)
Краевые условия первого рода учитываются фиксацией соответст-
вующих весов qt (i — глобальные номера узлов сетки, лежащих на
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках 249
границе с краевым условием первого рода, q, — u;i каким либо
из способов, описанных в разделе 5.2.2.
5.2.5. БИКУБИЧЕСКИЕ ЛАГРАНЖЕВЫ БАЗИСНЫЕ ФУНКЦИИ
Бикубические базисные функции на прямоугольном лагранже-
вом конечном элементе могут быть построены аналогично рассмот-
ренным выше биквадратичным функциям. Этот элемент будет иметь
4 х 4 = 16 узлов, как это показано на рис. 25. Заметим, что для опре-
деления базисных функций на таком элементе нет необходимости вы-
писывать общий вид бикубической функции (аналогично соотноше-
нию (5.32) для биквадратичной)1, поскольку гораздо удобней (в том
числе и для вычисления локальных матриц) определить каждую бику-
бическую базисную функцию в виде произведения двух одномерных
базисных функций (аналогично (5.33) для би квадратичных функций)
Ф? р(») •
(5-44)
При этом целочисленные функции р. и v в соответствии с нумерацией
узлов, приведённой на рис. 25, определяются соотношениями
ц (г) = ((г - 1) mod 4) + 1, и (г) = |+ 1 > (5-45)
в которых (как и в соотношении (5.38)) a mod 6 - остаток от деления
а на 6, [с] - целая часть а.
Нетрудно убедиться, что локаль-
ные матрицы для определённых таким
образом бикубических элементов вы-
числяются через элементы матриц
жёсткости и и массы и
одномерных кубических элемен-
тов с помощью тех же самых соот-
ношений (5.34)-(5.35), а локальный
вектор правой части - с помощью
соотношений (5.39)- (5.40) (в которых
вектор f значений функции J в узлах
элемента имеет, естественно, размер-
ность 16, совпадающую с числом уз-
лов на бикубическом элементе).
Учёт краевых условий для бикуби-
Рнс. 25. Расположение узлов
на прямоугольном конечном элементе
с бикубическими базисными
функциями
ческих лагранжевых элементов в целом ничем не отличается oi учёта
краевых условий для биквадратичных и билинейных элементов
1 Впрочем, и для биквадратичной функции её общий вид (5 3?) мы, в об-
щем-то, никак не использовали.
250
5 Двумерные скалярные задачи
5.2.6. БИКУБИЧЕСКИЕ ЭРМИТОВЫ БАЗИСНЫЕ ФУНКЦИИ
Значительный интерес при решении некоторых практических за-
дач могу г представлять бикубические эрмитовы конечные элементы,
обеспечивающие непрерывность производных глобальных базисных
функций на границах конечных элементов. Локальные базисные функ-
ции для этих элементов также мо>ут быть построены в виде произве-
дения кубических функций одномерных эрмитовых элементов (см.
раздел 4.6),
Обозначим через X] (ж) кубическую базисную функцию, равную
единице при ж = хр , нулю при х = х.ч t и имеющую нулевые произ-
водные при х = хр и х = жр+1 , т.е. (ж) - это функция (ж), рас-
смотренная в разделе 4.6. Через Х2(х) обозначим одномерную куби-
ческую функцию ф-2 (ж) из раздела 4.6 (она равна нулю при х = .ту, и
= ж/Н. । , и её производная равна единице при х = хр и нулю при
х = / р н ), через (х) - функцию ф3 (ж), а через Х4 (х) - функцию
ф4 Ст). Аналогично на интервале (у5,ул-+1) введём кубические функ-
ции ) 1 (//), У2 (у), Уз (у) и У4 (у) (У] (у) - это Ф, (</) ит д.).
Тогда бикубические функции могу г быть представлены в виде
(5.44), при этом целочисленные функции р, и v определим соотноше-
ниями
р (i) = 2^X=J ]тосГ2^ + ((/ — 1) тос12) -|- ] , (5.46)
v(i) = 2p^| Д[0=-фпо<12) + 1 . (5.47)
В результате каждая бикубическая функция ф.г (ж,//) фактически опре-
д’Ф,. (*, У)
дсляегся своими значениями и значениями производных -----
(9ф. (х,у) д2ф. (ж, у)
---сЬ—:— И —(). 'ch В четь,Рёх веРшинах конечного элемента
Qps = 'р+1 х [у.оУ.-н-ib причём у каждой из функций -фДж,?/)
только одно из этих значений и только в одной вершине равно едини-
це, а остальные 15 значений равны нулю. Так, у функции
Ф1 (ж,?/) = (ж)У1 (?/) единице равно се значение в вершине
(при этом в трёх остальных вершинах она равна нулю и во всех чсты-
<Э'ф|(ж, ?/) d^i(x.y)
рёх вершинах значения её производных -------—- и
5.2.Построение МКЭ-аппроксимаций на прямоугольных сечках
251
у функции
дх
"~дхду Равнь1 НУЯЮ)- У функции ф2 (х,у) = (х) A (yj единице
д^2(х>у) / \
равно значение -------—- в вершине (хр,уя),
s z \ xz тл / \ <Уфз (х, у)
я’з \Х>У) — А (х)1<2 \У) единице равно значение -в всР|1|ине
У функции ф4 (х,у) — Х-2 (х) У2 (у) единице равно значение
а2ф4 (х, у)
дхду
единице равно её значение в вершине i
i|)G (х, у) = Х4 (х)У[ (у) единице равно значение —-д—
в вершине (хр, ys). У функции ф5 (х, у) = Х3 (х) У] (у)
x„+i,y.,), У функции
5фс (х, у)
---------------------------------------------------- в вершине
VVm>//aJ ит-д-
Локальные матрицы жёсткости G и массы М для бикубических
эрмитовых элементов так же, как и для лагранжевых (см. соотношения
(5.34), (5.35)), удобнее всего вычислять через элементы матриц жёст-
кости <7', и (. и массы М", и М;' ( одномерных эрмитовых кубиче-
ских элементов (см (4.34) и (4.35)). Для постоянных па конечном эле-
менте коэффициентов X и это можно сделать с помощью соотно-
шений (5.34)-(5.35), в которых функции ц и и определяются соотно-
шениями (5.46)-(5.47).
Локальный вектор правой части b бикубического эрмитова эле-
мента тоже (как и лагранжева) можно вычислить с помощью соотно-
шения (5.1 1) через локальную матрицу С, которая определяется соот-
ношением (5.40) и совпадаете локальной матрицей М при = 1 (как
это было описано в разделе 5.1 4). При этом компоненты вектора р,
являющиеся коэффициентами разложения функции f на конечном
элементе Q/M., могут быть определены как коэффициенты бикубичс-
10
ского интерполян га ^р/Ф/ функции f, т.е. pt, р5, р9 и р13 - эю
значения функции f
df
р14 — значения в
дх
в соответствующих вершинах Q/ s., /?>, pCl, ри} и
- „ . - dj
них, р3, р7, ри и Pis - значения -j—
/'я.
Pi 2 и Ас - значения .
252
5.Двумерные скалярные задачи
Рассмотрим теперь проблему построения глобальных базисных
функций и сборки глобальной матрицы из локальных. Каждая гло-
бальная базисная функция получается в результате сшивки всех ло-
кальных базисных функций тех конечных элементов, которые содер-
жат узел, соответствующий рассматриваемой глобальной базисной
функции (т.е. сшиваются все локальные базисные функции, ассоции-
рованные с одним и тем же узлом). Фактически от способа сшивки
зависит гладкость получаемой глобальной функции. В соответствии с
этим осуществляется и сборка глобальной матрицы из локальных (т.е.
занесение компонент локальных матриц в глобальную осуществляется,
как обычно, по соответствию локальных номеров локальных базисных
функций на элементе номерам «сшитых» из них глобальных базисных
функций).
Если эрмитовы конечные элементы применяются для решения за-
дачи с непрерывным коэффициентом диффузии X, то наиболее есте-
ственной сшивкой является следующая В каждом узле сетки опреде-
лим по четыре глобапьные базисные функции. Первая базисная функ-
ция получается путём сшивки локальных базисных функций, равных
единице в этом узле на всех примыкающих к нему элементах. Вторая -
путём сшивки тех функций, у которых производная по х равна едини-
це, третья — путём сшивки тех функций, у которых производная по у
равна единице, а четвёртая — путём сшивки тех функций, у которых
д2
смешанная производная равна единице.
Полученные в результате такой сшивки глобальные кусочно-
бикубические базисные функции порождают конечномерное про-
странство Vh функций v1' , имеющих не только непрерывные первые
duh
производные -Ч — и —у, но и непрерывные смешанные производные
Использование таких конечных элементов может быть особен-
но эффективно в том случае, koi да в качестве результата решения
краевой задачи необходимо получить значения именно производных
решения в заданных точках расчётной области. Кроме того, функции
?/' порождаемого такими элементами пространства V1'' являются до-
пустимыми и для решения вариационных задач, эквивалентных крае-
вым задачам для бигармоническш о уравнения (т.е. для дифференци-
ального уравнения четвёртого порядка).
Однако на практике часто встречаются задачи, в которых коэффи-
циент диффузии X является разрывной функцией координат, и соот-
ветственно па каждой границе разрыва X разрывной является и нор-
мальная к этой границе производная решения. В этом случае, как пра-
вило, используют лагранжевы элементы. Гем не менее иногда бывают
ситуации, когда требуется получить более гладкое решение в области
непрерывности коэффициента X. Чуть ниже мы покажем, как можно
построить базис на кубических элементах, который позволял бы полу-
чать решение с непрерывными производными в отдельных подобла-
дхд и
5 2 Построение МКЭ-аппроксимаций на прямоугольных сетках 253
стях расчётной области и с разрывами в нормальных производных на
границах разрыва коэффициента X. Мы рекомендуем ознакомиться с
этим материалом ещё и потому, что он позволяет глубже понять неко-
торые теоретические и практические аспекты МКЭ.
5.2.7. ИСПОЛЬЗОВАНИЕ БИКУБИЧЕСКИХ ЭРМИТОВЫХ ЭЛЕМЕНТОВ
ПРИ РЕШЕНИИ ЗАДАЧ С РАЗРЫВНЫМ КОЭФФИЦИЕНТОМ ДИФФУЗИИ
Покажем, как можно использовать бикубические эрмитовы ба-
зисные функций на примере аппроксимации решения задачи с коэф-
фициентом диффузии X, разрывным по х .
В каждом узле, лежащем на границе разрыва х = const определим
не четыре глобальные базисные функции (как это было сделано для
эрмитовых элементов с непрерывной производной), а шесть.
Первая базисная функция получается путём сшивки локальных ба-
зисных функций, равных единице в этом узле на всех примыкающих к
нему элементах (так же, как для стандартных эрмитовых элементов с
непрерывной производной).
Вторую функцию получим сшивкой тех локальных базисных функ-
ций, у которых производная по х равна единице и которые определе-
ны на примыкающих к рассматриваемому узлу прямоугольниках, ле-
жащих слева от границы разрыва X (заметим, что если к рассматри-
ваемому узлу примыкают два лежащих слева от границы разрыва пря-
моугольника, то сшиваются две локальные функции, в противном слу-
чае эта глобальная базисная функция порождается фактически только
одной локальной базисной функцией). Справа о г границы разрыва X
рассматриваемая глобальная базисная функция определяется тождест-
венно равной нулю (очевидно, что полученная таким образом функция
непрерывна, имеет непрерывную производную по у и разрывную
только на границе х = const производную по х — слева значение её
производной по х равно единице, а справа - нулю).
Третью функцию получим аналогично второй, т.е. сшивкой тех ло-
кальных базисных функций, у которых производная по х равна еди-
нице и которые определены на примыкающих к рассматриваемому
узлу прямоугольниках, лежащих справа от границы разрыва X Слева
от границы разрыва X эта базисная функция определяется тождест-
венно равной нулю (таким образом, построенная функция непрерывна,
имеет непрерывную производную по у и разрывную только на грани-
це х = const производную по х - слева значение её производной по
х равно нулю, а справа — единице).
Четвёртая базисная функция строится путём сшивки локальных ба-
зисных функций, производная которых по у равна единице в этом
узле на всех примыкающих к нему элементах (так же, как была по
строена третья базисная функция для эрмитовых элементов с непре-
рывной производной, см. с. 252).
Пятая же и шестая базисные функции, отвечающие cooi веге гвшню
за значения смешанной производной слева и справа от ip.uinm.i p.npi i-
ва X, строятся аналогично второй и третьей базисным функциям пу-
тём сшивки локальных базисных функций, отвечающих за шачсния
254
5.Двумерные скалярные задачи
смешанной производной на каждом конечном элементе. При этом пя-
тая функция получается путём сшивки локальных базисных функций,
определённых на лежащих слева от границы разрыва элементах, а шес-
тая - справа.
11а рис. 26 приведён пример нумерации глобальных базисных функ-
ций ф, (г = 1...50) для случая, когда сетка состоит из пяти конечных
элементов и границей разрыва X является линия а; = 2. Для этой сет-
ки вес построенные глобальные базисные функции обладают непре-
рывными производными Эф?у<9у/. Непрерывными производными
дх^^дх обладают только функции с номерами 1—13, 16, 19-27,30.33-
41,44, 47—50. Значение производной ди1'/дх при х = 2 — 0 (т.е. слева
от границы разрыва X) для функций и'1 из порождаемого таким обра-
зом конечномерного пространства определяется в разложении //' по
базису {ф,} весами при базисных функциях с номерами 6, 14, 28 и 42,
а при х — 2 4- 0 (т.е. справа от границы х — 2) - с номерами 15, 29 и
ПЛ “ -
43. Аналогично, значение смешанной производной q~q j ПРИ
г = 2 — 0 определяют веса при базисных функциях с номерами 8, 17,
3 1 и 45, а при х = 2 4- 0 - с номерами 18, 32 и 46.
Обратим внимание ещё на одно
обстоятельство, связанное с приме-
нением эрмитовых элементов для
задач с разрывным коэффициентом
диффузии в ситуации, когда граница
разрыва коэффициента диффузии
имеет прямой угол. Примеры таких
ситуации показаны на рис. 27, где
X], Х’2 и Х3 — некоторые постоян-
ные значения коэффициента диффу-
зии, не совпадающие между собой.
В ситуации, изображённой на
рис. 27,<7, в точке Р с координатами
(х^Ур) точное решение и имеет
производную dujdx, непрерывную
по .т при у = + 0 и разрывную
по г при у = ур —0 (аналогично в этом случае ведёт себя и произ-
водная ди./Оу) В ситуации, изображенной на рис. 27,6, в точке Р
точное решение и имеет производную dujдх, разрывную по х как
при у = ур -|- 0, так и при у = ур — 0, по при этом сами значения
разрыва нс совпадают (производная же diddy ведёт себя так же, как и
в предыдущем случае). Очевидно, что возможны и другие ситуации с
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках 255
дыдущем случае). Очевидно, что возможны и другие ситуации с раз-
рывно-нспрсрывн|ыми в узле, Р производными1.
Рис. 27. Примеры ситуаций с разрывно-непрерывными в узле Р производными
В такого рода случаях при использовании эрмитовых элементов мы
рекомендуем делать такую сшивку локальных базисных функций, что-
бы производные dujclx и dufdij (и, естественно, д2и/дхду) полу-
ченных глобальных базисных функций были разрывными, т.е. опреде-
лить в узле девять глобальных базисных функции.
Первая функция образуется сшивкой всех четырёх локальных ба-
зисных функций, отвечающих за значение решения в узле Р . Вторая
получается в результате сшивки двух локальных базисных функций,
отвечающих за значение производной по х на левом нижнем и левом
верхнем конечных элементах (из четырёх элементов, примыкающих к
узлу Р). Третья получается в результате сшивки двух локальных ба-
зисных функций, отвечающих за значение производной по х на пра-
вом нижнем и правом верхнем элементах. Четвертая получается сшив-
кой двух локальных базисных функций, отвечающих за значение про-
изводной по у на левом нижнем и правом нижнем элементах, а пятая —
сшивкой двух локальных базисных функций, отвечающих за значение
производной по у на левом верхнем и правом верхнем элементах.
Остальные четыре базисные функции получаются из локальных ба-
зисных функций, отвечающих за значение смешанной производной па
каждом из примыкающих к узлу Р конечных элементов, при этом
носителем каждой из этих функций является только один соответст-
вующий конечный элемент (т.е. на остальных элементах она доопреде-
ляется нулём).
Заметим, что для решения задач с разрывным коэффициентом диф-
фузии, в принципе, можно попытаться использовать эрмитовы элемен-
ты с непрерывной производной, однако сходимость к точному pel нс
нию в этом случае оказывается очень плохой (что будет проиллюсгри
ровано на приведённом ниже примере, см. раздел 5.2.9.2).
1 естественно, во всех этих ситуациях предполагается, чю р.кт м.нрннле
мыс производные в точке Р отличны от нуля
256
5. Двумерные скалярные задачи
5.2.8. УЧЁТ КРАЕВЫХ УСЛОВИЙ ДЛЯ БИКУБИЧЕСКИХ ЭРМИТОВЫХ
ЭЛЕМЕНТОВ
Процедуры учёта естественных краевых условий для эрмитовых
элементов, в оощем-то, ничем не отличается от соответствующих про-
цедур для лагранжевых элементов. Единственным отличием является
то, что не совсем очевидно, какие из базисных функций на ребре Г не
равны тождественно нулю.
Локальная матрица для третьего краевого условия имеет размер
1 х 1, и её компоненты вычисляются как
(5.48)
Г
где - функция, равная единице в первом (в локальной нумерации)
узле ребра Г, ф2 “ функция, производная которой вдоль Г равна еди-
нице в первом узле, - функция, равная единице во втором узле Г,
ф4 — функция, производная которой вдоль Г равна единице во втором
узле.
Обратим внимание па то, что узлам рассматриваемого ребра Г, во-
обще говоря, соответствуют восемь базисных функций, но четыре из
них, отвечающих за значения нормальной к ребру производной и сме-
шанной производной, на самом ребре тождественно равны нулю.
Таким образом, локальная матрица для третьего краевого условия
(в случае, когда 0 = const на I ) фак1ически является матрицей массы
одномерного эрмитова элемента (см раздел 4 6):
156 22/1. 54 — 13/1
~ о fl/> 2211 4Л2 13Л —ЗЛ2
А6:’ = , (5.49)
420 51 13/1 156 -22Л ’ V 7
-13/1 -З/i2 —22Л 4Л2
где h — длина ребра Г. Занесение локальной матрицы (5.49) в гло-
бальную, очевидно, должно делаться как обычно, но соответствию
введённых нами на ребре локальных номеров базисных функций гло-
бальным.
Соответственно определяются и локальные векторы правых частей
при учете вторых и третьих краевых условий (т.е. фактически это ло-
кальные векторы правых частей одномерных кубических эрмитовых
элементов, см. раздел 4.6).
При учёте же первых краевых условий (1.2) следует обратить вни-
мание на то, что значение функции и1 на ребре определяется не толь-
ко значениями весов базисных функций, равных единице в узлах сёт-
ки, но и значениями весов базисных функций, отвечающих за значения
в вершинах ребра 1 касательных к Г производных. Действительно,
базисные функции, отвечающие за значения в вершинах Г касатель-
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках
257
ных к Г производных, хотя и равны нулю в узлах (вершинах) ребра,
вовсе не равны нулю на всём ребре. Поэтому, если зафиксирован, веса
только у двух (отвечающих за значения и1' в узлах) базисных функ-
ций, то первое краевое условие не будет выполнено.
Таким образом, для учёта первого краевого условия на ребре I
нужно зафиксировать веса четырёх базисных функций, две из которых
равны единице в вершинах Г, а другие две имеют равную единице
касательную к ребру Г производную в его вершинах. При этом веса
первых двух функций можно, например, задать равными значениям
функции и,. (х,у) в соответствующих узлах Г, а веса остальных двух
функций - значениям касательной к Г производной функции д(/ (.т, ?/).
Например, если ребро Г с вершинами, имеющими координаты
(1,7) и (3,7), является частью границы S) с краевым условием
и L, = и.ч (ж> у} ~ е2> + У (5.50)
и если вершинам Г соответствуют глобальные базисные функции с
номерами 21,22, 23, 24 и 53, 54, 55, 56 (тут мы используем описанную
выше, в разделе 5.2.6 на с. 252, нумерацию, когда в каждом узле пер-
вой нумеруется функция, отвечающая за значение в этом узле, вто-
3 д2
рой - за производную , третьей - за и четвёртой - за ), то
для учёта этого краевого условия веса можно зафиксировать следую-
щим образом:
<721 = uy/(1J) = e2 + 7,
<753 = (3,7) = eG + 7,
(722 —
Эх
= 2е2,
954 “ дх
= 2ес.
3,.у=7
1,//=7
Если же ребро Г, являющееся частью границы с краевым усло-
вием (5,50), было бы ориентировано вдоль оси Y, например, его вер-
шины имели бы координаты (1,7) и (1,9), то при той же нумерации
соответствующих его вершинам глобальных базисных функций веса
можно было бы зафиксировать следующим образом:
<721 = «7/(1,7) = е2 +7,
<753 = uf/(l,9) = е2 +9,
<7?3 Qy
= 1,
1,//=7
dU!l
ду
Вообще говоря, можно было бы
весов из условия минимизации
находить значения фиксируемых
по этим весам (функционала
258
5.Двумерные скалярные задачи
J(и" — и;1У dS (т.е. аппроксимировать функцию и,, на 5] сплайном,
S1
имеющим минимальное среднеквадратичное отклонение от и,), но
такая процедура является гораздо более трудоёмкой и поэтому на
практике применяется довольно редко.
5.2.9. ПРИМЕРЫ РЕШЕНИЯ ЭЛЛИПТИЧЕСКИХ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ
БИКУБИЧЕСКИХ ЭРМИТОВЫХ ЭЛЕМЕНТОВ
5.2.9.1. ТЕСТОВЫЙ ПРИМЕР
Рассмотрим краевую задачу для уравнения (5.1) с параметрами
Х = 1, 4 = 2,
/ = -24 (от/3 + х3у) - Wy - 1 I- 2 (I r+ 5.г'2// + 2//2 + ю). (5.51)
Расчётная область, в которой будем искать решение, представлена
на рис. 28. На границах расчетной области определим следующие
краевые условия:
и | = 0.004т3 + 0.5т2 + 10.02, (5 52)
= — 5а;2, (5.53)
OTl Is] V
ХМ2=-(12по^+|о°»)> <5-54>
X + и Is - 36800// - 2//2 - 2200// - 10 = 0. (5.55)
IS., з
Т
«2
13-16
Рис. 28. Расчётная область
Нетрудно убедиться, что аналитическим решением этой задачи яв-
ляется функция
и (ж, у) = 1а;3?/3 + 5а;2?/ + 2у2 + 10 . (5.56)
Пусть конечноэлементная сетка состоит из одного конечного эле-
мента, совпадающего с расчётной областью. Поскольку при использо-
вании бикубических эрмитовых элементов каждому узлу соответству-
5.2.Построение МКЭ-аппроксимаций на прямоугольных, сетках 259
ет четыре неизвестные (см. раздел 5.2.6), введём нумерацию неизнес i
ных так, как это показано на рис. 28.
Как уже говорилось в разделах 5.2.1-5.2.6, для прямоугольных >лс
ментов двумерные матрицы жёсткости и массы удобно собирать ш
матриц одномерных элементов. Для эрмитовых бикубических элемен-
тов алгоритм сборки двумерной матрицы элемента из одномерных
определяется соотношениями (5.34)-(5.35) и (5.46)-(5.47).
Используя соотношения (4.34) и (4.35) (см. раздел 4.6), построим
матрицы жёсткости и массы одномерных эрмитовых элементов. Mai-
рицы жёсткости и массы для одномерного конечного элемента, ориен-
тированного вдоль .г, будут иметь вид (с учётом того, что
h. = h, = 10):
0.12 0.1 -0.12 0.1 26 7 ПО 21 9 7 65 21
0.1 4 -0.1 ПО 200 65 _50
3 3 , м = 21 21 21 7
-0.12 -0.1 0.12 -0.1 9 65 26 ПО
4 7 21 7 21
0.1 -0.1 65 _50 110 200
3 3. . 21 7 21 21
(5.57)
а для одномерного конечного элемента, ориентированного вдоль у (и
с учётом того, что h = hu = 0.1), - следующий вид:
12 0.1 -12 0.1 0 1 -0 1 —— 1 300 300 -12 -0.1 12 -0.1 01 "300 "01 300 26 11 9 6э
’ мУ - ш 7 11 210 9 7 65 210 2 2100 65 2100 5 7 65 2100 26 7 11 2100 5 7000 11 210 2
. 2100 1000 210 2100
(5.58)
Используя соотношения (5.34)-(5.35) и (5.46)-(5.47) и одномерные
матрицы жёсткости и массы (5.57) и (5.58), вычислим значения компо-
нент двумерной матрицы жёсткости и массы. Вычислим таким спосо-
бом, например, компоненту Z58 локальной матрицы рассматриваемого
двумерного элемента (числа, записанные не в дробях, приводятся с
окру! лением):
&>8 = G^ + = <-о. d • + 0.1 • (-Ш) =
= -О 00005238 - 0.52380952 = -0.5238619,
Мщ = 'fC'se = = 2(-Ш) (-LU) = —0.00548752,
Д58 = G58 + Л?58 = -0.5238619 - 0.00548752 = —0.5293491 .
Остальные компоненты локальной матрицы А вычисляются ана ю
। ичпо.
260
5.Двумерные скалярные задачи
Компоненты локального вектора правой части b вычислим путём
умножения двумерной матрицы массы на вектор весов f разложения
по эрмитову бикубическому базису функции f(x,y), определяемой
соотношением (5.51):
b = Cf.
Обратим внимание, что вектор f содержит не только значения
функции /(.?, у) в узлах конечного элемента, но и значения её частных
производных по х и по г/, а также значение смешанной производной
Вид матрицы Л = А и вектора правой части b = b приведены на
рис. 29.
Как уже говорилось выше (см. раздел 5.2.1, с. 234), вклады в матри-
цу и вектор правой части конечноэлементной СЛАУ от краевых усло-
вии второго и третьего рода могут быть представлены (для двумерных
задач) в виде локальных матриц и векторов ребер, на которых заданы
эти условия (напомним, что при использовании прямоугольных сеток
рёбра - это одномерные конечные элементы, ориентированные вдоль
одной из осей координат).
11ри использовании эрмитовых бикубических элементов на любом
ребре ненулевыми будут только четыре базисные функции: это функ-
ции, отвечающие за значения решения в узлах ребра, и функции, отве-
чающие за его производные по касательной к ребру (см. раздел 5.2.8).
Рассмотрим учёт второго краевого условия, заданного на границе ,
состоящей из одного ребра (см. рис 28). Это ребро ориентировано вдоль
, поэтому ненулевыми на нём будут глобальные функции с номерами 1,
2, 5 и 6 (функции ф| и ф5 отвечают за значения решения и на ребре
имеют локальные номера 1 и 3, а функции ф2 и Фо отвечают за произ-
водную решения по т и на ребре имеют локальные номера 2 и 4).
Вычислим локальный вектор правой части для ребра Sj с помощью
соотношения
И=М-Ч)', (5.59)
где М — матрица массы одномерного эрмитова элемента (см. (5.57)),
а О1 - вектор весов разложения по одномерным эрмитовым базисным
функциям правой части О1 (ж) = —Ьх2 второго краевого условия
(5.53), т.е.
б| = О1 (10) = -500, Gi = ^(Ю) = -100,
GJ = О1 (20) = -2000, 6J =^-(20) = -200.
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках 261
Таким образом, локальный век щий вид: 26 ПО 9 _65 7 21 7 21 . НО 200 65 _50 _ 21 21 21 7 9 65 26 ПО тор рс -500 ' -100 -2000 бр< а S] б 13000’ 3 25000 3 22000 удет иметь следую-
7 21 7 21 _65 _50 110 200 , 21 7 21 21 , -200 3 32500 3
'51
Локальный вектор b 2 заносится в глобальный вектор b по соот-
ветствию нумерации локальных базисных функций ребра глобальным.
„^1 -'S'l
т.е. компонента 2 добавляется к bj, b22 - к Ь2, Ь32 - к 65 и Ь4 ’ - к
Точно так же выполняется учёт второго краевого условия на грани-
це S2 . Здесь вектор b 2 вычисляется как произведение М 0 , где
вектор (см. краевое условие (5.54)) имеет следующий вид:
б2 = (о, -100, -1 1.2, -13б) .
При занесении в глобальный вектор правой части конечноэлемент-
ной СЛАУ компоненты вектора Ьл’2 с номерами 1, 2, 3 и 4 добавляют-
ся к компонентам вектора b с номерами 1, 3, 9 и 11 соответственно.
Рассмотрим учёт третьего краевого условия. Для этого необходимо
занести в глобальную матрицу А локальную матрицу А >3 (фактиче-
ски являющуюся матрицей массы ребра, ориентированного в данном
случае вдоль у) и в глобальный вектор b - вектор b'S;{. При этом ком-
поненты матрицы А’3 и вектора b 3 вычисляются следующим обра-
зом:
А53 =0М?/, Ь>5;’ =0М"й(1,
где й({ — вектор весов разложения по одномерным эрмитовым базис-
ным функциям заданной на 5;1 функции
(?/) = 36800т/3 + 2у2 + 2200т/ + 10, определяющей зретье краевое
условие на границе S3 (см. (5.55)), т.е.
«К, = (°) = Ю- «fe = ^(0) = 2200>
(0.1) = 266.82, = ^-(0.1) = 330 I I.
262
5 Двумерные скалярные задачи
Поскольку 0 = 1 (см. (5.55)), получаем, что матрица А5’ и вектор
кг3 имеют следующий вид (в числах приводятся все знаки без округ-
ления):
26 1! 9 65
7 210 7 2100
JJL 2 65 5_
_ 1 210 2100 2100 7000
100 9 65 26 Ц_
7 2100 7 210
65 __5_______11 2
. 2100 7000 210 2100 .
82.5628
- с , 1 78867
21 188.7712
-2.66914
Занесение компонент матрицы Л'1 и вектора b 3 в А и b произ-
водится по соответствию нумерации локальных базисных функций
ребра глобальным (для этого ребра номера одномерных локальных
функций I, 2, 3 и 4 соответствую г номерам двумерных глобальных
функций 5, 7, 13 и 15). Так, например, элемент А713 глобальной мат-
рицы А после учёта третьего краевого условия примет вид (числа,
записанные не в дробях, приводятся с округлением):
А 13 =“ 0.369092 LJ + А>'\= —0.3690921 11 ... 0 3687826 ,
•’l,J Z1UUUU
a wicmcht вектора правой часi и b примет значение
615 = 29.925501 + 64 = 29.925501 - -- - = 29.7984021 .
Для учёта первого краевого условия, заданного на границе Sj, фик-
сируются веса глобальных базисных функций с номерами 9, К), 13 и
14. Для этого на их диагональ ставятся единицы, а все остальные эле-
менты обнуляются. При этом компонентам вектора b с номерами 9 и
13 присваивается значение искомой функции (5.56) в соответствую-
щих узлах, а компонентам вектора Ь с номерами 10 и 14 - значение
производной по х искомой функции (5.56) в этих узлах (см. раз-
дел 5.2 8, с. 256).
Таким образом, после учёта всех краевых условий матрица Л и
вектор правой части b конечпоэлсментпой СЛАУ будут иметь вид,
изображенный на рис 30 (числа в матрице и векторе правой части
приведены с окружением, а компоненты матрицы, изменённые после
учёта третьего краевого условия, выделены жирным шрифтом).
Решением полученной коиечноэлсментной СЛАУ будет следую-
щий вектор (числа приведены точно без округления)’
q = 110, О, 500. НИ). 10. (). 20011, 200. 64.02, 11.2, «20.4, 136. 242.02, 24.S. 2960.4, 341
263
Рис. 29. Матрица и вектор правой части до учёта краевых условий
264
Рис. 30. Матрица и вектор правой части после учёта краевых, условий
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках 2ь5
Заметим, что для полного тестирования конечноэлсмепгнои процс
дуры решения краевой задачи с использованием бикубических шемен
тов следует проверить её на всех полиномах вида х'у1, ? = (),. 3,
.7 = 0...3.
5.2 9.2. ПРИМЕР РЕШЕНИЯ ЗАДАЧИ С РАЗРЫВНЫМ КОЭФФИЦИЕНТОМ
ДИФФУЗИИ
Рассмотрим следующую краевую задачу для уравнения (5.1) с
коэффициентами:
1,
10, (т,
4 = 0, f = о.
(5.60)
Расчётная область, в которой будем решать задачу, представлена на
рис. 31.
На границе расчётной области зададим следующие краевые усло-
вия:
Х^-1 =-тте^, (5.61)
Х-^1 = ттел sin (5.62)
Х-ё^- = —tv sin тт, (5.63)
on s:'
+ “k +0.1е^ = 0. (5.64)
Нетрудно убедиться, что аналитическим решением рассматривае-
мой краевой задачи будет функция
е‘к?/ sin tv.t;, (а*, у) £ Q1 = [0,1 х [0,1],
и(х,у) = (5.65)
0. le747 sin тгт, (а?, у) £ Q2 = [0,1] х [1,1.5].
Как видно из рис. 31, расчетная область состоит из двух подобла-
стей Q1 и Q, при этом Q1 совпадаете конечным элементом Оь л U
разбита на два конечных элемента Q2 и Узлы пронумерованы
слева направо, затем снизу вверх (их номера па рис. 31 показаны жир
пым шрифтом). Рядом с номерами узлов (курсивом, в скобках) пока in
ны глобальные номера базисных функций, привязанных к узлу Hi
помним, что при использовании стандартных бикубических ipMiiioin.ix
элементов к каждому узлу привязано четыре базисные функции пер
вая отвечает за значение решения в узле, вторая за значение в ном
266
5 Двумерные скалярные задачи
узле частной производной по х , третья - за значение частной произ-
водной по </, четвёртая - за значение смешанной производной.
Рис. 3 I. Расчётная область, нумерация
узлов и базисных функций
случае при рс
торых коэфф|
расчётной об
Напомним, что в одномерном
•ешении задач, в ко-
шциент диффузии в
'ласти имеет разрыв
(см. разделы 4.9—4.10), базис из
эрмитовых функций строился
таким образом, чтобы узлу разры-
ва коэффициента X соответство-
вало не две. а три функции: функ-
ция, отвечающая за значение ре-
шения, функция, отвечающая за
значение производной слева, и
функция, отвечающая за значение
производной справа.
В двумерном случае будем по-
ступать аналогичным образом.
Заметим, что в двумерном случае
на линии разрыва коэффициента
X разрывна не только производная по нормали к ней, но и смешанная
производная. Поэтому в узлах с номерами 2 и 6 мы вместо двух функ-
ций, отвечающих за частную производную д/8х и за смешанную про-
и модную d'jdxdy, введём четыре глобальные базисные функции так,
чтобы производные djdx и д21дхду конечноэлементпого решения
могли стать разрывными (см. раздел 5.2.7).
I аким образом, в узле с номером 2 глобальная базисная функция ф5
отвечает за значение решения и строится путём сшивки локальной
функции ф5 первого элемента с локальной функцией ф[ второго эле-
мента.
Глобальная функция фс отвечает за значение в этом узле частной
производной djdx слева и определяется локальной функцией фГ) пер-
вого элемента, а на остальных элементах доопределяется нулём.
Глобальная функция ф7 отвечает за значение частной производной
д'дх справа и определяется локальной функцией 'ф2 второго элемен-
та, а на остальных элементах доопределяется нулём.
Глобальная функция ф8 отвечает за значение частной производной
djdy и строится путём сшивки локальной функции ф7 первого эле-
мента с локальной функцией ф3 второго элемента.
5.2.Построение МКЭ-аппроксимаций на прямоугольных сетках 267
Глобальная функция ф9 отвечает за значение смешанной произ-
водной д1jdxdy слева и определяется локальной функцией ф8 перво-
го элемента, а на остальных элементах доопределяется нулём.
И, наконец, глобальная функция ф1() отвечает за значение смешан-
ной производной д' ]дхду справа и определяется локальной функцией
ф4 второго элемента, а на остальных элементах доопределяется нулём.
Аналогично определяется шесть базисных функций в узле с номе-
ром 6.
Локальная нумерация базисных функций на каждом из элементов
выполняется слева направо и снизу вверх так, как это было сделано в
предыдущем примере (см. раздел 5.2.9.1).
Сборка локальных матриц в глобалы1ую выполняется по соответст-
вию локальной и глобальной нумерации базисных функций. На рис. 32-
34 показана структура глобальной матрицы после занесения очередной
локальной матрицы (обратим внимание, что на каждом из этих рисунков
приведена только та часть глобальной матрицы, которая изменилась
после занесения матрицы очередного элемента). Компоненты локальной
матрицы конечного элемента Q/ обозначены как А1Ч .
Рассмотрим процедуру занесения локальной матрицы второго эле-
мента (см. рис. 33).
Прежде всего обратим внимание на то, каким глобальным функци-
ям соответствуют локальные функции этого элемента. Так, локальная
базисная функция ф^ соответствует глобальной с номером 5, ф2 -
глобальной функции с номером 7, фз - глобальной функции с номе-
ром 8, а ф4 - глобальной функции с номером 10. Локальные функции
с номерами 5-8 соответствуют глобальным номерам 1 1-14. Локальные
функции 9,10,1 1 и 12 соответствуют глобальным 23,25,26 и 28. И, на-
конец, локальные функции с номерами 13-16 соответствуют глобаль-
ным функциям с номерами 29-32.
Аналогично, по соответствию локальной и глобальной нумерации
базисных функций, в глобальную матрицу заносится матрица третьего
элемента (см. рис. 34).
Учёт третьего и вторых краевых условий, определяемых соотноше-
ниями (5.61)-(5.64), выполняется аналогично тому, как это было пока-
зано в разделе 5.2.9.1.
Решением полученной в результате конечноэлементной СЛАУ 6}
3G
ДС! функция и'1 = 52 7? ф/. •
i=i
268
7j 1 1 2 3 4 5 6 7 S 9 1011121314 1516 17 18 19 20 21 22 23 2-4 25 26 27
4', 4'2 4!з 4‘, 4 . 4.7 A's 4 9 4.0 4.u 4 ,2 4и 4,н 4.5 4.6
2 и4з 4.14,4» 4 7 4.я 4.9 4.10 4.и 4.12 4.13 4.11 4.15 4.16
3 4.3 4.4 AU 4.6 4.7 4.5 4.9 4.Ю 4и 4.12 4.13 4.и 4.В д1 Л3,1Ь
4 4л 4..5 4.6 4.7 4.s 4 9 4.11) 4.11 4.12 4.1з 4л. 4лз 4.16
Г, 4.5 4,г. 4.7 4,я 4.9 4.Ю 4п 4.12 4.1з 4.и 4.15 4лб
6 4.6 4.7 4 л 4.9 4.10 4 и 4.12 4.1з 4.И 4.5 416
7
8 4 7 4> 4.9 4.Ю 4.п 4.12 4.13 4.н 4лз 4.16
9 4 s 4,9 4 id 4.П 4,2 4.13 4.и 4,15 4.16
10
и
12
13
1-4
15
1G
17
is
19
20
21
22
23
24
25
26
27
4.9 4.10 4.11 4.12 4.13 4'1 4.15 4.1b
4o.lO Ao.l! К1Л2 4o.l3 Ao.ll Ao.15 4o.I6
j1 j1 j1 Д1 j1 j1
-4ll.ll Л11.12 Al.1.3 Л1| 14 A1.I5 ЛПЛЬ
^12.12 Аглз A2.11 4гл5 Агль
А.3.13 4з.Н Аз.1а АзТб
А| 14 А1.15 А 1.16
4.5.15 4’,.16
4 ь.1ь
Рис. 32. Занесение локальной матрицы первого элемента
5 я; 5 6 7 5 4X4 8 9 10 И 12 7-4з4.54л4,4б 13 4г 14 4- 1516171М 19 4„ 20 4.Ю 21 4.П 22 4 и 23 41з -4,. 24 4.11 25 26 4 ю 4.1) ’4 и 27 4.16 28 4 12 29 А..3 30 А 14 31 .4.’.. 32 А ,6
g 4.6 4; 4л 4 о Ало Ал А и 4 13 4.п А; и 416
7 4 2 4з А 9 4.Ю 4 и 4.2 4лз А) .14 4.з 4.16
8 4 7 4.з va, 4. । 4.» 4 6 44 4, 4.9 4 ш 4.1, 4.„ А и -4 о 4 и Ало 4 D-А и А.,6 Al 12 4« 4,4 At и A io
9 4-, 4л 4.5 4.6 4 4„ 4 9 А. ц> 4n 4,2 4 ,з 4n 4.!.) 4.1й
10 4 । 4 л 4 с 4- 4, 4 9 А ю Ал 4 Г2 Айз А 14 4.15 4.16
11 4S4.6 4- 4 4 о 4 ш 4.П 4.2 А |з 4.4 4 .5 4.6
12 4.6 4.7 4, 4,п А к, 4. п 4.12 А13 А п 4 г, А .6
13 4.7 4, А\ 4 № 4 и 4Z 12 А.и 4и 4.15 4.Ю
14 4. 4 0 410 4 ц А 12 4,з 4и 4.1.) A ,s
16
16
17
18
19 4.9 4.Ю 4.П 4.12 4 и А и А.,) 4.6
20 Ао.ю Au. и Ао.12 All.lJ Ao.ii ^10.15 4олб
21 •Ain Al.12 4 1.13 41.14 41 is 4) 16
22 4г.12 4) 13 42.11 4) 15 41 •42.16
23 Азл ' Ад Аз.14 A.I0 4з.Г1 ' А, н Аз к. А |) А13 А,, и A is A. io
24 41 л|| 11 •A'l.l) А) .б
23 4о ю 4.> п All 12 Ао.13 Ао 14 Аолз Aq, 16
26 4,15 - 4i.ii Аз io 4l.l2 л2 ^п.ы •Ч1Л1 4.35 А, io
А/лг Аз.» Аз.и 4; 15 4з.1б
Aj.13 А II Аз.15 Аз 16
4i.ii А1 г> 4д и.
4-п4\.1в
А
Рис. 33. Занесение локальной матрицы второго элемента
Рис. 34. Занесение локальной матрицы третьего элемента
5.2.Построение МКЭ-аппроксимаций на прямоугольных ссгкях 271
Получим решение этой же краевой задачи на сетках с шагами Л/2
(т.е. шаги по обеим координатам измельчены вдвое) и Л/8 (т.е. т.н и но
обеим координатам измельчены в восемь раз), а также на сетке ///8, но
при использовании эрмитова базиса с непрерывными производными
Значения полученных на разных сетках конечноэлементных решений
и их производных в некоторых узлах сетки приведены в табл. 13 15.
Для точки, в которой коэффициент диффузии терпит разрыв, приводя i-
ся значения соответствующих производных слева и справа. В первых
строках этих таблиц указаны координаты точки, в которой даются зна-
чения решения и его производных. Во вторых строчках - значения точ-
ного решения (5.65). В последующих строках - значения одного из при-
ближённых решений и его производных (каких именно, указано во вто-
рых строчках) в виде значений соответствующих компонент вектора q .
В строке h]3 с приведены результаты для стандартного эрмитова базиса
с непрерывными производными (на сетке с шагом Л/8). Значения точ-
ного и приближённых решений в табл. 13-15 даны с округлением.
Приведённые в табл. 13-15 результаты показывают, что при ис-
пользовании эрмитова базиса со специальными дополнительно вве-
дёнными базисными функциями в точке разрыва коэффициента диф-
фузии на сетке с шагом /i/2 в конечноэлементном решении не везде
был получен даже один точный знак, а на сетке с шагом Л/8 — почти
везде три точных знака. При этом в случае использования эрмитова
базиса с непрерывными производными значение конечноэлементного
решения (и особенно производных по х ) довольно далеки от истин-
ных.
Рассмот рим теперь, как можно получить значения конечноэлемент-
ного решения в некоторой произвольной точке.
Например, вычислим в точке (0.3,0.4) значение конечноэлемент-
ного решения и его частных производных, полученного на сетке с ша-
гом Л/8 при использовании эрмитова базиса с дополнительными ба-
зисными функциями в узлах, лежащих на линии разрыва коэффициен-
та диффузии.
Напомним, что для вычисления значения конечноэлементного ре-
шения и его производных в некоторой произвольной точке вначале
необходимо определить, в какой элемент попадает точка. Так, для се г
ки с шагом /г/8 точка (0.3,0.4) попадает в элемент с номером 75 Ik
нулевыми на этом конечном элементе являются глобальные функции с
номерами 315-322 и 417-424.
272
5.2 Построение МКЭ-аппроксимаций на прямоугольных сетках 273
На элементе с номером 75 функция иУЬ (являющаяся конечно эле-
ментным решением на сетке с шагом h/8) может быть представлен i в
виде линейной комбинации шестнадцати локальных базисных функ-
A/S,Si7fi
ций элемента с весами q/ , полученными из компонент bckio-
ра q с номерами 315-322 и 417—424:
qV84V> = (2.3, 7.22,7.22,22.7,3.,3.91,9 43,12.3,3.4.10.7,10.7,33.6,4.44,5.78,13.96,18.2)Г .
В точке (0.3,0.4) вектор-функция -ф^75 , составленная из базисных
функций с номерами 315-322 и 417-424, и её частные производные
принимают следующие значения (числа приводятся с округлением):
- ф^75 (0.3.0.4) = (о.6,О.О16.1.04 10-2,2.9 10-4,0.315,-1.075-10-2,5.6-Ю“3,
- 1.9 1.0“4,0.067,0.002,-0.0026,-7.240-5,0.037,-1.25-Ю-3,-1.410-3,4.810-5) ,
(9'ф^75 . . / о о
—-----(0 3,0.4) = (-10.3,-0.1075,-0.18,-1.9 10-д,10.3,-0.29,0.18,-5.1-10 15,
-1.2, -0.0125. 0.046. 4.8-10-4,1.2. -0.033, -0.046,1.3-10-3)" .
---(0.3.0.4) = (-4.9S,-0.14, 0.21.5.8-10-3,-2.7.0.092,0.11,-3.8-10-3 ,
ду k
4.98, 0.14, -0.18, —5.04-10-3, 2.7, -0.092, -0.099, 3.4-10-3 f
Таким образом, значение конечноэлементного решения и' и его
производных в точке (0.3,0.4) может быть вычислено следующим
образом (числа приводятся с округлением):
Л8 (0.3,0 4) = ^qf'^'^7'' (О.з,0.4) = 2.84167 ,
i=i
^-(0.3,0.4) = ^Ч0-3.0-4) = 6-48558'
1=1
^1(0.3,0.4) = (0.3,0 4) = 8.92501.
При этом значения аналитического решения и его ирон «водных
имеют вид (числа приводятся с округлением)
и (0.3,0.4) = 2.84255 , (0.3,0.4) = 6.48812 , (о 3,0.4) 8 9.101 I
274
5 Двумерные скалярные задачи
Как видно, в точке (0.3,0 4) при использовании сетки с шагом /г/8
и эрмитова базиса с дополнительными базисными функциями в узлах,
лежащих на линии разрыва коэффициента диффузии, в конечноэле-
ментном решении и его первых производных получено 3 точных знака.
При использовании же стандартного эрмитова базиса с непрерыв-
ными производными в конечноэлементном решении и его произ-
водных получаются только один—два точных знака (числа приводятся с
округлением):
(0.3.0.4) = 2.66114 , (0.3,0.4) = 6.50674 , (0.3,0.4) = 8.856026 .
Таким образом, при решении задач с разрывным коэффициентом
диффузии при использовании эрмитова базиса необходимо вводить
дополнительные базисные функции в узлах, лежащих на границе раз-
рыва коэффициента диффузии Использование базиса, состоящего
только из функций, имеющих непрерывные производные, в таких за-
дачах совершенно нецелесообразно.
5.3. ПРИМЕНЕНИЕ МКЭ ДЛЯ РЕШЕНИЯ ДВУМЕРНЫХ КРАЕВЫХ ЗАДАЧ
НА ТРЕУГОЛЬНЫХ СЕТКАХ
Рассмотренные выше подходы к решению двумерных краевых
задач с использованием прямоугольных сеток довольно просты и удоб-
ны для реализации. Но во многих практических задачах подобласти
имеют сложные границы, которые не могут быть с достаточной точно-
стью аппроксимированы на прямоугольных сетках. В этих ситуациях
довольно часто используют сетки, состоящие из треугольных элемен-
тов В данном разделе мы рассмотрим построение конечноэлементной
аппроксимации на сетках с треугольными ячейками.
Будем считать, что треугольная сетка задана в виде набора узлов
(вершин) и набора треугольников Каждый узел сетки описывается
двумя координатами 27. и ук, а каждый треугольник Q,„ — четырьмя
числами, первые три из которых - номера узлов сетки, являющихся
вершинами рассматриваемого треугольника, а четвёртый - номер по-
добласти расчётной области, служащий для определения значений
параметров X, -у и f дифференциального уравнения (1.1) внутри
данного треугольника.
Будем также считать, что границы S2 и S-] представлены наборами
ребер, каждое из которых описывается гремя целыми числами, причём
первые два числа — это номера узлов сетки, являющихся вершинами
рассматриваемого ребра, а третье число служит для определения значе-
ний параметров заданного на ребре краевого условия второго или
третьего рода. Границу же опишем набором пар целых чисел, в кото-
ром первое число каждой пары является номером узла, лежащим на S[,
а второе служит для определения значения параметра этого краевого
5.3.11римепспис МКЭ для решения двумерных краевых мдач 275
условия (хотя для эрмитовых конечных элементов может оказан.ся м>
лес удобным представление границы Si в виде набора ребер).
Для вычисления компонент локальных матриц на треугольных эле
ментах очень удобно использовать так называемые £-координаты.
Поэтому в следующем разделе будет дано определение £ -коордтип и
рассмотрены основные соотношения, позволяющие вычислять инте-
гралы от их произведений по треугольному элементу.
5.3.1. £ -КООРДИНАТЫ НА ТРЕУГОЛЬНИКЕ
Рассмотрим треугольник Q„( с вершинами (x’i,2/i), и
(х3, 2/3) • Введём на нём три линейные функции
£,(х, у) = оф + а\х + а2</, г = 1...3, (5.66)
такие, что функция £{ равна единице в вершине и нулю в двух
остальных вершинах , функция £} равна единице в вершине
(£'2,у-}) и нулю в двух остальных вершинах , а функция £$ равна
единице в вершине (£3,^3) и нулю в двух остальных вершинах .
Тогда, очевидно, справедливы следующие соотношения:
ао+ = 1,
«о+ 4- o^j/i = О,
»o+ оц X'i + ojf/! = 0,
0-1^2 + а2& — О,
cy?)+ a?Z2 + cv2?/2 = 1,
CY(3)+ + ^2Z/2 = 0,
otj)+ оцх3 + a-2^3 = 0,
cv’ijT cvfx3 4- a‘^z/3 = 0,
oto4- 011X3 T ot2^3= 1,
которые могут быть переписаны в матричном виде:
1 1 1) f >
оф Оц »2 1 1 1 1 0 0
«о cy'i ot2 .74 X-2 X-i — 0 1 0
«0 af qJ fh y-2 Уз 0 0 1
(5.67)
Из (5.67) сразу следует, что все коэффициенты функций (5 66) яв-
ляются компонентами матрицы (L, обратной к определяемой только
координатами вершин треугольника матрице
(5 6Х)
У1 У'2 Уз
Tib
5.Двумерные скалярные задачи
Cl] <*2 1 1 1 -1
а = <*0 а? — fl д д
СХо <*1 »2 У\ к У'2 Уз
(5.69)
Соотношения (5.66) можно записать в матричном виде
которые с учетом (5.69) примут вид
(5-70)
Из (5.70) сразу следует
(5-71)
д
д
д
ttQ
т.е. для £ -координат справедливы соотношения1
1 Эти соотношения в принципе можно получить и из других соображений.
Любая линейная комбинации функций Д, Д и Д является на Q,„ линейной
функцией, а две двумерные линейные функции совпадают тогда и только
тогда, когда совпадают их значения в трёх точках, не лежащих на одной пря-
мой. Левая же часть первого из уравнений (5.72) является линейной функци-
ей, которая в трёх вершинах треугольника принимает значения, равные еди-
нице, и поэтому это линейная функция v(x,y) — 1 . Левая часть второго из
уравнений (5.72) является линейной функцией, которая в трёх вершинах тре-
угольника принимает значения, равные т;-координате каждой вершины, и
поэтому это линейная функция v(x,y) = х. Из тех же соображений левая
часть третьего из уравнений (5.72) является линейной функцией г» (.г, т/) = у .
5.3.Применение МКЭ для решения двумерных краевых чадам
Д + &2 + Д — 1,
ДА 4- £2ъ2 + ДА = я,
(5.72)
* ДА + &2У2 + ДА — У-
Через матрицу D, определяемую соотношением (5.68), может быть
вычислена площадь треугольника Qw с вершинами {А»А}> {.T2J/2} и
{А, А}
mes Q7Zt — -i |det D|,
(5.73)
где detD - определитель матрицы D. Значения detD и компонент
D4 , являющихся коэффициентами ot, функций £j, Д и £3 (см. (5.66)
и (5.69)), легко вычисляются из определения (5.68) матрицы D :
det D = (Д - А) (Уз - У1) - LA - А) (У-z ~ У1)
АА ~ ^зУ-2
D-1
_ 1
detD
ад - АЙ
А А -ад
У2 - Уз А - А
Уз ~ У[ А - А
У1 - У2 А - А
/
(5.74)
(5-75)
Функции Д, £2 и £2 называются £ -координатами, а также ба-
рицентрическими или естественными координатами треугольника.
Они удобны тем, что для них существуют очень простые формулы,
позволяющие вычислять интегралы от произведений Д в произволь-
ных степенях по треугольнику Q7Zt:
/ (Д Г (£2Г <Ыу = (vi+72!;2-^2) ,|detD|, (5.76)
Qzzz
где под 0! понимается значение 1 и значение detD можно вычислить,
например, с помощью соотношения (5.74).
Обратим внимание на ещё одну проблему, возникающую при ис-
пользовании нерегулярных сеток с треугольными ячейками. Для гою
чтобы вычислить значение конечноэлемешного решения в произвол!,
ной точке Р с координатами (хр,ур) (не обязательно являющейся у»
лом сетки), требуется определить, в какой из конечных элементов попа
ла эта точка. Для определения попадания точки в выпуклы11 мною
угольник обычно используют следующий простой факт сумма и нмцл
лей треугольников, образованных рассматриваемой точкой I и каждой
стороной многоугольника, равна площади самого мноюуюльннка в юм
с ну час. если Р находится внутри или на границе мною}! одышка, н
больше площади многоугольника, если Р находится снаружи
278
5.Двумерные скалярные задачи
Для проверки попадания произвольной точки Р в треугольник
очень удобно использовать соотношения (5.73) и (5.74). Действитель-
но, из (5.73) и (5.74) следует, что удвоенная площадь треугольника,
образованного точкой Р — (хр,у1') и стороной треугольника с верши-
нами (£,,?/,), , может вычисляться как
sy (хр,У1’) = |(% - х,) (ур -уг)~ (хр - х.) (т/у - уг)|. (5.77)
Поэтому удвоенная сумма площадей может быть вычислена как
S12 (<</'') + S23 (я",у") + S31 (.г",у"), (5.78)
а удвоенная площадь треугольника - как модуль (5.74). Естественно,
при практической реализации разности, входящие в (5.78) и (5.74),
вычисляются один раз.
Заметим, что если для определения попадания точки Р в треуголь-
ник вычислялись все значения (5.77) и (5.74), то для вычисления зна-
чения функций £[, £>2 и Д; в этой точке можно использовать соотно-
шения [9]:
т.е. у £ -координат есть очень простой геометрический смысл - значе-
ние координаты £. в произвольной точке треугольника Q„( равно от-
ношению площади треугольника, образованного этой точкой и сторо-
ной треугольника, противоположной вершине (Д,т/д), к площади тре-
угольника Q,„ .
5.3.2. ЛИНЕЙНЫЕ ТРЕУГОЛЬНЫЕ ЭЛЕМЕНТЫ
Получим соотношения для вычисления локальных матриц и век-
торов на треугольных элементах с линейными базисными функциями.
На каждом элементе Qw треугольной сетки определим три локаль-
ные базисные функции
фг (х,у) = 4- сф; + с^у , г = 1...3, (5.79)
5.3.Применение МКЭ для решения двумерных краевых задач . . 279
и нулю в двух других, ф2 равна единице во второй (с коор-
Фз равна
и нулю в
базисные
Рис. 35. Поведение
локальной базисной функции
на треугольном элементе
такие, что ф} равна единице в первой (с координатами (xi,//i)) вер-
шине
динатами (Т;2, т/2)) вершине и нулю в двух остальных, а
единице в третьей (с координатами (£’з,Уз)) вершине П.„,
двух остальных.
Очевидно, что определённые таким образом локальные
функции ф» на треугольнике фактически
являются £ -координатами этого треуголь-
ника (5.66), т.е. ф{ (г-,?/) = £., (х,у), и поэтому
коэффициенты оф функций ф,; могут быть
вычислены по формулам (5.69), а при вычис-
лении интегралов от произведений вида ф,:ф7
по треугольнику Q,„ можно использовать
соотношение (5.76). Поведение локальной
базисной функции на треугольном конеч-
ном элементе изображено на рис. 35.
Получим выражения для локальных мат-
риц жёсткости G и массы М конечного эле-
мента Q,„. Учитывая представление (5.79) функций ф£ на Q,Z1 и заме-
няя параметр X некоторым постоянным на конечном элементе
(например, осреднённым по нему) значением X, получим
с. - f у И’,
О' I А ГЛ ГЛ I ГЛ ГЛ &
' J ох ох оу оу
^П1 ' '
— X J 4-oc-jouj) dQ = X^otia-j + ot^ct.^mesQ,,,.
Ли
Учитывая соотношение (5.73), получим
<?,, =X^^(aja/+aio>). i = 1...3, j = 1...3, (5.80)
где матрица D определяется соотношением (5.68), а её определи!ель
соотношением (5./4).
Столь же просто вычисляются компоненты локальной матрицы М
Будем считать, что параметр также заменяется на QM, пскшорым
постоянным значением . Тогда, используя соотношение ’6), ио ц
ним
280
5.Двумерные скалярные задачи
Q,
_____2!.0!Д.!_____ldetDI =
(2 + 0 + 0 + 2)!1 1
J ^»м
Q,
= -____1Ш01
1/1 II I Л I
2|detD|
24
12 , 1-1...3,
24
(581)
2 1
1 2
1 1
1
1
2
Получим выражения, определяющие локальную матрицу и вектор
ребра Гт, на котором задано краевое условие третьего рода. Очевид-
но, что на этом ребре ненулевыми являются только две базисные
функции. Введём на ребре Г/н локальную нумерацию его вершин и
обозначим через ф} базисную функцию, которая равна единице в пер-
вой вершине ребра, а через ф2 ~ во второй. Обратим внимание на то,
что ф»! и ф)2 на ребре Г,м фактически являются одномерными линей-
ными базисными функциями (равными единице в одной вершине и
нулю - в другой).
Будем считать, что параметр [3 на Г,„ постоянен и равен (3, а пара-
метр «р представлен в виде линейного интерполянта ^нф^ + тф2ф2
(где «|U и й(12 - значения параметра в вершинах ребра Гш). Тогда
компопен гы локальной матрицы А’3 и вектора Ь’3 ребра Г,„ опреде-
ляются соотношениями
4J3 = Р J фгф'/Г, btSi =fij (йщф)! + ^12ф2)ф?т/г . (5.82)
П» Г т
Очевидно, что локальный вектор Ь"3 может быть вычислен через
А"! по формуле
bS;‘
= А'?3
(5 83)
5.3.Применение МКЭ для решения двумерных краевых задач ... 281
Поскольку и ф2 на ребре Г/п - одномерные линейные базисные
функции, они имеют вид:
^(0 = 4^. =
где /i„t = mesF,„ =Л/(^-£1)2+(у2 ~^1)2 - длина ребра Г,„
((£'1, </]) и (£’2,2/2) ~ координаты вершин ребра Г,„) и 0 < £ < hin (т.е.
координаты х и у точек ребра связаны с переменной £, соотноше-
ниями х — хх + -Д-(£2 — £]), У ~ У1 + т^~ (у-2 ~ 2/1) и переменная
•Ьн
фактически определяет параметрическое представление ребра). Тогда
и5;| _ А Г fyn ~ 6, hln ~ _ А кщ
11 “ J k,rl hfrl ~ 3 ’
Л12 -Л1 -(J hm
t С h
т.е. А 3 фактически является матрицей массы одномерного элемента
(сравните с (4.10)). В результате локальные матрица и вектор ребра
Г,„, являющегося частью границы S3, имеют вид:
А53
&hin
6
'2 Г
1 2
£ S;{ ___ Р кп1
6
2Й|И + U(J2
/1(11 + 2и((2>
(5-84)
Аналогично вычисляется локальный вектор ребра Гш с заданным
на нём краевым условием второго рода (при условии, что параметр 0
заменяется на Г,п своим интерполянтом OjTpi Т Ог'Фг, гДе ^1 и "
значения параметра 0 в вершинах ребра Г,„):
20i +621
0i+202
/
(5 85)
282
5.Двумерные скалярные задачи
5.3.3. ПРИМЕРЫ РЕШЕНИЯ ЭЛЛИПТИЧЕСКИХ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ
ЛИНЕЙНЫХ ТРЕУГОЛЬНЫХ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Рассмотрим следующую краевую задачу для уравнения (5 1) с
параметрами:
Ю,
(г-, ?/) е Q1,
Е Q2,
4 = 0, f(x,y) =
-20, (.г-,?/) Е Q1,
0, (z,*/)eQ2.
(5 86)
Расчётная область Q = Q1 ПГ? представлена на рис. 36. На нём
глобальные номера узлов приведены в прямоугольничках (например,
□), а локальные номера узлов каждого из трёх конечных элементов
Q,„ (Qj = Q1, Q2U Q3 = О. ) - в кружочках (например, @ ).
Рис. 36 Расчётная область и сетка из трёх конечных элементов
На границах Sj, S'2, S3 заданы следующие краевые условия
“Is , = "2’ (5.87)
\ дп = 20, (5.88)
Хдп = о, (5.89)
\ Oil Х дп ,,+2(“| S;i -20?/ + 27) = 0. (5.90)
Можно убедиться, что аналитическим решением поставленной
краевой задачи будет функция
5.3.Применение МКЭ для решения двумерных краевых шдпч
283
У2,
20?/-19, (x,?/)eQ2.
(5 91)
Очевидно, что функция (5.91) непрерывна на всей расчётной облас-
ти Q = Q1 П Q2 (на границе Г21з между подобластями Q1 и Q2 и свср
ху и снизу она принимает одинаковые значения и(х,у) = 1). Для нее
также выполняется условие непрерывности потока на Г2,з:
— \ дц1
дп\
п „ „ ду2
Действительно,
х
5п|//=;1_п
д (20?/ - 19)
ду
Используя соотношения (
кальных матриц и векторов конечных элементов. Учитывая значения
параметров (5 86) решаемой дифференциально-краевой
чим, что локальные матрицы и векторы правых частей
ментов, изображённых на рис. 36, имеют вид
= 20 и
.'/=1-о
= 20.
.'/=1+0
(5.80) и (5 81), вычислим компоненты ло-
задачи, полу-
конечных эле-
-5
As21 = -5 10
-5
0
-5
5
А“2 =
1
3
6
. 6
_1
6
5
6
_2
3
_1
6
_2
3
6.
AQ:1 =
1
G
0
6
о
1.5
-1.5
_1
6
-1.5
5
3
1у/=1+()
5
о
bQ1 =
10
3
10
3
10
3 .
о
b ’2 = о
о
о
о
о
Сборку локальных матриц в глобальную будем выполнять по соот-
ветствию локальной и глобальной нумерации (см. рис. 36). У первого
элемента номера локальных функций совпадают с глобальными, по-
этому глобальная матрица после занесения в неё матрицы первого
элемента будет иметь вид
А1? 4г 42 0 о'
Ag 0 0
А = Ф 42 0 0
0 0 0 0 0
0 0 0 0 0
5 -5 ооо
-5 10 -5 0 0
0-5 500
О О 0 0 0
О О 0 0 0
284
5.Двумерные скалярные задачи
У второго элемента локальная функция фт соответствует глобаль-
ной ф5, ф-2 соответствует *ф3, а ф3 соответствует ф4 . Учитывая это,
после занесения локальной матрицы А51’2 в глобальную получим:
Ai' Д$21 Л12 Аз 0 1 0 5 -5 0 -5 10 -5 п гЛ
2^1 Л21 ДА Л22 ДА Лзз 0 0 и 0 и 0
Д521 Ли <21 Д$Ь । ДА Л13 f Л22 ДА Лгз АЙ — 0 -5 С _2 3 6
0 0 Ай ДА Лзз АЙ -Nl-ro —<|< 1 1 о о о о 5 6 __1 6 1
0 1 0 АЙ АЙ АЙ к О 6 з,
Учитывая, что у третьего элемента локальным номерам 1, 2 и 3 со-
ответствуют глобальные номера 4, 3 и 2, локальную матрицу А !;1 за-
носим в глобальную следующим образом:
А1.' ДА Л 2 АЙ 0 0
7i21 2Q1 । Д»з Л22 + А33 Ай + А$ 4? о
А = Ай ДА I ДА Л12 ‘ Л23 Ай + AJ? + Л£ Д^2 I Д^З Д^2 Л23 +Л21 ЛГ2
0 ДА1 Лз АЙ + АЙ Д^2 I Д^23 Д^22 Лзз Ли
0 0 АЙ Д*г2 Д^2 Аз Ли
Сборка локальных векторов в глобальный проводится аналогично.
Таким образом, после сборки локальных матриц и векторов всех ко-
нечных элементов получаем:
Выполним учёт краевых условий. Используя соотношение (5 85),
вычислим локальный вектор b 2 ребра Г45, соединяющего узлы с
номерами 4 и 5:
5.3.Применение МКЭ для решения двумерных краевых задач 285
И =
mes Г4 5
6
2of2 + 6.f2
0^ + 20^
где of2 = бз2= 20 (см. (5.88)), a mes Г4 5=^/(з;4 - ж5 )2 + (</4 — Уь)2--г’
длина ребра, соединяющего узлы с номерами 4 и 5. С учётом этого
получаем, что
bS2 =
50
50
Добавление локального вектора ребра в глобальный вектор конеч-
ноэлемептной СЛАУ также выполняется по соответствию локальной и
глобальной нумерации. В данном случае локальным номерам I и 2
ребра Г4 5 соответствуют глобальные номера 4 и 5. Таким образом,
после учёта второго краевого условия на границе S'] глобальный век-
тор правой части примет вид
Ь = -ф. 50. 5о)Т.
Очевидно, что однородное второе краевое условие, заданное на гра-
нице 6'2 (см. (5.89)), не даёт никаких вкладов в глобальный вектор.
Рассмотрим учёт третьего краевого условия. Из соотношения (5.90)
видно, что коэффициент [3 равен 2, коэффициент = 20//— 27 , а
длина ребра Г;}5, соединяющего узлы с номерами 3 и 5,
mes Г3>5 = ~ Т5)2 Т (//з - Уг>? = 5 -
Используя соотношения (5.84), получаем, что локальная матрица
А6:| и локальный вектор Ь5;| ребра, соединяющего узлы с номерами 3
и 5, имеют следующий вид:
3 • mes Г3 5 (2
6 1
'10 <
3 3
5 10
< з з;
3- mesEj r, 2^П + йр2
G «[ji+2t7[]2
2^[2-(-7)+53
6 -7+2-53
65
165
После занесения локальной матрицы АЛ;! и вектора Ь в i лоба н,
ныс (здесь локальным номерам 1 и 2 соответствуют глоба и пыс номе
ра 3 и 5) получим:
286
5.Двумерные скалярные задачи
5 -5 0 0 0
-5 35 3 -6.5 _1 6 0
А = 0 -6.5 32 3 _2 3 1.5
0 6 _2 3 1 6
0 0 1.5 6 11 3 .
10
3
185
3
50
215
к
ю'
3
Учёт первых краевых условий, определяемых соотношением (5.87),
выполняется следующим образом. Диагональным элементам Ли и А33
присваивается значение I, а все внедиагональные компоненты строк с
номерами 1 и 3 обнуляются (номера 1 и 3 - это номера узлов границы,
где задано первое краевое условие и для которых веса базисных функ-
ций фиксируются). При этом компонентам и 63 вектора правой
части присваиваются значения, определяемые первым краевым усло-
вием, - в данном случае это значения функции у2 (см. (5.87)) в первом
и третьем узле соответственно, т.е. 6] — 0 , а 63 = 1.
После учёта первых краевых условий конечноэлементная СЛАУ
примет окончательный вид:
1 и 0 0 0 / 0
-5 35 3 -6.5 6 0 10 3
А = 0 0 1 0 0 , Ь = 1
0 6 _2 3 1 _1 6 50
0 0 1.5 _1 6 11 3 215
Решением этой конечноэлементной СЛАУ будет вектор весов q
разложения и1' по линейным базисным функциям на треугольниках
(обратим внимание, что компоненты вектора q приводятся с округле-
нием):
q = (о, 1.1432, 1. 61.024, 61.001)Т.
Заметим, что полученное конечпоэлементное решение содержит
некоторую погрешность. Это связано с тем, что в качестве аналитиче-
ского решения рассматриваемой краевой задачи на части расчётной
области был взят полином второй степени, который не представим без
погрешности в используемом линейном базисе. Очевидно, что для
тестирования конечноэлементной процедуры, использующей линей-
ное оазисные функции, нужно брать такие задачи, решениями которых
являются кусочно-линейные функции.
Рассмотрим ещё один пример построения конечноэлементного ре-
шения с использованием линейных базисных функций на треугольни-
5.3.Применение МКЭ для решения двумерных краевых задач ... 28 -
ках. Расчётная область Q. в которой будем искать решение красной
задачи для уравнения (5.1), показана на рис. 37. Подобласть Q1 рас-
чётной области Q включает в себя конечные элементы Q2, и
П4, а подобласть Q2 - элементы Q5, Qc, Q7, Q8 и ^о-
Параметры дифференциального уравнения и краевые условия опре-
делим следующим образом:
5, (ж,?/) G Q1,
О, (ж, у) £ Q2,
5а; + 30т/ — 10, (ж, у) Е Q1,
°, € Q2,
«|Si =бг/ + 2,
х^|,
= -6,
ди
дп si
ди
дп s]
288
5 Двумерные скалярные задачи
ХМ. +ю«-бг/-21) = о.
Построим локальные матрицы и вектор и по соответствию локаль-
ной и глобальной нумерации занесём их в глобальные. После учёта
краевых условий (аналогично тому, как это было сделано в предыду-
щем примере) получим глобальную матрицу и вектор в виде:
5 3 43 48 0 __7_ 48 5 24 0 0 0 0 0 2323 96
43 ' 48 599 120 77 240 0 _7_ 8 25 24 0 0 0 0 2241 16
0 0 1 0 0 0 0 0 0 0 32
_ _7_ 48 0 0 487 120 163 48 0 -0.1 0 0 0 1177 96
А = 5 24 _7 8 0 163 48 931 120 13 240 2 -0.1 0 0 ъ = 1595 16
0 0 0 0 0 1 0 0 0 0 38
0 0 0 -0.1 _ 1 2 0 131 60 _7_ 12 -1 0 —2
0 0 0 0 -0.1 И 3 __7_ 12 931 60 0 2 3 1022
0 0 0 0 0 0 -1 0 5. 4 _1 4 33 4
0 0 0 0 0 0 0 2 3 4 25 4 . 1809 4
Матрицу этой системы легко сделать симметричной, исключив не-
нулевые внедиагональные элементы из третьего и шестого столбца:
3 43 48 0 _7_ 48 21 0 0 0 0 0 ' 2323 96
__13 48 599 120 0 0 _7 8 0 0 0 о 0 7217 80
0 0 ] 0 0 0 0 0 0 0 32
7 48 0 0 487 120 163 18 0 -0.1 0 0 0 1177 96
5 7 о 163 931 о 1 -0.1 о 0 25559
А = 24 8 48 120 2 , ь = 210
0 0 0 0 0 1 0 0 0 0 38
0 0 0 -0 1 2 0 131 60 __7_ 12 -1 0 -2
0 0 0 0 -0.1 0 __7_ 12 931 60 0 2 3 2618 3
0 0 0 0 0 0 -1 0 5 4 4 33 4
0 0 0 0 0 0 0 2 3 _1 4 25 4 . 1809 1
Решением копечноэлементной СЛАУ Aq = b будет вектор весов
5.3.Применение МКЭ для решения двумерных краевых задач К"
q = (29, 29.5, 32, 35, 35.5, 38, 50, 53, 59, 62^.
Нетрудно убедиться, что полученное конечноэлемешчое реш ине
ю
/?' = ( фг — это кусочно-линейные базисные функции на ipi
г—1
угольниках) совпадает с аналитическим, имеющим вид
и (х, у) = х + 6г/ - 2.
На практике при решении задач на нерегулярных сетках для храпе-
ния матриц конечноэлементных СЛАУ, как правило, использую шя
специальные форматы. Одним из таких наиболее распространенных
форматов хранения конечноэлементпых матриц является так называе-
мый разреженный строчно-столбцовый формат, который будет рас-
смотрен ниже в разделе 10.4.4. Тем не менее здесь в качестве примера
мы покажем, как выглядит полученная нами симметричная конечно-
элементная матрица в разреженном строчно-столбцовом формате.
Массивы ig (указатели на начала строк нижнего треугольника мат-
рицы) и jg (номера столбцов с ненулевыми элементами нижнего тре-
угольника матрицы) имеют следующий вид:
i(j = 1. 2, 3, 4, 7. 10, 12, 15, 16, 1э),
jg = (l, 2, 1, 1, 2. 4. 2. 3. 5. 4, 5, 5, 6. 7, 7. 7, 8, э) .
Массив di с диагональными элементами и ggl с ненулевыми вне-
диагональными элементами нижнего треугольника имеют вид
д. = (5 599 . 487 931 1 131 931 5 25)
\3’ 120* ’ 120' 120’ ’ 60’ 60 4’ 1/’
= (_м. о. _х a. _z о. о. -о. l -1. -о. I. о. -х о. |.4).
Алгоритмы построения портрета и сборки глобальной матрицы,
хранящейся в разреженном строчно-столбцовом формате, а также ос-
новные алгоритмы работы с ней (используемые при решении CJ1AV)
описаны в разделах 10.4.5 и 10.5.
5.3.4. ТРЕУГОЛЬНЫЕ ЭЛЕМЕНТЫ С КВАДРАТИЧНЫМИ БАЗИСНЫМИ
ФУНКЦИЯМИ
Кроме линейных базисных функций на 'треугольных конечных
элементах иногда - используются базисные функции более высоких
порядков. В этом случае узлами конечноэлементной сетки, в которых
определяются значения базисных функций, являются нс только вер
шины треугольников, по и точки на их рёбрах и внутри i рсуго. Пашков.
Рассмотрим построение квадратичной базисной функции и i ipc
угольнике. Для определения шести коэффициентов полною квазра
тичного полинома необходимо задать его значения в ineciii узлах, и
поэтому на треугольнике Q„, кроме трёх его вершин в йпчед гве узлов
290
5.Двумерные скалярные задачи
конечноэлементной сетки берутся также середины трёх его сторон.
Базисные функции квадратичного элемента, так же, как и линейного,
удобно выразить через £ -координаты:
Ф1 (*,</) = 4(24-1),
Фз (я,</) = 4? (24? ~ 1),
Ф-2 (^ у) = 4 (24 -1),
Ф4 (^ у) = 444,
Рис. 38. Расположение узлов
на треугольном конечном
элементе с квадратичными
базисными функциями
Фс> у) = 444
(5-92)
Здесь первые три базисные функции соот-
ветствуют узлам в вершинах треугольни-
ка, а последние три - узлам в серединах
его сторон. Локальная нумерация узлов
показана на рис. 38, а две локальные ба-
зисные функции изображены на рис. 39.
В принципе, можно использовать и
обычное представление базисных функ-
ций высоких порядков в виде полиномов
пространственных координат. Коэффици-
енты каждого из этих полиномов можно
вычислить по значениям базисной функ-
ции в узлах треугольника, а при вычиспе-
нии интегралов от базисных функций и их
производных по треугольнику Q,„ можно
воспользоваться соотношениями (5.72), позволяющими заменить пе-
ременные х и у на линейные комбинации £ -координат (чтобы мож-
но было воспользоваться соотношением (5.76) для вычисления соот-
ветствующих интегралов по ).
Рис. 39. Поведение квадратичных локальных базисных функций фг и фр
на треугольном конечном элементе
5.3.Применение МКЭ для решения двумерных краевых задач ... 291
Однако представление (5.92) является более удобным для вымпеле
ния локальных матриц и векторов конечного элемента1.
Поскольку подынтегральные выражения компонент матрицы м i
кости содержат производные базисных функций, покажем, как можно
получить эти производные для функций, записанных через £ -
координаты в виде (5.92). Сначала приведём частные производные £ -
координат, воспользовавшись представлением (5.66):
Тогда частные производные функций (5.92) вычисляются достаточно
просто:
^^ = ^(2^-4)=}.^- ох дх\ > ох д£{ дх = 4а}Д - q.[ , (5.94)
Ш^ = ^(2^_д) = 4Д^-- оу оу\ ' оу д£{ ду = 4о12£1 - , (5-95)
Й2 &У) ‘2 д'Ф-2 & дх дУ у) = 4<^£2 -а?, (5-96)
дФз fey) . зр з дфз (х, Ox ду >У) = 4а? - а?, (5.97)
1 Представление (5.92) можно довольно просто объяснить. Прежде всего
надо учесть, что каждая £-координата является линейной функцией коорди-
нат, и поэтому все шесть определяемых соотношением (5.92) функций дейо-
вительно являются квадратичными функциями. При этом у функции пер-
вый сомножитель равен нулю на противоположном первому узлу ребре и
поэтому ф] равна нулю в узлах с номерами 2, 3 и 5. На серединах рёбер, у
которых первый узел является вершиной, принимает значение 0.5, и по-
этому второй сомножитель 2£j — 1 у Ф1 равен нулю в узлах с номерами 4 и
6. В первом же узле Д принимает значение 1, и поэтому в этом узле так-
же равна единице. С помощью аналогичных рассуждений легко убедиться,
что квадратичная функция ф2 равна единице в узле с номером 2 и пулю в
остальных пяти узлах, а квадратичная функция ф3 равна единице в у<лс с
номером 3 и нулю в остальных пяти узпах. У функции ф4 сомножитель f'
равен нулю в узлах с номерами 2, 5 и 3, а сомножитель £ в у пых с п«»ме
рами 1, 6 и 3. В результате ф4 отлична от нуля только в одном in пн* in ны
бранных узлов (четвёртом), в котором её сомножители £t и Л равны О 5, и
поэтому -ф| в четвёртом узле равна единице. Аналогичные рж х ь к-ния i ирл
ведливы и для функция Фг> и ф(;.
292
5 .Двумерные скалярные задачи
2^L^l = 4[^-£2 + ^^-] = 4((>|£2+af^), (5.98)
с).г ( их ox I ' '
^МД^ = 4(^-Д+£|^-] = 4(а^2+а|£|), (5.99)
<9// {оу Оу ) ' >
= 4 («^ + а?£2), = 1 (с^Д + «2£2 ), (5.100)
a'M-'-.y)=4(tt!£1+a3A). £^112 = 4(а1£,+«3д). (5.101)
В качестве примера покажем, как вычиеляется компонента G)д ло-
кальной матрицы жёсткости при условии, что на конечном элементе
U,„ коэффициент диффузии X = X = const:
й,я + -
Ц/и ^'111
= X J |(4cv}£1 — о ]) • 4 (cy{£2 I-<+Д) +
+ — 0'2 j 4 \^2^2 + j (Ixdy =
—l(cv}a? + a-M) f ^'(Ь/ ‘(НГ+М)2) f £2dxdy +
o,)i.
+ 16
(<»Н+аМ) /'(Д)2^.</ + ю((«1)2+(«2)2)У £|Дй-гф/ .(5.102)
^z»z
S2.
Поскольку (см. (5.76))
f £,,Шу = f (£, У (£2)° ^'d-rd,/ = (1+10!”!00!b2)!RD| = M
$2j,t
f £2d.,dy =jT (£t)"d.rdy = (о/Д^мИВ! =
s\„.
f W2dxdy = f (Д )2(£2)"(£з)"л«/!/ =
QNi
2!0J0!_ |detD| =
12+0+0+2)!
|detD|
12
5.3.Применение МКЭ для решения двумерных краевых <адач
2‘Н
J f&dxdy =f (^(^X^dxdy =
^lll. ^4н
, 1!1!f1! ' |det D| =
(1+1+0+21!
|d<l l>|
' I
окончательно получаем
<?14 = WetD|(a’oci + c^o^), (5.103)
где detD может быть вычислен с помощью соотношения (5.74), а ко-
эффициенты а/ - с помощью соотношений (5.69) и (5.75).
Остальные компоненты G вычисляются аналогично.
Заметим, что если коэффициент X является некоторой (не кусочно-
постоянной) функцией координат, то на элементе Q,/t он может быть
заменен своим квадратичным Интерполянтом.
с
^1ц,„ = ^З^Ф* ’
/=1
где Xz - значения X в соответствующих узлах элемента Qf„ . В этом
случае вычисление компонент локальной матрицы жёсткости G ста-
новится более громоздкими. Каждая компонента G,, представляется в
виде суммы шести слагаемых вида Х//^, , где
Rij = J Ф/ grad ф, • grad ф .
Вычислим для примера Дс4 (выкладки для получения
grad ф( • grad ф4 были сделаны в (5 102)):
ДС4 = J Фс grad Ф1 ’ grad Ф4^ =
^,1
= -4(c\[af J (4ДД) J^dxdy -
4м.
- 4 ((c\{ у2 + (c4)2 j J (4Д £3) £2dxdy +
Q)(1
+1б(а}с</ +^2) j (4Д£3)(А)2 dxdy +
294
5 Двумерные скалярные задачи
Поскольку
J (4^£з ; Qdxdy = 4 J (Д)2 £$d.xdy =
1Ж.
в итоге получим
Я?4 — + <^2а2) + ((°4) +(аз) ))|de(.D|.
Остальные элементы Кг14 вычисляются аналогично.
Обозначим через гд и i]2 два выражения:
711 = cvlfYl + а2<*2 ’ 112 = (™1)2 + (<4)2 • (5.104)
Тогда
Л’и = (I1!!+^i]2)|cletD|, /?f4 =(--^'П1 -
= “ 90Tl2)ldetDl’ = (п^1 +^ n2)klctD|,
Ян =(^ 4! — ^Ti2)|det D|, Л& =(^T|1+^i]2)|cletD|.
В резулыагс
5.3.Применение МКЭ для решения двумерных краевых мдач . 295
30
Л2 4Хд
15 90 4.5
4Хг 2ХГ
45 45
712 |de(D| .
(5.IOS)
Очевидно, что выражение (5.105) должно совпасть с (5.103), если па
X = X = X, = const, в чём мы и рекомендуем убедиться читателю
самостоятельно.
Заметим, что по сравнению с (5.103) соотношение (5.105) является
значительно более вычислительно трудоемким (по числу операции
компьютера) и поэтому его имеет смысл использовать только тогда,
когда изменения коэффициента X на действительно существенны
Очевидно, что компоненты локальной матрицы массы также удоб-
но вычислять с использованием соотношения (5.76).
При обработке краевых условий второго и третьего рода следует
учитывать, что локальные матрицы и векторы соответствующих рёбер
фактически являются локальными матрицами и векторами одномер-
ных квадратичных элементов (аналогично тому, как это было для ли-
нейных элементов). Например, для краевого условия третьего рода при
условии, что параметр р на ребре Гш постоянен и равен |3, а параметр
представлен в виде квадратичного интерполянта
йщФ1 + йрг'Фг + «рз'Фз (где , С^2 и
узлах ребра Г„,), локальная матрица
ребра Г,„ примут вид
йрз - значения параметра в
А?3 и локальный вектор Ъ 3
(5.106)
Цтз
где h,n = mes Гш - длина ребра Г,„.
5.3.5. ТРЕУГОЛЬНЫЕ ЭЛЕМЕНТЫ С КУБИЧЕСКИМИ ЛАГРАНЖЕВЫМИ
БАЗИСНЫМИ ФХ ПКЦНЯМН
Для определения десяти коэффициентов полного кубического по-
линома необходимо задать его значения в десяти узлах, и поэтому на
треугольнике Q,,, кроме трёх его вершин должно быть еще семь узлов
Как правило, эти дополнительные узлы ставятся по два на каждом ребре
треугольника и один в его центре масс. В этом случае базисные функции
могут быть выражены через £. -координаты следующим образом
V1 (ж,;у) = |д(.^ -1)(3£, -2),
(г,») = идз^-1)(з£2-2).
’К = 2).
296
5.Двумерные скалярные задачи
-ф4 (.:,>/) = |£ А (ЗД-1),
Фе (*• и) = j A A (ЗА ~ 1),
ф8(.т,.у) = |АА (3£3-1),
•ф5(л») = |АА(ЗА-1).
Фг («>!/) = f АА (3А ~ 1),
^(^У) = ^£зА (ЗА -1),
Ф11)(ж,!/) = 27ААА,
(5.107)
Рис. 40. Расположение узлов
на треугольном конечном
элементе с квадратичными
базисными функциями
где первые три базисные функции соот-
ветствуют узлам в вершинах треугольни-
ка, следующие шесть — узлам на трёх его
рёбрах, а последняя — узлу в центре масс
(рис. 40).
Технология расчёта локальных матриц
и векторов для кубических лагранжевых
элементов практически ничем не отлича-
ется от рассмотренной нами выше техно-
логии для квадратичных элементов.
5.3.6. 1РЕУГОЛЫ1ЫЕ ЭЛЕМЕНТЫ
( КУБИЧЕСКИМИ ЭРМИТОВЫМИ
Ь УЗИСИЫМИ ФУНКЦИЯМИ
Рассмотрим возможности использо-
вания эрмитовой интерполяции решения
на треугольных конечных элементах, т.е
так называемых эрмитовых треугольных элементов. В этом случае в
вершинах и (^:ь?7з) треугольника Qw определяются
не только значения базисных функций, но и значения их производных.
Для эрмитовых треугольных конечных элементов локальные базисные
функции на треугольниках также очень удобно представлять в виде
полиномов £. -координат. Например, базисные функции треугольного
кубического эрмитова элемента можно записать в виде [9]:
4>i(z,Z/) = Д(ЗД -2^-7ДД),
Ф2(^?/)-^(3^2-24-7АА),
ф3 &у) = £л (3^-2^-74£2),
4>4 Сг‘,2/) = 27£| £2£3
4’5 («-’,//) = Д ((.Т1 -i’i)^2 № - + Й -Х-3)£з (А - Д))>
Фо (т, у) = 4 ((х2 - х3) £3 (Д - £3) + (я2 - (£3 - £2)),
ф7 (х,у) = £3((£'з - (£2 -2?з) + (.г'з - i2)£2 (Д - Д)),
ф8 (х,у) = Д ((Гд - У-з)£2 (^3 - А) + (т-Уз)£з(£2 “4))’
5.4.Четырёхугольные элементы
297
4’9 Wу) = & ((у-2 - у-з) А (4 - А) + (у-2 - У1) А (Аз - А)),
Ч’К) (л у) = А ((у-з - У\) А (Аз - Аз) + (у-з - У2) а2 (А - Аз)) •
При этом первые три функции отвечают за значения решения в верши
нах элемента, четвёртая - за значение решения в центре масс, пятая,
шестая и седьмая - за производную по х в вершинах элемента, а вось-
мая, девятая и десятая — за производную по у в его вершинах.
Обратим внимание, что у кубического эрмитова элемента произ-
водные глобальных базисных функций хотя и непрерывны в узлах, по
могут иметь разрывы на рёбрах элемента. Это означает, что такие ба-
зисные функции порождают конечномерное пространство функций,
имеющих только первые суммируемые с квадратом производные (на-
помним, что глобальные базисные функции бикубических эрмитовых
элементов на прямоугольниках и функции из порождаемого ими ко-
нечномерного пространства имеют суммируемые с квадратом вторые
производные и поэтому пригодны, например, для решения бигармопи-
ческих уравнений). Чтобы на треугольниках обеспечить непрерыв-
ность производных глобальных оазисных функций во всей области,
необходимо использовать полиномы более высокого порядка (как ми-
нимум пятого [9J). При решении краевых задач для дифференциальных
уравнений второго порядка использовать столь высокие степени поли-
номов для построения базисных функций обычно не только неудобно,
но и, как правило, довольно неэффективно. Поэтому эрмитовы тре-
угольные элементы используются на практике довольно редко.
5.4. ЧЕТЫРЁХУГОЛЬНЫЕ ЭЛЕМЕНТЫ
5.4.1. БАЗИСНЫЕ ФУНКЦИИ Н \ ЧЕТЫРЁХЪ БОЛЬНЫХ ЭЛЕМЕНТАХ
Четырехугольные элементы применяют, как и треугольные, для
решения задач в областях с криволинейными границами (внешними и
внутренними). Эти элементы сочетают в себе преимущества прямо-
угольных элементов в точности аппроксимации решения с возможно-
стями треугольников при описании
расчётных областей со сложными
границами.
Будем считать, что область Q раз-
бита на выпуклые четырёхугольники
Q/, и каждый четырёхугольник задан
координатами его четырёх вершин
), 2 = 1...4. При этом вершины
чолжпы быть пронумерованы так,
чтобы на одной стороне четырёх-
угольника нс лежали первая и четвёр-
тая вершины (и соответственно вторая
и третья). 1 [ример такого чстырсх-
у тельника показан па рис. 41.
Рис. II. Распочижсппс \ i шн
на чегырёхмо и.пом конечном
HICMCIIIV
298
5 .Двумерные скалярные задачи
Построим па четырёхугольном конечном элементе Q;. локальные
базисные функции с помощью билинейных функций, заданных на
шаблонном элементе £1Е, являющемся единичным квадратом:
= (ft,-п)|0 <^<1, 0<л<1). (5.108)
Отобразим £1Е в четырёхугольник О.к с вершинами (£,,уг) с по-
мощью следующих соотношений:
* = +U1- У ^2 +(1-УлЛз h6,7]T4, (5.109)
У = U - 0 (! - У У\ 44(1- >1)г/2 4-(1-Оп?7з 4-У1?/4- (5.110)
Соотношения (5.109) и (5.110) переводят границу £ = 0 квадрата
1.4 в границу четырёхугольника Ц , заключённую между вершинами
(£’1,</1) и (^з>У)- При этом граница 6, = 1 переходит в границу между
(X2J/2) и (^Лй), граница т] = О - в границу между (хъух) и (х2,у2),
а граница т| = 1 - в границу между (т3, у) и (.£4,7/4).
Введём на £1‘ билинейные базисные функции
Ф1 4 л) = (У Щ (л), ф2 а, Т]) = W2 (У Щ (л),
Фз fe Т1) = ИЛ1 (У ™2 М , Ф4 »У = (У И<2 (У ,
где и 1К2 — одномерные функции следующего вида:
(У = 1-С = С (5.111)
Тогда базисные функции на четырёхугольнике можно опреде-
лить с помощью соотношений
*Ф1 4 у) = И1 (£ 4 У)) IИ (т) (х, У), (5.112)
Ф-2 4 У = 4 (^4 у)) Щ (л 4 У), (5.113)
Фз (z,y) = Wj (Ут,:у))И<2 014У). (5.1 14)
ф4 (.т, у) = И<2 (е, (т, 7/)) 11/2 (т] (ж, у)), (5.115)
где Ут, У и т\(х,у) - функции, определяемые из соотношений
(5.109)-(5.1 10).
Нетрудно убедиться, что каждому узлу четырёхугольника Qk соот-
ветствует одна базисная функция, принимающая значение 1 в нём и
значение 0 в остальных узлах В дальнейшем мы будем называть
аппроксимацию с помощью функций (5.111)—(5.115) билинейной. Эта
аппроксимация, строго говоря, не является билинейной в координатах
5.4.Четырёхугольные элементы
299
{./;,(/}, но в координатах {£>, л] используемые нами локальные банк
ные функции действительно являются билинейными.
В принципе, соотношения (5.109)-(5.110) иногда использую и я и
для невыпуклых четырёхугольников. Однако в этом случае соо[ноше-
ния (5.109)-(5.110) не точно переводят квадрат О,Е в четырёхугольник
с вершинами (.г\,7/,) (поскольку часть единичного квадрач i
этим отображением переводится в подобласть, лежащую снаружи нс-
выпуклого четырёхугольника Qj.). Поэтому мы не рекомендуем поль-
зоваться полученными здесь соотношениями для певыпуклых четы-
рёхугольников. На наш взгляд, лучше либо не допускать появления
таких элементов, либо разбивать их на два треугольника (диагональю,
исходящей из максимального угла).
5.4.2. О СХОДИМОСТИ АППРОКСИМАЦИЙ НА ЧЕТЫРЁХУГОЛЬНЫХ КОНЕЧНЫХ
)Л ЕМ ЕН ГАХ
Итак, па четырёхугольных элементах базисные функции
(5.1 12)—(5.115), строго говоря, нс являются полиномами координат х и
у. Соотношения же (3.76), (3.77) и (3.86) дают оценку погрешности
конечноэлементного решения, которое ищется в виде кусочно-
нолииомиалыюй функции пространственных переменных. Поэтому
для рассмотренных выше четырёхугольных элементов вопрос сходи-
мости аппроксимаций требует отдельного обсуждения.
Вообще говоря, использование неполиномиальных базисных функций
нс является строго обязательным для сходимости конечпоэлементных
аппроксимаций к точному решению. На самом деле, для выполнения оце-
нок (3.76), (3.77) и (3.86) достаточно, чтобы на конечном элементе любой
полином степени т мог быть приближен линейной комбинацией базис-
ных функций этого элемента с точностью не ниже в энергетиче-
ской норме (3.60) (‘Или с точностью нс ниже С* (/г7"41) в норме (3.73))1.
Поэтому для того чтобы аппроксимации на четырехугольных элементах с
базисными функциями (5.112)-(5.115) имели погрешность С* (/г2) в нор-
ме (3.73), достаточно убедиться в том, что произвольный линейный поли-
ном может быть приближен линейной комбинацией функций (5.112)
(5.115) с весами, равными значениям этого полинома в соответствующих
узлах элемента, с погрешностью, нс превышающей Ch2 в норме (3.73).
Кроме того, аппроксимационные свойства элементов с нсполино-
миальными базисными функциями можно проверить на модельных
задачах. Для этого нужно построить задачу с некоторым п шеечным
решением, решить сё на последовательности сеток с уменыпающнхни я
характерными размерами элементов (например, Л, А/2, ///1 и i г),
jL Idl h/4
вычислить погрешности (г , г ' , г ' и т.д.) получаемых решении и
1 Здесь /?., как и ранее, - характерный размер элемента
300
5.Двумерные скалярные задачи
убедиться, что они убывают как минимум пропорционально квадрату
уменьшения характерного размера.
5.4.3. ЛОКАЛЬНЫЕ МАТРИЦЫ ЧЕТЫРЁХУГОЛЬНЫХ КОНЕЧНЫХ ЭЛЕМЕНТОВ
ПЕРВОГО ПОРЯДКА
Получим соотношения для вычисления элементов локальных
матриц массы и жёсткости четырёхугольного элемента первого поряд-
ка. Основная трудность здесь заключается в том, что базисные функ-
ции ф, (т,у) не представлены в аналитическом виде. Поэтому при
вычислении интегралов мы воспользуемся заменой переменных х и у
на £, и т|, что позволит перейти от интегрирования по четырёхуголь-
нику ГД. к интегрированию по квадрату где аналитический вид
базисных функций нам известен.
Для упрощения выкладок будем считать, что коэффициенты X и л
постоянны на ГД, поэтому, чтобы не загромождать выкладки, они бу-
дут опущены в формулах.
Сначала получим формулы для вычисления локальной матрицы
массы.
Так как функция ф, (.г’,'(/) на элементе ГД - это образ функции
ф,: ft, л) > определённой на шаблонном элементе , то
Д/ = ff Ф, (-С2/)Ф7 (xty)dxdy =
i 1
= f f Ф,. ft ft, л), У ft, л)) Ф7 ft ft, п), У (Ч, л)) \J\ =
() о
1 1
= f f<Pi ft,Tl)T, ft^PM^i], = (5 116)
о о
Вычислим якобиан J преобразования координат (5.109)-(5.110):
дх ду
dx d)y
с?л ^Л
(1 - л) ft’2 - .г-1) + Л ft4 - -Фз) (1 - л) (г/2 -2/1)4- л (г/4 - Уз)
(1-0(тз -A)4-e,ft4 -£2) 0 -0(</з -M + Udk -у-2)
= а() Та^ + ^л,
5.4.Четырёхугольные элементы
301
где коэффициенты а(), оц и а2 имеют следующий вид:
сх0 = (.т2 - ) (</з - ух) - (у2 - ) (£’з - i’i)
= (#2 - £i)fe -Уз)~ (У2 ~ У1)(^4 - £з) >
с*2 = (Уз -а-1)(?/4 -у-г)- (51 । ')
Из (5.117) нетрудно увидеть геометрический смысл коэффициен тов
ot(), а1т cy-2 . Если cq = 0, то параллельны стороны четырёхугольника,
лежащие между первой и второй и между третьей и четвёртой его
вершинами. Если же сх2 = 0, то параллельны стороны четырёхуголь-
ника, лежащие между первой и третьей и между второй и четвёртой
его вершинами. Таким образом, если Од. - параллелограмм, то cq = О
И (X j - 0 .
Если стороны четырёхугольника, прилежащие к первой вершине,
не являются параллельными, то ап 0.
Таким образом, якобиан J является линейной функцией координат
и т| и компоненты матрицы массы, определяемые соотношени-
ем (5.116), вычисляются элементарно. При этом следует учесть, что
якобиан J в силу взаимной однозначности отображения
(5.109)-(5.110) на нигде не обращается в ноль и поэтому не меняет
знак. Тогда модуль якобиана может быть вычислен как
И = sign(J) J = sign («и) J,
поскольку J = ex,) при £ = т] = 0 (здесь и далее мы полагаем, что сто-
роны четырёхугольника, у которых первая вершина является общей, не
лежат на одной прямой).
В результате матрица массы для аппроксимации с использованием
билинейных функции (5.112)-(5.115) может быть представлена в виде:
М = sign (а()) / а() 36 4 2 2 1' 2 2 +^ 72 2 2 1 1' 2 6 13 112 2 Q2 72 '2 1 1 2 2 1 2 1 6 1Y 2 3
2 2 4 1 1 4
к 1 2 2 4 13 2 6 к 1 2 3 61
Рассмотрим, как можно вычислить компоненты локальной матрицы
жёсткости:
G,.
= sign(a0) J J
, о о
= J gradip,; • gradxpjdQ —
d(pj (6,(ж,у),т](.т, у)) d(p.j (6,
дх
’— •/«/? (/ц |
их
302
5.Двумерные скалярные задачи
ду
f Г дф, (Е, (а, X/), т| (.т, у)} 5ф(ф ?/), 1] (л;, у
ду
о о
Вычислим производные и Используя правила диффе-
ренцирования сложной функции, получим
дф, дф, дх 5ф, ду
д^ дх д^ ду д^ ’
дф, = 5,?; , дфг ду_
5i] дх с>1| ду 51]
Применяя формулы Крамера (их применение возможно в силу того,
что <7 0), получаем
дф, _ 1 дф-,. дК ду 1 дфг
д.г J дф,. ду J
5г] 5т]
дх дф,
дф. 1 д^ _ 1 'дф,
ду J дх дф, J , ^1|
51] 511
'Д~(Рот1 4- 04 )J,
(05'П + 0-2) --^(0rX + 0i) ,
где
Pi = з-’з - 3'1>
j32=f2-£’Ij Рз =.2/3 -Z/b P4=fo-#i,
^з+^b 0G = </l — 3/2 — ?7з H-X/4 • (5.118)
Когда
( 1 1
ign(<'o) j f ^-М + в:1)-^-(Рсч + ₽4) х
, (J о 1
X ^-Ш + Рз)-^-(Рс,П + 04)3
rZ^dT] +
( 1 1
J f ^(^ + ^)-^(РЛ + Р1) *
Д) О I
5.4.Четырёхугольные элементы
303
Х + + у^П-
(5 119)
В этих соотношениях для билинейной аппроксимации (5 III)
(5.115) входящие в них функции
функциями координат 6, и
дф, дф;
и являются линейными
(УТ)
т, (5|l = ,1-1, =
1 <96, б/т)
_ 1 __ ^£2
<эе а>|
= —6, и т.д.), и поэтому для компонент Gy может
быть получен аналитический вид. Однако такой подход очень редко
применяется на практике, поскольку во-первых, соответствующие
формулы имеют довольно громоздкий вид и требуют очень большого
числа арифметических действий, а во-вторых (и это главное), они ста-
новятся вычислительно неустойчивыми, когда четырехугольник при-
ближается по форме к трапеции, т.е. когда cv, « 0 или cy2 и 0.
Поэтому интегралы в соотношениях (5.119) лучше вычислять чис-
ленно. Для этого можно использовать, например, метод Гаусса. Квад-
ратурные формулы при интегрировании по прямоугольнику (с тремя
узлами по каждой из координат) имеют следующий вид:
*>1+1 1U+1 iSh') 3 3
6, д,
где
i- _ £,<:+! +
: -----2----+ ^T’
= 0, t2 =0.774596669241483 37,
= Лж - Д,
I _ 4J+1 + д Ч'
- 2 +tl~T
h = ~h >
_ 8 _ 5
1 9’ 2 3 9‘
(5.120)
(5-121)
Для шаблонного элемента = [0,1] x [0,1] эти формулы прини-
мают вид:
j / (5
О () /,:=!/= I
где коэффициенты и т^. определяются соотношениями (S I ’()) и
(5.121).
304
5.Двумерные скалярные задачи
В качестве примера приведём локальную матрицу жёсткости для
конечного элемента ABCD с вершинами Л = (1,1), В = (5,3),
С = (2,5), В = (4,5), компоненты которой вычислялись с использо-
ванием квадратурных формул с тремя узлами по каждой из локальных
координат:
0.3982285392 -0.04645707836 -0.1205713479 -0.2312001129 '
-0.04645707836 0.8429141567 -0.5088573041 -0.2875997743
-0.1205713479 -0.5088573041 0.9264283699 -0.2969997178
-0.2312001129 -0.2875997743 -0.2969997178 0.8157996049
5.4.4. ВЫЧИСЛЕНИЕ ЗНАЧЕНИЯ КОНЕЧНОЭЛЕМЕНТНОГО РЕШЕНИЯ
В ПРОИЗВОЛЬНОЙ ТОЧКЕ РАСЧЁТНОЙ ОБЛАСТИ ДЛЯ СЕТКИ
С ЯЧЕЙКАМИ В ВИДЕ ЧЕТЫРЁХУГОЛЬНИКОВ
Рассмотрим проблему вычисления значения конечноэлементного
решения в произвольной точке Р расчётной области для сетки из вы-
пуклых четырёхугольных элементов. Для этого нужно сначала опреде-
ли гь, в какой из четырёхугольников попала точка Р. Эта проблема
может быть решена так же, как и для сетки из треугольных элементов.
I кшример, можно использовать тог факт, что точка Р тогда и только
тогда находится внутри или на границе выпуклого четырёхугольника
(как, впрочем, и любого выпуклого многоугольника), когда сумма
площадей треугольников, образованных этой точкой и каждой сторо-
ной четырёхугольника, равна площади самого четырёхугольника. Для
вычисления же площадей треугольников можно использовать соотно-
шения (5.73)-(5.74), приведённые в разделе 5.3.1 (а площадь четырёх-
угольника, естественно, легко вычисляется как сумма площадей двух
треугольников). При практической реализации используются различ-
ные процедуры ускорения анализа ситуаций, когда точка Р не попа-
дает в рассматриваемый четырёхугольник. Об этих процедурах будет
сказано в разделе 10.7.1.
После того как для точки Р найден содержащий её четырёхуголь-
ник, необходимо в этой точке вычислить значения базисных функций
(5.112)—(5.1 15). Для этого нужно получить координаты точки
единичного квадрата, которая отображается в точку Р = (хруур^ с
помощью соотношений (5.109)—(5.1 10), т.е. фактически нам нужно
получить из соотношений (5.109)-(5.1 10) выражения для вычисления
6, и т] через х и у.
Перепишем соотношения (5.109)-(5.1 10) в виде:
я = £‘1 + Е, (-4’1 4- £-2) 4- Т1 (-3) + £3) 4- €»т) (а) - х2 - £3 4- £4)>
У = У\ 4- 6, (-//! 4- у2) 4- т) (-4/1 4- уз) 4- е,п (у{-- у2 - Уз 4- у4)
или с учётом обозначений (5.1 18)
5.4. Четы рёху гол ы i ы е элементы
305
х = х} + 34 + 0ГП +
У = У1 + 34 + ЗзЛ + Зс^л
(5.123)
Очевидно, что из первого уравнения системы (5.123) можно исключить
член с произведением ^т|. Для этого нужно умножить первое уравне-
ние на 3g, второе на (35 и вычесть из первого уравнения второе. 1 (осле
элементарных преобразований получим уравнение
«4 - а2т) = w (ж, у), (5.124)
где
™ у) = Зс О - £1) - Рз (у - У1),
а коэффициенты eg и а2 определяются соотношениями (5.117).
В зависимости от значений коэффициентов уравнения (5.124) зна-
чения 6, и т) могут быть вычислены одним из следующих способов.
Пусть og = ot2 = 0. Это соответствует случаю, когда четырёх-
угольник представляет собой параллелограмм и Зб — Зс = 0 . Тогда
значения Е, и т) определяются соотношениями
. _ 0з(ж-®1)-31(г/-й) = 02(з/-й)-Р4
Р2Р3-РА ’ 11 Р2Р3-Р1Р4
Если од = 0, а сх2 О (т.е. параллельны только стороны четырёх-
угольника, лежащие между первой и второй и между третьей и четвёр-
той его вершинами), то
а2 (х - а?!) + 3xw (ж, у)
«А - Зб™ У)
Т]= -
W (ж, у)
а2
Если же од 0, a ot2 = 0 (т.е. параллельны только стороны четы-
рёхугольника, лежащие между первой и третьей и между второй и чет-
вёртой его вершинами), то
= w (ж, у) = og (y-yi)-&iw(x,y)
аг ’ 11 од|33 + 0Gw (ж, у)
И, наконец, в случае, когда од 0 и об2 0, значения G, и ц мо-
гут быть определены из соотношений
P5CW+ («2p2+aiPi+Psw (3;>!/)] Т) + сч(х1—а.-) + p2w (х,у) = I). (5.125)
зФл). (5126)
од од
306
5.Двумерные скалярные задачи
Заметим, что уравнение (5.125) может иметь два корня. Очевидно,
нам нужно выбрать такой, чтобы, во-первых, для него выполнялось
условие 0 < 1) < 1 и, во-вторых, для вычисленного по нему из соот-
ношения (5.126) значения £, выполнялось аналогичное условие
0<^<1.
5.4.5. ОБ ОДНОМ ОБЩЕМ СПОС ОБЕ ВЫЧИСЛЕНИЯ ЗНАЧЕНИЙ И ПРОИЗВОДНЫХ
КОНЕЧНО ЭЛЕМЕНТНОГО РЕШЕНИЯ, ПОЛУЧЕННОГО НА НЕРЕГУЛЯРНОЙ
С ЕТКЕ, С ИСПОЛЬЗОВАНИЕМ НЕРЕИНТЕРПОЛЯЦИИ
Как правило, на практике при использовании нерегулярных се-
ток (с четырёхугольными и тем более с шестигранными ячейками,
включая ячейки с искривлёнными границами) довольно редко приме-
няются рассмотренные в разделе 5.4.4 (и аналогичные им в трёхмер-
ном случае) процедуры, позволяющие точно вычислять значения ко-
нечноэлементного решения (или его производных) в произвольной
точке расчётной области. Гораздо проще и эффективней можно решить
эту проблему, например, через построение интерполянтов (как прави-
ло, сглаживающих). Для этого в нужной нам подобласти (где мы хотим
получить значения конечноэлементного решения или его производ-
ных) в некотором (достаточно большом) наборе точек, являющихся
определёнными точками конечных элементов, выдаются значения ре-
шения (или его производных), затем по ним строится сглаживающий
ингерполянт (например, на прямоугольной сетке) и уже по нему вы-
числяются значения решения (или его производных) в произвольной
точке.
I ем самым мы избавляемся от необходимости не только искать
нужный нам конечный элемент, но и (что ещё важнее) определять зна-
чения его локальных координат (для четырёхугольника - это две коор-
динаты и т], для шестигранника - три т] и CJ по глобальным
координатам (ж, у или х, у и z) для нужной нам точки. При этом
как процедура поиска нужной ячейки в прямоугольной сетке (на кото-
рой построен интерполя!тт), гак и процедуры вычисления значения
кусочно-полиномиальных функций на прямоугольнике или прямо-
угольном параллелепипеде очень просты и требуют минимальных вы-
чис. ипнелъных затрат.
Продемонстрируем на простейшем примере процедуру переиптер-
поляцин решения с сетки с четырёхугольными ячейками на прямо-
угольную сетку. На рис. 42 сплошными линиями показана сетка из
шести четырёхугольников Q,, на которой получено конечноэлемент-
ное решение (это может быть как вся расчётная область, так и любая её
подобласть), а штриховыми - регулярная прямоугольная сетка для
псрсинтерполяции решения. Точками показаны узлы (а^;,уд), по кото-
рым будет строиться интерполянт на прямоугольной сетке — эти узлы
поставлены в тех точках четырёхугольников, по которым обычно вы-
полняется численное интегрирование с использованием формулы Га-
усса (с п = 5 значения локальных координат 6, и ц для этих точек в
5.4.Четырёхугольные элементы
307
каждом четырёхугольнике определяются соотношениями оо!б«лоо77,
£.2=0.230765345, £.3=0.5, ^=0.769234655, ^=0.953089923, Т), £., )
Рис. 42. Вид исходной сетки из четырёхугольников
и регулярной прямоугольной сетки при переинтсрполяции решения
Очевидно, узлы переинтерполяции могут быть выбраны и другим
способом - важно лишь то, чтобы достаточно просто определялись их
локальные координаты в каждом четырёхугольнике.
Интерполянт и4’ на прямоугольной сетке может быть построен по
значениям конечноэлементного решения (или какой-либо интересую-
щей нас производной) в узлах точно так же, как нами бып по-
строен сглаживающий сплайн (см раздел 4.17.2). Для этого интерпо-
лянт и,ч> представляется в виде линейной комбинации базисных функ-
ций прямоугольных конечных элементов: и'1’ = 52 (/^'Ф/* •
/
Веса 7/’ разложения игр по могут быть найдены из ус пиши
минимизации следующего функционала (сравните с (4.101) и (4 10 ))
52 52 > У к) - Ч
2
iui)i
ч1'1
к
308
5.Двумерные скалярные задачи
где сх — параметр регуляризации1, цд. - веса, с помощью которых мож-
но регулировать близость и.'1' к значениям интерполируемой функции
в узлах (.тд., ук), a Q - вся расчётная область или её подобласть, на
которой выполняется переинтерполяция.
Под ик понимаются либо значения ик конечноэлементного реше-
ния в узлах переинтерполяции (лд, </*.), либо значения той производ-
ной решения д , которая нас интересует. Очевидно, значения могут
быть получены из решения СЛАУ2
Aq'p=b, (5.127)
компоненты матрицы А и вектора правой части b которой определя-
ются соотношениями (сравните с (4.108), (4.109))
4=1
k
J"
п
dx dx
dy dy
c/Q,
b< = •
A
Значения параметра регуляризации ct {при недостаточном покры-
тии прямоугольной сетки узлами {хк,ук)) следует выбирать такими,
чтобы, с одной стороны, нс возникало серьёзных проблем при решении
СЛАУ (5.127) (из-за близости сё матрицы к вырожденной), а с другой
стороны, чтобы при изменении параметра а в несколько раз (или даже
на порядок) сумма квадратов отклонений
изменялась очень незначительно.
Е -EoytWA-)
А: ( 7
Генерацию матрицы и вектора СЛАУ (5.127) можно выполнять по
технологии МКЭ - проходом по прямоугольникам формировать их
локальные матрицы и векторы (по узлам (ад, р/,), попавшим в обраба-
тываемый прямоугольник, и значениям в них vk конечноэлементного
решения или интересующей нас производной) и стандартным образом
собирать из них глобальные матрицу и вектор (об этом также шла речь
в разделе 4.17).
1 При достаточном покрытии прямоугольной сетки узлами {хк, по зна-
чениям в которых делается переинтерполяция на прямоугольную сетку, пара-
метр си может быть взят равным нулю.
2 Подтверждающие это рассуждения полностью аналогичны тем. которые
были проведены нами в разделе 4.17.2 при построении одномерных сглажи-
вающих сплайнов.
5.4.Четырёхугольные элементы
309
Для псреинтсрполяции в качестве базисных функций ф'/' можно
использовать как простые билинейные базисные функции, гак н функ
ции более высоких порядков, например, эрмитовы бикубические
тогда переитерполированная функция (само решение или какая- шбо
его производная) получится очень гладкой. Вычислять же значения (в
любых точках интересующей нас подобласти) функции ,
I
определённой на прямоугольной сетке, очевидно, не представляет ни-
какого труда.
Рассмотренный здесь подход помимо сеток с четырёхугольными и
шестигранными ячейками довольно удобен и эффективен и для любых
других нерегулярных сеток с ячейками в виде треугольников, тетраэд-
ров, призм.
Заметим, что у рассмотренной процедуры персинтергюляции есть и
определённые «подводные камни». Так, если подобласть из четырёх-
угольных ячеек имеет сложную форму и некоторые прямоугольники
полностью или большей своей частью нс попадают внутрь этой подоб-
ласти, то при нулевом коэффициенте регуляризации с\ матрица СЛАУ
(5.127) может получиться вырожденной. Использование же ненулевого
коэффициента ct может привести к увеличению отклонений ингерпо-
лянта от значений в узлах (гг/.,?д.). Выходом здесь может служить
либо выборочное введение ненулевого cv (только на прямоугольниках,
выходящих за обрабатываемую подобласть), либо фиксация значений
q'7' в определённых узлах прямоугольной сетки, являющихся верши-
нами только тех прямоугольников, которые полностью (или почти
полностью) лежат вне обрабатываемой подобласти.
5.4.6. ЧЕТЫРЁХУГОЛЬНЫЕ ЭЛЕМЕНТЫ ВЫСОКИХ ПОРЯДКОВ
Не представляет особого груда построить четырёхугольные ко-
нечные элементы высоких порядков. Здесь возможно несколько под-
ходов.
Один из подходов заключается в том, что на единичном квадрате в
качестве шаблонных базисных функций используются функции высо-
кого порядка, а отображается единичный квадрат в четырёхугольник
по-прежнему с помощью билинейных функций, т.е. отображение еди-
ничного квадрата Q7i в четырёхугольник Q/,. остаётся билинейным
(см. соотношения (5.109)-(5.1 10)) и может быть записано в виде:
Я' = (Ъ1]) £1 +Ф-2 fen)2-2 + Фз (^Т])£з + Ф? (^т1) ^ь (5 I2K)
'/ = Ф1' (£.,п)У1 + Фг(Ьфъ + Фз (C,'l)«/3 +ф4 (5 W
где
Ф1' = (1 — — П), Ф2 (£>• п) = U1 “ ч)-
Ф'з (£»,п) = (1 — On»* Ф^ n) =
( I О))
310
5.Двумерныс скалярные задачи
являются стандартными билинейными функциями на квадрате.
Базисные же функции на квадрате можно определить, например,
как стандартные оиквадратичные:
Ф? fen) = ИДУ ИДУ, Ф5<|(Сп) = 11/2(У1Иг(11), Ф7Ьч(Сп) = 1Ь(Е.)1ИзМ, Ф54 (Е..П)= Илз(Ю’К3(л), где m(Q = 2(q-i)«-i), 1К3(С,) = 2C(<-i). ₽2ЬЧ(СТ1) = »2(О^(’1), Д" fe п) = иду иду. Ф? fe ч) = ^з (У Щг(п), Ф^(СУ=^2 (У^З (л), (5.131) ”<2 (У = -4С(С-1), (5.132)
Аналогично можно построить четырёхугольный элемент и третьего
порядка.
Другой подход к построению четырёхугольных элементов высоких
порядков заключается в том, что и при построении отображения шаб-
лонного элемента в координатах (£,, тг|) в конечный элемент в коорди-
натах (гс,</) используются нс билинейные функции (5.130), а функции
более высоких степеней. Это даст возможность строить конечные эле-
менты с криволинейными границами.
5.5. ДВУМЕРНЫЕ КОНЕЧНЫЕ КЛЕМЕНТЫ
С КРИВОЛИНЕЙНЫМИ ГРАНИЦАМИ
Будем считать, что отображение единичного квадрата f/ в ко-
нечный элемент осуществляется с помощью соотношений
9 9
v ’ у = , (5.133)
/=| z=i
где ф;Х| - стандартные бн квадратичные функции на
(см. (5.131) (5.132)), а (.т,, у,) - координаты девяти узлов элемента Q/..
Это отображение переводит квадрат О/' в четырёхугольник (Д с кри-
волинейными границами так. как это показано на рис. 43.
Очевидно, что мы можем использовать такой подход для построе-
ния конечноэлементпых сеток с ячейками, имеющими криволинейные
границы (с целью более точной аппроксимации подобластей, имею-
щих криволинейные границы). Покажем па примере, как можно с по-
5.5.Двумерные конечные элементы с криволинейными i р.пищами 3 I 1
мощью соотношений (5.133) построить конечный элемент, аппрокси
мирующий некоторую подобласть с криволинейными границами hoi
пример проиллюстрирован на рис. 44.
Рис. 43. Пример отображения единичного квадрата в четырёхугольник
с криволинейными границами Од.
На рис. 44,а показана некоторая подобласть О/, имеющая две кри-
волинейные границы (верхняя - часть гиперболы, правая - часть ок-
ружности). На границы подобласти Q' поставлены девять точек
(£„$,), которые фактически и будут определять аппроксимирующий
Q' конечный элемент £2д.. Эти точки (на рис. 44,6 они приведены с
номерами) интерпретируются как образы точек щ) (рис. 44,в) еди-
ничного квадрата <дЕ (рис. 44,г). Отображение (5.133) переводит еди-
ничный квадрат в конечный элемент Q/., границы которого пока-
заны на рис. 44,6 сплошными линиями. На этом же рисунке пунктир-
ными линиями показаны границы исходной криволинейной подобла-
сти Q'. Обратим внимание на то, что верхняя граница, являющаяся
частью гиперболы, аппроксимирована с довольно заметной погрешно-
стью, а правая граница Од. практически совпала с соответствующей
границей О', являющейся частью окружности (левая и нижняя грани-
цы О', являющиеся отрезками прямых, аппроксимированы, естествен-
но, абсолютно точно).
Базисные функции на конечном элементе Q.f. с криволинейными
границами можно построить точно так же, как это было сделано в раз
деле 5.4.1 для обычного четырёхугольника (с прямыми сторонами), i с
через задание шаблонных функций фг (£», п) на единичном квадриге
Наиболее естественно в этом случае использовать в качестве базисных
те же биквадратичные функции (5.131), с помощью которых бы ю но
строено отображение (5.133). Но это, вообще говоря, нс ооя iaie паю
312
5.Двумерные скалярные задачи
Рис. 44. Пример построения конечного элемента,
аппроксимирующего подобласть с криволинейными границами
5.5.Двумерныс конечные элементы с криволинейными грлпмцпмн 3 13
Например, в ситуации, когда конечноэлементная сетка состоит в
основном из четырёхугольников с прямыми границами, a четырех-
угольники с криволинейными границами используются только щя
аппроксимации небольших участков расчётной области (нсносредст
венно примыкающих к криволинейным границам), можно и на четы
рёхугольниках с криволинейными границами ввести базисные функ-
ции, получаемые из билинейных функций единичного квадрата. В дом
случае будет автоматически обеспечена согласованная стыковка всех
конечных элементов.
С другой стороны, можно на единичном квадрате 0е, который пе-
реводится в конечный элементе помощью биквадратичных функций, в
качестве базисных использовать, например, кубические функции. Ес-
тественно, для этого на нужно кроме четырёх его вершин поста-
вить ещё 12 узлов, как это делалось на обычном бикубическом элемен-
те (см. с. 249). В этом случае на фактически должно быть два на-
бора узлов и соответственно функций ф, - один набор узлов для
биквадратичных функций, определяющих отображение £1Е в ГД., а
второй — собственно для определения базисных функций на (и
соответственно на Г2д).
Очевидно, что криволинейные элементы можно строить с помощью
не только биквадратичных, но и бикубических функций. Эти элементы
могу г, например, более точно аппроксимировать и такие криволиней-
ные границы, на которых есть точки перегиба.
Аналогично тому, как мы определили четырёхугольный элемент с
криволинейными границами, можно определить и треугольный эле-
мент с криволинейными границами. В этом случае в качестве шаблон-
ного треугольника удобно использовать прямоугольный треуголь-
ник с единичными катетами, изображённый па рис. 45,а, поскольку на
нем имеют очень простой вид £ -координат ы:
S =4, д = 1-е,-п. (5.134)
На рис. 45 показано, как шаблонный треугольник можно ото-
бразить в криволинейный треугольник с помощью соотношения:
С G
х = 12$ ’ у = 12$ ’ (5.135)
7=1 7=1
где ф-1 — стандартные лагранжевы квадратичные функции па чс
угольнике Q* , определяемые соотношениями (сравните с (5 92))
= Ш -1), ФДе.,т1) = -е2(^2-1).
Й (Е., Т1) = А (2£3 -1), ФЗ (Е., п) = 4ад,
ФЧДЕ,т1) = 4£2£!, фЗ(^п) = 4£,£1. (5. Но)
314
5.Двумерные скалярные задачи
в которых £ -координаты определяются формулами (5.134).
Несмотря на то, что конечные элементы с криволинейными грани-
цами могут давать определённые преимущества, поскольку позволяют
заметно точнее описывать геометрию сложных областей, при работе с
Рис. 45. Пример отображения шаблонного треугольника (а)
в треугольник с криволинейными границами Qj. (б)
Например, используемые при построении элементов с криволиней-
ными границами отображения могут оказаться не взаимно однознач-
ными, а иногда могут приводить и к построению конечных элементов с
пересекающимися сторонами. При этом такие ситуации довольно
трудно проконтролировать. На рис. 46 приведён пример конечного
элемента (Д. (рис. 46,0, построенного по точкам подобласти, изобра-
жённой на рис. 46//, и полученного отображением (5.133) через стан-
дартный единичный квадрат Q . У полученного элемента пересе-
каются верхняя и правая стороны, что приводил' к неоднозначности его
локальных базисных функций.
Непростой является и проблема выдачи значения конечноэлемент-
ного решения в произвольной точке Р расчётной области. Основной
причиной этого является отсутствие относительно простых способов
вычисления координат {^р, по исходным координатам (хр ,ypyj
точки Р, поскольку из соотношений (5.133) (или (5.135)) очень трудно
выразить 6, и т] через х и у. Одним из возможных путей решения
этой проблемы является подход, рассмотренный нами в самом конце
раздела 5 4.4 и основанный на псреинтерполяции полученного конеч-
ноэлементного решения на прямоугольную сетку.
При решении трёхмерных задач также можно использовать элемен-
ты с криволинейными границами. Техника построения таких элемен-
тов мало чем отличается от рассмотренной в данном разделе. Трудно-
сти же, связанные с использованием трёхмерных элементов с криволи-
нейными границами, имеют ту же природу, что и рассмотренные здесь
для двумерных элементов, но преодолевать их ещё сложнее.
5.6.Вычисление локальных матриц ...
315
Рис. 46. Пример конечного элемента с пересекающимися сторонами
5.6. ВЫЧИСЛЕНИЕ ЛОКАЛЬНЫХ МАТРИЦ МАССЫ И ЖЁСТКОСТИ
ПРИ ПРЕОБРАЗОВАНИИ СИСТЕМЫ КООРДИНАТ.
ИНВАРИАНТНОСТЬ ЛОКАЛЬНЫХ МАТРИЦ МАССЫ
И ЖЁСТКОСТИ К ПОВОРОТУ И ПАРАЛЛЕЛЬНОМУ ПЕРЕНОСУ
ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ
Покажем, что в декартовых координатах значения компонент
матриц массы и жёсткости не меняются при повороте и параллельном
переносе системы координат.
Обозначим через х вектор переменных в исходных координатах, а
через х' - вектор переменных, полученный в результате преобразова-
ния координат.
Функциональная матрица J этого преобразования имеет вид1
дх{ дх',
дх^ дх1
дх{ дх'н
k дхп dx,, t
Определитель этой матрицы (якобиан) обозначим через J .
Тогда компоненты локальной матрицы массы Mz в преобразован
ной системе координат, определяемые соотношением
1 Обратим внимание, что записанная нами функциональная млтрвцп янпя
стся транспонированной к традиционно используемой в русском ii.i'inoii ди re-
pa гуре матрице Якоби, см., например, [4], а в литературе по МК') именно
приведённую нами матрицу J обычно называют матрицей Якоби |25|
316
5.Двумерные скалярные задачи
M'lf. = J ф-(х')ф'(x')dQ',
u;„
где Q'„ - конечный элемент в новой системе координат, могут быть
вычислены с помощью соотношения
M'j = J фт (х)ф7 (x)|JpZQ, (5.137)
поскольку ф'(х') z = ф'(х'(х))| = ф, (х)| (т.е. функция ф-(х')
К 11п 1$ lnl И 2/к
на элементе Q',, — это образ функции ф,(х) элемента Q,rt) и
dQ' = |J|dQ.
При любом преобразовании координат градиент произвольной
функции /(х) преобразуется следующим образом:
grad/(x) = d/(x) dxA df(x) dx u j = а/(х(х')) dx- dx[ I 4 1 gf(x(x')) dx' dx.„ = J df' (xz) dx[ df (x') = J grad'/',
где J — функциональная матрица перевода координат т, в т- . Поэто-
му элементы матрицы жесткости G' могут вычисляться следующим
образом (при этом скалярное произведение grad- grad запишем в мат-
ричном виде (grad)T grad как произведение строки (grad)T на столбец
grad ):
Gij = f (grad'ф')Т grad'ф'с/Q' =
= J" (J" 1 grad ф, j J-1 grad ф7'J|dQ =
= J (grad ф,) (J-1)T J-1 ёгас1Ф7 \J\d^ =
$ lni
— J (grad ф^ (JJT) 1 gradф7 |./| dQ. (5.138)
5.6.Вычисление локальных матриц ..
317
Таким образом, соотношения (5.137) и (5.138) позволяют вычислять
локальные матрицы массы и жёсткости конечных элементов через ба-
зисные функции шаблонных конечных элементов1.
Наиболее удобны шаблонные элементы в тех случаях, когда они
переводятся в нужные нам конечные элементы линейным преобразо-
ванием вида
x' = Rx + a, (5.139)
где R - невырожденная матрица с постоянными коэффициентами, а
вектор констант. В этом случае функциональная матрица J преобра-
зования координат (5.139) совпадает с матрицей R.
Отдельно рассмотрим случай, когда задача решается в декартовой
системе координат и преобразование (5.139) является линейным пре-
образованием поворота со сдвигом. В этом случае R - ортогональная
матрица вращения, т.е. для неё выполняются соотношения
RRT = E, |R| = 1. (5.140)
Тогда из соотношений (5.137) и (5.138) сразу же следует, что
М:,=Мц, (5.141)
G',j = J" (grad ф,- )Т (RR')'1 grad ф/Ю =
= Г (grad ф, ) grad ф?бЮ = Gy. (5.142)
Таким образом, при аппроксимации краевых задач для эллиптиче-
ского уравнения (1 1) в декартовых координатах не возникает никаких
проблем, если в конечноэлементной сетке есть повёрнутые элементы
(это могут быть прямоугольники или прямоугольные параллелепипеды
с непараллельными координатным осям сторонами, прямые призмы,
оси которых не параллельны ни одной из осей координат, и т.д.). Такие
ситуации, например, могут возникать, если в расчётной области есть
прямоугольные подобласти, стороны которых не параллельны друг
другу, и для решения задачи используются комбинированные сетки (из
треугольников и прямоугольников или из тетраэдров, прямых призм и
параллелепипедов и т.п.). Из инвариантности локальных матриц к по-
вороту и смещению с очевидностью следует, что для любого конечно-
го элемента можно вычислять его локальные матрицы в удобной для
этого локальной системе координат, полученной поворотом и смете
нием глобальной декартовой системы координат.
Обратим особое внимание на то, что при использовании шаблон-
ных элементов нужно быть очень аккуратным при определении cooi
всгствия узлов требуемого нам элемента и шаблонного Например,
если повёрнутый прямоугольник, изображённый на рис. 47, определен
1 Фактически именно эти соотношения и были испольюнапы нами выше
ши построения локальных матриц четырёхугольного конечною люмены
318
5.Двумерные скалярные задачи
Рис. 47. Пример повёрнутого
элемента
набором узлов с глобальными номерами 22, 27, 35 и 49, то, казалось
бы, наиболее естественной и удобной (по возрастанию глобальных
номеров) локальной нумерацией должна быть нумерация, при которой
глобальный номер 22 соответствует локальному номеру 1, глобальный
номер 27 - локальному номеру 2, глобальный номер 35 - локальному
номеру 3 и глобальный номер 49 - локальному номеру 4. Если же при
этом на шаблонном элементе была использована другая локальная
нумерация (которую мы рассматривали
ранее, см. рис. 22 на с. 231), то, очевидно,
локальная матрица шаблонного элемента
не совпадёт с требуемой матрицей (и,
естественно, будет грубой ошибкой зане-
сение этой локальной матрицы в глобаль-
ную просто по указанному выше соответ-
ствию локальных и глобальных номеров).
Воспользоваться же матрицей шаблонно-
го элемента можно в том случае, если
сменить локальную нумерацию узлов
изображённого на рис. 47 конечного эле-
мента так, чтобы после поворота его ло-
кальная нумерация совпадала с нумераци-
ей шаблонного элемента. Например, мо-
гут быть использованы следующие соот-
ветствия глобальных и локальных номеров: 22-1, 49-2, 27-3, 35-4 или
27-1, 22-2, 35—3, 49-4 (читатель может легко построить ещё два по-
добных соответствия1).
Вообще говоря, если в сетке используются повёрнутые элементы,
го правильность использования шаблонного элемента можно обеспе-
чить следующими способами. Проще и лучше всего хранить элементы
гак, чтобы номера их глобальных вершин всегда перечислялись в пра-
вильном порядке (т.е. так. чтобы после поворота вершина с первым
перечисляемым номером совпадала с первой вершиной шаблонного
элемента, вершина со вторым перечисляемым номером — со второй
вершиной шаблонного элемента и т.д.2). Если же при построении сетки
элементы были записаны с произвольным перечислением глобальных
номеров вершин, то нужно изменить порядок перечисления этих номе-
ров. Например, для изображенного на рис. 47 элемента для этого дос-
таточно вычислить расстояние между первой (по порядку перечисле-
ния) вершиной и тремя остальными и на четвёртое место в списке
вершин элемента поставить номер вершины, расстояние до которой
максимально (в результате будез построена такая локальная нумерация
анример, для изображенного на рис. 47 элемента для этого дос-
1 На самом деле, поскольку матрица отражения тоже является ортогональ-
ной и её определитель равен +1 или -1, из соотношений (5.137) и (5.138) сле-
дует инвариантность матриц жёсткости и массы и к преобразованию отраже-
ния; поэтому правильным (для принятого нами шаблонного элемента) соот-
ветствием локальной и глобальной нумерации будет ещё и соответствие 22-1,
27-2, 49-3, 35-4 и т.д.
! Как правило, эго обеспечивается программой построения сеток.
5.7.Тестирование процедур конечноэлементного решения
319
вершин элемента, что шаблонный элемент можно будет получить из
этого элемента поворотом или отражением).
Естественно, всё сказанное здесь о преобразованиях системы коор
динат и об использовании шаблонных элементов (с локальными м<н
рицами и векторами, полученными при использовании на них локаль-
ных систем координат) справедливо и для трёхмерного случая.
5.7. ТЕСТИРОВАНИЕ ПРОЦЕДУР КОНЕЧНОЭЛЕМЕНТНОГО РЕШЕНИЯ
ДВУМЕРНЫХ ЗАДАЧ
Тестирование правильности реализаций конечноэлементных
процедур решения двумерных задач базируется, в общем-то, на тех же
принципах, которые были рассмотрены нами в четвёртом разделе при
построении тестовых задач в одномерном случае.
Прежде всего, конечноэлементную процедуру следует протестиро-
вать на задачах, решениями которых являются полиномы или кусоч-
ные полиномы, точно представимые в виде линейной комбинации гло-
бальных базисных функций. При этом желательно подбирать в качест-
ве тестовых такие функции, которые хотя бы в одной из подобластей
расчётной области являются полным полиномом требуемой степени
Например, при тестировании копечноэлементной процедуры, ис-
пользующей квадратичные базисные функции на треугольниках, одну
из тестовых задач следует выбрать так, чтобы её решение (хотя бы в
одной из подобластей расчётной области) имело вид:
и — сх0 -I- Орг- 4- <м2у + аз-г7/ + + ^У2 (5.143)
При тестировании же биквадратичных прямоугольных элементов
соответствующий полный полином имеет вид:
и = (\0 -I- cipT + а2У + а3ху + а4а,-2 4- o5j/2 +
4-ctC3,;2// + а7ху2 4- ct8.T27/2. (5.144)
Схема построения тестовой задачи в двумерном случае, в общем,
аналогична описанной в разделе 4.14 схеме для одномерного случая.
Расчётная область разбивается на несколько подобластей. В них опре-
деляются коэффициенты X и либо как некоторые константы, либо
как некоторые кусочно-полиномиальные функции. Внутри каждой
подобласти решение определяется в виде полинома, степень которого
не выше порядка базисных функций тестируемых элементов (и, как
уже говорилось, хотя бы в одной из подобластей решение желательно
задать в виде соответствующего тестируемым элементам полного по-
линома). При этом полиномы в подобластях должны быть заданы гак,
чтобы сшитая из этих полиномов функция и (определяемая нами как
решение тестовой задачи) на границах между подобластями была не-
прерывна, а её нормальная производная была либо непрерывна
(если на границе непрерывен коэффициент X), либо имела шкон ска-
320
5.Двумерные скалярные задачи
чок, чтобы непрерывной была величина Х-|^ (в случае с разрывным
X). После этого в каждой из подобластей вычисляется правая часть f
+ ''р и
дифференциального уравнения f =
выбираются такие параметры краевых условий, чтобы им удовлетво-
ряла функция и.
В качестве такого рода тестовых задач для линейных треугольных
элементов, например, вполне могут быть использованы задачи, опи-
санные в этом (пятом) разделе на с. 282-283 и с. 286-288
Задача же, рассмотренная в самом начале раздела 5.2 (расчётная
обл<1сть показана на рис. 21) с параметрами, определёнными в разделе
5.2.3, вполне может служить одним из тестов для прямоугольных би-
линейных элементов. Эгу задачу легко модифицировать так, чтобы
тестовое решение в одной из подобластей стало полным билинейным
полиномом. Для этого искомую функцию и в подобласти QJ
(см рис. 21) определим в виде
щ = 2х — у + 0.5ал/ — 3.6 .
Коэффициент X зададим так, чтобы он был разрывным по х :
1 в Q1
X = 10 в Q2
10 в Q3
С учётом требования непрерывности решения и и потоков Х-^-
на границах между подобластями ГУ поведение и в подобластях ГУ и
Q3 определим с помощью соотношения:
U2 = 0.2.г — 0 1у 4- 0.05ал/.
Jlci ко убедиться, что полученная функция и непрерывна во всей
расчётной области [|ГУ, а на границах между Q1 и Q2 и Q1 и Q3
г
непрерывен поток Х^-:
Х^- = 2 4-0.5?/ = =10(0.2 + 0.05?/).
^.т=2-о 5.г,;=2+о v '
В качестве примера тестовой задачи для процедуры, использующей
бикубические эрмитовы элементы, в самом простейшем случае может
быть использована, например, задача, приведённая в разделе 5.2.9.1.
При этом необходимо помнить, что так же, как и в одномерном случае.
5.7.Тестирование процедур конечноэлемептного решения ... 321
при построении теста для процедуры, использующей стандартные эр-
митовы оазисные функции, необходимо учитывать требование непре-
рывности частных и смешанной производных решения
На базе рассмотренной разделе 5.2.9.1 задачи нетрудно построить
тест, в котором решением будет полный бикубический полином Для
этого можно взять, например, функцию
и = 8 4- 0.2т 4- 15г/ 4- 2ху 4- 0.03т2 4-150/ 4- 0.5т2?/ 4-
4- 20т/ + т2/ 4- 0.001т3 4- 9000?/ + 0.07т3?/ 4-
4- 500т/ 4* 0.8т3/ 4- 25т2/ 4- 6.т3?/3. (5.145)
Коэффициенты этого полинома выбраны так, чтобы каждое слагае-
мое имело примерно одинаковый порядок (это желательно делать при
построении полиномиальных тестов). Для этого каждое слагаемое
хку"1 в полиноме (5.145) было умножено на коэффициент порядка
0.1* • 10"' (поскольку в нашем тесте т меняется от 10 до 20, а ?/ — от
0 до 0.1, порядок произведений 0.1А: • т* и 10"' • у"' одинаков и соот-
ветствует 1, а значит, и все слагаемые полинома (5.145) имеют одина-
ковый порядок).
Из вида полинома (5.145) (и в соответствии с рис. 28 и с учётом
значения коэффициента X = 1) получаем параметры краевых условий:
“Is, = 20 4-1.1т 4-0.115т2 4-0.022т3, (5.146)
Хдп = -(15 4-2т 4-0.5т2 4-0.07т3), (5.147)
\ ди. дп = -(1.14- 33г/ 4- 280?/ + 2800г/3), (5.148)
Х дп 4- и SA | - 34.6 - 921г/ - 8370/ - 85700/ = 0. (5.149)
Соответственно правую часть f дифференциального возьмём в виде f = -&L- + 2и = -284.06 - 39.606т - 53971л - д.г2 ду2 — 2996.49т?/ — 1.94т2 + 298у2 — 149т2?/ + 35.2ту2 + уравнения
4- 2т2/ - 1.598т3 4- 17950/ - З5.86т3?/ + 964т?/3 I
4- 1.6т3/ 4- 50т2/ 4- 12т3/.
322
5.Двумерные скалярные задачи
Вектор q решения СЛАУ, полученной в результате конечноэле-
ментной аппроксимации этой тестовой задачи с использованием эрми-
товых базисных функций, должен иметь вид
q = (14, 1 1. 155, 33, 32, 2.6, 815, 106.64.5, 10, 1080, 173, 264, 32.1, 4595, 571)Т ,
поскольку компоненты <71,75,79 и 713 являются значениями функции
и в узлах, компоненты 72>9giQio и (714 - значениями её производной
по ж, компоненты q^,q7,qn и 715 - значениями её производной по у,
а компоненты 74,73,712 и 716 - значениями смешанной производной.
Очевидно, что размерность СЛАУ в тесте легко увеличить дробле-
нием расчетной области на более мелкие элементы (что следует делать
и для проверки правильности сборки глобальной матрицы из локаль-
ных). 1хли, например, разбить изображённую на рис. 28 область на
четыре элемента (т.е. уменьшить шаги по каждой координате вдвое) и
узлы сетки пронумеровать слева направо и снизу вверх, то вектор ре-
шения конечноэлементной СЛАУ (размерности 36) будет иметь вид:
q (l4, 1.1, 155, 33, 21.125. 1.775. 393.75, 64.25,32, 2.6, 815, 106, 27.6875,
3.8,448.75,82,54.546875, 7.125, 1049.0625, 163, 100.75, 11.5375, 2127.5, 273.25 ,
64 5. 10, 1080, 173,136.625, 19.4, 2340, 341.25, 264, 32.1, 4595, 571)Т.
В случае же, когда коэффициент диффузии X является разрывной
(например, кусочно-постоянной) функцией и для нее используется
специальный базис из эрмитовых полиномов (см. разделы 5.2.7 и
5.2.9.2), необходимо подбирать соответствующие тесты. В качестве
таких тестов могут быть использованы, например, следующие задачи.
В первой задаче возьмём коэффициент X разрывным вдоль линии
х — const, а во второй — вдоль линии у = const. Расчётные области
для этих задач показаны на рис. 48.
Будем считать, что в обеих задачах в подобласти Q1 коэффициент
X равен 2, а в подобласти Q2 - равен 0.5 . Коэффициент в подоб-
ласти Q1 возьмём равным 0.1, а в подобласти Q2 - равным нулю.
В качестве решения в первой задаче возьмём кусочный полином
1 +.г + у+ JTI/+X2 Ту2 +я2у+ху2 +.с2у2 +х3 + уЛ +
II =
+хлу +хул+хлу2 +х2ул+хлу\
— 121+GS.r—121у+68а;у—121у2+68.гу2-121у3 +68ту3, (.T,y)cfi2,
а во второй - кусочный полином (чтобы уменьшить выкладки, мы не
будем использовать в этой задаче полный бикубический полином):
5.7.Тестирование процедур конечноэлементного решения
323
xs + ху + I/2 + 4,
ж3 — Зж + 4жу + 8у — 3.
с разрывными производными
Соответственно правая часть f дифференциального уравнения и
параметры краевых условий (в соответствии с рис. 48ж?) для первой
задачи будут иметь вид
-7.9 - 15.9(ж + у) - 23.9жу - 3.9 (ж2 + у2 + ж3 4- у3) -
-11.9 (ж3 у + ху3 + х2у + жу2) +
+0.1 (ж2 у2 + ж3у2 + х2у3 + ж3у3),
121 — 68ж + ЗСЗу - 204жу,
(ж, у) € Q1,
(+?/) 6 Q2,
ди
дп
S'
= -2(1 + ^ + ^2+!/3),
si
= 172(1 +i+ .? + a:;1).
= 2924а: - 5203,
on s-<
дп
дп
= -34(1 + г + а:2 + .г:').
ди
dns*
-578ж +1028.5,
+^|с -151(1 +у + у2 +у3) = 0,
on .1 ' '
324
5 Двумерные скалярные задачи
а для второй (в соответствии с рис. 48,6)- вид
f = 0.1.т3 -З.г, + 0.1ху — 12 л; + 0.1у2 — 3.6, (х,у) е Q1 (х,у) е Q2
и Is = х3 + 4, \ ди Хдп 4 = -6-2?/,
X <Эд| дп = ~2у, \ ди дп «2 " 37.5 + 2?/,
X = 7.875 + 2?/, х ди дп 2а: + 4 .
Будем считать, что в обеих задачах конечноэлементная сетка состо-
ит из двух конечных элементов Qj и Q2 > совпадающих с подобластя-
ми О1 и Q2.
Тогда размерность конечноэлсментной СЛАУ в обеих задачах бу-
дет равна 28, и вектор решения для первой задачи должен иметь вид
q = (15. 15, 17, 17, 225, 255. 1020. 255. 289, 1156, 1755. 1020. 1989. 1156,156,156,
86, 86, 2340, 2652, 10608,1290, 1462, 5848, 18252. 10608, 10062. 584s)T . (5.150)
В векторе (5.150) компоненты 9i, 75,911,915,91g и являются значе-
ниями функции и в узлах, компоненты 92>912>71б и #26 - значениями
се производной по х в узлах с номерами 1,3,4 и G, компоненты % и
920 - значениями её производной по х слева в узлах 2 и 5, компо-
ненты 97 и 921 - значениями её производной по х справа в узлах 2 и
5, компоненты 9з,98> 913’917’922 и 927 “ значениями её производной
по //, компоненты 94>914)918 и 928 _ значениями смешанной произ-
водной в узлах с номерами 1,3,1 и 6, компоненты 99 и - значе-
ниями смешанной производной слева в узлах 2 и 5 , а компоненты qll}
и 92ц — значениями смешанной производной справа в узлах 2 и 5 .
Для второй задачи вектор решения конечноэлементной СЛАУ дол-
жен иметь вид
q = (5. 3. 1, 1, 19.625, 18.75, 2.5, 1, 7, 4, 3, 12, 1, 4, 23.125, 19,75.
1.5, 18. I. 4. 55, 20. 12, 4, 95.125, 35.75. 18, 4^ .
(5.151)
В нём компоненты 91 >9б> 99’915» 921 и 925 являются значениями функ-
ции и в узлах, компоненты 92,9б>9кь91б>922 и 926 ~ значениями её
производной по х, компоненты 93,97,9-23 и 927 - значениями её про-
5.7.Тестирование процедур конечноэлементного решения .
325
изводной по у в узлах с номерами 1,2,5 и 6, компоненты ун и цц
значениями ее производной по у слева в узлах 3 и 4, компоненты у|?
и у18 - значениями её производной по у справа в узлах 3 и I, ком по
ненты q^q^q-M и <728 - значениями смешанной производной в узлах с
номерами 1,2,5 и 6, компоненты qri и у19 — значениями смешанной
производной слева в узлах 3 и 4, а компоненты у14 и <?2о — значения
ми смешанной производной справа в узлах 3 и 4.
Для более тщательной проверки правильности сборки глобальной
матрицы и вектора СЛАУ следует использовать сетки с достаточно
большим количеством элементов.
Например, можно в первой из рассмотренных здесь задач (см.
рис. 48,<я) конечноэлементную сетку сделать вдвое подробней по оси
.г (с координатами узлов: Tj = 0, = 1, т8=2, т4=2.75,
л5 = 3.5) и в четыре раза подробней по оси у (с координатами узлов:
уА = 2, у-2 = 2.75, уз = 3.5, у4 = 4.25, у5 =5). Конечноэлементная
СЛАУ и вектор q в этом случае будут иметь размерность 110 (с учё-
том того, что узлы при х = 2 имеют 6 степеней свободы, а все осталь-
ные - по 4). Значения вектора q, естественно, могут быть получены
путём вычисления значений функции и и её производных в узлах сет-
ки. Мы приведём значения лишь некоторых из них:
уг = 15 , у2 = 15, у3 = 17, у4 = 17, у5 = 60, ус = 90, q7 = 68,
Уз = 102, у9 = 225, у1() = 255, уп = 1020, у12 = 255, у13 = 289,
у14 = 1156, ..., у75 = 1501.171875, у7С = 1701.328125,
у77 = 6805.3125, у78 = 955.3125, у79 = 1082.6875, у8() = 4330.75.
Вообще говоря, для тестов, в которых искомая функция точно пред-
ставима в виде линейной комбинации базисных функций ф,, совер-
шенно не обязательно решать конечноэлементную СЛАУ для провер-
ки правильности генерации сё матрицы и вектора (тем более, что для
некоторых задач матрица конечноэлементной СЛАУ может быть вы-
рождена и найти её решение не так уж просто) В принципе, вполне
достаточно умножить конечноэлементную матрицу А на вектор q
весов разложения тестового решения по базису {ф£} и сравнить ре-
зультат с вектором правой части b конечноэлементной СЛАУ. Оче-
видно, в рассматриваемой ситуации эти векторы Aq и b должны сов-
пасть полностью (с точностью до ошибок округления), и такой способ
проверки правильности решения тестовой задачи является наиболее
удобным.
При тестировании процедур решения задач в цилиндрических ко-
ординатах следует помнить, что при подстановке в дифференциальное
уравнение в качестве решения некоторого полинома правая часть мо-
жет получиться не полиномиальной функцией. Например, уравнение
—div (X gradu) = f в цилиндрических координатах имеет вид
326
5 .Двумерные скалярные задачи
1,д9_/ \ ди\______д_(\ ди\ _
гл I ' Л n I гл I
г Ur\ or] oz\ dz]
(5.152)
и если в качестве тестового решения взять функцию и = г, то правая
часть f должна быть равна — 1/г. В этом случае конечноэлементное
решение совпадёт с тестовым только тогда, когда интегралы
= будут вычислены точно (т.е. Ь, должны быть точно
о
вычислены как интегралы J , а не получены в результате
и
замены f на каждом конечном элементе интерполянтом У^Дф^ , как
J
эго довольно часто делается при аппроксимации правой части, см
раздел 3.8). Этой проблемы для уравнения (5.152) не возникает, если в
качестве тестовой функции берётся полином г" при п > 2. Тем не
менее аппроксимацию уравнения (5.152) на линейных и билинейных
функциях все-таки можно протестировать, взяв, например, коэффици-
ент X равным г, если, конечно, при построении локальных матриц
коэффициент X (но не X?’) на каждом конечном элементе заменялся
своим интерполянтом У Х/ф/, а не аппроксимировался своим сред-
I
ним значением.
Аналогичные проблемы возникают и при тестировании процедуры
решения задачи для уравнения
(5.153)
Здесь в качестве тестового решения мы можем выбрать функцию
и. = г, и при этом правая часть / будет равна нулю. Однако в этом
случае конечноэлементное решение совпадёт с тестовым только тогда,
когда вклады в матрицу массы в виде интегралов
= jy--^'^i'^.jrdrdz будут вычислены точно (либо ана-
о/,. г цк г
литически, либо численно, но с использованием большого числа узлов
интегрирования на каждом конечном элементе Q*.). При использова-
нии же аппроксимации коэффициента —, например, его интерполян-
том Ф/ полученное конечноэлементное решение на относительно
I
грубой сетке будет довольно сильно отличаться от тестового из-за не-
совпадения — с У — Ф/ .
г Г/
5.7.Тестирование процедур конечноэлементного решения ..
327
Кроме задач с решениями в виде кусочно-полиномиальных функ-
ций, при тестировании двумерных задач имеет смысл использован.
близкие к ним по смыслу одномерные задачи. Так, если решается зада-
ча для уравнения (5.152) с зависящими в основном от переменной г
коэффициентом X и правой частью f, при тестировании процедуры
решения такой краевой задачи можно использовать в качестве ree l оно-
го решение одномерной задачи для уравнения
Ц_
г dr
ID dulD
=flD
(5.154)
в котором flD и X10 - это функции только переменной у . Выбирать эти
функции желательно так, чтобы они были максимально близки к функци-
ям f (г, z) и X (г, z) из исходной двумерной задачи для уравнения (5.152).
В этом случае двумерная тестовая задача может быть сформулирована в
прямоугольной области с краевыми условиями Xduldn = 0 на границах
z = const и с параметрами f и X, совпадающими с flD и X1D — тогда
конечноэлементное решение двумерной тестовой задачи будет соответст-
вовать решению одномерной задачи. На прямоугольной сетке при одина-
ковых разбиениях расчётной области по г в двумерной и одномерной
задачах и при использовании однотипных элементов (линейных - били-
нейных, квадратичных - биквадратичных и т.д.) решение «двумерной»
(тестовой) задачи должно совпасть с решением одномерной задачи в со-
ответствующих узлах. При использовании же треугольной сетки можно
проверить только сходимость решения «двумерной» задачи к решению
одномерной при дроблении сетки.
Анало! ично, при тестировании процедуры решения двумерной за-
дачи для уравнения (5 153) можно использовать одномерную задачу
для уравнения
= /1О (5|55)
г dr \ dr Jr2
Одномерная задача для уравнения (5.154) может быть использована
и для тестирования процедуры решения двумерной задачи для уравне-
ния в декартовой системе коороинат
д (\ ди\___д I х ди
дх \ дх/ ду I ду
(5.156)
Действительно, решение uXD (г) одномерной задачи для уравнения
(5.154) является двумерной функцией х и у, если учесть, чю
г = ^т2 + у2 . И поэтому в тестовой задаче для уравнения (5 I д») щс
таточно взять параметры X и f в виде
\{х,у) = Xw
[yjx2 +у2^,
f(x,y) = f'1' I .'/)
328
6.Трёхмерные скалярные задачи
6. ТРЁХМЕРНЫЕ СКАЛЯРНЫЕ ЗАДАЧИ
Технологии построения конечноэлементных аппроксимаций
трёхмерных скалярных задач не слишком принципиально отличаются
от соответствующих технологий для двумерных задач. Наиболее зна-
чительно различаются методы построения сеток — если построение
двумерной сетки, как правило, не столь уж сложная (хотя нельзя ска-
зать что и очень простая) проблема, то в трёхмерном случае генерация
сетки довольно часто является одним из самых сложных этапов реше-
ния задачи.
При построении же дискретных аналогов (матрицы и вектора пра-
вой части конечноэлементной СЛАУ) отличия между двумерными и
трёхмерными задачами не столь уж существенны. Особенно схожи
процедуры сборки глобальных матриц и векторов конечноэлементных
СЛАУ матрицы обычно хранятся в одинаковых форматах (чаще все-
го разреженных) и в трёхмерном случае сборка глобальных матриц и
векторов из локальных осуществляется по соответствию локальной и
глобальной нумерации базисных функций (для лагранжевых элемен-
тов- узлов) на конечных элементах абсолютно идентично тому, как
это делалось при решении двумерных задач. Фактические отличия
процедур генерации конечноэлементных СЛАУ для дву- и трёхмерно-
го случаев определяются лишь соотношениями, используемыми при
вычислении локальных матриц и векторов конечных элементов.
Иногда при решении трёхмерных задач используются постановки, в
которых дифференциальное уравнение и расчётная область задаются
не в декартовой, а в какой-либо другой, например цилиндрической или
сферической, системе координат Это актуально в тех случаях, когда
расчётная область в этой системе координат имеет более простую
структуру (например, состоит из параллелепипедов) и для построения
дискретных аналогов используются методы, в которых ячейки сетки
должны быть прямоугольными (например, метод конечных разностей
или простейшие варианты метода конечных объёмов). При использо-
вании же МКЭ с великолепными возможностями применения элемен-
тов различной формы только в очень редких случаях удаётся получить
сколь-нибудь заметный положительный эффект за счёт перевода трёх-
мерной задачи из декартовой в какую-либо другую систему координат
(в которой она остаётся также трёхмерной). Поэтому в отличие от дву-
мерного случая в этом разделе мы не будем останавливаться на осо-
бенностях построения конечноэлементных аппроксимаций трёхмер-
ных задач в криволинейных системах координат.
329
Двумерные же задачи в криволинейных системах координм рас-
сматривались нами столь подробно потому, что при переходе в декар-
тову систему координат эти задачи становятся существенно трёхмер-
ными. Различия же в вычислительных затратах при решении двумер-
ных и трёхмерных задач очень велики, и переход от трёхмерной задачи
к двумерной позволяет сократить требуемые вычислительные ресурсы
на порядок и более. Поэтому в такого рода ситуациях использование
криволинейной системы координат не только оправдано, но и просто
необходимо. Кроме того, двумерные (а иногда и одномерные) задачи в
криволинейных системах координат могут давать очень хорошие при-
ближения реально трёхмерных практических задач, и в таких случаях
их решение необходимо при использовании технологий построения
конечноэлементных решений трёхмерных задач с выделением основ-
ной части поля, которые будут рассмотрены нами в девятом разделе.
Если же всё-таки возникнет необходимость решения какой-либо
трёхмерной задачи в криволинейной (цилиндрической или сфериче-
ской) системе координат, то, в общем-то, рассмотренного нами мате-
риала в этом и предыдущем разделах вполне достаточно, чтобы по-
строить соответствующие конечноэлементные аппроксимации (в трёх-
мерном случае особенности построения конечноэлементных аппрок-
симаций эллиптических краевых задач при использовании криволи-
нейных систем координат практически ничем не отличаются от рас-
смотренных нами особенностей использования криволинейных систем
координат в двумерном случае — это учёт якобианов и соответствую-
щие изменения дифференциальных операторов).
Итак, в декартовой системе координат {.т, у, z} дифференциальное
уравнение (1.1) в трёхмерном случае может быть записано в виде
д I\ ди\__д [\ ди|__д (\ ди\
дх\ дх/ ду[ ду] dz\ dz]
+ Т* = f .
(6-1)
Выражения для вычисления компонент локальных матриц (см. со-
отношения (3.55)-(3.56)) в этом случае принимают вид:
<э-Ф, d^:j [ а-ф. Й.7 [ й/
дх дх ду ду dz dz
dxdydz,
(6.2)
M.jj = j ^.^.jdxdydz .
ft*
(6.3)
Компоненты локального вектора правой части Ъ конечного эле-
мента Qa. определяются выражением
b.j = J f^>j dxdydz .
(6 1)
330
б.Трёхмерные скалярные задачи
Интеграл в выражении (6.4), как и в двумерном случае (см. раз-
дел 5.1.4), будем вычислять с учётом того, что функция f на конечном
элементе представлена в виде разложения по базисным функциям
п.
ру ф), , где п - число локальных базисных функций конечного эле-
v 1
мента Q/.. Тогда локальный вектор b может быть вычислен через мат-
рицу С, фактически являющуюся матрицей массы М элемента
при = 1
Ъ = Ср. (6.5)
В дальнейшем мы так же, как и в одномерном и двумерном случа-
ях, при построении конечноэлементных аппроксимаций трёхмерных
задач в основном будем полагать, что правая часть / на элементе
заменяется её полиномиальным иптерполянтом. Очевидно, что тогда
для лагранжевых элементов веса ру нужно задавать как значения fy
правой части / дифференциального уравнения в соответствующих
узлах элемента О,,..
6.1. ПОСТРОЕНИЕ МКЭ-АППРОКСИМАЦИЙ НА СЕТКАХ
1В ПРЯМОУГОЛЬНЫХ ПАРАЛЛЕЛЕПИПЕДОВ
Пусть требуется решить краевую задачу для дифференциального
уравнения (6.1) в трёхмерной области Q. состоящей из фрагментов в
виде прямоугольных параллелепипедов.
Рассмотрим аппроксимацию этой краевой задачи па прямоугольной
сетке. При этом ячейками дискретизации являются прямоугольные
параллелепипеды Q>psr= [•'Е/,,.г’/,+1] х [ys, ?/л.+1] х [zr,zr+lj, т.е. ячейки
этой сетки строятся в виде прямого (декартова) произведения незави-
симых цруг от друга одномерных сеток {ii,...,xllt }, ,
Тогда выражения для вычисления компонент локальных
матриц (6.2)-(6.3) принимают вид:
ох ох оу оу OZ OZ
(6.6)
(6.7)
6.1.Построение МКЭ-аппроксимаций на сетках из ...
331
6.1.1. ТРИЛИНЕЙНЫЕ БАЗИСНЫЕ ФУНКЦИИ
Трилинейные базисные функции на прямоугольном параллеле-
пипеде Q/JSJ. строятся аналогично билинейным, т.е. как линейные по
каждой из трёх координат. На отрезках , [уч, ys+l ] и [z,., z, (। j
задаются по две одномерные линейные Функции:
Х} (т) = - X Х2 (т)= х — хр /1./; ^р > (6 8)
hx
(у) = y.s+i ~ У hy ’ М») = У_ — у» hy = y.s+А ~ Ул, (6-9)
Z1 (г) = z,.+i - Z Z -Z,. = z, +i - z,.. (6 10)
hz ’ Z2(Z) — hz ’
Как и при построении билинейных функций, трилинейные локаль-
ные базисные функции на конечном элементе представляются в
виде произведения функций (6 8)-(6.10):
Введём на прямоугольном параллеле-
пипеде локальную нумерацию узлов так,
как это показано на рис. 49, и определим
целочисленные функции р(ф, н(г) и 0 (г)
таким образом, чтобы базисные функции
(6.11) на элементе Qpxr были равны еди-
нице в узле с локальным номером i, рав-
ным номеру локальной базисной функции,
и нулю в остальных узлах:
(6 11)
Рис. 49. Расположение узлов
на конечном элементе
с трилинейными базисными
функциями
I1 G) — ((г- — 1) тос12) + 1,
v (г) = ~-1 j mod 2^ + 1,
°(г’)=[М+1’
(6-12)
(6.13)
(6.14)
где, как обычно, a mod 6 - остаток от деления а на Ь, [д] - целая
часть числа а. Очевидно, что целочисленные функции р(г), п(/) и
'О(г), определяемые соотношениями (6.12)—(6.14), принимают только
два значения: I или 2 (для г < 8 ).
Покажем, что при использовании трилинейных базисных функции
компоненты локальных матриц жёсткости (6.6) и массы (6.7) так же,
как и в двумерном случае, удобно вычислять через компоненты матриц
жёсткости и массы линейных одномерных элементов. Будем считать,
что параметры X и на элементе заменяются своими осреднёнными
332
б.Трёхмерные скалярные задачи
значениями X и у Тогда, учитывая представление базисных функций
(6,11), из (6.6) получаем формулу для вычисления матрицы жёсткости:
-------о к--------dxdudz =
ri у .
V ах^ эх.
J дх
zi +1
V
1>
дх J v6P«'(j
У.ч
rim I _________________v '
J ду ду
Ух
1/s
J +
zr
^+1
' j ^{i)^i]{j)dz +
z,
V rf,
I гч rv (.bZ .
J ду dy
zr
Обозначим через Gr, G- и G* локальные матрицы жёсткости, a
через M' , М'' и М? — локальные матрицы массы соответствующих
одномерных линейных элементов, т.е.
G' ^y-G1 А.,. I\r (6-15)
G!> /?7/ M?' = /iyMl, (6.16)
Gz = y-Gl dz Mz = /izM1 , (6-17)
где G1 = ' 1 -1 -1 1 I J , M1 = 1[2 1 6 12 (6.18)
Тогда
6.1 .Построение МКЭ-аппроксимаций на сетках из ...
333
(6 19)
+Л7и(/.)и(ЭМр(?)р( •
Аналогично вычисляется матрица массы:
Воспользовавшись обозначениями (6.15)-(6.17), получим.
11 ' 1|'(')||0) в(г)и(у) ‘’(ФКА
(6.20)
Сборка глобальной матрицы и вектора правой части конечноэле-
ментнои СЛАУ из локальных матриц и векторов конечных элементов
так же, как и в случае одномерных и двумерных элементов, выполня-
ется по соответствию локальной и глобальной нумерации базисных
функций. Напомним, что локальный вектор правой части может быть
вычислен с помощью соотношения (6.5), где С - это матрица массы
(6.20) при = 1, а компоненты вектора р - это значения fv правой
части f дифференциального уравнения в соответствующих узлах xv
конечного элемента (что соответствует замене f на конечном элемен-
те её интерполянтом X'i’v )
Технология вычисления локальных матриц и вкладов в вектор пра-
вой части при учёте краевых условии второго и третьего рода анало-
гична рассмотренной технологии вычисления локальных матриц и
векторов для двумерного случая. При этом вычисление интеграла по
грани прямоугольного параллелепипеда - это фактически вычисление
интеграла по прямоугольному конечному элементу, на котором заданы
билинейные базисные функции. Поэтому все необходимые интегралы
могут быть получены с использованием компонент одномерных мат-
риц массы и Мс из соотношений (6.15)-(6.17) (под 6, и С, пони-
маются две координаты из {.т, у, z}, которые изменяются па рассма т-
риваемой грани)
Па заключительном этапе должны быть учтены краевые условия
первого рода Соответствующая процедура ничем не отличаемся oi
той, которая была описана в разделе 5.2 2 для двумерного случая.
334
б.Трёхмерные скалярные задачи
6.1.2. ЛАГРАНЖЕВЫ БАЗИСНЫЕ ФУНКЦИИ ВЫСОКИХ ПОРЯДКОВ
НА ПРЯМОУГОЛЬНЫХ ПАРАДЕЛЕПИПЕДАХ
Кроме трилинейных базисных функций на прямоугольных па-
раллелепипеидальных конечных элементах довольно часто использу-
ются полиномиальные функции более высоких порядков - триквадра-
тичные и трикубические. Определим их по аналогии с биквадратич-
ными и бикубическими базисными функциями через соотношение
(6.11), т.е. как произведение одномерных базисных функций соответ-
ствующего порядка
Как и для трилинейных базисных функций, целочисленные функ-
ции [I, ц и О для других трёхмерных лагранжевых параллелепипеи-
дальных элементов определяются так, чтобы функции (6 11) были рав-
ны единице в узле с локальным номером, равным номеру локальной
базисной функции, и нулю в остальных узлах. Например, для триквад-
ратичных базисных функций, если локальная нумерация узлов конеч-
ного элемента определена в соответствии с рис. 50, эти функции име-
ют вид:
р (г) = ((?' - 1) mod 3) + 1,
и (г) = mod 3 j + 1,
(6.21)
(6 22)
(6.23)
где, как и ранее, a mod b — остаток от деления числа а на число Ь,
[а] - целая часть числа a, i. - номер локальной базисной функции
Рис. 50. Расположение узлов на конечном элементе
с триквадратичными базисными функциями
6.1 .Построение МКЭ-аппроксимаций на сетках из ...
335
Если параметры X и на элементе постоянны (и равны X и со-
ответственно), то компоненты локальных матриц жёсткости и массы
лагранжевых элементов высоких порядков так же, как и для трилиней-
ных элементов, определяются соотношениями (6.19) и (6.20), в кото-
рых G;'^, G;^, G*fi, и - компоненты локальных мат-
риц жёсткости и массы соответствующих одномерных конечных эле-
ментов.
6.1.3. ТРИКУБИЧЕСКИЕ ЭРМИТОВЫ БАЗИСНЫЕ ФУНКЦИИ
Как и бикубические эрмитовы конечные элементы в двумерном
случае, трикубические эрмитовы конечные элементы обеспечивают
непрерывность первых и смешанных производных глобальных базис-
ных функций на гранях конечных элементов Локальные базисные
функции для этих элементов также могут быть построены в виде про-
изведения кубических функций одномерных эрмитовых элементов (см.
раздел 4.6).
Локальную базисную функцию ф.г трикубического эрмитова эле-
мента определяют через её значения и значения её производных
<Эф7
<9ф, <9ф, <92ф7
ду ’ dz ’ дхду ’
печного элемента
<Э2ф, Э2ф7 <93ф,
„ А и „ „ Д в восьми вершинах ко-
oyoz oxoz oxoyoz
ftps,- = [я/,, я>+1 ] X [&, 2/.S+1 ] X \zr, zr+1 ], причём у
каждой из функций ф7- только одно из этих значений и только в одной
вершине равно единице, а остальные 63 значения равны нулю
Обозначим через (х) одномерную кубическую базисную функ-
цию, равную единице при х = хр, нулю при х = ж/>+1 и имеющую
нулевые производные при х = х.р и х = хр+\, т.е. АД (.т) - это функ-
ция ф! (:г), рассмотренная в четвёртом разделе на с. 153. Через Х± (х)
обозначим одномерную кубическую функцию ф2 (она равна нулю
при х = хр и х = хр+1 и её производная равна единице при х = хр и
нулю при х — х.р+1), через Х3 (т) - функцию ф3 (ж), а через Х$ (х) -
функцию *ф4 (т). Аналогично на отрезках [?/.s,?/.s+i] и [zr,z,.+i] введём
одномерные кубические функции УД (//), УД?/), Уз (?/) , У1 (у) и
ZL(z), Z2(z), £3(2), (z) (УД?/) и (z) - это соответственно
Ф1 (?/) И Ф1 (2) И Т.Д.).
Тогда трикубические функции могут быть представлены в виде
(6 11) и являющиеся индексами целочисленные функции р(?), п(') 11
г) (?) проще всего определить таблично (см. табл. 16):
336
б.Трёхмерные скалярные задачи
Таблица 16
г 1 2 3 4 5 6 7 8 9 10 II 12 13 14 15 16
Р- 1 2 1 1 2 1 2 2 3 4 3 3 4 3 4 4
V п- I ЛГ “Г Л- “Т- ~Г "Т" “I- ~Т~ “Г" ~Т~
0 I 1 1 2 I 2 2 2 1 1 I 2 1 2 2 2
1 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
Р I 2 1 I 2 1 2 2 3 4 3 3 4 3 4 4
V “З- 3 “З- 3 4“ ~т~ "З- 4 "3“ 4 ' Т“
0 I 1 1 2 I 2 2 2 1 1 1 2 1 2 2 2
i 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
Р I 2 I I 2 I 2 2 3 4 3 3 4 3 4 4
V Т" 1 1 "Л- ~Т~ 1 —Г" ~т~ Т- ~т~ 1 "Л-
0 3 3 3 4 3 4 4 4 3 3 3 4 3 4 4 4
i. 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
Р- 1 2 I 1 2 I 2 2 3 4 3 3 4 3 4 4
V "3“ —4“ "3“ 4 —I- “3~ “3“ "3“ л 3 ~т~
0 3 3 3 4 3 4 4 4 4 3 3 4 3 4 4 4
11струдно убедиться, что таким образом определённые функции
фактически ставятся в соответствие номерам узлов конечного элемен-
та, изображённого на рис. 49, следующим образом. В каждом узле оп-
ределено по 8 локальных функций, при этом в каждой восьмёрке пер-
вая функция (т.е. функции с номерами {1,9,17,25,33,41,49,57}) отве-
чаю! за значение решения в соответствующем узле, вторая — за значе-
ние производной по х, третья — за значение производной по у, чет-
вёртая - за значение производной по z , пятая - за значение смешанной
д2
производной п • шестая — за значение смешанной производной
д '1 7 ~ - д2
п , седьмая - за значение смешанной производной о и вось-
OyiJz oxdz
д3
мая - за значение „ 7. п--.
dxdyoz
Заметим, что табличный способ задания функций р. (/), v(i) и 9 (г)
мог быть применён и для рассмотренных выше лагранжевых элемен-
тов высокого порядка (а также и для двумерных лагранжевых и эрми-
товых элементов). Но в тех случаях формулы для вычисления соответ-
ствующих целочисленных функций получить было совсем не сложно
(в отличие от рассматриваемого здесь спучая).
Локальные матрицы жёсткости G и массы М для трик>бических
эрмитовых элементов так же, как и для лагранжевых, удобнее всего
вычислять через элементы матриц жёсткости и G^ и массы
6.2.Тетраэдральные конечные элементы
337
и одномерных эрмитовых кубических элементов (см.
раздел 4.6). Для постоянных на конечном элементе коэффициенте X
и это можно сделать с помощью соотношений (6.19) и (6.20) (и со-
ответственно (4.34) и (4.35)).
Формирование глобальных функций из локальных эрмитовых прак-
тически не отличается от двумерного случая, поэтому вопросы как
построения эрмитова базиса с непрерывной производной, так и ис-
пользования эрмитовых элементов при решении задач с разрывным
коэффициентом диффузии решаются аналогично тому, как это было
сделано в разделе 5.2. Обратим только внимание на то, что при форми-
ровании глобальной функции из локальных в трёхмерном случае нуж-
но добиваться требуемой непрерывности самой функции или её произ-
водных уже не на линиях, а на поверхностях - гранях элементов.
6.2. ТЕТРАЭДРАЛЬНЫЕ КОНЕЧНЫЕ ЭЛЕМЕНТЫ
6.2.1. ТЕТРАЭДРАЛЬНЫЕ СЕТКИ
Аналогом двумерных треугольных конечных элементов в трёх-
мерном случае являются четырёхгранные элементы с треугольными
гранями, которые принято называть тетраэдрами. Их вид изображен
на рис. 51. Как и в двумерном случае для сеток с треугольными ячей-
ками, разбиение расчётной области на тетраэдральные элементы ино-
гда называют трёхмерной триангуляцией. Основное преимущество
тетраэдральных сеток состоит в том, что они предоставляют хорошие
возможности для достаточно точного описания сложных (в том числе
и искривлённых) границ расчётной области.
Будем считать, что трёхмерная триангуля- ж?
ция, как и двумерная, задана в виде набора /\К
узлов (вершин) и набора тетраэдров. Каждый / \ N.
узел сетки описывается тремя координатами / \
.7,7., уд. и zt., а каждый тетраэдр О,1П — пятью / \
числами, первые четыре из которых - номера / \ X, 4
узлов сетки, являющихся вершинами рассмат- / \ - */
риваемого тетраэдра, а пятый - номер подобла- / 1" " /
сти расчётной области, служащий для опреде- 1^""’ \ /
ления значений параметров X, q и / диффе-
ренциального уравнения (1.1) внутри данного
тетраэдра. Будем также считать, что границы А/с. 51. Тетраэдральная
о о tz ячейка
52 и £>3 представлены наборами треугольни-
ков, каждый из которых описывается четырьмя
целыми числами, причём первые три числа - это номера узлов сетки,
являющихся вершинами рассматриваемого треугольника, а четверто
число служит для определения значений параметров заданного ня рас-
сматриваемом треугольнике краевого условия второго или третьего
рода. Границу же будем считать представленной набором пар це-
лых чисел, в котором первое число каждой пары является номером
338
б.Трёхмерные скалярные задачи
узла, лежащим на Sj, а второе служит для определения значения па-
раметра utJ этого краевого условия (иногда S) представляют набором
пар чисел, в каждой из которых первое число — целое и является номе-
ром узла, а второе — вещественное и является значением и, в этом
узле).
Для расчёта компонент локальных матриц на тетраэдральных эле-
ментах, как и на треугольниках в двумерном случае, вводятся трёх-
мерные £ -координаты. Поэтому ниже мы рассмотрим основные со-
отношения, позволяющие вычислять интегралы от любых их произве-
дений по тетраэдральному элементу.
6.2.2. £ -КООРДИНАТЫ НА ТЕТРА ЭДРЕ
Рассмотрим невырожденный тетраэдр Qm (т.е. тетраэдр с нену-
левым объёмом) имеющий вершины (£1,2/1,21), (£’2> 2/2^2) > (£‘з»^з>^з)
и (£4,2/4,24). Введём на нём четыре линейные функции
£t (x,y,z) = оф +оца; + 0^2/ 4-сфг, г = 1...4 (6.24)
такие, что каждая и? функций £, равна единице в вершине ) и
нулю в трёх остальных вершинах .
Очевидно, что из этих условий может быть получено 16 уравнений
вида
О() +сч|.£7 4-a.^jiJ = l..A, (6.25)
где Ь(j — символ Кронекера.
Соотношения (6.25) могут быть записаны в матричном виде:
a}) а} <4 <4 ' 1 1 1 г 1 0 0 0'
а? а\ al X) Х-2 £3 £4 0 10 0
ч ч ч ч <4 Ot? С*2 <4 У} У2 Уз У4 0 0 10 (6.26)
4 4 4 4 ОЦ) оц (*3 Z] Z2 z3 г4 к > 0 0 0 1 1
откуда сразу следует, что все коэффициенты функций (6.24) являются
компонентами матрицы (L, обратной к определяемой только коорди-
натами вершин тетраэдра матрице
6.2.Тетраэдральные конечные элементы
339
fl 1 1 1 )
т.е.
of, а} а-i о3
о» cy? о^ <4
о,3 cy3 с^ ot3
4 4 4 4
о() аг а] cy^
Соотношения (6.24)
£2
^3
А
ж3 х4
УЗ ?/4
z3 z4
(6.27)
'1111
X! Х2 Х3 Х4
У1 У-2 Уз Уь
Z1 Z-2 z3 Z4
(6.28)
можно записать в матричном виде
о о
О?)
О?)
О()
al
af
<4
<*2
<*2
02
Оз
о'з
Оз
Оз
которые с учётом (6.28) примут вид
Л' '1 1 1 Г -1 'Г
£2 .'£’1 Х‘2 Х-^ х4 X
^3 У1 У2 Уз У4 У
Z\ Z2 i3 z4 z
(6-29)
Из (6.29) сразу следует
(О 30)
X
У
Z
т.е. дпя £ -координат тетраэдра справедливы cooi ношения
340
6 Трехмерные скалярные задачи
Д + -^2 + Д? + £4 — 1, (6.3 1)
£^1 + £2т2 + -бз^з + Д^4 — х > (6.32)
А’Л + ^2 + А#3 + -&1У4 = У, (633)
Azi Т £2z2 + А-^з + А-^4 = z (6-34)
Через матрицу D, определяемую соотношением (6.27), может быть
вычислен объём тетраэдра Qm с вершинами (.fj, ух, zx), (ж2, 3/2» За),
(а'зЛ/зЗз) и (t4,?J4, z4):
mesQ„t = i|detD|, (6.35)
где detD — определитель матрицы D. Значение detD легко вычисля-
ется из определения (6.27) матрицы D
det D = (z-2 ~ Zi) {(7/3 ~ X/1) fe - ) - (у4 - Z/i) (23 - ii)} T
+ (y-2 -X/i){(23 -2i)(t4 -£i)-(24| -2i)fe ~*i)} +
+ (2-2 -21){(я3 -£i)G/4 -У1) -(£4 -£1)йз -&)} • (636)
Рассмотренные нами трёхмерные функции Д, £2, £$ и Д назы-
ваются £ -координатами, а также барицентрическими или естест-
венными координатами тетраэдра. Как и для двумерных барицен-
трических координат, для них существуют очень простые формулы,
позволяющие вычислять интегралы от любых произведений £t по
тетраэдру Qzn:
f (£, )''l(^),'2(4),':'(A)'',rf.rf!/dz = [detD| (6 37)
il)U ^1+v2+^3+v4+3)!
где под 0! понимается значение I и значение detD можно вычислить,
например, с помощью соотношения (6.36).
Кроме объёмных интегралов вида (637) нам потребуется для вы-
числения вкладов от естественных краевых условий вычислять инте-
гралы вида
f (£t)'''(£2)''2(£j)',Jiir
Г
по треугольным граням Г, определяемым тремя вершинами (х’ь t/i>2i),
fe,^2,22), («3,^3, 23).
Очевидно, что на Г трёхмерные функции £^, £2 и £3 фактически
являются двумерными естественными координатами треугольника Г
(так как они линейны на этом треугольнике и равны единице в одной
6 2 Тетраэдральные конечные элементы
341
из его вершин и нулю в остальных). Поэтому для этих функций при
переходе к двумерным координатам в плоскости Г станет справедли-
вой формула (5.76).
Заметим, что фактически переводить трёхмерные коордишпы вер-
шин в двумерные для вычисления определителя матрицы в (5.76) вовсе
не нужно. Можно воспользоваться соотношением (5.73), связывающим
значение этого определителя с площадью треугольника. Действитель-
но, площадь треугольной грани в трёхмерном пространстве можно
вычислить, например, как половину модуля векторного произведения
векторов, образующих стороны этого треугольника:
mes Г = 11(±2- £1, У-2- Уъ ) х (.f3- .гь у3- уг, z3- z} )| =
= ^Р,!2 +Р}/2 +Pz2 , (6-38)
где
Рт. = (у2- 2/1) (*3“ | - (^3- 2/1)(z-2- *1) , (6-39)
Ру = (*3- £'1) (*2“ ^1) - (^2- ) (*3“ *1) , (6.40)
Pz = (^2“ *1) [уз~ У\) - (^з- £1) [у-2~ У1) - (6.41)
Тогда интегралы по граням можно вычислять с использованием
формулы:
Ml 1 ! М3 •
1^2”^ м3+ 21!
2 mes Г,
Г
(6-42)
где mes Г может быть вычислена с помощью соотношений
(6.38)46.41).
6.2.3. ЛИНЕЙНЫЕ ТЕТРАЭДРАЛЬНЫЕ ЭЛЕМЕНТЫ
Получим соотношения для вычисления локальных матриц и век-
торов на тетраэдральных элементах с линейными базисными функ-
циями.
На каждом элементе Q,„ тетраэдральной сетки определим четыре
локальные базисные функции
ф7(т,?/) = оф + afc + а£т/+ , г = 1...4, (6.43)
такие, что ф, равна единице в г-й (с координатами (xltynzt)) верши-
не Q/n и нулю в трёх других. Очевидно, что определённые гаким обра-
зом локальные базисные функции ф\ на тетраэдре фактчсски
являются £-координатами этого тетраэдра (6.24), г.е.
342
б.Трёхмерные скалярные задачи
ф,\x,y,z) = (х, у, z), и поэтому коэффициенты оф функций ф,; мо-
гут быть вычислены по формуле (6.28), а при вычислении интегралов
от произведений вида ф,:ф7 по тетраэдру Qm можно использовать
соотношение (6.37).
Получим выражения для локальных матриц жёсткости G и массы
М тетраэдрального конечного элемента Q„(. Учитывая представление
(6.43) функций ф,: на и заменяя параметр X его осреднённым (по-
стоянным на ) значением X, получим
J дх дх ду д у dz dz
^iln \ J
= X J (cqO^ -h офо^ + офоф)(70 = X (oqCVj' + сфоф + ot3Ct^jmesQnt.
Учитывая соотношение (6.35), получим
G1J= X+a^ + офо^), i = 1...4, j = 1...4, (6.44)
где матрица D определяется соотношением (6.27), а её определитель -
соотношением (6.36).
Столь же просто вычисляются компоненты локальной матрицы М
Будем считать, что параметр также заменяется на тетраэдре Qm
своим осреднённым значением ф = const. Тогда, используя соотно-
шение (6.37), получим
Ч, = f й(4>;)2 ж = ij W2dQ =
SKu SIjh
>2»Q!d!0! Idetbl — ^ldetPl ?-l 4
’ (2+0+0+0+3)! loeLJJl go ’ 1
Mjj = J — T J J£.,£jdQ.=
Ku Ku
т.е.
6.2.Тетраэдральные конечные элементы
343
'2 1 1 1
- 7|detP| 12 11
120 1121
1112
(6 15)
Учёт краевых условий на треугольных гранях рассмотрим на при-
мере краевого условия третьего рода. Получим выражения, опреде-
ляющие локальную матрицу и вектор грани Г.„д, на которой задано
краевое условие третьего рода. Очевидно, что на этой грани ненуле-
выми являются только три базисные функции. Введём на грани Г„£
локальную нумерацию её вершин и обозначим через ф,- базисную
функцию, которая равна единице в i-й вершине грани Заметим, что
функции , ф2 и фз на грани Г„, фактически являются двумерными
барицентрическими координатами треугольника Г„, и для них спра-
ведпиво соотношение (6.42).
Будем считать, что параметр |3 на Г„, постоянен и равен (3, а пара-
метр представлен в виде линейного интерполянта
й«1Ф1 + «рг'Фг + Цгз'Фз (где fyi , йр2 и ^03 — значения параметра в
вершинах грани Г7„) Тогда компоненты локальной матрицы As $ и
вектора Ь'’3 ребра Г,„ определяются соотношениями
А* =ё/wr,
г„,
Sf3 =&f (%Ф1 Т ЙргФг + ^1з4’з)'<МГ.
Г„,
(6.46)
Очевидно, что в этом случае локальный вектор b‘s-1 может быть вы-
числен через А 3 по формуле
(6.47)
Используя соотношение (6.42), получим
Д?’ = f ₽(V = W2dr =
Г г
1 ГП 1 111.
344
6 Трёхмерные скалярные задачи
— А 2!0!0! о р _ A meS Г/п , — 1 Q
р (2+0+0+2)! 2 meS 1 р 6 ’ г ~ ‘ ’
= J М>.Ф/г = р f £,£,аг =
г т ГН1
— А 1?1!0! 2mes Г = 0 Iliesi ,
Р (14-1+0+0+2)! Ше31 Р 12 ’ 1 3 >
те А фактически является матрицей массы двумерного треугольно-
го элемента (сравните с (5.81)). В результате локальная матрица грани
Г,„ , принадлежащей границе 53 , имеет вид:
A m 2 11
АЛ* = ! 2 !
1 1 2
(6.48)
Читатель может легко убедиться, что локальный вектор, опреде-
ляющий вклад от заданного на Г,„ краевого условия второго рода, при
замене на Г,„ параметра 0 линейным интерполянтом
Орф Тб-з'Фг + бз'Фз (6, - значения 6 в вершинах Гш) имеет вид:
I?2
mes Г,„
12
261 + + 63
ё1+2ё2н-ё3
ё] + ё’2 + 2ё3
(6.49)
6.2.4. ТЕТРАЭДРАЛЬНЫЕ ЭЛЕМЕНТЫ С БАЗИСНЫМИ ФУНКЦИЯМИ ВЫСОКИХ
ПОРЯДКОВ
Рис. 52. Расположение узлов
на тетраэдральном конечном
элементе с квадратичными
базисными функциями
Как и для треугольных конечных эле-
ментов в двумерном случае, на тетраэдрах
могут быть построены элементы более
высоких порядков. В этом случае узлами
конечноэлементной сетки, в которых оп-
ределяются значения базисных функций,
являются не только вершины тетраэдров,
но и точки на их ребрах и гранях.
Рассмотрим построение квадратичной
базисной функции на тетраэдре. Для оп-
ределения десяти коэффициентов полного
квадратичного полинома необходимо за-
дать его значения в десяти узлах, и поэто-
му на тетраэдре О.т кроме четырёх его
вершин в качестве узлов конечноэлемепт-
ной сетки берутся также середины шести
6.3.Конечные элементы на треугольных призмах
345
его рёбер. Базисные функции квадратичного элемента так же как и
линейного, удобно выразить через £ -координаты (сравните с (5.92)):
Ф, (X, У, ?) = £ (2Л - 1), г = 1... 4, (6.50)
Ф,: (я,!/,2) = 4^|(.^(г), г = 5...10, (6.51)
где целочисленные функции р(г) и н(г) определяют локальные номе-
ра вершин ребра, центру которого соответствует базисная функция с
номером i. Если локальная нумерация узлов элемента выбрана так,
как показано на рис. 52, то эти целочисленные функции можно опре-
делить табл. 17:
______ ________________________ Таблица 17
г 5 6 7 8 9 10
I1 1 1 1 2 2 3
и 2 3 4 3 4 4
Аналогично строятся с использованием барицентрических коорди-
нат и базисные функции более высоких порядков [9]. Способы вычис-
ления локальных матриц и векторов для базисных функции, выражен-
ных через естественные координаты, практически ничем не отличают-
ся от тех, что подробно рассматривались для двумерного случая в раз-
деле 5.3.4.
5.3.4.
6.3. КОНЕЧНЫЕ ЭЛЕМЕНТЫ НА ТРЕУГОЛЬНЫХ ПРИЗМАХ
6.3 1 ОБ ИСПОЛЬ1ОВАНИИ ПРИЗМ В КАЧЕС ГВЕ ЯЧЕЕК СЕТКИ
Рассмотренные выше тетраэдральные конечные элементы до-
вольно удобны в случаях, когда расчетная область имеет сложные на-
клонные и искривлённые границы. Однако на сетках с примерно рав-
ным числом узлов при одинаковых вычислительных затратах они, как
правило, заметно уступают по точности прямоугольным нараллелепи-
пеидальным элементам. Поэтому при решении задач в областях,
имеющих только параллельные координатным плоскоетям границы
(внешние и внузренние), чаще всего используются именно параллеле-
пипеидальные сетки (которые ещё и очень просто задавать). В некото-
рых же случаях удобно использовать сетки с ячейками в виде прямых
призм.
Мы будем рассматривать призматические сетки с ячейками только
в форме прямой призмы, у которой две параллельные друг другу гра-
ни, — основания - являются одинаковыми двумерными фигурами, а
все остальные - боковые - грани являются прямоугольниками. Про
стсйшей из прямых призм является призма с треугольным основанием,
изображённая на рис. 53. Такую призму в дальнейшем будем называн.
треугольной и будем считать, что ось Z системы коор цшлг перпен-
дикулярна основаниям призмы
346
б.Трёхмерные скалярные задачи
6.3.2. ЭЛЕМЕНТЫ ПЕРВОГО ПОРЯДКА НА ТРЕУГОЛЬНЫХ ПРИ ШАХ
Рис. 53. Расположение узлов
на призматическом конечном
элементе с треугольным основанием
Определим на прямой треугольной призме QJ с вершинами
(Яц&Л)» (x^y^ZX), (xx,yx,Z2), (£-2.У-2^2) и (ж3,Уз,22)
шесть линейных базисных функций
фг (x,y,z), равных единице в одной
вершине призмы с соответствующим
номером и нулю во всех остальных.
Для этого зададим на двумерном
треугольнике с вершинами
(£1,2/1), (£’2,1/2), (£з,2/з), являющем-
ся основанием призмы Q.,„, двумер-
ные линейные базисные функции
Ф1(я,?/)> &2(Х>У) и фз (;е,?/), равные
единице в одной из этих вершин и
нулю в остальных. Очевидно, что эти
функции фактически являются дву-
мерными £ -координатами треуголь-
ника , определяемыми соотноше-
нием (5.66). Кроме того, зададим на
отрезке [i],z2] одномерные линейные
базисные функции:
zi Ю = Z\ Z, z2 (z) = ~ 21 ’ ^=22-Zi. (6.52)
Тогда функции (т. y,z) можно записать в виде
^&’,2/^) = , (6-53)
где целочисленные функции р(г) и и(г) определяются либо табл. 18,
__________________________________Таблица 18
либо формулами
i 1 2 3 4 5 6
И 1 2 3 1 2 3
и ~Г Т 1 ~т~ ~Т~
р (г) = (г — 1) mod 3 +1,
(6.54)
Нетрудно убедиться, что определённые соотношением (6.53) базис-
ные функции действительно равны единице только в одном узле приз-
мы, номер которого совпадает с номером функции, и нулю в осталь-
ных узлах. Кроме того, эти функции на прямоугольных гранях являют-
ся билинейными, а на треугольных-линейными.
6.3.Конечные элементы на треугольных призмах
347
Вычислим локальные матрицы элемента Q,„ . Будем считать, что
параметры X и на нём заменяются своими осреднёнпыми значе-
ниями X и Тогда, учитывая представление базисных функций
(6.53), выражение (6.2) можно преобразовать следующим образом.
f Jak &1b i Й. ^'i , M
и J дх дх ду ду dz dz
k /
С 7 дфр( „ дфц.( Д
J dx Zy& дх ду Z'4’) ду Zy^
. dZy(i) dZ^ _
+T|..(i) dz Чф.(.Ю dz
Г ^Фр(г)
J dx dx
Z\
Г . - а а. *ГdZ^) dZ'W
+ J ^.(^(j^dyj dz dz
dz.
Л Чп.
Z1
Обозначим матрицы жёсткости и массы соответствующих двумер-
ных и одномерных линейных элементов следующим образом:
G^’= Г -~--d£l = [ оца/ + ) mes >
lJ J dx дх ду ду \ 1 2/
(6-55)
(6.56)
(6.57)
где mesfij можно вычислить с помощью соотношения (5.73) и (5 I),
а коэффициенты о-, для треугольника определяются соотношени-
ем (5.69).
Тогда компоненты локальной матрицы жёсткости элсмснi.i 42,„ мо-
гут быть вычислены через компоненты матриц G"7, М , G , М ,
определяемых соотношениями (6.55)-(6.57), следующим обра ом
348
б.Трёхмерные скалярные задачи
G = \(g:'I' , ЛМ* , . + М'К,> ,ЛС* , V (6.58)
где целочисленные функции р и v определяются либо табл. 18, либо
формулами (6.54).
Нетрудно убедиться, что и компоненты локальной матрицы массы
элемента Q„, очень просто вычислять с помощью матриц М"' и М
Мп = ^Мг-' , , л. (6.59)
6.3.3. ЭЛЕМЕНТЫ ВЫСОКИХ ПОРЯДКОВ НЛ ТРЕУГОЛЬНЫХ ПРИЗМАХ
Очевидно, что представление базисных функций ф/, (.т, </, z) в
виде (6.53) на треугольной прямой призме возможно не только с ис-
пользованием линейных функций фр (.г,т/) и Zv(z), но и квадратич-
ных, кубических и т.д. Более того, функции фр (.т, у) и Zv (z) могут
быть даже разных порядков. При этом локальные матрицы прямой
треугольной призмы QT„ с вершинами (£1}?/i,zi), (£2,2/2,4),
(-4,2/1, £2), (^2,3/2,h) и (£з,2/з,^) также могут вычислять-
ся с использованием соотношений (6.58) и (6.59), в которых под G"7 и
М'?/ понимаются локальные матрицы жёсткости и массы (с единич-
ными коэффициентами X и 4 ) треугольного конечного элемента
(с вершинами (.4,3/1), (£2,2/2), (£з,2/з)), а под и М -локальные
матрицы жёсткости и массы (также с единичными коэффициентами X
и 4) одномерного элемента (z1?z2). Целочисленные же функции ц(г)
и м(г) можно в общем случае определить как
г - L
. ПА .
I1 (*-) — (7- ~ 1) mod пд +1,
17 (г) =
+ 1,
(6.60)
где под т?д понимается число локальных базисных функций, опреде-
лённых на треугольном конечном элементе
Например, на могут быть заданы квадратичные лагранжевы ба-
зисные функции, а на (4,2-2) - кубические. Тогда =6, базисные
функции фу </), i — 1 ...6 определяются соотношением (5.92), а
функции (z), у = 1...4 - соотношениями (4.30) Нумерация узлов
такого элемента, соответствующая функциям (6.60), приведена на
рис. 54.
6.4.Шестигранные элементы
349
Локальный вектор правой части
можно, как обычно, вычислить через
матрицу массы, если считать, что функ-
ция f заменяется на своим интер-
полянтом ; (fj ~ значение пра-
вой части [ дифференциального урав-
нения (6.1) в j -м узле элемента П7/,),
т.е.
Ь = Ср, С„ = ,MZ (Л.
Заметим, что если в качестве одно-
мерных функций Z.j (z) взять кубиче-
ские эрмитовы базисные функции, то
определённые соотношением (6 60)
функции р(г) и и (г) фактически задают
такую локальную нумерацию базисных
функций на призме, что функции, отве-
Рис. 54. Расположение узлов
на квадратично-кубическом
призматическом элементе
с треугольным основанием
чающие за значение решения и за его производную djdz в одном и
том же узле, будут иметь не соседние номера (как это традиционно
делается для эрмитовых элементов), а отличающиеся на . Переоп-
ределить функции р(г) и м(г) так, чтобы они задавали более привыч-
ную нумерацию, совсем не сложно, и мы предлагаем читателю сделать
это в качестве упражнения
6.4. ШЕСТИГРАННЫЕ ЭЛЕМЕНТЫ
Как уже было сказано, тетраэдральные
элементы несколько уступают по точности
прямоугольным параллелепипеидальным
элементам, хотя и гораздо лучше аппрокси-
мируют криволинейные границы расчётной
области В этом смысле ситуация полностью
аналогична ситуации с треугольниками и
прямоугольниками в двумерном случае. В
двумерном случае элементом, объединяю-
щем в себе возможности треугольников по
описанию искривлённых границ с возмож-
ностями прямоугольников получать более
точное решение на сетке с теми же узлами,
являлся четырёхугольник (см. раздел 5.4). В
Рис. 55. Локальная нумерация
вершин шее ин раннина
350
б.Трёхмерные скалярные задачи
трёхмерном случае похожими свойствами обладает элемент с шестью
четырёхугольными гранями — шестигранник1 * * * Покажем, как можно
построить базисные функции для такого элемента и вычислить его
локальные матрицы.
Пусть область П разбита на шестигранники . На рис. 55 пока-
зана локальная нумерация восьми вершин одного из таких шестигран-
ников. Как и для четырёхугольника в двумерном случае, локальные
базисные функции шестигранника можно получить, отображая на него
базисные функции, определённые на единичном кубе
={(^,0)1 0 <£.<!, О <!)<!, О<0 < 1}. (6.61)
Введем на О/' трилинейные базисные функции
ft, П 6) = ^.(0 (Ю И;{0 (пМб) (в) > г = 1... 8, (6.62)
где
1Ц (а) = 1 — а , W-2 (а) — а., (6.63)
а целочисленные функции p(z), v(?) и -О(г) определяются соотноше-
ниями (6.12)-(6.14).
Тогда отображение единичного куба Q7 в шестигранник с
вершинами (гг,, упгг' можно определить через базисные функции ф, в
виде
8 8 8
= 52^'Л‘П’0)’ У = 52 ^Л’^’0)’ г = 52^А>П0), (664)
/=1 /=1 ?:=1
а базисные функции на шестиграннике Q.„, можно определить с по-
мощью соотношения:
Ф, (-^?Л^) = Z/,^),T|(a7,^,^),0(х’,х/,^)), г = 1 — 8, (6.65)
в котором £, = Е,(.т, */,z), т] — 7](х,у,z) и Q = $(x,y,z) - функции, за-
данные (неявно) выражениями (6.64). Нетрудно убедиться, что каждо-
му узлу шестигранника Q,n соответствует одна базисная функция,
принимающая значение 1 в нем и значение 0 в остальных узлах .
Получим соотношения для вычисления элементов локальных мат-
риц массы и жёсткости элемента QTZ, с базисными функциями (6.65).
Как и в случае четырёхугольного элемента (см раздел 5.4.3), при вы-
числении интегралов по шестигранному элементу можно воспользо-
1 Вообще говоря, формально шестигранником является и, например, пи-
рамида с пятиугольным основанием Мы же всегда будем понимать под шес-
тигранником только тело с шестью четырёхугольными гранями (т.е. призму с
четырёхугольным основанием).
6.4 Шестигранные элементы
351
ваться заменой переменных ж, у и z на Т| и 0, что позволит пе-
рейти от интегрирования по шестиграннику Пп1 к интегрированию по
кубу Q , где известен аналитический вид базисных функции.
Получим соотношения для вычисления компонент локальной мат-
рицы массы Будем считать, что коэффициент постоянен на Q„, и
равен , тогда
= Ч fff 'Ф. У,z) 'Ф; (ж, У> dxdydz =
Qu.
1 1 1
о о о
где J — якобиан преобразования координат (6.64), т.е. определитель
функциональной матрицы
(6.66)
J =
дх ду дг
dt, dt
дх ду dz
Зт] Зт| Зт)
дх ду dz
30 dQ
Очевидно, что якобиан J является полиномом переменных , Т) и
0, и поэтому компоненты Мг] матрицы массы, определяемые соотно-
шением (6.66), в принципе могут быть вычислены аналитически.
Аналогично могут быть получены и выражения для вычисления
компонент локальной матрицы жёсткости:
G, = X grad ф,- (а;, у, z) • grad ф7- (ж, у, z) dxdydz =
Qn
1 1 I
= ^f J К^^фД,т),0)|7|^т]<Ю.
о о о
(6-67)
Однако аналитическое вычисление локальных матриц шести! ран-
ни ка, как и четырёхугольника, довольно редко применяется на пракш-
ке, поскольку соответствующие формулы являются достаточно i ро-
моздкими и не только требуют очень большого числа арифметических
действий по сравнению с численным интегрированием, но п в некото-
рых случаях могут становиться вычислительно неустойчивыми.
Рассмотрим одну довольно часто встречающуюся па ирам икс си
туацию, когда четыре боковые грани шестигранника являкнся прямо-
угольниками В этом случае шестигранник фактически является пря-
352
6.Трёхмерные скалярные задачи
мой призмой с четырёхугольным основанием Сетка из таких элемен-
тов легко может быть построена, например, тиражированием двумер-
ной сетки из четырёхугольников вдоль третьей оси координат.
Очевидно, что для такого шестигранника в виде прямой призмы
при вычислении его локальных матриц удобнее использовать базисные
функции не в виде (6.65), а в виде (6.53). При этом целочисленные
функции (i( i) и м(/) в (6.53) могут быть определены соотношениями
р («)= (г — 1) mod 4 + 1, v(i) = 1, г = 1...8, (6.68)
а ф, (.г, у/) являются базисными функциями четырёхугольного элемен-
та с вершинами (i‘2,2/г), (^З)Й) и Ул) Естественно, в
этом случае локальные матрицы такого элемента можно вычислять не
через соотношения (6.66)—(6.67), а с использованием формул
(6.58) (6.59), в которых матрицы G’ и М2 определяются соотноше-
ниями (6.57), а матрицы G'77 и М'/у - это матрица жёсткости и матри-
цы массы (вычисляемые для коэффициентов Х = ^ = 1) четырёх-
угольного элемента QfjJ (их вычисление рассматривалось в разде-
ле 5.4). При таком способе вычисления локальных матриц шестигран-
ника численное интегрирование можно использовать только для вы-
числения матрицы G7// (и при этом интегрировать только по четырёх-
угольнику, а не по всему шестиграннику). В результате компоненты
локальных матриц шестигранника можно вычислять с помощью полу-
ченных численно компонент матриц G7// и аналитических выражений
для компонент матриц М7//, G и М более экономично, чем при ис-
пользовании численного интегрирования по всему шестиграннику.
Поэтому рассмотренный способ для шестигранника в виде прямой
призмы вычислительно гораздо более эффективен, чем способ, осно-
ванный на общей схеме с численным интегрированием по всему шес-
тиграннику.
6.5. ТЕСТИРОВАНИЕ ПРОЦЕДУР КОНЕЧНОЭЛЕМЕПТНОГО РЕШЕНИЯ
ТРЁХМЕРНЫХ ЗАДАЧ
Основные принципы тестирования конечноэлемензных проце-
дур решения трёхмерных задач в целом мало отличаются от рассмот-
ренных в разделе 5.7 принципов тестирования процедур решения дву-
мерных задач. При тестировании трёхмерной процедуры точно так же
очень важным является этап проверки правильности её работы на за-
дачах, решениями которых являются полиномы (или кусочные поли-
номы) соответствующей степени При этом так же, как и в двумерном
случае, желательно хотя бы в одной из подобластей расчётной области
в качестве тестовых решений использовать полные полиномы.
Прежде всего, имеет смысл протестировать правильность генера-
ции локальных матриц и векторов. Например, для тестирования три-
линейных элементов можно использовать следующую краевую задачу
6.5.Тестирование процедур конечноэлементного решения ...
353
в параллелепипеде Q = [10,20] х [0,8] х [0,1]. Типы заданных на грани-
цах этого параллелепипеда краевых условий показаны на рис. 56, где,
как обычно, через обозначены границы с краевым условием второ-
го рода, а через 8% - границы с краевым условием третьего рода. Па
рис. 56 жирным шрифтом обозначены номера узлов.
Рис. 56. Простейшая расчётная область для тестирования трилинейных элементов
Выберем в этой тестовой задаче значения коэффициентов X и 7 в
виде
(6.69)
Х = 5, 7 = 0.4,
а в качестве решения - полином
и = 5 + 0.2а; + у + 30г + 0.5а:?/ + xz Т 10?/г 4- xyz . (6.70)
Исходя из этого (т.е. с учётом (6.69) и (6.70) и рис. 56) определим
правую часть f дифференциального уравнения и параметры краевых
условий:
+ уи =
f ____д /\ ди\____д [ \ ди
дх \ дх) ду [ ду
= 0.4(5 4- 0.2а; 4- у 4- 30г 4- 0.5а;?/ 4- xz 4- 10?/г 4- xyz),
Ч- =х^г
152 дп
г <9(5 4- 0.2а; 4- у 4- 30г 4- 0.5а;?/ 4- а;г 4- 10//г 4- xyz)
— о
дх
10
= — 1 — 2.5?/— 5г — 5?/г,
_ \ ди
-ft— = 5 4-2.5а: 4-50г 4-5.тг,
дп S2
354
6.Трёхмерные скалярные задачи
0 I , = X-g^ = 150 4- 5х + 50т/ 4- 5ггт/,
,52 дп
3 (u - = -1 - 2.5?/ - 5z - 5yz,
3 (и — Ujj)|52 = 5 + 2.5.Т + 50z + 5xz ,
3 (и, — 3 = 150 + 5т + 50?/ 4- 5xy,
15.,
и если взять, например, 3 = 10, то t получим в виде
= 9.1 4-11-25?/4-50.5z 4-30 5yz,
72(J 2 = 4.5 — 0.05.Т 4- 25z + 0.5a;z ,
= —10 —О.Зх —4?/ .
Очевидно, что вектор q решения конечноэлементной СЛАУ, ап-
проксимирующей эту тестовую задачу, должен иметь следующий вид
(это значения решения (6.70) в узлах сетки)
q = (7, 9, 55, 97, 47, 59, 255, 387) • (6-71)
Чтобы проверить правильность генерации конечноэлементной
СЛАУ, как уже говорилось на с. 325, совсем не обязательно её решать
и сравнивать полученный вектор решения q с вектором (6.71), можно
(и такой путь даже лучше) просто умножить сгенерированную матри-
цу на вектор q и сравнить полученный вектор Aq с вектором b пра-
вой части этой конечноэлементной СЛАУ. При этом, если какая-либо
из строк конечноэлементной СЛАУ сгенерирована неправильно, то
именно для этой строки результат её умножения на вектор q не совпа-
дёт с соответствующей компонентой вектора Ь, в го время как после
решения конечно элементной СЛАУ при наличии ошибки даже только
в одной се строке искаженными могут быть многие (или даже все)
компоненты вектора q.
Например, для рассмотренной нами тестовой задачи матрица А и
вектор b конечноэлементной СЛАУ должны иметь вид (для уменьше-
ния громоздкости матрица и вектор умножены на один и тот же коэф-
фициент, равный 216):
6.5.Тестирование процедур конечноэлементного решения
355
' 31702 15707 14426 7141 -8149 -4146.5 -4787 -2129 5'
15707 33622 7141 15386 -4146.5 -7189 -2429.5 -1307
14426 7141 29302 14507 -4787 -2429.5 -9349 -4716 5
7141 15386 14507 31222 -2429.5 -4307 -4746.5 -8389
А = -8149 -4146.5 -4787 -2429.5 12502 6107 4826 2341 •>
-4146.5 -7189 -2429.5 -4307 6107 14422 2341 5786
-4787 -2429.5 -9349 —4746.5 4826 2341 10102 4907
-2429.5 -4307 -4746.5 -8389 2341 5786 4907 12022
ь = ( -939164, -607624, -1405180, -810320, 2491196,3328936,3809980,5224641))1 . (6.72)
Если бы была допущена ошибка в генерации, например, пятой стро-
ки этой СЛАУ, то после умножения матрицы А на вектор q только
пятая компонента вектора Aq отличалась бы от соответствующей
компоненты вектора правой части b Это указывало бы на наличие
ошибки именно в пятой строке конечноэлементной СЛАУ (т.е. в пятой
строке матрицы А или в пятой компоненте вектора Ь) В то же время
если мы решим СЛАУ с матрицей А , такой что все компоненты Ач,
кроме Л5 7 и А7 5 , совпадают с соответствующими компонентами А/у,
и только (с учётом коэффициента 216) = /17 5 = 2666 (а не
4826 ), то в качестве решения СЛАУ Aq = b с вектором правой части
(6.72) получим вектор
q ~ (22.42, 4 576, 61 22, 95.63, 111.8, 33.07, 265.6, 385.3d) ,
в котором все компоненты отличаются от правильного вектора (6.71).
А если бы мы умножили матрицу А на вектор (6.72), то в векторе Aq
только пятая г/ седьмая компоненты, равные 1940396 и 3708460,
отличались бы от соответствующих компонент = 2491196 и
= 3809980 вектора b, что и указывало бы на ошибки генерации
именно в пятой и седьмой строках конечноэлементной СЛАУ.
Если при вычислении локальных матриц какие-либо из параметров
задачи X, /, 0, заменялись своими интерполянтами, то имеет
смысл построить соответствующий тест.
Например, проверить правильность замены на каждом конечном
элементе коэффициентов X и ч интерполянтами ^Х/ф^ (.г,//, ?) и
j
(а;,т/,z) (ф7 - лагранжевы базисные функции X и им
чепия X и в узлах конечного элемента) можно па следующей тесто-
356
б.Трёхмерные скалярные задачи
вой задаче, определённой в изображённой на рис. 56 расчётной облас-
ти Q.
Выберем значения коэффициентов X и в виде
X = xyz , = z , (6.73)
а в качестве решения - полином
и = За; + 5у — 10. (6.74)
Исходя из соотношений (6.73) и (6.74) определим правую часть f
дифференциального уравнения:
f — 2yz — 2xz — 10z.
Параметр 6 вторых краевых условий на границах Sj и Sj (см.
рис. 56) получим в виде
О* = -ЗОт/z, 01 = 40tz , 02 = 0 •
При формировании третьих краевых условий выберем параметр
[3 = 1, тогда параметр определяется следующими соотношениями
= 60 + + 60Уг ~ 10 > ^»|iS2 = ~ 10, = Зж + 5?/ - 10 .
Вектор решения для этой задачи имеет вид
q = (20, 50, 60, 90, 20, 50, 60, 9о)Т.
Обратим ещё раз внимание на то, что при построении тестовых за-
дач, конечноэлементные решения которых должны полностью совпа-
дать с точным решением, следует помнить о том, что в полученной
тестовой задаче при представлении (в программах генерации локаль-
ных матриц и векторов) параметров в виде соответствующих линей-
ных комбинаций базисных функций эти линейные комбинации долж-
ны точно совпадать со своими исходными значениями на каждом
конечном элементе, т.е. У^Х/ф; (~т,у,z) должна на каждом конечном
j
элементе совпадать с X, У^чА' ~ совпадать с
j
У2 // / (ж» У'~ совпаДать с f , 0уФ; (z, z) ~ совпадать с 0 и т.д.
i I
Чаще всего об этом забывают по отношению к f . Например, в тес-
те для трилинейных элементов могут взять тестовое решение
и, = За; + 5т/ — 10z , коэффициент X = xyz, коэффициент = z (все
они точно представимы в базисе трилинейных функций) и полу-
чить f = 2yz — 2xz — 10z2, которая не представима точно в базисе
6.5.Тестирование процедур конечноэлементного решения
357
трилинейных функций. Естественно, в этом случае совпадения Лц с
b может и не быть. Хотя, в принципе, в некоторых случаях и при не-
совпадении f с вектор Aq может совпадать с b - например,
j
в ситуациях, когда при любых значениях г интегралы У^ J
точно совпадут с интегралами У^ J* У^ /7ф(где, как обычно,
к J
ф; - локальная базисная функция, ф, - глобальная базисная функ-
ция).
Покажем, как можно построить более сложную тестовую задачу,
проверяющую, например, правильность учёта разрывов в X, и f и
работу процедур сборки конечноэлементной СЛАУ в относительно
сложной области (составленной из нескольких простых подобластей).
В качестве примера такой тестовой задачи рассмотрим краевую задачу
в расчётной области Q, состоящей из трёх прямоугольных подобла-
стей Q1 = [0,1] х [0,2.5] х [0,2], Q2 = [1,5] х [0,2.5] х [0,2] и
Q3 = ,0,1] х [0,2.5] х [2,7] и изображённой на рис. 57.
Рис. 57. Расчётная область для тестирования трилинейных
элементов при разрывных коэффициентах
Коэффициенты X и дифференциального уравнения (6.1) ыд.щим
в виде:
358
б.Трёхмерные скалярные задачи
1, вП1,
2, в fi2,
ufi3,
О
4, в Q1,
О, bQ2,
1, в Q3.
(6.75)
Вид тестового решения и в подобласти Q1 выберем следующим
образом:
и, = 2х (yz + z -|- у + 1).
(6.76)
Поскольку коэффициент X разрывен на границе х = 1 между по-
добластями О1 и fi2, решение и должно иметь разрывную нормаль-
ную к этой границе производную (естественно, само значение и долж-
но быть непрерывно). А так как нормаль к границе х — 1 направлена
вдоль оси х, то нормальной производной к границе будет Вели-
о
чину разрыва в ~ легко определить из условия непрерывности пото-
о | Q I
ка Х-тр- = X , и с учётом значений X справа и слева от
сдг|.7=1_() (7.r|x=i+()
х — I
2&|
— ди.
1+о дт
= 2(yz + z + у + 1).
1-0
(6.77)
Поэтому в подобласти Q2 тестовой решение и возьмём в виде
и = 1 + х + у + z + ху -|- xz 4- yz + xyz . (6.78)
Легко убедиться, что на границе х = 1 функция, определяемая со-
отношениями (6.76) и (6.78), непрерывна и удовлетворяет условию
Аналогично, с учётом непрерывности функции и и потока
X = X на границе z = 2 тестовое решение в подобласти Q3
возьмём в виде
и — З.та (у + 1I.). (6.79)
С учётом вида тестовой функции, определяемой соотношениями
(6.76), (6/8) и (6.79), и вида коэффициентов X и (см. (6.75)) опре-
делим параметры краевых условий (см. рис. 57) и правую часть / диф-
ференциального уравнения (6.1) (в скобках указаны номера узлов, оп-
ределяющих соответствующую границу):
6.5.Тестирование процедур конечноэлементного решения ...
359
Вектор решения q полученной конечноэлементной СЛАУ должен
иметь следующий вид:
q = (о, 2, 6, 0, 7, 21, 0, 6, 18. О, 21, 63, 0, 21, 0, 73.5^.
Для более тщательного тестирования сборки конечно micmciii нон
СЛАУ следует использовать более или менее подробные сечки, в koio-
рых по каждой координате сделано не менее четырех шип inaiов
360
6.Трёхмерные скалярные задачи
При тестировании тетраэдральных элементов имеет смысл задавать
границы отдельных подобластей расчётной области непараллельными
координатным плоскостям. Например, можно использовать в качестве
расчётной область Q, изображённую на рис. 58. Построим в ней тесто-
вую задачу для линейных тетраэдральных элементов. Так же, как и в пре-
дыдущем примере, жирным шрифтом на рис. 58 выделены номера узлов.
Рис. 58. Расчётная область для тестирования тетраэдральных элементов
Будем считать, что расчётная область, изображённая на рис 58, раз-
бита на 9 тетраэдральных конечных элементов (в скобках указаны
номера узлов, определяющих конечный элемент): Qj = (4,5,1,6),
П2 = (4,5,9,6), Q3 = (5,9,10,6), П4 = (1,2,5,6), Q5 = (2,5,6,7),
=(5,6.7,10), Q7 =(3,4,1,6), Q8 = (3,4,8,6), Q9 = (4,8,9,6).
Коэффициенты X и дифференциального уравнения (6.1) зададим
в виде
Х = 2, ^ = 5. (6.80)
Вид тестового решения и выберем следующим образом.
« = 10 + 2х — Зч/ + 5z . (6.81)
С учётом (6.80) и (6.81), а также рис. 58 определим правую часть f
и параметры краевых условий в виде
/ = 5(10 + 2.r-3// + 5z), u| =7 + 2;г + 5г,
еЦ = -ю, в|.Ч2 =6, е|^ = -4, e|S4 = ю,
6.5.Тестирование процедур конечноэлементного решения ...
361
Р = 4, = 12.6 + 2х — Зу + 5z .
Заметим, что для определения параметра необходимо было
вычислить величину X ^-| . Поскольку граница S2 не перпендику-
лярна ни одной из осей координат, величина может быть вы-
числена следующим образом:
дгь
=X(gradu.n),
где п - единичная внешняя нормаль к границе S3, которая, в свою
очередь, может быть найдена, например, с помощью векторного про-
изведения двух ребер границы S^, выходящих из одной вершины. На-
пример, нормированное векторное произведение ребер 3-1 и 3-8 равно
вектору п с координатами (—о.б.о,—0.8). Определить знак нормали мож-
но следующим образом. Из рис. 58 видно, что вектор 6-2 направлен в
сторону, противоположную направлению внешней нормали, следова-
тельно, скалярное произведение вектора нормали и вектора 6-2 должно
быть отрицательным. Вектор 6-2 имеет координаты (-4.0,о). Очевидно,
что скалярное произведение векторов п и 6-2 равно —2.4. Следова-
тельно, вектор внешней нормали противоположно направлен вектору
п и имеет координаты
П = (о.б, 0, 0.8) .
Заметим, что на практике (при наличии большой сетки) для опреде-
ления направления нормали можно использовать вектор, началом ко-
торого является любая вершина грани тетраэдра, где задаётся краевое
условие, а концом - та вершина тетраэдра, которая нс лежит на г рани с
краевым условием.
Нетрудно убедиться, что вектор решения q должен иметь следую-
щий вид
q = ^29, 25, 22, 14, 10, 26, 22, 19. 11, 7^.
Изображённую на рис. 58 область можно использовать и для гсс пи-
рования треугольных призм, основание которых лежит в плоскости
у = const. Для таких призм полный полином имеет вид
и = с() + СрТ + С2у + C’3z 4- с4ху + c3yz ,
и это следует учесть при построении тестовых задач.
При тестировании некоторых трёхмерных задач очень полезными
могут быть осесимметричные задачи. Это задачи, которые определены
362
6 Трехмерные скалярные задачи
в области, состоящей из цилиндров, и решения которых не зависят от
координаты ф в цилиндрической системе координат {г, ip,z} . Приме-
ром может служить задача в расчётной области, изображённой на
рис. 59,а.
В этой задаче можно задать значения параметров дифференциаль-
ного уравнения(1.1) в виде
Хт в Q1,
Х2 в Q2,
вО1, /] в Q1,
f = ‘
^2 В О2, Лв^2,
(6.82)
(6-83)
Рис. 59. Расчётные области для тестирования трёхмерных задач
Очевидно, что решение этой задачи может быть найдено в виде
двумерной функции u2D (г, z) в расчётной области, изображённой на
рис. 59,6. Для этого достаточно решить двумерную задачу для уравне-
ния
1_д_
/ дг
д
dz
+ yu2D = f
(6.84)
I J
с параметрами, определяемыми теми же соотношениями (6.82) и (6.83),
в которых эти параметры (X, , /, 0 и т.д.) фактически являются
функциями координат г и z ;
6.5.Тестирование процедур конечноэлементного решения ...
363
^1 в Q2% 41 в П2^1, /1 в Q2D’*
X = э = f =
^2 в Q2D’2, 42 в Q2Z?’2, h в Q2r’2
и
dii2D — \ du2D
ди. — v-2 dn
= 62,
u2D|
1г,
dn г()
12
Решение этой задачи в декартовой системе координат является
трёхмерной функцией, и качество полученного в трёхмерной области
(см рис. 59,й) конечноэлементного решения uh можно оценить путём
сравнения с трехмерной функцией u3D (х, у, z), полученной пересчё-
том из решения u2D(r,z) осесимметричной задачи (6.84) с помощью
соотношения
u3D (ж, t/, г) = u2D [у/х2 + у2, г).
Такие проверки особенно полезны и важны тогда, когда решаемые
трёхмерные задачи в некотором смысле близки к каким-либо осесим-
метричным задачам.
В целом же, следует помнить, что никакие тесты не дают стопро-
центной гарантии отсутствия ошибок. Многие программные реализа-
ции, содержащие несущественные (незначительные) погрешности мо-
гут успешно проходить различные тесты и давать вполне приемлемые
(очень правдоподобные) результаты. И только глубокое понимание
теории мКЭ и немалый практический опыт может позволить разра-
ботчику программного комплекса или исследователю, использующему
конечноэлементный пакет для решения сложных задач, понять, что в
программе есть ошибки реализации, из-за которых МКЭ не даёт точ-
ности или скорости сходимости, которые гарантирует его теория при
безошибочной реализации соответствующих вычислительных схем
Выявление таких ошибок - это уже искусство, требующее очень высо-
кого профессионализма.
364
7 Применение МКЭ для решения нестационарных задач
7. ПРИМЕНЕНИЕ МКЭ ДЛЯ РЕШЕНИЯ
НЕСТАЦИОНАРНЫХ ЗАДАЧ
В данном разделе мы рассмотрим некоторые способы аппрокси-
мации начально-краевых задач для уравнений параболическою типа
cr^--div(Xgradu) = / (7.1)
и для уравнений гиперболического типа
x4# + a^7-div(XgradM) =/• (7-2)
dt ит.
7.1. О ДИСКРЕТИЗАЦИИ ПО ВРЕМЕНИ
При построении дискретных аналогов начально-краевых задач
для дифференциальных уравнений (7.1) и (7.2) будем полагать, что ось
времени t разбита на так называемые временные слои значениями ,
j = 1...J , а значения искомой функции и и параметров X, о, х и f
дифференциальных уравнений (7.1) и (7.2) на j -м временном слое (т.е.
при t = /,) будем обозначать соответственно через w7, X7, ст7, х7 и
,/7, которые уже не зависят от времени t, но остаются функциями
пространственных координат (например, в двумерных задачах
и3 = и3 (ж, у) = u(x,y,tj), X = X7 (т, у) = X (ж, y,tj) И т.д.).
Помимо краевых условий вида (1.2)-(].4) начально-краевая задача
для уравнения (7.1) должна включать в себя начальное условие
wlz=/.() =у[\ (7.3)
где и() — заданная функция пространственных координат
(wl) = ti° (ж, у) в двумерном случае), а начально-краевая задача для
уравнения (7.2) должна включать в себя два начальных условия, в ко-
торых задаются значение искомой функции и в начальный момент
времени /,(1 (в виде соотношения (7.3)) и значение производной и по
времени в тот же момент t = . Очевидно, что из этих двух началь-
ных условий легко получить приближённое значение на временном
7.2.Аппроксимация начально-краевых задач ...
365
слое : и1 и" + Ду (t — /0). Поэтому в начально-краевой задаче
для уравнения (7.2) мы будем использовать два начальных условия в
виде (7.3) и в виде
u\f-tl=ul, (7.4)
причём функция и[ из (7.4) может быть либо задана непосредственно,
либо пересчитана по значениями и{] и Ду указанным выше спосо-
lt=/0
бом.
Для описания вычислительных процедур построения копечноэле-
ментных решений начально-краевых задач для уравнении (7.1) и (7.2)
удобно ввести две глобальные матрицы, получающиеся в результате
соответствующей аппроксимации отдельных членов дифференциаль-
ного уравнения эллиптического типа: матрицу жёсткости G как ап-
проксимацию члена —div^Xgrad uj и матрицу массы М как аппрок-
симацию члена уи., т.е.
-div(Xgradu) МКЭ-аппроксимация , G q (7 5)
-,И ---МКЭ-аппроксимация , м. q (7 6)
где q — вектор весов разложения конечноэлементного решения и1' по
базисным функциям, зависящим только от пространственных коорди-
нат. Как и прежде, через b будем обозначать вектор, определяющий
вклад в вектор правой части конечноэлементной СЛАУ от правой час-
ти f дифференциального уравнения (7.1) или (7.2) и краевых условий.
7.2. АППРОКСИМАЦИЯ НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО
ТИПА
Рассмотрим аппроксимацию дифференциального уравнения (7 1)
по времени с использованием следующих схем:
о 11J ------div(Xgradt?) =/', j = (7.7)
о- ---------div (Х grad j = (7.8)
° ll> 1 ~div X grad U’ = +2~—’ J = <7-9)
1дс А/ = tJ —t'~[ (здесь и далее мы будем считать, что параметры
дифференциального уравнения (7.1) не зависят от времени, а правая
366
7.Применение МКЭ для решения нестационарных задач
часть f — зависит. Не представляет труда записать схемы, аналогич-
ные (7.7)—(7.9), и в случае зависимости параметров о и X от t).
Соотношение (7.7) определяет неявную схему аппроксимации па-
раболического уравнения, соотношение (7.8) - явную схему, а соотно-
шение (7.9)- схему Кранка-Николсона1 *.
Чтобы построить вычислительные процедуры численного решения
полученных уравнений, воспользуемся введёнными ранее глобальны-
ми матрицами жёсткости G и массы М (см. (7.5)Ц7.6)), причём в
соотношении (7.6) под будем понимать параметр о.
Обозначим через q7 вектор весов разложения конечноэлементного
решения по базисным функциям (т.е. для лагранжевых элементов - это
значения решения в узлах конечноэлементной сетки). Тогда в резуль-
тате копечноэлементной аппроксимации краевой задачи для диффе-
ренциального уравнения (7.7) (с краевыми условиями вида (1.2)—(1.4),
наложенными на функцию и1) для каждого j = мы получим
матричное уравнение следующего вида:
Mq7 -^Mq7"'1 + Gq7 +M,<7;‘q-' = *>', (7.10)
где М/>3 - вклады в глобальную матрицу конечноэлементной СЛАУ от
краевых условий третьего рода, запись Ь7 означает, что этот вектор
сформирован по значениям функции f и краевых условий на j -м вре-
менном слое.
Если считать вектор q7-1 известным (его компоненты являются ве-
сами разложения по базисным функциям решения на (J —1)-м вре-
менном слое), то матричное уравнение (7.10) фактически является
СЛАУ для вектора неизвестных q7 :
М + G + М5:{)q7 = b7 4-^-Mq7-1. (7.11)
И матрица А в этой СЛАУ (7.11) - это сумма матриц
М 4- G 4- М^3, а вектор правой части - это вектор Ь7 4- -^yMq7-1.
Учитывая, что компоненты вектора q11 можно определить с помо-
щью функции г/. из начального условия (7.3) (для лагранжевых эле-
ментов - это значения в узлах пространственной сетки), получаем
следующую вычислительную процедуру.
Сначала па основе МКЭ генерируются матрицы G, М и М‘5;1 и
вектор Ь1. Из матриц G, М и М^3 формируется матрица
А — М 4- G -Ь М'?3 . Затем формируется вектор d = b1 4- -^-Mq" и
1 Мы используем традиционное для русскоязычной литературы название
этой схемы, хотя в последнее время её стали называть и схемой Кранка-
Николсон.
7.2.Аппроксимация начально-краевых задач ...
367
из решения СЛАУ Aq = d находится вектор решения q' на первом
временном слое.
Далее из матриц G, М и М‘5;$ формируется новая матрица1 А и
новый вектор d = b 4-7 Mq , и затем из СЛАУ Aq = d находится
вектор решения q на втором временном слое. Продолжая этот про-
цесс, получаем решение начально-краевой задачи на всех интересую-
щих нас временных слоях , j = 1...J .
Аналогично строятся процедуры решения уравнений (7.8) и (7.9).
Для уравнения (7.8) получаем матричное уравнение
^(М + М«')ч' =b>-1 +(7J7M-G)q'-‘, (7.12)
а для уравнения (7.9) - матричное уравнение
(^M+jG+jM^Jq(7.13)
Если бы в результате аппроксимации но пространству матрицы М
и имели ненулевые элементы только на главной диагонали (чго
возможно получить при использовании специальных подходов к по-
строению МКЭ-аппроксимации, которые применяются в основном для
решения начально-краевых задач для гиперболических уравнений), то
компоненты вектора решения qJ уравнения (7.12) можно было бы
явным образом (а не в результате решения СЛАУ) выразить через ком-
поненты вектора решения q на предыдущем временном слое (в связи
с чем схему (7.8) и называют явной). Отметим, однако, что для устой-
чивости вычислительного процесса при использовании явной схемы
необходимо соблюдать определённое соотношение между шагом но
времени и размерами ячейки дискретизации в пространственной сетке:
с уменьшением размеров ячейки дискретизации максимально допус-
тимый для устойчивого счёта шаг по времени должен быть уменьшен
пропорционально квадрату размера ячеек дискретизации.
Такого рода ограничений нет в неявной схеме (7.11) и в схеме
Кранка-Николсона (7.13) (которая по своей сути также является неяв-
ной схемой), и поэтому, несмотря на то, что при их использовании на
каждом временном слое необходимо решать соответствующую СЛАУ,
в суммарном итоге эти схемы чаще всего оказываются более эконо-
мичными по времени счёта, чем явная схема даже без решения СЛАУ
(из-за гораздо большего числа временных слов в явной схеме, необхо-
димого для обеспечения её устойчивости).
По сравнению с неявной схемой (7.11) схема Кранка-Николсона
(7.13) обладает гораздо более быстрой сходимостью при измельчении
1 Причём новая матрица А формируется только в том случае, если ымс-
нился шаг по времени или коэффициенты X , о или и ; если же ни л/ , ни
X , ни ст, ни р не изменились, то матрица А также нс меняется и перефор-
мировывать её не нужно.
368
7.Применение МКЭ для решения нестационарных задач
шага по времени, но при недостаточно малых временных шагах она
может давать довольно большую погрешность в виде осцилляций ре-
шения по времени (чаще всего это происходит тогда, когда довольно
резко меняется поведение решения во времени). Неявная же схема
(7 11) даёт гладкое решение по времени. В связи с этим значительный
интерес представляют схемы, обладающие достоинствами неявной
схемы и схемы Кранка-Николсона, т.е. схемы с высокой скоростью
сходимости при измельчении шага по t (как схема Кранка-
Николсона) и в то же время практически не имеющие осциллирующих
по времени погрешностей численного решения (как и у неявной схемы
(7.11). Такими достоинствами обладают неявные многослойные схемы.
Рассмотрим процедуру построения неявной трёхслойной схемы для
решения дифференциального уравнения параболического типа.
Будем считать, что функция и является функцией двух простран-
ственных координат а; и у (хотя это совершенно не принципиально,
так как все дальнейшие рассуждения останутся справедливыми и для
одномерных, и для трёхмерных начально-краевых задач).
Представим искомое решение и на интервале в следую-
щем виде:
u(x,y,t) ж uJ~2 (.т,у)^ (0 + UJ~[ (х,у)^ (t) + u-> (х,у)т}{} (£). (7.14)
В аппроксимации (7.14) функции пространственных координат
uJ~2, и и* являются значениями искомой функции и при
t = > и * — соответственно. Зависящие только от вре-
мени функции т\1 (t) являются квадратичными полиномами t, причём
тЕ (t) равна единице при t = tj_2 и нулю при t = tj_} и t = tJt функ-
ция Tfj (t) равна единице при t = tj_^ и нулю при t = tj_2 и t = tj, а
функция T|q (/) равна единице при t = tj и нулю при t = tj_2 и
t = . Таким образом, соотношение (7.14) определяет аппроксима-
цию функции и по времени как квадратичный интерполянт сё значе-
ний на временных слоях t = tj_2 , t = tj^ и t = tj.
Очевидно, что функции ij’ (i), (t) и тЗ (£) — это базисные квад-
ратичные полиномы Лагранжа (с двумя корнями из набора значений
времён tj_2 , tj_x vt tj, см. (4.20)), которые могут быть записаны в виде
(7.15)
(7.16)
(7.17)
7.2. Аппроксимация начально-краевых задач ...
369
где
Д^ tj tj_‘2f Д£| tj_-y tj_-2, tj tj_^. (7.18)
Применим представление (7.14) для аппроксимации производной
по времени параболического уравнения (7.1) на временном слое t - I
^(uJ 2 у)'П2 (О + и3 1 (x'iу)л/ (О + (а;,у)лй (0) -
— div (X grad = f'. (7-19)
Вычислим производные по t функций (7.15)-(7.17) при t = tf (с
учётом обозначений (7.18)):
(7.20)
(7.21)
(tj ^7-1) +(^/ ^J-2) _ Д/ + Д/q
д£л/() д7д£()
(7.22)
С учётом (7.20)-(7.22) уравнение (7.19) может быть переписано в
виде
ft цУ-1 + Д^+Д^о J — div (X grad цН = fJ. (7.23)
д£д^ д^д^ л/д£п V / J v '
Выполняя конечноэлементную аппроксимацию краевой задачи для
уравнения (7.23), получим СЛАУ следующего вида:
(д£+Мо м
I Д^Д^о I
= bJ -7777-W2 +тгЬ-, (7.24)
где, как и раньше, М - ма]рица массы, G - матрица жесткости,
M?s’3 - матрица вкладов от краевых условий третьего рода, Ъ7 - вектор
370
7.Применение МКЭ для решения нестационарных задач
правой части, построенный по значениям функции / и параметрам 0
и Pizp краевых условий на текущем временном ( j -м) временном слое,
q/-2 и qJ-1 - решение на двух предыдущих слоях по времени, q7 -
искомое решение на текущем слое по времени.
Очевидно, что воспользоваться схемой (7.24) для нахождения функ-
ции и на j -м временном слое мы можем лишь в том случае, когда нам
известны значения и на двух предыдущих временных слоях, т.е. по
схеме (7.24) мы можем вычислять q2 (зная q1 и q°), q3 (зная q2 и
q1) и т.д. Для вычисления же ql (q° нам известно из начального ус-
ловия) можно воспользоваться, например, неявной двухслойной схе-
мой (7.11).
Рассмотренный метод построения трёхслойной схемы очень удобен
и при аппроксимации начально-краевых задач по явной схеме при ис-
пользовании неравномерного по времени шага (это будет показано
ниже для уравнения гиперболического типа), но для уравнений пара-
болического типа неявная трёхслойная схема (7.24), как правило, на-
много эффективней любой явной схемы.
Аналогично может быть построена и четырёхслойная схема. В ней
функция и представляется в виде
и (я, у, t) uJ~3 (.т, у) (£) + uJ~2 (.т, у) -Г]* (£) +
+ и-7"1 (т,7/)т]1 (О + uJ (0> (7.25)
где функции т]/, (t) являются кубическими полиномами и имеют сле-
дующий вид (фактически это базисные кубические полиномы Лагран-
жа с тремя корнями из набора значений времён L-_3, L-_2 > t-i-i и tj ,
см. (4.20)):
j (/) =
G./-3 ~ <7-2) (^-3 — ^.7-1) (^j-3 ~
f'j-2 ~ ^-з)(^-2 — ^-l)(^-2
(t ~ tj-3 ) (^ ~ ^'-2 ) (^ ~ ^7)
//-1 — ^’-з)(^7—1 — tj—2)(^j-l ~ ^j)
(z - ) (* ~ tj-2) (^ - )
— ^.7-3) (^.7 ~ ^-2) (h ~ ^./-1)
(7.26)
(7.27)
(7.28)
(7.29)
7.3.Тестирование процедур решения начально-краевых задач ... 371
7.3. ТЕСТИРОВАНИЕ ПРОЦЕДУР РЕШЕНИЯ НАЧАЛЬНО-КРАЕВЫХ
ЗАДАЧ ДЛЯ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА
Для проверки правильности процедур построения коиечноэлс-
ментных решений начально-краевых задач удобно использовать тесто-
вые задачи, решениями которых являются полиномы пространствен-
ных координат и времени t. При этом, если порядок полинома по про-
странственным координатам не превышает порядка используемых
базисных функций (см. раздел 4.14), а порядок полинома по времени
соответствует порядку точности используемой временной схемы, то
получаемое численное решение должно полностью совпадать с точ-
ным решением тестовой задачи. Поэтому при тестировании двухслой-
ной схемы целесообразно использовать полиномы первой степени по
t, схемы Кранка-Николсона и трёхслойной схемы - полиномы второй
степени, а при тестировании четырёхслойной схемы — кубические по-
линомы t.
Построим тестовую задачу для схемы, аппроксимирующей началь-
но-краевую задачу для одномерного уравнения (7.1). Будем считать,
что в качестве схемы аппроксимации по времени использована трёх-
спойная неявная схема, а для аппроксимации по пространству - линей-
ные базисные функции. В качестве решения этой тестовой задачи вы-
берем функцию вида
и = гк:12 + 2t. (7.30)
Выберем параметры X и о уравнения (7.1) следующим образом:
Х = 1, о = 2.
Тогда для того чтобы функция (7.30) стала решением уравнения (7.1),
его правая часть f должна иметь вид
f = 2О.т« + 4.
Будем считать, что расчётная область Q представляет собой отре-
зок П = [0,10], и на ней построена равномерная конечноэлементная
сетка, состоящая из пяти конечных элементов. Сетка по времени со-
стоит из четырёх временных слоев:
«() = 0, ^=0.1, t2=0.3, «з=0.7. (7.31)
Учитывая вид решения (7.30), зададим начальное и краевые усло-
вия:
ц|, = 0, -^1 = -5«2, -^1 +Д |п-55/2 - 2/= 0 .
Как было сказано выше, воспользоваться зрехслойпои схемой мож-
но лишь в случае, если известны значения па двух предыдущих вре-
менных слоях. Для нахождения же решения </1 па временном слое
L = (функция и1} известна из начального условия) при решении
372
7.Применение МКЭ для решения нестационарных задач
практических задач можно пользоваться двухслойной схемой. Однако
если бы мы для нахождения и1 воспользовались двухслойной схемой,
то получили бы решение с погрешностью (поскольку решением
тестовой задачи является полином второй степени по £ , а двухслойная
схема точно аппроксимирует решения, зависящие от £ линейно). Это
не даст нам возможности проверить правильность трёхслойной схемы
при вычислении решений и2 и и 1 на последующих слоях. Поэтому в
данном случае (именно для тестирования трёхслойной схемы) зада-
дим и значение ?? = и |} = 0.05.-е + 0.2. Соответствующий и1 век-
тор весов ql имеет вид:
q1 = (о.2 0.3 0.4 0.5 0.6 0.7)Т.
Вычислим q2 как решение СЛАУ вида (7.24) с матрицей
А = М + G + MS:1 1 (7.32)
( Д£Д£() J
и вектором
d = Ь2----^Д-Mq1’ + -р- Mql. (7.33)
д£д^ д£1д£() 4 v 7
Нетрудно убедиться, что коэффициенты в формулах (7.32) и (7.33)
на временном слое £ = t2 имеют вид (см. значения tj, определяемые
соотношениями (7.3 I)):
д£-|-Д£() _ 25 Ыр д£ 20 /734ч
д£д£() 3 ’ д£д£х ’ д^д^ 3 ’ 17
Пользуясь выражениями (4.8), (4.10) и (4.11) для локальных матриц
и векторов, после их стандартной сборки в глобальные с учётом соот-
ношений (7.32) и (7.33) и вкладов от краевых условий, получим СЛАУ
Aq2 = d для вектора неизвестных q2 (т.е. на втором временном слое)
с матрицей А и вектором d следующего вида:
209 18 91 18 0 0 0 0 14.55'
91 209 91 о о о 50
18 9 18
А = 0 0 91 18 0 209 9 91 18 91 18 >09 9 0 91 18 0 0 , d = 80 ПО
0 0 0 91 18 209 9 91 18 140
0 0 0 0 91 18 227 18 J 85.55 1 J
7.4.Примеры решения начально-краевых задач ...
373
Нетрудно убедиться, что решением этой СЛАУ является вектор
q = (о.б. 1.5, 2.4, 3.3, 4.2, 5.1^ .
Вычислим решение на временном слое t = . Поскольку на этом
временном слое
At+Afu = 25 Afo = 25 а£ = 5
a£a£q 12 д£д/| 4 д£|Д^о 3
решением СЛАУ Aq3 = d (где матрица А определяется формулой
(7.32), а вектор правой части d - аналогичной (7.33) формулой
d = Ь3----Mq1 Ч--------Mq ) будет вектор:
ДьДц ДцДц)
q3 =(1.4, 6.3, 11.2, 16.1, 21, 25.э)Т.
Как видно, решение на всех временных слоях совпадает с точным
решением, определяемым формулой (7.30).
Заме тим, что и другие схемы по времени (в том числе и явные) тес-
тируются аналогично, при этом для четырёхслойной схемы при тести-
ровании следует задавать решение на трёх предыдущих временных
слоях.
7.4. ПРИМЕРЫ РЕШЕНИЯ НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
ДЛЯ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА
Продемонстрируем поведение рассмотренных выше схем ап-
проксимации по времени на примере решения задачи остывания неод-
нородного неравномерно нагретого теплоизолированного с боков
стержня длиной 0.04 м. Стержень состоит из трёх частей. Первая
часть с теплопроводностью X = 30 имеет длину 0.001 м, вторая часть
с теплопроводностью X = 0.1 - длину 0.004 м, а третья часть имеет
теплопроводность X = 0.02 и длину 0.035 м. Произведение рср коэф-
фициентов плотности р и теплоёмкости ср в первой части равно 107,
а во второй и третьей частях - равно 10Г). Левый конец стержня тепло-
изолирован, а на правом конце задано условие теплоотдачи со средой с
коэффициентом теплоотдачи 0 = 5 и температурой окружающей сре-
ды Up = 20. В начальный момент времени первая часть стержня iimcci
температуру 500 градусов, а вторая и третья - температуру 20 i раду-
сов^равную температуре окружающей среды
Таким образом, распределение температуры в стержне описывается
начально-краевой задачей для дифференциального уравнения
-#(>Да) + Р<'!.Дт = О (7.35)
дх\ дх) 1 dt
374
7.Применение МКЭ для решения нестационарных задач
с краевыми условиями
= °> Х1Н +5(“ 1,-04 -20) = 0
C?7l|;(;=o Cmls=().4 ' lj—°-4 '
и начальным условием
'500, х е (0,0.001),
u\t,=(}- u - 20j х е (0.001,0.04).
(7.36)
(7.37)
Для аппроксимации по пространству будем использовать элементы
с линейными базисными функциями. Поскольку начальное условие и1’
представляется в виде линейной комбинации базисных функ-
I
ций ч|?е (в которой веса q” = и} (ж,), xt - узлы сетки), для адекватного
учёта его разрыва в точке х = 0.001 (см. (7.37)), справа от неё необхо-
дим хотя бы один достаточно мелкий шаг (на котором функция
меняется линейно от значения 500 до значения 20). Поэтому
справа от точки х = 0.001 был задан один элемент длиной
/?, = 0.00001, а все остальные элементы сетки были взяты длиной
/г, = 0.001, вполне достаточной для получения требуемой точности
аппроксимации по пространству.
На рис. 60 приведены графики зависимости решения от времени t
в точке х = 0.01 для двух временных сеток (с шагами дискретизации
Д£ = 500 и Д£ = 100) и трёх схем аппроксимации по t: полностью
неявной двухслойной схемы (7.7), схемы Кранка-Николсона (7.9) и
полностью неявной трёхслойной схемы (7.23). Кроме того, на этом же
рисунке показан график решения, полученного на очень подробной
сетке по пространству и по времени (на рисунке этот график назван
точным решением).
Из рис. 60 видно, что для сетки с шагом дискретизации Д£ = 500
схема Кранка-Николсона даёт численное решение, колеблющееся во-
круг точного с довольно большой погрешностью. Двухслойная полно-
стью неявная схема хотя и даёт гладкое численное решение, но погреш-
ность его заметно выше, чем у осциллирующего численного решения,
полученного по схеме Кранка-Николсона. Самое же близкое к точному
численное решение даёт на этой сетке трёхслойная полностью неявная
схема. При дроблении сетки по времени схема Кранка-Николсона и
полностью неявная трёхслойная схема очень быстро (примерно с одина-
ковой скоростью) сходятся к точному - графики этих решений для
Д£ = 100 на рис. 60 практически слились с графиком точного решения.
Двухслойная же полностью неявная схема сходится к точному решению
с гораздо меньшей скоростью и даже на сетке с шагом Д£ = 100 даёт
довольно значительную погрешность (сопоставимую с погрешностью
трёхслойной схемы на сетке с шагом Д t = 500).
7.4.Примеры решения начально-краевых задач ...
375
Рис. 60. Графики зависимости решения от времени в точке х = 0.01
Несмотря на то, что схема Кранка-Николсона теоретически облада-
ет довольно высокой (квадратичной) скоростью сходимости1, при её
применении для задач, решение которых имеет довольно резкие изме-
нения по времени, осциллирующая погрешность может даже с дробле-
нием затухать очень медленно в некоторых подобластях расчётной
области. Такие довольно резкие изменения по времени имеет, напри-
мер, решение рассматриваемой нами задачи (7.35)-(7.37) в небольшой
части расчётной области, примыкающей к её левой границе.
Проанализируем поведение по времени численных решений, полу-
ченных с использованием рассматриваемых нами трёх схем (полно-
стью неявных двухслойной и трёхслойной и схемы Кранка-
Николсона), в точке х = 0.005. Графики этих решений приведены на
рис. 61.
На рис. 61,а приведены графики численных решений, полученные
на сетке с шагом = 50 . Из этого рисунка видно, что схема Крапка
Николсона в точке х = 0.005 при — 50 даёт очень большие ос-
цилляции в решении (размах этих осцилляций заметно превышас! да-
же погрешность двухслойной схемы), тогда как в точке / 0.01 чис-
1 Её погрешность с дроблением шага по времени Л/ убывает
как 6>(д/2)
376
7.Применение МКЭ для решения нестационарных задач
ленное решение, полученное с
Николсона даже на сетке с шагом
точным.
использованием схемы Кранка-
Д£ = J 00 , практически совпадало с
Рис. 61. Графики зависимости решения от времени в точке х — 0.005 при — 50
В принципе, можно предложить довольно простой приём для
уменьшения осциллирующей погрешности в численном решении, по-
лученном с использованием схемы Кранка-Николсона. Для этого зна-
чения решения нужно выдавать не в узлах временной сетки tj, а в се-
рединах iy+y-2 — (t/ +^'/+1)/2 интервалов [t.j, в виде полусуммы
значений на соответствующих временных слоях:
+ н(^+1))/2 • График решения в точке х = 0.005
для Д£ = 50 , полученного таким способом, приведён на рис. 61,6. Для
сравнения на нем также показаны решения, приведённые па рис. 61,а
(для возможности более детального анализа поведения сравниваемых
численных решений на рис. 61,6 использован укрупнённый масштаб).
Из этого рисунка видно, что осцилляции в решении, полученном с
использованием схемы Кранка-Николсона и выданном в точках |_у2,
значительно уменьшились. Рис. 62 иллюстрирует сходимость числен-
ных решений в точке х = 0.005 при дроблении шага по времени: на
рис. 62,а приведены графики численных решений для шага Д< = 25,
на рис. 62,6- графики численных решений для шага Д£ = 5, а на
рис. 62,в - графики численных решений для шага Д£ = 1 . Из этих ри-
сунков видно, что схема Кранка-Николсона в точке х = 0.005 даст
приемлемое по точности решение только при шаге Д£ = 1, в то время
как при использовании трёхслойной полностью неявной схемы реше-
ние с этой точностью было получено уже при шаге /\t = 25. Полно-
стью же неявная двухслойная схема, хотя и имеет монотонную сходи-
мость и даёт гладкие решения при всех рассмотренных шагах по врс-
7.4.Примеры решения начально-краевых задач ...
377
мени, всегда очень сильно уступает по точности полностью неявной
трёхслойной схеме а на подробных сетках и схеме Кранка- 11иколсона
в г
Рис. 62. Графики зависимости решения от времени в точке х = 0.005
а - AZ = 25 ; б- Д< = 5; с- Д£ = 1; г- At = 1 (укрупнённый масштаб)
Преимущество трёхслойной схемы над двухслойной полностью не-
явной и схемой Кранка-Николсона особенно ощутимо при решении
задач, в которых необходимо отслеживать изменение решения во вре-
мени на несколько порядков. К таким задачам относятся, например,
задачи зондирования Земли, основанные на изучении нестационарного
электромагнитного поля. На рис. 63 приведены графики зависимости
от времени численных решений, полученных с использованием двух-
слойной и трёхслойнои полностью неявных схем и схемы Кранка-
Николсона, для одной из таких задач и при использовании одинаковых
сеток как по пространству, так и по времени.
378
7.Применение МКЭ для решения нестационарных задач
Таким образом, для решения параболических задач как наиболее
эффективная может быть рекомендована полностью неявная трёхслой-
ная схема.
7.5. АППРОКСИМАЦИЯ НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ГИПЕРБОЛИЧЕСКОГО ТИПА
При решении начально-краевых задач для уравнения гиперболи-
ческого типа (7.2), в котором коэффициент о либо равен нулю, либо
принимает такие значения, что член oduldt оказывает на решение
уравнения заметно меньшее влияние, чем член xc?2w/c^2, наиболее
часто используют две схемы аппроксимации этого уравнения по вре-
мени: явную схему и схему, аналогичную схеме Кранка-Николсона.
При условии, что шаг по времени = tj — нс изменяется на всем
временном интервале, где ищется решение задачи, явная схема ап-
проксимации уравнения (7.2) по времени имеет вид
X u'-2u-^‘+u' - + 0 - div (\ grad а'-1) = Д'1, (7.38)
а схема, аналогичная схеме Кранка-Николсона, следующий вид:
и' — + uj~2 , и> — 1- к 1 и' + ?/7-2
X-------—2------+ а —--------div [X grad —----- =
= L—4-----> (7.39)
7.5.Аппроксимация начально-краевыхзадач ...
379
где uJ является значением искомой функции и на временном слое
t — tfi причём значения и' и t? должны быть заданы в качестве на
чальных условий.
Выполняя конечноэлементную аппроксимацию соответствующих
задач для уравнений (7.38) и (7.39), получим матричные уравнения
следующего вида (здесь и далее для простоты будем считать, что вкла-
дов от краевых условий в глобальную матрицу нет):
ArMXq' - A-M'q7'1 + ДуМ^"2 +
Af2 Ai2 Ai2
+ Д-МПЧ7 -ДмпЧ7~2 + Gq7-1 =b'"', (7.40)
2д£ 1 2/\t
-iyMV - A-Mxqbl + A-Mxq'~2 + J-rMV -
Ai2 Ai2 Af2 2At
--i-MV’2 + |Gq7 +Gq7-2 = |b' + |b7"2, (7.41)
где G. как и в предыдущем пункте, - матрица жёсткости, получаю-
щаяся в результате аппроксимации члена — div(X grad и), а Мх и
Мп - матрицы массы, получающиеся в результате аппроксимации
членов и ои соответственно.
Вычислительные процессы решения уравнений (7.38) или (7.39)
строятся так же, как и для рассмотренных в предыдущем пункте урав-
нений (7.7)-(7.9). Матричное уравнение (7.40), аппроксимирующее
краевую задачу для уравнения (7.38), фактически является системой
линейных алгебраических уравнений для вектора q;/ с матрицей:
А = Д-МХ + ДГМ
АГ 2Д/
и вектором правой части
d = b7"1 + -4j-Mxq/_1 - -1-MXq'-2 + Д-МПЧ7"2 - Gq7'1.
Ai2 Ai2 2a«
Конечноэлементные аппроксимации уравнения (7.38) обычно при
водят к матрицам массы М и М’ с ненулевыми компонентами, рас
положенными не только на главной диагонали, и поэтому на первый
взгляд использование МКЭ в сочетании с явной схемой аппроксима
ции по времени представляется очень неэффективным. Однако к на-
стоящему времени разработаны и довольно широко используются на
практике различные приёмы, позволяющие без заметного ущерба для
точности получаемого численного решения заменять мафицы Мч и
Мп маярицами М и М с ненулевыми компонентами только на
главной диагонали. В этом случае и у матрицы А =
Л* 1-Л-- М
А/ 2а/
СЛАУ Aq7 = d ненулевые компоненты будут только на главной диа-
380
7.Применение МКЭ для решения нестационарных задач
гонали, и поэтому решение на каждом временном слое легко вычисля-
ется без решения СЛАУ. Преимущества такой аппроксимации очевид-
ны: из вычислительной процедуры, реализующей построение числен-
ного решения на каждом временном слое, устраняется один из наибо-
лее трудоёмких этапов - этап решения СЛАУ, и вычислительные за-
траты на построение численного решения определяются в основном
затратами на вычисление вектора а .
Затраты же на построение матриц Мх , Мп и G в целом сравни-
тельно невелики, так как эти матрицы одинаковы на всех временных
слоях (если, конечно, соответствующие параметры задачи не зависят
от времени) и поэтому они могут быть построены перед началом про-
цесса движения по временным слоям (если количество временных сло-
ев будет хотя бы около 30-40, что выполняется практически для всех
реальных задач, то вычислительные затраты на обработку матриц Мх ,
М и G уже стану! примерно на порядок меньше затрат на вычисле-
ние вектора d на всех временных слоях).
Матричное уравнение (7.41), аппроксимирующее краевую задачу
для уравнения (7.39), является системой линейных алгебраических
уравнений для вектора q7 с матрицей
а = -Дм* + -Дм° +|g
Al ZAt 2
и вектором правой части
<1 =lb' +lb'-2 +-2-Mxq'-‘
2 2 ЛГ At2
+ 2Z7M"qJ’2_2Gq'’2-
Очевидно, что при конечноэлементпых аппроксимациях члена
— div (X grad и) матрица жёсткости G будет иметь ненулевые элемен-
ты вне главной диагонали (и при этом не существует корректных про-
цедур устранения ненулевых внедиагональных элементов G ). Поэто-
му вычислительная процедура построения численного решения на базе
такой аппроксимации по времени обязательно будет включать в себя
этан решения СЛАУ на каждом временном слое. Преимуществом же
такой аппроксимации по времени является то, что получаемая схема
абсолютно устойчива при любых сочетаниях шагов по времени и про-
странству (хотя при недостаточно малых шагах по времени она может
давать довольно большую погрешность численного решения в виде его
осцилляций по t), в то время как явная схема устойчива лишь при
определённом соотношении шагов по времени и пространству, которое
может приводить к значительному росту количества необходимых для
устойчивого счёта временных слоев при использовании пространст-
венных сеток с мелкой ячейкой дискретизации (особенно в случае
применения пространственных сеток с локальными сгущениями уз-
лов).
7.5.Аппроксимация начально-краевых задач ...
381
При аппроксимации начально-краевой задачи для уравнения гипср-
болического типа на сетке с неравномерным шагом по времени удобно
использовать тот же подход, который был использован чуть выше при
построении трёхслойной или четырёхслойной схемы для уравнения
параболического типа. В этом случае решение и также должно быть
представлено в виде (7.14) для трёхслойной схемы или в виде (7.25)
для четырёхслойной схемы, причём полиномы T\l(t) определяются
соотношениями (7.15)-(7.17) или (7.26)-(7.29) соответственно.
Чтобы получить явную схему аппроксимации уравнения (7.2) с не-
равномерным шагом по времени, вычислим значения первой и второй
производных функций (7.15)-(7.17) при t = :
^]2 (*) Af() d\i (0 2
dt f=h-i AZA/j ’ dt2 /=6-i AfAij ’
^Ti (0 A tj) — A tj d2v{ (t) 2
dt A tj A /() dt2 A/[At(j
rfq/j (i) At( ct2^ (t) 2
dt AiAi0 ’ dt2 f=6-i ~ AiAi0 ‘
Поскольку с учётом представления (7.14)
водные по времени аппроксимируются как
первая и вторая произ-
сб/,1
z-2 (*)
dt
+ uJ 1
d'n! (0
dt
, *У) (0 = _ At» j-2 At» - Ati
dt AtAt] A^At»
/=6—1
A 6
AtA^j
t/7,
i d2^) (0
Я/2
2- -
AZ-Atj
—± J. u'
A t(j
+ 2 U
aZa/b
аппроксимация дифференциального уравнения (7.2) по времени может
быть записана в виде
2 ?—2 2 /-1 . 2
X —т~г и' г—и 3 ~г~г
л(а/Д^ AtjAto А/Д/ц
382
7.Применение МКЭ для решения нестационарных задач
(АЛ) >_9 , Afn — Aii 1 । )
---у^у- UJ z Н---у —L и-1 1 + -у-1; U1 -
ДСДц Дб|Дц) ДгДЦ) у
— div^Xgrad u7-1) = jf7-1. (7 42)
Конечноэлементная аппроксимация краевой задачи для уравнения
(7.42) приведёт к матричному уравнению вида
—2—M'qJ-2 - - 2 г МУ'-1 +—2—MxqJ --^-M"q'~2 +
Д/-А£] AijAio AiAi() 4 AiAi] 4
+ ^P^-NTq'-! + —yy—Mnq7 +Gq'-1 = b', (7 43)
ДцДц)
которое фактически является СЛАУ для вектора q7 с матрицей А и
вектором правой части d следующего вида:
А = —Ят-Мх +-^-Мп,
AtAi() A^Aifj
d = b7 Д— Mxq7~2 +--2- JVPq7"1 +
Af Afj Ai)A^)
+ -4~мпч7~2 - Gq'-1-
А£Л/Л A^Ato ч 4
Аналогично может быть построена чстырсхслойная неявная схема
аппроксимации уравнения (7.2). Для этого нужно представить решение
и в виде (7.25) и вычислить при t — tj первые и вторые производные
функций (7.26)-(7.29 Полученная в результате этого неявная схема в
отличие от схемы (7.39) обычно даёт заметно меньшие осцилляции
численного решения, и, кроме того, опа позволяет в процессе счёта
изменять шаг по времени, что, в свою очередь, даёт возможность по-
высить эффективность используемых вычислительных процедур при
решении некоторых практических задач.
7.6. ОБ ОЧЕРЁДНОСТИ ВЫПОЛНЕНИЯ АППРОКСИМАЦИИ
ПО ВРЕМЕНИ И ПРОСТРАНСТВУ ПРИ РЕШЕНИИ
НЕСТАЦИОНАРНЫХ ЗАДАЧ
До сих пор при построении численного решения нестационарной
задачи мы использовали подход, в котором сначала выполнялась дис-
кретизация дифференциального уравнения по времени, а затем приме-
нялся МКЭ для вычисления решения на каждом временном слое. При
использовании неявных схем на каждом временном слое фактически
решалась эллиптическая краевая задача, и поэтому получаемое конеч-
ноэлементное решение было ближайшим (среди всех функций про-
странства, порождаемого набором базисных функций ф,) в энергети-
7.6.06 очерёдности выполнения аппроксимации по времени ...
383
ческой норме к функции, являющейся решением этой эллиптической
задачи при заданных значениях и на предыдущих временных слоях1
В принципе же, можно изменить очерёдность выполнения аппрок-
симации нестационарных задач по времени и пространству. Соответ-
ствующие эквивалентные вариационные формулировки для na4ajii.no-
краевой задачи параболического типа имеет вид
J X grad и grad ifodQ + J а — vodQ + J fiui\}dS =
Q Q S3
= J fvl}dQ + f 6v()dS + JVv0 e (7.44)
Q S2 S;{
а для задачи гиперболического типа - вид
f X grad и • grad v[}dQ + Г о Ду- v{]dQ + [f fiuv{}dS =
J J eft J Qt/ J
ц о о s3
— J + J &ul}dS + J" Vv0 e (7.45)
n s-2 s3
В соотношениях (7.44) и (7.45) искомое решение и является функ-
цией как пространственных координат х, у и z, так и времени t, а
пробные функции т() - функциями только пространственных перемен-
ных.
Конечноэлементное решение и1' вариационных уравнений (7.44) и
(7.45) будем искать в виде
uh = &(0 • ?/,z), (7.46)
где ф,- — базисные функции МКЭ, a - их веса, являющиеся функ-
циями только времени t .
Как обычно, подставляя в вариационные уравнения (7.44) и (7.45) вме-
сто и функцию и" (представленную в виде (7.46)), а вместо пробных
функций v() поочерёдно базисные функции фг (точнее те из них, которые
равны нулю на S{ \ получим конечноэлементные системы в виде сисгем
обыкновенных дифференциальных уравнений для весов q./t'):
Gq + Мп + M5’q = bQ + bS2 + bS(, (7.47)
Gq + Mn + Mx + MS;tq = bJ2 + l/’2 + bS:l , (7.18)
dt dt2
1 Этим очень удобно воспользоваться при изучении погрешности полу-
чаемого численного решения.
384
7.Применение МКЭ для решения нестационарных задач
где G , Мп, М и М 3 - стандартные глобальные матрицы жёсткости
и массы (М^3 - глобальная матрица вклада от краевого условия
третьего рода), определяемые соотношениями
Gy = J X grad ф,; • grad фjdQ, М" = J ,
Q n
= f ₽ф,ф/5,
Q 5:1
a b , b‘S2 и bS;1 - глобальные вектора правой части (bu - вклады от
конечных элементов, Ь$2 и Ь3 - вклады от границ со вторыми крае-
выми условиями):
Ь? = f /фгйП, bf2 = fo^dS, bf3 = Jpu^dS.
n s3
Если для решения систем обыкновенных дифференциальных урав-
нений (7.47) и (7.48) использовать какую-либо из рассмотренных нами
ранее схем аппроксимации по времени, то для вычисления значения
qz = qli,) на текущем временном слое будет получена точно та же
конечноэлементная СЛАУ, которую мы получали при другой очерёд-
ности выполнении аппроксимации по пространству и времени. Запись
же конечноэлементной системы в виде (7.47) или (7.48) (т.е. системы
обыкновенных дифференциальных уравнений для весов <?,(/)) обычно
используется из-за её большей наглядности.
7.7. РЕШЕНИЕ ЗАДАЧ С ГАРМОНИЧЕСКИМИ ПО ВРЕМЕНИ
ИСТОЧНИКАМИ
7.7. L ПОСТАНОВКА ЗАДАЧИ
Рассмотрим задачу для уравнения (7.2), в котором правая часть
/ представима в виде
f (ж, (/, z, t) — f !i (ж, у, z) sin wf -ь /' (ж, т/, 2) cos art . (7.49)
Если остальные параметры рассматриваемого уравнения (7.2) не за-
висят от времени, то тогда и его решение и может быть представлено
в виде
и (ж, у, z,t) — и” (ж, у, 2) sin wt 4- иг,(ж, 7/,2)coscL)i, (7.50)
где us и л' - две зависящие только от пространственных координат
функции, удовлетворяющие системе уравнений
7.7.Решение задач с гармоническими по времени источниками
385
—div(X grad u5) — - w2yus = f ,
—div (X grad ) + uo?/ — w2xur = f‘.
(7.51)
To же самое можно сказать и о решении краевой задачи, если нс
только f, но и параметры краевых условий являются гармонически
изменяющимися по времени функциями с одной и той же частотой ш:
uq (х, у, z,t) = и* (х, у, z) sin + uq (з:, т/, z) cos wt, (7.52)
О (x, y, z, t) — 6* (x, 7/, z) sin wf + 0r (x, т/, z) cos wi, (7.53)
up (x, ?/, z, i) = г/р (ж, у, z) sin wi + (x, y, z) cos wt. (7.54)
В этом случае функции us и ис должны удовлетворять краевым усло-
виям
ди*
дп 8-л
и- |Si = и.,,
ди*
дп
-О'
S2
151 = w-
дис
. = &’>
дп S2
ди( । .-j
дп s-л
Is-j
(7.55)
(7.56)
(7.57)
Ьз
7.7.2. ПОСТРОЕНИЕ КОНЕЧНОЭЛЕМЕНТНОЙ АННРОКСИМАЦИ
Выполним конечноэлементную аппроксимацию краевой задачи
(7.51), (7.55)—(7.57).
Сначала получим эквивалентную вариационную формулировку.
Для этого умножим каждое из уравнений системы (7.51) на пробную
функцию v и применим формулу Грина (интегрирования по частям).
В результате получим систему двух вариационных уравнений:
J (Х grad и* • grad v — voucv — u2x»Cvj dQ + f \3usvd,S =
= J /'vdQ + J Q*vdS + J ^'u^vdS,
Q S2 S.i
J (X grad ur grad v + wou,s’v — w2xwrt»j dQ T J ^urvdS =
Q
= f frvdQ + J&vd.S + f
о S-2 S-л
(7.58)
Уравнения (7 58) должны выполняться для aioGoit о G II , у ювле-
гворяющей однородному первому краевому условию па i рапицс .S', .
386
7.Применение МКЭ для решения нестационарных задач
Построим конечноэлементную аппроксимацию па основе вариаци-
онной формулировки (7.58) Пусть ('фг} - набор базисных функций
(г = !...«). Чтобы получить конечноэлементную СЛАУ, заменим в
(7.58) каждую из искомых функций us и иг на функции
п и
ия h = 7 ' ф.; и uc,h — , а вместо пробной функции подста-
г=1 Л=1
вим поочередно базисные функции ф, (дальнейшие рассуждения о
формировании копечноэлементной СЛАУ будем проводить для ситуа-
ции, когда в задаче нет первых краевых условий1):
— / <тфг tyjdQ
grad ф7 — ш2хФ?Ф/) dCl +
(7.59)
ib J (х srad
+ loаф,ф7йО
J=4n
i = 1...77..
(7.60)
В результате мы получили систему из 2п уравнений с 2/г неиз-
вестными q* и (]' . Чтобы определить матрицу и вектор правой части
полученной конечноэлементной СЛАУ, пронумеруем её уравнения и
неизвестные следующим образом. Уравнения из (7.59) и (7.60) будем
нумеровать поочерёдно таким образом, что »-е уравнение из (7.59)
будет иметь номер 2i — 1, а z-е уравнение из (7.бб) - номер 21. Соот-
ветственно пронумеруем и неизвестные этой системы, которые обо-
1 При наличии в задаче первых краевых условии, как обычно (см. рассуж-
дения на с. 235-237), из вариационных уравнений (7.58) заменой пробной
функции v на базисные функции ф, не должны формироваться уравнения
конечиоэлементнон СЛАУ, соответствующие фиксируемым (обеспечиваю-
щим выполнение главных краевых условий) весам (ц и q,:t .
7.7.Решение задач с гармоническими по времени источниками
ЗК7
значим qt, j = 1...2?/ (т.е. неизвестные q* и q\ системы уравнений
(7.59) и (7.60) мы объединяем в один вектор q ):
= <l'j, 42 j = (i'j> j = •
Обозначим
P,:I = f (X grad ' grad “ ^Х'ФхФ./)^ + [ ^),^.jdS, (1.61)
Q 6’:$
cit = w Г оф/ф^И . (7.62)
Q
Тогда матрица копечноэлементной СЛАУ будет иметь следующую
структуру:
'Рп ~С11 Pl2 -С12 Р\п.
Си Р11 <42 Р\2 <Ап Р\п
?21 -С21 Р22 -Q2 Р2п ^2)1
А = Qi Р21 с22 Р22 c2it Р2,<
Рп1 С/» 1 Рп2 сп2 Рпп
С»1 к Рп1 С„2 Р„2 Рпп /
Очевидно,
2x2 вида
что в этой матрице явно выделяются блоки размера
P'.i с'.1
% p,j
для хранения которых достаточно только двух ячеек памяти. Каким
образом, для хранения всей матрицы в блочном формате с учетом
структуры блока А требуется практически в два раза меньше намял и,
чем при хранении её покомпонентно. Поэтому при программной рса
лизации в таких случаях, как правило, используются блочные формана
хранения данных, в том чиспе и с учётом разреженной cipyici vpi i м.н
рицы. Более подробно о технологиях работы с матрицами, храпящими
ся в разреженном блочном формате, будет рассказано в дес я i ом ра к-
ле.
Заметим, что при решении задач, у которых в большей чк in । к
чётной области коэффициент о равен нулю, iimcci смьк i kiucih ih.i
типа блоков. Если блок А'7 соответствует узлам / и у, xoim бы о шн
388
7 Применение МКЭ для решения нестационарных задач
из которых не лежит внутри или на границе области с о 0 , то он
будет иметь структуру
А’> =
'р„ О'
.° р‘J’
и для его хранения достаточно только одной ячейки памяти.
В принципе, решение гармонических задач можно искать с исполь-
зованием комплексных чисел. Действительно, если считать us дейст-
вительной, а ис мнимой частями комплекснозначной функции и (а
можно и наоборот, с соответствующим знаком у мнимой части), то и
веса можно интерпретировать как комплексные числа с
действительной частью q'j и мнимой q'- . Аналогично и блоки А.'3 мат-
рицы А конечноэлементной СЛАУ можно интерпретировать как ком-
плексные числа с действительной частью p,.t и мнимой частью сг/.
Заметим, однако, что для задач, у которых в большой части расчётной
области коэффициент ст равен нулю, при представлении компонент
конечноэлементной матрицы в комплексном виде невозможно допол-
нительно сэкономить память за счёт заведомо нулевой мнимой части у
большинства этих компонент.
Сборку глобальной матрицы (и вектора правой части) для гармони-
ческих задач также удобно выполнять из локальных матриц конечных
элементов. Мы проиллюстрируем это в следующем разделе на примере
решения одномерной гармонической задачи, описывающей электро-
магнитное поле в задачах магнитотеллурического зондирования в го-
ризонтально-слоистой среде.
7.7.3. ПРИМЕР РЕШЕНИЯ ОДНОМЕРНОЙ ГАРМОНИЧЕС КОИ ЗАДАЧИ
Как уже говорилось в разделе 1.3.4, нестационарное электромаг-
нитное поле может быть описано с помощью вектора-потенциала. В
данном примере источником электромагнитного поля являются гармо-
нические токи, текущие в одном направлении (примем за это направ-
ление ось х ) в плоскости z = const: J — 0,0), где .7,. = sinwi.
Поскольку свойства среды изменяются только вдоль оси г, задача
становится одномерной, а вектор-потенциал имеет одну ненулевую
компоненту, зависящую от z: А = (Д (г),0,0). Заметим также, что
поскольку при магнитотеллурическом зондировании изучаются до-
вольно низкие частоты, при моделировании электромагнитных про-
цессов можно пренебречь токами смещения (т.е коэффициент е поло-
жить равным нулю).
Таким образом, электромагнитное поле при моделировании процес-
сов магнитотеллурического зондирования в горизонтально-слоистой
среде может быть описано следующими уравнениями:
7.7.Решение задач с гармоническими по времени источниками
389
—div grad A* j — wo А!'. = О,
—div Pj-grad A'I: j + wo А]. — О,
причём параметры этих уравнений и краевых условий имеют вид
р, = р() = 4-rvlO 7
0.01, zGiAUQ3,
0.1, 2GQ2,
cj = 2т • 0.01,
а расчётная область, в которой будем ис-
кать решение этой системы уравнений,
состоит из четырёх подобластей и пред- х-----
ставлена на рис. 64.
Построим конечноэлеменгную сетку,
состоящую из четырёх конечных элемен- рис 6i ]‘печения область
то в. При этом подобласть Q1 разобьём на
два конечных элемента Q| = 2• IO0,—10'1 j и Q2 = f—IO5,— 2 IO'1 j, a
конечные элементами Q3 и О4 будут совпадать с подобластями .О2 и
.0 соответственно. Для конечноэлементной аппроксимации будем
использовать линейные базисные функции Проиллюстрируем сборку
локальных матриц этих элементов в глобальную матрицу.
Учитывая соотношения (7.61)-(7.62), получим локальную матрицу
первого элемента:
Рп -cQ1 С11 р\1 -cQi 1 С 12 IO5 ВО 20-п 3 юГ| 14) -IflA 3
г”1 ,Д1 Ah 20тг ю5 1()п
А"’ = С11 С12 ??12 3 1'0 3 ~ НО
J2i J*i 10Г| 10~п юГ| 20 п
^21 С21 ^22 С22 1М) 3 1'0 3
J*1 Ютт И)-' 20 д юг‘
21 ^21 22 ^22 3 1'0 3 1*11 .
Аналогично вычисляются
конечных элементов:
;.“2 = Ah = 1-25-105
*4 ^22 11.П
компоненты локальных матриц остальных
*12
о2 1.25- 1О5
> =--------------------
21 ц„
390
7.Применение МКЭ для решения нестационарных задач
АЪ сп - = С22 Ют А1-2 3 ’ С12 = rQ2 21 _ 8т 3 ’
Рп’ = р 11 104 Ро ’ = ^21 = ю4 Ро
си - Юз = С22 20т лъл 3 ’ 12 = Юз С21 _ Ют 3 ’
= Р h = 22 Ю4 Л Ио ’ Р'г — Ю1 2 21 = ю4 Ро ’
- AU - ~ С22 — 2т о4 3 ’ 12 = Ю« zl — 2L 3 '
После элементов занесения локальных матриц первого и глобальная матрица примет вид: второго конечных
Ю5 14) 20-к 10Г1 3 )Ц) IQit 3 0 0 0 0 0 0
20к 3 Ю5 М() Юк 3 ю'1 МО 0 0 0 0 0 0
Ю5 14) Юк 2.25-10'Г| 3 цо 36к 3 1.25105 МО 8к 3 0 0 0 0
А = Ютт 3 0 Юг 14) 0 36к 3 1.25-10'5 М-о 2.25-105 МО 8к 3 8 т 3 1.25-Ю5 Но 1,25105 МО Юк 3 0 0 0 0 0 0 0 0
0 О 0 0 8 ту 3 0 1.25-105 1-4) 0 ] 6 т 3 0 1.25-Ю5 Мо 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
(т.е., например, в компоненту А33 глобальной матрицы заносятся ком-
поненты A33] и ripj2 локальных матриц конечных элементов и
в компоненту Л34 - компоненты и Л^2 и т.д.).
Аналогично заносятся локальные матрицы третьего и четвёртого
элементов. После занесения локальных матриц всех конечных элемен-
тов и учёта краевых условий конечноэлементная СЛАУ с матрицей А
и вектором b будет иметь вид:
7.7.Решение задач с гармоническими по времени источниками 391
1 0 о 0 0 0 0 О О ()
0 1 о 0 0 0 0 (I 0 И
1()5 14) Юту 3 2.25105 14) 36ту 3 1.25105 14) _8ту 3 () о () о
Юту 3 К)5 14) 36 ту 3 2.25-105 14) 8 ту 3 1.25-1 С)5 14) о 0 о О
0 0 1.25-1()5 14) _8тг 3 1.35105 14) 36-п 3 1()4 14) Юту 3 о ()
А = 0 0 8 ту 3 1.25105 14) Збтг 3 1.35105 14) Юту 3 Ю4 14) о 0
о 0 О 0 1()4 14) Юту 3 2104 14) 22ту 3 1()4 14) _ту 3
0 0 0 0 Юту 3 К)4 14) 22ту 3 2104 14) ТУ 3 1()4 14)
о 0 о 0 О О К)4 14) _ту 3 К)4 14) 2ту 3
0 0 о о () () ТУ 3 ю4 14) 2 ту 3 К)4 14)
/ \т
b = (о, О, О, О, О, О, О, О, J. 0]
Решением полученной конечноэлементной СЛАУ будет вектор
q = _l_(o. 0, -0.31, 0.137, -0.172, -1.07, 0.507, -1.27, 1.71, —1.32)Т .
На рис. 65,а приведены графики конечноэлементных решений
а/' = ^2 921-14’/: и 4/ — Х2672/. Фа Рис- ^5,6 для сравнения пока-
1=1 1=1
5 h 18
заны графики конечноэлементных решений А/ = 721-1'Ф/. 11
1=1
<h 18
А,’ = полученных на подробной сетке, содержащей 18 уз-
1=1
лов.
Приведём значение в точке z = 0 конечноэлементного решения,
полученного на подробной сетке (значения приводятся с округлением)
а;;7' (о) = о.о179, А'г7' (о) = -0.0135.
Заметим, что в точке z = 0 в конечноэлементном решении на грубой
сетке получено практически два точных знака.
Отмстим, что тестирование процедуры решения гармопнчс! кии <а
дачи может выполняться аналогично процедурам юстирования ш uni
гичсских задач, т.е. с использованием полиномов пенсии, равной пе-
псин используемых базисных функций (см. раздел III). В ыином
392
7.Применение МКЭ для решения нестационарных задач
случае задаются две искомые функции us и и' в виде кусочных поли-
номов, эти функции подставляются в соотношения (7.51) и (7.55)—
(7.57) и из них определяется вид правых частей fs и f и правые час-
ти краевых условий.
Кроме этого, процедура решения гармонической задачи может быть
протестирована и с помощью решения соответствующей нестационар-
ной задачи. Однако в этом случае следует помнить, что для сопостав-
ления решения нестационарной задачи с решением гармонической при
расчёте процесса как нестационарного (т.е. путём решения параболи-
ческой задачи) необходимо выбирать такие значения времени, чтобы
решение в интересующих нас пространственных точках уже практиче-
ски не менялось на соседних временных периодах.
7.7.4. ОБ ОШИБКЕ ЛППРОКС ИМАЦИИ КОНЕЧНОЭЛЕМЕПТПЬ*К РЕШЕНИЙ
ГАРМОНИЧ1 ( КПХ ИД\Ч
Здесь мы получим оценку погрешности коиечноэлемеитиого ре-
шения гармонической задачи для случая, когда вторая производная по
времени в исходной нестационарной задаче отсутствует1, т.е. изучае-
мый процесс описывается системой дифференциальных уравнений
—div (X grad us‘) — = /s’,
- div (X grad и' ) + wu5 = f .
(7.63)
1 Эта задача является начально-краевой задачей для уравнения параболи-
ческого типа.
7.7.Решение задач с гармоническими по времени ис гопниками
393
Для простоты будем считать, что краевые условия в решаемой за-
даче только первого и второго рода и только однородный. I огда точ-
ное решение {u,s’,ur} краевой задачи для системы уравнении (7 63)
будет удовлетворять системе вариационных уравнений
а. ( ия ,4) — ш (о и‘:, v) = (f s, v) у \/v G Hx,
a(ur, v) + и (ст ия, v) = (f‘ ,v)t Vv G H\
где билинейная форма a(u,w) определяется соотношением
a (v, w) = J X grad v • grad wdQ., (7.65)
а под записью (и, w) понимается стандартное скалярное произведение
пространства L2 :
= J vwdQ. (7.66)
о
Напомним, что если в решаемой задаче есть границы, где заданы
краевые условия первого рода (т.е. mes Si ^0), билинейная форма
(7.65) является скалярным произведением, которое мы называли энер-
гетическим,
Конечноэлементное решение (где us'h G Vh и
urJ> е vb, vh — конечномерное подпространство гильбертова про-
странства Н1 ) ищется из решения системы вариационных уравнений
= V? £ у’, (7.67)
а(и''‘У') + ш(аи’’Л,«‘) = (Г,1/’), Vi/'eO'. (7.68)
Чтобы оценить погрешность конечноэлементного решения, нам
нужно получить оценку отклонения функции ия'1, от функции //’ и
функции uc'h от функции ис . Эту оценку мы будем искать в Hicpieiii
ческой норме, порождаемой энергетическим скалярным произведены
ем (7.65):
||7/||э = Ja (и, v) . (769)
Мы будем также использовать и норму пространства 1 . оирс в
лённую через скалярное произведение (7.66):
1 Хотя полученные результаты будут справедливы и дня i ыч с нецдпо
родными краевыми условиями, в том числе и гретьего рода.
394
7.Применение МКЭ для решения нестационарных задач
M = (7.70)
Рассмотрим функции us,h G V1' и й,:,1> G такие, что
а (и:4 — й8'1', irs — й,1) = min а [и* — vll , ufl — vh),
а (и1 — uc,ll,uc — ucJl) = min а (и* — v1'', иг — vh},
V ’ „i'.eVh \ Г
т.е. функции йЛ'7' и йг,/' являются ближайшими (среди всех функций
?/' G V1') в энергетической норме (7.69) к функциям и* и и' соответ-
ственно.
Нетрудно убедиться, что эти функции iT'1' и й1'1 удовлетворяют
уравнениям Галёркина
a(us,h,vh} — — ^f\vhy \/vbeVh, (7.71)
4- Vi? G Vh . (7.72)
Действительно, поскольку функция пЛ фактически является реше-
нием уравнения Галёркина
a(u\v) = (Fs, г), VvG#1, (7.73)
в правой части которого стоит функция
F‘s = fs + wouc, (7.74)
то его конечноэлементное решение й5,Л находится из решения вариа-
ционного уравнения
a(us'll,vh j = (Fs,vhy \/vhEVh, (7.75)
и, с учётом того, что (см. (7.74))
(Fs,vh) = (/5 + иои‘\ vh^
функция й8’1'', очевидно, удовлетворяет уравнению (7.71). При этом
йЛ’71 как конечноэлементное решение уравнения (7.73) должна быть
функцией, ближайшей в энергетической норме к функции us.
Абсолютно так же можно доказать, что ближайшая (среди всех
функций vh G V1') в энергетической норме к иг функция Uc'h удовле-
творяет вариационному уравнению (7.72).
Запишем вариационные уравнения (7.71) и (7.72) в виде
a(us’h, uh) — = (f'\vhy 4vheVl1, (7.76)
7.7.Решение задач с гармоническими по времени источниками
395
где
а , v1' j 4- со (ой'4'11, vk) = (fc, v1'),
Vvh G Vh,
(7.77)
fs = fs + wo(uc -uc'h},
fc = fc — coo (us — US'k^ ,
(7.78)
(7.79)
т.е. функции йА’/л G Vh и uc'h G V1' являются конечноэлеменi ними
решениями гармонической задачи с «возмущённой» правой частью
{7‘\7'}, определяемой соотношениями (7.78)-(7.79), и эта «возму-
щённая» правая часть {7's,7r} отличается от правой части f }
исходной задачи тем меньше, чем точнее представимы функции ия и
и' в пространстве V1'где ищутся их конечноэлементные приближе-
ния и*'1' и и1'1'' (напомним ещё раз, что us'b - это ближайшая к us
среди всех ?/* G V1', а й,:'1' - ближайшая к ис среди всех ir G V1).
Оценим отклонения конечноэлементных решений для задач с «на-
стоящей» и «возмущённой» правыми частями. Для этого вычислим
квадрат энергетической нормы разности функций й‘*,А и и'4,1' (восполь-
зовавшись соотношениями (7.6/) и (7.71), в которых в качестве произ-
вольной функции v1' берётся функция us'h— и4’1):
+ (7‘ч, usJ'— usJ'^ — и:4'1’^ — (fs, us'h— usJl^ =
= (7s- fs,us'h- + w (o(uc'h- u1’1'), vsJl- us>h). (7 80)
Аналогично, воспользовавшись соотношениями (7.68) и (7 72), но
лучаем
Тогда с учётом того, что
о
396
7.11рименение МКЭ для решения нестационарных задач
из (7.80) и (7.81) получаем
= I r,us-h- ; Г- . (7.82)
Воспользуемся неравенством Коши-Буняковского
(v, w) < yl(u,v) • y/(w, w) = llvll • llwll
для оценки правой части соотношения (7.82):
В результате из соотношений (7.82) и (7.83) получим
Теперь воспользуемся тем фактом, что для произвольной функции
v Е Н[ её норма |р;|| пространства L2 (определяемая соотношениями
(7.66) и (7.70)) может быть оценена через энергетическую норму ||г;||э
(определяемую соотношениями (7.65) и (7.69)) следующим образом:
7.7.Решение задач с гармоническими по времени источниками
397
II" К ФИ,- (7 85)
где к > 0 - некоторая константа, зависящая только от расчёinoii об-
ласти и коэффициента диффузии X решаемой задачи’.
С учётом (7.85) неравенство (7.83) примет вид
1 Например, в качестве к в неравенстве (7.85) может быть взята величина
^1/Piiiin , гДе Pniiu > 0 - минимальное собственное число оператора
L = —div(X grad), который действует на заданные в расчётной области Q
функции, удовлетворяющие однородным главным краевым условиям на гра-
нице iS'i.
2 Вывод соотношения (7.87) можно интерпретировать также как доказа-
тельство устойчивости конечноэлементной аппроксимации для рассматри-
ваемых гармонических задач (полученных из нестационарных задач для урав-
нений параболического тина), т.е. доказательство того, что малым изменени-
ям правой части будут соответствовать и малые изменения конечно-
элементного решения. Вообще говоря, устойчивость копечпоэлемен той ап
проксимации в некотором смысле является следствием корректности Варна
ционной задачи (7.64), которая заключается в том, что малым изменениям
параметров задачи (и в том числе правой части {/“ ,/' }) соответствую г ма
лые изменения решения {ич,и‘ }. При этом та часть доказательства коррскг
ности вариационной задачи (7.64), где нужно изучить реакцию решения
на малые изменения правой части {/'*,/' }, ничем нс будет <н ш
чаться от рассмотренного нами доказательства справедливости сот ношения
(7.87), и в этом доказательстве не является принципиальным ю, иi какого
пространства (IIх или I '') берутся решения (для «настоящей» и «boimmhch
ной» правых частей) и пробные функции. Поэтому вместо г и ii.ocpioii.i про
странства /71 2 можно взять его подпространство I h важно го и.ко, чтооы
пробные функции и решение были элементами одного к тоги »«< функции
пильного пространства. И тогда из условия корректное ш исконной варнлпи
онпой задачи по правой части мы сразу же получим усчопне устойчивости
(7.87) консчноэлсмсптноп аппроксимации
398
7.Применение МКЭ для решения нестационарных задач
В нашем случае с учётом вида (7.78)-(7.79) «возмущённой» правой
части неравенство (7.87) примет вид1
и, ещё раз воспользовавшись соотношением (7.85), получаем оценку
отклонения конечноэлементного решения , д',/1} от функций
р7Л'/', и.'1' |, ближайших в энергетической норме к точному решению, в
следующем виде:
где а11МХ - максимальное значение параметра о в расчётной облас-
ти Q.
11олученное неравенство (7.89) приводит нас к следующему оче-
видному результату. Конечноэлементное решение , ие1' | будет
сходиться в энергетической норме к точному решению {д',и‘ } с тем
же порядком, с каким сходя тся к функциям id и ?/.' ближайшие к ним
функции idJl и й‘ h из соответствующих (шагу дискретизации h и
порядку конечных элементов) конечномерных подпространств Vh. А
поскольку кусочно-полиномиальные интерполянты функций id и id
схотятся к этим функциям в энергетической норме со скоростью
O(hk\ (к - порядок конечных элементов), то
= <2 (/?*).
1 Заметим, что с помощью неравенства (7.88) не представляет особого тру-
да доказать, что в норме пространства Ь2 конечпоэлементное решение
, и''-1'} сходится к точному со скоростью О (Л?11). Для этого, правда,
потребуется «противоположное» (7.85) неравенство ||?л,|| < С|р ||, где С > О
так же, как и к. в (7.85), константа, зависящая только от расчётной области и
коэффициента диффузии решаемой задачи.
7.7.Решение задач с гармоническими по времени источниками 399
Неравенство (7.89) позволяет сделать ещё один практически важ-
ный вывод: погрешность конечноэлементного решения рассматривае-
мой гармонической задачи зависит оттого, нисколько о пики к функ-
циям и5 и ис ближайшие к ним функции из подпространства \г/‘.
Поэтому выполнять дробление ячеек сетки или повышать порядок
элементов нужно в тех местах расчётной области, где функции и” и
и‘ хуже всего аппроксимируются кусочными полиномами соответст-
вующей степени. Чуть позже мы рассмотрим некоторые технологии
уточнения конечноэлементного решения для эллиптических задач,
некоторые из которых (например те, где контролируется скачок нор-
мальной производной на границах конечных элементов или сравнива-
ются решения на дроблёных сетках) будут вполне пригодны и при
решении гармонических задач рассмотренного здесь типа.
Заметим, что для уравнений (7.51), отличающихся oi уравнений
(7.63) наличием в них слагаемых —ц?хм'* и —ш2хвопрос о кор-
ректности вариационной постановки (и соответственно устойчивости
конечноэлементной аппроксимации) решается уже несколько иначе.
Аналогичное рассмотренному доказательство с введением билинейной
формы
a (v, w) = Г X grad и grad wdQ — ш2 J \vwdQ, (7.90)
Q О
может пройти только в том случае, когда ш2х111ах < р«де
Xi.iw = maxx , a ll,,,;,. > 0 - минимальное собственное число опера-
/V. 111 • IX rX. I
гора I/ -—div(Xgrad). Если же неравенство w2x.l(mx <1’111111 ,,с вь,_
полняется, то билинейная форма (7.90) может уже не бын положи-
тельно определённой и, например, когда о = 0 и значение ш2\ равно
одному из собственных значений оператора L = div(Xgrad), гар-
моническая задача с нулевой правой частью будет имен ненулевое
решение (в виде собственной функции, соответствую щеп иычению
ш2х ). И в результате будет уже невозможно доказан., что малым из-
менениям правой части должны соответствовать малые изменения
решения (поскольку если ц — собственное число оператора
— div (X grad) и w - решение уравнения — div (X grad) — |и/= / , то
этому же уравнению будет удовлетворять и функция и и. I- , где
z/p — собственная функция, соответствующая собственному числу р).
Разумеется, вес эги особенности гармонических задач вида (7.51) (с
ненулевыми слагаемыми —ш2х^Л и — w2X'Uf ) проявляются при вычис-
лении их конечноэлсментпых решений - в отличие от задач (7.63) при
их решении может наблюдаться отсутствие сходимости при измельче-
нии сетки и «странное» поведение получаемых конечноэлементных
400 7.Применение МКЭ для решения нестационарных задач
решений. В принципе же сложные электромагнитные задачи1 с суще-
ственными токами смещения в основном решаются либо как неста-
ционарные, либо как задачи на собственные значения и собственные
функции (часто называемые модами), и в этих случаях применение
МКЭ даёт прекрасные результаты как по точности получаемых при-
ближённых решений, так и по возможностям решения задач самой
высокой сложности.
1 Обычно это так называемые «полевые» задачи, т.е. задачи, в которых
ищется распределение электромагнитного поля.
8.1.Типы сосредоточенных источников
101
8. СОСРЕДОТОЧЬ ИНЫЕ ИСТОЧНИКИ
В СКАЛЯРНЫХ ЗАДАЧАХ
8.1. ТИПЫ СОСРЕДОТОЧЕННЫХ ИСТОЧНИКОВ
Как мы уже могли убедиться, при использовании МКЭ не возни-
кает никаких принципиальных трудностей при аппроксимации источ-
никового члена f дифференциального уравнения (I I), если f Е П"
(где Н° = L2 (Q) - пространство суммируемых с квадратом на Q
функций) Ситуация, когда f Е Н , соответствует случаю так назы-
ваемого распределённого источника, т.е. случаю, когда выделяемая в
любом объёме Qe источником f мощность J fdQ, стремится к нулю,
если к нулю стремится объёмная мера Qc :
J fdO —> 0 при mesQ. = j d£l —* 0 . (8.1)
При этом функцию f называют также объёмной плотностью источ-
ника. Чаще всего объемная плотность f задастся в виде кусочно-
постоянной функции либо в виде зависимости от каких-либо физиче-
ских характеристик.
Однако оывают ситуации, когда необходимо вычислить поле и ,
порождаемое так называемыми сосредоточенными источниками
источниками, выделяющими ненулевую мощность на множестве mi pi i
ноль (естественно, имеется в виду объёмная мера этого множеч тип)
Так, если ненулевая мощность выделяется на некоторой новермнн in
S , лежащей внутри трёхмерного объёма Q, то такой источник обычно
называют поверхностным. Если ненулевая мощность вы де лисп. i на
некоторой линии L (не обязательно прямой) в трёхмерной об ьк и 42,
то мы будем называть такой источник сосредоточенным на ihiiiiii
Если же ненулевая мощность выделяется в некоторой точке
р = (хр,ур,гр} трёхмерной области Q, то такой источник мы будем
называть точечным (заметим, что в данных нами опр< де в инях указа-
ние на принадлежность линии L и точки р ////>< \ ui’/u/oh оонле ти Ц
402
8.Сосредоточенные источники в скалярных задачах
является принципиальным - более подробные пояснения по этом}
вопросу мы дадим чуть позже).
Обычно сосредоточенные источники связывают с понятием
Ь-функции. Мы рассмотрим fi-функции трёх типов (в соответствии с
тремя типами рассмотренных нами выше сосредоточенных источив
ков).
Под поверхностной fi-функцией, сосредоточенной па поверхности
S , мы будем понимать функцию fi,s = b‘s (z, у, z) такую, что объёмный
интеграл от неё но произвольной подобласти Ц равен площади по-
верхности S, - Qc QS, i с. площади той части поверхности S, кото
рая лежит внутри Q, :
f bsdQ = J' dS , St = Qc П S . (8.2)
Соответственно мы будем говорить, что поверхностный источник
fs = Г (ж, //, z) = [)'s 6,ъ ( г, т/, z) имеет поверхностную плотное и,
p,s, значения которой определены лишь в точках поверхности S , и
такой поверхностный источник в произвольной трёхмерной подобна
сти выделяет мощность
f fsdQ = JpsdS , Sc = Qe П S. (8.3)
Под сосредоточенной на линии L fi-функцией мы будем пони
мать функцию bL = b/ (;i\ipz) такую, что объёмный интеграл от псе
по произвольной подобласти Пг равен длине линии Д = Пе П С, т.е.
длине той части линии L , которая лежит внутри :
JbLrfQ = Jdl. , /. = Qe П L (8.4)
Qe 4
(здесь криволинейный интеграл j d,L означает длину линии Д)
Соответственно будем говорить, что сосредоточенный на линии ис-
точник у7' = fL (ж, у, z) = р1 Ь! (;г:,у,г) имеет плотность р7, (значения
pL определены лишь в точках линии L ), и такой источник в произ-
вольной подобласти QE выделяет мощность
J fLdQ = f pLdL , Lc = Qe П L . (8.5)
8.1.Типы сосредоточенных источников
ЦП
И, наконец, под сосредоточенной в точке р 6-функцией (или го-
чечной 6-функцией) мы будем понимать функцию бр = б7'(.г,//, z)
такую, что интеграл от неё по произвольной трёхмерной подобласти
Qr равен единице только в том случае, если точка р лежи г внутри
Qe, а в противном случае интеграл от б7' равен нулю:
J Ъ1’(1£1 =
1,
О,
если р 6 Qc,
если р 0 Qe.
(8.6)
Соответственно под сосредоточенным в точке р (или точечным)
источником с мощностью р7' мы будем понимать источник
/7' = р7'б7'(ж, t/, z), который в произвольной трёхмерной подобласти
Qr выделяет мощность, равную р7’, лишь в том случае, если точка р
лежит внутри Qc (в противном же случае такой источник в Qe выде-
ляет нулевую мощность):
если р G Qc,
если р 0 Qc.
(8.7)
Введённые нами понятия поверхностной 6-функции, сосредото-
ченной на линии или в точке разделяют не всегда. Например, если в
данном нами определении точечной 6-функции (8.6) подобласть Qc не
считать обязательно трёхмерной, то это определение включит в себя и
сосредоточенную па линии б-функцию (если подобласть Ос считать
двумерной), и поверхностную б-функцию (если подобласть Qr счи-
тать одномерной). Мы же всё-таки будем разделять эти понятия, по-
скольку для поверхностных и сосредоточенных на линии или в точке
источников по-разному решается вопрос о сходимости МКЭ-решений.
Так, для задач с поверхностными источниками не возникает ника-
ких проблем с обоснованием сходимости копечноэлементной аппрок-
симации к точному решению. Для этого достаточно выбрать кусочно-
полиномиальные базисные функции подходящего типа, и конечноэле-
ментные решения с дроблением сетки будут сходиться к точному в
строгом соответствии с порядком полиномов, определяющих базисные
функции, и скоростью уменьшения размеров конечных элементов.
При использовании же МКЭ для решения трёхмерных за ыч с со-
средоточенными на линии или точечными источниками вопрос сходи-
мости коиечноэлемептных аппроксимаций к точному решению во всей
расчётной области не столь прост: в окрестности этих источников точ-
ное решение неограниченно растёт и не имеет суммируемых с квадра-
том первых производных, т.е. точное решение не является )лсментом
гильбертова пространства Я1 , а все рассмо!репные нами рапсе теоре-
тические результаты, посвящённые сходимости конечно элементных
404
8.Сосредоточенные источники в скалярных задачах
аппроксимаций к точному решению, были получены при условии, что
точное решение принадлежит пространству Н[ . Тем не менее МКЭ
позволяет довольно успешно решать и такого рода задачи, и ниже мы
рассмотрим некоторые из возможностей, которые предоставляет МКЭ
для построения приближённых решений задач с сосредоточенными на
линии и точечными источниками.
8.2. КОНЕЧНО ЭЛЕМЕНТНЫЕ АППРОКСИМАЦИИ ТРЁХМЕРНЫХ ЗАДАЧ
С ( (К РЕДОТОЧЕННЫМИ ИСТОЧНИКАМИ
Сначала рассмотрим случай поверхностного источника. Пусть
правая часть дифференциального уравнения (1.1) является суммой
распределённого источника /° — f'} (.г, y,z) и поверхностного источ-
ника /' = рг6] (:r,y,z) (т.е. /’ имеет плотность р1 на поверхности
I ). Тогда при использовании метода Галёркина эквивалентная крае-
вой задаче (1.1)-(1.4) вариационная формулировка примет вид
J X grad и. • grad i\}d.Q + j ^uvl}dD. + j fiuVudS = J fnvnd,Q +
Q Q S3 Q
+ (>rvi}dS -}• J" 0vlydS + J" V'Po G TTp. (8.8)
г S2 S3
Уравнение (8.8) может быть легко получено из уравнения (1.1) при
подстановке в него вместо [ суммы + ./' и учёте того, что
J frviydQ, — j' р1 b1 v()dQ = J р1 v[}dS
п п г
(8.9)
(сравните (8.9) с (8.3) и учтите, что в (8.9) в качестве Sc выступает
поверхность Г, ps = рг ).
Проанализируем вклад J р1 i>l}d,S в уравнение (8.8) от поверхност-
г
ного источника f] . Сравнивая его с вкладом j Ovl}dS от заданного на
S-2
поверхности S2 краевого условия второго рода, убеждаемся в их пол-
ной идентичности. Это означает, что поверхностный источник, задан-
ный на поверхности Г, должен обрабатываться точно так же, как и
заданное па Г второе краевое условие с 0 = рг .
Поэтому при построении конечпоэлементной СЛАУ техника учёта
вкладов от поверхностных источников ничем не отличается от техники
учёта вкладов от краевого условия второго poja. Гак, если конечно-
элементная аппроксимация краевой задачи проводится с использова-
нием тетраэдральной сетки, то поверхность Г, на которой задан по-
8.2.Конечноэлементные аппроксимации трёхмерных задач ...
105
верхностный источник с плотностью рг, удобно представим, набором
треугольников 5^, являющихся гранями соответствующих ютращров
конечноэлементной сетки (т.е. поверхность Г аппроксимируется 1 ра-
нями тех тетраэдров, у которых как минимум три вершины леж-л на
Г). Очевидно, список треугольников, аппроксимирующих Г, лучше
всего формировать при выполнении процедуры генерации конечно-
элементной сетки.
Вклады в вектор правой части конечноэлементной СЛАУ от тре-
угольников , как и при учёте краевых условий второго рода, удобно
представить в виде локальных векторов, и тогда соотношения, опреде-
ляющие эти вклады, ничем не будут отличаться от соотношений, опре-
деляющих вклады от вторых краевых условий.
Например, при использовании для конечноэлементной аппрокси-
мации кусочно-линейных базисных функций вклад от треугольника
S}', аппроксимирующего часть границы Г, может быть представлен в
виде вектора
bs =
mes S?
12
2рГ + Р2 + Рз
р| + 2р2 + Рз
pF + Р2 + 2Рз
(8.10)
г г
где р* — значения плотности поверхностного источника р в верши-
нах треугольника Sf (с учётом того, что плотность рг на аппрок-
симирована своим кусочно-линейным интерполяптом в виде разложс-
3
ния по базисным функциям р* = ^Р/Ф/ )•
Аналогично могут быть получены эквивалентные вариационные
постановки (в виде уравнений Галёркина) и конечноэлемептныс ап-
проксимации для задач (1.1)-(1.4), в которых источниковый член
кроме распределённого источника с объёмной плотностью /*’ имеем в
виде слагаемого сосредоточенный на линии L источник
fL'= pLbL z) или точечный (сосредоточенный в точке
р = (хр, ур, zp) ) источник fp = ррЬр (.т, у, z).
Уравнение Галёркина при наличии сосредоточенного на iihhhi /
источника (с плотностью pL ) имеет вид
J X grad 1/. • grad + J ^uu[}dQ.-b J = J |
ц n S-д
406
8.Сосредоточенные источники в скалярных задачах
Qvl}dS +
V«(, € Я,1,,
(811)
а при наличии точечного (сосредоточенного в точке р = ур ,zp})
источника (мощностью р1") - вид:
grad и • grad 4- / fiu,ul}dS = I f^v^dQ,
+
O Q S3 Q
I pz'w() (тр,ур,гр) + JQvl}dS + J [3?/(|V()dS Vm() G Яп- (8.12)
Si Si
Рассмотрим технику учёта вкладов в конечноэлсментную СЛАУ от
сосрсдоточсиного на линии L источника. 11ри этом будем считать, что
линия L аппроксимирована рёбрами, являющимися рёбрами тетраэд-
ральных конечных элементов с заданными на них кусочно-линейными
базисными функциями. Тогда вклад от ребра Ц. в вектор правой части
конечпоэлементной СЛАУ может быть представлен в виде локального
вектора (при условии, что pL представлена на Lk в виде линейной
комбинации р{'Ф1 + р2фг базисных функций ф] и ф2, соответствую-
щих вершинам этого ребра, н с учётом того, что фг и ф2 на ребре Lk
являются линейными функциями):
mesLk +Р2
b = —,
6 [pi I- 2р-г
(8.13)
Если же линия L представлена в виде совокупности отрезков Lk,
не совпадающих с ребрами конечных элементов, то учет вкладов от
несколько усложняется. В этом случае каждому отрезку Lk необ-
ходимо поставить в соответствие один конечный элемент1, внутри (или
на границе) которого лежш Lk. Затем нужно вычислить значения т|д
и д/2 каждой базисной функции ф; в первой (ц4) и второй (ц/2)
вершинах . И, наконец, предполагая, что р1 представлена па Lk в
виде линейной комбинации ррф] + р2ф2 двух линейных на ребре Lk
1 Если отрезок Lk лежит внутри или на (ранице нескольких конечных
элементов, то сто всегда можно разбить на несколько подотрезков, каждый из
которых лежит только в одном конечном элементе. Поэтому в дальнейшем
мы будем считать, что каждый отрезок Lk линии L лежит внутри или на
границе только одного конечного элемента.
8.2.Конечноэлементные аппроксимации трёхмерных ia uin
107
функций ipj и ф>2 » изменяющихся от 0 до 1 на этом ребре, можно вы
числить вклады в соответствующие компоненты вектора правой час in
= f (pf^l + Р2Ф2) • Ф// = f (pf<Pl + Р2ф2)(п./1Ф1 + 4^2.)^
U- Lk
= (2рЬ] д + рЬ1./2 + рЬдт + 2р^т]/2) (К । 0
(где под можно понимать как локальные, так и глобальные базис-
ные функции).
Обратим внимание ещё на одну довольно важную деталь для случая,
когда линия, на которой задан сосредоточенный источник, не состоит из
отрезков прямых (т.е. имеет криволинейные участки) и сумма длин ре-
бер Г' , аппроксимирующих Г, не равна длине Г . В этом случае можно
довольно существенно улучшить точность приближённого решения,
если на отрезках Г1, аппроксимирующих криволинейные участки I
кривой Г (т.е. на к G К Г* ~ Г , где К - множество соответствующих
индексов), задать эквивалентный по мощности источник. Для этого на
криволинейных участках Г нужно задать такую плотность р1 сосредо-
точенного источника, чтобы выполнялось соотношение •
JprrfS= £ f prdS,
р A* G A рА’
т.е. на рёбрах ГА: нужно таким образом изменить плотность источника,
чтобы его суммарная мощность по объединению ребер Г1 , аппрокси-
мирующих криволинейный участок границы Г, была равна мощности,
выделяемой на Г исходным источником. При этом, естественно, рас-
пределение плотности р1 на U ГА , аппроксимирующих Г, должно
z.e
быть максимально близким к р1 . Эта коррекция может быть особенно
эффективна тогда, когда решение задачи изучается в удалённых от
источника подобластях.
Вообще говоря, коррекцией плотности источника можно заменю
улучшить точность конечноэлементною решения и в некоторых га ычах
с сосредоточенными на искривлённых поверхностях источниками (осо
бепно тогда, когда интерес представляют значения искомого решении в
удаленных от поверхностного источника подобластях). В »iom t is41г
Q
также плотность р поверхностного источника на искрив к ипой но
всрхности S можно скорректировать так, чтобы суммарная моиивн и.
заданного па S источника совпала с суммарной мощностью ис гочпикл
заданного на аппроксимирующих S поверхностных элсмсчилх
В принципе, то же самое можно сказать и о распре inn-ином в обьсмс
источнике, если соответствующая подобласть (с ним нс пищиком) пме
408 8,Сосредоточенные источники в скалярных задачах
ет искривлённые границы и сумма объёмов аппроксимирующих эту
подобласть конечных элементов не совпадает с объёмом подобласти.
Процедура учёта сосредоточенного в точке р (точечного) источни-
ка наиболее проста. Если точка р = (ж1", ур, zp) является узлом сетки,
соответствующим глобальной функции ф?, то сосредоточенный в точ-
ке р источник J1' с плотностью рр учитывается добавлением значе-
ния рр к 7-й компоненте глобального вектора правой части. Если же
точка р нс совпадает с узлом сетки, то необходимо найти содержащий
её конечный элемент (при этом точка р может попасть не только
внутрь элемента, но и на его грань или ребро), затем вычислить значе-
ния q7 = ф7 (xp,yp,zp) каждой глобальной базисной функции ф7,
отличной от нуля в точке р, и занести значения ррт] • в соответствую-
щие (у-е) компоненты вектора правой части конечноэлементной
СЛАУ.'
Значения т)7 удобно вычислять через значения в точке р соответ-
ствующих глобальным функциям ф7 локальных функций конечного
элемента, в который попала точка р. Если точка р лежит на границе
между элементами, то можно выбрать любой (но только один) из этих
элементов.
Как мы убедились, техника учёта сосредоточенных источников в
МКЭ относительно проста. При учёте поверхностных источников наи-
более технологически трудоёмким является этап формирования граней
конечных элементов, аппроксимирующих поверхность с источниками
(заметим, что технология формирования таких поверхностей обычно
абсолютно идентична технологии формирования поверхностей со вто-
рыми и третьими краевыми условиями). При учёте сосредоточенных
на линии источников необходимо либо сформировать набор рёбер ко-
нечных элементов, аппроксимирующих линию L, и воспользоваться
соотношением (8.13), либо искать пересечения отрезков, на которые
разбивается L (или которыми она аппроксимируется), с конечными
элементами и воспользоваться соотношением (8.14). Наиболее проста
технология учёта сосредоточенного в точке источника - здесь доста-
точно определить либо узел сетки, совпадающий с источником (или
ближайший к нему), либо любой конечный элемент, внутри или на
границе которого лежит источник.
Обратим внимание на некоторое различие рассмотренных вариан-
тов обработки поверхностных и сосредоточенных на линии источни-
ков. Действительно, если при учёте поверхностного источника мы рас-
смотрели лишь вариант, в котором поверхность Г аппроксимируется
только гранями конечных элементов (и это накладывает некоторые
ограничения на процедуру генерации конечноэлементной сетки), то
при учёте сосредоточенного на линии £ источника было рассмотрено
два варианта: когда линия L аппроксимируется рёбрами конечных
элементов (и узлы аппроксимирующих L отрезков совпадают с узла-
8.2.Конечноэлемен1ные аппроксимации трёхмерных гадач
4 09
ми конечных элементов) и когда линия L произвольным образом пе-
ресекает конечные элементы (т.е. рёбра аппроксимирующих / отрез-
ков могут не совпадать с рёбрами конечных элементов).
Дело в том, что точное решение задачи с поверхностным источни
ком является элементом гильбертова пространства И1 и имеез раз-
рывные на поверхности Г нормальные (т.е. вдоль нормали к 1 ) про-
изводные. При совпадении аппроксимирующих Г поверхностных
элементов Sf с гранями конечных элементов мы получаем такое ко-
нечномерное подпространство V1' пространства Н[, которое содер-
жит функции с разрывными на S] (а значит, и на Г) нормальными
производными, что даёт возможность заметно улучшить аппроксима-
цию искомого решения и ускорить сходимость приближённых реше-
ний к точному при измельчении сетки (особенно в окрестности источ-
ника). А если бы элементы S[. не совпадали с гранями конечных эле-
ментов, то помимо серьёзных технологических трудностей реализации
этого варианта (связанных с поиском пересечений поверхности Г с
конечными элементами) поверхностный источник как бы «размазы-
вался» по тем конечным элементам, внутрь которых попадали бы S[ ,
и это могло лишь ухудшить аппроксимацию.
Несколько иная ситуация возникает при наличии в задаче сосредо-
точенного на линии или точечного источника. И в том и в другом слу-
чае точное решение и эллиптического уравнения уже не является эле-
ментом пространства Н1 , поскольку в окрестности сосредоточенного
на линии L источника функция (grad?i)2 ведёт себя как -у (где г -
г
расстояние до линии L), а в окрестности точечного источника
(grad-л)2 ~ Д- (где г - расстояние до точечного источника). Дейст-
г4
вительно, для сосредоточенного на линии L источника интеграл о г
(grad и)2 по некоторому цилиндру радиуса 7,, с осью, являющейся
частью линии L , может быть оценен как
4)
Г (grad л)2 dQ ~ J -у rdr = оо , (К-15)
оц о 7
а для точечного источника интеграл от (grad л)2 по шару О.п| радиу-
сом Го и с центром в точке задания точечного источника можс« бы и»
оценен как
4)
J (gradu)2dQ~ Jr2dr = ос>, (8.16)
о
410 8.Сосредоточенные источники в скалярных задачах
т.е. точное решение для этих источников не имеет суммируемых с
квадратом производных, и вследствие этого перестают быть обосно-
ванными рассмотренные в третьем разделе теоретические оценки схо-
димости конечноэлементных решений к точному.
Однако на практике ситуация с точностью конечноэлементных ре-
шений при наличии в задаче сосредоточенных на линии и точечных
источников вовсе нс так плоха. Дело в том, что для многих практиче-
ских задач решение требуется вычислять на некотором (как правило,
довольно значительном) расстоянии от сосредоточенного на линии или
точечного источника. Конечноэлементное же решение имеет очень
большую (лучше даже сказать, совершенно неприемлемую) погреш-
ность лишь вблизи сосредоточенных на линии или точечных источни-
ков (в районе нескольких ближайших к источникам ячеек сетки), а на
некотором расстоянии от этих источников погрешность конечноэле-
ментного решения становится вполне приемлемой и даже может вести
себя в соответствии с рассмотренными в третьем разделе теоретиче-
скими оценками (если погрешность конечноэлементного решения оце-
нивать в подобластях, удалённых от сосредоточенных на линиях или
точечных источников). В принципе, этому факту можно дать объясне-
ние, хотя и не вполне строгое, но полезное для понимания поведения
конечноэлементных решений в окрестностях сосредоточенных в точ-
ках и на линиях источников.
Проанализируем ситуацию с точечным источником. Для опреде-
лённости будем считать, что используются лагранжевы конечные эле-
менты1 и точка р, в которой задан точечный источник, совпадает с
узлом сетки, имеющим глобальный номер I. Тогда вкладом от него в
правую часть конечноэлементной СЛАУ является вектор Ь?, у кото-
рого лишь одна компонента Ь[ равна мощности источника р/;, а ос-
тальные компоненты — нулевые. Нетрудно показать, что абсолютно
такой же вклад в глобальный вектор правой части может дать распре-
делённый по объёму расчётной области Q источник (где
j
ф, - базисные функции, wf - значения плотности этого распределён-
ного источника в узлах сетки2), если веса w.j вычислить как решение
СЛАУ с матрицей массы М :
Mw = tC. (8 17)
Действительно, если бы мы взяли распределённый источник со зна-
чениями его плотности wt в узлах сетки и представили его в виде ку-
сочно-полиномиального интерполянта , то вклад в г-ю ком-
поненту глобального вектора правой части имел бы вид
1 Хотя аналогичные рассуждения можно провести и для элементов других
типов.
2 Напомним, что сейчас мы рассматриваем лагранжевы конечные элементы.
8.2.Конечноэлементные аппроксимации трёхмерных задач
411
/ Z2 = 52 Mijwi ’ (8.18)
Q j J
где M.tJ = ^'ф/ф7с1П — компоненты стандартной матрицы массы, т.е.
вкладом в глобальный вектор правой части от такого распределенного
источника являлся бы вектор Mw. А поскольку коэффициенты
определялись из решения СЛАУ (8 17), становится очевидным, что
построенный нами распределённый источник 52 Даёт в гло-
бальный вектор правой части конечноэлементнои СЛАУ точно такой
же вклад Ы', что и точечный источник pz'6/J (т,т/, z).
Аналогичные рассуждения можно провести и для сосредоточенного
на линии источника.
Интересно поведение распределённых источников, эквивалентных
сосредоточенным на линии и точечным источникам. Так, при использо-
вании кусочно-линейных базисных функций плотность эквивалентного
распределённого источника максимальна в ближайших к точке р или
линии L узлах сетки. При удалении на один шаг сетки от ближайших к
точке р или линии L узлов плотность эквивалентного распределённого
источника уменьшается столь резко, что у неё, как правило, даже меня-
ется знак. При удалении от р или L ещё на один шаг сетки значение
распределённого источника опять значительно уменьшается по модулю
и опять чаще всего с изменением знака и т.д. Таким образом, плотность
эквивалентного распределённого источника чаще всего ведёт себя при
удалении от р или L как осциллирующая функция (шаг осцилляции -
ячейка сетки) с быстрым затуханием амплитуды колебаний. Соответст-
венно и конечноэлементные решения могут иметь существенные осцил-
ляции в ближайших к точке р или линии L узлах сетки (иногда вило и»
до смены знака конечноэлементного решения в тех узлах, где мспяс!
знак эквивалентный распределённый источник). На некотором же уда-
лении от точки р или линии L плотность эквивалентного распределен
ного источника становится довольно малой и конечноэлементное решс
ние реагирует в основном на суммарную мощность, выделенную в окрт
стности точки р или линии L, и поэтому осцилляции в конечно l ie
ментном решении практически прекращаются и его точное и. тисню
улучшается. Поэтому несмотря на то, что вблизи сосредоточенных в
точке р или линии L источников МКЭ может давать решение с огром
пой погрешностью (что можно объяснить именно осциллиниями п ки
пости эквивалентных распределённых источников), на искоюром (по
рядка 4-5 ячеек сетки) удалении от р или L точносп конечно» и мчи
ного решения может стать вполне приемлемой.
Этим же можно объяснить тот факт, чго с дроблением сежи по
грешность конечноэлсментного решения в некоторой <ч р.1ниченной
412
8.Сосредоточенные источники в скалярных задачах
подобласти, удалённой от точки р или линии L, может убывать со-
гласно рассмотренным в третьем разделе теоретическим оценкам даже
несмотря на то, что точное решение и не является элементном гиль-
бертова пространства Я1 функций, имеющих суммируемые с квадра-
том первые производные во всей расчётной области (но при этом и
имеет суммируемые с квадратом первые производные в любой подоб-
ласти расчётной области, не содержащей точку р или линию L вме-
сте со сколь угодно малой их окрестностью).
Рис. 66. Поведение эквивалентных
На рис. 66 приведены графики поведе-
ния эквивалентных распределенных ис-
точников для трёхмерной задачи в одно-
родном пространстве с сосредоточенным
в точке р источником. Эти графики по-
строены вдоль линии, проходящей через
точку р. Соответствующие конечноэле-
ментные решения (как и значения пока-
занных на рис 66 эквивалентных распре-
деленных источников) были получены на
двух параллелепипеидальных сетках с
разными размерами ячеек и приведены на
рис. 67 (длины ячеек сетки вдоль линии,
точечному распределённых для которой были приведены графики
источников для двух сеток значений эквивалентных распределенных
источников и конечноэлементных решений, сразу видны на приведён-
ных рисунках по осцилляциям значений этих источников и решений).
I Га рис. 68 также для двух сеток с различными длинами ячеек пока-
зано поведение эквивалентных распределенных источников и конечно-
элементных решении вдоль линии L', перпендикулярной линии L
(источник сосредоточен на линии L ).
Рис. (Я Поведение конечноэлемептных решений и1'’1, г//1,2 на двух сетках (а)
и их погрешность относительно точного решения и (б) i
8.2.Конечноэлементные аппроксимации трехмерных шдач . 113
Рис. 68. Поведение эквивалентных сосредоточенному на линии распределённых
источников (а), конечноэлементных решений (б) и их погрешностей относительно
точного решения («) для двух сеток
Отметим, что описанное поведение конечноэлементных решений
для задач с сосредоточенными источниками практически ле зависит от
того, совпала ли точка р с узлом сетки и аппроксимируется ли линия
L или нет рёбрами конечных элементов (хотя программная реализа-
ция варианта, основанная на совпадении р и L с узлами и рёбрами
конечноэлементной сетки, наиболее проста). Поэтому при обработке
сосредоточенных в точке или на линии источников выбирается наибо-
лее удобный для решения конкретной задачи вариант. Так, вариант с
заданием точечного источника в узле сетки или сосредоточенного на
линии источника на ребрах конечных элементов более удобен и прост
в реализации. Однако если, например, необходимо решить серию задач
в одной и той же расчётной области, но с различным расположением
сосредоточенных источников, то привязывать их к узлам сетки или
рёбрам конечных элементов оказывается совершенно нецелесообразно.
В этом случае гораздо более удобным является вариант с независимым
от конечноэлементной сетки расположением сосредоточенных в точке
или на линии источников.
Вообще же рассмотренные в данном разделе методы построения
конечноэлементных аппроксимаций для задач с сосредоточенными на
линии или в точке источниками с учётом их в виде cootbcicibs ioiiiiix
б-функций в эквивалентных вариационных постановках являю н я
далеко не самыми лучшими по точности при ограниченных вычи< ш
тельных затратах. В девятом разделе будут рассмотрены i орал к» оо ire
эффективные методы решения задач с сосредоточенным и iu iohiihk.i
ми, основанные на выделении из искомых решений нолей спереди к»
чепных источников в более простых (но в определенном смы» ie (о
вольно близких к требуемым в исходных задачах) расчетных об i.icimx
414
8.Сосредоточенные источники в скалярных задачах
8.3. СОСРЕДОТОЧЕННЫЕ ИСТОЧНИКИ
В ДВУМЕРНЫХ И ОДНОМЕРНЫХ ЗАДАЧАХ
Довольно часто при решении задач с сосредоточенными источ-
никами расчётная область имеет такую структуру, что решение может
быть описано некоторой двумерной или даже одномерной функцией
соответствующих координат (чаще всего цилиндрических, но иногда
декартовых или сферических). При этом даже в случае, когда решени-
ем задачи является трёхмерная функция, нередко у нес существует
довольно хорошее двумерное или одномерное приближение (в окрест-
ности сосредоточенного источника такое приближение существует
практически всегда). Таким образом, определённый интерес представ-
ляют задачи с сосредоточенными источниками в областях меньшей
(чем три) размерности В связи с этим излагаемый здесь материал мож-
но также считать вспомогательным для рассматриваемого в следую-
щем разделе метода решения задач с сосредоточенными источниками
на основе выделения из искомых трехмерных полей близких им в не-
котором смысле полей меньшей размерности.
Сначала рассмотрим двумерные задачи, описывающие поля в трёх-
мерных областях с неизменяющимися по оси Z геометрией и пара-
метрами исходной краевой задачи.
Примером такой задачи может служить эллиптическая краевая за-
дача в области Q, изображённой на рис. 69,<з. Будем считать, что на
поверхностях Г] и Г-2 задано краевое условие dujdn = Ou-ldz = 0, на
поверхностях Г3 и Г4 — краевое условие и = u,(l(x,y), на поверхно-
стях Г5 и Гс - краевое условие (?/) и
= = а на В||У'|Ре1П,еи поверхности Г7 — поверхно-
1Г(| •
стный источник с плотностью ё 7 = р5 (?;) • 8Л (т, ?/, г) . Будем также
считать, что коэффициент диффузии X — Х(.г,//) не зависит от коор-
динаты z , а коэффициент равен пулю.
Тогда функция и , являющаяся решением этой задачи, также не бу-
дет зависеть от координаты z и может быть найдена как решение
краевой задачи, заданной в двумерной области Q, являющейся сече-
нием исходной трёхмерной области Q плоскостью z = const
(рис. 69,6). При этом в двумерной задаче и краевые условия, и источ-
ник на внутренней границе формально оказываются заданными на
линиях Г5, Гс и Г7 (являющихся линиями пересечения исходных
поверхностей Г5, Гс и Г7 с плоскостью z = const).
Соответственно и при обработке краевых условий на Г5 и Гр и ис-
точника на Г7 в МКЭ вклады от них вычисляются как интегралы по
линиям (что формально похоже на обработку сосредоточенных на ли-
ниях источников в трёхмерных задачах). Однако по сути источник на
8.3.Сосредоточенные источники в двумерных ...
415
Г7 является все-таки поверхностным, что подтверждается поведением
решения и и в окрестности Г7. Действительно, и имеет ограничен
ные (и соответственно суммируемые с квадратом) первые производ-
ные, причём производная по нормали к Г7 имеет на Г7 конечный
скачок (равный рЛ), т.е. функция а не имеет никаких особенноеicii,
присущих решениям трёхмерных задач с сосредоточенными па линиях
источниками (таких, как неограниченный рост решения и несумми-
руемость квадратов его первых производных в окрестности сосредото-
ченного источника).
Рис. 69. Расчётные области с поверхностным источником на Г7
(о) -трёхмерная; (б) -двумерная
Таким образом, в двумерном случае заданные на линиях источники
по сути являются поверхностными (т.е. фактически сосредоточенными
на поверхностях, получаемых при движении двумерных линий вдоль
третьей координаты, отсутствующей в двумерной задаче), и проблемы
точности конечпоэлементной аппроксимации этих задач (связанные с
построением сеток, сгущениями узлов, выбором базисных функций)
аналогичны соответствующим проблемам при решении трехмерных
задач с поверхностными источниками (хотя, конечно, в двумерных
задачах эти проблемы решаются гораздо проще).
Аналогичная ситуация возникает и для осесимметричных задач, ко
гда их решением является функция двух координат г и z в цнлин ipn
ческой системе координат {г, ф, z] .
В качестве примера рассмотрим эллиптическую краевую тдачх д !Я
уравнения — cliv(Xgradiz) + =/*3 в цилиндрической об час i п ,
изображённой на рис. 70. В ней линии г = const фак1ичссьн пипсы
вают боковые поверхности цилиндров, а линии z = const новерхпо
сти торцов цилиндров. Будем считать, что на границах 1 и I oo i.it
ти заданы краевые условия второго рода с правыми час iumii 0, (? )
и 02 соответственно, на остальных внешних границах краевые
416
8.Сосредоточенные источники в скалярных задачах
условия первого рода или однородные краевые условия второго рода, а
на внутренней границе Г3 — сосредоточенный источник с плотностью
р(г). Тогда эквивалентная формулировка в форме Галёркина для этой
задачи примет вид:
J X grad и grad ш/Q + yuudQ, =J 0\vdS +J G^vdS + J pvdS, (8 19)
?! Г-2 r;1
где элемент расчётной области dCl = rdrdz фак-
тически является элементом объёма, a dS — это
элементы границ Fj, Г-2 и Г3 (обратим ещё раз
внимание на то, что заданный на линии Г3 ис-
точник фактически оказывается поверхностным
и учитывается в вариационной постановке абсо-
лютно так же, как и краевое условие второго
рода).
В общем случае, когда поверхностные источ-
ники (или краевые условия второго рода) в осе-
симметричной задаче заданы на произвольных
линиях Г, элемент поверхности dS определяет-
ся соотношением rdl, где dl - длина элемен-
тарного участка Г. При построении конечно-
элементной аппроксимации интегралы по этим
линиям заменяются на сумму интегралов по
Рис. 70. Расчётная
область с поверхностным
источником на Г;(
отрезкам, являющимся рёбрами соответствующих конечных элемен-
тов, и, например, при использовании кусочно-линейных базисных
функций интеграл но одному из таких ребер Г/ для базисной функции
фг, равной единице в одном из узлов этого ребра, может быть вычис-
лен следующим образом:
J0ф,</.8 —Jb^rdl =J вф,. (»;Ф/ + т-ф^dl = 0 (8.20)
рА: рА’ рА:
где (rt, 2,) и - координаты узлов ребра Г*’, ф,: и ф, - базисные
функции, равные единице в соответствующих узлах ребра Г\
/1 = л/(7' ~ rj)2 + (zi ~ zi'f ~ ДЯИ||а ребра Г1. При вычислении инте-
грала (8.20) предполагалось, что параметр 0 был аппроксимировано на
ГЛ значением 0 = const, а якобиан г был представлен в виде линей-
ной комбинации базисных функции г = туф; 4-г;ф7-, и было также
учтено, что ф,- и -ф - две линейные на Г1 функции, изменяющиеся от
I до 0 и от 0 до 1 соответственно при движении по Г' от узла
до узла В принципе не составляет особого труда посчитать
8.3.Сосредоточенные источники в двумерных ...
417
значение этого интеграла в случае представления параметра 0 в виде
линейной комбинации базисных функций ф, и ф,.
Сосредоточенные источники, заданные в точке, в двумерных зада-
чах фактически являются аналогом источников, сосредоточенных на
линии в трёхмерных задачах. Решения двумерных задач с источника-
ми, сосредоточенными в точке, ведут себя точно так же. как решения
трёхмерных задач с источниками, сосредоточенными налипни.
Например, магнитное ноле от бесконечной (по г) токовой линии,
определяемой уравнениями х = .т(), у = у1}, в неизмсняющейся но z
среде описывается уравнением
— div
— grad и
М'
где плотность тока / является б-функцией, определённой в точке
Если бы свойства среды изменялись вдоль оси z, то задачу
нужно было бы решать в трёхмерной области с источником, сосредо-
точенным на линии
Очевидно, что решение двумерной задачи с сосредоточенным в
точке источником будет иметь особенность в окрестности этой
точки - оно и его производные будут неограниченно расти при при-
ближении к точке (т(),?/() ) и его производные не будут суммируемы с
квадратом в любой подобласти, содержащей точку (Х(},У(}). Тем не
менее МКЭ позволяет вычислять приближенные решения и таких за-
дач, причем на некотором удалении от (.Toj/o) получаемое конечно-
элементное решение может быть довольно точным.
При решении двумерных задач техника учёта сосредоточенных в
точке (д;о,З/о) источников очень проста (фактически она одинакова в
задачах любой размерности): в те компоненты глобального вектора
правой части, которым соответствуют не равные нулю в точке ( г(), //п)
глобальные базисные функции, заносится мощность источника, умно
женная на значение соответствующей глобальной базисной функции в
этой точке (.тп, т/о).
Решение же одномерной задачи с сосредоточенным в точке ш
точником ведёт себя так же, как решение трёхмерной задачи с поверх
ностным источником, заданным на плоскости х = const Гочное рг
шение такой задачи уже будет иметь суммируемые с квадратом первые
производные, и соответственно полученные на основе Nil ) npin> п«
жённые решения с дроблением сегки будут сходиться к го*пюм\ в н>> i
ном соответствии с оценками из третьего раздела.
418
9.Конечноэлементные процедуры решения краевых задач ...
9. КОНЕЧНОЭЛЕМЕНТНЫЕ ПРОЦЕДУРЫ РЕШЕНИЯ
КРАЕВЫХ ЗАДАЧ С ВЫДЕЛЕНИЕМ ЧАСТИ ПОЛЯ
9.1. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ С ВЫДЕЛЕНИЕМ ЧАСТИ ПОЛЯ
Рис. 71. Вид осесимметричной
конструкции
Для многих практических задач,
описываемых сложными математиче-
скими моделями, как правило, сущест-
вуют достаточно хорошие приближения,
которые могут быть получены с исполь-
зованием более простых моделей и соот-
ветственно с гораздо меньшими вычис-
лительными затратами. Этим обстоя-
тельством можно воспользоваться для
построения более экономичных (по вы-
числительным затратам) и точных про-
цедур решения сложных задач. Проде-
монстрируем идею построения таких
процедур на примере решения следую-
щей относительно простой (модельной)
задачи.
Рассмотрим задачу определения ста-
ционарного температурного поля в осе-
симметричной конструкции, изображённой на рис. 71 Соответствую-
щая расчётная область, состоящая из трёх подобластей Q , Q2 и Q3,
представлена на рис. 72. Стационарное температурное поле в области
Q — Ql U Q2 U fr описывается дифференциальным уравнением
—div (X grad it) = f, (9.1)
которое для нашей задачи в цилиндрической системе координат при-
нимает вид
1 д ( \ ди\_____д I\ ди\ _
•\ 1 ' Г\ 1 ГХ I А гх J
г от \ от I oz\ OZ )
(9.2)
Будем считать, что коэффициент теплопроводности X и плотность
теплового источника У имеют вид
9.1.Примеры решения задач с выделением части поля
419
50
1
0.2
в Q1,
в Q2,
в Q3,
5 • 104 (е4000’ — 1) вП1,
0 в О2 U О3.
(9.3)
Будем также считать, что на границах S\ и б1-2 задана адиабата:
= о,
ди
= 0,
(9.4)
а на границе 5) задана температура
«I. =20.
151
Можно считать, что на границе
г = 0 задано условие = 0 (хотя,
вообще говоря, эта граница имеет по-
верхностную меру нуль и любое задан-
ное на ней конечное значение плотности
потока не изменит решения задачи).
Решение u(r,z) этой осесимметрич-
ной задачи имеет довольно хорошее
приближение в виде решения u1/?(r)
одномерной краевой задачи для уравне-
ния
l_d_
г dr
ID duW
dr
(9.6)
с параметрами
50, г 6(0,0.002),
1, г 6(0.002,0.01),
(9-5)
Рис. 72. Расчётная об мен.
и конечноэлсмсппмя сены
ID
104
'4000г
г 6 (0,0.002),
г 6 (0.002,0.01)
(9.7)
дп S2
и краевым условием
=20.
1г=0.01
(9.8)
420
9.Конечноэлементные процедуры решения краевых задач ...
Очевидно, что по сравнению с двумерной задачей (9.2)-(9.5) одно-
мерная задача (9.6)-(9.8) может быть решена с очень высокой точно-
стью при гораздо меньших вычислительных затратах. Покажем, как
можно, используя решение одномерной задачи, получить нужное по
точности решение двумерной задачи (9.2)-(9.5) с значительно мень-
шими вычислительными затратами.
Обозначим через u+(r, z) разность между u(r, z) и г?1 (г, z), где
двумерная функция «/“ (?’, z) полностью определяется функцией
uiD (?'):
и° (r,z) = н1/) (г) Vz.
(9.9)
Аналогично обозначим через Xl}(r,z) и /()(r,z) параметры, задан-
ные в двумерной области П и совпадающие в ней с одномерными
функциями Х1£> (г) и fi!) (г):
X°(r,z) = X,/?(r), /°(r,z) = /w(r) Vz .
Очевидно, что коэффицисн i X() отличен от X в подобласти Q3 и сов-
падает с X в подобластях Q1 и Q2, а правая часть / " полностью сов-
падает с f (см. (9.3) и (9.7)).
Функция u+(r, z) может быть найдена как решение следующей
осесимметричной краевой задачи:
—div (X grad и+ I = — div((X” — X) grad j, (9-Ю)
\ &и+ — дп я* 0. х^- дп = 0, <?2 г>2 (9.Н)
«+| =0. 15] (9.12)
Читатель может легко убедиться, что функция и° 4- и+ удовлетво-
ряет уравнению (9.2) и краевым условиям (9.4)-(9.5). Для этого нужно
записать уравнение (9.6) в виде
—div(X° grad u()j — /°
и сложить его с уравнением (9.10), а также сложить соответствующие
краевые условия. При этом следует учесть, что правые части /() и /
уравнений (9.6) и (9.10) тождественно равны, а также то, что на грани-
не .5’, Х(,4^ =Х"4^-
on 5 oz
(г, z) = uiL> (г) нс зависит от z .
= 0,
поскольку функция
9.1.Примеры решения задач с выделением части поля
421
Построим численное решение рассматриваемой осесимметричной
задачи двумя способами: как решение, полученное в результате конеч-
ноэлементной аппроксимации задачи (9.2)-(9.5), и как решение, полу-
ченное в виде суммы решения одномерной задачи (9.6)-(9.8) и конеч-
ноэлементного решения задачи (9.10>—<9.12).
Покажем, как можно построить решение задачи (9.10)-(9.12)
Будем считать, что функция получена как решение одномер-
ной задачи на достаточно подробной сетке. Получим эквивалентную
вариационную формулировку для задачи (9.10)-(9.12). Для этого, как
обычно, умножим обе части уравнения (9.10) на пробную функцию v,
проинтегрируем по области Q и применим формулу Грина (интегри-
рования по частям). Учитывая, что на границах Q в задаче
(9.10)-(9.12) заданы однородные краевые условия (т.е. соответствую-
щие поверхностные интегралы обратятся в ноль), получим
J X grad и+- grad vein, = J ^Х() — X) grad ??’• grad vdQ Vv G . (9.13)
Q П
Представив u+ и в виде линейных комбинаций и
.7
базисных функций (где ql- - значения д” в узлах сетки) и за-
меняя пробную функцию 17 на базисную функцию ф,:, из вариационно-
го уравнения (9.13) получаем z-ю строку конечноэлементной СЛАУ:
(9.1 1)
Таким образом, матрица А полученной конечноэлемептноп ( 1АУ
является стандартной матрицей жёс!кости. Вектор же правой час in 1>
может быть получен в результате сборки локальных векторов
b = GAXq°, (9 15)
где GAX - локальная матрица жёсткости конечного темен га , ком
поненты которой определяются соотношением
= J (Х° ~ X)grad Фр. • grad ф,ДП, (9.16)
а компоненты ф’’ локального вектора q — эго знамени < и1 н coot нс !-
ствующих узлах конечного элемента Q/.. Гстссгнснно, cooiношения
422
9 Конечноэлементные процедуры решения краевых задач ...
(9.14)-(9.16) определяют только те уравнения конечноэлементной
СЛАУ, номера которых не совпадают с номерами узлов, лежащих на
границе Sj с первым краевым условием (для узлов, лежащих на S[,
формируются уравнения вида q “0, см. (9 12)).
Конечноэлементное решение, полученное по схеме (9.14)-(9.16),
фактически аппроксимирует поле и1' , источник которого для рассмат-
риваемой нами задачи находится в подобласти Q3 * * * (точнее, на её гра-
ницах), и поэтому аппроксимация поля и+ может существенно отли-
чаться по точности от аппроксимации поля и .
Сравним по точности конечноэлементные решения задачи
(9.2)-(9.5), полученные на одной и той же сетке (показанной на рис. 72
и имеющей 143 узла) по стандартной схеме и по схеме (9.14)-(9.16),
реализующей решение задачи (9.10)-(9.12). Для этого сначала решим
задачу (9.2)-(9.5) (с использованием стандартной схемы) на очень под-
робной сетке, имеющей 48441 узел. Па рис. 73 показано поведение
вдоль линий z = —0.016 и г = 0.009 полученного на подробной сетке
конечноэлементного решения и1' (будем называть его «точным»). На
этом же рисунке показан график решения и1, полученного на грубой
(изображенной на рис. 72) конечноэлементной сетке, график решения
у/’/2, полученного па сетке, вложенной к грубой, а также график реше-
ния мл'"'/'7'а построенного путём сложения решения и+’" задачи
(9.10)—(9.12), полученного на грубой сетке, и решения и<),Л одномер-
ной задачи (9.6)-(9.8) (см. (9 9)). Очевидно, что решение прак-
тически совпадает с точным решением. Полученное же на грубой сетке
решение и.1' отличается от точного на линии z = —0.016 при неболь-
ших г даже больше, чем решение одномерной задачи, при этом даже
решение на вложенной (имеющей в четыре раза больше узлов) сетке
и'!2 имеет довольно большую погрешность.
Таким образом, на очень i рубой сетке за счёт выделения одномер-
ной части поля нам удалось построить конечноэлементное решение, не
уступающее по точности конечноэлементному решению, полученному
на очень подробной сетке, в то время как на грубой сетке решение за-
дачи «напрямую» даёт совершенно неудовлетворительный по точно-
сти результат (сравнимый лишь с одномерным приближением)1. Заме-
тим, что для получения эквивалентного икп,п,1‘ по точности решения
(путём «прямого» решения задачи (9.2)-(9.5)) вычислительные затраты
1 При решении задач «напрямую» мы заменяли источник f его интерпо-
ляптом п 11 эго давало большую часть погрешности. Погрешность в
этой задаче можно довольно существенно уменьшить только за счёт более
точного учета источника на конечном элементе (например, при вычислении
компонент локального вектора с использованием численного интегрирова-
ния).
9.1 .Примеры решения задач с выделением части поля
423
Рис. 73. Графики конечноэлементных решений вдоль линий
z = -0.016 (а) и г = 0.009 (б)
В случае, когда на границе расчётной области задано третье краевое
условие, нужно соответствующим образом сформулировать краевое
условие в задаче на добавочное поле. Так, если в рассмотренном нами
примере на внешней границе г = 0.01 (которую мы теперь обозначим
как S3) задано условие теплообмена с окружающей средой, имеющей
температуру = 20 с коэффициентом теплоотдачи 0 = 5 :
+5(u L — 20) = 0, (9.17)
дп \ 15з /
то аналогичное условие необходимо задать в соответствующей одно-
мерной задаче:
+5(uw| -20) = 0. (Ч1К)
dr ,=<>.01 * Ul,°1 1
Очевидно, что в двумерном аналоге этой одномерной задачи (i .c в
задаче для функции и(|. определённой в двумерной ооп.ц ш
Q = [0.0.01] х [—0.02,0.02]) краевое условие (9.18) будет имен, ни i
1 Эти данные по уменьшению вычислительных ипр.н ииннск ibmui < tv
чаю, когда компоненты локального вектора вычислялись i 111 но 11.1011.1111км
численного интегрирования, а не при замене правой час 1 и / пнн-рпопми
том.
424 9.1<онечноэлсме1пные процедуры решения краевых задач ...
4-б(ип| — 2о) = О. (9.19)
\ is3 /
Чтобы получить краевое условие на этой границе в задаче на доба-
вочное поле, нужно в (9.17) вместо функции и подставить и+ 4- ип :
откуда
SA
X ^и+
S3
эл _ X с1ц()
5 дп
д(и+ 4- j
дп
+<
-20 = 0,
-г.
= 0.
(9.20)
Таким образом, на границе S3 для функции н+ должно быть зада-
но краевое условие третьего рода (9.20):
х^
дп S:,
+ Р(“+к -“р)
= о.
(9.21)
в котором
= 20-^4^ -а(,| .
5 Dll 5j IS;j
Заметим, что если коэффициент Х° во всех прилегающих к границе
S3 подобластях совпадает с X, то lit = 0 и краевое условие (9.21)
принимает вид
(9.22)
В результате в вариационную постановку (9.13) должны быть
включены соответствующие слагаемые, являющиеся поверхностными
интегралами по границе, где задано третье краевое условие:
J X grad и+ grad vdQ 4- J fiu+ud£l =
Ъ S3
= J [X[) — X) grad u." • grad vdQ 4- f (3^+vdQ V t» € Я1 . (9.23)
о s3
В рассмотренном нами примере расчётные области в исходной за-
даче для и, и в задаче, определяющей её приближение имели одну
и ту же внешнюю границу. В принципе же, это условие не является
9.1.Примеры решения задач с выделением части поля
425
обязательным для применения технологии выделения поля и ш ис-
комого решения и. Продемонстрируем до на примере следующей
задачи.
Рассмотрим задачу стационарного распределения темпера гуры в
расчётной области Q = Q1 UQ2, вид которой показан на рис. 74,</. )io
температурное поле описывается дифференциальным уравнением (9J)
в декартовой системе координат. Будем считать, что коэффициент ген
лопроводности является кусочно-постоянной функцией (X = Х( в Q
и X = Х2 в Q?), а плотность объёмного источника f отлична от нуля
только в подобласти Q1 и принимает в ней постоянное значение
Д = 10G . Будем также считать, что на внешней границе задано первое
однородное краевое условие и = 0.
Хорошим приближением этой задачи может служить задача в кру| е
ГУ = Q1 и О2', изображённом на рис. 74 Д с кусочно-постоянным ко-
эффициентом теплопроводности Х(), равным X] в Q1 и Х2 в Q2',
плотностью источника f, принимающей ненулевое значение только в
Q1 (равное 10е), и с краевым условием iz()| =0. Очевидно, что
решение л,° (х, у) такой задачи в круге ГУ зависит только от
г = yjx2 4- у2 и может быть получено как решение одномерной задачи
для функции uw (г) :
X[D =
10,
0.1,
1 d w dulD] _ AD
(9.24)
r e (0,0.002),
r 6(0.002,0.01),
log, re(0,0.002),
0, r 6(0.002,0.01),
(9.25)
uw| =0, (9.26)
lz-0.01
и значение u° в любой точке двумерной области ГУ может быть полу
чено как
7’ (т, у) = ulD ^/х2 + у2 ). (9,27)
Таким образом, решение исходной задачи имеет смысл иск пь как
сумму решения одномерной задачи и добавочного поля и' Функ
ция и4 (.т, у) может быть найдена как решение следу 1ощсн щи'Ш
—d iv (X grad и+) = 0 в П ,
(9.28)
426
9.Конечноэлементные процедуры решения краевых задач ...
hl’
(9.29)
в которой значения функции и" (х,у) на границе вычисляются че-
рез значения одномерной функции ulD с помощью соотношения
(9.2 "Э- При этом одномерная функция и1Г> может быть получена как
аналитически, так и численно с необходимой точностью при незначи-
тельных вычислительных затратах.
-0 01 -0.005 0 0.005 х
в
Рис. 74 Вид расчётных областей и копечноэлементпых сеток
9.1.Примеры решения залам с выделением части ноля
427
Рис. 75 Графики конечноэлементных решений вдоль линии .т = 0 :
а - общий вид, б - укрупнённый масштаб
Рис. 76. Общий вид трёхмерной
расчётной области для шлами
с выемкой
На рис. 75 приведены графики пове-
дения решений вдоль линии х = 0. Ре-
шения и!1 и и'1"’"1'1' двумерных задач
получены на сетке, изображённой на
рис. 74,в, а решения и' и и ‘ на сет-
ках, полученных двумя последователь-
ными дроблениями изображённой на
рис 74,в сетки, т.е. сетка после первого
дробления имела в 4 раза больше тре-
угольников и узлов (эта сетка показана
на рис. 74,?), а после второго - в 16 раз
больше треугольников и узлов, чем сет-
ка, на которой было получено решение
ustrm.,h _ 7/о,л u+,h . Эквивалентное же
по точности функции us"m,h решение
задачи (9.1) (при её решении «напря-
мую») удаётся получить лишь на сетке
после трёх вложенных дроблений исход-
ной (изображённой на рис. 74,в) сетке и имеющей примерно в 60 p.ri
большее число узлов и треугольников по сравнению с исходной cvi-
кой
Технология выделения поля ещё более эффективна при решении
трёхмерных задач. Примером может служить задача нахож (спин < ы
ционарного температурного поля в цилиндрической облает итобра
жённой на рис. 76. Сечением этого цилиндра плоскостью, нернен тку
лярной сё оси, является двумерная область, изобра псиная на риг 7-1 ,</
Очевидно, что если все параметры дифференциальною у равнения (9 I )
и краевых условий на боковой поверхности цилиндра нс зависят of
координаты 2, а на основаниях цилиндра заданы одноро nn.ie вторые
428
9.1<онечноэлементпые процедуры решения краевых задач ...
краевые условия = то эта заЛача может быть решена как
двумерная (которая только что была рассмотрена нами). Если же эти
условия не выполняются (т.е. либо параметры дифференциального
уравнения или краевого условия на боковой границе зависят от z, ли-
бо краевое условие хотя бы на одном из оснований не является одно-
родным краевым условием второго рода), эта задача становится трёх-
мерной. При этом хорошим приближением такой трёхмерной задачи
Рис. 77. Расчётная область
для основного ПОЛЯ
является осесимметричная задача в круговом цилиндре, поперечное
сечение которого приведено на рис. 74,о. Очевидно, что решение зада-
чи в круговом цилиндре может быть найдено как решение u2D (г, z)
осесимметричной задачи, определённой в двумерной области, изобра-
женной на рис. 77, и тогда решение исходной задачи с требуемой точ-
ностью может быть найдено с гораздо мень-
шими вычислительными затратами в виде
суммы решения осесимметричной задачи
и” (.?;,;//. z) = u2D \у]х2 + у2, г) и задачи на
добавочное поле (соответствующие вычис-
лительные затраты для такого рода трёхмер-
ных задач могут быть уменьшены уже более
чем па порядок).
Заметим, что рассмотренные двумерная
(рис. 74.и) и трёхмерная (рис. 76) задачи
имеют плоскость симметрии х = 0, на кото-
рой может быть задано однородное краевое
условие второго рода. В результате расчёт-
ная область может быть уменьшена вдвое -
соответственно практически вдвое умень-
шится (рсбуемое для достижения необходи-
мой точности число ячеек и узлов в конечно-
элементной сетке. Таким образом, учёт сим-
метрии позволяет дополнительно сократить
вычислительные затраты и никак не мешает
применению технологии выделения части
поля.
9.2. ОБЩАЯ СХЕМА ПОСТРОЕНИЯ КОНЕЧНОЭЛЕМЕНТНЫХ
ПРОЦЕДУР РЕШЕНИЯ ЗАДАЧ С ВЫДЕЛЕНИЕМ ЧАСТИ ГЮЛЯ
Рассмотрим эллиптическую краевую задачу, определённую в об-
ласти Q с границей 0Q = U S? U S3 :
—div (X grad u) + = f, (9.30)
(9.31)
9.2.Общая схема построения конечноэлементных процедур
429
Х#^| = 0, (9.32)
ls2
xM;,+(3(uU-4>)=0- (9-33)
Будем считать, что область Q полностью включается в область W
(или совпадает с ней), и в области Q' с границей дО/ — S'/ U S2 U S'/
определена функция w°, являющаяся решением краевой задачи
—div \() grad и °) + ^V = /% (9.34)
W"| , hl' (9.35)
^0 0UU ди = 0°, S-2 (9-36)
х о ди1) дп + 3° Sa (9.37)
Будем также считать, что функция может быть получена с го-
раздо меньшими вычислительными затратами либо численно, как ре-
шение задачи меньшей размерности, либо даже аналитически, и при
этом она достаточно хорошо приближает искомое решение и задачи
(9.30)-(9.33). Тогда решение и исходной задачи (9.30)-(9.33) имес!
смысл искать в виде суммы решений и1 «основной» задачи (9.34)--
(9.37) и задачи на «добавочное» поле и+ :
—div (X grad и+) + =
= f-f" -div((X() -X)gradu°) + (7’ (9.38)
“1 = U+ t a!l ’ (9.39)
x du* X dn - =e+, 6’2 (9 10)
x du+ dn + 3 Sa (‘» ID
При этом параметры краевых условий (9.39)—(9.41) онредслякнен с ic
дующими соотношениями:
(9 1?)
430
9.Конечноэлементные процедуры решения краевых задач ...
е+=0-Х^- , (9.43)
-“V (9-44)
*3
В зависимости от того, совпадают ли границы S|, S2 и S3 исходной
области с соответствующими границами S/, S-J и S3 области Q', в
которой определена задача для un, а также от того, совпадает или нет
коэффициент X с коэффициентом Х() в примыкающих к S2 и S3 по-
добластях расчётной области Q, параметры , 0+ , могут вычис-
ляться по более простым формулам. Так, на участке границы S{, сов-
падающем с соответствующим участком границы S/, параметр и*
можно вычислить по формуле
Ч/ lLH 4*7
Аналогично можно упростить выражения для вычисления 0+ и u(j
на участках границ S2 и S3, совпадающих с соответствующими уча-
стками границ S-2 и S3 . При этом, если коэффициенты X и Х() не
совпадают, параметры 6 н и можно вычислять по формулам
е+ =о-А-е",
х"
а если коэффициенты X и Х(| совпадают, то параметры 0+ и
удобней всего вычислять по формулам
()+ =0-0°,
U(l+ = Up — Up .
Таким образом, соотношениями (9.42)-{9.44) нм.еет смысл пользо-
ваться только на тех участках границ Sj, S2 и > которые не совпа-
дают с соответствующими участками границ S/, S-2 и S. /.
Получим эквивалентную вариационную постановку (в форме Га-
леркина) для задачи на добавочное поле. Для этого, как обычно, диф-
ференциальное уравнение (9.38) решаемой краевой задачи умножим на
9.2.Общая схема построения конечноэлементных процедур ...
431
пробную функцию1 * * v € (т.е. v должна удовлетворять однородному
первому краевому условию на <?[). проинтегрируем его левую и пра-
вую часть по области Q и после этого применим формулу Грина (ин-
тегрирования по частям). В результате получим
J X grad и+ grad v dQ — J X vdS + j* yu+v dQ =
Q S Q
= f (f-fn)vdQ + f(\n — X) grad u” • grad v d£l —
Q SI
- J(X° - X)^-vdS + f (4° - 4) A dQ Vt) G H(\. (9 45)
S ' Si
Учитывая, что v |5 =0, а также краевые условия (9.40)-(9.41),
преобразуем входящий в левую часть уравнения Галёркина (9 45) по-
/о +
X ~^~vdS к виду (см. (9.43)-(9.44)):
S
(' X^-vdS = Г X^^vdS + Г X^-vdS =
J on J on, J on
S S2 S;j
= Jo+vdS-fp(u+ -u+y)udS = flo-X^}vdS +
S-2 S.i S2 V
+j(-fiu+ -грцц -X^--(3i?’^dS \/v e Я/),
Si n I
Входящий в правую часть уравнения Галёркина (9 45) поверхност-
ный интеграл также разобьём на сумму интегралов по границам S\ , S
и S3 (напомним, что v на равна нулю):
J(x" - x)^’dS = J (х° - x)i£vds+f (x" -x) tr ‘"ls
s s2 s3
Объединяя оба поверхностных интеграла уравнения (9.4Ч), но нча
ем:
1 Здесь мы, чтобы не загромождать формулы лишними пн к-ксами нс бу-
дем использовать обозначения vtl (с нижним индексом «0») лпя ирон шильно-
го элемента пространства Я().
432
9 Конечноэлементные процедуры решения краевых задач ...
f X vdS - f (Х° - X) vdS =
J дп J ' ' ОП
S S
= f[^-X^}vdS- П\п -\\^-vdS +
J ‘ on / J \ ’ дп
S'2 -S'2
+fl-(5u+ + Pw0 -X^-pu°kdS - J(x° -X)^-vdS =
= f (б - X() "dS + I + 0Ц» - x° 4^ - pu'^ vdS.
J on / J p on
S-2 S-t
Таким образом, эквивалентная вариационная постановка для задачи
на добавочное поле (9.38)-(9 41) имеет вид
Г X grad и4 • grad v dQ Т / ^7/,4«jdQ + f fiu+vdS =
n \i s;,
= f U~ v + f (Х” “ X) Sracl u° ’ Sracl v dQ +
+f (т° - t) ul}v dQ + J10 - X” j vdS +
Ц s2 ' 7 7
+J‘^|J-X,1^--Pu,,jrdS УиеН}}. (9.46)
s3 V n
В случае, когда Q совпадает c Q' (и соответственно S2 совпадаете
S2 , а 5*3 - с S-i ) вид поверхностных интегралов в вариационном
уравнении (9 46) (с учётом краевых условий (9.36) (9 37)) может быть
упрощен:
j X grad и т • grad и dQ + J* ь и dQ Т J' рu+vdS =
Q Q S:l
= J‘(f - fe) v dQ tJ(X°- X) grad a” • grad v dQ +f 4) u"u dQ +
Q О Q
+f (0 - e(1) vdS + f P - //,';) udS Vv G 7/(i. (9.47)
S'2 S.i
Вообще говоря, требование о совпадении или полном включении
расчётной области Q в область Q' (в которой решалась задача для г?1)
не является обязательным для формирования задачи на добавочное
9.2.Общая схема построения конечноэлементных процедур ... 433
Рис. 78. Общий вид трёхмерной
расчётной области с добавленной
подобластью
поле. Покажем на примере, как может быть сформулирована задача на
добавочное поле в ситуации, когда Q не включается в Q'.
Рассмотрим задачу нахождения тем-
пературного поля в трёхмерной области
Q, изображённой на рис. 78. Эта область
представляет собой соединение кругово-
го цилиндра Q' с небольшой подобла-
стью О.'1.
Будем считать, что источник поля и
коэффициент теплопроводности в Q'
являются осесимметричными (т.е. зави-
сят только от радиальной координаты г
и осевой координаты z). Будем также
считать, что и краевые условия па боко-
вой цилиндрической поверхности и на
торцах Q' зависят только от г йот z.
Очевидно, что хорошим приближени-
ем решения рассмотренной трёхмерной
задачи является решение осесимметрич-
ной задачи в цилиндре Q'. Как обычно,
обозначим решение задачи в цилиндре
Q' через ип (т.е. ul](x,y,z) - трёхмерная функция, получаемая пере-
счётом решения u2D (r,z) осесимметричной задачи из цилиндриче-
ской в декартову систему координат, т.е.
Ut} (.Е, !/,1) = UiD [у/х2 + Д z) ).
Покажем, как можно доопределить функцию и{] в подобласти
=Q\Q'. Будем искать и[} в О!1 в виде решения краевой задачи
для уравнения
-div (Х grad u()) = f ,
т.е. в подобласти Q'z параметры дифференциального уравнения вои>-
мём из исходной задачи. На границах О.'1, которые являются !раннца
ми области Q , краевые условия также должны быть взяты из исходной
задачи, а на границе S'1 между П' и О.'1 (лежащей внутри области $2)
за (атим первое краевое условие, правая часть которого опрсделяегся
как решение осесимметричной задачи в области Q':
= uw(R.zY
1Дс Н радиус цилиндра Q'.
Таким образом, функция в области .0 удовлетворяет решению
уравнения (мы полагаем, что в fi' X11 = X, а /() = / ):
434
9.1<онечноэлементныс процедуры решения краевых задач ...
- div(X grad = f + fs<l, (9.48)
где fs = р5 - поверхностный источник и 65 — поверхностная б-
функция, сосредоточенная на Sd. Поверхностная плотность р5’7 по-
rS'1
верхностпого источника / определяется как
ди1]
ди"
дп s,i-
дп s,i+ '
(9.49)
Чтобы в этом убедиться, нужно проинтегрировать уравнение (9.48)
по объему , являющемуся окрестностью некоторого участка грани-
цы Sd,
J" —div (X grad и"= J fdCl 4- J fs<l '0,
I [рсобразуем левую часть полученного уравнения с помощью фор-
мулы Остроградского-Гаусса
где и Sd+i*1 - две части границы d$ld, лежащие по разные сто-
роны от границы Sd, а п~ и у?.4 - внешние (по отношению ) нор-
мали к границам Sd~bii и соответственно.
Объёмный интеграл от fs по Qd в соответствии с определением
поверхностного источника (см. раздел 8.2, соотношение (8.9)) преобра-
зуется к интегралу по поверхности Sd
J fs<ldQ = f ps'fbs''dQ = J ps"'dS.
a'l s'J
Стягивая Q(.z к Sd, получим, что Sd и Sd+Hl станут границами
St и St (T.c. совпадут c Sd), а интеграл от f no (с учётом ог-
раниченности f в Q) обратится в нуль.
В результате получим
9.3.Применение технологии выделения основного ноля
435
где ll |5а- означает, что значение разрывной на S'J функции II бсрс г-
ся с одной стороны S,1, а П’|^/+ - с другой.
Учитывая, что п~ = — п+ и выбирая нормаль п совпадающей с
п+, получаем
откуда в силу произвольности S? следует соотношение (9.49).
Обратим внимание на то, как направлена нормаль п в формуле
(9.49). Поскольку мы выбирали её совпадающей с направлением п.+ (а
п+ была внешней по отношению ВЗ), она должна «емтреть» в сто-
рону, противоположную от S”/-. Чтобы это подчеркнуть, в дальней-
шем нормаль п будем обозначать п * .
Таким образом, эквивалентная вариационная постановка для задачи
на добавочное поле будет иметь следующий вид:
Vr6/7(i, (9.50)
т.е. источником в задаче на добавочное поле фактически является по-
верхностный источник с поверхностной плотностью (9.49)
Нс представляет труда сформулировать задачу на добавочное но ic
и построить соответствующую ей эквивалентную вариациошцю по
становку для случая, когда Q не включается в Q' (т.е. П f 1 О ) и
коэффициенты дифференциального уравнения и параметры краевых
условий исходной задачи не совпадают с соответствующими iiapaxici
рами задачи для . В этом случае вариационное уравнение о\ ь i ео
держать соответствующие слагаемые из уравнений (9 17) и (9 >())
9.3. ПРИМЕНЕНИЕ ТЕХНОЛОГИИ ВЫДЕЛЕНИЯ О( HOBIIOI О IK) 1Я
ДЛЯ РЕШЕНИЯ ЗАДАЧ С СОСРЕДОТОЧ1 ИНЫМИ IK lOMHIlk \МЦ
Как уже говорилось в восьмом разделе, учё> Яосредстциц inn ix и
линии и в точке источников «напрямую» (с введением их в пр тую
часть вариационного уравнения в виде inirci p.i'ioii но шнпям или в
436
9.Конечноэлементные процедуры решения краевых задач ...
виде значений в точках) при построении конечноэлементных аппрок-
симаций является далеко не самым эффективным способом решения
такого рода задач. Существенного снижения вычислительных затрат
можно добиться выделением части поля, создаваемой сосредоточен-
ным источником в более простой, но достаточно близкой к требуемой
среде. При этом простая среда должна быть такой, чтобы поле от со-
средоточенного источника можно было получить с небольшими (го-
раздо меньшими, чем при решении исходной задачи) вычислительны-
ми затратами (либо аналитически, либо при решении задачи меньшей
размерности).
I акие подходы уже достаточно давно применялись, например, при
решении задач электроразведки методом интегральных уравнений. В
методе конечных элементов некоторым эквивалентом выделения части
поля являются постановки, основанные на использовании неполного
скалярного потенциала при решении задач магнитостатики (эти задачи
будут рассмотрены нами в шестнадцатом разделе). Выделять же поля
сосредоточенных источников при использовании метода конечных
элементов для решения задач электроразведки (описываемых уравне-
ниями эллиптического и параболического типа) было предложено в
работах [19, 20].
Покажем, как может быть построена конечноэлементная схема с
выделением поля сосредоточенного источника на примере нахождения
постоянного электрического поля в проводящей среде.
Пусть электрическое поле создастся в проводящем полупростран-
стве точечным источником, моделирующим ток, втекающий в это по-
лупространство из расположенной на его поверхности точки. Прово-
дящее полупространство представляет собой однородную по проводи-
мости вмещающую среду, содержащую один или несколько трёхмер-
ных объектов с отличающейся (от вмещающей среды) проводимостью
Электрическое поле Е = — grad и в этом случае полностью описыва-
ется электрическим потенциалом и , удовлетворяющим дифференци-
альному уравнению
— div (X grad и) — fp, (9.51)
где X — электрическая проводимость среды с объектами (являющаяся
трехмерной кусочно-постоянной функцией), = рр5р - сосредото-
ченный в точке р с координатами (.г’р,yjnzp\ источник, рр - величи-
на стекающего из р тока.
Будем искать решение и уравнения (9.51) в виде суммы двух функ-
ций и” и и |-, где а” - электрический потенциал, описывающий поле в
однородном полупространстве с проводимостью X" . При этом значе-
ние X" является проводимостью вмещающей среды (т.е. Х() совпадает
с X вне трёхмерных объектов). Таким образом, и{} является решением
уравнения
9.3.Применение технологии выделения основного ноля
437
—Aw” =
Х()
(где А — оператор Лапласа) и определяется формулой
Очевидно, что добавочное поле и+ = и — и{1 удовлетворяет урав-
нению
— div (X grad = — div^X — Х) grad и J . (9.53)
Определим расчётную область 0 в задаче для и+, исходя из гак
называемого принципа большого объёма. Для этого возьмём Q в виде
параллелепипеда с достаточно удаленными от объектов нижней и бо-
ковыми границами, на которых влияние трёхмерных объектов пренеб-
режимо мало (верхняя граница параллелепипеда лежит на единствен-
ной границе полупространства). Будем считать, что па нижней и боко-
вых границах параллелепипеда Q функция и. совпадает с а1). Тогда на
этих границах для добавочного поля и+ должно быть задано однород-
ное краевое условие первого рода. На верхней границе П должно бы ть
задано условие невытекания тока из проводящей среды. Поэтому на
этой границе для функций и и и'] справедливо однородное краевое
условие второго рода, откуда следует, что и для функции а4 на верх-
ней границе Q должно быть задано однородное краевое условие вто-
рого рода.
В результате эквивалентная вариационная постановка для красвон
задачи, определяемой уравнением (9.53) с однородными краевыми
условиями первого и второго рода, примет вид
f X grad и grad v dEl = f ^X(1 — Xj grad u[>- grad v d£l Vv E . (9.5 I)
Вообще говоря, в правой части вариационного уравнения (9 > 1)
grad и11 можно было бы заменить вектор-функций, составленной из
cooI ветствующих производных функции (9.52). Однако можно нос г\
пигь и намного проще - формировать правую часть конечно пемс hi
ной СЛАУ умножением соответствующей матрицы жёс1кос)П на вгк
юр q", компоненты которого являются весами разложения (|>mikiiiih
по базисным функциям (для лагранжевых элементов вес » 7 но
значения функции и" в соответствующих ф, узлах соки см июню
шспия (9.13)-<9.16)).
Пе представляет особого труда применить icxibvioi 1110 поля вы г
лспия точечного источника и в случае, кот ia bmcih.hoih.i 11 ере 1.1 имею
438
9.Конечноэлементные процедуры решения краевых задач ...
более сложную структуру. Например, в задачах геофизики очень часто
вмещающие среды являются так называемыми горизонтально-
слоистыми средами, в которых проводимость является кусочно-
постоянной функцией одной координаты z. В этом случае функция
может быть найдена как решение осесимметричной задачи с точеч-
ным источником в горизонтально-слоистой среде. В свою очередь,
решение осесимметричной задачи тоже может быть найдено с исполь-
зованием технологии выделения поля. В этом случае в качестве основ-
ного может быть взято поле точечного источника в однородном полу-
пространстве с проводимостью, равной проводимости слоя, в котором
находится точечный источник. Таким образом, рассмотренная техно-
логия двухэтапного выделения поля позволяет добиться дополнитель-
ного сокращения вычислительных затрат.
Другие примеры использования многоэтапной технологии выделе-
ния поля будут показаны в следующем разделе 9.4.
11ри решении нестационарных задач электроразведки источником
поля может быть токовая петля. Фактически этот источник является
источником, сосредоточенным на линии. Технология решения такой
задачи с разделением поля на основное (поле вмещающей среды) и
добавочное (поле влияния объектов) будет рассмотрена в четырнадца-
том разделе.
9.4. МНОГОЭТАПНАЯ ТЕХНОЛОГИЯ ВЫДЕЛЕНИЯ НОЛЯ
При решении некоторых сложных задач существенного сниже-
ния вычислительных затрат можно добиться с помощью схемы по-
этапного выделения поля, суть которой состоит в следующем. Сначала
выделяется поле, создаваемое в максимально упрощенной (относи-
тельно исходной) среде и, возможно, с упрощенным источником. Эта
задача может быть определена в области меньшей размерности, т.е,
вместо трёхмерной стать двумерной (осесимметричной) или даже од-
номерной. Её решение берётся в качестве основного поля первого
уровня. На базе этого основного поля формируется задача на добавоч-
ное поле, в которую включается часть неоднородностей исходной за-
дачи, дающих максимальный вклад в искомое решение. Используемая
для нахождения этого добавочного поля сетка строится таким образом,
чтобы оптимально учесть влияние источников, порожденных вклю-
ченными на этом этапе неоднородностями.
Па втором этапе в качестве основного поля второго уровня исполь-
зуется сумма основного и добавочного полей первого уровня. Доба-
вочное поле второго уровня определяется в результате включения (в
задачу второго уровня) следующей (по влиянию на решение исходной
задачи) части неоднородностей. Этот процесс продолжается до тех
пор, пока не будут учтены все неоднородности исходной задачи.
Таким образом, технологию выделения части поля можно приме-
нять несколько раз, что позволяет использовать на каждом этапе сетку,
оптимальную для нахождения добавочного поля этого уровня, в то
время как при решении задачи с одноэтапным выделением основного
поля сетка должна была бы дробиться в районе всех неоднородностей
I
9.4.Многоэтапная технология выделения поля
439
сразу. Особенно большое сокращение вычислительных затрат за счёт
применения многоэтапной технологии выделения поля можно полу-
чить при решении обратных задач, когда требуется вычислять доволь-
но много полей влияния отдельных неоднородностей.
Продемонстрируем это на примере следующей относительно про-
стой задачи электроразведки. В горизонтально-слоистой среде нахо-
дятся два объекта параллелепипеидальной формы. Среда имеет три
слоя. Толщина первого слоя 100 м (т.е. он лежит в промежутке
—100<z<0), его удельная проводимость 0.01 См/м. Второй слой
лежит в промежутке —300 < z < —100 и имеет удельную проводи-
мость 0.005 См/м. Третий слой распространяется от z — —300 в глубь
Земли и имеет проводимость 0.05 См/м. Первый (большой) объект
является параллелепипедом [—450,450] х [—400,400] х [—200,— 15] и
имеет удельную проводимость 0.1 См/м. Второй (малый) объект явля-
ется параллелепипедом [1500,1900] х [—250,150] х [—70,—40] и имеет
удельную проводимость 0.5 См/м. Электрическое поле возбуждается
током, стекающим из точки р с координатами ж7'=100, г/7'=0,
z7’ = 0.
Задача заключается в оценке влияния малого объекта при измере-
ниях электрического поля по поверхности Земли (например, для опре-
деления его наличия во вмещающей среде). Это можно сделать, решив
две трёхмерные задачи - задачу, когда вмещающая среда содержит оба
объекта, и задачу, когда вмещающая среда содержит только большой
объект. Разность решений задач с двумя и одним объектом будет яв-
ляться полем влияния малого объекта. Однако для этого обе задачи
должны быть решены с достаточно высокой точностью, чтобы поле
влияния малого объекта заметно превышало погрешности решения
этих задач. Например, при использовании тетраэдральных сеток, сече-
ния которых плоскостью у — 0 показаны на рис. 79, разность решений
этих трёхмерных задач на поверхности Земли (т.е. на линии
= 0, z ~ 0}) в районе эпицентра малого объекта сопоставима с по-
грешностью их решения. Чтобы убедиться в этом, достаточно ренииi.
обе задачи на более подробных сетках. Так, на сетке с уменьшенным
вдвое (по всем координатам) размером ячеек изменение решения зам
чи с одним большим объектом в районе эпицентра малою объема
будет не меньше, чем разность решений задач с одним и двумя ойьск
там и (на сетках, показанных на рис. 79).
На рис. 80 приведены графики значений потенциала элем рнчсскнх
полей, рассчитанных на разных сетках. Значения потенции и нрнно
дятся на поверхности Земли (т.е. при z = 0) вдоль липин // И I ра
фик, обозначенный черным прямоугольником, предо!авансi ново книг
решения задачи с одним (большим) объектом, полученною и i cciki
показанной па рис. 79,а и содержащей 6796 узлов I рафик, обо пьгн и
ный белым прямоугольником, представляет поведение решения нон
же задачи, полученного на гораздо более подробной ccikc, содержа
щей 52073 узла Графики, обозначенные черным и бе »ым ipt \ю наш
ком, представляют поведение решений за 1ачн с ли>мя ооьеыамп, по
440
9.Конечноэлементные процедуры решения краевых задач ...
лученных соответственно на грубой (11721 узлов, см. рис. 79,Д) и под-
робной (90655 узлов) сетках. Из этих чэафиков видно, что при исполь-
зовании сеток, приведённых на рис. 79, как погрешность решений за-
дач с одним и двумя объектами, так и их разность значительно превы-
шают поле влияния малого объекта (являющееся разностью значений,
представленных в виде графиков на рис. 80, которые обозначены бе-
лым прямоугольником и белым треугольником)
Рис. 79. Сечение конечноэлементных сеток плоскостью у = 0
для задач с одним (я) и двумя (б) объектами
Таким образом, чтобы получить поле влияния малого объекта хотя
бы правильного порядка, задачу с большим объектом необходимо ре-
шать на сетке, содержащей около 52000 узлов, а задачу с двумя объек-
тами - на сетке, содержащей около 90000 узлов. Заметим, что в рас-
смотренных задачах было выделено поле точечного источника в гори-
зонтально-слоистой среде (т.е. была использована одноэтапная техно-
логия выделения поля), в противном случае потребовались бы гораздо
более подробные сетки (имеющие как минимум на порядок большее
количество узлов).
Покажем, как эта задача может быть решена с использованием мно-
гоэтапной технологии выделения поля.
На первом этапе вычислим поле в среде, содержащей только боль-
шой объект. Это поле, естественно, будем искать в виде суммы двух
полей - основного поля как поля точечного источника в горизонталь-
но-слоистой среде и добавочного поля как поля влияния большого
объекта. Очевидно, что основное поле описывается осесимметричной
задачей и может быть найдено с высокой точностью при небольших
вычислительных затратах. Добавочное поле (поле влияния большого
объекта) будем вычислять на сетке, показанной на рис. 79,а. Эта сетка
9.4.Многоэтапная технология выделения поля
441
является вполне подходящей для
решаемой задачи, поскольку она
сгущена к краям большого объек-
та, где сосредоточены источники
вычисляемого добавочного поля.
На втором этапе в качестве ос-
новного поля будем использовать
полученное на первом этапе сум-
марное поле (т.е. сумму поля то-
чечного источника и поля влия-
ния большого объекта). Для вы-
числения добавочного поля (поля
влияния малого объекта в среде с
большим объектом) трёхмерная
сетка должна быть сгущена к кра-
ям малого объекта, в большом же
объекте шаг может быть доста-
точно грубым. Поэтому добавоч-
ное поле вычислим на сетке со
сгущением только к краям малого
узлов, её сечение плоскостью у — 0 показано на рис. 81.
Рис. 80. Конечпоэлементные решения
задач с одним и двумя объектами
на разных сетках
объекта. Эта сетка содержит 14320
Рис. 81. Конечпоэлементные сетки для задачи на добавочное поле малого объекта
На рис. 82 приведены график значений потенциала поля влияния
малого объекта вдоль линии (у — 0, z = 0} . Сравнивая график, приве-
дённый на рис. 82, с разностью приведённых на рис. 80 графиков, обо-
значенных черными треугольником и прямоугольником (поле влияния
объекта как разность полей на грубых сетках), а также с разноси.к»
графиков, обозначенных белыми треугольником и прямо) i олышком
(поле влияния объекта как разность полей на подробных сечках), мож
но сделать следующий вывод. Полученное на грубой сетке с ш пиль
зованием многоэтапной технологии поле влияния малою <нц..'м i со
поставимо по точности с решением, полученным как разноси, по ни
(поля от двух объектов и поля от большого объекта), вычыс н-нпых на
подробных сетках.
Заметим, что при вычислении поля влияния ма нно ooi.ckij в ви к-
разности двух полей нами были использованы две не «.ник имыс ccikh,
построенные со сгущением к источникам cooibcic гиующих по н и («ак.
в задаче с двумя объектами сетка сгущалась к обоим обьсмам, а в за-
442
9 Конечноэлементные процедуры решения краевых задач ...
даче с одним объектом сетка сгу-
щалась только к нему). В резуль-
тате для получения приемлемого
по точности решения потребова-
лись очень подробные сетки. Од-
нако такой способ (через разность
решений двух задач) всё-таки
может быть применён для нахож-
дения поля влияния малого объ-
екта и при использовании доволь-
но грубых сеток (как, например,
сетка, показанная на рис. 79,6), но
эти сетки должны быть построены
специальным образом. В разде-
ле 9.5 мы сформулируем условие,
которое нужно соблюдать при
п ,, построении таких сеток, и дадим
Рис. 82 Конечноэлементное решение _________„„______ . ’ ' '
задачи на добавочное поле малого объекта обоснование, почему выть нение
этого условия позволяет получать
поля влияния объектов с довольно высокой точностью.
9.5. ВЫЧИСЛЕНИЕ ПОЛЕЙ ВЛИЯНИЯ
9.5.1. ОСНОВНЫЕ ТИПЫ ЗАДАЧ, ТРЕБУЮЩИХ ВЫЧИСЛЕНИЯ ПОЛЕЙ ВЛИЯНИЯ
Как уже говорилось в разделе 9 4, вычисление полей влияния не-
больших неоднородностей является важной составной частью многих
процедур решения обратных задач (электроразведки, дефектоскопии и
т.д.). При этом под обратными задачами понимаются задачи, в кото-
рых по значениям поля нужно определить параметры (коэффициенты
и правые части) дифференциального уравнения и краевых условий,
описывающих это поле В этом случае сами дифференциально-краевые
задачи, в которых для заданных коэффициентов и правых частей диф-
ференциальных уравнений и краевых условий нужно найти их реше-
ние, называют прямыми .
Как правило, в процедурах, реализующих решение обратной зада-
чи, присутствует этап, на котором определяется, насколько вносимые в
параметры прямой задачи изменения влияют на её решение. При этом
для уточнения параметров краевой задачи может понадобиться оценка
влияния многих небольших изменений искомых параметров. Очевид-
но, что такие задачи лучше всего решать с выделением полей влияния
каждого из вносимых изменений
Кроме того, выделение поля влияния может быть использовано при
решении некоторых сложных нелинейных задач (например, трёхмер-
ных задач магнитостатики), в которых на фоне большого «внешнего»
поля (порождаемого «большими» источниками и объектами) требуется
вычислить поле, порождённое некоторым относительно небольшим
объектом со своими («внутренними?') источниками, и при этом пара-
метры этого объекта зависят от суммы «внешнего» и порождаемого
«внутренними» источниками полей.
9.5.Вычисление полей влияния
443
Здесь мы рассмотрим и обоснуем метод вычисления полей влияния
отдельных объектов в существенно трёхмерных задачах, который нс
требует разработки специальных формулировок для задачи расчёта
добавочного поля.
9.5.2. ОПЕРАТОРНАЯ ФОРМА ЗАДАЧИ, ОПРЕДЕЛЯЮЩЕЙ ПОЛЕ ВЛИЯНИЯ
Запишем решаемую дифференциально-краевую задачу в оператор-
ном виде:
Lu = f, (9.55)
где и -трёхмерное поле, учитывающее влияние исследуемого объек-
та.
Пусть и” — трёхмерное поле, не учитывающее наличие в задаче ис-
следуемого объекта, и определяющая его дифференциально-краевая
задача в операторной форме имеет вид
LV=/°. (9.56)
Будем считать, что области действия дифференциально-краевых
операторов L и £1) совпадают. Тогда поле и+ = и — и0 влияния ис-
следуемого объекта удовлетворяет операторному уравнению
Lu+ = f- f° + (L() - l). (9.57)
Чтобы убедиться в этом, достаточно вычесть уравнение (9.56) из
уравнения (9.55) и провести элементарные преобразования.
Таким образом, ноле и4 влияния исследуемого объекта может быть
найдено из решения задачи (9.57) с тем же дифференциально-краевым
оператором, что и в «полной» задаче (9.55), и источником, определяе-
мым разностью источников f и f и воздействием разности операто-
ров (/Г — L на поле а" .
9.5.3. ПОСТРОЕНИЕ КОНЕЧНОЭЛЕМЕНТНОЙ С ЛАУ, АППРОКСИМИРУЮЩЕЙ
ПОЛЕ ВЛИЯНИЯ
Сначала построим конечноэлементныс СЛАУ, аппроксимирующие
задачи (9.55) и (9.56). При этом для аппроксимации обеих задач будем
использовать одну и ту же конечноэлементную сетку (с одним и нн и
Dice набором базисных функции) В результате получим две С. IAV
Aq = b, (9.58)
A°q()=b°, (9.S9)
где А и А11 - конечноэлементные матрицы, являющиеся днскр<-| ними
аналогами дифференциально-краевых операторов / и 1 . 1> и 1»
векторы правых частей конечноэлементных ( HAV, л <| н q некю
ры, являющиеся решениями СЛАУ (9.58) и (9.59) соогш п ibciiiio и
444
9.Конечноэлементные процедуры решения краевых задач ...
определяющие конечноэлементные решения и1' = q4p и
ui}'h — [q")' ф дифференциально-краевых задач (9.55) и (9.56) (ф -
вектор, составленный из базисных функций ф£).
Поскольку СЛАУ (9.58) и (9.59) получены в результате конечно-
элементной аппроксимации задач (9.55) и (9.56) на одной и той же
сетке, мы можем провести над ними ге же операции, которые прово-
дили выше для операторных уравнений (9.55) и (9.56). Сначала вычтем
СЛАУ (9.59) из СЛАУ (9.58), а затем из левой и правой частей полу-
чившейся системы вычтем вектор Al’q°. После элементарных преоб-
разований получим
Aq ь = b — b" + (А" - A) q” ,
(9.60)
где q+ = q - q° .
Сравнивая (9.60) с (9.57), убеждаемся, что вектор q+ является ре-
шением СЛАУ
Aq^=b+ (9.61)
с матрицей, получающейся в результате конечноэлементной аппрок-
симации дифференциально-краевои задачи (9.57), и с вектором правой
части
bh = b-b" +(л° -A)q".
(9.62)
Таким образом, при использовании одной и той же сетки для вы-
числения конечноэлементных решений uk и и'1'1' дифференциально-
краевых задач (9.55) и (9.56) их разность = и'1' — и,"-11 является
конечноэлсментным решением дифференциально-краевой задачи
(9.57) на той же конечноэлементной сетке, причём и+’" = (q *ф
может быть найдено и как разность конечноэлсментных решений двух
задач (исходной и задачи для основного поля па одной и той же сетке),
и в результате решения СЛАУ (9.61) с правой частью (9.62). В послед-
нем случае при вычислении b вектор весов q ' может быть получен
не из решения СЛАУ (9.59), сгенерированной при аппроксимации за-
дачи для основного поля на той же (что и при аппроксимации исход-
ной задачи) сетке, а любым другим способом - подробнее об этом чуть
ниже.
9.6. О РАЗ ЛИЧНЫХ СПОСОБАХ ВЫЧИСЛЕНИЯ
ПОЛЕЙ влияния и ИХ ЭФФЕКТИВНОСТИ
Задача (9.57) и сё дискретный аналог (9.61) в каком-то смысле
обобщают результаты, полученные ранее в этом (девятом) разделе. В
тех случаях, когда расчётная область Q исходной задачи совпадает с
9.6 О различных способах вычисления полей влияния ...
445
расчётной областью Q' задачи для основного поля, можно нс задумы-
ваться о специальных формулировках задачи на добавочное поле, а
воспользоваться СЛАУ (9.61) с правой частью (9.62). При этом матри-
ца А этой СЛАУ должна быть получена в результате консчпоэле-
ментной аппроксимации исходной задачи, а матрица А" - при аппрок-
симации на той лее сетке задачи, в которой в подобластях, описы-
вающих объект, заданы параметры основного поля. Аналогично век-
тор b должен учитывать все источники' исходной задачи, а вектор
b“ — источники задачи для основного поля. Вектор же q' — это веса
разложения основного поля по базису {фд}, который был использован
при построении матриц А и А (ив разложении по которому ищется
поле м+,“).
Очевидно, что при использовании для нахождения добавочното по-
ля конечноэлементной СЛАУ (9.61) с правой частью (9.62) основное
поле может быть получено любым способом — как из решения двумер-
ной (или даже одномерной) задачи, так и из решения трехмерной зада-
чи на другой сетке (учитывающей источники и поведение основного
поля). Для подстановки этих полей в правую часть (9.62) СЛАУ (9.61)
нужно только выполнить пересчёт основного поля с сетки, на которой
оно получено, на сетку, которая используется для вычисления и4 (ес-
тественно, для вычисления вектора правой части b 1 нужно будет так-
же сгенерировать матрицу Ан и вектор Ь1’, соответствующие задаче
для основного поля).
С помощью полей влияния можно построить очень простую, но
вместе с тем весьма эффективную процедуру уточнения конечноэле-
ментного решения практически любой трёхмерной задачи, имею-
щей хорошее приближение в виде решения одномерной или дву-
мерной задачи или определённое в виде некоторой аналитической
функции.
Для этого мы воспользуемся тем фактом, что разность конечноэле-
ментных решений исходной задачи (9.55) и задачи для основного поля
(9.56), полученных на одной и той же сетке, является консчпоэлс-
ментным решением задачи (9.57) на той лее сетке, в которой в качс
стве нормального поля подставлено конечноэлементнос решение
задачи (9.56), полученное на этой лее сетке.
Обозначим через решение, аппроксимирующее на юн те
сетке, на которой получено конечноэлементное решение и1'. Гоз за и 1,
определяемое соотношением
«л = й" + uh - и"’1', (•> 61)
будет аппроксимировать точное решение и с гораздо бо кс iii.icommi
точностью, чем конечноэлементнос решение и', зе i зя iioivkiiiih
более точного решения нужно к полю являющемуся vx i л очно
1 В том числе и заданные с помощью естестве иных красных loiutft
446
9.Конечноэлементные процедуры решения краевых задач ...
хорошим приближением искомого поля и, добавить разность конеч-
ноэлементных решений исходной и приближающей её задач, получен-
ных на одной и той же сетке (с одним и тем же набором базисных
функций).
Итак, фактически мы рассмотрели три подхода к вычислению по-
лей влияния (на основе которых легко построить и соответствующие
процедуры существенного повышения точности конечноэлементных
решений).
Первый подход основан на использовании специальных постановок
для добавочного поля. Он предоставляет самые широкие возможности
и позволяет добиться наилучших результатов, но требует при работе
большой аккуратности и глубокого понимания, поскольку можно не-
чаянно внести «лишние» источники (чаще всего появляющиеся из-за
несбалансированности их положительных и отрицательных частей при
неаккуратной обработке источникового члена — L) д() в тех случа-
ях, когда этот источник является двуполярным с нулевой суммарной
мощностью).
Второй подход, основанный на решении СЛАУ (9.61) с правой ча-
стью (9.62), фактически фиксирует способ учёта источникового члена
— L^u{} в задаче на добавочное поле - в нём в качестве и{> высту-
пает функция, представленная в виде разложения по тому же базису
{гр; }, который используется и для представления добавочного поля
и+ (хотя при этом д() может быть получена из решения задачи мень-
шей размерности или на другой сетке), а оператор L° — L аппрокси-
мируется точно так же, как и воздействующий на и+ оператор L . И
благодаря именно этому устраняются практически все проблемы, свя-
занные с появлением «лишних» несбалансированных источников, ко-
торые могут возникать при неаккуратной «свободной» аппроксимации
члена (L() — L) д” .
Третий подход, основанный па вычислении и+ как разности ко-
нечноэлементных полей и и и. \ полученных на одной и той же сетке,
фактически является одним из вариантов второго подхода - эти подхо-
ды совпадут, если во втором подходе в качестве поля г/.11 взять конеч-
ноэлсментное решение соответствующей задачи, полученное на той же
сетке, которая используется для нахождения конечноэлементного при-
ближения добавочного поля д4 . Недостатки этого подхода очевид-
ны- если используется достаточно грубая сетка для нахождения поля
и+ (которая может быть вполне пригодной для нахождения именно
поля д+ , а не д или д’), то погрешность вычисления поля д() на этой
сетке может негативно сказаться и на точности вычисления добавочно-
го поля д+ .
Таким образом, второй подход, основанный на решении СЛАУ
(9.61) с правой частью (9.62), можно признать оптимальным по крите-
рию «надёжность+точность».
9.6.0 различных способах вычисления полей влияния ...
447
Очень важным является тот факт, что все изложенные здесь рассу-
ждения, касающиеся полей влияния, справедливы не только для задач,
описываемых эллиптическим уравнением. Эти схемы можно столь же
успешно применять при вычислении полей влияния и во многих не-
стационарных задачах, и в задачах, описываемых системой дифферен-
циальных уравнений в частных производных (векторных задачах).
Соответствующие примеры таких задач будут приведены ниже.
Обратим особое внимание читателя на то, что рассмотренные в
этом (девятом) разделе методы построения конечноэлементных реше-
ний, основанные на использовании как специальных процедур вычис-
ления добавочных полей, так и довольно простой общей схемы вычис-
ления поля влияния через решение СЛАУ (9.61) с правой частью (9.62)
или схемы уточнения решения с помощью соотношения (9.63), позво-
ляют добиться такого увеличения точности решения задачи, которое
для такого рода задач не может быть достигнуто ни за счёт оптимиза-
ции сеток, ни за счёт повышения порядка конечных элементов, при-
чём не только при сопоставимых вычислительных затратах, но и при
их увеличении в несколько раз, а иногда даже в десятки и сотни раз.
448 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
10. СТРУКТУРЫ ДАННЫХ, СЕТКИ И АЛГОРИТМЫ РАБОТЫ
С НИМИ В МКЭ
10.1. ОСНОВНЫЕ МЕТОДЫ ОПИСА1111Я РАСЧЁТНОЙ ОБЛАСТИ
Описание расчётной области в МКЭ необходимо для последую-
щего построения конечноэлемсптной сетки и определения значений
параметров дифференциального уравнения (т.е. его коэффициентов и
правой части) в подобластях. Кроме того, это описание должно содер-
жать информацию, необходимую для обработки краевых условий.
В настоящее время разработчики базирующихся па применении
МКЭ программных средств используют в основном два способа опи-
сания геометрии расчётной области. Один из них — метод конструк-
тивной геометрии. В этом подходе расчётная область представляется
с помощью базовых примитивов (например, для двумерного случая это
может быть многоугольник, окружность, эллипс и т.д.) и операций над
ними (объединение, пересечение, геометрические преобразования и
т.п.). Достоинства этого метода очевидны:
• малый объём исходных данных, если моделируемые объекты хо-
рошо описываются базовыми примитивами;
• возможность создания довольно простого языка для описания гео-
метрии области.
В основном метод конструктивной геометрии применяется в ком-
плексах конечноэлементного моделирования, предназначенных для
решения задач в областях с различными (возможно, пересекающими-
ся) телами стандартной формы (таких, как параллелепипед, цилиндр,
шар, конус и т.д.;.
Вторым распространенным подходом к описанию расчетной облас-
ти является метод описания границ. В этом подходе геометрия расчёт-
ной области задаётся путём описания всех границ сё подобластей.
Главным достоинством этого метода является хорошая возможность
стандартизации всех процедур задания границ подобластей расчётной
области и конечноэлементных ссгок, что позволяет создавать эффек-
тивные интерактивные графические системы для решения задач с гео-
метрией практически любой сложности.
В этом (десятом) разделе мы рассмотрим один из простейших вари-
антов метода конструктивной геометрии, предназначенный для описа-
ния расчётной области с прямоугольными подобластями, и дадим
очень короткий обзор методов, основанных на различных способах
10.2.Структуры данных для описания двумерных задач.
449
описания геометрии расчётной области через границы сё подобластей
Кроме того, будут довольно детально представлены структуры дан-
ных, предназначенные для описания расчётных областей и хранения
конечноэлементных сеток и матриц конечноэлементных СЛАУ, а так-
же рассмотрены некоторые наиболее важные алгоритмы работы с сет-
ками, матрицами и конечноэлементными решениями
10.2. СТРУКТУРЫ ДАННЫХ ДЛЯ ОПИСАНИЯ ДВУМЕРНЫХ ЗАДАЧ.
ДВУМЕРНЫЕ СЕТКИ
10 2.1. ОПИСАНИЕ ДВУМЕРНЫХ РАСЧЁ Т ПЫХ ОБЛАСТЕЙ С ПРЯМО' Г ОЛЫ1ЫМП
ПОДОБЛАСТЯМИ
Пусть расчётная область состоит из прямоугольных подобластей
ТУ/. ТУ2,.... Построим следующую структуру данных
Сначала сформируем массивы
АН| и У1' значений всех верти-
кальных и горизонтальных границ
подобластей Wt. Например, для
показанной на рис. 83 расчётной
области Q = ТУ/ U 11'2 U ТУз мас-
сивы А11 и У” будут иметь сле-
дующий вид: Xй = {1.,2.,6.} и
У"' = {1.,2.,4.,5.}.
Каждая из подобластей ТУ/
представляется набором из пяти
целых чисел, первое из которых
означает номер подобласти, вто-
рое- номер элемента в массиве
л , определяющего ,т -
координату левой границы подоб-
ласти ТУ,, третье - номер элемента в массиве X1 , определяющего г -
координату правой границы ТУ/, четвёртое - номер элемента в массиве
У' , определяющего у -координату нижней границы ТУ/, юное номер
элемента в массиве У1' , определяющего ?/-координату верхней грани-
цы ТУ/.
Таким образом, полное описание расчётной облает, состоящей из
набора прямоугольников с различными значениями парные фон диффе-
ренциального уравнения в них, может быть представлено в файле сле-
дующей структуры: первое число TV*1 (целое) озпачас! длин} массива
Х' ; следующие N вещественных чисел - элементы массива X ;
далее число X,' (целое) - длина массива У1 ; следующие N вещест-
венных чисел - элементы массива Уи ; затем число / (целое) - коли-
450 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
б.
чество подобластей из которых состоит расчётная область
Q; далее L наборов по 5 целых чисел, описывающих все подобласти
IKj.H'y,.... При использовании такого подхода расчётная область, пред-
ставленная на рис. 83, может быть описана следующим образом:
3
1. 2.
4
1. 2.
3
1
2
3
4 .
5.
2
3
3
4
3
4
1
2
3
1
2
2
Конечно, при описании границ отдельных подобластей вместо но-
меров элементов массивов Xй и У1* можно указывать их значения.
11о такое представление исходных данных может быть источником
ошибок при интерпретации этих данных в ситуациях, когда границы
подобластей задаются дробными числами, которые могут округляться.
Действительно, если при задании вертикальной (или горизонтальной)
границы двух смежных подобластей расчётной области одно и то же
число (например, т) округлить по-разному (например, при описании
одной подобласти задать а:-координату границы равной 3.14, а при
описании второй подобласти - равной 3.1415), то при интерпретации
таких данных в обрабатывающей геометрию расчётной области про-
грамме эти подобласти будут иметь несовпадающую границу - в ре-
зультате в расчётной области могут появиться дыры, искажающие её
геометрию. Нели не предусмотреть специальных мер контроля таких
ситуаций, то расчёт по заданным таким образом данным может приво-
дить к серьёзному искажению результата. Описание же границ подоб-
ластей через номера элементов массивов и Уп исключает воз-
никновение такого рода проблем.
Рис. 84. I [пнмер расчётной об. 1асти.
содержащей две подобласти
с одинаковыми значениями
параметров в них
Заметим, что номера подобла-
стей в рассмотренном подходе к
представлению расчётной области
нужны фактически для того, чтобы
вычислить значения параметров
(коэффициентов и правой части)
дифференциального уравнения — в
каждой из подобластей Ш эти па-
раметры могут быть либо различ-
ными константами, либо функциями
координат или решения. Поэтому
если в двух геометрически разне-
сенных подобластях расчётной об-
ласти параметры задачи одинаковы
(в том смысле, что в каждой из >тих
подобластей они либо равны одним и тем же константам, либо их зна-
чения могут быть вычислены по одним и тем же формулам), то у этих
10.2.Структуры данных для описания двумерны к задач .,.
451
подобластей удобно задать один и тог же номер. Но при ном каждая
из этих подобластей должна быть включена в описание расчсикч! об-
ласти. Например, расчётная область, показанная на рис. 84, будет опи-
сана следующим образом:
4
1. 2. 4. 6.
6
1. 2. 2.2 2.8 3. 3.5
4
112 16
2 2 4 1 2
3 2 3 3 4
2 2 4 5 6
Как видно из приведенного выше описания расчётной области Q,
две из сё четырёх подобластей имеют один и тот же номер, равный
двум. Очевидно, что при таком подходе под номером подобласти фак-
тически понимается номер формул, определяющих параметры диффе-
ренциального уравнения в рассматриваемой подобласти.
Аналогичный подход может быть применён для описания границ
расчётной области с заданными на них краевыми условиями первого,
второго или третьего рода. Каждый фрагмент границ , S2 и мо-
жет быть описан шестью целыми числами:
• тип краевого условия (1 означает принадлежность фрагмента гра-
нице /д, 2 - границе S2,3 - границе S3);
• номер границы (т.е. номер формул, задающих параметры краевого
условия на рассматриваемом фрагменте границы);
• номер элемента массива , с которого рассматриваемый фраг-
мент границы начинается по оси х ;
• номер элемента массива X4' , которым рассматриваемый фрагмен
границы заканчивается по оси х ;
• номер элемента массива У1И, с которого рассматриваемый фр<п-
мент границы начинается по оси у:
• номер элемента массива У,г, которым рассматриваемый фрагмеш
границы заканчивается по оси у.
При использовании такого подхода границы расчётной обиде т.
представленной на рис. 83, могут быть описаны следующим образом
(содержимое массивов ¥ и У1' - то же самое, что п в описании
самой расчётной области на с. 450):
112 2 12
1 2 2 3 2 2
3 112 4 4
3 2 2 3 4 4
3 3 1114
2 1 3 3 2 3
2 1 3 3 3 4
2 2 12 11
452 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
Очевидно, что если параметры краевых условий являются констан-
тами, то вместо номеров границ можно задавать значения этих пара-
метров. Однако если в решаемой задаче есть параметры краевых усло-
вий в виде некоторых функций, то задать их по номеру границы гораз-
до проще. Возможно и комбинирование двух подходов. Например,
если номер границы положителен, то он задаёт номер формулы, по
которой должны вычисляться параметры краевого условия, если же
отрицателен, то значения параметров краевого условия задаются в
следующих за этим номером вещественных числах (т.е. одним числом
для краевых условий первого и второго рода и двумя числами для
краевых условий третьего рода). Аналогичные модификации возмож-
ны и при описании расчётной области - после номера подобласти
можно зарезервировать место под необходимое количество вещест-
венных чисел, которые в случае отрицательного номера подобласти
интерпретируются как значения параметров.
10.2.2. ОБЩИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ СТРУН ГУР ДАННЫХ
ДЛЯ ХРАНЕНИЯ КОНЕЧНО ЭЛЕМЕНТНЫХ СЕТОК
Как было показано выше, наиболее эффективным способом фор-
мирования конечпоэлементной СЛАУ является её поэлементная сбор-
ка из локальных матриц. Поэтому хранение конечноэлементной сетки
должно быть таким, чтобы можно было достаточно просто организо-
вать цикл по элементам. При обработке каждого элемента нужен про-
стой доступ к координатам его вершин и к информации о значениях
параметров дифференциального уравнения на элементе (для вычисле-
ния локальных матриц и векторов), а также нужны глобальные номера
локальных базисных функций этого элемента (для занесения локаль-
ных матрицы и вектора в глобальные). Могут ещё также понадобиться
глобальные номера ребер и граней конечных элементов, а также неко-
торая дополнительная информация об особых узлах при наличии в
сетке несогласованных элементов (подробнее о том, для чего конкрет-
но нужна такая информация, будет сказано в следующих разделах).
Вся необходимая информация о копечноэлементной сетке хранится
в специальных структурах данных. При этом организация структуры
данных очень сильно зависит от типа сетки Наиболее простыми явля-
ются структуры данных для регулярных конечноэлементных сеток.
10.2.3. ХРАНЕНИЕ РЕГУЛЯРНЫХ ПРЯМОУГОЛЬНЫХ СЕТОК
При использовании двумерных регулярных прямоугольных се-
ток можно довольно просто определять положения ячейки и координа-
ты узлов по её номеру. Для этого дополнительно к описанию области
достаточно хранить только координатные линии х — хр и у = ys,
определяющие прямоугольную сетку. При этом кажцый конечный
элемент фактически определяется двумя соседними координатными
линиями по :г (.г = х„ и х = .тр+1) и по у (у = t/s. и у = уя+1). Зна-
чения же :гр и j/5, задающие координатные линии сетки, удобно хра-
нить в двух одномерных массивах V и Y .
10.2.Структуры данных для описания двумерных задач. ...
453
Эти массивы обычно формируются из массивов X и 1 , с по-
мощью которых определяются границы элементарных подобластей и
которые задаются в файле описания расчётной области (см. с. 149
450). Для этого достаточно каким-либо образом определить разбиение
интервалов между соседними точками в массивах X11 и У 11 . Это
можно сделать, например, задав количество подынтервалов, на кото-
рые должен быть разбит каждый интервал между соседними точками в
массивах X1' и У11 . Чтобы иметь возможность делать сгущения или
разрежения узлов, на каждом интервале между соседними точками
массивов Хп и У1’ можно также задавать коэффициент растяжения
(сжатия) подынтервалов.
Информацию о разбиениях на подынтервалы всех интервалов меж-
ду соседними точками в массивах X и У можно задавать в файле
со следующей структурой.
Пусть TVj’ —длина массива X11 , a Ny -длина массива У11 . Пер-
вые N ' — 1 пар чисел задают разбиение интервалов между соседними
точками в массиве X ’ . При этом первое в каждой паре число (це-
лое)- это количество подынтервалов, на которое должен быть разбит
очередной интервал. Второе же число в этой паре (вещественное) -
коэффициент изменения длины подынтервалов при разбиении каждого
интервала.
Следующие хранящиеся в этом файле Ny — 1 пар чисел точно так
же задают разбиение интервалов между соседними точками в массиве
уЩ
Приведём пример файла, определяющего разбиение показанной на
рис. 84 расчётной области. Учитывая, что N^ — 4, a TV,1/ =6 (см.
описание расчётной области на с. 451), нужно задать три пары чисел
для определения сетки по х и пять пар чисел для определения сетки
по у:
5 1. 41.25 41.
51. 11. 31. 11. 21.
Тогда массивы X и У будут иметь вид
X = (1, 1.2, 1.4, 1.6, 1.8, 2, 2.35, 2.78, 3.32 4, 4.5, 5. 5.5, (>},
У = {1, 1.2, 1.4, 1.6, 1.8, 2, 2.2, 2.4, 2.6, 2.8, 3, 3.25, ЗТ»}.
Обратим внимание на то, что в рассматриваемом нами примере
часть узлов (тр,?/Л.) и ячеек ^p+i] х [?/л.,7/л.+1 ] регулярной при
моугольной сетки не попадает в расчётную область. Гем нс менее чю
бы работать с этой сеткой как с регулярной, мы должны пронумеровать
все ячейки и все узлы. Так, в рассмотренном нами примере в расчетную
область не попали, например, узлы (2.2,4.5), (2.2,5) и т т (всею 16
узлов из 182), а также 28 ячеек из 156.
454 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
Узлы регулярной сетки, не попавшие в расчётную область, обычно
называют фиктивными.
Поскольку не попавшие в расчётную область ячейки не являются
конечными элементами, от них нет вкладов в глобальную матрицу.
Поэтому для фиктивных узлов в конечноэлементной СЛАУ генериру-
ются полностью нулевые строки, и, чтобы избежать вырожденности
СЛАУ, на главную диагональ таких строк (соответствующих фиктив-
ным узлам) можно, например, поставить единицу (и тогда в иктив-
ных узлах после решения конечноэлементной СЛАУ получатся нуле-
вые веса)1 * *.
1 аким образом, данных, хранящихся в массивах Хи' ив файле
описания области, достаточно для получения всей необходимой ин-
формации о конечных элементах в регулярной прямоугольной сетке
при указанном выше способе нумерации узлов (с введением фиктив-
ных узлов сетки при непопадании их в расчетную область).
Покажем, как можно получить всю необходимую информацию для
построения конечноэлементной аппроксимации при использовании
регулярной прямоугольной сетки с биквадратичными элементами
Обозначим через NI; количество координатных линий :г = хр, яв-
ляющихся вертикальными границами конечных элементов (и храня-
щихся в массиве X), а через 7V(/ количество координатных линий
у = ys, являющихся горизонтальными границами конечных элементов
(и хранящихся в массиве Y ). Тогда число биквадратичных конечных
элементов будет равно (N — 1)(Х(/ — 1 , а количество неизвестных q,
будет равно (2Х.(. — 1)[2Х(/ — 1).
Будем считать, что локальная нумерация узлов на биквадратичном
элементе определена в соответствии с рис. 24 на с. 246, а глобальная
нумерация всех узлов ссгки (включая внутренние) выполнена по
принципу возрастания их номеров сначала по х, затем по у. Тогда
координаты узлов конечного элемента с номером г можно определить
с помощью соотношений
р = ((•/ - 1) mod (N,. - 1)) + 1,
•7> = -V(/?), Vh = (? + У ’ ул = V(s),
(Ю.1)
Vi = П* + 0, (Ю.2)
_ xp 4- .ry,+1 _ ys + 7/., + 1
I'+i 2 ’ ,y-'+j 2
(10.3)
Номер подобласти IK,,,, которой принадлежит конечный элемент
Q,, можно легко получить, проверив, в какую из подобластей попал
1 Можно также после генерации копечноэлсмснтной СЛАУ с фиктивными
уравнениями и неизвестными сделать её сжатие, удалив из неё строки и
столбцы с номерами, соответствующими фиктивным узлам.
10 2.Структуры данных для описания двумерных задач
455
центральный узел Q?; с координатами
2;/?+l,Z/44_i j (лог номер необ-
ходим для вычисления значений параметров дифференциального урав-
нения).
Глобальные номера девяти локальных базисных функций конечно-
го элемента можно легко вычислить с помощью целочисленной
функции
/<(0 = 2
г — 1
N.- 1
(27У/; - 1) + 2 ((г - 1) mod (Nx - 1)) -|-1.
(10/1)
Так, узлу (тр,?/Л.) соответствует глобальная базисная функция с но-
мером К (г), узлам
xP+^ysj и (vn>&)
- глобальные функции со
следующими двумя номерами К (г) +1 и /<(/)+2. Узлу , 3/Л_|_± J
соответствует глобальная базисная функция с номером
К (/) + 2N.r — 1, узлам
и
•s+l
глобальные
функции со следующими двумя номерами. И, наконец, узлам
(хр j Уя+1)> угр+|’ ^Л+1
и (з'р+ь i/.s+i ’ - глобальные базисные функции
с тремя последовательными номерами, начиная с номера
/Цг)-|-2(2Уг-1).
Здесь мы рассмотрели способ, который позволяет получить всю не-
обходимую информацию о любом конечном элементе Q?; по номеру i
из структур данных, описывающих расчётную область и регулярную
сетку.
Однако чаще всего при работе с регулярными сетками проход по
конечным элементам организуют не одшш циклом по г (i — номер
обрабатываемого конечного элемента), а двумя (в двумерном случае)
или тремя (в трёхмерном) вложенными циклами. Самый внутренний
цикл - по р от 1 до Лг:, —1 (N— количество координатных линии,
определяющих границы конечных элементов по координате г и хра
нящихся в массиве X ). Внешний к нему цикл - по .ч о г 1 до Л I
(Nt/ - количество координатных линий по ?/, хранящихся в массиве
Y). И если задача трёхмерная, самый внешний цикл но r от I ю
N — 1 ( Nz - количество координатных линий но z, которые дол кны
храниться в массиве Z).
В этом случае координаты вершин обрабатываемою конечною > гс
мента определяются совсем просто - это компоненты массивов V , )
или Z с номером, равным значению соответствуй иней переменной
цикла р, s или г. Координаты узлов на ребрах и ви\|рн конечною
456 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
элемента определяются через координаты его вершин по формулам
вида (10.3).
Так же просто определяются глобальные номера локальных базис-
ных функции. Для биквадратичного элемента (при нумерации узлов по
принципу возрастания их номеров сначала по х, затем по у) узел
и соответствующая ему глобальная базисная функция имеет
номер (.$ — 1) (2/Vг — 1) 4- р , узлы
и (^р+ьХ/.ч) - следующие
ja ним номера, узел
имеет номер s (2N.i: — 1) 4- р , узлы
и
;^.ys+i
следующие за ним номера, а
(хр, i/.s+i) имеет номер (s 4- 1) (‘2N:l. — 1) + р (и соответственно
узел
узлы
— следующие за ним номера).
Номер же подобласти, которой принадлежит обрабатываемый эле-
мент, можно, как это было описано выше, определить с помощью цен-
трального узла сравнениями ею координат с хранящимися в массивах
Х,г и у" (и в трёхмерном случае в массиве Zw) координатами ли-
ний, определяющих границы подобластей 1К„,.
Однако если подобластей И',( довольно много, то количество опе-
раций, необходимое для определения номера подобласти, может сталь
довольно значительным. Ускорить эту процедуру можно, заменив
сравнения вещественных координат на целочисленные сравнения пе-
ременных цикла р, s (и г в трёхмерном случае) с номерами коорди-
натных линий, ограничивающих подобласти 1У,П .
Для того чтобы определять принадлежность конечного элемеша
той или иной подобласти, нужны два (в двумерном случае) целочис-
ленных массива 1ХЦ' и Л’1 , сформированных следующим образом.
В ячейку массива /Xй с номером j должен быть занесён номер ячей-
ки массива X, в которой хранится га же точка, что и в j -й ячейке
массива V11 (напомним, что в массиве X хранятся х -координаты
линий сетки, а в массиве X хранятся х -коор шпаты границ подобла-
стей ). Аналогично должен быть сформирован и массив IYW (а
также массив 7Z11 в трёхмерном случае). Очевидно, эти массивы
удобней всего формировать в тог момент, когда создаются массивы X
и Y по информации из массивов Xй и У1( и из файла, определяю-
щего сетку (через дробление интервалов между соседними точками в
массивах Xй и Yw ).
Покажем в качестве примера вид массивов 1Х]} и IY" для облас-
ти, изображённой на рис. 84. Описывающая эту область структура
10.2.Структуры данных для описания двумерных задач.
457
данных была приведена па с. 451. Будем считать, что разбиение згой
расчётной области определяется файлом, представленным па с 15.3
(сразу же за этим файлом приведены массивы X и Y с коорднн нами
линий сетки). Тогда массивы 1ХЛ и /У11 будут иметь вид:
/Xй = {], 6, 10, 14}, 7У,Г={1, 6, 7, 10, 11, 1з}.
Теперь, чтобы определить, попадает ли конечный элемент
х [т/5, ys+l в подобласть llz7n , нужно взять из описания
расчётной области номера т~, и т~, т* ограничивающих 1Г„,
координатных линий (это со второй по пятую компоненты т -й строки
массива MW (5,*), описывающего все подобласти, т.е.
77/,“ — М11'/(2,т), т+ = 717^(3,771), т~ = МТУ (4, т) и
777,+ =. и проверить, лежат ли внутри целочисленного от-
резка L?77,.“,777.^j значения р и р + 1, а также лежат ли значения s и
5 + 1 внутри целочисленного отрезка [т“,77г+ ]'.
10.2.4. ОПИСАНИЕ ДВУМЕРНЫХ ОБЛАСТЕЙ С КРИВОЛИНЕЙНЫМИ ГРАНИЦАМИ
Чаще всего двумерные области с криволинейными границами
задаются с помощью метода описания границ. При этом для описания
подобластей удобно использовать понятие элементарной подобласти.
Элементарная подобласть - это участок области, со всех сторон
окружённый границами области (внутренними или внешними) или их
фрагментами и не имеющий границ или их фрагментов внутри себя.
Очевидно, что в том случае, когда граница задаётся только из отрезков
прямых, элементарная подобласть является многоугольником (воз-
можно, нсвыпуклым Для задания каждой элементарной подобласти
Расчётной области обычно указывается одна точка, лежащая внутри сё.
раницы же элементарной подобласти чаще всего определяются авто-
матически с использованием только списка всех границ расчётной
области и координат одной точки, лежащей внутри этой элементарной
подобласти.
Рассмотрим один из возможных вариантов структуры данных для
описания областей с криволинейными границами Будем считать, что
вес внутренние и внешние границы расчётной области разбиты на уч i
стки - фрагменты границы.
1 При этом проверку на попадание конечного элемента в иодоблас и. И
лучше начинать с той же подобласти, в которую попал предыдущий конечный
элемент. Это может значительно сократить вычисли тельные чацкпы. необхо-
димые для поиска нужной подобласти. Особенно большую жономню можно
получить при сильных дроблениях расчётной области, поскольку в ном с iy-
чае ситуация, когда два соседних элемента лежат в одной но юб inc in, будсл
встречаться гораздо чаше, чем ситуация, когда ни два элемента разделяет
вну греппяя граница.
458 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
Описание каждого фрагмента границы должно содержать инфор-
мацию о координатах его концов (удобнее всего в виде номеров точек
в соответствующем массиве, где хранятся координаты этих точек), о
геометрических характеристиках этого фрагмента (например, если
фрагментом является дуга окружности, то это может быть информация
о её центре и радиусе), а также о заданных на нём краевых условиях и
их параметрах. Кроме того, для некоторых алгоритмов построения
сетки требуется информация о разбиении всех границ расчётной об-
ласти, и поэтому для каждого фрагмента границы довольно часто хра-
нят и информацию о его разбиении. Например, это может быть число
интервалов, на который требуется разбить фрагмент, и коэффициент
изменения тага (растяжения или сжатия) от начала фрагмента к концу
(т.е. коэффициент 1.2 означает, что каждый следующий шаг должен
быть в I 2 раза больше предыдущего)1.
Приведём пример формата текстового файла, хранящего такую
структуру данных. В первой строке задаётся одно целое число N, оз-
начающее длину массива точек - концов фрагментов границ. Начиная
со следующей строки задаются /V пар вещественных чисел — это мас-
сив координат этих точек. Затем задаётся целое число М - число
фрагментов границы. Далее следует At блоков информации о всех
фрагментах границы.
Каждый блок информации о фрагменте границы начинается с цело-
го числа, определяющего тип фрагмента (0 - отрезок прямой, 1 - дуга
окружности и т.д.). Следующие два целых числа - это номера началь-
ной и конечной точек фрагмента границы в массиве точек (концов
фра1 ментов границ). Затем задаются вещественные числа - геометри-
ческие характеристики фрагмента, количество которых, естественно,
зависит ог типа фрагмента. Например, для отрезка прямой никакая
дополнительная информация вообще не нужна. Для дуги же окружно-
сти достаточно хранить одно число - отношение а расстояния от се-
редины дуги до середины её хорды (т.е. отрезка, соединяющего концы
фрагмента границы) к длине этой хорды. При этом знак а может оп-
ределять, какая из двух дуг задаётся - слева или справа от направлен-
ного отрезка (хорды).
Следующее целое число означает тип краевого условия, которое за-
дано на фрагменте границы (0 - внутренняя граница или вспомога-
тельная линия для управления построением сетки, 1 — краевое условие
первого рода, 2 - краевое условие второго рода и т.д.). Затем для всех
типов краевых условий (кроме типа 0) задаётся одно целое число -
номер границы (т.е. номер формул, задающих параметры краевого
условия на рассматриваемом фрагменте границы).
1 В некоторых интерактивных системах информация о разбиении привя-
зывается не к с?1мому фрагменту границы, а к сто концам, т.е. задастся тре-
буемый шаг возле каждой точки, являющейся концом какого-либо фрагмента.
Эта, безусловно, очень удобная возможность описания сетки фактически мо-
жет быть реализована как интерактивная надстройка над описываемой струк-
турой данных, поскольку по заданным шагам у начала и конца фрагмента
границы легко определяются число интервалов и коэффициент изменения
шага на этом фрагменте.
10.2.Структуры данных для описания двумерных тадач
459
Последние два числа блока определяют параметры разбиения фраг-
мента границы: первое число (целое) определяет число интервалов, па
которые разбивается фрагмент, а второе (вещественное) ко »ффицп
ент изменения (растяжения или сжатия) шага. Часто для удобства да-
ётся возможность при описании разбиения фрагмента границы щ ы-
вать отрицательный коэффициент, который означает, что изменение
шага задано не от первой точки («начала») фрагмента ко второй («кон-
цу»), а от второй («конца») к первой («началу»).
Следующее за описанием фрагментов границы целое число А оз-
начает количество элементарных подобластей в расчетной области.
Затем задастся К троек чисел, первое из которых (целое) означат
номер формул, определяющих параметры дифференциального уравие
ния в элементарной подобласти, а два остальных (вещественные)
координаты произвольной внутренней точки этой элементарной по-
добласти.
Приведём пример файла с такой структурой для изображённой па
рис. 85 прямоугольной расчётной области с круглым отверстием, со-
стоящей из двух подобластей ГЦ и ГЦ. Будем считать, что точки, яв-
ляющиеся концами фрагментов границ, и сами фрагменты пронумеро-
ваны так, как это показано на рис 85. При этом номера точек указаны
в прямоугольничках, а номера фрагментов - в кружочках. Будем также
считать, что па границах-окружностях расчётной области заданы крае-
вые условия третьего рода, а на всех остальных внешних границах -
краевые условия первого рода. В этом случае содержимое файла будет
следующим:
8
0. 0. 8. 0. 0. 6. 2. 6.
5. 6. 8. 6. 0. 11. 8. 11.
10
012 1141.
0 13 11 4-1.5
026 114 -1.5
0 3 4 0 3 1.
1 45 0.5 31 41.
0 5 6 0 4 1.
1 45 -0.5 31 41.
037 1 1 4 1.5
068 1 1 4 1.5
078 1141.
2
1 3. 2.
2 3. 10.
Рассмотренная структура данных является достаточно универе.i и
ной и может быть использована в программных комн к*ксах, которые
предназначены для построения сеток с треугольными ячейк *мп чти
любых других сеток, допускающих произвольные сгущения \ пюн в
460 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
расчётной области1. Естественно, эта структура данных является не
единственно возможной для описания областей со сложными граница-
ми. Рассмотрим, например, структуру текстового файла данных, пред-
назначенного для систем построения сеток с четырёхугольными ячей-
ками.
Рис. 85. Пример расчётной области
с криволинейными границами
Обычно сетки с четырёхуголь-
ными ячейками используются для
дискретизации областей, пред-
ставляемых в виде объединения
элементарных подобластей, кото-
рые сами тоже являются псевдо-
четырёхуголышками. Под пссв-
дочетырёхугольником мы пони-
маем фигуру, у которой так же,
как у четырёхугольника, можно
выделить четыре стороны, но эти
стороны могут быть не отрезками
прямых, а ломаными линиями.
При этом противоположные сто-
роны таких элементарных подоб-
ластей (псевдочетырёхугольни-
ков) разбиваются одинаково (на
одно и то же число интервалов).
Таким образом, аналогами коор-
динатных линий в этом случае
являются «горизонтальные» и
«вертикальные» ломаные, а эле-
ментарные подобласти в виде
нссвдочетырёхугольников задаются номерами этих координатных (ло-
маных) линий, между которыми они находятся. Поэтому соответст-
вующая структура данных больше похожа нс на рассмотренную на
с. 458-459 универсальную структуру данных для описания областей с
криволинейными границами, а на рассмотренную в разделе 10.2.3
структуру для описания областей с прямоугольными подобластями.
Фактически всё отличие заключается лишь в том, что вместо границ,
параллельных осям координат, требуется описать ломаные линии -
апало! и координатных линий.
Итак, в первой строке файла, в котором хранится соответствующая
структура данных, задаются два целых числа N™ и Ny . Число 7Vjl
означает число узлов на ломаных вдоль «горизонтального» направле-
ния (по аналогии сточками на горизонтальных координатных линиях в
прямоугольной сетке), а число JV” - вдоль «вертикального» (по ана-
логии с точками на вертикальных координатных линиях). Затем следу-
1 Например, это могут быть несогласованные сетки из четырёхугольников
или смешанные сетки из прямоугольников и треугольников. Подробно о несо-
гласованных и смешанных сетках мы расскажем в одиннадцатом и двенадца-
том разделах.
10.2.Структуры данных для описания двумерных задач
461
ет х N™ пар вещественных чисел - координа! узлов ломаных,
при этом N\v узлов, соответствующих каждой из «горизонталь-
ных» ломаных, задаются последовательно. При этом А:-я «вершкаль-
ная» ломаная определяется парами координат с номерами А:,
(n\v + к), (2^’г + к),..., ((Д^ -1) N"' + А;) .
После них в файле хранится информация об элементарных подоб-
ластях в том же виде, как и при описании прямоугольных подобластей,
т.е. число L (целое) - количество подобластей из которых
состоит расчётная область Q; далее L наборов по 5 целых чисел, они
сывающих все подобласти 1К2,..., первое из которых означает но-
мер формул, определяющих параметры дифференциального уравнения
в подобласти, второе - номер «вертикальной» ломаной, определяющей
левую границу подобласти , третье - номер «вертикальной» лома-
ной, определяющей правую границу IV,,,, четвёртое - номер «горизон-
тальной» ломаной, определяющей нижнюю границу W„,, и пятое -
номер «горизонтальной» ломаной, определяющей верхнюю границу
W
r r in •
Покажем, как будет выглядеть файл с описанной структурой для
изображённой на рис. 86 расчётной области. Эта расчётная область
отличается от изображённой на рис. 85 только тем, что круглое отвер-
стие заменено восьмиугольным. Соответствующий файл будет иметь
вид:
5 5
0.0. 2.0. 4.0. 6.0. 8.0.
0. 5.27 2.44 4.94 3.5 4.5 4.56 4.94 8. 5.27
0. 6. 2. 6. 3.5 6. 5. 6. 8. 6.
0. 6.73 2.44 7.06 3.5 7.5 4.56 7.06 8. 6.73
0. 11. 2. 11. 4. 11. 6. 11. 8. 11.
6
112 13
12 4 12
14 5 13
2 12 3 5
2 2 4 4 5
2 4 5 3 5
Совсем несложно изменить последнюю структуру данных ык что
бы она позволяла более точно описывать криволинейные ipaiinnu об
ласги. Для этого достаточно организовать хранение «горизонтальных»
и «вертикальных» ломаных таким образом, чтобы их участками moi мп
быть не только отрезки прямых, но и дуги окружное гей (ими какие
нибудь другие кривые, описываемые, например, кубическими силан
нами). В этом случае все генерируемые на сторонах нссндочс1 ырёх-
угольника с криволинейными границами внугренпне узлы можно ста-
вить точно па границы (т.е. с учётом их возможною искривления).
462 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
Читатель может попробовать создать соответствующую структуру
данных в качестве упражнения1.
10.2.5. РЕГУЛЯРНЫЕ СЕТКИ С ЧЕТЫРЁХУГОЛЬНЫМИ ЯЧЕЙКАМИ
Рассмотренные в разде-
ле 10.2.3 подходы к построению
регулярных прямоугольных сеток
можно с не слишком большими
изменениями использовать и для
построения регулярных сеток с
ячейками в виде четырёхугольни-
ков, если для описания расчётной
области использована структура
данных, рассмотренная в конце
раздела 16.2.4 на с. 460-461.
В этом случае разбиение об-
ласти на ячейки задаётся, как и
для прямоугольной сетки (см.
с. 453), с помощью файла, в кото-
ром содержится информация о
разбиениях на подынтервалы всех
интервалов между соседними
точками на «горизонтальных» и
«вертикальных» ломаных, опре-
деляющих границы подобластей
%,-
Покажем, как можно задать
четырёхугольную сетку для об-
ласти, показанной на рис. 86
Рис. 86. Пример расчётной облас ги
с разбиением на четырёхугольные
элементарные подобласти
(файл её описания приведён на е. 461).
Пусть разбиение эюй области определяется следующим файлом
21. 11. 11. 31.
3 -1.5 11. 11. 3 1.5
Содержимое этого файла определяет следующее разбиение расчёт-
ной области. Интервалы между первыми двумя узлами всех «горизон-
тальных» ломаных должны быть разбиты на два подынтервала (на это
указывает первое число в первой паре), при этом длины подынтерва-
лов нс должны меняться (поскольку второе число в первой паре - ко-
эффициент растяжения - равен единице). Следующие два интервала на
всех горизонтальных линиях вообще не разбиваются (поскольку в сле-
дующих двух парах чисел первые числа, определяющие количество
подынтервалов, равны единице). Четвёртые же интервалы на всех го-
ризонтальных ломаных разбиваются на три подынтервала с равномер-
ным (поскольку коэффициент растяжения равен единице) шагом.
1 Один из возможных вариантов такой структуры данных будет приведён
нами чуть ниже, на стр. 466.
10.2.Структуры данных для описания двумерных задач. ...
463
Рис. 87, Пример ре!улярпой
четырёхугол ьной сетки
Следующие четыре пары чисел аналогичным образом определяют
разбиение интервалов «вертикальных» ломаных на подышервалы.
Каждый первый интервал всех «вертикальных» ломаных разбивается
на 3 подынтервала, причём так, что каждый последующий подынтер-
вал должен быть в 1.5 раза меньше предыдущего. На это указывает
коэффициент растяжения, равный -1.5 (отрицательные коэффициенты
растяжения интерпретируется нами как соответствующие коэффици-
енты сжатия или, что го же самое, коэффициент растяжения не от пер-
вой точки интервала ко второй, а, наоборот, от второй к первой - об
этом уже говорилось на с. 459)1.
На рис. 87 показана регулярная
четырёхугольная сетка, построен-
ная для изображённой на рис. 86
расчётной области (с файлом её
описания, приведённым на с. 461,
и с учётом рассмотренного здесь
файла, определяющего эту сетку).
Ячейки этой сетки, как и прямо-
угольной, образуются соседними
«горизонтальными» и «верти-
кальными» линиями. Однако опи-
сать эти линии уже невозможно с
помощью двух независимых мас-
сивов, аналогичных массивам X
и Y . Очевидно, это можно сде-
лать так же, как были заданы «го-
ризонтальные» и «вертикальные»
линии в описании расчётной об-
ласти, — для этого нужно перечис-
лить номера всех узлов сетки по-
следовательно вдоль «горизон-
тальных» линий слева направо,
передвигаясь от одной «горизон-
тальной» линии к другой снизу вверх.
Координаты узлов регулярной четырёхугольной сетки можно вы
числить по довольно простои схеме. Сначала можно расставить у глы
на «основных» «горизонтальных» и «вертикальных» линиях, зд ганных
в файле расчётной области, с учётом количества подынтервалов и ко
эффициентов растяжения-сжатия Благодаря регулярное^ сетки »тн
узлы можно ставить сразу же на нужные места в формируемом м.цч и
ве координат узлов сетки. После этого не представляет никакою ip\ ы
сформировать все остальные узлы. Для этого достаточно сформиро
вать «вспомогательные» «горизонтальные» линии между у» ымн, но
ставленными на «основных» «вертикальных» линиях на пре на lymcM
1 В принципе, вместо числа -1 5 можно было задан, 'ни к> I I х но oooi
всгствовало бы такому «растяжению» шага, при котором кал ii.ni «ле ц'ющий
отличался бы от предыдущего в 0 6667 раза, т.е <|»ак 1 ина ки было бы 1 шно
сжатие Использование отрицательного коэффициент у юбисс нм. что про
щс задавать симметричные сжатия-растяжения ячеек ccikii
464 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
этапе, и разбить их точно так же, как и «основные», с учётом количе-
ства подынтервалов и коэффициентов растяжения-сжатия, соответст-
вующих рассматриваемому интервалу «основной» «горизонтальной»
линии.
Для примера, изображённого на рис. 87, на первом этапе в массив
узлов будут по этой схеме занесено 60 узлов. Первый узел (с номе-
ром 1) совпадает с первым узлом первой «горизонтальной» ломаной из
файла описания расчётной области - его координаты ^=0,^ = 0.
Координаты второго узла (с номером 2) получаем из условия, что пер-
вый интервал всех «основных» «горизонтальных» линий разбит на два
подынтервала с единичным коэффициентом растяжения, - это коорди-
наты х-2 = 1, Уч — 0 - Аналогично получаются координаты узлов с
номерами 3-х до 8-и, от 25-и до 48-и и от 65-и до 72-х.
Координаты узла с номером 9 получаются с учётом того, что пер-
вый интервал всех «основных» «вертикальных» линий разбит на три
подынтервала с коэффициентом растяжения -1.5, — его координаты1 2
.Гд =0, </д = 2.5. Следующим заносится узел с номером 11. Его коор-
динаты также вычисляются с учетом разбиения первого интервала
«основных» «вертикальных» линий па три подынтервала с коэффици-
ентом растяжения —1.5. Поскольку этот интервал заключён между точ-
ками (2,0) и (2.44,4.94), узел с номером 11 будет иметь координаты0
.Тц = 2.21, T/ц — 2.34. Аналогично вычисляются координаты узлов с
номерами 12,13.16,17,19 и т.д.
На втором этапе будут сформированы координаты узлов с номера-
ми 10, 14, 15, 18, 22 и т.д. Например, координаты узла с номером 10
можно определить с учётом то<о, что интервал между уже сформиро-
ванными узлами с номерами 9 и 11 должен быть разбит на два подын-
тервала с коэффициентом растяжения-сжатия ое = 1, как и все первые
1 Ч гобы вычислить координаты этого узла, достаточно най.и длину перво-
го шага A.J и сдвинуться на Л, из узла с номером 1 (с координатами (0,0)),
являющегося начальной точкой разбиваемого интервала, в направлении к
точке с координатами (0,5.27), являющейся концом разбиваемого интервала.
„ , , , , (1 — а)
Длину шага /ц можно определить по формуле = d-f-----где d - длина
(1-а )
разбиваемого интервала, а - коэффициент растяжения-сжатия, п - количе-
ство подынтервалов (для рассматриваемого узла d = 5.27, а = ] /1.5 , п = 3,
и поэтому = 2.5). Очевидно, следующий шаг в этом же направлении
1ъ2 = &h} = 1.66 - это расстояние между узлом с номером 9 и узлом с номе-
ром 17 (т.е. по значению /г2 можно легко определить координаты узла с но-
мером 17).
2 При этом х - и у -координаты узла можно вычислить независимо друг от
друга, разбивая для .г интервал ^2, 2.44), а для у - интервал (d, 4.94) с од-
ним и тем же коэффициентом растяжения —1.5 (т.е. сжатия 1.5 ).
10.2.Структуры данных для описания двумерных задач
465
интервалы «горизонтальных» ломаных, описывающих расчётную об-
ласть. Таким образом, .Тщ = 1.115, т/И) = 2.42.
Обозначим через N.r количество точек па каждой «горизонталь-
ной» линии сегки, а через Ny — количество точек на каждой «вфрти-
калыюй» линии сетки (с учётом разбиения на подынтервалы интерва-
лов всех «горизонтальных» и «вертикальных» линий из описания рас-
чётной области). Таким образом, в полученной четырёхугольной сетке
будет Nr х Ny узлов и (N — 1) х — 1) ячеек.
Проход по конечным элементам для регулярных сеток с четырёх-
угольными ячейками удобней всего, как и для регулярных прямо-
угольных сеток, осуществлять двумя вложенными циклами: внутрен-
ний цикл по р от 1 до N,. — 1, внешний - по s от 1 до Ny — 1 . Опре-
делять же принадлежность ячейки той или иной подобласти (для вы-
числения значений параметров дифференциального уравнения) имеет
смысл с использованием стратегии, основанной на целочисленных
сравнениях номеров «горизонтальных» и «вертикальных» линий из
описания расчётной области с номерами «горизонтальных» и «верти-
кальных» линий сетки. Эго можно сделать с помощью массивов /Xй
и /У|И , которые формируются точно так же, как это было описано для
прямоугольных сеток па с. 456.
Для рассмотренного нами примера (см. рис. 87) массивы IX 11 и
/Уп будут иметь вид:
ZY” = {1,3,4,5,8} , IYW = {1,4,5,0,9}.
Стратегия определения номера подобласти для четырёхугольных
сеток ничем не отличается от соответствующей стратегии для прямо-
угольных сеток (см. с. 457).
Обратим внимание на то, что некоторые ячейки и узлы регулярной
четырёхугольной сетки (так же, как и при использовании прямоуголь-
ных сеток) могут не попадать в расчётную область. Для приведённого
на рис. 87 примера это четыре ячейки вну1ри «дырки» и узел с номе-
ром 36 (в самом центре «дырки», на рис. 87 он обозначен незакрашен-
ным кружком). Очевидно, что для узлов регулярной сетки, лежащих
вне расчётной области, не будут' сгенерированы консчноэлсмснiныс
уравнения, и обработка этой ситуации может быть проведен! iai< же,
как и в случае регулярных прямоугольных сеток (см. с. 454).
Ещё одна важная особенность сеток с четырёхугольными ячейками
заключается в возможности уточнения описания криволинейных i р.т
ниц при измельчении ячеек сетки. В рассмотренном нами прим ।
(рис. 86) круглое отверстие (см. рис. 85) было заменено пр ши и.ном
восьмиугольником. В этом случае дальнейшее дробчснис е.счки нс
приведёт к уточнению границ расчётной облает < (т.е новый \ cii.i бу
дут ставиться на отрезки, соединяющие вершины мшии\iо h.ihik.i) В
принципе же, при описании расчётной области от тс.и ныс уч и 1ки «и,-
риюнтальпыч» и «вертикальных» ломаных, опрс ic ihkhiihx »r> ot
lacib, можно хранить как некоторые кривые (ча (и окр\ гпбстсч! па
рабоЯ, сплайнов и т.д.). Это можно делать, например. вве кшп м ш ко
466 Ю.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
торого массива, в котором задаются номера «горизонтальных» лома-
ных и номера тех их интервалов, которые являются дугами окружно-
стей, и для этих интервалов задавать параметры соответствующей дуги
(либо в виде координат центра окружности1, либо в виде одного чис-
ла- отношения расстояния от середины дуги до середины её хорды к
длине этой хорды, см с. 458 о параметре а ) Аналогично можно опи-
сывать криволинейные участки и на «вертикальных» ломаных. Задание
вместо отрезков «горизонтальных» и «вертикальных» ломаных частей
парабол, сплайнов и других кривых можно организовать точно так же
с помощью соответствующих дополнительных массивов.
Рис. 88. Пример расчётной области и построение в ней четырёхугольной сетки
с учётом криволинейной границы
Проиллюстрируем возможность бопее точного учёта криволиней-
ных границ при измельчении сеток с чегырёхугольными ячейками на
примере разбиения области, изображённой на рис 88,я Для описания
этой области будем использовать практически такую же структуру
данных, которая была рассмотрена на с. 460. В ней сначала задаются
два целых числа и , а затем 7V?' х пар вещественных
чисел (координат узлов), определяющих «горизонтальные» и «верти-
кальные» ломаные:
3 4
0. 0. 5. 0. 7. 0.
0. 2.59 5.59 2.59 7. 2.
0. 4. 5. 4. 7. 4.
0. 6. 5. 6. 7. 6.
1 На самом деле, эта информация (две координаты центра окружности) яв-
ляется даже избыточной, поскольку дуга должна пройти через две точки (кон-
цы интервала). В принципе, возможно некорректное задание центра окружно-
сти, если он не равноудалён от концов интервала, и эту ситуацию надо специ-
ально обрабатывать - можно сообщать об ошибке в задании, а можно коррек-
тировать координаты центра так, чтобы он при максимальной близости к
указанному в файле описания области был равноудалён от концов интервала.
10.2.Структуры данных для описания двумерных задач. .
467
После этого задается информация об элементарных подобластях:
3
112 14
12 3 12
2 2 3 3 4
И наконец, дополнительно (по отношению к рассмотренной на
с. 460 структуре данных) зададим информацию о криволинейных уча-
стках «горизонтальных» и «вертикальных» ломаных в следующем
формате. Первым идёт число М, определяющее общее количество
криволинейных участков границ. Далее следуют М пятёрок чисел,
определяющих каждый участок. Первое число каждой четверки - при-
знак того, является ли линия «горизонтальной» (тогда это число рав-
но 1) или «вертикальной» (тогда это число равно —1) Второе число
номер ломаной, третье - номер интервала. Последние два числа - эго
параметры дуги (координаты центра окружности). Для рассматривае-
мого примера эта информация имеет вид
2
-1227. 4.
1 2 2 7. 4.
На рис. 88,6 показана сетка, получаемая при её построении по фай-
лу следующего вида:
4 -1.5 2 1.
3 -1.4 3 1.25 2 1.5
Обратим внимание на то, что при разбиении криволинейных участ-
ков узлы были поставлены нс на хорды, а на сами дуги, и узлы на
вспомогательных линиях генерировались с учётом этого.
Дополнительным преимуществом регулярных сеток является го,
что не только для хранения их самих, но и для хранения матриц ко-
нечноэлементных СЛАУ, получаемых в результате аппроксимации на
регулярных сетках, можно использовать самые экономичные структу-
ры данных (такие, как диагональный формат хранения матриц, кото-
рый будет рассмотрен чуть ниже в этом же, десятом разделе).
Сетки с ячейками в виде треугольников, тетраэдров и призм, как
правило, являются нерегулярными, и для их хранения обычно исполь-
зуются специальные структуры данных. Довольно часто такие cipxi<-
туры данных используются для хранения сеток с ячейками в виде »к
тырёхугольников и шестигранников, а иногда и для прямо)iони ix
сеток, когда расчётная область имеет большие «дыры» и слишком
много узлов регулярной сетки не попадает в расчё гпую об.п кн. (к*
при использовании регулярной сетки они должны сыпонищн фнк
тивпыми). Кроме того, когда в регулярных сетках делаю к я и ные
дробления (в частности, в прямоугольных сетках с поив iciihvm в них
468 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
несогласованных ячеек1), их регулярность также, как правило, наруша-
ется
Заметим, что идея набрасывания регулярной сетки (из прямоуголь-
ников или четырёхугольников в двумерном случае либо из параллеле-
пипедов или шестигранников в трёхмерном случае) может быть до-
вольно плодотворной даже при формировании нерегулярных конечно-
элементных сеток в областях с существенно изрезанными внешними
границами и большими «дырами». В таких случаях в конечноэлсмснт-
ную сетку можно не включать ячейки и узлы исходной регулярной
сегки, нс попавшие в расчётную область, но для описания регулярной
сетки и организации прохода по её ячейкам (для записи в конечноэле-
ментную сегку только тех из них, которые попали в расчётную об-
ласть) можно использовать рассмотренные нами выше структуры дан-
ных и алгоритмы работы с регулярными сетками.
10.2.6. ХРАНЕНИЕ НЕРЕГУ ЛЯРНЫХ СЕТОК
Для нерегулярных сеток наиболее удобным является поэлемент-
ный способ хранения При таком способе сетка задаётся в виде набери
вершин и набора элементов. Каждая вершина сетки описывается набо-
ром координат (двумя координатами х^. и в двумерном случае или
тремя координатами хк, у/. и zk в трёхмерном случае), а каждый эле-
мент Q/;/ - набором из нескольких целых чисел. Например, каждый
конечный элемент можно хранить в виде набора следующих чисел:
• номеров узлов, являющихся вершинами рассматриваемого элемента;
• глобальных номеров базисных функций элемента;
• номера подобласти расчётной области, служащего для определения
значений параметров дифференциального уравнения внутри данно-
го элемента.
Естественно, в случае совпадения номеров глобальных базисных
функций с номерами вершин элементов (или при возможности их про-
стого вычисления по этим номерам) нет никакой необходимости хра-
нить глобальные номера базисных функций элемента. Например, для
элементов первого порядка, у которых число базисных функций сов-
падает с числом вершин, для каждого элемента хранится ровно I + 1
целых чисел, где I — количество вершин элемента, а последнее
(/4-1) -е число — номер подобласти, которой принадлежит элемент
Для хранения сеток с лагранжевыми конечными элементами поряд-
ка выше первого, когда количество геометрических вершин не совпа-
дает с количеством узлов (к которым привязаны локальные базисные
функции), можно использовать различные варианты структур данных.
Мы рассмотрим два из них. В первом варианте массив узлов содержит
все узлы сетки, включая те, которые не являются геометрическими
вершинами элементов. Во втором же варианте в массиве узлов хранят-
ся только геометрические вершины конечных элементов, а координаты
узлов, к которым привязаны базисные функции, вычисляются через
1 Подробнее о таких несогласованных элементах и локальных дроблениях,
в результате которых они могут получаться, см. в одиннадцатом разделе
10.2.Структуры данных для описания двумерных задач. ... 469
координаты вершин элемента. Очевидно, что первый варит и позволя-
ет экономить время на вычисление координат узлов, а второй - память
на их хранение. Однако экономия вычислительных затрат в обоих слу-
чаях достаточно мала но сравнению с общими вычислительными за-
тратами на решение задачи, и выбор обычно делается в пользу первого
варианта как более простого для реализации.
Очевидно, что кроме информации о конечных элементах для реше-
ния задачи требуется еще и информация о краевых условиях Для не-
регулярных сеток границы чаще всего также хранятся поэлементно
рёбрами в двумерных задачах и гранями в трёхмерных.
Краевые условия второго и третьего рода представляются наборами
таких граничных элементов. Каждый граничный элемент (ребро или
грань), являющийся частью границы с заданным на ней краевым усло-
вием второго или третьего рода, описывается набором целых чисел
номерами ненулевых па этом граничном элементе глобальных базис-
ных функций1 и числом, которое служит для определения значении
параметров краевого условия (0 для второго краевого условия или [3 и
Up для третьего).
Краевое же условие первого рода чаще всего представляется набо-
ром пар целых чисел, в котором первое число каждой пары является
номером узла, лежащим на границе, а второе служит для определения
значения параметре! «г/ этого краевого условия. Заметим, что для эр-
митовых конечных элементов или при необходимости выполнения
дополнительных дроблений сетки информацию о границе S) лучше
хранить всё-таки в виде набора граничных элементов (рёбер или гра-
ней2) так же, как и в случае границ со вторым и третьим краевыми ус-
ловиями.
Рассмотрим два варианта структур данных, предназначенных для
хранения сеток из треугольных элементов первого и второго порядка.
Простейшие примеры таких сеток показаны на рис. 89 (с треугольни-
ками первого порядка) и 90 (с треугольниками второго порядка). 11а
обоих рисунках треугольники с номерами3 .1 — 3 лежат в подобласти
1Ц , а треугольник с номером 4 - в подобласти 1И2 • Будем считать, что
в обоих примерах на горизонтальных (нижней и верхней) границах
расчётной области заданы краевые условия второго рода (с разными
значениями параметра 0), а на левой (вертикальной) и праной (на
1 Для лагранжевых элементов эти номера совпадают с глобапьнымн номе
рами лежащих на рассматриваемой границе узлов.
2 На самом деле информацию о граничных элементах hiioi ы ну мш хрл
нить даже не в виде рёоер (или граней), а в виде некоторых кривых (it in по
верхностей) - в этом случае при выполнении дополниu ii.hi.ix ции» ц-ннй
новые (получаемые в результате этих дроблении) узлы мо кни ci шип. нс на
рёбра и грани, а именно на эти искривлённые границы, \ ючпяя их пре н iait
пение (подробнее об этом будет сказано ниже, см. i 621)
3 Номера конечных элементов па рис. 89 и рис 9(1 \k.ii.ihi.i в кр\ точках, а
номера узлов - в прямоугольничках.
470 Ю.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
клонной) границах — краевые условия первого рода (также с разными
значениями параметра и(/)
Для первого примера массив узлов состоит из следующих шести
пар вещественных чисел:
1. 1. 3. 1. 4. 1. 6.
Рис. 89 Пример сетки из треугольных
элементов первого порядка
чисел:
1251 2651 23
1. 3. 4. 3.
Будем считать, что каждый
треугольник первого порядка
описывается четырьмя целыми
числами: тремя номерами узлов,
являющихся его вершинами, и
номером подобласти, которой он
принадлежит. Тогда информация
о всех треугольниках сетки может
быть представлена массивом,
состоящим из четвёрок целых
чисел, и для сетки, изображённой
на рис 89, этот массив будет
содержать следующие четвёрки
6 1 3 4 6 2
Краевые условия второго рода для элементов первого порядка
можно хранить в отдельном массиве тройками целых чисел, первые
два из которых - номера вершин ребра, а третье - номер формулы, по
которой должно вычисляться значение параметра 0. Для рассматри-
ваемой нами задачи (в которой краевые условия второго рода заданы
на нижней и верхней границах расчётной области и параметр 0 на этих
границах может определяться разными формулами) и для сетки, изо-
бражённой на рис. 89, массив с информацией о вторых краевых усло-
виях примет вид
121 231 341 562
Информация о краевых условиях первого рода при использовании
элементов первого порядка может быть задана массивом пар целых
чисел, в которых первое число номер узла, а второе - номер форму-
лы, по которой должно вычисляться значение параметра ид В нашем
примере (соответствующем рис. 89) этот массив будет содержать че-
тыре нары целых чисел:
11 51 42 62
Для сеток с квадратичными (и более высокого порядка треуголь-
ными элементами) в массиве узлов можно хранить парами координаты
всех узлов сетки, включая узлы, не являющиеся вершинами треуголь-
ников Тогда для сетки, изображённой на рис. 90, этот массив будет
иметь вид:
10.2.Структуры данных для описания двумерных задач. ..
471
1. 1. 2. 1.
5. 1. 6. 1.
4. 2. 5. 2.
3. 1. 3.5
1. 2. 2.
1. 3. 2.5
Треугольники в этом случае
можно хранить набором семёрок
целых чисел. В каждой семёрке
чисел (описывающей один тре-
угольный конечный элемент) пер-
вые три числа - эго номера вер-
шин треугольника, являющихся
вершинами треугольника, сле-
дующие три - глобальные номера
1. 4. 1.
2. 3.5 2.
3. 4. 3.
।---1-----1-----1-----1-----'
1. 2. 3. 4. 5. 6 г
Рис. 90. Пример сетки из треугольных
элементов второго порядка
з. 38 с. 290. Последнее (седьмое)
которой принадлежит конечный
узлов, расположенных на середи-
нах рёбер. Такое перечисление
узлов квадратичного треугольни-
ка соответствует локальной нуме-
рации его узлов, приведённой на р
число означает номер подобласти
элемент.
Для сетки, изображённой на рис. 90, массив треугольников примет
вид:
1 3 13 2 9 8 1 3 15 13 10 14 9 1
3 5 15 4 11 10 1 5 7 15 6 12 11 2
Краевые условия второго рода для треугольных элементов второго
порядка можно хранить в массиве четвёрками целых чисел, первые два
из которых - номера вершин (граничных узлов) ребра, третье - номер
центрального узла ребра, четвёртое - помер формулы, по которой
должно вычисляться значение параметра 0 на рассматриваемом ребре
Для сетки, изображённой на рис. 90, этот массив с информацией о
краевых условиях второго рода имеет вид
1321 3541 5761 13 15 14 2
Информацию о краевом условии первого рода, как и для элементов
первого порядка, можно хранить парами целых чисел (первое число
номер узла, второе - номер формулы для вычисления д(/). Для се г км,
изображённой на рис. 90, соответствующий массив примет вид
11 81 13 1 15 2 12 2 72
Заметим, что чаще всего программы построения сеток формируют
данные, в которых содержатся только геометрические вершины »ie
ментов и ячейки как геометрические объекты (треугольники, прямо
угольники, тетраэдры и т.п.), заданные только номерами icoMeipirii
ских вершин и номером подобласти. В этом случае дли no-ijniпня они
санных выше структур данных необходимо внести в i 1рмы\рм ыи
ных, сформированные программами-пос трои гелями сл юк. пс пч i но
щую информацию о номерах всех ненулевых иг каждом конечном
элементе глобальных базисных функции Алгоритмы нумерации i ю
472 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
бальных базисных функций (или, что то же самое, неизвестных q,,
являющихся весами базисных функций ф, в представлении прибли-
жённого решения и'1 в виде ) мы рассмотрим несколько позже.
i
10.2.7. ПОСТРОЕНИЕ НЕРЕГУЛЯРНЫХ ТРЕУГОЛЬНЫХ СЕТОК
Как уже говорилось выше, сетки с треугольными ячейками
обычно используют в тех случаях, когда расчётная область имеет
сложные границы. Кроме того, треугольные сетки позволяют довольно
эффективно делать локальные дробления в отдельных местах расчёт-
ной области. Это даёт возможность уменьшать погрешность аппрок-
симации, не вводя в сетку так называемые «лишние» узлы, в результа-
те чего могут быть значительно сэкономлены вычислительные ресур-
сы1.
Существует очень много различных подходов к построению грс-
угольных сеток. Простейшие из них основаны на формировании ячеек
треугольной сетки из прямоугольных или четырёхугольных ячеек ре-
гулярной сетки, набрасываемой на расчётную область. Треугольные
конечные элементы получаются разбиением каждой прямоугольной
или четырёхугольной ячейки на два треугольника. При этом, естест-
венно, не попадающие в расчётную область ячейки и узлы регулярной
сетки сразу же игнорируются (из таких ячеек не формируются ячейки
треугольной сетки, а не попадающие в расчётную область узлы не за-
носятся в список узлов)
Возможны различные модификации таких подходов, когда, напри-
мер, регулярная прямоугольная сетка набрасывается на расчётную
область с криволинейными или наклонными границами и вершины
прямоугольников перед разбиением их на треугольники могут пере-
мещаться на внутренние и внешние границы расчётной области, пере-
секающие этот прямоугольник. При перемещении вершин из прямо-
угольников могут получаться нс только выпуклые, но и невыпуклые
четырехугольники - для разбиения на треугольные ячейки это не так
уж принципиально.
Однако такие подходы хотя и позволяют учитывать довольно слож-
ную геометрию расчетной области, но могут порождать довольно
большое число «лишних» узлов (из-за регулярности первоначальной
сетки) и поэтому не очень экономичны.
При сравнении различных методов построения сеток самым пра-
вильным критерием качества сечки является соотношение между по-
грешностью решения задачи, полученного с её использованием, и тре-
буемыми для вычисления решения затратами (т.е. оптимальная сетка
1 При выполнении локальных дроблений сечки от «лишних» узлов можно
избавиться и тогда, когда используются сетки с ячейками в виде прямоуголь-
ников п четырёхугольников, но в этом случае необходимо использовать несо-
гласованные сетки — эти вопросы детально будут рассмотрены чуть позже, в
одиннадцатом разделе. Поэтому основное преимущество сеток с треугольны-
ми ячейками по сравнению с прямоугольными сетками состоит всё-таки в
возможности учёта сложной геометрии расчётной области.
10.2.Структуры данных для описания двумерных задач. ... 473
должна обеспечивать либо минимальную погрешность решения при
равных вычислительных затратах, либо минимум вычислительных
затрат на получение решения требуемой точности) Однако на практ и-
ке использовать такой критерий можно лишь для сравнения качества
уже построенных сеток, да и то при решении далеко не каждой (а чаще
всего модельной) задачи, поэтому для контроля качества сетки в про-
цессе её построения нужны другие критерии.
При сравнении качества треугольных сеток (обычно их называю!
триангуляциями) с одним и тем же набором узлов довольно часто
используют следующий критерий: одна сетка считается лучше дру1 ой,
если значение самого острого угла среди всех треугольников у неё
больше (поскольку именно слишком острый угол треугольника можс)
существенно ухудши!ь свойства конечноэлементной СЛАУ [22]). Из-
вестно, что по этому критерию для заданного набора узлов наилучшеи
является триангуляция Делоне [14].
Триангуляцией Делоне называется такая триангуляция, в которой
для любого треугольника внутри описанной вокруг пего окружности
не содержится ни одного узла сетки. Для построения триангуляции
Делоне по заданному набору узлов можно использовать, например,
широко известный алгоритм Ватсона. Основная суть этого алгоритма
состоит в следующем. В уже существующую триангуляцию (начиная с
одного треугольника, охватывающего всю расчётную область) после-
довательно (по одной) добавляются новые точки с удалением всех тре-
угольников, для которых новая точка находится внутри описанной
вокруг них окружности. Вместо удалённых из триангуляции треуголь-
ников строятся новые путём соединения вставляемой точки со сторо-
нами многоугольника, полученного после удаления из триангуляции
ненужных треугольников.
Известно, что время работы алгоритма Ватсона пропорционально
7V2 - квадрату числа узлов. Поэтому много работ посвящено его уско-
рениям, которые основаны на хранении дополнительной информации,
ускоряющей поиск треугольников. Однако даже с ускорениями трудо-
ёмкость соответствующих алгоритмов относительно числа узлов /V по
числу операций остаётся на уровне N In /V .
Особо следует отметить, что при решении многих задач триангуля
ция Делоне не является наилучшей конечноэлементной сеткой для
аппроксимации решения. Например, в тех случаях, когда решение
очень мало меняется по одной пространственной координате и ре «ко
меняется по другой, для улучшения аппроксимации имеет смысл ис-
пользовать вытянутые треугольники, и применение методов, требую
щих максимизации острых углов треугольников в процессе построения
триангуляции, может не только не улучшить, но и ухудшить ючшм и.
получаемого конечноэлементного решения Кроме того, ipii.ini\ пнщя
Делоне по её определению не учитывает наличия в обдаст i'ii\iprit
них границ (т.е. границ подобластей, в которых ио-рачном\ мш\ i он
рсделяться параметры решаемой задачи), и поэтом) при iioctpocnim
триангуляции в области с внутренними границами методы оснонйн
ные на получении триангуляции Делоне, нередко окл ii.ib.iioich очень
неэффективными.
474 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
И совсем малонлодотворными представляются нам попытки при-
менить используемые пои построении триангуляции Делоне принципы
для генерации тетраэоралъных сеток, так как в трёхмерном случае
заложенные в её основу принципы не гарантируют даже построения
невырожденных (т.е. имеющих ненулевой объём) тетраэдров. Это про-
исходит по следующей причине. В трёхмерном случае для построения
каждого тетраэдра фактически выбираются такие 4 узла, которые ле-
жат на одной сфере и для которых внутрь этой сферы не попадает ни
одного другого узла. При этом триангуляция Делоне никак не контро-
лирует ситуацию попадания четырёх вершин тетраэдра на одну
плоскость (или их близость к одной плоскости), что и можег приво-
дить к вырожденности (или почти вырожденности) получаемых тет-
раэдров
Существуют гораздо более эффективные подходы, в которых три-
ангуляция строится на основе алгоритмов непосредственной локаль-
ной оптимизации сетки по какому-либо критерию. Дополнительным
преимуществом этих методов является то, что генерацию узлов в них
можно проводить непосредственно при построении сетки. По такому
принципу работает большинство алгоритмов, строящих сетки фрон-
тальны и методом.
Довольно часто при использовании фронтальных методов расчёт-
ная область задастся в виде набора элементарных подобластей, сетка в
которых строится отдельно с автоматической стыковкой но их грани-
цам путём задания одного и того же разбиения каждой из внутренних
границ для смежных (по этой внутренней границе) элементарных по-
добластей. При этом разбиения границ элементарных подобластей
обычно задаются как исходные данные для фронтального метода.
Продемонстрируем использование фронтального метода для гене-
рации сетки в выпуклом четырёхугольнике, на двух противоположных
сторонах которого задано одинаковое число узлов.
11усть задан выпуклый четырёхугольник с вершинами А, В, С и
D, на его сторонах АВ и ВС задано по т внутренних узлов, на сто-
роне АВ - пдр узлов, на стороне ВС - пПС узлов. Пример такого
четырехугольника приведён на рис. 91,а, где m = 3, nAD — 4,
= 7 -
Чтобы построить сетку, разобьем сначала четырёхугольник АВСВ
на т -|- 1 полосу непересскающимися отрезками Р/>( , соеди-
няющими узлы Pt-11' и Р/ на противоположных сторонах АВ и
DC, где задано одинаковое количество (по т ) узлов (см. рис. 91,6).
Количество узлов на а-м отрезке ТУ1/;Р/)Г (/ = 1...т) будем
вычислять по формуле
I1--тт™
\ 777 4- L /
^Ппвс '
(10.5)
10.2.Структуры данных для описания двумерных задач
475
где [с] — целая часть числа а (т.е. та- меняется почти линейно or зна-
чения пАВ до значения пвс при движении от стороны AD к стороне
ВС , см. рис. 91,6)
Рис. 91.11ример генерации узлов сетки на макрочетырсхугольник
Если на сторонах AD и ВС заданы коэффициенты растяжения-
сжатия шага qAB и qBC соответственно, то коэффициент q, растяже-
ния-сжатия шага на ?-м отрезке РА1' Р^ (естественно, в направлении
от стороны АВ к стороне DC) будем вычислять, считая его измене-
ние линейным при движении от стороны AD к стороне ВС по анало-
гичной формуле1
91 _(1-^Тт)9лс+7Гн‘9вс’-
(10.6)
В приведённом на рис. 91 примере заданы следующие коэффицисн
ты растяжения-сжагия <Мд=0.75, qBc~^ (1dc~®-75 и = Hi
рис 91,6 показаны внутренние узлы, сгенерированные по форму him
(10 5)—(10.6) - эти узлы сгенерированы на отрезках РВ (обоим
ченных пунктирными линиями).
Треугольную сетку в четырёхугольнике ABCD (с равным чш ном
узлов на двух его противоположных сторонах АВ и DC) можно но
строить, заполняя треугольниками попосы, на которые »ioi чнырёх
1 При этом, естественно, отрицательные коэффициенты р.пзимния
сжатия (т.е. коэффициенты q <— 1, означающие сжатие iimi.i при ihhmihih
от А!) к ВС) должны быть предварительно прсойраюи.шы в tooiiu н oiyio-
щне положительные 1/Ы .
476 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
угольник был разделен отрезками РА1' P,D( . Это полосы между сторо-
ной AD и отрезком РА L , между отрезками Р/ Р/ и Р^Р^
= — 1) и между отрезком PAL Р®с и стороной DC
(см. рис. 91,6).
Рис. 92. Процесс заполнения треугольниками одной полосы
Рассмотрим алгоритм заполнения треугольниками одной полосы.
Этот алгоритм проиллюстрирован на рис. 92 и заключается в следую-
щем. Сначала выбирается любое из двух рёбер, являющихся коротки-
ми (т.е. без внутренних узлов) i раницами полосы. Первый треугольник
строится присоединением к вершинам этого ребра одного из двух со-
седних с ним узлов. При этом выбирается такой узел, чтобы была ми-
нимальной длила нового ребра, соединяющего этот узел с лежащим на
противоположной (длинной) стороне полосы узлом старого ребра (яв-
ляющегося границей полосы).
10.2.Структуры данных для описания двумерных задач ..
477
Каждый следующий треугольник строится по тому же принципу: к
вершинам ребра, соединяющего два узла на противоположных (длин-
ных) сторонах полосы и полученного при построении предыдущего
треугольника, добавляется один из двух соседних с ними узлов какой,
что длина нового ребра является минимальной (см. рис. 92). Очевидно,
что на последнем шаге этого алгоритма получается сра^у два i ре-
угольника.
Рис. 93. Процесс построения сетки на четырёхугольнике
с равным числом узлов па противоположенных сторонах
Процесс построения сетки в четырёхугольнике с равным чис юм
узлов на двух его противоположных сторонах ирон iiioi ipiipou.ni hi
рис. 93. Один шаг этого процесса вполне можно Пронин pupciировли.
как генерацию слоя новых треугольников на фронпи \ м inni роенных
треугольников (с перемещением фронта ог стороны 1/> ч pioi] ней
Р, '* Р/ к стороне БС). Поэтому paccMoipciinxio пропс 1\ р\ генеря
478 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
ции сетки в четырёхугольнике можно отнести к классу фронтальных
методов.
Рассмотренный метод можно достаточно просто адаптировать для
генерации треугольной сетки в фигуре, представляющей собой тре-
угольник (макротреугольник) с заданными на его сторонах узлами,
если количество узлов хотя бы на двух сторонах этого макротреуголь-
ника совпадает. Будем считать, что равное количество узлов располо-
жено на сторонах АВ и АС макротреугольника АВС (см. рис. 94,а).
Для построения сетки в этом макротреугольнике достаточно сначала
отсечь ребром РАП РА( треугольник РАП РАС А , а затем использовать
рассмотренный выше алгоритм построения треугольной сетки в четы-
рёхугольнике РАПВСРА с равным числом узлов на сторонах РАВ В
и РА( С. Пример построения такой сетки проиллюстрирован на
рис. 94,6.
Рис. 94. Процесс построения сетки на треугольнике
с равным числом узлов на противоположенных сторонах
С некоторыми доработками (касающимися в основном способов
построения линий между узлами РАВ и Рвс для четырёхугольника и
узлами PAD и РАС для треугольника) рассмотренные методы можно
применять и для построения треугольных сеток внутри псевдочеты-
рёхугольников и псевдотреугольников, стороны которых не являются
отрезками прямых. Соответствующие примеры приведены на рис. 95.
10.2.Структуры данных для описания двумерных задач. ...
479
Рис. 95. Построение треугольных сеток внутри
пссвдочетырёхугольников и псевдотреугольников
Рис. 96. Построение треугольных сеток внутри фигур
с различным числом узлов на всех их сторонах
На основе рассмотренных алгоритмов построения сеток в чс ii.ipex
угольниках (и псевдочетырсхугольниках) с равным количсывом \ i ioi
на двух противоположных сторонах можно построить довольно про
стой алгоритм генерации треугольной сетки и в чегырёхмо ii.iiiim с
неодинаковым числом узлов на его противоположных стропах [hi
этого достаточно разбить исходный четырёхугольник на ин новых
четырёхугольника, у которых уже есть по две стропы с ранным ко ш
чеством узлов Это можно сделать, если провести через и»с иронию
положные стороны исходного четырёхугольника о шх iiihhio ык. что
бы в одном из новых четырехугольников (на koiopin прово him • i ш
480 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
ния разбивает исходный четырёхугольник) появилось две стороны с
равным числом узлом (чего, очевидно, всегда можно добиться на двух
сторонах одного из новых четырёхугольников, смежных с линией,
разбивающей исходный четырёхугольник). На самой же линии (разби-
вающей исходный четырёхугольник на два новых) нужно сгенериро-
вать столько же узлов, сколько их расположено на противоположной
этой линии стороне второго нового четырёхугольника. Соответствую-
щий пример приведён на рис. 96,а (АВСЬ — исходный четырёхуголь-
ник. A13EF и EFCD - новые четырёхугольники с равным числом узлов
на двух противоположных сторонах).
Аналогичный подход можно применить и для построения треуголь-
ных сеток внутри фигур в виде треугольников или псевдотреугольников
с различным числом узлов на всех их сторонах — соответствующий при-
мер приведён на рис. 96,6 (для построения сетки добавлена линия АВ).
10.3. СТРУКТУРЫ ДАННЫХ ДЛЯ ОПИСАНИЯ ТРЁХМЕРНЫХ ЗАДАЧ.
ТРЁХМЕРНЫЕ СЕТКИ
10.3.1. ОПИСАНИЕ ТРЁХМЕРНЫХ ОБЛАСТЕЙ И ПРИНЦИПЫ ПОСТРОЕНИЯ
ТРЁХМЕРНЫХ СЕТОК С ЯЧЕЙКАМИ В ВИДЕ ПАРАЛЛЕЛЕПИПЕДОВ
И ШЕСТИГРАННИКОВ
Как и в двумерном случае, способы описания трёхмерных облас-
тей довольно тесно связаны с методами построения конечноэлемент-
ных сеток. Если расчётные области содержат только подобласти в виде
прямоугольных параллелепипедов и для них предполагается использо-
вать соответствующие прямоугольные сетки, то применяются структу-
ры данных, аналогичные описанным в разделе 10.2.1. Фактически в
ращеле 10.2.3 уже было сказано, как распространить алгоритм по-
строения регулярной прямоугольной сетки на трёхмерный случай (т.е.
для построения сетки с ячейками в виде прямоугольных параллелепи-
педов). При этом описание расчётной области кроме массивов AHl и
У11 должно содержать ещё и массив У1’ , а наборы чисел, описываю-
щие каждую элементарную подобласть T7Z (в виде параллелепипеда),
должны содержать не по пять целых чисел, а по семь. Аналогично и в
файл описания сетки к массивам координатных линий сетки X и У
должен быть добавлен массив Z (и при работе с сеткой к массивам
/А'” и /У” должен быть добавлен массив IZW ). Сами же алгоритмы
построения трехмерных параллелепипеидальных сеток (как регуляр-
ных, так и нерегулярных) в целом ничем не отличаются от алгоритмов
построения двумерных прямоугольных сеток, рассмотренных в разде-
ле 10.2.3 (и в копие раздела 10.2.5 в случае генерации нерегулярных сеток).
Если расчётная область имеет не параллельные координатным плоско-
стям границы (в том числе в виде изогнутых поверхностей) и для её дис-
кретизации предполагается использовать сетки с шестигранными ячей-
ками, то можно использовать структуры данных, аналогичные описанным
в разделе 10.2.5 для построения сеток с четырёхугольными ячейками.
Рассмотрим чуть более детально возможные структуры данных для опи-
сания расчёт ных областей и хранения сеток с шестигранными ячейками
10.3.Структуры данных для описания трёхмерных задач
481
Простейшую структуру данных можно построить в случае, koi да
все внутренние и внешние границы расчётной области либо перпенди-
кулярны одной из осей (назовём её осью z), либо параллельны ей. В
этом случае в качестве базовой можно взять структуру данных, кото-
рая была рассмотрена нами при описании двумерных областей, со-
стоящих из четырёхугольных подобластей (см. с. 460-461 или с 166),
и добавить к ней одномерный массив Z1, , определяющий границы
элементарных подобластей по оси z. Например, на базе двумерной
расчётной области, изображённой на рис. 88,а, трёхмерная расчётная
область, состоящая из пяти подобластей и изображённая на рис. 97,г/,
может быть описана с помощью следующей структуры данных (срав-
ните со структурой данных, приведённой на с. 466).
Рис. 97. Трёхмерная расчётная область (а) и шестигранная сетка в ней (б)
3 4
0. 0. 5. 0. 7. 0.
0. 2.59. 5.59 2.59 7. 2.
0.4. 5. 4 . 7.4.
0. 6. 5. б. 7. 6.
4
0. 3. б. 11.
5
113 12 12
2 13 12 3 4
3 1 2 2 3 1 4
4 1 3 3 4 1 4
5 2 3 2 3 1 3
2
-1227. 4.
1227.4.
482 Ю.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
Первые пять строк определяют опорные узлы базовой плоскости
(являющейся фактически некоторым обобщённым сечением расчётной
области плоскостью z — const) точно так же, как задавались узлы при
описании четырёхугольной области (см. с. 466). Два целых числа в
первой строке задают значения N'' и N\l , а в следующих = 4
строках перечислены парами х- и у -координаты опорных узлов (оп-
ределяющих «горизонтальные» и «вертикальные» ломаные) последо-
вательно по «горизонтальным» ломаным (по TVj.' = 3 пар в каждой
строке).
Далее (в нашем примере это шестая строка файла описания облас-
ти) задаётся значение Ng , определяющее количество плоскостей
z - const, необходимых для задания подобластей расчётной области.
В следующей строке задаются значения z -координат этих плоскостей
(т.е. содержимое массива Z11 ).
После этого (в нашем примере с восьмой по двенадцатую строках)
задаётся информация об элементарных подобластях - сначала их ко-
личество L, а затем L семёрок чисел, определяющих каждую подоб-
ласть U7/.. 11срвое число каждой семёрки задаёт номер формул, опре-
деляющих параметры краевой задачи в 1ИЛ.. Следующие два числа
определяют номера «вертикальных» ломаных (которые фактически
определяют поверхности, ограничивающие подобласть I1 слева и
справа, эти границы можно интерпретировать как границы «по а;»),
четвёртое и пятое число — номера «вертикальных» (в базовой плоско-
сти) ломаных (границы «по //»), и, наконец, шестое и седьмое числа
определяют границы подобласти Щ по z .
В самом конце файла задаётся информация о криволинейных уча-
стках «горизонтальных» и «вертикальных» ломаных в формате, кото-
рый был описан при описании двумерных областей на с. 467. В нашем
примере это три последние строки. Их содержимое означает следую-
щее. Криволинейными1 являются два участка ломаных (поскольку
первое число в этом блоке информации равно двум). Первый участок
является участком «вертикальной» ломаной (поскольку имеет признак
— 1), расположен он на второй ломаной и является её вторым участ-
ком. Этот участок является частью окружности с центром в точке
х — 7 , у = 1. Второй участок - это участок «горизонтальной» лома-
ной (поскольку имеет признак 1). Он расположен на второй «горизон-
тальной'* ломаной, является сё вторым участком и представляет собой
дугу той же окружности с центром в точке х = 7 , у = 4 .
Для задания трёхмерной lcikh с ячейками в виде шестигранников
можно использовать те же принципы, которые были описаны нами для
сеток с ячейками в виде прямоугольников и четырёхугольников (см.
с. 453). При этом к данным, описывающим разбиение «горизонталь-
’ Напомним, что в рассматриваемом нами формате криволинейными уча-
стками могут быть только дуги окружности; естественно, можно, немного
усложнив формат, ввести несколько типов криволинейных участков.
10.3.Структуры данных для описания трёхмерны тдач. ..
483
ных» и «вертикальных» ломаных на базовой плоское!и, доблвляклея
данные, описывающие разбиение каждого интервала по z (мкье в
виде количества подынтервалов и коэффициентов растяжения слип ня)
Для сетки, изображённой на рис. 97,6 (и построенной в рассмотренной
выше трёхмерной области), файл её описания выгляди! следующим
образом:
4 -1.5 2 1.
3 -1.4 3 1.25 2 1.5
3 -1.2 21. 4 1.5
Теперь рассмотрим более общий случай, когда границы «по z » мо-
гут не быть плоскими и перпендикулярными оси z, а так же. как и
границы «по х » и «по у» (которые в предыдущем случае определя-
лись соответственно через «вертикальные» и «горизонтальные» лома-
ные базовой плоскости), могут являться некоторыми поверхностями.
По-прежнему расчётную область будем описывать с помощью
опорных узлов. Однако теперь эти узлы будем задавать не на базовой
плоскости, а сразу в трёхмерном пространстве {тремя их координата-
ми). Перечислять опорные узлы будем, как и прежде, в строго уста-
новленном порядке, с помощью которого фактически будут опреде-
ляться и все границы (внутренние и внешние) расчётной области
«по х », «по у» и «по z». При этом сначала перечисляются (последо-
вательно) 7V,. узлов первой «горизонтальной» ломаной первой по-
верхности «по z », затем 7VU узлов второй «горизонтальной» ломаной
и далее вплоть до N у -и «горизонтальной» ломаной первой поверхно-
сти «по z ». После информации обо всех опорных узлах первой по-
верхности «по z» персчисляются все «горизонтальные» ломаные вто-
рой поверхности «по z» (в том же порядке), третьей и далее вплоть до
N\[ -й поверхности «по z ». Таким образом задаются все опорные уз-
лы (их количество TV]1' х N'^ х ТУ" ).
Информация об элементарных подобластях задаётся абсолютно i ik
же, как и в предыдущем варианте (когда опорные узлы задавались на
базовой плоскости, а получаемые из неё границы были строго перпен-
дикулярны оси z). Только здесь шестое и седьмое числа каждой се-
мёрки чисел, описывающих элементарную подобласть, будут опреде-
лять номера не плоскостей, а поверхностей «по z ».
Приведём пример описания расчётной области с пснлоскнми
«по z» границами (обратим внимание, что теперь в первой строке
задаётся три числа , Ny и N ' , а за ними слсдуеп уже
• Ny • №/ троек вещественных чисел координат всех опорных
узлов):
3 4 4
0. 0. 0. 5. 0. 0. 7. 0. 0.
0. 2. 0. 5.59 2.59 0. 7. 2. 0.
0.4.0. 5. 4. 0. 7.4.0.
484 1О.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
0. 6. 0. 5 . 6. 0. 7 . 6. 0.
0. 0. 3. 5. 0. 3. 7 . 0. 3.
0. 2. 3. 5.59 2.59 3. 7 . 2. 3.
0. 4 . 3 . 5. 4 . 3. 7 . 4 . 3.
0. 6. 3. 5. 6. 3. 7 . 6. 3.
0. 0. 6. 5. 0. 6. 7 . 0. 6.
0. 2. 6. 5.59 2.59 6. 7 . 2. 6.
0. 4 . 6. 5. 4 . 6. 7 . 4 . 6.
0. 6. 6. 5. 6. 6. 7 . 6. 6.
0. 0. 9. 5. 0. 9. 7. 0. 9.
0. 2. 11. 5.59 2.59 11. 7 . 2. 11
0. 4 . 11. 5. 4 . 11. 7 . 4 . 11
0. 6. 8. 5. 6. 8 . 7 . 6. 8.
5
1 1 3 12 1 2
2 1 3 12 3 4
3 1 2 2 3 1 4
4 1 3 3 4 1 4
5 2 3 2 3 1 3
2
-1 2 2 7. 4 .
1 2 2 7 . 4 .
Вид этой расчётной обпасти показан на рис. 98,а.
Рис. 98. Трехмерная расчётная область («) и шестигранная сетка в ней (б)
а
Структура файла задания сетки для этого варианта задания расчёт-
ной области ничем не отличается от структуры файла задания сетки
для предыдущего варианта. На рис. 98,о изображена сетка, описывае-
мая файлом, приведённым на с. 483.
Не представляет труда модифицировать рассмотренный вариант
описания расчётной области так. чтобы можно было задавать искрив-
10.3.Структуры данных для описания трёхмерных задач. ... 485
ленные участки не только ломаных «вдоль х » и «вдоль //» (которые в
предыдущих вариантах мы называли «горизонтальными» и «верти-
кальными» ломаными), но и «вдоль 2». Для этого нужно ввести при-
знак искривления линии «вдоль 2». Напомним, что признак искривле-
ния линии «вдоль ху> (т.е. вдоль «горизонтальной» ломаной) был вве-
дён нами ранее как значение I, а признак искривления липин
«вдоль у» («вертикальной» ломаной) - как значение -1. Введём при-
знак искривления1 линии «вдоль z » как значение -10.
Для удобства определения положения искривлённой линии введем
понятие номера поверхности «по 2». Будем считать, что первые
TV1/ * N™ опорных узлов определяют поверхность «по 2» с номе-
ром I, следующие TV1/ х опорных узлов (с номерами от
TV? TV11' +1 до 27V.J1' Ny ) — поверхность «по г» с номером 2 и г.д.
Тогда опорный узел, из которого исходит искривлённый участок, удоб-
но определить тремя целыми числами: первое число — это номер по-
верхности «по 2», второе и третье числа —соответственно номера «го-
ризонтальной» и «вертикальной» ломаных (на этой поверхности), на
пересечении которых лежит определяемый нами узеп.
Заметим, что раньше мы определяли местоположение криволиней-
ных участков чуть иначе - заданием номера кривой и номера участка
этой кривой. В принципе, задание искривлённых участков «вдоль .г»
(т.е. горизонтальных ломаных) осталось практически тем же. посколь-
ку номер участка фактически совпадает с номером вертикальной ло-
маной и мы к этой информации добавили только номер поверхности
«по 2». Искривлённые же участки «вдоль //» теперь задаются чуть
иначе (раньше при задании таких участков первым задавался номер
«вертикальной» линии, а после него — номер «участка», фактически
являющегося номером «горизонтальной» линии, на которой лежал
опорный узел, т.е. здесь мы фактически поменяли эти номера места-
ми). Это сделано для того, чтобы единообразно определять пошцню
опорного узла для искривлённых участков по любому направлению
(как но старым двум направлениям - «вдоль ху> и «вдоль у», так п но
новому для этой структуры данных направлению - «вдоль I »)2.
1 Мы по-прежнему считаем, что искривлённые линии задакнея к» в
виде дуг окружностей, хотя, как уже говорилось, не представляо <но<юн>
труда ввести при описании расчётной области несколько типов п< крин н ннн
линий (кроме дуг окружностей это могут быть параболы, сил lilin.i и i ,i )
2 Вообще говоря, можно было бы просто ука ты ван. помер шнтрпоы» \ t ь
из которого исходит искривлённый участок. Однако при ошв шин р.ич< нюП
области всё-таки удобней задавать номер iz повермкд ш «по • » и номера
ломаных iy «вдоль т» и г,, «вдоль г/», чем задавнь «I но(ы ii.in.ui помер
опорного узла Z. который связан с номерами i , ty и », пч hh iiii.im гоопв»
шепнем i = г, — 1) A^Jr I (г. — 1)/V'1/V 1
486 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
Рассмотрим пример задания расчётной области с изогнутыми гра-
ницами не только «по х » и «по у», но и «по z ». Пусть файл описания
расчётной области имеет вид:
3 4 4
0. 0. 0. 5. 0. 0 . 7 . 0. 0.
0 . 2. 0. 5.59 2.59 0 . 7 . 2. 0.
0. 4 . 0. 5. 4 . 0. 7 . 4 . 0.
0. 6. 0. 5. 6. 0. 7 . 6. 0.
0. 0. 3. 5. 0. 3. 7 . 0. 3.
0. 2. 3. 5.59 2.59 3. 7 . 2. 3.
0. 4 . 3. 5 . 4 . 3. 7 . 4 . 3.
0. 6. 3. 5. 6. 3. 7 . 6. 3.
0. 0. 6. 5 . 0. 6. 7 . 0. б.
0. 2. 6. 5.59 2.59 6. 7 . 2. б.
0 . 4 . 6. 5 . 4 . 6. 7 . 4 . б.
0. 6. 6. 5. 6. 6. 7 . 6. 6.
0. 0. 9. 5. 0. 9. 7 . 0. 9.
0. 2. 11. 5.59 2.59 11. 7 . 2. 11
0. 4 . 11. 5. 4 . 11. 7 . 4 . 11
0. 6. 8 . 5 . 6. 8 . 7 . 6. 8.
5
113 12 12
2 13 12 3 4
3 1 2 2 3 1 4
4 1 3 3 4 1 4
5 2 3 2 3 1 3
14
1 1 2 2 7. 4 . 0.
1 2 2 2 7 . 4 . 3.
1 3 2 2 7 . 4 . 6.
1 4 2 2 7 . 4 . 11.
-1 1 2 2 7 . 4 . 0.
-1 2 2 2 7 . 4 . 3.
-1 3 2 2 7. 4 . б.
-1 4 2 2 7 . 4 . 11.
-1 4 3 1 0 . 2. 7.5
-1 4 3 2 5. 2. 7.5
-1 4 3 3 7 . 2. 7.5
-10 1 1 1 0. 3. 1.5
-10 1 1 2 5 . 3. 1.5
-10 1 1 3 7 . 3. 1.5
Вид этой расчётной области изображён на рис. 99,а. На рис. 99,6
показана сетка, описываемая тем же файлом (см. с. 483).
Итак, рассмотренные способы описания расчётных областей и се-
ток с шестигранными ячейками позволяют решать трехмерные задачи
в областях с достаточно сложными границами. Таким образом, исполь-
зование сеток с шестигранными яченками является разумным компро-
миссом, позволяющим наряду с широкими возможностями описания
сложной геометрии расчётной области сохранить простоту и удобство
её дискретизации, особенно если при этом реализована возможность
10.3.Структуры данных для описания трёхмерных задач
487
согласования элементов на несогласованных ячейках, например, с ис-
пользованием технологии Т-преобразования, которая будет описана
нами ниже, в одиннадцатом разделе.
Рис. 99. Трёхмерная расчётная область (а) и шестигранная сетка в ней (6)
Однако в некоторых ситуациях даже шестигранные ячейки могут
оказаться неудобными для дискретизации расчётной области из-за
очень сложной геометрии её границ. В таких случаях в качестве ячеек
дискретизации можно использовать тетраэдры. Нередко применяю! и
прямые призмы с треугольным основанием, если все изогнутые по-
верхности являются цилиндрическими с параллельными друг другу
образующими, или используют комбинированные сетки в виде тетра-
эдров и призм.
Ниже мы рассмотрим один из наиболее часто используемых спосо-
бов построения сеток с ячейками в виде призм и тетраэдров — метод
тиражирования сечений*.
10.3.2. МЕТОД ТИРАЖИРОВАНИЯ СЕЧЕНИЙ
В методе тиражирования сечений описание геометрии и конем
поэлементной сетки практически полностью совмещено и cencj i ipo
ится по сечениям. Под сечением понимается пересечение пско <>рои
(не обязательно плоской) поверхности с расчётной областью I рс\
* Заметим, что рассмотренные нами методы построения сеток С шее in
гранными ячейками в какой-го мере могут интерпретироваться кик ринопнд
ность метода тиражируемых сечений (там, например, было вис юно iioiihiml*
базовой плоскости и геометрию расчётной области можно 5ыпо бы и ihi.hi.
последовательно по сечениям «по 2»), Но все-таки paciMoipriini.ic нами ме
годы ближе к методу конструктивной геометрии, поскольку по ню in в ней
ыдаются через указание их границ «по т», «по //» и «по : », им ымим юле
являющихся некоторыми поверхностями, и б.нов 1я пжими п. яи иен я шип.
инструментом описания этих поверхностей.
488 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
мерная сетка строится заполнением конечными элементами простран-
ства между соседними сечениями, на которых построена сетка из дву-
мерных фигур, чаще всего треугольников. Принципиально возможно
создание алгоритма, для которого треугольные сетки на соседних се-
чениях строятся совершенно независимо, однако невысокая скорость
работы и сложность программной реализации такого алгоритма прак-
тически полностью перекрывают все его преимущества. Поэтому
большинство реализации метода тиражирования сечений требует по-
добия треугольных сеток и неизменности количества узлов на всех
тиражируемых сечениях, за исключением случаев, когда из триангуля-
ции выбрасываются узлы и треугольники, попавшие в полости, не вхо-
дящие в расчётную область При этом двумерная треугольная сетка, на
основе которой строится трёхмерная сетка, обычно называется базо-
вым сечением или базовой плоскостью.
Пространство между двумя сечениями с подобными треугольными
сетками (т.е. допускающими соответствие каждому треугольнику од-
ной сетки одного и только одного треугольника другой) заполняется
сначала треугольными призмами, каждая из которых затем разбивается
на три тетраэдра (с учётом согласованности разбиения соседних призм
по смежным граням, более подробно это будет рассмотрено ниже).
Если все призмы, построенные между двумя сечениями с треугольны-
ми сетками, оказываются прямыми, то в качестве ячеек сетки можно
оставить эти призмы (не разбивая их па тетраэдры).
Кроме того, возможны достаточно простые реализации метода ти-
ражирования сечений, когда допустимо тиражирование не всего сече-
ния, а лишь его части.
Тиражируемые сечения в рассматриваемом подходе могут быть
двух типов — основные и промежуточные. Основными называются
сечения, которые необходимы для описания геометрии области.
Для задания основного сечения удобно использовать преобразова-
ние базового сечения или уже созданных других основных сечений с
помощью специальных средств перемещения узлов без изменения то-
пологии сетки (что позволяет изменять границы подобластей на сече-
нии и делать его некоторые искривления), а также средств изменения
точек привязки информации о параметрах решаемого уравнения.
Промежуточные сечения - это сечения, которые генерируются ав-
томатически между двумя основными сечениями и обеспечивают нуж-
ную подробность сетки вдоль траектории тиражирования
Таким образом, процедура построения трёхмерной сетки после за-
дания базового сечения состоит из следующих этапов:
• описание поверхностей основных сечений и задание на них воз-
можных смещении узлов сетки;
• задание положения основных сечений в пространстве;
• задание количества промежуточных сечений и некоторых парамет-
ров, определяющих положение этих сечений между основными се-
чениями (например, это могут быть параметры кривых, по которым
должны генерироваться узлы между сечениями);
• непосредственное формирование конечных элементов.
10.3.Структуры данных для описания трехмерных задач. ... 489
10.3.3. ПОСТРОЕНИЕ ТЕТРАЭДРАЛЬНЫХ СЕТОК
МЕТОДОМ ТИРАЖИРОВАНИЯ СЕЧЕНИЙ
Как уже говорилось, при использовании метода тиражируемых
сечений трёхмерная конечноэлементная сетка формируется из специ-
альной двумерной сетки, в качестве которой удобно использовать пло-
скую триангуляцию, заданную на так называемой базовой плоскости
На базовой плоскости задаётся триангуляция с учётом того, что из
неё нужно будет формировать не только ячейки сетки, но и все грани-
цы (внешние и внутренние) расчётной области. Эти границы получа
ются либо как некоторые участки создаваемых в процессе тиражиро-
вания сечений, либо в результате тиражирования определённых линий,
заданных на базовой плоскости специально для формирования таких
«боковых» границ.
Также на базовой плоскости обычно задаются сгущения или разре-
жения узлов в тех местах, которые соответствуют местам сгущений
или разрежений узлов в трёхмерной сетке.
Рассмотрим построение согласованной тетраэдральной сетки между
двумя соседними сечениями (для простоты мы не будем здесь разли-
чать основные и промежуточные сечения), полученными тиражирова-
нием одной базовой плоскости.
Для построения тетраэдральной сетки между двумя сечениями сна-
чала строится сетка из треугольных призм с основаниями, полученны-
ми из одного и того же треугольника базовой плоскости1 *. Если призма
не вырождена (т.е. все её вершины различны), то каждая четырёх-
угольная грань призмы может быть разбита на два треугольника. При
этом из двух возможных диагоналей этой четырёхугольной грани для
её разбиения выбирается та, которая короче. Если диагонали близки по
длине (т.е. грань почти прямоугольная), то строится диагональ из вер-
шины с максимальным (из четырёх вершин грани) номером. Всего
возможно 8 (23) вариантов разбиения граней призмы. Эти варианты
показаны на рис. 100 и 101. Для шести из них призму всегда можно
разбить на 3 тетраэдра (см. рис. 100): для варианта на рис. 100,с/, это
тетраэдры 12 3 5, I 3 5 6 и 145 6; для варианта на рис. 100,6 - тетра-
эдры 123 5, 1345 и345 6; для варианта на рис. 100, в — тетраэдры
123 6, 1256и 145 6; для варианта на рис. 100,г - тетраэдры I 2 3 I,
2345и345 6; для варианта на рис. 100,6 - тетраэдры 12 3 6, 1216
и 2 4 5 6; для варианта на рис. 100,в - тетраэдры 1 2 3 4, 2 3 16 и
2 4 5 6. В двух оставшихся случаях (см. рис. 101) ставится дополни
тельный узел внутри призмы и строится 8 тетраэдров.
Таким образом, в рассмотренном способе согласованная icipui
ральная сетка строится без сохранения информации о ipey ioni.nnk.ix
на боковых гранях призм. При программной реализации ного ано
ритма необходимо, однако, учитывать, что при обработке общей гы
1 Безусловно, термин «призма» в данном случае не и по пк к<»|. реки и, по
скольку её основания могут оказаться не конгруэнтными л боковые грани нс
параллелограммами из-за возможных перемещении углов пл инетннх сече-
ниях. Однако получаемая в таких случаях фигура очень похожа ил пртму, и
поэтому для неё (наряду с «настоящими» призмами) ш пощнукп ггот термин.
490 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
двух призм грани в тех случаях, когда грань близка к прямоугольной,
из-за погрешностей округления может оказаться, что для одной из
призм разбиение произойдет по нумерации узлов, а для другой - по
длинам диагоналей. Чтобы этого не произошло, можно создать опре-
деляющую способ разбиения грани призмы подпрограмму, координа-
ты вершин в которую передаются в порядке нумерации узлов сетки
Рис. 100. Разбиение призмы на 3 тетраэдра для всех
случаев разбиения rpaiicii. когда оно существует
Информация о краевых условиях второго и третьего рода формиру-
ется в виде списка треугольников - трёх номеров вершин граничного
треугольника и номера формул для определения параметров соответ-
ствующего краевого условия. При этом треугольники, заносимые в
списки краевых условий второго и третьего рода, должны быть согла-
сованы с тетраэдрами, т.е. треугольники, аппроксимирующие границы
S-2 и с заданными на них краевыми условиями второго и третьего
рода, должны быть гранями ячеек конечноэлементной сетки.
Рассмотренная процедура разбиения граней призмы позволяет за-
писывать согласованные с конечноэлементной сеткой граничные тре-
10.4.Структуры данных для хранения матриц ...
491
угольники независимо от обработки самих конечных темен гон, если
краевые условия либо приписаны к рёбрам треугольников сечения
(тогда формируются по два треугольника от боковых гранен призмы),
либо заданы на самих треугольниках сечения.
а б
Рис. 101. Случаи разбиения граней призмы,
когда разбиений па 3 тетраэдра нс существует
Отметим, что в МКЭ задание однородного краевого условия второ-
го рода на некоторой грани не вносит никаких изменений в конечно-
элементную СЛАУ, поэтому не имеет никакого смысла сохранять ин-
формацию о таких гранях.
10.4. СТРУКТУРЫ ДАННЫХ ДЛЯ ХРАНЕНИЯ МАТРИЦ
КОНЕЧНОЭЛЕМЕНТНЫХ СЛАУ
10.4.1. ОСОБЕННОСТИ МАТРИЦ КОНЕЧНОЭЛЕМЕНТНЫХ СЛАУ
Важной особенностью матрицы Л конечноэлсментной СЛАУ
является её сильная разреженность, т.е. небольшое (относигелию
общего числа компонент) число ненулевых компонент в каждой строке
матрицы. Действительно, ненулевыми в г-й строке матрицы А явля
ются только компоненты в столбцах с номерами j, для которых
базисные функции ф, являются ненулевыми на тех же конечных > ie
меигах, на которых отлична от нуля базисная функция ф, 11о>к»м\
при программной реализации МКЭ для хранения матриц конечно! ic
ментных СЛАУ имеет смысл использовать формами, по и«> imiohuic
хранить только ненулевые компоненты матриц пли хотя бы to и.ко ic
компоненты, которые могуг стать ненулевыми в процесс! решения
СЛАУ (при использовании прямых методов решения ('ЛА\ )
Другой особенностью матрицы конечпоэлемешнои ( М \У, коюрро
можно учитывать при её хранении, является ciiMMvipiriiioi и. р.н поло-
жения ненулевых компонент. В самом деле, если в м ирит \ ненулс
492 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
вой является компонента Д , то это означает, что неизвестная i и неиз-
вестная j соответствуют одному конечному элементу (это тот конеч-
ный элемент, на котором обе глобальные базисные функции и ф/
отличны от нуля), и тогда компонента Afl также, скорее всего, будет
ненулевой. Кроме того, для большинства задач матрица конечноэле-
ментной СЛАУ является симметричной (т.е. Ач = Л/7 ), и поэтому хра-
нить можно только нижний (или только верхний) треугольник матрицы.
Мы будем излагать форматы хранения и алгоритмы работы с ними
для общего случая, когда матрица является несимметричной. При этом
будем считать, что компоненты нижнего треугольника матрицы хра-
нятся в массиве с именем ggl, а компоненты верхнего — в массиве с
именем дди.
Заметим, что формат хранения матрицы СЛАУ может зависеть и от
метода решения СЛАУ: если предполагается использовать какой-либо
из прямых методов (таких как LIA - или LU -разложение! то в процессе
решения СЛАУ необходима память для размещения профиля матрицы.
Под профилем понимаются тс компоненты матрицы, которые рас-
положены между первой ненулевой компонентой каждой строки ниж-
него треугольника и главной диагональю, и соответственно между
первой ненулевой компонентой каждого столбца верхнего треугольника
и главной диагональю.
При использовании же итерационных методов, в которых основная
операция - это умножение матрицы на некоторый вектор, имеет смысл
хранить только ненулевые компоненты матрицы.
Поскольку в МКЭ элементы главной диагонали матрицы СЛАУ
практически всегда не равны нулю, для их хранения удобно выделить
отдельный массив di длиной N (N - размерность СЛАУ). Далее при
описании всех форматов мы не будем специально обращать ваше вни-
мание на то, что они различаются только способом хранения внедиаго-
нальных элементов матрицы, а элементы главной диагонали всегда
хранятся отдельно в массиве di.
10.4.2. ПРОФИЛЬНЫЙ ФОРМАТ ХРАНЕНИЯ МАТРИЦЫ СЛАУ
Для хранения матрицы в профильном формате нам кроме масси-
ва di. потребуется ещё три массива: ggl и дди — для хранения самих
ненулевых элементов нижнего и верхнего треугольников матрицы (без
главной диагонали), и гд — массив для вычисления адресов ненулевых
элементов. При этом мы будем считать, что ненулевые элементы мат-
рицы А расположены симметрично (т.е если AtJ ^0,тои Аг/ 0 ).
В массиве ggl будем хранить все элементы профиля нижнего тре-
угольника матрицы по строкам (последовательно друг за другом), а в
массиве дди - все элементы профиля верхнего треугольника матрицы
по столбцам. В i -м элементе массива гд будем хранить номер элемента
в массиве ggl (или дди), с которого начинается г-я строка нижнего
(или г-й столбец верхнего) треугольника профиля матрицы. При этом
10.4.Структуры данных для хранения матриц ...
493
длина массива гд должна быть равна N +1 (N - размерность СЛАУ),
и последний его элемент будет содержать целое число, на единицу
большее числа элементов в массиве ggl (и дди ). Например, матрица
1. 2. 0 3. 0 0
4. 5. 0 6. 0 7.
0 0 8. 0 0 9. (Ю7)
10. 11. 0 12. 13. 0
0 u 0 14. 15. 0
0 16. 17. 0 0 18.
в профильном формате примет вид:
(Н = {l.,5.,S.,12.,15.,19.} , ig = {1,1,2,2,5,6,10} ,
ggl = {4.,10.,11.,0,14.,16.,17.,0,0} , дди = {2.,3.,6.,0,13.,7.,9.,0,0}.
Рассмотрим некоторые приёмы работы с матрицами, хранящимися
в профильном формате. В этом формате количество ненулевых эле-
ментов в г-й строке нижнего треугольника может быть вычислено как
ig(i + 1) —гр(г), а номер столбца, в котором находится первый нену-
левой элемент этой строки, - как г — (г<?(г 4- 1) — гд(г)) . Аналогично
вычисляется количество ненулевых элементов в г-м столбце (также
равное ig (г + 1) — ig(i)) и номер строки, в которой находится первый
ненулевой элемент этого столбца (тоже равный i — (ig (г + 1) — ig (г))).
В качестве примера работы с профильным форматом приведём на
языке Фортран подпрограмму занесения числа а в компоненту .1Г/
глобальной матрицы А .
subroutine AddElement(N,di,ig,ggl,ggu,i,j,a)
dimension di(N),ggl (*),ggu(*),ig(N+l)
if(i.eq.j)then
di(i)=di(i)+a
return
end i f
if(i.It.j)then
ind=ig(j+1)-(j-i)
* мы предполагаем, что портрет правильный, и
* поэтому ошибки не контролируем (очевидно
* ind должен быть не меньше ig(j))
ggu(ind)=ggu(ind)+a
else
ind=ig(i+1)-(i-j )
ggl(ind)=ggl(ind)+a
end i f
end
494 Ю.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
а
10.4.3. ЛЕНТОЧНЫЙ ФОРМАТ ХРАНЕНИЯ МАТРИЦЫ СЛАУ
При работе с регулярными сетками вместо профильного формата
хранения матрицы можно использовать более простой ленточный
формат. Например, если прямоугольная расчётная область регулярно
разбивается на прямоугольные конечные элементы с билинейными
базисными функциями, то при регулярной нумерации узлов, например,
слева направо и снизу вверх (как, впрочем, и при нумерациях снизу
вверх и слева направо, или справа налево и снизу вверх, или других,
аналогичных им) матрица конечноэлементной СЛАУ будет девятидиа-
гональной. Для сетки, представленной на рис. 102,6/, структура матри-
цы конечноэлементной СЛАУ показана на рис. 102,6 (крестиком обо-
значены ненулевые компоненты, точкой - нулевые).
'X X . . X X...........’
XXX. XXX........... ...
. XXX. XXX..............
. .XX. .XX..............
XX. .XX. .XX............
XXX. XXX, XXX...........
.XXX. XXX. XXX. . . .
. . XX. .XX. XX. . .
. . . XX .XX. .XX. .
. . .XXX. XXX. XXX.
........XXX . XXX . XXX
XX. .XX. .XX
...........XX. XX..
............XXX XXX.
..............X X X X X X
..............XX. .XX
б
Рис. 102. Структура матрицы конечноэлементной СЛАУ (б)
для регулярной прямоугольной сетки (а)
Поскольку в матрицах такого типа профиль имеет практически по-
стоянный размер, отпадает необходимость в хранении массива гд,
достаточно хранить одно число - полуширину ленты lw (в приведён-
ном примере полуширина лепты равна пяти). При вычислении адреса в
массиве ggl (или дди.) любой компоненты матрицы нужно только
учесть, что в первых lw строках нижнего треугольника (или столбцах
верхнего треугольника) число хранимых элементов на единицу мень-
ше номера строки (или столбца), а в остальных строках (или столбцах)
число хранимых элементов равно lw .
10.4.Структуры данных для хранения матриц ... 495
Таким образом, при ленточном формате хранения глобальной мат-
рицы А конечноэлементной СЛАУ подпрограмма занесения числа а
в компоненту +L будет выглядеть следующим образом:
subroutine AddElement(N,lw,di,ggl, ggu,i,j,a)
dimension di(N),ggl(*),ggu(*)
if(i.eq.j)then
di(i)=di(i)+a
return
end i f
if(i.It.j)then
if(j.le.lw)then
* количество значений в предыдущих столбцах
* можно посчитать как ind = — 1) =--------
ind=(j-1)*(j-2)/2 + i
ind=lw*(lw-1)/2+lw*(j-lw-1)+ i
end if
* мы предполагаем, что портрет правильный, и
* поэтому ошибки не контролируем
ggu(ind)=ggu(ind)+а
else
if (i.le.lw)then
ind=(i-l)*(i-2)/2+j
ind=lw*(lw-1)/2+lw*(i-lw-1)+j
end if
ggl (ind)=ggl(ind)+a
end if
end
10.4.4. РАЗРЕЖЕННЫЕ ФОРМАТЫ ХРАНЕНИЯ МАТРИЦ СЛАУ
Разреженные строчный, столбцовый и строчно-столбцовый
форматы нацелены на хранение только тех элементов матрицы, кото
рые не равны нулю. В этих форматах хранят, как правило, м:нрпцы
таких СЛАУ, для решения которых будут использованы итерационные
методы, не изменяющие портрет матрицы, т.е. местоноложент ес
ненулевых элементов.
Здесь мы так же, как и при описании профильного формата. бу км
считать, что портрет матрицы симметричный, и для храпения ни,кт ю
треугольника матрицы используется разреженный строчный формат,
а для хранения верхнего — разреженный столбцовый формат I акои
формат мы будем называть разреженным стройно сю юцоным и ш
просто разреженным форматом.
Для хранения матрицы в разреженном строчно сю кщоном форма
те нам потребуется, кроме массива di с/inaroH.ini.ными комнопснгамн
матрицы А, еще четыре массива: цц! и <1Ч" ми хранения самих
496 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
ненулевых компонент нижнего и верхнего треугольников матрицы А,
а также ig и jg- массивы для определения строк и столбцов ненуле-
вых компонент матрицы А.
В массиве ggl будем хранить последовательно по строкам все не-
нулевые элементы нижнего треугольника матрицы, а в массиве дди —
по столбцам все ненулевые элементы верхнего треугольника матрицы.
При этом в г-м элементе массива ig должен храниться номер элемен-
та в массиве ggl (и дди), с которого начинаются компоненты г-й
строки нижнего (и /-го столбца верхнего) треугольник*) матрицы.
Длина массива гд должна быть равна 7V 4- I (А -размерность СЛАУ),
и последний его элемент должен содержать число, на единицу большее
длины массива ggl (и дди).
Массив jg служит для определения номеров столбцов элементов
нижнего треугольника матрицы А и номеров строк элементов её
верхнего треугольника. Длина массива jg совпадает с длиной масси-
вов ggl и дди. Элемент jg(j) содержит номер столбца, в котором
расположена компонента матрицы ggl(J), и номер строки, в которой
находится компонента ggu(j). Например, матрица (10.7) в разрежен-
ном формате имеет вид:
(Il = {l..5.,8..12.,15..19.}, ig = {1.1.2,2.4,5.7} , jg = {l.L2,4,2.3} ,
= {4..10.,11.,14.,16..17.} , дди = {2.,3.,6.,13.,7.,9.} .
Приёмы работы с матрицами, хранящимися в разреженном форма-
те, довольно похожи на приёмы работы с матрицами в профильном
форма।с. Как и в профильном формате, количество хранящихся эле-
ментов в / -и строке нижнего треугольника (i-м столбце верхнего тре-
yi одышка) может быть вычислено как ig (г -Ь 1) — гд (г) .
Чтобы найти адрес ячейки в массиве ggl, в которой хранится зна-
чение компоненты Atl из нижнего треугольника матрицы А (т.е. при
i > j), нужно сначала найти элемент со значением j в массиве jg,
просматривая jg с элемента с номером ig(i) до элемента с номером
i.g(i + l) — 1. Индекс I элемента jg (/), равного j, и будет номером
искомой ячейки (содержащей значение Д,) в массиве ggl. Аналогич-
но определяются адреса ячеек массива дди, в которых хранятся ком-
поненты A,f верхнего треугольника матрицы А (т.е. при i < j).
Алгоритм умножения матрицы, хранящейся в разреженном (строч-
но-столоцовом) формате, на вектор х выглядит следующим образом
(результат заносится в вектор у ):
* умножаем главную диагональ матрицы
do i = 1,N
у(i) =di(i)*x(i)
10.4.Структуры данных для хранения матриц ...
497
end do
* цикл по строкам нижнего и столбцам верхнего
* треугольника матрицы
do i = 1,N
do j = ig(i),ig(i+1)-1
* умножаем компоненту нижнего треугольника /1д
* на хк, где к = jg(j)
у (i) =у (i)+ggl(j)*х(jg (j))
* умножаем компоненту верхнего треугольника Akl
★ на х, , где k = jg(j)
y(jg(j))=y(jg(j)) +ggu (j) *x (i)
end do
end do
Обратим внимание на то, как умножается верхний треугольник мат-
рицы на вектор х . Поскольку при выбранном способе хранения мат-
рицы поиск элементов одной строки её верхнего треугольника затруд-
нён, умножение на компоненты вектора х верхнего треугольника мат-
рицы проводится проходом по его столбцам — очередной (j-й) нену-
левой элемент г-го столбца матрицы умножается на .с (г) и добавляет-
ся к компоненте у (к} с номером к = jg(j).
Очевидно, что для хранения симметричных матриц достаточно од-
ного массива ggl, поскольку ggu в этом случае полностью совпадёт с
ним. При этом рассмотренный чуть выше алгоритм умножения матри-
цы на вектор совершенно не изменится - достаточно лишь заменить
массив ggu на ggl (если этот алгоритм оформлен в виде подпрограм-
мы с формальными параметрами ggl и ggu, то достаточно при обра-
щении к этой подпрограмме подставить в качес тве фактического пара-
метра название одного и того же массива и для ggl, и для ggu ).
Для некоторых методов решения СЛАУ рассмотренный разрежен
ный (строчно-столбцовый) формат хранения матриц с симметричным
портретом может оказаться не очень удобным. К таким методам о тио
сится, например, метод релаксации.
Конечно, процедуру решения СЛАУ даже при использовании мето-
да релаксации всё-таки можно организовать так, чтобы избежан. попе
ков элементов матрицы и в случае хранения её в рассмотренном нами
выше разреженном формате. Для этого нужно уравнения ( 1АУ обрл
батывать последовательно снизу вверх. При любой другой схеме обрл
ботки уравнений СЛАУ (например, при необходимости opi шнюнлн.
выборочную релаксацию) без процедур поиска ненулевых > немец гон
строк верхнего треугольника уже будет трудно обой rm i. В пом ел\
чае можно потратить дополнительную память пл увеличение (вдвое)
массива jg и хранить компоненты матрицы в одном млее ине </д, при-
чём все компоненты каждой строки хранить последе мин с илю (включая
и компоненты из верхнего треугольника матрицы), i с храпим. матри-
цу в разреженном строчном формате.
498 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
В некоторых же случаях самым удобным может оказаться разре-
женный столбцовый формат, в котором все ненулевые компоненты
матрицы хранятся в массиве дд последовательно по столбцам, в мас-
сиве jg хранятся соответствующие номера строк для этих компонент,
а в массиве ig хранятся адреса ячеек массивов дд и jg, с которых
начинаются столбцы матрицы. Примеры хранения матриц с использо-
ванием такого формата будут приведены ниже (см. раздел 11.6.4,
с. 545, 549).
10.4.5. АЛ! ОРИТМЫ ЗАНЕСЕНИЯ ЛОКАЛЬНЫХ МАТРИЦ
В ГЛОБАЛЬНУЮ МАТРИЦУ, ХРАНЯЩУЮСЯ В РАЗРЕЖЕННОМ ФОРМАТЕ
Рассмотрим одну из основных процедур МКЭ - процедуру сбор-
ки глобальной матрицы из локальных - для глобальной матрицы, хра-
нящейся в разреженном формате.
В принципе, для занесения компонент локальной матрицы в гло-
бальную можно было бы воспользоваться следующей достаточно про-
стой подпрограммой занесения числа а в компоненту Ду глобальной
матрицы (аналогичную той, что была приведена в качестве примера
для профильного формата в конце раздела 10 4.2):
subroutine AddElement(N,di,ig,jg,ggl,ggu,i,j,a)
dimension di(N),ggl(*),ggu(*),ig (N+l), j g ( *)
if(i.eq.j )then
di(i)=di(i)+a
return
end if
if (i.It.j)then
do ind=ig(j),ig(j+1)-1
if (jg(ind) .eq.i)exit
end do
мы предполагаем, что портрет правильный, и
поэтому ошибки, связанные с отсутствием
* нужной компоненты в портрете матрицы, не
кон тролируем;
на самом деле, попадание в это место
* подпрограммы означает, что нужной
* компоненты нет в портрете
ggu(ind)=ggu(ind)+a
else
do ind=ig(i),ig(i+1)-1
if(jg(ind).eq.j)exit
end do
ggl (ind)=ggl(ind)+a
end i f
end
Однако этот способ не всегда эффективен. Конечно, основные за-
траты машинною времени при генерации конечноэлементной матрицы
приходятся на вещественные операции, которые необходимо сделать
10.4.Структуры данных для хранения матриц ...
499
при вычислении компонент локальных матриц. Но для некоторых ти-
пов конечных элементов, для которых в строке глобальной матрицы
может оказаться достаточно много ненулевых компонент (как, напри-
мер, для элементов высоких порядков), цикл поиска индекса в массиве
jg может занимать заметное время, не только сравнимое со временем
вычисления компонент локальных матриц, но и даже превышающее
его. В этом случае процедуру занесения локальной матрицы в глобаль-
ную можно ускорить следующими способами.
Во-первых, можно сделать так, чтобы элементы массива jg, соот-
ветствующие одной и той же строке нижнего треугольника (и, естест-
венно, одному и тому же столбцу верхнего треугольника) были упоря-
дочены по возрастанию. Такое упорядочение никак не изменит проце-
дуры умножения матрицы на вектор, но позволит ускорить поиск в
массиве jg нужного индекса при занесении одной компоненты ло-
кальной матрицы в глобальную (например, можно использовать про-
стейший способ ускоренного поиска в упорядоченном массиве - дихо-
томию).
Во-вторых, можно ускорить процедуру занесения компонент ло-
кальной матрицы в глобальную, если заносить эти компоненты не по
одной, а все вместе. При этом без всяких дополнительных действий
(и даже без упорядочения массива jg) для несимметричных матриц
поиск легко ускоряется практически в два раза, поскольку для симмет-
рично расположенных компонент локальной матрицы индекс в jg
можно будет искать один раз. Но гораздо большего ускорения можно
добиться в том случае, если на конечном элементе номера локальных
базисных функций упорядочить по возрастанию соответствующих им
глобальных номеров, т.е. если пронумеровать локальные базисные
функции так, чтобы базисная функция с минимальным глобальным
номером имела на конечном элементе локальный номер 1, базисная
функция со следующим по величине глобальным номером - локаль-
ный номер 2 и т.д. Рассмотрим алгоритм, реализующий такое занесе-
ние локальной матрицы в глобальную.
Будем считать, что массив jg соответствующим образом упорядо-
чен, а локальная матрица А размера к х к конечного элемента с уно
рядоченными локальными номерами базисных функций прсдсз авлспа
двумя массивами: двумерным вещественным массивом А размер.! kxk
и целочисленным массивом L длины к. При этом элемеш Г. (i ) по
номер глобальной базисной функции, соответствующей JioK.i ii.noif
базисной функции с номером i. Тогда подпрограмма занесения к»
кальной матрицы в глобальную может быть следующей
subroutine AddLocal (N,di,ig,jg,ggl,ggu , k, I., A)
dimension di (N),ggl(*),ggu(*), ig(NH), jg(*
dimension L(k),A(k,k)
* заносим диагональные элементы
do i = l,k
di(L(i))=di(L(i))+A (i,i)
500 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
end do
* начинаем цикл по строкам нижнего (и
* одновременно по столбцам верхнего)
* треугольника локальной матрицы
do i=l,k
* устанавливаем начальное значение нижней
* границы поиска. Поскольку локальные номера
* упорядочены, для каждого последующего
* элемента строки начинать поиск можно с уже
* найденного индекса
ibeg=ig(L(i))
* начинаем поиск дихотомией по строке нижнего
* (и по столбцу верхнего) треугольника
do j=l,i-1
iend=ig(L (i)+1)-1
do while(jg(ibeg).ne.L(j))
ind=(ibeg+iend)/2+1
if(jg(ind).le.L(j))then
ibeg=ind
else
iend=ind
end if
end do
ggl(ibeg)=ggl(ibeg)+A(i,j)
ggu (ibeg)=ggu(ibeg)+A(j,i)
ibeg=ibeg+l
end do
end do
end
Заметим, что упорядочение локальных номеров базисных функций
по возрастанию их глобальных номеров необходимо только для уско-
рения работы с глобальной матрицей, т.е. ускорения процесса сборки и
алгоритма построения портрета матрицы, который будет рассмотрен
позже. Для вычисления же самой локальной матрицы упорядочение
локальных базисных функций может оказаться даже нежелательным
(например, при использовании шаблонных элементов со «своей» ну-
мерацией базисных функций). Поэтому в некоторых случаях имеет
смысл использовать сразу две локальные нумерации базисных функ-
ций конечного элемента: одну в соответствии с нумерацией базисных
функций шаблонного элемента, вторую — по возрастанию глобальных
номеров базисных функций.
Программа же занесения локальной матрицы в глобальную может
очень мало отличаться от рассмотренной выше. Для этого достаточно
(на каждом конечном элементе) ввести целочисленный массив LL дли-
ны к такой, что в первой его ячейке хранится локальный номер базис-
ной функции с минимальным глобальным номером, во второй - ло-
кальный номер базисной функции со следующим по величине гло-
бальным номером и т.д. Тогда в рассмотренной выше программе нуж-
10.4.Структуры данных для хранения матриц ...
501
но просто заменить обращение к компонентам А (1 , i ), Л (i , j) и
A(j,i) обращениями A(LL(i),LL (i)), A (LL ( i) , 1.1. ( j) ) и
A (LL (j ) , LL (i) ) соответственно, что и обеспечит зансссшк компо-
нент локальной матрицы в глобальную строго по возрастанию гло-
бальных номеров базисных функций.
10.4.6. ДИАГОНАЛЬНЫЙ ФОРМАТ ХРАНЕНИЯ МАТРИЦЫ СЛАУ
Разреженные форматы могут оказаться не самыми эффективны
ми для матриц СЛАУ, полученных при решении задачи на конечно-
элементной сетке с регулярной структурой. Для матриц такого типа
более эффективными являются форматы, учитывающие закономерно-
сти расположения ненулевых компонент. К таким форматам относи гея
диагональный формат хранения разреженных матриц, имеющих регу-
лярную структуру.
По-прежнему будем считать, что матрица имеет симметричный
портрет. В диагональном формате в двумерных массивах ggl и дди
размером Nd х (TV — 1) хранятся элементы ненулевых побочных диа-
гоналей матрицы A (Nd — число таких диагоналей в одном из тре-
угольников матрицы А, N - размерность СЛАУ). Во вспомогатель-
ном массиве ig длиной Nd хранятся смещения ненулевых диагоналей
относительно главной (т.е. фактически уменьшенные на единицу но-
мера строк, с которых начинаются диагонали нижнего треугольника,
или уменьшенные на единицу номера столбцов, с которых начинаются
диагонали верхнего треугольника).
Например, матрица
1. 2. о з. о о
4. 5. 6. 0 7. 0
0 S. 9. 0. 0 11.
(10.8)
12. 0 13. 14. 15. 0 47
0 16. 0 0. 18. 19.
0 0 20. 0 21. 22.
в диагональном формате имеет вид (на место несуществующих эле-
ментов в массивы ggl и дди занесены нули):
di = {1.,5.,9.,14.,18.,22.} ,
tg = {1.з},
дди =
2. 6. 0. 15. 19.
3. 7. 11. 0. 0.
дд1 =
4. 8. 13. 0. 21.
12. 16. 20 0. 0
Приёмы работы с матрицей в таком формате yiocraio'itio npocn.i.
Например, программа умножения матрицы на вектор для hoi о форма-
та может иметь следующий вид:
do i = 1,N
у (i) =di (i) *x (i)
502 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
end do
do i = l,Nd
do j = l,N-ig(i)
ir=j+ig(i)
у (ir)=y(ir)+ggl(i,j)*x (j)
У(j)=У(j)+ggu(i,j)*x(ir)
end do
end do
Рассмотрим, как можно найти местоположение компоненты Д,
матрицы А в массиве ggl (это необходимо, например, при сборке гло-
бальной матрицы). Сначала в массиве ig нужно найти значение i — j
(заметим, что если в ig такого значения нет, то это означает, что
Д7 = 0 и эта компонента не хранится). Индекс элемента массива ig,
равного i — j, обозначим через А: (т.е. ig(k) = i — j). Тогда ggl(k,f)
будет искомым элементом массива ggl, в котором должно храниться
значение компоненты Ду.
10.4.7. БЛОЧНЫЕ ФОРМАТЫ ХРАНЕНИЯ. РАЗРЕЖЕННЫЙ БЛОЧНЫЙ ФОРМАТ
При решении некоторых типов задач методом конечных элемен-
тов получаемая СЛАУ имеет матрицу с явно выделяющимися блоками
одного фиксированного размера пь. Примером может служить матри-
ца конечноэлемеитной СЛАУ, получаемая при аппроксимации гармо-
нической краевой задачи (7.51), (7.55)—(7.5/). Если учесть блочную
структуру матрицы при хранении её в разреженном формате, то можно
сэкономить как минимум память в массивах индексов. Кроме того,
довольно часто не требуется хранить все компоненты блока, поскольку
некоторые из них либо являются фиксированными числами (например,
пулями в гармонической задаче в случае, когда коэффициент о на всех
прилегающих к узлу конечных элементах равен нулю, см. с. 388), либо
совпадают друг с другом (например, для хранения блока (с. 387) вме-
сто четырёх его элементов можно хранить только два числа). Форматы
хранения матрицы СЛАУ, учитывающие описанные особенности, на-
зывают разреженными блочными.
Мы рассмотрим блочные форматы на примере блочной модифика-
ции разреженного строчно-столбцового формата, рассмотренного в
разделе 10.4.4.
Под блок-строкой мы будем понимать несколько последователь-
ных строк матрицы. Если все блок-строки содержат одинаковое коли-
чество строк щ, то первая обычная строка в Л-й блок-строке имеет
номер (А: — 1) пь + 1 , k = 1... Nb , где Nh — блочный размер матрицы
(т.е. Nb = N/щ,). Аналогичным образом определяется и блок-
столбец.
Для хранения матрицы в разреженном блочном формате нам потре-
буется семь массивов: ggl и дди — для хранения самих ненулевых
10.4.Структуры данных для хранения матриц ...
503
элементов нижнего и верхнего треугольников матрицы А, ig, jg и
ijg - массивы для вычисления адресов в ggl и дди ненулевых (блоч-
но-) внедиагональных элементов матрицы, di — для хранения ненуле-
вых элементов диагональных блоков матрицы и idi - для вычисления
адресов этих диагональных блоков в массиве di. ГТри этом будем счп
тать, что матрица А имеет симметричный блочный портрет, т.е. бло-
ки в матрице расположены симметрично и количество чисел, которые
нужно хранить для каждого из двух симметрично расположенных бло-
ков матрицы, одинаково.
Рассмотрим, каким образом можно хранить конечноэлементную
матрицу А с помощью массивов ggl, дди, ig , jg, ijg, di и idi. В
массиве ggl, как обычно, будем хранить элементы блоков нижнего
треугольника матрицы, а в массиве дди — элементы блоков верхнего
треугольника матрицы. При этом все элементы одного блока матрицы
должны быть расположены в этих массивах подряд и в строго уста-
новленном порядке.
Массив ijg служит для определения номеров ячеек в массивах ggl
и дди, с которых начинается очередной блок. Элемент ijg(j) массива
ijg содержит номер элемента в массиве ggl (и дди ), с которого начи-
нается информация о блоке матрицы с номером j . Обратим внимание
на то, что номер j - это не номер блок-строки или блок-столбца, а
просто порядковый номер блока среди хранящихся в массивах ggl и
дди блоков (соответственно длина массива ijg определяется общим
числом блоков нижнего или верхнего треугольника матрицы А ).
Для определения номера блок-столбца нижнего {блок-строки верх-
него) треугольника матрицы, в котором находится интересующий нас
блок, служит массив jg . В jg (j) содержится номер блок-столбца ниж-
него (блок-строки верхнего) треугольника матрицы, в котором распо-
ложен блок с номером j. Число элементов, которое хранится в ggl и
дди для этого блока, определяется, очевидно, как ijg (j + 1) — ijg {j}
Элемент гд(г) массива ig содержит номер элемента в массивах д/
и ijg, с которого начинается информация о блок-строке нижнею
(блок-столбце верхнего) треугольника матрицы с номером г.
Длина массива гд равна TV/, + 1, и последний его элемент содержи!
число, на единицу большее длины массива jg , т.е. длина массив . /
равна ig{Nb +1) — 1 (это общее число блоков в нижнем или верхнем
треугольнике матрицы А). Длина же массива ijg па с щницх но п nir
(т.е. равна ig(Nb +1))- Последний элемент массива ijg со п-ржич чш
ло, на единицу большее длины массива ggl (и дди ) i < i шил м.н ива
ggl (и дди ) равна ijg(ig(Nb + 1)) - 1.
504 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
Как уже говорилось, главная блок-диагональ матрицы в рассматри-
ваемом нами разреженном блочном формате хранится в массивах di и
idi (тоже упаковано). Значения элементов диагональных блоков хра-
нятся в массиве di. (аналогично тому, как хранится информация в мас-
сивах ggl и дди ). В массиве idi (длиной N/, + 1) элемент с номером i
содержит номер ячейки, с которой в массиве di начинаются элементы
диагонального блока с номером г. В последней ячейке массива idi
содержится число, на единицу большее длины массива di . Число эле-
ментов, которые хранятся для г-го блока, определяется, естественно,
Рис. 103. Сетка
и нумерация ее узлов
В общем случае для определения типа блока
(от которого может зависеть способ определения
значении компонент матрицы через хранимые в
массивах ggl, дди и di. числа) следует хранить
ещё два массива. Назовём эти массивы Ид и
Udi и будем хранить в них типы матричных и
диагональных блоков соответственно. Очевид-
но, что длина массива Ug должна быть
ig(Nb + 1) ~ 1, а массива Udi - Nh. Однако на
практике чаще Bcei о оказывается возможным
определять тип блока по числу хранящихся для
него элементов. Например, для рассмотренных в
разделе 7.7 гармонических задач матрица конеч-
ноэлементной СЛАУ состоит из блоков двух
типов (см. раздел 7.7.2, с. 387-388), причём для
блока первого типа нужно хранить два значения,
а для блоков второго типа — одно. Очевидно, в этом случае вполне
можно обойтись без массивов Ug и itdi .
Рассмотрим в качестве примера хранение в разреженном блочно
формате матрицы конечноэлементной СЛАУ, полученной при аппрок-
симации I армонической задачи (7.51), (7.55)—(7.57) на треугольной
сетке, изображённой на рис. 103.
Пусть треугольники {1,5,3} и {1,2,5} лежат в подобласти, в кото-
рой значение коэффициента о равно нулю. Введём (как и в разде-
ле 7.7) обозначения
Р,, = f gl'ad ’
сч = f .
Q
(Ю.9)
(10.10)
Тогда матрица конечноэлементной СЛАУ будет иметь вид:
10.4.Структуры данных для хранения матриц ...
505
>11 0 1 И2 0 ' ИЗ 0 1 0 1 0 | И5 0 '
0 Pu ! 0 P12 ! 0 Из ! 0 0 ! 0 । И5
P21 0 \P22 -022 ! 0 0 ; P24 ~c24 ; z’25 -C25
0 P21 ! 022 P22 ! ° i 0 ; o>4 । P24 ! C25 J T>25
Р31 0 0 P31 ! o ! о 1 0 0 ! Рзз ! о । 0 РЗЗ ! 0 ! 0 1 0 0 ! P35 ! 0 1 0 ?35 (10.11)
0 0 ;P42 —c42 ! о i 0 j P44 ' 44 ]P45 C45
0 0 ' C42 ?42 i 0 1 0 j c44 P44 ; c45 P45
P51 0 ; P52 -C52 ; P53 0 ;p54 C54 ; Д55 -C.55
0 P51 | c52 7’52 I ° P53 j O54 P54 । c55 P55
В разреженном блочном формате эта матрица примет вид:
idi = {1,2,4,5,7,9} , di = {pi 1, р22, С22, р33<р44 , С44, р55, С55 } ,
ig = {1,1,2,3,4,8} , jg = {1,1,2,1,2.3,4} , ijg = {1,2,3,5,6,8,9,11} ,
ggl = { P21, Рзь ?42, C42.P51> Pb2»c52, ИЗ> ?54 , <T,4 },
ggu = {pj 2, Pl 3, P24, C-24, И 5» P25, c25, P35: P45, C45 } •
Обратим внимание на то, что для гармонических задач фактически
нет необходимости хранить массив дди, поскольку (как это с очевид-
ностью следует из соотношений (10.9) и (10.10)) ptJ = p.j, и = с(£,
и, следовательно, для этих задач дди = ggl.
При работе с матрицами в разреженном блочном формате необхо-
дима информация о том, как располагаются в матрице А числа, хра
нящиеся в массивах di, ggl и дди. Эта информация фактически опре-
деляет алгоритм умножения блока матрицы на соответствующий
фрагмент вектора (который мы будем называть бпок-вектором).
Приведём пример подпрограммы умножения блока маарнцы па
блок-вектор для гармонической задачи, т.е. для случая, когда ig, 2 и
Р
с
—сА
0)
блоки могут быть только двух типов: вида
И ВПД.1
I'
, при-
Р
О
чём для блока первого типа хранится два числа, р и г, а для шорою -
одно число р.
subroutine MultBlock(b,k,x, у)
integer К
506 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
real b(к),х(*),у(*)
умножает блок В на блок-вектор X
Результат добавляет в блок-вектор Y
if(к == 1)then
у (1) =у (1)+b (1) *х (1)
у (2)=у(2)+Ь(1) *х(2)
else
y(l)=y(l)+b(l)*x(l)-b(2)*x(2)
y(2)=y(2)+b(2) *x(l)+b(l) *х(2)
end if
end subroutine MultBlock
Очевидно, аналогичную подпрограмму умножения одного блока
матрицы на блок-вектор можно написать и для блоков другого типа.
Тогда программа умножения матрицы на вектор становится очень по-
хожей на программу умножения матрицы на вектор в обычном разре-
женном строчно-стол* цовом формате:
* Nb-число блоков
* k-размер блока
do i = 1, Nb
ib=k*(i-1)+1
do j=l,k
у(ib+j-l)=O.
end do
isize=idi(itl)-idi(i)
call MultBlock(di(idi(i)),isize,x(ib),у(ib))
end do
do i = 1,Nb
ib=k*(i-1)+1
do j = ig(i),ig(i+1)-1
jb=k* (jg (j)-1)+1
isize=ijg(j+1)-ijg(j)
* в нашем случае ggu^ggl, и поэтому для
* хранения значений компонент матрицы нужен
* только один массив, его имя - gg
call MultBlock(gg(ijg(j)),isize,x(jb), у(ib))
call MultBlock(gg(ijg(j)),isize,x(ib),у(jb))
end do
end do
10.4.8. ПРОЦЕДУРА СБОРКИ ГЛОБАЛЬНОЙ МАТРИЦЫ, ХРАНЯЩЕЙСЯ
В РАЗРЕЖЕННОМ БЛОЧНОМ ФОРМАТЕ
В принципе, процедуру сборки матрицы, хранящейся в разре-
женном блочном формате, можно сделать аналогичной процедуре
сборки матрицы, хранящейся в обычном разреженном формате, т.е
собирать глобальную блочную матрицу из локальных блочных матриц.
Но если в матрице блоки имеют разную структуру, то такая технология
является не очень удобной. Например, для рассмотренных нами гар-
монических задач локальная матрица может иметь блок с только двумя
10.4.Структуры данных для хранения матриц ...
507
(диагональными) ненулевыми компонентами (равными друг другу), а
соответствующий блок глобальной матрицы (в который должен быть
занесён рассматриваемый блок локальной матрицы) при этом имеет
четыре ненулевых компоненты (с ненулевыми внедиагональными ком-
понентами). Такая ситуация возникает для всех связей по рёбрам, ле-
жащим на границах между проводящими (о^О) и непроводящими
(су = 0) подобластями расчётной области. Необходимость контроля и
обработки такой ситуации лишает подход, основанный на сборке гло-
бальной блочной матрицы из локальных блочных матриц, главного (и
практически единственного) его преимущества — универсальноети.
поскольку соответствующие алгоритмы обработки практически всегда
определяются структурой блока.
Поэтому гораздо удобнее собирать блочные матрицы не из локаль-
ных блочных матриц, а из стандартных локальных матриц конечных
элементов — чаще всего это матрицы жёсткости и массы (хотя в четыр-
надцатом разделе будут рассмотрены задачи, в которых используются
локальные матрицы и других типов - см соотношения (14.34)-( 14.38)).
Приведём пример программы сборки глобальной матрицы для гар-
монической задачи (7.51), (7.55)-(7.57). Поскольку для этой задачи
матрица обладает определённой блочной симметрией, для хранения
значений её компонент будет использоваться только один массив дд
(который может быть проинтерпретирован и как ggl, и как дди ).
Будем считать, что массив jg соответствующим образом упорядо-
чен, а локальные матрицы Р и С размером к х к конечного элемента
с упорядоченными (по возрастанию соответствующих глобальных
номеров) локальными номерами базисных функций содержат компо-
ненты, определяемые соотношениями вида (10.9) и (10.10), и пред-
ставлены двумерными массивами Р и С размером kx к (к - число ба-
зисных функций конечного элемента). Соответствие локальных но-
меров базисных функций глобальным (фактически это соответствие
локальных номеров базисных функций номерам блок-строк и блок-
столбцов глобальной матрицы) задано массивом L длины к. Когда
подпрограмма занесения локальной матрицы в глобальную mo;kci
быть следующей:
subroutine AddLocal(N, di, idi, ig, jg, gg,
ijg, k, L, P, C)
dimension di(*),gg(*)
dimension ig(N+l),jg(*), ijg(*),idi(N+l)
dimension L(k),P(k,k),C(k,k)
logical itype
* Если на диагонали матрицы С стоит нуль ш>й
* элемент, то её не надо заносить. Проверим >т«
* и запомним тип занесения в перемени >й iiyj •
itype= C(l,l).ne.0.
* заносим диагональные элементы
do i=l,k
ind=idi(L(i))
508 Ю.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
di(ind)=di(ind)+P(i,i)
if(itype) di(ind+1)=di(ind+1)+C(i,i)
end do
* начинаем цикл по строкам нижнего (и
* одновременно по столбцам верхнего)
* треугольника локальной матрицы
do i=l,k
* устанавливаем начальное значение нижней
* границы поиска. Поскольку локальные номера
* упорядочены, для каждого последующего
* элемента строки начинать поиск можно с уже
* найденного индекса
ibeg=ig(L(i))
* начинаем поиск дихотомией по строке нижнего
* (и по столбцу верхнего) треугольника
do j=l,i-l
iend=ig(L(i)+1)-1
do while(jg(ibeg).ne.L(j))
ind=(ibeg+iend)/2+1
if(jg(ind) .le.L (j))then
ibeg=ind
else
iend=ind
end if
end do
ind=ijg(ibeg)
gg(ind)=gg(ind)+P(j,i)
if(itype) gg(ind+1)=gg(ind+1)+C(j,i)
ibeg=ibeg+l
end do
end do
end
10.5. ПОСТРОЕНИЕ ПОРТРЕТА КОНЕЧПОЭЛЕМЕНТНОЙ МАТРИЦЫ
Для работы с матрицей в разреженном формате нужно сначала
построить ее портрет (т.е. сформировать массивы гд и jg ).
Построение портрета матрицы фактически означает нахождение в
конечноэлементной сетке для каждой глобальной базисной функции
фг номеров j всех базисных функций, для которых J ф^ф^ * 0 или
Г grad ф, • grad фу 0, т.е. номеров всех глобальных базисных функ-
о „
ций, не равных нулю на хотя бы одном из тех конечных элементов, па
которых не равна нулю глобальная базисная функция ф^.
10.5.Построение портрета конечноэлементной матрицы
509
В дальнейшем две глобальные базисные функции, которые обе не
равны нулю хотя бы на одном конечном элементе, будем называл, свя-
занными (так же будем называть и соответствующие таким базисным
функциям веса - компоненты вектора неизвестных конечноэлемен той
СЛАУ).
Алгоритм построения портрета матрицы может быть реализован с
помощью массива списков. Его основная идея заключается в следую-
щем. Создастся массив из N списков, где N - число глобальных ба-
зисных функций. При прохождении по конечным элементам добавля-
ем в каждый список, соответствующий ненулевой на этом элементе
глобальной базисной функции, номера всех остальных ненулевых па
этом элементе глобальных базисных функций. Естественно, при каж-
дом добавлении в список следует проверять, нет ли уже в нём добав-
ляемого номера базисной функции Кроме того, если портрет симмет-
ричный и строится только для одного из треугольников матрицы, па-
пример для нижнего треугольника с хранением компонент матрицы
конечноэлементной СЛАУ по строкам, то добавлять в каждый список
нужно только те глобальные номера функций, которые меньше номе-
ра самого списка.
Однако прямая программная реализация описанного алгоритма с
использованием списков является не самой эффективной, причём не
столько из-за затрат дополнительной памяти на реализацию списков,
сколько из-за затрат времени на работу с ними (поскольку операции
динамического выделения/освобождения памяти в языках высокого
уровня являются достаточно затратными) Поэтому мы продемонстри-
руем реализацию этого алгоритма с однократным выделением памяти
под весь список.
Будем считать, что для обращения к структурам данных определе-
ны следующие функции: функция NumberOf Unknowns (I), которая
возвращает число глобальных базисных функций, ненулевых на эле-
менте с номером г, и функция IndexOf Unknown (I, J), которая
возвращает глобальный номер j -й локальной базисной функции на
элементе с номером i.
Тогда программа на языке Фортран, реализующая алгоритм но
строения портрета (т.е. формирующая массивы гд и jig), можеч бы и.
следующей:
subroutine GeneratePortrai t (ig, j g, N, Kel, list.)
* N - число глобальных базисных функций в
* конечноэлементной сетке
* Kel - число конечных элементов в сетке*
dimension ig (N+l),jg (*),list(2, *)
* list - временный массив для хранени i спи ы.
* для этого массива должно быть выделено
* вдвое больше памяти, чем для массива щ.
* Для упрощения программы мы нс будем
* проверять, что алгоритм не выходит *ы гранит
* выделенной памяти, хотя в реальной nj 1 р »мм»«
* это всё-таки надо бы делать.
510 Ю.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
* Элементы list(l,:) будут хранить
* номер базисной функции, a list(2,:)
* следующего элемента в массиве list.
* Номер 0 означает конец списка
номер
ALLOCATABLE listbeg(N)
ALLOCATE listbeg
* временный массив listbeg будет хранить
* номера элементов массива list, с которых
* начинаются списки для каждой из базисных
* функций
listsize=0
* listsize - текущая длина массива list
do i=l,N
listbeg (i) = 0
end do
* цикл формирования списка одним проходом по
* элементам.
do ielem=l,Kel
do i=l,NumberOfUnknowns(ielem)
k=IndexOfUnknown(ielem,i)
do j=i+l,NumberOfUnknowns(ielem)
indl=k
ind2=IndexOfUnknown(ielem,j)
if(ind2.It.indl)then
indl=ind2
ind2=k
end if
* заносить будем связь большего номера с
* меньшим, т.е. ind2 с indl
iaddr=listbeg(ind2);
if(iaddr.eq.0)then
* списка ещё не было, создаём его
listsize=listsize+l
listbeg(ind2)=listsize
list(1,listsize)=indl
list(2,listsize)=0
else
* список уже был. Ищем в нём indl.
do while(list(l,iaddr).It.indl.and.
list(2,iaddr).gt.O)
iaddr=list(2,iaddr)
end do
if(list(1,iaddr).gt.indl)then
* не нашли и встретили элемент с большим
* номером. Добавляем перед ним, чтобы список
* оставить упорядоченным
10.5.Построение портрета конечноэлементной матрицы
511
listsize=listsize+l
list (1,listsize)=list(1,iaddr)
list (2,listsize)=list(2, iaddr)
list (1,iaddr)=indl
list(2,iaddr)=listsize
else
if(list(1, iaddr).It.indl)then
* не нашли, а список закончился.
* Добавляем в конец списка
listsize=listsize+l
list (2,iaddr)=listsize
list (1,listsize)=indl
list (2,listsize)=0
end if
end if
end if
end do
end do
end do
* Создание портрета по списку
ig(1)=1
do i=l,N
ig(i+1)=ig(i)
* ig(i+l) фактически указывает на ячейку
* массива jg, куда надо поместить следующий
* элемент
iaddr=listbeg(i)
do while(iaddr.ne.0)
jg (ig(i + 1))=list(1, iaddr)
ig (i + 1)=ig(i + 1)+1
iaddr=list(2,iaddr)
end do
end do
Заметим, что приведённый алгоритм является практически универ
сальным в том смысле, что он нс привязан к типу конечных элемента,
и позволяет использовать в одной конечноэлементной сетке элсмсшь!
с различным числом базисных функций. Единственным о> рапиченш м,
делающим этот алгоритм не совсем универсальным, является пре ню
ложение о том, что все локальные базисные функции на одним > н-мгн
те являются связанными между собой (т.е. пред г юл ;п ас i с я, что щя
любых двух функций с локальными номерами i и / > юм<»т I,, ю
калькой матрицы А нс равен нулю). Однако эго oi раннчениг юсы
точно просто ликвидируется введением дополни i с H.noii ф\нкпии,
проверяющей перед занесением связи в список сё на шчие \ оор.ю.111.1
ваемого элемента. Соответствующие изменения в npoip.iMMi мы пре
доставляем сделать читателю в качестве упри ми пня
512 1 ©.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
Обратим внимание, что приведённый алгоритм сразу строит массив
jg так, что номера элементов одной строки нижнего треугольника
упорядочены в нём по возрастанию, что удобно нс только для приве-
дённого выше алгоритма сборки матрицы, но и для методов решения
СЛАУ с использованием неполной факторизации (см. семнадцатый
раздел).
Кроме того, рассмотренный нами алгоритм формирования портрета
разреженной матрицы может быть положен в основу алгоритма по-
строения упорядоченного массива рёбер конечных элементов, который
будет рассмотрен в разделе 10.6.3.
10.6. АЛГОРИТМЫ НУМЕРАЦИИ БАЗИСНЫХ ФУНКЦИЙ, ГРАНЕЙ
И РЕБЕР КОНЕЧНЫХ ЭЛЕМЕНТОВ
10.6.1. НУМЕРАЦИЯ ГЛОБАЛЬНЫХ БАЗИСНЫХ ФУНКЦИЙ
Все базисные функции рассмотренных ранее типов конечных
элементов можно условно подразделить на следующие основные клас-
сы:
I) функции, связанные с геометрическими вершинами элементов
сетки, — это функции, отвечающие за значения в узлах, совпадаю-
щих с геометрическими вершинами сетки для лагранжевых элемен-
тов, и все привязанные* к вершинам элементов функции эрмитовых
элементов;
2) функции, ненулевые внутри только одного элемента, - это все
базисные функции, ассоциированные с внутренними узлами конеч-
ных элементов;
3) функции, ассоциированные с рёбрами элементов, - это все базис-
ные функции, привязанные к узлам сетки, лежащим на рёбрах эле-
ментов и не совпадающим с геометрическими вершинами элемен-
тов;
4) функции, ассоциированные с гранями трёхмерных элементов, -
эго все базисные функции, привязанные к узлам сетки, лежащим на
гранях элементов и не совпадающим с геометрическими вершинами
элементов и узлами на их рёбрах.
Очевидно, что нумерация оазисных функций первого класса не пред-
ставляет особой сложности, поскольку исходная информация о сетке
уже содержит номера геометрических вершин каждого конечного эле-
мента. Для простейшего (и наиболее частого) случая, когда каждой вер-
шине соответствует одно и то же число к базисных функций, никакой
алгоритм нумерации вообще не нужен, поскольку для i-й вершины
глобальный номер её j -й базисной функции (j = 1...А-) может опреде-
ляться по номеру вершины /. как к (г — 1)4- j. Для остальных случаев
возможен очень простой алгоритм нумерации, когда первой функции,
1 В МКЭ вместо термина «привязанный» чаще употребляется его синоним
«ассоциированный», т.е. вместо «функции, привязанные к вершинам» говорят
«функции, ассоциированные с вершинами». В дальнейшем мы будем пользо-
ваться в основном термином «ассоциированный».
10.6.Алгоритмы нумерации базисных функций, граней и ребер . 513
соответствующей (г +1) -й вершине, присваивается номер
— 72, + А:г,где А:д - число функций, соответствующих / и вершине
Так же просто пронумеровать базисные функции второго класса Для
простейшего случая, когда число базисных функций kt, ассоциирован-
ных с внутренними узлами любого конечного элемента, одинаково и
равно А:, глобальный номер первой локальной базисной функции эле-
мента Q, можно определить как 7i() + к {г — 1) + I, где ??() - общее чис-
ло уже пронумерованных функций других классов. Для остальных слу-
чаев возможен, как и для функций первого класса, алгоритм нумерации,
когда первой функции, ассоциированной с внутренним узлом элемен та
Q,+1, присваивается номер n1+J = 727 -|-А;г, где кг - число функций,
ассоциированных с внутренними узлами элемента Q,.
Нумерация же функций третьего и четвертого классов может быть
выполнена аналогично только в том случае, если предварительно про-
нумерованы соответствующие граничные элементы {рёбра и грани)
всех конечных элементов Тогда в массивах, размерности которых
определяются числом соответствующих граничных элементов, можно
сохранить значения к, - число функций, привязанных к внутренним
узлам / -го граничного элемента, и, как и ранее, определить номер пер-
вой функции на z Т 1 -й границе как тз,+] = 72, + А:д. Однако подсчёт и
нумерация рёбер конечных элементов и их трёхмерных граней являют-
ся отдельной проблемой, которую мы рассмотрим чуть ниже.
Необходимо отмстить, что рассмотренные здесь методы могут при-
водить к нумерации базисных функций, которая является далеко нс
лучшей для решения СЛАУ Дело в том, что при использовании этих
методов связанные между собой базисные функции могут получить
далёкие друг от друга номера, что, в свою очередь, можег заметно ос-
ложнить процесс решения конечноэлементной гЛАУ из-за роста разме-
ра профиля при использовании как прямых, гак и некоторых итсрацион
ных методов (например, с предобусловливанием на основе неполной
факторизации). Поэтому построенная нами нумерация должна рассмат-
риваться, в общем-то, как первичная, позволяющая лишь дать одиноко
вые (и вместе с тем уникальные) номера базисным функциям, ненуле-
вым на нескольких элементах. Для получения же оптимальной нумера
ции должны быть применены какие-либо алгоритмы сортировки
Подробное рассмотрение алгоритмов сортировки нсизвссшых 11я
уменьшения профиля матрицы С.1АУ выходит за рамки данной iciini и
Мы рассмотрим только простейшую идею перенумерации баян них
функций, ассоциированных с узлами сетки (причём с любыми i t i imu л
не только с геометрическими вершинами).
Запишем в массив точек все узлы сетки, с которыми ассоциированы
базисные функции, так, что адрес точки в массиве будсч опрс к ып.ся
номером ассоциированной с ней функции (т.е ка к пли \ ц-i ниишем
столько раз, сколько функций к нему привязано) I к рсч оргирм м юч
ки в этом массиве по возрастанию каждой из их кооршни (и in но
бым другим способом, при котором узлы, распо юмппыс в конечно
элементной сетке недалеко дру1 от яру i а, окажу ня и юс шючно близ-
514 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
ко расположенными друг к другу в сформированном массиве узлов).
Новый номер каждой оазисной функции определим как адрес соответ-
ствующей этой функции точки в пересортированном массиве (естест-
венно, для этого у каждой хранящейся в массиве точки должен быть
известен её старый номер, т.е. порядковый номер этой точки в массиве
узлов до его пересортировки).
На самом деле, этот очень простой алгоритм нумерации базисных
функций является достаточно универсальным, поскольку практически
всегда можно считать, что базисные функции, ассоциированные с рёб-
рами, гранями или самими элементами1, ассоциированы с определён-
ными узлами на этих рёбрах или гранях или с узлами внутри элемен-
тов. Однако с ростом числа базисных функций (при дроблении сетки
или повышения порядка элемента) он может стать довольно затратным
как по объёму памяти, так и по количеству машинных операций. По-
этому ниже (на с. 518) мы рассмотрим гораздо более эффективный
алгоритм нумерации базисных функций, основанный на использова-
нии упорядоченных списков рёбер, граней и конечных элементов.
Упорядочение рёбер, граней и конечных элементов необходимо
также и при использовании так называемых иерархических базисных
функций, которые будут рассмотрены нами в двенадцатом разделе.
Зги базисные функции порождают подпространство, совпадающее с
подпространством, натянутым на базисные функции лагранжева типа.
Однако они имеют определённые преимущества перед функциями
лагранжева типа, о которых будет сказано в разделах 12.2 и 12.4. Ие-
рархические базисные функции удобно ассоциировать с рёбрами, гра-
нями и самими конечными элементами. Поэтому для работы с иерар-
хическими базисными функциями необходимы соответствующие спи-
ски рёбер2 и граней3 (список же конечных элементов создаётся на эта-
пе построения сетки, и он является основой для формирования списков
драней и рёбер). Кроме того, при наличии упорядоченных списков рё-
бер и граней можно гораздо быстрее упорядочить и пронумеровать и
лагранжевы базисные функции на элементах высоких порядков - соот-
ветствующий алгоритм будет изложен на с. 518. Поэтому ниже (в раз-
делах 10.6 2 и 10.6 3) мы рассмотрим алгоритмы, позволяющие из спи-
ска конечных элементов (заданных номерами их вершин) построить
список всех граней и список всех рёбер
10.6.2. ПОСТРОЕНИЕ СПИСКОВ ГРАНЕЙ ТРЁХМЕРНЫХ КОНЕЧНЫХ ЭЛЕМЕНТОВ.
ИСПОЛЬЗОВАНИЕ УПОРЯДОЧЕННОГО СПИСКА ГРАНЕЙ ДЛЯ УСКОРЕНИЯ
ПРОЦЕДУРЫ НУМЕРАЦИИ БАЗИСНЫХ ФУНКЦИЙ
Кроме того, что построение списка граней элементов может ока-
заться необходимым для первичной нумерации базисных функций,
1 Такие функции используются, например, в иерархических элементах
(см. двенадцатый раздел).
2 Список рёбер необходим также и при работе с векторными базисными
функциями (edge-функциями), которые мы рассмотрим в пятнадцатом разделе.
3 Список граней также используется в векторном МКЭ при работе с эле-
ментами высоких порядков (или с так называемыми face-элементами).
10.6.Алгоритмы нумерации базисных функций, гранен и ребер .. 515
ассоциированных с этой гранью1 (или её узлами2, ни являющимися
вершинами элемента или узлами его рёбер), список i ранен может по-
требоваться для построения поверхности, разделяющей подобласти с
различными свойствами. Это используется, например, в noci процессо-
рах для отрисовки поверхностей отдельных подобластей расчётной
области. Список граней также может понадобиться при решении <адач,
вариационная постановка которых включает поверхностные ин тег ралы
по внутренней границе, например, см. 8.2, 15.13, 16.6.3.
Построить список граней можно многими способами. Мы кратко
опишем один из них.
Сначала нужно приписать каждой грани каждого конечно! о эле-
мента номер смежного по этой грани конечного элемента (что требус!,
естественно, дополнительного объёма памяти для хранения почти
целых чисел, где к — общее число граней конечных элементов). Для
регулярных сеток, а также для некоторых алгоритмов построения не-
регулярных сеток информация о соседях каждого конечного элемента
известна на этапе построения сетки и может быть сохранена соответ-
ствующим препроцессором. Мы же рассмотрим, как можно получить
эту информацию в наиболее часто встречающемся случае, когда она не
была сформирована на этапе генерации сетки, а конечноэлсментная
сетка хранится поэлементно и каждый элемент задаётся только номе-
рами своих узлов.
Поставим в центр каждой грани по одной точке на каждом из ко-
нечных элементов (естественно, центр одной и той же грани на двух
смежных конечных элементах должен определяться по одному и тому
же алгоритму, чтобы соответствующие точки совпали или почти сов-
пали3 4)- Проходя по списку конечных элементов, запишем эти точки в
массив (назовём этот массив Р ). Затем упорядочим массив Р любым
способом по значениям координат (например, сначала по возрастанию1
координаты х , при одинаковых значениях координаты х - по возрас-
танию значений у и затем по возрастанию z). В упорядоченном мас-
сиве Р одинаковые точки окажутся на соседних местах, и поэтому
повторяющиеся точки легко можно обнаружить и удалить. Теперь но-
мером грани можно считать номер точки в полученном после удаления
повторов массиве Р.
Теперь рассмотрим, как можно приписать к каждой грани но гва
смежных по ней конечных элемента. Создадим для этого целомнс icii
ный массив ind номеров элементов длиной к , где к - общее чш ю
граней конечных элементов (которое равно длине массива Р после
удаления повторов). Запишем в массив ind нулевые значения la i< м
пройдём по конечным элементам и для каждой грани каждою конем
ного элемента (обозначим номер элемента через т) онреде шм номер
1 Это может понадобиться при использовании иерархических itiii некюр
ных базисных функций.
2 При использовании лагранжевых базисных функции
3 В пределах ошибки округления.
4 Естественно, с учётом ошибок округления шачепим, р 11 нич лк nil исс» на
уровне ошибки округления, должны считаться оОннамты мн
516 1О.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
i точки - центра этой грани (в упорядоченном массиве Р это можно
сделать достаточно быстро). Если ind (г) равно нулю, то присвоим
ind (г) значение т, а если in.d(ij не равно нулю, то ind (г) — номер
элемента, смежного по рассматриваемой грани с элементом т, и в
структуру данных, хранящую информацию о конечных элементах,
нужно внести соответствующую информацию (о номерах соседей) для
обоих элементов.
Недостатком такого способа поиска соседей является не столько
существенный объём дополнительной памяти (если считать, что веще-
ственное число занимает вдвое больше памяти, чем целое, то может
потребоваться до 2 • з 2 • к = Г2к целых чисел1 под массив Р ), сколько
затраты на упорядочение вещественного массива координат «центров»
граней.
Несколько более эффективным по памяти и быстродействию явля-
ется следующий алгоритм.
Для каждого узла сетки подсчитаем число конечных элементов, ко-
торые его содержат. Для этого нам понадобится массив ig целых чи-
сел длиной п, где п - число узлов в сетке. Присвоим элементам этого
массива нулевые значения. Затем пройдём в цикле по всем конечным
элементам, и в нём будем добавлять единицу к тем элементам ig (г)
массива ig , у которых значение индекса г является номером вершины
обрабатываемого конечного элемента.
Теперь создадим массив jg из п подмассивов переменной длины,
причём длина г-го подмассива должна быть равна ig(i) (т.е. общая
длина массива jg — это сумма значений всех элементов массива ig ).
Мы не случайно дали массивам такие имена, структура данных дейст-
вительно похожа на структуру для хранения портрета разреженной
матрицы.
Значения элементов массива гд(г) пересчитаем так, чтобы они ста-
ли не длинами массивов, а адресами начал этих массивов в массиве
jg-
Заполним массив jg номерами конечных элементов, содержащих
каждую (г-ю) вершину, записав эги номера в jg по адресам от ig(i)
до ig (i + 1) — 1. Для этого пройдём в цикле по всем конечным элемен-
там, записывая номер конечного элемента (равный, естественно, зна-
чению индекса цикла) в каждый из подмассивов массива jg с номера-
ми, равными номерам вершин обрабатываемого конечного элемента.
Для формирования этой информации можно ввести ещё один целочис-
ленный массив длины п, в г-й ячейке которого должно храниться
количество номеров конечных элементов, уже занесённых в г-й под-
1 Поскольку кроме того, что вещественное число занимает вдвое большую
память по сравнению с целым (первый сомножитель - двойка), нужно хра-
нить 3 координаты узла (сомножитель - тройка) и один и тог же узел может
принадлежать двум (смежным) граням (последний сомножитель - двойка).
10.6.Алгоритмы нумерации базисных функций, граней и ребер . .. 517
массив массива jg . Процесс формирования массива jg завершим упо-
рядочением каждого из п его подмассивов.
С помощью созданной структуры данных поиск соседей конечного
элемента по любой из его граней можно выполнять следующим обра-
зом.
Пусть р - число вершин обрабатываемой грани m-го конечного
элемента. Берём из первой ячейки подмассива массива jg с номером,
равным номеру первой вершины обрабатываемой грани, хранящееся
там значение номера конечного элемента. Обозначим этот номер через
ct. Проверяем, присутствует ли номер а во всех остальных (р — 1) -м
подмассивах с номерами, равными остальным номерам вершин обра-
батываемой грани (для ускорения этого поиска и было сделано упоря-
дочение номеров конечных элементов в подмассивах массива jg).
Если хотя бы в одном из подмассивов значение а не найдено, то пере-
ходим к следующему элементу первого подмассива. Если ct найдено
во всех подмассивах, то а и есть номер конечного элемента, соседнего
с т -м по обрабатываемой грани (естественно, значение а, совпа-
дающее с т, должно пропускаться).
Очевидно, что параллельно с поиском смежных конечных элемен-
тов можно без всякого труда и пронумеровать все грани, давая новый
номер только той грани обрабатываемого конечного элемента, для
которой ещё не был найден номер смежного по ней элемента (естест-
венно, при обработке других конечных элементов).
Сравним оба рассмотренных нами алгоритма формирования списка
смежных (по граням) конечных элементов по требуемому для их рабо-
ты объёму памяти. Подсчитаем объём памяти, необходимый для рабо-
ты последнего алгоритма. Для простоты будем считать, что все эле-
менты содержат одно и то же число вершин ц и граней и. Обозначим
через 6 общее число элементов. Тогда длина массива jg равна цО,
поскольку в нём номер каждого элемента хранится столько раз, сколь
ко у него вершин. Очевидно, что если большинство граней внутрен-
•Л
ние, то их общее число можно оценить как к, . Это означает, что
массив jg для любого из рассмотренных нами типов конечных > ic
ментов занимает меньше памяти, чем массив Р из первого алгоритма,
поскольку массив Р занимал около 12к = Gv6 ячеек целочисленно! о
массива, а для конечных элементов практически любого гппа ( rcipa >;i
ров, призм, шестигранников) значение 6v в несколько раз npcBi.iiii.ie i
значение ц . Кроме того, последний алгоритм имеет пренмуиц то и в
скорости. Действительно, вместо полного упорядочения бо н-шою г..
щественного массива и поиска в нём нужных значений (Koopum.ii
точек) для определения номера обрабатываемой грани в первом j ио-
ритме во втором алгоритме нужно сделать лини, частнчшн упорядо-
чение целочисленного массива и относительно небольшое чш чо це Kt-
численных сравнений при поиске смежного но обраб;цынлемон ipaiin
конечного элемента.
518 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
Однако второй алгоритм имеет и один существенный недостаток -
в нём грани нумеруются без учёта их расположения в пространстве, в
то время как в первом алгоритме они уже в процессе их нумерации
упорядочиваются именно по геометрическому принципу. Геометриче-
ская же упорядоченность граней является довольно важным фактором
в том случае, когда по номерам граней определяются номера ассоции-
рованных с ними базисных функций, и тогда предпочтительными яв-
ляются такие нумерации, у которых базисные функции с пересекаю-
щимися носителями имеют близкие глобальные номера. В то же время
этот принцип должен выполняться для всех базисных функций сразу
(ассоциированных с вершинами, рёбрами, гранями и самими конечны-
ми элементами), и поэтому нумерацию базисных функций с упорядо-
чением их по геометрическому принципу всё равно нужно делать от-
дельно1. Однако это упорядочение можно сделать гораздо быстрее,
если вершины, рёбра и грани предварительно упорядочены по геомет-
рическому принципу. При этом, естественно, нужно использовать спе-
циальный (очень быстрый) алгоритм, который упорядочивает узлы,
хранящиеся в нескольких упорядоченных массивах.
Па самом деле, упорядочить глобальные функции по геометриче-
скому принципу можно нс только путём геометрического упорядоче-
ния сразу всех узлов, с которыми эти базисные функции ассоциирова-
ны. Очень хороший результат (по критерию геометрической близости
носителей базисных функций, имеющих близкие глобальные номера)
можно получить и другими способами, основанными па работе, в ос-
новном, с целочисленными массивами.
Например, можно по значениям координат упорядочить только
вершины конечных элементов, а грани, рёбра и сами конечные элемен-
ты упорядочивать уже по возрастанию минимальных номеров опреде-
ляющих их вершин. Если же две грани (так же, как два ребра или два
конечных элемента) имеют вершины с одинаковыми минимальными
номерами, то их можно упорядочить по номерам других вершин (так-
же по возрастанию их номеров)2. Конечно, прежде чем упорядочивать
таким способом все грани (рёбра или конечные элементы), нужно сна-
чала упорядочить по возрастанию номера определяющих их вершин.
11ослс этого упорядочение всего массива граней (рёбер или конечных
элементов) можно выполнить очень быстро и с использованием толь-
ко целочисленных сравнений номеров вершин.
Окончательная же нумерация всех базисных функций может быть
выполнена уже совсем просто. Первый номер даётся базисной функ-
ции. ассоциированной с вершиной с первым номером. Далее нумеру-
ются все базисные функции, ассоциированные с ребрами3, гранями4 и
1 Об этом было упомянуто чуть выше на с. 513.
2 В принципе, грани, рёбра и конечные элементы с одинаковыми мини-
мальными номерами вершин можно записать и в произвольном порядке, но
тогда серьёзно увеличится трудоёмкость алгоритмов поиска нужных элемен-
тов в соответствующих массивах.
•3 Или с узлами на рёбрах для лагранжевых элементов.
4 Или с узлами на гранях для лагранжевых элементов.
10.6.Алгоритмы нумерации базисных функций, i ранен и ребер 519
конечными элементами1, содержащими эту вершину Следующий по-
сле них номер даётся базисной функции, ассоциированной со второй
вершиной. За ней нумеруются все базисные функции, ассоциирован-
ные с рёбрами, гранями и конечными элементами, у которых мини-
мальный номер определяющих их вершин равен двум и т.д. (г.с после
нумерации базисной функции, ассоциированной с z-й вершиной, но-
меруются все базисные функции, ассоциированные с рёбрами, i ранями
и конечными элементами, у которых минимальный помер определяю-
щих их вершин равен i (если таковые ещё есть)). Последний п^-й
номер получит базисная функция, ассоциированная с пв-й вершиной
(где пв - количество вершин в сетке).
Заметим, что при использовании такого алгоритма глобальной ну-
мерации базисных функций имеет смысл использовать и соответст-
вующие алгоритмы работы с гранями, рёбрами и конечными элемен-
тами, которые упорядочивают их по минимальным номерам вершин,
определяющих эти грани, рёбра и конечные элементы. Очевидно, что
рассмотренный в данном разделе первый алгоритм построения списка
смежных по граням конечных элементов очень легко модифицировать
с учётом того, что грань определяется нс координатами расположен-
ной на ней точки, а номерами вершин. В этом случае при упорядоче-
нии граней будут выполняться только целочисленные сравнения, а
после работы этого алгоритма мы получим уже упорядоченный массив
граней, готовый к использованию в рассмотренном только что алго-
ритме упорядочения всех базисных функций (ассоциированных с вер-
шинами, рёбрами, гранями и конечными элементами). Это требование
(упорядоченность по минимальным номерам вершин; может быть без
особого труда выполнено и при построении списка рёбер.
10.6.3. ПОСТРОЕНИЕ СПИСКА РЁБЕР КОНЕЧНЫХ ЭЛЕМЕНТОВ И ИХ НУМЕРАЦИЯ
Рассмотренный в разделе 10.6.2 метод нумерации граней через
геометрическое упорядочение узлов, ассоциированных с этими граня-
ми, в принципе, можно было бы использовать и для нумерации рёбер
конечных элементов. Но даже в двумерном случае такой алгоритм нс
очень эффективен как по памяти, так и по быстродействию. В грех
мерном же случае он оказывается крайне неэффективным, поскольку
каждое ребро может принадлежать большому количеству конечных
элементов, что приведёт к резкому увеличению длины массива у шов
из-за повторных их записей (три вещественные координаты как юю
узла будут записаны столько раз, скольким конечным элемен там при
надлежит ребро), и, следовательно, к чрезмерно большим вычисли
тельным затратам на упорядочение очень длинного веннч твенно.о
массива. Поэтому мы рассмотрим другой, гораздо более эффскншныи
алгоритм нумерации ребер, который пригоден как в двумерном, ык и в
трёхмерном случае, очень быстр и экономичен но намят
Обратим внимание на то, что портрет матрицы конечно » icmchiiioh
СЛАУ в разреженном строчно-столбцовом формат (дня >лемепгов
первого порядка) фактически содержит информацию о наличии свжен
1 Или с узлами внутри конечных элементов л.п ран.кспа шил
520 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
между базисными функциями. Действительно, если для некоторых г и
j (пусть для определённости i> j) между глобальными функциями
ф,- и ф; существует связь (т.е. существует конечный элемент, на ко-
тором их произведение или произведения их производных не равны
нулю), то элемент Д:/ конечноэлементной матрицы А не равен нулю.
Тогда в массиве jg по адресам от ig(i) до ig(i + 1) — 1 (включительно)
должно быть значение, равное j . Обозначим через г (лежащее в диа-
пазоне ig(ij < г < гд{г + 1)) такой номер элемента в массиве jg, что
jg(.r) = j. Очевидно, что для каждой связи между базисными функ-
циями существует своё значение г, и поэтому это значение может
рассматриваться как номер соответствующей связи. Количество таких
связей, очевидно, совпадает с длиной массива jg .
Таким образом, алгоритм построения портрета является фактически
алгоритмом подсчёта и нумерации связей между глобальными базис-
ными функциями. Поэтому его достаточно легко модифицировать так,
чтобы он подсчитывал и нумеровал ребра элементов, которые в каком-
то смысле тоже являются «связями» между вершинами элементов. Для
этого нужно везде в приведённой на с. 509-51 1 программе заменить
вызов функции NumberOf Unknowns (m), возвращающей число ло-
кальных базисных функций на элементе с номером т, на вызов функ-
ции, возвращающей число вершин элемента, а вызов функции
IndexOf Unknown (m, i), возвращающей глобальный номер базис-
ной функции с локальным номером г, на вызов функции, возвращаю-
щей номер геометрической вершины в конечноэлементной сетке. Кро-
ме того, для каждой пары вершин элемента нужно проверить, есть ли
между ними ребро, для чего в двух местах программы после строки
ind2=IndexOfUnknown(NumElem,j)
достаточно вставить строку
IF ( .NOT.IsEdgeExist(NumElem,indl,ind2))CYCLE ,
где логическая функция IsEdgeExist возвращает значение . TRUE.
в том случае, если у элемента с номером NumElem есть ребро между
вершинами indl и ind2.
Итак, если нам нужно определить номер ребра, вершины которого
имеют номера i и j (г > у), то с помощью массивов гд и jg мы мо-
жем сделать это так же, как, например, определялся номер ячейки мас-
сива дд, содержащей значение компоненты А матрицы, хранящейся
в разреженном формате. В этом случае номером ребра будет номер г
(лежащей в диапазоне ig(jj) < г < ig(i + 1)) ячейки массива jg, в ко-
тором хранится значение j .
При этом дополнительную информацию о каждом из рёбер сетки
(например, о количестве базисных функций, ассоциированных с этим
ребром, или о номерах этих базисных функций) можно хранить в
10.7.Алгоритмы работы с конечноэлементными решениями
521
структурах данных, аналогичных тем, которые используются для хра-
нения матриц в разреженных форматах.
Очевидно, что рассмотренный алгоритм (практически совпадаю-
щий с алгоритмом построения портрета нижнего треугольника матрп
цы в разреженном строчном формате) даёт упорядочение ребер но
максимальным номерам определяющих их вершин. Мы предлагаем
читателю в качестве упражнения написать программу формирования
рёбер, упорядоченных по минимальным номерам определяющих их
вершин1.
10.7. АЛГОРИТМЫ РАБОТЫ С КОНЕЧНОЭЛЕМЕНТНЫМИ РЕШЕНИЯМИ
Под конечноэлементным решением л/' мы, как обычно, понимаем
функцию, являющуюся линейной комбинацией базисных функций, при-
чём веса в этой линейной комбинации определяются из решения конеч-
ноэлементной СЛАУ. Естественно, не возникает никаких проблем с
получением значений в точках, являющихся вершинами элементов, по-
скольку для всех рассмотренных ранее типов элементов значение в вер-
шине элемента совпадает с одним из весов (для лагранжевых столь же
легко получаются значения во всех узлах — это значение компоненты
вектора весов, номер которой совпадает с номером узла).
Однако очень часто требуется получить значение решения краевой
задачи не в узле сетки, а в произвольной точке пространства, и при
этом может понадобиться получить даже не само решение, а его про-
изводные или интегралы от него или его частных производных по от-
дельным подобластям или их границам. Здесь мы рассмотрим именно
такого рода проблемы, связанные с обработкой конечноэлеменгных
решений, и возможные пути их решения.
10.7.1. ПОИСК КОНЕЧНОГО ЭЛЕМЕНТА В НЕРЕГУЛЯРНОЙ СЕТКЕ
При использовании нерегулярных конечноэлементных сеток ос-
новной проблемой выдачи значений решения в произвольной точке
пространства (после того как найден вектор весов разложения но ба
зисным функциям) является поиск конечного элемента, в который по-
падает эта точка. Действительно, когда элемент в сетке найден, то ша
чение решения в любой его точке вычисляется как значение в пей ли
нейнои комбинации локальных базисных функций найденного копеч
ного элемента, причём коэффициентами этой линейной комбинации
являются компоненты вектора весов q с номерами, определяемыми по
соответствию глобальной и локальной нумерации узлов (точнее. ба
зисных функций) на найденном конечном элементе.
Естественно, делать полный перебор всех конечных HicMviiioit г
проверкой, в какой из них попала точка, можно только для сеток с не
большим числом элементов. При работе же с более пли менее нодроб
1 Этот алгоритм будет практически повторять алгоршм п<х ipoctnin порт-
рета нижнего треугольника матрицы в разреженном с iou(»hoiiom формате,
или, что то же самое, портрета верхнего треугольника м.при цы в р.прежен-
ном строчном формате.
522 Ю.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
ными сетками, вычислительные затраты при использовании такого
подхода могут стать неприемлемо большими.
Повысить эффективность поиска элементов позволяет создание спе-
циальной вспомогательной структуры данных для хранения информа-
ции о местоположении ячеек конечноэлементной сетки в пространстве.
Покажем, как можно реализовать такой подход с использованием спе-
циальной структуры для двумерной конечноэлементной сетки.
Ускорить поиск конечных элементов можно, основываясь на сле-
дующем очевидном факте. Необходимым условием попадания точки в
сам конечный элемент является условие попадания её в содержащий
этот элемент прямоугольник, стороны которого параллельны осям
координат.
Создадим специальный список непересекающихся прямоугольни-
ков, каждому из которых будет соответствовать массив ссылок на оп-
ределённое число конечных элементов (в виде их номеров). Эти непе-
рссекающиеся прямоугольники (из списка) далее будем называть ос-
новными. Основной прямоугольник должен содержать ссылку на ко-
нечный элемент, если центр масс этого элемента попадает в него. Про-
ходя по всем конечным элементам, будем приписывать ссылки на них
к основным прямоугольникам. Сами же основные прямоугольники
будем динамически переформировывать следующим образом. В слу-
чае появления слишком большого количества ссылок (превосходящего
некоторое заранее фиксированное число) на конечные элементы в со-
ответствующем основному прямоугольнику массиве этот прямоуголь-
ник разбивается пополам прямой, параллельной одной из координат-
ных осей. При этом оси должны чередоваться - при каждом новом
разбиении прямоугольника должна выбираться та ось, которая не была
использована при разбиении того прямоугольника, из которого данный
прямоугольник был получен. В качестве начального списка основных
прямоугольников при таком способе их формирования можно взять
список, содержащий один прямоугольник, описанный вокруг всей рас-
чётной области
Для того чтобы можно было определить попадание точки внутрь
самих конечных элементов, после формирования списка основных
прямоугольников припишем к каждому основному прямоугольнику
ещё и внешний прямоугольник. Границы этого внешнего прямоуголь-
ника зададим гак, чтобы он содержал все прямоугольники, описанные
вокру! каждого конечного элемента, соответствующего основному
прямоугольнику, Теперь непопадание точки внутрь описанного вокруг
конечного элемента прямоугольника можно предварительно контро-
лировать через непопадание этой точки во внешний прямоугольник
вспомогательно!। структуры (непопадание точки во внешний прямо-
угольник гаран гирует непопадание этой точки внутрь любого конечно-
го элемента, ссылка на который хранится в соответствующем этому
внешнему прямоугольнику основном прямоугольнике).
Очевидно, что рассматриваемый метод хранения двумерных эле-
ментов требует значительных накладных расходов, поскольку при его
реализации необходима дополнительная память для хранения как са-
мих прямоугольников, так и соответствующих им массивов ссылок на
10.7.Алгоритмы работы с конечноэлементными решениями 523
конечные элементы. Кроме того, при попадании точки во внешний
прямоугольник необходимо просматривать все конечные элементы,
ссылки на которые содержатся в соответствующем массиве Однако
если точек, в которых требуется выдать конечноэлементнос решение,
достаточно много, накладные расходы компенсируются существенным
ускорением поиска нужных конечных элементов.
Отметим, что рассмотренный алгоритм построения вспомогатель-
ного списка прямоугольников очень удобно использовать для сеток с
локальными сгущениями, к которым он адаптируется автоматически.
Если же коиечпоэлементная сетка в достаточной степени регулярная,
то этот алгоритм может быть существенно упрощен, например, за счс!
генерации вспомогательных прямоугольников одинаковых размеров.
Обратим также внимание на то, что рассмотренный алгоритм поис-
ка конечных элементов с использованием вспомогательной структуры
данных вполне пригоден и для трёхмерных конечноэлементных сеток,
только вместо прямоугольников в нём должны быть использованы
прямоугольные параллелепипеды1.
И конечно, очень эффективным способом выдачи значений конеч-
ноэлементного решения, полученного на нерегулярной сетке, является
рассмотренный в разделе 5.4.5 способ выдачи решения, полученного
на сетке с четырёхугольными ячейками, с переинтерполцией его на
регулярную прямоугольную сетку (см. с. 306-J09). Этот способ, оче-
видно, с тем же успехом может быть использован и при работе с ячей-
ками другой формы - треугольными, тетраэдральными, шестигранны-
ми (в трёхмерном случае переинтерполяция делается, естественно, на
регулярную сетку с ячейками в виде прямоугольных параллелепипе-
дов). Он практически снимает проблему поиска нужной ячейки сетки в
исходной нерегулярной сетке. При этом на регулярной сетке из прямо-
угольников или параллелепипедов можно использовать более гладкие
базисные функции (эрмитовы), что позволит сразу же и существенно
улучшить гладкость получаемого решения.
Таким же способом можно выдавать и значения производных ко-
нечноэлементного решения - подробнее об этом чуть позже.
10.7.2. ПОСТРОЕНИЕ ПРОИЗВОДНЫХ КОНЕЧНОЭЛЕМЕНТНОГО РЕШЕНИЯ
Следующей проблемой, которую мы рассмотрим, является про-
блема дифференцирования полученного конечноэлементного решения.
Естественно, наиболее простым (но далеко не самым лучшим) спосо
бом построения производных решения является прямое дифферент!
рование линейной комбинации базисных функций (весами в поп ш
нейной комбинации являются компоненты вектора пепзвсс тых ко
нечноэлементной СЛАУ). Однако полученные таким способом нроня
водные являются разрывными на дэаницах элементов (если, конечно,
для построения конечноэлементнои аппроксимации были и поп.зона
ны не эрмитовы элементы). А в случае, когда грсбусгся нолучнн.
старшие производные решения, такой способ и вовсе и< но»моыю нс-
1 В этом случае дробление основных параллелепипедов ну ici ocymcciB
ляться плоскостями, перпендикулярными одной in ipex осей с их им 'гсдова
гсльным чередованием.
524 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
пользовать, поскольку базисные функции (лагранжевы и иерархиче-
ские) имеют разрывные первые производные.
Одним из путей решения этой проблемы является использование
для конечноэлементной аппроксимации исходной задачи эрмитовых
базисных функций необходимого для построения требуемой произ-
водной порядка. Однако во многих случаях решение исходной задачи с
использованием эрмитовых элементов может оказаться слишком за-
тратным (из-за резкого возрастания размерности и заполненности ко-
нечноэлсмсптной СЛАУ). Поэтому обычно используют другие (специ-
альные) способы построения производных решения.
Довольно простой и распространённый способ - это построение со-
гласованных результантов. Он уже был рассмотрен нами для одно-
мерного случая (см. раздел 4.18). Суть его не меняется и для дву- и
трёхмерного случая. Здесь также ищется разложение искомой произ-
п
ВОДНОЙ WIl = по тем же самым базисным функциям, которые
«=1
были использованы для вычисления конечноэлементного решения
п
и1' = У2<7ГФл , причём веса q-" определяются из минимизации функ-
z=l
ционала
(1012)
Q’" ' '
где 6, - любая из переменных ж, у или z, a Q'"' — некоторая подоб-
ласть расчётной области исходной задачи, в которой ищется производ-
ная решения и где искомая производная непрерывна. Минимизация
функционала (10 12) фактически сводится к решению СЛАУ
Cq’"=b, (10.13)
с матрицей массы С с компонентами
Сг) = f ‘ФхФ/Р (10.14)
О’"
и вектором правой части b с компонентами
" с 51b
6, = У2 I —<г fZQ •
>1
Второй способ вычисления производных конечноэлементного ре-
шения фактически является обобщением первого. Он заключается в
том, что при минимизации функционала (10.12) w1 ищется в виде раз-
ложения не по тем функциям ф.,, с помощью которых было получено
конечноэлсмсптпое решение и.'1, а по каким-либо другим базисным
10.7.Алгоритмы работы с конечноэлементными решениями
525
функциям ф™, т.е. wh = У^дГФГ' • В этом случае компоненты мигри-
7 = 1
цы массы С и вектора правой части b СЛАУ (10.13) размерное г и п„,
имеют вид
Сг] = (10.15)
ц"'
Ь, = £>“ <1016)
J=1 Qw
Заметим, что при вычислении производных конечноэлементного
решения вторым способом базисные функции ф™ могут, в принципе,
определяться и на другой сетке, например прямоугольной в двумерном
случае и параллелепипеидальной в трёхмерном. В этом случае при
вычислении интегралов (10.16) придётся находить пересечения эле-
ментов одной сетки с элементами другой сетки, и поэтому чаще всего
интегралы в соотношении (10.16) вычисляются численно.
Третьим способом построения производных конечноэлементного
и
решения ц7' = ^"фг является дифференцирование ближайшей к
г=1
нему функции w/l = J ^"Фг" из конечномерного пространства, натя-
7=1
нутого на базисные функции ф’" с непрерывной производной. В этом
случае минимизируется не функционал (10.12), а функционал
J (uh -urfda, (10.17)
o’"
Минимизация функционала (10.17) эквивалентна решению СЛАУ
(10.13) с матрицей массы С, компоненты которой определяются соси
ношением (10.15), и вектором правой части b с компонентами
'-= Е •ФГ'Ф/п-
7=1 fl’"
(10 18)
При этом для снижения вычислительных затрат на поиск перси чепия
конечных элементов (если базисные функции ф-" и ф; определены па
разных сетках) для вычисления интегралов в (10.18) мог\ i примени и.
ся процедуры численного интегрирования, в коюрых шачсни
E«"t>
J=1
II)
просто вычисляется в нескольких
iочках (например.
526 10.Структуры данных, сетки и алгоритмы работы с ними в МКЭ
дву- и трёхмерные аналоги квадратурных формул Гаусса, см., напри-
мер, с. 303, 705, 753).
И, наконец, как некоторая модификация второго способа может
быть предложен, пожалуй, самый эффективный способ выдачи произ-
водных решения, основанный на переинтерполяции с использованием
регулярной сетки с ячейками в виде прямоугольников (в двумерном
случае) или прямоугольных параллелепипедов (в трёхмерном случае).
Для четырёхугольных конечных элементов этот подход уже обсуждал-
ся в разделе 5.4.5. Соответствующие формулы (в трёхмерном случае)
для вычисления компонент матрицы С и вектора b СЛАУ (10.13)
имеют вид
Сч = Z2 'fe- > У к > Ч) , У к, Ч) + f & gracl Ф1"- grad ф"Ж,
к о
(10.19)
7
что соответствует замене минимизируемого функционала (10.12) на
функционал
(10.20)
где 6, — переменная , у или z), производную по которой (от реше-
ния) необходимо построить, ,yk,z^.) — узлы, по значениям в кото-
рых с троится нужная нам производная w = — (т.е. это узлы, в кото-
рых мы требуем близости интерполянта wh
к Чд ), - веса (вели-
чина регулирует близость значения wh к в узле (.тд., ук, zk)),
а - параметр регуляризации (который при достаточном числе узлов
(.г\, Ук> Ч.) может быть принят равным нулю, см. раздел 5.4.5).
Последний способ привлекателен не только своей простотой и
удобством для реализации, а также отличными возможностями для
получения сглаженных значений производных решения. Совсем нема-
ловажным в этом способе является то, что при его использовании пол-
ностью отпадает необходимость поиска конечного элемента в нерегу-
лярной сетке, где лежит точка, в которой нужно выдать значение про-
10.7.Алгоритмы работы с конечноэлементными решениями
527
изводной - это значение выдаётся по регулярной прямоу! ольной сетке,
для которой затраты на поиск ячейки практически отсутствую! Во
втором и третьем способах проблема поиска конечного элемента, в
который попадает нужная нам точка, при выдаче решения также сни-
мается (если базис {ф’"} соответствует регулярной прямоугольной
сетке), но зато при вычислении интегралов в соотношениях (10.16) или
(10.18) (даже численном) она остаётся (в первом способе - согласован
ных результантах - эта проблема остаётся при выдаче значений произ-
водных). Поэтому последний способ при работе с конечноэлсмсш ни-
ми решениями, полученными на нерегулярных сетках, имеет огромные
преимущества по трудоёмкости и вычислительным затратам по срав-
нению со всеми остальными рассмотренными здесь методами вычис-
ления производных конечноэлементных решений.
Обратим внимание на то, что все рассмотренные способы вычисле-
ния производных требуют обычно гораздо меньше вычислительных
затрат по сравнению с решением исходной краевой задачи. Действи-
тельно, исходная задача решается в расчётной области Q, а задачи
минимизации (10.12), (10.17) или (10.20) - в некоторой (чаще всего
относительно небольшой) её подобласти Q’" . Поэтому размерность п.„,
СЛАУ (10.13) может быть намного (на порядок и более) меньше раз-
мерности п матрицы конечноэлементной СЛАУ, аппроксимирующей
исходную краевую задачу. Да и итерационные методы решения СЛАУ
с матрицей вида (10.14), (10.15) или (10.19) сходятся, как правило,
очень быстро.
В принципе, возможно многоэтапное применение рассмотренных
здесь процедур для вычисления старших производных конечноэле-
ментных решений. На первом этапе по конечноэлементному решению
и строится его производная w = , на втором - с помощью той
же процедуры по w1' строится производная
ди)1'
, фактически являю-
Л’2 //
щаяся аппроксимацией и Т-Д- Однако пользоваться такими мно-
гоэтапными процедурами следует с определённой осторожностью
если решение недостаточно гладкое, а конечноэлементная сетка до
вольно грубая, то даже на втором этапе полученные значения прот
водных могут серьёзно отличаться от соответствующих производных
точного решения. Контролировать точность здесь можно, как обычно,
дроблением сеток, причём измельчать сетки нужно нс только при вы
числении w1',
и т.д., по и при вычислении uh.
528
11 Комбинированные и несогласованные сетки
11. КОМБИНИРОВАННЫЕ И НЕСОГЛАСОВАННЫЕ СЕТКИ
11.1. СОГЛАСОВАННЫЕ И НЕСОГЛАСОВАННЫЕ СЕТКИ
И КОНЕЧНЫЕ ЭЛЕМЕНТЫ
Несмотря на то, что у прямоугольных билинейных и треуголь-
ных линейных элементов порядок аппроксимации (см. раздел э.6) оди-
наков (поскольку одинаков максимальный порядок полностью пред-
ставимых через их базисные функции полиномов), тем не менее при
использовании сеток с одинаковым числом узлов (т.е. имеются в виду
треугольные сетки, полученные из прямоугольных разбиением каждо-
го прямоугольника на два треугольника) конечноэлементное решение
на прямоугольных элементах довольно часто оказывается заметно точ-
нее, чем па треугольных. Однако с помощью треугольных элементов
можно существенно точнее (по сравнению с прямоугольниками) опи-
сать криволинейные границы, и поэтому для задач, решаемых в облас-
тях с криволинейными границами, гораздо выгоднее использовать
треугольные элементы (см раздел 3.9).
В ситуациях же, когда расчётная область состоит в основном из
прямоугольников, но при этом имеет и криволинейные границы, ока-
зывается выгодно использовать комбинированные сетки, в которых
внутри областей используются прямоугольные элементы, а около кри-
волинейных границ — треугольные Метод конечных элементов может
быть без особых проблем применён для решения задач на такого рода
сетках. 11ри этом для так называемых согласованных сеток не возника-
ет никаких проблем с построением соответствующих конечноэлемент-
ных аппроксимаций.
До сих пор мы неявно полагали, что все ячейки конечноэлементных
сеток являются геометрически одинаковыми (например, треугольни-
ками или прямоугольниками) и на них однотипно определено одина-
ковое количество локальных базисных функций. В принципе же, при
решении многих задач иногда удобно использовать конечные элемен-
ты не только с ячейками разного типа (прямоугольники с треугольни-
ками, тетраэдры с призмами или с параллелепипедами и т.п.), но даже
и с разнотипными локальными базисными функциями. В связи с этим
имеет смысл уточнить понятия «сетка» и «конечный элемент», кото-
рые мы до сих пор использовали интуитивно.
В дальнейшем будем считать, что сетка - это объединение непересе-
кающихся по своим внутренним точкам ячеек. При этом под ячейкой
11.1 .Согласованные и несогласованные сетки ...
529
сетки будем понимать некоторую подобласть расчётной области, у ко-
торой есть границы и узлы. Под узлами будем понимать множество
выделенных точек ячейки, используемых как для описания геометрии
ячейки, так и для определения базисных функций на ней. Часть узлов,
определяющих геометрию ячейки, будем называть геометрическими
вершинами. И, наконец, под конечным элементом будем понимать
ячейку сетки с заданными на ней локальными базисными функциями.
Здесь, как и ранее, под расчётной областью мы понимаем (в зависимо-
сти от контекста использования этого термина) либо область О, в кото-
рой решается краевая задача, либо её аппроксимацию О,1' в виде обьс-
динения всех ячеек сетки. При этом подразумевается, что границы
аппроксимируют соответствующие границы Q (либо полностью совпа-
дают с ними), т.е. в пет дополнительных границ, появившихся за
счёт «дырок» в сетке, а некоторое несовпадение границ и Q может
получиться исключительно из-за искривлённости границ Q .
Заметим, что ранее мы называли ячейки сетки конечными элемен-
тами, явно не разделяя этих понятий, поскольку на всех ячейках базис-
ные функции определялись однотипно (тем не менее мы не считали
эти понятия полностью эквивалентными, всегда подразумевая, что
конечный элемент не определяется без заданных на нём базисных
функций). Такое разделение становится необходимым при работе
именно с несогласованными сетками, поскольку на несогласованной
сетке можно за счёт специального определения базисных функций
определить согласованные конечные элементы.
В дальнейшем под согласованной сеткой будем понимать сетку,
для ячеек которой выполняется условие: любая граница одной ячейки
либо точно совпадает с границей только одной другой ячейки, либо
является фрагментом внешней границы расчетной области. При этом
под границами ячеек, например, у треугольников, понимаются три его
стороны, у прямоугольника - четыре его стороны, у многогранника —
его грани и т.д.
На рис. 104 приведены примеры согласованной и несогласованной
треугольной сетки. Сетка па рис. 104,6 является несогласованной по-
тому, что сторона Г, треугольника Q] не совпадает (точно) с какой-
либо одной стороной другого треугольника. Заметим, что, как и ранее,
в дальнейшем мы будем называть стороны ячеек двумерной сетки
(треугольников и прямоугольников), также и рёбрами (как и стороны
граней многогранников), т.е. под ребром мы всегда будем понимать
линию, соединяющую две вершины ячейки сетки как в двумерном, так
и в трёхмерном случае.
В этом (одиннадцатом) разделе мы уделим особое внимание воз-
можности использования несогласованных сеток для решения краевых
задач. При этом конечноэлементная аппроксимация на несогласован-
ных сетках будет строиться путём согласования конечных элементов,
т.е. глобальные базисные функции будут формироваться из локальных
функций конечных элементов так, чтобы все функции порождаемого
ими конечномерного пространства были непрерывными во всей рас-
чётной области и поэтому допустимыми для вариационной формули-
530
11 .Комбинированные и несогласованные сетки
ровки (см. с. 86). Фактически для выполнения этого требования необ-
ходимо будет добиваться того, чтобы глобальные базисные функции
были непрерывными па границах конечных элементов.
Заметим, что иногда в МКЭ используют несогласованные конечные
элементы на согласованных сетках, если они выдерживают так назы-
ваемое кусочное тестирование [9, 22]. Мы не являемся сторонниками
такого подхода, поскольку считаем эту ситуацию несколько искусст-
венной (на согласованной сетке всегда не представляет особого труда
построить согласованные конечные элементы). На самом деле, доволь-
но часто при решении сложных практических задач бывает совсем
непросто построить оптимальную согласованную сетку. Поэтому го-
раздо более важными, по нашему мнению, являются те разделы МКЭ,
которые позволяют строить качественные конечноэлементные аппрок-
симации именно на несогласованных сетках, и именно этому вопросу
будет в основном посвящён весь этот раздел.
11.2. КОМБИНИРОВАННЫЕ СОГЛАСОВАННЫЕ СЕТКИ
ИЗ ТРЕУГОЛЬНИКОВ И ПРЯМОУГОЛЬНИКОВ
С БАЗИСНЫМИ ФУНКЦИЯМИ ОДНОГО ПОРЯДКА
Рассмотрим ситуацию, когда согласованная конечноэлементная
сетка состоит из треугольников и прямоугольников с определёнными
на них локальными базисными функциями первого порядка, т.е. на
треугольниках заданы линейные функции, а на прямоугольниках —
билинейные. Как и в случае сеток с однотипными элементами (т.е.
состоящих из только треугольных или только прямоугольных ячеек)
каждая глобальная базисная функция привязывается к узлу сетки и
определяется через локальные оазисные функции прилегающих к это-
му узлу конечных элементов.
Тогда очевидно, что базисная функция ф, в узле Рг, к которому
примыкают как треугольные, так и прямоугольные конечные элементы
(фрагмент сетки с таким узлом Р, и вид глобальной базисной функции
Ф,, например, изображён на рис. 105), окажется непрерывной на всех
границах между элементами. Действительно, на ребре Гу, соединяю-
11 ^.Комбинированные согласованные сетки. .
531
щем узлы P.j и Р, и являющемся границей между треугольником П/. и
прямоугольником обе соответствующие узлу Р, локальные ба-
зисные функции элементов и Q/fl являются одномерными линей-
ными функциями, равными единице в узле Р, и нулю в узле Р..
Поэтому глобальная базисная функция ф,, определяемая на каж-
дом из элементов .0;. и как соответствующая локальная базисная
функция этих элементов (т.е. так же, как это обычно делается для сеток
с однотипными элементами), является непрерывной на границе Г4/
между элемен гами .0/ и .
Рис. 105 Фрагмент комбинированной ссгки (а)
и вид глобальной базисной функции ф, (б)
Таким образом, глобальная матрица и вектор конечноэлементной
СЛАУ могут быть стандартным образом собраны из локальных матриц
и векторов треугольных и прямоугольных элементов по соответствию
локальных номеров базисных функций глобальным (или локальных
номеров узлов элементов глобальным номерам узлов сетки).
То же самое справедливо и при использовании комбинированной
сетки с треугольными и прямоугольными элементами более высокого
порядка (т.е. с квадратичными базисными функциями па треугольни-
ках и биквадратичными базисными функциями на прямоугольниках,
кубическими на треугольниках и бикубическими на прямоугольниках
и т д.). В этом случае глобальные базисные функции также оказывают-
ся непрерывными на рёбрах конечных элементов при сшивке соответ-
ствующих одному и тому же узлу локальных функций, поскольку эти
532
11 .Комбинированные и несогласованные сетки
локальные функции являются на ребре одинаковыми одномерными
полиномами. Обратим внимание на то, что при построении квадратич-
ных и кубических лагранжевых базисных функций введённые нами на
рёбрах треугольников и прямоугольников дополнительные узлы были
поставлены одинаково - это и обеспечивает совпадение соответст-
вующих одномерных полиномов на ребре, по которому граничат тре-
угольник и прямоугольник.
11.3. ОБ ИС ПОЛЬЗОВАНИИ НЕСОГЛАСОВАННЫХ СЕТОК В МКЭ
На практике несогласованные сетки применяются обычно тогда,
когда в качестве ячеек сетки используются прямоугольники, паралле-
лепипеды, четырёхугольники, шестигранники или призмы. Для дву-
мерных сеток с треугольными ячейками несогласованные сетки, как
правило, используются очень редко, поскольку вместо процедуры со-
гласования конечных элементов на несогласованной треугольной сетке
можно без особого труда построить согласованную сетку, доразбив
ячейки с вершинами внутри рёбер на более мелкие треугольники (и
избавиться гем самым от вершин внутри рёбер). То же самое можно
сказа ть и о сетках с тетраэдральными ячейками.
Далее мы рассмотрим процедуры построения согласованных ко-
нечных элементов для сеток с прямоугольными ячейками При этом
мы рассмотрим два способа построения согласованных конечных эле-
ментов, которые будут продемонстрированы на соответствующих
примерах. 11срвый из них базируется на том, что используются локаль-
ные матрицы стандартных прямоугольных элементов и согласование
элементов осуществляется фактически па этапе сборки глобальной
матрицы, а второй - на введении так называемых переходных конеч-
ных элементов специального вида, для которых строятся специальные
локальные базисные функции и соответственно локальные матрицы.
11.4. III СОГЛАСОВАННЫЕ СЕТКИ С ПРЯМОУГОЛЬНЫМИ ЯЧЕЙКАМИ
Для решения практических задач, как правило, используются не-
равномерные сетки, поскольку они позволяют заметно уменьшить вы-
числительные затраты на получение решения необходимой точности.
При этом если используются сетки с прямоугольными ячейками, то
можно дополнительно снизить вычислительные затраты, избавившись
от так называемых «лишних» узлов, которые практически не влияют на
точность решения задачи. Такие («лишние») узлы часто появляются
при использовании регулярных неравномерных сеток с прямоуголь-
ными ячейками Причины появления такою рода узлов поясним на
следующем примере.
На рис. !06,<7 показана регулярная прямоугольная сетка для реше-
ния задачи с тремя прямоугольными объектами в прямоугольной рас-
чётной области (подобласти-объекты изображены на этом рисунке
жирными линиями). Эта сетка была получена следующим образом. На
координатных осях были поставлены точки {а;,} и через них
11.4.Несогласованные сетки с прямоугольными ячейками
533
проведены координатные линии х = х., и у = у, и получены ячейки
сетки в виде прямоугольников [а;,;,^+1] х\yJy у., и j При лом гонки
{ж,} и были поставлены так, чтобы объекты были разбила па
мелкие ячейки, а с удалением от объектов шаг дискретизации плавно
увеличивался (с коэффициентом разрядки kr = 1.2 , т.е. с удалением от
объектов каждый последующий шаг больше предыдущего в А; раз).
Очевидно, что при использовании такой регулярной прямоугольной
сетки в отдельных местах расчётной области появляются ячейки,
имеющие довольно большой размер по одной координате и очень ма-
ленький по другой - это подобласти , 1И2, 1И3, . Таким образом,
изображённая на рис. 106,<7 сетка содержит довольно много узлов, ко-
торые никак не улучшают качество аппроксимации и только увеличи-
вают вычислительные затраты. Эти узлы могут быть удалены, как это,
например, показано на рис. 106,6, но получаемая сетка будет несогла-
сованной.
Рис 106. Удаление «липших» узлов из регулярной прямоугольной сетки:
а - стандартная регулярная сетка; б - нерегулярная прямоугольная сетка,
полученная после удаления «лишних узлов»
Несогласованные прямоугольные сетки используются и в тех слу-
чаях, когда необходимо повысить точность конечноэлементного реше-
ния за счёт локальных вложенных дроблений сетки. Пример исходной
регулярной сетки показан на рис. 107,<7, а двух сеток, полученных по-
сле одного и двух вложенных локальных дроблений - на рис. 107,6 и
рис. 107,в соответственно.
Очевидно, что в получившейся несогласованной сетке присутству-
ют узлы двух типов: обычные узлы, являющиеся только узлами ячеек
(одной или нескольких), и так называемые терминальные узлы. Тер-
534
1 I Комбинированные и несогласованные сетки
минальный узел - это учел, находящийся на границе хотя бы одной
стандартной ячейки, узлом которой он не является (см. рис. 108).
Заметим, что если в двумерном случае несогласованные сетки с
прямоугольными ячейками можно легко преобразовать к согласован-
ным, разбив отдельные ячейки1 сетки
на треугольники, и после этого стро-
ить конечноэлементное решение на
комбинированной сетке, то в трёхмер-
ном случае сделать совсем непросто.
Поэтому имеет смысл рассмотреть
возможности построения конечноэле-
ментных аппроксимаций на несогласо-
ванной сетке с прямоугольными ячей-
ками (в трёхмерном случае сетка с
ячейками в виде прямоугольных парал-
лелепипедов часто тоже называется
прямоугольной, мы уже пользовались
этим и будем пользоваться далее).
Рис. 108. Пример сетки Способы согласования конечных
с герминальными узлами элементов на несогласованных сетках,
в принципе, мало различаются в дву-
мерном и трёхмерном случаях. Поэтому идею такого согласования мы
рассмотрим ддя двумерного случая. Вначале же на небольшом приме-
ре поясним, почему на несогласованной сетке при использовании
обычной процедуры сборки конечноэлементной СЛАУ из стандартных
локальных матриц получаются несогласованные конечные элементы.
11.5. , ПРИМЕР НЕСОГЛАСОВАННОЙ СТЫКОВКИ ЭЛЕМЕНТОВ
НА НЕСОГЛАСОВАННОЙ ПРЯМОУГОЛЬНОЙ СЕТКЕ
Пусть сетка состоит из трёх прямоугольных элементов Qj, Q2 и
Из, как это изображено на рис 109. На этих элементах введём стан-
1 Речь идёт о тех ячейках, в которые попали терминальные узлы.
1 1.5.Пример несогласованной стыковки элементов
535
дартные билинейные локальные базисные функции ф*<4 , / । . I,
к = 1...3 . Номера этих локальных базисных функции сот истовую!
локальным номерам узпов на каждом конечном элементе, которые
показаны на рис. 109 в кружках. При этом глобальные номера узлов
сетки указаны в прямоугольничках.
Очевидно, что на правой границе Г элемента 0} (т.е. на линии, со-
единяющей узлы сетки с глобальными номерами 2 и 7) локальные ба
зисные функции элементов Qj и граничащих с ним элементов О2 11
Q3, соответствующие одним и тем же узлам сетки, не совпадают. Дей-
ствительно, функция ф-2 линейно изменяется от значения 1 в узле с
глобальным номером 2 до значения 0 в узле с глобальным номером 7.
Соответствующая этому же узлу (с глобальным номером 2) функция
фр2 на Г линейно изменяется от значения 1 в узле с глобальным но-
мером 2 до значения 0 в узле с глобальным номером 4 (т.е., например,
в узле с глобальным номером 4 функция ф?21 равна 0.5, а функция
ф{*2 - нулю). Для узла же с глобальным номером 4, который является
терминальным, на элементе вообще нет соответствующей локаль-
ной базисной функции.
Если для рассматриваемого
случая собрать матрицу и вектор
конечноэлементной СЛАУ из ло-
кальных матриц и векторов эле-
ментов Q2 и ^з обычным
способом (т.е. по соответствию
глобальной и локальной нумера-
ции), то полученная конечноэле-
ментная СЛАУ фактически будет
аппроксимировать исходную ва-
риационную задачу па простран-
стве с разрывными базисными
функциями. Действительно, такой
сборке соответствует глобальная базисная функция ф2" , линейная на
границе Г со стороны элемента Qj и кусочно-линейная1 со стороны
элементов О2 и ^з (верхний индекс «по» у ф2" означает, что эта
функция не непрерывна).
То же самое можно сказать и о глобальной функции фу". Базисная
же функция ф^’ на ребре Г со стороны Q1 вообще равна нулю, по-
скольку на этом элементе нет соответствующей рассматриваемому
узлу локальной функции.
Рис. 109. Пример несогласованной сетки
1 Она изменяется линейно от значения 1 в узле с глобальным номером 2 до
значения 0 в узле с глобальным номером 4 и равна нулю на отрезке между
узлами с глобальными номерами 4 и 7.
536
11 .Комбинированные и несогласованные сетки
Таким образом, соответствующий стандартной сборке базис {ф”с}
содержит разрывные функции, и поэтому функции порождаемого им
пространства не являются допустимыми для вариационной задачи (см.
с. 86), а конечные элементы становятся из-за этого несогласованными.
Ниже мы рассмотрим два способа, позволяющих на такой сетке по-
строить базис {ф'} из непрерывных функций и тем самым согласо-
вать конечные элементы. Первый способ будет заключаться в построе-
нии базиса {ф-‘} без изменения локальных базисных функций элемен-
тов (т.е. терминальным узлам на элементе нс будут ставиться в соот-
ветствие никакие локальные базисные функции), а второй - во введе-
нии стыковочных элементов со специальными локальными базисными
функциями, соответствующими терминальным узлам.
11.6. ПОСТРОЕНИЕ СОГЛАСОВАННЫХ КОНЕЧНЫХ ЭЛЕМЕНТОВ
( III ( ОГЛ U ОВАННЫМИ ЛОКАЛЬНЫМИ БАЗИСНЫМИ
Ф> нкцпями
Здесь мы рассмотрим первый из упомянутых в конце разде-
ла 1 1.5 способов построения согласованных конечных элементов.
11.6.1. UAIOIK ГР\ЦИЯ РАССМАТРИВАЕМОГО СПОСОБА СОГЛАСОВАНИЯ
НА ПРОСИ iilHErt ПРЯМОУГОЛЬНОЙ СЕТКЕ
Для сетки, изображённой на рис. 109, построим непрерывные
глобальные базисные функции, соответствующие узлам с глобальными
номерами 2 и 7, следующим образом. Для простоты будем считать, что
терминальный узел с глобальным номером 4 стоит точно посередине
ребра I Функцию ф2 определим как ФГ+тФГ, а функцию ф?
определим как фуг 4 ^ФГ • Нетрудно убедиться, что полученные гло-
бальные базисные функции ф2 и ф? являются линейными функциями
на ребре I как со стороны так и со стороны Q2 UH3, значения
каждой из них в узлах с глобальными номерами 2 и 7 со стороны Q,
совпадают со шачепиями со стороны Q2 UQ3, и поэтому эти функции
непрерывны на I
Базисные же функции ф, для ?. = 1,3,5,6,8 определим равными
ФГ . Таким образом, в базисе {ф-} содержится только 7 базисных
функций. При этом для того чтобы одинаковые функции в базисах
Ф»} и {ФГ } имели одинаковые номера, в базисе {ФУ} базисные
пункции пронумерованы не подряд — в нём отсутствует базисная
функция с номером 4 Соответственно и вектор искомых весов разло-
жения по этому базису,будет иметь 7 компонент, при этом их номера,
естественно, должны быть равны номерам базисных функций, и по-
этому компонента вектора весов q = ЛвГ фактически будет
фиктивной.
1 1.6 Построение согласованных конечных элементов
537
Построим конечноэлементную аппроксимацию с использованием
базиса {ф, }. /Vй1 этого, как обычно, в эквивалент ной вариационной
постановке (в форме Галёркина) искомое решение и заменим iHiicii-
ной комбинацией базисных функций uh = q^i и вместо пробной
», 2^4
функции в вариационное уравнение будем подставлять поочерёдно
базисные функции {ф^}. Очевидно, что если считать номера уравне-
ний совпадающими с номерами базисных функций, то в получаемой
конечноэлементной СЛАУ будет отсутствовать уравнение с номером 4.
Таким образом, мы получим следующую систему уравнений (мы
полагаем, что вкладов от естественных краевых условий нет, посколь-
ку они никак не повлияют на паши рассуждения - на внешних грани-
цах все ф£ просто совпадают с ф •" ):
8
= ^4.
1 Hi
о
Очевидно, что если номера * и j не равны 2 или 7, то компонента
A'j матрицы А‘ этой СЛАУ совпадает с соответствующей компонен-
той А"' матрицы А'" СЛАУ, собранной из локальных матриц по
стандартной технологии (для уменьшения выкладок будем считать,
что ч — 0 ):
Ag = = J X grad ф”г • grad Ф77Й2, i, j = 1,3,4,5,6,8 .
Q
Если же хотя бы один из номеров г или j равен 2 или 7, то А'; не
совпадает с A"j,:, но при этом А'- может быть вычислен через компо-
ненты матрицы А"' . Покажем это.
Рассмотрим случай, когда г = 2, a j * 2 и j * 7 .
A!2j = f grad 'Фг • grad ф'?с/П = J X grad (ф£г + | ф™') grad ф“гсЙ2 =
= У2 f Х grad (ф£г + | ф£') • grad ф"' dQ.
Теперь, когда мы перешли на интегрирование по отдельным конеч-
ным элементам, мы можем заменить grad(<+l<) на
grad ф^"’ + ^grada|>4r. При этом обратим особое внимание на то, что
538
11 .Комбинированные и несогласованные сетки
J' X grad ip2C • grad Ф/ dQ * У X grad ф2с * grad ф™’сЮ
о Л=1Цд.
из-за разрывности ф2п на границе Г (между Qj и О2 U Q3 )• То же
самое справедливо и для функции ф^. Таким образом,
з з
A'2j = У2 / X grad ф2/г • grad ф’-''dQ +1У2 / Х Srad Ф^' • grad ф"'сЮ .
*=1ПЛ
Учитывая, что компоненты матрицы Апг были определены нами
как
3
< = Е J X grad ф"'г • grad (H.l)
/с=1 А
получаем
ле _ дпс л2] (И.2)
Аналогично
+ |A“', J*2hj#7, (11.3)
^2=Л^ + Ф A'41', i 2 и г> 7 (HA)
4- Ф A'4 , i 2 и i 7 (11.5)
^2 = ^2 + 2 A?4 + 2 A14 > (116)
А27 = ‘ ^24 + 7 Al 7 + 4 A44 , (H-7)
А72 — А$ + 2 A74 + Ai 2 + A4 4 , (11.8)
А77 — А77 4- Ф А74 + -i А47 + -Ф А44 . (H.9)
Таким образом, все компоненты матрицы А' могут быть вычисле-
ны через компоненты матрицы Аш; (собранной из локальных матриц
несогласованных элементов стандартным способом). Очевидно, что
это возможно и для любой другой аналогичной ситуации, когда эле-
менты непрерывного базиса {ф'} формируются как линейные комби-
нации разрывных функций ф“г, получаемых формальным объедине-
нием локальных базисных функций соседних конечных элементов. В
1 1.6.Построение согласованных конечных элементов
539
разделе 11.6.2 мы получим соотношения, позволяющие вычислять
компоненты матрицы А' через компоненты матрицы А " для общего
случая.
11.6.2. ОБЩАЯ СХЕМА ПОСТРОЕНИЯ КОНЕЧНОЭЛЕМЕНТНОЙ СЛАУ
ПРИ СОГЛАСОВАНИИ ЭЛЕМЕНТОВ НА НЕСОГЛАСОВАННЫХ СЕТКАХ
С ИСПОЛЬЗОВАНИЕМ МАТРИЦЫ ПЕРЕХОДА
Пусть базисные функции ф[ выражаются через функции ф’"’ с
помощью соотношения
ф': =Тфш:, (11.10)
где фш; - вектор, составленный из функций ф“г, г = 1...п (п — чис-
ло узлов в сетке), фг — вектор, составленный из функций ф':,
г = , а Т — матрица размера п(. х п перехода от базиса {ф"'г} к
базису {Ф^ } Тогда
Ас = [ |Х grad (фг) grad (ф' )г + 7 (ф') (фг )т J dQ =
о
= f {\ grad (Гф’“:) grad (Т-ф+ ч(Тф'‘Э(Тф',г)т}<Ю.
Чтобы вынести матрицу Т (компоненты которой являются кон-
стантами) за интеграл, необходимо перейти от интеграла по всей рас-
чётной области к сумме интегралов по конечным элементам, посколь-
ку фг — непрерывные, а ф"г - разрывные функции, и для них (!)
J X grad (ф"с) grad (фмг)'dQ J X grad (ф"г) grad (фш:)тdQ .
Q к
Таким образом,
А' = Е Лх g™1 ) grad (Т'Ф'"' )т+ ч (Т<'') (Т^“ )Т } ^ =
к hk
= У2 f {><т 6га(1 ('Ф"г) grad (#"')Т Тт+ тТфкг (Ф"г )т тт } dQ =
к ^к
= Т Е f {Хgrad(-ф"')grad+ 7Ф"'(i|)“ )т}Тт.
Учитывая, что матрица Аш: фактически была нами определена как
540
11 .Комбинированные и несогласованные сетки
А’"' =Е f {Xgra<l(4|>"')gi-a<l('l|;"c)T+Tl’“('4’"':)T}df5> (СП)
k Пк
окончательно получим
Аг = ТА'"'ТТ. (Н.12)
Аналогично преобразуется и вектор правой части:
Ьг = ТЬ"Г. (11.13)
Скажем несколько слов о том, как можно вычислить компоненты
матрицы перехода. Для этого сначала поясним, как в общем случае
может быть построена функция ф'; при стыковке двух элементов с
одним. На ребре Г, являющемся границей между одним элементом
(«большим») и объединением нескольких других («маленьких»),
функция ф' определяется как базисная функция «большого» элемента.
Пол ому фактически на этой границе мы должны представить каждую
ненулевую базисную функцию ф-’ (которая на Г является локальной
базисной функцией «большого» элемента) через базисные функции
ф"‘ , полученные стандартной сшивкой локальных базисных функций
«маленьких» элементов. А это уже сделать довольно просто. Действи-
тельно, весами разложения линейной (как, впрочем, и любой полино-
миальной) базисной функции «большого» элемента по кусочно-
линейным (или соответственно по кусочно-полиномиальным лагран-
жевым) базисным функциям, полученным стандартной сшивкой ло-
кальных базисных функций «маленьких» элементов, являются значе-
ния разлагаемой функции в узлах «маленьких» элементов.
Например, для несогласованной сетки, изображённой на рис. 109,
функция ф'> в узлах, лежащих па границе Г (Г = ГД П (ГД СЮз)),
принимает значения ф2 (х-^у?} = 1, ф2 {хд,Уд) — 0-5 , ф>2 (ж7 >'//?) = 0 ,
и поэтому через базисные функции фф она выражается следующим
образом:
Ф-2 (•'•’, //) = Ф2 (^2,2/2) ФГ у) + ф-2 (^4, Уд ) ФГ у) +
+ Ф-2 (3’7, У7 ) ФГ (®, у) = ФГ у) + 0.5ф^‘ (х, у) .
Отсюда становятся очевидными значения ненулевых компонент
второй строки матрицы перехода Т: УД = 1 и 7^4 = 0.5.
Аналогично вычисляются и компоненты седьмой строки матрицы Т.
Таким образом, для рассматриваемого нами примера (т.е. для сетки,
изображённой на рис. 109) матрицу перехода Т можно записать в ви-
де:
11.6.Построение согласованных конечных элемспюн ...
541
1 0 0 0 0 0 0 0
0 1 0 0.5 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 0
т = 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0.5 0 0 1 0
0 к 0 0 0 0 0 0 1
(H.I4)
Нетрудно убедиться, что соотношения (11.2)-(1 1.9) могут быть по-
лучены из (11.12) с помощью матрицы (1 1.14).
В матрице (1 1.14) четвёртая строка является полностью нулевой -
это произошло потому, что мы хотели оставить у функций (и соот-
ветственно у весов q,j) номера, равные номерам узлов сетки (заметим,
что ф’/г имеют именно такие номера). Очевидно, что в этом случае
п(. = п и матрица А' имеет размер п х п (где п — число узлов в сет-
ке) и при этом у неё имеются нулевые строки и нулевые столбцы, со-
ответствующие терминальным узлам.
Рассмотрим, как можно преобразовать получаемую конечноэле-
ментную СЛАУ, сделав её матрицу невырожденной. Простейший спо-
соб — поставить на места диагональных элементов нулевых строк еди-
ницы. Однако тогда значения весов с номерами, соответствующими
нулевым строкам, получатся равными нулю (т.е. при вычислении ре-
шения на конечном элементе в виде линейной комбинации его локаль-
ных базисных функций этими весами всё равно нельзя воспользовать-
ся, а в матрице СЛАУ остались «лишние» строки и столбцы).
Другой способ заключается в том, что матрица Т сразу задаётся
прямоугольной (т.е. п,. п и п(. — число нетерминальных узлов). То-
гда номера функций ф' (и, естественно, весов) становятся не равными
номерам узлов. В этом случае для рассматриваемого нами примера
матрица Т имела бы вид:
(П-15)
При таком способе построения преобразования Т матрица Аг ко-
нечноэлементной СЛАУ уже не будет иметь нулевых строк и столб-
542
1 1 .Комбинированные и несогласованные сетки
нов. И хотя в этом случае номера 1лобальных функций ф£ (и соответ-
ственно компонент q\ вектора весов q' = (Аг) 1 Ь' ) становятся не
равными номерам узлов, это нс является большой проблемой для на-
хождения значений компонент вектора весов qMr, номера которых
соответствуют глобальным номерам узлов, поскольку qnr может быть
получен из q' с помощью матрицы преобразования Т :
qz" = TTqr. (11.16)
Докажем справедливое и. соотношения (1 1.16). Действительно, нам
нужно получи н> закон вектор qw , который бы при скалярном умно-
жении на ф"г давал копечноэлементное решение uhкоторое имеет
вид и.'1 = (q1 )' ф' (q' - вектор решения конечноэлементной СЛАУ),
т.е. такой q , что
(<!'" )т ф'" = (q')T ф' . (11.17)
Нетрудно убедиться, что вектор q'"', вычисленный с помощью со-
отношения (I 1.1о), удовлетворяет равенству (11.17) (с учётом связи
(11.10)):
(q'")' >!’"' = (Т'<Г)‘ #“ = (qf)ТТ-ф'" = (Ч')тф‘ .
После вычисления же q”c (с помощью соотношения (11.16)) не
представляет никакой сложности вычислить значение конечноэле-
меитши о решения внутри любого конечного элемента — нужное нам
значение будез линейной комбинацией значений локальных базисных
функции (в этой точке), коэффициенты которой - это соответствую-
щие компоненты вектора весов q"r (полученные по соответствию ло-
кальных номеров базисных функций рассматриваемого конечного
элемента номерам функций ф.-" ).
11.6.3. АЛГОРИТМ ( БОРКИ МАТРИЦЫ КОПЕЧНОЭЛЕМЕНТНОЙ СЛАУ
ИЗ ЛОКАЛЬНЫХ М \ I РИЦ ЭЛЕМЕНТОВ С НЕСОГЛАСОВАННЫМИ
ЛОКАЛЬНЫМИ Ь\ПИ НЫМИ ФУ НКЦИЯМИ
Заметим, что при практической реализации довольно неудобно
пытаться вычислять матрицу Лг напрямую по формуле (11 12) через
предварительно собранную матрицу А”г . Конечноэлементные матри-
цы обычно хранятся в упакованных форматах, учитывающих меезопо-
ложепие их ненулевых элементов, и поэтому форматы упаковки А и
А,,г могут не совпадать. В принципе, можно вообще не собирать мат-
рицу А , а при реализации процедуры решения СЛАУ учитывать, что
её матрица является произведением трёх матриц (см. (11.12)). Естест-
11.6.Построение согласованных конечных элементов
543
венно, это приводит к заметному увеличению вычислительных шграг1
и определённым неудобствам при использовании некоторых схем нрс-
добусловливания (см. семнадцатый раздел). Поэтому более выгодными
являются процедуры, позволяющие сразу (без формирования Л" )
генерировать А' .
Покажем, как может быть организована процедура генерации мат-
рицы А‘ , когда А' собирается сразу из локальных матриц конечных
элементов
Пусть узлы сетки пронумерованы так, что первые п,. функций ф’"
соответствуют тем же самым узлам, что и функции ф':, т.е. терми-
нальные узлы (которым не соответствует ни одной функции -ф';‘) будут
иметь номера с п(. + 1 до п (для рассматриваемого нами примера
узел, который имел номер 4, в новой нумерации должен иметь номер 8,
а узлы с номерами от 5 до 8 в новой нумерации должны иметь номера
на единицу меньше).
Тогда, во-первых, матрица Т имеет более простой вид (её первые пс
столбцов образуют единичную подматрицу). Во-вторых, на каждом ко-
нечном элементе очень легко определить по глобальному номеру узла,
какая из его локальных базисных функций нестандартным образом уча-
ствует в построении глобальной (как ф^ ’ и -ф,21 в нашем примере).
В этом случае не представляс г особого труда построить алгоритм ге-
нерации глобальной матрицы А' , чтобы из стандартных локальных мат-
риц формировались непосредственно её компоненты, а не компоненты
матрицы A'tr . Например, этот алгоритм может быть следующим.
• Каждая компонента А~- локальной матрицы А добавляется стан-
дартным образом в компоненту Д', глобальной матрицы А' (по
соответствию локальных номеров i и j глобальным i и j), если
i < П,. И J < П(. .
• Если i > п(. и j < 7\., то компонента добавляется с весами 7Д
ко всем компонентам А^ с такими значениями индекса р., для ко-
торых Titi 0.
• Если i < п(. и j > пе , то компонента Ац добавляется с весами TVj
ко всем компонентам А!а) с такими значениями индекса и, для ко-
торых TVJ 0.
• Если i > пс и j > п(., то компонента А-- добавляется с весами
Т^г TVJ ко всем компонентам A['IV с такими значениями индексов
1 Поскольку увеличивается число действий при выполнении умножения
матрицы на вектор, являющегося одной из основных и наиболее затратных
операций во многих итерационных методах.
544
1 1 .Комбинированные и несогласованные сетки
р и v, для которых 7J,,: ^0 и Т1Ч 0.
Ниже, в разделе 11.6.5, мы продемонстрируем работу этого алго-
ритма на примере с достаточно сложной несогласованной прямоуголь-
ной сеткой.
В заключение скажем несколько слов о возможных процедурах
сборки правой части конечноэлементной СЛАУ. В принципе, можно
получить вектор правой част умножением матрицы перехода на век-
тор b"r (см. (11.13)) - в отличие от генерации матрицы, эта процедура
не требует больших дополнительных вычислительных затрат. Тем не
менее мы рекомендуем использовать всё-таки процедуру прямой сбор-
ки, аналогичную сборке матрицы:
• Если i < п,., каждая компонента /т локального вектора b добавля-
ется стандартным образом в компоненту Ь- глобального вектора
Ь' (по соо тветствию локального номера г глобальному «).
• Если i >п,., го компонента Ь- добавляется с весами Т)и ко всем
компонентам с такими значениями индекса р,, для которых
Щи 0 .
11.6.4. СП<)( ОЬЫ \P\IH ПНЯ МАТРИЦЫ ПЕРЕХОДА
II АЛГОРИТМ II Н(>( 1 РОЕНИЯ
Очевидно, что для рассмотренного нами способа занесения ло-
кальных матриц не нужно (да и неудобно) хранить матрицу Т в виде
прямоугольного массива Достаточно хранить только ненулевые компо-
ненты сё последних и — п, столбцов (с номерами j > п(.) вместе с но-
мерами строк, в которых эти компоненты находятся. Поэтому для рабо-
ты с матрицей Т удобно использовать разреженный столбцовый фор-
матам. раздел 10.4. I) для хранения её последних п — п(. столбцов. Для
этого нужно три одномерных массива: массив ig указателей на начала
столбцов (длины п — и,. | 1 ), массив gg для хранения только ненуле-
вых компонент последних п — п,. столбцов матрицы Т и соответст-
вующий ему массив номеров строк jg , в которых находятся эти ненуле-
вые элементы.
Для рассмотренного памп примера матрица Т после соответст-
вующей перенумерации узлов примет вид
'1000000 о'
1 о
О I
о о
о о
0 0 0 0 0.5
о о о о о
10 0 0 о
0 10 0 0
(11.18)
0 0 0 0 0 1 0 0.5
0 0 0 0 0 0 1 о
11.6.Построение согласованных конечных элементов
545
и в разреженном столбцовом формате (без учёта единичной подматри-
цы) она может быть представлена массивами
«£7 = {1,3}, j<7 = {2,6}, да = {0.5,0.5} .
Вообще говоря, рассмотренную процедуру согласования конечных
элементов обычно применяют для несогласованных сеток, в которых
каждое граничное ребро или грань любой ячейки сетки либо является
частью одного граничного ребра (грани) другой ячейки, либо можея
быть объединением нескольких граничных рёбер (граней) других яче-
ек. Примеры таких двумерных сеток приведены на рис. 1 10 и III.
Обратим внимание на то, что для сетки с «перехлёстом» границ,
пример которой приведён на рис. 112, хотя формально рассмотренная
процедура согласования и может быть применена, результат может
получиться довольно плохим по точности, поскольку конечноэлемент-
ное решение в этом случае будет как бы игнорировать все узлы сетки
между вершинами с номерами 2 и 10 (для билинейных базисных функ-
ций при х = 5 оно будет линейно по у на всём отрезке 1 < у < 13 ).
Построим матрицу перехода для сетки, изображённой на рис. 1 10. В
этой сетке из 21 узла только с 15 ассоциированы базисные функции ф,
(т.е. п,. — 15). Эти 15 узлов в соответствии с приведённым выше опи-
санием алгоритма прямой генерации матрицы А' (без использования
матрицы А"г) пронумерованы первыми. Поэтому для матрицы пере-
хода Т необходимо сформировать только пять последних столбцов.
Покажем, как могут быть вычислены компоненты этих четырёх по-
следних столбцов матрицы Т.
Обоснование метода вычисления компонент матрицы перехода Т
было приведено на с. 540. Но там фактически был описан способ фор-
мирования матрицы Т по строкам, т.е. именно компоненты г-й стро-
ки Т вычислялись как значения глобальной базисной функции ф' в
узлах сетки (очевидно, что для всех узлов с номерами j < п,. функция
ф': принимает ненулевое значение только в узле с номером j = i., что
и делает левую подматрицу матрицы Т единичной матрицей). Однако
технологически гораздо эффективнее формировать матрицу I по
столбцам, поскольку нам нужно фактически вычислять только ненуле-
вые компоненты Т, а их гораздо проще находить именно по столбцам.
Поэтому ниже на примере мы продемонстрируем, как работает алго-
ритм формирования матрицы Т по столбцам.
Сначала сформируем столбец с номером 16 матрицы Т . Поскольку
узел с номером 16 находится на ребре между узлами с номерами 2 и 9,
ненулевые значения в 16-м столбце Т должны попасть во 2-ю и 9-ю
строки и соответствующие компоненты должны быть значениями гло-
бальных базисных функций ф- в узле с номером 16. Таким образом,
^2,16 —
У9 - У16
У9 ~ У2
- 0.375 и
^9.16 —
Z/1G - У-2
У9 - У2
6-1
9-1
0.625
(здесь уг - это значение у -координаты узла сетки с номером г
)
546
11 .Комбинированные и несогласованные сетки
Теперь сформируем столбец с номером 17 матрицы Т. Поскольку
терминальный учел с номером 17 находится на ребре между узлами 7 и
18, ненулевые значения в 17 столбце должны были бы попасть в 7-ю и
18-ю строки и соответствующие компоненты должны были бы быть
значениями глобальных базисных функций ф£ в узле с номером 17.
Таким образом, Ту 17 = —— = -у.~—j5 = 0.625 (х, - значение
.1 |я — 13 — ।
х -координаты узла сетки с номером г). Если бы узел с номером 1 8 не
был терминальным (и ему соответствовала бы одна из функций базиса
{фу}), то соответствующая компонента матрицы Т (обозначим её
718,17 ) приняла бы значение — -—— = ~J = 0.375 . Но в матри-
це Т только 15 строк, поскольку в базисе {ф-;} только 15 функций.
Поэтому теперь нам нужно определить, какие базисные функции из
{ФУ} принимают ненулевые значения в терминальном узле с номе-
ром 18 (и, следовательно, и в узле с номером 17). Очевидно, что для
рассматриваемого нами примера это функции ф£ и фф. Значение в
узле с номером 17 функции ф8 определяется как произведение значе-
ния Ть 18 = ——— = 11 ~ —0.5 на значение Т18 17.
2/10-2/5 11-1
11.6.Построение согласованных конечных элементов
547
Рис. 112. Несогласованная сетка
с «перехлёстами»
Рис. 111. Несогласованная сетка,
в которой граничное ребро одного
конечного элемента контактирует
с граничными рёбрами сразу трёх
конечных элементов
Действительно, функция ф8 была построена так, что она линейно
изменяется от значения I в узле с номером 5 до нулевого значения в
узле с номером 10 (именно поэтому её значение в узле с номером 18
равно ———). Вдоль ребра, соединяющего узлы с номерами 18 и 7,
Z/io ~ Уъ
эта функция также является линейной и меняется от того значения,
которое она приняла в узле с номером 18 (напомним, что это значение
Т518 ) до нулевого значения в узле с номером 7. И поэтому её значение
в узле с номером 1 7 определяется как произведение её значения в узле
с номером 18 на значение Д8Д7 линейной функции х(.т), принимаю-
щей единичное значение в узле с номером 18 и нулевое значение в
узле с номером 7 (т.е. на значение х(.т18) = ——— = Т[7 18 ). В ре-
.Т18 -
зультате мы получаем Д 17 = Т518 • Т1817 = 0.5 • 0.375 = 0.1875 .
Аналогично:
710.17 = 310,18 • 7*18,17 = 7~71«,17 = °-5 ' 0-375 = °-1875 •
Z/1U — 4/5
Таким образом, в 17-м столбце матрицы Т три ненулевых элемен-
та: Т5Д7 = 0.1875, Т7>17 = 0.625 и Т1()>17 = 0.1875.
548
1 I .Комбинированные и несогласованные сетки
В столбце с номером 18 матрицы Т ненулевыми являются только
два элемента: 7518 и is • Они Уже были получены нами при вычис-
лении элементов 17-го столбца: Т5д8 — 0-5 и 7](ц8 — 0.5 .
Определим, в каких строках должны будут находиться ненулевые
компоненты 19-го столбца. Поскольку терминальный узел с номе-
ром 19 стоит на ребре, соединяющем узлы с номерами 7 и 21, положе-
ние одной из ненулевых компонент очевидно: она должна находиться
в 7-й строке. Строки же с номером 21 в матрице Т нет (так как
21 > п,. = 15 ), и поэтому мы должны определить номера вершин реб-
ра, на котором стоит 21-й узел. Очевидно, это узлы с номерами 10 и 20.
Поскольку 20 > на данном этапе очевидно положение только ещё
одной ненулевой компоненты 19-го столбца — она находится в 10-й
строке (т.е. па данный момент известно, что в 19-м столбце ненулевые
компонен ты находятся как минимум в 7-й и 10-й строках). А для узла с
номером 20 должны быть определены номера вершин ребра, на кото-
ром он расположен. Это узлы с номерами 9 и 13. Таким образом, нену-
левыми в 19-м столбце Т являются компоненты строк с номерами 7, 9,
К) и 13.
("ответственно могут быть вычислены и значения компонент 7g 19,
7'к).1<) и /'13,19 (компонента Т7>19 вычисляется сразу же как значение в
узле с номером 19 линейной на ребре между узлами с номерами 7 и 21
функции, равной единице в узле с номером 7 и нулю в узле с номе-
ром 21: 77 19 = —---— = 0.4). Компонента 79 19 вычисляется в виде
'3/21 “ У7
(по цепочке, которая привела от узла с номером 19 к узлу с номе-
ром 9):
^9,19 — ^21,19 ^20,21 • 2g,20 , (1 119)
т.е.
3/19-3/7 ^10-^21 . 3/13 - 3/20 = 3 . 6 . 3 = 0 216
3/21 - 3/7 -ЛО - ж20 3/13 - 3/9 5 10 5
Аналогично компонента Тф 19 вычисляется как
гр ________ rf' т1 _____________ 3/19 3/7
110.19 — /21.19 • 110,21 — -------------Г"
3/21 — 3/7
Si^o = ^.A = o.24
г И1 - -'с2<> 5 10
а компонента Т1319 — как
гр _________ гр гр гр _______________________ 3/19 3/7
-/13,19 — -/21,19 ‘ -/20,21 ’ -/13,20 — ---------------~
3/21 ~ 3/7
^10 ~ -с21 . 3/20 — 3/9
^10 ~ ж20 3/13 ~ 3/9
— 3 . JL. 2 __ q
5 10 5
Компоненты остальных столбцов (20-го и 21-го) фактически нами
уже получены (при вычислении компонент 19-го столбца):
11.6.Построение согласованных конечных элементов ...
549
^9,20 — 0-6, 213,20 — 0-4 ;
2j),21 = 220,21’29,20 — 0-36, 2]() 21 = 0.4 , 2}з 21 = 220,2Г ^'13.20 = 0.2 I .
Таким образом, матрица Т в разреженном столбцовом форм нс
(без единичной левой подматрицы) будет иметь вид:
гд = {1,3,6,8,12,14,17},
jg ~ {2,9,5,7,10,5,10,7,9,10,13,9,13,9,10,13} ,
дд = {0.375,0.625,0.1875,0.625,0.1875,
0.5,0.5,0.4,0.216,0.24,0.144,0.6,0.4,0.36,0.4,0.24}. (1 1 .20)
Обратим внимание на следующую деталь при формировании нену-
левых компонент матрицы Т. Напомним, что при формировании i-й
строки Т мы должны вычислить значение функции во всех узлах
сетки, где она принимает ненулевое значение. То, как определить но-
мера узлов, в которых ф-; принимает ненулевые значения, рассмотрим
на примере вычисления компонент 9-й строки для сетки, изображён-
ной на рис. 110.
Так как узлы с номерами 16 и 20 стоят на рёбрах, содержащих вер-
шину с номером 9, то -фд принимает в этих узлах ненулевые значе-
ния - это и есть значения 7g 1С и 2g го- Узел с номером 16 не является
вершиной никакого ребра, на котором стояли бы терминальные узлы,
и поэтому идущая через него цепочка ненулевых элементов 9-й строки
на нём заканчивается.
Узел же с номером 20 является вершиной ребра, на котором стоит
терминальный узел с номером 21, и поэтому в 9-й строке Т ненулевой
будет и компонента Tq 2j , причём её значение вычисляется по ведущей
к ней цепочке: Т9 2J = 29;2() Т2о,21 •
Узел с номером 21 также является вершиной, из которой исходит
ребро, содержащее терминальный узел. Это узел с номером 19, и по-
этому значение очередной ненулевой компоненты 9-й строки Т919
также может быть вычислено по ведущей от 9-го узла к 19-му (через
20-й и 21-й узлы) цепочке:
2д,19 — 2g,20 ’ 220,21 221,J 9 (11.21)
Поскольку узел с номером 19 не является вершиной никакого реб-
ра, содержащего терминальные узлы, на нём заканчивается и эта це-
почка, поэтому в 9-й строке больше ненулевых элементов нет. Таким
образом, мы показали, как матрицу Т можно было бы сформировать
по строкам.
Однако для работы этой процедуры, как мы убедились, требуется
такая структура данных, которая бы позволяла по номеру узла опреде-
лять исходящие из него рёбра, содержащие терминальные узлы. А по-
скольку чаще всего конечноэлементная сетка хранится в виде множе-
550
11 .Комбинированные и несогласованные сетки
ства ячеек, определяемых узлами, гораздо проще и удобнее сформиро-
вать структуру данных, которая для каждого терминального узла по-
зволяет определить номера вершин ребра, на котором он находится
Кроме того, заносить компоненты локальных матриц сразу (напрямую)
в матрицу А' намного удобнее, если элементы матрицы Т хранятся
по столбцам, а нс по строкам. Именно поэтому сначала мы привели
подробный пример, в котором матрица Т строилась по столбцам, с
движением по цепочке узлов от терминального узла к узлам, с кото-
рыми ассоциированы базисные функции, не равные нулю в рассматри-
ваемом терминальном узле. Очевидно, что в этом случае элементы
цепочки, определяющей значение искомой компоненты матрицы, по-
лучались в обратном порядке - сравните (11.19) с (1 1.21).
Обобщим всё сказанное выше о формировании матрицы Т. Будем
считать, что в качестве исходных данных мы имеем конечноэлемент-
ную сетку в виде множества ячеек, каждая из которых задана перечис-
лением номеров её узлов. При этом в локальной нумерации узлов
ячейки перечисляются не только узлы, определяющие локальные ба-
зисные функции этого элемента, но и герминальные узлы, попавшие
на |рапицы этого элемента1. Будем также считать, что все терминаль-
ные узлы имеют глобальные номера, большие п,..
11ри хранении сетки в таком виде проходом по конечным элемен-
там очень легко сформировать структуру данных (обозначим её (5 ), в
которой для каждого терминального узла с номером j хранятся те
глобальные номера узлов i конечного элемента (содержащего этот
терминальный узел), которым соответствуют локальные базисные
функции ф;- (где i - локальный номер узла с глобальным номером г),
принимающие ненулевые значения в рассматриваемом терминальном
узле с глобальным номером j. Напомним, что значения ф,- в терми-
нальном узле с номером j мы обозначали как Тч (если узел с номе-
ром / нс герминальный) или как Тч (если узел с номером i терми-
нальный). Очевидно, что это как раз те значения, которые нам потре-
бую!ся для формирования всех ненулевых компонент матрицы Т, и
поэтому их имеет смысл сохранить вместе с номерами узлов i. Когда
такая структура данных построена, алгоритм формирования Т может
быть следующим
Выбираем очередной номер столбца j (начиная с j = п,. 4-1 ). Для
него определяем номера узлов i и берём соответствующие им значе-
1 Удобнее всего информацию о конечном элементе хранить так, чтобы но-
мера его узлов, определяющих локальные базисные функции элемента, хра-
нились первыми.
11.6.Построение согласованных конечных элемент on
551
ния T,j или из сформированной ранее структуры данных1 б. Г.сли
i < то Tt заносится в матрицу Т. Для тех же номеров которые
больше п(., начинается построение цепочек номеров узлов, необходи-
мых для вычисления последующих ненулевых компонент столбца /.
При этом для каждой цепочки выделяется ячейка памяти ЭЛ,, в кото-
рой будет накапливаться произведение вида (11.19), и в неё заносится
значение 7} . Далее, по структуре данных 6 для номера узла 1. опре-
деляем номера узлов I. Взятые из & значения 7/, (при I < п,. ) или 7J,
(при I > п(.) домножаем на содержимое соответствующей ячейки па-
мяти ЭЛ, . Для тех I, которые не превосходят значения п,. (т.е. для
I < п(.), полученные значения произведений 7}, на содержимое соот-
ветствующей ячейки памяти ЭЛ, заносим в матрицу Т как оконча-
тельно сформированные новые (не хранящиеся в &) компоненты 7}у.
Для тех же номеров I, которые больше п(., заводим «свои» ячейки
памяти ЭЛ/ и в них переносим содержимое ячейки ЭЛ.,, умноженное
на Тц . Далее выбираем любую из неоконченных цепочек и продолжа-
ем её, обращаясь к структуре б и определяя новые номера, соответст-
вующие последнему в этой цепочке номеру. При этом, очевидно, це-
почка оканчивается, если все номера, полученные из структуры б,
окажутся меньшими либо равными п(..
После того, как все начатые цепочки будут окончены, j -й столбец
матрицы Т будет окончательно сформирован и можно переходить к
формированию следующего столбца.
Очевидно, что описанная нами процедура фактически является раз-
новидностью алгоритма обхода по дереву (который может быть реали-
зован как обход по дереву в ширину или в глубину).
Обратим особое внимание, что описанный здесь алгоритм форми-
рования матрицы Т построен так, что он вполне пригоден нс только
для несогласованных двумерных конечноэлементных сеток с элемен-
тами первого порядка, но и для несогласованных двумерных и даже
трёхмерных конечноэлементных сеток с элементами любого порядка.
1 Мы используем одно и то же обозначение Ту для компонент формируе-
мой матрицы Т и для значений, хранящихся в структуре данных б не слу-
чайно (точнее, вполне намеренно). Дело в том, что хранящиеся в структуре
данных б значения Тг. при i < пг действительно являются компонентами
Ту матрицы Т (и должны быть просто перенесены из б в Т ). Проблема в
том, что в 6 хранятся далеко не все ненулевые компоненты матрицы Т, и
именно на вычисление не хранящихся в б компонент Ту и нацелен наш
алгоритм (при этом для вычисления таких Ту используются как значения 7}./,
так и значения Тц, хранящиеся в 6).
552
1 1 .Комбинированные и несогласованные сетки
Заметим, что для рассмотренных нами примеров с двумерными конеч-
ными элементами первого порядка обходимое в алгоритме дерево все-
гда является двоичным, а при использовании элементов более высоких
порядков или трёхмерных элементов из каждой вершины дерева может
исходить больше двух цепочек (в соответствии со структурой (5, в
которой для каждою герминального узла хранятся значения всех ба-
зисных функций, не равных нулю в этом узле).
Заметим также, что рассмотренный алгоритм формирования матри-
цы Т применим только в том случае, когда цепочки, формируемые по
структуре 6, образуют именно дерево, т.е. граф без циклов. Поэтому
этот алгоритм нс будет работать для несогласованных сеток «с пере-
хлёстом» (такая сетка приведена, например, на рис. 112). На самом
деле, такие сетки лучше не применять вообще (главным образом но
причине резкого ухудшения аппроксимационных свойств сетки в мес-
тах «перехлёста», о чём было сказано выше, на с. 545), и поэтому, в
общем-1 о, нс имеет какого-либо смысла усложнять рассмотренный
алгоритм для учёта возможных «перехлёстов» в сетке. Гем не менее
кош роль ситуации «перехлёста», которая приведёт к зацикливанию
рассмотренного алгоритма, лучше включить в реализацию этого алго-
ршма, гем более что сделать это чрезвычайно просто: достаточно про-
верять, не появилась ли в цепочке какая-либо вершина второй раз.
В заключение в качестве ещё одного примера приведём вид матри-
цы перехода Т (в разреженном столбцовом формате) для сетки, изо-
бражённой на рис. Ill:
ig {l.3.5.7}, j(} = {7,14,7,14,13,14}, gg — {0.75,0.25,0.375,0.625,0.6.U.4} .
11 6.5. ПРИМЕР СБОРКИ ГЛОБАЛЬНОЙ МАТРИЦЫ СЛАУ
С ИСПОЛЬЗОВАНИЕМ МАТРИЦЫ ПЕРЕХОДА
Продемонстрируем работу описанного выше алгоритма прямой
генерации глобальной матрицы А (т.е. без формирования матрицы
А ) с использованием матрицы перехода на примере занесения в неё
локальных матриц некоторых элементов для сетки, изображённой па
рис. I 10.
Рассмотрим элемент с вершинами, имеющими глобальные номе-
ра I, 2, 8 н 9. Обратим внимание на то, что терминальный узел с гло-
бальным номером 16 не является узлом этого элемента (ему не соот-
ветствует пн одна локальная базисная функция этого элемента). Таким
образом, для рассматриваемого элемента все глобальные номера его
узлов меньше п,. (?ir = 15), и поэтому компоненты его локальной мат-
рицы заносятся в матрицу А' обычным способом - по соответствию
локальных и глобальных номеров.
Теперь рассмотрим конечный элемент с вершинами, имеющими
глобальные номера 9, 19, 20 и 21. Будем считать, что при формирова-
нии локальной матрицы этого элемента была использована локальная
нумерация «слева направо, снизу вверх», т.е. локальный помер 1 соот-
ветствует глобальному номеру 9, локальный номер 2 - глобальному
номеру 19, локальный номер 3 - глобальному номеру 20, локальный
номер 4 - глобальному номеру 21.
11.6.Построение согласованных конечных элементов ..
553
Занесём в А' компоненту Ац локальной матрицы рассмгггрпвас-
мого элемента. Поскольку локальный номер 1 соответствует глобаль-
ному номеру 9 и 9 < 'пг, компонента А1Л заносится в Л' обычным
образом - добавлением её к компоненте Ад 9.
Рассмотрим, как должна заноситься в А' компонента Д >. По-
скольку локальный номер 2 соответствует глобальному номеру 19 и
19 > 71,., компонента А12 должна быть добавлена с весами 7’,д9 ко
всем элементам Ад,, с номерами н, для которых 7J,jg 0 . Эти значе-
ния v и соответствующие им веса 7],дд легко могут быть получены из
массивов (1120), являющихся представлением матрицы перехода в
разреженном столбцовом формате. Для этого по номеру столбца (рав-
ному 19) определяем элемент в массиве гд, содержащий адрес начала
искомого столбца в массивах jg и дд. Поскольку первые п(. столбцов
матрицы Т не хранятся, это элемент гд(19 — ?><), т.е. гд(4) = 8 . Ко-
личество ненулевых элементов в столбце с номером 19 определяется
как ig (5) — ig (4) = 4 . В результате для столбца с номером 19 имеем
четыре значения v (7, 9, 10 и 13) и соответствующие им значения
^ia19 (0.4, 0.216, 0.24 и 0.144). Таким образом, занесение компоненты
Д , в матрицу А выполняется следующим образом: к компоненте
Ад 7 добавляется значение 0.4 А12, к компоненте А£д - значение
0.216-Д 2> к Ag l() - значение 0.24 • А12 и к Ад13 - значение
0.144-Л1>2.
Аналогично заносятся компоненты Aj 3 и А114 :
0.6 Д з —+ Ag g, 0.4 • А13 —»Адд3;
0.36 Д д —> Ад,д > 0.4 /1) 4 —> Аддд , 0.24 А1 4 —> Адд3 .
Наиболее сложной является процедура занесения для случая, когда
обоим локальным номерам i и j компоненты А; , соответствуют
глобальные номера, большие п(.. Кратко рассмотрим этот случай на
примере занесения компоненты Д2,з (соответствующие глобальные
номера - 19 и 20). Для занесения этой компоненты нам понадобится
столбец с номером 19 (который был выписан выше) и столбец с номе-
ром 20, для которого ig (5) = 12, ig (6) — ig (5) = 2 , v = {9,13},
T^2() =. {0.6,0.4}. В результате схема занесения компоненты Д23 вы-
глядит следующим образом:
554
11 Комбинированные и несогласованные сетки
0.6-0.4-Л,зЛ4’,7,
0.6 -0.216 - Л2 3 Л A5t9,
0.6-0.24-Л2,я2» Лдш,
0.6 0.144 Л zV)|13
0.4 • 0.4 • А2 3 —* Л[з 7 ,
0.4-0.216-43^^13,9,
0.4 • 0.24 • zl2 з —> Д'здо,
0.4 0.144 • —* Лздз .
11.7. СОГЛАСОВАНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
НА НЕСО1 ЛАС ОВАННОЙ СЕТКЕ
С ИСПОЛЬЗОВАНИЕМ ПЕРЕХОДНЫХ ЭЛЕМЕНТОВ
Рассмотренная нами в разделе 11.6 технология согласования ко-
нечных элементов на несогласованной сетке была нацелена на исполь-
зование локальных матриц стандартных элементов. В результате она
потребовала разработки специальных процедур сборки глобальной
СЛАУ с использованием матрицы Т преобразования базиса {ф”г} в
базис ' ф' } . В дальнейшем мы будем называть такую технологию тех-
Т) И Е; р ,10]
ц 1 4 г Q2 г 1 Qi В— и
ш г П d D | 8 |
нологией Т-преобразования (или просто Т-технологией).
Теперь же мы покажем, как можно решить проблему согласования
элементов с другой стороны: ввести специальные переходные элементы
(с нестандартными локальными базисными функциями), оставив
стандартной сборку глобальной матрицы.
Проиллюстрируем идею по-
строения переходного элемента
на примере несогласованной сет-
ки, изображённой на рис. 113.
Будем считать, что Q1? Q3 и -
это стандартные конечные эле-
менты с билинейными локальны-
ми базисными функциями. На
ячейке же Q2 определим пять
локальных базисных функций так,
„ чтобы стандартная сшивка их с
локальными базисными функ-
циями соседних элементов давала
непрерывные глобальные функции.
Будем считать, что на О2 локальная нумерация узлов задана так,
как это показано па рис. 113 (как и прежде, на этом рисунке локальные
номера узлов приведены в кружочках, а глобальные — в прямоуголь-
ничках). При этом локальную нумерацию узлов стандартных элемен-
тов мы не приводим, считая её прежней, т.е. на стандартном элементе
узлы пронумерованы слева направо, снизу вверх.
На элементе Q2 локальные базисные функции ф^2 и ф^2 опреде-
лим как стандартные билинейные базисные функции прямоугольного
элемента:
11.7.Согласование конечных элементов . .
555
f2 - X УЗ - У ТИ2 _ ^2 У- У\
- hx Л, ’ - Л, h., '
где х.„уг - координаты узла с локальным номером z, h.r — х} j j,
hy = y3 — yY. Локальные же базисные функции ф^2 > Ф42 и 'Фа 2 опре-
делим соотношениями:
Ф22
Ф?
\т - Ж! Уь - У
к hT
О,
О,
ж - .TJ у -
х-хх у-у-2
h:>: 1^Т
X - J’l Ул - У
У < Уз,
У > Уз,
У < Уз,
У > Уз,
У < Уз,
У > Уз,
где hf = fe- у2, h* = //., - /;5 .
Эти функции построены по тому же принципу, что и стандартные
билинейные функции V (.г) У (г/), только функция-сомножитель У (</)
у них определена не как линейная, а как кусочно-линейная на интерва-
ле (^2,2/4) функция. Так, у функции ф22 сомножитель У (*/) прини-
мает значение единица при у = у2, линейно убывает до нуля при из-
менении у от у-z к у3 и равен нулю при у > у3 . Аналогично, у функ-
ции ф42 сомножитель У (•//) принимает значение единица при у = у^,
линейно убывает до нуля при изменении у от у^ к у3 и равен нулю
при у < уГ). У функции же ф^2 сомножитель У (у) фактически явля-
ется стандартной кусочно-линейной функцией (см., например, (2.45)):
он линейно изменяется от нуля до единицы при изменении у от у2 до
уь и от единицы до нуля при изменении у от у3 до у4 .
Очевидно, что локальные функции этого элемента па его ребре, со-
единяющем узлы с локальными номерами 2 и 4, совпадают с соответ-
ствующими локальными базисными функциями соседних элементов
Q3 и Q4. Тогда глобальная базисная функция ф5, определяемая как
ф“2 на и как 'Ф^3 на ^з> является непрерывной. Аналогично, не-
прерывной является глобальная функция ф7, определяемая как ф42
556
11 .Комбинированные и несогласованные сетки
на П2 и как Фз4 на ^4* а также глобальная функция фс, определяе-
мая как Ф52 на П2, как ф3;! на Q3 и как на Q4. В результате на
несогласованной сетке с помощью переходного элемента Q2 с0 специ-
альным локальным базисом мы построили согласованные конечные
элементы, и поэтому сборку глобальной матрицы (а также и построе-
ние её портрета) можно проводить стандартными способами.
В отличие OI 1с\нологии Т-преобразования, при использовании
технологии согласования конечноэлементных сеток через переходные
элементы герминальным узлам мы поставили в соответствие гло-
бальные оашеные функции (увеличив тем самым размерность конеч-
номерного пространства, на котором ищется приближённое решение).
Поэтому на одной и гой же сетке при использовании этих технологий
будет различным количество степеней свободы — неизвестных весов
q, в разложении приближённого решения по базисным функциям. Тем
нс менее увеличение числа степеней свободы в технологии переход-
шах элемснюв не является сколько-нибудь серьёзной проблемой, так
как при сё использовании некоторое увеличение размерности вектора
неизвестны^ (и, естественно, размерности СЛАУ) может сопровож-
дайся coo I встствующим улучшением конечноэлементной аппрокси-
мации.
| Аналогично переходному элементу
—-------------------------- с терминальным узлом на правой сто-
СО (5J роне (см. рис. 113) не представляет
никакого труда определить переход-
ные элементы в случаях, когда терми-
(6)"---- нальный узел находится на любой из
других трёх сторон прямоугольника.
Более сложной является ситуация,
когда переходной прямоугольный эле-
мент содержит терминальные узлы на
смежных границах. Пример такого
Рис. 114. Шееiny шопов переходной элемента приведён на рис. 114. Если
жмет на этом элементе определить только
шесть локальных базисных функций
(так, чтобы они непрерывно сшивались с локальными базисными
функциями всех соседних элементов) с помощью соотношений
h - Д Уз - и
j - Л //G - У
h‘- Vr
о,
У > Уб,
(11.22)
(11.23)
У < Z/G,
11^.Согласование конечных элементов . .
557
Фз =
'&> ~х у-щ
hT \
О,
х < £'з,
х > z5,
(1 1.24)
ф4 =
х - х-5 У ~ Уб
hr hr ’
о,
X > Хго и у > у к
X < х.ь или у < yG
х-хх у-уг
hr Ч
Х-2 - X у - У1
hr h!f
х < f5,
•^5,
(П-25)
(11 26)
Фо =
X - ^1 У- У-2
hx If
X-Xj Уд - у
hx hr
У < Уб,
У > Уб,
(11.27)
X
где h.r = -т5 - х{, ЬГ = х2 - х5
ЬГ = Уб - У1, h„*= Уз~ Уб, чо
окажется, что на этом элементе нельзя
точно представить, например, посто-
янную функцию и — const. В этом
очень легко убедиться Действительно,
каждая из функций (11.22)—611-27)
равна единице только в одном узле и
нулю во всех остальных, и поэтому
весами разложения константы по та-
кому базису могут быть только значе-
ния этой константы. Для базиса же
(11.22)—(11.27) сумма всех функций,
очевидно, не совпадает с функцией
v = 1, в чём можно убедиться, вычис-
лив значение этой суммы
G
S (ж, у) = фг (т, у), например, в
г=1
точке с координатами х — , у = у6:
Рис. 115. Шестиузловой переходной
элемент с разбиением
на треугольники
s(xro, yG) = У2 Ф, fe Уб) = ^Г~^Г + ° + ° + ° + ~hT + 1 ‘
Таким образом, при использовании шестиузлового элемента с ба-
зисными функциями (11.22)—(11.27) могут существенно ухудшиться
558
11 Комбинированные и несогласованные сетки
аппроксимационные свойства получаемого численного решения (в
этом случае перестают работать оценки погрешности конечноэлемент-
ной аппроксимации, приведённые в третьем разделе, см. (3.76), (3.77),
(3.86))>.
Рис. 116. Пятнузловой переходной
JJICMCIH с рл(биением
па(реугольпики
Тем не менее корректный переход-
ной элемент с двумя терминальными
узлами на смежных сторонах постро-
ить можно. Например, этот элемент
можно было бы разбить на треуголь-
ники. как это показано на рис. 115, и
на этих треугольниках определить
стандартные локальные базисные
функции. В результате локальная мат-
рица переходного элемента размерно-
сти 6x6 может быть получена стан-
дартной сборкой из четырёх локаль-
ных матриц соответствующих тре-
угольных элементов (размерности
3x3). Замс him. что точно таким же способом можно было бы постро-
ить нягпузловой переходной элемент, разбив его на три треугольника,
как это показано н i рнс 116.
Рис. 117. Ссмиу «попой переходной
>пемен)
Вообще говоря, такое определение
переходного элемента через объедине-
ние нескольких простых стандартных
элементов по аппроксимации эквива-
лентно построению согласованной
комбинированной сетки 11емного раз-
личаются лишь структуры данных,
используемые для хранения сетки, и
соответствующие процедуры их обра-
ботки. Однако технология переходных
элементов имеет заметные преимуще-
ства ещё и в тех случаях, когда пред-
полагается дробить ячейки сетки на
себе подобные в отдельных подобла-
стях расчетной области для уменьшения погрешности решения. В этом
случае построение комбинированной сетки (т.е. замена в сетке всех
переходных элементов их разбиением на простые подэлементы) не
позволит разбивать переходные элементы на себе подобные (посколь-
1 Вообще говоря, представимость функции v = const на элементе не яв-
ляется строго необходимой для обеспечения хорошей аппроксимации и вы-
полнения оценок (3.76), (3.77), () 86). Например, на четырёхугольном «били-
нейном» элементе (см. разделы 5.4.1, 5.4.2) может быть не представима точно
линейная функция, однако эти оценки остаются справедливыми, поскольку с
дроблением сетки погрешность представления линейной функции уменьша-
ется не медленнее, чем отклонение точного решения от линейной функции на
каждом элементе (то же самое можно сказать и об элементах более высокого
порядка на четырёхугольнике) Но здесь всё-таки несколько другой случай.
1 1.7.Согпасование конечных элементов ...
559
ку в комбинированной сетке уже нет информации и переходных эле-
ментах, из которых она была получена).
Если же мы не хотим включать в сетку элементы другого ины, го
переходной элемент с терминальными узлами на двух смежных ребрах
всё-таки можно построить и с использованием естественных для пря-
моугольника билинейных базисных функций. Для этого нужно ввести
дополнительный (седьмой) узел внутри элемента (см. рис. I 17) и опре-
делить на нём следующие базисные функции:
£3 ~Ув-У , a-Tj ус-у
hf hj: hf hf
хГ) - ху-у!
h,
^•2 - х Уб - У
h... Кг
(1 1.28)
£5 - х Уз - У
/lyy
О,
У < Уб,
У > Уб,
х >
(1 1.29)
(1 1.30)
.г-25 y-yG
0,
X < 25 ИЛИ у < у6,
(11.31)
х > 25 И у > yG,
2-21 У~У1
hf
2-2 - X у -ух
h? h!,
X
(11.32)
560
11 .Комбинированные и несогласованные сетки
а ~ А У ~ У 2
А,. hf
I' - -И У4 - У
к
У < Уб,
У > Уб,
x>x5ty< yG,
X < %5,У > Уб,
(11.33)
Фс =
Рис. [ 18. Разбиение семиузлового
переходного >лемепта
2- — 2>5, У < Уб,
(П-34)
2> — 3*5 ,У > Уб,
В принципе, базисные функции и
локальные матрицы переходных эле-
ментов можно получать и с использо-
ванием технологии Т -преобразова-
ния, которую мы в этом случае будем
называть технологией локального
Т -преобразования (поскольку она
будет использоваться для построения
локальных матриц переходных эле-
ментов). Покажем, как с помощью
этой технологии можно построить
локальную матрицу того же самого
семиузлоього переходного элемента с двумя терминальными узлами на
смежных сторонах (см. рис. I 17).
Разобьём рассматриваемый элемент на четыре прямоугольника так,
как это показано на рис. 118 В результате его узлы с номерами 5 и 6
перестанут быть терминальными, а добавленные узлы с номерами 8 и
9, наоборот, стануi терминальными. Вклад этого элемента в глобаль-
ную матрицу можс! быть вычислен как сумма вкладов от четырёх его
частей (стандартных прямоугольных элементов) с помощью техноло-
гии Т-преобразования. Матрица Т, соответствующая изображённой
на рис. 118 нумерации узлов, с учётом того, что терминальными явля-
ются узлы с номерами 8 и 9, выглядит следующим образом:
11.7.Согласование конечных элементов ...
561
1 0 0 0 0 0 0 V ''11
0 1 0 0 0 0 0 hx Kt 0
0 0 1 0 0 0 0 0 by
Т = 0 0 0 1 0 0 0 0 0 (11.35)
0 0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0
Таким образом, чтобы получить локальную матрицу рассматривае-
мого переходного элемента, надо собрать из четырех матриц стандарт-
ных прямоугольных элементов «глобальную»’ матрицу и умножить её
слева и справа на матрицы Т и Тт соответственно.
Например, чтобы получить матрицу жёсткости (при коэффициенте
диффузии X = 1), мы должны воспользоваться матрицей жёсткости
стандартного элемента в виде
(11.36)
и собрать из четырёх таких матриц «глобальную» матрицу G в соот-
ветствии с нумерацией узлов, приведённой на рис. 118.
Локальная матрица жёсткости G переходного элемента получается
после умножения матрицы G слева и справа на матрицы Т и Тт.
Получим выражения для нескольких элементов G. Для этого сна-
чала получим первую строку матрицы S, являющуюся произведением
Т на G . Так как в первой строке матрицы Т ненулевыми являются
только 1-я, 8-я и 9-я компоненты, то
h=* ~
Sik=Glk+-^-Gsk+-j-
(11.37)
•
' Глобальную в смысле сетки из четырёх прямоугольных элементов, обра-
зующих рассматриваемый переходной элемент.
562
11 .Комбинированные и несогласованные сетки
Вычислим теперь компоненту Сц. Для этого нужно умножить пер-
вую строку матрицы S на первый столбец матрицы Тт (т.е. фактиче-
ски на первую строку Т). Учитывая, что в первой строке Т только 3
ненулевых компоненты, получим:
^11 — 3 Ь ЗДщ —(7ц
Поскольку матрица G симметрична, полученное выражение можно
несколько упрости н> (оставив компоненты только нижнего треуголь-
ника G ):
^41 = £ц I 2-—--()Н| 1 '£'91 +
л > I7 - /т V ~ V )2 ~
<1L38)
Лнало! ично можно получить выражение для G{,:
G-2 —
I
(11.39)
При получении окончательного выражения для (712 мы учли, что в
матрице G некоторые компоненты (в частности, (712 и (7д2) равны
нулю.
Так как в матрице Т все строки, начиная с четвёртой, имеют един-
ственную ненулевую компоненту (диагональную и равную единице),
то, начиная с G’14, все компоненты первой строки совпадают с соот-
ветствующими компонентами первой строки S.
Очевидно, что аналогичными действиями может быть построена
вся матрица Заметим, что в соответствии со структурой матрицы Т
(см. (11.35))
11.7.Согласование конечных элементов ...
563
= Су при г, j = 4...7.
(I 1.40)
В принципе, можно было бы получить выражения для компонент
G в явном виде, подставляя в полученные формулы вида (11.38)-
(11.40) выражения для компонент матрицы G. Например, соответст-
вующее выражение для может быть получено из (11.38) следую-
щим образом.
Компонента Gji фактически является компонентой Cfj локальной
матрицы конечного элемента с вершинами 1, 8, 9 и 7 (см. рис. 118), т.е.
+
3 ЛГ 3
но компоненты G^,
. Компоненты С81, С91 и С798 - это соответствен-
ен и (7з2 локальной матрицы этого же элемента.
Компонента ё88 - это сумма двух компонент: компоненты G22 конеч-
ного элемента с вершинами 1, 8, 9 и 7 и компоненты (7^ конечного
элемента с вершинами 8, 2, 7 и 6, а компонента G99 - сумма компо-
ненты G33 конечного элемента с вершинами 1, 8, 9 и 7 и компоненты
Gfi конечного элемента с вершинами 9, 7, 3 и 5. Таким образом, вы-
ражение (11.38) примет вид
Тем не менее этой способ вычисления матрицы G, основанный на
использовании полученных в явном виде выражений для её компонент
(типа (11.41)), являясь довольно громоздким, не позволяет существен-
но сократить число действий за счёт упрощения этих выражений. По-
этому, на наш взгляд, всё-таки нс стоит получать эти выражения в ви-
де, подобном (11.41), а лучше пользоваться выражениями, опреде-
ляющими компоненты G через компоненты G (т.е. выражения вида
(1 1.38)-(11.40)) и учитывающими, что некоторые из компонент матри-
цы G равны нулю.
Таким образом, матрицу G лучше сформировать «в числах» стан-
дартной сборкой из четырёх локальных матриц вида (11.36) и умноже-
564
11 Комбинированные и несогласованные сетки
нием её на матрицу Т и Т' слева и справа получить (также «в чис-
лах») матрицу G. Безусловно, такой способ существенно упрощает
процедуры построения локальных матриц любых типов переходных
элементов, получаемых из локальных матриц стандартных элементов с
помощью Т-технологии.
В принципе, матрицу G можно было бы получить по алгоритму
прямой сборки из четырех локальных матриц вида (11.36) (см. раз-
дел 11.6.3). Рекомендуем читателю проделать это для лучшего пони-
мания алгоритма прямой сборки.
Кроме того, в качестве упражнения читатель может вычислить хотя
бы несколько компонент локальной матрицы жесткости переходного
элемента напрямую но стандартным формулам (см., например, (5.2)),
используя явный вид (I 1.28) (I 1 34) его локальных базисных функций.
Рекомендуем вычисли и, таким способом хотя бы элемент (711 и срав-
нить его с выражением (II II) (хотя бы по значению при некоторых
фиксированных координатах узлов переходного элемента). Очевидно,
что такой способ iребусi большого количества рутинной работы (свя-
занной с взятием интегралов) для вычисления локальной матрицы жё-
сткости каждою переходною элемента и при этом не даёт сколь-
нибудь заметного снижения вычислительных затрат.
Таким образом, матрицу переходного элемента всё-таки лучше
строить но технологии локального Т-преобразования (неважно, ум-
ножением на матрицы Т и 'Г' или по алгоритму прямой сборки), по-
скольку это нс только освобождает от рутинной работы по вычисле-
нию интегралов, но и может избавить от неприятностей, связанных с
построением переходных элементов с плохими аппроксимационными
свойствами (как, например, рассмотренного выше шестиузлового пе-
реходного элемента с базисными функциями (1 1.22)-(1 1.27)).
Очевидно, что и для любого пятиузлового прямоугольного пере-
ходного элемента локальные матрицы проще всего строить с исполь-
зованием технологии локального Т-преобразования (разбив пятиузло-
вой элемент на 2 С1андаргных прямоугольных элемента). При этом
базисные функции переходных элементов можно даже не получать в
явном виде1.
Таким образом технология локального Т-преобразования позволя-
ет достаточно просто созда н, довольно универсальный и в то же время
не приводящий к дополни тельным вычислительным затратам алгоритм
формирования локальной матрицы А переходного элемента. Напри-
мер, такой алгоритм носiроения локальной матрицы А переходного
элемента из его «глобальной» матрицы А реализует следующая про-
цедура на языке Фортран:
1 Заметим, что и при вычислении конечноэлементно! о решения в любой
точке переходного элемента можно обойтись без построения локальных ба-
зисных функций переходного элемента в явном виде - для этого можно вос-
пользоваться либо соотношением (11.10), либо соотношением (11.16).
11 .7.Согласование конечных элементов ...
565
SUBROUTINE MultTAT(Ag,Al,ig,jg,gg,N,Nc)
INTEGER N,NC,ig(N-NC+1),jg(*)
REAL Ag(N,N),Al(Nc,Nc),gg(*)
* Программа для вычисления нижнего
* треугольника матрицы А = ТАТТ
* Массив Ад - А, массив А1 - А,
* Массивы ig,jg и дд - матрица перехода в
* разреженном столбцовом формате
* Вычислим сначала диагональ А:
DO i=l,Nc
Al(i,i)=Ag(i,i)
DO k=Nc+l,N
DO L=ig(k-Nc),ig(k-Nc+1)-1
if(jg(L).eq.i)then
Al(i,i)=A1(i,i)+Ag(k,k)*gg(L)**2
Al (i, i) =A1 (i, i) + 2*Ag (i , k) *gg (L)
DO kk=Nc+l,k-l
DO LL=ig(kk-Nc),ig(kk-Nc+1)-1
if (jg(LL) .eq.ijthen
Al(i, i)=A1(i,i)+ 2*Ag(k,kk)*gg(LL)*gg(L)
end if
end do
end do
end if
end do
end do
end do
* Теперь вычислим нижний треугольник А .
* Сначала умножаем на единичную подматрицу
DO i=2,Nc
DO j=l,i-1
Al(i,j)=Ag(i,j)
END DO
END DO
* Затем умножаем на всё остальное
DO k=Nc+l,N
DO L=ig(k-Nc),ig(k-Nc+1)-1
DO kk=l,NC
Il=min(j g(L),kk)
I2=max(jg(L),kk)
if (Il.EQ.12)cycle
Al(12,I1)=A1(12,II)+Ag(k, kk) *gg(L)
end do
DO kk=Nc+l,k-1
DO LL=ig(kk-Nc),ig(kk-Nc+1)-1
Il=min(jg(L),jg(LL))
I2=max(jg(L),jg(LL))
566
11 .Комбинированные и несогласованные сетки
if(II.EQ.12)cycle
Al(12,II)=А1(12,II)+Ag(k,kk)*gg(LL)*gg (L)
end do
end do
DO LL=ig (k-Nc),L-1
Il=min(jg(L),jg(LL))
I2=max(jg(L),jg(LL) )
if(Il.EQ.12)cycle
Al(12, II)=A1(12,11)+Ag(k,k)*gg(LL)*gg(L)
end do
end do
end do
END SUBROUTINE MultTAT
Puc. 119. I IpeoGpa имшнис сетки
с «перехлёстом»
В принципе, незначительно услож-
нив этот алгоритм, можно учесть и
наличие в матрице А заведомо нуле-
вых компонент (соответствующих
двум не связанным узлам, т.е. таким
узлам, для которых нет ни одного
общего подэлемента).
Обратим внимание ещё на одну
довольно важную деталь. Фактически
мы показали, что во многих случаях
при использовании технологии
Т-преобразования и при использова-
нии технологии переходных элемен-
тов может быть получена одна и та же
конечноэлементная аппроксимация.
Но для этого должны быть использо-
ваны не полностью совпадающие сет-
ки (т.е. сетки с разным количеством
узлов), поскольку терминальные узлы
в этих технологиях несут разную смы-
словую нагрузку - в одной технологии
степени свободы, соответствующие
терминальным узлам, удаляются, а в другой — сохраняются. Например,
для сетки «с перехлёстом» (изображённой на рис. 112), напрямую
Т-технологию применять нецелесообразно, поскольку она приводит к
фиксации функции и. как линейной вдоль линии «перехлёста», см.
рассуждения на с. 545. Гсхноло! ия же переходных элементов для этой
сетки вполне приемлема.
Тем не менее можно достаточно просто преобразовать рассматри-
ваемую сетку (добавив терминальные узлы с номерами 17-21, как это
показано на рис. 1 19), и уже для неё применить Т-технологию и полу-
чить ту же аппроксимацию, что и при использовании технологии пере-
ходных элементов.
Однако при практической реализации Т-технологии обработка си-
туаций, связанных с продлением линий, является не такой уж простой,
11 ^.Несогласованные трехмерные сетки
567
поскольку при этом могут появляться вырожденные элементы - в ча-
стности, если линии продлеваются с двух противоположных ребер
одного элемента. Иллюстрирующий эту ситуацию пример изображён
на рис. 120. Очевидно, что если точки Д и Р2 имеют почти совпа-
дающие у -координаты, то продление линий приведёт к появлению
практически вырожденного прямоугольника. Соответственно при
стандартной обработке матрица конечноэлементной СЛАУ может
быть испорчена огромными вкладами от локальной матрицы жёстко-
Рис. 120. Проблема продления
линий
сти этого почти вырожденного элемента.
Контролировать такую ситуацию на
глобальном уровне может оказаться до-
вольно сложно, в то время как при приме-
нении технологии переходных элементов
все проблемы могут быть решены на ло-
кальном уровне. Даже если потребуется
создать переходной элемент с большим
количеством терминальных узлов с произ-
вольным расположением их на любых гра-
ницах переходного элемента, этот элемент может быть достаточно
просто построен (либо через рассмотренный здесь способ с использо-
ванием технологии локального Т -преобразования, либо путём разбие-
ния на какие-либо стандартные элементы - треугольники или четы-
рёхугольники). Это преимущество технологии переходных элементов
является ещё более значимым в трёхмерном случае.
11.8. НЕСОГЛАСОВАННЫЕ ТРЁХМЕРНЫЕ СЕТКИ
Покажем, как может быть использована Т -технология для со-
гласования трёхмерных сеток с несогласованными ячейками. На
рис. 121 приведены примеры ситуаций, характерные для нерегулярных
трёхмерных сеток с терминальными узлами и ячейками в виде прямо-
угольных параллелепипедов (рис. 121,а) и прямых призм (рис. 121,6) .
Обратим внимание на то, что в трёхмерном случае при использова-
нии элементов первого порядка с терминальными узлами структура
данных О (см. с. 550) несколько усложняется по сравнению с двумер-
ным случаем. В двумерном случае для элементов первого порядка в
структуре данных (5 для каждого терминального узла хранится ровно
два глобальных номера — это номера тех узлов конечного элемента,
которым соответствуют локальные оазисные функции, принимающие
ненулевые значения в рассматриваемом терминальном узле. В трёх-
мерном же случае таких функций может быть больше двух. Так, для
узла, находящегося внутри грани элемента (например, это узел с номе-
ром 18 на рис. 121//) таких функций четыре (это функции, соответст-
вующие узлам с номерами 2, 6, 10 и 14).
Поскольку для изложенного в разделе 11.6.4 алгоритма построения
матрицы перехода Т была использована структура данных 6 в общем
виде (а не в виде двоичного дерева, которым она является только для
несогласованных двумерных сеток с элементами первого порядка), этот
568
11 .Комбинированные и несогласованные сетки
Рис 121 I lpitMcpi.1 си гуаций. характерных для нерегулярных трёхмерных сеток с
элементами в виде параллелепипедов (а) и в прямых треугольных призм (б)
В качестве примера приведём матрицы перехода Т для сеток, изо-
бражённых на рис. 121 (как обычно, в разреженном столбцовом фор-
мате без хранения единичной подматрицы).
Будем считать, что для се пси из параллелепипедов, изображённой
на рис. 121//, //-координата узла с номером 1 (а также узлов с номера-
ми 2, 3, 8, 9 и т.д.) равна 0, //-координата узла с номером 4 (а также
узлов с номерами 16, 18, 19 н гд.) равна 3 и //-координата узла с но-
мером 5 (а также узлов с номерами 6, 7 и т.д.) равна 5. Будем также
считать, что z -координата узла с номером 1 (а также узлов с номера-
ми 2, 3, 4 и т.д.) равна 0, z -координата узла с номером 8 (а также узлов
с номерами 17, 18 и 19) равна 1, a z -координата узла с номером 9 (а
также узлов с номерами 10, II и т.д.) равна 4. Тогда матрица Т для
этой сетки представляется в виде:
11.8.Несогласованные трехмерные сетки
569
Ig z= {1,8,5,9,11,13} , jg = {2.6,2,10,2,6,10,14,4,12,10,11} ,
gg = {0.4,0.6,0.75.0.25,0,3,0.45,0.1,0.15,0.75,0.25,0.4,0.0} .
Для сетки же из призм (рис. 121,6) будем считать, что координаты
узлов заданы табл. 19.
Таблица 19
“Ж" 1 2 3 4 5 6 7 8 9 10 11 12 13
X 0 5 11 0 10 0 0 5 11 0 10 5 0
У 0 0 0 4 5 0 0 0 0 4 5 0 4
Z 0 0 0 0 0 3 5 5 5 5 5 3 Г~
Тогда матрица перехода для этой сетки имеет вид
ig = {1,3.5} , jg = {2,8,4,10}, gg = {0.4,0.6,0.4,о.б} .
Несогласованные трехмерные сетки довольно удобны для построе-
ния локальных сгущений и в ситуации, когда в качестве ячеек сеток
используются шестигранники. Однако здесь наряду с проблемой «пе-
рехлёстов» (характерной также и для сеток с ячейками в виде паралле-
лепипедов) есть еще одна проблема, связанная с ограничениями, на-
кладываемыми на форму стыкуемых граней. Остановимся на этой про-
блеме более подробно.
Будем использовать в дальнейшем следующую терминологию. Ко-
нечный элемент, к одной грани которого примыкают сразу несколько
других элементов, будем называть «большим», а примыкающие к его
одной грани элементы - «маленькими». Аналогично гоань, к которой
примыкают сразу несколько конечных элементов, будем называть
«большой», а контактирующие с ней грани примыкающих («малень-
ких») элементов - «маленькой». Напоимер, в изображённой на рис. 122
сетке шестигранный элемент {1,2,5,6,9,10,13,14} является «большим»1,
элементы {2,3,16,4,17,8,18,19}, {17,8,18,19,10.11,20,12} и {16,4,6,7,20,
12,14,15} - «маленькими», грань {2,6,10,14} - «большой», а грани
{2,16,17,18}, {17,18,10,20} и {16,6,20,14} - «маленькими».
Чтобы при использовании Т-технологии согласования конечных
элементов на несогласованной сетке с шестигранными ячейками полу-
ченные базисные функции ф' стали действительно непрерывными,
необходимо выполнение следующего требования.
Все рёбра «маленьких» граней, контактирующих с «большой» гра-
нью, должны лежать на «координатных линиях» этой «большой» гра-
ни, те. при отображении ячейки с «большой» гранью на шаблонный
кубик = [0,1] х[0,1]х[(),1] лежащие на этой i рани ребра контакти-
рующих с ней «маленьких» граней должны попасть на линии
1 Очевидно, один и тот же элемент может быть «большим» для контакта
по одной его грани и «маленьким» для контакта по другой. Например, эле-
мент {16,4,6,7,20,12,14,15} является «большим» для контакта по грани
{16,4,20.12} и «маленьким» для контакта по грани {16,6,20,14}. В этом случае
применяемый термин («большой» или «маленький») будет однозначно опре-
делять, о каком именно контакте идёт речь.
570
11 .Комбинированные и несогласованные сетки
£, = const или (, = const (естественно, для тех граней шестигранника,
которые отображаются в одну из граней т| = const шаблонного кубика
Qr). Несколько «координатных линий» на одной из граней шести-
гранника, полученных отображением линий £, = 0.125, £, = 0.25,
£, = 0.325, £, = 0.5, £, = 0.625, £, = 0.75, £, = 0.825 и линий С = 0.2,
С, = 0.4 , С, = 0.6 и ( = 0.8 , показаны (тонкими линиями) на рис. 123.
Рис. 122 Примеры опунций. характерных для нерегулярных трёхмерных сеток
с «исмснтами в виде шестигранников
На рис. 124 приведены примеры до-
пустимого и недопустимого несогласо-
ванного контакта «большого» шести-
гранника с двумя «маленькими», а на
рис. 125-е тремя Тонкими линиями на
этих рисунках показаны «координатные
линии» «большого» шестигранника на
грани несогласованного контакта (т.е.
линии, в которые на грани1 £, = const
переходят линии С, = const и т| = const
при отображении шаблонного кубика
в «большой» шестигранник).
Как видно из этих рисунков, при до-
пустимых несогласованных контактах
каждое ребро «маленьких» граней лежит
строго на одной из «координатных линий» «большой» грани, а при
недопустимых хотя бы одно ребро «маленьких» граней пересекает
«координатные линии» «большой» грани.
1 Это именно та грань кубика , которая является прообразом грани
«большого» шестигранника, контактирующей с «маленькими».
11.8.Несогласованные трёхмерные сегки
571
Рис. 124. Пример допустимого (а) и недопустимого (б) контакта «большого»
шестигранника с двумя «маленькими»
а б
Рис. 125. Пример допустимого (а) и недопустимого (б) контакта «большого»
шестигранника с тремя «маленькими»
Естественно, следить за соблюдением этого ограничения (т.е. непе-
ресечения «координатных линий» «больших» граней ребрами «ма-
леньких») лучше всего на этапе построения сетки. Однако и уже по-
строенную несогласованную сетку можно скорректировать соответст-
вующим образом, либо несколько передвинув рёбра «маленьких» гра-
ней, либо сделав доразбиение «большой» ячейки, которое фактически
перенесёт «большую» грань на противоположную сторону «большой»
ячейки (и эта «большая» ячейка перестанет быть таковой). Соответст-
вующие примеры приведены на рис. 126.
Проблема же «перехлёстов»1 в трёхмерном случае тоже может быть
решена доразбиением соответствующих ячеек (аналогично тому, как
это делалось в двумерном случае, см., например, рис. 1 19 на с. 566). Но
технически в трёхмерном случае устранять «перехлёсты» намного
труднее, чем в двумерном, и поэтому лучше всё-таки нс допускать их
1 Под «перехлёстом» мы понимаем ситуацию, когда объединение контак-
тирующих с «большой» гранью «маленьких» граней не совпадает полностью
с этой большой гранью (т.е. «маленькие» грани «вылезают» за границы «ооль-
шой»).
572
1 1 .Комбинированные и несогласованные сетки
возникновения на этапе генерации сетки (как, впрочем, и пересечений
«координатных» линий «большой» грани рёбрами «маленьких»).
Рис. 126. Возможные способы коррекции: а - недопустимый контакт «большой»
ячейки с «маленькими», о коррекция сдвигом рёбер «маленьких» граней;
в- коррекция доразбиенисм с переносом «большой» грани на противоположную
сторону
Таким образом, при использовании несогласованных трёхмерных
сеток рассмотренную выше технологию Т-преобразований можно
применять практически без изменений. При использовании несогласо-
ванных сеток с шее।игранными ячейками необходимо лишь кроме
нсдоп 1цсния «нерсхлёс гов» следить за тем, чтобы координатные ли-
пин «больших» гранен нс пересекались рёбрами «маленьких», и в слу-
чае нарушения лих условии соответствующим образом модифициро-
вать сетку.
11.9. КОМБИНИРОВАННЫЕ ТРЁХМЕРНЫЕ СЕТКИ
Здесь мы рассмо1рим, как можно для комбинированной сетки с
ячейками в виде тетраэдров и прямоугольных параллелепипедов со-
гласовать конечные элементы. Возможно, для практики этот случай
имеет не слишком большое значение (поскольку в ситуациях, когда
часть подобласти удобно разбить па параллелепипеды, а часть прихо-
дится разбивать на тетраэдры из-за искривлённости или изломанности
границ, удобнее всего использовать шестигранные ячейки, обладаю-
щими близкими к тетраэдрам возможностями учёта сложной геомет-
рии и такими же как у параллелепипедов аппроксимационными свой-
11 ^.Комбинированные трёхмерные сетки
573
ствами1). Однако излагаемый здесь материал может быть очень поле-
зен для более глубокого понимания тех довольно важных и сложных
разделов МКЭ, которые связаны с построением согласованных конеч-
ных элементов на несогласованных сетках.
При использовании комбинированных сеток тетраэдры и паралле-
лепипеды, в отличие от треугольников и прямоугольников, нс согла-
суются автоматически2. Поэтому наша задача будет состоять в гом.
чтобы построить согласованные конечные элементы на комбиниро-
ванной сетке из параллелепипедов и тетраэдров.
Рис. 127. Пример стыковки параллелепипеда с тетраэдрами по одной грани
Сначала рассмотрим простейшую ситуацию, когда параллелепипед
с трилинейными базисными функциями стыкуется с тетраэдрами пер-
вого порядка по одной грани. Пример такой ситуации приведён на
рис. 127. На нём изображён параллелепипед с вершинами
{1,2,3,4,5,6,7,8} и тетраэдры {6,7,8,11}, {5,6,7,9}, {6,7,9,10}. Очевидно,
что локальные базисные функции параллелепипеда и тетраэдра, привя-
занные к одному и тому же узлу, в этом случае не могут быть сшиты в
непрерывную глобальную базисную функцию. Однако мы можем, не-
сколько изменив базис тетраэдрального элемента, сделать представи-
мой билинейную функцию на той грани тетраэдра, по которой он сты-
1 Фактически единственным значимым преимуществом параллелепипедов,
тетраэдров и прямых призм над шестигранниками является то, что их локаль-
ные матрицы могут быть вычислены без использования численного интегри-
рования, что существенно ускоряет генерацию конечноэлементной СЛАУ, и
это может стать важным фактором в том случае, когда генерация СЛАУ зани-
мает существенную часть от полного времени решения задачи.
2 Поскольку в трёхмерном случае глобальные базисные функции должны
быть непрерывны на гранях, а не только на рёбрах, как в двумерном случае.
574
11 .Комбинированные и несогласованные сетки
куется с параллелепипедом. Для этого достаточно ввести дополни-
тельную квадратичную базисную функцию вида , где г и j - это
локальные номера узлов тетраэдра, лежащих на ребре, которое являет-
ся диагональю грани стыковки параллелепипеда и тетраэдра. Функция
вида .£.7?, должна быть введена в базис всех тетраэдров, содержащих
такое ребро (являющееся диагональю грани стыковки). На рис. 127 это
ребро, соединяющее узлы с (лобальными номерами 6 и 7, и поэтому
квадратичная функция должна быть добавлена в базис тетраэдров
{6,7,8,11} (у этого гстраэдра это функция , поскольку на нём вер-
шины с глобальными номерами 6 и 7 имеют локальные номера I и 2),
{5,6,7,9} (у него это функция £2£3)и {6,7,9,10} (функция Д-С2)-
Нетрудно убедиться, что на каждом из
двух треугольников, получаемых при
разбиении прямоугольника одной из его
диагоналей, любую билинейную функ-
цию можно точно представить в виде
линейной комбинации трёх линейных
базисных функций треугольника и квад-
ратичной функции вида £,j£i (где i и j -
эго локальные номера узлов диагонали)
Будем считать, что прямоугольник разбит
диагональю на два треугольника так, как
это показано на рис. 128. На этом рисунке
в прямоугольничках приведены локаль-
ные номера узлов прямоугольника в
Рис. 128. I p.ilи», по коюроП
происходит CH.IKOliKil
параллелепипеда с ic'ipa > (рамп
треугольничках — локальные номера узлов левого треугольника Q2, в
кружочках - локальные номера узлов правого треугольника Q3 . Тогда
локальная базисная функция прямоугольника ф^1 на треугольниках
П2 и Q3 может бы и, представлена через базисные функции треуголь-
ников
4>i‘2 = 4!'2. = А'1. Ф$/2 = 412, Ф“2 = 412 ’ ф2 3 = ’ Фз3 = 4 ' > ф“2 = (11.42) (Н.43)
—
в виде
Фр1 =ф;22 _ф»2 на q2> (11.44)
< на Q3. (Н-45)
Аналогично представляется функция ф^ 1.
Ф? =<2 -Ф? "а «2. (11.46)
11 ^.Комбинированные трёхмерные сетки
575
< = на Г23. (11.47)
Функции же ф21 и Ф31 представляются в виде
наП2, (11.48)
Ф21=Фз:?+Ф?5 наО3, (11.49)
ф“1 = ф“2 + ф^2 * на q2 ? (1 1.50)
ф£321=ф^ наП3. (11.51)
Справедливость соотношений (11.44)—(11.51) можно доказать на-
прямую на основе явных представлений базисных функций прямо-
угольника и треугольников Приведём это доказательство для соотно-
шения (11.44).
Исключительно для упрощения выкладок будем считать, что левый
нижний угол прямоугольника имеет координаты* х = 0, у — 0. Тогда
(11.52)
где /г,,, и h.lf - размеры прямоугольника Qj. Функции же фр2 и ф^'2 (с
учётом (11.42)) на О2 имеют вид
<г=1-ф, <
откуда
-ih^2 — 1 У.— 1 —У_ — j —2-------У—।—2L. .У— (] ] 53)
-1 hy hy]h:i: h.f hv+hx hy-
Сравнивая (11.52) с (11.53), убеждаемся в справедливости (1 1.44).
Справедливость остальных соотношений (11.45)—(11.51) можно дока-
зать абсолютно аналогично.
Вообще говоря, соотношения (11.44)-(11.51) могут быть получены
из следующих соображений. Любая билинейная функция является
неполным квадратичным полиномом на прямоугольнике. С другой
стороны, любой квадратичный полином представим в базисе квадра-
тичных треугольных элементов. Значит, любая билинейная функция
должна быть точно представима через базисные функции квадратич-
ных треугольных элементов. Однако нам желательно, чтобы в квадра-
тичном базисе треугольного элемента присутствовали линейные функ-
1 Это нисколько не уменьшает общности дальнейших рассуждений вслед-
ствие инвариантности матриц конечных элементов к их переносу, которая
была доказана в разделе 5.6.
576
11 .Комбинированные и несогласованные сетки
ции. Квадратичный базис такого тина нетрудно построить - он являет-
ся базисом иерархического треугольного элемента, который получает-
ся добавлением к трём линейным базисным функциям элемента ещё
трёх квадратичных базисных функций вида £г£1. Более подробно ие-
рархические базисы мы рассмотрим несколько позже в следующем
разделе. Здесь же для представления билинейных функций нам доста-
точно воспользоваться лишь свойством его полноты (в смысле пред-
ставимости любой квадратичной функции). С учётом этого свойства
любая билинейная функция ф° точно представима в виде линейной
комбинации шести базисных функций ф^ квадратичного иерархиче-
ского треугольного >лсмента:
G
= (|L54)
7=1
где ф^ представляются через £ -координаты треугольника в виде
ФС=£., ф£=£2, ф£ = Д,
Наши же коэффициенты </• в этом случае довольно просто - для
этого достаточно приравнять значения левой и правой части соотно-
шения (11.54) сначала в трёх вершинах треугольника (в результате
сразу будут получены значения (р , q2 и q3, поскольку в каждой из
вершин ненулевой является только одна из шести базисных функций
G
ф^ ), а затем приравнять ф° и <7/фу в серединах трёх ребер тре-
7=1
угольника (с учётом уже найденных значений , q2 и 9з). Значения
д4 > 95 и 9g будут найдены также без решения системы, поскольку на
каждом из рёбер ненулевой является только одна из базисных функ-
ций ф4, ф£ и ф$ и какие-то две из функций ф^ , ф-f и фз (но их
веса q±, q2 и q3 к лому моменту уже будут найдены и поэтому для
нахождения q4 , qr> или q(i из значения ф° в середине соответствую-
щего ребра нужно вычесть значение дхф^ + q24’-2 + 9з”Фз и поделить
его на 4, поскольку (функции ф^1 для j > 4 в середине «своего» ребра
равны у ).
Проведённые выше рассуждения о том, как можно получить фор-
мулы представления билинейной функции через квадратичные функ-
ции треугольника с использованием иерархического базиса, полезны
тем, что этот подход вполне может быть использован и для представ-
ления биквадрагичных функций (и функций более высокого порядка)
11.9.Комбинированные трёхмерные сетки
577
через иерархические базисы треугольных элементов к ситуации, когда
нужно стыковать параллелепипеды и тетраэдры высоких порядков.
Однако более тщательно обдумать эту ситуацию мы рекомендуем чи-
тателю уже после того, как он ознакомится с принципами построения
иерархических базисов в следующем разделе.
Теперь вернёмся к проблеме согласования базисных функций па-
раллелепипеда и примыкающих к его грани тетраэдров для элементов
первого порядка. Для построения согласованных элементов нам необ-
ходимо получить непрерывные глобальные базисные функции. Стан-
дартная же сборка локальных матриц в глобальную фактически будет
означать, что использован базис {ФГ } сразрывными функциями (раз-
рывные функции привязаны к узлам грани стыковки). Поэтому в этот
базис нужно добавить функции вида (эти функции должны быть
пронумерованы, как всегда, после всех функций, привязанных к вер-
шинам конечных элементов). Тогда на основе соотношений вида
(11.44)-(1 1.51) вместо разрывных функций ф’"' можно построить не-
прерывные базисные функции ф*'. Так для ситуации, изображённой на
рис. 127, разрывными являются функции ф$г, фс"‘, ф”г и ф^, и из
них (с учётом соотношений (11.44)—(11.51)) непрерывные функции
получаются с помощью кусочно-квадратичной базисной функции ф}2
(имеющей на тетраэдрах {6,7,8,11}, {5,6,7,9}, {6,7,9,10} вид , i и
j — локальные номера вершин ребра {6,7}) в виде
ф£=ф!Г-Ф12, -Фс=<+Ф12,
Ф^ = ФГ+Ф^> Ф£=ФГ-«.
Очевидно, что матрица Т такого преобразования базисов в разре-
женном столбцовом формате без учета единичной подматрицы будет
иметь вид
ig = {1.5), .19 = {5.6,7,8}, дд = {-1.1.1.-1}.
На рис. 129 приведён пример стыковки параллелепипеда с тетраэд-
рами по двум прямоугольным граням. Матрица Т-преобразования в
этом случае (также в разреженном столбцовом формате без учёта еди-
ничной подматрицы) будет вид
ig = {1,5,9} , jg = {5,6,7,8,2,4.6.s} , дд = {-1,1,1-1,-1,1.1-1} .
Таким образом, для согласования параллелепипедов с тетраэдрами
нам понадобятся тетраэдральные конечные элементы с пягыо локаль-
ными базисными функциями1:
Ф1=Д. ф2=£2, Фз = £3, ф4 = Д, ф5=££7,
1 Эти элементы, в общем-то, можно интерпретировать как переходные
между стандартными параллелепипеидальными и тетраэдральными элемен-
тами.
578
11 Комбинированные и несогласованные сетки
где г и j' - это локальные номера узлов ребра, являющегося диагона-
лью прямоугольной грани стыковки рассматриваемого тетраэдра с
параллелепипедом. Очевидно, что локальные матрицы жёсткости G и
массы М этого элемента в качестве подматрицы 4x4 содержат соот-
ветствующие локальные матрицы стандартного линейного тетраэд-
рального элемента (см. формулы (6.44), (6.45)). Компоненты же пятой
строки (и пятого столбца) имеют следующий вид1:
67/5 = G51 = X ' 9 j ' Ч (° 1 + CY1 ) + 06-2 ^Ot2 + С*2 ) + Ot3 ((*3 4- QT.J )),
если I i и I j,
если I = i и I j или I = j и I i .
Puc. 129. Пример стыковки параллелепипеда с тетраэдрами по двум граням
1 В принципе, эти матрицы могут быть получены из стандартного квадра-
тичного иерархического элемента при удалении из него трёх квадратичных
базисных функций, ассоциированных с тремя «ненужными» нам рёбрами, т.е.
выбрасыванием соответствующих строк и столбцов. Эта процедура является
стандартной при согласовании иерархических базисов различных порядков и
более детально обсуждается в следующем разделе.
12.1 .Использованиетехнологии ...
579
12. ПОСТРОЕНИЕ КОНЕЧНОЭЛЕМЕНТНЫХ
АППРОКСИМАЦИЙ НА СЕТКАХ С ЭЛЕМЕНТАМИ
РАЗНЫХ ПОРЯДКОВ. ИЕРАРХИЧЕСКИЕ БАЗИСЫ
Как мы уже говорили, повышения точности конечпоэлементной
аппроксимации можно добиваться двумя путями: уменьшением разме-
ров элементов или повышением их порядка (т.е. повышением степени
полиномиальных базисных функций). Более подробно соответствую-
щие технологии будут обсуждаться в следующем разделе. Для этих
технологий очень важной является возможность изменения порядка не
всех элементов сетки, а только некоторой их части. Поэтому в данном
разделе мы рассмотрим, как можно построи ть согласованную конечно-
элементную аппроксимацию при наличии в сетке элементов разных
порядков.
12.1. ИСПОЛЬЗОВАНИЕ ТЕХНОЛОГИИ Т-ПРЕОБРАЗОВАНИЯ
ДЛЯ СОГЛАСОВАНИЯ ЭЛЕМЕНТОВ РАЗНЫХ ПОРЯДКОВ
Рис. 130. Пример сетки с элементами
разных порядков
Покажем, как может быть использована рассмотренная нами в
предыдущем разделе технология Т -преобразования для согласования
элементов разных порядков на
простейшем примере, когда били-
нейный и биквадратичный эле-
менты граничат друг с другом.
Эта ситуация изображена на
рис. 130. Как и ранее, в кружках
показана локальная нумерация
узлов (и базисных функций), а в
прямоугольничках — глобальная.
Очевидно, что стандартная
сборка в этом случае будет озна-
чать, что в базис включены функ-
ции ф-2Г, Фе" и 'Фи * разрывные
вдоль ребра Г, являющегося гра-
ницей между билинейным элементом {Д и биквадратичпым элементом
0-2- Действительно, в этом случае (т.е. при стандартной сборке) гло-
бальная базисная функция Ф2" на ребре Г со стороны элемента
580 12.Построение конечноэлементных аппроксимаций на сетках ...
является локальной базисной функцией ф^1 и поэтому линейна на Г
(и, например, в узле с глобальным номером 11 она равна 0.5), а со сто-
роны Q2 Фг" является локальной базисной функцией фр2 и поэтому
квадратична (в узле с глобальным номером 11 она равна нулю). То же
самое можно сказать и о функции ф^' . Функция же ф]'[ на вообще
равна нулю (поскольку ей не соответствует никакая локальная базис-
ная функция), а на Q2 это квадратичная базисная функция, равная
единице в узле с глобальным номером 11
Устранить разрывы в глобальных базисных функциях можно ана-
логично тому, как это было сделано в предыдущем разделе - преобра-
зованием базиса {ф™ } в базис {ф^}, содержащий только непрерыв-
ные функции. Функции ф‘ будем строить из ф'"‘, как и в предыдущем
разделе, с помощью матрицы перехода Т :
фс = Тф"е, (12 1)
। де, как и ранее, ф'" - вектор, составленный из функций ф',г,
г = 1...П (п - число узлов в сетке), фг — вектор, составленный из
функций ф£, г = 1... п(., а Т - матрица перехода размера п(. х п .
Чтобы сделать непрерывной глобальную функцию, соответствую-
щую узлу с глобальным номером 2, нужно, очевидно, сделать её ли-
нейной вдоль Г со стороны Q2 (поскольку, наоборот, получить на Г
квадратичную функцию как линейную комбинацию линейных базис-
ных функций элемента Q1 невозможно). Это можно сделать, предста-
вив ф2 в виде
Ф2 =ФГ +0 5ФГГ
Аналогично может быть получена глобальная функция :
= ФГ+0.5Ф1Т.
Остальные базисные функции ф’,г (естественно, для г < 10 ) были
непрерывными, и поэтому соответствующие функции ф[ должны про-
сто совпасть с ними
Таким образом, матрица перехода имеет вид
12.1 .Использование технологии ...
581
1 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0 0.5
0 0 1 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0 0
т = 0 0 0 0 1 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 1 0 0 0.5
0 0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 и 0 0 0 1 0
I 1-го
Рис. 131. Пример сетки с тремя
биквадратичпыми и одним
билинейным элементом
Очевидно, что компоненты
столбца (соответствующего (фактиче-
ски удалённой из базиса {ф' } (функ-
ции), как и при обработке терминаль-
ных узлов, являются значениями ло-
кальных базисных (функций линейного
элемента в узле, который фактически
отсутствует на линейном элементе.
Это является общим правилом для
стыковки любых лагранжевых эле-
ментов - если, например, на ребре Г
стыкуются биквадратичный элемент с
бикубическим, то терминальными
становятся узлы бикубического эле-
мента (на ребре Г) и компоненты
матрицы Т вычисляются как значе-
ния в этих терминальных узлах би-
квадратичных функций (номер стро-
ки- это глобальный номер биквадра-
тичной функции, номер столбца -
глобальный номер терминального
узла).
Приведём ещё один, чуть более сложный, пример построения мат-
рицы перехода при стыковке лагранжевых элементов первого и второ-
го порядка На рис 13 I изображена ситуация, когда два биквадрагич-
ных элемента (И2 и ^з) стыкуются с одним билинейным (П,). В та-
ком случае матрица Т в разреженном столбцовом (формате будет
иметь вид (напомним, что в этом формате не хранится левая верхняя
единичная подматрица матрицы Т):
ig = {1,3,5},
j(J = {2,8,7,8} ,
582 12.Построение конечноэлементных аппроксимаций на сетках ...
В принципе, технология Т -преобразований вполне применима и
для стыковки лагранжевых элементов с эрмитовыми. Пример такой
ситуации приведён на рис. 132. Обратим внимание на то, как пронуме-
рованы функции ф.,;. Функции ф1 и - это стандартные билиней-
ные, а ф5 4- ф8 и 'Ф1з4-ф1с - стандартные бикубические функции.
Функция ф2 отвечает за значение решения в узле 2, ф3 — за его произ-
водную в узле 2 на элементе Q2 (на элементе эта функция рав-
о2
на нулю), ф4 - за производную в узле 2 на элементе Q2 (на
элементе она тоже равна нулю), ф1() - за значение решения в уз-
ле 5, фп - за его производную в узле 5 на элементе Q2 > Ф12 ~ за
производную в узле 5 на элементе П2 (фп и *ф12 на Qj равны
нулю). Функции же ф17 и ф18, построенные из локальных функций
•ф‘/1 и и отвечающие в узлах 2 и 5 за значение производной вдоль
ребра Г, пронумерованы последними потому, что в непрерывном ба-
зисе [ф* } такого типа функции отсутствуют.
фд Ф1(),Ф11»Ф18»Ф12 Ф13>Ф14>Ф15>Ф16
Рис. 132. Пример сетки с билинейным и эрмитовым бикубическим элементами
И в этом случае для построения матрицы Т нужно выразить на
общем ребре Г линейные функции через кубические эрмитовы. Не-
трудно убедиться, что
ф-2 = ФГ - ф Фп - ФК, ФК = ФК + ФК + Ф ФК,
где Л(/ - длина ребра Г. Соответственно матрица Т в разреженном
столбцовом формате будет иметь вид
12.2.Иерархические базисы ....
583
гр = {1,3,5}, jg = {2,10,2,10}, gg =
1 1
Л hy
1 1
Ь'у
12.2. ИЕРАРХИЧЕСКИЕ БАЗИСЫ.
СОГЛАСОВАНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ РАЗНЫХ ПОРЯДКОВ
Как было показано выше, если конечноэлементная сетка содер-
жит лагранжевы элементы разных порядков, то их можно согласовы-
вать с помощью специальных технологий, таких, как технология
Т-преобразования (а можно воспользоваться и технологией переход-
ных элементов). Однако элементы разных порядков можно согласовы-
вать и гораздо проще, если использовать на них в качестве базисных
функции специального вида - так называемые иерархические базисные
функции. Определяется иерархический базис следующим образом.
На конечном элементе иерархическим называют такой базис,
который содержит все базисные функции этого элемента более низко-
го порядка.
12.2.1. ИЕРАРХИЧЕСКИЕ БАЗИСЫ ОДНОМЕРНЫХ ЭЛЕМЕНТОВ
Об иерархических базисных функциях мы уже упоминали в раз-
деле 4.4.1 (с. 139) при построении одномерного элемента второго по-
рядка. Напомним, что в этом случае для построения квадратичного
конечного элемента к двум линейным базисным функциям добавля-
лась одна квадратичная. В дальнейшем (как это принято в большинст-
ве монографии и учебников по МКЭ) при построении иерархических
базисов в качестве шаблонного мы будем использовать одномерный
элемент = [—1,1]. На этом элементе линейные базисные функции
имеют вид
= Фг(У = ЦК (12.2)
т.е. иерархические базисные функции конечного элемента первого
порядка просто совпадают с лагранжевыми базисными функциями.
Иерархический базис конечного элемента второго порядка опреде-
лим добавкой к функциям (12.2) квадратичной функции, равной нулю
на концах Р :
<₽3(о=1-е- • ('гл
Для построения иерархического базиса каждого следующего по-
рядка р нужно добавить к базису элемента предыдущего порядка лю-
бой полином степени р, равный нулю на концах , например поли-
ном
V„+1(O = V'-2(1-^). (12.4)
584 12.Построение конечноэлементных аппроксимаций на сетках ...
зис, в котором
Очевидно, что эта формула определяет и функцию (12.3) элемента
второго порядка (при р = 2 ), и поэтому построенный иерархический
базис определяется соотношениями (12.2) и соотношением (12.4) при
р > 2.
Рассмотренный иерархический базис не является единственно воз-
можным, поскольку существует множество полиномов степени р > 3 ,
равных нулю на концах 0е . Полиномы вида (12.4) имеют очень про-
стую форму, но коэффициенты при них в разложении конечноэле-
ментного решения по такому иерархическому базису не имеют какой-
либо очевидной интерпретации (как, например, значение этого реше-
ния в узлах или значение его каких-либо производных). Как мы пока-
жем позже, при согласовании иерархических элементов на несогласо-
ванных сетках это не очень удобно, поскольку может приводить к до-
вольно ощутимым дополнительным вычислительным затратам. По-
этому в таких ситуациях лучше использовать такие базисы, которые
позволяют находить коэффициенты разложения по базисным функци-
ям относительно простыми способами. Например, это может быть ба-
определяются формулой1:
если р чётно,
(12.5)
если р нечётно.
Нетрудно убедиться, что у функций, определяемых соотношением
(12.5), в точке Е, = 0 все производные не ниже второго порядка, кроме
производной порядка р, равны нулю, и только производная порядка р
равна единице. Это позволяет легко вычислять коэффициенты разло-
жения любого полинома по такому базису. Позже мы покажем, как
удобно это свойство базисных функций при согласовании иерархиче-
ских элементов на несогласованных сетках в двумерном и трёхмерном
случаях.
Можно также построить такой иерархический базис на одномерных
элементах, что почти у всех базисных функций первые производные
будут ортогональны друг другу (т.е. интегралы по от произведе-
ний первых производных разных базисных функций будут равны ну-
лю). Базис такого типа можно построить с помощью ортогональных
полиномов Лежандра.
Полином Лежандра степени р может быть определён на с по-
мощью соотношения
Зии для р > 2
Фр+1(У =
(12.6)
1 Первые две функции определяются, как и ранее, формулами (12.2)
12.2.Иерархические базисы ....
585
Кроме того, для полиномов Лежандра справедливо рекуррентное
соотношение
Р„ (0 = (Е.) - Р„-2 (О, (12.7)
которое позволяет вычислить любой полином Лежандра, если извест-
ны первые два из них:
Ж) = 1. Л(0 = С (12.8)
Приведём ещё несколько полиномов Лежандра:
P2(E.) = i(3^-l)> Р3(О = Ж3-ЗЕ,),
Р4(Е,) = |(35^-30£,2+з), Р5(О = |(бЗ£.5-7О^+15^). (12.9)
Иерархические базисные функции с ортогональными производны-
ми (начиная с квадратичной) могут быть получены из полиномов Ле-
жандра по формуле
фр+1(У = <7Н1 f Рр-.Дт])^, р >2, (12.10)
-1
где ср+1 - произвольная ненулевая константа. Можно также опреде-
лить эти функции по формуле
<₽„+1(У = с;,+1(Р/,(0-Р„_2(0), р>2. (12.11)
Коэффициент с„,+1 в соотношении (12.10) (так же как и коэффици-
ент с'р+1 в (12.11)) можно выбрать так, чтобы базисная функция имела
удобный вид. Приведём вид нескольких (первых) базисных функций с
ортогональными производными:
Фз(0 = С2-1. Ф4(О=43-Е.
Ф5(О = б^-0^+1, фс(О = 7^-10^+ЗЕ.. (12.12)
Заметим, что производные этих функций ортогональны также и
производным линейных функций (12.2). Неортогональными в системе
функций (12.2), (12.10) являются производные только двух линейных
функций (12.2). Кроме того, обратим внимание читателя па то, что
функции фз и ф4 из (12 12) с точностью до коэффициента совпадают
с соответствующими функциями, определяемыми соотношением
(12.5), те в системе функций (12.5) квадратичная и кубическая функ-
ции также имеют производные, ортогональные друг другу и произ-
водным линейных функций (12.2). Это свойство ортогональности про-
изводных может быть учтено при построении локальных матриц жёст-
кости. Если с помощью таких функций строятся базисные функции
586 12,Построение конечноэлементных аппроксимаций на сетках ...
двумерных или трёхмерных элементов, то и в их локальных матрицах
жёсткости будет достаточно много нулевых компонент, которые не
нужно хранить в глобальной матрице жёсткости.
12.2.2. ИЕРАРХИЧЕСКИЕ БАЗИСЫ НА ПРЯМОУГОЛЬНИКАХ
На прямоугольных элементах иерархические базисы высоких
порядков можно строить из одномерных иерархических базисов точно
так же, как это было сделано при построении лагранжевых (и эрмито-
вых) элементов. Так, биквадратичный иерархический базис на шаб-
лонном1 элементе £1Е =
функции:
К.
2
Лу hy
содержит следующие
(12.13)
(12.14)
(12.15)
(12.16)
(12.17)
Очевидно, что первые четыре функции - это стандартные билиней-
ные функции на прямоугольнике, и поэтому этот элемент действи-
тельно является иерархическим.
Функции ф5, фс, ф7 и ф8 являются линейными по одной коорди-
нате и квадратичными по другой. Эти четыре функции на границах
элемента отличны от нуля каждая только на одном «своём» ребре: ф5
на левом, фс па правом, ф7 на нижнем и ф8 на верхнем. Поэтому
функции ф5, фС1, ф7 и ф8 удобно ассоциировать не с узлами элемен-
та, а с соответствующими рёбрами прямоугольника (на которых они
отличны от нуля).
1 В данном случае под шаблонным понимается прямоугольный элемент с
размерами /г,. и h,y и центром в начале координат, т.е. любой прямоугольный
элемент О,„ получается из этого шаблонного только сдвигом и поворотом, и
поэтому локальные матрицы жёсткости и массы любого прямоугольного эле-
мента О,,, совпадут с локальными матрицами шаблонного элемента (см. раз-
дел 5.6)
12.2.Иерархические базисы ....
587
Функция же грд является биквадратичной и отлична от нуля внутри
элемента и равна нулю на всех его границах.
Так же как иерархический базис прямоугольного элемента второго
порядка был получен добавкой к базису (12.13)-(12.14) элемента пер-
вого порядка пяти функций (12.15)-(12.17), иерархический базис пря-
моугольного элемента третьего порядка должен быть построен добав-
лением базисных функций к базису (12.13)-(12.17). Очевидно, что, как
и в случае лагранжевых элементов, полный бикубический базис дол-
жен содержать 16 функций.
Добавляемые функции строятся1 в виде произведения одномерных
иерархических функций предыдущих порядков от одной координаты
на кубические от другой и произведения двух одномерных кубических
функций от ж и у:
Ф10 = Ф1
- У
h
V1').
Фи (х,у) =
Ф13 у) = Ф>4
/т
Ф14 &у) = Фз
(12.18)
(12.19)
(12.20)
(12.21)
Функции ф1(), фп , Ф12 и Ф13 (так же, как и ф5, фс, ф7 и ф8 ) от-
личны от нуля каждая только на одном «своём» ребре, и поэтому они
также ассоциируются с этими рёбрами. Остальные функции, очевид-
но, равны нулю на всех границах элемента (они ассоциируются, как и
ф9, с внутренней частью элемента).
Аналогично строятся иерархические базисы на прямоугольных
элементах более высоких порядков- добавляются функции, являющие-
ся произведениями одномерных иерархических функции предыдущих
порядков от одной координаты (.г или у) на одномерный иерархиче-
ский полином высшей степени от другой координаты (у или х ), и ещё
одна функция, являющаяся произведением двух одномерных полино-
мов высшей степени от х и у соответственно.
Локальные матрицы иерархических элементов так же, как это дела-
лось для лагранжевых и эрмитовых элементов, удобно строить из локаль-
ных матриц одномерных элементов (см. с. 233 и разделы 5.2.4—5.2.6).
Заметим, что определённые таким способом иерархические базисы
порождают те же самые конечномерные пространства функций, что и
1 Аналогично тому, как строились и добавляемые к билинейным базисные
функции б и квадратичного иерархического элемента.
588 12.Построение конечноэлементных аппроксимаций на сетках ...
базисы из лагранжевых функций. Но иногда используют и иерархиче-
ские базисы с меньшим количеством функций. Например, на элементе
второго порядка можно не вводить функцию ф9, поскольку при уда-
лении этой функции хотя и перестаёт быть представимым полный би-
квадраптчный полином, но при этом не нарушается представимость
любых полиномов до второй степени. Точно так же на элементе
третьего порядка можно не вводить функции ф9, ф14, ф15 и ф1С. Но
при этом функция ф9 должна присутствовать в базисе элемента чет-
вёртого порядка, поскольку без неё уже не будет представим произ-
вольный полином четвёртой степени.
Очевидно, что иерархические базисы на прямоугольнике с умень-
шенным числом функций1 имеют как достоинства, так и недостатки по
сравнению с полными биквадратичными, бикубическими и т.п. бази-
сами. К очевидным достоинствам относится уменьшение размерности
конечноэлементной СЛАУ, а к недостаткам - возможное снижение
точности получаемого конечноэлементного решения.
12.2.3. ИЕРАРХИЧЕСКИЕ БАЗИСЫ НА ПРЯМОУГОЛЬНЫХ ПАРАЛЛЕЛЕПИПЕДАХ
Покажем, как строятся иерархические базисы на прямоугольных
параллелепипедах. Для
hy hy
2“,-2
Q /? _ _ ^:г. Ь':г
2’2
этого введём шаблонный элемент
/г2 hz
2’2'
Иерархические базисные
х
X
функции на этом элементе так же, как и лагранжевы базисные функ-
ции (см. раздел 6.1), могут быть построены через одномерные шаблон-
ные иерархические функции фА. (6,) (определённые соотношением
(12.2) и любым из соотношений (12.4), или (12.5), или (12.10) или
(12.1 1)) с помощью формулы
•фДж,?/, г) = ф|1(2)
(12.22)
где p((), v(i) и '0 (?’) - целочисленные функции, определяемые для
элементов до третьего порядка включительно следующей табл. 20:
Таблица 20
1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
в 1 2 1 2 1 2 1 2 1 2 3 3 1 2 3 3
V 1 1 Т" ~Т 1 1 2 Г ~Т 1 2 3 3 1 2
0 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2
1 Вообще говоря, эти базисы порождают те же пространства, что и базисы
так называемых серендиповых элементов |4, 10].
12.2.Иерархические базисы ....
589
i 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
Н 1 2 1 2 1 2 3 3 3 3 3 1 2 4 4 1
V 1 1 ~Т~ ~т~ 1 Т~ 3 ~Т" 4 “Т“ “7Г-
0 3 3 3 3 3 3 3 3 1 2 3 1 1 1 1 2
i 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
И 2 4 4 1 2 1 2 1 1 1 2 2 2 3 4 4
V 4 1 2 1 1 2 2 3 4 4 4 1 1 1
г) 2 2 2 4 4 4 4 4 3 4 4 3 4 4 3 4
i 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
li 3 4 4 3 4 4 3 4 4 4 3 3 4 4 3 4
V Т~ ~Т ~Т~ 4 3 4 3 4 ~Т~ 4 Т- 4
'0 4 3 4 1 1 1 2 2 2 3 3 4 3 4 4 4
Таким образом, первые 8 из функций (12.22) являются базисными
для элемента первого порядка. Эти 8 и следующие 19 (т.е. первые 27)
функций являются базисными для элемента второго порядка (триквад-
ратичного). Базис элемента третьего порядка (трикубического) получа-
ется добавлением к 27 функциям триквадратичного элемента следую-
щих за ними 37 функций (т.е. этот базис содержит 64 функции). Для
элемента четвёртого порядка добавляется 61 функция (в нём 53 = 125
функций) и т.д.
Обратим внимание, что в трёхмерном случае иерархические базис-
ные функции удобно ассоциировать не только с узлами и рёбрами, но
и с гранями элементов Принцип ассоциирования остаётся тем же: если
базисная функция равна нулю на всех гранях, кроме одной, то она с
этой гранью и ассоциируется. Функции, равные нулю на всех границах
элемента, можно ассоциировать с центром элемента. Информация о
том, с каким узлом, ребром или гранью ассоциирована базисная функ-
ция, необходима для глобальной нумерации
Табл. 20 фактически определяет следующее соответствие базисных
функций узлам, рёбрам и граням параллелепипеда, с которыми эти
оазисные функции ассоциируются (для иерархических элементов до
третьего порядка). Первые 8 функций ассоциируются с вершинами (и
их номера совпадают с локальными номерами вершин). Информация о
том, какие функции соответствуют каким рёбрам, приведена в табл. 21.
В табл. 22 приведена информация о функциях, ассоциированных с
гранями. Оставшиеся функции ассоциированы с центром элемента —
это функции с номерами 27, 58-г64 (индексы р, v и '0 в (12.22) для
этих функций принимают значения 3 или 4).
590 12.Построение конечноэлементных аппроксимаций на сетках ...
Таблица 21
рёбра .г=—Л(у2 У=~Лу/2 а;=Л-,у2 y=-h,,f2 Г £=—ht j! I V=hyp x~hrl'2 y=hy/2
значе- НИЯ индек- сов Н 1 2 1 2
и “Г“ 1
0 3,4 3,4 3,4 3,4
номера базис- ных функций 17,36 18, 37 19, 38 20, 39
рёбра |у=-Л,//2 z——hzJ'2 J У=Л?// 2 z=-hz/2 У=~^1'2 z=hzj'2 У=Ьу/2 z—hzl'2
значе- НИЯ индек- сов Н 3,4 3,4 3,4 3,4
V 1 ~т~ 1
0 1 1 2 2
номера базис- ных функций 11, 30 12, 31 15, 34 16,35
рёбра x——ht/2 z=-hz/2 x=htj'2 z——hz]2 z=hz/2 x=A;i;/2 z=h,j2
значе- ния индек- сов к i 2 1 2
V ~"3, 4 3,4 3,4
0 1 I 2 2
номера базис- ных функций 9, 28 10, 29 13, 32 14, 33
Таблица 22
грани У=-^чр y^hv/'2 ^-hzp. z=hzJ2
значения индексов И 1 2 3,4 3,4 3,4 3,4
17 3,4 3,4 Г" Т~ 3,4 ~^4
0 3,4 3,4 3,4 3,4 1 2
номера базис- ных функций 21,40, 41,42 22, 43, 44,45 23,46, 47, 48 24, 49, 50, 51 25, 52, 53, 54 26. 55, 56. 57
12.2.4. СОГЛАСОВ \IIIIE ИЕРАРХИЧЕСКИХ ЭЛЕМЕНТОВ РАЗНЫХ ПОРЯДКОВ
НА ПРЯМОУГОЛЬНИКАХ И ПАРАЛЛЕЛЕПИПЕДАХ
Иерархические элементы удобны тем, что позволяют очень легко
согласовывать элементы разных порядков. В качестве примера пока-
жем, как согласуются элементы второго и третьего порядка на прямо-
угольнике.
12.2.Иерархические базисы ....
591
а б
Рис. 133. Локальная нумерация базисных функций на элементах второго («)
и третьего (б) порядка
На рис. 133 слева изображён элемент второго порядка, а справа -
элемент третьего порядка. Для согласования этих элементов достаточ-
но на элементе третьего порядка удалить из базиса одну функцию,
ассоциированную с левым ребром и являющуюся на этом ребре куби-
ческой. В соответствии с принятой нами локальной нумерацией
(см. раздел 12.2.2) это функция с номером 10. Таким образом, ненуле-
вые на этом ребре глобальные базисные функции получаются сшивкой
локальных базисных функций ф2, *4’4 и Фс левого элемента с локаль-
ными базисными функциями ,
Фз и ф>5 правого элемента соот-
ветственно. Полученные в резуль-
тате такой сшивки глобальные
Рис. 134 Глобальная нумерация
после согласования биквадратичпого
и бикубического элементов
базисные функции являются не-
прерывными, и поэтому конечные
элементы оказываются согласо-
ванными.
На рис. 134 перечислены все
глобальные базисные функции (с
привязкой к вершинам, рёбрам и
центрам элементов, с которыми
они ассоциированы) после согласования квадратичного и кубического
элемента1. Таким образом, с левым ребром кубического элемента (по
которому этот элемент стыкуется с квадратичным) ассоциирована
1 Фактически для нумерации глобальных базисных функций мы использо-
вали принцип геометргтеского упорядочения точек, к которым они привяза-
ны (см. с. 513). При этом функции, ассоциированные с рёбрами, мы привязали
к точкам на серединах этих ребер, а функции, ассоциированные с центрами
элементов, к точкам в центре элементов. Упорядочение точек делалось снача-
ла по у, а затем по х для уменьшения ширины ленты (или профиля) матри-
цы. Функции, привязанные к одной и той же точке на ребре или в центре эле-
мента, упорядочивались по возрастанию их порядка (т.е. степени полинома).
592 12.Построение конечноэлементных аппроксимаций на сетках ...
только одна (квадратичная) глобальная базисная функция (в отличие
от остальных его рёбер, с которыми ассоциировано по две функции). В
результате вся процедура согласования выродилась в исключение из
базиса правого элемента локальной базисной функции *ф1() (и поэтому
ей и не нужно было давать никакого глобального номера).
Согласование иерархических элементов разных порядков на парал-
лелепипедах идейно выполняется так же. Однако в этом случае согла-
сование нужно проводить по объектам двух типов: рёбрам и граням1.
Рассмотрим изображённую на рис. 135 ситуацию, когда контакти-
руют элемент второго порядка (с вершинами {7, 8, 10, II, 13, 14,
15, 16}) и два элемента третьего порядка (это элемент П2 с вершинами
{1, 2, 4, 5, 7, 8, 10, 11} и элемент Q3 с вершинами {2, 3, 5, 6, 8, 9, И,
12}). Поскольку грань {7, 8, 10, 11} является общей для элементов
разных порядков, с ней должны быть ассоциированы только глобаль-
ные базисные функции, соответствующие элементу более низкого по-
рядка. В нашем случае это означает, что с ней должна быть ассоцииро-
вана только одна базисная функция (из иерархического базиса элемен-
та второго порядка, являющаяся биквадратичной на этой грани), а из
базиса элемента П2 должна быть исключена ассоциированная с этой
гранью базисная функция элемента третьего порядка (являющаяся на
ней бикубической). При этом ассоциированная с гранью {2,5,8,11}
бикубическая (на ней) функция остаётся в глобальном базисе (и соот-
ветственно как локальная базисная функция элементов П2 и ^з)-
11а всех четырёх рёбрах, которые являются общими для элементов
третьего и второго порядка (это рёбра {7,8}, {7,10}, {8,1 1} и {10,1 1}),
нс должно быть ассоциированных с ними кубических базисных функ-
ций. Именно поэтому из базиса элемента П2 должны быть удалены 4
кубические (на каждом из рёбер {7,8}, {7,10}, {8,11} и {10,11}) ло-
кальные функции. Поскольку ребро {8,11 ; принадлежит ещё и элемен-
ту Q3, из сто локального базиса тоже должна быть удалена кубическая
функция, ассоциированная с этим ребром.
1 Если на параллелепипедах используются иерархические базисы не выше
третьего порядка, аналогичные серендиповым, то согласование по граням не
нужно проводить, поскольку в этом случае нет ассоциированных с гранями
базисных функций.
12.2.Иерархические базисы ....
593
Рис. 135. К согласованию иерархических элементов
разных порядков на параллелепипедах
Итак, процедура согласования иерархических базисов разных по-
рядков и в трёхмерном случае фактически свелась к исключению из
локального иерархического базиса элемента некоторых функций, ас-
социированных с рёбрами и гранями (для тех рёбер и граней, по кото-
рым рассматриваемый элемент граничит с элементами более низкого
порядка). Поэтому фактически при занесении локальной матрицы эле-
мента в глобальную соответствующие строки и столбцы в ней должны
быть просто проигнорированы (и поэтому они могут даже и не генери-
роваться).
Таким образом, основной проблемой при согласовании иерархиче-
ских базисов является создание процедуры, позволяющей для каждого
элемента определять глобальные номера всех ненулевых на нём базис-
ных функций (т.е. установление соответствия локальных номеров его
базисных функций глобальным). Это проблема может решаться раз-
ными путями.
Можно, например, для каждого элемента наряду со списком всех
его вершин и номеров глобальных базисных функций хранить номера
всех элементов, смежных с ним по граням и рёбрам. В этом случае
процедура глобальной нумерации может быть реализована следующим
достаточно простым способом. Первые N номеров получаю! базис-
ные функции, ассоциированные с вершинами элементов (N общее
число вершин элементов). Затем нумеруем все базисные функции пер-
вого элемента и номера функций, ассоциированных с сю гранями и
рёбрами, заносим в соответствующие места1 списка номеров глобаль-
1 Мы подразумеваем, что на каждом элементе единым образом введена
локальная нумерация вершин, рёбер, граней и ассоциированных с ними ба-
зисных функции, и поэтому у соседнего элемента эти «соответствующие мес-
та» определены однозначно.
594 12.Построение конечноэлементных аппроксимаций на сетках ...
ных базисных функций смежных элементов То же самое делаем для
всех остальных элементов, но при этом новые глобальные номера по-
лучают только те локальные базисные функции, которые не были про-
нумерованы ранее.
Другой путь решения этой проблемы базируется на том, что наряду
с глобальной нумерацией вершин вводится глобальная нумерация всех
ребер, граней и самих элементов. Для каждого элемента в этом случае
хранятся не глобальные номера его базисных функций, а глобальные
номера его вершин, ребер и iраней. Глобальные же номера базисных
функций приписываются к рёбрам и граням, что автоматически обес-
печивает их совпадение для смежных элементов Способы нумерации
рёбер и граней были рассмотрены нами в разделах 10.6.2 и 10 6.3.
12.2.5. ИЕРАРХИЧЕСКИЕ БАЗИСЫ ИЛ ( ИМПЛЕКСАХ. СОГЛАСОВАНИЕ
ТРЕУГОЛЬНЫХ И ТЕТРА )ДРАЛЫ1ЫХ ИЕРАРХИЧЕСКИХ ЭЛЕМЕНТОВ
РАЗЛИЧНЫХ ПОРЯДКОВ
Покажем, как можно ввести иерархические базисы на симплек-
сах (т.е. треугольниках в двумерном случае и тетраэдрах в трёхмер-
ном). Удобнее всего это сделать с использованием £ -координат.
Для треугольного конечного элемента иерархические базисные
функции можно записать в следующем виде.
Первые три базисные функции - это £ -координаты треугольника:
= А, Ф2 = Д, Фз = А
В элементе второго порядка добавляются три ассоциированные с
рёбрами (и квадратичные на них) базисные функции
Ф4=ДД, Ф5 = ДД, ФС = АА-
В элементе третьего порядка добавляются ещё три ассоциирован-
ных с рёбрами (и кубические па них) функции
Ф7 = (Д — Д), Фе = ДД । д — Д),
4>0 =£2£)(А -Д) (12.23)
и одна функция, ассоциированная с центром элемента:
Ф1о — ДД Д
Приведём общие формулы для построения иерархического базиса
треугольного элемента любого1 порядка р. Этот базис строится из
всех базисных функций элемента предыдущего порядка ( р — 1) с до-
бавлением к нему трёх базисных функций, ассоциированных с рёбрами
элемента, и р — 2 функций, ассоциированных с центром элемента.
1 На самом деле эти формулы имеет смысл использовать в случае р > 4,
хотя они справедливы и при р = 2, и при р = 3 .
12.2.Иерархические базисы ....
595
Добавляемые к базису элемента порядка р — 1 три базисные функ-
ции порядка р, ассоциированные с рёбрами элемента, могут быть по-
лучены, например, по формулам [33]:
=А-е2 Х,,(Д-Д), (12.24)
Ф.,+2=АД-Хр(^-Д), (12.25)
ф.,+3 =^А'Х„№“А). (12.26)
Здесь s — количество базисных функций элемента порядка р — 1, ко-
торое можно вычислить по формуле
з = 3(Р-1) + ^-2^-3),
а функция Хр (О определяется через одномерные иерархические ба-
зисные функции фг соотношением:
Х„ (О = (12.27)
Обратим внимание на следующий факт, являющийся очень важным
для практического использования соотношений (12.24)-( 12.26). Вхо-
дящая в соотношение (12.27) одномерная иерархическая базисная
функция фр+i ((;) является полиномом степени р при р > 2 (см. со-
отношения (12.4), или (12.5), или (12.10)—(12 12)). Любой же из поли-
номов ф//+1 (£,) при р > 2 обязательно имеет сомножитель — 1.
Действительно, все эти полиномы были определены на интервале
{—1,1] так, чтобы на его концах они принимали нулевое значение (и
поэтому значения £ = i 1 являются корнями полиномов фР+1 (6,))
Таким образом, соотношение (12.27) определяет Хр (0 как полином
степени р — 2, и поэтому в правых частях соотношений (12.24)—
(12.26) стоят только полиномы Л -координат (например, для базиса
(12 4) функция (12.27) определяется совсем просто: Хр (0 = V 2 )•
Наконец, приведём формулу, определяющую вид р — 2 базисных
функций порядка р, ассоциированных с центром элемента и добав-
ляемых к базису элемента порядка р — 1 [33].
Ф.,+3+. = ^£з^-1(4-А)^-2-.(2Д-1). i = l...p-2, (12.28)
где Pj (^) - некоторый полином (от одной переменной) степени j .
596 12.Построение конечноэлементпых аппроксимаций на сечках ...
Аналогично строится иерархический базис для тетраэдральных
элементов. Так, элемент второго порядка строится добавлением к че-
тырём линейным базисным функциям
ф„ = A, s = 1...4 (12.29)
шести квадратичных базисных функций, ассоциированных с рёбрами:
К = -ЧА, Фс = Фт = £1-С| ,
4’8 = £2£з , -фд = ад, ф10 = ад. (12.30)
Элемент порядка р строится добавлением к базису элемента по-
рядка р — 1 шести функций, ассоциированных с рёбрами, 4(р —2)
1 ~ г л \ (Р ~ 'А (р ~
функции, ассоциированных с гранями, и (при р >4)------------------
функций, ассоциированных с центром.
Обозначим через s количество базисных функций элемента поряд-
ка р — 1. Шесть функций порядка р, ассоциированных с рёбрами,
можно определить с помощью соотношений:
ФлЧ-1 = А А • Хр (А ~АА
'Фл+2 = А А Хр (А — £3),
'фл-+з = А А -хР(А - А),
фл.44 = А А - Хр (А ~АА
Фл+з |= АА хР(А -АА
Ф.ч+б = АА • Хр (А-А),
где (6,) - тот же полином степени р — 2 , который был использован
при определении базисных функций на треугольниках, см. (12.27).
Базисные функции, ассоциированные с гранями, можно определить
с помощью соотношений1:
Ф.ч+с+/ — АААА-1 {А — А) А>~2-> А^А — 1)> i = 1...р — 2,
'Фх+С + р-2+7 AAAA-i (А - А) Рг-2-г (2Д -1), i = 1... р - 2,
'Фл+С+2(р-2)+/ = AAA Pi-} {А - A)Pp-2-i (% А “ 1) , г = 1 • --Р — 2 ,
Ф.ч+с+з(р-2)+/. — АААА-i (А - А) Рр-2-i (2Д1 -1), г = 1 • -.р — 2.
1 На самом деле, индексы, естественно, можно упростить, но мы не сдела-
ли эго намеренно, чтобы был виден принцип индексации.
12.2.Иерархические базисы ....
597
Базисные функции, ассоциированные с центром, можно определить
соотношением
Ф , = ДДААД-1(Д-Д)А-1(2Д-1)х
.sTG4-4(/;-'2)+—---+j
xP7,_2_j_t(2A-1), г = 1...р —3, ; = 1...р-3-г (1231)
Выпишем в качестве примера несколько базисных функций, ассо-
циированных с центром элемента. Первая базисная функция такого рода
появляется у элемента четвёртого порядка, и она имеет вид (учтём, чго
s = 20 - число базисных функций элемента третьего порядка):
Фзз = 44444 (4 - 4) 4 (24 -1) ри (24 -1) = 4444 ,(12.32)
поскольку Р() (Q - это полином нулевой степени, т.е. Р() (£,) = 1.
У элемента пятого порядка будет уже четыре базисные функции,
ассоциированные с центром, три из которых — полиномы пятой степе-
ни (учтём, что число базисных функций элемента четвёртого порядка
5 = 35 и =
Фз4 = ДДААД (2Д ~ 1) >
ф55 = ДАААЛ(2Д-1),
Фзо — АДА АД (А — А) •
Элементы же шестого порядка будут иметь уже десять базисных
функций, ассоциированных с центром, шесть из которых — полиномы
шестой степени. Приведём первые два из таких полиномов шестой
степени
Фй1 — А ДАДД (2А — 1),
ф82 = Д ДА АД (2Д -1) д (2А -1) •
Таким образом, полученные соотношения позволяют получить вид
всех базисных функций иерархического элемента на тетраэдре любого
порядка. При этом они фактически определяют и локальную нумерацию
всех базисных функций иерархических элементов высоких порядков:
первые шесть номеров (после всех базисных функций до (р — 1)-го по-
рядка) определяют локальные базисные функции р -го порядка, ассо-
циированные с ребрами, следующие 4(р —2) номера определяют ло-
кальные базисные функции у?-го порядка, ассоциированные с гранями,
и последние (р — 3)(р — 2)/2 номера (при р > 4 ) определяют локаль-
ные базисные функции р -го порядка, ассоциированные с центром
598 12.Построение конечноэлементных аппроксимаций на сетках ...
Заметим, что на практике крайне редко используются элементы
выше четвёртого порядка из-за большой размерности локальной мат-
рицы и соответственно высокой заполненности (ненулевыми элемен-
тами) глобальной матрицы. Поэтому, хотя приведённые соотношения
принципиально позволяют создать единую процедуру вычисления
локальных матриц любого порядка, на практике вовсе не обязательно
реализовывать такой общий (но довольно сложный) алгоритм, а мож-
но, зафиксировав максимальный порядок элемента, выписать конкрет-
ный вид всех его базисных функций (как, например (12.29), (12.30) или
(12.32)) и вычислить аналитически каждую компоненту локальной
матрицы жёсткости и массы (как это было сделано, например, для ла-
гранжевых элементов, см. раздел 5.3.4).
Обратим внимание на ещё одну чрезвычайно важную деталь. В со-
отношениях, определяющих иерархические базисные функции на сим-
плексах, знак локальной функции зависит от того, в каком порядке
берутся £ -координаты. Это означает, что если на двух соседних сим-
плексах, смежных по грани или ребру, локальная нумерация вершин
сделана не однотипно, то сшитая из таких локальных базисных функ-
ций глобальная функция может оказаться разрывной. Покажем это на
простейшем примере.
Пусть на двух треугольниках, имеющих общее ребро Г, введена
локальная нумерация вершин так, как это показано на рис. 136. Тогда
кубическая локальная базисная функция фд1 элемента ассоцииро-
ванная с ребром Г, будет иметь вид (см. (12.23)) фд^ДА (А — А) , а
ассоциированная с этим же ребром кубическая локальная базисная
функция Ф72 элемента О2 будет иметь вид ф?2 — ДА (Д — Д) •
Нетрудно убедиться, что эти функции при движении вдоль ребра [
будут принимать одинаковые по модулю, но разные по знаку значения
(так как на Г функция £2 элемента совпадает с функцией Д эле-
мента О.-2, а функция Д элемента Qj совпадает с функцией Д эле-
мента Q2). В результате сшитая стандартным образом1 из этих локаль-
ных функций глобальная базисная функция получится разрывной, что
приведёт к нарушению одного из важнейших условий, налагаемых на
базисные функции, и, как следствие, к очень далёкому от истинного
конечноэлементному решению.
1 Обычно мы полагаем, что глобальная базисная функция ф,-, полученная
сшивкой двух локальных базисных функций ф?*1 элемента QZ] и фж эле-
мента Qz., , определяется как ф, — фр'1 на QZ) и фг = ф* - на Qz., (аналогич-
но и при большем числе сшиваемых локальных базисных функций), и все
стандартные алгоритмы сборки глобальных матриц основаны на этом факте.
12.2.Иерархические базисы ....
599
То же самое можно сказать и о функци-
ях, ассоциированных с рёбрами и гранями
тетраэдров. При этом ассоциированные с
гранью функции четвёртого и больших
порядков могут оказаться разрывными,
если, например, вершины этой грани на
одном конечном элементе имеют локаль-
ные номера 1,2,4, а на смежном с ним ко-
с ошибочном для иерархических
элементов локальной нумерацией
Рис. 136. Пример ситуации
ошибочной для иерархических
вершин треугольников
нумерацию вершин на каж-
нечном элементе эти же вершины имеют
локальные номера 1,4,3 («правильными» на
втором элементе будут нумерации 1,2,3,
или 1,3,4, или 2,3,4, или, естественно, 1,2,4).
Эту проблему можно очень просто
решить следующим образом. Локальную
дом конечном элементе нужно ввести так, чтобы большему локальному
номеру вершины обязательно соответствовал больший глобальный
номер. Для этого достаточно при задании тетраэдральной сетки в мас-
сив элементов (в котором хранятся номера вершин элементов, см. раз-
дел 10.2.6) заносить номера вершин каждого тетраэдра в порядке воз-
растания. На самом деле, при построении формул для базисных функ-
ций мы учитывали эту особенность иерархических базисов, и читатель
может убедиться, что определённые нами локальные базисные функ-
ции сшиваются в непрерывные глобальные функции при выполнении
сформулированного выше правила локальной нумерации вершин эле-
ментов.
Иерархические базисы на симплексах также позволяют очень про-
сто согласовывать элементы разных порядков. Процедура согласова-
ния в общем-то ничем не отличается от рассмотренной нами в разде-
ле 12.2.4 процедуры согласования на прямоугольниках и параллелепи-
педах. Точно так же на иерархическом треугольном или тетраэдраль-
ном элементе должны устраняться «лишние» (более высоких поряд-
ков) базисные функции, ассоциированные с рёбрами (для треугольни-
ка) или с рёбрами и гранями (для тетраэдра), по которым этот элемент
является смежным с элементами более низких порядков. При этом
надо решать те же проблемы, связанные с идентификацией рёбер и
граней на различных конечных элементах, например, через введение
их глобальной нумерации. Более подробно об этом мы говорили также
в разделе 12.2.4 (в самом его конце).
12.2.6. ИЕРАРХИЧЕСКИЕ БАЗИСЫ НА ПРЯМЫХ ПРИЗМАХ
Иерархический базис на прямой треугольной призме можно по-
строить аналогично тому, как был построен базис из функций лагран-
жева типа (см. раздел 6.5). Каждая иерархическая базисная функция на
треугольной призме строится в виде прямого произведения одномер-
ной иерархической функции и иерархической базисной функции тре-
угольника.
600 12.Построение конечноэлементных аппроксимаций на сетках ...
Для простоты будем считать, что основания призмы лежат в плос-
костях z = const •. Тогда с рёбрами и гранями, лежащими в плоскостях
оснований призмы, ассоциируются иерархические функции вида
Ф (т, у, z) = фд (х, у) -Z(z),
где фЛ (а:, у) — это функции вида (12.24)-( 12.26) или (12.28), a Z (z) -
линейные одномерные функции вида (z2 — z)jhz или (z - Zi )/Л,2
(hz — z-2 — zx — высота призмы, a Zj и z-2 — z-координаты её основа-
ний).
С рёбрами же и гранями, перпендикулярными основаниям призмы,
ассоциируются иерархические функции вида
ф(я,2/,г) = (x,y)-(p(z),
где - одна из £ -координаттреугольного основания, a <p(z) -
одномерная иерархическая функция, определяемая либо соотношени-
ем (12.4), либо (12.5), либо (12.10) или (12.11).
С центром призмы ассоциируются функции вида
Ф(т, у, z) = фЛ (т, у)- ip(z). (12.33)
Заметим, что при переходе от иерархического базиса (р — 1) -го по-
рядка к иерархическому базису р -го порядка добавляется 2 (р — 2) 4-1
(т.е. 2р — 3 ) функций, поскольку «новые» ассоциированные с центром
элемента функции получаются умножением функции фЛ (а;, р) р-го
порядка на все функции tp(z) от второго до (р — 1)-го порядка и ум-
ножением функции ip(z) р-го порядка па все функции фЛ (а;,р) от
второго до (р — 1)-го порядка, а также умножением функций фЛ (X </)
и <p(z) р-го порядка.
Абсолютно аналогично может быть построен иерархический базис
на прямых призмах с четырёхугольным основанием (фактически яв-
ляющихся шестигранниками определённого вида). Для этого доста-
точно построить иерархические базисные функции на четырёхуголь-
нике. Эти функции могут быть построены точно так же отображением
чсгырсху гол bn иков в единичный квадрат, как это было сделано для
лагранжевых элементов (см. раздел 5.4.1). Соответственно через ото-
бражение единичного куба в шестигранник может быть построен ие-
рархический базис на шестигранных элементах, не являющихся пря-
мыми призмами.
1 Очевидно, что этого вполне достаточно для построения локальных мат-
риц любых прямых треугольных призм, поскольку, как уже было показано в
разделе 5.6, локальные матрицы жёсткости и массы инвариантны к поворотам
конечных элементов.
12.3.Согласование иерархических конечных элементов ...
601
12.3. СОГЛАСОВАНИЕ ИЕРАРХИЧЕСКИХ КОНЕЧНЫХ ЭЛЕМЕНТОВ
НА НЕСОГЛАСОВАННЫХ СЕТКАХ
В разделе 12.2 нами были рассмотрены базисные функции, по-
зволяющие очень просто согласовывать элементы различных поряд-
ков. Здесь же мы коснемся вопросов, связанных с использованием ие-
рархических базисов на несогласованных ячейках. Такие ситуации
возникают тогда, когда для уточнения конечноэлементного решения
одновременно используется и локальное дробления ячеек сетки и по-
вышение порядка некоторых элементов1. При этом, если для треуголь-
ников и тетраэдров локальные дробления можно выполнять, не нару-
шая согласованности сетки, то для сеток с ячейками в виде прямо-
угольников, параллелепипедов (а довольно часто и четырёхугольни-
ков, шестигранников и прямых треугольных призм) локальные дроб-
ления сетки приводят к появлению несогласованных ячеек.
а
Рис. 137. Пример стыковки иерархических элементов высоких
порядков на параллелепипедах: а - вид стыкуемых параллелепипедов
(4 параллелепипеда сверху стыкуются с одним параллелепипедом снизу);
б - нумерация функций на грани стыковки
Очевидно, что при согласовании иерархических элементов на пря-
моугольниках проблему построения непрерывных глобальных функ-
ций нужно решать только для функций, ассоциированных с вершина-
ми и рёбрами2. Поэтому мы рассмотрим, как можно согласовывай»
иерархические конечные элементы на несогласованных параллслспи-
ледах — в этом случае непрерывные глобальные функции нужно стро-
ить как для функций, ассоциированных с вершинами и рёбрами, гак и
для функций, ассоциированных с гранями.
1 Подробнее на этом мы остановимся в следующем, тринадцатом разделе
(см. раздел 13.3, где рассматриваются p-h-технологии).
2 При этом ассоциированные с вершинами базисные функции иерархиче-
ских элементов тождественно совпадают с лагранжевыми базисными функ-
циями элементов первого порядка и проблема согласования для них решается
точно так же, как это было показано в разделе 12.2.4.
602 12.Построение конечноэлсментных аппроксимаций на сетках ...
Покажем, как можно согласовать иерархические конечные элемен-
ты на параллелепипедах, когда к одной грани параллелепипеда примы-
кают четыре параллелепипеда, как это показано на рис. 137,<7. Этот
случай является наиболее показательным, поскольку он включает в
себя практически все ситуации, возникающие при согласовании иерар-
хических элемен тов на прямоугольниках и параллелепипедах.
Будем считать, что на согласуемых параллелепипедах заданы ие-
рархические базисы третьего порядка1. Будем также считать, что гло-
бальные базисные функции ф”г (из базиса несогласованных элемен-
тов), ассоциированные с вершинами, рёбрами и гранями, лежащими в
плоскости стыковки «большого» параллелепипеда с четырьмя «ма-
ленькими», пронумерованы следующим образом. С вершинами ассо-
циированы трилинейные функции ф“г 4- ф™’ (на «большом» паралле-
лепипеде они совпадают с соответствующими функциями непрерыв-
ного базиса {ф'}) и трилинейные функции ф"? 4-фг£ (это функции
«маленьких» параллелепипедов, и они будут включаться в виде сла-
гаемых в функции ф? при определении их на «маленьких» параллеле-
пипедах). С рёбрами ассоциированы квадратично-билинейные2 функ-
ции фг-г 4-Фз" и кубически-бил инейные функции ф^’ 4- ф"з (они ас-
социированы с рёбрами «большого» параллелепипеда), а также квад-
ратично-билинейные функции фзе 4- Ф37 и кубически-билинейные
функции Ф42 4- фг$ (они ассоциированы с рёбрами «маленьких» па-
раллелепипедов). И, наконец, с гранью «большого» параллелепипеда
ассоциированы биквадратично-линейная функция фдг (опа линейна
по направлению от грани внутрь «большого» параллелепипеда), куби-
чески-квадратично-линейныс функции ф^ и Ф15 и бикубически-
линейная функция ф$ . С гранями же «маленьких» параллелепипедов
ассоциированы биквадратично-линейные функции фз'д 4- ф^ , кубиче-
ски-квадратично-линейные функции Ф54 4- Фс1 и бикубически-
линейные функции ф^ 4- . На рис. 137,6 показаны номера базис-
ных функций ф”,: на грани, по которой выполняется стыковка одного
параллелепипеда с четырьмя. При этом стрелочки указывают на цен-
тры рёбер и граней (принадлежащих соответственно «большому» и
«маленьким» параллелепипедам), с которыми ассоциированы функции
с перечисленными номерами.
1 Если согласуемые элементы имеют различный порядок, то перед согла-
сованием по сетке выполняется очевидное согласование по порядку ненуле-
вых на согласуемых гранях базисных функций (путём исключения из элемен-
тов высоких порядков «лишних» базисных функций).
2 Под квадратично-билинейными функциями мы, естественно, понимаем
функции, квадратичные по одной координате (в данном случае это координа-
та, ось которой совпадает с направлением ребра) и линейные по двум осталь-
ным координатам. Аналогично определяются кубически-билинейные, би-
квадрагично-линейные и другие такого рода функции.
12.3.Согласование иерархических конечных элементов
603
Обратим ещё раз внимание на то, что на грани, по ко юрой стыку-
ются параллелепипеды, все базисные функции ф; тожде ткенно сов-
падают с соответствующими функциями ф”' «большого» параллеле-
пипеда, т.е. для нашего примера на грани (тыковки
ф[ = ф”‘ > а = 1---16 Этим фактом мы будем постоянно пользоваться
при построении базисных функций ф'‘ на маленьких параллелепипе-
дах.
Компоненты матрицы Т-преобразования, переводящего базис {Ф"г}
в базис {ф/} непрерывных функций, могут быть найдены (см. разде-
лы 11.6.2 и 11.6.4) как коэффициенты представления функций ф' в виде
линейных комбинаций функций ф"' (на грани, по которой проводится
стыковка). Получим эти коэффициенты для некоторых функций.
Рассмотрим сначала функцию ф[ . Эта функция, очевидно, является
билинейной на грани стыковки, и поэтому на «маленьких» параллеле-
пипедах может быть представлена в виде линейной комбинации ку-
сочно-билинейных на этой грани функций Ф17 , Ф18, Ф26 , Ф21 (веса
которых равны значению функции ф’/' в соответствующих этим
функциям вершинах; веса же остальных кусочно-билинейных на грани
функций Ф19 , ф-22 4- Ф25 являются нулевыми, поскольку ф"' в соот-
ветствующих вершинах равна нулю):
Ф1 = Ф17 + 0-6ф1'8г + 0.7фЖ + 0.42ФЗГ. (12.34)
Заметим, что веса всех остальных функций ф'"’, являющихся на
грани функциями более высокого порядка, должны быть нулевыми,
поскольку эти функции таковы, что если хотя бы один из их весов не
будет равен нулю, то линейная комбинация 71,гФГ уже не будет
г
на грани билинейной функцией'.
1 Поскольку не существует такого набора коэффициентов (среди которых
хотя бы один ненулевой), что линейная комбинация иерархических базисных
функций порядка не ниже р станет полиномом порядка р — i .
604 12.Построение конечноэлементных аппроксимаций на сетках ...
Аналогичным образом1 определяются веса разложений функций
Ф2, Фз и Ф4 п0 базису {ф-"'} .
В линейной комбинации ТЬл'ФГ , определяющей функцию ф£,
ненулевыми могут быть веса только у функций до второго порядка
включительно (исключая биквадратичпые на грани функции). По-
скольку не равна нулю только в вершинах, с которыми ассоцииро-
ваны функции Ф20 и Ф21, веса у остальных кусочно-билинейных на
грани функций должны быть нулевыми (в противном случае линейная
комбинация, представляющая ф£, окажется не равной нулю в соответ-
ствующих вершинах). Таким образом, значение 7^20 будет равно зна-
чению фз' в вершине, где ф.д) равна единице, а значение Т})21 будет
равно значению фз': в вершине, где ф.-j" равна единице, т.е.2
.20 — 0.84, а Т5 21 = 0.504 .
Остальные веса можно найти, приравнивая, например, значения
функции фз" к линейной комбинации У^Т51Уф'" в точках на середи-
нах ребер «маленьких» параллелепипедов, поскольку в этих точках
ненулевой является только одна (ассоциированная с рассматриваемым
1 Мы не включили в представление ф,’ (см. (12.34)) в качестве слагаемого
функцию ф1' (оговорив, что даём представление ф[ на «маленьких» парал-
целепипедах). На самом деле, поскольку функции фр, ф'/х , фг» и Ф2" опре-
делены только на «маленьких» параллелепипедах (и на «большом» равны
пулю), го в представлении ф) во всей расчётной области, конечно же, долж-
на в качестве слагаемого участвовать и функция ф”' , которая наоборот опре-
делена только на «большом» параллелепипеде (включая грань контакта), а на
«маленьких» равна нулю. Таким образом, компонента 7]д тоже должна быть
равна единице. Строго говоря, ф)’ в расчётной области должна быть опреде-
лена как линейная комбинация пяти функций фТ , фр, ф"£, ф*о и ф-21 ,
причем награни контакта фр, ф{", ф.”» и Ф2" следует определить равными
пулю и лишь в пределе (при движении от внутренних точек «маленьких» па-
раллелепипедов к «рани контакта) линейная комбинация (12.34) должна сов-
пасть с ф{" - это позволяет строго обосновать непрерывность функции ф]
(при наличии в её представлении наряду с фр, ф}", фэд, Ф-^ и функции
Ф1"‘ с весом Т1Л = 1) во всей расчётной области. То же самое можно сказать
и об остальных функциях ф' (т.е. фактически в представлении каждой из них
свесом 7], =1 участвует функция ф"' ).
2 Будем считать, что иерархический базис построен на основе одномерных
функций (12.4).
12.3.Согласование иерархических конечных элементов ...
605
ребром) из квадратично-линейных на грани функций. Таким образом,
взяв точку с координатами х = 1, у = 2.3 (где ф2д (2\ у)1 2 равна еди-
нице и из остальных функций линейной комбинации ненулевыми мо-
гут быть только функции ф2о > Ф21 ), получим
•ФЬЖГ (1, 2.з) = 0.51,
£ Т^-ф” = Ts.20® (1, 2.3) + ТЬ,21® (1, 2.3) + Т5,26® (1, 2.3),
i
и в результате
Ts.26 = ® (1, 2.3) - 7Ь.2„® (1, 2.з) - T^i® (1, 2.з) =
= 0.51 - 0.84 • 0.5 - 0.504 • 0 = 0.09.
Аналогично могут быть найдены коэффициенты Т5>27 (по точке с
координатами х = 1, т/ = 3.3), Т528 (по точке с координатами
х = 1.4 , у = 2.3 ) и Т5,2д (по точке с координатами х = 1.4 , у = 3.3 ).
Веса остальных квадратично-линейных на грани функций фзо -? фз7 в
представлении ф”г в виде ^Т^ф™ > очевидно, должны быть равны
нулю, поскольку фзс является линейной функцией координаты х, а
функции фз/, 4- Ф37 - квадратичные иерархические функции этой ко-
ординаты2.
В представлении биквадратичной на грани функции фд ненулевы-
ми будут веса только у биквадратичных (на своих участках грани)
функций фз8 4- Ф41 и у кусочно-билинейной на грани функции ф2[.
Вес Tq2i сразу же находится из значения функции фд': в узле с коор-
динатами х = 1.4, у = 2.6 (поскольку все остальные функции линей-
ной комбинации в этой точке равны нулю). Веса же 38 -г 7g 41 могут
быть найдены как разность значений функции фдг и Гд-21ф2{ в тех
точках грани, где только одна из функций фз8 -г ф41 равна единице
(это точки (1.2,2.3), (1.7,2.3), (1.2,3 3) и (1.7,3 3)).
1 Естественно, функция ф."£ является функцией трёх координат, но на рас-
сматриваемой грани z = const, и поэтому на ней ф-“й зависит только от х и
у . Таким очевидным сокращением числа аргументов у базисных функций мы
в данном разделе будем пользоваться и далее.
2 И их линейная комбинация с хотя бы одним ненулевым коэффициентом
не может быть линейной функцией.
606 12.Построение конечноэлементных аппроксимаций на сетках ...
К сожалению, коэффициенты представлений иерархических базис-
ных функций третьего порядка находить ещё сложнее Здесь также
ещё существуют точки, с помощью которых можно поочерёдно опре-
делять веса оазисных функций в линейной комбинации, представляю-
щей разлагаемую функцию. Однако для элементов четвёртого порядка
это уже станет невозможным, и для нахождения коэффициентов ли-
нейных комбинаций придётся решать СЛАУ небольших размерностей.
В принципе, коэффициенты разложения одних базисных функций
по другим можно искать не только по значениям самих функций в оп-
ределённых точках, но и по значениям их производных. Покажем, как
это можно сделать в рассматриваемом нами примере для функции
третьего порядка.
Рассмотрим кубически-линейную на грани функцию фф. Значения
весов билинейных функций ф^ и ф^ находятся (как и для других
функций) из значений функции фф в точках (1,2.6) и (1.4,2.6), т.е.
^10,2(1 = 'ФГо (I,2-6), а 7jo,21 = 'Фю (1-4,2.6). Веса квадратично-
линейных функций ф2с 4- Ф29 проще всего найти по значениям фф: в
точках (1,2.3), (1,3.3), (1.4,2.3) и (1.4,3.3) (поскольку все кубически-
линейные функции в этих точках равны нулю). И, наконец, веса куби-
чески-л инейных функций Ф42 4- Ф45 можно найти по значениям про-
изводных j- в тех же четырёх точках (1,2.3), (1,3.3), (1.4,2.3) и
пЗ
(1.4,3.3), поскольку производная отлична от нуля в каждой из
ду
этих точек только у одной из кубически-линейных функций.
Например, продифференцируем трижды функцию Ф1о и линейную
комбинацию ^2Л())7ФГ в точке (1,2.3). Будем считать, что функции
Z
ф’,г построены на основе одномерных иерархических базисных функ-
ций ф, (6.) вида (12.4). Тогда фф‘ (я,?/) = ф1 q 5 5)фд (у ~ 3), и
д3фщ
ду3
=1(-6)(1)3=-6.
Аналогично вычисляется значение производной Т1()>/;ф"<: в точке
1.
(1,2.3) (при этом следует учесть, что производная d^jdy3 в точке
(1,2.3) отлична от нуля только у функции Ф42 ):
12.3.Согласование иерархических конечных элементов ... 607
,т=1,|/=2.3
В результате получаем Tio.42 = 0.027.
Для элементов же более высоких порядков именно за счёт использо-
вания значений производных можно избежать решения СЛАУ при по-
иске коэффициентов Д ;. В этом случае сначала ищутся веса функций
максимального порядка по значениям производных соответствующего
порядка в точках, расположенных на серединах ребер и граней (с помо-
щью этих производных из линейной комбинации фактически исключа-
ются все функции меньшего порядка). Затем с использованием уже по-
лученных коэффициентов и производных меньших порядков определя-
ются веса функций меньших порядков. Веса билинейных функций оп-
ределяются, как всегда, по значениям в вершинах элементов.
Обратим особое внимание на то, что если иерархический базис по-
строен на основе одномерных функций (12.5), то практически все ком-
поненты матрицы Т могут быть довольно просто получены с помо-
щью значении производных соответствующих порядков в определён-
ных точках.
Действительно, одномерные шаблонные иерархические функции
фр+1 (С,), определяемые соотношениями (12.5), в точке £ = 0 имеют
равные нулю производные любого порядка, кроме первого и р-го.
Производная же в этой точке равна единице.
Покажем, как можно, используя это свойство одномерного иерар-
хического базиса вида (12.5), вычислять компоненты матрицы Т (даю-
щей представление функций ф' через функции ф'-г ).
Рассмотрим сначала функции ф'“' , ассоциированные с рёбрами, ле-
жащими в плоскости стыковки. Каждая из этих функций является на
грани стыковки произведением линейного полинома одной координаты
и полинома степени р (р > 2) другой координаты. Тогда компоненты
Ту, являющиеся весами этих функций ф"г в линейной комбинации,
представляющей ф'-:, можно вычислить с помощью соотношения
(а, у)
дхр
<Эрф"г (х, у)
dxv
(12.35)
608 12.Построение конечноэлементных аппроксимаций на сетках ...
если ребро ориентировано вдоль х , или соотношения
дрт$ (ж, у)
дур
<9"ФГ Ы)
ду”
(12.36)
если ребро ориентировано вдоль у. В этих соотношениях (ж/, у') -
координаты центра ребра, с которым ассоциирована функция ф'?" .
Очевидно, что ненулевыми в соотношениях (12.35)—(12.36) будут
только те компоненты, которые связывают ф'и с функцией ф'\ ассо-
циированной либо с ребром того же направления (что и для функции
ф" ), либо с центром грани.
Преобразуем выражения (12.35) и (12.36) с учётом представления
функций ф''г и ф'‘ в виде произведения одномерных шаблонных
функций. Обозначим через h'. длину ребра, с которым ассоциирована
функция ф”г. Тогда на ребре, ориентированном вдоль х, ассоцииро-
ванную с ним функцию ф"г можно записать через одномерную шаб-
лонную функцию в виде
= (12.37)
I и. О/ Ь^-
Теперь получим выражение для функции ф; через одномерные
шаблонные функции. Обозначим через (a\.,t/f.) координаты центра
грани «большого» параллелепипеда, а через h.,. и hy размеры прямо-
угольника, являющегося гранью этого параллелепипеда. Будем счи-
тать, что функция ф' является полиномом степени р, от координаты
х (очевидно, что рт должно быть не меньше р; в противном случае
7] у = 0 и его не нужно вычислять). Тогда функция ф- может быть
записана в виде
(a.v) = T/,)+i о 5/ ' о 5/^ > (12.38)
где ру некоторое число, определяющее при ру > 2 степень исходного
полинома ф£ (.с, у) от координаты у, а при ру = 0 или ру = 1 одну из
линейных базисных функций (12.2).
Из (12.37)
12.3.Согласование иерархических конечных элементов ...
609
/ \
™ . х - х'(.
дЩг-(х,у) _ 1₽',+Ц 0.5Л,; J
За? , , " дх”
г-1-с .У=Уг.
г- х — х(.
Вводя переменную Е, = -^z--, получаем
_Э"ф„+1(£.) рЕ,
Рс,У=Ус
др^-е (х,у)
дхр
_2_У'
h',
(12.39)
(х^ у\
Аналогично вычислим значение
дх'1'
представления (12.38) и используя замену
1 0.5L, ’
д''< У)
дх1'
дх1’
, учитывая
переменных Е, = п р,
U &ГЬЧ
- У______________________и
^+1(0.5А
У=У<-
= д7'ФЕ,+1(Е,) ГдЕ.|
д^1> дх)
Е=
Ус -Ус
— 1 с 1>.г - v .
(Р.,. - Р)-
?/<-?/<
0.5/д,
0.5/lj;
J>.r~V
= (ж;. - х(.
(Рг - р)
Из (12.35) с учётом (12.39) и (12.40) окончательно получаем
. xi’-i -p
(12.40)
Гп У( ~ у‘-
’^+1| 0.5/^
Ус ~
'^+I [ 0.5Лу
Т
-Г 7. I
(Р.г ~ Р)
где фР}/+1(Е,) определяется соотношениями (12.2) для р№ <2
ношениями (12.5) для >2.
(12.41)
и COOT-
610 12.Построение конечноэлементных аппроксимаций на сетках ...
Абсолютно аналогично можно преобразовать соотношение (12.36)
и получить простые выражение коэффициентов 7] для любой функ-
ции ф™‘, ассоциированной с ребром, ориентированным вдоль у:
(р,, - J')!
1 ^7/ )
с;. — х(.
0.5/г,.
(12.42)
Коэффициенты Т, для функций ф"г, ассоциированных с гранями,
могут быть вычислены следующим образом:
д‘‘ + ФИ^~, у)
дхр:г ду1'11
дхР:г дуРу
где (ф, у'.) - координаты центра грани «маленького» параллелепипе-
да, с которой ассоциирована функция ф"с, а р'. и р' - степени поли-
номов от х и от у, определяющих функцию ф'"’ (в виде
i
+i ["(Щ;
(12.5)).
Тогда
т
л- I и
V ~ Че
0.5/^
через одномерные функции вида
,1'г
V.!
(«! -
(р»-р.0!
(12 43)
2 V l
к
где, как и в соотношениях (12.41) и (12 42), р,. и р - степени поли-
номов от я: и от у, определяющих функцию ф': (в виде (12 38)),
(а;;,у,.) - координаты центра прямоугольника, являющегося гранью
«большого» параллелепипеда, a h,. и Д(/ - размеры этого прямоуголь-
ника
Таким образом, соотношения (12.41 )-(12.43) позволяют достаточно
просто вычислять все ненулевые компоненты матрицы Т (опреде-
ляющие представления ф-’ через ф"с) для функций ф“г, ассоцииро-
ванных с рёбрами и I ранями. Если же функция ф"': ассоциирована с
вершиной, значение Tt t определяется по значению ф-' в узле, с кото-
рым ассоциирована ф';" .
12.3.Согласование иерархических конечных элементов ...
611
Обратим внимание на то, что хотя соотношения (12.41)—(12.43) бу-
дут давать правильные результаты для любых сочетаний функций ф)
и ф'“ , ассоциированных с рёбрами и гранями, тем не менее не стоит
использовать эти соотношения для вычисления заведомо нулевых
компонент матрицы Т.
Так для любой функции ф;, ассоциированной с ребром, ненулевы-
ми являются лишь тс компоненты 7] , матрицы Т, которые, во-
первых, отвечают за связь с функциями ф?“ , ассоциированными толь-
ко с рёбрами, либо являющимися частью определяющего ф' ребра,
либо лежащими внутри «большой» грани и являющиеся параллельны-
ми определяющему ф •’ ребру, а во-вторых, отвечают за связь с кусоч-
но-билинейными функциями ф™:, ассоциированными с вершинами,
которые лежат либо внутри определяющего ф-: ребра, либо внутри
«большой» грани.
Для функций ф'-, ассоциированных с гранью, ненулевыми являют-
ся лишь те компоненты Tt f матрицы Т, которые определяют её связь
с функциями ф7/' , ассоциированными только с рёбрами и вершинами,
лежащими внутри «большой» грани, а также с функциями ф”с, ассо-
циированными с гранями «маленьких» параллелепипедов.
Кроме того, коэффициент Тг} будет заведомо нулевым, если либо
р.,. < р'Г, либо р;1 < р'и (где, как и прежде, р.,. и ру - степени полино-
мов от л: и от у, определяющих функцию ф':, а р!г и р' - степени
полиномов от х и от у, определяющих функцию ф' ).
Для билинейных же на грани стыковки функций ф' ненулевыми
являются только те компоненты 7} матрицы Т, которые отвечают за
её связь с кусочно-билинейными функциями ф'-г, и значение Tt ) оп-
ределяется по значению ф-: в узле, с которым ассоциирована ф'“'.
Таким образом, для одного из иерархических базисов нами получе-
ны удобные соотношения (12.41)—(12 43), позволяющие использовать
технологию Т-преобразования для согласования иерархических эле-
ментов на несогласованных сетках с параллеленипеидальными ячей-
ками. Основные процедуры формирования матрицы Т в ситуациях,
когда непрерывная па одной стыкуемой грани функция (и для нее
строится представление через разрывные на этой грани функции ф"г )
не является непрерывной во всей расчётной области (и её нужно согла-
совывать с другими базисными функциями на других гранях или рёб-
рах), при использовании иерархических базисов хотя и усложняются,
но в целом аналогичны рассмотренным в разделах 11.6.4 и 11 8 проце-
дурам для элементов первого порядка.
612 12.Построение конечноэлементных аппроксимаций на сетках ...
Скажем несколько слов о том, как можно осуществлять локальные
дробления сеток с треугольными и тетраэдральными ячейками при
использовании элементов высоких порядков. Принципиально возмож-
но несогласованно разбивать соседние ячейки и в таких сетках и ис-
пользовать технологию Т-преобразования для согласования конечных
элементов па несогласованных ячейках сетки. Однако чаще всего это
дел ать не i (елссооб р аз но.
Сетки с треугольными и тетраэдральными ячейками используются
обычно при решении задач, в которых границы подобластей не явля-
ются прямыми или плоскими. Пример аппроксимации такой границы
ребром двух смежных треугольников приведён на рис. 138/г. Пусть
один из треугольников в результате локального дробления ячеек по-
добласти 1Г| был разбит на четыре ячейки так, как это показано на
рис. 138,6. Очевидно, что можно построить согласованные элементы
на полученных пяти треугольниках с помощью Т-преобразования.
Однако в этом случае аппроксимация криволинейной границы оста-
нется столь же «плохой», как и до дробления треугольника из подоб-
ласти II7! . Поэтому целесообразно сместить «новый» (попавший на
аппроксимирующее криволинейную границу ребро) узел на криволи-
нейную границу и разбить смежный треугольник из подобласти на
два треугольника, получив, к тому же, и согласованную сетку (как это
показано на рис. 138,е).
Обратим внимание на еще одну особенность, возникающую при не-
скольких последовательных локальных дроблениях треугольных сеток
Если в следующем после изображённого на рис. 138«? дроблении тре-
12.3.Согласование иерархических конечных элементов ...
613
буется разбить треугольник из подобласти \V-2 путём дробления других
его двух рёбер пополам, то лучше это делать так, как показано на
рис. 138,г, т.е. разбить исходный треугольник подобласти 1И2 на наи-
более подобные ему треугольники (аналогично тому, как был разбит
треугольник из подобласти ). Очевидно, сделать это не очень труд-
но, если хранить треугольники, у которых разбито только одно или два
ребра, как переходные элементы (или так называемые макроэлементы,
т.е. в виде объединения обычных треугольных элементов) до тех пор,
пока дополнительные узлы не будут поставлены на середины всех трёх
их «первоначальных» ребер, и лишь после этого разбить макроэлемент
на четыре треугольника рёбрами, соединяющими середины всех трёх
его сторон. При этом следует контролировать возможность возникно-
вения таких ситуаций, когда после «вытягивания» узла на криволиней-
ную границу для треугольника из И2 ег0 последующее разбиение на
четыре может стать совершенно некорректным. Это может произойти,
например, если рёбра треугольника из 1И2 пересекают «настоящую»
(криволинейную) границу. Возможность появления такой некоррект-
ной ситуации проиллюстрирована на рис. 139.
Рис. 139. Пример некорректной ситуации, возникающей после дробления
и «вытягивания» узла на границу
То же самое можно сказать и о согласовании элементов после ло-
кальных дроблений сеток с тетраэдральными ячейками. При этом,
приведённые выше доводы о преимуществе согласования симплексов
путём дробления смежных с ними ячеек1, а не за счёт использования
Т-технологии, становятся ещё более весомыми для тетраэдров ещё и
потому, что применение технологии Т-преобразования на тетраэдрах
(особенно при использовании иерархических базисов высоких поряд-
ков) является гораздо более трудоёмким, чем на треугольниках.
В заключение скажем несколько слов о согласовании (после ло-
кальных дроблений) элементов высоких порядков для сеток с ячейка-
ми в виде прямых треугольных призм. На наш взгляд, удобнее всего в
плоскостях, параллельных основаниям призм, проводин, согласование
треугольной сетки с помощью дополнительных дроблений смежных с
измельченными треугольников (как это обычно делается при работе с
1 Что позволяет улучшать аппроксимацию изогнутых поверхностей.
614 12.Построение конечноэлементных аппроксимаций на сетках ...
треугольной сеткой). В плоскостях же, перпендикулярных основаниям
призм, согласуемые грани являются прямоугольниками, и для них не
представляет особой сложности (в том числе и для иерархических ба-
зисов) применить процедуру согласования с помощью технологии
Т-преобразования
12.4. СРАВНЕНИЕ ЛАГРАНЖЕВЫХ И ИЕРАРХИЧЕСКИХ ЭЛЕМЕНТОВ
При использовании элементов высоких порядков чаще всего
применяют лагранжевы и иерархические базисы. Очевидно, что ла-
гранжевы базисные функции не только заметно проще строятся, но и
делают более наглядной интерпретацию получаемых в результате ре-
шения конечноэлементной СЛАУ значений компонент вектора неиз-
вестных - это просто значения приближённого решения и1' в узлах
сетки. Кроме того, для лагранжевых элементов можно использовать
более простые процедуры нумерации глобальных базисных функций.
Иерархические же базисы позволяют гораздо проще согласовывать
элементы различных порядков на согласованных сетках.
В локальных матрицах иерархических элементов высоких порядков
на прямоугольниках и параллелепипедах появляется немало нулевых
элементов. Причина заключается в том, что одномерные иерархиче-
ские функции чётного и нечётного (выше первого) порядков сами яв-
ляются ортогонал ьными и имеют ортогональные производные для всех
рассмотренных нами базисов (12.4), (12.5) и (12.10) (или (12.11)). В
результате для любых двух функций вида
Ф< (х, т/,^) = ФМг+1
(х — х(.)
[ 0.5/?,,. J
' ^Ч/+1
[у-Ус
[ °-5Ч ,
z — z(.
0.5hz
Фгг+1
и
, \ - (.т — X.. ) „ Гу — у..\ „ (z — Z.. )
ф./ (-А//, г) - (р/<+1 0 5 I -(Щ- -^/4+1
\ \ .7 V * /
соответс гвующие компоненты матрицы жёсткости и массы будут ну-
левыми, если либо рг — чётное (но не равное нулю), a p!t — нечётное
(но большее единицы) или наоборот (при этом ру , p';t, pz , p'z - лю-
бые, включая и равные нулю), либо р:/ - чётное 0), а р'п - не-
чётное (ру ^1) или наоборот (при этом р.г, р'г, pz , pz - любые),
либо pz — чётное (р? 0), а р'г - нечётное 1) или наоборот
12.4.Сравнение лагранжевых и иерархических элементов 615
(при этом р.,., р'1;, р;1, р';1 - любые)1. Это, в свою очередь, приводит к
меньшей заполненности глобальной матрицы конечноэлементной
СЛАУ.
При согласовании элементов высоких порядков на несогласован-
ных ячейках трудоёмкость реализации стыковки для иерархических
базисов, быть может, несколько выше2, чем для лагранжевых, но при
использовании иерархических базисов заполненность и матрицы Т
ниже (для элементов третьего порядка и выше), что, в свою очередь,
также можно использовать для некоторого снижения вычислительных
затрат.
Но самым главным преимуществом иерархических базисов являет-
ся то, что при абсолютно одинаковых аппроксимационных свойствах
лагранжева и иерархического базисов (т е. тождественного совпадения
конечномерных пространств, натянутых на эти базисы) сходимость
многих наиболее эффективных и часто используемых для решения
конечноэлементных СЛАУ итерационных методов может оказаться
заметно выше в случае, когда эти СЛАУ получены с использованием
иерархических базисов (т.е. для иерархических базисов не только
уменьшается заполненность матрицы СЛАУ, по и уменьшается коли-
чество итерации при решении этой СЛАУ). А поскольку этап реше-
ния СЛАУ является обычно самым вычислительно трудоёмким, ис-
пользование иерархических базисов может привести к заметной эко-
номии затрат машинного времени на получение решения с требуемой
точностью.
1 При использовании одномерных шаблонных функций вида (12.10) (или
(12.11)) в локальной матрице жёсткости количество заведомо нулевых эле-
ментов максимально (хотя в двумерных и особенно трёхмерных задачах это
преимущество использования функций вида (12.10) или (12.11) существенно
уменьшается), но, к сожалению, соответствующие компоненты матрицы мас-
сы могут быть ненулевыми.
2 Хотя при использовании одномерных шаблонных функций вида (12.5)
процедура вычисления компонент матрицы Т не столь уж сложна, поскольку
в достаточной степени формализована (см. соотношения (12.41)-( 12.43) и
рассуждения после них).
616
13 .Основные способы уменьшения погрешности ...
13. ОСНОВНЫЕ СПОСОБЫ УМЕНЬШЕНИЯ
ПОГРЕШНОСТИ КОНЕЧНОЭЛЕМЕНТНЫХ РЕШЕНИЙ
ДВУ- И ТРЁХМЕРНЫХ ЗАДАЧ
13.1. О НЕКОТОРЫХ СТРАТЕГИЯХ ПОВЫШЕНИЯ ТОЧНОСТИ
КОНЕЧНОЭЛЕМЕНТНЫХ РЕШЕНИИ
В четвёртом разделе нами были рассмотрены два способа умень-
шения погрешности конечноэлементных решений одномерных задач -
это уменьшение размера элемента и повышение его порядка (т.е. по-
вышение степени полиномов, используемых в качестве базисных
функций). Эти способы остаются основными и при решении много-
мерных (дву- и трёхмерных) задач. Однако если в одномерном случае
при дроблении всех ячеек сетки вдвое вычислительные затраты воз-
растали также примерно вдвое (в соответствии с ростом количества
узлов и неизвестных), то при решении многомерных задач дробление
сетки приводит к гораздо большему росту вычислительных затрат.
В двумерном случае при дроблении всей сетки вдвое только коли-
чество узлов (и соответственно размерность СЛАУ) увеличивается в
четыре раза. При этом несколько изменяется структура матрицы (уве-
личивается ширина её ленты), растёт количество итераций при реше-
нии СЛАУ итерационными методами, что приводит к росту вычисли-
тельных затрат уже более чем в четыре раза
Ещё быстрее происходит рост вычислительных затрат при дробле-
нии всей сетки в трёхмерном случае. В этом случае число узлов увели-
чивается в восемь раз, и рост вычислительных затрат на решение
СЛАУ может увеличиться даже более чем на порядок.
Аналогичная ситуация возникает и при повышении порядка всех
элементов сетки. В двумерном случае при изменении порядка элемен-
тов с первого на второй не только в четыре раза увеличивается число
неизвестных, по и происходит заметный рост заполненности (ненуле-
выми элементами) матрицы конечноэлементной СЛАУ. В трёхмерном
случае увеличение порядка элемента приводит к ещё более значитель-
ному увеличению размерности СЛАУ и заполненности её матрицы
Поэтому при решении многомерных практических задач, как пра-
вило, не удаётся использовать стратегии повышения точности конеч-
ноэлементного решения за счёт нескольких дроблений всех элементов
сетки (или за счёт увеличения порядка некоторых элементов). Гораздо
более эффективными здесь являются стратегии, основанные на ис-
13.2.Соотношения, позволяющие проводить сравнения ...
617
пользовании неравномерных сеток и локальных дроблений ячеек сетки
(или за счёт увеличения порядка всех элементов) в тех местах расчёт-
ной области, где конечноэлементное решение имеет максимальную
погрешность. Однако для реализации этих стратегий нужно иметь воз-
можность достаточно просто сравнивать погрешности решений, полу-
ченных на сетках сразличными размерами ячеек и с элементами раз-
личных порядков. Такие возможности были рассмотрены нами уже в
третьем разделе и продемонстрированы на решении одномерных задач
в четвёртом разделе. Здесь мы покажем, как они могут быть использо-
ваны при решении многомерных задач.
13.2. СООТНОШЕНИЯ, ПОЗВОЛЯЮЩИЕ ПРОВОДИТЬ СРАВНЕНИЯ
ПОГРЕШНОСТЕЙ КОНЕЧНОЭЛЕМЕНТНЫХ РЕШЕНИИ
Как было показано в третьем разделе, сравнить погрешности
двух конечноэлементных решений и'1'1 и uh>2. полученных на различ-
ных сетках (как с различными размерами ячеек, так и с элементами
различных порядков), можно на основе соотношения
<i3j)
если в задаче нет неоднородных главных краевых условий, и соотно-
шения
= f (и'1'2) - / '1) - L (w9, u'1'2) + L (ш“, и'1'1), (13.2)
если в задаче есть неоднородное краевое условие первого рода (см.
с. 122, соотношение (3.100)).
Входящие в соотношения (13.1) и (13.2) линейная форма f (и) и
билинейная форма L(u,v) — это фактически левая и правая части урав-
нения Галёркина
L(i/,, v) = /(v),
определяющего эквивалентную вариационную постановк для решае-
мой краевой задачи, т.е. (см. соотношение (3.11) или (3.37))
L(w, v) = J X grad w grad vdQ + J ywvd£l + J fiwvdS, (13.3)
q Я 53
f (v) = J fudQ-\- J QvdS + J fiupvdS . (13-4)
я s2 5;j
Функция же w!l в соотношении (13 2) - это произвольная функция
(из гильбертова пространства 771), удовлетворяющая главным крае-
618
13.Основные способы уменьшения погрешности ...
вым условиям, т.е. = ufI.
Значения линейной и билинейной форм могут
быть легко вычислены с помощью матрицы А и вектора b, получае-
мых в процессе генерации конечноэлементной СЛАУ. Действительно,
поскольку и1' ищется в виде линейной комбинации базисных функций
71
ф,- (т.е. uh — У^^'ф, ), значение формы можно получить как
,:=1
результат скалярного произведения вектора весов q" на вектор b :
./(??') = (q7')T ь,
причем компоненты вектора b определяются соотношением (которое
п
сразу следует из (3.22) с учётом uh = У^д7-'ф>: )
7=1
= J + J + J Рг/^ф^б',
12 5’2 S;j
т.е. b./ фактически являются компонентами глобального вектора пра-
вой части конечноэлементной СЛАУ, полученными в результате её
сборки до учёта главных краевых условий.
Гочно так же можно убедиться, что если функция wa точно пред-
ставима в базисе {ф,:} (т.е.
= 0 ), значение билиней-
2=1
ной формы Llw^u1' 1 можно легко вычислить с помощью соотноше-
ния
Z,(w"X) = (q"’)T Aq'',
в котором </" и q'1 - веса разложения по базису {ф,} функций wfJ и
и1' соответственно, а матрица А - глобальная матрица конечноэле-
ментной СЛАУ без учёта главных краевых условий (чтобы в этом убе-
диться, достаточно подставить в соотношение (3.21) в качестве w
и II
функцию w9 = 22<7/''ф7 , а в качестве и - функцию и1' = У^д.-'ф7 )•
1аким образом, для сравнения погрешностей двух решении
и'1'1 = и и'1'2 — д-',2ф''^‘‘,/'2 , полученных на различных
4=1 7 = 1
13.2.Соотношения, позволяющие проводить сравнения ...
619
конечноэлементных сетках (с базисами и |ф*"елЛ2} соответ-
ственно), соотношения (13.1) и (13.2) можно записать в виде
||u —— ||?г — w/l,2|| = (q/l,2j b7'’2 — (q6’1j b7'*1, (13.5)
IIй—u/I,1li—IIй—и''2II = (q,l>2) 2—^Л1 —
— (q'"’1 )Т A/l,2q/l’2 -f- (q'"’2)T A/l’1q/1’1, (13.6)
где А7'’1 и Ь7'’1 - глобальные матрица и вектор для первой сетки, а
А71’2 и ЬЛ’2 - для второй (взятые до учёта главных краевых условии со
сборкой всех уравнений, включая так называемые фиктивные).
Обратим особое внимание на те ограничения, которые необходимы
для справедливости соотношений (13.5) и (13.6).
Во-первых, параметры краевой задачи не должны изменяться при
переходе от одной сетки к другой. Это может случиться, если один из
параметров (например, J) заменяется своим интерполянтом
»»1 71-2
53.А1'ФГеА/,Л на первой сетке и 53на второй, и при этом
4=1 1=1
"1 7/.-2
* 53 То же самое можно сказать и об осталь-
2=1 4=1 _
ных параметрах уравнения и краевых условий. Для выполнения этих
ограничений как минимум необходимо, чтобы геометрия расчётной
области не изменялась при переходе от одной сетки к другой (напри-
мер, из-за различной аппроксимации её криволинейных внешних или
внутренних границ).
Во-вторых, при наличии в задаче неоднородных первых краевых
условий функция wf> должна быть точно представима в базисах
r^/ne.s/ii} и | пространств, соответствующих сравниваемым
конечноэлементным решениям uh'1 и и'1'2 (т.е.
i
= 0 и
™’-Е7Г2'ФГ'‘2
= 0).
Если указанные выше ограничения не выполняются, то, строго го-
воря, соотношения (13.5) и (13.6) перестают быть справедливыми. По-
этому в ситуациях, когда дробление сетки приводит к некоторому из-
менению параметров задачи, сравнить по точности два конечноэле-
ментных решения г?1’1 и и'1'2 можно, вычислив, например, их погреш-
ность относительно третьего, заведомо более точного, решения и’1'3 .
Для этого нркно представить конечноэлементныс решения и1'1 и и11,2
в виде их разложений по базису, на котором получено более точное
решение и'1,3 :
620
13 Основные способы уменьшения погрешности ...
7. i
т.е. q/1,1 и q-1'2 - веса разложений и'1'1 и и'1’2 по базису {ф™™Л3}. При
этом веса q-1'1 и г;/1’2 могут быть вычислены как значения и'1'1 и uh'2 в
узлах сетки, определяющей базис |'ф"1ел7г31. Это означает, что если
сетка, определяющая базис s/t3}, является вложенной, например, к
сетке, определяющей базис }, и базисы и |ф”‘ел’,13|
однотипны (т.е. определяют элементы одного порядка), то и"'[ = й'1'1.
То же самое можно сказать о функции и'1'2. Очевидно, что размер-
ность векторов q/tJ и q’1'2 будет совпадать с размерностью векто-
ра q/l’3.
Квадрат энергетической нормы разности решений и’1'3 и uh,i мо-
жет быть вычислен следующим образом:
||<,Л3 - «*•'£ = (q"'3 - q'-’1)7 A'*’3 (q'‘-3 - q'В * * 11), (13.7)
где А' 3 - глобальная матрица, построенная для базиса (и
взятая до учёта главных краевых условий).
Аналогично может быть вычислен квадрат энергетической нормы
разности решений г?1,3 и йЛ’2 :
р-3 - й'12£ = (q'‘-3 - Ч«)Т A'1’3 (q*>3 - qA’2) . (13.8)
Сравнением значений (13.7) и (13.8) легко определить, какое из ре-
шений i//*’1 или и1'2 является более точным (и насколько).
Соотношения (13.7) и (13.8) позволяют сравнивать погрешности
решений в энергетической норме. Однако в некоторых ситуациях
удобней оценивать погрешность приближённого решения и" в норме
пространства L2 (Q):
В этом случае вычислить норму разности двух конечноэлементных
решений можно с помощью матрицы массы.
Пусть по-прежнему uh'1 и и1'2 - два конечноэлементных решения,
которые мы хотим сравнить по точности, а иЛ)3 - заведомо более точ-
ное решение, полученное на более подробной сетке. Обозначим через
С матрицу массы, компоненты которой определяются соотношениями
13.2.Соотношения, позволяющие проводить сравнения ...
621
J (13.9)
Очевидно, что эта матрица может быть стандартным образом собра-
на из локальных матриц конечных элементов на сетке, где определен
базис |ф'"Г5/'3} . Тогда квадрат отклонений uhA и uh'2 от и1'"* в норме
пространства L? (Q) может быть вычислен следующим образом'
|,Л3 _ £ = (qM _ qM )т С".3 (q'*'3 - q'1?), (13 10)
||„м - й.,‘-2||3 = (qM-q«)Tc'‘-3(qM_qM)i (13 l,)
где по-прежнему q^1 и qz''2 - веса разложения uhA и и11,2 по базису
Соотношения (13.10) и (13.11) можно использовать для оценки по-
грешности решения в отдельной подобласти Q расчётной области О..
Для этого достаточно собирать матрицу массы только но конечным
элементам, принадлежащим подобласти Q. Кроме того, если при
оценке погрешности точность решения в одних подобластях расчётной
области более важна, чем в других, это можно учесть введением в со-
отношение (13.9), определяющее матрицу массы, весовой функции ш:
c];f = J (13.12)
Q
Очевидно, соотношение (13.12) можно использовать и в ситуации,
когда мы не хотим учитывать погрешность в каких-либо подобластях
расчётной области - достаточно в этих подобластях задать функцию ш
равной нулю, поскольку правая часть соотношения (13.10) с матрицей
С1,3, имеющей компоненты (13.12), фактически определяет
В заключение обратим внимание читателя на следующий довольно
важный факт; При дроблениях сетки можег несколько изменяться расчет-
ная область за счёт уточнения аппроксимации её криволинейных границ.
Например, если двумерная расчётная область имеет криволинейную гра-
ницу Г, которая при разбиении на конечные элементы (например, тре-
угольники первого порядка) аппроксимируется отрезками, го при дробле-
нии сетки дополнительные узлы должны ставиться не на отрезки, аппрок-
симирующие криволинейную границу, а на саму границу. Эта ситуация
показана на рис. 140, причем на рис. 140// показаны ячейки сетки до
дробления и этому рисунку соответствует конечноэлементное решение
u,hA . 1 la рис. 140,6 крестиками показаны места, куда при дроблении ребер
должны быть поставлены дополнительные узлы, а на рис. 140,в — сетка
622
13 .Основные способы уменьшения погрешности ...
после дробления и переноса узлов с граничных ребер на криволинейную
границу. Штриховыми линиями на этом рисунке показаны рёбра грубой
сетки вблизи криволинейной границы.
Рис. 140. Дробление сетки около криволинейной границы
Будем считать, что рис. 140,в соответствует конечноэлементное
решение uh,z и покажем, как можно получить веса функций и7’’1 для
оценки (с помощью формулы (13.10)) погрешности конечноэлементно-
го решения, соответствующего сетке, изображённой на рис. 140,<7. Оче-
видно, что в узле Д значение функции й7'’1 просто совпадает со зна-
чением решения и1'"1 в этом узле (и поэтому вес ), в узле
Рп, лежащем на середине ребра значение функции и1*'1 вы-
числяется как полусумма значений uk,} в узлах и Р5 (и соответст-
венно вес дуу1 = 0.5 ), а в узле Р7 w7'’1 вообще не опреде-
лено, и его имеет смысл определить так же, как и в случаях, когда узел
подробной сетки попадает на ребро грубой сетки, т.е.
^ = о,5 + д!р).
Аналогично можно поступать и в ситуациях, когда дробление рёбер
делается неравномерно, и подобным же образом пересчитывать решение
во внутренних узлах ребер и элементов, примыкающих к криволиней-
ным границам, при дроблении сеток с элементами высоких порядков.
13.3. р -ТЕХНОЛОГИИ, h -ТЕХНОЛОГИИ И p-h -ТЕХНОЛОГИИ
УТОЧНЕНИЯ РЕШЕНИЙ. АДАПТИВНЫЕ СЕТКИ
Как уже говорилось выше, существует два основных способа по-
вышения точности аппроксимации конечноэлементного решения -
дробление ячеек сетки и повышение порядка элементов. Соответст-
венно технологии, в которых уточнение конечноэлементного решения
13.3.p-технологии, h-технологии и p-h-гехнологии ... .
623
основано на дроблении ячеек сетки, называют /г-технологиями, а
технологии, в которых уточнение конечноэлементного решения осно-
вано на повышении порядка элементов, — р-технологиями. Гели же
для уточнения конечноэлсментного решения одновременно использу-
ются и дробление ячеек сетки и повышение порядка элемен гов, то та-
кие технологии называют р -h -технологиями.
Рассмотрим некоторые стратегии, которые могут быть применены
при использовании р-, h - и р-h -технологий уточнения консчноэлс-
ментных решений.
Мы будем считать, что возможны локальные дробления сетки (т.е.
дробление части элементов) или повышение порядка только у части эле-
ментов. При использовании двумерных сеток с прямоугольными (или
четырёхугольными) ячейками или трёхмерных сеток с ячейками в виде
параллелепипедов, прямых призм или шестигранников в результате ло-
кальных дроблений будут появляться несогласованные сетки и для согла-
сования конечных элементов может быть применена технология
Т-преобразования или переходных элементов (см. одиннадцатый раз-
дел). Согласование же элементов разных порядков удобней всего выпол-
нять при использовании иерархических базисов (см. двенадцатый раздел).
Наименее затратной стратегией уточнения копечноэлементного
решения является стратегия, основанная на контроле потоков через
границы смежных конечных элементов. В ней по полученному конеч-
поэлементному решению вычисляются потоки X с двух сторон
каждой границы Sk{_k2 — ППА;2 , разделяющей два конечных эле-
мента ГД и СД2, и вычисляется величина v\k{^k2 несовпадения пото-
ков, например, в виде
т1А.1-А-2
(13.13)
или
(13-14)
Для тех элементов, которые содержат грани с большими (превы-
шающими некоторый порог1 ri](v) значениями критерия (13.13) или
(13.14), либо выполняется их дробление (в /г-технологии), либо по-
вышается их порядок (в р -технологии). После этого вычисляется ре-
1 Этот порог может быть определён, например, как ад111ах , ot- некоторый
коэффициент в диапазоне 0 < а < 1, дшах - максимальное значение т]*1_д;2 .
624
13.Основные способы уменьшения погрешности ...
шение на новой сетке с раздробленными ячейками или с элементами
более высокого порядка и процедура повторяется. Критерием останова
является либо превышение отведённых для решения задачи лимитов
вычислительных ресурсов, либо достижение ситуации, когда макси-
мальное по всем границам значение становится меньше задан-
ного минимального порога т]111;11 (при использовании критерия (13.13)
в качестве критерия останова можно использовать соотношение
< Лг > означающее, что сумма всех несовпадений потоков не
превосходит некоторого порогового значения лг )
При использовании же р -h -технологии стратегия, основанная на
понижении значений критериев (13.13) или (13.14), может выглядеть
следующим образом. После того как определены конечные элементы с
границами, на которых критерий принимает значения, превы-
шающие порог Ли, сначала выполняется дробление этих элементов и
считаются новые значения Ла^-а^ а затем повышается порядок этих
элементов (до их дробления) и также вычисляются значения Ла^-А;2
Предпочтение отдаётся повышению порядка только в том случае, ко-
гда значения Ла.1-а2 за счёт повышения порядка элементов уменьши-
лись заметно сильнее, чем при дроблении этих элементов. Это объяс-
няется тем, что повышение порядка элементов, как правило, приводит
к большему росту вычислительных затрат1.
Основанные на минимизации критериев (13.13) или (13.14) страте-
гии в ряде случаев могут давать сгущение сеток или повышение по-
рядка элементов не совсем в тех местах, которые максимально влияют
на точность получаемого конечноэлементного решения (особенно если
требуемая точность необходима в какой-то небольшой части расчёт-
ной области), а в некоторых случаях и вовсе неприменимы. Например,
при использовании эрмитовых элементов на прямоугольниках или
параллелепипедах потоки между элементами являются всегда непре-
рывными2 (естественно, и в тех случаях, когда конечноэлементное
решение имеет погрешность). Это может служить довольно серьёзным
аргументом против того, что несовпадение потоков напрямую связано
с точностью получаемого решения.
Действительно, при использовании лагранжевых бикубических или
трикубических базисных функций при решении задач с непрерывным
коэффициентом диффузии точность получаемого конечноэлементного
1 В принципе, можно сравнивать результаты нескольких вложенных дроб-
лений с результатами одного повышения порядка, выполняя при этом столько
дроблений, чтобы соответствующие им вычислительные затраты были близки
к вычислительным затратам, необходимым для выполнения одноэтапного
повышения порядка.
2 Исключения составляют случаи, когда в задаче есть разрывы в коэффи-
циенте X и применены специальные базисные функции, см. с. 155 и разде-
лы 4.9-4.10. В этом случае разрывы в потоках будут только на границах, и в
целом ситуация останется той же самой, что и при использовании стандарт-
ных эрмитовых элементов (с непрерывными производными).
13.3.p-технологии, h-технологии и p-h-технологии
625
решения в энергетической норме, по крайней мере, нс ниже (а обычно
заметно выше), чем при использовании эрмитовых базисных функций
на той же сетке (так как на одной и той же сетке пространство, натяну-
тое на базис из эрмитовых функций, полностью включается в про-
странство, натянутое на базис из лагранжевых функций той же степе-
ни). Но у конечноэлементного решения, полученного на эрмитовых
элементах, нет никаких разрывов в потоках, а у решения на лагранже-
вых элементах эти разрывы есть практически всегда (за исключением
задач с решениями в виде полиномов невысокой степени), и при этом
точность решения на эрмитовых элементах может быть ниже.
Кроме того, при наличии в задаче локальных источников, особенно
если они сосредоточены в точках или на линии, при использовании кри-
терия (13.14) дробление сетки (или повышение порядков элементов) все
время будет происходить в окрестности этих источников. Мы же в вось-
мом разделе показали, что для получения нужного по точности решения
на некотором удалении от источника дробление в окрестности локальных
источников не является необходимым. Лишние дробления при использо-
вании критерия (13.14) могут выполняться также в окрестностях угловых
точек границ, на которых является разрывным коэффициент X.
Если же используется критерий (13.13), то необоснованные дробле-
ния (или повышения порядков элементов) могут выполняться на тех
участках, где используются элементы больших размеров, и при этом на
качество решения в областях с небольшими ячейками эти дробления
могут не оказывать почти никакого влияния1.
Рассмотрим другую стратегию повышения точности конечноэле-
ментных решений. Эта стратегия основана на определении мест сетки,
в которых дробление определённого {относительно небольшого) числа
элементов приводит к максимальному снижению погрешности конеч-
ноэлементного решения. При этом для вычисления погрешности могут
быть использованы либо соотношения (13.5) (или (13.6)), либо соот-
ношения (13.7)-( 13.8) или (13.10)-(13.11).
Разобьём расчётную область на прямоугольники (в двумерном слу-
чае) или на параллелепипеды (в трёхмерном случае) так, чтобы в каж-
дый прямоугольник (или параллелепипед) попадало примерно одина-
ковое количество «центров» конечных элементов (определяемых, на-
/
пример, как Р^ = уУ^РУ1'
Z /=1
где Ppk - вершины конечного элемента
Q/.., I — их количество). Алгоритм разбиения расчётной области па
такие прямоугольники или параллелепипеды был описан нами в разде-
ле 10.7.1 (естественно, эти прямоугольники или параллелепипеды не
обязательно должны быть согласованными, как конечные элементы, и
их объединение может не совпадать с расчётной областью).
1 Тем не менее заметим, что у многих конечноэлементных решений задач с
распределёнными источниками всё-таки есть довольно устойчивая связь ме-
жду их точностью и величиной разрывов потоков на границах элементов, и
высокая экономичность технологии, основанной на контроле потоков, делает
её довольно эффективной в таких случаях.
626
13.Основные способы уменьшения погрешности ...
Пусть пц/ - количество прямоугольников или параллелепипедов
И /, на которые разбита расчётная область. Решим поочерёдно щу
задач, в которых выполнено дробление только тех ячеек сетки (или
повышен порядок только тех элементов), чьи центры попали в один из
таких прямоугольников (или параллелепипедов), и оценим погреш-
ность каждого из получаемых конечноэлементных решений. При этом
рассмотрим случай, когда для сравнения погрешности можно исполь-
зовать соотношения (13.5) или (13.6).
Припишем каждому прямоугольнику Wi число di, являющееся моду-
лем разности погрешностей конечноэлементных решений с раздроблен-
ными и нераздрооленными элементами1 *, центры которых попали в пря-
моугольник W[. Величина dt легко считается по формуле (13.5) (или
(13.6), если в задаче есть неоднородные первые краевые условия). Затем
ищется номер т, для которого drH = max(cZ/), и выбирается сетка, в
которой были раздроблены ячейки с центрами, лежащими в прямоуголь-
нике . Таким образом, мы выбрали сетку, которая за счёт дробления
относительно небольшого числа конечных элементов сильнее всего по-
зволяет уменьшить погрешность конечноэлементного решения.
Чтобы продолжить процедуру оптимального дробления сетки, ра-
зобьём прямоугольник 1И„, на несколько прямоугольников
IV,Н],...,так, чтобы количество ячеек новой сетки с центрами,
лежащими в каждом из «новых» прямоугольников 1И,П, примерно
совпадало с количеством ячеек с центрами, лежащими в каждом из
остальных прямоугольников IV/ (для т ). Для выбора же нового
места сетки, в котором будут наиболее эффективны дальнейшие дроб-
ления, нам нужны «новые» значения tZz, полученные в результате
дроблений конечных элементов по участкам, определяемым новым
набором прямоугольников (в котором вместо прямоугольника Wirl
взяты «новые» прямоугольники ,...,Иф,ч).
Хотя для новой сетки значения dt, полученные для «старых» пря-
моугольников на предыдущем этапе, могут несколько измениться,
можно всё-гаки получить значения только для «новых» прямо-
угольников И7,»] ,...,1И7,Ц (решением s задач с поочерёдными дробле-
ниями сетки в местах, определяемых прямоугольниками Иф,( ,...,1УШ ).
Тогда максимальное значение dm можно выбрать с использованием
только s «новых» значений dt и остальных «старых» значений ф (по-
лученных для неизмененных прямоугольников IV/ на старой сетке; т.е.
«старые» значения ф для новой сетки фактически можно считать не-
которыми оценками «настоящих» значений ф). При этом имеет смысл
1 Для р -технологии - с увеличенным и неувеличенным порядком элемен-
тов в этом прямоугольнике.
13.3.p-технологии, h-технологии и p-h-технологии . . 627
по-разному обрабатывать ситуации, когда значение d„, попадает на
одно из «новых» значений, а когда - на одно из «старых».
Если dril находится среди «новых» значений, то можно сразу же
приступить к очередной итерации дробления сетки, начиная с разбие-
ния соответствующего dlrl прямоугольника на s «новых» прямоуголь-
ников.
Если же d.in находится среди «старых» значений, то имеет смысл
обновить его значение (путём перевычисления погрешности по фор-
муле (13.5) или (13.6) для новой сетки с дроблением соответствующих
ячеек и без этого дробления). Если обновленное значение остаётся
максимальным, то можно приступить к очередной итерации, а если
нет— то выбрать прямоугольник, соответствующий новому макси-
мальному значению, и обрабатывать эту ситуацию в зависимости от
того, является ли dm «настоящим» значением погрешности или только
его оценкой, взятой с предыдущего этапа.
Рассмотренный итерационный процесс прекращается, когда либо
все погрешности dt (или их сумма) становятся ниже заданного порога,
либо достигается предел отведённых для решения задачи вычисли-
тельных ресурсов.
Таким образом, один шаг построенного нами итерационного про-
цесса фактически заключается в определении места сетки, дробление в
котором конечных элементов приводит к максимальному снижению
погрешности численного решения.
Заметим, что только на первом шаге рассмотренного итерационно-
го процесса надо решать ??.|И задач (где nw - первоначальное количе-
ство прямоугольников или параллелепипедов), а на каждом после-
дующем — можно решать только четыре задачи для двумерного случая
или восемь для трёхмерного (плюс, возможно, одну или несколько
задач для обновляемых «старых» прямоугольников или параллелепи-
педов). При этом на каждом шаге число элементов в сетке будет уве-
личиваться примерно в (тщ/ + З^щу раз для двумерного случая и при-
мерно в (щ|/ + T)[n.w - Для трёхмерного (где /г1И - количество прямо-
угольников или параллелепипедов на предыдущем шаге). Количество
же прямоугольников увеличивается в среднем на 3, а параллелепипе-
дов— в среднем на 7 на каждом шаге итерационного процесса. Оче-
видно, что относительная скорость роста количества элементов в сетке
убывает на каждом шаге итерационного процесса (и она, конечно же,
несопоставимо меньше, чем при дроблении всех элементов сетки), а
сами дробления с каждым шагом становятся всё более локальными
Итак, мы рассмотрели случай, когда для сравнения погрешности
можно использовать соотношения (13.5) или (13.6) (в этом случае рас-
сматриваемая стратегия является либо наименее затратной, либо наи-
более обоснованной).
Теперь покажем, как можно использовать эту стратегию в ситуа-
ции, когда для оценки погрешности нельзя использовать соотношения
(13.5) или (13.6), а получить оценку погрешности можно только с по-
628
13.Основные способы уменьшения погрешности ...
мощью соотношений (13.7)—(13.8) или (13.10)-(13.1 1), т.е. путём срав-
нения решений, вычисленных на различных сетках. При этом в соот-
ношениях (13.7) (13.8) или (13.10)—(13.11) и11'1 и и11'2 можно интер-
претировать как сравниваемые решения (и7*’1 - как решение на сетке с
текущего шага, и1'2 - как решение на сетке с локальными дробления-
ми ячеек сетки текущего шага, центры которых попали в выбранный
прямоугольник Wi), a uh,i — как заведомо более точное решение. В
этом случае d; может определена либо как разность (13.8) и (13.7),
либо как разность (13.11) и (13.10). Естественно, чтобы воспользовать-
ся соотношениями (13.7)-(!3.8) или (13.10)—(13.1 1), необходимо вы-
полнять (как об этом было сказано в разделе 13.2) пересчёты сравни-
ваемых решений и!1'1 и и'1'2 в функции й7'11 и и11,2, определённые на
сетке, на которой было получено решение и,,,л .
В принципе, при использовании соотношений (13.7)—(13.8) или
(13.10)-(13.1 1) для оценки точности решений с локальными дробле-
ниями в качестве более точного решения и.'3 можно взять решение на
сетке, полученной дроблением всех ячеек сетки с текущего шага. Од-
нако такое дробление в двумерном случае увеличивает количество
узлов и элементов примерно в четыре раза, а в трёхмерном — примерно
в восемь раз, и, как следствие этого, на каждом шаге итерационного
процесса вычислительные затраты возрастут многократно, что делает
такую технологию очень неэффективной и фактически неприемлемой
для практического использования. Тем не менее возможны её модифи-
кации, несколько менее обоснованные, но позволяющие сделать вы-
числительные затраты близкими к ситуации, когда используются соот-
ношения (13.5) или (13.6).
Эти модификации базируются на следующем (почти всегда под-
тверждающемся на практике) предположении, которое заключается в
следующем. Если раздробить исходную сетку в двух различных по-
добластях расчётной области, то отклонение от решения и,1,[, полу-
ченного на исходной сетке, конечноэлементиых решений и- и и7'13,
полученных при дроблениях исходной сетки в двух разных подобла-
стях, будет больше для того из решений и1,2 и и1'3 , которое ближе к
точному. 11оэтому в рассмотренном выше итерационном процесса
можно определить (7/ как квадрат нормы разности решения и7'1, полу-
ченного на ссгке с текущего шага, и решения г/'*2, полученного на
сетке с локальными дроблениями тех ячеек сетки текущего шага, цен-
тры которых попали в прямоугольник , т.е.
di = ||?t/l 2 — и1*'11|' = |q7,2 — q71’1) A7t’2 (q7*’2 — q7'’1) (13.15)
или
dt = p’2 - = (У-2 - q^f C"’2 (q"-2 - q"-1), (13.16)
13.3.p-технологии, h-технологии и p-h-технологии . . .
629
где А7'2- матрица конечноэлементной СЛАУ (взятая до учёта первых
краевых условий, см. раздел 13.2), соответствующая сетке с локальны-
ми дроблениями (на которой было получено и'1'2), С1,2- матрица мас-
сы для этой же сетки (построенная, возможно, с использованием пара-
метра ш, см. (13.12)), a q7'’1 - веса разложения й7*’1, полученные пере-
счётом и1''1 с сетки текущего шага (без дробления) на сетку с локаль-
ными дроблениями.
Очевидно, при использовании соотношений (13.15) или (13.16) вы-
числительные затраты вполне соответствуют вычислительным затра-
там, когда для сравнения точности решений берутся соотношения
(13.5) или (13.6). Однако следует помнить, что если при использовании
соотношений (13.5) или (13.6) ф показывает действительную раз-
ность отличий двух приближённых решений и'1,1 и и11'2 от точного
решения и, то соотношения (13.15) или (13.16)- это только некоторая
оценка, позволяющая судить, какое из множества решений и'1,2 (каж-
дому из которых соответсгвует своё локальное дробление и своё г//)
может оказаться наиболее близким к точному.
Рассмотренную стратегию, основанную на разбиении расчётной
области на прямоугольники или параллелепипеды , с помощью ко-
торых производится оценка влияния конечноэлементной сетки на по-
грешность получаемого решения, будем называть -стратегией.
W[ -стратегию можно столь же успешно использовать и тогда, когда
уточнение решения проводится на основе р -технологии. В этом слу-
чае вместо дроблений конечных элементов, центры которых попали в
прямоугольник (или параллелепипед) И), повышается их порядок.
Разбиение же прямоугольника , для которого повышение порядка
соответствующих ему конечных элементов привело к максимальному
снижению погрешности, выполняется следующим образом. В каждом
из «новых» прямоугольников (полученных в результате
разбиения W„,) общее количество степеней свободы1 конечных эле-
ментов, соответствующих каждому из этих прямоугольников
, должно стать близким к общему количеству степеней
свободы конечных элементов, соответствующих 1Г„, до его разбиения
(а значит, и общему количеству степеней свободы конечных элемен-
тов, соответствующих каждому из «старых» прямоугольников И) ).
Принципы использования -стратегии для p—h -технологии ана-
логичны рассмотренным выше принципам использования для p-h-
технологии стратегии, основанной на контроле потоков (см. с. 624).
Здесь также следует учитывать, что повышение порядка элементов
1 Под общим количеством степеней свободы для каждого прямоугольника
IV/ мы понимаем количество ненулевых глобальных базисных функций на
конечных элементах, соответствующих .
630
13.Основные способы уменьшения погрешности ...
может быть вычислительно гораздо более затратным, чем одно вло-
женное дробление Поэтому при оценке того, что является более эф-
фективным- дробление ячеек или повышение порядка элементов,
имеет смысл ввести поправочные коэффициенты к получаемым оцен-
кам погрешности, пропорциональные вычислительным затратам1.
Вообще говоря, при использовании p-h -технологии имеет смысл
сначала выполнять дробление сетки (особенно в ситуациях, когда в
расчётной области есть криволинейные границы) и переходить к по-
вышению порядка элементов только после того, как ячейки сетки ста-
ли достаточно мелкими и искривлённые границы аппроксимированы
достаточно точно2. При этом использовать элементы выше четвёртого
порядка, как правило, нецелесообразно (из-за колоссального роста
вычислительных затрат), т.е. после доведения элементов, попадающих
в прямоугольник , до третьего или четвёртого порядка, для даль-
нейшего уточнения решения имеет смысл вернуться к их дроблению.
По сравнению со стратегией, основанной на контроле потоков,
-стратегия является более универсальной. Например, П} -стратегию
можно применять при использовании эрмитовых элементов, когда
стратегия, основанная на контроле потоков, неприменима вообще.
Кроме того, далеко не во всех задачах точность решения напрямую
связана с непрерывноегыо потоков - примером могут служить вектор-
ные задачи, рассмотренные в четырнадцатом и пятнадцатом разделах
П /-стратегия является более гибкой из-за больших возможностей в
выборе различных критериев оценки точности получаемых решений.
Например, в качестве нормы отклонения двух приближённых решений
трёхмерной задачи можно использовать интеграл от модуля отклоне-
ния этих решений или каких-либо их производных не только но части
подобласти расчётной области, но и по некоторой поверхности, по
которой, например, проводится измерение характеристик изучаемых
полей. Эти возможности делают IV/ -стратегию довольно удобной и
при решении векгорнььк задач, когда решением является вектор-
функция, а изучаются характеристики, являющиеся производными
искомой вектор-функции (причём, как правило, на некоторой внутрен-
ней поверхности расчётной области).
Рассмотренные в данном разделе стратегии уточнения конечноэле-
ментных решений нацелены фактически на построение так называе-
мых адаптивных сеток, те. сеток, в которых по какому-либо крите-
рию пршнводится дробление части ячеек с целью максимального сни-
жения по1 рсшности конечноэлементного решения.
1 Или вместо повышения порядка элементов делать несколько вложенных
дроблений с эквивалентными повышению порядка суммарными вычисли-
тельными затратами, как об этом уже говорилось на с. 6/4
2 Естественно, при дроблении рёбер (и граней), аппроксимирующих ис-
кривлённые (изогнутые) участки границы, новые узлы должны переноситься
на искривлённую (изогнутую) границу, как это было показано, например, на
рис. 140 (с. 622).
631
14. ПРИМЕНЕНИЕ УЗЛОВОГО МКЭ
ДЛЯ РЕШЕНИЯ ВЕКТОРНЫХ ЗАДАЧ
Под векторными задачами мы будем понимать задачи, в кото-
рых решением является некоторая вектор-функция Примеры таких
задач были рассмотрены нами в первом разделе - это были задачи,
описывающие трёхмерные электромагнитные поля. Кроме того, к это-
му классу могут быть отнесены трёхмерные задачи теории упругости и
др. В данном разделе будут рассмотрены такие векторные задачи, ре-
шениями которых являются вектор-функции с компонентами, каждая
из которых удовлетворяет дифференциальному уравнению второго
порядка и как минимум непрерывна. Таким образом, каждая из компо-
нент искомой вектор-функции может быть найдена в виде линейной
комбинации непрерывных базисных функций, которые использовались
при решении скалярных задач. Такие базисные функции обычно назы-
вают узловыми (к ним относятся не только лагранжевы и эрмитовы
базисные функции, но и иерархические1). Соответственно и МКЭ, ис-
пользующий при нахождении численного решения такие базисные
функции, называю т узловым2.
Технологию построения конечпоэлементных аппроксимаций век-
торных задач на основе узлового МКЭ мы рассмотрим на примере
задачи (1.56)—(1.57), описывающей нестационарное электромагнитное
поле в однородной по магнитной проницаемости среде (и без учета
токов смещения).
1 Хотя при рассмотрении иерархических базисов мы ассоциировали часть
базисных функций с рёбрами и гранями, их вполне можно было бы, в общем-
то, ассоциировать и с некоторыми узлами на этих рёбрах или гранях; иерар-
хические же функции, ассоциированные с центрами элементов, вполне можно
считать ассоциированными с узлом в центре элемента. Тем не менее формаль-
но было бы правильней называть такие базисные функции не узловыми, а
скалярными (и конечные элементы с такими функциями называть скалярны-
ми, даже если они используются при решении векторных задач). В настоящее
время используется оба этих термина, мы же, в основном, будем пользоваться
термином «узловой» (применительно как к базисным функциям, так и к ко-
нечным элементам) даже при использовании иерархических базисов
2 В следующем разделе будут рассмотрены процедуры построения конеч-
ноэлеменгных решений задач, основанные на использовании в качестве ба-
зисных разрывных вектор-функций. Такой МКЭ обычно называют вектор-
ным.
632
14.Применение узлового МКЭ для решения векторных задач
14.1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И ВАРИАЦИОННАЯ ПОСТАНОВКА
Рассмотрим задачу определения трёхмерных функций
А,. = A,. (x,y,z,t), = A;i(x,y,z,t), Az = Az(x,y,z,t) и
У = У (.т, у, 2, £), удовлетворяющих в расчётной области Q системе
уравнений1
—i-ДД. 1 Po 0 М 1 дУ di. дх = 7CT J X У (14.1)
— АД, 4 14) 11 0 дА dt / , дУУ ду — J у > (14.2)
-Ьд,1 | 14) 0 VAZ . дУ dt dz t rcr Z 5 (14.3)
div(o grad 1') — div [ Si J = — div JCT, (14.4)
а на границе S области Q — краевым условиям
Ч=0, ’/ь=о- <|4-5>
Для простоты будем считать, что div JCT = 0.
Сначала выполним аппроксимацию системы уравнений (14.1)-
(14.4) по времени. Для этого можно воспользоваться неявной двух-
слойной или трёхслойной схемой (см. соотношения (7.7) и (7.24)). Да-
лее будем обозначать через А = А (я, у, z, t.^ значение вектор-
потенциала на текущем временном слое, а через A<J = А (я, г/, z, £,_])
и А<=2 = А.(т, ?/, z, ~ значение вектор-потенциала на двух преды-
дущих временных слоях. Аналогично под У будем понимать значение
скалярного потенциала на текущем (7 -м) временном слое. Тогда для
значений А и У на текущем временном слое получаем систему диф-
ференциальных уравнений:
_-i-AAr+^+a|K = Fa;; (14.6)
= (14.7)
T4) и У
-J-ДА, +чА + о£Е = Д, (14.8)
Ц() OZ
1 Под Д здесь понимается оператор Лапласа, т.е. Д = div grad .
14 1 .Математическая модель и вариационная постановка
633
— div (о grad V) — div^Aj = F] , (14.9)
где коэффициент , вектор-функция
F = F (ж, у, z) = (F.,: (ж, у, z) , Fy (.т, у, z), Fz (т, у, z))T
и функция Fl = Fv (х, у, z) определяются схемой аппроксимации по
времени. Так, для двухслойной полностью неявной схемы коэффици-
ент , вектор-функция F и функция F1 имеют вид
F = JCT + ,
Fv = div (тА^1),
а для трёхслойной полностью неявной схемы
tj_ i t 2
G'./— ^.7-2)
(14.10)
(14-11)
(14-12)
(14.13)
(14.14)
(14.15)
(14.16)
F = jcr +^1A<=1 T^A^2,
Fv = div (^A^1 +^2A^2),
Получим для системы уравнений (14.6)-(14 9) эквивалентную ва-
риационную постановку. Для этого умножим каждое из уравнений на
пробную функцию v G IIо , проинтегрируем по области Q и применим
формулу Грина (интс! рирования по частям)
— / grad А,. grad ш/Q +J ^A,:vdCl +J1 =J F:i.vdFl, Q Q Q (14.17)
J- f grad А • Го J о grad udQ T J ^AyVdQ. +J 0 vdCl —J Ff/vdFl , (14.18)
— / grad Az Го J О grad vdFl +J ^Azvd£l +J oQ^-vdFl —J FzvdSl, Ц Q Q (14.19)
J о grad У • grad vdFl + J ^A • grad vdFl — J Fv vd£l. (14.20)
634
14.Применение узлового МКЭ для решения векторных задач
Заметим, что с учётом вида функции F правую часть уравнения
(14.20) лучше также преобразовать с использованием формулы интег-
рирования по частям. Тогда в случае двухслойной схемы
У F[ vd£l — f 1 grad vtZQ, (14.21)
о n
а в случае трёхслойной
f FvvdQ =
Q
J Аф 1 • grad vdQ + J*
• grad vdQ.
(14.22)
14.2. ПОСТРОЕНИЕ КОНЕЧНОЭЛЕМЕНТНОЙ АППРОКСИМАЦИИ
ЗАДАЧИ, ОПИСЫВАЕМОЙ СИСТЕМОЙ ВАРИАЦИОННЬЬХ
УРАВНЕНИЙ
Будем считать, что расчётная область Q разбита на конечные
элементы П,„ и в ней определены финитные базисные функции ф7
i — 1..лг (т.е. каждая функция ф, определяется в виде сшивки соот-
ветствующих локальных базисных функций нескольких соседних ко-
нечных элементов и является ненулевой только на этих конечных эле-
ментах). Трёхмерные функции А,., , Az и V будем искать в виде
линейных комбинаций базисных функций ф7:
а = Е«м><. А = £?"*,. д = £«м>;, v = (14.23)
*=1 4=1 ?.= 1 4=1
Подставляя выражения (14.23) в вариационные уравнения (14.17)-
(14.20) и заменяя пробную функцию v поочерёдно на базисные функ-
ции *ф7 i = 1.../tn (7?п - количество базисных функций, равных нулю
на границе S области fl), получаем
1 п Г ” Г
— 52 Й / ёга<1 Фj • Sracl + 52 ТФ>Ф^ +
И,) 7=1 Q 7=1 ’ Q
р ® Ф1 р
J g ф/Zfl = J F,; l|.’zdfl,
12 12
i = 1...77(),
52 (Jj j 6rad Ф> ‘ Srad Ф»'Й2 + эФ^Фт^ +
° 7=1 Q 7=1 Ц
< p p
J ° Ф^п = j i = l.. .?iu ,
7=1 О У Q
(14.24)
(14.25)
14.2.Построение конечноэлементной аппроксимации задачи ...
635
Fz^\dQ,, г = 1...пц,
(14.26)
52 [ а grad -ф; • grad фг<Ю + 52 7; f уФj ^7 +
J=1 Q i=l Q
+Е чу, f тф, +£,<ij / =
J=1 Q У 7=1 Ц
= J Fvi\)id£l, г = l...?i().
о
(14.27)
Очевидно, система (14.24)-( 14.27) - это система из 4п0 уравнений
для 4?г неизвес1ных. Недостающие 4 (гг — 7г0) уравнений, как всегда,
должны быть сформированы в результате учёта главных краевых ус-
ловий, и поскольку в задаче только однородные краевые условия, не-
достающие уравнения имеют вид
7г = 0, д? =0, дх=0, =0, i - ??()
Как уже говорилось в разделе 5.2.2, при генерации конечноэле-
ментной СЛАУ чаще всего употребляется схема, в которой генериру-
ются так называемые «фиктивные» уравнения, полученные при замене
пробной функции v базисными функциями фх с номерами
г = п(} + 1,..,,7?.. Это делает схему сборки конечноэлемеитной СЛАУ
более однородной, т.е. локальные матрицы конечных элементов зано-
сятся в глобальную вне зависимости от того, является элемент гранич-
ным (с локальными функциями, соответствующими глобальным функ-
циям фг с номерами i > nQ ) или нет Мы будем использовать именно
такую схему.
Итак, рассмотрим как можно построить матрицу и вектор правой
части конечноэлементной СЛАУ размерности 4??, уравнения которой
определяются соотношениями (14.24)-( 14.27).
Пронумеруем уравнения этой системы следующим образом. Будем
нумеровать их поочерёдно так, чтобы г-е уравнение из (14.24) получи-
ло номер 4 г — 3, г-е уравнение из (14.25) - номер 4г — 2 , Се уравне-
ние из (14.26) - номер 4 г — 1, а Се уравнение из (14.27) - помер 4г.
Соответственно пронумеруем и неизвестные этой системы, которые
обозначим Qj, j = l,...,4?i (т.е. неизвестные (?', q", qz и q^ объеди-
ним в один вектор q размерности 4/г):
636
14.Применение узлового МКЭ для решения векторных задач
= Q'h q^j-2 = (fj^ q4j-i=qj, Q4j=qj, j = i...n.
Учитывая то, что коэффициент является произведением пара-
метра задачи о на коэффициент (3, (см. (14.10) или (14.13)), который
зависит только от величины временных шагов и определяется исполь-
зуемой схемой аппроксимации по времени, уравнение (14.27) можно
разделить на [3/ (это позволит нам в дальнейшем получить конечно-
элементную СЛАУ с сгимметричной матрицей). После деления уравне-
ния (14.27) на (3Z получаем
А" £ ?!' f ° grad J ‘ grad + £ f
1 z J=1 о Q
|^dQ +
(JX
Обозначим:
+ = (14.28)
P,j = 77- / grad ф,: • grad ф dQ +
Po J
о
(14.29)
о grad фг • grad rp;dQ,
(14.30)
vr Г ^Ф? n Г ^Ф/ , Г СЛЬ,
d-j = I сгф., —^-d- d£l, d/ = I сгф • —-d- dQ dp. = I огр, n 7 dQ . (14.31)
J J dx ,J J dy 1 J oz
о о Q
Тогда матрицу конечноэлементной СЛАУ можно представить в блоч-
ном виде с блоками размером 4x4 следующего вида'
0 0 dj
A'J = 0 Рч 0
0 0 Ри
d- d.7'z ГЧ
i,j = 1... п .
(14.32)
Компоненты вектора правой части удобно вычислять с помощью
матрицы массы. Обозначим через g вектор размерности 4п с компо-
14.2.Построение конечноэлементной аппроксимации задачи ...
637
нентами, являющимися весами разложения1 вектора сторонних токов
JCT по базисным функциям ф,;:
Z7 = 52^4г-зФ/., б^-гФх , Лст = 52<74,:-1'Ф. •
/:=1 z=i z=i
Компоненты g4i (г = 1...п) не используются и могут быть взяты,
например, равными нулю.
Обозначим через С и М матрицы размера 4п х 4п, состоящие из
блоков размера 4x4 следующего вида:
('ГЛ.;.; 0 0 0)
Cij ООО ч/
0 0 0
0 Cjj 0 0 и
Cij = , м^' = 0 0 m„- 0 , г, j' = 1,..., n
0 0 dj 0 fj
0 0 0 0 d:,jj d1' d'-T J1 J1 r n
h. Р/, J
где t/ji, d1--, dZjt — определяются соотношением (14.31), а сг/ и -
это элементы матриц массы:
с.у- = ф,ф7^О, тп^ = J сифф^П.
о ц
Обозначим через q^1 вектор решения на предыдущем2 (t = )
временном слое, а через q< 2 - вектор решения на слое t = ^_2 . Тогда
вектор правой части b размерности 4п для двухслойной схемы (с
учётом соотношения (14.21)) может быть вычислен в виде
b = Cg + P1Mq*1,
а для трехслойной схемы (с учётом соотношения (14.22)) — в виде
1 Строго говоря, это разложение корректно использовать лишь в том слу-
чае, если JCT является непрерывной вектор-функцией. Если же вектор-
функция JCT разрывна (например, разрывными являются её касательные со-
ставляющие), то такое разложение можно делать на каждом конечном эле-
менте и соответственно получать локальный вектор правой части путем
умножения локальной матрицы на локальный вектор весов разложения JCT на
(это будет продемонстрировано ниже, см. с. 642).
2 Здесь мы по-прежнему будем обозначать через t.l временной слой (j -
номер слоя), и индекс j у tt, естественно, никак не связан с индексом j у
базисных функций и компонент матриц.
638
14.Применение узлового МКЭ для решения векторных задач
b = Cg 4- ftMq^1 4- p/'Mq^2,
где р,, Р, и pf - коэффициенты, определяемые соотношениями (см.
(14.10) и (14.16))
д = 1 = 1 А' = 21 =
р// _ 42 ____________________
° (^—^-2)(^-1~^-2)
Довольно часто при решении электромагнитных задач в расчётную
область включается непроводящее пространство (воздух или другие
диэлектрики). В этом случае расчётная область содержит подобласти с
коэффициентом проводимости ст = 0 . Очевидно, в этих подобластях
четвёртое уравнение системы (14.6}-(14.9) не определено1 и соответст-
венно в них не ищется скалярный потенциал V . Естественно, изменя-
ется и структура блоков конечноэлементной матрицы, соответствую-
щих непроводящим подобластям. Если блок А';/ соответствует узлам
i и j, хотя бы один из которых не лежит внутри или на границе об-
ласти с а * 0 (при г = j соответствующий узел также не должен ле-
жать внутри или па границы области с 0), то он будет иметь
структуру
Plj 0 0 0 '
0 Pij 0 0
А'1 = 0 0 Рч 0 , (14.33)
0 0 0 V
gradi]), • gracUJy/Q (сравните с (14.29) и учтите, что на
где ptJ
носителях функций ф, и ф7 о — 0, а значит и = 0), 67/ - символ
Кропекера. На диагональ строк, соответствующих скалярному потен-
циалу V и узлам, лежащим в непроводящей области, ставится едини-
1 Строго говоря, расчётная область Q' для потенциала Iz отличается от
расчетной области Q для вектор-потенциала А при наличии в ней непрово-
дящих подобластей, и поэтому краевые условия для V должны быть сформу-
лированы на границах Q1 Однако эти краевые условия получаются из усло-
вия нсвытекания тока в непроводящую среду и выполняются естественным
образом для вариационного уравнения (14.20) (с правой частью (14.21) или
(14.22)) с заменой в нем Q на О1 .
14.3.Хранение и сборка глобальной матрицы
639
ца, чтобы конечноэлементная матрица была невырожденной (очевид-
но, что в таком случае в этих узлах мы получим (ft = = 0 )'.
14.3. ХРАНЕНИЕ И СБОРКА ГЛОБАЛЬНОЙ МАТРИЦЫ
Хранить матрицу А конечноэлементной СЛАУ (14.24)-( 14.27)
выгодней всего в разреженном блочном формате (см. раздел 10.4.7).
При этом для хранения блока (14.32) необходимо 8 ячеек памяти, а для
хранения блока (14.33) - только одна. В диагональных же блоках нуж-
но хранить либо 5 чисел, либо только одно. Кроме того, достаточно
хранить только нижний треугольник матрицы А, поскольку блоки А7’
верхнего треугольника (при j < ?’) являются транспонированными к
соответствующим блокам Аг? нижнего треугольника (г.е.
А* = (А’-')Т).
Собирать глобальную матрицу А удобно из обычных локальных
матриц жесткости и массы и трёх несимметричных матриц с элемен-
тами вида (14.31).
Рис. 141. Расчётная область
Покажем на примере, как выглядит в разреженном блочном форма-
те глобальная матрица для сетки из двух параллелепипеидальных эле-
ментов. На рис. 141// показана глобальная нумерация вершин этих
двух параллелепипедов. Будем считать, что в элементе определяе-
мом вершинами {1/2,4,5,7,8,10,11}, коэффициент о отличен от нуля,
а в ’ определяемом вершинами {2,3,5,6,8,9,11,12}, коэффициент о
равен нулю. Будем также считать, что локальная нумерация узлов элс-
1 В принципе, неизвестные q4l, соответствующие узлам в непроводящей
области, можно вообще удалить из вектора неизвестных q. однако в этом
случае нарушится однородность структуры векторов q и b (и для работы с
ними потребуются дополнительные структуры данных, например портрет).
640
И.Применение узлового МКЭ для решения векторных задач
ментов Qz соответствует изображённой на рис. 141,6. Тогда массивы
idi, ig,jg, ijg, di и gg, определяющие матрицу А в разреженном блоч-
ном формате, будут иметь вид:
idi = {1.6.11.12,17,22.23,28,33,34.39,44,45}
_ fn$h л'ЛЬ j»4ii 7)$h 1 ЭЪ j.v5h jz,$1i _,$li „$1-2
ai ~ ]P11 ’“11 ’“11 ’ “11 ’ 711 ’ P22 ' Tn >«22 ’“22 ’“22 ’ 722 ’P22 ’
Ql jT.$4 jySli jz.44 44 Q] 1 $12 jj,$1j jy.$4 rlz^l rill -nQ2 I
P33’“33 ’“'33 ’“33 ’733 ’^44 ' T33 ’ “44 ’“44 ’“44 >r44 ’T44 ’•••/
ig = {1,1,2.3.5,9,12.16,23,28,34,44.51}
jg — {1,2,1,2,1,2,3,4,2,3,5,1,2,4,5,1,2,3.4,5,6,7,2,3,5,6,8,
1,2,4,5,7,8,1,2,3,4,5,6,7,8,9,10,2,3,5,6,8,9,11}
VT — {1,9,10,18,26,34,42.43.51,52,53,54,62,70.78,86,94,102,103,111,
119,120,128,129,130,131,132,133,141,149,157,165,173,181,189,197,198,
206,214,215,223,231,'232,240,241,242,243,244,245,246,247}
nn _ /„Hi ./«,$*! j?/,$h >»/,Qi >2,$^ Qi Q-2
99 — |P12’“12 ’“12 ’“12 ’“21 ’“21 ’“21 ’ r12 >P12 ’
Ql j.t,Q| n/,Qi j.r,Qi j.V,$h Qi
P13’“13 ’“13 ’“13 ’“31 ’“'31 ’“31 ’ 713 ’
Q! jr.Q} j»/.Qi jz,$2i jx.Qj jz.Qi
P-23 ’ “23 ’ “23 ’ “23 ’ “32 ’ “'32 ’ “32 ’ '23 ’
Ql rr,Hi j?/, $1] jz,Q! jj-^l! n/,$li jz.Qi Sli
“14 ’“l4 ’“14 ’“14 ’“'41 ’“41 ’“41 ’ 714 ’
7)ul ,5*2 л ';511 j?/,$11 jz.ll} »x,$li i?/,$li jz,$l} $1! $12
P-24 + T13 ’“24 ’“24 ’“24 ’“42 ’“42 ’“42 ’724 ’Т23 ’
$?1 »x,$li j?/,$li 7^,111 jx,$1[ 7?/,$1; iZ.Qi $1! $12 $12 $1-2 1
Г34’“34 ’“34 ’“34 ’“43 ’“43 ’“43 ’734 ’P14 ’?24 ’Т34 ’•••/
где
$^-
Ру =
если о 0 на Q/i:,
— G.j, если о = 0 на Q?,
р() А’
если о 0 на Q/.,
= Р/.
8/у, если ст = 0 на
(14.34)
(14.35)
Мк
G и С — стандартные матрицы жёсткости и массы параллелепипеи-
дального элемента , определяемые через его локальные функции ф7
с помощью соотношений
14.4.Применение процедуры выделения поля ...
641
Gy = J grad'ф, • grad , Cjj = J ф^ф^/П, (14.36)
«А: ^k
а значения d^lk, и df.fik вычисляются через локальные матрицы
Dr, D7 и D2 с компонентами
Г - chb; ~ С - 5ф. - Г - <9ф.
Щ = / фг-^-бЮ, = I фг £>2 = I ^—J-da (14.37)
J J дх J J ду J J dz
iik Ъ
по формулам (см. (14.3 1))
=&£>;, d^1' =dD»,, ^=dbt,. (14.38)
При получении соотношений (14.34), (14.35) и (14.38) мы полагали,
что коэффициент о является постоянным на каждом конечном эле-
менте Q;. и принимает на нем значение о.
Соотношения (14.34)-(14.38) фактически определяют локальные
матрицы элементов любого типа, с помощью которых можно не толь-
ко легко собрать глобальную матрицу конечноэлементной СЛАУ
(14.24)—(14.27), но и формировать локальные векторы (о чём будет
сказано ниже, в разделе 14 4).
14.4. ПРИМЕНЕНИЕ ПРОЦЕДУРЫ ВЫДЕЛЕНИЯ ПОЛЯ
ПРИ РЕШЕНИИ ВЕКТОРНЫХ ЗАДАЧ
Как и в случае сложных трёхмерных скалярных задач, многие
векторные задачи имеют довольно хорошие приближения в виде ре-
шении гораздо более простых двумерных или даже одномерных задач.
Для решения таких векторных задач применение технологии выделе-
ния основного поля может привести к сокращению фебуемых вычис-
лительных ресурсов (памяти и времени счёта) на несколько порядков.
Будем считать, что задача (14.1)—(14.5) имеет довольно хорошее
приближение в виде более простой задачи, определяющей электриче-
ское поле Ё() = — dA^jdt — grad V(>. Тогда добавочное поле
Е+=— <9 А+ dt — grad lz+ (и равное разности Ё и Ё°) описывается
системой уравнений
—L А Я,1 + о = JCT _ JO + А _ о0 j go
р() \dt дх ) • \ /
—L ДД+ + + (а - а") В",
р() 7 I dt ду v '
(14.39)
(14.40)
642
14.Применение узлового МКЭ для решения векторных задач
--Гдл+ ++ = Л"-Л° +(о-о")Е",
Ро (от dz I z \ / 2
— div (о grad 1/+) — div
dt
= — div
((о-оп)Ё"),
(14.41)
(14.42)
о
где о° и Jn - проводимость среды и вектор сторонних токов, соответ-
ствующие полю F11 (для простоты мы считаем, что div J = 0 так же,
как и div .Iе1 = 0). В дальнейшем также будем (для простоты) считать,
что JCT = .7°.
Вариационная постановка для задачи (14.39)-(14 42) строится абсо-
лютно аналогично тому, как была построена вариационная постановка
для задачи (14.1)—(14.5). В результате получается система вариацион-
ных уравнений, аналогичная системе (14 17)-( 14.20) с дополнитель-
ными слагаемыми в правой части: в первые три уравнения этой систе-
мы должны быть добавлены слагаемые
|’(o-o°)Z?>dQ, J (o-a°)£jWQ, J (о - (14.43)
Q U Q
соответственно, а в четвёртое — слагаемое
J (о — о'^Ё" • grad?;dQ. (14.44)
Q
При построении конечноэлсментной аппроксимации учёт слагае-
мых (I 1.13)—(14.44) удобней делать на локальном уровне. Вклады в
локальный вектор правой части Ь, имеющий размерность 47 (/ - ко-
личество локальных базисных функций элемента П/.), будут иметь вид
^-1, .$ = = ,
j=i j=i
Vi =
./=1
+ D^ +b^y (14.45)
г i
где c’, ё!- и ct - веса разложения по базису конечного элемента
i
Qj. функций Е1,., Еу и соответственно (т.е. Е' =52^ ^ и т.д.),
C.,j - компоненты локальной матрицы массы, определяемые соотно-
14.5.Тестированис конечноэлементных процедур
643
шением (14.36), а , £)' и Ь^г - компоненты локальных матриц D',
D7 и D2, определяемые соотношениями (14.37).
В принципе, не представляет труда получить вклады в локальный
вектор правой части и от слагаемого JCT — J0, если1 2 JCT J0. В этом
случае вклад2 от JCT — J° в компоненту локального вектора бу-
/
дет иметь вид — в компоненту ~ вид
7=1
/ „ /
а В КОМПОнеНТУ 64z-l - ВИД 52^4^1 где
>1 .7=1
д - , д!' и gZj — веса разложения на конечном элементе функций
7.-, Л/ и 7^т по его базису {'Ф,}, а 11, д!'А и gzA} - веса разложе-
ния на Q/.. по его базису функций J*, 7” и 7а •
14.5. ТЕСТИРОВАНИЕ КОНЕЧНОЭЛЕМЕНТНЫХ ПРОЦЕДУР
РЕШЕНИЯ ВЕКТОРНЫХ ЗАДАЧ
Как и в случае скалярных задач, тестирование конечпоэлсмент-
ных процедур решения векторных задач лучше всего начинать с тес-
тов, имеющих полиномиальные или кусочно-полиномиальные реше-
ния. Способы построения таких тестов мы подробно рассматривали в
разделах 4.14, 5.7, 6.5, 7.3 и они вполне пригодны (с небольшими оче-
видными модификациями) и в случае векторных задач.
Следующим этапом тестирования должен быть этап, на котором ре-
шаются более или менее реальные задачи. При этом лучше использовать
задачи, решение которых можно получить другим (желательно наиболее
простым) способом. Для векторных задач существуют довольно много
ситуаций (при определённом виде источников поля и коэффициентов
уравнений), когда решаемая векторная задача вырождается в скалярную
задачу, причём меньшей размерности. Покажем, как это можно сделать
для рассмотренной в этом разделе векторной задачи.
Будем считать, что электромагнитное поле возбуждается круговым
током, а вмещающая среда имеет круговую симметрию. Тогда при
условии однородности среды по магнитной проницаемости электро-
магнитное поле полностью описывается одной компонентой
Д (r,z, £) вектор-потенциала А (в цилиндрической системе
1 Точно так же следует учитывать слагаемое с Jc в постановке (14.24)—
(14.27), если J 1 является разрывной вектор-функцией.
2 Естественно, формулы (14.45) тоже определяют вклады в локальный век-
тор правой части, которые должны суммироваться с приводимыми ниже вкла-
дами от JCT — J°.
644
14.Применение узлового МКЭ для решения векторных задач
координат), и эта функция Ay(r,z, t) может быть найдена из решения
двумерного уравнения (см. с. 326):
+ = J (14.46)
Но р()г и*
Таким образом, в качестве тестовой задачи может быть выбрана за-
дача нахождения распределения вектор-погенциала в цилиндрической
области Q, состоящей из нескольких подобластей с различными
значениями в них коэффициента о (т.е. о = оА. = const в ). В од-
ной из подобластей, описывающей кольцо, можно задать Е = 1 , а в
остальных - отсутствие стороннего тока, (т.е. .7 = 0).
Эту же трёхмерную задачу можно использовать и для тестирования
процедуры, реализующей схему с выделением поля. Для этого в каче-
стве о" можно взять кусочно-постоянную функцию, совпадающую с
о во всех подобластях QZ: кроме одной (т.е. о” — о будет отлична от
нуля только в одной подобласти). Входящий же в правые части урав-
нений (14.39)—(14.42) вектор Е может быть получен из функции
дА^ (г, z, t)
E^{r,z,t) =------------- но стандартным формулам преобразования
векторов при переходе из цилиндрической в декартову систему коор-
динат:
Е{! (х, у,z, £) = -Е” (yjx2 + у2,z, У , (14.47)
V ' у]х2 + у2
(,т, у, z, t) = Е” (у]х2 + у2, z, t) . х , (14.48)
7 Jx2 + у2
Ez (x,y,z,t) =Л). (14.49)
Вектор-потенциал А ' , являющийся решением задачи на добавоч-
ное поле (14.39)-( 14.42), нужно сравнивать с вектор-потенциалом,
полученным после пересчёта в декартову систему координат разности
решений А^ (в среде с о") и Др (в среде со) двух двумерных задач.
Пересчёт А^ в А — (А, (х,у, z, i), А,/ (т, у, z,t),Az (а;, ?/, z,t)^ (а также и
Др и Др —Д^) выполняется по формулам, аналогичным (14.47)—
(14.49).
К сожалению, тестовые задачи, основанные на решении уравнения
(14.46), не позволяют проверить правильность аппроксимации членов
уравнений (14.1)—(14.3), содержащих скалярный потенциал V , а также
правильность аппроксимации уравнения (14.4) и связей между всеми
уравнениями системы (14.1)-—(14.4). Наиболее полное тестирование
!4.5.Тестирование конечноэлементпых процедур ...
645
системы (14.1)-(14.4) можно осуществить на основе другой осесим-
метричной скалярной задачи.
Рассмотрим задачу моделирования электромагнитного поля так на-
зываемой вертикальной электрической линии (ВЭЛ) в проводящей
среде. Сторонний ток в этой задаче течёт вдоль отрезка, параллельного
оси z, и вытекает из этого отрезка в проводящую среду с одного его
конца, а втекает - с другого. Поле ВЭЛ в осесимметричной среде
может быть описано следующим уравнением:
- di V (1 grad Я J + -L (1) + р .^ = 0, (14.50)
= 4 = °’ <14'51>
где I - сторонний ток в ВЭЛ (текущий вдоль оси z в подобласти
/ < г},, не входящей в расчётную область), гь - значение г-
координаты левой границы прямоугольника (являющегося расчёт-
ной областью для задачи (14.50)—(14.51)), Г' - часть левой границы
, соответствующая ВЭЛ, а Г - остальные границы Q43.
Заметим, что двумерное уравнение (14.50) содержит член
д д,
---г От ' о ’ Фактически являющийся сосредоточенным на поверхно-
стях />1п| (где о терпит разрыв) источником с плотностью ,
где Ш - скачок на S[n], а п,. — г-компонента вектора единичной
нормали к S1^]. С особенностями решения краевых задач вида (14.50)-
(14.51), включая построение эквивалентных вариационных постановок
и конечноэлементных аппроксимаций, читатель может познакомиться,
например, в работах [18].
Значения компонент напряжённости электрического поля могут
быть получены по значениям с помощью соотношений (следую-
щих из уравнения rotH == оЕ ):
. 1ряф , Яф]
о dz ' z о Or т
(14.52)
Если решать эгу задачу в декартовой системе координат, то она, ес-
тественно, будет описываться системой трёхмерных уравнений (14.1)-
(14.4), и в решении (-А,у) этой системы ненулевыми окажутся все три
компоненты вектор-потенциала А и скалярный потенциал К. Таким
образом, с помощью рассмотренной задачи для ВЭЛ можно наиболее
полно протестировать процедуры решения системы уравнений (14.1)—
646
14.Применение узлового МКЭ для решения векторных задач
(14.4). При этом сравнивать можно как значения Е, которые из реше-
ния (А, V) задачи (14.1)-(14.4) можно получить в виде
E = -^-gradV,
а из решения Ну задачи (14.50)—(14.51) с помощью соотношений
(14.52) и пересчёта функций Е,. (г, z, t) и Ez(r, z, Z) в декартову систе-
му координат по формулам:
Д. (ж, У, z, t) = Е,. \Jx2 + у2, Z, I х \fx2 + у2 (14.53)
Ку У, Z, 1) = Я,, ^у/х2 + у2, Z, 1 у (14.54)
у[х2 + у2 1
Яг (т, у, z, t) = Ez [ylx2 + у2 ,z,t^ (14.55)
так и значения Н, которые из решения задачи (14.1)—(14.4) можно
получить в виде Н = — rotA , а из решения Яф (r,z,i) задачи (14.50)—
Ро
(14.5 I) его пересчётом в компоненты Я7., Ну и Hz вектора Н по фор-
мулам
/Л,, (.г, у, z, 0 = -Ну 1у]х2 + у2, z, ,
v 7 + у2
НУ (я, У, z, t) = Ну (dx2 + у2, г, - х ,
V ' yjx + у2
Hz (x,y,z,t) = 0.
Аналогичным образом можно построить и тесты для задачи
(14.39)-( 14.42) на добавочное поле.
15.1 .Векторные дифференциальные уравнения второго порядка ... 647
15. ВЕКТОРНЫЙ МКЭ ДЛЯ РЕШЕНИЯ ЗАДАЧ
ЭЛЕКТРОМАГНЕТИЗМА
15.1. ВЕКТОРНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО
ПОРЯДКА С РАЗРЫВНЫМИ РЕШЕНИЯМИ
В предыдущем разделе была рассмотрена математическая мо-
дель электромагнитного поля, определяемого потенциалами ^А, PJ,
которые удовлетворяют системе дифференциальных уравнений второ-
го порядка (14 1)-(14.4) и являются непрерывными функциями. Поэто-
му при построении конечноэлементных аппроксимаций задач, описы-
ваемых с помощью этих непрерывных потенциалов, все искомые
функции (три компоненты вектор-потенциала А и скалярный потен-
циал V) представлялись в виде линейных комбинаций стандартных
скалярных (кусочно-полиномиальных) базисных функций1.
Однако математическая модель в виде системы уравнений
(14.1)—(14.4) не описывает электромагнитные процессы в средах с из-
меняющимся коэффициентом магнитной проницаемости, а также она
непригодна в ситуациях, когда нельзя пренебрегать влиянием токов
смещения2. В этих случаях для описания электромагнитного поля мож-
но использовать модель в виде одного векторного уравнения (см. раз-
дел 1.3.4)
rot (— rot а] + оДД- + — JCT . (15.1)
UL J dt dt1
Модель электромагнитного поля на основе векторного уравнения
Q5.1) позволяет решать самые сложные задачи электромагнетизма.
Она корректно описывает электромагнитные поля в ситуациях, когда
среда содержит любые неоднородности с изменёнными электрически-
1 Напомним, что в четырнадцатом разделе мы назвали такие базисные
функции узловыми.
2 Хотя эта модель является довольно показательной именно для МКЭ, по-
скольку описанные в четырнадцатом разделе схемы можно использовать и
при решении многих других задач, которые описываются системами диффе-
ренциальных уравнений в частных производных для нескольких неизвестных
функций (например, задачи теории упругости и др.)
648
15.Векторный МКЭ для решения задач электромагнетизма
ми и магнитными свойствами. На основе этой модели можно рассчи-
тывать распространение электромагнитных волн с учётом конечной
скорости их распространения и отражения от объектов с изменёнными
свойствами как в непроводящих, так и в проводящих и в смешанных
(т.е. содержащих непроводящие и проводящие подобласти) средах.
Уравнение (15.1) позволяет решать и нелинейные электромагнитные
задачи, в которых коэффициенты (чаще всего магнитная проницае-
мость р ) зависят от значений вычисляемого поля. Таким образом, при
изучении процессов электромагнетизма уравнение (15.1) играет одну
из самььх важных ролей.
Однако векторное уравнение (15.1) имеет определённые особенно-
сти (к ним относится, например, возможная разрывность А), приво-
дящие к серьёзным трудностям при попытках воспользоваться рас-
смотренными ранее схемами построения конечноэлементных аппрок-
симаций. Гем нс менее в последние годы были предложены новые
подходы, которые позволяю! успешно применять МКЭ и для решения
этого уравнения. Изучению таких подходов и будет посвящён данный
раздел.
Прежде чем приступить к построению конечноэлементной аппрок-
симации начально-краевой задачи для уравнения (15.1) по пространст-
ву, мы. как обычно, выполним аппроксимацию уравнения (15.1) по
времени1.
Обозначим через А = А (т, y.z^t.^ значение вектор-потенциала на
текущем временном слое, а через А^1 = А (я, у, z, ,
А^2 = А (я, у, z, tj-2.) и А 3 = А(т, y,z, — значение вектор-
потенциала на трёх предыдущих временных слоях. Тогда в результате
аппроксимации по времени уравнения (15.1) получим векторное урав-
нение
rot — rot А р чА = F,
(15.2)
где коэффициент -у и вектор-функция F определяются схемой ап-
проксимации по времени. Например, для трёхслойной полностью не-
явной схемы коэффициент и вектор-функция F имеют вид
v(2t:i -£;2) + 2е
(^7 — ^7-! )(/;7 “ ^7-2 )
(15.3)
1 Основные принципы аппроксимации нестационарных уравнений по вре-
мени были изложены нами в седьмом разделе. Несколько позже мы обсудим и
другой подход, когда для нестационарных векторных уравнений сначала вы-
полняется аппроксимация по пространству (см. раздел 15.14).
15.1 .Векторные дифференциальные уравнения второго порядка ... 649
Заметим, что при решении задач с несущественными токами сме-
я2 д
щения е ; у (в этих задачах обычно полагают е = 0 ) лучше исполь-
dt,
зовать трёхслойную полностью неявную схему. При решении же задач
с существенным влиянием токов смещения целесообразнее использо-
вать четырёхслойную полностью неявную схему.
Особенность векторного уравнения (15.2) состоит в том, что, хотя
оно и является дифференциальным уравнением второго порядка, его
решение А имеет разрывные нормальные составляющие на граница,х
разрыва коэффициента (а значит, и коэффициентов о и е, т.е. на
границах сред с различной проводимостью или диэлектрической про-
ницаемостью)1. Поэтому при решении векторного уравнения (15.2)
имеет смысл использовать такие базисные функции, которые позволя-
ют достаточно хорошо аппроксимировать разрывные вектор-функции.
’ Естественно, если эти нормальные составляющие А не равны нулю на
границах разрыва о и е, а нормальная составляющая плотности сторонних
токов 5СТ на этих границах непрерывна. Разрывность нормальных состав-
ляющих А на границах разрыва о или е следует из непрерывности нор-
мальных составляющих плотности полного тока J = JCT
(9 А <92А
dt di2 '
650
15 Векторный МКЭ для решения задач электромагнетизма
Ниже мы покажем, как могут быть построены базисные функции тако-
го типа.
15.2. ВАРИАЦИОННАЯ ПОСТАНОВКА
Будем считать, что на границе S = S) U S-2 расчётной области
Q, в которой определено уравнение (15.2), заданы краевые условия
двух типов:
х п) = А!1 х п,
•'Isj
— rot Л х и
(V
= И. ’ х ii,
(15.7)
(15-8)
где «х» - знак векторного произведения, п - вектор нормали к по-
верхности б) или S2, а А'7 и II ’ — известные вектор-функции.
Условие (15.7) фактически задаёт равенство касательных состав-
ляющих искомого вектор-потенциала А касательным составляющим
заданной на S) вектор-функции А'7, а условие (15.8) — равенство каса-
тельных составляющих напряжённости магнитного поля Н (с учётом
представления вектора индукции магнитного поля В в виде В = rot А
и связи В с Н в виде соотношения В = pH) касательным составляю-
щим заданной на S2 вектор-функции Н° .
Нетрудно убедиться, что условия равенства нулю касательных либо
нормальных составляющих вектора магнитной индукции В (а это наи-
более часто используемые условия симметрии и условия, задаваемые
на границах большого объёма) являются частным случаем краевых
условий (15.7) и (15.8).
Действительно, поскольку В представляется в виде В = rot А, ус-
ловие
В х п| = О
ls2
(15.9)
равенства нулю касательных составляющих вектора индукции магнит-
ного поля В на участке S2 границы S расчётной области Q является
частным случаем краевого условия (15.8): условие (I 5.9) будет выпол-
нено, если в (15.8) положить Нн = 0 .
Условие же равенства нулю нормальных составляющих индукции
магнитного поля
15.2.Вариационная постановка
651
В • й| = О
I.S1
(15.10)
на участке границы S выполняется при постоянном значении каса-
тельных составляющих А на (чго сразу следует из определения опе-
рации rot),т.е. для выполнения (15.10) достаточно в (15.7) взять А'7 =0.
Эквивалентная вариационная формулировка в форме Галёркина для
уравнения (15.2) с краевыми условиями (15.7) и (15.8) имеет вид
J* — rot А • rot Фт/Q + А Фс?О =
= Г(Йехп)-Ф</5 (15.11)
о 52
где запись R Р означает скалярное произведение вектор-функций1 R
и Р, а «х » по-прежнему - знак векторного произведения.
Решение А и пробные вектор-функции Ф должны принадлежать
пространству H,ut, содержащему все вектор-функции Ф, которые
сами суммируемы с квадратом на Q (т.е. ^Ф Н О = £ф Фг/Q < сю ) и
о ц
для которых на Q существуют и суммируемы с квадратом вектор-
функции го1Ф (т.е. 1го1Ф}' d.Q = J rot Ф • rot Фс/Q < сю ).
Пространство же Н™’ пробных вектор-функций Ф является под-
множеством всех вектор-функций из пространства Hrot таких, что их
касательные составляющие равны нулю на границе Sj (т.е. для всех
Ф G должно выполняться (Ф х ri) = 0, сравните с (15.7)).
\ /ISi
Решение А вариационного уравнения (15 11) следует искать на
множестве H‘7ot всех тех вектор-функций из пространства Hlot, кото-
рые удовлетворяют краевому условию (15 7) Заметим, что при
А'7 = 0 на Si пространство H}jot тождественно совпадает с Н™1, а
если в решаемой задаче отсутствуют краевые условия вида (15.7), то
оба пространства HJyot и Н™1 тождественно совпадают с пространст-
вом Hrot.
1 Обратим внимание на то, что rot А и гоЬФ гоже век тор-функции и в
подынтегральном выражении первого слагаемою левой части уравнения
(15.11) стоит их скалярное произведение.
652
15.Векторный МКЭ для решения задач электромагнетизма
Докажем эквивалентность вариационного уравнения (15.11) век-
торной краевой задаче (15.2), (15.7), (15.8).
Преобразуем первое слагаемое вариационного уравнения (15.11) с
использованием векторной формулы Грина:
J* rot Ц- rot А • Ф rfQ + j — rot Л х в | • tyclS + p,A-'PdQ =
= Jr-^dQ-T р;й(>хйУ VdS УФеН,?’. (15.12)
о s-2
Поскольку пробные век iop-функции Ф являются произвольными
элементами Но’1, мы можем выбирать из них вектор-функции Ф”,
касательные составляющие которых равны нулю на всей границе S .
Для таких вектор-функции поверхностные интегралы в уравнении
(15.12) оказываются равными нулю, и это уравнение принимает вид
— rot А 4-чА— F Ф"<7П = О
U1 ) J
УФ() 6 H(r)ot : Ф(,хв| =0,(15.13)
откуда следует, что для век гор-нотенциала А почти всюду1 в области
Q выполняется дифференциальное уравнение (15.2).
Мы показали, что для вектор-функции А, удовлетворяющей ва-
риационному уравнению (15.1 I), почти всюду выполняется дифферен-
циальное уравнение (15.2). Тогда, учитывая что S = U S2 и то, что
сумма объемных интегралов в уравнении (15.12) равна нулю (посколь-
ку нами уже доказана справедливость уравнения (15.2)), из уравнения
(15.12) получим:
Так как касательная составляющая Ф на границе равна нулю
(по определению пространства II Но’1), то с учётом того, что
— rot А х в
U1
• Ф = — — rot А-(фхв) = — — rot АО = 0,
р \ / р
1 Т.е. за исключением подобластей с объёмной мерой нуль, таких, как, на-
пример, поверхности, линии и точки в трёхмерном случае или линии и точки
в двумерном.
15.3.Приближение решения на подпространствах
653
первое слагаемое в (15.14) обращается в нуль. Поэтому
rot А х п — Нн xnl Ф^ = 0 V^GH{)Ot. (15.15)
s2 '
Отсюда следует, что на границе S2 выполняется (почти всюду1) крае-
вое условие (15.8).
Краевое же условие (15.7) выполняется по определению простран-
ства , в котором ищется решение А .
Итак, мы доказали, что решение А е HJ;ot вариационного уравне-
ния (15.1 1) действительно удовлетворяет и уравнению (15.2), и крае-
вым условиям (15.7) и (15.8). Чтобы доказать обратное утверждение,
достаточно провести рассмотренные выше рассуждения в обратном
порядке (и мы предоставляем читателю провести такое доказательство
самостоятельно в качестве несложного упражнения). Это и завершит
доказательство эквивалентности вариационного уравнения (15.11) век-
торной краевой задаче (15.2), (15.7), (15.8).
15.3. ПРИБЛИЖЕНИЕ РЕШЕНИЯ НА ПОДПРОСТРАНСТВАХ
Общая схема построения приближённого решения векторной ва-
риационной задачи (15.11) в целом мало чем отличается от схемы вы-
числения приближенно! о решения скалярной вариационной задачи
(3.37).
Чтобы использовать метод Галёркина для нахождения решения
уравнения (15.1 1), мы должны прежде всего определить конечномер-
ное подпространство Vn,(' бесконечномерного пространства Н‘°1.
Соответственно обозначим через V*'ot подмножество всех функций из
Vrut, удовлетворяющих главному краевому условию.
Приближённое решение уравнения Галёркина (15.11) определяется
как вектор-функция A/l, принадлежащая подмножеству2 * * * * V(‘uL конеч-
номерного подпространства Vrot пространства Hrot, такая, что соот-
1 Т.е. за исключением частей поверхности S2 с поверхностной мерой
нуль - линии и точки в трехмерном случае или точки в двумерном.
2 V‘ot при этом может быть также и подмножеством пространства Н"" ,
если в Vl“' есть функции, точно удовлетворяющие главному краевому усло-
вию (15.7); в противном случае VJ°* - подмножество всех функций из конеч-
номерного пространства V1"’, удовлетворяющих главному краевому условию
с функцией А'/,а х п в правой части, где А';,/' - это приближение А7 такое,
что в Vr<” есть вектор-функции, у которых касательные к 5| совпадают с
А'/Ахп (о некоторых способах построения такой вектор-функции А бу-
дет сказано чуть ниже).
654 15.Векторный МКЭ для решения задач электромагнетизма
ветствующее вариационное уравнение должно выполняться для любой
вектор-функции из подпространства1 * У™1 пространства Н},01, т.е
= Jf*$\/Q4- Дйн хп) ф'1й5 V^/lGV0rot. (15.16)
и 's2
Как правило, конечномерное пространство Vlot определяется как
линейное пространство с базисом из п вектор-функций ар, и, естест-
венно, любые функции из У(/ ! и У™1 могут быть представлены в
виде линейной комбинации базисных вектор-функций ф,;. Поэтому
приближённое решение Л? ищется в виде линейной комбинации ба-
зисных вектор-функций ф,:
А''=Е'аД- (1517)
J=I
Функция А'' в виде линейной комбинации (15.17) подставляется в
вариационное уравнение (15.11), а пробная вектор-функция Ф в этом
уравнении заменяется поочерёдно на все базисные функции простран-
ства Vg11 . В результате получается система линейных уравнений вида
J -у rot фу rot, ф/ZQ 4- у\ф j ф/Zfi
Q.i =
I F • ф/Ю 4
Q
хп) ф,(/£}
$2
(15.18)
i € ZV(),
где N - множество всех номеров от 1 до п (напомним, что п - раз-
мерность пространства V’’4 ), а А() - подмножество N с удалёнными
из него п — По номерами i тех базисных вектор-функций ф конеч-
номерного пространства Vlot, которые не входят в пространство V()Ot
(т.е. размерность конечномерного подпространства У™* равна п(), а
его базисные функции - это базисные вектор-функции ф, G Уго* с
номерами z Е А() ).
1 У)'4 тоже является подмножеством функций из У“4, но удовлетво-
ряющих однородному главному краевому условию на .
15.3.Приближение решения на подпространствах
655
Краевые условия (15.8) являются естественными, поскольку учи-
тываются автоматически в вариационной постановке. Вклады от них,
как и от краевых условии второго рода в узловом МКЭ, идут только в
правую часть СЛАУ (15 18) (в компоненты её вектора правой части с
такими номерами I, для которых базисные вектор-функции ф, имеют
на S-2 отличные от нуля касательные к S2 составляющие).
Краевое же условие (15.7), как и в узловом МКЭ, называется глав-
ным Здесь мы рассмотрим, как можно учесть главное краевое условие
(15.7) для наиболее часто встречающегося на практике случая, когда
оно является однородным (т.е. А7 х в = 0 ).
Как мы увидим чуть позже, при решении уравнения (15.2) с исполь-
зованием векторного МКЭ базисные вектор-функции ф, строятся так,
что все базисные функции конечномерного пространства Vrot с ин-
дексами i Е Ao имеют нулевые касательные к S) составляющие (они
же и образуют базис подпространства V™1). Поэтому для выполнения
однородных главных краевых условии достаточно к н.(| уравнениям
системы (15.18) добавить и — п0 уравнений вида
</, =0, zG7V\A(1. (15.19)
Таким образом, если конечноэлементная СЛАУ была сгенерирова-
на с фиктивными уравнениями (т.е наряду с уравнениями (15.18) для
L С А() генерировались аналогичные уравнения и для i G N \ А()), то
учесть однородные главные краевые условия можно одним из сле-
дующих двух очень простых способов. Можно либо вместо сгенериро-
ванных строк с индексами i G N \ А() вставить строки вида (15.19)
(т.е. с единицей на диагонали матрицы и нулями во всех внедиаго-
нальных элементах этих строк и в соответствующей компоненте век-
тора правой части). 11осле этого можно очень легко симметризовать
матрицу С полученной системы, обнулив все её компоненты Су с
индексами j € N Nf} (в этом случае мы сохраним соответствие но-
меров компонент вектора весов q номерам базисных функций). А
можно просто перенумеровать неизвестные q.. так, чтобы в получае-
мой СЛАУ остались только те веса q., которые в исходной нумерации
имели номера i Е А(). В этом случае номера компонент вектора весов
после решения полученной СЛАУ с квадратной матрицей размерности
не будут соответствовать номерам «своих» базисных функций, и
поэтому нужно либо после решения конечноэлсментной СЛАУ вер-
нуться к исходной нумерации весов, либо перенумеровать базисные
функции так, чтобы все ю функции, которые в исходной нумерации
имели номера z Е А \ А(), после перенумерации получили бы номера
z < (напомним, что — количество номеров в множестве А() ).
656
15.Векторный МКЭ для решения задач электромагнетизма
Если же по какой-либо причине необходимо решить задачу с неод-
нородным главным краевым условием (на практике этот случай встре-
чается чрезвычайно редко, например, при тестировании конечных эле-
ментов или при решении задачи «внутри» известного внешнего поля
без использования технологии выделения поля), то процедура учёта
таких главных краевых условий уже не столь проста и будет рассмот-
рена нами в следующем разделе.
15.4. УЧЁТ НЕОДНОРОДНЫХ ГЛАВНЫХ КРАЕВЫХ УСЛОВИЙ
Для учёта неоднородного главного краевого условия (15.7), как и
в случае однородного, к п1} уравнениям системы (15.18) мы можем
добавить еще п — линейных (относительно весов <?,-) уравнений,
которые и должны обеспечить необходимую близость на S) касатель-
ных составляющих приближенного решения А/‘ = к каса-
jeN
тельным составляющим век гора А'7.
Эти уравнения можно получить, например, из условия близости
Ah хп кА’хп на S\ в среднеквадратичном:
Si
V2
- А-7 х п (is =
mm
ieN\Ni}
(15.20)
f
S] l/ew
где под квадратом вектор-функции мы, как обычно, понимаем скаляр-
ное произведение её на себя.
Как мы уже говорили, базисные вектор-функции ф; в векторном
МКЭ будут строиться так, что для j 6 No вектор-функции ф; будут
иметь только нулевые касательные к Si составляющие. Поэтому усло-
вие (15.20) можно записать в виде
( У2
f У? 9? (фу х й) — А'7 х n dS—
min
f Z ч'Н'ФзХй)
- A-'7 X n dS,
(15.21)
15.4.Учёт неоднородных главных краевых условий
657
т.е. п — 7?о весов д“ с индексами j 6 N \ могут быть найдены в
результате минимизации по ним квадратичного функционала
= f (Ф/х п)-
Sj (je7V\M)
ч2
A"xn dS.
(15.22)
Минимизация же квадратичного функционала (15.22) эквивалентна
решению СЛАУ с матрицей М'\ компоненты которой определяются
выражением
i,je N\ А()
(15.23)
и правой частью Ь'7, компоненты которой определяются выражением1 *
Ь!> = ffi, xn).(A5 xnjdS, ieN\N(). (15.24)
S]
Перенумеруем неизвестные q} с индексами присвоив
им номера от 1 до п — п(), и обозначим соответствующий вектор (раз-
мерности п — п{}) через q . Соответственно перенумеруем и базисные
вектор-функции с индексами j Е N \ - в результате получим
набор базисных вектор-функций гр, с номерами от 1 до п — п() (т.е.
— это базисная вектор-функция 4>t с таким номером i, что среди
всех номеров к < i ровно j — 1 номер принадлежит множеству
У\У()).
В результате нужные нам веса q!)t , доставляющие минимум функ-
ционалу Iя, могут быть найдены из решения СЛАУ размерности
п — п{} с матрицей М7 и вектором правой части Ы, компоненты ко-
торых определяются соотношениями (сравните с (15.23) и (15.24))
х nj • х njf/S1, i, j — 1 ...?г — n(), (15.25)
b-1 — J (-ф,x nV(Av x nj dS, i = 1...71 — n(). (15.26)
Si '
1 В этом можно легко убедиться дифференцированием (q) по qf и при-
равниванием полученных производных нулю.
658
15.Векторный МКЭ для решения задач электромагнетизма
Заметим, что эта СЛАУ имеет, как правило, очень маленькую (по
сравнению с конечноэлементной СЛАУ (15.18)) размерность и не
большую, чем у матрицы системы (15.18), заполненность ненулевыми
элементами.
После того, как мы найдём вектор q7, являющийся решением
СЛАУ MQq7 — b7 с матрицей (15.25) и вектором правой части (15.26),
можно вернуться к исходной нумерации неизвестных и по q7 сформи-
ровать вектор q размерное ги п. Тогда для учёта краевых условий
(15.7) к уравнениям (15.18) можно будет добавить уравнений
вида
Однако для учета неоднородных главных краевых условий в век-
торном МКЭ можно использовать гораздо более простую и удобную
для реализации процедуру Основная её идея заключается в том, что
вектор-функция А7 из правой части краевых условий (15.7) заменяет-
ся некоторым интерполя и гом А' представленным в виде линейной
комбинации базисных вектор-функции:
А"" =^2^,. (15.27)
J
Веса (}-' в разложении (15.27) можно находить следующим спосо-
бом. Как уже говорилось чуть выше, базисные вектор-функции ф, в
векторном МКЭ строятся таким образом, что на поверхности S\ нену-
левые касательные имеют только п — 7?.п базисных вектор-функций ф7
с номерами i € N \ . При этом для каждой из таких вектор-функций
ф, (с номером i G N АГ()) на поверхности S) существует точка
(^,.>2//,^) и проходящий через эту точку касательный к поверхности
S{ вектор т7 такой, что
4/ т, 0, фДа\,&,?,:)• т, = О, (15.28)
Тогда, умножая левую и правую части равенства (15.27) скалярно
на вектор т,;, в точке (э;,,?/,, с учётом (15.28) получаем
А"’Л (хг, y1yZi) т, = ^'ф, (х/5 у„ z.,) • тг. (15.29)
Полагая, что в точках (.г;,?/,, z.z) значения проекций на т7 интерпо-
лянта А7,/' должны совпадать со значениями проекций на тг вектор-
15.4 Учёт неоднородных главных краевых условий
659
функции А-9 (из правой части краевого условия (15.7)), получаем из
(15.29) выражение для вычисления значений весов qf':
Т/:
Теперь при учёте главного краевого условия потребуем равенства
касательных составляющих Ак хп искомой вектор-функции A/l не
касательным составляющим A!l х п вектор-функции А°, а касатель-
ным составляющим А-9,л х п вектор-функции
А"Л = S А- (1531)
ieW\/V()
Таким образом, построенная нами вектор-функция Аг/ /', опреде-
ляемая соотношениями (15.31) и (15.30), как бы интерполирует на
касательные составляющие вектор-функции А' (с совпадением их в
точках ).
Учитывая, что приближённое решение также ищется в виде линей-
ной комбинации базисных вектор-функций
А = 52^^
i
и что на только вектор-функции с номерами i 6 N \ NG имеют
отличные от нуля касательные к составляющие, получаем, что ус-
ловие
А1' х n ‘ = A!,'h х п
будет выполнено, если выполняются следующие уравнения для ве-
сов 7, :
<?,=<)?, ie2V\(V0,
или с учётом (15.30)
_ АС7 /> ) ‘
Ом/Л,^)- т, ’
i G N \ N()
(15.32)
(напомним, что (.г;, y^zt) и т, - это такие точки на S{ и касательные
к S{ векторы, для которых выполняются соотношения (15.28)).
660
15.Векторный МКЭ для решения задач электромагнетизма
Итак, для учёта краевого условия (15.7) к п0 уравнениям системы
(15.18) нужно добавить п — п1} уравнений вида (15.32), которые дают в
матрице конечноэлементной системы строки с единственной ненуле-
вой (равной единице) компонентой на главной диагонали.
Таким образом, учёт главных краевых условий в векторном МКЭ
можно выполнить абсолютно аналогично тому, как мы это делали в
узловом МКЭ — либо генерировать СЛАУ размерности п, собирая её
сначала вместе с фиктивными уравнениями (с номерами i Е N \ ) и
затем заменяя эти уравнения на уравнения вида1
</, =7,’, (15.33)
либо уже в момент сборки матрицы и вектора правой части конечно-
элементной СЛАУ учитывать соотношения (15.33) и не генерировать
фиктивные уравнения для i. Е N \ Nq . Последний вариант наиболее
просто реализуем в случае, когда базисные вектор-функции имею-
щие на границе ненулевые касательные к ней составляющие, про-
нумерованы последними (т.е. i > п{} для всех i Е N \ N(l ), и становит-
ся особенно привлекательным (очень простым и экономичным) в слу-
чае однородных главных краевых условий.
15.5. ЭНЕРГЕТИЧЕСКОЕ СКА ЛЯРНОЕ ПРОИЗВЕДЕНИЕ
И ПОГРЕШНОСТЬ ПРИБЛИЖЁННОГО РЕШЕНИЯ
В ЭНЕРГЕТИЧЕСКОЙ НОРМЕ
Рассмотрим билинейную форму, определяющую левую часть
уравнения Галёркина (15.11):
л(а,ф)= Г —rot А • rot Ф<Ю + ^А-ФйП. (15.34)
о ц
Нетрудно убедиться, что при > 0 эта билинейная форма удовле-
творяет всем аксиомам скалярного произведения. Поэтому мы можем
определить скалярное произведение двух произвольных вектор-
функций Ф и Ф из множества2 * * Нго1 в виде
1 Правые части этих уравнений (15.33) в случае однородных главных
краевых условий просто должны быть равны нулю, а в случае неоднородных
главных краевых условий могут быть найдены либо из условия минимизации
отклонения касательных к SA составляющих искомого решения А1 от каса-
тельных составляющих А", либо из условия равенства касательных состав-
ляющих А7' и А-; на определённом наборе точек границы Sy.
2 Напомним, что Н1<>| - это множество таких вектор-функций Q , которые
сами суммируемы с квадратом на Q и для них существуют и суммируемы с
квадратом функции rotQ, см. с. 651.
15.5.Энергетическое скалярное произведение и погрешность ...
661
(Ф,Ф)Э = J^rot<-rot$dfi + ФсЮ. (15.35)
О Q
Это скалярное произведение будем называть энергетическим. Со-
ответственно энергетической нормой вектор-функции Ф будем на-
зывать норму, порождаемую скалярным произведением (15.35):
||ф[ = 7(Ф,Ф), . (15.36)
Определённые соотношениями (15.35) и (15.36) энергетическое ска-
лярное произведение и энергетическая норма (так же, как и энергети-
ческие скалярные произведения и норма (3.4) и (3.60), введённые нами
в третьем разделе для скалярных задач) очень удобны для изучения
погрешности ||.А7' — а|| приближённого решения А7', которое ищется
как решение уравнения (15.16). При этом техника оценки этой по-
грешности, которую мы изложим чуть ниже, практически не отличает-
ся от рассмотренной нами в третьем разделе техники оценки погреш-
ности ||i? — w|| приближённого решения уравнения (3.26) (сравните с
рассуждениями на с. 111—112).
Запишем уравнения (15.11)и(15.16)в виде
(Х,ф) = /(ф) УФ 6 (15.37)
(а7',Ф7') =/(фл) УФ7'Jj V(}’ot, (15.38)
где f — линейная форма, определяемая следующим соотношением
(сравните с правыми частями уравнений (15.11) и (15.16)):
/(ф) = jF-SdQ-b J^xn^^dS. (15.39)
о S-2
Поскольку V()Ot является подпространством пространства H(l)Ot,
уравнение Галёркина (15.11) справедливо и для всех пробных вектор-
функций Ф7' из V()Ot:
(а,фЧ = /(ф7') УФ7' G ЧГ. (15.40)
Тогда, из (15.38) и (15.40) получаем
(а7'-А,Ф7') =0 УФ^еХ)01, (15.41)
15.5.Энергетическое скалярное произведение и погрешность ... 663
662 15.Векторный МКЭ для решения задач электромагнетизма
т.е. приближённое решение А7'' является ортогональной' проекцией
точного решения А на подпространство V(’ot (V,}ot подмножество
вектор-функций из VIot, удовлетворяющих главному краевому усло-
вию (15.7)).
С учётом соотношения (15.41) не представляет труда доказать, что
решение А7' уравнения (15.16)- ближайшая в энергетической норме к
точному решению А (уравнения (15.11)) вектор-функция среди всех
вектор-функций Ф7' из Vf,ot .
Действительно, для любой вектор-функции Ф7' G Vf,ot справедливо
|'а —ф7,||2 = (а-ф7/,л-ф7') =
= (А-А/'4-А/'-Ф/')А-А/'+А/1-Ф/') =
' >з
= (А-А^А-А7'), | 2(Л—А,1,АЛ—ФЛ) + (а7'-Ф7',А7'-Ф7'') =
\ /э \ 'з
= ||А-А/1|2 + ||а7' - Ф"||2 +2(а- Ал,А7' -Ф7') .
Поскольку А7' и Ф7' являются элементами пространства век-
тор-функций, удовлетворяющих на S) одному и тому же неоднород-
ному краевому условию, их разность удовлетворяет на S) однородно-
му главному краевому условию и поэтому вектор-функция
Ф = А — Ф7' является элементом пространства V™1 1 2, и тогда из
(15.41) сразу следует, что (А — А;', АЛ — Ф'')э = 0 .
Учитывая это, получаем
||а-ф'‘||2 = ||а — ал|| + |а" -ф'*||2 уф'* ev,”1,
откуда
||а-А'‘|2 =||а-Ф'’||2 — ||Ал-ф'*|2 V4'‘6V~‘, (15.42)
т.е.
||А - А* ||2 < ||А - Ф'’ j2 vi'1 € V“. (15.43)
1 В смысле энергетического скалярного произведения.
Итак, вектор-функция А7', полученная как решение уравнения
(15.I6)1, действительно является вектор-функцией, ближайшей (в
энергетической норме) к А (точному решению, удовлетворяющему
уравнению (15.11)2) среди всех вектор-функций из пространства Vjut .
Таким образом, при построении приближённого решения нам нуж-
но лишь позаботиться о том, чтобы в конечномерном пространстве
Vjot в принципе были функции, достаточно близкие к искомому ре-
шению А, а метод Галёркина обеспечит выбор из всех функций про-
странства Vf'ul самой близкой к А (в энергетической норме) вектор-
функции A7i. Пространство же Vr<jt (и, естественно, его подмножест-
во V(Jot) в векторном МКЭ (как и в скалярном) определяется сеткой и
видом определённых на ячейках сетки локальных базисных вектор-
функций.
Сделаем ещё одно замечание о сути введённой нами энергетиче-
ской нормы. Па самом деле, квадрат энергетической нормы разности
точного А и приближённого А7' решений имеет и довольно важный
физический смысл. Рассмотрим его.
Будем считать, что для аппроксимации производных искомого век-
тор-потенциала А по времени используется четырёхслойная полно-
стью неявная схема аппроксимации по времени и значения точного и
приближённого решении на предыдущих временных слоях (которые
мы, по-прежнему, будем обозначать через АЛ1 , А и АГ3) совпа-
дают. При этом только для уменьшения громоздкости выкладок шаг по
времени будем считать постоянным и равным А/>. Тогда энергетиче-
ская норма разности А и А7' на текущем временном слое может быть
записана в следующем виде:
|| А - А'* ||2 = (А - А'*, А - А'ф =
1 Это уравнение может быть записано через энергетическое скалярное
произведение (15.35) и линейную форму (15.39) в виде (15.38).
2 Это уравнение также может бьпь записано через энергетическое скаляр-
ное произведение (15.35) и линейную форму (15.39) в виде (15.37).
664
15.Векторный МКЭ для решения задач электромагнетизма
Т-Дг fe A —A? ) (10.
Д/ J \ /
О
С учётом того, что1 rot А = В, rot А'1 = В7' и
где Ё и Ё7' - аппроксимации производных по времени — dAjdt и
— дА4 dt по четырёхслойной полностью неявной схеме, получим
+ Ш/е(Ё-ЁЛ) dQ. (15 44)
о
Поскольку метод Галёркина ищет ближайшую (в энергегичсской
норме) к А вектор-функцию А1' среди всех вектор-функций
Ф7' 6 VJ',L (см. (15.43)), из (15.44) видно, что одновременно с миними-
зацией ||а — А/'1| обеспечивается близость вычисляемых через А7'
индукции магнитного поля В и напряжённости электрического поля
Е к «точным»2 значениям индукции В и напряжённости Ё .
1 В - вектор индукции магнитного поля, Ё - вектор напряжённое!и элек-
трического поля.
2 Слово «точные» взято нами в кавычки потому, что точными значения В
и Е на текущем временном слое всё-таки следует считать условно, поскольку
Е вычисляется как аппроксимация производной вектор-потенциала по вре-
мени. И даже точное решение А дифференциального уравнения (15.2) на
текущем временном слое содержит в себе погрешность от аппроксимации
входящих в уравнение (15.1) производных по времени. Тем не менее на осно-
ве приведенных здесь результатов не представляет особого труда доказать
сходимость получаемых приближений А1', В/( и ЕЛ и к «абсолютно точным»
значениям А, В и Е соответственно.
15.5.Энергетическое скалярное произведение и погрешность ... 665
Таким образом, фактически в рассматриваемом нами варианте век-
торного МКЭ в качестве приближённого решения будет находиться
такой векгор-потенциал А'', который на каждом временном слое бу-
дет минимизировать функционал
(В - В'' )2dQ + ^rrf°(Ё - Ё/г)\ю + Д^е(Ё - ЁлdQ , (15.45)
Q О й
те будут минимизироваться взвешенные квадраты отклонений индук-
ции магнитного поля и напряженности электрического поля от своих
«точных» значений.
Обратим внимание на го, что в функционале (15.45) перед вторым
слагаемым есть сомножитель Ai. Вообще говоря, входящие в (15.45)
слагаемые имеют смысл физических энергий — первое слагаемое мо-
жет быть сопоставлено с энергией магнитного поля
jBHtZQ = j уВ2<Ю, второе слагаемое - с потерями энергии элек-
й о
тромагнитного поля JоЕ'э/Q, связанными с переходом этой энергии в
й
тепло, и третье слагаемое - с энергией электрического поля I eE2<ZQ .
й
При этом в балансе энергии электромагнитного поля энергии магнит-
ного и электрического ноля дифференцируются по времени, а потери —
нет Фактически это мы видим и в функционале (15.45) - сомножитель
Ai перед вторым слагаемым делает пропорции между входящими в
(15.45) погрешностями аналогичными пропорциям соответствующих
энергий в балансе энср! ии электромагнитного поля1.
Сделаем ещё одно очень важное замечание о единственности реше-
ния задачи (15.2) и эквивалентного ей вариационного уравнения
(15.11) (и соответственно уравнения (15.16) для нахождения прибли-
жённого решения).
При решении задач, в которых токи смещения являются несущест-
<Э2 А
венными, в уравнении (15.1) слагаемое е полагается равным ну-
лю При этом, хотя коэффициент е по физическому смыслу является
ненулевым для любых материалов, в задачах с несущественными то-
ками смещения удобно именно е сделать равным нулю - в этом случае
и для задачи с несущественными токами смещения остаются справед-
ливыми рассмотренные нами аппроксимации, приводящие к вариаци-
онным задачам (15.11) и (15.16).
Коэффициент же удельной проводимости о может принимать ну-
левые значения (в том числе и по его физическому смыслу) в отдель-
1 Эго также можно считать обоснованием уместности применения к норме
(15 36) (определяемой через скалярное произведение (15.35)) термина «энер-
гетическая».
666
15.Векторный МКЭ для решения задач электромагнетизма
ных подобластях расчётной области. Тогда при несущественных токах
смещения и наличии в расчётной области непроводящих подобластей
уравнение (15.1) будет иметь не единственное решение.
Действительно, если А удовлетворяет уравнению (15.1), то для
любой скалярной функции и, равной нулю в подобластях с ненуле-
вым о и отличной от нуля в подобластях, где коэффициент о равен
нулю, уравнению (15.1) будет удовлетворять также и вектор-функция
А + grad U . Очевидно, го же самое можно сказать и о решении урав-
нения Галёркина (15.1 I) - если к вектор-функции А, удовлетворяю-
щей этому уравнению, добавить градиент скалярной функции и та-
кой, что U равна нулю в подобластях с ненулевым и отлична от
нуля в тех подобластях, где равен нулю, полученная вектор-
функция также будет удовлегворять уравнению (15.11).
Однако при несущественных токах смещения (когда в уравнении
(15.1) коэффициент е полагается равным нулю) в подобластях, где
равен нулю и коэффициент о, физический смысл имеет лишь rot А , а
производная по времени всктор-потенциала А (как и сам вектор-
потенциал А) никакого физического смысла не имеет. Поэтому (при
е = 0 ) мы можем найти любой из те,х элементов А7* пространства
V“’1, которые в подобластях с нулевым о обеспечивают максималь-
ную близость В7' = rot А7' к В = rot А .
Очевидно, что именно такой вектор-потенциал A7' = и бу-
дет найден в результате решения системы (15.18) (с добавленными к
ней уравнениями, обеспечивающими выполнение главных краевых
условий). Действительно, как было показано чуть выше, приближён-
ное решение минимизирует энергетическую норму разности точного
А и приближённого А7' решений (см. (15.43)). А при е = 0 квадрат
этой нормы может быть записан в виде
||а
rot А — rot А7'
\2)
-A7') dQ,
(15.46)
где Qn - объединение всех подобластей расчётной области Q, в кото-
рых коэффициент о равен нулю. Очевидно, что минимизация (15.46)
не гарантирует близости в подобласти Q() приближённого решения
15.6.Принципы построения базисных вектор-функций ...
667
А7' к некоторому1 фиксированному точному решению А . Но это и не
нужно - по смыслу задачи вполне достаточно получить такой А ,
чтобы в подобласти Q() вычисленная по А7' индукция магнитного
поля В7' = rot А7' была максимально близка к В = rot А, что с успе-
хом и обеспечивает метод Галёркина.
Тем не менее при численной реализации метода Галёркина (для за-
дач с несущественными токами смещения и наличием подобластей с
нулевой проводимостью) возникают определённые трудности, связан-
ные с вырожденностью системы уравнений (15.18) (которая остаётся
вырожденной даже после добавления в неё уравнений, обеспечиваю-
щих выполнение главных краевых условий). Для решения таких задач
нужно либо использовать специальные методы решения СЛАУ, учи-
тывающие её возможную вырожденность, либо изменять постановку
задачи так, чтобы устранить вырожденность полхченной СЛАУ (такие
постановки будут рассмотрены нами в разделе 15.13).
15.6. ПРИНЦИПЫ ПОСТРОЕНИЯ БАЗИСНЫХ ВЕКТОР-ФУНКЦИЙ
ИЗ ПРОСТРАНСТВА Hrot НА ДВУМЕРНЫХ СЕТКАХ
15.6.1. ОБЩИЕ ПРИНЦИПЫ
Базисные функции в векторном МКЭ, как и в узловом, строятся в
виде полиномов пространственных координат, определяемых на ячей-
ках сетки. Однако векторный МКЭ имеет одно довольно существенное
отличие - базисные функции в нём нс должны быть полностью непре-
рывными. Допустимыми для вариационной задачи (15.11) являются
вектор-функции, у которых на границах конечных элементов непре-
рывны только касательные к этим границам составляющие. Разрыв-
ность же нормальных составляющих базисных вектор-функции не
только не создаёт проблем при построении конечноэлементного реше-
ния, но во многих случаях является даже необходимым свойством.
Дело в том, что при решении многих практических задач довольно
часто возникают ситуации, когда напряжённость электрического поля
Ё = — 8^81 имеет разрывные нормальные составляющие - тогда и
точное решение А краевой задачи (15.2) или вариационной задачи
(15.11) будет иметь разрывы в своей нормальной составляющей (на тех
границах, где разрывен коэффициент ).
1 Поскольку в подобласти П() точное решение уравнения (15.1) определя-
ется не единственным образом, а лишь с точностью до слагаемого вида
grad U , где U - произвольная скалярная функция.
668
15.Векторный МКЭ для решения задач электромагнетизма
Здесь мы рассмотрим основные принципы построения базисных
вектор-функций, используемых для конечноэлементной аппроксима-
ции вариационного уравнения (15.11)1.
15.6.2. БАЗИСНЫЕ ВЕКТОР-ФУНКЦИИ НА ПРЯМОУГОЛЬНИКЕ
Проще всего можно построить базисные вектор-функции, опре-
деляющие конечномерное пространство Vrut, на конечноэлементной
сетке с прямоугольными ячейками.
Рассмотрим прямоугольный конечный элемент
Qr5 = х изображённый на рис. 142. Определим на
нём четыре локальные базисные вектор-функции:
0 ( 0 )
Ф1 = т,.+ | - X , Фг = х — хг
к
p/.s-1-l ~У\ (У ~ У.ч ]
Фз = Ily > Ф4 = Ьу
0 0
(15-47)
Очевидно, что базисные век-
тор-функции *4?! и ф2 направлены
ВДОЛЬ ОСИ у и ИХ модули ф]
и
меняются линейно вдоль оси
— от единицы на ребре 1
до нуля на ребре 2, а ф-2 - от
единицы на ребре 2 до нуля на
ребре 1).
Аналогично базисные вектор-
функции ф3 и ф4 направлены
на прямоугольном конечном элементе
вдоль оси х и их модули меняются линейно вдоль оси у.
Каждая из базисных вектор-функций (15.47) только на одном ребре
прямоугольника Qrs. имеет ненулевую касательную составляющую:
1 Эти базисные функции, очевидно, являются элементами пространст-
ва Hn,f.
15.6.Принципы построения базисных вектор-функций ...
669
- на ребре 1, *ф2 - на ребре 2 и т.д. Поэтому такие базисные век-
базисных вектор-функций
тор-функции ассоциируют с соответствующими рёбрами (на которых
их касательные составляющие не равны нулю) и иногда называют рё-
берными (или edge-) функциями, а конечные элементы с такими ба-
зисными функциями - edge-элементами.
Как мы увидим чуть ниже, тер-
мин «edge» вполне уместен для
базисных вектор-функций из Hrot и
соответствующих конечных эле-
ментов первого порядка. Базисные
же вектор-функции высоких поряд-
ков могут быть ассоциированы уже
не только с рёбрами, но и с самими
элементами (или с их гранями в
трёхмерном случае), и поэтому для
таких функций более корректным
является название «базисные век-
тор-функции из Hrut» (которое мы
в основном и будем использовать)1.
Глобальные базисные edge-
функции2 также ассоциируются с
рёбрами (поскольку имеют ненуле-
вую касательную составляющую
только на одном ребре). Каждая из
таких вектор-функций получается в
результате сшивки соответствую-
щих локальных базисных вектор-
функций двух конечных элементов,
содержащих это ребро, и не равна
нулю только на этих (двух) элемен-
тах. Для сетки, изображённой на
рис 143, на рис. 144 показан вид двух глобальных базисных вектор-
функций, одна из которых -ф7 ассоциирована с ребром, параллельным
оси х, а другая *ф4 - с ребром, параллельным оси у. Очевидно, что
определённые таким образом глобальные базисные вектор-функции (и
соответственно любые их линейные комбинации) будут иметь непре-
рывные касательные составляющие во всей расчётной области.
На рис. 145 в качестве примера изображена вектор-функция
f = ф1 4- ф2 ~ 1-5фз — 0.6ф4 + 1.5ф5 — 0.2-фб — 0-2ф7 —
— 0.5ф8 — 0.2ф9 + 0.5ф1О — 0.4фп — 0.4*ф12 ,
1 В конце этого (пятнадцатого) раздела мы обсудим другие возможные на-
звания вектор-функций различных типов (см. с. 825).
2 Здесь мы оставили название «edge-функции» потому, что речь идёт о
функциях первого порядка.
670
15.Векторный МКЭ для решения задач электромагнетизма
являющаяся линейной комбинацией базисных вектор-функций, нуме-
рация которых соответствует нумерации рёбер на рис. 143. Эта вектор-
функция может быть проинтерпретирована, например, как напряжён-
ность некоторого электрического поля в области с разрывным (на рёб-
рах 6 и 7, см. рис. 143) коэффициентом удельной проводимости о (или
разрывным коэффициентом диэлектрической проницаемости е), при-
чём отношение значений соответствующего коэффициента (взятых из
разных подобластей) на этой границе равно примерно 3 (и таким же
является отношение на этой границе нормальных составляющих f).
Рис. 144. Вид глобальных базисных вектор-функций на прямоугольной сетке
Рассмотренные нами глобальные базисные вектор-функции, поро-
ждённые из локальных вектор-функций вида (15.47), являются вектор-
функциями наименьшей степени, которые допустимы для решения
вариационной задачи (15.11) на прямоугольной сетке. В векторном
МКЭ эти функции обычно называют функциями первого порядка, хо-
тя, очевидно, они не представляют точно даже такие векторные поля, у
которых х -компонента линейно зависит от .г, а ^-компонента линей-
но зависит от у. Тем не менее такие базисные вектор-функции позво-
ляют аппроксимировать любые векторные поля с погрешностью 6>(Л)
в энергетической норме (/г - характерный размер конечного элемен-
15.6.Принципы построения базисных вектор-функций ...
671
Рис. 145. Вид линейной комбинации
глобальных базисных вектор-функций
та), т.е. конечные элементы с эти-
ми базисными вектор-функциями
имеют первый порядок аппрокси-
мации1.
Базисные вектор-функции вы-
соких порядков определяются, как
и в узловом МКЭ, с помощью по-
линомов соответствующей степе-
ни. При этом степень полинома у
той компоненты вектор-функции,
которая соответствует её направ-
лению, берётся обычно на едини-
цу меньше.
Покажем, как могут быть по-
строены базисные вектор-функции
высокого порядка на прямоуголь-
ном элементе. При этом мы будем
использовать те принципы, по
которым строились иерархические
базисные функции в узловом
МКЭ2 (напомним, что принципы
построения иерархических базис-
ных функций были рассмотрены
нами в двенадцатом разделе).
Вид иерархических базисных
вектор-функций высокого порядка
приведём для шаблонного элемен-
та 0е =
На шаблонном элементе базисные вектор-функции первого по-
рядка (см. (15.47)) имеют следующий вид:
1 + rf
2
О
ф4 =
(15.48)
Для построения прямоугольного векторного элемента второго по-
рядка необходимо добавить к локальным базисным вектор-функциям
(15.48) ещё 8 вектор-функций вида
1 И это делает уместным определение таких функций как функций первого
порядка.
2 Естественно, базисные вектор-функции высоких порядков можно стро-
ить и с помощью полиномов Лагранжа - их вид будет даже несколько проще,
но иерархические базисы обладают определёнными преимуществами, о кото-
рых мы уже говорили в двенадцатом разделе для узловых конечных элемен-
тов.
672
15 Векторный МКЭ для решения задач электромагнетизма
Ф10 =
'Рс —
ФГ2
О
(15.49)
i + n/
9
Очевидно, что квадратичные базисные вектор-функции ip9 4- ф>12
имеют нулевые касательные составляющие на всех рёбрах конечного
элемента, и поэтому их имеет смысл ассоциировать с самим конечным
элементом (т.е к ним уже совершенно не подходит термин «edge»).
Заметим также, что квадратичные глобальные базисные вектор-
функции, построенные из вектор-функций вида ф>д4-<р12, являются
ненулевыми только на одном конечном элементе, т е. они равны од-
ной из локальных базисных вектор-функций внутри конечного элемен-
та и тождественно равны нулю вне его. Это же справедливо для всех
базисных вектор-функции высоких порядков, ассоциированных не с
ребрами, ас самим конечным элементом.
Приведём общий вид шаблонных иерархических базисных вектор-
функций прямоугольного конечного элемента р-го порядка'. В этот
базис входят все 2р(р — 1) базисных вектор-функций элемента
(р — 1)-го порядка и ещё 1р вектор-функций (для р > 3 ):
Ф2р(/>-1)+4—
1Р2р(р-1)+2
О
,£1-2(1-(.2)
Ф2р(р-1)+4+1
Ф2р(/>-1)+4+2
1 При этом мы будем пользоваться одномерными иерархическими функ-
циями вида (12.2)-(12.4).
15.6.Принципы построения базисных вектор-функций ...
673
(15.50)
из которых первые четыре вектор-функции ассоциируются с рёбрами
конечного элемента, а остальные 4р — 4 вектор-функции — с самим
элементом.
Очевидно, что базисные вектор-функции -ф, (ж, у) произвольного
конечного элемента Qrs. = [тг,тг+1] х [?/.s,3/s+i] могут быть легко полу-
чены из вектор-функций (£,, i]) заменой переменных
6, — 2\Х З'г-Ы/г)/hj: •> — ^r+l Хг ’ (^Т + ^r+l )/^ >
Л = 2 [у - ys+i/2}/fiy , hy = ys+i - ys, &+1/2 = (ys + ys+i )/2,
т.е.
2^-^+1/г)
К.
2 [У ~ V.s+l/2 j
674
15.Векторный МКЭ для решения задач электромагнетизма
15.6.3. БАЗИСНЫЕ ВЕКТОР ФУНКЦИИ НА ТРЕУГОЛЬНИКЕ
Рассмотрим, как можно построить базисные вектор-функции из
Нг‘' на треугольных конечных элементах. Для этого удобно использо-
вать векторы grad Д , где Д - это £ -координаты треугольника Q/M .
Действительно, вектор-функция
gracl^Q имеет нулевую касательную со-
ставляющую на ребре с номером 2, со-
единяющем вершины с номерами 2 и 3
(рис. 146), поскольку линии равного
уровня Д параллельны этому ребру. То-
гда вектор-функция £2grad£( будет
иметь нулевые касательные составляю-
щие уже на двух рёбрах с номерами 2 и 3
(поскольку функция Д па ребре 3 равна
нулю). Таким образом, вектор-функция
Д grad Д имеет ненулевую касательную
составляющую только на ребре I. При
2
Рис. 146. Локальная нумерация
узлов и рёбер на треугольном
конечном элементе Q.,,,
этом значение касательной составляющей вектор-функции Д grad£t
на ребре 1 меняется линейно от нуля в точке 1 до значения
(gradrj vj (где Д - единичный вектор, направленный вдоль реб-
ра 1) в точке 2. Покажем, что значение (grad Д) - Vi в точке 1 равно
y/j (или — 1/Zj в зависимости от ориентации вектора Д), где
1\ = ~^2) +Й1-2/2) - длина ребра I.
Напомним (см. раздел 5.3.1), что £-координаты являются линей-
ными функциями декартовых координат:
д = «о + сф; + сДт/, i = 1, 2, з,
где
1 1 11 Г1
«0 «2 1 1 1
«о «2 = а = d 1 = Z1 ^2
«0 »2 7 У\ 1 У-2 Уз 7
Поэтому grad Д = («1,012) > и, учитывая, что
Vi = (Д ,
получаем
(grad Д) Д = (а} (Д - Д>) + <4 (ft - У2 ))Д
(15.51)
(15.52)
(15.53)
(15.54)
15 6.Принципы построения базисных вектор-функций ...
675
Но, из (5.69)
схо сх{ а2 / ( ч 111 10 0
«о о? а2 Д .^2 £’3=0 1 0
Q?) (Y? Oi2 / У\ У2 Уз 0 0 1 V
т.е. в результате умножения первой строки матрицы (L на первый и
второй столбцы матрицы D получаем
aj) + о^Д + = 1, (15.55)
«о + а}Д + c4?/2 = 0. (15.56)
Вычитая (15.56) из (15.55). получаем
a} (Д - Д) + (У1 ~ У2) = 1,
т.е. с учётом (15.54)
(grad Д) vj = l/Zj . (15.57)
Абсолютно аналогично можно доказать, что для вектора Vj, на-
правленного вдоль первого ребра треугольника Q,n и определяемого
соотношением (15.53), будет справедливо равенство
(grad£2)- vj = -1Д ,
и поэтому касательная составляющая вектор-функции Д grad Д на
ребре 1 будет меняться линейно от значения — 1/Zi в точке 1 до нуля в
точке 2. При этом вектор-функция Д grad Д так же. как и вектор-
функция Д grad Д, имеет нулевые касательные составляющие на дру-
гих рёбрах треугольника, поскольку grad Д перпендикулярен к ребру
с номером 2, а функция Д равна нулю на ребре с номером 3 (см.
рис. 146).
Поэтому вектор-функция
Ф1 = Д grad Д - Д grad Д (15.58)
имеет постоянное, равное , значение касательной составляющей на
ребре 1 и нулевые значения касательных составляющих на ребрах 2
и 3
На самом деле, доказать то, что вектор-функция ф] имеет постоян-
ную касательную па ребре 1, можно и другим, очень простым спосо-
676
15 Векторный МКЭ для решения задач электромагнетизма
бом. Для этого достаточно выразить из тождества Д + Д + Д = 1
функцию Д :
*Ф1 = -С? grad Д - Д grad Д = Д grad Д - Д grad (1 - Д - Д)
и учесть, что на этом ребре Д + Д = 1, т.е,
*Ф1 = ^2 grad Д 4 Д grad Д + Д grad Д = grad Д + Д grad Д
на ребре 1.
Тогда, учитывая, что функция grad£3 перпендикулярна ребру 1
(т.е. grad Д v, = О, Д - касательный к ребру 1 единичный вектор,
см. (15.53)), касательная к этому ребру составляющая вектор-функции
*Ф1 будет равна
“Ф1 ’ Vi = grad Д • Д + Д grad Д • Д = grad Д Д =
4 4
(сравните с (15.54)).
Но для нас очень важным является и тот факт, что величина
оц (Д — Д) + (\2 (Hi ~ У-1) пе зависит от координат вершины тре-
угольника, ни лежащей на ребре 1, с которым ассоциирована векпюр-
функция rpj, а доказательство этого и составляет основную часть про-
ведённых нами выше рассуждении (см. соотношения (15.55), (15.56)).
Очевидно, чго на треугольнике Q,„ можно ввести ещё две локаль-
ные базисные вектор-функции, ассоциированные с ребром 2 и реб-
ром 3 соответственно (см рис. 146)
Фг = A grad Д - Д grad Д, (15.59)
Фз = A grad Д - Д grad Д (15.60)
Точно так же, как и для вектор-функции -ф1, можно доказать, что
вектор-функции ф2 и ф3 имеют постоянные касательные составляю-
щие на рёбрах, с которыми они ассоциированы, и нулевые касательные
составляющие на двух других рёбрах
Из локальных вектор-функций такого вида можно построить мини-
мально допустимый базис конечномерного подпространства Vrot,
определяемого для сетки с треугольными ячейками. Действительно,
так как локальные базисные вектор-функции вида (15.58)~(15.60), ас-
социированные с ребром Г, на двух треугольниках О.Ш] и , смеж-
15.6.Принципы построения базисных вектор-функций ...
677
ных по этому ребру, имеют касательные составляющие, равные 1/Z
(Z — длина Г), то в качестве глобальной базисной вектор-функции,
ассоциированной с ребром Г, можно взять следующую вектор-
функцию. На треугольниках Q„4 и Ош., она должна быть равна ло-
кальным базисным вектор-функциям, ассоциированным с ребром Г, а
на всех остальных ^треугольниках эта гло-
бальная базисная вектор-функция должна
быть тождественно равна нулю.
Очевидно, что определенные таким об-
разом глобальные вектор-функции имеют
ненулевые (и непрерывные) касательные
составляющие только на одном ребре, с
которым они ассоциированы, и поэтому
они сами и любые их линейные комбина-
ции являются элементами пространства
Hrut. Пример одной из таких глобальных
базисных вектор-функций (для сетки из
треугольных конечных элементов) приве-
дён на рис. 147.
Обратим внимание на одну деталь,
очень важную при работе с треугольными
edge-элементами (это замечание актуально
при использовании любых нерегулярных
сеток с edge-элементами). Непрерывность
касательной составляющей глобальной
базисной вектор-функции на ребре, с ко-
торым она ассоциирована, оказывается
зависящей от локальной нумерации вершин
треугольников, смежных по этому ребру.
Покажем это на примере сигуации, изо-
бражённой на рис. 148.
Рассмотрим глобальную базисную век-
Рис. 147. Вид глобальной
базисной вектор-функции
на треугольной сетке
тор-функцию, ассоциированную с ребром, соединяющим вершины с
глобальными номерами 2 и 3. На треугольнике Qj (с вершинами,
имеющими глобальные номера 1,2,3) эта базисная вектор-функция
определяется как
Фз1 = A grad - £2 grad ,
а на треугольнике (с вершинами, имеющими глобальные номе-
ра 3,2,4) - как
Ф'/ = A grad Д - grad £2
Но локальная вектор-функция ф^1 на ребре {2,3} имеет касатель-
ную составляющую, направленную отточки с глобальным номером 3 к
678
15.Векторный МКЭ для решения задач электромагнетизма
точке с глобальным номером 2, а локальная вектор-функция -ф^2 на
этом же ребре - касательную составляющую, направленную от точки с
глобальным номером 2 к точке с глобальным номером 3. Вид глобаль-
ной вектор-функции, полученной в результате «формальной» сшивки
этих двух локальных вектор-функции, приведён на рис. 148,6. Очевид-
но, что полученная глобальная век тор-функция имеет разрывную каса-
тельную составляющую на ребре, с которым она ассоциирована.
Рис. 148. Глобальная и локальная нумерация базисных вектор-функций
на треугольнике (а) и вид глобальной базисной вектор-функции, полученной
«формальной» сшивкой локальных базисных вектор-функций ф^1 и ф^2 (б)
Заметим, что аналогичная проблема уже рассматривалась нами в
двенадцатом разделе для иерархических базисных функций и решить
её можно тем же самым способом - специальным упорядочением ло-
кальных номеров вершин на конечном элементе. Так, если на тре-
угольных конечных элементах локальную нумерацию вершин прово-
дить строго по возрастанию их глобальных номеров, то локальные
базисные вектор-функции, примыкающие к одному и тому же ребру,
всегда будут направлены в одну и ту же сторону, и касательные со-
15.6.Принципы построения базисных вектор-функций ...
679
ставляющие получаемых глобальных вектор-функций будут непре-
рывны1.
Иногда вместо базисных вектор-функций (15.58)—<15.60) использу-
ют нормированные вектор-функции
(^2 gratis - Д grad £2) > (15.61)
Ф-2 = grad£[ -Д grad£3), . (15.62)
Фз = (^3 grad £>2 - £2 grad £3 ), (15.63)
где Zj, I2 и (з ~ длины соответствующих рёбер. Эти вектор-функции
удобней тем. что в случае их использования не возникает никаких про-
блем при решении задачи на смешанной сетке, состоящей из прямо-
угольных и треугольных ячеек. Действительно, касательная состав-
ляющая глобальной базисной вектор-функции, ассоциированной с
ребром, которое является общим для прямоугольника и треугольника,
будет равна единице как на прямоугольнике, так и на треугольнике.
Это и обеспечит непрерывность такой глобальной векгор-функции
(полученной формальной сшивкой локальных базисных вектор-
функций прямоугольника и треугольника) на ребре, с которым она
ассоциирована, и тем самым обеспечит принадлежность её простран-
ству Hrut.
Следует отметить ещё одну особенность базисов, построенных с
помощью соотношений (15.58)—(15.60) (или, что практически то же
самое, (15.61)—(15.63)). На этих базисах плохо представимыми являют-
ся даже вектор-функции, линейно изменяющиеся по одной из про-
странственных координат. Поэтому могут возникать серьёзные труд-
ности при решении задач со скин-эффектом, когда необходимо ап-
проксимировать функцию, резко меняющуюся вблизи некоторой гра-
ницы. В этом случае обычно используют конечные элементы, вытяну-
тые в направлении, касательном к границе, и очень сжатые в направ-
лении нормали к этой границе. При использовании же вектор-функций
(15.58)-( 15.60) (и (15.61)—(15.63)) на вытянутых треугольниках реше-
ния задач со скин-эффектом обычно аппроксимируются с очень боль-
шой погрешностью.
1 Обратим внимание на то, что локальные базисные вектор-функции на
треугольном конечном элементе сразу были введены нами так, чтобы их каса-
тельные составляющие на рёбрах, с которыми они ассоциированы, были на-
правлены от вершины с большим номером к вершине с меньшим. Если бы мы
не придерживались этого правила и задали бы базисные вектор-функции про-
извольно (например, вместо (15.59) определили
Ф-2 = £\ grad £.1 ~ £< grad Д ), то не удалось бы согласовать локальные базис-
ные вектор-функции двух соседних элементов столь простым способом (пу-
тём синхронного возрастания локальных и глобальных номеров вершин ко-
нечных элементов).
680
15.Векторный МКЭ для решения задач электромагнетизма
В принципе, на треугольных конечных элементах совсем несложно
построить такой базис, с помощью которого можно точно представить
любую линейную вектор-функцию. Однако в этом случае нужно ис-
пользовать шесть локальных базисных вектор-функций. Например, это
могут быть вектор-функции следующего вида:
”Ф| = Д grad Д, -ф2=Ддгас1Д, ч[>з = Д grad Д.
•фл = Д grad Д , -ф5 = Д grad Д, -фс = Д grad Д, (15.64)
где вектор-функции и ч|?2 имеют ненулевые касательные только на
ребре 1 (см. рис. 146) и поэтому ассоциируются с этим ребром, вектор-
функции чрз и чр4 имеют ненулевые касательные только на ребре 2 (и
ассоциированы с ребром 2), а вектор-функции чр5 и чр6 — только на
ребре 3 (и ассоциированы с ним). При этом касательные составляющие
этих вектор-функций меняются от значения 1/Z (или —I// в зависимо-
сти от ориентации ребра, I - длина ребра) в одной вершине ребра, с
которым они ассоциированы, до нуля в другой вершине этого ребра.
Глобальные базисные вектор-функции получаются (как и в случае
базиса (15.58)—(15.60)) сшивкой двух локальных базисных вектор-
функций, ассоциированных с одним ребро м и отличных от нуля в од-
ной it той же вершине этого ребра. Так. например, вектор-функция
яр! будет сшиваться с такой функцией смежного с (см. рис. 146)
треугольника, которая ассоциирована с ребром 1 и отлична от нуля в
той вершине, которая на Q/n имеет локальный номер 2. Поэтому каж-
дую из таких 1лобальпых вектор-функций можно считать ассоцииро-
ванной одновременно с одним ребром и одной вершиной.
Эквивалентный (15.64) базис может быть построен добавкой на ка-
ждом конечном элементе к базису (15.58)—(15.60) ещё трёх линейных
базисных вектор-функций (т.е по иерархическому принципу - новый
базис получается добавкой базисных функций к набору функций ста-
рого базиса). Можно, например, к вектор-функциям (15.5 8)-(15.60)
добавить первую, третью и пятую вектор-функции из набора базисных
вектор-функций (15.64). А можно добавить вторую, четвёртую и шес-
тую. Но обычно к вектор-функциям (15.58)-( 15.60) добавляются век-
тор-функции следующего вида:
'Фд = Д grad Д + Д grad Д, (15.65)
Фз = A grad Д + Д grad Д, (15.66)
Фо = Д grad Д + Д grad Д. (15.67)
Каждая из вектор-функций (15.65)-(15.67) также имеет ненулевую
касательную только на одном ребре (с которым она и ассоциируется),
15.6.Принципы построения базисных вектор-функций ... 681
и эта касательная изменяется вдоль соответствующего ребра линейно
от значения —1 в одной его вершине до значения 1 в другой.
Базисные вектор-функции треугольных конечных элементов высо-
кого порядка можно построить, например, в виде
(А(1 -£,)** (£2)‘!| (1 - £_,)'- (£,)1Г1 (1 - £;)‘" g™l£, . (15.68)
При построении таких базисов необходимо следить, чтобы все ба-
зисные функции были линейно независимыми и давали любую поли-
номиальную вектор-функцию нужного порядка. Однако на симплексах
элементы высокого порядка используются довольно редко. Чаще все-
го, если для повышения точности расчёта выбирается путь, связанный
с повышением порядка элемента, в качестве конечных элементов ис-
пользуются либо прямоугольники или параллелепипеды, либо четы-
рёхугольники или шестигранники (с четырёхугольными гранями).
Сделаем ещё одно довольно важное замечание относительно ис-
пользования edge-элементов на ячейках различных типов. При исполь-
зовании базисов вида (15.64) или (15.58)- (15.60) и (15.65)-(15.67) чис-
ло глобальных базисных вектор-функций ровно вдвое больше числа
рёбер сетки. Кроме того, возрастает и количество связей между гло-
бальными вектор-функциями, что приводит к увеличению заполненно-
сти матрицы конечпоэлементной СЛАУ почти вчетверо. Поэтому в
ситуациях, когда при использовании минимального оазиса (15.58)-
(15.60) не удаётся получить решение задачи (например, в случае скин-
эффекта и необходимости использования вытянутых ячеек), треуголь-
ные edge-элементы являются далеко не самыми эффективными. В этом
случае лучше использовать либо прямоугольные edge-элементы (если
геометрия задачи позволяет это делать), либо четырёхугольные edge-
элементы, которые, пожалуй, наиболее эффективны для решения дву-
мерных задач в областях со сложной геометрией.
15.6.4. БАЗИСНЫЕ BI К ГОР ФУНКЦИИ ИА ЧЕТЫРЁХУ1 ОДЫШКЕ
В векторном МКЭ, как и в скалярном, четырёхугольный конеч-
ный элемент сочетает в себе основные достоинства прямоугольных и
треугольных элементов: высокое качество аппроксимации (как у пря-
моугольных элементов) и возможность работы со сложной геометрией
(как у треугольных элементов).
Основной принцип построения базисных вектор-функций на четы-
рёхугольнике остаётся тем же (как и на прямоугольнике или треуголь-
нике): каждая базисная вектор-функция должна иметь отличную от
нуля касательную составляющую не более чем на одном ребре1. Наи-
более удобно строить такие базисные вектор-функции через отображе-
ние на четырёхугольник базисных вектор-функций шаблонного эле-
мента в виде квадрата = [0,1] х [0,1] или = [—1,1]х[—1,1| (при
работе с лагранжевыми базисами обычно используется квадрат
QE =[0,1] х [0,1], а при работе с иерархическими базисами чаще ис-
1 У элементов высокого порядка есть базисные вектор-функции, которые
имеют нулевые каегггельные на всех рёбрах.
682
15.Векторный МКЭ для решения задач электромагнетизма
Рис 149. Расположение узлов
на четырёхугольном конечном
элементе
пользуют квадрат QE = [—1,1] х [—1,1], поскольку одномерные иерар-
хические базисные функции удобней задавать на отрезке [—1,1]). Мы
будем пользоваться шаблонным элементом = [—1,1] х [—1,1], пола-
гая, что элементы высоких порядков будут строиться с помощью рас-
смотренных в разделе 15.6.2 базисных вектор-функций вида (15.50).
Рассмотрим некоторый (произ-
вольный) четырёхугольный конечный
элемент Q„, с вершинами
(т,,?/,;), г = I...4 . Будем считать, что
его вершины и ребра пронумерованы
так, как это показано на рис. 149 (при-
чём в прямоугольничках стоят ло-
кальные номера вершин, а в кружоч-
ках — локальные номера рёбер)
Прежде чем определить базисные
вектор-функции на ffe, установим
между точками (т, у) четырёхуголь-
ника Qm и точками (£., т}) шаблонного
элемента С1Е = [— 1,1] х [— 1,1] взаим-
но однозначное соответствие с помощью формул
X = Х1ф1 (е., Т]) + ±2ф2 fe л) + ^ЗФЗ (6.) Л) + feT>4 fe, л) >
У = fe, л) + У2Ч>2 (k, л) + Z/зФз fe, л) + Р4Ф4 fe л),
(15.69)
где ф, — это стандартные узловые билинейные базисные функции:
ф1=
(1-Q (i-п) ,, _ (i+О (i-ц) ,, _ (1-0 (1+л) ,, _ (1+0 (1+л)
—------2“> -----2----— • ^3------2----2“’ ----2-----2~
Так как определяемые нами на базисные функции являются
векторами, то чтобы задать на Q,n базисные вектор-функции через
стандартные базисные вектор-функции шаблонного конечного элемен-
та £1е :
' 0 '
^2 = 1 + е, ’
' о '
Ф1 = i-e, ’
Фз =
1 — Т]
ф4 =
(15.70)
2
2
2
0
1 +Л
2
0
(сравните с (15.47)), надо определить, как векторы, заданные на О/ (в
координатах {fe, т|} ), отображаются в векторы на ffe (в координатах
'{®»2/})-
15.6.Принципы построения базисных вектор-функций ...
683
Например, отображение вектора w, заданного в точке (^/,,7),,)
квадрата (т.е. точка — начало вектора w), в вектор v с
началом в точке (точка из Q,„ является отображени-
ем1 точки (б./л'Пр) из ) можно определить с помощью соотношения
v =
(15.71)
где J (6., 1]) - функциональная матрица отображения (15.69), т.е.
дх
дх
дт\
ду'
ду
дту
^4^(®г- (®4~ (®2“ й)+ (®4- Уз)
ф i2) ф fe)
Тогда любой вектор, касательный к стороне £ = — 1 квадрата Q7, бу-
дет отображаться в вектор, касательный к ребру 1 четырёхугольника
(см. рис. 149), любой вектор, касательный к стороне £ = 1 квадра-
та £1Е, - в вектор, касательный к ребру 2 четырёхугольника П„Л, лю-
бой вектор, касательный к стороне т] = — 1 квадрата - в вектор,
касательный к ребру 3 четырёхугольника Q,n, а любой вектор, каса-
тельный к стороне т] = 1 квадрата , - в вектор, касательный к реб-
ру 4 четырёхугольника Q„t.
Однако если базисные вектор-функции ч|\ (х,у) конечного элемен-
та Q,,, определить как
*Фг у) = JT(U^ У) 1 Л (я> */)) Фг у) , Л (г‘, у)) , (1 5-73)
где ф, (6,, т|) - базисные вектор-функции, заданные на шаблонном эле-
менте Q£ (см. (15.70)), a ^(х,у) и т](х,у) - функции, определяющие
обратное к (15.69) отображение, то эти вектор-функции могут иметь
ненулевые касательные не на одном ребре, с которым они ассоцииро-
ваны, а ещё на двух смежных с ним рёбрах. Действительно, вектор-
1 Это отображение определяется соотношениями (15.69).
684
15.Векторный МКЭ для решения задач электромагнетизма
функция (ж, у) (полученная из
вектор-функции ф] (£, т|) по фор-
муле (15.73)) в первом узле (£[,?/])
четырёхугольника Q,„ (см.
рис. 149) будет направлена вдоль
ребра 1 и поэтому будет иметь
ненулевую касательную к ребру 3
(если ребро 3 не ортогонально
ребру 1). Аналогично, (.г, ?/) в
узле (.г’з,?/з) будет иметь ненуле-
вую касательную к ребру 4 (если
ребро 4 не ортогонально ребру 1)
Поведение такой вектор-функции
Рис. 150. Вид «неправильной» базисной
вектор-функции, определяемой
соотношением (15.73)
на изображено на рис. 150. То
же самое можно сказать и о трёх
остальных вектор-функциях, опре-
деляемых соотношением (15.73).
Чтобы получить нужные нам
базисные векюр-функции (с нуле-
выми касательными на трёх рёбрах
Q„,), воспользуемся следующим фактом. Значение скалярного произ-
ведения любой вектор-функции *ф(ж,у) на произвольный вектор v в
любой точке (^,?//?) может быть вычислено как
J w = > (15.74)
где w — вектор, полученный из v отображением, обратным к (15.71),
т.е. w = J T v , а (^у,,т|р) ~ точка в координатах {£,, т|} , которая
при преобразовании координат т|} в координаты {ж, у} отобража-
ется в точку (жр, ур^.
Таким образом, если в качестве локальных базисных вектор-
функций четырёхугольника П,„ взять вектор-функции
Фа (ж, у) = J4(e, (ж, у) , 7] (ж, у)) & (£, (ж, у) , 7] (ж, у)) ,
(15.75)
то каждая из таких вектор-функций *ф7 (ж, ?/) будет иметь ненулевые (и
при этом постоянные) касательные только на одном ребре с номером i
(с которым она и должна быть ассоциирована).
15.6.Принципы построения базисных вектор-функций ...
685
Действительно, если для вектор-функции •ф1 (:г, у) в качестве век-
тора v взять вектор единичной длины, направленный вдоль ребра 1, то
с учётом (15.74) и (15.75) в любой точке (тр,ур), лежащей на ребре 1
четырёхугольника ,
= ’ (15.76)
где w - вектор, направленный вдоль стороны 6, = — 1 шаблонного
квадрата 0е, т.е. w = (0, d)T. При этом значение d одинаково для
всех точек ребра 1, поскольку
- £1 - Зз)
- У1 )+^^(у4~Уз)
>з-А)
Цуз~У1)
Jfe -£i У
2 [(Уз - У} У
т.е. d не зависит от координаты т)р (координата же равна — 1 на
ребре 1). С учётом того, что v - вектор единичной длины,
d = 21М1 =
7(*з -i’i)2 + (уз - J/l)2 11
где Zj - длина ребра 1.
Таким образом, значение касательной составляющей вектор-
функции -фДт, у), определяемой формулой (15.75), на ребре 1 четы-
рёхугольника Q„, может быть вычислено как (см. (15.76))
*Ф1Л =(ф1 (-1,л)>
и с учетом того, чю ф] (—1, т]) =
о
d
и w —
, получаем
Фьу) = d = 2-
т.е. вектор-функция фДт, у) имеет на ребре 1 постоянную, равную
686
15.Векторный МКЭ для решения задач электромагнетизма
2/Z] , касательную составляющую1.
На остальных рёбрах (т,//) имеет нулевые касательные состав-
ляющие. Действительно, если взягь в качестве v единичный вектор,
направленный вдоль ребра 3, то его прообразом будет вектор
Рис. 151. Поведение локальных базисных вектор-функций, определяемых
соотношением (15.75), на четырёхугольнике Q,„
1 Если бы мы использовали в качестве шаблонного элемента единич-
ный квадрат [o,i]x[o,i], то касательная составляющая на первом ребре
была бы равна l//t .
15.6.Принципы построения базисных вектор-функций ...
687
Аналогично | гфь v ] = 0, если вектор v направлен вдоль ребра 4.
На ребре же с номером 2 вектор-функция имеет нулевую касатель-
ную, поскольку на нём ф| = 0 .
Точно так же можно доказать, что и остальные базисные вектор-
функции, определяемые соотношением (15.75), имею! ненулевые (и
постоянные, равные 2/Z, ) касательные на рёбрах, с которыми они ас-
социированы, и нулевые касательные на остальных рёбрах четырёх-
угольника И,,,. На рис. 151 показано поведение на локальных ба-
зисных вектор-функций. На рис. 152 показан вид одной глобальной
базисной вектор-функции в расчётной области при использовании в
качестве элементов лискпетизании четырёхугольников.
Рис. 152. Поведение одной из глобальных базисных вскгор-функций
при использовании сетки с четырёхугольными ячейками
Очевидно, что вместо вектор-функций (15.75), у которых касатель-
ная составляющая на ребре (с которым она ассоциирована) равна 2/Z, ,
можно ввести нормированные базисные вектор-функции с единичны-
ми касательными:
Ф, (я, ?/) = тр ‘ (-П у) , Л (я, у)) Ф,. (С, (•*, У) > Л (т, у)),
(15.77)
где lj — длина г-го ребра.
Вектор-функции вида (15.77) имеет смысл использовать, например,
в тех случаях, когда в конечноэлементной сетке наряду с четырех-
угольниками есть и прямоугольники, и при этом локальные матрицы
прямоугольных элементов вычисляются не через шаблонные элемен-
ты, а напрямую по функциям, определённым в разделе 15.6.2.
688
15.Векторный МКЭ для решения задач электромагнетизма
Рассмотрим, как можно ввести базисные вектор-функции па криво-
линейном четырёхугольнике. Задать криволинейный четырёхугольник
можно (так же как и четырёхугольник с прямыми сторонами) через
некоторое отображение шаблонного квадратного элемента. Например,
криволинейный четырёхугольник можно задать отображением шаб-
лонного элемента (У = [—1,1] х [—1,1] (аналогично рассмотренному в
разделе 5.5 отображению квадрата Q = [0,1] х 0,1], см. рис. 43) с
помощью соотношений
9 9
г’= EXbq (^’71)Л , У = 52 Ф?4 (£,?])&(15.78)
1=1 г=1
где фь‘* - стандартные лагранжевы биквадратичные (узловые) функ-
ции на , a (rrt,?/,) — координаты девяти узлов элемента £2„,. Тогда
определяемые соотношением (15.75) базисные вектор-функции ic
функциональной матрицей J, полученной для отображения (15.78)
будут иметь ненулевые касательные составляющие также только на
одной стороне криволинейного четырёхугольника, и эти касательные
будут зависеть от координат только тех узлов четырёхугольника Qy;/,
которые лежат на этой стороне*.
Базисные вектор-функции высокого порядка на четырёхугольнике
(в том числе и на криволинейном) также удобно вводить через базис-
ные вектор-функции высокого порядка шаблонного элемента 0е. Для
этого можно, например, использовать шаблонные вектор-функции
иерархического типа, которые были введены нами в разделе 1 5.6.2 (см.
соотношения (15.48)-( 15.50)). Базисные же вектор-функции высокого
порядка фДз;, у) конечного элемента получаются из вектор-
функций т]) шаблонного элемента (У с помощью того же соот-
ношения (15.75).
И в заключение обратим внимание на то, что нумерация узлов век-
торного четырёхугольника (которая косвенно определяет нумерацию
его базисных вектор-функций) не может быть абсолютно произволь-
ной, поскольку это может привести к разрывности глобальных базис-
ных вектор-функций (из-за того, что касательные составляющие ло-
кальных вектор-функции одного и того же ребра могут оказаться на-
правленными в разные стороны). Здесь, к сожалению, проблему нельзя
решить столь же просто, как для треугольников (т.е. использовать
только такие локальные нумерации вершин, которые упорядочены по
возрастанию соответствующих им глобальных номеров). Простейшим
выходом для четырёхугольников может быть использование таких
нумераций узлов и рёбер, которые подобны нумерациям в стандартных
1 Это принципиально для обеспечения непрерывности касательных со-
ставляющих при построении соответствующих глобальных базисных функ-
ций на криволинейных сторонах четырёхугольника.
i 5.7.0 некоторых возможностях построения ...
689
прямоугольных сетках1 (что и позволит для любых двух смежных че-
тырёхугольников автоматически обеспечить одинаковую направлен-
ность локальных базисных вектор-функций, ассоциированных с реб-
ром, по которому эти четырёхугольники являются смежными).
15.7 . О НЕКОТОРЫХ ВОЗМОЖНОСТЯХ ПОСТРОЕНИЯ
НА ПРЯМОУГОЛЬНЫХ EDGE-ЭЛЕМЕНТАХ базисных
ВЕКТОР-ФУНКЦИЙ (ИЗ H,ot) С НЕПРЕРЫВНЫМИ
НОРМАЛЬНЫМИ СОСТАВЛЯЮЩИМИ
Несколько выше (в разделе 15.6.2) нами были рассмотрены такие
базисные вектор-функции на прямоугольных edge-элементах первого
порядка, которые являются постоянными вдоль одной из координат
(ось которой совпадала с направлением вектор-функции). Очевидно,
что даже некоторые линейные вектор функции не могут быть точно
представлены в виде линейной комбинации базисных вектор-функции
этого типа.
В принципе, в качестве базисных вектор-функций на прямоуголь-
ных еаее-элементах первого порядка можно использовать и другие
вектор-функции. Например, на прямоугольном конечном элементе
Q,.s = х [i/.s.,2/.s+i] можно ввести 8 линейных базисных вектор-
функций следующего вида:
О
У ~ У s ЗУ-Н ~ х
hy h,:i:
х - хг у - ys
(15.79)
На рис. 153 показан вид первых двух из этих вектор-функций.
1 Например, слева направо и снизу вверх по координатным линиям сетки
690
15.Векторный МКЭ для решения задач электромагнетизма
Рис. 153. Вид локальных вектор-функций и
Очевидно, что если к четырём базисным всктор-функциям (15.47)
добавить ещё четыре вектор-функции типа фв-т-фд, то полученный
базис будет эквивалентен базису 615.79) (читатель может самостоятель-
но убедиться, что каждая век гор-функция из одного базиса представля-
ется в виде линейной комбинации двух вектор-функций из другого).
1 г т f , 1 1 1 I 1 III». 1 1 t I 1 tilt. 1 t 1 1 , till, .it' 1.1 1 1 1 1 'till, 'till, t t t 1 1 (II..
Рис. 155. Вид двух глобальных вектор-функций базиса, порождаемый вектор-
функция.ми (15.47) и типа 4- из (15.49)
Глобальные вектор-функции, порождаемые из локальных вектор-
функций (15.79), будут иметь ненулевые касательные составляющие
15.7.0 некоторых возможностях построения ...
691
только на одном ребре, с которым они ассоциированы, и при этом их
значения будут меняться от нуля в одной вершине ребра до единицы в
другой. Таким образом, с каждым ребром будут ассоциированы две
глобальные базисные вектор-функции, каждая из которых будет не
равна нулю только на двух конечных элементах, смежных по этому
ребру На рис. 154 приведён вид двух таких глобальных базисных век-
тор-функций, ассоциированных с одним и тем же ребром. Заметим, что
и глобальный базис, порождаемый вектор-функциями (15.47) и типа
Фз из (15.49), также имеет по две вектор-функции, ассоцииро-
ванные с одним ребром1. Пример двух глобальных’базисных вектор-
функций этого базиса, ассоциированных с одним и тем же ребром,
приведен на рис. 155.
Vs+2
Очевидно, что с помощью гло-
бальных вектор-функций, получен-
ных сшивкой тех локальных вектор-
функций (15.79), которые ассоции-
рованы с одним и тем же ребром и
имеют совпадающие на нём каса-
тельные составляющие, уже можно
точно представить любую кусочно-
линейную вектор-функцию2. Но
пространство VIot, порождаемое
такими глобальными вектор-
функциями, будет иметь вдвое боль-
шую размерность, чем пространст-
во, определяемое глобальными ба-
зисными вектор-функциями, по-
)р-функции (15.47) (при этом
.У возрастёт уже почти в не-
7s + l
^r,s+\. Г4 ^/+l,.s+]
Г) Г2
Ц. Г3 ^Г+1,.5-
У.ч
Хг -Тг + 1 ‘^г+2
Рис. 156. Обозначения элементов
и ребер сетки для построения
векторных базисных функций
строенными только из локальных векто]
заполненность конечноэлементной СЛА.
тыре раза, поскольку практически вдвое увеличится ещё и количество
связей между глобальными базисными вектор-функциями).
Однако с помощью локальных базисных вектор-функции (15.79)
можно построить другой глобальный базис. Каждую глобальную ба-
зисную вектор-функцию в этом базисе можно определить с помощью
локальных базисных вектор-функций двух сонаправленных соседних
(имеющих общую вершину) рёбер. Покажем это на примере, изобра-
жённом на рис. 156
Мы будем исходить из того, что нумерация локальных базисных
вектор-функций каждого конечного элемента выполнена в соответст-
вии с соотношениями (15.79). Тогда глобальную базисную вектор-
функцию, ассоциированную с рёбрами 1\ и Г2, можно определить
следующим образом На конечном элементе .0,.ч она должна быть рав-
1 Очевидно, оба этих глобальных базиса порождают одно и то же про-
странство V“>f.
2 То же самое можно сказать и о глобальном базисе, который можно по-
строить из локальных вектор-функций (15.47) и вектор-функций типа
фГ) 4- из (15.49).
692
15.Векторный МКЭ для решения задач электромагнетизма
на ф^’5 — его четвертой локальной вектор-функции (см. соотношения
(15.79)), на конечном элементе Qr+i..s — его второй локальной вектор-
функции -фэг+1’5, на Q,iS+i - равна ’,Л+1, на Qr+ls.+1 - равна
ф^г+1’л+1 ? а на остальных конечных элементах эта глобальная базисная
вектор-функция должна быть равна нулю. На рис 157 показан вид
двух глобальных базисных вектор-функций, одна из которых ассоции-
рована с рёбрами Г\ и Г2 (рис. 157,а), а другая - с рёбрами Г3 и Г4
(рис. 157,6).
а б
Рис. 157. Вид двух глобальных базисных вектор-функций
с непрерывными как касательными, так и нормальными составляющими
Очевидно, такие глобальные базисные вектор-функции уже позво-
ляют точно представлять любые кусочно-линейные функции (так же,
как глобальные базисные вектор функции, полученные непрерывной
(по касательной составляющей) сшивкой локальных вектор-функций
(15.79)). При этом размерность порождаемого ими конечномерного
пространства Vrot будет практически совпадать с размерностью про-
странства, порождаемого глобальными базисными вектор-функциями,
полученными из локальных вектор-функций (15.47). Однако глобаль-
ные базисные вектор-функции, построенные в результате сшивки че-
тырех локальных вектор-функций вида (15.79), не позволяют получать
решения с разрывными нормальными составляющими на границах, где
разрывен коэффициент . Эту проблему можно решить следующим
образом. В подобластях, где коэффициент непрерывен, можно ис-
пользовать глобальные вектор-функции, полученные сшивкой четырёх
локальных вектор-функций вида (15.79). Если же два ребра, с которы-
ми ассоциирована такая глобальная вектор-функция, разделены грани-
цей, где терпит разрыв, то вместо одной вектор-функции, ассоции-
рованной с этими двумя рёбрами, следует ввести две вектор-функции,
каждая из которых получена сшивкой только двух (ассоциированных с
соответствующим ребром) локальных вектор-функций вида (15.79)
15 8 Конечноэлементные матрицы и векторы ... 693
(пример таких вектор-функций приведён на рис. 154). Очевидно, это
несколько увеличит размерность пространства Vrot, но зато даст воз-
можность гораздо точнее аппроксимировать разрывные решения1.
Заметим, что при решении практических задач с разрывной удельной
электрической проводимостью о (или диэлектрической проницаемо-
стью е, если существенны токи смещения) рассмотренные здесь гло-
бальные базисные вектор-функции с непрерывной нормальной состав-
ляющей не применяются из-за усложнения технологии сборки матрицы
конечноэлементной СЛАУ. При этом и порядок аппроксимации у ко-
нечных элементов с такими базисными вектор-функциями остаётся пер-
вым, как и у элементов с базисными вектор-функциями вида (15.47). Но
всё же при использовании edge-функций с непрерывными нормальными
составляющими2 конечноэлементное решение, очевидно, является более
гладким и поэтому может быть более точным3, чем конечноэлементное
решение, получаемое с использованием базисных вектор-функций вида
(15.47). Однако следует учесть, что при использовании одной и той же
сетки, хотя размерность конечноэлементной СЛАУ будет почти одина-
ковой, заполненность её матрицы ненулевыми компонентами для edge-
функций с непрерывными нормальными составляющими окажется при-
мерно в 2.5 раза больше, чем для edge-функций вида (15.47).
15.8 КОНЕЧНОЭЛЕМЕНТНЫЕ МАТРИЦЫ И ВЕКТОРЫ,
ПОЛУЧАЕМЫЕ ПРИ РЕШЕНИИ ДВУМЕРНЫХ ВЕКТОРНЫХ ЗАДАЧ
С ИСПОЛЬЗОВАНИЕМ БАЗИСНЫХ ВЕКТОР-ФУНКЦИЙ
ИЗ ПРОСТРАНСТВА H,ot
15.8.1. ОСОБЕННОСТИ ВАРИАЦИОННОЙ ПОСТАНОВКИ
ДЛЯ ДВУМЕРНОЙ ВЕКТОРНОЙ ЗАДАЧИ
Двумерная векторная задача, вообще говоря, является частным
случаем трёхмерной векторной задачи, в которой у искомого решения
только две компоненты являются ненулевыми функциями, каждая из
которых зависит только от двух (соответствующих этим компонен-
там) координат. Примером такого рода задач могут служить задачи
моделирования в проводящей среде нестационарного электромагнит-
ного поля, вектор электрической напряжённости Е которого лежит в
плоскости XY и не изменяется вдоль координаты z, т.е.
Ё = (Д7; (т, у), Еу (х, у), о)Т. Очевидно, и вектор-потенциал А такого
1 В принципе, аналогичный подход был описан в разделах 5.2.7 и 5.2.9.2
при использовании скалярных эрмитовых элементов для аппроксимации ре-
шений с разрывными производными.
2 Естественно, на рёбрах, примыкающих к границам разрыва коэффициен-
та 'у, должны быть использованы глобальные вектор-функции с разрывными
нормальными составляющими.
3 Особенно в точках, близких к границам (и тем более углам) конечного
элемента.
694
15.Векторный МКЭ для решения задач электромагнетизма
поля будет иметь аналогичный вид А = (Д. (ж,?/), А,, (ж,з/),0)Т, а век-
тор индукции В = rot А будет иметь единственную ненулевую ком-
дА,. ЭА. -* хт
поненту Bz = ----(т.е. В = (О,О,Вг) )'. То же самое можно
сказать и об осесимметричных электромагнитных полях, у которых в
цилиндрической системе координат напряжённость электрического
поля не имеет ф -й составляющей и зависит только от координат г и
z, т.е. Е = (Е,. (г, z) , О, Ez (г, г))1 (для таких полей В — (О, 0)Т,
дА,. dAz .
~~dz
Поэтому в двумерных векторных задачах в естественном краевом
условии (15.8) значением векторного произведения rot Ах п является
вектор, касательный к границе двумерной области Q (поскольку
rot А — вектор, перпендикулярный к плоскости, в которой задана рас-
чётная область Q, a ii лежит в этой плоскости и перпендикулярен к
границе ). Этот вектор может быть представлен в виде
rot А х п = 0
(15.80)
где п.,. и п,, — компоненты вектора нормали (т.е. для двумерной рас-
чётной области п = ), а 0 — третья (и единственная ненуле-
вая) компонента вектора rot А , т.е.
дА,, дА,:
дх ду
(15.81)
Чтобы убедиться в справедливости соотношения (15.80), нужно
векторы rot А и п рассматривать как трёхмерные. В этом случае
rot А = (О,О,0)Т (где 0 определяется соотношением (15.81)), а вектор
п лежит в плоскости XY (где задана расчётная область Q ) и поэтому
п = п„, 0)Т . Тогда rot А х п — 0n?/,07ia;,O)T и этот вектор, оче-
видно, лежит в плоскости XY и фактически является двумерным, и
поэтому его вполне можно записать в виде (15.80).
Таким образом, вариационное уравнение (15.11) в двумерном слу-
чае можно записать в виде
1 Это, вообще говоря, довольно известный факт - у «плоских» (т.е. зави-
сящих от двух пространственных координат) нестационарных электромагнит-
ных полей напряжённость электрического поля ортогональна индукции маг-
нитного поля.
15.8.Конечноэлементные матрицы и векторы ...
695
rot А rot Фс?П + ~уА • Фг/О ---
о
= Гг-ФсЮ + f ±&r-4fdS
J J p,
S-2
УФ G
(15.82)
где т — (—n!t, nx)T - касательный к S2 вектор (n = (n7;,TZ;(/)T - внеш-
няя по отношению к Q нормаль к S2 ), а скалярная функция 0 — пра-
вая часть краевого условия, заданного на S2 в виде1
дх
ад
а?/
J >S2
= е.
(15.83)
Произведение rot А • rot Ф в первом слагаемом вариационного
уравнения (15.82) фактически является произведением третьих (и
единственных ненулевых) компонент трёхмерных векторов rot А и
rot’I' (поэтому в двумерных векторных задачах rot А и гс^Ф до-
вольно часто вообще считают скалярными функциями, заданными в
двумерной области Q).
Главные же краевые условия в двумерных векторных задачах зада-
ются в виде
Д|„ =(Ат)1 = и!1,
151 1 ;|S1
(15.84)
где т — вектор, касательный к Д (который также может быть опреде-
лён через компоненты вектора п внешней по отношению к Q нормали
-> / \Т
к Д как т = I— ).
Конечноэлементная аппроксимация вариационного уравнения
(15.82) приводит к СЛАУ следующего вида (сравните с (15.18)):
J — rot ф7 • rot ф^П + J\ф7- фг^П qj =
Hui 11
о
1 На самом деле, естественное краевое условие в трёхмерной постановке
обычно задаётся как значение касательной составляющей напряжённости
магнитного поля Н , т.е. в виде p-rot Ахп = Н° х п ; соответственно в дву-
мерном случае вместо (15.83) можно задать условие
±т
(1 дх
— <г)г, где
дА,.'
дУ t
& связано с 0 из (15 83) очевидным соотношением О' = — 0 .
696
15.Векторный МКЭ для решения задач электромагнетизма
— ff + f - От ipjdS', г е NG , (15.85)
•j j u
O S-2
где n — общее число базисных вектор-функций (размерность Vrot),
No — множество номеров базисных вектор-функций *ф,, которые не
ассоциированы с рёбрами, лежащими на границе Д (эти базисные
вектор-функции порождают подпространство V(jot пространства Vrot
размерностью nJ ).
Остальные п — п() уравнений имеют вид
(15.86)
где и? — значение веса ассоциированной с ребром (из ) базисной
вектор-функции "ф,: (для г 0 7У() ) такое, что касательная составляющая
вектор-функции является максимально близкой к касательной
составляющей решения А на этом ребре1. Если используются базис-
ные вектор-функции с единичными касательными на рёбрах, то иг- —
некоторое (осреднённое либо взятое в центре ребра) значение Д на
рассматриваемом ребре.
Таким образом, матрица основной части (15.85) конечноэлементной
СЛАУ (15.85)—(15.86) может быть представлена в виде суммы матриц
жёсткости G и массы М, компоненты которых определяются соот-
ношениями
1 Обратим особое внимание на то, что в качестве и'- берётся касательная
составляющая А только в том случае, если на рассматриваемом ребре Гш
ненулевую касательную имеет только одна глобальная базисная вектор-
функция ф,. Значение тф при Д const на Г7/1 в этом случае может быть
вычислено как gf по формуле (15.30). Если же используются базисные век-
тор-функции высоких порядков, то с одним ребром Г,(1 могут быть ассоции-
рованы несколько базисных вектор-функций (имеющих на нём ненулевые
касательные), и в этом случае при учёте неоднородного главного краевого
условия на Гш веса всех ассоциированных с ним базисных вектор-функций
могут быть получены либо как значения касательных составляющих решения
в определённых точках ребра (а также грани в трёхмерном случае), либо из
условия максимальной близости к Д линейной комбинации (с этими весами)
соответствующих базисных вектор-функций (подробнее об этом см. раз-
дел 15.4). Для однородных же главных краевых условий всё совсем просто -
веса всех вектор-функций, ассоциированных с соответствующими ребрами,
просто обнуляются.
15.8.Конечноэлементные матрицы и векторы ...
697
G.jj — J" — rot • rotipycZQ, Му = . (15.87)
Компоненты же вектора b правой части основной части конечно-
элементной СЛАУ (без учёта вкладов от переноса в правую часть сла-
гаемых, умножаемых на qt, j /V(1) определяются соотношением
S-2
— ©т .
Jf • ф.2с?П +
о
=
(15.88)
15.8.2. ЛОКАЛЬНЫЕ МАТРИЦЫ И ВЕКТОРЫ
ПРЯМОУГОЛЬНЫХ EDGE-ЭЛЕМЕНТОВ
Получим формулы для вычисления локальных матриц прямо-
угольного конечного элемента Q,s. = [т,.,а;г+1] х [?/.s-, </.s.+i] с базисом
(15.47).
Сначала вычислим роторы1 локальных базисных вектор-функций
на Q,.s.:
rotz'ip1= у-—- = — у-, rotz3p2= -у- Х ,Х-~ = у-, (15.89)
z дх h.t: hx z dx hi: h.i:
го1г-ф3= — 7----= 7-, rotz^4= i V* ~ -~A~- (15.90)
dy hy /?,,/ zN4 dy hy hy
Тогда локальная матрица жёсткости этого элемента при постоянном
значении на нём коэффициента ц (т.е. р = р на Q75) имеет вид:
h:t; h.t:
hx
hy hy
(15.91)
1 Как мы уже говорили, в двумерном случае rot-ф имеет единственную
ненулевую компоненту rot^-ф.
698
15.Векторный МКЭ для решения задач электромагнетизма
На Qrs базисные вектор-функции зф и ф2 ортогональны базис-
ным вектор-функциям -ф3 и ф4, и поэтому соответствующие скаляр-
ные произведения ф, • ф (при i = 1,2, j = 3,4 и г = 3,4, 7 = 1,2)
будут равны нулю. В результате ненулевыми у М являются только
компоненты Л7,у для г, j = 1,2 и г, j = 3,4, и при постоянном значе-
нии на Q,.s, равном ,
'2 1 О О'
h.ll.. 12 0 0
м = ч-Н-
6 0 0 2 1
0 0 12
(15.92)
Вычислим теперь компоненты локального вектора правой части b
конечного элемента Qrs. Для этого представим правую часть F диф-
ференциального уравнения (15.2) в виде интерполянта
F ~ Fy ^.,?/ч+|)'ф1 + Fy ^у+1,т/ч+^'ф.2 +
+ F,: (.т ,+1, уя j ф3 + F, , </.s.+l j ф4,
(15.93)
где +ij, F:l.^:r+^yNj и - оче-
видно, значения касательной составляющей F в серединах рёбер, с
которыми ассоциированы , ф2, *Фз и '4’4 соответственно.
В принципе, в качестве коэффициентов разложения F по базисным
вектор-функциям ф, можно использовать и некоторые средние значе-
ния его касательных составляющих на рёбрах. Например, если считать,
что касательная составляющая F на каждом из рёбер Q,.s. ведёт себя
как квадратичная парабола, то в соотношении (15.93) вместо коэффи-
циента (.'Ey-, перед ф( можно поставить «среднеинтегральное»
значение этой параболы в виде
гральное» значение
g Fy (зт+1
, перед ф2 - «среднеинте-
y.s) + 4ДУ ^r+1, ys+i j + Fy (xr+i, ys+l)
15.8.Конечноэлементные матрицы и векторы ...
699
и т.д. (эти коэффициенты получаются после интегрирования аппрок-
симирующей касательную составляющую F параболы, проходящей
через три точки ребра, й деления полученного значения интеграла на
длину ребра).
Локальный вектор правой части Ъ при использовании представле-
ния F в виде (15.93) может быть вычислен с помощью локальной мат-
рицы массы М1:
Ь=М’
£фг,У,+|)
( £>+ 1 ’ j
F,. I х , 1, уч)
' \ r+2 J' )
Fx[xr+^ys^
(15.94)
где М’ - матрица массы, определяемая соотношением (15.92) при зна-
чении коэффициента равном единице (т.е. у М по сравнению с М
из соотношения (15 92) отсутствует сомножитель )
Получим теперь вклады в вектор правой части от естественного
краевого условия (15.83). Эти вклады определяются слагаемым
Г — 0т- ф^/э из правой части уравнения (15.85). Пусть Г,„ - ребро,
S-2
являющееся часть границы S2. Интеграл f —©т-'ф//*? будет нену-
г И
1 т -»
левым только для той глобальной базисной вектор-функции -ф,, кото-
рая ассоциирована с ребром Гм (поскольку на ребре Г,„ скалярное
произведение т-ф/5 для всех остальных базисных вектор-функций
будет равно нулю). Таким образом, при использовании базиса (15.47)
локальный вектор правой части для ребра Г,„ имеет размерность, рав-
ную единице (т.е. фактически является скаляром), и его значение оп-
ределяется соотношением (р и 0 полагаем константами па Г,,, )1
] РЛ
1 Если естественное краевое условие задано в виде
р дх
дЛ,'
ду
= ©, то
в соотношении (15.95), очевидно, будет отсутствовать сомножитель 1/р .
700
15.Векторный МКЭ для решения задач электромагнетизма
-7г//Г
п.,.
6Г"‘ = !©/,„
р
Г(±2 - )/4п '
(У1 - У\ )/1;п
=-^0(-7г(/(.т2 -^1) + ^, (?/2 -&)), (15.95)
где 1т - длина ребра Г„г, и, и п — компоненты вектора п внешней
(по отношению к расчётной области) нормали к Г7„, :ct и у; - коор-
динаты вершин ребра Г„,, причём очерёдность задания этих координат
имеет принципиальное значение - они должны быть заданы так, чтобы
направление вектора (.^ — >\,У2 ~/71)' совпадало с направлением каса-
тельной к Г,„ составляющей базисной вектор-функции (заметим,
что сомножитель (- nf/ (.i’2 — .i?!) + п:1. (у-2 — ij])) в соотношении (15.95)
принимает значение либо - 1т, либо 1„, в зависимости от того, как
соотносятся направления внешней нормали к Г.„( и касательной со-
ставляющей ф,). Очевидно, значение 6Г’" должно быть занесено в I-
ю компоненту глобального вектора правой части конечноэлементной
СЛАУ.
Заметим, что при использовании базисных вектор-функций вида
(15.79) и базисных вектор-функций высоких порядков локальные век-
торы правой части рёбер Гш Е S2 уже будут иметь размерность, боль-
шую единицы, поскольку в этих случаях ненулевые касательные со-
ставляющие на каждом ребре будут иметь несколько базисных вектор-
функций (для линейного базиса с вектор-функциями (15.79) и квадра-
тичного базиса размерность локального вектора Ь1 будет равна
двум, для кубического базиса трём и т.д.).
В целом же, на особенностях вычислений локальных матриц и век-
торов при использовании векторных базисов высоких порядков мы
остановимся чуть позже, при рассмотрении четырёхугольных элемен-
тов, сочетающих в себе лучшие качества двумерных элементов (см.
раздел 15.8.4).
15.8.3. ЛОКАЛЬНЫЕ МАТРИЦЫ И BI КI ОРЫ ТРЕУГОЛЬНЫХ EDGE ЭЛЕМЕНТОВ
Рассмотрим треугольный cclge-элемент с локальным базисом
(15.58)—(15.60) В общем виде локальные вектор-функции из этого
базиса можно записать как
*Ф/ = Д(0 grad £i)(() - £{)(/) grad Д(0, i = 1... 3, (15.96)
где v(i), — две целочисленные функции, определяемые табл. 23
15.8.Конечноэлементные матрицы и векторы ...
701
Таблица 23
г 1 2 3
ц(г) 2 3 3
fl (г) 1 1 2
Вычислим ротор базисной вектор-функции тр,, определяемой соот-
ношением (15.96). С учётом (5.66)
где коэффициенты а’’ легко могут быть получены из соотношений
(5.69), (5.74), (5.75)1.
Теперь получим соотношения для вычисления компонент локаль-
ных матриц жёсткости G и массы М элемента (при постоянных
на Q,„ значениях коэффициентов р=р и = ч):
G.tj = Г irotTp, rotipy/Q =
11
= -a^’a^’lldetDI, (15.97)
(Lx1 \ 1 /1
= J = 4 f (д(1) grad Д(у))(Д0) grad £a(y))dQ-
$ i/ll J
J (д(г) grad 4(z))(4(j) grad£,.j0))dQ-
S lvl
-T J (A(z) grad^(i))(^(>) grad ^(j))dQ +
—- i Kn
+T f (Д)(.) grad^(i))(4(/) grad 4(j))dQ =
1 Фактически это компоненты матрицы, обратной к матрице D, состав-
ленной из единиц и координат вершин треугольника; формула для вычисле-
ния D 1 приведена в разделе 5.3.1, см. (5.75).
702
15.Векторный МКЭ для решения задач электромагнетизма
(15.98)
—^0(/:),u(7)mi/(z),f)(j) + 5i/(i),v( j) ) j
где коэффициенты определяются соотношением
9ki = grad A grad = otf а{ + а£а?2,
mki — это компоненты матрицы массы узлового треугольного конечно-
го элемента первого порядка, определяемые соотношением (5.81) (при
этом подразумевается, что при вычислении в соотношении (5.81)
значение коэффициента было принято равным единице), a detD и
коэффициенты а’’ могут быть вычислены по формулам (5.74) и (5.75)
(с учётом (5.69)).
Локальные векторы треугольных edge-элементов можно вычислять
через матрицу массы аналогично тому, как это было сделано в разде-
ле 15.8.2 для прямоугольных edge-элементов, см. соотношение (15.94).
Для этого нужно получить значение Д касательной составляющей F
на ребре треугольника с локальным номером j . Проще всего это мож-
но сделать с помощью соотношения
/; = т Ь^г (15.99)
где (£>,?/,) и (i;s,y.s) — координаты вершин j -го ребра (г и s - их ло-
кальные номера), а вектор т в (15 99) — это единичный вектор, направ-
ленный вдоль j -го (в локальной нумерации) ребра треугольника Q(/l:
т = (яг-xs,yr(15.100)
- длина j -го ребра.
Обратим особое внимание на то, что направление вектора т долж-
но совпадать с направлением касательной составляющей базисной
вектор-функции г|^, ассоциированной с соответствующим ребром.
Таким образом, локальный вектор правой части треугольника
может быть вычислен с помощью соотношения (сравните с (15.94))
b-M'f, (15.101)
где М1 — это матрица массы при значении коэффициента , равном
единице, a f - вектор с компонентами fj, являющимися коэффициен-
тами разложения F по базисным вектор-функциям -гр, и определяе-
мыми, например, соотношением (15.99).
15.8.Конечноэлементные матрицы и векторы ...
703
Получим вклады в вектор правой части от естественного краевого
условия, заданного на ребре Гто 6 S2. При использовании базиса
(15.58)-(15.60) локальный вектор правой части для ребра Г„( будет
иметь размерность, равную единице. С учётом того, что значение каса-
тельной составляющей базисной вектор-функции ф, на Г,„ равно
1/7,п (Д, -длина Г„,, см. раздел 15.6.3), вклад от ребра Г,„ е S2 для
базиса (15.5 8)-( 15.60) будет иметь вид (сравните с (15.95))
ЬГ’" =^^(~п!/^'2-х1) + п.л:(у2-у1)), (15.102)
И Чп
где п.,. и пу — компоненты вектора п внешней (по отношению к рас-
чётной области) нормали к Гш, яу и y-f - координаты вершин ребра
Г.„г, заданных в таком порядке, что направление вектора
(х2 — , у2 — ?/i j совпадает с направлением касательной к Г,„ со-
ставляющей ф,.
Для базиса же (15.61)-(15.63) вклад Ьг"' будет, очевидно, опреде-
ляться соотношением (15.95).
15.8.4. ЛОКАЛЬНЫЕ МАТРИЦЫ И ВЕКТОРЫ
ЧЕТЫРЁХУГОЛЬНЫХ EDGE-ЭЛЕМЕНТОВ
Локальные матрицы и векторы четырёхугольных edge-элементов
будем вычислять с использованием шаблонного элемента
= [— 1,1] х [— 1,1]. Напомним, что локальные базисные вектор-
функции фг произвольного четырёхугольника П7„ мы определили
через базисные вектор-функции ф>, шаблонного элемента с помощью
соотношения
Фг (я, у) = J’1 (А (я, у)>Т] у)) Фг (6, у), Л (т, у)), (1 5.1 03)
где
дх
дх
5 т]
ду
ду
(15.104)
— это функциональная матрица отображения, переводящего шаблон-
ный элемент Q7 в четырёхугольник П,„ . Отображение Q7 в Q,„ мо-
жет определяться, например, соотношениями (15.69) для четырёх-
угольника с прямыми сторонами или соотношениями (15.78) (см. так-
же (5.133)) для криволинейного четырёхугольника.
704 15.Векторный МКЭ для решения задач электромагнетизма
Сначала получим выражения для вычисления компонент локальной
матрицы массы М элемента Q7ZJ.
Будем считать, что на Qnt коэффициент принимает значение
5 = const. Для вычисления значения интеграла по Qm воспользуемся
заменой переменных (15.69):
М, — f'уФ, ‘ Ф/^7 = 7
ц,
<,lE
Компоненты матрицы J1 могут быть достаточно просто получены
через компоненты матрицы J :
J1
h‘2
-J-21
12
Убедиться в том. что
ду
ду
дг\ dt,
дх
дх
, dr] <9^
(15.105)
матрица (15 105) действительно является об-
ратной к матрице J , можно простым умножением её на J
гг т дх ду ди Qr.
того, что якобиан J — ~ ~ ):
dt, от] dt, дх]
ду&и_ду&а
<Эт] dt, dt, ch]
(с учётом
ду dy
<Эт] dt,
дх ду
dt, dt,
lLl djL
G?T] ch]
векторного четырёхугольника первого порядка компо-
_ CLx'd]L>
ch] dt, dt, ch]
. дт] dt, ,
Тогда для
ненты матрицы массы можно вычислить по формулам
-<Л2—,<А1 —
7 7 1-Ч
-Л2 2 )
/1 с
= 1
п
1
0
1
о
1 о
0 1
-1 _1 «Л ч
.2 1 ~^2'
’ 4
и т.д.
В принципе, интегралы в полученных выражениях для Мч можно
посчитать и аналитически. Однако кроме того, что в этом случае необ-
ходимо выполнить огромный объём аналитических преобразований
(при этом для отображений (15.69) и (15.78) эти аналитические преобра-
зования будут разными), в результате будут получены очень громоздкие
аналитические выражения, которые не только потребуют большого ко-
15.8.Конечноэлементные матрицы и векторы ...
705
личества операций для вычисления каждой компоненты матрицы массы,
но и могут оказаться вычислительно довольно неустойчивыми для че-
тырёхугольников определённой конфигурации (например, для четырёх-
угольников, две противоположные стороны которых почти параллельны
друг другу). Поэтому обычно значения компонент матрицы М четы-
рёхугольника вычисляют с помощью численного интегрирования. Кро-
ме того, при использовании численного интегрирования процедура вы-
числения компонент локальных матриц практически не усложняется и
при включении в базис функций высоких порядков
Численные значения интегралов по = [—1,1]х[—1,1] можно по-
лучить, иапример, с помощью квадратурных формул Гаусса. Для схе-
мы с девятью точками (три по каждой координате) формула численно-
го интегрирования произвольной функции т]) по имеет вид
(сравните с соотношениями (5.120)—(5.122) для шаблонного элемента
= [0,1]х[0,1]):
11 3 3
f Г/(Ы^1~ЕЁ>т№-г1). (15.Ю6)
к=11=1
где
i1==0, t2 =0.77459666924148337, t3=-t2i (15.107)
Ti=f, Т2=т3 = |. (15.108)
Теперь получим выражения для вычисления компонент локальной
матрицы жёсткости G четырёхугольного элемента Q„t. Для этого
воспользуемся тем, что значения вектор-функций го1“фг (в координа-
тах {т, у}) в любой точке ^хр,ур^ четырёхугольника Q,n совпадают со
значением -уго!ф, (в координатах {6,, г|} ) в точке (Ду,,т]р) шаблонно-
го элемента О.1 , являющейся прообразом точки (при отобра-
жении Q7 в О,ь). Доказательство этого факта будет приведено чуть
ниже при рассмотрении векторных шестигранных элементов.
Тогда при р, = ц — const на Qm
и
1 1
-- rot *ф, rot -ф = •= J J -j rot ф, -j rot ф, | J\ d^dv\ —
Л и-1-1
1 1
rot ф, rot d£dv\. (15.109)
706
15.Векторный МКЭ для решения задач электромагнетизма
Введём матрицу R с компонентами R,.j = rotip, rot^. Поскольку
rot — const на Q' для всех базисных вектор-функций первого по-
рядка (см. соотношения (15.48)), все компоненты матрицы R не зави-
сят от переменных £ и т]:
-1 -1 1'
1 1 -1
1 1 -1
-1 -1 1
/
В результате мы получаем очень простые выражения для вычисле-
ния матрицы жёсткости векторного четырёхугольника первого по-
рядка:
1 1
6 =
1—1—1 f
4r = 4 -1 1 1 -1
|1 4|1 —1 1 1 -1
1-1-1 1
/
где значение
1 1
-1-1I
может быть получено с помощью численного интегрирования (напри-
мер, по формулам (15.106)—(15.108) при f (£,,т]) = ?—~—гт).
И л)|
Для элементов высоких порядков компоненты матрицы R уже бу-
дут зависеть от £ и т] и поэтому при вычислении всех тех компонент
Gj.j матрицы жёсткости, для которых хотя бы одна из вектор-функций
ф или ip7 является вектор-функцией порядка, выше первого, имеет
смысл использовать численное интегрирование. Формулы, опреде-
ляющие базисные вектор-функции иерархического типа для шаблон-
ного элемента высокого порядка, были приведены нами в разде-
ле 15.6.2 (см. соотношения (15.48)-( 15.50)).
Компоненты локального вектора правой части четырёхугольного
элемента можно вычислять через его матрицу массы М1 (М1 - это
матрица массы при = 1) аналогично тому, как мы делали это для
прямоугольных и треугольных элементов (см., например, соотношение
(15.101)). Для этого вектор-функцию F нужно также заменить её при-
ближением в виде линейной комбинации локальных базисных вектор-
15.8.Конечноэлементные матрицы и векторы ...
707
функций четырёхугольника Qm. Коэффициенты J этой линейной
комбинации (являющиеся компонентами вектора f из (15.101)) для
векторного четырёхугольника первого порядка могут быть получены
по тем же формулам (15.99)-( 15.100), что и для векторного треуголь-
ника первого порядка.
При использовании элементов высоких порядков компоненты ло-
кального вектора правой части можно вычислять, выполняя численное
интегрирование по £1Е скалярного произведения вектор-функции
F (z (£>, Т|), г/(£,, т])) на J 1фг (£,, т)) (естественно, с домножением на мо-
дуль якобиана |7|), т.е. вычислять
bi = /г(.г'(^т1),?у(^1з))(г](рД^т]))|7|^б/т], (15.110)
используя соотношения (15.106)-(15.108), в которых в качестве /(6,, т])
берётся подынтегральное выражение из (15.110).
Особо следует отметить, что для тех составляющих вектор-
функции F, которые определяются значениями решения па предыду-
щих временных слоях (А^1, А4^2 и АЛ3, см. соотношения (15.4) и
(15.6)), вклады в локальный вектор правой части должны вычисляться
только через матрицу массы1. Так, вклад Ь< 1 в локальный вектор b от
слагаемого rfjA^1 (где - некоторый коэффициент, зависящий от
значений коэффициентов а и е на и схемы аппроксимации по
времени2) должен быть вычислен в виде
1 Вообще говоря, это касается не только четырёхугольных конечных эле-
ментов, но и всех рассмотренных нами ранее. Мы не делали на этом акцента
при обсуждении векторных прямоугольников и треугольников лишь потому,
что рассматривали там способ генерации вектора b именно через матрицу
массы. Если же для учёта вкладов в вектор b правой части конечноэлемент-
ной СЛАУ от той составляющей правой части F уравнения (15.2), которая
определяется сторонними токами (т.е. JC1 из (15.1)), применяется численное
интегрирование, то для учёта вкладов от тех составляющих F, которые опре-
деляются значениями решения на предыдущих временных слоях (т.е. А' 1,
А^2 и А^3) следует использовать рассматриваемый здесь подход.
2 Например, для рассмотренной в разделе 15.1 трёхслойной схемы коэф-
о(^- t.j_21 -h 2е
фициент dy определяется формулой dx— -------у---------г-, см. (15.4). При
\j~ Л-2)
этом мы считаем, что о и е являются константами на конечном элементе
. В противном случае имеет смысл ввести две локальные матрицы массы,
в каждую из которых входит свой коэффициент ( о или е ).
708
15.Векторный МКЭ для решения задач электромагнетизма
Ь^* 1 = ^М1^1,
где q1-1 - локальный вектор решения с предыдущего временного слоя.
Аналогично учитывается слагаемое Д?А<2 (и для четырёх-
слойной схемы по времени):
Ь^2 = с^М1^2 , Ь^3 = ДД1^3.
Таким образом, локальный вектор b генерируется в виде
b = b^J + b'2 + b^3 + bjCT = М1 (^q^1 + d2q^2 + + ЬдСТ ,
г JCT
где компоненты вектора b вычисляются с использованием числен-
ного интегрирования скалярного произведения вектора
JCI г fe л) > ?/fe л)) на вектор J (здесь JCT - вектор сторон-
них токов, см. (15.4) и (15.6))
^/СТ = f Jvr П),7/т1))’ (^л))И^Т] (15.111)
(не путайте вектор сторонних токов JCT из правой части дифференци-
ального уравнения (15.1) с функциональной матрицей J отображения
квадрата f/ в четырёхугольник Q,n ).
И в заключение рассмотрим, как можно вычислить вклады в вектор
правой части конечноэлементной СЛАУ от естественного краевого
условия. Вклад в вектор правой части (см. (15.88)) от ребра Г„‘ 6 S2
определяется формулой1
Для базисных вектор-функций первого порядка вклад от ребра Г,„
идёт только в одну компоненту вектора b (поскольку только одна гло-
бальная базисная вектор-функция имеет ненулевую касательную на
этом ребре), и поэтому локальный вектор правой части имеет размер-
ность, равную единице. Единственная компонента этого локального
вектора (при 0 = const на Г,„ ) отличается от &г"' для базиса (15.58)—
1 Ещё раз обратим внимание на то, что для естественного краевого усло-
1 [дА ал J ,
вия, заданного в виде — ------ = 0 , вклад в вектор правой части от
|t дх ду I
ребра Г7„ будет определяться формулой 6£г"‘ = J 0'т 'ф/AS1 .
Г
Х 7»
15.8.Конечноэлементные матрицы и векторы ...
709
(15.60) векторных треугольников только сомножителем 2 (сравните с
(15.95))
6"Г'“ = (~ПУ ) + П., (у-2 - )) ,
к Чп
поскольку ассоциированная с ребром Г„( базисная вектор-функция ф
(первого порядка) была определена нами так, что на Гт у неё каса-
тельная составляющая равна (по-прежнему 1т — длина ребра Г,п,
п.,. и - компоненты вектора й внешней нормали к Гт, Xj и у., -
координаты вершин ребра Гш, заданных в таком порядке, что направ-
ление вектора (.г2 — — 3/i)T совпадает с направлением касатель-
ной составляющей вектор-функции ф./;.
При использовании базисов высоких порядков каждом на ребре Г.,„
ненулевые касательные составляющие имеют р вектор-функций ( р -
порядок базиса), и поэтому размерность локального вектора Ъ1"' рав-
на р. Будем считать, что на Г„, введена следующая локальная нуме-
рация глобальных базисных вектор-функций1: локальный номер век-
тор-функции (имеющей на Г„, ненулевую касательную) равен р. Та-
ким образом, при использовании иерархического базиса второго по-
рядка локальный вектор ребра Г„( будет иметь две компоненты, но
при этом вторая компонента (при © = const на Г„г) будет равна нулю.
Для иерархического базиса третьего порядка
и т.д.
Обратим внимание на ситуацию, когда конечноэлементная сетка
содержит криволинейные четырёхугольники и граница S2 аппрокси-
мируется криволинейными рёбрами. В этом случае при вычислении
интегралов по Гш необходимо учитывать, что касательные состав-
1 Мы будем считать, что базис высокого порядка построен по иерархиче-
скому принципу, и напомним, что во введённых нами иерархических базисах
вектор-функция первого порядка имеет постоянную касательную на ребре, с
которым она ассоциирована. В базис второго порядка добавляются вектор-
функции, которые имеют касательную составляющую, линейно изменяющую-
ся вдоль «своего» ребра (от значения — гД,£ до значения 2/Zm ). Добавляемые
(к базису второго порядка) вектор-функции третьего порядка имеют каса-
тельную составляющую в виде квадратичного полинома, равного нулю в
вершинах «своего» ребра и значению 2//т в его центре, и т.д.
710
15.Векторный МКЭ для решения задач электромагнетизма
ляющие базисных вектор-функций гф на Г„, могут уже не быть поли-
номами, как их прообразы ф7 на соответствующих рёбрах-прообразах
Поэтому при вычислении интегралов по криволинейным рёбрам Г,,,
/1 д
— Gt
г и
1 т
вычислять как
7 И(ж(-1,п),у(-1.ч)) t W=|_rfj ,
если ребро Г,„ получено отображением левой стороны шаблонного
элемента (при этом мы учли, что внешняя нормаль к этому ребру
направлена «влево», и поэтому вектор т направлен «вниз», т.е. его
прообраз w имеет отрицательную ^-компоненту), или
если ребро Г,„ получено отображением нижней стороны Q7 (и анало-
гично для правой и верхней сторон QF), и т.д. При этом значение
строго положительного параметра d, определяющего вектор w,
должно быть получено из условия, что длина вектора J 1 w равна еди-
нице (в каждой точке ребра, по которому ведётся интегрирование).
15.9. ПРИМЕР СБОРКИ ГЛОБАЛЬНОЙ МАТРИЦЫ И ВЕКТОРА ПРАВОЙ
ЧАСТИ СЛАУ И УЧЁТА КРАЕВЫХ УСЛОВИЙ В ВЕКТОРНОМ МКЭ
Рассмотрим следующую тестовую задачу. Зададим в расчётной
области Q = [1,6] х [1,6] конечноэлементную сетку из четырёх конеч-
ных элементов и пронумеруем её рёбра и соответствующие им базис-
ные вектор-функции так, как это показано на рис. 158.
Пусть в уравнении (15.2) коэффициенты р. и равны единице, а
правая часть определена как F =
х — 6 и у — 1 заданы главные краевые условия
+ У
0
При этом на границах х — 1,
A|I=1=o, AU=o, 4|s=1=2,
(15.112)
15.9.Пример сборки глобальной матрицы и вектора ...
711
а на границе у = 6 - естественное краевое условие (в двумерном слу-
- _ дА„ дА
чае вместо rot А х п задаётся ------—, см. рассуждения на с. 693—
дх ду
695 и соотношение (15.83)):
'dA,f дА,
дх ду
= -1.
(15.113)
4-----
14-
У
6—
Рис. 158. Конечноэлементная сетка
и глобальная нумерация рёбер
для тестовой задачи
u—G
Обратим внимание на то, что в
главных краевых условиях вместо
векторов А х п заданы скаляры
Д = А • т, где т — единичный ка-
сательный к рассматриваемой гра-
нице вектор1. Такой способ задания
главных краевых условий является
наиболее удобным для ситуаций,
когда используются edge-элементы.
В этом случае главное краевое усло-
вие учитывается включением в ко-
нечноэлементную СЛАУ уравнения,
определяющего вес базисной век-
тор-функции чф, ассоциированной с
ребром Г С Д (на котором учитыва-
ется главное
значение Д
рассуждения
рассуждения
вые условия
ков'
Решением рассмотренной краевой задачи является вектор-функция
краевое условие), через
на этом ребре. Общие
на эту тему были приведены нами в разделе 15.4 (эти
дают представления о том, как учитывать главные крае-
и при использовании векторных базисов высоких поряд-
0
, в чём легко убедиться непосредственной подстановкой
этой вектор-функции в уравнение (15.2) (при р = 1, ^ = 1 и
) и в краевые условия (15.112), (15.113).
О
F =
Построим конечноэлемензную аппроксимацию рассмазриваемой
тестовой задачи с использованием базисных вектор-функции первого
порядка.
Локальные матрицы жёсткости G, массы М и локальный вектор
правой части b прямоугольного конечного элемента могут быть вы-
1 См. также с. 695, пояснения к формуле (15.84).
712
15.Векторный МКЭ для решения задач электромагнетизма
числены по формулам (15.91)-(15.94). Для конечного элемента они
имеют следующий вид:
3/2 -3/2 -1 1' 1 1 0 o' ' 0 '
Gqi = -3/2 3/2 1 -1 , MQl = 12 0 0 bJ>1 = 0
-1 1 2/3 -2/3 0 0 2 1 9 12
1 -1 -2/3 2/3 0 0 12 k J
После занесения этих локальных матриц GU1, 1 и вектора bQ1 в
глобальную матрицу С и глобальный вектор b получим:
<s/3 0 -1 1 0 1/3 0 0 0 0 0 0 ' 9'
0 0 0 0 0 0 0 0 0 0 0 0 0
-1 0 7/2 -1/2 0 1 0 0 0 0 0 0 0
1 0 -1/2 7/2 0 -1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
0 = 1/3 0 1 -1 0 8/3 0 0 0 0 0 0 , b = 12
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 2 0 l У
Вычислим локальные
матрицы и локальный вектор элемента 02 :
Занесём вклады от этого элемента в глобальную матрицу и вектор:
15.9.Пример сборки глобальной матрицы и вектора ...
713
’ 8/3 0 -1 1 0 У3 0 0 0 0 0 0 ' 9 '
0 4 0 -1 1 0 1/2 0 0 0 0 0 27/2
-1 0 7/2 -1/2 0 1 0 0 0 0 0 0 0
1 -1 -1/2 15/2 1/2 -1 1 0 0 0 0 0 0
0 1 0 1/2 4 0 -1 0 0 0 0 0 0
С - У3 0 1 -1 0 8/3 0 0 0 0 0 0 Ь = 12
0 1/2 0 1 -1 0 4 0 0 0 0 0 18
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
1
Вычислим локальные матрицы и локальный вектор правой части
элемента Q3 и занесём их в глобальную матрицу и вектор:
1 -1 -ji 1' '1 1 0 О' ' о'
0
1 1 1 -1 2 1 2 0 0
GU;1 MQ3 — bQ:l 34
1 1 1 -1 3 0 0 2 1 3
1 -1 -1 1 0 0 1 2 38
———
1 3 J
' 8/3 0 -1 1 0 У3 0 0 0 0 0 0 ' 9
0 4 0 -1 1 0 1/2 0 0 0 0 0 27/2
-1 0 7/2 -1/2 0 1 0 0 0 0 0 0 0
1 -1 -1/2 15/2 1/2 -1 1 0 0 0 0 0 0
0 1 0 1/2 4 0 1 0 0 0 0 0 0
С = У3 0 1 -1 0 15/3 0 -1 1 0 -1/3 0 ь = 70/3
0 1/2 0 1 -1 0 4 0 0 0 0 0 3 18
0 0 0 0 0 -1 0 7/3 -У3 0 1 0 0
0 0 0 0 0 1 0 -1/3 7/3 0 -1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 -У3 0 1 -1 0 7/3 0 38/3
0 0 0 0 0 0 0 0 0 0 0 0 0
Для последнего элемента Q4:
714
15 Векторный МКЭ для решения задач электромагнетизма
2/3 -2/3 -1 1' '2 1 0 О’ 'o'
G”4 = -2/3 2/3 1 -1 , мп-> = 12 0 0 bQ< 0
-1 1 3/2 —3/2 0 0 2 1 17
1 -1 -3/2 3/2 0 0 12 I > 19
3/3 0-110 1/3 0 0 0 0 0 0 ' 9 ’
0 4 0-11 0 1/2 0 0 0 0 0 27/2
-1 0 7/2 -1/2 0 1 0 0 0 0 0 0 0
1 -1 -1/2 15/2 1/2 -I 1 0 0 0 0 0 0
0 1 0 1/2 4 0-10 0 0 0 0 0
с = 1/3 0 1-10 15/3 0 -1 1 0 -1/3 0 b 70/3
0 1/2 0 1 -1 0 15/2 0 -1 1 0 — 1/2 35
0 0 0 0 0 -1 0 7/3 -1/3 0 1 0 0
0 0 0 0 0 1 -1 -1/3 15/3 1/3 -1 1 0
0 0 0 0 0 0 1 0 1/3 8/3 0 -1 0
0 0 0 0 0 -1/3 0 1 -1 0 7/3 0 38/3
1 0 0 0 0 0 0 -1/2 0 1 -1 0 7/2 19
Учтём естественное краевое условие (15.1 13), заданное на рёбрах с
номерами 11 и 12. Вклад от ребра с номером 11 равен 2 (см. (15.95),
р, = 1, 0 — — 1, пг = 0, // = 1, х2 — = 2, у2 — У1 — 0 ) и должен
быть добавлен к одиннадцатой компоненте вектора b От ребра с но-
мером 12 вклад в соответствующую (двенадцатую) компоненту равен
3. В результате глобальный вектор правой части консчноэлсментной
СЛАУ имеет вид:
1 / 27 70 44 \Т
Ь = 9, —, 0, 0, 0, —, 35, 0, 0, 0, —, 22 .
\ 2 3 3 /
Осталось учесть главные краевые условия (15.1 12), которые факти-
чески заданы на рёбрах с номерами 1,2. 3, 5, 8 и 10 Для этого вместо
строк с этими номерами1 запишем в конечноэлементную СЛАУ стро-
ки, фиксирующие значения весов базисных вектор-функций чф, ф2,
'ф3, чф , *ф8 и чр1(), которые и обеспечат выполнение главных крае-
вых условии
1 Фактически сгенерированные уравнения с номерами I, 2, 3, 5, 8 и 10 яв-
ляются фиктивными, поскольку они не могут быть получены из вариацион-
ной постановки, так как все пробные функции ф € Иц* должны иметь нуле-
вые касательные на Sj.
15.9.Пример сборки глобальной матрицы и вектора ...
715
1 0 0 0 0 0 0 0 0 0 0 0 1 г 2
0 1 0 0 0 0 0 0 0 0 0 0 2
0 0 1 0 0 0 0 0 0 0 0 0 0
1 -1 -1/2 15/2 1/2 -1 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0 0 0 0
с = 1/3 0 1 -1 D 15/3 0 -1 1 0 -1/3 0 ъ = 70/3
0 1/2 0 1 -1 D 15/2 0 -1 1 0 -1/2 35
0 0 0 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 1 -1 -1/3 15/3 1/3 -1 1 0
0 0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 -1/3 0 1 -1 0 7/3 0 44/3
0 к 0 0 0 0 0 -1/2 0 1 -1 0 7/2 22
Нетрудно убедиться, что решением СЛАУ Cq = = Ь является вектор
весов
Ч = (
2, 2. О, 0, 0, 5. 5, 0, 0, 0, 7, 7
+ У
О
рассмотренной
12
определяющий конечноэлементное решение Д ' — <7 Ч*, , полно-
/=1
стью совпадающее с точным решением А =
тестовой задачи.
Теперь покажем, как можно собрать матрицу конечноэлементной
СЛАУ без генерации фиктивных уравнении (соответствующих рёбрам
с главными краевыми условиями). Для этого перенумеруем рёбра (и
соответствующие им базисные вектор-функции) так, чтобы все рёбра,
принадлежащие поверхности S) (где заданы главные краевые усло-
вия), были пронумерованы последними (т.е. имели номера I > ?i()).
Очевидно, что в этом случае глобальная матрица конечноэлементной
СЛАУ может сразу собираться как матрица размера п() х д.() (в рас-
сматриваемом нами примере п{} = 6). При этом вклады в компоненты
Сп и bi с индексами ? > просто игнорируются, а вклады в компо-
ненты С с индексами i < д0 и j> п() либо игнорируются, сели со-
ответствующее ребро принадлежит границе с однородным главным
краевым условием, либо умножаются на число и вычитаются из
г-й компоненты вектора b (напомним, что для нормированных век-
716
15.Векторный МКЭ для решения задач электромагнетизма
тор-функций первого порядка и9 — значение касательной составляю-
щей решения в середине ребра, подробнее см. с. 696).
Таким образом, процесс сборки без строк, соответствующих базис-
ным вектор-функциям с номерами i > 71^ , выглядит следующим обра-
зом. На рис. 159 показана сетка с перенумерованными рёбрами (рёбра,
принадлежащие , пронумерованы последними). После занесения
локальных матриц и вектора элемента Qj (они приведены на с. 712)
глобальные матрица и вектор примут вид
7/2 -1 -1 8/3 0 0 0 0 0 0 0 0
С = 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
' —2
34/3
О
О
О
О
к
Рис. 159. Конечноэлементная сегкя
с перенумерованными рёбрами
Здесь, очевидно, в глобальную
матрицу и вектор не заносились
строки с локальными номерами 1 и 3
(им соответствуют глобальные но-
мера 9 и 7), а компоненты G23 и
ТИ2з умножались на и9 = 2 (см.
(15.112)) и вычитались из компонен-
ты Ъ} вектора правой части; компо-
ненты G43 и Л/4з также умножались
на и9 — 2 и вычитались из компо-
ненты Ь-2 вектора правой части.
Компоненты же G21, М21 и G41,
М41 соответствуют ребру с гло-
бальным номером 9, которое при-
надлежит границе с однородным
главным краевым условием, и поэтому просто игнорируются.
В результате занесения локальных матриц и вектора элемента П2
(они приведены на с. 712) получаем (здесь не заносятся строки с ло-
кальными номерами 2 и 3 и в правую часть переносятся1 компоненты
^13’ ^13 и ^43’ -^43
1 Перенос осуществляется после умножения эш\ компонент на соответст-
вующее и4 и с обратным знаком (на этом ребре и!1 тоже равно двум, см.
(15.112)).
15.9.Пример сборки глобальной матрицы и вектора ...
717
'15/2 -1 1 0 0 (р о'
-1 8/3 0 0 0 0 34/3
1 0 4 0 0 0 17
с = 0 0 0 0 0 0 , Ь = 0
0 0 0 и 0 0 0
0 к 0 0 0 0 0 0 1 7
После обработки элемента Q3 (его локальные матрицы и вектор
приведены нас. 713)
' 15/2 -1 -1 15/3 1 0 0 1 0 -1/3 о' 0 ' о' 68/3
1 0 0 1 4 0 0 7/3 0 -1 0 0 , ь — 17 0
0 0 -1/3 0 0 0 -1 D 7/3 и 0 0 38/3 0 к
После обработки (его локальные матрицы и вектор приведены
на с. 714)
' 15/2 -1 1 0 0 0 о'
1 15/3 0 1 -1/3 0 68/3
1 0 15/2 -1 0 -1/2 , ь -; 34
0 1 -1 15/3 - 1 1 0
0 -1/3 0 -1 7/3 0 38/3
0 0 -1/2 1 0 72 19 к /
Никаких изменений в учёте второго краевого условия в этом слу-
чае, очевидно, нет (следует учесть только изменение глобальной нуме-
рации рёбер), и после учёта второго краевого условия
Ь — ( О, 74/3, 34,
О, 44/3, 22 )Т.
При реализации такого метода сборки1, как правило, перед генера-
цией матрицы и вектора правой части формируется вектор весов дли-
ны пI в котором значения первых ?г() компонент несущественны (мо-
гут задаваться нулевыми), а последние п — т?0 задаются равными зна-
чениям и”. Так, для элементов первого порядка в компоненты q,
(/' > п(}) нужно занести значения и/ касательных составляющих ре-
1 Естественно, если в задаче есть неоднородные i чавные краевые условия.
718
15.Векторный МКЭ для решения задач электромагнетизма
шения на соответствующих рёбрах (эти веса мы обозначали также и
как qf- ). Для элементов же высоких порядков соответствующие значе-
ния весов qt (2 > п{] ) могут быть найдены с использованием методов,
которые были рассмотрены нами в разделе 15.8.1 (см. сноску на с. 696)
и в разделе 15.4. Хранящимися в векторе весов q значениями q!-
(i> п{} ) очень удобно пользоваться при генерации СЛАУ размерности
т?.() для обработки компонент локальных матриц, у которых номера
столбцов соответствуют глобальным номерам, большим 7?.() (т.е. для
умножения этих компонент на q!tl при переносе их в правую часть
СЛАУ).
Отметим, что и для вычисления значения приближённого решения
11
А" = Е д,/ф, в отдельных гонках расчётной области (принадлежащим
г=1
конечным элементам, примыкающим к границам с главным краевым
условием) нам также необходимы эти значения q![ весов qL (при
г > п()).
15.10. О РАНГЕ ГЛОБАЛЬНОЙ МАТРИЦЫ ЖЁСТКОСТИ В ВЕКТОРНОМ
МКЭ И СВЯЗАННЫХ С ЭТИМ ТРУДНОСТЯХ РЕШЕНИЯ
СТАЦИОНАРНЫХ И НЕКОТОРЫХ НЕСТАЦИОНАРНЫХ
ЭЛЕКТРОМАГНИТНЫХ ЗАДАЧ
Обратим внимание па одно важное свойство глобальной матри-
цы жёсткости в векторном МКЭ, которое заключается в том, что ранг
этой матрицы может быть намного меньше её размера’.
Рассмотрим следующую тестовую задачу. В уравнении (15.2) по-
ложим коэффициент р равным единице, а коэффициент - равным
нулю. Расчётную область и сетку в ней возьмём из примера, рассмот-
ренного в разделе 15.9 (они изображены на рис. 159). При этом будем
считать, что на всех границах этой расчётной области заданы главные
(например, однородные) краевые условия, и воспользуемся технологи-
ей сборки глобальной матрицы, при которой строки, соответствующие
рёбрам с главными краевыми условиями, не включаются в конечно-
элементную СЛАУ.
Тогда глобальная матрица жёсткости будет иметь вид
1 Напомним, что в узловом МКЭ ранг матрицы жёсткости мог быть только
на единицу меньше её размера, и достаточно было задать главное краевое
условие хотя бы на одном участке границы, чтобы матрица жёсткости пере-
стала быть вырожденной.
15.10.0 ранге глобальной матрицы жёсткости в векторном МКЭ ... 719
5/2 -11 0 '
-1 5/3 0 1
1 0 5/2 -1
0 1-1 5/3
(15.1 14)
Очевидно, что если умножить эту матрицу на ненулевой вектор
q = (2, 3, -2, -з)Т,
(15.115)
то мы получим нулевой вектор. Таким образом (в отличие от матрицы
жёсткости для узловых элементов), матрица жёсткости для векторных
элементов является вырожденной даже после учёта главных краевых
условий. Этого, в принципе, следовало ожидать, поскольку при ,
равном нулю, уравнению (15.2) даже в случае задания главных крае-
вых условий на всех границах расчётной области удовлетворяет мно-
жество решений. Доказать это чрезвычайно просто.
Пусть, например, уравнению (15.2) (при — 0) и некоторым крае-
вым условиям удовлетворяет вектор А(). Тогда этой краевой задаче
удовлетворяет и любой вектор вида А() + grad I , где V — любая ска-
лярная функция, равная константе на границе (где заданы главные
краевые условия), т.е. для V должно выполняться единственное усло-
вие: (grad V х п)|л, = 0 .
Читатель может легко убедиться, что приведённый нами чуть выше
вектор q (см. (15.115)), умножение на который матрицы жёсткости G
(см. (15.114)) даст нулевой вектор, определяет вектор-функцию
4
Q Ф/ > равную grad У, при V = 6ф(.г*, у), где ф{а;. у) — узловая
билинейная функция, ассоциированная с «центральным» узлом
(имеющим координаты х — 3 , у — 4 ).
Вырожденность глобальной матрицы жёсткости1 в векторном МКЭ
создаёт серьёзные трудности (связанные с необходимостью примене-
ния специальных методов решения СЛАУ с матрицами низкого ранга)
при его использовании не только для решения стационарных задач (в
которых = 0 во всей расчётной области), но и при решении многих
нестационарных электромагнитных задач (включая гармонические), в
которых токи смещения несущественны и расчётная ооласть содержит
непроводящие подобласти (т.е. подобласти с нулевым значением в них
коэффициента удельной электрической проводимости о).
1 Да ещё такая, что ранг этой матрицы может быть существенно меньше её
размера.
720 15.Векторный МКЭ для решения задач электромагнетизма
Поэтому при решении стационарных задач (задач магнитостатики)
в подавляющем большинстве случаев гораздо более эффективными
оказываются постановки, основанные на использовании скалярных
потенциалов магнитного поля (особенно постановка с использованием
полного и неполного скалярного потенциалов, которая будет рассмот-
рена нами в шестнадцатом разделе). Исключение здесь составляют
лишь такие стационарные задачи, в которых ток течёт внутри ферро-
магнитных материалов (с коэффициентом магнитной проницаемости
ц, отличным от коэффициента магнитной проницаемости вакуума р,()
да ещё и зависящим от индукции магнитного поля) — в таких задачах
использование скалярных потенциалов имеет свои довольно сущест-
венные трудности.
Для решения же нестационарных электромагнитных задач при не-
существенных токах смещения и при наличии в расчётной области
непроводящих подобластей (где коэффициент о равен нулю) можно
использовать специальные постановки, в которых магнитное поле в
непроводящих подобластях описывается скалярным магнитным по-
тенциалом, а в проводящих — вектор-потенциалом (см. раздел 1.3.6).
Такие постановки во многих случаях позволяют не только существен-
но сократить размерность конечноэлементной СЛАУ, но и устранить
её вырожденность. Методы построения конечноэлементных аппрокси-
маций, основанные на постановках с совместным использованием ска-
лярного и векторного магнитных потенциалов, будут рассмотрены
нами чуть ниже, в разделе 15.13.
15.11. БАЗИСНЫЕ ВЕКТОР-ФУНКЦИИ ИЗ ПРОСТРАНСТВА Hrot
НА ТРЁХМЕРНЫХ СЕТКАХ
Общие принципы построения базисных вектор-функций из про-
странства H,ot на трёхмерных сетках практически ничем не отличают-
ся от принципов построения базисных вектор-функций на двумерных
сетках (см. раздел 15.6.1). Здесь мы рассмотрим, как эти базисные
функции строятся на наиболее часто употребляемых типах трёхмерных
конечных элементов (при этом мы будем существенным образом опи-
раться на сведения, представленные в разделе 15.6).
15.11.1. БАЗИСНЫЕ ВЕКТОР-ФУНКЦИИ НА ПАРАЛЛЕЛЕПИПЕДЕ
Базисные вектор-функции из пространства Hrot на параллелепи-
педах строятся наиболее просто (по сравнению с трёхмерными конеч-
ными элементами других типов), и основные принципы построения
этих вектор-функции практически ничем не отличаются от принципов
построения базисных вектор-функций на прямоугольниках (см. раз-
дел 15.6.2).
Рассмотрим параллелепипед Q,.s.p = [.г,.,.тг+1 ] х [t/s., ?/s.+1 j х , zp+l j.
Определим на нём двенадцать (ассоциированных с рёбрами) базисных
вектор-функций таких, что каждая из них имеет направление строго
вдоль одной оси координат, параллельной ребру, с которым она ассо-
15.11.Базисные вектор-функции из пространства ...
721
циирована. При этом модуль каждой базисной вектор-функции внутри
Q является билинейной функцией двух других координат, направ-
лению осей которых она перпендикулярна.
Например, базисная вектор-функция, ассоциированная с ребром
= уч1 z = , имеет вид
-Ф1 =
Уч+[ У ^>+1
Ч hz
о
о
где h = уя+1 —ys, fiz = ур+1 — ур. Очевидно, эта базисная вектор-
функция имеет ненулевые касательные составляющие только на двух
гранях Q - это грани у = уя и z — zp. При этом на каждой из эт их
граней она изменяется линейно по нефиксированной (и не совпадаю-
щей с х ) координате от значения 1 на ребре, с которым она ассоции-
рована, до нуля на противоположном ребре. Тем самым обеспечивает-
ся непрерывная сшивка касательных этих базисных вектор-функций в
параллелепипеидальной сетке (и принадлежность полученных функ-
ций пространству Hrut).
Параллеленипеидальный векторный элемент, кроме того, что он
имеет определённую самостоятельную ценность для решения электро-
магнитных задач в областях с границами, параллельными координат-
ным осям, является основой для построения векторного шестигранного
элемента (в том числе и с искривлёнными гранями), наиболее эффек-
тивного по точности и возможностям учёта сложной геометрии рас-
чётной области. Поэтому то, как строятся базисные вектор-функции
высоких порядков, мы покажем па примере шаблонного элемента-
кубика 0е = [— 1,1]х[— 1,1]х[—1,1], который является базовым1 при
построении векторных базисных функций на шестигранных элементах.
Заметим, что в векторном МКЭ, как и в узловом (см. раздел 12.4), ие-
рархические базисы по сравнению с лагранжевыми базисами того же
порядка гораздо более удобны при использовании у?-технологии2
уточнения конечноэлементного решения, могут дава.ь меньшую за-
полненность конечноэлементной СЛАУ и более быструю сходимость
итерационных методов её решения.
1 Мы по-прежнему будем рассматривать базисы высоких порядков, по-
строенные по иерархическому принципу, и только поэтому в качестве шаб-
лонного элемента мы берём не единичный кубик QE = [0,1] х [□, 1 ] х [0,1], а
более удобный для построения иерархических базисов шаблонный элемент
= [—1,1] х [—1,1] х [- 1,1].
2 И некоторых вариантов h - р -технологии.
722
15.Векторный МКЭ для решения задач электромагнетизма
Введём одномерные скалярные иерархические функции:
1-й . /пч 1 + й
Ф- (й) = , Ф+ (й) = ——,
фр (0) = -0/?~2 (1 — О2), р>2.
(15.116)
Базис первого порядка на содержит, как уже говорилось, 12
вектор-функций, которые через одномерные функции ф_ (Ф) и ф+ ($)
могут быть записаны в виде
Ф-Сп) Ф-К) Ф+(п)Ф_К) ф_(т])ф+К)
£1 = 0 > £-2 = 0 > £з = о
0 J 0 0
ф+Юф+кУ 0 0
£4 = 0 , £5 = Ф-К) Ф-К) , £с = Ф+К)Ф-К) ,
0 0 k > 0
0 0 0
£? = Ф-ЮФ+К) > £8 = Ф+КЖК) > £9 = о
0 0 Ф-К) ф_(т])
0 0 ( \ 0
£ю — 0 > £п = 0 > £12 — 0
Ф+К)Ф-К) ) Ф_(0Ф+Ы Ф+К) Ф+KD
и все эти вектор-функции ассоциированы с рёбрами конечного элемен-
та.
Для построения иерархического базиса второго порядка к уже
имеющимся двенадцати вектор-функциям первого порядка добавляет-
ся 12 вектор-функций, ассоциированных с рёбрами, 24 вектор-
функции, ассоциированные с гранями, и 6 вектор-функций, ассоцииро-
ванных с самим конечным элементом.
Добавляемые вектор-функции, ассоциированные с рёбрами, полу-
чаются следующим образом. Каждая вектор-функция первого порядка
умножается на координату, вдоль которой она направлена
£13 = ££1>
£17 = W.5 >
£•21 — С£э,
£14 = ^.£-2 ’
£18 = WG >
£22 = С£к),
£15 =
£19 = W? >
£•23 = С£и,
£ic — ^£4>
£20 = л£8=
£•24. = С£12
15.11.Базисные вектор-функции из пространства ...
723
Очевидно, каждая из этих вектор-функций имеет ненулевые каса-
тельные составляющие только на двух гранях, смежных по ребру, с
которым эта вектор-функция ассоциирована.
Ассоциированные с гранями вектор-функции второго порядка име-
ют следующий вид. С гранью £ = — 1 ассоциируются вектор-функции
О
О
^ИФ-Д)
4=25
О
ФгЮФДО
О
4=26= W25 >
4=27 —
4=28— ^4=27
С гранью = 1 ассоциируются
О
SP29 = ФгЮФ+Й.) > Фзо= П^29>
о
С гранью т] = — 1 ассоциируются
4=31 =
О
О
ФгС'л) Ф+(0
> 4=Ъ— СФ31 •
ФгШ-Сп)
О
О
С гранью т] = 1 ассоциируются
ФгЮФ+Сп)
О
О
С гранью С, — — 1 ассоциируются
Ф2(л)Ф-Ю
о
о
С гранью С, = 1 ассоциируются
Ф2('Г1)Ф+Ю
О
о
4=зз —
4=37 —
> Фзз>
> Фз8~ ^4=37 >
Ч=>41 =
, ^42=^41>
4=35 =
4=39 —
О
О
Фг(У Ф-Сп)
О
О
ф2(ОФ+('г1)>
, Фзб= СФ>35 •
> 4=40“ С/Рзо •
О
Ф43 = ФгСОФ-Ю , ^44= 'ПР43 •
о
4=45 =
о
Ф47 = Фэ(О Ф+(0 ’ 4=48= 414=47
О
, <Р4С= ^4£
Очевидно, что все эти вектор-функции ф>25 4=48 имеют ненулевые
касательные только на одной грани, и поэтому соответствующие гло-
бальные вектор-функции получаются сшивкой только двух локальных
вектор-функций
И, наконец, вектор-функции второго порядка, ассоциированные с
самим элементом, имеют вид
724
15.Векторный МКЭ для решения задач электромагнетизма
Ф49 —
Ф2(л) Ф2(С)
О
О
$50= ’
Ф51
О
Ф2(ЮФ2(С)
О
Фм= Фзз<
Фб2- Ф.51Л,
Ф2(^)Ф2(л)]
Все эти вектор-функции имеют пулевые касательные на всех гранях
конечного элемента, и поэтому каждая из них фактически является
прототипом глобальной вектор-фу нкцией, отличной от нуля внутри
только одного конечного элемента.
Рассмотрим, как может быть построен иерархический базис />-го
порядка путём добавления недостающих вектор-функций в иерархиче-
ский базис (р — 1)-го порядка. Пусть иерархический базис (р — 1)-го
порядка содержит к вектор-функций1. Покажем, что для построения
базиса р-го порядка к базису (р — 1)-го порядка должны быть добав-
лены 12 вектор-функций, ассоциированных с рёбрами, 24 (/) — 1) век-
гор-функций, ассоциированных с гранями, и 9р2—21р + 12 вектор-
функций, ассоциированных с самим элементом.
Для удобства записи базисных вектор-функций кроме одномерных
функций ф_(-0), ф+(0) и фр('О) для р>'2 (см. (15.116)) введём ещё
две одномерные функции
ф„(0) = 1, Ф1 (о) = о.
Добавляемые к базису (р —1)-го порядка вектор-функции, ассо-
циированные с рёбрами, строятся аналогично тому, как это было сде-
лано для вектор-функций второго порядка. Каждая вектор-функция
первого порядка умножается на функцию ф/?_1(0), где 0 - координа-
та, вдоль которой направлено соответствующее этой вектор-функции
ребро, т.е.
Фл+1 = Фр-1(0Ф1 , ФА.-+12 = Фр-1(0 Ф12 •
Добавляемые к базису (у? — 1) -го порядка вектор-функции, ассо-
циированные с гранями, строятся по следующему принципу. Па каж-
дой грани строятся вектор-функции двух направлений, совпадающих с
направлениями рёбер этой грани (по 2(р — I) вектор-функции каждого
направления). У этих вектор функций, как и у всех остальных, только
одна ненулевая компонента Эта компонента является произведением
1 Чуть позже мы увидим, что к = Зр2 (р — 1).
15.11.Базисные вектор-функции из пространства ...
725
одномерных функций координат Е,, т] или Q, одна из которых являет-
ся функцией ф_(-0) или ф+("0) (где 0 - то из направлений т| или
, которое перпендикулярно рассматриваемой грани, а индекс «—»
или « + » у ф определяет положение грани, т.е. « —» - это грань
О = — 1. а « + » - грань 0 = 1).
Остальные два сомножителя являются одномерными иерархиче-
скими функциями двух оставшихся координат. При этом для каждого
из двух направлений (касательных к грани и определяемых оставши-
мися координатами) оазисные вектор-функции являются функциями
двух типов
В вектор-функциях первого типа вторая одномерная функция-
сомножитель координаты, вдоль которой направлена вектор-функция,
является иерархическим полиномом степени р — 1, а третья одномер-
ная функция-со множитель - полиномом от оставшейся третьей коор-
динаты степени от 2 до р — 1 Например, для грани £ = — 1 это век-
тор-функции
ФА+12 + /-1
О
Ф_(У Фр-чОМЮ
о
i = 2... р — 1
Фа + г2+г-2+»:-1
О
Ф_(ЮФр-1(С)ФХ'п)>
i = 2... р — 1,
из которых, очевидно, первые р — 2 вектор-функции направлены
вдоль координаты ц, а последние р — 2 вектор-функции — вдоль ко-
ординаты .
В вектор-функциях второго пипа вторая одномерная функция-
сомножитель координаты, перпендикулярно оси которой направлена
рассматриваемая вектор-функция1, является иерархическим полино-
мом степени р, а третья одномерная функция-сомножитель - полино-
мом от оставшейся третьей координаты степени от 0 до р — 1, из кото-
рых неиерархическими являются только полиномы нулевой и первой
степени. Так, для грани £ = — 1 это вектор-функции
Т)А+12+2(р-2)+/.Ч
О
Ф_(ОФ/>К)Фг(п) >
о
г = 0.../? — 1,
1 Но при этом её направление, естественно, должно быть касательным к
рассматриваемой грани
726
15.Векторный МКЭ для решения задач электромагнетизма
А’+Г2+'2(р—2)+/>+?+!
О
о
Ф-(б,)Ф//т1)Фг(О>
г = 0... р — 1.
Очевидно, первые р из этих вектор-функций направлены вдоль ко-
ординаты з], а последние р — вдоль координаты С,. Всего же на одной
грани получается 2 (;> — 2) + 2р = 4 (р — 1) новых вектор-функций.
Таким образом, к иерархическому базису (р —1)-го порядка долж-
ны быть добавлены 24(р — 1) новые вектор-функции, ассоциирован-
ные с гранями.
И, наконец, рассмотрим добавляемые к базису (р — 1)-го порядка
вектор-функции, ассоциированные с самим элементом, — это вектор-
функции зрёх направлений (т.е каждая вектор-функция по-прежнему
имеет лишь одну ненулевую компоненту, являющуюся произведением
трёх одномерных полиномов от координат т] или С,). Такие вектор-
функции (каждого из трёх направлений) можно условно разбить на два
типа по виду образующих их ненулевые компоненты одномерных
функций-сомножителей.
В вектор-функциях первого типа первая одномерная функция-
сомножитель - это иерархический полином ф j от координаты, вдоль
оси которой направлена вектор-функция, а вторая и третья одномер-
ные функции-сомножители - это иерархические полиномы от остав-
шихся координат степени от 2 до р — 1. Так, вектор-функции этого
типа, направленные вдоль оси координаты - это вектор-функции
вида
ФЛ-г24/> -12+(/»—2)(z—2)+1
Ф/>-1(ОФ,.('11)Ф7(С)
О
О
М = 2...р —1.
В вектор-функциях второго типа первая функция-сомножитель-
это один из полиномов степени от 0 до р — 1 (из которых неиерархи-
ческими являются только полиномы нулевой и первой степени) от той
координаты, вдоль оси которой направлена вектор-функция. Вторая
одномерная функция-сомножитель - это иерархический полином сте-
пени р от одной из оставшихся координат. Третья же одномерная
функция-сомножитель является полиномом степени от 2 до р от по-
следней оставшейся координаты. Вектор-функции этого типа, направ-
ленные вдоль координаты имеют следующий вид (при этом мы
последними пронумеруем те вектор-функции, у которых сомножители
являются полиномами р-й степени и от т], и от С,, и поэтому эти век-
тор-функции мы определим отдельной строкой):
15.11.Базисные вектор-функции из пространства ...
727
^>Z+24/»-12+(p-2)'2+»(/>-2)+j-l
^А-+24/»-12+(р-2)24-2р(р-2)+«
ФХУ ФДУФ/О
О
о
^А+24р—12+(/>—2)2 +]i(ji—2)+i(]i—'2)+ /-1
ФХУ ФР(0 Ф/л)
о
о
фху Ф/Д)ф7/о
о
о
2=0...р—1, j=‘2...p—1,
2=0...р-1, 7=2...р-1,
2 = О...р — 1 .
Итак, к базису (р — 1)-го порядка добавляется
(р — 2)2 4-2р(р — 2) Т-р = Зр2 — 7р + 4 ассоциированных с самим
элементом вектор-функций одного направления
Аналогично строятся добавляемые к базису (р — 1)-го порядка и
ассоциированные с самим элементом вектор-функции двух других
направлений, и всего получается 9р2—21р4-12 новых вектор-
функций, ассоциированных с самим элементом.
Таким образом, для построения иерархического базиса р-го поряд-
ка к вектор-функциям (р — 1)-го порядка должно быть добавлено
9р2 + Зр новых вектор-функций. Общее же количество вектор-
функций в базисе р -го порядка равно Зр (р 4- I)2 .
В заключение приведём вид лагранжевых базисных вектор-
функций высокого порядка на шаблонном элементе , которые не
только заметно проще строятся, но и более удобны при использовании
А-технологий уточнения решения с применением Т-преобразования
(см^раздел 15.15.6).
При построении лагранжева базиса в качестве шаблонного элемен-
та мы будем использовать единичный кубик = [0,1] х [0,1] х [0,1],
поскольку одномерные лагранжевы базисные функции удобней зада-
вать на отрезке [0,1].
Введём на отрезке [0,1] стандартные одномерные базисные поли-
номы Лагранжа р-й степени (р > 1; для р = 0 ф[] (9) = 1):
А ( ° “
Ф''(О = П
[i/p - j/p]
i — 0...р .
728
15.Векторный МКЭ для решения задач электромагнетизма
На параллелепипеде в лагранжевом векторном базисе р -го порядка
так же, как и в иерархическом, по р (р +1)2 вектор-функций каждого
из трёх направлений (т.е. всего Зр(р + 1)2 вектор-функций). Единст-
венная ненулевая компонента вектор-функций одного направления
является произведением трёх одномерных лагранжевых полиномов.
Два из них - это полиномы р-й степени о г координат, оси которых
перпендикулярны направлению рассматриваемой вектор-функции, а
третий - полином (р — 1)-й степени координаты, ось которой парал-
лельна направлению рассматриваемой вектор-функции, т.е.
о
о
г=О...р—1, j,l=O...p,
/'(Р+1 )2 + Ч>( 7'+1) +J (7J+1)+1 +1
^27?(/л] )2+ ф(/л1)+/>+7+1
Ф1ЖШй
о
г, 1=0...р, j=O...p—1,
О
О
жИ^фпо
г, j=0... р, 1—0... р—1.
В лагранжевом базисе с рёбрами ассоциируются вектор-функции, у
которых в ненулевой компоненте нижние индексы обоих одномерных
полиномов степени р принимают крайние значения 0 и р (это вектор-
функции
фгШймфЖ)
о
о
ФЖШ'Ю
о
ФГШ^ЖЮ
о
о
о
Ф£ШГШ;(О
о
и т.д.). С гранями ассоциируются вектор-
функции, у которых среди трёх сомножителей-полиномов ненулевой
компоненты нижний индекс только одного из одномерных полиномов
степени р принимает крайние значения 0 и р (это вектор-функции
о
о
о
о
о
15.1 1.Базисные вектор-функции из пространства ...
729
О
О
о
о
к 0 и к р).
ФГЧШШФШ
о
о
ф?;(уфгяфж)
фгШ-ыфж)
о
о
фгюфГмфш
И т.д.,
Все остальные вектор-функции ассоциированы с самим конечным
элементом.
Отметим, что информация о том, с чем (ребром, гранью или самим
конечным элементом) ассоциирована локальная базисная вектор-
функция, может быть очень полезна для глобальной нумерации базис-
ных вектор-функций на сетках с шестигранными ячейками и опреде-
ления соответствия между локальной и глобальной нумерациями ба-
зисных вектор-функций на каждом конечном элементе. Фактически
это соответствие и определяет глобальные базисные вектор-функции
как сшивку локальных и, как следствие, сборку глобальных матрицы и
вектора из локальных1.
Соответствие между локальной и глобальной нумерацией лагран-
жевых базисных вектор-функций можно установить и без привязки их
к рёбрам, граням и элементам, а по всем узлам, в которых только одна
глобальная вектор-функция отлична от нуля. Такой способ, конечно,
проще и применяется для регулярных сеток2, но для нерегулярных
сеток он является вычислительно гораздо более затратным.
Информация о том, с каким ребром или гранью ассоциирована ба-
зисная вектор-функция, нужна при реализации технологии
1 Заметим, что в базисах высоких порядков с каждым ребром и гранью
может быть ассоциировано по несколько локальных вектор-функций, и по-
этому необходимо иметь правило выбора нужной локальной вектор-функции,
ассоциированной с рассматриваемым ребром или гранью, при построении
соответствующей глобальной вектор-функции. В иерархических базисах это
правило очень простое: в глобальную вектор-функцию, ассоциированную с
рассматриваемым ребром или гранью, объединяются локальные вектор-
функции этого ребра или 1рани одного порядка. В лагранжевых же базисах в
глобальную вектор-функцию объединяются те локальные вектор-функции
ребра или грани, которые отличны от нуля в одном и том же узле этого ребра
или грани. Так, например, для ребра, направленного (в локальных координа-
тах) вдоль оси , сшиваться должны те ассоциированные с ребром вектор-
функции, которые отличны от нуля в одном и том же узле с координатой
i=y(p-l), г = 0...7>-1 (дляр>2).
2 Этот способ для регулярных сеток будет, пожалуй, самым эффективным,
если каждый узел хранить в виде трёх целых чисел - номеров «координат-
ных» плоскостей, на пересечении которых этот узел находится (о соответст-
вующих сетках, см. раздел 10.3.1 об опорных узлах и пример на с. 482, рис. 97
и 98).
730
15.Векторный МКЭ для решения задач электромагнетизма
Т -преобразования для согласования векторных конечных элементов
на несогласованных сетках с шестигранными ячейками (и, как следст-
вие, при реализации /г-, р- и р—h -технологий уточнения конечно-
элементных решений).
Итак, рассмотренные нами здесь базисы высоких порядков на шаб-
лонном элементе-кубике являются основой для реализации векторного
МКЭ на шестигранных сетках (включая и элементы с искривлёнными
гранями)1. А поскольку шестигранный элемент очень удобен для опи-
сания сложной трёхмерной геометрии, рассмотренный здесь материал
служит основой для создания многих эффективных алгоритмов реше-
ния сложных практических задач.
15.11 2 Б \ЛК НЫЕ ВЕКТОР-Ф} НКЦПП НА ТЕТРАЭДРЕ
базисные вектор-функции на тетраэдре, как и на треугольнике,
удобно определить через £ -координаты. В качестве направлений этих
базисных вектор-функций можно взять векторы grad£?, Z = 1...4.
Нетрудно убедиться, что каждый из векторов grad перпендикуля-
рен грани, противоположной узлу с локальным номером г2. Поэтому
вектор-функции вида £ grad Д (z^J) имеют нулевые касательные
уже на двух гранях, противоположных вершинам тетраэдров с локаль-
ными номерами i, и j (поскольку на грани, противоположной верши-
не с локальным номером j , функция = 0).
Таким образом, вектор-функция £ grad£z имеет ненулевые каса-
тельные только на двух гранях, которые содержат ребро, соединяющее
вершины с локальными номерами i и j. Покажем, что касательные
вектор-функции £, grad XI, к каждой из этих граней зависят только от
координат вершин тетраэдра, лежащих на рассматриваемой грани (и
никак не зависят от координат вершины, противоположной этой гра-
ни).
Рассмотрим в качестве примера вектор-функцию £2 grad Д. Оче-
видно, эта вектор-функция имеет ненулевые касательные составляю-
щие только на гранях, содержащих вершины тетраэдра с локальными
номерами 1 и 2, т.е. на гранях (1,2,3} и {1,2,4} (к грани {2,3,4} век-
тор gradjCj ортогонален, а на грани {1,3,4} функция £2 равна нулю).
1 Подробнее векторные шестигранные элементы будут рассмотрены чуть
ниже.
2 На этой грани £, — 0, а значит, и производные £, по любому направле-
нию т, касательному к этой грани, равны нулю; но производная £, по на-
правлению т равна скалярному произведению grad£z на вектор т, т.е.
grad 2^ т = 0 на грани, где Д,=0, что и означает перпендикулярность
grad £ рассматриваемой грани.
15.11.Базисные вектор-функции из пространства ...
731
Покажем, что на грани {1,2.3 касательные составляющие вектор-
функции grac^ не зависят от координат (Д,у4,Д) четвёртой верши-
ны тетраэдра. Для этого вычислим два скалярных произведения
grad Д • v12 и grad Д v13, в которых векторы
V12= , v13= (Д-Д/ДН/зЛ-Д) (15.117)
направлены вдоль рёбер, соединяющих вершины с локальными номе-
рами 1 и 2 и с локальными номерами 1 и 3.
Воспользуемся тем, что коэффициенты сД, определяющие £ -
координаты в виде
Д = сД + суД’+ су2?/+ сДг, (15.118)
являются компонентами матрицы CL, обратной к составленной из ко-
ординат вершин тетраэдра матрице D (см. раздел 6.2.2, соотноше-
ние (6.28)):
<4 с*} <4 «г (1 1 1 п '1 0 0 О'
4 4 «1 <4 <4 <4 <4 д У1 д У2 Уз д Ул = 0 0 1 0 0 1 0 0 (15.119)
4 °3 СУ.] <4 *2 Z-3 Д 1 / 0 0 0 1
Из соотношения (15.119) получаем (как результат умножения пер
вой строки CL на первый и второй столбец матрицы D ):
сД, -ь су}.Д + су2Д + СУ3Д = 1, (15.120)
OL() + Су] Д 3* 3“ ^3^2 ~ 0 . (15.121)
Вычитая (15.121) из (15.120), получаем равенство
<4 (Д - Д) + суТ2 (Д - у2) + <4 (Д - Д) = 1,
которое с учётом обозначения (15.117) и представления Д в виде
(15.118) может быть записано в виде
gi-абД v12 =1, (15.122)
т.е. проекция вектора gradД на единичный вектор v12//12 (где
^12 = 7(^1+(?Л-1/2 )2 3-(Д -z2)2 - длина вектора v12 ) не
зависит от координат четвёртой вершины тетраэдра (и зависит толь-
ко от координат первой и второй его вершин).
732
15.Векторный МКЭ для решения задач электромагнетизма
Абсолютно аналогично доказывается, что
grad v13 =1, (15.123)
т.е. проекция вектора grad Д и на единичный вектор v13/Z13 (где /13 -
длина вектора vl3 ) не зависит от координат четвёртой вершины тет-
раэдра (а зависит только от координат первой и третьей его вершин).
С учётом неколлипсарности векторов v12 и vI3 из (15.122) и
(15.123) сразу следует, что проекция вектора grad Д па любой вектор,
лежащий в плоскости грани {1,2,3} (т.е. грани, определяемой верши-
нами тетраэдра с локальными номерами 1, 2 и 3), не зависит от коор-
динат (т4,/;4, Д) четвёртой вершины тетраэдра, а значит, и касатель-
ная составляющая вектора grad Д на грани {1,2,3} не зависит от ко-
ординат вершины с номером 4. При этом в ходе доказательства мы
фактически получили, что касательная к грани {1,2,3} составляющая
трёхмерной £. -координаты Д ведёт себя абсолютно так же, как и
градиент соответствующей двумерной' £-координаты треугольника
{1,2,3}.
Очевидно, и вектор-функция £2grat^ на грани {1,2,3} будет
иметь касательную, не зависящую от четвёртой вершины тетраэдра
(поскольку функция Д па этой грани также нс зависит от четвёртой
вершины тетраэдра - она линейно меняется от единицы во второй
вершине до нуля в вершинах с номерами I и З)1 2.
Таким образом, вектор-функция Д^п^Д награни {1,2,3} ведёт
себя следующим образом. Её касательная к этой грани не зависит от
координаты четвёртой вершины (а, точнее, ведёт себя как соответст-
вующая двумерная вектор-функция треугольника {1,2,3}), и при этом
её проекция на единичный вектор v 2/Z12 (направленный вдоль ребра,
соединяющего вершины с номерами 1 и 2) также линейно изменяется
1 Под двумерной £ -координатой в данном случае мы, естественно, пони-
маем линейную функцию двух координат, оси которых лежат в плоскости
рассматриваемой треугольной грани, и равную единице в одной вершине этой
грани и нулю в двух других.
2 На самом деле, касательная к грани {1,2,3} составляющая трёхмерной
вектор-функции £2 grad будет двумерной вектор-функцией треугольника
(причём того же вида) в координатах, оси которых лежат в плоскости этой
грани. Это сразу же следует из того, чго скалярное произведение grad£ на
векторы v12 и V|3 совпадают в двумерном и трёхмерном случаях (сравните
соотношения (15.57) и (15.122) и учтите, что V] - нормированный вектор, а
vI2 - нет) и трёхмерная функция £2 на грани {1,2,3} ведёт себя как стан-
дартная двумерная £ -координата.
15.1 1.Базисные вектор-функции из пространства ... 733
от значения 1Д2 в вершине с номером 2 до нуля в вершине с номе-
ром 1.
Абсолютно аналогично можно доказать, что и касательная к грани
{1,2,3} составляющая вектор-функция grad£2 не зависит от коор-
динаты четвертой вершины тетраэдра, а её проекция на единичный
вектор линейно изменяется от значения —1/^12 в вершине с
номером 1 до нуля в вершине с номером 2. Поэтому проекция вектор-
функции £ grad£г — Д grad £2 на ребро, соединяющее вершины с
локальными номерами 1 и 2, будет постоянной на этом ребре и равной
1//12 (как и у соответствующей функции треугольного элемента).
Очевидно, что на грани {1,2,4} касательная к ней составляющая
вектор-функция £> grad £ — Q grad £> нс будет зависеть от координат
третьей вершины тетраэдра (и будет вести себя на этой грани как соот-
ветствующая вектор-функция двумерного треугольного элемента).
Поэтому, если на каждом тетраэдре, содержащем некоторое ребро
Г, определить базисную вектор-функцию в виде
£tgrad£ - £J grad Д (где i и j - локальные номера, соответствую-
щие глобальным номерам вершин рассматриваемого ребра Г), то эта
вектор-функция будет иметь непрерывные (ненулевые) касательные
составляющие на всех гранях, содержащих ребро Г. На всех же ос-
тальных гранях тех тетраэдров, которые содержат Г, эта вектор-
функция будет иметь нулевые касательные составляющие. Гем самым
будет обеспечена непрерывность касательных составляющих зр/ во
всей расчётной области (естественно, *фд. = 0 во всех тетраэдрах, не
содержащих ребро Г).
В результате при использовании такого базиса на одном тетраэдре у
нас будет определено шесть1 локальных базисных вектор-функций *ф
вида
•фр = £t grad £f — £ grad £t, (15.124)
ассоциированных с соответствующими рёбрами тетраэдра. Номера р
этих локальных вектор-функций - это локальные номера рёбер тетра-
эдра, которые могут быть определены через локальные номера i и j
вершин этого ребра. Например, можно ввести следующую локальную
нумерацию рёбер тетраэдра: первое ребро соединяет вершины с ло-
кальными номерами I и 2, второе - вершины 1 и 3, третье - вершины 1
и 4, четвёртое — вершины 2 и 3, пятое - вершины 2 и 4 и, наконец, шес-
тое ребро соединяет вершины с номерами 3 и 4.
1 Это количество рёбер тетраэдра и соответственно число глобальных ба-
зисных вектор-функций, ненулевых на одном тетраэдре.
734 15.Векторный МКЭ для решения задач электромагнетизма
Для обработки тетраэдрального векторного элемента (построения
его локальных матриц и вектора) удобно связать локальные нумерации
его вершин и рёбер заданием двух целочисленных функций и
j(p), которые по локальному номеру р ребра позволяют определять
локальные номера i и j его вершин. Для рассмотренной нами чуть
выше нумерации эти функции определяются табл. 24.
_______________________________Таблица 24.
р 1 2 3 4 5 6
i(p) 1 1 1 2 2 3
j(p) 2 3 4 3 4 4
Рассмотренный нами базис минимального порядка на тетраэдраль-
ных векторных конечных элементах (построенный с использованием
только вектор-функций вида (15.124)) обладает теми же недостатками,
что и аналогичный базис па треугольных векторных элементах. Эдин
из наиболее принципиальных - это резкое ухудшение аппроксимаци-
онных свойств при появлении в сетке вытянутых тетраэдров (включе-
ние которых в сетку обычно требуется, например, при наличии в рас-
чётной области вытянутых подобластей, при решении задач со скин-
эффектом и т.д.). Избежать этих эффектов (при появлении в сетке вы-
тянутых тетраэдров) можно путём добавления в локальный базис тет-
раэдра шести дополнительных (также ассоциированных с его рёбрами)
вектор-функций вида
-фс+р = Д grad Д Ч-Д grad Д , (15.125)
где i = г(р) и j = 7(79) - целочисленные функции, определяемые (как
и для вектор-функций (15.124)) табл 24.
В принципе, эквивалентным1 базису (15.124)-(15.125) на тетраэдре
является базис, построенный из двенадцати вектор-функций вида
'ф/( = Д grad Д, (15.126)
в котором с каждым ребром, соединяющим вершины с локальными
номерами i и j, также ассоциированы две вектор-функции: это век-
тор-функция Д grad/? и вектор-функция Д grad£,.
Заметим, что базис с векгор-функциями (15 124)—< 15.125) (в отли-
чие от базиса с вектор-функциями (15.126)) построен, вообще говоря,
по иерархическому принципу и позволяет использовать в одной и той
же сетке как элементы с шестью локальными базисными вектор-
функциями вида (15.124), так и элементы с добавленными к ним ба-
зисными вектор-функциями вида (15.125). Это, естественно, даёт та-
1 Естественно, в смысле порождаемого им конечномерного пространства
Vn,t. Что же касается свойств конечноэлементных матриц, то эти базисы,
конечно, не являются эквивалентными.
15.11.Базисные вектор-функции из пространства ...
735
кому базису заметные преимущества (по сравнению с базисом
(15.126)1 так как позволяет включать в него дополнительные (вида
(15 125)) вектор-функции не на всех, а только на вытянутых (и, есте-
ственно, примыкающих к ним) тетраэдрах
Обратим внимание на то, что на векторном тетраэдре (как и на век-
торном треугольнике) необходимо следить за направлением локальной
базисной вектор-функции (т.е. за тем, чтобы локальные базисные век-
тор-функции одного и того же ребра имели одинаково направленную
касательную к этому ребру). Решить эту проблему проще всего так же,
как и на векторных треугольниках: локальную нумерацию вершин
каждого тетраэдра проводить строго по возрастанию их глобальных
номеров.
В целом же, даже при использовании минимального базиса (с един-
ственной вектор-функцией на ребре вида (15.124))' тетраэдральные
векторные элементы обычно уступают векторным шестигранникам
(при примерно одинаковом количестве узлов в сетке) как по точности
получаемых конечноэлементных решений, так и по вычислительным
затратам (из-за гораздо большего количества рёбер в тетраэдральной
сетке по сравнению с сеткой из шестигранников). При этом геометрия
расчётной области (даже при наличии в ней сложных границ) с помо-
щью шестигранных элементов может быть описана, в общем-то, не
хуже, чем при использовании тетраэдральных элементов1 2. Единствен-
ным преимуществом тетраэдральных элементов, как мы уже говорили,
является возможность разрежения шага сетки в любых направлениях.
Однако использование несогласованных сеток в совокупности с техно-
логией Т-преобразования позволяет очень эффективно решать и эту
проблему на сетках с шестигранными ячейками. К преимуществам
сеток с шестигранными ячейками можно отнести и то, что на них про-
ще реализуются элементы высоких порядков3. Поэтому для решения
практических задач шестигранные элементы (в совокупности с техно-
логией Т -преобразования) являются, пожалуй, наиболее эффективны-
ми.
15.11.3. БАЗИСНЫЕ ВЕКТОР ФУНКЦИИ НА ТРЕУГОЛЬНОЙ ПРИЗМЕ
Рассмотрим, как могут быть определены базисные вектор-
функции на прямой призме с треугольным основанием (наклонные
призмы с треугольным основанием мы рассматривать не будем, по-
скольку вместо них удобнее использовать шестигранные элементы).
Базисные вектор-функции первого порядка на призме (как и на па-
раллелепипеде и тетраэдре) мы будем строить так, чтобы каждая из
1 Не говоря уже о ситуациях, когда в базис требуется включать по две век-
тор-функции, ассоциированные с одним ребром.
2 При этом можно использовать шестигранные элементы и с изогнутыми
гранями (подробнее об этом мы расскажем чуть позже).
3 Идея построения базисных вектор-функций высокого порядка на тетра-
эдрах в целом аналогична той, которая была нами рассмотрена для треуголь-
ных векторных элементов (т.е. умножением полиномов £ -координат соот-
ветствующих степеней на векторы grad £,, см. соотношение (15.68)).
736
15.Векторный МКЭ для решения задач электромагнетизма
них имела ненулевые касательные только на двух гранях, пересекаю-
щихся по ребру, с которым эта вектор-функция ассоциирована
Будем считать, что основания призмы перпендикулярны оси z (ле-
жат в плоскостях z = const). Пронумеруем рёбра призмы так, как это
показано на рис. 160 (эти номера указаны в кружочках) Базисные век-
тор-функции, ассоциированные с ребрами, имеющими номера от 1
до 6, определим следующим образом:
Чй - (£2grad4 А&тас,£2) 2, h (15.127)
Ф-2 = (A gradA gr«icl £3) 2 h (15.128)
Фз = (А grad A A erad А) 2, > п. (15.129)
Ф4 = (£2 grad £1 “ £1 grad А) , 1 > (15.130)
Ф5 - (£з grad 4 4 grad А) , 1 > к (15.131)
Фо = (Д erad £i A grad £3) , 1. 11 (15.132)
Рис. 160. Локальная нумерация узлов
и рёбер на призме
где h — z2 — — высота призмы (Zj и
£2 - z -координаты нижнего и верх-
него сё оснований), а £t = £.j(.r,y') -
двумерные £ -координаты треуголь-
ника, являющегося основанием приз-
мы (коэффициенты а1- двумерных £-
координат вычисляются через х - и у-
координаты1 трёх вершин призмы
любого из оснований но стандартным
формулам (5.69)). Под grad£z в фор-
мулах (15.127)-(15.132) понимается
стандартный трёхмерный grad-
вектор:
grad £,
дх
д£,{^у) 0 т
ду
1 Это значения (£1уУ1) - х- и у -координаты перкой и четвёртой вершин
призмы, (£2,7/2) “ х ~ и //-координаты второй и пятой вершин призмы и
(£з,#з) _ х~ 11 У -координаты третьей и шестой вершин призмы.
15.11 .Базисные вектор-функции из пространства ...
737
Очевидно, что каждая из вектор-функций (15.127)—(15 132) имеет
нулевые z-составляющие и вектор-функции (15.127)-(1 5.129) на ниж-
ней грани z = Zj, а вектор-функции (15 ! 30)—(15.132) на верхней грани
z — z2 полностью совпадают со стандартными базисными вектор-
функциями треугольника, являющегося основанием призмы Сомно-
жители —------ и ------ (в соотношениях (15.127)-(15.132)) делают
h h
эти вектор-функции убывающими от значений, равных значениям
стандартных базисных вектор-функций треугольника на «своём» осно-
вании, до нуля на противоположном.
В результате каждая из вектор-функций (15.127)-(15.132) имеет не-
нулевые касательные только на двух гранях, которые пересекаются по
ассоциированному с ней ребру (это одно из оснований призмы и боко-
вая её грань). При этом на боковой (вертикальной) грани эти вектор-
функции ведут себя как базисные вектор-функции прямоугольника, а
на основании, как уже говорилось, - как базисные вектор-функции
треугольника.
Базисные вектор-функции, ассоциированные с вертикальными рёб-
рами 7,8 и 9 (см. рис. 160), определим в виде
ф, = (0,0,^)Т, ф8=(0,0,|^)Т, = (0,0,1£3)Т, (15.133)
где Д = £, (ж,у) - те же двумерные £-координаты треугольника,
являющегося основанием призмы (множитель h в этих функциях по-
ставлен для того, чтобы edge-функции призмы были определены в
некотором смысле единообразно, т.е. их касательные составляющие на
соответствующих рёбрах были равны длине ребра).
Вектор-функции (15.133), очевидно, перпендикулярны основаниям
призмы, и каждая из них имеет ненулевые касательные составляющие
только на двух боковых гранях, смежных по ребру, с которым она ас-
социирована При этом (по свойствам £-координат треугольника)
модуль каждой из вектор-функций (15 133) линейно по х и у убывает
от значения h на вертикальном ребре, с которым она ассоциирована,
до нуля на остальных двух вертикальных рёбрах (и, естественно, на
вертикальной 1рани, содержащей эти два вертикальных ребра! Таким
образом, векгор-функции (15.133) на боковых (вертикальных) гранях
ведут себя как базисные вектор-функции прямоугольника.
Заметим, что для вектор-функций (15.127)-(15.132) так же, как и
для вектор-функций треугольника и тетраэдра, необходимо следить за
тем, чтобы ассоциированные с одним и тем же ребром локальные век-
тор-функции этого типа на двух смежных призмах были направлены в
одну и ту же сторону
Конечные элементы в виде призм с векторными базисными функ-
циями (как и с узловыми) применяются обычно для таких задач, у ко-
торых расчётные области имеют довольно сложное сечение, перпенди-
кулярное одной из координатных осей, и это сечение очень слабо ме-
няется при движении вдоль оси, которой оно перпендикулярно. При
738 15.Векторный МКЭ для решения задач электромагнетизма
этом так же, как и при использовании векторных треугольников (с
базисными вектор-функциями вида (15.58)—(15.60)), аппроксимацион-
ные качества треугольных призм с векторными базисными функциями
вида (15.127)—(15.132) резко ухудшаются, если в основании призмы
лежит вытянутый треугольник.
Устранить этот недостаток треугольной призмы можно введением
на ней дополнительных базисных вектор-функций вида
*ф/; = (Д grad £ + £f grad Д) Z (z),
где Z(z) - одна из линейных функций вида (z2 — z}/h и (z — z^fh.
Но при этом и заметно возрастёт как число степеней свободы, так и
заполненность матрицы конечноэлементной СЛАУ. Гораздо более
выгодным вариантом может стать использование прямых призм с че-
тырёхугольным основанием, являющихся (как и параллелепипед) од-
ним из частных случаев, пожалуй, наиболее удобного и эффективного
(по соотношению вычислительных затрат и точности аппроксимации)
векторного конечного элемента - шестигранника.
15.11.4. БАЗИСНЫЕ ВЕКТОР-ФУНКЦИИ НА ШЕСТИГРАННИКЕ
На шестиграннике так же, как и на четырёхугольнике, базисные
вектор-функции удобней всего строить с помощью шаблонного эле-
мента. Обычно в качестве шаблонного элемента берут кубик
[0,1] х [0,1] х [0,1] при использовании базиса лагранжева типа или ку-
бик [—1,1] х [—1,1] х [—],!] при использовании иерархического базиса.
Мы рассмотрим, как строятся базисные вектор-функции с использова-
нием шаблонного кубика = [—1,1] х [—1,1] х [—1,1].
Рассмотрим некоторый (произвольный) шестигранник с вер-
шинами (Д, уг, zt), i = 1... 8 .
Зададим отображение шаблонного кубика в шестигранник
соотношениями
8 8 8
х =12 О, О ’ У ‘П’ 0 У г > z =Z2 0^,(15.134)
2=1 2=1 2=1
где tp, ((,т],() — стандартные скалярные трилинейные базисные функ-
ции, определённые на шаблонном элементе О,Е (каждая функция
ф- С) является произведениями трёх линейных одномерных функ-
1 — Ю 1 + 0
ций (, т] и ( вида 1+_(0) = или 1Г+(0) = —-— и равна едини-
це в одной вершине 0е, которая отображается в узел (Д, Д,Д), и ну-
лю в остальных вершинах).
15.11.Базисные вектор-функции из пространства
739
Определим отображение базисных вектор-функций ф, (£,, Т), (,) шаб-
лонного элемента QE на шестигранник . При этом нам желательно
отобразить ф,- таким образом, чтобы у полученных на вектор-
функций фг касательные составляющие были ненулевыми только на
тех гранях, на прообразах которых шаблонные вектор-функции ф,
имеют ненулевые касательные. Этому условию будут удовлетворять
вектор-функции ф-, полученные из ф- следующим образом:
Ф, &y,z) = J ’ф, */,*)), (15.135)
где
дх ду dz
¥ дК ¥
дх ду dz
<9т] <9т) <9т|
дх ду dz
А 1
(15.136)
- функциональная матрица' преобразования координат, переводящего
кубик .О7 в шестигранник (сравните с функциональной матрицей
(15.72) преобразования квадрата в четырёхугольник).
Доказательство того, что базисные вектор-функции (15.135) будут
перпендикулярны всем тем граням шестигранника, которые являются
образами граней 0е , где шаблонные вектор-функции ф, имеют нену-
левые касательные, в целом мало отличается от соответствующего
доказательства для четырёхугольника. Это доказательство базируется
на том, что в любой точке шестигранника скалярное произ-
ведение любой вектор-функции ф на произвольный вектор v может
быть представлено в виде скалярного произведения вектора
Лф(жр,yf),на вектор w, связанный с v соотношением v = J'w,
1 Компоненты функциональной матрицы (15.136), вообще говоря, являют-
ся функциями координат 6,, т] и С,, но в выражении (15.135) под J подразу-
мевается матрица J = J(^(x,y,z) ,T)(x,y,z),(,(.t,y,z)) , которая, как и вектор-
функция ф,-(б.(з;,у,z),t](.t,у,z),C.(x,y,z)), зависит уже от координат х, у и
z . Тем самым правая часть в (15.135), как и левая, определяется как вектор-
функция координат х, у и z .
740
15.Векторный МКЭ для решения задач электромагнетизма
где J = Л^Р,Ур^рУх}[хр,ур,г.рУ^хр,у1>угр)У
Действительно,
(4 (аф, Ур, zv) л) = (ф (жр> Ур, zp),JTwj = (J-ф (жр, yp, zpj ,w j, (15.137)
и из (15.137) сразу следует, что если вектор 1ф(а;/п2/р,2р) перпенди-
кулярен вектору w, то и ф(.тр, ур, z,^ будет перпендикулярна вектору
V. Но если в качестве Лф(.г, у, z) взять одну из базисных вектор-
функций ф,ав качестве вектора w произвольный вектор, касатель-
ный к тем граням QF, которым перпендикулярна ф.г, то, во-первых,
вектор v будет касательным к грани шестигранника Qm, являющейся
образом соответствующей грани кубика 0е , а во-вторых, вектор-
функция ф, на этой грани шестигранника будет ему перпендику-
лярна (см. (15.137)). Если отображение в является взаимно
однозначным, то, очевидно, для любого вектора v, касательного к
какой-либо грани Г шести! ранника, можно найти вектор w , лежащий
на грани-прообразе Г и являющийся прообразом v (этот вектор
w = J Tv ). В результате из (15 137) следует, что вектор-функция ф?;,
I з
определённая как J (см. (15.135)), будет ортогональна всем гра-
ням шестигранника О.т, являющимся образами тех граней кубика 0е,
которым ортогональна .
Таким образом, каждая из вектор-функций -ф-, полученных из
шаблонных вектор-функций первого порядка (это вектор-функции
ф 4-ф,ч из раздела 15.11 1), будет иметь ненулевые касательные
только на двух гранях, пересекающихся по ребру шестигранника Q,M ,
являющегося образом ребра кубика 0е', с которым ассоциирован её
прообраз ф,- (к граням Qm, являющимся образами граней О , кото-
рым перпендикулярна ф,;, вектор-функция ф, будет перпендикулярна
в соответствии с (15.137), а на остальных двух гранях, не содержащих
рассматриваемое ребро, ф./; будет равна нулю, поскольку на гранях,
являющихся их прообразами, ф, равна нулю). Очевидно, вектор-
15.11.Базисные вектор-функции из пространства ...
741
функции *фг; = J ip-, г = 1...12, как и их прообразы ср-, имеет смысл
ассоциировать с соответствующими ребрами шестигранника.
Точно так же доказывается, что образы -ф,; ассоциированных с рёб-
рами и гранями шаблонных вектор-функций cpt высокого порядка
имеют ненулевые касательные либо только на двух смежных по одно-
му ребру гранях (если вектор-функции ассоциированы с этим ребром),
лиоо только на одной грани, с которой они ассоциированы (все же
ассоциированные с самим конечным элементом О,т вектор-функции
высоких порядков просто равны нулю на всех его гранях).
Не представляет особого труда определить базисные вектор-
функции и на шестиграннике с изогнутыми гранями1. Например, для
описания трёхмерной геометрии расчётной области с изогнутыми гра-
ницами удобно использовать шестигранник, полученный из шаблонно-
го кубика 0е — [— 1,1] х [— 1,1] х [-1,1] отображением вида
27 27 27
=12 ’ у =12 у,. , , (15.1 з 8)
z=l z=l
где cp-A - эго стандартные триквадратичные лагранжевы базисные функ-
ции2, заданные на 0е , a (£-,у,, z-), z = 1...27, — координаты узлов кри-
волинейного конечного элемента , восемь из которых являются его
вершинами, а остальные девятнадцать задаются для определения искрив-
ления рёбер и граней (двенадцать узлов на «серединах»3 рёбер, шесть
узлов в «центрах»4 граней и один узел в «центре»5 элемента).
1 Строго говоря, под шестигранником обычно понимают геометрическое
тело с плоскими гранями. Мы же тем не менее будем использовать понятие
«шестигранник» для обозначения тел, топологически подобных параллелепи-
педу и имеющих границы в виде не только плоских, но и изогнутых четырёх-
угольников.
2 Каждая функция ф/' (£,т], С,) является произведениями трёх квадратич-
ных одномерных функций координат Е,, 1] и ( вида ИфО) = 0(Ю —1)/2,
Ц/2(тЭ) = 1 — Ю2 или Wj(-O) = 0(1 + 0у2 и равна единице в одной вершине
, которая отображается в узел (iz,^,z;), и нулю в остальных вершинах.
3 Имеется в виду точка на ребре шестигранника , в которую отобража-
ется середина соответствующего ребра кубика Q£; естественно, точка
на «середине» ребра может быть не равноудалённой от его вершин.
4 Точно так же имеется в виду точка на грани шестигранника Q,„ , в кото-
рую отображается центр соответствующей грани кубика QE .
5 Этот узел фактически фиксирует вид отображения внутренних точек ку-
бика 0е в точки шестигранника .
742
15.Векторный МКЭ для решения задач электромагнетизма
Базисные вектор-функции на шестиграннике с изогнутыми гранями
также определяются с помощью соотношения (15.135), в котором -
это базисные вектор-функции шаблонного элемента любого порядка (в
том числе и первого), a J - функциональная матрица преобразования
(15.138).
В заключение отметим, что все получаемые из шаблонных вектор-
функций ip, по формуле (15.135) локальные базисные вектор-функции
яр, автоматически сшиваются в глобальные вектор-функции с непре-
рывными на границах между двумя шестигранниками касательными
составляющими (если они, естественно, ассоциированы с одним и тем
же ребром или одной и той же гранью, являются однотипными1 и «од-
нонаправленными»-2).
Ключевым в доказательстве этого утверждения, опять же, является
соотношение (15.137), а также и следующий факт.
Пусть Г - граница между шестигранными элементами Q и fy
(возможно, изогнутая). Если на гранях rf и Г-f шаблонного элемента
С1Е, которые переводятся в одну и ту же грань Г при отображениях
0е в fy и fy соответственно, взять такие касательные к ним век-
торы и w2, что они совпадают при совмещении rf с ГЕ, то обра-
зом этих векторов будет один и тот же вектор3 v, касательный к по-
верхности Г.
В таком случае из (15.137) в одной и той же точке ур, zp^ грани
Г для любого касательного к Г вектора v
(4у) = (&f 4"“)л).
1 Для иерархических базисов это вектор-функции одного порядка, а для
лагранжевых — это те локальные вектор-функции ребра или грани, которые
отличны от нуля в одном и том же узле этого ребра или грани.
2 Напомним, что под «однонаправленными» мы понимаем такие вектор-
функции, у которых совпадают направления проекций на ребро или любой
касательный к грани вектор, с которым (ребром) или с которой (гранью) эти
функции ассоциированы.
3 В этом проще всего убедиться для наиболее часто встречающегося при
использовании шестигранных сеток случая, когда прообразы rf и rf одной
и той же грани двух смежных шестигранников - это две параллельные друг
другу грани шаблонного элемента 0е (т.е. перпендикулярные одной и той же
координатной оси 6,, д или С,) и векторы Wi и w2 получаются друг из друга
параллельным переносом вдоль оси, которой перпендикулярны rf и Г-f ; но
это останется справедливым и для случая, когда прообразами одной грани Г
являются и две смежные грани rf и Г-f шаблонного элемента 0е .
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 743
(Ф"“2 (х„, у,„ 2„) (ф*, , ф“2), w2),
где (ф4 ,tlp”4 Лр"4 ) и (ф”2 >ф“2 Х^”'2) _ прообразы одной и той же
точки ^xp,yin z.p^ на грани Г, ф^’М1 и фу’"'2 — сшиваемые (по Г) в
одну глобальную вектор-функцию локальные вектор-функции элемен-
тов Q и Q, а и - их прообразы.
Тогда из условия
/Ц,,, \ ^111-2 с^т.2\ |
1^/ |Ч>/; iHp Ар I» W1 I — l^j Лр pW2b
которое является естественным для прообразов сшиваемых вектор-
функций, и следует сразу же равенство
('ФГ'"1 (Хр> Ур, zp ) > v) = (фу "‘2 (тр, ур, zp), V j ,
означающее непрерывность касательных составляющих глобальных
вектор-функций, получаемых сшивкой локальных вектор-функций
ф“"'1 И фу "‘2 .
Таким образом, из определённых нами с помощью соотношения
(15.135) локальных базисных вектор-функций для любых шестигран-
ных1 элементов (в том числе и с изогнутыми гранями) получаются
глобальные вектор-функции любых порядков с непрерывными на гра-
ницах элементов касательными к ним составляющими.
15.12. ГЕНЕРАЦИЯ КОНЕЧНОЭЛЕМЕНТНОЙ СЛАУ В ВЕКТОРНОМ МКЭ
ПРИ РЕШЕНИИ ТРЁХМЕРНЫХ ЗАДАЧ
Мы приведём здесь локальные матрицы и векторы наиболее час-
то употребляемых трёхмерных edge-элементов (с вектор-функциями
первого порядка) и покажем, как можно вычислять компоненты ло-
кальных магриц при использовании базисных вектор-функций высо-
ких порядков на наиболее эффективных векторных элементах - шести-
гранниках. Кроме того, мы покажем, как следует обрабатывать правую
часть векторного уравнения при наличии в ней слагаемых вида </,A ,
j *’ г
d2A и т.д. (получаемых при аппроксимации по времени исходной
1 Естественно, под любыми шестигранными элементами мы понимаем те-
ла, которые могут быть получены с помощью взаимно однозначного отобра-
жения (в них) кубика QE; это, например, отображение (15.134) или (15.138)
или отображение такого же вида с использованием других узловых функций
лагранжева типа.
744
15.Векторный МКЭ для решения задач электромагнетизма
нестационарной задачи, А - решения на предыдущих временных
слоях), и рассмотрим особенности учёта краевых условий.
15.12.1. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ
КОНЕЧНОЭЛЕМЕНТНЫЕ МАТРИЦЫ И ВЕКТОРЫ
Формулы для вычисления компонент глобальных матриц жёст-
кости G и массы М, определяющих глобальную матрицу С — G + М
конечноэлементной СЛАУ, очевидно, имеют вид (см. формулу
(15.18)):
= J — rot-ф; • rot-Qy/Q, Mtl: = J ^ф,; ф^сЮ. (15.139)
и lL ц
Соответственно вклады в G и M от конечного элемента опре-
деляются соотношениями
G,, = f — rot-ф,; • rot-ф dQ, (15.140)
= /эФ; • Ф/Q, (15.141)
tyn
где G и М - локальные матрицы жёсткости и массы конечного эле-
мента Q,„ , а ф( - его локальные базисные вектор-функции.
Компоненты глобального вектора b конечноэлементной СЛАУ
(15.18), очевидно, определяются соотношением
b.j = Ji ф-dO, + J*х п^-ф,с15. (15.142)
ц s.2
Таким образом, глобальный вектор правой части b собирается из
локальных векторов конечных элементов Q.,n с компонентами вида
JF ф,фП и из локальных векторов участков S2 границы S2 с ком-
понентами вида J Н J х п) • ^jdS .
a in
15.12.2. ЛОКАЛЬНЫЕ МАТРИЦЫ ПАРАЛЛЕЛЕПИПЕДА
С ВЕКТОРНЫМИ БАЗИСНЫМИ ФУНКЦИЯМИ
При вычислении компонент локальных матриц параллелепипеда
с векторными базисными функциями (так же, как и с узловыми) обыч-
но пользуются тем, что все подынтегральные функции представляются
в виде произведения одномерных полиномов, и поэтому объемные
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 745
интегралы можно вычислять как произведение одномерных интегра-
лов.
Наиболее простой вид имеет локальная матрица массы М (см.
(15.141)1 векторного параллелепипеда. Поскольку локальные базисные
вектор-функции параллелепипеда частично ортогональны друг другу,
эта матрица содержит довольно много нулей. При принятой нами ну-
мерации локальных базисных вектор-функций первого порядка на па-
раллелепипеде (эта нумерация была определена нами на шаблонном
элементе — см. вектор-функции 4-ф12 в разделе 15.11.1) ненулевые
компоненты локальной матрицы массы сосредоточены возле её глав-
ной диагонали, и сама матрица М (при = const на ) имеет
вид:
4 2 2 1 0 0 0 0 0 0 0 0'
2 41 2 00000000
214 2 0 0 000000
12 2 400000000
000042210000
hrJv,.h7 000024120000
М —
1 36 000021420000’
00001 2 240000
0 0 0 0 0 0 0 0 4 2 2 1
00000000241 2
000000002142
000000001 2 2 4
/
где h.,., и hz — размеры параллелепипеда.
Матрицу М можно записать в более компактном виде. Для этого
введём подматрицу D размера 4x4:
4
2
2
1
2
4
1
2
D =
2 1'
1 2
4 2
2 4
Тогда
где О - состоящая из нулей подматрица размера 4x4.
746
15.Векторный МКЭ для решения задач электромагнетизма
Локальную матрицу жёсткости G (см. (15.140)) векторного парал-
лелепипеда сразу приведём в компактном виде. Для этого определим
три подматрицы размера 4x4:
2 1 -2 -1' 2 -2 1 -Г -2 2 -1 Г
1 2 -1 -2 -2 2 -1 1 -1 1 —2 2
Gi- — 2 -1 2 1 > G2— 1 -1 2 —2 > G3— 2 -2 1 -1
-1 -2 1 2 -1 к 1 -2 2 > i к -1 2 -2 /
Тогда (при р = р, = const на О,т )
^х^у q hxhz
6hz I 6liy
--^G9
6 2
. h.yhz
~r~i—' TT—
0 h-% 6
Q
-TF 1
G2
"У qT
6 3
Как удобнее всего вычислять локальные матрицы параллелепипе-
дов с базисными вектор-функциями высоких порядков (через компо-
ненты матриц шаблонных элементов), мы покажем чуть ниже, когда
будем рассматривать построение локальных матриц шестигранных
элементов.
15.12.3. ЛОКАЛЬНЫЕ МАТРИЦЫ ТЕТРАЭДРА
С ВЕКТОРНЫМИ БАЗИСНЫМИ ФУНКЦИЯМИ
Локальные базисные вектор-функции тетраэдрального edge-
элемента (Д с вершинами (i7;|&;,z/.:) (& = 1...4) имеют вид (см.
(15.124)):
Фр = Д(Р) grad £j( f>) - grad £,;(p), p = 1... 6,
где Д (к — 1...4) - £-координаты тетраэдра Q,„, а целочисленные
функции г(р) и j(p) определяются табл. 24, нас. 734.
Вычислим векторы rot :
rot-ф^ = rot(£4p) §racl А(р) ~ grad£4p)) =
= 2 (grad х grad£J1(w)) = (od(p) x
где c?; = (cti, c*2, аз) — векторы, составленные из компонент матри-
цы d , определяемой соотношением (6.28).
Тогда компоненты локальной матрицы жёсткости (см. (15.140)) век-
торного тетраэдра будут иметь вид (при р = р = const на О,1Г1)
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 747
Gps=J" =• rot ф7/ rot = -= mes (ct'^x схАр^ (od(A)x ct-7(5)
in
где mesQ„, =^|detD| - объём тетраэдра Qm (матрица D определя-
ется через координаты вершин тетраэдра соотношением (6.27), а её
определитель cletD — соотношением (6.36)).
Компоненты локальной матрицы массы (см. (15.141)) могут быть
вычислены с использованием формул интегрирования £ -координат
(см. (6.37)) и определяются соотношением (при — const на О,т )
Mps=J Ч ф(/ (mi(p).(s)g.j(p)j(s) -
> (15.143)
где коэффициенты ды определяются соотношением
9ki = grad Д • grad Д = о? • а1,
a mpi — это компоненты матрицы массы узлового тетраэдрального
конечного элемента первого порядка, определяемые соотношени-
ем (6.45) (при этом подразумевается, что при вычислении mki в соот-
ношении (6.45) значение коэффициента было принято равным еди-
нице).
Очевидно, локальные матрицы векторного тетраэдрального элемен-
та первого порядка имеют размер 6x6 (поскольку тетраэдр имеет 6
рёбер).
Если на тетраэдре задано 12 базисных вектор-функций (т.е. к шести
вектор-функциям вида (15.124) добавлено шесть вектор-функций вида
(15.125)), то локальные матрицы, очевидно, будут иметь размер
12x12. Но поскольку для вектор-функций вида (15.125) го!ф/ = 0,
ненулевыми компонентами матрицы жёсткости такого конечного эле-
мента будут лишь те компоненты Gif, для которых обе базисные век-
тор-функции являются функциями вида (15.124).
Компоненты же матрицы массы тетраэдрального элемента с таким
набором базисных вектор-функций будут определяться следующими
соотношениями. Если ф? и фл. являются вектор-функциями вида
(15.124), то Мря определяется соотношением (15.143). Если фр явля-
ется вектор-функцией вида (15.124), а ф5 - вектор-функцией вида
(15.125), то Мрч определяется соотношением
748
15 Векторный МКЭ для решения задач электромагнетизма
Мр» [mi(p),i(.s)9~ m7(p),^G4)ffi(p)J(.4) 4~
Если же обе вектор-функции -фр и -фя являются вектор-функциями
вида (15.125), то
Mps ^{^т1(р),-1(м)9?(/>),./(.*) Т
4~ mi(p),jlst9j(p),Hs') 4“ mj(p), j(.4')9i.(p),i(s)j
15.12.4. ЛОКАЛЬНЫЕ МАТРИЦЫ ТРЕУГОЛЬНОЙ ПРИЗМЫ
С ВЕКТОРНЫМИ БАЗИСНЫМИ ФУНКЦИЯМИ
Прежде чем вычислять компоненты локальных матриц тре-
угольной призмы П,„, введём следующие обозначения. Вектор-
функции Д grad - £.j grad £ (где Д - двумерные £ -координаты
треугольника), фактически являющиеся двумерными базисными век-
тор-функциями лежащего в основании призмы треугольника (с припи-
санной нулевой третьей компонентой), обозначим через -ф/Л . Тогда
первые три базисные вектор-функции призмы могут быть записа-
ны в виде (см. рис. 160 и формулы (15.127)-(15.132))
Фр - Фр 2'2 д 2 ’ р = 1...3,
а следующие три - в виде
Ф7> = фр_3 Z- , р = 4...6,
где h = z-2 — - высота призмы (fj и z2 — z -координаты нижнего и
верхнего её оснований).
Получим выражения для компонент матрицы массы призмы Q„, .
Обозначим через Мл матрицу массы (размера 3x3) векторного тре-
угольника, лежащего в основании призмы. Компоненты этой матрицы,
очевидно, определяются соотношением (15.98) (при этом подразумева-
ется, что в этом соотношении коэффициент равен единице). Тогда
компоненты М , матрицы массы призмы для z, j = 1...6 определяют-
ся соотношениями (при = const на Q,„ )
ТИц = J тФ/' • фу(7П ~ Т J Фг" • Ф| I д ] dQ. =
Нт
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 749
— Т f ' ''frjdQb С Р2 , dz =
kJ kJ \ П/ I О
Mi3 = 4 f -Й Ф-з
tyll
i = 1... 3, j = 4... 6,
4 = ч f &-з ф
4 L, и
i = 4... 6, j — 1... 3,
M„ = 4 f 4?-3 fcA)dn = ^Л'ёз.^3, i,J = 4...6,
kJ \ lb I О
i hll
где Q^, — треугольник, являющийся основанием призмы Q,„ (т.е.
Q;n = Q* x[z1}i.2]).
Значения MLJ для ?’ = 1...6, j = 7... 9 и i = 7... 9, j = 6 будут
равны нулю, поскольку соответствующие вектор-функции ф, и фу
орт огональны друг другу. И, наконец,
*2
р- J* ^-G^-GtZQ = ~jf f dz =
Urn 4
^-mesQ*, i = j = 7. ..9,
-^-mesQ*., i j, ij = 7...9,
где mesQA - площадь треугольного основания призмы. Таким обра-
зом, компоненты М,., при i, j = 7... 9 - это разделённые на h компо-
ненты матрицы1 Мл (размера 3x3), которая является матрицей мас-
сы треугольника с узловыми (скалярными) базисными функциями.
Компоненты матрицы МЛ определяются соотношением (5.81) (в кото-
ром коэффициент нужно положить равным единице).
1 Не путать с матрицей массы МЛ векторного треугольника.
750
15.Векторный МКЭ для решения задач электромагнетизма
В результате локальную матрицу массы М векторной треугольной
призмы можно записать в виде
2Ма Мл О
М = ^ МА 2МЛ О ,
О о
I h ,
где О - подматрица размера 3x3, состоящая из нулей.
Вычислим теперь компоненты G- матрицы жёсткости. Сначала
получим выражения для rot Ф :
rot ф.
rot-ф,
—— фд
h
z2 — Z , 7 д
h rot2 ф,
I ^7,-3
-|^-3
z - 7 Д
- — ~rotz ф?_3
2 = 1...3,
2 = 4...6,
rot Ф,;
_ Jl /i-G
h 2
1 i—G
h 1
0
2 = 7...9,
где ф^ 7 и фу, - х- и у -компоненты базисной вектор-функции ф^
векторного треугольника Гф,, являющегося основанием призмы , а
07 - коэффициенты, определяющие £ -координаты треугольника
(см. соотношения (5.66) и (5.69)).
Обозначим через GA матрицу жёсткости (размера 3x3) векторно-
го треугольника , лежащего в основании призмы. Компоненты этой
матрицы, очевидно, определяются соотношением (15.97) (при этом
подразумевается, что в этом соотношении коэффициент р равен еди-
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 751
нице). Под Мл по-прежнему будем понимать матрицу массы вектор-
ного треугольника, лежащего в основании призмы. Тогда компоненты
матрицы жёсткости призмы определяются соотношениями (при
ц — jl: const на ):
Gjj — •=• Г rot гр; rot =
И it
= ip- J ('Ф+ (Л - z)2 rot2$? rot^jdfi =
*ф7л xjjjdQ + J rot^xjjA rot2xjj^JQJ J ' dz
= 1(1
ц \A
G/-' = + 3 G-V3)
Gij = jl (“ h M^~3 +1 G^~3)1
Gli = jl (“ h + 3 G*~3’j) ’
M = 4...6,
i = 1... 3, j = 4... 6,
i = 4... 6, j = 1... 3,
= J (-<«Г° + =
Q.„, V '
= S'/((-4“2 + £2а})с<Г0 +(Да! -^)af°)dn =
= (—Ch.2^2~G + + ОцО^-6 — Ot2Ot(-G)mesQ^,
Oil \ /
г = 1...3, J = 7...9,
G;. = Jj-(ar3c<fc -c<i-3afc -аГ3а/-е +«r3c<';)mes<C,
i = 4... 6, j — 7... 9,
Gi3 = J i(cY.rcCYfG + arcaf-G)dQ =
= + «ГМ”6)mesi,j = 7...9.
752 15.Векторный МКЭ для решения задач электромагнетизма
Аналогично можно получить выражения для компонент матрицы
массы и жёсткости треугольной призмы с дополнительными базисны-
ми вектор-функциями на рёбрах оснований1 (построенными из базис-
ных вектор-функций треугольника вида (15.65)-( 15.67)).
Не представляет также особого труда получить выражения для мат-
риц жёсткости и массы, если в основании прямой призмы лежит четы-
рёхугольник. Очевидно, компоненты этих матриц можно вычислять
через матрицы векторного и скалярного четырёхугольника.
Заметим, что прямая призма с четырёхугольным основанием явля-
ется одной из разновидностей шестигранника и, естественно, её ло-
кальные матрицы могут быть получены по схемам, которые мы рас-
смотрим чуть ниже для шестигранных элементов. Однако применение
формул, основанных на разложении трехмерных базисных функций в
прямое произведение двумерных и одномерных, позволяет заметно
сократить количество машинных операций при вычислении компонент
локальных матриц и тем самым улучшить качество программы генера-
ции конечноэлемент ной СЛАУ.
15.12.5. ЛОКАЛЬНЫЕ МАТРИЦЫ ШЕСТИГРАННИКА
С ВЕКТОРНЫМИ БАЗИСНЫМИ ФУНКЦИЯМИ
Как мы уже не раз отмечали, векторный шестигранник обладает,
пожалуй, самыми лучшими аппроксимационными свойствами среди
всех рассмотренных нами векторных элементов.
Напомним, что базисные вектор-функции *ф,.(я,у,z) шестигранно-
го конечного элемента Q„, были определены с помощью соотношения
(15.135) через вектор-функции <р>/(£,, i], Q шаблонного кубика О.Е и
функциональную матрицу J отображения О.Е в Q,„. Особо отметим,
что изначально компоненты функциональной матрицы J и вектор-
функций ip,; были определены как функции переменных т] и ( и
только при определении век гор-функций -ф., (я, у, z) переменные т)
и £ у компонент матрицы J и у вектор-функций ip, заменялись функ-
циями £ (я, г/, z), т](я, у, z) и (фя, у, z). Эти функции фактически опре-
деляют отображение Q,„ в О.Е, обратное к исходному отображению
вида (15.134) или (15.138) (или подобных им отображений с ещё боль-
шим набором узлов (я.,,y^z,) и отображающих функций Ф т], Q),
являющихся полиномами Лагранжа).
Таким образом, при выполнении замены переменных я, у и z на
переменные г] и С, вектор-функции
1 Такие вектор-функции имеет смысл вводить, если в основаниях призмы
лежат вытянутые треугольники и хотя бы один из параметров ст или е на
призме Q,„ не равен нулю (эти ситуации могут возникать при наличии в рас-
чётной области вытянутых объектов или при наличии скин-эффекта).
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 753
должны быть просто заменены на определённые в координатах £, Т] и
вектор-функции J 1 (£,,')],(,)'?’/ (£,,т],С,) И поэтому компоненты локаль-
ной матрицы массы М шестигранника П,„ могут быть получены с
помощью следующего выражения:
1 1 1
= /\ф» • Ф/^
$17/,
(15.144)
-1-1 -1
где компоненты матрицы J, вектор-функции ф, и модуль якобиана
| J\ — это функции своих «родных» координат 8,, г) и С,.
Если коэффициент на Q { является некоторой функцией коорди-
нат х , у и z , то при интегрировании по под , естественно, под-
разумевается функция ч (ж (£ Т], <), у (£, Т], Q, z (£., Т], Q) .
Для произвольных шестигранников интегралы в соотношении
(15.144) берутся численно. Соответствующая схема вычисления значе-
ния интеграла от произвольной функции /(6., т],С) по с использо-
ванием квадратурных формул Гаусса имеет вид
f f f f(^Qd^d^~Y^ (15.145)
-1-1-1 Л:=1 Z=.’ r-=l
Её точность зависит от числа п, определяющего количество узлов
интегрирования. При п = 2 параметры tv и тр определяются соотно-
шениями
£]— 0.5773502692, t2 = ~tx , Tj: = T2 = 1 . (15.146)
В этом случае формула (15.145) даёт точное значение интегралов
для функций /(£.,!],Q, являющихся произведением любых полиномов
от £, Т]
Для
НИЯМИ
С, до третьей степени включительно.
= 3 значения tv и т„ в (15.145) определяются соотноше-
и
п
(15.147)
(15.148)
= 0, £.2=0.77459666924, £3 = ~t2 ,
Т1 = f, Т2 =т3 = |.
При п — 3 формула (15.145) абсолютно точна для функций
являющихся произведением любых полиномов от , т] и до пятой
754
15.Векторный МКЭ для решения задач электромагнетизма
степени включительно (заметим, что схемы с этим значением п наи-
более часто используются при численном интегрировании).
Для п — 4
^=—0.8611363116, t2 = — 0.3399810436, t3 =-t2, t4 = -tx, (15.149)
T1 — T4 — 0.3478548451, T2 = T3 = 0.6521451549 (15.150)
и формула (15.145) будет абсолютна точна для функций-полиномов до
седьмой степени включительно
И последними приведём значения tv и тр для п = 5 :
^=-0.9061798459, t2 = — 0.5384693101, t-3— 0, t4= —t2, tr= (15.151)
Ti = T5 — 0.2369268851, T2 = T4 = 0.4786286705, T3 = 0.5688888889.(15.152)
В этом случае формула (15.145) будет абсолютна точна для функций-
полиномов до девятой степени включительно.
Для элементов первого порядка обычно применяются схемы чис-
ленного интегрирования с п — 2 или п = 3. При использовании эле-
ментов высоких порядков схемы численного интегрирования с п — 2
или п = 3 могут оказаться очень неточными. В этих случаях лучше
использовать схемы интегрирования с большими п. Однако с ростом
п очень быстро (пропорционально п3) растут вычислительные затра
ты на получение значения каждой компоненты локальной матрицы
Поэтому не следует как пользоваться схемами численного интегриро-
вания с малыми п для элементов высоких порядков, так и использо-
вать схемы численного интегрирования с большими п для элементов
невысоких порядков.
Теперь рассмотрим, как можно вычислить компоненты матрицы
жёсткости векторного шестигранника . Для этого так же, как и при
вычислении матрицы массы, удобно воспользоваться заменой пере-
менных х , у и z (определяющих точки в П,„ ) на переменные £,, т) и
С, (определяющие точки в Q^). Однако здесь возникает проблема,
связанная с определением вида функции rot ф., при замене перемен-
ных (.т, у, z) на (£,, -г], Q.
Чтобы воспользоваться заменой переменных (х,у, г) на (£., г], С) ПРИ
вычислении компонент матрицы жёсткости, нам нужно получить вы-
ражение скалярного произведения rot фг rot фу в координатах
(£>Л>0- И ПРИ этом мы, конечно, должны воспользоваться тем, что
вектор-функции ф,: после замены переменных (ж, т/, z) на (6,, бу-
дут иметь вид (см. (15.135))
Ф» (я ЛЛ), У (£, Л, Q),z Л, Q) = ЛЛ) ЧЛ (^Л<) - (15.153)
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 755
Обратим внимание на то, что, хотя в левой части соотношения
(15.153) и стоит вектор-функция координат (6,, Т), С,), тем не менее её
компоненты являются проекциями на оси х , у и z . И нам желательно
получить аналогичное выражение для вектор-функции rot я|1,, т.е. мы
бы хотели получить вектор-функцию Rip,-, компоненты которой сов-
падали бы с проекциями rot яр, на оси ж, у и z, но при этом были
определены как функции переменных (£,, т], С,) (это обеспечило бы пра-
вильное вычисление скалярных произведений rot яр, rot яр, при заме-
не переменных (.?, у, z) на (£,,лЛ))- И, кроме того, нам желательно
получить такое выражение для вектор-функции Кяр?-(G,, т],С)> которое
позволило бы вычислять её через воздействие оператора rot в коор-
динатах (р, Т), С) на базисную вектор-функцию <£,: (£,, т], С,) (а не через
воздействие оператора rot в координатах (t,?/,z) на базисную вектор-
функцию (fyx, у, Z),T)(Z, у, z),C.(z, т/, г))).
Покажем, что выражение, определяющее вектор-функцию
R-ф. (£,, Л,С) через rot ф.( (6,, т], С,), имеет вид:
I^Pi (tuQ = jJTrot(p,, (15.154)
где оператор rot воздействует в координатах (8,, т], С,) и функциональ-
ная матрица J и вектор-функция ф, , естественно, также заданы в ко-
ординатах (8., Т|Л)-
Обозначим через яр|^ вектор-функцию
= Фг (^,ЛЛ),ЖЛ,О^(£>>ЛЛ))> (15.155)
т.е. компоненты вектор-функции яр, совпадают с компонентами век-
тор- функции яр.,, но при этом компоненты яр,^ являются явно задан-
ными функциями переменных 6,, л и Q (в отличие от компонент век-
тор-функции яр,, которые являются явно заданными функциями пере-
менных х , у и z , а зависимость яр, от £, г] и С, фактически является
параметрической).
756 15.Векторный МКЭ для решения задач электромагнетизма
Заметим, что именно вектор-функция была определена нами
как J ф>7, где ф, (£,,r),Q - стандартная базисная вектор-функция шаб-
лонного элемента т.е. (это с очевидностью следует из соотноше-
ний (15 153) и (15.155))
Ф?е(£.. <К) = ЛиО & (U0 • (15.156)
Чтобы убедиться в справедливости (15.154), нужно получить выра-
жения для компонент вектор-функции Иф; в переменных 8,, т] и (^ и
сравнить их с компонентами вектор-функции yJTrot<pt, стоящей в
правой части (15 154).
Получим выражения для R/ф, в переменных 6,, т] и С Прежде все-
го, воспользовавшись правилом дифференцирования сложной функ-
ции, выразим производные компонент вектор-функций ф- по пере-
менным 6,, т) и С, через производные соответствующих компонент
вектор функций ф\ по переменным х, у и z (с учётом соотношения
(15.155)):
at
Эп
дх д^ ду ЭЕ, dz
ду д^Цх,у,г)
ду Эт) + dz
ду д(^ + dz
дх Эт)
dz
dz
сЛп ’
(15.157)
(15.158)
____________________________________________dz_
д(^ дх д(^ "и ду д^ "г dz дС,
и аналогично для остальных двух компонент
функции -ф*^.
Из соотношений (15.157)-(15.159) и аналогичных им для у- и z-
компонент вектор-функций ф-2 и ф, получим выражения, связы-
вающие производные компонент вектор-функций ф,2 по переменным
, Г] и с производными соответствующих компонент вектор-
функций фх по переменным х, у и z, в виде:
дх
(15.159)
•фу,г вектор-
И
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 757
4r.t 4г,.
дх
4“f dip.,- i
сф dy
4’?f 4.г,<
ас. dz
4g, 4B,i
дх
4g,f Эт] = J 4j/,l ду
4gf 4В,» dz
д^г^ 4г,«
dk дх
4gf 4г,.
dr] = J ду
д&£ 4г,7
dz
где J - функциональная матрица (15.136).
Из этих трёх систем уравнений по правилу Крамера получаем вы-
ражения для производных компонент вектор-функций ф7 по перемен-
ным х , у и z :
4“t A 2
4^ _ 1 . . дх j dqt dr] 7’22 J-2.A
ас Ай J-.VA
7 ' Ai дк -Аз
4ri 1 -4^ = 4 det dy J J J Э71 Аз J
J 1 An
^'Фу/,г 4gf 4gf 712 Аз 7, >
dx - j det Эт| J22 J23 5
4gf d<^ Ай A13
и т.д. (здесь, очевидно, — компоненты функциональной матрицы
J , т.е. Ап = *Л -2 = и т-Д-> а «7 - якобиан, т.е. J = det J ).
de,
С помощью этих выражений для частных производных компонент
вектор-функций ф, уже легко получить выражения для всех грех ком-
понент вектора Rip . Получим, например, соотношение, определяю-
щее первую компоненту вектора Яфг:
758
15.Векторный МКЭ для решения задач электромагнетизма
, 1
ду dz J
<9т)
дК
—р2зЛи )н—ф^“(711^33-Лп Лз)+
a-^v
+ 1J2a)--^г~ р21^3'2 -^22^31 )~
(Z Z 7 , X p r J J \
—1J12JH - JH<32j-----------P1IJ22 -^21J12)
(15.160)
Получим теперь выражение для первой компоненты вектора, стоя-
щего в правой части (15.154). Для этого сначала получим выражение
для вектора :
j 1+712 + 7 ГЗ'Фгд
л()Е З-Фг = 72i4>-/,i + 7-224’w,ii + 7234>z,?: 7314>“.f +7з2ф”? +7зз*Фг,? ?
Используя равенства
а7ц _dJ-n 5q ' de* t)t> ’ dQ д‘Г] ’
dJ\-2 = ^J22 <9^12 _ ^7з2 9J22 _ ас ас ’ ас д.1-А2 aq ’
dJ13 gJ23 0T] d^ ’ а<^1з _ a J33 aj-23 ~~дС=~дС ’ “ас^=' 9J.H ал ’
(15.161)
сразу следующие из определяющего функциональную матрицу J со-
отношения (15.I36)1, и вычисляя нужные производные (по 6,, т] и 0
компонент вектора (15.161), получаем следующие выражения для ком-
—• I Т "7 (
понент вектора rot ip2 = rot J-ф,
I Поскольку и т.д.
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 759
( a^i2f a^?f a-4>"f a4>“f +J- an 721 a^’ i ~
1 J:ti ап +-^ 32 ) th]
Л ajyf + 713 -7з1 -732 g -7зз
rottp,= ас. к + 7.2 !722
^zf ^rlf ^zf .4. 7.,.. z>’ 7 7. ,, •,y'1 7., Z’’
Al ai] +12 +1.» J
Из этого соотношения легко получить выражения для всех компо-
нент вектора, стоящего в правой части доказываемого нами равенства
(15.154). Например, первая его компонента получается умножением
первой строки матрицы JT на полученный вектор rot ср., и делением
на якобиан, т.е. имеет вид
a^f
----J21J33 + J31J21 -ffiT- + J31J22 ~ ~ + Ли723
a^/f a^”f a^>“f _ j a$“f
~J31J11 —------J31J12 —Щ----Ли Аз “J (A1J32-J12J31) +
ai]< а^Л
+ (-^21^32+^317-22) Ч-----(-^217зз+7з17'2з)
Сравнивая полученное выражение с (15.160). убеждаемся в их пол-
ной идентичности. Точно так же можно убедиться в совпадении вто-
рой и третьей компонент векторов R-ф, и -у J rotip,.
Итак, мы убедились в справедливости соотношения (15.154) и с ею
помощью можем выполнить замену переменных (.г, у, z) на (£,,?],С)
при вычислении компонент матрицы жёсткости’
760
15 Векторный МКЭ для решения задач электромагнетизма
1 1 1
Gi} = J 1 rot ф, rotapydQ = f J /1кф,аф,р|<^<м; =
u... -1-1-Г
1 1 1
-ff J“;(j jTrotsP>) (j'jTrot<P/)lJl^ri'nd^ =
-1-1-Г
i i i
(15.162)
Интегралы в выражении (15.162) чаще всего вычисляются с помо-
щью формул численного интегрирования1, которые были приведены
нами чуть выше (см. соотношения (15.145)-(15.152)). Коэффициент р,
при этом может как заменяться своим средним значением р на конеч-
ном элементе , так и вычисляться как сложная функция координат
(tnO:
р. = р. (.г ft, т), Q), у ft, т),О, z ft, т), С,)).
Очевидно, формулы (15.144) и (15.162) справедливы для шестигран-
ных элементов с базисными вектор-функциями любых порядков Они
также довольно удобны для вычисления матриц массы и жёсткости пря-
моугольных векторных параллелепипедов высоких порядков. В этом
случае функциональная матрица J является диагональной (на её диаго-
нали стоят числа htp, hyl2, ) и компоненты локальных матриц
массы и жёсткости удобно вычислять в виде суммы трёх слагаемых
z-f 2/lp г У с I
~ ТГ7Г I . I -^L^i-rot^jd^d-qdC, +
nTJnz _j р
2lly г l- L- I
+ 7Г7Г I ( •/ +
2А. 1 * 1
+ т~Г~ I -I J .
1Сл _ hyhz г * 1 * *
2,гх
1 Исключениями являются случаи, когда либо могут быть получены доста-
точно простые аналитические выражения для компонент матрицы жёсткости
(например, когда шестигранник является прямоугольным параллелепипедом),
либо возможны существенные упрощения этих формул (например, когда шес-
тигранник является прямой призмой с четырёхугольным основанием).
15 12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 761
hrh, I 1 1. - ~ hxhy 11 I. „
+ ~^~J .1 j ^Фуз'ФуА^^ + J J J А^А .
ЛГ1у -1-1-1 z -1-1-1
причём значения достаточно легко получить для шаблонных базисных
вектор-функций ф, любых порядков, исходя из их вида (см. с. 721-729).
Таким образом, локальные матрицы жесткости и массы векторных
параллелепипедов любых порядков могут быть представлены в виде
суммы трёх числовых матриц1 с коэффициентами в виде некоторых
произведений /ix, Л,у, hz или обратных к ним величин.
Обратим также внимание на то, что локальные матрицы параллеле-
пипедов, вычисленные по рассмотренным здесь формулам, будут от-
личаться от матриц, приведённых в разделе 15.12.2. Причина заключа-
ется в том, что базисные вектор-функции параллелепипедов вводились
нами так, что их касательные были равны единице на соответствую-
щих рёбрах (и в соответствующих точках граней элемента Q,„ для
функций высоких порядков). Здесь же ецинице на соответствующих
рёбрах и в точках равны шаблонные вектор-функции ф,, которые
после отображения в Q./(z становятся локальными базисными вектор-
функциями с касательными, равными не единице, a 2//i,., или
2piz (в зависимости от направленности ребра).
И в заключение получим с помощью формулы (15.154) выражение
для R/ф , которым мы фактически воспользовались в соотношении
(15.109) при вычислении матрицы жесткости векторного четырех-
угольника ЭР. Для этого построим шестигранник в виде прямоуголь-
ной призмы , основанием которой является четырёхугольник Qp'.
Высоту призмы Q.,„ (т.е. ее размер по z) возьмём равной единице. На
Q„, определим векторные базисные функции которые в плоско-
стях оснований Q.„, совпадают с базисными вектор-функциями четы-
рёхугольника и при этом не изменяются по z (т.е зависят только
от переменных х и //). Очевидно, вектор rot фр будет иметь нулевые
х - и у-компоненты (поскольку х- и ^-компоненты каждой вектор-
функции ф не изменяются по 2, a z -компонента фс равна нулю), а
значит, и у вектора R-ф ($,, т|.(,) будут нулевыми первые две компо-
ненты. Третья же компонента этого вектора в соответствии с формулой
(15.154) может быть получена как результат умножения третьей строки
матрицы J* (где J — функциональная матрица преобразования, псре-
1 Т.е. матриц, компоненты которых являются числами.
762 15.Векторный МКЭ для решения задач электромагнетизма
водящего шаблонный элемент [—1,1] х [— 1,1] х [0,1] в призму Q,n ) на
вектор rot ф, и деления на якобиан. Отметим, что размер шаблонного
элемента по третьей координате взят единичным и совпадает с разме-
ром призмы Q„, по z , и поэтому функциональная матрица такого пре-
образования имеет вид
(1° 1CJ JY2 0
J = тО "'21 J22 0
0 к 0 1
(15.163)
где J° - компоненты функциональной матрицы J° преобразования,
переводящего двумерный шаблонный элемент [— 1,1] х [—1,1] в четы-
рёхугольник .
Учитывая, что J = JL (J - определитель функциональной матри-
цы (15.163), a J‘J - определитель Л;/), из (15.154) получаем выраже-
ние для третьей (единственной ненулевой) компоненты вектора R-ф
в виде
1 [бфрр
Я.
Эт|
(15.164)
где ф, и ф°,; - компоненты вектор-функции ф3 двумерного шаб-
лонного элемента [— 1,1] х [— 1,1], отображаемого в четырёхугольник
Q'7
Таким образом, единственная ненулевая компонента вектора1
roti]?;7 для двумерной базисной вектор-функции ф77 четырёхуголь-
ника после замены переменных (.г, у) на (6,, т|) примет вид
(15.164) (или в другой форме —туго!ф°), чем мы, собственно, и вос-
пользовались в соотношении (15.109).
Заметим, что проведённые здесь рассуждения могут быть полезны
при создании специальных методов генерации матрицы жёсткости и
массы векторных шестигранников, являющихся прямыми призмами с
четырёхугольными основаниями. Для таких векторных шестигранни-
ков так же, как и для прямых призм с треугольными основаниями, ло-
кальные матрицы могут быть сгенерированы с помощью локальных
1 Этот вектор перпендикулярен плоскости, в которой лежит , и поэто-
му его можно считать скаляром, что мы и делали при рассмотрении двумер-
ных векторных элементов.
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 763
матриц векторных и скалярных четырёхугольников. Очевидно, интел-
лектуальная трудоёмкость такого подхода несколько выше (по сравне-
нию с подходом, основанным на численном интегрировании), но зато
это позволяет довольно существенно снизить вычислительные затраты
при генерации конечноэлементной СЛАУ, особенно если учесть, что
для обращения матрицы J существуют очень простые формулы
(15.105). Эти формулы имеет смысл использовать и в том случае, когда
компоненты матрицы массы шестигранника (являющегося прямой
четырёхугольной призмой) вычисляются с помощью численного ин-
тегрирования.
15.12.6. ГЕНЕРАЦИЯ ВКЛАДОВ ОТ КОНЕЧНЫХ ЭЛЕМЕНТОВ
В ВЕКТОР ПРАВОЙ ЧАСТИ
Компоненты глобального вектора правой части b определяются
соотношением (15.142). Здесь мы рассмотрим, как генерируются вкла-
ды в b, определяемые объёмным интегралом. При этом мы учтём при-
роду вектор-функции F, являющейся правой частью уравнения (15.2)
и входящей в подынтегральное выражение объёмного интеграла в фор-
муле (15.142).
При решении нестационарных задач вектор-функция F — это сум-
ма вектора плотности сторонних токов Jcr (являющегося правой ча-
стью исходного нестационарного уравнения (15.1) и взятого на теку-
щем временном слое) и линейной комбинации FA — У^^.А^ реше-
к
ний А , А и др. на предыдущих временных слоях1:
F = JCT 4- Fa .
Поэтому в случае, когда уравнение (15.2) получено в результате ап-
проксимации нестационарной задачи, вклады в глобальный вектор b
правой части конечноэлементной СЛАУ от JCT и FA учитываются по-
разному. Так как решения А на предыдущих временных слоях были
найдены в виде А'1 = У^ q, *ф/ , то
i
Jfa -ф/ю = Id^K • = У2 • 4/^
П к Q к Q I
1 Коэффициенты ф. определяются через параметры задачи о и е и по-
этому могут быть (как и о и е) функциями пространственных координат;
конкретный вид ф. определяется типом используемой схемы аппроксимации
по времени.
764
15.Векторный МКЭ для решения задач электромагнетизма
и вклады от Fa в глобальный вектор b лучше всего вычислять через
матрицу массы1. При этом возможны несколько путей.
Можно сгенерировать глобальные матрицы массы Мп и Мс с ком-
понентами
— Jcnj>7 -ф/с/П , MfL — , (15.165)
Q Q
и сформировать вклады от FA в глобальный вектор правой части ум-
«=л-
ножением этих матриц на соответствующие векюры весов q , полу-
ченные на предыдущих временных слоях. Например, для трёхслойной
схемы аппроксимации по времени
-|-Мс
2
+ bJ'T, (15.166)
где bJ - вектор, определяемый составляющей JCT правой части F
уравнения (15.2)
Очевидно, в этом случае нужно будет хранить в памяти компьютера
три глобальные матрицы2: наряду с глобальной матрицей С конечно-
элементной СЛАУ Cq = b , которую для рассматриваемой нами трёх-
слойной схемы можно представить3 в виде
с = G + 1 м" + Т-
(15.167)
2___дг
нужно хранить еще и глобальные матрицы М'1 и МЕ .
Бели же память компьютера является довольно дефицитным ресур-
сом. то вклады в вектор b правой части конечноэлементной СЛАУ от
составляющей FA правой части F уравнения (15.2) можно учитывать
1 Вообще говоря, это самый правильный путь. Другие способы, когда
вклады от и FA вычисляются не одинаково, могут привести к гораздо
большим ошибкам аппроксимации.
2 Или в лучшем случае две, если либо коэффициент п равен нулю во всей
расчётной области, либо можно пренебречь токами смещения (и тогда е = 0).
3 При этом совсем не обязательно вычислять С как сумму трёх матриц,
она может формироваться из локальных матриц С конечных элементов, уже
являющихся суммой соответствующих локальных матриц жёсткости и массы,
т е., например, для трёхслойной схемы аппроксимации по времени
С = G + + 7-----Д------?М (сравните с (15.167)).
15.12 Генерация конечноэлементной СЛАУ в векторном МКЭ ... 765
и на локальном уровне. Например, для трёхслойной схемы аппрокси-
мации по времени
где Мг и Мс - локальные матрицы массы конечного элемента Q„,,
г 1ст
b - вклад в локальный вектор правой части от стороннего тока на
Q,tt, a q - локальные векторы, определяющие на 0,1П конечноэлс-
ментное решение на предыдущих временных слоях
В последнем случае, очевидно, при генерации глобального вектора
правой части будет сделано большее количество арифметических опе-
раций. но зато не нужно хранить глобальные матрицы массы М'
и МЕ.
Заметим, что основанные на использовании матриц массы методы
учёта вкладов в глобальный вектор правой части конечноэлементной
СЛАУ от составляющей FA вектор-функции F реализуются совер-
шенно одинаково для любых типов конечных элементов (любой гео-
метрии и с базисными вектор-функциями любого порядка).
Теперь рассмотрим, как учитываются вклады в глобальный вектор
правой части конечноэлементной СЛАУ от составляющей Jct вектор-
функции F. Эти вклады, естественно, удобнее всего вычислять в виде
локальных векторов bJ конечных элементов . Компоненты век-
тора bjC1 , очевидно, должны вычисляться по формуле
(15.169)
^tii
Интегралы в правой части (15.169) могут вычисляться различными
способами. Простейший из них основан на том, что вектор плотности
сторонних токов JCT аппроксимируется на конечном элементе не-
которым вектором-константой. Обычно в качестве такого вектора-
констангы берётся значение Ju в центре конечного элемента О.,п . Этот,
безусловно, вычислительно самый малозатратный метод целесообразнее
всего применять в случаях, когда вектор плотности сторонних токов JCI
постоянен1 или почти постоянен на конечном элементе, а также при
1 Для многих практических задач довольно характерной является ситуа-
ция, когда JCT - кусочно-постоянная вектор-функция, а значит, на каждом
конечном элементе этот JCT является вектором-константой.
766 15 .Векторный МКЭ для решения задач электромагнетизма
использовании векторных тетраэдральных элементов первого порядка
(и особенно с «минимальным» базисом, в котором нет вектор-функций
вида (15.125), - на таких элементах этот метод практически не отличает-
ся по точности от метода вычисления локального вектора через локаль-
ную матрицу массы, который мы рассмотрим чуть ниже).
Приведём формулы для вычисления компонент локального вектора
тетраэдрального конечного элемента О,т, основанные на способе с
заменой JCT на вектор-константу на Qin .
Пусть (±r,?/r,zf.) - координаты центра тетраэдра с вершинами
1 4 1 4 1 4
(т-е. , у,- = ’ £• = >• Тогда с Учё"
д=1 i=l j = 1
том вида (15.124) локальных базисных вектор-функций тетраэдрально-
г 1СТ
го элемента компоненты его локального вектора будут иметь вид
= f ‘ (Д(/>) §rad Л(р) ~ £j(p) £rad ^(р) )=
^111
= Зст (£•. Ус, К. ) • (аД- <У-'М) , (1 5.170)
где detD — определитель матрицы D, значение которого может быть
вычислено с помощью соотношения (6.36) (сама матрица D определя-
ется через координаты вершин тетраэдра соотношением (6.27)),
а/ = — векторы, составленные из компонент матрицы
CL, определяемой соотношением (6.28), a j(p) и г{р) - локальные
номера вершин тетраэдра, определяющие ребро тетраэдра Q,„ с ло-
кальным номером р. Таким образом, каждая компонента вектора bjCT
вычисляется как скалярное произведение вектора JCT и раз-
ности векторов — о/7')), умноженное на коэффициент
|detD|/24 .
Второй способ вычисления локального вектора bJtT конечного эле-
мента основан на представлении JCT на Q,zl в виде разложения по
базисным вектор-функциям, т.е.
^«ЕМ- (15.171)
J
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 767
тст
При использовании этого способа локальный вектор b может
быть получен в результате умножения матрицы массы1 М1 на вектор
f, компонентами которого являются коэффициенты f:j разложения
JCT на по базису {'Ф/ j (см. (15.171)), т.е.
bjCT=M‘f. (15.172)
Вообще говоря, формула (15.172) справедлива для любых типов
конечных элементов (любой геометрии и с базисными функциями лю-
бого порядка). Основной проблемой здесь является получение значе-
ний коэффициентов /у в разложении (15.171). Для edge-элементов
(элементов первого порядка) каждый вес /у может быть получен, на-
пример, как значение в середине ребра Гу проекции на него вектор-
функции JCT, где Гу - ребро, с которым ассоциирована базисная век-
тор-функция -фу, т.е.
7 (15.173)
где xi.yl.z'. - координаты центра2 ребра Гу, v7 - вектор, направлен-
ный вдоль ребра3 4 Гу и с(Л1 оправленный* с базисной вектор-функцией
-ф/5 a — длина вектора vy.
Для тетраэдральных элементов первого порядка при наличии в их
базисе функций типа (15.125) соответствующие веса могут быть вы-
числены как полуразность касательных к ребру Гр составляющих
1 Напомним, что под М1 мы понимаем матрицу массы (15.141) конечного
элемента при = 1.
2 Каждая из координат х{,-это полусумма соответствующих коор-
динат вершин Гу.
3 Например, в качестве vy может быть взят вектор с координатами, рав-
ными разности соответствующих координат вершин ребра Г,.
4 Очень важно проследить, чтобы направление вектора v; было таким,
что скалярное произведение v, • ф/ было положительным.
768 15.Векторный МКЭ для решения задач электромагнетизма
вектор-функций JCT в вершинах этого ребра*. Если же на тетраэдрах
используются базисные функции типа (15.126), то, очевидно, в качест-
ве двух ассоциированных с этим ребром весов fap-i и Лр можно
брать касательные к ребру Гф составляющие JCT в соогвегствующих
его вершинах.
В принципе, для элементов первого порядка значения fj можно
вычислять и по более сложной схеме, через значения касательной со-
ставляющей JCI в нескольких точках ребра (это можно делать как для
параллелепипедов, так и для других элементов - тетраэдров, призм,
шестигранников). Например, значение (т.е. значение веса вектор-
функции фу, ассоциированной с ребром Г7, в разложении Jcr по ба-
зису первого порядка см- (15.171)) может быть получено как
взвешенная сумма значений касательной к Гу составляющей JCT в
вершинах ребра Гу, взятых с весом 1/6, и значения касательной к Гу
составляющей JCT в центре этого ребра, взятого с весом 2^,3 (как это
было сделано для прямоугольного элемента, см. с. 698).
При использовании же базисов высоких порядков значения /у, по-
зволяющие достаточно точно представить JCT в виде (15.171) на Q/n,
вычисляются относительно просто в тех случаях, когда на конечном
элементе без особого труда можно указать точки (х3у3, , в
каждой из которых все базисные вектор-функции ф/. при k j либо
равны нулю, либо ортогональны базисной вектор-функции фу, т.е.
ф7 (х3, у3,z3 фА [х3, у3 ,z3^ = 0 \/к j . (15.174)
В этом случае значения весов f в разложении (15.171) вектора
плотности сторонних токов JCT по базисным вектор-функциям ф-
1 Очевидно, при вычислении этой полуразности значение JCT • v касатель-
ной составляющей плотности токов в ней должно браться «с плюсом» в вер-
шине, где ф - v > 0, и «с минусом» в вершине, где ф - v < 0 (v - вектор,
направленный вдоль ребра, ф - соответствующая рассматриваемому ребру
базисная вектор-функиия, определяемая соотношением (15.125)).
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 769
могут быть вычислены по формуле
fj = (Лст(ж< у3,z3) • чЦж-', у3, z3))Iу3, zJ) • чЦя-', у3, z3 j) .
Однако довольно просто определить точки, в которых выполняется
соотношение (15.174), можно только при использовании параллелепи-
педов с базисными вектор-функциями лагранжева типа. На других же
типах конечных элементов (тетраэдрах, призмах, шестигранниках)
точек, в которых выполняется соотношение (15.174), может просто не
существовать. Кроме того, даже для элементов первого порядка метод,
.. г 1СТ
основанный на вычислении локального вектора о через матрицу
массы М1 по формуле (15.172) (с вычислением fj по формуле
(15.173)), может оказаться довольно неточным1 из-за относительно
большой погрешности представления JC1 на . Таким образом, ме-
тод, основанный на использовании для генерации bJ формулы
(15.172), на практике целесообразно применять лишь для векторных
параллелепипедов.
Гораздо более универсальным и при этом позволяющим обеспечить
представление JCT на Q/n практически с любой необходимой точно-
стью является следующий метод.
Введём на Q,n скалярные лагранжевы базисные функции ф-,
i, = 1...71*1’' . Координаты узлов, определяющих эти скалярные базис-
ные функции, обозначим через (x^y'^z^j (г = l...n,lh ), т.е.
1, к = г,
О, к i.
Обозначим также через /лс\., JJV, значение соответствующих
компонент вектор-функции JCT в узлах [x^y'^zf^ (т.е.
ит-д-)-
Порядок базисных функций *ф* выберем такой, чтобы вектор-
функция
1 В принципе, для элементов первого порядка этот метод мало отличается
по точности от рассмотренного нами чуть выше метода с заменой JCT на Q.,„
вектором-константой, а по количеству операций он является заметно более
трудоёмким.
770
15,Векторный МКЭ для решения задач электромагнетизма
(15.175)
была на достаточно близка к вектор-функции Jcr.
Определим на Q/(t вектор-функции
Тогда JCT может быть представлен в виде (см. (15.175))
= (15.177)
1=1
где
a3k_2 = J“k, a3k^=J^k, a3k=J^.. (15.178)
В результате, заменяя в формуле (15.169) вектор-функцию JCT на её
покомпонентный интерполянт JCT, определяемый соотношением
(15.177) (в котором коэффициенты щ определяются соотношением
(15.178), а базисные вектор-функции - соотношением (15.176)), полу-
“L JCT
чаем выражение для вычисления компонент вектора b
ьГ = I (15.179)
/=1 О
Интегралы в соотношении (15.179) для любых рассмотренных нами
элементов (любого порядка), кроме шестигранников, можно вычис-
лить аналитически. Это позволяет добиться высокой точности вычис-
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 771
г 1СТ
ления компонент локального вектора b при относительно невысо-
кой трудоёмкости машинных вычислений.
Для шестигранников же интегралы в (15.179) обычно вычисляют с
использованием шаблонного элемента (поскольку именно на нём оп-
ределён аналитический вид базисных вектор-функций), и поэтому по-
лучить их значения аналитически чрезвычайно сложно из-за сложного
вида матрицы J ( J - функциональная матрица преобразования шаб-
лонного кубика QE в шестигранник Qw). Исключением могут быть
некоторые специальные случаи, например, когда шестипэанник явля-
ется прямой призмой (с четырёхугольным основанием). Если же шес-
тигранник не является прямой призмой, то и даже тогда, когда для
значений интегралов в (15.179) аналитические формулы получены, они
могут оказаться очень громоздкими и вычислительно неустойчивыми.
Поэтому для шестигранных элементов (особенно, если они имеют
изогнутые границы и на них заданы базисные вектор-функции высо-
ких порядков) обычно используют также достаточно универсальный и
относительно простой метод, основанный на численном интегрирова-
нии. Рассмотрим его.
гг г Iег
Компоненты локального вектора о на шестигранном элементе
Qr„ вычисляются с использованием отображения Qw в шаблонный
элемент (которое фактически является обратным к отображению
Q* в Q,„, определяемому соотношениями (15.134), или (15.138), или
аналогичными им с другими скалярными функциями фу). С учётом
того, что базисные вектор-функции ф. на шестиграннике Qm опреде-
ляются через шаблонные (определённые на QE) вектор-функции ф, с
помощью соотношения (15.135), выражение для компоненты bf* при-
мет вид1
б/ = J" JCT (:Г,1/,г) • Яр.,; (x,y,z)dQ, =
—J* JCT(:c,y,2) (J fe(.c,y,c),T](a;,y,z),C(a: y,z}) ф/(£,(:Е,(/1£),т](.г\1/,2),С>(.т,у,г))^ dxdydz =
= f J Ф/ И d^dtydC, .
1 Ещё раз обратим ваше внимание на то, что JCT = JCT (.г,у,z) - это вектор
плотности сторонних токов, a J = J (£», т), С,) _ функциональная матрица, опре-
деляемая соотношением (15.136).
772
15.Векторный МКЭ для решения задач электромагнетизма
Для вычисления последнего интеграла (по кубику О,Е) можно ис-
пользовать рассмотренные нами ранее стандартные формулы числен-
ного интегрирования (см. соотношения (15.145)-(15.152)).
15.12.7. УЧЁТ КРАЕВЫХ УСЛОВИЙ
Рассмотрим, как учитываются естественные краевые условия (за-
данные в виде (15.8)) в векторном МКЭ. Эти краевые условия дают
вклады в вектор правой части конечноэлсмснтной СЛАУ (см. соотно-
шение (15.142)).
Компоненты локального вектора Ь'2 вклада от грани1 , яв-
ляющейся участком границы S'2 (где заданы естественные краевые
условия (15.8)), определяются соотношением
1 = f (Йв хпЦ4 (15.180)
°2
где зр, — локальные базисные функции поверхностного элемента S*.
Под зр.,, очевидно, подразумеваются вектор-функции, определяемые
как значения тех глобальных базисных вектор-функций, у которых
касательные к грани S™ отличны от нуля на S-2 .
Сначала скажем несколько слов о возможных способах хранения
граней S-2 . Один из них заключается в задании каждой грани S-2l но-
мерами узлов сетки (абсолютно аналогично тому, как задаются конеч-
ные элементы Q„,). Такой способ довольно часто используется при
хранении граней тетраэдральной сетки. Однако только трёх вершин
треугольной грани S-2 недостаточно, чтобы получить значения вкла-
дов от неё в вектор правой части конечноэлсмснтной СЛАУ, посколь-
ку для вычисления этих вкладов нужен вектор единичной нормали п с
определённым направлением (п должен быть направлен из расчётной
области Q). Для этого можно, например, хранить вершины грани в
строгом порядке (так, чтобы по векторному произведению рёбер мож-
но было однозначно определить направление внешней нормали). Для
векторных тетраэдров этот способ очень неудобен, поскольку он мо-
жет вступать в противоречие со способом определения направления
базисной вектор-функции (так как направление базисной вектор-
функции также наиболее удобно связать с порядком перечисления
вершин). Поэтому для однозначного определения направления внеш-
ней нормали наряду с номерами вершин, задающими грань S-2 , можно
хранить ещё и номер узла, по которому можно однозначно определить
направление нормали. Для тетраэдральных сеток в качестве номера
1 Для рассмотренных нами типов трёхмерных конечных элементов гранью
<5’2", очевидно, может быть прямоугольник, треугольник, четырёхугольник (в
гом числе и изогнутый).
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 773
такого узла удобнее всего хранить номер четвёртой (не принадлежа-
щей S!{1) вершины тетраэдра ГД., гранью которого является участок
S-2 границы S-2.
Другой способ хранения граней S%1, из которых состоит граница
.$2, заключается в следующем. Каждая грань определяется двумя це-
лыми числами. Одно из этих чисел — номер к конечного элемента ГД,
которому принадлежит грань S™, а второе - локальный номер нужной
нам грани в этом конечном элементе.
Очевидно, второй способ является очень экономичным и позволяет
практически без затрат получать всю информацию о базисных вектор-
функциях на S-2 и направлении нормали из структуры данных, в ко-
торой хранится информация о конечном элементе ГД.. Единственное (и
го очень относительное) неудобство этого способа состоит в том, что
нужных (с ненулевыми касательными составляющими) нам базисных
вектор-функций на S^' меньше, чем число локальных базисных век-
тор-функций на ГД, и поэтому на S™ нужно либо ввести еще одну
локальную нумерацию1 (как поднумерацию) локальных ба гисных
функций конечного элемента ГД., либо сделать локальную нумерацию
базисных вектор-функций на S™ точно такой же, как на ГД, и форми-
ровать локальный вектор Ь^2 большей длины с нулями в тех компо-
нентах, которые соответствуют локальным базисным вектор-функциям
конечного элемента Q/. с нулевыми касательными составляющими на
S-21. Очевидно, любой из этих путей реализуется очень просто.
* s,il
Вернёмся к проблеме генерации локального вектора b 2 грани
S'>'. Прежде чем приступить к обсуждению методов вычисления инте-
гралов в соотношении (15.180), определяющем компоненты локально-
го вектора Ь2 , рассмотрим, как можно вычислять внешнюю нормаль
п. Для некоторых типов конечных элементов нормали к их граням
определяются очевидно. Например, если S^' - это грань прямоуголь-
ного параллелепипеда, то вектором нормали является один из векторов
(1.0.0)т или (—1,0,0)1, либо (0,1,0)т или (0.— 1,0)т, либо (0,0,1)' или
(0,0, —1)т. Для других же типов конечных элементов (тетраэдра, приз-
мы и шестигранника) задача нахождения нормалей п к граням хоть и
не очень сложна, но не является совершенно тривиальной.
1 Для того, чтобы по ней сначала определять локальный номер рассматри-
ваемой базисной вектор-функции на конечном элементе ГД , а потом по этому
номеру брать хранящийся в информации об ГД глобальный номер соответст-
вующей базисной вектор-функции и по нему заносить компоненту локального
вектора грани S-2 в нужную компоненту глобального вектора правой части
конечноэлементной СЛАУ.
774 15.Векторный МКЭ для решения задач электромагнетизма
Рассмотрим, как можно вычислить единичную нормаль п к участ-
ку S21 границы S-2 , являющемуся гранью тетраэдра Q/.. Здесь можно
воспользоваться несколькими довольно простыми способами.
Во-первых, нормаль п можно получить через векторное произве-
дение vt х v2 двух векторов, направленных вдоль двух любых рёбер
треугольника S?{1 . Нужный знак у этого векторного произведения
(чтобы нормаль была внешней) можно определить, умножив его ска-
лярно на вектор v3, соединяющий любую из трёх вершин грани 5'2" с
четвёртой вершиной1 тетраэдра С/,, гранью которого и является уча-
сток S-2 . Будем считать, что вектор v3 направлен в сторону четвёртой
(не принадлежащей <S'21) вершине тетраэдра. Тогда, если
(vt х v2) • v3 < 0, то единичной внешней нормалью будет вектор
n = (vA х v2)J V! х v2||. В противном случае п = —, vj х v2 )/l|v, х v2||.
Нормаль п к участку S21, являющемуся гранью тетраэдра О/.,
можно также получить через его £ -координаты. Напомним, что век-
тор grad Д перпендикулярен грани тетраэдра, противоположной его
вершине с номером г. Поэтому, учитывая, что grad Д = (oif, а2, cd))Г,
получаем
Способ вычисления п через о^ удобен тем, что через а также
определяются базисные вектор-функции *ф2 на треугольнике 52" , т.е.
эти коэффициенты всё равно будут нужны для вычисления компонент
1 Здесь мы подразумеваем, что грань S-^ хранится последовательностью
номеров четырёх вершин тетраэдра первые три из которых - вершины
грани S'". Если же грань S™ хранится как набор двух номеров (номера к
тетраэдра QA. и локального номера грани в этом тетраэдре), то вместо четвёр-
той вершины тетраэдра Q*., очевидно, должна быть взята та его вершина,
которая не лежит на нужной нам грани.
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 775
' S1'" / о Л -*
локального вектора b 2 (при интегрировании (Н хп1-ф4 по грани
)-.
На участках S2 границы S2, являющихся гранями прямых тре-
угольных призм, единичная внешняя нормаль определяется не сложнее,
чем для граней тетраэдров. Нормали к треугольникам, являющихся
основаниями призмы, - это, очевидно, векторы, направленные вдоль
«боковых» (перпендикулярных основаниям) рёбер призмы. Нормали
же к боковым граням призмы могут быть найдены либо как векторные
произведения векторов, направленные вдоль двух смежных ребер гра-
ни, либо через векторы grad Д , где Д — это £ -координаты треуголь-
ников, являющихся основаниями призмы.
Рассмотрим, как можно вычислить единичную нормаль п к грани-
це S2 для участка S'2, являющегося гранью шестигранника Ид . Как
всегда, будем считать, что шестигранник Q*. задан некоторым отобра-
жением (например, (15.134) или (15.138)) единичного кубика .
Грань S2 — это поверхность, в которую отображается одна из шести
сторон шаблонного кубика (которая для
= [— 1,1] х [— 1,1] х [— 1,1] определяется одним из соотношений
^ = — 1, 6, = 1, Т] = — 1, т] = 1, Д = — 1 или С, : 1).
Для определённости будем считать, что грань S2 получена ото-
бражением стороны 6, = — 1 кубика . Получим выражение для вы-
числения й в точке (.тр, y^z^, в которую отображается некоторая
точка с координатами q = qp и С, = Д,, лежащая на стороне 6, = — 1
кубика . Для этого воспользуемся тем фактом, что любой вектор
w = (0,)т, лежащий на границе £, = — 1 кубика , с помощью
функциональной матрицы J = J (Д, rg С,) преобразования в Од. пе-
реводится в вектор v = JT(— 1, ЛрЛр) w , являющийся касательным к
грани S2 в точке . Тогда направление vn нормали й мо-
жет быть получено с помощью векторного произведения отображён-
ных векторов Wj = (0,1,0)т и w2 = (0,0,1)т, т.е.
V» = (jT(—ПрЛр) Wi) х (15.181)
1 Напомним, что все коэффициенты с?7 находятся как компоненты матри-
цы, обрат ной к матрице D, составленной из координат вершин тетраэдра, см.
раздел 15.11.2.
776
15.Векторный МКЭ для решения задач электромагнетизма
а сама единичная нормаль - как1
Й = - vn/||vn||.
С учётом вида векторов Wj и w2 вектор vn, определяющий на-
правление нормали (к граням, полученным отображением сторон
6, = — 1 и С = 1 кубика Q£ ), примет вид
дх ду Qz
<Эт] ’ <Эт| ’ <Эт|
х
[ дх ду gH
К’дс’дс]
£.=-1
[ду dz dz ду
d(^ <Эт) д(^ ’
дг_дх_ дх dz
<Эт] at, дт] ЭС, ’
дх ду
<Эт] ас,
ду дх
ал ас, у
Для граней S'}1, полученных отображением сторон т] = +1 и
С — +1 кубика , направления нормалей, очевидно, определяются
соотношениями
[ дх ду дИ
1А’ ae/acj
[ дх ду
[ас ’ ас’ aj
Т)=-1
f ду dz dz ду
[ас ас ас, ас, ’
Эд Э:с dx dz
d^ d{ d^ SC ’
дхду__ду_дх^
st, ос, oi, ас, ’
1|=-1
(dx dy Qz\
[ас1 ac’ aej
^[dx dy dz\
* n 1 n , -7Г-1
1 Вектор vn в данном случае будет направлен внутрь шестигранника, по-
скольку в векторном произведении (15.181) перемножаемые векторы направ-
лены вдоль «координатных линий» шестигранника и их последовательность
такова, что по правой тройке вектор, получаемый в результате векторного
произведения, должен быть направлен в ту же сторону (по соответствующей
координатной линии), что и вектор (1,0,0)т в кубике QE . Очевидно, при тех
же векторах wi и w2 на грани С = 1 единичная внешняя нормаль п на соот-
ветствующей грани Qz. будет определяться формулой п = ^„/ЦуцЦ .
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 777
®V_dz__ dz ду
д^ <9т] д^ <Эт) ’
dz дх дх dz
д^ dr) д^ <9т| ’
дх ду
д^ <Эт]
ду дх
д^ дт\
Л=')//
С=-1
соответственно. Сама единичная нормаль й через vn определяется
соотношением
n = =Fvn/||vn||,
где знак «минус» используется для сторон т) = — 1 и С, = — 1, а знак
«плюс» — для сторон 1| = 1 и С, = 1 -
Рассмотрим теперь непосредственно методы вычисления компо-
~ gm
нент локальных векторов Ь'2 граней S™ . Они в целом мало чем от-
т JCT
личаются от методов вычисления компонент локальных векторов b
конечных элементов Q„, - это методы, основанные на замене Нн
(точнее, Нв х й ) вектором-константой на S-^, на представлении
Н° хп в виде разложения по локальным базисным вектор-функциям
грани S-2 (т.е. через матрицу массы поверхностного элемента S^' ), на
замене вектор-функции Ннхп покомпонентным интерполянтом (с
использованием узловых базисных функций) и на использовании чис-
ленного интегрирования
Метод, основанный на замене Н° х й вектором-константой на
S!{1 , даёт самые простые формулы для вычисления компонент Ь6'2 :
b-* = J (15.182)
qm
где вектор-константа w вычисляется по формуле
w = Нв (х(.,у,.,4) х й(хс,у,.,zr),
в которой (.£,., у(., z(.) — точка на S^', где берутся значения Нв и Й
(как правило, координаты этой точки вычисляются как среднее ариф-
метическое координат вершин S-j").
Например, для элемента S",1 , являющегося треугольной гранью тет-
раэдра , формула (15.182) примет вид (сравните с выражением
(15.1 70) для компоненты локального вектора тетраэдра)
fyf2 = Jw (Д(/,) grad - £j{p} grad Д(р)) dS =
778 15.Векторный МКЭ для решения задач электромагнетизма
= те8Д-(йв (я,., у,., z(.) х n (f(., 7/,., z(.)) • ,
где сс = (04,012,013) - векторы, составленные из компонент матрицы
CL, определяемой для Qj. (с нумерацией вершин, соответствующей их
нумерации на S2 1) соотношением (6.28), a j(p) и i(p) - локальные
номера вершин грани S™, определяющие её ребро с локальным номе-
ром р.
Рассмотрим, как может быть вычислен локальный вектор Ь'2 с
Л gm.
помощью стандартной матрицы массы М 2 грани S2‘ (как поверх-
ностного элемента), компоненты которой определяются соотношения-
ми
qm
В этом случае локальный вектор Ь^2 может быть получен умно-
жением MS‘2 на вектор 0 , т.е.
- счи. Л С’’11 ~
1>2 =М2е. (15.183)
Компонентами 0/ вектора О являются веса разложения вектора
шхп по локальным базисным вектор-функциям фу поверхностного
элемента S™ , т.е. (сравните с (15.171))
Нв Х11^ 52м, - (15.184)
.7
При использовании базиса первого порядка каждую компоненту 0у
вектора 0 можно вычислить как значение проекции вектора Й() х п
на ребро Г,, с которым ассоциирована базисная вектор-функция фу, в
середине этого ребра:
07 = (ЙВ (я/, у]., z->) х п , у?.., )) • V j/lj ,
где xl,y?.,zl — координаты центра ребра Гу, vy — вектор, направлен-
ный вдоль ребра Гу и сонаправленный с базисной вектор-функцией
a lj — длина вектора v?.
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 779
Значения 07 могут быть вычислены и по более сложным (но и чуть
более точным) формулам, использующим значения проекции вектор-
функции Н° х й на ребро Гу в нескольких точках ребра (как, напри-
мер, при вычислении коэффициентов /7 в разложении (15.171),
см. с. 769, 698 699).
gm
Для базисов высоких порядков вычислять b 2 через матрицу мас-
сы поверхностного элемента S™ довольно просто лишь в том случае,
когда на S'2" существуют точки, в каждой из которых ненулевую каса-
тельную к S-2 имеет только одна базисная вектор-функция. Тогда вес
0, этой базисной вектор-функции ф7 в разложении (15.184) можно
вычислить по формуле
где значения Н(), й и ф, берутся в соответствующей точке. Однако
такие точки легко указать лишь для прямоугольных граней и базисных
вектор-функций высокого порядка лагранжева типа. Для многих же
наиболее часто используемых типов конечных элементов (например,
тетраэдров и шестигранников) таких точек на их гранях может вообще
не существовать даже для базисных вектор-функций лагранжева типа.
Поэтому такой метод почти никогда не применяется при использова-
нии элементов высоких порядков (за исключением параллелепипедов с
базисами лагранжева типа).
/ч gill
Чтобы получить соотношения для вычисления Ь'2 с помощью за-
мены вектор-функции Н ’ хЙ покомпонентным интерполянтом, оп-
ределим на грани S^1 вектор-функции ф , каждая из которых имеет
только одну ненулевую компоненту (см (15.176)). Функции ф7 , яв-
ляющиеся компонентами вектор-функций ф , - это определённые на
узловые базисные функции лагранжева типа. Порядок функций
ф7 выбирается таким, чтобы каждая компонента вектор-функции
Н ’ хй могла быть достаточно точно представлена в виде линейной
комбинации функций ф7 .
Представим Н() х й в виде покомпонентного интерполянта:
3nv
Нв х п ^2 а7ф?, (15.185)
7=1
780
15.Векторный МКЭ для решения задач электромагнетизма
где «з/_2 - х -компонента вектор-функции Н хп в I -й точке (в ко-
торой ф/ равна единице, а все остальные ф*. равны нулю), а3к_х -
у -компонента этой вектор-функции в /-й точке, а азк - её z -компо-
нента.
Подставляя (15.185) в (15.180), получаем (сравните с (15.179))
bt'2 = ^(lj I ф. -4V,dS. (15.186)
J=I
Метод с покомпонентной интерполяцией Н°хп является доволь-
но универсальным. Входящие в соотношение (15 186) поверхностные
интегралы для многих типов граней S2 можно вычислять аналитиче-
ски, что позволяет добиваться высокой точности вычисления компо-
цент локального вектора b 2 при относительно невысоких вычисли-
тельных затратах. Трудности при получении соответствующих анали-
тических выражении возникают обычно в тех случаях, когда базисные
вектор-функции (да и скалярные функции ф/ ) на конечном эле-
менте Од (гранью которого является S2 ) определены с использовани-
ем преобразования координат (с помощью которого конечный элемент
О? получается из шаблонного элемента Оу ). Эта ситуация характерна
для сеток с шестигранными ячейками.
При работе с шестигранными конечными элементами наиболее
удобным способом вычисления компонент локальных матриц и векто-
ров является численное интегрирование. Этот способ остаётся очень
удобным и при вычислении вкладов от естественных краевых условий,
если участки S™ границы S2 являются гранями (в том числе и изо-
гнутыми) шестигранных конечных элементов.
Пусть участок S'2 границы S-2 является одной из граней ‘шести-
гранного конечного элемента Од., и этот шестигранник Од. определён
как отображение1 шаблонного кубика О; =[—1,1 х [—1,1] х[-1,
1] j
заданного в координатах (£,,т|}С,).
Будем считать, что грань S2l получена отображением стороны
= — 1 шаблонного кубика О^. Тогда интеграл по поверхности S-2 в
выражении (15.180) может быть вычислен как
1 Это отображение может быть построено с помощью трилинейных, трик-
вадратичных или других скалярных базисных функций, заданных на шаблон-
ном кубике О£ , см., например, (15.134) или (15.138)
15.12.Генерация конечноэлементной СЛАУ в векторном МКЭ ... 781
. С”1
V2
пт
д2
>,»,з)Л(;г>У»г)) JcZjS'—
S-2l
1
-1 -1
(15.187)
где J - функциональная матрица преобразования шаблонного кубика
Qe в шестигранник - шаблонные базисные вектор-функции, а
02 и Зз - функции, определяемые соотношениями:
(дх i < (dy i i_
IaJ
02=
(/ <2 \2 / V2)
I дх I . dy i dz I
IaJ
03 =
dx-dx, дУ dy I dz dz
дт\ dC,^ dq d^ "г <Эт]
(15.188)
Очевидно, соотношения, аналогичные (15.187)-(15.188), можно по-
лучить для любой из оставшихся пяти сторон (( = 1, q = — 1, Г] = 1,
С, — —1 и С, = 1) кубика .
Для вычисления интеграла по квадратику [— 1,1] х [— 1,1] в соотно-
шении (15.187) можно использовать стандартные формулы численного
интегрирования. Например, при использовании девятиточечной схемы
это формулы (15.106)-(15.108). Если же используются базисные век-
тор-функции высоких порядков, то лучше применять более точные
формулы:
1 1 п и.
Iff n)d^} ~ 52 T'T^ (*/• > fi) >
(15.189)
в которых значения параметров tv и т„ зависят от п (при п = 3 па-
раметры tv и т,, определяются соотношениями (15.147)—(1 5.148), при
п = 4 — соотношениями (15.149)—(15.150), при п = 5 - соотношения-
ми (15.151)-(15.152)).
И в заключение скажем несколько слов об учёте главных краевых
условий.
782
15.Векторный МКЭ для решения задач электромагнетизма
Различные способы учёта неоднородных главных краевых условий
были рассмотрены нами достаточно подробно в разделе 15 4 и в разде-
ле 15.Ф (см. с. 715-718); однородные главные краевые условия учиты-
ваются очень просто — либо обнуляются все компоненты соответст-
вующих строк и столбцов (с номерами i е N \ N()), либо эти компо-
ненты просто игнорируются (если все номера i G N \ NQ — последние,
т.е. г > п()).
15.13 . ПОСТРОЕНИЕ КОНЕЧНОЭЛЕМЕНТНЫХ АППРОКСИМАЦИЙ
ПРИ СОВМЕСТНОМ ИСПОЛЬЗОВАНИИ СКАЛЯРНОГО
И ВЕКТОРНОГО ПОТЕНЦИАЛОВ МАГНИТНОГО ПОЛЯ
15.13.1. ПОСТАНОВКА ЗАДАЧИ
В разделе 1.3.6 была рассмотрена математическая модель с со-
вместным использованием векторного А и скалярного U магнитных
потенциалов, очень удобная для решения нестационарных задач элек-
тромагнетизма, в которых поле формируется в основном за счёт вих-
ревых токов в отдельных проводящих объектах, окружённых непрово-
дящей средой.
Электромагнитное поле в этой модели на каждом временном слое
описывается системой из двух уравнений: векторного уравнения1
rot | у rot A j + = F (15.190)
дчя векпюр-пот енциала А, определённого в подобласти ПА, и ска-
лярного уравнения
—div (pgrad U) = 0 (15.191)
для скалярного потенциала U, определённого в подобласти . В
подобласть Q.,J должны бы гь включены только такие подобласти рас-
чётной области, в которых коэффициент удельной проводимости су
равен нулю. Подобласть же QA должна включать в себя все «прово-
дящие» подобласти (в которых о 0) и, возможно, некоторые «не-
проводящие» подобласти, являющиеся перемычками, не позволяющи-
1 Напомним, что уравнение (15.190) получается в результате аппроксима-
ции по времени уравнения (15.1). Коэффициент и вектор-функция F в
(15.190) определяются схемой аппроксимации по времени, а само решение А
является значением вектор-потенциала на текущем временном слое.
15.13 Построение конечноэлементных аппроксимаций ... 783
ми обходить ненулевые токи1 по области О,и. Таким образом, расчёт-
ная область Q представляется в виде объединения двух (возможно,
неодносвязных) подобластей QA и Qf/, не пересекающихся по своим
внутренним точкам.
На (возможно, неодносвязной) поверхности Яг'— ПАП , являю-
щейся границей между QA и Qt7, должны выполняться следующие
условия сопряжения:
— rot А х n = — (grad U х п) _,п ,
(15.192)
(15.193)
где и - нормаль к поверхности S'r (в дальнейшем мы будем считать,
гч т т
что она является внешней по отношению к QA), -------производная U
on
по нормали п (т.е. = grad U • ri).
Условие (15.192) обеспечивает непрерывность касательных состав-
ляющих напряжённости магнитного поля Н на поверхности б”' (по
которой Qa граничит с ), а условие (15 193) - непрерывность нор-
мальной составляющей индукции В на Я .
Будем считать, что на внешней границе Я расчётной области Q,
которая состоит из четырёх частей S,A, 5'А, и Я12 (т.е.
Я = 5,aU Яи , и граница S*A = S,A US2A - часть границы Я, примы-
кающей к QA, а граница Яи = Я[} US2 - часть границы Я, примы-
кающей к ), заданы однородные краевые условия следующего вида:
(15.194)
(15.195)
1 Вводить такие перемычки имеет смысл только для предотвращения об-
хода ненулевых вихревых токов. Не допускать обход по области Я1и ненуле-
вых известных (сторонних) токов (например, токов в обмотках) лучше с ис-
пользованием поверхностей разрыва потенциала U - подробнее об этом мы
поговорим чуть ниже в разделе 15.13.3.
784
15.Векторный МКЭ для решения задач электромагнетизма
Таким образом, электромагнитное поле на каждом временном слое
описывается системой из двух дифференциальных уравнений (15.190)-
(15 191) с условиями сопряжения (15.192)-(15.193) и краевыми усло-
виями (15 194)—(15.195).
Краевая задача (15.190)—(15.195) эквивалентна системе двух вариа-
ционных уравнений
ОЛ
sn
уф g н;<*
ЦА
ФхйА)| =0, (15.196)
/15,Л
fpgrad U • grad^dQ — j*
rot А • n) <J>dS = О
Ол
УФЕ =0. (15.197)
В соотношениях (15.196)-(15.197) через й обозначена внешняя по
отношению к QA нормаль к поверхности Sr' (являющейся границей
между ОЛ и 9/ ). Под Н'^ понимается пространство определённых
на QA пробных вектор функций Ф, которые сами суммируемы с
квадратом и имеют суммируемые с квадратом роторы (т.е.
ею). При этом касательные всех
J Ш<оо и J
ЦА ол
пробных вектор-функций Ф должны быть равны нулю на границе Sf
(в соотношении (15.196) йА - нормаль к ).
Под понимается гильбертово пространство скалярных проб-
ных функций Ф, определённых в подобласт и и имеющих интегри-
руемые с квадратом первые производные (т.е. j* (gratis)2 dQ < сю ).
Все пробные функции Ф Е H< Lf должны быть равны нулю на грани-
це .
Доказательство эквивалентности1 системы вариационных уравне-
ний (15.196) (15.197) дифференциально-краевой задаче (15 190)-
(15.195) в целом мало чем отличается от соответствующих доказа-
тельств эквивалентности вариационного уравнения (15.11) краевой
* Это доказательство можно найти, например, в работе [21].
15.13.Построение конечноэлементных аппроксимаций ...
785
задаче для векторного уравнения (15.190) и эквивалентности вариаци-
онного уравнения
J*pgradt/-grad^dQ = Je<PdS Wety, Ф|5г = О
краевой задаче для скалярного уравнения (15.191). Небольшой отличи-
тельной особенностью является то, что после использования формулы
Грина (интегрирования по частям) в подынтегральных выражениях
поверхностных интегралов по поверхности 5 , являющейся границей
между подобластями QA (где определён вектор-потенциал А) и Q1 2 3 *
(где определён скалярный потенциал U ), появляется произведение
невязок условий сопряжения на соответствующие пробные функции
(векторные и скалярные). Это и позволяет доказать, что из справедли-
вости вариационных уравнений (15.196) и (15.197) следует справедли-
вость не только дифференциальных уравнений (15.190) и (15.191) и
естественных краевых условий (заданных на и ), но и условий
сопряжения (15,192)-(15.193) (и, естественно, наоборот, т.е. что усло-
вия сопряжения дают соответствующие слагаемые в вариационные
уравнения).
В заключение заметим, что краевые условия (15.194) и (15.195) яв-
ляются наиболее часто используемыми условиями симметрии и усло-
виями, задаваемыми на границах «большого объёма»1. Если же по
смыслу задачи на внешней границе Q необходимо задать ненулевое
значение касательной составляющей Н (на S^) или нормальной со-
ставляющей В (на S% ), то в вариационную формулировку
(15.196)-(15.197) необходимо добавить соответствующие слагаемые
вида J* (Й° х й) ФdS или J 0$dS .
S2 S2
15.13.2. ПОСТРОЕНИЕ КОНЕЧНОЭЛЕМЕНТНЫХ АППРОКСИМАЦИЙ
ПРИ СОВМЕСТНОМ ИСПОЛЬЗОВАНИИ ВЕКТОРНЫХ И УЗЛОВЫХ
БАЗИСНЫХ ФУНКЦИЙ
На конечных элементах, попавших в область QA, введём век-
торные базисные функции? ф,, а на конечных элементах, попавших в
область , - узловые базисные функции' фг.
1 Под «большим объёмом» обычно понимается такая расчётная область,
что при задании на её границах любых однородных краевых условий элек-
тромагнитное поле практически не меняется в интересующих нас точках.
2 Для конечных элементов первого порядка каждая из этих вектор-
функций ассоциируется с одним из рёбер.
3 Для элементов первого порядка (и лагранжевых элементов любого по-
рядка) каждая из этих функций ф, ассоциируется с одним узлом.
786
15.Векторный МКЭ для решения задач электромагнетизма
Будем искать решение (A,U) системы вариационных уравнений
(15.196)—(15.197) в виде разложения по базисным вектор-функциям ф
и скалярным функциям ф/ .
Пусть ??,.ф — количество базисных вектор-функций ф?;, а тъф - коли-
чество базисных функций ф,-. Обозначим через q вектор весов раз-
мерности ?г.ф + , в котором первые 77,ф компонент — это веса в раз-
ложении вектор-потенциала А по базису {-фД, а следующие ком-
понент- это веса в разложении скалярного потенциала U по бази-
су {ф.у} :
.7=1
л.„,
= IS п.ф •
.7="'ф+1
(15.198)
Подставляя в систему вариационных уравнений (15.196)-(15.197)
вместо А и U их представления в виде разложений (15.198) по соот-
ветствующим базисам {’Фу} и {ф7} и заменяя пробные вектор-
функции Ф в вариационном уравнении (15.196) поочерёдно на базис-
ные функции -ф,; и пробные функции Ф в вариационном уравнении
(15.197) поочерёдно на базисные функции ф,, получаем СЛАУ
"r+''ф
+ 12 f (ёга<1Ф./-«.|,х й) • ^ids =
IS f Р'ёГас1Ф.7-/'Ф ‘ grad<K-RL -
.7 = "ф+1
7 = 1... 7?„ф,
tl;..
-ISJ (rot 'Ф? fi)ф^-"VdS =0 ’ = 74+1> I7/'-ф+пф-
7=1
Таким образом, значения весов q.j в разложениях (15.198) могут
быть найде ны из решения СЛАУ
Cq = b,
15.13.Построение конечноэлементных аппроксимаций ...
787
в которой компоненты вектора b определяются соотношениями
Jf • x^dQ, г=1...тг.ф,
оА
О, г = п.ф+1,...,тгч|)-рЛф,
(15.199)
а матрица С состоит из четырёх подматриц:
0ф<|/
СФ
где Сф - симметричная матрица размера п.ф х п.ф, С'фф - матрица раз-
мера л,.ф хпф, Сфф - матрица размера х п.ф и — симметричная
матрица размера Пф х Пф. Компоненты этих матриц определяются со-
отношениями
Сф = J* — rotxf\ • rot-ij^dQ + г,у = 1...п.ф, (15.200)
qa |L oa
= f (sra<% х й) пП ?: = 1...7г.ф, _7 = 1...пф, (15.201)
о = ~f (rot Фг й) еП г = 1...Пф, 7 = 1...п.ф, (15.202)
tj с* = ^gradc^ • grack^dQ, Qf/ (15.203)
В формулах (15.200 )-(l 5.203), определяющих компоненты глобаль-
ной матрицы С, соотношения (15.200) и (15.203)— это стандартные
вклады от векторных и скалярных конечных элементов. Вклады в век-
тор правой части (15.199) от векторных элементов вычисляются также
стандартным образом. Нестандартными являются только формулы для
вычисления вкладов в глобальную матрицу С от поверхностных инте-
гралов (15.201) и (15.202). В качестве примера вычислим эти вклады
для тетраэдральных элементов первого порядка с шестью edge-
функциями для тетраэдров, лежащих в QA, и четырьмя узловыми
функциями для тетраэдров, лежащих в Qf/ .
Пусть Sk — треугол ьная грань тетраэдра, лежащая на поверхности
Sn . Тогда на S1' ненулевую касательную имеют 3 базисные вектор-
функции хр,:. Обозначим через ф7 локальные базисные вектор-
функции, соответствующие глобальным базисным вектор-функциям
788
15.Векторный МКЭ для решения задач электромагнетизма
ф,; с ненулевыми на Sk касательными, и соответственно через ф, -
локальные скалярные функции, соответствующие ненулевым на Sk
скалярным глобальным базисным функциям ф,.
Тогда
У* (gradtj^ х nj • ^dS — - - (о? x nj • (ct17^ — ctx^ j,
sn
—J (rot фу n^$7dS = — -in^Sl^ (cd'O) x n,
sn
где mesS'/' - площадь треугольника Sk, n - нормаль к плоскости тре-
угольника Sk', внешняя по отношению к QA, v(i) и X(z) — локальные
номера вершин треугольника Sk, определяющие его ребро с локаль-
ным номером i, а векторы коэффициентов с?:, определяемые соотно-
шением (6.28), вычисляются для содержащего треугольную грань Sk
тетраэдра из QA.
15.13.3. ПОСТРОЕНИЕ КОНЕЧНОЭЛЕМЕНТНЫХ АППРОКСИМАЦИЙ
ДЛЯ ЗАДАЧ С РАЗРЫВНЫМ СКАЛЯРНЫМ ПОТЕНЦИАЛОМ
При моделировании электромагнитных полей довольно часто
возникают ситуации, когда вектор напряжённости магнитного поля в
среде, где отсутствуют токи, может быть представлен в виде градиента
скалярного магнитного потенциала U лишь при условии, что этот
потенциал разрывен. Такие ситуации могут возникать как при решении
нестационарных электромагнитных задач (с несущественными токами
смещения), так и в задачах магнитостатики (которые будут рассмотре-
ны в шестнадцатом разделе).
Основной причиной, по которой в той части расчётной области, где
магнитное поле представляется через скалярный потенциал, нужно
задавать разрыв этого потенциала, является тот факт, что по той части
подобласти, где скалярный магнитный потенциал непрерывен, не
должно быть пути обхода ненулевого тока (подробно это мы обсужда-
ли в разделе 1 .J.6).
Поэтому при моделировании некоторых типов электромагнитных
полей в расчётной области, где магнитный потенциал U удовлетворя-
ет уравнению
—div (pgrad U) = 0 , (15.204)
могут быть заданы поверхности S1', на которых для U должны вы-
полняться условия (см. (1.81))
=U\s^ +/’ (15.205)
15.13.Построение конечноэлементных аппроксимаций ...
789
где I - полный ток, который может быть обойдён по контуру, полно-
стью лежащему в области определения потенциала U, a Sp и 5^ -
две стороны поверхности S1'.
Таким образом, при аппроксимации уравнения (15.204) нам нужно
учитывать то, что искомое решение должно иметь разрыв на поверх-
ности S1'.
Рассмотрим, как можно построить конечноэлементную процедуру
вычисления такого решения.
Для простоты будем считать, что на внешней границе области Q, в
которой определено уравнение (15.204), заданы либо первые, либо
однородные вторые краевые условия1.
Покажем, что для краевой задачи, определяемой уравнением
(15.204) и условиями (15.205) и (см. (1.82))
(15.206)
на поверхности S1’ разрыва U , эквивалентная вариационная поста-
новка будет иметь вид:
J pgradt/-gracWQ = 0, (15.207)
где искомая функция U имеет разрыв I на S1' (см. (15.205)) и удов-
летворяет главным краевым условиям на внешней границе Q, под
Q \ S1’ понимается область Q с вырезанной поверхностью Sl> (на
которой, естественно, не определено значение gradH ), а Ф — пробная
функция, удовлетворяющая однородным первым краевым условиям на
внешней границе Q и непрерывная во всей области О, включая Sp .
Для доказательства эквивалентности вариационного уравнения
(15.207) задаче (15.204)—(1 5.206) воспользуемся скалярной формулой
Грина (интегрирования по частям). При этом учтём, что поверхность
S1' фактически разрезает область определения потенциала U и обе её
стороны являются границами О \ Sp, а значит, при интегрировании по
Л г/
частям появятся два поверхностных интеграла от с разных
сторон от S1’, т.е. интеграл от I11 Ф со стороны 5^ и интеграл от
1 В принципе, на внешней границе Q, в которой определён скалярный по-
тенциал U , могут быть заданы не только неоднородные вторые краевые усло-
вия, но и условия сопряжения вида (15.193). Очевидно, в этом случае в вариа-
ционной постановке просто появятся дополнительные слагаемые. На рассуж-
дения же об учёте разрыва потенциала U на поверхности S1' это, в общем-то,
никак не повлияет (исключение составляет тот случай, когда поверхность
разрыва S1' соприкасается с поверхностью Sr>, на которой заданы условия
сопряжения).
790
15.Векторный МКЭ для решения задач электромагнетизма
р“ со стороны Sp (напомним, что Ф непрерывна на S1’ и по-
этому принимает один и те же значения с обеих её сторон). Таким об-
разом, с помощью формулы Грина уравнение (15.207) преобразуется к
виду
— J div (|tgrad U) <Z>dQ+j]t+ —j-— Ф(Ю—^рГ Фс/Q = 0. (15.208)
О' S'1 S’’ S’’
Выбирая пробные функции Ф, равные нулю на Sp, убеждаемся в
справедливости дифференциального уравнения (15.204) почти всюду
в Q.
Далее, учитывая справедливость уравнения (15.204), из (15.208) по-
лучаем
f (i<4 4Г- - =° >
J \ дп дп /
s’’
откуда ввиду произвольности пробных функций Ф следует справедли-
Обратим особое внимание на то, что условие непрерывное пт проб-
ных функций Ф на Sv является ключевым для того, чтобы из вариа-
ционной постановки (15.207) следовала справедливость соотношения
(15.206).
Будем искать приближённое решение1 U1’ вариационного уравне-
ния (15.207) в виде линейной комбинации стандартных (непрерывных)
базисных функций ф;. При этом, чтобы обеспечить разрывность U1'
на S1’ (т.е. выполнение условия (15.205)), на всех тех конечных эле-
ментах, которые расположены со стороны S4 и узлы которых лежит
на поверхности Sp , будем вместо веса qt использовать вес q + 1 .
Таким образом, на каждом конечном элементе У/,, касающемся по-
верхности S1' со стороны S4 , конечноэлементиое решение Uh пред-
ставляется в виде
и''= Е (<?>+’) Ф; + Е «А- (15.209)
jeNQk\NS1‘
где Nilk - множество номеров узлов конечного элемента ГД , a Ns> -
множество номеров узлов, лежащих на поверхности2 * Sp .
Это, очевидно, обеспечит нам, с одной стороны, скачок потенциала
U" на Sp, равный 7, а, с другой стороны — непрерывность пробных
1 При этом U1' должно удовлетворять условиям (15.205) как главным.
2 Заметим, что на S1' у нас не «двойные», а обычные «одинарные» узлы,
т.е. узел считается одним и тем же как со стороны ST, так и со стороны Sp .
15.13.Построение конечноэлементных аппроксимаций ...
791
функций (поскольку все базисные функции ф7 останутся непрерыв-
ными).
В результате при подстановке Uh в вариационное уравнение
(15 207) и заменяя пробные функции Ф на базисные функции фу (ес-
тественно, включая и те, которые ассоциированы с узлами, лежащими
на поверхности S1' ), с учётом (15.209) получаем, что разрыв U на Sp
даёт вклад от конечного элемента Од. в компоненту Ь, вектора правой
части b конечноэлементной СЛАУ в виде
Ь^к = / j*p.grackf)j - grac^dQ. (15.210)
nN5''
Ещё раз обратим внимание, что в формуле (15.210) суммирование
ведётся только по гем номерам j базисных функций конечного эле-
мента Од., которые соответствуют лежащим на поверхности S1’ узлам,
и при этом сам конечный элемент должен примыкать к S1 со стороны
Sp . Очевидно, вклады очень удобно вычислять на локальном
уровне через компоненты локальной матрицы жёсткости конечного
элемента Од..
Описанная процедура учёта разрыва потенциала остаётся точно та-
кой же и в задачах с двумя потенциалами (скалярным и векторным),
если поверхность разрыва Sp не пересекается с поверхностью S ,
которая является границей между подобластями определения вектор-
ного и скалярного потенциалов. Если же Sp и S соприкасаются, то
для узлов, которые лежат одновременно на Sp и S' и с которыми
ассоциированы базисные функции ф7, разрыв потенциала U даст до-
бавки в компоненты Ь, вектора правой части в виде поверхностных
интегралов
52 ZJ( grack^j х п) iptdS, (15.211)
jeN5* nN5'* 5P
где Sp - те участки поверхности Sn , которые имеют хотя бы один
общий узел с S1’ (и при этом Sp должен примыкать к Sp со стороны
5О
Sp ), N z - множество номеров скалярных базисных функций фу,
ненулевых на участке Sp, -ф, - базисные вектор-функции, имеющие
на Sp ненулевые касательные составляющие, п - нормаль к Sp. Оче-
видно, вклады (15.211) также удобно вычислять с использованием со-
792
15.Векторный МКЭ для решения задач электромагнетизма
ответствующих компонент матрицы конечноэлементной СЛАУ
(см. (15.201)).
15.14 . ОБ ОЧЕРЁДНОСТИ ВЫПОЛНЕНИЯ В ВЕКТОРНОМ МКЭ
АППРОКСИМАЦИИ НЕСТАЦИОНАРНЫХ ЗАДАЧ
ПО ПРОСТРАНСТВУ И ВРЕМЕНИ
До сих пор при построении дискретных аналогов нестационар-
ных векторных задач мы сначала выполняли аппроксимацию по вре-
мени, а потом на текущем временном слое строили конечноэлемент-
ную аппроксимацию полученной «стационарной» задачи. Удобство
такого подхода заключается не только в том, что техника построения
дискретного аналога полученной «стационарной» задачи мало чем
отличается от соответствующей техники построения конечноэлемент-
ного решения обычной стационарной задачи1 * *, но и главным образом в
том, что при изучении погрешности приближённых решений неста-
ционарных задач можно использовать очень сильные результаты, по-
лученные для соответствующих стационарных задач (мы использовали
такой подход, например, в рассуждениях, приведённых на с. 663-665).
Однако довольно часто при решении нестационарных векторных
задач методом конечных элементов их аппроксимацию по времени
выполняют не до, а после аппроксимации по пространству.
Например, при решении нестационарной задачи для уравнения
(15.1) эквивалентная вариационная постановка может быть записана в
виде (сравните с (15.11))
о
I dt
= JjCT-^rfQ+ Днвхп)-Ф^
О S-2
УФ €
(15.212)
где вектор-потенциал А является функцией не только пространствен-
ных переменных х , у и z , но и времени t, а пробная вектор-функция
Ф является функцией только пространственных переменных.
Соответственно конечноэлементное решение А? вариационного
уравнения (15.212) ищется в виде линейной комбинации
А7' = 52 ’
1 Отличия состоят лишь в учёте тех слагаемых правой части дифференци-
ального уравнения «стационарной» задачи, которые связаны со значениями
решения на предыдущих временных слоях.
15.14.06 очерёдности выполнения в векторном МКЭ ...
793
где гр.Л - базисные вектор-функции конечномерного пространства
VrotC Hrot, зависящие только от пространственных переменных, а
компоненты вектора весов q(£) являются функциями времени.
Таким образом, система уравнений, получаемая в результате ко-
нечноэлементной аппроксимации вариационного уравнения (15.212)
по пространству, принимает вид
dq(i) d2q(C Тст <?
Gq(0 + M°—+ М--— bJ +b\ (15.213)
dt dt2
где G - стандартная глобальная матрица жёсткости (компоненты Gti
которой определяются соотношением (15 139)), Мп и Мс — глобаль-
ные матрицы массы (их компоненты определяются соотношениями
(15.165)), a bJ' и Ь,<?2 - вклады в глобальный вектор от правой части
JC1 дифференциального уравнения (15.1) и от второго краевого усло-
вия (15.8).
В результате конечноэлементная система (1 5.213) фактически явля-
ется системой обыкновенных дифференциальных уравнений для век-
тора весов q(i). Если для её решения использовать какую-либо из не-
явных схем (трёх- или четырёхслойную), то для вычисления вектора q
на текущем временном слое будет получена абсолютно та же конечно-
элементная СЛАУ, которую мы получали ранее. При этом глобальная
матрица С этой СЛАУ будет суммой матриц G, Мп и Мс (у М и
ML будут сомножители, зависящие от схемы аппроксимации по вре-
мени), а в вектор правой части b кроме b и Ь' 2 войдут вклады в
виде произведений матриц М' и ML (также с соответствующими со-
множителями, зависящими от схемы аппроксимации по времени) на
значения вектора весов q с предыдущих временных слоёв.
Таким образом, результат будет абсолютно одинаковым (т.е. оче-
рёдность выполнения аппроксимации по пространству и времени ни-
как не влияет на окончательный результат), а запись вариационной
постановки и конечноэлементной системы с производными по времени
(как, например, (15.212) и (15.213)) в некоторых случаях является даже
более наглядной.
Естественно, все приведённые здесь рассуждения об очерёдности
выполнения аппроксимации по пространству и по времени справедли-
вы и в тех случаях, когда для решения нестационарных векторных
задач используется МКЭ с узловыми базисными функциями (т.е. ис-
пользуются подходы, аналогичные рассмотренному в четырнадцатом
разделе).
794
15.Векторный МКЭ для решения задач электромагнетизма
15.15 ОСОБЕННОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ ТЕХНОЛОГИЙ МКЭ
ПРИ ИСПОЛЬЗОВАНИИ ВЕКТОРНЫХ БАЗИСНЫХ ФУНКЦИЙ
При решении задач с использованием векторных, базисных функ-
ций, так же как и в узловом МКЭ, необходимо решать проблемы опен-
ки точности получаемых решений, разрабатывать технологии дробле-
ния сеток для уточнения приближённых решений, согласовывать ко-
нечные элементы на несогласованных сетках, выделять поля, описы-
ваемые более простыми задачами, и т.д. Для этого можно использо-
вать, в общем-то, практически те же технологии, которые применяют-
ся в узловом МКЭ и были рассмотрены нами в предыдущих разделах.
Здесь мы обратим внимание па особенности применения этих техноло-
l ий в векторном МКЭ.
15 15.1. ОБ ОЦЕНКЕ ТОЧНОСТИ KOIH ЧНОЭЛЕМЕНТНЫХ РЕШЕНИЙ
В ВЕКТОРНОМ МКЭ
Как мы показали в разделе 15.5, вектор-функция А7', получаю-
щаяся в результате решения уравнения (15.2) с применением векторно-
го МКЭ, является ближайше йх к точному решению А этого уравнения
в энергетической норме, определяемой соотношением
(15.214)
Поэтому для того, чтобы оцепить, как будет вести себя погреш-
ность А —А с дроблением сетки, можно воспользоваться оценкой
А — П', где П - кусочно-полиномиальная вектор-функция, являю-
щаяся, например, некоторым интерполянтом А. Действительно, для
А (как ближайшей к А в энергетической норме) выполняется
||а-а"|э<||а-п"|1, (15.2,5)
где П7' - кусочно-полиномиальный интерполянт А, представимый в
базисе |-ф, ! (т.е. ф, - это те базисные вектор-функции, в виде линей-
ной комбинации которых ищется приближённое решение:
1 Средн всех функций вида ф, , |ф, | - базис конечномерного под-
пространства Vrotc Hr,,t
15.15.Особенности применения различных технологий МКЭ
795
Таким образом, для того чтобы оценить погрешность IА — А ,
нам достаточно получить оценку погрешности представления точного
решения А своим кусочно-полиномиальным интерполянтом.
Для этого мы можем воспользоваться следующим фактом. Любая
достаточно гладкая вектор-функция Ф, определённая в области Q,
может быть приближена своим кусочно-полиномиальным интерполян-
том Гг с погрешностью
Ф-П'1) = С>(//+1), (15216)
где h — характерный размер подобластей , на которые разби га об-
ласть Q, к - степень полиномов, из которых на каждом Q,„ строится
интерполянт Пл, а под || • ' понимается норма1 *:
Ф" = [Ji Фс/Q. (15.217)
V и
Из определения норм (15.214) и (15.217) легко получить следующее
соотношение:
НИМЫЧ)- (,5-218)
где С = max I max /1/ц, max
\ J2 V _/ Q
А поскольку rotn,z является кусочным полиномом степени к — 1
(если Г1' — кусочный полином степени А:), из (15.215) и (15.216) с
учётом (15.218) получаем
(15.219)
Соотношение (15.219) определяет скорость сходимости приближён-
ного решения А7' к точному для векторных конечных элементов раз-
личных типов - тетраэдров, призм, параллелепипедов, шестигранников
Теперь мы можем объяснить, почему таким, на первый взгляд до-
вольно странным, образом были построены конечные элементы высоко-
го порядка на параллелепипедах (и соотетственно шестигранниках).
Напомним, что единственная ненулевая компонента оазисных век-
тор-функций *ф на параллелепипедах строилась как произведение
трёх полиномов, каждый из которых является функцией только одной
1 Это норма пространства IL? вектор-функпнй, интегрируемых с квадра-
том.
796 15.Векторный МКЭ для решения задач электромагнетизма
из координат (т.е. в виде X(x)Y (y')Z(z)). При этом степень к одно-
мерного полинома от той координаты (х, у или г), вдоль которой
направлена вектор-функция, была на единицу меньше степени двух
других одномерных полиномов, хотя, казалось бы, можно было взять в
качестве базисных вектор-функций такие функции ф+, у которых сте-
пень всех одномерных полиномов, определяющих единственную нену-
левую компоненту, равна к. Однако компоненты вектор-функций
го1ф+ (после соответствующего дифференцирования ф+) будут ку-
сочными полиномами той же степени к —А., что и компоненты век-
тор-функций rot'll?, . Это значит, что в норме (15.217) вектор-функция
rot А в базисах {rot ф,} и {rot'ip+j будет аппроксимироваться с оди-
наковым порядком. Соот ветственно в энергетической норме вектор-
функция А будет аппроксимироваться в базисах и (ф+ ] также
с одинаковым порядком.
Поэтому степень к у полиномов от той координаты (ж, у или z ),
вдоль которой направлена локальная базисная вектор-функция парал-
лелепипеда, является в некотором смысле «лишней», так как добавле-
ние соответствующих вектор-функций в базис увеличивает размер и
заполненность матрицы конечноэлементной СЛАУ, но не приводит к
повышению порядка аппроксимации конечноэлементного решения в
энергетической норме (хотя, конечно, его точность при этом может
всё-таки несколько повыситься).
15.15.2. ТЕХНОЛОГИИ УМЕНЬШЕНИЯ ПОГРЕШНОСТИ ПРИБЛИЖЁННЫХ
РЕШЕНИЙ В ВЕКТОРНОМ МКЭ
Для улучшения точности конечноэлементного решения в век-
торном МКЭ применяются в общем-то те же подходы, что и в узло-
вом. - дробление ячеек сетки и повышение порядка элементов.
Очевидно, при решении трёхмерных задач даже однократное дробле-
ние всех ячеек сетки или повышение хотя бы на единицу порядка элемен-
та приводит к резкому скачку требуемых для получения решения вычис-
лительных затрат. Поэтому и дробление сеток, и повышение порядка эле-
мента чаще всего выполняется локально, в тех местах, которые дают наи-
больший вклад в общую погрешность конечноэлементного решения
Таким образом, для того чтобы улучшить точность конечноэле-
ментного решения, желательно сначала определить те места расчётной
области, где дробление ячеек сетки (или повышение порядка элемента)
даст наиболее значимое уменьшение погрешности.
В разделе 13.3 были рассмотрены различные технологии определения
мест дробления сетки (или мест, где имеет смысл повышать порядок эле-
ментов) при использовании узлового МКЭ для решения скалярных задач.
Один из этих способов базировался на контроле поведения нор-
мальной производной (определяющей поток) гшиближённого решения
на границах между конечными элементами. Поскольку точное реше-
ние должно было иметь непрерывный поток на границах между эле-
15.15.Особенности применения различных технологий МКЭ
797
ментами’, величина скачка потока на этих границах могла служить
критерием точности приближённого решения.
В векторном МКЭ аналогичным критерием может служить кон-
троль поведения касательных составляющих rot А? на границах меж-
ду элементами. Действительно, для точного решения А должно вы-
полняться условие непрерывности касательных составляющих вектора
i-rotA. Поэтому, контролируя величины разрывов R-rotAz'jxn (где
п - нормаль к границе между соседними конечными элементами),
можно определить места, где погрешность приближённого решения
А наиболее велика и где поэтому имеет смысл провести дробления
ячеек сетки или увеличить порядок элементов2.
Другой подход, позволяющий определять те места дробления сетки
или повышения порядка элемента, которые дадут наибольшее умень-
шение погрешности конечноэлементного решения АЛ , может базиро-
ваться на сравнении величин погрешности, полученных на различных
сетках (для скалярных задач этот подход был рассмотрен нами на
с. 625-629). Для этого нам нужно уметь сравнивать по точности ко-
нечноэлементные решения, полученные на разных сетках.
Способы сравнения конечноэлементных решений, полученных на
разных сетках, в векторном МКЭ, в общем-то, аналогичны рассмот-
ренным нами способам сравнения по точности приближённых реше-
ний в скалярном МКЭ (см. раздел 13.2).
Во-первых, для векторного МКЭ остаётся справедливым тот факт,
что энергетическая норма разности точного решения А уравнения
(15.2) и его конечноэлементного решения А" (при однородных глав-
ных краевых условиях) равна разности значений правой части уравне-
ния Галёркина (15.1 1) при Ф, равном А, и Ф,равном А1 2' :
||а-а'‘||2 = /(а.)- г(а'-),
где (см. уравнение (15.11))
/(а) = jF-AdQ + J'^xn^AdS,
О Si
f ( a'') = Jr A7'dQ + J(Йв x n) AlldS .
Q S-2
(15.220)
1 Если, конечно, на этих границах не задан поверхностный источник.
2 Заметим, что для любого конечноэлементного решения АЛ нормальные
составляющие вектора В/; = rot. А6 на границах между элементами всегда
непрерывны в силу свойств операции rot.
798 15.Векторный МКЭ для решения задач электромагнетизма
Это сразу следует из вариационных уравнений (15.37) и (15.38) при
подстановке в (15 37) вместо Ф решений А или А? и в (15.38) вместо
Ф7' конечноэлементного решения A/l:
|а-а'1|2 = (а-а\а-Ал) =(а,а) -2(а,Ал) + (а\ал) -
= / A|-2/(A,t; + /(ал) = /(а)-/ а'1)
Таким образом, разность погрешностей двух решений
АЛл = У^^'ф и А ,2 = У^<?.2ф2, полученных на разных сетках, мо-
жет быть вычислена с помощью соотношения
|| А - А'1’1
£-и-^=
/(а'1’2)-/(а'1’1).
(15.221)
Значения же / (А'1’1) и /(А'*’2) получить совсем просто - это ска-
лярное произведение соответствующих весов и правых частей конеч-
ноэлементных СЛАУ:
/(А?’1) = (b])Tq\ /(аМ) = (b2)Tq2.
Однако соотношение (15.221) корректно лишь в том случае, когда
правая часть F уравнения (15.2) (и соответственно правая часть Н
естественного краевого условия) аппроксимируются «одинаково», те.,
если, например, используются их разложения по базисным вектор-
функциям, эти разложения должны быть одинаковыми на разных сет-
ках. Этому, конечно, довольно трудно удовлетворить при решении
нестационарных задач (когда в правую часть F входят слагаемые со
значениями решения на предыдущих временных слоях), а также при
решении задач в областях с изогнутыми границами.
Поэтому при решении практических задач более подходящим явля-
ется другой способ сравнения погрешностей на двух сетках. Погреш-
ности двух решений А7*’1 и А71,2 можно сравнить по их отклонениям
от некоторого эталонного решения А '*в, являющегося заведомо более
точным, чем А 1 и А?’2 (например, полученного на сетке, вложенной
к обеим сеткам, на которых вычислялись А71,1 и А/г’2). При этом саму
энергетическую норму отклонений А71’1 и А71’2 от А/и® можно вычис-
лить с помощью матриц конечноэлементпой системы, используемой
для получения АЛ® (сравните с (13.7) и (13-8)):
15.15.Особенности применения различных технологий МКЭ 799
||дЛ® _ дЛ,1||2 = (q© _ qi,®)T (G© + M®)(q® - q1-®), (15.222)
||аЛ’® _ д/г,2||2 = (q& _ q2,©)T (G® + M®)(q® - q2’®), (15.223)
где G ® и Мш - матрицы жёсткости и массы конечноэлементной сис-
темы (G® +M®)q® = b®, в результате решения которой вычисляется
вектор весов q®, определяющий эталонное решение АЛ’® — ^q®^® ,
I
|ф® | - базис, в котором ищется A/l,e, a q1’® и q2’® - веса разложения
приближённых решений А71’1 и А"'2 по базису {'ф®1:
а'*1 = 52 , ал’2 = 5>;2’®ф® . (15.224 >
i г
Основные трудности этого подхода, очевидно, состоят в том, что,
во-первых, для сравнения по точности решений А7'’1 и А71,2 нужно
иметь заведомо более точное решение А71’® и, во-вторых, для того,
чтобы можно было воспользоваться соотношениями1 (15.222) и
(15.223), решения А7' 1 и А7*’2 должны быть точно представимы в ба-
зисе |*ф®| (и, кроме того, эти разложения (15.224) должны быть явно
построены).
Для определения же мест, в которых дробление ячеек сетки или по-
вышение порядка элементов наиболее эффективно, могут быть приме-
нены те же подходы, которые были рассмотрены нами на с. 625-630 в
тринадцатом разделе как составные элементы IV/ -технологии. Заме-
тим, что и все остальные аспекты этой технологии практически без
1 Хотя, конечно, погрешности ||а *® — А/м|| и ||а7'® — ДЛ2| можно вы-
числить и без использования конечно элементных матриц G® и М® (напри-
мер, используя численное интегрирование на ячейках сетки, где вычислялось
А7'1®), но соответствующая процедура может стать очень трудоёмкой и$-за
того, что значения А71,1 и А71’2 придётся вычислять в огромном количестве
точек, не зная, в каких конечных элементах соответствующих сеток они нахо-
дятся. Тем не менее такая процедура всё-таки возможна, и в ней уже совсем
не обязательно использовать энергетическую норму - можно сравнивать ре-
шения либо только по значениям Brt = rot А7', либо только по значениям
Ё7' = — причём нс во всей области, а только в отдельных наиболее
интересующих нас подобластях.
800 15.Векторный МКЭ для решения задач электромагнетизма
изменений могут быть использованы при решении задач векторным
МКЭ'.
15.15.3. ТЕСТИРОВАНИЕ ПРОЦЕДУР ПОСТРОЕНИЯ КОНЕЧНОЭЛЕМЕНТНЫХ
АППРОКСИМАЦИЙ
Прежде всего правильность построения конечноэлементных
матриц и векторов в векторном МКЭ, точно так же как и в узловом,
проверяется на тестовых полиномиальных (или кусочно-
полиномиальных) решениях. Для этого подбираются такие параметры
задачи, чтобы её решением была вектор-функция, являющаяся поли-
номом (или кусочным полиномом) степени не выше, чем порядок ис-
пользуемых конечных элементов. Очевидно, в этом случае конечно-
элементное решение должно полностью совпасть с точным решением
тестовой задачи.
Соответствующие примеры для узлового МКЭ были достаточно
подробно рассмотрены нами в разделах 4.14, 5.7, 6.5, 7.3. При этом
некоторой особенностью векторного МКЭ является вырожденность
матрицы жёсткости, и поэтому при её тестировании обычно не решают
СЛАУ (для нахождения вектора весов q), а выполняют умножение
этой матрицы на тот вектор q, который даёт разложение точного ре-
шения по базису '['Ф/j (и затем полученный результат сравнивают с
вектором правой части конечноэлементной СЛАУ1 2). Значения же весов
q , как и в узловом МКЭ, определяют по значениям тестового решения
в тех точках, где только одна базисная вектор-функция3 имеет некото-
рую характеристику, отличную от нуля, — для векторных элементов это
обычно значение касательной к некоторой прямой (для элементов пер-
вого порядка — к их рёбрам).
При тестировании матрицы массы можно проверять её с помощью
уравнения ^A = F, где А - заданная вектор-функция, компоненты
которой являются полиномами требуемой степени. Веса q,j разложения
А по базису j, с одной стороны, могут быть получены по значе-
ниям А (точнее, её определённых касательных) в характерных точках,
а, с другой - из решения СЛАУ
1 Обратим внимание, что векторный МКЭ используется в основном для
решения нестационарных задач, и мы, в общем-то, не предполагаем, что ко-
нечноэлементная сетка может меняться на каждом временном слое. Обычно
сетка не меняется при движении по временным слоям, но при этом подбира-
ется так, чтобы получить решение нужной точности в нужном диапазоне вре-
мен.
2 Такой способ, кроме того, что снимает проблемы тестирования вырож-
денных конечноэлементных матриц, даёт дополнительные удобства при поис-
ке ошибок - он фактически указывает, в каких строках матрицы могут нахо-
диться неверные компоненты, см. рассуждения на с. 325 и с. 354-355.
3 Или их минимальное количество в случае иерархических базисов.
15.15.Особенности применения различных технологий МКЭ
801
Mq = b,
где М — стандартная матрица массы, а компоненты вектора правой
части b, = J F • ф7бЮ вычисляются «прямым» интегрированием по-
п
линомов, полученных как скалярное произведение тестового полинома
F = ^А. на фА (т.е. без разложения F по базису |*ф,}).
Заметим, что такого рода процедуры тестирования матриц массы не
являются особенностью векторного МКЭ - аналогичные им применя-
ются и в уз новом МКЭ.
Обратим внимание ещё на одну деталь, связанную с шестигранными
элементами. Эта деталь также не является особенностью только вектор-
ного МКЭ, но при рассмотрении узловых шестигранников мы не акцен-
тировали на ней внимание (хотя о близкой проблеме мы упоминали при
рассмотрении четырёхугольных узловых элементов, см. раздел 5.4.2).
Очевидно, при использовании шестигранных конечных элементов
полиномы (кусочные полиномы), определённые в области Q, не пред-
ставляются точно в виде линейной комбинации базисных функций
(если, конечно, шестигранники не являются прямоугольными паралле-
лепипедами), поскольку сами базисные вектор-функции не являются
кусочными полиномами в Q. Это справедливо как для узлового, так и
для векторного МКЭ. Действительно, базисные вектор-функции ф.,
строятся через вектор-функции ф(, которые являются полиномами от
локальных координат £, т] и на шаблонном элементе, и после соот-
ветствующего преобразования переменных полученные функции
ф, (ж, y,z} могут не быть полиномами от «новых» координат х, у и
z . Соответственно если в качестве тестовой берётся задача с решени-
ем в виде полинома от переменных х, у и z, то её конечноэлемент-
ное решение может не совпадать с точным. Тем не менее тесты с ре-
шениями, являющимися полиномами от координат х, у и z, пред-
ставляют определённый интерес и для шестигранных сеток. Как ми-
нимум с помощью этих тестов можно убедиться, что на шестигранной
сетке (при её дроблении) достигается необходимый порядок аппрок-
симации.
Следующий (после проверки на полиномиальных решениях) уро-
вень тестирования связан с построением таких тестовых задач (близ-
ких в некотором смысле к интересующим нас векторным задачам),
решение которых может быть получено в других постановках, допус-
кающих либо аналитические решения, либо достаточно простые спо-
собы построения численных решений. Это могут быть задачи меньшей
размерности, и при этом они могут быть сформулированы в другой
системе координат (например, в цилиндрической или сферической).
Рассмотрим примеры такого рода тестовых задач. Неплохим тестом
для проверки правильности процедур, реализующих конечноэлемент-
ное решение векторного уравнения (15.1), может служить задача, в
802
15.Векторный МКЭ для решения задач электромагнетизма
которой электромагнитное поле в цилиндрической системе координат
описывается единственной ненулевой компонентой Др = •
Это поле может быть получено из решения скалярной задачи для урав-
нения
- div grad Др j - j Д, + о + е = J(15.225)
в двумерной цилиндрической области.
Недостатками тестовых задач, основанных на решении уравнения
(15.225), является то, что, во- первых, ненулевыми в этих задачах будут
только компоненты Д. и Ду, и, во-вторых, коэффициенты р , о и е
не должны зависеть от координаты tp , а поскольку токи в такой поста-
новке направлены только по ip , невозможно протестировать ситуации,
когда токи пересекают границы разрыва параметров задачи.
Эти недостатки отсутствуют в тестовых задачах, основанных, на-
пример. на решении уравнения
- div (1 grad ) - A(X) Я, + = 1 ГОМ-, (15.226)
где - единственная ненулевая компонента напряжён-
ности магнитного поля в цилиндрической системе координат, а вектор
сторонних токов J в цилиндрической системе координат имеет две
ненулевые компоненты:
Зст = (Лст(г,г,О,о,Лст(г,г,<))т.
Задача, основанная на решении уравнения (15.226), должна быть
определена в такой расчётной области, в которой коэффициент удель-
ной проводимости о везде отличен от нуля. Кроме того, в этой поста-
новке токи смещения должны быть пренебрежимо малы.
Напряжённость электрического поля, получаемая в результате ре-
шения уравнения (15.226), может быть вычислена как
Е = -i^rotH — JCTj, и, значит, в декартовой системе координат Ё име-
ет все три ненулевые компоненты, которые являются функциями всех
координат, и поэтому при разрывных ц и о токи уже будут пересе-
кать границы разрыва этих параметров.
Аналогично можно протестировать ситуацию, когда токи смещения
существенны и коэффициент диэлектрической проницаемости £ мо-
жет иметь разрывы (расчётная область неоднородна по е). В этом слу-
чае тестовую задачу можно построить на основе решения уравнения
- div (1 grad Яф ) - -S- н+ + и = 1 гоЦ, JCT. (15.227)
15 15.Особенности применения различных технологий МКЭ
803
При этом предполагается, что во всей расчётной области коэффи-
циент удельной проводимости о равен нулю (здесь мы, в отличие от
предыдущей задачи, полагаем, что коэффициент р не может зависеть
от поля и поэтому он вынесен за производную по времени).
Заметим, что для построения конечноэлементных аппроксимаций
начально-краевых задач для двумерных скалярных уравнений вида
(15.225)-( 15.227) лучше всего использовать схемы, в которых не воз-
никает необходимость специального учёта слагаемого с производной
от разрывных коэффициентов1 (это слагаемое
4 в (15.225),
ат (гр) N
либо слагаемое -Д-(—'\Н.п в (15.226), либо слагаемое — в
от\го/ дг\гЕ/
(15.227)). Такие схемы мы обсудим чуть позже, в шестнадцатом разде-
ле (см. с. 852-856), поскольку они очень удобны и для решения нели-
нейных задач (в которых коэц фициенты уравнения зависят от искомо-
го поля).
Не представляет труда построить также тесты, когда поля являются
двумерными в декартовой системе координат, причём их можно ори-
ентировать так, чтобы для двух любых выбранных координат вектор-
потенциал имел две соответствующие им ненулевые компоненты, ка-
ждая из которых была бы функцией этих двух координат.
Например, в качестве тестовой можно взять задачу, в которой един-
ственной ненулевой компонентой вектора напряжённости магнитного
поля Н будет Hz — Hz{x^yyt), и эта компонента Hz является реше-
нием двумерной начально-краевой задачи для уравнения
- <liv grad Hz) + - ° = £ rotj JCT, (15.228)
,dj? 9J?
где, очевидно, rot~J = —---
ax ay
В этом случае двумерная расчётная область Q может быть состав-
лена из подобластей с различной удельной проводимостью ст и маг-
нитной проницаемостью р (в том числе зависящем от Н = (Яг|). В
эквивалентной же векторной постановке вектор-потенциал А будет
иметь две ненулевые компоненты А1; и At), являющиеся функциями
двух пространственных координат2 х и у, и при этом вектор-функция
А будет иметь разрывы нормальной составляющей на границах скачка
коэффициента о.
1 Фактически это слагаемое содержит в себе 6 -функцию, заданную на
границах разрыва соответствующего коэффициента.
2 И, естественно, времени t.
804
15.Векторный МКЭ для решения задач электромагнетизма
15.15.4. СОСРЕДОТОЧЕННЫЕ ИСТОЧНИКИ В ВЕКТОРНЫХ ЗАДАЧАХ
В трёхмерных векторных электромагнитных задачах плотность
стороннего тока может быть сосредоточена на поверхности или на
линии.
Пусть сторонний ток JCI имеет две составляющие J' r,S! и JcrS,
причем JctQ - это распределенный по объёму ток, a JCT,S - сосредо-
точенный на поверхности ток с объёмной плотностью
Jcl-,<?= ps bs (a:,y,z), в которой р5 - поверхностная плотность тока
(определённая только на поверхности S^), a 6‘5(z, г/, z) — соответст-
вующая поверхностная б -функция (см. раздел 8.1).
Тогда эквивалентная вариационная постановка для уравнения (15.1)
(с естественным краевым условием, заданным на S2 ) будет иметь вид
rot А rot Ф cZQ +
ФгЮ =
J Jcr’u Фс/Q + ffis • Ф(15 + J(Йе x й) VdS,
i 2 St, S-2
(15.229)
где Ф, как обычно, пробная векгор-функция, а р имеет только ка-
сательные к Sb составляющие (р • п = 0 на ).
Таким образом, в сравнении с учётом естественного краевого усло-
вия учёт поверхностного тока технически мало чем от него отличается
(а фактически является даже более простым). При этом точное реше-
ние А соответствующей задачи будет иметь суммируемый с квадра-
том rot А, т.е. наличие поверхностного тока не нарушает принцип
допустимости функций для вариационной постановки (по которому
решение должно, как и пробные функции, лежать в пространстве
H"'f). Поэтому все результаты, касающиеся сходимости приближён-
ного решения к точному, остаются справедливыми и при наличии в
задаче поверхностного тока.
Несколько иной (по крайней мере, в теоретическом плане) является
ситуация, когда J содержит в качестве слагаемого сосредоточенный
на линии сторонний ток, т.е. JCT = JCT-Q-р JCT’£ , где
J L= pz' bL (x,y,z), p — определённая на L плотность сосредото-
ченного на L стороннего тока JCT , а б^(з;, г/, z) - сосредоточенная на
линииЛ б-функция (см раздел 8.1).
В принципе, и в этом случае можно записать вариационное уравне-
ние, в некотором смысле эквивалентное исходной задаче:
15.15.Особенности применения различных технологий МКЭ
805
^^Фг/П =
о dt
rot А • rot Фб/Q + JoФc/Q + Je
n
= JjCT’Q^tZQ +
JpL • ФгД, + J(Йв x n) Фг/S',
L S-2
(15.230)
Однако здесь мы должны учитывать, что вектор-функция А уже не
является элементом пространства Hrot (поскольку rot А не является
суммируемым с квадратом). Поэтому для конечноэлементных аппрок-
симаций. построенных на основе вариационного уравнения (15.230),
уже могут не быть справедливыми результаты, связанные со скоро-
стью сходимости приближённого решения А" к точному.
Тем не менее и с помощью вариационного уравнения (15.230) мож-
но получать вполне приемлемые по точности конечноэлементные ре-
шения на некотором расстоянии от линии L . Рассуждения, которые
могут объяснить этот факт, мало чем отличаются от проведённых нами
в восьмом разделе (с. 410-413) рассуждений (о фактическом «размазы-
вании» сосредоточенных на линии и в точке источников в консчноэлс-
ментной постановке) для сосредоточенных источников в скалярных
задачах
Но все-таки лучше всего сосредоточенные на линиях сторонние то-
ки учитывать с помощью техники выделения поля, когда из трёхмер-
ной задачи выделяется поле с особенностью, определяемое сосредото-
ченным на линии источником.
15.15.5. О ВЫДЕЛЕНИИ ПОЛЯ В ВЕКТОРНОМ МКЭ
При решении многих векторных электромагнитных задач суще-
ственного повышения точности получаемого решения (причём такого,
которое за счёт только дробления сетки или повышения порядка ко-
нечных элементов может оказаться недостижимым даже в случае уве-
личения вычислительных затрат и мощности компьютера на несколько
порядков) можно добиться в результате использования методов реше-
ния, основанных на выделении из искомого поля достаточно близкого
к нему поля меньшей размерности.
Довольно подробно такие подходы были рассмотрены нами для уз-
лового МКЭ в девятом разделе и в разделе 14 4. В принципе, эти под-
ходы не слишком сильно меняются при использовании векторного
МКЭ при решении электромагнитных задач.
Рассмотрим векторное уравнение (15.1). Будем считать, что изу-
чаемое электромагнитное поле, полностью описываемое всктор-
потенциалом А (т.е. В = rotA, Ё — ), может быть представ-
лено в виде суммы двух полей, каждое из которых описывается «сво-
им» вектор-потенциалом А” (основное поле) и А (добавочное ноле),
т.е. В° = rotA1’, Ё° = -dA.l}/dt, В+ = rotA+J Ё+ = -dA+/dt.
806
15.Векторный МКЭ для решения задач электромагнетизма
Будем также считать, что поле А' может быть получено из реше-
ния более простой, чем исходная, задача (например, двумерной или
даже одномерной), и при этом оно достаточно близко к полю А Тогда
поле A 1 может быть найдено как решение векторного уравнения
rot (— rot А+ ] + о + е А+ = jCT — JCT-° -|-
U1 J dt dt2
Trot -L- —— rotA + (ct° - crV^— + (e° - e) , (15.231)
H|tl) I v ’ dt v ’ dt2
где |i.°, a1’, e1) и Jcr,° - параметры среды и плотность сторонних то-
ков, соответствующие полю А
Эквивалентная вариационная постановка для уравнения (15 231) (с
однородными краевыми условиями) имеет вид
а2л+
dt2
rot SPdQ + /о - А • Фс/Q + Ге
J di J
о о
— rot А ' rot V₽dQ +
+Да"- a) . ф rffi +Де11- е) Ф УФ 6 Н(Т‘. (15.232)
si ' а °1
Если поле А можно с достаточной точностью и без особых труд-
ностей представить в виде линейной комбинации базисных вектор-
функций ф/, которые используются при вычислении приближённого
решения
д+./А = ^2^ (/)-ф, (.T,?/,z),
то в результате конечноэлементной аппроксимации вариационного
уравнения (15.232) мы получим систему для вектора весов q+(£)
dq dqH 0
Gq b + Мп—у— 4- Мс--— = bJ "J +
dt dt2
[Л-1! , .. )rfq° / - Л"
+G1'1 “ q" + M<n 4- + M(c -*>-4-,
dt dt2
(15 233)
15.15.Особенности применения различных технологий МКЭ
807
где qn(7) — вектор1 весов в разложении вектор-потенциала А ' по ба-
зисным вектор-функциям *ф,, т.е.
(15.234)
lj_ .11
a G, Ма, Мс, G'1' ’* *, М^° -п), М^г -е' и bjCT-jCT’° - матрицы жёст-
кости и массы и вектор правой части, компоненты которых определя-
ются соотношениями
G,y — Г— rot • rot tyjdQ ,
J LL
Q
71?;, = У'е'Ф, • *ф7с?Г7,
= J (on- oj ф7; • = У (en—e) ф.,: • ф7тЮ,
о Q
bt = (15.235)
Система обыкновенных дифференциальных уравнений (15.233)
может быть аппроксимирована по времени с помощью какой-либо
неявной схемы (особенно если распространение поля изучается в сре-
де, содержащей объекты с отличной от нуля удельной проводимо-
стью), и тогда вектор весов на текущем временном слое может быть
определён из решения соответствующей СЛАУ:
Cq'=b, (15.236)
где qz = q+'(4) (т.е. Q*' - значение вектора весов q+ на k-м времен-
ном слое).
Например, при использовании трёхслойной полностью неявной
схемы аппроксимации по времени с равномерным шагом Д? матрица
и вектор правой части СЛАУ (15.236) будут иметь вид:
c = g+^m"+^m-;
1 Точнее, q°(£) -это векгор-фупкция времени.
808
15 Векторный МКЭ для решения задач электромагнетизма
b = bJ"-lF!0 +^M’qw
+G'
—Ц-mV1
(AZ)2
----TMcqt-2 +
(AZ)2
, „ . <Zq°(Z)
q°( h) + M<" -o) - „ + г
t=tk
d2q°(i)
dt2
t=ik
где qk 1 и q 2 — значения q на двух предыдущих временных слоях
(т.е. при i = Iк I и t = tk- -2 соответственно), a q'’(/) - вектор (вектор-
функция времени), компоненты которого являются весами в разложе-
нии вектор-потенциала А” но базису (см. (15.234)).
В общем-то, в качестве основного поля не обязательно брать поле
меньшей размерности Очень хороший эффект можно получить и то-
гда, когда в качестве основного берётся трёхмерное поле, которое мо-
жет быть достаточно просто и с хорошей точностью вычислено более
простым способом.
Примером этого может служить ситуация, когда нужно вычислить
нестационарное поле, порождаемое сторонними токами JCT, текущими
в сложных обмотках, и искомое поле изменяется во времени довольно
медленно. И при этом возникающие в проводящих подобластях вихре-
вые токи, хотя и оказывают влияние па результирующее поле, но не
слишком кардинально изменяют его. В этом случае в качестве основ-
ного поля может быть взято ноле А4, порождаемое токами J'' в од-
нородной (ц° = ро) непроводящей среде. Тогда вектор-потенциал А
очевидно, удовлетворяет уравнению
— rot irot А()) = J'
(15.237)
Ро \ 1
При этом плотность сторонних токов JC1 должна, очевидно, удов-
летворять соотношению divJ 1 = 0 (которое сразу следует из (15.237)
после применения к его левой и правой части операции div). Тогда
вектор-функция А1), удовлетворяющая уравнению (15.237), может
быть найдена из решения уравнения
—ЛА() = р() JCT,
где Д - оператор Лапласа (поскольку решение А'1 уравнения (15.238)
при divJcr = (J удовлетворяет соотношению div А 1 = 0 и из справед-
(15.238)
15.15.Особенности применения различных технологии МКЭ
809
ливости (15.238) и тождества rot (rot$> = — ДФ 4- grad(div<Jj для А*'
сразу следует справедливость (15.237)).
Таким образом, компоненты вектор-функции А1 * *’ в произвольной
точке (т.т/, z) могут быть вычислены по формулам (заметим, что об
этом мы уже говорили в первом разделе, см. соотношения (1.32)—
(1.34))
где Q7 - область, в которой плотность сторонних токов JCT отлична
от нуля.
В некоторых случаях компоненты вектор-потенциала А1), удовле-
творяющего уравнению (15.238) (и соответственно (15.237)), бывает
проще вычислить в результате решения трёх эллиптических краевых
задач (с использованием, например, узлового МКЭ), чем по формулам
(15.239>-(15.241). Дело в том, что подынтегральные выражения в соот-
ношениях (15.239)- 15.241) имеют особенность, и хотя эта особен-
ность интегрируема, нужно, например, с большой аккуратностью при-
менять формулы численного интегрирования для вычисления А(> по
формулам (15 239)—(1 5.241) в тех точках (x,y,z), которые принадле-
жат Q7 (те. там, где плотность сторонних токов JCT отлична от ну-
ля)1. Поэтому в тех случаях, когда область Q7 достаточно велика и при
этом в исходной нестационарной задаче удельная проводимость о
внутри Q7 не является нулевой, значения вектор-потенциала Ап мо-
жет оказаться гораздо проще и выгоднее (по вычислительным затра-
там) получать в результате численного решения трёх скалярных эл-
липтических краевых задач для уравнений ДД”=р,07£г,
ДА” = P()JyT и ДД” = в «большом объёме» (с использованием,
например, узлового МКЭ).
1 Нельзя использовать стандартные формулы численною интегрирования
для ячейки, содержащей точку (x,y,z), а нужно специальным образом учиты-
вать особенность в подынтегральном выражении
810 15.Векторный МКЭ для решения задач электромагнетизма
С помощью соотношений (15.239)-(15.241) можно очень легко по-
лучить выражения для вычисления значений векгор-потенциала А°,
описывающего магнитное поле в однородном непроводящем про-
странстве, в случае, когда сторонние токи сосредоточены на некоторой
поверхности S или на некоторой линии (или наборе линий) L .
Так, если сторонний ток сосредоточен на линии (наборе линий) L ,
его объёмная плотность может быть представлена в виде
JCT’L— pL . ^x,y,z) (где pL - определённая на L плотность сосредо-
точенного на L стороннего тока JCT,L, а б£ (х\у,z) — сосредоточенная
на линии L б-функция). Тогда выражения (15.239)—< 15.241) преобра-
зуются к виду
А() ДО Г^-dL, Az° = ^- f — dL, (15.242)
• 4tv J г ’ hJ r z 4tv J r v 7
L L L
где r — — x'}2 + (y — y*f+ (z — z’)2 , x , у и z — координаты точ-
ки, в которой вычисляются А,', Ау и А2, а х', у' и z' — координаты
точки на линии L .
Если контуры L, по которым текут сосредоточенные на них токи,
имеют сложную конфигурацию, то для вычисления значений вектора-
потенциала А() по формулам (15.242) имеет смысл использовать чис-
ленное интегрирование. В простейшем варианте каждый контур разби-
вается на элементарные участки Д и значение каждой компоненты
А1) получается в виде суммы значений соответствующего подынте-
грального выражения в точках (т;,?/;,2(), являющихся центрами уча-
стков Д , умноженных на длины l.j этих участков Д :
и аналогично для остальных двух компонент. При этом желательно,
чтобы точки (x.ny.jyZj) были не слишком близки к тем точкам, в кото-
рых вычисляются значения А11, поскольку в них поле A(J может быть
получено с довольно большой погрешностью. Но на практике конту-
ры, по которым тек) г сторонние токи, как правило, не соприкасаются с
проводящей средой, а значения поля Ап (как основного при использо-
вании его в процедуре выделения поля) необходимы только в тех точ-
ках, где проводимость исходной задачи отлична от нуля.
Заметим, что в принципе не обязательно представлять основное по-
ле в виде потенциала Ап (такого, что В° = rotA11 и Е() = — <9A()/<9i) и
15.15.Особенности применения различных технологий МКЭ
811
для этого Аи получать веса г/’1 в его разложении по базисным функци-
ям -ф,, используемым при вычислении поля А+ (соответствующие
процедуры вычисления А° и в некоторых случаях могут быть со-
всем не простыми и вычислительно довольно трудоёмкими).
Если основное поле получено в виде значений Н° и Е° (т.е. на-
пряжённости электрического и магнитного полей), то эквивалентная
вариационная постановка для вычисления поля А+ (определяющего
добавочные к Н1) и Ё() поля Н+ = —rotA4 и Ёь =—<ЭА4/д/) может
быть записана в виде
^^•Фс/П-1- Ге
at J
ц
и0)-
+ f 1--Ь_ н()
dt2
• rot Ф +
S2
Д^-.фбЮ УФбН(1)01 (15.243)
и вклады в вектор правой части b от слагаемых, содержащих Нн и
Ё(), могут вычисляться, например, с использованием численного ин-
тегрирования.
Выделение поля может быть очень эффективным и во многих других
ситуациях, когда, например, для описания электромагнитного поля при-
меняется постановка с совместным использованием векторного и ска-
лярного потенциала (эта постановка была рассмотрена в разделе 15.13)
или так называемой II-ф-постановкой (она будет рассмотрена чуть
ниже), для которых конечноэлементные аппроксимации строятся также
с использованием векторного МКЭ. При этом техника построения зада-
чи на добавочное поле в целом не слишком отличается от рассмотрен-
ной здесь, хотя, конечно, при решении практических задач бывает очень
много нюансов, которые могут довольно сильно повлиять на то, на-
сколько выделение поля позволит улучшить окончательный результат (в
несколько раз, на один порядок или на несколько порядков).
15.15.6. ИСПОЛЬЗОВАНИЕ СЕТОК С НЕСОГЛАСОВАННЫМИ ЯЧЕЙКАМИ
В ВЕКТОРНОМ МКЭ
Как мы уже говорили, при использовании векторного МКЭ (как
и узлового) основными способами улучшения точности получаемого
конечноэлементного решения является повышение порядка конечных
элементов и дробление ячеек сетки. При этом на практике дробление
сетки применяется гораздо чаще, чем повышение порядка конечных
элементов.
812
15 Векторный МКЭ для решения задач электромагнетизма
Чтобы избежать появления большого количества «лишних» степе-
ней свобод (приводящих к существенному росту размерности конечно-
элементной СЛАУ и практически не влияющих на точность конечно-
элементного решения), дробление сегки нужно проводить локально,
разбивая (возможно, неоднократно) лишь отдельные группы ячеек.
На сетках с ячейками определённых типов (в виде прямоугольни-
ков, четырёхугольников, призм, параллелепипедов и шестигранников)
локальные дробления могут приводить к появлению несогласованных
ячеек, т.е. могут возникать ситуации, когда стороны, по которым гра-
ничат две смежные ячейки, имеют не один и те же вершины. Доволь-
но подробно проблемы, связанные с использованием несогласованных
сеток в узловом МКЭ, мы обсуждали в одиннадцатом разделе. Анало-
гичные проблемы при использовании сеток с несогласованными ячей-
ками возникают и в векторном МКЭ.
Очевидно, стандартная сборка глобальной матрицы и вектора пра-
вой части конечноэлементной СЛАУ из локальных при наличии в сет-
ке несогласованных ячеек в рассмотренном нами варианте векторного
МКЭ1 фактически будет означать, что используются базисные вектор-
функции ф'" , имеющие разрывные на границах между несогласован-
ными ячейками тангенциальные (касательные) составляющие.
Рассмотрим, как в таких случаях можно только посредством пере-
организации процедуры сборки глобальных матрицы и вектора из ло-
кальных переопределить оазисные вектор-функции так, чтобы все
функции из порождаемого эт им базисом конечномерного прост ранства
V (на котором ищется конечноэлементное решение) стали допусти-
мыми для вариационной постановки. Фактически нам нужно сделать
так, чтобы все глобальные базисные вектор-функции ф, 6 V имели
непрерывные тангенциальные составляющие и в результате простран-
ство V стало подпространством Vrut' пространства Hrot.
Реализующая такой подход процедура согласования edge-элементов
на несогласованных ячейках может быть построена по технологии
Т-преобразования, практически полностью аналогичной соответст-
вующей технологии согласования конечных элементов на несогласо-
ванных сетках в узловом МКЭ, которая была рассмотрена нами в раз-
делах 11.6-11.8.
Покажем на простейшем примере, как могут быть согласованы
edge-элементы на несогласованной двумерной прямоугольной сетке.
Пусть прямоугольная сетка имеет три ячейки и к правой стороне
одной из ячеек (которую мы, как и прежде, будем называть «боль-
шой») примыкают сразу две другие ячейки (их мы будем называть
«маленькими»). Эта ситуация изображена на рис. 161. Па этом же ри-
1 Здесь имеется в виду такая постановка, в которой конечноэлементное
решение (и соответственно базисные вектор-функции) имеет непрерывные
касательные составляющие; в следующем разделе будет кратко рассмотрен
другой вариант векторного МКЭ, в котором у части базисных вектор-функций
непрерывны нормальные составляющие, а касательные составляющие могут
быть разрывными.
15.15.Особенности применения различных технологий МКЭ
813
сунке показана глобальная нумерация узлов сетки и рёбер — номера
узлов приведены в кружочках, а номера рёбер - в квадратиках, т.е.
ребру1 {1,2} дан глобальный номер 1, ребру {2,3} - глобальный но-
мер 2, ребру {4,5} - номер 3, ребру {6,7} - номер 4, {7,8} - номер
5, {1,6} - номер 6, {2,7} - номер 7, {3,5} - номер 8, {5,8} - номер
9, {2,4} — номер 10, {4,7} - номер
Обратим особое внимание на то,
что правому ребру «большого»
прямоугольника2 и левым рёбрам
«маленьких»3 даны разные гло-
бальные номера, поскольку они не
совпадают друг с другом.
Базис |ф'' j первого порядка,
соответствующий указанной на
рис. 161 глобальной нумерации
рёбер, будет порождать конечно-
мерное пространство V, очевидно,
не являющееся подпространством
Hrot
Рис. 161. Несогласованная
прямоугольная сетка из трёх ячеек
, поскольку вектор-функции ф“г, фц, и ф"{ имеют разрывные
на ребре {2,7} касательные составляющие. Действительно, фуг на
ребре {2,7} в пределе слева имеет касательную составляющую, рав-
ную единице4, а справа — касательную составляющую, равную нулю.
Вектор-функции же фд, и фп , наоборот, справа на соответствующих
частях этого ребра имеют касательные составляющие, равные единице,
а слева — касательные составляющие, равные нулю.
Введём вместо вектор-функций ф’уг, ф"() и ф"{ вектор-функцию
фу, которая на «большом» прямоугольнике совпадает с вектор-
функцией фу" , а на «маленьких» — с вектор-функциями ф^ и ф"['
соответственно. Очевидно, эта вектор-функция фу может быть записа-
на в виде
^7 = 'Ф?Г + Ф1() + Фи ,
1 В фигурных скобках указаны глобальные номера узлов.
2 С номерами вершин {1,2,6,7}.
3 С номерами вершин {2,3,4,5} и {4,5,7,8}.
4 Или 2/Z (где I - длина ребра), если вектор-функция получена отображе-
нием из шаблонного элемента 0е = [—1,1] х [—1,1]; в дальнейших рассужде-
ниях мы будем считать, что касательные составляющие вектор-функций на
соответствующих им рёбрах равны единице.
814
15.Векторный МКЭ для решения задач электромагнетизма
и она уже будет иметь непрерывную касательную составляющую на
ребре {2,7}.
Определив остальные вектор-функции ф'у- равными вектор-
функциям ф'-г (j = 1,...,6,8,9), получим базис {ф;}. 1 д, порож-
дающий конечномерное пространство Vrut С Hlot.
Согласование трёхмерных edge-элементов по сути ничем не отли-
чается от только что рассмотренной нами процедуры для двумерного
случая, хотя, конечно, технически эта процедура в трёхмерном случае
намного сложнее, чем в двумерном.
Рассмотрим, как в общем спучае на несогласованной сетке можно
построить базисные вектор-функции с непрерывными касательными
составляющими. При этом, однако, наложим некоторые (совсем не
жёсткие) ограничения на то, каким образом могут контактировать друг
с другом несогласованные ячейки.
Будем считать, что при построении несогласованных сеток не до-
пускаются так называемые «перехлёсты». Под ^перехлёстом», как и
раньше, мы понимаем ситуацию, когда к одной стороне «большой»
ячейки примыкают несколько других («маленьких») и при этом соот-
ветствующие стороны маленьких ячеек не лежат целиком на контак-
тирующей с ними стороне «большой» ячейки. Пример несогласован-
ной трёхмерной сетки с «перехлёстом» показан на рис. 162.
Рис. 162. Несогласованная параллелепипеидальная сетка с «перехлёстом»
При отсутствии таких «перехлёстов» технология преобразования ба-
зиса |ф"‘‘ j, соответствующего стандартной сборке локальных матриц и
векторов в глобальные (и порождающего конечномерное пространство
15.1 5.Особенности применения различных технологий МКЭ
815
V с вектор-функциями, не лежащими1 в Нго* ), в базис {'Ф/ J конечно-
мерного пространства Vrot С Hrot может быть следующей (мы рас-
смотрим трёхмерный случай, поскольку в двумерном случае эта техно-
логия является слишком простой и не вполне показательной2).
Перед тем, как приступить к непосредственному описанию техники
построения матрицы Т-преобразования базиса в базисе |-ф' |,
определим следующий способ нумерации вектор-функций исходного
базиса |,ф-'г|. У контактирующих друг с другом конечных элементов
базисные вектор-функции, ассоциированные с рёбрами и гранями,
получают одни и те же глобальные номера в том и только в том слу-
чае, если эти рёбра и грани полностью совпадают друг с другом. При
этом последовательность присвоения вектор-функциям глобальных
номеров лучше всего сделать такой.
Сначала должны быть пронумерованы те глобальные вектор-
функции, которые ассоциированы с «большими» рёбрами (т.е. рёбрами,
не являющимися частью каких-либо других рёбер и не попадающими
внутрь каких-либо граней). Если используются элементы высоких по-
рядков и есть ассоциированные с гранями базисные вектор-функции, то
те вектор-функции, которые ассоциированы с «большими» гранями,
также должны получить меньшие номера, чем любая из базисных век-
тор-функций, ассоциированных с «маленькими» рёбрами (являющимися
частями каких-либо «больших» рёбер или лежащими внутри какой-либо
грани) или «маленькими» гранями (являющимися частью «большой»
грани). И также до вектор-функций, ассоциированных с «маленькими»
рёбрами и гранями, должны быть пронумерованы все вектор-функции,
ассоциированные с конечными элементами (если таковые имеются).
Так, для несогласованной сетки, изображённой на рис. 163, сначала
следует пронумеровать базисные вектор-функции, ассоциированные с
рёбрами {1,2}, {2,3}, {4,5}, {6,7}, {7,8}, {1,6}, {2,7}, {3,5},
{5,8}, {1,9}, {2,10} , {3,11}, {5,13}, {6,14}, {7,15}, {8,16}, {9,10},
{10,11}, {12,13}, {14,15}, {15,16}, {9,14}, {10,15}, {11,13}, {13,16}
(и с гранями {1,2,6,7}, {2,3,4,5}, {4,5,7,8}, {1,2,9,10}, {2,3,10,11},
{4,5,12,13}, {6,7,14,15}, {7,8,15,16}, {1,6,9,14}, {2,7,10,15},
{3,5,11,13}, {5,8,13,16}, {9,10,14,15}, {10,11,12,13}, {12,13,15,16},
а также со всеми конечными элементами), и только после этого — ба-
зисные вектор-функции, ассоциированные с рёбрами {2,4}, {4,7},
{10,12}, {12,15}, {4,12} (и гранями {2,4,10,12}, {4,7,12,15}).
1 И, значит, недопустимыми для вариационной постановки.
2 Некоторые аспекты этой технологии, возникающие в трёхмерном случае,
для двумерных задач могут отсутствовать вовсе; при этом все ситуации, кото-
рые могут возникнуть в двумерном случае, обрабатываются абсолютно анало-
гично тому, как это делается в трёхмерном случае.
816
15.Векторный МКЭ для решения задач электромагнетизма
Рассмотрим, как можно сформировать матрицу Т, преобразующую
базис {ф'/} в базис |ф, j пространства кусочно-полиномиальных
вектор-функций с непрерывными касательными составляющими
Рис. 163. Несогласованная параллелепипеидальная сегка из трёх ячеек
Пусть п(. — число базисных вектор-функций ф”г, ассоциированных
с «большими» рёбрами (и с «большими» гранями и с конечными эле-
ментами для базисов высоких порядков).
Очевидно, при описанном нами чуть выше способе нумерации век-
гор-функций в базисе {4?" } эти базисные вектор-функции будут
иметь номера j < п(.. Именно на их основе мы и будем строить базис-
ные вектор-функции ф' , т.е. каждая из базисных вектор-функций ф;
будет иметь в качестве слагаемого вектор-функцию ф-'г (с тем же
номером /').
Каждая ф' должна точно совпадать с ф-"’, если ф"' не имеет раз-
рывов касательных составляющих (и эти вектор-функции ассоцииро-
ваны с геми рёбрами или гранями, по которым ячейки сегки стыкуют-
ся согласованно). Остальные же вектор-функции ф£ будут иметь в
качестве слагаемого вектор-функцию ф'" и несколько вектор-
функций1 ф"г с номерами j > п( (эти вектор-функции ассоциированы
с «маленькими» рёбрами или гранями).
Таким образом, для всех век гор-функций ф'-г при j > п(. необхо-
димо получить значения коэффициентов Тг/ в линейных комбинациях
1 С некоторыми сомножителями.
15.15.Особенности применения различных технологий МКЭ
817
> которые позволят вместо вектор-функций 'ф'"' с разрыв-
j>‘Hc
ными касательными составляющими (для i < п,.) получить вектор-
функции
& = + Е 'Л/Е
j>n(.
с непрерывными касательными составляющими.
Эти значения Tt. могут быть получены с помощью практически той
же технологии, которая была рассмотрена нами в одиннадцатом разде-
ле для согласования узловых конечных элементов на несогласованных
ячейках (см. разделы 11.6.4 и 11.8)
Будем считать, что для несогласованной сетки сформированы сле-
дующие структуры данных. Для каждого «маленького» ребра (т.е. реб-
ра, являющегося частью некоторого «большого» ребра или лежащего
внутри какой-либо грани) хранится либо номер «большого» ребра,
частью которого является это «маленькое» ребро, либо номер «боль-
шой» грани, внутри которой лежит рассматриваемое «маленькое» реб-
ро. Вместе с номером грани хранятся номера всех базисных век гор-
функций, ассоциированных как с самой («большой») гранью, так и со
всеми её рёбрами (ограничивающими эту «большую» грань). Кроме
того, хранится также набор чисел, каждое из которых является весом в
разложении соответствующей базисной вектор-функции, ассоцииро-
ванной с «большой» гранью или одним из ограничивающих её рёбер,
по базисным вектор-функциям «маленьких» рёбер и граней, контакти-
рующих с этой «большой» гранью.
Заметим, что некоторые рёбра могут быть одновременно и «боль-
шими» и «маленькими», если, с одной стороны, части этих рёбер яв-
ляются другими рёбрами, а с другой стороны, эти рёбра лежат внутри
некоторых граней. Это, например, ребро {8,13} для сетки, изображён-
ной на рис. 164. Действительно, оно является «большим» для рёбер
{8,10} и 110,13} и «маленьким», поскольку лежит внутри грани
{7,9,12,14}, и в структуре данных для него (как для «маленького»
ребра) должна храниться информация о содержащей его грани. При
этом если «маленькое» ребро одновременно является частью какого-
либо ребра и лежит внутри какой-либо грани (как, например, ребро
{8,10} - оно является частью ребра {8,13} и лежит внутри грани
{7,9,12,14}), то для него в структуре данных хранится информация
только о соответствующем «большом» ребре (т.е. о ребре {8,1.1}),
поскольку информация о грани может быть получена уже через это
«большое» ребро (которое является «маленьким» для грани
{7,9,12,14}).
Таким образом, для сетки, изображённой на рис. 164, для вектор-
функции, ассоциированной с «маленьким» ребром {8,10}, должны
818
15.Векторный МКЭ для решения задач электромагнетизма
храниться номера только тех вектор-функций, которые ассоциированы
с ребром {8,13} (и соответствующие веса - для элемента первого по-
рядка это один вес, равный единице). Для ребра же [8,13} должны
храниться номера всех базисных вектор-функций, ассоциированных с
рёбрами {7,12} и {9,14} (и с гранью {7,9,12,14} при использовании
базисов высоких порядков), и столько же вещественных чисел, каждое
из которых является весом вектор-функции, ассоциированной с рас-
сматриваемым «маленьким» ребром {8,13}, в разложении соответст-
вующей вектор-функции (ассоциированной с каким-либо из рёбер
{7,12} или {9,14} или с гранью {7,9,12,14}). При использовании
базиса первого порядка это будет всего два веса, равные значениям
касательных (к рассматриваемому «маленькому» ребру {8,13}) со-
ставляющих базисных вектор функций с «большой» грани
{7,9,12,14 }, ассоциированных с ребрами {7,12} и {9,14}.
Очевидно, что при использовании базисов высоких порядков по-
добную структуру данных проще всего формировать для вектор-
функций ла! ранжева типа. Основной принцип здесь, в общем-то, тот
же, что и при работе с узловыми базисными функциями
(см. с. 545-552). Веса вектор-функций, ассоциированных с «маленьки-
ми» рёбрами и гранями, в разложении на рассматриваемой «большой»
грани вектор-функций, ассоциированных с её рёбрами и с ней самой,
могут быть получены как значения соответствующих касательных
составляющих вектор-функций этой «большой» грани в определённых
точках — это точки, в каждой из которых только одна из вектор-
функций. ассоциированных с «маленькими» ребрами и гранями, имеет
отличную от нуля соответствующую касательную составляющую.
Несколько сложнее построить процедуру формирования рассмат-
риваемой структуры данных для векторного иерархического базиса.
Основные трудности в этом случае имеют практически тот же харак-
15.15.Особенности применения различных технологий МКЭ
819
тер, что и трудности, возникающие при работе с узловыми иерархиче-
скими элементами на несогласованных сетках. Поэтому и алгоритмы
формирования этой структуры для векторных иерархических элемен-
тов (на несогласованных сетках) в целом идентичны рассмотренным
нами в разделе 12.3 алгоритмам для узловых иерархических элементов
Итак, будем считать, что для несогласованной конечноэлементной
сетки построена структура данных, в которой для каждой вектор-
функции, ассоциированной с «маленьким» ребром или с «маленькой»
гранью, хранятся номера вектор-функций, ассоциированных с рёбрами
«большой» грани и с самой этой гранью1, а также хранятся числа, каж-
дое из которых является весом этой вектор-функции (ассоциированной
с «маленьким» ребром или гранью) в разложении на «большой» грани
соответствующей вектор-функции, ассоциированной с «большим»
ребром или с самой «большой» гранью2.
Тогда для формирования матрицы Т, преобразующей базис ф, [
в базис |ф'}, можно использовать те же самые процедуры, которые
были рассмотрены нами в разделе 1 1.8 для согласования узловых ба-
зисных функций на несогласованных сетках. Здесь точно так же можно
строить «цепочки», по которым уже совсем просто построить матрицу
Т - соответствующие алгоритмы были описаны нами в разделе 11.6.4.
В качестве примера приведём вид матрицы Т для сетки, изобра-
жённой на рис. 164. Нумерация глобальных базисных вектор-функции
•ф"' и соответствующих им рёбер определяется табл. 25 (заметим, что
п(. — 33). При этом будем считать, что используются элементы перво-
го порядка и отношения длин рёбер (эта информация необходима для
вычисления Ttj и Тч) следующие: длина ребра {2,7} к длине ребра
{7,16} как 0.3 к 0.7, длина ребра {8,10} к длине ребра {10,13} как 0 6
к 0.4, а рёбра {7,8} и {8,9} имеют одинаковую длину. Тогда в разре-
женном столбцовом формате матрица Т имеет вид (при этом левая
единичная подматрица размера пе х п(. матрицы Т, как всегда, не хра-
нится}
ig = {1,2,3.4.6,7,8,11.14,15,17,20,22,23,24,25,26,27,28}
jg = {6,12,14.5,25.6,14,5,16,25,5,16, 25,16,14,19,5,16,25,15,20,16,19,12,19,27,27}
1 Ещё раз напомним, что «маленькие» грани примыкают к «большой» гра-
ни при контакте несогласованных ячеек сетки, а каждое «маленькое» ребро
является либо частью «большого» ребра, либо лежит внутри «большой» гра-
ни.
2 Удобнее всего формировать такую структуру в процессе генерации сет-
ки, особенно если измельчение отдельных участков сетки выполняется с по-
мощью локальных дроблений. Однако возможно и использование специаль-
ных алгоритмов, основанных на обработке уже построенной несогласованной
сетки (но при этом, конечно, хотя бы информацию о контактирующих «несо-
гласованно» рёбрах и гранях лучше всё-таки формировать в процессе генера-
ции конечноэлемснсной сетки).
820 15.Векторный МКЭ для решения задач электромагнетизма
дд = {1,1,1,0.7,0.3,1,1,0.35,0.5,0.15,0.35,0.5, 0.15,1,0.4,0.0,0.35,0.5,0.15,0.4,0.0,1,1,1,1,1,1}
номер ребра 1 2 3 4 5 6 7 8 9 10 II 12 13 14 15 16 17
номера вершин 1,2 1,4 1. 15 2, 3 2. 5 2, 16 3, 6 3,9 4,5 4,21 5,6 5,22 6, 14 7,9 8, 17 9, 14 9, 18
Таблица 25
номер ребра 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
номера 11, 12, 13, 14, 15, ‘ 15, 16, 16, 17, 17, 18, 19, 20, 21, 22, 23, 2, 7
вершин 20 14 23 24 16 21 17 22 18 23 20 20 24 22 23 24
номер ребра .35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
номера вершин 5, 12 7,8 7, 12 7. 16 8,9 8, 10 8, 13 9, Н ю, II ю, 13 ю, 19 11. 14 12, 13 12, 22 13, 14 17, 19 19, 23
В заключение рассмотрим вопросы, связанные с использованием
несогласованных сеток с ячейками другой формы.
Наиболее полезной для многих практических задач является воз-
можность согласования конечных элементов на несогласованных сет-
ках с шестигранными ячейками, поскольку использование шестигран-
ных ячеек позволяет достаточно просто и вместе с тем довольно каче-
ственно разбивать области со сложными границами, а возможность
включения в шестигранную сетку несогласованных ячеек позволяет
достаточно эффективно избавляться от «лишних» узлов при локальных
сгущениях или при разрежениях сетки.
Очевидно, что рассмотренные нами подходы для согласования ба-
зисных вектор-функций на несогласованных параллелепипедах могут
быть практически без изменения применены для согласования базис-
ных вектор функций на несогласованных шестигранниках Однако при
этом должно быть выполнено ещё одно (кроме отсутствия «перехлё-
стов») ограничение для тех границ шестигранников, по которым кон-
тактируют несогласованные ячейки, - это условие попадания рёбер
«маленьких» граней строго на «координатные линии» соответствую-
щей «большой» грани. Это ограничение необходимо для того, чтобы
касательную составляющую каждой базисной вектор-функции «боль-
шой» грани можно было бы точно представить в виде линейной ком-
бинации касательных составляющих базисных вектор-функций при-
мыкающих к этой грани «маленьких» шестигранников. Примеры до-
пустимого и недопустимого несогласованного контакта «большого»
шестигранника с «маленьким» были рассмотрены нами в разделе 11.8
(см. рис. 124 и 125), они вполне актуальны и для векторного МКЭ
Способы преодоления соответствующих проблем при работе с вектор-
ными и скалярными несогласованными шестигранными элементами
также практически ничем не различаются.
То же самое можно сказать и о принципах согласования конечных
элементов различных порядков с векторными базисными функциями.
В целом они остаются теми же. что и для элементов с узловыми базис-
ными функциями. Здесь также при использовании в согласованной
15.16.Другие возможности векторного МКЭ для решения ...
821
сетке конечных элементов различных порядков очень удобны иерар-
хические базисы. Реализация соответствующих подходов (фактически
являющихся некоторыми вариантами р -технологии уточнения конеч-
ноэлементного решения) очень проста. Как и в узловом МКЭ, в этом
случае достаточно убрать из локального базиса каждого конечного
элемента высокого порядка, граничащего с конечным элементом более
низкого порядка, те базисные вектор-функции, которые не с чем
«сшить» на границе контакта этого элемента высокого порядка со
смежным конечным элементом (являющимся элементом другого, бо-
лее низкого порядка).
Преимущество векторных иерархических базисов (по сравнению с
лагранжевыми) при использовании h-р -технологии на несогласован-
ных сетках может состоять, как и в случае узлового МКЭ, только в
более быстрой сходимости применяемых для решения конечноэле-
ментных СЛАУ итерационных методов, поскольку при стыковке век-
торных конечных элементов разных порядков на несогласованных
ячейках работать с иерархическими базисами даже сложнее, чем с ла-
гранжевыми. Трудности здесь, в общем-то, аналогичны тем, которые
были рассмотрены нами в разделе 12.3 для узловых конечных элемен-
тов.
15.16. ДРУГИЕ ВОЗМОЖНОСТИ ВЕКТОРНОГО МКЭ ДЛЯ РЕШЕНИЯ
НЕСТАЦИОНАРНЫХ ЗАДАЧ ЭЛЕКТРОМАГНЕТИЗМА
15.16.1. О ПОСТАНОВКАХ С СОВМЕСТНЫМ РЕШЕНИЕМ УРАВНЕНИЙ
ДЛЯ НАПРЯЖЁННОСТИ МАГНИТНОГО ПОЛЯ И ДЛЯ СКАЛЯРНОГО
МАГНИТНОГО ПОТЕНЦИАЛА
Кроме рассмотренной в разделе 15.13 постановки с векторным
А и скалярным U магнитными потенциалами, при моделировании
нестационарных электромагнитных полей в областях с проводящими и
непроводящими подобластями можно использовать и другие поста-
новки, не приводящие к вырожденным конечноэлементным СЛАУ.
Например, в проводящих подобластях (где коэффициент удельной
проводимости о не равен нулю) вместо векторного уравнения (15.1)
для вектор-потенциала А можно использовать векторное уравнение1
для напряжённости магнитного поля Н:
1 Это уравнение легко получить из системы уравнений Максвелла
(1.9)—(1.12) при е = 0 после деления уравнения (1.9) на о, применения к его
обеим частям оператора rot и подстановки в него вместо rotE значения
— — (из уравнения (1.10)); при этом после нахождения
вектор-функции Н напряжённость электрического поля может быть получе-
на как Ё — 2-lrotH — JCTj (опять же из уравнения (1.9) при е = 0).
822
15.Векторный МКЭ для решения задач электромагнетизма
, . а(ин) . .
rot(^rotH|H—- - = rot(-^Jj. (15.244)
Такие постановки рассмотрены, например, в работе [26]1. Однако в
этих постановках, в отличие от постановок с совместным использова-
нием вектор-потснциала А и скалярного потенциала U , в подобла-
стях с нулевой о электромагнитное поле может быть описано только
скалярным потенциалом. Это может привести к гораздо более серьёз-
ным (по сравнению с рассмотренной в разделе 15.13 постановкой для
потенциалов А и U ) трудностям в тех случаях, когда в решаемой за-
даче возможны обходы ненулевых токов2 по подобластям с нулевой
проводимостью. В постановках же с потенциалами А и U в таких
ситуациях можно в подобластях с нулевой о ввести специальные тон-
кие прослойки-перемычки («разрезающие» контуры возможных обхо-
дов ненулевых токов), в которых поле В определяется вектор-
потенциалом А, и основной трудностью здесь будет только вырож-
денность получаемой конечноэлементной СЛАУ. При этом линейно
зависимых уравнений в полученной конечноэлементной СЛАУ будет
относительно немного — пропорционально числу степеней свободы
конечных элементов в прослойках-перемычках. А поскольку нас уст-
раивает любое из решений3 конечноэлементной СЛАУ, проблема её
вырожденности фактически переходит в проблему вычислительных
затрат на получение одного из решений. Довольно часто это решение
может быть получено (хотя и за довольно большое число итераций)
наиболее часто употребляемыми итерационными методами, такими
как MCG (метод сопряжённых градиентов), BiCG (метод бисопряжён-
ных градиентов) и его модификации, GMRES и др. (см. семнадцатый
раздел) даже с использованием самых примитивных схем предобу-
словливания. В принципе же, можно использовать и процедуры регу-
ляризации для ускорения сходимости соответствующих итерационных
процессов решения таких СЛАУ.
Тем не менее постановки с совместным использованием уравнений
(15.244) и (15.191) могут оказаться довольно эффективными при реше-
нии некоторых типов задач. К ним относятся, например, задачи (в том
числе и нелинейные), в которых проводящие конструктивные элемен-
ты не имеют сквозных отверстий (и, значит, по непроводящим подоб-
ластям нельзя обойти ненулевой вихревой ток, наводимый в любой из
проводящих подобластей).
1 Там они называются Н—<Ь-постановками, поскольку через ф там обо-
значен скалярный магнитный потенциал.
2 Особенно вихревых, т.е. тех токов, которые определяются в процессе
решения задачи (как оЕ ).
3 Напомним, что в векторном МКЭ конечноэлементная СЛАУ может
иметь множество решений А', но при этом любое из этих решений даёт одно
и то же поле Вл = rot Ал .
15.16.Другие возможности векторного МКЭ для решения ...
823
Соответствующая системе дифференциальных уравнений (15.191).
(15.244) эквивалентная вариационная постановка' включает в себя два
вариационных уравнения
Г1 _ г<э(рй) _
I — rotH • го1Ф dQ + / —^-'Ф(Ю= I — JCTrot’SfdQ —
Jo J dt Jo
ЦН S2H uH
-J’(ljCTxnH)<'d5 УФсН^, (фхп)|п=0, (15.245)
5n
Jpgradl7grad<Z>dQ-О УФ 6 Я^ (15.246)
Uu 5P
и условие
(Н х пн )|ьП = - (g?a<l U х nH )|^,. (15.247)
Здесь S(\ как и в постановке (15.196)-(15.197), граница между по-
добластями Q11 и (QH - область определения уравнения (1 5.244),
a - область определения уравнения (15.191)).
Условие же (15.247) может быть проинтерпретировано как главное
краевое условие. И при построении конечноэлементной СЛАУ это
условие может быть учтено практически так же, как в МКЭ учитыва-
ются главные краевые условия. Например, при использовании элемен-
тов первого порядка вместо тех строк, которые соответствуют базис-
ным вектор-функциям ф,,: с ненулевыми касательными составляющи-
ми на 5П, в конечноэлементную СЛАУ можно вставить уравнения для
весов (/, этих базисных вектор-функций вида
-?„)// = О, (15.248)
где i — номер уравнения и edge-функции ф,, ассоциированной с реб-
ром Г.,: (на котором ф, имеет равную единице касательную состав-
ляющую), a j\ и j-2 - номера узловых базисных функций фд и фи,
ассоциированных с вершинами ребра Г,, и I - длина ребра Г, . Знаки
в уравнении (15.248) соответствуют случаю, когда касательная edge-
функций ф? направлена от той вершины, с которой ассоциируется
базисная функция фл, к той, с которой ассоциируется базисная функ-
ция ф>2.
1 Мы опустим вклады от краевых условий на внешней границе расчётной
области QH U Qu .
824
15.Векторный МКЭ для решения задач электромагнетизма
15.16.2. ОБ ИСПОЛЬЗОВАНИИ БАЗИСНЫХ ВЕКТОР-ФУНКЦИЙ
ИЗ ПРОСТРАНСТВА Hd,v
Здесь мы рассмотрим возможности использования в векторном
МКЭ базисных вектор-срункций из различных функциональных про-
странств.
До сих пор для решения векторных уравнений мы использовали ба-
зисные вектор-функции ф/; из пространства Hrot (напомним, что каж-
дая вектор-функция Ф из пространства Hvot должна быть сама сум-
мируема с квадратом и иметь суммируемый с квадратом го1Ф). С
помощью таких базисных вектор-функций фл мы получали конечно-
элементные решения электромагнитных задач, которые описываются
одним векторным уравнением вида (15.1). Это уравнение является до-
вольно универсальным и позволяет моделировать практически любые
нестационарные электромагнитные процессы, включая нелинейные
(трудности при его использовании возникают в основном тогда, когда
в область входят подобласти с ст = 0 и токи смещения являются несу-
щественными; для этих случаев нами были рассмотрены специальные
постановки, описанные в разделах 15.13 и 15.16.1).
Однако иногда моделирование нестационарного электромагнитного
поля проводится на основе других математических моделей. Примером
одной из таких моделей может служить следующая система из двух
дифференциальных уравнений первого порядка (см., например, [29])
eM = rot Й -оЕ -JCT, (15.249)
сч I |i J
4^ = -rotE, (15.250)
которая обычно используется только в тех случаях, когда в модели-
руемом электромагнитном процессе существенны токи смещения.
Эквивалентная вариационная постановка для системы (15.249)-
(15.250) включает в себя два вариационных уравнения
(15.251)
(15.252)
где напряжённость электрического поля Е и пробная вектор-функция
Ф являются элементами пространства Hrot, а индукция магнитного
15.16.Другие возможности векторного МКЭ для решения ...
825
поля В и пробная вектор-функция Ф — элементами пространства H<liv
вектор-функций, которые имеют суммируемые с квадратом диверген-
ции (т.е. для \/Ф G H<liv J dQ < оо).
Q
При построении конечноэлементной аппроксимации в качестве ба-
зисных вектор-функций подпространства Vrot С Hlot, очевидно, мо-
гут быть взяты рассмотренные нами в этом (пятнадцатом) разделе век-
тор-функции ф, с непрерывными касательными составляющими. В
качестве же базисных вектор-функций пространства V'llv С Н'11' (че-
рез линейную комбинацию которых будет искаться приближённое
решение В1' и на которые будет заменяться пробная вектор-функция
Ф при построении конечноэлементной системы) берутся вектор-
функции ф; с непрерывными нормальными составляющими на смеж-
ных гранях.
На векторных элементах первого порядка эти (>ункции, естествен-
но, ассоциируются с гранями, и поэтому они эыли названы face-
функциями1. Однако, как мы уже убедились, на элементах высоких
порядков некоторые из базисных вектор-функций и из пространства
Hrot также удобно ассоциировать с гранями (т.е. таким вектор-
функциям также вполне подошло бы название «face-функции»). В
принципе же, основным характерным признаком базисных вектор-
функций из пространства Hrut и из пространства H<l,v является не то,
с каким геометрическим объектом эти вектор-функции ассоциируются,
а то, что одни из них имеют непрерывные касательные составляющие,
а другие - нормальные. При этом, очевидно, базисные вектор-функции
из Hrot имеет смысл ассоциировать с рёбрами, гранями или конечны-
ми элементами, а базисные вектор-функции из Н‘,v - только с граня-
ми или конечными элементами. Поэтому, наверное, вполне правильно
было бы называть edge-функциями только те базисные вектор-
функции из Hrot, которые ассоциированы с рёбрами, а к названию
«face-функция» добавлять признак принадлежности её к тому или ино-
му пространству. Например, ассоциированную с гранью базисную
вектор-функцию из пространства Н'°* можно называть face-т-
функцией (т — это признак того, что непрерывными являются танген-
циальные составляющие), а ассоциированную с гранью базисную век-
тор-функцию из пространства H‘,lv - face-n-функцией (п - это при-
знак того, что непрерывными являются нормальные составляющие).
Аналогично, ассоциированные с конечным элементом базисные век-
1 Заметам, что использовать векторные edge- и face-функции для решения
задач электромагнетизма впервые предложил Неделек (Nedelec, см. его работы
[27, 28]).
826
15.Векторный МКЭ для решения задач электромагнетизма
тор-функции из пространства Hrot удобно называть volume-T-
функциями, а из пространства Н'|п - volume-n-функциями1.
Покажем, как могут быть построены базисные вектор-функции из
пространства H(llv на сетку прямоугольных параллелепипедов.
Определим на параллелепипеде Пга7,={.тг,жг+1] х [г/Л.,т/ч+1, x[zp,zp+1]
шесть вектор-функций:
hr.
о
о
о
о
zp+\ -z
hz
О
О
где h.r = хг+1 - xr, hy = ys+1 - ys, hz = ?/p+1 - yp. При этом вектор-
функцию ф будем ассоциировать с гранью х = хг параллелепипеда
Q,.S7,, вектор-функцию ф., - с гранью х = хг+1, вектор-функцию ф.( -
с гранью у — уя и т.д. Таким образом, каждая из локальных вектор-
функций ф, имеет ненулевую нормальную составляющую только на
одной грани, с которой она ассоциирована.
Каждую из глобальных базисных вектор-функций ф; также будем
ассоциировать с одной гранью и определим в виде сшивки ассоцииро-
ванных с этой гранью двух локальных вектор-функций параллелепи-
педов, смежных по этой грани (если грань является участком границы
расчётной области, то ассоциированная с ней глобальная вектор-
функция определяется, естественно, соответствующей локальной век-
тор-функцией одного параллелепипеда).
Набор определённых таким образом вектор-функций ф может
служить базисом простейшего конечномерного пространства
1 На это в последних работах обращают внимание и многие английские
авторы; например, в работе [301 векторные элементы с базисными вектор-
функциями из пространства Нг"' предлагается называть «vector tangential
element», а элементы с базисными вектор-функциями из пространства H<I1V -
«vector normal element».
15.16.Другие возможности векторного МКЭ для решения ...
827
V,1IV С Hrllv. Очевидно, любая вектор-функция из этого пространства
Vdlv имеет непрерывные нормальные составляющие и разрывные ка-
сательные
Не представляет особого труда построить конечномерное простран-
ство V IV с базисными вектор-функциями высоких порядков Основной
принцип остаётся тем же - каждая из базисных функций должна иметь
на границах конечных элементов непрерывные нормальные составляю-
щие (при этом базисные вектор-функции высоких порядков уже могут
быть ассоциированы не только с гранями, но и с самими элементами).
На сетках с шестигранными ячейками базисные вектор-функции из
пространства Н (так же, как и базисные вектор-функции из про-
странства Hrot) удобно определять через базисные вектор-функции
шаблонного кубика. Техника работы с face-n-функциями и volume-n-
функциями в целом мало чем отличается от рассмотренной нами тех-
ники работы с базисными вектор-функциями из пространства Hrot
(т.е. с edge-функциями, face-т-функциями и volume-т-функциями)1.
В заключение заметим, что электромагнитные процессы, описы-
ваемые моделью (15.249)—(15.250), без каких-либо особых проблем
могут быть промоделированы с помощью одного векторного уравне-
ния (15.1). При этом преимущества использования вариационной по-
становки (15.212) по сравнению с вариационной постановкой (15.251)-
(15.252) очевидны: при использовании одной и той же сетки для по-
строения конечноэлементных аппроксимаций соответствующих ва-
риационных задач вычислительные затраты для постановки (15.212)
значительно меньше, чем для постановки (15.251)-( 15.252) (и по коли-
честву степеней свободы, и по общему числу ненулевых компонент
матрицы) Преимущества же постановки с двумя вариационными
уравнениями могут состоять в том, что получаемые с её помощью ко-
нечноэлементные решения сразу дают поля В и Е (для постановки
(15.212) В и Е получаются дифференцированием А по пространству
и времени) и, возможно, в более быстрой сходимости методов решения
конечноэлементных СЛАУ. Однако вряд ли можно получить какое-
либо теоретическое обоснование последнего утверждения (да и, скорее
всего, преимущество какого-либо из рассмотренных подходов в скоро-
сти получения конечноэлементного решения2 фактически будут зави-
1 Более подробно о лагранжевых face-n-функциях и volume-n-функциях на
сетках с шестигранными ячейками можно посмотреть в работе [29] .
2 Особенно, при использовании неявных схем аппроксимации по времени;
при использовании же явных схем (которые являются относительно эффек-
тивными, как правило, только при о = 0 или при изучении быстроменяю-
щихся электромагнитных процессов в почти непроводящих средах) для реше-
ния уравнения (15.1) довольно часто пользуются процедурами диагонализа-
ции матрицы массы (простейшая из которых состоит в том, что в каждой
строке матрицы массы к диагональному элементу добавляются все внедиаго-
нальные элементы этой строки с последующим их обнулением), и тогда вы-
числительные затраты определяются только числом ненулевых компонент
матрицы жёсткости.
828
15.Векторный МКЭ для решения задач электромагнетизма
сеть от типа решаемой задачи), а негативные последствия дифферен-
цирования А для получения В и Е в отдельных интересующих ис-
следователя точках легко снимаются путём применения простейших (и
в целом относительно малозатратных) процедур сглаживания.
И, наконец, пожалуй, самым важным преимуществом постановки с
одним уравнением (15.1) (и соответственно вариационной постановки
(15.212)) является её универсальность: с использованием её можно не
только моделировать любые нестационарные поля (с различным уров-
нем влияния токов проводимости и токов смещения), но и решать не-
линейные1 электрома! нитные задачи практически любого уровня
сложности.
1 Подробнее об этом будет сказано в следующем разделе, посвящённом
решению нелинейных 1адач
16.1 Нелинейные эллиптические краевые задачи
829
16. РЕШЕНИЕ НЕЛИНЕЙНЫХ ЗАДАЧ
16.1. НЕЛИНЕЙНЫЕ ЭЛЛИПТИЧЕСКИЕ КРАЕВЫЕ ЗАДАЧИ
Нелинейными называют такие дифференциально-краевые зада-
чи, у которых параметры дифференциального уравнения или краевых
условий зависят от решения.
В общем виде нелинейное дифференциальное уравнение эллипти-
ческого типа можно записать следующим образом:
-div (X(u) gradu) + и — f (tz), (16.1)
т.е. параметры X, и f являются некоторыми функциями от и .
Как правило, отдельно рассматривается ситуация, когда один из ко-
эффициентов (чаще всего это коэффициент диффузии X ) зависит от
производных решения, например, X = X(gradu). Хотя формально за-
пись Х(и) может означать не только непосредственную зависимость X
от решения и (заданную аналитически, таблично или каким-либо ещё
способом), но и зависимость X от каких-либо производных и (напри-
мер, от gradiz или от |gradw| = J(gradiz)2 ), тем не менее при реализа-
ции соответствующего метода решения нелинейной задачи очень важ-
ным является то. как именно задана зависимость X от решения — непо-
средственной зависимостью X(zz) или как-то иначе, например, зависи-
мостью X(|gradtz|).
Заметим также, что нелинейность дифференциального уравнения
(16.1), порождаемая зависимостью коэффициента от и , можно трак-
товать как нелинейность модифицированной правой части
/(u) =/(u) — ^(tz)tt. (16.2)
Однако при переносе члена (w) и в правую часть методы решения
соответствующей нелинейной задачи чаще всего уступают по эффек-
тивности подходам, в которых нелинейный член уравнения
(16.1) обрабатывается отдельно от правой части f (.и). И поэтому луч-
ше нелинейность ^(tz)tz обрабатывать с учётом ее вида, а не как со-
ставляющую нелинейной правой части.
830
16.Решение нелинейных задач
В этой книге мы рассмотрим наиболее часто встречающиеся па
практике ситуации, когда коэффициент диффузии X и правая часть f
являются некоторыми функциями решения, оставив читателю для са-
мостоятельного осмысления ситуации с нелинейностью, порождаемой
зависимостью от и.
Краевая задача может оказаться нелинейной не только в том случае,
когда параметры дифференциального уравнения X, -у и f зависят оз
решения и , но и тогда, когда параметры краевых условий 0, р ил и
зависят от и . Так, краевое условие второго рода делает краевую зада-
чу нелинейной, если параметр 0 зависит (не линейно) от и :
Х^- = 0(Ю. (16.3)
on
Краевое условие же третьего рода является нелинейным, если его
параметры 3 или зависят от и. В общем случае нелинейное крае-
вое условие третьего рода может быть записано в виде.
Х^-+ 0(u)(u — (w)) = 0 (16.4)
(при этом, естественно, предполагается, что — не линейная
функция и).
В результате конечноэлементной аппроксимации нелинейной краевой
задачи (16.1), (16.3), (16.4) получается система нелинейных уравнений
A(q)q = b(q), (16.5)
у которой компоненты матрицы A(q) и вектора правой части b(ql
определяются следующим образом:
(q) = J X (иЛ (q)j grad ф7 • grad ф/ZQ +
+ + f 0(w,z (q)) ф/ф,.^, (16.6)
Q S3
(q) = j f(i'h (q)^;dQ + f (q)^:dS +
Q S2
+ f 3(^'(q)) (q)) (16.7)
S’3
где
(<1) = • (16.8)
./
Рассмотрим методы решения этой системы нелинейных уравнений.
16.2.Метод простой итерации
831
16.2. МЕТОД ПРОСТОИ ИТЕРАЦИИ
16.2.1. СХЕМА МЕТОДА
Наиболее простым для решения системы нелинейных конечно-
элементных уравнений (16.5) является так называемый метод простой
итерации. Он заключается в следующем.
Выбирается некоторое начальное приближение - функция и° (или
вектор весов q^°^ разложения по базису { ф,-} ) Это начальное при-
ближение обычно выбирается на основе некоторых априорных данных.
С помощью выбранного начального приближения q" вычисляют-
ся коэффициенты конечноэлементной матрицы Ау (q ' j и вектора
правой части / (q(l (см. соотношения (16.6)-(16 8)) При этом пара-
метры дифференциального уравнения и краевых условий, зависящие
от решения и, могут быть представлены на каждом конечном элемен-
те Q/ в виде линейной комбинации базисных функций (см. раздел 3.8).
Например, коэффициент диффузии может быть представлен интерпо-
ля нтом
j
где (в случае использования элементов лагранжева типа)
(q((")) ~ значение коэффициента X^uh (q(‘”)) в j ~м узле, ф7- -
базисная функция, соответствующая j -му узлу.
Довольно часто при решении нелинейных задач для вычисления
компонент конечноэлементной матрицы и вектора правой части ис-
пользуется численное интегрирование. В этом случае значения реше-
ния в узлах интегрирования, по которым вычисляются параметры за-
дачи Х(и), ^(и) и f (и), берутся как значения в этих узлах интегри-
рования линейной комбинации локальных базисных функций фг с
весами q,, полученными на предыдущей итерации по нелинейности
или из начального приближения.
Итерационный процесс в методе простой игераиии строится сле-
дующим образом. Па первом шаге решается система линейных алгеб-
раических уравнений Atq^’ iqf = b,q1'"' В результате решения
этой СЛАУ находится новое приближение q’ 1 решения нелинейной
системы (16.5), которое, в свою очередь, используется для нахождения
компонент матрицы Д, q1"^ и вектора b, (q('^ , затем решается сис-
тема A-qW '-qC2) = b q<L>) и т.д.
832
16.Рсшение нелинейных задач
16.2.2. ОСТАНОВ ИТЕРАЦИОННОГО ПРОЦЕССА
Решение на А:-й итерации можно считать решением систе-
мы нелинейных конечноэлементных уравнений (16.5), если выполня-
ется условие:
где е - некоторое малое число, выбранное как требуемая точность реше-
ния нелинейной задачи. В данном случае норма абсолютной невязки не-
линейной системы делится на норму её правой
части для того, чтобы в качестве е можно было бы использовать относи-
тельное. а не абсолютное значение порога невязки, что гораздо удобнее
при решении большинства практических задач. При этом в качестве век-
тора b можно брать как вектор b^q^j, вычисленный по начальному
приближению, так и вектор b(q^), вычисленный по значению q^\
полученному на текущей итерации по нелинейностям.
В ряде случаев в качестве критерия выхода можно использовать ус-
ловие — q^'_1)||/||q^|| < 6, где 6 — некоторое малое число. Это
условие означает, что при переходе к следующей итерации решение
почти не меняется. Однако следует помнить, что такое условие выхода
не । арантирует получение решения нелинейной задачи с требуемой
точностью и может использоваться в «аварийных» случаях, когда ите-
рационный процесс по нелинейностям начинает стагнировать. Можно
также для остановки итерационного процесса по нелинейностям при
его стагнации предусматривать выход по количеству итераций.
16.2.3. ИСПОЛЬЗОВАНИЕ РЕЛАКСАЦИИ
Для ускорения сходимости процесса решения нелинейной зада-
чи, а во многих случаях и для её обеспечения может быть использован
принцип релаксации. В этом случае каждое последующее приближе-
ние решения строится как
q'M = +(1-(16.10)
где о? - коэффициен т релаксации, a - решение системы
A(q(A:-’))qW=b(q^-1)).
Значение коэффициента релаксации и/ можно получать в результате
минимизации по с? невязки нелинейной системы (16.5) (при подстанов-
ке в неё вместо q значения q^z\ определяемого соотношением (16.10)):
16.3.Метод Ньютона
833
Я(сУ') + (1 - i/Jq^^i/qM + (1 - wA')q^-1^ -
-b (c/q^ + (1 - wZ:) q(A-1)][. (16.11)
Для минимизации функционала (16.11) по ш/,: может быть исполь-
зован любой метод одномерной оптимизации.
Метод простой итерации очень прост по программной реализации, но,
как правило, требует выполнения большого количества итераций, а в ряде
случаев вообще не даёт возможности получить решение нелинейной за-
дачи, особенно в случаях с существенной зависимостью параметров зада-
чи от решения (или его производных). Метод же Ньютона, хотя и являет-
ся значительно более сложным для программной реализации, обладает
гораздо лучшей сходимостью при решении многих нелинейных задач.
16.3. МЕТОД НЬЮТОНА
Метод Ньютона основан на линеаризации нелинейных уравне-
ний системы (16 5) с использованием разложения в ряд Тейлора. Суть
такой линеаризации заключается в следующем.
Каждый нелинейный член уравнений системы (16.5) представляет-
ся в виде разложения в ряд Тейлора в окрестности точки q() (q° - век-
тор весов, полученный на предыдущей итерации по нелинейностям
или являющийся начальным приближением), причём этот ряд ограни-
чивается членами с первыми производными. Так, слагаемые левой
части уравнений системы (16.5) представляются в виде
Ач (ч)<ъ
4(Ч"И+Г
г
д(Аи(ч )Qj)
dq,.
а компоненты вектора правой части - в виде
9bj (q)
dq,
Я~Я
В результате из системы (16.5) получается система линейных ал-
гебраических уравнений
АЛЧ = ЬЛ, (16.12)
которую мы будем называть линеаризованной по методу Ньютона
конечноэлементной системой.
Сразу заметим, что при программной реализации линеаризацию
уравнений системы (16.5) после сборки глобальной матрицы выпол-
нять чрезвычайно сложно, поскольку процедуру сборки глобальной
матрицы конечноэлементной системы уравнений легко запрограмми-
ровать тогда, когда компоненты локальных матриц и векторов являют-
834
16.Решение нелинейных задач
ся числами, а не некоторыми функциями вектора решения q. Поэтому
линеаризацию отдельных слагаемых уравнений системы (16.5) нужно
проводить на уровне локальных матриц и векторов, и только после
этого собирать из них глобальные матрицу А и вектор правой части b
линеаризованной конечноэлементной системы.
Рассмотрим конечный элемент Q./n . Как обычно, обозначим через
А локальную матрицу элемента через b — его локальный вектор
правой части, а через q — подвектор глобального вектора q, состоя-
щий из весов (в локальной нумерации) базисных функций конечного
элемента О7/(.
Представим слагаемое A в виде разложения в ряд Тейлора в
окрестности значения q() и ограничимся членами с первой производной:
Л, (Ч И;
Л,(ч")$+Е
7-1
д(Л(ч Ч)
(q )
дф.
q=q()
(16.13)
где п - размер локальной матрицы (и, естественно, вектора) элемента
, a q() - значение q на предыдущей итерации1 метода Ньютона.
Аналогично линеаризуются и компоненты локального вектора пра-
вой части:
1 На первой итерации в качестве q(] обычно берут коэффициенты разло-
жения начального приближения гЛ() по локальным базисным функциям -ф.,
п
конечного элемента , т.е. и, например, для лагранжевых.
>1
элементов в качестве д!- можно взять значения w/l,° в соответствующих узлах
конечного элемента .
16.3.Мет од Ньютона
835
Mfr(g)
(16.14)
q=q°
Из соотношения (16.13) видно, что в результате линеаризации сла-
гаемого A.. (q }qt появляются слагаемые, содержащие кроме qj ещё и
другие компоненты вектора решения. Это значит, что в результате
линеаризации слагаемого A. (q )<7? мы получим вклады не только в
компоненту локальной матрицы A.L линеаризованной СЛАУ, но и
в другие компоненты г-й строки AL. Так, например, даже если и
^4 (q )
7^1 слагаемое ——-
д(Ц
q =q()
— д?) даст вклад в компоненту
u . ^Aj(q )
A , равный --——-
dqi
qU (это множитель перед д, ). Кроме того,
lq =q()
правая часть (16.13) имеет слагаемые, не содержащие компоненты
вектора решения, а значит, являющиеся добавками в правую часть
dA (q)
линеаризованного уравнения. Так, все слагаемые —------
яв-
iq=q()
появляющиеся в результате линеаризации слагаемого А{ (q }q.j
ляются вкладами в компоненту локального вектора правой части b,L
линеаризованной конечноэлементной системы.
В свою очередь, из соотношения (16.14) видно, что в результате ли-
неаризации компоненты bt (q) вектора правой части появляются сла-
гаемые, содержащие компоненты вектора решения. Это означает, что в
результате линеаризации компонент вектора правой части системы
46 5) появляются добавки в компоненты матрицы линеаризованной
т ЗД (q)
конечноэлементнои системы. 1ак, слагаемые —
РЪ
qr из правой
q=q°
db (л 1
части разложения (16.14) дают вклады вида----'
dqr
ненты Af'. локальных матриц линеаризованной системы.
Таким образом, линеаризованная система (16.12) собирается из ло-
кальных матриц A.l и локальных векторов bL следующего вида.
в компо-
q=q()
836
16.Решение нелинейных задач
а 4 (м)
^7/
(16.15)
b!j
дЬ, (q)
dqr
(16.16)
Итерационный процесс в методе Ньютона строится аналогично то-
му, как бып построен итерационный процесс в методе простой итера-
ции. Очередной его шаг заключается в генерации по q‘ (на первой
итерации q формируется из начального приближения, на последую-
щих в качестве q ' берётся q'r ) линеаризованной системы (16.12) и
её решении, в результате чего (возможно, с использованием релакса-
ции (16.10)) находится новое приближение q^^. После этого проверя-
ется критерий останова (16.9), и в случае его невыполнения осуществ-
ляется переход к следующей итерации метода Ньютона.
Обратим внимание на то, что при оценке невязки используются
матрица и вектор нелинеаризовапной системы. Это значит, что при
вычислении невязки должны быть использованы пе матрица А и
вектор Ь£, собираемые из локальных матриц и векторов вида (16.15) и
(16.16), а матрица A (q) и вектор b(q), компоненты которых вычис-
ляются, как и в методе простой итерации, по формулам (16.6)-(16.8), и
в эт их формулах в качестве вектора q берётся вектор q,A), получен-
ный в результате решения линеаризованной системы (16.12).
Вообще говоря, полученный на А;-й итерации в результате решения
линеаризованной системы (16.12) вектор q не гарантирует уменьше-
ния невязки исходной нелинейной системы (16.5), вычисленной как
A^q(/ ' |q — b‘q’' j||, по сравнению с невязкой
A(q iq b(q' ' ' на предыдущей итерации. Увеличение
невязки может произойти в том случае, когда нелинейность в коэффи-
циентах задачи значительная, и вектор q'fc-1\ по которому1 вычисляют-
ся компоненты матрицы и вектора линеаризованной системы, довольно
далёк от решения нелинейной системы. В результате решение q^ ли-
неаризованной системы (16.12) может значительно отличаться от векто-
ра q'z 11 (по которому выполнялась линеаризация) и попасть в область
таких значений, где невязка линеаризованной системы уже очень сильно
1 При генерации вкладов в линеаризованную систему этот вектор был обо-
значен нами как q'1.
16.3.Метод Ньютона
837
отличается от невязки исходной нелинейной системы. В этом случае
вектор, доставляющий нулевую невязку линеаризованной системе, мо-
жет дать очень большую невязку в исходной нелинейной системе.
Чтобы не допустить этого, можно ограничивать отход вектора q1'
от вектора q( = q' по которому выполняется линеаризация, т.е.
оставлять век гор q в зоне, где невязка линеаризованной системы ещё
достаточно близка к невязке исходной нелинейной системы.
Нетрудно убедиться, что для достижения этой цели можно брать
вектор qH по формуле (16.10), т.е. использовать нижнюю релакса-
цию. Очевидно, что при значении коэффициента релаксации с/ , близ-
ком к нулю, значение q^ будет близко к q° = q^-1\ линеаризован-
ная система будет также близка к исходной нелинейной системе и по-
нижение невязки линеаризованной системы должно приводить к по-
нижению невязки нелинейной системы. Лучше всего коэффициент
релаксации о/ выбирать из условия минимума невязки 7?|^соА’), опре-
деляемой соотношением (16.11).
Заметим также, что при использовании метода Ньютона из-за осо-
бенностей вычисления производных по и зависимостей X (?/.), /(w) и
других коэффициентов нелинейной краевой задачи (производные
д\(.и) Of (и)
—и другие входят, как мы покажем чуть позже, в выра-
жения, определяющие в соотношениях (16 15) и (16.16) производные
(q )
dQj
dbj (q)
и
) результирующая линеаризованная матрица Az (в
отличие от А [ q' ' |) может перестать быть положительно опреде-
лённой. Избежать этого можно введением так называемого коэффици-
ента «демпфирования» м Е (0,1], который ставится перед добавками с
производными (сравните с (16.15) и (16 16)).
На каждой итерации коэффициент v выбирается сначала равным
единице. Если на очередном шаге итерационного процесса матрица
перестаёт быть положительно определённой (что сопровождается, как
правило, резким ухудшением сходимости итерационного процесса
838
16.Решение нелинейных задач
решения линеаризованной системы), коэффициент v уменьшают и
перевычисляют матрицу и вектор Ь; линеаризованной системы.
При этом на следующем шаге итерационного процесса коэффициент и
снова может быть взят равным единице.
16.4. ПРИМЕР РЕШЕНИЯ ОДНОМЕРНОЙ НЕЛИНЕЙНОЙ ЗАДАЧИ
С КОЭФФИЦИЕНТОМ ДИФФУЗИИ, ЗАВИСЯЩИМ ОТ РЕШЕНИЯ
Рассмотрим одномерную задачу для уравнения следующего ви-
да:
= <|619>
Зависимость коэффициента X от решения и может быть задана
либо явно (в виде некоторой аналитической функции), либо (что чаще
всего встречается на практике) таблично. При этом будем считать, что
параметры 'у и f не зависят от и .
Разобьём расчётную область Q на конечные элементы
Q,/( = [ж,п,ж,„+1] узлами xt, i = l...n, и выполним конечноэлемент-
ную аппроксимацию краевой задачи для нелинейного уравнения
(16.19) с использованием кусочно-линейных базисных функций.
Рассмотрим конечный элемент О.1П . Введём на нем локальную ну-
мерацию узлов и базисных функций: = х1П, х2 = Ф1 — Фш,
ф2 = Ф///+1 (Ф-z ~ глобальные кусочно-линейные базисные функции).
Коэффициент Х(а) на элементе представим в виде линейного
интерполянта
Х$2"'(г? (q, ж)} = Xй'"(q, )j ф] (x) + XQ"' (uh (q, x2)) ф2 (ж),
7t
где г?' (q, ж) — u!l (q, x) = , и в нашем случае
Z=1
и'1 (q, z) = £1Ф1(ж) 4- <72ф2(ж)
Тогда компоненты локальной матрицы А конечного элемента О,т
могут быть вычислены следующим образом:
Д:/ (q) = j {и>1' (4> )) Ф1 grad фу grad ф?^П +
+ j Х$2ш ('{?' (q, х2)) ф2 grad фу • grad ф-^И + J тфу-фДО .(16.20)
16.4.Пример решения одномерной нелинейной задачи ...
839
Как было показано выше, для построения матрицы и вектора пра-
вой части линеаризованной системы (16.12) (см. соотношения (16.15) и
dA.. (q )
(16.1 6)) необходимо вычислить частные производные ——-
dqj
и
q=q()
db (д)
. Так как правая часть в рассматриваемой задаче не зависит
q=q°
db (q)
от решения, то----
= 0.
5^. „
с
Вычислим производные по qy компонент локальной матрицы:
q=q()
дД/- (д )
dq.
q=q°
Ф1 grad ф,- • grad ф,.сК1 +
q=q()
Q,
dq.
ф2 grad ф,; • grad . (16.21)
Таким образом,
q=q()
нам необходимо вычислить производные
dq.
, которые уже не зависят от неизвестных q.j и
lq=q()
фактически являются константами на О,/н, и вычислить интегралы
J ф, grad ф, • grad .
^in.
Нетрудно убедиться, что интеграл
У 'ф/ grad ф?; grad ф,.сЮ равен
Д- при I = Г и — при i г.
2п, r 2h
Значения производных от коэффициента диффузии можно полу-
чить следующим образом:
dq
q=q(1
dX^1" (и)
du
duh (q,S)
, (16.22)
q=q°
и
где значение производной приближённого решения и11 по неизвест-
ной qj
840
16.Решение нелинейных задач
ди1' (q, Т/) 9^2 ) 7'
д q:i q=q() dqj
(16.23)
q=q”
т.е. для любых лагранжевых элементов оно равно единице при I = j и
нулю при I j.
зависит от
«=7?(q,.T/)
(и)
Способ же вычисления производной ----v
того, каким образом задана зависимость X от и . Если эта зависимость
задана таблично, то обычно строится аппроксимирующий её сплайн
(чаще всего кубический сплайн с непрерывными первыми производ-
ными, см. раздел 4.17), и по нему вычисляется значение производной
дХ{и)!ди. Этот случай является наиболее общим. В частных же слу-
чаях, когда зависимость X от и задаётся аналитически (формулой),
производную дХ(и)/ди можно вычислять аналитически.
Таким образом, полученные значения производных (16.22) под-
ставляются в выражение (16 21) для вычисления производных
АД,- (4 )
dqj
вьтажения для вычисления компонент локальных матриц и векторов
(16 15) и (16.16) (или (16 17) и (16.18)), из которых и собирается ли-
неаризованная система (16.12).
Пусть зависимость Х(и) задана аналитически, в виде формулы:
X(u) = u2 + 1. (16.24)
, а эти производные, в свою очередь, подставляются в
q=q°
Вычислим производные
дХп"' (ц)
ди
чаем:
. Исходя из того, что
q=q()
= 2uh (q, i/) (см. (16.24)), и учитывая (16 23), полу-
dq:i
dq
о,
(16.25)
q=q'
Таким образом, из (16.21) с учётом (16.25) получаем
и
и
16.4.Пример решения одномерной нелинейной задачи ...
841
дА}! (q) q=q() — in0 hqi ’ аЛц (q) q=q° - hq2’
а д(12
с>Л}2 (q) - 1 dA}2 (q) 1 n°
a 9i q=q° dq.2 q=q()
^Л1 (q) - 1 /7° ^21 (q) — - Xn" h q'2 ’
a 9i q=q() “ /Л1’ dq2 q=q°
9А22 (q) -In0 - hУ| ’ ^22 (q) 1 n()
a9i q=q° dq-2 4=q() - hq2-
(16.26)
Подставляя выражения (16.26) в соотношения (16.15) и (16.16), по-
лучаем, что компоненты локальных матриц KL и локальных векторов
правой части bL, из которых собирается линеаризованная система
(16.12), для зависимости X от и, заданной соотношением (16.24), вы-
числяются следующим образом:
aL _ 1 i э'К 1 _1_ h
Ai — ) +(?2) + 214-^-91 + ч у,
AL2 = - ((Й1)2 + (Й)2 + 2) 4-1$ ($ “ $) + У*7"
4г! = + (Й)2 + 2) 4- 1$ (-$ 4- $) 4- Vй |,
Ш+И+2)+1 И+|,
Z//и / \ / / fl, \ / О
= 1(2/1 + h) + |(« + (^)2)(Й' - &“),
^2 = g- (71 + 2/а) + ^((?1) + (Й) )(—Й' + й'), (16.27)
где, как обычно, использованы обозначения f = f(ii) (т.е. f/ - значе-
ния f в узлах $i), а - среднее значение на конечном элементе
П,„ . При вычислении вкладов от f в Ь (и соответственно в Ь71) функ-
цию f (х) мы заменяли интерполянтом //4)Z(x).
1
842
16.Решение нелинейных задач
Пусть расчётная область Q = [5,15] разбита равномерно на 5 ко-
нечных элементов, коэффициент X в дифференциальном уравнении
(16.19), как уже было сказано, определяется соотношением (16.24),
коэффициент 'у является константой, равной единице, правая часть
задана в виде функции / = —х, а на краях расчётной области заданы
первые краевые условия и1ж=5 = 5 и wljiMs — 15 . Нетрудно убедить-
ся, что решением такой нелинейной краевой задачи является функция
и — X .
Продемонстрируем на примере решения этой тестовой задачи ме-
тод Ньютона и сравним его по скорости сходимости с методом про-
стой итерации. При этом выход из итерационного процесса (по нели-
нейностям) и в методе Ньютона, и в методе простои итерации будем
осуществлять при достижении относительной невязкой R нелиней-
ной конечноэлементной системы A(q)q — b значения е = 10~13 (т.е.
при Rk — || A (q(*)) q(Z:) — b|||/||b||| < icr13).
В качестве начального приближения выберем постоянную функ-
цию, удовлетворяющую краевому условию слева: ц,° Я 5. Для него
Л,| = |а(ч<11>)ч<|’>-ь|/||Ь|| = 1.48.
При использовании метода Ньютона было сделано 7 итераций. В
табл. 26 показано, как менялась по итерациям относительная невязка и
коэффициент релаксации ш (который, начиная со второй итерации,
уменьшался только в том случае, когда невязка нелинейной системы не
уменьшалась по сравнению со значением на предыдущей итерации*).
Таблица 26
А; 1 2 3 4 5 6 7
Bk 9.67 8.43 1.31 8.23-IO’2 6.75-10’4 4.72-10‘8 610’15
1 0.5 1 1 1 1 1
Приведём значения компонент локальной матрицы и вектора пра-
вой части для первого конечного элемента Qj = [5,7] на нескольких
итерациях метода Ньютона, а также значения векторов q(A:).
С учётом того, что начальное приближение w() является константой,
равной пяти, по формулам (16.27) получаем на первой итерации по не-
линейностям локальную матрицу и вектор конечного элемента :
'13-13'1 (о o'] Го.667 о.ззз'
-13 13 + 0 о1+ 0.333 0.667
-5.667'
-6.333
'-5.667
-6.333
13.667
-12.667
-12.667'
13.667
/
1 При этом на следующей итерации ш снова брался равным единице.
16.4.Пример решения одномерной нелинейной задачи ...
843
Вектор весов q^, определяющий приближённое решение
uh = на первой итерации, выглядит следующим образом:
i
qW = (5., 3.022, 2.626, 4.066, 7.884,15
Заметим, что вклады в матрицу и вектор правой части на первой
итерации, полученные в результате линеаризации, для данного приме-
ра являются нулевыми, поскольку в качестве начального приближения
выбрана константа (см. (16.27)). Следовательно, для данного примера
после первой итерации решение, полученное методом Ньютона, сов-
падёт с решением, полученным методом простой итерации.
На второй итерации метода Ньютона локальная матрица и вектор
конечного элемента Qi имеют вид:
Al =
' 9.033 —9.033) 4.946
-9.033 9.033 + -4.946
\ / \
2.989'
-2.989
0.667 0.333'
0.333 0.667
\
' 14.645 -5.7104'
-13.645 6.7104
bL -
-5.667'
-6.333
33.7603 '
-33.7603
/
' 28.094 '
-40.094
/
Вектор весов решения на второй итерации выглядит следующим
образом:
q(2‘ = 15., 4.918,9.717,11.531,11.44,15.
Как видно из табл. 26, на второй итерации значение коэффициента ре-
лаксации было выбрано равным 0.5. Это было максимальное из значений
0.1, 0.2, 0.3,...,0.9 (т.е. из значений ш G (0,1], взятых с дискрете й 0.1),
при котором невязка на второй итерации стала меньше, чем на первой.
И, наконец, приведём локальную матрицу и вектор конечного эле-
мента полученные на шестой итерации:
A/j=
19.002 -19.002) (—5.0013 -7.0023) (0.667 0.333'
19.002 19.002 + 5.0013 7.0023 0.333 0.667
/ \ \
' 14.667 -25.67'
-13.667 26.67
ЬЛ
— 5.667) (-74.026'
"С
-6.333 74.026
/ \
—79.692'
67.692
Глобальный вектор весов на шестой итерации q^6^ совпадает с век-
* /
тором весов q = 15., 7., 9., 11., 13., 15.1 разложения точного реше-
ния по базису {ф7} с точностью до 8 знаков.
В табл. 27 показано, как по итерациям изменялась невязка нелиней-
ной системы при её решении методом простой итерации (коэффициент
844
16.Решение нелинейных задач
релаксации ш на всех итерациях был равен единице). Как видно из
этой таблицы, для уменьшения относительной невязки до значения
1013 в методе простой итерации понадобилось уже 26 итераций (по
сравнению с семью итерациями метода Ньютона).
______________________________________Таб j । и ца 2 7
к I 2 3 4 5 7
Rk 9.67 4.3 2.42 0.46 0.15 1.04 IO'2
к 8 12 15 19 25 26
Rk 2.3 103 1.23 10'5 1.93 10'7 941O10 3.67 IO'13 8.55-10'14
16.5. О СХОДИМОСТИ КОНЕЧНОЭЛЕМЕНТНЫХ РЕШЕНИЙ
НЕЛИНЕЙНЫХ КРАЕВЫХ ЗАДАЧ
Рассмотрим скалярную нелинейную краевую задачу для эллип-
тического уравнения
—div (Xgradw) + уи = f . (16.28)
Будем считать, что нелинейной эту задачу делает зависимость коэф-
фициента X от решения и (хотя заметим, что проводимые ниже рас-
суждения останутся справедливыми и в случаях, когда от и зависят
коэффициент -у, правая часть / и параметры краевых условий).
При решении нелинейной краевой задачи для уравнения (16.28) ме-
тодом Галеркина приближение и'1 искомой функции и ищется как
решение вариационной задачи (для сокращения длины формул будем
считать, что на границах расчётной области Q заданы первые или од-
нородные вторые краевые условия):
J (х (uh) graduh grad</' + yu^v1'j dQ = J fuhdQ, (16.29)
где приближённое решение uh и пробная функция ?/' — являются эле-
ментами конечномерного пространства Vh с базисом {ф,} .
Конечноэлсменгное решение uh — д^ф<: фактически определя-
г
ется вектором весов q, который находится из решения системы нели-
нейных уравнений
A(q)q = b,
компоненты матрицы которой и вектора правой части определяются
соотношениями
Л = f gradxh grad^j + 7ФгФ?
q I \ r
= J f^idQ .
16.5.0 сходимости конечноэлементных решений ...
845
Рассмотрим линейную краевую задачу с теми же краевыми усло-
виями, что и в исходной нелинейной задаче, для уравнения
—div (х(иЛ) grad uj + -уй = f (16.30)
Очевидно, что функция и1' будет конечноэлементным решением и
этой краевой задачи, и поэтому uh будет в энергетической норме1
ближайшей к й среди всех функций vh из конечномерного простран-
ства Vh, т.е.
||иЛ — й|| < ||д/г — й|| Vi/1 G V1' .
Итак, при решении нелинейной задачи методом Галёркина мы по-
лучаем такую функцию ?//', которая является ближайшей в энергети-
ческой норме к точному решению й линейной задачи с параметром
X = Х(иЛ).
В результате конечноэлементное решение ий нелинейной задачи
является функцией, самой близкой (среди всех функций vh eV1') в
энергетической норме к точному решению й той задачи, параметры
которой (зависящие от решения) определены по этой ближайшей к й
функции uh.
Поэтому, если конечноэлементная сетка, на которой вычисляется
решение достаточна подробна, то функция и1' будет достаточно
близка к функции й, и при выполнении некоторых (совсем не «жёст-
ких») ограничений на зависимость X(w) значения коэффициента
X (uh ) будут близки к значению X(й) (то же самое будет справедливо
для других параметров задачи, зависящих от решения), т.е. функцию
й можно признать «почти решением» исходной нелинейной задачи.
Погрешность этого решения й (как решения нелинейной задачи) фак-
тически будет определяться погрешностью в задании параметров зада-
чи, зависящих от и, и при определённых ограничениях на зависимость
X (и других параметров) от и она будет тем меньше, чем лучше
функции из конечномерного пространства V' могут принципиально
приблизить функцию й. Таким образом, для того чтобы функция й
была близка к точному решению и, достаточно, чтобы в конечномер-
ном подпространстве V" в принципе были функции, хорошо аппрокси-
мирующие й (напомним, что и1' — это функция, ближайшая к й среди
всех функций V11' Е V1' ). И чем ближе окажется и1'' к «своему» й , тем
больше оснований считать это й решением исходной нелинейной за-
1 Эта норма, очевидно,
||v ||“ = ^(x^'^gr.idv)2 +Т,2)Й£
S2
определяется
соотношением
846
16.Решение нелинейных задач
дачи — ведь параметры задачи, которой удовлетворяет й , определяют-
ся по очень близкой к и функции и1.
В итоге, происходящее при дроблении конечноэлементной сетки
сближение функций uh с соответствующими функциями й одновре-
менно обеспечивает и приближение и1' к решению исходной нелиней-
ной задачи и ). При этом скорость сходимости и1' к и в основном за-
висит от сходимости и,1' к соответствующим функциям й . А эго зна-
чит, что и при решении нелинейной задачи скорость сходимости uh к
и будет во многом определяться типом используемых базисных функ-
ций, и при увеличении их порядка вполне можно ожидать соответст-
вующего увеличения скорости сходимости 1//'' к и, т.е. убывания по-
грешности ||//. — ?//'Ц как □ (/?), где h - характерный размер конеч-
ных элементов, а к - степень полиномов, используемых в качестве
локальных базисных функций1.
Убедиться в том, что с дроблением сетки (или повышением порядка
элементов) и,1' сходится к «своему» й, можно, например, следующим
образом.
Сначала вычисляется конечноэлементное решение и1'' на некоторой
сетке 9Л[ (как решение нелинейной вариационной задачи (16.29)). За-
тем ешка дробится, но при построении конечноэлементной аппрокси-
мации параметры задачи вычисляются по решению и1'', полученному на
сетке QJlj. Сравнивая полученные таким образом решения на различных
сетках, можно получить оценку погрешности й — и11 на сетке .
Затем берётся новая, более мелкая сетка ЭД?2 и рассмотренная про-
цедура оценки погрешности й — повторяется для неё. Сравнивая
полученные оценки погрешности й — uh на сетках QJlj и Ш12 (и, воз-
можно, на ещё более подробных сетках), можно сделать вывод о схо-
димости (или i с отсутствии) uh к «своему» й с дроблением сеток.
Аналогичным образом можно проанализировать сходимость uh к
«своему» й и при повышении порядка элемента.
Заметим, однако, что для практического использования рассмотрен-
ная процедура проверки сходимости uh к «своему» й не очень-то
удобна. Дело в том, что процедуры, реализующие вычисление конечно-
элементного решения вариационных задач вида (16.29), обычно строят-
ся таким обраюм, чтобы значения параметров задачи, зависящих от её
решения, вычислялись по значениям конечноэлементного решения, оп-
ределённого именно на той сетке, на которой ищется решение.
Поэтому на практике обычно используются гораздо более простые
процедуры контроля сходимости и}> к и. Сравниваются решения и1',
1 Если, конечно, в зависимостях параметров нелинейной задачи от и нет
каких-либо особенностей, связанных с возможными резкими изменениями их
значений при малых изменениях и.
16.6.Вычислительные схемы решения нелинейных задач ...
847
получаемые в результате конечноэлементной аппроксимации нелиней-
ного вариационного уравнения1 на различных сетках. Если конечно-
элементное решение г?' «стабилизируется» при переходе на всё более
подробные2 сетки (т.е. изменения в его значениях с каждым новым
дроблением происходят во всё более «дальних» знаках), то с очень
большой долей уверенности можно полагать, что функция и1'' сходится
к и. При этом, если используются вложенные сетки, то погрешность
и — и1' убывает примерно тем же темпом, с каким изменяется и1' при
переходе с одной сетки на другую.
Из проведённых рассуждений можно также сделать вывод, что при
решении нелинейных задач основные рекомендации к процедурам
измельчения конечноэлемен'гных сеток остаются в целом такими же,
что и при решении линейных задач: дробить ячейки сетки нужно там.
где из соответствующих используемой сетке базисных функций нельзя
построить функцию, с необходимой точностью аппроксимирующую
функцию й. Обычно это происходит в тех местах расчётной области,
где функция и1' наиболее резко изменяет свои производные при пере-
ходе с одного конечного элемента на другой (если, конечно, на грани-
це между такими элементами нет скачка в коэффициенте диффузии X
или на этой границе не задан сосредоточенный источник).
16.6. ВЫЧИСЛИТЕЛЬНЫЕ СХЕМЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ ЗАДАЧ
МАГНИТОСТАТИКИ
16.6.1. ПРИМЕНЕНИЕ МЕТОДА НЬЮТОНА ДЛЯ РЕШЕНИЯ ДВУМЕРНЫХ
НЕЛИНЕЙНЫХ ЗАДАЧ МАГНИТОСТАТИКИ
Рассмотрим двумерную задачу магнитостатики в декартовой
системе координат. Как уже говорилось в разделе 1.3.3.1 (с. 32-33), в
этих задачах предполагается, что вектор плотности токов имеет только
одну ненулевую компоненту JZT, зависящую от координат .т и у, и
при этом магнитная проницаемость ц зависит также только от коор-
динат х и у. В этом случае магнитное поле полностью определяется
только одной компонентой Az — Az(x,y) вектор-потенциала А, кото-
рая является решением двумерной краевой задачи для уравнения
— div | — grad Az | = Jzr . (16.31)
Задача магнитостатики является нелинейной, если коэффициент
магнит ной проницаемости зависит от вектора индукции В магнитно-
го поля. Мы будем считать, что ц зависит от модуля В = 4- By
вектора магнитной индукции В (в двумерном случае Bz =0).
1 Например, вида (16.29).
2 Лучше всего вложенные друг в друга.
848
16.Решение нелинейных задач
В результате конечноэлементной аппроксимации (по методу Галёр-
кина) краевой задачи для нелинейного уравнения (16.31) получаем
систему алгебраических уравнений:
G(q)q = b, (16.32)
компоненты матрицы и вектора правой части которой определяются
как
Gj., — f —-—• grad ф, grachpjdQ. Ь,— Г . (16 33)
Конечноэлементным приближением Az (х, у) искомой функции
Az (к, у) является линейная комбинация базисных функций -ф.2 (ж, у):
А'г (х,у) = - (16.34)
Z
Уравнения системы (16.32) не являются линейными относительно
неизвестных qt, поскольку компоненты матрицы G (см. (16 33)) зави-
сят от q, ( гак как р зависит от В = в|, а В определяется как iotAj и
А^ = £у/,-ф7 )-
i
Поскольку в двумерном случае вектор-потенциал А имеет одну
ненулевую компоненту Az, вектор индукции определяется соотноше-
нием
Рассмотрим случай, когда на каждом конечном элементе коэф-
фициент ц.(В) аппроксимируется константой, вычисляемой по неко-
торому среднему значению на модуля В =
(34 )2
ду ) [ дх
вектора индукции В.
Если для конечноэлементной аппроксимации в качестве базисных
функций -ф, используются линейные базисные функции на треуголь-
никах! (см. раздел 5.3.2), то значение магнитной индукции
1 Заметим, что треугольные конечные элементы первого порядка довольно
часто используются для решения многих нелинейных практических задач,
например, при расчёте электродвигателей, в которых расчётной областью
является поперечное сечение, имеющее довольно сложную геометрию.
16.6.Вычислительные схемы решения нелинейных задач ...
849
В = z , —является постоянным на конечном элементе Q„. и
( ду ox J
соответственно значение магнитной проницаемости р также будет
постоянной величиной на .
Но и в более общих случаях, когда вычисляемый по модуль
' 0 А1^
ду + дх
В =
вектора индукции не является константой на
(например, если используются базисы высоких порядков или ко-
нечные элементы в виде прямоугольников или четырёхугольников),
подход, основанный на аппроксимации коэффициента р на каждом
конечном элементе Qzrt некоторой постоянной, вычисляемой по сред-
нему на значению модуля В вектора индукции, чаще всего почти
не уступает по точности получаемого решения нелинейной задачи дру-
гим подходам, в которых коэффициент р аппроксимируется некото-
рой функцией (например, Интерпол я нтом, построенным с помощью
базисных функций). С учётом же простоты и универсальности реали-
зации для элементов любых типов и порядков этот подход является
наиболее привлекательным (причём при решении не только двумер-
ных, но и трёхмерных задач).
Итак, значения р на каждом О,/; будем вычислять по среднему зна-
'э/Н2
чению В модуля В =
вектора индукции магнит-
. ду ,
дх
ного поля на этом элементе. Однако алгоритмически удобнее на ко-
нечных элементах вычислять В2 - среднее значение квадрата модуля
индукции.
Получим выражения для вычисления значения В2 на конечном
элементе 0,„. Представим В2 в виде:
_ 1 Г
mesQ,„ J
о
дА^ V
1
mesQ.,
1
mesQ
дх
дА\
ду
(16.35)
rfQ =,
где mesQ,,, - площадь конечного элемента Q„(.
Учитывая представление (16.34) функции А? в виде линейной ком-
бинации базисных функций получаем, что среднее значение квад-
рата модуля вектора магнитной индукции на ттг-м элементе представ-
ляется в виде следующей квадратичной формы:
850
16.Решение нелинейных задач
^2 _ 1
mesQw
1=1 j=l
(16.36)
где I — количество базисных функций ф,2 конечного элемента Qm,
qt - компоненты локального вектора весов q (в разложении у)
по локальным базисным функциям фг на элементе Qm), а компоненты
матрицы П определяются соотношениями:
U = / grachpi • grad'WjdQ.
(16.37)
С другой стороны, элементы G, глобальной матрицы G конечно-
элементной СЛАУ (16.32) формируются как суммы соответствующих
компонент локальных матриц G конечных элементов Qy„, причём
компоненты локальных матриц G определяются следующим образом:
у J
—Lgrad^ • grad^ 4Q.
(16.38)
Сравнивая выражения (16.37) и (16.38), получаем, что при
р.(В) = \\ В = const на конечном элементе Q,n локальные матрицы
G и II связаны следующим простым соотношением:
0 = ^11.
Р
(16.39)
Выполним линеаризацию члена Glf (q)g,. Для этого так же, как мы
это делали в разделе 16.3 (см. соотношение (16.13)), представим сла-
гаемое Gr/ (q)qj в виде разложения в ряд Тейлора и ограничимся чле-
нами с первой производной:
dGtJ (q)
' dq.
q=qG
^gq(q)
q=q°
Z'i д9г
q=q°
(16.40)
16.6.Вычислительные схемы решения нелинейных задач ...
851
где q°, как и прежде, локальный вектор решения на предыдущей ите-
рации метода Ньютона (на первой итерации q() — локальный вектор,
определяющий начальное приближение на Q7„ ).
Учитывая, что компоненты матрицы П не зависят от q,., из (16.39)
получаем:
3^(4) _ - 5(ХЛ) _ 4УИ) dB2
dqr () “ " dq, dB2 dq,.
4=4
Производные Л? вычислим, дифференцируя (16.36):
q>-
dB2
dq,.
(16.41)
(16.42)
= ____2___X^II.n"
Подставляя (16.41) и (16.42) в (16.40), получаем
—2— ли.^п..у2{Чг -'л')Е'М! • (|6-43)
mes(Q„J dB2
Из соотношения (16.43) видно, что так же, как и в рассмотренной
ранее одномерной задаче, в результате линеаризации вклада Gtj (q)gz
появляются слагаемые, содержащие кроме j -й ещё и другие компо-
ненты вектора решения, а также слагаемые, не содержащие компонен-
ты вектора решения и поэтому являющиеся добавками в правую часть
линеаризованного уравнения. Таким образом, линеаризованная систе-
ма
Gzq = bfj (16.44)
собирается из локальных матриц GL и локальных векторов о 7 сле-
дующего вида:
_ d(l/ph * if i
+-----Vv-W ЕЧ«'Й ЕХ'Й (16.45)
<i6-46)
852
16.Решение нелинейных задач
где Q*.1 - компоненты локального вектора решения qu с предыдущей
итерации метода Ньютона, a (q’ J и Ьг — компоненты локальных
матрицы G и вектора b конечного элемента , определяемых соот-
ношением (сравните с (16.33))
CL- = f — grachpj • gradikdQ , Ьг = Г J^^dQ, (16.47)
J J p J J
S Bi
в котором ц, (а точнее, 1/p)1 вычисляется по среднему на значе-
нию В, полученному на предыдущей итерации метода Ньютона, т.е.
по значению (см. (16.36))
s = =J^EEW • <16-48’
V г—1 p=i
Глобальная матрица GL и вектор bL линеаризованной конечно-
элементной СЛАУ собираются из локальных матриц G1 и векторов
конечных элементов стандартным образом. Сам же итерационный
процесс метода Ньютона при решении двумерных нелинейных задач
магнитостатики выполняется так, как это было описано в разделе 16.3
(с контролем точности получаемого решения по невязке
|G(q!‘>)q'‘)-bhb|| и с включением в случае необходимости релак-
сации и демпфирования).
Рассмотренная схема решения двумерной нелинейной задачи маг-
нитостатики с небольшими модификациями применима и для решения
двумерных нелинейных краевых задач в цилиндрической системе ко-
ординат.
Пусть необходимо найти распределение стационарного магнитного
поля в осесимметричной области Q, и сторонний ток имеет единст-
венную ненулевую компоненту J^= в цилиндрической сис-
теме координат. Тогда вектор индукции магнитного поля В будет
иметь в цилиндрической системе координат две ненулевые компонен-
ты Вг и Bz , которые могут быть получены как компоненты вектора
1 Так как в двумерных задачах магнитостатики гораздо удобнее задавать
(таблично и в виде сплайна) именно зависимость 1/|l от В, а не зависимость
ц от В .
16.6.Вычислительные схемы решения нелинейных задач ...
853
rotA, где А — вектор-потенциал, имеющий (в цилиндрической систе-
ме координат), как и вектор плотности стороннего тока
JCT = (о,«7у,0)Т, единственную ненулевую компоненту Д. = Др(г,г).
Двумерная скалярная функция ДДг,г) может быть найдена из реше-
ния уравнения
”dlV 7^)ёГас1^ = (16.49)
Отличительной особенностью уравнения (16.49) (по сравнению с
уравнением (16.31) в декартовой системе координат) является наличие
д
в нем слагаемого —
В = (Д,В2)
_ 1
dr [гр,(В)
в этой задаче
Ар, к тому
же вектор индукции1 2
определяете я как
rotA =
dz ’ dr
и значение В2
не будет равно
(grad4p , Поэтому форма записи нелинейной осесимметричной зада-
чи магнитостатики в виде уравнения (16.49) для скалярной функции
Др(г, z) является не самой удобной для построения на её осн< >ве экви-
валентной вариационной постановки и итерационного процесса полу-
чения конечноэлементного решения с использованием метода Ньюто-
на2.
Гораздо удобнее для этого оказывается запись уравнения для век-
тор-потенциал а А, определённого в цилиндрической системе коорди-
нат, в векторном форме (которая сразу следует из уравнения
rotH - JCT):
rot
rotA
= JCT.
(16.50)
Методы построения эквивалентных вариационных постановок для
векторных уравнений (с соответствующими краевыми условиями) бы-
1 В дальнейшем мы, учитывая двумерность задачи, будем записывать
только ненулевые компоненты векторов В , rotA и grad Ар.
2 Отметим, что при использовании вариационной постановки, построен-
ной для уравнения (16.49), получить представление В2 в виде квадратичной
Формы также можно, по сделать это не так просто.
’ j
854
16.Решение нелинейных задач
ли подробно рассмотрены нами в пятнадцатом разделе. Для уравнения
(16.50) эквивалентное вариационное уравнение имеет вид1 (см (15.11)):
f-JL-rotArot$dn= ГЗСТФ<Й1 (16.51)
о о
Учитывая, что вектор-потенциал А в цилиндрической системе ко-
ординат имеет только одну ненулевую компоненту Др(г, z), вариаци-
онное уравнение (16.51) можно записать в виде
Г 1
Jr (В)
РА- АД/дФ , Ф)
dr г \ dr г )
. ^Ар <ЭФ
dz dz
/
(16.52)
где Ф = Ф(г, z) - vp-компонента пробной вектор-функции Ф. Это
означает, что в качестве пробных вектор-функций мы взяли вектор-
функции Ф = (0,Ф(r,z),0f , в которых Ф(г,г) - произвольные ска-
лярные функции из пространства Hf} (т.е. Ф(г,г) имеют в О сумми-
руемые с квадратом первые производные и удовлетворяют на границе
Sj однородным главным краевым условиям).
Компоненты матрицы G и вектора правой части b нелинейной
системы уравнений
G(q)q = b,
полученной в результате конечноэлементной аппроксимации вариаци-
онного уравнения (16.52), определяются следующими соотношениями:
с = f 1 [Р^ , , ФД, Э<М.,О
« j аг + г Д дт г J+ dz dz ’
— J JytyidQ,
где ф, - глобальные базисные функции.
Соответственно локальная матрица конечного элемента Q7(I будет
иметь вид
Мы будем считать, что в краевой задаче заданы либо краевые условия
первого рода, либо однородные краевые условия второго рода (на практике
обычно используются такие краевые условия как условия на границе «боль-
шого объёма» или на плоскости симметрии).
16.6.Вычислительные схемы решения нелинейных задач ...
855
где ф, - локальные функции конечного элемента.
При этом, если значения ц(В) (или —(B)) на конечном элементе
И
Qw вычисляется по среднему на Q?n значению В модуля индукции
магнитного поля, то его квадрат (с учётом разложения вектор-
потенциала А по локальным базисным вектор-функциям
ф2 = 0, фг (г,z), О I элемента Qw) может быть вычислен следующим
образом (сравните с (16.35) и (16.36)):
В2 =----— f rotA rot AfZQ =
mcsSL. J
Q
J Lm
= f rot E • rot E =
Urn i 3
1
rnesQ,,,
J rot ф,; • rot фр/Q =
S iin
= 1
mesQ,„
dr
oz dz
r
= —E (i> q Ла»
rnesQ,,. 7 '
i,j
где фг (r,z) - скалярные базисные функции элемента Q,„ (через кото-
рые фактически определяются вектор-функции фг).
Таким образом, значение В2 может быть вычислено через локаль-
ную матрицу П, компоненты которой отличаются от компонент ло-
кальной матрицы жёсткости G конечного элемента Q,rt только отсут-
ствием сомножителя 1/р, (сравните с (16.53)):
<Эф, ф?; <Эф/
дг г дг
Фу
дг г
UZ OZ
(16.54)
и, поскольку мы принимаем, что на значение р = щВ' = const,
локальные матрицы G и П оказываются связанными простым соот-
ношением
856
16.Решение нелинейных задач
G = ln, (16.55)
полностью идентичным соотношению (16.39) для случая декартовых
координат.
Очевидно, что дальнейшие рассуждения при использовании метода
Ньютона для решения нелинейной осесимметричной задачи магнито-
статики ничем не будут отличаться от рассмотренных нами чуть выше
рассуждений для двумерной нелинейной задачи в декартовых коорди-
натах вплоть до вида локальных матриц (16.45') и векторов правой час-
ти (16.46) линеаризованной системы, а также формулы (16.48) для вы-
числения В на .
Отметим, что рассмотренный нами подход к решению стационар-
ной нелинейной осесимметричной задачи, в общем-то, почти без изме-
нений может быть применён как к решению соответствующих осесим-
метричных нестационарных нелинейных задач, описываемых уравне-
ниями вида
rot^
р(2?)
г СТ
ip ,
где А = (О, Д, (г, z), 0)Т или
rotjp (^гош) + -Д (рЯ^) = rotlpJCT,
где Н = (0,Яф (г,z),0^T, так и для моделирования трёхмерных элек-
тромагнитных полей (как стационарных, так и нестационарных), опи-
сываемых векторным уравнением (16.50) или
rot
rotA
(ЭА __ тст
dt
(16.56)
1
и при использовании для решения этих уравнений векторного МКЭ.
Однако обратим внимание на тот факт, что при моделировании ста-
ционарного нелинейного магнитного поля (а для нестационарного при
наличии в расчётной области подобластей с о = 0 ) матрица системы
конечноэлементных уравнений будет вырождена так же, как и при
решении соответствующих линейных задач. Поэтому для решения
трехмерных нелинейных задач магнитостатики чаще всего применяют
подход, основанный на представлении напряжённости магнитного
поля в виде градиента скалярного потенциала. Преимущества такого
подхода заключаются не только в том, что матрица конечноэлемент-
ной системы в этом случае получается невырожденной, но и в том, что
для построения конечноэлементной аппроксимации используются ска-
лярные базисные функции.
16.6.Вычислительные схемы решения нелинейных задач ...
857
16.6.2. РЕШЕНИЕ ТРЁХМЕРНЫХ ЗАДАЧ МАГНИТОСТАТИКИ
С ИСПОЛЬЗОВАНИЕМ НЕПОЛНОГО СКАЛЯРНОГО ПОТЕНЦИАЛА
Сначала рассмотрим подход к решению трёхмерной задачи маг-
нитостатики, в котором напряжённость магнитного поля Н ищется в
виде (см. (1.40))
Н = Нс — grad С/, (16.57)
где Нг - напряжённость магнитного поля оттоков J в вакууме, опре-
деляемая соотношением (1.43), a U - неполный скалярный магнит-
ный потенциал, удовлетворяющий уравнению
— div (р, grad t/) =—div fpH'J, (16.58)
в котором р - относительная магнитная проницаемость среды (т.е. в
вакууме р = 1).
Получим для уравнения (16.58) эквивалентную вариационную фор-
мулировку. При этом будем считать, что на границах расчётной облас-
ти для искомой функции U заданы однородные краевые условия пер-
вого или второго рода (что соответствует наиболее часто встречаю-
щимся случаям условий на плоскостях симметрии или условий на гра-
ницах «большого объёма»).
Домножим уравнение (16.58) на пробную функцию Ф и проинтег-
рируем по расчётной области П Применив формулу Грина (интегри-
рования по частям), получим1
J р grad U • grad Фгй7 = JpHr .gradtfdQ. (16.59)
п ц
Конечноэлементная аппроксимация уравнения (16.59) приводит к
системе уравнений с матрицей G и вектором b , компоненты которых,
очевидно, определяются соотношениями:
Gy = р grad • grad фубЮ, b,: = J pHf grad ,
Q Q
1 При этом мы полагаем, что на внешних границах расчётной области, где
U 0, вместе с соотношением dUldn = 0 (которое может быть записано
также в виде grad U • п — — Нкгш1- п = 0) выполняется и соотношение
Н'- п — 0, и поэтому соответствующий поверхностный интеграл не появится
после интегрирования по частям не только члена J div (р grad [/) ФdQ , но и
о
SI
858
16.Решение нелинейных задач
где "ф/ - глобальные базисные функции.
Рассмотренная постановка позволяет получать вполне приемлемые
результаты при необходимости вычисления значений поля вне ферро-
магнитных материалов. Внутри же этих материалов (в которых отно-
сительная магнитная проницаемость р 1) значение поля Н может
вычисляться с очень низкой точностью. Причина этого заключается в
следующем.
Внутри ферромагнитных материалов с большой относительной маг-
нитной проницаемостью р абсолютные значения напряжённости Н
магнитного поля могут быть на несколько порядков меньше соответст-
вующих значений поля Hf, создаваемого теми же токами и в тех же
точках пространства при замене рассматриваемой ферромагнитной
среды на неферромагнитную. В рассматриваемой же нами модели зна-
чения искомого поля Н внутри ферромагнетика получаются как сумма
значений поля Нг и поля Hgrad = — gradt/, вычисляемого в результа-
те решения краевой задачи для уравнения (16.58). Очевидно, что, по-
скольку значения Н намного меньше значений Нг, мы должны полу-
чить значения H';ri,d, близкие по абсолютной величине к Нг и обрат-
ные по знаку. Но значения Hgrad вычисляются с погрешностью (опре-
деляемой ошибкой конечноэлементной аппроксимации), и если для
самих значений Hgrad эта погрешность составляет проценты (или даже
доли процента), то после сложения Hgrad с Нг погрешность в Н мо-
жет стать не только сопоставимой с получаемыми значениями поля Н,
но и даже превосходить их.
Поэтому, если нам нужно решить нелинейную задачу, в которой
магнитная проницаемость ферромагнетиков зависит от значений поля
И, то мы должны вычислять поле Hgrad в этих ферромагнетиках с
достаточно высокой точностью, чтобы обеспечить необходимую точ-
ность вычисления коэффициента р(Я).
Таким образом, процедуры решения нелинейных задач магнитостати-
ки, основанные на использовании только одного (неполного) скалярного
потенциала, как правило, довольно неэффективны и требуют чрезмерно
высоких вычислительных затрат из-за необходимости сильного дробле-
ния сетки в тех местах расчётной области, где р зависит от Н.
Заметим, что схема, основанная на использовании неполного по-
тенциала, фактически является схемой выделения поля (поля влияния
тел с магнитной проницаемостью, отличной от магнитной проницае-
мости вакуума), но это как раз тот случай, когда схема выделения поля
не только не улучшает, а значительно ухудшает точность получаемого
решения. Причина очевидна - если мы считаем основным полем маг-
нитное поле в среде без ферромагнитных материалов (поле токов в
вакууме), то добавочное поле должно кардинально изменить значения
поля в местах, где расположены ферромагнетики. В результате иско-
16.6.Вычислительные схемы решения нелинейных задач ...
859
мое (суммарное) поле внутри ферромагнетиков будет намного меньше
каждого из составляющих его полей - и основного (поля токов в ва-
кууме), и добавочного (поля влияния ферромагнитных тел), и в резуль-
тате взаимовычитания этих полей ошибка в искомом поле (внутри
ферромагнетиков) может стать очень большой. Поэтому для нелиней-
ных задач магнитостатики при отсутствии токов в ферромагнетиках
нужно использовать другую схему, в которой поле в ферромагнетиках
представляется напрямую в виде градиента некоторого скалярного
потенциала. Этот подход мы сейчас и рассмотрим.
16.6.3. РЕШЕНИЕ ТРЁХМЕРНЫХ НЕЛИНЕЙНЫХ ЗАДАЧ МАГНИТОЛ 1А ГИКИ
С ИСПОЛЬЗОВАНИЕМ ДВУХ СКАЛЯРНЫХ ПОТЕНЦИАЛОВ
Разобьём расчётную область Q на две подобласти и Qp.
Подобласть должна включать в себя все подобласти, где плотность
сторонних токов J отлична от нуля. Напряжённость II магнитного
поля будем искать в виде
HL = Hc-gradP в 0е7,
HF=-gradP bQp,
(] 6.60)
где 1Г, как и прежде, поле от токов J в вакууме, определяемое соот-
ношением (1.43).
На границе Sn, являющейся границей между подоблас тями Q/z и Qp
(т.е. Sn = QPDQP), должны выполняться условия непрерывности нор-
мальной составляющей В = pH и тангенциальной составляющей Н:
=Ир-а)к!г₽
(aMlsn=(йМЬ
(16.61)
(16.62)
где й - нормаль к поверхности Sr' (мы будем считать её внешней по
отношению к подобласти Qp ,т.е. п - пр = — пг, йр и пи - внешние
нормали к Qp
и соответственно), а запись
в левой
части соотношения (16.61) означает, что значения р берутся на по-
верхности Sn со стороны подобласти (аналогично в правой части
(16.61) значения р берутся на Sn со стороны Qp).
Напряжённость магнитного поля Н определяемую соотношением
(16.60) и удовлетворяющую условиям (16.61) и (16.62), будем искать
как решение уравнения
div(pH) = 0.
860
16.Решение нелинейных задач
Умножим это уравнение на пробную функцию Ф и проинтегриру-
ем его по всей расчётной области Q:
f div(pfi^dQ = 0. (16.63)
Учитывая, что Q = QrU , перепишем вариационное уравнение
(16.63) в виде
J div(pH^dQ + f div (р.Н/?) Ф<Ю = 0 . (16.64)
Qf/ QP
Будем считать, что в подобласть неполного потенциала не вхо-
дят феррома! петики (подобласть же полного потенциала включает
в себя все ферромагнетики, но может включать и не ферромагнетики).
Тогда в Ст относительная магнитная проницаемость р равна едини-
це, и
div^pH^) = div^H^ + ЕГ J = div (grad P),
поскольку для поля Hf, определяемого по закону Био-Савара
формулой (1.43), справедливы соотношения
rotHr = JCT, diviF = 0. (16.65)
В результате вариационное уравнение (16.64) примет вид
— J div (grad U) ФгЮ — J div (pgradP) Фс/Q = 0. (16.66)
QP QP
Применив к обоим слагаемым левой части уравнения (16.66) фор-
мулу Грина (интегрирования по частям) и полагая по-прежнему, что на
внешних фаницах Q для U и Р заданы либо первые, либо однород-
ные вторые краевые условия, получим
J grad U grad\?$? —J (grad U- nu^dS +
& sn
-+ J pgradP grat^dQ —J (pgradP Ф<Р> = 0. (16.67)
ilp Sn V
Учитывая, что = — nu = n , и объединяя поверхностные инте-
гралы в уравнении (16.67), получаем
j* grad U gracwdQ + J pgradP • gradФdQ 4-
16.6.Вычислительные схемы решения нелинейных задач ...
861
4- J ((grad U — pgradP) • й) tydS = 0,
(16.68)
где в поверхностном интеграле (по Sn) grad Р берётся со стороны
подобласти £lu , a pgradP, естественно, со стороны .
Преобразуем подынтегральное выражение поверхностного инте-
грала из (16.68) с учётом того, что в подобласти £1и (включая и её гра-
ницу Sn) gradP = IT — (см. (16.60)):
((grad U - pgradP) п)|5П = ^Нг - 4- рЙр ) • й)
Й-^
Из (16.61) (с учётом того, что р = 1 внутри £1и ) получаем
а значит,
((grad U - pgradP) й)| = (Йг й)| р .
D \ /|<у
Таким образом, вариационное уравнение (16.68) принимает вид
j* grad U grad\l/dQ + J pgradP grad^dQ = —J (Йг- nj tydS . (16.69)
Qp sn
Вариационное уравнение (16.69) обеспечивает выполнение уравне-
ния divB = 0 в каждой из подобластей П,1' и О,р и непрерывность
нормальных составляющих В на границе Sn между ними. Уравнение
же rotH = JCI в каждой из подобластей выполняется потому, что поле
Н'; удовлетворяет уравнению rotHc = JCT (см. (16.65)) и для любой
функции IV справедливо rot grad W = 0 (и при этом JCT = 0 в по-
добласти Пр).
Таким образом, нам осталось выполнить последнее требование к
полю Н, определяемому соотношением (16.60), - обеспечить непре-
рывность его касательных составляющих, т.е. обеспечить выполнение
соотношения (16.62), которое можно переписать в виде
Н'
(16.70)
где т - произвольный вектор, касательный к Sn .
862
16.Решение нелинейных задач
Рассмотрим определённую на поверхности Sr' функцию R, удов-
летворяющую уравнению
9R
ду
(16.71)
Тогда, если на S' связать неполный потенциал U с полным Р со-
отношением
U = PpR, (16.72)
то соотношение (16.70) выполнится автоматически.
Таким образом, для того чтобы обеспечить выполнение условия не-
прерывности на поверхности Sn касательных составляющих Н, мы
можем найти функцию R, удовлетворяющую на этой поверхности
уравнению (16.71), и связать значения потенциалов U и Р на Sn со-
отношением (16.72). Такая функция R называется скачком потен-
циала.
Вариационное уравнение (16.69) можно записать в более удобном
для построения конечноэлементной аппроксимации виде:
f pgradH • gradtfdQ = -J (н,:-п) , (16.73)
Q\5n Sn
где U — скалярный потенциал, определённый во всей расчётной об-
ласти Q и имеющий на поверхности Sn разрыв, равный скачку R :
= U\so_>np +R, (16.74)
т.е. искомая функция U имеет на Sn «заданный»1 разрыв R .
Обратим также внимание на то, что пробная функция Ф должна
быть непрерывна2 во всей расчётной области Q, включая Sn, — имен-
но это обеспечит выполнение условия (16.61).
Таким образом, мы получили задачу, практически полностью ана-
логичную рассмотренной нами в разделе 15.13.3 задаче с разрывом
скалярного потенциала. Отличие заключается лишь в том, что там раз-
рыв был константой, определяемой величиной обходимого тока, а
здесь разрыв является функцией, удовлетворяющей уравнению (16.71).
Поэтому конечноэлементная аппроксимация вариационного уравнения
(16.73) с условием (16.74) приведёт к системе уравнений с матрицей G
и вектором правой части b, компоненты которых определяются соот-
ношениями:
1 Этот разрыв определяется уравнением (16.71).
2 Пробная функция Ф должна быть элементом пространства функций,
имеющих суммируемые с квадратом производные на всей области Q, а реше-
ние U - функция, имеющая суммируемые с квадратом производные только
на Q \ .
16.6.Вычислительные схемы решения нелинейных задач ...
863
Grj = J* р grad фг grad ф7<7Н, = bR—J (нг- rij ф,///?,
» 5n
(16.75)
где bR — вклады в соответствующие компоненты глобального вектора
b от скачка R. Значения bR удобнее всего заносить в глобальный
вектор b в виде вкладов от конечных элементов Q,n, которые лежат в
подобласти Qt и узлы которых попадают на границу Sn . Компоненты
соответствующих локальных векторов b (которые определяют вкла-
ды bR в компоненты 6, глобального вектора b) могут быть вычисле-
ны по формуле (сравните с (15.210))
Ър = 52 J -grad^dQ,
,/е^Л о,„
(16.76)
где Nr — множество локальных номеров узлов (точнее, базисных
функций) конечного элемента О,1П, лежащих на границе Sr', a qR -
значения скачка R вэгихузлахЕ
Рассмотрим теперь, как можно вычислить скачок R . Будем искать
его в виде линейной комбинации тех же базисных функций, которые
используются для конечноэлементной аппроксимации вариационной
задачи, т.е. в виде
Rh = 52 = ф = ф <г >
. ..<<1
(16.77)
где N - множество номеров глобальных базисных функций, отлич-
ных ог нуля на Sr .
Значения весов qR следует находить из условия максимальной бли-
Г) с) R1’’
зости на S значений к значениям Щ — Н' • т, где т - произ-
вольный касательный к Sn вектор.
Минимизировать отклонение dRh /дт от можно, например, по
1 То, что q^ являются значениями скачка R. в узлах на поверхности ,9",
справедливо, естественно, для лагранжевых элементов. Если используются
элементы других типов (например, иерархические), то qR - это значения
весов базисных функций ф7, делающие линейную комбинацию
J
максимально близкой к функции R на Sn.
864
16.Решение нелинейных задач
всем рёбрам* е.т конечных элементов, лежащим на № . В этом случае
минимизируемый функционал можно записать в виде (используя в
качестве векторов т все рёбра е.т )
= (16.78)
Чн
Подставляяв функционал (16.78) вместо R1' его выражение в виде
линейной комбинации базисных функций (16.77), получаем
Г//1
Минимизируя этот функционал по д,- , получаем СЛАУ
gV = ьп,
в которой компоненты матрицы и вектора правой части определяются
соотношениями
Gn = V Г= V fEk H1' de
" de„, de,„ de"‘ ’ de,„
e-in
Очевидно, что ненулевыми в матрице G' будут только те столбцы и
строки, номера которых являются номерами базисных функций, отлич-
ных от нуля хотя бы на одном из рёбер е7„ . В принципе, для нахождения
вектора весов q1' имеет смысл так перенумеровать все базисные функции
(и соответственно веса qf ), чтобы те функции, которые отличны от нуля
хотя бы на одном из рёбер е,„ , были пронумерованы первыми.
В результате такой перенумерации мы получим СЛАУ
Gnq/?=bn (16.79)
гораздо мсныней размерности с невырожденной и по-прежнему сильно
разреженной матрицей G (фактически компоненты матрицы G и
вектора Ъ являются компонентами G и Ь'1, и связь между индекса-
ми соответствующих компонент определяется перенумерацией).
1 Так очень удобно посгупать для любых элементов первого порядка; если
же используются элементы более высоких порядков с базисными функциями,
ассоциированными с точками поверхности 6'" , не лежащими на рёбрах, то и
в этом случае можно использовать минимизацию по рёбрам, но при этом
нужно обязательно построить дополнительные рёбра, на которых эти функ-
ции отличны от нуля (например, соединив точки, с которыми они ассоцииро-
ваны, с точками на рёбрах, лежащих на Sn ).
16.6.Вычислительные схемы решения нелинейных задач ...
865
После решения СЛАУ (16.79) компоненты вектора q 1 (размерно-
сти, равной размерности исходной задачи) могут быть получены из
компонент вектора q77 в результате обратной перенумерации.
Численное решение Uh определяется соотношением
ЕлА в Q7’,
./
52 (<7., в Q",
J
в котором вектор q имеет ту же размерность, что и вектор q (т.е. для
всех функций ф7, равных нулю на , q1} — 0).
Итак, мы рассмотрели схему построения конечноэлементного ре-
шения трёхмерной задачи магнитостатики, в которой поле в ферромаг-
нитных материалах представляется в виде градиента скалярной функ-
ции U . При этом коэффициенты получаемой конечноэлементной сис-
темы определяются соотношениями (16.75)—(16.76), и, очевидно, если
коэффициент магнитной проницаемости р зависит от значений поля
Н (как правило, эта зависимость задаётся в виде ц(Я), где Н - мо-
дуль вектора Н), то конечноэлементная система является нелинейной.
Для решения нелинейной системы
G(q)q = b,
в которой компоненты матрицы и вектора определяются соотноше-
ниями (16.75), можно применять практически те же методы, которые
были рассмотрены нами при решении двумерных нелинейных задач
магнитостатики. Наиболее эффективным здесь также является метод,
основанный на линеаризации слагаемых Gr/(q)^z, причём, как и в
двумерных задачах, выполнять линеаризацию этих слагаемых удобнее
всего на уровне локальных матриц.
Чтобы получить выражения для вычисления компонент линеаризо-
ванных локальных матриц, сначала получим выражение для среднего
значения квадрата модуля напряжённости магнитного поля на конеч-
ном элементе Q.,n С (т.е. лежащего в подобласти, где находятся все
ферромагнитные материалы):
__ 1 j
mesQ,,. J
о,
grad U grad Ud£l
1
mesO„,
^in
grad -grad
d.Q =
866
16.Решение нелинейных задач
= Л £ f gri^- ’ ° 6-80)
"' lj it,,,
где, как и в двумерном случае, матрица П — локальная матрица жёст-
кости для среды с р = 1 :
Д7/ — / gracl^ • gradij^dQ.
(16.81)
В результате при решении трёхмерной нелинейной задачи магнито-
статики выражения, определяющие компоненты локальных матриц
Gl и векторов Ь' конечных элементов Q.„., из которых собирается
линеаризованная система, практически ничем не будут отличаться от
соответствующих выражений для двумерного случая1 (сравните с
(16.45)-( 16.46) с учётом того, что мы вернулись к более привычным
индексам для компонент матрицы, поменяв индекс г на индекс j ):
с!: - g,3(ч")+ d^2 E^" E^“ (l682)
ь,£ = ь. +- Ей1IzPZXll (16.83)
mes(Qw) dHl "
где, как и прежде, q() - локальный вектор весов конечного элемента
Q„?, полученный на предыдущей итерации2 метода Ньютона, I - чис-
ло локальных базисных функций конечного элемента QHl, a G^ (qrJ и
lljj - компоненты локальных матриц, определяемые соотношениями
(16.75), (16.76) и (16.81), причём компоненты (ч°) вычисляются
при значениях р. = р(я), где значение Н вычисляется с помощью
соотношения (16.80), т.е.
я = ^ЕЕ^ ое-H
Скажем несколько слов о возможности выделения поля в трёхмер-
ных задачах магнитостатики.
1 Вывод этих выражений практически полностью совпадаете выводом со-
ответствующих выражений для двумерного случая, см. с. 850-852, формулы
(16.40Н 16.46).
2 Или из начального приближения.
16.6.Вычислительные схемы решения нелинейных задач ...
867
Как мы уже говорили, использование только неполного скалярного
потенциала можно трактовать как выделение поля гоков в однородной
по р среде, но эго не только не улучшает точность решения нелиней-
ной задачи магнитостатики, а может катастрофически сё ухудшить
Тем не менее для многих практических нелинейных задач магнитоста-
тики «правильное» выделение основного поля
повысить точность получаемого решения.
Продемонстрируем это на следующем
очень простом примере. Пусть необхо-
димо решить задачу магнитостатики для
конструкции, изображённой на рис. 165.
Обмотка, в которой течёт ток, является
усечённым круговым полым цилиндром,
а магнитный материал - соосным с ним
ферромагнитным цилиндром с выемкой.
Очевидно, хорошим приближением ис-
комого поля будет являться поле в кон-
струкции с ферромагнитным цилиндром
без выемки Это поле может быть полу-
чено в результате решения соответст-
вующей осесимметричной задачи для
потенциала . Тогда искомое поле мо-
может существенно
жет быть получено в виде суммы поля Рис. 165. Вид конструкции
Н279 осесимметричной задачи и поля
Н379 = —grad U, которое может быть вычислено путём решения сле-
дующей нелинейной задачи
— div (р grad [7) = — div ^р — р279 ] Н 79 j,
(16.85)
где р279 - распределение магнитной проницаемости, соответствующее
двумерной задаче, а значения р = р(Н) вычисляются по значениям
модуля напряжённости Н = H'D + Н379 суммарного поля. При этом
вычислительную схему решения нелинейной задачи следует модифи-
цировать, с учётом того, что р в ферромагнитном материале вычисля-
ется не по одному полю Н ' = — grad 7/, а по сумме двух полей -
известному полю Н279 и искомому полю Н379. Однако в отличие от
ситуации с неполным потенциалом, здесь поля Н279 и Н379 уже не
взаимоуничтожаются, а поле Н379 действительно дополняет поле
Н279. В результате при удачном выборе аппроксимирующей двумер-
ной задачи поле Н будет вычисляться заметно точнее (а во многих
случаях и намного точнее), чем в схеме с двумя потенциалами без вы-
деления осесимметричной (или двумерной) части поля.
868
16.Решение нелинейных задач
16.6.4. ЗАДАНИЕ КРИВЫХ НАМАГНИЧИВАНИЯ
и вычисление производных (1/ц)/dB2 И d^jdH2
При решении задач магнитостатики кроме геометрии расчётной
области необходимо задавать магнитные свойства ферромагнетиков,
входящих в изучаемую конструкцию. Как правило, магнитные свойст-
ва материалов представляются в виде кривых намагничивания В(Н)
(В - модуль индукции магнитного поля, Н — модуль напряжённости
магнитного поля). Пользуясь этими кривыми, несложно получить не-
обходимые для описанных выше вычислительных процедур зависимо-
сти р;(В) ИЛИ р(Я).
Обычно зависимости 1/р от В и р от Н задаются таблично. По-
этому в процессе решения задачи магнитостатики при вычислении
значения ур или р , а также их производных по В или Н (если обра-
ботка нелинейностей выполняется с использованием метода Ньютона)
удобно использовать кубический сплайн1 (как правило, сглаживаю-
щий, см раздел 4.17.2).
По этому сплайну для любого значения В или Н можно вычис-
лить значение 1/р или р, а также его производную d{l/[i^dB или
. Сами же значения В или Н на любом конечном
можно получить с помощью формул (16.48) или (16.84).
Необходимые для вычисления локальных матриц GL и
элементе
векторов
и вектора
1 Поскольку при вычислении компонент локальной матрицы GL
b линеаризованной системы необходимо вычислять значения производных
1/р по В2 или р по Я2 (а значения В1 и Я2 могут быть получены непо-
средственно из формул (16.36) и (16 80)), может показаться, что для реализа-
ции описанных выше вычислительных схем наиболее подходящим является
кубический сплайн, аппроксимирующий зависимость 1/р от В2 или р от
Я ' . Однако эго не так. Кубический сплайн, построенный по набору значений
1/р и В2 или р и Н2, может иметь участки немонотонности (особенно в
конце кривой намагничивания), не характерные для реальной зависимости
магнитной проницаемости от величины магнитного поля, в то время как у
кубического сплайна, построенного по набору значений 1/р и В или р и Я,
такие участки немонотонности могут и не появиться. Заметим, что наличие
участков немонотонности в зависимости 1/р и В2 или р и Я2 приводит к
существенному замедлению сходимости итерационного процесса Ньютона и
возникновению в нем плохо затухающих осцилляций. Поэтому в подавляю-
щем большинстве случаев кубический сплайн лучше строить по набору зна-
чений 1/р и В или р и Я.
16.6 Вычислительные схемы решения нелинейных задач ...
869
b£ значения производных1 d^y^dE2 или dyjdH2 (см. соотношения
(16.45)-(16.46) или (16.82)—(16.83)) можно вычислить следующим об-
разом:
dB2
1 ГЛ
2В dB
dy
~dH2
в=в
в=в
= 1_ fZ|L
Н=Н 2Я dH
н=п
Ещё одной проблемой при работе с кривыми намагничивания явля-
ется то, что очень часто соответствующие таблицы данных обрывают-
i R
ся в том месте, где величина • • уГг- становится достаточно близкой к
y{]dH
единице, а при решении практической задачи величина В или Н (по
которой на конечном элементе вычисляется значение 1Дс или р. и зна-
чение соответствующей производной) может превысить последнее
табличное значение В„ или Нп .
Получим выражения, позволяющие вычислять значения ХДс и про-
изводные 1Дь по В и по В2 для В > Вп при условии, что для В > В„
справедливо соотношение 1 (где Но — магнитная проницае-
мость вакуума).
С одной стороны, мы имеем очевидное равенство (напомним, что че-
рез р мы обозначаем относительную магнитную проницаемость среды):
f = НоЯ.
С другой стороны, при условии, что для В > Вп справедливо
== 1, для В > В„ будет справедливо и соотношение
(16 86)
АВ = |.1()Д н,
где АН = Н — Нп, АВ = В — Вп. и поэтому
|Х()Н = Но (Я„ + ДЯ) = Г + ДВ = + в - Б,
где р,п - значение относительной магнитной проницаемости при
В = В„ (т.е. В„ = Ц„.Ц()ЯН ).
(16.87)
1 Значения этих производных, очевидно, нужно вычислять при В = В и
Н = Н.
870
16.Решение нелинейных задач
Сравнивая выражения (16.86) и (16.87), получаем:
откуда
1
Р
_1
-1
+ 1.
(16 88)
Из (16.88) очень легко получить выражения для вычисления произ-
водных 1Д1 по В и по В2:
dB В2 [р« J
dB2
i 4LAi)_ b„ (i j
2B dB 2Z?3 (prt
(16.89)
(16.90)
Таким образом, выражения (16.88)—(16 90) позволяют получить зна-
чения
1Д1, d {1/i^/dB и d (1Дь1 dB для В > Вп.
Аналогично в случае, когда зависимость коэффициента р, от Н за-
дана только для значений Я < Нп, можно получить выражения для
вычисления значений ц и его производных по Я и по В2 при значе-
ниях II > II,,:
|1 = J
_4l _ i ^р J л, п ни
(щ2 2Н dH ц" 4 2Н3 ‘
Нередко при решении практических задач сходимость метода Нью-
тона можно заметно улучшить (если норма невязки нелинейной систе-
мы перестала монотонно и достаточно быстро убывать), если исполь-
зовать «демпфирование» (см с. 837) и для тех участков зависимости
1Дь от В (или ц, от Я), где В > Вп (или Я > Нп). В этом случае
можно, например, вместо (16 90) использовать соотношение
dB2
в2
2 В4
-Т-1
tPw
в
> Р it
т.е. в качестве коэффициента «демпфирования» взять v =
Blt/B.
17.1.Прямые методы решения СЛАУ
871
17. МЕТОДЫ РЕШЕНИЯ СЛАУ, ПРИМЕНЯЕМЫЕ В МКЭ
Здесь мы очень кратко рассмотрим методы, наиболее часто при-
меняемые для решения конечноэлементных СЛАУ.
17.1. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
Прямые методы решения СЛАУ применяются в основном при
решении одномерных задач, поскольку в этом случае получаемая мат-
рица СЛАУ является профильной с заполненным профилем. 11ри ре-
шении же большинства двумерных и особенно трёхмерных задач пря-
мые методы чаще всего оказываются малоэффективными из-за силь-
ной разреженности матрицы СЛАУ, поэгому используются только в
очень редких случаях.
Пусть дана система линейных алгебраических уравнений:
Ах = Ь. (17.1)
Прямые методы, как правило, основаны на разложении исходной
матрицы на произведение нескольких матриц специального вида, на-
пример.
• LU -разложение: L — нижняя треугольная матрица, U - верхняя
треугольная матрица с единицами на главной диагонали;
• LI -разложение (метод квадратного корня): L - нижняя треуголь-
ная матрица;
• LDLT -разложение: L — нижняя треугольная матрица, Ln = 1, D -
диагональная матрица.
Выбор того или иного метода разложения зависит от свойств мат-
рицы А (таких, как симметричность, положительная определенность)
После построения разложения процедура нахождения решения
СЛАУ (17.1) очень проста. В качестве примера рассмотрим решение
системы (17.1) методом, основанным па LU -разложении.
Предположим, что нам удалось построить матрицы L и U такие,
что
А = LU . (17.2)
Подставляя (17.2) в (17.1), получаем:
LUx = b. (17.3)
Обозначим через у вектор Ux, тогда
872
17.Методы решения СЛАУ, применяемые в МКЭ
Ly = b. (17.4)
Таким образом, решение системы (17.1) сводится к трем основным
этапам:
1) по значениям элементов матрицы А найти значения элементов
матриц L и U;
2) решить систему (17.4) с нижней треугольной матрицей L (прямой
ход);
3) решить систему Ux = у (где у - решение системы (17 4)) с верх-
ней треугольной матрицей U (обратный ход).
Очевидно, основные вычислительные затраты в этой процедуре
приходятся на первый этап'. Затраты же второго и третьего этапа экви-
валентны затратам обратного хода метода Гаусса, когда в очередном
обрабатываемом (z-м) уравнении неизвестной остаётся только одна
(г-я) переменная t/, (в системе Ly = b) или хг (в системе Ux = у ).
17.1.1 . LU РАЗЛОЖЕНИЕ
Покажем, как получается алгоритм построения LU -разложения.
Матрицы L и U будем искать в следующем виде:
Ln 0 0 ... 1 ^12 On -
^21 А22 0 ... 0 1 о23 ...
I ; и = (17.5)
^31 ^32 ^33 0 0 1 ...
Воспользуемся равенством (17.2). Будем последовательно умно-
жать строки матрицы L на столбцы матрицы U. В результате полу-
чим п1 2 соотношений (?z — размерность СЛАУ), позволяющих после-
довательно вычислять все значения2 L}j (z = l...n, j — и Url
(i — 1... ii, j = i 4-1... n ):
An = L] (; / получим значение Лц /
Дл = 7>21; / получим значение /
А12 = Iqi • ; / получим значение U12 /
Л22 = L2i ' О12 + А22*>! получим значение Л22 !
Л3] = Л31; Л32 = Lj] • U12 -Ь Б32 ; / получим значения Л31 и Л32 /
4з=АгО13; А23=л21-и134-Л22-^23;/получим значения [/13 и Л23/
А33 = Л31 U13 + Л32 • U23 + Ь33 ; / получим значение Л33 /
1 Если, конечно, матрица А не имеет очень узкий профиль.
2 Их, очевидно, также п2 .
17.1.Прямые методы решения СЛАУ
873
Из этих соотношений можно получить общие формулы для нахож-
дения элементов матриц L и U. Полагаем равным Ап . Далее для
г от 2 до п последовательно находим:
j-i
Lij — Aj ^3 LikUkj > 7 = 1,- .,г- 1, (И.6)
k=l
J-l
Uji ~ L , 7 = 1,- i — 1, (17-7)
A=1
i—
-Azi у АДА, j (17.8)
k-1
т.е. сначала формируется Д] (равный Ап), после чего в цикле по г от
2 до п по формуле (17.6) вычисляются все внедиагональные элемен-
ты г-й строки матрицы L, затем по формуле (17.7) — все внедиаго-
нальные элементы г-го столбца матрицы U и, наконец, по формуле
(17.8) диагональный элемент Д, (напомним, что ULi = 1 Vz).
Очень удобен для построения LU -разложения профильный формат
хранения матрицы СЛАУ. Ниже мы приведём фрагмент программы на
языке Фортран, реализующей алгоритм LU -разложения матрицы,
хранящейся в профильном формате. Результат разложения записыва-
ется на место исходной матрицы (при этом в массив di записывается
диагональ матрицы L).
do i =2,N
sumdi=0
jO=i- (ig (i + 1)-ig (i))
do ii=ig(i), ig(i+1)-1
j=ii-ig(i)+j0
jbeg=ig(j)
j end=ig(j +1)
if(jbeg.It.jend)then
jOj=j-(jend-jbeg)
jjbeg=max(jO,jOj)
jjend=min(j,i-1)
cl=0
do k=0,jjend-jjbeg-1
indggu=ig(j)+ j jbeg-j 0j+k
indggl=ig(i) + jjbeg-j 0 + k
cl=cl+ggu(indggu)*ggl(indggl)
end do
ggl(ii)=ggl(ii)-cl
cu=0;
do k=0,jjend-jjbeg-1
indggl=ig(j)+j jbeg-j 0j + k
indggu=ig(i)+jjbeg-jO+k
874
17.Методы решения СЛАУ, применяемые в МКЭ
cu=cu+ggu(indggu)*ggl(indggl)
end do
ggu(i i)=ggl(ii)-cd
end if
ggu(ii)=ggu(ii)/di(j+1)
sumdi=sumdi+ggl(ii)*ggu(ii)
end do
di(i)=di(i)-sumdi
end do
17.1.2 . LLT -РАЗЛОЖЕНИЕ
Это разложение может быть построено только для симметричной
положительно определённой матрицы А. Формулы для вычисления
элементов нижней треугольной матрицы L приведём без их вывода:
(17.9)
LL -разложение называют также разложением Холесского1 (или
Холецкого), а основанный на нём метод решения СЛАУ - методом
Холесского.
17.1.3 . LDLT-РАЗЛОЖЕНИЕ
Такое разложение можно построить для симметричной, но не
обязательно положительно определённой матрицы. В этом случае диа-
гональные элементы матрицы L берутся равными единице (т.е.
= 1 V/.), и в результате элементы диагональной матрицы D опре-
деляются однозначно.
А.= 1
А? г) А/ у
Jj jt=l
j < i-(17.10)
Очевидно, для положительно определённой матрицы А все эле-
менты диагональной матрицы D должны быть положительными.
17.2. НЕПОЛНЫЕ РАЗЛОЖЕНИЯ МАТРИЦ
Для ускорения сходимости многих итерационных методов обыч-
но используют предобусловливание матрицы А системы
Ах = Ь. (17.11)
Одним из наиболее часто используемых методов предобусловлива-
ния является так называемый метод неполной факторизации матри-
цы. Он заключается в следующем.
Вместо системы (17.11) решается «эквивалентная» ей система
1 В английском написании Holessky.
17.2.Неполные разложения матриц
875
S-]AQ“1y = f, (17.12)
в которой S — нижняя треугольная, a Q — верхняя треугольная матри-
цы такие, что матрица SQ в некотором смысле близка к матрице А .
Например, матрицы S и Q могут быть построены так, что их порт-
реты (т.е. места расположения ненулевых элементов) совпадают с
портретами нижнего и верхнего треугольников матрицы А соответст-
венно, и при этом значения ненулевых элементов матриц S и Q вы-
числяются таким образом, чтобы все ненулевые элементы матрицы А
совпали с соответствующими элементами матрицы SQ . Нулевые же
элементы матрицы А могут не совпасть с соответствующими элемен-
тами матрицы SQ, и именно поэтому такое разложение называется
неполным.
Очевидно, если очень многие элементы матрицы SQ совпадут с
соответствующими элементами матрицы А, то система (17.12) будет
иметь матрицу, близкую к единичной. Действительно, если L и U
нижняя и верхняя треугольные матрицы полного разложения А, то в
этом случае S L и Q^U (т.е. S-1L^E и UQ-1^E, где Е -
единичная матрица), и тогда матрица S^AQ-1 = S 'LIJQ 1 системы
(17.12) будет близка к единичной матрице Е, что может существенно
ускорить сходимость многих итерационных методов решения СЛАУ.
Систему (17.12) мы назвали эквивалентной исходной системе
(17.11) потому, при f = S-1b с помощью вектора решения у системы
(17.12) можно довольно просто получить вектор решения СЛАУ
(17.11) в виде х = Q *у - фактически вектор х получается из реше-
ния системы Qx = у с верхней треугольной матрицей Q . Вектор же f
системы (17.12) может быть достаточно просто получен из решения
системы Sf = b с нижней треугольной матрицей S.
Ниже приводятся тексты программ, реализующие решение СЛАУ
Sy = С с нижней треугольной матрицей S и Qy = f для матриц S и
Q, хранящихся в разреженном ^прочно-столбцовом формате
(см. раздел 10.4.4).
♦решение СЛАУ с нижней треугольной матрицей (прямой ход)
do i i = IfN
sum-0.
in ig(ii)
ik=ig(ii+1)-1
if (in.le.ik)then
do jj=in,ik
sum=sum+cggl(jj)*y(jg(jj))
end do
end if
876
17.Методы решения СЛАУ, применяемые в МКЭ
y(ii)=(r(ii)-sum)/cdi(ii)
end do
^решение СЛАУ с верхней треугольной матрицей (обратный ход)
do kk=l,N
ii=N+l-kk
yii=y(ii)/cdi(ii)
у (ii)=yii
in=ig(ii)
ik=ig(ii+1)-1
if(in.le.ik)then
do jj=in,ik
nst=jg(jj)
у(nst)=y(nst)-egg(jj)*yii
end do
end i f
end do
Замелим, что при использовании неполной факторизации для пре-
добусловливания СЛАУ с несимметричными матрицами довольно
часто используют такой вариант неполного LU -разложения, при кото-
ром диагональные элементы матриц S и Q (S « L и Q ~ IJ) совпа-
дают (т.е. S\,= Qu Vi)-
Этот вариант неполной факторизации особенно целесообразно при-
менять в тех случаях, когда матрица А решаемой СЛАУ довольно
близка к симметричной и для решения СЛАУ используются такие ме-
тоды, как GMRES, локально-оптимальная схема или метод бисопря-
жённых градиентов (см. раздел 17.3).
Формулы, реализующие неполную факторизацию матрицы А с ус-
ловием равенства диагональных элементов нижней треугольной мат-
рицы S и верхней треугольной матрицы Q (SQ ~ А), имеют вид
А» ~ F SikQti
Обратим внимание па то, что, поскольку диагональные элементы
матриц S и Q совпадают, то вместо диагональных элементов Q ис-
пользуются соответствующие элементы S, а диагональные элементы
Q не хранятся.
17.3.Итерационные методы решения СЛАУ...
877
17.3. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
С РАЗРЕЖЕННЫМИ МАТРИЦАМИ
17.3.1 МЕТОД С ОПРЯЖЁНПЫХ ГРАДИЕНТОВ
Одним их наиболее эффективных методов решения симметрич-
ных конечноэлементных СЛАУ с разреженными матрицами является
метод сопряжённых градиентов (МСГ). Его классический алгоритм
для решения системы уравнений (17.11) с симметричной положитель-
но определённой матрицей А выглядит следующим образом.
Выбирается начальное приближение х и полагается
г” = Ь — Ах°, (17.14)
z° = г°. (17.15)
Далее для к = 1,2,... производятся следующие вычисления:
Г А-1,
к (A.zfc-1,zfc-1) ’ V 7
хА = х1-1 (17.17)
г* = г*-1 -c^Az*"1, (17.18)
z* = г* + foz*-1. (17.20)
где х 1 - вектор начального приближения; хА - вектор решения на А. -Й
(текущей) итерации; г; - вектор невязки на к-й (текущей) итерации;
z'1 - вектор спуска (сопряжённое направление) на к-й итерации; оц ,
Рд - коэффициенты.
Выход из итерационного процесса (17.16)-(17.20) осуществляется
либо но условию малости относительной невязки:
|rlj|/M<£- <17-21>
либо (аварийно) по превышению максимально допустимого числа ите-
рации А-|11а, .
Нетрудно убедиться, что применение итерационного процесса
(17.14)—(17.20) к предобусловленной СЛАУ с матрицей S ‘AS 1 и
вектором S b после соответствующих переобозначении приводе! к
следующему итерационному процессу:
г° = Ь — Ах°, (17.22)
878
17.Методы решения СЛАУ, применяемые в МКЭ
Z° = М'1!-0,
“‘ = (Аг1-1,^'-') ’
хк = хА;—1 + CtfcZ*-1 ,
rk = rA:-1 — oq.Az*-1,
(м-V,/)
Pt
zA‘ = M-1/ + fo.z^-1,
(17.23)
(17.24)
(17.25)
(17.26)
(17.27)
(17.28)
где xA: и rA: — вектор решения и вектор невязки исходной (не предобу-
словленной) СЛАУ, а М = SST - матрица предобусловливания. При
этом запись М-1р в соотношениях (17.23), (17.24), (17.27) и (17.28)
означает1, что в них вместо М-1р должен быть подставлен вектор q,
который определяется из решения системы SS'q ~р, т.е. сначала
вычисляется вектор v из системы Sv = р, а затем — вектор q из сис-
темы Srq = v . Очевидно, матрицу S следует выбирать таким образом,
чтобы эти системы можно было решить без серьёзных вычислитель-
ных затрат (например, в качестве S брать нижнюю треугольную мат-
рицу)
Ускорение сходимости процесса (17.24)-( 17.28) во многом зависит
от выбора матрицы М и от её близости к А .
Можно, например, взять М = D, где D - матрица, в которой нену-
левой является только её главная диагональ, равная главной диагонали
матрицы А (в этом случае, очевидно, не нужно строить матрицу S).
Такое предобусловливание называют диагональным. Диагональное
предобусловливание несколько улучшает сходимость МСГ в случае,
когда строки матрицы очень разномасштабные.
Гораздо более эффективным является предобусловливание непол-
ным разложением Холесского. Для него матрица S является нижней
треугольной и строится по формулам, полностью аналогичным форму-
лам LLr-разложения (см. (17.9)). При этом портрет нижней треуголь-
ной матрицы S либо полностью совпадает с портретом нижнего тре-
угольника матрицы А, либо лишь незначительно отличается от него.
Ниже приведён текст программы, реализующий построение матрицы
S неполного разложения Холесского.
rumen=Id-55
nerazl=0
с nerazl - k-во неразложенных эл-тов СЛАУ
1 Если, конечно, М - не диагональная матрица.
17.3.Итерационные методы решения СЛАУ...
879
do ii=l,N
naii=ig(ii)
koii=ig(ii+1)-1
sumdi=0.
do while (naii.le.koii)
do i=naii,koii
с вычисляет cgl(i) и cgu(i)
suml=0.
sumu=0.
j j=jg(i)
if(i.eq.naii)goto 6
najj=ig(jj)
kojj=ig(jj+1)-1
if(najj.gt.kojj)goto 6
с утножает ii-ю строку ggl на jj-й столбец ggu
с и jj-ю строку ggl на ii-й столбец ggu
nggi=naii
с nggi - нотер текущего эл-та в шассиве ggl в ii-й
строке
nggj=najj
с nggj - нотер текущего эл-та в тассиве ggu в jj-m
столбце
1 continue
if (jg(nggi) .It.jg(nggj))then
nggi=nggi+l
if(nggi.It.i)goto 1
goto 6
end if
if(jg(nggi).eq.jg(nggj)
suml=suml+cgl (nggi) *cgu (nggj )
sumu=sumu+cgl(nggj)*cgu(nggi)
nggi=nggi+l
if(nggi.ge.i)goto 6
end if
nggj=nggj+l
if(nggj.le.kojj)goto 1
6 cgl(i)=(ggl(i)-suml)*cdi(jj)
cgu (i) = (ggu(i)-sumu)*cdi(j j)
end do
с утножает ii-ю строку на ii-ю
do i=naii,koii
sumdi=sumdi+cgl(i)*cgu(i)
end do
r=di(ii)-sumdi
if(r.gt.abs(di(ii)*rumen))goto 12
cgl(naii)=0.
cgu(naii)=0.
nerazl=nerazl+l
880
17 Методы решения СЛАУ, применяемые в МКЭ
naii=naii+l
sumdi=0.
end do
r=abs(di(ii))
12 cdi(ii)=ld0/sqrt(r)
end do
Ещё раз обратим внимание на то, что при использовании в качестве
предобусловливания неполного разложения Холесского не требуется
фактическое построение матрицы М, участвующей в формулах
(17.23)-(17.28) (и тем более её обращение). Здесь просто ищется век-
тор q как результат решения системы Mq = г' с матрицей М, яв-
ляющейся произведением нижней треугольной матрицы S и верхней
треугольной матрицы Sr, т.е. сначала вычисляется вектор v из систе-
мы Sv = р (с нижней треугольной матрицей S), а затем - вектор q из
системы S'q = v (с верхней треугольной матрицей ST ), и этот вектор
q и есть требующийся нам вектор М 'г
17.3.2. ЛОКАЛЬНО-ОПТИМАЛЬНАЯ СХЕМА
Метод сопряжённых градиентов с предобусловливанием непол-
ным разложением Холесского эффективен для решения СЛАУ с раз-
реженными симметричными положительно определёнными матрица-
ми.
Для решения СЛАУ с несимметричными разреженными матрицами
также существуют итерационные методы, схемы которых довольно
похожи на схему МСГ, и при этом в тех случаях, когда матрица А
решаемой СЛАУ довольно близка к симметричной, эти методы по эф-
фективности могут приближаться к МСГ.
Здесь мы рассмотрим одну из таких схем, относящуюся к классу
локально-оптимальных (см., например, Г16|). Эта схема была предло-
жена в работе [32], и в несколько модифицированном (и оптимизиро-
ванном) виде она выглядит следующим образом.
Выберем начальное приближение xh и вычислим
г° = z() = b-Ах°, р° = Аг() (17.29)
Далее для /с = 1,2,... будем вычислять приближения х" с помощью
следующего итерационного процесса:
хА: = хА: 1 + ot.k1k 1,
гА = ГА'-1 — Oq-p*"1 ,
(17.30)
(17.31)
(17.32)
17.3.Итерационные методы решения СЛАУ...
881
(рА: ^А/')
Zk = Гк + Рл2А- 1 ,
р = Ага + pzpA-1,
(17.33)
(17.34)
(17.35)
где рА = Az - вспомогательный вектор, который вычисляется не
умножением матрицы на вектор, а пересчитывается рекуррентно с
помощью соотношения (17.35) (т.е. на каждой итерации процесса
(17.30)-( 17.35)) делается только одно умножение матрицы на вектор
при вычислении Ага ).
Процесс заканчивается, если величина (г‘;,гА(квадрат нормы не-
вязки) становится достаточно малой (т.е., например, если выполняется
соотношение (17.21)). При этом квадрат нормы невязки можно вычис-
лять с помощью рекуррентного соотношения1
(гА:,гА) = (гА:-1,гА'-1) —с^ (рА-1,рА:_|). (17.36)
Ещё раз обратим внимание на то, что схема (17.29)—(17.36) особен-
но эффективна в тех случаях, когда матрица А близка к симметрич-
ной.
Можно показать, что при использовании матриц неполной факто-
ризации S и Q (таких, что матрица SQ в некотором смысле близка к
А) локально-оптимальная схема (17.29)—(17.36) (при применении сс к
СЛАУ с матрицей S"1 AQ1) преобразуется к следующему виду.
Выбирается начальное приближение х и вычисляются
г() — S-1 [b — Ах°), z° =Q“1f°, pn = S“1Az1’.
Далее для к = 1,2,... производятся следующие вычисления:
хА = хк 1 -ь ctkzk 1,
fА = fА:-1 — ,
(17.37)
(17.38)
(17.39)
(17 40)
1 Заметим, что рекуррентный пересчёт невязки может с ростом числа ите-
раций накапливать довольно значительную ошибку, и поэтому после опреде-
лённого числа итераций имеет смысл делать так называемое «обновченис»
итерационного процесса, т.е. пересчитать тк по формуле г b Axz и,
кроме того, можно взять z* — гА и pz = Azz.
882
17.Методы решения СЛАУ, применяемые в МКЭ
(p*-1,s-1AQ~lf*)
гк = Q-if* +0fcZfc"1,
рА = S-1AQ-Iffc d-fop*-1,
(17-41)
(17.42)
(17.43)
где х1 - вектор решения исходной (не предобусловленной) СЛАУ, а
гк - вектор невязки СЛАУ S“ ]Ах = S-1b .
Процесс заканчивается, если величина [гА:,гА) стала достаточно
малой1, причём ' гА , гА ) можно вычислять по рекуррентной формуле
(pt-iy-l)
При построении матриц S и Q лучше воспользоваться такой схе-
мой неполной факторизации, при которой диагональные элементы
матриц S и Q совпадают2 (см. (17.13)).
17.3.3. GMRES
Одним из наиболее надёжно сходящихся итерационных методов
решения конечноэлементных СЛАУ с несимметричными разрежен-
ными матрицами является метод GMRES (аббревиатура от Generalized
Minimum Residual method) [31].
Приведём схему этого метода, использующую предобусл о вливание
СЛАУ неполной факторизацией с матрицами3 * * S и Q , т.е. для решения
СЛАУ вида (S-1AQ_1)x = S b (где х = Qx).
Выбирается начальное приближение х° и полагается
x"=Qx°, г° =S~1(b-Ах”). (17.44)
Далее для k = 1,2,... выполняются итерации метода. На каждой
итерации вычисляются элементы двух вспомогательных матриц - мат-
рицы V размера п х т и матрицы Н размера (m + 1) х т, где п -
1 Здесь для выхода из итерационного процесса вместо соотношения (17.21)
следует использовать соотношение г < е2 .
2 Это позволит получить довольно бпизкую к симметричной матрицу
S-1AQ-1 предобусловленной системы, если матрица А имела значительную
симметричную часть; для симметричной матрицы А это разложение факти-
чески совпадёт с неполным разложением Холесского (т.е. даст Q = S7 ).
3 Здесь также наилучший эффект обычно даёт неполное разложение с ис-
пользованием формул (17 13), дающих треугольные сомножители S и Q с
равными диагональными элементами.
17.3.Итерационные методы решения СЛАУ...
883
размерность решаемой СЛАУ, ат- размерность подпространства
Крылова, которая является параметром1 метода
Обозначим через vz г-й столбец матрицы V. Первый столбец V
формируется по формуле
v1 = гА-1/||гА:-1||. (17.45)
Для р = 1,2,...,т выполняются следующие действия.
1. Вычисляется вектор
w = (s-1AQ-1v1'). (17.46)
2. Вычисляются элементы р -го столбца верхнего треугольника
матрицы Н:
ff>,1-vx-w, Х = 1......|л. (17.47)
3. Определяется вспомогательный вектор
v|l+1 = S-1AQ_1v'‘ - £НХ,ЛХ . (17.48)
Х=1
4. Находится значение поддиагонального элемента матрицы Н :
Д.+ц. =||v"+'||- (17.49)
5. Если 77(1+111 = 0, процесс построения матрицы Н заканчивается,
и за т принимается текущее значение2 р В противном случае опре-
деляется новый столбец матрицы V :
v'L+1 = —L-v'l+1. (17.50)
Через определённую таким образом матрицу Н новое приближение
х' определяется следующим образом.
Вычисляется вектор dfc == (||гА-1||,О,...,о) размера т 4- I . Вектор
параметров z/ формируется как решение задачи наименьших квадра-
тов:
1 Число т называют также глубиной метода. Обычно значение этого па-
раметра берут в диапазоне от нескольких единиц до нескольких сотен, а чаше
всего - в диапазоне 5-г30.
2 В этом случае для нахождения вектора параметров (об этом речь пой-
дёт чуть ниже) будет достаточно решить СЛАУ Hz' = <1 с квадратной мат-
рицей Н , в которой нижний треугольник содержит единственную ненулевую
диагональ рядом с главной диагональю (и при этом уже совсем нс обязатель-
но применять метод вращения).
884
17.Методы решения СЛАУ, применяемые в МКЭ
|dA — Hz' || = min
после чего вычисляется
хА = х*-1 + VzA:.
Новая невязка рассчитывается как
rfc = S-1 b-AQVj.
(17.51)
(17.52)
(17.53)
После окончания итерационного процесса решение исходной
СЛАУ определяется как
x = Q ]х, (17.54)
т е из решения Qx = х с верхней треугольной матрицей Q .
Обратим внимание на то. что матрица Н, для которой необходимо
решать задачу минимизации (17.5 1). является прямоугольной матрицей
размера (///,+ 1)х т, у которой все элементы Ннижнего треуголь-
ника при i.> j + 1 равны нулю. Поэтому для решения задачи (17.51)
лучше всего воспользоваться следующим способом [31].
Приведём матрицу Н к верхнему треугольному виду, обнуляя по-
очерёдно все элементы Я?+17, г = 1,...,т + 1, с помощью ортого-
нального преобразования вращения:
Н(,)> = Н,
где В - матрица вращения размера (?п + 1) х (m + 1), у которой
ненулевыми являются только элементы главной диагонали и элементы
^'й-1 и ^•’|)м ’тс-
I
1
Cj Si
-Si G
1
1
17 3 Итерационные методы решения СЛАУ...
885
н,-+м
Si = I =, c.j = r- .... ". . = .
^(я’Г11)2 + (Hi+1,.)2 + (w.+i,,)2
Обозначим через H квадратную матрицу размера т х т, получен-
ную из матрицы Н " отбрасыванием последней строки, а через d
вектор размера т + 1, полученный из вектора d последовательным
умножением на него слева матриц R ’ , г = 1,...,т + 1. Тогда решени-
ем задачи минимизации (17 51) является вектор zA:, полученный из
решения СЛАУ
HzA=d, (17.55)
где d - вектор размера т, полученный из d отбрасыванием по-
следнего элемента.
17.3.4. ДРУГИЕ МЕТОДЫ
Для решения конечноэлементных СЛАУ с несимметричными
матрицами иногда применяются различные варианты метода бисоп-
ряжённых градиентов. Схема одного из таких вариантов (она счита-
ется наиболее классической) выглядит следующим образом.
Выбирается начальное приближение х и полагается
г° = Ь —Ах°, (17.56)
рп = г(), (17.57)
z°=r°, (17.58)
s° = r°. (17.59)
Далее для к = 1,2,... производятся следующие вычисления:
pL ],гА’ ]) (17.60)
X* = Xt-1 + Otj-Z*-1, (1761)
rk = rfc-1 — ct^Az'-1, (17 62)
pA = pA'-1 — ctji.ATsfc-1, (17.63)
(р*,Г*) ™ („к-l _fc—1\ ’ (17.61)
Ip , Г 1 zk = rk 4- foz^1. (17.65)
886
17.Методы решения СЛАУ, применяемые в МКЭ
sk =рк +^.SA“1. (17.66)
где х1’ - вектор начального приближения; х; - вектор решения на к -й
(текущей) итерации; гА и z/,: - вектор невязки и вектор спуска на А -й
итерации; рА и sA: - вспомогательные векторы; а/., - коэффициен-
ты.
Очевидно, на каждой итерации метода бисопряжённых градиентов
делается два умножения матрицы на вектор (самой матрицы А на век-
тор zA:-1 и транспонированной к ней матрицы на вектор sA:“l).
При использовании для предобусловливания неполного LU -
разложения в рассмотренной выше схеме можно заменить матрицу А
на матрицу S-1AQ-1, а вектор правой части b на вектор S b После
того как будет получено решение предобусловленной системы х, ре-
шение х исходной системы можно вычислить из решения системы
Qx = х с верхней треугольной матрицей Q (невязку г, соответст-
вующую исходной системе, также можно получить из невязки г пре-
добусловленной системы после умножения её на нижнюю треуголь-
ную матрицу S: г = Sr).
Заметим, что если при решении конечноэлементной СЛАУ с не-
симметричной матрицей какой-либо из вариантов метода бисопряжён-
ных градиентов сходится, то его скорость сходимости может быть за-
метно выше, чем у GMR.ES или локально-оптимальной схемы Однако
довольно часто бывают случаи, когда GMR.ES и локально-оптимальная
схема сходятся, а все варианты метода бисопряжённых градиентов -
нет (обратных же случаев почти не бывает).
В некоторых случаях, когда не удаётся добиться сходимости к ре-
шению (для СЛАУ с несимметричной матрицей) ни одним из рассмот-
ренных выше методов, можно попытаться воспользоваться методом
релаксации. В простейшем варианте (метода последовательной ре-
лаксации) его формулы выглядят следующим образом:
= 2’f
co
О < СО < 2,
где к - номер итерации, а со — параметр релаксации, с помощью кото-
рого можно регулировать скорость сходимости приближённого реше-
ния х‘ к точному х (п по-прежнему-размерность СЛАУ).
Более быстрой сходимости можно добиться, если использовать так
называемую блочную релаксацию. Для этого нужно разбить матрицу
А на блоки А,? гак, чтобы диагональные блоки Ап можно было легко
разложить на множители L, и U, и количество ненулевых элементов в
17.3.Итерационные методы решения СЛАУ.
887
этих множителях примерно совпадало с количеством ненулевых эле-
ментов в диагональных блоках1.
Тогда соответствующий блок-строке с номером i подвектор х,
вектора решения х вычисляется по формуле (для последовательной
блочной релаксации)2
xj+1= (1 -ш)х*+ ш(Ай)' 1
г—1 т
ь.-ЕМ+1-Е М
7=1 J=i+1
, 0<ш<2,
где по-прежнему к — номер итерации, ш — параметр релаксации, т —
количество блок-строк, а произведение подматрицы (А,,)1 на под-
г—1 ш
вектор р (в нашем случае р b — А/х/, ' 1 - У^ А,/Х; ) вычис-
7=1 7=i+l
ляется путём решения двух систем: L,y - р с нижней треугольной
матрицей L, и U,q = у с верхней треугольной матрицей L\ (и, оче-
видно, q = (А,:/)-1р)
Существуют и другие итерационные методы решения СЛАУ с раз-
реженными матрицами. Некоторые из них могут по скорости сходимо-
сти заметно превосходить рассмотренные здесь методы, если матрицы
решаемых СЛАУ обладают определёнными дополнительными свойст-
вами (см, например, [16], [5]). Однако по универсальности они всё-
таки значительно уступают таким методам, как метод сопряжённых
градиентов, локально-оптимальная схема и GMRES.
1 Вообще-то, при разбиении матрицы А на блоки А,у можно использовать
более общий критерий - нужно, чтобы очень быстро, с минимальными вы-
числительными затратами, решались системы A„q = р .
2 Обратите внимание на то, что подвектор х(, который в квадратной скоб-
ке должен быть умножен на диагональную подматрицу А„ , вынесен из неё -
это может довольно существенно сократить вычислительные затраты
888
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1 . Жданов М.С., Спичак В.В. Математическое моделирование элек-
тромагнитных полей в трёхмерно-неоднородных средах. - М.: Наука,
2 . Захаров Е.В. Интегральные уравнения в краевых задачах элек-
тродинамики. - Изд-во Моск, ун-та, Москва 1987.
3 . Зенкевич О. Метод конечных элементов в технике. - М.:Мир,
1975.
4 . Зенкевич О., Морган К. Конечные элементы и аппроксимация. -
М.: Мир, 1986.
5 . Ильин В.П. Методы неполной факторизации для решения алгеб-
раических систем. - М.: Физматлит, 1995.
6 . Кулон Ж.-Л., Сабоннадьер Ж.-К. САПР в электротехнике: Пер. с
франц. -М.: Мир, 1988.
7 . Марчук Г.И., Агошков В.И Введение в проекционно-сеточные
методы.-М.: Наука, 1981.
8 . Матвеев А.Н. Электричество и магнетизм: Учеб, пособие. - М.:
Высш, школа, 1983.
9 . Митчелл Э., Уэйт Р. Метод конечных элементов для уравнений с част-
ными производными -М.: Мир, 1981.
10 . Норри Д., де Фриз Ж. Введение в метод конечных элементов. -
М.: Мир, 1981.
11 .Обэн Ж.-П. Приближённое решение эллиптических краевых за-
дач. - М.: Мир, 1977.
12 .Оден Дж. Конечные элементы в нелинейной механике сплош-
ных сред. - М.:Мир, 1976.
13 .Ортега Дж. Введение в параллельные и векторные методы реше-
ния линейных систем. - М.: Мир, 1991.
14 . Препарата Ф., Шеймос М. Вычислительная геометрия: Введе-
ние.-М.: Мир, 1989.
15 .Сабоннадьер Ж.-К., Кулон Ж.-Л. Метод конечных элементов и
САПР: Пер. с франц. - М.: Мир, 1989.
16 .Самарский А.А., Николаев Е.С. Методы решения сеточных урав-
нений. - М.: Наука, 1978.
17 .Сильвестер П., Феррари Р. Метод конечных элементов для ра-
диоинженеров и инженеров-электриков - М.: Мир, 1986.
18 .Соловейчик ЮГ., Персова М.Г., Тригубович Г.М. Математиче-
ское моделирование процесса становления осесимметричного поля
вертикальной электрической линии. И Сибирский журнал индустри-
альной математики. - Новосибирск, 2003. -Т.6. -№2(14)-С. 10/-125.
19 .Соловейчик Ю.Г., Рояк М.Э., Моисеев В.С., Васильев А.В. Ма-
тематическое моделирование на базе метода конечных элементов
трёхмерных электрических полей в задачах электроразведки // Изв
РАН, Сер.: Физика Земли.-№9, 1997.-С. 67-71.
20 .Соловейчик Ю.Г., Рояк М.Э., Моисеев В.С., Тригубович Г.М.
Моделирование нестационарных электромагнитных полей в трёхмер-
889
ных средах методом конечных элементов И Изв. РАН, Сер.: Физика
Земли. - № 10, 1998. - С. 78-83.
21 .Соловейчик Ю.Г., Рояк М.Э. Совместное использование узловых
и векторных конечных элементов для расчёта трёхмерных нестацио-
нарных электромагнитных полей И Сибирский журнал индустриальной
математики.-2004.-Т. 7.-№ 3(19)-С. 132-147.
22 .Стренг Г., Фикс Дж. Теория метода конечных элементов. — М.:
Мир, 1977.
23 .Сьярле Ф. Метод конечных элементов для эллиптических за-
дач,- М.: Мир, 1980.
24 .Треногин В.А. Функциональный анализ. - М.:Наука, 1980.
25 .Фихтенгольц Г.М. Курс дифференциального и интегрального
исчисления: В 3 томах. - М.: Физматлит, 2001.
26 .Bossavit A. Computational Electromagnetism: Variational Formula-
tions, Complementarity, Edge Elements. - Academic Press (Boston), 1998.
27 J.C.Nedelec. A new family of mixed finite elements in R3 // Numer.
Math. №50, 1986 .-PP.57-81.
28 .J.C.NedeIec. Mixed finite elements in R3 П Numer. Math. №35,
1980. - PP.315-341.
29 . R.N. Rieben, G.H. Rodrigue, D.A. White. A high order mixed vector
finite element method for solving the time dependent Maxwell equations on
unstructured grids 11 Journal of Computational Physics vol.204, 2005. -
PP.490-519.
30 .Ren Z. , Ida N. High Order Differential Form-Based Elements for the
for the Computation of Electromagnetic Field // IEEE Transactions On
Magnetics, VOL. 36, No. 4, 2000. -PP. 1472-1478.
31 . Saad Y. Iterative methods for sparse linear systems. - SIAM, 2003.
32 . Soloveichik Y.G. Iterative method for solving finite element systems
of algebraic equations // Computers Math. Applic.- Vol.33, 1996-
PP.87-90.
33 . Szabo B., Babuska I. Finite Element Analysis. — John Wiley and
Sons, New York, 1991.
890
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
алгоритм Ватсона 473
- занесения локальных матриц
в разреженную
глобальную 498, 499, 507
— нумерации базисных
функций 512,514,518
------, ассоциированных
с узлами 513
------с элементами 513
— граней элементов 515,516
— рёбер 519
- поиска элемента
в нерегулярной сетке 522
- построения
LU-разложения 872, 873
- матрицы перехода 544,550
- портрета матрицы 509
- регулярной трёхмерной
сетки 480
- тетраэдральной сетки 488,489
поузловой сборки 74, 108
- поэлементной сборки 74, 108
— сборки двумерных локальных
матриц из одномерных 233
— матрицы для несогласованных
элементов 543
- триангуляции
макротреугольника 478
— макрочетырёхугольника 476
- - псевдотреугольника 479
— псевдочетырёхугольника 479
— умножения блок-матрицы
на блок-вектор 505
— матрицы в разреженном
формате на вектор 496
— формирования локальной
матрицы переходного
элемента 564
- фронтальный
построения триангуляции 474
аппроксимация на конечно-
мерном подпространстве 101
-повремени 381
-Ритца 102
-уравнения Галёркина 106
ассоциирование базисных
функций с гранью 514, 729, 825
- с ребром 514, 587, 729, 825
-----с узлом 252, 513
-----с элементом 729
базис иерархический 139, 583
- кусочно-полиномиальный 54
- лагранжев 147
-тригонометрический 51
-эрмитов 149
базовая плоскость 488
блок-столбец 502
блок-строка 502
вариационная постановка 57, 84
— в форме
Галёркина 64, 86, 97, 404
---Ритца 57,62,86
— для векторной задачи
с векторными базисными
функциями 651
-------с векторными
и узловыми
базисными функциями 784
-------с узловыми
базисными функциями 633, 642
-----нестационарной
задачи с векторными
базисными функциями 792
— для двумерной
скалярной задачи 226
— для задачи
с выделением поля 432, 642, 811
-----с разрывным
скалярным потенциалом 789
-----с сосредоточенными
источниками 404, 405,406, 804
— для одномерной
скалярной задачи 128
891
— для скалярной
гармонической задачи 385, 393
— для скалярной задачи
с выделением поля 421, 432, 435
— для скалярной
начально-краевой задачи 383
вариационная формулировка см.
вариационная постановка
вектор правой части
СЛАУ локальный 77
-------глобальный 76
вектор-потенциал 30, 37, 39, 43,
663, 782
- в модели с одним
векторным уравнением 647
- в нестационарной
задаче 632,663
- для двумерной задачи 32, 803
- для осесимметричной
задачи 33,644
вычисление
через плотность тока 32
выдача решения в произвольной
точке в нерегулярной сетке 522
-------криволинейного
элемента 314
-----с использованием
переинтерполяции 306
-------четырёхугольного
элемента 304
выделение поля для векторной
задачи с векторными
базисными функциями 805
-------с узловыми
базисными функциями 641
— для скалярной
эллиптической задачи 428
— многоэтапное 439
— сосредоточенного
источника 436,810
— , операторная форма 443
вырожденность
матрицы в векторном МКЭ 719
генерация СЛАУ 140
геометрическая вершина 529
глубина GM RES 883
дискретный аналог 64
задача вариационная 57, 97
- векторная 631,693
- гармоническая 384, 388, 504
-двумерная 32, 226, 693, 847
-интерполяции 204
- краевая 24, 86, 111, 3 84
- магнитостатики 29, 847
- начально-краевая 25, 26, 364, 648
- нелинейная 37, 99, 829, 838, 847
- нелинейная нестационарная 856
- нестационарная 26, 364, 632, 763
-обратная 442
-одномерная 128,388,838
- осесимметричная 32, 227, 645,
802
- прямая 442
- сглаживания 208
- трёхмерная 329, 796
- электростатики 27
-эллиптическая 24, 128
закон Био-Савара 32, 35, 860
источник поверхностный 401,404
-распределённый 401
-сосредоточенный 401
— в точке 401,406
— на линии 401,405
— на поверхности 401,406
-точечный 401,406
конечный элемент 54, 68, ЮЗ, 529
— , поворот 318
координаты
барицентрические 277, 340
- глобальные 306
- естественные 277, 340
-локальные 306,350,754
£ -координаты 277,338
коэффициент диффузии 24. 168
892
- изменения шага сетки 458
краевое условие главное 95, 655
— естественное 79, 95, 655
макротреугольник 478
матрица глобальная 74, 107,365
-жёсткости 107, 108
-локальная 75, 108
— вклада от краевого
условия третьего рода 234
-массы 107, 108
-разреженная 107
- функциональная 315
- Якоби 315
метод бисопряжённых
градиентов 885
- блочной релаксации 886
- Бубнова-Галёркина 63
-Галёркина 63, 104. 117
— коллокации 81
- конечных
элементов векторный 631
----узловой 631
- конструктивной геометрии 448
- наименьших квадратов 47
- неполной факторизации 874
- Ньютона 833
- описания границ 448
- проекционный 117
- простой и терации 83 I
- релаксации 886
- Ритца 62, 104
- сопряжённых градиентов 877
-тиражирования сечений 487
-GMRES 882
МКЭ-решение 102
невязка дифференциального
уравнения 58, 60, 97
-системы нелинейных конечно-
элементных уравнений 832, 837
-СЛАУ 877
норма пространства 393
- соболевская 113
- энергетическая 110, 661
нормаль 773
носитель 70, 83
нумерация базисных функций 512
----глобальная 76
----локальная 75
----на основе
упорядоченных списков 514
—, ассоциированных
с гранями 515,516
----,-с рёбрами 519
----,-с узлами 513
----,-с элементами 513
- вершин шестигранника 349
— неизвестных для учёта
первого краевого условия 236
- рёбер
на прямоугольном элементе 668
— на треугольнике 674
- на четырёхугольнике 682
— тетраэдра 733
-узлов и рёбер на призме 736
— на квадратично-кубическом
призматическом элементе 349
— на квадратичном тетраэдре 344
— на параллелепипеидальном
элементе 331
- на призматическом
элементе 346
— на прямоугольнике 231
— на прямоугольном
биквадратичном элементе 246
— на прямоугольном
бикубическом элементе 249
— на прямоугольном
триквадратичном элементе 334
— на треугольном
квадратичном элементе 290
— регулярной сетки 454
— с введением фиктивных 454
оператор Лапласа 30, 167,437,808
- нелинейный 64
- несамосопряжёпный 64
893
- эллиптической
дифференциально-
краевой задачи 85, 114
плотность источника
объёмная 401
— поверхностная 402
погрешность МКЭ-решения 110
— в норме пространства 1% 116
— в энергетической норме 114
- при аппроксимации границ 126
полнота кусочно-
полиномиального базиса 226
полунорма 112
портрет матрицы 495
— в диагональном формате 501
- в разреженном
строчном формате 496
- - в столбцовом формате 516
- симметричный блочный 503
- построение 508
порядок аппроксимации 116
-сходимости 110, 116
— МКЭ-решения для
векторных
конечных элементов 795
- для гармонической
задачи 398
- для эллиптической
задачи 114
-точности 110
потенциал векторный 30, 37, 39,
43, 663, 782
-скалярный магнитный 35
---неполный 857
- полный 35, 782
- электрический 27
предобусловливание 874
- диагональное 878
- неполным разложением
Холесского 878
призма треугольная 345, 599
пространство 87
- Н1" 60, 84
- Hrut 651
- H,liv 825
- гильбертово 60
- конечномерное 70
— , натянутое на
базисные функции 101
- пробных функций 97
профиль 492
псевдочетырёхугольник 460
псевдотреугольник 479
разреженность СЛАУ 491
разрыв потенциала 788, 791
расчётная область 529
ребро 529
решение конечноэлементное 102
-приближённое 49, 102
-точное 102
сборка двумерных локальных
матриц из одномерных 233
- матрицы и вектора СЛАУ 140
поузловая 74, 108
поэлементная 74, 108
сетка 528
-адаптивная 630
- вложенная 164, 533
- несогласованная 529
- прямоугольная 534
- согласованная 529
сечение 487
- базовое 488
-основное 488
- промежуточное 488
система
вариационных уравнений 784
-линеаризованная 833
-уравнений Максвелла 26
894
скалярное произведение
пространства 393
— энергетическое 87,94,661
скачок потенциала 862
согласованный результант 218
сплайн кубический
интерполяционный 204
— сглаживающий 204, 208
степень свободы 158,556
стратегия уточнения решения 623
----, контроль
касательных составляющих 797
----, контроль потоков 623
----, Wi -стратегия 629, 800
суперсходимость 178
схема аппроксимации по времени
Кранка-Николсон(а) Зо7,375
- неявная 366
-------двухслойная 370
— трёхслойная 368
-------четырёхслойная 370
----явная 367
-------трёхслойная 378
сходимость 110
порядок см. порядок
сходимости
сшивка локальных
базисных функций 225, 252, 721
тестирование на кусочно-
полиномиальных
решениях 185, 326, 801
- на задачах
меньшей размерности 327, 801
тетраэдр 337
технология Т-преобразования 554
-локального
Т-преобразования 560
Т -технология согласования
шестигранных элементов,
условие корректности 569
h-технология 623
р-технология 623
p-h-технология 623
триангуляция 473
-Делоне 473
-трёхмерная 337
узел сетки 529
— терминальный 533
— фиктивный 454
упорядочение геометрическое 518
- граней 514, 515,519
— индексов
в портрете матрицы 499
- локальных
номеров вершин 678, 688
- рёбер 514, 521
-узлов 519
-элементов 514
уравнение
в слабой форме 57, 58, 97
- вариационное 56,86, 695
-Галёркина 64,97, 100
-Лапласа 31
- Пуассона 3 1
- фиктивное 68, 79, 236
учёт второго краевого
условия как главного 180
- главных
краевых условий 68, 236
------в узловом МКЭ
для векторной задачи 635
для эрмитовых элементов 257
- естественных
краевых условий 79, 333
- в векторном МКЭ 772
для эрмитовых элементов 256
- неоднородных главных
краевых условий
в векторном МКЭ 658. 782
895
- однородных главных
краевых условий
в векторном МКЭ 655, 782
- однородных естественных
краевых условий 285,491
формат матрицы
разреженный блочный 502
— столбцовый 498, 544
— строчно-столбцовый 289, 495
----строчный 497
функция базисная 48, 83
— на треугольнике 279
— узловая 631
- биквадратичная 245
- бикубическая лагранжева 249
- бикубическая эрмитова 250
- билинейная 230
- глобальная 109, 225
- допустимая 54, 86, 226, 529
- квадратичная на тетраэдре 344
— на треугольнике 290
- кубическая лагранжева 148
----на треугольнике 295
— эрмитова 150.154
— на треугольнике 296
-кусочно-квадратичная 138
-кусочно-линейная 70
-локальная 75, 109
- пробная 54
- рёберная 669
- триквадратичная 334
- трикубическая эрмитова 335
-трилинейная 331
-финитная 68, 102
-формы 109
b-функция поверхностная 402
- сосредоточенная на линии 402
- точечная 403
edge-функция 669, 825
face-функция 825
face-т-функция 825
face-n-функция 825
volume-т-функция 826
volume-n-функция 826
функции с пересекающимся
носителем 518
характерный размер 112
шестигранник 350
элемент второго порядка 128,136
- двухузловой кубический 149
-криволинейный 310
-лагранжев 137
-несогласованный 110
-одномерный 131, 136, 137, 149
- параллелепипеидальный 331,334
- первого порядка 128
- переходной 532,554,557
- призматический 345
- прямоугольный 230
- согласованный 109, 225
-тетраэдральный 337,730
-треугольный 278,290,295,296
- четырёхугольный 297
- шаблонный 136
- шестигранный 349
- эрмитов 149
элемент-прототип 136
edge-элемент 669
элементарная подобласть 457
якобиан 300,315,351
ячейка сетки 529
УЧЕБНОЕ ИЗДАНИЕ
Юрий Григорьевич Соловейчик
Михаил Эммануилович Рояк
Марина Геннадьевна Персова
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
ДЛЯ РЕШЕНИЯ СКАЛЯРНЫХ И ВЕКТОРНЫХ ЗАДАЧ
Учебное пособие
Редактор И.Л. Кескевич
Технический редактор Н.В. Гиврилова
Художник-дизайнер А.В. Ладыжская
Лицензия ИД№04303 от 30.03.01
Подписано в печать 09.03.07
Формат 60 х 90 1/16. Бумага офсетная
Уч.-изд. л. 67,2. Печ. л. 56
Тираж 3000 экз. (1-й з-д 1-500 экз.). Заказ № 433
Издательство Новосибирского государственного
тех н ич сского у н н вере итета
630092, г. 11овосибирск, пр. К. Маркса, 20
Тел. (383)346-31-87
E-mail: office @ publish.nstii.ru
Отпечатано в типографии
Новосибирского государственного технического университета
630092, г. Новосибирск, пр. К. Маркса, 20