А.П. КАРП
К борник
W ЗАДАЧ
по АЛГЕБРЕ
и нячяляпп
янялизя
КОМПЛЕКСНЫЕ ЧИСЛА

А.П. КАРП
I I5OPHUK
W ЗАДАЧ
no АЛГЕБРЕ
U НАЧАЛАМ
АНАЛиЗА
Учебное пособие
для учащихся школ и классов
с углубленным изучением математики
Рекомендовано
Главным управлением развития
общего среднего образования
Министерства образования Российской Федерации
МОСКВА «ПРОСВЕЩЕНИЕ» — АО «УЧЕБНАЯ ЛИТЕРАТУРА» 1995
УДК 373.167.1
ББК 22.14я72
К26
Рецензенты:
заслуженный учитель России Л И. Звавич,
учитель-методист школы № 218 Москвы А. Д. Блинков,
методист ОНМЦ Северного округа Москвы А. 3. Гурвиц
Карп А. П.
К26 Сборник задач по алгебре и началам анализа: Учеб,
пособие для учащихся шк. и классов с углубл. изуч.
математики.— М.: Просвещение, 1995.— 176 с.: ил.— ISBN
5-09-006589-6.
Книга содержит задачи (и примеры их решения) по всем основным раз-
делам курса алгебры и начал анализа, а также варианты выпускных эк-
заменационных работ как для базовой школы, так и для классов с углуб-
ленным изучением математики. К большинству задач даны ответы, указа-
ния, а к наиболее трудным решения. Сборник окажет помощь учащимся
10—11 классов, абитуриентам и учителям.
К	Уточн. пл- 1995> № И4(2) ББК 22.14я72 + 22.161я72
103(03)—95
Учебное издание
Карп Александр Поэлевич
СБОРНИК ЗАДАЧ
ПО АЛГЕБРЕ И НАЧАЛАМ АНАЛИЗА
Зав. редакцией Т. А. Бурмистрова. Редактор Л. Н. Белоновская. Младший ре-
дактор Н. Е. Терехина. Художники В. В. Костин, Ю. В. Пахомов. Художествен-
ный редактор Е. Р. Дашук. Технический редактор О. А. Куликова.
Корректоры Н. В. Белозерова, И. В. Чернова
ИБ № 16019
Сдано в набор 19.06.95. Изд лиц № 010001 от 10.10.91 Подписано к печати
13.1195 Формат 60Х90*/16 Бумага офсетная № 2. Гарнитура Литературная
Печать офсетная Усл. печ. л. 11,04-0,25 форз. Усл кр.-отт. 11,75. Уч-изд
л 9,184-0,35 форз. Тираж 50 000 экз. Заказ 1259.
Ордена Трудового Красного Знамени издательство «Просвещение» Комюета Россий-
ской Федерации по печати. 127521, Москва, 3-й проезд Марьиной рощи, 41.
АО «Учебная литература». 117571, Москва, проспект Вернадского, 88. Москов-
ский педагогический государственный университет.
Саратовский ордена Трудового Красного Знамени полиграфический комбинат Комитета
Российской Федерации по печати 410004, Саратов, ул. Чернышевского, 59.
ISBN 5-09-006589-6
© Карп А. П., 1995
ПРЕДИСЛОВИЕ
Предлагаемый вниманию читателя сборник содержит задачи
по всем основным разделам курса алгебры и начал анализа
10—11 классов с углубленным изучением математики.
По замыслу автора, в первую очередь задачник должен дать
материал для работы на уроке при формировании основных по-
нятий, введении в новые разделы, преодолении типичных оши-
бок, демонстрации основных приемов и алгоритмов и т. п. Зада-
чи объединены в серии — блоки, в каждом из которых с разных
сторон рассматривается одна математическая идея. Большин-
ство серий начинается указаниями, а наиболее трудные (или не-
традиционные) примерами решения. Решать задачи серии реко-
мендуется подряд — вырванные из контекста, они окажутся
труднее, да и сам процесс поиска сходства и аналогии не менее
важен, на наш взгляд, чем его результат. Ко всем задачам при-
ведены ответы, а для наиболее сложных даны указания и ре-
шения.
Задачник составлен так, чтобы по возможности облегчить его
использование при изучении курса в различных последовательно-
стях и по различным программам — «избыточные» или «несвое-
временные» разделы и серии могут быть пропущены без ущерба
для остального.
Надеемся, что сборник задач может быть использован и в об-
щеобразовательной школе (на занятиях кружков и факультати-
вов, в работе с сильными учащимися), а также при подготовке
к вступительным экзаменам.
В качестве приложения помещены проверочные работы по
материалу задачника, варианты экзаменационных работ, прове-
денных в Санкт-Петербурге, и задания для повторения, в кото-
рых также использованы задачи экзаменов.
В конце книги дан список изданий, близких по целям к за-
дачнику, или таких, из которых можно почерпнуть теоретические
сведения, материалы для закрепления изученного, а также для
предэкзаменационной тренировки. Эти книги были использова-
ны автором при работе над задачником, хотя, конечно, восстано-
вить происхождение каждой идеи не представляется воз-
можным. Отметим лишь, что нами также широко использова-
лись задачи вступительных экзаменов и математических олим-
пиад.
Автор выражает благодарность рецензентам книги за полез-
ные замечания, а также своим бывшим ученицам А. Б. Балашо-
вой и О. В. Лебединцевой за помощь в подготовке рукописи к пе-
чати.
3
§ 1. ВЕЩЕСТВЕННЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА
I.	Иррациональные числа
В заданиях 1.1 —1.12 требуется доказать иррациональность
данных чисел. В заданиях 1.1 —1.9 при этом приходится исполь-
зовать соображения делимости и свойства рациональных чисел.
Пример. Докажите иррациональность числа a = ~\j4k-}-2,
где
Доказательство. Так как любое целое число при деле-
нии на 4 может давать лишь остатки 0, 1, 2, 3, то квадрат целого
числа может иметь лишь остатки 0 и 1 при делении ца 4. Поэто-
му a$Z. Но пусть 0 = ^-— несократимая дробь. Тогда т2 =
= (4& + 2) /г2, а отсюда получим, что т-2 и п\2— противоречие.
1.1.	Уз. 1.2. Уз + 1.	1.3. УЗ+УГ 1.4. д/2.
1.5.	У2+Уз. 1.6. У^, где р — простое число.
1.7.	УЗА: Н-2, где k£N. 1.8. Уб^ + З, где k£N. ЕЭ.УЗ^З
1994 тройки
Для доказательства иррациональности чисел, данных в зада-
ниях 1.10 — 1.12, достаточно показать, что соответствующие дро-
би непериодичны.
Пример. Докажите иррациональность числа 0,1234... (по-
дряд выписаны все натуральные числа).
Доказательство. Предположим, что данная дробь пери-
одична и имеет период, состоящий из п знаков. Но в этой дроби
найдется место в периодической части, состоящее из 2п-\-\ ну-
лей. На нем, очевидно, должен укладываться целый период, сле-
довательно, он должен состоять из одних нулей, но этого, очевид-
но, не может быть.
1.10.	0,101001000... (после п-и единицы стоит п нулей).
1.11.	0,369121518... (выписаны подряд все числа, кратные 3).
1.12.	0,392781... (выписаны подряд степени числа 3).
4
1.13.	Числа а и Ь рациональные, а числа х и у иррациональные.
Выясните, могут ли указанные ниже числа быть рацио-
нальными, могут ли они быть иррациональными:
а) а + &; б) а + %; в) ab\ г) ах\ д) х-\-у\ е) ху.
1.14.	Докажите, что между любыми двумя рациональными чис-
лами найдутся как рациональные, так и иррациональные
числа.
II.	Метод математической индукции
В заданиях 1.15— 1.18 требуется доказать данные равенства
для всех натуральных п.
1.15.	24-44-6 + ... + 2/z = /z(/z+ 1).
1.16.	14-4 + 9 + - + «2= ~—--б(-^'1)'
1.17.	— 4—L-4- 4----------!------=—“—
1 -3	3-5	{2п- 1) (2/г-Ь 1)	2п+1 ’
1.18.	Ы! 4-2.2! 4-...4-/г./г! =(//4-1)!- 1.
В заданиях 1.19— 1.21 требуется доказать данные неравен-
ства.
1.19.	3">5лг4-1, ">3.	1.20. 3">/г2, n^N.
1.21. (14-й)п>14-/гй, n^N, h^~\.
В заданиях 1.22 — 1.24 требуется доказать данные утвержде-
ния о делимости чисел.
1.22. 18"— 1:17.	1.23. 33" + 24-7"; 10.	1.24. 7-52"4-12-6"; 19.
III. Комплексные числа. Их геометрический смысл.
Действия с комплексными числами
1.25. Вычислите:
a) (/324-/5)(/34-/~3); б) (/4-1)16:
в) /(/4-3);
. 2Z—1
е) 3/4-1 ’
1.26. Найдите числа z —Rez4-/Imz из данных условий:
а) /4-Rez = /z; б) i (г4-1)4-2 Re z = z2.
1.27. Изобразите на чертеже множество всех точек комплексной
плоскости, для которых выполнены данные условия:
а) Imz = 2; б) Rez= —1; в) Im(z4-/) = 0; r) Imz^O;
д) RezsC3; е)	ж) Re(z4-2)>0; з) Re2z>0;
(Re z<2;
и) Im2z=l; к) Re iz = 1; л) Rez-j-Imz^l.
5
1.28.	Рассматриваются все точки z комплексной плоскости, та-
кие, что Rez=Imz. Изобразите множество всех точек и,
удовлетворяющих данным условиям:
a) u = z-\-\\ б) u = z — ц в) u = z-\-2i— 1.
1.29.	Пусть М — совокупность всех точек и комплексной плоско-
сти, таких, что (Re и)2 + (Im и)2= 1. Изобразите на чертеже
множество всех точек г, таких, что М — совокупность точек
вида u = z-{-i + 1.
1.30.	На комплексной плоскости отмечены точки Л, В, D, соответ-
ствующие числам = 0, z2 = 24-/, z3= 1 4-3/. Найдите ком-
плексное число г, такое, что соответствующая ему точка
С будет вершиной параллелограмма ABCD. Решите ту же
задачу для 21 = 14-2/.
1.31.	Для каждой данной ниже тройки чисел z2, г3 проверьте,
лежат ли на одной прямой соответствующие им точки ком-
плексной плоскости:
а)	^! = 0; г2 = /4-2; г3 = 2/4-4;
б)	2j= — 14-/’» z2=14-5/; г3 = 3/.
1.32.	Докажите, что точки, соответствующие числам zb г2, г3, ле-
жат на одной прямой тогда и только тогда, когда имеются
такие не все равные нулю одновременно вещественные
числа с2, с3, что
c1z14-c2z24-c3z3 = 0, а сх 4-с24-с3 = 0.
Пример. Пусть М — совокупность всех точек и комплекс-
ной плоскости, таких, что Imu=l. Изобразите на чертеже мно-
жество всех точек г, удовлетворяющих условию z = tr, где и£М.
Решение. Ясно, что все числа и из М имеют вид и — х-{-Ц
где х вещественное. Поэтому имеем равенства
z = aA-bi = x?— 14- 2х/,
а отсюда Ь = 2х, а = х?—\=^—1 (рис. 1).
6
1.33.	Изобразите на чертеже множество всех точек комплексной
плоскости, удовлетворяющих данным условиям:
a) Rez2 = 0; б) Imz2 = 0; в) Re-^ = 0; г) Im^=l.
1.34.	Пусть М — совокупность всех точек и комплексной плоско-
сти, таких, что Reu = 0. Изобразите на чертеже множество
всех точек г, удовлетворяющих данным условиям:
a) z = u2, где и£М; б) z = (u + I)2, где и£М.
1.35.	Пусть точка и пробегает интервал с концами в точках uQ =
= 0 и h!=14-z. Изобразите на чертеже совокупность всех
. 1
точек, пробегаемых при этом числом г = —.
1.36.	Пусть и пробегает все точки квадрата с вершинами в точ-
ках Uj = O, u2 = i, u3=14-Z, ^4=1. Изобразите на чертеже
совокупность всех точек, которые при этом пробегает чис-
ло z = u2.
IV. Сопряженные комплексные числа.
Модуль и аргумент комплексного числа.
Тригонометрическая форма комплексного числа.
Действия в тригонометрической форме
1.37.	М — совокупность всех чисел г, таких, что \z — i\ = 1.
а)	Изобразите на чертеже множество М.
б)	Изобразите на чертеже множество всех u = z, где z£M.
1.38.	Изобразите на чертеже множество всех точек комплексной
плоскости, для которых выполнено данное условие:
a) z + z = I;	б) iz-\-iz=l\ в) z-z = l;
г) z-z 4-2z4-2z = 0; д)	е) z2-z2 — bz-z — 4.
1.39.	Пусть a — комплексное число, b — вещественное. Выясни-
те, какую фигуру задает на комплексной плоскости урав-
нение az-\- a - z = b. Докажите, что любую прямую можно
задать таким уравнением.
1.40.	Изобразите на чертеже множества А и В комплексных чи-
сел, удовлетворяющих соответственно уравнениям
z- zA--^ = ® и а+ z = 2л/2”, где « = 0,5(1—/).
а
Найдите все общие точки множеств А и В.
1.41.	Изобразите на чертеже множество всех точек комплексной
плоскости, удовлетворяющих данным условиям:
Re z	2 . .
а) —— = 0,5; б) Im-—
' Z-Z	Z— 1
7
1.42.	Пусть zx = 44-3/, z2 = 34-4Z. Изобразите на чертеже множе-
ство всех точек комплексной плоскости, удовлетворяющих
данным условиям:
a)	\zxz —	= |z2z — zxz2\\
б)	\iz — izx | = \2z — 2z2\.
1.43.	Данными ниже условиями определяются различные сово-
купности комплексных чисел z. Для чисел z из каждой со-
вокупности определите наименьшее значение величины \z\
(при этом полезно иметь в виду геометрический смысл этой
задачи):
a) \z — 2/1 = 1; б) \z — 2| = |z — 4|; в) z-\-z= — 1;
г) z-z-{-2i(z — z)= 1; д) \z — 6/| = \z — 8|.
1.44.	Для чисел z из тех же совокупностей, что и в задании 1.43,
определите наименьшие значения величины \z— 1— i\.
1.45.	Выясните, какие значения может принимать модуль комп-
лексного числа г, если известно, что |z4-/4-ll=j.
1.46.	Найдите все комплексные числа г, удовлетворяющие одно-
временно двум условиям:
I z — 1 — 11	| z 4-1 4- /1 и | z — 211	Д/2*-
1.47.	Пусть z — комплексное число. Точки 4, В, С соответствуют
числам г, г2, г3(г#=0, г#=1).
а)	Докажите, что если |г| = 1, то треугольник АВС равно-
бедренный.
б)	Найдите все такие комплексные числа г, что треуголь-
ник АВС равносторонний.
в)	Найдите все такие числа г, что треугольник АВС равно-
бедренный.
1.48.	Изобразите на чертеже множества всех чисел z комплекс-
ной плоскрсти, удовлетворяющих данным условиям:
a) argz = i; б) argz=^; в) arg^ = ^;
г)	arg iz = y; д) 0<argz<y; е) arg(z — i+ l)=j.
1.49.	Найдите все комплексные числа г, удовлетворяющие одно-
временно двум условиям:
arg z = — и \z— 11 = 1.
1.50.	Представьте данные ниже числа в тригонометрической
форме:
а) 14-/; б) 1— Д/З /; в) 14-3/; г) -24-/;
д)	sin 75° 4-/cos 75°; е) (sin 75° 4-/cos 75°)/;
ж) sin 35°4~/cos 145°;
8
sin 24°-H cos 156°
cos 35° — i sin 35°
ч . 2л . .Л	2л \
и) sin —+ H 1 —cos —J ;
v . 2л . . /. . 2л\ ч 7	\	7/
к) sin—+ q 1 4-cos —); л) ------.
□ у	□ у	i i
1.51.	Вычислите:
a)	(1+V3i)'995; 6) (1-z)988; в) (Д/3-z)1917.
1.52.	Пользуясь формулами Муавра и бинома Ньютона, выведи-
те формулы, выражающие sin па и cos па через sin а и
cos а.
1.53.	Докажите, используя выведенные в задании 1.52 формулы,
что cos \ °£Q.
1.54.	Найдите следующие суммы:
а> C0S 2Th+C0S 2*+t + - + C0S 2k + Tn
6)	1 + e + s2 + ••• + ъп~\ где 8 — корень п-и степени из еди-
ницы;
в)	l+28 + 382+... + ^"1.
V. Комплексные числа
и преобразования плоскости
1.55.
Пусть 2j=2, z2 = -^, z3 = z, z4 = cos 4 + * sin , z5 =
о	о
= 2 ^cos j + * sin у). Для каждой из следующих точек г по-
стройте на чертеже точки г-г, z=l, 2, 3, 4, 5:
a) z= 1; б) г = 2;
в) z = i
г) z = cos у + * sin у; д)
1.56. Пусть Л4, Р, К соответственно множества всех точек комп-
лексной плоскости, удовлетворяющих условиям Reu=l,
Imu = 2 и Imu = Reu. Для каждого числа zh z=l, 2, 3, 4,
5, из задания 1.55 изобразите на чертежах совокупности
всех точек вида zru для и£М, для и£Р и для и£К.
1.57. Пусть М — множество всех точек zx комплексной плоско-
сти, таких, что |z2i +V2| =1 К — множество всех точек z2
этой плоскости вида z2 = rz1, где zx£M. Найдите расстояние
между фигурами М и К.
Пример. z0 = 2 (cos 75°-Н sin 75°). Рассмотрим функцию ф,
такую, что ф(г) = г0-г для всех z. Изобразите на чертеже фигу-
ру, в которую функция ф переводит фигуру, задаваемую уравне-
нием |г —z—1|==у.
9
Решение. Функции ф соответству-
ет композиция поворота на угол в 75°
и гомотетии с коэффициентом 2 (рис. 2).
1.58. Пусть z0 = cossin. Рас-
смотрим функцию ф, такую, что
ф(г) = г0-г для всех г. Изобразите
на чертежах фигуры, в которые
эта функция переводит фигуры,
задаваемые данными ниже усло-
виями:
а) |г| = 1;	б) |г — i \ = 1;
в) Im г<2 Re г + 2.
Решите ту же задачу для
г0 = 2 и для z0=1+l
1.59. Пусть Л, В, С — точки, соответствующие числам = 1,
г2=и, г3 = 3 + 2/. Постройте фигуры, в которые переводит-
ся треугольник АВС функциями ф (г) = ^соз -^ + i sin г,
ф(г) = 2г и т (г) = (’\/з' + 0 г-
1.60.	Постройте образ окружности |г —1| = 1 при следующих
преобразованиях:
а) ф(г) = /г; б) ф(г) = 2/г; в) т (г) = 2/г + /+ 1.
1.61.	Рассматривается функция ф(г) = г2, выясните:
а)	какие точки комплексной плоскости она оставляет непо-
движными;
б)	в какую фигуру она переводит фигуру, задаваемую на
комплексной плоскости уравнением Кег=1шг;
в)	есть ли на комплексной плоскости окружности, которые
этой функцией переводятся в себя.
1.62.	Рассматривается функция ф(г) = ~.
1)	Найдите неподвижные точки этой функции.
2)	Выясните, в какие фигуры она переводит фигуры, зада-
ваемые уравнениями:
a) Im z = Re г; б) |г| = 1; в) |г— 11 = 1.
VI. Некоторые задачи с параметрами
Пример. Найдите все вещественные а, такие, что система
уравнений |г —а| = 1 и |г —/|=^- не имеет решений.
Решение. Заметим, что при а<0 решений, очевидно, нет,
а при a = Q есть. Выясним, при каких положительных а система
имеет решения. Для этого заметим, что каждое из данных урав-
нений задает на комплексной плоскости окружность; условие на-
личия у них хотя бы одной общей точки — то, что расстояние
10
между центрами не меньше модуля разности радиусов и не боль-
ше суммы радиусов
11|< уа2+1 <1+1,
т. е. За^4. Таким образом, система не имеет решений
_ 4
и при а>* — •
Ответ. (—оо; O)U0-i + °°)«
1.63.	Найдите все вещественные числа а, такие, что любое комп-
лексное число г, удовлетворяющее неравенству \z — ai\ < 1,
удовлетворяет и неравенству \z — 1|<3.
1.64.	Найдите все вещественные числа а, такие, что найдется хо-
тя бы одно комплексное число г, удовлетворяющее одно-
временно следующим условиям:
\z-ai\=a-\-4 и \z — 21 < 1.
1.65.	Найдите все вещественные числа а, такие, что существует
ровно одно комплексное число г, удовлетворяющее одно-
временно следующим условиям:
\z — z|^3 и \z — За|	2а.
1.66.	Найдите все такие вещественные числа а, при которых не-
совместна система неравенств
(\z\	\z— 1 — i\
11г|	|г + а2 + (6 — a)i\.
1.67.	Найдите все вещественные числа а, такие, что всякое комп-
лексное число г, удовлетворяющее неравенству
|г — 11	|г —а — (а + 1) i\,
удовлетворяет и неравенству \z—1|^1.
§ 2. ПОСЛЕДОВАТЕЛЬНОСТИ.
' ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ.
ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
I. Последовательности.
Свойства последовательностей
2.1. Выпишите по пять первых членов последовательностей, за-
данных ниже формулами общего члена или рекуррентно:
а) а„ = + -1; б) ая = 2"; в)
г) a„+1 = 3a„, а, =2; д) ап+1 = а„ — 2, а, = 3;
е) ап+х = ап-\- п\ aj=l; ж) ап = 2ап~\ если	ах—— 1;
3) a„+2 = a„ + an+l, at= — 1, а2 = 0;
и) а„+2 = а„-а„+!, а, = 2, а2 = 3.
В заданиях 2.2—2.13 требуется выяснить, какие из данных
последовательностей являются монотонными.
Пример. Дана последовательность ап = ——, n£N. Вы-
У1п2 + 2п
ясните, является ли она монотонной.
Решение. I способ. Заметим, что функция у = х2-}-2х
возрастает на множестве [1; + оо), поэтому функция
y = ^Jx2-\-2x также возрастает на нем, а функция у== ! на
Д/х2 -f-2x
нем убывает. Очевидно тем самым, что и функция натурального
аргумента ап = —-------- также является убывающей.
АД2-|-2/?
II способ. Убедимся непосредственно в том, что последо-
вательность (ап) является убывающей. Для этого достаточно про-
верить, что разность ап+1 — ап является отрицательной при
всех n£N\
3 ,___	3---------------
__У/п2-|-2л — у(/?4-1)2-}-2 (/i-f-l)
ап +1 ап 3 ...........  --2Г~з~	•
У(я-Н)24-2(/7-Н) -W + 2/г
3 Г7-----~	3 I----------------
И, так как \п2-\-2п < у(^+ I)2 + 2 (/z+ 1), очевидно, что
_|_ 1 &п < 0.
2.2.	ап = п2-{-{.	2.3. an = nz— 1.	2.4. an = yfn.
2.5.	2.6. а.~.	2.7. 0, = 2-.
2.8.	«.-GY’"-. 2.9. а.= (“2+'’
' '	[n2-f-2n) если п/2.
2.10.	ап + х = ап~ 1, если п^\, ^ = 1.
2.11.	ап^1=3ап, ах= — 1.	2.12. ап^1 = ап-{-п1 ^ = 1.
2.13.	ап^2 = ап + ап^х — 1, ttl = 1, а2 = 2.
Пример. Дана последовательность (ап):
=	ах = а. а2 = Ь.
Выясните, при каких положительных а и b последователь-
ность (ап) является возрастающей.
12
Решение. Заметим, что все члены последовательности (ап)
положительны и для всех п^\ выполняется равенство ап4_2 —
— an+i=an+i (ап— 1). Отсюда ясно, что, для того чтобы последова-
тельность была возрастающей, числа а и b должны быть больше
1, но если это условие выполнено, то для любого п>2
йп йп_ 1 * ^п — 2	1 И 4-2Я/t-г 1 •
Ответ. Ь>а>\.
2.14.	Дана последовательность ап±} = 5ап1 а} — а. Выясните, при
каких значениях параметра а она будет возрастающей.
2.15.	Дана последовательность	— а2-}-ап — 1, ах = а. Выясни-
те, при каких положительных значениях а она будет возра-
стающей.
2.16.	Дана последовательность ап+2 = ап4.14-2an, а{ — а, а2 = Ь.
Выясните, при каких значениях а и b она будет возраста-
ющей.
а,.,!
2.17.	Дана последовательность йп+2 = ——, а} = а, а2 = Ь.
ап
Выясните, существуют ли такие положительные числа
а и Ь, что последовательность (ап) является возрастающей.
В заданиях 2.18 — 2.24 требуется выяснить, какие из данных
последовательностей являются периодическими.
2.18.	=	2.19. ап = п2—\.	2.20. cz„ = sin п.
2.21.	ап+2 = ап, а{=\, а2= — 1.
2.22.	апЛ.{ = ап_{ для ах — 4, а2 = 2.
2.23.	ап+2 = ^, а, = 1, а2 = 2.
2.24.	ап+1=^ + у/ал — а2„ ,
2.25.	Дана последовательность (ап):
a„+i = a«> а{ = а.
Выясните, при каких значениях а последовательность (ап)
является периодической.
2.26.	Дана последовательность (ап):
ап+2 = 2ап^г4-3апч а} = а, а2 = Ь.
Выясните, существуют ли такие положительные а и 6, что
последовательность (ап) является периодической.
13
В заданиях 2.27 — 2.37 требуется установить, какие из дан-
ных последовательностей являются ограниченными.
Пример 1. Дана последовательность (ап):
ап±2 = ап+х-ап, ах = 2, а2 = 5.
Выясните, является ли она ограниченной.
Решение. Так как все члены последовательности — нату-
ральные числа, отличные от единицы, очевидно, что
^ + 2 = ^+1‘^>^4-1 (ПРИ ВСеХ
Предположим, что последовательность (ап) является ограни-
ченной, но тогда найдется такое натуральное число /<, что ап<К
при всех п. Но рассмотрим член последовательности ак. Ясно,
что ак>ак_х
ах, а2, ..., ак — К различных натуральных чисел. Отсюда
ак>К — противоречие.
Ответ. Последовательность не является ограниченной.
Пример 2. Дана последовательность ап+2 — —, 0i = L
ап
а2 = 2. Выясните, является ли она ограниченной.
Решение. Выпишем несколько первых членов последова-
тельности:
1,2,	2, 1,1,1, 1,2.
Ясно, что последовательность (ап) периодична и |ап|	2 при
всех п.
Ответ. Последовательность ограниченная.
2.27.	ап = п+1.	2.28. ап = -2 .	2.29. ап=-£-.
п	п -f- 3
2.30.	ап=1+2 + '.: + п.	2.31.	1 + ‘ +...+ ' .
п2	У2 \1п
2.32.	a„ = [Vn2+ 1 ].	2.33. ап = sin п.
2.34.	j = ап /2, ах = — 1.	2.35. i — /2 • ип1 их = 1.
2.36.	ап+х — а\ —— Ь 2.37. ап + х = • . 2 + 1, £] = !.
ип I
2.38.	Дана последовательность ал+1 = а2п-\-2ап, ах — а. Приведите
примеры таких чисел а, что последовательность (ап) явля-
ется ограниченной. Докажите, что при а = 2 и а = 3 после-
довательность (ап) неограниченная.
2.39.	Последовательность (ап) ограниченная. Выясните, какие из
следующих последовательностей обязательно являются
ограниченными, какие могут быть ограниченными:
а) *„ = -1; б) хп = Чап\ в) х„=|а„|;
ип
г) Хя=|а„4-3|; д) x„ = sin ; е) х„=^.
14
2.40.	Последовательность (ап) неограниченная. Выясните, какие
из следующих последовательностей обязательно являются
неограниченными, какие могут быть неограниченными:
а) хп=±-\ б) х„ = 2ая; в) х„=|а„|; г) хп = |ап + 31;
ип
д) x„ = sin ап; е) хп=^ .
2.41.	Последовательности (ап) и (Ьп) ограниченные. Выясните, ка-
кие из следующих последовательностей обязательно огра-
ниченные, какие могут быть ограниченными:
а) хп = ап + Ьп; б) хя=-^;	в) хп=ал-Ьп;
3 /	/'  	л — Vh
г) Х„ = 2а„ + 3й„; д)	=д/аГ 4-е) хп= 
Un Г ип
2.42.	Последовательность (ап) ограничена, а последовательность
(Ьп) неограничена. Выясните, какие из следующих последо-
вательностей обязательно неограниченные, какие могут
быть неограниченными:
а) хп = ап + Ьп, б)хя = ^;	в) хп = ап-Ьп;
г) хя = 2а„ + 36я; д) хп = -\/а^ + \]Ьп; е) х„= °	" .
I
2.43.	(ап) и (Ьп) — неограниченные последовательности. Выясни-
те, какие из следующих последовательностей обязательно
являются неограниченными, какие могут быть неограни-
ченными:
а) хп = ап + Ьп; б) xn = j-;	в) х„ = ап-Ьп;
г) Х„ = 2ая + 36„; д) хп = д/а? + VV. е) хп= "	" .
ип I ип
2.44.	Дана последовательность (ап). Рассматриваются последо-
вательности
%п	Уп &2п — i»	&2п 4-4»
а)	Пусть последовательность (ап) ограничена. Выясните,
какие из последовательностей (xj, (z/J, (zn), (ип) являются
ограниченными.
б)	Пусть последовательности (хп) и (уп) ограничены. Дока-
жите, что (ап) также ограничена.
в)	Пусть последовательности (уп) и (zn) ограничены. Дока-
жите, что и (ап) является ограниченной.
г)	Пусть последовательности (хп) и (ип) ограничены. Выяс-
ните, обязательно ли (ап) является ограниченной.
15
II	. Предел последовательности
2.45.	Решите данные неравенства в натуральных числах для
8==То и 8 = Тоо :
Ч 1	.X 1	Ч 1
а) -<е;	б) —гт<8;	в) ~з<8-
' п	7 п 4-1	л3
2.46.	Докажите, что для любого 8>0 найдется натуральное
N, такое, что для всех n>N выполнены данные неравенства.
Выясните, сколько существует таких натуральных JV:
. 1 _	..	1	ч	1 _
а) — <8;	б)	—— <8;	в)	-г<8.
' п	7	п -f-1	7	п3
2.47.	Докажите, что lim ап = 0 для последовательностей (ап), за-
данных ниже:
а) Т; б» “-=i; в> “-“тт? г) “-=wr
2.48.	Докажите справедливость следующих равенств:
a) lim (3 + — ) = 3; б) lim 4тг = 2; в) lim -|- оо;
г) lim V^.±-L —2; д) lim 2п = Д- °°; е) lim Д//г2Д-1 = + °°-
П —► оо	п —оо	и -> оо
В заданиях 2.49—2.52 требуется доказать, что данные после-
довательности не имеют предела.
2П, если п-2,
2.51.	= sign cos/г	2.52. xn = sinn.
2.53.	Дана последовательность (хД, такая, что последователь-
ность (|хД) сходится. Выясните, верно ли, что и последова-
тельность (хЛ) обязательно сходится.
2.54.	Дана последовательность (хп), такая, что последователь-
ность yn = sinxn сходится. Выясните, обязательно ли схо-
дится последовательность (хп).
2.55.	Дана последовательность (ап). Рассматриваются последо-
вательности хп = а2п, уп = а2п_ь гп = а2п+4, ип = а3п.
а)	Пусть последовательность (ап) сходится к числу А. Выяс-
ните, какие из последовательностей (хД, (уп), (zn), (ип) явля-
ются сходящимися.
б)	Пусть А = lim хп = lim уп. Докажите, что А= lim ап.
в)	Выясните, верно ли, что если последовательность (хД
сходится, то и последовательность (гД сходится.
г)	Выясните, верно ли, что если последовательность (гД
сходится, то и последовательность (хД сходится.
16
д)	Выясните, верно ли, что если последовательности (хп)
и (уп) сходятся, то и (ап) сходится.
е)	Пусть А = lim хп, В= lim уп, С— lim ип. Докажите, что
П —>- оо	п —>- оо	п —>- оо
А = В = С= lim ап.
П —оо
2.56.	Приведите примеры (если это возможно) последовательно-
стей:
а) неограниченных, но не стремящихся к бесконечности;
б) стремящихся к бесконечности, но ограниченных;
в) таких, что из них можно извлечь подпоследовательности,
сходящиеся к 0, 1, 2.
2.57.	Последовательность (хп) такова, что ПРИ всех
Выясните:
а)	может ли она не иметь предела;
б)	может ли она иметь предел, отличный от нуля;
в)	может ли она иметь предел, равный 1.
2.58.	Последовательность (хп) такова, что limxn=l. Выяс-
ните, может ли эта последовательность содержать отрица-
тельные числа; 10 отрицательных чисел; 100 отрицательных
чисел; бесконечно много отрицательных чисел.
2.59.	Последовательность (xj такова, что lim хп——2. Выяс-
п 4- °°
ните:
а)	можно ли из нее извлечь бесконечную последователь-
ность, все члены которой положительны;
б)	можно ли из нее извлечь расходящуюся подпоследова-
тельность.
2.60.	Выясните, могут ли последовательности (хп) и (уп) сходить-
ся к одному и тому же числу, если:
а) хп<Уп ПРИ всех n£N\
б) множества их значений не пересекаются.
2.61.	Сходящиеся последовательности (хп) и (z/J имеют одинако-
вые множества значений. Обязательно ли lim хл = lim уп1
Обязательно ли lim хп= lim уп, если к тому же все члены
каждой последовательности различны?
2.62.	Выясните, верно ли, что lim хп=-|"°°, если:
а)	в последовательности (хп) содержатся все натуральные
числа;
б)	все члены последовательности (хл)—натуральные чис-
ла;
в)	все члены последовательности (хп)— различные на-
туральные числа.
17
В заданиях 2.63—2.66 требуется доказать данные утвержде-
ния при условии, что lim хп = 2
П—* оо
’	*4-1	3
Пример. Докажите, что lim-^—— (при условии,
что lim хп = 2).
П —оо
Решение. Рассмотрим модуль разности:
I Хп + 1	3 I
U + 3 5|
5хл 4- 5 — Зхл — 9
5(х„ + 3)
2 1х„ —2|
5 |хл + 3|
Возьмем произвольное 8|С ^0; 0. Ясно, что существует такое
натуральное число N, что для любого n>N
|xn — 2|<8Н 0<5 — 8j < Хп + 3< 5 +8Н
поэтому для всех n>N
3 I 2et 4et
*н + 3	5 J 5 (5 —61)	45
45е
Возьмем теперь произвольное 8>>0 и рассмотрим	(мо-
жем считать, что 8 таково, что ei<0- Тогда, как сказано выше,
найдется такое N, что для всех n>N
I *л+ 1	3 I 4ej
I хл + 3	5	45
^ + 2 _
Хп + 1
2.63.	lim (хпЦ-3) = 5.
П оо
2.65.	Птд/л~=У2.
п ОО
2.64.
lim
п оо
2.66.	lim х^ — 4.
£
3 '
2.67.	Приведите, если это возможно, примеры последовательно-
стей, удовлетворяющих данным ниже условиям. В случае,
если это невозможно, объясните почему:
а)	(хп) и (уп)—расходящиеся, lim (xn + z/J= 1;
б)	(хп) — сходящаяся, (уп)—расходящаяся, (хп-уп) — схо-
дящаяся;
в)	(хп) и (уп)—расходящиеся, (хп-уп) — сходящаяся;
г)	(хп) и (уп)—расходящиеся, lim (хп-уп) = 1;
п —оо
д)	(хп) — сходящаяся, (уп) — расходящаяся, (~ ) — сходя-
щаяся;
е)	(%Д и (г//;) — сходящиеся, (—) — расходящаяся;
\ У п /
18
ж)	lim хп— + оо, (уп)— сходящаяся и lim //ПУ=О,
П —оо	П —оо
(хп • Уп) — сходящаяся;
з)	lim хп= 4- оо, (уп) — сходящаяся, (хп-уп) — сходящаяся;
и) (хп) и (уп) не являются сходящимися к нулю,
lim (х„-«/„) = 0;
к) (х„) и (у„) — расходящиеся, (х„+у„) и (хп-уп) — сходя-
щиеся;
л) (Хп + Уп) и (хп — уп) — сходящиеся, (хп) — расходящаяся;
м) (хп) и (2xn4-3//J — сходящиеся, (уп) — расходящаяся;
н) (хп) и (—) — расходящиеся, lim yn=i;
о) (хп) — расходящаяся, lim уп= 1, lim — = 1.
П —оо	П -> оо Уп
В заданиях 2.68—:2.73 требуется вычислить данные пределы,
пользуясь теоремами о пределе суммы, произведения, частного
и т. п.	______
Пример. Вычислите lim 1 — Д/^ + З ).
П -> оо
Решение. Пт(Д//г24- 1 —Ум2 + 3 )= lim . '	, но
V	д/п2+1 +V«2 + 3
lim ("\//i24- 1 +Д/п24-3 )= + °°-
П -> оо
Ответ. 0.
2.68.
lim
П -> ОО
И-Ы
п-|-2
2.69.
lim
п оо
п2 — Зп
гг 4-3
2.70.
.. п2 4- 5п
lim —------------
г-^оо Зл2 —7л 4-1
2.71.
lim	.
п-+ оо л34-4/г — 2
2.72. lim (д/л-Д/л- 1 )•
П —оо
2.73.
..	2П4-3Г
lim ——:-------
оо Зп+ 1 4-2'
в	заданиях 2.74—2.80 требуется построить на координатной
плоскости совокупности точек с координатами, удовлетворяющи-
ми данным уравнениям.
2.74.	у = Нт — .	2.75. у= lim —-—. П оо	п оо 1 4*
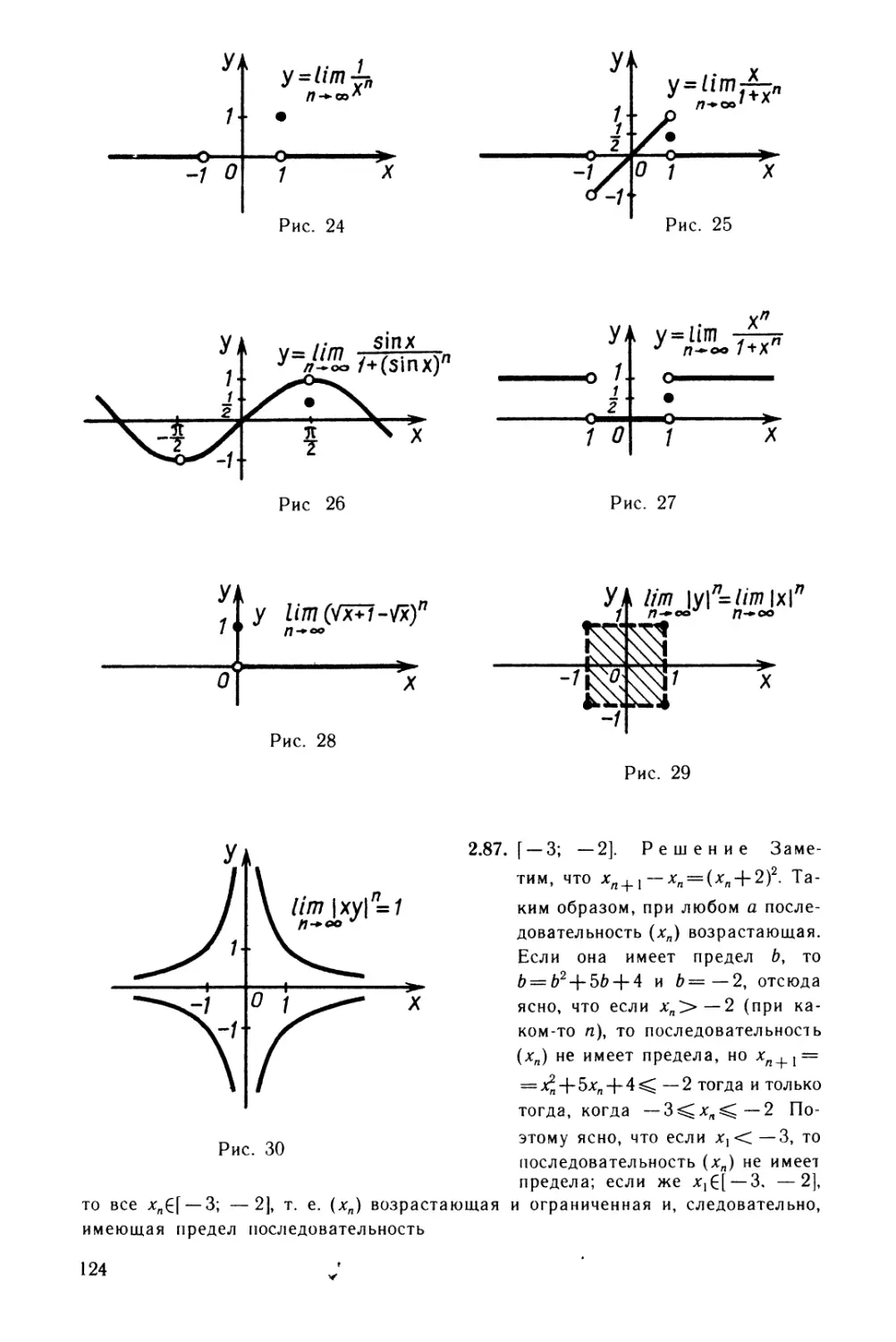
2.76.	1-	sin х	а--	..	х" и= lim	.	2.77. и= lim	. п^оо 1 +(sin X)"	п+оо 1+х"
2.78.	у= Нт С\/х+ * — У-Й".	2.79. lim |г/|л= lim |х|". Л-^-оо	Л-»-оо	л-»-оо
2.80.	lim |xz/|" = 1. П оо
19
В заданиях 2.81—2.85 требуется доказать, что данные после-
довательности имеют пределы, и найти их (при этом следует вос-
пользоваться теоремой о том, что любая ограниченная и моно-
тонная последовательность имеет предел).
2я
Пример 1. Докажите, что последовательность ап = — имеет
предел, и найдите его.
Решение, -у- = --—у1, поэтому последовательность (яп)
убывающая, она ограничена снизу нулем. Поэтому сущест-
вует а= lim а„, но а= lim ал + 1 = lim (—-ап\ = а lim = 0.
Ответ. 0.
Пример 2. Докажите, что последовательность (хп):
хя+1 = ^ + 4х„ + 2, х,= — |
имеет предел, и найдите его.
Решение. Рассмотрим разность хп+1 — хп = х^ + Зхп + 2. Яс-
но, что хп+1 —хп^0, если — 2^xn^ —1. Заметим теперь, что
при всех п
хя+1 = х^ + 4хя4-2^ —2,
так как (xn-f-2)2^0.
Но из соотношения —2<Xj< —1, рассуждая по индукции,
получаем, что -2<хя+1<хя<-1. Итак, последовательность
(хп) убывающая и ограниченная, поэтому имеет предел. Пусть
а= lim xnt тогда	*
П —оо
a— lim хя+|= lim. (х^ + 4хя4-2) = а2 + 4а + 2,
П —► оо	п -> оо
з
откуда а—— 2 или а— — 1. Но все хп<——, поэтому
lim хп= —2.
Ответ. —2.
2.81.	2.82. ая = 4- 2.83. ая+1 = а2 + 5О„ + 3, а,=-2.
о	п
2.84.	ая+, =|(ал+±), а, = 3.	2.85. а„ +, = д/бН- , а, = 2.
2.86.	Докажите, что последовательность (хп):
хя+1 = ^ + 6х„ + 6, Х| = 4
не имеет предела.
2.87.	Выясните, при каких значениях а последовательность (хп):
x„ + i = x^-j-5xn + 4, хх = а имеет предел.
20
III.	Предел функции
2.88.	Постройте графики данных функций / и укажите, при
каких значениях аргумента выполняются неравенства
|/(х) —/ (х0)| < е для 8=1 и для е =
a) f(x) = x2, xQ = 0; 6) f(x) = y[x, х0=1; в) = хо— *•
2.89.	Докажите, что данные последовательности имеют указан-
ные пределы при условии, что lim хп = а:
п —сю
a)	lim х^ = а2;
П —сю
б)	lim д/хГ = У/а (д^О);
п —► сю
В) lim (а=И=°)-
2.90.	Решите неравенство !/(х)— А |<е для данных функций
/ и данных чисел А;
а) /(х) = х2, Л=а2; б) [(х) = у[х, А—л/а (а^О);
в) =	^=7 (а=#0).
2.91.
2.92.
2.93.
2.94.
Для функций y = f(x) и чисел А из задания 2.90 подберите
числа б>>0, такие, что из неравенства |х — а|<б следует
неравенство |/(%)-- А | <£. Объясните, сколько таких чисел
б можно подобрать.
Постройте график функции f (х) = -—у и для любого
8>0 укажите какое-либо число б>-0, такое, что для всех
х, таких, что |х—1| <б, хУ=1, выполнено неравенство
|/(X)- 1 | <8
Докажите следующие утверждения:
a) lim(x+2) = 5; б) limx3 = a3; в) lim (х + ~) = 2.
х-+ 3	X а	Х-+ \ \ х /
Постройте графики данных функций f и докажите, что не
существует предела (конечного) lim/(x):
2.95.
а) /(х) =
х, если х^ 1,
— х, если х< 1;
б) /(•*)=-—г
В) /U)“T
Докажите, что функция
1,
0,
/(х)==
если xf/?\Q,
если xfQ
не имеет предела ни в какой точке.
2.96.	Постройте график функции у — —гт+1 и докажите следу-
х. -j- 1
ющие утверждения:
а)	для любого M>Q найдется такое число б, что для любо-
го числа х, такого, что |хЦ-1|<Сб, выполнено неравенство
/(х)>А4;
21
Рис. 3
б)	для любого 8>0 найдется число Л4>»0, такое, что для
всех чисел х, больших М, выполнено неравенство
|/(х)- 1 I <8.
2.97.	На рисунке 3 изображены графики функций, отмечены чис-
ла а и А. Укажите, для каких функций справедливы следу-
ющие утверждения:
а) Нт/(х) = Л; б) lim / (х)= + °°; в) lim/(x)= —оо;
х->~ а	х-+ а	а
г) не существует lim/(x); д) lim f (х)= + оо;
х—> а	х4- оо	*
е) lim f(x) — Л; ж) не существует lim /(%).
х -> 4- оо	х->4*°°
2.98.	Приведите, если это возможно, примеры функций /, таких,
что lim/(x) = 2 и справедливы следующие утверждения
х-+ 2
(если это невозможно, объясните почему):
а)	существует число х#=2, такое, что
|х-2|<-гЪ, |/(х) —2| > 100;
б)	для любого б>>0 и для любого х, такого, что |х —2| <б,
выполнено неравенство /(х)<0;
в)	для любого числа б>*0 найдется число х, такое, что
|х —2| <6 и /(х)<0;
22
г)	для любого n£N найдется число хп1 такое, что
|х„ —2| <1 и 7(х„)>п;
д)	для любого n£N найдется число хп, такое, что f(xn)>ri.
2.99.	Приведите, если это возможно, примеры функций /, таких,
что lim /(х)=4-°° и выполнены следующие утвержде-
х-> + оо
ния (если это невозможно, объясните почему):
а)	для любого М >0 найдется число /<, такое, что для всех
х<К выполнено неравенство /(%)<Л4;
б)	для всех К>0 и для всех х<К выполнено неравенство
/(х)<2;
в)	для всех чисел /<>>0 найдется такое число х<К, что
выполнено неравенство /(х)<2;
г)	для всех чисел /<>>0 найдется число х>К, такое, что
/UX2;
д)	можно выбрать такую последовательность х2, ..., хЛ, ...,
что последовательность f (xj, f (х2), ..., f (хл), ... стремит-
ся к 2;
е)	можно выбрать такую последовательность хн х2, ..., хя, ...,
что lim хп= + оо и lim (/(хп)) = 2.
2.100.	Вычислите данные пределы, используя теоремы о дейст-
виях с пределами:
a) lim(3x2 + 5x —2); б) lim-^Ц-; в) lim - * ;
х->2	х->2 *~3	-1
х .. х2 —5x-f-6 ч ..	— 3 ч .. Vx + 3 — Д/2*~3
Г> |ПЧ л2—9 ; Д) 1|т4 х-4 ; е) 11ПД-*Нт==Г------------
х + 3	9	х->4	Х^б д/х + 2 -2
2.101.	Исследуйте данные функции на асимптоты:
х	1	^х	х2 х	х2 —4x-f-3
а) У =----о ; б) у —------в) y = -z------!;
7	х — 3	7 57 х—1	7	х2 — 5x4-6
х	х2 —X	х	|х|	х	х2
г> 9 =	д) 9 = ^Т; е> 9 =
х sin х	.	X	х	.1
ж) у = —j- ;	з) у =---; и) y = xsm — .
х	sin х	х
2.102.	Приведите, если это возможно, примеры функций, графи-
ки которых имеют:
а)	три вертикальные асимптоты;
б)	две различные горизонтальные асимптоты;
в)	две различные наклонные асимптоты;
г)	наклонную и горизонтальную асимптоты.
2.103.	Приведите, если это возможно, примеры функций /, таких,
что не существует lim/(x) и выполнены следующие
х а
ут	верждения (если это невозможно, объясните почему):
а) существует lim |/(х)|;
23
б)	существует lim ((/(х))2-|- 1);
х—* а
в)	существует lim ((/(х))2 + 2/(х) + 3);
х —а
г)	существует lim sin f (х).
х-+ а
2.104.	Приведите, если это возможно, примеры функций f и g,
таких, что выполнены следующие утверждения (если это
невозможно, объясните почему):
а)	не существуют lim/(x) и limg(x), но существует
lim(f(x).g(x));
х-> 1
б)	не существуют lim/(х) и limg(x), но существует
lim(f (x) + g(x));
X1
в)	существуют lim (/ (x) + g (%)) и lim(/(x) — g(x)), но не
X —1	X —► 1
существуют lim/(x) и limg(x);
Х-> 1	X1
г)	существуют limg(x) и lim --- , но не существует
х-+ 1	х-> 1 ё (х)
lim / (х).
2.105. Вычислите следующие пределы, нахождение которых свя-
.. sin х *
зано с равенством lim---=1:
х+ 0 х
ч	sin 2х a) lim	; х->0 х 1	. л sin х —sin — 1- sin х	\ г	$ б) lim	;	в) lim—		; Х_»„х-Л	5х-л 5
1 Sin X —— г) lim	; л Л	V	 X — л	с 6	6	ч ..	tg X— 1 д) hm	§	 л 2 cos х— у2 Х^~4
IV. Непрерывные функции
2.106. Исследуйте данные функции на непрерывность:
а) у = sin (х+ 1); б) у = [х]\
в) у = sign х\
О У =
xsin —, если х#=0,
X
0, если х = 0;
д) z/ = sign {%};
х2—1, если х>0,
х, если х^О;
ж) у =
если х>»1,
x-f*1	<
—J—, если х=С1;
4
24
2.107.
2.108.
2.109.
2.110.
3) у =
к) У —
, если х^4 ,	। если
’ 1, если xefi\Q;
sin X
, если %-
%2, если xfQ,
4х — 3, если *ex\Q.
Приведите, если это возможно, примеры функций, непре-
рывных:
а) ровно
б) ровно
в) ровно
Найдите
ные функции непрерывны:
одной точке;
двух точках;
трех точках.
все значения параметра а, такие, что дан-
а) /(х) =
, если х^а,
1
—, если х = а;
4
. х4- 1, если
б) (*)=\ о
( 2х, если х<а;
----, если х>а,
х — а
х3 + 4, если х^а.
Найдите все значения параметра а, такие, что данная
функция f непрерывна ровно в двух точках:
{х? — 2ах, если х£О,
— 3, если x£R\Q;
/ х (х3—*2, если
б*) f(x) = \
(ах—1, если x£R\Q.
Найдите все значения параметров а и bt такие, что данная
функция f непрерывна на всей числовой оси:
в) /(*) =
^(х)—ax-\-b, если 0
2,
л
7 ’
в
в
в
2.111.	Известно, что функция f непрерывна. Докажите, что не-
прерывны следующие функции:
\ if / м	( f (*), если /(х)^0,
а)//=1/(х)|; б) </ = ]'	. 'v в y = f(\x\).
( 0, если /(х)<0;	7
25
V*. Свойства непрерывных функций
В заданиях 2.112—2.114 полезно иметь в виду, что если функ-
ция непрерывна в точке х0, то для любой последовательности
(хД, стремящейся к х0, верно, что lim / (хД = /( lim хп).
П —оо	П —оо
2.112.	Функция f непрерывна. Рассматривается последователь-
ность xn = f (xn_j)(n^2), хх = а. Известно, что существует
предел этой последовательности. Докажите, что уравне-
ние /(х) = х имеет решение.
2.113.	Функция f непрерывна и такова, что при любом x£R вы-
полнено равенство /(х) = / Докажите, что функция
f постоянная.
2.114.	Н айдите все непрерывные функции /, такие, что при лю-
бом x£R выполнено равенство
/(х2) + /(х)==х2 + х.
Для решения заданий 2.115—2.125 полезно использовать тот
факт, что если непрерывная на отрезке функция / такова, что
/(а) = Л, f (Ь) = В, то для любого С£(Л; В) на интервале
(я; Ь) найдется такое число с, что f(c)=C.
Пример. Докажите, что уравнение х = sin x-f-1,2 имеет хо-
тя бы одно решение.
Решение. Рассмотрим функцию f(x) = x— sin х— 1,2. Яс-
но, что f (0) = —1,2<0, а /(10)>0, поэтому на интервале
(0; 10) найдется хотя бы один корень уравнения /(х) = 0.
2.115.	Докажите, что уравнение 2х = 4х имеет по крайней ме-
ре два корня.
2.116.	Докажите, что любой многочлен нечетной степени имеет
по крайней мере один корень (вещественный).
2.117.	Функция непрерывна на отрезке [0; 1], и множество ее
значений на этом отрезке есть отрезок [0; 1]. Докажите,
что уравнение /(х) = х имеет на этом отрезке корень.
2.118.	Докажите, что если уравнение /(х) = х (где [—непре-
рывная функция) не имеет корней, то и уравнение
/(/(х)) = х также не имеет корней.
2.119.	Функции f и g определены и непрерывны на отрезке [0; 1].
Известно, что f (0)<g (0), f (l)>g(l). Докажите, что име-
ется такое число с, что f (c) = g (с).
2.120*	. Функции f и g определены и непрерывны на отрезке
[0; 1] и отображают его в отрезок [0; 1]. Известно, что для
любого х£[0; 1] выполнено равенство f (g (x)) = g (f (x)). До-
кажите, что найдется такое число с, что f (с) = g (с).
26
2.121*	. Функция f непрерывна и такова, что для любого х най-
дется такое натуральное п, что выполняется равенство
/(/(.../(х))...) = 1.
п раз
Докажите, что: а) уравнение f(x) = x имеет хотя бы одно
решение; б) / (1 )= 1.
2.122.	Выясните, существуют ли непрерывные функции /, не име-
ющие корней, и такие, что при всех значениях х выполня-
ются условия:
а)	(/«-/(х)<0; б)
в)	/(х)4-/(х+1)/(2х)/(2х+1)=0;
г)	/(х+1)/(х) + /(х+1)+1=0.
2.123.	Функция f непрерывна на отрезке [1; 2] и принимает толь-
ко иррациональные значения. Известно, что
Найдите f (1).
2.124.	Выясните, имеется ли такая непрерывная функция /, что
число f (х) рационально тогда и только тогда, когда число
/(*+1) иррационально.
2.125.	Выясните:
а) существует ли непрерывная функция /, принимающая
в иррациональных точках иррациональные значения,
а в рациональных — рациональные;
б*) существует ли непрерывная функция /, принимающая
в рациональных точках иррациональные значения, а в ир-
рациональных — рациональные.
В заданиях 2.126—2.127 используется ограниченность непре-
рывной функции на отрезке.
2.126.	Функция f непрерывна на [0; 4-оо) и lim f (х)==3. До-
%-> + оо
кажите, что функция f ограничена на [0; +°°)-
2.127.	Функция f непрерывна на (1; 3] и lim f (х) = 2. Докажите,
X —► 1
что функция f ограничена на [1; 3].
2.128.	Функция f непрерывна на R и такова, что для любых
хну выполняется равенство f (x-{-y) — f (х) + / (#)• Дока-
жите, что:
а)	найдется такое число a£R, что для всех x£Q выполнено
равенство f(x) — ax\
б)	если значения двух непрерывных функций совпадают
в рациональных точках, то они совпадают во всех точках;
в) найдется такое число a£R, что f(x) = ax при всех x£R.
27
2.129.	Найдите все непрерывные функции /, удовлетворяющие
уравнению f (% + //) = / (x)-f (у) (при всех х и у из R).
2.130.	Найдите все непрерывные на (0; + 00) функции /, такие,
что при всех х и у из (0; + 00) выполняется равенство:
a) f(xy)=f(x)+f(y); б) f(xy)=f(x)f(y).
§ 3. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
I.	Определения производной и дифференциала.
Вычисление производных
В заданиях 3.1—3.6 требуется:
а)	вычислить приращения ф(й) = / (x04-ft) — f (х0) для дан-
ных функций у = f (х) и данных точек х0=1 и х0= —1;
б)	построить соответствующие графики функций £/ = ср (Л);
в)	построить графики функций ф (h) =
г)	найти Нтф(Л), если он существует.
й — о
3.1.	/(х) = 2х + 3.	3.2. /(х)-х2.	3.3. /(х) = х2-2х.
3.4.	/(х)=Ц.
3.5.	f(x) =
3.6.	/(х)=|х4-1|.
х, если xZ> 1,
— х, если х< 1.
В заданиях 3.7—3.10 требуется для данных функций
y — f(x) и данных точек х0=1 и х0= — 1 выполнить следующие
задания:
ч	f// \	1-	+ —/(х0)
а)	вычислить производные f (x)=lim ----------------;
h-+Q	Л
б)	составить выражение т (h) = f (х0Ц- /г) — f (х0) — f' (х0) h и до-
казать, что Нтт(/г) = 0;
Л-»- о
в)	наити lim —— .
Л + 0 h
3.7.	f(x)=3x-l.	3.8. f(x) = x2 + x.	3.9. /(х) = -1^_
3.10.	f(x) = ’\[x + 2.
В заданиях 3.11—3.15 требуется выяснить, для каких из дан-
ных функций у = [(х) найдется такое число fe, что при всех
h функция ф(й) = /(х0 + й) —/(х0) (при х0= 1) может быть пред-
ставлена в виде ф (h) = kh-\-x (ft), где:
а) Птт(й) = 0;	б) lim^-^- = 0.
h -> 0	h -> 0 "
3.11.	f(x) = 5x-\.	3.12. /(х)=х2-6х+3.	3.13. f(x)=\x-\\.
3.14.
{2х, если х^ 1,
x-f-1, если х<
3.15.
х, если х^ 1,
— х, если х< 1.

28
В заданиях 3.16—3.18 требуется'сравнить значения прира-
щения ср — f (x0 + h) — f (х0) и дифференциала df = f'(x0)h для
данных функций y — f(x), точек х0=1 и х0= — 1 и значений
й = 0,1 и Л = 0,01.
3.16.	Цх)=-2x4-1.	3.17. 7(х) = 2х24-3. 3.18. /(х)=—!—.
В заданиях 3.19—3.21 требуется найти дифференциалы дан-
ных функций у = f (х) и с их помощью вычислить приближенно
значения данных функций в указанных точках хн
3.19.	/(х) = д/х, х,= 17.	3.20.	х, = 1,003.
3	Г-
3.21.	/(х) — ух, х1 = 9.
3.22.	Приведите примеры функций, имеющих производные везде,
кроме:
а) одной точки; б) двух точек; в) трех точек; г) целых
чисел.
3.23.	Выясните, какие из данных функций имеют производную
в точке хо = О:
а) /(х) = -	( . 1 . Л sin — , если х#=0,
	X
	0, если х = 0;
б) /(%)=•	Г . 1	, А х sin—, если х=#0.
	X 0, если х = 0;
в) /(%)='	х2 sin —, если х=#0
	X 0, если х = 0;
г) /(*) = •!	г х + 1, если х^0, k х2-^ 1, если х<0; Г х, если х^0,
Д) /(*) = )	[ х2 + х, если х<0.
3.24.	Найдите все значения параметров а и Ь, такие, что данные
функции: 1) непрерывны в х0=1; 2) дифференцируемы
в х0 — 1:
ч	f х f X, если х> 1,
a) f(x)=l
( ахЦ- р, если х< 1;
{х, если 1,
ах^Ьх, если х<1;
29
в) f (х)=
1 - 1
—, если 1,
х
ах-{-Ь, если x<Z 1.
д) /(*)={
3.25.	Исследуйте данные функции на дифференцируемость:
а) у = х\х\', б) у= lx2 — 4хЦ-3|;	в) у= |sin х|;
г) у — |х| -sin х;
х, если xfQ,	J х2, если xfQ,
О, если x£R\Q\	( 0, если x£R\Q.
3.26.	Приведите, если это возможно, примеры функций f и g,
удовлетворяющих данным условиям (если это невозможно,
объясните почему):
a)	f и g не дифференцируемы в точке х0, f + g дифференци-
руема в х0;
б)	/ дифференцируема в точке х0, g не дифференцируема
в точке х0, f + g дифференцируема в х0;
в)	/+ Я дифференцируема в х0, g дифференцируема в точ-
ке х0, f — g не дифференцируема в х0;
г)	/ + Я дифференцируема в х0, f — g дифференцируема
в х0, f не дифференцируема в точке х0;
д)	f дифференцируема в точке х0, g не дифференцируема
в точке х0, f-g дифференцируема в х0;
е)	f не дифференцируема в точке х0, g не дифференцируема
в точке х0, f-g дифференцируема в х0;
ж)	f не дифференцируема в точке х0, /2 дифференцируема
в точке х0;
з)	/ дифференцируема в точке х0, g дифференцируема
в точке х0, ~ не дифференцируема в точке х0;
и)	/ дифференцируема в точке х0, g не дифференцируема
f
в точке х0, не дифференцируема в х0;
к)	f не дифференцируема в точке х0, g дифференцируема
в точке х0, дифференцируема в х0;
л)	f дифференцируема в g (х0), g не дифференцируема
в точке х0, y — f{g (х)) дифференцируема в х0;
м) f не дифференцируема в g(x0), g не дифференцируема
в точке х0, y = f(g(x\) дифференцируема в х0;
н) */ = /(£(*)) дифференцируема в х0, z/ = g(/(x)) не диф-
ференцируема в х0.
3.27.	Докажите следующие утверждения:
а)	производная нечетной функции — четная функция;
б)	производная четной функции — нечетная функция;
в)	производная периодической функции — периодическая
функция.
30
II.	Геометрический смысл производной.
Касательная
В заданиях 3.28—3.32 для данных функций y = f(x) требует-
ся написать уравнения касательных у = 1(х) к их графикам
в точках с абсциссой х0 = 2, записать разность /(х) —/(х) и про-
г /(х)—Z(x)
верить, что lim ----------= 0.
Х~Х0
3.28.	/(х) = х2 + 2х.	3.29. / (х) = х3.	3.30. f (х) = —.
3.31.	/(х) = д/2х.	3.32. /(х) = sin лх.
3.33.	Напишите уравнения касательных к графику функции
/---- А/2~
f \ — х2 в точках с абсциссами xQ — 0 и х0 =	По-
стройте график функции f и эти касательные.
3.34.	Напишите уравнение касательной к графику функции
— х— 1, если х< —1,
—х2, если |х|<1,
х— 1, если х> 1,
в точках с абсциссами хо = О и хо = 2~' Выясните» сколько
общих точек имеют эти касательные и график функции [.
Пример. Напишите уравнения касательных к графику фун-
кции f (х) = х? — 4х, проходящих через точку (—2; 11).
Решение. Заметим, что данная точка не лежит на графике
функции /. Пусть проходящая через нее касательная касается
графика функции в точке с абсциссой х0, тогда ее уравнение
= —4х0 + (2х0 —4)(х —х0), Т. е. z/ = (2x0 —4) х —х^. Так как
точка ( — 2; 11) лежит на этой касательной, имеем 11 = —4х0 +
4-8 — х^, отсюда х0= — 1 и х()=—3.
Ответ. у=—6х—1; у= — 10х — 9.
3.35.	Напишите уравнения касательных к графику функции
у=-х^ — 2х2, параллельных прямой у—— х-|-3.
3.36.	Напишите	уравнения	касательных	к	графику	функции
у — -, перпендикулярных прямой z/ = 4x-(-3.
3.37.	Напишите	уравнения	касательных	к	графику	функции
у = х?4-ЗхЦ-2, проходящих через точку с координатами
(2; 8).
3.38.	Напишите уравнение общей касательной к параболам
z/ = x2 + 2x и у = х? — 4х.
3.39.	Напишите уравнение прямой, касающейся графика функ-
ции у — х2 — 2 |х—1| в двух точках.
31
3.40.	Пусть Mk — множество точек, через которые проходит ров-
но k различных касательных к графику функции // = х2.
Изобразите на координатной плоскости множества точек
Mk для & = 0, 1, 2, 3... .
3.41.	Выясните, является ли прямая у = 3х — 2 касательной в ка-
кой-либо точке к графику функции у = х3.
3.42.	Найдите все значения параметра а, при которых прямая
у = ах— 16 касается графика функции у = х?.
3.43.	Найдите все значения параметра а, при которых прямая
у = ах-\-$а—1 и график функции /(х)== л/х касаются.
3.44.	Найдите все значения параметров а, Ь, с, таких, чтобы име-
лась прямая, касающаяся графика непрерывной функции
х2+ Юх + 8, если х<-2,
У =
ах? -\-bx-\-c, если — 2<х<0,
х^Зх, если х^О,
ровно в трех точках.
В заданиях 3.45—3.46 требуется определить углы между
кривыми, т. е. углы между касательными к кривым в точках их
пересечения.
3.45.	Найдите, под какими углами парабола у = х2-{-3x4-2 пере-
секает ось абсцисс.
3.46.	Найдите, под какими углами пересекаются графики функ-
ций:
а)	/(х) = х3 —х и g (х) = х4-4;
б)	/(х) = х3 —х и g (х)=х? — 10;
в)	f(x) = sinx и g(x) = cosx.
III.	Исследование функций с помощью производной
В заданиях 3.47—3.50 требуется исследовать данные функ-
ции на монотонность, при этом целесообразно пользоваться эле-
ментарными теоремами о монотонности функций.
Пример. Исследуйте на монотонность функцию
f (х) = у/х4 — 4х.
Решение. Так как функция у = у[х монотонно возрастает,
достаточно исследовать функцию g(x) = x4— 4х.
g' (х) = 4х3 — 4. Исследуя знаки производной g', находим, что
функция g убывает на [— оо; 1] и возрастает на [1; 4- 00 )• Учи-
тывая область определения функции /, получаем ответ.
3 г—
Ответ. Функция f возрастает на [Д/4; 4- °°) и убывает на
(-оо; 0].
32
3.47.	/ (x)=^2S-i5^ + Mx.	3.48. f (x)=(%_2)2'(x_3)2 •
3.49.	/(x) = 23^5-'0?+2.	3.50. /(x)=sin7;r.'
I X | —ox “f* D
В заданиях 3.51—3.54 требуется исследовать на моно-
тонность функции, заданные на разных множествах разными
формулами.	х2 —4х, если х^О,
3.51. Цх) = -	х + —, если х<0. X
3.52. f(x) = -	Г	з.	 1 — у(х— I)2, если х^2, хД/1—х+2, если х>2.
3.53. /(х) = -	х + 2 Д/5 — х, если х^5, Зх—х3, если х>5. Г	1	. х	— если х^С 1,
3.54. /(%) = •	2/ , х5 — 5х, если х> 1.
В заданиях 3.55—3.63 требуется установить, при каких зна-
чениях параметра а выполняются данные условия.
Пример. Выясните, при каких значениях параметра
а функция
f (х) = х3 — ах2 -{-(За — 3) х4-2
возрастает на множестве [4; +°°)-
Решение. Рассмотрим производную /' (х) = 3х2 — 2ах-{-
4-За — 3. Данное условие эквивалентно выполнению неравенст-
ва Зх2 —2ах + 3а —3^0 при всех xj>4, но оно выполняется при
всех х^4 в следующих ситуациях:
а)	уравнение Зх? -2ах-{-За — 3 = 0 имеет не более одного
корня, т. е. D= а2 — 9а + 9^0;
б)	оба корня этого уравнения не больше 4, но это условие эк-
Г (4)^0
вивалентно системе « ^^0
Л<4-
Отсюда получаем ответ.
Ответ. ( — оо; 9].
3.55.	/(х) = х3 —ах2 + 3ах+1 возрастает на /?.
3.56.	f (х) = х3 — ах?-}-(6а — 1) х + 3 убывает на [1; 2].
2 Заказ 1259
33
3.57. / (х) = х3 —2ЯХ2 —5ах + 3 возрастает на [4; + <х>).
3.58. / (х) = х3 —ах2 + (2а —3) х + 2 возрастает на [ — 2; —1].
3.59. /(х) = х4~ возрастает на (2; Ц-оо).
3.60. f (х) = (х — af(x — 2а + 4)3 возрастает на [0; 1].
	' х4-3, если х< 1,
3.61. /(х) =	[ х3 ++Зах, если х^1, возрастает на /?.
	х3Ц-Зх—3, если х<;1,
3.62. /(х) = <	2х4-Л, если 1<х<3, Л
	2х-\-а, если х^З,	возрастает на R.
3.63. Уравнение х3 — (а-{-2) х?-\-Зах=Ь при любом b имеет ров-	
но один корень.	
В заданиях 3.64—3.69 требуется найти наибольшие и наи-
меньшие значения данных функций на данных множествах (если
они существуют).
3.64.	/(х) = х3-6х24~2 на [ — 3; 3].	3.65. /(х) = х4-| на [1; 3].
3.66.	f (х) = 3х4 — 8?4-6/4-2 на [-1; 2].
3.67.	/(x) = cos2x—2 cos х на [—у;
3.68.	/(х) = 5х —4х на [1; 2].
{х4 + 4х3, если х=С — 1,
х —6х, если х> — 1, на R.
3.70.	Представьте число 3 в виде суммы двух положительных
слагаемых, таких, чтобы сумма их четвертых степеней бы-
ла наибольшей.
3.71.	Найдите наибольшее значение площади равнобедренного
треугольника с периметром 2.
3.72.	Н айдите на параболе у — ^ точку, ближайшую к точке
с координатами (3; 0).
3.73.	Найдите на кривой у = у[х точку, ближайшую к точке
с координатами (3; 6).
3.74.	Найдите наименьшее расстояние между точками параболы
у = х^ и прямой у — 2х — 2.
В заданиях 3.75—3.77 требуется определить все значения
параметра а, такие, чтобы выполнялись данные условия о наи-
больших и наименьших значениях данных функций на указан-
ных отрезках.
Пример. Выясните, существует ли такое значение парамет-
ра, что наибольшее и наименьшее значения функции [ (х) =
= 2х3 —Зах2 на отрезке [—1; 1] достигаются внутри него.
34
Решение. Возьмем производную f' (х) — 6х(х — а). Таким
образом, критические точки х = 0 и х = а. Из условия ясно, что
в них и достигаются наибольшее и наименьшее значения, отсюда
а6(-1; 1). Но / (0) = 0, / (а)= —а3, / ( — 1 )= —2 —За, / (1) = 2 —
— За. Возможны следующие варианты:
а)	0<а< 1. Но тогда значение f (а) = — а3 должно быть наи-
меньшим, но — а2> — 1 и — 2 —За<—2— противоречие;
б)	— 1<а<0. Но тогда f (а)= — а3 должно быть наиболь-
шим значением, но — а3<1, а 2 — За>2— противоречие.
Ответ. Таких а нет.
3.75.	Наименьшее значение функции f(x) = x3 — 12х на отрезке
[0; а] достигается в правом конце. Найдите все значения
параметра а.
3.76.	Наибольшее значение функции f (х) = х-\-~ на отрезке [1; 2]
достигается в его правом конце. Найдите все значения па-
раметра а.
3.77.	Наибольшее и наименьшее значения функции /(х) = 2х3 —
— 3 (а-{- \ ) х?-{-бах на отрезке 2^ достигаются внутри
него. Найдите все значения параметра а.
3.78.	Дана функция f (х) = х3 — 3 (а + 1)	12ах. Постройте
график функции y = g(a), где g (а)— наименьшее значение
функции f на отрезке [0; 4].
3.79.	Выясните, при каком значении параметра а наименьшее
значение функции /(х) = х2 + ^- на отрезке [1; 2] больше 6.
3.80.	Выясните, при каких значениях параметра а наибольшее
значение функции f(x) = (x— а)2 (х— 3) на отрезке [0; 4] не
4
превосходит —.
3.81.	Выясните, при каких значениях параметра а наименьшее
значение функции f (х) = 2х3 — 3ax?-f-3a на отрезке [0; 2] бу-
дет наибольшим.
3.82.	Выясните, при каких неотрицательных значениях парамет-
ра а наибольшее значение функции f (х) = ах-\-^ на отрез-
ке [ — 2; —1] будет наименьшим по модулю.
3.83.	Постройте график функции y = g(x), определенной сле-
дующим условием: g(x)— наименьшее значение функции
/(/) = /3 —3/ на отрезке [х; х-|-2].
В заданиях 3.84—3.87 требуется найти наибольшие или наи-
меньшие члены данных последовательностей, при этом полезно
переходить к функциям вещественного аргумента.
Пример. Найдите наименьший член последовательности
ап = (п2 — 4п) (а + 3)2.
35
Решение. Рассмотрим функцию /(х) = (х2 —4х)(х + 3)2. Ее
производная f' (%) = 2 (х + 3) (2Х2 —Зх —6). Критические точки
о 3 —л/бт” 34-V57 ~
Xj=— 3, х2 —-----—, х3 =-----. Отсюда ясно, что на отрезке
L 3 + W1 Д. £ .	Гз-ьд/^т- .	\
0;---— функция / убывает, а на луче ---------; + оо \ возра-
о 3+V57"
стает, но 2<С----—<3, поэтому достаточно сравнить числа
а2= — 100 и а3= — 108.
Ответ. Наименьший член последовательности а3= —108.
3.84. Найдите наименьший член последовательности а=п2-}-^-.
п
37
3.85. Найдите наименьший член последовательности а=п-\--------.
п	п
3.86.	Найдите наименьший член последовательности
ап = и3 — 18/г2 + Зп + 2.
3.87.	Найдите наибольший член последовательности
ап = у/п^ + ЗОп — 2п.
В заданиях 3.88—3.91 требуется найти области значений
данных функций.
Пример. Найдите область значений функции
/ (х) = х4 + 32х.
Решение. (х) = 4х3 + 32. Отсюда ясно, что наименьшее
значение функции [( — 2) — —48, но lim /(х)= + оо. С учетом
непрерывности функции f получаем ответ. .
О т в е т. [ —48; + оо ).	\
3.88.	/(х)=-^т.	3.89. /(х) = х+д/3-х.
3.90.	/(х) = 42+Ц •
1 v 1 г+зх+г
3.91. /(х) =
Зх4 —4х3 —24х2 + 48х, если
8х3+12х2 + 2, если х<~.
3.92.	Выясните, при каких значениях параметра а область зна-
чений функции / (х) = (х—1 )3 (Зх —4&+1) содержится во
множестве [—16; + оо ).
3.93.	Выясните, при каких значениях параметра а область зна-
чений функции /(х) =	‘	„ содержится во
оХ — oQ-X -j- 1 ZQ. л U
множестве 0;	.
36
В заданиях 3.94—3.96 требуется доказать наличие корней
данных уравнений.
Пример. Докажите, что уравнение х6 —6х5 = — 1 имеет два
корня.
Решение. Рассмотрим функцию f (х) = х6 — 6х5 + 1, ее про-
изводная (х) = 6х4 (х —5). Функция f имеет при х=5 минимум
//=—3124, но lim	Поэтому из непрерывности
Х-+ ± оо
функции f ясно, что уравнение имеет по одному корню на луче
(—оо; 5] и на луче [5; Ц-оо). Так как функция f монотонна на
этих лучах, то на каждом из них она имеет ровно по одному
корню.
3.94.	Докажите, что уравнение х4 —4хЦ-2 = 0 имеет по крайней
мере два корня.
3.95.	Докажите, что уравнение (х + 1)3(х-р2)2 = —3 имеет ровно
один корень.
3.96.	Выясните, сколько корней имеет уравнение
< : лД+ 1 = 1.
В заданиях 3.97—3.100 требуется доказать данные неравен-
ства.
2_
Пример. Докажите неравенство Зх3 — 1^2х.
2
Решение. Рассмотрим функцию f (х) = 2х — Зх3 + 1-
______________i_
/'(х) = 2 —2х 3, х=1—точка минимума, /(1) = 0, поэтому
при всех х>>0 /(х)^0, что и требовалось доказать.
5 _
3.97.	5 ух^х + 4 при х^О.
3.98.	Зх4 + 4х3// —бх2//2^ 12х//3—11//4 при х2>0, y>Q.
3.99.	cosx^l—4".	3.100. In х> 1—- при х>1.
2	х г
В заданиях 3.101—3.106 целесообразно построить графики
данных функций f и с их помощью ответить на поставленные во-
просы.
Пример. Дана функция /(х) = х3 —бх2. Постройте ее гра-
фик и выясните, сколько корней имеет уравнение [ (х) — а в зави-
симости от а.
Решение. (х) = 3х2 — 12х = 3х(х — 4). Исследуя знаки
производной, находим, что функция [ возрастает на [4; + оо)
и (—оо; 0] и убывает на [0; 4].
Схематично построим график (рис. 4).
Проводя теперь прямые у = а и рассматривая точки их пере-
37
сечения с построенным графиком, легко дать ответ на поставлен-
ный вопрос.
Ответ. Если a<Z —32, то один корень; если а= — 32, то два
корня; если —32<а<0, то три корня; если а = 0, то два корня;
если а>0, то один корень.
3.101.	Дана функция / (х) = х5—12,5х3 + 32,5х. Выясните, сколь-
ко корней имеет уравнение f(x) — a в зависимости
от а.
3.102.	Дана функция f	. Выясните, сколько корней име-
ет уравнение f(x) = a в зависимости от а.
3.103.	Дана функция f (х) = х(х— I)3. Выясните, сколько поло-
жительных корней имеет уравнение f(x) = a в зависимо-
3.104.
сти от а.
Дана
3.105.
имеет
Дана
х I 2
функция f(x) = —==. Выясните, сколько корней
уравнение f(x) = a на отрезке [1; 2].
функция /(х)-— -
параметра а
ниях
/ (х)^а будет луч.
Выясните, при каких значе-
(х-7)2	и
множеством решений неравенства
3.106.	Дана функция f (х) = у2х3Ц-9х2. Выясните, при каких
значениях параметра а множеством решений неравенства
[ (х)^а будет отрезок.
38
В заданиях 3.107—3.109 также полезно применять графиче-
ский метод.
Пример. Выясните, при каких значениях параметра а урав-
нение х3 — ах — а = 0 имеет три корня на отрезке [ — 2; 4].
Решение. Уравнение х3— ах— а = 0 эквивалентно уравне-
х3
нию а = —. Для схематичного построения графика функции
, х2 (2x4-3)	_	,
а найдем а (х) =-------. Отсюда ясно, что функция а име-
U4-1)
27	3
ет минимум — при х= ——,
возрастает на
и
(1; + оо ), убывает на оо; — —j (рис. 5).
Так как а (4) = -^-, а ( —2) = 8, ясно, что прямые a = const,
параллельные оси абсцисс, будут пересекать график в трех точ-
ках с абсциссами, принадлежащими отрезку [ — 2; 4], при
а
Ответ.
3.107.	Выясните, при каких значениях параметра а уравнение
х4 — ах34-27 = 0 имеет хотя бы один корень, больший 4.
3.108.	Выясните, при каких значениях параметра а уравнение
1) х2 + (За + 2) х+(а — 1) = 0 имеет два корня на
Г1 о!
отрезке —; 3 .
3.109.	Выясните, при каких значениях параметра а из
неравенства	а> х-\-У] х? — 16	следует неравенство
а 4- 2 >2%.
§ 4. ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
I. Нахождение первообразных
В заданиях 4.1—4.5 требуется выяснить, являются ли ука-
занные функции F первообразными для данных функций f (за-
данных на соответствующих множествах D (f)).
4.1 F(x) = x2+l, f (х)=2х, D(f) = R.
4.2. F (x) = |x- 11, /(x)=l, D(/) = ( —oo; 0].
{2%4- 1, если x^ 1,
9	, Z =	D(f) = R.
2x— 1, если x< 1,
39
4.4. F(x) =
x3 + x+L если x^O,
y + если x<0,
c/ 4 f Зх2-|- 1, если xZ>0,
= \	। i
( %+ 1, если x< 1,
D(f) = R.
	2Х2 — 7х-Н, если х^4,
4.5. Л(х)=.	— -у 4-2x4-5, если х<4,
/(*) = {	х—7, если х^4, ~х + 2 если х<4	= Я Л> |	£* VVvlrl Л,	а у
В заданиях 4.6—4.9 требуется отыскать первообразные
F данных функций /, удовлетворяющие данным условиям.
4.6. /(х)=-^, F(l)= 1, F(- 1)= - 1.
4.7. /(х) =
х2^ 1, если 1,
2х, если х< 1,
4.8. 7(х)=|х-1|, F(2) = 3.
л л г/ X I Vх» еСЛИ х>2,
4.9. f(x) = < у
( х— 1, если х<2,
F(2) = 0.
F(9)=18, F(-4)= -6.
4.10.	Выясните, обязательно ли первообразная четной функции
/ нечетная. Может ли она быть нечетной? Обязательно ли
среди первообразных четной функции есть нечетная? От-
ветьте на те же вопросы при условии, что функция / непре-
рывна на всей числовой оси.
4.11.	Выясните, обязательно ли первообразная нечетной функ-
ции / четная. Может ли она быть четной? Обязательно ли
среди первообразных нечетной функции есть четная? От-
ветьте на те же вопросы при условии, что функция 7 непре-
рывна на всей числовой оси.
4.12.	Докажите, что если непрерывная на всей оси функция 7 та-
кова, что ее график имеет ось симметрии х — а, то график
ее первообразной имеет центр симметрии.
4.13.	Докажите, что если непрерывная на всей оси функция f та-
кова, что ее. график имеет центр симметрии (а; 0), то гра-
фик ее первообразной имеет ось симметрии.
4.14.	Выясните, обязательно ли первообразная периодической
функции 7 периодична. Может ли она быть периодичной?
Обязательно ли среди первообразных периодической функ-
ции есть периодическая?
40
4.15.	Выясните, обязательно ли первообразная возрастающей
функции f возрастающая. Может ли она быть возрастаю-
щей? Обязательно ли среди первообразных возрастающей
функции есть возрастающая?
4.16.	Выясните, могут ли определенная на всей оси функция и ее
первообразная быть периодичными, но иметь несовпадаю-
щие наборы периодов.
4.17.	Выясните, может ли график функции совпадать с графи-
ком какой-то ее первообразной.
4.18.	Выясните, может ли график какой-то функции пере-
секаться с графиком ее первообразной ровно в одной точке,
ровно в двух, ровно в трех.
4.19.	Найдите все значения параметра а, такие, что первообраз-
ная функции
/(Л) = х24-2(а —3)х + 2а + 9
будет возрастающей на всей числовой оси функцией.
р ( 0, если %У=0,
4.20.	Докажите, что функция/(%) = < 4	. не имеет пер-
[ 1, если х = 0
вообразной.
4.21.	Выясните, возможно ли выполнение для каких-то функций
f и g следующих условий:
а)	функция у = [(х) не имеет первообразной, а функция ви-
да y = kf(x) (k£R) имеет первообразную;
б)	функция / не имеет первообразной, а функция /2 имеет
первообразную;
в)	функции f и g не имеют первообразных, а функция f-\-g
имеет первообразную;
г)	функции fg и f — g имеют первообразные, а функция
/ не имеет.
В заданиях 4.22—4.31 требуется отыскать все функции /,
удовлетворяющие данным условиям.
4.22.	(/' (х))3 + /' (*) = 0 при всех x£R.
4.23.	При всех x£R выполняются равенства
П(х)-/(х+1) = 0
\Г(х) + Г(х+1) = 0.
4.24.	Функция y — f(x) дифференцируема, и при всех зна-
чениях x£R выполняется равенство / (%)•/'(х) = 0.
4.25.	Функция / непрерывна на /?, и при любых выполня-
ется неравенство
/ (Х2) —/ (х,)
Х2 —X]
<sin I/(х2) —/ (х,)|.
41
4.26.	Функция f такова, что имеется число а > 0, такое, что
при всех х2=£х} выполняется неравенство
I/(^2> — /(*1)1 < |Х2 —*1|1+“-
4.27.	Дифференцируемая функция f такова, что при всех
х и h выполняется равенство
f (% + Л) = Г(х).
4.28.	Дифференцируемая функция f такова, что при всех значе-
ниях х и h выполняется равенство
4.29.	Функция / трижды дифференцируема и такова, что при
всех x£R выполняется равенство
/(%)./'(*)7"(*) = 0.
4.30.	Дифференцируемая функция f такова, что при всех х вы-
полняются равенства
/(*) + /(*— 1) = 4х,
Л(х) + 2/'(х-1) = 6.
4.31.	Дифференцируемая функция [ такова, что при всех
х и h выполняется равенство
f(x+h)—f(x) = hf' (*+4)-
В заданиях 4.32—4.34 требуется доказать данные равенства.
Пример. Докажите тождество arcsin х + arccos х = у •
Доказательство. Рассмотрим функцию
f (%) = arcsin х + arccos х.
Ее производная ['(х) = г 1—--1— — 0. Отсюда f(x) — c при
Vi-x2 Vi-x2
всех xGD(f), но, подставив х=1, находим f (1) = у, поэтому
с = у. Итак, arcsin х+arccos х = у при всех х£[— 1; 1].
4.32.	arctg х+ arcctg х = ^ •
4.33.	arctg arctg= при х>0.
1	л
4.34.	arctg %+ arctg — — — у при х<0.
42
II. Определенный интеграл
В заданиях 4.36—4.42 требуется вычислить определенные ин-
тегралы, при этом ответ может быть получен из геометрических
соображений.
4.35.	1		 -	3		 Д/1—х2 dx.	4.36. yl&x — х?~8 dx. -1	2
4.37.		^=dx.	4.38. W2-X2 dx. Л '+VT-X-	)
4.39.	(1 — |x|)dx.	4.40.	|х—l|dx. -1	0
4.41.	з J ( |х — 1 | + | X — 2 | )dx. 0
4.42.	4 min(x; 4 — x)dx, где min (а; b) — наименьшее из чисел а и Ь, в случае их равенства min (а; Ь) = а = Ь.
4.43.	Постройте график функции g(x) = ^ \t — 2| dt, х^О.
4.44.	Постройте график функции £(*) = $ (|/-2|4-|/-3|)d/, х>0. 0
4.45. Вычислите площади фигур, ограниченных линиями, зада-
4.46.	ваемыми следующими уравнениями: а)	у = х2 — 4x-j-3, х— 0, г/= 0; б)	z/ = x2 — 4х + 3, z/= 0; в)	у — х2 — 4x4-3, //= — !, х — 0; г)	// = х2 —4x4-3, у = 2х — 5. Докажите следующие утверждения для интегрируемой на любом отрезке функции /: а а)	если функция f нечетна, то f (х) dx = 0 (при а>»0); — а а	а б)	если функция f четна, то	f (х) dx = 2^ f(x)dx — а	0 (при а>0);
43
в) если функция f периодична с периодом Г, то для любых
а и b выполнено равенство
ь	ь+т
f (х) dx = f (x) dx.
a	a + T
4Al. Выясните, при каких значениях параметра а выполняются
следующие равенства:
а	1
а) (%+ 1) dx=^ ; б) \x — a\dx = ^.
о	о
4.48.	Выясните, при каких значениях параметра а инте-
а
грал (Зх2 — 10% + 6) dx положителен.
о
4.49.	Найдите, при каких значениях параметра а интеграл
2а
(2х — \)dx принимает наименьшее значение.
а
4.50.	Найдите наибольшее значение интеграла
а
(Зх2 — 4ахЦ-3^) dx
о
при положительных а.
4.51.	А и В — точки на параболе у = х?, такие, что прямые АО
и ВО взаимно перпендикулярны (О — начало координат).
Найдите наименьшее значение суммы площадей фигур,
ограниченных дугами параболы и хордами АО и ВО.
В заданиях 4.52—4.53 требуется найти суммы, в которых
присутствуют интегралы от взаимно обратных функций.
1	1
Пример. Найдите сумму д/х" dx + ^ х? dx.
о	о
Решение. Разумеется, нетрудно вычислить каждый из этих
1
интегралов, но заметим, что интеграл х2 dx равен площади фи-
о
гуры, ограниченной графиком функции у = х?, осью абсцисс
1
и прямой х=1, а интеграл у[х dx равен площади фигуры,
о
ограниченной графиком функции у — х2, осью ординат и прямой
у — 1. Отсюда ясно, что искомая сумма равна площади квадрата
со стороной 1.
Ответ. 1.
44
2	1
4.52.	arcsin xdx.
о	0
л
1	f	5r-
4.53.	\ sin5xdx + \ arcsin yx dx.
о	0
I	2
f	f	10 /—
4.54.	Докажите, что \ x10dx + \	dx^2.
о	0
4.55.	Пусть f и g — взаимно обратные возрастающие функции,
определенные на [0; +оо), интегрируемые на любом отрез-
ке [0; с] и такие, что f (0) = g (0) = 0. Докажите, что для всех
положительных а и Ь выполнено неравенство
а	b
f(x)dx-{-^ g (х) dx^ab.
о	о
4.56.	Пусть числа а и b положительны, р и q таковы, что —-|— =
= 1 и р>\, q>\. Докажите, что выполнено неравенство
--—^ab.
р я
§ 5. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
И ТЕОРИИ ВЕРОЯТНОСТЕЙ
I.	Простейшие комбинаторные задачи
5.1.	Известно, что 80% учениц данной школы любят читать сти-
хи, а 70% любят есть пирожные. Укажите, какие из следу-
ющих утверждений обязательно верны, какие, вообще гово-
ря, неверны. Объясните почему.
а)	Для того чтобы ученица данной школы любила стихи,
достаточно, чтобы она любила пирожные.
б)	Для того чтобы ученица данной школы любила стихи,
необходимо, чтобы она любила пирожные.
в)	Любая ученица данной школы любит пирожные или
стихи.
г)	По крайней мере 50% учениц данной школы любят и пи-
рожные, и стихи.
5.2.	Известно, что а% учеников данной школы любят ходить
в филармонию, а Ь% учеников данной школы любят стре-
лять из рогатки. Назовите все пары а и />, такие, чтобы сле-
дующие утверждения были обязательно верны.
45
а)	Для того чтобы ученик данной школы любил ходить
в филармонию, достаточно, чтобы он любил стрелять из ро-
гатки.
б)	Для того чтобы ученик данной школы любил ходить
в филармонию, необходимо, чтобы он любил стрелять из
рогатки.
в)	Любой ученик данной школы любит ходить в филармо-
нию или стрелять из рогатки.
г)	По крайней мере 50% учеников данной школы любят
и ходить в филармонию, и стрелять из рогатки.
5.3.	Пусть множество А содержит т элементов, а множество
В содержит п элементов.
а)	Выясните, сколько элементов в множестве ЛХ^ всех
пар вида (а, 6), где а£Л, Ь^В.
б)	Выясните, сколько существует отображений из Л в В.
в) Выясните, сколько существует взаимно однозначных
отображений из Л в Л.
г)	Выясните, сколько существует взаимно однозначных
отображений из Л в В.
д)	Рассматриваются все взаимно однозначные отображе-
ния из Л в В. Выясните, сколько существует различных об-
ластей их значений.
е)	Рассматриваются все отображения из Л в В. Выясните,
сколько существует различных областей их значений.
5.4.	Пусть имеется пг различных ящиков и п шариков. Ответьте
на следующие вопросы:
а)	Сколькими способами можно распределить все шарики
по ящикам так, чтобы в каждом ящике лежало не более од-
ного шарика (шарики считаются одинаковыми)?
б)	Сколькими способами можно распределить все шарики
по ящикам так, чтобы в каждом ящике лежало не более од-
ного шарика, если шарики считаются различными?
в)	Сколькими способами можно распределить все шарики
по ящикам, считая шарики одинаковыми?
г)	Сколькими способами можно распределить все шарики
по ящикам, считая шарики различными?
5.5.	В этой задаче действуют следующие персонажи: экономные
мамы, не дающие детям больше чем по одной шоколадке;
несправедливые мамы, раздающие шоколадки как угодно;
и справедливые мамы, раздающие шоколадки так, чтобы
у каждого ребенка была хотя бы одна шоколадка.
а)	Пусть мама раздает т детям п шоколадок. Выясните,
какими должны быть числа т и п, чтобы мама, решившая
быть экономной, оказалась и справедливой; чтобы мама,
решившая быть справедливой, оказалась и экономной,
б) У каждой из мам, справедливой, экономной и неспра-
ведливой, по п детей и соответственно по k, I и т одинако-
46
вых шоколадок. Укажите, сколько у них способов их раз-
дать.
в) У экономной и несправедливой мам по п детей и по
/ и т различных шоколадок. Выясните, сколько у мам спо-
собов их раздать. Какими должны быть числа т и п, чтобы
у несправедливой мамы было больше 10 возможностей?
г) У справедливой мамы двое детей и п различных шокола-
док. Выясните, сколько у мамы способов их раздать.
д) У справедливой мамы трое детей и п различных шоко-
ладок. Выясните, сколько у мамы способов их раздать,
е) У справедливой мамы три девочки, два мальчика и пять
различных шоколадок. Выясните, сколько у мамы способов
их раздать так, чтобы шоколадки «Сникерс», «Марс»
и «Баунти» достались девочкам.
ж) У экономной мамы п детей и k различных шоколадок.
Выясните, сколько у нее способов раздать шоколадки так,
чтобы старшему не достался «Сникерс».
з)	У несправедливой мамы п детей и k различных шокола-
док. Выясните, сколько у нее способов их раздать так, что-
бы младшему не досталась шоколадка «Баунти».
и)	У двух экономных мам по т и k детей соответственно
и по п шоколадок (/г^т, n^.k). Экономные мамы решили
детей, которым не достались шоколадки, сводить в зоопарк.
Выясните, сколько у них способов сформировать группу,
идущую в зоопарк.
к)	У двух несправедливых мам по т и k детей и по п шоко-
ладок (/г^т, n^k). Несправедливые мамы решили детей,
получивших шоколадки, еще и в зоопарк сводить. Выясни-
те, сколько у них способов сформировать группу, идущую
в зоопарк.
5.6.	Круг разделен на 4 равных сектора. Имеются две краски,
которыми можно красить круг, закрашивая сектор целиком
одной краской. Ответьте на следующие вопросы:
а)	Сколько существует различных способов раскрасить
круг?
б)	Сколько существует различных способов раскрасить
круг, который разрешается поворачивать на 180° (раскра-
ски считаются различными, если они не совмещаются при
повороте)?
в)	Сколько существует различных способов раскрасить
этот круг, если его разрешается поворачивать на углы,
кратные 90°?
5.7.	Круг разделен на р равных секторов (р — простое число).
Имеется п красок. Ответьте на следующие вопросы:
а)	Сколько существует различных способов раскрасить не-
подвижный круг?
б)	Сколько существует одноцветных раскрасок круга?
47
в)	Сколько различных раскрасок неподвижного круга соот-
ветствует одной неодноцветной раскраске круга, который
2л
разрешается поворачивать на углы, кратные углу в — ра-
диан?
г)	Сколько существует различных раскрасок круга, кото-
2 л
рый разрешается поворачивать на углы, кратные ?
5.8.	Рассматривается прямоугольная сетка квадратов размера-
ми т на /г, состоящая из тп квадратов, разделенных верти-
кальными и горизонтальными прямыми. Ниже подразуме-
вается, что из одного узла сетки в другой можно двигаться
только по отрезкам вертикальных и горизонтальных пря-
мых.
а) Назовите число кратчайших путей, ведущих из нижнего
левого угла (точки (0; 0)) в правый верхний (точку (т; п)).
б) Назовите число кратчайших путей, ведущих в точку
(fe; n — k) из точки (0; 0) и проходящих через точки
(fe; n — k— 1) и (k— 1; п — k) соответственно. Выведите отсю-
да рекуррентное соотношение для полученных чисел.
в) Выясните, сколько кратчайших путей ведет из точки
(0; 0) в точку (/г; /г). Заметьте, что каждый такой путь про-
ходит ровно через одну точку вида (k; n — k), где O^Zk^Ln.
Выведите отсюда соотношение
ся2л= I (С*)2
6 = 0
(Ckn — число неупорядоченных подмножеств //-элементного
множества, состоящих из k различных элементов).
5.9.	Докажите следующие рекуррентные соотношения:
а)	+
б)	Ckn--=Ckn~' где Ckn — число неупорядоченных набо-
ров из k не обязательно различных элементов //-элементно-
го множества;
в)	Dn = (n—1)(£\_| + Dn_2), где Dn — число перестановок
//-элементного множества, таких, что ни один элемент не
остается неподвижным;
п — 1
г)	Кп = £ КтКп^т, где Кп — число способов расставить
т = 1
скобки в выражении х}- х2-хп, К} = К2=
5.10.	Докажите следующие равенства:
а)	(!+%)”= £ Cknxk-
6 = 0
48
б)	«(Ц-х)”-^ £ feC*?-1;
k= I
(1+х)я+1 _ V c‘**+' .
B' n+1	A+l ’
1	k = 0
r) 7^7=1 +l+-+"4-..„ |X|<1;
«•)	W<‘-
5.11.	При решении следующих задач полезно использовать соот-
ношения, доказанные в задании 5.10, подставляя в них те
или иные вещественные или комплексные числа, или, на-
пример, представляя выражение (14-х)Л в виде произведе-
ния (1 -f-х)*(1 4-х)"-* для различных k и приравнивая ко-
эффициенты в разложениях. Докажите равенства:
a) f С>2Я; б) £(- 1^ = 0;
в) £ (-iO = 22cos^; г) £ (-l)A.3^C“ = 2'1cos|n;
k=0	k=Q
п	п г* ап+1
л) £ К! = ».2-’;
k=l	k = 0
ж) £ ( — 1)*(2&+ 1) С2к+1 = п-2 2 cos(я—1);
k = 0
оо pk	k	п
з) I -^ = 2"; и) Ск+т=£ C'n.Ck-!- к) l Скп.Сп~к = Сп2п.
k = 0 2	1 = 0	k = 0
II. Простейшие задачи теории вероятностей
5.12.	В классе учится т человек, среди них п отличников. От-
ветьте на следующие вопросы:
а)	Наудачу выбирают одного ученика. Какова вероятность,
что он будет отличником?
б)	Наудачу выбирают k учеников. Какова вероятность, что
среди них будет ровно s отличников?
5.13.	Калиф—Аист забыл волшебное слово «мутабор» и произ-
носит слова наудачу. Ответьте на следующие вопросы для
случаев, когда Калиф делает одну попытку и когда он де-
лает 10 попыток.
49
а)	Какова вероятность, что он угадает, если он помнит дли-
ну заветного слова и все его буквы?
б)	Какова вероятность, что он угадает, если он все верно
помнит про все буквы заветного слова, кроме буквы «р»,
про которую не уверен, одна она в слове или их там две?
в) Какова вероятность, что он угадает, если он помнит, что
в слове не было никаких букв, кроме «м», «у», «т», «а», «б»,
«о», «р», и помнит длину слова (входили ли эти буквы
в слово и по скольку раз, он не помнит)?
г) Какова вероятность того, что Калиф произнесет слово,
в котором будет сочетание букв «табу», если он помнит
длину слова и все входящие в него буквы?
5.14.	Нарисуйте два таких подмножества А и В квадрата со сто-
роной длины один, что два события — попадания в эти фи-
гуры при стрельбе по квадрату — будут независимыми.
5.15.	Приведите примеры (если это возможно) таких событий 4,
А2 и А3, что выполнены следующие условия:
а)	Р(ДЛ/) = Р(Л1)Р(Л/),	/, /=1, 2, 3, но Р(4Л2Л3)=#
=#Р(Л1).р(Л2).р(4з);
б)	Р (А[А2А3) = Р (А{) Р (А2) Р (А3), но неверно, что
р (AlAj) = Р (Д) Р (Лу) для всех i=/=j\ i, /=1, 2, 3.
5.16.	Два стрелка стреляют по мишени. Вероятность попадания
в цель при одном выстреле у первого 0,7, у второго 0,8. От-
ветьте на следующие вопросы:
а)	Какова вероятность, что цель будет поражена дважды,
если каждый стреляет по одному разу?
б)	Какова вероятность, что цель будет поражена ровно
один раз, если каждый стреляет по одному разу?
в)	Какова вероятность, что цель будет поражена ровно три
раза, если каждый стреляет ровно два раза?
5.17.	Два стрелка стреляют по мишени. Вероятность попадания
в цель при одном выстреле у первого а у второго р2.
а) Найдите если р2 = 0,6, а вероятность ровно одного
попадания в цель при том, что стреляют по одному разу,
0,5.
б)	Найдите и р2, если вероятность того, что цель пора-
жена ровно один раз при условии, что каждый стреляет по
одному разу, 0,46, а вероятность того, что цель не пораже-
на ни разу при том же условии, 0,42.
5.18.	Известно, что 50% всех преступлений в Лондоне соверша-
ют люди Мориарти, 25% — шайка Сильвиуса и лишь
25% — остальные преступники. Известно, что лишь в 10%
преступлений люди Мориарти идут на убийство, у шайки
Сильвиуса и остальных преступников убийством отягоще-
ны соответственно 20% и 30% преступлений. Ответьте на
следующие вопросы, помня, что вместе названные преступ-
ные сообщества не работают:
50
а)	Какова вероятность того, что случайно выбранное пре-
ступление в Лондоне отягощено убийством?
б)	Известно, что наудачу выбранное лондонское преступ-
ление отягощено убийством. Какова вероятность того, что
оно совершено людьми Мориарти?
5.19.	В Скотланд-Ярде дежурят Лестрейд, Хопкинс и Грегсон.
Лестрейд забирает половину всех дел, Хопкинс и Грег-
сон — по четверти. Вероятности раскрытия преступления
у них соответственно рх, р2, р3. Вместе сыщики не работают,
а) Выясните, в каких границах лежит вероятность раскры-
тия преступления Скотланд-Ярдом, если известно, что чис-
ла рх и р2 лежат в пределах от 0,2 до 0,5, a p3f [0,1; 0,4].
б) Найдите число pXl если р2 = 0,3,р3 = 0,4, а вероятность
раскрытия преступления Скотланд-Ярдом равна 0,5.
в)	Известно, что вероятность того, что наудачу выбранное
раскрытое преступление окажется раскрытым Лестрейдом,
у. Ответьте, не стоит ли выгнать Грегсона и Хопкинса, по-
ручив все дела Лестрейду.
г)	Выясните, какой должна быть вероятность того, что рас-
крытое преступление было раскрыто Лестрейдом, чтобы
предложенное выше сокращение кадров было оправдано.
5.20.	Круг разделен на п равных секторов. В круг наудачу бро-
сают шарик.
а)	Пусть п = 3. Выясните, сколько раз надо бросить ша-
рик, чтобы вероятность попадания хотя бы один раз в отме-
ченный сектор была больше 0,5.
б)	Пусть /г = 3. Выясните, какова вероятность того, что при
10 бросаниях шарика будет ровно два попадания в отме-
ченный сектор.
в)	Шарик бросают в круг п раз. Докажите, что вероят-
ность рп того, что при этом не будет ни одного попадания
в отмеченный сектор, меньше 0,5.
г*) Найдите в условиях предыдущего пункта lim рп.
III.	Геометрические вероятности
5.21.	Наудачу выбирают неотрицательное число %, такое, что
х^З. Какова вероятность того, что х^1?
5.22.	Наудачу выбирают числа хи//, такие, что х£ [0; 2], //f [0; 1].
Ответьте на следующие вопросы:
1	2
а)	Какова вероятность того, что х^—, //^^-?
<3	о
б)	Какова вероятность того, что //^2х?
в)	Какова вероятность того, что х//^^-?
г)	Какова вероятность того, что z/^sinx?
51
5.23.	На отрезке АВ выбираются наудачу точки С и D. Ответьте
на следующие вопросы:
а)	Какова вероятность того, что точка D правее точки С?
б) Какова вероятность того, что BD^ACl
в)	Какова вероятность того, что AC^BD и D лежит спра-
ва от С?
г)	Какова вероятность того, что D лежит справа от С и из
трех отрезков AC, CD и DB можно сложить треугольник?
5.24.	Наудачу составляют квадратный трехчлен х? Р*-\- Ц, та-
кой, что |р| =С5, |^| с:5. Ответьте на следующие вопросы:
а) Какова вероятность того, что этот квадратный трехчлен
имеет вещественные корни разных знаков?
б)	Какова вероятность того, что этот квадратный трехчлен
имеет вещественные корни?
в)	Какова вероятность того, что этот квадратный трехчлен
имеет два положительных корня?
г)	Какова вероятность того, что этот квадратный трехчлен
имеет два корня, большие единицы?
5.25.	Два незнакомых мафиози пытаются убить друг друга. Пер-
вый приходит к месту встречи от 12.00 до 13.00, мгновенно
и незаметно оставляет мину, которая взорвется через
10 мин, ждет 5 мин и уходит, второй также приходит от
12.00 до 13.00, оставляет свою мину, которая взорвется че-
рез 15 мин, ждет 10 мин и уходит. Ответьте на следующие
вопросы:
а)	Какова вероятность того, что мафиози встретятся?
б)	Какова вероятность гибели второго мафиози?
в)	Какова вероятность гибели первого мафиози?
г)	Какова вероятность гибели обоих мафиози?
§ 6.	МНОГОЧЛЕНЫ И УРАВНЕНИЯ
I.	Простейшие понятия.
Метод неопределенных коэффициентов
6.1.	Найдите все значения параметра а, такие, что многочлены
Р и Q равны, если
Р (х) = х34-* — 1,
Q (х) = х34-(а2 — 5а+ 6) х24-(«2 — 8) х4-2а —7.
6.2.	Найдите все значения параметров а и Ь, такие, что мно-
гочлены Р и Q равны, если
Р (х)=х34-(а4-/?) х24-(/?2 — а) х-\-Ь,
Q(x) = x34-(2&— Ох2 4-3x4-За — 1.
52
6.3.	Найдите все значения параметров а, Ь, с, такие, что
многочлены Р и Q равны, если
Р (х) = х3-|-ах2-|-(а4-6) х + с — 5,
Q (х) = х3 4-Ьх2 + cx-j-(a — 2c).
6.4.	Найдите все значения параметров а, />, с, такие, что вы-
полняются следующие равенства (при всех х):
а)	х = а(х — 2) (х — 3) + й (х — 1) (х — 3) + £ (* — 2) (х — 1);
б)	х2 = а(х2+ 1)-р (/?хс) (х — 1);
v	1	_ ах-\-Ь . с
(х2 + х4-1)(х-2)—^-2 ’
6.5.	Найдите все значения параметров а, Ь, с, такие, что при
всех значениях х выполняются следующие равенства:
а) х2 —4х + 2 = а(х—1)2 + й(х—1) + с;
б)	х3 — Зх = (х? + ах-]-Ь)(х — 1) + с.
6.6.	Найдите все значения параметров а, Ь, такие, что найдется
многочлен Q, для которого выполняется равенство
х3 + ах24-&х4-2 = (х2Ц-х+ 1) Q (х).
6.7.	Найдите все значения параметров а, b и с, такие, что
многочлен х* + ах? + Ьх + а является кубом двучлена х + ^.
6.8.	Найдите многочлен Р третьей степени со старшим коэффи-
циентом единицей и такой, что Р (1) = О, Р(2) = 0, Р(3)=1.
6.9.	Найдите многочлен Р третьей степени с двумя старшими ко-
эффициентами, равными единице, у которого единица — ко-
рень кратности 2.
6.10.	Найдите:
а)	многочлен второй степени Р, такой, что Р (0) = 0, Р(1) =
= 2, Р(2) = 6;
б)	многочлен третьей степени Р, такой, что Р(0) = 0,
а)	Придумайте такой многочлен Р степени, не большей п,
что P(xl) = yi для любого Z = 0, 1, 2, ..., п.
б)	Выясните, обязательно ли существует такой многочлен
степени п.
в)	Выясните, сколько существует таких многочленов Р, что
p^xi) — yl для всех х( (/ = 0, 1, 2, ..., п).
53
II.	Теорема Безу. Следствия из нее
6.12.	Проверьте, выполняются ли данные ниже условия:
а) х34-3х24-5х —9:‘х—1; б) х4 —	+ — 3;х4-3;
в) х34-2х+7;х-2; г) х™+ ?>х*+ 7+ Ь\х? + 1.
6.13.	Докажите, что выполняются данные ниже условия:
а)	х4 х3 — х — \ х2 — \ \
б)	x3 — 2x2 — 5x + 6;x2 —4x4-3;
в)	х3 — 2х24-* — 2-х2+ 1.
6.14.	Найдите все значения параметров а, Ь, при которых выпол-
няются данные ниже условия:
а) х34-3х24-ах4- 1 \х — 2; б) х5 4-а2-*2 4-За 4- 1 -х— Г,
в) х3 + 3ах24-йх4-2.:х2—1; г) х34-2ах24-^х4-1 -х^1.
6.15.	Найдите все натуральные п, такие, что выполняются дан-
ные ниже условия:
а)	(х2+16Г-(х + 2)2п;х-3; б) (х+ 1У + U~ 1 Г:х;
в)	(х24-х— If — (х2 — х+ l^-x2 — х;
г)	(x2 + 3f — 3(2xf 4-2-х—1.
6.16.	Для данных ниже многочленов Р, Q, R найдите все значе-
ния параметров а и Ь, такие, что остаток от деления Р на
Q равен R:
а)	Р (х) = х3 — 5х + а, Q(x) = x — 2, /?(х) = 7;
б)	Р (x) = x3 + a2x2 — 4f Q(x) = x—1, /? (х)= 1;
в)	Р (х) = х3 + 3 (а + Ь) х2 + (Ь — а) х 4- 2, Q (х) — х2 — 1,
/?(х) = 2х + 3.
6.17.	Известно, что остаток от деления многочлена Р (х) на х—1
равен 2, от деления Р (х) на х —3 равен 1. Найдите
остаток от деления Р (х) на х2 —4x4-3.
6.18.	Остаток от деления многочлена Р (х) на х —2 равен 3, от
деления Р (х) на х—3 равен 4, от деления его на х —4 ра-
вен 5. Найдите остаток от деления многочлена Р (х) на
(х —2)(х —3)(х —4).
6.19.	Найдите остаток от деления многочлена Р (х) = х100 —
— 2х514-1 на Q(x) = x2—1.
6.20.	Найдите многочлен Р четвертой степени со старшим коэф-
фициентом единицей, у которого число —2 является кор-
нем кратности 3, а остаток от деления многочлена Р (х) на
х —3 равен — 1.
54
6.21.	Многочлен Р (х) с целыми коэффициентами представлен
в виде
Р(х) = (х —	— х2)(х—х3) Q (%)+ 1,
где хь х2, х3— различные целые числа, a Q (х) — некий
многочлен. Выясните, может ли многочлен Р (х) иметь це-
лые корни.
6.22.	Многочлен Р (х) с целыми коэффициентами принимает зна-
чение 5 в пяти различных целых точках. Выясните, может
ли он иметь целый корень.
6.23.	Многочлен Р (х) с целыми коэффициентами имеет целый
корень. Выясните, в скольких целых точках максимума он
может принимать значение р2, где р — простое число.
III.	Теорема Виета
6.24.	Найдите коэффициенты многочлена третьей степени со
старшим коэффициентом единицей, имеющего:
а) корни 1, 2, 3;
б)	корень 1 кратности 2 и корень 3.
6.25.	Пусть х1? х2, х3—корни многочлена Р(х) = х3 — бх2 —
— 15x4-1. Найдите:
а) х?4-х^4-4; б) х3 4-х2 4~
X 1 I 1 I 1
в)--------------------
x,-f-x2	Xj+%3 х2 + х3
6.26.	Найдите сумму квадратов корней уравнения
г,995-25г34-2г-(/4-3) = 0.
6.27.	х, у, z — вещественные корни уравнения третьей степени
с рациональными коэффициентами. Докажите, что
£у + ^z + y^z + y^x + z^x + ^y — рациональное число.
6.28.	Известно, что уравнение
ах3 4- йх2 4- сх 4- 6 = О,
где имеет 3 различных целых отрицательных корня.
Найдите а,
6.29.	Известно, что уравнение
х44-(а2 —4) х3 —4х24-« = 0
имеет 4 вещественных корня, сумма которых равна 0. Най-
дите а.
6.30.	Известно, что уравнение
х34-(а2— 1) х2 — 7ах4-3 (а 4~ 1 ) = 0
имеет 3 вещественных корня, сумма которых равна 0. Най-
дите а.
55
6.31.	Известно, что уравнение
х4 — (За + 6) %24-а2 —2 = 0
имеет 4 вещественных корня, произведение которых равно
2. Найдите а.
6.32.	Известно, что уравнение
х3 4- я*2 4- Ьх 4- с = 0
имеет 3 вещественных корня, причем а<0, с>-0. Опреде-
лите знаки корней.
6.33.	Докажите, что уравнение х3-\-ах*-\-bx-\- с = 0, где 6^0,
с=С0, а — произвольное вещественное число, не может
иметь двух положительных корней.
6.34.	Докажите, что при а>0 и произвольном вещественном
b уравнение х34-ах4-й = 0 имеет только один вещественный
корень.
6.35.	Докажите, что уравнение х3 —2х24-5х4-а = 0 при любом
a£R имеет только один вещественный корень.
IV.	Уравнения
В заданиях 6.36—6.68 требуется найти все комплексные кор-
ни данных уравнений.
В заданиях 6.36—6.39 целесообразно пользоваться теоремой
о рациональных корнях уравнения.
6.36.	х3 —4х24-5х —2 = 0.	6.37. х34-2х2- 14х-3 = 0.
6.38.	2х3 — х24-4х-2 = 0.	6.39. 6х44-13х3-6х2-5х4-2 = 0.
6.40.	г2 —4г4-5 = 0.	6.41. г2 — г(2z*4-1 ) + i— 1 =0.
6.42.	г2-2 (z'4- 1) г-2 = 0.
В заданиях 6.43—6.54 полезно применять замену переменной.
6.43.	х4- 5х24-4 = 0.	6.44. хб-28х34-27 = 0.
6.45.	(3x4-1)4— 10(3x4-1)24-9 = 0.
6.46.	(х24-4х)2-3(х24-4х)-10 = 0.
6.47.	(х24-4)4 —6(х24-4)2 —27 = 0.
6.48.	(х2-х-1)24-Зх2 = Зх4-7.
6.49.	2 (х2 —7х4-3)2 = 3 (х —3) (х —4).
6.50.	(х- 1)х(х4- 1)(х4-2) = 24.
6.51.
6.52.
6.53.
6.54.
(х4-4)(х4-5)(х4-7)(х4-8) = 4.
зег-М)2 4x2-f-4
(х2 —2х + 3)2	х2 —2x4-3
х24-Зх4-5 .	4x4-8	__ г
*4-2	' х24-3x4-5 ~
1	2	_ 7
х24-4х	х24-4х— 1 Ю
56
(х+|) + 62 = 0.
В уравнениях из заданий 6.55—6.59 полезны замены пере-
k
менных вида t =	—, где k£R.
Пример. Решите уравнение 5х4 —Збх3 4-62Х2 —36x4-5 = 0.
Решение. Поделив данное уравнение на х2, получим
-36
Введем обозначение / = х4- — • Имеем
X
5(/2-2)-36/ + 62 = 0,
5/2 —36/+ 52 = 0, /, = 2, /2=^-.
Отсюда Xj = 1, х2 = 5, х3 = ~.
э
Ответ. Xj = 1, х2 = 5, х3 = -~.
D
6.55.	6х4—13? + 12л2— 13x4-6 = 0.
6.56.	2х4—15? + 40? —45х+18 = 0.
6.57.	6х4 — 25х3 4-12?+ 25x4-6 = 0.
6.58.	2?-Зх4-?-?-Зх + 2 = 0.
6.59.	5х=Т—16’
Уравнения из заданий 6.60—6.63 могут быть решены как од-
нородные.
Пример. Решите уравнение
6(х2-4)24-5(х2-4)(х2-7х4-12)4-(х2-7х4- 12)2 = 0.
Решение. Поделим на (х2 — 7x4-12)2 (ясно, что значения
х такие, что х2 —7x4-12 = 0 решениями не являются).
х2 —4
Теперь обозначим ------= /.
г	х2 —7x4-12
Имеем 6/24-5^4-1 =0, t\ — ~~• Отсюда
Z	о
х2 —4	___ 1 х2 —4	_ 1
х*-7х+12 ~ И х2 —7x4*12 ~ ~"3 ’
Ответ. Х] = 0, х2=1|, х3=1, х4=1у.
6.60.	20х4 — 28? (?+ 1 ) + 9 (?+ 1 )2 = 0.
6.61.	(?-4х+5)2 + 4(? —4х+5)(х-1) —5(х- 1)2 = 0.
6.62.	(х —2)2(х+I)2 —(х —2)(?—1) —2(х—1)2 = 0.
6.63.	2(? + 2)2 = 9(?+ 1).
57
Уравнения из заданий 6.64—6.68 могут быть решены при по-
мощи разложения на множители их левых частей.
6.64.	х — х24-4х —4 = 0.	6.65. х3+ 10х+11=0.
6.66.	х3 —Зх24-Зх-2 = 0.	6.67. Зх34-Зх24-Зх4-1=0.
6.68.	х44-2х34-2х24-2х4-1 =0.
Задания 6.69—6.75 сводятся к исследованию квадратных
уравнений. В заданиях 6.69—6.75 под корнями понимаются
лишь вещественные корни, a£R.
6.69.	Найдите все значения параметра а, при которых уравнение
х4 — 4х2 4- о2 — 1 = 0
имеет ровно 3 различных корня.
6.70.	Найдите все значения параметра а, при которых уравнение
х4 4- Зх2 4- а — 3 = 0
имеет ровно один корень.
6.71.	Найдите все значения параметра а, при которых уравнение
х4 —2 (а —2) х24-2а4-4 = 0
имеет ровно 2 различных корня.
6.72.	Найдите все значения параметра а, при которых уравнение
х4-2 (а4-3) х24-2а4-9 = 0
имеет ровно 4 различных корня.
6.73.	Найдите все значения параметра а, при которых уравнение
х4 + 2(а-1)х24-3а + 6
х— 1
имеет ровно 3 различных корня.
6.74.	Выясните, при каких значениях параметра а все корни
уравнения
х44-2 (а —3) х2-2а4-9 = 0
по модулю меньше 3.
6.75.	Выясните, при каких значениях параметра а все корни
уравнения
х4 —2(а4-1)*2 —а4-1=0
больше —2.
В заданиях 6.76—6.81 удается найти требуемые значения па-
раметра, пользуясь особенностями указанных корней уравнений.
6.76. Известно, что число 14~Л/2 является корнем уравнения
х3 —а2х24-(2а— 1) х4- 1я| =0,
где a£Q. Найдите а и остальные корни уравнения.
58
6.77.	Известно, что число д/б" 4-2 является корнем уравнения
х3-(а + ^)х2 + (3/?-За)х+1=0
с рациональными коэффициентами. Найдите числа а,
b и остальные корни уравнения.
6.78.	Известно, что число 1-Н является корнем уравнения
х3 — ах2 + (2а — 2) х — 4 = 0,
где а — вещественное число. Найдите а и остальные корни
этого уравнения.
6.79.	Известно, что уравнение
х3 — х2 4-(а 4-3) х — 4а = 0,
где а — вещественное число, имеет чисто мнимый корень.
Найдите а и корни этого уравнения.
6.80.	Известно, что уравнение
х3 — 4Х2 + 9х — 2а = 0,
где а — вещественное число, имеет корень г, такой, что
Rez = -^Imz. Найдите а и корни этого уравнения.
6.81.	Известно, что уравнение
х3 — 4Х2 + 8х — а — 0,
где а — вещественное число, имеет корень, модуль которого
равен 2. Найдите а.
§ 7.	ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА.
СТЕПЕННЫЕ ФУНКЦИИ
I. Основные свойства степенных функций
В заданиях 7.1—7.6 требуется найти области определе-
ния данных функций.
7.1.	// = Д/х2-5х+б.	7.2. у = У/х-5.
_1_ ____________________________ _________
7.3.	у = (х-2)\	7.4. г/ = Д/х2-4х-5 + yj2x-x2.
7.5.	z/ = Vx2-4x + 3 Н-Д/х2-7x+ 12 .	7.6. y = ^x-3~.
В заданиях 7.7—7.11 требуется найти множества значений
данных функций.
Пример. Найдите множество значений функции
у = х-^-А^/х — 1 .
59
Решение. Обозначим t =~\J х— 1 . Ясно, что область значе-
ний данной функции совпадает с областью значений функции
y — t2-\-M-\-\ при /^0. Но из свойств квадратного трехчлена
ясен ответ.
Ответ. [1; + оо ).
7.7.	у = Ух-2.	7.8. у = V/ + 3 __L9. у = Vx2-4x+3 - 1.
7.10.	t/ = x —2д/х. 7.11. z/ = x2 + 2Д/х2 —3.
В заданиях 7.12—7.18 требуется исследовать данные функ-
ции на монотонность. При этом целесообразно использовать тео-
ремы о монотонности композиции монотонных функций.
Пример. Исследуйте на монотонность функцию
х2 — 6х 4- 2 Л/х2 —6x-f-8
Решение. Обозначим t (x) = \Jx? — $x-{-8 (/^0).
Функция y = t2-\-2t — 8 монотонно возрастает на луче
[0; +°°), поэтому функция у = ——------- убывает на множестве
t 4* 2/ — 8
[0; 2) и на множестве (2; + °о). Так как функция у = У[х возра-
стает на луче [0; + оо), а функция у = х? — 6x4-8 возрастает на
луче [3; + 00) и убывает на (—оо; 3], то функция t(x) =
= V*2 —6x4-8 возрастает на [4; 4- °°) и убывает на ( — оо; 2]. Так
как t(x) — 2 при x = 3zbV6~» по теореме о монотонности компози-
ции монотонных функций получаем ответ.
Ответ. Функция f возрастает на ( — оо; 3 —д/б") и (3 — д/б"’, 2]
и убывает на [4; 34-Д/б") и (34-Д/б^ + 00 )•
7.12.	i/ = Vx2-4. 7ЛЗ. у=л]х-3 +Д/х-4.
7.14.	у = Д/х2 —4х—12 + Ух2-7х+12 .	7.15. у=Д/х2-7х.
7.16.	i/ = x + Vx- 1 .	7.17. г/ = х —2 Д/х + 3 .
В заданиях 7.19—7.33 требуется построить графики данных
уравнений. В заданиях 7.19—7.28 это удается сделать с по-
мощью геометрических преобразований.
7.19.	г/ = Д/х-2.	7.20. у=\2х-4.	7.21. у = ^2 |х| - 4 .
7.22.	i/=V|2x-4| . 7.23. z/ = V|2|x| -4| . 7.24. у= |Д/2х-4 -2|.
7.25.	|г/| =Д/2х-4.	7.26. | у - 21 = Д/2х-4.
7.27.	|z/-Д/2х-4 | =Д/2х-4. 7.28. \у-У2х-4 | = Д/2х-4 -2.
60
В заданиях 7.29—7.33 для построения графиков достаточно
провести исследование предложенных функций.
7.29.	у = д/х2 —6x4-5.	7.30. у = У]х—5 +	1 .
7.31.	у = Л]х? — 4х +V%2 + 4x.	7.32. y = x + '\jx— 1 .
7.33.	у = 8х2 — 4у[х.
II. Эквивалентность уравнений
В заданиях 7.34—7.42 требуется выяснить: а) являются ли
данные уравнения следствиями уравнения (х—2)(х —3) = 0;
б) следует ли оно из них.
7.34. х —3 = 0.	7.35.	=
х— 2
7.37. %2~5х+6 =0.
х — 4
7.39. (х — 3) (х — 4) = 0.
0.	7.36. х —4 = 0.
7.38.	5—6 = 0.
7.40.	(х — 3)(х — 4)(х — 2) = 0.
7.41.	(х2 + 2)(х-3)(х —2) = 0.	7.42. х2 + 2 = 0.
В заданиях 7.43—7.49 требуется установить, могут ли при пе-
реходе к данным уравнениям от уравнения f (х) = g (х): а) по-
явиться лишние корни; б) потеряться корни.
7.43.	/(x) + g(x) = 2/(x).	7.44. / (x)-g (x) = (g (х))2.
7.45.	(f(x))2 = (g(x))2.	7.46.
7.47.	=	7.48. Vx-l/(x) = V7=Tg(x).
7.49.	дД-2 f(x)=y/x-2 g(x).
III.	Область допустимых значений уравнения
В заданиях 7.50—7.55 требуется решить данные уравнения.
7.50.	у/х — 5 = д/х —5.	7.51. У/х — 4 + Д/3 —х = 2.
7.52.	ДД-З +Д/5х —х2 —6 +Д/2х + 3 =3.
7.53.	(х2-6х)Д/2х- 1 =0.	7.54. (х-5)Д/х2-7х + 6 =0.
7.55.	Д/х2 —4х = д/х2 —Зх —2.
7.56.	Выясните, при каких значениях параметра а данные урав-
нения имеют ровно один корень:
а)	(х — а)У/х — 5 =0; б) (х— 1)у/х — а =0;
в)	(х — а) л/х+~2а~ = 0;
г)	(х— 1) Д/х2— 2ах4-3а — 2 = 0;
д)	у/х — 2а-\-3 • Д/х2 —(5а —3) х + 4а2 — За =0;
61
e)	У/х2-2ах-\-2 = У/х? — 2х, ж) yjx2 — 2x-{-a ='\jx2 — x\
з)	~\/2х?—х = ‘\]х?-{-ах—а ;	и) Д/х2—х = Д/(5а — 1) х—4а2;
к) у/х2-4х-{-3 =л/2 (а —2) % —4а + 3 .
7.57.	Выясните, при каких значениях параметра а данные урав-
нения не имеют решения:
(х — а) д/х — За 4- 1	п	г:---z- /-----
а) ---т===— = 0;	б) у2х —3 = ух —а;
ух —2а —5
в) Д/^“Зх4-3 —а =yjx—a; г) д/х2—(4а + 1) х-\-а =^х— 1 .
7.58.	Выясните, при каких значениях параметра а число 2а яв-
ляется корнем уравнения
Д/2х —а —2 • д/х —а2 + 3а —4 • д/х — 5а + 11 — 0.
7.59.	Выясните, при каких значениях параметра а урав-
нение
Л]х — а2 «д/х —4а + 3 =0
не имеет корней, больших 2.
7.60.	Найдите все значения параметра bt такие, что найдет-
ся значение параметра а, при котором число 1 является
корнем уравнения
Д/2х —ах+ 1 =У/х-Ь-{-а .
7.61.	Найдите все значения параметра bt такие, что при
любом значении параметра а число а является корнем
уравнения
V(3&-3)x+2Z> =У/х2-(а+\)х + аЬ + 2Ь2.
IV. Область возможных решений
В заданиях 7.62—7.64 требуется решить данные урав-
нения. При этом полезно иметь в виду, что решением урав-
нения вида y/f (х) =g (х) может быть только такое число х0,
при котором g(xo)^O.
7.62.	V4-X2 = - 1.	7.63. Л/4- х2 = х - 3.
7.64.	Л]х2-4 +V8-X3 = х-2.
7.65.	Найдите все значения параметра а, при которых уравнение
Д/^ + я2 — х — а
имеет решение.
62
7.66.	Найдите все значения параметра а, при которых уравнение
V^2 + 2a+ 1 = 1
имеет решение.
7.67.	Найдите все значения параметра а, при которых данные
уравнения не имеют решения:
а)	Д/2ах —- х — а2 — а 4-1 = х— 1;
б)	д/(4 —4а) х — а — 8 = х — 1.
V. Различные методы решения
иррациональных уравнений
В заданиях 7.68—7.88 требуете^ решить данные уравнения.
Для выполнения заданий 7.68—7.74 достаточно возводить
в соответствующие степени обе части уравнений.
7.68.	д/2%2—11x4-13 = х — 3. 7.69. Д/* + 3 4-^/2x4-7 = 5.
7.70.	У/7х-5 -Д/2х-3 =2. 7.71.	-2х+"б =х-1.
7.72.	Д/Эх2 —8x4-7 = х4- 1.	7.73. (24-х)= 625х.
Д/х+13	д/х+13 _ 128	—7
'	х-7	'20	5 V
При решении заданий 7.75—7.78 полезно проводить замену
переменной.
Пример. Решите уравнение
Д/2 —х -4-Л/х4-7 =3.
Решение. Введем новые переменные
и = Л/2 — х, v = = Д/х4- 7 .
т-	( u + v — 3
Имеем систему уравнений < _
( u + tr = 9.
(	и — 2 ( и = 1
Решая ее, находим <	<
(	v= I, ( v = 2.
Ответ. х=1, х= — 6.
7.75. д/х” —2д/х" = 3.	7.76. х2 —6х = 5Д/х2 —6x4-12 — 16.
7.77.	+ 6	= 5. 7.78. л/5^7+л/Т+4 = 3.
63
В заданиях 7.79—7.81 полезно домножать выражения в ле-
вой части на сопряженные.______
7.79.	Убх2 4-2x4- 1 — yj5x2 + 2x — 8 = 1.
7.80.	У]4^ + 7х + 3 -Д/^ + бх + б = 3 —х.
7.81.	У/х2 — 4x4*5 4-V*2 — 5x4-6 = х — 1.
Выполняя задания 7.82—7.83, полезно иметь в виду, что так
как равенство а3-{-Ь3-\-с3 = ЗаЬс выполняется тогда и только тог-
да, когда а-\-Ь-{-с = 0 или а = Ь = с, то уравнение вида
+^g(x) =h(x) эквивалентно уравнению f(x)+g(x)-
3 ________________
-(/i(x))3=-3 y/(x)g(x) h(x) при условии, что не существует,
таких х, что f (x) = g (х) = — (h (х))3 (это важно иметь в виду
в случаях, когда затруднительно сделать проверку).
7.82.	~\15 + х +Д/4 —% =3.
7.83.	Д/х + З + Д/5 —х = — ДЯ-
Для решения заданий 7.84—7.88 целесообразно использовать
свойства соответствующих функций.
Пример 1. Решите уравнение
Ух2 —4x4-5 4-Д/2Х2-8x4-17 = 4.
Решение. Заметим, что Д/х2 — 4х4~5 =У(х— 2)24- 1	1,
а У2х2-8х4-17~ = У2(х-2)2 + 9 >3, поэтому функция /(х) =
= Д/х2 —4x4-5 4-V2X2 —8x4- 17 при нимает только значения, не
меньшие 4. Ясно, что равенство достигается только при х = 2.
Ответ. х = 2.
Пример 2. Решите уравнение
81---------------------
Д/х + 2 = — 2 —Зх.
Решение. Заметим, что х= — 1 — корень данного уравне-
8/---------------------
ния, но функция у=\х-{-2 возрастает на луче [ — 2; + 00)»
8 у--
а функция у = —2 — Зх убывает на нем, поэтому \х4-2 > 1 > .
81----
Х>—2 —Зх при х> — 1, — 2 —Зх> 1 >ух4-2 при х<— 1
и других решений данное уравнение не имеет.
Ответ. х= — 1.
7.84.	д/х-1 — 5—-2х.	7.85. У^х-2 ^[О-х2.
7.86.	У5х4-6 +Д/х24-4х-3 = 11-2х.
7.87.	Vх24-2x4-5 +3jx2 + 6x+ 10 =3.
7.88.	Ух2 —4х-}-7 4- 3 УЗх4-7 = 17 - х.
64
VI. Системы иррациональных уравнений
В заданиях 7.89—7.96 требуется решить данные системы
уравнений.
7.89.	= 0	790	=0
( х2 — у2 = 9.	(х2 = 4г/.
7.91.
\j3x-\- у =х — 2
х+у = 1.
У — х = 2
Д/х2-4г/+ 12 + V//-4 = Д/11—х.
'ЗД/15-у =х+13
. У/Зух — 2у2 = х — 2у.
7.95.
х — у + У/х—у + 3 =3.
Л/х3+1 =Уу3 + 3//2 + Зу + 2________
. Д/х2 —4xz/ + 4i/2+ 1 +Д/2Х2 —8xz/ + 8i/2 + 4 =3.
VII. Иррациональные неравенства
В заданиях 7.97—7.114 требуется решить данные неравенст-
ва. Они решаются либо непосредственно, либо с помощью мето-
да интервалов (при этом, разумеется, сначала приходится ре-
шить соответствующие уравнения).
7.97.	Д/Зх + 4 > —1.	7.98.	V3x4-4 >1.
7.99.	Д/Зх+4 >2х —4.	7.100.	ДЧх-З < -1.
7.101.	дЧх-З <1.	7.102.	"\/4x —3 <2x— 3.
7.103.	VXZ2 <2.	7.104.	Vx+2 t
	х— 5		x — 4
7.105.	(х2 —9х+ 14) у/х —	5 >0.	
7.106.	(х —3) Д/х? — 6х-Н	j >0.	
7.107.	(х2 —8x4- ^(Л/х2-	- 10x4-21 >0.	
7.108.	(х2 — 5 х + 4) "V х2 —	7x4-10	>0.
7.109.	Д/20 —2х —x-f-6 х — 7		
3 Заказ 1259
65
7.110.	Л/5х+1 +Д/2х-2 >Д/10х4-6.
7.111.	Д/д/% + 7 -х<Д/х-1 . 7.112. x2 —2 Д^-Зх-! >44-3x.
7.113.	л/^±4 4-2Д/^| <3. 7.114. Д/4х4- 1 >^±i.
у x — 3	v *4-3	v	x
VIII. Иррациональные уравнения
и неравенства с параметром
В заданиях 7.115—7.117 требуется установить, сколько кор-
ней имеют данные уравнения в зависимости от а. Для решения
этих заданий полезно построить графики соответствующих ле-
вым частям уравнений функций.
7.115.	Д/|2х —2| — 1=а.	7.116. Д/2х —х2 = а.
7.117.	Д/х2— 5x4-4 4-Д/х24-5х—6 = а.
В заданиях 7.118—7.120 требуется решить данные урав-
нения.	______
7.118.	yjx—a =а. 7.119. Д/2х —а =х. 7.120. Д/Зх—а =а — 2х.
В заданиях 7.121—7.124 требуется решить данные неравен-
ства.
7.121.	7.122. (д/х — а) (д/х—1 — 2а)>0.
7.123.	>а- 7124- Д/4х + а >х.
7.125.	Выясните, при каких значениях параметра а уравнение
д/1 —х2 — х — а
имеет единственное решение.
7.126.	Выясните, при каких значениях параметра а уравнение
д/х — 1 = х — а
имеет два решения.
7.127.	Выясните, при каких значениях параметра а уравнение
Д/х —3 — а — | х |
имеет решение.
7.128.	Выясните, при каких значениях параметра а множеством
решений неравенства
V-Ч /	2
х—а Д/х ах— а
будет отрезок длины меньше единицы.
66
§ 8. ЛОГАРИФМИЧЕСКАЯ И ПОКАЗАТЕЛЬНАЯ ФУНКЦИИ.
ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
И НЕРАВЕНСТВА
I. Область определения логарифмической функции
В заданиях 8.1—8.8 требуется найти области определения
данных функций.
8.1.	z/ = lnx2.	8.2. z/ = lg(x —5).
8.3.	z/ = lg(x—2)4-log2(3 — х). 8.4. z/ = lg (х2 —5x4-6).
8.5.	i/='n	•	8-6’ У = ^~{ >og2(x4-2).
8.7.	i/ = logx 3.	8.8. «/ = logx+4(x2— 1).
В заданиях 8.9—8.11 требуется решить данные уравнения.
8.9.	(х+ 1) log2 х = 0.
8.10.	log2 (х2 —4х—1 )= log2 (2Х2 —6).
8.11.	logx(x2 + 4x — 4) = 2.
8.12.	Выясните, при каких значениях параметра а функция
z/ = log2(x — а)
определена на множестве (1; +°°)-
8.13.	Выясните, при каких значениях параметра а функция
у = In (х2 —4х + 3)
определена на луче [а; +°°)-
8.14.	Выясните, при каких значениях параметра а функция
i/=lg(x2 —2(а-ь 1)х-ь 1—а)
определена на отрезке [0; 2].
8.15.	Выясните, при каких значениях параметра а функция
In (%2 —2ax-f-a)
У х-\-а
определена на отрезке [1; 2].
II.	Основные свойства логарифма и степени
В заданиях 8.16—8.20 требуется изобразить множества точек
с координатами (х; //), для которых выполняются данные
условия.
8.16.	Iog2xz/ = log2x4-log2 у.
8.17.	log2x// = log2( —х)4-log2 ( — //).
8.18.	Iog2x24-log2у2 = 2 log2 |х| 4-2 log2 |z/|.
67
8.19.	log^2 2 + log? 2 =| logx 2 + 1 logj, 2.
8.20.	Iog?«/2 = logx(— y).
В заданиях 8.21—8.24 требуется выяснить, всегда ли верны
предлагаемые равенства, а если не всегда, то установить, могут
ли они быть верны для каких-то чисел.
8.21.	Iog2(x+ i/) = log2 x + log2 у. 8.22. 2'°g2X = x.
8.23.	log2 xz/ = log2 x log2 y.	8.24.	=
В заданиях 8.25—8.31
требуется упростить данные вы-
ражения.
8.25. Iog2 16 у/2.
8.26.
8.28.
3 + log J
~2
8.29.
logl255V5. 8.27. 3log9'3.
l0g4 7	'°g<a-|Og°3
------	log । a
'°g4A/3 . 8.30. 3log23. 8.31. a
log8 9
5
В заданиях 8.32—8.35 требуется найти значения данных вы-
ражений при указанных условиях.
8.32.	log2 20, если log25 = a.
8.33.	log36, если log2 3 = €/.
8.34.	log6 125, если log25 = a, log3 25 = &.
8.35.	log26, если log2 15 = a, log8 75 = &.
III. Свойства логарифмической
и показательной функций
В заданиях 8.36—8.55 требуется исследовать данные функ-
ции на монотонность.
В заданиях 8.36—8.48 исследование проводится элементар-
ными средствами с помощью теоремы о монотонности компози-
ции монотонных функций.
Пример 1. Исследуйте на монотонность функцию
/(x)=log1(x2 —6х + 8).
2
Решение. Ясно, что функция */ = log} t убывает на луче
~2
(0; +°°), а функция / (х) = %2 —6x4-8 возрастает на луче
[3; 4" 00) и убывает на луче (— оо; 3). Учитывая область опреде-
68
ления логарифмической функции, по теореме о монотонности
композиции монотонных функций получаем ответ.
Ответ. На луче (— оо; 2] функция f возрастает, а на луче
[4; + оо ) убывает.
Пример 2. Исследуйте на монотонность функцию
/(x) = log^x —4 log2 х.
Решение. Введем новую переменную /(x)=log2x. Ясно,
что функция t возрастает на множестве (0; +°°), а функция
у (t) = t2 — 4t возрастает на луче [2; 4-оо) и убывает на луче
( — оо; 2]. Поэтому по теореме о монотонности композиции моно-
тонных функций получаем ответ.
Ответ. Функция / возрастает на луче [4; 4- оо) и убывает на
промежутке (0; 4].
8.36. г/ = 2?~6х+4.
8.38. y=\OgL^±l.
8.40. y = \ogl х — 8 log3 х + 2.
8.42. у = "\/log2 х —9.
8.37. y — log2(x2 — 5x+4).
x+l
8.39. z/ = 2x“'.
8.41. i/ = 4x —2x+3.
8.43. у
1
2х —8 ’
8.44.
8.46.
8.48.
8.45. у
1
9х — 2-Зх+2 ’
log2 X — 1
log2 4x
__________1________
Vlog2 X — 2 log, X
7	7
8.47. у
3
6 In х— In2 х —5
В заданиях 8.49—8.55 предполагается исследование функций
на монотонность с использованием производных.
8.49.	z/ = log3 х—3 log2 х. 8.50 т/= 35х — 5 - 27х + 2.
log2, х — 2
2
8.53.	у = ех— х4-1.	8.54. г/ = 4х — 3-2Х+* 4-х In 16+1.
8.55.	z/ = ln(x24-3)4-ln(x + 3) — 2.
В заданиях 8.56—8.68 требуется найти множества значений
данных функций.
69 •
В заданиях 8.56—8.65 для этого полезно вводить новые пере-
менные.
Пример. Найдите множество значений функции
/(x)=log2(x2 — 4x4-6).
Решение. Функция / определена при всех значениях пере-
менной х. Множество значений функции / (х) = х2 —4x4-6— луч
[2; 4-°°)- Но функция z/ = log2t на этом множестве принимает
все значения из множества [1; 4-°°) и только такие значения.
Ответ. [1; 4- 00 )•
8.56.	у — log2 х — 4 log2 х4-1-	8.57. // = Д/1п2 х4-2 .
8.58.	z/ = 4x4-2x+2.	8.59. у = -±— .
2	3
8.60.	у= х 2	1-----— •	8.61. z/ = log2(x2 —4х+3).
*°g2 *Ч~2 log2 x-f-3
8.62. y = log1(7x-x2-12).	8.63. z/ = log2^l-.
8.64. z/ = (l)x2-6x.	8.65. z/ = log2(9x —Зх4-2).
В заданиях 8.66—8.68 предполагается применение произ-
водной.
8.66. z/= 1 п х — х4"2.	8.67. у = х-ех. 8.68. у = х\п х— х.
В заданиях 8.69—8.93 г
функций.
В заданиях 8.69—8.86
преобразования.
8.69. у = log2 х — 1.
8.71. у= log2 | х| — 1.
8.73. у= Ilog2 |х| - 11.
8.75. z/ = log2(x—1)—1.
8.77. z/ = log2(l-x)-l.
8.79. // = log2 I |х| — 11 — 1.
8.81. z/ = 2x+1.
8.83. z/ = 2'-|x|.
8.85. z) = 2lxl + l.
ребуется построить графики данных
полезно применять геометрические
8.70.	«/=log2( —х)— 1.
8.72.	у — |log2x— 11.
8.74.	z/ = 2 (log2(2x)—1).
8.76.	z/ = log2(|x|-l)-l.
8.78.	у = log2 |х— 11 — 1.
8.80.	z/ = log2(2x— 1)— 1.
8.82.	у = 2'~х.
8.84.	z/ = 2|l-xl.
8.86.	у= |2x+1 - 11.
В заданиях 8.87—8.90 для построения графиков достаточно
провести исследование данных функций элементарными мето-
дами.
8.87.	у= '°g2% .	8.88. z/==4x —2х+1.
Iog2 х —3
70
8.89. i/ = log1(x2 + 2x).	8.90. y= log2(x+ 1)+ log±(x — 1).
2	7
В заданиях 8.91—8.93 для построения графиков приходится
использовать производные.
8.91. z/ = 8x —3-2Х.	8.92. У = ^-	8.93. у = х-е~х.
IV. Решение логарифмических
и показательных уравнений
В заданиях 8.94—8.132 требуется решить данные уравнения.
Задания 8.94—8.98 могут быть решены логарифмированием
данных уравнений.
8.94. 2Х = 4Х+3.	8.95. 32х“3-5 3х-2 = |.
8.96. 3х • 5х-1 = 1.	8.97. 32х+' • 52х~1 = 4.
8.98.	x'gx=10 000.
Задания 8.99—8.102 могут быть решены с помощью потенци-
рования данных равенств. При этом полезно переходить к одно-
му основанию логарифмов.
8.99.	Iog2x4 = 4.	8.100. log2 (2Х+ 1 )=х+ 1.
8.101.	log2x + log2(x — 4)=log25.
8.102.	Iog2(x— l)+log4(x+ 1 )2 + logt (x —2) = 3.
7
В заданиях 8.103—8.115 для решения данных уравнений по-
лезно применять метод замены переменной.
8.103. 2х+44-2х+1+3-2х+2= 120.
8.104. 4х —7x+2 = 7x+1 — 2-4х+1.
8.105. 4х-|-2х+2 + 4 = 0.	8.106. ^-j- + 2‘-x = 2.
8.107. 9-4х— 13-6х + 4-9х = 0.
8.108. 10-4х —9-2х(4х+ 1 ) + 2 (16х + 2-4х+ 1 ) = 0.
8.109. log2 % + logs 2%+ logs 8х = 7.
8.110. log2 х2 + 2 log4 %2 + logi6 *4 = 5.
8.111. 1g2 х — 31gx + 2 = 0.	8.112. log2 x— logx 16= — 3.
8.113. —!-----1----—= —2. 8.114. -^2.---------— =—.
lgx-1	Igx — 3	log,- В * 1о?24* log2, X — 4
4	2
8.115. Iog2(3x+1)4-2 log4(3х-1) = 3.
71
Задания 8.116—8.121 удается решить, представляя данные
выражения в виде произведений.
8.116.	In х lg х — 2 = lg х— 2 In x.
8.117.	Iog5 x log6 x + 12 = log5 x4 + log6 x3.
8.118.	Iog2 4x log3 log3 3x — log2 32x.
8.119.	6x + 3 = 3(3x-'4-2z).
8.120.	2х-log2 x + 1 =2X+ log2 x-
8.121.	3-x'°8^ = ~Qlog2X.
Уравнения из заданий 8.112—8.132 удается решить, исполь-
зуя свойства соответствующих функций.
Пример. Решите уравнение log2x = 6 — х.
Решение. Заметим, что х = 4, очевидно, является корнем
данного уравнения. Но функция f (х)= log2 х возрастает на луче
(0; + оо ), а функция g (х) = 6 — х убывает на этом же множестве,
поэтому для всех х>4
f(x)>f(4), a g(x)<g(4) = /(4);
для всех х<4
/(х)</(4), a g(x)>g(4) = /(4).
Следовательно, других решений данное уравнение не имеет.
Ответ. х = 4.
8.122. Зх+1 = 11—2х.
8.124. 2х + 5х = 7х.
8.126.	log3(x + 5) = log^x4-4
8.128.	2 log2 |х| =5 — х2.
8.130.	2*+2	5х4~3 X
8.132.	6 —Зх’!	10 х	2х— 1
8.129. 2^ + ^2 — х2.
8-123-(!)'+©'='
8.125. Iog2x=3~x + |.
8.127. х log2 х = 24.
8.131. log2(Зх + 4) = 2-5х.
V. Решение логарифмических
и показательных неравенств
В заданиях 8.133—8.162 требуется решить данные неравенст-
ва. При этом достаточно сначала решить соответствующие урав-
нения, пользуясь всеми перечисленными выше методами, а по-
том применить метод интервалов.
72
8.133.	2х2+4х+4>2.	8.134. 2х-Зх“2>4-
8.135.	х1е х> 10.	8.136. (х —3) log2 х>0.
8.137.	(х+ 1) log2(x2+ 1)>0.
8.138.	(x2-4x-5)log2(x2-4x + 4)>0.
8.139.	(х —4)log2(x — 3)>0.	8.140. (х —3) log2(x—2)<0.
8.141.	(х2 —5x4-6) log2(х2 —Зх + 3)<0.
8.142.	(х— 1)(2Х — 2)>0.
8.143.	(х2 + 4х4-3)((|)х-8)<0.
8.144.	(|у-2х+1>3“х-2.
8.145.	Iog2 х log3 х> log3 х34- log2 х2 —6.
8.146.	2х- log3 х4- log3 x<2x+1 -|-2.
8.147.	4-3x-logj x4-36 log2 x-|-9>3x.
7
8.148.	2x+4 + 3-2x-2>67.	8.149. 4х-5-2x + 4>0.
8.150. log2 x4-3 log, x—10^0.
3	3
log2, x—4
8.151.	4‘— 1	8.152. —		 log] X— 1	<0.
8.153.	2 log, 2 4			2 log2 2-r2	
	log2 X — 2 log2 X	l°g2|	
8.154. log2(9x-2-3x+,4-7)> 1. 8.155. Q)x '4-1>2x.
8.156. log2x4-3^(-0x
8.157. 512'\/x2-6x4-i0 2xX^26x.
8.158.
2x+l-7	10
x — 1	3 — 2x
Задания 8.159—8.162 связаны с решением неравенств вида
log }g(x)>a и f (х)ё b. Они решаются или переходом к но-
вому основанию, или непосредственным рассмотрением случаев,
когда /(%)>» 1 и когда
Пример. Решите неравенство logx(х2-{-2х)> 1.
Решение. Область допустимых знамений неравенства
(0; 1)U(1; +оо).
73
На ОДЗ неравенство эквивалентно совокупности
1
Ответ. х> 1.
8.159. Iogx+1 (х2 —4%4-1)> 1.	8.160. log2x+3 х2
8.161. logx+2 (х2 —Зх)^ logx+2 х. 8.162. х2х~5>1.
В заданиях 8.163—8.167 требуется построить множества то-
чек с координатами (х; у), удовлетворяющими данным условиям.
8.163. logxz/^l. 8.164. Iogx+y 2у 1. 8.165. logx (2х + у)^ 2.
8.166. log^^ + i/2)^ 1.	8.167. log?+j/2 у^\.
2
VI. Системы логарифмических
и показательных уравнений
В заданиях 8.168—8.179 требуется решить данные системы
уравнений.
f х4-« = 6	(х— у—1
8.168.	{ ,	, , о 8.169. I
log2 х+ log2 у = 3.	[4'4-2*= 18.
х2-|-*/2 = 68	(Зх+* = 9
log2x-log2z/ = 2.	‘	’ [ log2(x-|- l)4-log2(i/4- 1) = 2.
, log3(х — у)— 1
8.172. ё У’
10-25*-5Х~ = 125.
8.170.
8.173.
log2x4-2 log4 у = 3
3 log8(x+ 1) — log^(z/— l)=log13.
2
| 92х+* — 9х-3* = 6
8’174' I logx+i (// + 3)4-logx+l (г/ + * + 4) = 3.
О1__ ( log2x2 + log3 </3 = 7
0.1 /О. S
[ log2 х —2 10g3z/ = 4.
74
8.176.
8.178.
8.179.
Iogx_2(xz/ — x—2«/4-2) + | logy-j (x2 —4x + 4) = 3
. Iogx+1 (y + x — 2) — logj/+2(x2+z/2)= — 1.
logx+i (xy + %+//+ 1) + logx+jZ(z/ + 2) = 4
2 •ogx+i (У+ 0 — logx+jz(t/2 + 2x + xi/ + 2//) = 2.
xy = y2x
x3 = y2 (x
&=y*x
VII. Исследование логарифмических
и показательных уравнений и неравенств
8.180.	Найдите все значения параметра а, при которых данные
уравнения имеют ровно один корень:
а) (2х — a) log2 х = 0; б) (х— 1) log2 (х — а) = 0;
r)10gi(2x_0)=l.
8.181.	Найдите все значения параметра а, при которых данные
уравнения имеют хотя бы одно решение:
Га^4х —2 (а + 3)-2х —а-|-9 = 0;
б' У-2(а+\).У + 2а+1 = Q
^^ioga(^—2«)= 1;
Г) log2(x—a)—log2(x —За)= 1;
д) log2(x2 — 3x + a)=log2(x — 3).
8.182.	Найдите все значения параметра а, при которых каждое
из данных уравнений: 1) имеет хотя бы один корень, боль-
ший 2; 2) не имеет корней, меньших 2:
а) т-2—тт---------=0’ б) ———=°;
log2 X — 2а log2 X — a	log2(x—а)—1
Q (2х — а) (зх — ^--а^ = 0; г) (2х — a) log2(x + a) = 0;
д) 9х —2 (а —2)-Зх + а = 0; е) iog2(x2 — 4ах + а-\-1) = 0;
ж) log2 х —2а log2 х-|-4а —3 = 0;
iog2 х— 2а log2 %4-За
7^4	= ‘
75
В заданиях 8.183—8.186 требуется
выяснить, сколько корней имеют данные
уравнения в зависимости от а. Для реше-
ния данных заданий целесообразно ис-
пользовать графики.
S.,83. (1)-6 (1)-=а.
8.184.	log2 х — 4 log2 х = а.
8.185.	8х —3-4Х —9-2х+1=а.
8.186.	log3 х— 12 log3 х = а.
Для решения заданий 8.187—8.189
полезно построить множества всех точек
с координатами (х; а), удовлетворяющи-
ми данным уравнениям.
Пример. Выясните, при каких
значениях параметра а уравнение
logx-2 (х2 + ^) = 2 имеет единственное решение.
Решение. Данное уравнение эквивалентно системе
х>2
х=/= 3
а = 4 — 4х.
Построим множество точек с координатами (х; а), удовлетво-
ряющими этой системе (рис. 6). Из чертежа ясен ответ.
Ответ. (—оо; —8)0(—8; —4).
8.187.	Выясните, при каких значениях параметра а уравнение
logx_, (?4-а)= 1
не имеет решений.
8.188.	Выясните, при каких значениях параметра а уравнение
(*+«) = 1
имеет хотя бы одно решение.
8.189.	Выясните, при каких значениях параметра а уравнение
|0§2х+2<г(^ + а2)=1
имеет единственное решение.
Задания 8.190—8.194 посвящены исследованию неравенств.
8.190. Выясните, при каких значениях параметра а неравенство
log2 х — 2 (а + 1) log? x + a-f- 3>0
выполняется при всех х>0.
76
8.191.	Выясните, при каких значениях параметра а неравенство
2(а + 2)-2х-4х + а<0
выполняется при всех значениях х.
8.192.	Выясните, при каких значениях параметра а неравенство
log2*-l <Q
log2 х — а
выполняется на интервале (2; 3).
8.193.	Выясните, при каких значениях параметра а неравенство
3х-5а
выполняется на интервале (1; 2).
8.194.	Выясните, при каких значениях параметра а неравенство
9х — 2(а —3)-3Х — а-4-5^0
выполняется на отрезке [1; 2].
§ 9. ЭЛЕМЕНТЫ ТРИГОНОМЕТРИИ
I.	Преобразования тригонометрических выражений
9.1.	Найдите sin 2а, если sin а — cosa = a.
п о тт «	2 sin а4~3 cos a	Q
9.2.	Найдите -------------, если tga = 3.
3sin а —5 cos а
9.3.	Известно, что Найдите tg а.	sin a —cos а 	 1
		2sin a4~cos а 4
9.4.	Известно, что	2 sin a4-cos а 1
		5sin a —cos а 3
Найдите cos 2а и sin 2а. ;
9.5.	Найдите cos^~+a^, если cosa = -| и а£^ — ; 0^.
9.6.	Найдите tg^+2a^, если tga = 3.
9.7.	Найдите cos(a + P), если cosa = 4-, cos Р = тг и углы
э	о
аир лежат в первой четверти.
9.8.	Найдите cos а, если cosp=y, cos (а +Р) = ^ и углы
аЦ-Р и р лежат в первой четверти.
9.9.	Докажите, что a + Р— , если 0<а<у, 0<Р<у и
1	д/з”
sina = —, sin р = -^---.
3	3 о
3
9.10.	Известно, что tg2a=——. Найдите tg а.
77
В заданиях 9.11—9.20 требуется найти данные произведения
и частные.
sin 1° sin 2° ... sin 90°	g 12 sin 1° sin 2° ... sin 45° cos 46° cos 47° ... cos 89°
sin 91° sin 92° ... sin 179°	
ctg 1° ... ctg 179°.	9.14. tg l°tg2°... tg89°.
sin 80° — sin 40°	_ .	sin 70° -f- sin 20° 9.16. 	r=	. cos 35°4-y3 sin 35°
cos 70°	
cos 20° cos 40° cos 80°.	Л i o	л	2л 9.18. cos — cos — . 5	5
sin 10° sin 30° sin 50°sin 70° sin 90°.
л 4л 5л
cos — cos — cos — .
9.11.
9.13.
9.15.
9.17.
9.19.
9.20.
В заданиях 9.21—9.26 требуется найти данные суммы.
9.21.	sin 10° cos ll°+cos 35° cos 54° —sin 46° sin 65°.
9.22.	sin!70“+-itg20"sin 140“.
9.23.	10. cos 20.
sin 20°
9.24.	cos— cos Дг-.
9.25.	cos 24° + cos 48° — cos 84° — cos 12°.
9лл	2л * 4л * 6л
.26. cos—+ cos—+ cos —.
9.27.	Докажите, что
/гг-f-l \ . гга
sin —al sin —
sin a + sin 2a + --- + sin na =------------ .
sin У
В заданиях 9.28—9.31 требуется построить графики данных
функций. Для этого полезно проводить преобразования соответ-
ствующих выражений.
9.28.	z/ = sin2 %4-cos2 х.	9.29. // = tg x-ctg x.
9.30.	z/ = ^i±Z±2!±_lsin 2x.	9.31. y=-----—-------.
cos x— sin x Z	(tg 2x— tg x) cos 2x
Задания 9.32—9.43 связаны с обратными тригонометрически-
ми функциями. В заданиях 9.32—9.36 требуется вычислить ука-
занные значения.
9.32.	a) sin^arcsin^; б) arcsin ^sin^.
9.33.	a) sin arcsin sin ; б) sin arcsin sin ДД .
1	3
9*34. sin2arctg3. 9.35. cos arcsin —.	9.36. tg arccos — .
о	Ь
78
9.37.	Найдите arcsin х, если arctgx = -^-.
9.38.	Докажите выполнение следующих равенств:
ч . 3 .	5	.63
a)	arcsin — + arccos — = arcsin — ;
7	5	13	65
б)	4arctg|-arctg^9=^-^
в)	arctg| + arctg| + arctgy + arctg-^ = ^-.
В заданиях 9.39—9.43 требуется построить графики данных
уравнений.
9.39.	у = sin (arcsin х).	9.40. у = arcsin sin х.
9.41.	arcsin х= arcsin у. 9.42. z/ = sin (arccos х).
9.43. arcsin х= arccos у.
II. Основные свойства
тригонометрических функций
В заданиях 9.44—9.53 требуется найти области определения
данных функций.
q 44	—	1	q 45 n —	sin x-f-sin 3x „ . „	1 -	 Ч 4П // 		
		
	sin x	sin 2x	tg2 x-f-1
q 47 .. —	1	q 48	—	;	!	 q 4Q и — яrcsin
U.T I . у		
	sin x2	sin (x2-2x) '
9.50. i/ =	arcsin 4x	_ _ . 6i_, . 9.51. y-	^arctgx + y.
9.52. y =	1	1 arcsin x4-arccos — . X	9.53. y — arcsin (x2 — 4x4-4).
В заданиях 9.54—9.76 требуется найти области значений
данных функций.
Пример. Найдите область значений функции
sin3 х — 3 sin2 х+2 sin х
у =--------:---;------•
sin X— 1
Решение. Очевидно, у = sin2 % —2 sin х (sin х=/= 1). Поэтому
достаточно найти область значений функции
y = t2 — 2t при /£[— 1; 1).
Ответ. (— 1; 3].
9.54.	f/ = sin2 а:.	9.55. z/ = sinxcosx.
9.56.	у = 2 sin х4-3 cos х.	9.57. z/ = cos2 х — 6 cos х4-5.
9.58.	у —2 sin2 х— sin х на [0; л].
9.59.	z/ = tg2 х —3 tg х на [ —J -^]'
79
9.60.	У	_ 1	9.61.	y—	2 cos x-h1
		cos2 X				cos x —3
9.62.	У	= A/cos х+ 1 .	9.63.	y=	Д/cos X— 1 . fx — sin2 x
9.64.	У	= У]4 cos2 х —cos x.	9.65.	It		\	6/
				У	Л
9.66. 9.68. 9.70. 9.71. 9.73.	У	sin2 x— sin x	9.67. 9.69. 9.72. 9.74.	11 		x 6" sin 2x —2 sin x
		sin x— 1 sin2 x— sin x		У	cos x — 1 arcsin 2x. arctg x-h 1
	У У	sin2 x — 3 sin x-f-2 = arcsin2 x —2 arcsin x. arccos x		У = 11 		
	У У	arccos x-p3 = y/arctg x.		у — У —	2 arctg x-f-3 arcsin ^x2 —2x + -|
9.75.	У	x arcsin x	9.76.	У —	x-h 1 Я Г С P П Q 	'	
		X			Q 1 V V С/ О	• 2 (x— 1)
В заданиях 9.77—9.84 требуется исследовать данные функ-
ции на периодичность, отыскивая наименьший период там, где
он есть.
Пример. Исследуйте функцию /(x) = cos2x на периодич-
ность.
Решение. Так как функция y — cosx периодична с перио-
дом 2л, функция f периодична с периодом л. В самом деле, для
любого х имеем cos 2 (х +tt) = cos (2х + 2л) = соз 2х. Докажем те-
перь, что л — наименьший период данной функции. Предполо-
жим противное: пусть Т — период данной функции и 0<Т<л.
Но тогда для всех х имеем cos 2 (х + T) = cos 2х. В том числе это
равенство должно выполняться и для х = 0, отсюда cos 2Т = 1, но
таких Т£(0; л) нет — противоречие.
Ответ. Данная функция периодична, наименьший период л.
9.77.	£/ = sin Зх. 9.78. z/ = sin2x. 9.79. z/ = VC0S х •
9.80.	у — sin x + cos х.	9.81. z/ = cos+cos j •
9.82.	у = sin 6x + cos 9x.	9.83. // = соэлх.
9.84.	y = cos x-J-cos лх.
В заданиях 9.85—9.89 требуется определить промежутки
знакопостоянства данных функций.
9.85.	у = sin (х+у).	9.86. z/ = cos (х —-0 sin ^2x + j).
9.87.	y = tg х sin (х— 1).	9.88. у = sin2 х— sin х.
9.89. у
COS X
2 cos х— 1
ЙО
В заданиях 9.90—9.94 требуется исследовать данные функ-
ции на четность и нечетность.
9.90. £/ = sin jc2. 9.91. z/ = sin х3.	9.92. у = a resin х3.
9.93. у — arcsin tg 2х.	9.94. z/= —-c-s-n* .
sin х
В заданиях 9.95—9.105 требуется исследовать данные функ-
ции на монотонность. В заданиях 9.95—9.102 для этого достаточ-
но использовать теоремы о монотонности композиции монотон-
ных функций.
Пример. Исследуйте на монотонность функцию
f (x) = cos (х2 + х)
на отрезке [—1; 1].
Решение. Функция у = х2-[-х убывает на отрезке 1; —-i-j
от 0 до —и возрастает на отрезке [ — ; 1J от — ~ до 2. Так
как функция y — cosx на отрезке [ — у; oj возрастает, а на от-
резке [0; л] убывает, по теореме о композиции монотонных фун-
кций получаем ответ.
Ответ. На отрезках 1; —и 1] функция f убывает,
на отрезке [ —oj функция f возрастает.
9.95. z/ = sin2x. 9.96. у =....-S-— .	9.97. // =-----!----.
sin x-f-1	sin x-f-cos x
3	I ^1
.98. z/ = sinx на отрезке — —; — .
9.99.	z/ = sin2 x — sin x на отрезке |\);
9.100.	z/ = cos2 x — 4 cos x на отрезке —т]*
9.101.	z/ = arcsin (х2 —6x4-9).
9.102.	у —2 arcsin2 х— arcsin х.
В заданиях 9.103—9.105 приходится использовать произ-
водные.
9.103.	z/ = %4-sin х.
9.104.	z/= cos х cos 2х на [ — л; л],
it 1 ас	। sin 2х
9.105.	// = sin %4-5—•
81
III. Графики тригонометрических функций
в	заданиях 9.106—9.116	требуется	построить графики дан-
ных уравнений. В заданиях		9.106—9.113 для этого целесообраз-	
но пользоваться геометрическими преобразованиями.			
9.106.	у — sin 2х.	9.107.	z/ = sin(2x — у).
9.108.	II сл Б’ * 1	9.109.	z/ = sin 2х —4 . 1	4 1
9.110.	У = sin | 2 |х| —y|-	9.111.	у— sin ( 2х —4) . 1 X	4/1
9.112.	l*/l =sin f2x—	9.113.	у = sin % + cos х.
В заданиях 9.114—9.116 для построения графиков приходит-
ся проводить исследование данных функций.
9.114. у— ——.	9.115. z/ = sin2 %4-2 sin х.
9.116. у — sin х sin 2х.
IV. Тригонометрические уравнения
В заданиях 9.117—9.118 требуется решить данные урав-
нения.
Задания 9.117—9.120 сводятся к простейшим уравнениям.
9.117. ^ = 0.	9.118. sin(x2-4x)cos(x+1) = 0.
9.119.	5 sin х — 3 cos х. 9.120. sin %4-cos x= 1.
Задания 9.121—9.128 целесообразно решать с помощью за-
мены переменной.
9.121.	2sinx~3-=—1	9.122. 2 sin2 х —5 sin % + 3 = 0.
3sinx+l 5
9.123.	—~-----1--— =--------!-.
cos2 X— 1	2 cos x— 1	cos x— 1
9.124.	sin2 x — 5 sin x cos x-J-4 cos2 x — 0.
9.125.	3 sin 2x — 4 cos2 x— 1.
9.126.	sin 2x —2 \/2~ sin %== 2 x/2~ cos x—3.
9.127.	tg(x+i) + 2tg(x-i)=l.
9.128.	——Hcos2x= -2.
Задания 9.129—9.137 могут быть решены при помощи пред-
ставления соответствующих выражений в виде произведений.
9.129. sin х-{-sin 2х — 0.
82
9.130.	sin 2%+sin 6% + cos 3x — cos 5x = 0.
g 121 sin x+sin 2x  j
sin 3x
9.132.	sin2 x+sin2 3x= 1 + cos 4x.
9.133.	cos 3x cos 6x = cos 4x cos 7x.
9.134.	sin 3x cos 2x = sin 5x+ sin x.
9.135.	cos2 x — sin2 x= cos x-|- sin x.
9.136.	tg x-f- 1 =sin x + cos x.
9.137.	sin3 x-J-cos3 x= 1 — j sin 2x.
В заданиях 9.138—9.145 целесообразно использовать свойст-
ва соответствующих тригонометрических функций (монотон-
ность, ограниченность синуса и косинуса).
Пример 1. Решите уравнение sin x + cos х— 1,5.
Решение. Заметим, что sin x + cos х = д/2" sin fx-hно
sin fx + v	1, а д/2~<1,5.
I X 4 / I
Ответ. Нет решений.
Пример 2. Решите уравнение cosx = x —
Решение. Ясно, что х = — корень этого уравнения, но на
отрезке [0; л] функция у = х — у возрастает, а функция //==
= cos х убывает, поэтому на этом отрезке уравнение других корней
не имеет, но так как |cosx| ^1, а при х^л и х^О верно
J х — у > 1, то оно их и вообще больше не имеет.
Ответ. х = •
9.138.	sin х cos х= sin 35°.
9.139.	cos 2x-|-sin2 х—0,5 = cos 40°.
9.140.	sin5 x + cos9 x= 1.
9.141.	sinx+sinx = x + —•
2	2	x
9.142.	x2 —2 cos 2лх-х+1 =0.
9.143.	x2 —2 (cos лг/4-cos лг) x+4 +	+	(z/ + -z — l)=0.
9.144.	sinx=x —л.	9.145. |tgx|— у—1.
Для решения заданий 9.146—9.149 полезно доказывать вы-
полнение алгебраических неравенств.
Пример. Решите уравнение
sin2 Зх + j sin2 x=sin Зх sin х.
83
Решение. Заметим, что sin2 3x4-^-sin2 x^sin Зх sin х, так
как а2-{- b2^2ab, причем равенство достигается только, если а =
— Ь, т. е. sin Зх = ^-sin х. Отсюда ответ.
Ответ. |л£, ( — ip arcsin	+ k, mfzj.
9.146.	tg2 x + ctg2 х = 2.
9.147.	tg2 x+ctg2 x= 1 4-cos3 (x —у).
9.148.	sin4 x-J-cos4 x = -^ .
9.149.	2 | sin x| + sin2 2x+ I cos x| =3 sin 2x.
Задания 9.150—9.158 связаны с обратными тригонометриче-
скими уравнениями.
5тс
Пример. Решите уравнение 3 arcsin 2x4-2 arccos 2х = — .
Решение. Так как arcsin 2x4-arccos 2х = у ПРИ всех
xf [ — 4 ; -П, имеем arcsin 2х = 4 , но отсюда sin (arcsin 2х) = ^- .
[ 2 2 J	4	'	2
Ответ. х = -2т-.
4
9.150.	arcsin (х2 —4х) = 0.
9.151.	5 arctg Зх — 2 arcctg Зх = -^ .
9.152.	arccos2 х4-2 arcsin х arccos х = 4гт- .
оо
9.153.	arcsin (х2 —3x) = arcsin ( — 2х).
9.154.	arcsin sin х = 4х —3.
9.155.	arcsin 2х= arccos х.
я2
9.156.	arcsin х arccos х = 4^ •
Io
9.157.	arcsin (3 —2x)4- arccos (x2 — 1 ) = л.
9.158.	arcsin у =
V. Тригонометрические неравенства
В заданиях 9.159—9.163 требуется построить графики дан-
ных неравенств.
9.159.	sin (х—z/)>>0.	9.160. cos х cos у>0.
9.161.	-^<0.	9.162. arcsin (х4-//)<0.
sin у
9.163.	arcsin xy>Q.
84
В заданиях 9.164—9.186 требуется решить неравенства..
9.164. sin—Ц->0 на [ —т?; 41-
х— 1	L 2 5J
9.165.	tg (х2-4х)<0 на [0; 3].	9.166.	на [—я; я].
9.167.	(х — (sin х — -0>О на [0; 2я].
л < q s i п х 1	~	л < л л 2 с о s х 4~	АГ	1
9.168.		<0.	9.169. --------— >0 на Г — я; я].
2 sin х— 1	tg х — 2
9.170. 5s"1% <2.	9.171. 2 cos2 % + cos x- 1 <0.
2 sin x4~ 1
9.172.	6 sin2 x — 7 sin x-f- 2^0.
9.173.	sin2 x —2 sin 2x +3 cos2 xj>0.
9.174.	——4 sin x <^2.	9.175. sinxsin2x<0.
cos 2x-hcos x
9.176.	sin x4~sin 5x^2 sin 3x. 9.177. sin 3xcos x^sin 4x.
9.178.
9.180.
9.181.
9.183.
9.185.
cos x+sin x^cos 2x.
9.179.
sin x —cos х^д/2*.
sin x4-4 sin 2x4-5 sin 4x< 10.
arcsin x<4.
О
3 arccos x —2л
2 arcsin x—л
<0.
sin x arcsin x>»0.
9.182.
9.184.
9.186.
IO	•
arccos x + 3 arcsin x>— .
6
arcsin2 x —3 arcsin x=C —2.
arccos 2x> arcsin x.
9.187.
9.189.
9.190.
9.191.
VI.	Системы тригонометрических уравнений
В заданиях 9.187—9.207 требуется решить данные системы
уравнений.
(х2 —Злх)(х-г/)	х-\-у = ^
(cos X— 1) (cos у 1)	9.188. <
sin xcos у = 0.	sin *4-cos (j-y)= 1.
6 — 7 sin x = 5 cos (4// —2)
2f/ = x-h 1.
sin 3x—sin y-}-2 sin x = 0
у1 — 6xy + 5x2 = 0.
z/24-nx = (j4-2x) г/
COS X COS 3x J
cos 3г/ cos у
85
9.192.
9.193.
9.194.
9.196.
9.197.
9.199.
9.200.
9.201.
9.202.
9.203.
9.205.
9.206.
9.207.
cos (2x+z/)= 1 +(xy — yf
х — у = 3я.
у — х — 2л
sin % + sin (у — 4x) = cosi 2 x4-2.
sin (x — y) = 0
cos y = cos x2.
9.195.
sin x j
sin x — sin у
COS x = cos2 y.
9.198.
f tg n%4-tg ny=\ — tg nx tg ny
( sin x cos y = sin у cos x.
' sin %4-sin y= 1
sin x
k sin у
sin2 (x+y) + sin (x + y) = 2
2 cos (x—у)— 1   1
cos (x—r/)-f-2	2
{sin 2%4-sin 2y = 0
cos (2%4-//)4-cos // = 0.
| sin2 (x4-//)4- sin (x4-//) = cos2(x4-//)4-cos (x-\-y)
( 1 4-cos (x — y) = 2 sin2(2x4-//).
'	3
sin %4-2 sin y — ~2
< sin2 % + cos2 y= 1.
cos (2x + 3i/)4-sin (x—y) = 2
cos (x+«/)4-sin (x + 3z/)= —2.
arcsin x+ arcsin у = л o 9n4 J arcsin x+ arccos y = л
x2 —z/2=0.	(x + z/=l.
i + 3л
arcsin x + arctg y = —
arccos x4- arctg y — ~^ •
arcsin (x2 —x + 1) = arcsin у
arccos-----5----= arcsin------------.
2	2
cos 2.nx + cos 2m/ = sin 2л (x-^-y)
arccos (x + z/) + arcsin 4 (x — z/)=y .
86
VII.	Уравнения и неравенства с параметрами
9.208.	Выясните, при каких значениях параметра а данные урав-
нения имеют ровно один корень (на указанном множестве
или, если оно не указано, на всем множестве /?):
а)	(х—1) arcsin (х — а) = 0; б) (х2 — 4х) arcsin (х — а) = 0;
в)	(а2 — 5а + 6) sin х — а — 3 на [0; 2л];
. (х — а)(х— 1)	а \	9 ,
г)		Ч------= 0; д) cosx=r + a;
sin х
е)	cos % + cos ах = 2.
9.209.	Выясните, при каких значениях параметра а дан-
ные уравнения имеют четное число решений на отрезке
[ — 2л; 2л]:
a) cos2x = a;	б) (х — a)sinx = 0;
. sin2 х —2а sin —2 п
г) (sin -i — За+ Q (cos х — а) = 0.
В заданиях 9.210—9.213 требуется установить, сколько реше-
ний имеют данные уравнения на указанных промежутках в зави-
симости от а. Для их решения полезно строить графики соответ-
ствующих функций.
Пример. Выясните, сколько кор-
ней имеет уравнение
cos2 хcos х = а
на отрезке [0; 2л] в зависимости от а.
Решение. Проведя замену пе-
ременной t — cos х, построим график
z/(/) = /2-H на отрезке [—1; 1]
(рис. 7).
Заметим, что при всех &#= — 1 урав-
нение cosx=/> имеет ровно два реше-
ния на отрезке [0; 2л], а урав-
нение cos х= — 1 имеет на этом отрез-
ке ровно одно решение. Теперь, выяс-
няя, сколько точек пересечения имеют
прямые у = а с построенным графиком,
и анализируя, какие абсциссы имеют
эти точки, получаем ответ.
Ответ. Если a<Z —р то нет решений; если а= —то два
решения; если —-^-«СЖО— четыре решения; если а — 0— три
решения; если 0<а^2 — два решения; если а>2— нет
решений.
87
9.210.	2 cos2 x — cos х — а	на [0; л].
9.211.	tg3 x — 3 tg x = a на (“у» у)-
9.212.	sin2x —sinx = a на [0; 2л].
9.213.	cosx~' =a на [-£; ol .
cos x-f-1	L 2 J
Задания 9.214—9.217 сводятся к исследованию квадратных
трехчленов.
9.214.	Выясните, существуют ли такие значения параметра а,
при которых уравнение
sin2 % —2 (а — 1) sin х + я+ 1 = 0
имеет ровно 4 различных корня на отрезке [0; 2л].
9.215.	Выясните, при каких значениях параметра а неравенство .
sin2 х — 2а sin x-f-4a — 3^0
выполняется при всех значениях х.
9.216.	Выясните, при каких значениях параметра а неравенство
sin2x —2(а —2)sinx4-0^O
не имеет решений на отрезке [0; л].	]
9.217.	Выясните, при каких значениях параметра а неравенство |
cos2 х—2 (а —3) cos х + 2а+ 9^0	I
выполняется на отрезке 0;	|
I о J	J
9.218.	Выясните, существуют ли такие значения параметров 1
а и Ь, что при всех значениях х выполняются следующие I
неравенства:	|
a) a sin х + b cos х> 1;	б) a cos х— b cos 2х> 1;	1
в) a sin2x+6 cos2 х> 1.	|
9.219.	Найдите все значения параметра а, при которых уравне- |
ние (I) следует из уравнения (II):	1
a)	(I): sin2x=l, (II): asinx=l;	I
б)	(I): sin Зх + cos 5х —cos Зх = а, (II): sin x = a sin x2;	|
в)	(I): (sin x —a2 + a)(cos2 x —2a) = 0,	1
(II): sin2 x —(2a-H I) sin x + a2 + a = 0.	1
ПРИЛОЖЕНИЯ
1. ПРОВЕРОЧНЫЕ РАБОТЫ
ПО КУРСУ АЛГЕБРЫ И НАЧАЛ АНАЛИЗА
10—11 КЛАССОВ
Ниже мы приводим варианты заданий для проверки усвое-
ния материала предыдущих параграфов. При использова-
нии их в качестве контрольных работ следует иметь в виду, что
они составлены с избытком, и потому оценка «отлично» может
быть поставлена даже в случае невыполнения каких-то заданий.
Работа 1. Комплексные числа
Вариант 1
1 d	°	1 -Н* . 2
1.	Выполните действия у—т + — •
2.	Дано число г = д/3~ + ^
а)	Запишите z в тригонометрической форме.
б)	Вычислите Im г1995.
3.	Найдите все вещественные хи//, такие, что
х (1 -J- i) 2/ (х — iy -|- 1) = 1	/.
4.	Пусть М — множество всех комплексных чисел z, таких, что
|z—14-/| = 1.
а)	Изобразите на чертеже множество М.
б)	Найдите наименьшее значение выражения \z— 311
для z£M.
в)	Изобразите на чертеже множество всех чисел z, таких, что
z£M.
г)	Изобразите на чертеже множество всех чисел и, таких, что
и = — iz, где zfМ.
5.	Пусть и — такое комплексное число, что Imu = 2Reu. Изоб-
разите на чертеже, множество всех комплексных чисел z — u\
Вариант 2
1.	Выполните действия ууу —у-
2.	Дано число z=l+V^z-
а)	Запишите z в тригонометрической форме.
б)	Вычислите Re z1995.
89
3.	Найдите все вещественные хи//, такие, что
х(1 — /) + 3/ (ix-\-y — 1) = 1 — I.
4.	Пусть М — множество всех комплексных чисел z, таких, что
\z+l-i\ = \.
а)	Изобразите на чертеже множество М.
б)	Найдите наибольшее значение выражения \z — 2/| для
z£Af.
в)	Изобразите на чертеже множество всех чисел z, таких, что
zf М.
г)	Изобразите на чертеже множество всех чисел и, таких, что
u = —iz, где zfМ.
5.	Пусть и — такое комплексное число, что Imu = 3Reu. Изоб-
разите на чертеже множество всех комплексных чисел z — u2.
Работа 2. Предел последовательности. Предел
Непрерывность функции
функции.
Вариант 1
1.
Вычислите:
v ।.	х2 4* 7х 4-11
a)	lim—2----——;
оо 2Х2 —5x-f-1
б)	lim
х-> -3
х2 —4х —21
в) lim
х — -2
x-f-2
tg х
г) lim
х"*° 2 cos (Х4-4)- 1
О
2.
Дана функция /(х) =
— fe2x, если х<С — 1,
&Х2, если — 1^х^2,
kx — 4, если х>2.
а)	Найдите все значения fe, такие, что функция f непрерывна
на [— оо; 0].
б)	Найдите все значения fe, такие, что функция / непрерывна
на R.
в)	Рассматривается последовательность an — f(n). Найдите
все значения fe, такие, что существует конечный предел
этой последовательности.
3. Приведите, если это возможно, пример последовательности
(ап), такой, что lim (|ал14-1) = 2, a lim (п (ап+ 1 ))= 1-
1.
Вычислите:
Вариант 2
х Зх2 4-5x4-13
a) lim —;
х->оо X2-7x4-2
б)
lim
-> -4
х2 —Зх —28.
х2— 16
90
lim ----------------------------
' + 3	—Zsinu + i-!
О
2. Дана функция f(x) =
9 ,	1
— kx, если x< — 1,
D
kx — 2, если — l^x^2,
fe2*2 — 4fex— 2, если x>2.
а)	Найдите все значения fe, такие, что функция f непрерывна
на [0; + оо ).
б)	Найдите все значения k, такие, что функция f непрерывна
на R.
в)	Рассматривается последовательность an — f( — п). Найдите
все значения fe, такие, что существует конечный предел этой
последовательности.
3. Приведите, если это возможно, пример последовательности
(ап), такой, что lim (|аЛ| + 1 ) = 3, a lim (и (an4-2))= 1.
Работа 3. Элементы дифференциального исчисления
Вариант 1
1.	Найдите все пары чисел а и Ь, такие, что функция
{ах24-4х, если
хг — 2х-{-Ь, если х<1,
дифференцируема на R.
2.	Дана функция f =	.
а)	Найдите наибольшее и наименьшее ее значения на отрезке
[-2; 0].
б)	Исследуйте функцию f на монотонность.
в)	Постройте график функции /.
г)	Укажите, сколько решений имеет уравнение f(x) — a в за-
висимости от а.
3.	Выясните, существует ли касательная к графику функции
z/ = x4 — 2Х2, имеющая с ним 3 общие точки.
Вариант 2
1.	Найдите все пары чисел а и Ь, такие, что функция
р	( ах2 — 2х + Ь, если — 1,
/(•*)=< ,. . .
(;г4-4х, если х> — 1,
дифференцируема на R.
91
2.	Дана функция f (х) — ——^7 .
а)	Найдите наибольшее и наименьшее ее значения на отрезке
[0; 3].
б)	Исследуйте функцию / на монотонность.
в)	Постройте график функции /.
г)	Укажите, сколько решений имеет уравнение f(x) = a в за-
висимости от а.
3.	Выясните, существует ли касательная к графику функции
у = х4—12Х2, имеющая с ним 3 общие точки.
Работа 4. Элементы интегрального исчисления
Вариант 1
1	а
1.	Найдите число а, такое, что	Д/х + 3 dx=^\[x dx.
-3	о
2.	Найдите первообразную функции
/(*) =
д/% + 3, если х^1,
— х-{-— , если 1,
О	о
график которой проходит через точку с координатами (0; 1).
3.	Найдите площадь фигуры, ограниченной графиками функций
у = У/х+3 и z/=lx+-|..
О о
о
4.
Вычислите min (у/х-[-3 ; у х + -|) dx, где min (а; Ь) — наи-
-з
меньшее из чисел а и b и min (а; Ь) = а = Ь, если а — Ь.
5.
Найдите
наименьшее значение
5 (lx+l)dx
-10
1. Найдите число а, такое, что
Вариант 2
5	а
Л]х — 1 dx = ^y/x dx.
1	о
2.	Найдите первообразную функции
У/х— 1 , если х^2,
/(*)={ 1.1 ~
— % + тг, если х<2,
4	2
график которой проходит через точку с координатами (0; — 1).
92
3.	Найдите площадь фигуры, ограниченной графиками функций
z/ = Vx—1 и у=1х+|.
10
4.	Вычислите max (у/х— 1 ;	+ где max (а; Ь) — наи-
1
большее из чисел а и b и max (а; Ь) = а = Ь, если а = Ь.
а
5.	Найдите наименьшее значение j x-\-^j dx.
-4
Работа 5. Элементы комбинаторики
и теории вероятностей
Вариант 1
1.	Семь различных открыток произвольным образом раздают
Коле, Толе и Оле. Выясните:
а)	сколько существует способов это сделать;
б)	какова вероятность того, что Коля останется без открытки.
2.	В классе 7 девочек и 17 мальчиков. Наудачу выбирают 8 че-
ловек. Определите вероятность того, что среди выбранных
будет ровно 5 девочек.
3.	Илья Муромец выбирает путь. Вероятность того, что он пой-
1	1	5
дет налево, — — , прямо —— , направо — — , а вероятности то-
го, что на выбранном пути он станет богатым, соответственно
1 1 1 ~ Л
— , — , — . Определите, какова вероятность того, что он станет бо-
1U О D
гатым.
ю
4.	Найдите сумму £ 2k Cf0.
k = Q
5.	Наудачу выбирают два числа х и у из числового отрезка
[0; 2]. Определите, какова вероятность того, что
Г х + у^2
I у — х^ 1.
Вариант 2
1.	Шесть различных картинок произвольным образом раздают
Грише, Мише, Саше и Наташе. Выясните:
а)	сколько существует способов это сделать;
б)	какова вероятность того, что Наташа останется без кар-
тинки.
2.	В классе 24 человека. Из них 18 учатся без троек. Наудачу
выбирают 7 человек. Определите, какова вероятность того,
что среди них будет ровно 3 троечника.
93
3.	Старик обращается к золотой рыбке с тремя различными
просьбами. Вероятность того, что он попросит новое корыто,
в первый раз — 0,7, во второй раз —0,2, в третий раз —0,1. Ве-
роятность того, что рыбка исполнит* первую просьбу,— 0,8,
вторую — 0,3, третью—0,1. Определите, какова вероятность
приобретения стариком нового корыта.
12	ck
4.	Найдите сумму £ (-1)*—^-.
л=о	2
5.	Наудачу выбирают два числа х и у из числового отрезка
[ — 3; 0]. Определите, какова вероятность того, что
Г у — х< — 1
I у + *> —3.
Работа 6. Многочлены. Уравнения
Вариант 1
1.	Проверьте справедливость следующего утверждения:
(х2 —4)n —(2х—1 )п;х —3
при любом n£N.
2.	Найдите остаток от деления многочлена
Р (х) = хи — 16/+ х — 3 на многочлен Q (х) = х? — 3x4-2.
3.	Решите уравнение 2х34-Зх2 — 29% + 30 = 0.
4.	Известно, что число 14-Д/3~ является корнем многочлена
Р (х) — х3 + ах? + Ьх— а
с рациональными коэффициентами. Найдите числа а и Ь.
5.	Числа хь х2, х3—корни многочлена х3 —Зх—1. Найдите
/4~ /4~
6.	Выясните, существует ли вещественное число а, такое, что
не имеет вещественных корней.
Вариант 2
1.	Проверьте справедливость следующего утверждения:
(х2 + 3)п— (х3—1)п-х—2
при любом n£N.
2.	Найдите остаток от деления многочлена Р (х) = х13 + 32х8 +
4-х + З на многочлен Q (х) = х24-Зх4-2.
3.	Решите уравнение Зх3 —8лг — 13x4-30 = 0.
94
4.	Известно, что число 1 + является корнем многочлена
Р (х) = х3 — ах? -\-bx-\-2a
с рациональными коэффициентами. Найдите числа а и Ь.
5.	Числа х2, х3—корни многочлена х3 —5x4-1. Найдите
6.	Выясните, существует ли вещественное число а, такое, что
л?4-(а— 1) х2 — ах— 2
уравнение ----------—:--------= 0
не имеет вещественных корней.
Работа 7. Иррациональные уравнения
и неравенства. Степенные функции
Вариант 1
1.	Дана функция /(х)=Л/х^^Т-
а)	Постройте ее график.
б)	Решите неравенство (х — 5) f (х)^0.
в)	Решите уравнение /(х) = 3х.
г)	Определите, при каких положительных значениях парамет-
ра а уравнение f(x) = ax имеет два решения.
д)	Выясните, при каких значениях параметра а уравнение
f(x) = a имеет два решения, большие — 1.
2.	Решите неравенство 2	+ 3	>5.
3.	Решите уравнение ЛД2-6x4-6 +У]2х — 1 =9 —х.
Вариант 2
1.	Дана функция f (х)= ух24-2х.
а)	Постройте ее график.
б)	Решите неравенство (х4~3)/(х)=С0.
в)	Решите уравнение /(х) = -^х.
г)	Определите, при каких положительных значениях парамет-
ра а уравнение f(x) = ax имеет ровно одно решение.
д)	Выясните, при каких значениях параметра а уравнение
f(x) — a имеет два решения, меньшие 1.
2.	Решите неравенство
V—-	V7/- -
3.	Решите уравнение ух2 —4x4-7 -{-У/Зх — Б = 13 —х2.
95
Работа 8. Логарифмическая и показательная функции.
Логарифмические и показательные уравнения
и неравенства
Вариант 1
Дана функция f (%) = log2 (2 — х) + log2 (5 — х).
1.	Найдите значение /( — 1), если /(— 4) = fe.
2.	Исследуйте функцию / на монотонность.
3.	Решите уравнения: a) f (х) = 1 — logj (%+ О» б) /(х) = 2\
2"
4.	Решите систему уравнений
У = [(х)
3*----—
3“—7
5.	Решите неравенство 2х / (х) + 2>/(х) + 2х+1.
6.	Выясните, при каких значениях параметра а уравнение
(2х — a)(j(x)— 2) = 0 имеет единственное решение.
Вариант 2
1.
2.
3.
Дана функция f (х) = log3 (2 + х) + log3 (8 + х).
Найдите значение /(4), если /(10) = 6.
Исследуйте функцию f на монотонность.
Решите уравнения:
a) f (х)=log^(x + 2) + 2; б) /(х)=(|)Х 2.
4.
Решите систему уравнений
' y = f(x)
2У-----— = 2
2*—5
5. Решите неравенство Зх+3 / (х) + 3^/(х)4~Зх+4.
6. Выясните, при каких значениях параметра а уравнение
(3х —а)(/(х) —3) = 0
имеет два решения.
Работа 9. Элементы тригонометрии
Вариант 1
1.	Вычислите:
a) cos 50° cos 40° — sin 35° sin 25°;	6) sin 2 arccos .
2.	Решите уравнения:
. sin 3%4-sin bx ~	n 2	। i л • n
a) ----z-----= 0;	6) 6 cos %+ 1 =4 sin 2x.
sin 6x — sin 2x
3.	Решите неравенство -------->2.
1 — sin x
96
4.	Дана функция f (х) = 4 sin2 х— sin х.
а)	Найдите множество ее значений.
б)	Выясните, при каких значениях параметра а уравнение
f(x) = a имеет два решения на отрезке — у; у .
Вариант 2
1.	Вычислите:
a) sin 110° cos 70° —sin 5° cos 35°; б) cos 2 arcsin .
2.	Решите уравнения:
. sin 10x-4-sin 6%	.	.	?	.
a) -------------;	6) 1 — 4 cos x= sin 2x.
sin 20x—sin 12x
3.	Решите неравенство -----!—>2.
1 4-cos x
4.	Дана функция f (x) = 3 cos2 x + cos x.
а)	Найдите множество ее значений.
б)	Выясните, при каких значениях параметра а уравнение
f(x) = a имеет ровно одно решение на отрезке [0; л].
2. ЗАДАНИЯ ДЛЯ ПОВТОРЕНИЯ
КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА
Ю—11 КЛАССОВ
Ниже мы отмечаем «звездочкой» наиболее трудные зада-
ния и «ноликом» — задания, представляющиеся нам легкими
для классов с углубленным изучением математики.
1.	Дано число a = (sincos-^0 .
а)	Запишите число а в алгебраической форме.
б)	Изобразите на чертеже совокупность всех таких комплекс-
ных чисел г, что | az| > 1.
в)	Найдите число г, такое, что его аргумент равен р а
Re (az) = 1.
г)	Изобразите на чертеже совокупность всех комплексных чи-
сел г, таких, что az-\-az = 2.
2.	Пусть С — множество точек z комплексной плоскости,
удовлетворяющих условию: |iz + 2 + 2i| = 1.
а)	Постройте множество С.
б)	Найдите все точки множества С, расстояние от которых до
13
мнимои оси равно —.
в)	Найдите область значений модуля z для точек множест-
ва С.
г)	Найдите область значений аргумента z для точек множе-
ства С (считая, что аргумент вычисляется в промежут-
ке [0; 2л)).
4 Заказ 1259
97
3*. Даны 3 комплексных числа:
д/з" , з . д/з" . 1 . д/з" -1 •
21 —	2 z’ г2—	2 + 2 z’ гз— 2	2 1'
а)	Найдите расстояние от точки г2 до фигуры, задаваемой
уравнением \z — z3| = 1.
б)	Изобразите на чертеже множество точек z комплексной
плоскости, таких, что |z2z —ZjzJ = |z3z —z2z3|.
в)	Пусть z пробегает все точки отрезка с концами в точках г2
и г3, a U и V — множества точек, которые при этом пробегают
соответственно u = z2-z и v = z3-z. Изобразите пересечение
множеств U и V.
г)	Пусть z пробегает все точки отрезка с концами в точках z{
и г3. Изобразите множество всех точек, которые пробегает
при этом w = z2.
4*. Обозначим через S множество всех комплексных чисел г, та-
ких, что \z\ = 1.
а)	Докажите, что все решения уравнения z64-z3+ 1 =0 при-
надлежат множеству S.
б)	Найдите те решения уравнения 2г3 + iz2 + 2£г = 1, которые
лежат в множестве S.
в)	Выясните, при каких значениях a£R уравнение z64-z2 = a
имеет решения, лежащие в множестве S.
г)	Выясните, при каких значениях c£S уравнение z64-z2 = c
имеет решения, лежащие в S.
5. Дана последовательность an = 2n-34-9«23~п, n£N.
а)	Докажите, что 22па2п4_1;5 при всех n^N.
б)	Найдите наименьший член последовательности (ап).
в)	Докажите, что при всех n^N выполнено равенство
4-1	2 (#и4-2 “Н ^)-
г)	Найдите формулу для общего члена последовательности (сп),
удовлетворяющей такому же соотношению 5сп+1 = 2 (cn+2 + cJ,
но при условии q = 0, с2 = 3.
6*. Последовательность задана рекуррентно
хх = а, хпЛ.х = х?п — хп — 3 при всех n£N.
а)	Докажите, что если a£Z, то хп— нечетное число при всех
п^2.
б)	Выясните, при каких значениях а последовательность (хп)
является постоянной.
в)	Выясните, при каких значениях а последовательность (хп)
является геометрической прогрессией.
г)	Пусть а = 4. Докажите, что последовательность (хп) не име-
ет предела.
7°. Дана функция f (х) = '\[х + 2.
а)	Решите уравнение f(x) = x.
б)	Постройте график функции y = f(x).
98
в)	Найдите площадь фигуры, ограниченной осью ординат,
графиком функции f и прямой у — х.
г)	Найдите наибольшее значение функции y = f(x) — x.
8°. Дана функция f (х) = ^(х4 — 4х3 + 7).
а)	Постройте ее график.
б)	Найдите наибольшее и наименьшее значения функции f на
отрезке [ — 1; 4].
в)	Напишите уравнение касательной / к графику функции
f в точке графика с абсциссой хо = О.
г)	Найдите площадь фигуры, ограниченной прямой / и графи-
ком функции [.
9. Дана функция [ (х) = х2 — 4 ~\[х.
а)	Напишите уравнение касательной / к графику функции
f в точке А графика с абсциссой 4.
б)	Найдите первообразную функции /, график которой прохо-
дит через точку А.
в)	Постройте график функции /.
г)	Найдите площадь фигуры, ограниченной графиком функ-
ции /, касательной I и осью абсцисс.
10*. Дана функция f(x) = ex, рассматриваемая на отрезке [0; 1].
а) Докажите, что любая касательная к графику этой функ-
ции пересекает ось ординат в точке С с неотрицательной ор-
динатой.
б)	Обозначим через S(x) площадь прямолинейной трапеции,
ограниченной касательной в точке х, осью абсцисс и прямы-
ми х = 0, х=1, вычислите S (х).
в)	Докажите, что функция y = S(x) принимает наибольшее
значение в середине отрезка [0; 1].
г)	Сформулируйте и докажите аналогичное утверждение для
функции g(x) = x4 + 3.
11*. Дана функция f(x) = x? и точка В с координатами (3; 5).
а) Через точку В проводятся касательные к графику функ-
ции [. Найдите координаты точек касания.
б)	Пусть А —та из точек, найденных в предыдущем пункте,
у которой абсцисса меньше, а С — точка с координатами
(3; 9). Найдите площадь треугольника АВС.
в)	Докажите, что площадь криволинейного треугольника
АВС, образованного дугой параболы АС и отрезками АВ
2
и ВС, составляет у от площади, найденной в предыдущем
пункте.
г)	Сформулируйте и докажите аналогичное утверждение для
произвольной точки В, лежащей ниже графика функции /.
12*. Дана функция f(x) = y[x. Точки пересечения прямой х = пг
с графиком функции [ и осью абсцисс обозначаются соответ-
ственно А (т) и В (т), а касательная к графику функции
f в точке А (т) обозначается 1(т).
99
а)	Докажите, что площадь фигуры, ограниченной графиком
2
функции /, осью абсцисс и прямой х=т, равна — mf(m).
б)	Пусть С (т) — точка пересечения прямых / (т) и Ох. Най-
дите отношение площадей криволинейного треугольника
АОС и прямолинейного треугольника АВС.
в)	Пусть М и N— точки графика функции, такие, что пря-
мая MN параллельна /(4). Докажите, что площадь фигуры,
ограниченной прямой A4N, осью Ох и перпендикулярными ей
прямыми, проходящими через М и N, не превосходит 32.
г) Пусть y = g(x)— непрерывная неотрицательная функция,
определенная на луче [0; Ц- оо), такая, что g(4) = 2 и при
любом значении т площадь фигуры, ограниченной графиком
функции g, осями координат и прямой х—т, равна
2	I—
— mg (т). Докажите, что g(x)=\x.
13. Дана функция f (х) = (хД-2)4 — х4.
а)	Докажите, что функция f возрастает на всей числовой
оси.
б)	Решите неравенство /(х)^ 16%+16.
в)	Найдите все такие числа а, что функция g (х) = f (х — а)
нечетна.
г)	Выясните, при каких значениях параметра k уравнение
f (x} — k(x-\-\) имеет три различных корня.
14*. Дана функция f (х) = х3Ц-Зх2.
а)	Докажите, что фигуры, ограниченные отрезками горизон-
тальных касательных к графику функции f и дугами этого
графика между точками пересечения касательных с графи-
ком, имеют равные площади.
б)	Докажите, что график функции f симметричен от-
носительно точки Л( —1; 2).
в)	Пусть прямая I касается графика функции f в точке с аб-
сциссой х0, где х0У= — 1. Выясните, сколько еще общих точек
она имеет с графиком функции /. Найдите их координаты,
г) Докажите, что всякая прямая, пересекающая график дан-
ной функции в трех точках, одна из которых является сере-
диной отрезка между двумя другими, проходит через точ-
ку А.
15°. Дана функция f (х) = Д/х + 5 + 1-
а)	Решите уравнение f (х) = 4Д- х.__
б)	Решите неравенство f (х)<У]х? — Зх + 1-
в)	Постройте график функции /.
г)	Выясните, какое из следующих чисел ближе к 4:
/(2) или /(5).
16°. Дана функция [ (х) = ^--*^ .
а)	Найдите область определения функции [.
100
б)	Решите уравнение /(х) = 2 — х.
в)	Сравните значения 3/(3) и 2/(4).
г)	Решите неравенство (/ (x))2<z х^4-Зх4-2.
17.	Дана функция / (х) = Д/8 —х 4- Д/2^4-8.
а)	Найдите область определения функции /.
б)	Найдите множество значений функции /.
в)	Решите уравнение / (х) = 2л/б\
г)	Решите неравенство / (х)> у5х4-16.
18.	Дана функция / (х) = Д/*2 —4x4-3 + Д/х2-7х4-6 .
а)	Найдите область определения функции /.
б)	Решите уравнение / (x) = y/~V5.
в)	Решите неравенство / (х)^У]х— 1 .
г)	Найдите все значения параметра а, такие, что уравнение
f(x) = a имеет два корня.
19°. Дана функция /(x) = logj (6х —%2 —5).
Т
а)	Найдите область определения функции /.
б)	Вычислите значение 3/(3).
в)	Решите уравнение /(х) = 2 logj (5 —х)4-1.
Т
г)	Решите неравенство /(х)^ — 1.
20°. Дана функция / (х) = log2 (i? — 5х + 4).
а)	Решите уравнение /(х) = 2.
Л \ D	£ ( 5 4“ 1 \
б)	Вычислите значение /(-----—1.
в)	Решите неравенство /(x)4-logj (2х —6)>0.
7
( y = f(x)
г)	Решите систему уравнений <
21.	Дана функция / (х)= logj.
а)	Найдите область определения функции /.
б)	Решите уравнение /(x) = log2 3—74 •
в)	Найдите промежутки монотонности функции /.
г)	Выясните, сколько корней имеет уравнение f{x) — a в за-
висимости от а.
22.	Дана функция /(х)= log2-^4-logi >^4-2.
а)	Решите уравнение /(х) = 0.
б)	Решите неравенство / (х)^3.
в)	Найдите область значений функции /.
г)	Выясните, при каких значениях параметра а уравнение
f(x) = a имеет два корня.
101
23*. Дана функция f (х) = log2 х — 3 log2 х.
а)	Решите неравенство /(х)^0.
б)	Решите уравнение f(x)= — 4.
в)	Найдите все значения параметра а, такие, что неравен-
ство /(x)<alog2x выполняется при всех х из отрезка
[2; 4Л/Т].
г)	Выясните, сколько корней имеет уравнение f(x) = a в за-
висимости от а.
24*. Дана функция /(x)=loga+2x(x2— 1).
а)	Пусть а = 0. Решите уравнение /(х)=1.
б)	Пусть а= — 1. Решите неравенство /(x)J> —1.
в)	Изобразите на чертеже множество всех пар (х; а), таких,
что /(х)= 1. Выясните, при каких значениях параметра а это
уравнение имеет решения.
г)	Выясните, при каких положительных значениях парамет-
ра а уравнения f(x) = n имеют решения при всех натураль-
ных п.
25°. Дана функция /(х) = 2 sin2 х —sin 2х.
а)	Вычислите значение f
б)	Упростите выражение f (х) + / (х —
в)	Решите уравнение /(х) = 0.
г)	Напишите уравнение касательной к графику функции
в его точке с абсциссой х0 = ^«
и 4
26°. Дана функция f (x) = sin 4х cos 2х. ’
а)	Решите уравнение f (х) = 3 sin2 2х.
/(a) —sin 2a
б)	Упростите выражение ----------.
2/ (a) — sin 6а
/ (%)
в)	Решите неравенство —
г)	Упростите выражение	— cos2xcos4x и вычисли-
те его значение при х =
27.	Дана функция /(x) = cos22x — cos2 х.
а)	Докажите, что при любом х из отрезка ^0; yj
/ (х)
б)	Решите уравнение ----= 0.
sin х
в)	Решите неравенство f (х)^0 на отрезке [0; 2л].
г)	Найдите наибольшее значение функции f.
28.	Дана функция /(x) = cos 2x + cos х — 4 cos2^-.
а)	Выразите y = f(x) как функцию от cos х.
102
б)	Решите уравнение f(x)= — 3.
в)	Докажите, что при любом х /(х)^0.
г)	Выясните, сколько корней имеет уравнение f(x) = a на от-
резке [0; л] в зависимости от а.
29*. Дана функция f (х) — sin х sin Зх.
а)	Решите уравнение /(х) = ^-.
б)	Найдите наименьшее положительное решение системы
уравнений
|/(х) = 0
( cos Ьх— 1.
в)	Найдите множество значений функции f.
г)	Пусть g (х)— наименьшее значение функции f на отрезке
р;	Найдите наибольшее значение функции у =
= g(t) на множестве вещественных чисел.
30*. Даны функции f (x) = cos х, g(x) = cos2x.
а)	Найдите площадь фигуры, ограниченной графиками дан-
ных функций и прямыми х =	х = у.
б)	Пусть А (т) и В (т)— это точки пересечения прямой
х=т с графиками функций f и g. Выясните, при каких
значениях т длина отрезка с концами в этих точках равна
единице.
в)	Выясните, существует ли отрезок, концы которого лежат
на графике функции /, а середина совпадает с точкой
г)	Изобразите на координатной плоскости множество сере-
дин отрезков, концы которых лежат на графике функции /.
3. ВАРИАНТЫ ВЫПУСКНЫХ ЭКЗАМЕНОВ
Мы приводим ниже варианты выпускных экзаменов по мате-
матике, проводившихся в 1992—1994 гг. в Санкт-Петербурге. За-
дания в них объединены в блоки-«сюжеты». Все публикуемые
варианты для классов с углубленным изучением математики
и варианты для базовой школы 1993 г. состоят из «обязательной
части» и «сюжетов на выбор». Каждый учащийся должен был
выбрать из предложенных ему «сюжетов на выбор» один, соста-
вив, таким образом, «свой» вариант из трех сюжетов (двух обя-
зательных и одного выбранного) (12 пунктов). При решении вари-
антов для базовой школы 1994 г. учащиеся также должны были
выбрать три сюжета (12 пунктов), но из всех четырех предло-
женных сюжетов.
103
Для получения оценки «5» достаточно было верно и пол-
ностью решить любые 10 из выбранных 12 пунктов, для получе-
ния оценок «3» и «4» соответственно достаточно было решить
6 и 8 пунктов. Продолжительность экзамена 5 4s.
Задания для базовой школы
1993 г.
Вариант 1
Обязательные задачи
1.	Дана функция f (x) = cos х cos Зх.
а)	Докажите, что f (х) = ^ (2 cos2 2x + cos 2х — 1).
б)	Решите уравнение /(х) = 0.
в)	Упростите выражение f (%) + f (у +	и вычислите его зна-
чение при =	•
\ п	/(*).!	г	-I
г)	Решите неравенство ---->— на отрезке [ — л; л].
cos Зх
2.	Дана функция / (х) = (-Г)* — (-0* 2.
а)	Вычислите f ( log, 3^.
7
б)	Решите уравнение f(x)= — 3.
в)	Найдите область определения выражения log5/(x).
г)	Решите неравенство log5/(x)^l.
Сюжеты на вы бор
3.	А. Дана функция f (х) = Д/25 — х2.
а)	Найдите область определения функции /.	I
б)	Решите уравнение f (х) = х+ 1.	1
в)	Найдите наибольшее значение функции f на отрезке I
[ —1;	I
г)	Выясните, при каких значениях параметра а уравнение I
f(x) = a имеет ровно одно решение.
З.Б. Дана функция /(х) = х3 —Зх.
а)	Постройте график функции /.
б)	Найдите первообразную для функции /, график которой
проходит через точку с координатами (1; 0).
в)	Напишите уравнение касательной I к графику функции
[ в точке графика с абсциссой х0= —1.
г)	Найдите площадь фигуры, расположенной во 2-й коор- i
динатной четверти и ограниченной	графиком функции /,	J
касательной I и осью ординат.	1
104	I
Вариант 2
Обязательные задачи
1.	Дана функция f (х) = sin х sin Зх.
а)	Докажите, что f (х) = -^ (cos 2х — 2 cos2 2%+ 1 )•
б)	Решите уравнение f (х) = 0.
в)	Упростите выражение /(%) + / (у —	и вычислите его зна-
Зл
чение при х = —.
г 16
/ (х)	д/2~
г)	Решите неравенство ----на отрезке [0; 2л].
sin Зх
2.	Дана функция f (х) = 9х — Зх+1.
а)	Вычислите /(log3 2).
б)	Решите уравнение f (х)= — 2.
в)	Найдите область определения выражения logj f (х).
~2
г)	Решите неравенство log, f (х)^—2.
~2
Сюжеты на выбор
3.	А. Дана функция f(x)=\J—-—.
а)	Найдите область определения функции [.
б)	Решите уравнение /(%)=—%4-3.
в)	Найдите наименьшее значение функции f на луче
[2; +оо).
г)	Выясните, при каких значениях параметра Ь уравнение
f(x) = b имеет 2 различных корня.
3.	Б. Дана функция f (х) = 3х? — х3.
а)	Постройте график функции [.
б)	Найдите первообразную для функции /, график которой
проходит через точку с координатами ( — 1; 0).
в)	Напишите уравнение касательной / к графику функции
f в точке графика с абсциссой х0 = 2.
г)	Найдите площадь фигуры, расположенной в 1-й коорди-
натной четверти и ограниченной графиком функции /, каса-
тельной / и осью ординат.
1994 г.
Вариант 1
1.	Дана функция / (%) = sin Зх cos 4х.
а)	Вычислите f —
.. __	sin 2х cos 5x-f-sin x cos 2x
б)	Упростите выражение ----------д—j---------
105
в)	Решите уравнение / (х) = sin Зх sin 4х.
хп	/(*) ^Д/2"	Г л л!
г)	Решите неравенство ----на отрезке — —; 0 .
sin Зх	L Ь J
2.	Дана функция f (х) = log2 (х— №+ 12).
а)	Найдите наименьшее целое число х из области определе-
ния функции /.
б)	Докажите, что f = — 2 + 2 log2 7.
\ п	/ 1 \/(х)	/ 1 \log2 (Зх+12)
в)	Решите неравенство ( —У —1
г)	Решите уравнение f (х) = [ (х — 2).
3.	Дана функция / (х) = (х+1 )2 (х—2).
а)	Решите уравнение f(x) — x— 2.
б)	Постройте график функции [.
в)	Найдите наименьшее и наибольшее значения функции f на
отрезке [ — 2; 1,5].
г)	Найдите площадь фигуры, расположенной в 3-й коорди-
натной четверти и ограниченной графиком функции f и пря-
мой у = х — 2.	__________
4.	Дана функция f (х)= ух2 + 8х + 7 .
а)	Найдите область определения функции /.
б)	Найдите координаты точек пересечения графиков функций
y = f(x) и у= —Зх— 1.
в)	Сравните числа f (-0 и 2/^—0.
г)	Найдите все значения параметра а, при которых уравнение
f(x) = a имеет два различных корня.
Вариант 2
1.	Дана функция f (x) = cos Зх cos 2х.
а)	Вычислите —J0-
б)	Упростите выражение ----------------------.
sin х sin 4х —cos х cos 2х
в)	Решите уравнение f (х) = sin Зх cos 2х.
\ п	/(*)	1	Гл
г)	Решите неравенство -----> — на отрезке 0; — .
cos Зх	L 4 J
2.	Дана функция / (х)= logj (2Х2 — Зх— 2).
~2
а)	Найдите наибольшее целое отрицательное число х из обла-
сти определения функции /.
б)	Докажите, что / ( —0= —3 —2 logj 3.
~2
log j (Зх —2)
в)	Решите неравенство 3/(х)^3 2
г)	Решите уравнение f (x) = f (х + 3).
106
3.	Дана функция / (х) = (х—1 )2 (х + 2).
а)	Решите уравнение f (х) — х-{-2.
б)	Постройте график функции f.
в)	Найдите наименьшее и наибольшее значения функции f на
отрезке [ — 3; 1,5].
г)	Найдите площадь фигуры, расположенной в 1-й коорди-
натной четверти и ограниченной графиком функции f и пря-
мой # = х4-2.
4.	Дана функция f (х) = Д/3 + 2х —%2.
а)	Найдите область определения функции f.
б)	Найдите координаты точек пересечения графиков функций
y = f(x) и у = 3х — 1.
в)	Сравните числа 2/^-0 и 3/( —-0.
г)	Найдите все значения параметра Ь, при которых уравнение
f(x) = b имеет ровно один корень.
Задания для классов
с углубленным изучением математики
1992 г.
Вариант /
Обязательные задачи
1 п л.	их W + Scosx
1.	Дана функция f(x) =--------=.
2 cos х— уЗ
а)	Решите уравнение f(x)= — 1.
б)	Найдите все решения неравенства /(х)^0 из отрезка
[л 5л 1
в)	Докажите, что / (x) = ctg (-^+0 ctg — 0.
г)	Найдите множество значений функции / на отрезке ; л].
2.	Дана функция /(x)=log2(4 — х2).
а)	Решите неравенство /(х)^СО.
б)	Решите уравнение /(x) = 2 1og4(7 — 4х).
в)	Найдите промежутки монотонности функции /.
г)	Выясните, сколько корней имеет уравнение f (х) = а (в зави-
симости от а).
Сюжеты на выбор
3.	А. Дана функция f (х) = х —Д/*+2.
а)	Напишите уравнение касательной / к графику функции
f в точке с абсциссой 7.
б)	Найдите наибольшее и наименьшее значения функции f на
отрезке [ — 2; 2].
107
в)	Постройте график функции f на отрезке [ — 2; 8].
г)	Найдите площадь фигуры, ограниченной графиком функ-
ции /, касательной I и осью абсцисс.
3.	Б. Даны комплексные числа z0 = i и г^д/з".
а)	Изобразите на чертеже множество М всех таких комплекс-
ных чисел 2, что \z — 20| = 1.
б)	Изобразите на чертеже множество К всех таких комплекс-
ных чисел 2, ЧТО | 2 — 20 | = | 2 — 2j |.
в)	Найдите все числа, содержащиеся и в К и в М.
г)	Среди чисел, принадлежащих множеству /<, найдите число
с наименьшим модулем.
3.	В. Дана функция f(x) = x3 — (а + О %2 + («2 —3) х + 2.
а)	Решите уравнение f (х) = 0 при а —2.
б)	Решите относительно а неравенство f
в)	Решите уравнение f(x) = 0 при условии, что один из его
корней равен 2.
г)	Выясните, при каких значениях а уравнение f(x) = b имеет
единственный корень при любом Ь.
Вариант 2
Обязательные задачи
1.	Дана функция f (х) = -—- .
1 4-2 sin х
а)	Решите уравнение f(x)= — у.
б)	Найдите все решения неравенства /(х)^0 из отрезка
Г л 3л1
L ¥ ’ TJ
в)	Докажите, что f(x)=tg -0 ctg (-утг+у)-
г)	Найдите множество значений функции f на отрезке [(J; yj.
2.	Дана функция f (х)= logj (4х— %2).
з
а)	Решите неравенство f (х)^ — 1.
б)	Решите уравнение / (х) = 2 log9	1	.
в)	Найдите промежутки монотонности функции /.
г)	Выясните, сколько корней имеет уравнение f(x) = a (в за-
висимости от а).
Сюжеты на выбор
3.	А. Дана функция f (х) = Д/х — 1 — х-|-3.
а)	Напишите уравнение касательной пг к графику функции
f в точке с абсциссой 2.
108
б)	Найдите наибольшее и наименьшее значения функции f на
отрезке [1; 5].
в)	Постройте график функции f на отрезке [1; 7].
г)	Найдите площадь фигуры, ограниченной графиком функ-
ции /, касательной т и осью абсцисс.
3.	Б. Даны комплексные числа г0= 1 +1^/3 и z{ = 2.
а)	Изобразите на чертеже множество К всех таких комплекс-
ных чисел г, что \z — z0| = l.
б)	Изобразите на чертеже множество Р всех таких комплекс-
ных чисел г, что \z — г0| = |г — z} |.
в)	Найдите все числа, содержащиеся и в К и в Р.
г)	Среди чисел, принадлежащих множеству /<, найдите число
с наибольшим модулем.
3.	В. Дана функция
f (Х) = х3 - х2 + (^2-4) х — (Ь 4-2).
а)	Решите уравнение f (х) = 0 при b= — 1.
б)	Решите относительно b неравенство /(6)^0.
в)	Решите уравнение — 0 при условии, что один из его
корней равен — 1.
г)	Выясните, при каких значениях b уравнение f(x) = a имеет
единственный корень при любом а.
1993 г.
Вариант /
Обязательные задачи
1.	Дана функция /(x) = cos 2х—sin х.
а)	Докажите равенство ——= 14-sinx.
1 — 2 sin х
б)	Решите уравнение f (x) = cos х.
в)	Найдите все решения неравенства /(х)>1 из отрезка
[л Зл 1
“У’ ~2]
г)	Выясните, при каких значениях параметра а уравнение
/(х) = а имеет четыре корня на отрезке [ — л; 0].
I°g2-~l°g2(4x)
2.	Дана функция f (х) =-----------.
log2(2x)
3 log j х
а)	Решите уравнение /(х) =-------—р.
4
б)	Решите неравенство /(х)<2,4.
в)	Найдите промежутки монотонности функции [.
г)	Найдите множество значений функции [ при х£0-; 2j.
109
Сюжеты на выбор
З.А. Рассматриваются комплексные числа
z. Zi = z-\-2i и u = z-zl.
а)	Найдите все числа г, такие, что и = 0.
б)	Изобразите на чертеже множество всех таких чисел г, что
вещественная и мнимая части числа z} равны.
в)	Изобразите на чертеже множество всех таких чисел г, что
вещественная и мнимая части числа и равны.
г)	Пусть |г| = 1. Найдите наименьшее значение \и\.
З.Б. Дана функция / (х) = х2 —2|х—4|.
а)	Постройте график функции /.
5
б)	Найдите значение ^f(x)dx.
з
в)	Напишите уравнение прямой /, касающейся графика функ-
ции f в двух различных точках.
г)	Найдите площадь фигуры, ограниченной графиком функции
f и прямой /.
З.В.	Дана функция [ (х) = д/2% + 6 — а’\/х—2.
а)	Решите неравенство /(х)^0 при а=1.
б)	Решите уравнение /(х) = 4 при а=1.
в)	Выясните, при каких значениях параметра а система урав-
нений	,	£	.
(//=/(*)
( у = а "\/2х4-6 — у/х — 2
имеет решения.
г)	Выясните, при каких значениях параметра а множество ре-
шений неравенства /(x)J>0 будет лучом.
dариант £
Обязательные задачи
1.	Дана функция f (x) = cos х — cos 2х.
f (*)
а)	Докажите равенство --------=1— cos х.
2 cos х -f- 1
б)	Решите уравнение / (х)—sin х = 0.
в)	Найдите все решения неравенства /(%)<! из отрезка
г)	Выясните, при каких значениях параметра а уравнение
с / \	Г Л Л ]
f(x) = a имеет четыре корня на отрезке	-у .
9
logs---logs (Эх)
2.	Дана функция /(*) =-----------------
iog3 4
О
но
3 ,og< x
а) Решите уравнение f(x) =-----------.
,ogVTx”2
б)	Решите неравенство /(x)> 1,25.
в)	Найдите промежутки монотонности функции /.
г)	Найдите множество значений функции f при х£ |^; з).
Сюжеты на выбор
З.А. Рассматриваются комплексные числа
г, 21 = г —2 и u = z-z}.
а)	Найдите все числа г, такие, что и = 0.
б)	Изобразите на чертеже множество таких чисел z, что веще-
ственная и мнимая части числа z} противоположны.
в)	Изобразите на чертеже множество всех таких чисел z, что
вещественная и мнимая части числа и равны.
г)	Пусть |z| = 1. Найдите наибольшее значение |и|.
З.Б. Дана функция f (х) = 2|х — 3| — (х + 1 )2-
а) Постройте график функции /.
4
б)	Найдите значение ^f(x)dx.
2
в)	Напишите уравнение прямой /, касающейся графика функ-
ции f в двух различных точках.
г)	Найдите площадь фигуры, ограниченной графиком функции
f и прямой /.
З.В. Дана функция f (х) = Ьу]х — 3 — Д/2х-|-4.
а)	Решите неравенство /(х)^0 при Ь — \.
б)	Решите уравнение /(х) + 4 = 0 при Ь=1.
в)	Выясните, при каких значениях параметра b система урав-
нений
У= —f(x)
y = -Ь А/2х + 4
имеет решения.
г)	Выясните, при каких значениях параметра b неравенство
f (х)^0 не имеет решений.
1994 г.
Вариант 1
Обязательные задачи
1.	Дана функция / (х) = 2 sin х cos2	—-0.
а)	Решите уравнение /(х) = 0.
б)	Решите неравенство /(x)^2sinx на интервале (— л; л),
в) Найдите наименьшее значение функции /.
111
f (x)
г)	Выясните, сколько корней имеет уравнение —-—-— = 0 на
sin х — а
отрезке [ — л; yj в зависимости от а.
2x+2_l. 1
2.	Дана функция f(x)= ох | , .
а)	Вычислите fl-----
\l°g32
б)	Решите уравнение /(х) = 3.
в)	Найдите множество значений функции /.
г)	Постройте график функции f на луче (— оо; 0].

Сюжеты на выбор
З.	А. Дана функция f (х) = У1х? — х + 4 .
а)	Решите уравнение f(x) = 2x.
f W
б)	Решите неравенство ^^l.
в)	Проверьте, является ли точка с координатами (2,5; 3) сере-
диной какого-либо отрезка, концы которого лежат на графике
функции /.
г)	Найдите все значения параметра а, такие, что функция g,
где g (х) = f (х — а), является четной.
З.Б. Дана функция f =
Z л
а)	Найдите первообразную функции / на множестве (0; + оо),
график которой проходит через точку 4(1; —6).
б)	Постройте график функции /.
в)	Проверьте, является ли прямая /, заданная уравнением
//=-15x4-23,5, касательной к графику функции /.
г)	Найдите площадь фигуры, ограниченной графиком функции
/, осью абсцисс и прямыми / и х = 3.
З.В.	Дано комплексное число а=14-*.
а)	Изобразите на чертеже множество всех таких комплексных
чисел г, что |z4-^l = l^l-
б)	Проверьте, являются ли числа а или —а корнями уравне-
ния z4 — Зг3 — Зг24-10 = 0.
в)	Изобразите на чертеже множество М всех комплексных чи-
сел г, таких, что az-\-az = |а|.
г)	Найдите наименьшее значение выражения \z — а\4-|г4-^1
для z£M.
Вариант 2
Обязательные задачи
1.	Дана функция f (х) = 2 cos х cos2
112
а)	Решите уравнение f(x) = O.
б)	Решите неравенство /(x)^2cosx на интервале
в)	Найдите наибольшее значение функции [.
г)	Выясните, сколько корней имеет уравнение —— = 0 на
Z>-f-cos х
отрезке [— у; jtJ в зависимости от Ь.
зх+1 । ।
2.	Дана функция f(x) =—.
\ D	£ / ,0^5 4
а)	Вычислите т[------
\log53
б)	Решите уравнение f (х) = 2.
в)	Найдите множество значений функции /.
г)	Постройте график функции / на луче ( —оо; 0].
Сюжеты на выбор
З.	А. Дана функция f (х)= ух? — 2*4-9 .
а)	Решите уравнение /(х) = 3 —2*.
б)	Решите неравенство 2х\_ । •
в)	Точка М (1; 3) является серединой отрезка с концами на гра-
фике функции /. Найдите координаты концов отрезка.
г)	Найдите все значения параметра Ь, такие, что функция g,
где g (x) = f (х-\-Ь\ является четной.
З.Б. Дана функция /(х) = х34--р
а)	Найдите первообразную функции f на множестве (0; 4- °°)»
график которой проходит через точку 4(1; 2).
б)	Постройте график функции /.
в)	Проверьте, является ли прямая /, заданная уравнением
у = 11,25х— 13, касательной к графику функции /.
г)	Найдите площадь фигуры, ограниченной графиком функции
/, осью абсцисс и прямыми / и х = 0,5.
З.В.	Дано комплексное число b —
а)	Изобразите на чертеже множество всех таких комплексных
чисел г, что \z — b\ = \b\.
б)	Проверьте, являются ли числа b или — b корнями уравнения
Зг44-г3-г2 4-14 = 0.
в)	Изобразите на чертеже множество К всех таких комплекс-
ных чисел г, что bz— bz=\b\ i.
г)	Найдите наименьшее значение выражения |z4-^l 4- |z —61
для
5 Заказ 1259
113
ОТВЕТЫ. УКАЗАНИЯ. РЕШЕНИЯ
§ 1.	Вещественные и комплексные числа
1.3.	Указание Доказательство сводится к доказательству иррационально-
сти \/б”.
К)
/1)	' Рис. 8
114
1.5.	Доказательство. Пусть число л = дАГ-}-Д/з' рациональное, но тогда
имеем г3 — Зг2 Д/з”-f-9г2 — 3 Д/з" = 2 и
Р + Эг2-^
Д/3 =—з 2-|2'з—— противоречие.
1.9.	Указание. Подкоренное выражение делится на 3 и не делится на 9.
1.12.	Указание. Достаточно, например, доказать, что в записи данного числа
содержатся сколь угодно длинные наборы из нулей, т. е. достаточно дока-
зать, что для любого n^N найдется такое k£N, что Зк—1:10", а это может
быть доказано с помощью принципа Дирихле.
1.13.	а) Обязательно рациональное; б) обязательно иррациональное; в) обязатель-
но рациональное; г) если а = 0, то рациональное; если а=#=0, то иррацио-
нальное, д) может быть и рациональным и иррациональным; е) может быть
и рациональным и иррациональным.
1.14.	Указание. Пусть а и b — рациональные числа, Ь>а, достаточно рас-
а-\-Ь	, Ь — а
смотреть числа —-— и а-]—.
1.24.	Д о к а з а т е л ь с т в о. При гг = О имеем 7-f-12jl9. Пусть утвержде-
ние верно при n = k. Но 7-52(А+1)+12-6* + 1 = 7-52А-25+12-б‘-6 =
= 6 (7-52* + 12-6*) + 19-7-52*, поэтому из истинности утверждения при n = k
вытекает его истинность при л = &-}-1, поэтому утверждение верно при
всех гг^О.
1.25.	а) 0; б) 256; в) -1+3»; г) д) 3-»; е) -Ц!.
1.26.	a) z=l—z; б) z= —1.
1.27.	См. рис. 8. 1.28. См. рис. 9. 1.29. См. рис. 10. 1.30. 3-f-4/, 2-f-2z.
1.31.	а) Лежат на одной прямой; б) лежат на одной прямой.
1.33.	См. рис. 11.	1.34. См. рис. 12.	1.35. См. рис. 13.
1.36.	См. рис. 14.	1.37. См. рис. 15.	1.38. См. рис. 16.
1.40.	См. рис. 17. Общая точка Д/2~ — Д/2~/. 1.41. См. рис. 18. 1.42. См. рис. 19.
а)
115

1.43.	a) 1; б) 3; в) 0,5; г) 2; д) 1
5
1.44.	а) Д/2"— 1; 6) 2; в) 1,5; г) л/5 -^2; д) I-L
5
1.45.	[V2-|; VS'+I] • '-46. -1+«.
1	1 л/з 2*
1.47.	б) \z\ = 1, или |z-f- 1| = 1, или z—— — b£R\ в) — —-f-i. 4
1.48.	См. рис. 20. 1.49. 1-f-i.	|
1.50.	a) д/7 (cosy + isin-^, б) 2 (cos ( —	+ < sin ( — у)),	*
___ #
в)	уТо (cos arctg 3-Н sin arctg 3);	|
г)	Vs" (cos (л —arctg-04-/ sin (л — arctg-0) ;	|
116
О)
Рис. 15
д) cos 15°-f-zsin 15°; е) cos 105°-Hsin 105°;
ж) cos (—55°)-Н sin (— 55°); з) cos ( —31°)-Н sin ( —31°);
и) 2 sin —
5
л , . . л
cos —-Н sin —
5	5
. _ л / Зл . Зл
, к) 2 cos— cos—+ 1 sin —
о у 10	1U
л) л/2 sin


117
a)
б)
6)
1тпд
д)
Рис.
Рис. 17
е)
16
1.51.	а) — 21995; б) — 2494; в) 21917<.
1.52.	Указание.
cos ла = Re (cos a-f-* sin а)", a
sin па = Im (cos а-Н sin а)п.
1.53.	У к а з а н и е. Выразите cos 30°
через cos 1°.
1.54.	а) 0,5; б) если е= 1, то л; если
8^=1, то 0; в) если 8=1,
л(л-|-1)	л
то —; если 8 =#= 1, то-------- .
2	8—1
Указание. Достаточно пред-
ставить данную сумму в виде
суммы нескольких геометриче-
ских прогрессий.
118
Рис. 19
1.56.	Для и£М. См. рис. 21.
1.57.	1 1.58. Пусть z0 = coscosСм рис. 22. 1.60. в) См. рис. 23.
6	6
1.61.	a) 2 = 0, 2=1; б) в луч Re2 = 0 Im 2 = 0, в) есть: \z\ = 1.
1.62.	1) z=±l; 2) а) в прямую Im z ——Re z без точки 0, б) в окружность
|z| = l; в) в прямую Re z==^-
1.63.	[—W; У/З]. 1.64. (-2-^;', -fY t65- a = 0’ д=6+У^~ .
у 10	6/	5
1.66.	a—— 3, a = 2. 1.67. a^l, — 1.
§ 2. Последовательности. Предел последовательности.
Предел функции. Непрерывность функций
2.2. Возрастающая.
2.5. Возрастающая.
2.8. Убывающая
2.11. Убывающая
2.3. Возрастающая.
2.6. Убывающая.
2.9. Возрастающая.
2.12. Возрастающая
2.4. Возрастающая.
2.7. Возрастающая.
2.10. Убывающая.
2.13. Возрастающая.
119
Im a
0<argz<^-
Рис. 20
2.14.	a>0 2.15. a>l. 2.16. 6>a>0. 2.17. He существуют.
2.18.	Периодическая. 2.19. He является периодической.
2.20.	He является периодической Решение. Предположим, что сущест-
вует такое	что sin (/? + k)= sin п при всех n£N, но тогда
k / k \
sin — cos In4-— ) = 0 при всех n£N, но &=#2л/ и 2n-f-k = 2ns-f-
4~л (s£Z)—противоречие.
2.21.	Периодическая. 2.22. Периодическая * 2.23. Периодическая.
120
IS!
гг эиа
(5
ay
----i:z 9-
v Ш1
/=ZU»I
'' Ш1
f=zay
v LUI
V Ш1

2.24. Периодическая. Решение. Заметим, что
ап^±- при всех n£N\
Период равен 2
2.25. а — 0, а—\. Решение. По крайней мере, начиная с а2 все члены после-
довательности неотрицательны, но ап_^1—ап = ап(ап—1). Поэтому если
а2> 1, то все ап> 1 (п^2) и последовательность (ап) возрастающая и, следо-
вательно, непериодическая; если 0<а2< 1, то все ал<1 (гг^>2) и последо-
вательность (ап) убывающая и, следовательно, непериодическая; если же
я2=1 или я2 = 0, последовательность, очевидно, периодическая.
2.26. Не существуют. 2.27. Неограниченная. 2.28. Ограниченная.
2.29. Ограниченная. 2.30. Ограниченная.
2.31. Неограниченная. Решение
'п
но последовательность Ьп = У[п неограниченная.
2.32.	Неограниченная.	2.33. Ограниченная	2.34. Неограниченная.
2.35.	Неограниченная.	2.36. Неограниченная.	2.37. Ограниченная.
2.38.	Например- а — 0, а— — 1, я = 0,5 — в самом деле,	—1, так как
ал4-2ал^ — 1, но при — 1 <а<0 последовательность (ап) убывает, поэтому
при а£[ — 1; 0] ап£ [—1; 0]. Пусть а = 2, по индукции доказывается, что
ал>>2п, следовательно, (ап) неограниченная.
2.39.	а) Не обязательно, но может быть ограниченной; б) обязательно ограничен-
ная; в) обязательно ограниченная; г) обязательно ограниченная; д) обяза-
тельно ограниченная; е) обязательно ограниченная
2.40.	а) Не обязательно неограниченная, но может быть неограниченной; б) обя-
зательно' неограниченная; в) обязательно неограниченная; г) обязательно
неограниченная; д) обязательно ограниченная, е) не обязательно неограни-
ченная, но может быть неограниченной
2.41.	а) Обязательно ограниченная; б) не обязательно ограниченная, но может
быть ограниченной; в), г) обязательно ограниченная; г) обязательно ограни-
ченная; д) обязательно ограниченная; е) не обязательно ограниченная, но
может быть ограниченной
2.42.	а) Обязательно неограниченная, б) не обязательно неограниченная, но мо-
жет быть неограниченной, в) не обязательно неограниченная, но может
быть неограниченной; г) обязательно неограниченная; д) обязательно не-
ограниченная; е) не обязательно неограниченная, но может быть неограни-
122
ченной. Решение. Пусть ап = 1, Ьп = п, тогда
— 2п
тт
= —24~-------, очевидно,
14-п
1х„| <2.
Пусть а„=-. Ь„ =
п, если л/2,
—-Н—~ , если п-2.
п п2
Заметим, что х2п = 3п — 2, т. е. (хл) неограниченная.
2.43.	а) — е) Не обязательно неограниченная, но может быть неограниченной.
2.44.	а) Все; г) не обязательно. Например,
{1, если п-2 или л-З,
л, если л/2, л/З.
2.45.	а) 10, п> 100; б) л >9, л >99; в) л >2, л >4.
2.51.	Указание. Достаточно заметить, что в последовательности yn = cosn
сколь угодно далеко от начала есть как положительные, так и отрицатель-
ные числа.
2.52.	Решение. Можно рассуждать аналогично заданию 2.51.
Другое решение таково: пусть А = lim sin п, но тогда A — lim sin(«-f-2),
fl —► ОО	П-* оо
отсюда lim (sin (п -f- 2) — sin п) = 0, но тогда lim cos (п -f-1 ) = 0,
fl —► ОО	п -* оо
lim sin 2п — А—0 и lim (sin2 л-f-cos2 л) = 0—противоречие.
п оо	п -* оо
2.53.	Нет, например хп = ( — 1)".	2.54. Нет, например хп — пп.
2.55.	а)	Все; в) да;	г) да;	д) нет, например ап — (— 1)".
2.56.	а)	Например,	хп =(( — 1 )"-f-1) п\ б) таких нет; в) 0, 1, 2, 0, 1,	2,	...	.
2.57.	а)	Да; б) да;	в) нет. 2.58. Да, да, да, нет. 2.59.	а)	Нет; б)	нет.
2.60.	а)	Да; б) да.	2.61.	Нет, да. 2.62. а) Нет; б) нет;	в)	да.
2.67.	а) Например, х„ = п+1, уп = — п; 6) х„=-\, уп = п; в) х„=(( — 1)л+ 1)п,
п
' п, если п-2,	( п, если л/2,
«/„=((—ir+’ + lJn; г) жя = 1 1	у„ = (|
— , если л/2,	— , если п-2;
п	I л
д) хп=—, уп = п; е) хл=1, уп=—\ ж) таких последовательностей нет;
п	п
з) х„ = п, у„ = о-, и) X„ = ((-1)”+I)n, </„ = ((- 1)я+1 + 1)п; К) х„=( —1)“,
у„=(— 1)'1+1; л) таких последовательностей нет; м) таких последовательно-
стей нет; н) уп~1, хп = п\ о) таких последовательностей нет.
2.68.	1.	2.69. 4-оо.	2.70. у.	2.71.	0.	2.72.	0.	2.73.	1.
2.74.	См.	рис. 24.	2.75. См. рис	25.	2.76. См.	рис.	26.
2.77.	См.	рис. 27.	2.78. См. рис.	28.	2.79. См.	рис.	29.
2.80. См. рис. 30. 2.81. 0. 2.82. 0. 2.83. —3 2.84. а = 2. 2.85. 3.
2.86. Решение. Легко доказывается по индукции, что последовательность
(хл) возрастает, если Xj=4, но если последовательность (хл) имеет предел а,
то а = а2-|-6а-f-6, т е. а = 3 или а = 2, но все хп^4 — противоречие.
123
Рис. 25
Уд
7"
У
Zim (УГй-Ух)"
ОТ
Рис. 28
2.87. [ — 3; —2]. Решение Заме-
тим, что хп+1—хп = (*л4-2)2. Та-
ким образом, при любом а после-
довательность (хп) возрастающая.
Если она имеет предел Ь, то
b — Ь24-5Ь4-4 и Ь= — 2, отсюда
ясно, что если х„>—2 (при ка-
ком-то п), то последовательность
(хп) не имеет предела, но хп^_1 =
= х^4-5хл4-4^—2 тогда и только
тогда, когда — 3^хя^—2 По-
этому ясно, что если х} <—3, то
последовательность (хп) не имеет
предела; если же XjC[ — 3. —2],
то все хлЕ[ — 3; —2], т. е. (хл) возрастающая и ограниченная и, следовательно,
имеющая предел последовательность
124
2.98. а) Например, /(x) =
103, если |x-2|>^,
2, если |x_2|<-JL;
б) это невозможно;
в)	взять /(2)<0; г) невозможно; д) например, lim f (х) = 4- оо.
х-»- оо
2.99.	а) Например, /(х) —х; б) невозможно, в) /(х) = х; г) невозможно;
д) /(х) = х; е) невозможно.
2.100.	а) 20; б) -3; в) -2; г) 4; д) 1; е) — 2.
о 6
2.101.	а) Горизонтальная // = 0, вертикальная х = 3, б) вертикальная х=1, на-
клонная f/ = x4-l; в) горизонтальная у=\, вертикальная х = 2; г) горизон-
тальная i/=l, вертикальные х=—2, х= — 1; д) горизонтальные ^=1,
//= — 1, вертикальная х— 1; е) наклонные # = х, у= —х; ж) вертикальная
х = 0, горизонтальная # = 0, з) вертикальные х=л£, k£Z\ и) горизонталь-
ная у — 1.
1	| х|	х2
2.102.	Например:	а) у=~—3—— ;	б) у=-----;	b)z/ = —==,
х(Г—1)	х— 1	V^+l
ч 1
г)	У = ~г-;— ..
Vx2+ 1 —х
1, есл и x£Q,
1, если x^Q\
( 0, если x£Q,	( 0, если x£Q,
В) /(х)—I _2 ес^и	г) Н*)—если X^Q
Заметим, что во всех случаях а — любое число.
{1, если х£О,
1	SM = f(x)\
— 1, если x£Q,
{1, если x£Q,
i	dn SM=-f(x)’
— 1, если x£Q,
в) невозможно, г) невозможно
2.105.	а) 2; б) —1; в) -i- cos ~; г) ; д) — Д/^”-
5	5	2
2.106.	а) Непрерывна везде; б) разрывна в x£Z\ в) разрывна в нуле; г) непрерыв-
на везде; д) разрывна в x£Z; е) разрывна в нуле; ж) непрерывна везде;
з) непрерывна везде; и) непрерывна в х= 1; к) непрерывна в х=1, х=3.
Решение. Пусть х0#=1, х0=#3, но, рассматривая последовательности
хь х2, ..., хя, ...—>х0 и /ь /2, ..., /л, . .->-х0, такие что xt£Q (i£N), видим, что
lim /(xt) = x§, a lim /(/л) = 4х0 —3, но x^=#4x0 —3. Таким образом, функ-
л -* оо	л —* оо
ция разрывна в х0 Для х0=1 и х0 = 3 аналогичные последовательности
имеют общий предел, а тем самым и для любой последовательности (хл),
стремящейся к х0, имеем, что lim /(хл) = / (х0).
125
2.107.	а) См., например, 2.106 (и); б) см., например, 2.106 (к);
{0, если x£Q,
х(х— 1)(х — 2), если x£Q.
2.108.	а) а = 2; б) а=1; в) а=—2.
2.109.	а)	а<.—У[з\ б) а=1.
Решение. Требуется, чтобы уравнение х3 — х2 = ах—1 имело ровно
два корня, т. е. имело корень х} кратности два и корень х2, но тогда
xfx2= —1, 2х!4-х2=1, а отсюда Xj=l.
2.110.	а = 3, b= — 1. 2.113. Указание. Заметьте, что
t(x}=f )=Мf	<°>-
/ п—»-оо \ £ J \п °°	/
2.114.	/(х) = х. Указание. Рассмотрите функцию g(x) = /(x)— х.
2.118.	Д о к а з а т е л ь с т в о. Пусть для какого-то х = х0 верно неравенство
/ (х0)>х0, но тогда /(х)>»х для всех х (иначе для непрерывной функции
g(x) = /(x) —х нашлись бы два значения аргумента, в которых она прини-
мает значения разных знаков). Но тем самым f (f (х))>»/(х)>»х при
всех х.
2.119.	Указание. Рассмотрите функцию /г(х) = /(х) — g(x).
2.120.	Доказательство. Предположим противное, но тогда при всех хЕ [0; 1]
выполнено, например, неравенство /(x)>g(x). Пусть теперь / (а) — наи-
меньшее, a f (Ь)—наибольшее значение функции /. Имеем g(/(a)) =
= /(g(fl))>/(a), g (f (£)) = / (g (^)Х/(b). Поэтому существует такое с0,
что g (f — f (с0). Рассмотрим теперь последовательность сп = f (c/J_1).
Ясно, что g(c„) = g(f(c„_|)) = /(g(c„_|)) = /(cn_1) = c„, и так как с„ =
=	a j = g (сп_ 0, то сп>сп_х. Итак, имеем возрастаю-
щую и ограниченную последовательность, следовательно, существует
с— lim сп. Из непрерывности очевидно, что f(c) = c, a g(c) = c, т. е.
п -* оо
/ (c) = g(c) — противоречие.
2.121.	Д о к а з а т е л ь с т в о. Рассмотрим функцию F (х) = /(х) — х. Если она
нигде не обращается в нуль, то, например, /(х)>»х при всех х
и f (f (... f (х))...) >х для любого п и для любого х, в частности для х— 1 —
п раз
противоречие. Поэтому существует х0 = /(х0), но тогда /(/.../(х))...) = х0
п раз
для любого п. Отсюда х0=1.
2.122.	а) Да; б) нет; в) нет; г) нет. 2.123. У/2
2.124.	Нет. Решение. Предположим, что такая функция имеется, но рас-
смотрим непрерывные функции
„ е(„_1<±Ц<£+1>.
Так как эти функции принимают только иррациональные значения, то они,
а тем самым и их сумма, постоянны, т. е. /(x) = const, очевидно, противо-
речие.
126
2.125.	а) Да; б) нет. Решение. Рассмотрим функцию h (x) = f (х) — х. Мно-
жество ее значений состоит только из иррациональных чисел, поэтому
h (х) = с — const, отсюда f (х) = x-f-c, но / (c) = 2c£Q.
2.128.	Указание. Пусть /(1) = а, рассуждая по индукции, покажите, что
f(n) = any /(x14-...-f-xJ = /(x1)4- . + /(хл) для любых хь х2, . ., х„, а от-
f/1\ а	. /т\ т
сюда / ( — )=—, наконец, — ] = а — .
уп / п	х п / п
2.129.	/(х) = 0 при всех х и f(x) = ax.
2.130.	а) / (х) = 0 и / (х)= loga х; б) f (х) = 0 и f (x) = xa. a£R. Указание. Ес-
ли f отлична от нулевой, рассмотрите функцию g (x)=ln / (х).
§ 3.	Элементы дифференциального исчисления
3.6.	При х0= —1:	а) q(h)=\h\\ б) см. рис. 31; в) см. рис 32;
г) не существует.
3.10.	При х0= —1: а) 0.5; 6) т(й) = УмТ- 1 -у h; в) 0.
{2/z, если Zz^O,	( h, если /z^O,
. ь. а) Например, k = 1; x(h)=<
/г, если /г<0.	[0, если /г<0.
lim т(/г) = О; б) такого k нет.
Л-^0
{/г, если /г^0,
а) — б) Такого k нет
-/г-2, если Zz<0.
3.16.	б//(/г) = ф(/г). 3.17. Для х0= 1 ф (Zz)-df (/г) = 2/г2.
/г2	1	1
3.18.	Для х0=1 ф(/г)-^(/г)=^—3.19. 4-. 3.20. 0,991. 3.21. 2 — .
3.22.	а) г/=|х|; б) z/= |х|-f-|х—11, в) z/ = |х| -f- |х— 11 -f- |х— 2|
3.23.	а) Не имеет производной; б) не имеет производной, в) имеет производную;
г) не имеет производной; д) имеет производную.
{а= 1	( а = 0	( а= — 1
б) a-b^=l, { в) 1, {
/? = 0; 7	I /?=1; 7	(/7 = 2
127
Рис. 34
3.25.	а) Везде дифференцируема, б) дифференцируема везде, кроме точек х=1,
х = 3; в) дифференцируема везде, кроме точек х = л£, k£Z\ г) везде диффе-
ренцируема; д) нигде не дифференцируема; е) дифференцируема в нуле.
3.26.	а) /(х) = Iх|, g(x) — — |х|, х0 = 0; б) — г) это невозможно; д) хо = О, /(х) = 0,
g(x)=|x|; е) /(x)=g(x)=|x|, хо = О, ж) /(х)=|х|; з) /(х)=1, g(x) = x,
хо = 0; и) / (х)= 1, g (x)==sign х, хо = О, к) это невозможно; л) f (х) = 0, g (х) =
= |х|, хо = О,
м) /(х)=
1, есл и х =# ± 1,
2, если х— ± 1,
g(x) =
1, если х= 1,
— 1, если х#= 1,
-*о=1;
н) f(x)=|x|, g(x)=|x— 1|, Хо = О.
3.28.	Z(x)=6x—4 3.29. Z(x)=12x—16. 3.30. Z(x)=l —х. 3.31. /(х)=-^х+1.
3.32.	Z(x) = n(x —2). 3.33. Z|(x)=l, Z2(x) = VF-x (рис. 33).
3.34.	lx (х)= 1 имеет три общие точки с графиком функции /, 12(х) = У/2 — х име-
ет две общие точки с графиком функции /.
4	19	11
3.35.	у=— х, у=—х + —. 3.36. z/=—-х + -, z/=—-х + -.
9
3.37.	</ = 3x4-2, у=\\х— 14. 3.38. у=-х--. 3.39. </ = 2х-2.
3.40.	См рис. 34. Mk — ф, k — 3, 4, ..	3.41. Да, в точке х0=1
3.42.	а=12 3.43. а = 4. 3.44. а=1, Z> = 6, с = 0. 3.45. 4. ~Т-
4	4	4
3.46.	a) arctg 11 — ~ ; б) arctg-^|; в) 2 arctg .
3.47.	На	[0; 2] и	на [3,	-f-°о) возрастает, на [2; 3) убывает.
3.48.	На	( —оо ;	2), на	[2,5; 3) возрастает, на (2, 2,5], на (3;	4-оо)	убывает.
3.49.	На ( — оо; —V^"] и на +00) возрастает, на [ — \2 ; д/2”] убывает.
3.50.	На	(—оо;	—2] и	на	[0, 2] возрастает, на [—2, 0] и на [2,	4- оо)	убывает.
3.51.	На	(—оо,	—1] и	на	[2; + °°) возрастает, на [—1, 0) и на (0, 2]	убывает.
3.52.	На (—оо, 1] возрастает, на [1, -f-oo] убывает
3.53.	На (—оо, 4] возрастает, на (4, 4-оо) убывает.
3.54.	На (—оо; —1], на (0, 1] и на (1; 4~°°) возрастает, на [ — 1, 0) убывает.
128
И I
2 J
3.55. [О, 9]. 3.56. ( - оо;
3.57. f — оо; 2	. 3.58. [0; -f- оо ).
3.59.	(—оо, 4]. 3.60. (—оо; 0]U	|; + «>). 3.61.	+ «>).
/—	2
3.62.	[0; 1]. 3.63. [1, 4]. 3.64. 2, — 79. 3.65. 2 Д/2 , Зу. 3.66. 19, 2.
3.67.	— 1,5; VF 3.68. 1, 17 3.69. Наименьшее значение —32, наибольшего нет.
3	3	1	1
3.70.	3.71. —=. 3.72. (1, 1) 3.73. (4, 2). 3.74. -4= .
2 2 зл/з^	л/5
3.75.	(0. 2]. 3.76. (—оо, 2]. 3.77. pl; 2^
3.78.	См рис. 35. Решение Найдем производную
f'(x) = 3x? — 6(а4- l)x-f-12a = 3(x2 —2(а4-1)х-}-4а).
Корни производной х1=2а, х2 = 2. Вычислим несколько значений функции
f (0) = 0; / (4)= 16; f (2) = 12а — 4, / (2а) = — 4a3-f- 12a2 и сравним эти зна-
чения:
/(2)<f(0)^12a<4^a<l
О
/(2а)</ (0)<^4a2(3 — а)<0^>а>3 (т. е. 2a>6>4).
Используя это, получаем, что если a-SZ— , то g (a) = 12a— 4, а если —-^Ja,
О	о
то g(a) = 0.
г~	Г 2	1
3.79.	а>2у2. 3.80.	4----—; 4|. 3.81. а=1. Решение. Возьмем
L зд/з^ J
производную /'(л) = 6х2— 6ах = 6х(х— а). Ясно, что если а 6(0; 2],
то наименьшее значение функции на отрезке [0; 2] достигается в точке а;
если а^2, то в точке 2, если а^0, то в нуле. Итак, наименьшее значение
на [0; 2] равно За, если а^0, —а34-За, если 0^а^2; 16 —9а, если
129
а^2. Исследуем теперь функцию у=— а34-За на [0; 2]. Так как
у' = —3a2-f-3, получим, что наибольшее на [0; 2] значение достигается при
а=1, z/(l) = 2, но ясно, что 16 — 9а<0 при а^2, а За^О при а^О.
3.82.	а = 0. 3.83. См. рис. 36. 3.84. а5 = 75. 3.85. аб=12 4-.
о
3.86.	а12= - 826. 3.87. а2 = 4. 3.88. (-оо; 0]U[4; + оо).
3.89.	(-оо; 3jl . 3.90. [-17 + 2^/72", + oo)U(-oo; -17 — 2Д/тУ].
3.91.
3.101.
3.102.
(-оо; 6]и[16; 4-оо). 3.92. [—1; 3]. 3.93. а>3. 3.96. Два.
Если a<Z— 21 или а>21, то 1 корень; если а= ±21, то 2 корня; если
6,5 "\/б,5 <а<21 или — 21 <а< — 6,5Л/б,5 , то 3 корня; если
то 4 корня; если — 6,5 Д/б,5 <а <6,5 Д/б,5 , то 5 корней.
1
а = —, то 1 корень;
а= ±6,5 у 6,5 ,
Если
—, то нет корней; если а — 0 или
3.103.
если
то 2 корня.
Если
"2 ’
27	„	27
—— , то нет корней, если а=— —— или
256	н	256
г/ 27
тельный корень; если —"256 ’
то 2 положительных корня.
3.104.
Если а С
, то один корень; при других значениях а — ни од-
ного.
130
3.105.	а<13,5. 3.106. а>ЗУ13. 3.107. а>^—.
4	64
(0; -^-V 3.109. а^4, а^8. Решение Построим графики функций
10/
а1(х) = 2х — 2 и а2 (х) = х + V*2~ 16 . Для этого заметим, что
х
так как аПх)=1-]__________ то у = а2(х) монотонно возрастает на луче
V?-16
[4; -f-оо) и убывает на луче (— оо, —4], у = а1(х) возрастает на всей оси
(рис. 37). Заметим теперь, что пары (х; а), удовлетворяющие первому не-
равенству, лежат над графиком функции у = а2(х), а пары, удовлетворяю-
щие второму неравенству, лежат над графиком функции у = а}(х). Так
как условие задачи выполняется при таких значениях а, что множество ре-
шений первого неравенства является подмножеством решений второго, по-
лучаем указанный ответ.
§ 4.	Элементы интегрального исчисления
4.1.	Да. 4.2. Нет. 4.3. Нет. 4.4. Да. 4.5. Нет.
—-4-2, если х>0,
*
----2, если х<0.
х
F(X) =
— 4-х —4 — , если х>1,
3	3
х2 —4 -i-, если х< 1.
О
4.8. /?(х) =
4.9. F (х) =
—— 4-x-f-2, если х<1.
2 лГТ
— у/хт, если х>2,
х2
——х— 18, если х<2.
4.10.	Не обязательно нечетная, но может быть нечетной. Среди первообразных
обязательно есть нечетная функция. Для непрерывной функции f те же от-
веты.
4.11.	Для разрывной на R функции: не обязательно четная, но обязательно есть
четная функция среди первообразных. Для непрерывной на всей оси функ-
ции /• обязательно четная.
4.14.	Не обязательно периодичная, но может быть периодичной.
Пример. /(x) = sinx-f-l и /(x) = sinx.
4.15.	Нет, да, нет. 4.16. Нет. Решение Пусть F — первообразная функция /.
Очевидно, если — период F, то и /. Пусть Т — период /, не являющийся
периодом F, но тогда при всех х:
F (x-f- Т) — F (х)= С=#=0 и F (пТ) — F (0)4-лС
(n£N). F — неограниченная. Противоречие, так как F — непрерывна и пери-
одична.
4.17.	Да. 4.18. Да 4.19. [0; 8].
131
4.20.	Решение. Предположим противное: пусть F—первообразная функции
/, но тогда по теореме Лагранжа для всех х<0 и всех х>0 имеем F(x) —
— F (0) = 0-(х — 0), т. е. F (х) = F (0) при всех х,гно тогда F' (х) = 0 при всех
х — противоречие.
{1, если х=#0,
— 1, если х = 0;
{0, если х=#0,
g (*) = /(*)> г) нет
1, если х = 0,
4.22.	/ (х)—с (const). 4.23. f(x) — c. 4.24. f(x)=c. 4.25. f(x) = c. 4.26. f(x) = c.
4.27.	f(x) = kx+l IER). 4.28. f(x) = kx+l (k£R, l£R).
4.29.	f (x) = ax-\-b (a£R, b£R). Решение. Предположим, что вторая произ-
водная не везде равна нулю, но тогда, так как она непрерывна, найдется
интервал, на котором она не обращается в нуль. Ясно, что в какой-то точ-
ке этого интервала первая производная не обращается в нуль, но тогда
найдется целый интервал, на котором первая и вторая производные не об-
ращаются в нуль, но тогда на нем сама функция / везде принимает нуле-
вое значение, но тем самым и ее производные тоже равны нулю — проти-
воречие. Итак, /"(х) = 0 для всех х.
4.30.	/ (x) = 2x-f-1- 4.31. / (x) = ax2-f- bx-\- с, a£R, b£R, c£R.
4.35.	4.36. 4- 4-37- 2-4- 4-38- ^+4- 4-39-	4-49- • 4-4»- 5. 4.42. 4.
2	4	2	4	2
4.43. g(x) =
( x — 9?
--------Ь 2, если x>2
(рис. 38).
Рис. 38
132
'х(5 — х), если 0^х<2,
4.44. g(x) =
4 4-х, если 2^х^3,
х2 — 5x4-13, если 3<х
(рис 39).
4.45.	а) I (ед2); б) 1 -J- (ед2), в) 2-|- (ед.2); г) 1	(ед2)
О	О	О	О
4.47.	а) а= — 3, а=1, б) а=-^. 4.48. (0; 2)(J(3; 4-оо).
4.49.	а=1 4.50. 4. 4.51. 1 4.52. — 4.53. —.
6	3	2	2
§ 5.	Элементы комбинаторики и теории вероятностей
5.1.	а) Неверно, 6) неверно; в) неверно; г) верно.
5.2.	а) а—100 или /? = 0; б) b — 100 или а = 0; в) а=100 или £=100,
г) а4-/?> 150
5.3.	а) тпу б) пт\ в) т\ г) -—д) С"; е) С™
(п — ту
5.4.	а) С- б) Л- в) Сл; г) тп.
5.5.	а) т — п, б) Ckn~~n, если kZ^n, иначе 0; С1п, если 1^л, иначе 0, С™;
в) А1п, Аг^ — пгп, пары (п; т) могут быть любыми, кроме пар вида (1; т),
(п, 1) (где	10) и пар (2; 2), (2, 3), (3, 2); г) 2л-2; д) Зл —3-2Л —3;
е) 12, ж) если k^n, то (n— 1)если k>n, то 0; з) (п— \)nk~
и) C-.q; к) (2m—l)(2fe—1).
rtP_л
5.6.	а) 16; б) 10, в) 6. 5.7. а) пру б) п\ в) р, г)-\-п.
Р
5.8.	а) С"+„; б) С‘_„ С*~\, (*_, +	= С‘.
5.9.	а) Указание. Достаточно, например, заметить, что Ckn — это число
кратчайших путей, ведущих из точки (0; 0) в точку (k; n — k) (см 5.8),
причем каждый такой путь проходит ровно через одну точку вида
(£—1; п — k — т), где О^т^п — k.
в) Решение. Рассмотрим произвольную перестановку множества
1, 2, ..., . ., п, такую, как в условии. Пусть на первом месте стоит элемент k,
k=£ 1. Возможны два варианта 1 стоит на &-м месте, тогда остальные места
можно заполнить Dn_2 способами, или 1 стоит не на fc-м месте, но тогда
числа 2, 3, .., k—\, 1, k, .., п должны занять места со второго по л-е, при-
чем каждое должно поменять свое место, отведенное ему в предыдущей за-
писи,— для этого имеется Dn_x способов. Так как k пробегает значения
от 2 до п, всего имеем (п — 1) (Dn_ j -\~Dn_2) способов.
г) Указание. Заметьте, что если знак последнего выполняемого умно-
жения стоит после хтУ то скобки можно расставить Кт-Кп_т способами.
5.10. б) Указание. Продифференцируйте формулу из 5.10 (а).
в) Указание. Проинтегрируйте формулу из 5.10 (а).
д) Указание. Перемножая равенства из 5.10 (г), определите коэффи-
циент при х*.
133
5.11. Указание. В заданиях а)—г) достаточно подставить в формулу бинома
Ньютона указываемые ниже значения: а) х=1; б) х =— 1; в) x — i\
г) х — Л/Зц д) подставьте в формулу из 5.10 (б) х= 1; е) подставьте в форму-
лу из 5.10 (в) х = 1; ж) подставьте в формулу п. 3.5.10 (б) x=i, з) подставьте
в формулу из 5.10 (б) х = г, з) подставьте в формулу из 5.10 (д)	>
и) воспользуйтесь равенством (1 -f-x)'n + n = (l 4-х/"-(1 4-х)л и формулой би-
нома Ньютона, определите коэффициент при х*, к) воспользуйтесь
1	1	1	е / X
равенством ---------— ------------------и равенством из 5.10 (д).
(1-х)2л	(1-х)" (1-х)"
/->s	— S
5.12. а) б) 	.
™ Ckm
5.13.
Ответы даются для случая одной попытки: а) ~; б) ; в) ; г) —.
1!	5 • 7!	7	2.10
5.14. См. рис 40.
5.15. Решение, а) Например, пусть 3 грани тетраэдра покрашены в красный,
синий и зеленый цвета, а четвертая грань — во все 3 цвета, Ah А2, А3—
попадания на грань, содержащую соответственно красный, синий и зеле-
ный цвета (при попадании на поверхность тетраэдра); б) например, пусть
в ящике 2 красных и 3 белых шара. Вытаскивают 2 шара. Ah А2, А3— со-
5.16.
5.18.
5.20.
ответственно такие исходы, при которых среди вытащенных есть белый
шар, есть красный шар, есть зеленый шар.
а) 0,56; б) 0,38; в) 0,4256. 5.17. а) Р1 = 0,5; б) рх = 0,3, р2 = 0,4.
2	1
а) 0,175; б) 5.19. а) [0,175; 0,475]; б) 0,65; в) не стоит; г) больше — .
5.21.
/	1V	1
г) lim ( 1-)
л-»- оо \	П /	в
2	117	1
-. 5.22. а) —; б) -; в) --- In 8; г)
3	7 8	7 8	7 8	8	7
1 -f-cos 2
2
Рис. 40
134
5.23.
a>i;O)±;B>±;r)±	r>
101—40Д/5
600
5.25.	а) —— ; б) —. Решение. Пусть х—время прихода первого ма-
288	72
фиозо, у — второго (х и у считаем принадлежащими отрезку [0; 1]). Ясно,
что условием гибели второго мафиозо является выполнение неравенства
х<у<~х-\-^~ . Изобразим соответствующие множества пар (х; у) (рис. 41).
о
Так как площадь всего квадрата 1, а площадь фигуры, задаваемой указан-
ным неравенством,
11
72 ’
получаем
11	ч	19
ответ:	—;	в)	——;	г)	0.
72	'	288	7
§ 6.	Многочлены и уравнения
6.1.	а = 3. 6.2. а=1, & = 2. 6.3. а = 6=1, с = 2.
„ „ ч 1 <_	3 ,,	,	1	1	,	3	1
6.4.	а) а=-, Ь=— 2,	б* а=ь=с=2’ в) «=—у. Ь= —с = - .
6.5.	а) а = 1, Ь=— 2, с— — Г, б) а=1, Ь = с—~2. 6.6. а = Ь = 3.
6.7.	aj = />! = £!=(); а2 = ЗУ/з, Ь2 = 9, с2=\/з'; а3~ — ЗД/з~. &3 = 9, с3—— у/з.
6.8.	(х- 1)(х— 2)(х —2,5). 6.9. (х—1)2(х —3). 6.10. а) х2-^; б) x3-f-2x.
Д (х-х0)(х— Х|)-...-(х-х,_1)(х- х,+ 1)...(х-х„)
.1 . а) р X — ^у, (Х,_ХО)(Х._Х1).....(X,—x.^HXi—x(+I)...(х, —х„) ’
б) не обязательно; в) бесконечно много.
6.12.	а) Да; б) да; в) нет; г) да.
2	1
6.14.	а) —10,5; б) — 1, а2= — 2; в) а= — у, b= — 1, г) а = —, 6=1.
6.15.	а) п — любое; б) п—нечетное; в) п — четное; г) п = 1.
6.16.	а) а = 9; б) а= ±2; в) а= — , 6 = -|-.
О о
6.17.	—0,5x4-2,5. 6.18. х4-1. 6.19. -2x4-2. 6.20. (x-f-2)3 (х— 3-ууг) 
6.21.	Нет. 6.22. Нет. 6.23. В четырех.
6.24.	а) х3 — бх2-f~11х— 6 = 0; б) х3 —5x2-f-7x —3
21
6.25.	а) 66; б) 483; в) — —. 6.26. 0. 6.28. а=1. 6.29. а = 2. 6.30. а=1.
6.31.	а = 2. 6.32. Один отрицательный корень, два положительных.
6.34.	Решение. Предположим противное, но тогда данное уравнение имеет
три вещественных корня хь х2, х3, причем Xj-|-х24-х3 = 0, а x^-f-x^-f-
4-х2х3>0, тогда x?4-x^4-x^ = (xl4-x24-x3)2 —2(х1х24-х1х34-х2х3)<0 — про-
тиворечие.
6.36.	{1; 2}. 6.37. |з;	6.38. Ц, ±УГЛ .
6.39.	(1;	- IztVF) • 6.40. {2±i}. 6.41. {<; *4-1}.
I Л о	)
135
6.42. {1±У\/2+1+1(1±У\/2<Л)}. 6.43. {±2; ±1}
6.50.	{-3; 2; -'А'.У*! | 6.51. { — 6; — бгЬЛДП •
{1 л/ТТ	__)
2	; -i±i V2 Г •
... ( - . -14±Wol л„ 3 2 4
6.54.	•> —5; 1, --—----- ? 6.55.	±/; —; — } .
6.56.	{1; 1-1; 2. 3 j . 6.57. { —2; -1; 3 j .
6.58.	{±<; 2; 1; -1}. 6.59. |1; 3; -51-V*1 | .
6.60.	{±1; ±3}. 6.61. { —1; 0; 2, 3}. 6.62. {0; 3; ±д/3).
6.63.	{1; 1; ~~2^" | ' Указание х24-2 = х-|-1 4-х2—х-|-1, а х34-1 =
=(х+1)(х2-х4-1).
6.64.	{1; ±2/}. 6.65. { — 1; ld=1 . 6.66. ^2;
6.67.	J-ч—!—; 1(\Т-\/2'-2±<л/з’(А/4’+^))1 
I fc+1 6	J
3
Указание. Зх3-f-Зх2-f-Зх-f-1 =(x-f-1 )3-f-( у2 х)3 =
= (0/24 1) х+ 1) (О/Г--\/2’+ 1) а^ + (2-Д/Г) х+ 1).
6.68.	{—1; ±i). 6.69. а=±1. 6.70. а = 3. 6.71. а<-2, а = 6.
9
6.72.	а>0. 6.73. а= — 1, а= — 2 6.74. а> — - 6.75. а<1.
4
6.76.	а = 2, х2=1— л/2, х3 = 2. 6.77. а = 2, /? = 3, х2 — 2 —	х3=1. 6.78. а = 4,
х2= 1 —х3 = 2.
6.79.	а = 1, X! = 1, х2 = 2/, х3 = — 2L
6.80.	flj =0, корни 0, 2±;iyf5, а2 = 5, корни- 2, 1 ±2г, а3 = 4455, корни: 22,
— 9±18/
6.81.	aj = 8, а2= — 40.
136
§ 7.	Иррациональные уравнения и неравенства.
Степенные функции
7.1.	(-оо; 2]U[3; + оо). 7.2. (-оо; + оо). 7.3. [2; + оо ).
7.4.	0. 7.5. (-оо; 1]Щ4; + oo)|j{3}. 7.6. [4; + оо). 7.7. [0; + оо)
7.8.	[Д/3\ 4-оо). 7.9. [-1; 4-оо). 7.10. [ — 1,4- оо). 7.11. [3;4*оо)
7.12.	На ( —оо; —2] убывает, на [2; 4~ °°) возрастает.
7.13.	На [4, 4-°о) возрастает.
7.14.	На (—оо; —2] убывает, на [6; 4~ °°) возрастает.
7.15.	На (—оо; 3,5] убывает, на [3,5, 4-°°) возрастает.
7.16.	На [1; 4-°о) возрастает.
7.17.	На [—3; —2] убывает, на [—2; 4-°°) возрастает.
7.18.	На [5, 9] убывает, на [9; 4-°°) возрастает.
7.19.	См. рис. 42.
7.22.	См. рис. 45.
7.25.	См. рис. 48.
7.28.	См. рис. 51.
7.31.	См. рис. 54.
7.34. а) Нет; б) да.
7.37. а) Да; б) да.
7.40.	а) Да; б) нет.
7.43.	а) Нет; б) нет.
7.46.	а) Нет; б) да.
7.49.	а) Да; б) нет.
7.53.	[1; б| . 7.54.
7.20.	См рис 43
7.23.	См. рис. 46
7.26.	См. рис. 49.
7.29.	См рис 52
7.32.	См. рис. 55.
7.35. а) Нет, б) да.
7.38. а) Да; б) да.
7.41. а) Да; б) да.
7.44. а) Да, б) нет.
7.47. а) Нет; б) нет.
7.50. [5, 4- оо )
{1; 6). 7.55. 0.
7.21. См рис. 44.
7.24. См. рис. 47. 7.27. См. рис. 50. 7.30. См. рис. 53. 7.33. См. рис. 56. 7.36. а) Нет; б) нет.	
7.39.	а) Нет; б) нет.
7.42.	а) Нет; б) да.
7.45.	а) Да; б) нет.
7.48.	а) Да, б) да.
7.51. 0.	7.52. х = 3.
3
7.56.	а) а ^5; б) 1; в) а^О, г) 1 ^а<2; д) а<0, а>3; е) а< 1, 1 <а<— ;
ж) а>1, а^О; з) 0<а<-^, а = 1; и)	а = 0;
к) а = 0, а —4, а< — , а>4,5.
7.57.	а) [— 5; 6]; б) ; 4-	» в) (3; 4- °° )» г) (— оо; 0). 7.58. а= 1, а = 3 у .
7.59.	£ — УГ; 1-^-j . 7.60. ft<4. 7.61. fr=l. 7.62. 0 . 7.63. 0 . 7.64. х = 2
7.65.	а<0. 7.66.	—1. 7.67. а) а<0; 6) а>0. 7.68. х = 4.
7.69.	х=1. 7.70. {2, 1; 68}. 7.71. {5; УТо"}. 7.72. {1; 2; 3).
7.73.	(4-; —-Д. 7.74. Ь-ДЗ 7.75. {З8}.
(62	63 /	(51/
5;
О J
7.78.	{-3, 4}. 7.79. I—у; 2^ 7.80. {3}.
137
138
у=\!х-5+>12Х-1
139
7.81.	<2; 3 —> . Указание. Домножив на сопряженное выражение и учи-
V	)
тывая, что х=1 не является корнем уравнения, получим
Д/х2 —4x4-5 — Д/х2 —5x4-6 = 1
Д/х2 —4x4-5 -f-Д/х2 —5x4-6 = х— 1
Отсюда 2 Д/х2 —4x4-5 = х и т. д.
7.82.	{-4; 3}. 7.83. 0 . 7.84. х = 2. 7.85. х=3. 7.86. х = 2.
7
7.87.	0. 7.88. х = 3. Решение. ОДЗ: х^> — Ясно, что х = 3 — корень
уравнения, и так как функция у = Д/х2 — 4x4-7 -f-3Д/Зх-f-7 на луче
[2; -f-оо) возрастает, а функция у = 17 — х убывает, то на луче [2; -f-оо)
других корней нет. Но на отрезке [0; 2]
Д/х2 —4x4-7 4*ЗД/Зх4*7 <ЗД/Й+V?< 15< 17-х,
а на отрезке
Д/х2-4x4-7 4-3V3X4-7 С-^-4-ЗД/т"<17-х.
О
Поэтому и там уравнение не имеет других корней.
7.89.	(5; 4), (5; —4). 7.90. (4; 4), (2; 1). 7.91. (34-МГ -2-Д/б").
7.92.	(3; 2). 7.93. (3; 5). 7.94. (—1; —1). 7.95. (0; — 1), (4; 5).
7.96.	(2; 1). 7.97. х> — 1Д 7.98. х>-1
О
7.100.	0. 7.101. R; 1Y 7.102. (3; 4- оо). 7.103. [2; 5)0(6; 4-оо).
7.104.	(4; 7). 7.105. [7; 4-oo)U{5). 7.106. [6; 4-oo)|j{l}.
7.107.	(-оо; 2]U[7; 4*«>)U{3}. 7.108. (-оо; 1)0(5; 4-°° )•
7.109. (7; 8). 7.110. (3; 4- оо). 7.111.
2;
1 +Л/29~]
7.112.	(-оо; — 2]0(5; 4-оо). 7.113. (5; 4-оо). 7.114. Г-1; C0U(2; 4-°° )•
7.115.	Если а < — 1, то нет корней; если а — — 1, то один корень; если а>» — 1, то
два корня.
7.116.	Если а> 1 или ж0, то нет корней; если а=1, то один корень; если
0^а<1, то два корня
7.117.	Если ж0 или ОсаСД/ЗО", то нет корней; если а = 0 или д/30~СаСД/дГ,
то один корень, если	то два корня
7.118.	Если Ж0, то нет корней; если а^0, то х=а24-а-
7.119.	Если а>1, то нет корней; если	то х( 2= 1 ±Д/1 —а , если Ж О,
то х = 1 4- VТ — а •
140
7 юл е* —--а	°	а	4а4*3 — \ISa-f-9*
7.120.	Если а<0, то нет корней; если а>(), то х =--------.
(2а2 4- 1
—о----’	“ 1
а — 1
если а=1, то — 1; если а>1, то (—оо, — 1]U(—з-------------♦ 4“ 00 )•
\ а — 1	/
7.122.	Если а<0, то [1; -f- оо); если а = 0, то (1, 4-оо); если 0<а^1, то
(4а24-1; 4-°0); если а>1, то [1; а2)0(4а24-1, 4~ 00)
7.123.	Если а<0, то ( — оо; 2]; если 0^ а< 1, то ( — оо, 24-(а — 1) а2); если а = 1,
неравенство не определено; если а>»1, то (24-а2(а—1); 4~ 00 )•
Рис. 61
141
7.124.	Если а^ —4, то нет решений; если — 4<а^0, то
(2-V4+T; 2 + V4 + а), если а>0, то £ —	2 +Д4 + а).
7.125.	(—1, l](j{ — Д/2”) • Указание. В этом и последующих заданиях це-
лесообразно пользоваться геометрической интерпретацией условия.
(3	1
—, 11. 7.127. [3; -f-оо). Решение. Нарисуем схематично графики
функций у = а— |х| и у = у/х— 3 (рис. 57). Теперь ясно, что графики име-
ют точку пересечения только если а^З.
7.128.	(0; 1)и(1;	.
§ 8.	Логарифмическая и показательная функции.
Логарифмические и показательные уравнения
и неравенства
8.1.	х=#0. 8.2. х>5. 8.3. 2<х<3 8.4. х>3; х<2.
8.5.	2<х<3, 3<х<5. 8.6. -2<х< - 1; х>1
8.7.	х>0; х=#=1. 8.8. —4<х<—3; —3<х< —1; х>1.
8.9.	х=1. 8.10. х=—5. 8.11. 0. 8.12. а<1. 8.13. а>3.
8.14.	а<0. 8.15. а< — 2; — 1<а<1.
8.16.	См. рис. 58	8.17. См. рис. 59.	8.18. См. рис. 60.
8.19.	См. рис. 61	8.20. См. рис. 62.
8.21.	Верно не всегда; например, при х=у = 2 верно. 8.22. Верно при х>0.
8.23.	Верно не всегда, например, при х = у=\ верно.
8.24.	Верно не всегда; например, при z/=100, х= 10000 верно.
5 __
1	1	.—	д/q	з	«—
8.25. 4 у 8.26. ~. 8.27. Д/Тз . 8.28.	. 8.29. у. 8.30. Д7 .
8.31.	-4= 8.32. а+ 2 8.33.
УЗ
8.36.	На ( — оо; 3] убывает,
8.37.	На ( —оо; 1) убывает,
8.38.	На (-оо; -1) и
8.39.	На (—оо; 1) и на (1;
8.40.	На (0; 81] убывает, на [81; 4~ °°) возрастает.
8.41.	На (—оо; 2] убывает, на [2; -f- оо) возрастает.
—!—. 8.34. —:—-. 8.35. 2а —3/?-f-l.
а	2а + Ь
на [3; 4-оо) возрастает.
на (4, + оо) возрастает.
на (2; 4-оо) возрастает
4- ею) убывает
8.42. На
убывает, на [8; 4~ 00) возрастает
8.43.	На (—оо ; 3) и на (3; 4" 00) убывает.
8.44.	На ( —оо; —log3 2) и на (—log32; 4~ 00) убывает.
8.45.	На ( —оо; 0] возрастает, на [0; 4" 00) убывает.
142
8.46.
8.47.
8.48.
На
На
На
и на
возрастает.
(0; е) и на (е; е3] убывает, на [е3; е5) и на (е°; 4-оо) возрастает.
возрастает, на (1;
4- оо) убывает
4 ’
8.49.	На (0; 1] и на [4; 4-00) возрастает, на [1; 4] убывает.
8.50. На
— оо
_и
2J
убывает, на
возрастает.
2 ’
8.51.	На ( — оо; 0] и на [log2 3; 4- 00) возрастает, на [0; 1) и на (1; log2 3] убывает.
8.52.	На ^0;	и на	; 4~°°^ убывает.
8.53.	На (—оо; 0] убывает, на [0; 4-00) возрастает.
143
8.54.	На (—оо, 0] и на [1; -f- оо) возрастает, на [0; 1] убывает.
8.55.	На (—3; 4- оо) возрастает. 8.56. [ — 3, 4-оо). 8.57. [ д/2~, 4-оо).
8.58.	(0; 4-оо). 8.59. (в; -0 8.60. (в; £| . 8.61. (— оо, -|- оо)
8.62.	[2; 4- оо). 8.63. ( — оо; 0). 8.64. (О, З9].
8.65.	|log2I; 4- оо \ 8.66. (-оо; 1]. 8.67. Г-1; -(-оо')
8.68.	[—1; 4-оо).	8.69. См рис. 63.	8.70. См. рис 64
8.71.	См. рис 65	8.72. См рис 66.	8.73. См. рис. 67
144
8.74. См
8.77. См
8.80. См
8.83. См.
8.86. См.
8.89. См
8.92. См.
8.94. х =
рис 68.
рис 71
рис 74.
рис 77.
рис 80.
рис 83
рис 86
-6
8.75. См.
8.78. См
8.81. См
8.84. См
8.87. См.
8.90. См
8.93. См.
8.95. х =
рис. 69
рис 72
рис 75
рис 78
рис. 81
рис 84
рис 87
8.76. См. рис. 70.
8.79. См
8.82. См
8.85. См
8.88. См
8.91. См
рис 73
рис 76.
рис. 79
рис 82.
рис 85
8.97. x = l|og15^
8.96. х — logj5 5
8.99. {±2}
6 Заказ 1259
145

8.100.	х=0. 8.101. х = 5 8.102. {3, 5}. 8.103. х = 2.
56
8.104.	x=log4-^-. 8.105. {0; 2}. 8.106. {-1, 1}.
7
8.107.	{0; 2} 8.108. {0; 1; -1} 8.109. {2} 8.110. {±2}
8.111.	{10, 100} 8.112. {2, ДД . 8.113. {1, 100}. 8.114. {8}
I 16 1
8.115.	{1} 8.116. Д 8.117. {125; 1296}. 8.118. Н; 9
8.119.	{0,1}. 8.120. {2}. 8.121. (1; у}. 8.122. {!}. 8.123. {1}
8.124.	{1}. У к а з а н и е. Поделите левую и правую части на 7х.
8.125.	{2}. 8.126. {4} 8.127. {8} 8.128. {±2}. 8.129. {0}.
8.130.	{±1} 8.131. 0 . 8.132. 0. 8.133. (-00, —3)U(—1; +°о).
8.134.	[1; 4-оо). 8.135. (j);	+00)
8.136.	(0; 1)U(3; 4~ <» )• 8.137. (-1; 0)U(0; 4-°°)
8.138.	(-00, -1JUH, 2)U(2; 3JU[5; 4-00)
8.139.	(3; 4)U(4; 4-00). 8.140. {3}. 8.141. (1; 2)(J(2, 3).
8.142.	(-00; 1)U(1, 4-00 ) 8.143. {-3)U[— 1. 4-0°)
8.144.	[ —log32; 0]. 8.145. (0; 8](J[9; 4-°°) 8.146. (0; 9]
8.147.
. 8.148. [2; 4-oo). 8.149. (-00, 0]U[2; -|-oo)
8.150.	|1; 243| 8.151. (-00, 0)U[2, 4-00).
8152.	|)|Д4; 4-00) 8.153. Л); -7=]U(1, 4)U(4, 4-00).
8.154.	(—00; 0]U[log35; 4-00 ). 8.155. (-00, 1].
8.156.	[2; 4-0°) 8.157. {3}. 8.158. (1;	8.159. (5, 4-00).
8.160.	-•) U(~l. 3). 8.161. (3; 4]
8.162.	(0; 1)U(2,5; Д- oo) 8.163. См рис. 88 8.164. См. рис. 89 8.165. См. рис 90.
8.166.	См. рис. 91. 8.167. См. рис 92.
8.168.	(2, 4), (4; 2). 8.169. (2; 1) 8.170. (8, 2)
8.171.	(1; 1) 8.172. (4; 1). 8.173. (2; 4). 8.174. (1, -1)
(5	\
8-27, -Д- 1. 8.176, (4; 3) 8.177. (2; 8).
Л/з" /
8.178.	(1; 1), (9; 27). 8.179. (1, 1), (j •
8.180.	а) а^О, а = 2, б) а^1, а = 0, в) а = 0, а= — 1, г) а>0, а=/=1.
8.181.	a) а>0; б) а> — —, а=£\, а=£0, в) а>0, а^=\, г) а>0, д) а<0
147
4
8.182.	a) 1) a=^=— , 2) a — любое, 6) 1) a<3 и 2) a — любое, в) 1) a>4,
5
1 5
2) a^O, a^6; r) 1) Ж —1, a>4, 2)	—1, a^4, д) 1) a>6 —,
1 /
2) 0^a<4, e) 1)	, 2) 0<a<—, ж) 1) a<l, a^3, 2) a 1,
7	4
з) 1) a<_ — 1, a^3, 2) a>0
8.183. Если a<Z — 9, то нет решений, если a=— 9 или cz^O, то одно решение;
если —9<а<0, то два решения Указание Достаточно построить
график y(t)=t2 з) — 6t на множестве (0; 4- оо) и исследовать, сколько точек
пересечения он имеет с прямыми у = а
148
8.184.	Если а<_ — 4, то нет решений, если а= — 4, то одно решение; если
а>—4, то два решения
8.185.	Если a<Z —26, то нет решений; если а= —26 или 1, то одно решение;
если — 26<а<1, то два решения
8.186.	Если а< —16 или а>*16, то одно решение; если а= — 16 или а=16, то
два решения; если — 16<а<16, то три решения.
8.187.	—1. а=— 3. 8.188. — 1<а<1-Д/Г,
8.189.	I 1+У/2,	0> 8.190. (-2; 1) 8.191. (-оо, -1].
I	4	4 J
3	32
8.192.	[log23, 4-ОО). 8.193. (-00, -]U[4, 4-00) 8.194. (-00, —).
5	7
§ 9.	Элементы тригонометрии
9.1.	1—а2 9.2. 2 4- 9.3. 2,5. 9.4. sin 2а =—44, cos 2а =—44-
4	61	61
9.5.	^ 9.5. 25^-48.9.7. '-8^.
10	39	15
Qfi	1+2V30-
9.8. cos а =-------------------.
Решение, cos a = cos ((а4- Р)— P)=cos (а4- Р) cos р 4-
4-	sin (а4- Р) sin р, но sin р = ——, a sin (а4~ Р) = -^—•
9.10.	3 или —1. 9.11. 1. 9.12.	9.13. 0. 9.14. 1. 9.15. 1
3	2
9.16.	9.17. 4- 9.18. 4- 9.19. 2_ 9.20. 4 9.21. 0. 9.22. 1.
2	8	4	16	8
9.23.	1 9.24. 2.. 9.25. 2.. 9.26. —2.. 9.28. См. рис 93.
9.29.	См. рис 94. 9.30. См. рис. 95.	9.31. См рис. 96.
Ум
____________
1
~0
Рис. 93
3~ -Л Л 0
2
Зя я fi*
Рис. 94
ЗЯ 5Л-Л ЗЯ Л Л 0 Л Л ЗЯ Л 5Л	X
” 2~ 4 "4“2“4	4 2 4	4
Рис. 96
149
Ун y=$in(arcsinx)
Рис. 97
9.32.	а) б) -2-. 9.33. а)1,б)|. 9.34. 1. 9.35.	.
0	0	2 Z	э	о
4	т
9.36.	у. 9.37.	9.39.	См рис	97.	9.40. См рис 98
9.41.	См рис 99.	9.42.	См рис	100	9.43. См рис. 101
9.44.	х^лк, k£Z	9.45.	xj=^k,	k£Z	9.46. х^^ + лк, k£Z.
9.47.	х=£±У/лк,	fe = 0,	1, 2,	. 9.48. х#=1+УГ+^Г,	k = 0, 1. 2, 3.
’« Н I] •“ И i]
9.51.	[—1, 4-oo). 9.52. x= + i. 9.53. [1, 3] 9.54. |0, 1]
9.55.	Г_ 1, 11. 9.56. [-УТз"; У/13\ 9.57. |0, 12]
I 4	£ J
150
9.58.
. 9.60. [1; 4-оо).
9.61.	j] 9.62. [0; У/2]. 9.63. {0}.
9.64.	[О, д/ЁГ]. 9.65. [0; 1]. 9.66. [ — 1; 1] 9.67. [-1; 2].
9.77. Т=— 9.78. Т = л.
9.79.	7 = 2л 9.80. 7 = 2л. 9.81. 7 = 8л. 9.82. Т = ^-. 9.83. 7 = 2.
О
9.84.	Функция непериодическая Решение. Предположим, что функция пе-
риодичная с периодом 7, но тогда при всех вещественных х выполняется ра-
венство
cos %4-cos лх = cos (х4~ Г)-f-cos л (x-f- Г),
отсюда, полагая х = 0, получаем cos Т4*cos лТ = 2, но тем самым
( cos Т = 1
<	те. Т = 2л&, лГ = 2л& при каких-то k£N, n£N, но тогда
( cos л7 = 1,
л=-^-£ф — противоречие.
k
9.85.
На интервалах
Н+М;
где k = 0, ±1, ±2, ..., положительна.
9.86.	На интервалах
(-Т+Ы;
-^-4-2л^, -^-4-2л&\ где k = Qy
— -^-4-2л&),	( — ^-4-2л&;
о / у о
±1, ±2, ..., положительна.
Т+“)-
9.87.	На интервалах ^2л&4-1, у4-2л£^, (л4~2л/г, л4-14~2л&),
л4-2лk, 2л(&4-1)^, где 6 = 0, ±1, ±2, ., положительна.
9.88.	На интервалах ^2л&; -^-4~2л&^, 0^-4-2л£, л4~2л&^, где 6 = 0, ± 1, ±2, ...,
отрицательна
9.89.	На интервалах ( — -^-4~2л&, 2л&4~Y (^4~2л^-^4-2л&\ где&==0, ± 1,
\ О	О / у Z	Z	/
±2, . , положительна
9.90.	Четная. 9.91. Нечетная 9.92.И-1ечетная 9.93. Нечетная.
151
9.94. Четная. 9.95. На отрезках
л/г, ~ 4- nk , где k = 0, ± 1,
±2, возрастает,
на отрезках
у +	л 4- лЛ I, где k = 0, ± 1, ±2,
убывает
9.96. На у — у4"2л&, -^-4~2л/гр где /г = 0,	±1, ±2,
Г л Зл \
1“4-2л&, -^-4"2л/гк где /г = О, ±1, ±2,	, убывает
, возрастает, на
(j ПГ	> ’’Т	I I л
----^-4-2л6, — —^-4-2л/г| и 44-2л6,
4	4	]	4
-^-4-2л/г1 где /г = 0, ±1,
9.100. На
убывает, на
возрастает
9.101. На [2, 3] убывает, на [3, 4] возрастает.
9.102. На
убывает, на
возрастает
9.103.	Возрастае! на R
9.104. На
возрастает; на
, 1	/ 2\	1	/	2\1	Г	1	/2'
— л 4~— arccos | —— ), —— arccos ( — — ) ,	0,	— arccos ( ——
2	\3/	2	\	3 7 J	L	2	\ 3,
— arccos
убывает
9.105.
4+2-^
О
, где Z? = 0,
. , возрастает, на
, убывает
9.106.
См рис 102	9.107. См рис 103	9.108. См. рис. 104
152
ESI
Z9i/ ‘ ‘| ‘О 'I ~	Щ--+I-7- ‘?b' + fr/\. + 3| *811'6
Z9^pv + ^-+j *ZH*6	311
OH awd из ЦГ6	601
ZOI and нэ lire	901
601 эин
Jud	«э	*911'6	III	3Hd	WD	SI 1’6
3Hd	irj	*8||*6	801	3nd	из	*gn*6
•эиб	wo	*oi Г6	SOI	3t<d	ИЭ	’60Г6
801 3Hd
ZOI 3Hd
|(±-хг)шг|=Л |л
|i-|x|?|t//s=X
A
SOI 3Hd	tOI DHd
Z
301 3Md
SOI 3Hd
$-xzXis=^
x?uis=A
(	3	I	'I	(	л	I
9.119.	I arctg — Ц-л/г I k£Z> 9.120. { 2л/г, -^-4-2л/? k^Z, n^Z
I	5	I	I	I	2	|
9.121.
(-1)*-^+л& k£Z\. 9.122.
-^- + 2л/г 1 k£Z
9.123.
0 9.124.	+ arctg4 4-nn &EZ, n£Z
9.125.	1у4-л/г, arctg 5 + л/z I k£Z, n£Z
9.126. 1^ + 2лН k£Z
I 4
Указание Положите t = sin x-\~ cos x
9.127.	{arctg y-f-л&, -^-4-л/г| k^Z, /?£/}>.
9.128.	| — arctg-|+ л/г, arctg2-HT/?| k^Z, n£Z
154
9.129.	|л&, ± —Ч-2лл| k£Z, n£Zj.
9.130.	№k, ( —If+'.^ + nnLeZ, n£Z
9.131.	0 9.132.	+ v k, I *64 n^Z
I o 4	2 I
9.133. JAj k$z\. 9.134.
l+yd k^z> n^z
9.135.	| — — 4-л/?, —-^-4-2лгг, 2лт k£Z, n£Z, m£zl.
<42	I	)
9.136.	|2л&, — -?• 4-л/г I k£Z, rzczk 9.137. 12л&, -^-4-2лгг k£Z, nEzl.
(	4 I	J	<	2	|	)
9.138.	0	9.139. 0	9.140. |у4-2л&, 2лгг | k£Z, n£z}.
9.141.	x= ± 1 9.142. x = 1 9.143. (—2, —1; —1). Решение. Ясно, что
%2 —2 (cos лг/4-cos лг) x-f-4^0 при всех х, у, z, так как
Z) = (cos Л//4-СО8 лг)2 — 4^0, причем равенство нулю достигаекя только
если cos лу4-cos лг = 2 (тогда х — 2) или cos лу 4-cos лг= —2 (тогда
х— —2). Но \/х24~//24~224~2 (y + z—l) ^0 при всех х, у, z, таких, что это
выражение определено. Поэтому данное уравнение эквивалентно следую-
щей совокупности систем уравнений-
х = 2
< COS лу 4- COS Л2 — 2
У1^ + у2 + ^ + 2(у + г—1) =0
х= —2
cos лу 4- cos лг = —2
V^ + ^2 + z2 + 2(z/ + z— 1) =0.
Подставляя х— ±2, получаем (#4~ 1 )24~(24" 1 )2 = 0. Отсюда z = y =
= — 1 и х— — 2
9.144.	х = л 9.145. х = -. 9.146. I ± 4~ nk kЕZI 9.147. 144- 2лк LЕz\.
4	I 4	| J <4 I )
9.148.	{ zb “4-	| k£Z^. Указание Воспользуйтесь неравенством
2(а24-^2)>(а4-^)2
155
Рис 113
Рис 114
^ПП^ПП^
I
2Я|
„Д1
^<0
siny u
X
|Л 2я| X
I
I
Рис 115
156
9.149.	0. Указание. Воспользуйтесь неравенством
з___________________________________________
а 4-& 4-с > 3 Д/абс (а>0, 6>0, с>0).
9.150.	{О, 4}. 9.151. х=-^ 9.152. х= ±3^1 9.153. х = 0.
9.154.	х=1 9.155. х=—!= 9.156. х=4= 9.157. х= 1 9.158. х=1.
у5	У/2
9.159.	См рис. 113 9.160. См рис. 114. 9.161. См. рис 115
9.162.	См. рис 116 9.163. См. рис. 117 9.164. £ — i; 0 /	1	\	Н.4Л1
9.165.	(О; 2 — \/4-j Ш(2-У4-л, 2+Д/4-л)	
9.166.	(-»• -т>(4;,,)и(т'-*)	
9.168.	(-2-+2Я*. J+2n^u(y + 2nA!, -^ + 2л*), k£Z.	
9.169.	£ —л, —	— n + arctg 2; —-0u(arctg2, у	
9.170.	(- — + 2л/г, ^ + 2лЛ /г = 0, ±1, ±2, . . . \ 6	6	/	
9.171.	^-|-4-2л&; л4-2л/г^и^л4~2л&, -^4~2л&^, k^Z.	
9.172.	Г	2	2	] Г 5л I arcsin — 4~2л&; л — arcsin — 4~2л& U 1 — 4~2л&; I	3	3	116	1 Чтт	1 _±i+2nfe , ktz. 0	J
9.173. I arctg 3 +л (/г — 1); j+nk . kCZ
9.174.
— -у + 2лА; у + 2л/г^и р^~ + 2л/г, л 4-2лА:^U(^п + 2л£, 4^- + 2nfej, k(zZ
9.175.	(y + 2nA>; л + 2лЛ^и(я-|;2л*; -^- + 2^, k£Z
q 17fi Г-"» ,2л'	2я(£+1)1	_
9.17b.	| —4--г-«, ------I,
[ 3	3	3	J
9.177.
— л + 2лА>, — -52- + 2л/г] U [—у + 2лй,
— ^-4-2л^ U |4лй;
? + Н и
иЦ-н-гл*, ^+2л*|, кг.
9.178.	|-^-+2лй, — — 4-2лА| U |2л*. —+ 2nJ, k£Z.
I 2	4	114 I
157
9.179.
9.182.
9.185.
9.188.
9.189.
9.190.
9.191.
9.192.
9.194.
9.195.
9.197.
9.198.4
-^4-2лй Lgzj. 9.180. R 9.181. Г-1;
9.183. Г—1; —Л. 9.184. [sin 1, 1)
[- 1, 0)U(0, 1J 9.186.
_1_ 1 A
2 ' Д/5/
. 9.187. х = 3л, у ^=л-]-2лк (k£Z)
{^2л&,	+	^у-}-2ля, — у 4-2лгг^ | k£Z, n£Z
(( — 1)‘ arcsin ^4-л/г, ( — 1)‘~ arcsin т + 4 + ^Г \k^z
I	и	£	D £	£ I
{(,_„• 2+A(-„.21 + l + j^|i6z}.
Gh tHK ’«}
(Зя; 0) 9.193. /fi+гл. ^ + 2я(*+|А | *ez|
^±У1+Ь(» + 2я>	(t + 2n>0 iEZ п(Л
— 1 + \J\ —4л (k — 2m)
2

0.9.196.	l+A-.-l'ALez, n^z\.
w |\8 2	2	8 2	2 /1	J

( — 1)г^-4-л/г,
158

9.200.	{(i + ,,4. 4 + .™). (444. ^4>),	+
n£Z, l£Z
9-20L {(те+т‘; -к+т'4^41)’ (т+?‘; ~тЧ(4"-4>)
(%; л4-2л& — x)\k£Z, n£Zy x£R}.
9.202.	0 9.203. x = y=l. 9.204. (1, 0) 9.205. (1, 1)
9.200.	<0. „ 9.20,. (A.±). (-A.-A). (l.A). (±4).
9.208.	a) a<0, a >2, a=l, б) a = 0, a = 4, a>5, a<_ — 1, 1<а<3, в) a=l,
r) a=l, a = nky k£Z, д) a=l, e) a£R\Q.
2
9.209.	a) a=/=V, б) (—2л; — л)0( —л; 0)U(0, л)О(л; 2л), в) a=/=l, а=/=—,
О
Г) (2	1=^="3* ’ &	0
9.210.
Если а< — — или а>3, то нет решений; если а= — — или 1 <а^3, то од-
8	8
_1_
8
но решение; если
<а^1, то 2 решения.
9.211.	Если а< — 2 или а >2, то одно решение; если а= — 2 или а = 2, то 2 ре-
шения; если —2<а<2, то 3 решения.
9.212.
Если а< —- или а>2, то
4
нет решений; если а = 2, то одно решение, если
а—---или 0<а<2, то
4
2 решения, если
'---<а^0, то 4 решения.
9.213.	Если а>0 или а< —1, то нет решений; если — 1^а^0, то одно
решение.
9.214.	Нет, не существуют. 9.215. а^1 9.216. (0; 5).
9.217.	—12-^- 9.218. а) Нет; б) нет; в) да.
9.219. а) | — 1; 1]; б) а = 0 Указание Заметьте, что х=0 — корень уравне-
ния (II), в) а>1, а< —2, а = 0, а=л/2— 1.
Приложение 1
Работа 1
Вариант 1
1. — i 2. а) 2 ^cos -^-4"i sin -^0, б) 21995 3. х= — , у = ^. а) См рис 118,
б) уДТ — 1, в) см рис 119, i) см рис. 120 5. См рис. 121.
Вариант 2
1. 2/. 2. а) 2 fcos ~ + * sin б) —21995 3. х = — -i-, У = ~^ 4. а) См. рис. 122,
\ О	и /	Л	Л
б) Д/2 + 1, в) см рис 123, г) см рис. 124 5. См рис 125
Работа 2
Вариант 1
I. а) 1, б) 14; в) -1, г)----С 2, a) k = 0, k = -2, б) k = -2, в) А> = 0
2	3	д/з
3. Например, ап= — 1+ —
Вариант 2
11	1	2
1. а) 3; б) —; в) -, г) —— 2. a) £ = 0, £ = 2,5, б) £ = 2,5; в) £ = 0.
8	4	уз
3. Например, ап——24- —
п
Работа 3
Вариант 1
I- ч= -2, Ь = 3. 2. а) унаи6 = -1, г/наим = —2, б) на (- оо; —1] и на [3; + оо)
возрастает, на [ — 1, 1) и на (1, 3] убывает, в) см рис 126, г) если — 1 <а<7,
то нег решений, если а— — 1 или а —7, ю одно решение, если а>7 или
a<Z — 1, то два решения 3. Да, например, // = 0
Вариат 2
1. а= -2, Ь=— 3 2. а) yHJIl6 = 7, 1/найм =3, б) на (- оо, —4] и на [2; + оо) воз-
растает, на [—4, — I) и на (—1, 2| убывает, в) см рис 127, г) если —9<а<3,
то нет решений, если а= — 9 или а = 3, то одно решение, если —9
или а>3, то два решения 3. Да, например, г/ = 0
160
>
Рис 125
161
Работа 4
Вариант 1
1. а = 4 2. Л(х)=<	%2	5 если х<1, о 3	1	1	9S /		 3. 1 (ед2). 4. 31 5. 2 V(* + 3)3	5	,	6	3	6 3		2.ес;,их>1
Вариант 2	г2 1 	1— х— 1, если х<2,
1. а = 4 2. F(x) = - )	8 2	 3. |(ед2). 4. 18^-.5. сел» х»2 3 "	6
Работа 5
Вариант 1
“Г 1О о ‘ СО - |1Л со со •—• 00 СЧ о сч см |со o' СО со
Вариант 2
а) б) (J) 2. 6 18 3. 0,63 4.	5. 1
162

Работа 6
Вариант 1
1. Справедливо 2. 16х —33. 3. ^2, 1
4. а= — 4, Ь = 2 5. 6. 6. Да
Вариант 2
{2	1
3; 1 — , — 2 >.
О	J
4. а = 4, b = 0. 5. 10. 6. Нет.
Работа 7
Вариант 1
1. а) См рис. 128; б) [5; 4-oo)|j{0, 4); в) {0}; г) (0; 1); д)	.
2. (0; 4]U(— оо, —5). 3. х = 5.
Вариант 2
1. а) См. рис. 129, б) (—оо; — 3]|j{ —2, 0}, в) х = 0, г) (0; 1]; д) 0<а<^3”-
2. [4, 4- оо) 3. х = 3.
Работа 8
Вариант 1
1.	• 2. Убывает на (—оо; 2) 3. а) х=1; б) х=1.
4. (1; 2). 5. (0; 1) 6. (-оо, 0]U{2}U|4, + оо)
Вариант 2
1. b— 1 2. Возрастает на (—2; 4-оо) 3. а) х=1, б) х—\.
4. (1; 3). 5. (-2; 1] 6. Д;з)и(3, + оо)
163
Работа 9
Вариант /
L.>1 6)1^ 2. а) {т + i* I «4
3. С- + 2л»; i+zAfi+ 2л»; ^-+2л»). »tz.
у о	2	/ у 2	о /
4. а) Г-4х< 5]; б> ~ -4-<а<3.
I 10 I	10
Вариант 2
' а> 7;»>S 2'а| {т+т‘ I «4
б)’! —-^-4-лб, агс!^34-лгг | ky n^Z
3. ^-^-4-2л&; л + 2л^и(л4-2л^, 4^-4-2л&^, k£Z.
4. а) [--4]; б) fl=—f2-2<fl<4
Приложение 2
1. а) —	, б) см рис 130; в) (Д/б” — V^") fcos + 5’п т*\ г) см Рис
2	2	у о о /
131 2. а) См. рис. 132, б) г, = -2-|+ 1 4 i, z,= —2^ + 2^i; в) [2^-1;
5	5“	55
[3ni	1 Зпс	1	"1
— — arcsin---— , —4-arcsin----== 3. а) 1; б) см рис.133;
4	2^2	4	2Д/2 J
\[% А/2" а/2~	а/2~
в) см. рис. 134, г) см. рис 135 4. б)--—\-1	, — -i , в) { — 2; 0; 2);
г)	5. б) а5 = 6-|. Г) с„ = 2" —22-". 6. б) а = 3, а=-1;
в) {3, —1, +У/3} 7. а) х=4, б) см. рис 136, в) (ед.2), г) 24
о	4
8.	а) См. рис. 137; б) унзнм = -10, </наиб=6, в) z/ = 3,5; г) 4^- (ед2).
9.	а) у = 7х— 20, б) j/ = 4-—8^" +8, в) см рис. 138, г) 44 (ед.2)
О	о	/1
10.	б)4-(3-2х) 11. а) (1; 1), (5; 25), б) 4 (ед.2).
164
12. б) 1. 13. б) [-2, -1]U|O, + оо); в) а= 1; г) fe>8.
14. в) Одну, (—3 —2х0, — 2х0(3 + 2х0)2) 15. а) {— 1}, б) [ — 5, — 1)0(5; +оо);
в) см. рис. 139, г) /(5).
16. а) (-оо, -7)01-1; + оо); б) 4-Д/т’. в) 3/(3)>2/(4); г) ( — 1, + оо)
165
17. a) [ —4, 8]; б) [2 Д/з"; 6]; в) (в, -2-||. г)
I	О J
-з|,4\ 18.а)(—оо, 1]Щ6, 4-оо),
б) Н-, б|, в) [6, 4- oo)U{l} ; г) [Л/ПГ; 4-0°) 19- а) (1; 5); б) 1, в) {2};
г) (1; 2]U[4; 5). 20. а) {0, 5}, б) 3, в) (5; 4-°°). О [х = 5
Ъ = 2.
21. а) — оо, — J|j(2, 4-оо ), б) {3}; в) на оо, —J возрастает, на (2, 4- оо ) воз-
растает; г) если а=/= — 1, то один корень; если а= — 1, то нет корней.
22. а) {2, 8}, б) (0; 1]U[16; 4-оо), в) [—1, 4-оо ); г) а> — 1 23. а) х=1, х>8,
166
1
| Л|	cos a |
Рис 140
6)
(I J 4	5
г) если a<Z. —4 или a>0, то один корень; если a =
= 0 или a — — 4, то два корня, если —4<а<0, ютри корня. 24. а) {1
б)	Г1 ; + оо Y. в)(—2, 1 -2 V2)U( 1 -2V2, +00),
г) (2, 1 + 2д/з")и( 1 +%у/2; + оо). 25. а) 0, б) 2, в) Infe, -2- + nn | k, nCZ
г) у — ‘2х —у.	26. а)
Ikez' nez\-б) cos4a'
,	( А , 5л Зл I Ли/ А , Зл |3л I Л Кг 7	>	«	1
в)	(л*+-Т7’ “г +nk )и( +-7* ’ -Г5" + ЯЧ’ k^Z' Г> —cosbjc- — ТС-
27.	б) I k£Z, fe/з); в) R-, -^]иГ^Г- Л”! и{0; л’ 2л}’ Г) *•
[31	J L	J L	J
28.	a) y = <2t2— t — 3, где / = cosx; б) <-^-4-л/г,
+ у-}-2лгг J k£Z, n£Z
г) если а< — 3 — или а>0, то нет
8
корней; если а = — 3 — или — 2<а<0, то
8
один корень, если
— 3 ~<о< — 2, то два корня
8
I я л	я	I	I	Г	91
29.	а) < —+ — k-, + — + лп п, keZ>; б) 2л, в) —1, — , г) 0
^42	о	I	J	L	io J
л/з"
зо. а) 1—(ед2),
4
{л , л _	1 — \/17 р.
— 4-ля; + —Ч~2лгг; iarccos------[-2лт
2	о	4
ет, например, отрезок с концами в точках с координатами (0, 1) и (),
г) см рис 140.
Приложение 3
Задания для базовой школы
ky п, m£Z>, в) существу-
1993 г.
Вариант /
L б){|4^ I ftez|.B)cos4x,^,r) (-Д.-^иГ-Д	л)
(о 3 I )	2	\ з 6/ \ 6 6/ \6 3/
167
2. a) —3, б) (0, logj 3-1, в) (— оо, — 2); г) Flogj 5; — 2\
I 2 J	L 2	/
3. А. а) | — 5, 5], б) {3}, в) 5, г) а = 5.
И Зг2 5	3
3. Б. а) См рис. 141, б) —----------—	у==^' г) ~4
Вариант 2
1	I аг Л \ л W х /л л\н/л 2л\ /2л Зл\
'• б) Ь- I 6 Г в) ~со ’ r) U' зМз; ~М-; т)
2. а) — 2, б) {0, log3 2}; в) (1, + оо), г) (1, log3 4].
3. А. а) ( —оо, — 1]U[1, + оо), б) {2}; в) 1, г) й>0.
у4 5
3. Б. а) См. рис 142, б) х3——4~—, в) г/ = 4, г) 4 (ед2)
1994 г.
Вариант 1
1. а) , б) I, в)
(nk .л лп I •	1 Г л \
w i6+v И4лб2гг) [-16•°;
2.	а) —2, в) (-3, 2JU10. 4), г) {1,5}.
3.	а) {—2, 0, 2}; б) см рис 143, в) —4 и 0, г) 4 (ед2)
4.	а) (-оо; —71Uf— 1, + °°). б)	в) /(1)<2/(-1), г) а>0
Вариант 2
а) -3^. б1	2L+- |	г> [о.
168
2.	a) -1; в) (2; 3]; г)
3.	а) {— 2; 0; 2}; б) см рис. 144, в) —16 и 4; г) 4 (ед2 3 *)
4.	а) [-1; 3]; б) (1, 2); в)	г) ft = 2.
Задания для классов
с углубленным изучением математики
1992 г.
Вариант 1
I- а) U+л* I ktz\- б)	D [-1. 7-4<]
2 I J [о	о J у о о/
2. а) ( — 2;	— д/з”] U [Д/з\	2)» б) {Ч»	в) на (“2;	0] возрастает,	на |0;2) убывает,
г) если а<2, то два корня; если а — 2, то один корень; если а>2, то
корней нет.
5	11	7
3. А. а) у=— х------б) —2,25 и 0; в) см рис 145; г) — (ед.2).
6	6	30
169
3. Б. а) См
---| при а = 0, {2,
I+W
2
Вариант 2
(--И^тр [-!•']
2. а) (0; 1]U[3; 4); б) {3}, в) на (0, 2] убывает, на [2; 4) возрастает;
г) если а < log j 4, то нет корней, если a = log1 4, то один корень; если
з	"з
a^logj 4, то два корня.
“з
1	1	5
3. А. а) у=— — *4-3, б) 0 и 2 — ; в) см. рис. 148; г) — (ед2).
170
з л/Т з з л/Т
3. Б. а) См. рис. 149, б) см. рис. 150; в) —г)	----
3. В. а) {— 1, 1 ±у/2}; б) (- оо; - 1JJ[_1; 2] ; в) {— 1; 1 ± д/2~) при b= — 1,
1993 г.
Вариант 1
1. б) 1 — -^-4-я&; 2я/и; —-^-4-2лгг	k£Z, m£Z, n£Z(; в) f	-5-
14	2	J X 6	/ \	6
г) ( — оо, — 1,5].
3. А. а) {0; 2/}; б) см. рис. 151; в) см рис 152; г) 1.
2	2
3. Б. а) См. рис 153, б) 30 — , в) у = 8х— 17; г) — (ед2)
о	<5
3. В. а) х>2, б) {40 + 8Д/22'}; в) а=1, г) а^У/2
171
Вариант 2
1. б) + 2лт, у + 2лгг J k£Z, m£Z, n£Z
[- »(>•
Г' 1<°<|
2-.) -i; «) (о.
г) (-оо; -1,5]
3 д/27*), в) убывает
на (0; 3) и на (3, + оо),
3. А. а) {0; 2}; б) см рис 154, в) см рис 155, г) 3.
2	2
3. Б. а) См рис. 156, б) —30 — , в) //=-8x4-9: г) — (ед2)
<5	о
3. В. а) х>3; б) {41 + 8^22“}, в) b= -1, г) Ь^У/2
172
1994 г.
Вариант 1
1.	а) |л&, —у4-2лгг | k£Z,	б) ( — л,	в) — ; г) если
а=/=0, а=/= — 1, то три корня, если а —0, то один корень; если а= — 1, то два
корня
7
2.	а) —; б) {!}; в) (1; 4); г) см рис. 157.
/2 —1
\3 ’ 8 ]
3. А. а) {1}, б)
, в) да, с концами в точках с координатами (1; 2) и
(4, 4), г) а= —i
173
у3 я 5
3. Б. а) —-4-1-; б) см
6x6
рис. 158; в) да, является; в точке с абсциссой
Q1
х0=1; г) 7-^_ (ед.2).
3.	Б. а) См. рис 159, б) число —а — корень уравнения; в) см. рис. 160; г) 2 ~\j2.
174
Вариант 2
1. а) <-^--}-л&, 2л/?	n£Z>, б) Г^,	в) г) если Ь=#0,
I Z*	I	I	| Z*	/	х
b=/= — I, то три корня, если Ь — 0, то один корень, если b = — 1, то два корня.
13
2. а) —, б) {!}; в)
о
’ з)’ г) СМ' РИС 161
3. А. а) {0}; б) (1, 2|; в) (0. 3), (2; 3), г) Z>=1.
3. Б. а)--Н3 1пх4~1 — ; 6) см рис 162, в) да, является, в точке с абсциссой
4	4
х0 = 2, г) 61п2—(ед2)
zooU
3. В. а) См рис 163; б) число b — корень уравнения,’в) см рис. 164. г) 2 ^/2
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Башмаков М И., Беккер Б М, Гольховой В. М Задачи по
математике Алгебра и анализ — М . Наука, 1982 — Вып 22 — (Библиотечка
«Квант»)
Болтянский В Г, Сидоров Ю. В, Шабунин М И Лекции
и задачи по элементарной математике — М Наука, 1971
Вавилов В В, Мельников И. И, Олехник С Н., П а с и-
ч е н к о П И Задачи по математике Алгебра Справочное пособие — М На-
ука, 1987
Вавилов В В, Мельников И И, Олехник С Н., Паси-
ченко П И Задачи по матемашке Начала анализа Справочное пособие —
М.. Наука, 1990
175
Вавилов В. В., Мельников И. И., Олехник С. Н., Паси-
ченко П. И. Задачи по математике. Уравнения и неравенства: Справочное по-
собие.— М.: Наука, 1987.
Виленкин Н. Я., Ивашов-Мусатов О. С., Шварцбурд С. И.
Алгебра и математический анализ для 10 класса: Учебное пособие для уча-
щихся школ и классов с углубленным изучением математики.— М.: Просвеще-
ние, 1995.
Виленкин Н. Я., Ивашов-Мусатов О. С., Шварцбурд С. И.
Алгебра и математический анализ для 11 класса: Учебное пособие для уча-
щихся школ и классов с углубленным изучением математики.— М.: Просвеще-
ние, 1995.
Галицкий М. Л., Гольдман А. М., 3 в а в и ч Л. И. Сборник за-
дач по алгебре для 8—9 классов: Учебное пособие для учащихся школ и классов
с углубленным изучением математики.— М.: Просвещение, 1995.
Галицкий М. Л., 'Мошкович М. М., Шварцбурд С. И. Уг-
лубленное изучение курса алгебры и математического анализа: Методические ре-
комендации и дидактические материалы.— М.: Просвещение, 1990.
Говоров В. М., Дыбов П. Т., Мирошин Н. В., Смирно-
ва С. Ф. Сборник конкурсных задач по математике.— М.: Наука, 1983.
Дорофеев Г. В., Потапов М. К., Розов Н. X. Пособие по мате-
матике для поступающих в вузы (Избранные вопросы элементарной математи-
ки).— М.: Наука, 1973.	1
Задачи письменного экзамена по математике за курс средней школы: усло-
вия и решения / Д. И. Аверьянов, Л. И. Звавич, В. К. Смирнова.— М.: Школа-
Пресс, 1993.—Вып. I.
Карп А. П. Сборник задач по алгебре для^ учащихся 8—9 классов школ
с углубленным изучением математики.— С.-Петербург: Образование, 1993.
Кречмар В. А. Задачник по алгебре.— М.: Наука, 1972.
Кудрявцев Л. Д., Кутасов А. Д., Чехлов В. И., Шабу-
нин М. И. Сборник задач по математическому анализу: Предел, непре-
рывность, дифференцируемость: Учебное пособие / Под ред. Л. Д. Кудрявцева/—
М.: Наука, 1984.
Ривкинд Я. И. Дифференциальное и интегральное исчисление в за-
дачах.— Минск: Вышэйшая школа, 1971.
Саакян С. М., Гольдман А. М., Денисов Д. В. Задачи по ал-
гебре и началам анализа для 10—11 классов.— М.: Просвещение, 1990.
Сборник задач по математике для поступающих во втузы / Под ред.
М. И. Сканави.— М.: Высшая школа, 1988.
Сивашинский И. X. Теоремы и задачи по алгебре и элементарным
функциям.— М.: Наука, 1971.
Ш а р ы г и н И. Ф. Решение задач: Учебное пособие для 10 класса общеоб-
разовательных учреждений.— М.: Просвещение, 1994.
Ш а рыгин И. Ф., Голубев В. И. Решение задач: Учебное пособие
для И класса общеобразовательных учреждений.— М.: Просвещение, 1995.
СОДЕРЖАНИЕ
Предисловие.......................................... 3
§ 1.	Вещественные и комплексные числа ....	4
§ 2.	Последовательности. Предел последовательно-
сти. Предел функции. Непрерывность функ-
ций ...........................................11
§ 3.	Элементы дифференциального исчисления .	28
§ 4.	Элементы интегрального исчисления	....	39
§ 5.	Элементы комбинаторики и теории	вероятно-
стей 	45
§ 6.	Многочлены и уравнения..............52
§ 7.	Иррациональные уравнения и неравенства. Сте-
пенные функции ................................59
§ 8.	Логарифмическая и показательная	функции.
Логарифмические и показательные уравнения
и неравенства ............................ 67
§ 9.	Элементы тригонометрии..............77
Приложения
1.	Проверочные работы по курсу алгебры
и начал анализа 10—11 классов .................89
2.	Задания для повторения курса алгебры
и начал анализа 10—И	классов ................97
3.	Варианты выпускных	экзаменов................103
Ответы. Указания. Решения	.....................114
Рекомендуемая литература	..................... 175
ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ
sin2a 4- cos2a = 1
sin (a + p) = sina cosp 4- sinp cosa
sin (a — p) = sina cosp — sinp cosa
cos (a + p) = cosa cosp — sina sinp
cos (a — p) = cosa cosp 4- sina sinp
sin2a = 2 sina cosa
cos2a = cos2a — sin2a
1 4- cos2a = 2 cos2a
1 — cos2a = 2 sin2a
a + p a — P
sina 4- sinp = 2 sin —— cos ——
. n , . a-p a+p
sina — sinp = 2 sin —-— cos—p-
cosa + cosp = 2 cos cos
cosa — cosp = — 2 sin ^-p^ sin
sina sinp =y (cos (a — p) — cos (a 4- p))
cosa cosp = ~ (cos (a — p) 4- cos (a 4- p))
sina cosp =-y (sin (a — p) 4- sin (a 4- p))
ЛОГАРИФМЫ И СТЕПЕНИ. ОСНОВНЫЕ ФОРМУЛЫ (a > 0; b > 0; х > 0; у > 0; a * 1)
au • av = au + v
au
bu
alogox = x
logaxy = logax 4- logay
(au)v = auv
au • bu = (ab)u
logay = log»*_ log»v
logaxa = a logax
logxb
logrtb = -----,
logxa
log_b = —-— ,
Уа logba
logakxk = logax,
m
logakXm=— l°gox, k*0
w	к
X * 1
b / 1
k*0