Автор: Сетна Дж.П.
Теги: сборники произведений разных авторов на разные темы серии сборники физика механика статистическая механика
ISBN: 978-5-91522-336-2
Год: 2013
Текст
УДК 082.1; 531
ББК 94.3; 22.317
С28
Серия: Фундаментальные основы нанотехнологий: лучшие зарубежные учебники
Главный редактор серии: академик А.Р. Хохлов
Ответственный редактор: канд. физ.-мат. наук А.В. Чертович
Редакционная коллегия:
Антипов Евгений Викторович, профессор химического факультета МГУ;
Гудилин Евгений Алексеевич, профессор факультета наук о материалах МГУ;
Клячко Наталья Львовна, профессор химического факультета МГУ;
Образцов Александр Николаевич, профессор физического факультета МГУ
Сетна Джеймс П.
С28 СТАТИСТИЧЕСКАЯ МЕХАНИКА. Энтропия, параметры порядка, теория
сложности / Пер. с англ. Тамм М.В., Бодрова А.С.; науч. ред. Ошанин Г.С. - М.: Научный мир,
2013 - 616 с: ил. - (Фундаментальные основы нанотехнологий: лучшие зарубежные
учебники). ISBN 978-5-91522-336-2
Учебник «Статистическая механика: энтропия, параметры порядка и сложность»,
написан профессором Корнелльского университета (США) Джеймсом Сетной и был
впервые издан на английском языке в 2006 году издательством Оксфордского
университета. За прошедшие годы он приобрел большую популярность не только у студентов-
физиков, но и у студентов смежных специальностей - химиков, математиков, биологов и
биофизиков. Эта популярность вполне заслужена: учебник написан живым и понятным
языком, при этом автор излагает доступным образом не только фундаментальные
концепции и методологию современной статистической механики, но и их связь с теорией
динамических систем, квантовой теорией, теорией информации, современной химией и
биологией, основополагающими проблемами финансовой математики. Дж. Сетна
предлагает читателям не только общее видение решенных проблем, но и целый ряд задач,
которые еще ждут своего исследователя. Каждая глава учебника содержит большой
набор интересных упражнений. Представляется, что книга Дж. Сетны на русском языке
окажется очень полезной для студентов, аспирантов и исследователей, работающих как
в области физики, так и в смежных областях.
Copyright О Oxford University Press, 2006
Great Clarendon Street, Oxford OX2 6DP
All rights reserved.
No part of this publication may be reproduced,stored in a retrieval system, or transmitted, in any form or
by any means,electronic, mechanical, photocopying, recording, or otherwise,without the prior permission
of Oxford University Press, or as expressly permitted by law, or under terms agreed with the appropriate
reprographics rights organization. Enquiries concerning reproduction outside the scope of the above should
be sent to the Rights Department, Oxford University Press, at the address above.
ISBN 978-0-19-856676-2 (англ.)
Все права защищены.
Никакая часть настоящей книги не может быть воспроизведена или передана в какой бы то ни было
форме и какими бы то ни было средствами, будь то электронные или механические, включая
фотокопирование и запись на магнитный носитель, а также размещение в Интернете, если на то нет
письменного разрешения правообладателя.
© Тамм М.В., Бодрова А.С., перевод
на русский язык, 2013
ISBN 978-5-91522-336-2 © Научный мир, издание на русском
языке, оформление, 2013
Оглавление
Предисловие к русскому изданию 5
Предисловие 6
1 Что такое статистическая механика? 10
Упражнения 13
2 Случайные блуждания и возникновение коллективного
поведения 36
2.1 Примеры случайных блужданий: универсальность и
масштабная инвариантность 37
2.2 Уравнение диффузии 44
2.3 Потоки и внешние силы 46
2.4 Решение уравнения диффузии 50
2.4.1 Преобразование Фурье 50
2.4.2 Метод функций Грина 52
Упражнения 55
3 Температура и равновесие 79
3.1 Микроканонический ансамбль 80
3.2 Микроканонический идеальный газ 83
3.2.1 Конфигурационное пространство 84
3.2.2 Импульсное пространство 87
3.3 Что такое температура? 92
3.4 Давление и химический потенциал 96
3.4.1 Материал повышенной сложности: давление в механике
и статистической физике 99
3.5 Энтропия, идеальный газ и пара уточнений для фазового
пространства 103
2 Оглавление
Упражнения 106
4 Динамика фазового пространства и эргодичность 123
4.1 Теорема Лиувилля 124
4.2 Эргодичность 128
Упражнения 135
5 Энтропия 148
5.1 Энтропия как необратимость: тепловые машины и смерть
Вселенной 148
5.2 Энтропия как мера беспорядка 157
5.2.1 Энтропия смешения: демон Максвелла и осмотическое
давление 157
5.2.2 Остаточная энтропия стекол: невыбранные дороги .... 160
5.3 Энтропия как неопределенность: память и теория информации 165
5.3.1 Неравновесная энтропия 166
5.3.2 Информационная энтропия 167
Упражнения 173
6 Термодинамические потенциалы 201
6.1 Канонический ансамбль 202
6.2 Невзаимодействующие системы и канонические ансамбли .... 209
6.3 Большой канонический ансамбль 213
6.4 Что такое термодинамика? 216
6.5 Механика: трение и флуктуации 222
6.6 Химическое равновесие и скорости реакций 223
6.7 Плотность свободной энергии идеального газа 229
Упражнения 234
7 Квантовая статистическая механика 256
7.1 Смешанные состояния и матрицы плотности 257
7.1.1 Материал повышенной сложности: матрицы плотности . 258
7.2 Квантовый гармонический осциллятор 263
7.3 Статистика Бозе и Ферми 265
7.4 Невзаимодействующие бозоны и фермионы 267
7.5 «Квантовое» распределение Максвелла—Больцмана 273
7.6 Излучение абсолютно черного тела и бозе-конденсация 276
7.6.1 Свободные частицы в сосуде 276
7.6.2 Излучение абсолютно черного тела 277
7.6.3 Бозе-конденсация 280
Оглавление 3
7.7 Металлы и ферми-газ 284
Упражнения 286
8 Моделирование и вычисления 307
8.1 Модель Изинга 308
8.1.1 Магнетизм 309
8.1.2 Бинарные сплавы 310
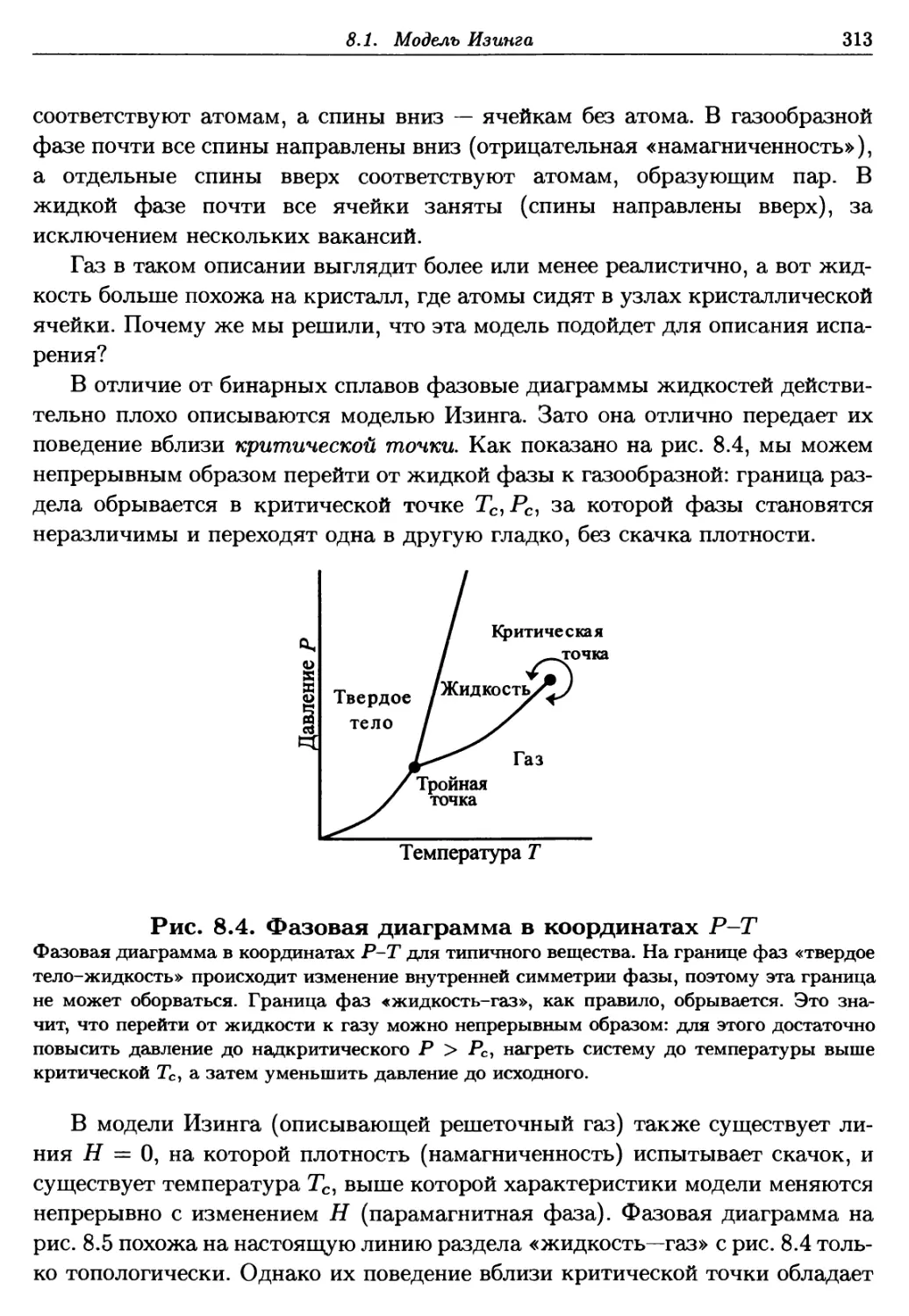
8.1.3 Жидкость, газ и критическая точка 312
8.1.4 Модель Изинга: как это решать? 314
8.2 Цепи Маркова 315
8.3 Теория возмущений: что такое фаза? 322
Упражнения 326
9 Параметры порядка, нарушение симметрии и топология 359
9.1 Нахождение нарушенной симметрии 361
9.2 Определение параметра порядка 362
9.3 Исследование элементарных возбуждений 368
9.4 Классификация топологических дефектов 373
Упражнения 383
10 Корреляции, отклик и диссипация 408
10.1 Корреляционные функции: мотивация 409
10.2 Экспериментальное измерение корреляций 414
10.3 Одновременные корреляции в идеальном газе 415
10.4 Гипотеза регрессии Онзагера и временные корреляции 419
10.5 Восприимчивость и линейный отклик 423
10.6 Диссипация и мнимая часть восприимчивости 424
10.7 Статическая восприимчивость 427
10.8 Флуктуационно-диссипационная теорема 431
10.9 Принцип причинности и соотношение Крамерса—Крёнига . . . 435
Упражнения 439
11 Скачкообразные фазовые переходы 460
11.1 Стабильные и метастабильные фазы 461
11.2 Правило Максвелла 464
11.3 Теория критического зародышеобразования 466
11.4 Морфология скачкообразных переходов 470
11.4.1 Динамика фазового разделения 470
11.4.2 Мартенситы 478
11.4.3 Дендриты 479
4 Оглавление
Упражнения 480
12 Непрерывные фазовые переходы 501
12.1 Универсальность 505
12.2 Масштабная инвариантность 515
12.3 Примеры критических точек 524
12.3.1 Критические явления в равновесных системах: энергия
против энтропии 524
12.3.2 Квантовые критические явления: нулевые колебания
против энергии 525
12.3.3 Динамические системы на пороге хаоса 526
12.3.4 Стекла: случайные, но замороженные системы 528
12.3.5 Перспективы 530
Упражнения 531
А Методы Фурье 565
АЛ Условные обозначения 566
А.2 Производные, свертки и корреляции 570
А.З Методы Фурье и пространство функций 572
А.4 Фурье и трансляционная симметрия 575
Упражнения 578
Литература 590
Предметный указатель 603
Предисловие к русскому
изданию
Я пишу это предисловие к русскому изданию моей книги с огромным
удовольствием и благодарностью. В течение длительного времени Россия и
Запад были независимыми центрами развития статистической физики и физики
конденсированного состояния. Современным пониманием физики металлов,
параметров порядка, сверхпроводников и свехтекучих жидкостей (см. главы
7, 9 и 12) мы в значительной мере обязаны Л.Д. Ландау, В.Л. Гинзбургу,
Н.Н. Боголюбову и их соотечественникам. Мой долг состоит в том, чтобы
поблагодарить Михаила Тамма, Анну Бодрову и Татьяну Низкую за то, что
они, отвлекаясь от собственной научной работы, посвятили много времени
переводу моей книги, и Глебу Ошанину за ее научное редактирование.
Насколько я знаю, ключевую роль в подготовке книги к печати сыграли также
Анна Соколова из издательства «Научный мир» и Владимир Стадничук
(которому пришлось взвалить на свои плечи обязанность по втискиванию всех
моих сносок и рисунков в формат, непохожий на английскую версию книги), я
им также очень благодарен. Благодаря всем этим людям нам удалось
преодолеть вслед за научным барьером — от физики к вычислительной математике,
биологии, техническим и социальным наукам — и барьер лингвистический:
от латинского алфавита к кириллице.
Джеймс П. Сетна,
Корнелльский университет,
март 2013
Предисловие
Границы научного знания со временем стремительно расширяются.
Обязанностью каждого следующего поколения ученых является синтез старого
знания с новыми концепциями и представлениями и передача следующим
поколениям очищенного набора ключевых идей. В этой книге я попытался
дать очищенное изложение развития статистической механики за последние
пятьдесят лет, которые были временем как большого расширения предмета
этой науки, так и важных обобщений в известных областях.
Эта книга рассчитана не только на физиков, я также ориентировался на
интересы и опыт продвинутых студентов и исследователей в таких областях,
как математика, биология, технические науки, вычислительная математика
и социальные науки. Именно поэтому в книге не предполагается наличие у
читателя большого опыта и знаний в области физики, в частности (за
исключением главы 7), явно не предполагается, что читатель знает квантовую
механику или интересуется ею. Основной текст посвящен изложению
предметов, относящихся к пересечению интересов всех групп читателей, в то время
как раздел упражнений охватывает объединение этих интересов. Следующее
поколение исследователей во всех перечисленных областях науки будет
изучать статистическую механику — либо целиком, либо какие-то из ее разделов
по отдельности. Делая статистическую механику понятной и полезной для
исследователей из различных областей, мы тем самым обогащаем ее предмет.
Действительно, в наше время многие ученые-физики по мере развития своих
исследований совершают вылазки в перечисленные смежные дисциплины.
Необходимость изложения новых концепций и приложений требует
сокращения некоторых традиционных тем. Так, термодинамика не играет уже
той ключевой роли в физике, которую она играла когда-то. Подобно судьбе
гидродинамики в предыдущем поколении, она продолжает оставаться
чрезвычайно полезной в некоторых областях, но исследователи, занимающиеся
этими областями, легко изучают ее самостоятельно. Кроме того,
термодинамика не оказала существенного влияния на области, далекие от физики и
Предисловие
7
химии: никто не пытается установить соотношения Максвелла для рынка
ценных бумаг или записать уравнения Клапейрона—Клаузиуса для алгоритмов
сжатия информации. Эти и другие важные темы, относящиеся к
термодинамике, были включены нами в состав упражнений, а не основного текста.
Также большинство книг по статистической механике опираются на
примеры из физики конденсированного состояния и физической химии — примеры,
которые впоследствии более подробно разбираются в других курсах. Между
тем даже мне, специалисту в физике конденсированного состояния,
представляется, что низкотемпературное поведение теплоемкости металлов — тема
гораздо менее занимательная, чем коллапс белых карликов, не говоря уже об
энтропии перетасовок игральных карт.
Первая часть книги посвящена обсуждению стандартных тем,
рассматриваемых под междисциплинарным углом. В большом количестве
упражнений развиваются новые приложения статистической механики:
теория случайных матриц, волатильность фондовых рынков, теорема
Колмогорова—Арнольда—Мозера, энтропия Шеннона в теории передачи
информации, рассуждения Дайсона о жизни в конце существования
Вселенной. Вторая часть книги содержит обсуждение метода Монте-Карло,
параметров порядка, линейного отклика и корреляций (включая
классический вывод флуктуационно-диссипационной теоремы), и теорию
скачкообразных и непрерывных фазовых переходов (теорию критического
зародышеобразования и теорию ренормализационной группы).
Книга предназначена для студентов старших курсов. Большая часть
текста будет доступна любому читателю, привычному к чтению научной
литературы и знакомому с частным производными и основами классической
механики. Исключение составляют глава 4 (требующая знания гамильтоновской
механики), глава 7 (требующая знания квантовой механики), раздел 8.2
(требующий знания линейной алгебры) и глава 10 (используемые в ней методы
преобразования Фурье изложены в Приложении). Односеместровый курс для
бакалавров может включать, например, главы 1-3, 5—7 и 9. Наиболее
трудолюбивые из магистров первого года в Корнелльском университете
смогли освоить за один семестр весь текст и примерно половину упражнений. Я
постарался удовлетворить потребности перечисленных разнообразных
категорий читателей с помощью сносок и примечаний, которые очень активно
используются в этой книге. Рассматривайте их как необязательные ссылки
на дополнительный материал, иногда более простой, иногда более сложный,
иногда — освещающий предмет с другой стороны по сравнению с основным
изложением. Упражнения градуированы по сложности, от φ (может быть
8
Предисловие
выполнено простым усмотрением) до ©(повышенной трудности);
упражнения, помеченные @(многие из них — это лабораторные работы на
компьютере), не следует задавать слишком часто. Большая часть глав 1-3, 5 и б была
сочинена для факультативного курса «волны и термодинамика», читаемого
второкурсникам; эти главы, а также упражнения, помеченные фи©, могут
быть рекомендованы амбициозным студентам младших курсов. Курс,
предназначенный для междисциплинарной аудитории, мог бы сфокусироваться в
большей степени на таких темах, как энтропия, параметры порядка и
критические явления, и включать главы 1-3, 5, б, 8, 9 и 12. Компьютерные
упражнения, приведенные в книге, являются результатом трех различных односе-
местровых курсов компьютерного практикума. Мы надеемся, что указания
и инструкции к компьютерным упражнениям, приведенные на сайте
книги [132], упростят включение этих упражнений в подобные курсы в других
университетах.
Английский текст книги доступен в виде pdf-файла в интернете. Я также
планирую выложить используемые в книге картинки в таком виде, чтобы
заинтересованным в этом лекторам было удобно их использовать в своих
презентациях.
На протяжении всей моей научной жизни я учился статистической
механике у моих друзей и коллег. Настоящая книга является учебником, а не
монографией, поэтому по умолчанию предполагается, что авторство
излагаемых идей и концепций мне не принадлежит: просто эти идеи стали
настолько центральными в данной области науки, что постоянное упоминание об их
авторстве будет утяжелять повествование. Я старался включать ссылки на
литературу только в тех случаях, когда, как я полагаю, это поможет моему
предполагаемому читателю. В наше время заинтересованный читатель (и
сочинитель учебника) может с использованием поисковых систем легко найти
информацию о ключевых идеях и статьях по любой теме, достаточно
всего лишь знать, как эта тема называется. Учебник в наше время в большей
степени, чем когда-либо — это всего лишь основа для дальнейшего
самообразования. Я благодарю всех, кто в течение многих лет терпеливо объяснял мне
свои идеи и методы, как лично, так и через статьи или с помощью интернета.
Я должен в особенности поблагодарить тех многих людей, которые
существенно помогли мне в написании этой книги. Я хотел бы поблагодарить
Национальный Научный Фонд и Лаборатории атомной физики и физики
твердого тела Корнелльского университета за их поддержку при написании этого
текста. Я хотел бы поблагодарить Памелу Дэвис Киверслон за великолепное
Предисловие
S
оформление обложки. Я хотел бы поблагодарить Эанну Фланаган, Эрика Си-
джиа, Сола Теколски, Дэвида Нельсона, Пола Гинспарга, Винная Амбегаока-
ра, Нейла Эшкрофта, Дэвида Мермина, Марка Ньюмэна, Курта Готтфрида,
Криса Хенли, Барбару Минк, Тома Роквелла, Сабу Саки, Петера Лепейджа
и Берта Галперина за полезные и плодотворные обсуждения. Эрик Грэннан,
Пит Брауэр, Мишель Ванг, Рик Джеймс, Эанна Фланаган, Аира Вассерман,
Дейл Фиксен, Рэчел Бин, Остин Хедмэн, Ник Трефтен, Сара Шандера, Эл
Сивере, Алех Тэта, Пол Гинспарг, Джон Гакенхеймер, Дэе Штейн и Роберт
Вейсс оказали существенную помощь при составлении ряда упражнений. Мой
подход к объяснению метода ренормализационной группы (глава 12) был
развит совместно с Карин Дахмен, Крисом Майерсом и Ольгой Перкович.
Студенты, слушавшие мои курсы, существенно помогли в оттачивании текста
и проверке упражнений; Джонатан Маккой, Остин Хедмэн, Брет Хэнлон и
Кайден Хаззард в особенности заслуживают благодарности. Адам Беккер,
Сурачат (Йор) Лимкумнерд, Сара Шандера, Ник Тейлор, Квентин Мейсон и
Стефан Хикс, занимавшиеся вычиткой текста, оценкой сложности
упражнений и составлением указаний к ним, внесли большой вклад в очистку текста
от неточностей. Я хотел бы поблагодарить Джоэля Шора, Мохита Рандериа,
Марка Ньюмэна, Стефана Лангера, Криса Майерса, Дана Рокшара, Бен Ви-
дома и Алана Брея, прочитавших части текста и давших неоценимые советы,
которые позволили существенно улучшить изложение материала. Я хотел бы
поблагодарить Джулию Харрис из издательства Оксфорд Юниверсити Пресс
за внимательное отношение и техническую помощь на конечных стадиях
подготовки книги. Наконец, мы провели сотни часов вместе с Крисом Майерсом,
составляя многие компьютерные упражнения; его широкие знания в науке и
моделировании, тонкий вкус в выборе вычислительных методов и средств, и
его прекрасное чувство юмора сделали это взаимодействие приятным и
продуктивным. Все ошибки и неуклюжести, сохранившиеся в тексте (а также и
то, что я не упомянул в нем множество увлекательных тем), сохранились там
вопреки замечательному вкладу, сделанному этими друзьями и коллегами.
Я бы хотел отдельно поблагодарить Кэрол Девайн за советы, полезные
комментарии и вопросы, а также за то, что на протяжении последних двух
лет она в течение, наверное, тысячи часов стойко терпела обращенный в ее
сторону затылок ее мужа.
Джеймс П. Сетна,
Итака, Нью-Йорк,
февраль, 2006
Глава 1
Что такое статистическая
механика?
Многие из встречающихся в природе систем слишком сложны для
непосредственного анализа. Предсказать поведение всех атомов в куске льда, или
всех валунов на линии разлома во время землетрясения, или всех узлов
интернета попросту невозможно. Тем не менее, подобные системы в целом
часто демонстрируют удивительно простое поведение. Статистическая
механика объясняет такое простое поведение сложных систем.
Идеи и методы статистической механики проникли во многие области
науки, техники и математики: понятия об ансамблях, энтропии, методах Монте-
Карло, фазах, флуктуациях и корреляциях, зародышеобразовании и
критическом поведении являются центральными в физике и химии, но они же
играют ключевую роль и в теории динамических систем, в теории информации,
в биоинформатике и теории сложности. Квантовая статистическая механика,
хоть и не имеет прикладного значения, является основанием многих разделов
физики. Скажем здесь несколько слов о том, что же это за всепроникающие
идеи и методы.
Ансамбли. Главная хитрость статистической механики состоит в том,
что она изучает не единую систему, а большой набор, или ансамбль систем.
Зачастую оказывается, что, хотя и понимание поведения отдельной системы
невозможно, можно вычислить, как будет вести себя набор из большого числа
одинаково приготовленных систем.
Например, рассмотрим случайное блуждание (рис. 1.1). (Представьте
себе, что речь идет о траектории частицы в газе или конформации полимера
в растворе.) Хотя любая данная реализация траектории такого блуждания
Что такое статистическая механика?
11
нерегулярна и, как правило, непредсказуема, в главе 2 мы выведем
изящные законы, описывающие поведение множества всех возможных случайных
блужданий.
В главе 3 мы введем понятие о равновесной статистической механике,
используя ансамбль всех состояний системы с заданной энергией; в процессе
изучения этого ансамбля окажется необходимым ввести такие коллективные
характеристики, как температура, энтропия и давление. В главе 4 мы
приведем наиболее полное из известных на сегодняшний день математических
обоснований этого рассмотрения. В главе б будет развито понятие о
свободных энергиях, которые описывают поведение частей систем; учитывая только
важные (с точки зрения макроскопического наблюдателя — прим.
переводчика) степени свободы, мы получим новые простые законы, вырастающие из
сложного поведения на микроскопическом уровне.
Рис. 1.1. Случайные блуждания
Движение молекул в газе, бактерий в жидкости, фотонов внутри солнца описываются
случайными блужданиями. Конкретная траектория одного случайного блуждания (слева)
плохо поддается количественному описанию. Напротив, статистические свойства большого
набора случайных блужданий (справа: показаны положения концов траекторий
блужданий, начинающихся в начале координат) описываются довольно простыми законами.
Глубокий основополагающий принцип статистической механики состоит в том, что зачастую
значительно легче понять поведение ансамбля систем.
Энтропия. Энтропия — наиболее фундаментальное из понятий,
возникающих в статистической механике (см. главу 5). Изначально под энтропией
понималась термодинамическая величина, вводимая для тепловых машин и
необратимо возрастающая со временем. В дальнейшем она стала основной
мерой беспорядка и информации, используемой в разных областях наук и
позволяющей количественно описать все что угодно, от сжатия изображений
при размещении их в интернете до тепловой смерти Вселенной.
12
Гл.1. Что такое статистическая механика?
Квантовая статистическая механика, о которой пойдет речь
только в главе 7, подводит микроскопическое основание под значительную часть
астрофизики и физики конденсированного состояния. Мы используем ее для
описания устройства металлов и изоляторов, для объяснения работы лазеров,
коллапса звезд, природы и свойств микроволнового реликтового излучения,
унаследованного нами от ранней вселенной.
Методы Монте-Карло позволяют находить средние по ансамблю
значения тех или иных величин на компьютере в случаях, когда система слишком
сложна для того, чтобы описать ее аналитически. Эти методы, изобретенные
и разработанные в статистической механике, используются повсюду в науке
и технологии — от моделирования процессов, происходящих внутри
ускорителей элементарных частиц, до моделирования транспортных потоков или
дизайна компьютерных микросхем. В главе 8 мы введем понятие о методе
Монте-Карло, модели Изинга и обсудим математику так называемых цепей
Маркова.
Фазы. Статистическая механика объясняет существование и свойства
фаз. По мере развития науки число известных фаз выросло от трех
наиболее распространенных фаз материи (твердых тел, жидкостей и газов) до
сотен: от сверхтекучих жидкостей и жидких кристаллов до вакуумных
состояний Вселенной вскоре после Большого Взрыва или фаз «связанных» и
«скользящих» сбросов во время землетрясений. В разделе 8.3 мы объясним
глубокую связь между понятием фазы и теорией возмущений. В главе 9 мы
введем понятие о поле параметров порядка внутри заданной фазы, которое
описывает ее свойства, возникающие в ней возбуждения и топологические
дефекты.
Флуктуации и корреляции. Статистическая механика описывает не
только усредненное поведение ансамбля систем, но и полное распределение
возможных типов поведения. В главе 10 мы используем корреляционные
функции для описания того, как системы флуктуируют и развиваются в
пространстве и времени. В этой главе мы также выведем очень полезные
тонкие связи между корреляциями, откликом на внешние воздействия и
диссипацией в равновесных системах.
Скачкообразные фазовые переходы. Переходы между разными
фазами приводят к формированию красивых пространственных структур.
Большинство таких переходов относятся к разряду скачкообразных:
лед остается твердым кристаллическим веществом до момента, когда
он (по крайней мере, часть, находящаяся непосредственно на границе
кристалла) внезапно становится жидкостью. В главе 11 мы изучим
Гл.1. Упражнения
13
образование зародышей новых фаз и экзотические структуры, которые
могут формироваться при скачкообразных фазовых переходах.
Критические явления. Другим классом фазовых переходов являются
непрерывные переходы. На рис. 1.2 изображен снимок одной конкретной
модели при температуре непрерывного перехода Тс. Обратите внимание на
самоподобные, фрактальные структуры; система не может решить, остаться ли
ей серой или разделиться на белую и черную фазы, так что она флуктуирует
на всех масштабах, демонстрируя то, что называется критическим
поведением. Траектория случайного блуждания также является самоподобным,
фрактальным объектом; увеличенное изображение маленького участка случайного
блуждания статистически выглядит подобно начальному изображению (см.
рис. 1.1 и 2.2). В главе 12 мы развиваем скейлинговые и ренорм-групповые
методы, которые объясняют эти самоподобные фрактальные свойства. Эти
методы также объясняют универсальность: многие свойства непрерывных
фазовых переходов оказываются на удивление не зависимыми от
конкретных деталей системы, в которой происходит переход.
Научное знание растет путем накопления информации, однако для
применения науки необходимо не только последовательное накопление, но и ее
«дистиллирование», выработка на основе накопленной информации новой
системы понятий.
Статистическая механика проникла своими ответвлениями во множество
областей науки и математики (см., например, рис. 1.3). Основная часть
каждой главы представляет собой дистиллированную версию: изложение
системы понятий, представляющих фундаментальное значение для всех
приложений. Накоплению информации посвящен раздел «упражнения»: он содержит
развернутое введение в различные приложения статистической механики к
мезоскопической физике, астрофизике, теории динамических систем, теории
информации, физике низких температур, статистике, биологии, лазерной
физике и теории сложных систем.
Упражнения
Первые три упражнения содержат краткую информацию о вероятностях
и распределениях вероятностей — математических понятиях, играющих
центральную роль в статистической механике. В упражнении Квантовые
игральные кости исследуются дискретные распределения, которые можно
рассматривать как первое знакомство со статистиками Бозе и Ферми. В упражнении
Распределения вероятностей вводятся ключевые распределения
вероятностей для непрерывных распределений, вычисляются их моменты, вводятся
14
Гл.1. Что такое статистическая механика?
Рис. 1.2. Модель Изинга в критической точке
Двумерная модель Изинга, описывающая магнит при температуре ферромагнитного
перехода Тс. При более высоких температурах система находится в немагнитном состоянии,
магнитный момент в среднем равен нулю. При температуре, соответствующей рисунку,
система как раз «решает», выбрать ей положительное (показано белым цветом) или
отрицательное (показано черным) направление магнитного момента.
понятия свертки и многомерного распределения. Упражнение Времена
ожидания иллюстрирует парадоксы, к которым можно прийти, если перепутать
величины, усредненные по разным ансамблям.
Упражнение Формула Стпирлинга посвящено выводу полезной
приближенной формулы п\ ~ y/brn(n/e)n\ более сильные студенты могут перейти
после него к упражнению Формула Стпирлинга: асимптотическое
разложение и изучить вопрос о нулевом радиусе сходимости этого разложения —
ситуации достаточно распространенной для вычислений в статистической
механике методом теории возмущений.
Последние три упражнения несколько более трудны. Для их понимания
не требуется никаких знаний по статистической механике, но тем не менее они
иллюстрируют сквозные темы этой науки и широту ее приложений.
Упражнение Теория случайных матриц содержит краткое введение в эту активно
развивающуюся область исследований, имеющую приложения в ядерной
физике, мезоскопической физике и теории чисел; часть (а) представляет собой
хороший пример использования гистограмм и ансамблей, остальные, более
продвинутые части, посвящены таким темам, как отталкивание уровней,
гипотеза Вигнера, универсальность и возникновение симметрии. В
упражнении Шесть рукопожатий вводится ансамбль так называемых малых миров,
широко используемых в общественных науках и в эпидемиологии для
описания связанности различных групп. При выполнении этого вычислительного
Гл.1. Упражнения
15
Рис. 1.3. Возникновение хаоса
Механические системы могут переходить от простого, предсказуемого поведения (слева)
к хаотическому состоянию (справа) по мере изменения некоторого внешнего параметра
μ. Многие совершенно различные системы описываются общим, универсальным скейлин-
говым поведением вблизи точки возникновения хаоса (обратите внимание на
самодублирующиеся структуры вблизи μοο)· Понимание этой универсальности возможно благодаря
использованию инструментария, развитого для изучения непрерывных фазовых переходов
в жидкостях и газах. В свою очередь, теория хаоса дает наилучшее объяснение явлению
роста энтропии в статистической механике.
упражнения вы познакомитесь с сетевыми структурами данных, алгоритмом
поиска по ширине, понятием о непрерывном пределе и впервые
познакомитесь с понятием скейлинга. В упражнении Правильные раскраски карты мы
сформулируем такие важные и трудные задачи информатики, как раскраска
графов и логическая совместимость. Эти задачи связаны с поиском
решения на ансамбле возможных конфигураций, подобном ансамблю состояний в
статистической механике.
1.1 Квантовые игральные кости.1 (Квантовая теория) (2)
У вас есть несколько «трехсторонних» игральных костей, т.е. таких, что
при их бросании может выпасть сторона с одной, двумя или тремя точками.
С помощью этих костей можно играть в три игры: Различимые, Бозоны и
Фермионы. В каждый ход любой из этих игр игрок бросает кости одну за
другой, «перебрасывая», если того требуют правила, пока не получится
разрешенная комбинация. В игре Различимые разрешены любые комбинации.
В игре Бозоны комбинация считается разрешенной только в том случае,
если следующее выпавшее число не меньше предыдущего. В игре Фермионы
Упражнение составлено совместно с Сарой Шандера.
16
Гл.1. Что такое статистическая механика?
разрешены комбинации, в которых следующее число строго больше
предыдущего. На рис. 1.4 изображена таблица разрешенных комбинаций для двух
костей.
Такие правила бросания костей аналогичны правилам квантовой
статистики неразличимых частиц.
Рис. 1.4. Квантовые игральные кости
Бросаем две кости. В игре Бозоны разрешены только варианты из квдратов,
заштрихованных светлым; они имеют одинаковую вероятность 1/6. В игре Фермионы принимаются
только комбинации в квадратах заштрихованных темным (не включая диагональ от левого
нижнего до правого верхнего угла), все они имеют вероятности 1/3.
(а) Пусть кости «честные»: каждое число выпадает ровно в 1/3 случаев.
Какова вероятность р(4) того, что при бросании двух костей в игре Бозоны в
сумме выпадет 4? А в игре Фермионы!
\ (Ь) Если мы теперь бросаем три «трехсторонние» кости по правилам игры
Фермионы, чему равна вероятность р(6) того, что в сумме выпадет 6?
(Указание: обратите внимание на то, что работает принцип запрета: в игре
Фермионы запрещены комбинации, в которых на каких-либо двух костях выпадают
одинаковые числа.) Примером фермионов являются электроны; два
электрона не могут находиться в одном и том же состоянии.
При игре в Бозоны для двух костей существует шесть различных
разрешенных комбинаций (11), (12), (13), ..., (33); половина из них соответствует
дублям (оба числа равны), в то время как для старой доброй игры
Различимые только треть комбинаций соответствует дублям2; т.е. вероятность
выкинуть дубль в игре Бозоны двумя костями увеличивается в 1.5 раза. Если
2В игре Фермионы дублей, конечно, не бывает.
Гл.1. Упражнения
17
бросать три кости, правила игры Бозоны дают десять разрешенных
комбинаций (111), (112), (ИЗ), ..., (333). Можно показать, что при бросании Μ
костей, каждая с N сторонами, игра Бозоны дает число разрешенных
комбинаций, определяемое биномиальным коэффициентом
(Ν + Μ - 1\ _ (JV + M-1)!
V Μ )~ Μ\(Ν-1)\'
(с) Во сколько раз вероятность выбросить триплет (три одинаковых числа)
при бросании трех костей по правилам Бозонов повышается по сравнению с
игрой Различимые! А для произвольного М, во сколько раз повышается
вероятность М-кратного мультиплета (на всех костях — одинаковое число) при
бросании Μ костей?
Обратите внимание на то, что в игре Бозоны состояния костей (т.е.
выпавшие на них числа) склонны принимать равные значения, кластеризоваться.
Примерами того, как настоящие бозоны собираются в одно и то же состояние,
являются бозе-эйнштейновская конденсация (раздел 7.6.3) и лазеры
(упражнение 7.9).
1.2 Распределения вероятностей. Q)
Большинство людей чаще сталкиваются с вероятностями дискретных
событий (например, при бросании монетки или в карточных раскладах), чем
с распределением вероятностей непрерывных переменных (например, роста
людей или скоростей атомов). Три непрерывных распределения, которые
наиболее часто встречаются в физике, следующие: (i) равномерное: pUniform(#) =
1 при 0 < χ < 1, р(х) = 0 в другом случае (генератор случайных чисел на
компьютере генерирует случайную величину, распределенную именно так);
(ii) экспоненциальное: Pexponential(^) = ехр(—£/т)/т при t > 0 (известное из
закона радиоактивного распада и используемое в теории столкновений в
газах); и (iii) гауссово (нормальное): pgaussian(^) = ехр(—у2/2а2)/(у/2ка) (эта
формула описывает распределение скоростей молекул в газах,
распределение положения броуновской частицы на больших временах, распределение
суммы равнораспределенных случайных величин и решение уравнения
диффузии).
(а) Правдоподобие. Чему равна вероятность того, что случайная величина,
выбранная из равномерного распределения на отрезке [0,1) окажется в
интервале от χ = 0.7 до χ = 0.75? Что радиоактивное ядро не распадется в течение
времени, вдвое превышающего типичное время распада г? Что ваша оценка на
экзамене, результат которого распределен по Гауссу, будет более чем на 2σ выше
среднего значения? (Указание: /2°°(1/\/2π) ехр(—ν2/2) dv = (1 — erf (\/2))/2 ~
0.023.)
18 Гл.1. Что такое статистическая механика?
(b) Нормировка, среднее и среднеквадратичное отклонение.
Покажите, что перечисленные распределения вероятности нормированы:
f p(x)dx = 1. Чему равно среднее хо для каждого из этих распределений? А
среднеквадратичное отклонение JJ (χ — хо)2р(х) άχΊ (Используйте формулы
J^0(l/^F)exp(-V2/2)dt; = lH
J^ *2(1/л/^)ехр(-*72)Л; = 1.)
(c) Сумма независимых случайных переменных. Нарисуйте график
распределения вероятности для суммы χ + у двух случайных величин, независимо
выбранных из плоского распределения на [0,1). Покажите, что в общем случае
сумма ζ = х + у двух случайных величин с распределениями р\{х) и Р2(у) имеет
распределение p(z) = f p\(x)p2(z — x)dx (так называемая свертка функций р\
и Р2)·
Многомерные распределения вероятностей. В статистической механике
зачастую исследуются распределения вероятностей для нескольких
переменных одновременно (например, для всех компонент скоростей всех атомов в
заданном объеме). Рассмотрим, например, распределение скоростей только
для одной молекулы. Если компоненты vx, vy и vz скорости молекулы
независимы друг от друга и распределены в соответствии с распределением
Гаусса с σ = y/kT/M (раздел 3.2.2), то полное распределение как функция трех
переменных описывается произведением трех гауссовых функций:
*^·ν"> = (2.(fcr)M))3/2 exP(-MvV2fcr)
/ Μ f-Mvl\
Ι Μ f-Mv2z\
ХУ2МеХр{-2йг)-
(d) Используя ваш ответ о среднеквадратичном отклонении для
распределения Гаусса (см. вопрос (Ь)), покажите, что средняя кинетическая энергия равна
кТ/2 в расчете на одно измерение (одну степень свободы). Покажите, что в
трехмерии распределение вероятности того, что модуль скорости равен ν = |ν|
— это распределение Максвелла
PMaxweii(^) = \^(у2/а3) exp(-v2/2σ2). (1.2)
(1.1)
Гл.1. Упражнения
19
(Указание: какую форму имеет область трехмерного пространства скоростей,
в которой |v| находится между ν и ν + δν? Площадь сферы радиуса R равна
4тгЯ2.)
1.3 Времена ожидания.3 (Математика) @
В среднем по шоссе за час проезжает 12 автобусов и 12 легковых
автомобилей. Автобусы ходят по расписанию: каждый следующий автобус проезжает
ровно через 5 минут после предыдущего. Машины же проезжают случайным
образом: вероятность проезда машины в течение короткого интервала dt
равна di/r, где τ = 5 минут. Имеется наблюдатель, который подсчитывает число
проехавших машин и автобусов.
(a) Проверьте, что, действительно, среднее число машин, проезжающих за
час мимо наблюдателя, равно 12.
(b) Чему равна вероятность Рьив{п) того, что за произвольно выбранный
десятиминутный интервал мимо наблюдателя проедет η автобусов? А вероятность
^саг(^) того, что за это же время мимо него проедет η машин? (Указание:
для случая машин можно, например, разделить весь промежуток времени
на маленькие интервалы d£; в течение каждого из этих интервалов с
вероятностью dt/τ машина проезжает, а с вероятностью 1 — dt/r « e~dt/T - не
проезжает. Независимо от того, каким образом вы решали задачу, вы
должны получить в результате распределение Пуассона РСаг(тг) = апе~а/п\ См.
также упражнение 3.9.)
(c) Найдите распределения вероятности pbus» Pear того, что длина интервала
между двумя последовательными автобусами (соответственно, машинами)
равна Δ. Чему равны средние от этих двух распределений? (Указание: чтобы
записать распределение вероятности для автобусов, вам понадобится ί-функция
Дирака.4)
(d) Представьте теперь, что другой наблюдатель прибыл на шоссе в
некоторый произвольный момент времени. Каково распределение вероятности времени
Δ, которое ему придется прождать до прибытия первого автобуса? А до
прибытия первой машины? (Указание: каким будет это распределение в момент,
когда предыдущая машина только что проехала? А зависит ли оно вообще
от того, когда именно проехала предыдущая машина?) Чему равны средние
от этих двух распределений?
3 Упражнение составлено совместно с Питом Вроуэром.
4£-функция δ(χ — хо) - это распределение вероятности, соответствующее тому, что
событие с вероятностью 100% попадет в любой интервал, содержащий хо; поэтому δ(χ — хо)
равна нулю если χ φ жо> и f f(x)S(x — χο)άχ = /(хо), если только область
интегрирования включает хо- Математически ^-функция не является функцией в обычном смысле, она
является распределением или мерой.
20
Гл.1. Что такое статистическая механика?
Среднее время ожидания между двумя машинами равно 5 минутам.
Среднее время ожидания следующей машины наблюдателем, только что
вышедшим на дорогу, тоже равно 5 минутам. Достаточно лишь немного подумать,
чтобы убедиться, что и среднее время, прошедшее с того момента, когда
проехала предыдущая машина, до момента появления наблюдателя, тоже
должно быть равно 5 минутам. Но 5 + 5 φ 5! Как такое может быть?
Одна и та же физическая величина может иметь разные средние
значения в зависимости от того, в каком ансамбле она усредняется! Среднее время
между машинами в части (с) было средним по количеству интервалов,
каждый интервал между машинами входил в него с одинаковым весом. Среднее
время до следующей машины в части (d) было средним по времени: второй
наблюдатель прибывает с равной вероятностью в каждый момент времени, а
значит он попадет во в два раза более длинный интервал между машинами
со в два раза большей вероятностью.
(е) В части (с) pfaf(A) была вероятностью того, что наугад выбранный
интервал имеет длину Δ. Запишите выражение для р£™е(Д) - вероятности того,
что второй наблюдатель, прибывая на шоссе в произвольный момент времени,
попадет на интервал длины Δ. (Указание: убедитесь, что ваша вероятность
отнормирована.) Используя /o£™e(A)f вычислите взвешенную по времени
среднюю длину интервала между машинами, измеряемую вторым наблюдателем.
1.4 Формула Стирлинга. (Математика) Q)
Приближение Стирлинга [126] для п!, верное при больших п, чрезвычайно
широко используется в статистической механике.
Покажите, преобразуя сумму в интеграл, что log(n!) = ^2^=1 log fc ~ (η +
l/2)log(n + 1/2) — η — 1/2 log(l/2). (Как обычно в этой книге, log означает
натуральный логарифм, а не log10.y) Убедитесь в том, что этот результат не
противоречит более точной и более широко известной формуле п\ « (п/е)п\/2пп.
Для этого достаточно доказать, что разница между первой формулой и
логарифмом от второй стремится к константе при η —> оо. Покажите также, что вторая
формула не противоречит выражению, используемому нами в упражнении 1.5,
η! ~ (2^(n+l))1/2e~(n+1)(n+l)n"hl, в том смысле, что разность между
соответствующими логарифмами стремится к нулю при η —> оо. (Полезные формулы:
J log xdx = χ log χ — χ, и log(n + 1) — log(n) = log(l + 1/n) ~ 1/n с точностью
до членов порядка 1/n2.)
1.5 Формула Стирлинга. Асимптотический ряд. (Математика) (§)
Формула Стирлинга (которая на самом деле была впервые получена де
Муавром) может быть уточнена и записана в виде степенного ряда.
Гл.1. Упражнения
21
Важно, что это не обычный ряд Тейлора, а так называемый
асимптотический ряд. Асимптотические ряды находят применение во многих областях
прикладной математики, статистической механики [124] и теории поля [125].
Итак, мы хотим получить разложение п! при больших п. Для того чтобы
сделать это, нам нужно превратить факториал в непрерывную функцию,
интерполировать его значения на дробные числа. Такая непрерывная функция
(с точностью до сдвига аргумента на единицу) называется гамма-функцией:
Τ(ζ) = (ζ — 1)! Существует множество эквивалентных формул,
определяющих Г(г); собственно, методами комплексного анализа можно показать, что
любая формула, задающая аналитическую функцию и удовлетворяющая
рекуррентному соотношению Τ(ζ+1) = ζΤ(ζ) и нормировке Г(1) = 1, порождает
одну и ту же функцию. Типичное определение (которое мы не будем здесь
использовать) гласит T(z) = J0°° e_tiz_1 d£; интегрируя по частям, можно
показать, что Г(г + 1) = zT(z).
(a) Используя рекуррентное соотношение Γ(ζ + 1) = ζΓ(ζ), покажите, что
Γ(ζ) имеет сингулярности (стремится к бесконечности) при всех целых
отрицательных значениях аргумента.
Формулу Стирлинга можно продолжить [7, р. 218] до следующего
изящного разложения Γ(ζ) по степеням 1/ζ = ζ'1:
Γ[ζ] = (ζ-1)!
- (2π/ζ)1/2β_*ζ*(1 + (1/12)·*-1
+ (1/288)ζ~2 - (139/51840)ζ~3
- (571/2488320)гГ4
+(163879/209018880)ζ-5
+ (5246819/75246796800)ζ~6
- (534703531/902961561600)ζ-7
- (4483131259/86684309913600)ζ-8
+ ...)· (1-3)
Это разложение выглядит как ряд Тейлора по степеням 1/г, но между ним и
обычным рядом Тейлора имеется одно тонкое различие. Зададимся вопросом
о радиусе сходимости [128] этого ряда. С точки зрения комплексного
анализа, радиус сходимости ряда - это расстояние от точки, вокруг которой мы
разлагаем функцию в ряд до ближайшей сингулярности этой функции на
комплексной плоскости (см. замечание 27 на стр. 325 и рис. 8.7(a)).
(b) Пусть <7(£) = Г(1/С); тогда с точностью до множителя формула
Стирлинга представляет собой ряд Тейлора по степеням ζ. Нарисуйте на комплексной
22
Гл.1. Что такое статистическая механика?
плоскости ζ полюса (сингулярности) д(С), которые вы нашли в части (а).
Покажите, что радиус сходимости обобщенной формулы Стирлинга для д должен
быть равен нулю, и что, следовательно, какое бы большое z мы ни взяли,
формула Стирлинга для этого ζ в конце концов разойдется.
Действительно, при больших j коэффициенты при z~J начинают очень
быстро расти, в книге [7, р. 218] показано, что нечетные коэффициенты (А\ =
1/12, А^ = —139/51840, ...) асимптотически растут как
A2j+1 ~ (-l)''2(2j)!/(27r)2(''+1>. (1.4)
(c) Используя признак сходимости Даламбера и формулу (1.4), покажите
в явном виде, что радиус сходимости формулы Стирлинга действительно равен
нулю5.
Все это вовсе не означает, что формула Стирлинга бесполезна!
Асимптотический ряд длины η неограниченно приближается к /(г), когда ζ стремится
к бесконечности, но при каждом конкретном конечном ζ этот ряд расходится
при η —> сю. Собственно говоря, асимптотические ряды очень распространены
и часто оказываются полезными в гораздо более широкой области
параметров, чем ряды Тейлора.
(d) Чему равен 0!? Вычислите 0! по формуле Стирлинга, суммируя Д/v для
нескольких первых N. Формула работает очень неплохо, учитывая, что она
вообще-то соответствует разложению вокруг бесконечно удаленной точки!
На сегодняшний день область науки, которая дает наиболее точные
количественные предсказания — это квантовая электродинамика. Физики
суммируют огромное количество фейнмановских диаграмм, для того чтобы точно
количественно предсказать свойства фундаментальных квантовых явлений.
Ф. Дайсон показал, что квантово-электродинамические вычисления
оперируют с асимптотическими рядами [125]; таким образом, наиболее точные
вычисления в науке имеют форму расходящихся рядов. Многие другие
важные разложения на самом деле представляют собой асимптотические ряды;
например, закон Гука в теории упругости имеет нулевой радиус
сходимости [15,16].
5 Если вы не помните свойств радиуса сходимости, обратитесь к [128]. В этой задаче
вы рассматриваете только нечетные члены ряда, поэтому радиус сходимости будет равен
y/\A2j-i/A2j+i\.
Гл.1. Упражнения
23
1.6 Теория случайных матриц.6 (Математика, квантовая теория) @
Одним из необычных и активно развивающихся приложений понятия
ансамбля является теория случайных матриц, используемая для описания
явлений ядерной физики, мезоскопической квантовой физики и теории волн7.
Теория случайных матриц была изобретена в результате смелой попытки
описать статистику энергетических уровней в атомном ядре. Во многих случаях
статистическое поведение квантовых систем с очень сложным и запутанным
взаимодействием собственных векторов и собственных значений может быть
удовлетворительно количественно описано с использованием ансамблей
матриц, элементы которых представляют собой случайные, совершенно
некоррелированные числа!
Для этого упражнения вам понадобится программное обеспечение, с
помощью которого удобно (1) строить гистограммы и рисовать графики функций
на одной картинке, (2) находить собственные значения матриц, сортировать
их, вычислять и запоминать разности между соседними уровнями и (3)
генерировать симметричные случайные матрицы с гауссовыми и
целочисленными элементами. Хорошими примерами такого программного обеспечения
являются Mathematica, Matlab, Octave или Python. Для тех из вас, кто мало
знаком с подобными программными пакетами, мы приводим несколько
полезных советов по выполнению этого задания в разделе, посвященном
компьютерным упражнениям на веб-сайте этой книги, под заголовком «Random
matrix theory» [132].
Наиболее часто используемым ансамблем случайных матриц является
гауссов ортогональный ансамбль (ГОА). Построение матрицы if,
принадлежащей к ансамблю таких матриц размера Ν χ Ν, состоит из двух этапов.
• Постройте матрицу ΝχΝ, элементы которой суть независимые гауссово
распределенные случайные величины со средним 0 и
среднеквадратичным отклонением σ = 1.
• Сложите матрицу с транспонированной, чтобы сделать ее
симметричной.
Напомним, что гауссово распределение с нулевым средним - это
распределение, генерирующее случайное число из интервала вокруг χ с плотностью
вероятности
**-£?-""■ («)
6 Упражнение составлено совместно с Питом Вроуэром.
7 В последние 10-15 лет активно развиваются также приложения теории случайных
матриц к задачам комбинаторики, теории броуновского движения и так называемых детерми-
нантных процессов. — Прим. переводчика.
24
Гл. 1. Что такое статистическая механика?
Одно из наиболее удивительных свойств больших случайных матриц - это
характерное для них распределение расстояний (щелей) между собственными
значениями.
(a) Постройте ансамбль из Μ = 1000 (или около того, чем больше, тем
лучше) случайных матриц размера N = 2, 4 и 10 из ГОД. Найдите
собственные значения каждой матрицы Лп и упорядочите их по возрастанию. Найдите
разность между соседними собственными значениями λη+ι — λη для η, скажем,
равного8 Ν/2. Постройте гистограмму распределения щелей между уровнями,
при этом выберите шаг гистограммы достаточно малым, чтобы были
заметны флуктуации. (Указание: для отладки программы используйте Μ = 10, и
только потом замените его на Μ = 1000.)
Обратили внимание на спад на гистограмме вблизи нуля? Это явление
называется отталкиванием уровней.
Для N = 2 распределение вероятности для расстояния между уровнями
достаточно легко вычислить непосредственно. Пусть наша матрица имеет вид
м = 0-
(b) Покажите, что разность собственных значений Μ равна
λ = у/(с — а)2 + 4Ь2 = 2\/d2 + Ь2, где d = (с - а)/2, а след матрицы с + а
на нее не влияет Таким образом, распределение вероятностей на множестве
матриц Μ (с точностью до значения следа, не влияющего на результат)
может быть записано как функция двух переменных рм{а,Ъ). Какая область
на плоскости (Ь, d) соответствует разностям собственных значений, лежащим
в интервале (λ, λ + Δ)? Докажите, что если рм непрерывна и конечна при
d = b = 0, то плотность вероятности р(Х) вблизи значения λ = 0 стремится
к нулю (это и есть отталкивание уровней). (Указание: d и Ь должны
одновременно обратиться в ноль, чтобы λ оказалась равна нулю. Перейдите
к полярным координатам, используя λ в качестве радиуса.)
(c) Вычислите аналитически величину среднеквадратичного отклонения для
диагональных и недиагональных элементов случайной матрицы из ГОА
(полученного симметризацией гауссовых матриц с σ = 1). Для проверки вашего
ответа вы можете построить предсказываемые вами гауссовы кривые совместно
с гистограммами распределений Нц и Н\2 для матриц, использованных вами
в части (а). Вычислите аналитически величину стандартного отклонения для
d = (с —α)/2, определенной в части (Ь) для матриц из ГОА с N = 2, покажите,
что оно равно стандартному отклонению для Ь.
8Почему мы не используем разности между всеми соседними парами собственных
значений? Средняя разность между соседними значениями может плавно меняться по спектру
матрицы, что приведет к некоторому смазыванию распределения.
Гл.1. Упражнения
25
(d) Получите в явном виде распределение вероятности расстояния между
собственными значениями матриц из ГОД с N = 2, проинтегрировав формулу
для собственных значений с весом рм{а,Ъ). (Указание: используйте и здесь
полярные координаты.)
Полученное в части (d) распределение просветов по ширине можно
перемасштабировать так, чтобы среднее значение просвета оказалось равным
единице. Проделав это, вы получите:
PWignerW = ye—2/4. (1.6)
Это выражение называется гипотезой Вигнера; для случайных матриц с
N > 2 оно предсказывает распределение расстояний между собственными
значениями с ошибкой, не превышающей 2%9.
(e) Постройте график формулы (1.6) поверх гистограммы для N = 2,
полученной вами в части (а), а также поверх гистограмм для N = 4 и N = 10.
Насколько полученный результат зависит от конкретных деталей
определения ГОА? Можно ли надеяться, что это результат универсален, т.е.
описывает и другие ансамбли вещественных симметричных матриц? Определим
ансамбль симметричных случайных матриц (назовем его «±1»), состоящий
из симметричных матриц размера NxN, элементы которых могут принимать
значения ±1 с равной вероятностью и независимо друг от друга.
(f) Постройте ансамбль из Μ = 1000 симметричных матриц с N = 2, 4 и
10 и элементами, равными ±1 с вероятностью 1/2. Аналогично части (а)
постройте распределение просветов между собственными значениями. Получились
ли результаты универсальными (т.е. не зависящими от ансамбля с точностью до
величины среднего просвета) для N = 2 и 4? Похожи ли они на (почти)
универсальные10 (т.е. почти такие же, как для ГОА в части (а)) при N = 10? Начертите
формулу Вигнера поверх вашей гистограммы для N = 10.
Ансамбль ГОА обладает рядом красивых статистических свойств.
Например, он инвариантен относительно ортогональных преобразований:
H-+RTHR RT = R-\ (1.7)
(g) Покажите, что Тг[НТΗ] равен сумме квадратов всех элементов Н.
Покажите, что этот след инвариантен относительно ортогонального преобразования
9 Распределение для больших случайных матриц также известно и является
универсальным. Однако вычислить его существенно сложнее.
10Обратите внимание на «выброс» в нуле. Этот эффект связан с тем, что существует
малая, но конечная вероятность того, что наша случайная матрица имеет пару в точности
совпадающих столбцов (или строк). Однако эта вероятность быстро стремится к нулю с
ростом N.
26
Гл.1. Что такое статистическая механика?
координат (т.е. такого, что Η —> RTHR и RT = R г). (Указание:
вспомните или выведите формулу циклической инвариантности следа: Тг[Л.ВС] =
Тг[САВ\.)
Обратите внимание на то, что для симметричной матрицы такой след
равен сумме квадратов диагональных элементов плюс удвоенной сумме
квадратов недиагональных элементов из правого верхнего угла. Это свойство
чрезвычайно удобно, т.к. в ГОА дисперсия (квадрат среднеквадратичного
отклонения) недиагональных элементов как раз вдвое меньше, чем у диагональных
(см. часть (с)).
(h) Запишите, в терминах следа, введенного в части (g), распределение
вероятности р{Н) того, что сумма квадратов элементов матрицы из ГОА равна Н.
Используя вашу формулу и инвариантность, доказанную в части (g), покажите,
что ансамбль ГОА инвариантен относительно ортогонального преобразования:
p(RTHR) = р(Н).
Это первый раз, когда мы сталкиваемся со спонтанно возникающей
симметрией. Во многих различных ансамблях случайных матриц, по мере того
как размер матрицы N стремится к бесконечности, возникают распределения
собственных значений и собственных функций, которые инвариантны
относительно ортогональных преобразований координат, несмотря на то, что
сам ансамбль матриц не обладает такой симметрией. Аналогично, когда
в задаче о случайных блужданиях на решетке число шагов N стремится к
бесконечности, в ней возникает сферическая симметрия, хотя, конечно, сама
решетка сферической симметрией не обладает. То же верно и для
крупномасштабных свойств решеточной модели Изинга при критической температуре.
1.7 Шесть рукопожатий.11 (Теория сложности, моделирование) (§)
Одной из самых популярных тем в теории случайных сетей является
исследование вопроса о степени их связности. Фраза про «шесть
рукопожатий» часто используется для описания того, насколько сильно связанными
являются сети знакомств в человеческом обществе: целый ряд исследований
(правда, не вполне корректно поставленных) показал, что для любой наугад
выбранной пары жителей Земли можно построить связывающую их цепочку
из небольшого количества людей (как правило, их оказывается около
шести), последовательные участники которой достаточно хорошо знакомы друг
с другом (скажем, хотя бы раз здоровались друг с другом за руку). Если
представить себе людей в виде узлов некоторой сети, а их знакомства в виде
связей между этими узлами, то эта задача сводится к исследованию
связности «сети знакомств».
Упражнение составлено совместно с Кристофером Майерсом.
Гл.1. Упражнения
27
Множество интересных задач возникает при изучении сетей,
сгенерированных случайным образом. Сеть (или граф) представляет собой набор узлов
(или вершин) и связей (ребер), каждая из которых соединяет два узла. При
этом любой узел может, вообще говоря, участвовать в сколь угодно большом
количестве связей (рис. 1.5). Случайная сеть — это сеть, созданная с
помощью каких либо фиксированных, но вероятностных по своей природе правил;
изучение таких сетей, как правило, продуктивно вести в терминах ансамбля
возможных сетей, в котором каждой сети приписывается вес, равный
вероятности ее образования. Таким образом, рассматриваемый класс задач
включается в сферу применимости идей статистической механики. В этом упражне-
Рис. 1.5. Сеть
Сеть представляет собой набор узлов (точек) и связей (линий, соединяющих точки).
нии мы построим некоторый ансамбль случайных сетей и вычислим для этих
сетей распределение расстояний между вершинами. Мы изучим так
называемые тесные миры12 [96,145] — теоретическую модель, объясняющую, почему
добавление небольшого количества связей между далекими частицами
(например, необычных международных или межкультурных контактов) может
радикально снизить типичное расстояние между двумя произвольными
вершинами сети. Наконец, мы увидим как в большой сети с малым количеством
таких «далеких» связей возникает простое и универсальное скейлинговое
поведение.
В разделе компьютерных упражнений на сайте книги [132] вы найдете
несколько файлов с указаниями и графическими шаблонами, упрощающими
работу с этим упражнением. Мы планируем сделать этот сайт многоязычным
и поддерживающим разные операционные системы.
Построение сети типа «тесный мир». Пусть L вершин сети
расположены по кругу и пусть есть два вида связей. С одной стороны, из каждого
узла выходит Ζ коротких связей, соединяющих его с его ближайшими по
12В англоязычной литературе используется близкий по смыслу термин «Small Worlds».
28
Гл.1. Что такое статистическая механика?
кругу (расположенными не расстоянии не более Ζ/2). Кроме того, имеется
ρ χ L χ Ζ/2 длинных связей, которые соединяют произвольные наугад
выбранные узлы (рис. 1.6). (Эта модель является упрощенным вариантом [96]
модели, предложенной в [145].)
(а) Определите на компьютере объект «сеть». Узлы в пределах этого
упражнения мы будем обозначать целыми числами. Введите класс «сеть», в котором
определите пять функций:
(1) HasNode(n), которая проверяет, принадлежит ли узел η сети;
(2) AddNode(n), которая добавляет в сеть новый узел η (если он в нее еще не
входит);
(3) AddEdge(nl, п2), которая добавляет в сеть новую связь между узлами п\
и п2;
(4) GetNodesO, которая возвращает список всех узлов сети; и
(5) GetNeighbors(n), которая возвращает полный список соседей узла п.
Рис. 1.6. Тесный мир
В этой сети семь длинных связей. При ее построении использовалось pLZ/2 = 8; но одна
из добавленных связей или совпала с существующей короткой, или соединила узел с ним
же самим.
Напишите процедуру построения тесного мира, который (при заданных
значениях L, Ζ и р) добавляет сначала узлы и короткие связи, а потом случайным
образом расставляет длинные связи. Используйте программный шаблон с
нашего сайта, чтобы изобразить полученную сеть на рисунке. Проверьте, что вы
Гл.1. Упражнения
29
правильно применяете периодические граничные условия: каждый узел г должен
быть связан с узлами (г — Ζ/2) mod L,..., (г + Ζ/2) mod L)13.
Измерение минимального расстояния между узлами. При изучении
тесных миров чаще всего интересуются распределением кратчайших расстояний
между узлами. В отсутствие длинных связей кратчайшее расстояние между
г и j будет соответствовать движению вдоль короткой дуги окружности,
соединяющей эти узлы, с шагами длины Zj2\ это расстояние всегда меньше,
чем L/Z (расстояние между двумя диаметрально противоположным
точками окружности), а распределение р{£) этих расстояний £ будет равномерным
на отрезке 0 < £ < L/Z. Естественно ожидать, что добавление длинных
связей приведет к сдвигу распределения в сторону более коротких путей.
(Ь) Определите следующие три функции, которые помогут вам находить и
анализировать распределение длин кратчайших путей.
(1) FindPathLengthsFromNode(graph, node), которая возвращает список
кратчайших расстояний от узла node до всех узлов node2 из сети graph.
Эффективным способом формирования этого списка является алгоритм
поиска в ширину. Идея метода заключается в переборе вершин путем
последовательного наращивания оболочек вокруг узла node. Текущая
оболочка (список currentShell) включает узлы, расстояние до которых
от node равно £. В список nextShell сохраняются узлы «следующей»
оболочки (т.е. соответствующей £ + 1). Прежде чем удалиться на
очередной шаг от начального узла, мы пробегаем «в ширину» все узлы
текущей оболочки, формируя заготовку для следующего шага:
- Начните с i = О (расстояние от node до него самого равно нулю) и
положите currentShell = [node].
— Пока описанная ниже процедура порождает непустой список
currentShell:
* введите новый список nextShell нулевой длины;
* для каждого соседа каждого узла из currentShell проверьте, не
присвоено ли ему уже расстояние до node (т.е. не встречался ли
он в предыдущих обол очках). Если нет, добавьте его в nextShell
и присвойте ему расстояние £+1;
13Здесь (г — Ζ/2) mod L — это целое число 0 < η < L — 1, которое отличается от г — Ζ/2
на число, кратное L.
30
Гл.1. Что такое статистическая механика?
* после того, как все узлы из currentShell обработаны таким
образом, добавьте единицу к £ и переименуйте nextShell в
currentShell.
— Верните список расстояний.
Эта процедура стартует из node и последовательно заметает все узлы сети,
измеряя их расстояния до стартового узла. Название алгоритма
объясняется тем, что мы сначала перебираем оболочку «в ширину», проверяя все
узлы, находящиеся на равном расстоянии от стартовой точки, и только
потом переходим к следующей оболочке. (Указание: протестируйте вашу
программу для сетей с малыми L и р. Для этого сравните полученные
расстояния для нескольких узлов с расстояниями, посчитанными
вручную с помощью рисунка, построенного в части (а).)
(2) FindAllPathLengths(graph), которая, последовательно выполняя
процедуру FindPathLengthsFromNode, создает список расстояний между
всеми парами узлов в заданной сети. Проверьте себя, построив гистограмму
распределения длин путей при ρ = 0. Убедитесь в том, что, как и было
предсказано выше, это распределение постоянно при 0 < £ < L/Z. Теперь
создайте графы с L = 1000 и Ζ = 2 при ρ = 0.02 и ρ = 0.2; постройте
соответствующие изображения графов и гистограммы распределения
расстояний. Приглядитесь к гистограмме. Насколько сильно она меняется с
ростом pi Какое значение ρ необходимо для того, чтобы сеть
удовлетворяла правилу «шести рукопожатий»?
(3) FindAveragePathLength(graph), которая вычисляет среднюю длину пути
(£) между двумя узлами. Вычислите значения (£) для нескольких
реализаций сетей с Ζ = 2, L = 100 и ρ = 0.1; ваши результаты должны оказаться в
районе £ = 10. Обратите внимание на существование значительных
флуктуации от сети к сети. Каково примерное число длинных связей в вашей
системе? Логично ли ожидать появления флуктуации при таком числе?
(с) Постройте график средней длины пути £(р) (отнормированной на £(р =
0)) в зависимости от вероятности ρ при Ζ = 2 и L = 50. Используйте
полулогарифмическую шкалу по ρ в пределах от ρ = 0.001 до ρ = 1. (Указание: ваша
кривая должна быть похожа на кривую Ваттса и Строгатса [145, fig. 2] со
сдвигом значений ρ в 100 раз; см. ниже обсуждение непрерывного предела.)
Почему при малых ρ график выходит на константу, равную единице?
Большие L и возникновение непрерывного предела. Перенормировка £(р) в
части (с) становится понятной, если рассмотреть непрерывный предел
задачи. В этом пределе, когда количество узлов L неограниченно увеличивается,
Гл.1. Упражнения
31
а количество длинных связей Μ = pLZ/2 остается конечным, задача имеет
изящное решение, в котором расстояния измеряются в радианах ΑΘ —
единицах длины дуги окружности. Нормировка I на £(р = 0) « L/(2Z), собственно,
и соответствует переходу к таким единицам длины, т.к. Δ0 = πΖί/L.
(d) Постройте изображение вашей сети из части (с) (Z = 2, L = 50) для
ρ = 0.1 в виде круговой диаграммы; постройте аналогичные диаграммы для
графов Ваттса и Срогатса с Ζ = 10, L = 1000 и ρ = 0.1 и ρ = 0.001. Какая из их
систем кажется вам статистически более похожей на вашу? Постройте (можете
использовать процедуру перенормировки, предложенную на сайте) график
перенормированной средней длины пути πΖί/L как функцию общего числа длинных
связей Μ = pLZ/2, для 0.001 < ρ < 1, при L = 100 и 200, a Z = 2 и 4.
В непрерывном пределе среднее расстояние между точками (Δ0)
оказывается зависящим только от Μ = pLZ/2. Поскольку Ватте и Строгатс [145]
использовали значение ZL в 100 раз превышающее наше, то, соответственно,
для того, чтобы получить такое же Μ, нам надо взять в 100 раз большее
р. Ньюмэн и Ватте [100] выводят результаты для непрерывного предела с
помощью ренорм-группового анализа (см. главу 12).
(e) Реальные сети. Выберите реальную сеть — самостоятельно или с
помощью нашего сайта [132]14, и вычислите для нее среднее расстояние между
вершинами и гистограмму распределения расстояний.
В сети, описывающей тесный мир, наличие всего нескольких длинных
связей играет принципиально важную роль в эффективном распространении
сигналов (распространении информации в компьютерных сетях,
распространении инфекционного заболевания в социуме, ...). Во многих случаях важно
понять насколько существенен тот или иной узел для распределения
кратчайших путей. Будем говорить, что некоторый узел является «посредником»
между двумя другими, если он принадлежит кратчайшему пути между
ними (для определенности договоримся также включать начальный и конечный
узлы в число промежуточных). «Посредничеством» данного узла будем
называть общее число кратчайших путей, которые через него проходят (рис. 1.7).
(Если между двумя узлами есть К различных кратчайших путей одинаковой
длины, договоримся включать каждый из этих путей с весом 1/К.)
Эффективный алгоритм вычисления посредничества аналогичен описанному выше
алгоритму вычисления кратчайшего пути.
14В числе примеров на сайте вы найдете сети киноактеров (узлы этой сети — это актеры,
а наличие связи означает, что актеры играли в одном фильме), «Шесть шагов до Кевина
Бэйкона», сеть бейсболистов (здесь связь соответствует тому, что они играли в одной и той
же команде).
32
Гл.1. Что такое статистическая механика?
Рис. 1.7. Посредничество
Тесный мир с L = 500, К = 2 и ρ = 0.1, размеры узлов и толщины связей пропорциональны
квадратному корню из их посредничества.
(f) Посредничество (повышенной трудности). Прочитайте [48,97], где
обсуждаются алгоритмы вычисления промежуточности. Примените эти алгоритмы к
построенному вами тесному миру, а также к сети из реальной жизни, которую
вы анализировали в упражнении (е). Изобразите ваши результаты графически с
помощью программного обеспечения, предлагаемого на сайте книги [129].
1.8 Правильная раскраска карты.15 (Информатика, моделирование,
математика) (3)
Многие задачи информатики заключаются в поиске допустимого решения
среди огромного множества возможных вариантов. Примером такой задачи
является задача о трех красках (рис. 1.8). Можно ли раскрасить все N
вершин графа в три цвета (скажем, красный, синий и зеленый) таким образом,
чтобы никакие два узла, связанные между собой, не были окрашены в один
цвет16? Для графа из N вершин можно, конечно, проверить все 3N
возможные раскраски, но время такого решения растет экспоненциально с ростом
N. Пока, к сожалению, не известно можно ли радикально сократить это
время. Ни один из существующих сегодня алгоритмов не позволяет проверить
Упражнение и связанное с ним программное обеспечение созданы совместно с
Кристофером Майерсом, с помощью Барта Селмана и Карлы Гомес.
16Напомним знаменитую теорему о четырех красках, гласящую, что любая карта может
быть раскрашена в четыре цвета. Это означает, по сути, что любой планарный граф можно
раскрасить в четыре цвета.
Гл.1. Упражнения
33
раскрашиваемость графа из N вершин в три цвета за время, гарантированно
не превосходящее (для любого графа) конечной степени 7V.17
Рис. 1.8. Раскраска графа
Два простых примера графов с N = 4 вершинами, один из них можно раскрасить в три
цвета, а другой — нельзя.
Еще одним хорошим примером является задача о логической
совместимости (SAT). Представьте, что имеется длинное логическое выражение,
содержащее N логических переменных. В этом логическом выражении могут
использоваться операции НЕ(-«), И (Л) и ИЛИ (V). Такое выражение
называется совместным, если существует такой набор значений переменных
(Истинно или Ложно), что все выражение в целом оказывается Истинно.
Можно ли придумать такой алгоритм решения задачи о совместности, чтобы
время решения (даже в наихудшем возможном случае) росло с ростом числа
переменных N медленнее, чем экспоненциально? Выполняя это упражнение,
вы покажете, что задача о логической совместимости как минимум так же
вычислительно сложна, как и задача о трех красках. Точнее, вы покажете,
что существует соответствие между задачей о трех красках на графе из N
вершин и задачей о совместимости уравнения с 37V переменными, так что
наличие полиномиального (а не экспоненциального) по времени алгоритма
для задачи SAT приведет к наличию такого же полиномиального (до сих
пор неизвестного) алгоритма для задачи о трех красках.
Введем логические переменные Ац^.в, обозначающие, что вершина
графа А окрашена в красный, зеленый или синий цвет, соответственно. Тогда,
17Поскольку задача о трех красках является NP-полной (см. упражнение 8.15),
нахождение такого полиномиального по времени алгоритма для этой задачи эквивалентно
нахождению полиномиального по времени алгоритма для решения задачи коммивояжера или
задачи нахождения основного состояния спинового стекла.
34
Гл.1. Что такое статистическая механика?
например, логическое выражение -<(ЛдЛ Ас) соответствует тому, что
вершина А не окрашена одновременно и в красный, и в зеленый цвет, а выражение
Ar V Aq V Ав истинно, если А окрашена хотя бы в один из трех цветов18.
Для того чтобы записать задачу о трех красках на языке логической
совместимости, необходимо записать три набора уравнений: что каждая
вершина А окрашена в какой-то цвет (см. выше), что каждая вершина окрашена
не более чем в один цвет, и что любые соседние по графу вершины А и В
окрашены в разные цвета.
(a) Запишите логическое выражение, утверждающее, что А окрашено ровно
в один цвет. Запишите логическое выражение, утверждающее что А\л В
окрашены в разные цвета. (Указание: оба выражения должны оказаться
конъюнкцией (пересечением с помощью И, Л) трех вариантов, каждый из которых
включает две переменные.)
Любое логическое выражение можно записать в стандартном виде,
который называется конъюнктивной нормальной формой. Назовем литералом
выражение, состоящее из одной переменной или из ее логического отрицания;
говорят, что логическое выражение записано в конъюнктивной нормальной
форме, если оно представлено в виде конъюнкции утверждений, каждое из
которых является литералом, либо дизъюнкцией (объединением с помощью
ИЛИ, V) нескольких литералов.
(b) Покажите, что зависящее от двух логических переменных X и Υ
выражение -|(-Х"ЛУ) эквивалентно дизъюнкции двух литералов (-iX)V(-«y). (Указание:
просто проверьте все четыре значения). Запишите ваши ответы из части (а) в
конъюнктивной нормальной форме. Сколько литералов входит в каждое
утверждение? Является ли это число литералов максимальным для задачи о трех
красках на произвольном графе?
В части (Ь) вы показали, что в общем случае задача о трех красках
сводится к задаче логической совместимости в конъюнктивной нормальной форме,
каждое слагаемое которой содержит не более трех литералов. При этом общее
количество логических переменных втрое больше, чем число вершин в графе,
задачу о раскраске которого мы решаем. (Можете считать это указанием к
части (Ь).) Задача логической совместимости в конъюнктивной нормальной
форме которой каждое слагаемое содержит не более к литералов, называется
задачей kSAT.
18Напомним, что логическая операция ИЛИ (V) соответствует включающему или —
результат этой операции ложен, только если обе входящие в нее переменные (посылки)
ложны. В обычной русской речи используется как включающее или (в ответ на «Дайте мне
ручку или карандаш» можно дать И то, И другое), так и исключающее (назойливый гость,
спрашивающий ребенка «Ты кого больше любишь, маму или папу?», будет недоволен
ответом «Обоих!»). — Прим. переводчика.
Гл.1. Упражнения
35
(с) Покажите, что время, необходимое для того, чтобы свести задачу о трех
красках на произвольном графе к задаче 3-SAT, в самом худшем случае
пропорционально квадрату числа вершин в графе Μ (т.е. для больших Μ оно не
превышает аМ2 с некоторым фиксированным а). (Указание: количество ребер
в графе не превышает М2.) Пусть имеется алгоритм, гарантирующий решение
любой здачи 3-SAT от N переменных за время, не превышающее Τ(Ν).
Получите ограничение сверху на время решения задачи трех красок на графе из Μ
вершин с использованием этого алгоритма. Покажите, что если Τ(Ν)
полиномиально по N (т.е. это время не превышает Νχ для некоторого целого х), то и
задача трех красок будет решаться за время, полиномиальное по Μ. Мы
вернемся к вопросам о задачах логической совместимости, kSAT и NP-полноте
в упражнении 8.15. Там мы обсудим статистический ансамбль задач kSAT
и исследуем фазовый переход, соответствующий изменению доли
совместимых слагаемых, а также расходимость типичной вычислительной сложности
задачи вблизи этого перехода.
Глава 2
Случайные блуждания и
возникновение коллективного
поведения
Что делает физику возможной? Почему математические законы,
описывающие наш макроскопический мир, настолько просты? Физические законы
нашего мира не являются прямыми утверждениями о реальности
микроскопической Вселенной. Напротив, наблюдаемые нами простые закономерности
являются следствием лежащего в их основе куда более сложного
микроскопического поведения.1 Статистическая механика дает набор мощных
инструментов для изучения простого коллективного поведения, вырастающего из
сложного поведения отдельных элементов.
В этой главе, мы исследуем возникновение такого коллективного
поведения на примере случайных блужданий. Случайные блуждания — это
траектории, чьи последовательные шаги направлены в случайных направлениях.
Вы могли бы подумать, что закон всемирного тяготения Ньютона или его уточненная
версия, предложенная Эйнштейном, более фундаментальны, чем уравнение диффузии. Вы
были бы правы: гравитация действует на все объекты. Но простой макроскопический
закон тяготения возникает, как считается, на квантовом уровне из обмена огромным числом
виртуальных гравитонов, точно так же, как уравнение диффузии возникает из множества
длинных случайных блужданий. Уравнение диффузии и другие континуальные законы
статистической механики специфичны для конкретных систем, но механизм
возникновения, вырастания этих законов из микроскопической теории очень похож на механизм
возникновения макроскопических законов гравитации или других фундаментальных законов.
Этот механизм и является источником удивительно простых математических законов
природы [148].
2.1. Примеры случайных блужданий...
37
Они часто возникают в статистической механике: как суммы
флуктуирующих величин, как траектории частиц, претерпевающих случайные
столкновения, как формы длинных связанных цепей, например полимеров. В этих
системах можно отметить два типа возникающего крупномасштабного
поведения. Во-первых, отдельное случайное блуждание, если оно содержит
достаточно большое количество шагов, становится фрактальным или масштабно
инвариантным (это явления объясняется в разделе 2.1). Во-вторых,
распределение вероятности для положения конечной точки блуждания подчиняется
простому континуальному закону — уравнению диффузии^ которое вводится в
разделе 2.2. Оба эти свойства практически не зависят от микроскопических
деталей блуждания, другими словами, они являются универсальными. Мы
используем случайные блуждания во внешнем поле как первый пример
появления уравнения непрерывности, линейного отклика и распределения Больц-
мана (см. раздел 2.3). Наконец, в разделе 2.4, для того чтобы решить
уравнение диффузии, мы вводим понятия о преобразовании Фурье и функциях
Грина. Таким образом, случайные блуждания послужат нам удобной
иллюстрацией для многих идей и методов статистической механики.
2.1 Примеры случайных блужданий:
универсальность и масштабная инвариантность
Во многих задачах статистической механики интерес представляют
суммы или средние значения рядов флуктуирующих величин: sn = Σι=ι ^i-
Внутренняя энергия вещества равна сумме энергий молекул, из которых оно
состоит; ваша оценка на письменном экзамене — это сумма баллов,
набранных вами при ответе на отдельные вопросы. Представьте себе, что вы
добавляете слагаемые в сумму по одному, тогда последовательность частичных
сумм si, S2, · · · представляет собой пример одномерного случайного
блуждания. Мы приведем три примера случайных блужданий: бросание монетки,
траектория пьяницы и конформации полимеров.
Бросание монетки. Например, рассмотрим эксперимент, в котором
человек бросает монетку и запоминает разность бдг между числом выпавших
орлов и решек. Каждое бросание монетки соответствует добавлению к сумме
нового члена 1% = ±1. Какой результат для s^ = Σϊ=ι h — (орлы-решки) вы
ожидаете получить после N бросаний?
Среднее значение s^, очевидно, равно нулю (положительные и
отрицательные слагаемые встречаются с равной вероятностью), поэтому это среднее
— плохая количественная характеристика суммы. Можно измерить среднее
38 Гл.2. Случайные блуждания и возникновение коллективного поведения
значение2 модуля (|«дг|), но оказывается, что более удобная в
использовании характеристика — это средний квадрат суммы или среднеквадратичное
отклонение, л/^дг)· После одного бросания среднеквадратичное отклонение
равно
<5?) = 1=Л(-1)2 + ±(1)2; (2.1)
после двух и трех бросаний
<4>=3=|(-3)2 + |(-1)2 + |(1)2 + |(3)2
(2.2)
(например, вероятность получить два орла после трех бросаний монетки
равна трем восьмым: OOP, ΟΡΟ и POO). Можете ли вы угадать, чему будет
равно (s2), не вычисляя его?
Сохранится ли эта простая закономерность и в дальнейшем? Чтобы
выяснить это, попробуем выразить среднеквадратичное отклонение на N-ou шаге
через отклонение на N — 1 шаге и характеристики последнего шага.
Поскольку среднее от суммы равно сумме средних, находим
(4) = ((sn-1 + Ϊν?) = (4-i> + 2(sN.1 iN) + (£2N). (2.3)
С другой стороны, £n равно ±1 с вероятностью 1/2, независимо от того,
что происходило на предыдущих шагах (а значит, и независимо от sjy-i).
Поэтому (s^v-i $>n) = \$N-\ (+1) + 2sN-i(—1) = 0. Кроме того, мы знаем, что
£2N = 1, так что
(4) = <4-1> + 2is^rt^+ (4) = (4-1> + Ι- (2-4)
Таким образом, предполагая, что (s^r-i) = Ν— 1, мы доказали, что (s^) =
N индукцией по N.3
Таким образом, квадратный корень из среднего квадрата (количества
орлов минус количество решек) равен квадратному корню из числа бросаний
монетки:
yf^) = VN. (2.5)
2Угловыми скобками {·) мы обозначаем среднее по ансамблю. В этом случае наш
ансамбль состоит из 2N возможных последовательностей из N бросаний монетки.
3Вычисление среднего модуля (|$лг|) не было бы настолько простым. Именно поэтому
для измерения флуктуации обычно вычисляют корень из их среднего квадрата.
2.1. Примеры случайных блужданий...
39
Траектория пьяницы. Случайными блужданиями являются также и
траектории, претерпевающие множество последовательных случайных
поворотов (связанных, например, со столкновениями); например, траектория
молекулы духов в воздухе4 (см. упражнение 2.4). Поскольку воздух —
сильно разреженная среда, а силы взаимодействия молекул короткодействующие,
движение молекулы будет состоять из редких коротких столкновений, сильно
меняющих ее скорость, и сравнительно длинных участков, в течение которых
она движется равномерно. После нескольких столкновений скорость
молекулы будет совершено нескоррелированной с начальной скоростью. Траектория
такой молекулы будет изломанным случайным блужданием в трехмерном
пространстве.
Случайное блуждание молекулы духов состоит из шагов случайной
длины, совершаемых в случайном направлении со случайной скоростью. Более
удобно изучать ситуацию, в которой шаги имеют равную длину и происходят
через равные промежутки времени,5 поэтому мы рассмотрим классическую
задачу о траектории пьяницы (рис. 2.1). Пусть пьяница начинает свой путь от
фонарного столба, расположенного в начале координат, χ = у = 0. Через
равные промежутки времени он совершает шаги ijy длины L каждый. Поскольку
он пьян, совершаемые им шаги направлены в абсолютно произвольную
сторону и никак не скоррелированы с предыдущими шагами. Количественно, это
отсутствие корреляции означает, что среднее скалярное произведение любых
двух шагов £т и £п равно нулю (это следует из равновероятности всех углов
θ между этими шагами): (£т · £п) = L2(cos(0)) = О.6 Отсюда следует, что
скалярное произведение £/у и s^_i = Σπϊ=\ £т равно нулю. Как и в прошлом
разделе, это позволяет нам написать по индукции:
(s&) = ((sjv-i + £N)2) = (s&.jl) + (2s^_i · £N) + (φ
= (s2N_1) + L2 = ... = NL\ (2.6)
так что среднеквадратичное пройденное пьяницей расстояние равно vNL.
На примере случайных блужданий мы впервые встречаемся с понятиями
масштабной инвариантности и универсальности.
4Реальный залах в реальной комнате будет, в основном, распространяться за счет
конвекции; в жидкостях и газах, как правило, диффузия доминирует только на малых
масштабах. В твердых телах конвекции нет, поэтому тепло- и электропроводность в твердых
телах были бы более точным, хотя и менее ярким, примером случайных блужданий.
5То есть случайным остается только выбор направления. — Прим. переводчика.
6Вообще говоря, если между двумя переменными нет корреляции, то среднее от их
произведения равно произведению средних; в нашем случае имеем (im · in) = (im) · (in) =
0 0 = 0.
40 Гл.2. Случайные блуждания и возникновение коллективного поведения
Рис. 2.1. Траектория пьяницы
Пьяница стартует у фонарного столба и делает последовательные шаги длины L каждый
под произвольным углом к предыдущему.
Масштабная инвариантность. Как выглядит траектория частицы,
которая за N шагов проходит расстояние всего лишь порядка y/N? Траектории
случайных блужданий выглядят изломанными и запутанными. Настолько,
что если вы увеличите маленький кусочек траектории, увеличенная версия
выглядит настолько же изломанной и запутанной, как траектория в целом,
см. рис. 2.2. Каждая из этих увеличенных траекторий, конечно, не совпадает
с начальной, как не совпадают и два случайных блуждания равной длины.
Однако ансамбль случайных блужданий длины N будет очень похож на
ансамбль блужданий длины ЛГ/4, пока N не уменьшится настолько, что станут
различимы отдельные шаги. Случайные блуждания масштабно
инвариантны: они выглядят одинаково на всех масштабах.7
Универсальность. Оказывается, что на удаленных масштабах, когда
отдельные шаги (и любые корреляции между соседними шагами) становятся
неразличимы, все случайные блуждания выглядят одинаково. На рис. 2.2
изображено блуждание пьяницы; однако любое двумерное случайное
блуждание будет иметь те же статистические свойства. Если, например, бросать
две монеты различного достоинства и откладывать разность орлов и решек
7Кроме того, во всех пространствах размерности больше двух, они представляют собой
фракталы размерности два. Это попросту означает, что случайное блуждание «объема»
V = N шагов умещается внутри сферы радиуса R ~ sn ~ N1^2 (рис. 2.2). Фрактальная
размерность D этого объекта, определяемая как RD = V (размерность Хаусдорфа), равна,
соответственно, двум.
2.1. Примеры случайных блужданий...
41
Рис. 2.2. Случайные блуждания: масштабная инвариантность
Траектории случайных блужданий представляют собой сильно изломанные фрактальные
линии, чей общий вид не меняется при изменении масштаба. Здесь на каждом
последующем рисунке изображена первая четверть блуждания, изображенного на предыдущем,
увеличенная в два раза. Самое короткое блуждание состоит из 31 шага, самое длинное —
из 32 000. Левая часть рис. 1.1 представляет собой то же самое блуждание, продолженное
до 128000 шагов.
для рублевой монетки по оси х, а для пятирублевой — по оси у, то, на
масштабах намного превышающих размер одного шага, мы получим статистически
тот же самый ансамбль случайных траекторий. В трехмерном пространстве
фотоны8 внутри Солнца (см. упражнение 2.2) или в стакане молока
совершают случайное блуждание с фиксированной скоростью с между
столкновениями. Тем не менее, после нескольких шагов их траектории становятся
статистически неотличимыми от траектории молекулы духов, которая движется
с переменной скоростью. Эта независимость поведения от микроскопических
деталей называется универсальностью.
8На случай, если вы не знаете: фотоны — это кванты света и другого электромагнитного
излучения.
42 Гл.2. Случайные блуждания и возникновение коллективного поведения
Случайные блуждания — достаточно простой случай, в котором мы
можем напрямую показать, что все индивидуальные случаи ведут себя
одинаково. В разделе 2.2 мы обобщим наши рассуждения о росте
среднеквадратичного смещения пропорционально \A/V, так чтобы они работали одновременно
и для бросаний монетки, и для траектории пьяницы; при некотором усилии
можно также учесть непостоянство времен между поворотами и
флуктуации скоростей на прямых участках, что позволит распространить наши
рассуждения на случай фотонов и молекул газа. Кроме того, если вычислить
величины, характеризующие изломанность и запутанность траекторий этих
системах, то можно убедиться в том, что и они тоже совпадают для всех
ансамблях после достаточно большого количества шагов. Мы отложим пока
этот вопрос и вернемся к нему в главе 12 (а именно, в упражнении 12.11),
где мы дадим глубокое и интуитивно понятное объяснение того, почему все
перечисленные системы обладают масштабной инвариантостью и
демонстрируют универсальное поведение на больших масштабах. Универсальность и
масштабная инвариантность объясняются там с помощью ренорм-групповых
методов, разработанных изначально для исследования непрерывных фазовых
переходов.
1985 Ϊ990 1995^ " 2000 " 2005
1Ьд
Рис. 2.3. Нормализованный индекс S&P 500
Временной ряд дневных цен закрытия биржевого индекса Standard &· Poor's 500,
откорректированный на инфляцию и деленный на среднюю доходность за указанный период
(6.4%). Поведение биржевых индексов часто описывают случайными блужданиями со
сносом (см. упражнение 2.11). Обратите внимание, что флуктуации цен индивидуальных
бумаг (и соответствующие риски) будут, как правило, существенно большими. Усреднение по
500 бумагам приводит к тому, что флуктуации подавляются, при этом средняя доходность
сохраняется, см. [85,86]. Для сравнения приведена траектория одномерного так
называемого геометрического случайного блуждания.
Полимеры. Наконец, случайными блужданиями описываются конфор-
мации полимеров. Полимеры — это длинные молекулы (например, ДНК,
РНК, белки и многие пластики), состоящие из множества небольших звеньев
(называемых мономерными звеньями), соединенных между собой в длинную
2.1. Примеры случайных блужданий...
43
цепь. Тепловое движение приводит к наличию флуктуации углов между
соседними звеньями, если эти флуктуации доминируют по сравнению с
энергией взаимодействия звеньев,9 то полимерная цепь принимает форму (конфор-
мацию) траектории случайного блуждания. В данном случае шагу
блуждания соответствует не шаг по времени, а шаг вдоль цепи или номер
мономерного звена.
Случайные блуждания, соответствующие конформациям полимеров
в разбавленном растворе, не похожи по своим свойствам на случайные
блуждания из первых двух примеров; они принадлежат другому
классу универсальности.10 Это связано с тем, что полимеры не могут
самопересекаться; блуждания, траектории которых подразумевают, что два
звена находятся в одном и том же месте в пространстве, запрещены. То есть
полимеры — это несамопересекающиеся случайные блуждания. В двумерном
и трехмерном пространстве оказывается, что самопересечения играют
роль, не сводимую к деталям структуры на микроуровне, их влияние
«выживает» при переходе к большим масштабам, существенно меняя
свойства случайных блужданий.11 Можно показать, что эти запрещенные
самопересечения будут часто происходить между сильно удаленными по
цепи друг от друг участками полимера, и что их запрещение изменяет
зависимость среднеквадратичного размера полимера (s^) от числа звеньев
9Полимеры не всегда формируют случайные блуждания. Пластмассы при низких
температурах могут переходить в частично-кристаллическое состояние; белки-ферменты и РНК
часто собираются в плотные структуры строго предсказуемой формы. С другой стороны,
расплавленные пластики и денатурированные белки являются примерами систем, в
которых полимерные молекулы принимают форму случайных блужданий. Двойная спираль
ДНК является примером очень жесткого полимера, для раствора ДНК шаг случайного
блуждания имеет длину в несколько сотен нуклеотидов (мономерных звеньев ДНК), см.
упражнение 2.10.
10Все сказанное в этом абзаце верно для разбавленных растворов полимеров в режиме,
когда притяжение между звеньями достаточно мало (так называемый режим хорошего
растворителя). Более аккуратный анализ показывает, что в полимерных системах
встречаются как режимы с несамопересекающимися конформациями, так и режимы, в которых
конформации полимеров на больших масштабах совпадают с траекториями обычных
самопересекающихся случайных блужданий, таких как бросание монетки или траектория
броуновской частицы. Например, в приведенном выше примере расплава пластика
конформации индивидуальных цепей совпадают с конформациями обычных случайных блужданий
(это утверждение называется теоремой Φ лори). Более подробно прочитать о
статистических свойствах полимерных молекул можно, например, в [153,155]. — Прим. переводчика.
11 Говорят, что отсутствие самопересечений — это релевантное возмущение, которое
меняет класс универсальности. В (нефизическом) случае пространства размерности больше
четырех, самопересечение становится иррелевантым; воображаемые гиперполимеры в
пятимерном пространстве будут вести себя на больших масштабах в точности как обычные
случайные блуждания.
44 Гл.2. Случайные блуждания и возникновение коллективного поведения
N (см. упражнение 2.10). Степенная зависимость \/(s%) ~ Nu сохраняется,
но индекс ν меняется: вместо обычного для случайных блужданий ν = 1/2
появляется большее значение (у = 3/4 в двумерном пространстве и ν « 0.59
— в трехмерном [90]). Степенные законы играют центральную роль при
изучении масштабно-инвариантых систем; ν — это наш первый пример того,
что называется универсальным критическим индексом (см. гл. 12).
2.2 Уравнение диффузии
В непрерывном пределе, когда пространственные и временные масштабы
велики, в ансамбле нерегулярных, изломанных случайных блужданий
возникает простое коллективное поведение; их эволюция описывается уравнением
диффузии:12
g=PW=pgf. (2,,
Уравнение диффузии описывает изменение со временем плотности р(х, t)
облака духов, когда составляющие это облако молекулы совершают
случайные блуждания под действием столкновений с молекулами воздуха. С другой
стороны, оно описывает и распределение вероятности расположения одной
индивидуальной частицы, совершающей блуждание в пространстве;
действительно, если частицы не взаимодействуют между собой, распределение
вероятности для одной частицы одновременно задает (с точностью до числового
множителя) и плотность всех частиц.
В этом разделе мы выведем уравнение диффузии, перейдя к
непрерывному пределу для ансамбля случайных блужданий. Рассмотрим обычное
некоррелированное случайное блуждание, в котором через каждый шаг времени
At положение частицы χ меняется на £:
x{t + At) = x{t)+£(t). (2.8)
Пусть распределение вероятности для одного шага равно χ(£).13 Будем
считать, что χ имеет нулевое среднее и стандартное отклонение а, так что
первые моменты14 χ равны
12 В оставшейся части этой главы мы ограничимся для простоты рассмотрением
одномерного случая. Кроме того, мы заменим обозначение переменной s на ж, чтобы подчеркнуть,
что она имеет смысл пространственной координаты.
13В двух наших примерах распределение χ(^) было дискретным; его можно записать
с помощью <5-функции Дирака (см. сноску 4 на стр. 19). Для бросания монетки, χ(£) =
\δ(1 + 1) Η- \δ(ί — 1); для пьяницы, что соответствует равномерному распределению на
окружности радиуса L.
14п-ым моментом функции р(х) называется (хп) = f xnp(x)dx.
2.2. Уравнение диффузии
45
/ ζχ{ζ)
dz = l,
άζ = О, (2.9)
z)dz = а2.
Как выглядит распределение вероятности положения частицы р(х, ί + Δί)
после одного шага, если задано начальное распределение вероятности р{х\ ί)?
Для того чтобы частица перешла из положения х1 в момент времени t в
положение χ в момент времени t + Δί, шаг £(t) должен быть равен χ — хт.
Вероятность этого равна χ(χ — χ'). Умножив ее на плотность вероятности
того, что частица первоначально находилась в χ1 (p(xr>t)), и интегрируя по
всем возможным начальным положениям я/, получаем
/оо
р(х', t)x(x - χ') άχ'
-оо
p(x-z,t)X(z)dz, (2.10)
-/_
оо
оо
где мы ввели переменную ζ = χ — χ'.15
Допустим теперь, что распределение ρ достаточно широкое: длина шага
очень мала по сравнению с масштабом, на котором меняется ρ (рис. 2.4). мы
можем использовать разложение уравнения (2.10) в ряд Тейлора по ζ:
Рис. 2.4. Непрерывный предел для случайных блужданий
Мы считаем, что размер шага а мал по сравнению с масштабами, на которых меняется
р(ж), так что мы можем использовать ряд Тейлора по пространственным производным р.
15Обратите внимание, что άζ = —άχ\ но пределы интегрирования меняются на /^ —У
f^0°° = — J^o> так что минусы сокращаются. Такие вещи часто происходят при
вычислениях, обращайте на них внимание.
46 Гл.2. Случайные блуждания и возникновение коллективного поведения
P(x,t + At)*J[P(X,t)-zfx + Z^
χ{ζ)άζ
άζ
=p(x,i)+^S°2' (2n)
где мы использовали моменты χ из уравнения (2.9). Теперь, если мы
допустим, что ρ еще и медленно (по сравнению с длиной одного шага At)
меняется со временем, мы можем использовать приближение р(х, t + At) — р(х, t) «
(dp/dt) Δί, и в результате получаем
*e = jL*e (212)
dt 2Atdx2' У ]
Это и есть уравнение диффузии16 (уравнение 2.7), в котором
D = a2/2At (2.13)
Уравнение диффузии описывает все случайные блуждания, в которых
распределение вероятности меняется во времени и пространстве достаточно
медленно по сравнению с индивидуальными шагами17.
2.3 Потоки и внешние силы
Во всех рассматриваемых нами случаях частицы, совершая случайные
блуждания, не исчезают и не возникают из ничего, можно говорить об их
локальном сохранении.18 Пусть р(х) — плотность сохраняющейся величины.
16D должно быть больше нуля. Случайные блуждания и диффузия стремятся
выровнять неровности распределения плотности. «Горки» на распределении соответствуют
отрицательным значениям второй производной (д2р/дх2 < 0) и они должны опускаться
(dp/dt < 0), «ямки» соответствуют положительной второй производной и должны
подниматься.
17Предполагается также, что между шагами блуждания нет дальнодействующих
корреляций. Например, несамопересекающиеся случайные блуждания не подчиняются
уравнению диффузии, т.к. требование отсутствия самопересечений накладывает такие дально-
действующие корреляции. — Прим. переводчика.
18Некоторая величина локально сохраняется, если, во-первых, ее интеграл (нулевой
момент) не зависит от времени, и, во-вторых, она переносится непрерывно от точки к точке
(т.е. запрещена ее «телепортация»). Например, плотность вероятности р(х) того, что
отдельная частица, совершающая случайное блуждание, находится в заданной точке х, также
локально сохраняется; как и полная плотность частиц, вероятность не может создаваться
и уничтожаться, она может только «переползать с места на место».
2.3. Потоки и внешние силы
47
Тогда правило, по которому она изменяется (рис. 2.5), можно записать в
терминах потока J(#), проходящего через точку х:
Здесь поток J — это скорость, с которой некая «субстанция» течет
вправо через точку х; поскольку количество этой «субстанции» сохраняется, ее
плотность может измениться только за счет перетекания из одного места в
другое. Уравнение диффузии (2.7) получается из уравнения непрерывности
(уравнения 2.14) и предположения, что поток19 пропорционален локальному
градиенту плотности:
«/diffusion = -^т-, (2.15)
что естественно ожидать для системы с линейным откликом.20 Случайное
блуждание частиц приводит к тому, что они в среднем диффундируют из
областей высокой плотности в области низкой плотности.
J(x)-k p(jc) Δχ —4-* J(x +Δχ>
Рис. 2.5. Сохраняющийся поток
Пусть р(х, t) — плотность некоторой сохраняющейся величины (числа молекул, массы,
энергии, вероятности и т.д.), зависящая от пространственного положения х, a */(х) —
полный поток этой величины через точку х. Количество «материала» в малом элементе объема
(χ, χ + Ах) равно η = ρ(χ) Δχ, приток в эту область слева равен */(х), а отток справа равен
J(x + Δχ), так что
^=J(x)-J(x + Ax)^^Ax,
σι σι
откуда и получаем уравнение непрерывности:
dp _ J(x + Δχ) - J (χ) _ _dJ_
dt Ax дх
Во многих приложениях помимо случайного блуждания имеется еще и
постоянный снос. В некоторых случаях (например, при вычислении
итоговой оценки в экзаменационном тесте, см. упражнение 2.1) естественным
образом возникает ненулевое среднее значение для каждого отдельного шага
случайного блуждания. В других случаях имеется внешняя сила F, которая
19Из уравнения диффузии следует, что поток J = —D др/дх + С, но постоянная
составляющая потока С, не зависящая от р, не имеет физического смысла в случае случайных
блужданий.
20См. примечание 43 на с. 232.
48 Гл.2. Случайные блуждания и возникновение коллективного поведения
нарушает симметрию между направлениями движения; средний снос в этом
случае равен произведению F At и подвижности η:
x(t + At) = x(t) + F^At + £{t). (2.16)
При наличии микроскопической модели поведения системы можно
вывести явную формулу для этой подвижности. Например, если воздух
разрежен, а диффундирующая молекула имеет малый размер, мы можем
считать, что между столкновениями, разделенными интервалами Δί, она
движется равноускоренно; мы можем также считать, что после столкновения
скорость совершенно не зависит от скорости до него. В таком случае
дополнительный снос за счет внешней силы в расчете на один прямой участок
будет равен ускорению F/m, умноженному на половину квадрата времени:
\(F/m)(At)2 = F At(At/2m), следовательно η = {At/2m). Используя
уравнение (2.13), получаем
7" Ъп V &) ~ τη(α/Δί)2 " ^2' ( }
где ν = a/At — скорость случайного блуждания без сноса. С другой стороны,
если воздух не разрежен и размер диффундирующей в нем частицы не мал,
мы можем рассматривать воздух как вязкую среду с динамической
вязкостью η; в случае, если частица — это просто сфера радиуса г, из механики
жидкости для подвижности известен ответ η = 1/(6πητ).
Исходя из уравнения (2.16), можно провести переход к непрерывному
пределу, совершенно аналогично тому, как мы сделали это в уравнениях (2.10-
2.12), и получить уравнение диффузии в системе с внешней силой:21
что соответствует потоку вида
J = 1Fp-D^. (2.19)
21 Обратите внимание на то, что если поле силы неоднородно, эволюция системы зависит
также от градиента силы:
Э2,
др = _д£= dF(x)p(x) cfp_
dt дх Ί дх дх2
dF „др^-Рр
2.3. Потоки и внешние силы
49
Знак вновь появившегося члена легко объяснить качественно: если ρ
растет как функция χ (имеет положительный наклон др/дх) и сила тащит
частицы вперед (F > 0), то ρ будет уменьшаться со временем, т.к. более плотные
области будут со временем удаляться в положительном направлении оси х, а
их место будут занимать менее плотные области.
Уравнение диффузии описывает, как системы случайно блуждающих
частиц приходят к равновесию (см. гл. 3). Уравнение диффузии в отсутствие
внешних сил описывает эволюцию распределения плотности духов в
комнате. Не зависящее от времени равновесное распределение р*? в соответствии
с уравнением диффузии (2.7), должно удовлетворять условию д2р*/дх2 = 0
и должно поэтому иметь вид р*(х) = ро + Вх. Если духи не могут
проникать сквозь стены, то на границе комнаты должно быть др* /дх ос J = 0,
следовательно В = 0. Итак, как и следовало ожидать, плотность духов
стремится к довольно скучному равновесному состоянию р*[х) = ро, в котором
они распределены равномерно по всей комнате.
При наличии постоянной внешней силы (например силы тяжести)
равновесное состояние оказывается более интересным. Пусть χ — высота над
землей и F = —тд — сила тяжести. Тогда, исходя из уравнения (2.18),
равновесное распределение р* удовлетворяет
dp* dp* d2p*
°-δΓ-™£ + 0ΊΡ- (2·20)
Общее решение этого уравнения имеет вид р*(х) = Aexp[—(y/D)mgx] 4- Β.
Будем считать, что концентрация наших духов В в дальнем космосе равна
нулю,22 так что концентрация духов экспоненциально спадает с высотой:
р*{х) = Аехр (-j-mgx\ . (2.21)
Сила тяжести тянет молекулы духов вниз и они не оседают на землю только
потому, что совершают случайные блуждания. Если перейти теперь от
молекул духов к молекулам кислорода (и пренебречь градиентами температуры
и погодой), то мы получим простейшее объяснение того, почему при подъеме
в горы становится тяжелее дышать.
Аналогичные проблемы возникают, и если коэффициент диффузии зависит от
плотности или от положения в пространстве. Работая с сохраняющейся величиной,
сначала записывайте уравнения в терминах потока, чтобы гарантировать ее сохранение:
J = —D(p, x)Vp + 7(x)^(x)p(x)· Автору и его студентам случалось терять до недели
рабочего времени в случаях, когда они забывали про это правило.
22 Ненулевое значение В соответствовало бы дождю духов постоянной интенсивности.
23 В главе 6 мы выведем распределение Больцмана, которое гласит, что для системы в
равновесии вероятность иметь энергию mgh = Ε пропорциональна ехр(—Е/квТ), где Τ
50 Гл.2. Случайные блуждания и возникновение коллективного поведения
2.4 Решение уравнения диффузии
Сделаем небольшое математическое отступление и расскажем вкратце о
двух важных методах решения дифференциальных уравнений:
преобразовании Фурье и методе функций Грина. Оба эти метода опираются на то,
что уравнение диффузии линейно: если известен некоторый набор решений
рп(х,£), то любая их линейная комбинация ^2no>npn(x^t) также является
решением. Если нам удастся разложить начальное условие р(х, 0) по функциям
из этого набора р(х,0) = Σ)ηαηρη(χ, 0), мы автоматически получаем
формальное решение уравнения.
Методы Фурье чрезвычайно эффективны с вычислительной точки
зрения, благодаря существованию алгоритмов быстрого преобразования Фурье
(БПФ), позволяющего переходить от распределений в обычном координатном
пространстве к функциям в пространстве решений. Метод функций Грина
более важен для аналитических вычислений и поиска приближенных
решений.24
2.4.1 Преобразование Фурье
Преобразование Фурье состоит в разложении функции ρ в ряд по плоским
волнам pk(t)elkx.
Уравнение диффузии не меняется при сдвиге координат; наша система
трансляционно инварианта. Другими словами, если некоторое р(х, t)
является решением, то р(х — Δ, t) также является допустимым решением уравнения,
которое описывает эволюцию системы с начальными условиями, сдвинутыми
— температура, а кв — постоянная Больцмана. Этот ответ совпадает с нашим
уравнением (2.21), если
£>/7 = квТ. (2.22)
Это равенство называется соотношением Эйнштейна. Постоянные D и 7 в
(неравновесном) уравнении диффузии связаны друг с другом, поскольку плотность должна в пределе
стремиться к равновесному распределению, задаваемому статистической механикой. Наша
грубая оценка (уравнение 2.17) дает соотношение D/j = την2. Сравнивая его с
уравнением (2.22), мы можем предположить, что квТ равно удвоенной кинетической энергии частиц
вдоль оси х; это утверждение также верно и является частным случаем теоремы о
равнораспределении (см. раздел 3.2.2).
24 Стоит отметить, что значительная часть квантовой теории поля и квантовой механики
многих тел формулируется в терминах объектов, которые тоже называются функциями
Грина. Однако методы этих теорий — весьма затейливые дальние родственники простых
методов теории линейных дифференциальных уравнений (см. упражнение 10.9).
2.4- Решение уравнения диффузии
51
на Δ в направлении оси х.25 Линейное дифференциальное уравнение,
описывающее трансляционно-инвариантную систему, имеет, при очень общих
дополнительных условиях, решение в форме плоской волны р(х, t) = pk(t)elkx.
Мы докажем это важное утверждение в Приложении (раздел А.4). Здесь
же мы просто воспользуемся им, не заботясь о деталях. Подставляя плоскую
волну26 в уравнение диффузии (2.7), получаем
^ = -Dk%, (2.24)
P*(t) = P*(0)e-Dfc2t. (2.25)
Сами по себе полученные решения нефизичны; нам нужно скомбинировать их
подобающим образом, чтобы получить осмысленный ответ. Прежде всего, эти
решения — комплексные, нужно сложить решения с волновыми векторами к
и — fc, чтобы получить косинусоидальные волны, или вычесть и разделить на
2i, чтобы получить синусоидальные. Косинусы и синусы сами по себе тоже
не могут быть плотностями (потому что они меняют знак), но их тоже
можно складывать между собой (например, слагаемое при к = О соответствует
постоянной плотности ро)> чтобы получить осмысленные ответы.
Действительно, можно сложить решения для всех возможных волновых векторов и
получить общее решение в виде
1 Г°°
Р(х, t) = — J pk(0)eikxe-Dk ' dfc. (2.26)
Здесь коэффициент Pfc(O) — это просто преобразование Фурье от начального
распределения плотности (см. уравнение А.9):
/оо
p(x,0)e-ikx dx, (2.27)
-ОО
и мы видим, что уравнение (2.26) — это обратное преобразование Фурье
(уравнение АЛО) от решения, временная эволюция которого в пространстве
25Не забывайте, что преобразование g(x) = f(x — Δ) сдвигает функцию в положительном
направлении; например, новая функция ρ(Δ) имеет в Δ такое же значение, какое старая
имела в начале координат ρ(Δ) = /(0).
26 Многим читателям эта процедура знакома по решению волновых уравнений или
уравнения Шрёдингера. Действительно, уравнение Шрёдингера в свободном пространстве —
это то же самое, что уравнение диффузии с мнимым коэффициентом D.
52 Гл.2. Случайные блуждания и возникновение коллективного поведения
Фурье известна (уравнение 2.25). Итак, записав ρ в виде суперпозиции
плоских волн, мы вывели простой закон: коротковолновые вклады в р,
соответствующие волновому вектору fc, подавляются с течением времени t по закону
e-Dk2t
2.4.2 Метод функций Грина
Метод функций Грина состоит в разложении ρ по семейству решений
G(x — y,f), где G описывает эволюцию начального состояния,
концентрированного вокруг одной точки у, то есть, в данном случае, диффузию частиц,
стартующих из заданной точки у.
Рассмотрим сперва случай, когда все частицы стартуют из начала
координат. Рассмотрим единицу количества вещества духов, испущенную из
начала координат в момент времени t = 0. Как записать такое начальное
условие p(x,t = 0)? ρ равно нулю всюду, кроме точки χ = 0, но
интеграл J*p(x, 0)dx = 1, так что р(0,0) явно должно быть бесконечным.
Функция, устроенная таким образом, называется дельта-функцией Дирака δ(χ)
(см. примечание 4 на стр. 19), %indexdelta-function, Dirac@5-function, Dirac
математически она задает интегральный оператор, который, будучи
применен к произвольной функции, возвращает ее значение в нуле:
/
/(!/)%) dy = /(0). (2.28)
Определим функцию Грина G(x,£) как функцию, описывающую эволюцию
начальной плотности G(x,0) = δ(χ) (что соответствует концентрации всего
вещества в начале координат). Естественно, G(x,f) подчиняется уравнению
диффузии dG/dt = Dd2G/dx2. Вычислим G(x,t) с помощью метода Фурье,
описанного в предыдущем разделе. Преобразование Фурье при t = 0 дает
G*(0) = / G(x, 0)е~'1кх dx= i S(x)e-[kx dx = 1 (2.29)
(независимо от к). Соответственно, _ зависимость решения в
Фурье-пространстве от времени имеет вид Gk(t) = e~Dk *, а в реальном
пространстве
G(x, t) = ±- (eikxGk(0)e~Dk2t dk = i- / ^e~Dk2t dfc. (2.30)
2π J 2π J
2·4· Решение уравнения диффузии
53
Здесь последний интеграл — обратное преобразование Фурье от
распределения Гаусса,27 которое можно вычислить непосредственно28 и получить новую
гауссову функцию
G(x, t) = -Д= e"*2/4Dt. (2.32)
Это и есть функция Грина для уравнения диффузии. Функция Грина явно
задает распределение конечных точек случайных блужданий, стартующих из
начала координат (см. рис. 2.6).
• Функция Грина полностью задает вероятностное распределение по
расстояниям. Для случайного блуждания из N звеньев длины а мы
получили в разделе 2.1, что у/(х2) = VNa; получается ли этот ответ из
функции Грина? В заданный момент времени t функция Грина
(уравнение 2.32) — это гауссова функция со стандартным отклонением σ(ί) =
y/2Dt\ подставляя сюда значение коэффициента диффузии из
уравнения 2.13 D = α2/2Δ£, получаем среднеквадратичное расстояние σ(ί) =
ay/t/At = αχ/ϊν, где Ν = ί/Δί — количество шагов блуждания; таким
образом, оба наших метода дают согласованные результаты.
• Наконец, поскольку уравнение диффузии обладает трансляционной
симметрией, эволюция случайных блужданий, стартующих из
произвольной точки у (что соответствует начальному условию
27Физики называют ехр(—х2) функцией, или распределением Гаусса, а соответствующий
интеграл — гауссовым интегралом. В статистике соответствующее распределение
вероятности (1/\/27г)ехр(—х2/2) называется нормальным распределением. Полезно помнить, что
преобразование Фурье от функции Гаусса (1/ν/2πσ) ехр(—χ2/2σ2) — тоже функция Гаусса
ехр(—σ2&2/2), но со стандартным отклонением l/σ и без множителя перед экспонентой
(см. уравнение 2.32).
28Возьмите выражение \кх — Dk2t в показателе экспоненты из формулы (2.30) и
дополните его до квадрата —Dt(k — ix/(2Dt))2 — x2/(4Dt), затем сделайте замену переменных
к = к- ix/(2Dt):
G0M) = ^e-*& (2.31)
/
oo-ix/(2Dt) .
e~DtK- άκ.
-oo-ix/(2Dt)
Если мы сможем сдвинуть пределы интегрирования вдоль мнимой оси так, чтобы они
совпали с действительной осью, то интеграл окажется равен <\/n/Dt, откуда и следует
уравнение (2.32). То, что этот сдвиг пределов интегрирования можно сделать, вообще говоря,
совсем не очевидно. Чтобы его выполнить, нужно воспользоваться теоремой Коши,
позволяющей деформировать контуры интегрирования на комплексной плоскости (см. рис. 10.11
в разделе 10.9). Мы проделаем аналогичную процедуру для обратного преобразования (от
реального пространства к Фурье-пространству) в примечании 24 к упражнению А.4.
54 Гл.2. Случайные блуждания и возникновение коллективного поведения
Рис. 2.6. Множество случайных блужданий
10000 конечных точек случайных блужданий длины 1000, стартующих из начала
координат. Обратите внимание, что после 1000 шагов распределение конечных точек похоже на
гауссово. Собственно, уже после пяти шагов распределение, за исключением своих дальних
хвостов, чрезвычайно близко к гауссову.
δ(χ — у)), будет описываться функцией G(x — y,t). Поскольку любое
начальное распределение р(х, 0) можно представить как суперпозицию
5-функций:
р(х, 0) = J p(y, 0)δ(χ - у) dy = J p(y, 0)G(x - у, 0) dy, (2.33)
то общее решение уравнения диффузии р(х, t) записывается в виде
р(х, t)= p(y, 0)G(x - у, t) dy
= /р(з/,0)ехр(-(х - y)2/4Dt)/V4nDtdy. (2.34)
Это уравнение утверждает, что текущее значение плотности в
некоторой точке определяется начальным распределением плотности вокруг
нее, сглаженным («размазанным») с весом G. Таким образом, записав
ρ в виде суперпозиции точечных источников, мы получили, что
уравнение диффузии сглаживает «острые углы» и неровности начального
распределения. Распределение через время t есть ни что иное, как
начальное распределение, усредненное на масштабе порядка типичного
расстояния, пройденного за это время случайным блужданием, y/2Dt.
Гл.2. Упражнения
55
Уравнение (2.32) представляет собой центральную предельную теорему:
сумма многих независимых случайных величин сходится к распределению
Гаусса.29'30
Упражнения
Упражнения Случайное блуждание в пространстве оценок, Диффузия
фотонов внутри Солнца и Молекулярные моторы посвящены описанию
случайных блужданий, возникающих в различных контекстах. Упражнение
Блуждание молекулы духов посвящено исследованию траектории отдельной
молекулы методами молекулярной динамики. В упражнении Моделирование
случайных блужданий численно исследуется возникновение симметрии в
случайных блужданиях и центральная предельная теорема. Упражнения
Преобразование Фурье и функции Грина и Диффузия с периодическими
начальными условиями качественно иллюстрируют поведение функций
Грина и свойства преобразования Фурье для уравнения диффузии. В
упражнениях Теплопередача и Сковородка выводится уравнение диффузии
для задачи теплопроводности, которое затем используется для решения
практической задачи кулинарной физики. Упражнение Полимеры и
случайные блуждания посвящено исследованию случайных блужданий без
самопересечений; мы увидим, что в двумерии запрет на самопересечения
приводит к появлению новых критических индексов и нового класса
универсальности (см. также гл. 12).
В упражнении Акции, волатильность и диверсификация мы оценим
флуктуации на рынке ценных бумаг и выясним, как диверсификация
снижает риски, не изменяя средней доходности активов. В упражнении
Финансовая математика: деривативы мы сфокусируемся на одном шаге
случайной эволюции цены акций и вычислим цену так называемого опциона
на эту акцию.
Наконец, упражнение Построение перколяционной сети приводит еще
один пример (собственно перколяционные сети) объекта, который, подобно
случайным блужданиям, демонстрирует самоподобие и степенной скейлинг;
мы изучим непрерывный предел для задачи перколяции (демонстрирующий
более тонкие эффекты) в гл. 12 и упражнении 12.12.
29Поэтому, видимо, статистики и называют распределение Гаусса нормальным: в
нормальных, обычных условиях сумма или среднее от многих измерений флуктуирует по
закону, описываемому распределением Гаусса.
30Вообще говоря, центральная предельная теорема в ее классической формулировке
требует существования конечных первого и второго моментов у слагаемых. — Прим.
переводчика.
56 Гл.2. Случайные блуждания и возникновение коллективного поведения
Наука о случайных блужданиях имеет множество приложений. На
вебсайте книги [129] мы планируем привести несколько дополнительных
упражнений, (i) Поиск питательных веществ бактериями (хемотаксис) устроен как
направленное случайное блуждание, предполагающее случайные переходы из
состояния направленного движения (плывущего состояния,
соответствующего шагам случайного блуждания) в состояние кувыркания (более или менее
беспорядочного изменения направления скорости) и обратно, см. [10]. (ii)
Случайные блуждния с редкими, очень длинными шагами могут принадлежать
к другим классам универсальности, как, например, блуждания Леей,
которые не описываются уравнением диффузии и не подчиняются центральной
предельной теореме.31
2.1 Случайное блуждание в пространстве оценок, φ
Построим модель распределения оценок на письменном экзамене. Будем
считать, что экзамен представляет собой тест с вариантами ответов,
состоящий из 10 вопросов, каждый — стоимостью по 10 баллов. Все вопросы имеют
одинаковую сложность, и средняя оценка за экзамен равна 70. Какое
различие оценок на таком экзамене может объясняться удачей, а какое является
отражением различия в знаниях и навыках экзаменуемых? Чтобы оценить
это, будем считать, что все студенты одинаковы и каждый из них отвечает
на каждый ответ случайным образом и дает правильный ответ с
вероятностью 0.7.
(a) Чему равно среднее и среднеквадратичное отклонения для оценок на
таком экзамене? (Найдите значения среднего и отклонения для одного вопроса,
а потом примените наши теоремы для случайного блуждания из 10 шагов.)
Должно получиться, что экзамену со средней оценкой 70 соответствует
типичное среднеквадратичное отклонение порядка 15.
(b) Какой физический смысл вы можете приписать отношению реально
наблюдаемого среднеквадратичного отклонения и отклонения, вычисленного для
системы, в которой ответы студентов случайны?
2.2 Диффузия фотонов внутри Солнца. (Астрофизика) ®
Большая часть энергии термоядерного синтеза в Солнце генерируется
вблизи его центра. Радиус солнца примерно равен 7 · 105 км. Считается, что
в его внешней трети перенос энергии происходит в основном за счет
конвекции, в то время как на большей глубине (скажем, до радиуса R = 5 · 108 м)
доминирующий механизм переноса — это диффузия (случайное блуждание)
31 Точнее, блуждания Леви все же подчиняются некоторым предельным теоремам, но эти
теоремы отличаются от классической центральной предельной теоремы. — Прим.
переводчика.
Гл.2. Упражнения
57
рентгеновских фотонов. (Фотон — это квант, порция энергии: вы можете
рассматривать его как частицу, которая всегда двигается со скоростью света с.
Коэффициентом преломления вещества внутри Солнца можно в этой
задаче пренебречь.) Считайте, что среднее расстояние £, которое проходит фотон
между соударениями, равно £ = 5 · 10~5 м.
Сколько шагов N длины I понадобится фотону, чтобы достигнуть
расстояния R, на котором начинает работать конвекция? Сколько примерно лет At
понадобится ему на это? (Можете предположить, что фотоны совершают шаги
в произвольных направлениях, и что все шаги имеют равную длину £.)
Полезные формулы: с = 3 · 108 м/с; (х2) ~ 2Dt; (s2) = ησ2 = n(s^).
В году 31556925.9747 ~ π · ΙΟ7 ~ 3 · 107 секунд.
2.3 Молекулярные моторы и случайные блуждания.32
(Биология) (2)
Внутри клеток вашего тела можно найти несколько типов молекулярных
моторов, которые могут направленно двигаться, перетаскивать предметы и
копировать молекулы (рис. 2.7). В их числе молекулярные моторы, благодаря
которым сокращаются наши мускулы, моторы, которые копируют
(транскрибируют) ДНК в РНК, копируют (транслируют) РНК в белки, моторы,
которые переносят грузы внутри клетки. Все эти моторы обладают рядом общих
свойств: (1) они двигаются по некоторой линейной «рельсе» (микротрубке,
ДНК, ...), совершая дискретные шаги вдоль нее из одного
низкоэнергетического положения в другое; (2) при движении они поглощают энергию в виде
АТФ (аденозинтрифосата) или НТФ (нуклеотидтрифосфата), что позволяет
им развивать направленную движущую силу; и (3) их механические
свойства можно изучать путем приложения к ним внешней силы и наблюдения
за изменениями в их движении.
Рис. 2.7. Белок-мотор
Когда мотор переносит какой-либо груз («собирает» РНК или белок, ...)> он движется
против внешней силы /ext, совершая работу. Необходимую для этого энергию он получает
из молекул АТФ (аденозинтрифосфата), которые расщепляются на АДФ (аденозиндифос-
фат) и ион фосфата с помощью реакции гидролиза.
Это упражнение было составлено совместно с Мишель Ванг.
58 Гл.2. Случайные блуждания и возникновение коллективного поведения
§
Он
д
(Г)
ΙΟ
о
со
U
Расстояние χ
Рис. 2.8. Эффективный потенциал, соответствующий движению
вдоль ДНК
Энергия (точнее — свободная энергия Гиббса) молекулярного мотора как функция
координаты вдоль ДНК. Сразу после того как мотор копировал один нуклеотид в РНК, он
оказывается в низкоэнергетическом состоянии. Чтобы транскрибировать следующий
нуклеотид, нужно преодолеть энергетический барьер V. Асимметрия энергии δ есть сумма
вкладов от связывания нуклеотида РНК, сжигания АТФ, и отсоединения мотора после
окончания его работы. Экспериментатор может менять эту асимметрию, прикладывая к
мотору внешнюю силу, наклоняющую потенциал влево и замедляющую транскрипцию.
Для того чтобы транскрибировать ДНК в РНК, мотор движется
шагами длиной в один нуклеотид (А, Т, G или С); длина шага Δχ примерно
равна 0.34 нм. Чтобы присоединить новый нуклеотид, мотор должен
преодолеть асимметричный потенциальный барьер (рис. 2.8). Ванг с соавторами
(рис. 2.9) показали, что мотор можно остановить, приложив к нему силу
27 пН (т.е. 27 пикоНьютонов).
(а) Чему равна разность энергии между соседними минимумами потенциала,
вызванная наличием такой внешней силы, приложенной к бусине (рис. 2.9)?
Будем считать, что эта внешняя останавливающая сила компенсируется внутренней
силой «сползания» — силой, которую развивает мотор и которая толкает его в
выделенном направлении транскрипции. Что можно сказать в таком случае об
отношении вероятностей перехода вперед и назад в отсутствие внешней силы от
оптического пинцета при температуре 300 К? (кв = 1.381 · 10~23 Дж/К.)
(Указание: Если бы ансамбль моторов находился в тепловом равновесии, полный
поток вперед и назад был бы одинаковым; полный поток из потенциальной
ямы равен числу частиц в ней, умноженному на вероятность выхода;
наконец, любой отдельно взятый мотор не знает, является он частью равновесного
ансамбля или нет.)
Возникновение силы, увлекающей мотор в направлении транскрипции,
связано с химическими реакциями, сопровождающими движение мотора от
Гл.2. Упражнения
59
Рис. 2.9. Эксперимент с оптическим пинцетом
Лазерный луч сфокусирован в одной точке (лазерной ловушке)] полистирольная бусинка
втягивается в область, где интенсивность света наибольшая (диэлектрик всегда
втягивается в электрическое поле). Рельсом служит молекула ДНК, присоединенная к бусинке,
мотор — это молекула РНК-полимеразы, связанная на стеклянной подложке. Когда мотор
копирует ДНК в РНК, он тянет за ДНК, вытягивая бусинку из ловушки, что создает силу,
препятствующую движению.
одной пары нуклеотидов к следующей. Для того чтобы присоединить
очередной нуклеотид к РНК, мотор окисляет одну молекулу нуклеотрифосфата
(НТФ) с выделением пирофосфата. Полная энергия, высвобождаемая в этой
реакции, зависит от детального устройства системы и принимает значения
между 2 · 10~20 и 5 · 10~20 Дж. Собственно говоря, эта величина — изменение
свободной энергии Гиббса в этой реакции, но для целей этого упражнения вы
можете обращаться с ней как с обычной энергией.
(Ь) Эффективность молекулярного мотора не может быть совершенной: не
вся химическая энергия превращается в силу, развиваемую мотором. Из вашего
ответа на вопрос (а) и приведенных значений энергии реакции оцените
коэффициент полезного действия мотора — отношение его полезной работы
(развиваемая сила, умноженная на пройденное расстояние) к потребленной энергии.
Многие модели молекулярных моторов основываются на задаче Фейнмана
о храповике и собачке [43, 1.46], при разборе которой он прозорливо
обсуждает вопрос о том, как была бы устроена работа шестеренок и храповиков на
молекулярном уровне.
2.4 Блуждание молекулы духов.33 (Моделирование) (2)
Траектория молекулы духов в воздухе при отсутствии ветра, как и
траектория любой другой молекулы в разреженном газе — это случайное
33Это упражнение и соответствующее программное обеспечение были разработаны
совместно с Кристофером Майерсом.
60 Гл.2. Случайные блуждания и возникновение коллективного поведения
блуждание, запутанная ломаная линия, состоящая из множества
практически прямых сегментов, разделенных точками столкновения. На
веб-сайта книги [132] вы найдете программы, которые моделирующие
молекулярную динамику [30], порождающую такие случайные блуждания.
Запустите модель разреженного газа из взаимодействующих атомов,
положив среднюю скорость атомов равной нулю.34 Пронаблюдайте за
движением одного выделенного атома («атома духов»). Обратите внимание, что,
когда атом выходит за границу области моделирования, он немедленно
появляется с противоположной стороны: в нашей модели используются
периодические граничные условия.^ В вашей программе должна быть возможность
построить и проанализировать «развернутую» траекторию ти = (хи,Уи,ги)
выбранного атома, т.е. траекторию без скачков координат, вызванных
периодическими граничными условиями.
(a) Посмотрите на траекторию выбранного атома. Качественно, похожа ли
она на траекторию случайного блуждания? Начертите xu{t) как функцию t и
xu{t) как функцию yu{t). Время, через которое частица полностью забывает
первоначальное направление — это время между столкновениями. Длина между
столкновениями — это расстояние, проходимое атомом за это время. Оцените
(можно грубо) эти величины.
(b) Постройте г^(£) как функцию от t для нескольких частиц (убедившись
в том, что их средняя скорость равна нулю). Наблюдаете ли вы какую-либо
регулярность в росте каждой из этих величин по отдельности? Постройте теперь
(г^) как функцию t, где треугольные скобки соответствуют усреднению по всем
частицам. Растет ли эта величина линейно со временем? Оцените коэффициент
диффузии D.
2.5 Моделирование случайных блужданий.36 (Моделирование) @
Случайные блуждания можно эффективно моделировать и
анализировать на компьютере.
(а) Напишите процедуру, генерирующую случайное блуждание из N шагов в
d-мерном пространстве. Каждый шаг вашего блуждания по каждой из координат
34 Атомы взаимодействуют посредством парного потенциала Леннарда—Джонса,
который является хорошим приближением для описания взаимодействия молекул благородных
газов.
35Периодические граничные условия — это искусственный прием, придуманный для того,
чтобы эффективно симулировать поведение бесконечно большой системы, используя
систему конечного размера. Он состоит в том, что моделирование проводится в прямоугольной
области, противоположные грани которой математически отождествляются между собой:
(х,у, ζ) = (χ ± L,у, ζ) = (х,у± L,ζ) = (χ,y,z± L).
36Это упражнение и соответствующее программное обеспечение созданы совместно с
Кристойером Майерсом.
Гл.2. Упражнения
61
должен представлять собой случайную величину, равномерно распределенную
на отрезке (—1/2, 1/2). (Сначала сгенерируйте все шаги и запишите их в виде
матрицы Ν χ d, а затем просуммируйте их так, чтобы получилась траектория
блуждания.) Постройте xt как функцию t для нескольких случайных
блужданий из 10 000 шагов. Постройте траектории на плоскости (х, у) для нескольких
двумерных блужданий с N = 10, 1000 и 100000. (Старайтесь, чтобы отношение
масштабов по осям было близко к единице.) Можно ли сказать, что
увеличение числа шагов в 100 раз приводит к десятикратному увеличению типичных
значений координат?
Каждое индивидуальное случайное блуждание непредсказуемо и
отличается от остальных, однако ансамбль блужданий обладает элегантными
предсказуемыми свойствами.
(Ь) Напишите процедуру для вычисления положений концов W случайных
блужданий из N шагов в пространстве d измерений. Постройте на одном
графике положения конечных точек для 10000 случайных блужданий с N = 1 и
10. Убедитесь, что распределение более длинных блужданий обладает круговой
симметрией, несмотря на то, что распределение после одного шага квадратное
(рис. 2.10).
Рис. 2.10. Возникновение сферической симметрии
Конечные точки многих траекторий случайных блужданий после одного (центральный
квадрат из ярких точек) и десяти (все остальные точки) шагов. Видно, что хотя
индивидуальные шаги не обладают вращательной симметрией (шаги вдоль диагоналей длиннее),
конечные точки случайных блужданий из многих шагов такой симметрией обладают.
Сферическая симметрия возникает спонтанно с ростом числа шагов.
Мы наблюдаем возникновение симметрии: несмотря на то, что шаги
блуждания вдоль диагоналей квадрата длиннее, после нескольких шагов
62 Гл.2. Случайные блуждания и возникновение коллективного поведения
случайное блуждание обладает почти точной симметрией относительно
вращения.37
Наиболее важным свойством случайных блужданий является
центральная предельная теорема. Конечные точки ансамбля одномерных случайных
блужданий из N шагов среднеквадратичной длины а в пределе N —У оо
распределены в соответствии с гауссовым (нормальным) распределением
р(х) = -j=- βχρ(-χ2/2σ2), (2.35)
где σ = y/Na.
(с) Вычислите среднеквадратичную длину а для одномерных шагов,
равномерно распределенных на отрезке (—1/2, 1/2). Напишите процедуру, которая
строит гистограмму распределения конечных точек W одномерных случайных
блужданий из N шагов, а также (на том же графике) распределение,
предсказываемое уравнением (2.35). Используйте χ в интервале (—3σ, 3σ), и пусть
в гистограмме будет, скажем, 50 колонок. Постройте такие гистограммы для
W = 10000 и N = 1, 2, 3 и 5. Насколько быстро распределение конечных точек
сходится к распределению Гаусса?
2.6 Преобразование Фурье и функции Грина, φ
Пусть начальный профиль плотности некоторой системы p(x,t = 0)
представляет собой небольшое возмущение однородной плотности ро,
показанное на рис. 2.11. Плотность подчиняется уравнению диффузии
др/dt = Dd2p/dx2, где D = 0.001 м2/с. Возмущение вблизи χ = 5 имеет
гауссову форму ехр(—х2/2)/\/27г, а возмущение вблизи χ = 15 — это волна
cos(10x), домноженная на гладкую функцию с компактным носителем.
(а) Метод Фурье. Попытаемся угадать, как будет эволюционировать
плотность, изображенная на рис. 2.11. В качестве первого шага рассмотрим
простую синусоидальную волну. Если начальное распределение плотности равно
Pcos(z50) = cos(10x), какой вид будет иметь это распределение плотности
через t = 10с? Полезные формулы: p(k,t) = p(k,tr)G(k,t — t')\ G(k,t) =
exp(-DkH).
37 «Квадратная» асимметрия шагов — это возмущение, которое не является
релевантным на больших временных и пространственных масштабах (см. гл. 12). Если разложить
в ряд дискретное уравнение диффузии в непрерывном пределе и сохранить старшие
члены до четвертых производных включительно, то получится dp/dt = DV2p + EV2 (V2p) +
F (dAp/dxA + d*p/dy4), где F обладает «квадратной», а не сферической симметрией.
Однако типичный масштаб этого члена — Δί/α4, так что на масштабах, больших, по сравнению
с а, он становится исчезающе мал.
Гл.2. Упражнения
63
(b) Метод функций Грина. В качестве второго шага проверим, сколько
времени потребуется возмущению, для того чтобы распространиться на расстояние,
равное типичному масштабу гауссовой кривой в левой части рисунка. Пусть в
некоторый предыдущий момент времени t = —to, распределение плотности
имело вид й-функции, локализованной в точке χ = О, р(х, —ίο) = δ(χ). Каким нужно
выбрать время ίο» чтобы получить в момент времени t = О гауссово
распределение плотности р(х,0) = ехр(—х2/2)/у/2п, если коэффициент диффузии равен
D = 0.001 м2/с? Полезные формулы: p(x,t) = f p(y,t')G(y — x,t — t')ay\
G(x,t) = (l/V^X)exp(-x2/(4Dt)).
(c) Рисунки. Рассмотрим теперь, как изменится распределение плотности
за следующие 10 секунд. Начальный профиль плотности p(x,t = 0) показан
на рис. 2.11. Какой из вариантов на рис. 2.12 описывает профиль плотности в
момент t = 10с? (Указание: сравните t = 10с с временем ίο из части (Ь).)
Полезные формулы: (χ2) ~ 2Dt.
5 10 15
Положение χ
Рис. 2.11. Начальный профиль плотности
На графике показаны отклонения от среднего значения.
2.7 Диффузия с периодическими начальными условиями. (2)
Рассмотрим одномерное уравнение диффузии dp/dt = Dd2p/dx2, с
периодическим начальным условием, состоящим из й-функций при всех хп = nL:
(а) Используя метод функций Грина, получите приближенное выражение для
плотности, верное для малых времен при —L/2 < χ < L/2 и состоящее из
одного челна (а не имеющее вид бесконечной суммы). (Указание: сколько
гауссовых функций дают существенный вклад в распределение плотности в
рассматриваемой области на малых временах?)
64 Гл.2. Случайные блуждания и возникновение коллективного поведения
Ί0
15 20 25
Положение χ
5 10 15
Положение χ
(с)
5 10 15
Положение χ
5 10 15
Положение χ
(е)
Рис. 2.12
Гл.2. Упражнения
65
(b) Используя ряд Фурье38, получите приближенное выражение для
распределения плотности, верное на больших временах и состоящее из двух (а не
бесконечного числа) слагаемых. (Указание: сколько длин волн дают существенный
вклад в ответ на больших временах?)
(c) Определите, в терминах L и D, характерное время г, такое, что ответ из
части (а) верен для t <С г, а ответ из части (Ь) — при t » т.
2.8 Теплопередача. ©
Поток энергии в веществе с теплопроводностью kt и распределением
температур Т(х, у, z, t) = T(r, t) задается уравнением J = — ktVT\39 Энергия —
локально сохраняющаяся величина, поэтому плотность энергии Ε
удовлетворяет уравнению dE/dt = — V · J.
(a) Пусть вещество обладает постоянной теплоемкостью Ср и плотностью р,
так что Ε = СррТ. Покажите, что в этом случае температура Τ удовлетворяет
уравнению диффузии дТ/dt = kt/(cpp) V2T.
(b) Поместив вещество в полость, в которой возбуждены стоячие
микроволны (т.е. в микроволновую печь), мы нагреваем его неоднородно по объему,
точнее — периодически модулированным образом, так что Τ = sin(fc:r) при t = 0.
Пусть в момент t = 0 микроволновая печь выключается. Покажите, что
амплитуда модуляции температуры экспоненциально спадает со временем. Как
характерное время этого спадания зависит от длины волны модуляции λ = 2n/kl
2.9 Сковородка, φ
Железная сковородка быстро нагревается на плите до температуры
400°С. Оцените (скажем, с точностью до множителя порядка двух), через
какое время ее ручка нагреется до такой температуры, что к ней нельзя
будет прикасаться? (Задача заимствована из [116, р. 40].)
Проведите оценку тремя способами.
(a) Угадайте ответ из вашего повседневного опыта. Если вы всю жизнь имели
дело только с алюминиевым сковородками, посоветуйтесь с родителями или
друзьями.
(b) Получите грубую оценку методом размерного анализа. Вам нужно
перенести количество теплоты CppVAT через поперечное сечение ручки А = V/Ax.
Сколько тепла будет переноситься через эту площадь за единицу времени, если
градиент температуры по порядку величины равен ΑΤ/ΑχΊ Сколько времени St
38Вы можете использовать и непрерывное преобразование Фурье, но вы обнаружите, что
фурье-образ р(к, 0) равен нулю всюду, кроме к = 2пт/Ьу где он описывается δ-функцией.
39Мы могли бы вывести это уравнение, рассмотрев случайные блуждания фононов в
веществе. Однако, мы не будем здесь этого делать.
66 Гл.2. Случайные блуждания и возникновение коллективного поведения
понадобится для того, чтобы такой поток перенес количество теплоты,
необходимое для нагревания всей ручки?
(с) Методом функции Грина (см. упражнение 2.6) вычислите время,
необходимое для того, чтобы тепловой импульс распространился по бесконечному
металлическому стержню из χ = О на среднеквадратичное расстояние σ(ί),
равное длине ручки. Используйте этот результат для оценки времени нагревания.
Указание: Теплоемкость железа равна Ср = 450 Дж/(кг К), его плотность
ρ = 7900кг/м3, теплопроводность kt = 80Вт/(м К).
2.10 Полимеры и случайные блуждания. (Моделирование, физика
конденсированного состояния) @
Полимеры — это длинные молекулы, как правило состоящие из
одинаковых небольших звеньев, называемых мономерами, связанных друг с другом в
длинную одномерную цепь. Будучи погруженной в растворитель, полимерная
цепь часто принимает конформации, напоминающие траектории случайных
блужданий. Как правило, углы между отрезками, соединяющими соседние
мономерные звенья, достаточно малы; память о направлении цепи
пропадает на масштабе, как минимум, нескольких звеньев. Однако при рассмотрении
достаточно крупномасштабных свойств цепей можно, вместо того чтобы
учитывать поведение этих малых углов, заменить цепь эквивалентной, в которой
вся гибкость сконцентрирована в небольшом количестве изломов. Мы будем,
таким образом, приближать полимер некоррелированным случайным
блужданием из прямолинейных шагов длиной в несколько мономерных звеньев.
Такая эквивалентная длина шага называется персистентной длиной.*0
(а) В двойной спирали ДНК на одну комплементарную пару приходится
длина в 3.4 А, а персистентная длина ДНК равна 50 нм. Считая, что конформация
ДНК адекватно представляется случайным блужданием, вычислите среднекв-
дратичное расстояние y/{R2) между концами фрагмента цепи (гена) длиной в
100000 комплементарных пар.
Полимеры в растворе, как правило, непредставимы в виде простых
случайных блужданий. Случайные блуждания — особенно в пространствах
малой размерности — часто пересекают друг друга. Одиночные полимеры в
растворе представляют собой несамопересекающиеся случайные блуждания:
полимер «исследует» только те конформации, которые не пересекают сами
себя.
Разные авторы определяют персистентную длину немного по-разному, но все
определения совпадают с точностью до множителя порядка единицы.
Гл.2. Упражнения
67
Выясним, влияет ли отсутствие самопересечений на статистику конфор-
маций полимера в пространстве двух измерений. В частности, будет ли
типичное расстояние между концами цепи по-прежнему расти пропорционально
корню из длины цепи полимера L, R ~ y/Ll
(b) Двумерное несамопересекающееся случайное блуждание. Приведите
короткое убедительное рассуждение, отвечающее на вопрос о том, возвратно ли
обычное (самопересекающееся) блуждание в двух измерениях, т.е. вернется ли
(после некоторого большого числа шагов) типичное случайное блуждание в
начальную точку. (Указание: до какого типичного расстояния от начальной
точки «доходит» случайное блуждание из N шагов? Сколько раз оно
посещает каждую точку из доступного для него объема?)
Запустите код, ссылка на который приведена на сайте книги [132] в
разделе 'Self-avoiding random walks'. Эта программа моделирует двумерное
случайное блуждание как последовательность шагов единичной длины на
квадратной решетке (при этом шаги назад запрещены). Каждое случайное
блуждание начинается в начале координат и распространяется до тех пор, пока не
посетит какую-либо ячейку решетки дважды, после чего блуждание
«выкидывается». Среднеквдратичный размер несамопересекающегося блуждания
длины η вычисляется усреднением по блужданиям, «выжившим» к п-ому
шагу.
(c) Запустите программу на некоторое достаточно большое время, затем
остановите ее и распечатайте результат. Похоже ли на то, что R ~ VT? Если
нет, то какую оценку вы можете дать для показателя степени i/f связывающего
Re L1 Как полученный вами результат соотносится с предсказанием теории для
двумерной системы: ν = |?
2.11 Акции, волатильность и диверсификация.41 (Финансы,
моделирование) (2)
Динамика цен акций достаточно хорошо приближается случайными
блужданиями. Индекс Standard and Poor's 500 (S&P 500) — это взвешенное
41 По мнению переводчика, описание динамики фондовых индексов, даваемое автором
в этом упражнении, является лишь очень грубым приближением к реальности. Обратите
внимание на то, что наличие «тяжелых хвостов» в распределении недельных, месячных и
т.д. изменений индекса Standard and Poor's (см. часть (b) упражнения) связано с
наличием долгосрочных корреляций между шагами. Такие долгосрочные корреляции связаны, в
частности, с воздействиями внешнего мира на фондовый рынок; в свою очередь,
представляется более разумным описывать эти воздействия на языке непрерывного распределения
шоков разного масштаба, а не в терминах «либо огромная катастрофа, либо ничего
особенного», как это делает автор. Более подробно о финансовых рынках и используемой для
их описания математике можно узнать из [13]. — Прим. переводчика.
68 Гл.2. Случайные блуждания и возникновение коллективного поведения
среднее цен пятисот больших компаний, торгуемых на фондовом рынке
США.
Воспользуйтесь ссылкой 'Stock market' на сайте упражнений к этой
книге [132] и скачайте файл SandPConstantDollars.dat, а также файлы с
указаниями для того языка программирования, которым вы собираетесь
воспользоваться. Каждая строчка в файле данных соответствует одному буднему дню
(торги на бирже не проводятся по субботам и воскресеньям). Первая колонка
— это время t (измеренное в днях начиная с середины октября 1982), вторая
— значение индекса Standard and Poor's SP(t) для этого дня,
скорректированное на инфляцию, с использованием индекса потребительских цен для
соответствующего месяца.
Являются ли флуктуации цен акций случайными или они вызваны
внешними обстоятельствами?
(а) Начертите зависимость цены акций от времени. Обратите внимание на
пик в районе 2000 года. 11 сентября 2001 года (день номер 6903 в списке)
произошла атака террористов на башни-близнецы в Нью-Йорке. Похоже ли, что
падение цен на фондовом рыне после 2000 года было, в основном, связано с
этим внешним событием?
Иногда крупные флуктуации являются следствием внешних событий;
флуктуации размеров популяций в экологии также имеют достаточно
случайный характер, но исчезновение динозавров было определенно
вызвано падением метеорита.42
Если понимать изменение индекса S&P 500 как некоторое случайное
блуждание, то каков шаг этого блуждания? Это зависит от определения: от
того, спрашиваем ли мы, на сколько индекс изменился за год, за неделю
или за день.
Возникает еще дополнительный технический вопрос: измеряем мы время
в обычных календарных днях, или в торговых днях? Мы будем
придерживаться принятого в финансовом сообществе правила и рассматривать только
торговые дни. Определим шаг времени между измерениями t равным
одному торговому дню для однодневных изменений (даже если между торговыми
днями есть выходной или праздник), пяти для недельных изменений и 252
(типичное число торговых дней в году) для годовых изменений.
42 Это далеко не единственное возможное объяснение исчезновения динозавров. — Прим.
переводчика.
Гл.2. Упражнения
69
(b) Напишите процедуру Ре, которая находит в базе все пары моментов
времени, разделенные временным интервалом At = £, и возвращает список
процентных изменений индекса
для этих пар. Постройте гистограмму дневных, недельных и годовых изменений.
На каком временном масштабе имеет смысл инвестировать в бумаги,
привязанные к индексу Standard and Poor's 500 (т.е. на каком масштабе средний рост
индекса становится существенным на фоне его флуктуации)? Кроме того, как
вы думаете, почему гистограмма годовых изменений выглядит настолько
сложнее остальных? (Указание к последнему вопросу: сколько лет покрывает ваша
база данных? Независимы ли шаги SP(n) — SP(n — £) и SP(m) — SP(m — £),
если η — т < £? Масштаб флуктуации зависит не от общего числа шагов, а
от эффективного числа независимых шагов случайного блуждания.)
Распределения, полученные вами в части (Ь) для коротких промежутков
времени, должны выглядеть достаточно похоже на распределение Гаусса, что
хорошо согласуется с нашим анализом случайных блужданий на языке
функций Грина и центральной предельной теоремы. Однако люди, занимающиеся
финансовой математикой, более заинтересованы в изучении отклонений от
ожидаемого поведения. Они заметили, что хвосты этих распределений
существенно отклоняются от распределения Гаусса.
(c) Покажите, что логарифм от распределения Гаусса — это парабола с
ветвями вниз. Постройте логарифм от гистограммы распределения, полученной в
части (Ь). В полученной гистограмме больше или меньше редких больших
отклонений, чем в распределении Гаусса? (Указание: далеко на хвостах
распределения количество измерений оказывается невелико и данные флуктуируют
между нулями и единицами. Обращайте внимание не на эту область, а на
область несколько ближе к центру распределения, для которой имеется
достаточная статистика.)
Некоторые акции, инвестиционные фонды и индексы более рискованны,
чем остальные. Это не означает, что они в среднем приносят меньший доход;
напротив, как правило, средняя доходность, рискованных вкладов выше, чем
консервативных и надежных. Рискованные бумаги имеют менее
предсказуемую доходность: иногда они растут быстрее, чем ожидалось, но иногда резко
падают в цене. У рискованных бумаг велико среднеквадратичное
отклонение доходности. В финансах это среднеквадратичное отклонение называют
волатильностью
ve=yJ({Pt{t)-Pe)2).
70 Гл.2. Случайные блуждания и возникновение коллективного поведения
(d) Вычислите среднюю дневную, недельную и месячную волатильность для
данных индекса S&P 500 с поправкой на инфляцию. Постройте график волатиль-
ности и ее квадрата как функции времени между измерениями для временного
шага от 0 до 100 дней. Ведет ли себя волатильность так, как она должна себя
вести для случайного блуждания?
Волатильность акции зачастую вычисляют, измеряя флуктуации ее цены
в течение одного дня, после чего ее умножают на квадратный корень из 252,
для того чтобы оценить ожидаемые флуктуации в течение года.
Отдельные акции, входящие в индекс S&P 500, как правило, имеют
гораздо большую волатильность, чем индекс в целом.
(e) Пусть 500 бумаг, учитываемых в индексе S&P 500 имеют среднегодовую
доходность mi и волатильность σι каждая. Пусть они входят в индекс с равным
весом и пусть их флуктуации не коррелированны. Чему будет равна средняя
доходность и волатильность всего индекса? Не имея дополнительной инсайдерской
информации43 и догадок о том, какие из акций могут оказаться более
доходными, что выгоднее — покупать какую-то одну акцию, или бумагу, привязанную к
значению индекса как целого? Какая из этих бумаг имеет меньшую
волатильность?
Инвестиционные консультанты подчеркивают важность диверсификации
портфелей. Флуктуации разных акций не независимы друг от друга,
особенно если это акции предприятий одной отрасли; необходимо распределять
свои вложения между разными секторами экономики, между акциями,
облигациями и другими видами бумаг — это позволяет снизить рискованность и
волатильность вложений.
2.12 Финансовая математика: деривативы.44 (Финансы) φ
Предположим, что вы выбрали дом, который вы хотите купить, но вы
хотите сделать это не сейчас, а через два года, когда закончите университет. Вы
беспокоитесь, что за это время понравившийся вам дом может подорожать (у
вас на его покупку есть «всего» $100,000), но покупать его сейчас вы тоже не
хотите. Более того, нельзя исключать, что ваши планы за два года
изменятся. То, что вам нужно — это так называемый колл-опцион (от английского
call option),45 т.е. договор, по которому вы выплачиваете несколько тысяч
долларов нынешнему владельцу дома, а он в ответ обязуется (если вы того
Использование инсайдерской информации при торговле на бирже незаконно.
44 Это упражнение было разработано совместно с Эриком Граннаном на основе книги [64].
45Точнее говоря, это так называемый европейский колл-опцион, американский опцион
позволял бы вам купить дом в любой момент в течение двух лет, а не только по их
окончании.
Гл.2. Упражнения
71
захотите) продать вам свой дом через два года за $100,000. Вашим
родителям, которые собираются через 15 лет выйти на пенсию, может
понадобиться пут-опцион (от put option), который, за определенную плату, позволит
им продать дом по фиксированной цене через пятнадцать лет. Эти опционы
не представляют сами по себе права на какую-либо материальную
собственность, их цена выводится из цены какой-то другой собственности (в данном
случае — дома). Поэтому их принято называть производными ценными
бумагами, или деривативами (от англ. derivative — производная). В торговле
недвижимостью деривативы редки, но в торговле акциями и валютой они
используются очень широко.46
Покупатель опциона защищает себя от риска, продавец опциона получает
деньги за то, что принимает на себя риск того, что цена на торгуемый товар
в будущем неожиданно вырастет или упадет. Какую цену продавец должен
запросить за взятие на себя этого риска? Довольно элегантный ответ на этот
вопрос дает модель Блэка—Шоулза [101], благодаря появлению которой
развилась многомиллиардная индустрия торговли деривативами.
Блэк и Шоулз сделали несколько допущений: непрерывность изменения
цен на рынке, мгновенное проведение сделок и т.д. При этих
предположениях существует безрисковая стратегия и справедливая цена дериватива, при
которой ни одна из сторон не извлекает прибыли. Рассмотрим здесь частный
случай теории.
• Пусть в мире есть только два возможных объекта инвестиции:
рискованный актив, который мы будем называть акцией, и деньги (безрисковый
актив). В начальный момент времени цена акции равна Хо; цена денег
равна единице.
• На момент истечения опциона цена акций может принять одно из двух
значений, Хи > Xd·47
• Ставка рефинансирования равна нулю, так что цена денег в момент
истечения опциона по-прежнему равна 1. (Это предположения не меняет
ничего фундаментального.)
• Мы можем брать в долг и одалживать деньги под процент, равный
ставке рефинансирования (то есть равный нулю) и мы можем покупать и
46Если вы продаете ваш товар за доллары, а зарплату платите в песо, у вас может
возникнуть желание купить страховку от того, что доллар резко упадет по сравнению с
песо между данным моментом и моментом, когда вам заплатят за произведенный товар.
47Это ограничение — наличие только двух возможных финальных цен — позволяет
упростить вычисления. Индексы и и d соответствуют английским словам up (верх, вверх) и down
(низ, вниз).
72 Гл.2. Случайные блуждания и возникновение коллективного поведения
продавать акции (даже если у нас их нет; это называется продажа без
покрытия). Транзакционных издержек нет.48
Пусть Vu и Vd — две возможные цены опциона в момент его истечения.49
Пусть Vo — справедливая начальная цена опциона, которую нам надо
определить.
Рассмотрим портфель инвестиций V, который включает дериватив и
некоторое количество α акций. Начальная цена V равна Р0 = Vq + аХ$. На
момент истечения опциона цена портфеля может быть либо Vu + olXu, либо
Vd + aXd.
(a) При каком значении а конечные цены портфеля равны между собой?
Чему равна эта постоянная финальная цена PfI
(b) При какой начальной цене дериватива Vo начальная цена портфеля
инвестиций равна конечной цене? (Выразите ваш ответ в терминах Рр, # и Хо,
затем подставьте ответы из части (а).) При этом значении начальной цены
ни продавец, ни покупатель дериватива не извлекают никакой прибыли; в
среднем доходность дериватива такая же, как доходность денег.
(c) Зависит ли ваш ответ от значения вероятностей ри и pd того, что конечная
цена будет равна Хи и Xd, соответственно?
Рассматриваемый портфель — это взвешенное среднее дериватива и самих
акций, чья цена сохраняется, т.е. его владелец оказывается полностью
безразличен к изменению цены акции. Таким образом, этот портфель является
безрисковым активом. А значит, его цена должна расти со скоростью
безрискового роста; в этом состоит смысл так называемой арбитражной оценки.
(Грубо говоря, арбитражные операции — это операции, при которых можно
заработать денег бесплатно; т.е. существует стратегия обновления портфеля,
для которой некоторые конечные состояния имеют положительную
доходность по сравнению с безрисковыми инвестициями, и никакие состояния не
имеют отрицательной доходности. Если рынок эффективен, то арбитражные
операции на нем невозможны; предполагается, что инвесторы уже
проторговали на нем достаточно времени, чтобы «бесплатных» денег не осталось.)
То есть на организацию продажи или покупки того или иного актива ресурсы не
тратятся. — Прим. переводчика.
49Например, если рассматриваемый дериватив — это колл-опцион, позволяющий
держателю купить акцию по цене X/, где Хи > Xf > Xdi то цена опциона в момент его
истечения равна Vu = Хи — Xf в случае, если финальная цена акции равна Хи, или Vd = О,
если финальная цена акции равна Xd (потому что в этом случае опцион останется
неиспользованным) .
Гл.2. Упражнения
73
Можно обобщить приведенную аргументацию на большее число шагов
по времени, рассматривая их последовательно, начиная с конечного
состояния (в котором цена дериватива известна), и шаг за шагом возвращаясь к
начальному состоянию; это называется оценкой опционов методом
биномиального дерева. Если рынок эффективен, средняя цена акции будет расти
со скоростью безрискового актива, так что неизвестна только ее волатиль-
ность (величина флуктуации ее цены, см. упражнение 2.11). В непрерывном
пределе это дерево превращается в знаменитое уравнение Блэка-Шоулза в
частных производных.
2.13 Построение перколяционной сети.50 (Теория сложности,
моделирование) @
На рис. 2.13 показано, как будет выглядеть большой лист бумаги с
закрепленными концами, если последовательно делать в нем множество небольших
дырок в случайных местах. Усреднение по ансамблю в данном случае будет
означать усреднение по всевозможным случайным положениям дырок;
рисунок соответствует моменту, когда лист бумаги почти готов развалиться на
части. При некотором расположении дырок лист распался бы на две части
существенно раньше (например, если бы дырки располагались последовательно
поперек листа), при некоторых других (расположение в шахматном порядке)
— несколько позже, но подавляющее большинство членов нашего ансамбля
соответствуют расположениям дырок, схожим с показанным на рисунке. Как
и в случае случайных блужданий, проанализировать поведение всего
ансамбля расположений дырок существенно проще, чем описать какое-то
конкретное расположение.
Теория перколяции — это теория, изучающая, как качественно меняется
связность большой системы при случайном удалении ее частей. За пределами
физики эта задача часто рассматривается как архетипический пример
применения теории непрерывных переходов и критических явлений. По-видимому,
этот статус объясняется простой формулировкой задачи и тем, что ее
исследование не требует предварительного изучения равновесной статистической
механики.51 В этом упражнении мы изучим перколяцию по связям и по узлам
(рис. 2.13 и рис. 2.14, соответственно) на двумерной решетке.
50Это упражнение и связанное с ним программное обеспечение разработано совместно с
Кристофером Майерсом.
51С формальной точки зрения, перколяция является равновесным фазовым переходом.
Можно показать, что задача перколяции является предельным (соответствующим q —У 1)
случаем модели Поттса — модели, в которой каждому узлу решетки сопоставляется спин,
способный находиться в q различных состояниях (случай q = 2 соответствует модели Изин-
га) [19, section 8.4]. Однако для постановки задачи перколяции и ее изучения не обязательно
знать, что такое статсумма или распределение Больцмана.
74 Гл.2. Случайные блуждания и возникновение коллективного поведения
ιιπιιμϊ:
-{тд:гпг
1 #-# · · 11 · # #
-•-1 μ· · 1 · · A-
-#•14·· · · · ·
Рис. 2.13. Сеть перколяции по связям
Каждая связь на квадратной решетке размера 10 χ 10 присутствует с вероятностью ρ = 0.4.
Это ниже порога перколяции для бесконечной решетки ρ = 0.5, и действительно, сеть
связей распадается на индивидуальные кластеры (окрашенные в разные цвета). Имейте в виду,
что используются периодические граничные условия. Обратите внимание на то, что
имеется множество маленьких кластеров и лишь немного больших. А именно, мы наблюдаем
12 кластеров размера 5=1, три кластера размера S = 2, и один (черный) кластер
размера S = 29. На большой решетке вблизи точки перколяционного перехода распределение
кластеров по размерам p(S) спадает по степенному закону52(см. упражнение 12.12).
На сайте книги [132] в разделе компьютерных упражнений вы найдете
файлы с указаниями и графическими шаблонами, которые помогут вам при
выполнении этого упражнения.
Перколяция по связям на квадратной решетке.
(а) Определите на компьютере сеть перколяции по связям для двумерной
решетки размера L x L с периодическими граничными условиями и
вероятностью связи, равной р. В этом упражнении узлы решетки будет удобно
представлять парами целых чисел (i,j). Вам понадобится функция GetNeighbors(n),
возвращающая список соседей заданного узла п. Программное обеспечение,
выложенное на сайте, позволяет нарисовать сеть перколяции по связям для
различных значений ρ и L. С помощью этих рисунков проверьте, что вы правильно
определили периодические граничные условия. (Есть два разных способа
построения сети. Вы можете начать с пустой сети и последовательно добавлять
в нее узлы (процедура AddNode) и связи (процедура AddEdge), вертикальные
52Строго говоря, степенной закон для p(S) на всех масштабах наблюдается только в
самой точке перехода ρ = рс, вблизи точки перехода степенное затухание наблюдается как
промежуточная асимптотика. А именно, вероятность найти кластер заданного размера
спадает степенным образом только для промежуточных, средних кластеров, для очень
больших кластеров спадание существенно более быстрое. — Прим. переводчика.
Гл.2. Упражнения
75
или горизонтальные (см. упражнение 1.7). Другой, более традиционный
подход состоит в том, чтобы задать двумерный массив вертикальных и
горизонтальных связей, тогда функция GetNeighbors(n) будет возвращать список
соседей узла η = (i,j) в соответствии с тем, имеются ли связи на
соответствующих местах в матрице связей.)
Перколяционный переход и дуальность. В большинстве случаев
нахождение точного положения точки перехода само по себе оказывается непростой
задачей. Мы выбрали для анализа именно перколяцию на квадратной
решетке, потому что можно показать, что в большой системе точка перколяцион-
ного перехода — это рс = 1/2. Для доказательства этого факта используется
дуальная решетка.
Узлами дуальной решетки являются центры квадратных ячеек между
первоначальными узлами. Связи дуальной решетки — это те связи между ее
узлами, которые не пересекают связи первоначальной решетки. Поскольку
каждая из возможных связей дуальной решетки пересекает ровно одну
возможную связь первоначальной решетки, вероятность р* того, что связь на
дуальной решетке реализуется, равна 1 — р, где ρ — вероятность реализации
связи на начальной решетке. Если мы сможем показать, что перколяция на
дуальной решетке наблюдается тогда и только тогда, когда она не
наблюдается на начальной решетке, это и будет означать, что рс = 1/2. Проще всего
заметить это из рисунка.
(b) Сгенерируйте и напечатайте небольшую перколяционную сеть с ρ = 0.4,
выбрав такую реализацию, в которой нет кластера, покрывающего всю решетку
сверху вниз или справа налево (можете просто распечатать рис. 2.13).
Начертите маршрут на дуальной решетке, соединяющий верхнюю и нижнюю (правую
и левую) стороны решетки. (Вы увидите, что это действие аналогично поиску
крысой пути в лабиринте.) Стало ли очевидным, что в больших системах
перколяция на дуальной решетке наблюдается тогда и только тогда, когда она не
наблюдается на первоначальной?
Поиск кластеров.
(c) Запрограммируйте следующие две функции, которые позволят вам
находить кластеры связей на решетке.
(1) Функцию FindClusterFromNode(graph, node, visited), которая по
заданному узлу node в сети graph возвращает кластер, содержащий этот
узел, и помечает все узлы этого кластера маркером visited. Кластер —
это массив узлов, объединяющий начальный узел node, его соседей,
соседей соседей и т.д. Смысл использования метки visited заключается в
том, чтобы избежать многократной проверки одних и тех же узлов. Для
построения кластера эффективным алгоритмом является поиск в ширину:
76 Гл.2. Случайные блуждания и возникновение коллективного поведения
мы начинаем из узла node и проходим весь граф, двигаясь по оболочкам
— множествам узлов, равноудаленных от начального. Нам понадобится
массив currentShell, состоящий из узлов текущей оболочки, чьи соседи
еще не проверены, и nextShell, в который помещаются узлы, подлежащие
рассмотрению на следующем шаге (сначала поиск по всей оболочке, затем
переход к следующей — отсюда название «поиск в ширину»). Алгоритм
работает следующим образом:
— Определите visited [node] = True,
cluster = [node] и
currentShell
= graph.GetNeighbors(node).
— Пока в оболочке currentShell есть узлы,
* создайте пустой список nextShell;
* для каждого узла текущей оболочки currentShell, если он еще
не был посещен (т.е. если он не помечен как visited),
• добавьте этот узел к кластеру cluster,
• пометьте его маркером visited,
• и добавьте всех его соседей к nextShell;
* присвойте currentShell значения nextShell.
— В качестве результата работы функции верните массив cluster.
(2) Функцию FindAllClusters(graph), которая для всех узлов присваивает
маркеру visited значение False, вызывает FindClusterFromNode(graph,
node, visited) последовательно для всех узлов, которые помечены как
непосещенные (visited = False), и запоминает полученные кластеры.
Если хотите, вы можете дополнительно рассортировать кластеры по
размеру от самых больших до самых маленьких, это удобно при их отрисовке,
а также при поиске самого большого кластера.
Проверьте ваш код, запустив программу при малых значения L и используя
предлагаемые на сайте книги графические шаблоны. Правильно ли отрисовываются
кластеры? Если ваша программа работает корректно, они должны изображаться
разными цветами.
Перколяция по узлам на треугольной решетке. Принцип
универсальности утверждает, что статистические свойства перколяционных кластеров на
больших масштабах не должны зависеть от микроскопических деталей
модели. Другими словами, удаление связей на квадратной решетке должно вблизи
рс приводить к образованию такой же фрактальной картины дырок, что и в
Гл.2. Упражнения
77
задаче о вырезании круглых отверстий из листа бумаги вблизи точки, где
лист распадается на части. Ничто в алгоритмах, реализованных вами в
части (с), не зависело от того факта, что у каждого узла было по четыре соседа,
ни даже от того, что узлы соответствовали вершинам квадратной решетки.
Давайте рассмотрим задачу перколяции на треугольной решетке (рис. 2.14);
узлы на ней заняты с вероятностью р, при этом каждый узел связан с
теми из его шести соседей, которые тоже заняты (удаление узла на такой
решетке соответствует вырезанию шестиугольного отверстия из листа бумаги).
Треугольная решетка тоже удовлетворяет соотношению дуальности, поэтому
вновь рс = 0.5.
С вычислительной точки зрения, удобно нумеровать узлы треугольной
решетки следующим образом. Узел, расположенный в точке (#,у)
треугольной решетки, пометим числами [г, j], где χ = i+j/2 и у = (x/3/2)j. Добавляя
теперь периодические граничные условия и считая, что i,j — целые числа
и 0 < г < L, 0 < j < L, мы получим покрытие нашей области ромбами, у
которых меньший из углов равен 60°.53 Каждая вершина [i,j] имеет шесть
соседей: [i,j] ± е, где е = [1,0], [0,1], [-1,1].
(d) Сгенерируйте сеть перколяции по узлам на треугольной решетке.
Первый способ построения этой сети состоит в том, чтобы добавлять вершины по
одной, используя каждый раз процедуру AddNode с вероятностью р, а затем
использовать функцию HasNode(k) (возвращающую значение True или False в
зависимости от того, занят ли узел fc), чтобы определить, с какими из соседей
к следует построить связи. Второй способ состоит в том, чтобы сразу, за один
проход, сгенерировать матрицу случайных чисел, определяющую, какие узлы
заняты, а какие свободны, добавить соответствующие узлы (с помощью
процедуры AddNode) и расставить связи между ними. Проверьте правильность работы
вашей процедуры для маленьких L с помощью программы визуализации.
(Обратите внимание на сдвиг периодических граничных условия по вертикали, см.
рис. 2.14.) Используйте процедуры, написанные вами в части (с) для поиска
кластеров, и проверьте их (в частности, на соответствие периодическим граничным
условиям) с помощью программы визуализации.
(e) Сгенерируйте небольшой кластер (скажем, для решетки 30 χ 30)
перколяции по связям на квадратной решетке и сравните его с небольшим кластером
перколяции по узлам на треугольной решетке. Вы увидите, что эти кластеры
5 Графическая программа использует такие периодические граничные условия, что эти
ромбы эффективно превращаются в прямоугольники.
78 Гл.2. Случайные блуждания и возникновение коллективного поведения
Рис. 2.14. Сеть перколяции по узлам
Каждый узел на треугольной решетке размера 10 х 10 занят с вероятностью ρ = 0.5, что
соответствует точке перколяционного перехода на бесконечной решетке. Обратите внимание
на то, что граничные условия обеспечивают периодичность по горизонтали и
периодичность со сдвигом по вертикали.
отличаются друг от друга по многим параметрам. Теперь сгенерируйте
большие54 кластеры обоих типов, скажем, на решетке 1000 χ 1000 (или посмотрите
на рис. 12.7). Согласны ли вы с тем, что они в целом выглядят очень похоже
(если смотреть издалека и не слишком приглядываться к деталям)?
В гл. 12 и упражнении 12.12 мы обсудим теорию перколяции более
подробно.
54Время работы вашей программы, если она написана правильно, должно быть
пропорционально общему числу узлов решетки N. Если вам кажется, что время выполнения
программы растет быстрее, чем в 4 раза при удвоении линейных размеров решетки,
попробуйте найти неэффективные процедуры и оптимизировать вашу программу.
Глава 3
Температура и равновесие
Обратимся теперь к изучению равновесной статистической механики —
триумфатору девятнадцатого столетия. В равновесной статистической
механике вводится фундаментальное понятие температуры и изучаются законы,
определяющие поведение всех известных жидкостей и газов.1 В этой
главе мы будем рассматривать как общую теорию, так и ее применение для
описания конкретной системы — идеального газа. Идеальный газ является
наглядным примером, иллюстрирующим использование формального
подхода, а его анализ даст предварительное представление о материале, который
будет изучаться в следующих главах.
Говорят, что система, не подверженная внешнему воздействию,2 достигает
равновесия? если на больших временах она переходит в состояние, не
зависящее от начальных условий (за исключением постоянных величин, таких как
полная энергия.)
Статистическая механика описывает равновесное состояние как
усреднение по всем возможным состояниям в фазовом пространстве, в соответствии
с законами сохранения. Данный микроканонический ансамбль вводится в
разделе 3.1. В разделе 3.2 мы, используя микроканонический ансамбль, изучим
свойства идеального газа. В разделе 3.3 мы определим понятия энтропии и
Для описания твердых тел при низких температурах используется квантовая
статистическая механика.
2 Если на систему оказывается внешнее воздействие (т.е. на нее действуют внешние
силы или потоки), то ее конечное состояние мы будем называть стационарным.
3Если система является достаточно большой, то ее равновесное состояние не будет
меняться с течением времени и будет достаточно «спокойным», отсюда и возникает этот
термин. Малые системы будут продолжать заметно флуктуировать даже в состоянии
равновесия.
80
Гл.3. Температура и равновесие
температуры для равновесных систем, а также покажем с помощью
микроканонического ансамбля, что потоки тепла максимизируют энтропию и
выравнивают температуры. В разделе 3.4 мы выведем формулу для давления
через энтропию и дадим определение химического потенциала. Наконец, в
разделе 3.5 мы вычислим энтропию, температуру и давление идеального газа
и приведем две поправки к нашему определению объема фазового
пространства.
3.1 Микроканонический ансамбль
Статистическая механика позволяет получить решение многих задач,
описывающих поведение системы как целого, что невозможно при подходе, в
котором рассматриваются индивидуальные частицы. В данной главе мы
исследуем универсальное поведение N атомов в сосуде объема V —
произвольных атомов в произвольном внешнем потенциале.4 Давайте предположим для
простоты, что стенки сосуда гладкие и твердые, так что энергия атомов при
их соударении со стенкой сохраняется. Таким образом, наша система
является изолированной, т.е. не зависящей от окружающего мира.
Каким образом можно исследовать поведение наших атомов? Мы можем,
в принципе, определить координаты5 Q = (#ι,2/ι>ζι>#2, · · · ,^лг,Улг,^лг) =
(<7ъ · · · > Qsn) и импульсы Ρ = (pi, · · · ,Рзлг) частиц в любой момент времени,
если известны их координаты и импульсы в начальный момент времени, с
использованием законов Ньютона:
Q = m"1P, P = F(Q) (3.1)
(где F — ЗЛ^-мерная сила, действующая со стороны других частиц и стенок
сосуда, am — масса частиц).6
Очевидно, что решение этих уравнений в общем случае невозможно по
следующим причинам:
• Многие системы, представляющие интерес, состоят из такого большого
числа частиц, что рассчитать их траектории не представляется
возможным.
4 Однако мы не будем использовать квантовую механику вплоть до главы 7.
537У-мерное пространство координат Q называется конфигурационным. ЗТУ-мерное
пространство импульсов Ρ носит название импульсного. 67У-мерное пространство (Р, Q) —
фазовое пространство.
6 Здесь m — диагональная матрица, если не все частицы имеют одинаковую массу.
3.1. Микроканонический ансамбль
81
• В большинстве систем, представляющих интерес, движение является
хаотическим, то есть эволюция системы с течением времени
становится все более чувствительной к начальным условиям — вы никогда не
сможете знать о системе достаточно, для того чтобы предсказать ее
поведение в будущем.
• Даже если бы расчет траекторий всех частиц был бы возможен,
такое решение было бы бесполезным для большинства приложений. Нас
гораздо больше интересует среднее число атомов, соударяющихся со
стенкой, чем, например, точное время удара конкретной частицы.
Каким образом можно простым способом извлечь важную информацию
из сложных траекторий движения этих атомов? Хаотическое движение
будет приводить к перемешиванию траекторий7вне зависимости от того, что мы
знали о начальных условиях нашей системы, при этом известными остаются
лишь постоянные во времени величины; для нашей системы это полная
энергия E.s Вместо того чтобы исследовать поведение системы с конкретным
набором начальных условий, давайте предположим, что энергия — это все, что
нам необходимо для описания равновесного состояния. Это приводит нас к
статистико-механическому описанию равновесного состояния нашей системы
как ансамбля систем со всевозможными начальными условиями с энергией
Ε — микроканонического ансамбля.
Рассчитаем свойства нашего ансамбля, усредняя по состояниям с
энергией, принадлежащей слою (Ε, Ε+δΕ), взяв предел9 δΕ —> О (рис. 3.1). Давайте
определим функцию Ω,(Ε) как объем фазового пространства данного тонкого
слоя, деленный на δΕ:10
Ω(Ε)δΕ= I dPdQ. (3.2)
JΕ<Η(ΡΛ)<Ε+δΕ
Равновесие и достигается именно вследствие этого перемешивания.
8В бесконечной системе полный импульс и момент импульса также сохраняются,
наличие сосуда нарушает вращательную и трансляционную инвариантность.
9Что же будет в квантовой механике, в которой энергетические уровни ограниченной
системы дискретны? В этом случае (гл. 7) мы должны брать достаточно большое δΕ по
сравнению с разницей в собственных энергетических состояниях, но малое по сравнению с
полной энергией.
10 Более формально, можно записать энергетический слой Ε < Ή(Ρ, Q) < Ε+δΕ,
используя ступенчатую функцию Хевисайда θ(χ), где θ(χ) = 1 при χ > О, и θ(χ) = 0 при χ < 0.
82
Гл. 3. Температура и равновесие
Здесь Ή(Ρ, Q) — гамильтониан нашей системы.11 Нахождение среднего
(О) некоторой величины в микроканоническом ансамбле производится при
усреднении 0(Р, Q) по тому же самому энергетическому слою:
<°>* = oTW^W i 0(P,Q)dPdQ. (3.6)
Обратите внимание, что при усреднении по всем состояниям в фазовом
пространстве, совместимым с нашим знанием о системе (иными словами, с
сохранением энергии), мы сделали скрытое предположение о том, что все
точки в фазовом пространстве (с данной энергией) являются a priori
равновероятными, то есть при усреднении имеют одинаковый вес. В разделе 3.2,
Можно увидеть, что Θ(Ε + δΕ — Ή) — Θ(Ε — Ή) равно единице именно внутри
энергетического слоя (рис. 3.1). В пределе δ Ε —У О, можно записать Ω(Ε) как производную:
П(Е)6Е = [ dP dQ = / dP dQ [Θ(Ε + δΕ-Η)-θ(Ε- Щ
= 6E-£EJdFdQe(E-H),
а математическое ожидание некоторого оператора О как
(О) = щщ j dPdQ [Θ(Ε + 8Ε-Ή)- Θ(Ε - Щ 0(P,Q)
(3.3)
_J д_
Ω(Ε) дЕ
ίdPdQ Θ(Ε - П)0(Р,Q).
(3.4)
Для дальнейшего изложения важно отметить, что производные в уравнениях (3.3) и (3.4)
взяты при постоянных N и V: (d/dE)\vtN- Наконец, нам известно, что производной
функции Хевисайда является δ-функция Дирака (см. примечание 4 на стр. 19). Таким образом,
мы получаем:
П(Е)= fdPdQS(E-H(P,Q)), (О) = —?— J dPdQ δ (Ε - W(P,Q))0(P,Q). (3.5)
Итак, микроканонический ансамбль может быть записан как плотность вероятности
δ (Ε - Ή(Ρ, Q)) /Ω(Ε) в фазовом пространстве.
11 Гамильтониан Ή, является функцией Ρ и Q и представляет собой полную энергию
системы. В нашем случае она будет иметь вид:
Р2 3N г>2
E- + u(Q)= У^
2m vv; ^2т
α=1
+ t/(gi,...,g37v),
где сила в законах Ньютона (уравнение 3.1) выражается через потенциальную энергию
следующим образом: Fa = —dU/dqa.
3.2. Микроканонический идеальный газ
83
О
Рис. 3.1. Энергетический слой
Слой энергий между Ε и Ε + δΕ может иметь неоднородную «толщину». Объем этого слоя
в 6 TV-мерном фазовом пространстве, деленный на δΕ, и есть определение Ω(Ε). Обратите
внимание, что при вычислении среднего по микроканоническому ансамблю более широкие
области имеют больший вес. В разделе 4.1 мы покажем, что, подобно тому, как капля воды
в реке проводит большую часть времени в глубоких зонах, где вода течет медленнее, так
же и траектория в фазовом пространстве проводит больше времени в широких областях.
рассматривая случай идеального газа, мы покажем, что это предположение
достаточно адекватно описывает поведение системы.12 Мы полностью
обоснуем предположение равных весов в главе 4, в которой мы также обсудим
более интригующий вопрос, почему такое большое количество систем
действительно достигает равновесия.
Тот факт, что микроканоническое распределение описывает равновесные
системы, должен показаться вам удивительным. Поведение равновесной
системы на больших временах и есть типичное поведение всех систем с
одинаковыми значениями сохраняющихся величин. Эта фундаментальная «регрессия
к среднему» и представляет собой основу статистической механики.
3.2 Микроканонический идеальный газ
Мы можем говорить об абстрактной совокупности атомов и выводить для
них общие уравнения, но для расчета конкретных свойств нужно выбрать
определенную систему. Наиболее типичной системой в статистической
механике является одноатомный13 идеальный газ. В качестве хорошей
аппроксимации подобного идеального газа можно рассматривать атомы гелия при
12 В разделе 3.5, мы добавим две поправки к нашему определению объема
энергетического слоя Ω(Ε).
13Воздух представляет собой смесь газов, но состоит преимущественно из двухатомных
молекул: Ог и N2, с небольшой примесью трехатомного СОг и одноатомного Аг. Свойства
двухатомных идеальных газов лишь незначительно сложнее по сравнению с одноатомным
84
Гл. 3. Температура и равновесие
высоких температурах и низких плотностях — при этих условиях атомы
имеют очень слабые дальнодействующие взаимодействия и редко соударяются.
Идеальный газ представляет собой предельный случай, когда взаимодействие
между частицами исчезает.14
В случае идеального газа энергия не зависит от пространственной
конфигурации частиц Q. Это позволяет изучать позиции частиц (раздел 3.2.1)
отдельно от их моментов (раздел 3.2.2).
3.2.1 Конфигурационное пространство
Поскольку энергия не зависит от конфигурации частиц, веса всех
конфигураций в нашем микроканоническом ансамбле одинаковы. Иными словами,
вероятность того, что все частицы будут находиться в малой окрестности
радиуса е центра сосуда, равна вероятности того, что они будут находиться в
е-окрестности любой другой конфигурации.
Чему равна плотность вероятности p(Q) того, что частицы идеального
газа будут находиться в некоторой конфигурации Q £ №?N внутри сосуда
объема V? Нам известно, что ρ — константа, не зависящая от конкретной
конфигурации. Мы знаем, что атомы газа находятся в некоторой
конфигурации, удовлетворяющей условию J pdQ = 1. Интеграл по координатам для
каждой из N частиц равен V, таким образом p(Q) = l/VN.
Тот факт, что нахождение всех частиц в одной половине сосуда имеет
такую же плотность вероятности, что и более разумные конфигурации, может
показаться противоречащим здравому смыслу. Пусть две
невзаимодействующие частицы находятся в кубическом сосуде размерами L χ L χ L. Поместим
начало координат в центр сосуда. Чему равна вероятность того, что обе
частицы находятся на его правой половине (или имеют координату χ > 0)?
Вероятность нахождения обеих частиц справа есть интеграл от функции ρ = 1/L6
по шестимерному объему, в котором обе частицы имеют координату χ > 0.
Объем этого пространства составляет (L/2) x L x L x (L/2) χ L χ L = L6/4,
таким образом вероятность равна 1/4, как при подбрасывании монетки для
газом. Для них необходимо также учитывать внутренние вращательные и, при высоких
температурах, колебательные степени свободы.
14 Если нет взаимодействий между частицами, то каким образом идеальный газ может
достичь равновесия? Если частицы никогда не сталкиваются, то они вечно будут двигаться
со скоростями, заданными в начальный момент времени произвольным образом. Мы
подразумеваем взятие предела бесконечных времен прежде взятия предела бесконечно слабых
взаимодействий, таким образом, мы можем допустить установление равновесного
распределения.
3.2. Микроканонический идеальный гае
85
каждой частицы. Вероятность того, что N таких частиц находятся справа,
составляет 2~N — как это можно предположить интуитивно. Не путайте
плотность вероятности с вероятностью! Маловероятные состояния для молекул
не есть состояния, обладающие малой плотностью вероятности. Скорее, это
состояния с малой полной вероятностью, поскольку они соответствуют
конфигурациям и моментам частиц, занимающим лишь незначительный объем
в полном фазовом пространстве.
Обратите внимание, что конфигурационное пространство, как правило,
имеет размерность в несколько раз большую числа Авогадро.15 Векторные
пространства огромного размера обладают необычными свойствами,
следствием которых являются важнейшие законы статистической механики.
Например, в большинстве конфигурационных пространств практически
ровно половина координат χ > О (что соответствует расположению в правой
части сосуда). Если бы в сосуде было 2JV невзаимодействующих частиц, то
какова была бы вероятность нахождения N + т из них с правой стороны?
Существует 22Ν равновероятных способов разместить различные частицы по
двум сторонам коробки. Из них в (Л^п) = {2N)\/((N + m)\(N — m)\) случаях
справа будут находиться т дополнительных частиц.16 Таким образом,
Ρ -2-™( 2Ν λ 2~™ {2Ν}[ (37)
Ут~2 \N + m)~Z (N + m)\(N-m)\' [Л)
Можно посчитать флуктуацию числа частиц с правой стороны, используя
формулу Стирлинга17
п! ~ {п/е)пу/Ът ~ (п/е)п. (3.8)
Для наших целей мы будем использовать второе, менее точное
приближение; сохранение сомножителя у/Ъгп дает постоянный коэффициент в
окончательном выражении (упражнение 3.9), который мы получим при нормировке
полной вероятности на единицу. С использованием формулы Стирлинга
выражение (3.7) приобретает вид:
15 Грамм водорода состоит из примерно N = 6.02 · 1023 атомов, это число называется
числом Авогадро. Таким образом, типичный размер конфигурационного пространства 3iV
составляет 1024.
16 (£) — это число способов выбрать неупорядоченную группу q частиц из набора ρ частиц.
Существует р(р — I) · · · (р — q + I) = ρ!/(ρ — ς)! способов выбрать упорядоченный набор,
поскольку ρ — число способов выбрать первую частицу, ρ — 1 — вторую, ... Для каждого
неупорядоченного набора число упорядоченных групп составляет q\> таким образом (р) =
р!/(«!(р-«)!)·
17Формула Стирлинга говорит нам о том, что -«среднее» число в факториале п! = п(п —
1) ■ · · 1 приблизительно составляет η/e; см. упражнение 1.4.
86
Гл. 3. Температура и равновесие
= ЛГ2ЛГ(ЛГ + m)-^N+m\N - m)-^-m)
= (1 + m/Arj-^+^il - m/JV)-(JV_m)
= ((1 + m/AO(l - m/N)yN (1 + m/N)-m(l - m/JV)m
= (1 - m2/N2)-N(l + m/N)-m(l - m/N)m. (3.9)
Поскольку \m\ >C N, мы можем сделать замену 1 + е *=» ехр(с), получив
Рш « (е"7"2/^2)"^ (е7"/")"™ (е-т'"У « P0exp(-m2/N), (3.10)
где Ро — сомножитель, потерянный из-за использования упрощенной
формулы Стирлинга. Известно, что сумма вероятностей должна
быть равна единице, таким образом для \т\ <§; N мы получаем
1 = Στη Рт * /f^o -Ро ехр(—m2/iV) dm = PqVttN. Следовательно,
«•-ι/Ι* «■»(-£)· с·1»
Это замечательный результат: он говорит о том, что флуктуации числа
частиц подчиняются распределению Гаусса, или нормальному распределению18
(ΐ/\/2πσ) βχρ(—χ2/2σ2) со стандартным отклонением σ = y/N/2. Если число
частиц равно числу Авогадро N ~ 1024, тогда относительная флуктуация
составляет σ/Ν = 1/V2N ~ Ю-12 = 0.0000000001%. В конфигурационном
пространстве размерности Μ3Ν практически ровно половина всех координат
находятся в правой половине их возможного диапазона. В разделе 3.2.2 мы
рассмотрим другое необычное свойство пространств высокой размерности.
Вообще говоря, относительные флуктуации большинства величин в
равновесной статистической механике, представляющих интерес, имеют
зависимость от числа частиц 1/y/N. Для многих величин, характеризующих
макроскопические системы, отклонения от средней величины очень малы19
18Мы снова получили центральную предельную теорему. Мы вывели ее в разделе 2.4.2,
используя случайные блуждания и континуальное приближение вместо формулы
Стирлинга; распределение Гаусса представляло собой функцию Грина для числа выпадений
орла при подбрасывании монеты 2N раз. Мы еще раз выведем ее в упражнении 12.11 с
использованием методов ренормализационной группы.
19Мы покажем это в общем случае в разделе 10.7, см. уравнение (10.50).
3.2. Микроканонический идеальный газ
87
3.2.2 Импульсное пространство
Изучение микроканонического распределения импульсов намного
увлекательнее20 и нагляднее, чем изучение конфигурационного пространства
идеального газа, описанного в предыдущим разделе. Здесь мы будем изучать
геометрию сфер высоких размерностей.
Кинетическая энергия взаимодействующих частиц имеет вид
α=1 α=1
где в последнем равенстве предполагается, что все атомы имеют одинаковую
массу га. Таким образом условие, что система частиц одинаковой массы имеет
энергию U7, эквивалентно тому, что система находится на сфере радиуса R =
\/2тЕ в импульсном пространстве размерности 3Ν.
Математики21 называют это 3Ν—1-мерной сферой (гиперсферой), §^-1·
Если энергия системы находится в малом диапазоне между Ε и Ε + δΕ, то
каким будет ее объем в импульсном пространстве? Объем μίδ^ Ι ί — 1-
мерной сферы (в ^-мерном пространстве) радиуса R составляет22
μ (s^1) = тг€/2Я7(^/2)! (3.13)
20Численные коэффициенты не будут играть здесь существенную роль; их проще
сохранить, чем объяснить, почему мы не должны этого делать. Обратите внимание на
сомножители, зависящие от R. В разделе 6.2 мы обнаружим, что те же самые вычисления намного
проще провести с использованием канонического распределения.
21 Математики любят давать названия поверхностям, или многообразиям, по числу
измерений или локальных координат многообразия, а не по числу измерений пространства,
в котором находится многообразие. Ведь в любом количестве измерений (вплоть до двух)
можно нарисовать сферу. Таким образом, баскетбольный мяч представляет собой
двумерную сферу S2, круг — одномерную сферу S1, а нуль-мерная сфера §° состоит из двух точек
±1.
22Дает ли это выражение правильную площадь двумерной сферы? Факториал
определяется для дробных чисел (см. упражнение 1.5) следующим образом: (3/2)! = Зу/п/4.
Подставляя это выражение в уравнение (3.13), получаем правильный ответ. Общая формула
— хорошее упражнение на многократное интегрирование с применением метода
математической индукции. Совет: проще вычислять одновременно интегралы в двух измерениях.
88
Гл.3. Температура и равновесие
Объем тонкого слоя23 между Ε и Ε + δΕ задается формулой
μ (§31ϊζ1 ^ - μ (б^±)
Объем СЛОЯ _ V V2m(E+6E)J \ V2mEJ
IE " δΕ
= KV^EJ = ^ (^/2(2mB)W/(3JV/2)!)
= ^^(SNm^mE)3^2-1/ (37V/2)!
= (3Nm)n3N/2RSN~2/ (ЗЛГ/2)! (3.14)
В нашем микроканоническом ансамбле, в котором все состояния с энергией
Ε имеют одинаковый вес, плотность вероятности некоторого определенного
набора моментов частиц Ρ обратно пропорциональна объему этой оболочки.
Давайте проведем некоторые наглядные расчеты с использованием
нашего микроканонического ансамбля. Рассчитаем плотность вероятности ρ(ρι)
того, что х-компонента импульса первого атома равна pi.24 Плотность
вероятности того, что этот момент составляет pi, а энергия лежит в диапазоне
(Ε, Ε + δ Ε), пропорциональна площади кольцеобразной области на рис. 3.2.
Радиус этой сферы составляет R = \/2тЕ, таким образом, по теореме
Пифагора, радиус круга равен R! = уЪпЕ — ρϊ2. Объем кольцевой области в
импульсном пространстве представляет собой разность площадей двух
«кругов» (3N—2-мерных сфер) с импульсом р\ и энергиями Ε и Ε+δΕ. Мы можем
использовать уравнение (3.13) с ί = 3Ν — 1:
площадь кольца = Лзлг-2 λ /dE
δΕ μ\ у/2тЕ-р^) /
= Α (π(^-υ/2(2τηΕ -ΡιψΝ~^2/ [(3Ν - l)/2]l)
= ^3N-1^2(3N-l)m(2mE-p21)^N-^2/ [(3N - 1)/2]!
= (3ΛΓ - l)m^N-^l2R!3N~3/ [(3ΛΓ - 1)/2]! (3.15)
23Почему это не то же самое, что и площадь поверхности? Поскольку толщина слоя
— это бесконечно малое приращение энергии δΕ, не равное бесконечно малой толщине
SR « SE(dR/dE) = 6E(R/m). Это различие не имеет значения для идеального газа (обе
величины имеют однородную плотность вероятности по всем направлениям Р), но оно
важно для взаимодействующих систем (в которых меняется толщина энергетического слоя, см.
рис. 3.1).
24По негласному соглашению физиков ρ используется для обозначения плотности
вероятности всевозможных сортов. Ранее мы использовали ее для обозначения плотности
вероятности в ЗТУ-мерном конфигурационном пространстве; здесь мы используем ее для
обозначения плотности вероятности одной переменной. Аргумент функции ρ говорит нам
о том, какая именно плотность вероятности имеется в виду.
3.2. Микроканонический идеальный газ
89
Рис. 3.2. Энергетическая поверхность
Энергетическая поверхность в импульсном пространстве представляет собой 3N—1-мерную
сферу радиуса R = у/2тпЕ. Учитывая, что х-компонента импульса атома #1 — pi, мы
должны рассматривать круг (точнее, 3N—2-мерную сферу) радиуса R' = \JlmE - pi2.
Условие, что энергия принадлежит слою (.Ε, Ε + δΕ), приводит к рассмотрению кольцевого
слоя, показанного на вложенном рисунке.
Плотность вероятности ρ(ρι) того, что кольцевая область имеет высоту
pi, равна ее площади, деленной на объем слоя в уравнении (3.14):
ρ(Ρι) = площадь кольца/объем оболочки
_ (ЗЛГ - ljm^3*-1)/2^3*-3/ [(37V - 1)/2]!
3Ντηπ3Ν/2Β?Ν-2/ (37V/2)!
ос (R2/R'3)(R'/R)3N
= (R2/R's)(l - Pl2/2mE)3N/2. (3.16)
Плотность вероятности ρ(ρι) будет равна нулю практически везде, если
только R'/R = y/l — pi2/2mE не стремится к единице, поскольку эта величина в
уравнении 3.16 возводится в огромную степень (3iV, порядка числа Авогад-
ро). Мы можем упростить R2/R'3 « \/R = Ι/у/ЪпЕ и 1 -p\2/2mE = 1 - ε «
ехр(—б) = ехр(— pi2/2mE), получив
'«"'"^-(ет)· <зл7)
Плотность вероятности ρ(ρι) представляет собой распределение Гаусса
со стандартным отклонением y/2mE/3N; коэффициент пропорциональности
можно задать таким образом, чтобы нормировать распределение Гаусса,
получив
р(Р1) = . * ехр (^-Ш) ■ (3-18)
Данная формула представляет собой распределение вероятности для любой
компоненты импульса любой частицы, независимо от ее номера. Используя
90
Гл. 3. Температура и равновесие
микроканонический ансамбль, мы получили распределение импульсов,
зависящее от Е, N и га, не рассматривая при этом траектории отдельных частиц.
Именно поэтому аппарат статистической механики является таким мощным.
Формула (3.18) говорит нам о том, что основная часть площади
поверхности сферы большой размерности расположена очень близко к экватору!
Представим себе р\ как широту сферы. Диапазон широт, содержащий
большую часть площади, имеет вид δρ « ±y/2mE/3N, а полный диапазон широт
составляет ±у/2тЕ. Поделив его на δρ, получаем корень из числа Авогад-
ро. Это верно вне зависимости от выбора экватора, даже для пересечения
нескольких экваторов. Геометрия большого числа измерений очень необычна.
В рамках статистической механики это представляется намного менее
странным. Типичная конфигурация газов такова, что кинетическая
энергия примерно одинаково распределена между всеми компонентами
импульса. Конфигурации, в которых одному атому принадлежит вся кинетическая
энергия (расположенные далеко от экватора), исчезающе редки.
Формула (3.18) предвосхищает четыре ключевых результата, которые мы
получим в следующих нескольких главах, детально изучая равновесную
статистическую механику.
(1) Температура. В наших вычислениях мы рассматривали
распределение энергии, имеющейся в системе, между одной из компонент
импульса и оставшимися степенями свободы идеального газа. В разделе 3.3
мы будем изучать распределение энергии между двумя подсистемами и
обнаружим, что баланс энергии характеризуется температурой.
Температура Τ нашего идеального газа будет определяться формулой (3.52)
квТ = 2Ε/3Ν.25
Из уравнения (3.18) следует важная формула
M-jdm'vi-i&rY (319)
(2) Распределение Больцмана. Вероятность того, что координата χ
импульса первой частицы имеет кинетическую энергию К = р\/2т,
пропорциональна ехр(—К/квТ) (уравнение 3.19). Это наш первый пример
распределения Больцмана. В разделе 6.1 мы увидим, что вероятность
25 Мы увидим, что температура естественным образом измеряется в энергетических
единицах. Исторически мы измеряли температуру в градусах, а энергию — в других различных
единицах (Джоули, эрги, калории, электронвольты, футофунты и т.п.); постоянная
Больцмана кв = 1.3807·Ю-23 Дж/К является стандартным коэффициентом пропорциональности
между температурой и энергетическими единицами.
3.2. Микроканонический идеальный газ
91
того, что малая подсистема находится в некотором определенном
состоянии26 с энергией £", в общем случае будет также пропорциональна
ехр(-Е/квТ).
(3) Теорема о равнораспределении. Средняя кинетическая энергия
(Pi/2m), как следует из уравнения (3.19), составляет квТ/2.
Это представляет собой пример теоремы о равнораспределении
(раздел 6.2): каждая гармоническая степень свободы равновесной
классической системы имеет среднюю энергию квТ/2.
(4) Общее классическое27 распределение импульсов.
Наш вывод будет проводиться в рамках одноатомного идеального
газа. Но мы могли бы провести аналогичные вычисления для системы
нескольких газов с различными массами. В этом случае наша сфера
импульсов превратилась бы в эллипсоид, но распределение импульсов
задавалось бы той же самой формулой. Что еще более удивительно, мы
увидим (используя канонический ансамбль в разделе 6.2), что наличие
взаимодействий также не имеет значения до тех пор, пока система
остается классической:28 плотности вероятности для моментов по-прежнему
определяются той же самой формулой, не зависящей от потенциальных
энергий. Распределение импульсов по формуле (3.19) верно
практически для всех классических равновесных систем. Наличие
взаимодействий влияет на конфигурацию частиц, но не на их скорости.
26Это отличается от вероятности того, что энергия подсистемы равна Е, которая
представляет собой произведение больцмановской вероятности и числа состояний с этой
энергией.
27 Молекулярные газы обладают внутренними колебательными модами, которые не очень
хорошо описываются классической механикой. При низких температурах они часто
заморожены. Учет вращательных и трансляционных степеней свободы, но игнорирование
колебаний является хорошим приближением для воздуха при комнатной температуре (см.
прим. 13 на с. 83).
28Релятивистские эффекты, магнитные поля и квантовые взаимодействия приводят к
изменению распределения скоростей. Уравнение (3.19) будет достаточно точным для всех
газов при разумных температурах, во всех жидкостях, за исключением гелия, и многих
твердых тел, которые не достаточно холодные. Обратите внимание, что практически все
вычисления с использованием метода молекулярной динамики классические:
распределение импульсов в них определяется уравнением (3.19).
92
Гл.З. Температура и равновесие
3.3 Что такое температура?
Наш повседневный опыт говорит о том, что поток энергии направлен от
горячего к соседнему холодному телу до тех пор, пока они не достигнут одной
и той же температуры.
Статистическая механика утверждает, что распределение тепла между
двумя телами определяется микроканоническим распределением, что все
возможные состояния с фиксированной полной энергией для двух тел
равновероятны. Согласованы ли между собой эти два утверждения? Можем ли мы
определить температуру таким образом, чтобы она была одинаковой для двух
тел большого размера, находящихся в равновесии друг с другом?
Рассмотрим произвольную изолированную систему с полной энергией Е,
состоящую из двух частей 1 и 2. Каждая подсистема имеет фиксированный
объем и фиксированное число частиц. Они энергетически слабо связаны друг
с другом, то есть мы пренебрегаем зависимостью энергии Е\ первой
подсистемы от состояния S2 второй подсистемы и наоборот.29 Таким образом, наш
микроканонический ансамбль постулирует, что при равновесии
всевозможные состояния двух подсистем с полной энергией Ε имеют одинаковый вес.
Некоторое определенное состояние системы как целого задается парой
состояний (si,S2) с энергией Ε = Е\ Η- Ε2. Из этого непосредственно следует, что
состояние s\ первой подсистемы с энергией Е\ будет реализовано с
плотного
стью вероятности0"
ρ(*ι)(χΩ2(#-#ι), (3.20)
где Ωι(£Ί) δЕ\ и Q2(i?2) ^2 — объемы энергетических слоев для двух
подсистем в фазовом пространстве. Объем энергетической поверхности всей
системы с энергией Ε получится при сложении произведений объемов подсистем
для пар состояний, сумма энергий которых составляет Е:
ЩЕ) = ΙάΕχ Ωι(£?ι)Ω2(£? - #ι), (3.21)
29Макроскопическая система, связанная с внешним миром посредством стенок, слабо
с ним взаимодействует, поскольку энергия взаимодействия принимает большие значения
только вблизи поверхности, в пренебрежимо малой части полного объема. Что еще более
удивительно, импульсы и координаты в немагнитных и неквантовых системах
представляют собой две несвязанные друг с другом подсистемы: в гамильтониане отсутствуют члены,
зависящие одновременно как от импульсов, так и от координат (хотя они, безусловно,
связаны в процессе динамической эволюции).
30Таким образом, если мы сравним вероятности двух состояний sf и s\ подсистемы 1 с
энергиями ΕΪ и Е\, и если Ω2(£ - Εγ) в 50 раз больше, чем Ω2(£ - Е\), тогда p(sf) =
50p(si), поскольку в этом случае существует в 50 раз больше партнеров, с которыми можно
скооперироваться, чтобы получить свою долю вероятности.
3.3. Что такое температура?
93
что является интуитивно понятным.31 Обратите внимание, что
подынтегральное выражение в уравнении (3.21), нормированное на полный
интеграл, представляет собой плотность вероятности32 того, что подсистема
имеет энергию Е\:
р(Ег) = Ω1(Ε1)Ω2{Ε - Ег)/П(Е). (3.23)
Если все подсистемы содержат большое количество частиц, то оказывается,
что33 р(Е\) — функция с очень острым пиком вблизи максимума при Е*.
Таким образом, при равновесии энергия в подсистеме 1 определяется (за
исключением малых флуктуации) максимальным значением подынтегральной
функции Ωι(^ι)Ω2(-Ε' —-ΕΊ). Максимум находится путем приравнивания нулю
производной (άΩχ/άΕι) Ω2 — Ωι (сШг/сЩг), то есть:
1 άΩι
Ωιά#ι
1 άΩ2
Е+ Ω2 di?2
(3.24)
31 Это также легко получить при помощи ^-функции Дирака (упражнение 3.6). Мы также
можем вывести это более сложным способом с использованием энергетических слоев:
П(Е) = ^- [ dPi dQi dP2 dQ2 =
otj Je<Hi+h2<e+se
= /dPidQif-ί / dP2dQ2>) =
J \0ί^ Je-Hi<H2<E+6E-'Hi /
= /dPi dQi Q2(E - «i(Pi,Qi)) =
= Σ f dPidQifi2(^-Wi(Pi,Qi))= (3.22)
J \0b Je1<Hi<E1+6E /
= iaEiQi(Ei)n2(E-Ei)y
где мы заменили суммирование интегрированием Ση f(n^E) « (1/δΕ) f dEif(Ei).
32Обратите внимание: снова мы допускаем небольшую небрежность: мы используем p(si)
в уравнении (3.20) для плотности вероятности того, что подсистема находится в некотором
определенном состоянии βι, и мы используем р(Е\) в уравнении (3.23) для обозначения
плотности вероятности того, что подсистема находится в некотором из многих частных
состояний с энергией Е\.
33 Аналогично тому, как число частиц идеального газа в правой половине сосуда
флуктуирует лишь незначительно, так же энергия Ει первой подсистемы очень мало флуктуирует
вблизи значения ΕΙ, при котором вероятность имеет максимум. Мы это детально покажем
в упражнении 3.8, и более абстрактно в примечании 37 ниже.
94
Гл. 3. Температура и равновесие
Более удобно работать не с величиной Ω, а с ее логарифмом. Дадим
определение равновесной энтропии
Sequil(#) = kB \og(Sl(E)) (3.25)
для каждой из наших систем.34 Аналогично полной энергии, объему и числу
частиц, энтропия большой системы, как правило, пропорциональна ее
размеру.35 Подобные величины, линейно зависящие от размера системы,
называются экстенсивными. (Величины, такие как температура, давление и
химический потенциал, определенный ниже, которые остаются постоянными при
увеличении объема системы, называются интенсивными.)
Таким образом, dS/dE = кв(1/П) (сЮ/сШ), и уравнение (3.24) сводится к
простому утверждению
d (S1(E1) + S2(E-E1)) = dSl
άΕχ ν iV L' ^ χ" άΕχ
aS2
Ε·
dE2
О, (3.26)
что полная энтропия Si + S2 увеличивается.36 Мы хотим дать определение
температуры таким образом, чтобы она становилась одинаковой для двух
подсистем, достигающих состояния равновесия. Мы видим, что
dE\ αϋ/2
в термическом равновесии. Поскольку dS/dE уменьшается при увеличении
энергии, в статистической механике температура определяется следующим
34 Снова постоянная Больцмана кв — коэффициент преобразования единиц, выраженный
в единицах [энергия]/[температура]. Энтропия безразмерна, за исключением того случая,
когда температура и энергия измеряются в различных шкалах (см. примечание 25 на
с. 90).
35Это можно показать, используя тот факт, что большинство крупных систем могут
быть разложены на много маленьких слабо взаимодействующих подсистем, для которых
энтропии складываются. (Для систем с дальнодействующими взаимодействиями, такими
как гравитация, разделение системы на большое количество слабовзаимодействующих
подсистем невозможно, в этом случае энтропия и энергия будут неэкстенсивными
величинами.) Аддитивность энтропии для невзаимодействующих систем выполняется в
каноническом ансамбле (раздел 6.2), а также для макроскопических систем в
микроканоническом ансамбле. Из уравнения (3.28) следует П(Е) и Ωι(£7ι)Ω2(£3) Je~iEl~Ei)2/2trE άΕι
= Ω\(ΕΙ)Ω2(Ε£)/(\/2πσΕ)ι таким образом, полная энтропия системы составляет
Stot(E) = кв \ogQ(E) «&(Я?) + S2(E - Ει) + кв log(\/2W).
Она экстенсивна, за исключением пренебрежимо малой поправки к в \og(\/2naE)
(возникающей за счет увеличения флуктуации энергии при объединении двух подсистем).
36Энтропия — это именно максимум, а не просто экстремум, поскольку в уравнении (3.26)
под знаком логарифма стоит вероятность (уравнение 3.23), имеющая максимум в точке Е{.
3.3. Что такое температура?
95
образом: 1/Т = dS/dE. Мы проводили наши расчеты для постоянного объема
и числа частиц. Для произвольной системы37
I- as
Т~ дЕ
Величина, обратная температуре, — это цена покупки энергии у внешнего
мира. Чем ниже температура, тем сильней уменьшается энергия. Энтропия
— это уплаченная валюта. За каждую единицу купленной энергии δΕ мы
платим δΕ/Τ = SE(dS/dE) = δΞ — за счет уменьшения энтропии
внешнего мира. Обратная температура — это стоимость покупки единицы энергии
в единицах энтропии.38 «Внешний мир» часто называют термостатом; это
источник и сток теплоты, он фиксирует температуру. Все термостаты
эквивалентны между собой, различаются только величиной фиксируемой
температуры.
Точнее говоря, поведение системы в состоянии равновесия, слабо
связанной с внешнем миром, не зависит от того, как именно устроен внешний мир
— она зависит только от температуры мира. Это глубокая правда.
37Действительно ли плотность вероятности р(Е\) имеет острый пик, как мы
предположили? Можно разложить по формуле Тейлора числитель в уравнении (3.23) в окрестности
максимума Ει = El и использовать тот факт, что температуры выравниваются при El,
таким образом, можно не учитывать члены, линейные по Ει — Е{:
Ωι(Ει)Ω2(Ε - Ει) =
= exp (Si(Ei)/kB + S2(E - Ex)/kB) =
» exp [(Λ(Εί) + \{Ει - Е{)2Щ + S2(E - El) + \{El - Е1)2Щ} /*в] =
= ni(£?i)ib(£S)exp ((Si - ЯГ)2 (Щ + Щ) /(2*b)) - (3.28)
Итак, флуктуации энергии гауссовы: р{Е\) = (Ι/χ/^πσ^ε-^1-^ /2<τε, со стандартным
отклонением σε, задаваемым формулой 1/σ% = —(l/kB)(d2Si/dEi+d2S2/dE2).
(Обратите внимание на знак минус; d2S/dE2 = д(1/Т)/дЕ, как правило, имеет знак минус,
поскольку обратная температура уменьшается при увеличении энергии. Это также
свидетельствует о том, что S(E) выпукла вниз.) Поскольку как S, так и Ε являются
экстенсивными величинами, они пропорциональны числу частиц iV, и σ% ос \/(d2S/dE2) ос N (т.к.
в числителе одна 5,ав знаменателе — две Е). Таким образом, флуктуации энергии на
частицу σε/Ν очень малы; они имеют зависимость l/y/Ν. Данное поведение типично для
флуктуации в статистической механике.
38 Если говорить более корректно, то плата производится в отрицательной энтропии: при
покупке δΕ из окружающего термостата мы получаем энтропию δΕ/Τ .
(3.29)
96
Гл.З. Температура и равновесие
3.4 Давление и химический потенциал
Энтропия S(E, V, Ν) является нашим первым примером
термодинамического потенциала.39 В термодинамике все макроскопические свойства могут
быть рассчитаны при взятии производных от термодинамических
потенциалов по другим аргументам. Часто полезно представлять
термодинамические потенциалы в виде поверхностей. На рис. 3.4 изображена поверхность в
пространстве S,E,V (при постоянном числе частиц N). Энергия E(S,V,N)
представляет собой другой термодинамический потенциал, полностью
эквивалентный S(E, V, TV); это та же самая поверхность, но направленная «вверх».
В разделе 3.3 мы определили температуру через производную
(dS/dE)\yy]sf. Как насчет других двух первых производных — (dS/'dV)\E,N
и (dS/dN^Ey? To есть, как меняется энтропия при обмене объемом
или частицами между двумя подсистемами? Изменение энтропии при
небольшом сдвиге АЕ, AV, и AN из подсистемы 2 в подсистему 1 (рис. 3.3)
имеет вид
AS =
dSi
dEi
dS2
V,N
дЕ2
АЕ +
dSx
V,N;
dVi
dS2
Ε,Ν
dV2
AV
Ε,Ν j
+
dSi
dNx
dS2
ЕУ
dN2
AN.
(3.30)
Ey,
Первый член, так же как и ранее, составляет (1/ΤΊ — \/Т2)АЕ\ обмен
энергией выравнивает температуры и увеличивает энтропию. Аналогично обмену
энергией, если две подсистемы могут обмениваться объемом и числом частиц,
то энтропия также будет увеличиваться при изменении этих величин, если
не учитывать небольшие флуктуации. Приравнивая производные по объему,
мы получаем статистико-механическое определение давления Р:
Ρ
Τ
as
dV
(3.31)
Ε,Ν
а приравнивание производных по числу частиц дает определение химического
потенциала μ:
.40
Т
as
dN
(3.32)
ЕУ
39Большинство других термодинамических потенциалов, которые мы будем
использовать в дальнейшем, чаще называют свободными энергиями.
40 Эти выражения часто объединяются в формуле dS = (1/Т) dE + (Ρ/Τ) dV — (μ/Τ) dN
(см. раздел 6.4).
3.4- Давление и химический потенциал
97
Рис. 3.3. Две подсистемы
Две подсистемы, изолированные от внешнего мира, могут обмениваться энергией
(открытая дверь с изоляционной прослойкой), объемом (поршень) или частицами (небольшие
дырочки).
Эти определения несколько непривычные. Обычно давление и
химический потенциал определяются через изменение энергии Е, а не энтропии
S. Можно связать наши определения с более стандартными, используя
одно важное математическое тождество, которое мы выведем в упражнении
3.10: если / — функция переменных χ и у, то (рис. 3.4):41
дх
дх
fdf
= -1.
(3.33)
Запомните, что если мы зафиксируем все переменные, кроме одной, то
частная производная аналогична обычной, а именно
df
дх
I df
Используя это тождество для S(E, V) и фиксируя N, мы получаем
-1
dS_
dV
Ε,Ν
dV_
дЕ
или
S,N
дЕ
W
д£
dS
V,N
-P.
(3.34)
(3.35)
(3.36)
S,N
Обратите внимание, что именно этот результат, взятый с обратным знаком, вы бы
получили, если бы сократили df, дх, и ду в «числителе» и «знаменателе», производные
похожи по своим свойствам на дроби, но не совсем.
98
Гл. 3. Температура и равновесие
Таким образом, давление — это приращение энергии, деленное на приращение
объема при постоянной энтропии, взятое с обратным знаком. Аналогично,
-i=ds
ΘΝ
dN
ЕудЕ
дЕ
s,vds
μ
N,V T
дЕ
~dN
Г,
(3.37)
syj
таким образом
дЕ
sy
μ;
(3.38)
химический потенциал — увеличение энергии при добавлении частицы при
постоянной энтропии.
Рис. 3.4. Поверхность состояния
Энтропия S{E, V, Ν) является функцией энергии Ε и объема V (при фиксированном числе
частиц Ν). Если посмотреть с другой стороны, эта поверхность также определяет энергию
E(SjV,N). Три кривые представляют собой линии при постоянных 5, Ε и V\ тот факт,
что они должны замыкаться, дает выражение
dS_
дЕ
VyN
дУ
S.7V
ду_
dS
= -1
(см. упражнение 3.10).
Химический потенциал неизвестен большинству новичков в
статистической механике. Мы можем почувствовать давление и температуру, когда
наши тела обмениваются объемом с воздушными шариками и теплом с
кофейными чашками. Большинство из нас не имеет аналогичного чувственного
3.4· Давление и химический потенциал
99
опыта с обменом частицами.42 Вы можете рассматривать химический
потенциал как некую «силу», связанную с изменением числа частиц таким же
образом, как давление — это сила, связанная с изменением объема, а
температура — сила, связанная с изменением энергии; различие в μ, Ρ, и Τ приводят
к возникновению потока частиц, объема или энергии из одной подсистемы
в другую. Химические потенциалы играют решающую роль в химических
реакциях; то, будет ли протекать реакция, в частности, зависит от
относительной стоимости продуктов реакции и реагентов, измеряемой разницей в их
химических потенциалах (раздел 6.6). Они являются причиной
осмотического давления, которое удерживает мембраны клетки натянутыми. Химические
потенциалы также играют ключевую роль в расчетах невзаимодействующих
квантовых систем, для которых число частиц в каждом квантовом
состоянии может варьироваться (гл. 7). По мере изучения химических потенциалов
ваши интуитивные представления о них улучшатся.
3.4.1 Материал повышенной сложности: давление в механике
и статистической физике
Наше представление о давлении мы получили из механики: энергия
подсистемы увеличивается при уменьшении объема согласно АЕ = — PAV. В
нашем статистико-механическом определении давления (Р = —(dE/dV)\s,N,
уравнение 3.36) утверждается, что изменение энергии производится при
фиксированной энтропии — что не так общеизвестно.
Не всякое механическое изменение объема пригодно для измерения
давления. При измерении давления не должен происходить обмен теплом.
(Изменение объема при добавлении тепла для поддержания фиксированной
температуры, например, приводит к совершенно другим результатам.) Сжатие
должно происходить медленно. Если объем уменьшается настолько быстро,
что равновесие подсистемы нарушается (например, если поршень движется
со скоростью, близкой к скорости звука), то соответствующее приращение
энергии будет также включать в себя энергию создания звуковых и ударных
волн, что неприемлемо для измерения давления. Мы называем
адиабатическим процесс, происходящий без обмена теплом и достаточно медленный,
для того чтобы система оставалась равновесной.
В этом параграфе мы, используя микроканонический ансамбль,
покажем, что механическое определение давления (степень изменения
средней внутренней энергии при медленном изменении объема,
42 Можно привести наглядный пример для химического потенциала одного из газов.
Наши легкие меняют углекислый газ на кислород. Высокий химический потенциал CCfe в
крови приводит к тому, что мы активно дышим.
100
Гл. 3. Температура и равновесие
Рт = —AE/AV) эквивалентно определению давления в статистической
механике (Pstat = T(dS/dV)\EjN = -(dE/dV)\s,N, уравнения 3.31 и 3.36).
Таким образом, адиабатическое измерение давления происходит при
постоянной энтропии.
Доказательство это достаточно технично и абстрактно, для него
требуются методы, которые не используются в оставшейся части книги. Почему этот
вопрос важен, за исключением уточнения нашего определения давления? В
гл. 5, мы увидим, что энтропия — фундаментальная мера необратимости.
Поскольку система остается в равновесии при адиабатическом изменении объе-
ма, ее энтропия не должна меняться.
Мы возвращаемся здесь к истокам макроскопического закона об
отсутствии вечных двигателей. В результате наших рассуждений мы получим
микроскопические законы, демонстрирующие, что равновесные системы
(изменяющиеся адиабатически, медленно, термически изолированные), имеют
постоянную энтропию.44
Рассмотрим вывод формулы для механической силы на единицу площади
Рт в рамках статистической механики. Рассмотрим некоторую произвольную
изолированную от внешнего мира жидкость или газ, объем которой медленно
меняется от V до V 4- AV.
Для нахождения механического давления нужно рассчитать, насколько
изменится энергия при изменении объема. Исходная система при t = 0
представляет собой микроканонический ансамбль объема V, равномерно
заполняющий фазовое пространство в диапазоне энергий Ε <Н < Ε + δ Ε с
плотностью 1/Ω(Ε, V). Частью этого расширяющегося ансамбля является
траектория P(£),Q(£), эволюционирующая во времени при изменении гамильтониана
Ή(Ρ, Q, V(t)). Скорость изменения энергии этой выделенной траектории
имеет вид
di _ д¥Г+ dQ4+ dV'dt· (όό9)
43Имеется в виду, что энтропия всей системы как целого, включая механический прибор,
меняющий объем, не должна уменьшаться. Мы используем тот факт, что прибор может
быть сделан из небольшого количества движущихся частей, взаимодействующих с нашей
системой, а энтропией системы с небольшим числом степеней свободы можно пренебречь.
(Обратите внимание, что энтропия всегда в Nks раз больше логарифма. Логарифм —
медленно меняющаяся функция, таким образом энтропия представляет собой всегда
достаточно малую константу, умноженную на N и на кв. Если система состоит только из
небольшого числа движущихся частей iV, то ее энтропия всего в несколько раз больше к в
— следовательно, ей можно пренебречь.)
44 В наших рассуждениях мы не будем использовать тот факт, что параметр V
представляет собой объем. Любое адиабатическое изменение в системе происходит при постоянной
энтропии.
3.4· Давление и химический потенциал
101
Частные производные гамильтониана частиц с кинетической энергией
Р2/т/2 и потенциальной энергией U(Q) имеют вид дН/д¥ = Ψ/m = Q и
дН/dQ = dll/dQ = —Ρ, таким образом в правой стороне уравнения (3.39)
первые два члена сокращаются.45 Таким образом, изменение энергии этой
выделенной траектории имеет вид:
dt dVK 'v; at K }
Итак, производная от энергии вдоль траектории равна математическому
ожиданию частной производной dH/dt в текущей точке траектории: нам не
нужно следить за движением отдельных частиц.
Нам по-прежнему необходимо усреднить это изменение энергии по
равновесному ансамблю начальных условий. В общем случая это невозможно, пока
мы не сделаем второго предположения, связанного с адиабатическим
измерением давления: пусть потенциальная энергия меняется настолько медленно,
что система находится в равновесии при данном объеме V(t) и энергии E(t).
Это позволит нам рассчитать среднее по ансамблю изменение энергии как
среднее в состоянии равновесия при текущем фиксированном объеме:
т. = т\ *к. (з.41)
di \0V/E(t),v(t) di
Поскольку это изменение энергии равно — Рт (dV/dt), мы получаем
(уравнение 3.5):
-р-={Щ=mJdVdQS{E-n''-<i-v))^- (342)
Перейдем теперь к расчету производной, представляющей интерес для
статистико-механического определения температуры:
as
dV
д и ι /п\ кв 5Ω
(3.43)
Ε,Ν
45 Это уравнения Гамильтона. Взаимное сокращение имеет место для гамильтоновых
систем в общем случае, даже для систем, не представимых в ньютоновском виде.
102
Гл.З. Температура и равновесие
Используя уравнение (3.3) для записи Ω через θ-функцию, можно изменить
порядок дифференцирования:
дП
dV
Ε,Ν
dV
дЕ
—I
E,N°E\VN
fd¥d®e(E-n(F,Q,V))
;nJ
д
dPdQ — θ(Ε-Μ(Ψ,®,ν))
dV
V,N
I
S(E-H(¥,®,V))-^.
(3.44)
Но интеграл по фазовому пространству в последнем уравнении
представляет собой в точности тот же самый интеграл, который появляется в нашей
формуле (3.42) для давления: это Ω(Ε)(—Рт). Таким образом
dV
Ε,Ν
дЕ
дЕ
(П(Е)Рт)
V,N
Рт+П
дРт
V,N
дЕ
(3.45)
V,N
и мы получаем
dS_
dV
Ε,Ν
-fcBlog(0) = - —
рт + п
дР„
dkBiog(n)
дЕ
Рт + кв
V,N
дРт
дЕ
V,Nj
V,N
дЕ
dS_
дЕ
Рт + кв
дРп
V,N
дЕ
V,N
V,N
Рт^и дРт
-¥ + кв-дЁ
(3.46)
V,N
Ρ и Τ — интенсивные величины, но Ε — экстенсивная величина (линейно
возрастающая с размером системы). Следовательно, Р/Т порядка единицы
для большой системы, а кв(дР/дЕ) — порядка Ι/iV, где N — число частиц.
(Например, мы увидим, что для идеального газа PV = 2/ЗЕ — ΝΗβΤ, таким
образом кв(дР/дЕ) = 2kB/ZV = 2P/3NT = 2P/3NT < Р/Т для больших
N.) Следовательно, вторым членом для систем большого числа частиц можно
пренебречь, что дает нам требуемое соотношение:
05
dV
Ε,Ν
1 m
Ύ'
(3.47)
Производная энтропии S(E, V, Ν) по V при постоянных Ε и N в самом деле
есть механическое давление, деленное на температуру.
3.5. Энтропия, идеальный газ и пара уточнений для фазового пространства 103
3.5 Энтропия, идеальный газ и пара уточнений для
фазового пространства
Давайте вычислим температуру и давление идеального газа, используя
наш микроканонический ансамбль. Затем мы введем две небольшие поправки
к объему фазового пространства (одну квантовомеханическую и одну для
одинаковых частиц), которые не влияют на температуру или давление, но
важны для энтропии и химического потенциала.
Мы вывели объем Ω(Ε) энергетического слоя в фазовом пространстве
в разделе 3.2; он представляет собой произведение46 объема в импульсном
пространстве (уравнение 3.14) и объема в конфигурационном пространстве
V^. До введения поправок
Псшае(Е) = V" (^) n^(2mE)^/(3N/2)\
« νΝπ3Ν'2(2τηΕ)3Ν/2/ (37V/2)!. (3.48)
Обратите внимание, что во второй строчке уравнения (3.48) мы выкинули
член 3Ν/2Ε, он делит объем фазового пространства на незначительную
величину (две трети энергии на одну частицу).47 Энтропия и ее производные
имеют вид (до введения поправок)
Scrude(S) = кв log (уыж™1\2тЕ)™'2/ (ЗЛГ/2)|)
NkB log(F) + ^^ log(27rm£7) - кв log[(3iV/2)!], (3.49)
I- ЕЁ
Т~ дЕ
L-ЁЁ
Τ ~ dV
_ WhB
V,N 2E
= NkB
Ε,Ν V '
(3.50)
(3.51)
а температура и давление задаются следующим образом:
46Разделение на сомножители происходит вследствие равенства нулю потенциальной
энергии.
47Умножение Ω(Ε) на число, не зависящее от числа частиц, эквивалентно прибавлению
к энтропии постоянной величины. Энтропия типичной системы настолько велика (порядка
числа Авогадро, умноженного на кв)> что добавление константы, не зависящей от числа
частиц, несущественно. Обратите внимание, что это означает, что объем Ω(Ε) настолько
велик, что умножение его на константу не меняет его значение существенным образом
(упражнение 3.2).
104
Гл. 3. Температура и равновесие
квТ=—, (3.52)
PV = NkBT. (3.53)
Первая строчка представляет собой выражение для температуры,
обещанное при формулировке уравнения (3.19). На каждую компоненту скорости
частиц в идеальном газе приходится средняя энергия, равная 1/2квТ.
Вторая формула — это уравнение состояния*8 идеального газа. Уравнение
состояния — это соотношение между макроскопическими величинами
равновесной системы, верное в пределе большого числа частиц. Сила на единицу
площади, с которой идеальный газ воздействует на стенку, флуктуирует с
течением времени вокруг давления Р(Т, V, N) = NksT/V^ заданного
уравнением состояния. Величина флуктуации исчезающе мала при увеличении
размера системы.
В общем случае, необходимо сделать две поправки к нашему
определению объема энергетического слоя в фазовом пространстве. Во-первых, объем
фазового пространства имеет размерность ([длина][импульс])37V; объем
энергетического слоя мультипликативно зависит от величин, выбранных для
длины, массы и времени. Изменение выбора этих единиц будет приводить к
добавлению константы, умноженной на 37V, к соответствующему выражению
для энтропии. Более физические свойства, такие как температура и
давление, зависят только от производных энтропии, таким образом, наличие
константы не будет на них влиять. В самом деле, нулевое значение энтропии не
определено в рамках классической механики.
Наводит на размышление тот факт, что [длина] [импульс] — это единицы
постоянной Планка /ι, и мы увидим в гл. 7, что квантовая механика
действительно задает нулевое значение энтропии. Мы увидим в упражнении 7.3, что
деление49 Ω (Ε) на h3N замечательным образом приравнивает нулю плотность
энтропии в равновесных квантовых системах при абсолютном нуле
температур.
Во-вторых, в квантовой физике есть тонкость при рассмотрении
идентичных частиц. Два электрона или два атома гелия (одинаковые изотопы) не
просто трудно различимы между собой, они целиком и полностью
идентичны (см. рис. 7.3). Мы увидим в разделе 7.3, что правильный с точки зрения
48Достаточно редко бывает, чтобы «уравнение состояния» было записано в виде
точного уравнения! Только в очень специфических случаях (таких как невзаимодействующие
системы, подобные идеальному газу) можно записать в явном виде термодинамические
потенциалы, уравнения состояния или другие величины.
49 Это эквивалентно использованию единиц, для которых h = 1.
3.5. Энтропия, идеальный газ и пара уточнений для фазового пространства 105
квантовой механики учет идентичности частиц предполагает усреднение по
всевозможным состояниям с использованием статистики Бозе и Ферми.
В классической физике возникает аналогичная проблема при
рассмотрении одинаковых частиц. Одинаковые классические частицы аналогичны
идентичным (неразличимым) частицам при высокой температуре, когда
статистики Бозе и Ферми становятся несущественными (гл. 7). Мы используем
термин «одинаковые» для описания частиц, которые в принципе не являются
идентичными, но которые имеют один и тот же гамильтониан и одинаковые
свойства при измерении (например, пылинки и коллоидные частицы). Для
системы двух одинаковых частиц точки фазового пространства (р^, Рв, Чл> Чв)
и (Ρβ·>Ρα,4β·>4α) не должны учитываться одновременно; объем фазового
пространства Ω(Ε) должен быть наполовину меньше того, который
получается, если учитывать различие между частицами. Для N одинаковых частиц
объем фазового пространства надо поделить на Ν!, полное число способов
пронумеровать частицы. и
В отличие от учета сомножителя h3N , деление объема фазового
пространства на N\ существенным образом меняет предсказания классической
статистической механики.
Мы увидим в разделе 5.2.1, что увеличение энтропии при объединении
сосудов с частицами различного типа будет огромным, в то время как
увеличение энтропии при объединении сосудов, наполненных одинаковыми
частицами, будет близко к нулю. Этот результат получается при делении Ω(Ε) на
Ν\ для каждого набора N одинаковых частиц. Мы называем
результирующий ансамбль статистикой Максвелла—Больцмана, для того чтобы отличить
ее от статистики различимых частиц и от квантово-механической статистики
Бозе и Ферми.
Учет этих двух поправок дает нам корректное выражение для объема
энергетического слоя классических одинаковых частиц вместо уравнения
(3.2):51
Ω(Ε) = ί
JE
E<H(F,Q)<E+SE N! h3N
dPdQ (3.54)
50 N\ иногда называют коэффициентом Гиббса
51 Обратите внимание, что мы также выкинули δ Ε из левой части. Так же как в уравнении
(3.48), в котором мы не учли сомножитель 3Ν/2Ε для идеального газа, чтобы упростить
формулы (то есть делая энтропию экстенсивной величиной), сомножитель δ Ε
пренебрежимо мал, когда число частиц большое (см. примечание 47).
106
Гл. 3. Температура и равновесие
Для идеального газа, Ω0Γ11<ιΘ в уравнении (3.48) превращается в
П(Е) = (VN/N\) (nSN/2(2mE)SN/2/ (ЗЛГ/2)!) (l/h)SN, (3.55)
S(E) = NkB log
h3 (2πτηΕ)3/2
kBlog[N\(3N/2)\]. (3.56)
Мы можем привести наше выражение для энтропии идеального газа к более
удобному виду, используя формулу Стирлинга log(iV!) ~ NlogN — TV, верную
для больших N:
S(E, V, Ν) = ^Nks + NkB log ^ (^У^] ■ (3-57)
Это стандартная формула для энтропии идеального газа. Мы можем
привести ее к более простому виду, выражая через плотность числа частиц ρ =
N/V:
S = NkB (I - ΜρΑ3Λ , (3.58)
где52
А = h/y/4nmE/3N (3.59)
называется термической волной де Бройля. Она играет большую роль для
квантовых систем при низкой температуре (гл. 7).
Упражнения
Интересно обсудить большие и малые числа, которые появляются в
статистической механике. Мы исследуем их в упражнениях Температура и энергия
и Большие и очень большие числа.
В упражнении Вторая космическая скорость изучается, почему Земля
не является газовым гигантом, подобно Юпитеру. В Расчете давления
выводится давление идеального газа непосредственно из рассмотрения ударов
молекул о поверхность. В Газе твердых сфер делается следующий шаг за
рамки приближения идеального газа.
52Де Бройль обнаружил, что материя может вести себя как волна; частица с импульсом
ρ имеет длину волны AqUantum = h/p. Среднеквадратичная компонента импульса в нашем
газе имеет вид р2 = 2m(E/3N), таким образом, наши частицы имеют квантовую длину
волны h/y/2mE/3N = \/2πAthermai· Эти значения достаточно близки, чтобы λ тоже присвоить
имя де Бройля.
Гл. 3. Упражнения
107
Следующие четыре упражнения посвящены статистическим свойствам и
флуктуациям слабо взаимодействующих систем. Объединение двух
макроскопических систем иллюстрирует практичность использования 5-функции при
выводе закона для произведения объемов энергетических слоев в фазовом
пространстве. Смесь газов и Флуктуации энергии в микроканоническом
ансамбле демонстрируют, что флуктуации энергии малы, вначале в
специфическом, затем — в общем случае. В распределении Гаусса и Пуассона исследуется
влияние внешнего мира на эти флуктуации.
В Цепном соотношении Эйлера и Соотношениях Максвелла
рассматриваются некоторые хитрые соотношения для частных производных в
термодинамике. Наконец, Решение дифференциальных уравнений: движение маятника
знакомит с численными методами, используемыми в молекулярной
динамике, которые могут быть использованы для моделирования реальных газов (а
также жидкостей и твердых тел), делая акцент на достоверности, точности
и устойчивости.
3.1 Температура и энергия, φ
В каких единицах [джоулях, миллиджоулях, миллиджоулях,
микроджоулях, наноджоулях, ..., зептоджоулях (10~21 джоулей), йоктоджоулях (10~24
джоулей)] мы бы измеряли температуру, если бы мы использовали
энергетические единицы вместо того, чтобы вводить постоянную Больцмана кв =
1.3807 · 10"23 Дж/К?
3.2 Большие и очень большие числа, φ
Числа, встречающиеся в статистической механике, могут поставить в
тупик ваш калькулятор. Например, гугол — 10100 (единица со ста нулями).
Гуголплекс — это число 10googo1.
Рассмотрим один моль одноатомного идеального газа (число частиц N =
число Авогадро, 6.02 · 1023) при комнатной температуре Τ = 300 К, объемом
V = 22 А л (соответствующим атмосферному давлению).
(a) Какие величины (S, Τ, Ε и Ω(Ε)), характеризующие наш образец газа,
превышают гугол? А гуголплекс? Имеет ли значение, какие единицы измерения
вы используете, в разумных пределах?
Некоторые величины, характеризующие газ, являются интенсивными (не
зависящими от N для больших TV), другие — экстенсивными
(пропорциональными 7V), а некоторые увеличиваются даже еще быстрее с ростом N.
(b) К какой категории (интенсивные, экстенсивные, нелинейные) относится
каждая из величин из задания (а)?
108
Гл.З. Температура и равновесие
3.3 Вторая космическая скорость. (2)
Молекулы атмосферы планет медленно уходят в открытый космос.
Траектория каждой молекулы представляет собой случайное блуждание,
характерный шаг которого увеличивается при удалении от планеты, когда ее
атмосфера становится более разреженной. Давайте используем для расчета утечки
молекул грубое приближение идеального газа, пренебрегающее
соударениями между частицами, за исключением столкновений частиц с поверхностью
самой планеты.
В этом упражнении мы рассмотрим двухатомный кислород как
одноатомный идеальный газ, масса частиц которого в два раза
больше массы атома кислорода то2 = 2то- (Это не является грубым
приближением, поскольку вращение и колебания не влияют на траекторию
центров масс.) Предположим, что распределение z-компонент импульса
частиц °° такое же, как и для идеального газа, приведенное в уравнении
3.19: p(pz) = \/у/2-ктквТ exp(-p2z/2mkBT). Для вашего удобства приводим
значения констант: кв = 1.3807 · 1СГ16 эрг/К, то2 = 5.3 · 10"23 g и Τ = 300 К.
(a) Какова среднеквадратичная скорость в вертикальном направлении \/Jvf)
молекулы О2? Если молекула стартовала с поверхности Земли с данной
среднеквадратичной скоростью, насколько высоко она поднимется, если пренебречь
столкновениями с другими частицами? Сколько времени ей потребуется, чтобы
снова упасть на Землю? (Полезная константа: д = 980см/с2.)
(b) Найдите вероятность того, что вертикальная компонента скорости
молекулы О2 превышает вторую космическую скорость (порядка 11 км/с).
(Подсказка: f£° e_i dt « е~х /2х для больших х.)
(c) Если пренебречь столкновениями молекул и предположить, что скорость
молекулы термализуется (принимает случайное значение, согласно максвеллов-
скому распределению по скоростям) каждый раз, когда она сталкивается с
Землей (приблизительное время между двумя последовательными соударениями
можно взять из задания (а)), то какую долю молекул кислорода мы теряем
каждый год? Должны ли мы беспокоиться о том, что мы можем лишиться нашей
атмосферы? (Полезно знать, что в году примерно π · 107 секунд.)
Попробуйте провести аналогичные вычисления для водорода Нъ и вы
обнаружите существенную утечку. Именно поэтому основная часть атмосферы
Юпитера состоит из водорода, а для Земли это не так.
То есть мы не учитываем ветер и вращение Земли.
Гл.З. Упражнения
109
3.4 Расчет давления.54 (Моделирование) ®
С микроскопической точки зрения, давление возникает при соударениях
атомов с поверхностью. Давайте вычислим это микроскопическое давление
идеального газа как аналитически, так и с использованием компьютерного
моделирования методом молекулярной динамики. Вы можете скачать
соответствующую программу [30] с нашего сайта [132].
Проведите моделирование идеального газа в системе с отражающими
стенками. Каждый раз, когда атом сталкивается со стенкой, происходит
зеркальное отражение, при котором составляющие импульса, параллельные
стенке, остаются неизменными, а перпендикулярные составляющие меняют
свой знак на противоположенный.
(a) Вспомните, что давление Ρ = F/A — это сила на единицу площади,
а сила F = dp/dt = (]ΓΔΡ)/Δί — изменение импульса в единицу времени.
Предположим, что стенка площадью А с координатой χ = L удерживает
атомы с координатами χ < L внутри сосуда. Запишите выражение для давления
через pc{Px)f ожидаемое число соударений частиц с ^-компонентой импульса рх
со стенкой в единицу времени. (Подсказка: обратите внимание на пределы
вашего интеграла, а также на двойку перед интегралом. Вносят ли вклад
отрицательные компоненты импульса?)
Моделирование предоставляет нам «наблюдателя», который записывает
характеристики всех соударений со стенкой в течение заданного интервала
времени.
(b) Постройте гистограмму числа соударений со стенкой в течение интервала
времени At с переносом импульса Δρ. На что вы должны умножить рс(Рх) из
задания (а), чтобы получить эту гистограмму?
В отличие от распределения импульсов в газе, вероятность рс{Рх)
столкновения со стенкой частицы с импульсом рх стремится к нулю при стремлении
рх к нулю. Неподвижные атомы и реального газа не соударяются со стенкой.
Плотность распределения частиц с импульсом рх есть произведение полной
концентрации частиц N/V и вероятности того, что частица обладает
импульсом рх (уравнение 3.19Ί.
У^шдгехр{-^) (360)
(c) Насколько далеко от стенки должны быть расположены атомы с
импульсом рх, чтобы успеть с ней столкнуться за время At? Какой будет
результирующая формула для рс{Рх)? Согласуется ли она с вашей гистограммой из задания
54Это упражнение и соответствующее программное обеспечение было разработано
совместно с Кристофером Майерсом.
по
Гл.З. Температура и равновесие
(Ь)? Какое результирующее выражение для давления Ρ вы получили?
Согласуется ли оно с уравнением состояния идеального газа?
3.5 Газ твердых сфер. (2)
Мы можем внести поправки к приближению идеального газа,
рассматривая атомы малого радиуса. Пусть потенциальная энергия непересекающихся
сфер равна нулю, а потенциальная энергия пересекающихся —
бесконечности, что соответствует приближению твердых сфер, таким образом, сферы не
могут перекрываться. Давайте рассмотрим двумерную систему. Трехмерная
система не является более сложной, но ее сложнее визуализировать.
Пусть в двумерном сосуде размером L x L с жесткими стенками находится
газ N твердых дисков радиуса г <С L (рис. 3.5). Рассмотрим достаточно
разбавленный газ, для которого Nnr2 «С L2. Пусть А — эффективная доступная
для дисков площадь коробки (см. рис. 3.5): А = (L — 2г)2.
(а) Площадь, доступная второму диску, составляет А—7г(2г)2 (рис. З.б), если
не учитывать небольшие поправки, возникающие, когда исключенный объем
первого диска перекрывается с исключенным объемом вблизи стенок сосуда. Чему
равен доступный 2ЛГ-мерный объем в конфигурационном пространстве системы
твердых сфер с нулевой энергией в пределе малой концентрации? Не учитывайте
малые поправки, когда исключенный объем вокруг одного из дисков
перекрывается с исключенным объемом вокруг других дисков или вблизи стенок сосуда.
Не забудьте о сомножителе 1/7V! для неразличимых частиц. Оставьте свой ответ
в виде произведения N сомножителей.
Рис. 3.5. Газ твердых сфер
Гл.З. Упражнения
111
Рис. 3.6. Исключенный объем вокруг твердого диска
(b) Чему равна конфигурационная энтропия для твердых дисков?
Приведите свой ответ к такому виду, чтобы он не зависел от суммы N членов, но был
верным в первом приближение по площади дисков кг2. Покажите, что для
больших N это хорошо аппроксимируется функцией Sq = Л/7гя(1 + log(A/N — b)),
где b — эффективный исключенный объем за счет присутствия других дисков.
(Выведите формулу £^=1 log (Л - (п - 1)е) = Nlog(A -(Ν- \)е/2) + 0{е2).)
Чему равно Ь, если выразить его через площадь одного диска?
(c) Найдите давление газа твердых сфер в приближении больших N из
задания (Ь). Сводится ли оно к уравнению состояния идеального газа при 6 = 0?
3.6 Объединение двух макроскопических систем. @
Рассмотрим изолированную систему с энергией Е, состоящую из двух
макроскопических подсистем, каждая из которых имеет постоянный объем V
и число частиц N. Подсистемы слабо связаны между собой, сумма их энергий
составляет Е\ + Ε<ι = Ε (рис. 3.3, где возможен только обмен энергией).
Используя й(х)-функцию Дирака (см. примечание 4 на с. 19), мы можем
задать объем энергетической поверхности системы с гамильтонианом Ή,:
П(Е) = J ^ δ (Ε - ?ί(Ρ, Q)) (3.61)
_ Γ dPidQidP2dQ2
~J h3N> h3N*
χδ(Ε- (Wi(Pi,Qi) + ft2(P2,Q2))) · (3.62)
Выведите формулу (3.21), Ω(Ε) = J άΕχ Ωι(Ει)ίΐ2(Ε—Εχ) для объема
энергетической поверхности всей системы, используя J-функцию Дирака (вместо
использования энергетических слоев, как в уравнении 3.22) (Совет: подставьте
/ δ{Εχ - 7ii(Pi,Qi)) άΕχ = 1 в уравнение 3.62.)
112 Гл. 3. Температура и равновесие
3.7 Смесь газов. ©
Рассмотрим смесь одноатомного (Не) и двухатомного (Н2) газа.
Используем модель идеального газа для их описания. Таким образом, мы можем
рассматривать гелий как отдельную систему, невзаимодействующую с
водородом (за исключением их перемешивания в пространстве). Мы показали,
что для одноатомного идеального газа из N атомов Ω\(Ει) ос Ег .В
случае двухатомной молекулы Ω2(Ε2) ос Е2 ·55
(a) Рассчитайте плотность вероятности того, что энергия системы 1
составляет Е\ (уравнение 3.23). Для смеси этих двух газов, при какой энергии Εψ**
плотность вероятности будет максимальной?
(b) Приведите ответ на задание (а) к гауссову виду, раскладывая логарифм
в ряд Тейлора log (ρ(ϋα)) « log (p(£'flax)) + (Εχ - Ε™3*) +... вплоть до второй
производной, а затем снова, взяв экспоненту от обеих частей. В этом
приближении, чему равна средняя энергия (-ΕΊ)? Какова величина флуктуации энергии
на одну частицу \/{{Е\ — E™**)2)/N1 Действительно ли они очень малы
(пропорциональны l/\/N)l
Для подсистем с большим числом частиц N температура и плотность
энергии очень четко определены, поскольку Ω(Ε) для каждой из
подсистем очень быстро растет с увеличением энергии, таким образом, что
Ωι(£Ί)Ω2(-Ε' — -ΕΊ) имеет очень острый пик вблизи максимума.
3.8 Флуктуации энергии в микроканоническом ансамбле. (2)
Мы обсуждали в разделе 3.3, что флуктуации энергии в двух слабовзаимо-
действующих подсистемах — порядка y/N. Давайте получим для них точное
выражение.
Из уравнения (3.28) видно, что для двух подсистем с энергией Е\ и Е2 =
Ε — Ει плотность вероятности энергии Е\ — гауссова, с дисперсией
(стандартное отклонение в квадрате):
σ\χ = -кв/ (д^г/дЕ^ + d2S2/dEl). (3.63)
(а) Покажите, что
J^^S_ _ 1 1_
квдЕ2 " kBTNcvT'
55Это верно при h2/21 <С квТ <С Ьы, где ω — частота молекулярных колебаний, а /
— момент инерции. Нижний предел отвечает классическому вращению, а верхний —
отсутствию колебательных степеней свободы. Таким образом, в нашей системе остаются три
моды, отвечающие трансляционному движению и две вращательные моды — всего пять
степеней свободы.
(3.64)
Гл. 3. Упражнения
113
где 1/су — величина, обратная удельной теплоемкости при постоянном
объеме. (Удельная теплоемкость Су равна энергии, требуемой для увеличения
температуры одной частицы на одну единицу: Ncy = (дЕ/дТ)\у^.)
Знаменатель в правой части уравнения (3.64) представляет собой
произведение двух энергий. Второй сомножитель NcyT — это энергия на масштабе
всей системы. Это полная энергия, которая требовалась бы для того, чтобы
увеличить температуру системы с абсолютного нуля до данного значения,
если бы удельная теплоемкость Су не зависела от температуры. Однако первый
сомножитель квТ — это энергия на масштабе одного атома, не зависящая от
N. Таким образом, флуктуации энергии пропорциональны среднему
геометрическому этих двух сомножителей, взятому по двум подсистемам в
уравнении (3.28) и, таким образом, пропорциональны y/N. Флуктуации полной
энергии на частицу приблизительно равны 1/y/N, умноженному на среднюю
энергию частицы.
Эта формула достаточно примечательна. Она представляет собой
флуктуационно-диссипационное соотношение (см. раздел 10.7). Согласно
определению теплоемкости, для того чтобы ее измерить, нужно добавить
небольшое количество энергии в систему и измерить изменение
температуры. Данная формула позволяет нам рассчитать удельную
теплоемкость системы, изучая равновесные флуктуации энергии. Эти
флуктуации очень малы в типичных образцах, изучаемых в экспериментах,
но в компьютерном моделировании могут быть весьма существенными.
(Ь) Пусть Су ' и Су — удельные теплоемкости двух подсистем, каждая из
которых состоит из N частиц. Покажите, используя уравнения (3.63) и (3.64),
что
1 1 NkBT2
(1) + (2) " σ2
Ш + 7(2) = ~Λ~· (3·65)
Данные две системы могут даже не взаимодействовать между собой.
Координаты и импульсы в моделировании методом молекулярной динамики
(изучающей атомы, подчиняющиеся ньютоновским законам движения)
можно рассматривать как две невзаимодействующие подсистемы, поскольку их
кинетическая энергия не зависит от их конфигурации Q, а потенциальная
энергия не зависит от импульсов Р.
Пусть, моделируя методом молекулярной динамики N
взаимодействующих частиц с постоянной энергией, находящихся в состоянии равновесия, мы
измерили кинетическую энергию как функцию времени56 и обнаружили, что
В системе с твердыми стенками полный импульс и момент импульса не сохраняются.
114
Гл.З. Температура и равновесие
средняя кинетическая энергия составляет К = (-ΕΊ), а стандартное
отклонение — σκ·
(с) Используя теорему о равнораспределении, выразите температуру через
К. Покажите, что с4 = 3&в/2 для импульсных степеней свободы. Зная К и
<?к, рассчитайте удельную теплоемкость системы, исследуемой методом
молекулярной динамики (конфигурационную и кинетическую).
3.9 Распределение Гаусса и Пуассона. ®
Глубокой правдой, лежащей в основе равновесной статистической
механики, является тот факт, что поведение больших, слабо взаимодействующих
систем во многом не зависит от окружающей среды. Какого рода термостат
окружает систему, не столь существенно, если он обладает четко
определенной температурой, давлением и химическим потенциалом.
Это не относится, однако, к флуктуациям вокруг среднего значения, если
только термостат не превышает существенным образом по размерам нашу
систему. В этом упражнении мы будем исследовать флуктуации числа частиц
в подсистеме, объем которой в К раз меньше объема полной системы.
Давайте вычислим вероятность нахождения η частиц в подсистеме объема
V системы объема KV с полным числом частиц Τ = К No. При К = 2 мы
получим наш предыдущий результат, уравнение (3.11), включая префактор.
При К —> сю мы получим результат для бесконечного объема.
(a) Получите точную формулу для вероятности того, что η находятся в
подсистеме объема V, принадлежащей системе объема KV, состоящей из Τ частиц.
(Совет: какова вероятность того, что первые η частиц попадут в подсистему
V, а оставшиеся Τ — η частиц окажутся снаружи в объеме (К — 1)V7 Чему
равно число способов выбрать η частиц из Т?)
Распределение Пуассона
рп = апе-а/п\ (3.66)
встречается во многих практических приложениях. Оно возникает повсюду,
где встречается большое число возможных событий Т, каждое из которых
имеет малую вероятность а/Т, например, число машин, проезжающих через
заданную точку в течении часа по практически пустой улице, число
космических лучей, падающих в данную секунду и т.д.
(b) Покажите, что распределение Пуассона является нормированным:
ΣηΡη = 1- Выразите среднее по распределению (п) через а. Рассчитайте
дисперсию (стандартное отклонение в квадрате) ((п - (п))2).
(c) Покажите, что вероятность нахождения η частиц в подсистеме объема V
при К —У оо подчиняется распределению Пуассона (З.бб). Что характеризует а?
Гл. 3. Упражнения
115
(Совет: вы можете использовать формулу е~а = {е~1/к)Ка —> (1 — 1/К)Ка при
К —> оо и тот факт, что η «С Т. Здесь нет необходимости предполагать, что η
велико, распределение Пуассона верно даже для небольшого числа событий.)
Выполняя задания (Ь) и (с), вы обнаружите, что изменение числа частиц
в объеме V внутри бесконечной системы равно TVq, среднему числу частиц в
объеме:
((n-{n))2) = N0. (3.67)
Это в два раза больше, чем квадрат флуктуации в случае, когда объем V
занимает половину полного объема (уравнение 3.11). Это не противоречит
здравому смыслу, поскольку частицы могут флуктуировать более свободно в
бесконечном объеме, чем в удвоенном.
Если Nq велико, будет ли вероятность Рт того, что Л/о + га лежат вне
нашего объема, по-прежнему гауссовой? Давайте проверим это для
произвольного К. Во-первых, давайте, так же как и в разделе 3.2.1, используем
простейший вид приближения Стирлинга (уравнение 3.8) без квадратного
корня: п\ ~ (п/е)п.
(d) Используя результаты расчетов из задания (а), запишите точную
формулу для log(Pm). Используйте простейший вид формулы Стирлинга.
Разложите ваш результат в ряд Тейлора в окрестности га и покажите, что log(Pm) «
—πι2/2σ'κ, что дает распределение Гаусса
Pm~e-m2/2< (3.68)
Чему равна σχ? В частности, G2 и σοο? Результат ваших расчетов для съ
должен совпадать с результатом, полученным в разделе 3.2.1, а σ^ — с
уравнением (3.67).
Наконец, давайте рассчитаем нормировку распределения Гаусса.
Обратите внимание, что отношение более точного и менее точного выражений для
формулы Стирлинга в уравнении (3.8) имеет вид ν/2πη. Мы можем
использовать это для того, чтобы получить нормировку 1 / \/2πσχ распределения
Гаусса.
(e) Какой вклад внес бы квадратичный сомножитель, если бы вы сохранили
его в формуле Стирлинга в заданиях (a)-(d)? Выразите его через Тип. (Он
будет иметь вид соотношения, состоящего из трех сомножителей вида \2πΧ.)
Используя уравнение (3.68), покажите, что флуктуации малы: m = n — No <£i No
для больших No. Пренебрегая этими флуктуациями, положите η = No в вашем
выражении и найдите коэффициент перед распределением Гаусса в уравнении
(3.68). (Подсказка: ваш ответ должен быть нормированным.)
116
Гл.З. Температура и равновесие
3.10 Цепное соотношение Эйлера. (Термодинамика, математика) Q)
В традиционной термодинамике давление определяется как
изменение энергии при изменении объема, взятое с обратным знаком,
Ρ = —(dE/dV)\isrts, а химический потенциал — как изменение энергии
при изменении числа частиц μ = (dE/dN)\vts- Дифференциал полной
внутренней энергии имеет вид:
άΕ = Τ dS - Ρ dV + μ dN. (3.69)
(a) Покажите, выражая dS из уравнения (3.69), что (dS/dV)\isrε = Ρ/Τ и
(0S/dAO|v,E = -M/T.
Я никогда не любил манипулировать с дифференциалами cLATs.57 Можно
ли вывести эти выражения, используя специфические соотношения для
частных производных? Наше уравнение состояния S(E, V, Ν) при фиксированном
N представляет собой поверхность в трехмерном пространстве. На рис. 3.4
изображен треугольник на этой поверхности, который можно использовать
для вывода цепного соотношения Эйлера для частных производных.
(b) Покажите, что, если / — функция χ и у, то
(dx/dy)\f(dy/df)\x(df/dx)\y = -1.
(Совет: Рассмотрите треугольник на рис. 3.4. Первая сторона треугольника
начинается в точке (#о,У(ь/о) и при постоянном / продолжается в
точку у о + Ду. Результирующая вершина будет иметь координаты
(хо + {9x/dy)\fAy,yo Η- Δ?/,/о). Вторая сторона при постоянном χ
возвращается в точку уо, а третья сторона — при постоянном у обратно в
(хо, Уо> /о)· Кривая должна быть замкнутой, если / — однозначная функция.
Записывая условие замкнутости, получаем цепное соотношение Эйлера.)
(c) Используя «традиционные» определения Ρ и μ, подставьте в формулу
из задания (b) S при фиксированном Ε и выведите два соотношения из задания
(а). (Вычисление, обратное последнему, было проведено в разделе 3.4.)
3.11 Соотношения Максвелла. (Термодинамика, математика) (3)
Рассмотрим микроканоническую формулу для равновесной энергии
E(S,V,N) некоторой произвольной системы.58 Известно, что вторые
производные Ε симметричны. При фиксированном N мы получим тот же
57Действительно, существуют дифференциальные формы, коварные с математической
точки зрения (см. примечание 23 на с. 219).
58Можно вывести эту формулу, выражая Ε из известного уравнения S = S(N,V,E). Оно
будет представлять собой ту же самую поверхность в четырех измерениях, что и S(N, V, Ε)
(рис. 3.4), но с другим направлением нормали.
Гл.З. Упражнения
117
самый ответ вне зависимости от порядка взятия частных производных по S
(а) Используйте это условие для вывода соотношений Максвелла
dV
S,N dS
(3.70)
V,N
(Эти вычисления должны занять у вас не более двух строчек.) Выведите две
аналогичные формулы, взяв частные производные Ε по другим переменным.
Существует множество подобных соотношений [53].
(Ь) Статистико-механическая проверка соотношений Максвелла. Используя
уравнение (3.57), выведите формулы для E(S,V,N), T(S,V,N) = {dE/dS)\VjN
и P(S,V,N) = —{dE/dV)\syN для идеального газа. (Обратите внимание на то,
что Τ и Ρ — функции Ν, V и S, а не Е.) Покажите, что соотношение Максвелла
(3.70) выполняется.
3.12 Решение дифференциальных уравнений: движение
маятника.59 (Моделирование) (§)
Физические системы, как правило, описываются функциями,
непрерывными с течением времени. Движение систем задается
дифференциальными уравнениями. Численно можно получить лишь приблизительное
решение дифференциальных уравнений, поскольку шаги по времени дискретны.
В этом упражнении мы рассмотрим наиболее распространенный и важный
метод компьютерного моделирования — молекулярную динамику, а также
коротко обсудим другие программы, используемые для решения произвольной
системы дифференциальных уравнений.
Мы будем изучать динамику маятника:
^ = 0 = -|sin(0). (3.71)
Данное уравнение описывает движение маятника, представляющего собой
стержень нулевой массы длины L, на конце которого расположен груз
бесконечно малого размера.60 Его легко получить с использованием силовой схемы
свободного тела.
Зайдите на наш сайт [132] и скачайте файлы на том языке
программирования, который вы хотите использовать. На анимации вы увидите
осциллирующий маятник, стартующий с начальными условиями #о = 2π/3, θ = 0.
Уравнение решается для значений параметров д = 9.8 м/с2 и L = 1 м.
59Это упражнение и сопутствующее программное обеспечение были разработаны
совместно с Кристофером Майерсом. См. также Numerical Recipes [102, chapter 16].
60Уравнение движения стержня конечной массы, но без груза на конце, имеет
аналогичный вид.
118
Гл.З. Температура и равновесие
Существует три независимых критерия хорошего алгоритма для решения
дифференциальных уравнений: достоверность, точность и устойчивость.
Достоверность. В алгоритме с дискретным временным шагом мы не
можем идти простейшим на первый взгляд путем — использовать текущее
значение (6(t), #(£)), чтобы получить (θ(ί+δ), θ(ί+δ)). Вместо этого мы действуем
следующим образом: зная 0(£), определяем ускорение и новое значение
скорости θ{ί) —> 6(t + 5), а затем, зная θ{ί + 5), рассчитываем новую координату
0(t)->0(« + 5):
θ(ί + δ) = θ(ί) + θ(ήδ, (3.72)
θ{ί + δ) = θ(ί) + θ(ί + δ)δ. (3.73)
Не проще было бы задавать θ и θ сразу же, зная их текущие значения,
таким образом уравнение (3.73) имело бы вид θ{ί+δ) = θ(ί)+θ{ί) δ? Этот
простейший из всех пошаговых алгоритмов называется методом Эйлера. Его не
следует использовать для решения обыкновенных дифференциальных
уравнений (хотя зачастую он используется для решения уравнений в частных
производных).
(а) Проведите вычисления методом Эйлера. Во-первых, изучите, каким
образом изменение порядка вычисления θ и Θ,
e{t + S) = 9{t) + 0{t)S,
0(i + δ) = 0(t) + θ(ί) δ,
в коде, который вы скачали, приведет к изменению поведения системы.
Поменяйте местами эти две строчки в коде и вы увидите, что вначале маятник будет
колебаться несколько раз, а затем начнет описывать петлю. Является ли новый
алгоритм столь же хорошим, как предыдущий? (Обратите внимание на то, чтобы
вернуть эти две строчки в исходный вид.)
Новая схема настолько же точна, как и предыдущая, но она нефизична.
По некоторым причинам, которые мы здесь не обсуждаем, изменение θ
перед изменением θ приводит к тому, что в нашем алгоритме с достаточной
степенью точности моделируется гамильтонова система.61 Данный алгоритм
называется симплектическим.62 Улучшенные версии этого алгоритма, такие
61 Уравнение (3.73) представляет собой гамильтонову динамику невзаимодействующих
частиц, а га, умноженное на уравнение (3.72), — закон эволюции импульса ρ = F для
системы частиц с бесконечной массой.
62 Он сохраняет симплектическую форму.
Гл. 3. Упражнения
119
как алгоритм Верле, приведенный ниже, часто используются для
моделирования систем с постоянной энергией, поскольку они точно63 моделируют
динамику гамильтоновых систем, сохраняя основные физические свойства.
Точность. В большинстве численных методов для решения
дифференциальных уравнений (и других задач, таких как интегрирование) вводится
размер шага δ. Вычисление становится более точным при уменьшении δ. Но
существенной является не ошибка на каждом временном шаге, а точность
ответа после фиксированного промежутка времени Т, где ошибка
накапливается на протяжении Τ/δ шагов. Если ошибка меняется как йп, то точность
алгоритма — порядка п. Точность нашего алгоритма обладает не очень
высоким порядком!
(b) Выразите 6(t + δ) через 6(t), 6{t) и 6{t) в уравнениях 3.72 и 3.73 для
нашего ступенчатого алгоритма. Сравните с рядом Тейлора x(t + τ) = x(t) +
ντ + \ατ2 + 0(τ3) для функции θ(ί). Какой будет ошибка вычисления θ за
один временной шаг? Глядя на уравнение 3.73, определите, какой будет ошибка
за один шаг по времени для ΘΊ Считая, что наибольшая из двух ошибок будет
задавать полную точность и что ошибка за один шаг по времени накапливается в
течение большего количества шагов при уменьшении шага, определите порядок
точности для нашего ступенчатого алгоритма.
(c) Постойте траекторию движения маятника для временных шагов δ = 0.1,
0.01, и 0.001. Сравните значения функции в одной из точек (например при t = 1)
для трех различных δ. Можно ли предположить, что траектория будет
сходиться64 при 5 —» 0? Какого порядка сходимость: улучшается ли каждая кривая в 10,
100, 1000... раз?
Перегруппировка вычислений в процессе одного временного шага
(уравнения 3.72 и 3.73) дает нам алгоритм Верле:
θ{ί + δ/2) = θ{ΐ)+1-θ{ί)δ,
θ{ί + δ) = θ{ί) + θ{ί + δ/2)δ, (3.75)
0(ί + δ) = θ(ί + δ/2) + \θ(ί + δ)δ.
Секрет, который делает этот алгоритм столь эффективным, заключается в
искусном разделении увеличения скорости на две части, причем первая
задается ускорением в предыдущий момент времени, а вторая — в последующий.
(Инициализируйте θ один раз, прежде чем начать цикл.)
63За исключением ошибок округления.
64 Вы можете заметить, что приблизительные решения сходятся к точному ответу. Можно
использовать этот факт для ускорения сходимости к правильному ответу. Это называется
экстраполяцией Ричардсона и является основой метода Булирша—Стоера.
120
Гл. 3. Температура и равновесие
(d) Покажите, что N шагов нашего ступенчатого алгоритма эквивалентны
алгоритму Верле, если мы сдвинем скорости до и после временного шага на
=Fl/250.
(e) Как и в задании (Ь), запишите θ(ί+δ) для скоростей Верле через функции,
зависящие от t. Точность какого порядка это дает?
(f) Реализуйте алгоритм Верле и постойте траекторию для временных шагов
δ = 0.1, 0.01 и 0.001. Какого порядка точность вычисления?
Устойчивость. Во многих задачах высокая точность не является
решающим фактором. Что мешает нам брать большие временные шаги? В данной
задаче, как правило, существует наименьший характерный отрезок
времени, определяемый периодом колебаний (как в нашем упражнении), а также
скоростью роста или распада. Когда наш временной шаг начинает занимать
значительную долю этого характерного отрезка времени, алгоритмы,
подобные нашему, зачастую становятся нестабильными. На протяжении первых
нескольких шагов точность еще является допустимой, но малые ошибки
экспоненциально накапливаются до тех пор, пока ошибка не становится
неприемлемой (в самом деле, зачастую первым предупреждением о наличии проблем
является переполнение массивов).
(g) Постройте траекторию маятника θ(ί) для временных шагов δ = 0.1, 0.2,
..., 0.8 для колебаний с малой амплитудой во = 0.01, #о = 0.0, вплоть до
£тах = 10. При каком значении δ€ решение становится неустойчивым? Найдите
отношение йс к характерному периоду маятника. Насколько точно
рассчитывается амплитуда осцилляции при йс/2?
(Необходимо рассмотреть несколько периодов для оценки максимальной
амплитуды решения.)
При изучении больших нелинейных систем (например,
дифференциальных уравнений в частных производных и проведении
молекулярно-динамических расчетов) устойчивость зачастую представляет
собой основную проблему. Максимальная величина шага зависит от
локальной конфигурации, так, часто в сильно нелинейных областях система
становится неустойчивой существенно раньше, чем этого можно ожидать.
Максимально возможный размер шага с точки зрения устойчивости часто
дает огромную точность, существенно большую необходимой.
Алгоритм Верле не сложно запрограммировать. Существуют симплекти-
ческие алгоритмы более высокого порядка для гамильтоновых систем, но они,
как правило, используются в нестандартных приложениях, таких как
движение планет, в которых требуется высокая точность, поскольку эти алгоритмы,
как правило, значительно менее устойчивы. В системах дифференциальных
уравнений, в которых энергия не сохраняется, или даже в гамильтоновых
Гл.З. Упражнения
121
системах (таких как соударяющиеся частицы с высокой энергией), в
которых точность на малых временах существенно важнее, чем достоверность на
больших временах, мы используем общие методы.
Программы для решения обыкновенных дифференциальных уравнений.
Программы для решения дифференциальных уравнений в общем
случае различаются в базовых алгоритмах (метод Рунге—Кутты, метод
«предиктор-корректор», ...), методах поддержки и увеличения точности
(переменный временной шаг, экстраполяция Ричардсона). Существуют
также неявные схемы для решения жестких систем обыкновенных
дифференциальных уравнений. Система является жесткой, если существует
большое различие между наибольшим и наименьшим характерным
временем. Неявные схемы зачастую позволяют брать временные шаги,
намного большие наименьшего характерного промежутка времени (в
отличие от явного алгоритма Верле, рассмотренного в задании (d), который
становится нестабильным.) Большие, сложные вычислительные пакеты для
решения дифференциальных уравнений разрабатывались на протяжении
многих лет. Они решают систему уравнений dy/dt = dydt (у, ί), где в
нашем случае у = [0,0] и dydt = [0,0]. Они, как правило, включают в себя
функции и подпрограммы, зависящие от следующих аргументов:
• начальных условий уо,
• правой части — функции вектора у и времени £, которая возвращает
вектор, задающий текущую скорость изменения у,
• начального и конечного времени, а также, возможно, промежуточных
времен вывода траектории y(t).
Они обладают следующими опциями:
• требуют задать точность вычислений, как правило, относительную и
абсолютную точность, иногда отдельно для каждой из компонент у,
• возвращают производную и информацию о временном шаге в
заданных точках (для возможности эффективного повторного запуска после
промежуточных стадий вычисления),
• запрашивают программу, которая рассчитывает производные dydt по
текущим компонентам у (используется в жестких схемах
интегрирования),
• предоставляют информацию о методах, временном шаге и
характеристиках алгоритма.
122
Гл.З. Температура и равновесие
Вам будет предоставлен один из подобных общих алгоритмов и инструкции
по его использованию.
(h) Запишите функцию dydt, используйте общую программу для расчета
движения маятника, как в заданиях (а)-(с), проверьте, насколько точным
является вычисление траектории.
Глава 4
Динамика фазового
пространства и эргодичность
До сих пор обоснованием использования микроканонического ансамбля
была неопределенность: все что мы знаем о сложном движении системы —
это то, что ее энергия сохраняется. Таким образом, мы усредняем по
всевозможным состояниям фазового пространства, энергия которых одинакова.1 В
этой главе мы приведем более убедительное обоснование
микроканонического ансамбля и, следовательно, всей равновесной статистической механики.
В разделе 4.1 мы покажем, что усреднение по поверхности равной энергии2
для классических систем согласовано с временной эволюцией системы.
Согласно теореме Л иу вилл я, объем в фазовом пространстве сохраняется, таким
образом, траектории только движутся по энергетической поверхности, но не
меняют относительные веса различных частей поверхности. В разделе 4.2
мы введем понятие эргодичности; поверхность равной энергии эргодической
системы практически полностью покрыта траекториями. Используя
теорему Л иу вил л я и предполагая эргодичность, мы покажем,3 что усреднение по
микроканоническому ансамблю согласовано с типичным поведением системы
на больших временах, которое мы называем равновесием.
Если вы принимаете на веру правильность усреднения по поверхности равной энергии,
то оставшаяся часть книги не будет опираться на результаты этой главы.
2Поверхность равной энергии можно представить как энергетический слой Ε <
T-L(F,Q) < Ε + δΕ, в пределе δ Ε —У 0. Мы здесь будем рассматривать поверхность
равной энергии, а не энергетический слой, поскольку в процессе эволюции траектории не
переходят на поверхности с другими энергиями.
3Мы не стремимся к математической строгости, мы представим на качественном
физическом уровне доказательства результатов, полученных более строгим способом; см. [81].
124
Гл.4. Динамика фазового пространства и эргодичность
4.1 Теорема Л иу вил ля
В главе 3 мы показали, что равновероятный учет всех состояний с
заданной энергией в фазовом пространстве дает разумные предсказания для
идеального газа, но мы не показали, что этот демократичный подход является
заведомо правильным. Теорема Лиувилля, справедливая для всех гамильто-
новых систем, покажет нам, что все состояния действительно равноправны.
Системы точечных частиц, подчиняющиеся законам Ньютона, в которых
отсутствует диссипация, представляют собой пример гамильтоновых
динамических систем. В этих системах сохраняется энергия, заданная
гамильтонианом Ή(Ρ, Q). Зная Ή, можно получить законы движения с помощью
уравнений Гамильтона:
qa = dH/dpa,
ра = -dU/dqa,
где используется стандартное обозначение X = dX/dt. Типичным примером
гамильтониана, а также единственным примером, который будет
рассматриваться в данной книге, является гамильтониан частиц, взаимодействующих
с потенциальной энергией U:
W(P,Q) = Σρα2/2τηα + U(qu · · · ,<Z37v). (4.2)
α
В этом случае из уравнений Гамильтона, как и ожидалось,
непосредственно следуют ньютоновские уравнения движения:
<?а = дН/дра = Ра/та,
Ра = -&H/dqa = -dU/dqQ = /α(βι, · · ·, Q3n),
где fa — сила, действующая на частицу а. Гамильтонианы более общего
вида4 возникают, например, при изучении движения твердых тел или
механических объектов, соединенных шарнирами и стержнями, где естественными
переменными являются углы и относительные позиции, а не координаты в
пространстве. Гамильтонианы также играют ключевую роль в квантовой
механике.5
4 Вы будете детально изучать гамильтонову динамику в более продвинутых курсах
классической механики. Тех, кто еще не знает ничего о гамильтонианах, мы спешим заверить,
что мы не будем использовать ничего, кроме гамильтониана простейшего вида для
ньютоновских точечных частиц. Для целей, преследуемых в данной книге, нет необходимости
рассматривать общий случай.
5В разделе 7.1 мы обсудим теорему Лиувилля для квантовых систем.
4.1. Теорема Лиувилля
125
Гамильтоновы системы отличаются от произвольных систем,
описываемых дифференциальными уравнениями. В них не только сохраняется
энергия, но они также обладают многими необычными свойствами.6 Теорема
Лиувилля определяет наиболее важные из этих свойств.
Рассмотрим эволюцию общей плотности вероятности в фазовом
пространстве:
p(P,Q) = ρ(ςι,... ,дзлг,Ръ ■ - · ,Рзлг). (4.4)
(В микроканоническом ансамбле ρ равно константе в бесконечно малом
диапазоне энергий и нулю вне этого диапазона.) Эта плотность вероятности
локально сохраняется: вероятность не может создаваться или разрушаться, она
может только перемещаться по фазовому пространству.
В качестве аналогии рассмотрим жидкость с трехмерной массовой
плотностью Рзб(#) со скоростью v{x). Поскольку массовая плотность локально
сохраняется, рзБ должно удовлетворять уравнению непрерывности дрзо/дЬ =
—V· J, где J = P3DV — поток массы (рис. 4.1). Аналогично, плотности
вероятности в 67V измерениях соответствует поток вероятности в фазовом
пространстве (рР, pQ) и, следовательно, она удовлетворяет уравнению непрерывности
#Р = _ у^ (д(РЯа) д{рРа)\
£?г \dqa α dqQ дра Q dpaJ'
Теперь становится ясно, что означает dp/dqa, поскольку ρ является
функцией всех qa и ра. Но что подразумевается под dqQ/dqa7 Для наших точечных
частиц qa = ρα/τη не зависит от qa\ и также ра = /а(дь..., Qsn) не зависит
от момента ра·7 Следовательно, оба загадочных члена в уравнении (4.5)
исчезнут для ньютоновских точечных частиц. Более того, применяя уравнения
Гамильтона (4.1), мы увидим, что они сокращаются и для произвольной га-
мил ьтоновой системы:
dqQ/dqQ = d{dn/dpQ)/dqQ = d2U/dpadqa = d2H/dqadpa
= d(dH/dqQ)/dpQ = д(-ра)/дра = -дра/дра. (4.6)
Для математически подкованных читателей: гамильтонова динамика сохраняет сим-
плектическую форму ω = dq\ Λ dpi + ... + dq3N Λ άρ3Ν· Отсюда можно получить теорему
Лиувилля, поскольку объем в фазовом пространстве составляет ω3Ν.
7 Зато он будет практически всегда зависеть от координаты qa.
126
Гл. 4- Динамика фазового пространства и эргодичность
Рис. 4.1. Сохраняющиеся потоки в 3D
Рассмотрим потоки, втекающие и вытекающие из малого объема AV в пространстве.
Изменение плотности внутри объема dp3O/dtAV должно быть равно потоку
материала через поверхность, взятому с обратным знаком, который по теореме Гаусса равен
-JVJdV~-VJAV.
Таким образом, мы получаем выражение
| + Σ^ + |^=^0. (4,,
Это и есть уравнение Л иу вилл я.
Что представляет собой dp/dt и чем отличается от dp/dt? dp/dt
называется полной производной ρ по времени; она представляет собой
эволюцию ρ для частицы, движущейся вместе с потоком. В трехмерном потоке
dp3D/d£ = dp/dt + ν · Vp = dp/dt + Σί=ι Xi(dp/dxi); первый член
представляет собой изменение ρ вследствие ее временной эволюции в фиксированной
точке, а второй член — это изменение р, которое почувствовала бы частица,
движущаяся со скоростью ν, если бы поле ρ не менялось с течением
времени. Уравнение (4.7) описывает точно такой же физический процесс, но в
6ЛГ-мерном фазовом пространстве.
Какую информацию дает нам теорема Лиувилля dp/dt = 0 о гамильтоно-
вой динамике?
• Потоки в фазовом пространстве несжимаемы.
В механике жидкостей, если производная плотности арзв/dt = 0, это
означает, что жидкость несжимаема. Плотность малого элемента
жидкости не меняется по мере ее движения; следовательно, этот малый
элемент не сжимается и не расширяется. Теорема Лиувилля означает тоже
4.1. Теорема Лиувилля
127
самое. Малый объем в фазовом пространстве может изменять форму,
он может вытягиваться, скручиваться или сворачиваться, но его объем
будет оставаться неизменным (рис. 4.2).
Рис. 4.2. Несжимаемый поток
Малый объем в фазовом пространстве может быть вытянут и сжат под воздействием
потока, но теорема Лиувилля показывает, что величина объема остается неизменной.
• Отсутствие аттракторов. В других динамических системах большая
часть состояний системы обычно являются переходными, и система в
конце эволюции может находиться в достаточно малом числе
состояний, называемых аттрактором. Движение маятника с затуханием
останавливается; его аттрактор — нулевая скорость и вертикальный
угол (упражнение 4.2). Затухающий маятник под воздействием внешней
силы начинает осциллировать с определенной амплитудой; его
аттрактор представляет собой окружность в фазовом пространстве. Может со-
здасться впечатление, что исчезновение этих неустойчивых состояний в
диссипативных системах происходит аналогично установлению
состояния равновесия в статистической механике, в которой на больших
временах все начальные состояния сводятся к статическому равновесному
поведению.8 Но это совсем не так, мы только что доказали, что переход
к состоянию равновесия в статистической механике происходит по
совершенно другому механизму! В равновесной статистической механике
все состояния равновероятны; переходные состояния являются
временными только потому, что они очень нетипичные, с течением времени
они исчезают, чтобы снова возникнуть в качестве редких флуктуации.
• Микроканонические ансамбли не зависят от времени.
Изначально однородная плотность в фазовом пространстве будет
оставаться однородной. В более общем смысле, поскольку энергия сохраняется,
8Мы неоднократно будем возвращаться к вопросу о том, каким образом необратимость
и затухание появляются в статистической механике, в оставшейся части этой книги. Это
всегда будет связано с введением различных приближений микроскопической теории.
128
Гл.4- Динамика фазового пространства и эргодичность
однородная плотность в малом энергетическом слое (Ε, Ε 4- δΕ) будет
оставаться однородной.
Теорема Лиувилля говорит нам о том, что поверхность равной энергии
может быть возмущена, но относительные веса различных частей
поверхности определяются их объемами в фазовом пространстве (см. рис. 3.1) и не
меняются. Это свойство является необходимым условием того, чтобы можно
было описывать равновесное состояние системы, не зависящее от времени, с
помощью микроканонического ансамбля.
4.2 Эргодичность
При усреднении по энергетической поверхности в статистической
механике делается предположение, впервые сформулированное Больцманом. Грубо
говоря, предположение состоит в том, что траектории на поверхности равной
энергии полностью перемешиваются с течением времени, т.е. поверхность не
разделяется на несколько несмешиваемых областей (рис. 4.3). Такая
полностью перемешанная система называется эргодической.9 Оригинальный способ
определения эргодичности был предложен Больцманом. Адаптируя его
определение, мы получаем
Определение 1: В эргодической системе, траектория практически
любой10 точки фазового пространства в некоторый промежуток времени
может подойти сколь угодно близко11 к любой другой точке (с
определенными координатами и импульсами) на поверхности равной энергии.
Математики различают эргодичность и смешивание; здесь мы предполагаем только
эргодичность. См. [81] для дальнейшей информации об эргодичности.
10Что означает практически любая? Формально это означает любая, за исключением
набора точек нулевого объема (нулевой меры). По существу, термин «почти»
употребляется здесь для того, чтобы избежать проблем с необычными, специфическими начальными
условиями, такими как частицы, движущиеся ровными рядами с совершенно одинаковыми
скоростями.
11 Почему это не то же самое, что и предположение о прохождении через любую точку
на поверхности равной энергии? Больцман предполагал изначально именно это. Однако
можно показать, что гладкая кривая (наша траектория, зависящая от времени) не
может заполнить целиком весь объем (поверхность равной энергии). В эргодической системе
траектория очень плотно покрывает поверхность равной энергии, но не полностью.
4.2. Эргодичность
129
Рис. 4.3. КАМ-торы и неэргодическое движение
Сечение Пуанкаре фазовой траектории движения Земли (рис. 4.8) в проблеме трех тел
(упражнение 4.4), где масса Юпитера примерно в 70 раз больше своего реального значения.
Замкнутые петли соответствуют траекториям, формирующим торы в фазовом
пространстве, сечение которых выглядит с нашей точки зрения как деформированные окружности.
Заполненная область сложной формы — это сечение одиночной траектории, выполняющей
хаотическое движение, она соответствует эргодической области. Можно показать, что
торы, каждый из которых также представляет собой эргодическую область, занимают
ненулевой объем в фазовом пространстве при малых массах Юпитера. Обратите внимание, что
данная система неэргодична в соответствии с нашими определениями. Траектории на торе
никогда не попадут в оставшуюся часть энергетической поверхности. Область Я,
сформированная хаотическими доменами, инвариантна по отношению к временной эволюции; она
имеет положительный объем, а область вне R также имеет положительный объем.
Наиболее важным следствием эргодичности является равенство среднего
по времени среднему по микроканоническому ансамблю.12
Интуитивно ясно, что, поскольку траектория (P(t),Q(£)) целиком
покрывает поверхность равной энергии, то среднее любой величины 0(Р(£), Q(t)) по
времени — то же самое, что и усреднение О по поверхности равной энергии.
Тем не менее, оказывается, что это утверждение достаточно сложно
доказать. С математической точки зрения проще работать с другим,
эквивалентным определением эргодичности. Это определение, грубо говоря, говорит о
том, что поверхность равной энергии не может быть разделена на непере-
мешиваемые подмножества. Давайте определим эргодическую компоненту R
12Если эргодическая система приходит к равновесию (т.е. не осциллирует вечно), среднее
по времени будет определяться поведением в положении равновесия; таким образом,
эргодичность подразумевает, что равновесные свойства равны средним по микроканоническому
ансамблю.
130
Гл.4. Динамика фазового пространства и эргодичность
множества13 S как его подмножество, остающееся инвариантным под
воздействием потока (таким образом, r(i) Ε R для всех r(0) Ε R).
Определение 2: Эволюция в подмножестве S является эргодической
в том и только в том случае, если все эргодические компоненты R в S
имеют либо нулевой объем, либо объем, равный объему S.
Мы можем дать объяснение на интуитивном уровне, почему эти два
определения эквивалентны (однако это сложно доказать). Траектория r(t)
должна лежать внутри одиночной эргодической подобласти. Если r(t) плотно
покрывает поверхность равной энергии (определение 1), то «нет больше
места» для второй эргодической компоненты с ненулевым объемом
(определение 2).14
И наоборот, если есть только одна эргодическая компонента R с объемом,
равным S (определение 2), то любая траектория, стартующая в Д, должна
бесконечно близко подойти ко всем точкам в R (определение 1), иначе точки
в Д, расположенные далеко от траектории (вне границы траектории), будут
представлять собой инвариантное множество ненулевого объема.
Используя второе определение эргодичности, мы можем доказать, что
средние по времени должны быть равны средним по микроканоническому
ансамблю. Давайте обозначим среднее по микроканоническому ансамблю
наблюдаемой О как (O)s, а среднее по времени с начальными условиями (Р, Q)
как O(P(0),Q(0)) = limT-*x> (1/Г) /0Т 0(P(t), Q(t)) d*.
Доказательство того, что среднее по времени О равно среднему по
ансамблю (О) s для эргодической системы (с использованием второго
определения), состоит из трех частей.
(1) Средние по времени на траекториях принимают постоянные
значения. Если О — «достаточно хорошая» функция (т.е. не принимает
бесконечные значения на энергетической поверхности), тогда
O(P(0),Q(0)) = O(P(t),Q(t)); (4-8)
среднее по времени в будущем не зависит от значений О в течение
конечного промежутка времени (0, t). Таким образом, среднее по времени
О постоянно вдоль траектории.15
13 Здесь S — поверхность равной энергии.
14Математикам нужно быть очень аккуратными в определениях и доказательствах,
чтобы исключить наличие различных инвариантных подмножеств, которые бесконечно близко
переплетены.
15Если бы мы могли показать, что б — непрерывная функция, то мы могли бы
использовать первое определение эргодичности для того, чтобы показать, что средние по времени
4.2. Эргодичность
131
(2) Средние по времени постоянны на энергетической
поверхности. Рассмотрим теперь подмножество Ra энергетической поверхности,
в котором О < а для некоторого значения а. Поскольку О постоянно
вдоль траектории, любая точка в Ra с течением времени переходит в
другую точку в области Да, таким образом, Ra является эргодической
компонентой. Если динамика на энергетической поверхности является
эргодической, это означает, что объем области Ra равен либо нулю, либо
объему всей энергетической поверхности. Следовательно, О принимает
постоянное значение на энергетической поверхности (за исключением
области нулевого объема), это значение равно а*, минимальному
значению, когда Да* занимает всю энергетическую поверхность. Таким
образом, равновесное, среднее по времени нашей наблюдаемой О не зависит
от начальных условий.
(3) Среднее по времени равно среднему по микроканоническому
ансамблю. Равно ли это равновесное значение среднему по
микроканоническому ансамблю по S? Нам нужно показать, что траектории не
задерживаются в некоторых областях энергетической поверхности
больше времени, чем должны (исходя из толщины энергетического слоя,
(см. рис. 3.1). Теорема Лиувилля в разделе 4.1 говорит нам о том, что
микроканонический ансамбль не зависит от времени, таким образом,
среднее по ансамблю равно среднему по времени и равно среднему по
ансамблю от среднего по времени. Но среднее по времени постоянно (за
исключением области нулевого объема), таким образом, в эргодической
системе среднее по ансамблю равно среднему по времени повсюду (за
исключением областей нулевого объема).16
постоянны на энергетической поверхности, поскольку наша траектория бесконечно близко
подходит к каждой точке на поверхности. Но непрерывность О не является очевидной.
Например, она не непрерывна для неэргодических гамильтоновых систем. Из рис. 4.3 мы
можем увидеть, рассматривая два различных начальных условия на двух близлежащих
точках, одна из которых находится внутри хаотической области, а другая — на КАМ-торе.
Средние по времени на этих двух траекториях будут совершенно различными, О будет
претерпевать скачок на границе.
16В формуле (0)s = (0(t))s = (0(P(i),Q(i)))s интеграл для среднего (-)s берется по
различным начальным условиям (P(0),Q(0)), но оценивается О в точке (P(£),Q(£)).
Усреднение по всем временам и использование того факта, что среднее по времени О = а*
132
Гл.4. Динамика фазового пространства и эргодичность
Можем ли мы доказать эргодичность нашей системы? Как правило, нет.17
Эргодичность была доказана для соударения твердых сфер, а также для
геодезического движения на конечных поверхностях с постоянной
отрицательной кривизной,18 но для многих систем, важных для практических
приложений, это невозможно. В самом деле^ в некоторых фундаментальных
проблемах действительно фигурируют неэргодические системы.
• КАМ-торы и проблема трех тел. Поколения математиков и
физиков работали над гравитационной проблемой трех тел.19 Основную
сложность представляло доказательство того, что взаимодействия
между планетами не запутывают их орбиты на больших временах.
Следует отметить, что «запутывание орбит» — это как раз то, что должно
происходить в эргодической системе! (Такой же объем фазового
пространства при постоянной энергии будет занимать конфигурация, при
которой Земля и Венера поменяются местами, и во много раз больший
— если Земля улетит в межзвездное пространство.) В прошлом веке20
была доказана так называемая теорема КАМ (теорема Колмогорова,
Арнольда и Мозера), показывающая, что (для малых межпланетных
взаимодействий и при определенных начальных условиях) планеты
движутся по слабовозмущенным эллипсам вокруг Солнца (КАМ-торы, см.
рис. 4.3). Другие начальные условия, сложным образом переплетенные
со стабильными, приводят к хаотическому движению. Упражнение 4.4
посвящено исследованию КАМ-торов и хаотического движения в
численном моделировании.
(практически повсюду), дает нам
{0)s = lim ψ f <0(P(t),Q(t)))sdi
Т-юо 1 JQ
4-moo^r°(IP(i)'W))di)5
= (0(P,Q)>s = (Os = a*. (4.9)
17To есть нельзя доказать для микроскопической динамики, но зачастую достаточно
легко бывает доказать эргодичность для численных алгоритмов, моделирующих достижение
состояния равновесия (см. раздел 8.2).
18Геодезическое движение на сфере представляет собой движение с постоянной
скоростью по большим кругам. Геодезия — это наиболее короткий путь между двумя точками.
В общей теории относительности падающие тела совершают геодезическое движение в
пространстве-времени.
19Ньютон решил гравитационную проблему двух тел, получив эллипсы Кеплера.
20 То есть в двадцатом столетии.
4.2. Эргодичность
133
Из теоремы К AM и изучения хаоса в этих системах мы узнаем, что га-
мильтоновы системы с малым числом частиц часто, даже практически
всегда, не являются эргодическими — в них возникают области,
представляющие собой торы ненулевого объема, которые не смешиваются с
оставшейся частью энергетической поверхности.
• Ферми, Паста, Улам и КдФ.
Вы можете предположить, что эти необычные эффекты возникают при
наличии небольшого числа частиц в системе. Если частиц будет много,
исчезнет ли это странное поведение? На одном из первых компьютеров,
разработанных для Манхэттенского проекта, Ферми, Паста и Улам
проверили это предположение [39]. Они рассматривали одномерную
цепочку атомов, связанных ангармоническими потенциалами и попытались
понять, термализуется ли такая система или нет. Ниже приведена
цитата из их работы: [39, р. 978] :
Скажем прямо, что результаты наших расчетов с самого
начала оказались неожиданными для нас. Вместо ожидаемого
непрерывного перехода энергии из первой в более высокие
моды, поведение системы оказалось совершенно иным.
Вместо постепенного появления более высоких мод энергия в
основном распределяется между небольшим количеством
определенных мод. Следовательно, очень сложно найти скорость
«термализации» или перемешивания в нашей задаче, а это
было изначальной целью наших расчетов.
Оказалось, что их система в непрерывном пределе описывается
нелинейным дифференциальным уравнением в частных производных
(уравнение Кортевега де Фриза), обладающим еще более
удивительными свойствами, чем уравнения, описывающие движение
планет. Это уравнение имеет бесконечное число сохраняющихся
величин. Может быть найдено точное решение этого уравнения,
представимое в виде комбинации волн, называемых солитонами.
Предполагалось, что данный тип неэргодичности, найденный в
уравнении Кортевега де Фриза, возникает только в специфических
одномерных системах. Обнаружение ангармонических локализованных мод в
универсальных трехмерных системах [117,136,138] означает, что
неэргодичность может возникать в достаточно реалистичных решеточных
моделях.
134
Гл.4- Динамика фазового пространства и эргодичность
• Фазы с нарушенной симметрией. Многие фазы обладают
нарушенной симметрией. В магнитах, кристаллах, сверхтекучих жидкостях и
жидких кристаллах, к примеру, нарушается эргодичность, поскольку
они могут находиться лишь в одном из многих основных состояний с
одинаковой энергией (см. гл. 9). Например, жидкость может попасть
в любую точку фазового пространства с заданной энергией, но
бесконечный кристалл (с идеальной решеткой атомов, ориентированных
определенным образом) никогда не сможет флуктуировать таким
образом, чтобы изменить свою ориентацию или (в трехмерном
пространстве) порядок атомов. Таким образом, трехмерный кристалл обладает
нарушенной ориентационной и пространственной симметрией.
Реальная система может находиться только в одной эргодической области
фазового пространства (определенном положении и ориентации
кристалла), и мы должны это учитывать при построении теории подобных
систем.
Стекла. Существуют другие примеры нарушения эргодической
гипотезы. Например, стекла покидают положение равновесия, когда
остывают, они больше не могут, согласно эргодической гипотезе, оказаться
в любой точке фазового пространства, но лишь осциллируют вокруг
одного из многих метастабильных стеклообразных состояний.
Используя определенные модели стеклообразных и неупорядоченных систем,
можно показать нарушение эргодичности, причем не только распад на
небольшое число макроскопических состояний, как в обычных фазовых
переходах с нарушением симметрии, но и на бесконечное число
различных, неупорядоченных основных состояний. Остается открытым
вопрос, действительно ли в стеклах происходит нарушение эргодичности
при бесконечно медленном остывании или они являются просто очень
медленными «замороженными» жидкостями.
Должны ли мы беспокоиться о том, что мы не можем доказать
эргодичность наших систем? Довольно увлекательно выявить пробелы в основах
статистической механики, особенно если они связаны с таким количеством
важнейших задач математики и физики. Мы подчеркиваем, что эти пробелы для
большинства задач представляют интерес лишь с чисто теоретической точки
зрения. Статистическая механика на удивление хорошо описывает большую
часть систем с огромным числом взаимодействующих степеней свободы.
Гл.4. Упражнения
135
В самом деле, степень точности здесь удивительная. В различных
приложениях статистической механики мы очень редко тщательно исследуем
вопрос применимости теоремы Лиувилля к данному ансамблю и предполагаем,
что эргодичность выполняется для равновесных термических систем.
Упражнения
Достижение состояния равновесия показывает, что в реальном
компьютерном моделировании методом молекулярной динамики действительно
достигается состояние, предсказанное нашей равновесной теорией.
В теореме Лиувилля и затухающем маятнике, а также Инвариантной
мере рассматриваются аналоги теоремы Лиувилля для диссипативных и
хаотических систем. В первом упражнении изучается, как нарушается теорема
Лиувилля при наличии диссипации, во втором рассматривается сложный,
сингулярный ансамбль, сформированный сворачиванием и растяжением
хаотического отображения.
Юпитер! и теорема К AM наглядно иллюстрируют нарушение
эргодичности в движении планет; эргодическая солнечная система была бы крайне
неудобным местом для жизни.
4.1 Достижение состояния равновесия.21 (Моделирование) Q)
Можем ли мы проверить, что реальная система атомов действительно
достигает состояния равновесия? Как мы упоминали в разделе 4.2, нам
неизвестно, как доказать эргодичность подобной системы. К тому же фазовое
пространство огромно, и невозможно обосновать эргодичность, проверяя в
компьютерном моделировании, что траектория движения частиц пройдет вблизи
всех возможных точек фазового пространства.
(а) Можем ли мы проверить, что траектория движения 20 частиц,
находящихся в кубическом сосуде объемом L x Lx L, подойдет сколь угодно близко к
любым возможным конфигурациям для данной системы? Будем считать
«близкими» или одинаковыми две пространственные конфигурации, если
соответствующие атомы для двух конфигураций находятся в одной и той же части сосуда
объемом (L/10) x (L/10) x (L/10). Сколько будет возможных различных
конфигураций в этом случае? Предположим, что у нас есть компьютер, который может
обработать 1012 конфигураций в секунду. Сколько лет займет проверка данного
числа конфигураций? (Подсказка: для удобства, в году приблизительно π· 107
секунд.
21 Это упражнение и сопутствующее программное обеспечение были разработаны
совместно с Кристофером Майерсом.
136
Гл.4· Динамика фазового пространства и эргодичность
Решая ньютоновские уравнения движения с использованием
молекулярной динамики, мы можем проверить предсказания равновесной теории,
основанные на предположении эргодичности. Скачайте программу по
молекулярной динамике и ее описание с сайта [132].
Проведите моделирование достаточно разреженного газа частиц
с постоянной энергией (микроканоническое), взаимодействующих с
потенциалом Леннарда-Джонса (приблизительно соответствующим
аргону или другому инертному газу). Пусть атомы стартуют с нулевыми
скоростями (нетипичное, неравновесное состояние), но в произвольной
конфигурации (за исключением того, чтобы два атома в начальной
конфигурации не перекрывались, то есть чтобы расстояние между двумя
атомами было не меньше |Δγ| = 1). Атомы, находящиеся вблизи, начнут
быстро двигаться, со временем соударяясь с другими, более отдаленными
атомами, до тех пор пока газ не придет в равновесное устойчивое состояние.
Мы вывели распределение компонент импульса (рх,ру,рг) в равновесном
идеальном газе (уравнение (3.19) раздела 3.2.2),
р{рх) = 7ШЩТехр ("2^г) · (410)
Это распределение импульсов верно также для систем взаимодействующих
частиц, таких как система, изучаемая в данном упражнении (мы покажем
это в гл. 6)
(Ь) Постройте гистограммы распределения импульсов в данной системе,
умножая для каждого из новых графиков среднее время расчета на четыре.
Пусть начальное среднее время расчета равно одному шагу по времени. На
малых временах эта гистограмма будет иметь максимум вблизи нуля, поскольку
в начальной конфигурации атомы покоились. Приближается ли гистограмма к
распределению Гаусса (уравнение 4.10) на больших временах? Оцените время
достижения состояния равновесия, зная зависимость распределения скоростей
от времени. Оцените конечную температуру из вашей гистограммы.
Частицы, строго подчиняющиеся уравнениям Ньютона,
самопроизвольно эволюционируют в соответствии с предсказаниями равновесной
статистической механики. С точки зрения динамической теории данный факт
кажется необычным, тем не менее, такое поведение типично для статистико-
механических систем. Однако на рис. 4.3 и в упражнении 4.4
рассматриваются системы взаимодействующих частиц (планет), которые не приходят к
состоянию равновесия.
Гл.4· Упражнения 137
4.2 Теорема Лиувилля и затухающий маятник. (Математика) (2)
Сила — 7Р, пропорциональная импульсу затухающего маятника,
замедляет его движение. Уравнение движения маятника имеет вид:
χ = р/М,
Ρ = ~ΊΡ — -К" sin (я)
На больших временах маятник будет стремиться к равновесному
стационарному состоянию с нулевой скоростью их = 0 (или множеству эквивалентных
позиций χ = 2τηπ, где т — целое число.) (р, х) = (О,0) представляет собой
аттрактор для затухающего маятника. Рассмотрим ансамбль затухающих
маятников, стартующих с различными начальными условиями, распределенными
с вероятностью р(ро, #о)· На больших временах все маятники придут в
равновесное стационарное состояние. Совершенно очевидно, что теорема Лиувилля
в данном случае не выполняется.
(a) Какие условия нарушаются в выкладках (4.5-4.7) для затухающего
маятника? Почему теорема Лиувилля к нему неприменима? Более конкретно, чему
равны частные производные др/др и dq/dql
(b) Найдите выражение для полной производной dp/dt для затухающего
маятника. Изучите эволюцию области фазового пространства с начальным
объемом А = Ар Ах. Как будет меняться ее объем с течением времени?
4.3 Инвариантная мера.22 (Математика, сложные системы) @
Теорема Лиувилля говорит нам о том, что при усреднении гамильтоно-
вой системы по времени все доступные точки в фазовом пространстве имеют
одинаковый вес. Как происходит эволюция негамильтоновых систем? Как
правило, подобные системы не проходят все возможные точки фазового
пространства, на больших временах они попадают в подпространство,
называемое аттрактором.
Рассмотрим логистическое отображение единичного интервала (0,1).23
f(x) = 4μχ(1 - χ). (4.12)
Рассмотрим траекторию, начинающуюся в точке хо, как последовательность
точек хо, f(xo), /(/(#о)), · · · > /'η'(χο), Одна итерация аналогична
одному шагу по времени (подобно одной итерации для отображения Пуанкаре в
упражнении 4.4 или одному шагу по времени At в алгоритме с дискретным
временным шагом в упражнении 3.12).
22 Это упражнение и сопутствующее программное обеспечение были разработаны
совместно с Кристофером Майерсом; см. [68]. Описание доступно на сайте [132].
23Мы также будем изучать это отображение в упражнениях 5.9, 5.16 и 12.9.
(4.11)
138
Гл.4. Динамика фазового пространства и эргодичность
Точечный аттрактор. При малых μ аттрактором нашего отображения
является фиксированная точка х* = f(x*)· Эта точка устойчива, если малые
возмущения затухают после ряда итераций:
\f(x* + e)-x*\*\f'(x*)\e<e, (4.13)
что происходит в случае, если производная [/'(я*)! < I.24
(а) Моделирование. Пусть μ = 0.2; выполните ряд итераций для / для
нескольких начальных точек из отрезка 0 < хо < 1 на ваш выбор и убедитесь,
что ноль является аттрактором. Постройте / и прямую у = χ на одном и том
же графике. Есть ли другие точечные аттракторы помимо χ = 0? Проделайте те
же самые вычисления для μ = 0.4 и 0.6. Каким будет результат?
Аналитика. Найдите ненулевой аттрактор χ*(μ) отображения (4.12),
покажите, что он будет стабильным при 1/4 < μ < 3/4. Если вы достаточно
целеустремленный человек или если у вас есть программа по вычислительной
алгебре, покажите, что существует устойчивый двухпериодический цикл при
3/4 < μ < (1 + ч/б)/4.
Системы с точечным аттрактором являются полной противоположностью
систем, для которых теорема Лиувилля выполняется. В системах с точечным
аттрактором все начальные точки являются переходными, за исключением
одной, системы с любыми начальными условиями приходят в конечном
итоге в одно и то же состояние, не зависящее от времени. (С другой стороны,
точно такое же поведение мы ожидаем в статистической механике на
макроскопическом уровне, система приходит в равновесное состояние, не зависящее
от времени! Все микросостояния эквиваленты, но подавляющее большинство
возможных микросостояний соответствуют одному и тому же
макроскопическому поведению в большинстве систем большого числа частиц.) Мы можем
задать тривиальный «равновесный ансамбль» для данной системы, который
состоит из одиночной точки х*\ среднее по времени любой величины 0(х)
будет составлять (О) = 0(х*).
При больших значениях μ поведение системы становится более сложным.
При μ = 1 система заполняет весь отрезок, динамика является эргодической
и аттрактор будет включать в себя все возможные состояния. Однако, в
отличие от гамильтоновых систем, не все состояния будут иметь одинаковый
вес (т.е. теорема Лиувилля не будет выполняться).
24 Для многомерных отображений достаточным критерием устойчивости является то, что
собственные значения якобиана по модулю меньше единицы. Непрерывная временная
эволюция dy/at = F(y) будет устойчивой, если dF/dy меньше нуля или если действительные
части собственных значений якобиана DF меньше нуля (для многомерных систем).
Гл.4- Упражнения
139
Мы можем найти среднее по времени для функций χ двумя способами:
усредняя по времени (проводя множество итераций отображения) или взяв
интеграл по χ с весом р(я), где р(х) — инвариантная плотность, a p(x)dx
представляет собой вероятность того, что точка траектории будет лежать в
промежутке между χ и χ + dx. Для того чтобы численно найти ее, проведем
около тысячи итераций (A^transient)? стартуя в некоторой типичной точке хо?25
для того чтобы прийти в точку ха, принадлежащую аттрактору, а затем
построим длинную траекторию из миллиона шагов {Ncyc\es). Гистограмма этой
траектории задает р{х). Усреднение с плотностью р(х) аналогично
усреднению по времени по траектории из миллиона точек. Мы называем р(х)
инвариантной, поскольку она не меняется при отображении /. Воздействуя / на
р, мы только уберем первую точку ха и добавим одну дополнительную точку,
принадлежащую аттрактору, в конце траектории.
(Ь) Инвариантная плотность. Пусть μ = 1; проведите ряд итераций / и
постройте гистограмму значений, задающих плотность р(х) точек вдоль
траектории, вы обнаружите, что точки χ вблизи границ попадаются значительно чаще,
чем точки вблизи центра.
Аналитика. Используя тот факт, что усредненное по времени значение р(х)
не зависит от времени, проверьте, что при μ = 1 плотность точек составляет
№= А—г <4л4>
Пу/ Х(1 — X)
Сравните теоретическую кривую с численной гистограммой. (Подсказка: точки
в окрестности dx точки χ переходят под воздействием / в окрестность dy =
f'(x) dx отображения у = f(x). Каждая итерация отображает две точки ха и
хь = 1 — ха в у, и таким образом, отображает плотность p(xa)|dxa| и р(хь)Их&|
в р(у) dy. Итак, вероятность р(у) dy должна быть равна p(xa)|dxa|+p(xb)|dx5|5
следовательно
p(f(Xa)) = p(Xa)/\f'(Xa)\ + р(*ь)/|/'Ы|· (4.15)
Подставьте уравнение (4.14) в уравнение (4.15). Вы должны будете
разложить многочлен на сомножители.)
То есть мы не должны выбирать в качестве начальной точки, например, неустойчивый
точечный аттрактор или неустойчивую периодическую орбиту!
140
Гл.4- Динамика фазового пространства и эргодичность
Математики называют плотность вероятности р(х) dx инвариантной
мерой аттрактора.26 Для того чтобы получить среднее по времени для
некоторой функции О(х), можно использовать тот факт, что
(0)= fo(x)p(x)dx. (4.16)
Для математиков мера является способом найти вес различных областей при
взятии интеграла, что в точности соответствует р(х) dx. Обратите внимание,
что для точечного аттрактора р(х) = δ(χ*).27
Пики инвариантной плотности. При значениях μ, незначительно
меньших единицы, инвариантная плотность нашего отображения приобретает
достаточно сложный вид.
(с) Найдите инвариантную плотность (как описано выше) при μ = 0.9. Пусть
длина вашей траектории будет достаточно большой Ncyc\es, а размер столбца
достаточно малым, чтобы можно было увидеть интересные структуры. Обратите
внимание, что аттрактор больше не заполняет весь интервал (0,1); найдите,
в каких пределах расположен аттрактор. Обратите внимание на пики функции
р(х) на границах аттрактора, а также внутри аттрактора. Отметьте наиболее
выдающиеся пики (рис. 4.4).
Рис. 4.4. Инвариантная плотность
Инвариантная плотность в хаотической области (μ = 0.95).
Аналитическое описание пиков.
Обратите внимание, что /'(1/2) = 0, таким образом, из уравнения (4.15)
следует, что p(f(x)) > p{x)/\f(x)\ имеет сингулярность вблизи χ = 1/2: все
точки вблизи χ = 1/2 под действием оператора / сжимаются и переходят
практически в одну точку. Дальнейшие итерации этой сингулярности
порождают большее число пиков, причем каждый из следующих пиков
уменьшается по величине и размывается.
(d) Пусть μ = 0.9. Рассчитайте /(1/2), /(/(1/2)), ... и сравните результаты
расчетов с пиками, полученными в задании (с). (Постройте пики, полученные
26Для некоторых аттракторов существует множество инвариантных мер, одной из них
является мера SRB (John Guckenheimer, приватное обсуждение).
27
В случае точечного аттрактора мера имеет точечный вес в точке х*.
Гл.4- Упражнения
141
аналитически и путем численных расчетов на одном и том же графике.)
Бифуркационная диаграмма. Эволюция аттрактора и его инвариантной плотности
при изменении μ для значений μ, близких к единице, представлены на
бифуркационной диаграмме на рис. 4.5. Одной из замечательных особенностей
данного графика являются четкие бифуркационные кривые,
сформированные пиками инвариантной плотности.
Рис. 4.5. Бифуркационная диаграмма в хаотической области
Обратите внимание на кривые, пронизывающие диаграмму. Они соответствуют пикам,
сформированным отображением точки χ = 1/2 (см. [68]).
(е) Бифуркационная диаграмма. Постройте аттрактор как функцию μ (вы
должны получить график, аналогичный изображенному на рис. 4.5) при 0.8 <
μ < 1. (Для значений параметра μ, взятых через равные промежутки δμ,
проделайте ntransient итераций, затем запишите траекторию для следующих Псу^
итераций и постройте график, выбирете ntransient и nCyCies больше 100, а δμ < 0.01.)
На том же самом графике, для тех же значений μ постройте первые восемь
отображений χ = 1/2, то есть, /(1/2),/(/(1/2)), Соответствуют ли
кривые, которые вы видите на рисунке, пикам? Что происходит на бифуркационной
диаграмме, когда эти кривые пересекаются? (См. [68].)
4.4 Юпитер! и теорема КАМ. (Астрофизика, математика) @
См. также сайт, посвященный Юпитеру: [123].
В основе статистической механики лежит эргодическая гипотеза: любая
система, состоящая из большого числа частиц, будет занимать всю
энергетическую поверхность. Мы рассматриваем большие системы, поскольку хорошо
известно, что многие системы с небольшим числом взаимодействующих
частиц не являются эргодическими.
Классическим примером неэргодической системы является Солнечная
система. Юпитер обладает достаточной энергией, чтобы отправить другие
планеты за пределы Солнечной системы. Большая часть фазового пространства
142
Гл.4- Динамика фазового пространства и эргодичность
энергетической поверхности соответствует таким конфигурациям, при
которых все планеты уйдут за пределы Солнечной системы, и только один
Юпитер продолжит вращаться вокруг Солнца. Таким образом, согласно эргоди-
ческой гипотезе, наша планета была бы обречена на долгую суровую зиму.
Итак, возникает большой вопрос: почему Земля не находится в межзвездном
пространстве?
Ученые, занимающиеся математической физикой, изучали эту проблему
на протяжение столетий. Для простоты они рассматривали проблему трех
тел: например, Солнце, Юпитер и Землю. Ранние (неудачные) попытки
заключались в применении теории возмущений к силам взаимодействия между
планетами. Гравитационная сила Юпитера, действующая на Землю, не
является малой. Если бы эта сила действовала как постоянный тормоз или
ускоритель, наша орбита была бы сильно искажена за пару тысяч лет. А раз это
не так, то воздействие Юпитера должно достаточно точно уравновешиваться
с течением времени ...
Данное упражнение в основном описательное и носит дискуссионный
характер, нужно ответить только на пару вопросов. Скачайте программу
Jupiter из списка компьютерных упражнений на сайте [132]. Убедитесь, что
Юпитер не выталкивает Землю за пределы Солнечной системы. Попробуйте
увеличить массу Юпитера до 35 000 масс Земли.
Снова запустите программу (или снова задайте массу Юпитера равной
317.83 массы Земли). Рассмотрите траекторию Земли, немного подождите и
попробуйте увидеть малые эффекты действия Юпитера на движение Земли.
Обратите внимание на то, что положение Земли сдвигается в зависимости от
того, находится Юпитер на той же стороне от Солнца, что и Земля, или нет.
(а) Насколько изменится расстояние от Земли до Солнца на протяжении
первого юпитерианского года (около 11.9 лет)? Насколько увеличится это
относительное изменение на протяжении следующей сотни юпитерианских лет?
Юпитер сворачивает орбиту Земли в подобие спирали вокруг некоторой
трубки. Эта орбита в физическом трехмерном пространстве является
проекцией соответствующей «трубки» в βΝ-мерном фазовом пространстве. Трубка
в фазовом пространстве существует уже для безмассовых планет.
Давайте рассмотрим вначале приближение невзаимодействующих планет
(т.е. предположим, что Земля и Юпитер обладают нулевой массой). В этом
приближении орбиты Земли и Юпитера становятся окружностями, или,
точнее, эллипсами. В топологии эллипс и окружность являются эквивалентными
(неразличимыми) объектами, растянутая резиновая лента произвольной
формы является окружностью, до тех пор пока она образует замкнутую кривую.
Подобным образом, тор (поверхность пончика) топологически эквивалентен
Гл.4· Упражнения
143
любой замкнутой поверхности, содержащей дырку внутри (подобной
поверхности кофейной чашки с отверстием в ручке). Убедитесь, что в приближении
невзаимодействующих планет в шестимерном фазовом пространстве орбита
Земли остается окружностью с точки зрения топологии.28
(Ь) Если пренебречь взаимодействием между планетами, то какой
топологической поверхности в восемнадцатимерном фазовом пространстве будет
соответствовать траектория движения трех тел? Возможные варианты: (i)
сфера, (ii) тор, (ш) бутылка Клейна, (iv) тор с двумя дырками и (ν) комплексная
проективная плоскость. (Подсказка: эта фигура определяется как
произведение двух окружностей, параметризованных двумя независимыми углами —
один представляет собой время в течение земного года, а другой — время на
протяжении юпитерианского года. Используйте рис. 4.6 и задание (с), если
мысленно это трудно себе представить.) Сколько раз Земля обернется вокруг
этой поверхности в течение каждого юпитерианского года? (Это отношение лет
называется числом кручения.^
Рис. 4.6. Тор
Орбита Земли вокруг Солнца после адиабатического увеличения массы Юпитера до 50000
земных масс.
Математическое решение задачи трех тел было получено в прошлом
столетии Колмогоровым, Арнольдом и Мозером. Их доказательство основано
на топологической целостности тора в фазовом пространстве (который
теперь носит название КАМ-тора). Они смогли доказать стабильность тора в
случае, если число кручения (отношение года на Юпитере и года на Земле)
28Подсказка: Постройте орбиту в плоскостях (ж, у), (ж,рх) и других. Она должна
выглядеть как проекция окружности на различные оси.
144
Гл.4· Динамика фазового пространства и эргодичность
является достаточно «хорошим» иррациональным числом 9 Более
конкретно, они смогли доказать, что при достаточно малых массах планет в фазовом
пространстве существует деформированный тор вблизи невозмущенного,
вокруг которого траектории планет движутся по спирали с теми же числами
кручения (рис. 4.6).
(с) Насколько можно увеличить массу Юпитера, чтобы орбита Земли
перестала выглядеть как тор (рис. 4.7)? Запускайте каждую новую массу с теми же
самыми начальными условиями, иначе ваш ответ будет зависеть от начального
положения Юпитера. Изучите удивительную траекторию, возникающую, когда
масса становится достаточно большой.
Рис. 4.7. Траектория Земли
Траектория Земли вокруг Солнца, если бы масса Юпитера внезапно увеличилась в 100
раз.
Таким образом, для «малых» масс Юпитера траектория в фазовом
пространстве немного искажается и закручивается, так что ее тороидальная
форма видна, если наблюдать лишь за положением Земли.
Тот факт, что тор не разрушается, представляет собой серьезную
проблему для статистической механики! Орбита неэргодически заполняет всю
Достаточно «хорошее» иррациональное число χ не может быть аппроксимировано
рациональным числом p/q с точностью, превышающей ос Ι/q : если задано хорошее
иррациональное число ж, существует такое С > 0, что \x — p/q\ > C/q2 для любых целых чисел ρ и
q. Практически все действительные числа являются хорошими иррациональными числами,
и теорема КАМ для них выполняется. Для тех читателей, которые слышали о разложении
в цепную дробь: лучшее приближение χ рациональным числом представляет собой обрыв
разложения в цепную дробь. Распространненным иррациональным числом является
золотое сечение, (1 + >/5)/2 = 1/(1 + 1/(1 + 1/(1 + ...))).
Гл.4· Упражнения
145
доступную энергетическую поверхность. Это является контрпримером к эр-
годической гипотезе Больцмана. Это означает, что средние по времени не
равны средним по энергетической поверхности; наш климат был бы очень
некомфортным, если бы наша орбита была эргодической.
Давайте теперь построим сечение Пуанкаре, чтобы исследовать торы и
хаотические области между ними. Если динамическая система возвращается
к окрестности начальной точки в фазовом пространстве, можно взять
поперечное сечение фазового пространства и рассмотреть отображение в себя
этого поперечного сечения (рис. 4.8).
Рис. 4.8. Сечение Пуанкаре
Сечение Пуанкаре тора представляет собой круг. Динамика на торе становится
отображением круга самого в себя.
Сечение Пуанкаре, показанное на рис. 4.8, является сечением плоскостью
в трехмерном фазовом пространстве. Можем ли мы свести нашу задачу к
рассмотрению сечения Пуанкаре в трех координатах фазового пространства? В
изначальной задаче фазовое пространство имеет восемнадцать размерностей.
В системе центра масс — двенадцать размерностей. Если мы ограничимся
рассмотрением движения на плоскости, она сведется к восьмимерной. Если
мы предположим, что масса Земли равна нулю (ограниченная задача трех
тел на плоскости), то у нас остается пять необходимых координат
(координаты ху Земли и скорости, а также положение Юпитера на своей орбите).
Если мы удалим еще одну координату, переходя во вращающуюся вместе с
Юпитером систему координат, наша модель будет задаваться четырьмя
числами: двумя координатами и двумя компонентами импульса Земли. Мы
также можем убрать еще одну переменную, учитывая сохранение «энергии». На
самом деле энергия Земли не сохраняется (поскольку Земля находится в
периодическом потенциале), но существует сохраняющаяся величина, подобная
энергии, во вращающейся системе отсчета, более детальное описание дано на
146
Гл.4. Динамика фазового пространства и эргодичность
сайте [123] под заголовком «Описание задачи трех тел». Таким образом,
задача сводится к трехмерной (и для малых масс Юпитера мы получаем тор,
вложенный в трехмерное пространство). Наконец, мы строим сечение
Пуанкаре. Мы рисуем точку траектории каждый раз, когда Земля проходит точно
между Юпитером и Солнцем. Мы откладываем расстояние до Юпитера по
горизонтальной оси и компоненту скорости по направлению к Юпитеру вдоль
вертикальной оси. Перпендикулярная компонента скорости не показана (она
задается значением «энергии»).
Выберите тип выводимого изображения Пуанкаре. Положите массу
Юпитера равной 2000 и проведите моделирование до 1000 лет. вы должны
увидеть два эллиптических поперечных сечений тора. При увеличении массы
(каждый раз задавая заново начальные условия) пронаблюдайте за тем, как
разрушаются поперечные сечения торов. Проведите моделирование до двух
тысяч лет при Mj = 22000Me, обратите внимание на то, что тороидальные
поперечные сечения превращаются в три окружности.
Фиксируя массу Mj = 22000Me, давайте изучим зависимость вида
планетарных орбит от начальных условий. Задайте хаотическую траекторию
(Mj = 22000Me) и изучите сечение Пуанкаре. Запустите траектории из
различных начальных положений при фиксированной «энергии» и постройте
сечение Пуанкаре.30 Вы сможете, таким образом, увидеть траектории на
двумерном сечении трехмерной поверхности с постоянной «энергией». Обратите
внимание, что, когда вы стартуете с некоторых начальных условий, в этом
случае в сечении Пуанкаре медленно образуются замкнутые кривые. Они
соответствуют КАМ-торам, которые сжимаются и скручиваются подобно
резиновым лентам. Продолжайте до тех пор, пока вы не обнаружите, что
некоторые орбиты могут заполнять всю область, что соответствует хаотическим
орбитам.31
(d) Если вы можете сделать снимок экрана, распечатайте сечение Пуанкаре
с начальными условиями как на КАМ-торах, так и в хаотических областях,
отметьте на рисунке, каким кривым они соответствуют. См. рис. 4.3, на котором
3 Это может быть сделано при нажатии кнопки на дисплее в зависимости от типа
реализации. В текущей реализации вы можете выбрать начальные координаты и скорость в
направлении Юпитера, перпендикулярная компонента скорости будет задана
автоматически с учетом сохранения «энергии». Если вы выбирете начальное положение, в котором
энергия не может сохраняться, то программа выдаст предупреждение.
31 Обратите внимание, что хаотические орбиты не выталкивают Землю из Солнечной
системы. Хаотические области вблизи бесконечности и вблизи наших начальных условий
не связаны между собой. Это может быть артефактом нашей модели с малым числом
измерений. В больших системах предполагается, что все хаотические области (на связанной
энергетической поверхности) связаны между собой посредством диффузии Арнольда.
Гл.4- Упражнения
147
представлен небольшой сегмент изображения, который вам следует
сгенерировать.
Оказывается, что доказательство того, что влияние со стороны
Юпитера компенсируется, основано на усреднении по поверхности тора. Если год
на Юпитере равен году на Земле, умноженному на рациональное число, то
орбита замыкается по прошествии нескольких лет, и невозможно провести
усреднение по всему тору, только по замкнутой спирали. Рациональные числа
кручения, как мы теперь знаем, приводят к хаосу, когда включены
взаимодействия между планетами. Большая хаотическая область, найденная вами
выше, соответствует невозмущенной орбите с числом кручения 3:1 (поэтому
вы получили три круга). Рациональные числа расположены очень плотно.
Между любыми двумя КАМ-торами существуют хаотические области всего
лишь потому, что между любыми двумя иррациональными числами
присутствуют рациональные. Более того, оказывается, что числа, очень близкие к
рациональным (числа Лиувилля, такие как 1 +1/10 +1/1010 +1/1010 +··.)>
также могут привести к хаосу. Было очень сложно показать, что множество
торов выживает несмотря ни на что. Вы можете себе представить, почему
понадобились сотни лет, для того чтобы понять это (особенно при отсутствии
компьютеров, дающих возможность графически проиллюстрировать торы и
хаос).
Глава 5
Энтропия
Энтропия — это наиболее важное понятие в статистической механике. Что
она представляет собой? Можем ли мы понять это на интуитивном уровне?
В этой главе мы увидим, что существуют три связанные друг с другом
интерпретации понятия энтропии.1
Энтропия является мерой беспорядка в системе] в разделе 5.2 мы
проиллюстрируем это, изучая энтропию смешения и остаточную энтропию стекол.
Энтропия характеризует величину недостатка информации о системе; в
разделе 5.3 мы рассмотрим различные примеры из теории неравновесных
систем и теории информации. Но начнем мы в разделе 5.1 с исходной трактовки
этого понятия, возникшей в девятнадцатом столетии при изучении тепловых
машин, холодильников и конца Вселенной. Энтропия является мерой
необратимых изменений в системе.
5.1 Энтропия как необратимость: тепловые машины
и смерть Вселенной
В начале 1800-х годов произошел прорыв в понимании устройства
двигателей и тепловых машин. В частности, ученых интересовал
фундаментальный вопрос: насколько эффективной может быть тепловая машина? Вопрос
Равновесие — слово, имеющее положительный оттенок, по-видимому, потому что оно
позволяет легко рассчитать различные свойства системы. Энтропия и величины,
которые она характеризует: беспорядок, недостаток информации, неопределенность — слова,
имеющие отрицательный оттенок, возможно, потому что энтропия мешает изготовлению
эффективных тепловых машин. Заметьте, что эти смысловые оттенки не всегда
оправданы; например, в теории информации, высокая энтропия Шеннона — это хорошо, она
соответствует лучшему сжатию данных.
5.1. Энтропия как необратимость: тепловые машины и смерть Вселенной 149
был очень непростым, поскольку для ответа на него необходимо было
открыть два важных закона:2 закон сохранения энергии и закон возрастания
энтропии.3
Для некоторых типов двигателей только сохранение энергии является
важным. Например, существуют электродвигатели, преобразующие
электроэнергию в механическую работу (движение электричек), а генераторы
преобразуют механическую работу (например, вращающейся ветряной мельницы)
в электроэнергию.4 Для подобных электромеханических двигателей
абсолютный предел задается законом сохранения энергии: мотор не может произвести
механическую работу, превышающую потребленную электроэнергию, а
генератор не может выработать больше электрической энергии, чем получает
механической. Идеальный электромеханический двигатель может
преобразовать всю энергию из одной формы в другую.
Паровые двигаетели более сложные. Ученые в начале 1800-х
обнаружили, что теплота является формой энергии. Паровой двигатель, приводящий в
действие электростанцию или локомотив старого образца, преобразует часть
тепловой энергии из горячего пара («горячего термостата» или
«нагревателя») в электроэнергию или механическую работу, но часть тепловой энергии
всегда теряется — выбрасывается в воздух или холодную воду для
электростанций («холодный термостат» или «холодильник»). Действительно, если
бы единственным ограничением работы теплового двигателя было
сохранение энергии, то можно было бы сделать двигатель, использующий тепловую
энергию камня, в конечном итоге получая полезную работу и очень холодный
камень.
Энергия явно становится менее полезной, как только она
превращается в теплоту. При распределении энергии между всеми атомами в большом
количестве материла не всю ее можно извлечь обратно для произведения
полезной работы. Энергия более полезна для генерации электричества,
когда она распределена между горячим паром и холодным озером, чем в виде
воды однородной, средней температуры. В самом деле, в большинстве
случаев, когда мы используем механическую или электрическую энергию, энергия
переходит в теплоту, возникающую из-за трения и других диссипативных
процессов.
2Это первый и второй закон термодинамики, соответственно (см. раздел 6.4).
3Некоторые педантичные люди сказали бы, что правильнее говорить, что энтропия
никогда не убывает, поскольку в равновесии энтропия системы постоянна. Тем не менее,
фраза «энтропия всегда возрастает» представляется более благозвучной.
4Электродвигатели — это по сути тоже самое, что и генераторы, только работающие в
противоположном направлении; при вращении турбины электромотора можно
генерировать электроэнергию.
150
Гл.5. Энтропия
В результате установления равновесия между горячим и холодным телами
в изолированной системе образуются два теплых тела. Этот процесс
является необратимым; невозможно вернуться в начальное состояние, не произведя
внешнюю работу над системой. Карно в своих публикациях 1824 года
обнаружил, что для изготовления максимально эффективной тепловой машины
нужно избегать необратимости. Тепловая машина, работающая в обратном
направлении, представляет собой холодильник; он использует механическую
работу или электричество для перекачки тепла из холодного термостата в
горячий. Полностью обратимая тепловая машина была бы способна
производить работу за счет перехода тепла из горячего термостата в холодный, а
затем использовать ту же самую работу для возвращения тепла в горячий
термостат.
Если бы у вас была тепловая машина более эффективная, чем обратимая,
вы могли бы ее запустить одновременно с обратимой тепловой машиной,
работающей как холодильник (рис. 5.1). Эта пара двигателей производила бы
работу по извлечению энергии из горячего термостата (как из нашего
вышеупомянутого камня) без поступления теплоты в холодный камень. После
использования этой работы мы могли бы перевести оставшуюся теплоту из
трения в горячий термостат, получив вечный двигатель, который совершал
бы полезную работу, ничего не потребляя. В термодинамике мы постулируем
невозможность подобных вечных двигателей.5
Рис. 5.1. Вечный двигатель и цикл Карно
Как использовать машину, производящую на Δ больше работы, чем в цикле Карно, для
построения вечного двигателя, производящего работу Δ за цикл.
При расчете свойств этой обратимой тепловой машины Карно нашел
фундаментальный предел для КПД тепловых машин и открыл то, что
впоследствии назвали энтропией.
Карно рассмотрел модель тепловой машины (рис. 5.2), состоящей
из поршня с внешним давлением Р, двух термостатов с высокой Т\ и
низкой Т% температурами, и некоторого газа внутри поршня. В течение
одного цикла количество теплоты Q\ поступает из горячего термостата,
5 Этот постулат представляет собой одну из формулировок второго закона
термодинамики. Он эквивалентен более стандартной формулировке возрастания энтропии.
5.1. Энтропия как необратимость: тепловые машины и смерть Вселенной 151
количество теплоты Qi уходит в холодный термостат, а поршень совершает
полезную работу W = Q\ — Q2· Для того чтобы тепловая машина Карно
была обратимой, нужно избегать следующих процессов: (i) трения, (ii)
соприкосновения горячих деталей машины с холодными, (iii) расширения
систем с высоким давлением за счет уменьшения объема систем с
низким давлением, (iv) слишком быстрого движения стенок контейнера
(приводящего к возникновению звуковых или ударных волн).
Рис. 5.2. Модель тепловой машины
Поршень с внешним приложенным давлением Р, движущийся через изолированный
цилиндр. Цилиндр можно поместить в термический контакт с одним из двух термостатов:
горячий термостат с температурой Т\ (скажем, горящий уголь на электростанции) и
холодный термостат при температуре Тг (скажем, вода в холодном озере). В течение одного
цикла движения поршня внутрь и наружу, количество теплоты Q\ поступает в систему,
производится механическая работа W, и количество теплоты Q? вытекает из системы в
холодный термостат.
Карно, будучи теоретиком, мог не принимать в расчет практические
трудности. Он рассматривал поршень, движущийся в течение цикла без трения
с бесконечно малой скоростью. Поршень использовался как для совершения
работы, так и увеличения и уменьшения температуры. Карно соединял газ с
термостатом, только когда его температура становилась равной температуре
термостата, таким образом, его тепловая машина полностью обратима.
Цикл Карно, в течение которого поршень движется наружу и внутрь,
состоит из четырех стадий (рис. 5.3).
• (а—>Ь) Сжатый газ соединен с горячим термостатом, поршень движется
наружу при постоянном давлении, количество теплоты Q\ поступает в
систему для поддержания постоянной температуры газа Т\.
152
Гл.5. Энтропия
• (b—>с) Поршень продолжает двигаться в ту же сторону при переменном
давлении, охлаждая газ до температуры Т^ без передачи тепла.
• (с—к!) Разреженный газ соединяется с холодным термостатом и
сжимается; газ расходует количество теплоты Q<i для поддержания постоянной
температуры Т^.
• (d—»а) Поршень сжимается, нагревая газ до температуры Т\ без
передачи тепла, возвращаясь в исходное состояние.
Рис. 5.3. Цикл Карно. P—V диаграмма
Четыре стадии цикла Карно: а—^Ь, поступление количества теплоты Qi при постоянной
температуре Ti; b—X:, расширение без обмена теплом; с—^d, отдача количества теплоты Qi
при постоянной температуре Тг; и d—»a, сжатие без обмена теплом, приведение в состояние
с исходным объемом и температурой.
Закон сохранения энергии говорит нам о том, что количество теплоты,
поступившее в поршень, Q\ — Q2, равно работе поршня W:
Q1=Q2 + W. (5.1)
Работа, производимая поршнем, есть интеграл силы, умноженной на
перемещение. Сила может быть представлена как площадь поверхности поршня,
умноженная на давление, а перемещение, умноженное на площадь
поверхности поршня, есть изменение объема, что дает следующий результат:
W = I Fax = j(F/A)(Adx) = I PdV = area inside FFloop. (5.2)
J J J cycle
Таким образом, если мы построим зависимость Ρ от V для четырех стадий
нашего цикла, то площадь внутри результирующей замкнутой кривой будет
представлять собой работу, совершенную поршнем над внешним миром (см.
рис. 5.3).
5.1. Энтропия как необратимость: тепловые машины и смерть Вселенной 153
\
Карно обнаружил, что все обратимые тепловые машины, работающие с
одними и теми же горячим и холодным термостатами, производит одно и
то же количество работы при заданном потоке теплоты (поскольку все они
абсолютно эффективные). Это позволяет рассматривать в качестве рабочего
тела простейшее вещество — одноатомный идеальный газ, для которого
известна связь между давлением, объемом и температурой. В разделе 3.5 мы
получили уравнение состояния идеального газа
PV = NkBT (5.3)
и увидели, что его полная энергия равна кинетической, задаваемой теоремой
о равнораспределении
E=^NkBT=^PV. (5.4)
При переходе а—»Ь, когда мы добавляем в систему количество теплоты
Qi, мы получаем P{V) = NkBT\/V. Используя закон сохранения энергии,
имеем
Q1 = Eb - Еа + Wab = ^PbVb - ^PaVa + J PdV. (5.5)
Ho PaVa = NUbT\ = РьЦ), таким образом, первые два слагаемые
сокращаются, при расчете интеграла в последнем слагаемом получаем
Ql = f^fLaV = NkBTliog(^. (5.6)
Аналогично,
(I)·
Q2 = NkBT2log -^ . (5.7)
Для изучения двух других стадий нашего цикла мы должны знать, как
ведет себя идеальный газ при расширении и отсутствии тепловых потоков
как внутрь, так и наружу. Опять же, по закону сохранения энергии на малом
участке пути, работа по малому изменению объема —PdV равна изменению
энергии di?. Используя уравнение (5.3), —PdV = -(NkBT/V)dV, и (5.4),
d^E = 3/2NkBdT, получаем dV/V = -3/2dT/T. Интегрируя обе части от b
до с, находим
таким образом, Vc/Vb = {Ά/Τ2)3/2. Аналогично, Vd/Va = (7ι/Τ2)3/2.
Получаем Vc/Vb = Vd/Va, и следовательно
Vc^VcVb^VdVb = Vb
vd vbvd vavd va' (by)
154
Гл.5. Энтропия
Мы можем подставить отношение объемов в расширенном и сжатом
состояниях (уравнение 5.9) в соотношения для потоков тепла (уравнения 5.6 и 5.7)
и получить
Щ-Яквь(%)-»*,*(%) -Щ. (5.10,
Это фундаментальный результат Карно. Его цикл и, следовательно,
любая обратимая тепловая машина удовлетворяют условию
| = |· (5.11)
Позднее ученые договорились определять6 изменение энтропии как
отношение потока тепла к температуре:
AStfiermo = ψ· (5·12)
Для обратимой тепловой машины поток энтропии Q\/T\ из горячего
термостата в поршень равен потоку энтропии из поршня в холодный термостат
Q2/22, энтропия не создается и не исчезает. Любая реальная тепловая
машина создавала бы7 дополнительную энтропию в течение цикла, никакая
тепловая машина не может уменьшить энтропию Вселенной.
Необратимое увеличение энтропии не является законом природы на
микроскопическом уровне. В частности, микроскопические законы природы
являются обратимыми во времени: законы, регулирующие движение атомов,
6 Термодинамическая энтропия определяется через поток тепла АЕ = Q при
фиксированной температуре Т, таким образом, наше определение температуры в статистической
механике 1/Т = dS/dE (уравнение 3.29) эквивалентно термодинамическому определению
энтропии 1/Т = AS/ΔΕ => AS = Q/T (уравнение 5.12).
7Например, малая утечка тепла из горячего в холодный термостат, составляющая δ за
один цикл, создавала бы
т2
энтропии в течение цикла.
5.1. Энтропия как необратимость: тепловые машины и смерть Вселенной 155
не зависят от того, движется ли время в прямом или обратном
направлении.8 Микроскопические законы не дают нам понятия о стреле времени.
Направление времени, при котором энтропия возрастает, есть наше определение
будущего.9
Это непонятное утверждение можно проиллюстрировать на примере
игры в бильярд. Если пренебречь трением, то траектории бильярдных шаров
также являются обратимыми во времени. Если бы скорости шаров вдруг во
время партии поменяли направление, они бы начали двигаться обратно до
тех пор, пока весь импульс не сконцентрировался бы в одном шаре, который
затем остановился бы при ударе о кий. В бильярде основным свойством,
позволяющим различить течение времени в прямом и обратном направлении,
является большая упорядоченность системы на начальных временах;
вначале весь импульс сконцентрирован в одном шаре, а познее он
распределяется между всеми шарами, участвующими в соударениях. Аналогично,
единственной причиной существования стрелы времени, определяющей различие
прошлого и будущего, является тот факт, что в начальном состоянии
Вселенная находилась в состоянии с необычайно низкой энтропией, и необратимо
движется к равновесию.10 (Можно предположить, что во время Большого
Взрыва энтропия была высокой. В самом деле, система была очень горячей
(высокая энтропия в пространстве импульсов), но плотной (низкая энтропия
в конфигурационном пространстве), и в сумме энтропия была меньше,11 чем
сейчас.)
8Если говорить более корректно, то законы природы инвариантны только при СРТ-
преобразовании: изменении направления времени (Т), пространственной инверсии (Р) и
замены материи на антиматерию (С). Радиоактивный бета-распад и другие силы слабого
взаимодействия не являются инвариантными при обратимости времени. Однако основным
парадоксом статистической механики является следующее: мы не можем сказать исходя
только из микроскопических законов, являемся ли мы материей, которая живет в прямом
направлении времени, или антиматерией, которая живет в обратном направлении времени,
в зеркальном отражении. Время, бегущее в обратном направлении, с макроскопической
точки зрения, казалось бы странным, даже если бы мы состояли из антивещества.
9В электромагнетизме тот факт, что волны испускаются источниками гораздо чаще,
чем сходятся в точке, в которой находится источник, тесно связан с проблемой различия
прошлого и будущего.
10Предположим, что по просшествии долгого времени, по космологическим меркам,
возникнет спонтанная флуктуация равновесной системы с образованием упорядоченного
состояния с низкой энтропией. В момент времени, предшествующий этому событию, с очень
большой степенью вероятности, будет казаться, что все наши законы макроскопической
физики идут в противоположном направлении. Наиболее вероятным путем образования
упорядоченного состояния из равновесия является обращенный во времени наиболее
вероятный путь перехода этого упорядоченного состояния обратно в состояние равновесия.
156
Гл.5. Энтропия
Различие температур и давлений, которые мы сейчас наблюдаем,
являются отголоском этого состояния с низкой энтропией в далеком прошлом.
Космические приложения необратимости возрастания энтропии также
обсуждались ведущими учеными XIX века. В 1854 году Гельмгольц предсказал
тепловую смерть Вселенной: он предположил, что со временем вся энергия
во Вселенной перейдет в теплоту, все температуры выравняются, и все вокруг
«погрузится в вечный покой». В 1895 году Г.Д. Уэллс в своем произведении
Машина времени [147, chapter 14] рисовал такую картину Земли в далеком
будущем:
... солнце, кровавое и огромное, неподвижно застыло над
горизонтом, оно походило на огромный купол, горевший тусклым светом
... Земля перестала вращаться, она была обращена к Солнцу
одной стороной, точно так же, как в наше время обращена к Земле
Луна. ... Не было ни прибоя, ни волн, так как не чувствовалось
ни малейшего дуновения ветра. Только слабая ровная зыбь слегка
вздымалась и опускалась, море как будто тихо дышало, сохраняя
еще признаки своей вечной жизни...
Этот мрачный прогноз подвергся пересмотру в последнее время. Оказалось,
что благодаря тому, что Вселенная расширяется, существуют другие
сценарии развития. В то время как смерть Солнца и звезд и в самом деле не
подлежит сомнению, возможно, что если жизнь эволюционирует таким образом,
чтобы приспособиться к окружающей среде, цивилизация, память и
мышление будут существовать еще неопределенно долгое время (упражнение 5.1).
Если предположить, что Вселенная остается в равновесном состоянии при
расширении, энтропия будет оставаться постоянной. В самом деле, энтропия фотонов остается
постоянной при расширении Вселенной (упражнение 7.15). Однако для ядер это неверно:
первичный ядерный синтез — образование тяжелых ядер из протонов и нейтронов
останавливается после образования небольшого количества легких элементов [146]. (Подобно
тому как в идеальном газе при резком расширении газ остается более горячим, чем
если бы он производил работу при адиабатическом расширении при наличии поршня, так
же и фотоны, испускаемые звездами, вырабатывающими железо-56 из водорода и гелия,
имеют более высокую частоту и температуру, чем фотоны, смещенные в красную сторону,
которые испускались при тех же самых процессах во время гипотетически равновесного
Большого Взрыва.) В работе [107] обсуждается, является ли основным источником
низкой энтропии при Большом Взрыве соответствующее специфическое начальное состояние
пространства-времени.
5.2. Энтропия как мера беспорядка
157
5.2 Энтропия как мера беспорядка
Второй интуитивной интерпретацией понятия энтропии является мера
беспорядка в системе. Мамы-ученые говорят своим детям, чтобы они
понижали энтропию, убираясь в комнатах. Интуитивно ясно, что жидкости имеют
большую энтропию, чем кристаллы, поскольку позиции атомов в них менее
упорядочены.12 Мы проиллюстрируем эту интерпретацию, вначале вычислив
энтропию смешения, а затем обсудив энтропию стекол при нулевой
температуре.
5.2.1 Энтропия смешения: демон Максвелла и осмотическое
давление
Взбивание яйца является типичным примером необратимости, вы не
можете снова отделить белок от желтка после перемешивания. Модель
взбивания показана на рис. 5.4 и 5.5: смешение частиц двух различных типов.
Здесь изменение энтропии при перемешивании является мерой увеличения
беспорядка.
Го ~
о о
о о
о
[о о
• · у\
•
•
• #
• ·|
Рис. 5.4. Неперемешанные атомы
Состояние перед перемешиванием: N/2 белых атома с одной стороны, N/2 черных атома
— с другой.
Рассмотрим сосуд, разделенный перегородкой на две равные части
объема V. На одной стороне расположены N/2 неразличимых белых атомов,
образующих идеальный газ, на другой — 7V/2 неразличимых черных атомов.
12Существуют интересные примеры систем, упорядочивающихся при увеличении
энтропии. В этих системах увеличение видимого порядка (например кристаллического или ори-
ентационного) приводит к увеличению беспорядка другого типа (например вибрационных
степеней свободы). Энтропия является точной мерой беспорядка, но не единственно
возможной и не всегда удобной.
158
Гл.5. Энтропия
1 · о
о
о
I ·
•
о
•
о
•
•
•
2V \
о
о
о 1
• 1
Рис. 5.5. Перемешанные атомы
Смешанное состояние: N/2 белых и 7V/2 черных атомов, распределенных в объеме 2V.
Конфигурационная энтропия этой системы (уравнение 3.55, без учета
энтропии импульсного пространства) равна
Summxed = 2 кв log[VN/2/(N/2)\], (5.14)
и представляет собой удвоенную конфигурационную энтропию N/2
неразличимых атомов в объеме V. Предположим, что черные и белые атомы имеют
одну и ту же массу и одинаковую полную энергию. Рассмотрим теперь
изменение энтропии при удалении перегородки и перемешивании двух наборов
атомов. Поскольку температура и давление одинаковы в обеих частях,
удаление перегородки не приводит к необратимому излучению звука или переносу
тепла, любое изменение энтропии происходит за счет перемешивания
черных и белых атомов. В смешанном состоянии13 энтропия увеличивается до
величины
Smixed = 2kB \og[(2V)N'2/(N/2)\], (5.15)
равной удвоенной энтропии N/2 неразличимых атомов в объеме 2V.
Поскольку log(2mx) = га log 2+log я, изменение энтропии за счет смешения составляет
Admixing = Smixed ~ ^unmixed = kB log 2^ = NkB log 2. (5.16)
Мы получаем выигрыш в энтропии fc#log2 каждый раз, когда помещаем
атом в произвольную из двух коробок. В более общем случае, мы можем
определить счетную энтропию:
Counting = &в^(число конфигураций) (5.17)
для систем с дискретным числом равновероятных конфигураций.
13Социальная политика здесь ни при чем. Энтропия смешения нескольких миллиардов
человек не будет заметна на глаз.
5.2. Энтропия как мера беспорядка
159
Этот тип дискретного выбора часто возникает в статистической
механике. В равновесной квантовой механике (для конечной системы) состояния
квантованы, и добавление новой частицы (невзаимодействующей с другими)
в одно из т вырожденных состояний добавляет к в log m к энтропии
системы. В теории передачи информации (раздел 5.3.2, упражнения 5.14 и 5.15)
каждый бит, передаваемый по каналу, может находиться в одном из двух
состояний, таким образом, энтропия случайного потока битов длины N
составляет AS = ksN log2.14
В более общем случае состояние, в котором может находиться одна из
частиц, существенно зависит от конфигурации остальных частиц. Тем не
менее, равновесная энтропия по-прежнему определяется логарифмом числа
различных состояний, в которых может находиться система. Например,
наша равновесная статистико-механическая энтропия 5βςωΐ(Έ) = kB^og(fl(E))
(уравнение 3.25) представляет собой логарифм числа состояний с энергией
Е, каждое из которых занимает объем h3N в фазовом пространстве.
Что случится, если убрать перегородку, разделяющую N/2 черных атомов
на одной стороне и N/2 черных атомов на другой стороне?
Начальная энтропия та же самая, что и в предыдущем случае
S'immixed = 2 кв log[VN/2/(N/2)\], но конечная энтропия теперь составляет
^mlxed = ^в log((2V)N /N\). Обратите внимание, что теперь в знаменателе
под логарифмом стоит ЛП, а не ((7V/2)!)2, как в уравнении (5.15), поскольку
все наши частицы теперь неразличимы. 7V! = {N)(N — l)(N — 2)(TV — 3)...,
a ((ΛΓ/2)!)2 = (N/2)(N/2)[{N - 2)/2][(N - 2)/2]...; они отличаются
приблизительно в 2N раз, что компенсируется изменением энтропии
вследствие удвоения объема. В самом деле, раскладывая логарифм по
формуле Стирлинга logn! « n log η — η, мы увидим, что энтропия на один
атом остается неизменной.15 Именно поэтому мы вводим сомножитель
Ν\ для учета неразличимых частиц в разделе 3.2.1; без него энтропия
уменьшалась бы каждый раз на 7Vlog2 при разделении контейнера на две
части.16
Каким образом мы можем на интуитивном уровне понять связь энтропии
смешения и термодинамической энтропии поршней и тепловых двигателей
в разделе 5.1? Можем ли мы использовать нашу энтропию смешения для
14Постоянная Шеннона ks определяется в разделе 5.3.2.
15 Если удерживать члены более высоких порядков в формуле Стирлинга, вы увидите,
что энтропия незначительно увеличивается при ликвидации перегородки. Это происходит
вследствие того, что становятся возможными флуктуации числа частиц на обеих
сторонах. См. упражнение 5.2 для малых систем, в которых увеличение энтропии за счет этого
эффекта является существенным.
16 Этот эффект часто называют парадоксом Гиббса.
160
Гл.5. Энтропия
производства работы? Для того чтобы это сделать, нужно различать два
типа атомов. Предположим, что перегородка на рис. 5.4 является мембраной,
непроницаемой для черных атомов, но позволяющей проходить белым.
Поскольку как черные, так и белые атомы представляют собой идеальный газ,
белые атомы распределились бы однородно, заполнив весь объем, в то время
как черные атомы были бы сконцентрированы с одной стороны. Это
привело бы к нарушению баланса давлений. Если полупроницаемая перегородка
использовалась бы как поршень, то она могла бы произвести работу,
увеличивая объем той части, в которой находятся черные шары, до тех пор пока
эта часть не заполнила бы весь объем.17
Что бы произошло в случае более активного разделения? Максвелл
предложил идею некоторого микроскопического разумного существа (позднее
получившего название Демон Максвелла), который управлял бы маленькой
дверцей между двумя частями сосуда. Если черный атом приближался бы
к дверце с левой стороны или белый атом — с правой, демон открывал бы
дверцу, в противоположной ситуации дверца была бы закрыта. С течением
времени эта сортировка привела бы к сегрегации системы и понижению ее
энтропии. Этот процесс не может происходить сам по себе в
термодинамике, поскольку работа такого демона требовала бы потребления энтропии. В
самом деле, с помощью подобного мысленного эксперимента можно
определить нижний предел того, сколько энтропии должно создать разумное
существо, чтобы осуществить процесс сортировки такого рода (рис. 5.6 и
упражнение 5.2).
5.2.2 Остаточная энтропия стекол: невыбранные дороги
В отличие от кристалла, каждый атом которого находится в определенной
позиции, при формировании стекла всегда возникают совершенно различные
конфигурации атомов. Таким образом, стекло обладает остаточной
энтропией, при стремлении температуры к абсолютному нулю энтропия стекла не
исчезает, но принимает значение fcBlogQgiasg, где £lg\ass — число
конфигураций при нулевой температуре, в которых может оказаться стекло.
Что такое стекло? Стекла неупорядоченные, подобно жидкостям, но
твердые, подобно кристаллам. Они не находятся в состоянии равновесия, они
образуются при остывании жидкостей, слишком быстром для возможности
17Такие полунепронецаемые мембраны достаточно распространены, но не для газов, а
для разбавленных растворов ионов в воде, некоторые из которых могут проходить через
мембрану, а другие — нет. Результирующая сила давления на мембрану называется
осмотическим давлением.
5.2. Энтропия как мера беспорядка
161
Рис. 5.6. Ионный насос
Реализацией демона Максвелла в биологии является Na+/ К+-АТФазз>1 фермент,
встроенный в мембраны практически каждой клетки в нашем организме. Этот фермент
поддерживает повышенную концентрацию ионов калия (К+) внутри клетки и ионов натрия
(Na+) снаружи. Фермент обменивает два иона К+, поступающих снаружи, на три иона
Να+, находящихся внутри, используя в качестве топлива одну АТФ (аденозин с тремя
фосфатами), превращающуюся в АДФ (два фосфата). Если вы едите слишком много соли
(Na+ C/~), то избыточные ионы натрия в крови увеличивают осмотическое давление на
клетки, увеличивают количество воды в крови и повышают ваше кровяное давление. На
рисунке (Toyoshima и др., © Nature 2000) показана структура аналогичного фермента —
кальциевой АТФазы [26]. Линией показано изменение ее формы при удалении двух ионов
Са+.
формирования равновесного кристаллического состояния, вы хорошо знако-
1 О
мы со стеклами, сделанными из кремния, такими как оконное стекло и
Ругех™.19 Вы также сталкивались с молекулярными стеклами, такими как
леденцы (стекла, сделанные из сахара). Многие другие вещества (даже
металлы) могут перейти в стеклообразное состояние при быстром остывании.
Как определить остаточную энтропию стекла? Во-первых, нужно оце-
90
нить энтропию жидкости в состоянии равновесия, и затем измерить поток
энтропии Q/T из стекла в процессе остывания из состояния жидкости до
абсолютного нуля. Разность
18Окна сделаны из натровой извести (кремния (SiCb), смешанного с оксидами натрия и
кальция).
19 Ругех™ представляет собой боросиликатное стекло (оксиды бора и кремния) с
малым коэффициентом теплового расширения, оно используется для изготовления мерных
кружек, которые не трескаются при наполнении кипящей водой.
20 Можно получить SiiquidCTi), медленно нагревая кристалл от абсолютного нуля и
измеряя поступающее в систему J0 £ dQ/T.
162
Гл.5. Энтропия
^residual = *Sliquid(7>) ~ / f~JTat = ^liquid№) ~ / ψ~^ΤάΤ (5.18)
задает остаточную энтропию.
Какова остаточная энтропия типичного стекла? Остаточная энтропия
составляет порядка кв на одну молекулу стекла (например, S1O2 или
молекулу сахара). Это означает, что число возможных конфигураций в
стеклообразном состоянии eslkB огромно (упражнение 5.11).
Как можно измерить число возможных стеклообразных состояний
системы, которые она не выбрала?
В конце концов, стекло переходит в какую-то конкретную конфигурацию.
Каким образом можно использовать данные измерения потока тепла из
жидкости при ее переходе в стеклообразное состояние, для того чтобы определить
число Qgiass возможных стеклообразных состояний? Иными словами, каким
образом статистико-механическое определение энтропии *Sstat = кв log figiagg
связано с термодинамическим определением ASthermo = Q/ΤΊ
Для того чтобы ответить на этот вопрос, нам необходима упрощенная
модель того, как стекло выходит из состояния равновесия при остывании.21
Рассмотрим стекло как набор независимых молекул. Пусть каждая молекула
обладает двухъямной потенциальной энергией: при варьировании некоторой
внутренней координаты qi существует два минимума энергии с разницей в δι и
разделенные барьером V{ (рис. 5.7). Изменение этой внутреннней координаты
может соответствовать вращению молекулы сахара в леденце или сдвигу в
положении атома водорода в S1O2 в оконном стекле.
Рассмотрим поведение одной из этих степеней свободы с двухъямным
потенциалом. При охлаждении системы термическое возбуждение молекулы,
необходимое для преодоления потенциального барьера, происходит все реже
и реже. До тех пор пока скорость охлаждения Гсоо1 мала по сравнению со
21 Стеклование не является резким фазовым переходом. Жидкость становится все более
вязкой при остывании, ее динамика — все более медленной, до тех пор пока степень
остывания не становится слишком быстрой, для того чтобы атомы успевали перестраиваться для
поддержания состояния равновесия. В этот момент происходит плавный переход,
приводящий к тому, что эффективная вязкость становится бесконечной, а стекло — связанным.
Наша модель не очень хорошо подходит для описания самого процесса стеклования, но
она достаточно неплохо описывает термическое перераспределение (β - релаксацию) при
температурах ниже температуры стеклования, а также является прекрасной моделью в
квантовой динамике (туннелировании), описывающей свойства стекол при температуре
порядка нескольких градусов Кельвина. См. раздел 12.3.4 о том, насколько мало мы знаем
о стеклах.
5.2. Энтропия как мера беспорядка
163
Ы
►
«1
Рис. 5.7. Двухъямный потенциал
Модель потенциальной энергии для одной из координат ς» в стекле. Два состояния
разделены барьером V* с малой разницей в энергиях 6%. В равновесии атому в ехр(—6г/квТ) раз
менее выгодно находиться в верхней яме. В случае потенциальных барьеров с Vi ^> квТ
молекула большую часть времени будет совершать колебания в одной из ям и редко будет
переходить через барьер.
скоростью возбуждения, наша молекула будет оставаться в состоянии
равновесия. Однако при температуре Т{, когда эти скорости выравниваются,
переходы между двумя состояниями прекращаются, и молекула застывает в
каком-то определенном положении. Если скорость охлаждения ГСОО! очень
мала по сравнению с частотой молекулярных колебаний (как это обычно
бывает),22 то скорость возбуждения будет быстро меняться с изменением
температуры, и наша система перейдет в стеклообразное состояние в малом
диапазоне температур вокруг Гг.23 Число молекул, находящихся в верхней
потенциальной яме, равно фактору Больцмана е_(5'/*БГ', умноженному на число
молекул в нижней яме. Таким образом, молекулы, для которых δι » &βΤί,
будут преимущественно находиться в основном состоянии (и,
следовательно, практически в состоянии равновесия). Однако рассмотрим N молекул с
потенциальными барьерами, величина которых велика по сравнению с
разницей в энергии потенциальных ям δι <С квТ^. Когда стекло остывает, эти
молекулы одна за другой случайным образом замораживаются в одном из
22Время колебаний атома порядка 10~ секунд, а время охлаждения, как правило,
составляет от секунд до нескольких лет, таким образом, скорость охлаждения действительно
мала по сравнению с характерными временами на микроскопических масштабах.
23Это можно вывести напрямую, используя уравнение Аррениуса (раздел 6.6) для двух
переходов.
164
Гл.5. Энтропия
двух состояний (рис. 5.8). Оба состояния этих молекул будут примерно
одинаково заселены, когда равновесие нарушается, таким образом, каждое будет
добавлять примерно к в log 2 в остаточную энтропию. Таким образом, N
молекул, для которых Ti > δι/кв·, будут вносить вклад порядка fc#log2 ~ кв в
7*
Ц
п
η
ц
п
7*
Рис. 5.8. Дороги, не выбранные стеклами
Ветвящиеся пути стеклообразных состояний в нашей модели. Энтропия (как
статистическая, так и термодинамическая) пропорциональна числу ветвлений, которые проходит
стекло при охлаждении. Конкретное стекло будет двигаться по одной из траекторий на
этой сетке, тем не менее термодинамическая энтропия измеряет полное число состояний.
Меньше ли поток термодинамической энтропии AS = J dQ/T из
стекла, чем из равновесной системы? По-видимому, да, поскольку часть энергии
остается в стекле у молекул, которые находятся в верхних потенциальных
ямах. Равен ли этот остаток статистической остаточной энтропии?
Молекулы с квТг <С <Si> которые переходят в основное состояние раньше, чем
замораживаются, вносят тот же самый вклад в поток энтропии в термостат, как
и для равновесной системы. С другой стороны, каждая молекула с квТ » δι
не будет отдавать (в половине случаев) энергию δι в термостат, в отличие от
бесконечно медленного (равновесного) охлаждения. Поскольку при
равновесном охлаждении эта теплота была бы передана термостату при температуре
порядка δί/кв, недостающий поток энтропии для этой молекулы составляет
AQ/T ~ 6г/(6{/кв) ~ кв- Снова, каждая из iV молекул вносит порядка кв в
(экспериментально измеряемую) термодинамическую остаточную энтропию
*^thermo·
24Мы теряем коэффициенты порядка log 2, поскольку не учитываем молекулы, для
которых квТг ~ δι и которые частично застывают в потенциальных ямах с более высокой
энергией, но распределение между основным и возбужденным состояниями неэквивалентное.
Термодинамическая и статистическая энтропии, безусловно, количественно согласуются
при тщательном расчете, за исключением неравновесных эффектов.
остаточную статистическую энтропию S^at-
5.3. Энтропия как неопределенность: память и теория информации 165
Таким образом, поток тепла для конкретной конфигурации стекла
определяется числом дорог, не выбранных стеклом в его путешествии в
охлажденное состояние.
5.3 Энтропия как неопределенность: память и
теория информации
Наиболее общая интерпретация понятия энтропии — мера недостатка
информации о системе. Равновесное состояние системы обладает
максимальной энтропией, поскольку теряется вся информация о начальных условиях,
за исключением сохраняющихся величин. Максимум энтропии
соответствует максимуму недостатка детальной информации о системе. Энтропия
стекла или нашей смеси белых и черных атомов, есть мера числа состояний, в
которых могут находиться атомы и, следовательно, мера неопределенности
состояния системы.26 Данная интерпретация предполагает, что энтропия не
является свойством самой системы, а характеризует информацию о системе,
которой мы обладаем27 (представлена ансамблем различных возможностей),
что явным образом разрешает многие сбивающие с толку спорные
вопросы. Атомы в стекле находятся в некоторой данной конфигурации, которую
мы могли бы определить, используя некоторую футуристическую технику
рентгеновской голографии. Если бы мы так сделали, наша неопределенность
исчезла бы, и остаточная энтропия стала бы для нас равной нулю.28 В
принципе мы могли бы использовать наше знание о позициях атомов в стекле для
извлечения дополнительной работы из стекла, невозможной до измерения
позиций атомов (упражнение 5.2).
25 В теории информации используется альтернативный термин неопределенность,
который может быть спутан с соответствующим понятием из квантовой механики.
Неопределенность Гейзенберга не связана с энтропией.
26Опять же, энтропия является точной мерой недостатка информации о системе, но не
обязательно самой подходящей для любых целей. В частности, энтропия не
характеризует полезность информации. Изотермическое сжатие моля газа до половины его объема
уменьшает неопределенность на 1023 бит, что соответствует намного большему изменению
энтропии, чем при запоминании всех рукописных работ в истории человечества.
27Энтропия равновесной системы является исключительно свойством структуры
системы, поскольку информация, которой мы обладаем о системе, фиксирована (при нуле).
28Процесс рентгеновской голографии, естественно, должен был бы создавать как
минимум столько же энтропии в течение измерения, сколько теряется стеклом.
166
Гл.5. Энтропия
До этого момента мы ограничивались рассмотрением случая, в котором
неопределенность максимальна, то есть все возможные конфигурации
системы равновероятны. Как же быть с системами, некоторая информация о
которых нам известна, в которых некоторые конфигурации более вероятны, чем
другие? Можно сделать эффективное обобщение определения энтропии для
произвольных распределений вероятности, которое мы введем в разделе 5.3.1
для обычных статистико-механических систем. В разделе 5.3.2 мы покажем,
что эта неравновесная энтропия является общей мерой неопределенности для
множества различных систем и используется в большом количестве
приложений за пределами традиционной физики.
5.3.1 Неравновесная энтропия
Во втором законе термодинамики говорится о том, что энтропия
увеличивается, что подразумевает наличие определения энтропии для систем, не
находящихся в состоянии равновесия. В общем случае мы можем описать
нашу систему с помощью распределения вероятности р, характеризующего
анамбль состояний.
Давайте начнем с распределения вероятностей по дискретному набору
состояний. Из раздела 5.2.1 нам известно, что энтропия Μ равновероятных
состояний (уравнение 5.17) составляет S(M) = fc#logM. В этом случае
вероятность каждого состояния равна pi = 1/М. Если мы запишем S(M) =
—fcBlog(l/M) = — fc#(log(p{)), то получим достаточно приятное обобщение
для счетной энтропии в случае, когда щ не является константой:
^discrete = ~М1оёРг) = ~кВ ^Рг logPi- (5.19)
г
Мы увидим в разделе 5.3.2 и упражнении 5.17, что это обобщение энтропии
для неравновесных систем является корректным.
Что же будет в случае непрерывного распределения? Любое
неравновесное состояние классической гамильтоновой системы может быть описано с
помощью плотности вероятности р(Р, Q) в фазовом пространстве.
Неравновесная энтропия в этом случае принимает вид:
Snonequil = ~^в(1оёР) = ~кВ /pbgp
-кв I
JE
Ε<Η(Ψ,®)<Ε+δΕ
-^p(P,Q)logp(P,Q). (5.20)
5.3. Энтропия как неопределенность: память и теория информации 167
Для микроканонического ансамбля, в котором pequil — ^-/(ЩЕ)бЕ)^
неравновесное определение энтропии отличается от равновесного S = кв log Ω на
пренебрежимо малую величину кв log(SE)/N на одну частицу:29
Smicro = ~кВ bg Pequil = kB log(fl(E)SE)
= кв log(il(E)) + kB log(SE). (5.21)
В квантовых системах неравновесная энтропия записывается с
использованием матрицы плотности ρ (раздел 7.1):
^quantum =
-kBTr(plogp). (5.22)
Наконец, обратите внимание, что Snoneq и «Squantum определены для
микроскопических законов движения, которые (раздел 5.1) обратимы во времени.
Таким образом, мы можем предположить, что эти микроскопические
энтропии не будут зависеть от времени, поскольку на микроскопическом уровне
система не знает о том, в каком направлении по времени энтропия должна
увеличиваться.30 Никакой информации не теряется (в принципе) при
эволюции замкнутой системы с течением времени. Энтропия (и наш недостаток
информации о системе) возрастает только в теориях, в которых мы
игнорируем или исключаем некоторые степени свободы. Эти степени свободы могут
быть внешними (информация уходит в окружающую среду или термостат)
или внутренними (информация уходит в микроскопические степени свободы,
которые игнорируются в теории при огрублении масштаба).
5.3.2 Информационная энтропия
Понятие неопределенности является ключевым во многих областях!
Энтропия как мера неопределенности используется повсюду, начиная от
перемешивания карт (упражнение 5.13), заканчивая восстановлением изображений
с помехами. Для данных приложений связь с температурой не имеет
значения, таким образом, нет необходимости использовать постоянную Больцмана.
Вместо этого энтропия нормируется с постоянной ks = l/log(2):
29Произвольный выбор ширины энергетического слоя в микроканоническом ансамбле,
таким образом, связан с произвольным выбором нулевого значения энтропии в
классических системах. В отличие от (экстенсивного) сдвига вследствие изменения единиц фазового
пространства (раздел 3.5) этот сдвиг является микроскопическим.
30Вы можете это подробно показать в упражнениях 5.7 и 7.4.
168
Гл.5. Энтропия
Ss = -ks Y^Pi logpi = - Y^Pi log2Pi, (5.23)
г г
таким образом, энтропия измеряется в битах.31
Эта нормализация была введена Шенноном [134], и формула (5.23)
называется энтропией Шеннона в теории информации. Шеннон писал, что
эта энтропия в применении к ансамблю возможных сообщений или
изображений задает фундаментальный предел сжатия данных32 для
эффективного использования пространства дисков или каналов передачи информации
(упражнения 5.14 и 5.15). Файл данных с низкой энтропией очень
предсказуем. Имея некоторый поток информации, мы можем предсказать содержимое
данных в следующей порции с некоторой степенью достоверности, подобно
тому, как близнецы и супруги, давно состоящие в браке, часто заканчивают
предложения друг за друга. В передаче изображений, если последние шесть
пикселей были белыми, то изображаемая область может оказаться белым
фоном, а следующий пиксель — тоже белым. Нам необходимо лишь передать
или сохранить данные, которые не соответствуют нашим ожиданиям.
Энтропия характеризует степень неопределенности, насколько ошибочными будут
наши предсказания об оставшейся части сообщения.
Энтропия настолько полезна в различных отраслях, потому что она
является единственной в своем роде (непрерывной) функцией, обладающей тремя
ключевыми свойстами.33 В этом разделе мы расскажем, в чем заключаются
эти три свойства и почему они естественны для любой функции,
характеризующей неопределенность. Мы также увидим, что наша неравновесная
энтропия Шеннона удовлетворяет этим свойствам. В упражнении 5.17 вы сможете
показать, почему энтропия является единственной подобной функцией.
В качестве наглядного примера неопределенности предположим, что ваш
сосед по комнате потерял ключи и просит у вас совета, где их найти. Вы
хотите предсказать успехи соседа в поисках ключей, измеряя неопределенность с
помощью некоторой функции Si. Предположим, что есть Ω возможных мест
31 Каждый бит удваивает число возможных состояний Ω, таким образом, log2 Ω есть число
битов.
32Схемы сжатия данных без потерь (файлы с расширением gif, png, zip, и gz) убирают
избыточную информацию в оригинальных файлах, а их эффективность ограничена
энтропией ансамбля сжимаемых файлов (упражнение 5.15). Схемы сжатия файлов с потерями
(файлы с расширением jpg, mpg, и трЗ) также ликвидируют информацию, которая
предполагается несущественной для людей, смотрящих или слушающих файлы (упражнение
5.14).
33Единственная с точностью до констант ks или кв.
5.3. Энтропия как неопределенность: память и теория информации 169
Ah, в которых он мог оставить ключи, вероятность нахождения в которых
вы оцениваете как р^ = Р(А^), причем JZi pi = 1.
Какими тремя ключевыми свойствами должна обладать наша функция
неопределенности 5/(ρι,... ,Ρω)?
(1) Энтропия максимальна при равных вероятностях, если отсутствует
какая-либо дополнительная информация. Безусловно, лучшим планом для
вашего соседа было бы посмотреть вначале в наиболее вероятных местах, в
которых pi максимальна. Ваша неопределенность будет максимальной, если
все Ω мест имеют одинаковую вероятность:
Sl ( Ω'' " ' Ω ) > 5/^Ь "'' 'ΡΩ^ UnleSS Pi = n for aU *' (5*24^
Ω
Удовлетворяет ли энтропия Шеннона уравнению (5.24) и условию (I)?34
Заметим, что функция f(p) = — ρ logp является вогнутой (выпуклой вниз,
рис. 5.9). Для вогнутой функции среднее значение f(p) по набору точек pk
меньше или равно / от среднего по р^:35
й]ЕЛ»>*/(й2>)· (5-25)
Но это означает, что
<**«/(£ Σ j
Ω
26)
(2) Энтропия не зависит от состояний с нулевой вероятностью. Если
ключи не могут находиться в ваших ботинках (место Aq), to ваша степень
34 В упражнении (6.6) мы попросим вас показать, что энтропия Шеннона Ss имеет
экстремум при равных вероятностях. Здесь мы приводим более строгое доказательство, что
она имеет глобальный максимум, используя выпуклость χ log x (примечание 35).
35Уравнение (5.25) представляет собой неравенство Йенсена. Оно может быть доказано
методом математической индукции с использованием определения вогнутой поверхности
(уравнение 5.28). Для Ω = 2 положим А = 1/2, а = р\ и Ь = р2 и покажем, что /((pi +
Рг)/2) > (/(ρι) + /(ρ2))/2. Для произвольной Ω положим А = (Ω —1)/Ω, α = (Σι _1 рк)/(П —
170
Гл.5. Энтропия
0.4| ■ 1 ■ 1 ■ 1 ■ г
Рис. 5.9. Энтропия представляет собой вогнутую поверхность
При χ > 0, функция f(x) = —ж log ж является выпуклой вниз (вогнутой). Таким образом,
для 0 < λ < 1 линейная интерполяция лежит ниже кривой:
/ (λα + (1 - λ)6) > λ/(α) + (1 - λ)/(6). (5.28)
Мы знаем, что / вогнутая, поскольку ее вторая производная, — 1/ж, всюду отрицательна.
неопределенности не изменится, если вы включите вашу обувь в число мест,
в которых могут находиться ключи:
S/(pi, · · · ,ΡΩ-ι, 0) = S7(pi,... ,ρω-ι). (5.29)
Энтропия Шеннона обладает свойством (2), поскольку Ρω log Ρω —> 0 при
Ρω->0.
(3) Изменение энтропии для условных вероятностей. Это последнее
свойство нашей функции неопределенности требует введения нового
понятия условной вероятности.36
Для того чтобы помочь в поисках ключей, вы, наверное, спросите соседа,
где он был последний раз, когда видел ключи. Предположим, что существует
1), и 6 = ρςχ и покажем, что
/ \~~0~) = f { » П-1 + ΩΡΩ] * —f \~^Γ) + Ω/(ΡΠ)
\fc=l / fc=i
где мы использовали справедливость уравнения 5.25 при Ω — 1 для доказательства его
справедливости при Ω методом индукции.
36Если вы считаете обсуждение условной вероятности сложным, а третье свойство
функции неопределенности (уравнение 5.35) менее очевидным, чем первые два, то вы в хорошей
компании. Обобщения энтропии, модифицирующие третье условие, иногда бывают
полезными.
5.3. Энтропия как неопределенность: память и теория информации 171
Μ мест Βι, где он мог быть (открывал дверь комнаты, вел машину, находился
в подвальном помещении для стирки, ...) с вероятностями qi. Безусловно,
вероятность того, что ключи находятся в кармане пальто больше, если сосед
был на улице, когда видел ключи последний раз. Пусть гм = Р(Ак и В^) —
вероятность, что ключи находятся в месте fc, а последний раз их видели в
месте I. Пусть37
— условная вероятность того, что ключи последний раз видели вВ^,а сейчас
они находятся в А^. Естественно,
YJP{Ak\Bi) = Yjcki = l\ (5.31)
к к
что говорит о том, что где бы (в каком месте [£]) сосед ни видел ключи в
последний раз, сейчас они находятся где-нибудь с вероятностью единица.
Прежде чем вы спросите соседа, где он последний раз видел ключи, у вас
есть степень неопределенности Si(A) = 5j(pi,... ,ρη) о месте нахождения
ключей и степень неопределенности Sj(B) = 5/(ςι,... , дм) о том, где
ключи видели последний раз. Общая степень неопределенности об этих двух
вещах дается функцией степени неопределенности, примененной ко всем Ω χ Μ
условным вероятностям:
Si(AB) = 5/(γιι,γι2,...,γιμ,^2ι,···^ωμ)
= Si(cnqi, Ci292, · · ·, cim9m, 02ΐ9ι>..., cqmQm)· (5.32)
После того как сосед ответил на ваш вопрос, ваша степень
неопределенности о том, где в последний раз видели ключи, сводится к нулю (уменьшается
на Si (В)). Если ключи последний раз видели в прачечной (место В$),
вероятность, что ключи находятся в А&, становится равной с^ и ваша степень
неопределенности о том, где сейчас находятся ключи, составляет теперь
SI(A\Bi) = SI(cli,...,ciii). (5.33)
Таким образом, ваша общая степень неопределенности уменьшается с Sj(AB)
до Sj(A\Bi). Мы можем измерить полезность ваших вопросов как ожидаемую
величину уменьшения вашей степени неопределенности о том, где находятся
37Условная вероятность Р(А\В) (читается как «вероятность события А при условии
события β»), умноженная на вероятность события В, есть вероятность того, что произойдут
оба события А и Б, таким образом, Р(А\В)Р(В) = Р(А и В) (или Ckeqe = гы).
172
Гл.5. Энтропия
ключи. Ожидаемая степень неопределенности после того, как на вопрос
ответили, получается при добавлении веса qe — вероятности ответа — к каждому
ответу Bf.
(Si(A\B£))B = Σ QiSi{A\Bt). (5.34)
г
Это дает нам третье ключевое свойство функции степени
неопределенности. Если мы начнем с общего распределения АВ, а затем измерим В, будет
неплохо, если в среднем ваша общая степень неопределенности уменьшится
на изначальную неопределенность В:
(Si{A\Bt))B = Sj(AB) - S^B). (5.35)
Удовлетворяет ли энтропия Шеннона уравнению 5.35, свойству (3)?
Условная вероятность Ss(A\B£) = —fcsj^c^logc^, поскольку ск£ есть
распределение вероятностей для Ак мест при условии изначального
местоположения L Таким образом,
SS(AB) = -ks^2ckeq£\og(ckeqe)
м
= ~ks I Y^ckeqtlog(cke) -\-^2ckeqelog(qe) 1
V Μ ki J
= Σqe I ~ks Σсы los(c^) I - ks Σqe los(^) ΙΣ^)
t \ к ) t Xk )
= Y^qeSs(A\Be) + Ss(B)
£
= (Ss(A\B£))B + Ss(B), (5.36)
и энтропия Шеннона удовлетворяет условию (3).
Если А и В нескоррелированны (например, если они являются
результатами измерений в невзаимодействующих системах), то вероятность А не
изменится при измерении В, таким образом, Si(A\Bi) = SiCA). Тогда наше
третье условие предполагает Si(AB) = Si(A)-\-Sj(B); наша степень
неопределенности о невзаимодействующих системах аддитивна. Это просто-напросто
является условием того, что энтропия — экстенсивная величина. Мы
обсуждали, что энтропия слабо взаимодействующих систем в равновесии должна
быть аддитивной, в разделе 3.3. Наше третье условие подразумевает, что это
верно в общем случае для некоррелированных систем.
Гл.5. Упражнения
173
Упражнения
В упражнениях рассматриваются четыре основных аспекта энтропии.
Энтропия устанавливает фундаментальные пределы. Мы исследуем
энтропийные пределы мышления в Жизни и тепловой смерти Вселенной,
измерений в Сжигании информации и демоне Максвелла, вычислений в
Обратимом вычислении и памяти в Термодинамике черных дыр. Мы будем
упражняться в вычислении энтропийных пределов КПД тепловых машин в P-V
диаграмме и Холодильнике Карно.
Энтропия - это величина, возникающая при переходе к
макроскопическому описанию системы. Мы показали, что из инвариантности относительно
обращения времени следует, что при полном микроскопическом описании
замкнутой системы не может происходить потери информации, следовательно
энтропия должна быть постоянной величиной. Вы сможете в явном виде
показать это в упражнении Возрастает ли энтропия? Энтропия возрастает,
поскольку содержащаяся в начальных условиях информация быстро
становится иррелевантной вследствие хаотического движения, это наглядно
проиллюстрировано в Отображении «кот Арнольда» и численно (для дисси-
пативной системы) в упражнении Хаос, Ляпунов и возрастание энтропии.
Энтропия также возрастает в теориях, в которых при огрублении
масштаба пренебрегается микроскопическими степенями свободы, пример этого мы
увидим в упражнении Возрастание энтропии: диффузия.
Энтропия имеет также ощутимые проявления в экспериментах. В
Энтропии стекол мы покажем, как в эксперименте можно определить верхний и
нижний пределы энтропии, возникающие из-за огромной степени
неопределенности о конфигурации атомов в стекле при нулевой температуре. В
Резиновой ленте мы обнаружим, что энтропия случайного блуждания может
приводить к возникновению сил.
Энтропия является общей мерой неопределенности, с огромным
количеством приложений в различных областях. В упражнении Сколько раз нужно
перетасовать карты? мы используем ее для тасования карт (где
неопределенность является целью). В Информационной энтропии и Энтропии
Шеннона мы рассмотрим ключевую роль энтропии в теории передачи
информации и алгоритмах сжатия данных. Во Фрактальных размерностях мы
определим важную величину, характеризующую фрактальные множества в
диссипативных системах, близко связанную с энтропией. Наконец, в Выводе
энтропии вы воспроизведете знаменитое доказательство того, что энтропия
Шеннона является уникальной мерой неопределенности с тремя ключевыми
свойствами, изложенными в разделе 5.3.2.
174
Гл.5. Энтропия
5.1 Жизнь и тепловая смерть Вселенной. (Астрофизика) @
Фримен Дайсон [36] писал о том, как должна эволюционировать жизнь,
чтобы приспособиться к наступлению холода и темноты, ожидаемых при
тепловой смерти Вселенной.
Обычно под живыми организмами подразумеваются существа,
потребляющие энергию для того, чтобы выживать и размножаться. Конечно, так
говорить некорректно: энергия сохраняется, а не потребляется. Живые существа
препятствуют потокам энтропии, они используют источники энергии,
обладающие низкой энтропией (например, растения потребляют
высокотемпературную солнечную радиацию, а мы — шоколадные батончики), и выделяют
формы той же самой энергии с высокой энтропией (теплота тела).
Дайсон не интересовался вопросами выживания и размножения, его
интересовало мышление перед смертью Вселенной. Он предполагал, что разумное
существо генерирует определенное количество энтропии AS за одну мысль.38
Энергия, необходимая на одну мысль. Предположим, что существо
потребляет теплоту Q из горячего резервуара температурой 7\ и излучает его
в холодный резервуар температурой Τ*}.
(a) Чему будет равна минимальная энергия Q, требуемая для производства
одной мысли, выраженная через AS и Τ<ρ. Пусть температура Т\ очень большая.
Полезные формулы: AS = Q2/T2 — Qi/7\; Qi — Q2 = W (закон сохранения
энергии).
Время излучения энергии за одну мысль. Дайсон показал, используя
теорию, которую мы здесь не приводим, что мощность излучения нашего
разумного существа как производителя энтропии не превышает СТ^ то есть
константу, умноженную на температуру холодного резервуара в кубе.39
(b) Запишите выражение для максимального количества мыслей в единицу
времени dH/dt (обратно пропорционального времени At на одну мысль),
выражая его через AS, С и Т^.
Число мыслей экологически эффективного существа. Наша Вселенная
расширяется, радиус R растет приблизительно линейно с течением
времени t. Микроволновая фоновая радиация имееет характерную температуру
Каждая мысль может обладать произвольной сложностью, единственная энтропия,
которая с необходимостью должна быть сгенерирована, связана с записью ответа
(упражнение 5.3).
39Эта константа пропорциональна числу электронов в существе, таким образом, наш
ответ Δί — это время на одну мысль на один моль электронов.
Гл.5. Упражнения
175
©(f) ~ Д-1, которая понижается при расширении Вселенной, что
соответствует красному сдвигу вследствие эффекта Доплера. Экологически
эффективное существо, естественно, постаралось бы использовать как можно
меньше теплоты и выбрать таким образом, наименьшее возможное Τ*}. Оно не
может испускать тепло при температуре, меньшей Т2 = 0(t) = A/t.
(c) Сколько мыслей Η может произвести экологически эффективное
существо между текущим моментом времени to и бесконечностью. Выразите Η через
AS, С, XI
Бесконечное время: алчные существа. Дайсон хотел бы, чтобы его
существа были способны продумать бесконечное число мыслей перед концом
Вселенной, но потребить ограниченное количество энергии. Он предположил,
что его существа должны успеть продумать свои мысли до того, как
кончится мир, и что они выделяют энергию при температуре Тг(£) ~ Г-3/8, которая
уменьшается с течением времени, но не быстрее, чем θ(ί) ~ t~l.
(d) Покажите, что в схеме охлаждения Дайсона полное число мыслей
бесконечно, но полная потребляемая энергия конечна.
Мы должны отметить, что существует множество поправок к идеям
Дайсона. Могут возникнуть различные сложности, например, за счет наличия
квантовых пределов охлаждения и распада протона. Возможны различные
варианты, зависящие от того, по какому пути пойдет эволюция системы в
будущем. Большое сжатие (коллапс Вселенной самой в себя) потребует
адаптации к нагреву и давлению, в то время как темная энергия может привести
к ускорению расширения, и в конце концов наша Вселенная будет пустынной
и практически необитаемой.
5.2 Сжигание информации и демон Максвелла. (Информатика) @
Существует ли минимальная энергетическая стоимость измерения? В
этом упражнении мы опишем работу Беннетта [9], представленную в книге
Фейнмана [42, chapter 5].
Мы снова рассмотрим связь между информационной и
термодинамической энтропией. Можем ли мы сжигать информацию как топливо?
Рассмотрим очень экономичный тип цифровой записи, в которой один
атом используется для записи одного бита (рис. 5.10). Она представляет
собой набор ячеек, каждая из которых содержит один атом идеального газа.
Каждая ячейка разбита на две одинаковые части подвижной центральной
перегородкой. Если атом находится в ее верхней части, это соответствует
единице, если в нижней части — то нулю. Верхняя и нижняя стенки
представляют собой поршни без трения, которые могут быть использованы для
сдвигания атомов.
176
Гл.5. Энтропия
Если мы знаем положение атома в n-й ячейке, то мы можем сдвинуть
стенку, убрать перегородку и постепенно вернуть поршень в исходное
положение (рис. 5.11) — тем самым мы уничтожим информацию о нахождении
атома, но произведем полезную работу.
0
■
т
-τ-
0
|
т
-τ-
1
■
•
"ΤΟ
■
т
—τ-
0
■
т
-τ-
0 1
■ ■
•
т
-τ
ΓΙ
■
•
-τ-
0
■
•
—τ-
0
■
m
-τ-
0
■
m
—τ—
1
I
•
-τ-
0
I
Ш
-τ-
0
■
•
-τ—
Рис. 5.10. Экономичный тип памяти
Положение одного атома идеального газа кодирует один бит. Если он находится в верхней
половине ячейки с перегородкой, бит равен единице, в противоположном случае — нулю.
Верхняя и нижняя стенки перегородки представляют собой поршни, которые могут быть
использованы, для того чтобы задавать положение атомов или извлекать энергию из
сохраненных битов. Числа, написанные над ячейками, не являются частью нашей системы,
они всего лишь означают, какой бит соответствует данной позиции.
Рис. 5.11. Ячейка с подвижными стенками
Извлечение энергии из сохраненного бита состоит из трех стадий: сжатие пустой
половины коробки, ликвидация перегородки, отведение назад поршня и извлечение работы Ρ dV
из одного атома идеального газа. (Можно снова поместить перегородку, для того чтобы
вернуться в состояние, подобное исходному, но с большей неопределенностью.) В данном
процессе теряется один бит информации (какая именно сторона перегородки занята
атомом).
(a) Сжигание информации (рис. 5.12). Предполагая, что газ расширяется при
постоянной температуре Т, какую работу совершит атом при обратном движении
поршня?
Итак, это минимальная работа, требуемая для того, чтобы задать
состояние бита, которое в данный момент неизвестно. Однако известный бит может
быть перезаписан без затраты энергии (рис. 5.13).
(b) Перезапись бита. Задайте последовательность движений перегородки, а
также верхней и нижней стенок, обратимо преобразующих нулевой бит (атом
внизу) в единичный бит (атом наверху), без совершения над системой
дополнительной работы.
Гл.5. Упражнения
177
Рис. 5.12. Мишина, сжигающая информацию
Данный тип памяти может быть использован как тепловая машина. Если машина знает или
может угадать информацию, записанную в памяти, она может извлечь полезную работу в
обмен на потерю этой информации.
Рис. 5.13. Поршень, заменяющий ноль на единицу
Таким образом, единственное необратимое действие для данного типа
памяти происходит при потере информации о состоянии бита (что эквивалентно
тому, чтобы убрать, а затем снова вернуть на место перегородку).
(с) Потеря информации о состоянии бита. Предположим, что
местоположение атома в n-й ячейке изначально неизвестно. Чему равно изменение энтропии,
если убрать перегородку и удвоить объем, доступный атому? Рассчитайте как
термодинамическую энтропию (зависящую от кв), так и информационную
энтропию (зависящую от ks = l/log2).
Эта энтропия характеризует стоимость упущенной возможности извлечь
работу из бита (как в задании (а)).
Что не дает демону Максвелла использовать атом с неизвестным
расположением для выполнения работы? Демон должен сначала узнать, на какой
стороне ячейки находится атом. В ранних исследованиях предполагалось, что
178
Гл.5. Энтропия
существует минимальная энергетическая стоимость этого измерения, равная
энергии, полученной при уничтожении одного бита (задание (а)). Беннетт [9]
показал, что нет необходимости расходовать энергию в процессе измерения.40
Почему второй закон термодинамики при этом не нарушается?
(d) Демонические состояния. Известно ли состояние демона после
уничтожения бита?41 Чему равна его энтропия? Сколько энергии потребуется для
возвращения демона в исходное состояние при температуре Т? Нарушается ли при
этом второй закон термодинамики?
Демон может извлечь неограниченное количество полезной работы из
записи с неизвестной последовательностью битов, если он обладает достаточно
большим количеством внутренних состояний, для того чтобы запомнить
последовательность — в сущности, он может скопировать информацию на
другую, внутреннюю, последовательность ячеек. Но та же самая работа должна
быть затрачена для того, чтобы занулить эту внутреннюю пленку,
приготовив ее для нового использования.
Идеи Беннетта могут показаться очевидными, всегда необходимо
заплатить за энергию из термостата увеличением энтропии. Однако следствия этих
идей играют большую роль в теории вычислений (упражнение 5.3).
5.3 Обратимое вычисление. (Информатика) @
Существует ли минимальная энергетическая стоимость вычислений?
Это упражнение также основано на работе Беннетта [9] и
Фейнмана [42, chapters 5, 6].
Компьютер, созданный для общих целей, может быть построен из
определенных элементарных логических схем. Многие из этих схем уничтожают
информацию.
(а) Необратимые логические схемы. Рассмотрим схему «Исключающее
ИЛИ», показанную на рис. 5.14. Сколько бит информации теряется в
процессе действия этой схемы? Предполагая, что четыре возможных входных
параметров равновероятны, чему равна минимальная работа, требуемая для
проведения этой операции, если схема работает при температуре Т? (Совет:
подобно демону в упражнении 5.2(d), схема затрачивает энергию для
приведения системы в более определенное состояние.)
40Он моделировал демона как систему с двумя возможными состояниями (например,
другая ячейка, разделенная перегородкой). Если начальное состояние демона известно, то
можно скопировать состояние ячейки в ячейку демона, не затрачивая ни энергии, ни
энтропии при адиабатическом движении стенок и перегородки. Демон таким образом, может
узнать положение атома и извлечь работу из ячейки.
41 Имеется в виду, известно ли оно окружающему миру, а не только самому демону?
Гл.5. Упражнения
179
АШВ=(Различнь»€?)
Рис. 5.14. Схема «Исключающее ИЛИ»
Логическая схема «Исключающее ИЛИ» аналогична употреблению слов в разговорном
английском: либо А, либо В, но не оба одновременно. Схема «Исключающее ИЛИ»
выдает единицу (верно), если А и В различные, и выдает ноль (неверно) в случае, если они
одинаковые.
В ранних работах в этой области предполагалось, что данные логические
операции требуют определенных затрат энергии. Беннетт обнаружил, что
они могут быть сделаны без дополнительных энергетических затрат путем
добавления дополнительных выходов к схемам. Конечно, отслеживание этих
дополнительных выходов требует наличия дополнительной памяти —
происходит обмен энергетической стоимости на выигрыш в энтропии. Однако
результирующая схема теперь становится обратимой.
(Ь) Обратимая схема. Добавьте дополнительный выход к схеме
«Исключающее ИЛИ», который просто копирует состояние входа А (С = A, D = А 0 В).
(Эта схема называется Контролируемое Отрицание (C-NOT) — одна из трех
схем, которые Фейнман предлагал для создания универсальной вычислительной
машины, см. [42, chapter б])
Нарисуйте таблицу, задающую четыре выхода (С, D) данной схемы для
четырех возможных входов (А, В) = (00,01,10,11). Если мы зададим выходы
(С, D) схемы в качестве входов другой схемы «Контролируемое Отрицание»,
какая операция в результате будет произведена?
Полностью обратимый компьютер, таким образом, может быть
сконструирован из этих новых схем. Компьютер производит вычисление, затем аккку-
ратно копирует результат в буфер выхода, а затем производит обратное
вычисление. В обратимом вычислении вся информация о дополнительных битах
может быть повторно использована, как в задании (Ь). Единственная
энергетическая или энтропийная стоимость вычисления заключается в записи
ответа.
Эти рассуждения позже привели к идее квантовых компьютеров.
Квантовые компьютеры являются обратимыми по своей природе, и могли бы
стать гораздо более мощными для выполнения некоторых видов расчетов,
чем обыкновенные компьютеры.
ЛВ^
180
Гл.5. Энтропия
5.4 Термодинамика черных дыр. (Астрофизика) ©
Астрофизики длительное время изучали черные дыры — конечное
состояние массивных звезд, слишком тяжелых для того, чтобы сопротивляться
действию гравитации (упражнение 7.16). Когда вещество продолжает падать
в центр, в конечном итоге вторая космическая скорость может стать равной
скорости света. После этого падающее вещество не в состоянии даже
обмениваться информацией с внешним миром. Радиус черной дыры массой Μ
49
составляет
Ra = G—, (5.37)
где G = 6.67 · 10~8см3/гс2 — гравитационная постоянная, а с = 3 · 1010см/с
— скорость света.
Хокинг, используя методы квантовой механики и общей теории
относительности, рассчитал эмиссию излучения из черной дыры.43 Он получил
удивительный результат: черные дыры испускают излучение, аналогичное
излучению абсолютно черного тела при температуре
Не3
Thh = ^GMks' (5·38)
В соответствии с теорией Эйнштейна, энергия черной дыры составляет Ε =
Мс2.
(a) Рассчитайте удельную теплоемкость черной дыры
Теплоемкость черной дыры является отрицательной. То есть ее
температура уменьшается при добавлении энергии. В обычных материалах это
приводит к нестабильности. Холодные области будут поглощать теплоту и
становиться еще холоднее. Действительно, популяция черных дыр является
нестабильной, большие дыры будут поглощать маленькие.44
(b) Рассчитайте энтропию черной дыры, используя определение
температуры 1/Т = dS/dE и предполагая, что энтропия равна нулю, когда масса черной
дыры составляет Μ = 0. Выразите ваш результат через площадь поверхности
42Это радиус Шварцшильда горизонта событий для черной дыры, не обладающей
моментом импульса или зарядом.
43Ничто не может покинуть черную дыру, излучение возникает вследствие колебаний
вакуума снаружи черной дыры; эти колебания вакуума и являются источником частиц.
44Термически изолированный стакан ледяной воды также имеет отрицательную
теплоемкость. Поверхностное натяжение искривленной поверхности льда будет немного уменьшать
температуру сосуществования (см. раздел 11.3), чем больше теплоты поступает в систему,
тем меньше становится ледяной куб, тем больше он искривлен и тем ниже результирующая
температура [92].
Гл.5. Упражнения
181
А = 4nR%, измеренный в единицах планковской длины L* = y/hG/c? в квадра^
те.
Как это иногда случается, Бекенштейн вывел эту формулу для энтропии
несколько ранее, рассматривая аналогии между термодинамикой, теорией
информации и статистической механикой.
С одной стороны, когда черные дыры взаимодействуют или
обмениваются зарядом и угловым моментом, можно показать, используя классическую
общую теорию относительности, что площадь поверхности может только
увеличиваться. Таким образом, имело смысл предположить, что энтропия
может быть пропорциональна этой площади. Затем он обнаружил, что, если
вы имеете некоторое количество ненужного мусора с высокой энтропией, от
которого вы хотите избавиться, вы можете отправить его в черную дыру и не
вспоминать больше о нем. В самом деле, если считать, что энтропия
характеризует недостаток информации о состоянии системы, то как только материя
попадает в черную дыру, можно сказать, что наше знание о системе
полностью исчезает.45 (Более конкретно, энтропия черной дыры характеризует
недоступность информации о том, из чего она состоит.) Погружая
различные физические системы в черную дыру (теоретически) и измеряя
увеличение площади по сравнению с увеличением энтропии, он смог вывести эти
формулы исключительно с помощью методов статистической механики.
Мы можем использовать эти результаты, для того чтобы найти
фундаментальный предел для хранения памяти.
(с) Рассчитайте максимальное число битов, которые могут храниться в сфере
радиусом один сантиметр.
Наконец, в качестве одного из первых физических предсказаний теории
струн ваша формула для энтропии (задание (Ь)) была выведена
микроскопически для черных дыр определенного типа.
5.5 Р—V - диаграмма. (Термодинамика) (2)
Пусть одноатомный идеальный газ в сосуде под поршнем проходит цикл,
представленный на P-V - диаграмме на рис. 5.15.
Кривая а соответствует охлаждению при постоянном объеме при
взаимодействии с термостатом температурой Тс; кривая b соответствует нагреванию
при постоянном давлении при взаимодействии с термостатом температурой
2V, кривая с соответствует сжатию при постоянной температуре при
взаимодействии с термостатом температурой Т^;
45За исключением массы, момента импульса и заряда. Таким образом, предполагается,
что барионное число, например, не сохраняется в квантовой гравитации. Обсуждалось,
что, когда все барионы исчезают, то Дайсону трудно создать его вторичную частицу из
электронов и нейтрино (упражнение 5.1 ).
182
Гл.5. Энтропия
Какие из следующих шести утверждений являются верными?
1) Цикл обратим, во Вселенной не производится дополнительная энтропия.
2) Цикл действует как холодильная машина, использующая работу поршня
для перекачки энергии из холодного в горячий термостат, охлаждая холодный
термостат.
3) Цикл действует как тепловая машина, переводящая тепло из горячего в
холодный термостат и производящая положительную работу над внешним
миром.
4) Работа за цикл равна по модулю \W\ = PoVo |41og4 — 3|.
5) Теплота Qc, поступающая в холодный термостат, по модулю равно \QC\ =
(9/2)P0V0.
6) Сумма теплоты, поступающей из горячего термостата Qh, и
произведенной над газом работы W равна теплоте, поступающей в холодный термостат.
06мм V
Рис. 5.15. P—V - диаграмма
Полезные формулы: PV = NkBT; U = (3/2)NkBT; AS = Q/T; W =
— J PdV] AU = Q + W. Обратите внимание, что знаки различных слагаемых
зависят от направления потоков тепла, вы должны выбирать знак исходя из
физических соображений.
5.6 Холодильник Карно. (Термодинамика) ®
Размеры нашего холодильника составляют примерно 2мх1мх1м, а
толщина изоляционной прослойки порядка Зсм. Изоляция скорее всего сделана
из полиуретана с теплопроводностью около 0.02 Вт/м К. Пусть
температура внутренней части холодильника равна 270 /Г, а комнатная температура —
300 К.
(а) Чему равна мощность, утекающая через изоляционную прослойку
холодильника?
Гл.5. Упражнения
183
Наш холодильник работает при 120 В, максимальный ток составляет 4.75
А. Электродвигатель компрессора включается время от времени на несколько
минут.
(Ь) Предположим, что (i) мы не открываем дверь холодильника, (ii)
термические потери в основном происходят за счет утечки через полиуретан, а не через
изоляционную прослойку вокруг дверей, (iii) наш холодильник работает по
циклу, обратному циклу Карно. Какая мощность в среднем будет необходима для
работы холодильника? Какую долю времени должен работать электродвигатель
компрессора?
5.7 Возрастает ли энтропия? (Математика) ©
Второй закон термодинамики говорит о том, что энтропия всегда
возрастает. Однако мы можем показать, что в изолированной системе, вне
зависимости от того, стартует ли она в неравновесных условиях, энтропия,
рассчитанная при наличии полного микроскопического описания, остается постоянной
во времени.
Теорема Лиувилля говорит нам о том. что полная производная плотности
вероятности равна нулю. Вдоль траектроии системы локальная плотность
вероятности никогда не меняется. Плотность вероятности равновесных
состояний зависит только от энергии и их числа. Что-то тут не так. Если плотность
вероятности изначально неоднородна, как она может стать однородной?
Покажите, что
^ = -ν[/ωνι
где / — некоторая функция, а V = (P,Q) — 6ЛГ-мерная скорость в фазовом
пространстве. Таким образом (используя теорему Гаусса в 6ЛГ-мерном
пространстве), покажите, что J{df(p)/dt) dPdQ = 0, предполагая, что плотность
вероятности стремится к нулю для больших импульсов и координат, и /(0) = 0.
Покажите, что отсюда следует, что энтропия S = —кв Jplogp постоянна и не
меняется с течением времени.
В упражнении 7.4 мы увидим, что энтропия квантовых гамильтоновых
систем также постоянна. Некоторые глубокие истины не являются
микроскопическими, факт того, что энтропия возрастает — эмерджентное свойство.
184
Гл.5. Энтропия
5.8 Отображение «кот Арнольда». (Математика) ©
Почему мы думаем, что энтропия возрастает? Точки в фазовом
пространстве не движутся по кругу, они растягиваются, скручиваются и
сворачиваются в сложные структуры, в особенности в системах, в которых
выполняются законы статистической механики. Арнольд, подражая Шредингеру с его
котом, предложил следующую аналогию. Вместо того чтобы рассматривать
непрерывное преобразование фазового пространства самого в себя,
сохраняющее 6ЛГ-мерный объем, давайте изучим отображение квадрата на плоскости
η у. η самого в себя (рис. 5.16), сохраняющее площадь.46
Рис. 5.16. Отображение «кот Арнольда»
см. Рооп [108] и фильм на сайте [114].
Рассмотрим отображение (рис. 5.16)
r(:)=(*++;bd- <"·>
Проверьте, что Г сохраняет площадь. (Собственно говоря, это отображение
представляет собой умножение на матрицу Μ = (п). Чему равен ее
определитель?)
46Нелинейные отображения плоскости, сохраняющие площадь, часто рассматриваются
как динамические системы, сходные с гамильтоновыми. Сохраняющие площадь
отображения соответствуют сечениям Пуанкаре гамильтоновых систем (4.4), в которых площадь
взвешивается с величиной, обратной скорости, с которой система проходит через
поперечное сечение. Они, в частности, важны в изучении ускорителей частиц с высокой энергией,
где отображение задает мгновенный срез частиц после совершения одной орбиты вокруг
кольца.
Гл.5. Упражнения
185
Покажите, что оно берет квадрат η χ η (или изображение η χ η пикселей)
и отображает его самого в себя с периодическими граничными условиями.
(Делая некоторое количество вырезаний и вставок, его можно рассматривать как
отображение тора самого в себя.) Как для линейного отображения, найдите его
собственные значения и собственные векторы. Покажите, что небольшая
окрестность (например круг в центре картинки) будет вначале вытянута вдоль
направления, соответствующего иррациональному углу, в тонкую полоску (рис. 5.17).
Рис. 5.17. Растяжение отображения Арнольда
Малая круглая окрестность вытягивается вдоль иррационального угла под воздействием
отображения «кот Арнольда». Центр картинки находится в начале координат χ = О, у = 0.
Когда эта тонкая полоска достигает границы, она делится на две части.
В случае квадрата η χ η дальнейшие итерации растягивают и рассекают
начальный круг в тонкую линию, равномерно покрывающую плоскость.
В случае картинки, состоящей из пикселей, количество пикселей черного,
белого цвета и всех оттенков серого сохраняется, они просто так
перемешиваются, что картинка кажется однородного цвета. Таким образом, задавая
предел разрешения нашего измерения (ошибки округления в компьютерных
вычислениях, например) или вводя небольшую связь с внешним миром,
можно увидеть, что конечное состояние стремится к равновесию, что
противоречит утверждениям упражнения (упражнение 5.7).
186
Гл.5. Энтропия
5.9 Хаос, Ляпунов и возрастание энтропии. (Математика, сложные
системы) ©
Хаотические динамические системы существенным образом зависят от
начальных условий. Это часто описывают как «эффект бабочки» (согласно
Лоренцу, придумавшему аттрактор Лоренца): взмах крыльев бабочки в
Бразилии может с течением времени привести к торнадо в Техасе. В этом
упражнении мы рассмотрим эту сильную зависимость от начальных условий для
конкретной системы (логистического отображения)48 и охарактеризуем эту
зависимость с помощью показателей Ляпунова. Логистическое отображение
преобразует интервал (0,1) сам в себя:
/(χ)=4μχ(1-χ), (5.40)
где временная эволюция определяется как последовательность итераций
отображения:
х0, χι, Χ2, · ■ ■ = яо, Дхо), ДДхо)), · · · · (5.41)
В частности, при μ = 1 оно сворачивает вдвое единичный отрезок и
растягивает его (неоднородным образом), покрывая исходную область.
Математическое сообщество рассматривает динамические системы как
законы непрерывной динамической эволюции, так и дискретные
отображения.49 Растяжение и сворачивание, рассмотренное на примере
логистического отображения в данном упражнении, часто можно наблюдать в физических
системах, подверженных внешнему воздействию, в которых не выполняются
законы сохранения.
В этом упражнении мы рассмотрим значения μ вблизи единицы, при
которых движение является преимущественно хаотическим. Хаос часто
определяется как движение, при котором конечная конфигурация существенным
образом зависит от начальных условий. Две траектории, изначально
разделенные расстоянием €, как правило, с течением времени удаляются друг от
друга на расстояние eext, где λ — показатель Ляпунова для хаотической
динамики.
47Это упражнение и сопутствующее программное обеспечение были разработаны
совместно с Кристофером Майерсом.
48Мы также изучаем это отображение в упражнениях 4.3, 5.16 и 12.9.
49Сечение Пуанкаре (рис. 4.8) сводит непрерывную рециркуляционную динамическую
систему к отображению первого возвращения, позволяя рассматривать отображения и
законы непрерывной эволюции вместе. Подобное здесь напрямую неприменимо, поскольку
логистическое отображение (4.12) не является обратимым, оно не задается сечением
Пуанкаре гладкого дифференциального отображения. (Помните теоремы существования и
единственности из математики? Необратимость следует из единственности.)
Гл.5. Упражнения
187
Вначале задайте μ = 0.9. Возьмите две соседние точки, хо и j/o — #о + е,
расположенные между нулем и единицей. Исследуйте траектории
яо,/(яо),/(/(яо)),···,/^^) и yo,/(i/o), Насколько быстро они
расходятся? Почему они прекращают расходиться? Оцените показатель
Ляпунова. (Подсказка: е можно задать в несколько раз большим, чем
точность машинного вычисления (около Ю-17 для вычислений двойной
точности), если вы не находитесь вблизи максимума / в точке хо = 0.5.)
Многие гамильтоновы системы являются хаотическими. Две
конфигурации классических атомов или бильярдных шаров, начальные позиции и
скорость которых практически одинаковы, будут быстро расходиться, по мере
того как соударения будут увеличивать изначально небольшие различия в
углах соударений и скоростях. Это хаотическое растяжение, сворачивание и
перемешивание фазового пространства лежит в основе нашего объяснения
того, почему энтропия возрастает.
5.10 Возрастание энтропии: диффузия. @
Мы видели, что формально энтропия не возрастает для замкнутых
классических и квантовых систем с произвольным гамильтонианом. Однако мы
можем показать, что энтропия возрастает в большинстве используемых на
практике теорий с огрублением масштаба. Когда мы избавляемся при
интегрировании от некоторых степеней свободы, информация о начальных
условиях становится нерелевантной с течением времени. В данном упражнении
вы покажите, что энтропия возрастает в уравнении диффузии.
Пусть p(x,t) удовлетворяет уравнению диффузии др/dt = Dd2p/dx2.
Предположим, что плотность ρ и ее градиенты стремятся к нулю при χ =
±оо.50
Получите выражение для производной энтропии по времени
S = — кв f p(x)logp(x)dx и покажите, что она действительно возрастает с
течением времени. (Подсказка: проведите интегрирование по частям.
Вы должны будете получить интеграл от положительно определенной
величины.)
5.11 Энтропия стекол. (Физика конденсированного состояния) @
Стекла не находятся в состоянии равновесия. Если вы поместите стекло
в изолированный сосуд, оно нагреется (очень медленно), поскольку
микроскопические перестановки атомов будут понижать потенциальную энергию.
Таким образом, стекла не обладают четко определенной температурой или
теплоемкостью. В частности, потоки тепла при охлаждении или нагревании
50Также, вы можете предположить, что дпр/дхп log ρ стремится к нулю при χ = ±оо,
даже если log ρ стремится к — оо.
188
Гл.5. Энтропия
(dQ/dT)(T) будут варьироваться в зависимости от конкретного образца (но
их интегралы будут подчиняться закону сохранения энергии).
Томас и Парке сделали предположение (рис. 5.18), что удельная
теплоемкость стекла равна dQ/dT, т.е. измеренный поток количества теплоты из
стекла, деленный на изменение температуры термостата. Они обнаружили,
что удельные теплоемкости, измеренные таким образом, при нагревании и
охлаждении стекла, не совпадают.
Пусть исходная жидкость находится в состоянии равновесия при
температуре 325 °С как перед охлаждением, так и после нагревания (таким образом,,
ее энтропия Siiquid одна и та же в этих двух случаях).
(a) Остаточная энтропия стекол (уравнение 5.18) в эксперименте,
представленном на рис. 5.18, принимает большее значение при нагревании или
охлаждении? (Совет: используйте тот факт, что интегралы под кривыми
/0 е (dQ/dT) dT задают потоки тепла, которые в случае выполнения закона
сохранения энергии должны быть равны по модулю при нагревании и
охлаждении. На кривой нагрева на рис. 5.18 вес сдвигается в область
высоких температур, это приводит к увеличению или уменьшению
интеграла J{l/T){dQ/dT)dT?)
(b) Используя второй закон термодинамики (энтропия может только
возрастать), покажите, что в случае охлаждения и последующего нагревания
равновесной жидкости остаточная энтропия, измеренная при охлаждении, всегда будет
меньше, чем остаточная энтропия, измеренная при нагревании.
Ваше доказательство применимо к общему случаю любых систем, не
находящихся в состоянии равновесия. (Совет: рассчитайте поток энтропии из
стекла при остывании жидкости и ее переходе в стеклообразное состояние.
Сравните его с потоком энтропии из внешнего мира при нагревании стекла и
его переходе в жидкость. Жидкость находится в равновесии как в начальном,
так и в конечном состоянии, см. [79].)
Остаточная энтропия типичного стекла — порядка кв на одну молекулу.
Она характеризует, сколько различных атомных конфигураций материала
существует в «замороженном» состоянии.
(c) В моделировании методом молекулярной динамики с сотней
неразличимых частиц, предполагая, что остаточная энтропия составляет fc^log2 на один
атом, вычислите вероятность того, что два различных охлаждения в состояние
с нулевой энергией приведут к эквивалентным атомным конфигурациям (с
точностью до перестановок)? В системе с 1023 молекулами, с остаточной энтропией
fcelog2 на одну молекулу, сколько различных охлаждений потребуется для того,
чтобы снова вернуться в начальную конфигурацию с вероятностью 1/2?
Гл.5. Упражнения
189
Рис. 5.18. Удельная теплоемкость стеклования
Удельная теплоемкость стекла В2О3, измеренная при его нагревании и охлаждении [142).
Стекло сначала быстро охлаждается из расплава (500°С —> 50°С за полчаса), затем
нагревается, начиная с температуры 33 °С —> 345 °С, за 14 часов, охлаждается, начиная с
температуры 345 °С, до комнатной температуры за 18 часов (ромбы) и, наконец, снова
нагревается, начиная с температуры 35 °С —У 325 °С (крестики). См. [77].
5.12 Резиновая лента. (Физика конденсированного состояния) φ
На рис. 5.19 показана одномерная модель резины. Резина состоит из
длинных полимерных молекул, конформации которых в недеформированном
материале аналогичны траекториям броуновского движения. При растяжении
резины конфигурация молекул меняется, они вытягиваются в направлении,
параллельном приложенной внешней силе. Рассмотрим простую модель, в
которой молекулы состоят из N звеньев размером dy с равной вероятностью
направленных либо параллельно, либо антипараллельно к предыдущему
звену. Пусть расстояние между концами цепи равно L. Когда молекула
растягивается, L увеличивается, а энтропия молекулы уменьшается.
(а) Выразите энтропию данной системы через d, N и L. (Совет: сколько
существует способов разделения N звеньев на Λί, направленных вправо, и
N — Μ, направленных влево, при которых полная длина молекулы равна L?)
Рис. 5.19. Резиновая лента
Простая модель резиновой ленты с N = 100 звеньями. Начало полимера расположено
сверху, конец — снизу, вертикальные смещения приведены для наглядности.
190
Гл.5. Энтропия
Пусть внешняя среда находится в равновесии при температуре Т. Пусть
на молекулу действует внешняя сила, направленная вправо. Молекула будет
воздействовать на среду с равной и противоположно направленной
энтропийной силой F.
(b) Найдите выражение для силы F, с которой молекула воздействует на
внешнюю среду, выражая ее через энтропию термостата. (Совет: температура
термостата составляет 1/Т = dSbath/dE, а сила, умноженная на
перемещение — это энергия.) Используя тот факт, что длина L должна соответствовать
максимальной энтропии Вселенной, запишите общее выражение для F через
внутреннюю энтропию молекулы.
(c) Используя модель молекулы из задания (а), общее выражение из задания
(Ь) и формулу Стирлинга log(n!) « η log η — η, запишите закон для силы F(L)
нашей молекулы при больших N. Чему равна жесткость К в законе Гука F =
—KL для нашей молекулы для малых L?
В нашей модели отсутствует внутренняя энергия, эта сила носит
исключительно энтропийный характер.
(d) Если мы увеличим температуру нашей резиновой ленты, находящейся
под воздействием внешней нагрузки, растянется она или сократится? Почему?
В более реалистичных моделях резиновой ленты энтропия состоит
преимущественно из конфигурационной энтропии случайного блуждания и
энтропии колебательных степеней свободы молекул. Если мы растянем
резиновую ленту при отсутствии потоков тепла, то полная энтропия будет
оставаться практически постоянной. (Резина достаточно упругая, небольшое
количество необратимой энтропии создается в ряде последовательных растяжений
и сжатий, если деформация не очень резкая.)
(e) Верно или нет?
1) При растяжении резиновой ленты она будет охлаждаться.
Конфигурационная энтропия случайного блуждания будет уменьшаться, приводя к
уменьшению энтропии колебательных степеней свободы и, следовательно, к уменьшению
температуры.
2) При растяжении резиновой ленты она будет охлаждаться.
Конфигурационная энтропия случайного блуждания будет уменьшаться, приводя к увеличению
энтропии колебательных степеней свободы и, следовательно, к уменьшению
температуры.
3) При снятии внешней нагрузки с резиновой ленты она будет охлаждаться.
Конфигурационная энтропия случайного блуждания будет увеличиваться,
приводя к уменьшению энтропии колебательных степеней свободы и, следовательно,
к уменьшению температуры.
Гл.5. Упражнения 191
4) При снятии внешней нагрузки с резиновой ленты температура не будет
уменьшаться, поскольку энтропия не изменится
Эта более реалистичная модель подобна идеальному газу, который тоже не
обладает конфигурационной энтропией.
5) Аналогично идеальному газу, температура будет изменяться вследствие
работы, совершенной над системой.
6) В отличие от идеального газа работа над резиновой лентой будет
положительна, когда резиновая лента растягивается.
Вы можете проверить ваши выводы экспериментальным путем. Возьмите
резиновую ленту (лучше всего толстую и эластичную), поднесите ее к губам
(которые очень чувствительны к температуре), затем растяните ее и
отпустите.
5.13 Сколько раз нужно перетасовать карты? (Математика) ©
Сколько раз нужно перетасовать колоду из 52 карт, чтобы их порядок
стал случайным?
До сих пор не существует четкого ответа на этот вопрос, он зависит от
того, как рассчитывать количество информации, остающееся в картах.
Некоторые говорят, что необходимо семь перемешиваний, другие — что достаточно
шести.51 Рассмотрим вычисления, изложенные в работе [144], и
охарактеризуем возрастающую случайность, используя понятие информационной
энтропии.
Пусть вначале карты в колоде упорядочены (A4k, 24k, ..., KJk).
(а) Чему равна информационная энтропия перед перемешиванием? А после
того, как порядок становится абсолютно случайным?
Рассматривать перемешивание с математической точки зрения проще
всего в обратном порядке.52
Рассмотрим колоду после перемешивания. Каждая карта в колоде
попадает либо из верхней половины или из нижней половины колоды в начальный
51 Говоря более конкретно, когда число карт N —> оо, при некоторых способах измерения
информации происходит резкий переход вблизи 3/2 log2 Ny в то время как при других
способах измерения информация теряется постепенно, и большая ее часть исчезает при
log2 TV перемешиваниях.
52 При перемешивании карт вначале разделяют колоду на две части. В соответствии с
биномиальным распределением, вероятность выбрать η карт для верхней части составляет
2_52(5^). Затем карты из обеих частей сбрасываются в определенной последовательности,
причем вероятность того, что карта из данной части будет сброшена, пропорциональна
числу карт, остающихся в данной части. Вы можете проверить, что таким образом, любая
из 252 конфигураций при рассмотрении перемешивания в обратном порядке равновероятна.
192
Гл.5. Энтропия
момент времени. Перемешивание делает каждую из 252 возможных
конфигураций (число способов распределения карт по двум частям в начальный
момент времени) равновероятной.
(b) Пренебрегая вероятностью того, что два одинаковых перемешивания
могут привести к одной и той же конечной последовательности карт, чему равна
информационная энтропия после одного перемешивания?
Вы можете убедиться, что единственный способ, при котором два
перемешивания могут привести к одной и той же конечной последовательности,
это когда вначале сбрасываются все карты из нижней половины, а затем —
все карты из верхней половины.
(c) При каком количестве из 252 возможных перемешиваний вначале
сбрасывается вся нижняя половина, а затем — вся верхняя половина, оставляя порядок
карт неизменным. Отсюда, чему равна реальная информационная энтропия
после одного перемешивания? (Подсказка: используйте ответ, найденный вами
к заданию (Ь).)
Мы можем определить нижний предел числа перемешиваний,
необходимый для того, чтобы уничтожить всю информацию, предполагая, что
увеличение энтропии остается постоянным при дальнейших перемешиваниях.
(d) Снова, не учитывая вероятность того, что две различные
последовательности т перемешиваний приведут к одной и той же конечной
последовательности карт, рассчитайте, сколько перемешиваний понадобится для того, чтобы
превысить энтропию полностью случайной колоды?
5.14 Информационная энтропия. (Вычислительная математика,
математика, сложные системы) ©
Энтропия является мерой неопределенности состояния системы, мерой
недостатка информации. Она имеет огромное значение в технологии
коммуникаций: сообщения проходят через сетевые средства передачи информации,
сокращающие информационную энтропию для получателя.
Пусть ваш дедушка послал вам e-mail. Из заголовка сообщения вы видите,
что оно состоит из 1000 символов. Вы знаете, что каждый символ состоит из
8 бит, что дает 28 = 256 различных букв или символов.
(а) Предполагая, что все возможные сообщения от вашего дедушки
равновероятные (типичное сообщение будет выглядеть как С*те'!8\/[Ьеер]...), чему
может быть равно число N различных сообщений? Чему равен соответствующий
верхний предел Smax информационной энтропии ks log TV?
Ваш дедушка обычно пишет довольно скучные сообщения, они все
похожи друг на друга. Возможно всего 16 различных равновероятных вариантов
Гл.5. Упражнения
193
сообщений от него.53 После того как вы прочтете сообщение, вы так или
иначе забудете, в какой последовательности были расположены слова, вы будете
помнить лишь основную суть сообщения.
(Ь) Чему равно реальное изменение информационной ЭНТрОПИИ Ai>Shannoni
которому вы подвергаетесь, читая сообщение? Если ваш дедушка пишет одно
сообщение в месяц, чему равно минимальное число 8-битных символов в год,
которые потребуются для записи сообщений от вашего дедушки? (Вы можете
закодировать различные сообщения одним символом.) (Подсказки: ASghannon
— разница в энтропии до и после того, как вы узнали, каким из 16 возможных
было данное сообщение. Длина 1000 не имеет значение в этом случае.)
Замечание: это экстремальная форма сжатия данных с потерями, подобно
используемой в изображениях jpeg, анимации mpeg и аудио файлах трЗ.
Мы спрашиваем о числе символов в год, требуемых для оптимально сжатого
сигнала.)
5.15 Энтропия Шеннона. (Информатика) ©
Языки, на которых мы говорим, информационно избыточные: число
имеющих смысл английских предложений, состоящих из пятидесяти букв,
существенно меньше, чем 2650, а число различимых десятисекундных разговоров
по телефону намного меньше, чем число звуковых сигналов, которые
могут быть с помощью частот до 20 000 Гц.54 Это непосредственно наводит на
мысль о теории сжатия сигналов. Если вы можете перекодировать алфавит,
сократив наиболее общеупотребимые сочетания букв и увеличив длину более
редких, вы можете существенно сократить пропускную способность канала
связи, требуемую для передачи данных. (Это сжатие данных без потерь,
подобно zip, gz и gif.) Пусть некий язык АЪд! для передачи данных на
большие расстояния состоит только из трех звуков: громкого крика А, сильного
хлопока В и щелчка С. Пусть в типичном сообщении крики и хлопки
попадаются одинаково часто (р = 1/4), а щелчки в два раза более распространены
(р = 1/2). Предположим, что во всем остальном сообщения представляют
собой случайную последовательность.
53В каждом сообщении говорится о том, что они выиграли партию в бридж (с
вероятностью 50 на 50), о том, что они хотят, чтобы вы им чаще писали (каждый раз), и о том,
кто, по их мнению, выиграет чемпионат по баскетболу среди женских команд различных
колледжей в их районе (случайным образом выбирая одну из восьми команд в лиге).
54 В телефонах, например, не заполняется весь диапазон возможных частот: нижний
предел составляет 300-400 Гц, а верхний предел 3000-3500 Гц. Вы можете по-прежнему
понимать слова, эта грубая форма сжатия данных приводит только к потере невербальных
нюансов общения. (Paul Ginsparg, приватное сообщение).
194
Гл.5. Энтропия
(a) Чему равна энтропия Шеннона для этого языка? Более конкретно, чему
равна величина энтропии Шеннона — fcsX)pmlogpmt передаваемая за один звук
или символ?
(b) Покажите, что канал связи, передающий биты (единицы и нули), не
может передавать больше чем одну единицу энтропии Шеннона на один бит.
(Совет: для этого нужно сначала показать, что для N = 2п сообщений энтропия
Шеннона максимальна при рт = 1/N. Мы доказали это уже более сложным
образом (примечание 35 на стр. 169). В этом упражнении вы должны
показать, что это точка локального экстремума, используя множители Лагранжа
или непосредственно полагая рн = 1 — Σπι=ιΡ™>·)
(c) В общем случае покажите, что энтропия Шеннона задает минимальное
число битов, необходимых для передачи ансамбля сообщений. (Совет: сравните
энтропию Шеннона N оригинальных сообщений с энтропией Шеннона N
(коротких) перекодированных сообщений.) Рассчитайте минимальное число битов на
символ, требуемое в среднем для передачи сообщений для канала связи АЪ^!.
(d) Найдите схему сжатия (правило, которое переводит сообщение АЪ^! в
нули и единицы, которое может быть обратимо для восстановления
оригинального сообщения), удовлетворяющую пределу, найденному в задании (Ь). (Совет:
рассмотрите схему для кодирования сообщения, сжимающую один символ в
единицу времени. Не все буквы будут сжиматься в одно и то же число битов.)
Шеннон также вывел меру пропускной способности провода с помехами,
обсуждал возможные коды, корректирующие ошибки и т.д.
5.16 Фрактальные размерности.55 (Математика, сложные системы) @
В науке встречается большое количество различных странных множеств.
В статистической механике такие множества часто возникают в непрерывных
фазовых переходах при появлении самоподобных пространственных
структур (см. гл. 12). В хаотических динамических системах аттрактор (множество
точек, которые занимает система на больших временах, когда прекращается
переходный процесс) часто бывает фрактальным (подобный аттрактор
называется странным аттрактором). Эти множества зачастую разреженные и
изрезанные, с дырками на всевозможных масштабах длины, (см. рис. 12.2,
12.5 и 12.11).
Эти странные множества часто характеризуют с помощью понятия
размерности. Два совершенно не похожих друг на друга множества могут иметь
55Это упражнение и сопутствующее программное обеспечение были разработаны
совместно с Кристофером Майерсом.
Гл.5. Упражнения
195
одинаковую размерность. Считается, что путь случайного блуждания (в
пространстве трех и более измерений) может представлять собой двумерное
множество (примечание 7 на стр. 40), но он сильно отличается от поверхности.
Однако если два множества имеют различные размерности (определяемые
одним и тем же образом), то они совершенно точно будут различными.
Существуют разные способы определения размерности. Грубо говоря,
странные множества зачастую бывают пространственно неоднородными,
и определяемая размерность зависит от того, как взвешивать различные
части множества. В этом упражнении мы рассчитаем информационную
размерность (близко связанную с неравновесной энтропией) и емкость
(изначально носящую название размерности Хаусдорфа, а также иногда
называемую фрактальной размерностью).
Для генерации нашего странного множества наряду с более стандартными
множествами мы будем использовать логистическое отображение.56
/{χ) = 4μχ(1-χ). (5.42)
Аттрактор логистического отображения представляет собой периодическую
орбиту (нулевой размерности) при μ = 0.8 и хаотическую плотность с пиками,
заполняющую два интервала (единичной размерности) при μ = 0.957
При появлении хаоса при μ = /Zoo ~ 0.892486418 (упражнение 12.9) эта
размерность становится промежуточной между нулем и единицей, это
странное самоподобное множество называется аттрактором Фейгенбаума.
Как информационная размерность, так и емкость определяются через
число Рп занятых ячеек размера е в пределе е —> 0.
(а) Напишите программу, которая при заданном μ и множестве ячеек размера
6 делает следующее.
• Проводит сто или тысячу итераций / (для того чтобы попасть в область
аттрактора)
• Проводит большое число итераций A^tot. накапливая точки аттрактора.
(При μ < /Хоо вы можете просто проинтегрировать 2П раз, где η
достаточно большое.)
• При любом € строит гистограмму, характеризующую вероятность Pj того,
что точки попадут в j-\o ячейку.
• Возвращает множество векторов Pj[e].
Мы изучаем это отображение также в упражнениях 4.3, 5.9 и 12.9.
196
Гл.5. Энтропия
Вы можете протестировать вашу программу, задав μ = 1 (при
котором распределение должно выглядеть как р(х) = \/ку/х(\ — я), упражнение
4.3(b)) и μ = 0.8 (при котором распределение выглядит как две 5-функции,
каждая из которых содержит половину точек).
Емкость. Определение емкости мотивировано идеей, что необходимо по
меньшей мере
Wcover = V/eD (5.43)
ячеек размера eD, для того чтобы покрыть D-мерное множество объема V.58
Взяв логарифм от обеих частей, можно получить logA^cover ~ log V + Dloge.
Емкость определяется как предел
D . log iVcover / r л л ч
capacity = Jim , (5.44)
но сходимость медленная (ошибка составляет порядка log V/ log е). Более
быструю сходимость можно получить при расчете тангенса угла наклона в
зависимости log TV от log e:
П _1™dl°g7Vcover
■^capacity — 11Γ^
e-)O d log 6
= 1.mlogA^±i-log^
е-Ю l0g€i+l ~log€i
(b) На основе программы из задания (а) напишите программу для расчета
N[e], считающую количество непустых ячеек. Постройте зависимость Ampacity
из быстро сходящегося уравнения (5.45) от средней точки l/2(logei+i + log£i).
Сходится ли она к D = 1 при μ = 0.9? 59
Сходится ли она к D = 0 при μ — 0.8? Постройте эти две кривые, а
также кривую для μοο· Сходится ли последняя к D\ « 0.538, емкости аттрактора
Фейгенбаума, известной из литературы? Насколько малое отклонение от /Хоо
требуется взять, для того чтобы увидеть переход к целым размерностям при
численном расчете?
57См. упражнение 4.3. Хаотическая область логистического отображения не имеет
странного аттрактора, поскольку отображение ограничено одним измерением. Каскады
удвоения периодов в динамических системах более высоких размерностей имеют фрактальные
странные аттракторы в хаотических областях.
58Представьте себе покрытие поверхности сферы в трехмерном пространстве
маленькими кубиками. Число кубиков будет стремиться к площади поверхности (двухмерной),
деленной на е2.
59 В хаотических областях сохраняйте число ячеек малым по сравнению с числом
итераций. Иначе вы обнаружите множество пустых ячеек между точками и скорее всего
получите нулевую размерность.
Гл.5. Упражнения
197
Энтропия и информационная размерность. Плотность вероятности
p(xj) ~ Pj/e = (l/e)(Nj/Ntot). Переходя от интегрирования к суммированию
в формуле для энтропии (5.20), получаем
S = -кв / р{х) \og{p{x)) dx
—Σ ?"*(?)«
3 '
= -]Tp,logP,+log6 (5.46)
3
(для удобства полагая кв = 1)·
Вы можете решить, что энтропия фиксированной точки равна нулю, а
энтропия m-периодического цикла равна кв log га. Однако это неверно. Если
существует фиксированная точка или периодический предельный цикл, то
аттрактор принадлежит множеству нулевой размерности (набор точек), а не
единичной. Энтропия должна стремиться к минус бесконечности,
поскольку у нас есть точная информация о том, где будет находиться траектория
на больших временах. Для того чтобы оценить энтропию fc^logm «нулевой
размерности» численно, мы должны использовать дискретную формулу для
энтропии (уравнение 5.19), суммируя по ячейкам Pj, вместо того чтобы
интегрировать по х:
Sd=0 = - Σ PJ 1об(^) = Sd=i ~ МО. (5.47)
з
В более общем случае достаточно «естественным» представляется
определение энтропии для множества размерностью D следующим образом:
SD = - Σ PJ 1οβ(ρί) + D 1оё(£)· (5·48)
3
Вместо того чтобы использовать эту формулу для определения энтропии,
математики используют ее для определения информационной размерности
D™ = ES (Σ pi loe pi) / loe(6)· (5·49)
Информационная размерность согласуется с обычной размерностью для
множеств, которые локально имеют вид ЖР. В отличие от емкости (5.44), в
которой одинаково учитывается каждая занятая ячейка, информационная раз-
лгерность учитывает более занятые части (ячейки) аттрактора с большим
198
Гл.5. Энтропия
весом. Снова мы можем ускорить сходимость, обратив внимание на то, что,
согласно уравнению (5.48), сумма ^2jPj^ogPj является линейной функцией
log € с наклоном D и точкой пересечения Sp с осью ординат. Измеряя наклон
напрямую, находим
Anf = !^o dloge · (5·50)
(с) Аналогично заданию (b), напишите программу, которая строит Z?inf из
уравнения (5.50) как функцию средней точки log б при увеличении числа ячеек.
Постройте кривые для μ = 0.9, μ = 0.8 и /Хоо. Согласуется ли информационная
размерность с обычной для первых двух значений μ? Сходится ли кривая для
Моо к Di « 0.517098, информационной размерности аттрактора Фейгенбаума,
известной из литературы?
Большая часть фракталов в «реальном мире» обладает широким
спектром различных характерных пространственных размерностей, они
являются мультифракталами.
5.17 Вывод энтропии. (Математика) ©
В этом упражнении вы покажите, что существует единственная
непрерывная функция Si (с точностью до константы fc#), удовлетворяющая трем
ключевым свойствам (уравнения 5.24, 5.29 и 5.35), для того чтобы служить
хорошей мерой неопределенности:
Si(^,...,^]>SI(Pu...,Pu) (5.51)
если pi = 1/Ω для всех г,
*5/(Рь · · · >ΡΩ-ι, 0) = Sj(pi,... ,ρω-ι), (5.52)
Здесь
(Si(A\Be))B = Sj(AB) - Sj(B). (5.53)
Si{A) = SI(pi,...,Pa),
Si (В) = Si(qi,...,qni),
(Si(A\Be))B = Σ qtSiiae,..., cat),
ι
Si(AB) = Si(cuqi, · · ■ ,спмдм)·
Гл.5. Упражнения
199
Таким образом, вы покажете, что эта функция и есть наша неравновесная
энтропия (5.19). Наше доказательство основано на замечательной небольшой
книге Хинчина [70].
Для удобства положим L(g) = 5/(1/(7,..., 1/g).
(a) Для любых рациональных вероятностей пусть д будет наименьшим общим
кратным числом их знаменателей и пусть qe = де/д для целых д£. Покажите, что
SI(B) = L(g)-^q£L(ge). (5.54)
е
(Совет: считайте, что АВ состоит из д событий с вероятностью 1/д каждое,
В характеризует определенную группу событий размера ge, a A — конкретное
событие из де событий группы £, рис. 5.20.)
(b) Покажите, что в случае L(g) = kstogg уравнение (5.54) представляет
собой энтропию Шеннона (5.23).
Зная, что Si (А) — энтропия Шеннона для рациональных вероятностей и
предполагая, что Si (А) непрерывна, можно тем самым показать, что Si (A)
является энтропией Шеннона. Таким образом, мы свели нашу задачу к тому,
чтобы показать, что L(g) является логарифмом с точностью до константы.
Л*
В1
Рис. 5.20. Рациональные вероятности и условная энтропия
Пусть вероятности qe = (1/6,1/3,1/3,1/2) состояния Be рациональные. Мы можем
разделить полную вероятность на д = 12 одинаковых частей (кругов с вероятностью Гке = 1/12
каждый), где дк = (2,3,3,4) — количество кругов для соответствующей реализации Be.
Мы можем, таким образом, записать нашу неопределенность Si (В) через (максимальную)
равновероятную неопределенность L(g) = Si(\/g,...) и L(gk) и, используя формулу
изменения энтропии в свойстве для условной вероятности (5.35), получить нашу меру
неопределенности Si (В) (5.54).
200
Гл.5. Энтропия
(c) Покажите, что L(g) монотонно возрастает с увеличением д. (Совет:
используйте оба первых ключевых свойства.)
(d) Покажите, что L(gn) = nL(g). (Совет: рассмотрите η независимых
распределений вероятности для д равновероятных событий. Примените
рекурсивно третье свойство.)
(e) Покажите, используя задания (с) и (d), что при 2т < sn < 2m+1
- < Ш < —· <«■«>
η L(2) n
(Совет: как L(2m) соотносится с L(sn) и L(2m+1)?) Покажите, что
т/п < log(s)/log(2) < (т + 1)/п. Покажите, что отсюда следует, что
\L(s)/L(2) — log(s)/log(2)| < 1/n и, следовательно, L(s) = fclogs, где к —
некоторая константа.
Таким образом, наша функция неопределенности Sj совпадает с
формулой для неравновесной энтропии (с точностью до константы).
Глава 6
Термодинамические
потенциалы
В этой главе мы расскажем, как описывать различные части статистико-
механических систем. Если мы не рассматриваем большую часть нашей
системы, то есть договариваемся не учитывать некоторые степени свободы, то
статистико-механическое описание оставшихся частей системы
производится с помощью статистических ансамблей и соответствующих
термодинамических потенциалов. Использование термодинамических потенциалов, как
правило, упрощает вычисления и позволяет доступным образом объяснить
поведение системы. Что конкретно мы не учитываем в нашем рассмотрении?
Мы не рассматриваем внешний мир. Большинство систем не являются
изолированными, они часто обмениваются энергией, объемом или частицами
с внешним миром в состоянии равновесия (часто называемом термостатом).
Если связь с внешним миром слабая, то можно ее не учитывать.
Канонический 1 ансамбль с постоянной температурой (раздел 6.1) и свободная энергия
Гельмгольца возникают в системах, которые могут обмениваться энергией
с термостатом. Большой канонический ансамбль (раздел 6.3) и большой
термодинамический потенциал используются для описания систем, которые
также обмениваются частицами при фиксированном химическом потенциале. В
больших системах эти различные ансамбли предсказывают в среднем одно и
то же поведение (за исключением незначительных флуктуации). В принципе
большую часть представляющих интерес вычислений мы могли бы провести
1 Канонический (Оксфордский английский словарь): ...4. общ. Подчиняющийся
правилам или канонам: соответствующий общепринятым авторитетным источникам,
традиционный, достоверный, общепринятый, стандартный. 5. Мат. Подчиняющийся общим
правилам и формулам.
202
Гл.6. Термодинамические потенциалы
при постоянной энергии и числе частиц. Однако вычисления могут
существенно упроститься за счет использования подходящих термодинамических
потенциалов (раздел 6.2).
Мы не учитываем несущественные внутренние степени свободы. В
изучении, скажем, химических реакций, магнитов или движения больших
механических объектов движение отдельных атомов, как правило, не
представляет интереса. Для того чтобы не учитывать их в механических системах,
вводят понятия трения и шума (раздел 6.5). Для того чтобы не рассматривать
движение атомов в химических реакциях, была создана теория скоростей
химических реакций (раздел 6.6).
Мы огрубляем масштаб. Многие системы не являются однородными из-за
определенных начальных или граничных условий. Их свойства
варьируются во времени и пространстве. Если эти системы локально находятся вблизи
состояния равновесия, мы можем не учитывать внутренние степени
свободы малых объемов, то есть огрублять масштаб нашего описания, сохраняя
только континуальные поля, описывающие локальное состояние.2 Например,
в разделе 6.7 мы рассчитаем плотность свободной энергии для идеального
газа и с помощью нее (снова) получим уравнение диффузии.
В этой главе мы получим в явном виде выражение для свободной энергии
для некоторых важных случаев. Запомните, что термодинамические
потенциалы являются очень важным методом исследования, даже в системах, в
которых в силу их сложности невозможно аналитическое решение. Мы
приведем примеры, в которых точное решение возможно, в частности для того,
чтобы мотивировать вывод термодинамических потенциалов в
континуальном приближении для систем, в которых невозможно произвести вычисления
на микроскопическом уровне.
6.1 Канонический ансамбль
Канонический ансамбль задает равновесное поведение системы при
фиксированной температуре. Мы определили понятие температуры в разделе 3.3,
рассматривая систему, состоящую из двух слабовзаимодействующих частей,
с координатами в фазовом пространстве (Pi,Qi) и (P2,Q2), которые могут
обмениваться энергией. Теперь мы сосредоточим внимание на поведении
одной из частей — (системы); предположим, что вторая часть (термостат)
слишком большая. Мы не интересуемся измерением свойств, зависящих от
термостата, и хотим получить статистический ансамбль системы, который
усредняется по соответствующим состояниям термостата.
2Это поля параметра порядка, которые мы будем изучать в главе 9.
6.1. Канонический ансамбль 203
Рис. 6.1. Канонический ансамбль
Канонический ансамбль описывает равновесные системы, которые обмениваются энергией
с термостатом. Температура термостата Т. Вероятность состояния s системы с энергией Е3
составляет p(s) = exp(—Es/kBT)/Z. Термодинамика канонического ансамбля описывается
с помощью свободной энергии Гельмгольца А(Т, V, Ν) = Ε — TS.
Как зависит вероятность того, что наша система находится в состоянии
s, от ее энергии Е3? Как мы обсуждали в разделе 3.3, плотность вероятности
того, что наша система находится в некотором определенном состоянии s,
пропорциональна объему энергетической оболочки термостата с энергией Е —
Es:
p(s) ос Ω2(Ε - Ea) = exp (S2{E - Es)/kB), (6.1)
поскольку состояние s разделяет микроканоническую вероятность с любым
партнером-термостатом, с которым оно может сосуществовать при полной
фиксированной энергии Е.
Сравним вероятность двух типичных состояний А и В нашей
равновесной систмы. Мы знаем, что флуктуации энергии малы и предполагаем, что
термостат очень большой. Поэтому предположим, что обратная температура
I/T2 = dS2/dE2 постоянна в диапазоне энергий (Е — Ε α, Ε — Ев)·
Следовательно,
р(8в)/р(8А) = П2(Е - ЕВ)/П2(Е - ЕА)
_ e(S2(E-EB)-S2(E-EA))/kB _ e(EA-EB)(dS2/dE)/kB
= e(EA-EB)/kBT2 /62ч
204
Гл.6. Термодинамические потенциалы
Это есть общий вывод распределения Больцмана. Вероятность состояния
системы3 с энергией Е8 составляет
p(s) ос exp(-Ea/kBT). (6.3)
Мы знаем, что вероятность является нормированной величиной, таким
образом,
р(8) = ехр(-Я,/*вГ)/ J ^2i expi-W^Pj, Qi)/kBT)
= exp(-Es/kBT)/J2exp(-En/kBT)
П
= exp(-Es/kBT)/Z, (6.4)
где нормировочный множитель
Z(T,N, V) = Y^exp(-En/kBT) = j ^ffi1 ехр^М^РиОО/квТ) (6.5)
называется статистической суммой.4
Уравнение (6.4) является определением канонического ансамбля,5
который используется для расчета свойств системы, обменивающейся энергией с
внешним миром температурой Т.
Статистическая сумма Ζ представляет собой всего лишь нормировочный
множитель, который обеспечивает равенство полной вероятности единице.
Вас может удивить тот факт, что этот нормировочный множитель играет
ключевую роль в теории. В самом деле, большинство представляющих
интерес величин может быть рассчитано двумя различными способами: как сумма
по всевозможным состояниям или через производную статистической суммы.
Давайте рассмотрим это, используя Ζ для расчета средней энергии, удельной
теплоемкости и энтропии произвольной системы.
3Для классической системы она используется вместо вероятности на объем фазового
пространства η .
4Для того чтобы не усложнять формулы интегралами, мы будем записывать их как
«непрерывную сумму» f dFdQ/h3N —*■ J^n до окончания этой главы. Это обозначение
используется в квантовой механике (гл. 7), в которой уровни энергии дискретны для
связанных систем. Дискретное суммирование используется также в решеточных системах, таких
как модель Изинга (раздел 8.1), в которых все континуальные степени свободы
исчезают при интегрировании. Никаких затруднений в преобразовании сумм в уравнениях этой
главы обратно в интегралы по фазовому пространству возникнуть не должно.
5 Формальным методом вывода канонического ансамбля является частичный след,
удаляющий степени свободы термостата из микроканонического ансабля. Для того чтобы
посчитать математическое ожидание оператора В, зависящее только от координат системы
6.1. Канонический ансамбль
205
Внутренняя энергия. Для того чтобы рассчитать среднюю
внутреннюю энергию нашей системы,6 (Е), мы каждое состояние учитываем с весом,
равным его вероятности. Обозначая β = 1/(квТ), получаем:
(Pi,Qi), мы начнем с усреднения по энергетической оболочке всего пространства
(уравнение 3.2), включающего как координаты системы, так и координаты термостата (F2yQ2):
Ω(Ε) = -^= [ dPi dQi dP2 dQ2 =
°E JΕ<Ηι+Η2<Ε+δΕ
= ίάΕι Ω1{Ε1)Ω2(Ε - Εχ). (6.6)
<Б> = ЙТШр ί dPl dQiSiPbQOdPaclQa =
Ы{П)0П JΕ<Ηι+Η2<Ε+δΕ
= ^JdF1dQlB(FuQl)n2(E-n1(FuQi)). (6.7)
(Коэффициенты неразличимости частиц и постоянная Планка в уравнении (3.54)
несущественно усложняют вывод.) Опять-таки, если термостат достаточно большой, небольшие
изменения энергии Ει — (Ει) не изменяют его температуру. Поскольку \/Т2 = dS2/dE2
является постоянной величиной, имеем 8Ω2(Ε — Ei)/dEi = —(1/Α;βΤ)Ω2. Решая это
дифференциальное уравнение, можно получить
Ω2(Ε - Ει) = Ω2(Ε - (Ει)) exp(-(#i - (Ei))/kBT). (6.8)
Таким образом,
Ω(Ε) = ίάΕιΩ1(Ει)Ω2(Ε - (Ei))e-(El-{El))/kBT =
= Ω2(Ε-(Ει))β{Ει)/ι'ΒΤ idEiili(Ei)e~El/kBT = (6.9)
= Ω2(Ε-(Ει))β(Ει)/*ΒΤΖ
а также
(В) = /^1^1Д(Рь-01)П»(Д-<Д1>)е-^^Ла)-№>)/*дТ^№ _ {Ei)) e<El)/kBrz =
= -| /dPidQiBiPi.Qi) exp(-Hi(Pi,Qi)/kBT). (6.10)
Интегрируя по F2 и Q2, мы получаем канонический ансамбль (уравнение 6.4) из
микроканонического. Вычисление распределения импульсов ρ(ρι) в разделе 3.2.2 было сделано
подобным образом. Мы интегрировали по всем остальным степеням свободы и получили
распределение Больцмана для ж-компоненты импульса частицы номер один. Этот процесс
называется исключением путем интегрирования степеней свободы в термостате и
является стандартным способом вывода термодинамических потенциалов.
6 Угловые скобки означают усреднение по каноническому ансамблю.
206
Гл.6. Термодинамические потенциалы
(Ε) = ΣΕηΡη = ^ψ = -
ΘΖ/θβ
= -dlogZ/dp. (6.11)
Удельная теплоемкость. Пусть Су — удельная теплоемкость на частицу
при постоянном объеме. (Удельная теплоемкость — это энергия, требуемая
для увеличения температуры на одну единицу д(Е)/дТ.) Используя
уравнение (6.11), получаем
Nr =^1 = 9Ш^1 = L_ W = 1 d2l°&Z (а 10Ч
^ дТ δβ dT kBT> δβ квТ2 θβΐ · κ '
Представляя предпоследнюю формулу в этом выражении в виде суммы,
получаем интересный результат
„ = 1_д(Е1 = 1 д ΣΕη*-βΒη
* квТ* δβ ΗΒΤ*δβ Σε~βΕ"
Ζ*
квТ*
= ^[(EV(E>2] = ^, (6.13)
где ое — среднеквадратичная флуктуация7 энергии нашей системы при
постоянной температуре.
Уравнение (6.13) является достаточно примечательным,8 поскольку оно
связывает макроскопическую восприимчивость (с^, изменение энергии при
изменении температуры) и микроскопические флуктуации (σβ, флуктуация
энергии при тепловом равновесии). В общем случае, флуктуации связаны с
характеристиками отклика аналогичным образом. Эти соотношения крайне
полезны, например, при расчетах восприимчивости в численном
моделировании. Например, для измерения удельной теплоемкости нет необходимости
проводить незначительные изменения температуры и измерять поток тепла.
Достаточно изучить флуктуации энергии в состоянии равновесия
(упражнения 3.8 и 8.1).
7Мы используем стандартный прием σ\ = ((Ε - (Ε))2) = (Ε2) - 2(Ε(Ε)) + (Ε)2 =
(Ε2) — (Ε)2, поскольку (Ε) — постоянная величина, которую можно вынести за скобки при
усреднении по ансамблю.
8 Мы должным образом введем понятие восприимчивости (линейного отклика) и
рассмотрим другие известные соотношения в главе 10.
6.1. Канонический ансамбль
207
Аналогичны ли результаты расчетов с использованием канонического и
микроканонического ансамблей? Уравнение (6.13) говорит нам о том, что
флуктуации энергии на частицу
σΕ/Ν = V\Е2) - (Ε)2/Ν = у/(квТ)(суТ)/у/м (6.14)
очень малы. Они составляют 1/\/7ν, умноженное на геометрическое среднее
двух микроскопических энергий: квТ (две трети кинетической энергии на
частицу) и СуТ (энергия на одну частицу при нагревании от абсолютного нуля,
если удельная теплоемкость не зависит от температуры). Эти малые
флуктуации не меняют свойств макроскопической системы. Ансамбли с постоянной
энергией (микроканонический) и постоянной температурой (канонический)
предсказывают одинаковое поведение системы.
Энтропия. Используя универсальную формулу статистической
механики9 для энтропии (5.20), находим
9 В качестве альтернативы можно использовать микроканоническое определение
энтропии полной системы и уравнение (6.8) и показать, что
S =kB\ogfdEi Ωι(Ει)Ω2(Ε - Ει)
=kB\og[dEl Ωι(£ι)Ω2(£ - (Ει))
exp(-(Ei-(Ei))/kBT)
=kB\ogn2(E-(E1))
+ kB\og(exp((E1)/kBT))
+ kB\ogfdElQl(El)
expi-Ex/квТ)
=kB\ogQ2(E2)
+ kBpE1+kB\ogZl
=S2 + E1/T-A1/Ty
таким образом,
Si =Ei/T + fcBlogZi
= Ei/T-Ai/T, (6.15)
Итак, мы получаем тот же самый результат, не используя неравновесную энтропию.
208
Гл.6. Термодинамические потенциалы
Σβχρ(-βΕη)(-βΕη - logZ)
= -кв-
Ζ
= kBP(E) + kBlogζΣβχΡ^ βΕη) = <|> + fcfJlogζ (6 16)
Обратите внимание, что формулы для (£7), Су и S содержат logZ и его
производные. Это обуславливает10 введение термодинамического
потенциала для канонического ансамбля, называемого свободной энергией Гелъмголъ-
ца:
А(Г, V, Ν) = -kBT log Ζ = (Ε) - TS. (6.17)
Энтропия представляет собой производную А по Т, взятую с обратным
знаком. А именно,
дА
дТ
дквТ log Z rr.dlogZdp
Ny = дт~ = -k*lo*z- квТ-дГдт
= -kBlogZ- kBT(E)/(kBT2) = -kBlogZ- (E)/T
= -S. (6.18)
Почему этот термодинамический потенциал называется свободной
энергией? Во-первых, квТ имеет размерность энергии. Во-вторых, он
представляет собой доступную (свободную) энергию для совершения работы.
Тепловая машина, в которую поступает из нагревателя энергия Ε = Qi,
должна передать холодильнику энтропию S = Q2/T2 и может совершить работу
W = Q\ — Q2 = Ε — T2S. Таким образом, А = Ε — TS представляет собой
энергию, свободную для совершения полезной работы (раздел 5.1).
Мы видим, что ехр(—А(Т, V, N)/kBT) = Ζ аналогично статистическому
весу Больцмана exp(—Es/kBT). Первое выражение представляет собой объем
фазового пространства, или вес всех состояний с заданным числом частиц N
и объемом V. Последнее — это вес, соответствующий определенному
состоянию s. В общем случае термодинамические потенциалы не учитывают все
степени свободы, за исключением X. Объем фазового пространства,
соответствующий X, составляет exp(—F(K)/kBT).
Исторически термодинамика и различные термодинамические потенциалы появились
раньше, чем статистическая механика.
6.2. Невзаимодействующие системы и канонические ансамбли 209
6.2 Невзаимодействующие системы и канонические
ансамбли
Рис. 6.2. Невзаимодействующие системы с общим термостатом
Расчет свойств двух слабо взаимодействующих подсистем проще проводить в
каноническом, чем в микроканоническом ансамбле, поскольку каждая из подсистем обменивается
энергией с термостатом и не влияет на энергию других подсистем.
Канонический ансамбль, как правило, более удобен для выполнения
вычислений, поскольку для систем, гамильтониан которых разделяется на
невзаимодействующие компоненты, статистическая сумма разбивается на
сомножители, каждый из которых может быть вычислен независимо.
Давайте это покажем.
Предположим, что у нас есть система, состоящая из двух слабо
взаимодействующих подсистем L и Д, соединенных с термостатом, для которого
β = 1/квТ. Состояние полной системы представляет собой пары состояний
(sf,sj*) двух подсистем с энергиями Е\ и Е^, соответственно.
Статистическая сумма полной системы составляет
Ζ = Χ>χρ {-β{Ε$> + Ε?)) = £У^е-^
υ
-βΕ?
(6.19)
Таким образом, для невзаимодействующих систем статистическая сумма
распадается на сомножители. Свободная энергия Гельмгольца, таким образом,
состоит из двух независимых слагаемых
А = -квТ log Z = -kBTlog(ZL · ZR) = AL + AR,
(6.20)
210
Гл.6. Термодинамические потенциалы
подобно энтропии, средней энергии и другим экстенсивным величинам,
пропорциональным размеру системы.
Это намного проще, чем аналогичное вычисление в микроканоническом
ансамбле! В микроканоническом ансамбле каждая подсистема соревнуется с
другой за имеющуюся полную энергию. Даже несмотря на то, что подсистемы
не связаны между собой (энергия одной из них не зависит от состояния
другой), невозможно провести раздельные вычисления для каждой из них при
использовании микроканонического ансамбля. Позволяя каждой подсистеме
получать энергию из большого термостата, канонический ансамбль дает
возможность проводить независимые расчеты для каждой из подсистем.
Теперь мы можем непосредственно рассмотреть несколько важных
примеров невзаимодействующих систем.
Идеальный газ. Различные атомы в идеальном газе не
взаимодействуют между собой. Статистическая сумма N различимых атомов идеального
газа массой га в кубическом сосуде объема V = L3 представима в виде
произведения интегралов по всем степеням свободы а:
= (Ly/2nmkBT/h2)3N = (L/X)3N.
Здесь
λ = h/^2nmkBT = y/2nh2/mkBT (6.21)
— термическая длина волны де Бройля (уравнение 3.59).
Средняя внутренняя энергия идеального газа составляет
{Е) = JJ^ . -| ,og(r3»/2) _ W _ 3_NkβΓι (6 22)
что позволяет получить теорему о равнораспределении для импульсов без
необходимости расчета объемов сфер в ЗЛ^-мерном пространстве (раздел
3.2.2).
Для N одинаковых частиц мы посчитали каждую возможную
конфигурацию Ν\ раз для различных перестановок частиц, таким образом, мы должны
поделить Z^feal на Λ/Ί, точно так же, как мы это делали при расчете объема
фазового пространства Ω в разделе 3.5:
ЗДГ = (L/XfN/N\.
(6.23)
6.2. Невзаимодействующие системы и канонические ансамбли 211
Это не влияет на внутреннюю энергию, но меняет свободную энергию Гельм-
гольца:
43Й* =-kBT\og{(L/XfN/N\)
= -NkBT\og(V/X3) + kBT\og(N\)
~ -NkBTlog(V/X3) + kBT(N log Ν - ΛΓ)
= -NkBT(log(V/NX3) + l)
= NkBT(\og(pX3)-l), (6.24)
где ρ = N/V — средняя концентрация, и мы использовали формулу
Стерлинга log(7V!) ~ Nlog N - N.
Наконец, энтропия N неразличимых частиц в каноническом ансамбле
составляет
S . _«* . -NkB 0^., - ,) - NkBTa-^l
= NkB (5/2 - log(pA3)) , (6.25)
— то же самое выражение, которое мы получили (затратив гораздо большие
усилия) с использованием микроканонического ансамбля (уравнение 3.58).
Классический гармонический осциллятор. Электромагнитное
излучение, колебания атомов в твердых телах, а также возбужденные состояния
многих других систем вблизи состояния равновесия могут быть приближенно
описаны как совокупность невзаимодействующих гармонических
осцилляторов.11 Статистико-механические вычисления с использованием
канонического ансамбля для этих систем проводятся по отдельности для каждой моды.
Полная энергия гармонического осциллятора массой т и частотой ω
равна
W(p, q) = ρ2/2т + mu2q2/2. (6.29)
11 Например, при температурах, малых по сравнению с температурой плавления, твердое
тело или молекула с произвольным многочастичным потенциалом взаимодействия V(Q),
как правило, находятся в окрестности минимума потенциала Qo Разложение потенциала
вблизи минимума дает
V(Q) »V(Qo) + ]T(Q - Qo)«ft»V
а
+ £|(Q-Oo)e(Q-Oo)/>
α,,2
x ΘαΘβν + .... (6.26)
Поскольку потенциал имеет минимум при Qo, градиент потенциала в этой точке должен
быть равен нулю, и второй член в правой части исчезает. Третий член представляет собой
огромную квадратичную форму 37V x 37V, которую можно диагонализовать, приведя ее к
212
Гл.6. Термодинамические потенциалы
Статистическая сумма одного подобного осциллятора составляет (где мы
обозначили h = h/2n)
- h (6·30)
Поскольку свободная энергия Гельмгольца классического осциллятора юавна
Αω(Τ) = -kBT\ogZ = kBT\og{hw/kBT), (6.31)
внутренняя энергия имеет вид
(Ε)ω(Τ) = ~д-Щ^ = ^β(^β + log Μ = Ι/β = kBT, (6.32)
и, следовательно, cv = д(Е)/дТ = kB. Это является основным
утверждением теоремы о равнораспределении:12 средняя энергия каждой гармонической
степени свободы (р и q считаются за две) в классической равновесной системе
составляет квТ/2.
Классическое распределение скоростей Следует отметить, что как
для идеального газа, так и для гармонического осциллятора каждая
компонента импульса дает сомножитель ^/2πτη/β в статистической сумме. Как
мы пообещали в разделе 3.2.2, это происходит в любой классической
системе, в которой импульсы не связаны с координатами, то есть где часть полной
энергии, зависящая от импульсов частиц, имеет стандартный вид ΣαΡα/2τηα
нормальным модам qk. (Если не все массы атомов одинаковы, то нужно
перемасштабировать компоненты Q — Qo на квадратный корень соответствующей массы перед диаго-
нализацией.) Гамильтониан совокупности несвязанных осцилляторов, выраженный через
нормальные моды, имеет вид:
П = ΣρΙ/2τη + τηωΙ<£/2. (6.27)
к
При достаточно высоких температурах, когда квантовые эффекты малы, можно, используя
уравнение (6.30), найти полную статистическую сумму нашей гармонической системы
Z = Y[Zk = Y[(l/Phwk). (6.28)
к к
(В разделе 7.2 мы рассмотрим квантовомеханический осциллятор, который во многих
случаях достаточно точно описывает атомные колебания в широком диапазоне температур
вплоть до точки плавления.)
12Мы ознакомились с этой теоремой для импульсов ρ в разделе 3.2.2.
6.3. Большой канонический ансамбль
213
(неквантовые, нерелятивистские, немагнитные частицы). В этих системах
распределение по скоростям всегда максвелловское (уравнение 1.2), вне
зависимости от конфигурации системы.
Это очень важное и противоречащее интуиции утверждение. Равновесное
распределение скоростей атомов, пересекающих барьеры в химических
реакциях (раздел 6.6) или окружающих горные вершины, точно такое же, как
и в ямах с низкой энергией.13 Каждый атом замедляется, когда
поднимается наверх, и наверху оказываются только обладающие наибольшей энергией.
Плотность атомов наверху, таким образом, меньше, но распределение
кинетической энергии остается тем же самым (упражнение 6.1).
6.3 Большой канонический ансамбль
Рис. 6.3. Большой канонический ансамбль
Описывает равновесные системы, которые могут обмениваться энергией и частицами с
термостатом. Вероятность системы находиться в состоянии s с Na частицами и энергией Еа
составляет p(s) = ехр(—(Еа — μ7νβ)/(&βΤ)) /Ζ. Термодинамика большого канонического
ансамбля описывается большим термодинамическим потенциалом Ф(Т, V, μ).
Большой канонический ансамбль позволяет разделить вычисления для
систем, которые могут обмениваться как энергией, так и частицами с
окружающей средой.
Рассмотрим систему в состоянии s с энергией Е8 и числом частиц Ns,
а также термостат с энергией Е2 = Ε — Es и числом частиц N2 = N —
13Вершины гор не были бы холоднее, если бы атмосфера находилась в состоянии
равновесия.
214
Гл.6. Термодинамические потенциалы
Ns (рис. 3.3). По аналогии с уравнением (6.3), плотность вероятности, что
система будет находиться в состоянии s, пропорциональна
p(s)cxn2(E-Es,N-Ns)
= exp ((S2(E -ES,N- Ns)) /kB)
= exp (-Es/kBT + Ν3μ/1ζΒΤ)
= exp (-(Es - μΝ3)/1ζΒΤ), (6.33)
где
μ = -TdS/dN (6.34)
— химический потенциал. Обратите внимание на сомножитель —Т,
преобразующий изменение энтропии в изменение энергии. Учитывая, что άΕ =
TdS — PdV + μάΝ, можно увидеть, что μ = (dE/dN)\sy — не что иное как
изменение энергии при адиабатическом добавлении дополнительной
частицы, при котором система (N + 1) частиц остается в равновесии. При низких
температурах данная система будет заполняться частицами до тех пор, пока
энергия, необходимая для того чтобы поместить следующую частицу, не
достигнет μ. После этого число частиц останется постоянным, за исключением
термодинамических флуктуации.
Так же, как и в случае канонического ансамбля, в выражении для
плотности вероятности присутствует нормировочный множитель, называемый
большой канонической статистической суммой
Ξ(Γ, V, μ) = Σ e-tEn-»N'MkBTi (6.35)
η
плотность вероятности состояния Si имеет вид p(si) = ^Εί~μΝ^^ΒΤ/Έ.
Большой термодинамический потенциал
Ф(Г, V, μ) = -kBTlog(E) = {Ε) -TS-μΝ (6.36)
вводится по аналогии со свободной энергией Гельмгольца А(Т, V,N). В
упражнении вы выведете соотношение Эйлера Ε = TS — PV + μΝ, и
покажете таким образом, что Φ(Τ,μ, V) = —PV.
Частичные следы.14 Между прочим, заметим, что мы можем записать
большую каноническую статистическую сумму как сумму по каноническим
14 Интегралы по фазовому пространству в классической механике превращаются в
суммы (следы) по состояниям в гильбертовом пространстве в квантовой механике.
Несущественные степени свободы в квантовой механике исчезают при взятии частичного следа по
6.3. Большой канонический ансамбль
215
статистическим суммам. Представим сумму по состояниям η нашей системы в
виде двойной суммы — внутренней суммы15 по состояниям с фиксированным
числом частиц Μ в системе и внешней суммы по М. Пусть состояние s^m,m
имеет энергию £^М)а/> таким образом,
Ξ(7\ ν,μ) = Y^Y^e-(E<M>M-vM)/kBT
\
= Υ" J2e-EiMtM/kBT ^цМ/квТ
м \ем )
= Y^Z{T,V,M)e»M'kBT
м
= V е-(Мту,м)-»м)/квт ^6 37)
Μ
Снова отметим, что свободная энергия Гельмгольца в последнем уравнении
играет точно такую же роль, как энергия в уравнении (6.35). ехр(—Еп/квТ)
представляет собой вероятность того, что система находится в определенном
состоянии п, в то время как ехр(—А(Т, У,М)/квТ) — вероятность того, что
система находится в произвольном состоянии с Μ частицами.
Использование большого канонического ансамбля. Большой
канонический ансамбль особенно полезен для описания невзаимодействующих
квантовых систем (см. гл. 7). В них каждое собственное энергетическое
состояние может быть представлено как отдельная подсистема, не зависящая от
других, за исключением конкуренции между собственными состояниями за
число частиц. Схожий ансамбль также встречается в химических реакциях
(раздел 6.6).
Пока что, для того чтобы проиллюстрировать использование большого
канонического ансамбля, давайте рассчитаем величину флуктуации числа
частиц. Среднее число частиц в системе составляет
ENme~(Em~*lNmVkBT кпТд" дФ
Y,me-^Em-^m)lkBT ~ Ε θμ~ δμ 1 >
Подобно тому, как флуктуации энергии связаны с удельной теплоемкостью
(величина изменения энергии при малом изменении температуры, раздел
состояниям (см. гл. 7). Название «частичный след» для интегрирования по
несущественным степеням свободы также стало использоваться в классической статистической физике
(см. примечание 5 на с. 204).
15 Эта сумма аналогична интегрированию по внутренним степеням свободы.
216
Гл.6. Термодинамические потенциалы
6.1), флуктуация числа частиц связана с величиной изменения числа частиц
при малом изменении химического потенциала:
d(N) _ д £тЛГте-^™-^™>/^т
θμ θμ Ξ
ι {ΣτηΚ™*-{Ε™-μΝ™)βΒΤΐ
Ξ2 kBT
1 Σ Nm2e"(Em"^m)/fcsT
+
(6.39)
fcBT Ξ
(Ν2) - (7V)2 _ ((Ν - (Ν))2)
kBT kBT
6.4 Что такое термодинамика?
Исторически термодинамика и статистическая физика очень тесно
связаны, и часто они изучаются одновременно. Что же такое термодинамика?
(0) Термодинамика {Oxford English dictionary): Теория соотношений
между тепловой и механической энергией и преобразований одной из
данных форм энергии в другую.
(1) Термодинамика — это теория, являющаяся следствием
статистической механики в пределе очень больших систем. Статистическая
механика возникла как вывод термодинамики на основе атомной теории, на
микроскопическом уровне (незадолго до того, как существование атомов
стало общепризнанным). Можно сказать, что термодинамика является пределом
статистической механики при стремлении числа частиц N -> оо.16
Рассчитывая относительные флуктуации величин, таких как энергия или давление, и
показывая, что они исчезающе малы, согласно 1/\/Ν, мы тем самым даем
обоснование термодинамики на микроскопическом уровне. Термодинамика
является статистической механикой систем, находящихся вблизи состояния
равновесия, без учета флуктуации.
В данной книге мы сформулируем основные методы и результаты
классической термодинамики в упражнениях (см. «Упражнения, термодинамика»
в алфавитном указателе книги). Исследование параметров порядка (см. гл.
9) дает термодинамические законы, вообще говоря, для широкого спектра
состояний вещества.
Статистическая механика имеет существенно большую область
применения, чем термодинамика. В частности, в приложениях к другим областям,
Предел N —> оо поэтому часто называется термодинамическим пределом.
6.4- Что такое термодинамика?
217
таким как теория информации, динамические системы и теория сложности
вычислений, статистическая механика описывает многие системы, в
поведении которых далеко не всегда можно проследить связь с термодинамикой.
(2) Термодинамика является самосогласованной теорией.
Термодинамика может быть получена на основе аксиом. Она основана на так
называемых трех законах термодинамики, которые для полноты должны быть
дополнены «нулевым» законом. Их можно выразить в следующих нестрогих
формулировках:
(0) Транзитивность состояния равновесия. Если две системы находятся в
состоянии равновесия с третьей системой, то они находятся в состоянии
равновесия друг с другом.
(1) Закон сохранения энергии. Полная энергия изолированной системы,
включая тепловую, сохраняется.
(2) Энтропия всегда возрастает. В изолированной системе могут
происходить необратимые процессы, характеризуемые функцией состояния,
называемой энтропией.
(3) При абсолютном нуле температур энтропия стремится к нулю.
Энтропия на одну частицу в любых двух равновесных системах с большим
числом частиц стремится к одному и тому же значению17 при
стремлении температуры к абсолютному нулю.
Нулевой закон (транзитивность состояния равновесия) становится
основой определения понятия температуры. Наш вывод температуры в рамках
статистической мееханики в разделе 3.3 дает обоснование нулевого закона на
микроскопическом уровне: системы, которые могут только обмениваться
теплом, находятся в равновесии друг с другом, если у них одинаковое значение
1/Г = (dS/dE)\VtN.
Первый закон термодинамики (сохранение энергии) является
фундаментальным физическим законом. Термодинамика автоматически наследует его
из микроскопической теории. Исторически понимание того, как работа
переходит в теплоту, в рамках термодинамики было важным для установление
факта сохранения энергии. Тщательный анализ передачи и преобразования
энергии при тепловых потоках и совершении механической работы18
является ключевым в термодинамике.
17 Это значение приравнивается нулю при измерении объема фазового пространства в
единицах h3N (раздел 3.5).
18Мы сталкивались с этим при анализе цикла Карно в разделе 5.1.
218
Гл.6. Термодинамические потенциалы
Второй закон (энтропия всегда возрастает) — основа термодинамики.19
Он обсуждался в гл. 5.
Третий закон (энтропия стремится к нулю при Τ = О, также известный
как теорема Нернста) по существу отражает тот факт, что квантовые
системы при абсолютном нуле температур находятся в основном состоянии.
Поскольку число основных состояний в квантовой системе, как правило, очень
мало,20 а число частиц велико, в равновесных системах при абсолютном нуле
температур энтропия на одну частицу равна нулю.
Законы термодинамики имеют много эквивалентных способов записи.21
Каратеодори [17,18], например, формулировал второй закон теомодинамики
следующим образом:
Существуют состояния системы, бесконечно мало отличающиеся
от заданного, в которые невозможно перейти из заданного
состояния при любом квазистатистическом адиабатическом22 процессе.
Эта аксиоматическая формулировка привлекала внимание математиков со
времен Каратеодори. В данной книге мы не будем рассчитывать свойства
систем с использованием аксиоматического подхода или из законов
термодинамики, мы сконцентрируемся на изучении статистической механики.
(3) Термодинамика представляет собой «зоопарк» частных
производных, преобразований и соотношений. Более чем в любой другой
области науки, литература по термодинамике изобилует различными
частными производными и хитрыми соотношениями между различными
физическими величинами.
19В Двух Культурах Ч.П. Сноу говорил, что знание второго закона термодинамики в
науке то же самое, что чтение произведений Шекспира — в искусстве. (Люди, не
принадлежащие к англоязычной культуре, возможно, не согласятся с данным утверждением.)
Запоминание того, какой номер соответствует какому закону, несущественно, но само
понятие энтропии и ее неизбежного возрастания в самом деле является ключевым.
20Некоторые системы имеют несколько вырожденных основных состояний, но число этих
состояний, как правило, мало или очень медленно возрастает с увеличением размера
системы, таким образом, энтропия на одну частицу стремится к нулю. Стекла обладают большой
остаточной энтропией (раздел 5.2.2), но они не находятся в состоянии равновесия.
21 Иногда можно услышать первый и второй закон в следующем виде: (1) Вы не можете
выиграть; и (2) Вы даже не можете остаться при своих. ((1) you can't win; и (2) you can't
break even — первые две строчки из популярной песни Майкла Джексона «You can't win». —
Прим. переводчика).
22Каратеодори использовал термин адиабатический для обозначения состояния, в
котором отсутствуют тепловые потоки. Мы используем его также для бесконечно медленных
(квазистатистических) переходов.
6.4· Что такое термодинамика?
219
Это возникает, в частности, из-за того, что существует несколько
альтернативных возможностей выбора термодинамических потенциалов. Для
описания молекулярных систем используются не только энтропия (или
внутренняя энергия), свободная энергия Гельмгольца и большой термодинамический
потенциал, но также свободная энергия Гиббса, энтальпия и другие.
Существуют специальные термодинамические потенциалы для изучения
магнитных систем, где вместо частиц исследуется локальная намагниченность или
спины. В литературе обозначения и даже названия различных
термодинамических потенциалов мало согласованы друг с другом.
Как можно провести преобразования от одного термодинамического
потенциала к другому? Давайте запишем свободную энергию Гельмгольца более
детально:
А(Т, V,N)=E- TS(E, V, Ν). (6.40)
Величины, стоящие в правой части уравнения, зависят от четырех
переменных: Т, V, N и Е. Почему А не является функцией Е1 Рассмотрим
производную А — Es — TbSs(Es) по энергии системы Es при фиксированной
температуре термостата Ту.
dA/dEs = 1 - TbdSs/dEs = 1 - Ть/Т3. (6.41)
Поскольку А описывает систему, находящуюся в состоянии равновесия,
температуры системы и термостата должны совпадать и, следовательно,
дА/дЕ = 0, таким образом, А не зависит от Е. С физической точки зрения,
передача энергии происходит до тех пор, пока А не достигнет минимума, и
Ε не является больше независимой переменной. Это является примером
преобразования Лежандра (упражнение 6.7). Преобразования Лежандра
позволяют переходить от представления в рамках одного типа энергии или
термодинамического потенциала к другому, меняя один набор независимых
переменных (в данном примере, £", V и Ν) на другой (Г, V и Ν).
Термодинамика кажется довольно запутанной, но при этом она
является действительно мощным аппаратом. Практически любая представляющая
интерес макроскопическая величина может быть получена при взятии
производных от термодинамических потенциалов. Взяв первые производные
энтропии, энергии или свободной энергии, можно получить такие величины, как
температура и давление. В термодинамике используется сокращенная
система записи для упорядочения этих частных производных. Например, запись23
άΕ = TdS -PdV + μάΝ (6.42)
23Точный смысл этих формул раскрывается в дифференциальной геометрии, где άΧ
представляют собой дифференциальные формы. В термодинамике различаются полные
220
Гл.6. Термодинамические потенциалы
означает, собственно говоря, что E(S, V, Ν) удовлетворяет уравнениям
3.29, 3.36 и 3.38:
as
= г,
N,V
8V
= —Ρ, and
7V,5
дЕ
dN
= μ.
(6.43)
v,s
Соответствующее уравнение для свободной энергии Гельмгольца А(Т, V, N)
имеет вид
cL4 = d(E -TS) = dE-TdS-SdT
= -8άΤ-ΡάΥ + μάΝ,
(6.44)
что соответствует
дА
дТ
S,
Ny
дА
8V
τν,τ
-Ρ, and
Μ
dN
μ.
(6.45)
ν,τ
Рис. 6.4. Ансамбль Гиббса
G(T, Ρ, TV) описывает термодинамику системы, которая может обмениваться с термостатом
как теплом, так и объемом. Энтальпия Η(S, Ρ, Ν) используется для систем, которые могут
обмениваться лишь объемом.
дифференциалы, такие как dS, и неполные дифференциалы, такие как работа и
количество теплоты, которые не являются производной функции состояния и величина
которых зависит от пути интегрирования. В математике различают замкнутые и полные
дифференциальные формы, которые (в односвязном пространстве) соответствуют полным
дифференциалам в термодинамике. Соотношения между замкнутыми и полными
дифференциальными формами рассматриваются в теории когомологий и т.п. Эти вопросы не
являются ключевыми в статистической механике и не будет рассматриваться в данной
книге.
6.4· Что такое термодинамика?
221
Аналогичным образом, в системах, в которых температура и давление
постоянны (в том числе в большинстве биологических и химических систем),
минимизируется свободная энергия Гиббса (рис. 6.4)
G(T, Ρ, Ν) = Ε - TS + PV, dG = -S άΤ + V άΡ + μ dN. (6.46)
В системах с постоянной энтропией и давлением минимизируется
энтальпия
H(S, P,N)=E + PV, <1Я = Г dS + V dP + μ dN. (6.47)
Наконец, как было сказано в разделе 6.3, системы с постоянной температурой,
объемом и химическим потенциалом описываются большим
термодинамическим потенциалом
Φ(Τ,ν,μ) = Ε-Τ8-μΝ, άΦ = -S dT - Ρ dV - Ν Αμ. (6.48)
В термодинамике есть много сложных, не очевидных на интуитивном
уровне соотношений. Первые производные должны составлять маленький
замкнутый треугольник (см. рис. 3.4), что задает определенное соотношение
для их произведения (уравнение 3.33, упражнение 3.10).
Вторые производные свободной энергии определяют такие величины, как
удельная теплоемкость, коэффициент объемного сжатия и магнитная
восприимчивость. Вторые производные должны обладать свойством симметрии
(д2 /дхду = д2/дудх), что задает соотношения Максвелла между
различными величинами, которые на первый взгляд кажутся совершенно не
связанными друг с другом (упражнение 3.11). Существуют и другие сложные
соотношения, возникающие при взятии производных по «неестественным
переменным»,24 а также множество неравенств, полученных из условия стабильности
системы.
Безусловно, статистическая механика ничем не отличается от
термодинамики в том плане, что она наследует у нее весь набор этих сложных
соотношений. Более того, в статистической механике существуют свои
соотношения, связывающие равновесные флуктуации с транспортными свойствами
и восприимчивостью, такие как соотношение Эйнштейна для флуктуации и
диффузионного потока (раздел 2.3) и флуктуационно-диссипационная
теорема, которую мы выведем в гл. 10. Тем не менее, в статистической механике
основной упор делается не на общие соотношения между величинами, а на
изучение свойств конкретных систем.
24Например, существует полезный прием взятия производной от S(E, V, Ν) по Ρ при
постоянной Т, не выражая ее через Ρ и Τ [53].
222
Гл.6. Термодинамические потенциалы
6.5 Механика: трение и флуктуации
Рассмотрим груз массой га, подвешенный на конце пружины с
коэффициентом жесткости К и длиной в недеформированном состоянии /ίο, под
действием гравитационного поля д. Насколько сильно растянется пружина? Мы
решали огромное количество упражнений такого типа в курсе механики.
Пружина растянется до длины Л,*, где — тд = K(h* — ho). При h* силы,
действующие на пружину, сбалансированы, а энергия системы минимальна. Какой
физический принцип здесь используется? В физике энергия сохраняется, а
не минимизируется! Должны ли мы заключить, что груз будет вечно
осциллировать с постоянной амплитудой?
И* Л0
Рис. 6.5. Груз на пружине
Груз на пружине в состоянии равновесия расположен очень близко к положению с
минимумом энергии.
Настал тот момент в вашем образовании физика, когда мы наконец
можем объяснить, почему груз приходит в состояние, соответствующее
минимуму энергии. Наша система (масса и пружина)25 связана с очень большим
числом N внутренних атомных и молекулярных степеней свободы.
Колебания груза взаимодействуют с этими степенями свободы (за счет наличия
трения) и обмениваются с ними энергией. Колебания атомов есть теплота, таким
образом, за счет трения происходит диссипация энергии маятника, которая
переходит в теплоту. В самом деле, поскольку потенциальная энергия
пружины является квадратичной, мы можем использовать теорему о
равнораспределении: в равновесии K(h — h*)2/2 = квТ/2. Для пружины с
коэффициентом жесткости К = ΙΟΝ/m при комнатной температуре (квТ = 4 · 10~21 J)
y/({h - /ι*)2) = у/квТ/К = 2 · Ю-11 m = 0.2 А. Положение маятника в самом
25Мы подразумеваем, что полная система, исследуемая в данной задаче, состоит из двух
подсистем: макроскопической конфигурации массы и пружины и составляющих ее атомов,
которые рассматриваются как часть окружающей среды.
6.6. Химическое равновесие и скорости реакций
223
деле определяется минимумом энергии с погрешностью меньшей, чем радиус
атома, возникающей из-за тепловых флуктуации.26 Каким образом связано
это статистико-механическое представление с коэффициентом трения
затухающего гармонического осциллятора?
Тщательный статистико-механический анализ (упражнение 10.7) дает
закон движения груза в виде
h = - — (h - h*) -ΊΚ + ξ(ί), (6.49)
m
где 7 представляет собой коэффициент трения или диссипации, а ξ(ί) —
случайная, зависящая от времени сила, возникающая за счет внутренних
колебательных степеней свободы системы. Это пример уравнения Ланжевена.
Величина случайной силы ξ зависит от коэффициента трения η и
температуры Г, что приводит к формированию распределения Больцмана в
стационарном состоянии. В общем случае как ξ, так и η зависят от частоты, мы
будем подробно рассматривать эти вопросы в гл. 10.
6.6 Химическое равновесие и скорости реакций
При изучении химических реакций интерес, как правило, представляет
число молекул различного типа как функция времени, а не точное значение
координат или импульсов молекул. В этом разделе мы с помощью метода
термодинамических потенциалов получим законы химического равновесия, в
частности, закон действующих масс. Затем мы обсудим, когда именно
происходят химические реакции и обоснуем закон Аррениуса для скоростей
протекания термоактивируемых реакций.
При химических реакциях происходит замена одного типа молекул на
другой. Например, аммиак (ΝΗ3) может быть получен из водорода и азота
посредством реакции (рис. 6.6)
ЗН2 + N2 U 2NH3. (6.50)
Все химические реакции в принципе обратимы, но скорость обратной
реакции может существенно отличаться от скорости прямой реакции. При
химическом равновесии27 концентрации [X] различных молекул X (выраженные
26 Мы вернемся к рассмотрению флуктуирующего гармонического осциллятора в
упражнении 10.3.
27Эксперименты, как правило, производятся при постоянном давлении, что существенно
усложняет расчеты, но не вносит концептуальных изменений.
224
Гл.6. Термодинамические потенциалы
Рис. 6.6. Соударение с образованием аммиака
Простейшим обоснованием закона действующих масс служит рассмотрение реакции как
одновременного соударения всех реагентов.
как число частиц на единицу объема) удовлетворяет закону действующих
масс28
w=^(r)- (6·51)
Простейшим образом можно обосновать закон действующих масс,
рассматривая химическую реакцию как одновременное столкновение всех
реагентов. Вероятность того, что одна молекула азота и три молекулы водорода
столкнутся в малом объеме, в котором возможно протекание реакции,
пропорциональна концентрации азота и концентрации водорода в кубической
степени, таким образом, прямая скорость реакции в единице объема будет
составлять /ГррМгПНг]3. Аналогично, обратная реакция будет протекать со
скоростью АГв[МНз]2, пропорциональной вероятности того, что две молекулы
ΝΗ3 столкнутся. Баланс этих двух реакций приводит к установлению
стационарного состояния, для которого верно уравнение (6.51), где Keq = Кр/Кв-
Эта простейшая аргументация может быть неприменима в реальных
реакциях, протекающих как последовательность некоторых кратковременных
промежуточных состояний, ни в одном из которых не происходит одновре-
2Q
менное соударение всех реагентов.
28 В более общем случае химическая реакция может быть записана в виде ^Zi ν%Αχ =
0. Здесь Vi — стехиометрические коэффициенты, представляющие собой число молекул
типа Л,, претерпевающих изменения при реакции (где Vi < 0 для реагентов и ι/, > 0 для
продуктов реакции). Закон действующих масс в общем случае имеет вид ПЛ^*]"* = ^*q·
29Процесс Хабера-Боша, используемый для промышленного производства аммиака,
состоит из нескольких промежуточных стадий. Молекулы азота и водорода адсорбируются
на железную подложку и диссоциируют на атомы. Атом азота присоединяет атомы
водорода один за другим. В конечном итоге молекула NH3 испаряется (покидает поверхность
подложки). Атомы железа действуют как катализатор, понижая энергетический барьер
6.6. Химическое равновесие и скорости реакций
225
Каким образом можно строго вывести закон действующих масс с
использованием методов статистической механики?
Поскольку нас не интересуют ни координаты, ни импульсы частиц,
наша система при фиксированном объеме и температуре может быть описана с
помощью свободной энергии Гельмгольца A(T,V,Nh2,Nn2,Nniis). При
протекании химической реакции меняется число всех трех молекул, что приводит
к изменению свободной энергии Гельмгольца системы:
9А А АГ 9А АКТ дА А лт
АА = tm2AN»>+ w^AN">+ m^sAN™>
= -З/ХН2 - μΝ2 + 2Μνη3) (6.52)
где μ χ = дА/дХ — химический потенциал молекулы X. Реакция протекает
до тех пор, пока свободная энергия не достигнет минимума, таким образом,
в равновесии
-3/хн2 - W2 + 2/XNH3 = 0· (6-53)
Для вывода закона действующих масс необходимо сделать
предположение, что молекулы нескоррелированны в пространстве.30 Таким образом,
молекулы каждого типа можно рассматривать как самостоятельный идеальный
газ. Свободная энергия Гельмгольца каждого из трех газов может быть
представлена в виде
Α{Ν, V, Τ) = NkBT [log({N/V)X3) - l] + NF0, (6.54)
где λ = к/у/2птпквТ — термическая длина волны де Бройля. Первые два
члена возникают за счет вклада в статистическую сумму координат и
импульсов молекул (уравнение 6.24). Последний член NFq соответствует
внутренней свободной энергии молекул.31 Таким образом, химический потенциал
имеет вид
и ускоряя реакцию, не участвуя в ней. (В биологии белковые катализаторы называются
ферментами.)
30 Это предположение зачастую является справедливым для ионов и атомов в растворе.
Если межионным взаимодействием можно пренебречь и растворитель (вода) не играет
существенной роли, то ионы можно с некоторой степенью приближения рассматривать как
идеальные газы, с поправками за счет интегрирования по степеням свободы растворителя.
31 Для атомов в основном состоянии Fo равна энергии Fo основного состояния. Для
небольших молекул без спина при комнатной температуре внутренняя свободная
энергия Fo, как правило, определяется основным энергетическим состоянием молекулы Fo,
а также вкладом за счет классического вращательного движения. Колебание и
внутреннее возбуждение электронов при этом практически отсутствуют. В этом режиме
свободная энергия гомоядерных двухатомных молекул составляет Fo = Fo — квТ\о^{1Т/Н ), где
/ — момент инерции. Для молекулы аммиака, обладающей тремя моментами инерции,
Fo = Fo - kBTlogiVSnT^hhh/^3) (см. [74, sections 47-51]).
226
Гл.6. Термодинамические потенциалы
ВА
μ{Ν, V,T) = — = kBT [log((N/V)X3) - l] + NkBT(l/N) + F0
= kBT\og((N/V)Xs) + F0
= kBTlog(N/V) + с + F0, (6.55)
где константа с = kBTlog (λ3) не зависит от концентации. Подставляя
уравнение (6.55) в уравнение (6.53), разделив на квТ, записывая концентрации
в виде [X] = Νχ/V и перенося в правую часть слагаемые, не зависящие от
концентраций, мы получаем закон действующих масс:
-31og[H2] - log[N2] + 21og[NH3] = log(tfeq),
[NH3]2
ww ■,· (6·56)
Мы также получили, что константа равновесия экспоненциально зависит от
разницы внутренних свободных энергий AFnet = — 3F0 2 — F0 2 + 2F0 3
реагентов и продуктов реакции:
Keq = К0 exp(-AFnet/kBT) (6.57)
где
К = Щ?к = —fm™3 к г-з (б 58)
слабо зависит от температуры.
Согласно больцмановскому фактору, e~AFn€t/kBT конечное состояние, в
котором свободная энергия молекул на AFnet ниже, чем в начальном
состоянии, является более выгодным. Температурная зависимость множителя перед
экспонентой Ко (возникающая за счет того, что энтропия четырех молекул
в импульсном пространстве выше, чем у двух) и температурная зависимость
свободных энергий молекул Fo (см. примечание 31), как правило, малы по
сравнению с экспоненциальной зависимостью от разницы энергий основных
состояний молекул AEnet:
Keq ос exp(-AEnet/kBT), (6.59)
где для реакции синтеза аммиака AEnet — 92.4кДж/моль.32 Константы
равновесия в большинстве случаев подчиняются уравнению (6.57), что
соответствует термически активируемым реакциям.
32Реакция синтеза аммиака экзотермическая, она проходит с выделением теплоты.
Обратная реакция, при которой из аммиака образуется азот и водород, является
эндотермической.
6.6. Химическое равновесие и скорости реакций
227
Давайте выйдем за пределы химического равновесия и рассмотрим
скорости прямых и обратных реакций. Для того чтобы это сделать,
необходимо определить, к каким молекулам принадлежат данные атомы в данный
момент времени. То есть в какой именно момент на траектории движения
происходит реакция?
Химическая реакция, вовлекающая Μ атомов, как правило, представляет
собой траекторию в ЗМ-мерном конфигурационном пространстве. Обычно в
химии выбирается одна «координата реакции» X и строится зависимость
энергии (проминимизированной по оставшимся ЗМ—1 координатам) от X.
Подобный график изображен на рис. 6.7.33
Рис. 6.7. Потенциальный барьер
Энергия Ε как функция некоторой координаты реакции X в химической реакции. Точками
схематически обозначено количество атомов в каждой позиции. Реагенты (слева)
отделены от продуктов реакции (справа) энергетическим барьером высоты В. Можно оценить
скорость реакции, рассчитывая число реагентов, пересекающих барьер в единицу времени.
Обратите внимание на энергетический барьер В, отделяющий реагенты от
продуктов реакции. Атомная конфигурация, соответствующая вершине
барьера, называется переходным состоянием. (В ЗМ-мерном
конфигурационном пространстве этот барьер представляет собой седловую точку. Для
отделения реагентов от продуктов реакции требуется построение (ЗМ—1)-мерной
Рисунок 6.7 встречается в исследованиях перехода через барьер в широком круге
явлений, таких как диффузия в кристаллах и атомные переходы между метастабильны-
ми состояниями (в стеклах, раздел 5.2.2, биомолекулах, упражнение 6.4 и нанопереходах,
упражнение 10.5). В каждой из этих систем после взятия частичной суммы (следа) остается
дискретный набор состояний.
228
Гл.6. Термодинамические потенциалы
разделяющей поверхности, определяющей переходное состояние.) Наша
свободная энергия A(T,V,Nu2,N^2,N^n3), собственно говоря, представляет
собой частичную сумму (след), в которой все конфигурации слева от
переходного состояния В соответствуют реагентам, а все конфигурации справа —
продуктам реакции. Насколько быстро будет протекать наша химическая
реакция, если она начнется в неравновесном состоянии при наличии
избыточного количества реагентов? В разбавленных системах, в которых выполняется
закон действующих масс, скорость прямой реакции является хорошим
приближением, вне зависимости от концентрации продуктов реакции.34
Скорость реакции не может превышать полное число атомов,
пересекающих в единицу времени энергетический барьер из состояния реагента в
состояние продукта при равновесии. (Она может быть меньше, если траектории,
пересекающие барьер, сразу же возвращаются обратно, прежде чем перейти
в состояние равновесия на обратной стороне).35 Количество таких повторных
переходов минимизируется при надлежащем выборе разделяющей
поверхности переходных состояний.36 Концентрация частиц на вершине барьера
меньше, чем концентрация на дне потенциальной ямы, в ехр(—В/квТ) (фактор
Больцмана) раз. Скорость реакции, таким образом, подчиняется закону Ар-
рениуса:
Г = Г0ехр{-В/квТ), (6.60)
с коэффициентом перед зкспонентой Го, пропорциональным произведению
концентраций реагирующих веществ по аналогии с законом действующих
масс (например, Го ос [H2]2[N2] для нашей реакции получения аммиака).
Тщательно рассчитывая число атомов в потенциальной яме, а также их число и
скорости вблизи вершины барьера, можно получить формулу для константы
пропорциональности (упражнение 6.11).
Закон Аррениуса для термически активируемого движения применяется
для расчета не только скоростей химических реакций, но и других
макроскопических величин, таких как коэффициенты диффузии и скорости зароды-
шеобразования (раздел 11.3).37
34При больших концентрациях картина может быть иной. Например, если в качестве
катализатора используется подложка, а продукт реакции ее не покидает, то реакция может
прекратиться в случае заполнения продуктом активной поверхности.
35 Повторный переход через барьер дает динамическую поправку к теории переходных
состояний, см. [57].
36При низких температурах важно, прежде всего, чтобы эта поверхность была
перпендикулярна нестабильному «направленному вниз» собственному направлению гессиана
(матрицы вторых производных) потенциальной энергии при переходном состоянии.
37В физике существуют различные типы медленных процессов. (1) Большие системы
могут медленно реагировать на внешние изменения, поскольку возмущение не сразу
передается в отдаленные части системы, примером является медленное затухание при больших
6.7. Плотность свободной энергии идеального газа
229
6.7 Плотность свободной энергии идеального газа
Мы начали нашу книгу (раздел 2.2) с изучения уравнения диффузии. Как
оно связано с термодинамическими потенциалами и ансамблями? Вообще
говоря, неоднородная неравновесная система также может быть описана с
использованием статистической механики, если пространственные и временные
градиенты достаточно малы, а система близка к локальному равновесию. Мы
можем описать локальное состояние системы с помощью полей параметра
порядка. Каждой величине (плотности, температуре, намагниченности)
соответствует поле, характеризующее состояние макроскопического тела. Мы
можем описать неоднородную систему, находящуюся в состоянии, близком
к равновесному, используя плотность свободной энергии, зависящую, как
правило, от полей параметра порядка и их градиентов. Свободная энергия
неравновесной системы рассчитывается при интегрировании плотности
свободной энергии.38
Мы рассмотрим поля параметра порядка и плотность свободной энергии
для большого количества сложных систем в главе 9. Мы будем
использовать симметрию и градиентное разложение для вывода плотности свободной
энергии, поскольку зачастую прямой расчет является очень сложным. В этом
разделе в качестве наглядного примера мы явным образом вычислим
плотность свободной энергии для неравновесного идеального газа.39
Обратите внимание, что удобно записать свободную энергию Гельмгольца
идеального газа (уравнение 6.24) через концентрацию ρ = N/V и
термическую волну де Бройля λ:
Α(Ν, V, Τ) = NkBT [log(pA3) - l] . (6.61)
длинах волн в уравнении диффузии (раздел 2.2) и модах Голдстоуна (раздел 9.3). (2) В
радиоактивных ядрах период полураспада может составлять миллиарды лет вследствие
медленного квантового туннелирования через потенциальные барьеры. (3) Системы могут
быть медленными, поскольку для перехода через барьер требуется термическая активация
(со скоростью, подчиняющейся закону Аррениуса (6.60)).
38Строго говоря, каждому полю параметра порядка s(x) соответствует функционал
F{s}, определяющий свободную энергию системы. (Функционал — это отображение
пространства функций на пространство действительных чисел.) Запись этого функционала
как интеграла по плотности свободной энергии (как мы это обычно делаем) может быть
некорректной не только в силу дальнодействия полей, но также вследствие наличия
расходимости, (упражнение 9.3).
39 Мы также будем использовать плотность свободной энергии идеального газа при
изучении корреляционных функций в разделе 10.3.
230
Гл.6. Термодинамические потенциалы
Следовательно, плотность свободной энергии щ = p(x.j)AV атомов в малом
объеме AV имеет вид
Яаеа1(р(х,·),Т) = A(n,^tT) = р(ъ)квТ [ΐοβ(ρ(χ,)λ3) - 1]. (6.62)
Вероятность для заданной плотности частиц р(х) составляет
Р{р} = e-/»/dVJ"-(p(*))/z. (6.63)
Как обычно, свободная энергия F{p) = J T(p(x))dx аналогична энергии в
распределении Больцмана. Мы избавляемся от микроскопических степеней
свободы (координат и скоростей отдельных частиц) при интегрировании и
заменяем их полем р(х). Плотность свободной энергии в уравнении (6.62)
может использоваться для расчета любого равновесного свойства системы,
которое может быть выражено через концентрацию р(х).40
Плотность свободной энергии также используется для описания эволюции
систем с неоднородной концентрацией p(x,t). Если в каждом малом объеме
AV система близка к равновесию, то ее временная эволюция может быть
описана с использованием равновесной статистической механики, даже
если глобально система не находится в состоянии равновесия. Если
концентрация неоднородна, то возникает сила, стремящаяся ее выровнять. Полная
свободная энергия будет уменьшаться при переходе частиц из областей с
высокой концентрацией в области низкой концентрации. Мы можем
использовать плотность свободной энергии для расчета этой силы, а зная эту силу —
вывести законы эволюции системы.
Химический потенциал неоднородной системы имеет вид
_ дА _ дА/У _ дТ
β " ΘΝ " ΘΝ/V " dp
и представляет собой изменение свободной энергии при изменении средней
концентрации р. Для неоднородной системы локальный химический
потенциал в точке χ
μ(χ) = ^ (6.64)
является вариационной производной41 плотности свободной энергии по р.
40Например, в гл. 10 мы вычислим корреляционные функции (р(х)р(х')) и обсудим их
связь с восприимчивостью и диссипацией.
41 Производная в пространстве функций дает линейное приближение JF{p + δ ρ} — Т{р}
(см. примечание 7 на с. 416). Мы будем редко встречаться с использованием вариационных
производных в данной книге.
6.7. Плотность свободной энергии идеального газа
231
Рис. 6.8. Огрубление масштаба плотности в пространстве
Поле концентрации р(х) учитывает все возможные конфигурации точек Q, приводящие
к данному среднему значению концентрации. В плотности свободной энергии ^аеа1(р(х))
содержится вклад всех микросостояний (Р, Q), приводящих к надлежащему числу частиц
в малом объеме. Вероятность того, что концентрация данной системы будет именно
такой, пропорциональна интегралу по всевозможным конфигурациям Q частиц на рис. 6.9,
которые задают данное значение концентрации.
Поскольку свободная энергия идеального газа не зависит от градиентов
р, вариационная производная δΤ/δρ равна частной производной дТ/др:
£ τ-ideal β
μ(χ) = -д— = Тр (рквТ [log(PA3) - 1])
= kBT[log(pX3)-l]+pkBT/p
= kBTlog(p\3). (6.65)
Химический потенциал аналогичен давлению: частица может понижать
свободную энергию, перемещаясь из области с высоким химическим
потенциалом в область с низким химическим потенциалом. Градиент химического
потенциала —θμ/дх, таким образом, представляет собой градиент давления,
эффективную статистико-механическую силу, действующую на частицу.
Как меняется концентрация частиц за счет этой силы μ(#)? Если наша
концентрация есть концентрация всего газа, то атомы будут ускоряться под
действием силы, приводя к образованию звуковых волн.42 Их момент будет
сохраняться, так же как и концентрация частиц. Если наши частицы могут
В этом случае необходимо также учитывать поле локальных скоростей при описании
локальных свойств системы.
232
Гл.6. Термодинамические потенциалы
Рис. 6.9. Флуктуации концентрации в пространстве
Если rij — число точек в объеме AV с центром в точке Xj, то p(xj) = rij/AV.
создаваться и уничтожаться, уравнение эволюции концентрации будет
включать слагаемое dp/dt = —ημ, не имеющее отношения к потоку частиц. В
системах, энергия которых сохраняется (или практически сохраняется),
эволюция будет определяться гамильтоновыми уравнениями движения для
плотности свободной энергии. В магнитах внешняя сила вызывает прецессию. В
сверхтекучих жидкостях градиенты химического потенциала приводят к
закручиванию и раскручиванию фазы поля параметра порядка (возникновение
вихрей)...
Давайте рассмотрим малую концентрацию духов в большом количестве
неподвижного воздуха. Число частиц сохраняется, но импульс существенно
уменьшается (поскольку частицы духов рассеиваются молекулами воздуха).
Скорость наших частиц пропорциональна эффективной силе, действующей
на них — ν = —η(8μ/8χ), где η — подвижность.43 Следовательно, поток
3 = ρν частиц имеет вид
43 Это представляет собой пример линейного отклика. Потоки в системах, близких к
состоянию равновесия, как правило, пропорциональны градиентам соответствующих
величин. В качестве примеров можно привести закон Ома, в котором электрический ток
пропорционален градиенту электромагнитного потенциала / = V/R = (1/Я)(аф/ах),
термическую проводимость, для которой поток тепла пропорционален градиенту температуры
J = acVT, и вязкие жидкости, скорость сдвига в которых пропорциональна касательному
напряжению. Мы будем более подробно изучать системы с линейным откликом в гл. 10.
6.7. Плотность свободной энергии идеального газа
233
3=ΎΡ(χ) (--<£) =-ΊΡ(χ
dkBTlog(PX3)
дх
-W^g-^-g, <«>
и скорость изменения ρ описывается уравнением диффузии
!=-*·'-*·*& ^
Обратите внимание, что
• мы снова вывели уравнение диффузии (уравнение 2.7)
др/dt = Dd2p/dx2. В этот раз мы использовали плотность свободной
энергии, полученную в равновесной статистической механике, и
предполагали линейный закон, связывающий скорость и приложенную
силу.
• Мы снова получили соотношение Эйнштейна (уравнение 2.22) D =
jkBT-
•
Мы предположили, что —θμ/дх действует как внешняя сила, несмотря
на то, что мы используем μ для идеального газа, который сам по себе
не обладает потенциальной энергией (см. упражнения 5.12 и 6.13).
Наша плотность свободной энергии для идеального газа имеет гораздо
более простой вид, чем плотность свободной энергии произвольной системы,
поскольку идеальный газ не является упругим (т.е. свободная энергия не
зависит от градиентов концентрации). Наш вывод основывался на разделении
пространства на малые области. В общем случае эти области не будут
являться независимыми системами, и будет дополнительное изменение
свободной энергии, зависящее от изменения полей от объема к объему (например
(свободная) энергия сжатия упругого стержня), что приведет к появлению
членов, зависящих от градиентов полей.
234
Гл.6. Термодинамические потенциалы
Упражнения
Термодинамические потенциалы являются основными рабочими
лошадками статистической механики и термодинамики. Существует огромное
количество практических приложений различных термодинамических
потенциалов в химии, физике конденсированного состояния и инженерии. В
упражнениях, представленных ниже, эти приложения глубоко не изучаются, скорее
в них делается акцент на рассмотрение универсальных задач и методов.
В Экспоненциальной атмосфере, Системе с двумя состояниями и
Отрицательной температуре изучаются наиболее фундаментальные проблемы
статистической механики. В последних двух также рассматривается связь
между каноническим и микроканоническим ансамблями. В Молекулярных
моторах и термодинамических потенциалах приводится пример из области
биофизики, как можно сконструировать необходимые термодинамические
потенциалы в системах, обменивающихся чем-то другим, помимо энергии,
объема и числа частиц, а также вводится понятие телеграфного шума для систем
с двумя устойчивыми состояниями.
Лаплас, Лагранж и Лежандр расскажут вам о важнейших
математических методах термодинамики и их связи со статистической механикой. Эйлер,
Гиббс и Дюгем, а также Клаузиус и Клапейрон попросят вас вывести
фундаментальные термодинамические соотношения, названные в их честь.
В Переходе через барьер рассматриваются количественные методы
расчета скоростей химических реакций. Михаэлис, Ментен и Хилл предлагают
еще один пример создания эффективной теории за счет исключения
несущественных степеней свободы. В этом упражнении также выводятся два
выражения для скоростей химических реакций, часто встречающиеся в
молекулярной биологии. В Пыльце и твердых квадратах приводится пример
энтропийного термодинамического потенциала, имеющий точное решение.
К сожалению, статистика практически не перекрывается со
статистической механикой, несмотря на то что их задачи очень близки; это касается как
их аудитории, так и лексикона. Статистическая механика и статистика
— это слабая попытка заполнить этот пробел, рассматривая байесовский
анализ.
Каким образом можно рассчитать энтропию или термодинамические
потенциалы при помощи компьютера? Вероятность каждого возможного
состояния в ансамбле оценить не представляется возможным, нужно использовать
альтернативные методы [8,67,95]. Упражнение по компьютерным
вычислениям по этой теме планируется разместить на веб-странице книги [129].
Гл.6. Упражнения
235
6.1 Экспоненциальная атмосфера.44 (Моделирование) (2)
Когда вы забираетесь на горную вершину, воздух становится холодным
и разреженным и, как правило, достаточно ветреным. Описываются ли эти
эффекты с помощью статистической механики? Ветер — нет, поскольку он
связан с неоднородным нагреванием и испарением в достаточно удаленных
областях. Мы определили, что в равновесной статистической механике два
тела, находящиеся в контакте, должны иметь одну и ту же температуру,
даже когда одно находится над другим. Но молекулы газа падают вниз под
воздействием гравитации....
Этот пример рассматривался в [43, 1.40], где Фейнман использовал его
для вывода множества формул равновесной статистической механики.
Давайте воспроизведем его доказательство. Скачайте нашу программу по
молекулярной динамике с сайта [132] и описание к этому упражнению. Проведите
моделирование идеального газа в сосуде с отражающими стенками под
воздействием гравитации. Поскольку идеальный газ не приходит к состоянию
внутреннего равновесия, моделирование начинается в равновесном ансамбле
с температурой Т.
(а) Выглядит ли распределение визуально статистически стационарным? Как
возможно поддержание стационарного распределения по высоте, несмотря на то
что на все атомы постоянно действует ускорение, направленное вниз? После
проведения некоторого количества итераций постройте гистограмму распределения
по высоте и распределения скоростей. Стационарны ли эти распределения, за
исключением статистических флуктуации? Согласуются ли они с равновесным
распределением Больцмана?
Равновесное термическое распределение не зависит от времени, даже
если нет соударений для поддержания состояния равновесия. Число атомов,
проходящих плоскость при постоянном ζ сверху вниз, должно совпадать с
числом атомов, проходящих снизу вверх. Снизу атомов больше, но многие из
них не обладают достаточной кинетической энергией, для того чтобы высоко
подняться.
С макроскопической точки зрения, мы можем использовать уравнение
состояния идеального газа (PV = 7Vfc#T или P(z) = р(г)квТ), для того чтобы
вывести распределение Больцмана, определяющее зависимость плотности от
высоты.45
44Это упражнение и сопутствующее программное обеспечение были разработаны
совместно с Кристофером Майерсом.
45Фейнман отмечал, что это макроскопическое доказательство может быть применено
для любой внешней силы! Если F — сила, действующая на каждый атом, то в равновесии
давление должно уравновешивать плотность внешней силы Fp. Следовательно, изменение
давления составляет Fpax = άΡ = а(квТр) = квТар. Если сила представляет собой
236
Гл.6. Термодинамические потенциалы
(b) Давление увеличивается при понижении высоты вследствие увеличения
веса верхних слоев воздуха. Чему равна сила, действующая за счет гравитации
на слой толщиной Az и площадью ΑΊ Чему равна разность давлений в точках ζ
и ζ — Azl Используя это, а также уравнение состояния идеального газа,
найдите зависимость плотности газа от высоты. Совпадает ли она с распределением
Больцмана?
Фейнман затем выводит распределение импульсов частиц из баланса
потоков частиц вниз и наверх, упоминаемых в задании (а). Он начинает с
обсуждения того, что в равновесии вероятность того, что данный атом имеет
определенную скорость νζ в вертикальном направлении, не зависит от
высоты.46 (Атомы на различных высотах имеют одинаковую температуру, они
отличаются только общей плотностью. Поскольку они не взаимодействуют,
они ничего не знают о плотности, и распределение атомов по скоростям не
может зависеть от ζ.)
(c) Пусть некоторое неизвестное распределение по скоростям составляет
Ρν(νζ)· Запишите общее равновесное распределение вероятности p(vz,z,t)
через распределение Больцмана по высоте, полученное в задании (Ь) и pv(vz).
Теперь рассмотрим47 атомы со скоростью в вертикальном направлении vz
в слое газа площадью А между ζ и ζ + Az в момент времени t. Их плотность
вероятности (на единицу скорости в вертикальном направлении) составляет
p(vz,z, t)AAz. По прошествии промежутка времени At этот слой приобретает
скорость vz — gAt и проходит расстояние h + vzAt, таким образом,
p{vz,z, t) = p{vz - gAt, z + vzAt, t + At). (6.68)
(d) Используя тот факт, что ρ(νζ, ζ, t) не зависит от времени в состоянии
равновесия, запишите соотношение между dp/dvz и dp/dz. Используя ваш
результат из задания (с), получите равновесное распределение скоростей в идеальном
газе.
градиент некоторого потенциала £/(х), то в некоторой локальной точке χ имеем — VC/ =
F = kBT(dp/dx)/p = kBT(d\ogp)/dx = kBTV log p. Отсюда log ρ = С - U/kBT and ρ ос
exp(—U/kBT). Фейнман, таким образом, делает резкий скачок от рассмотрения идеального
газа (в котором отсутствует внутренняя потенциальная энергия) к взаимодействующим
системам ...
46 В момент прочтения этой части книги вы уже знаете формулу распределения по
скоростям для классической системы и то, что она не зависит от положения частиц. Но
Фейнман, как мы помним, выводит все с самого начала. Также обратите внимание на то, что
ρ в задании (Ь) соответствует массовой плотности, а здесь мы используем эту букву для
обозначения плотности вероятности.
47 Фейнман приводил сложное доказательство без использования частных производных
и с осторожностью вводя распределения вероятности, но доказательство с использованием
математики представляется более понятным.
Гл.6. Упражнения
237
Фейнман затем утверждает, что взаимодействие и соударения между
частицами не изменяют распределение по скоростям.
(е) Проведите моделирование взаимодействующего газа в сосуде с
отражающими стенками под воздействием гравитации. Задайте температуру и
плотность, при которой на дне образуется слой жидкости (подобно воде в стакане).
Постройте распределение по высоте (в котором будут четко видны эффекты за
счет взаимодействия) и импульсное распределение. С помощью последнего
определите температуру. Действительно ли наличие взаимодействий не приводит к
изменению вида импульсного распределения?
Что происходит с атомами, которые испаряются из жидкости? Только
атомы, обладающие очень высокой энергией, могут покинуть жидкость и
стать молекулами газа. Они, однако, расходуют практически всю излишнюю
энергию (в среднем) на то, чтобы покинуть жидкость. Их распределение по
кинетической энергии точно такое же, как в жидкости.48 Фейнман
заканчивает свою главу, подчеркивая, что классическое распределение Больцмана,
несмотря на то что оно достаточно хорошо описывает многие свойства, не
согласуется с экспериментами по удельной теплоемкости в газах, что приводит
к необходимости использования квантовой механики.49
6.2 Система с двумя состояниями, φ
Рассмотрим статистическую механикку небольшого объекта, который мо-
жет находиться только в двух возможных дискретных состояниях, первом
— с энергией Е\ и втором — с более высокой энергией Е^ > Е\.
(а) Отношение больцмановских вероятностей. Найдите отношение
равновесных вероятностей Р2/Р1 обнаружить нашу систему в двух состояниях, когда она
слабо взаимодействует с термостатом температурой Т. Чему равна предельная
вероятность при Τ —> оо? А при Τ —> 0? Полезная формула: больцмановская
вероятность = Z(T)exp(-E/kT) ос ехр(-Е/кТ).
48Если пренебречь квантовомеханическими эффектами.
49Квантовая механика важна для описания внутренних колебаний внутри молекул, в
которые переходит энергия при нагревании газа. Квантовые эффекты не имеют большого
значения для описания давления и других свойств газа, определяемых преимущественно
движением центров масс молекул.
50Представьте его себе как небольшую асимметричную монетку, которая может
находиться в состоянии «орел» или «решка», но в которой отсутствуют внутренние колебания
и движение центра масс. Многие системы хорошо моделируются набором подобных систем
с двумя состояниями: некоторые парамагнетики, окись углерода на поверхности, стекла
при низких температурах, ...
238
Гл.6. Термодинамические потенциалы
(Ь) Вероятности и средние. Вычислив нормировку распределения
вероятности (учитывающую, что система должна находиться в том или другом
состоянии), найдите р\ и р2· (Для этого найдите Z(T) из «полезной формулы» к
заданию (а).) Чему равно среднее значение энергии Е?
6.3 Отрицательная температура. @
Рассмотрим систему N атомов, каждый из которых может находиться в
основном или возбужденном состоянии. Для удобства определим нулевое
значение энергии таким образом, что энергии двух возможных состояний атома
составляют ±ε/2. Пусть атомы изолированы от внешнего мира и
существует только слабая связь между ними, достаточная для того, чтобы привести
атомы в состояние внутреннего равновесия, но больше никак не влияющая
на их состояние.
(a) Микроканоническая энтропия. Если полная энергия системы составляет
Ε (соответствующая числу возбужденных атомов га = Ε/ε + Ν/2), чему
равна микроканоническая энтропия нашей системы? Упростите ваше выражение,
используя формулу Стирлинга logn! ~ n log η — η.
(b) Отрицательная температура. Найдите температуру системы, используя
упрощенное выражение из задания (а). Что произойдет с температурой при Ε >
О?
Энергия Ε > О соответствует инверсии заселенности. Инверсия
заселенности является основным движущим механизмом лазеров.
Для многих величин термодинамические производные проще всего
проинтерпретировать, рассматривая их как сумму по состояниям. Проще всего
увидеть это в малых системах.
(c) Канонический ансамбль, (i) Возьмите один из наших атомов и соедините
его с термостатом температурой квТ = l/β. Запишите точные выражения для
^сапоп. ^сапоп и £саП0п как сумму по двум состояниям атома. (Е представляет
собой энергию каждого состояния, умноженную на вероятность рп этого
состояния, a S — сумму по — ^BPnlogPn·) (ϋ) Сравните ваши результаты с теми,
что вы получите, используя термодинамические соотношения. Возьмите Ζ из
суммы по состояниям, рассчитайте свободную энергию Гельмгольца A, S как
производную А и Ε из соотношения А = Ε — TS. Совпадают ли выражения,
полученные методами термодинамики и статистической физики?
(d) Что случится с Ε в каноническом ансамбле при Τ —> оо? Обнаружите ли
вы режим с отрицательной температурой, обсуждаемый в задании (Ь)?
(e) Связь канонического и микроканонического ансамблей. Найдите
энтропию для канонического распределения N атомов, связанных с внешним миром,
используя ваш ответ к заданию (с). Объясните значение S(T = оо) — S(T = 0)
Гл.6. Упражнения
239
при подсчете состояний. Используйте приблизительное выражение для
энтропии из задания (а) и температуры из задания (b)f покажите, что канонические и
микроканонические энтропии совпадают: SmiCro(E) = SC8inon(T(E)). (Полезная
формула: arctanh(x) = log ((1 + x)/(l — χ)) /2.) Обратите внимание, что на рис.
6.10 они не совпадают, поскольку выражение для формулы Стирлинга, которое
мы используем в задании (а), не является достаточно точным при N = 50.
Объясните словами, почему микроканоническая энтропия меньше канонической.
Рис. 6.10. Отрицательная температура
Энтропия и флуктуации энергии для системы с N = 50 атомами. Каноническое
распределение вероятности приводится для (Ε) = —10ε и квТ = 1.207ε. Вы можете сравнить ваши
расчеты с данным графиком.
(f) Флуктуации. Рассчитайте среднеквадратичные флуктуации энергии в
нашей системе в каноническом ансамбле. Оцените их при Т(Е) из задания (Ь).
Являются ли флуктуации Ε малыми по сравнению с Ε при больших N1
6.4 Молекулярные моторы и термодинамические потенциалы.51
(Биология) (2)
На рис. 6.11 представлена экспериментальная установка, изучающая
молекулярный мотор РНК-полимеразу, который производит транскрипцию
ДНК в РНК.52 Выбор хорошего ансамбля для описания этой системы
представляет собой непростую задачу. На систему действуют две
постоянные силы (F и давление), в ней происходят сложные химические и
биологические процессы. Тем не менее, вам известны некоторые факты,
основанные на фундаментальных принципах. Давайте будем рассматривать
оптическую ловушку и удаленную жидкость как часть внешней среды, а
51 Это упражнение было разработано совместно с Michelle Wang.
52РНК, рибонуклеиновая кислота, представляет собой длинный полимер, подобный
ДНК, выполняющий множество различных функций в живых клетках. Он состоит из
четырех мономерных звеньев (A, U, С и G: аденин, урацил, цитозин и гуанин). ДНК содержит
Τ (тимин) вместо урацила. При транскрипции происходит точное копирование
последовательности ДНК в РНК, с заменой Τ на U.
240
Гл.6. Термодинамические потенциалы
под «системой» будем подразумевать локальную область: ДНК, РНК,
мотор, а также жидкость и локальные молекулы в области, находящиеся в
непосредственной близости от данных объектов, как показано на рис. 6.11.
Рис. 6.11. Молекулярный мотор РНК полимераза
Молекулярный мотор РНК полимераза, соединенный с предметным стеклом, движется
вдоль молекулы ДНК (производя ее транскрипцию в РНК). Противоположный конец
молекулы ДНК соединен с бусинкой, на которую оптическая ловушка воздействует с
постоянной внешней силой F. Пусть расстояние от мотора до бусинки составляет х; таким образом,
мотор стремится уменьшить х, а сила — увеличить х.
(а) Пусть мы больше ничего не знаем о химических и биологических
процессах в системе. Какие из данных утверждений будут верны в любом случае?
1) Полная энтропия Вселенной (системы, бусинки, ловушки, лазерного пучка,
...) должна возрастать либо оставаться неизменной с течением времени.
2) Энтропия Ss системы должна возрастать с течением времени.
3) Полная энергия Ег Вселенной должна уменьшаться с течением времени.
4) Энергия Es системы должна уменьшаться с течением времени.
5) Gs — Fx = Es — TSs + PVs — Fx должна уменьшаться стечением времени,
где Gs — свободная энергия Гиббса системы. Полезная формула: G = E — TS+
PV. (Подсказка: ровно два утверждения являются правильными.)
Последовательность мономеров в РНК может кодировать информацию
для строительства белков, а также приводить к тому, что РНК
сворачивается в различные структуры, важные для выполнения ее функций. Одной из
наиболее важных подобных структур является шпилька (рис. 6.12).
Экспериментаторы изучают прочность этих шпилек, подвергая их внешнему
воздействию (например, с помощью лазерных щипцов). Под воздействием
достаточно большой силы шпилька раскрывается. Вблизи предела раскрытия
шпильки РНК начинает переходить между состояниями с закрытой и раскрытой
Гл.6. Упражнения
241
Рис. 6.12. Шпильки в РНК
Длинная РНК при соединении с комплементарной цепочкой сразу же сворачивается,
образуя шпильку. (Опубликовано с разрешения Liphardt et al. [112], ©2001 AAAS.)
шпильками, производя телеграфный шум 53 (рис. 6.13). Подобно току в
телеграфном сигнале, который должен быть либо включен, либо выключен, эти
системы являются бистабильными и совершают переход из одного состояния
в другое, они представляют собой системы с двумя состояниями.
Две конфигурации РНК, по-видимому, обладают различной энергией
(EZ,EU), энтропией (SZ,SU) и объемами (VZ,VU) в локальной области вблизи
состояний с закрытой и раскрытой шпильками, соответственно. Пусть
внешний мир имеет температуру Τ и давление Р. Пусть L = Lu — Lz —
дополнительная длина ДНК в раскрытом состоянии. Пусть pz — доля
времени, которое молекула проводит в закрытом состоянии при заданной
внешней силе F, а ри = 1 — pz — доля времени в раскрытом состоянии.
(Ь) Какие из нижеприведенных утверждений являются верными, если
предположить, что РНК под воздействием внешней силы находится в равновесии?
1) Pz/Pu = exp((Slot - Slot)/kB), где S** и S™ - полная энтропия
Вселенной, когда РНК находится в закрытом и раскрытом состоянии, соответственно.
2) Pz/Pu = ехр(-(#* " Еи)/квТ).
53 Подобно тому, как телеграфный ключ включается и выключается в различные
промежутки времени, для того чтобы посылать точки и тире, система с телеграфным шумом
переходит в то или другое состояние из двух возможных через случайные промежутки
времени.
242
Гл.6. Термодинамические потенциалы
»»-.»■» , ,. .■ ■..,'. .»""' " и,. 13.2pN
14.2 ρΝ
jUUiifijuunj ги·*·»"
Рис. 6.13. Телеграфные шумы при переходе РНК между двумя
состояниями
При возрастании внешней силы доля времени, которое РНК проводит в закрытом
состоянии, уменьшается. (Напечатано с разрешения Liphardt et al. [112], ©2001 AAAS.)
3) PzlPu = exp(-(Gz - Gu)/kBT). где GZ = EZ- TSZ + PVZ *GU = EU-
TSU + PVU — термодинамические потенциалы Гиббса в двух состояниях.
4) pz/pu = ехр(—(Gz — Gu + FL)/fc^T)f — где L - дополнительная длина
закрытой РНК, a F — приложенная сила.
6.5 Преобразование Лапласа.54 (Термодинамика) (2)
Преобразование Лапласа функции f(t) является функцией х:
гоо
£{/}(*)= / f(t)e~xtdt. (6.69)
Jo
Покажите, что каноническую статистическую сумму Ζ(β) можно записать
как преобразование Лапласа микроканонического объема энергетического слоя
Ω(Ε).
6.6 Множители Лагранжа.55 (Термодинамика) ©
Метод множителей Лагранжа позволяет найти экстремум функции /(х)
при заданном условии связи д(х) = до. Производную функции
/(x) + A(</(x)-so) (6.70)
по λ и х полагают равной нулю. Производные по χ таким образом, включают
в себя члены, зависящие от λ, что позволяет учесть условие связи. Полагая
производную по λ равной нулю, можно получить λ.
54Pierre-Simon Laplace (1749-1827). См. [89, section 4.3].
55Joseph-Louis Lagrange (1736-1813). См. [89, section 12, p. 331].
Гл.6. Упражнения
243
Давайте используем множители Лагранжа, для того чтобы найти
максимум неравновесной энтропии
S=-kBjp(F,Q)logp(F,Q)
= -kBTr(pbgp)
с учетом условия нормировки, а также определенной энергии и числа
частиц. Вы можете использовать любую форму записи энтропии, которую вы
предпочитаете. В случае записи энтропии в виде интеграла Вам потребуется
вариационное исчисление, расчеты для дискретной формы попроще.
(a) Микроканонический ансамбль. Используя множители Лагранжа, для
того чтобы учесть условие нормировки ΣιΡ* = 1» покажите, что распределение
вероятностей, максимизирующее энтропию, представляет собой константу
(микроканоническое распределение).
(b) Канонический ансамбль. Интегрируя по всем Ρ и Q, используйте другой
множитель Лагранжа, для того чтобы зафиксировать среднюю энергию (Е) =
ΣιΕίΡι. Покажите, что каноническое распределение максимизирует энтропию
при заданных условиях нормировки и фиксированной энергии.
(c) Большой канонический ансамбль. Суммируя по различным числам
частиц N и добавляя условие, что их среднее число составляет (Ν) = Σΐ^Ρί,
покажите, что большое каноническое распределение соответствует максимуму
энтропии.
6.7 Преобразование Лежандра.56 (Термодинамика) ©
Преобразование Лежандра функции f(t) представляет собой
минимизацию f(x) — хр по я, таким образом, ρ характеризует наклон (р = df/dx):
д(р) = min{/(x) - хр}. (6.72)
X
Мы уже знакомились в книге с тем, что в термодинамике преобразованием
Лежандра энергии является свободная энергия Гельмгольца 5Т
А(Т, N, V) = min {E(S, V, Ν) - TS} . (6.73)
Ε
Имеет ли это отношение к статистико-механическому выражению из
упражнения 6.5, которое связывает Ω = ехр(5/&в) и Ζ = ехр(—А/квТ)?
Термодинамика, грубо говоря, это статистическая механика без учета флуктуации.
56Adrien-Marie Legendre (1752-1833).
57Вообще говоря, в уравнении (6.40) Ε была независимой переменной. Как это обычно
бывает в термодинамике, мы можем выразить E(S> V, Ν) через S(E> V, Ν).
244
Гл.6. Термодинамические потенциалы
Используя преобразование Лапласа из уравнения (6.5), найдите уравнение
для Етах, максимизирующее подынтегральное выражение. Совпадает ли эта
энергия с энергией, минимизирующей преобразование Лежандра (6.73)?
Найдите приближение для Ζ(β) в вашем преобразовании Лапласа, взяв
подынтегральное выражение в точке максимума (т.е. не учитывая флуктуации). Получается
ли при этом преобразование Лежандра (6.73)?
6.8 Соотношение Эйлера. (Термодинамика, химия) (2)
(а) Используя тот факт, что энтропия S(N, V, Ε) экстенсивна для больших
систем, покажите, что
N
as
dN
V,E
dv
+ Ε
Ν,Ε
дЕ
= s.
Ν,V
Покажите отсюда, что в общем случае
S=(E + PV- μΝ)/Τ
(6-74)
(6.75)
и, следовательно
Ε = TS - PV + μΝ. (6.76)
Это соотношение Эйлера58
(Ь) Проверьте это в явном виде для идеального газа. Используйте формулу
для энтропии идеального газа (уравнение 3.57)
S(N,V,E) = -NkB
+ NkB log
V /4тгт£\3/2
Nh* \ SN )
(6.77)
для вывода выражений для Г, Ρ и μ через Ε, Ν и V и проверьте уравнение
(6.75).
6.9 Соотношение Гиббса—Дюгема. (Термодинамика, химия) (2)
Поскольку Ε является функцией состояния, она должна зависеть только
от 5, V и N. Но в уравнении (6.76) присутствует также явная зависимость
от Τ, Ρ и μ, как такое может быть?
Для того чтобы ответить на этот вопрос, рассмотрим небольшое
изменение всех шести переменных. Нам известно, что (Ш = TdS — ΡάΥ-\-μάΝ. При
58Леонард Эйлер (1707-1783), Вообще говоря, это одно из многих фундаментальных
соотношений, названных в честь Эйлера, другие соотношения Эйлера включают в себя число
граней, ребер и вершин при полигонализации поверхности, а также полярное
представление комплексных чисел.
Гл.6. Упражнения
245
варьировании переменных в уравнении Эйлера мы получаем dE = TdS —
Ρ dV + μ dN + S dT — V dP + Ν άμ. Это дает соотношение Гиббса—Дюгема
0 = 8άΤ-νάΡ + Νάμ. (6.78)
Это соотношение говорит о том, что интенсивные величины Τ, Ρ и μ не
являются независимыми. Небольшое изменение μ приводит к небольшим
изменениям Τ и Р.
(a) Запишите μ как производную свободной энергии Гиббса G(T,P,N).
Таким образом, μ становится функцией трех переменных Τ, Ρ и N.
Соотношение Гиббса—Дюгема говорит от том, что оно не должно зависеть от
N.
(b) Докажите, что изменение числа частиц в большой системе при
фиксированной температуре и давлении не должно приводить к изменению химического
потенциала. (Подсказка: удвоение числа частиц при фиксированных Τ и Ρ
приводит также к удвоению размера и энергии системы.)
Тот факт, что как G(T, Ρ, Л/"), так и N экстенсивны, говорит о том, что
G должно быть пропорционально N. Мы использовали эту экстенсивность
для доказательства соотношения Эйлера в упражнении 6.8. Таким образом,
мы можем использовать соотношение Эйлера для записи формулы для G
напрямую.
(c) Используйте соотношение Эйлера (уравнение 6.76) для записи выражения
для G = Ε — TS + PV. Оно в самом деле будет пропорциональным N1 Как
насчет вашего выражения для μ из задания (а), будет ли оно зависеть от N1
6.10 Уравнение Клаузиуса—Клапейрона. (Термодинамика, химия) ©
Рассмотрим фазовую диаграмму на рис. 6.14. Вдоль равновесной фазовой
границы температуры, давления и химические потенциалы различных фаз
должны совпадать, иначе через межфазную границу проходило бы тепло,
или происходило бы смещение в сторону или утечка частиц, соответственно
(что нарушало бы предположение равновесия).
(а) Примените соотношение Гиббса—Дюгема (6.78) для обеих фаз при
малом сдвиге ΔΤ вдоль фазовой границы. Пусть si, v\, S2 и V2 — молекулярные
энтропии и объемы (s = S/N, ν = V/N для каждой фазы). Выведите уравнение
Клаузиуса·—Клапейрона для тангенса угла наклона линии сосуществования фаз
на фазовой диаграмме
dP/dT = (sl-s2)/(vl-v2).
(6.79)
246
Гл.6. Термодинамические потенциалы
П
Температура
Рис. 6.14. Типичная фазовая диаграмма
Типичная фазовая диаграмма, демонстрирующая кривые сосуществования фаз для
твердых тел, жидкостей и газов.
Сложно экспериментально измерить энтропию на одну частицу, у нас нет
энтропийного термометра. Но, как вы помните, изменение энтропии при
фазовом переходе AS = Q/T связано с потоком тепла Q, требуемом для
фазового перехода. Пусть латентное (скрытое) тепло L представляет собой поток
тепла на одну молекулу.
(Ь) Запишите выражение для dP/dT, не содержащее энтропию.
6.11 Переход через барьер. (Химия) (2)
В этом упражнении мы выведем закон Аррениуса (уравнение 6.60),
Т = Т0ехр{-Е/квТ)) (6.80)
определяющий скорость, с которой химические реакции проходят через
энергетические барьеры. Экспоненциальная зависимость от высоты барьера Ε
представляет собой относительную больцмановскую вероятность того, что
частица находится вблизи вершины барьера (и, следовательно, в состоянии
через него перейти). В данном упражнении мы тщательно вычислим префак-
тор Го-
Рассмотрим систему с энергией U(X), имеющей локальный минимум в
точке X = Xoj в которой величина энергии составляет U(Xo) = 0.
Предположим, что существует энергетический барьер высоты U(Xb) = В, через
который частицы могут переходить.59 Пусть температура системы намного
59Данный потенциал может описывать химическую реакцию, где X - координата
реакции. Другой пример: он может описывать утечку газа со спутника Юпитера, где Χ —
расстояние от спутника в направлении Юпитера.
Критическая
точка
Гл.6. Упражнения
247
меньше В/кв· Для того чтобы произвести наши вычисления, необходимо
сделать некоторые упрощения. (1) Мы предполагаем, что атомы, движущиеся
направо и переходящие через барьер, не попадают обратно в потенциальную
яму. (2) Мы предполагаем, что атомы, находящиеся на дне ямы, находятся
в состоянии локального равновесия. (3) Мы предполагаем, что число частиц,
движущихся направо и переходящих через барьер, задается равновесным
распределением внутри потенциальной ямы.
(a) Пусть плотность вероятности того, что координата частицы равна X,
составляет р(Х). Чему равно отношение плотностей вероятности р(Хв)/р(Хо),
если предположить, что частицы вблизи вершины барьера находятся в равновесии
с частицами на дне потенциальной ямы? Полезная формула: распределение
Больцмана ρ ос ехр(—Е/квТ).
Если высота барьера В ^> fc^T, то большинство частиц в яме находятся
вблизи ее дна. Зачастую потенциал вблизи дна достаточно хорошо
описывается квадратичным приближением U(X) « Μω2(Χ — ΛΌ)2/2, где Μ — масса
нашей системы, а ω — частота малых осцилляции в яме.
(b) Чему равна в данном приближении плотность вероятности р(Х) вблизи
дна ямы (рис. 6.15)? Чему равна р(Хо), плотность вероятности нахождения в
самой низкой точке потенциальной ямы? Полезная формула: гауссово
распределение вероятности (1/ν2πσ2)βχρ(—χ2/2σ2).
Рис. 6.15. Распределение вероятности в потенциальной яме
Приблизительное распределение вероятностей для атомов внутри потенциальной ямы.
248
Гл.6. Термодинамические потенциалы
Зная ответы к заданиям (а) и (Ь), мы можем получить распределение
вероятности р(Хв) на вершине барьера.60 Нам также необходимо знать
вероятность того, что частицы вблизи вершины барьера имеют скорость V,
поскольку наиболее быстро движущиеся частицы вносят больший вклад в
поток вероятности через барьер (рис. 6.16). Как обычно, поскольку
полная энергия представляет собой сумму кинетической и потенциальной,
полная больцмановская вероятность представима в виде двух сомножителей.
Равновесное распределение частиц по скоростям будет иметь вид p(V) =
l/y/2nkBT/Mexp{-MV2/kBT/2).
Рис. 6.16. Переход через барьер
Диапазон координат атомов, движущихся вправо со скоростью υ, которые перейдут через
вершину барьера за время Δί.
(с) Вначале запишите выражение для Г — вероятности того, что в
единицу времени данная частица будет двигаться вправо и перейдет через барьер
при неизвестной плотности вероятности р(Хв)р(У) как интеграл по скорости
V. Затем, используя ваши формулы из заданий (а) и (Ь), оцените Г для нашей
системы. Полезная формула: f£° χ ехр(—х2/2σ2) dx = σ2.
Каким образом можно, обобщить нашу одномерную модель? В прежние
времена Крамере изучал различные одномерные модели, меняя способы
взаимодействия системы с внешним термостатом. С помощью компьютера можно
60Точнее, мы рассчитали распределение частиц р(Хв) в равновесии, половина из которых
(движущихся вправо) в нашем предположении переходит через барьер в неравновесных
реакциях.
Гл.6. Упражнения
249
избежать рассмотрения термостата в отдельности и напрямую работать с
полным конфигурационным пространством высокой размерности, что приводит
к построению теории переходных состояний. Формула, полученная в теории
переходных состояний, очень похожа на ту, которую вы получили в задании
(с), за исключением того, что префактор содержит произведение всех частот
на дне ямы и всех положительных частот в седловой точке на вершине
барьера (см. [57]). Другие обобщения возникают при переходе через барьеры со
сложной структурой [66] или в неравновесных системах [84].
6.12 Уравнения Михаэлиса—Ментен и Хилла. (Биология,
моделирование) @
Скорости химических реакций часто достигают насыщения. Клетка
должна быть чувствительна к введению нового химического вещества S, но ее
отклик не должен неограниченно расти при возрастании концентрации нового
химического вещества [*S].61 Другие биологические реакции действуют как
переключатели. Переключатель реагирует на изменение концентрации
химического вещества S, резко меняя скорость реакции или свое состояние.
Подобные реакции являются хорошим примером того, как можно получить
эффективную динамическую теорию, избавляясь от некоторых степеней свободы.
В данном случае мы не огрубляем масштаб некоторой большой статистико-
механической системы, а исключаем из уравнений только один фермент Е,
для того чтобы получить эффективную скорость реакции.
Скорость химической реакции
NS + B-+C, (6.81)
где N молекул субстрата S соединяются с молекулой В, образуя молекулу С,
будет подчиняться закону действующих масс:
^ = k[S]N[B). (6.82)
Насыщение и уравнение Михаэлиса—Ментен. Насыщение не наблюдается
в обычной кинетике химических реакций. Обратите внимание на то, что
скорость реакции стремится к N-ft степени концентрации [S]. Скорость реакции
растет линейно или еще быстрее с ростом концентрации, что весьма далеко
от состояния насыщения.
61 [S] представляет собой концентрацию S (число частиц на единицу объема). S
обозначает субстрат.
250
Гл.6. Термодинамические потенциалы
Основным примером реакции с насыщением в биологических системах
является реакция Михаэлиса—Ментен. Реакция такого типа преобразует
химическое вещество S (субстрат) в продукт Ρ со скоростью
d[P] Vm^[S]
dt KM + [S\*
(6.83)
где Км — константа Михаэлиса (рис. 6.17). Эта реакция при малых
концентрациях ведет себя подобно обычной химической реакции с N = 1 и к =
Утах/Км, но скорость реакции стремится к насыщению Vmax при [S] —> оо.
Константа Михаэлиса Км представляет собой концентрацию [5], при
которой скорость реакции равна половине той скорости, при которой происходит
насыщение (см. рис. 6.17).
Концентрация субстрата [S]
Рис. 6.17. Скорости реакций,
Михаэлиса—Ментен и Хилла
описываемых уравнениями
Мы можем вывести уравнение Михаэлиса—Ментен, предполагая наличие
катализатора или фермента Е, количество которого ограничено. Пусть
фермент частично свободен и способен к взаимодействию (концентрация [Е]), а
частично связан с субстратом (концентрация [Е : *5]),62 помогая произвести
из него продукт. Полная концентрация [Е] + [Е
Реакции имеют следующий вид:
S] = Etot фиксирована.
E + S
'кг
E.S *¥ Е + Р.
(6.84)
Предположим, что количество субстрата очень большое, и его концентрация
медленно меняется с течением времени. Предположим также, что
концентрация [Е : S] стационарна, и избавимся от нее как от степени свободы.
'Двоеточие обозначает связанное состояние двух молекул, называемое димером.
Гл.6. Упражнения
251
(а) Пусть скорости реакции связывания в уравнении (6.84) имеют
стандартный вид (уравнение 6.82), с константами к\, к-\ и fccat» где N = 1 или N = О
Запишите уравнение для d[E : S]/dt, положите эту производную равной нулю
и используйте это выражение, для того чтобы исключить [Е] в уравнении для
dP/dt. Выразите Vmax и Км в уравнении Михаэлиса—Ментен (6.83) через fcs и
Интуитивно легко понять причину этого насыщения: когда все ферменты
связаны с субстратом, добавление большего количества субстрата не может
ускорить течение реакции.
Кооперативностъ и резкое переключение: уравнение Хилла. Гемоглобин
— это то, что делает кровь красной. Этот белок, содержащий железо,
способен присоединять до четырех молекул кислорода в легких, а затем он
переносит их в ткани тела, где освобождается от них. Если бы связывание всех
четырех молекул кислорода было независимым, то зависимость
концентрации [О2] от концентрации связанного кислорода подчинялась бы уравнению
Михаэлиса—Ментен. Чтобы полностью освободить гемоглобин (НЬ) от
кислорода, требовалась бы очень маленькая концентрация кислорода в ткани.
Что будет в том случае, если связывание НЬ кислородом будет скорее
сигмойдальным - достаточно резкий переход между состоянием, при
котором связаны четыре кислорода при высокой концентрации [О2] (в легких) и
практически полном отсутствии связывания при низких концентрациях
кислорода. Это возникает из-за того, что связывание кислорода увеличивается
при наличии других связанных молекул кислорода. Это происходит не
потому, что молекулы кислорода слипаются каким-либо образом друг с
другом, а из-за того, что каждая молекула кислорода деформирует НЬ, таким
образом, что он становится нелокально аллостерическим^ меняя
конфигурацию и сродство к другим центрам связывания. Уравнение Хилла было
введено для гемоглобина для описания данного типа кооперативного
связывания. Подобно уравнению Михаэлиса—Ментен, оно также используется
для описания скоростей реакций, где вместо носителя НЬ имеется фермент
или, например, последовательность центров связывания при транскрипции
(см. упражнение 8.11).
Мы выведем уравнение Хилла исходя не из аллостерического
связывания, а с точки зрения реакции с насыщением, включающей η одновременно
связываемых молекул. Согласно уравнению Хилла, скорость реакции имеет
вид
63Аллостерический происходит от Alio (другой) и steric (структура или пространство).
Аллостерические взаимодействия могут быть кооперативными, как в гемоглобине, или ин-
гибирующими.
252
Гл.6. Термодинамические потенциалы
d[P) Vmax[S)n rfiR_.
~dT ~ щ + [s]» (6·85)
(см. рис. 6.17). Для НЬ концентрация молекул, связанных с η молекулами
кислорода, задается правой частью уравнения (6.85). В обоих случаях переход
становится все больше похож на переключатель, где реакция (или
способность НЬ принимать или отпускать кислород) включается строго при
определенных концентрациях (см. рис. 6.17). Переход может становиться более
или менее резким при увеличении или уменьшении п.
Уравнение Хил л а может быть получено с использованием упрощения, что
η связываются в течение одной реакции:
E + nS tJ*E\{nS\ (6.86)
где Ε в нашем примере соответствует гемоглобину, a S — молекулам Ог- Снова
существует фиксированное полное число £tot = [Щ + [Е ·' п^]·
(Ь) Пусть две реакции в уравнении (б.86) имеют стандартный
хи ми ко-кинетически и вид (уравнение 6.82), где N = О или N = п. Запишите
равновесное уравнение для Ε : (nS), затем исключите [Е], зная фиксированное
полное число £tot· Выразите Vmax и Кц через къ, ки и Etot.
Как правило, в частности для гемоглобина, эта кооперативность не
является настолько жесткой. Наряду с полностью свободными и полностью
связанными состояниями существуют состояния с одной, двумя и тремя
молекулами О2 · Такие системы можно также приближенно описывать с
использованием уравнения Хилла, но η при этом становится подгоночным параметром.
Например, для НЬ η « 2.8.
Уравнения Хилла и Михаэлиса—Ментен часто используются в моделях
биологических реакций, даже если не известны точные механизмы
(ферменты, кооперативное связывание), генерерующие реакции.
6.13 Пыльца и твердые квадраты. @
Между объектами, погруженными в газ, на небольших расстояниях
возникает эффективная сила притяжения в случае, когда молекула газа не может
больше находиться между объектами. Можно рассматривать это явление как
нарушение баланса давления (с одной из сторон отсутствуют соударения) или
как энтропийное притяжение.
Давайте рассмотрим энтропийное притяжение между пыльцой и
стенкой, представляя жидкость в виде двумерного идеального газа классических
неразличимых частиц. Для удобства представим себе, что пыльца и жидкость
представляют собой квадратные частицы, сонаправленные с осями сосуда,
размером ВиЬ, соответственно (рис. 6.18).
Гл.6. Упражнения
253
Рис. 6.18. Квадратная пыльца
Квадратная пыльца в жидкости ориентированных квадратных молекул вблизи стенки.
Тонкие линии обозначают область исключенного объема вокруг пыльцы и стенки.
Предположим, что молекулы идеального газа не взаимодействуют
между собой (в отличие от системы, рассматриваемой в упражнении 3.5), но
потенциальная энергия бесконечна, если молекула газа перекрывается с
пыльцой или со стенкой. Пусть ячейка площадью L x L содержит одну частицу
пыльцы и N молекул газа.
Пусть пыльца находится вблизи одной из стенок. Пусть расстояние от
стенки до ближайшей поверхности пыльцы равно Q. (Похожая задача с
квадратной частицей, взаимодействующей с малыми молекулами,
рассматривалась в работе [45].)
(a) Чему равна площадь A(Q » 0), доступная молекулам газа, когда
пыльца находится далеко от стенки? Чему равно пересечение исключенных объемов
А(0) - А(ос), когда пыльца соприкасается со стенкой, Q = 0? Получите
выражение для A(Q) как функции Q при Q <Ь и Q > Ъ.
(b) Чему равен доступный молекулам объем в конфигурационном
пространстве Q(Q) (размерности 27V)? Чему равна конфигурационная энтропия
идеального газа, S(Q)7 (Выразите ваш ответ через A(Q).)
Ваши ответы к заданию (Ь) определяют свободную энергию пыльцы после
суммирования по степеням свободы газа.
(c) Чему равна результирующая свободная энергия пыльцы J*(Q) = Ε —
Τ S(Q) при Q > b и Q <Ы Зная J*(Q), найдите силу, действующую на пыльцу
при Q <Ъ. Эта сила положительная (направленная от стенки) или
отрицательная? Почему?
254
Гл.6. Термодинамические потенциалы
(d) Рассчитайте явным образом силу, возникающую вследствие давления
идеального газа на дальнюю сторону пыльцы, выраженную через A(Q).
Сравните ее с силой, полученной через свободную энергию в задании (с). Почему
с другой стороны отсутствует балансирующая сила? Чему равна эффективная
«длина» дальней стороны пыльцы?
6.14 Статистическая механика и статистика.64 (Статистика) ©
Рассмотрим задачу аппроксимации экспериментальных данных
теоретической моделью. Пусть наша модель Μ предсказывает зависящую от времени
функцию y^M'(t). Пусть имеется N экспериментально определенных точек yi
в моменты времени U со стандартным отклонением σ. Мы предполагаем, что
экспериментальные ошибки данных независимы и распределены по Гауссу,
таким образом, вероятность того, что теоретическая модель воспроизводит
наблюдаемые точки (вероятность P(D\M) данных, задаваемых моделью),
составляет
P(D\M) = ТТ -Д=- е-(У(М)М-У*)2/2°2. (6.87)
(a) Верно или нет: Плотность вероятности соответствует распределению
Больцмана с энергией Η и температурой Т, где Η = Σί=ι(ν^Μ\ίί) — Уг)2/2 и
квТ = σ2.
В статистике существует два подхода. Среди семейства моделей
сторонники частотного подхода выбирают модель Μ с наибольшим P(D\M) (оценка
максимальной вероятности). Ансамбль наиболее подходящих моделей затем
выбирается в согласии с диапазоном входных данных (полученным из
ошибок σ). Байесианцы имеют другую точку зрения. Они доказывают, что нет
причины a priori верить тому, что все модели обладают одинаковой
вероятностью. (В пространстве моделей не существует аналога теоремы Л иу вил л я
(см. гл. 4)). Предположим, что вероятность модели (prior) равна Р(М). Они
используют теорему
P(M\D) = P(D\M)P(M)/P(D). (6.88)
(b) Докажите теорему Байеса (уравнение 6.88), используя тот факт, что
Р(А и В) = Р(А\В)Р(В) (см. примечание 37 на с. 171).
Байесианцы зачастую выбирают максимум P(M\D) как модель для
экспериментальных данных. Но с данной точки зрения более естественным
представляется рассмотрение полного ансамбля моделей, взвешенного с функцией
Это упражнение было разработано с участием Роберта Вейсса.
Гл.6. Упражнения
255
Р(М|D), для наилучшего описания данных. Это среднее по ансамблю
естественным образом определяет величину ошибок, а также оценку различных
величин.
Рассмотрим задачу аппроксимации линией двух точек данных.
Предположим, что у нас есть следующий набор экспериментальных точек: t\ = О,
у\ = 1 и ^2 — 1, J/2 = 2, где оба значения у имеют некоррелированные
гауссовы ошибки со стандартным отклонением σ = 1/2, как предполагалось выше
в уравнении (6.87). Наша модель М(т,Ь) задается уравнением y(t) = mt + b.
Наш байесианский статистик знает, что как га, так и Ъ лежат между нулем и
двойкой, и предполагает, что во всем остальном распределение вероятностей
однородно, Р(т, Ъ) = 1/4 при 0<га<2иО<Ь<2.
(с) Какой из контурных графиков, представленных на рис. 6.19, представляет
собой распределение вероятностей Р(М\D) для модели, задаваемой
наблюдаемыми данными? (Расстояние между контурными линиями произвольно).
(е)
Рис. 6.19
Глава 7
Квантовая статистическая
механика
Квантовая статистическая механика является основой физики твердого
тела (описывающей поведение металлов, полупроводников и стекол), а
также имеет огромное значение в молекулярной физике и астрофизике (белые
карлики, нейтронные звезды) Она объясняет явления, которые дали толчок
к созданию квантовой механики (теория Планка излучения абсолютно
черного тела), а также другие интересные квантовые феномены (конденсация
Бозе, сверхтекучие жидкости и сверхпроводники)
Приложения квантовой статистической механики являются важными
компонентами курсов по этим различным предметам. Мы рассмотрим эту
важную тему только в одной главе, чтобы избежать перекрытий с другими
курсами по физике и химии, а также чтобы наша книга была понятна для
непосвященных в тайны квантовой механики.
В этой главе мы предполагаем, что читатель знаком с основами
квантовой механики. Мы будем идти от абстрактного к конкретному, используя
ряд упрощений. Мы начнем (в разделе 7.1) с введения смешанных
состояний для квантовых ансамблей и матриц плотности — темы повышенной
сложности (для неравновесных квантовых систем, которые нельзя
представить как смеси энергетических собственных состояний). Мы рассмотрим
смешанные состояния в разделе 7.2 на примере квантового гармонического
осциллятора с конечной температурой. Мы изучим статистическую
механику одинаковых частиц (раздел 7.3). Мы сделаем затем сильное упрощение,
предполагая, что частицы не взаимодействуют между собой (раздел 7.4),
получив распределения Бозе—Эйнштейна и Ферми для заполнений
собственных состояний одиночных частиц. Мы сравним статистику Бозе, Ферми и
7.1. Сметанные состояния и матрицы плотности
257
Максвелла—Больцмана в разделе 7.5. Мы покажем, насколько удивительно
полезным оказывается приближение невзаимодействующих частиц в
квантовых системах для решения классических проблем: излучения черного тела,
конденсации Бозе (раздел 7.6), а также для описания поведения металлов
(раздел 7.7).
7.1 Смешанные состояния и матрицы плотности
Классические статистические ансамбли представляют собой
распределения вероятности p(P,Q) в фазовом пространстве. Как обобщить их в
случае квантовой механики? Тут сразу возникают две проблемы. Во-первых,
принцип неопределенности Гейзенберга говорит нам о том, что невозможно
определить координату и импульс квантовой частицы в одно и то же
время. Состояния нашей квантовой системы не будут представлять собой точки
в фазовом пространстве. Во-вторых, в квантовой механике уже
присутствуют плотности распределения вероятности. Даже для систем, находящихся
в определенном состоянии1 Ψ(($), вероятность распределена между
различными конфигурациями |Ψ((ί)|2 (или импульсами |Ф(Р)|2). В статистической
механике нам нужно ввести второй тип вероятности, для того чтобы
описывать ансамбль, который может находиться в различных квантовых
состояниях ^n(Q) с вероятностями рп. Ансамбли в квантовой механике называются
смешанными состояниями. Они представляют собой суперпозиции не
различных волновых функций, а некогерентных смесей.2
Предположим, что мы хотим рассчитать математическое ожидание
оператора А. В некотором определенном состоянии Фп квантовое математическое
ожидание имеет вид
(А)риге = J *;(Q)A*n(Q) d3"Q. (7.1)
Таким образом, математическое ожидание для ансамбля составляет
гВ квантовых системах с большим количеством частиц волновые функции
представляют собой функции координат всех частиц (или импульсов всех частиц, в импульсном
пространстве).
2 Например, если \V) соответствует вертикально поляризованному фотону, а \Н) —
горизонтально поляризованному фотону, то суперпозиция (1/\/2) (\V) + \Н)) представляет
собой диагонально поляризованный фотон, в то время как неполяризованный фотон
представляет собой смесь половины \V) и половины |/f), описываемую матрицей плотности
(|У)(У| 4- \Н)(Н\)/2. Суперпозиция находится в обоих состояниях, а смесь — либо в одном,
либо в другом (упражнение 7.5).
258
Гл.7. Квантовая статистическая механика
(А) = ^Рп / *;(Q)A*n(Q) d3ArQ. (7.2)
За исключением некоторых отдельных упражнений, в оставшейся части
книги мы будем рассматривать смешанные состояния (уравнение 7.2). В
самом деле, для большинства равновесных ансамблей Фп могут
рассматриваться как энергетические собственные состояния, а рп — либо константы
в малом энергетическом диапазоне (для микроканонического ансамбля),
либо βχρ(—βΕη)/Ζ (для канонического ансамбля), либо βχρ(—β(Εη — Νημ)) /Ξ
(для большого канонического ансамбля). Вы можете прервать здесь чтение
данной книги и перейти к разделу, посвященному квантовому
гармоническому осциллятору, так как информация, изложенная в следующем разделе, не
является необходимой для большинства практических приложений.
7.1.1 Материал повышенной сложности: матрицы плотности
Что произойдет, если мы выйдем за пределы смешанных состояний? Во-
первых, существует большое количество систем, которые не могут быть
описаны как смесь энергетических собственных состояний. (Например, каждое
такое смешанное состояние будет обладать свойствами, не зависящими от
времени.) Во-вторых, несмотря на то, что можно определить общий, не
зависящий от времени ансамбль через более общий базис Фп, возможность
производить преобразования между различными базисами оказывается довольно
полезной. В самом деле, в сверхтекучих жидкостях и сверхпроводниках
присутствует удивительный недиагональный дальний порядок в пространстве
координат (упражнение 9.8). В-третьих, мы увидим, что для правильного
обобщения теоремы Лиувилля требуется более изящный подход, основанный на
использовании операторов.
Нашей целью является избежание проведения расчетов, привязанных к
определенным состояниям Фп. Вместо этого запишем среднее по ансамблю
(уравнение 7.2) через А и оператор р, матрицу плотности. В этом
разделе мы будем использовать обозначения Дирака, с помощью которых можно
записать среднее по ансамблю смешанных состояний следующим образом: 3
(А) = 5>η<Ψη|Α|Φη). (7.3)
П
3В обозначении Дирака (Ф|М|Ф) = / Ф*МФ.
7.1. Сметанные состояния и матрицы плотности
259
Выберем некоторый полный ортонормированный базис Фа. Тогда
тождественный оператор будет иметь вид
1 = Σ|Φβ)(Φβ| (7.4)
α
Подставляя тождественный оператор (7.4) в уравнение (7.3), находим
(А) =£><Фп| (Х>«)<Фа|) А|Ф„>
η \ а /
η а
= Σ>ΩΑ|(5>η|Φη)<Ψη|)|Φα)
Q \ П /
= Tr(Ap), (7.5)
где4
представляет собой матрицу плотности.
Матрица плотности обладает следующими свойствами:
Достаточность. В квантовой механике во всех измеряемых процессах
определяются математические ожидания операторов. Наша матрица
плотности, таким образом, достаточна для описания всего, что нам нужно знать о
наших квантовых системах.
Чистые состояния. Матрица плотности чистого состояния с
определенной волновой функцией Φ имеет вид рриге = |Ф)(Ф|. В координатном базисе
|Q) матричные элементы матрицы плотности, характеризующей чистые
состояния, имеют вид ppure(Q,Q0 = (QIPpurelQO = *W)*(Q). В частности,
зная матрицу плотности чистого состояния, можно вычислить его волновую
функцию5 с точностью до физически неизмеряемой фазы. Поскольку наша
4 След матрицы представляет собой сумму ее диагональных элементов. Он не зависит
от выбора базиса. То же самое верно и для операторов. Мы суммируем по диагональным
элементам Тг(М) = Σα(φ"ΙΜΙφ")·
5В частности, поскольку Φ является нормированной, |Ф*(<0/)|2 = /dQ|p(Q»Q')|2 и> сле"
довательно,
»(Q) = *Q.g> (7.7)
V/dQ|p(Q,Q')|2
с точностью до фазы </>*(Q') для каждой координаты Q'.
260
Гл.7. Квантовая статистическая механика
волновая функция является нормированной, (Ф|Ф) = 1, мы видим, что
квадрат матрицы плотности чистого состояния равен самой матрице плотности:
Р£иге=|Ф><ФЦФ><Ф| = |Ф><Ф|=Рриге·
Нормировка. След матрицы плотности чистого состояния Тгрриге = 1,
поскольку мы можем выбрать такой ортонормированный базис, в котором
первым матричным элементом будет сама волновая функция Ф, а
оставшиеся элементы будут равны нулю. Таким образом, след произвольной матрицы
плотности будет также равен единице, поскольку она характеризует
распределение вероятности для матриц плотности чистых состояний:
Тгр = ΊΗ5>η|Φη)(Φη|) =£ί^&(|Ψη)<Ψη|) = £>„ = 1. (7.8)
\ п / η η
Каноническое распределение. Каноническое распределение
представляет собой смесь энергетических собственных состояний \Еп) с
больцмановским весом βχρ(—βΕη). Таким образом, матрица плотности
Рсапоп диагональна в энергетическом базисе:6
П
Мы можем записать каноническую матрицу плотности в виде, не зависящем
от выбора базиса, используя оператор Гамильтона Н. Во-первых,
статистическая сумма представима в виде следа7
Ζ = £>хр(-№) = Σ(Εη\βχρ(-βΗ)\Εη) = Tr(exp(-0W)). (7.11)
η η
Во-вторых, числитель имеет вид
Σ \Еп) еМ-РЕп)(Еп\ = Σ \Еп) ехр(-/?Н)<Я„| = exp(-j9W), (7.12)
6Обратите внимание, что состояния Фп в произвольной смеси не обязательно должны
представлять собой собственные состояния и даже быть ортогональными.
7Чему равна экспоненциальная функция от матрицы Μ? Можно определить ее в виде
разложения в ряд ехр(М) = 1 + Μ + М2/2! + М3/3! + ..., но проще выбрать такой базис,
в котором матрица Μ диагональна. В этом базисе любая функция /(М) имеет вид
//(рп) 0 0 ...\
/(р)=1 0 /(р22) 0 ...I. (7.10)
Затем можно снова вернуться к исходному базису. С помощью подобной процедуры можно
также определить log M (уравнение 7.14).
1.1. Смешанные состояния и матрицы плотности
261
поскольку оператор Η (и, следовательно, ехр(—βΗ)) диагоналей в
энергетическом базисе. Таким образом,
- - еМ~т (7.13)
rcanon ^(βχρί-^))
Энтропия. Энтропия для произвольной матрицы плотности имеет вид
S = -kBTr(plogp). (7.14)
Временная эволюция матрицы плотности. Временная эволюция
матрицы плотности определяется временной эволюцией чистых состояний,
составляющих ее:8
др ^ /^|*„>/φ I , |ф чЗ<*«|\ ,71.ч
ж = L·»· I-аг(Фп| + ^п)~дГ) ■ (715)
Временная эволюция кет-вектора волновой функции |ФП) происходит под
действием гамильтониана:
а временная эволюция бра-вектора волновой функции (Фп| определяется
временной эволюцией Ψ* (Q):
^-(£)'-(**··)'--**·*·· <717>
Поскольку оператор 7ί эрмитов, получаем
Таким образом,9
η
= ^[«.p]· (7·19)
8pn — вероятности качала эволюции в состояниях Φη· Очевидно, что они не меняются
с течением времени.
9 Коммутатор двух матриц имеет вид [А, В] = АВ — В А. Обратите внимание, что
уравнение (7.19) — это взятая со знаком минус формула, характеризующая временную
эволюцию операторов в представлении Гейзенберга.
262
Гл.7. Квантовая статистическая механика
Квантовая теорема Лиувилля. Этот закон временной эволюции
(7.19) представляет собой квантовую версию теоремы Лиувилля. Это
можно увидеть, используя уравнения Гамильтона (4.1) qa = дН/дра и
ра = —dH/dqa, а также определение скобок Пуассона
г л rv τ^ΟΑ дВ дА дВ
{Д В}Р = V 7г- ~ я-л"· 7·20
Приравнивая нулю полную производную (4.7), можно получить уравнение
для частной производной:
dp _ dp ^ dp . dp ,
dt " ~dt +2^^α+^Ρ
таким образом
= др ^(^дН_др_дН\
dt^^\dqadpa dVadqa)' У ■ >
^ = {П,р}р. (7.22)
Принимая во внимание соотношения между скобками Пуассона и
коммутатором { }р «-»■ (l/ift)[ ], можно показать, что закон временной эволюции (7.19)
является аналогом теоремы Лиувилля (7.22).
Квантовая теорема Лиувилля и статистическая механика.
Квантовая версия теоремы Лиувилля не так полезна, как классическая. В
классической теореме, как вы помните, утверждается, что dp/dt = 0. Вдоль
траектории любой точки ρ постоянна. Если траектория покрывает всю
энергетическую поверхность (эргодичность), то плотность вероятности постоянна на
всей энергетической поверхности, что обосновывает справедливость
использования микроканонического ансамбля.
Для изолированной квантовой системы эта аргументация больше не
работает. Условие, что равновесное состояние стационарно, не является очень
строгим. В самом деле, dp/dt = [Η, ρ] = 0 для произвольной смеси
многочастичных энергетических состояний. В принципе, изолированные
квантовые системы не являются эргодическими, и необходимо включить
взаимодействие с внешним миром, чтобы вызвать переходы между многочастичными
собственными состояниями, необходимыми для достижения состояния
равновесия.10
10 Многочастичное собственное состояние большой системы имеет ряд особенностей.
Рассмотрим атом в возбужденном состоянием, помещенный в большой сосуд. Мы, как правило,
7.2. Квантовый гармонический осциллятор
263
7.2 Квантовый гармонический осциллятор
Гармонический осциллятор является отличной иллюстрацией применения
статистической механики к квантовым системам. Рассмотрим осциллятор с
частотой ω. Его энергетические собственные состояния имеют вид Еп = (п +
l/2)huj (рис. 7.1). Таким образом, его статистическая сумма представляет
собой геометрическую прогрессию Σ#η, сумма которой равна 1/(1 — х):
Рис. 7.1. Энергетические уровни гармонического осциллятора
Энергетические уровни гармонического осциллятора эквидистантны.
считаем, что атом находится в энергетическом собственном состоянии, переходящем с
течением времени в основное состояние, излучая при этом некоторое количество фотонов.
Очевидно, что атом только приблизительно находится в собственном состоянии (или его
энергия не будет затухать). Он находится в резонансе, представляющем собой
собственное состояние, если мы не учитываем взаимодействие с электромагнитным полем.
Многочастичные состояния системы представляют собой странные суперпозиции состояний с
фотонами, поглощенными атомом, и атомом, излучающим фотоны, что в конечном итоге
приводит к установлению стационарного состояния. Если начать учитывать большее
количество атомов и другие взаимодействия, то реальные многочастичные собственные
состояния, как правило, достаточно бесполезны (за исключением основного состояния и наиболее
низких возбужденных состояний). Слабые взаимодействия с внешним миром разрушают
эти многочастичные собственные состояния и, как правило, приводят к установлению
равновесия.
264
Гл.7. Квантовая статистическая механика
оо
а-/ЗМ"+1/2)
Ζφ0 = Σ*-βΕη = Έ*
п=0 п=0
оо 1
= 6-βΠω/2 у^ L-β^Υ = Β~β^/2 L
βϋω
η=0
1 1
efihu,/2 _ е-/?йи,/2 2 sinh(/?/iu>/2)'
Средняя энергия составляет
dlogZqho _ д
(7.23)
(-E')qho = —
δβ δβ
^-βΠω
ij9ftw + log(l-e-^)
=^G+i37w)=*-(b^)· (7·24)
что соответствует среднему уровню возбуждения
<n>qh° = ^йсгзу· (7·25)
Таким образом, удельная теплоемкость квантового гармонического
осциллятора имеет вид (рис. 7.2)
?*L-k ( *" V е~Пы,квТ
дТ~ В\квТ) (1_е-^АвТ)2·
су = ^ = кв — ——о· (7.26)
При высоких температурах е~^/квТ « 1 — huj/квТ, таким образом, Су —>·
fc#, что соответствует классическому гармоническому осциллятору (и
задается теоремой о равнораспределении). При низких температурах ег^/ЬвТ
экспоненциально мало, и удельная теплоемкость быстро стремится к нулю,
когда энергия приближается к энергии нулевых колебаний huj/2. Существует
энергетическая щель11 huj между нулевым и первым возбужденным
состоянием. Таким образом, вероятность перехода системы в возбужденное состояние
пропорциональна е~^/квТ
11В физике твердого тела он называется запрещенной зоной и соответствует
минимальной энергии, необходимой для перехода системы в возбужденное состояние. В квантовой
теории поля, в которой возбужденные состояния соответствуют частицам, он называется
массой частицы гас2.
7.3. Статистика Возе и Ферми
265
kBT/h<u
Рис. 7.2. Удельная теплоемкость квантового гармонического
осциллятора
7.3 Статистика Бозе и Ферми
В квантовой механике идентичные частицы не только сложно различить.
Их квантовые волновые функции одни и те же, с точностью до изменения
фазы12 при перестановке координат (рис. 7.3). В частности, волновые функции
бозонов13 не меняются при перестановке, таким образом
Ф(гьг2,...,глг) = Ф(г2,Г1,...,глг) = *(rPl,rp2,...,rP7V)
(7.27)
для любых перестановок Ρ целых чисел 1,..., N. Для фермионов14
Φ(Γ1,Γ2,...,ΓΝ) = -Φ(Γ2,Γ1,...,ΓΝ) = σ(Ρ)Φ(Γρ1,Γρ2,...,ΓρΝ), (7.28)
12 В трехмерном пространстве это изменение фазы составляет ±1. В двухмерном
пространстве могут быть любые фазовые изменения, таким образом, там присутствуют не
только фермионы и бозоны, но еще и энионы. Энионы возникают как возбуждения в
дробном квантовом эффекте Холла.
13Примерами бозонов являются мезоны, Не4, фононы, фотоны, глюоны, W± и Ζ
бозоны, а также (предположительно) гравитоны. Последние четыре соответствуют
фундаментальным взаимодействиям — электромагнитному, сильному, слабому и гравитационному.
В теореме о спиновой статистике (не обсуждаемой в данной книге) утверждается, что у
бозонов целые спины.
14 Большинство распространенных элементарных частиц являются фермионами:
электроны, протоны, нейтроны, нейтрино, кварки и т.д. У фермионов полу целые спины.
Частицы, состоящие из четного числа фермионов, являются бозонами.
266
Гл.7. Квантовая статистическая механика
где <г(Р) — знак, соответствующий перестановке Р.15 Собственные состояния
систем идентичных фермионов и бозонов представляют собой подмножество
собственных состояний различимых частиц с тем же самым гамильтонианом:
НЪп = Еп*п; (7.29)
В частности, они определяются различимыми собственными состояниями,
которые обладают соответствующими свойствами симметрии при
перестановках. Несимметричное собственное состояние Φ с энергией Ε может быть
симметризовано, давая собственное состояние Возе при суммировании по
всевозможным перестановкам Р:
*sym(ri,r2,...,r;v) = (normalization) ^ Φ (rPl, гр2,..., τΡν) (7.30)
ρ
или антисимметризовано, образуя собственное состояние фермиона
Фаауш(гь г2,..., τΝ) = (normalization) ^ σ(Ρ)Φ(ΓΡι, гр2,..., γΡν), (7.31)
ρ
если при симметризации или антисимметризации сумма не становится равной
нулю. Поскольку эти состояния являются комбинацией собственных
состояний с энергией £7, их энергия также равна Е.
В квантовой статистической механике одинаковых частиц суммирование
по ансамблю проводится исключительно по симметричным волновым
функциям для бозонов или антисимметричным волновым функциям для
фермионов. Таким образом, статистическая сумма для, например, канонического
ансамбля по-прежнему имеет вид
Ζ = Ίί(έ-βΗ)=Σβ-βΕ", (7.32)
П
но теперь след берется по полному набору симметричных (или
антисимметричных) состояний, а суммирование проводится по симметричным (или
антисимметричным) многочастичным энергетическим состояниям.
15 Перестановка {Pi, Р2, · · ·, Ρ/ν} — это изменение порядка целых чисел {1,2,...,iV}. Знак
σ(Ρ) перестановки +1, если Ρ четная, и —1, если Ρ — нечетная перестановка. Если
поменять два числа местами и оставить все остальные без изменения, то это будет нечетная
перестановка. Можно показать, что для двух перестановок их знаки перемножаются.
Таким образом, нечетные перестановки соответствуют перемене мест нечетного числа пар
чисел, а четные — перестановке четного числа пар чисел.
7.4- Невзаимодействующие бозоны и фермионы
267
Η
Рис. 7.3. Диаграмма Фейнмана: идентичные частицы
В квантовой механике два электрона (или два атома одного и того же изотопа)
фундаментально идентичны. Мы можем схематически проиллюстрировать это, рассматривая
сложнейшую тему, основанную на квантовой теории поля и теории относительности.
Рассмотрим рассеяние фотона на электроне в двух системах отсчета. Отложим время по
вертикальной оси, а координату — по горизонтальной. Слева мы видим два «различных» электрона,
один из которых рождается вместе с анти-электроном или позитроном, а другой позже ани-
гилирует с позитроном. Справа мы видим то же самое событие в другой системе отсчета.
Здесь есть только электрон, рассеивающий два фотона. (Электрон является виртуальным
и движется быстрее скорости света между соударениями. Это допустимо в
промежуточных состояниях при квантовых переходах. Два электрона слева не только неразличимы,
они представляют собой одну и ту же частицу*. Античастица также является электроном,
но движущимся во времени в обратном направлении.)
7.4 Невзаимодействующие бозоны и фермионы
Квантовая статистическая механика большого числа частиц очень
сложна. Мы сделаем следующее предположение: будем считать, что квантовые
частицы не взаимодействуют друг с другом. Так же, как и в случае
классического идеального газа, это существенно упростит вычисления.
Гамильтониан невзаимодействующих частиц представим в виде суммы
квантовых гамильтонианов Η для одной частицы:
Нт = Σ Н(РМ) = £ ^Vj + ν{τΛ). (7.33)
j=l j=l
Пусть фк — одночастичное собственное состояние i/, тогда
Нфк{т) = екМт)- (7-34)
В случае различимых частиц многочастичные собственные состояния могут
быть записаны в виде произведения ортонормированных одночастичных
собственных состояний:
N
*S£t(ri>r2>...>rJV) = IJ^(rj)> (7.35)
3=1
268
Гл.7. Квантовая статистическая механика
где частица j находится в одночастичном собственном состоянии kj.
Собственные состояния невзаимодействующих бозонов задаются с помощью
симметризации по координатам г у.
N
фЫ8оп(гьг2,-··,^) = (normalization) ^Д^(гр^), (7.36)
ρ j=i
и, естественно, собственные состояния фермионов определяются при
антисимметризации по всевозможным N\ перестановкам16
1 N
Cmion(ri,r2)...,r^) = -=Σ <Г(Р)Ц^Р>)· С7'38)
ViV* Ρ j=\
Рассмотрим две частицы в ортонормированных одночастичных
энергетических состояниях фк и Φι- Если частицы различимые, то
существуют два собственных состояния Φη{τι)Φι(τ2) и φΐζ{τ2)Φΐ{τ\)· Если
частицы являются бозонами, то собственное состояние представимо в
виде [\/у/2) {φ^Υ\)φι{τ2)+Φη{τ2)Φι{^ι))- Если частицы — фермионы, то
собственное состояние имеет вид (1/%/2) (φΐζ{τ\)Φι{*2) ~ Φη(τ2)Φι{υι))·
Что произойдет, если частицы находятся в одном и том же одночастичном
собственном состоянии ф{1 Для бозонов собственное состояние φι{τ\)φι{τ<ι)
уже является симметричным и нормированным.17 Для фермионов
антисимметризация состояния, при котором обе частицы находятся в одном и том же
состоянии, дает ноль: φι(τι)φι(τ2) — Φι(^2)Φΐ(τι) — 0. Это принцип запрета
Паули: вы не можете обнаружить два фермиона в одном и том же квантовом
состоянии.18
Как построить статистическую механику невзаимодействующих
фермионов и бозонов? В данном случае наиболее удобно использовать большой
канонический ансамбль (раздел 6.3). В этом ансамбле можно рассматривать
16 Эта антисимметризация может быть записана в следующем виде
(7.37)
уЩ
^fci(n) ··· ^*ι(Γν)
Фк2(Г1) ... V>fc2(rN)
^kN(ri) ... ^(γν),
называемом определителем Слэтера.
17Обратите внимание, что нормировка волновой функции бозонов зависит от того,
сколько одночастичных состояний заняты несколькими частицами.
18Поскольку спин электрона может иметь два направления ±1/2, это означает, что в
каждом одночастичном собственном состоянии могут находиться два электрона.
7.4- Невзаимодействующие бозоны и фермионы
269
каждое собственное состояние как населенное независимо от других
собственных состояний, в котором обмен частицами происходит напрямую с внешним
термостатом (аналогично рис. 6.2). Большая статистическая сумма имеет,
таким образом, вид:
к
Большой канонический ансамбль позволяет тем самым рассматривать
каждое собственное состояние отдельно.
Бозоны. Для бозонов допустимы всевозможные числа заполнения η&.
Каждая частица в собственном состоянии ψ^ дает вклад ε& в энергию и — μ
в химический потенциал, таким образом
Hboson = £ е-^-"К = £ (e-*«*-O)Bfc = t _ β_^_μ) (7.40)
пк=0 пк=0
и большая статистическая сумма для бозонов имеет вид
-boson = 11 ι _ρ-/3(ε*-μ)· \^ЛЧ
к
Большой термодинамический потенциал (Ф = —fc#TlogH,
уравнение 6.36) представим в виде суммы больших термодинамических
потенциалов для каждого одиночного состояния:
SbLn = Σфктт = Σ k*T 1оё i1 ~ *-β{ε*-μ)) · (7-42)
k k
Поскольку заполнение различных состояний происходит независимо, мы
можем найти среднее число частиц в состоянии ψ^. Из уравнения (6.38) следует
ДфЬовоп _/3e-/3(sfc-M) ι
<"*> = ~4Г = -*'ri-r^-» " ^5^ΓΓί· <7"3>
Полученное выражение называется распределением Бозе—Эйнштейна
(рис. 7.4)
(п)ве = е^)_г (7.44)
Распределение Бозе—Эйнштейна характеризует заполнение одночастичных
собственных состояний невзаимодействующими бозонами. Для состояний с
низкой населенностью, для которых (п) «С 1, (п)ве ~ β~^ε_μ', заселенность
270
Гл.7. Квантовая статистическая механика
бозонов согласуется с уравнением Больцмана.19 Условие малой заселенности
имеет вид ε^ — μ » fcgT и реализуется, как правило, при высоких
температурах20 (когда частицы распределены среди большего числа состояний).
5
4
Та
ι
(ε-μ)/*,Γ
Рис. 7.4. Распределения Бозе—Эйнштейна, Максвелла—Больцмана
и Ферми—Дирака, (η)(ε)
Числа заполнения одночастичных собственных состояний как функция отклонения
энергии ε от химического потенциала μ. Распределение Бозе—Эйнштейна расходится при
стремлении μ κ ε, а среднее число заполнения для распределения Ферми—Дирака стремится к
единице при малых μ.
Обратите внимание, что (п)ве —► оо при μ -» ε&, поскольку знаменатель
стремится к нулю (и становится отрицательным при μ > ε&). В системах
невзаимодействующих бозонов μ всегда меньше или равно наименьшему из
собственных значений энергии одиночных частиц.21
Обратите внимание, что среднее возбуждение (п)ф0 квантового
гармонического осциллятора (7.25) задается распределением Бозе—Эйнштейна (7.44)
при μ = 0. Мы используем этот факт в упражнении 7.2 для того, чтобы
показать, что возбуждения гармонических осцилляторов (колебания) можно
рассматривать как частицы, подчиняющиеся распределению Бозе (фононы).
19 Мы выведем это из распределения Максвелла—Больцмана в разделе 7.5.
20Может показаться, что это находится в противоречии с формулой для распределения
Бозе. Однако при увеличении Τ μ становится отрицательным и растет по модулю быстрее,
чем температура. Это происходит (при фиксированном числе частиц), поскольку большее
число состояний при высоких температурах становится доступным для заселения, таким
образом, давление μ, необходимое, для того чтобы сохранять их заполненными,
уменьшается.
21 Химический потенциал подобен давлению, действующему на атомы в системе. Когда
уровень реки становится равным высоте полей, на вашей ферме происходит наводнение.
1 1
1
:
.
Бозе-Эйнштейн
* * * Максвелл-Больцман
— Ферми-Дирак
7.4- Невзаимодействующие бозоны и фермионы
271
Фермионы. Для фермионов допустимо только п^ = 0ип^ = 1. Большая
статистическая сумма для фермиона в одиночном состоянии имеет вид
1
^fermion _ V^ e-/?(efc-^)nfc _ j _μ ^β(^-μ) (7.45)
пк=0
а большая статистическая сумма для всех фермионов в системе:
а^ = П(1+е~Л*~'°)· <7·46)
к
Суммируя всего лишь по двум состояниям, находим:
^ Eifc=oexp(-^(£fc-^)nfe) l + e-«-*-iO &«-») +ϊ [7Α7)
Полученное выражение называется распределением Ферми—Дирака
/(e) = (n>FD = 6β(ε_1) + 1, (7.48)
где /(ε) называется функцией Ферми (рис. 7.5). Так же как и в случае
бозонов, когда средняя заселенность состояния грк мала, она задается
распределением Больцмана β~^ε~μ\ В данном случае химический потенциал
может быть либо больше, либо меньше, чем любое данное собственное значение
энергии Ek- В самом деле, при низких температурах химический потенциал
μ отделяет заполненные состояния с энергией Ek < μ от пустых состояний.
Только состояния с энергией, отличающейся от μ на квТ, являются лишь
частично заполненными.
Химический потенциал μ играет существенную роль в этих вычислениях.
Как его определить? Как правило, вы знаете ожидаемое число частиц N и
меняете μ до тех пор, пока не получите это число. Таким образом, μ
играет роль внешнего давления, которое меняется до тех пор, пока система не
становится заполненной надлежащим образом.
Удивительная эффективность теории невзаимодействующих
бозонов и фермионов. Классический идеальный газ играет важную роль в
статистической механике и хорошо описывает поведение многих газов, но
никто не ожидает от этой модели, что она будет также объяснять свойства
жидкостей и твердых тел. Приближение отсутствия взаимодействий в квантовой
механике является намного более мощным по неясным на первый взгляд
причинам.
272
Гл.7. Квантовая статистическая механика
1
to
)
-т=о
— МалиеГ
<г-Ы~квТ
Энергия ε/μ
Рис. 7.5. Распределение Ферми /(ε)
Уравнение (7.48). При низких температурах состояния с энергией, меньшей μ, заселены.
Состояния с энергией, большей μ, — не заселены, а состояния, с энергией, отличающейся
от μ на квТ, — заселены частично.
В случае бозонов приближение отсутствия взаимодействий между
частицами работает в трех важных случаях: для описания фотонов, фононов и
разреженного бозе-газа. В разделе 7.6 мы рассмотрим две фундаментальные
задачи, посвященные невзаимодействующим бозонам: излучение твердого
тела и бозе-конденсацию. Поведение сверхпроводников и сверхтекучих
жидкостей также имеет ряд свойств, схожих с поведением бозе-газа.
Трудно встретить в реальной жизни систему невзаимодействующих фер-
мионов. Электроны заряжены, и электромагнитное отталкивание между
ними в атоме, молекуле или материале всегда вносит наибольший вклад в
энергию. Между нейтронами возникает сильное взаимодействие, таким образом,
ядра и нейтронные звезды — не лучшие кандидаты для использования
теории, в которой пренебрегается взаимодействием между частицами.
Нейтрино трудно упаковать в сосуд.22 Проводился ряд экспериментов с холодными
разбавленными газами атомов-фермионов, но модель невзаимодействующих
фермионов, казалось бы, подходит лишь для малого числа приложений.
Поразительно то, что невзаимодействующий ферми-газ описывает все эти
системы (атомы, металлы, диэлектрики, ядра и нейтронные звезды) на
удивление хорошо. Взаимодействующие системы фермионов в большинстве
случаев ведут себя как набор невзаимодействующих фермионов в некотором
эффективном потенциале. Это приближение является настолько мощным, что
в большинстве случаев мы просто пренебрегаем взаимодействиями. Вне
зависимости от того, рассматриваем ли мы возбуждение IS электрона в атоме
22Нейтрино — достаточно неуловимая частица. Свинцовая стена, которая могла бы
остановить половину испускаемых нейтрино, должна быть толщиной со световые годы.
7.5. «Квантовое» распределение Максвелла—Больцмана
273
кислорода или пару электрон-дырка в полупроводнике, мы можем
использовать приближение невзаимодействующих электронов. Объяснение этого
удивительного факта дает теория Ландау для ферми-жидкостей.23
7.5 «Квантовое» распределение Максвелла—
Больцмана
В классической статистической механике мы рассматриваем
неразличимые частицы как различимые, но делим объем фазового пространства (или
статистическую сумму в каноническом ансамбле) на N\:
оМВ _ 1 odist
Ν ~~ τνΤ '
ZT = ^Z%st. (7.49)
Это необходимо, для того чтобы энтропия оставалась экстенсивной
величиной (раздел 5.2.1). Это приближение также иногда используется в квантовой
статистической механике, но мы должны подчеркнуть, что оно не описывает
ни бозоны, ни фермионы, ни любую другую физическую систему. Эти
фиктивные частицы подчиняются распределению Максвелла—Больцмана.24
23Ландау описывал взаимодействующие системы фермионов (например электронов) при
температурах, малых по сравнению с энергией Ферми, начиная с
невзаимодействующего ферми-газа и потихоньку «включая» взаимодействие (Энергия Ферми составляет
£f = μ(Τ = 0), см. раздел 7.7.) Возбужденные состояния невзаимодействующего газа
соответствуют электронам, перешедшим в состояния с энергией выше энергии Ферми и оставив
внизу дырки. Они эволюционируют двумя способами при включении взаимодействий. Во-
первых, возбужденные электроны и дырки создают экранирующее облако, которое одевает
чистое возбуждение в квазичастицы. Во-вторых, эти квазичастицы имеют определенное
время жизни. Они становятся уже не собственными состояниями, а резонансами.
Квазичастицы являются полезным описанием до тех пор, пока взаимодействия могут быть
включены достаточно медленно, для того чтобы сформировалось экранирующее облако, но
достаточно быстро, для того чтобы квазичастицы не затухли. Это выполняется для электронов
и дырок вблизи энергии Ферми, времена жизни которых достаточно долгие, поскольку
они могут перейти только в энергетические состояния, находящиеся еще ближе к энергии
Ферми [6, р. 345]. В более поздних работах идеи Ландау обрели вид
систематизированных расчетов в рамках теории возмущений, в которых квазичастицы представляют собой
особые точки квантовой функции Грина (см. упражнение 10.9 для классического примера
того, как это работает). Недавно исследователи использовали приближение ренорм-групп
для интерпретации идей Ландау, в котором при операциях по огрублению масштаба
удаляются состояния вдали от энергии Ферми и система эффективно приближается к состоянию
невзаимодействующего ферми-газа (см. гл. 12 и упражнение 12.8).
24Иногда говорят, что различимые частицы подчиняются статистике Максвелла—
Больцмана. Многие величины не зависят от наличия N1 в знаменателе в уравнении (7.49),
274
Гл.7. Квантовая статистическая механика
Чему равна каноническая статистическая сумма для N
невзаимодействующих различимых квантовых частиц? Если статистическая сумма для одной
частицы
Zi = £e"*fc, (7.50)
к
то статистическая сумма для N невзаимодействующих различимых (но во
всем остальном похожих) частиц составляет
zNi,dist = ^ e_^(efci+efc2+...+efcjv) = -q / £у^ J = ΖΛ (7.51)
kiyk2y...ykn j=l \ kj J
Таким образом, статистическая сумма Максвелла—Больцмана для
взаимодействующих частиц имеет вид
ΖΝΙ,ΜΒ = ΖχΝ/ΝΙ (? 52)
Давайте проиллюстрируем соотношение между тремя различными
распределениями, рассматривая канонический ансамбль для двух
невзаимодействующих частиц в трех различных энергетических состояниях ει, ε<2. и £з-
Статистическая сумма Максвелла—Больцмана для этой системы будет иметь
вид
ΖΝΙ,ΜΒ = | ^-βει +е-р£2 +е-Резу
- Ip-2/?ei . 1р-2/?е2 , Ιρ-2/?ε3
~2 +2Θ +2Θ
+ Θ-^(ε1+ε2) + Θ-^(ει+ε3) + Θ-/?(ε2+ε3) (7 53)
Сомножитель 1/ΛΓ! фиксирует веса одночастичных состояний.25 Каждое
имеет единичный вес в статистической сумме Максвелла—Больцмана. Но каждое
состояние, занятое двумя частицами, в котором обе частицы имеют одну и
ту же волновую функцию, входят в сумму с весом 1/2.
Существует два способа модифицировать полученный результат. Первый
заключается в том, чтобы прекратить дискриминацию состояний со
множественной заселенностью и обходиться с ними демократическим образом. Тем
самым мы получим невзаимодействующие бозоны:
такие как заселенность (п) одночастичных собственных состояний (уравнение 7.60). Но
этот сомножитель влияет на другие величины, такие как энтропия смешения и
свободная энергия Гельмгольца, таким образом, мы оставим термин распределение Максвелла—
Больцмана для одинаковых частиц (раздел 3.5).
25Говоря более точно, мы имеем в виду многочастичные состояния, в которых одноча-
стичные состояния заняты одной частицей или свободны.
7.5. «Квантовое» распределение Максвелла—Болы^мана
275
^NI,boson _ e-20ei + β~2βε2 +e"2fe +e"/3(ei+e2) + β~β(ει+ε3) +β-β(ε2+ε3) (7.54)
Другой способ — это вообще не учитывать состояния со множественной
заселенностью. Таким образом, мы получаем фермионы:
^NI,fermion _ ^-β(ει+ε2) + ^_/3(ει+ε3) + ^-β(ε2+ε3) (7.55)
Итак, в распределении Максвелла—Больцмана состояния со множественной
заселенностью рассматриваются как некий компромисс между
демократичными бозонами и запрещающими фермионами, не имеющий физического
смысла. Мы сравнили различные распределения для канонического
ансамбля. Что будет в случае большого канонического ансамбля, который мы и
используем для вычислений?26 Большая каноническая статистическая
сумма для статистики Максвелла—Больцмана имеет вид
(\ М
Ve-^M βΜβμ
k )
-Σά(Σ.*-)" —(Σ—-)
= JJexp(e-^£fc-^). (7.56)
k
Большой термодинамический потенциал имеет вид
φΝΙ,ΜΒ = _fcBTlogSNI,MB = £ фк (? 5?)
к
где одночастичный большой термодинамический потенциал равен
Ф* = -kBTe-fcb-ri. (7.58)
Наконец, ожидаемое27 число частиц в одночастичном собственном состоянии
с энергией ε составляет
{п)мв = ~=е-^е-^. (7.60)
26 См. упражнение 7.1, в котором рассматриваются три ансамбля для четырех различных
типов распределений.
27Интересно отметить, что невзаимодействующие частицы заполняют одночастичные
энергетические состояния в соответствии с одним и тем же законом
<»> - е«-1>+с' (7·59)
где с = — 1 для бозонов, с = 1 для фермионов и с = 0 для статистики Максвелла—Больцмана.
276
Гл.7. Квантовая статистическая механика
Это и есть как раз фактор Больцмана для заполнения состояний для
невзаимодействующих различимых частиц. Коэффициент неразличимости N\ не
влияет на заполнение одночастичных состояний при отсутствии
взаимодействия.
7.6 Излучение абсолютно черного тела и
бозе-конденсация
7.6.1 Свободные частицы в сосуде
В данном, а также в следующем разделе, посвященном фермионам, мы
будем проводить дальнейшие упрощения. Мы рассмотрим частицы, которые
не только не взаимодействуют между собой и являются идентичными, но
также еще и свободными. Таким образом, они не подвержены действию внешних
потенциалов, за исключением помещения в сосуд объемом L3 = V с
периодическими граничными условиями.2**
Рис. 7.6. Частица в сосуде
Квантовые состояния частицы в одномерном сосуде с периодическими граничными
условиями представляют собой синусоидальные и косинусоидальные волны ψη с η возможными
длинами волн, kn = 2nn/L. В реальном сосуде (с нулевыми граничными условиями вблизи
стенок) были бы только синусоидальные волны, но на половине расстояния между двумя
волновыми векторами кп = πη/L, давая ту же самую плотность состояний.
Одночастичные квантовые собственные состояния такой системы
представляют собой произведение синусоидальных и косинусоидальных волн по
28Таким образом, значение φ вблизи стенок не обязательно должно быть равно нулю (как
для бесконечного квадратного потенциала), но оно должно быть одинаковым на
противоположных сторонах сосуда: ψ(0, у, ζ) = ^(Ь, у, ζ), ψ(χ, О, ζ) = ψ(χ, L, z) и ψ(χ, у, 0) = ψ(χ, у, L)
Периодические граничные условия, как правило, нереализуемы в экспериментах, но их
удобно использовать в моделировании.
1.6. Излучение абсолютно черного тела и бозе-конденсация
277
трем направлениям — например, для любых неотрицательных целых чисел
щ
, /2\3/2 /2тгп1 \ /2πη2 \ /2πη3 \ _1Ч
^ = ( у I cos I ——χ 1 cos I ——у J cos I ——z I . (7.61)
Существует восемь подобных состояний с одной и той же энергией,
получающихся при подстановке синусов вместо косинусов во всевозможных
комбинациях по трем направлениям. Наиболее удобно записать это, используя
комплексную экспоненту вместо синусов и косинусов:
Vk = (l/L)3/2exp(ik.r), (7.62)
где к = (2π/Ζ/)(ηι,η2,η3), а гц — любое целое число.29 Допустимые одноча-
стичные собственные состояния образуют регулярную сетку на пространстве
волновых векторов к со средней плотностью (L/2n)3 на единицу объема в
/с-пространстве:
концентрация плоских волн в k-пространстве = V/8n . (7.63)
В большом сосуде объемом V сетка является достаточно мелкой, таким
образом, можно использовать континуальное приближение, при котором число
состояний в k-пространстве определяется объемом сосуда, умноженным на
плотность (уравнение 7.63).30
7.6.2 Излучение абсолютно черного тела
В качестве первого приложения нашей теории рассмотрим
электромагнитное излучение, состоящее из мод плоских волн, подобных (7.62). Каждая
плоская волна движется со скоростью света с, таким образом, ее частота
равна иь = c|k|. Существуют две моды на каждый волновой вектор к, по одной
для каждой поляризации. При квантовании электромагнитного поля каждая
мода становится квантовым гармоническим осциллятором.
29Восемь вырожденных состояний определяются теперь выбором знака для трех целых
чисел.
30Собственно говоря, континуальный предел работает только потому, что форма сосуда
(задающая допустимые вектора к) не играет роли, если сосуд очень большой. По той же
причине энергия одночастичного собственного состояния не зависит от направления. Она
будет пропорциональна |к| для безмассового фотона и пропорциональна к2 для бозонов и
электронов, имеющих массу (рис. 7.7). Это и позволяет провести вычисления, изложенные
в следующих разделах.
278
Гл.7. Квантовая статистическая механика
Рис. 7.7. к-сфера
Допустимые точки в k-пространстве с периодическими граничными условиями образуют
регулярную сетку. Точки с одинаковой энергией лежат на сфере.
До появления квантовой механики люди не могли понять причину
установления равновесия электромагнитного излучения. Теорема о
равнораспределении предсказывает, что если вы приходите к равновесию, то энергия
каждой моды будет составлять квТ. Поскольку гораздо большее количество
волновых векторов присутствует в ультрафиолетовом и рентгеновском
диапазоне,31 то, открывая печную дверцу, вы теоретически должны были бы
получить загар или даже кое-что похуже (что соответствует так
называемой ультрафиолетовой катастрофе). В экспериментах наблюдается спектр,
который согласуется с данным предсказанием лишь для малых частот, но
обрезан (к счастью) на высоких частотах.
Давайте получим равновесное распределение энергии внутри нашего
сосуда при температуре Т. Число одночастичных собственных плосковолновых
состояний д(и) άω в малом диапазоне do; составляет32
9И^ = («*)(^)(^), (7.64)
31 Существует в тысячи раз больше волновых векторов, удовлетворяющих условию |А;| <
lOfco, чем условию |А;| < ко. Нижняя и верхняя границы диапазона оптических частот и
волновых векторов отличаются примерно в два раза, таким образом, существует в восемь
раз больше мод для оптических волн, чем для радио- и инфракрасных волн.
32 Мы поступим достаточно неряшливо и будем использовать обозначение д(и) для
числа состояний фотонов на единицу частоты, а в дальнейшем мы будем обозначать д(е)
число одночастичных собственных состояний на единицу энергии. Обратите внимание, что
9ω(ω) άω = ge(huj) d/ϊω, таким образом, дш = hge.
7.6. Излучение абсолютно черного тела и бозе-конденсация
279
где первый сомножитель соответствует площади поверхности сферы
радиуса fc, второй — толщине сферической оболочки для малых do;, а последний
— плотности одночастичных собственных волновых векторов плоских волн,
умноженной на два (поскольку существует две поляризации фотонов на кал\—
дый волновой вектор). Зная к2 = ω2/(? и d|k|/du; = 1/с, можно найти
плотность собственных состояний (плоских волн) на единицу частоты:
Vu2
9{ω) = да. (7.65)
Итак, число фотонов не фиксировано, они могут рождаться и
уничтожаться, таким образом, их химический потенциал μ равен нулю.33 Их энергия
εk = foujk· Наконец, с достаточно хорошей степенью точности они
представляют собой идентичные невзаимодействующие бозоны, таким образом,
число фотонов на одно собственное состояние с частотой ω составляет (п) =
l/(e^/fcaT — 1). Это дает нам число фотонов:
(# of photons) όω = ehwfki^_1 όω. (7.66)
Электромагнитная энергия на единицу объема и(ш) дается выражением
(рис. 7.8).
(7.67)
Л.2С3 efiw/feBT _ ι ■
Это и есть знаменитая формула Планка для излучения абсолютно
черного тела.34 При малых частотах можно сделать следующее приближение:
ейш/квт _|й fju/квТ, получив формулу Рэлея—Джинса
VtiRj(w) do; = V I -g-g ) ω2 άω
= квТд(ш). (7.68)
33См. упражнение 7.2 для вывода этого в рамках модели квантового гармонического
осциллятора.
34Почему оно называется излучением черного тела? Черная поверхность поглощает все
излучение на всех частотах. В равновесии поглощаемая энергия на данной частоте должна
быть равна излучаемой. (Это называется принципом детального равновесия, раздел 8.2.)
Следовательно, если пренебречь охлаждением поверхности при излучении, черное тело
излучает тепловое распределение фотонов (см. упражнение 7.7).
280
Гл.7. Квантовая статистическая механика
I
се
I
Частота ω
Рис. 7.8. Планковский спектр излучения абсолютно черного тела
Пунктирной линией обозначено приближение Рэлея—Джинса, справедливое для малых
частот ω.
Как и следовало ожидать из теоремы о равнораспределении, на каждый
классический гармонический осциллятор приходится энергия квТ.
Для колебаний с частотами, существенно превышающими квТ/h,
теорема о равнораспределении не выполняется. Наличие запрещенной зоны Ηω,
так же как и при расчете удельной теплоемкости при низких
температурах в разделе 7.2, приводит к тому, что вероятность возбуждения
подавляется больцмановским фактором е~^/квТ (уравнение 7.67, таким образом,
1 / (e/kJ/fcBT — 1) « е-й*>/квТу Открытие Планком того, что квантование
энергии предотвращает ультрафиолетовую катастрофу, легло в основу квантовой
механики и послужило причиной того, что константа h носит его имя.
7.6.3 Бозе-кон денсация
Как изменятся наши вычисления в том случае, если
невзаимодействующие свободные бозоны могут рождаться и уничтожаться? Предположим, что
наши бозоны не имеют спина, обладают массой га, и нерелятивистские, таким
образом, их энергия составляет ε = ρ2/2m = — 7i2V2/2ra. Если мы поместим
их в сосуд с периодическими граничными условиями, мы можем сделать то
же самое континуальное приближение для плотности состояний, как и в
случае излучения абсолютно черного тела. В уравнении (7.63) число собственных
плосковолновых состояний на единицу объема в пространстве векторов к
равно ν/8π3, таким образом, плотность в импульсном пространстве ρ = ftk
составляет ν/(2π/ι)3. Для наших массивных частиц de/d|p| = |р|/га = у/2е/т,
7.6. Излучение абсолютно черного тела и бозе-конденсация
281
таким образом, число собственных плосковолновых состояний в малом
диапазоне энергий άε равно
*>*-С"Л(%Ч(<ЗЯ50
= (4.(2m£))(y|de)(^5)
-$£**■ (7М)
где первый сомножитель соответствует площади поверхности сферы в
пространстве р, второй — толщине сферической оболочки, а третий —
плотности собственных плосковолновых состояний на единицу объема в
пространстве р. Теперь пусть среднее число частиц в каждом из этих одночастичных
плосковолновых состояний задается распределением Бозе—Эйнштейна с
химическим потенциалом μ, \/{^\е~^)1квТ _ ι). Полное число частиц 7V, таким
образом, имеет вид
Ν(μ) = Г
Jo
9{£) de. (7.70)
Θ(ε-μ)ΑβΤ _ I
Будем изменять μ в этом уравнении, чтобы получить правильное число
частиц N. Для бозонов, как упоминается в разделе 7.4, μ не может превышать
наименьшую собственную энергию одночастичного состояния (здесь εο = 0),
таким образом, μ будет все время отрицательным. Для большего числа
частиц мы увеличим μ, благодаря чему большее количество частиц окажется
в каждом одночастичном состоянии. Существует, однако, предел того, как
сильно мы можем давить. Когда μ = 0, число частиц в основном состоянии
расходится. Для свободных бозонов в трехмерном пространстве интеграл для
Ν(μ = 0) имеет конечный предел.35 Таким образом, наибольшее число частиц
^rriax ϊ которое мы можем поместить в сосуд в рамках нашего континуального
приближения для плотности состояний, можно получить из уравнения (7.70)
при μ = 0:
35 При μ = 0 знаменатель в подынтегральном выражении в уравнении (7.70) составляет
приблизительно ε/квТ для малых ε, но числитель пропорционален y/ε, таким образом,
интеграл сходится в нижнем пределе: /0 ε-1'2 ~ (ε ' )|0 /2 = VX/2.
282
Гл.7. Квантовая статистическая механика
ATcont= / iQ άε
** J ее/квТ - 1
= Vm3'2 f°° у/ё
V h J vWo eZ-!
= (JO) C(3/2). (7.71)
Здесь ζ — дзета-функция Римана,36 С(§) ~ 2.612, а λ = h/y/brmk^T —
термическая длина волны де Бройля (3.59). Что-то новое должно произойти при
критической плотности:
N££ = 03/2) = 2.612 частиц
V λ3 объем де Бройля
Существует изящная интерпретация: квантовая статистика частиц
становится определяющим фактором, когда они находятся в пределах расстояния
порядка термической длины волны де Бройля друг от друга.
Что случится, если мы попытаемся добавить еще частиц? Наше
приближение для континуального распределения собственных состояний больше не
будет работать. На рис. 7.9 показана схематическая иллюстрация первых
нескольких одночастичных собственных состояний. Когда расстояние
между μ и нижним уровнем εο становится существенно меньшим, чем
расстояние между нижним и следующим уровнем ει, континуальное приближение
становится качественно неверным. Низкоэнергетические состояния,
появляющиеся в континуальном пределе, не могут вместить избыточные бозоны.
Вместо этого все частицы, когда их число начинает превышать N£££c,
попадают в состояние с наименьшей энергией.37 Это называется конденсацией
Бозе—Эйнштейна.
36Дзета-функция Римана ζ(β) = [l/(s — 1)!] /0°° ze-1/(e2 — 1) άζ известна по многим
причинам. Она связана с распределением простых чисел. Она фигурирует в знаменитой
недоказанной до сих пор гипотезе Римана, что ее нули на комплексной плоскости, за
исключением четных, отрицательных и целочисленных, имеют действительную часть, равную
1/2.
37Стоит отметить, что существуют незначительные поправки к некоторым состояниям
вблизи состояния с наименьшей энергией.
7.6. Излучение абсолютно черного тела и бозе-конденсация
283
ε,
tf&uffnhhti _ μ
Рис. 7.9. Бозе-конденсация
Химический потенциал μ здесь настолько близок к энергии основного состояния εο, что
континуальное приближение для плотности состояний больше не работает. Основное
состояние макроскопически заселено (то есть заполнено ненулевой долей полного числа частиц
Ν).
Как правило, мы не добавляем дополнительные частицы при
фиксированной температуре. Вместо этого мы понижаем температуру при
фиксированной концентрации N/V. Бозе-конденсация при этом происходит при
температуре
2πτη\νζ(3/2)) ' [7ЛО)
, ^вес h2 ( N \2/3
fcBTcBEC ' χ
Бозе-конденсация была впервые экспериментально осуществлена в 1995 г.
(см. упражнение 7.14).
Довольно долго считалось, что бозе-конденсация лежит в основе явления
сверхтекучести жидкостей. Жидкость Яе4 претерпевает необычный переход
при температуре порядка 2.176 К в невязкое состояние. Она будет
циркулировать до тех пор, пока продолжается охлаждение. При более
тщательном рассмотрении перехода в сверхтекучее состояние учитывается
взаимодействие между атомами гелия и используется метод скейлинга, который мы
введем в гл. 12. Но интересно отметить, что температура бозе-конденсации
для жидкости Яе4 (с массой т = 6.65 · 10~24 г и объемом на одну частицу
V/N = 27.6см3/моль) 3.13 К достаточно близка к температуре перехода в
сверхтекучее состояние.
284
Гл.7. Квантовая статистическая механика
7.7 Металлы и ферми-газ
В разделе 7.4 мы утверждали, что многие системы фермионов, между
которыми присутствует сильное взаимодействие, удивительно хорошо
описываются моделью невзаимодействующих фермионов. Давайте рассмотрим
свойства N свободных невзаимодействующих фермионов в сосуде.
Допустим, наши частицы нерелятивистские и имеют спин 1/2. Одноча-
стичные собственные состояния будут такими же, как и в случае бозонов, за
исключением того, что существует два состояния (спин вверх и спин вниз)
на каждую плоскую волну. Отсюда, плотность состояний будет в два раз
больше, чем следует из уравнения (7.69):
Полное число фермионов при химическом потенциале μ определяется
интегрированием функции #(ε), умноженной на среднее число фермионов в
энергетическом состоянии ε, задаваемое функцией Ферми /(ε) (7.48):
Ν(μ) = 1°° *(ε)/(ε) ds = jT e(£.,f/t)r + 1 6ε. (7.75)
При каком химическом потенциале полное число фермионов будет равно
Ν? При ненулевой температуре нужно произвести самосогласованные
вычисления, но при Τ = О можно найти 7V, вычисляя число состояний с энергией,
меньшей μ. В нулевом температурном пределе (см. рис. 7.5) функция Ферми
становится ступенчатой функцией /(ε) = θ(μ — ε). Все состояния ниже μ
заполнены, а все состояния выше μ пустые. Значение химического потенциала
при нулевой температуре называется энергией Ферми sf- Мы можем найти
число фермионов, интегрируя до μ = ε/τ:38
38Уравнение (7.77) можно вывести в пространстве к, где мы заполняем все состояния
с |к| < кг. Здесь волновой вектор Ферми Uf имеет энергию, равную энергии Ферми,
hkF/2m = рр/2т = €f, отсюда Uf = y/2eF~rn/h. Полученная сфера заполненных
состояний при Τ = 0 называется сферой Ферми. Число фермионов внутри сферы Ферми, таким
образом, равно объему сферы Ферми в k-пространстве, умноженному на плотность
состояний в к-пространстве,
^V=((4/3)^3)(^)=gv, (7.76)
что эквивалентно (7.77).
7.7. Металлы и ферми-газ
285
Рис. 7.10. Поверхность Ферми для алюминия
Поверхность Ферми для алюминия, с сайта [40]. Алюминий имеет энергию Ферми, равную
11.7eV, с тремя проводящими электронами снаружи заполненной оболочки неона.
Ранее мы упоминали, что приближение независимых фермионов на
удивление хорошо работает, даже несмотря на то, что взаимодействия не
являются малыми. Пренебрегая кулоновским взаимодействием между электронами
в металле или сильным взаимодействием между нейтронами в нейтронной
звезде, можно получить отличное описание их реального поведения. Однако
в наших вышеприведенных расчетах полагалось, что электроны
представляют собой свободные частицы, на которые не действует внешний потенциал. В
общем случае это приближение не вполне корректно. Взаимодействия в
атомном ядре важны, и именно из-за них один материал отличается от другого.
В частности, наличие атомов в кристалле обуславливает появление
периодического потенциала для электронов.39 Можно показать, что одночастичные
собственные состояния в периодическом потенциале являются
периодическими функциями, умноженными на exp(ik · г), с точно такими же волновыми
векторами, как и в случае свободных фермионов. Заполнение поверхности
Ферми в k-пространстве изменится только за счет того, что энергии этих
одночастичных состояний больше не будут изотропными. У некоторых
металлов (в частности щелочных, подобных литию на рис. 7.11) поверхность
Ферми практически сферическая, у некоторых довольно сложная, состоящая
из нескольких частей [6, chapters 9-11].
' Гораздо лучшую аппроксимацию, чем учет только кулоновского потенциала ядер,
дает рассмотрение вклада внутренней оболочки электронов в периодический потенциал, и
заполнение Ферми-пространства оставшимися электронами проводимости.
286
Гл.7. Квантовая статистическая механика
Рис. 7.11. Поверхность Ферми для лития
Поверхность Ферми для лития, с сайта [40]. Энергия Ферми для лития составляет 4.74
eV, с одним проводящим электроном снаружи заполненной оболочки гелия. Как и для
большинства металлов, энергия Ферми лития существенно превышает кв, умноженное на
температуру плавления (4.74 eV = 55 000 К, температура плавления 453 К). Следовательно,
она хорошо описывается поверхностью Ферми при Τ = 0, немного размытой функцией
Ферми (рис. 7.5).
Упражнения
Мы начнем с двух упражнений на различные виды статистики
одинаковых частиц: Ансамбли и квантовая статистика и Фононы и фотоны
являются бозонами. В упражнении Единицы фазового пространства и нуль
энтропии мы с помощью квантовой механики определим некоторые важные
параметры классической статистической механики, а затем спросим,
возрастает ли энтропия в квантовых системах? В матрицах плотности
фотонов и спиновой матрице плотности мы приведем простейшие примеры этого
сложного понятия.
Квантовая статистическая механика является основой множества
различных областей науки. Мы начнем с трех примеров из оптики: Излучение и
поглощение света, Коэффициенты Эйнштейна и Скопление бозонов:
сверхтекучие жидкости и лазеры. Мы приведем три фундаментальные для
физики конденсированного состояния вычисления: Дефекты в кристаллах,
Фононы на струне и Фермионы в полупроводниках. Мы сделаем два
упражнения на бозе-конденсацию: Бозе-конденсация в энергетической зоне и Бозе-
конденсация: эксперимент. В конце мы рассмотрим два базовых
астрофизических приложения: Вселенная с преобладанием фотонов и Белые карлики,
нейтронные звезды и черные дыры.
Гл.7. Упражнения
287
7.1 Ансамбли и квантовая статистика. (Квантовая физика) ©
Рассмотрим систему, характеризуемую двумя одночастичными
собственными функциями и энергиями Ео/кв = —10 и ϋ^/^Β — Ю. В процессе
эксперимента в эти два состояния попадают три невзаимодействующие частицы:
одинаковые фермионы со спином 1/2, идентичные бозоны без спина,
различимые частицы или одинаковые бесспиновые частицы, подчиняющиеся
статистике Максвелла— Больцмана. Пожалуйста, сделайте таблицу и запишите в
нее ответы на каждое из трех заданий для всех четырех случаев (статистики
Ферми, Бозе, различимых частиц, Максвелла—Больцмана). Возможно, вам
также понадобится сделать некоторые расчеты.
(а) Рассмотрим вначале систему с постоянной энергией. Какая из кривых на
рис. 7.12 отвечает энтропии фермионов как функции энергии? бозонов?
различимых частиц? частиц, подчиняющихся статистике Максвелла—Больцмана?
τ ■ 1 ■ г
2-30 -20 -10 0 10 20
Е/кв (градусы К)
Рис. 7.12. Три частицы микроканонического ансамбля
(b) Пусть теперь система находится при постоянной температуре. Какая из
кривых на рис. 7.13 соответствует средней энергии фермионов как функции
температуры? бозонов? различимых частиц? частиц Максвелла—Больцмана?
(c) Система находится при постоянной температуре, с химическим
потенциалом, заданным таким образом, чтобы среднее число частиц было равно трем.
Какая из кривых на рис. 7.14 иллюстрирует химический потенциал
фермионов как функцию температуры? бозонов? различимых частиц? статистики
Максвелла—Больцмана?
7.2 Фононы и фотоны являются бозонами. (Квантовая физика) ©
Фононы и фотоны представляют собой элементарные гармонические
возбуждения упругих и электромагнитных полей. Мы увидим в
упражнении 7.11, что фононы можно рассматривать как несвязанные
гармонические осцилляторы с распределением частот ω. Подобным образом
288
Гл.7. Квантовая статистическая механика
Рис. 7.13. Три частицы канонического ансамбля
«,80
^- 60
| 40
I 20
I 0
1-20
а-40
~"ν0 20 40 60
Τ (1радусы К)
Рис. 7.14. Три частицы большого канонического ансамбля
можно показать, что гамильтониан электромагнитного поля представим в
виде разложения по гармоническим нормальным модам, называемым
фотонами.
В этом упражнении мы объясним, почему фононы и фотоны считаются
частицами, а не возбуждениями гармонических колебаний.
(а) Покажите, что каноническая статистическая сумма для квантового
гармонического осциллятора с частотой ω равна большой канонической
статистической сумме для бозонов, заполняющих одно и то же состояние с энергией hu>,
где μ = 0 (с точностью до произвольного выбора нулевого значения полной
энергии системы).
Больцмановское заполнение гармонического осциллятора аналогично
заполнению бозонами одиночного квантового состояния согласно статистике
Бозе—Эйнштейна, с точностью до сдвига энергии Ηω/2, который называется
нулевой энергией. Возбуждения гармонического осциллятора зачастую
можно трактовать как частицы, подчиняющиеся статистике Бозе: η-e
возбуждение — это η бозонов, заселяющих квантовое состояние осциллятора.
Гл.7. Упражнения
289
Это аналогия с частицами становится даже более удобной в системах,
подобных фононам и фотонам, в которых присутствует множество
гармонических осцилляторов с различными волновыми векторами к (см.
упражнение 7.11). В самом деле, массивные бозе-частицы, подобные Не4, в свободном
пространстве характеризуются одночастичными квантовыми собственными
состояниями с дисперсионным соотношением40 ε& = h к2 /2т. Фононы и
фотоны — это набор гармонических осцилляторов с различными fc, с энергией
возбуждения ε& = hwk- Если мы, следуя подходу, изложенному в задании (а),
рассматриваем их как бозоны, заселяющие одночастичные состояния, то мы
видим, что они совершенно аналогичны обычным массивным частицам.
(Дисперсионное соотношение для фотонов такое же, как и для безмассовых бо-
юнов. Если устремить к нулю массу релятивистских частиц, то мы получим
ε = \/га2с4 - р2с2 ->· |р|с = Йс|к|.)
(Ь) Претерпевают ли фононы или фотоны бозе-конденсацию при низких
температурах и можете ли вы объяснить, почему? Можно ли в качестве
неравновесной бозе-конденсации фотонов рассматривать макроскопическое заселение
состояния с единственной частотой и импульсом?
7.3 Единицы фазового пространства и нуль энтропии. (Квантовая
физика) @
В классической механике энтропия S = кв log Ω стремится к минус
бесконечности, когда температура падает до нуля. В квантовой механике энтропия
на одну частицу стремится к нулю,41 поскольку состояния квантованные, а
основное состояние становится единственно заселенным. Это теорема Нерн-
ста, третий закон термодинамики.
Размерность классического объема бесконечно тонкого энергетического
слоя в фазовом пространстве Ω,(Ε) δΕ (уравнение 3.2) составляет
((импульс) χ (расстояние) )3Ν. Несколько некорректно брать логарифм
размерной величины. Данной размерностью обладает также величина
где h — постоянная Планка. Если мы измеряем объем фазового
пространства в единицах h на каждое измерение, то Ω,(Ε) δΕ будет
безразмерной величиной. Конечно, единицей измерения может быть /ι,
умноженная на любую константу, например Н.
Дисперсионное соотношение — это соотношение между энергией и волновым вектором,
здесь €k.
41 Если основное состояние является вырожденным, то энтропия не стремится к нулю,
но, как правило, остается конечной при возрастании числа частиц N. Таким образом, для
больших N энтропия на одну частицу стремится к нулю.
290
Гл.7. Квантовая статистическая механика
(a) Произвольное нулевое значение классической энтропии. Покажите, что
ширина энергетического слоя δΕ в определении Ω(Ε) не меняет
микроканоническую энтропию на одну частицу S/N = kB^og(Q(E))/N в большой системе.
Покажите, что выбор единиц в фазовом пространстве также не меняет
классическую энтропию на одну частицу.
Мы хотим выбрать единицы объема фазового пространства таким
образом, чтобы классическая энтропия совпадала с квантовой при высоких
температурах. Сколько квантовых собственных состояний будет приходиться на
единицу объема классического фазового пространства при больших
энергиях? Мы определим это, сравнивая квантовый результат с классическим для
определенной системы, а затем проверим, справедлив ли он для другой
системы. Давайте рассмотрим вначале случай свободных частиц.
(b) Плотность состояний для частицы в одномерном сосуде в фазовом
пространстве. Покажите, что квантовая плотность состояний в импульсном
пространстве в одномерном сосуде размера L с периодическими граничными уело-
виями равна L/h. Изобразите классическое фазовое пространство в этом
сосуде (р, х) и проиллюстрируйте прямоугольником длины L каждое квантовое
собственное состояние. Равна ли площадь, приходящаяся на одно собственное
состояние в фазовом пространстве, h, как мы предположили в разделе 3.5?
Это справедливо также для N частиц в трехмерном сосуде.
(c) Плотность состояний в фазовом пространстве для N частиц в сосуде.
Покажите, что плотность состояний для N свободных частиц в кубическом сосуде
объема V с периодическими граничными условиями равна VN/h3N и,
следовательно, фазовый объем на одно состояние равен hSN.
Давайте посмотрим, справедлив ли такой выбор единиц42 также для
гармонического осциллятора.
(d) Фазовая плотность состояний гармонического осциллятора. Рассмотрим
гармонический осциллятор с гамильтонианом Η = ρ2/2τη+πιω2ς2/2. Нарисуйте
энергетическую поверхность с энергией Ε и найдите объем (площадь)
охваченного ею фазового пространства. (Подсказка: площадь эллипса равна пг\Г2, где
2 Вы показали здесь, что в идеальных газах энтропия вычисляется с использованием
единиц фазового пространства, полагая h = 1. Для того чтобы показать, что это справедливо
для взаимодействующих систем, как правило, используется квазиклассическое
приближение [73, chapter 48, р. 170] или интегралы по траекториям [41]. Мы можем представить
себе измерение разницы в энтропии между взаимодействующими системами и идеальным
газом как медленное и обратимое включение взаимодействия между частицами путем
измерения потока энтропии в систему или из нее. Таким образом, определение нуля энтропии
для идеального газа задает его для всех систем.
Гл.7. Упражнения
291
г\ и Г2 —длина большой и малой оси, соответственно.) Чему равен объем на
одно энергетическое состояние, заключенный между Еп и ЕпЛ.\, для собственных
энергий Еп = (п + l/2)hwl
7.4 Возрастает ли энтропия в квантовых системах? (Математика,
квантовая физика) @
В упражнении 5.7 мы увидели, что в классических гамильтоновых
системах неравновесная энтропия »Snonequil = —кв J pl°gP является константой. В
данном упражнении вы покажете, что в процессе микроскопической
эволюции изолированной квантовой системы энтропия также является постоянной
величиной для произвольных зависящих от времени матриц плотности p(t).
Используя закон эволюции (уравнение 7.19) dp/dt = [H,p]/{ifo), покажите,
что S = Tr (plogp) не зависит от времени, где ρ — произвольная матрица
плотности. (Подсказка: покажите, что Тг(АВС) = Тг(САВ) для произвольных
матриц А, В и С. Также вы должны знать, что оператор Μ коммутирует с
любой функцией /(М).)
7.5 Матрицы плотности фотонов. (Квантовая физика) @
Запишите матрицу плотности для вертикально поляризованного фотона \V)
в базисе, в котором \V) = (J), а для горизонтально поляризованного
фотона \Н) = (j). Запишите матрицу плотности для диагонально
поляризованного фотона (Ι/λ/2, Ι/λ/2) и для неполяризованного света (см. примечание 2 на
стр. 257). Вычислите ΊΥ(ρ), ΊΥ(ρ2) и S = -fcBlr(plogp). Дайте физическую
интерпретацию этим величинам. (Подсказка: одно из них соответствует
проверке, является ли состояние чистым, другое — мере информации, а третье
— нормировке.)
7.6 Спиновая матрица плотности.43 (Квантовая физика) @
Пусть гамильтониан спина равен
U = ~B-ff, (7.78)
где σ = (σχ, συ, σζ) три матрицы Паули, а В можно рассматривать как магнитное
поле в единицах, в которых гиромагнитное отношение равно 1. Запомните, что
OiGj —OjOi = 2ieijk&k· Покажите, что любая матрица плотности размером 2x2
может быть записана в виде
р=\{1 + р-3). (7.79)
3Вопрос основал на экзаменационном задании, предложенном Бертом Гальпериным,
Гарвард, 1976.
292
Гл.7. Квантовая статистическая механика
Покажите, что уравнения движения для матрицы плотности ihdp/dt = [Η, ρ]
могут быть записаны в виде dp/dt = —В χ р.
7.7 Излучение и поглощение света. (Квантовая физика) (2)
В эксперименте, который изучал Планк, плотность энергии на единицу
частоты (уравнение 7.67) внутри сосуда не была получена напрямую.
Исследовалась энергия, излучаемая небольшим отверстием площадью А.
Предположим, что отверстие находится на передней стороне контейнера,
перпендикулярной оси ζ.
Чему равно распределение фотонов непосредственно внутри границ
отверстия? Отверстие практически не влияет на фотоны, движущиеся со
скоростью νζ > О, поскольку они излучаются с удаленных сторон резервуара,
для которых наличие отверстия представляет собой незначительное
возмущение. Таким образом, предполагая, что релевантные фотоны непосредственно
внутри отверстия распределены таким же образом, как в оставшейся части
сосуда (уравнение 7.67), какое их количество покинет его за время dt?
Фотоны, находящиеся в пределях расстояния vzdt от отверстия, покинут
резервуар за время dt (рис. 7.15). Вертикальная скорость vz = ccos(0), где
θ — угол между направлением скорости фотонов и вертикалью.
Распределение Планка изотропно, таким образом, вероятность того, что фотон будет
двигаться под углом 0, составляет 2π8ΐη(0) άθ/(4π) = sin(0) άθ/2.
Рис. 7.15. Эмиссия фотонов
Фотоны, которые находятся на расстоянии не более vz dt от отверстия, покидают резервуар
за время at.
(а) Покажите, что плотность вероятности ρ(υζ)44 того, что данный фотон
будет иметь скорость νζ, не зависит от νζ на интервале (—с, с) и равна, таким
образом, 1/2с. (Подсказка: ρ(νζ) Δνζ = ρ(θ) Δ0.)
Верхний предел энергии, излучаемой отверстием площадью Д
определяется энергией сосуда как целого (уравнение 7.67), умноженной на долю
Acdt/V объема в пределах расстояния cdt от отверстия.
4 Мы снова допускаем некоторую небрежность, обозначая одной и той же буквой ρ
плотности вероятности на единицу скорости и на единицу угла
Гл.7. Упражнения
293
(b) Покажите, что в действительности излучаемая энергия составляет
1/4 от верхнего предела. (Подсказка: вам нужно будет взять интеграл
foP(vz)vzdvz.)
Следовательно, равновесная мощность излучения через малое отверстие
составляет на единицу площади
Ры^(ш,Т) = у —е^/квТ_1. (7.80)
Почему это называется излучением черного тела? Безусловно, маленькое
отверстие в большом (холодном) резервуаре выглядит черным — любой свет,
проникающий внутрь, отражается там до тех пор, пока не будет поглощен
стенками. Предположим, что мы загородили отверстие некоторым черным
объектом — материалом, который поглощает излучение любой частоты при
любом угле падения. Этот объект будет поглощать излучение из резервуара,
повышая свою температуру, до тех пор пока не придет в равновесие с
резервуаром — испуская такое же количество излучения, сколько он поглощает.
Таким образом, полная мощность на единицу площади, излучаемая нашим
черным объектом в равновесии при заданной температуре, должна быть
равна мощности, излучаемой отверстием. Это также должно быть справедливо
в случае, если мы поместим селективный фильтр между отверстием и нашим
черным телом, пропускающий только определенный тип фотонов. Таким
образом, излучение и поглощение нашего черного тела и отверстия должны
быть сбалансированы для каждой фотонной моды. Это представляет собой
пример принципа детального баланса, который мы более детально обсудим в
разделе 8.2.
Какая мощность на единицу площади -PCoiored(^,T) излучается в
равновесии при температуре Τ красным или коричневым телом? белым? зеркалом?
Эти объекты различаются между собой долей падающего света, которую они
поглощают при различных частотах и углах α(ω, θ). Мы снова можем
использовать принцип детального баланса, помещая наш раскрашенный объект
рядом с черным телом и сравнивая поглощаемую и излучаемую мощность для
каждого угла и частоты:
Colored (ω, Γ, θ) = Pbiack(w, Τ)α(ω, θ). (7.81)
Наконец, мы вычислим Qtot(T), полную мощность на единицу площади,
излучаемую черным телом при температуре Т, интегрируя уравнение (7.80)
по частоте.
(c) Используя равенство /0°° х3/(ех — 1)скг = π4/15, покажите, что
PCX)
Qtot(T) = / iWk(", Τ) άω = σΤ\ (7.82)
Jo
294
Гл.7. Квантовая статистическая механика
а также получите выражение для постоянной Стефана—Больцмана σ. (σ =
5.67 · 10~5эргсм~2К~4с-1; используйте это, чтобы проверить ваш ответ.)
7.8 Коэффициенты Эйнштейна. (Квантовая физика, оптика,
математика) (3)
Эйнштейн, используя статистическую механику, вывел основные законы
взаимодействия света с материей на самой ранней стадии развития квантовой
механики. В частности, он установил, что наличие индуцированного
излучения необходимо для самосогласованности статистической механики, а также
получил выражения, определяющие относительные скорости поглощенного,
спонтанного и вынужденного излучения [43, 1.42-5].
Рассмотрим систему, состоящую из невзаимодействующих атомов, слабо
связанных с фотонами (электромагнитным излучением), в равновесии при
температуре fcgT = Ι/β. Атомы могут находиться в двух собственных
энергетических состояниях Е\ и i?2> причем средние заселенности каждого уровня
равны N\ и ЛГ2. Отношение заселенностей, как всегда, определяется
распределением Больцмана.
/^\=е-«*-*>. (7.83)
Плотность энергии электромагнитного поля задается распределением Планка
(7.67):
Атом в основном состоянии будет поглощать электромагнитную энергию
фотонов со скоростью, пропорциональной плотности энергии и(и), где
энергия возбуждения hw = Е2 — Е\. Давайте определим скорость поглощения на
один атом 2пВи(и).*5
Атом в возбужденном состоянии £?2 при отсутствии электромагнитного
воздействия переходит в основное состояние со скоростью А, излучив фотон.
Эйнштейн отметил, что ни А, ни В не должны зависеть от температуры.
Эйнштейн доказал, что при учете только этих двух процессов возникает
несогласованность.
(а) Рассчитайте среднее по большому временному интервалу N2/N1,
предполагая только наличие поглощения и спонтанного излучения. Покажите, что
даже в пределе слабого взаимодействия (при малых А и В) это уравнение не
согласуется со статистическими распределениями (7.83) и (7.84). (Подсказка:
45 В литературе также используется обозначение ^cycles (/), где / = ω/2π равна
числу циклов в секунду. Поскольку ucyc\es(f)df = η(ω)άω, скорость поглощения равна
Bucycies(f) = Bu(u))du>/df = 2πΒη(ω).
Гл.7. Упражнения
295
запишите выражение для dN\/dt и положите его равным нулю. Зависит ли
полученное отношение В/А от температуры?)
Эйнштейн решил эту проблему, учитывая вынужденное излучение. Грубо
говоря, атом под воздействием осциллирующего электромагнитного поля с
большей вероятностью будет излучать фотоны той же самой моды. Эйнштейн
получил, что вероятность вынужденного излучения равна константе 2πΒ',
умноженной на плотность энергии и(и).
(b) Запишите выражение для dNi/dt, включая поглощение (отрицательный
член), а также спонтанное и вынужденное излучение. Предполагая наличие
равновесия, с помощью данного уравнения, а также формул (7.83) и (7.84) выразите
В и В' через А. Полученные выражения называют коэффициентами
Эйнштейна.
Давайте выразим скорость вынужденного излучения через число
возбужденных фотонов на одну моду (см. альтернативный вывод в
упражнении 7.9(a)).
(c) Покажите, что скорость затухания возбужденных атомов А + 2πΒ'ν,{ω)
увеличивается в (п) + 1 раз по сравнению со скоростью при нулевой температуре,
где (п) — среднее число фотонов, колеблющихся с частотой hw = Е2 — Е\.
7.9 Скопление бозонов: сверхтекучие жидкости и лазеры.
(Квантовая физика, оптика, атомная физика) @
Добавление частицы в бозе-копдепсат. Предположим, что у нас есть
система невзаимодействующих бозонных атомов в сосуде с возможными одно-
частичными собственными состояниями ψη. Пусть в начальный момент
времени система находится в сконденсированном бозе-состоянии, при котором
все N бозонов находятся в состоянии ψο, таким образом,
ф1?](гь ...,rN) = Μη) ■ ■ ■ Μ*ν). (7.85)
Предположим, что в систему аккуратно помещается новая частица, в
состояние, представляющее собой суперпозицию Μ одночастичных состояний с
наименьшей энергией.46 Таким образом, если бы она была помещена в
пустой сосуд, то ее начальное состояние имело бы вид
46 В случае свободных частиц в кубическом сосуде V после добавления частицы в начало
координат ее состояние ф(г) = δ(τ) будет представлять собой суперпозицию всевозможных
плоских волн с одинаковым весом, δ(τ) = (l/^)Skelkx. (Используя обозначения теории
вторичного квантования, а*(х = 0) = (1/V)53kajc.) Мы аккуратно помещаем частицу в
начало координат, ограничиваясь суммированием по состояниям с низкой энергией.
Подобным образом обычно моделируется квантовое туннелирование (например, в переходе
Джозефсона или сканирующем туннельном микроскопе).
296
Гл.7. Квантовая статистическая механика
φ(τΝ+ι) = -j=(xp0(rN+1) + Vi(r;v+i)
+ ... + ^Af-i(rjv+i))· (7.86)
Состояние Φ(γι,.. .rw+i) частицы после ее помещения в бозе-конденсат,
состоящий из невзаимодействующих частиц, задается симметризацией
функции-произведения Ф^(γι, ..., τν)Φ(*ν+ι) (уравнение 7.30).
(а) Найдите симметризованное начальное состояние системы с добавленной
частицей. Покажите, что отношение вероятности, что новый бозон попадет в
основное состояние {ψο), больше вероятности попасть в пустое состояние (фт
для О < т < М) в N + 1 раз. (Подсказка: вначале сделайте это для N = 1.)
Таким образом, если макроскопическое число бозонов находится в одном
одночастичном собственном состоянии, то новая частица с большей
вероятностью тоже попадет в это же состояние, чем в какое-либо из микроскопически
заселенных состояний.
Обратите внимание, что ничто в вашем анализе не зависит от ψο —
низшего энергетического состояния. Если в начальный момент времени в системе
присутствует макроскопическое число частиц в одночастичном состоянии с
волновым вектором к (например, в сверхтекучей жидкости со
сверхпроводящим током в направлении к), новые добавленные частицы или частицы,
рассеянные неоднородностями, с большой вероятностью попадут в это же
состояние. Это альтернативный способ объяснения устойчивости
сверхпроводящих токов, комплементарный топологическому подходу (упражнение 9.7).
Добавление фотона в лазерный пучок. Эта «коммуникабельность»
бозонов лежит в основе принципа работы лазеров.47 В лазере N фотонов
находятся в определенной моде. Атом в возбужденном состоянии излучает фотон.
Фотон, который он излучает, с вероятностью, большей BJV+1 раз,
предпочитает присоединиться к лазерному пучку, а не попадать в другие доступные
моды. Здесь N соответствует вынужденному излучению, при котором
существующее электромагнитное поле извлекает энергию из возбужденного
атома, а +1 соответствует спонтанной эмиссии, которая происходит даже при
отсутствии внешних фотонов.
Представим себе одиночный атом в состоянии с энергией возбуждения Ε
и скоростью распада Г в кубическом сосуде объема V с периодическими
граничными условиями для фотонов. Согласно принципу неопределенности для
энергии и времени (АЕ At) > ft/2, энергия атома известна с точностью до
47Лазер — это акроним от английского слова «laser». Light amplification by the stimulated
emission of radiation — усиление света посредством вынужденного излучения.
Гл.7. Упражнения
297
соотношения АЕ ос КГ. Предположим для простоты, что в кубическом
сосуде, в котором изначально отсутствуют фотоны, атом при распаде испускает
фотон, частота которого с равной вероятностью принимает любые значения
в диапазоне Ε - КГ/2 < Κω < Ε + КГ/2.
(b) Предполагая, что сосуд большой, а скорость распада Г мала, получите
выражение для числа мод Μ на единицу объема V, конкурирующих за фотон,
испускаемый атомом. Оцените его для лазера с длиной волны λ = 619 нм и
толщиной линии Г = 104 рад/с. (Подсказка: используйте выражение (7.65)
для плотности состояний.)
Предположим, что лазер уже в работе. Таким образом, существует N
фотонов в объеме V вещества, излучающего в оптическом диапазоне, причем
все фотоны находятся в одинаковом плосковолновом состоянии (т.е. лазер
одномодовый).
(c) Используя ваш результат из задания (а), найдите число фотонов на
единицу объема N/V, которые будут находиться в генерирующей волне, для атома,
который с вероятностью 50% излучает в этой моде.
Основной задачей запуска лазера является создание популяции
возбужденных атомов. Усиление возникает при наличии инверсной заселенности,
при которой число возбужденных атомов больше, чем число атомов в низшем
энергетическом состоянии (что, естественно, представляет собой
неравновесное состояние). Это становится возможным при накачке атомов в
возбужденное состояние.
7.10 Дефекты в кристаллах. (Квантовая физика, физика
конденсированного состояния) (2)
Дефект в кристалле имеет одну центральную конфигурацию с нулевой
энергией и Μ внецентральных конфигураций с энергией е, причем между
состояниями практически нет квантового туннелирования. Гамильтониан
может быть записан в виде матрицы (M+l)x(M-fl)
/о о о -\
U = 0 € 0 . (7.87)
\0 0 с ···/
Пусть в кристалле N дефектов. Предположим, что каждый из них находится
в определенной позиции (следовательно, они различимы), а также, что они
не взаимодействуют между собой.
Запишите каноническую статистическую сумму Z(T), среднюю энергию
Е(Т), флуктуации энергии, энтропию S(T) и удельную теплоемкость С(Т)
как функции температуры. Постройте удельную теплоемкость на один дефект
298
Гл.7. Квантовая статистическая механика
C(T)/N при Μ = 6. Задайте е в качестве энергетической единицы и кв = 1
на вашем графике. Получите простое соотношение между Μ и изменением
энтропии при переходе от нулевой к бесконечной температуре. Проверьте это
соотношение, используя ваше выражение для S(T).
Скачок удельной теплоемкости системы с двумя состояниями называется
аномалией Шоттки.
7.11 Фононы на струне. (Квантовая физика, физика конденсированного
состояния) @
Непрерывная струна длиной L с массой μ на единицу длины под
воздействием напряжения г смещается по вертикали в поперечном направлении
на u(x,t). Плотность кинетической энергии (μ/2)(θυ,/θί)2, а потенциальной
(т/2)(ди/дх)2. Струна зафиксирована на границе в точках χ = О и χ = L.
Выразите кинетическую и потенциальную энергию через нормальные моды
Qk(t), где u(x,t) = Y^nqkn(t)8in(knx), kn = ηπ/L. Используя эти переменные,
покажите, что система представляет собой совокупность невзаимодействующих
гармонических осцилляторов. Вычислите плотность нормальных мод на единицу
частоты д{и) для длинной струны. Вычислите удельную теплоемкость струны
с(Т) на единицу длины в пределе L —у сю, считая, что осцилляторы квантовые.
Чему равна удельная теплоемкость струны в классическом пределе?
Выполняя похожие вычисления в трехмерном пространстве, можно
получить удельную теплоемкость кристаллов при низкой температуре.
7.12 Полупроводники. (Квантовая физика, физика конденсированного
состояния) @
Рассмотрим простую модель легированного проводника [6, chapter 28].
Рассмотрим кристалл кремния, легированного фосфором, состоящий из N —
Μ атомов кремния и Μ атомов фосфора. Каждый атом кремния добавляет
один свободный электрон в систему и может находиться в двух состояниях с
энергиями ±Δ/2 с энергетической щелью Δ = 1.16 эВ. Каждый атом
фосфора имеет два свободных электрона и два состояния, одно с энергией — Δ/2,
а другое с энергией Δ/2 — б, где е = 0.044 эВ немного меньше, чем
энергетическая щель.48 (В нашей модели не учитывается квантовомеханический
скачок между атомами, а также спин и химические процессы. Каждый атом
кремния на самом деле вносит четыре электрона и имеет четыре уровня, а
каждый атом фосфора — пять электронов и четыре уровня. Итак, в нашей
48Атом фосфора нейтрален, когда оба состояния заполнены. Верхнее состояние можно
представить себе как электрон, связанный с положительным ионом фосфора. Энергия е
соответствует кулоновскому притяжению электрона и иона фосфора. Она мала, поскольку
диэлектрическая постоянная достаточно большая [6, chapter 28].
Гл.7. Упражнения
299
системе присутствуют Ν + Μ бесспиновых электрона (максимум один
электрон на каждое состояние), N состояний валентной зоны с энергией — Δ/2,
Μ состояний примесной зоны с энергией Δ/2 — в и N — Μ состояний зоны
проводимости с энергией Δ/2).
(a) Получите выражение для числа электронов как функцию температуры Τ
и химического потенциала μ для энергетических уровней нашей системы.
(b) Чему равна предельная вероятность заполнения состояний при Г —у оо,
когда энтропия максимальна, а все состояния равновероятны? Используя это,
найдите выражение для μ(Τ), справедливое при больших Т, не зависящее от Δ
или е.
(c) Постройте диаграмму энергетических уровней, иллюстрирующую
заполненные и пустые состояния при Τ = 0. Найдите выражение для μ(Τ) в пределе
низких температур Τ —> 0, не зависящее от переменной Т. (Подсказка:
приравняйте число дырок в примесной зоне и число электронов в зоне проводимости.
Почему можно не учитывать валентную зону?)
(d) В одном кубическом сантиметре образца находится Μ = 1016 атомов
фосфора. Силикон содержит около N = 51022 атомов на кубический сантиметр.
Найдите μ при комнатной температуре (1/40эВ) из выражения, полученного
в задании (а). (Напишите соответствующую компьютерную программу.) Какая
доля атомов фосфора при данной температуре будет ионизована (т.е. их верхнее
энергетическое состояние будет незаполненным)? Чему равна плотность дырок
(незаполненных состояний с энергией —Δ/2)?
Фосфор представляет собой донор электронов, а наш образец —
полупроводник η-типа, поскольку основными носителями являются электроны.
Проводники р-типа легированы акцепторами, и основными носителями заряда в
них являются дырки.
7.13 Бозе-конденсация в энергетической полосе. (Атомная физика,
квантовая теория) (2)
Плотность одночастичных собственных состояний д(Е) системы
невзаимодействующих бозонов образует энергетическую полосу. Собственные
энергии ограничены диапазоном Ет[п < Ε < Emax> таким образом, плотность
д(Е) ненулевая в этом диапазоне и равна нулю в противном случае. Система
состоит из бозонов с конечной плотностью. Что из нижеприведенного
необходимо, для того чтобы в системе происходила бозе-конденсация при низких
температурах?
(a) д(Е)/(еМЕ-Е™^ + 1) имеет предел при Ε -> £~in.
(b) g(E)/(e^E-Emi^ - 1) имеет предел при Ε -> £~in.
(c) £min > 0.
300
Гл.7. Квантовая статистическая механика
(d) fE . g(E')/(E' — Em[n)dE' представляет собой сходящийся интеграл в
нижнем пределе £Ίηίη.
(e) Бозе-конденсация не может происходить в системе, состояния которой
ограничены энергетической полосой.
7.14 Бозе-конденсация: эксперимент. (Квантовая физика, атомная
физика) (J)
Андерсон, Эншер, Мэтьюс, Вьеман и Корнелл в 1995 году смогли
экспериментально произвести бозе-конденсацию разбавленного газа рубидия-87 [103].
(a) Является ли рубидий-87 (состоящий из 37 протонов и электронов и 50
нейтронов) бозоном или фермионом?
(b) Считая, что максимальная концентрация равна 2.5· 1012/см3, вычислите
температуру Т<Рге lctf при которой начнется бозе-конденсация.
Экспериментаторы обнаружили, что бозе-конденсация начинается при температуре fj^[iessw[ed —
170 нК. Это ниже или выше вашей оценки? (Полезные константы: h = 6.6262 ·
1(Г27 эрге, тп~тр = 1.6726 · 10"24 г, кв = 1.3807 · 1(Г16 эрг/К.)
Эффективная потенциальная энергия ловушки гармоническая по
трем направлениям, но анизотропнная с цилиндрической симметрией.
Частота вдоль цилиндрической оси составляет /о =120 Гц, таким образом,
с^о ~ 750 Гц, а две другие частоты меньше в γ/8 раз: ω\ ~ 265 Гц.
Бозе-конденсация наблюдалась при резком удалении потенциала ловушки49
и освобождении атомов газа. Изображение распыляемого облака было
получено через 60 мс при освещении лазером и использовании прибора с
зарядовой связью для изображения тени.
Основное состояние частицы массой т в одномерном гармоническом
осцилляторе с частотой ω имеет вид ψο(χ) = .(τηω/πΗ) ' е_та;ж /2Л,
а волновая функция в пространстве импульсов представима в виде
ψο(ρ) = (1/(πτηΗω)) ' е~р /2mfkJ. В данной трехмерной задаче решение
представимо в виде произведения соответствующих гауссиан по трем осям.
(c) Будет ли распределение импульсов шире вдоль высокочастотной оси (ωο)
или одной из низкочастотных осей (ωι)? Предположим, что вы можете
пренебречь малой шириной распределения начальных координат и что координаты на
рис. 7.16 отражают распределение скоростей, умноженных на время движения.
Какая из осей, χ или у на рис. 7.16, соответствует цилиндрической оси с высокой
частотой? Какого типа анизотропия возникнет в импульсном распределении при
высоких температурах (в классической статистической механике)? В
рассматриваемом случае бозе-конденсация проводилась не в свободном пространстве.
49На самом деле потенциал сначала медленно уменьшался в 75 раз, а затем резко
удалялся. Мы не учитываем это в нашем рассмотрении.
Гл.7. Упражнения
301
Атомы находились в потенциале гармонического осциллятора. Для
вычислений в свободном пространстве мы используем приближение континуальной
плотности состояний д(Е). Это имеет смысл, только если квТ велико по
сравнению с расстояниями между уровнями вблизи основного состояния.
Рис. 7.16. Конденсация Бозе—Эйнштейна
Конденсация Бозе—Эйнштейна при 400, 200 и 50 нано-Кельвинах. На рисунках
изображены пространственные распределения через 60 мс после удаления потенциала. Поле зрения
для каждого изображения составляет 200мкмх270мкм. Левое изображение практически
сферически симметрично и построено до бозе-конденсации. На среднем рисунке изображен
эллиптический бозе-конденсат, наложенный на сферический термический фон. На правой
картинке проиллюстрирован практически чистый конденсат. Перепечатано из [103].
Благодарен Physics 2000 team за разрешение использования изображения.
(d) Сравните huo с квТ при экспериментально полученной температуре бозе-
конденсации Tcmeasured. (h = 1.05459 · 10"27 эрг с; кв = 1.3807 · 10"16 эрг/К.)
Для бозонов в одномерном гармоническом потенциале с частотой ωο
очевидно, что д(Е) = \/(tvujQ). Число состояний в малом диапазоне АЕ равно
числу hwo, которые он содержит.
(e) Вычислите плотность одночастичных собственных состояний
/»оо
д(Е) = / (fcKfc2d£3 ^1(^1)^2(^2)^3(^3)
./о
χδ{Ε-(ε1+ε2 + ε3)) (7-88)
для трехмерного гармонического осциллятора с частотой по одному
направлению ωο, а по двум другим - ω\. Покажите, что она равна l/δΕ, умноженной на
число состояний в пространстве векторов ё*между энергиями Ε и Ε + δΕ. Равна
ли толщина данного треугольного слоя δΕΊ
В эксперименте N = 2 104 атомов находились в ловушке при конденсации.
(f) По аналогии с вычислениями в свободном пространстве, найдите
максимальное число атомов, которые могут находиться в трехмерном потенциале
302
Гл.7. Квантовая статистическая механика
гармонического осциллятора в задании (е) при отсутствии бозе-конденсации при
температуре Т. (Вам может понадобиться формула /0°° z2/(ez — 1) άζ = 2£(3) =
2.40411.) При какой температуре Т^°, согласно вашим вычислениям,
произойдет бозе-конденсация в реальной экспериментальной ловушке?
7.15 Вселенная с преобладанием фотонов.50 (Астрофизика) ®
В настоящее время Вселенная не находится в состоянии равновесия.
Однако радиация в микроволновом диапазоне частот с хорошей степенью
точности подчиняется распределению Планка при температуре 2.725 ± 0.001 К
(рис. 7.17).
Фоновая радиация в микроволновом диапазоне представляет собой
окно во времена примерно 380 000 лет спустя после Большого Взрыва,51 когда
температура понизилась достаточно сильно для возможности образования
атомов водорода из протонов и электронов. Свет проходит не очень далекий
путь в ионизированных газах. Он ускоряет заряды и рассеивается от них.
Таким образом, до этого времени наша Вселенная была похожа на равновесный
суп из электронов, ядер и фотонов.52 Образовавшиеся нейтральные атомы
были достаточно прозрачны, для того чтобы практически все возникшие в
то время фотоны путешествовали на протяжении следующих 13 биллионов
лет, попав в конечном итоге в наши детекторы.
Длина волны этих фотонов за прошедшее время сильно увеличилась.
Это произошло вследствие последующего расширения Вселенной. Начальное
планковское распределение фотонов менялось как из-за эффекта Доплера
(красное смещение, возникающее из-за кажущегося движения от нас
удаленного газа, излучающего фотоны), так и из-за рассредоточения фотонов
в большем объеме. Эффект Доплера уменьшает энергию фотона, а также
сжимает весь частотный диапазон фотонов (увеличивая число фотонов на
единицу частоты).
Могут возникнуть вопросы, почему современный микроволновой фон
является тепловым (см. рис. 7.17) и почему его температура так мала? ...
(а) Если размер сосуда равен L, а длины волн всех фотонов в сосуде
увеличиваются в / раз, чему станет равна частота и/ фотона с начальной частотой
ωΐ Если начальная плотность фотонов составляет η(ω), какое значение η'(ω')
она приобретет после расширения? Покажите, что планковское выражение для
числа фотонов на единицу частоты на единицу объема
50Это упражнение было разработано с участием Дэйла Фиксена и Еанна Фланагана.
51 Здесь приведены оценки времени, известные к моменту написания упражнения. См.
также [146], где описывается история ранней Вселенной.
52Нейтрино покинули состояние равновесия несколько раньше.
Гл.7. Упражнения
303
Частота (см1)
Рис. 7.17. Планковское микроволновое фоновое излучение
Планковское микроволновое фоновое излучение получено спутником СОВЕ [25].
Единицы измерения взяты из исходной статьи. По оси абсцисс отложены обратные сантиметры
вместо частот (для того чтобы получить частоты, нужно умножить на скорость света), а
по оси ординат — мега-Янский/стерадиан по (1 мега-Янский
соответствует распределению Планка при 2.725 К.
10"20Втм"2Гц"1). Линия
ω
1Р<?(&»/квТ _ 1)
(7.89)
(из уравнения 7.66) сохраняется, за исключением сдвига по температуре.
Чему равна новая температура Т\ выраженная через начальную температуру Г и
коэффициент расширения /? Как и ожидалось, при адиабатическом
расширении система остается в состоянии равновесия, но ее температура меняется.
(Ь) Какое количество фоновых микроволновых фотонов на кубический
сантиметр присутствует в системе? Сравните полученную плотность со средней
плотностью атомов во Вселенной (nmatter ~ 2.5 · 10~7 атомов/см3)? (Вы
можете использовать: f£°x2/(ex — l)dx = 2ζ(3) « 2.404. Полезные константы:
h = 1.05 · 10"27 эрг с, с = 3 · 1010см/с и кв = 1.38 · 10"16 эрг/К.)
Космологи утверждают, что в нашей Вселенной преобладают фотоны,
поскольку их сейчас намного больше, чем атомов.
Давайте приблизительно оценим относительный вклад атомов и фотонов
в другие характерные свойства Вселенной.
(с) Получите выражения для энтропии S, внутренней энергии Ε и давления
Ρ фотонного газа в объеме V и при температуре Т. Для простоты запишите их,
304
Гл.7. Квантовая статистическая механика
используя постоянную Стефана—Больцмана53 σ = п2к^/60Н3с2. Не
учитывайте нулевую энергию колебаний фотонов54 (поскольку иначе энергия и давление
были бы бесконечными, даже при нулевой температуре). (Подсказка:
используйте большой термодинамический потенциал Φ для фотонов. Для вашего
сведения, /0°° х3/(ех — 1) dx = π4/15 = —3 /0°° χ2 log(l — е~х) dx, где последний
интеграл может быть взят по частям.)
(d) Получите выражения для энтропии, плотности массы-энергии55 и
давления идеального газа, состоящего из атомов водорода, с плотностью nmatter
и с тем же объемом и температурой, что и для фотонного газа. Можем ли
мы не учитывать квантовые эффекты для атомарного газа? Поместите ответы
на задания (с) и (d) в таблицу и сравните значения соответствующих величин
для атомов и фотонов. В четырех столбцах таблицы приведите две
аналитические формулы, а затем численные значения для V = 1см3, современную
температуру фонового микроволнового излучения и современную плотность атомов.
(Подсказка: вам понадобится свободная энергия Гельмгольца А для атомов.
Другие полезные константы: σ = 5.67 · 10~5эргсм~2К~4с-1 и га# ^ тр =
1.673 -ИГ24 г.)
Вначале суп из света и материи удовлетворял волновому уравнению [63]:
Р-^ = ΒΨΘ. (7.90)
Здесь θ — локальная флуктуация температуры ΔΤ/Т. Константа ρ
представляет собой сумму трех вкладов: плотности материи, плотности энергии
фотонов E/V, деленной на с2, а также вклада Р/с2 за счет давления фотонов
Р.
(e) Покажите, что сумма двух вкладов фотонов в массовую плотность
пропорциональна E/(c2V). Чему равен коэффициент пропорциональности?
Постоянная В в нашем волновом уравнении (7.90) представляет собой
коэффициент объемного сжатия: В = -V(dP/dV)\s·56 После образования
53В законе Стефана—Больцмана утверждается, что черное тело излучает с мощностью
σΤ4 на единицу площади, где σ — постоянная Стефана—Больцмана, см. упражнение 7.7.
54Рассматривайте их как бозоны (уравнение 7.42) при μ = 0, а не как гармонические
осцилляторы (уравнение 7.23).
55 Убедитесь, что вы учли вклад гас2 в плотность энергии для атомов водорода.
56Важно отметить, что сжатие происходит адиабатически (при постоянной энтропии S),
а не изотермически (при постоянной температуре Т). (В этом заключалась ошибка
Ньютона.) Звуковые волны распространяются слишком быстро, и температура не успевает
выравниваться. В самом деле, можно предположить при достаточно больших длинах волн,
что переноса тепла не происходит (следовательно, мы можем использовать
адиабатическое приближение). Все это верно как для воздуха, так и для фотонных газов в ранней
Вселенной.
Гл.7. Упражнения
305
нейтральных атомов доминирующий вклад в давление (а также В) вносит
фотонный газ.
(f) Запишите Ρ как функцию S и V (исключая Τ и Е) и вычислите В
для фотонного газа. Покажите, что оно пропорционально плотности энергии
фотонов E/V. Чему равен коэффициент пропорциональности?
Пусть R — отношение pmatter к сумме вкладов фотонов в ρ из задания (е).
(g) Чему была равна скорость звука во Вселенной как функция R и с до
начала образования нейтральных атомов? (Подсказка: сравните с
уравнением (10.78) в упражнении 10.1 для проверки ваших ответов к заданиям (е)-
(g)·)
Упражнение 10.1 и анимация волн на сайте [141] иллюстрируют, каким
образом данное волновое уравнение объясняет многие наблюдаемые
флуктуации в микроволновом фоновом излучении.
7.16 Белые карлики, нейтронные звезды и черные дыры.
(Астрофизика, квантовая физика) @
Когда источники энергии в больших звездах израсходованы, а
температура стремится к нулю, окончательное состояние определяется
конкуренцией между гравитацией и химической или ядерной энергией, необходимой для
сжатия материала.
Упрощенная модель звездного вещества представляет собой озеро
Ферми невзаимодействующих электронов с достаточным количеством ядер для
баланса заряда. В качестве модели белого карлика (или черного карлика,
поскольку мы предполагаем нулевую температуру) рассмотрим ядра Не4 И
компенсирующие их заряд электроны, распределенные с однородной
плотностью. Пусть гравитация подчиняется закону Ньютона. Предположим, что
химическая энергия определяется исключительно энергией газа
невзаимодействующих электронов (заполняющих уровни до энергии Ферми).
(а) Предполагая, что электроны нерелятивистские, вычислите энергию
сферы радиусом R, содержащую N невзаимодействующих электронов при
нулевой температуре.57 Вычислите ньютоновскую гравитационную энергию
сферы, содержащую ядра Не4, с такой же по модулю, но противоположной по
знаку плотностью заряда. При каком радиусе полная энергия минимальна?
Более детальная версия этой модели изучалась Чандрасекаром и другими
в качестве модели белых карликов. Полезные величины: тр = 1.6726 · 10~24 г,
тп = 1.6749 · КГ24г, те = 9.1095 · 1(Г28г, h = 1.05459 · НГ27эргс, G =
57Вы можете предположить, что одночастичные собственные состояния имеют те же
самые энергии и плотность в k-пространстве в сфере объема V, как и в кубическом сосуде
объемом V. Граница не влияет существенным образом на объемные свойства.
306
Гл.7. Квантовая статистическая механика
6.672 · 1(Г8см3/(гс2), leV = 1.60219 · 1(Г12эрг, кв = 1.3807 · 1(Г16эрг/К, и
с = 31010см/с.
(b) Используя нерелятивистскую модель из задания (а), вычислите энергию
Ферми электронов в белом карлике массой, равной массе Солнца 2· 1033 г,
предполагая, что он состоит из гелия, (i) Сравните ее с характерной энергией
химической связи в атоме. Правильно ли мы делаем, что пренебрегаем
взаимодействиями электрон-электрон и электрон-ядро (то есть химическими)? (ii) Сравните ее
с температурой внутри звезды, например, 107К. Оправдано ли предположение,
что газ электронов является вырожденным (с температурой, близкой к нулевой)?
(iii) Сравните ее с массой электрона. Оправдано ли использование
нерелятивистской теории? (iv) Сравните ее с разницей в массах протона и нейтрона.
Электроны в больших белых карликах являются релятивистскими. Это
приводит к тому, что энергия растет намного медленнее с увеличением
радиуса и в конечном итоге достигает верхнего предела.
(c) Предполагая сильно релятивистские электроны, где ε = рс, вычислите
энергию сферы невзаимодействующих электронов. Обратите внимание, что эта
энергия не может сбалансировать гравитационное притяжение ядер, за
исключением особого значения массы М$. Вычислите М$. Как соотносится полученное
Mq с массой солнца, приведенной выше?
Звезда с массой, большей чем Мо, продолжает уменьшаться при
охлаждении. Электроны (см. (iv) в задании (Ь)) объединяются с протонами, сохраняя
практически постоянную плотность. Таким образом, звезда сжимается в шар,
состоящий практически из одних нейтронов (нейтронную звезду, часто
образующую пульсар из-за захваченных магнитных потоков). В недавних
работал [109] предполагается, что «нейтроний» будет и дальше преобразовываться
в разновидность кваркового супа, состоящего из многих странных кварков,
образуя прозрачный изолирующий материал.
При большей массе отталкивание Ферми между кварками не может
противостоять гравитационному давлению (кварки становятся
релятивистскими), и звезда коллапсирует в черную дыру. При этих массах общая теория
относительности начинает играть существенную роль, что выходит за рамки
данной книги. Однако базовая конкуренция между давлением вырождения
и гравитацией остается той же самой.
Глава 8
Моделирование и вычисления
Большинство моделей статистической механики не разрешимы в явном
виде.1 Даже в случае, когда точные решения неизвестны, статистическая
механика задает общие соотношения и определяет важные понятия, в терминах
которых корректно вести рассмотрение (температуру, энтропию, свободную
энергию, термодинамические соотношения). Однако бывают случаи, когда
важно получить количественный ответ, касающийся конкретной модели или
эксперимента.
Для получения этих ответов есть два основных способа. Первый способ —
численное моделирование. Иногда численная модель просто имитирует
поведение системы на микроуровне. Например, при моделировании молекулярной
динамики движение каждого атома рассчитывают явно, с помощью законов
Ньютона. Однако в этой главе мы не будем рассматривать такие модели.2
Дело в том, что часто нас интересует только равновесное состояние системы,
а подробности ее динамического поведения (то, как именно она приходит в
равновесие) не имеют значения. В этом случае методы типа Монте-Карло
позволяют найти равновесные свойства системы, минуя прямое
моделирование. Вы познакомитесь с этими методами в разделе 8.1 на примере модели
Изинга — самой популярной решеточной модели в статистической механике.
Мы не можем выписать аккуратную формулу для уравнения состояния, энтропии или
функции распределения.
2 Часто методы прямого моделирования сами используют результаты и идеи
статистической механики. Например, для имитации взаимодействия системы с термостатом в
микроскопическую модель добавляют трение и шум в пропорциях, приводящих к правильному
тепловому равновесию (соотношение Эйнштейна (2.22); см. также раздел 10.8 и
упражнение 10.7).
308
Гл.8. Моделирование и вычисления
В основе методов Монте-Карло лежит математическая теория цепей
Маркова, имеющая и многие другие приложения; теории марковских цепей
посвящен раздел 8.2.
Второй способ — это теория возмущений. Она позволяет вычислить
эффекты, возникающие при добавлении в разрешимую модель малых
дополнительных членов (возмущений). А для сложной модели — экстраполировать
ее свойства из предельного случая (например, бесконечно большой или
нулевой температуры), в котором они известны. Теория возмущений кратко
изложена в разделе 8.3, где обсуждается глубокая связь между сходимостью
соответствующих разложений и существованием фаз.
8.1 Модель Изинга
Решеточные модели образуют огромную индустрию в современной
статистической механике. В таких моделях переменная задана в узлах регулярной
решетки, а ее поведение описывается гамильнонианом или эволюционными
уравнениями. Критические явления и фазовые переходы (см. гл. 12),
решеточная КХД3 и квантовая теория поля, квантовый магнетизм и модели
высокотемпературных сверхпроводников, фазовые диаграммы для сплавов (см.
раздел 8.1.2), поведение систем с загрязнениями и беспорядком,
возникновение лавин и гранулярный шум (см. гл. 12)... Все эти и многие другие явления
могут быть описаны с помощью решеточных моделей.
В этом разделе мы познакомимся с моделью Изинга4 и рассмотрим три
физических системы (среди многих и многих), которые она описывает:
магнетики, бинарные сплавы и фазовый переход «жидкость—газ». Модель
Изинга — самая проработанная и изученная из решеточных моделей. Подобно
идеальному газу в предыдущих главах, она послужит нам доступной
«мишенью» для применения различных методов: методов Монте-Карло (в этом
разделе), низко- и высокотемпературных разложений (раздел 8.3,
упражнение 8.1), вывода соотношений между флуктуациями, восприимчивостью и
диссипацией (упражнения 8.2 и 10.6). На примере модели Изинга мы
сможем пронаблюдать образование зародышей при скачкообразном фазовом
переходе (упражнение 11.4), рост зародышей и разделение фаз (раздел 11.4.1,
упражнение 11.6), явление самоподобия при непрерывном фазовом переходе
(упражнение 12.1).
3Квантовая хромодинамика (КХД) — это теория сильного взаимодействия. Она
описывает силы, связывающие нуклоны в ядре.
4 Фамилия Ising действительно должна читаться как «Изинг», однако большинство
англоязычных физиков произносят ее как «Айзинг».
8.1. Модель Изинга
309
Модель Изинга представляет собой решетку из N клеток г, в каждой из
которых задана единственная переменная (степень свободы) Si с двумя
возможными значениями (состояниями) ±1. В основном нас будут интересовать
модели Изинга на квадратной и кубической решетке (двумерная и
трехмерная, соответственно, рис. 8.1). Гамильтониан модели Изинга имеет вид:
H = -YjJsisj-H^2sh (8.1)
(У) г
где сумма (ij) берется по всем парам ближайших соседей (на квадратной
решетке каждая клетка имеет четыре таких соседа),5 a J — константа
взаимодействия между соседями.
Рис. 8.1. Двумерная модель Изинга на квадратной решетке
Значения s» = ±1 традиционно обозначают разным цветом или стрелками вверх и вниз.
8.1.1 Магнетизм
Изначально модель Изинга использовалась для описания магнетиков.
Поэтому степень свободы Si по традиции называют спином, Η — внешним
полем, а сумму Μ = Σι si — намагниченностью.
Энергия пары соседних спинов —JsiSj равна —J, если спины сонаправле-
ны, и + J, если они противоположно направлены. Таким образом, при J > 0
(в обычном случае) соседним спинам выгодно быть направленными в одну
5При моделировании конечных систем мы используем периодические граничные
условия, чтобы избежать особых случаев на границе. Соседями граничных ячеек считаются
граничные ячейки на противоположной стороне области.
310
Гл.8. Моделирование и вычисления
сторону; такое взаимодействие называют ферромагнитным. При низких
температурах почти все спины выстраиваются в одном направлении, образуя
ферромагнитную фазу. При J < 0 взаимодействие называют
антиферромагнитным; в этом случае при низких температурах спины стремятся
выстроиться в шахматном порядке (для квадратной решетки) и образуют
антиферромагнитную фазу. При высоких температурах энтропия доминирует
независимо от знака J; в этой парамагнитной фазе спины флуктуируют
совершенно беспорядочно и удельная намагниченность т(Т) = M(T)/N равна
нулю (рис. 8.2).7
' ι •■~t —г-
Ферромагнетик
) 2 4
... ..,.,.. _, ,—.^
Парамагнетик
ι.Ι
6 8
Рис. 8.2. Намагниченность в модели Изинга
Удельная намагниченность в расчете на спин тп(Т) для трехмерной модели Изинга на
кубической решетке. При низких температурах присутствует ненулевая спонтанная
намагниченность, исчезающая при Τ > Тс ~ 4.5.
8.1.2 Бинарные сплавы
Модель Изинга является весьма убедительной моделью бинарного
сплава. Представим себе квадратную решетку, занятую атомами двух типов -
6Название «ферромагнетик» происходит от латинского названия железа (Fe), самого
распространенного материала со спонтанной намагниченностью.
7Параметры модели Изинга соответствуют микроскопическим, но отличаются от них
нормировкой. Спин Изинга Si = ±1 представляет собой удвоенную ζ-компоненту 1/2-спина
атома в кристалле: σ\ = Si/2. Таким образом, константа взаимодействия между спинами
в модели Изинга в четыре раза отличается от константы z-z взаимодействия между
физическими спинами: JsiSj = ±3σ\σ^. На микроуровне константа взаимодействия спина с
внешним магнитным полем равна р/хбЯ · σ\, где g — гиромагнитное отношение спина (для
электрона близкое к двум), а με = eh/2me — магнетон Бора. Таким образом, внешнее
поле в модели Изинга отличается от физического на множитель р/хб/2. Кроме того,
взаимодействие между спинами в большинстве материалов не обладает настолько сильной
анизотропией, чтобы можно было ограничиться z-компонентами; лучшую аппроксимацию
дает скалярное произведение σ» · σ^ = σ*σ* + σ?σ? + a\aZj, используемое в модели Гей-
зенберга. (В отличие от модели Изинга, где σ\ коммутирует с Ή и конфигурации спинов
соответствуют собственным состояниям оператора энергии, квантовая и классическая
модели Гейзенберга различны.) Некоторые материалы действительно обладают анизотропной
кристаллической структурой, и для них модель Изинга применима, хотя и приближенно.
8.1. Модель Изинга
311
А и В (рис. 8.3). (Реальным примером такого сплава может послужить β-
латунь, состоящая из меди и цинка, смешанных примерно поровну. При
низких температурах атомы разных элементов сидят каждый на своей решетке,
причем атомы цинка находятся в центре кубов, образованных атомами
меди. На языке модели Изинга они формируют «антиферромагнитную» фазу
на объемно-центрированной кубической решетке. При высоких
температурах атомы цинка и меди свободно меняются местами, что соответствует
парамагнитной фазе. Температура перехода равна примерно 733 °С (см. [150],
раздел 3.1.1).
Рис. 8.3. Модель Изинга для описания бинарного сплава
Атомы в кристалле располагаются в узлах решетки. В сплаве атомы разных элементов (в
данном случае А и В) могут выстраиваться различными способами, порождая множество
решеточных конфигураций.
Присвоим химическим элементам значения спинов А = +1 и В = —1.
Количество атомов каждого элемента обозначим Να и Νβ соответственно,
так что Να + Nb = N. Пусть энергия взаимодействия (прочность связи)
между соседними атомами равна Еда, Ebb и Еав, & число связей каждого
из трех возможных типов равно Να α, Νββ Ναβ· Тогда гамильтониан нашего
сплава можно записать в виде:
^binary = -EaaNaa - EbbNbb - ΕΑΒΝΑΒ· (8.2)
Каждая ячейка взаимодействует только со своими ближайшими соседями,
поэтому эта модель — всего лишь замаскированная модель Изинга.
Действительно, можно показать, что8 J = \(Еаа + Евв — %Еав) и Я = Еаа — Евв-
312
Гл.8. Моделирование и вычисления
Чтобы сделать эту модель верной количественно, необходимо учесть
эффекты релаксации атомов. Действительно, если атомы одного типа
«крупнее» атомов другого — они раздвинут соседей, сместив их положения
равновесия. Такой сдвиг можно учесть простой модификацией коэффициентов
гамильтониана (8.2). Мы также должны включить в гамильтониан
температурные флуктуации положений равновесия, превратив его в свободную
энергию.9 Для построения фазовых диаграмм реальных сплавов используют
более сложные модели Изинга [104] (с трехсторонним взаимодействием
ячеек, большим радиусом взаимодействия т.д.). Иногда взаимодействия за счет
релаксации и тепловых колебаний имеют существенные дальнодействующие
составляющие и могут приводить к качественным изменениям поведения —
например, изменить тип фазового перехода с непрерывного на
скачкообразный.
8.1.3 Жидкость, газ и критическая точка
Модель Изинга используют также для описания фазового перехода
«жидкость-газ». В этой модели решеточного газа спины вверх (si = +1)
8Убедитесь в этом сами. Добавив дополнительное постоянное слагаемое —CN к
гамильтониану модели Изинга, легко убедиться, что
nbini = -jY^8i8j-HY^8i-CN = -J(NAA + NBB-NAB)-H(NA-NB)-CN, (8.3)
(ij) i
поскольку Να — Νβ соответствует суммарной намагниченности, Ναα + Νββ — это число
сонаправленных соседей, a Nab — число противоположно направленных соседей. Теперь
воспользуемся тем фактом, что на квадратной решетке число связей «сосед-сосед» ровно
вдвое больше числа ячеек (Ναα + Νββ + Nab = 2iV), и что каждому атому типа А должно
соответствовать четыре связи, заканчивающихся на A: AN a = 2Naa + Nab (аналогично
AN в = 2Nbb + Nab)· Решив эту систему, вы избавитесь от Λ/\ Να и Νβ в гамильтониане и
сможете сравнить его с гамильтонианом для бинарного сплава (8.2); отсюда вы получите
значения J и Я, указанные выше, и С = \(Еаа + Евв + 2Еав)·
9Чтобы учесть тепловые флуктуации, мы должны проинтегрировать колебания атомов
вокруг их положений равновесия (как в разделе 6.6). Это позволит нам вычислить
эффективную свободную энергию для каждой конкретной конфигурации атомов^}:
(г Г р-п(РЛ)/квт\
Т{зг} = -kBT\og / dP / dQ ш = H{Si} - TS{Si}.
\J Уатомг, типа а, вблизи узла* п )
(8.4)
Энтропия £{5г} этих колебаний зависит от конфигурации s\ и часто может быть
вычислена явно (упражнение 6.11(b)). Тогда Τ\β%} принимает вид решеточного гамильтониана
с коэффициентами, зависящими от температуры; конфигурации атомов с большей
свободой колебаний имеют большую энтропию и становятся все более выгодными при высоких
температурах.
8.1. Модель Изинга
313
соответствуют атомам, а спины вниз — ячейкам без атома. В газообразной
фазе почти все спины направлены вниз (отрицательная «намагниченность»),
а отдельные спины вверх соответствуют атомам, образующим пар. В
жидкой фазе почти все ячейки заняты (спины направлены вверх), за
исключением нескольких вакансий.
Газ в таком описании выглядит более или менее реалистично, а вот
жидкость больше похожа на кристалл, где атомы сидят в узлах кристаллической
ячейки. Почему же мы решили, что эта модель подойдет для описания
испарения?
В отличие от бинарных сплавов фазовые диаграммы жидкостей
действительно плохо описываются моделью Изинга. Зато она отлично передает их
поведение вблизи критической точки. Как показано на рис. 8.4, мы можем
непрерывным образом перейти от жидкой фазы к газообразной: граница
раздела обрывается в критической точке ТС,РС, за которой фазы становятся
неразличимы и переходят одна в другую гладко, без скачка плотности.
Χ
Χ
Температура Τ
Рис. 8.4. Фазовая диаграмма в координатах Р-Т
Фазовая диаграмма в координатах Р-Т для типичного вещества. На границе фаз «твердое
тело-жидкость» происходит изменение внутренней симметрии фазы, поэтому эта граница
не может оборваться. Граница фаз «жидкость-газ», как правило, обрывается. Это
значит, что перейти от жидкости к газу можно непрерывным образом: для этого достаточно
повысить давление до надкритического Ρ > Рс> нагреть систему до температуры выше
критической Тс, а затем уменьшить давление до исходного.
В модели Изинга (описывающей решеточный газ) также существует
линия Η = О, на которой плотность (намагниченность) испытывает скачок, и
существует температура Тс, выше которой характеристики модели меняются
непрерывно с изменением Η (парамагнитная фаза). Фазовая диаграмма на
рис. 8.5 похожа на настоящую линию раздела «жидкость—газ» с рис. 8.4
только топологически. Однако их поведение вблизи критической точки обладает
Критическая
Твердое /Жидкость/^)
тело
Газ
Тройная
точка
314
Гл.8. Моделирование и вычисления
поразительным сходством. Как вы узнаете позже в гл. 12, некоторые аспекты
поведения системы «жидкость—газ» вблизи критической точки могут быть
точно описаны трехмерной моделью Изинга.
Вверх
Критическая
\точка
Вниз
в
' Температура Τ
Тс
Рис. 8.5. Фазовая диаграмма модели Изинга в координатах Н-Т
При температуре ниже критической Тс существуют «фазы» со спинами вверх и вниз,
разделенные скачком намагниченности при Η = 0. При температуре выше Тс зависимость от
Η становится гладкой.
8.1.4 Модель Изинга: как это решать?
Как же вычислить статистические свойства модели Изинга? Вариантов
несколько:
1. Решить одномерную задачу, как это сделал сам Изинг.10
2. Обзавестись гениальным мозгом. Онзагер решил двумерную задачу
Изинга умопомрачительно сложным методом. Вслед за ним другие
великие мыслители нашли более простые и элегантные решения, но
каждое из них занимает целую главу утомительных технических
выкладок. Трехмерную задачу Изинга так пока никто и не решил.
3. Запустить метод Монте-Карло на компьютере11.
Методы Монте-Карло12 основаны на случайном блуждании по
пространству конфигураций в поисках равновесия. Эти методы будут рассмотрены
10 Это типичное домашнее задание в учебниках вроде нашего; с небольшими подсказками
любой из вас с ним справится.
11 Или разложить решение в ряд при низких или высоких температурах, воспользоваться
методом трансфер-матрицы, методом точной диагонализации системы (если она
небольшая), разложить в l/iV-ряд по числу состояний на ячейку, в 4—б-ряд по числу размерностей
пространства, ...
12Монте-Карло - это город в Монако, известный своими казино. Каждый вечер там
генерируют тысячи случайных чисел.
8.2. Цепи Маркова
315
с большей степенью общности в разделе 8.2. Здесь же приведем алгоритм
одного из таких методов, известного как метод термостата (в русскоязычной
литературе он так же известен как метод «тепловой бани»).
Метод термостата для модели Изинга
• Выберите случайную ячейку решетки г = (#,у).
• Подсчитайте, сколько ее соседей имеют спин вверх:
4 (4 соседей со спином «вверх»),
2 (3 соседей со спином «вверх»),
О (2 соседей со спином «вверх»), (8-5)
—2 (1 соседей со спином «вверх»),
[—4 (0 соседей со спином «вверх»).
ГПг = }] Sj =
• Вычислите Е+ = —Jmi - Я и Е_ = +Jrrii + Η — энергию ячейки г в
состоянии +1 или —1 при неизменном окружении.
•
Присвойте ячейке г спин вверх с вероятностью е РЕ+/(е &Е+ +е &Е-)
и спин вниз с вероятностью е~&Е- /(е~&Е+ + е~*Е~).
• Повторите процедуру.
В этом алгоритме термостат «прикладывается» последовательно к
отдельным ячейкам решетки; спин такой ячейки меняется с вероятностью,
соответствующей температуре термостата, при условии, что спины соседей
фиксировал ы. С помощью этого алгоритма мы сможем исследовать
статистические свойства модели Изинга на компьютере, так же как исследовали
свойства идеального газа с помощью бумаги и ручки.
8.2 Цепи Маркова
Алгоритм тепловой бани или термостата является далеко не самым
эффективным (и даже не самым популярным) методом приведения модели
Изинга в равновесие. Вообще же все методы Монте-Карло представляют
собой частный случай цепей Маркова. В этом разделе мы выведем
некоторые математические свойства цепей Маркова и получим критерий,
гарантирующий сходимость алгоритма к равновесному состоянию.
Цепи Маркова являются довольно сложной темой, необязательной для
понимания остального текста. В этом разделе мы введем понятие
детального равновесия и еще раз обсудим понятие эргодичности. Марковские методы
316
Гл.8. Моделирование и вычисления
играют важную роль и в других разделал физики — они служат
математическим языком для описания случайных блужданий и других случайных
эволюционных процессов как в дискретных, так и в непрерывных системах.
В последнее время марковские цепи находят все больше применений в
биоинформатике и распознавании речи, где пытаются найти скрытую марковскую
модель, описывающую закономерности речи или генетического кода.
В этом разделе мы рассмотрим марковские цепи с конечным набором
состояний {а}, которые система проходит, двигаясь дискретными шагами п.13
В марковской цепи вероятность перехода системы в новое состояние зависит
только от ее текущего состояния. Иными словами, марковская система — это
система, не обладающая памятью.
Например, модель Изинга с N ячейками может находиться в одном из
2N состояний § = {si}. Марковская цепь для модели Изинга — это правило
перехода, определяющее вероятности Ps7^=S перехода из текущего состояния
§ в любое другое состояние §'.14 В алгоритме термостата вероятность
перехода Ps'<t=S отлична от нуля, только если §' и § отличаются значением спина
в единственной ячейке. Формулировку в терминах цепей Маркова допускают
и многие задачи, выходящие за рамки классической статистической
механики. Например, в упражнении 8.4 рассмотрена модель с 1001 возможным
состоянием (соответствующим различному количеству α красных бактерий),
а вероятности допустимых переходов суть Ρα+\^α·> Ρα-ι<=α и Ρ<χ<=α·
Запишем вероятности нахождения системы в каждом из состояний α на
шаге η в виде вектора ра{п). Тогда скорости Ρβα перехода из состояния α
в β (стрелку опустим) образуют матрицу. Умножая на эту матрицу вектор
вероятностей р, мы получим значение этого вектора в следующий момент
времени (уравнение (8.6)).
Обычно мы хотим узнать, к чему стремится вероятность нахождения
системы в различных состояниях на больших временах. При каких условиях
алгоритм, заданный матрицей Р, приведет нашу систему к
термодинамическому равновесию? Чтобы ответить на этот вопрос, нам понадобятся
некоторые свойства матриц перехода Р, их собственных значений и собственных
векторов. В общем случае матрица перехода Ρβα обладает следующими
свойствами:
13Существуют аналоги цепей Маркова с бесконечным набором состояний и/или
непрерывным временем.
14 В некоторых текстах индексы расположены в обратном порядке -Ps=>s'· В нашей
индексации переход к следующему состоянию соответствует умножению слева на матрицу Ραβ
(см. уравнение 8.6).
8.2. Цепи Маркова
317
• Эволюция во времени. Вектор вероятности на шаге η + 1 равен
Ρβ(η + 1) = ΣΡβ*ρα(η), ρ(η + 1) = Ρ · ρ(η). (8.6)
α
• Положительность. Элементами матрицы являются вероятности,
поэтому
О < Ρβα < Ι- (8.7)
• Сохранение вероятности. Система всегда находится в каком-либо
из заданных состояний, и из состояния α всегда переходит в одно из
состояний набора, поэтому
£>α = 1· (8.8)
β
• Несимметричность! В большинстве случаев Ρβα φ Ραβ.
Последнее свойство вовсе не удивительно; переход из состояния с высокой
энергией в состояние с низкой намного вероятней, чем наоборот. Однако это
асимметрия означает, что наша математическая интуиция и многие методы,
разработанные специально для эрмитовых и симметричных матриц, к
матрицам перехода Ραβ неприменимы. В частности, эту матрицу не всегда можно
привести к диагональному виду.
Что же нам известно о цепях Маркова и их несимметричных матрицах
Р? Ниже мы приведем ряд математических утверждений, доказывая лишь
самые важные и простые из них, а остальные «принимая на веру».
Итак, у нашей матрицы Ρ по-прежнему есть собственные значения.
Кроме того, каждому из различных собственных значений по-прежнему
соответствует как минимум один правый собственный вектор:
Ρ . рх = \рх (8.9)
и один левый:
σΛΤ·Ρ = λσΛΤ. (8.10)
Однако вырожденным собственным значениям не обязательно соответствует
несколько векторов,15 а правые и левые собственные векторы, как правило,
не совпадают.16
15Например, у матрицы (°J) есть кратное собственное значение, равное нулю. Но ему
соответствует всего один левый собственный вектор (01) и один правый (J).
16Это следует из одной специфической теоремы, доказательство которой мы опустим:
Любая матрица Μ может быть приведена к жордановой канонической форме (ничего
общего с каноническим ансамблем!) заменой базиса S: Μ = SJS~l. Матрица J является
318
Гл.8. Моделирование и вычисления
В частном случае матрицы перехода Ρ мы можем пойти еще дальше.
Если марковская цепь достигает на больших временах состояния равновесия
р*, то это состояние не должно меняться под воздействием матрицы
перехода. Таким образом, Ρ · ρ* = ρ* и равновесное распределение вероятностей
является правым собственным вектором с собственным значением, равным
единице. Можно показать, что наша матрица перехода действительно имеет
такой собственный вектор.
Теорема 8.1. Матрица Ρ имеет по крайней мере один правый собственный
вектор р* с собственным значением, равным единице.
Доказательство (для ленивых). Матрица Ρ имеет левый собственный
вектор <т* с собственным значением, равным единице — это вектор, состоящий
из одних единиц, σ*τ = (1,1,1,..., 1):
(σ*τ · P)Q = Σσ*βΡβα = γ^Ρβα = 1 = σ*β. (8.12)
β β
А раз матрица Р имеет собственное значение, равное единице, то она должна
иметь и соответствующий ему правый собственный вектор. Также можно
показать, что правые собственные векторы, соответствующие всем остальным
собственным значениям, имеют сумму компонент, равную нулю. Это следует
из условия сохранения вероятности.17
Теорема 8.2. Любой правый собственный вектор рх, соответствующий
собственному значению λ, отличному от единицы, имеет сумму компонентов,
равную нулю.
блочно-диагональной, причем каждому блоку соответствует одно собственное значение λ
(при этом одно и то же значение λ может соответствовать нескольким блокам). Например,
блок, соответствующий λ кратности три, может выглядеть так:
Iх 1 °\
О λ 1 . (8.11)
\0 0 λ/
Этому блоку соответствует только один левый и один правый собственный вектор
(пропорциональные первому столбцу и последней строке, соответственно).
17Теорему 8.2 можно рассматривать как утверждение о том, что все правые собственные
векторы, кроме р*, ортогональны левому собственному вектору ащ.
8.2. Цепи Маркова
319
Доказательство. Пусть рЛ — правый собственный вектор, то есть Ρ
рл = Арл. Тогда
λΣ^ = Σ Ы) = Σ fewA = Σ (ςρ*
β β β \ α / α V β
Ρλα
Σ^·
(8.13)
Из этого следует, что либо λ = 1, либо ^α Ρα = 0-
Марковская цепь может иметь несколько стационарных распределений
вероятности.18 Также она имеет невозвратные состояния, которые система
покидает однажды и больше в них не возвращается.19 Также в марковских
цепях возможны циклы, то есть распределения вероятностей, которые
система проходит по кругу 1—► 2 —> 3 —>····—>· 12 —>· 1, раз за разом возвращаясь в
исходное состояние. Все это затрудняет наш поиск термодинамического
равновесия. Чтобы избежать этих трудностей, мы ограничимся рассмотрением
только эргодических цепей Маркова.20
Марковская цепь с конечным числом состояний является эргодичной, если
в ней нет циклов и она неприводима: из каждого состояния α можно перейти
в любое другое состояние β за конечное число шагов.
Нам понадобиться следующая теорема (мы приводим ее без
доказательства).
Теорема 8.3. (Фробениуса—Перрона) Пусть А — матрица, состоящая из
неотрицательных элементов, и существует такое п, что все элементы Ап строго
18Дифференциальным аналогом этого утверждения является КАМ-теорема из
упражнения 4.4. Каждому КАМ-тору соответствует распределение вероятности, не зависящее от
времени.
19Невозвратные состояния очень важны в динамике диссипативных систем. В таких
системах все состояния, кроме лежащих на аттракторе, являются невозвратными.
20 Это определение является некоторым компромиссом между физическим и
математическим взглядами на марковские цепи. Физики обычно игнорируют циклы и называют
эргодичными алгоритмы, которые могут достичь любого состояния. Математики же
используют термин «эргодичный», чтобы исключить циклы и исключить уход вероятности
на бесконечность (в нашем случае такой проблемы нет, потому что число состояний
конечно). При этом они позволяют системе иметь невозвратные состояния; достижимым из
любой точки должен быть только аттрактор. Наше определение эргодичности для
конечных марковских цепей сводится к требованию того, чтобы некоторая степень матрицы
перехода Рп имела все элементы строго больше нуля; математики называют такие матрицы
регулярными.
320
Гл.8. Моделирование и вычисления
положительны. Тогда А имеет положительное собственное значение λο
единичной кратности, оба собственных вектора которого (левый и правый) имеют
строго положительные компоненты. Кроме того, это собственное значение является
максимальным: |λ| < λο для всех остальных собственных значений λ.
Для эргодичной цепи Маркова можно показать (с помощью теоремы 8.2),
что собственный вектор Фробениуса—Перрона со строго положительными
компонентами относится к λο = 1. Отнормировав этот вектор так, чтобы
сумма его компонентов была равна единице, мы получим единственное
равновесное распределение вероятностей р*.
Есть ли связь между определением эргодичной марковской цепи и
определением эргодичности из раздела 4.2, сформулированным через траектории в
фазовом пространстве? Эргодичность в фазовом пространстве означает, что
рано или поздно система пройдет через все состояния на поверхности с
заданной энергией. Для конечных цепей Маркова условие эргодичности более
сильное: оно означает, что вероятность перехода из любого состояния в любое
другое за конечное время отлична от нуля.21
Можно показать, что эргодичная цепь Маркова сходится к равновесию
из любого начального распределения вероятностей р(0), но доказательство
для общего случая довольно сложное. Его можно упростить, сделав
очередное предположение: что марковская цепь удовлетворяет условию детального
равновесия.
Марковская цепь удовлетворяет условиям детального равновесия, если
существует распределение вероятностей р* такое, что22
ΡαβΡβ = ΡβαΡ*α (8.14)
для любых состояний а и β. Иными словами, поток вероятности из состояния
α в β уравновешен потоком в обратном направлении, и это равенство верно
не только для суммы, но для каждого ее члена (каждой пары состояний).
Если изолированная физическая система инвариантна относительно
обращения времени (нет диссипации, нет магнитных полей), и ее состояния
также инвариантны (нет состояний с выделенной скоростью или моментом), то
ее динамика автоматически удовлетворяет условиям детального равновесия.
Действительно, если состояние равновесия остается таковым при обращении
21 Обратите внимание на то, что алгоритм с ненулевой вероятностью остаться в любом
текущем состояний (Раа > 0 для всех состояний) автоматически лишен циклов. Часы,
способные «пропускать» секунды, не могут оставаться синхронными.
22Альтернативное определение детального равновесия, не апеллирующее напрямую к
равновесному распределению р*, вы найдете в упражнении 8.5.
8.2. Цепи Маркова
321
времени, то поток вероятности β —> а должен быть равен обращенному
потоку а —> β. Квантовые системы, испытывающие переходы между
собственными состояниями энергии, удовлетворяют детальному равновесию, поскольку
энергетические состояния не зависят от обращения времени. Многие другие
модели (например, модель Изинга для бинарного сплава, см. раздел 8.1.2)
имеют состояния, зависящие только от конфигурации системы. Эти модели
также удовлетворяют условиям детального равновесия.
Условия детального равновесия позволяют нам найти полный набор
правых собственных векторов матрицы перехода Р. Действительно, поделим обе
части уравнения (8.14) на */p%Pa· Полученная матрица Qa^ будет
симметричной:
I р*
Qa/З = Ρ<*β\-£ = Ρ<#Ρ*β/\[&?β
γ Ρα. ν
= ΡβαΡ*α/Μ^=ΡβαΜ=Ωβα. (8.15)
' ν у Ρ β
Эта симметричная матрица имеет следующие собственные векторы: Q · тх =
а правые собственные векторы Ρ получаются из них простой
перенормировкой23 на \/р*:
~~ (8.16)
a a a \ V P<* J
= Σ (Q/»«t«) 4h=λ & \[ρΊ) = χρχβ· (8·17)
α
Теперь мы можем сформулировать главную теорему, лежащую в основе
всех методов поиска равновесия для решеточных моделей.
Теорема 8.4. Дискретная динамическая система с конечным числом
состояний гарантированно сходится к равновесному распределению вероятностей р*,
если вычислительный алгоритм:
• марковский (не обладает памятью),
23Чтобы получить правые собственные векторы Ρ из Q, необходимо проделать
описанную процедуру в обратном порядке. Чтобы получить рау нужно умножить т* на y/ρζ , а
чтобы получить σ* — поделить. Поэтому, если выполнены условия детального равновесия,
то σ* = Pa/pa- В частности, σ1 —■ σ* = (1,1,1,... )т, как следует из теоремы (8.1).
322
Гл.8. Моделирование и вычисления
• эргодичный (пробегает все состояния без циклов), и
• удовлетворяет условиям детального равновесия.
Доказательство. Пусть Ρ — матрица перехода нашего алгоритма. Так
как он удовлетворяет условиям детального равновесия, то Ρ имеет полный
набор собственных векторов рх. В силу эргодичности существует только один
правый собственный вектор р1 с собственным значением, равным единице.
Этот вектор мы выберем в качестве равновесного распределения р*;
напомним, что для всех остальных собственных значений |λ| < 1. Представим
начальные условия в следующем виде: р(0) = а\р* + Σ|λ|<ι αλΡΛ· Тогда24
р(п) = Р.р(п-1) = Рп. р(0) = а1Р* + £ ахХпр\ (8.18)
|А|<1
Так как сумма (конечного числа слагаемых) в правой части уравнения
стремится к нулю, плотность вероятностей сходится к а\р*. Из этого следует, что
а\ = 1 и состояние системы стремится к р* при η —>· сю.
Таким образом, чтобы построить алгоритм поиска равновесия (см.
упражнения 8.6 и 8.8), необходимо лишь убедиться в том, что он марковский,
эргодичный и удовлетворяет условиям детального равновесия.
8.3 Теория возмущений: что такое фаза?
Что такое фаза? Некоторые примеры нам уже известны. Вода — это
жидкая фаза Н2О, существующая при температурах от 0°С до 100 °С (при
атмосферном давлении); при замерзании и испарении равновесная плотность
Н2О изменяется скачком. Модель Изинга находится в ферромагнитной фазе
при температуре ниже Тс и в парамагнитной при более высокой температуре.
На рис. 8.6 показана удельная теплоемкость бозонного и фермионного газов
(частицы в обоих газах не взаимодействуют). Здесь хорошо видны
основные отличия между этими типами газов,25 и самое фундаментальное из них
24Чем ближе собственное значение к единице, тем медленней затухает соответствующая
мода. Характерное время сходимости алгоритма г можно оценить, найдя максимальное
|Атах| < 1 и приравняв λη = e~n^r.
25Удельная теплоемкость фермионного газа уменьшается при снижении температуры;
при низких температурах могут быть возбуждены только собственные состояния,
соответствующие единичным частицам с энергией в несколько квТ от энергии Ферми. Удельная
теплоемкость бозонного газа при снижении температуры сначала растет. Для обоих
газов Cv/N —> 0 при Τ —> 0 (по-другому не может быть, иначе бы расходилась энтропия
ffCv/TdT).
8.3. Теория возмущений: что такое фаза?
323
заключается в том, что бозонный газ имеет две фазы. Его удельная
теплоемкость испытывает излом при температуре конденсации, которая разделяет
нормальную и конденсированную фазы.
3/2
аГ
квТ1(П2рЪ1т)
Рис. 8.6. Удельная теплоемкость бозонного и фермионного газов
Кривая теплоемкости бозонного газа испытывает излом в точке Бозе-конденсации Тс.
Теплоемкость фермионного газа меняется без изломов.
Как мы определяем в общем случае, где заканчивается одна фаза и
начинается другая? В пределах одной фазы свойства материала не испытывают
скачков: его поведение при малых изменениях внешних условий можно
экстраполировать гладким образом. Иными словами, в пределах фазы работает
теория возмущений. Более строго это можно сформулировать так: в
пределах одной фазы физические свойства являются аналитическими функциями
внешних условий (т.е. их можно разложить в сходящийся ряд Тейлора).
Большая часть статистической механики (да и вообще теоретической
физики) состоит в построении разложений высокого порядка вокруг
предельных случаев, для которых решение известно. Линейную теорию возмущений
по пространственным и временным координатам мы рассмотрим в гл. 10.
Решеточные теории при высоких и низких температурах Τ строят в виде
разложений в ряд по степеням 1/Т или Т, а для пересчета всех возможных
конфигураций кластеров применяют диаграммы Фейнмана (рис. 8.7(b)). Для
разреженных газов при высоких температурах существуют вириальные
разложения.
Металлы при низких температурах описываются теорией
ферми-жидкости, где электроны заменяют на невзаимодействующие
квазичастицы, свойства которых приближенно учитывают
электрон-электронное взаимодействие.
Свойства систем вблизи точки непрерывного фазового перехода
описывают с помощью е-разложения , где возмущение ведется и вовсе по размерности
У /
s /
/ /
/ /
ι /
ι /
1 /
i/ . 1
— фермионный газ 1
— бозонный газ |
1 . 1
324
Гл.8. Моделирование и вычисления
физического пространства. Некоторые из этих разложений имеют нулевой
радиус сходимости; их называют асимптотическими рядами (упражнение 1.5).
Вот, например, первые члены низкотемпературного разложения [33,106]
для удельной намагниченности трехмерной кубической модели Изинга [119]
(раздел 8.1):
Рис. 8.7. Теория возмущений
(а) Низкотемпературные разложения для намагниченности кубической модели Изинга (см.
рис. 8.2) с различным числом слагаемых. (Ь) Высоко- и низкотемпературные разложения
для модели Изинга и других решеточных моделей можно представить в виде сумм по
кластерам частиц (фейнмановские диаграммы). При малых Τ типичные конфигурации
представляют собой маленькие кластеры из спинов вверх, погруженные в море спинов
вниз (или наоборот). Этот кластер из четырех ячеек кубической решетки вносит вклад в
коэффициент при х20 разложения (8.19), так как обращение такого кластера разрушает
20 связей.
га
Л-2х6- 12я10 + Ых12 - 90а:14 + 192s16 - 792s18 + 2148s20
- 7716s22 + 23262s24 - 79512s26 + 252054s28
- 846628s30 + 2753520s32 - 9205800s34
+ 30371124s36 - 101585544s38 + 338095596s40
- 1133491188s42 + 3794908752s44 - 12758932158s46
+42903505303s48 - 144655483440s50
+ 488092130664s52 - 1650000819068s54 + ..., (8.19)
где s = e~2J/kEtT — вероятность разрыва связи (перехода от сонаправлен-
ных спинов с энергией — J к противоположно направленным с энергией J).26
26На самом деле этот вычислительный подвиг (27 слагаемых!) был совершен вовсе не
для того, чтобы точно посчитать намагниченность при низких температурах. Различные
хитроумные методы используют эту экстраполяционную формулу, чтобы понять, что
происходит при фазовом переходе в точке Тс (гл. 12). Кривая га(Т) на рис. 8.2 и рис. 8.7(a) на
самом деле не является результатом прямых измерений, а построена с помощью
аппроксимации Паде порядка 9,10 [32].
8.3. Теория возмущений: что такое фаза?
325
Это разложение получено путем аккуратного анализа вероятностей
различных конфигураций малой энергии, которые получаются при обращении
кластеров спинов в различных комбинациях (см. рис. 8.7(b)). Оно позволяет
предсказать намагниченность при низких температурах, используя ее
значения в нуле; на рис. 8.7(a) видно, что намагниченность хорошо описывается
этим разложением при fcgT ^ 3J. Чтобы получить ряд, сходящийся при
более высоких температурах, необходимо построить разложение вокруг точки
Г ~ 3J/fc#.27 Однако ни одно разложение с конечным числом слагаемых не
может экстраполировать значения за Тс, при которой намагниченность
обращается в ноль. Это становится очевидным, если подходить к этой точке с
другой стороны: га(Т) = О при температурах выше Тс, поэтому любая
экстраполяция на температуры ниже Тс будет неизбежно давать ноль. Самые
впечатляющие достижения теории возмущений связаны как раз с
суммированием бесконечных рядов, позволяющих экстраполировать за пределы
критических точек.
Границы разделов фаз — это поверхности в пространстве параметров,
где свойства системы теряют гладкость. Экстраполяция свойств за границу
раздела не имеет предсказательной силы. Мы могли бы даже определить
фазы как области, в которых работает теория возмущений — но в этом случае
жидкость и газ пришлось бы считать одной фазой (так как от жидкости
к газу можно перейти непрерывно, обойдя критическую точку сверху, см.
рис. 8.4).
Эта идея лежит в основе важного экспериментального метода. Допустим,
вы создали новый экзотический жидкий кристалл. Как понять,
принадлежит ли он к какой-то уже известной фазе или нет? Чтобы ответить на этот
вопрос, нужно попытаться привести его к известному состоянию, гладко
изменяя внешние условия и вмешивая ингредиенты. Например, принадлежат
ли нефть и вода одной (жидкой) фазе? Можно ли перейти от воды к нефти
непрерывным образом, не испытывая фазовых переходов?28 Воду и нефть
смешать нельзя, но можно смешать нефть со спиртом, а уж воду со
спиртом — тем более. Плавно меняя концентрации, мы можем перейти от нефти
к чистому спирту, а затем от чистого спирта к воде. Это показывает, что
Радиус сходимости ряда меньше Тс, поскольку на комплексной плоскости
температуры имеется еще одна особенность, на меньшем расстоянии от нуля. Это похоже на ситуацию
с функцией 1/(1+ х2): несмотря на то что эта функция аналитична на действительной оси,
ее ряд Тейлора 1 — х2 + х4 — х6 + ... сходится только для — 1 < χ < 1; радиус сходимости
ограничен полюсами ±i на комплексной плоскости.
28 Такой переход иногда называют адиабатически непрерывным [4]. Фазы можно
также рассматривать как классы универсальности, соответствующие разным притягивающим
точкам ренорм-группы; см. гл. 12.
326
Гл.8. Моделирование и вычисления
обе жидкости принадлежат одной фазе (рис. 8.8). Такой прием часто
используют экспериментаторы, для того чтобы понять, какой из экзотических фаз
принадлежит созданная ими субстанция. Применим он и в теоретической
физике. Если можно плавно перейти от А (теории) к В (эксперименту), вводя
в коэффициенты теории различные поправки, то А и В принадлежат одной
фазе — можно публиковать!29
Рис. 8.8. Нефть, спирт и вода
Схематичная фазовая диаграмма тернарной смеси из нефти, воды и спирта. Каждая точка
треугольника представляет собой процентную смесь трех составляющих. Углы
треугольника представляют воду, спирт и нефть в чистом виде. Закрашенная область соответствует
расслоению фаз; при относительных концентрациях, лежащих в этой области, смесь
распадается на две фазы, концентрации в каждой из которых определяются значениями на
концах секущей линии. Нефть и вода не растворяются друг в друге. Однако мы можем
перейти от воды к нефти гладким образом, вмешивая спирт.
Упражнения
В упражнении Модель Изинга рассмотрены непрерывный и
скачкообразный фазовые переходы, происходящие в этой модели при изменении
температуры и внешнего поля. Упражнение Изинг: флуктуации и восприимчивость
посвящено вычислению линейного отклика модели на изменение внешних
параметров, связи между флуктуациями и откликом, а также
асимптотическому поведению модели при низких и высоких температурах.
29При этом некоторые невозмущенные поправками теории лучше других, даже если они
принадлежат одной фазе. Правильной теорией сверхпроводимости несомненно является
теория Бардина—Купера—Шрейфера (БКШ), хотя предыдущие модели (на основе бозе-
эйнштейновской конденсации электронных пар) не отделены от нее фазовым переходом.
Пространственные размеры куперовских пар велики по сравнению с расстоянием между
разными парами, из-за чего пары сильно перекрываются, что делает теорию БКШ
практически точной.
Гл.8. Упражнения
327
В упражнениях Розенкранц, Гильденстерн и Марков и Красные и
зеленые рассмотрены примеры неравновесных цепей Маркова. В упражнении
Детальное равновесие вам предстоит переписать условия детального
равновесия в форме, не включающей в себя вектор равновесного состояния.
Упражнение Алгоритм Метрополией посвящен одному из самых популярных
методов Монте-Карло, а в упражнении Реализация модели Изинга вам
предлагается реализовать метод термостата и метод Метрополиса самостоятельно. В
упражнениях Алгоритм Вольфа и Реализация алгоритма Вольфа
обсуждается один весьма изящный и эффективный алгоритм обращения кластеров
спинов.
В малых системах, таких как живые клетки, количество
взаимодействующих молекул так мало, что случайные флуктуации их количества становятся
заметными. В упражнениях Стохастические клетки и Репрессилятор мы
реализуем метод типа Монте-Карло (алгоритм Гиллеспи) для
стохастического моделирования химических реакций в таких системах. В упражнении
Энтропия растет! Цепи Маркова вам предстоит показать, что сглаженное
описание системы с помощью марковской цепи действительно приводит к
убыванию свободной энергии.
В упражнении Лавины и гистерезис мы представим неравновесную
решеточную модель для описания магнитов, а в Алгоритмах исследования
гистерезиса исследуем современный алгоритм порядка 0(N log N) для реализации
этой модели.
И наконец, в упражнении NP-полнота и k-SATмы исследуем класс задач,
наиболее сложных вычислительно, и опишем фазовый переход, в окрестности
которого реализуются действительно сложные случаи.
8.1 Модель Изинга. (Моделирование) φ
Для этого упражнения вам понадобится программа для моделирования
модели Изинга на квадратной решетке. Вы можете скачать ее на сайте
книги [132] в разделе компьютерных упражнений. Гамильтониан модели Изинга
имеет вид (см. уравнение 8.1):
w = - j Σ вд - н Έ Si> (8·2°)
(ij) г
где Si = ±1 — спин ячейки, а сумма Σ(ύ') берется по четырем ближайшим
соседям (каждая пара учитывается один раз). Обычно параметр
взаимодействия J и константу Больцмана кв выбирают равными единице, так что и
энергия, и температура измеряются в единицах J. Константу Η по
традиции называют внешним полем, а величину Μ = Σΐ &г ~ намагниченностью.
328
Гл.8. Моделирование и вычисления
В нашей компьютерной модели число ячеек со спином вверх не
сохраняется, поэтому она не очень подходит для описания бинарного сплава. Скорее
она описывает систему, обменивающуюся частицами с окружением (большой
канонический ансамбль) или модель поверхностного слоя, который
обменивается атомами с окружающим паром. Поэкспериментируйте с параметрами
модели. Вы увидите, что при высокой температуре спины скореллированы
слабо. При низкой температуре почти все они направлены в одну сторону,
что соответствует большим значениям намагниченности.
Приблизительно оцените Тс — максимальную температуру, при которой
удаленные друг от друга спины остаются в среднем параллельны при Η = 0. Что
происходит с системой при переходе через Тс? Меняется ли ее поведение плавно
или скачкообразно (как при замерзании воды)? Теперь проследите за
поведением системы при температуре Τ = 2 (ниже Тс), меняя внешнее поле от Η = —0.1
до Η = +0.1 (см. рис. 8.5).Что происходит при переходе через «границу фаз»
Η = 0? Является ли этот переход непрерывным?
8.2 Модель Изинга: флуктуации и восприимчивость.
(Моделирование) ©
Статистическая сумма для модели Изинга имеет вид Ζ = Ση ехР(—/^η)>
где индекс состояния η пробегает все 2Ν возможных конфигураций спинов
(см. уравнение 8.1), а свободная энергия равна F = —kTlogZ.
(a) Покажите, что средняя намагниченность Μ равна —(dF/dH)\T·
(Указание: выпишите статсумму в явном виде и продифференцируйте).
Выведите формулу для магнитной восприимчивости χο = {дМ/дН)\т в терминах
((М — (М))2) = (М2) — (М)2. (Указание: вспомните вывод формулы (6.13);
((E-(E)Y) = kBT2C.)
Загрузите симулятор модели Изинга из раздела компьютерных
упражнений на сайте книги [132]. Эта программа, помимо прочего, вычисляет средние
значения следующих величин: (|га|), ((га — (га))2), (е), ((е — (е))2).
Обратите внимание на то, что энергия е = E/N и намагниченность га = M/N
приводятся в расчете на один спин (так всегда делают в компьютерном
моделировании, чтобы результаты не зависели от размера системы). Формулы
же, полученные вами, относятся к системе β целом. Это следует иметь в
виду при сравнении результатов. Вы можете ускорить процесс вычисления,
уменьшив размер системы и частоту обновления графиков.
Прежде чем начинать усреднение, убедитесь в том, что система пришла
в равновесие!
(b) Корреляции и восприимчивость: численное исследование. Проверьте
формулы для теплоемкости С и магнитной восприимчивости χ из части
Гл.8. Упражнения
329
(а). Для этого вычислите средние значения и флуктуации величин при
фиксированных Η = О, Τ = 3, затем измените значения параметров на
АН = 0.02, ΔΤ = 0.1 и вычислите их снова. Выполните такую же проверку
при Г = 2, когда (Μ) φ О.30
Для модели Изинга существуют разложения при малых и больших
температурах, которые можно получить с помощью диаграмм Фейнмана (см.
раздел 8.3). Первые члены этих разложений хорошо известны и объясняют
многие физические явления.
Низкотемпературное разложение для намагниченности. При низких
температурах мы можем считать, что спины обращаются (меняют знак) по
одному, и полностью игнорировать наличие кластеров.
(c) Сколько энергии необходимо затратить для обращения одного спина в
противоположную по сравнению с его соседями сторону? Приведите систему в
равновесие при относительно невысокой температуре Τ = 1.0 и измерьте
намагниченность. Обратите внимание на то, что первые возникающие флуктуации -
это единичные обращения спинов. Выпишите формулу для намагниченности с
учетом того, что при низкой температуре «неправильно направленные» спины
разрежены (так что можно не рассматривать случаи их наложения или
соседства). Не забудьте, что каждое обращение спина меняет намагниченность на 2.
Сравните ваш результат с наблюдаемым. (Указание: воспользуйтесь
уравнением 8.19.)
Намагниченность (как и теплоемкость) в модели Изинга
экспоненциально мала при низких температурах, поскольку существует энергетический
барьер, который необходимо преодолеть для переключения спина.31 Такой же
эффект (запрещенная зона) наблюдается в полупроводниках и диэлектриках.
Высокотемпературное разложение для восприимчивости. При высоких
температурах мы можем сделать наоборот - полностью пренебречь энергией
связи соседних спинов.
(d) Получите формулу для восприимчивости свободного спина во внешнем
поле. Сравните ее с восприимчивостью модели Изинга при высокой температуре
Τ = 100, измерив, например, AM/АН при АН = 1 (почему в данном случае
АН = 1 можно считать малым возмущением?).
30Прежде чем начинать вычисления, убедитесь в том, что система пришла в равновесие!
При температуре меньше Тс это означает, что в области не должно оставаться красных
и черных доменов: она должна быть полностью однородной. Полоски, остающиеся при
низких температурах, можно убрать, приложив к системе слабое внешнее поле.
31 На самом деле, не у всех магнитов есть такая запрещенная зона. При наличии
вращательной симметрии спинов возможно возникновение спиновых волн произвольной энергии.
Спиновые волны похожи на звуковые, но вместо положений атомов в них колеблются
направления спинов.
330
Гл.8. Моделирование и вычисления
Полученная вами формула для восприимчивости известна под названием
«закона Кюри».
8.3 Розенкранц, Гильденстерн и Марков. (Математика) (2)
В пьесе Т. Стоппарда «Розенкранц и Гильденстерн мертвы» герои
проводят следующий простой опыт: подбрасывают монету до тех пор, пока не
выпадет решка.
(a) Рассмотрим два состояния Гильденстерна («продолжает бросать»
(flipping) и «закончил» (done)) как состояния марковской цепи. Тогда вектор
вероятности на текущем шаге имеет вид: ρ = I ^р111^ J. Выпишите матрицу
\ Pdone /
перехода Р, описывающую эволюцию Ρ · рп = рп+ь предполагая, что монета
без изъянов.
(b) Найдите собственные значения и правые собственные векторы Р. Какой
из этих векторов соответствует стационарному состоянию р*? Назовем
оставшийся вектор р. Для удобства перенормируем ρ так, чтобы его первый элемент
был равен единице.
(c) Запишем произвольное начальное состояние в виде ро = Ар* + Вр. Какое
условие следует наложить на А и В, чтобы ро было допустимым распределением
вероятности? Запишите рп как функцию А, В, р*, и р.
8.4 Красные и зеленые бактерии.32 (Математика) (2)
В начальный момент времени t = 0 в питательной среде находятся 500
красных и 500 зеленых бактерий. Раз в час каждая из бактерий делится на
две. Хищник-дальтоник поедает ровно 1000 бактерий в час.33
(a) На очень больших временах каково будет распределение вероятности
для числа красных бактерий а?
(b) Сколько примерно времени понадобится для достижения конечного
состояния?34
32 На основе задачи, предложенной автору на выпускном экзамене в Принстонском
университете осенью 1977.
33Эта задача специально поставлена нечетко. В качестве ответа на вопросы (Ь) и (с)
вполне подойдут приближенные оценки с точностью до множителя, меньшего двойки.
Разрешается использовать как аналитические, так и численные методы.
34При ответе на этот вопрос можно предположить, что одна бактерия делится и одна
съедается 1000 раз в час, либо - что в конце часа все бактерии делятся и 1000 из них
съедаются. Результат будет примерно одинаков в пределах заданной нами точности.
Первый способ размножения удобней для аналитических методов, связанных с нахождением
собственных векторов; второй способ может быть задействован для развития методов,
использующих диффузию вероятности, коэффициент которой зависит от а.
Гл.8. Упражнения
331
(с) Предположим, что зеленые бактерии нравятся хищнику на 1% больше,
чем красные (конкретную реализацию этого предпочтения можете выбрать
сами). Оцените, как это повлияет на равновесное состояние?
8.5 Детальное равновесие. (2)
Если система находится в равновесии, то любые два состояния α и β
(вероятности нахождения системы в которых назовем р£ и р£ соответственно)
удовлетворяют условиям детального равновесия (уравнение 8.14) :
Ρβ<=αΡα = Ρα<=βΡ*β, (8·21)
то есть поток вероятности из α в β равен потоку в обратном направлении (из
β в а). Условие детального равновесия можно переписать в изящном виде,
не используя равновесные вероятности. Рассмотрим три состояния системы:
α, β и 7·
(a) Предположим, что переход между любыми двумя состояниями из этой
тройки удовлетворяет условию детального равновесия. Исключив из уравнения
вероятности состояния, выведите следующую формулу для вероятностей
переходов:
Ρα^=βΡβ<=-γΡ^γ<=α = Ρα<=ηΡη<=βΡβ^=α· (8.22)
Если рассматривать состояния α, β и η как цикл, то полученное условие
означает равенство потоков по часовой и против часовой стрелки.
Можно доказать и обратное: если любая тройка состояний в марковской
цепи удовлетворяет условию (8.22), то она удовлетворяет условию
детального равновесия (точнее, существует хотя бы одно распределение плотности
вероятности р*, при котором потоки вероятности удовлетворяют условию
детального баланса), если только среди вероятностей переходов не встречаются
нули.
(b) Пусть Ρ — матрица перехода марковской цепи, удовлетворяющая
условию (8.22) для любой тройки α, β и η. Предположим, что существует
состояние а, скорости перехода в которое из всех других состояний δ положительны.
Постройте распределение вероятности р£, показывающее, что Ρ удовлетворяет
условию детального равновесия (уравнение 8.21). (Указание: пусть задан
вектор вероятностей р*а\ каким должен быть вектор р£, чтобы для этой пары
35Необходимое и достаточное условие состоит в том, что прямые и обратные
произведения в уравнении (8.22) для циклов любой длины совпадают (это условие
называется критерием Колмогорова). Система с ненулевым потоком в четырехзвенном цикле
1 -> 2 —>· 3 —► 4 —> \ удовлетворяет уравнению (8.22) (т.к. О = 0) для каждого трех-
звенного цикла, но нарушает условие детального равновесия. На это автору указал Нери
Мерхав.
332
Гл.8. Моделирование и вычисления
выполнялось условие равновесия? Покажите, что такое распределение
удовлетворяет условиям детального равновесия для любых двух состояний.)
8.6 Алгоритм Метрополиса. (Математика, моделирование) φ
Метод термостата, описанный в тексте главы, обрабатывает один спин за
шаг. Другой популярный метод такого типа — это алгоритм Метрополиса.
Он состоит из следующих шагов:
(1) выбрать произвольный спин;
(2) вычислить изменение энергии ΔΕ при обращении этого спина;
(3) если ΔΕ < 0, переключить спин; если ΔΕ > 0, переключить спин с
вероятностью е~^ЛЕ.
Покажите, что алгоритм Метрополиса удовлетворяет условию детального
равновесия. Так как процесс, заданный алгоритмом Метрополиса, эргодичный и
марковский (без памяти), он должен приводить к тепловому равновесию.
Является ли алгоритм Метрополиса более эффективным, чем алгоритм термостата
(позволяет ли он достичь равновесия за меньшее число действий)?
8.7 Реализация модели Изинга. (Моделирование) @
В этом упражнении мы займемся численным моделированием двумерной
модели Изинга на квадратной решетке с помощью алгоритмов термостата и
Метрополиса. В разделе компьютерных упражнений на сайте книги [132] вы
можете скачать файлы с заготовками программ и графические процедуры.
В заготовке к этому упражнению реализовано изображение квадратной
решетки, заполненной случайными спинами ±1 — так что у вас есть под рукой
пример использования графических процедур и генерации случайных чисел.
Алгоритм термостата обращает один спин на каждом шаге, приводя его
в состояние теплового равновесия с соседями: этот процесс подробно описан
в разделе 8.1.
(а) Напишите программу, реализующую алгоритм термостата для модели
Изинга. При задании температуры или внешнего поля следует сохранить в
массив heatBathProbUp[nUp] вероятности обращения спина вверх при условии, что
nUp его соседей обращены вверх (т.е. равны +1). (Таким образом, эти
вероятности не придется пересчитывать миллионы раз — при каждом обращении спина.)
Исследуйте поведение модели (как, например, в упражнении 8.1).
Алгоритм Метрополиса также обращает по одному спину за шаг, но при
уменьшении общей энергии спин обращается с единичной вероятностью:
подробности см. в упражнении 8.6.
Гл.8. Упражнения
333
(b) Напишите программу, реализующую алгоритм Метрополиса для модели
Изинга. В этом случае вам понадобится массив MetropolisProbUp[s,nUp],
хранящий вероятности того, что спин с текущим значением s изменит значение на
+1, если nUp из его соседей обращены вверх. Насколько этот алгоритм быстрее
алгоритма термостата?
Алгоритм Метрополиса всегда приводит к равновесию быстрее, чем
алгоритм термостата — но выигрыш в скорости очень невелик. Однако
существуют и другие алгоритмы, позволяющие существенно улучшить сходимость в
определенных условиях (см. упражнения 8.8 и 8.9).
8.8 Алгоритм Вольфа. (Математика, моделирование) @
Вблизи критической точки Тс, в которой система приобретает
намагниченность, динамика обращений единичных спинов становится очень
медленной (время корреляции расходится). Вольф [149], развивая идеи Свендсена и
Ванга [139], придумал остроумный способ переключать спины целыми
кластерами.
Переключение кластеров методом Вольфа
(1) Выбрать случайную ячейку, запомнить направление спина в ней D =
±1 и переключить его.
(2) Для каждого из четырех соседей, если его направление совпадает с D,
переключить его с вероятностью р.
(3) Для каждого из вновь переключенных на шаге (2) спинов применить
пункт (2) теперь уже к его соседям.
Поскольку существует конечная вероятность переключения каждого
спина, алгоритм Вольфа является эргодичным. Кроме того, процесс
переключения кластеров в целом является марковским. Давайте убедимся в том, что он
удовлетворяет условию детального равновесия, и выберем подходящее
значение ρ для заданной температуры.
(а) Для двух состояний А и В, изображенных на рис. 8.9 и 8.10, покажите,
что Ев — Еа = 2(щ — n±)J. Объясните, почему это верно для переключения
любого кластера из спинов, направленных вверх.
Обращение кластера может начаться из любой ячейки α кластера С.
Отношение скоростей перехода Та-^в/^в^а зависит от того, сколько раз
кластер не расширил своих границ. Обозначим Р£ вероятность того, что кластер
вырос из внутренней ячейки α до конечного размера С (игнорируя попытки
вырасти за пределы границы). Тогда
334
Гл.8. Моделирование и вычисления
Рис. 8.9. Кластер перед переключением
Область, ограниченная пунктиром, обращена за одну итерацию алгоритма Вольфа.
Назовем эту конфигурацию А.
Γ^β = Σ^(1-ρΓ, (8.23)
α
ΓΒ^Α = ΣΡΖ(1-Ρ)η\ (8.24)
α
поскольку кластер должен отказаться от роста щ раз, стартуя из состояния
А, и щ раз, стартуя из В.
Рис. 8.10. Кластер после переключения
Обозначим эту конфигурацию В, а кластер перевернутых спинов — С. На границе кластера
С η t= 2, a η l= 6.
Гл.8. Упражнения
335
(b) Каким должно быть значение р, чтобы алгоритм Вольфа удовлетворял
условиям детального равновесия при температуре Т?
Если вы не собираетесь реализовывать алгоритм Вольфа
самостоятельно (упражнение 8.9), скачайте симулятор Вольфа из раздела компьютерных
упражнений на сайте книги [132]. Запустите модель при Τ = 2.3, используя
алгоритм термостата для системы 500x500 или больше; убедитесь в том, что
характерный размер кластеров растет медленно. Запустите алгоритм
Вольфа, и вы увидите, насколько быстрее устанавливается равновесие. Обратите
внимание на то, что часто картина полностью меняется всего за один проход;
время корреляции в алгоритме Вольфа намного меньше, чем в алгоритмах с
обращением единичных спинов, таких как алгоритм термостата или Метропо-
лиса. (Более подробно алгоритм Вольфа описан в книге [99, sections 4.2-3].)
8.9 Реализация алгоритма Вольфа. (Моделирование) @
В этом упражнении мы займемся реализацией алгоритма Вольфа из
упражнения 8.8. В разделе компьютерных упражнений на сайте книги [132]
вы найдете заготовки и графические шаблоны, которые помогут вам в
работе.
Вблизи критической температуры Тс установление равновесия происходит
очень медленно, это называется критическим замедлением. Такое поведение
совершенно справедливо воспроизводится алгоритмами термостата и Метро-
полиса, обращающими по одному спину за шаг. Если нас интересует не
динамика процесса, а лишь само состояние равновесия, то можно попытаться
ускорить сходимость и сэкономить время расчета.
(a) Запустите двумерную модель Изинга (вы можете взять ее с сайта книги
или выполнив упражнение 8.7) при температуре, близкой кТс = 2/log(l + \/2),
используя алгоритм с обращением единичных спинов. Начните из
намагниченного состояния и увеличивайте температуру: система рано или поздно придет в
состояние, в котором только половина спинов направлена вверх. Начните с
высокой температуры и уменьшайте ее: вы увидите, как постепенно растут домены,
заполненные спинами вверх и спинами вниз. Однако для достаточно больших
систем вы рискуете не дождаться равновесия — вблизи критической точки процесс
сходится очень медленно.
Алгоритм Вольфа позволяет переключать большие кластеры спинов за
один раз, и таким образом избежать замедления сходимости в Тс. Он работает
только при нулевом внешнем поле. Подробности см. в упражнении 8.8.
(b) Напишите программу, реализующую алгоритм Вольфа. Этот алгоритм
имеет рекурсивную природу, однако программа с рекурсией работает
эффективно только для маленьких систем. Спины, подлежащие переключению, удобней
всего хранить в виде списка (назовем его toFlip). Также следует запомнить
336
Гл.8. Моделирование и вычисления
знак спина, с которого началось переключение.
Пока в списке toFlip остаются элементы,
если первый спин списка параллелен исходному,
переключите его, и
для каждого из его соседей,
если сосед параллелен исходному спину,
добавьте его в список toFlip с вероятностью р.
(c) Оцените «на глаз», сколько обращений кластеров требуется для
достижения равновесия при Тс. Действительно ли алгоритм Вольфа сходится быстрее
методов с обращением единичных спинов? Как соотносится их эффективность
при высоких температурах?
(d) Задав начальную конфигурацию случайным образом, понизьте
температуру до Τ = 1 и посмотрите, как алгоритм поспинового обращения
приводит систему в равновесие. Сравните с алгоритмом Вольфа (см. также
упражнение 12.3.) Какой алгоритм достигает равновесия быстрее? Меняется ли
качественно динамика происходящего?
8.10 Стохастические процессы в клетках.36 (Биология,
моделирование) @
Живая клетка — это удивительно сложная смесь различных сложных
молекул (РНК, ДНК, белков, липидов...), постоянно реагирующих друг с
другом. Совокупность этих реакций иногда сравнивают с работой компьютера:
клетка получает входные данные от внутренних и внешних сенсоров, которые
запускают соответствующую «программу» химических реакций,
обеспечивающую адекватный отклик. Например, клетки сетчатки ждут, когда на них
попадет свет, и генерируют в ответ нервный импульс.
Как правило, кинетику химических реакций описывают
дифференциальными уравнениями относительно концентраций реагентов: предполагается,
что количество молекул так велико, что статистически флуктуациями можно
пренебречь. Однако в клетке реагирующих молекул может быть очень мало.
Например, участок ДНК, отвечающий за конкретную реакцию,
существует (как правило) в единственном экземпляре. Поэтому очень важно понять,
можно ли (и если да, то при каких условиях) использовать понятие о
непрерывно меняющихся концентрациях, несмотря на то что реальное количество
молекул — конечное целое число.
Рассмотрим реакцию димеризации, при которой молекула Μ (мономер)
соединяется с другой такой же молекулой и образует димер D: 2M <—> D.
36 Это упражнение и соответствующая компьютерная программа разработаны совместно
с Кристофером Майерсом.
Гл.8. Упражнения
337
Белки в клетках часто образуют димеры; иногда (как в нашем случае)
соединяются два одинаковых белка (гомодимер), а иногда два разных (гете-
родимер). Пусть константа скорости прямой реакции равна fc^, а константа
скорости обратной реакции — ки. На рис. 8.11 этот процесс изображен в виде
сети (диаграммы) Петри [51]: каждой реакции соответствует прямоугольник,
исходные компоненты изображены как входящие стрелки, а продукты
реакции — как исходящие. Числа над стрелками обозначают количество
произведенных и поглощенных веществ — это стехиометрические коэффициенты.
В нашем случае есть две реакции: реакция диссоциации с удельной
скоростью ku[D] (каждый димер распадается с одинаковой скоростью ки) и
реакция димеризации с удельной скоростью fc&[M]2 (для образования связи два
мономера должны столкнуться, поэтому скорость реакции пропорциональна
концентрации мономеров в квадрате).
Рис. 8.11. Реакция димеризации
Диаграмма Петри для реакции димеризации, константа скорости димеризации равна кь,
константа скорости диссоциации — ки.
Квадратные скобки [.] здесь и далее обозначают концентрацию.
Предположим, что объем клетки таков, что одна молекула на клетку соответствует
концентрации 1нМ (Ю-9 молей на литр). Тогда можно выбрать наномоли в
качестве основной единицы измерения, и [М] будет в точности равно
количеству молекул в клетке. Пусть кь = 1нМ_1с-1 и ки = 2 с"1, а в начальный
момент времени t = 0 все N мономеров не связаны в димеры.
(а) Непрерывная димеризация. Запишите дифференциальное уравнение для
dM/dt, считая Μ и D непрерывными переменными. (Указание: не забудьте,
что для образования одного димера нужно две молекулы М.) Каковы будут
равновесные концентрации [М] и [D] для N = 2 молекул при использовании этих
уравнений и значений кь и ки, указанных выше? А для N = 90 или N = 10100
338
Гл.8. Моделирование и вычисления
молекул? Решите дифференциальное уравнение для Μ(t) численно при N = 2
и N = 90, и убедитесь, что решение сходится к найденным вами значениям.
Естественно ожидать, что непрерывные уравнения могут давать
правильный результат при большом числе молекул. Если же молекул всего несколько,
роль флуктуации будет велика. Такие флуктуации называют дробовым
шумом. Этот термин возник при исследовании электрического шума при слабом
токе, где единичные электроны создают шум, напоминающий стук дробинок.
Дробовой шум можно смоделировать с помощью алгоритма Монте-Карло.37
Пусть скорости каждой из реакций равны Г{, а суммарная скорость равна
Г tot = Σί IV Тогда среднее время ожидания реакции равно l/rtot, а
вероятность того, что эта реакция будет типа j, равна Tj/Ttot. Алгоритм
моделирования системы до времени tf таков:
(1) Вычислить скорости всех реакций.
(2) Найти суммарную скорость реакций Ttot-
(3) Выбрать случайный временной шаг twait из распределения
p(t) = rtotexp(-rtot*)·
(4) Если текущий момент времени t+tWait больше, чем ί/, то моделирование
окончено; выход.
(5) В противном случае:
— увеличить t на tWait,
— выбрать случайное число г из равномерного распределения на
отрезке [o,rtot),
— выбрать реакцию j, для которой Σί<7 ^* — т < ^2i<j-\-i Г» (так, что
г приходится на j-ft интервал суммы rtot),
— выполнить реакцию, пересчитав количества каждого из веществ в
соответствии со стехиометрическими соотношениями.
(6) Повторить.
37 В химическом моделировании этот алгоритм называют алгоритмом Гиллеспи [47]; для
модели Изинга такой же подход был реализован Бортцем, Калосом и Лебовицем [12], в
этом контексте он называется непрерывным методом Монте-Карло.
Гл.8. Упражнения
339
Важное изменение:38 скорость реакции для Μ мономеров в дискретном
случае должна быть равна кьМ(М — 1), а не кьМ2.
(b) Стохастическая димеризация. Реализуйте этот алгоритм для реакции ди-
меризации из части (а) упражнения. Выполните моделирование при N = 2,
N = 90 и N = 10100. Сравните несколько случайных реализаций с
непрерывным решением. Насколько большим должно быть число молекул Ν, для того
чтобы индивидуальные реализации хорошо описывались непрерывным
уравнением (скажем, чтобы флуктуации были меньше, чем ±20% на больших
временах)?
Измерить концентрацию молекул в отдельной клетке — непростая
техническая задача. Как правило, в эксперименте получают значения, усредненные
по большому числу клеток. Такая усредненная концентрация будет меняться
гладко, несмотря на то что значения в отдельных клетках флуктуируют.
Давайте посмотрим, описывается ли это «среднее по ансамблю» непрерывными
уравнениями.
(c) Усреднение стохастической димеризации. Вычислите средние значения
по результатам большого числа реализаций стохастической модели из части (Ь).
Для N = 2 и N = 90 сравните результат с детерминистическим решением.
Насколько случайный шум сдвигает значений концентраций на больших временах?
При каком значении N среднее по ансамблю от Μ(t) будет хорошо описываться
непрерывными уравнениями (погрешность менее 5% на больших временах)?
8.11 Репрессилятор.39 (Биология, моделирование) @
«Центральная догма» молекулярной биологии гласит, что информация в
клетке передается по цепочке ДНК-РНК-белки: ДНК транскрибируется в
РНК, которая затем транслируется в белок.
Сегодня, когда геном полностью секвенирован, можно считать, что у нас
есть полный список деталей клетки. Дело за малым — понять, как все эти
детали работают в сборке.
Белки, РНК и ДНК участвуют в сложной сети взаимодействующих
химических реакций, отвечающих за метаболизм, отклик на внешние воздействия,
размножение (пролиферацию), дифференциацию клеток растущего организма
на различные типы, и (если в функциях клетки происходит опасный сбой)
запускающих запрограммированную гибель клетки — апоптоз.
Мы узнаем о структуре этой сети реакций все больше и больше, однако
понимание их динамики остается до сих пор очень примитивным. Сложность
38В противном случае, если стартовое число мономеров нечетно, концентрация может
стать отрицательной!
39Это упражнение во многом основано на работе [37]. Упражнение и соответствующее
программное обеспечение разработаны совместно с Кристофером Майерсом.
340
Гл.8. Моделирование и вычисления
задачи объясняется, в частности, тем, что сети реакций в клетке нельзя
однозначно разбить на модули. Один и тот же белок может участвовать в
нескольких, на первых взгляд независимых, схемах регуляции. В этом упражнении
мы рассмотрим простейшую сеть регуляции генов — так называемый репрес-
силятор. Эта регуляторная сеть представляет собой три белка, каждый из
которых ингибирует производство следующего. Экспериментаторы
встраивают эти белки в бактерию Е. coli, стараясь минимизировать их влияние на
остальные механизмы клеточной жизни. Здесь мы реализуем стохастическую
модель, которую авторы [37] использовали для описания репрессилятора.
Эта модель позволит нам:
• проиллюстрировать на простом примере центральную догму и
принципы транскрипторной регуляции: управляющее воздействие белков на
экспрессию ДНК в РНК,
• ознакомиться с продвинутыми методами Монте-Карло, применяемыми
для моделирования стохастических реакций,
• ознакомиться со способами автоматического построения непрерывной
модели на основе скоростей реакции,
• пронаблюдать флуктуации типа дробового шума, обусловленные малым
числом молекул, и флуктуации типа телеграфного шума,
обусловленные конечными скоростями реакции прикрепления и открепления регу-
ляторных белков от регулируемой ДНК.
Рис. 8.12 представляет сеть реакций репрессилятора так, как ее видит
биолог. В системе из трех белков (TetR, ACI и Lad) каждый подавляет
выработку следующего. Мы увидим, что в определенных обстоятельствах это
может привести к спонтанным осцилляциям; каждый белок по очереди
переживает всплеск концентрации, угнетая выработку последующего белка и
стимулируя, таким образом, производство своего угнетателя. Это приводит к
понижению его концентрации и к всплеску концентрации следующего. Далее
процесс продолжается циклически.
В действительности за этой биологической схемой скрывается очень
сложная система реакций. Так, белок Lad может связываться с одним или двумя
сайтами транскрипционной регуляции, или сайтами-операторами,
расположенными перед геном, который кодирует мРНК tetR.40
40Матричная РНК (мРНК) используется для кодирования белков. Существуют и другие
формы РНК, которые играют роль энзимов или других элементов клеточной машинерии.
Белки в Е. coli принято называть теми же именами, что и кодирующие их мРНК — только
белки начинаются с большой буквы, а мРНК — с маленькой.
Гл.8. Упражнения
341
TetR
-/ Л
λα |LacI
Рис. 8.12. Репрессиляторная сеть глазами биолога
Затупленные т-образные стрелки означают, что белок в начале такой стрелки угнетает
производство белка, на который эта стрелка направлена. Таким образом, LacI (лак-ай)
подавляет выработку TetR (тет-ар), который в свою очередь подавляет λ CI (лямбда-си-
один). Это компактное описание скрывает за собой очень сложную систему реакций (см.
рис. 8.13).
В связанном состоянии он существенно замедляет трансляцию мРНК
tetR.41 Таким образом, пока белок LacI привязан к ДНК, уровень
tetR будет постепенно падать из-за ее естественного разложения. Как
следствие, все меньше TetR-белков будет транслировано из мРНК tetR.
Соответствующая сеть из десяти реакций приведена на рис. 8.13, который
представляет собой лишь треть репрессиляторной сети. Упрощенная схема,
используемая биологами (см. рис. 8.12), скрывает подробности того, как
именно конкретный белок подавляет производство следующего. Более
подробная диаграмма уже включает в себя две точки прикрепления
молекулы-репрессора, что дает три состояния (Ро, Р\, и Р2) промотора в
зависимости от того, сколько белков LacI к нему прикреплено.
Программный пакет для моделирования репрессилятора вы можете
скачать с сайта книги [132].
(а) Запустите компьютерную модель на 6000 секунд (или больше) и
постройте состояния белка, РНК и промотора как функцию от времени. Обратите
внимание на то, что
• количество белка действительно осциллирует, как на рис. [37, figure 1(c)],
• заметны существенные шумоподобные флуктуации,
• белков производится намного больше, чем мРНК.
41 РНК полимераза, молекулярный мотор, ответственный за транскрипцию ДНК в РНК,
должен прикрепиться к ДНК в сайте-промоторе. Связываясь с соседними сайтами-
операторами, белок-репрессор ингибирует эту связь и, таким образом, частично блокирует
транскрипцию. Неполное блокирование транскрипции называют «утечкой» (leakiness).
342
Гл.8. Моделирование и вычисления
Рис. 8.13. Репрессилятор с точки зрения моделирования
Сеть Петри [51] для трети репрессиляторной сети (репрессия белка LacI белком TetR).
Упрощенная биологическая схема (рис. 8.12) скрывает за собой удивительно сложную
систему! Соответствующие уравнения уже реализованы в численной модели, так что
подробное изучение этого рисунка необязательно. Синие вертикальные прямоугольники
обозначают реакции прикрепления А + В —> С, со скоростями &ь[А][£]. Контурные вертикальные
прямоугольники соответствуют реакциям открепления С —У А + В со скоростями fcu[C].
Горизонтальные прямоугольники — это реакции катализированного синтеза С —¥ С + Р,
происходящие со скоростью 7[С]"> темные соответствуют транскрипции (производству мРНК),
а более светлый — трансляции (производству белка). Черные вертикальные
прямоугольники соответствуют реакции распада А —> мусор со скоростью fcd[i4]. Белок LacI (сверху)
может прикрепляться к ДНК в двух сайтах-промоторах непосредственно перед геном,
кодирующим tetR; В связанном состоянии он почти полностью блокирует транскрипцию
(производство) мРНК tetR. Po обозначает состояние промотора без привязанных белков
LacI; Pi — состояние с одним блокированным сайтом, а Рч — с двумя блокированными
сайтами. LacI может привязываться к одному или обоим сайтам, изменяя состояние рецептора
с Pi на Pi+i, или открепляться. В свободном состоянии Ро мРНК tetR транскрибируется
быстро, а в связанных состояниях медленно (за счет неполного (leaky) подавления). мРНК
tetR, в свою очередь, катализирует производство белка TetR.
Чтобы оценить влияние флуктуации на систему, мы должны сравнить
результаты стохастического моделирования с гладкими решениями
дифференциальной модели (как мы делали в упражнении 8.10). В [37] авторы
приводят систему из шести дифференциальных уравнений, представляющих собой
непрерывный аналог стохастической модели. Для упрощения задачи они
интегрируют эту систему по состояниям промотора, получая в результате
уравнение Хилла (см. упражнение 6.12) для производства мРНК, и различным
образом перемасштабируют переменные. Вместо того чтобы записывать их
уравнения и перенормировки в явном виде, удобно (и полезно для понимания
процесса) написать процедуру, которая генерирует непрерывные
дифференциальные уравнения непосредственно из известных нам скоростей реакций.
Гл.8. Упражнения
343
(b) Создадим на основе репрессилятора детерминистическую программу,
аналогичную имеющейся стохастической. Напишите процедуру dcdt(c,t)f
реализующую следующий алгоритм:
• Присвоить количествам веществ в сети значения из массива с.
• Заполнить вектор dcdt (длина которого соответствует количеству
реагентов) нулями.
• Для каждой реакции:
— вычислить ее скорость;
— для каждого вещества, стехиометрический коэффициент которого
меняется в результате реакции, прибавить изменение коэффициента,
умноженное на скорость реакции, к соответствующей компоненте
dcdt.
Теперь запустите процедуру интегрирования полученного дифференциального
уравнения (как описано, например, в последней части упражнения 3.12) и
сравните полученный результат с результатами стохастического моделирования.
Вы увидите, что стохастическая модель порождает флуктуации,
существенные по отношению к непрерывному решению. Часть этих флуктуации
связана с тем фактом, что число молекул белков и мРНК конечно. В
частности, число молекул мРНК всегда существенно меньше числа белков.
(c) Напишите процедуру, которая создает такую стохастическую репрессиля-
торную сеть, в которой концентрации мРНК умножены на RNAFactor, а
непрерывные уравнения оставлены прежними (для этого достаточно умножить
начальные концентрации и скорости транскрипции на RNAFactor и поделить
скорость трансляции на RNAFactor.) Попробуйте повысить RNAFactor до 10 и до
100. Уменьшились ли флуктуации числа мРНК и белков? Этот шум вызван тем,
что молекул в клетке всегда дискретное целое число. Он аналогичен
дробовому шуму, который наблюдается в электрических цепях из-за дискретной
природы электрического заряда. Этот шум пропорционален, как и
большинство флуктуации, квадратному корню из числа молекул.
Особенно грубым приближением выглядит непрерывное описание
прикрепления белка к сайту-оператору ДНК: переменная, которая равна либо
нулю, либо единице, заменяется непрерывной величиной, принимающей все
значения из этого интервала. (Такой шум в других приложениях называют
телеграфным — по аналогии с телеграфом, который либо молчит, либо
посылает постоянный сигнал, когда оператор нажимает на ключ и замыкает
цепь.) Непрерывное описание работает в пределе, когда скорости связывания
344
Гл.8. Моделирование и вычисления
и отрыва велики по сравнению со скоростями остальных процессов. Тогда
действительно белки и мРНК со своего временного масштаба видят только
усредненную, локально-равновесную концентрацию. С другой стороны,
когда скорости связывания/отрыва малы по сравнению со скоростью
отклика мРНК и белков, профили концентраций последних принимают типичный
«телеграфный» вид.
(d) Встройте в модель параметр telegraphFactor, управляющий
скоростью связывания/отрыва белка от РНК. Запустите модель на 1000 секунд
с RNAFactor = 10 (чтобы подавить дробовой шум) и telegraphFactor = 0.001.
Заметны ли на кривых концентрации мРНК моменты связывания и отрыва
белков?
8.12 Энтропия растет! Цепи Маркова. (Математика) @
Выпуклость функций — один из основных инструментов доказательств в
формальной статистической механике. Например, функция f(x) = —χ log ж
является строго выпуклой вниз при χ > 0 (см. рис. 5.9); в этом легко
убедиться, вычислив вторую производную — она отрицательна во всей области.
(а) Выпуклость суммы функций. Пусть Σα^α = 1 и для всех α выполнено
μα > 0 и ха > 0. Индукцией по числу состояний Μ покажите, что если д(х)
выпукла вниз при χ > 0, то
(м \ м
α=1 / α=1
Это неравенство является обобщением неравенства Иенсена (уравнение 5.25), в
котором все μα равны между собой. (Указание: в определении выпуклости
вниз, /(λα + (1 — λ)6) > λ/(α) + (1 — λ)/(6), положите (1 — λ) = /хм+ι и
b = хм+i- Тогда α будет суммой Μ слагаемых, умноженных на некоторые
коэффициенты. Равна ли сумма коэффициентов при xQ в α единице? Можно
ли применить метод индукции?)
В упражнении 5.7 мы выяснили, что энтропия не растет в гамильтоновых
системах. Давайте покажем, что она растет в марковских цепях.42
Система, описываемая марковской цепью, неявно обменивается энергией
с термостатом температуры Т. Для доказательства роста их суммарной
энтропии достаточно показать, что AS — ΔΕ/Τ больше нуля, где AS — прирост
энтропии нашей системы, а ΔΕ/Τ — поток энтропии из термостата. Таким
42Мы знаем, что марковские цепи рано или поздно приходят к равновесному состоянию и
утверждали поэтому, что в таком состоянии свободная энергия системы минимальна. Здесь
мы покажем, что свободная энергия марковской цепи действительно монотонно убывает.
Гл.8. Упражнения
345
образом, рост энтропии для марковской цепи оказывается эквивалентен
убыванию свободной энергии Ε — TS.
Пусть Ραβ — матрица перехода для марковской цепи, удовлетворяющая
условиям детального равновесия с энергией Еа при температуре Т. Текущая
вероятность пребывания в состоянии α равна ра. Свободная энергия
вычисляется по формуле:
F = Ε - TS = Σ Р<*Еа + квТ Σ Ρα log Ρα· (8.26)
α α
(b) Покажите, что свободная энергия марковской цепи убывает. А
именно, с помощью уравнения (8.25) покажите, что свободная энергия состояния
Ρβ = ΣαΡβ<*Ρ<* меньше или равна свободной энергии состояния р(п\
Используйте свойства матрицы перехода Ρ (О < Ραβ < 1 и Σα^αβ = -О и УСЛ0В]ле
детального равновесия (Ραβρ*β = ΡβαΡα> гАе Pa = exP(—EQ/kBT)/Z).
(Указание: у вас может возникнуть соблазн использовать μα = Ραβ в
уравнении (8.25), но для вычисления энтропии нужны значения Ρβα, а эти две
матрицы не равны между собой. Чтобы перейти от Ραβ κ Ρβα, воспользуйтесь
условием детального равновесия.)
8.13 Гистерезис и лавины.43 (Сложные системы, моделирование) @
Если кусок магнетика поместить в растущее внешнее поле H(t) (рис. 8.14),
то намагничивание (рис. 8.15) будет происходить не плавно, а мелкими
скачками, которые принято называть лавинами (рис. 8.16). Эти лавины
возникают из-за неравномерного расширения магнитных доменов — границы домена
«протаскиваются» внешним полем по шероховатому ландшафту
потенциальной энергии, обусловленному наличием примесей и неоднородностей.
Магнитный сигнал, порождаемый такими лавинами, называют шумом Баркгаузена.
Для моделирования этого процесса мы будем использовать неравновесную
решеточную модель, модель Изинга со случайным полем. Гамильтониан этой
модели имеет следующий вид:
W = - Σ JsiSi " Σ (Я(*) + hi) Si' <8·27)
(iJ) i
где спины S{ = ±1 заданы на квадратной или кубической решетке с
периодическими граничными условиями. Константа взаимодействия J и внешнее
43 Большая часть этого упражнения взята из [65]. Упражнение и соответствующее
программное обеспечение разработаны совместно с Кристофером Майерсом.
346
Гл.8. Моделирование и вычисления
поле Η имеют тот же смысл, что и в классической модели Изинга (см.
раздел 8.1). Наличие беспорядка имитируется случайным полем h{, значение
которого в каждой ячейке независимо выбирается из распределения Гаусса со
среднеквадратическим отклонением R:
ρ(Λ)=νέ^/2* (8·28)
Тепловое равновесие нас больше не интересует (в этом случае никакой
гистерезис не возможен). Рассмотрим противоположную ситуацию: положим
температуру равной нулю. Начиная из состояния со всеми спинами вниз,
будем адиабатически (бесконечно медленно) увеличивать H(t) от —оо к оо.
Рис. 8.14. Шумы Баркгаузена
При приближении магнита к катушке (т.е. увеличении интенсивности поля H(t)) в нем
происходит переключение магнитных доменов в направлении внешнего поля. Скачки
результирующего магнитного поля можно преобразовать в электрический сигнал на катушке
индуктивности и прослушать с помощью обычных колонок. Шум Баркгаузена для нашей
компьютерной модели можно прослушать на сайте [72].
Правила переключения спинов просты: спин переключается в том случае,
если это уменьшает общую энергию системы. То есть, для переключения
спина необходимо, чтобы локальное поле в ячейке г
J J2 Sj + hi + H(t) (8.29)
jno соседям г
поменяло знак с отрицательного на положительный. Это может произойти по
двум причинам: при переключении кого-то из соседей (спины, захваченные
распространяющейся лавиной), либо при изменении внешнего поля
(зарождение новой лавины).
Файлы с указаниями и графические шаблоны для различных языков
программирования и систем будут доступны в разделе компьютерных
упражнений на сайте книги [132].
Гл.8. Упражнения
347
Рис. 8.15. Цикл гистерезиса с подциклами
Цикл гистерезиса с подциклами для нашей модели. При увеличении или уменьшении
внешнего поля намагниченность меняется с запаздыванием — это называется гистерезисом. На
макроуровне кривые намагниченности кажутся гладкими.
Рис. 8.16. Мелкие скачки: шум Баркгаузена
Рассматривая рис. 8.15 с большим увеличением, мы замечаем, что намагниченность растет
мелкими скачками — лавинами.
(а) Создайте массивы для хранения решеточных переменных s[m][n]
и h[m][n]. (Для кубической решетки индексов будет три.) Заполните
первый массив спинами вниз (—1), а второй — значениями случайного поля
(случайными действительными числами из распределения 8.28). Напишите
функцию FlipSpin, которая для заданных г и j меняет спин в соответствующей
ячейке с s = — 1 на s = +1 (и выдает ошибку, если спин уже переключен).
Напишите процедуру NeighborsUp, вычисляющую для заданной ячейки число
соседей со спинами вверх (учитывая периодические граничные условия).
В отличие от лабораторного эксперимента, на компьютере бесконечно
медленное изменение магнитного поля обеспечить легко. Чтобы вызвать
лавину, достаточно найти спин, наиболее близкий к переключению, и увеличить
Η ровно настолько, чтобы он смог переключиться. После этого лавина будет
распространяться сама.
348
Гл.8. Моделирование и вычисления
Распространение лавины
(1) Найдите спин г, который спровоцирует следующую лавину — то есть
направленный вниз спин с максимальным значением внутреннего поля
^Σ? по соседям г s3 + ^ индуцированного случайным полем в ячейке и
состоянием соседей.
(2) Увеличьте внешнее поле Η так, чтобы оно перевесило внутреннее, и
поместите спин в очередь (см. правую часть рис. 8.17).
(3) Возьмите спин из очереди по принципу FIFO («обслуживание в порядке
поступления»).
(4) Если спин еще не переключен,44 переключите его и поместите в очередь
всех его соседей с положительным локальным полем.
(5) Повторяйте шаги (3) и (4) до опустошения очереди.
(6) Повторяйте шаги, начиная с (1), пока все спины не будут переключены.
(b) Напишите процедуру BruteForceNextAvalanche для шага (1), которая
проверяет локальное поле во всех ячейках со спином —1 и возвращает
координаты ячейки, в которой возникнет лавина.
(c) Напишите процедуру Propagate Avalanche, которая моделирует
распространение лавины из заданной ячейки (шаги (3)-(5)) и выделяет цветом
переключенные спины. Запустите ее для системы 300 χ 300 при R = 1.4, 0.9 и 0.7
(или 503-системы при R = 4, R = 2.16 и R = 2) и посмотрите на возникающие
лавины. Если у вас быстрый компьютер, вы можете попробовать
смоделировать систему большего размера. Но увлекаться пока не стоит — в следующем
упражнении вы реализуете алгоритм с использованием сортированного
списка, который существенно ускорит вычисления.
Нам было бы интересно измерять многие свойства моделируемой нами
системы: размер лавин, корреляционные функции лавин, формы петель
гистерезиса, средние формы пиков при распространении лавин... Если встроить
все эти измерения во внутренний цикл программы, код получится слишком
громоздким. Вместо этого имеет смысл использовать шаблон
проектирования субъект-наблюдатель: при каждом обращении спина и в конце каждой
лавины субъект (наша численная модель) уведомляет об этом список
наблюдателей.
44Необходимо проверить, не был ли этот спин уже переключен, т.к. спины могут
оказываться в очереди по нескольку раз, см. рис. 8.17.
Гл.8. Упражнения
349
Решетка Очередь
Рис. 8.17. Распространение лавины в модели с гистерезисом
Слева: распространение лавины. Лавина спровоцирована спином номер 13. Он вызвал
переключение первой порции спинов 14, 8 и 12, которые спровоцировали вторую порцию
переключений: 15, 19, 7, 11 и 17, а те, в свою очередь, третью: 10, 20, 18 и 6. Справа:
очередь типа FIFO (first in - first out, «обслуживание в порядке поступления») во время
переключения спинов второй порции. (Числа показывают номера спинов,
спровоцировавших переключение спинов из очереди.) Спин в левом хвосте очереди будет переключен
первым. Обратите внимание на спин 20, который был добавлен в очередь дважды (два
соседних спина в предыдущей порции). Вставляя в очередь «маркеры» после каждой порции,
мы можем вычислить, сколько спинов в единицу «времени» опрокидывается при
распространении лавины (см. рис. 8.18).
(d) Скомпилируйте MagnetizationObserver (наблюдатель
намагниченности), который хранит внутреннюю намагниченность (изначально равную
—N) и увеличивает ее на 2 при каждом уведомлении. Скомпилируйте
AvalancheSizeObserver (наблюдатель размера лавины), который отслеживает
размер текущей лавины после каждого обращения спина, а по окончании
лавины добавляет итоговый размер в общую гистограмму. Встройте процедуры
NotifySpinFlip (оповещение об переключении спина) и NotifyAvalancheEnd
(оповещение о конце лавины) в программу и в коды соответствующих
наблюдателей. Постройте кривую намагниченности М(Н) и гистограмму
распределения лавин по размерам D(S) для трех систем, рассмотренных в
(с).
8.14 Гистерезис: алгоритмы.45 (Сложные системы, моделирование) @
По мере того как растет объем памяти и скорость компьютеров, выгода
от использования эффективных алгоритмов только возрастает. Рассмотрим
некоторую задачу для системы размера 7V; сложные алгоритмы, как правило,
работают медленнее, чем простые, при малых N. Но если время решения
45 Это упражнение также основано на работе [65]. Упражнение и соответствующее
программное обеспечение разработано совместно с Кристофером Майерсом.
350
Гл.8. Моделирование и вычисления
Рис. 8.18. Временной ряд лавины
Число опрокинутых спинов на каждом временном шаге приведено на рис. 12.5. Как
видите, несколько раз лавина практически останавливается. Будь внешнее поле чуть слабее
по отношению к беспорядку, лавина распалась бы на несколько маленьких. Тот факт, что
беспорядок мал ровно настолько, чтобы обеспечить рост лавины, свидетельствует о
близости фазового перехода и приводит к самоподобию. В критической точке частичная лавина
размера S провоцирует (в среднем) лавину такого же размера S.
задачи сложным алгоритмом растет как N, а простым — как 7V2, сложный
алгоритм оказывается выгоднее для решения больших задач.
В модели гистерезиса (упражнение 8.13) время, необходимое для поиска
зародыша лавины «в лоб», пропорционально N для каждой лавины.
Поскольку общее количество лавин примерно пропорционально N (большая часть
лавин имеет единичный размер, особенно в трехмерии), время поиска простым
перебором пропорционально N2. Можно ли избежать перебора всех ячеек
при поиске каждой новой лавины?
Ответ — можно, используя алгоритмы сортировки списков: для этого
нужно упорядочить46 список спинов в порядке возрастания случайных полей
(рис. 8.19). Если задан интервал значений поля (if, Η + Δ), то для решетки,
на которой у каждой вершины ζ соседей, достаточно проверять те спины, для
которых случайное поле лежит в интервале JS + Η < —hi < JS + (Η + δ)
для ζ + 1 возможного значения поля JS = {—Jz, —J(z — 2),..., J ζ),
создаваемого его соседями. Также полезно в каждый момент помнить положения в
списке тех ζ + 1 спинов, которые могут переключиться следующими.
Сортировку спинов можно провести за время N log TV, которое на практике почти
неотличимо от пропорционального 7V, что дает значительный выигрыш по
сравнению с алгоритмом простого перебора.
Пожалуйста, используйте прилагаемую нами процедуру для сортировки списка; это
самая медленная часть программы. Написать свою собственную процедуру для сортировки
списков очень легко, но значительно сложнее отладить ее так, чтобы она эффективно
работала для длинных списков.
Гл.8. Упражнения
351
Решетка Сорт, список
Номер
спина
hi
- о
- 1
- 2
-3,4
И
Рис. 8.19. Сортировка списка
Сортировка списка для поиска следующего спина в лавине. Окрашенные ячейки соот-
иетствуют уже переключенным спинам. В сортированном списке стрелки справа соответ-
гтвуют указателям nextPossible[nUp] — указателям на первый по списку спин, который
не переключится, если будет иметь ровно nUp соседей, направленных вверх, при текущем
ннсшнем поле. Некоторые из них указывают на уже перевернутые спины, это означает, что
они уже имеют больше направленных вверх соседей, чем соответствующее значение nUp.
(Вообще говоря, непереключенные спины не обязаны идти в списке подряд.)
Алгоритм с сортированным списком.
(1) Определите список указателей next Possible [nUp], каждый из которых
указывает на положение в сортированном списке того спина, который
переключится следующим, если у него будет nUp соседей, направленных
вверх. Изначально все указатели списка nextPossible [nUp] указывают
на спин с наибольшим случайным полем hi.
(2) Из ζ + 1 спина, на которые указывает nextPossible, выберите тот
nUpNext, чье внутреннее поле максимально nUp - nDown + hi =
= 2 nUp - ζ Λ- hi. Не проверяйте те значения nUp, для которых
соответствующие указатели «уползли» за границу списка, используйте
переменную stopNUP.
352
Гл.8. Моделирование и вычисления
(3) Сдвиньте указатель nextPossible [nUpNext] на следующий спин в
сортированном списке. Если вы добрались до конца списка, уменьшите
значение stopNUP на единицу.47
(4) Если спин nUpNext имеет в точности нужное количество соседей со
спином, направленным вверх, переключите его, увеличьте внешнее поле
H(t) и запустите следующую лавину. В противном случае просто
переходите к пункту (2).
Напишите программу, реализующую алгоритм поиска лавины по
сортированному списку. Обратите внимание на задержку перед началом симуляции;
большая часть времени тратится на сортировку списка. Сравните время расчета с
алгоритмом «в лоб» для системы умеренного размера, в которой этот
алгоритм начинает испытывать проблемы. Выполните расчеты для системы
большего размера48 (20002 при R = (0.7,0.8,0.9) или 2003 при R = (2.0,2.16,3.0))
и исследуйте распределение возникающих лавин по формам и размерам.
Для моделирования по-настоящему больших систем с миллиардами
спинов без использования гигабайт памяти существует еще один, так
называемый битовый алгоритм, который хранит спины в виде битов и никогда не
генерирует и не хранит случайное поле целиком (реализация этого алгоритма
описана в [65]).
8.15 NP-полнота и kSAT. (Вычислительная математика, моделирование,
математика) @
В этом упражнении вам предстоит численно исследовать фазовый
переход, возникающий в семействе задач математической логики, известных
под названием kSAT [5,29]. В частности, вы увидите, как возрастает
вычислительная сложность этих задач при приближении к критической точке.
Это упражнение связывает воедино ряд фундаментальных проблем из
теории критических явлений, вычислительной математики и математической
логики.
47Либо этот спин уже переключен (тогда мы переходим к следующему), либо он
запускает следующую лавину (переключить и перейти к следующему), либо у него пока не
достает правильно направленных соседей для переключения (переходим к следующему, а
этот перевернем, когда соседей станет больше).
48Предупреждение: Скорее всего, оперативная память компьютера закончится раньше,
чем ваше терпение. Если вы слышите, что компьютер часто обращается к жесткому диску
(характерный скрипучий шум), запустите систему меньшего размера.
49Это упражнение и соответствующее программное обеспечение разработаны совместно
с Кристофером Майерсом, при участии Барта Сельмана и Карлы Гомез.
Гл.8. Упражнения
353
Задача kSAT, которой посвящено это упражнение, относится к классу
гак называемых NP-полных задач. В предыдущих упражнениях вы уже
видели, что время работы алгоритмов по-разному зависит от размера системы
N (например, для сортировки списка из N элементов достаточно выполнить
NlogN операций сравнения). Специалисты в области вычислительной
математики делят все задачи на классы сложности', так, задача принадлежит
классу сложности Р, если любое ее решение может быть найдено за время,
растущее с размером системы N не быстрее, чем полиномиально.50 Задача
о сортировке списка, очевидно, принадлежит классу Ρ (время решения
ограничено сверху полиномом Ν2, так как NlogN < Ν2 для больших 7V); как
удалось доказать недавно, вопрос о том, является ли TV-значное число
простым, также принадлежит классу сложности Р. Задача принадлежит классу
ΝΡ51, если за полиномиальное время можно проверить, является ли
предложенное решение верным. Например, неизвестно, принадлежит ли классу
Ρ задача о разложении TV-значного числа на множители (так как
неизвестен алгоритм, позволяющий ее решить за полиномиальное время), однако
известно, что она принадлежит классу ΝΡ.52
(а) Пусть имеются два TV-значных числа. Мы хотим проверить, является ли
некое заданное число их произведением. Покажите, что число операций,
необходимых для такой проверки, не превышает С · Ν2, где С — константа.
Для многих задач класса ΝΡ неизвестен алгоритм решения с
полиномиальным временем. Удалось показать, что существует подкласс этих задач,
обладающих максимальной сложностью — так называемые NP-полные задачи.
Под максимальной сложностью имеется в виду то, что, научившись решать
эти задачи, мы сможем решить любую другую задачу класса ΝΡ. А именно,
любая задача класса ΝΡ может быть сведена (с использованием алгоритма
с полиномиальным числом операций) к одной из NP-полных задач. Та^им
образом, если удастся найти полиномиальный алгоритм для любой задачи
Классы Ρ и ΝΡ определены для детерминистических компьютеров с одним
процессором. Для некоторых задач (например, разложения на простые множители) существуют
алгоритмы с полиномиальным временем, предназначенные для квантовых компьютеров
(на случай, если их когда-нибудь изобретут).
51ΝΡ означает не «неполиномиальное», а скорее недетерминистски полиномиальное
время. То есть задачи из класса ΝΡ могут быть решены за полиномиальное время на
гипотетическом недетерминистском параллельном компьютере — машине с
неопределенным количеством процессоров, каждый из которых может обсчитывать свой подслучай.
52Сложность разложения больших чисел на множители лежит в основе некоторых
методов криптографии с открытым ключом. Благодаря этим методам, номер вашей кредитной
карты доступен интернет-магазину, но недоступен жуликам и ворам, прослушивающим
сеть. Является ли задача разложения на простые множители NP-полной — неизвестно.
354
Гл.8. Моделирование и вычисления
из класса NP-полных — это сделает все задачи класса NP разрешимыми за
полиномиальное время.
• Классическим примером NP-полной задачи является задача
коммивояжера. Пусть заданы N городов, и известна стоимость проезда между
каждыми двумя из них. Для заданного бюджета К необходимо найти
замкнутый маршрут с посещением каждого города стоимостью < К
(если такой существует). Лучший алгоритм решения этой задачи включает
в себя перебор путей, число которых растет экспоненциально с ростом
N — быстрее любого полинома.
• В статистической механике задача поиска конфигурации спинового
стекла с минимальной энергией53 также является NP-полной (см.
раздел 12.3.4).
• Еще один пример NP-полной задачи — это задача о трехцветной
раскраске графа (упражнение 1.8): можно ли раскрасить N вершин графа
в синий, красный и зеленый цвета так, чтобы ни одно из ребер не
соединяло вершины одного цвета?
Один из ключевых вопросов вычислительной математики заключается
в том, совпадают ли классы Ρ и NPnHbiMH словами, могут ли все эти
задачи быть решены за полиномиальное время? Большинство исследователей
склоняется к отрицательному ответу. Считается, что в худшем случае время
решения NP-полных задач растет с увеличением N экспоненциально.
Доказательство принадлежности задачи классу NP-полных состоит, как
правило, в том, чтобы свести ее к одной из уже известных NP-полных
задач (увеличив число операций не более чем на полином от N). В
упражнении 1.8 мы сформулировали задачу выяснения совместности (SAT)
булевских логических выражений. Коротко говоря, задача SAT заключается в
поиске набора N логических переменных (принимающих значения Истинно
или Ложно), при котором выражение истинно, либо в доказательстве того,
что такого набора не существует. Логическое выражение составляется из
переменных с помощью операторов ИЛИ (V), И (Λ) и НЕ (-■). В упражнении 1.8
мы рассмотрели особый класс логических выражений под названием 3SAT.
В выражениях этого класса требуется одновременное выполнение Μ условий
на N переменных, каждая из которых представляет собой три литерала,
связанных оператором ИЛИ (литерал представляет собой саму переменную или
ее отрицание). Например, ЗвАТ-выражение может начинаться так:
53С технической точки зрения, как и в задаче коммивояжера, нам следует
переформулировать задачу так, чтобы она стала задачей на принятие решения. Например, найти
состояние (если оно существует) с энергией меньше Е.
Гл.8. Упражнения
355
[(-.Хат) V Хм V Х3] А [(-.Х2) V Х43 V (-.Х21)].... (8.30)
В упражнении 1.8 мы показали, что задача 3SAT является NP-полной, при-
недя задачу трехцветной раскраски графа из N вершин к задаче 3SAT с 3N
переменными. Исторически SAT — это первая задача, для которой была
доказана NP-полнота; любая другая задача класса NP может быть отображена
па задачу SAT примерно таким же образом. Известно, что задача 3SAT
является NP-полной, в то время как задача 2SAT (т.е. такая, что входящие
в нее условия содержат два литерала) принадлежит к классу Р, т.е. может
быть решена за полиномиальное время.
Численное исследование Тот факт, что задача является NP-полной, вовсе
не означает, что типичный представитель этого класса будет сложен для
численного решения. Эта классификация основана на худших случаях, а не на
типичных представителях задачи. Если сложные случаи встречаются редко,
среднее время решения может быть вполне приемлемым, несмотря на то, что
решение некоторых задач потребует экспоненциально много времени
(большинство графов с парой сотен вершин удается либо быстро раскрасить в 3
цвета, либо быстро показать, что трех недостаточно; однако некоторые
конфигурации оказываются чудовищно сложными для анализа). Среднее время
решения таких задач и распределение задач по временам можно оценить с
помощью методов статистической механики.
В оставшейся части этого упражнения мы реализуем алгоритмы решения
kSAT-задач и применим их к случайному набору 2SAT- и ЗвАТ-задач с
Μ условиями. Мы увидим, что в пределе при больших N доля выполнимых
kSAT-выражений испытывает фазовый переход при росте числа условий на
переменную Μ/Ν. Каждое новое ограничение уменьшает набор возможных
решений. Случайное kSAT-выражение с малым числом условий на
переменную почти всегда совместно и его решение легко найти. Когда число
условий на переменную велико, выражение почти всегда несовместно, и это тоже
легко доказать. И только вблизи критической точки, когда среднее число
решений стремится к нулю при N —> сю, проверка совместности типичного
выражения становится по-настоящему сложной.
Логическое выражение над N переменными Хт в конъюнктивной
нормальной форме удобно представить в виде списка списков. Элементы
корневого списка представляют собой выражения, соединенные операторами
конъюнкции (И). Каждое такое выражение задано списком литералов,
соединенных операторами дисъюнкции (ИЛИ). Литералы же представлены целыми
356
Гл.8. Моделирование и вычисления
ненулевыми числами из [—Ν, Ν] (при этом — т соответствует -^Хт).
Например, список [[—3,1,2], [—2,3, —1]] соответствует выражению ((-^Xs)\/Xi VA"2)A
(№)νχ3ν№)).
Загрузите шаблоны программ и программы анимации из раздела
компьютерных упражнений на сайте книги [132].
(b) Выполните часть (Ь) упражнения 1.8. Сгенерируйте на компьютере
конъюнктивную нормальную форму, соответствующую трехцветной раскраске двух
графов, изображенных на рис. 1.8. (Указание: переменных должно
получиться N = 12, по три на каждую вершину.)
Алгоритм определения совместности Дэвиса—Патнема (DP-алгоритм,
см. рис. 8.20) имеет рекурсивную природу. Он заключается в следующем:
одной из переменных присваивают пробное значение Истинно, исключают
ее из всех условий и применяют DP-алгоритм к полученному упрощенному
выражению. Если выражение совместно — задача решена. Если нет,
значение стартовой переменной меняют на Ложно и применяют
DP-алгоритм к полученному условию.
Для реализации DP-алгоритма вам понадобятся: (i) структура данных,
хранящая для каждой переменной список условий, в которые входит она
сама, и список условий, в которые входит ее отрицание, (ii) запись, в которой
хранятся условия, выполненные автоматически при текущих значениях
входящих в них литералов. Также вам потребуется процедура исключения,
которая изменяет значение одной из переменных и возвращает преобразованные
переменные и условия. (Если алгоритм достигает тупика - противоречия в
одном из условий — эти изменения понадобятся вам для возврата к исходному
состоянию.) Рекурсивная программа, вызывающая процедуру исключения,
должна возвращать не только информацию о выполнимости выражения, но
и количество тупиков, в которые зашел алгоритм.
(c) Напишите программу, реализующую DP-алгоритм. Примените ее к
выражениям, соответствующим трехцветной раскраске графов из пункта (Ь).
Давайте посмотрим, как меняется вычислительная сложность типичной
задачи 3SAT при увеличении числа условий в расчете на переменную M/N.
(d) Напишите процедуру, принимающую три параметра fc, TV и Μ и
генерирующую Μ случайных kSAT-условий относительно N переменных. При этом
следует исключить случаи, при которых переменная появляется в одном условии
с собой или своим отрицанием. Для N =5, 10 и 20 вычислите долю совместных
2SAT- и ЗвАТ-выражений как функцию от Μ/Ν. Зависит ли доля
несовместных выражений от Μ/Ν1 В каком месте происходит переход от совместности к
Гл.8. Упражнения
357
Рис. 8.20. Алгоритм Дэвиса—Патнема
Схема алгоритма Дэвиса—Патнема в процессе выполнения. Черные кружки — это
свободные переменные, два оттенка серого обозначают пробные значения Истинно и Ложно,
присвоенные переменным. Связи обозначают условия, истинность которых еще не
выявлена.
несовместности? Исследуйте зависимость объема вычислений (количества
тупиков) от M/N: постройте графики среднего значения, среднеквадратичного
отклонения и облако точек, соответствующих отдельным запускам. Действительно
ли сходимость замедляется вблизи точки перехода? Сходимость DP-алгоритма
можно существенно ускорить, внеся в него небольшие усовершенствования.
Самое важное из них состоит в исключении синглтонов — условий, в
которых все переменные, кроме одной, имеют заданные значения. Такие условия
однозначно определяют значение этой оставшейся переменной.
(е) При исключении переменной из очередного условия проверьте, не
становится ли это условие синглтоном; если да, присвойте значение
соответствующей переменной и повторите процедуру. Протестируйте улучшенный алгоритм
на больших задачах. Заметно ли ускорение сходимости?
Тяжелые «хвосты» и случайный перезапуск. DP-алгоритм рано или
поздно выдаст либо решение, либо заключение о несовместности. Однако время,
затрачиваемое на поиск решения, варьируется очень сильно. Вы могли
заметить это на предыдущем графике — в нескольких случаях объем вычислений
был просто огромен по сравнению с остальными. Можно было бы
предположить, что эти точки соответствуют редким вычислительно сложным
случаям. Однако это не так. На самом деле время расчета сильно флуктуирует
даже при запуске алгоритма на одной и той же задаче [58].
358
Гл.8. Моделирование и вычисления
(f) Запустите DP-алгоритм для одной и той же 28АТ-задачи с N = 40
переменных и Μ = 40 условий, случайно меняя порядок выбора переменных.
Оцените показатель степенной функции p(t) ~ tx, описывающей вероятность
закончить вычисления за время t. Отсортируйте список переменных таким
образом, чтобы на каждом шаге для исключения выбиралась переменная, чаще
всего фигурирующая в условиях. Приводит ли это к ускорению алгоритма?
Попробуйте обратить порядок, выбирая каждый раз самую редкую переменную.
Замедляет ли это алгоритм?
Если изменение порядка исключения переменных так сильно влияет на
сходимость, то имеет ли смысл продолжать расчет до сходимости при
неудачно выбранной точке? Обнаружение «тяжелых хвостов» в распределении
времен расчета привело к идее включения в алгоритм [58] случайных
перезапусков] отбрасывая вычислительные затраты на поиск решения из неудачной
точки, можно улучшить средние показатели и избежать тяжелых хвостов.
Известно, что семейство задач 2SAT испытывает непрерывный фазовый
переход при M/N = 1, а семейство 3SAT— скачкообразный фазовый переход
(однако с критическими флуктуациями) вблизи M/N = 4.25. Считается, что
критическое замедление в задачах 3SAT не зависит от используемого
алгоритма. Вдалеке от точки фазового перехода сложные случаи, требующие
экспоненциального времени решения, встречаются экспоненциально редко;
DP-алгоритм в этой области обычно сходится быстро.
(g) Используя улучшенный алгоритм, постройте зависимость доли
совместных 28АТ-выражений от M/N при N = 25, 50 и 100. Приближается ли точка
фазового перехода к M/N = 1 при больших N1 Для задач 3SAT постройте
такие же зависимости при N = 10, 20, 30 и больше, если позволяет мощность
компьютера. Действительно ли фазовый переход происходит при M/N « 4.25?
Вблизи фазового перехода постройте зависимость объема вычислений
(встреченных тупиков) от N для 2SAT и 3SAT. Исходя из этих данных можно ли
предположить, что 2SAT принадлежит классу Р? Похоже ли, что время
решения задач 3SAT растет экспоненциально?
Другие алгоритмы. За прошедшее десятилетие произошел настоящий
прорыв в алгоритмах определения совместности. Так, в методе
WalkSAT [118] процесс исключения начинается с выбора случайной
конфигурации, для которой применяется метод Монте-Карло с
нулевой температурой, обращающий только переменные, входящие в
неудовлетворенные условия. Лучший из известных на сегодняшний день
алгоритмов,SP, был разработан физиками [50, 94] на основе методов,
используемых в статистической механике спиновых стекол.
Глава 9
Параметры порядка, нарушение
симметрии и топология1
В начальной школе нас научили, что существует три состояния вещества:
газ, жидкость и твердое тело. Древние считали, что таких состояний
четыре: воздух, вода, земля и огонь, что нас учили считать чистым
предрассудком. Автор помнит, что когда он сам учился в старших классах, он прочитал
книжку под названием Семь состояний материи [52]. Как минимум одним из
них была «плазма», из которой состояли звезды, а следовательно — большая
часть Вселенной,2 и которая была подозрительно похожа на огонь древних.
Первоначальные три состояния превратились в огромное множество.
Магнетики в важном и хорошо определенном смысле представляют собой
особую фазу вещества. Металлы отличаются от изоляторов. Сверхпроводники
и сверхтекучие жидкости представляют собой новые удивительные
состояния материи. Жидкий кристалл в ваших наручных часах находится в
одной из огромного множества разнообразных жидкокристаллических фаз [28]
(нематик, холестерик, голубые фазы I, II, смектики А, В, С, С*, D, I, ...).
Существует более 200 качественно различных типов кристаллов, и это не
считая квазикристаллов (рис. 9.1). Существуют неупорядоченные состояния
вещества типа спиновых стекол и состояния, в которых наблюдается
дробный квантовый эффект Холла с возмущениями заряда е/3, как у кварков.
Физики элементарных частиц утверждают, что вакуум, в котором мы
живем, в прошлом находился в существенно других состояниях; в последнем
из предыдущих вакуумов, например, могло распространяться четыре вида
*Эта глава представляет собой немного переработанную версию лекции, прочитанной
в Институте Санта-Фе [121].
2 Тогда еще ничего не знали о темной материи.
360
Гл.9. Параметры порядка, нарушение симметрии и топология
света [24] (переносимые тем, что мы теперь называем фотоном, W+, W и
Z-бозонами).
Рис. 9.1. Квазикристаллы
Кристаллы, без сомнения, являются наиболее старым примером фазы с нарушенной
симметрией. В последние десятилетия был открыт совершенно новый класс квазикристаллов,
на картинке приведен пример квазикристалла [55] с симметрией икосаэдра. Обратите
внимание на оси симметрии пятого порядка, запрещенные в обычных кристаллографических
категориях.
Когда у вещества было всего три состояния, мы могли изучить каждое из
них по отдельности и спокойно вернуться к изучению деления в столбик.
Однако теперь, когда они настолько размножились, нам пришлось развить для
них некоторое новое систематическое описание. Наша систематика все время
разрастается и уточняется, поскольку мы продолжаем находить все новые и
новые фазы, которые не вписываются в наши старые представления.
Поразительно, как пятисотое состояние вещества умудряется испортить систему,
замечательно работавшую для первых четырехста девяносто девяти.
Квазикристаллы, дробный квантовый эффект Холла и спиновые стекла заставили
нас серьезно поломать голову, прежде чем мы поняли: (1) почему они ведут
себя именно так, и (2) как встроить их в общую систему.
В этой главе мы расскажем вам об этой общей системе. Она состоит из
четырех главных шагов [93]. Во-первых, вам необходимо найти, какая
симметрия нарушена в исследуемой фазе (раздел 9.1). Во-вторых, вам надо
определить параметр порядка (раздел 9.2). В-третьих, вам следует исследовать
9.1. Нахождение нарушенной симметрии
361
элементарные возбуждения, возможные в системе (раздел 9.3). В-четвертых,
вы классифицируете топологические дефекты (раздел 9.4). Большая часть
того, о чем говорится в этой главе, взято из книг Мермина [93], Коулмана [24],
и де Женна и Про [28], все эти книги мы с удовольствием рекомендуем
читателю.
9.1 Нахождение нарушенной симметрии
Чем сотни различных состояний вещества отличаются друг от друга?
Почему мы говорим, что вода и оливковое масло находятся в одном и том же
состоянии (а именно, жидком), в то время как, скажем, алюминий и
(намагниченное) железо находятся в разных? Мы обнаружили, по материалам
многочисленных наблюдений, что, как правило, разные фазы отличаются своей
симметрией.3
Посмотрите на рис. 9.2, на котором изображены куб и сфера. Кто из них
более симметричен? Очевидно, что сфера имеет гораздо больше
преобразований симметрии, чем куб. Если повернуть куб на 90° в одном из многих
направлений, он будет выглядеть точно так же, сфера не изменится при
повороте не только на 90°, но вообще на любой угол.
(а)у
Рис. 9.2. Что более симметрично, куб или сфера?
(а) Куб обладает множеством симметрии. Он переходит в себя при повороте на 90°, 180° или
270° вокруг любой из трех осей, проходящих через центры противоположных граней, при
повороте на 120° или 240° вокруг оси, проходящей через две противоположных вершины, на
180° вокруг любой оси, проходящей через центр и любое из 12 ребер. (Ь) С другой стороны,
сфера переходит в себя при повороте на любой угол. Сфера инвариантна относительно
вращения: для нее все направления эквивалентны. Куб — фигура, нарушающая симметрию
вращения: в кубе (как в рассказе Оруэлла. — Прим. переводчика) некоторые направления
«более равны, чем другие».
3Это не означает, что разные фазы всегда имеют разную симметрию! Газы и
жидкости обладают одной и той же симметрией, некоторые флуктуационные фазы в
пространствах малой размерности не нарушают симметрию. С другой стороны, можно уверенно
утверждать, что если два состояния вещества обладают различной симметрией, то они
представляют собой разные фазы.
362
Гл.9. Параметры порядка, нарушение симметрии и топология
На рис. 9.3 нарисованы двумерные схематические изображения льда и
воды. Кто из них более симметричен? На первый взгляд кажется, что лед
более симметричен; регулярно расположенные атомы образуют в нем
правильную решеточную структуру. Лед обладает дискретной симметрией
вращения: при повороте на углы, кратные 60° (см. рис. 9.3(a)), переходит в себя.
Он также обладает дискретной трансляционной симметрией (т.е.
симметричен относительно сдвига): сдвиг картинки можно будет легко заметить, если
только вектор сдвига не равен целому числу шагов решетки. Вода выглядит
беспорядочно и нерегулярно. С другой стороны, если повернуть рис. 9.3(b)
на произвольный угол, он по-прежнему будет выглядеть как вода! На
самом деле, правильнее представлять себе воду не как мгновенный снимок,
представленный на рисунке; а как комбинацию, ансамбль всех возможных
подобных снимков. В то время как моментальный снимок воды не обладает
никакими симметриями, вода как фаза обладает полной трансляционной и
вращательной симметрией.
(Ь) о о
Вода
° °о
00 η
о о°
Рис. 9.3. Что более симметрично, вода или лед?
На первый взгляд кажется, что вода гораздо менее симметрична, (а) Картинка,
изображающая «двумерный» лед, очевидно, не инвариантна относительно вращения; ее можно
повернуть (так чтобы она перешла в себя) только на 120° или 240°. Точно так же, она
нарушает и трансляционную инвариантность; кристалл переходит в себя только при сдвиге
на определенные выделенные расстояния (равные целому числу шагов решетки). (Ь)
Картинка, изображающая воду, не обладает вовсе никакой симметрией; атомы расположены
случайно, без какого бы то ни было дальнего порядка. Однако вода как фаза обладает
полной трансляционной и вращательной симметрией: картина беспорядочного нагромождения
атомов будет выглядеть ровно так же, если ее сдвинуть или повернуть.
9.2 Определение параметра порядка
Физика элементарных частиц и физика конденсированного состояния —
науки с существенно разной философией. Физики элементарных частиц
неизменно интересуются кирпичиками, из которых состоит материя. Когда
оказалось, что протоны и пионы состоят из кварков, все внимание переключилось
9.2. Определение параметра порядка
363
на кварки. Теперь кажется правдоподобным, что кварки, электроны и
фотоны состоят из струн, которые трудно (пока) изучать экспериментально.
Физика конденсированного состояния, с другой стороны,
концентрируется на вопросе о том, как сложно устроенные совокупности огромного
множества электронов и ядер могут вести себя таким удивительно простым и
интересным образом. Для ученых, специализирующихся в этой области,
главный вопрос состоит не в том, чтобы установить основополагающие квантово-
механические законы, управляющие поведением частиц, а в том, чтобы
понять и объяснить то, как из взаимодействия многих частиц возникают новые
законы.4
Как нетрудно догадаться, мы далеко не всегда следим за перемещением
всех электронов и протонов. Мы всегда стремимся выделить из множества
переменных самые существенные, соответствующие важным степеням свободы
системы. В кристалле существенной переменной является смещение атомов
относительно узлов решетки. В магните существенной степенью свободы
является направление локальной намагниченности (вектор, указывающий, куда
смотрит северный полюс магнита вблизи данной точки). Локальная
намагниченность возникает в результате сложного взаимодействия между
электронами, отчасти она связана с существованием у электронов собственного
магнитного момента, отчасти — с тем, как именно электроны двигаются внутри
вещества; однако во многих случаях эти детали не имеют значения.
Существенные переменные образуют «поле параметров порядка». На
рис. 9.4 показано поле параметров порядка для магнита.5 В каждой
точке χ = (χ,?/,ζ) задано направление локальной намагниченности М(х).
Модуль Μ можно считать фиксированным для заданного материала, но
направление намагниченности может меняться. Став магнитом, материал
нарушает сферическую симметрию. Параметр порядка Μ указывает, какое
именно направление материал «выбрал» для нарушения симметрии.
Параметры порядка образуют поле; в каждой точке магнита М(х)
определяет локальное направление поля вблизи точки х. Почему направление
намагниченности в разных точках вещества будет различным? Как правило,
4 Физики элементарных частиц тоже используют поля параметров порядка. Главное
различие состоит в том, что они не знают, из чего состоят их поля. Для них должен быть
хорошей новостью тот факт, что наше более полное знание о природе полей в физике
конденсированного состояния оказывается зачастую достаточно бесполезным.
5 Большинство магнитов одновременное являются и кристаллами, соответственно,
сферическая симметрия в них уже нарушена. Однако для так называемых «гейзенберговских»
магнитов влияние кристаллической решетки на магнитные свойства мало. На самом деле
то, что отличает собственно магниты — это нарушение симметрии относительно обращения
времени: если изменить направление стрелы времени, то намагниченность меняет знак.
364 Гл.9. Параметры порядка, нарушение симметрии и топология
Рис. 9.4. Магнитный параметр порядка
В магнетике при заданной температуре величина локальной намагниченности |М| = Мо
практически неизменна, однако зачастую энергия почти не зависит от направления Μ =
М/Мо вектора намагниченности. Поэтому намагниченность может иметь разное
направление в разных точках вещества. (Именно из-за этого не все куски железа являются
магнитами!) Намагниченность — это то, что мы называем параметром порядка в магните; вы
можете представлять ее в виде стрелки, указывающей в направлении магнитного
момента каждого отдельного атома. Состояние магнита в каждый момент времени описывается
полем параметра порядка М(х). Можно представлять его себе в виде набора стрелок,
соответствующих всем точкам пространства, или в виде функции, которая ставит в
соответствие точкам пространства χ точки на поверхности сферы. Эта сфера S2 является
пространством значений параметра порядка для магнита.
наименьшей энергии соответствует однородное поле параметра порядка,
когда нарушение симметрии одинаково во всех точках пространства. На
практике, однако, зачастую наблюдается неоднородное нарушение симметрии.
Большинство тел, сделанных из железа, не выглядят магнитами просто потому,
что локальная намагниченность в разных точках направлена в разные
стороны. На атомарном уровне намагниченность присутствует; для того чтобы
сделать кусок железа магнитом, достаточно заставить магнитные моменты
разных частей указывать в одну сторону. Как мы увидим в этой главе, многие
виды интересного для нас поведения подразумевают изменение параметров
порядка как функции координат.
Поле параметра порядка М(х) удобно представлять себе двумя
различными способами. С одной стороны, можно представлять, что из каждой точки
пространства исходит маленький вектор. С другой стороны, можно говорить
о нем как об отображении реального пространства на пространство
параметра. Другими словами, Μ — это функция, которая переводит точки магнетика
в точки на поверхности сферы (см. рис. 9.4). Как мы упоминали ранее,
математики называют сферу S2, поскольку локально она имеет два измерения.
(Их не интересует, какова размерность пространства, в которое погружена
сфера.)
9.2. Определение параметра порядка
365
Выбор параметра порядка — это искусство. Как правило, мы изучаем
новые системы, поведение которых нам еще не понятно; в этом случае угадать
параметр порядка — значит сделать серьезный шаг к пониманию того, что
происходит. Кроме того, зачастую выбор параметра порядка неоднозначен.
В магнитах, например, можно рассматривать Μ как вектор фиксированной
длины из S2, маркирующий состояния с различно нарушенной симметрией.
Этот топологический параметр порядка хорошо описывает магнетики
при низких температурах, в области, в которой изучаются элементарные
возбуждения и топологические дефекты. Для того чтобы изучать переход из
режима низких в режим высоких температур, в котором намагниченность
равна нулю, лучше рассматривать Μ как «мягкий спин», т.е. вектор переменной
длины (вектор в пространстве R3, см. упражнение 9.5). Нахождение
простейшего описания, подходящего для ваших нужд, часто оказывается ключом к
решению проблемы.
Прежде чем обсуждать изменение параметра порядка в пространстве,
приведем еще несколько примеров. Жидкие кристаллы в
жидкокристаллических дисплеях (например в старых электронных часах) — это нематики.
Нематики состоят из длинных тонких молекул, которые склонны
выстраиваться таким образом, что их длинные оси параллельны. Нематические
жидкие кристаллы, подобно магнитам, нарушают сферическую симметрию.
Однако в отличие от магнитов взаимодействие здесь состоит не в том, чтобы
одинаково направить одноименные полюса, а в том, чтобы одинаково
направить оси (представьте себе на месте нематиков игральные карты,
симметричные относительно переворота верх-низ). Параметр порядка в этом случае —
не вектор М, а вектор без направления η = —п. Пространство параметров
порядка — это полусфера, противоположные точки экватора которой
совпадают (см. рис. 9.5(b)). Это пространство обозначается RP , математики (по
своим туманным причинам) называют его проективным пространством.
Для кристалла существенные степени свободы связаны с нарушением
трансляционной симметрии. Рассмотрим двумерный кристалл, основное
состояние которого (т.е. состояние с минимальной энергией) соответствует
квадратной решетке, но который немного деформирован (рис. 9.6). Эта
деформация может быть описана набором стрелок, соединяющих позиции
атомов в недеформированной идеальной решетке и их положения в
реальной решетке. Говоря более аккуратно, и(х) — это смещение, которое
необходимо совершить, чтобы локально, вблизи точки χ совместить
идеальную и реальную решетки. Сформулировав определение таким
образом, мы имеем возможность доопределить и между узлами решетки;
366
Гл.9. Параметры порядка, нарушение симметрии и топология
Рис. 9.5. Пространство параметра порядка в нематиках
(a) Нематики состоят из длинных тонких молекул, которые предпочитают выстраиваться
в одну сторону. (Дисплеи в часах с жидкокристаллическим экраном состоят из немати-
ков.) Поскольку для них неважно, каким именно концом вверх смотрят молекулы, то их
параметр порядка — не просто единичный вектор η в направлении предпочтительной
ориентации осей молекул, а вектор с присоединенным условием эквивалентности η = —п.
(b) Пространство параметров порядка нематика — это полусфера, противоположные точки
экватора которой отождествлены друг с другом. Поэтому, например, путь, изображенный
на полусфере, замкнут: два его пересечения с экватором соответствуют одной и той же
ориентации молекул нематика в пространстве.
в таких промежуточных точках тоже существует смещение, которое
наилучшим образом совмещает две решетки.
Параметр порядка и — на самом деле не совсем вектор, тут есть тонкость.
Существует неоднозначность в выборе узла решетки, который мы считаем
соответствующим заданному реальному атому. Как показано на рис. 9.6, когда
мы меняем референтный узел решетки («идеальный» атом), вектор
смещения и меняется на величину, пропорциональную шагу решетки а:
и = и + ах = и + max + nay. (9.1)
Поэтому множество существенно различных параметров порядка — это
квадрат с периодическими граничными условиями. Как показано на рис. 9.7,
квадрат с периодическими граничными условиями обладает такой же
топологической структурой, как и тор Т2.
Наконец, упомянем, что догадаться, какой именно параметр порядка (и,
соответственно, нарушение симметрии) надо выбрать — не всегда простая
задача. Например, прошло много лет, прежде чем кто-либо догадался, что
естественный параметр порядка для сверхпроводников и сверхтекучего гелия-4
— это комплексное число ψ.6 Модуль комплексного числа ψ фиксирован для
6Параметр порядка ψ(χ) представляет собой «волновую функцию» конденсата,
который, очень грубо говоря, представляет собой квантовое состояние, в котором
одновременно находится большая доля имеющихся в веществе атомов гелия или купервоских пар.
Соответствующее нарушение симметрии связано с числом частиц. В «симметричном»,
высокотемпературном состоянии гелия число атомов локально сохраняется; в сверхтекучем
9.2. Определение параметра порядка
367
Рис. 9.6. Двумерный кристалл
Кристалл состоит из атомов, выстроенных в регулярно повторяющиеся ряды и колонки.
При высоких температурах, а также если кристалл деформируется или содержит
дефекты, атомы несколько смещаются относительно своих «правильных» положений на решетке.
Это смещение и показано для одного из атомов. Еще лучше это можно сказать следующим
образом: можно рассматривать и(х) как вектор трансляции, который позволит локально,
в окрестности х, привести текущее положение атомов в соответствие с тем положением,
которые они должны занимать на идеальной решетке. Также на рисунке показана
неоднозначность определения и. Какой «идеальный» атом мы должны поставить в соответствие с
заданным реальным атомом? Эта неоднозначность приводит к тому, что нет разницы
между значениями параметра и и и + max + nay. Вместо того чтобы быть просто двумерным
векторным пространством, пространство параметра порядка для кристалла оказывается
квадратом с периодическими граничными условиями.
Рис. 9.7. Пространство параметра порядка для кристалла
Обратите внимание, что если склеить противоположные стороны квадрата (задавая таким
образом периодические граничные условия), то получится тор. Тором называется фигура,
представляющая собой поверхность пончика, автомобильной камеры или бублика
(выберите, что вам более знакомо).
гелии локальная концентрация атомов становится неопределенной величиной (см.
упражнение 9.8)
368 Гл.9. Параметры порядка, нарушение симметрии и топология
заданного вещества при заданной температуре, так что топологическое
пространство параметров порядка представляет собой множество комплексных
чисел с фиксированным модулем \ψ\. Другими словами, пространство
параметров порядка для сверхпроводников и сверхтекучих жидкостей — это круг
S1.
Рассмотрим теперь малые отклонения от однородного распределения
параметра порядка.
9.3 Исследование элементарных возбуждений
Люди — удивительно медлительные существа. За время, нужное, чтобы
моргнуть глазом, атомы, из которых состоят ваши ресницы, сталкиваются
миллионы миллионов раз. Поэтому неудивительно, что в физике
конденсированного состояния мы тратим большую часть времени на изучение
медленных явлений. Как правило, только коллективные движения огромного
количества атомов могут происходить достаточно медленно, чтобы человек
успевал их заметить.
Хороший пример такого явления — это звуковые волны. Мы не будем
здесь говорить о звуковых волнах в воздухе; воздух — среда с ненарушенной
симметрией, так что ему нечего делать в этой главе.7 Вместо этого
рассмотрим распространение звука в одномерном кристалле, показанном на рис. 9.8.
Мы описываем наше вещество полем параметра порядка и(х), где χ — точка
внутри вещества, χ — и(х) — положение на идеальной решетке,
соответствующее этой точке.
Далее, деформация идеального кристалла должна стоить сколько-то
энергии.8 Однородное смещение, однако, не будет стоить ничего; состояние
с и(х) = щ имеет ту же энергию, что и идеальный кристалл. (Сдвиг всех
атомов вправо на равное расстояние не вызывает изменения энергии.)
Таким образом, энергия будет зависеть только от производных функции
и(х). Простейшее возможное выражение для нее имеет вид9
п Г Л 1 fdu\2
с = / αχ -κ ι — ι ·
J 2 \dxj
Мы показываем здесь, что низкочастотные возмущения могут возникать из
спонтанного нарушения симметрии. Кроме того, они могут возникать и из законов локального
сохранения: поскольку воздух не возникает из ничего и не исчезает бесследно,
длинноволновая модуляция плотности не может быстро релаксировать.
8При конечных температурах имеется в виду свободная энергия.
9См. упражнения 9.5 и 9.6.
(9.2)
9.3. Исследование элементарных возбуждений
369
Рис. 9.8. Одномерная звуковая волна
Параметр порядка для одномерного кристалла — это локальное смещение и(х).
Длинноволновые возмущения и(х) соответствуют низким частотам и являются причиной звука.
Кристаллы являются твердыми телами из-за нарушения трансляционной симметрии.
(Стекла — тоже твердые вещества, но мы не понимаем фундаментальной причины их
твердости [133].) Твердость означает, что они сопротивляются смещениям. Поскольку существует
подлежащая трансляционная симметрия пространства, однородное смещение не
вызывает изменения энергии. Почти однородное смещение, соответственно, стоит совсем немного
энергии и будет, соответственно, иметь низкую частоту. Такие низкочастотные
элементарные возбуждения — это звуковые волны в кристаллах.
В низкочастотной области (т.е. области, различимой для человеческого уха)
более старшие производные не будут давать заметного вклада.10 Далее,
возможно, вы помните закон Ньютона F = та. Сила в данном случае — это
производная от энергии F = — (d£/dn). Роль массы играет плотность
вещества р. Проведя некоторые математические выкладки (вариационное
дифференцирование и интегрирование по частям, если вам интересно), можно
получить волновое уравнение
рй = K{d2u/dx2). (9.3)
Решение этого уравнения
и(х, t) = щ cos(kx — Ukt) (9.4)
соответствует звуковым волнам, или фононам. Длина звуковой волны λ =
2π/Α:, а частота (в радианах в секунду) — ω. Подставляя уравнение (9.4) в
уравнение (9.3), получаем соотношение
ω = у/к/ рк. (9.5)
Частота становится мала только тогда, когда длина волны стремится к
бесконечности. Это очень общее наблюдение: медленно могут происходит
10Члены, в которые входят высшие производные, становятся малы на больших
пространственных и временных масштабах; n-ая производная от функции, меняющейся на
масштабе порядка D, имеет порядок дпи/дхп ~ 1/Dn. (Проверьте это; возьмите 400-ю
производную от и(х) = cos(2nx/D).) Производные в степени η > 1 также становятся малы:
(ди/дх)п ~ l/Dn.)
370 Гл.9. Параметры порядка, нарушение симметрии и топология
только очень крупномасштабные шевеления огромного числа атомов.
Почему частота в этом случае становится малой? Дело в том, что однородное
смещение (а это то, во что уравнение 9.4 превращается для бесконечной
длины волны) вовсе не стоит никакой энергии. Почему однородное смещение не
стоит энергии? Потому что существует трансляционная симметрия: сдвиг
всех атомов на одинаковое расстояние не меняет их взаимодействий. Но не
говорили ли мы только что, что трансляционная симметрия у нас как раз
нарушена? В том-то и дело!
Значительно позже, чем было понято поведение фононов, Джеффри Гол-
дстоун начал размышлять о нарушении симметрии и параметрах порядка в
общем виде. Ему удалось показать, что в довольно общем случае, когда
имеется нарушение какой-то непрерывной симметрии (трансляционной,
вращательной, SU(3), ...), длинноволновые возмущения в направлении этой
симметрии обязаны быть низкочастотными (см. упражнение 10.9). Тот факт, что
основное состояние системы (т.е. состояние с минимальной энергией)
нарушает симметрию, означает, что система обладает жесткостью;
модулирование параметра порядка будет приводить к увеличению энергии в духе
уравнения (9.2). В случае кристаллов нарушенная трансляционная симметрия
приводит к возникновению сопротивления деформациям и к существованию
низкочастотных фононов (рис. 9.8). В магнитах нарушение симметрии
относительно вращения приводит к возникновению магнитной жесткости и
спиновых волн (рис. 9.9). В нематических жидких кристаллах нарушение
симметрии вращения приводит к возникновению сдвиговой жесткости (нематики
текут, но сопротивляются изгибу!) и волн кручения (рис. 9.10).
\ //М\\\ Utf
Рис. 9.9. Магнетики: спиновые волны
Магнетики нарушают симметрию вращения. Поскольку они сопротивляются локальному
кручению вектора намагниченности, но не сопротивляются однородному повороту, в них
могут возникать низкоэнергетичные возмущения типа спиновых волн.
В сверхтекучих жидкостях нарушенная симметрия — это довольно
экзотическая калибровочная симметрия.11 Нарушение этой симметрии приводит
к появлению нового вида жесткости, который и есть сверхтекучесть.
Сверхтекучесть и сверхпроводимость на самом деле — ничуть не более удивительное
явление, чем обычная жесткость твердых тел. Если вдуматься, то твердость,
скажем, стульев — совершенно удивительная штука. Надавите на несколько
11 См. упражнение 9.8.
9.3. Исследование элементарных возбуждений
371
Рис. 9.10. Нематические жидкие кристаллы: волны кручения
В нематических жидких кристаллах также существуют низкочастотные волны кручения.
атомов с одной стороны стула, и с другой стороны, на расстоянии в
миллиард атомов, они как миленькие начинают двигаться. Точно так же, изменение
потока сверхтекучей жидкости требует кооперативного изменения поведения
макроскопически большого числа атомов, и потому не может происходить
спонтанно, точно так же, как части стула не могут начать спонтанно
двигаться в разные стороны.12
Низкочастотные голдстоуновские моды в сверхтекучей жидкости — это
волны тепла! (Не завидуйте им; теплые волны в жидком гелии — это очень
холодные теплые волны.) Часто эти волны называют вторым звуком, но на
самом деле это просто периодические модуляции температуры,
распространяющиеся в веществе так же, как звук распространяется в кристаллах.
Чтобы закрыть тему, надо теперь обсудить ситуацию в
сверхпроводниках. В них тоже есть нарушение калибровочной симметрии, и они обладают
жесткостью, которая приводит к существованию незатухающих токов. Но как
быть с низкоэнергетическими возбуждениями? В сверхпроводниках их нет.
Постойте, а как же теорема Голдстоуна?
В теореме Голдстоуна, разумеется, есть дополнительные условия,
которые исключают сверхпроводники из области ее применимости. (Собственно
говоря, Голдстоун занимался как раз сверхпроводниками, когда вывел свою
12Переводчику приходилось быть свидетелем такого спонтанного движения, но,
справедливости ради стоит отметить, что в этот момент стул испытывал на себе давление человека,
который на нем сидел. — Прим. переводчика.
372 Гл.9. Параметры порядка, нарушение симметрии и топология
теорему.) Но, конечно же, все позабыли об этих дополнительных условиях и
запомнили только, что при нарушении непрерывной симметрии всегда
возникает низкочастотная мода. В физике конденсированного состояния мы всегда
знали, почему в сверхпроводниках нет голдстоуновской моды; Ф.У.
Андерсон показал, что ее отсутствие связано с наличием дальнодействующего ку-
лоновского взаимодействия и с эффектом Мейснера. В физике же высоких
энергий об этом особом случае забыли, и им пришлось переоткрывать этот
эффект самостоятельно. С тех пор это исключение из теоремы Голдстоуна
принято называть механизмом Хиггса, поскольку (откровенно говоря) Хиггс
и его товарищи из физики высоких энергий нашли более простое и элегантное
объяснение механизма, чем мы в физике конденсированного состояния.13
Завершим этот раздел обсуждением еще одно исключения из теоремы
Голдстоуна, исключения, о котором мы знаем даже дольше, чем о
сверхпроводниках, но которое так и не имеет красивого объяснения. Как быть с
ориентационным порядком в кристаллах? Кристаллы же нарушают не
только непрерывную трансляционную, но и непрерывную вращательную
симметрию. Фононы — это голдстоуновские моды, соответствующие сдвигу, но гол-
дстоуновских мод, соответствующих вращению, в кристаллах нет.ы
Волны кручения, подобные волнам в жидких кристаллах (см. рис. 9.10) в
обычных кристаллах запрещены; они разрывают решетку на больших масштабах.
На микроскопическом уровне мы это худо-бедно понимаем, но мы не знаем
красивого макроскопического объяснения этого базового свойства твердых
тел.
13Говоря языком физики конденсированного состояния, голдстоуновская мода
порождает волну зарядовой плотности, чье электрическое поле не зависит от длины волны.
Благодаря этому она обладает конечной частотой (так называемой плазменной частотой) даже
при большой длине волны. На языке физики высоких энергий можно сказать, что фотон
поглощает голдстоуновский бозон и приобретает массу. Эффект Мейснера связан со щелью
в спектре флуктуации параметра порядка (h умножить на плазменную частоту), которую
физики высоких энергий называют массой бозона Хиггса.
14 В двумерном пространстве кристаллы являются исключением из другого знаменитого
факта, так называемой теоремы Мермина—Вагнера. В 1960-х годах Хохенберг, Мермин и
Вагнер показали в серии работ, что двумерные системы с непрерывной симметрией не
могут при конечной температуре нарушать эту непрерывную симметрию. По крайней мере,
именно так обычно пересказывают их теорему; на самом деле они доказали ее для
нескольких частных случаев — для сверхтекучих жидкостей, сверхпроводников, магнетиков и для
трансляционного порядка в кристаллах. Действительно, в двумерии кристаллы не
нарушают трансляционной симметрии; при любой конечной температуре колебаний атомов
оказывается достаточно, чтобы на больших расстояниях их положения перестали в точности
соответствовать друг другу (корреляции в положении атомов медленно спадают с
расстоянием). Но при этом ориентационная симметрия в кристаллах нарушена: оси кристалла
во всех точках пространства указывают в одну сторону (В работе Мермина о кристаллах
этот вопрос обсуждается.) Близкодействующие корреляции в положении атомов (тот факт,
9.4- Классификация топологических дефектов
373
9.4 Классификация топологических дефектов
Когда автор учился в университете, самой модной темой были
топологические дефекты. Все кругом изучали группы гомотопий и выискивали, о
какой бы экзотической системе написать статью. В конечном итоге оказалось,
что это вполне полезное дело.15 Действительно, в большинстве приложений
вы сможете сообразить, каковы возможные дефекты, без всякой теории
гомотопий. Однако, чтобы убедить в этом окружающих, вам придется потратить
огромное количество времени на рисование картинок. И самое важное —
теория гомотопий помогает разбираться в дефектах.
Дефект — это разрыв в поле параметра порядка. Топологический дефект
— это разрыв, который невозможно залатать. Рассмотрим участок
двумерного кристалла, изображенный на рис. 9.11. Начиная с середины показанной
области, в ней появляется лишний ряд атомов. (Такой дефект называется
дислокацией.) Вдали от точки дислокации кристалл локально выглядит вполне
нормальным; он немного деформирован, но в нем нетрудно различить
квадратную решетку и определить для него параметр порядка. Можно ли как-то
передвинуть атомы в непосредственной близости от начала нового ряда, с
тем чтобы починить, залатать дефект?
Нет. Обратите внимание, что мы можем узнать о появлении нового ряда
атомов, и близко не подходя к центру рисунка. Естественный способ сделать
это — это нарисовать большую петлю вокруг дефекта и посчитать число
рядов, пересекающих эту петлю. Например, в петлю, изображенную на рис. 9.12,
входит два ряда атомов, а выходит — три; как бы далеко от дефекта мы ни
находились, справа всегда будет появляться дополнительный ряд.
Как обобщить эту базовую идею на другие системы с нарушенной
симметрией? Вспомним, что пространство параметра порядка для двумерного
кристалла — это тор (см. рис. 9.7), и что значение параметра порядка в
заданной точке — это вектор трансляции, сдвиг на который совмещает
вблизи рассматриваемой точки локально деформированную решетку с идеальной
квадратной решеткой. Далее, чему равно значение параметра порядка
намного левее дефекта (а) по сравнению с(#значением намного правее (d)? Решетка
справа сдвинута по сравнению с решеткой слева на половину шага решетки;
параметр порядка сдвинулся на половину окружности тора. Как показано
что локально они выстроены в ряды и колонки) порождают дальнодействующие силы,
заставляющие оси различных частей кристалла упорядочиться и указывать в одну сторону,
нарушая тем самым ориентационную симметрию.
15Следующая модная тема, теория катастроф, так никогда и не оказалась особенно
важной.
374 Гл.9. Параметры порядка, нарушение симметрии и топология
Рис. 9.11. Дислокации в кристаллах
Здесь изображен дефект в кристалле. Видно, что один из рядов атомов, идущих
справа, исчезает где-то посередине образца. Место, где он исчезает — это дефект, потому что
локально вблизи этого места кристалл выглядит совсем непохожим на идеальный. Это
топологический дефект потому, что никакое локальное движение не позволяет от него
избавиться. Никакая перестановка атомов в середине образца не может исправить тот факт,
что справа в образец «входят» пять рядов атомов, а слева «выходят» только четыре!
Вектором Бюргерса дислокации называется полное число таких добавочных рядов, собранное
в вектор (первая составляющая — столбцы, вторая — строки).
на рис. 9.12, при обходе верхней половины контура по часовой стрелке
параметр порядка (т.е. положение атома внутри элементарной ячейки)
сдвигается вверх, при обходе нижней половины контура он опять сдвигается вверх.
Таким образом, в целом параметр порядка делает полный оборот вокруг
тора. Число намотки вокруг тора — это полное число раз, которое контур в
пространстве параметра порядка опоясывает его за время, пока
соответствующий контур в реальном пространстве обходит дефект.
Почему мы называем дислокации топологическими дефектами?
Топология — это наука о свойствах поверхностей и кривых, не зависящих от изгибов
и деформаций. Поле параметра порядка, которое не опоясывает тор, каким
бы сложно и кособоко устроенным оно ни было, можно непрерывным образом
«разогнуть» и превратить в однородное поле. Если же вдоль какого-то, хотя
бы одного замкнутого контура параметр порядка меняется так, что он
опоясывает тор ненулевое число раз, то это означает, что внутри этого контура
есть дефект, который невозможно «разогнуть»; поскольку «число намотки»
— это целое число, оно не может гладко и непрерывно превратиться из не
нуля в нуль.
Как классифицировать дефекты в двумерных кристаллах с квадратной
решеткой? Видно, что имеются два целых числа, важных для их описания:
число витков вокруг центрального отверстия (т.е. вдоль внешней
окружности тора) и число витков через отверстие (вокруг внутренней окружности).
В традиционном описании эти два числа в точности соответствуют числу
дополнительных рядов и столбцов атомов. В старые времена эта комбинация
9.4- Классификация топологических дефектов
375
Рис. 9.12. Петля вокруг дислокации
Петля вокруг дислокации и ее отображение в пространство параметра порядка.
Рассмотрим петлю, замкнутый контур, нарисованный вокруг дефекта. Значение поля параметра
порядка и меняется, когда мы движемся вдоль этой петли. При движении вдоль нее
положения атомов по сравнению с их локально- «идеальными» положениями плавно
смещаются вверх. Такое движение соответствует некоторой траектории в пространстве параметра
порядка; а именно, траектории однократно опоясывающей отверстие тора. Обход вокруг
отверстия тора соответствует добавлению одного дополнительного столбца атомов.
Плавно сдвигая атомы, мы деформируем траекторию, но никакая непрерывная деформация не
может изменить того, сколько раз наша траектория опоясывает тор. С другой стороны, две
траектории, охватывающие тор одинаковое количество раз, эквивалентны, т.е. их можно
перевести друг в друга непрерывным преобразованием.
двух чисел называлась вектором Бюргерса и все прекрасно ее понимали без
всяких торов. Теперь мы называем ее гомотопической группой тора:
Πι(Τ2)=ΖχΖ, (9.6)
где Ζ обозначает целые числа. Другими словами, дефект можно описывать
двумя целыми числами (га, п), где га соответствует числу дополнительных
рядов атомов в правой части петли, а п — числу дополнительных столбцов в
нижней части.
На этом месте уместно поговорить о практическом значении
топологических дефектов. К сожалению, у нас нет возможности приложить к каждой
копии книги по мягкой медной трубке, с которой вы могли бы проэкспери-
ментировать. На своих лекциях автор делает именно так: такая трубка стоит
всего несколько центов, и механики двух континентов с удовольствием режут
их на кусочки для демонстраций, но упаковать такую трубку в книгу никак
376
Гл.9. Параметры порядка, нарушение симметрии и топология
не получается. Так или иначе, медь и большинство других металлов
обладают свойством, которое называется наклёп, или у жестчение при
деформации.16 Медную трубку очень легко согнуть, но удивительно трудно разогнуть
обратно. В начальном состоянии мягкая медь почти свободна от дефектов.
Чтобы согнуться, металлу приходится создать множество линейных
дислокаций, которые, двигаясь, и создают изгиб.17
Линейные дефекты запутываются между собой и мешают появлению
новых дефектов. Поэтому, когда вы пытаетесь разогнуть трубку, металл
становится гораздо жестче. Явление ужестчения при деформации оказало
существенное влияние на массовую культуру: волшебник без малейшего
усилия сгибает кусок металла, который не может потом разогнуть могучий
силач..., супермэн сгибает железный прут и превращает его в наручники
для преступников...
Прежде чем объяснить, почему дефекты образуют группу, приведем еще
несколько примеров топологических дефектов и того, каким образом их
можно классифицировать. На рис. 9.13 изображен дефект магнита, который
называется «ёж». Попросту говоря, намагниченность во всех направлениях
указывает от центра. Каким образом, не подходя близко к дефекту, узнать, что
он существует? Поскольку речь идет о точечном дефекте в трехмерном
пространстве, нам необходимо окружить его сферой. Когда мы двигаемся по
этой сфере в реальном пространстве, соответствующий параметр порядка
двигается в пространстве параметра порядка (которое, по совпадению, тоже
является в этом случае сферой радиуса |М|). Собственно говоря, при таком
обходе сферы, окружающей дефект, пространство параметра порядка
обходится полностью ровно один раз. Это число (в данном случае — один)
называется числом намотки и не меняется, когда мы непрерывно меняем поле
параметра порядка. Точечные дефекты в магнитах классифицируются по их
числу обертки:
П2(§2) = Z. (9.7)
16Некоторые скрепки тоже твердеют при изгибе, но не так сильно (отчасти потому, что
они уже согнуты). После нескольких изгибов, однако, они перестают твердеть и, наоборот,
на глазах начинают гнуться все легче и легче; это происходит оттого, что они начинают
ломаться на части.
17 Здесь опять играет роль загадочное отсутствие в кристаллах ориентационной голдсто-
уновской моды (см. прим. 14 на с. 372), если бы эта мода существовала, она бы и передавала
изгиб. См. также упражнение 11.5.
9.4- Классификация топологических дефектов
377
Здесь индекс 2 показывает, что мы говорим о второй гомотопической группе.
Это отражает тот факт, что мы окружаем дефект двумерной поверхностью,
а не одномерным контуром, как в случае дислокаций в кристалле.18
Рис. 9.13. Дефект «ёж»
В магнитах нет линейных дефектов (мяч невозможно заарканить), но в них есть точечные
дефекты. Здесь показан дефект типа «ёж», М(х) = Мо х. Точечный дефект в трехмерном
пространстве невозможно охватить петлей, но его можно заключить внутрь сферы. Поле
параметра порядка осуществляет отображение сферы, окружающей дефект, в
пространство параметра порядка. В случае если внутри сферы находится дефект ёж, это
отображение полностью однократно покрывает пространство параметра порядка (напомним, что
это пространство в данном случае — тоже сфера). Точечные дефекты в кристаллах
классифицируются по их числу намотки] вторая группа гомотопий сферы — это Z, целые числа.
Вам может показаться, что топологический дефект мощности семь — это
просто семь дефектов мощности 1, собранные вместе. В общем, вы не так
далеки от истины; иногда дефекты запутываются, но обычно мощные дефекты
распадаются на независимые части. Однако это не значит, что комбинация
двух дефектов всегда порождает более мощный дефект. В нематических
жидких кристаллах два линейных дефекта — это то же самое, что ни одного!
В магнитах не бывает линейных дефектов; замкнутый контур в реальном
пространстве никогда не охватывает что-либо, что нельзя было бы
выправить непрерывным преобразованием поля параметра порядка. Формально это
18Нулевая гомотопическая группа классифицирует доменные стенки. Третья
гомотопическая группа, приложенная к дефектам в трехмерных материалах, классифицирует
то, что в физике конденсированного состояния люди называют текстурами, а в физике
частиц иногда называют скирмионами. Четвертая гомотопическая группа, приложенная
к дефектам интегралов по траекториям в четырехмерном пространстве, классифицирует
типы инстантонов.
378 Гл.9. Параметры порядка, нарушение симметрии и топология
можно показать, заметив, что первая гомотопическая группа сферы состоит
из единственного нулевого элемента; любой замкнутый контур на
поверхности баскетбольного мяча можно стянуть в точку. В нематических жидких
кристаллах, однако, пространство параметров порядка — это полусфера. На
полусфере, как видно из рис. 9.5(b), существует контур, который
невозможно стянуть в точку вращениями или растяжениями параметра порядка. Этот
путь не выглядит замкнутым, но напомним, что противоположные точки на
экваторе полусферы на самом деле соответствуют одной и той же
ориентации нематика. При обходе дефекта направление поля директора η
поворачивается на 180°; на рис. 9.14 показана одна из типичных конфигураций,
соответствующих такому дефекту (называемая дефектом s = —1/2). Теперь,
если соединить два таких дефекта, они сокращаются (см. упражнение 9.1).
Нематические дефекты складываются по модулю 2:19
Πι(ΚΡ2) = Ζ2. (9.8)
Два параллельных дефекта могут слиться и «вылечить друг друга», даже
если каждый из них по отдельности стабилен; каждый дефект соответствует
половине оборота вокруг сферы; состоящий из двух частей полный оборот
можно стянуть в точку.
Наконец, почему мы утверждаем, что классы дефектов образуют
группу? Группа — это множество, на котором введена операция произведения,
не обязательно коммутативная, и в котором для каждого элемента есть
обратный ему относительно этой операции элемент.20 В первой гомотопической
группе элементами являются классы эквивалентности замкнутых контуров;
контуры считаются эквивалентными, если их можно перевести друг в друга
непрерывным преобразованием, при котором они не покидают пространство
параметра порядка.21 Например, любой контур, проходящий через отверстие
в торе сверху вниз (как вверху правого тора на рис. 9.15), эквивалентен
любому другому такому контуру. Чтобы перемножить контур и и контур ν, нужно,
прежде всего, деформировать их таким образом, чтобы они проходили через
19Подобно тому, как часы складываются по модулю 12.
20Кроме того, групповая операция должна быть ассоциативной: а(Ьс) = (аЪ)с и в группе
обязательно должен присутствовать единичный элемент, т.е элемент е, удовлетворяющий
ае = еа = а для любого элемента группы а. — Прим. переводчика.
21 Замкнутый контур — это непрерывное отображение окружности в пространство
параметра порядка: θ —> и(в), 0 < θ < 2π. Когда мы окружаем дефект замкнутой петлей, мы
тем самым порождаем замкнутый контур в пространстве параметра порядка, как
показано на рис. 9.4; θ —¥ х(0) — это петля в реальном пространстве, θ —► u(x(0)) — контур в
пространстве параметра порядка. Два контура эквивалентны, если существует
непрерывное однопараметрическое семейство кривых, соединяющих их друг с другом: и = υ, если
существует непрерывная по0ипоО<£<1 функция ut(6), такая, что ио = и, а и\ = v.
9·4· Классификация топологических дефектов
379
Рис. 9.14. Линейный дефект в нематическом жидком кристалле
Заарканить сферу нельзя, но можно заарканить полусферу! На рисунке изображен дефект,
соответствующий контуру, изображенному на рисунке 9.5(b). При обходе вокруг дефекта
по часовой стрелке, параметр порядка поворачивался бы против часовой стрелки на 180°.
Путь, изображенный на рисунке 9.5(b), соответствовал бы обходу правой стороны
полусферы. Обход вокруг левой стороны привел бы к появлению дефекта, соответствующего
повороту параметра порядка на 180° по часовой стрелке. Маршрут, изображенный на 9.5(b)
представляет собой нечто промежуточное и показывает, что эти два дефекта не являются
топологически различными (см. упражнение 9.1).
одну точку. Затем мы определяем новый контур и ® г>, который состоит из
последовательных обходов сначала контура и, а затем — контура v.22
Обратным контуром к контуру и является тот же самый контур,
пройденный в обратном направлении. Единичный элемент — это класс
эквивалентности контуров, которые не охватывают ни одну из «ручек» поверхности;
каждый из этих контуров может быть непрерывно стянут в точку (а
следовательно, и превращен в любой другой контур из этого класса
эквивалентности). Наконец, закон перемножения контуров имеет прямую физическую
интерпретацию: окружение двух дефектов мощностей и и ν полностью
эквивалентно окружению одного дефекта мощности и® ν (см. рис. 9.15).
Все это выглядит довольно абстрактно; возможно, обсуждение
пространств параметров порядка и замкнутых контуров в них приводит
к более ясному пониманию проблемы, но можно ли где-нибудь
непосредственно применить все это обсуждение групповой структуры
дефектов? Закончим эту главу обсуждением поразительного физического
следствия из законов группового умножения, описанных выше.
22Другими словами, если и и υ пересекаются при θ = 0 = 2π, мы определяем и <£) ν(θ) =
и(2в) при 0 < 0 <пии® ν(θ) = ν(2θ) при π < θ < 2π.
380
Гл.9. Параметры порядка, нарушение симметрии и топология
Рис. 9.15. Перемножение контуров
Произведение двух контуров — это контур, начинающийся от их пересечения и проходящий
сначала вдоль первого, а затем — вдоль второго. Контур, обратный данному — это тот же
самый контур, пройденный задом наперед; если умножить контур на его обратный,
результат, очевидно, сокращается. Такое определение задает групповую операцию на множестве
гомотопических классов. Это правило умножения имеет физическую интерпретацию. Если
два линейных дефекта сливаются, их гомотопический класс задается контуром, который
охватывает их обоих. Этот большой контур может быть деформирован таким образом,
чтобы его можно было разбить на два маленьких контура, так что гомотопический класс
объединения двух дефектов равен произведению гомотопических классов отдельных
дефектов.
Рис. 9.16. Два дефекта: могут ли они пересечься?
Может ли линейный дефект класса α пересечь дефект класса /3, не образовав
топологического зацепления?
9.4· Классификация топологических дефектов
381
Рис. 9.17. Стягивание петли с точки зацепления дефектов
Видно, что линейный дефект, смещающийся влево, оставляет за собой след — зацепление
за правый дефект. Можно ли считать что этот след (двойная линия: до левого дефекта,
вокруг него и назад) топологически эквивалентен единице, т.е. отсутствию дефекта?
Окружим двойную линию замкнутым контуром. Деформируя этот контур, можно заставить его
«съехать вниз» с двойной линии, но он все равно будет охватывать оба дефекта α и /3, как
показано на рисунке.
Могут ли два линейных дефекта пересечь друг друга? На рис. 9.16
показаны два непараллельных друг другу линейных дефекта мощности
(гомотопического типа) α и β. Пусть некоторая внешняя сила пытается перетащить
дефект α через дефект β. На рис. 9.17 показано положение двух дефектов.
Видно, что после пересечения остается след, зацепление дефектов, а может
пройти через β не зацепившись, только если этот след можно стереть. Что
для этого требуется? Требуется, чтобы суммарная мощность дефекта,
измеренная вдоль петли, показанной на рис. 9.17, была равна нулю.
Возьмите две проволоки и кусок нитки или веревки. Согните
проволоки таким образом, как показано на рис. 9.17. Веревку свяжите в
достаточно большую замкнутую петлю и обхватите ею точку зацепления проволок.
Покрутите веревку, попытайтесь стянуть ее с точки зацепления в область,
382
Гл.9. Параметры порядка, нарушение симметрии и топология
где проволоки параллельны. Вы увидите, что полностью стащить веревку с
проволок невозможно (помните, что перебрасывать петлю через концы
проволоки запрещено!), но что вы можете стащить ее вниз так, что она образует
конфигурацию, изображенную на рис. 9.18.
Рис. 9.18. Некоммутирующие дефекты
Гомотопический класс петли на рисунке — это βα/3_1α_1, что равно единице (соответствует
отсутствию дефекта) тогда и только тогда, когда βα = αβ. Таким образом, два линейных
дефекта могут проходить друг сквозь друга только в случае, если соответствующие
гомотопические классы коммутируют!
На этом рисунке мы видим, что каждая проволока обходится веревкой два
раза — один раз по часовой стрелке и один раз против. Сокращаются ли эти
обходы? Совсем не обязательно! Приглядевшись, вы увидите, что порядок
обхода дефектов таков, что полный гомотопический класс нашего
веревочного контура — это /3α/?_1α_1, такая комбинация равна единице тогда и только
тогда, когда β и а коммутируют. Поэтому вопрос о физическом зацеплении
дефектов напрямую связан со структурой группы контуров; коммутирующие
дефекты могут проникать друг сквозь друга, некоммутирующие дефекты
запутываются.
В этом месте было бы чрезвычайно красиво закончить утверждением,
что ужестчение меди при изгибе вызвано топологическим зацеплением
дефектов. Однако это неправда. Гомотопическая группа дислокаций в меди с
гранецентрированной кубической решеткой коммутативна. (Она очень
похожа на группу дислокаций в двумерном кристалле; пусть α = (τη, η) и
β = (°?Р)5 гДе яг,п,о,р — числа дополнительных строк и столбцов атомов,
тогда αβ = (τη + ο,η + ρ) = βα.) Причина, по которой дислокации в
меди не пересекают друг друга — энергетическая, а не топологическая. Линии
дислокаций сильно взаимодействуют между собой, и энергетически
связываются друг с другом, когда пытаются пересечься. Как вы помните, в начале
главы мы говорили, что в нашей теории есть дыры; топологическая теория
дефектов может предсказать, что некоторые вещи невозможно сделать, но
она ничего не знает о том, что некоторые возможные вещи сделать очень
сложно.
Гл.9. Упражнения
383
Нам бы очень хотелось сказать вам, что эта красивая связь между
коммутативностью группы и зацеплением линейных дефектов, тем не менее, очень
важна для множества других приложений. Но и это тоже неправда. Известно
два типа материалов, в которых, как считается, есть линейные дефекты,
которые могут запутываться между собой. Первый — это двуосные нематики,
вещества, которые детально изучены теоретиками, хотя их до сих пор никто
еще не нашел. Другой пример — это металлические стекла, для которых
Дэвид Нельсон построил теорию поведения линейных дефектов, отвечающих
за релаксацию фрустраций. Нельсоновские дефекты не коммутируют и,
соответственно, не могут проходить друг сквозь друга. Изначально он
надеялся объяснить замерзание металлических стекол в случайных конфигурациях
через запутывание линейных дефектов. Однако пока что никому не удалось
довести эту идею до стадии готовых формул.
Упражнения
Изображение и осознание структуры топологических дефектов в
различных системах — занимательная и интересная задача. В упражнении
Топологические дефекты в нематических жидких кристаллах мы сможем
визуализировать представления теории гомотопий и интегральный вид
топологических зарядов. Упражнение Топологические дефекты в модели XY
посвящено изучению закона умножения дефектов. Энергия и внутренняя структура
дефекта исследуются в упражнении Энергия дефектов и члены типа
полной дивергенции для случая точечных дефектов, и в упражнении Доменные
стенки в магнетиках для случая поверхностных дефектов.
В упражнениях Симметрии и волновые функции и Теория Ландау для
модели Изинга мы обсудим, как использовать законы симметрии для вывода
новых материальных закономерностей без использования какой-либо
информации о микроскопических свойствах вещества. Во втором из этих
упражнений получено наиболее общее выражение для свободной энергии, совместимое
с симметрией системы, в то время как в первом симметрия используется для
получения уравнений движения в явном виде.
Откуда берутся параметры порядка? В простых жидких кристаллах и
магнетиках природа нарушения симметрии в упорядоченном состоянии
понятна интуитивно. В упражнениях Порядок в сверхкритических жидкостях
384 Гл.9. Параметры порядка, нарушение симметрии и топология
и вихри и Сверхкритические жидкости: матрицы плотности и
недиагональный дальний порядок (последнее из них — достаточно сложное!) мы
введем комплексный параметр порядка для сверхкритических жидкостей и
обсудим нарушение калибровочной симметрии, характерное для
сверхкритических жидкостей. При этом изложение будет идти по пути постепенного
повышения уровня строгости.
9.1 Топологические дефекты в нематических жидких
кристаллах. (Математика, физика конденсированного состояния) Q)
Число намотки S — это число 0net/27r, где 6net — это угол, на который
поворачивается параметр порядка при обходе дефекта. Число намотки
положительно, если параметр порядка поворачивается в том же направлении, в
котором производится обход дефекта (рис. 9.19(a)), и отрицательным, если
поворот происходит в противоположном направлении (рис. 9.19(b)).
5-1/2 S—1/2
Рис. 9.19. Дефекты в нематических жидких кристаллах
(а) дисклинация с S = |, (Ь) дисклинация с S = — |. Точки не имеют физического смысла,
они приведены для того, чтобы вам было легче следить за поворотом направления
директора при обходе контура (начинайте с левой стороны контура и двигайтесь по часовой
стрелке); зачастую у молекул нематика имеются отличающиеся друг от друга головы и
хвосты, но никаких дальнодействующих корреляций между их положениями нет.
Из топологических соображений ясно (см. рис. 9.5(b)), что число намотки
не является, вообще говоря, топологическим инвариантом. Оно является
инвариантом для сверхтекучих жидкостей с гомотопической группой S1 и для
кристаллов с гомотопической группой TD, но не для гейзенберговых
магнитов и не для нематических жидких кристаллов (о которых здесь и идет
речь). Если рассматривать плоскость картинки как экватор полусферы
(пространства параметра порядка для нематиков), видно, что дефект S = 1/2
соответствует обходу левой половины экватора, а дефект S = —1/2 —
обходу правой половины экватора. Такие два контура могут быть непрерывным
образом переведены один в другой; контур, показанный на картинке,
изображающей пространство параметров порядка для нематика (рис. 9.5(b)) — это
как раз нечто промежуточное между двумя такими контурами.
Гл.9. Упражнения
385
Какой из рисунков 9.20 отвечает расположению молекул нематика в
реальном кристалле, соответствующему промежуточному положению между S = 1/2
и S = —1/2, т.е. промежуточному контуру, изображенному на рис. 9.5(b)?
(Изменение формы молекул на рисунке соответствует их повороту в третьем
измерении.)
9.2 Топологические дефекты в XY-модели. (Математика, физика
конденсированного состояния) ©
Пусть параметр порядка т(х,у) для двумерной XY-модели — это
единичный вектор на плоскости (тогда пространство параметра порядка — это
S1). Топологические дефекты классифицируются в соответствии с их числом
намотки s, т.к. Πι(§1) = Ζ. Число намотки — это число оборотов против
часовой стрелки, которые совершает параметр порядка при однократном обходе
дефекта против часовой стрелки.
(a) Чему равны числа намотки для двух дефектов, окруженных контурами А
и В, на рис. 9.21? Чему равно, в соответствии с правилами группового
произведения в Πι(§1), число намотки для контура С1
(b) Скопируйте картинку на отдельный лист бумаги и заполните
пространство снаружи от контуров А и В (вплоть до контура С и дальше) непрерывным,
гладким ненулевым полем, состоящим из единичных векторов. (Указание:
используйте ответ части (Ь) для проверки вашего ответа из части (а).)
Для числа намотки в двумерной XY-модели можно записать формулу,
выражающую его через интеграл по контуру, охватывающему дефект. Пусть
контур D направлен против часовой стрелки и охватывает дефект один раз
(рис. 9.22).
(c) Покажите, что число намотки задается следующим контурным
интегралом вдоль D:
1 / 2
s = — Φ /J(midjm2 - m2djmi)d£j, (9.9)
2?Г J j=i
где χι и Х2 — две координаты на плоскости, dj = д/dxj, a ij — это вектор,
касательный к контуру, вдоль которого производится интегрирование (так что
интеграл имеет форму ^v · d^). (Указания: Запишите m = (cos(0),sin(0));
интеграл от производной по направлению V/ · d£ равен разности значений
функции / на концах кривой интегрирования.)
386
Гл.9. Параметры порядка, нарушение симметрии и топология
(с)
Гл.9. Упражнения
387
Рис. 9.21. Пара дефектов в XY-модели
Два топологических дефекта, каждый из них охвачен контуром, направленным против
часовой стрелки (А и В, соответственно); контур С охватывает оба дефекта и также
направлен против часовой стрелки. Контур в пространстве параметра порядка, соответствующий
С и рассматриваемый как элемент гомотопической группы, равен групповому
произведению контуров, соответствующих А и В.
Рис. 9.22. Окружение дефекта замкнутым контуром
Кривая D однократно охватывает дефект; άί — это единичный вектор, касательный к D в
направлении обхода контура против часовой стрелки. Пусть φ — угол между единичным
вектором m и направлением оси х.
Существуют и другие подобные полезные формулы. Так, число намотки
для векторного параметра порядка и сферической поверхности П2(§2)
выражается через интеграл от якобиана поля параметра порядка.23
9.3 Энергия дефектов и члены типа полной дивергенции. (Физика
конденсированного состояния, математика) Q)
Пусть нематический жидкий кристалл описывается полем параметра
порядка п, представляющего собой единичный вектор в направлении осей
молекул. (Будем считать, что в этом нематике «головы» молекул выстраиваются
3Такие формулы используются, например, в интегралах по траекториям, для того чтобы
задать веса областей различной топологии.
388
Гл.9. Параметры порядка, нарушение симметрии и топология
в одном направлении.24) Плотность свободной энергии для такого нематика
обычно записывают в виде
^bulk[n] =—(divn)z + -g-in · rotn)z
+ ^(nxrotn)2. (9.10)
Пусть в центре сферической капли радиуса Rq находится дефект типа «ёж»
(см. рис. 9.13). так что поле параметра порядка имеет вид п(г) = г = т/\г\ =
(х, у, z)l\Jx2 + у2 + ζ2. «Ёж» — это топологический дефект, который
соответствует однократному оборачиванию сферы.
(a) Покажите, что для ежа rot ή = 0. Вычислите свободную энергию ежа,
проинтегрировав свободную энергию ^[п] по объему шара. Сравните эту
свободную энергию со свободной энергией идеально упорядоченного (ή — константа)
нематика того же объема (считайте, что ή направлен, скажем, в направлении
оси х).
Из каких соображений можно определить, какие именно члены входят в
выражения для свободной энергии, подобные приведенному выше? С одной
стороны, ясно, что некоторые слагаемые запрещены соображениями
симметрии. Но и многие разрешенные из соображений симметрии члены при
записи свободной энергии зачастую опускают. Это связано с тем, что эти члены
представляют собой так называемую «полную дивергенцию». Действительно,
в соответствии с теоремой Гаусса, всякий вклад в свободную энергию,
представляющий собой дивергенцию некоторого векторного поля, может быть
переписан в виде потока этого векторного поля через поверхность
рассматриваемого объекта. В случае периодических граничных условий вклад таких
членов обращается в ноль. Однако система, которую мы рассматривали
выше, в отличие от систем с периодическими граничными условиями, имеет
границу. Можно было бы предположить, что, тем не менее, для
достаточно больших систем вклады типа дивергенции несущественны, т.к. вклад от
потока поля через границу растет пропорционально площади границы, в то
время как вклад от других членов растет пропорционально объему. Но это
предположение не всегда верно.
(b) Добавим в выражение для свободной энергии J^n] новый (разрешенный
симметрией системы) член ^divt^l = Ko(divn) и посмотрим, к какому
результату это приведет. Вычислите вклад этого члена в свободную энергию ежа двумя
24Этот параметр порядка — такой же, как в гейзенберговом антиферромагнетике, однако
антиферромагнетик обладает дополнительной симметрией, в соответствии с которой
параметр порядка может вращаться независимо от вращения пространственных координат. В
жидком кристалле такой симметрии нет.
Гл.9. Упражнения
389
способами: интегрируя этот член по объему, а также используя теорему Гаусса и
вычисляя соответствующий интеграл по поверхности. Сравните полную энергию
/ ^buik + ^divd3^ с полной энергией однородного состояния η = χ, и с полной
энергией «анти-ежа» п(г) = —г. Какая из этих энергий минимальна при
больших значениях До? Как основное состояние при больших До зависит от знака
К01
Слагаемое с Ко из части (Ь), очевидно, никак нельзя считать
пренебрежимо малым! Во многих случаях для жидких кристаллов характерны так
называемые сильно связывающие граничные условия, которые
соответствуют тому, что угол между параметром порядка и поверхностью зафиксирован
и зависит от химической структуры поверхности. В этом случае некоторые
члены типа члена с Ко не включают в выражение для объемной свободной
энергии потому, что они становятся слишком большими: их роль состоит в
том, что они жестко задают граничные условия.25
9.4 Доменные стенки в магнетиках. (Физика конденсированного
состояния) @
Плотность свободной энергии изинговского магнетика с температурой
ниже Тс может быть грубо аппроксимирована двухъямным потенциалом (см.
формулу 9.19) с двумя минимумами в ±то:
Τ = \к{\/т)2 + (μ(Τ)/2)τη2 + (д/4\)т* (9.11)
= \к(\7т)2 + (д/4\)(т2 - т2)2. (9.12)
В этом упражнении мы обсудим структуру доменной стенки, разделяющей
области с положительной и отрицательной намагниченностью.
Будем считать, что намагниченность т(х) меняется только в
направлении оси х, и что га(—оо) = —то, а т(оо) = то- В промежуточной
области, намагниченность должна проходить через невыгодную область ст«0.
Жесткость К не дает намагниченности меняться слишком быстро; параметр
д стремится уменьшить область, в которой намагниченность отличается от
своего равновесного значения ±гпо. В части (а), мы дадим грубую размерную
оценку толщины доменной стенки в терминах параметров К, то и д из
соображений баланса между градиентным членом, который «не любит» тонкие
стенки, и барьерным членом, который «не любит» толстые стенки.
25Ср. механические связи: при рассмотрении шариков, связанных мягкой резинкой,
необходимо учитывать силу, действующую на них со стороны резинки; для шариков, связанных
бесконечно жесткой палкой, достаточно записать связь (граничное условие), что
расстояние между ними сохраняется. — Прим. переводчика.
390
Гл.9. Параметры порядка, нарушение симметрии и топология
Второе слагаемое в Τ — это двухъямный потенциал с барьером В (в
единицах энергии на единицу объема), разделяющим два минимума. Если
граница раздела между доменами с т = —то и т = +гао имеет толщину Δ, то
соответствующий «барьерный» энергетический вклад должен быть порядка
~ В χ Δ на единицу площади границы, следовательно, чтобы
минимизировать этот член, нужно сделать Δ как можно меньше. Первый член в Τ
соответствует жесткости параметра порядка га, его сопротивлению
быстрому изменению в пространстве, соответствующий вклад на единицу площади
границы раздела будет по порядку величины равен ~ К А х (mo/Δ)2.
(a) Используя эти грубые оценки, найдите В, минимизируя сумму двух
вкладов, и получите грубую оценку для энергии на единицу площади доменной стенки
в терминах параметров К, гао и д.
В оставшейся части этого упражнения мы используем вариационный
принцип для вычисления формы доменной стенки (подробнее о
вариационном исчислении вы можете узнать, например, из [89, chapter 12]).
(b) Найдите уравнение, которому должна удовлетворять функция га(х),
минимизирующая F = J Tdx и удовлетворяющая граничным условиям. (Это так
называемое уравнение Эйлера-Лагранжа из вариационного исчисления.)
(c) Покажите, что решение этого уравнения т(х) обладает тем свойством,
что
Ε = {K/2){dm/dx)2 - {д/Щт2 - т20)2 (9.13)
не зависит от х. (Указание: чему равно дЕ/дх?)
Функция Ε аналогична энергии частицы в перевернутой потенциальной
яме, причем χ играет роль времени. Двухъямный потенциал, таким
образом, превращается в потенциал с двумя горками в точках ±Шо· (Сохранение
этой «энергии» следует из трансляционной симметрии системы.) Поиск
минимизирующей функции т(х) соответствует поиску траектории классической
частицы в перевернутом потенциале; частица скатывается с одной горки и
закатывается на другую.
(d) Покажите, используя граничные условия, что Ε = 0. Используя этот
факт, найдите минимизирующую свободную энергию траекторию т(х),
удовлетворяющую граничным условиям т(±ос) = ±то. Была ли верной (с
точностью до порядка) оценка толщины стенки, сделанная вами в части (а)?
(Указание: если вы знаете, что dy/dx = /(у), то вы тем самым знаете и что
fdy/f(y) = fdx.)
Гл.9. Упражнения
391
9.5 Теория Ландау для модели Изинга. (Физика конденсированного
состояния) @
В этой главе основное внимание было уделено топологическим
параметрам порядка, характеризующим различные основные состояния системы со
спонтанно нарушенной симметрией. Для изучения «внутренности» дефектов,
поверхностей, а также высокотемпературных областей вблизи фазовых
переходов необходимо рассматривать параметры порядка с переменным модулем,
а не только направлением.
В разделе 6.7 мы вычислили в явном виде свободную энергию идеального
газа как функцию его плотности. Можно ли использовать соображения
симметрии и разложения свободной энергии в ряды по градиентам, для того
чтобы записать плотность свободной энергии для более реалистичных систем —
в том числе для систем, чье микроскопичечское поведение мы не понимаем?
Лев Ландау использовал такой подход для построения теории магнетиков,
сверхпроводников и сверхтекучих жидкостей во времена, когда
микроскопическая природа последних двух была еще неясна.26 В этом упражнении мы
построим теорию Ландау27 для модели Изинга.28
Мы приведем здесь общий рецепт построения теории и предложим вам
применить этот рецепт для случая модели Изинга. По ходу изложения мы
будем указывать на места, где предположения теории Ландау могут
нарушаться; зачастую это происходит ровно там, где предсказания теории были
бы наиболее интересными.
(1) Выберите поле параметра порядка.
Напомним, что в модели Изинга имеется высокотемпературная
парамагнитная фаза со средней намагниченностью в расчете на один спин га, равной
нулю, и низкотемпературная ферромагнитная фаза с ненулевой средней
намагниченностью на один спин ±га(Т), стремящейся к единице при Τ = 0.
Изинговский магнетик выбирает одно из двух равновесных состояний (со
спином, направленным вверх или вниз); другими словами, в нем происходит
спонтанное нарушение имеющейся в гамильтониане симметрии относительно
26Физики называют этот подход теорией Ландау. Очень похожие формализмы были
развиты во многих областях физики и техники, от жидких кристаллов до «рационально-
механического» подхода к изучению мартенситов (см. упражнения 11.7 и 11.8). Словарь
этих подходов может отличаться (вместо Ландау могут упоминаться Фрэнк, Эриксен и
Лесли, свободные энергии могут называться материальными соотношениями, параметры
порядка — внутренними переменными), но основа подхода сохраняется.
27Точнее говоря, теорию Гинзбурга—Ландау, т.к. мы будем включать градиенты в
выражение для свободной энергии, что было впервые сделано Гинзбургом в его совместной
работе с Ландау.
28См. также упражнение 12.5, в котором обсуждается более традиционная форма
приближения среднего поля.
392
Гл.9. Параметры порядка, нарушение симметрии и топология
направления спина. Поэтому естественный выбор параметра порядка29 — это
скаляр т(х), локальное значение намагниченности, усредненное по
некоторому объему Δν, полученное усреднением намагниченности на один спин в
маленьких объемчиках (см. раздел 6.7).
(a) Чему будет равна намагниченность га(х) при температурах, больших по
сравнению с параметром взаимодействия модели Изинга J? Чему она будет
равна при температурах, очень малых по сравнению с J?
(2) Запишите в общем виде выражение для локальной30 плотности
свободной энергии, удерживая только наиболее длинноволновые члены и
учитывая трансляционную симметрию.
Локальный вид выражения для свободной энергии подразумевает, что она
зависит от значения параметра порядка и его производных:
7"Ising{m, Г} = 7"(х, m, д,т, djdkm,...). (9.14)
Используем разложение в ряд Тейлора по производным, подобно тому, как
мы действовали в разделе 9.3.31 Сохраняя только члены до второго порядка
по т (и, для простоты, опуская градиенты температуры), получим
7*Ising{m, Г} =А(т, Т) + К(т, ТЩт
+ Bij(m,T)didjm
+ аа(т,Т)(дгтЩт). (9.15)
(b) Благодаря какой симметрии мы можем считать, что неизвестные
функции А, В, С и V не зависят от пространственных координат х? Если характерный
масштаб изменения намагниченности велик и равен D, насколько малыми будут
члены, включающие третьи производные, по сравнению с учитываемыми нами
членами, пропорциональными В и С?
(3) Учтите все симметрии задачи.
29Существует более систематический подход к выбору параметра порядка,
предложенный Ландау. Он основан на теории представлений групп и может быть весьма полезен при
рассмотрении более сложных систем.
30Возможно, к параметрам порядка придется добавить дальнодействующие кулоновские,
гравитационные и упругие поля. Для полного описания системы требуется параметр
порядка, учитывающий длинноволновые поля, сохраняющиеся величины и все нарушенные
симметрии системы.
31 Разложение в ряд по производным не работает вблизи границ раздела фаз и в
сердцевине дефектов, т.е. в областях, где параметр порядка существенно меняется на
микроскопическом масштабе. Тем не менее, теория Ландау, будучи точно решаемой, зачастую
все равно используется в этих областях как (неконтролируемое) приближение к реальному
поведению.
Гл.9. Упражнения
393
Модель Изинга обладает симметрией относительно направления спинов
(вверх или вниз),32 так что плотность свободной энергии должна
удовлетворять соотношению .FIsing{m} = Т{—т}. Следовательно, коэффициенты
А и С являются функциями га2, а В и V могут быть записаны в виде
Vi{m,T) = mvi(m2,T) и By(m) = тЬ^(т2,Т).
Двумерная модель Изинга на квадратной решетке симметрична
относительно поворота решетки на 90°. Следовательно, V{ — 0, поскольку никакой
ненулевой вектор не сохраняется при повороте на 90°. Аналогично, Ъ и С
должны коммутировать с этими поворотами, и следовательно должны быть,
с точностью до постоянного множителя, равны единичным матрицам.33
Поэтому имеем
7-Ising{m,T} = Л(т2,Г) + mb(m2,T)V2m
+ C(ra2,T)(Vra)2. (9.16)
Многие системы являются изотропными: плотность свободной энергии в
них должна сохраняться при любых поворотах. В изотропных системах
материальные константы (такие как функции Д Вц и Cij в уравнении 9.15)
должны сохраняться при поворотах. Все вклады в плотность свободной
энергии изотропной системы можно поэтому записать в терминах скалярных и
векторных произведений градиентов поля параметра порядка.
(с) Изменится ли выражение для свободной энергии (9.16) для случая
магнетика с полной вращательной симметрией?
(4) Упростите выражения, используя члены вида полной дивергенции.
По своей сути, плотность свободной энергии — до некоторой степени
произвольная величина. Если добавить к Τ градиент произвольной гладкой
функции V-£(m), полная свободная энергия (т.е. объемный интеграл от плотности
энергии. — Прим. переводчика) изменится лишь на член, равный
поверхностному интегралу /V · £(m)dV = J £(га) · dS. Во многих случаях такими
поверхностными членами можно пренебречь, (i) Если система удовлетворяет
периодическим граничным условиям, то интеграл f £(т) · dS = 0, поскольку
противоположные грани рассматриваемого объема дают противоположные и
сокращающиеся вклады, (ii) В больших системах поверхность занимает очень
32Равновесное состояние может не обладать этой симметрией, но модель — а
следовательно и свободная энергия — без сомнения, обладает.
33При повороте на 90° R = (_JJ), вектор ν переходит в R · v. Для того чтобы
вектор сохранился при этом повроте, должно быть (v\ V2) = (^i v2)(_iJ) = (—^2,^1),
следовательно vi = —V2 = —v\ = 0. Симметричная матрица С преобразуется в RCR~l =
(-io)(c1£cm)(i~o) = (-Сие") так что для ее инвариантности необходимо Сц = С22 и
С12 = 0, так что С действительно равна единичной матрице с точностью до множителя.
394
Гл.9. Параметры порядка, нарушение симметрии и топология
малую долю полного объема, так что поверхностные члены можно считать
пренебрежимо малыми /V · £(m)dV = J £(m) · dS ~ L2 <^ J FaV ~ Ls.
(iii) Добавление члена типа полной дивергенции можно «обменять» на
соответствующее изменение поверхностной свободной энергии, зависящей от
ориентации поля параметра порядка вблизи поверхности образца.34
Благодаря этому мы можем проинтегрировать вклады в свободную
энергию по частям; вычитая полную дивергенцию V(uv) из свободной энергии,
мы можем заменить член и Vv на член — ν Via. Например, мы можем вычесть
член —V · (rab(ra2,T)Vra) из свободной энергии (9.16):
7-Ising{m,T}
= A{m2,T) + mb{m2,T)V2rri
+ C(m2,T)(Vm)2
- V(rab(ra2,T)· Vra)
= A(m2,T) + C(m2,T)(Vm)2
- V(rab(ra2,T)) · Vm
= A{m2,T) + C{m2,T){Vm)2
- (b{m2,T) + 2m2b'(m2,T)) (Vm)2
= A(m2,T)
+ (С(т2,Г)-Ь(т2,Г)
- 2m2b/(m2,T))(Vm)2, (9.17)
что позволяет нам заменить (mb(m2, Τ)) (V2m) на эквивалентное слагаемое
— (Vra)(V(rab(ra2,T)Vra) · Vm). Таким образом, мы можем заменить член,
пропорциональный bV2m, на пропорциональный (Vm)2, при этом
возникает перенормированное значение коэффициента с = С(т2,Т) — Ь(тп2,Т) —
2т2г/(т2,Г)и
7"Ising{m, Г} = Aim2, Τ) + c{m2, T)(Vm)2. (9.18)
34См. упражнение 9.3 и [78]. Надо также проявлять осторожность в работе с членами
вида полной дивергенции для случая систем с топологическими дефектами,
перечисляющими внутренние поверхности раздела, см. [120].
Гл.9. Упражнения
395
(5) Предположите (попробуйте предположить), что параметр порядка
мал.
Если предположить, что т мало, можно разложить Аиспо степеням га2,
получая А(т2, Т) = /ο+(μ(Τ)/2)τη2+(<7/4!)τη4 и с(га2, Т) = \К, что приводит
к традиционному виду свободной энергии Ландау для модели Изинга:
Rising = }-K(Vm)2 + /о + (м(Г)/2)т2 + (g/4\)m\ (9.19)
где /ο,ρίί также могут зависеть от Т. (Множители 1/2 и 1/4! используются
по историческим причинам.)
Модель с плотностью свободной энергии, задаваемой уравнением (9.19),
— одна из самых изучаемых в физике. В теории поля обычно используют
обозначение ф, а не га, для параметра порядка и называют этот объект
«моделью ф4». Именно для этой модели (с добавлением флуктаций) Кен Вильсон
развил свою теорию ренормализационной группы (см. гл. 12).
Обратите внимание, что свободная энергия Ландау качественно меняется
при обращении коэффициента μ в ноль (рис. 9.23). При положительных μ
она имеет единственный минимум при га = 0; при отрицательных μ имеется
два минимума при га = ±у^—6μ/#. Не связано ли это изменение с переходом
модели Изинга из парамагнитной (га = 0) в ферромагнитную фазу при Тс?
Как мы предполагаем, наше выражение для плотности свободной
энергии уже учитывает флуктуации га на масштабах, малых по сравнению с
масштабом сглаживания W. Если игнорировать флуктуации на масштабах,
больших, чем W, то свободная энергия всей системы будет равна плотности
свободной энергии, умноженной на объем,36 и намагниченность при
температуре Τ будет задаваться минимумом плотности свободной энергии. Тогда
квадратичный член с μ(Τ) обращается в ноль при температуре Тс, и, разлагая
μ(Τ) ~ а(Т — Тс) + ..., получим га = ±у/6а/ду/Тс — Τ вблизи критической
температуры.
35 Обратите внимание, что это приближение не работает для скачкообразных фазовых
переходов, когда параметр порядка остается велик вплоть до точки перехода, и скачком
обращается в ноль при ее прохождении. Теории типа теории Ландау тем не менее часто
применяются и для скачкообразных переходов (см. рис. 11.2(a)), т.к., несмотря на наличие
неконтролируемых неточностей, они все равно проливают свет на происходящее.
36Полная свободная энергия является выпуклой функцией (см. рис. 11.2(a)). Наличие
максимума на графике плотности свободной энергии Τ (рис. 9.23) возможно, если граница
раздела фаз шире, чем характерный масштаб сглаживания. Заметим также, что истинная
полная свободная энергия имеет сингулярности в точках фазовых переходов, в то время
как Τ остается аналитической, это связано с тем, что Τ — это свободная энергия
конечной части системы; истинные фазовые переходы (сингулярности свободной энергии) могут
происходить только в термодинамическом пределе, т.е. в бесконечных системах.
396
Гл.9. Параметры порядка, нарушение симметрии и топология
* г
\
\ У
.... μ>0
— μ = 0
.-. μ<0
• "
"ν
/ '
■ У '
i
N
4_/
Удельная намагниченность m
Рис. 9.23. Свободная энергия Ландау
Плотность свободной энергии Ландау для модели Изинга (9.19) при положительном,
нулевом и отрицательном значении коэффициента μ.
Этот вывод верен качественно, но не количественно. Намагниченность
действительно обращается в ноль при температуре Тс по степенному закону
га ~ (Тс — Т)^, но показатель /?, вообще говоря, не равен 1/2; для двумерных
систем он равен /?2D = 1/8, а для трехмерных /?3D ~ 0.325. Эти показатели (в
особенности предположительно иррациональный показатель для
трехмерного случая) не могут быть получены, даже если мы будем учитывать члены
более высокого порядка в аналитическом разложении Ландау.
(d) Покажите, что показатель /^Landau — 1/2 не меняется в пределе Τ —>· Тс
даже если мы добавим к свободной энергии Ландау (уравнение 9.19)
дополнительный член (/i/6!)ra6. (Другими словами, покажите, что га(Т)/(Т — ТС)Р
стремится к константе при Τ —> Тс.) (Указание: получите квадратное уравнение
для га2. Рассмотрите корень, обращающийся в ноль при Τ = Тс, и
разложите его по степеням h.) Исследуйте также еще один тип фазового перехода, в
котором g = 0, но h > 0; чему равен показатель β для этого перехода?
Как мы видим из рис. 9.24, не существует такой длины W, что на
больших масштабах модель Изинга при Τ = Тс выглядит гладкой и
однородной. Существенные поправки к свободной энергии Ландау возникают на всех
пространственных масштабах; свободная энергия бесконечно большой
системы имеет сингулярность при Τ = Тс (из-за чего наше степенное разложение
jrismg перестает работать). Плотность свободной энергии Ландау — это
только первый шаг в изучении непрерывных фазовых переходов.37 Необходимо
37Важным исключением является сверхпроводимость, т.к. размер куперовских пар в
сверхпроводниках намного превышает типичное расстояние между парами. Благодаря
этому каждая куперовская пара перекрывается с большим числом соседей, что подавляет
флуктуации поля параметра порядка, и теория Ландау остается верна вплоть до очень
узкой окрестности точки перехода.
Гл.9. Упражнения
397
использовать методы ренормализационной группы, развитые в гл. 12, чтобы
научиться объяснять и предсказывать эти сингулярности.
Рис. 9.24. Флуктуации на всех масштабах
Фотография модели Изинга при температуре Тс. Обратите внимание на существование
флуктуации на всех масштабах.
9.6 Симметрия и волновые уравнения. @
Разложения по степеням производных и соображения симметрии можно
использовать не только для вывода новых выражений для свободной
энергии (см. упражнение 9.5), но также и для того, чтобы впрямую выводить
уравнения движения. Этот подход (иногда — с учетом флуктуации)
оказался успешен для ряда систем, находящихся вдали от равновесия [61,69,143].
В этом упражнении вы выведете уравнение движения для скалярного
параметра порядка y{x,t) в одномерной системе. Этот параметр порядка может
иметь смысл поперечного смещения во флуктуирующей одномерной струне,
или продольного смещения молекул в одномерном кристалле, или плотности
молекул одномерного газа.
Запишем закон движения в наиболее общем возможном виде. Начнем
с того, что запишем наиболее общее возможное уравнение эволюции. Такое
уравнение может записываться в терминах производной параметра порядка
по времени dy/dt = ..., как в уравнении диффузии, или в терминах
ускорения d2y/dt2 = ..., как в уравнении колебаний, или в каком-то еще более
общем виде. Перенеся все члены уравнения в левую часть, мы можем
записать его в терминах некоторой (вообще говоря, нелинейной) функции Q от
различных частных производных функции y(x,t):
398
Гл.9. Параметры порядка, нарушение симметрии и топология
б (ν,
ду ду д2у д^у д^у
» )=0· <9а»
Заметьте, что мы уже предположили, что наша система однородна во времени
и пространстве, иначе функция Q явно зависела бы от t и х, соответственно.
Прежде всего, давайте попробуем почувствовать на примере, скажем,
уравнения диффузии, как именно функция Q задает уравнение движения.
(a) Какое распространенное уравнение соответствует подстановке
G{o>iiQ>2, · · ·) — аз — Da± в уравнение (9.20)?
Сосредоточьте внимание на больших временах и масштабах:
используйте разложение по производным. Мы с вами — существа большие и
медленные. Мы в состоянии заметить только такие движения системы, которые
имеют низкие частоты и малые волновые векторы. Каждая производная по
времени (координате) делит нашу функцию на величину, равную
характерному масштабу времени (соответственно, координаты). Поэтому, если мы
хотим ограничиться рассмотрением больших временных и пространственных
масштабов, имеет смысл выкинуть из уравнения все члены с более чем
двумя производными (т.е. все, что соответствует многоточию в уравнении 9.20).
Мы также предположим, что функция Q — аналитическая функция у и его
производных и, следовательно, может быть записана как сумма
произведений своих аргументов. Другими словами, мы предполагаем следующий вид
уравнения
где /, <7, ..., η — какие-то аналитические функции у.
(b) Выпишите пропущеные члены, используя в качестве коэффициентов
функции j{y), k(y), ..., т{у).
Учтите симметрию системы.
Будем полагать, что наша система подобна колебанию струны или
одномерным фононам, так что сдвиг параметра порядка у —> у + Δ — это
преобразование симметрии, сохраняющее нашу систему инвариантной (рис. 9.25).
Из этого следует, что (/, а, следовательно, и /, д, ..., η не зависят от у.
Предположим также, что наша система инвариантна относительно
перемены знака параметра порядка у —> —у, а также относительно инверсии
Гл.9. Упражнения
399
координаты χ —» —χ (рис. 9.26). Точнее говоря, сохраним только те
члены уравнения (9.21), которые являются нечетными по параметру порядка и
четными по координате.
38
У(х,0+А
y(x,t)
Рис. 9.25. Симметрия сдвига
Мы предполагаем, что наша система симметрична относительно однородного сдвига поля
параметра порядка. Другими словами, если j/(x, t) — решение уравнения движения, то
у(х, t) + Δ тоже должно быть решением.
Рис. 9.26. Перевороты и инверсии
Мы предполагаем, что наша система симметрична относительно переворота (у -¥ —у) и
инверсии (х —У —х). Следовательно, если у(ху t) — решение, то у(—х, t) и — y(x,t) — тоже
решения.
(с) Какие три члена уравнения (9.21) выживают после учета этих симметрии?
Какой из них не является частью волнового уравнения d2y/dt2 = с2д2у/дх21
Этот третий член является источником трения. Например, если
колеблющаяся струна находится в вязкой среде (например, покоящемся воздухе),
то медленные колебания (соответствующие малым числам Рейнольдса)
будут затухать по закону, заданному разрешенным симметрией членом из
части (с). В системах, симметричных относительно обращения времени,
диссипации быть не может, и вы можете проверить, что ваш диссипативный член
38 Все члены уравнения движения обязаны иметь одну и ту же симметрию
относительно преобразования симметрии системы. У системы, симметричной относительно инверсии
координаты, уравнение движения может быть как четным, так и нечетным по отношению
к этой инверсии.
400
Гл.9. Параметры порядка, нарушение симметрии и топология
меняет знак при обращении времени t —У — t, в то время как два других члена
не меняются.
Этот третий член не может возникнуть, если струна колеблется в
вакууме. В частности, он неинвариантен относительно преобразований Галилея.
Говорят, что система обладает галилеевской инвариантностью, если она не
меняется при изменении скорости системы отсчета: если y(x,t) — решение,
то у(х, t) + vt — тоже решение.39 При наличии вязкой среды галилеевская
инвариантность не является обязательным требованием: действительно,
преобразование Галилея меняет скорость струны, но не среды, и, следовательно,
система не переходит в себя (относительная скорость струны относительно
воздуха меняется). С другой стороны, внутреннее трение в струне,
связанное с ее изгибом и деформацией, должно быть галилеевски инвариантно.
Такое трение описывается так называемым кельвиновским затуханием
(которое вы можете представлять себе как некий буфер, расположенный внутри
материала параллельно микроскопическим пружинкам, обеспечивающим его
жесткость).
(d) Покажите, что ваш диссипативный член неинвариантен относительно
преобразования Галилея. Покажите, что кельвиновское затухание, описываемое
членом d3y/dtdx2, инвариантно относительно преобразования Галилея и
преобразуется так же, как другие члены волнового уравнения, при сдвиге и перевороте
параметра порядка, а также при инверсии координаты.
9.7 Порядок в сверхтекучих жидкостях и вихри. (Квантовая физика,
физика конденсированного состояния) ©
Сверхтекучесть гелия тесно связана с бозе-конденсацией в идеальном
газе; сильные взаимодействия между атомами гелия меняют многие вещи
количественно, но многие качественные свойства совпадают. В частности, мы
описываем сверхтекучую жидкость в терминах ψ(τ) — комплексного
числа, которое мы интерпретируем как волновую функцию состояния, занятого
макроскопически большой долей атомов жидкости.
(а) Пусть N невзаимодействующих бозонов находятся в одном квантовом
состоянии х(г). Запишите выражение для полной плотности тока J(r).40
Комплексное поле х(г) можно записать в терминах его амплитуды и фазы
x(r) = |x(r)|exp(i^(r)). Плотность сверхтекучей компоненты жидкости равна
39 Эта инвариантность является предельным случаем лоренцевской инвариантности для
случая малых скоростей.
40Используйте стандартное квантово-механическое одночастичное выражение J =
(ih/2m)(ip\7ip* — V>*VV>) и умножьте его на число частиц; или многочастичную формулу
J(r) = (Ш/2га) f d3ri · · · ά3ΤΝ Σε <ΗΓ* ~~ г)(ФУ£Ф* — Ψ^Χ^Ψ), в которую нужно подставить
выражение для волновой функции конденсата Ψ (г ι, ..., rjv) = fj x(rn)·
Гл.9. Упражнения
401
ns = Ν\χ\2. Выразите поток J через φ и ns. Чему равна получившаяся
скорость сверхтекучей компоненты ν = J/nsl (Она должна получиться не
зависящей от ns.)
Традиционно принято нормировать параметр порядка Ландау для
сверхтекучей жидкости φ (г) таким образом, что его амплитуда равна
квадратному корню из плотности сверхтекучей компоненты; в терминах части (а)
ф(т) = VNX(r).
В равновесной статистической механике состояние, содержащее
макроскопическое число частиц, — это всегда основное состояние, которое всегда
является вещественным и, следовательно, не имеет связанных с ним потоков.
Однако можно создавать неравновесные состояния, в которых
макроскопическое число частиц конденсируется в каком-либо другом квантовом
состоянии. Например, экспериментатор может охлаждать движущийся контейнер
с жидким гелием, тогда основное состояние в движущейся системе
координат, связанной с сосудом, будет соответсвовать состоянию с ненулевым
потоком в лабораторной системе координат. Более распространено приготовление
сверхтекучего гелия во вращающемся состоянии.
(b) Рассмотрим тор с дыркой вдоль вертикальной оси, заполненный
идеальным бозе-газом при Τ = 0\ сверхтекучая жидкость конденсируется в состояние,
вращающееся вокруг дырки. Используя выражение, полученное в части (а), и то,
что φ + 2ηπ неотличимо от φ при любом целом п, покажите, что циркуляция
§ ν · dr вокруг дырки квантуется. Чему равен квант циркуляции?
Сверхтекучий гелий может завихряться только квантующимися
порциями! Обратите внимание, что это немедленно объясняет отсутствие вязкости в
сверхтекучей жидкости: скорость вдоль тора квантуется, следовательно, она
не может непрерывно стремиться к нулю; если жидкость начинает вращаться
вокруг тора с некоторым ненулевым вихревым числом п, она должна
сохранять это состояние вращения неограниченно долго.41 Именно поэтому такие
жидкости называются сверхтекучими.
В массе гелия это вихревое число определяет линейные дефекты,
называемые вихревыми линиями (рис. 9.27).
(c) Рассмотрим ф(г), фазу волновой функции бозе-конденсата, как
топологический параметр порядка сверхтекучей жидкости. Является ли пространство
значений этого параметра порядка замкнутой петлей S1? Классифицируйте
возможные типы вихревых линий в сверхтекучей жидкости. (Другими словами,
либо приведите первую гомотопическую группу пространства параметра порядка,
41 Или по крайней мере до того момента, когда произойдет какое-то драматическое
событие, которое изменит п, например, пока вихревая линия не пересечет тор, что потребует
энергии активации, пропориональной толщине тора. См. также упражнение 7.9.
402 Гл.9. Параметры порядка, нарушение симметрии и топология
либо перечислите возможные значения квантованной циркуляции при обходе
вихревой линии.)
14
К <Ί
Рис. 9.27. Вихревая линия в сверхтекучей жидкости
Скорость потока ν(χ) вокруг вихревой линии в сверхтекучей жидкости.
9.8 Сверхтекучие жидкости: матрица плотности и
недиагональный дальний порядок. (Физика конденсированного состояния, квантовая
физика) ©
В этом упражнении мы развиваем квантовую теорию параметров порядка
в сверхтекучих жидкостях и сверхпроводниках, следуя классическому
изложению Андерсона [2,3]. Мы вводим приведенную матрицу плотности,
недиагональный дальний порядок, нарушение калибровочной симметрии и
показываем, что состояние части объема сверхтекучей жидкости естественным
образом описывается как суперпозиция состояний с разным числом частиц.
Это упражнение потребует от вас усилий; в нем предполагается более
хорошее знание квантовой механики, чем в основном тексте, в нем встретятся
технически сложные вычисления, а рассматриваемые понятия будут тонкими
и глубокими...
Матрицы плотности. В упражнении 9.7 мы видели, что бозе-конденсат
идеального газа можно описать в терминах комплексного числа ^(г),
соответствующего чистому квантовому состоянию, занятому макроскопически
большим числом частиц. В гелии при его переходе в сверхтекучее состояние
атомы находятся в сильно взаимодействующем жидком состоянии. Однако
параметр порядка ψ(τ) можно определить и для взаимодействующей системы,
для этого нам понадобится приведенная матрица плотности.
Гл.9. Упражнения
403
Пусть наша система находится в смешанном состоянии, включающем
многочастичные состояния Фа с вероятностями Ра. Полная матрица плотности
в координатном представлении это, как вы помните,
p(ri,...,r^,ri,...,r^)
= ^РаФ*(г!,...,г^)Ф(п,...,г^). (9.22)
а
(Точнее говоря, это матричные элементы матрицы плотности в координатном
представлении; строки помечены индексом {г^}, а столбцы — {tj}.)
Приведенная матрица плотности р(г', г) (которую, начиная с этого места, я буду
называть просто матрицей плотности) получается, если положить г'· = Tj для
всех частиц, кроме одной, проинтегрировать по всем положениям и умножить
на N:
Ν ί d3r2---d3rN
χ ρ(γ\ r2 . ., rN, r, r2,..., rN). (9.23)
(Для наших целей неважно, почему этот объект называется матрицей;
думайте о р2 как об обычной функции двух переменных.)
(а) Как выглядит приведенная матрица плотности /^(γ',γ) для
бозе-конденсата невзаимодействующих частиц при нулевой температуре, если
эти частицы конденсировали в нормированное одночастичное состояние х(г)?
Альтернативная элегантная формулировка понятия матрицы плотности
состоит в том, чтобы вместо многочастичных волновых функций
использовать операторы рождения и уничтожения, принятые во вторичном
квантовании. Эти операторы а'(г) и а(г) добавляют и, соответственно, убирают бозон
в указанной точке пространства. Они подчиняются коммутационным
соотношениям
[a(r),at(r')] = i(r-r'),
[a(r),a(r')] = [at(r),at(r')] = 0;
поскольку в вакууме частиц нет, мы знаем также, что
a(r)|0)=0,
<0|а*(г) = 0.
t, , - (9·25)
Определим кет-волновую функцию как
404
Гл.9. Параметры порядка, нарушение симметрии и топология
|Ф) = (Ι/λ/JV!) / ά3η···ά3ΓΝ
χ Ф(гь ..., г*)а*(п). ·. a*(rN)\0). (9.26)
(b) Покажите, что кет-функция нормирована, если нормирована
симметричная волновая функция Бозе Ф. (Указание: используйте уравнение (9.24), для
того чтобы вытащить все α вправо от at в уравнении (9.26); у вас должна
получиться сумма N\ членов, каждый из которых — произведение N δ-функций,
приравнивающих некоторую перестановку г ι · · · гдг к г[· · -rfN.) Покажите, что
(Ф|а+(г/)а(г)|Ф), т.е. перекрывание а(г)|Ф) с а(г')|Ф) для чистого состояния
|Ф) равно приведенной матрице плотности (9.23).
Поскольку это верно для всех чистых состояний, это должно быть
верно также и для смешанных состояний; следовательно приведенная матрица
плотности — это то же самое, что и математическое ожидание (а^(г')а(г)).
В невырожденном бозе-газе в системе со статистикой Максвелла-Больц-
мана или в системе со статистикой Ферми можно вычислить /92(г7, г) и
показать, что она быстро стремится к нулю при |г' — г| —>· оо. Это естественно; в
большой системе а(г)|Ф(г)) порождает состояние, в котором недостает
частицы, локализованной вблизи г, это состояние не будет перекрываться с
состоянием а(г')|Ф), у которого недостающая частица локализована в удаленной
точке г'.
Недиагональный дальний порядок и параметр порядка сверхтекучего
состояния. Это неверно для сверхтекучих жидкостей; подобно бозе-конденсату
из части (а), сверхтекучие жидкости (несмотря на то что молекулы в них
взаимодействуют, а температура конечна) имеют приведенные матрицы
плотности с недиагональным дальним порядком (ODLRO, по первым буквам
английских слов off-diagonal long-range order, недиагональный дальний
порядок);
р2{т', г) -> ^{т'Щт) при |г' - г| -> оо. (9.27)
Это поведение называется дальним порядком, т.к. оно означает наличие
корреляций между пространственно удаленными точками; оно называется
недиагональным, т.к. диагонали матрицы плотности в координатном
представлении соответствует одинаковое положение в пространстве
г = г'. Параметр порядка сверхтекучей жидкости ψ(τ) описывает
дальнодействующую часть этих корреляций.
(c) Чему равна функция ^(г) для невзаимодействующего бозе-конденсата из
части (а), в терминах волновой функции конденсата х(г)?
Гл.9. Упражнения
405
Приведенная матрица плотности во многом аналогична корреляционной
функции плотность-плотность для газов С(г',г) = (р(г/)/9(г)) и
корреляционной функции для намагниченности (М(г/)М(г)) (см. гл. 10). Тот факт,
что р2 имеет неисчезающую на бесконечности часть, аналогичен тому, что
(М(г/)М(г)) ~ (М)2 при г' — г —> оо; дальний порядок для направления
намагниченности — аналог дальнего порядка в корреляциях фазы в
сверхтекучих жидкостях.
Сохранение числа частиц и ψ. Рис. 9.28 иллюстрирует тот факт, что
число частиц, локализованных внутри заданной части объема сверхтекучей
жидкости, — это неопределенная величина. Наше основное состояние локально
нарушает закон сохранения числа частиц.42 Если число частиц в заданной
области — плохо определенная величина, то, возможно, имеет смысл говорить
о локальном состоянии как о суперпозиции состояний с различным числом
частиц? Тогда, возможно, удастся факторизовать недиагональный дальний
порядок (at(r')a(r)) ~ ^*(г;)^(г) до (a^(r/))(a(r)), где^(г) = (а). (Эта
величина равна нулю в замкнутой системе, т.к. a(r) меняет полное число частиц.) В
таком случае немедленно возникает вопрос о том, каким образом
устанавливать относительные фазы между волновыми функциями, соответствующими
разному числу частиц. Рассмотрим область достаточно маленькую, чтобы
можно было не обращать внимания на пространственные вариации.
II
«(О
N бозонов
I
Рис. 9.28. Делокализация и ODLRO
Частицы в сверхтекучих жидкостях дел окал изованны: число частиц в заданной части
полного объема — это плохо определенная величина. Аннигиляция бозона в точке г в области I,
если только этот бозон принадлежит конденсату, эквивалентна его аннигиляции в точке г7.
Перекрывание вероятностей этих двух состояний в точности равно р2(г',г) = ψ*(τ')ψ(τ).
42 Это не то же самое, что разница между каноническим и большим каноническим
ансамблями. Большой канонический ансамбль — это смесь состояний с разным числом частиц,
взятых с некоторыми вероятностями; в сверхтекучих жидкостях имеется когерентная
суперпозиция волновых функций с разным числом частиц.
406
Гл.9. Параметры порядка, нарушение симметрии и топология
(d) Рассмотрим бозе-конденсат из N невзаимодействующих частиц при
нулевой температуре, заключенный в такую небольшую область. Пусть
состояние, в которое бозоны конденсируются, пространственно однородно, %(г) = χ =
|x|exp(i<£). Чему равна фаза TV-частичного состояния бозе-конденсата?
Фаза exp(i^(r)) — это относительная фаза между компонентами
локального бозе-конденсата с числом частиц N и N — 1. Сверхтекучее состояние
— это когерентная суперпозиция состояний с различным числом частиц в
локальных областях. Как это странно!
Сохранение импульса происходит из трансляционной симметрии;
сохранение энергии происходит из однородности времени; сохранение момента
импульса — из изотропности пространства. Какая симметрия порождает
сохранение числа частиц?
(e) Рассмотрите гамильтониан Η системы, сохраняющей число частиц,
записанный на языке вторичного квантования (т.е. в терминах операторов рождения
и уничтожения). Покажите, что этот гамильтониан инвариантен относительно
следующей глобальной симметрии: умножения всех операторов рождения на
exp(iC), а операторов уничтожения — на ехр(—Ίζ). (Это соответствует
изменению фазы N-частичных волновых функций на βχρ(\Νζ). Указание: обратите
внимание, что все члены Η содержат равное число операторов рождения и
уничтожения.)
Величина |^(г)|2 описывает плотность сверхтекучей компоненты ns. Как
мы видели выше, для невзаимодействующего бозе-газа при нулевой
температуре ns — это полная плотность; для сверхтекучего гелия это примерно один
процент от полной плотности, а для сверхпроводников — порядка Ю-8. Если
записать φ (г) = y/ns(r) exp(i0(r)), то фаза ф(г) указывает, в каком именно
из состояний с нарушенной симметрией мы оказались.43
Нарушение калибровочной инвариантности. Здесь можно обнаружить
глубокую связь с квантовой электродинамикой, если превратить эту
глобальную симметрию в локальную. Посмотрим, что будет, если сдвинуть φ на фазу
С (я), зависящую от пространственной координаты. Это не изменит члены,
соответствующие потенциальной энергии, но изменит кинетическую энергию,
поскольку она включает градиенты. Рассмотрим чистое одночастичное
состояние. Наша волновая функция χ(χ) превратится в χ = βχρ(ιζ(χ))χ(χ), и
[p2/2m] χ = [((fi/i)V) /2ra] χ теперь включает члены, содержащие V£.
(f) Покажите, что одночастичный гамильтониан инвариантен относительно
преобразования, которое меняет фазу волновой функции на exp(iC(x)) и
одновременно заменяет ρ на ρ — Ηνζ.
43#0(г) — это параметр порядка Ландау; фаза ф(г) — это топологический параметр
порядка.
Гл.9. Упражнения
407
Эта инвариантность при умножении на фазовый множитель тесно
связана с калибровочной инвариантностью в электродинамике. Напомним, что в
классической электродинамике векторный потенциал А определен с
точностью до градиента произвольной функции Л: замена А —у А + VA сохраняет
магнитное поле и, следовательно, не меняет никаких наблюдаемых величин.
Выбор какого-то конкретного Л называется в этой науке выбором калибровки,
а произвольность этого выбора называют калибровочной инвариантностью.
Напомним также, как мы включаем электродинамику в гамильтониан
заряженных частиц: для частицы заряда q мы заменяем кинетическую энергию
на (p—(q/c)A)2/2m, используя «ковариантную производную» (h/i)V — (q/c)A.
В квантовой электродинамике число частиц не сохраняется, но
сохраняется заряд. Наша локальная симметрия, происходящая из локального
сохранения числа частиц, аналогична симметрии в электродинамике, если умножить
волновую функцию на exp(i(g/e)C(x)), где — е — это заряд электрона.
(g) Рассмотрим гамильтониан заряженной частицы в векторном потенциале
Η = ((fi/i)V — (q/c)A)2/2m + V(x). Покажите, что этот гамильтониан
инвариантен относительно преобразования, которое умножает волновую функцию на
exp(i(g/e)C(x)) и производит подходящее калибровочное преобразование А.
Каким должно быть это подходящее преобразование?
Подводя итог, мы показали, что сверхтекучесть приводит к состоянию,
в котором количество частиц локально не определено. Мы увидели, что
состояния локальных областей сверхтекучей жидкости естественно описывать
как когерентные суперпозиции состояний с различным числом частиц.
Амплитуда параметра порядка ^(г) = (а(г)) определяется корнем из плотности
сверхтекучей компоненты, а его фаза exp(i0(r)) задает относительную фазу
между квантовыми состояниями с разным числом частиц. Мы увидели, что
гамильтониан симметричен относительно однородных изменений ф; основное
состояние сверхтекучей жидкости нарушает эту симметрию точно так же, как
низкотемпературное состояние магнетика нарушает симметрию
относительно вращения. Наконец, мы увидели, что превращение этой глобальной
симметрии в локальную требует дополнительных изменений в гамильтониане,
которые полностью аналогичны калибровочным преобразованиям в
электродинамике; сохранение числа частиц происходит из калибровочной симметрии.
Сверхтекучие жидкости спонтанно нарушают калибровочную симметрию!
В [2,3] вы можете найти продолжение этих рассуждений. В частности,
число частиц N и фаза φ оказываются сопряженными переменными. Это
подразумевает уравнение ihN = [Η, Ν] = idH/дф, которое дает ток Джозефсона
и которое также связано с уравнением для скорости сверхтекучей жидкости,
которое мы вывели в упражнении 9.7.
Глава 10
Корреляции, отклик
и диссипация
В этой главе мы рассмотрим, как системы флуктуируют, как реагируют
на внешние возмущения и рассеивают (диссипируют) энергию.1
Макроскопически вещество в состоянии теплового равновесия выглядит
однородным и неизменным во времени, однако на микроскопическом уровне
из-за тепловых флуктуации оно всегда флуктуирует, «подрагивает». Для
измерения таких подрагиваний в их развитии используют корреляционные
функции. В разделе 10.1 мы дадим определение корреляционных функций, а
в разделе 10.2 отметим, что их можно измерить непосредственно в
экспериментах по рассеянию (например, рентгеновских лучей, нейтронов и
электронов). В разделе 10.3 мы покажем на примере идеального газа, как можно
использовать методы статистической механики для вычисления одновременных
корреляционных функций. В разделе 10.4 мы используем гипотезу регрессии
Онзагера, для того чтобы вывести корреляционные функции, зависящие от
времени.
Во многих случаях важно знать, каким образом система реагирует на
какое-либо внешнее возмущение. Теория линейного отклика — это
систематический метод, позволяющий описывать реакцию равновесных систем на
слабые внешние возмущения. Используя методы статистической механики,
можно вычислить реакцию системы на приложенное механическое
напряжение, электрическое или магнитное поле, воздействие звуковой волны или
света. В каждом из этих случаев зависящий от координат и времени линейный
1 Дополнительную информацию на эту тему вы сможете найти для классических систем
в [22, chapter 8], а для квантовых — в [44,88].
10.1. Корреляционные функции: мотивация
409
отклик на зависящее от координат и времени внешнее воздействие
описывается величиной соответствующей восприимчивости (см. разел 10.5).
Существует очень тесная взаимосвязь между флуктуациями,
податливостью2 и диссипацией в равновесных системах. В разделе 10.6 мы покажем,
что податливость и диссипация — это в точности действительная и мнимая
части восприимчивости. В разделе 10.7 будет показано что статическая
восприимчивость пропорциональна одновременной корреляционной функции. В
разделе 10.8 мы выведем флуктуационно-диссипационную теорему,
описывающую динамическую восприимчивость в терминах корреляционной
функции, зависящей от времени. Наконец, в разделе 10.9 мы используем
принцип причинности (тот факт, что отклик на внешнее воздействие не может
произойти раньше этого воздействия), для того чтобы вывести соотношение
Крамерса—Крёнига, связывающее действительную и мнимую части
восприимчивости (податливость и диссипацию) между собой.
10.1 Корреляционные функции: мотивация
Мы научились выводить законы, предсказывающие равновесное
состояние термодинамической системы, и законы, описывающие приближение
систем к равновесию (рис. 10.1 и 10.2). Однако встает вопрос: как количественно
описать исследуемое нами поведение? Каким образом вытащить из
исследуемого ансамбля систем какие-либо проверяемые числа или функции,
описывающие возникающие пространственные паттерны и их развитие во времени,
числа и функции, которые можно было бы использовать для сравнения
теории с экспериментом?
На рис. 10.1 изображен мгновенный снимок модели Изинга при низкой
температуре, точки χ со спином 5(χ,ί), направленным вверх, покрашены
черным, со спином, направленным вниз — белым; черные и белые области
конкурируют между собой [127] за то, кто из них станет новым основным
состоянием с нарушенной симметрией. На рис. 10.2 изображена поверхность
золота, уплощающаяся из иррегулярного начального состояния за счет
тепловых флуктуации [27], показана высота поверхности /i(x, t). Эти рисунки
содержат богатое, полное описание индивидуальных представителей
соответствующих ансамблей, но на их основе очень сложно количественно
определить, насколько эксперименты совпадают с предсказаниями теории. В то же
время, можно количественно описать эволюцию двух этих развивающихся
2 Мы неформально используем слово «податливость» для описания синфазного
реактивного отклика, для описания которого, похоже, нет общепринятого официального термина
(см. раздел 10.6).
410 Гл.10. Корреляции, отклик и диссипация
Рис. 10.1. Фазовое расслоение
Фазовое расслоение в модели Изинга, в которой температура была резко понижена с
высокой до нулевой [127], что привело к замораживанию неоднородностей. Система быстро
разбивается на локальные кластеры («блобы») спинов, направленных вверх и вниз, затем
эти блобы растут и слипаются, образуя блобы все большего размера (см. раздел 11.4.1).
Рис. 10.2. Отжиг поверхности
Снимок поверхности, возникшей в результате бомбардировки пленки золота атомами
благородных газов и тепловой релаксации в течение некоторого времени (Татьяна Курчич и
Барбара Купер [27]). Разрешение рисунка позволяет видеть отдельные моноатомные слои,
каждая из стрелок указывает на яму одноатомной глубины внутри большей ямы.
Типичный размер островков и ям увеличивается по мере релаксации (уплощения) поверхности с
течением времени. Снимок сделан на сканирующем туннельном микроскопе.
10.1. Корреляционные функции: мотивация
411
во времени систем, измерив типичный размер неоднородности как функцию
времени. На рис. 10.3 изображена модель Изинга при критической
температуре Тс, когда флуктуации происходят на всех пространственных и временных
масштабах. В такой равновесной системе нам может понадобиться функция,
которая описывает вероятность того, что черная область простирается на
расстояние г или выживает в течение времени т.
Рис. 10.3. Критические флуктуации
Двумерная модель Изинга на квадратной решетке вблизи критической температуры Тс.
«Острова» однонаправленных спинов в этом случае могут иметь любой размер, а
равновесные флуктуации происходят на всех временных масштабах (см. гл. 12).
Обычно мы измеряем пространственную и временную связность в системе
с помощью корреляционных функций. Вернемся к задаче роста изинговских
блобов и рассмотрим значение двух спинов £(х, t) и £(х+г, t) на расстоянии г
друг от друга в один и тот же момент времени t (см. рис. 10.1. Если |г| намного
больше типичного размера блоба L(t), спины будут направлены в одну или
в разные стороны с вероятностью 50/50, так что их среднее произведение
будет равно нулю. Если |г| намного меньше размера блоба L, спины почти
наверняка будут направлены в одну сторону (оба вверх или оба вниз), так что
среднее от их произведения будет близко к единице. Одновременная спин-
спиновая корреляционная функция
сгЧг) = №,«№ +г, t)> (юл)
будет спадать от единицы при г = 0 до нуля при |r| ^> L(t), и пройдет через
1/2 на расстоянии, равном типичному размеру блоба L(t). В неравновесных
412
Гл.10. Корреляции, отклик и диссипация
задачах, подобных этой, состояние системы меняется со временем, поэтому и
одновременная корреляционная функция также меняется со временем.3
Вообще говоря, корреляционная функция содержит более подробную
информацию, чем просто размер блоба. Рассмотрим, например, равновесную
корреляционную функцию для модели Изинга
С(г, г) = (5(х, t)S(x + г, t + τ)).
(10.2)
Одновременная корреляционная функция С(г, 0) содержит информацию
о том, как отдельный спин влияет на состояние своих соседей. Даже при
высоких температурах, если выделенный спин направлен вверх, то его
ближайшие соседи будут с большей вероятностью направлены вверх, чем вниз.
При приближении температуры к температуре ферромагнитного перехода
Тс это предпочтение распространяется на все более и более дальних соседей
(рис. 10.4). Ниже Тс появляется дальний порядок: даже очень далекие спины
будут склонны выстраиваться в ту же сторону, что и выделенный спин,
потому что каждое из двух равновесных состояний с нарушенной симметрией
имеет ненулевую среднюю намагниченность тп в расчете на один спин. Выше
Тс одновременная корреляционная функция стремится к нулю на больших
расстояниях г; ниже Тс она стремится к га2, поскольку флуктуации спинов,
расположенных далеко друг от друга, становятся нескореллированными:
1
I \ ^^^^^ I
L \ — —— J
m
К '
\>^
ι \ ^^
\
\
1 \
«Ч
X.
1 '
.- выше Τ
с
— ниже Τ
с
«^ .
Ό ξ 4
Расстояние г
Рис. 10.4. Одновременная корреляционная функция
Схематическое изображение одновременной корреляционной функции С (г, τ = 0) при
температуре чуть выше и чуть ниже критической температуры Тс. При г = 0 корреляционная
функция равна (S2) = 1. (Расстояние £(Т), на котором корреляционная функция
экспоненциально спадает к своему пределу на больших расстояниях (т.е. нулю или т2), называется
корреляционной длиной. При температуре Тс корреляционная длина расходится, что
соответствует появлению флуктуации на всех пространственных масштабах, см. гл. 12).
3Мы более подробно обсудим рост зародышей в разделе 11.4.1.
10.1. Корреляционные функции: мотивация
413
£7(00,0) = lim (5(x,t)5(x + r,t)> = (5(x,t))(5(x+ r,t)> = m2.
г—юо
(10.3)
Что происходит при критической температуре? При Τ = Тс
одновременная корреляционная функция спадает на больших расстояниях по
степенному закону С(г, 0) ~ τ-(ά-2+η) (рис Ю.5), что соответствует наличию
корреляций на всех пространственных масштабах, своего рода
компромиссу между ближним и дальним порядком. Аналогично, зависящая от
времени спин-спиновая корреляционная функция (в одной точке пространства)
С(0, т) = (s(t)s(t + τ)) стремится при больших г к нулю, если Τ > Тс, к
га2, если Τ < Тс, а при Τ = Тс спадает по степенному закону с некоторым
новым показателем С(0, г) ~ τ~^ά~2+η^ζ. Мы обсудим, каким образом
можно объяснить появление этих степенных законов, в главе 12, где мы изучим
непрерывные фазовые переходы.
10
S"
£ -ι
υ ίο
г
г
— Τ вблизи Τ
с
— Т
с
1 ' ' ' ;
"\ -
\
\
\
\
">
10 ξ
Расстояние б
1000
Рис. 10.5. Степенное спадание корреляций
Схематическая корреляционная функция из рис. 10.4, перерисованная в логарифмических
координатах при температуре, равной Тс (прямая линия, соответствующая степенному
закону С ~ 7--(d-2+T7)) и выше Тс (где зависимость меняется на С ~ е"
превышающих корреляционную длину £(Т)), см. гл. 12.
г/ЦТ)
на расстояниях,
В других системах можно говорить о корреляционных функциях
плотность-плотность С(г,т) = (р(х + г, t + r)p(x,f)),4 корреляционной
функции высота-высота на поверхности (см. рис. 10.2), корреляционной
функции фазы для параметра порядка сверхтекучести, ...
43десь ρ(χ,ί) = Σι ^(х — xj) измеряет пространственное расположение атомов.
414
Гл.10. Корреляции, отклик и диссипация
10.2 Экспериментальное измерение корреляций
Во многих экспериментах по рассеянию корреляционные функции можно
измерить непосредственно. Рентгеновское рассеяние измеряет
корреляционную функцию электронной плотности, нейтронным рассеянием можно
измерить спин-спиновые корреляции и т.д. Упругое рассеяние дает
одновременные корреляционные функции, в то время как неупругое рассеяние позволяет
измерить корреляционные функции, зависящие от времени.
Опишем вкратце, как это работает, на примере упругого рентгеновского
рассеяния. При дифракции рентгеновских лучей5 (рис. 10.6) плоская волна
с волновым вектором ко рассеивается на образце, причем амплитуда
рассеянной волны с волновым вектором ко + к пропорциональна ре(к) —
преобразованию Фурье от электронной плотности ре(х) в образце.
Интенсивность рассеянного пучка |ре(к)|2 может быть измерена, например,
экспозицией в нем фотопленки. Но эта интенсивность задается преобразованием
Фурье от одновременной корреляционной функции электронной плотности6
Сее(г) = (Pe(x + r, £)ре(х, t)) (см. уравнение А.21):
\р(к)\2 = да*да = JdJ^pwJdxe-^pw
= fdxdx'e-ik(x-x'V(x>(x)
= ίdre"ikr /dx'/9(x>(x' + r)
= /dre-ikry(p(x),9(x + r)) = V idre-ikrC(r)
= VC{k). (10.4)
Таким же образом и в других экспериментах по рассеянию измеряются
двухточечные корреляционные функции, усредненные по всему рассеивающему
объему.
Микроскопия в реальном пространстве и дифракционные эксперименты
в fc-пространстве снабжают нас взаимно дополнительной информацией об
одной и той же системе. Изображения в реальном пространстве несут простую
5Обратите внимание, что используемые в медицине методы рентгенографии и
компьютерной томографии измеряют прохождение рентгеновских лучей, а не их дифракцию.
6Поскольку электроны, как правило, связаны с ядрами атомов, Сее(г) можно переписать
в терминах атом-атомных корреляционных функций (см. упражнение 10.2). Это делается
с помощью форм-факторов [6, chapter 6].
10.3. Одновременные корреляции в идеальном газе
415
Рис. 10.6. Рентгеновское рассеяние
Пучок с волновым вектором ко рассеивается на неоднородностях плотности р(х) с
волновым вектором к, в результате чего получается рассеянная волна с волновым вектором
ко + к; интенсивность в рассеянном пучке пропорциональна |р(к)|2 [6, chapter 6].
непосредственную информацию, легко воспринимаемую человеческим
мозгом. Они бесценны при изучении редких событий (информация о которых
потеряется при усреднении по ансамблю), распределении локальных
геометрий (форм отдельных элементов ансамбля, в противоположность
усредненным значениям) и физических динамических механизмов. С другой стороны,
методы в fc-пространстве соответствуют усреднению по всему образцу,
благодаря чему они могут давать очень точные результаты, тесно связанные с
вычислительными и аналитическими методами (о чем подробно пойдет речь
в этой главе). Действительно, во многих случаях оказывается полезным
сделать экспериментально полученным в реальном пространстве данным
численное преобразование Фурье, для того чтобы получить из них
корреляционные функции (см. упражнение 10.1).
10.3 Одновременные корреляции в идеальном газе
На протяжении оставшейся части этой главы мы будем рассматривать
только системы, находящиеся в равновесии или близкие к равновесию. В этих
случаях мы увидим, что существуют удивительно тесные связи между
корреляциями, откликом и диссипацией. Мы сфокусируемся на идеальном газе,
который представляет собой одновременно и самый простой, и самый
сложный случай. В разделе Упражнения вы исследуете корреляционные функции
более сложные с вычислительной точки зрения (см. упражнение 10.8), но
идеальный газ представляет собой одновременно фундаментальный и
концептуально тонкий случай. Начнем с вычисления одновременной корреляционной
функции Cideal (г, 0).
416
Гл.10. Корреляции, отклик и диссипация
Плотность свободной энергии Гельмгольца для идеального газа равна
J-ideaV(x), Т) = p(*)kBT [log(p(x)A3) - 1] (10.5)
(см. уравнение 6.62). Вероятность Р{р(х)} того, что в результате флуктуации
в системе будет наблюдаться некоторый заданный профиль плотности /э(х),
пропорциональна
Р{р(х)} ос β-βίΓ(ρ(*))**. (Ю.6)
Допустим, что флуктуации малы и разложим это выражение вблизи (р) —
Ро-
•F(p(x)) = То + -^
ч 1 δ2Τ
(Ρ - Ро) + ~
(Р ~ Ρ0Ϋ
Ро
2 V»
= Jb + μο{ρ - Ро) + 2α(Ρ ~ Ро)2, (Ю.7)
где7 μο = {δ^/δρ)\ρη — химический потенциал, а коэффициент перед квад-
д2Т\
'РО
ратичным членом равен
α =
dp2
квТ/ро = Po/pS (10.8)
Ро
(поскольку давление Ро = NksT/V = роквТ). В вероятность входит только
интеграл от свободной энергии
/V(p(x))dx = VTb + μο/^^ /-a(/9-/90)2dx, (10.9)
где член с μο обращается в 0, поскольку среднее от ρ равно ро. Свободный
член То также можно выкинуть, т.к. он просто сдвигает свободную энергию
всех состояний на константу и не меняет относительных вероятностей.8
Таким образом, эффективная свободная энергия для малых флуктуации
плотности идеального газа равна
Нр) = \<*(р-ро)2, (ю.ю)
7δΤ/δρ — это вариационная производная. Τ — это функционал, отображающий
функцию на число; при малом изменении аргумента δρ, Τ{ρ + δρ) — Т{р} = $(δΤ/δρ)δράχ..
Этот интеграл можно рассматривать как своего рода скалярное произведение δρ и δΤ/δρ
(см. раздел А.З, где обсуждаются произведения в функциональном пространстве), так что
вариационная производная — это своего рода градиент функционала, т.е. /(χ -Ι- δ) = V/ · δ.
Действительно, каждый больцмановский вес умножается на фактор e~^v^°, так что
статсумма Ζ умножается на тот же фактор, а отношение e~^vjr° /Ζ, которое и задает
вероятность, оказывается не зависящим от JO.
10.3. Одновременные корреляции в идеальном газе
417
а вероятность найти заданную флуктуацию плотности равна
Р{р(х)} ос e-£/H^°)2dx. (10.11)
Мы можем теперь вычислить математическое ожидание для
одновременной корреляционной функции плотность-плотность:
Cideal(r, 0) = (р(х, i)p(x + г, ί)) - pi = <(p(x, t) - ро)(р(х + г, t) - ро))· (10.12)
Здесь мы вычли квадрат средней плотности, с тем чтобы измерять только
флуктуации параметра порядка вокруг его среднего значения. (После
вычитания среднего получается так называемая связная корреляционная функ-
цая.) Если разбить идеальный газ на маленькие ячейки объема AV, то
вероятность обнаружить плотность p(xj) в j-u объеме равна
Это гауссово распределение со среднеквадратичной шириной
σ = y/l/(PaAV), так что средний квадрат флуктуации внутри одной
ячейки равен
«"-"fl-sav· (1014)
Флуктуации плотности в разных ячейках не скоррелированы. Это означает,
что Cldeal(r, 0) = 0, если г соединяет точки из разных ячеек, и Cideal(0,0) =
1/(βαΔν) внутри одной ячейки.9
Как понимать тот факт, что Cldeal зависит от размера ячейки AV?
Флуктуации становятся сильнее по мере уменьшения размера ячейки. Это для нас
не новость: мы видели при изучении микроканонического ансамбля (см.
раздел 3.2.1 и уравнение 3.67), что квадрат флуктуации числа частиц в
маленьком объеме идеального газа равен математическому ожиданию числа частиц
в этом объеме ((Ν— (Ν))2) = TV,10 так что относительные флуктуации l/y/N
становятся тем больше, чем меньше рассматриваемый объем.
Как записать корреляционную функцию в пределе AV —> 0? Она должна
быть равна бесконечности при г = 0 и нулю для других г. Точнее говоря, она
9Соответственно, корреляционная длина ξ равна нулю для идеального газа (см.
рис. 10.4).
418
Гл.10. Корреляции, отклик и диссипация
должна быть пропорциональна й-функции Дирака, на этот раз — трехмерной
6(r) = S(rx)S(ry)S(rz).
Одновременная корреляционная функция для идеального газа равна
Cideal(r,0) = -^-($(r). (10.16)
pa
Корреляционная функция некоррелированной системы — это белый шум.11
Для того чтобы увидеть, что постоянный множитель при й-функции
действительно равен 1//3α, можно использовать Cldeal для вычисления флуктуации
от полного числа частиц в заданном малом объеме AV (то есть интеграла от
ρ по этому объему):
<(Р - Ро)2>ьох = ( ( д^у Μχ) - Ро) dx)2)
= 7aW/ dx/ dx'((P(x) - PoKp(x') - A)))
= 7XT7N2 / dx / dx' τ-δ(* ~ x')
(AV)2 JAV JAV βα
в согласии с уже полученным нами результатом (уравнение 10.14).
10Согласуются ли два этих утверждения? Используя уравнение (10.8) и закон
Менделеева-Клапейрона PoV = NksT = Ν/β, получаем для флуктуации плотности
{(Р-Ро) ) - (Δν)2
N _ р0
(AV)2 AV
1
_ (p0/P0)(P0/p*)AV
_ 1
~ (ΝIPoV) aAV
= β^Αν (10·15>
в полном соответствии с нашим результатом, полученным из свободной энергии Jrldeal.
11 Белый свет — это смесь света всех частот с равными амплитудами и случайными
фазами (см. упражнение А.8). Наш шум обладает тем же свойством. Преобразование Фурье
от С(г,0), C(k, t = 0) = (l/V)\p(k)\2 (см. уравнение 10.4) — это константа, не зависящая
10.4. Гипотеза регрессии Онзагера и временные корреляции
419
10.4 Гипотеза регрессии Онзагера и временные
корреляции
Равновесная статистическая механика не определяет закон спадания
флуктуации однозначно.
Как воздух, так и небольшая примесь пахучего вещества в нем являются
хорошими примерами идеальных газов. Однако динамика флуктуации
плотности для них существенно различна: для воздуха они приводят к звуковым
волнам, а для пахучей добавки — к диффузии за счет рассеяния на
молекулах воздуха. Для того чтобы описать корреляции во времени, необходимо
помимо статистической механики привлекать какие-то еще дополнительные
сведения. Возможно два основных подхода. С одной стороны, можно идти
от микроскопических законов; действительно, большинство подходов к этой
теме основываются на квантовой механике [44]. С другой стороны, можно (и
мы пойдем в этой главе как раз по этому пути) исходить из макроскопических
законов эволюции.
Каким образом коррелированы во времени флуктуации в идеальном газе?
Например, пусть в момент времени t = О имеется редкая флуктуация,
увеличивающая концентрацию пахучего вещества в данной точке пространства
(рис. 10.7).Каким образом эта флуктуация будет рассасываться, переходить
к более типичному профилю с течением времени?
Макроскопически, концентрация подчиняется уравнению диффузии,
которое обсуждалось в гл. 2. Там мы вывели закон изменения искусственно
созданного неравновесного профиля плотности без учета спонтанных тепловых
флуктуации. Макроскопическое начальное условие (рис. 10.8) будет меняться
в соответствии с уравнением диффузии др/dt = DV2p. При переходе к
микроскопической плотности возникает дополнительная проблема (рис. 10.7): в
то время как старые флуктуации рассасываются, все время спонтанно
возникают новые тепловые флуктуации.
В этой книге мы довольно-таки вольно подходим к обозначению средних,
используя один и тот же символ (·) для усреднения по времени, по
координате, и для усреднения по микроканоническому, каноническому и большому
каноническому ансамблям. В этом разделе нам понадобится использовать
несколько различных средних, так что нам понадобятся для них
различающиеся обозначения. Средние по микроканоническому, каноническому или
от волнового вектора к. Следовательно, все моды имеют равную амплитуду. Чтобы
показать, что фазы случайны, можно выразить свободную энергию (уравнение 10.9) в Фурье-
пространстве, где она оказывается суммой независимых вкладов различных мод;
следовательно, в равновесии относительные фазы этих мод случайны (см. упражнение 10.8).
420
Гл.10. Корреляции, отклик и диссипация
Рис. 10.7. Затухание флуктуации в присутствии шума
Нетипичная флуктуация при t = 0 к более позднему времени τ затухнет до более типичного
состояния.
Рис. 10.8. Детерминированное затухание начального состояния
В отсутствие шума аналогичное начальное состояние плавно затухнет до нуля.
большому каноническому ансамблю не могут быть использованы для
вычисления величин, зависящих больше чем от одной временной переменной, т.к.
равновесные ансамбли независимы от динамики. Пусть (·) обозначает
одновременное равновесное среднее (т.е. среднее по равновесному ансамблю).
Зависящие от времени корреляционные функции определяются как средние
по равновесному ансамблю динамических траекторий (сценариев временного
развития системы), этот ансамбль может включать случайное воздействие
окружающей среды (тепловой шум). Обозначим такое среднее как (·)βν.
Таким образом, (-)ev обобщает (-)eq на случай величин, зависящих от более чем
одной временной переменной. Наконец, обозначим за [·] усреднение по
тепловому шуму от динамики системы с заданным распределением плотности
р(х, 0) = pi(x) в начальный момент времени. Таким образом, мы усредняем
все новые спонтанные тепловые флуктуации и рассматриваем только среднее
затухание заданной начальным условием флуктуации или созданного руками
начального условия.
10.4- Гипотеза регрессии Онзагера и временные корреляции
421
Будем считать, что это последнее среднее при заданном начальном
условии подчиняется тому же самому уравнению диффузии, которое управляет
эволюцией макроскопической плотности системы (см. рис. 10.7 и 10.8). Для
диффузии пахучего вещества, которую мы рассматриваем, это означает
|[p(x,i)]pi=DV2[p(x,i)]pj. (10.18)
Это предположение и есть в точности гипотеза регрессии Онзагера [105]:
... можно предположить, что спонтанно возникшее отклонение от
равновесия релаксирует по тому же закону, как если бы это
отклонение было создано искусственно.
Вычислим корреляционную функцию (р(г + г', t + ί')ρ(τ', t'))ev
следующим образом: возьмем эволюционное среднее при заданном
начальном условии [р(х, t)] , а затем усредним его по всем возможным
начальным условиям р(х, 0) = Pi(x)> считая их распределенными в
соответствии с тепловым равновесием. Используем тот факт, что наша
система однородна в пространстве и времени, так что можно зафиксировать
первую из рассматриваемых точек в начале координат:
С(г, τ) = ((/9(х + г, t + τ) - ро)(р(х, t) ~ Po))ev
= ((/9(r,r)-/90)(p(0,0)-po))ev
= (([P(r,r)]pi -p0)(Pi(0) -po))eq. (10.19)
Другими словами, усреднение и по тепловым флуктуациям, и по
начальным условиям (-)ev равносильно усреднению сначала по тепловому шуму [·].,
а потом по начальным условиям (-)eq. Гипотеза Онзагера говорит нам, что
-ar--(^[P(^)U(A(0)-po))eq
= (£>V2[p(r,i)]A(Pi(0)-po))
= DV2([p(r,i)]pi(Pi(0)-po))eq
= DV2((p(r,f)-po)(p(0,0)-p0))ev
= DV2Cideal(r,i). (10.20)
422
Гл.10. Корреляции, отклик и диссипация
Таким образом, корреляционная функция С подчиняется тому же
уравнению, которое описывает релаксацию искусственно созданного
начального условия. Это общее наблюдение.12
Таким образом, для того чтобы в произвольной системе найти
зависящую от времени корреляционную функцию С, необходимо в качестве
начального условия использовать одновременную корреляционную функцию
С(х, 0), вычисленную из равновесной статистической механики, а в качестве
закона изменения С во времени — соответствующий макроскопический
закон эволюции. В случае идеального газа духов одновременные корреляции
12Используем гипотезу регрессии Онзагера для вычисления корреляционной функции С
для произвольного параметра порядка s(x, t). Пусть макроскопический закон изменения
s(x, t) с точностью до первого порядка по отклонениям от его среднего значения s задается
некоторой функцией Грина (см. раздел 2.4.2):
«5 macro
= s- J dx'G(x-x',£)
X(smacro(x',0)-S). (10.21)
Положим для удобства s = 0. Эта свертка упростится, если мы перейдем к
преобразованию Фурье по координате х, но не по времени £, и используем правило свертки для
преобразований Фурье (см. уравнение А.23):
Smacro(k, t) = G(k, t)s(ky 0), (10.22)
где мы используем шляпку для обозначения преобразования Фурье по координате.
Гипотеза Онзагера гласит, что спонтанная тепловая флуктуация параметра порядка Si будет
эволюционировать по тому же закону
[*(М)]?1 = £(М)*(к)
= 6(M)s(M = 0), (10.23)
так что корреляционная функция
C(r,t) = (S(r,t)S(0,0))ev
= ([s(r,t)lisi(0))e (10.24)
меняется по закону
C(Kt) = ([s(kyt)]Sisi(0))eq
= (6(M)s(k,0)si(0))
= 6(M)C(k,0). (Ю.25)
Таким образом, корреляционная функция опять подчиняется тому же уравнению, по
которому происходит релаксация заданного начального условия.
10.5. Восприимчивость и линейный отклик
423
задаются уравнением (10.16): Cldeal(r, 0) = 1/{βα) <5(г), а закон эволюции —
это уравнение диффузии. Мы знаем, каково решение уравнения диффузии с
^-функциональным начальным условием: оно задается функцией Грина (см.
раздел 2.4.2). Функция Грина уравнения диффузии в одномерном
пространстве — это (см. уравнение 2.32) G(x,t) = (l/y/4nDt)e~x lADt. Для того
чтобы получить G в трехмерном пространстве, необходимо взять произведение
вкладов по осям х, у и ζ. Разделив на βα, получим окончательный ответ
С-(г,т) = iflfcr) = ± (^V'V- (10.26)
Это корреляционная функция для идеального газа, подчиняющегося
уравнению диффузии.
10.5 Восприимчивость и линейный отклик
Как наша система будет реагировать на внешнее воздействие, на удар?
Воосприимчивостъ х(г, τ) описывает отклик на расстоянии г через время г
на (малое) внешнее воздействие в начальный момент времени в начале
координат. Дадим определение понятию восприимчивости для общего случая
некоторого параметра порядка s(x, £), возмущаемого некоторым внешним
полем /(х, t). Другими словами, будем считать, что поле / появляется в
функционале свободной энергии в виде слагаемого
F^Fo + F/, (10.27)
где
Ff(t) = - I dx/(x,f)s(x,f). (10.28)
Вы можете считать, что / — это плотность силы, стремящейся увеличить s.
Если s — это плотность частиц р, то / — это минус потенциал внешнего поля
—V(x), действующего на эти частицы; если s — это намагниченность Μ в
модели Изинга, то / — это внешнее магнитное поле Н\ если s — поляризация
Ρ диэлектрика, то / — это приложенное внешнее электрическое поле Е(х, i).
Для удобства будем считать в этом разделе, что s = О.13
Как параметр порядка s будет реагировать на приложенное внешнее поле
/? Если поле мало, мы можем предполагать, что отклик будет линейным,
Вообще говоря, мы всегда можем определить s как отклонение от среднего значения
параметра порядка в отсутствие внешнего поля.
424
Гл.10. Корреляции, отклик и диссипация
хотя, возможно, и нелокальным в пространстве и времени. Таким образом,
s(x, £)будет зависеть от /(х', t') при всех более ранних временах if < t:
s(x, t)= i dx' / at' χ(χ - x', t - 0/(*', t'). (10.29)
Это нелокальное соотношение выглядит значительно проще, если сделать
преобразование Фурье14 от s, / и χ по координате и времени. Динамическая
восприимчивость х(к, ω) описывается соотношением
?(к,о;) = х(к,ш)7(к,а;), (10.30)
поскольку, как обычно, преобразование Фурье от свертки равно
произведению преобразований Фурье (см. уравнение А.23). Функция χ — это
восприимчивость параметра порядка s к внешнему полю /. Например, поляризация
во внешнем поле описывается поляризуемостью а:15 Р(к,а;) = а(к, а;)Е(к,а;),
намагниченность во внешнем поле равна М(к,ω) = х(к,о;)Н(к, ω), и так
далее.
10.6 Диссипация и мнимая часть восприимчивости
Восприимчивость в реальном пространстве χ(χ, t) — это действительная
функция, но у динамической восприимчивости
Х(к,ш) = y<ixdi е^е-*хХ(Х,<) = Х'(к,ш)+ ίχ"(Κω) (10.31)
есть как действительная χ' = Re[%], так и мнимая часть χ" = Im[%].16 Из
определения ясно, что χ(—к, — ω) = х*(к,о;); кроме того, для систем,
симметричных относительно преобразования инверсии χ <н> —х, верно еще и
14Для обозначения преобразования Фурье от функции Л(х, t) и по координате, и по
времени мы будем пользоваться волной: i4(k,cj). Также волной В(к) мы будем означать
преобразование Фурье по координате от функции #(х), не зависящей от времени. Однако
для преобразования только по координате χ от функции А(х, £), зависящей от коордианты
и времени, мы используем шляпку A(k, t).
15В теории электромагнетизма обычно используется не поляризуемость а, а
диэлектрическая проницаемость е. В системе СИ α = (б — 1)бо,
16Иногда используют определение преобразования Фурье, отличающееся от нашего
комплексным сопряжением (см. раздел АЛ), т.е. тем, что в преобразовании по времени стоит
—i вместо i. Однако в этом случае χ" определяется как минус мнимая часть от
преобразования Фурье обобщенной восприимчивости, в результате чего определение χ" не отличается
от нашего.
10.6. Диссипация и мнимая часть восприимчивости
425
χ(χ, t) = χ(—х, t) и, следовательно, %(к, —ω) = χ*(к, ω), так что χ' — четная
функция w, а χ" - нечетная, χ' описывает согласованный по фазе отклик на
синусоидальное внешнее воздействие, а χ" — отклик, отстающий по фазе.17
В общем случае мнимая часть восприимчивости χ" описывает
диссипацию энергии, вызванную наличием внешнего поля.18 Диссипацию можно
измерить непосредственно (например, измеряя сопротивление проводника как
функцию частоты) или исследуя затухание волн в среде (оптическое,
ультразвуковое затухание и т.д.). Как известно, «энергия» — это интеграл от
«силы» /, умноженной на «перемещение» ds, или сила, умноженная на
скорость ds/dt и проинтегрированная по времени. Пренебрегая для простоты
зависимостью от пространственных переменных, средняя по времени
рассеянная удельная (на единицу объема) мощность ρ равна
»-1&?Γ/<')£*-Λ!.ϊΓ-·(,)**· <ш'зз>
где мы усреднили по времени Τ и произвели интегрирование по частям,
полагая, что в пределе Τ —l· oo краевые члены малы. Полагая внешнюю силу
гармонической f(t) = Re^e-^'] = ^(/„е-1"* + /*е^), имеем
ρ(ω) = Ш^ i £ s{t)^(fwe-^ - £еМ) di, (10.34)
17Если приложить внешнее поле /(£) = cos(cji), т.е. /(ω) = |(£(ω) + δ(—ω)), то отклик
будет описываться s(u>) = χ(ω)/(ω), так что
*> = έ/
β-'ίω*8(ω)άω
= έ(8"ί"χ(ω)+8"χ(-"))
= ^(e"iwt(x,M + ix,,H)
+ eiwt(x,M-ix,/H))
= ^(x'McosM)
+ x"(cj)sinM))· (10.32)
Следовательно, χ' описывает согласованный по фазе отклик, а χ" — отстающий по фазе
на π/2.
18Действительную часть иногда называют реактивным откликом, а мнимую — диссипа-
тивпым.
426
Гл.10. Корреляции, отклик и диссипация
где перемещение s(t) вызвано, в свою очередь, силой, действовавшей в
предыдущие моменты времени:
/»оо
/оо
df'x(i-fW)
-оо
/оо
drX(T)f(t-r)
-оо
= Г dr ^(/ше-^-т) + /:е1ш('-т)). (10.35)
Подставляя уравнение (10.35) в уравнение (10.34), получаем
im — / di /
ρ(ω) = lim - / di / dr
°° ίωχ(τ)
т^сю Τ J0 J_00 4
x (/α,β-^4-') + /;е-(4-т))(/ше--' - /;eiwt)
Г00, ίωχ(τ) ,. 1 Γτ Λ
= άτ Α} ' lim - Ι at
x [/*e"iwi2t-T) - /*2е^24-т) + |/а,|2(е-^т - е^т)] . (10.36)
Первые два члена равны нулю, а третий — это синус,19 так что
Ф) = <^rI°JiT x(r)sin(u;r) = ^МхН]
= ^Х"Н· (10.37)
Поскольку рассеиваемая мощность обязана быть положительной, мы
получаем, что ωχ"(ω) > О.20
Обсудим эту формулу для хорошо знакомого случая выделения тепла на
проводнике, через который течет электрический ток. Под действием
(достаточно низкочастотного) гармонического напряжения V(t) = VLJcos(ut)
проводник с сопротивлением R рассеивает энергию с мощностью (Р) = (V2/R) =
19 В частности,
i(e-iwT-eiwT) = 2sin(u;r),
lim (Ι/Τ) I at e±2iwt = 0
lim (IIT) I at e0iwf = 1.
20Мы уже знаем (см. начало этого раздела), что χ" — четная функция; теперь мы также
знаем, что эта функция положительна при ω > 0.
10.7. Статическая восприимчивость
427
V^(cos2(u;£))/i? = \V2/R в соответствии с законами Ома и Джоуля—Ленца.
В проводнике длины L и поперечного сечения А возникает электрическое
поле Εω coscctf, где Εω = Уш/Ь, а его сопротивление равно R = L/(aA), где σ —
электропроводность металла. Таким образом, средняя удельная рассеиваемая
мощность равна ρ(ω) = (Ρ)/(LA) = \{(ΕωΙ.)2/(L/σΑ)) (I/LA) = \σΕ2ω.
Учитывая, что Εω играет роль силы /ω, а поляризуемость α(ω) — роль
восприимчивости χ(ω), уравнение( 10.37) можно интерпретировать в том смысле,
что статическая проводимость связана с низкочастотным пределом мнимой
части динамической восприимчивости: σ = Ιιτηω^ο ω αμ(ω).
10.7 Статическая восприимчивость
Во многих случаях представляет интерес, как система реагирует на
постоянную внешнюю силу — вместо того чтобы быстро толкнуть систему, мы
надавливаем на нее. Возмущение поля парамера порядка, вызванное
точечным надавливанием, описывается статической восприимчивостью Хо(г).
Если внешняя сила не зависит от времени (так что /(χ',ί') = /(χ')),
система достигнет некоторого сдвинутого состояния равновесия, и мы сможем
использовать равновесную статистическую механику для поиска возникшего
постоянного сдвига в поле параметра порядка s(x). Нелокальная связь между
s и слабым полем / задается статической восприимчивостью, χο:
*(х) = |dx'Xo(x - х')/(х')· (Ю.38)
Если сделать преобразование Фурье от s и /, можно выразить это
соотношение через Фурье-образ χο (см. уравнение А.23):
*к = Хо(к)/к. (10.39)
Например,21 плотность свободной энергии идеального газа в линейном
приближении раздела 10.3 равна Τ = \ot(p — Ро)2· При наличии зависящего
21 Уравнение (10.45) можно вывести в общем виде в результате следующего
(несколько абстрактного) рассуждения. Вычислим математическое ожидание (sic)eq для заданной
силы /к, а затем возьмем производную по /к и получим Хо(к). В свободной энергии,
заданной уравнением( 10.28), член, связанный со взаимодействием, превращается для случая
постоянной силы в
Ff = -[ dx/(x)e(x) = -V^/k?_k, (10.40)
<* к
где V — это объем системы (внутри периодических граничных условий), а суммирование
по к производится по всем разрешенным волновым векторам в ящике (см. приложение А).
(Мы используем ряд Фурье, а не непрерывное преобразование Фурье, поскольку это делает
428
Гл.10. Корреляции, отклик и диссипация
от координат потенциала внешнего поля /(х) = — V(x) эта свободная энергия
минимизируется р(х) = ро + /(х)/#, так что (сравнивая это выражение с
10.38), получаем для статической восприимчивости
X{,deal(r) = ί(Γ)/α,
(10.43)
что в Фурье-пространстве соответствует %o(k) = 1/ol. Здесь χο ~~ это как бы
«жесткость пружины», описывающая отклик на постоянную внешнюю силу.
рассуждение более интуитивно понятным; вместо <5-функций и бесконечностей мы
получаем в этом случае множители, пропорциональные объему.) Математическое ожидание
параметра порядка во внешнем поле равно
<*·<>«, =
ttfce-'fr-i^'-)] ldlogZ
"Ι'
■тЛе-Л(*Ь-УЕк
/k»-k)l
β dfk
(10.41)
где Тг соответствует интегрированию по всем возможным конфигурациям параметра
порядка s (формально речь идет об интеграле по траекториям в функциональном
пространстве). Восприимчивость получается дифференцированием уравнения (10.41):
Хо(к)
9(i).
/=о
в/к
Тг [?k(/?Vs_k)e
-/?(F0-V£k
/к«-к)1
/=о
TrL-^Fo-VEic/k^-k)!
Тг [ske-^(F°-v^^-k)]lV [(/3V?_k)e-^(F°-v^^-Ol
(10.42)
Tr[e-^(F°-v^/k«_k)l
= ^((Зкв-к) - <3к>(в-к» = /9V<(3k - (?k»2> = /3C(k,0),
/=o
где последнее равенство — это тождество Фурье, приравнивающее корреляционную
функцию к квадрату модуля флуктуации (уравнение А.21 со следующими уточнениями (i)
поскольку мы используем ряды, а не интегралы Фурье, возникают два дополнительных
множителя Vy и (ii) вычитание (sk) дает нам связанную корреляционную функцию, из которой
уже вычтено среднее s).
Заметьте, что все вычисление опять сводится к дифференцированию статистической
суммы; в уравнении (10.41) (sic) = (l/P)d\ogZ/dfk и уравнении (10.42) С(к,0) =
(l/fi2)d\ogZ/dfk. Корреляционные функции более высокого порядка могут быть
получены, в свою очередь, вычислением более старших производных от log Z. Это
распространенная техника в теоретической физике; для того чтобы вычислить корреляции в ансамбле,
добавьте в него соответствующее внешнее поле и вычислите производные по нему.
10.7. Статическая восприимчивость
429
Заметим, что статическая восприимчивость Xodeal(r) идеального газа и его
одновременная корреляционная функция Cldeal(r, 0) = δ(τ)/(βα)
пропорциональны друг другу: Xodeal(r) = /3Cldeal(r,0). Можно показать, что эта
пропорциональность сохраняется для всех равновесных систем (см. сноску 21):
Хо(г) = /ЗС(г,0). (10.44)
Другими словами, статическая восприимчивость χο, соответствующая ω = 0,
получается делением одновременной корреляционной функции С на квТ —
как в обычном, так и в Фурье-пространстве:
Хо(к)=0С(к,О). (10.45)
Эта связь между откликом и флуктуациями должна казаться интуитивно
понятной; система или ее мода, которая легко откликается на возмущение,
должна одновременно и сильно флуктуировать.
Каким образом статическая восприимчивость Хо(г) связана с
определенной нами ранее динамической восприимчивостью х(г,£)? Используем
динамическую восприимчивость (уравнение 10.29) для особого случая не
зависящей от времени силы
-М
ϊ(χ, t) = J dx' J at' χ(χ - x', t - t')/(x')
)
άτχ(χ-χ',τ)/(χ'), (10.46)
и получим выражение для χο:
/»оо poo
χο(Γ)=/ άίχ(Γ,ί)=/ dtX(r,i). (10.47)
JO J-oo
Мы используем здесь тот факт, что физический мир подчиняется принципу
причинности (никакой эффект не может предшествовать своей причине во
времени), и полагаем x(r,t) = 0 для t < 0 (см. рис. 10.9). Интегрирование
по времени в уравнении (10.47) приводит к выделению Фурье-компоненты с
ω = 0, так что зависящие от к компоненты статической восприимчивости —
это низкочастотные пределы динамической восприимчивости:
Xo(k) = x(k," = 0). (10.48)
430
Гл.10. Корреляции, отклик и диссипация
Рис. 10.9. Восприимчивость
Восприимчивость х(г = 0,£) для воображаемой системы с двумя временами релаксации.
Здесь х(г, t) описывает отклик на импульсное воздействие, случившееся в момент
времени t в прошлом; из принципа причинности следует, что на временах, предшествующих
импульсу, никакого отклика не должно быть, так что х(г, t) = 0 для t < 0.
Зачастую говорят об однородной восприимчивости системы — отклике
на внешнюю силу, не только постоянную во времени, но и однородную в
пространстве. Удельная теплоемкость, введенная в разделе 6.1, и магнитная
восприимчивость из упражнения 8.1 — это примеры однородной (т.е.,
соответствующей к = 0) статической восприимчивости к изменению температуры
и магнитного поля, соответственно). Для однородной статической
восприимчивости s = J*dx'xo(x - х')/ — Хо(к = 0)/, так что однородная
восприимчивость задается Хо(к) при к = 0. Зная, что Хо(к) = /ЗС(к, £ = 0) (см.
уравнение 10.45), можно связать однородную восприимчивость с длинноволновой
(к = 0) компонентой одновременной корреляционной функции. Но при к =
0 корреляционная функция равна среднему квадрату от пространственно-
усредненного параметра порядка (s)Space = (1/V) /s(x)dx:
kBTxo(k = 0) = C(k = 0, t = 0) = / dr (s(r + x)s(x))
= Jdr V|dxS(r + x)s(x)\
= V(^/dr,S(r,)^/dXS(x))
= V((s)s2pace>. (10.49)
Таким образом, мы связали однородный линейный отклик с флуктуация-
ми системы как целого. Мы уже получали такой результат для двух частных
случаев: в упражнении 8.1(b), где флуктуации намагниченности задавали
восприимчивость модели Изинга, и в уравнении (6.13), которое связывало
10.8. Флуктуационно-диссипационная теорема
431
флуктуации энергии с удельной теплоемкостью.22 Уравнение (10.49)
показывает, что, вообще говоря, флуктуации величин, усредненных по объему,
становятся исчезающе малыми в термодинамическом пределе V —> оо:
(WU> = *-!ψΆ· CM»)
если только однородная восприимчивость остается конечной.
10.8 Флуктуационно-диссипационная теорема
Обратимся теперь к вычислению динамической восприимчивости. Она
также связана с корреляционной функции, на этот раз — посредством
флуктуационно-диссипационной теоремы.
Как вычислить х(г, £), т.е. функцию, описывающую пространственно-
временную эволюцию системы после короткого импульсного воздействия в
точке г = t = 0? Мы знаем, что эволюция системы при заданных начальных
условиях задается функцией Грина G(r, t). Мы можем наложить на
систему начальное условие, приложив к ней постоянную во времени силу
/(х, t) = /(χ) при t < 0 и убрав ее при t = 0, так что /(х, t) = 0 при t > 0.
В таком случае мы можем установить соответствие23 между откликом,
22Флуктуации энергии в уравнении (6.13) не подчиняются этой формуле, но все же и они
связывают однородный отклик с флуктуациями.
23 Можно сделать это в общем виде для произвольного поля параметра порядка s(x,£).
Пусть имеется начальное условие, определяемое не зависящим от времени внешним полем
/(х) и задаваемое равенством ^(к,£ = 0) = хо(к)/(к). Последующая эволюция системы
задается сверткой начального условия с функцией Грина G(x,£) (см. уравнение 2.34), что
равносильно в Фурье-пространстве умножению на G(k, t):
5(k,i)=xo(k)/(k)G(k)t). (10.51)
Мы также можем получить уравнение на 5(k,t), используя динамическую
восприимчивость, уравнение (10.29) и тот факт, что /(*') = 0 при t' > 0:
s(x, t)= idx i di' χ(χ - χ', t - t')/(x', t') =
= 1^1 dt'x(x-x',i-t')/(jc')= (10.52)
= y'dx,y0OdrX(x-x,,T)/(x'))
S(k,t) = y°
drx(k,r)/(k). (10.53)
432
Гл.10. Корреляции, отклик и диссипация
задаваемым функцией Грина s(x, t) = f dx' G(x — x/,i)s(x/,0), и откликом,
задаваемым восприимчивостью s(x, t) = J^^ at' J dx' /(χ')χ(χ — χ', £ — tr).
Сделаем это для идеального газа, где Хо(г) = δ(τ)/α (см. уравнение 10.43),
так что р(х, 0) = /(х)/а. Последующая эволюция во времени задается
функцией Грина G(x, £), что, как мы видели, дает для идеального газа, в
соответствии с гипотезой регрессии Онзагера (см. уравнение 10.26), корреляционную
функцию Cideal(x,*) = G(x,t)/08a):
р(х, t) = ί dx' p(x', 0)G(x - x', t) = / dx' &^G(x - x', t)
= ί dx' /(xO/?Cideal(x - χ', ί)· (10.56)
Сравним это выражение с выражением для р(х, £), записанным в терминах
динамической восприимчивости. Поскольку /(х, t) = 0 при ί > 0, в формуле
будут стоять интегралы только по отрицательным временам; сделаем замену
переменных τ = t — t':
р(х, t) = j dx' У di' /(x')x(x - x', ί - ί')
= У dx'/(x') J°° dr χ(χ - x', τ). (10.57)
Сравнивая два выражения, получаем
άτχ(Γ,τ). (10.58)
Это верно для любой внешней силы /(к), так что получаем вместе с уравнением (10.51),
/t°°dr x(k, τ) = xo(k)G(k,£). Наконец, из последнего раздела (уравнение 10.45) мы
знаем, что Хо(к) = /ЗС(к,0). Гипотеза регрессии Онзагера утверждает, что функция Грина
G(k, t) для s зависит от времени по тому же закону, что и корреляционная функция С (см.
уравнение 10.25), следовательно C(k,0)G(k, t) = C(k,£). Поэтому
Г άτ x(k, τ) = /3C(k, 0)G(k, t) = β6(Κ t). (10.54)
Дифференцируя обе части этого выражения по времени, получаем флуктуационно-
диссипационную теорему в к-пространстве:
x(k,i) = -/?^%^· (10.55)
10.8. Флуктуационно-диссипационная теорема
433
Взяв производную от обеих частей, получим выражение, являющееся одной
из форм записи флуктуационно-диссипационной теоремы:
ideal
Xldeal(r,t) = -β
дС
ideal
dt
(t > о).
(10.59)
Флуктуационно-диссипационная теорема в такой форме верна для
линейного отклика в любых классических равновесных системах (см. сноску 23).
Линейная динамическая восприимчивость χ для любого поля параметра
порядка s(x, t) с корреляционной функцией С(х, t) равна
хьо—е?°£й ((>о).
(10.60)
Что происходит при t < 0? Корреляционная функция должна быть
симметрична во времени (рис. 10.10), поскольку состояние равновесия
инвариантно относительно обращения времени:
C(r, r) = (s(x, t)e(x + г, t + τ))
= (s(x, t)e(x + г, t - τ)) = C(r, -τ).
(10.61)
Но принцип причинности требует, чтобы χ была равна нулю при t < 0 (см.
рис. 10.9):
X(r,t)=0 (t<0). (10.62)
Рис. 10.10. Зависящая от времени корреляционная функция
Зависящая от времени корреляционная функция С(г = О, г) для той же воображаемой
системы, чья восприимчивость показана на рис. 10.9.
Чтобы понять, почему эта теорема называется флуктуационно-
диссипационной, посмотрим на то, как она выглядит в Фурье-координатах.
И в этот раз опустим для простоты зависимость от пространственных
координат. Используя уравнения (10.60) и (10.62) и интегрируя по частям,
получим
434
Гл.10. Корреляции, отклик и диссипация
dte
/оо poo
df χ(ί)βίωί =-/? / at
-oo J0
/•ОО
= - βΟ(ί)έω1\™ + Ίωβ / dt C{t)eluJt. (10.63)
Jo
Далее, первый член этого выражения действителен и C(t) = С(—£), так что
мы можем записать мнимую часть восприимчивости в виде
/•ОО
χ"(ω) = Im[x(u;)] = βω / di C{t) cos(ut)
Jo
= ^j~JtC{ty»< = ^C{u). (10.64)
Это динамическая форма (классической) флуктуационно-диссипационной
теоремы. Сформулируем ее еще раз:
χ"Η = ^С(ш). (10.65)
Используя этот результат и уравнение (10.37), связывающее рассеянную
мощность ρ(ω) и χ", получаем
= М^см. (Ю.66)
Мы получаем, таким образом, что мощность ρ(ω), рассеиваемая при
воздействии внешней силы /ω, выражается в терминах корреляционной функции
спонтанных тепловых флуктуации С (ω)] отсюда название флуктуационно-
диссипационная теорема.
Обратите внимание, что флуктуационно-диссипационная теорема
выполняется только для равновесных систем. (Существует несколько интересных,
но гораздо более спекулятивных попыток обобщить ее на неравновесные
системы.) Обратите также внимание, что мы совершенно не учитывали
квантовую механику в нашем изложении.24 Действительно, существуют квантово-
механические поправки к флуктуационно-диссипационной теореме; ее полная
квантовая версия гласит
24 Можно также вывести флуктуационно-диссипационную теорему из квантово-
механических соображений, а затем использовать ее для вывода гипотезы регрессии Он-
загера [44].
10.9. Принцип причинности и соотношение Крамерах—Крёнига 435
χ"(Κω) = 1т[х(к,ш)] = ^(1 - е~^)С(Ц,Ш). (10.67)
При высоких температурах 1 — е~^^ ~ βΗω и мы возвращаемся κ
классическому результату — уравнению (10.65).
10.9 Принцип причинности и соотношение
Крамерса—Крёнига
Статическая восприимчивость χ(£) (и в этот раз опустим для простоты
пространственную зависимость) — это вещественная функция на полупрямой
t > 0. Динамическая восприимчивость складывается из двух вещественных
функций χ'(ω) и χ" (ω), определенных на всей числовой прямой. Можно
использовать свойства симметрии χ(—ω) = —χ*(ω), для того чтобы свести ее
к двум вещественным функциям на полупрямой ω > 0, но даже и в этом
случае остается впечатление, что χ(ω) содержит вдвое больше информации,
чем x(t). Поэтому естественно возникает предположение, что χ' и χ" могут
оказаться не независимыми функциями. Пусть мы исследовали поглощающие
свойства материала в зависимости от частоты и получили х;/(к, ω). Можем ли
мы получить из этих данных вещественную часть восприимчивости χ'(к, ω)?
Замечательно, что можно найти формулу, выражающую χ'(ω) через
χ"(ω). Эта формула называется соотношением Крамерса—Крёнига, и она
следует из принципа причинности. Для того чтобы понять ее вывод, вам
понадобятся некоторые знания из области комплексного анализа.25
Мы знаем, что χ(ί) = 0 при t < 0, поскольку законы природы
подчиняются принципу причинности: отклик не может предшествовать
воздействию, которое его вызывает. К каким следствиям это приводит для χ(ω) =
J dt χ(£)θ1ωί? Рассмотрим функцию χ как функцию комплексной частоты
ω = и + Ίν:
/»оо
Х(и + iv)= / dt X{tyute-Vt. (10.68)
Jo
Она замечательно сходится при ν > 0, но выглядит подозрительной при ν < 0.
На комплексной плоскости ω быстрая сходимость при ν > 0 означает, что
χ(ω) — аналитическая функция в верхней полуплоскости.26 Также кажется
2бЕсли вы никогда раньше не слышали о теореме Коши, продолжайте читать: мы вкратце
дадим вам представление о главных фактах комплексного анализа.
26Название «аналитическая» означает сходимость разложения ряда Тейлора для
соответствующей функции. Удивительно, как много функций в физике — аналитические;
практически во всех случаях оказывается возможным пользоваться разложением в степенные
436
Гл.10. Корреляции, отклик и диссипация
вероятным, что в нижней полуплоскости (ν < 0) могут встретиться
сингулярности (например полюса) χ(ω).
Применим теперь одну глубокую теорему комплексного анализа. Пусть С
— замкнутая кривая (контур) на комплексной плоскости ζ, и пусть /(г) ана-
литична внутри некоторой области, целиком включающей этот контур и его
«внутренность», тогда теорема Коти утверждает, что контурный интеграл
от /(г) вдоль С равен нулю:
I
/(z')dz' = 0.
(10.69)
Теорема Коши (которую мы не будем доказывать) — это изумительное
утверждение, но оно имеет простую интерпретацию: оно представляет собой
условие существования интеграла от /(г) как хорошо определенной функции
комплексного переменного (рис. 10.11).
N
Re[z]
Рис. 10.11. Теорема Коши
Для того чтобы f(z) имела хорошо определенный комплексный интеграл в пределах от z\
до 22, контурные интегралы вдоль путей А и Ву соединяющих эти точки, должны
совпадать. Поэтому интеграл вдоль замкнутого контура С, состоящего из пути А, пройденного
вперед, и пути В, пройденного назад, должен быть равен нулю. Поэтому теорема Коши —
это условие существования хорошо определенного интеграла, не зависящего от конкретной
траектории, соединяющей точки z\ и z^.
Рассмотрим теперь интеграл
JcL
Χ(ω')
dw' = 0
ω' — ω
(10.70)
ряды. В разделе 8.3 мы обсуждали, что внутри фазы свойства материала являются
аналитическими функциями внешних параметров; в упражнении 9.5 мы обсуждали, что в
конечных системах (и при конечном сглаживании) свободная энергия является аналитической
функцией параметра порядка и его градиентов. Здесь нам встретилось новое объяснение
аналитичности некоторой функции — причинность!
10.9. Принцип причинности и соотношение Крамерса—Крёнига 437
Рис. 10.12. Контур Крамерса—Крёнига
Контур Сш на комплексной плоскости ω'. Горизонтальная ось — это Re[a/], а вертикальная
— Im[u/]. Контур интегрирования проходит вдоль вещественной оси от — оо до оо, за
исключением маленького полукруга, обходящего полюс в точке ω. Контур замыкается большим
полукругом на бесконечности, где χ(ω') быстро стремится к нулю. Этот контур не
охватывает никаких сингулярностей, так что по теореме Коши интеграл вдоль него обязан быть
равен нулю.
вдоль контура (7ω, изображенного на рис. 10.12. Этот интеграл равен нулю,
поскольку функция χ (о/) аналитична в верхней полуплоскости, а
следовательно аналитична и χ(ω')/(ω' — ω), за исключением точки ω' = ω,
которую мы обошли вдоль маленького полукруга радиуса е. Можно показать,
что вклад большого полукруга стремится к нулю при стремлении его
радиуса к бесконечности (R —> оо). Вклад маленького полукруга, обходимого по
часовой стрелке ω' = ω + 6exp(i0), π > θ > 0, равен
J email (jjr — (jj J small (jjr — (jj
= χ(ω) log(u/ - ω)
ια/=ω+€βχρ(ί0)
Ιΐι/=ω+€βχρ(ίπ)
= x(o;)[log€ - (log б + ίπ)] = -ίπχ(ω).
(10.71)
По мере того как R —У оо и е —> 0, вклад от двух горизонтальных участков
сходится к интегралу по всей вещественной оси:
lim
ηω -е /«оо 1 ~/ /ч /.оо ~/ /ч
/ + / ^Т-1-d" = PV / ^=-±- do;',
У_оо Λ,/+€ \ω' - ω у.оо ω' - ω
(10.72)
где левая часть — это определение главного значения (PV) интеграла, т.е.
предельного значения интеграла, при условии, что границы интегрирования
стремятся к полюсу симметрично с обеих сторон.
438
Гл.10. Корреляции, отклик и диссипация
Поскольку вклады от полукругов и горизонтальных участков обязаны, по
теореме Коши, в сумме давать ноль, уравнение (10.71) должно быть равно
минус уравнению (10.72), так что27
ХН = Л Г ψ-^άω', (10.74)
πι У.оо ω' - ω
где правую часть надо понимать в смысле главного значения интеграла.
Обратите внимание на i в знаменателе. Оно означает, что действительная
часть интеграла дает мнимую часть χ, и наоборот. В частности,
УМ = ReRM, ^-Γψ^^^-Γρύ.„J. (10.75)
π J_OQ ω' -ω π J_00 ω' - ω
Обчно принято дополнительно упрощать эту формулу с учетом того, что
χ"(ω) = —χ"{—ω) и, следовательно,
χΉ = - Г Χ"("') (V }—) do/
π Jo \ω' — ω —ω' —ω;
Таким образом, можно измерить мнимую, диссипативную часть
динамической восприимчивости и получить из нее вещественную, реактивную часть
путем вычисления простого интеграла. И наоборот,
Это и есть соотношения Крамерса—Крёнига. На практике применить их
бывает достаточно сложно; чтобы получить вещественную часть
восприимчивости, необходимо измерить (или приближенно оценить) мнимую
диссипативную часть во всем интервале частот, от глубокого инфракрасного диапазона
до рентгеновского.
27 Многие заметят, что этот результат связан с интегральной формулой Коши, которая
гласит, что
/ -№- άζ' = 2^/(*W (10.73)
Jc ζ — ζ
где Ν — число оборотов контура вокруг точки ζ в направлении против часовой стрелки.
Рассматриваемый случай (направленный против часовой стрелки полукруг, замкнутый
напрямую через точку ζ) соответствует N = ~.
Гл.10. Упражнения
439
Упражнения
В упражнении Реликтовое микроволновое излучение мы обсудим самую
первую из корреляционных функций, доставшуюся нам от Большого
Взрыва. В упражнении Парные распределения и молекулярная динамика мы
изучим парную функцию распределения атомов в пространстве, получаемую из
молекулярно-динамического моделирования жидкостей и газов.
Следующие пять упражнений посвящены флуктуациям во времени и
эволюции. В упражнениях Затухающий осциллятор и Спин мы изучим
разнообразные связи между корреляциями, откликом и диссипацией в двух
наиболее часто наблюдаемых и исследуемых системах. Упражнение Телеграфный
шум в наносочленениях связывает корреляционные функции с цепями
Маркова и детальным балансом, используя для этого современный
экспериментальный контекст. Упражнение Флуктуации и диссипация в модели Изинга
посвящено проверке нашей главной теоремы методом численного
моделирования. В упражнении Шум и уравнения Ланжевена исследуются тепловые
флуктуации в контакте с термостатом и то, как они возвращают в систему
энергию, потерянную при диссипации. Это упражнение содержит
теоретическое обоснование использования одной из моделей термостата в молекулярно-
динамическом моделировании.
В заключение мы рассмотрим две системы, флуктуирующие как в
пространстве, так и во времени. (Число необходимых преобразований Фурье в
результате удваивается, но концептуально ситуация не становится более
сложной.) В упражнение Динамика магнетика мы пройдем все этапы вычисления
корреляционных функций и восприимчивости для поля параметра порядка,
обладающего (в отличие от случая идеального газа) жесткостью по
градиентам. Наконец, упражнение Квазичастичные полюса и теорема Голдстоуна
посвящено моделированию ультразвукового затухания в газах и
показывает, как собственным модам с конечными временами жизни можно приписать
смысл сингулярностей восприимчивости при комплексных значениях
частоты.
10.1 Микроволновое реликтовое излучение.28 (Асторфизика) @
В упражнении 7.15 мы исследовали микроволновое реликтовое излучение.
Это излучение было испущено примерно через 380000 лет после Большого
Взрыва, когда заряженные электроны и протоны сформировали стабильные
нейтральные атомы и почти полностью перестали рассеивать протоны [146].
28Это упражнение было составлено с помощью Иры Вассерман, Эанны Фланаган, Рэчел
Вин и Дейла Фиксена.
440
Гл.10. Корреляции, отклик и диссипация
Как мы видели, спектр реликтового излучения почти полностью
совпадает со спектром излучения черного тела, что указывает на то, что в момент
расцепления фотоны находились в тепловом равновесии.
В то время Вселенная не просто находилась в состоянии локального
теплового равновесия, но, похоже, достигла одной и той же температуры во
всех направлениях (то есть достигла глобального равновесия). За вычетом
влияния нашей галактики (которая излучает в микроволновом диапазоне) и
нескольких других некосмологических точечных источников, в ранних
экспериментах не удавалось обнаружить никаких угловых флуктуации
температуры реликтового излучения. Такая однородность является аргументом в
пользу так называемой инфляционной модели. Согласно инфляционному
сценарию, пространство-время переживало в ранней Вселенной этап быстрого
расширения, в результате которого наблюдаемая Вселенная оказалась
пространственно однородной.
Дальнейшие более точные эксперименты позволили обнаружить допле-
ровский сдвиг в поле температур, который оказалось возможным
использовать для определения абсолютной скорости Солнца.29 Солнце обладает
абсолютной скоростью около полутора миллионов километров в секунду,
направленной в сторону созвездия Льва.
Последующие эксперименты наконец показали более интересные
неоднородности в микроволновом реликтовом излучении, показанные на рис. 10.13.
Мы интерпретируем эти флуктуации как неоднородности температуры, эво-
люционирующие в соответствии с волновым уравнением
Я2Й г2
(1 + *)™ = ^©, (10.78)
где с — скорость света в вакууме, θ — флуктуация температуры ΔΤ/Τ, t —
время, a R происходит от вклада материи в полную плотность вселенной (см.
упражнение 7.15 и [63]).
Какого рода корреляции между флуктуациями можно ожидать в
начальный момент, исходя из инфляционного сценария? В соответствии с
инфляционной теорией на очень ранних временах Вселенная находилась в состоянии
29В соответствии с теорией Эйнштейна всякое движение является относительным:
законы физики не зависят от того, насколько быстро Солнце движется относительно удаленных
галактик. Посредством реликтового излучения Большой Взрыв задает выделенную
систему отсчета. В разделе 5.1 мы обратили внимание, что Большой Взрыв ответственен также
и за стрелу времени; благодаря ему в нашем мире (очень существенно) нарушена
симметрия относительно обращения времени и (чуть-чуть) нарушена симметрия относительно
преобразований Лоренца.
30Мне говорили, что это уравнение соответствует «co-moving time-orthogonal
калибровке», что бы это ни значило.
Гл.10. Упражнения
441
Рис. 10.13. Карта микроволнового реликтового излучения
Карта микроволнового реликтового излучения, полученная научной командой
NASA/WMAP [141]. Показаны вариации температуры микроволнового реликтового
излучения после вычета постоянной части, дипольного вклада и излучения нашей
галактики, полученные WMAP (зондом микроволновой анизотропии Вилкинсона, the
Wilkinson Microwave Anisotropy Probe). Спутник находится в центре сферы. Порядок
величины флуктуации около одной 100000-й.
с очень маленькими случайными вариациями температуры и плотности и с
нулевыми начальными скоростями. Эти начальные вариации не были
независимыми (т.е. не были белым шумом). Напротив, в результате инфляционного
этапа Вселенная оказывается в состоянии с масштабно-инвариантным
начальным полем скоростей, распределенным по степенному закону
C(k, t = 0) = |§(к, t = 0)\2/V = Akn°-S, (10.79)
где ns « 1 для большинства инфляционных теорий. (Помните, что квадрат
модуля от преобразования — это преобразование от корреляционной
функции, |в(к, t)\2 ос С(к, £), см. уравнение А.21.)
Пусть Вселенная представляет собой одномерный ящик длины L с
периодическими граничными условиями. Решим задачу об эволюции
одновременной корреляционной функции во времени31 С(х — x\t) = (θ(χ,£)θ(χ',£))
при t = 380000 лет, при начальных условиях (dQ/dt)\t=o = 0 и случайном
«Время» здесь соответствует не разности времен между двумя измерениями, а времени,
прошедшем с момента, когда закончился инфляционный этап, до момента измерений (см.
аналогичное обсуждение сглаживания корреляционной функции в разделе 10.1).
442
Гл.10. Корреляции, отклик и диссипация
распределении S(x,t = 0) с масштабно-инвариантными корреляциями,
задаваемыми уравнением (10.79). Мы можем теперь посчитать, как
эволюционировала каждая из Фурье-компонент, и вычислить корреляционную функцию
в k-пространстве в момент расцепления.
(a) Пусть задано начальное значение 0(к, t = 0). Предположив, что
{dQ/di)\t=o = 0, вычислите в(к,t) из уравнения (10.78). Вычислите
С(к, t) = (|в(к, £)|2) в терминах А, с и R при условии, что ns = 1. Для
какого значения L (в световых годах и в метрах) &220 будет соответствовать
первому пику32 fc2C(k,£) в момент расцепления, если R = 0.7? (Указание:
с = 3 · 108м/с, t = 380000 лет, кроме того, оказывается, что в году примерно
π · 107 секунд.) L можно грубо интерпретировать как размер части
Вселенной, видимой реликтовым излучением в момент расцепления.
(b) Нарисуйте график 1(1 + \)C(kui) в момент расцепления для R = 0.7 и
А = 1 в области от / = 40 до / = 1500. Сравните его с рис. 10.14.
40 100 И» 400 800 1400
Мультипольмый момент Ц)
Рис. 10.14. Корреляционная функция реликтового излучения
в Фурье-пространстве, полученная научной командой NASA/WMAP [141]. Температурные
вариации микроволнового реликтового излучения разложены по сферическим
гармоникам (которые являются примерным аналогом преобразования Фурье по углам). Вы
можете интерпретировать мультиполный момент / как примерный аналог волнового вектора
ki = 2πΖ/Ζ/.33 Кривая линия соответствует теоретическому приближению, аналогичному по
смыслу содержанию данного упражнения, но более строгому и последовательному.
32Мы умножаем на А:2, чтобы примерно соответствовать вертикальной оси /(/ + \)Ci на
рисунке 10.14.
33Первый пик находится на / ~ 220; авторы предполагают, что второй пик расположен в
районе / = 546 ±10. Обратите внимание, что горизонтальная ось не является ни линейной,
ни логарифмической.
Гл.10. Упражнения
443
Ваша корреляционная функция должна выглядеть существенно менее
структурированной, чем полученная в эксперименте. На длинах волн,
больших по сравнению с произведением скорости света и времени жизни
Вселенной (/ < 160, примерно область до первого пика), волновое уравнение еще
не успело начать работать. На более коротких длинах волн (I > 1100) волны
затухли, из-за того что длина свободного пробега фотона между барионами
стала велика. Вычисление, во многом аналогичное вашему, но учитывающее
эти и еще некоторые (например гравитационные) эффекты, смещает
положение пиков и их амплитуды и приводит к результату, изображенному
сплошной линией на рис. 10.14. Более детально об этих результатах можно узнать
из [63,141].
10.2 Парные распределения и молекулярная динамика.34
(Компьютерное моделирование) @
Во многих экспериментах по рассеянию измеряются парные корреляции
между положениями атомов. Пусть имеется система 7V, заключенных в объем
\Л35 Средняя плотность системы, в которой атомы расположены в точках х*,
— это
p(x) = {Ji(x-Xi)), (10.80)
г
а корреляционная функция плотность-плотность36
с(х, х') = < Σ <Ηχ - х*Жх' - χ;)>· (10·81)
Две эти функции используются в определении парной функции распределения
5(х,х'):
, Л С(х,х') С(х-х') ,лпоп.
5(x'x)=^^=-(W· (10·82)
34Это упражнение было составлено в сотрудничестве с Нилом В. Ашкрофтом и
Кристофером Р. Майерсом.
35 Мы будем использовать периодические граничные условия, чтобы наличие у области
моделирования границ не нарушало трансляционной симметрии.
36Внимание, в теории жидкостей букву С обычно используют для другой величины —
прямой корреляционной функции Орнштейна-Цернике.
444
Гл.10. Корреляции, отклик и диссипация
Здесь последнее равенство выполняется для пространственно однородных си-
стем, таких как жидкости или газы. ',0°
(а) Покажите аналитически, исходя из уравнения (10.80), что в
однородной системе средняя плотность р(х) действительно равна N/V. Покажите, что
Я(х, х') = я(х - х') = g(r), где
»(Г) = (^Е*(Г-Г«)). (10-83)
a Tij = Xi — Xj — вектор, соединяющий положения г-ro и j-ro атомов. Пусть
система однородна и положения атомов не коррелированны (т.е., система является
идеальным газом). Покажите, что <7(г) = 1. Пусть теперь потенциальная энергия
системы есть сумма вкладов парных взаимодействий Ε(τ^). Запишите в этом
случае потенциальную энергию как интеграл по пространственной координате г,
включающий N, V, g(r) и Е(г).
Как правило, g(r) —> 1 при г —> оо; корреляции исчезают по мере роста
расстояния между частицами.
Жидкости и газы не только однородны, но и изотропны;
следовательно, парная корреляционная функция g должны быть инвариантна
относительно вращений, т.е. должна зависеть только от модуля расстояния между
частицами г = |г|. Обычно программа молекулярного моделирования
должна содержать быструю процедуру NeighborLocator, возвращающую список
Half Neighbor пар атомов j < г, расстояния между которыми \г^\ не
превышают заданный масштаб обрезания. Правильным образом
перемасштабированная гистограмма распределения этих пар по расстоянию — удобный
способ количественно оценить парную корреляционную функцию. Пусть число
h(rn) на гистограмме равно количеству таких пар с гп < г < гп + Лг в нашей
системе.
37Парная корреляционная функция описывает согласованные флуктуации положения
атомов и не учитывает группировку, связанную с равновесной неоднородностью плотности.
Например, в трехмерных кристаллах имеется нарушение трансляционной симметрии —
дальний порядок; функция /э(х) даже после усреднений по тепловым флуктуациям будет
иметь максимумы вблизи узлов кристаллической решетки.
38Автор, конечно же, имеет в виду жидкость и газ в отсутствие внешнего поля.
Например, газ в поле тяжести не является пространственно однородной системой. — Прим.
переводчика.
Гл.10. Упражнения
445
(b) Для изотропной пространственно однородной системы в трехмерном
пространстве покажите, что
Что изменится в этой формуле в случае двухмерного пространства?
Загрузите нашу программу для моделирования методом молекулярной
динамики [30] с сайта книги [132]. В нашей программе используется
потенциал Леннарда—Джонса, в соответствии с которым все атомы взаимодействуют
с силами короткодействующего отталкивания ~ 1/г12 и сравнительно даль-
нодействующего ван-дер-ваальсового притяжения ~ 1/г6:
iWr) = 4e((^)12-(^)6). (10.85)
Потенциал Леннарда—Джонса дает отличное приближение для описания
межатомного взаимодействия в благородных газах, например в аргоне. В
нашей программе масштабы измерения расстояния σ и энергии е выбраны
равными единице.
(c) Нарисуйте график зависимости потенциала Леннарда—Джонса от
расстояния между частицами г, выберите пространственный масштаб таким образом,
чтобы соответствующая притяжению потенцальная яма была хорошо видна.
Чему равно расстояние, на котором энергия взаимодействия минимальна?
Понимаете ли вы, почему это отталкивание называют «отталкиванием твердых сфер»?
Газ. Начнем с моделирования газа, выберем при этом давление достаточно
близким к давлению насыщенного пара.
(d) Промоделируйте двумерный газ с атомами, взаимодействующими с
потенциалом Леннарда—Джонса, при температуре Τ = 0.5б и плотности ρ =
0.05/σ2. Вычислите парную функцию распределения для такого газа при 0 <
г < 4σ. Обратите внимание на провал на малых расстояниях. Можете ли вы
обнаружить влияние притягивающей потенциальной ямы а) на глаз, б) на графике
парной функции распределения?
При малых плотностях и высокой температуре корреляции между
атомами в газе в основном связаны только с попарным взаимодействием атомов
(а не взаимодействием, «переданным» через третьи, четвертые, ... атомы).
Энергия парного взаимодействия атомов в нашей системе известна и равна
-E'pairi^), поэтому в этом пределе
5theory(r) ex ехр(-Е(г)/квТ). (10.86)
Поскольку Е(г) -40и д(г) —> 1 при г —> оо, коэффициент
пропорциональности должен быть равен единице.
446
Гл.10. Корреляции, отклик и диссипация
(е) Сравните g(r), полученную в части (d)f с ^theory для системы с
плотностью ρ = 0.05/σ2. Хорошо ли они согласуются? Будут ли они согласовываться
еще лучше при более высоких температурах и более низких плотностях, когда
многочастичные взаимодействия еще менее существенны?
Рис. 10.15. Парная функция распределения
Парная функция распределения g(r) для двумерной жидкости Леннарда—Джонса.
Жидкость. Обратимся теперь к исследованию жидкости, используем ту
же температуру, что и при моделировании газа, но повысим плотность.
(f) Промоделируйте жидкость при ρ = 0.75/σ2 и Τ = 0.5. На анимации
обратите внимание, что каждый атом все время находится в окружении
примерно шести ближайших соседей, расположенных на расстоянии, примерно
соответствующем минимуму энергии взаимодействия. Вычислите парную функцию
распределения. Можете ли вы объяснить особенности, которые вы
наблюдаете на графике (у вас должно получиться что-то вроде рис. 10.15), в терминах
ближайших соседей и «соседей через один»?
(g) Определим координационное число атома жидкости как число соседей
этого атома, расположенных на расстоянии, не превышающем расстояние до
первого минимума на графике g(r). Чему равно в таком случае среднее
координационное число атома в вашей двумерной жидкости?
В большинстве (трехмерных) простых одноатомных жидкостей так
определенное координационное число лежит между 11 и 11.5. (В кристаллах с
плотнейшей упаковкой число ближайших соседей равно двенадцати.)
Главным исключением являются элементы IV группы (углерод, кремний,
германий, ...), для которых связывание очень сильно зависит от углов взаимной
ориентации атомов, в результате чего число ближайших соседей в жидкости
существенно уменьшается, примерно до 5.5; в кристаллической фазе в этих
веществах атомы имеют по три или четыре ковалентно связанных соседа.
Гл.10. Упражнения
447
Кристалл. В трехмерном кристалле атомы колеблются вблизи
равновесны положений в узлах кристаллической решетки (только изредка
происходят перескоки между узлами решетки, когда атомы меняются местами или
свободная вакансия движется по объему кристалла). Если амплитуды этих
колебаний станут велики по сравнению с шагом решетки, то кристалл без
сомнения расплавится. Критерий Линдеманна состоит в том, что для
кристаллов простых веществ плавление обычно происходит тогда, когда амплитуда
тепловых колебаний становится равна примерно 10% межатомного
расстояния.
(Обратите внимание, как это удивительно. Трехмерный кристалл в
миллиарды атомов длинной, с тепловыми колебаниями, почти достаточными для
того, чтобы расплавиться, оказывается способен держать каждый из своих
атомов в строго определенном месте, с точностью до долей ангстрема.)
Это неверно для двумерных систем, где решетка не такая жесткая и
тепловые флуктуации более сильны.39 Критерий Линдеманна, конечно, также
подразумевает, что типичная вариация в расстояниях между ближайшими
соседями в трехмерном кристалле остается вплоть до точки перехода много
меньше, чем шаг решетки. Выполняется ли эта версия критерия Линдеманна
и для двумерных кристаллов?
(h) Промоделируйте кристалл при Τ = 0.1, выбрав в качестве начального
условия гексагональную упаковку с межатомным расстоянием, примерно
равным расстоянию до минимума парного потенциала. Вычислите усредненную по
углам парную корреляционную функцию.40 Насколько сильно (в процентах от
равновесной величины) флуктуирует расстояние между ближайшими соседями?
Малы ли эти флуктуации по сравнению с шагом рещетки? Кроме того, можете
ли вы опознать, какие атомы на гексагональной решетке соответствуют второму
и третьему пику на g(r)l
10.3 Затухающий осциллятор. @
Исследуем более подробно вопрос о флуктуациях груза на пружинке (см.
раздел 6.5). Благодаря взаимодействию макроскопического движения с
внутренними степенями свободы системы всякие имеющиеся в начальный момент
39Теория двумерных кристаллов и их плавления породила множество красивых
теоретических и экспериментальных работ; обратите внимание на работы по переходу
Костерлица-Тулесса-Гальперина-Нельсона-Юнга.
40Другими словами, используйте те же процедуры, что и для жидкостей и газов,
игнорируя тот факт, что р(х) в уравнении (10.82) зависит от направления, как
обсуждалось в примечании 37. Эта усредненная парная функция распределения по-прежнему дает
правильное значение для потенциальной энергии (т.к. потенциальная энергия от углов не
зависит).
448
Гл.10. Корреляции, отклик и диссипация
макроскопические колебания со временем затухнут; единственной
сохраняющейся формой движения будут микроскопические тепловые флуктуации.
Эти флуктуации, однако, могут играть существенную роль в наномеханиче-
ских и биологических системах. Кроме того, затухающий осциллятор — это
классическая модель многих физических процессов на атомных масштабах,
таких как диэлектрические потери в изоляторах (см. [88], где этот вопрос
рассмотрен автором модели).
Рассмотрим простой затухающий гармонический осциллятор,
подчиняющийся под действием внешней силы / уравнению движения
(a) Восприимчивость. Найдите динамическую восприимчивость χ{ω) для
осциллятора. Нарисуйте графики χ' и χ" для wo = m = 1 и 7 = 0.2, 2 и 5.
(Указание: сделайте преобразование Фурье от уравнения движения и решите его
относительно 0, считая / известной.)
(b) Причинность и критическое затухание. Проверьте, что при
положительных значениях коэффициента трения η ваша восприимчивость χ{ω)
удовлетворяет принципу причинности {x(t) = 0 при t < 0). Исследуйте для этого
положение сингулярностей восприимчивости на комплексной плоскости ω (см.
раздел 10.9). При каком значении 7 полюса «садятся» на мнимую ось? Когда
полюса становятся чисто мнимыми, всякие колебания в системе исчезают, и
система называется передемпфированной(?).
На этой стадии было бы естественно попросить вас проверить
соотношение Крамерса—Крёнига (уравнение 10.76) и явно показать, что вы можете
записать χ' в терминах χ". Однако это оказывается достаточно трудным как
аналитически, так и численно. Если вы достаточно амбициозны, попробуйте
это сделать.
(c) Диссипация и восприимчивость. Пусть задана внешняя сила
f(t) = Acos(cjt). Решите уравнение и найдите θ{ί). Вычислите среднюю
рассеиваемую мощность, проинтегрировав fdO/dt и используя полученную
формулу для θ{ί). Согласуются ли ваши ответы для мощности и χ" с общей
формулой для диссипации мощности (уравнение 10.37)?
(d) Корреляции и тепловое равновесие. Используя флуктуационно-
диссипационную теорему, вычислите корреляционную функцию
6(ω)
C(t-t') = (e(t)e(t')). (10.88)
Гл.10. Упражнения
449
из χη{ω) (см. уравнение 10.65). Найдите одновременную корреляционную
функцию С(0) = (Θ2) и покажите, что она удовлетворяет теореме о
равнораспределении. (Указание: наш осциллятор находится в потенциальной яме V{6) =
±πιω%θ2. Кроме того, (wg - ω2)2 + С2ш2 = (ω§ - ω2 + №ω)(ω$ - ω2 - Wu>)\
используйте контурное интегрирование.)
10.4 Спин.41 (Физика конденсированного состояния) @
Спин в твердом теле может принимать два значения: sz = ±1/2,
соответствующие намагниченностям Μ = ομΒ$ζ, где gμв — некоторая константа.42
Совершая тепловые флуктуации, спин может перескакивать между
положениями «вверх» и «вниз». Во внешнем магнитном поле Η каждый спин имеет
энергию — Μ · Η. Пусть Μ(t) — намагниченность спина в момент времени
t. При заданном небольшом зависящем от времени поле H(t) вдоль оси ζ
математическое ожидание Μ удовлетворяет уравнению
d [M(i)]Mi /at = -Г [M(t))Ml + ΓχοΗ(ί), (10.89)
где Г — скорость релаксации спина, χο — статическая магнитная восприим-
чивоть, усреднение [-]м. производится по тепловым флуктуациям окружения,
и имеется фиксированное начальное условие М\ = Μ(0).
(a) Пусть поле Η не зависит от времени. Используя равновесную
статистическую механику, определите зависимость М(Н). Используя эту формулу при
малых Н, определите χο (ответ должен получиться не зависящим от Н, но
зависящим от температуры).
(b) Используйте гипотезу регрессии Онзагера для вычисления
C(t) = (M(t)M(0))ev при нулевом внешнем поле Н = 0. Каким должен быть
ответ при t < 0? Чему равно С(и), преобразование Фурье от C(t)?
(c) Предполагая, что классическая флуктуационно-диссипационная теорема
верна, выведите динамическую восприимчивость %(£) и χ{ω).
(d) Вычислите энергию, рассеиваемую осциллятором во внешнем магнитном
поле H(t) = Hocos(ut).
10.5 Телеграфный шум в наносочленениях. (Физика
конденсированного состояния) ©
Во многих физических системах наблюдается телеграфный шум —
перескоки между двумя состояниями, происходящие через случайные
промежутки времени (как будто телеграфный ключ переходит из замкнутого в
разомкнутое состояние и обратно с различными интервалами для точек и для
41 Это упражнение является адалтированным вариантом экзаменационного вопроса,
задаваемого Бертом Гальпериным на экзамене в Гарвардском университете в 1976 году.
423десь д -- гиромагнитное отношение для спина, а μΒ = eh/2me — магнетон Бора.
450
Гл.10. Корреляцииj отклик и диссипация
тире). Наносочленение, поведение которого иллюстрируется рис. 10.16 имеет
два состояния а и β. Между этими состояниями в случайный момент времени
происходят переходы, вероятности этих переходов в единицу времени равны
Ρβ^α = Ρβα Для перехода из а в β и Ραβ для перехода из β в а.
Время
Рис. 10.16. Телеграфный шум в металлическом наносочленении
Зависимость сопротивления от времени R(t) для медной перемычки (источник [111]).
Обозначим состояние с малым сопротивлением а, соответствующее сопротивление — Яа>
состояние с большим сопротивлением /3, соответствующее сопротивление ΙΙβ. По-видимому,
эти два состояния соответствуют переходу атома или группы атомов в перемычке из одного
метастабильного состояния в другое.
Основное кинетическое уравнение. Рассмотрим ансамбль, состоящий из
многих идентичных копий рассматриваемой системы. Пусть состояние
ансамбля в момент времени t задается вектором p(t) = (ρα·>Ρβ), компоненты
которого — это вероятности того, что система находится в соответствующем
состоянии. Этот вектор эволюционирует во времени в соответствии с
основным уравнением
dp/dt = Mp. (10.90)
(a) Чему равна матрица Μ (размера 2x2) для нашей системы в
терминах Ра/3? На больших временах какую часть времени наша система проводит
в состоянии а, (ра) = Ит^-юо ρα(ί)? (Обратите внимание, что в отличие от
цепей Маркова, рассмотренных в разделе 8.2, в этой задаче мы
рассматриваем эволюцию в непрерывном времени. Помните также, что увеличение Ραβ
приводит к увеличению ра и уменьшению ρ β.)
(b) Найдите собственные значения и собственные векторы матрицы М.43
Какой из этих векторов соответствует стационарному состоянию Доо), найденному
в части (а)? Пусть при t = 0 система находится в состоянии а, ДО) = (1,0).
Запишите это начальное условие в базисе собственных векторов и выпишите закон,
по которому pa{t) эволюционирует во времени. Чему равно время релаксации
системы до стационарного состояния?
43Точнее говоря, правые собственные векторы Μ · р\ = \р\.
Гл.10. Упражнения
451
Переобозначим полученную вами вероятность pa(t) = Paa(t), чтобы
подчеркнуть тот факт, что она описывает вероятность того, что система
находится в состоянии а в момент времени t' +1 при условии, что в момент времени
t' она находится в состоянии а. Полезно проверить, что Раа(0) = 1 и что
Paa(t) -> (pa) При t -► 00.
(с) Корреляционная функция. Пусть R(t) — сопротивление как функция
времени, перескакивающее между состояниями Ra и Rp, как показано на рис. 10.16,
и пусть R — усредненное по времени сопротивление. Запишите формулу для
корреляционной функции C(t) = ((R(tf) — R)(R(tf + t) — R)) в терминах Paa(t)-
Можно не подставлять выражение для Paa из части (Ь). (Указание: чему
равно ((R(t') — Rβ)(R(t' +1) — Rfi)) в терминах Ραα(*)? А в терминах C(i)?)
Рекомендуем проверить, что ваш ответ C(t) —У О при t —у оо, и что С(0) =
(Pa)(Ra ~ R? + (Ρβ){ΙΙβ ~ R?·
Наносочленения зачастую, особенно при высоких температурах,
демонстрируют более чем два метастабильных состояния в экспериментально
доступной области.44 Обычно это связано с независимыми флуктуациями в
двух разных точках сочленения (передвижках атомов в точках, слишком
далеких, чтобы существенно взаимодействовать между собой), но иногда можно
увидеть и более сложное поведение. На рис. 10.17 показан телеграфный шум
для системы с тремя состояниями α, β и η (проиндексированными от более
низкого к более высокому сопротивлению). Из рис. 10.17 видно, что
вероятности переходов ΡΊβ и ΡβΊ наиболее велики, за ними следуют вероятности
ΡαΊ и ΡΊα. Переходов между состояниями аи/Зна графике не наблюдается.
lUroi iffffij imu
Время
Рис. 10.17. Телеграфный шум с тремя метастабильными
состояниями
Данные взяты из [110].
Через наносочленение течет большой ток (благодаря чему, собственно, и
можно измерить его сопротивление). В связи с этим встает вопрос о том,
Говорят, что шум в сочленении находится за пределами экспериментально доступной
области, если флуктуации происходят слишком быстро или слишком медленно, для того
чтобы зафиксировать их с помощью имеющегося оборудования.
452
Гл.10. Корреляции, отклик и диссипация
являются ли наблюдаемые переходы равновесными флуктуациями,
связанными, например, с зависимостью эффективной температуры от внешнего
поля, или они представляют собой неравновесные переходы, индуцированные
наличием тока. Это можно проверить, если измерить две последние
вероятности перехода и проверить соблюдение детального баланса. Если детальный
баланс нарушен, то система находится в неравновесном состоянии.
(d) Детальный баланс. Пусть условия детального баланса выполнены. Чему
должно быть равно отношение двух неизвестных вероятностей перехода Ραβ и
Ρβα в терминах четырех известных вероятностей? (Указание: см.
упражнение 8.5.)
10.6 Флуктуации и диссипация в модели Изинга. (Физика
конденсированного состояния) @
В этом упражнении нам опять придется моделировать модель Изинга;
вы можете использовать для этого программное обеспечение, приведенное на
сайте книги [132].
Рассмотрим гамильтониан модели Изинга во внешнем меняющемся поле
H(t),
(υ) ι
и исследуем флуктуации отклика на внешнее поле — зависящей от времени
намагниченности M(t) = Σί *%(*)· Программа компьютерного
моделирования модели Изинга должна быть способна выдать как намагниченность в
расчете на один спин как функцию времени m(t) = (1/N) Y^i Si, так и
зависящую от времени корреляционную функцию намагниченности
c(i) = ((m(0) - (τη)^)(τη(ί) - <т>ес))еу · (Ю.92)
Мы будем работать при температурах выше Тс, так что (m)eq = О.45
Зависящая от времени корреляционная функция должна быть
ненулевой при нулевом времени и должна стремиться к нулю при времени,
стремящемся к бесконечности. Пусть перед началом наблюдения имелось
маленькое ненулевое внешнее поле, которое мы выключаем при t = О, так что
H(t) = Ηοθ(—ί).46 Намагниченность m(t) будет отлична от нуля при t = О,
но будет стремиться к нулю с течением времени. В соответствии с гипотезой
регрессии Онзагера m(t) и c(t) должны затухать по одному и тому же закону.
45 Обратите внимание, что формулы в тексте приводятся в терминах полной
намагниченности Μ = Nm и ее корреляционной функции С = N2c.
463десь θ — функция Хевисайда: S(t) = 0 при t < 0, и θ(ί) = 1 при t > 0.
Гл.10. Упражнения
453
Промоделируйте модель Изинга при размере системы 200 χ 200.
Уравновесьте систему при Τ = 3 и Η = 0, после чего измерьте зависящую от
времени автокорреляционную функцию с достаточно хорошей точностью и
сохраните полученный график. (Перемасштабируйте его таким образом,
чтобы были видны малые времена, когда затухание еще не произошло.) Теперь
уравновесьте систему при Τ = 3, Η = 0.05, затем положите Η = 0 и измерьте
зависимость намагниченности от времени m(t).
(a) Похожи ли формы графиков релаксации намагниченности и
автокорреляционной функции, а также характерные времена релаксации? Измерьте с(0) и
т(0) и вычислите значения С(0) и М(0) для системы как целого.
Функции отклика и флуктуационно-диссипационная теорема. Функция
отклика x(t) определяет изменение намагниченности в ответ на бесконечно
малый импульс внешнего поля Н. Благодаря принципу суперпозиции мы
можем использовать χ(ί) для получения отклика на любое внешнее возмущение.
Так, в малом внешнем поле H(t) средняя намагниченность будет равна
Μ(ί) - (М)щ = f at' X(t - t')H(t'), (10.93)
J—oo
где (Μ) — равновесная намагниченность в отсутствие внешнего поля H(t)
(для нас это ноль, поскольку мы находимся выше Тс).
(b) Используя уравнение (10.93), запишите выражение для M(t) через χ(ί)
для случая ступенчатого внешнего поля H(t) = Ηοθ(—ί).
Флуктуационно-диссипационная теорема гласит, что
X(i) = -/?dC(t)/di,
где C(t) = <(М(0) - (M)eq)(M(i) - <M)eq))ev.
(c) Используйте уравнение (10.94) и ваш ответ из части (Ь), для того чтобы
предсказать связь между релаксацией намагниченности M(t) и корреляционной
функцией C(t), измеренную вами в части (а). Согласуется ли полученное вами
аналитически отношение этих функции при t = 0 с отношением, полученным
вами в части (а)?
10.7 Шум и уравнения Ланжевена. @
Мы ни разу не обсуждали явно вопрос о том, каким образом энергия,
потерянная системой при затухании, возвращается в нее. Между тем, это
необходимо для поддержки теплового равновесия. Приток энергии происходит
благодаря взаимодействию с тепловыми флуктуациями термостата. В этом
упражнении мы выведем уравнение Ланжевена, включающее одновременно
и тепловой шум, и диссипацию ( [22], раздел 8.8).
(10.94)
454
Гл.10. Корреляции, отклик и диссипация
Рассмотрим для начала систему с координатами Р, Q в фазовом
пространстве и с внутренней потенциальной энергией V(Q), линейно
взаимодействующую с термостатом посредством члена Q · ¥ в гамильтониане:
р2
Н=— + V(Q) + Wbathiift, 2/2, Уз,...)
1т
-Q-F(ift,...)· (10.95)
Предположим, что в отсутствие взаимодействия с нашей системой
термостат будет создавать тепловой шум ¥b{t) с нулевым средним. При
взаимодействии с нашей системой будет возникать ненулевое среднее значение
силы
(F(t)>= / dt'Xb(t-t')®(t'), (Ю.96)
J—oo
где Xb(t — t') — это восприимчивость термостата к движению системы Q(t).
Уравнение движения нашей системы в этом случае будет включать как
случайный тепловой шум F, так и неслучайное запаздывающее взаимодействие,
возникающее из-за \ь:
т® = "ΈΚ + ¥ь + [ dt' Xb{t - t')Q(t'). (10.97)
J—oo
"0Q
Мы можем записать эту восприимчивость в терминах корреляционной
функции шума в отсутствие взаимодействия с нашей системой:
Cb(t-t') = (¥b(t)¥b(t')), (10.98)
используя флуктуационно-диссипационную теорему
Xb(t-f') = -/^, t>t'. (10.99)
(a) Интегрируя по частям и сохраняя граничные члены, покажите, что
уравнение движения принимает вид
BV Гь
т® = -ш + ¥ь-Р at' съ(* - OQ(0· (lo.ioo)
Чему равен «потенциал средней силы» V, в терминах V и Сь?
(b) Пусть времена корреляции в термостате существенно меньше типичных
временных масштабов эволюции системы. Тогда в уравнении (10.100) можно
приближенно заменить Q(t') « Q(t), в результате чего получается сила вязкого
Гл.10. Упражнения
455
трения — 7Q. Как записывается формула для ηΐ И наоборот, покажите, что для
модельной системы с идеальным законом вязкого трения —7Q» при температуре
Т, тепловой шум с необходимостью должен быть белым шумом: Cb{t—t') ос S(t—
t'). Чему равен коэффициент при й-функции? Другими словами, из вязкого
трения получается, что термостат должен быть марковским, т.е. не иметь
памяти, и наоборот.
Уравнения Ланжевена полезны как для аналитических
вычислений, так и как метод поддержания постоянной температуры в
молекуярно-динамическом моделировании.
10.8 Динамика магнетика. (Физика конденсированного состояния) @
Одномерный классический магнетик при температуре выше
критической47 описывается плотностью свободной энергии
Т[М] = (C/2)(VM)2 + (£/2)М2, (10.101)
где Μ (χ) — намагниченность как функция единственной пространственной
координаты х. Средняя намагниченность равна нулю, а состоянию с
намагниченностью М(х) соответствует полная свободная энергия F[M] = J T[M] dx.
Методы, которые мы использовали для нахождения корреляционных
функций и восприимчивостей для систем, управляемых уравнением
диффузии, могут быть с небольшими модификациями применены для
описания этой (более математически сложной) магнитной системы.
Предположим для простоты, что магнит имеет длину L, и что имеются
периодические граничные условия. Мы можем записать разложение М(х) в
ряд Фурье (см. уравнение А.4)
оо
Μ(χ)= Σ Mnexp(ifcnz),
n=—00
где кп = 2nn/L и (см. уравнение А.З)
Mn = (l/L) [ M(x)exp(-iknx). (10.103)
Jo
Как обычно для линейных систем с трансляционной инвариантностью (см.
раздел А.4), свободная энергия F[M] распадается на независимые вклады
гармоник, по одному для каждого fcn.48
47Так в тексте. Вообще говоря, в одномерном магнетике нет перехода в упорядоченную
фазу ни при какой конечной температуре. — Прим. переводчика.
48Обратите внимание, что эта независимость означает, что в состоянии равновесия фазы
различных мод не коррелированны.
(10.102)
456
Гл.10. Корреляции, отклик и диссипация
(а) Выведите это разложение F\ покажите, что каждый член является
квадратичным. (Указание: единственным тонким местом является М^; разложите
его на действительную и мнимую части.) Чему, исходя из теоремы о
равнораспределении, равно (|МП|2> ? Покажите, что
(м-м">«, - ϊρ|ϊΒ)*~ (10104)
(Ь) Вычислите равновесную одновременную корреляционную функцию для
намагниченности, С(х, 0) = (Μ(χ,Ο)Μ(0,0)) . (Сначала найдите, в виде
суммы по п, формулу для магнита длины L. Затем преобразуйте сумму в
интеграл: f dk «-> Σ&^ = ^I^Ylk·) ^ам понадобится значение интеграла
J — с
еш7(1 + <гиг) аи = (π/α) exp(-|v|/a). (10.105)
Пусть магнитный параметр порядка не сохраняется, и система
передемпфирована, так что производная по времени [М]м. равна некоторой
постоянной 77, умноженной на вариационную производную от свободной энергии:
—дГ~ = -ηδΜ- (10106)
Μ меняется в том направлении, в котором действует приложенная сила.49
Член δΤ/δΜ — это вариационная производная:50
6F = F[M + δΜ] - F[M]
= I {T[M + δ Μ] - Τ[Μ}) άχ
= ί(δΤ/δΜ)δΜάχ. (10.107)
(с) Вычислите δΤ/δΜ. Подобно тому, как это делается при выводе
уравнение Эйлера-Лагранжа ([89], раздел 12.1), вам понадобится проинтегрировать
один из членов по частям, чтобы исключить δΜ.
49Напомним, что усреднение [М]м. производится по всем возможным сценариям
эволюции при заданном начальном условии Мх(х) = М(х,0).
50Эта формула аналогична взятию градиента скалярной или векторной функции, f(y +
δ) — f(y) ~ V/ · 6, с точностью до замены скалярного произведения в случае векторного
анализа на свертку (интеграл от произведения функций по х) в случае функционального
анализа.
Гл.10. Упражнения
457
(d) Используя ваш ответ из части (с), вычислите функцию Грина G(x,t)
для [М]м., описывающую эволюцию во времени ^-функционального начального
условия М[(х) = М(х,0) = G(x, 0) = δ(χ). (Указание: вам может помочь
использование преобразования Фурье.)
Гипотеза регрессии Онзагера говорит нам, что эволюция во времени
спонтанно возникших флуктуации (например таких, которые описываются
функцией С(х, 0) в части (Ь)) определяется той же формулой, что и эволюция
искусственно заданного начального условия (которая, в свою очередь,
определяется функцией Грина из части (d)):
C{x,t)=(M(x,t)M(0,0))w
= ([M(x,t)]MiM(0,0))eq
= / f°M(x', 0)G(x - χ', t)dx'M(0,0)\
V-oo / eq
/oo
C{x',0)G(x-x',t)dxf. (10.108)
-OO
(e) Используя гипотезу регрессии Онзагера, вычислите зависящую от
времени и координат корреляционную функцию C(x,t) = (M(x, £)M(0,0))ev. (Это
довольно сложная часть упражнения; ваш ответ должен выражаться через
функцию ошибок.) Если у вас есть подходящее программное обеспечение, постройте
график этой функции для малых и больших времен; верно ли, что она выглядит
похоже на ехр(—\у\) в одном пределе и на ехр(—у2) в другом?
Флуктуационно-диссипационную теорему можно использовать для того,
чтобы связать восприимчивость х(яг, t) к зависящему от времени внешнему
импульсу и корреляционную функцию С(х, t) (см. уравнение 10.60).
Пусть x{X)t) описывает обычный отклик Μ на внешнее поле H{x',t')
(уравнение 10.29), взаимодействие которого с намагниченностью
описывается энергией f M(x)H(x) dx.
(f) Вычислите восприимчивость χ(χ,ί), зная C(x,t). Сначала выпишите
общую формулу, затем подставьте ваш ответ из части (е).
10.9 Квазичастичные полюса и теорема Голдстоуна. @
Зуковые волны — это фундаментальные возмущения (или голдстоунов-
ские моды), связанные с трансляционной симметрией. Если система
инвариантна относительно однородного сдвига на вектор и, в ней должны
существовать низкочастотные возмущения, связанные с длинноволновыми полями
сдвига u(x,t) (см. раздел 9.3).
Звуковые волны обладают небольшой диссипацией (демпфированием),
называемым ультразвуковым затуханием. Если система, рассматриваемая
458
Гл.10. Корреляции, отклик и диссипация
нами, обладает также инвариантностью относительно преобразования
Галилея,51 эта диссипация стремится к нулю по мере стремления длины волны к
бесконечности. Проиллюстрируем это, вычислив явное выражение для
диссипации для одной конкретной модели распространения звука.
Пусть скорость звука в нашем веществе равна с, а его плотность — р.
Приложим к веществу внешнюю силу f(x, t). Будем моделировать
превращение энергии в тепло с помощью кельвиновского затухания с коэффициентом
затухания
д2и од2и ,7дд2и f(x,i) ,,Л <ПЛ.
«г = <?аР+*5а?+,· (10109)
Как мы заметили в упражнении 9.6, кельвиновское затухание — это дисси-
пативный член с самым меньшим количеством производных, допустимый из
соображений галилеевской инвариантности.
В отсутствие диссипации и внешних сил d= 0 = /(х, £), решения
волнового уравнения имеют форму плоских волн и(х, t) = exp (\(kx — Ukt)) с
дисперсионным соотношением Шк = ±cfc. Диссипация приводит к тому, что плоские
волны затухают с течением времени, что соответствует появлению мнимой
части частоты ω^ —> иь — ΪΓ. Определим добротность Qk как умноженное
на 2π число периодов осцилляции, укладывающихся в период времени, за
который энергия волны (пропорциональная и2) спадает в е раз.
(a) Покажите, что уравнение (10.109) в отсутствие внешней силы (/ = 0)
имеет решения типа затухающих плоских волн,
и(х, t) = exp (\(кх — uJkt)) exp(—Г&£)
= ехр(1(*;х-Пл«)), (10.110)
с комплексной частотой Ω& — ^к — il\. Найдите Ω&, решив квадратное
уравнение. Как выглядит новое дисперсионное соотношение для ω&? Чему равен
параметр затухания 1\? Покажите, что в длинноволновом пределе частота Uk ~ ±ск.
Пропорционально какой степени к расходится добротность при к —у 0?
Следовательно, чем ниже частота, тем меньше затухание колебаний. Голдстоуновские
моды становятся недиссипативными при ω —> 0.
(b) На какой частоте действительная часть частоты ω^ обращается в ноль?
(На этой частоте звуковые волны становятся передемпфированными; на
более коротких волнах деформации смещения релаксируют диффузионно, без
колебаний.)
51 Преобразование Галилея — это однородное изменение скорости всех точек системы на
v. u(x,i) -> гх(х, t) + vt (нерелятивистский предел преобразования Лоренца). Если система,
инвариантная относительно преобразования Галилея, движется с постоянной скоростью,
она этого не замечает.
Гл.10. Упражнения
459
Этот прием, поиск решений в форме затухающих волн, работает только
для линейных уравнений. Более общий подход состоит в том, чтобы
исследовать восприимчивость к внешним возмущениям. Если приложить к системе
без затухания внешнюю силу /(х, t) = cos(kx) cos(cfci), которая соответствует
волновому вектору и частоте ω = ск одного из фононов, амплитуда
соответствующей моды колебания будет неограниченно расти; другими словами,
восприимчивость в этом случае расходится. Посмотрим, что будет происходить
при наличии затухания.
(c) Чему равна восприимчивость \(к,и) для нашей системы с затуханием,
описываемой уравнением (10.109)? (Указание: перейдите к Фурье-переменным
к и ω, и задание превратится в простое алгебраическое упражнение.)
Проверьте, что ваше решение в отсутствие диссипации (d = 0) имеет полюса52 при
Uk = ±cfc для любого волнового вектора fc; при возмущении, соответствующем
резонансу, восприимчивость расходится. Проверьте, что эти полюса сдвигаются
в ilfc = (jfc - \Tk (в обозначениях части (а)) при включении диссипации.
(d) Проверьте, что все полюса восприимчивости лежат в нижней
полуплоскости, как того требует принцип причинности (см. раздел 10.9).
Преобразование Фурье от корреляционной функции в веществе С(к,и>)
можно измерять методом нейтронного рассеяния. Пусть для нашего вещества
с = 1000м/с, d = 10~3м/с2, ρ = 1г/см3 и Г = 300К; имейте в виду, что
постоянная Больцмана кв = 1.3807 · 10~23 Дж/К.
(e) С помощью флуктуационно-диссипационной теоремы
χ"(Κω) = ^6(Κω) (10.111)
(см. уравнение 10.65) вычислите С(к,и) — корреляционную функцию в нашем
веществе. Нарисуйте график С(к,ш) при ω = 108 (это соответствует примерно
16 МГц) для к от нуля до 2 · 105. Кажется ли вам, что будет сложно оценить
дисперсионное соотношение ω&, зная корреляционную функцию?
В сильно взаимодействующих системах элементарные возмущения
представляют собой квазичастицы: перенормированные электроны, фононы,
колебательные моды, не являющиеся чистыми многочастичными состояниями,
поскольку они затухают со временем (см. сноску 23 на с. 273). Эти
квазичастицы определяются как полюса пропагаторов или квантовых функций
Грина, тесно связанных с нашей классической корреляционной функцией C(fc, ω).
52Функция ψ(ζ) имеет полюс в точке ζο, если она расходится в точке ζο как константа,
деленная на ζ — ζο в целой положительной степени. Полюса особенно легко находить, если
φ представляется в виде отношения двух функций, каждая из которых остается гладкой
и конечной в рассматриваемой области; тогда нули знаменателя и есть полюса.
Глава 11
Скачкообразные фазовые
переходы
Большинство фазовых переходов происходят скачкообразно. В точке
скачкообразного перехода многие физические свойства системы испытывают
разрыв; плотность, сжимаемость, вязкость, теплоемкость, диэлектрическая
проницаемость, теплопроводность — все эти характеристики скачком
принимают новые значения. Более того, в большинстве случаев эти
переходы происходят без всяких промежуточных стадий, ничто не указывает
на то, что вот-вот произойдет переход; чистая вода не превращается в шугу
(незамерзшая смесь воды и льда. - Прим. переводчика) перед тем как
превратиться в лед,1 а в водяном паре при 101°С нет маленьких капелек
воды.2
В разделе 11.1 мы исследуем фазовые диаграммы и поведение
свободной энергии вблизи скачкообразных фазовых переходов. В разделе 11.2 мы
изучим правило Максвелла, используемое для определения точки
сосуществования двух фаз. В разделе 11.3 мы вычислим скорость, с которой происходит
образование зародышей новой фазы при скачкообразном переходе. Наконец,
в разделе 11.4 мы обсудим устройство трех типов микроструктур, связанных
Шуга возникает тогда, когда в воде есть примеси вроде соли или сахара; она
представляет собой лед, состоящий почти целиком из чистой воды (НгО) в окружении более
соленой воды. Наличие соли приводит к понижению температуры замерзания; при
замерзании воды из нее вымораживается соль, в результате чего температура замерзания для
оставшейся жидкости понижается.
2Точнее говоря, есть только экспоненциально редкие микроскопические капли,
возникающие в результате флуктуации. Наличие этих редких капель важно для зародышеобра-
зования (см. раздел 11.3).
11.1. Стабильные и метастабильные фазы
461
со скачкообразными переходами — динамических структур, возникающих
при разделении фаз, мартенситов и дендритов.
11.1 Стабильные и метастабильные фазы
Вода остается жидкостью при охлаждении вплоть до 0°С, когда она
внезапно замерзает и превращается в лед. При нагревании вода остается
жидкостью вплоть до 100°С, когда она внезапно превращается в пар.
С другой стороны, при выпаривании кастрюли с водой ничего внезапного
не происходит. Это связано с тем, что мы не можем напрямую
контролировать температуру воды, наше воздействие на систему состоит в том, что мы
подводим к ней постоянное количество тепла в единицу времени.3
Рассмотрим теплоизолированный сосуд с водой, в котором поддерживается
постоянное давление (при этом его объем может изменяться), и будем подводить к
нему тепло с небольшой скоростью. В момент, когда система достигнет точки
перехода жидкость—газ, в верхней части сосуда возникнет небольшой
пузырек газообразной фазы; по мере дальнейшего подвода энергии этот пузырек
будет плавно расти, заполняя все большую часть сосуда. Переход из
жидкого в газообразное состояние проходит через промежуточную двухфазную
область; температура системы будет меняться до тех пор, пока вся
жидкость не выкипит. Можно провести аналогичный эксперимент, зафиксировав
температуру и плавно меняя объем сосуда V. Получающаяся в результате
фазовая диаграмма показана на рис. 11.1(b); двухфазная область
возникает в результате минимизации свободной энергии Гельмгольца А(Т, V, 7V), как
показано на рис. 11.2(a).4
3 Скрытой теплотой перехода называется изменение энтальпии Ε + PV в точке
перехода. Для испарения воды эта теплота равна 2500 Дж/г = 600 кал/г. Таким образом, при
условии постоянства подвода тепла к системе на то, чтобы вся вода выкипела, понадобится
в шесть раз больше времени, чем на то, чтобы нагреть ее от 0°С до температуры кипения
((1 кал/г°С) · 100°С).
4То, что зависимость свободной энергии от объема в двухфазной области описывается
прямой линией, означает, что при увеличении объема и переходе жидкости в газ давление
Ρ = —(8Α/δν)\τ,Ν остается постоянным, точно так же как температура остается
постоянной, когда жидкость выкипает при заданном давлении. Свободная энергия любого
стабильного пространственно-однородного состояния всегда должна лежать ниже свободной
энергии смешанного двухфазного состояния с тем же объемом, энергией и числом частиц:
равновесная свободная энергия — это выпуклая функция.
462
Гл.11. Скачкообразные фазовые переходы
Рис. 11.1. Фазовые диаграммы в координатах Р-Т и T-V
Фазовые диаграммы в координатах Р-Т и T-V для типичного вещества, (а) Линия
сосуществования жидкость-газ задает давление насыщенного пара PV(T) и температуру
кипения жидкости TV(P). Для воды НгО линия равновесия жидкость-твердое тело имеет
отрицательный наклон, поскольку (в отличие от большинства других веществ в жидком и
твердом состоянии) лед имеет меньшую плотность, чем вода. (Ь) ТУ-диаграмма перехода
жидкость-газ при фиксированном TV, на диаграмме видна двухфазная область (см. также
рис. 8.8 и 12.6(a)). Область, заштрихованная горизонтальными штрихами, соответствует
фазовому расслоению; в этой области система будет разделяться на две фазы,
соответствующие жидкости и газу в состояниях, определяемых концами горизонтальной линии.
Диаграмма в координатах P-V выглядит похожим образом.
Чтобы избежать рассмотрения этих двухфазных областей, перейдем к
переменным Ρ и Τ и будем использовать свободную энергию Гиббса5
G(T, P,N) = E-TS + PV. (11.1)
Как обычно (см. раздел 6.5), побеждает то состояние, в котором G
минимально.6 Соотношение Эйлера Ε = TS — PV + μΝ говорит нам, что
G = μΝ (см. упражнение 6.9). Таким образом, состояние с наименьшим
химическим потенциалом оказывается предпочтительным и переход происходит
при /xiiq = /Xgas· Это выглядит логичным: на границе раздела жидкость-газ
фазы могут обмениваться энергией, объемом и частицами. Обмен энергией
будет происходить вплоть до выравнивания температур, обмен объемом —
вплоть до выравнивания давлений, а частицы будут переходить из жидкости
в газ до тех пор, пока не выровняются химические потенциалы двух фаз.
Вспомним теперь термодинамическое соотношение для дифференциалов
dE = TdS — PdV + μάΝ и, применив его к уравнению (11.1), получим aG =
5 Можно также обойти рассмотрение двухфазных областей, используя большой
термодинамический потенциал Ф(Т, V, N) = E — TS — μΝ. В большом каноническом ансамбле число
частиц может варьироваться, так что при превращении жидкости в газ лишние молекулы
просто удаляются.
6Минимизируя G для нашей системы, мы тем самым максимизируем энтропию
Вселенной в целом (т.е. системы и термостата, с которым она обменивается энергией и объемом,
см. раздел 6.5).
11.1. Стабильные и метастабилъные фазы
463
Рис. 11.2. Стабильные и метастабилъные состояния
(а) Свободная энергия Гельмгольца как функция объема. Пунктирная линия
соответствует метастабильным и нестабильным состояниям (рис. 11.3(a)). При соответствующих
значениях объемов равновесное состояние, показанное темной прямой линией, не является
пространственно однородным, а представляет собой смесь жидкости и газа. (Смесь XN
молекул стабильной газовой фазы и (1 — X)N молекул стабильной жидкой фазы будет
описываться линейной зависимостью на этом рисунке: V = AV^Slform + (1 — А)1^1Гогш, а
А = Aj4gas+(1 — А)Лнч плюс поверхностная свободная энергия, пренебрежимо малая для
достаточно больших систем.) (Ь) Свободная энергия Гиббса для жидкой и газовой фазы вдоль
изобары (линии постоянного давления, соответствующей горизонтальной пунктирной
линии на рис. 11.1(a)). Фазовый переход происходит в точке, где две кривые пересекаются.
—SdT + V άΡ + μάΝ. Меняя температуру при фиксированном давлении и
числе частиц, мы получаем, таким образом, что
dG
дТ
= -S. (11.2)
На рис. 11.2(b) показана свободная энергия Гиббса как функция
температуры для жидкости и для газа. В точке фазового перехода эти свободные
энергии равны. Различие в наклонах этих кривых равно различию в энтропии
жидкости и газа (см. уравнение 11.2). В соответствии с термодинамическим
определением энтропии S = dQ/T (см. раздел 5.1) получаем, что это
различие в энтропии равно скрытой теплоте перехода в расчете на одну частицу L,
умноженной на число частиц N и поделенной на температуру перехода Tv,
AS = LN/TV. (11.3)
Тот факт, что свободная энергия Гиббса имеет излом в точке перехода,
соответствует скачку энтропии при переходе из одной фазы в другую;
скачкообразным фазовым переходам соответствуют скачки первой производной
464
Гл.11. Скачкообразные фазовые переходы
свободной энергии. Именно поэтому во многих книгах их называют фазовыми
переходами первого рода.7
Обратите внимание на то, что мы продолжили рисовать кривые
свободной энергии жидкости и газа и с «неправильной» стороны от точки фазового
перехода. Экспериментально хорошо известно, что пар можно переохладить
существенно ниже точки конденсации.8 При тщательном проведении
эксперимента над достаточно чистыми системами можно также и существенно
перегреть жидкость. Это довольно тонкий вопрос с теоретической точки
зрения. Некоторые из теорий скачкообразных переходов порождают
хорошо определенные метастабильные фазы (показанные пунктирной линией на
рис. 11.2(a)). Однако совершенно определенно не существует равновесного
газообразного состояния при температуре ниже Tv. В более хитрых подходах
(которые мы не будем здесь обсуждать) свободным энергиям метастабильных
фаз приписывается, помимо действительной, еще и мнимая часть.9
11.2 Правило Максвелла
На рис. 11.3(a) показана зависимость давления от объема при
изотермическом расширении вещества. При увеличении объема, в момент, когда
давление в системе достигает давления насыщенного пара при
соответствующей температуре, жидкая фаза становится метастабильной. Аналогично, газ
становится метастабильным при прохождении того же давления в процессе
сжатия. Метастабильные состояния хорошо определены только вблизи точки
перехода, где зарождение новой фазы происходит медленно (см. раздел 11.3)
В этой книге мы избегаем этого названия и аналогичного названия переходы второго
рода для непрерывных фазовых переходов. Это связано не только с туманностью этих
названий, но и с тем, что второе из них попросту вводит в заблуждение: в точке непрерывного
перехода термодинамические функции имеют степенные или существенные особенности, а
не просто разрывы вторых производных (см. гл. 12). (Английское название «first(second)
order phase transition» — фазовый переход первого (второго) порядка — еще более явно
указывает на порядок соответствующей разрывной производной свободной энергии, чем
русское. —Прим. переводчика.)
8Именно это происходит в случаях, когда относительная влажность воздуха превышает
100%.
9 Аналогично тому, как время жизни резонанса в квантовой механике связано с мнимой
частью его энергии Ε + ШГ, мнимая часть плотности свободной энергии оказывается
пропорциональна вероятности (в единицу времени и в расчете на единицу объема) зарождения
новой фазы (см. раздел 11.3). Мы не будем обсуждать этот вопрос подробно, умолчим и
о связанной с этим формализмом существенной особой точке свободной энергии: более
подробную информацию можно получить в [15,75].
11.2. Правило Максвелла
465
и времена жизни метастабильных фаз остаются достаточно большими.
Пунктирной линией показана полностью нестабильная область; если искусственно
приготовить пространственно однородное распределение молекул с
характеристиками из этой области, такое состояние спонтанно развалится на густо
переплетенные нити двух фаз10 (см. раздел 11.4.1).
Рис. 11.3. Правило Максвелла
(а) Зависимость давления от температуры вдоль изотермы (соответствующей
вертикальной пунктирной линии на рис. 11.1(a)). При малых значениях объема вещество находится
в жидкой фазе; когда объем достигает двухфазной области на рис. 11.1(b), жидкая фаза
становится метастабильной. При больших объемах стабильной является газовая фаза и,
аналогично, она становится метастабильной при переходе в двухфазную область.
Точками показана линия сосуществования фаз, на которой давления и химические потенциалы
двух фаз равны. (Ь) Разность свободной энергии Гиббса между двумя точками с равными
давлениями равна разности площадей фигур на PV-диаграмме, заштрихованных разной
штриховкой.
Откуда мы узнали, что нужно нарисовать линию сосуществования фаз
на рисунке 11.3(a) именно при этом давлении? Как найти давление
насыщенного пара, при котором жидкость и пар сосуществуют при заданной
температуре? Из предыдущего раздела мы знаем, что сосуществование фаз
соответствует равенству свободных энергий Гиббса Gnq = Ggas. Напомним, что
dG = —SdT + VdP + μάΝ, так что при фиксированной температуре и числе
частиц (dG/dP)\ryN = V. Следовательно, мы знаем, что
AG= / V(P)dP = 0. (11.4)
Может показаться, что этот интеграл равен нулю по определению, т.к. оба
предела интегрирования равны давлению насыщенного пара F\iq = Pgas =
10 Это спонтанное разделение называется спинодалъным распадом. В былые времена
было принято называть конечные точки пунктирной кривой точками спинодали, однако есть
причины сомневаться, что в реальной жизни (в отличие от среднеполевых теорий)
существуют хорошо определенные точки перехода между режимами зародышеобразования и
синодального распада.
466
Гл.11. Скачкообразные фазовые переходы
PV(T). Однако в действительности эта формула равна сумме интегралов по
четырем фрагментам (см. рис. 11.3(b)):
AG = V{P) άΡ+ I V(P) άΡ
/*-*max /*-*gas
+ / V(P)dP+ V(P)dP, (11.5)
J *unst J fmax
где нестабильная точка соответствует максимуму барьера на рис. 11.2(a) и
Pliq = PUnst = Pgas в точке сосуществования фаз. Обратите внимание, что
первый и последний члены отрицательны, т.к. Р\щ > Pmin и Pmax > Pgas·
Эти четыре интеграла имеют красивый геометрический смысл, показанный
на рис. 11.3(b): сумма первых двух равна площади области, заштрихованной
правой штриховкой (зеленые штрихи, направленными направо вверх), а
сумма последних двух — площади области (со знаком минус), заштрихованной
левой штриховкой (красные штрихи, направленными направо вниз).
Площади этих двух областей должны, следовательно, быть равны при давлении
насыщенного пара. Это и есть правило равных площадей Максвелла.11
11.3 Теория критического зародышеобразования
Влажной ночью воздух может оказаться перенасыщен парами воды.
Каким образом этот метастабильный пар превращается в капли росы или в
микроскопические капельки, формирующие облака и туман?
Мы видели (см. рис. 11.2(b)), что разница между свободными энергиями
Гиббса для газа и жидкости увеличивается по мере понижения
температуры ниже Tv. Можно оценить разность химических потенциалов, являющуюся
движущей силой образования капель; мы знаем, что dG/dT = — S
(уравнение 11.2), a AS = LN/TV (уравнение 11.3), так что
Αμ = (Cgas - CbJ/N = (д{Се^С^\р^т\/м
= ASAT/N = (LN/TV)(AT/N) = LAT/TV. (11.6)
11 Следует помнить, что правило Максвелла имеет смысл только для среднеполевых
теорий, в которых имеется хорошо определенная нестабильная ветвь кривой P(V) (см.
рис. 11.2(a)).
11.3. Теория критического зародышеобразованил
467
Какой фактор препятствует формированию капель? Это поверхностное
натяжение σ между жидкой и газообразной фазами. Поверхностное
натяжение — это свободная энергия Гиббса на единицу площади поверхности раздела
между газом и жидкостью. Подобно натяжению нити, поверхностное
натяжение может вызывать силу, стремящуюся уменьшить площадь поверхности.12
Чтобы получить большую каплю, ее радиус необходимо нарастить от
нуля (рис. 11.4). Поскольку выигрыш в свободной энергии растет
пропорционально объему капли V, а цена образования капли (в виде поверхностного
натяжения) пропорциональна площади ее поверхности Л, для слишком
маленьких капель цена каплеобразования будет перевешивать выигрыш.
Рассмотрим сферическую каплю радиуса R. Поверхностная энергия Гиббса
равна σΑ. Пусть концентрация молекул жидкости равна р\щ частиц в единице
объема, и каждой частице соответствует выигрыш в свободной энергии
Гиббса, равный Δμ = LAT/TV, тогда полный выигрыш в свободной энергии равен
VpiiqA/x. Следовательно,
Gdropiet(fl) =σΑ- Υρχ^Δμ = 4πϋ2σ - (-nR3)P]iq(LAT/Tv). (11.7)
График этой свободной энергии изображен на рис. 11.5. Обратите
внимание на то, что при малых R (в области доминирования поверхностного
натяжения) свободная энергия растет квадратично, а при больших R (когда
доминирует объемный вклад, связанный с разностью химических
потенциалов) энергия спадает пропорционально кубу R. Газ будет оставаться газом
до тех пор, пока одна из редких тепловых флуктуации не позволит системе
перевалить через барьер и сформировать критическую каплю.
12 Как определяется поверхностное натяжение? Теоретически мы можем измерить
свободные энергии Гиббса жидкости Gee и газа Ggg в точке равновесия фаз, поместив их при
постоянном давлении в цилиндрические сосуды, поверхность которых предпочитает одну
фазу другой (например, в реальной жизни поверхность, покрытая воском, предпочитает
газ). После этого мы должны отрезать по половине каждого из сосудов и склеить их
между собой; в результате будет формироваться граница раздела площади А, равной площади
поперечного сечения сосудов. Мы измеряем теперь свободную энергию Гиббса при наличии
поверхности Geg и определяем поверхностное натяжение как σ = [Geg — \{Gee + Ggg)\/A.
Такая сложная процедура необходима для того, чтобы исключить поверхностные энергии
взаимодействия с боковыми стенками.
Обратите внимание, что определение поверхностного натяжения для изогнутых
поверхностей вдали от точки сосуществования фазы — более тонкая задача [74, chapter XV].
468
Гл.11. Скачкообразные фазовые переходы
Поверхностное
натяжение
Рис. 11.4. Пузырек пара
Зарождение новой фазы происходит в результате редкой тепловой флуктуации, при
которой возникает капелька новой фазы, достаточно большая, чтобы преодолеть
потенциальный барьер, изображенный на рис. 11.5.
в
*!,
droplet'
о
"
~Ry
l6na3T2/3p2L2A?
R \
Iе \
2<sTJpLAT \
~-r\
Рис. 11.5. Энергетический барьер
Энергетический барьер для формирования капель: свободная энергия как функция R
проходит через максимум.
Радиус критической капли Rc и величину барьера свободной энергии В
можно найти, максимизировав G(R):
dGd]
roplet
dR
Rc
= 8тгаДс - 4жр1щ(ЬАТ/Ть)Я% = О,
Rc —
В =
1σΤν
С Ρΐίς^ΔΤ'
16πσ3Γ2 Ι
3p2qL2 (ΔΤ)2·
(11.8)
(11.9)
(11.10)
Вероятность найти критическую каплю в единице объема газа равна
ехр(—В/квТ), умноженной на некоторый коэффициент. Скорость
11.3. Теория критического зародышеобразованил
469
зародышеобразования в единице объема — это полное число капель, чей
радиус достигает Rc в единицу времени, оно равно вероятности оказаться
на вершине барьера, умноженной на скорость пересечения барьера и
на корректирующий множитель, учитывающий обратные переходы.13
Поправочные коэффициенты важны для более точных теорий, но главный
вклад в экспериментально наблюдаемую зависимость дает экспоненциально
малая вероятность обнаружить каплю критического размера. Таким
образом, интересующая нас скорость зародышеобразования в единице
объема Г имеет вид
Г = (prefactors)e-B/fcBT. (11.11)
Обратите внимание на следующие особенности полученного результата.14
• Радиус критической капли равен Rc ос 1/ΔΤ. Если вы переохлаждаете
жидкость совсем чуть-чуть, то для того, чтобы преодолеть
поверхностное натяжение, вам понадобится большая капля.
• Высота барьера В ос 1/(ΔΤ)2. Энергетический барьер
зародышеобразования расходится при Τ = Τυ.
• Скорость зародышеобразования равна Г ос ехр(—С/(АТ)2). Для
слабого переохлаждения она может быть очень мала.15
Вычисленные нами скорости соответствуют однородному зародышеобра-
зованию: скорости образования капель новой фазы в совершенно чистой
системе без границ. На практике однородное зародышеобразование доминирует
редко. Поскольку зародышеобразование так сильно подавляется
поверхностным натяжением, система придумывает разнообразные ухищрения, чтобы
13См. упражнение 6.11, в котором рассмотрена аналогичная задача пересечения барьера
для задачи о вычислении скоростей химических реакций.
14 В предыдущих главах мы использовали статистическую механику для вычисления
средних характеристик фазы и типичных (гауссовых) флуктуации вокруг этих средних
характеристик. Теория образования критических капель (и ее квантовых аналогов — ин-
стантонов) позволяет нам, задаваясь вопросом о типичных флуктуациях вблизи точки
перехода между фазами, исследовать редкие флуктуации, находящиеся далеко в хвосте
распределения. В гл. 12 мы также будем исследовать редкие крупные события,
находящиеся далеко в хвосте распределения. В этом случае мы будем, по сути, отображать эти
редкие флуктуации рассматриваемой системы на более типичные флуктуации некоторой
другой, сглаженной системы.
15 Скорость распада метастабильной фазы имеет существенную особенность при Τν; т.е.
она равна в этой точке нулю во всех порядках теории возмущения по ΔΤ. В некотором
смысле именно поэтому мы можем изучать метастабильные состояния — теория
возмущений автоматически игнорирует тот факт, что они нестабильны.
470
Гл.11. Скачкообразные фазовые переходы
хотя бы частично снизить энергетический барьер. Именно поэтому капли
росы образуются на траве (или на вашем ветровом стекле), вместо того чтобы
формироваться в воздухе и только потом падать на землю; поверхностное
натяжение между водой и травой намного меньше натяжения между водой
и воздухом, так что можно сформировать примерно полусферическую
каплю и уменьшить энергетический барьер В вдвое. При формировании
облаков зародышеобразование происходит на микроскопических частицах пыли,
что, опять же, позволяет уменьшить площадь поверхности, необходимую для
формирования критической капли заданного размера.16
Отметим в заключение, что зародыши, возникающие при зарождении
кристаллических фаз, не будут, вообще говоря, иметь идеальную
сферическую форму. Поскольку поверхностное натяжение в кристаллах анизотропно,
форма зародыша, содержащего максимальное количество атомов при
заданной поверхностной энергии, будет не сферической, а так называемой
равновесной кристаллической формой (т.е. той формой, которую кристалл с таким
числом частиц примет в равновесии, рис. 11.6).
11.4 Морфология скачкообразных переходов
Что же происходит после образования зародыша новой фазы (а также в
тех случаях, когда переход происходит, минуя стадию зародышеобразования,
например, если переохлаждение очень велико)? Ответ на этот вопрос
составляет предмет огромной, богатой дисциплины, относящейся в значительной
степени к геологии, инженерной науке и науке о материалах, а не к
статистической механике. Мы дадим здесь лишь краткое введение в этот предмет,
подчеркивая те факты и области, которые используют идеи статистической
механики.
11.4.1 Динамика фазового разделения
Что общего между соусом для салата, чугуном и горной породой?
Фазовое разделение играет ключевую роль в понимании структуры всех этих
трех веществ. Если взболтать масло и уксус, они образуют смесь, состоящую
из маленьких капель. После прекращения взбалтывания микроскопические
16Кстати говоря, температура облаков во многих случаях так низка, что в них
зарождаются кристаллики льда, а не капельки воды. Некоторые растительные патогены
(Pseudomonas syringae) синтезируют белки, структура которых позволяет им эффективно
способствовать образованию зародышей кристаллов льда; эти бактерии используют
повреждения, наносимые растениям заморозками, для того чтобы проникнуть в них. Люди
используют такие же белки в снеговых пушках, применяемых на лыжных курортах.
11.4. Морфология скачкообразных переходов
471
Рис. 11.6. Равновесная форма кристалла
Равновесная форма кристалла свинца при температуре около 300°С [38,122]. Обратите
внимание на плоские грани, которые соответствуют низкоэнергетичным
высокосимметричным поверхностям. Имеется три интересных статистико-механических вопроса, связанных
с этими поверхностями, которые мы не будем здесь подробно обсуждать. (1) Части
поверхности кристалла с плоскими гранями находятся в другой фазе по сравнению с
закругленными частями; они находятся ниже точки перехода шероховатости. (2) Равновесную
форму кристалла, минимизирующую свободную энергию, можно рассматривать как
преобразование Лежандра от свободной энергии (построение Вулффа). (3) Для некоторых видов
взаимодействий при низкой температуре все грани равновесная форма кристалла могут
быть плоскими (ниже точек переходов округления граней и округления углов); в этой фазе
характерный пространственный масштаб будет расти со временем только логарифмически
(рис. 11.10).
капельки сливаются в более крупные капли, постепенно образуя все более и
более грубую смесь, до тех пор пока фазы не разделятся полностью и все
масло не соберется сверху.
В расплавленном железе, перед тем как его отливают, имеется довольно
значительная примесь растворенного углерода. При охлаждении железа
растворенный углерод осаждается, образуя множество зародышей (как описано
в разделе 11.3), которые начинают расти и продолжают свой рост, пока не
закончится весь примесный углерод. В результате углерод оказывается
распределенным среди железа в виде крупинок, чей размер и количество зависят
от процедуры охлаждения расплава. Твердость и хрупкость чугуна зависят
от характеристик этих частиц углерода, и поэтому зависят от того, каким
именно образом железо охлаждали.
Камни (куски горной породы) часто состоят из крупинок разных веществ:
для гранита это кварц, щелочные полевые шпаты и плагиоклазы; для
базальта — плагиоклазы и богатые кальцием пироксены... Типичные размеры этих
крупинок в разных породах отличаются.
472
Гл.11. Скачкообразные фазовые переходы
Горные породы, сформировавшиеся из лавы при извержениях вулканов,
состоят из наиболее мелких крупинок; породы, возникшие глубоко под
землей из очень медленно остывавшей магмы, состоят из крупных зерен. Для
того чтобы крупинка росла, образующие ее атомы должны находить ее,
диффундируя сквозь соседние крупинки, состоящие из других веществ — этот
процесс крайне замедляется, когда крупинки становятся большими.
Поликристаллы также формируются при охлаждении расплавов чистых веществ;
в разных частях жидкости будут возникать зародыши кристаллов разной
ориентации, которые будут затем расти, слепляясь друг с другом. В этом
случае одно из зерен может расти, забирая молекулы у соседа, не дожидаясь
того момента, когда нужные ему молекулы продиффундируют издалека.
Динамику фазового расслоения можно пронаблюдать и на компьютере.
На рис. 11.7 показаны два мгновенных снимка модели Изинга, замороженной
при нулевой температуре, в моменты времени, отличающиеся примерно в
десять раз. Обратите внимание на то, что морфология областей со спинами,
направленными вверх и вниз, выглядит похоже на обоих рисунках, однако
типичный масштаб длины L(t) растет с течением времени. В этом состоит
главная идея теорий, описывающих фазовое расслоение: статистически
система подобна самой себе в более поздний момент времени, меняется лишь
пространственный масштаб L(t), зависящий от времени.
Рис. 11.7. Динамика фазового расслоения
Конфигурация спинов двумерной модели Изинга (с несохраняющимся параметром
порядка) при Τ = 0 через время, соответствующее (а) примерно двадцати шагам времени (за
один шаг времени каждый спин пробуют переключить один раз) и (Ь) примерно 200
шагам. Обратите внимание на то, что морфология доменов выглядит похоже, однако в более
поздний момент времени типичный пространственный масштаб примерно втрое крупнее
(λ/Ϊ0«3).
Основные результаты, касающиеся динамики фазового расслоения,
можно получить путем простых рассуждений (они могут показаться вам даже
слишком простыми). Рассмотрим рис. 11.8, на котором изображены этапы
фазового расслоения. Большинство интересных особенностей на мгновенном
снимке имеют один пространственный масштаб R ~ L(t). Расслоение
состоит в процессе «огрубления масштаба», когда мелкомасштабные неровности
11.4· Морфология скачкообразных переходов
473
сжимаются до нуля, а выживают только структуры и неоднородности более
крупного размера. Таким образом, нам нужно понять, сколько времени
уходит на то, чтобы выступы и капли типичного размера R сжались до нуля.
Это позволит нам оценить, каким образом размер выживших неоднородно-
стей L(t) растет со временем. L(t), таким образом, имеет смысл размера До
самых мелких неоднородностей, которые имелись в системе в начальный
момент времени и не успели полностью сгладиться до момента времени t.
Θ
Рис. 11.8. Движение поверхности, вызванное ее кривизной
Поверхностное натяжение σ порождает на поверхности раздела напряжение (силу на
единицу площади) τ = 2σκ, которое пропорционально средней локальной кривизне
поверхности к в этой точке. Морфология двухфазной структуры, в которой происходит расслоение,
имеет характерный масштаб Я, так что типичная локальная кривизна поверхности равна
к ~ 1/R. В случае, когда параметры порядка не сохраняются, наличие этой силы приводит
к росту характерного масштаба по закону L(t) ~ t '2.
Сила, вызывающая огрубление масштаба и сглаживание
неоднородностей, — это поверхностное натяжение: система может уменьшить свою
свободную энергию, уменьшая площадь поверхности границы между различными
доменами. Рассмотрим наиболее легко решаемый случай — случай эволюции
сферического домена. Поверхностная энергия для сферы радиуса R равна
^surface = 4π/ΐ2σ, так что на поверхности действует сила на единицу площади
(напряжение) г, направленная внутрь сферы:
г = ^р/(4тгД2) = 2а/Д. (11.12)
Поверхность произвольного вида имеет два главных радиуса кривизны: Ri
и /?2j которые могут быть как положительными, так и отрицательными;
напряжение г направлено перпендикулярно поверхности и задается
формулой (11.12) с точностью до замены 1/R на среднюю кривизну \ [1/-Ri + I/-R2]·
S
474
Гл.11. Скачкообразные фазовые переходы
Задачи, связанные с динамикой фазового расслоения, можно разделить на
два больших класса: задачи с сохраняющимся и с ^сохраняющимся
параметром порядка. Смесь масла с уксусом, чугун и гранит имеют сохраняющиеся
параметры порядка; для того чтобы данный домен увеличился в размере, ему
нужно затащить к себе дополнительные молекулы сквозь домены другого
вещества. В однокомпонентных поликристаллах и модели Изинга, показанной
на рис. 11.7, параметры порядка не сохраняются; спины могут свободно
переключаться из положения вверх в положение вниз, а молекулы могут свободно
переходить из домена с одной кристаллической ориентацией в соседний домен
с другой ориентацией.
Для несохраняющихся параметров порядка можно ожидать, что
поверхность раздела будет двигаться со скоростью, пропорциональной напряжению
и подвижности поверхности η:
Можно решить это уравнение и найти время fy, при котором сфера полностью
исчезнет, что позволит нам узнать, по какому закону растет L(t) в случае
несохраняющихся параметров порядка:
/ RdR= -2σηάί,
JRo Jo
B*/2 = 2aVtf, (11.14)
L(t) ~ Ro = \J±or)t oc \ft.
Решить эту задачу в явном виде для более сложных геометрий с
выпуклостями, сужениями и т.д. невозможно, однако в общем случае неоднородности
масштаба порядка R рассасываются за время порядка t ос Д2, так что
типичный масштаб огрубленной структуры растет как L(t) ~ t@, где β = 1/2.
Исследование случая с сохраняющимся параметром порядка идейно очень
похоже (см. рис. 11.9). В этом случае кривизна поверхности задает градиент
химического потенциала др/дх, который вызывает диффузию молекул из
областей с большой положительной кривизной в области малой или
отрицательной кривизны.Скорости частиц задаются их подвижностью 7 — D/квТ
(соотношение Эйнштейна), умноженной на градиент химического
потенциала,
ν = ^Vp =>* J = pv = /07V/X, (11.15)
где J — поток частиц через единицу площади, а р — плотность числа частиц.
Изменение химического потенциала при переносе частицы из домена радиуса
11.4- Морфология скачкообразных переходов
475
R на плоскую поверхность равно в точности изменению свободной энергии
при удалении одной частицы из сферического домена; поскольку число
частиц в шаре равно Ν = |π/ϊ3ρ, то
Рис. 11.9. Огрубление для систем с сохраняющимися параметрами
порядка
Различие в локальной кривизне поверхностей раздела является движущей силой роста
структур и в случае сохраняющихся параметров порядка. Атомы будут диффундировать
из областей с большой положительной кривизной в области с малой или отрицательной
кривизной. На больших масштабах доминирует объемная диффузия (L(t) ~ t1'3); на малых
масштабах существенную роль может играть поверхностная диффузия (L(t) ~ ί1^4). Для
жидкостей имеют значение также гидродинамические потоки, что дополнительно
усложняет ситуацию [137].
Естественно ожидать, что типичное расстояние AR между нашей сферой
и другим, более плоским, участком той же фазы также имеет порядок R (это
соответствует нашему предположению, что в системе существует
единственный характерный масштаб), так что
'-"й-ж· (1117)
Скорость изменения объема сферической капли — это поток числа частиц
через единицу площади поверхности J, умноженный на площадь поверхности
капли и деленный на число частиц в единице объема р:
476
Гл.11. Скачкообразные фазовые переходы
dVdroplet _ 4
dt " 3
•И?)
^dropletJ _ (47ГД2)27<7 - 8π^σ
Ρ PR2 Ρ '
dR- 2'"'1 (11.18)
dt ρ Я2'
/"«•«И- Г"22*.
-*/.
следовательно
1/3
L(t) ~ До = Г—1\ ос f1/3. (11.19)
Это грубое рассуждение — почти на уровне анализа размерностей —
позволяет получить правильный вывод о том, что характерный масштаб в
системах с сохраняющимся параметром порядка должен огрубляться по закону
L(t) rv $, где β = ^ в случае, когда основной механизм огрубления — это
объемная диффузия.
Тема огрубления масштаба и роста доменов при фазовом расслоении
имеет еще множество деталей и поворотов.
• Поверхностная диффузия. Часто оказывается, что коэффициент
диффузии на поверхности раздела фаз значительно больше
коэффициента диффузии в объеме: энергия активации, необходимая
для перемещения вдоль поверхности, существенно меньше, чем
энергия, необходимая для того, чтобы полностью удалить молекулу
из домена. Поток приповерхностной диффузии пропорционален J,
умноженному на периметр (пропорциональный первой степени β),
вместо J А; повторяя те же рассуждения, получим L(t) ~ t1'4. В
принципе, на больших временах t —> оо поверхностная диффузия
становится менее значительной, чем объемная, но зачастую она
доминирует в экспериментально интересной области.
• Гидродинамика. В жидкостях имеются другие важные механизмы
роста доменов. Например, в бинарных смесях жидкостей (масла и воды)
при соотношении компонент, близком к 50/50, образуются две
непрерывные взаимнопроникающие сетеобразные фазы (т.е. фазы
макроскопического линейного размера, по каждой из которых можно пройти от
11.4- Морфология скачкообразных переходов
477
одной стенки сосуда до другой). Различные области этих сетей имеют
разную кривизну и, следовательно, разное давление, из-за чего в них
возникают гидродинамические потоки [137], приводящие к росту
доменов.
• Логарифмическое расслоение в стеклах. В основе изложенной
теории фазового расслоения лежит негласное предположение о том, что
элементарные перестройки морфологии доменов в процессе их роста
соответствуют изменению лишь небольшого числа степеней свободы,
и, следовательно, высота элементарных барьеров ограничена. В
случае, когда это неверно (например, если необходимо удалить целый слой
атомов, для того чтобы уменьшить свободную энергию), динамика
перестроений радикально замедляется при росте размеров слоев. Именно это
происходит в трехмерной модели Изинга с антиферромагнитным
взаимодействием ближайших соседей, упомянутой выше (рис. 11.10, [135]).
Высота энергетического барьера, который надо преодолеть, чтобы
переключить целый слой спинов, растет пропорционально L, что приводит
к логарифмическому закону L(t) ~ log(f). В некоторых работах
утверждается, что аналогичный механизм роста барьеров объясняет
медленную релаксацию в жидкостях, формирующих стекла (раздел 12.3.4).
Рис. 11.10. Логарифмический рост поверхности
Упрощенная модель поверхности, перпендикулярной объемной диагонали, во фрустриро-
ванной модели Изинга со взаимодействием ближайших соседей, в которой барьеры для
роста доменов расходятся с увеличением их размера [135]. Обратите внимание на то, что
понижение энергии поверхности происходит посредством образования «террас» —
плоских участков вдоль основных направлений решетки (что может считаться своеобразным
«огрублением» граней). Этот процесс существенно замедляется, когда грани
увеличиваются в размере, поскольку энергетический барьер для переключения всей грани целиком
пропорционален ее длине. Это замедление происходит раньше перехода округления углов,
описанного в подписи к рис. 11.6.
478
Гл.11. Скачкообразные фазовые переходы
• Неуниверсальность. Изучение процесса огрубления с точки зрения
физики было во многом мотивировано аналогией со степенными и скей-
линговыми законами, известными из теории непрерывных фазовых
переходов (см. гл. 12 и упражнение 12.3). Однако имеются и существенные
различия. Степенные законы, описывающие динамику фазового
расслоения, проще и в каком-то смысле универсальнее — степени \ и ^,
полученные нами выше, не зависят, например, от размерности
пространства. С другой стороны, морфологии зародышей и скейлинговые
законы для кристаллов не универсальны; они зависят отанизотропии
свободной энергии и подвижности граней [113]. Практически для любого
конкретного вещества при любой конкретной температуре
скейлинговые функции на больших временах будут новыми. Если вдуматься, это
даже радует; в минералогии и науке о материалах существует такое
удивительное многообразие микроструктур, что не имело никакого смысла
ожидать, что все они описываются одной скейлинговой функцией.
11.4.2 Мартенситы
Во многих кристаллах при охлаждении происходят скачкообразные
структурные перестройки — фазовые переходы между разными
кристаллическими структурами. Хорошим примером может быть
растяжение кубического кристалла вдоль одной оси и одновременное сжатие
вдоль двух других. Динамически такие переходы часто затруднены: когда в
части образца переход уже произошел, а в другой — еще нет, напряжение на
границе раздела фаз может привести к разрушению кристалла.
Во многих материалах (например в железе17) фазовые переходы между
кристаллическими группами обходятся без крупномасштабного накопления
напряжения между частями кристалла, образуя мелкомасштабные слоистые
структуры. На рис. 11.11 приведена фотография мартенсита, на которой
показано формирование микротекстуры, позволяющей материалу локально
вытянуться, не образуя напряжений на больших масштабах.
17Соответственно, структура стали усложнена не только наличием углеродных зерен, но
и мартенситной доменной структурой; обе эти особенности существенно влияют на
свойства стали, и обе они существенно зависят от конкретных процедур охлаждения и ковки,
которым сталь подвергалась при ее изготовлении.
11.4. Морфология скачкообразных переходов
479
Рис. 11.11. Мартенсит
Исключительно красивый образец структуры мартенсита, полученный Чу [23]. Светлые и
темные полосы соответствуют двум вариациям мартенсита, т.е. кристаллам, вытянувшимся
после фазового перехода в двух разных направлениях. Квадратная область, занимающая
большую часть фотографии, не может изменить свою форму как целое, не вызвав слишком
большого напряжения между собой и соседними доменами. В результате формирования
показанной полосатой структуры (называемой ламинатом), напряжения по разным осям
в мартенсите уравновешиваются и дают в результате нулевое полное напряжение.
Мартенситы изучают не столько с помощью статистической механики,
сколько с помощью математики.18 Главная цель, однако, остается той же
самой: минимизировать (невыпуклую) свободную энергию при заданных
граничных условиях (см. упражнения 9.5, 11.7, и 11.8).
11.4.3 Дендриты
Почему возникают снежинки [83]? Кристаллики льда, возникающие в
атмосфере, в момент зарождения имеют примерно сферическую форму. Однако
по мере их роста возникает неустойчивость: те точки, которые оказываются
наиболее выступающими из кристалла в окружающую область
перенасыщенного пара, будут расти быстрее. Это происходит по двум причинам: потому
что концентрация пара в этих местах выше, а также, потому что
выделяющееся при кристаллизации тепло быстрее всего рассеивается с выступов
структуры (см. упражнение 11.9). Типичная для снежинок шестиконечная
форма возникает из-за того, что кристаллы льда имеют ось симметрии
шестого порядка, а разные кристаллографические поверхности растут с разной
скоростью. Огромное разнообразие форм снежинок отражает разнообразие
условий (температуры и концентрации водяного пара), при которых они
растут.
18Удобным инструментом для изучения мартенситов оказались непрерывные нигде не
дифференцируемые функции, ранее считавшиеся лишь патологическим случаем из теории
функций вещественной переменной.
480
Гл.11. Скачкообразные фазовые переходы
Аналогичные разветвленные структуры, называемые дендритами,
формируются и при росте других кристаллов (по тем же самым причинам).
Морозные узоры на окнах — один из самых очевидных примеров; на
рисунке 11.12 показан другой пример — кристалл растворителя, растущий в смеси
растворителя и полимера. Здесь, в выемках оказывается захвачено не тепло,
а молекулы медленно диффундирующего полимера, что приводит к
замедлению кристаллизации в этих областях. Многие используемые на практике
металлы и сплавы микроскопически представляют собой плотно упакованные
дендритные структуры.
Рис. 11.12. Дендриты
Растущие кристаллы часто формируют разветвленные структуры (дендриты) из-за того,
что выступы растут быстрее, чем впадины. На этом рисунке показаны дендриты, растущие
в сторону расплава вещества в тонкой пленке, протягиваемой через область с градиентом
температуры (Боденшац, Уттер, Рагнарсон [11]).
Упражнения
Первые три упражнения, Правило Максвелла для модели
Ван-дер-Ваальса, Критическая точка уравнения Ван-дер-Ваальса и
Поверхностное натяжение в модели Ван-дер-Ваальса используют старую
классическую модель фазового перехода жидкость—газ для иллюстрации
общих свойств скачкообразных фазовых переходов. Следующие два
упражнения, Зародышеобразование в модели Изинга и Зарождение пар
дислокаций, исследуют явления, сходные с зародышеобразованием в
магнитных системах (численно) и в системах с пластической деформацией
(аналитически).
19Дендрон — это греческое слово, означающее «дерево».
Гл.11. Упражнения
481
В следующих четырех упражнениях мы рассмотрим морфологию и
эволюцию структур, возникающих при разделении фаз в фазовых переходах
первого рода. Упражнение Фазовое расслоение в модели Изинга посвящено
численному исследованию стандартной модели, используемой для изучения
роста корреляций при быстром охлаждении. В упражнениях
Микроструктура оригами и Минимизирующие последовательности и микроструктура
рассмотрены важные методы, используемые математиками и инженерами для
изучения мартенситов и других микроструктур, индуцированных
граничными условиями. Наконец, в упражнении Снежинки и линейная стабильность
вводится модель, описывающая формирование дендритов, и метод
исследования устойчивости решений к малым возмущениям.
11.1 Правило Максвелла для модели Ван-дер-Ваальса. (Химия) @
Уравнение Ван-дер-Ваальса
(Р + N2a/V2)(V - Nb) = NkBT (11.20)
часто используется в качестве приближенного уравнения состояния
жидкостей и газов. Происхождение множителя V — Nb связано с наличием
короткодействующего отталкивания между молекулами (см. упражнение 3.5);
слагаемое N2a/V2 учитывает основной вклад20 от дальнодействующего
притяжения молекул.
На рис. 11.13 показаны зависимости давления от объема для одного
моля воды в приближении Ван-дер-Ваальса. Для каждой из кривых выполните
приближенно построение Максвелла; обозначьте на PV-диаграмме примерную
область сосуществования жидкости и газа. Вы можете сделать это карандашом
прямо в книге, но лучше скачать электронную версию графика с сайта [129].
11.2 Критическая точка уравнения Ван-дер-Ваальса. (Химия) @
Верхняя точка кривой сосуществования фаз на рис. 11.13 соответствует
таким значениям плотности, давления и температуры, при которых различие
между жидкостью и газом исчезает. Этой точке посвящено множество
исследований, так как она является классическим примером критической точки, в
окрестности которой наблюдаются самоподобные флуктуации и скейлинговое
поведение.
(а) Найдите критическую точку на рис. 11.13. Константы уравнения Ван-
дер-Ваальса подобраны таким образом, чтобы воспроизвести
экспериментальные значения критической температуры и давления для воды: Тс = 647.3 К и
20Эти поправки к уравнению состояния идеального газа соответствуют слагаемым
первого порядка в теории возмущений по плотности газа: для разреженных газов они малы.
482
Гл.11. Скачкообразные фазовые переходы
6*10*
5*10*
^4 НЮ8
X 3 к 10*
1
3 2 к 10*
1 «10*
v 50 100 150 200 250 300
Молярный объем (см3)
Рис. 11.13. Изотермы газа Ван-дер-Ваальса в координатах P-V
Показаны изотермы для воды в приближении Ван-дер-Ваальса (уравнение 11.20),
параметры а = 0.55Джм3/моль2 (а = 1.52 · Ю-35 эрг см3 в расчете на одну молекулу) и
Ь = 3.04 · Ю-5 м3/моль (Ь = 5.05 · Ю-23 см3 на одну молекулу) подобраны таким
образом, чтобы воспроизводились значения критической плотности и температуры для воды.
Рс = 22.09 МПа = 220.9 · 106 дин/см2; проверьте, что ваша оценка для
параметров критической точки примерно совпадает с этими данными. Мне удалось
найти очень мало данных о критическом молярном объеме для воды, а те
данные, которые удалось найти, не согласуются между собой: один источник
называет цифру 50см3/моль, другой — 55. Отметьте истинную экспериментальную
критическую точку на Вашем графике. Достаточно ли хорошо уравнение Ван-
дер-Ваальса предсказывает критическую плотность воды?
(Ь) Рисунок, который вы нарисовали, выполняя упражнение 11.1, наверное,
недостаточно точен, чтобы это можно было по нему определить, но фазовые
границы, предсказываемые уравнением Ван-дер-Ваальса, сходясь в критической
точке, образуют квадратичный максимум: 1/ре~ 1/р9 ~ (Р — Рс)1/2, где pi и р9
— это молярные плотности жидкости и газа, находящихся в фазовом равновесии
при давлении Р. Аналогично можно показать, что уравнение состояния Ван-дер-
Ваальса предсказывает, что
ре - Ра ~ (Те - Τ)1'2 ~ (-ί)1/2. (11.21)
Гл.11. Упражнения
483
Сравните это предсказание с рис. 12.6(a). Какое значение критического индекса
β предсказывает теория Ван-дер-Ваальса в соответствии с уравнением (11.21)?
11.3 Поверхностное натяжение в модели Ван-дер-Ваальса.
(Химия) (3)
Уравнению состояния Ван-дер-Ваальса соответствует следующее
значение химического потенциала на одну частицу
μ\ρ] =~квТ + Р/р -ар + квТ log(A3/9)
-kBT\og(l-bp), (11.22)
где ρ = N/V — плотность газа.
(a) Покажите, что минимуму μ соответствует р, удовлетворяющее уравнению
Ван-дер-Ваальса.
(b) Используя значения параметров из подписи к рис. 11.14, найдите, какое
приближенное значение дает уравнение Ван-дер-Ваальса для давления
насыщенного пара воды при 373 К = 100°С? Насколько это давление близко к
настоящему давлению насыщенного пара при этой температуре? (Указание:
атмосферное давление примерно равно 1 бару = 0.1 = 106 дин/см . Что происходит,
когда давление насыщенного пара оказывается равным атмосферному?)
График на рис. 11.14 можно рассматривать как своего рода барьер
свободной энергии, который необходимо преодолеть для формирования границы
раздела жидкость-газ. Пусть μο — химический потенциал, общий для
жидкости и газа при заданной температуре. Тогда дополнительная свободная
энергия Гиббса, связанная с образованием профиля плотности р(х), равна
AG = J р(х) (μ[ρ(χ)} - μ0) d3z, (11.23)
поскольку p(x)d3x — это число молекул, расположенных в элементарном
объеме d3x и имеющих в связи с этим увеличенный химический потенциал
μ[ρ(χ)].
(c) При комнатной температуре граница раздела между водой и паром очень
узкая, ее толщина порядка размера молекулы. Это делает самую идею
использования сглаженной свободной энергии для ее исследования достаточно
сомнительной. Тем не менее, пусть толщина границы раздела порядка двух или трех
ангстрем. Используя ван-дер-ваальсовское выражение для химического
потенциала (рис. 11.14) и уравнение (11.23), оцените поверхностное натяжение воды
(т.е. добавочную свободную энергию Гиббса на единицу площади поверхности,
по порядку величины это толщина слоя, умноженная на высоту барьера).
484
Гл.11. Скачкообразные фазовые переходы
-6.0
Τ -6J
о
"3-6.4
""б α005 0Ж ΟΟΐΙ 1)02 ~0Ш5~0~Ю
Плотность (моль/см3)
Рис. 11.14. Химический потенциал в приближении Ван-дер-Ваальса
Химический потенциал μ[ρ] в приближении Ван-дер-Ваальса для воды при температуре
Τ = 373 К и соответствующем (по уравнению Ван-дер-Ваальса) давлении сосуществования
фаз Ρ = 1.5 · 107 дин/см2.
Как ваш ответ соотносится с экспериментальным значением поверхностного
натяжения воды в точке кипения, равным 59 дин/см? (Один моль равен 6.023·
1023 молекул.)
11.4 Зародышеобразование в модели Изинга. ©
Модель Изинга (см. раздел 8.1) — это не только архетипическая модель
для изучения непрерывных фазовых переходов; это также наилучшая из
имеющихся у нас моделей для изучения зародышеобразования (в этом
упражнении) и динамики фазового расслоения (в упражнении 11.6).
Модель Изинга можно использовать для изучения зарождения одной
фазы внутри другой. Можно показать, что существует аналогия между
переохлаждением воды (и ожиданием образования зародыша кристалла льда) и
изменением внешнего магнитного поля, действующего на магнетик с Hext > 0
на Hext < 0 при температуре Г < Тс. Еще лучшей аналогией является
переохлаждение водяного пара и ожидание образования дождевой капли.
Запустите программу моделирования системы изинга, скачав ее
предварительно с сайта книги [132]. Выберите размер системы 40 χ 40 и температуру
Τ = 1.5 (это ниже Тс), задайте начальное состояние, в котором все спины
направлены вверх. Включите внешнее поле Hext = —0.3 и наблюдайте за
спинами. Со временем они должны переключиться в положение «вниз», при этом
новая фаза будет зарождаться в виде небольших, более или менее круглых
кластеров спинов, которые затем будут расти, заполняя собой систему.21
21 Мы используем периодические граничные условия, поэтому может показаться, что
кластеры, образующиеся вблизи границы, состоят из нескольких независимых частей. Это
иллюзия.
Гл.11. Упражнения
485
(a) Используя график зависимости намагниченности от времени, измерьте
среднее (по десяти измерениям) время, необходимое для того, чтобы
намагниченность сменила знак (будем считать это время временем зарождения новой
фазы). Для ускорения моделирования имеет смысл уменьшить частоту
обновления графики. Тем же методом измерьте скорость образования новой фазы при
#ext = —0.2. Поскольку зародыш фазы может образоваться независимо в любой
точке системы, скорость зародышеобразоывания растет пропорционально числу
спинов в системе. Для обоих значений поля вычислите скорость зародышеобра-
зования в расчете на один спин Гехр(Я).
Для оценки скорости возникновения новой фазы можно использовать
теорию критического зародышеобразования (раздел 11.3). Слишком маленькие
капли новой фазы будут сжиматься из-за наличия поверхностного (в данном
случае — линейного) натяжения σ; большие капли будут расти из-за того,
что они дают выигрыш в объемной свободной энергии HextAM(T) на
единицу площади новой фазы (здесь ΔΜ — разница в намагниченности двух
фаз). Предполагая, что температура, размер зародыша и время наблюдения
достаточно велики (так что работает непрерывная теория), можно оценить
критический размер зародыша Rc.
(b) Запишите формулу для свободной энергии кластера перевернутых спинов
радиуса R как функцию σ, Η и AM. Выведите формулы для Rc (критического
размера зародыша, соответствующего максимуму энергии), высоты барьера
зародышеобразования В и скорости зародышеобразования Гtheory — ехр(—Б/Т),
считая, что коэффициент пропорциональности примерно равен единице, если
время меряется в шагах моделирования (один шаг моделирования равен
времени, за которое в среднем каждый спин пробовали переключить один раз). При
низких температурах ΔΜ « 2, т.к. система почти полностью намагничена, а
σ rsj 2J = 2 (т.к. на каждую связь с невыгодным расположением спинов на
границе раздела приходится энергетический проигрыш 2J). Для каждого из двух
значений поля, использованных при моделировании, запишите (в виде таблицы)
Н, Rc, В, rtheory. a также Гехр, полученное в части (а).
Предсказание должно получиться достаточно плохим. Достаточно ли
велико значение критического размера зародыша, чтобы можно было
использовать непрерывную теорию (он должен составлять хотя бы несколько шагов
решетки)?
Более действенный способ проверить теорию состоит в том, чтобы создать
в качестве начального условия домен спинов, направленных вниз, в
окружении спинов, направленных вверх, и проследить за эволюцией этого домена.
Используйте небольшую систему размера (40x40), сконструируйте нужное
начальное условие, сначала направив все спины вверх, а потом переключив
486
Гл.11. Скачкообразные фазовые переходы
спины внутри кластера круглой формы в центре области моделирования.
Сохраните созданное начальное состояние, чтобы его можно было
использовать еще раз. Графические предпочтения установите таким образом, чтобы
картинка перерисовывалась на каждом шаге времени, т.к. кластеры будут
сжиматься достаточно быстро.
(с) Положите Η = —0.2, Г = 1.5, а радиус кластера спинов вниз равным пяти
(диаметр, соответственно, равным десяти) и проведите десять запусков
программы. Что происходит чаще: схлопывание кластера или его рост? (Вы достаточно
быстро это увидите.) Поменяйте Η и проведите измерения еще раз, составьте
таблицу значений Η и доли схлопывающихся капель /. Подберите значение Η
таким образом, чтобы вероятность схлопывания была примерно равна половине;
найдите значение внешнего поля, при котором Rc = 5 с точностью до 0.1. При
каком значении поля теоретическое значение критического размера зародыша
равно Rc = 5 (при Г = 1.5)?
В части (Ь) мы обнаружили, что теория критического зародышеобразова-
ния плохо предсказывает скорость образования новой фазы. В части (с) мы
показали, что она работает достаточно неплохо (с точностью до множителя
порядка двух) в части предсказания связи между внешним полем и
критическим размером зародыша. Это различие в основном связано с тем, что
зависимость скорости от высоты барьера экспоненциальна, так что небольшая
ошибка в определении высоты барьера (и критического радиуса зародыша)
приводит к большой ошибке для скорости зародышеобразования. Вы
заметите, что теоретики в своих работах редко предсказывают скорости реакций.
Почти всегда они вместо этого будут сравнивать теоретические и
экспериментальные данные для высот барьеров (или радиусов зародышей, как в этом
случае). Это позволяет избежать неловких ситуаций.
Наличие таких барьеров зародышеобразования позволяет
переохлажденной жидкости и пересыщенному пару оставаться стабильными в течение
достаточно долгого времени.
11.5 Зарождение пар дислокаций. (Технические науки) @
Рассмотрим двумерный кристалл, подвергнутый сдвиговому напряжению
(рис. 11.15).22 Внешнее напряжение можно частично снять, сдвинув верхнюю
часть кристалла влево на один шаг решетки а по сравнению с нижней
частью. Если кристалл имеет длину L, высвобождающаяся при таком полном
сдвиге энергия равна \F\a = axyLa. В ситуации, изображенной на рисунке,
22 Аналогичная проблема для сверхтекучих жидкостей изучалась в [31, 35], см.
также [140]. Полное решение усложняется за счет того, что влияние других пар дислокаций
перенормирует константы упругости при высоких температурах.
Гл.11. Упражнения
487
сдвиг произошел только частично; сдвинулась только часть ряда длины R
между двумя дислокациями (дислокации показаны на рисунке
традиционным значком Т, отмечающим конец лишнего ряда атомов).
Таким образом, энергия, высвободившаяся в результате образования
дислокации, равна в этом случае
\F\aR/L = axyRa. (11.24)
Эта энергия является аналогом объемной свободной энергии жидкой капли
в переохлажденном газе.
Рис. 11.15. Пара дислокаций
Пара дислокаций в двумерном гексагональном кристалле. В контур, обходящий правый
дефект, снизу входит на один ряд атомов больше. Следуя принятой в материаловедении
договоренности (и считая, что дислокация «указывает» в направлении, перпендикулярном
рисунку, см. [60, Fig. 1.20, р. 23]), это краевая дислокация с вектором Бюргерса b = αχ,
где а — расстояние между соседними атомами. Аналогично, дефект слева соответствует
одному лишнему ряду атомов, входящему сверху, его вектор Бюргерса b = —ах. Центры
дефектов находятся на одной высоте на расстоянии R друг от друга. Кристалл находится
под действием внешнего напряжения оху = F/L, сила F = ±axyLy приложена к верхней и
нижней граням кристалла, как показано на рисунке, и кристаллу не дают поворачиваться.
(Рисунок предоставлен Николасом Бейли.)
Образование дислокаций, в свою очередь, стоит некоторого количества
энергии (эта энергия является аналогом поверхностной энергии капли). С
дислокациями связана фиксированная локальная энергия С, зависящая от
особенностей межатомного взаимодействия, и дальнодействующая энергия
взаимодействия дефектов, которая (для геометрии, изображенной на
рис. 11.15) равна
488
Гл.11. Скачкообразные фазовые переходы
Здесь μ — это двумерный модуль сдвига,23 a v — коэффициент Пуассона.
Температуру в этом упражнении будем считать достаточно малой, чтобы
энергии, задаваемые уравнениями (11.24) и (11.25), были хорошими
приближениями к соответствующим свободным энергиям. Вычитая энергию, выигранную
от образования дислокации из энергетической цены ее образования, получим
задачу о критическом радиусе зародыша Rc и высоте барьера зародышеобра-
зования В, аналогичную решенной нами ранее для образования зародышей
при скачкообразных фазовых переходах.
Какие из следующих утверждений истинны, а какие ложны?
1. Критический радиус зародыша Rc пропорционален 1/аху.
2. Энергетический барьер зародышеобразования равен \jo\y.
3. Скорость Г спонтанного, за счет тепловых флуктуации, образования
дислокаций, предсказываемая теорией критического зародышеобразования, имеет
вид Г = Го(Т) (σχν/μ)Ό^ΒΊ\ где Гп(Т) — некоторая зависящая от свойств
конкретного вещества функция, a D — константа.
Дислокации передают пластическую сдвиговую деформацию. В маленьком
образце каждая новая пара дислокаций расползается на противоположные края
системы и в конце концов приводит к сдвигу верхней поверхности образца
относительно нижней на одну постоянную решетки. Таким образом, при любой
ненулевой температуре и любом внешнем напряжении любой (двумерный)
кристалл будет «ползти», его крайние поверхности будут сдвигаться друг
относительно друга с ненулевой скоростью. Чем же тогда отклик кристалла на внешнее
напряжение отличается от отклика жидкости?
В соответствии с результатом нашего вычисления отклик двумерного
кристалла на внешнее напряжение неотличим от отклика жидкости; даже при низких
температурах скорость сдвиговой деформации пропорциональна приложенному
напряжению.
11.6 Динамика фазового расслоения в модели Изинга. @
В процессе разделения фаз поверхностное натяжение заставляет
маленькие капельки и выступы на поверхности раздела фаз сжиматься и исчезать,
что приводит к огрублению смеси, т.е. росту типичного пространственного
масштаба системы со временем.
Еще раз запустите модель Изинга на вашем компьютере (см. раздел,
посвященный компьютерным упражнениям на сайте книги [132]). Задайте
достаточно большую систему, дождитесь установления равновесия при
бесконечной температуре (Г = оо), после чего положите Г = 1.5 (это ниже Тс). (В
23Двумерные модули упругости μ и ν могут быть связаны с соответствующими
трехмерными значениями; в наших обозначениях μ имеет размерность энергии на единицу
площади.
Гл.11. Упражнения
489
начале моделирования установите графические опции таким образом, чтобы
изображение перерисовывалось на каждом шагу; по мере того как разделение
фаз будет прогрессировать, имеет смысл уменьшить частоту перерисовки.)
Статистически изображение в разные моменты времени выглядит похоже с
точностью до увеличивающегося во времени типичного размера элементов.
Каким образом можно определить этот типичный размер L(t)?
(a) Покажите, что при нулевой температуре разность между полной
энергией системы и энергией ее основного состояния пропорциональна периметру
линии раздела фаз со спинами, направленными вверх, и спинами,
направленными вниз.24 Покажите, что величина этого периметра на единицу площади — это
хорошая оценка для обратного значения типичного размера структуры L~l(t).
(b) Начав со случайного распределения спинов, положите температуру и
внешнее поле равными нулю, сделайте один шаг по времени и измерьте
среднюю энергию на единицу площади (Е). Измерьте эту энергию усреднением по
времени вплоть до момента t = 2, 4, 8, ... и 1024, перезапуская процедуру
усреднения перед каждым следующим расчетом.25 Составьте таблицу со столбцами
t, (E(t)) и L(t) ос 1/{(Е) + 2). Постройте график зависимости характерного
масштаба L(t) ос 1/((Е) + 2) от времени в логарифмических координатах. По
какому степенному закону растет характерный масштаб? Какую зависимость вы
ожидали увидеть?
11.7 Микроструктура оригами.26 (Математика, технические науки) @
На рис. 11.11 показана доменная структура тонкого слоя вещества,
претерпевшего мартенситный фазовый переход. Это фазовый переход, в
котором меняется форма элементарной кристаллической ячейки; например, в
высокотемпературной фазе ячейка могла быть кубической, а в
низкотемпературной — вытянутой вдоль одной оси и сжатой вдоль двух других. Три
возможных направления этой длинной оси называются вариантами. Части
большого высокотемпературного монокристалла могут, таким образом, при
понижении температуры локально перейти в один из трех возможных
вариантов.
Параметром порядка в мартенситном переходе является поле деформаций
у(х), описывающее конечное (послепереходное) положение точки у в
мартенсите как функцию ее начального положения χ в недеформированном и не
24При конечных температурах имеется вклад в энергию от тепловых флуктуации спинов
внутри фаз, который не имеет отношения к периметру границы раздела.
25Вы измеряете средний периметр линии раздела за вторую половину времени
измерения, но как функция времени это среднее значение ведет себя аналогично мгновенно
измеренному периметру.
26Это упражнение было составлено совместно с Ричардом Д. Джеймсом.
490
Гл.11. Скачкообразные фазовые переходы
повернутом образце. Варианты отличаются соответствующими градиентами
деформации Vy, которые описывают растяжение, сдвиг и поворот
элементарных ячеек при фазовом переходе.
В этом упражнении мы исследуем аналогию между мартенситами и
структурами, получающимися при сгибании бумаги. Рассмотрим лист
бумаги, белый с одной стороны и разлинованный с другой, лежащий на
столе. У этого листа бумаги есть два существенно различных основных
энергетических состояния: один вариант соответствует тому, что вверх
смотрит белая сторона листа, другой — тому, что линованная.
Плотность энергии (и свободной энергии) бумаги не зависит от
поворотов, но она быстро растет при деформациях растяжения или сдвига. Подобно
состоянию мартенсита, состояние бумаги можно описать полем деформаций
у(х), задающим положение у точки, начальная координата которой для неде-
формированного листа бумаги, положенного на стол линованной стороной
вверх, равна х. Разумеется, у(х) должна быть непрерывной функцией, иначе
это означает, что бумага разорвалась. Поскольку энергия листа бумаги не
зависит от его перемещения по столу как целого, она может зависеть только от
градиентов поля деформации. Учитывая только низшие производные поля
деформаций,27 можно записать плотность энергии как функцию градиента
деформации Vy = djyf.
Τ = a|(Vy)T Vy - I|2 = a(diyjdiyk - Sjk)2. (11.26)
Постоянная а велика, т.к. бумага плохо растягивается. В этом упражнении
мы будем рассматривать только основные состояния, т.е. состояния,
соответствующие наименьшей возможной энергии.
(а) Покажите, что основные состояния бумаги, чья свободная энергия
задается уравнением (11.26) включают оба варианта и любые их повороты, как
показано на рис. 11.16. В частности, покажите, что (1) любой поворот yi(xj) = RijXj,
где состояния «линованной стороной вверх, линии параллельны краю стола»
является основным состоянием (здесь Ду = (s^£~cos0£))» и (^) чт0
переворот бумаги белой стороной вверх и последующий поворот yi{xj) = RikPkjXj —
(5п0Г ~ссм0ад) (ο-ι) (Ξ) также сохраняет ее в основном состоянии. Наши два
варианта являются, таким образом, поворотами состояний, описываемых I =
В настоящих мартенситах имеются определенные правила {условия
совместности) для границ раздела между вариантами: если задан один вариант,
27Если включить в рассмотрение старшие производные поля деформаций, можно учесть
наличие линейной энергии, связанной со сгибами бумаги.
Гл.11. Упражнения
491
S0(2) S0(21-P
Рис. 11.16. Пространство параметра порядка для бумаги
Разрешенные (соответствующие нулевой энергии) значения градиентов деформации для
бумаги, лежащей на столе. Пусть θ — угол между направлением χ линий на бумаге и
стороной стола. Можно повернуть бумагу на любой угол θι (тогда градиент деформации —
это простое вращение, принадлежащее группе28 SO(2)). Кроме того, можно перевернуть
лист бумаги (это соответствует преобразованию (х, у) —» (ж,—у), т.е. умножению вектора
координат на матрицу Ρ = (о^)), а затем повернуть на угол 9W (в этом случае градиент
принадлежит множеству SO(2)P). Таким образом, два варианта структуры
соответствуют тождественному преобразованию И и отражению Р; основные состояния соответствуют
произвольным поворотам этих двух вариантов. Границе раздела между вариантами
соответствует сгиб бумаги под углом вс (рис. 11.17).
разрешены только некоторые, строго определенные направления для другого
варианта и границы раздела между ними. Для нашего листа бумаги граница
раздела между вариантами «линованной стороной вверх» и «белой стороной
вверх» — это просто сгиб бумаги, см. рис. 11.17.
Рис. 11.17. Сгиб бумаги
Для нашего листа бумаги поверхность раздела между двумя состояниями с ве = 0 и 9W —
это прямой сгиб под углом θс.
(Ь) Положите лист бумаги на стол, так чтобы его длинная сторона была
параллельна краю стола (что соответствует θι = 0). Придерживая левую часть
листа, так чтобы угол θι не менялся, сгибайте правую часть под разными
углами сгиба вс. Установите, как связаны угол сгиба вс и угол 0W, на который
поворачивается правая часть листа.
Пусть сгиб произведен в направлении с. Мы можем вывести условие
совместности на границе, потребовав, чтобы поле деформаций у оставалось
492
Гл.11. Скачкообразные фазовые переходы
непрерывным (не должно быть скачка при переходе из разлинованной к белой
поверхности), следовательно производные по направлению Dy ■ с = (с ■ V)y
должны совпадать.
(с) Покажите, что из условия, полученного вами в части (Ь), следует, что
разность производных по направлению (Dye — Dyw) равна нулю вдоль с, (Dy£ —
Dyw) · с = (djyf — djyf)cj = 0. (Указания: Dye — это единичная матрица,
cos(20) = cos2 θ - sin2 0, sin(20) = 2 sin θ cos θ.)
В общем случае, для того чтобы два варианта мартенсита с градиентами
деформации А и В могли быть соединены вдоль плоской поверхности,
перпендикулярной п, необходимо, чтобы существовали матрицы поворотов R^
и такие, что
5>,(;ч-е«^="<%. (11·27)
к к
где а ® η — это прямое произведение а и п. Это условие совместности
гарантирует, что производные от у по любому направлению с вдоль границы
(т.е. перпендикулярному п) одинаковы для обоих вариантов, (Dyi — Dy2)c =
(R^B — R^A)c = a(n · с) = 0 и, следовательно, поле деформаций
непрерывно на границе. Для нашего листа бумаги, Dy — это либо М, либо RP,
где R — некоторая матрица поворота, и, следовательно, уравнение (11.27) в
точности совпадает с тем, что мы доказали в части (с).
Как видно на рис. 11.11, в эксперименте мартенсит при переходе в
новое состояние не растянулся однородно вдоль одной из осей. Вместо этого он
образовал множество тонких слоев каждого из двух вариантов. Для
образования такой структуры не потребовалось большого количества энергии, т.к.
поверхностная энергия на границе раздела вариантов достаточно мала.
Мартенситы образуют такие ламинированные структуры для того,
чтобы удовлетворить граничным условиям. Мартенситные переходы происходят
в стали; когда кузнец охлаждает подкову, кристаллы железа локально
растягиваются вдоль одной из нескольких возможных осей. Однако
раскаленная подкова не меняет своей формы, когда ее погружают в холодную воду.
Это происходит по двум причинам. Во-первых, если бы одна часть
подковы начала растягиваться раньше другой, на границе раздела растянутой и
нерастянутой частей возникло бы огромное напряжение. Во-вторых,
подкова состоит из множества кристаллических зерен, оси которых направлены в
29Другими словами, их разность должна быть матрицей ранга один, собственные
значения которой вдоль всех направлений, перпендикулярных п, равны нулю.
Гл.11. Упражнения
493
разные стороны и, соответственно, направления растяжения для различных
зерен различны. Поэтому, вместо того чтобы растягиваться как целое,
железо в подкове переходит в состояние, являющееся в каждой точке смесью
различных вариантов и обеспечивающее, в хорошем приближении, отсутствие
крупномасштабных деформаций.
Это достигается образованием микроструктур, подобных ламинированной
структуре, показанной на рис. 11.П.30 На границе квадратной области
растяжение мартенсита должно быть равно нулю, для этого он образует такую
ламинированную микроструктуру, что растяжение в одном слое и сжатие в
другом соседнем слое взаимно сокращаются.
Лист бумаги из нашего примера может формировать подобные
микроструктуры, если потребовать, чтобы его граница лежала вдоль заданной
кривой, не совпадающей с его естественной границей.
(d) Скачайте с сайта книги [129] и распечатайте полноразмерную версию
рис. 11.18. Вырежьте шестиугольник и сложите его вдоль указанных на рисунке
сгибов. К чему стремится граница получающейся структуры?31
Математики и инженеры, изучающие подобные задачи, как правило,
работают в удобном пределе, в котором границы раздела между вариантами (в
нашем случае это сгибы бумаги) имеют энергию, равную нулю. В этом
пределе микроструктуры могут становиться бесконечно тонкими, так что
хорошо определенными остаются только величины типа отношения концентраций
вариантов в заданной точке. Эта задача является удивительным примером
того, как патологические функции, изучаемые в анализе функций
вещественной переменной, оказываются полезными при изучении реальных физических
явлений.
30Ламинированная структура настоящих мартенситов — это еще более математически
странный объект, чем структура бумаги. Если пренебречь поверхностной энергией на
границе вариантов, градиент деформации для мартенсита разрывен во всех точках; для
нашего листа бумаги градиент разрывен всего лишь во всех точках на границе. Более подробно
см. упражнение 11.8.
31 Доказательство того, что лист действительно можно сложить вдоль указанных сгибов,
— это частный случай общей теоремы (Ричард Д. Джеймс, частное сообщение) о том, что
в плоскую структуру можно сложить лист бумаги с любой сетью сгибов, такой, что в
каждом узле сходится по четыре сгиба и углы между противоположными сгибами в сумме
равны 180°. Эту теорему можно (хотя и не без труда) получить из уравнения (11.27). Форму
границы в результате сгибов можно вывести, рассматривая, каким образом накладываются
друг на друга треугольники на внешней границе листа.
494
Гл.11. Скачкообразные фазовые переходы
Рис. 11.18. Микроструктура оригами
Двумерный пример формирования микроструктуры на примере оригами, получен
Ричардом Д. Джеймсом.
11.8 Минимизирующие последовательности и
микроструктуры.32 (Математика, технические науки) @
Морфология мартенсита, показанная на рис. 11.11, представляет
собой тонко переплетенную смесь двух кристаллических вариантов.
Слоистая структура (называемая ламинатом) возникает в материале из-за
стремления минимизировать энергию натяжения, необходимую для того,
чтобы слепить вместе домены поликристалла. Если бы поверхностная
энергия, необходимая для образования границы между вариантами, была
равна нулю, слои могли бы стать бесконечно тонкими, что привело бы к
возникновению странной математической функции: поле растяжений у(х) в
этом пределе было бы непрерывным, и в каждой точке33 χ оно имело бы
градиент, соответствующий одному из основных состояний (вариантов).
Однако этот градиент был бы разрывен во всех точках, меняясь от
одного варианта к другому при каждом переходе через бесконечно густо
расположенные границы раздела.
Именно в этом странном пределе теория мартенситов становится
элегантной и понятной. Если вам кажется, что такой функции у(х) не существует,
вы правы; можно стремиться к нулевому значению энергии натяжения,
конструируя все более и более тонкие ламинированные структуры, но ни одна
32Это упражнение было составлено совместно с Ричардом Д. Джеймсом.
33За исключением границ раздела, которые (несмотря на их густоту) с математической
точки зрения образуют множество меры ноль.
Гл.11. Упражнения
495
функция у(х) не может соответствовать в точности нулевой энергии.
Подобно минимуму функции на рис. 11.19, предельная минимальная энергия
мартенсита существует, но ее невозможно достичь.
Минимизирующей последовательностью для функции д(х), имеющей
нижнюю грань значений, равную до, — называют последовательность
аргументов х\, χ<ι ..., для которой д(хп) > д{хп+\) и limg(xn) = д0.
41
Рис. 11.19. Функция, не имеющая минимума
Нижняя грань значений функции д(х) = < ' _ ' равна д = 0, но она никогда не
достигается.
(а) Найдите минимизирующую последовательность для (достаточно
примитивной) функции д из рис. 11.19.
Подобные микроструктуры часто возникают в системах, имеющих
невыпуклую плотность свободной энергии. Рассмотрим задачу, в которой энергия
у(х) задается функцией
■%]= Г[(2/,2-1)2 + 2/2]с1^ (11.28)
./о
с граничными условиями у(0) = у(1) = 0. Эта энергия мала, если у(х)
остается близкой к нулю, а производная dy/dx = у'{χ) — близкой к ±1. Именно из-за
последнего условия эта энергия является невыпуклой: имеются два
энергетически выгодных значения наклона, в то время как лежащие между ними
промежуточные значения энергетически невыгодны.34 Эта свободная энергия
34Функция f[x] называется выпуклой, если /[λα+(1 —А)6] < А/[а]+(1—А)/[6];
геометрически это означает, что если / — выпуклая функция, то любой отрезок, соединяющий точки
496
Гл.11. Скачкообразные фазовые переходы
подобна энергии сгибания двумерного листа бумаги (см. упражнение 11.7);
вы можете интерпретировать ее как энергию сгибания одномерного листа
(тогда у1 — ±1 отвечают состояниям «лицом вверх» и «лицом вниз»,
соответственно) во внешнем потенциале у2, который притягивает бумагу к началу
координат и заставляет ее смяться в маленький шарик.
Теорема о микроструктуре. Функция Т[у], задаваемая уравнением
(11.28), нигде не достигает своего минимума.
(b) Докажите теорему о микроструктуре.
• Покажите, что нижняя грань значений энергии Τ равна нулю.
• Постройте минимизирующую последовательность функций уп(х), для
которой Пт7"[уп] = 0.
• Покажите, что второе слагаемое в Т[у] обращается в ноль, только если
у(х) = 0, и эта функция не минимизирует Т.
Меры Юнга (материал повышенной трудности). Интуитивно понятно, что
любая последовательность, минимизирующая свободную энергию,
задаваемую уравнением (11.28), должна содержать функции, чей наклон стремится
к у1 « ±1, а значения стремятся к у « 0. С точки зрения математики, можно
ввести распределение вероятности (меру Юнга) vx(S) того, что точкам χ + е
вблизи заданного χ соответствует наклон функции, равный S = у'(х + в).
(c) Покажите, что любая последовательность, минимизирующая свободную
энергию (11.28), задается мерой Юнга vx(S) = ^S(S—1) + ^6(5+1). (Указание:
свободная энергия представляет собой сумму двух квадратов. Используйте
первое слагаемое для того, чтобы показать, что мера Юнга должна иметь
вид vx(S) = a(x)S(S — 1) + (1 — a(x))S(S + 1). Затем запишите (у(х)) в виде
интеграла, зависящего от а(х), и используйте второе слагаемое свободной
энергии, для того чтобы показать, что а(х) = ^.)
11.9 Снежинки и линейная устойчивость. (Физика конденсированного
состояния) (3)
Рассмотрим достаточно условную двумерную модель зародышеобразова-
ния и роста зародышей кристаллов льда (или любых других зародышей
кристалла в переохлажденной жидкости). Подобно тому, как происходит
фазовое расслоение в системе с сохраняющимся параметром порядка, движущей
силой расслоения является переохлаждение, а наиболее медленной стадией,
контролирующей скорость процесса, — диффузия. Когда кристаллики льда
(ayf[a\) и(6, f[b]) лежит выше графика /. Свободная энергия J7, описываемая уравнением
(11.28), является невыпуклой функцией наклона у'.
Гл.11. Упражнения
497
растут в атмосфере, они быстро поглощают весь водяной пар,
находящийся вблизи их поверхности; чтобы рост кристалла продолжался, новые
атомы воды должны диффундировать издалека. В других системах медленной
стадией, контролирующей скорость процесса, может быть диффузия
выделяющегося при кристаллизации тепла от поверхности или диффузия атомов
примеси (например соли), предпочитающей находиться в жидкой фазе.
Форма кристалла в заданный момент времени задается кривой χ(λ,ί),
определяющей текущее положение границы раздела жидкость-кристалл,
параметризованной неким параметром λ.35 Пусть η — единичный вектор,
нормальный к поверхности кристалла в данной точке и направленный в сторону
жидкости, a S(k) — локальная скорость роста кристалла как функция
локально кривизны поверхности ку тогда36
дх
η -Ц- = ЗД = Л + Вк - Ск\к\. (11.29)
dt
Уравнение (11.29) выбрано таким образом, что оно воспроизводит
известный нам результат для роста круглой капли радиуса R(t) и кривизны
к = 1/R.
(a) Обобщите закон роста зародышей для сохраняющегося параметра
порядка (уравнение 11.18) и формулу для критического размера зародыша
(уравнение 11.9) на случай двумерных капель. Если положить в уравнении (11.29)
А = В = О, какое значение С нужно взять, чтобы воспроизвести закон,
описывающий рост зародышей в двумерном пространстве? При каком значении А
получается правильный результат для критического размера зародыша?
Таким образом, параметр А отвечает за переохлаждение (за то, насколько
кристаллическое состояние предпочтительнее пара), в то время как С
отвечает за поверхностное натяжение.
(b) Рассмотрим поверхность, содержащую области как положительной, так и
отрицательной кривизны (как на рис. 11.20). В каком направлении поверхностное
натяжение пытается сместить части границы с положительной кривизной к на
выступах кристалла? А в каком направлении оно действует на части границы
в выемках (областях с отрицательной к)? Получили бы мы правильный ответ,
если бы подставили аналитический член Ск2 в уравнение (11.29)?
35Мы можем выбрать любую удобную нам параметризацию А. Например, А может быть
углом θ в полярных координатах или длиной дуги вдоль поверхности. Кривизна к и в
целом уравнения движения (11.29) должны быть калиброеочно инвариантны, т.е.
аккуратно записаны таким образом, чтобы они не зависели от способа (калибровки) измерения
положения точки А на кривой.
36 Составляющая dx/dt, параллельная поверхности, не влияет на ее рост; она влияет
только на то, как зависит от времени параметризация кривой.
498 Гл.11. Скачкообразные фазовые переходы
Рис. 11.20. Координаты для описания формы кристалла
Зародыш кристалла с шестью независимыми выростами (чтобы увидеть полностью
сформированный дендрит, посмотрите на рис. 11.12). Поверхность раздела жидкость-кристалл
в двумерном случае описывается параметрически заданной кривой х(А), например —
зависимостью R(6).
Член Вк ускоряет движение областей с положительной кривизной
(выступы кристалла) и замедляет рост в областях с отрицательной кривизной
(выемки). Он грубо имитирует диффузию тепла или примесей от
поверхности (рис. 11.21): выдающиеся вперед выступы кристалла оказываются в более
холодной и влажной области.
Мы назвали эту модель условной, потому что она пытается с помощью
локальной теории [46] имитировать существенно нелокальный эффект
диффузии [76]. Более точные микроскопические теории явно учитывают
теплопроводность в приповерхностном слое [14,34].37 Однако наша теория дает
результат, качественно очень похожий на более точные теории.
Рассмотрим теперь решение, соответствующее растущей круглой капле,
и исследуем поведение небольшого возмущения ее поверхности: будет ли оно
увеличиваться или уменьшаться со временем? Почти круглую каплю можно
параметризовать функцией i?(0, £). Кривизна поверхности задается в этих
координатах выражением
_ Д2 + 2 {dR/θθ)2 - R{&Rme2\
(и2 + (dR/θθ)2
Проверьте, что для идеального круга эта формула дает к = 1/R.
37В частности, именно поэтому нам понадобился неаналитичный член к\к\. Кроме того,
наш параметр Л, имеющий смысл скорости роста плоской поверхности, также не
реалистичен. Например, при ΔΤ < L/c выделяющееся при кристаллизации тепло слишком велико,
.3/2
(11.30)
Гл.11. Упражнения
499
Рис. 11.21. Поле диффундирующей величины в окрестности
растущей поверхности
Поверхности постоянной температуры, концентрации пара или концентрации соли в
жидкости вблизи растущей поверхности кристалла (показанной жирной кривой). Обратите
внимание, что градиенты малы в выемках структуры и велики на концах выступов; это
позволяет выступам расти быстрее. Поверхности внутри кристалла не показаны.
(с) Запишите левую часть уравнения (11.29), η · дтс/dt через dR/dt, R и
dR/дв. (Указания: η — это единичный вектор, перпендикулярный
локальной касательной к поверхности [d(Rcos6)/d6, d(Rsm6)/d6] и направленный
вовне. Здесь cbc/di указывает вдоль г поскольку мы выбрали θ в качестве
переменной параметризации.38 Ваш ответ не должен в явном виде зависеть
отв.)
Маленькие кристаллики льда коллапсируют, более крупные — растут. У
еще более крупных кристаллов растут выступы, в результате чего они
образуют дендриты (рис. 11.12). Для того чтобы понять, при каких условиях на
круглой капле начинают расти выступы, можно использовать метод
линейного анализа устойчивости. Этот метод состоит в том, чтобы взять известное
точно решение и посмотреть, устойчиво ли оно к малым возмущениям.
Разложим R(6,t) = Sm=-oor™(OexPOm0)· Для каждого возможного
числа выступов т нас будет интересовать, при каком значении радиуса го39
такие выступы начнут расти.
для того чтобы быть полностью скомпенсированным переохлаждением; конечное
состояние в этом случае представляет собой смесь льда и воды, так что расти могут только
узкие выросты на поверхностях (при этом они не могут находиться слишком близко друг
к другу).
8Возможно, будет более понятно, если мы скажем, что ^-координата не меняется при
изменении ί, поскольку параметризация обеспечивает ее постоянство.
39То есть Гт для т = 0.
500
Гл.11. Скачкообразные фазовые переходы
Рис. 11.22. Снежинка
© Кен Либбрехт, snowcrystals.com [82,83].
(d) Пусть rm(t) мало при га ^ 0. Разложите уравнение (11.29) (записав его в
полярных координатах, как вы делали с уравнением (11.30) и в части (с)) по гт и
их производным, удерживая члены до первого порядка малости. Запишите закон
изменения drm/dt в терминах гт и го (исключив гп с другими положительными
п). Выразите радиус го, при котором выступы начинают расти, через А, В и С.
(Указание: когда вы запишете линейное разложение, умножьте его на е~
и проинтегрируйте по 0; после этого используйте свойство ортогональности
преобразования Фурье, уравнение А.27.)
Вы всегда можете воспользоваться этим методом, если удается найти
простое точное частное решение некоторой задачи. Добавьте к решению малое
возмущение, используйте линейное приближение и посмотрите, затухают ли
соответствующие моды Фурье.
Характерная шестиугольная форма снежинок связана с наличием оси
симметрии шестого порядка в структуре кристаллов льда; скорость роста
поверхности кристалла зависит от угла — это еще один эффект, не учтенный
в нашей модели.
Глава 12
Непрерывные фазовые
переходы
Непрерывные фазовые переходы завораживают. При повышении
температуры магнетика намагниченность непрерывным образом уменьшается до
нуля при достижении критической температуры Тс. В критической точке Тс
наблюдаются большие флуктуации намагниченности (рис. 12.1); вместо того
чтобы выбрать одну из фаз — с намагниченностью вверх, вниз, или с нулевой
намагниченностью — изинговский магнетик в критической точке
представляет собой нечто подобное фракталу,1 в котором смешаны все три фазы. Это
удивительное поведение не характерно не только для равновесных фазовых
переходов при изменении температуры.
На рис. 12.2 изображен перколяционный переход.2 В ранней работе [80],
с которой началось активное изучение этого перехода, исследователи брали
проводящий лист бумаги, из которого в случайных местах вырезались
дырки, и изучали изменение проводимости листа в зависимости от концентрации
дырок. Было показано, что при приближении к некоторой критической
концентрации проводимость падала до очень маленькой величины, т.к. вблизи
точки, где лист распадался на части, проводящие пути были очень
немногочисленны и имели очень сложную форму. Таким образом, в этой модели
1 Термин фрактал используют для описания множеств, характерная размерность
которых не равна целому числу; с точки зрения математики он примерно соответствует
множествам с нецелой размерностью Хаусдорфа. Этот термин проник в массовую культуру и
повседневный язык и ассоциируется с рыхлыми шероховатыми множествами типа
изображенных на рисунках в этой главе.
2От английского слова to percolate — протекать. — Прим. переводчика.
502
Гл.12. Непрерывные фазовые переходы
Рис. 12.1. Модель Изинга при критической температуре Тс
Модель Изинга при критической температуре Тс, разделяющей спонтанно
намагниченную фазу при Τ < Тс и фазу с нулевой намагниченностью при Τ > Тс. Белым и черным
отмечены области с положительной и отрицательной намагниченностью (s = ±1),
соответственно. В отличие от скачкообразных фазовых переходов, рассмотренных в гл. 11,
намагниченность в этом случае непрерывно стремится к нулю при Τ —> Тс снизу.
также наблюдается непрерывный переход: качественное изменение
поведения в точке, вблизи которой свойства системы меняются непрерывным, а не
разрывным образом.
Во многих физических системах происходят события различных
масштабов, крупнейшие из которых могут иметь катастрофические последствия.
На рис. 12.3(a) показана энергия, высвобожденная в результате
землетрясений, как функция времени по наблюдениям за 1995 год. Находящиеся под
земной корой тектонические плиты медленно движутся (это соответствует
дрейфу континентов), земная кора реагирует на это движение резкими,
импульсными сдвигами — землетрясениями. Подобного рода импульсный шум
возникает во множестве систем, от сминаемой бумаги [62] до рисовых
хлопьев Rice Krispies [72] и магнетиков [131]. Число таких импульсных лавин
как функция их размера часто описывается степенным законом D(s) ~ s~T
в очень широком (несколько порядков) диапазоне размеров (рис. 12.3(b)). В
последние несколько десятилетий было обнаружено, что подобные системы
также можно рассматривать как разновидности критических точек — точек
непрерывного перехода между двумя качественно различными состояниями.
Большинство свойств больших лавин в подобных системах можно понять,
используя методы, развитые для изучения равновесных фазовых переходов.
503
Рис. 12.2. Перколяционный переход
Компьютерная модель перколяции, в которой вместо вырезания круглых дырок убирают
связи между узлами решетки. Пусть вероятность убрать связь равна 1 — р; тогда при р,
близком к единице (дырок нет), проводимость велика и она уменьшается с уменьшением
р. При достаточно большом количестве дырок (для этой модели — при рс = 1/2) самый
большой кластер связей еле-еле удерживает систему связанной, он имеет множество
отверстий на всех масштабах. При большей вероятности сохранения связей (р = 0.51, слева
внизу) наибольший кластер в целом хорошо связан и имеет только сравнительно
маленькие дырки; при меньшем ρ (ρ = 0.49, справа внизу; разные кластеры обозначены разными
оттенками) лист распадается на множество мелких фрагментов. Перколяция — это
фазовый переход при некотором рс, разделяющий связную и фрагментированную фазы (см.
упражнения 2.13 и 12.12).
Методы ренормализационной группы и скейлинга, используемые для
изучения критических точек, основаны на глубоких принципах и позволяют
получать множество нетривиальных результатов. Большая часть исследований
в этой области (как с исторической точки зрения, так и на современном этапе)
посвящена построению сложных схем, позволяющих применить эти методы
для той или иной конкретной системы. В настоящей главе мы остановимся
на наиболее важных ключевых идеях, необходимых для понимания
экспериментов и новых теоретических моделей. О конкретных методах вычисления
критических индексов мы говорить не будем.
504
Гл.12. Непрерывные фазовые переходы
Рис. 12.3. Размеры землетрясений
(а) Энергия, высвобожденная землетрясениями в 1995 году, как функция времени. Этот
временной ряд, если его проиграть через динамик (предварительно изменив характерные
частоты, так чтобы они попали в слышимую область), звучит подобно треску или
импульсному шуму [72]. (Ь) Гистограмма числа землетрясений в 1995 году как функция их
размера. Обратите внимание на логарифмический масштаб; наиболее слабые из
учтенных землетрясении в миллион раз слабее и в тысячу раз более вероятны, чем наиболее
сильные. Это распределение хорошо описывается степенным законом ~ S'-2'3, который в
данном контексте называется законом Гутенберга-Рихтера.
В разделе 12.1 мы исследуем удивительное явление универсальности: две
системы, абсолютно непохожие на микроскопическом уровне, могут
демонстрировать в точности одинаковое критическое поведение вблизи точек своих
фазовых переходов. Мы дадим качественное объяснение этого явления в
терминах ренормализационно-групповых потоков в пространстве всех
возможных систем.
Рис. 12.4. Модель землетрясений Варриджа-Кнопоффа
Модель, в которой разлом при землетрясении моделируется последовательностью грузов,
которые двигаются с трением вдоль нижней плоскости под действием горизонтально
направленной силы, приложенной к их подвесам. Как было показано Карлсоном и Лангером
[21], даже в случае, когда рассматривается регулярное расположение одинаковых грузов,
эта система приходит в состояние, в котором наблюдаются землетрясения в очень большом
диапазоне размеров.
12.1. Универсальность
505
В разделе 12.2 мы исследуем типичные самоподобные структуры,
наблюдаемые при непрерывных фазовых переходах. Самоподобие объясняет
наличие структур, подобных фракталам, в критических точках: система в
критической точке выглядит так же, как то, что получится из нее при изменении
пространственного (или временного) масштаба. Мы покажем, что
наблюдаемые степенные законы и скейлинговые функции имеют достаточно простое
объяснение в терминах самоподобия.
Наконец, в разделе 12.3 мы дадим обзор широкого многообразия
систем, поведение которых может быть понято с использованием
ренормализационно-групповых и скейлинговых методов.
12.1 Универсальность
Построение количественных физических теорий оказываются возможным
потому, что зачастую макроскопические явления не зависят от
микроскопических деталей систем, в которых они происходят. В гл. 2 мы убедились в
том, что уравнение диффузии практически не зависит от правил, по которым
происходят вызывающие диффузию случайные столкновения.
Гидродинамика основана на возникновении простого закона — уравнения Навье—Стокса
— из сложных микроскопических взаимодействий; если бы макроскопическая
динамика жидкости существенно зависела от форм и правил взаимодействия
составляющих жидкость молекул, было бы невозможно записать простые
макроскопические законы в непрерывной форме. Классическая квантовая
механика полагается на тот факт, что поведение электронов, ядер и
фотонов в основном не зависит от внутреннего устройства ядер;
нерелятивистская квантовая механика — это эффективная теория, к которой при низких
энергиях сводится более сложная теория объединения. В теории
элементарных частиц высоких энергий была предложена оригинальная концепция
перенормировки (ренормализации), которая объясняет, как такие эффективные
теории можно построить в релятивистских квантовых системах. Решеточная
квантовая хромодинамика (моделирующая сильное взаимодействие, которое
удерживает частицы в ядрах) оказывается полезна только благодаря тому,
что моделирование на решетке, нарушающее однородность и изотропность
пространства (а также лоренцову инвариантность) на больших масштабах
приводит к поведению, удовлетворяющему всем этим симметриям. В
каждой из перечисленных областей физики множество различных
микроскопических моделей приводят к одной и той же теории в пределе низких частот
и больших длин волн. Вблизи точек непрерывных переходов поведение
506
Гл.12. Непрерывные фазовые переходы
Рис. 12.5. Лавина среднего размера
Лавина среднего размера (в которой переключается 282 785 спинов) при моделировании
гистерезиса в магнетике [131] (см. упражнения 8.13, 12.13 и рис. 12.11). Окраска рисунка
соответствует временной развертке лавины: она началась в темной области внизу рисунка,
последние переключения спинов произошли в верхней области. Резкая смена оттенков
соответствует реально наблюдаемому явлению: разные оттенки отвечают разным сублавинам,
между которыми движение почти останавливается (рис. 8.18).
становится необычайно мало чувствительным к микроскопическим
деталям систем; настолько, что для этого явления имеется специальное
название, универсальность. На рис. 12.6(a) показано, что плотности
жидкостей ре(Т) и газов р9(Т) для большого количества различных
атомов и малых молекул выглядят очень похоже, если измерять их
температуру и плотность в единицах критических величин для
соответствующего вещества. Это сходство во многом объясняется
простыми причинами: взаимодействия между молекулами во многих
системах достаточно похожи, с точностью до масштабов энергии и
расстояния. Поэтому, скажем, аргон и угарный газ удовлетворяют
соотношению
рсо(Т) = АрАт{ВТ) (12.1)
при подходящем подборе параметров А, В. Однако на рис. 12.6(b)
показаны данные для совершенно другой физической системы —
системы взаимодействующих спинов во фториде марганца,
претерпевающем ферромагнитный переход. Кривые, описывающие данные для
магнетиков и для перехода жидкость-газ, совпадают, если помимо
изменения масштаба температуры Τ и параметра порядка (М и р,
соответственно) разрешить более общее преобразование координат
12.1. Универсальность
507
рАг(Г) = А(М{ВТ), Т) (12.2)
способное поворачивать оси.3
Природа не знает о том, что мы выберем именно ρ и Г в качестве
переменных. Вблизи критической точки перехода жидкость-газ естественная
мера плотности зависит от температуры, и А(М,Т) — это преобразование,
переводящее нас в эту естественную систему координат. За вычетом вопроса
о выборе переменных, поведение магнитного перехода и перехода жидкость-
газ вблизи критической точки совпадают.
В этом, пожалуй, не было бы ничего удивительного, если бы две
фазовые диаграммы были параболическими; локальный максимум аналитической
кривой общего положения4 выглядит как парабола. Но скачки
намагниченности и плотности вблизи Тс менются как (Тс — Т)& с одним и тем же
показателем β « 0.325, совершенно отличным от корневой особенности β = 1/2,
соответствующей аналитической кривой общего положения.
Кроме того, имеется множество других характеристик (восприимчивость,
теплоемкость, корреляционная длина), которые расходятся по степенным
законам вблизи критической точки, и все соответствующие показатели
степеней (так называемые «критические индексы») совпадают для перехода
жидкость-газ и для магнетиков. Это и есть универсальность. Когда две
различные системы имеют одинаковые расходимости вблизи критических точек,
мы говорим, что они принадлежат одному классу универсальности. Важно
отметить, что теоретическая модель Изинга (несмотря на то, что она
существенно упрощает взаимодействие и морфологию системы) принадлежит к
тому же классу универсальности, что и одноосные ферромагнетики, и
системы с переходом жидкость-газ, благодаря чему теоретические предсказания
для модели Изинга оказываются напрямую применимы к реальным
экспериментам.
33десь В = Т™ /Т*9 — это обычная перенормировка температуры, а А(М,Т) = а\М +
а2+а3Т = (pcpo/Mo)M+pc(l + s)-(pcs/T!9)T — это поворотное преобразование координат
от (р,Т1д) к (М,ТМ). Оказывается, что помимо этого имеется поправка,
пропорциональная (Тс — Т)1_а, где а ~ 0.1 — критический индекс для теплоемкости. Эту поправку тоже
можно рассматривать как своего рода поворот, учитывающий зависимость эффективного
коэффициента связи модели Изинга от давления. Для простых молекул, данные по
которым приведены на рис. 12.6(a), эта поправка мала, но она существенна для жидких
металлов [49]. Как поворот, так и эта поправка на 1 — α субдоминантна, т.е. они стремятся
к нулю при приближении к Тс быстрее, чем параметр порядка (Тс — Τ)β.
4Математический термин общего положения, грубо говоря, имеет смысл «за
исключением редких случаев, вероятность которых равна нулю», в данном случае — того, что
вторая производная функции в максимуме окажется нулевой.
508
Гл.12. Непрерывные фазовые переходы
Рис. 12.6. Универсальность
(а) Универсальность вблизи критической точки жидкость-газ. Линии сосуществования
жидкости и газа (в координатах р(Т)/рс и Т/Тс) для ряда атомов и малых молекул вблизи
их критических точек (Тс,рс) [56]. Кривая соответствует приближению данных по аргону
р/рс = 1 + s(i - Т/Тс) ± р0(1 - Τ/Τ0)β с s = 0.75, р0 = 1-75 и β = 1/3 [56]. (Ъ)
Универсальность: критическая точка перехода ферромагнетик-парамагнетик. Намагниченность
как функция температуры для одноосного ферромагнита M11F2 [59]. Мы начертили обе
ветви ±М(Т) и поменяли местами оси, чтобы сделать более заметной аналогию с
переходом жидкость-газ, показанным выше. Обратите внимание, что вблизи обеих
критических точек (и магнитной, и критической точки перехода жидкость-газ) параметр порядка
меняется как (1 — Т/Тс)^, где β « 1/3. (Кривые для перехода жикость-газ наклонены;
две кривые совпадут, если определить эффективную намагниченность вблизи
критической точки жидкость-газ как ред = р — 0.75рс(1 — Т/Тс) (тонкая линия в середине графика,
см. выше).) Это не случайность; обе системы принадлежат одному классу
универсальности, тому же, что и трехмерная модель Изинга. По современной оценке, для этой модели
β = 0.325 ± 0.005 [151, chapter 28].
12.1. Универсальность
509
Чтобы лучше почувствовать, откуда берется универсальность,
рассмотрим перколяцию по узлам и по связям, показанную на рис. 12.7. Здесь мы
видим (слева) две микроскопически различные системы, в которых на
больших масштабах обнаруживается (справа) практически одинаковое поведение.
Вблизи точки перехода, в которой системы разваливаются на несвязные
части, они оказываются похожими друг на друга! В частности, исчезают какие-
либо следы подлежащей структуры решетки и микроскопических правил
заполнения.5
Рис. 12.7. Универсальность в перколяции
Универсальность означает, что крупномасштабная морфология перколяционного кластера
в точке рс не должна зависеть от микроскопических деталей. Вверху показана перколяция
по связям, в которой связи, соединяющие узлы квадратной решетки, заняты с
вероятностью р\ вверху справа показан бесконечный кластер на решетке размера 1024 χ 1024 при
рс = 0.5. Внизу показана перколяция по узлам на треугольной решетке, где занятыми с
вероятностью ρ = рс = 0.5 являются ячейки, имеющие гексагональную форму. Несмотря на
то, что микроскопически решетки и правила размещения на них отличаются,
получающиеся большие кластеры статистически выглядят одинаково. (Можно заметить, что кластер
перколяции по узлам выглядит несколько менее темным. Универсальность соблюдается с
точностью до изменения общего масштаба, в данном случае — масштаба плотности.)
5 Обратите внимание, в частности, на возникновение симметрии в задаче.
Статистически большие перколяционные кластеры в точке рс трансляционно инвариантны и
изотропны, не зависимо от того, на какой решетке они расположены. Кроме того, мы увидим, что
возникает также масштабная инвариантность — подобие симметрии, связывающее
разные пространственные масштабы (мы отмечали это явление для случайных блужданий,
см. рис. 2.2).
510
Гл.12. Непрерывные фазовые переходы
Таким образом, мы видим, что в рассмотренных случаях различные
микроскопические системы выглядят похоже вблизи критических точек, если
пренебречь микроскопическими деталями и сконцентрировать внимание на
том, что происходит на больших масштабах. Для того чтобы
систематически исследовать это явление, нам необходим метод, позволяющий перейти к
чему-то вроде непрерывного предела, но с учетом того, что
рассматриваемые системы остаются неоднородными и флуктуирующими даже на самых
больших масштабах. Такой последовательный метод называется методом ре-
нормализационной группы.6
Метод ренормализационной группы описывает операции над весьма
абстрактным объектом — огромным «пространством систем». Различные точки
пространства систем соответствуют различным веществам в различных
экспериментальных условиях, а также различным физическим моделям этих
веществ, с различными законами взаимодействия и правилами динамики.
Таким образом, мы можем считать, например, что на рис. 12.8 изображено
множество всех моделей, описывающих лавины и гистерезис в трехмерных
системах. В этом пространстве систем имеется бесконечное множество
измерений, соответствующих всем возможным параметрам теоретических
моделей (беспорядку, константам взаимодействия, взаимодействию соседей через
один, дипольным полям, ...), а также всем возможным экспериментальным
параметрам (таким как химический состав вещества, температура, время
отжига, ...). При изменении одного параметра в эксперименте или в
теоретической модели соответствующая точка в пространстве систем будет двигаться
вдоль некоторой кривой; линия вверху рисунка могла бы, например,
соответствовать модели лавин из упражнения 8.13 с меняющимся параметром
беспорядка jR.
В методе ренормализационной группы исследуются свойства
отображения пространства систем на себя при огрублении масштаба. Операция
огрубления состоит в сжатии системы и удалении микроскопических степеней
свободы. Стирание микроскопических степеней свободы приводит к появлению
новой системы с таким же длинноволновым физическим поведением, но с
другими (перенормированными) значениями микроскопических параметров.
Например, на рис. 12.9 показано преобразование ренормализационной группы
6Слово ренормализация происходит из квантовой электродинамики, где эффективный
заряд электрона меняет свою величину (норму) при изменении масштаба. Слово группа,
как обычно считается, описывает семейство операций сглаживания (огрубления масштаба),
используемых в этом методе (при этом групповому умножению соответствует
последовательное применение операции). Однако операция, обратная сглаживанию, не определена,
так что ренормализационная группа не удовлетворяет обычному математическому
определению группы.
12.1. Универсальность
511
Рис. 12.8. Ренормализационная группа
Ренормализационная группа определяет отображение пространства систем на себя,
соответствующее огрублению масштаба. Рассмотрим пространство всех возможных моделей
лавин в гистерезисе [131]. При огрублении масштаба каждая из этих моделей переходит в
какую-то другую модель, такую, что в ней исчезают некоторые микроскопические
степени свободы, а правила переключения подстраиваются таким образом, что сохранившиеся
домены по-прежнему переключаются при тех же внешних полях. Неподвижная точка S*
этого отображения огрубления будет самоподобной (рис. 12.11), т.к. она переходит в себя
при изменении пространственного масштаба. Точки, подобные i?c, т.е. точки,
притягивающиеся к S*y также будут демонстрировать самоподобное поведение (с точностью до
коротковолновых степеней свободы, исключенных при огрублении по мере стремления точки
к S*). Модели, соответствующие Rc и S*, принадлежат одному классу универсальности.
Точки, близкие к критическим, по мере применения огрубляющего отображения
удаляются от S* вдоль одной и той же кривой ί/, благодаря чему они также обладают некоторыми
универсальными свойствами (рис. 12.12).
в реальном пространстве для модели Изинга, использующее «правило
большинства».7 Для реализации этой операции огрубления существует
несколько детально развитых математических техник: помимо ренормализационной
группы в реальном пространстве, это е-разложения в импульсном
пространстве, ренормализационные группы Монте-Карло и т.д. Эти конкретные
реализации технически сложны и приводят только к приблизительным
результатам; мы не будем обсуждать их в этой главе (см., однако, упражнения 12.9
и 12.11).8
7Мы не будем обсуждать здесь методы, используемые для получения параметров
эффективных взаимодействий между перенормированными спинами.
8Более подробно о техниках, используемых в методе ренормализационной группы, см.,
например, [154], [20]. — Прим. переводчика.
512
Гл.12. Непрерывные фазовые переходы
Рис. 12.9. Модель Изинга при критической температуре Тс:
огрубление масштаба
Последовательное огрубление мгновенного снимка двумерной модели Изинга при
критической температуре. Каждая операция огрубления меняет пространственный масштаб в
В = 3 раза. После огрубления спин в перенормированной ячейке принимает то состояние,
в котором пребывало большинство из девяти спинов, находившихся в соответствующей
области до перенормировки. Такого рода огрубление — это основная операция метода ре-
нормализационной группы в реальном пространстве.
12.1. Универсальность
513
Часто оказывается, что преобразование огрубления в пространстве систем
имеет неподвижную точку S* . В таком случае все системы, которые в
результате последовательного применения преобразования стягиваются в эту
неподвижную точку, будут иметь одни и те же длинноволновые свойства, а
следовательно — принадлежать к одному классу универсальности.
На рис. 12.8 изображены ренорм-групповые потоки в пространстве систем
(т.е. линии, вдоль которых движутся точки при преобразовании огрубления).
Рисунок изображает двумерную схему бесконечномерного пространства. Вы
можете понимать ее как двумерный срез пространства систем, выбранный
таким образом, чтобы он включал линию, соответствующую нашей системе до
перенормировки, и неподвижную точку S*. При такой интерпретации потоки
на рисунке соответствуют проекциям настоящих потоков на плоскость
рисунка, т.к. настоящие потоки направлены не точно в этой плоскости. С другой
стороны, можно рассматривать изображение как развертку криволинейной
поверхности, заметаемой нашей моделью при последовательном огрублении,
в таком случае следует игнорировать часть рисунка, расположенную ниже
кривой U.9
На рис. 12.8 показана неподвижная точка *S*, которой соответствует одно
неустойчивое направление, отталкивание в котором происходит вдоль кривой
U. Точки, отклоняющиеся от S* в этом направлении, не будут
притягиваться к неподвижной точке при преобразовании огрубления, а будут, напротив,
удаляться от нее. Неподвижные точки, имеющие такие неустойчивые
направления, соответствуют непрерывным переходам между качественно
различными состояниями. Для гистерезиса и связанных с ним лавин, существует фаза,
состоящая из моделей, в которых лавины малы, и другая фаза, состоящая из
моделей, в которых одна гигантская лавина разом переключает состояния в
существенной части системы. Поверхность С, состоящая из точек,
сходящихся к *S*, при преобразовании огрубления, представляет системы, находящиеся
в критической точке; таким образом, в точке Rc (в которой линия,
соответствующая нашим системам, пересекает С) система демонстрирует поведение
с лавинами на всех пространственных масштабах.10
В случаях, подобных переходу жидкость-газ, когда имеется два
«подгоночных» параметра (ТС,РС), определяющих критическую точку,
соответствующая неподвижная точка в пространстве систем будет иметь два
направления неустойчивости.
9Эта кривая является неустойчивым многообразием неподвижной точки S*.
10Поскольку S* имеет ровно одно неустойчивое направление, многообразие С имеет на
одно измерение меньше, чем пространство систем (на математическом языке говорят, что
С имеет коразмерность, равную единице), и, следовательно, разделяет пространство на
две фазы. Говорят, что С — это устойчивое многообразие для точки S*.
514
Гл.12. Непрерывные фазовые переходы
(·)
V'/1']—1 Y*V
Рис. 12.10. Общее и самоорганизующееся критическое поведение
(а) Часто встречаются неподвижные точки, устойчивые по всем направлениям. Такие
неподвижные точки описывают фазы, а не фазовые переходы. Большинство фаз соответствуют
простому поведению с флуктуациями, быстро спадающими на больших масштабах. Если
флуктуации остаются существенными на всех масштабах, соответствующие фазы
демонстрируют самоподобие и степенные законы, называемые общей масштабной
инвариантностью. (Ь) Критическое многообразие С в модели землетрясений, описываемой рисунком,
разделяет фазу залипания разломов и фазу скольжения. Переход из одной фазы в другую
вызывается внешним напряжением F, приложенным к разлому. Только вдоль С
наблюдается самоподобное поведение с широким спектром масштабов землетрясений, (с) Скорость
скольжения вдоль разлома будет вести себя как ν ~ (F — Fc)^ вблизи критического
значения силы Fc. Тем временем дрейф континентальных платформ приводит к тому, что
разломы скользят друг относительно друга с очень малой скоростью vs, что автоматически
приводит к развитию напряжения F, близкого к Fc, и порождает возникновение
землетрясений на всех масштабах; эта модель демонстрирует самоорганизующееся критическое
поведение.
Что происходит в случае, если неустойчивых направлений нет вовсе?
Неподвижная точка Sa на рис. 12.10 является точкой притяжения для целой
пространственной области систем, благодаря чему все соответствующие системы
имеют одинаковые длинноволновые свойства; эта точка представляет, таким
образом, фазу системы. Обычно для таких фаз не характерны флуктуации
на всех масштабах. Флуктуации возникают вблизи точки перехода, когда
система «не знает», какую из двух соседних фаз предпочесть. Однако бывают
ситуации, когда флуктуации имеются и внутри фаз, что приводит к явлению
общей масштабной инвариантности. Хорошим примером такой системы
является случайное блуждание,11 для которого большое количество различных
микроскопических правил движения приводит к одному и тому же
длинноволновому поведению, и флуктуации остаются важными на всех масштабах
вне зависимости от каких-либо подгоночных параметров.
пСм. раздел 2.1 и упражнения 12.10 и 12.11.
12.2. Масштабная инвариантность
515
Кроме того, бывают ситуации, когда внешние условия, воздействующие
на систему, естественным образом заставляют ее оставаться вблизи
критической точки, что приводит к формированию наблюдаемых флуктуации на всех
масштабах. Хорошим примером таких систем являются некоторые модели
динамики разломов при землетрясениях. На рис. 12.10(b) показаны ренорм-
групповые потоки для этих моделей землетрясений. Горизонтальная ось
соответствует внешнему напряжению на разломе землетрясения. При малых
внешних напряжениях разлом залипает, и землетрясения не происходит. При
большом напряжении в разломе начинается проскальзывание со средней
скоростью ν, при этом могут возникать небольшие неоднородности, но в целом
никаких резких событий не происходит. Неподвижная точка *S*q,
соответствующая землетрясениям, описывает переход от залипшей к скользящей фазе, в
этой точке наблюдаются землетрясения всех масштабов. В реальности не
существует механизма фиксации напряжения, приложенного к разлому; вместо
этого происходит постоянное относительное движение плит (дрейф
континентов) с чрезвычайно малой скоростью vs (порядка нескольких сантиметров в
год). На рис. 12.10(c) показана зависимость скорости от внешней силы для
этого перехода, можно видеть, как приложение в качестве внешнего условия
малой скорости естественным образом приводит систему к ее критической
точке, вызывая спонтанное возникновение критических флуктуации. Это
явление называется самоорганизующимся критическим поведением.
12.2 Масштабная инвариантность
Еще одной удивительной особенностью непрерывных фазовых переходов
является частое появление свойства самоподобия, или масштабной
инвариантности. Это явление ярко видно на изображении распределения спинов в
модели Изинга в критической точке (рис. 12.1), перколяционного кластера
(рис. 12.2) и лавин в модели гистерезиса (рис. 12.5). На всех этих рисунках в
критической точке неровности границ кластеров, иррегулярности и
вкрапления встречаются на всех пространственных масштабах. Происхождение этих
рыхлых фракталоподобных структур связано со скрытой симметрией
задачи: все эти системы (статистически) инвариантны относительно изменения
пространственного масштаба.
516
Гл.12. Непрерывные фазовые переходы
Рассмотрим рис. 2.2 и 12.11, иллюстрирующие самоподобие в случайных
блужданиях и в срезах лавин в модели гистерезиса. На каждом рисунке
верхнее правое изображение соответствует большой системе, в то время как
каждое последующее — это увеличенная в два раза часть предыдущего
изображения. Для модели гистерезиса на каждом рисунке мы видим большую
лавину, покрывающую всю систему (обозначенную черным цветом), и множество
меньших лавин разных цветов, имеющих на всех рисунках одинаково
нерегулярную структуру поверхности (см. рис. 12.5). Если не особенно
вглядываться и не обращать внимания на мелкомасштабные детали, рисунки выглядят
примерно одинаково. Это преобразование изменения масштаба и отвлечения
от мелких деталей и есть преобразование огрубления, применяемое в методе
ренормализационной группы. На рис. 12.9 показано одно из конкретных
правил, используемых для реализации этой операции огрубления, примененное
несколько раз к снимку модели Изинга при температуре Тс. И в этом случае
корреляции и флуктуации не меняют своего вида после изменения масштаба;
критическая модель Изинга статистически самоподобна.
Эту масштабную инвариантность можно рассматривать как симметрию,
возникающую при изменении масштаба. В трансляционно инвариантной
системе математическое ожидание любой функции, зависящей от координат
двух точек х\, Х2, может быть записано как функция разности координат
(g(x\,X2)) = G(%2 — #2)· Аналогичным образом, масштабная инвариантность
позволяет записать функции N переменных в терминах скейлинговых
функций N—1 переменной — с точностью до того, что эти скейлинговые функции,
как правило, дополнительно умножаются на некоторую степень одной из
переменных.
Начнем с рассмотрения функции одной переменной. Рассмотрим
распределение по размерам (объемам) D(S) лавин, скажем, в модели землетрясений,
соответствующей рис. 12.3(a), или в нашей модели гистерезиса в критической
точке. Рассмотрим ту же систему, но увеличим единицу длины, используемую
нами для измерений, — отступим назад, отбросим мелкие детали и посмотрим
на систему на огрубленном уровне. Пусть увеличение масштаба
соответствует умножению расстояния между делениями на нашей линейке на некоторое
небольшое число В = 1 4- е. Все масштабы в нашей системе (например
корреляционная длина ξ) после огрубления разделятся на В. Объем лавины S
после огрубления также станет меньше на некоторый множитель12 С = 1+се.
12 Если бы количество частиц в лавине было пропорционален кубу ее линейного размера,
то с было бы равно 3, поскольку (1+с)3 = 1+Зб+0(€2). В общем случае с — это фрактальная
размерность лавины.
12.2. Масштабная инвариантность
517
Рис. 12.11. Лавины: масштабная инвариантность
Изображения сечения лавин в нашей модели гистерезиса (упражнения 8.13 и 12.13), на
каждом следующем рисунке изображена (в увеличенном масштабе) нижняя правая
четверть предыдущего. Изначально в системе был миллиард ячеек (10003). Разные лавины
отличаются цветом. И здесь картинки (особенно на больших масштабах) выглядят
статистически схоже.
518
Гл.12. Непрерывные фазовые переходы
Наконец, значение D(S) после огрубления также перенормируется на
некоторый множитель А = 1 + ае.13 Таким образом, имеем в результате огрубления
ς? = ξ/Β = ξ/(ΐ + ε),
S' = S/C = S/(l+ce), (12.3)
D' = AD = D(l+ae).
Далее, вероятность того, что в огрубленной системе имеется лавина размера
S", равна перенормированной вероятности того, что в начальной системе была
лавина объема S = (1 + ce)S':
D'(S') = AD{S) = AD{CS') = (1 + ae)D((l + ce)S'). (12.4)
Здесь Df(Sf) — это распределение, измеренное с помощью новой линейки,
соответствующей меньшим лавинам и большим вероятностям. Поскольку мы
находимся в самоподобной критической точке, огрубленное распределение
D'(S') должно совпадать с D(S'). Устремляя теперь е к нулю, получаем
дифференциальное уравнение:
D(S') = D'(S') = (1 + ae)D((l + ce)S'),
AD
0 = aeD + ceS'—,
do
<±D _ aD
(12.5)
которое имеет общее решение14
D = DoS~a/c. (12.6)
Поскольку общие свойства внутри класса универсальности совпадают
только с точностью до выбора масштаба, константа Dq неуниверсальна,
т.е. различна для различных конкретных систем. С другой стороны,
константы а, с и а/с универсальны — не зависят от конкретного выбора
эксперимента в пределах одного класса универсальности. Некоторые из этих
13Сами лавины зарождаются или не зарождаются независимо от того, какую линейку
вы используете. Однако распределение вероятности по размерам D(S) меняется, т.к. из-за
условия нормировки вероятность большой лавины зависит от того, насколько маленькие
лавины вы можете измерить и учесть; кроме того, число лавин на единицу S меняется при
изменении масштаба S.
14Мы используем тот факт, что JdD/D = —a/cfdS/S, \ogD = К — (а/с) log S при
некоторой константе интегрирования К = log Dq.
12.2. Масштабная инвариантность
519
констант имеют стандартные названия: индекс с, задающий фрактальную
размерность лавины, обычно обозначают df или \/σν.
Индекс а /с, задающий распределение лавин по размерам, в задачах пер-
коляции и в большинстве моделей лавинообразования в магнетиках15
обозначается т, он связан с показателем Гутенберга-Рихтера для землетрясений16
(см. рис. 12.3(b)).
Большинство измеряемых величин, зависящих от одной переменной,
будут иметь такие степенные сингулярности в критической точке. Например,
корреляционная функция модели Изинга при Τ = Тс (см. рис. 10.4) в
пространстве размерности d спадает с расстоянием χ как С(х) ос x~(d~2+<n\ a
расстояние как функция времени для случайного блуждания (см. раздел 2.1)
растет как ί1'2, в обоих случаях появление степенного закона связано с
самоподобием системы.17
Мы ожидаем универсального поведения также и вблизи критической
точки. В этом случае при огрублении масштаба система становится
статистически похожа на саму себя, но при других значениях параметров. Например,
система, претерпевающая фазовое расслоение (см. раздел 11.4.1 и
упражнение 12.3), при огрублении масштаба становится подобна самой себе на более
ранних временах, когда домены были мельче, а перколяционный кластер в
точке чуть выше рс (см. рис. 12.2 слева внизу) при огрублении становится
похож на перколяционный кластер при условиях, более далеких от рс (т.е.
перколяционный кластер с меньшим количеством дыр).
Для магнетика при температуре немного ниже Тс18 после огрубления
масштаба на множитель В = 1 + в система становится похожей на систему,
находящуюся дальше от Тс в Ε = 1 + ее раз. В этом случае стандартным
обозначением для критического индекса служит греческая буква ν — 1/е (см.
рис. 12.12). Аналогично случаю с распределением лавин по размерам,
намагниченность огрубленной системы также надо перенормировать, умножив
15 За исключением нашей модели, в которой τ используется для обозначения параметра
распределения лавин по размерам при критических значениях поля и беспорядка; после
интегрирования по петле гистерезиса Ant ос 5,_т, где τ = τ + σβδ.
16Мы не претендуем на то, что нам удалось найти единственно правильное объяснение
закона Гутенберга-Рихтера. Существует много моделей, позволяющих получить значение
« 2/3 для показателя степенного закона, однако по-прежнему неясно, какая из них верно
описывает (если какая-то вообще описывает) реально наблюдаемые землетрясения.
17Это связано с тем, что только степенные функции самоподобны. Пусть f(x) = x_ot,
тогда при изменении масштаба χ в В раз имеем f(Bx) = В~ах~а ос /(х). (В [98] можно
прочитать больше о степенных законах.)
18В этом случае увеличение расстояния t до критической точки Тс соответствует
уменьшению абсолютной температуры Т.
520
Гл.12. Непрерывные фазовые переходы
f(Tc-Et.x) f{Tc-t.x)
0#ι
/[4'
ό *
-•уст
/'(Гс-/.х)
Рис. 12.12. Скейлинг вблизи критической точки
Если в результате преобразования ренорм-группы одна точка в пространстве систем
переходит в другую, то на больших масштабах их поведение должно быть подобно. Наша
система при разных температурах соответствует линии f(x) на рисунке (верхней прямой).
Рассмотрим систему при двух значениях температуры Тс — t и Тс — Et. Пунктирные
линии соответствуют последовательным огрублениям на множитель В; при таких
перенормировках / —> /' —> /" —> /^ ... На картинке система f(Tc — £, χ) после четырех
перенормировок переходит практически в то же состояние, что система /(Тс — Et,x) после
трех перенормировок. Мы видим, таким образом, что с точки зрения длинноволнового
поведения система f'(Tc — t,x) похожа на /(Тс — Et,x); система подобна самой себе при
других значениях внешних параметров. В частности, при каждой перенормировке χ
меняется на некоторый множитель В, а функция / — на некоторый множитель А, откуда
f'(Tc — t,y) = Af(Tc — t, By) = f(Tc — Et,y) для больших значений расстояния у.
12.2. Масштабная инвариантность
521
на F = (1 + /б) (где / = β/ι/), для того чтобы она совпала со значением
неогрубленной системы при более низкой температуре (см. рис. 12.12):
М'(ТС -t) = FM(TC -t) = M(TC - Et),
ί \ (12.7)
(1 +/€) М(ГС - t) = М(ТС - t(l +e€)J.
Устремив € к нулю, мы получим Μ ос t^e = t&, что объясняет
возникновение степенных законов вблизи точки перехода в магнетиках и в
окрестности критической точки жидкость-газ (см. рис. 12.6). Аналогичным образом,
теплоемкость, корреляционная длина, время релаксации, восприимчивость и
поверхностное натяжение равновесной системы будут иметь степенные
расходимости вида (Т — Тс)_х, критические индексы X которых традиционно
обозначаются как α, ι/, ζι/, η и —2ι/, соответственно. Также можно изучать
зависимость намагниченности от поля Η при критической температуре и
получить зависимость вида
Для специалистов в теории критических явлений центральной задачей
является вычисление этих критических индексов; во многих случаях
дискуссии крутятся вокруг разнообразных комбинаций этих греческих букв. Из-
19
вестно много аналитических подходов, позволяющих вычислять индексы,
их также легко измерить экспериментально (однако сделать это с хорошей
точностью значительно труднее, см. [115]).
Однако критическими индексами все не ограничивается. Из численного
моделирования легко извлечь множество других скейлинговых предсказаний.
Универсальность должна распространяться в том числе и на те свойства, для
которых нет простых степенных формул. В частности, существует множество
функций двух и более переменных, которые можно измерить. На рис. 12.13
показано распределение размеров лавин D-mt(S, R) в нашей модели
гистерезиса, проинтегрированное вдоль всей петли (см. рис. 8.15), для различных
значений беспорядка Д, больших Rc (см. упражнение 8.13). Обратите
внимание на то, что степенное распределение получается только при Rc « 2.16;
при больших значениях беспорядка имеется множество маленьких лавин,
после чего количество лавин резко спадает при достижении некоторого размера
*Ьтах(г£)·
Выведем скейлинговое выражение для Dint (5, R). Используя масштабную
инвариантность, мы можем записать эту функцию двух переменных в
виде произведения некоторой степени одной из переменных и универсальной
19Их можно выразить через собственные значения оператора огрубления,
линеаризованного вблизи неподвижной точки 5* на рис. 12.8 (см. упражнения 12.7 и 12.11).
522
Гл.12. Непрерывные фазовые переходы
Размер лавины S
Рис. 12.13. Распределение лавин по размерам
Распределение лавин по размерам для нашей модели гистерезиса. Обратите внимание на
то, что график построен в логарифмических координатах. (Мы можем измерять значения
D(S) вплоть до Ю-14, моделируя системы из миллиардов спинов и используя усреднение
по 5 с шагом AS ~ 105.) (i) Хотя распределение имеет чисто степенной вид только при
Rc « 2.16 (пунктирная линия, D(S) ос 5~т), даже при значениях беспорядка, вдвое
отличающихся от критического, имеются большие лавины размером порядка нескольких сотен
спинов, (ii) За исключением очень узкой окрестности критической точки, кривые имеют
неправильный наклон; имейте в виду, что степенные законы, верные на масштабе двух
порядков величин, часто дают неточные значения индексов (не смотря на это, они считаются
достаточно хорошими для публикации [115]). (iii) Скейлинговые кривые (тонкие линии)
хорошо работают даже вдали от Rc. На врезке показан график D(S)/S~T как функции
5σ(Λ — Rc)/R, что позволяет получить универсальную скейлинговую кривую Ό(Χ) (см.
уравнение 12.14). Подбирая значения Rc и критического индекса так, чтобы получить
хорошее совпадение кривых, можно достаточно точно измерить критические индексы даже
по измерениям вдали от i?c, т.е. по измерениям, для которых простая степенная
аппроксимация дает неверный результат (см. упражнение 12.12(g)).
функции одной комбинированной скейлинговой переменной. Из нашего
обсуждения Rc (см. уравнения 12.3) мы знаем, что
S' = S/{l + ce),
D' = £>(! +ас).
(12.8)
После огрубления масштаба система, изначально находившаяся при R — Rc+
г, окажется подобной системе с беспорядком, более далеким от критического:
R — Rc + Ef = Rc + (1 + ве)г, следовательно
D{S', Rc + Er) = D'{S\ Rc + r) = AD(CS', Rc + r),
D(S', Rc + (1 + ee)r) = (1 + ae) D ((1 + ce) S', Rc + r).
(12.9)
Для того чтобы облегчить вывод скейлинговой формы для функций
многих переменных, удобно заменить переменные на скейлинговые. Рассмотрим,
12.2. Масштабная инвариантность
523
например, комбинацию X = Se/Cr. После огрубления Sf = S/C и перехода к
более сильному беспорядку г' = Ег эта комбинация не меняется:
X1 = S,e'cr' = {S/C)e/c(Er) = (S/ (1 + се))е/с ((1 + ee)r)
=se/Cr ( (ϊτ^) = se/Cr+°(£2)=x+0(£2)- (1210)
Пусть D(S,X) = D(S,R) — распределение лавин по размеру как функция S
и X. Тогда огрубление D происходит аналогично огрублению функции одной
переменной, т.к. X остается неизменным. Уравнение (12.9) превращается в
D{S\ X') = D(S\ Χ) = (1 + ае) D ((1 + се) S*> X), (12.11)
так что
aD = -cS'^ (12.12)
и следовательно
D{S, X) = S~a/cV{X) = S~fV{X), (12.13)
где V(X) — некоторая скейлинговая функция. Эта функция является
аналогом неуниверсальной константы Do из уравнения (12.6), за исключением того,
что в этом случае скейлинговая функция является еще одним универсальным
предсказанием теории (универсальным с точностью до выбора единиц
измерения X и D). Переписав выражение в изначальных переменных и используя
общепринятые греческие обозначения для критических индексов (с = 1/σι/,
а = τ/σι/ и е = 1/ν), получим окончательное скейлинговое выражение для
распределения лавин по размерам:
D{S, R) ос S~fV{Sa{R - Rc)). (12.14)
Для того чтобы получить универсальную скейлинговую функцию из
данных эксперимента или компьютерного моделирования, используют так
называемый скейлинговый коллапс: если начертить D/S~T как функцию X =
Sa(R — Дс), кривые, соответствующие разным Д, накладываются друг на
друга (коллапсируют), как показано на врезке рис. 12.13.
Подобные универсальные скейлинговые функции появляются во многих
контекстах. Так, в равновесной модели Изинга имеется скейлинговая
функция для намагниченности М{Н,Т) = {%-ΤγΜ (Н/{ТС - Tfs),
корреляционной функции C(x,t,T) = x-&-d+7i)c (x/\T - Tc\~u,t/\T - Tc\~zv) и
эффектов конечного размера М(Т, L) = (Тс — ΤψΜ, (L/(TC — Т)_1/), в случае, если
рассматривается конечная кубическая система размера Ld.
524
Гл.12. Непрерывные фазовые переходы
12.3 Примеры критических точек
Идеи статистической механики нашли широкое применение во множестве
областей знания, зачастую лежащих очень далеко от изначальной тематики
статистической механики — изучения систем в тепловом равновесии. Идеи
скейлинга и ренормализационной группы оказались приложимы к особенно
широкому кругу проблем; в заключение этой главы мы дадим краткий обзор
таких приложений.
12.3.1 Критические явления в равновесных системах: энергия
против энтропии
Изначально методы скейлинга и ренормализационной группы были
разработаны для исследования непрерывных фазовых переходов в равновесных
системах. Модели Изинга, Поттса,20 Гейзенберга, фазовые переходы в
жидких кристаллах, смачивание, равновесные формы кристаллов (см. рис. 11.6),
плавление в двумерных системах — вот те объекты, на которых оттачивался
метод ренормализационной группы.
Переходы во всех этих системах происходят из-за конкуренции между
энтропией и энергией: более энергетически выгодное состояние побеждает при
низких температурах, но разрушается при высоких температурах из-за роста
энтропии. На рис. 12.14 показан результат удивительного классического
эксперимента — анализ перехода гелия в сверхтекучее состояние (этот переход
имеет такой же параметр порядка и принадлежит к тому же классу
универсальности, что и модель XY). Плотность сверхпроводящей компоненты
должна иметь вид
ps ос (Тс - Tf(l + d(Tc - Т)х), (12.15)
где χ — универсальная субдоминантная скейлинговая поправка. Поскольку
β ~ §, на рисунке по оси отложено ps/(T — Тс)2/3, чтобы отличия от
простого приближенного поведения были лучше видны. В верней части графика
кривая ведет себя почти прямолинейно и ее наклон отражает различие
между истинной измеренной величиной β = 0.6749 ± 0.0007 и использованным
для нормировки показателем |. Другие кривые показывают влияние
субдоминантной поправки, величина которой d растет с ростом давления.
Эксперименты по более точному измерению этой кривой проводятся в настоящее
время на международной орбитальной станции — это позволит уменьшить
влияние гравитации на наблюдаемое поведение.
20 Модель Поттса — это решеточная модель, подобная модели Изинга, но с числом
состояний каждого спина, равным N, а не двум.
12.3. Примеры критических точек
525
15Г7 1»29.09Ьаг
° 0.0001 0.001 0.01
г - 1-77Г
Рис. 12.14. Плотность сверхтекучей компоненты гелия: скейлинго-
вый график
Классический эксперимент [1, 54] 1980-го года по высокоточному измерению плотности
сверхтекучей компоненты гелия р9(Т). Обратите внимание на логарифмический масштаб
по горизонтальной оси; данные при наименьшем давлении (давление насыщенного пара
« 0.0504 бар) соответствуют изменению отклонения температуры от Тс на три порядка.
Вертикальная ось на рисунке отнормирована таким образом, чтобы сделать заметными
отклонения от ожидаемого степенного закона.
12.3.2 Квантовые критические явления: нулевые колебания
против энергии
При нулевой температуре не существует тепловых флуктуации, однако
существует множество хорошо изученных квантовых фазовых переходов,
возникающих из-за конкуренции потенциальной энергии и квантовых флуктуации.
Многие ранние исследования были посвящены переходу металл-изолятор и
явлению локализации, когда наличие беспорядка может приводить к тому,
что вещество является изолятором, несмотря на наличие состояний, лежащих
на поверхности Ферми. Методы скейлинга и ренормализационной группы
играли центральную роль в этих ранних исследованиях; например, состояния
вблизи порога мобильности (разделяющего локализованные и протяженные
состояния) самоподобны и фрактальны. Другие важнейшие вехи
включают эффект Кондо, микроскопическую квантовую когерентность
(подвергающую испытанию принципы теории квантовых измерений), переходы между
плато в квантовом эффекте Холла и переходы сверхпроводник-металл. На
рис. 12.15 показаны результаты недавнего эксперимента по изучению
прямого перехода из сверхпроводящего в изолирующее состоянии при изменении
толщины пленки. Ожидается, что сопротивление имеет скейлинговый вид
R{d, Τ) = RCT± ((d - dc)T-l'uz}; (12.16)
526
Гл.12. Непрерывные фазовые переходы
авторы представляют R(d,T) в виде функции t(d — dc), меняя t до тех пор,
пока кривые не совпадут (основная часть рис. 12.15(b)), после чего получают
значение Ι/ι/ζ из графика зависимости t от Τ (врезка). Ясно, что идеи скей-
линга и ренормализационной группы применимы в данной задаче; отметим
однако, что на момент написания настоящей книги не существовало никакой
теории, убедительно объясняющей приведенные конкретные наблюдения.
Рис. 12.15. Переход сверхпровоник-изолятор
(a) Тонкие пленки аморфного висмута являются изоляторами (их сопротивление
стремится к бесконечности при нулевой температуре), в то время как пленки толщиной более 12 А
— сверхпроводники (их сопротивление стремится к нулю при некоторой конечной
температуре).
(b) Скейлинговый коллапс. Сопротивление как функция перенормированной толщины слоя
для перехода сверхпроводник-изолятор, толщина перенормирована на некоторый
множитель £, подобранный независимо для каждого случая таким образом, чтобы добиться
наилучшего коллапса. Верхняя скейлинговая кривая Т- соответствует изоляторам с d < dCy
нижняя, J>, — сверхпроводникам с d > dc. На врезке показано, что t ~ т~1/игу где νζ ^ χ.2
(графики взяты из [87]).
12.3.3 Динамические системы на пороге хаоса
Как правило, в статистической механике наше внимание направлено на
системы с большим количеством частиц или на системы, находящиеся во
взаимодействии со сложным многочастичным окружением. Непрерывные
переходы могут, однако, возникать и в просто устроенных изолированных
системах с малым числом степеней свободы; в этом случае они называются
бифуркациями. Бифуркации — это качественные изменения поведения системы,
происходящие в момент, когда параметр в описывающей их системе
дифференциальных уравнений проходит через критическое значение. Бифуркации
изучаются в теории нормальных форм (см. упражнение 12.4).21 В теории
бифуркаций мы находим аналоги классов универсальности, критических
индексов и аналитических поправок к скейлингу.
21 См. также [152]. — Прим. переводчика.
12.3. Примеры критических точек
527
Динамические системы, даже в том случае, когда они включают
небольшое число степеней свободы, могут демонстрировать чрезвычайно сложное
хаотическое поведение. Траектории хаотических систем на больших
временах — аттракторы — часто представляют собой фрактальные множества,
для изучения которых применимы многие понятия и методы статистической
механики.22 Особенно яркий вклад в изучение систем на пороге хаоса внес
метод ренормализационной группы. На рис. 12.16 показана простая
динамическая система, претерпевающая последовательность бифуркаций и
переходящая в результате в хаотическое состояние. Фейгенбаум исследовал
последовательность этих бифуркаций с использованием ренормализационной
группы и огрубления, но не по пространственной, а по временной
координате (см. упражнение 12.9). И в этом случае поведение оказывается
универсальным — в точности та же последовательность бифуркаций (с точностью
до гладких замен переменных) происходит в других отображениях, а
также и в реальных экспериментально наблюдаемых системах. Другие
вычисления ренорм-группового типа существенно помогли при изучении перехода
от квазипериодического к хаотическому движению, а также в задаче об
исчезновении последней нехаотической области в гамильтоновых системах (см.
упражнение 4.4).
Рис. 12.16. Самоподобие на пороге хаоса
Аттрактор отображения Фейгенбаума f(x) = 4μχ(1 — χ) как функция μ. Для малых μ < μι,
последовательное применение / приводит к неподвижной точке χ*(μ). При увеличении μ
выше μι отображение сходится к двухточечному циклу; затем к четырехточечному циклу
после μ2, к восьмиточечному — после μ$... Эти бифуркации удвоения периода ведут себя
как геометрическая прогрессия: μ«> — μη ос 6~пу где δ = 4.669201609102990... —
универсальная константа. В точке μ«> система переходит в хаотическое состояние (см.
упражнение 12.9).
22Например, ансамбли из статистической механики становятся в этом случае
инвариантными мерами (см. упражнение 4.3), а для характеризации аттракторов используется
величина, связанная с энтропией (см. упражнение 5.16).
528
Гл.12. Непрерывные фазовые переходы
12.3.4 Стекла: случайные, но замороженные системы
Закончим этот раздел обсуждением непрерывного перехода, понимание
которого до сих остается неполным: перехода стеклования.
Стекла — это вещества, не находящиеся в равновесии; их времена
релаксации расходятся при охлаждении, и внутренние перестройки в них
прекращаются при некоторой характерной температуре, называемой температурой
стеклования. Многие другие неупорядоченные системы ведут себя подобно
стеклам: их времена релаксации становятся настолько велики, что они
застывают в неупорядоченном состоянии.23 Этот процесс замораживания иногда
описывают как появление дальнего порядка во времени, или как нарушение
эргодичности (см. раздел 4.2). Основной причиной того, что стеклообразные
системы замораживаются в неупорядоченном состоянии, являются
фрустрации. Изначально понятие фрустрации было введено для спиновых стекол
— веществ, которые формируются случайной подстановкой магнитных
атомов внутрь матрицы из немагнитного вещества. Взаимодействия магнитных
моментов атомов оказываются в этом случае случайными; некоторые пары
атомов предпочитают ориентироваться параллельно (как в
ферромагнетиках), некоторые — антипараллельно (как в антиферромагнетиках). Каждый
раз, когда образуется цикл из сильно взаимодействующих спинов, в котором
имеется нечетное число антиферромагнитных связей (рис. 12.17), этот цикл
оказывается фрустрированным: одна из связей неизбежно должна остаться
в невыгодном состоянии, поскольку число инверсий спина вдоль замкнутого
цикла всегда четно (см. рис. 12.17). Считается, что и для конфигурационных
стекол фрустрации имеют большое значение (рис. 12.18).
Изучение неупорядоченных магнитных систем очень сложно с
математической и вычислительной точки зрения. Например, точно доказано, что
равновесное основное состояние трехмерной модели Изинга со случайными
полями24 — это ферромагнитное состояние (что довольно скучно); однако
мы понимаем, почему при охлаждении в нулевом внешнем поле модель
замораживается в неупорядоченном состоянии, это связано с тем, что в процессе
разделения фаз энергетические барьеры, препятствующие релаксации,
расходятся. Методы, развитые для изучения замораживания спиновых стекол,
2 Стекла — это не то же самое, что неупорядоченные системы. В неупоряоченных
системах беспорядок фиксирован, он имеет место как в низко-, так и в высокотемпературном
состоянии; беспорядок в обычных конфигурационных стеклах появляется и
замораживается только при охлаждении. См. также раздел 5.2.2.
24Наша модель гистерезиса и лавин (см. рис. 8.18, 12.5, 12.11 и 12.13; упражнения 8.13,
8.14и12.13) — это та же самая модель Изинга со случайным полем, однако мы изучали ее
неравновесное состояние в растущем внешнем поле.
12.3. Примеры критических точек
529
А
A F
/ 8 1
Рис. 12.17. Фрустрация
В спиновых стеклах имеются магнитные атомы, взаимодействия между которыми имеют
случайный знак. На рисунке показан треугольник из изинговских (±1) спинов, в котором
имеется одна антиферромагнитная связь. При любой конфигурации спинов в этом
треугольнике как минимум одна из связей находится в невыгодном положении. Говорят, что
такая система фрустрирована.
имеют важные приложения в теории нейронных сетей (для которых
известен переход забывания при переполнении памяти), а в последнее время —
в теории алгоритмов для решения сложных (NP-полных) вычислительных
задач (см. упражнения 1.8 и 8.15). Однако мы по-прежнему не знаем ответов
на некоторые простые базовые вопросы. Например, до сих пор неизвестно,
конечно или бесконечно число равновесных состояний в спиновых стеклах —
будет ли число стеклообразных состояний по-прежнему велико, если
охлаждение проводится бесконечно медленно.25
В обычных конфигурационных стеклах вязкость и время релаксации
растут на десять-пятнадцать порядков в небольшом температурном интервале,
ограниченном снизу моментом, когда скорость охлаждения становится
выше скорости уравновешивания. По сути, мы не знаем, почему вязкость так
быстро расходится для такого большого количества различных веществ.
Существует как минимум три различных конкурирующих концепции перехода
стеклования.
(1) Он является проявлением равновесного перехода в идеальное
стеклообразное состояние с нулевой энтропией, состояние, которое сформировалось
25Существуют «кластерные» теории, в которых предполагается существование двух
(отличающихся знаком спина) основных состояний, и конкурирующие с ними теории,
основанные на методах «реплик» и «полости», предполагающие существование большого числа
основных состояний.
530
Гл.12. Непрерывные фазовые переходы
(а) (Ь)
Рис. 12.18. Фрустрации и кривизна
Одна из возможных форм фрустрации возникает в случае, когда энергетически
выгодная локальная упаковка оказывается несовместимой с формированием более крупных
структур. Здесь мы приводим два рисунка (любезно выполненных Памелой Дэвис Кавил-
сон [71]). (а) классическая проблема картографии: шкурку апельсина (или земную кору)
невозможно разместить на плоской поверхности, не растянув и не порвав ее. (Ь)
Аналогичная проблема, возникающая во многих стеклах металлов, атомы которых локально
предпочитают формировать маленькие симпатичные тетраэдры: невозможно склеить
икосаэдр из двадцати тетраэдров. Подобно тому, как шкурку апельсина можно без проблем
разместить на сфере, стекла металлов оказываются нефрустрированными в искривленном
пространстве [120].
бы при бесконечно медленном охлаждении. (2) Это чисто динамический
переход (в котором атомы или молекулы «запирают» друг друга). (3) Это вообще
не фазовый переход, а плавный переход в режим с намного большей
вязкостью (например, связанный с формированием долгоживущих ковалентных
связей между атомами).
12.3.5 Перспективы
Многие читатели этой книги сделают карьеру за пределами традиционной
физики. Физики продолжают играть существенную роль в финансовом мире
(в эконофизике, финансовой математике, на рынках деривативов), в
биологии (биоинформатике, моделировании экологии и эволюции),
вычислительной математике (моделировании дорожного движения и транспортных
процессов, разработке алгоритмов решения вычислительно сложных проблем)
и, до некоторой степени, в моделировании процессов в общественных науках
(построении моделей голосования и формирования консенсуса в обществе).
Методы и подходы статистической механики (в особенности скейлинговые
методы, используемые для изучения непрерывных переходов) являются,
возможно, наиболее полезными инструментами, приносимыми нами в эти
разнообразные области исследования. С другой стороны, я надеюсь, что эта книга
Гл.12. Упражнения
531
окажется полезным введением в эти методы и подходы для математиков,
биологов, инженеров и профессионалов в области финансов, чья
разнообразная деятельность продолжает расширять и обогащать область исследования
статистической механики.
Упражнения
Мы начнем этот раздел с того, что в упражнениях Самоподобие в модели
Изинга, Скейлинг и поправки к нему и Скейлинг и фазовое расслоение еще раз
обсудим явления и понятия, необходимые при изучении теории непрерывных
фазовых переходов. В упражнениях Теория бифуркаций, Теория среднего
поля и Порог генерации лазера мы обсудим несколько точно решаемых задач о
критических точках. То, как ренорм-групповые потоки определяют
критическое поведение, мы проиллюстрируем в упражнениях Траектории ренорма-
лизационной группы и Сверхпроводимость и ренормализационная группа; в
последнем из них качественно объясняются фундаментальные основы теории
Ферми-жидкостей. В упражнении Удвоение периода и двух версиях
упражнения Ренормализационная группа и центральная предельная теорема
обсуждаются важные приложения, в которых читатель сможет в явном виде и
полностью применить метод ренормализационной группы. В заключение мы
приводим два упражнения по компьютерному моделированию, Перколяция
и универсальность и Скейлинговые законы для гистерезиса и лавин, в этих
упражнениях читатель сможет провести полный анализ экспериментальных
данных, получив в результате критические индексы и скейлинговые функции,
подобно тому, как это делается при анализе данных реальных
экспериментов.
12.1 Самоподобие в модели Изинга. φ
Запустите модель Изинга (см. раздел компьютерных упражнений на сайте
книги [132]). Смоделируйте достаточно большую систему в нулевом внешнем
поле при температуре 1 = Тс = 2/log(l + \/2) « 2.26919. Выберите режим
перерисовки изображения, так чтобы графика не замедляла моделирование,
и дождитесь равновесия системы (для этого необходимо подождать
несколько сотен шагов). Вы должны увидеть достаточно самоподобную структуру, с
кластерами спинов, имеющих фрактальный вид: кластеры спинов вверх
будут вложены в более крупные кластеры спинов вниз, вложенные в еще более
крупные кластеры спинов вверх, и т.д. ...
Можете ли вы найти на картинке систему из трех последовательно вложенных
друг в друга кластеров? А из четырех?
532
Гл.12. Непрерывные фазовые переходы
12.2 Скейлинг и поправки к нему. (Физика конденсированного
состояния) ®
Вблизи критических точек самоподобие при изменении масштаба
приводит к возникновению характерных степенных зависимостей. Эти зависимости
могут, однако, быть скрыты за менее сингулярными поправками к скейлин-
говому поведению.
В эксперименте измеряют восприимчивость χ(Τ) магнетика при
температурах Г немного выше точки ферромагнитного перехода Тс. Оказывается,
что полученные данные хорошо приближаются формулой
Х(Г) = А(Т - Те)"1·25 + В + С(Т - Тс)
+ D(T-TC)1·71. (12.17)
(a) Предположим, что эта зависимость в окрестности Тс верна. Чему тогда
равен критический индекс 7?
При измерении функций двух переменных вблизи критических точек
получают универсальные скейлинговые функции, существование которых
предсказывается теорией.
Для некоторой другой трехмерной системы корреляционная функция
С(г,Т) = (S(x)S(x + г)) измерена при температурах немного выше Тс.
Оказывается, что эта функция сферически симметрична и имеет вид
С(г,Г) = r~l026C(r{T - Тс)°-65),
где функция С(х) примерно равна ехр(—х).
(b) Чему равен критический индекс vl А критический индекс 77?
12.3 Скейлинг и фазовое расслоение. (Физика конденсированного
состояния) ®
При изучении процесса фазового расслоения мы установили, что система
изменяется во времени, причем характерный масштаб в ней растет как
некоторая степень времени: L(t) ~ t1'2 для несохраняющегося параметра порядка
и L(t) ^t1/3 — для сохраняющегося. Эти показатели, в отличие от
критических индексов, могут быть выведены на основе аргументации типа анализа
размерности (см. раздел 11.4.1). С этими расходящимися
пространственными масштабами тоже связаны скейлинговые функции. В процессе фазового
расслоения система не остается подобной самой себе на разных масштабах
в один и тот же момент времени (как в случае равновесных непрерывных
переходов), однако она оказывается подобна, с точностью до изменения
пространственного масштаба, самой себе в другие моменты времени.
(12.18)
Гл.12. Упражнения
533
Пусть модель Изинга с несохраняющейся полной намагниченностью
заморожена при температуре Τ много ниже Тс. По прошествии длительного
времени to ее корреляционная функция принимает вид С£°аг(г, Т) = с(г).
Будем считать, что корреляционная функция на малых масштабах
С£оаг(0,Т, t) не зависит от времени и что корреляционная функция с
течением времени не меняет своей функциональной формы с точностью
до перенормировки длины. Запишите корреляционную функцию в момент
времени 2£о, С^г(г,Г)| в терминах с(г). Запишите корреляционную функцию
в скейлинговом виде
Cfcoar(r, Г) = Г"С{т/1р, Г). (12.19)
Используя независимость С^оаг(0,Т) от времени и тот факт, что параметр
порядка не сохраняется (см. раздел 11.4.1), определите численные значения
показателей а; и р.
Только недавно было выяснено, что скейлинговая функция С для
фазового расслоения зависит от температуры (и в частности, анизотропна при
низких температурах, когда доменные стенки выстраиваются вдоль
направляющих решетки). Фазовое расслоение в переохлажденной системе не
является «универсальным» в том смысле, в каком универсальны непрерывные
фазовые переходы (см. раздел 11.4.1); даже для одной модели различие в
температурах приводит к различию в скейлинговых функциях.
12.4 Теория бифуркаций. (Математика) ©
Теория динамических систем изучает временную эволюцию переменных,
подчиняющихся системам дифференциальных уравнений. Пусть χ(ί) —
вектор переменных, зависящих от времени t, λ — вектор параметров, от которых
зависит система дифференциальных уравнений, a Fa(x) - сама эта система
x=^ = FA(x). (12.20)
Как правило, предметом теории является не решение системы
дифференциальных уравнений в зависимости от начальных условий, а изучение
качественного поведения решений. Вообще говоря, наибольший интерес
представляют бифуркации — особые значения параметров А, при которых поведение
системы качественно изменяется.
(а) Рассмотрим дифференциальное уравнение относительно одной
переменной x(t) с одним параметром μ:
χ = μχ — χ3.
(12.21)
534
Гл.12. Непрерывные фазовые переходы
Докажите, что имеется бифуркация при /хс = 0, показав, что начальное условие
с малым ненулевым х(0) будет эволюционировать с течением времени
принципиально различным образом в случае μ > О и μ < 0. (Указание: хотя вы
могли бы решить это уравнение в явном виде, мы советуем вам рассуждать
качественно, используя бифуркационную диаграмму на рисунке 12.19; в этом
случае можно уложиться всего в несколько фраз.)
Теория динамических систем имеет много общего с изучением фаз и
фазовых переходов в равновесной статистической механике. Переход жидкость-
газ характеризуется набором внешних параметров λ = (Ρ, Τ, TV), а текущее
состояние системы характеризуется вектором χ = (ν,Ε',μ). Равновесным
фазам соответствуют неподвижные точки (χ*(μ), где х* = 0) динамической
системы, а фазовые переходы соответствуют бифуркациям.26 Например,
степенные законы, обнаруженные нами вблизи непрерывных фазовых
переходов, имеют более простые аналоги для динамических систем.
н
μ
Рис. 12.19. Диаграмма бифуркации типа «вилка»
Диаграмма потоков для бифуркации «вилка», описываемой уравнением (12.21).
Пунктиром отмечена линия неустойчивых неподвижных точек, жирными сплошными линиями —
кривые устойчивых неподвижных точек. Тонкие линии со стрелками описывают
динамику эволюции системы. Эта бифуркация называется «вилкой», потому что из одной линии
слева образуется три линии справа.
(Ь) Для бифуркации типа «вилка» найдите значение показателя /?,
определяемого как χ*(μ) ос (μ — μ€)^ при μ —>· μ0.
Теория бифуркаций также предсказывает универсальность: все «вилки»
демонстрируют вблизи точки перехода одно и то же скейлинговое поведение.
26В разделе 8.3 мы отметили, что в пределах одной фазы все свойства системы
являются аналитическими функциями внешних параметров. Аналогично, бифуркации — это
значения параметров А, при которых наблюдается неаналитичность динамики системы на
больших временах.
Гл.12. Упражнения
535
(с) Какому значению Ас соответствует бифуркация в дифференциальном
уравнении
га = tanh (Am) - га? (12.22)
Вблизи Ас подчиняется ли положение неподвижной точки га*(А) степенному
закону га* ~ |А — Ас|^ (с точностью до поправок более высокого порядка малости
по А —Ас)? Согласуется ли показатель β с аналогичным показателем для
бифуркации типа «вилка» в уравнении (12.21)?
Подобно тому, как существуют различные классы универсальности
непрерывных фазовых переходов, соответствующие различным неподвижным
относительно преобразования ренормализационной группы точкам, имеются
различные классы бифуркаций, имеющие различные так называемые
нормальные формы. Важными примерами таких нормальных форм (помимо
вилки) являются седловая бифуркация
χ = μ - χ2, (12.23)
транскритическая бифуркация
χ = μχ - χ2, (12.24)
и бифуркация Хопфа
*-(μ-(.» + »·)>«-».
у = (μ- (χΔ +у*))у + х.
12.5 Теория среднего поля. (Физика конденсированного состояния) Q)
В гл. 11 и упражнении 9.5 мы упоминали так называемые «теории
среднего поля». Этот термин используется в широком смысле для описания любых
теорий, которые пытаются описать флуктуации параметра порядка путем
включения в выражение для свободной энергии единственной
дополнительной степени свободы. В изначальном варианте теории среднего поля в
качестве такой степени свободы использовалось среднее поле, действующее на
данную частицу со стороны ее окружения, которое использовалось для
приближенного учета взаимодействия частиц.
В случае модели Изинга на квадратной решетке это соответствует
предположению о том, что каждый спин Sj = ±1 находится в окружении четырех
соседей, каждый из которых имеет среднюю намагниченность т = (sj), что
приводит к односпиновому гамильтониану вида
U = -4JmSj. (12.26)
536
Гл.12. Непрерывные фазовые переходы
(a) Считая температуру равной Т, вычислите среднее значение спина (sj),
описываемого гамильтонианом (12.26) при заданном значении га? При какой
температуре Тс теория среднего поля предсказывает фазовый переход?
(Указание: при каком значении температуры появляется ненулевое
самосогласованное решение га = (s)?) Покажите (подобно тому, как это сделано в
упражнении 12.4, часть (с)), что га ос (Тс — Т)& вблизи Тс. Согласуется ли предсказание
критического индекса β с реально наблюдаемым для модели Изинга в
двумерном (β = 1/8) или трехмерном (β « 0.325) пространстве?
(b) Покажите, что найденное вами в части (а) среднеполевое решение
соответствует минимуму зависящей от температуры эффективной свободной энергии
V(m) = квт{^- - log (cosh(4Jm/kBT)) ^-). (12.27)
Начертите на одном графике зависимости V(m) для \/{квТ) = 0.1, 0.25 и 0.5 в
интервале —2 < га < 2, убедитесь в наличии непрерывного фазового перехода.
Сравните полученный график с рис. 9.23.
(c) Как будет выглядеть эффективный среднеполевой гамильтониан для
модели Изинга на квадратной решетке во внешнем поле HI Покажите, что сред-
неполевая намагниченность соответствует минимумам27
V(т) = квт(^- - log (cosh((# + 4Jm)/kBT)) ^). (12.28)
Начертите на одном графике зависимости V(ra, Η) для β = 0.5 и Я = 0, 0.5,
1.0 и 1.5, найдите на графике метастабильные области и скачкообразный
фазовый переход. При каком значении Η метастабильное состояние становится
стабильным? Сравните ваш график с рис. 11.2(a).
12.6 Порог генерации лазера. (Квантовая физика, оптика,
математика) ©
Излучение в лазере находится в стационарном состоянии большой
плотности. Это состояние отличается от обычных термодинамических фаз не только
тем, что оно является состоянием поля, а не вещества, но и тем, что оно
является существенно неравновесным. Энтропия в лазере не достигает
максимума. Тем не менее, это состояние обладает устойчивостью и целостностью,
что делает его сходным с фазами равновесных систем.
27Надо сказать, что эта функция выглядит несколько непривычно: странно видеть
внешнее поле Η внутри эффективного потенциала, а не снаружи, в линейном по полю слагаемом
+га.
28 Это упражнение было составлено совместно с Алексом Гаэта и Алом Сиверсом.
Гл.12. Упражнения
537
В этом упражнении мы изучим систему возбужденных атомов,
взаимодействующую с фотонной модой на пороге возникновения лазерного излучения.
Мы увидим, что в этой системе наблюдается расходимость флуктуации и
скейлинговое поведение, сходные с тем, что мы изучали вблизи критических
точек.
Рассмотрим систему атомов, слабо взаимодействующую с фотонной
модой. Пусть N\ атомов находятся в состоянии с энергией £Ί, a 7V2 атомов
находятся в состоянии с большей энергией Е2\ при этом имеется сильное
взаимодействие этих атомов с окружением, которое поддерживает постоянство
этих заселенностей.29 Ниже порога лазерного излучения вероятность pn(t)
того, что в фотонной моде имеется η фотонов, подчиняется уравнению
—^ = α(ηρη-ιΝ2 - ηρηΝι - (η + 1)ρηΝ2
at
+ {η + 1)ρη^ιΝ1). (12.29)
Первое слагаемое в правой части описывает вероятность того, что в
присутствии η — 1 фотонов один из N2 возбужденных атомов испустит еще один
фотон; второе слагаемое описывает вероятность того, что один из Ν\ низко-
энергетичных атомов поглотит один из η фотонов; третье слагаемое
описывает излучение в присутствии η фотонов, а последнее — поглощение одного из
η + 1 фотона. Тот факт, что поглощение в присутствии га фотонов
пропорционально га, а излучение пропорционально га + 1, является общим свойством
бозонов (см. упражнения 7.8(c) и 7.9). Постоянная а > О зависит от времени
перехода и связана с коэффициентом Эйнштейна А (см. упражнение 7.8).
(а) Найдите простое выражение для d(n)/dt, где (n) = ^,т=отР™ ~~ это
среднее число фотонов в моде. (Указание: соберите вместе все члены,
содержащие рш.) Покажите, что в случае N2 > N\ ваше выражение приводит к
неограниченному росту среднего числа фотонов с течением времени, что
приводит к возникновению макроскопического числа заполнения одного фотонного
состояния, т.е. лазерного состояния. и
Рассмотрим теперь нашу систему непосредственно перед переходом в
лазерное состояние. Пусть е = (7V2 — Ν\)/Νι — мера того, насколько близко мы
29Другими словами, мы предполагаем, что имеется накачка в состояние N2,
компенсирующая релаксацию атомов из этого состояния за счет излучения, которое мы изучаем,
и любых других возможных каналов. Как правило, накачка предполагает возбуждение
атомов в какие-то еще третьи состояния.
30 В какой-то момент число фотонов перестанет расти из-за того, что поток энергии из
возбужденного состояния атомов N2 в фотонную моду превысит возможности накачки,
что приведет к невыполнению нашего базового предположения о постоянстве числа
возбужденных атомов.
538
Гл.12. Непрерывные фазовые переходы
подошли к точке лазерной неустойчивости. Можно ожидать, что величина
(п) будет расходиться при е —у О по закону e~v для малых е. Вблизи точек
фазового перехода, как правило, наблюдается критическое замедление: для
того чтобы прийти в равновесное состояние, системе приходится передавать
информацию на большие расстояния порядка корреляционной длины, для
чего требуется время, расходящееся в той точке, где корреляционная длина
расходится. Определим индекс критического замедления ζ для нашего
лазера, предположив, что типичное время релаксации в нем пропорционально
|б|~^ При € —> 0.
(b) Для € < 0, т.е. ниже точки неустойчивости, найдите из уравнения
части (а) стационарное значение (п), достигаемое на больших временах. Чему
равно ν для нашей системы? Решите уравнение и найдите закон, по которому
эволюционирует система из произвольных граничных условий. Ваше решение
должно экспоненциально сходиться к значению на больших временах.
Стремится ли время релаксации к бесконечности при е —> 0? Чему равно С?
(c) Найдите стационарное состояние р* при N2 < Ν\. (Ваша формула для
р* не должна содержать р*.) Пусть Ν2/Ν1 задается распределением Больцмана
при температуре Т. Будет ли р* в этом случае равновесным распределением
для квантового гармонического осциллятора при этой температуре? Внимание:
Число бозонов в фотонной моде задается распределением Бозе-Эйнштейна,
но вероятность наблюдения различных чисел заполнения квантового
гармонического осциллятора задается распределением Больцмана (см. раздел 7.2
и упражнение 7.2).
Можно предполагать, что вблизи неустойчивости вероятность наблюдать
η должна иметь скейлинговый вид
Р;(е)~п—Р(п|еГ). (12.30)
(d) Используя ответ из части (с), покажите, что при малых е существует скей-
линговая форма для р*, поправки к которой стремятся к нулю при е —> 0. Чему
равно г? Какой вид имеет функция Т>(х)1 (Указание: при выводе формулы
для Р, € мало, но nev — величина порядка единицы. Если бы вы были
экспериментатором и хотели пронаблюдать скейлинговый коллапс, вам следовало
бы начертить птрп как функцию χ = гг|е|~^; попробуйте заменить
переменные в выражении птрп так, чтобы вместо е в нем стоял бы ж, и выберите τ
так, чтобы исключить η при малых е.)
12.7 Траектории ренормализационной группы. ©
Модель Изинга вблизи критической температуры Тс описывается двумя
переменными: расстоянием до критической температуры t = (Τ — Тс)/Тс и
Гл.12. Упражнения
539
внешним полем h = Η/ J. При огрбулении масштаба х' = (1 — ε) χ система
оказывается подобна самой себе при измененной температуре t' = (1 + ae)t
и внешнем поле Ы — (1 + be) /ι, при этом Ь > а > О (таким образом,
имеются два релевантных собственных направления, причем внешнее поле более
релевантно, чем температура).
(a) На какой из приведенных на рис.12.20 диаграмм показаны потоки,
соответствующие случаю b > а > 0?
При той же процедуре огрубления масштаба намагниченность M(t,h)
перенормируется по закону М' = (1 + се) М, так что Μ ((1 + ае) £, (1 + be) h) =
(l + cc)M(t,/i).
(b) Пусть известны значения M(t, h) при t = t\, т.е. вдоль линии,
отмеченной закрашенными точками на рисунке из части (а). Запишите формулу для
Μ(2ίι,Λ) (вдоль линии, отмеченной пустыми кружками) в терминах M{t\,h').
(Указание: выразите скейлинговую переменную, постоянную вдоль ренорм-
групповых траекторий из части (а), через t и h. Запишите скейлинговое
выражение дял M(i, h) через эту скейлинговую переменную и выразите
критические индексы через a, b и с. После этого можно вычислить M(t,h) при
t = 2ίι, если известно значения намагниченности при t = t\.)
12.8 Сверхпроводимость и метод ренормализационной группы.
(Физика конденсированного состояния) ©
Обычно сверхпроводимость наблюдается при очень низких температурах;
в отличие от энергии фононов (сотни градусов Кельвина, умноженных на
кв) или электронов в атомах (десятки тысяч градусов Кельвина), фононная
сверхпроводимость в большинстве материалов наблюдается при
температурах, не превышающих несколько Кельвинов. Это в значительной степени
объясняется теорией сверхпроводимости Бардина—Купера—Шрифера
(теории БКШ), в соответствии с которой температура перехода в слабосвязанных
сверхпроводниках равна
Тс = 1.764 huDexp{-l/Vg{eF)), (12.31)
где ljd — характеристическая частота фононов, V — константа
передаваемого фононами притяжения между электронными парами, a 9{sf) — плотность
состояний электронного газа при энергии Ферми (см. уравнение 7.74).
Если V мало, множитель ехр(—\/Vg(eF)) становится экспоненциально малым,
что объясняет, почему переход в сверхпроводящее состояние, как правило,
происходит при таких низких температурах.
Между открытием сверхпроводимости и ее теоретическим объяснением
прошло несколько десятилетий. В течение этого времени много усилий было
540
Гл.12. Непрерывные фазовые переходы
(е)
Рис. 12.20
Гл.12. Упражнения
541
потрачено на поиск ее объяснений, в том числе таких, которые
основывались бы на взаимодействии электронов с фононами. Однако существовало
серьезное препятствие для такого объяснения: в результате изучения этого
взаимодействия было установлено, что вещество остается в металлическом
(т.е. не сверхпроводящем) состоянии во всех порядках теории возмущений.
(а) Разложите выражение для Тс (уравнение 12.31) в ряд Тейлора вблизи
V = 0+ (т.е. при бесконечно малых положительных V). Сделайте предположение
о значении всех членов разложения. Можем ли мы ожидать, что с помощью
теории возмущений по степеням V удастся объяснить сверхпроводимость при
положительных температурах?
Отсюда можно сделать два вывода.
• Если какое-то утверждение доказано во всех порядках теории
возмущений, это еще не значит, что оно верно.
• Поскольку фазы — это области, внутри которых теория возмущений
сходится (см. раздел 8.3), в этой теореме нет ничего особенно
удивительного. Она является, собственно, условием существования
металлической фазы с поверхностью Ферми.
В последнее время было развито ренорм-групповое описание состояния
жидкости Ферми и его неустойчивостей31 (см. сноску 23 на с. 273).
Обсуждение теории жидкостей Ферми, теории БКШ и этого ренорм-группового
описания завело бы нас слишком далеко в область сугубо технических вопросов.
Однако можно проиллюстрировать все эти три темы, рассмотрев модельную
систему с ренорм-групповыми потоками достаточно необычного вида.
Грубо говоря, ренорм-групповое описание жидкостей Ферми
утверждает, что поверхность Ферми является неподвижной точкой при огрублении
масштаба энергии. На входе имеется пространство систем, состоящее из
частично заполненных электронных зон ширины W по энергии, и включающее
все виды отталкивающего и притягивающего межэлектронного
взаимодействия. Огрубление масштаба состоит в исключении электронных состояний
вблизи границы зоны (интегрирования по соответствующим степеням
свободы),
W' = {\- S)W, (12.32)
с одновременным включением их влияния и взаимодействий в
перенормированные параметры взаимодействия оставшихся электронов. Эти
перенормированные взаимодействия задают ренорм-групповые потоки в пространстве
31В жидкости Ферми есть и другие неустойчивости. Например, зарядовые волны,
зависимость которых от параметра взаимодействия V также имеет характерный вид ехр(—1/aV).
542
Гл.12. Непрерывные фазовые переходы
систем. Уравнение на W задает изменение после одной итерации (п = 1);
можно сделать вид, что η — непрерывная переменная и перейти к пределу
δη —> О, в результате получим (W' — W)/S —> dW/dn и, следовательно,
dW/dn = -W. (12.33)
В результате соответствующих вычислений получается, что
• невзаимодействующий Ферми-газ, изученный нами в разделе 7.7,
является неподвижной точкой этого преобразования ренорм-группы. Все
взаимодействия в этой точке равны нулю. Пусть параметр V описывает
одно из этих взаимодействий;32
• тогда неподвижная точка является неустойчивой для притягивающего
взаимодействия V > О, и устойчивой для отталкивающего
взаимодействия V < 0;
• силы притяжения между электронами усиливаются при огрублении
масштаба и приводят к возникновению новых фаз, в то время как
силы отталкивания ослабевают при огрублении масштаба, в результате
чего система возвращается в состояние металлического Ферми-газа.
Этот результат существенно отличается от того, что получался у нас
выше при ренорм-групповом описании фазовых переходов: в том случае
релевантные направления, такие как температура и внешнее поле,
оказывались неустойчивы при огрублении, независимо от того, в какую сторону от
неподвижной точки происходило отклонение, в то время как другие, ирре-
левантные, направления оставались устойчивыми (см. рис. 12.8). Например,
температура нашего Ферми-газа является релевантной переменной, которая
при огрублении перенормируется по закону
Г = (1 + а6)Т,
К ' 12.34
dT/dn = аТ. к '
Здесь а > 0, так что при огрублении масштаба эффективная температура
системы повышается. Как можно получить переменную V, которая
увеличивается при V > 0 и уменьшается при V < 0?
• При изучении влияния преобразования ренормализационной группы на
параметр взаимодействия V оказывается, что он является
маргинальной переменной: с точностью до первого порядка он не увеличивается
и не уменьшается.
32 V имеет смысл параметра парного взаимодействия между электронами с
противоположно направленными спинами вблизи поверхности Ферми в сверхпроводниках.
Гл.12. Упражнения
543
2 (12.35)
Следующий разрешенный порядок разложения в ряд Тейлора вблизи
неподвижной точки дает нам уравнение для поведения взаимодействия при
огрублении:
V = (l + bSV)V,
dV/dn = bV
• Оказывается, что b > 0.
(b) Отметьте, истинно или ложно каждое из следующих утверждений? (см.
рис. 12.21).
При V > 0 (притяжение) взаимодействие растет с огрублением масштаба.
При V < 0 (отталкивание) огрубление масштаба приводит нас назад к
свободному Ферми-газу, что объясняет, почему Ферми-газ описывает состояние
металлов (см. раздел 7.7).
Температура — иррелевантная, но опасная переменная.
Скейлинговая переменная
х = τν1/βδ, (12.36)
где β и δ — универсальные критические индексы;33 не меняется при огрублении
масштаба (описываемом вторым из уравнений (12.34) и уравнением (12.35)) и,
следовательно, движение вдоль кривых на рис. 12.21 соответствует изменению
χ (х увеличивается в направлении, в котором указывают стрелки).
Скейлинговая переменная
y = Texp(a/(bV)) (12.37)
не меняется при огрублении масштаба, так что каждая из кривых на рис. 12.21
соответствует фиксированному значению у.
Далее, будем считать, что наша система переходит в сверхпроводящее
состояние при некоторой температуре TC(V) в случае, если взаимодействие
притягивающее (при этом мы можем ничего не знать о природе этого
сверхпроводящего состояния). При огрублении масштаба система, находящаяся в
точке перехода в сверхпроводящее состояние, переходит в систему, также
находящуюся в точке перехода.
(c) Какую функцию а/Ь нужно вычислить, чтобы получить из этих ренорм-
групповых соображений температуру перехода в соответствии с теорией БКШ
(уравнение 12.31)? Чему равно значение скейлинговой переменной (той, которую
вы выбрали в части (Ь)) вдоль TC(V)7
33Обратите внимание, что δ здесь — константа, а не обозначение бесконечно малого
изменения параметра.
544
Гл.12. Непрерывные фазовые переходы
g У, энергия связи, умноженная на DOS
Рис. 12.21. Ренорм-групповые потоки в теории Ферми-жидкостей
Ренорм-групповые потоки, описываемые уравнениями (12.34) и (12.35). Температура Τ
— релевантная переменная в неподвижной точке, соответствующей Ферми-газу; параметр
взаимодействия V — маргинальная переменная. Выделенная кривая — линия фазового
перехода TC(V). Например, ниже Тс система находится в сверхпроводящем состоянии; выше
Тс она представляет собой металл при конечной температуре.
Таким образом, выражение для температуры перехода при малых V из
теории БКШ (уравнение 12.31) можно объяснить, просто изучая газ Ферми,
не используя никакого представления о том, что такое сверхпроводящее
состояние*.
12.9 Удвоение периода.34 (Математика, теория сложных систем) @
В этом упражнении мы используем методы скейлинга и ренормализа-
ционной группы для изучения механизма возникновения хаоса. Существует
несколько путей, которыми динамическая система может прийти к
хаотическому состоянию; в этом упражнении мы рассмотрим каскад удвоений
периода^ который был впервые подробно изучен Фейгенбаумом.
Возникновение хаоса часто связывают с динамическим поведением,
состоящим в комбинации растяжений и наложений; при растяжении куска
ириски, движение крупинки внутри нее существенно зависит от ее начального
положения. Физику этого процесса можно представить, используя простое
отображение35
/(χ) = 4μχ(1-χ), (12.38)
определенное при χ Ε (0,1). Видно, что /(0) = /(1) = 0 и /(^) = μ. Таким
образом, при μ = 1 отображение складывает интервал (0,1) вдвое и растягивает
его так, чтобы целиком покрыть начальную область.
34 Это упражнение и связанное с ним программное обеспечение были разработаны в
сотрудничестве с Кристофером Майерсом.
35Мы также изучали это отображение в упражнениях 4.3, 5.9, и 5.16; части (а) и (Ь)
настоящего упражнения частично перекрываются с упражнением 4.3.
Гл.12. Упражнения
545
При изучении динамических систем (например, дифференциальных
уравнений или отображений, подобных уравнению 12.38) нас часто интересует
поведение системы на больших временах, когда ее траектории сходятся к
аттрактору. Возникновение и развитие хаоса можно изучать, наблюдая за
эволюцией аттрактора при изменении μ. При достаточно малых μ все точки
притягиваются к началу координат; начало координат — устойчивая
неподвижная точка, притягивающая весь интервал χ Ε (ОД)· При больших μ
сначала появляется новая неподвижная точка внутри интервала, а затем
происходит удвоение периода.
(а) Итерации: Положите μ = 0.2; выберите несколько начальных точек хо
и последовательно применяйте к ним отображение /. Вы увидите, что после
многих итераций все эти точки сходятся к нулю. Постройте на одном графике
функцию / и диагональную прямую у = х. Видите ли вы какие-нибудь
неподвижные точки, кроме χ = 0? Повторите процедуру для μ = 0.3, μ = 0.7 и 0.8.
Опишите, что происходит.
Постройте на одном графике функцию /, прямую у = χ и отрезки {#о,#о}»
{яо,/(яо)}. {/(яо),/(яо)}, {/(яо),/(/(яо))}, ...(иллюстрирующие путь, по
которому точка сходится к аттрактору; см. рис. 12.22). Покажите, чем отличаются
случаи μ = 0.7 и 0.8. Поэкспериментируйте с другими значениями μ.
Многократно проитерировав отображение, найдите какую-нибудь точку ао,
лежащую на аттракторе. Применяя к ао отображение /, постройте
последовательные итерации этой точки для μ = 0.7, 0.8, 0.88, 0.89, 0.9 и 1.0.
1
*Г
Г /
0
14
Х^ -У
/ >
X
А
1
1
Рис. 12.22. Цикл периода восемь
Итерации вокруг аттрактора отображения Фейгенбаума при μ = 0.89.
Видно, что при больших μ система перестает стремиться к стационарному
состоянию на больших временах. Неподвижная точка с f(x) = χ существует
546
Гл.12. Непрерывные фазовые переходы
для всех μ > \, но при больших μ она становится неустойчивой. Пусть х* —
неподвижная точка отображения (так что /(#*) = х*). Добавим к ней малое
возмущение: f(x* + е) « /(#*) + f(x*)t = х* + /'(#*)е; неподвижная точка
явл!»ется устойчивой (малые возмущения затухают), если \f(x*)\ < I.36
В данном случае, после того как неподвижная точка становится
неустойчивой, движение после многих итераций становится периодическим,
возвращаясь в одну и ту же точку после каждых двух итераций отображения, так
что f(f(x)) имеет две новые неподвижные точки. Это явление называется
удвоением периода. Обратите внимание на то, что по правилу
дифференцирования сложной функции df(f(x))/dx = /'(#)/'(/(#)), а в более общем
случае
d/W_d/(/(.../(x)...))
dx ~ dx li^yj
= /W(/(*)) ■■·/'(/(· ··/(*) ··■)).
так что устойчивость цикла периода N определяется произведением
производных отображения / во всех точках цикла.
(b) Аналитика: Найдите неподвижную точку χ*(μ) отображения (12.38) и
покажите, что она существует и устойчива в области 1/4 < μ < 3/4. Если вы
уверены в своих вычислительных способностях или умеете пользоваться программами
для аналитических вычислений, покажите, что цикл периода два устойчив при
3/4 < μ < (1 + л/б)/4.
(c) Бифуркационная диаграмма: Постройте аттрактор как функцию μ при
О < μ < 1; сравните с рис. 12.16. (Выберите фиксированный шаг δμ и для
каждого μ выполните ntransient итераций, после чего запомните следующие ncycies
шагов и отметьте их положения на графике. После отладки программы
установите каждое из чисел ntransient и ncycies большим ста, а δμ < 0.01.) Постройте
аттрактор для другого отображения с одним максимумом:
fsin(x) = Bsin(nx), (12.40)
при 0 < В < 1. Получились ли бифуркационные диаграммы похожими друг не
друга?
Обратите внимание на хаотическую область сложной структуры при
больших μ (мы изучали ее в упражнении 4.3). Каким образом осуществляется
36 В непрерывном случае возмущения затухают, если отрицательны все собственные
значения якобиана, составленного из производных отображения в неподвижной точке. Для
дискретных отображений возмущения затухают, если все собственные значения якобиана
меньше единицы.
Гл.12. Упражнения
547
переход от устойчивого аттрактора при μ < | к хаосу? Возникновение хаоса
в этой системе происходит в результате каскада удвоений периода. С ростом
μ наблюдается последовательность бифуркаций: при μι = f возникает цикл
периода два, который сменяется циклом периода четыре при μ2, циклом
периода восемь при μ% и т.д., образуя каскад удвоений периода. Наблюдается
геометрическая сходимость к предельной точке μ^:
μηπμοο-Αδ-η, (12.41)
так что
δ = lim (μη_ι - μη-2)/(μη - Μη-ΐ), (12.42)
η—too
вдоль оси х наблюдается такое же геометрическое самоподобие с
(отрицательным) масштабирующим множителем а, связывающим последовательные
поколения дерева (см. рис. 12.23).
Рис. 12.23. Самоподобие бифуркаций удвоения периода
Разность значений контрольного параметра между точками удвоения периода образует
геометрическую прогрессию μοο — μη ос (5~п, а аттрактор в цикле периода 2П подобен
половине аттрактора в цикле периода 2η+1, с точностью до обращения и изменения масштаба,
что соответствует перенормировке χ на множитель α и μ на множитель δ. Это
самоподобие иллюстрируется прямоугольниками на рисунке; содержимое прямоугольников подобно
с точностью до растяжения в δ раз вдоль горизонтальной оси μ и переворота и растяжения
в α раз вдоль вертикальной оси.
В упражнении 4.3 мы показали, что граница хаотической области
является образом точки χ = ^ · Нахождение образов этой точки полезно и при
изучении удвоения периода. Поскольку х = \ соответствует максимуму функции
/, то f'{\) = 0. Если эта точка является к тому же неподвижной точкой
изображения (как это происходит при μ = ^), то она будет не просто
устойчивой, а необычайно устойчивой: начальное условие, возмущенное на е
относительно неподвижной точки, переходит после одной итерации в точку на
расстоянии ef(\) + £2/2/"(^) = 0(е2) от χ = \. О такой точке говорят, что
548
Гл.12. Непрерывные фазовые переходы
она сверхустойчива. Если цикл период N проходит через χ = 2> так что
iV-ая итерация отображения fN(^) = /(.../(^)...) = ^, то
соответствующий цикл также оказывается сверхустойчивым, поскольку (в соответствии с
уравнением 12.39) производная по циклу равна произведению производных
от всех отображений вдоль него и, значит, в этом случае в точности равна
нулю.
Эти сверхустойчивые точки находятся примерно посередине между
точками бифуркациями, и найти их существенно легче, так как мы заранее
знаем, что χ = 2 принадлежит циклу. Используем их для исследования
геометрической сходимости и самоподобия бифуркационной диаграммы
удвоения периода, полученной в части (d). Для выполнения этой части (а
также части (h)) упражнения вам понадобится программа, вычисляющая корни
G(y) = 0 функций G одной переменной у.
(d) Универсальность и числа Фейгенбаума: С помощью численного
моделирования найдите для нескольких первых значений η значения μ*, при
которых циклы длины 2П сверхустойчивы. (Указание: введите функцию Ο(μ) =
/μ (^) — ^, и найдите ее корни в зависимости от μ. Для вычисления μ^+ι
следует искать корень в интервале (μ^ι+ε,μ^ι + (μ^ι—μ^ι_ι)/Α)1 хорошо
работает значение А ~ 3. Вычислите μο и μι аналитически.) Вычислите отношения
(Мп-1 — Μη-2)/(Μη ~ Μη-ι); похоже ли. чт0 они сходятся к числу
Фейгенбаума δ = 4.6692016091029909... ? Оцените μοο экстраполяцией с использованием
последних надежных значений μ^, которые вам удалось вычислить, и
уравнения 12.42. В сверхустойчивом цикле длины 2П ближайшая к χ = \ точка —
это /βη 1(^).37 Вычислите отношения сдвигов f^n \\) - \ для
последовательных значений п; похоже ли, что они сходятся к универсальному значению
α = —2.50290787509589284... ? Вычислите аналогичные отношения для
отображения /2(2) = Β$\Ί\(πχ)\ похоже ли, что числа α и δ являются универсальными
(т.е. не зависящими от конкретного отображения)?
Предельные значения α и δ не зависят от отображения, если только оно
соответствует однократному складыванию (отображение с одним максимумом)
с квадратичным максимумом. Такие же значения получаются и для
экспериментальных систем с большим числом степеней свободы, претерпевающих
каскад удвоений периода. Такое самоподобие и универсальность
подталкивают нас к поиску ренорм-группового объяснения этого явления.
(e) Огрубление масштаба времени. Постройте график f{f(x)) как функции
χ при μ = 0.8, начертите на том же графике прямую у — χ (или используйте
37Это следует из того, что в предыдущем сверхустойчивом цикле после 2П-1 итераций
мы возвращались в начальную точку χ =\.
Гл.12. Упражнения
549
и0 х 1
Рис. 12.24. Преобразование ренормализационной группы
Преобразование ренормализационной группы берет отображение д(д(х)) в маленьком окне
с верхним углом х*у переворачивает его и растягивает так, чтобы заполнить всю область
(0,1)х(0,1).
рис. 12.24). Обратите внимание на то, что устойчивый цикл периода два для /
превращается в пару устойчивых неподвижных точек для /'21. (Такое
преобразование соответствует огрублению масштаба времени — изучая f(f{x)) вместо /,
мы удаляем каждую вторую точку из исследуемого временного ряда.) Сравните
рисунок с графиком f(x) как функции χ при μ — 0.5. Обратите внимание на то,
что увеличенная область вблизи χ — \ для /И = /(/(#)) выглядит достаточно
похожей на все отображение / при меньшем значении μ — 0.5. Начертите Я4'(#)
при μ = 0.875; обратите внимание на то, что и здесь вблизи х = \ появляется
маленькое одногорбое отображение.
То, что сразу после бифуркации удвоения периода одногорбое
отображение появляется вновь в уменьшенном виде — это основная причина того,
что последовательные бифуркации так похожи друг на друга. Тот факт, что
многие свойства этих бифуркаций универсальны, связан с тем, что форма
маленьких одногорбых отображений после нескольких удвоений периода не
зависит более от начального отображения.
Определим это преобразование ренормлизационной группы Т,
отображающее функциональное пространство на себя. Грубо говоря, преобразование
Τ берет перевернутый горб функции f{f{x)) (см. рис. 12.24),
переворачивает его и растягивает так, чтобы покрыть весь интервал (0,1). Обратите
внимание, что на ваших графиках из части (g) прямая у = χ пересекает
график f(f(x)) не только в двух точках, соответствующих устойчивому циклу
длины два, но и (что естественно) в старой неподвижной точке /(#), x*[f] ·
Эта неустойчивая неподвижная точка играет для /'2' роль, которую начало
550
Гл.12. Непрерывные фазовые переходы
координат играет для /; наше ренорм-групповое изменение масштаба
должно отобразить (я*[/],/(#*)) = (х*,х*) в начало координат. Тот угол
отображения, который должен перейти в (1,0), чрезвычайно удобным образом
расположен в точке 1-х*, поскольку, к счастью, наше преобразование
симметрично38 относительно χ — -^. Для одногорбого отображения общего вида
д(х) с неподвижной точкой х*[д] сторона окна имеет, таким образом,
длину 2(х*[#] — ^). Чтобы подобающим образом растянуть и перевернуть его,
нам нужно, следовательно, умножить на а[д\ = —1/(2(х*[^] — ^)). Наше
преобразование ренормализационной группы Т[д], таким образом, отображает
функциональное пространство на себя и имеет вид
Т[д)(х) = а[д} (д (д(х/а[д] + х*[д})) - х*[д}). (12.43)
(То есть нужно перемасштабировать χ под размер окна, дважды применить
<7, сдвинуть угол окна в начало координат и умножить на а, чтобы заполнить
начальное окно (0,1) χ (0,1).)
(f) Скейлинг и ренормализационная группа: Напишите программу,
вычисляющую х*[д] и а[д], и определите преобразование ренормализационной группы
Т[д]. Начертите графики T[f], T[T[f]],... и сравните их. Приближаемся ли мы
к неподвижной точке /* в функциональном пространстве?
Этим объясняется самоподобие; в частности, значение а[д] сходится к
числу Фейгенбаума а = —2.5029..., когда д стремится к /*.
(g) Универсальность и ренормализационная группа: Используя
синус-отображение из уравнения (12.40), сравните T[T[/Sin]] и Т[Т[/]]
вблизи перехода в хаотическое состояние. Сходятся ли они к одной и той же
неподвижной точке?
Используя эту быструю сходимость в функциональном пространстве,
можно доказать, что (зачастую) будут наблюдаться бесконечные
геометрические прогрессии удвоений периода, приводящие к хаотическому
поведению, и что эти прогрессии будут иметь универсальные свойства
(показатели α и 5, формы кривых), не зависящие от конкретного вида
изначальной динамики.
12.10 Ренормализационная группа и центральная предельная
теорема: короткая версия. (Математика) @
Если вы хорошо знакомы с методом ренормализационной группы и
преобразованием Фурье, эту задачу можно сформулировать очень коротко. Если
нет, вам лучше обратиться к длинной версии упражнения 12.11.
38В асимметричных отображениях пришлось бы искать этот угол f(f(xc)) = x*
численно. Оказывается, однако, что нарушение этой симметрии не влияет на поведение вблизи
неподвижной точки.
Гл.12. Упражнения
551
Запишите ренормализационно-групповое преобразование Т, которое
отображает пространство распределений вероятности в себя и состоит в том, что
из начального распределения берутся две случайных величины, вычисляется их
сумма и делится на корень из двух [91]. Покажите, что распределение Гаусса
с произвольной шириной σ является неподвижной точкой этого
преобразования. Для преобразования Т, линеаризованного вблизи этой неподвижной точки,
найдите собственные функции /п и собственные значения λη. (Указание: это
легче сделать в Фурье-пространстве.) Объясните, в чем состоит физический
смысл релевантных и маргинальных собственных функций. Возьмите
биномиальное распределение с ρ = 1/2, вычтите из него устойчивое гауссово
распределение и найдите первую поправку к скейлинговому поведению как функцию х.
Какой собственной функции она соответствует? Почему в этом случае не
доминирует главное иррелевантное собственное значение?
12.11 Ренормализационная группа и центральная предельная
теорема: длинная версия. (Математика) @
В этом упражнении мы построим ренормализационную группу в
функциональном пространстве, которая позволит нам вывести центральную
предельную теорему [91]. Мы будем использовать отображения (подобные
нашему ренорм-групповому преобразованию Τ), которые переводят одну функцию
ρ от χ в другую функцию х; мы будем обозначать эту новую функцию Т[р]
или Т[р](х), если мы хотим подчеркнуть ее зависимость от х. Мы также будем
использовать преобразование Фурье (уравнение А.6)
Т[р](к) = £
оо
e-'lkxp(x) dx; (12.44)
Τ отображает функцию от χ в функцию от к. Там, где это удобно, мы будем
также использовать волну для обозначения образа Фурье: ρ = Τ[ρ], так что,
например (см. уравнение А.7),
1 Г°°
p0e) = 2W_ eikxP^dk- <12·45)
Центральная предельная теорема утверждает, что сумма многих
независимых случайных величин сходится к распределению Гаусса, независимо от
того как выглядело начальное распределение.39 Другими словами,
распределение Гаусса является для суммы большого числа слагаемых функцией,
39Для того чтобы центральная предельная теорема выполнялась, необходимо также,
чтобы математические ожидания и среднеквадратичные отклонения слагаемых были
однородно ограничены. — Прим. переводчика.
552
Гл.12. Непрерывные фазовые переходы
соответствующей неподвижной точке. Когда мы складываем много
случайных чисел, детали распределения индивидуальных слагаемых перестают
иметь значение; возникает простое поведение. Мы исследуем его с помощью
метода ренормализационной группы, используя это исследование как пример,
в котором ренорм-групповое преобразование может быть записано в явном
виде. В данном случае пространство систем — это пространство всех
возможных распределений вероятности р{х). Наше рассмотрение состоит из четырех
шагов.
1. Огрубление масштаба. Удалим некоторую часть (скажем, половину)
степеней свободы. В данном случае это будет соответствовать тому, что мы
попарно складываем случайные величины; распределение вероятности для
суммы N независимых случайных величин с распределением / совпадает с
распределением вероятности для суммы N/2 случайных величин с
распределением / * /, где * обозначает свертку.
(a) Покажите, что если р(х) — это вероятность того, что случайная величина
имеет значение х, то распределение вероятности для суммы двух случайных
величин, выбранных из этого распределения, задается сверткой
/оо
р(х - у)р(у) dy. (12.46)
-ОО
Помните, что преобразование Фурье от свертки равно произведению
преобразований Фурье частей (уравнение А.23), так что
Г[С[р}№ = №))2- (12-47)
2. Перенормировка. Поведение на больших масштабах, как правило, будет
таким же, как и поведение на малых масштабах, с точностью до сдвига
(перенормировки) некоторых констант. В данном случае по мере огрубления
масштаба среднее и ширина распределения будут увеличиваться. Ограничимся
здесь рассмотрением распределений с нулевым средним. Напомним, что
ширина (среднеквадратичное отклонение) распределения суммы двух
случайных величин, выбранных из р, будет в \/2 раз больше среднеквдратичного
отклонения одной случайной величины из р, и что, соответственно, типичная
высота распределения должна уменьшиться в л/2 раз, чтобы распределение
осталось нормированным. Определим оператор перенормировки Sk,
который снимает это уширение распределения вероятности:
S^ipKx) = V2p(V2x). (12.48)
(b) Покажите, что если ρ нормировано (интеграл от него равен единице),
то и S^fp] тоже нормировано. Покажите, что для преобразований Фурье верно
равенство
Гл.12. Упражнения
553
F[S^[p]№=p(k/V2). (12.49)
Наше преобразование ренормализационной группы — это композиция
этих двух операций,
Т\р](х) = ЗДОД](х)
/оо
р(л/2х-у)р(у)ау. (12.50)
-ОО
Распределение Гаусса должно быть неподвижной точкой этого
преобразования: сложение двух гауссовых случайных величин (свертка их
распределений) и перенормировка ширины должны возвращать нас назад к начальному
распределению Гаусса.
(c) Покажите, что распределение Гаусса
р*(х) = (1/>/2πσ) ехр{-х2/2а2) (12.51)
действительно переходит в себя под действием оператора Т, т.е. является
неподвижной точкой функционального пространства относительно этого
преобразования. Вы можете либо напрямую провести интегрирование, либо
воспользоваться известными свойствами свертки распределений Гаусса.
(d) Используя уравнения (12.47) и (12.49), покажите, что
F[T[p}№ = f[p\(k) = p(k/V2f. (12.52)
Вычислите преобразование Фурье от неподвижной точки р*(к) (или
воспользуйтесь упражнением А.4). Используя уравнение (12.52), покажите,
что p*(fc) является неподвижной точкой нашего оператора огрубления Τ в
Фурье-пространстве.40
Эти свойства оператора Τ и функции р* позволят вам выполнить
оставшуюся часть этого упражнения без использования тяжеловесных интегралов.
Центральная предельная теорема утверждает, что суммы случайных
величин имеют распределения вероятности, которые сходятся к распределению
Гаусса. Для того чтобы доказать это в рамках нашего ренорм-группового
подхода, нам нужно показать, что гауссова неподвижная точка является
притягивающей: что все близкие к ней распределения вероятности стремятся к р*
при последовательном применении Т.
40В явном виде оператор Τ задается выражением Τ = То Τ о .F-1, он задает
преобразование ренормализационной группы, переводящее пространство Фурье в себя.
554
Гл.12. Непрерывные фазовые переходы
3. Линеаризация вблизи неподвижной точки. Рассмотрим функцию,
близкую к неподвижной точке: р(х) = р*{х) + е/(х). В пространстве
Фурье р(к) = р*(к) + ef(k). Мы хотим найти собственные значения λη и
собственные функции /п производной преобразования Т, т.е. собственные
функции и собственные значения, удовлетворяющие уравнению
Т[р* + efn] = ρ* + Kef η + 0(e2),
T[p* + efn\=p* + \nefn + 0(e2).
(e) Используя уравнения (12.52) и (12.53), покажите, что Фурье-образы
собственных функций удовлетворяют соотношениям
%(к) = (2/Хп)Г(к/у/2)%(к/у/2). (12.54)
4. Нахождение собственных значений и вычисление критических
индексов.
(f) Покажите, что _
/„(*) = (ifc)V(fc) (12-55)
является преобразованием Фурье от собственной функции (т.е., удовлетворяет
уравнению 12.54.) Чему равно соответствующее собственное значение λη?
Оказывается, что наша неподвижная точка притягивает не все
окружающие распределения. Направления, соответствующие собственным значениям,
большим единицы, называются релевантными] эти направления
представляют опасность: они соответствуют отклонениям от нашей неподвижной точки,
которые увеличиваются с огрублением масштаба. Направления, которым
соответствуют собственные значения, равные одному, называются
маргинальными; отклонения в этих направлениях не уменьшаются (с точностью до
первого порядка), так что они тоже являются потенциально опасными.
Всегда, когда вы встречаетесь с релевантными или маргинальными операторами,
полезно разобраться в их физическом смысле.
(g) Собственная функция fo(x)t соответствующая наибольшему
собственному значению, соответствует нефизичному возмущению; почему? (Указание:
распределения вероятности должны быть нормированы на единицу.) Следующие
две собственные функции Д и /2 имеют важный физический смысл.
Покажите, что с точностью до членов первого порядка р* + efi соответствует сдвигу
среднего значения р, а р* + е/2 сдвигу среднеквадратичного отклонения ρ*, σ.
В данном случае релевантные возмущения переводят нас не в существенно
новые фазы, а в такие же гауссовы состояния с другим средним или другим
Гл.12. Упражнения
555
среднеквадратичным отклонением. Все прочие собственные функции
должны иметь собственные значения λη, меньшие единицы. Это означает, что
возмущения в этих направлениях будут сжиматься в результате применения
преобразования ренормализационной группы:
TN(p* + efn)-p*~\%efn. (12.56)
Поправки к скейлингу и бросание монетки. Можно ли получить из
этого рассмотрения какую-нибудь существенно новую информацию? Один из
интересных результатов, которые можно получить — это старшие
поправки к скейлингу. Существование неподвижной точки преобразования ренорм-
группы объясняет тот факт, что распределение результатов N бросаний
монетки сходится к распределению Гаусса при N —> оо. В свою очередь,
линейное разложение вблизи неподвижной точки позволяет дать систематическое
описание отклонений распределения от гауссового вида для больших, но
конечных N.
Обычно доминирующую роль играют наибольшие собственные значения.
Рассмотрим в нашем случае малые возмущения неподвижной точки /* в
направлении двух главных иррелевантных собственных функций, /з и /4:
р(х) = р*(х) + с3/з(х) + €*1а(х). (12.57)
Для этих собственных функций можно сделать в явном виде обратное
преобразование из fc-пространства (см. уравнение 12.55):
/з(х) ос ρ*(χ)(3χ/σ - χ*/σ%
/4(χ)<χρ*(χ)(3-6χ2/σ2 + χ4/σ*). ' )
Что произойдет с этими возмущениями после многократного применения
нашего преобразования ренормализационной группы Т? После t итераций
(что соответствует сложению 2е случайных величин) новое распределение
будет задаваться формулой
Те(р)(х) ~ р*(х) + Xie3f3(x) + X{e4f4(x). (12.59)
Поскольку 1 > Аз > λ4..., старшая поправка соответствует возмущению с
наибольшим собственным значением.
(h) Постройте график разности биномиального распределения (задающего
вероятность выпадения га орлов при N бросаниях монетки) и распределения
Гаусса с теми же значениями среднего и среднеквадратичного отклонения для
N = 10 и N = 20. (Среднее значение распределения Гаусса равно N/2, а
среднеквадратичное отклонение, равное y/N/2, можно получить экстраполяцией из
556
Гл.12. Непрерывные фазовые переходы
точки N = I.) Сходится ли эта разность к какой-то из собственных функций, /з
или /4 (см. уравнения 12.58)?
(i) Почему возмущение вдоль собственного вектора /з(я) не оказывается
асимптотически доминирующим? В силу какой симметрии оказалось, что €з =
О? Нарушится ли эта симметрия при бросании асимметричной монетки, у
которой орел выпадает чаще, чем в половине случаев?
Использование ренормализационной группы, возможно, не является
самым эффективным способом доказательства центральной предельной
теоремы, но оно позволяет получить качественное понимание того, как и почему
распределения вероятности сходятся к гауссову виду.
12.12 Перколяция и универсальность.41 (Теория сложных систем) @
Распределение кластеров по размерам: степенные законы в точке рс.
Система в точке перколяционного переходя рс является самоподобной. Если
посмотреть на нее на большем масштабе (например, используя линейку,
деления которой находятся в 1 + е раз дальше друг от друга, где е — бесконечно
малая величина), поведение больших перколяционных кластеров
статистически останется неизменным, нужно только одновременно правильным
образом перенормировать измеряемые величины. Пусть χ — длина (наибольший
пространственный размер), a S — объем (число элементов) перколяционного
кластера, и пусть n{S) — вероятность того, что наугад выбранный кластер
имеет объем S в точке рс·42 Кластер, измеренный с помощью новой линейки,
будет иметь длину х' = х/ (1 — б), объем Sf = S/ (1 + се), и будет встречаться
с вероятностью п' = (1 + ае) п.
(a) По аналогии с исследованием распределения размеров лавин
(уравнения 12.3-12.6) покажите, что распределение вероятности описывается
степенным законом n(S) ос S~T. Выразите г через α и с?
Для двумерных систем многие характеристики перколяционного перехода
вычислены точно. Например, известно, что43 г = 187/91. Вы можете
проверить этот результат численно, используя программу, которую вы написали
при выполнении упражнения 2.13, или программу с сайта книги [132].
(b) Вычислите распределение кластеров по размерам n(S) для перколяции
по связям на квадратной решетке и для перколяции по узлам на треугольной
Это упражнение и связанное с ним программное обеспечение были разработаны в
сотрудничестве с Кристофером Майерсом.
42Отсюда следует, что вероятность того, что наугад выбранный узел принадлежит
кластеру размера £, пропорциональна Sn(S).
43Совсем не очевидный результат!
Гл.12. Упражнения
557
решетке для большой системы (например, L χ L с L = 400) в точке ρ = рс.44
Начиная с некоторого не очень большого S, у вас перестанут появляться
кластеры соответствующего размера; постройте график log(n(S)) в зависимости от
log(*S) для перколяции по узлам и по связям и начертите на том же графике
степенной закон n(S) ос S-187/91, предсказываемый точной теорией. Чтобы полнее
использовать имеющиеся данные, следует объединять кластеры близких
размеров в группы, в особенности для больших размеров, которым соответствует
малое количество данных. Красиво реализовать эту процедуру довольно
непросто, на нашем сайте [132] есть программа, позволяющая сделать это. Постройте
графики еще раз, включив в них теперь все данные, и используйте объединение
кластеров в группы, начиная с 1 < S < 2, увеличивая размер группы на
каждом шаге в 1.2 раза. Вы должны ясно увидеть, что распределение кластеров
по размерам действительно выглядит как степенной закон (прямая линия
в логарифмических координатах), и более или менее убедительно
подтвердить, что показатель степени сходится к точному результату для больших S
и размеров системы.
Размер бесконечного кластера: степенные законы вблизи рс. Большая
часть интересных явлений в перколирующих системах при ρ выше рс касается
связного объекта, остающегося после удаления малых кластеров. Этот
объект часто называют перколяционным кластером. При ρ > рс этот
наибольший по объему кластер составляет конечную долю объема системы, которую
часто обозначают Р(р).45 Доля узлов, находящаяся в наибольшем кластере
при ρ > рс, во многом аналогична намагниченности Μ (Г) в магнетиках при
Τ < Тс (см. рис. 12.6(b)) и разности плотностей ρι(Τ) — рд(Т) вблизи
критической точки жидкость-газ (см. рис. 12.6(a)). В частности, значение Р(р)
непрерывно стремится к нулю при ρ —>· рс.
Системы, не находящиеся в точке рс, не являются самоподобными.
Однако имеется скейлинговое соотношение между системами с разными
значениями ρ — рс: при огрублении масштаба на 1 + е система оказывается подобна
другой, находящейся дальше от рс на множитель 1 + e/v. При этом доля
узлов Р, находящихся в перколяционном кластере, должна быть увеличена на
44Удачным образом, точка перколяции для обеих этих систем — это рс = |, см.
упражнение 2.13, часть (с). Это чрезвычайно упрощает скейлинговый анализ, т.к. нам не нужно
одновременно пытаться найти и критические индексы, и рс.
45При ρ < рс в системе тоже, конечно, имеется наибольший по размеру кластер, но его
размер не будет сильно расти при росте объема системы; доля Р(р) —>· 0 при росте размера
системы L —> оо, если ρ <рс.
558
Гл.12. Непрерывные фазовые переходы
множитель 1 + βε/ν. Эта последняя перенормировка отражает тот факт,
что в результате огрубления масштаба перколяционный кластер становится
более плотным, по мере того как имеющиеся в нем маленькие дырочки
заполняются или сглаживаются. Вы можете проверить, что в полной аналогии
с намагниченностью (см. уравнение 12.7)
Р(р)~(Рс-р)Р. (12.60)
В двумерных системах β = 5/36, a v = 4/3.
(c) Вычислите долю узлов Р(р), входящих в максимальный кластер, для
перколяции по узлам и по связям в последовательности точек ρ = рс + 2~п.
Используйте решетку настолько большого размера, насколько вы можете себе
позволить, и достаточно широкий интервал п. (После того отладки программы
значения η = 10 и размер решетки L x L с L = 200 должны быть подъемными
значениями.) Постройте в логарифмических координатах зависимость Р(р) от
р—рс и сравните ее с предсказанием теории, т.е. уравнением (12.60) с β = 5/36.
Вы увидите, что численные результаты в части (с) выглядят не слишком
убедительно даже для больших размеров решетки. Две получающиеся
кривые выглядят более-менее похоже на степенные законы, но наклоны /?eff в
логарифмических координатах не согласуются ни друг с другом, ни с
теорией. Хуже того, по мере приближения к рс видно (даже не смотря на шум), что
кривые определенно не стремятся к нулю. Это естественно; во всякой системе
всегда есть наибольший кластер, и только в пределе L —> сю относительный
объем этого наибольшего кластера стремится к нулю при ρ < рс.
Конечномерное масштабирование (упражнение повышенной трудности).
Можно получить более точные значения β из моделирования относительно
маленьких систем, если в явном виде включить в рассмотрение размер
системы L. Пусть Р(р, L) — доля узлов47 в наибольшем кластере для системы
размера L.
(d) Постройте на одном графике зависимости P(p,L) от ρ для перколяции
по связям при L = 5, 10, 20, 50 и 100, обращая особое внимание на область
вблизи ρ = рс, в которой кривые отличаются друг от друга. (Для L = 10 вам
понадобится изменять ρ в интервале от 0.25 до 0.75; для L = 50 интервал должен
46Мы еще раз напоминаем читателю, что выбор именно таких комбинаций греческих
букв вызван исключительно желанием получить в ответе общепринятые обозначения для
соответствующих критических индексов.
47Можно рассмотреть ансамбль, подобный микроканоническому, в который входят
системы, имеющие в точности 1?р занятых узлов или 21?ρ связей, однако проще использовать
среднее по ансамблю всех систем с заданным р, усредняя по результатам запуска
генератора случайных чисел.
Гл.12. Упражнения
559
быть примерно от 0.45 до 0.55 и т.д.) Достаточно получить пять-десять точек.
Вы увидите, что от образца к образцу результаты сильно флуктуируют (это еще
один эффект конечного объема), так что вам понадобится усреднить хотя бы по
десяти-двадцати реализациям для каждой точки.
Каждая из кривых Р(р, L) изгибается вблизи рс примерно там, где
характерный размер кластера достигает размера системы L. Этот изгиб сам по
себе является симптомом универсального поведения на больших масштабах,
так что можно изучать зависимость положения точки перегиба от L, с тем
чтобы получить более точное значение критического индекса β. Мы сделаем
это, используя скейлинговый коллапс: перенормируем горизонтальную и
вертикальную ось таким образом, чтобы все кривые легли на одну скейлинговую
функцию.
Для начала нам надо вывести скейлинговую функцию для P(p,L). Мы
знаем, что
L' = L/(l+e),
(Рс-рУ = {1 + *М(рс-р),
поскольку размер моделируемой системы L перенормируется так же, как
любой другой параметр размерности длины. Удобно сделать замену переменной
и перейти от ρ к X = (рс — p)Lxlv\ пусть Р(р, L) = P(L, (pc — p)Ll/u).
(e) Покажите, что X не меняется при огрублении масштаба
(уравнение 12.61). (Вы можете показать, что X1 = X с точностью до членов
порядка €2, или что dX/cfc = 0.)
Комбинация X = (рс — p)Lxlv — это еще одна скейлинговая переменная.
Переменная ξ = \р — pc\~v описывает то, каким образом длина расходится
вблизи точки перехода, она называется корреляционной длиной. Две систем
разного размера с различными значениями ρ становятся подобными, если их
размеры, измеренные в единицах £, равны. L в единицах £ — это L/ξ = Χν',
поэтому различные системы с одинаковым значением скейлинговой
переменной X статистически подобны друг другу. Это словесное рассуждение можно
записать в скейлинговом математическом виде, если посмотреть, каким
образом ведет себя P(L, X) при огрублении масштаба.
(f) Используя уравнение (12.61) и тот факт, что при огрублении масштаба Ρ
увеличивается на множитель (1 -Ь/Зб/ι/), запишите соотношение подобия для Р,
соответствующее уравнению (12.11) для D(S,R). Следуя нашему выводу
скейлинговой формы распределения лавин по размерам (вплоть до уравнения 12.14),
покажите, что P(L,X) = L~^/UV{X)1 где V(X) — некоторая функция X, и,
следовательно,
Р(р, L) ос Z-#T((p - pc)Ll'v)· (12.62)
560
Гл.12. Непрерывные фазовые переходы
Предполагая, что V(X) стремится к конечному пределу при X -» 0, выведите
степенной закон, описывающий размер перколяционного кластера L2P(pc,L)
как функцию L. Выясните, к какому степенному закону стремится V{X) при
X —> оо, используя тот факт, что Р(р, оо) ос (ρ — ρ0γ·
Мы можем теперь использовать уравнение (12.62), для того чтобы
определить, как следует перемасштабировать экспериментальные данные. Мы
можем найти функцию V, построив LP/vP{p,L) как функцию X = (p — pc)L1^
и положив опять ν = 4/3 и β = 5/36.
(g) Постройте график L^/uP{p,L) как функции X при X Ε [—0.8,+0.8],
рассчитав хотя бы пять точек для каждой кривой перколяции по связям и по
узлам, для размеров системы, равных L = 5, 10, 20 и 50. Усредните по большому
числу реализаций для маленьких систем (скажем, 400 для L = 5), и хотя бы по
десяти реализациям для самых больших.
Ваши точки должны лечь на две скейлинговые кривые, одну для
перколяции по узлам, другую — для перколяции по связям.48 Обратите внимание
на то, что кривые конечномерного масштабирования хорошо коллапсируют
для достаточно малых L. Для того чтобы явно проследить степенное
поведение Р(р), нам бы пришлось исследовать куда большие L (см. часть (с)).
Обратите также внимание на то, что кривые для перколяции по связям и
по узлам коллапсируют при одном и том же значении /?, несмотря на то,
что приблизительные степенные законы из части (с) казались различными.
В эксперименте (или в теории, для которой точные результаты не известны)
скейлинговый коллапс используют для оценки значений рс, β и v.
12.13 Скейлинг в задаче о гистерезисе и лавинах. (Теория сложных
систем) ©
Для выполнения этого упражнения скачайте с сайта книги [132]
программу Матта Кунца для моделирования гистерезиса или используйте программу,
написанную вами при выполнении упражнений 8.13 и 8.14.
Запустите моделирование на двумерной решетке размера 1000 χ 1000 с
беспорядком R = 0.9 или на трехмерной решетке размера 1003 при R = 2.16.49 В
этой программе используется упрощенную модель гистерезиса в магнетиках,
48 Эти две кривые тоже сколлапсировали бы при подобающей перенормировке
вертикальной и горизонтальной осей, если бы мы рассматривали треугольную решетку в квадратной
ячейке моделирования, а не в прямоугольной (полученной нами в результате сдвиговой
деформации решетки L x L). Кривые конечномерного масштабирования вообще существенно
зависят от граничных условий, в частности, от формы рассматриваемой области.
49Если ваша программа использует алгоритм прямого перебора, то вы, скорее всего,
сможете моделировать только системы небольшого размера, где-то около 503 узлов. При
наличии быстрого компьютера вам, возможно, удастся смоделировать систему большего
размера, но моделирование не должно становиться утомительно медленным.
Гл.12. Упражнения
561
описанная в [131] (см. также [130]). В начальный момент времени все спины
5г направлены вниз, они постепенно обращаются вверх при медленном
увеличении внешнего поля Η от минус бесконечности. Переключения зависят от
состояния спинов-соседей и локального случайного поля hi. При
переключении спины на картинке окрашиваются, причем каждая лавина окрашивается
в свой цвет. Лавина — это группа спинов, которые переключается вместе,
будучи запущенными переключением какого-то одного спина. Мерой
беспорядка является отношение R среднеквадратичного значения случайного поля
y(tif) к энергии ферромагнитной связи J между спинами:
R = у/Щ/J. (12.63)
Изучите кривые М(Н) и άΜ/άΗ для нашей модели. Индивидуальные
лавины выглядят ступеньками на первом графике и пиками на втором.
Такого рода временной ряд (последовательность пиков или выбросов с широким
распределением по размерам) на слух воспринимается как импульсный шум
или треск. На нашем сайте [72] вы можете прослушать звук, получаемый в
результате проигрывания временных рядов из нашей модели, а также
собранную нами коллекцию импульсных шумов: треск, возникающий при сминании
листа бумаги, треск огня, треск рисовых хлопьев Rice Krispies™n треск
Земли (последовательность землетрясений 1995 года, ускоренную до звуковой
частоты).
Изучите распределение лавин по размерам. По (непомеченной)
вертикальной оси на графике в логарифмических координатах откладывается число
лавин D(S, Д); по горизонтальной оси откладывается объем лавины S (S = 1
находится слева). При надлежащей нормировке D(S, R) — это вероятность
того, что заданная полученная в результате моделирования лавина имеет объем
S. График получен из гистограммы, кривая меняет цвет после первого шага
гистограммы, число лавин в котором равно нулю (после него значения
становятся гораздо менее надежными, и на них не стоит обращать внимания).
Если в программе есть такая возможность, изучите спин-спиновую
корреляционную функцию C(X)R). На графике в логарифмических масштабах
показана вероятность (по вертикальной оси) того, что лавина, начавшаяся в
точке хо, распространится до спина в точке χι на расстоянии χ = \/(xi — хо)2
(отложенного по горизонтальной оси).
Поведение на двумерной решетке очень интересно наблюдать, но мы до
сих пор не имеем хорошего понимания скейлингового поведения в этом
случае. Для динамики системы в трехмерном случае имеется достаточно данных,
чтобы сделать утверждение о наличии скейлингового и критического
поведения. На трехмерной кубической решетке имеется динамический фазовый
562
Гл.12. Непрерывные фазовые переходы
переход в точке Rc ~ 2.16. При беспорядке, намного меньшем Rc, почти все
спины переключаются в результате одной большой лавины. С другой
стороны, при беспорядке, намного большем Дс, все лавины достаточно малы; при
особенно высоком беспорядке каждый спин переключается в одиночку.
Критическое значение беспорядка — это такое значение, при котором при L —> оо
появляются покрывающие лавины, т.е. лавины, которые распространяются от
одной стороны области моделирования до другой.
Смоделируйте трехмерную систему при R = Rc = 2.16 для L = 100 (что
соответствует миллиону спинов; если у вас быстрый компьютер, можете
попробовать взять больше). Моделирование будет проходить быстрее, если вы
используете алгоритм с сортировкой списка (см. упражнение 8.14). На экране
вы увидите двумерные сечения лавин размера L x L. Обратите внимание на
то, что имеется множество совсем маленьких лавин и небольшое количество
больших. При беспорядке ниже Rc вы увидите, что формируется большая
однородно закрашенная область, служащая фоном для всего остального; это и
есть покрывающая бесконечная лавина. Посмотрите на кривую М(Н)
(нижнюю половину петли гистерезиса). На ней должно быть множество маленьких
скачков (лавин) и один большой (соответствующий покрывающей лавине).
(а) Какая доля спинов в системе переключается в результате одной большой
лавины в вашем моделировании? Сравните этот результат с кривой гистерезиса
при R = 2.4 > Rc. Имеется ли в этом случае такой же большой скачок, или
кривая выглядит непрерывной?
При беспорядке ниже Rc наблюдается большой скачок; выше Rc все
лавины малы по сравнению с размером системы. Мы считаем, что если бы размер
системы был достаточно велик, то доля спинов, переключаемая наибольшей
лавиной в точке Дс, стремилась бы к нулю. Тем не менее, эта наибольшая
лавина продолжала бы покрывать систему — подобно тому, как перколяци-
онный кластер в точке рс покрывает систему, но занимает (в пределе больших
систем) нулевую долю объема.
Распределение остальных лавин по размерам хорошо описывается
степенным законом; рассмотрим его подробнее. Запустите систему 10 раз (# Runs
10) при L = 100 и R = Rc = 2.16.50
50Если у вас медленный компьютер, делайте меньше запусков. Если быстрый —
рассмотрите систему с большим числом частиц. Следите за тем, чтобы при моделировании не
закончилась оперативная память (это можно заметить по характерному звуку,
издаваемому компьютером при обращении к жесткому диску); если это произойдет, переключитесь
на алгоритм bits, если он доступен в вашей программе. При крупномасштабном
моделировании алгоритм bits использует гораздо меньше памяти, чем алгоритм sorted list (с
сортировкой списка), но у него уходит много времени на поиск нескольких последних спинов.
Оба эти алгоритма работают намного быстрее, чем метод на основе прямого перебора.
Гл.12. Упражнения
563
Понаблюдайте за поведением лавинам. Обратите внимание на то, что в
некоторых случаях вторая по размеру лавина (первая соответствует
«фоновому цвету») порой оказывается достаточно маленькой; часто это связано с
тем, что более крупные лавины просто не проходят через наше сечение.
Посмотрите на распределение лавин по размерам. (Также вы можете посмотреть
как оно меняется в процессе усреднения по запускам.) Напечатайте его после
окончания моделирования. Вы увидите, что в точке Rc наблюдается
достаточно хорошее степенное распределение (прямая в логарифмических
координатах). Обозначим соответствующий критический индекс τ = т + σβδ:
D{S, Rc) ~ S~* = S-{t+<jP8\ (12.64)
(b) Измерьте эту комбинацию индексов по данным вашего моделирования.
Должно получиться что-то около двух. У вас получилось больше или меньше
двух?
Эта степенная зависимость для магнетиков аналогична закону
Гутенберга-Рихтера для землетрясений (см. рис. 12.3(b)), она естественным
образом возникает из самоподобия системы.
Исследуем теперь, каким образом распределение лавин по размерам
меняется при переходе к значениям выше Rc. Для этого мы выполним три-четыре
запуска моделирования при разных значениях R и построим распределение
лавин по размерам после некоторых трансформаций.
Запустите программу для R = 6 и R = 4 при L = 100 и убедитесь, что вы
получаете на выходе читаемые файлы с данными. Запустите программу для
Д = 3,Д = 2.5иД = 2.16 при L = 200.
(c) Скопируйте ваши файлы с распределением лавин по размерам и
отредактируйте их, обрезав гистограмму после появления первого нуля. Запустите
программу построения графиков и постройте распределения в логарифмических
координатах; при малых S зависимости будут похожи на степенные, но при
больших S они будут экспоненциально обрезаться.
Мы ожидаем, что распределение лавин по размерам имеет скейлинговый
вид
D{S, R) = S-(T+a/36)V{S{R - Rc)l/a) (12.65)
при значениях беспорядка, достаточно близких к Rc. Это предположение
отражает то, что система подобна самой себе при других значениях параметров;
система с 2(R — Rc) имеет такое же распределение, что и система ей- Дс, с
точностью до перемасштабирования вероятности в А раз и размера системы
в В раз, так что D(S, R-Rc)& AD{BS, 2(R - Rc)).
(d) Чему равны А и В в этом уравнении, если скейлинг задается
уравнением (12.65)?
564
Гл.12. Непрерывные фазовые переходы
При R = 4 и 6 поправки должны быть очень существенными! Посмотрим,
насколько хорошо работает такой коллапс.
(e) Для каждой кривой умножьте значения по вертикальной оси на ST+(T^.
После этого вы должны получить четыре кривые V(S(R — Rc)l/G), которые
(в логарифмических координатах) имеют примерно одинаковую форму, только
сдвинуты друг относительно друга по горизонтали (S перенормируется на
типичный максимальный размер лавины, пропорциональный 1/(R—Rc)1^a). Измерьте
положение максимума на каждой кривой. Составьте таблицу со столбцами R,
*Speak ий-Дс (где Rc ~ 2.16). В логарифмических координатах постройте
график R — Rc как функцию S^ak и оцените показатель σ ожидаемого степенного
закона 5реак ~ (Д - Rc)~l/(J.
(f) Проведите скейлинговый коллапс: начертите ST+(T^6D{S, R) как функцию
(R — Rc)l/a S для распределений лавин по размерам при R > Rc. Насколько
хорошо ваши точки ложатся на одну кривую?
Коллапс дает убедительные результаты только вблизи Дс, где для
получения хороших кривых надо проводить моделирование очень больших систем.
Приложение А
Методы Фурье
Почему важны методы Фурье? Почему настолько полезным оказывается
преобразование функций пространства и времени у(х, t) в функции частоты
и волнового вектора у (к, ω)?
• Частоты, воспринимаемые человеческим ухом. Человеческое ухо
анализирует изменение давления в воздухе на различных частотах.
Большие частоты воспринимаются как высокие звуки, малые частоты — как
низкие. Ухо, грубо говоря, производит преобразование Фурье давления
P(t) и передает |Ρ(ω)|2 в мозг.1
• Фурье-компоненты измеряются в экспериментах по дифракции.
Многие экспериментальные методы основаны на дифракции
электромагнитных волн (света, рентгеновских лучей, электронов или нейтронов) в
различных материалах (раздел 10.2). В этих экспериментах изучается
квадрат амплитуды Фурье после рассеяния исходного пучка на чем бы
то ни было.
• Многие математические операции становятся проще в Фурье-
пространстве. Производные, корреляционные функции и свертки
могут быть записаны в виде простых произведений после проведения
*На самом деле это только кажется, что ухо так работает, но в действительности оно
работает иначе. Во-первых, сигнал, передаваемый в мозг, зависит от времени, звуковысот-
ная информация меняется с течением времени при произнесении слов или воспроизведении
мелодии. Это, скорее, вейвлет-преобразование, дающее набор частот в различных
временных интервалах. Во-вторых, информация о фазах Ρ не теряется полностью: сила и высота
являются основными сигналами, но относительные фазы звуков различной высоты также
воспринимаются. В третьих, эксперименты показали, что механический отклик
человеческого уха нелинеен.
566
А. Методы Фурье
преобразования Фурье. Это использовалось нами при рассчете
корреляционных функций (уравнение 10.4), суммировании случайных
величин (упражнения 1.2 и 12.11) и расчете восприимчивостей
(уравнения 10.30, 10.39 и 10.53, упражнение 10.9). В каждом из этих
случаев мы сводили операции дифференцирования и интегрирования
к алгебраическим.
• Линейные дифференциальные уравнения для трансляционно
инвариантных систем имеют решения в пространстве Фурье.2
Мы использовали методы Фурье для решения уравнения диффузии
(раздел 2.4.1), а также для расчета корреляционных функций и
восприимчивостей (гл. 10).
В разделе АЛ мы введем стандартные обозначения, используемые в
физике для рядов Фурье, преобразования Фурье и быстрого преобразования
Фурье. В разделе А.2 мы получим их интегральные и дифференциальные
свойства. В разделе А.З мы рассмотрим преобразование Фурье как ортогональное
преобразование базиса в пространстве функций. И наконец, в разделе А.4 мы
объясним, почему методы Фурье так полезны для решения
дифференциальных уравнений, рассматривая их связь с трансляционной симметрией.
АЛ Условные обозначения
В этом разделе мы введем понятия ряда Фурье, преобразования Фурье и
быстрого преобразования Фурье, таким образом, как их обычно определяют
в физической литературе.
Ряд Фурье для периодической функции времени с периодом Τ имеет вид
1 г*
Ут = γ Ι У(0 exp(iumt) dt, (A.I)
где шш = 2πτη/Τ, am — целое число. Ряд Фурье может быть сведен к
исходной функции с помощью обратного преобразования Фурье:
оо
У(г)= Σ Vmexpi-iumt). (A.2)
771= —ОО
2 Трансляционная инвариантность в гамильтоновых системах подразумевает сохранение
импульса. Поэтому в квантовой механике преобразование Фурье преобразует волновые
функции в пространстве координат в волновые функции в импульсном пространстве даже
в системах, не являющихся пространственно инвариантными.
АЛ. Условные обозначения
567
Ряды Фурье для функций координат определяются с противоположным
знаком3 в комплексном показателе экспоненты. В трехмерном кубе объемом
V = LxLxLc периодическими граничными условиями эти формулы
приобретают вид
Ук = γ ί у(х) exp(-ik · χ) dV, (A.3)
и
У(х) = 5^ykexp(ik ■ χ), (Α.4)
k
где волновой вектор к принимает значения
Ь(т,п,о) = [2пт/Ц 2*п/Ц 2no/L). (A.5)
Преобразование Фурье определяется для функций, заданных на
бесконечной прямой:
/оо
y{t)exp{iut)dt, (A.6)
-ОО
где ω может теперь принимать всевозможные значения.4 Мы возвращаемся
к исходной функции с помощью обратного преобразования Фурье:
y(t)
1 f°°
= ττ / У(и) βχρ(-ίωί) άω. (Α.7)
Оно следующим образом связано с обратным рядом Фурье в континуальном
пределе (рис. АЛ):
^/с!^1уДа;=1у|ЛГ. (А.8)
3Это делается, для того чтобы волны, имеющие положительную частоту,
распространялись в прямом направлении, а не в обратном. Каждая компонента в обратном
преобразовании, elkxe~,wt = e^kx-wt)^ распространяется в направлении +ксо скоростью u>/|k|. Если
бы мы записали -И для преобразования Фурье как в координатном пространстве, так и во
времени, то е1^ χ+ωί) двигалась бы в обратном направлении (вдоль направления —к) при
ω >0.
4Почему перед рядом Фурье стоит коэффициент 1/Т или 1/L, но он отсутствует в
преобразовании Фурье? Представим себе систему в бесконечно большом сосуде. Ряды Фурье
используются для функций, определенных в данном объеме, таким образом, мы делим на
размер сосуда, чтобы сохранить их конечными при L -> оо. Преобразование Фурье обычно
используется для функций, которые быстро стремятся к нулю, таким образом, они
остаются конечными при увеличении размера сосуда.
568
А. Методы Фурье
Здесь коэффициент 1/Т компенсирует сомножитель Τ в определении
ряда Фурье. В трехмерном пространстве формула (А.6) остается практически
неизменной
у(к) = I у(х) exp(-ik · χ) dV, (A.9)
в то время как коэффициент перед интегралом в обратном преобразовании
Фурье возводится в куб:
1 Г°°
»(х) = Щз ]_„ УМ exp(ik ' х) dk' ίАЛ°)
Рис. А.1. Аппроксимация интеграла суммой
Аппроксимируя интеграл f y(u) exp(iut) άω суммой по эквидистантным точкам ит,
Στη ν(ω) exp(itJm£)Au, мы можем получить связь преобразования Фурье с рядом Фурье,
объяснив также наличие коэффициента 1/2π в уравнении (А.7).
Быстрое преобразование Фурье (БПФ) преобразует N равноудаленных
точек уе в новый набор комплексных чисел у^т:
7V-1
Ут™ = Σ νι<*Ρ№*™*/Ν), (A.ll)
£=0
где га = О, ...,TV — 1. Обратное преобразование БПФ задается следующим
образом:
1 Ν_1
W = Ν Σ УпГ exp(-i2nm£/N). (A.12)
m=0
БПФ, таким образом, отбирает дискретные значения функции y(t) в
равноудаленных точках ti = ίΤ/Ν, где I = 0,..., N — 1:
ΛΓ-1
Ут¥Т = Σ WexP(i^m^). (Α. 13)
£=0
АЛ. Условные обозначения
569
Из уравнения (А.11) видно, что y^J^v = Ут > таким образом, быстрое
преобразование Фурье является периодической функцией с периодом ω ν = 2πΝ/Τ.
Обратное преобразование может быть также записано в виде
Ν/2
У* = -й Σ У^Т exp(-i"mt*), (A.14)
m=-7V/2+l
где мы центрировали5 сумму по шт в точке ω = О, используя периодичность
функции.6
Часто значения y(t) (или наборы точек уе) представляют собой
действительные числа. В этом случае из уравнений (АЛ) и (А.6) следует, что
отрицательные амплитуды Фурье являются комплексными сопряженными
положительных: у(ш) = у*(—ω). Таким образом, для вещественных функций
реальная часть амплитуды Фурье будет четной функцией, а комплексная часть
— нечетной.7 Читатель может удивиться, почему существует столько разных
вариантов записи примерно одних и тех же операций Фурье.
(1) Функция y(t) может быть определена на ограниченном интервале (О, Т)
с периодическими граничными условиями (ряды Фурье, БПФ) или на
всем пространстве (преобразование Фурье). В периодическом случае
коэффициенты Фурье определены только для дискретных волновых
векторов шт = 2πτη/Τ, определяемых периодом функции, а для
бесконечных систем коэффициенты определены для всех ω.
(2) Функция y(t) может быть определена либо для дискретного набора N
точек tn = η At = ηΤ/Ν (БПФ), либо для всех точек t в диапазоне
(ряды Фурье, преобразование Фурье). Если функция определена только
для дискретного набора точек, коэффициенты Фурье являются
периодическими, причем u>n = 2π/Δ£ = 2πΝ/Τ.8
5Если TV представляет собой нечетное число, то сумма должна быть взята в пределах
-(N - 1)/2 < т < (N - 1)/2.
6Обратите внимание, что БПФ возвращает отрицательные коэффициенты Фурье в
последней половине массива, т = N/2 + l,N/2 + 2, (Это происходит из-за того, что
—N/2 + j и N/2 + j отличается на N вследствие периодичности БПФ.) Нужно обращать
на это внимание, используя преобразование Фурье в численных расчетах. Например, для
исследования эволюции плотности р(х) в уравнении диффузии (раздел 2.4.1) нужно
умножить первую половину массива рт на ехр(—Dk^t) = exp(—D[m(2n/L)]2t) и вторую
половину массива на ехр(—D(K — km)2t) = exp(—D[(N — πι)(2π/L)]2t).
7 Это позволяет написать более эффективный программный код для действительных
функций. За более быструю скорость нужно заплатить дополнительным действием по
распаковыванию результирующего спектра Фурье.
8Существует ее один вполне логичный вариант: дискретный набор точек, которые
заполняют все пространство. Классическим примером являются смещения атомов в бесконечном
570
А. Методы Фурье
В различных областях используются различные обозначения для методов
Фурье.
• Некоторые используют обозначение j = %/—Τ вместо i.
• Что более существенно, некоторые используют комплексные
сопряженные величины в наших формулах, заменяя —i на i в формулах,
проводящих преобразования во времени и пространстве. Это альтернативное
обозначение ничего не меняет для действительных величин.9
• Некоторые пишут симметричные коэффициенты \j\fT и 1/\/2π для
прямого и обратного преобразований Фурье.
• Некоторые используют частоту и длину волны (/ = 2πω и λ = 2п/к)
вместо угловой частоты ω и волнового вектора к. Это делает прямое
и обратное преобразование более симметричным, и позволяет избежать
наличия дополнительных коэффициентов.
Обозначения, используемые в данной книге, являются наиболее
общеупотребительными.
А.2 Производные, свертки и корреляции
Важнейшие дифференциальные и интегральные операции сводятся к
операции умножения в пространстве Фурье. Задачи математического анализа в
пространстве t или χ становятся алгебраическими упражнениями для ω или
к.
Интегралы и производные. Поскольку (d/dt)e~luJt = — iueluJt,
коэффициенты Фурье производной функции y(t) равны коэффициентам Фурье
данной фунуции, умноженным на — Ίω:
ay /at = Σ Ут (-iwm exp(-io;mt)) = ^(-iumym) exp(-icjm£), (A.15)
таким образом
= —\шуш. (А.16)
ω
кристалле. В пространстве Фурье такая система имеет непрерывный волновой вектор ку
но периодические граничные условия при ±К/2 = ±π/α (на границах зоны Бриллюэна).
9 Вещественные числа инвариантны относительно преобразования i «-► — i, но
комплексные величины заменяются на сопряженные. При замене i на — i в формулах для временных
рядов, например, в уравнении (10.31) получаем χ"(ω) = — Ιΐϊΐ[χ(ω)], а χ становится
аналитической в нижней полуплоскости (рис. 10.12).
dy
dt
Α. 2. Производные, свертки и корреляции
571
Это верно также для преобразования Фурье и для быстрого преобразования
Фурье. Поскольку производная интеграла равна подынтегральной функции,
ряд Фурье для неопределенного интеграла функции у задается делением на
—Ίω:
f
y(t)dt = ^ =i*i (A.17)
-ιω ω
за исключением точки ω = О.10
Эти соотношения очень полезны при решении многих линейных
дифференциальных уравнений в частных производных. Например, мы видели в
разделе 2.4.1, что уравнение диффузии
легко решаемо с использованием Фурье-преобразования от χ к к:
^ = -Dk?p, (A.19)
Pfc(«) = Pfc(O) exp(-Dk2t). (A.20)
Корреляционные функции и свертка. Квадрат амплитуды Фурье-
преобразования11 |y(w)|2 задается Фурье-преобразованием корреляционной
функции С{т) = (y(t)y(t + г)):
\у(и)\2 = у{и)*у{ш) = ldife-^'y(t')jdte^y(t)
= J di df e^-VyVMt) = Jdr e^T J at' y(t')y(t' + r)
= ί aTJ"TT(y{t)y{t + r)) =T /"dreiwTC(r)
= ΤΟ(ω), (Α.21)
10Существует два варианта: либо среднее значение у(и> = 0) равно нулю, либо не равно.
Если среднее значение функции равно нулю, то ι/(ω)/ω = 0/0 не определено при ω = 0.
Это утверждение имеет смысл, поскольку неопределенный интеграл задан с точностью до
произвольной константы интегрирования, которая соответствует произвольному значению
ряда Фурье при ω = 0. Если среднее значение функции у не равно нулю, то интеграл
функции будет включать член y(t — to). Таким образом, интеграл не будет периодической
функцией и он не будет раскладываться в ряд Фурье. (На бесконечном интервале у данного
интеграла не будет Фурье-преобразования, поскольку он не принадлежит множеству L2.)
11 Квадрат амплитуды Фурье-преобразования сигнала на временном отрезке называется
спектральной функцией.
572
А. Методы Фурье
где Τ — это полное время, в течение которого измеряется спектр Фурье.
Таким образом, эксперименты по дифракции, в которых измеряется квадрат
амплитуды преобразования Фурье в k-пространстве, дают нам возможность
получить пространственную корреляционную функцию системы (раздел 10.2).
Свертка 12 h(z) функций f(x) и д(у) определяется следующим образом:
h(z) = I f{x)g(z - х) dx. (A.22)
Фурье-преобразование свертки представляет собой произведение
Фурье-преобразований функций. В трехмерном пространстве13
/(к)» (k) = J e"ikx/(x) dx J e"iky <;(у) dy
= J e-ik-<x+^/(xMy) dx dy = J e~ikz dz j f(x)g(z - x) dx
= / e"ikz/i(z) dz = h(k). (A.23)
A.3 Методы Фурье и пространство функций
Существует замечательная аналогия между пространством векторов г в
трехмерном пространстве и пространством функций у(£), периодических с
периодом Т, помогающая понять суть разложения в ряды Фурье.
Рассмотрим пространство функций, включающее все комплексные функции y(t). (В
нашем пространстве также присутствуют комплексные плоские волны Фурье
e~1Urnt.) Давайте перечислим общие свойства этих двух пространств.
• Пространство векторов. Вектор г = (п,Г2,гз), принадлежащий
пространству R3, можно представить как вещественную функцию на
множестве {1,2,3}. И наоборот, функцию y(t) можно представить как
вектор с одной комплексной компонентой для каждого t Ε [О, Τ). С
математической точки зрения эта аналогия ужасна. Многие функции, которые
12 Свертка появляется, когда мы имеем дело с суммами и функциями Грина. Сумма
ζ = χ + у двух случайных векторных величин с функциями распределения /(х) и д(у)
имеет функцию распределения, задаваемую сверткой /ид (упражнение 1.2). Функция,
имеющая в начальный момент времени значение /(χ, ίο), в момент времени to -j- τ
определяется сверткой с функцией Грина #(у,т) (раздел 2.4.2).
13Свертка и корреляционные теоремы тесно связаны между собой. Мы производим
свертку во времени и исследуем корреляции в пространстве, для того чтобы показать, как
производить расчеты и в одномерном случае, и для векторных величин.
А.З. Методы Фурье и пространство функций
573
каждой точке t ставят в соответствие независимые случайные
величины, являются неопределимыми, неинтегрируемыми и вообще
патологическими. Пространство функций будет определено, если мы
ограничимся функциями у(£), квадраты модулей которых |з/(£)|2 = 2/(Оз/*(0
могут быть проинтегрированы. Обозначим данное векторное
пространство функций L2.14
• Скалярное произведение. Можно провести аналогию между
скалярным произведением двух трехмерных векторов г · s = r\S\ + r^sz + гз$з
и двух функций у и ζ:
νζ=ψ/ y(t)z*(t)dt. (A.24)
Это скалярное произведение можно себе представить как сумму
произведений ytzl во всех точках £, взятую с весом at/Т.
• Норма. Расстояние между двумя трехмерными векторами г и s
задается нормой разности |г — s|. Норма вектора представляет собой
квадратный корень скалярного произведения вектора с самим собой. Для
того чтобы распространить это определение на пространство функций,
мы используем тот факт, что скалярное произведение функции самой
с собой всегда является неотрицательной величиной. Именно поэтому в
нашем определении А.24 мы берем комплексное сопряженное z(t).
Данная норма в пространстве функций обозначается как норма L2:
|ь-Й
|y(i)|2dt. (A.25)
Поскольку мы ограничились рассмотрением квадратично
интегрируемых функций, норма всех функций в нашем пространстве конечна.15
14Преобразование Фурье, как правило, определяется HaL [R], а ряды Фурье — на L [О, Т\.
15Другим важным свойством является то, что единственным вектором с нулевой нормой
является нулевой вектор. Существует множество функций, квадраты которых при
интегрировании становятся равными нулю. В качестве примера можно привести функцию,
которая равна нулю всюду, за исключением точки Т/2, в которой она равна единице, а
также функцию, которая равна нулю в иррациональных точках и единице — в
рациональных. Математики преодолевают эту трудность, определяя векторы в L2 не как функции, а
как классы эквивалентности функций, относительное расстояние между которыми равно
нулю. Следовательно, нулевой вектор в L2 включает в себя все функции с нулевой
нормировкой.
574
А. Методы Фурье
• Базис. Простейшим выбором базиса в пространстве R3 является набор
трех единичных векторов χι, Х2, хз- Поскольку функции в
функциональном пространстве являются периодическими с периодом Т,
естественным представляется выбор базисных функций /т = е-*>ть^ где
ит = 2πτη/Τ.
• Ортонормируемость. Базис в пространстве R3 является ортонорми-
рованным, если х^ · Xj равно единице при г = j и нулю в
противоположном случае. Выполняется ли это для нашего базиса плоских волн? Они
являются нормированными:
ll/mlli = ^ViWmfdi = i· (А.26)
Они также ортогональны:
1 e-i(^m-u;n)i|T = 0) (A27)
-\{шт - ωη)Τ Ιο
за исключением т = η, поскольку e~^Urn~Un^T = e~l27r(m~n) = e~l0 = 1.
• Коэффициенты. Коэффициенты трехмерного вектора задаются
скалярным произведением с базисными векторами: гп = г · хп.
Аналогично в пространстве функций мы определяем коэффициенты Фурье (см.
уравнение АЛ):
1 fT
yrn = y-fm = j, Ι 2/(0 exp(iu;mi) at. (A.28)
• Полнота. Мы можем записать произвольный трехмерный вектор
г, суммируя базисные векторы, взвешенные с коэффициентами:
г = Y^rnStn. В пространстве функций данная процедура дает нам
формулу (А.2) для обратного ряда Фурье:
У = / j Ут]т·)
т=—оо
оо
y(t)= 5Z ymexp(-iumt).
(А.29)
A.4- Фурье и трансляционная симметрия
575
Говорят, что базис является полным, если любой вектор, принадлежа-
ищи данному пространству, может быть по нему разложен. Наши
функции fm представляют собой полный базис в пространстве L2.16
Выражение для коэффициентов Фурье (уравнение А.28) следует из
полноты (уравнение А.29) и ортонормируемости:
У1
= V'fi = \Σ Ут1т I ' h
= Y,ym(fm-h)=m (A.30)
m
или, выписывая подробно все сомножители,
= Σ *» (| jf e-^W dt) = т. (А.31)
Пространство функций, в котором скалярное произведение определено
согласно уравнению (А.24) (полное пространство со скалярным
произведением), называется гильбертовым пространством.
А.4 Фурье и трансляционная симметрия
Почему методы Фурье настолько полезны? В частности, почему решения
многих линейных дифференциальных уравнений могут быть представлены в
виде плоских волн: синусоид, косинусоид и elkx717 Большинство наших
основных уравнений выводятся для систем с трансляционной симметрией.
Инвариантность относительно переноса во времени имеет место в любой системе,
16Для доказательства полноты нужно показать, что не существует функций,
принадлежащих L2, которые были бы перпендикулярны всем модам Фурье. Это является одним из
примеров тех трудных задач, которые мотивируют развитие действительного анализа в
математике.
17 Это правда, мы очень часто используем так называемый метод разделения
переменных. Но почему этот метод так часто работает и почему полученные решения так часто
оказываются представимыми в виде синусоид и экспонент?
576
А. Методы Фурье
Ю/Х\таМЫ
Рис. А.2. Отображение 7д
Отображение 7δ переводит пространство функций в пространство функций, сдвигая
функцию вправо на расстояние Δ. Если решение системы уравнений, обладающей
трансляционной инвариантностью, сдвинуть вправо, оно по-прежнему будет являться решением
системы.
не подверженной внешнему воздействию, явным образом зависящему от
времени. Инвариантность относительно пространственного переноса
справедлива во всех однородных системах.
Почему плоские волны встречаются в системах с пространственной
инвариантностью? Плоские волны являются собственными функциями
оператора переноса. Определим оператор 7д, который отображает функциональное
пространство само в себя и сдвигает функцию на расстояние Δ вправо:18
Τδ{/}(ζ) = /(*-Δ). (Α.32)
Оператор 7д переводит любое решение /(я, t) уравнения с пространственной
инвариантностью в другое решение данного уравнения. Более того, 7д — это
линейный оператор (преобразование суммы является суммой преобразований
функций). Если мы представим себе оператор переноса в виде большой
матрицы, действующей на функциональное пространство, то какими будут его
собственные значения19 и собственные векторы (или собственные функции)
Л?
ТдШ(я) = fk(x ~ Δ) = Xkfk(x) (A.33)
Решения данного уравнения имеют вид комплексных плоских волн Д(х) =
elkx, а его собственные значени^ λ& = e~lkA.20
18То есть, если g = 7δ{/} и g(x) = f(x — Δ), το g — это /, сдвинутая вправо на Δ.
19Вы знакомы с собственными векторами симметричных матриц Μ 3 х 3, которые
преобразуются в коллинеарные векторы при умножении на Μ, Μ · en = Anen. Оператор 7δ
является линейным в пространстве функций, подобно тому, как Μ — линейный оператор
в пространстве R3.
20Вещественная экспонента еАх также является собственным состоянием с собственным
значением β~ΑΔ. В самом деле, уравнение диффузии является инвариантным относительно
трансляций во времени и имеет решения, экспоненциально затухающие с течением времени
(e_u,fctelfcx, где ω^ = Dk2). Решения, экспоненциально затухающие в пространстве, также
встречаются в некоторых задачах с пространственной инвариантностью, таких как
квантовое туннелирование и проникание электромагнитного излучения в металлы.
А-4- Фурье и трансляционная симметрия
577
Почему эти собственные функции настолько полезны? Временная
эволюция собственных функций должна иметь то же самое собственное значение λ!
Доказательство этого факта достаточно труднопроизносимо: трансляция
собственной функции, эволюционирующей с течением времени, имеет такой же
вид, что и эволюция транслированной собственной функции, равный
эволюционирующей с течением времени λ, умноженной на собственную функцию,
и также равный λ, умноженной на эволюционирующую с течением времени
собственную функцию.21
Наши вычисления работают именно потому, что различные собственные
значения не смешиваются при эволюции во времени. Временная эволюция
Аое1кх представляет собой величину, кратную A(t)elkx, поскольку существует
только одна собственная функция оператора трансляций, соответствующая
данному собственному значению. Как только мы свели дифференциальное
уравнение в частных производных к обычному дифференциальному
уравнению для нескольких амплитуд собственных состояний, расчет значительно
упростился.
Ученые, занимающиеся квантовой физикой, рассматривают
вышеприведенный тезис как утверждение об одновременно диагонализирующихся
коммутирующих операторах: поскольку оператор трансляции коммутирует с
оператором временной эволюции, можно найти полный набор собственных
состояний операторов трансляции, которые так же будут решениями для
временной эволюции. Математики рассматривают данное явление с точки зрения
теории представлений групп: решения трансляционно инвариантных
линейных дифференциальных уравнений образуют представление трансляционной
21 Записанная в виде уравнений, эта простая идея становится даже более запутанной.
Пусть lit — оператор временной эволюции для трансляционно инвариантного
уравнения (подобного уравнению диффузии в разделе 2.2). Таким образом, Ut{p}
преобразует функцию р{х,т) в р{х,т + t). (Ut — это не трансляция во времени, а эволюция во
времени.) Поскольку наша система является трансляционно инвариантной,
транслированные решения также являются решениями для транслированных начальных условий:
T&{Ut{p}} = ^*{7д{р}}. Теперь, если pfc(x,0) является собственным состоянием 7д с
собственным значением Afc, является ли рк(х, t) = Ut{pk){x) собственным состоянием с тем же
собственным значением? Ответ: да, в самом деле:
Ть{рк{х,1)} = TA{Ut{pk(x,0)}}
= Ut{TA{pk(x,0)}}
= Ut{\kPk(x,0)}
= \kUt{pk{x^)}
= \kpk(x,t), (A.34)
поскольку оператор эволюции Ut является линейным.
578
А. Методы Фурье
группы и, следовательно, могут быть разложены в неприводимые
представления этих групп. Эти подходы в общем эквивалентны и являются очень
мощными. Можно также использовать эти подходы для систем с другими
типами симметрии. Например, подобно тому как инвариантность
однородных систем при трансляциях приводит к решениям в виде плоских волн с
определенным волновым вектором fc, верно то, что:
• инвариантность изотропных систем (подобных атому водорода) под
воздействием группы вращений естественным образом даст решения,
включающие в себя сферические гармоники с определенными
угловыми моментами ί и га;
• инвариантность сильного взаимодействия при симметрии SU(3)
естественным образом приводит к наличию семейств мезонов и барионов;
• инвариантность Вселенной относительно группы Пуанкаре симметрии
пространства-времени (трансляции, вращений и др.) приводит к
наличию частиц с определенной массой и спином!
Упражнения
Мы начнем с трех упражнений, посвященных рядам Фурье: Звуковой
волны, Косинусов Фурье (численного упражнения) и Двойной синусоиды.
Затем мы поупражняемся в преобразовании Фурье с Фурье-преобразованием
гауссианы (численным упражнением) и Неопределенностью, делая акцент
на трансляции и перемасштабировании ширины преобразуемой функции. В
Соотношениях Фурье рассматривается нормировка, требуемая для перехода
от БПФ к рядам Фурье, а в Алиасинге и растекании спектра изучаются две
распространенные численные погрешности, возникающие в алгоритмах для
расчета БПФ. В Белом шуме рассматривается применение методов Фурье для
случайных функций. Сопоставление функции и ее Фурье-образа
представляет собой визуальный тест понимания методов Фурье. Наконец, в Феномене
Гиббса исследуется, что произойдет, если вы попробуете аппроксимировать с
помощью рядов Фурье функцию, имеющую разрыв первого рода.
А.1 Звуковая волна, φ
Музыкальный инструмент, играющий ноту частоты ω±, генерирует
периодическую волну давления P(t), период которой равен 2π/ω\: P(t) = P(t +
2π/ωι). Комплексный ряд Фурье, соответствующий этой волне (уравнение
А.2), равен нулю, за исключением точек ш = ±1и ±2, соответствующих
основной частоте ω\ и первому обертону. При га = 1 амплитуда Фурье равна
А. Упражнения
579
2 — i, при га = — 1 она составляет 2 + i, а при га = ±2 она равна 3. Чему
равно давление P(t): (А) ехр ((2 + Ί)ωιί) + 2ехр {Suit), (В) exp (2uit) exp (ίωχί) χ
2exp(3u;i£), (С) cos2u;i£ — sinu;i£+2cos3u;i£, (D) 4cosu;i£ — 2sincJi£+6cos2cJi£,
(E) 4coso;ii + 2sincJii + 6cos2cJii?
A.2 Косинусы Фурье. (Моделирование) (2)
В этом упражнении мы с помощью компьютера проиллюстрируем
некоторые свойства рядов Фурье и дискретного быстрого преобразования Фурье.
Скачайте программу для расчета преобразования Фурье и соответствующие
файлы с подсказками на сайте книги [132] в разделе компьютерных
упражнений. 22 Во-первых, мы рассмотрим ряды Фурье периодических функций
у(х) = у(х + L), где L = 20. Мы возьмем дискретные значения функции
в N = 32 точках, и используем БПФ для получения аппроксимации рядов
Фурье. Ряды Фурье будут построены как функции к в точках — fc/v/2, · · ·,
^τν/2-2ϊ fcyv/2-i· (Запомните, что га отрицательных точек задаются последней
половиной БПФ.)
(a) Аналитически (то есть с использованием ручки и бумаги) получите ряды
Фурье Ут в данном интервале для cos(k\x) и sm(kix). (Подсказка: они равны
нулю за исключением двух значений га = ±1.) Используйте пространственное
преобразование (уравнение А.З).
(b) Чему, по вашему предположению, равно расстояние Sk между точками
fcm? Чему равно fc/v/2? Оцените каждое из них аналитически как функцию L и
численно при L = 20.
Численно (при помощи компьютера) возьмите косинусоиду Acos(k(x —
хо)), где к = к\ = 2π/Ζ/, А = 1 и xq = 0, рассчитанную в 32 точках от χ = 0
до 20, как описано выше. Изучите ее ряд Фурье.
(c) Проверьте ваши расчеты из задания (а) для рядов Фурье функций
cos(fcix) и sm(k\x). Проверьте ваши расчеты из задания (Ь) для Sk и kN/2.
Уменьшайте fc, увеличивая тем самым число длин волн, но сохраняя
фиксированное число точек. Обратите внимание, что ряды Фурье выглядят
достаточно хорошо, но кривые в реальном пространстве начинают меняться по
амплитуде, подобно структурам, возникающим при биениях (наложении двух
волн с различной частотой). При увеличении числа точек вы можете увидеть,
что эффект биений возникает из-за малого числа точек, в которых мы
рассматриваем нашу функцию. Даже при большем количестве точек 7V биения
будут по-прежнему наблюдаться для очень маленьких длин волн (когда мы
22Если это упражнение используется в лабораторной работе по численным методам, то
можно в качестве предварительной подготовки сделать несколько аналитических
упражнений.
580
А. Методы Фурье
будем приближаться к /гдг/г)· Попробуйте взять различные количества волн
т до и после т = Ν/2.
А.З Двойная синусоида. (2)
Какая картинка на рис. А.З соответствует пространственному ряду Фурье
(уравнение А.4) функции f(x) = 3sin(x) + cos(2x)? (Сплошная линия отвечает
действительной части, пунктирная — мнимой части.)
А.4 Фурье-преобразование гауссианы. (Моделирование) (2)
В этом упражнении мы при помощи компьютера рассмотрим некоторые
свойства преобразования Фурье, изучая преобразование функции Гаусса,
но иллюстрируя, тем не менее, общий случай. Скачайте программу,
посвященную Фурье-преобразованиям и соответствующие файлы с
подсказками на сайте книги [132] в разделе компьютерных упражнений.23
Распределение Гаусса (также известное как нормальное распределение)
имеет вид
G(x) = -^- ехр (-(χ - χο)2/2σ2), (Α.35)
ν2πσ
где σ1 — дисперсия, а хо — среднее значение. Рассмотрим функцию Гаусса
G0(x) = -U ехр (-х2/2) (А.36)
ν2π
с нулевым средним значением и дисперсией σ1 = 1. Фурье-преобразование
Go тоже представляет собой функцию Гаусса с единичным стандартным
отклонением, но без нормировочного коэффициента:24
Go(fc) = exp(-fc2/2). (A.38)
23Если это упражнение используется в лабораторной работе по численным методам, то
можно в качестве предварительной подготовки сделать несколько аналитических
упражнений.
24Приведем вывод, кажущийся на первый взгляд элементарным. Выделим полный
квадрат под экспонентой и сделаем замену переменных χ на у = χ + \к:
1 Г
е ikx ехр(-х2/2) ах =
>
= -L Г ехр(-(х + ik)2/2) ax exp((ifc)2/2) = (А.37)
\/2π У-оо
exp(-fc2/2).
=[/
oo+ifc
exp(-y2/2)ch/
oo+ifc ν2π
Выражение в квадратных скобках равно единице (что дает e_fc '2), но, чтобы показать это,
мы должны изменить контур интегрирования с Im[y] = к на Im[y] = 0, применив теорему
Коши (см. рис. 10.11).
А. Упражнения
581
ι
1
So
iX°
-1
-2
2
1
Фл
^°
-1
-2
1 · 1 ι " г
ι i
I.I.I
■
|
L
1— ReQ?(A:
|·· Im[y(*
t
-2-10 1
Волновой вектор /
(a)
I " 1 ' 1 ■ Г
•
-Re[K*)]
·· Im(K*)]
-2-10 1
Волновой вектор \
(с)
2
1
-1
-2
1
ί
-2
ι
L
-1
Волновой
(е)
Рис. А.З
2
1
-1
-2
2
1
-1
1 · ι ' 1 · 1 ·
_L
ι
-Re[K*)]
-2-10 1
Волновой вектор к
(b)
-
J
_ J
1 -2
-ReD**)]
·· Im[y(*)]
. . l . L_
1 L
* ι .
-1 0 1
Волновой вектор к
1 I
(d)
I i
-Re|H* 1
·· Im[y(Jt |
0 1
вектор к
582
А. Методы Фурье
В этом упражнении мы рассмотрим, как меняется Фурье-преобразование
G(x) при изменении σ или xq.
Ширина. Если мы уменьшим ширину гауссианы (уменьшая σ), она
станет более заостренной. Меньшие длины соответствуют большим волновым
векторам, и мы ожидаем, что Фурье-преобразование станет шире.
(a) Начнем с функции Гаусса с σ = 1, численно измерим ширину Фурье-
преобразования на некоторой определенной высоте. (Разумно измерить ширину
на высоте, равной половине максимальной.) Возьмите σ, равное 2 и 0.1, измерьте
высоту и убедитесь, что ширина Фурье-преобразования обратно
пропорциональна ширине исходной функции.
(b) Покажите аналитически, что это правило верно в общем случае. Делая
замену переменных в уравнении (А.б), покажите, что если ζ(χ) = у(Ах), то
z(fc) = у(к/А)/А. Используя уравнение (А.36) и это общее правило, запишите
формулу для Фурье-преобразования гауссианы с центром в нуле и произвольной
шириной σ.
(c) Аналитически вычислите произведение АхАк ширины функции Гаусса
на уровне полумаксимума. (Ваш ответ не должен зависеть от величины σ.) Это
связано с принципом неопределенности Гейзенберга, Ах Ар ~ ft, который вы
изучали в квантовой механике.
Сдвиг. Обратите внимание, что узкая гауссиана с центром в достаточно
удаленной точке Хо является хорошим приближением б-функции. Таким
образом, мы ожидаем, что ее Фурье-преобразование будет похожим на плоскую
волну G(k) ~ exp(—ikxo), Фурье-образ функции 8{х — хо).
(d) Численно измените среднее значение гауссианы. Как изменится при этом
Фурье-образ? Убедитесь, что он умножается на ехр(—ikxo). Как меняется спектр
|G(u;)|2 при изменении хо?
0.4
0.3
§0.2
0.1
°.6 .4 -2 0 2 4
Координата х
Рис. А.4. Функции Гаусса в вещественном пространстве
А. Упражнения
583
4«^ Покажите аналитически, что это правило верно также в общем случае.
Производя замену переменных в уравнении (А.б), покажите, что если ζ(χ) =
у(х — хо), то z(k) = exp(—ikxo)y(k). Используя это общее правило, обобщите
свой ответ на задание (Ь), записав формулу для Фурье-преобразования функции
Гаусса шириной σ с центром в точке хо·
А.5 Неопределенность. (2)
Пунктирная линия на рис. А.4 соответствует функции
G0(x) = 1/л/2тг exp(-s2/2). (A.39).
Черной сплошной линией показана некоторая другая функция G(x).
Площади под двумя кривыми G(x) и Go(x) одинаковы. Пунктирная линия на
рис. А.5 соответствует преобразованию Фурье Go(k) = ехр(—к2/2). На каком
из рисунков сплошная линия иллюстрирует преобразование функции Фурье
G?
А.6 Соотношения Фурье. (2)
В этом упражнении мы рассмотрим связь между рядами Фурье и
быстрым преобразованием Фурье. В первом случае мы имеем непрерывную и
периодическую функцию в пространстве вещественных чисел и дискретный,
неограниченный набор амплитуд в пространстве Фурье. Второй случай
отвечает дискретности и периодичности как в вещественном пространстве, так и в
пространстве Фурье. Таким образом, мы снова имеем дело с преобразованием
интегралов в суммы (аналогично рис. А.1).
Если число точек N в БПФ стремится к бесконечности, то расстояние
между ними становится все меньше и меньше, и аппроксимация интеграла
суммой становится все лучше и лучше.
Пусть уе = y(te), где ti = £(T/N) = £(At). Аппроксимируйте интеграл А.1
суммой по j/£f (l/T)^^1 y(te)exp(—iumt£)At. Для малых положительных га
получите константу, связывающую у^Т с коэффициентом в разложении в ряд
Фурье Ут-
АЛ Алиасинг и растекание спектра. (Моделирование) Q)
В этом упражнении мы проиллюстрируем некоторые проблемы,
связанные с численной реализацией быстрого преобразования Фурье. Скачайте
программу по преобразованию Фурье и соответствующие файлы с подсказками
на сайте книге [132] в разделе компьютерных упражнений.25 Ряды Фурье ут
25Если это упражнение используется в лабораторной работе по численным методам, то
в качестве предварительной подготовки можно сделать несколько аналитических
упражнений.
584
А. Методы Фурье
1
0.8
0.6
0.4
0.2
θ'
■ ι ■ ι ■ /ι
G0(k)!
1
I
I
/ι
/ I
\
\
\
\
\
\
\ \
\
4
σ
^6 -4-2 0 2
Волновой вектор £
■^
&
Ι
0.8
0.6
0.4
0.2
θ'
(а)
/1
/ /
/ /
' /
' /
~ / /
- СоЩ' /
/ /
/ 1
Г\\
\\
\ \
\ \
\ \
\ \
\ \
\ \
'•"^ \ \
(Щ \
V ^^
-2 0
Волновой вектор к
(с)
-4-2 0 2
Волновой вектор к
-2 0
Волновой вектор к
(d)
Волновой вектор к
(е)
Рис. А.5
А. Упражнения
585
рассчитываются для всех целых га, а быстрое преобразование Фурье —
только для 0 < га < N. Это основное отличие можно проиллюстрировать тремя
способами: рассматривая размерность функционального пространства,
длины волн и наложение спектров.
Размерность функционального пространства. Пространство
периодических функций у(х) на 0 < χ < L бесконечно, но мы вычисляем их значения
только в N = 32 точках. Пространство всевозможных рядов Фурье также
должно иметь размерность N. Далее, каждый коэффициент БПФ является
комплексным (размерности два), но отрицательные частоты являются
комплексными сопряженными положительных, что соответствует двум
измерениям для двух волновых векторов кт и к-т = kjy-m). уо не имеет партнера,
но является вещественным (что соответствует одному измерению), а если N
четное, то у_лг/2 также не имеет партнера, но является вещественным. Таким
образом, N fc-точек соответствуют N вещественным точкам.
Длины волн. Точки, в которых мы рассчитываем нашу функцию,
разделены промежутками δχ = L/N. Имеет смысл останавливать расчет быстрого
преобразования Фурье, когда длины волн приближаются к δχ: в этом случае
невозможно различить волны, длины которых короче, чем расстояние между
точками, в которых вычисляется значение функции.
(a) Аналитически получите формулу для yi, для косинусоиды с волновым
вектором fcyv, первой длиной волны, не вычисляемой в нашем БПФ. После
упрощения должна получиться константа. Найдите также уе для fcyv/2- Численно
проверьте ваши расчеты yt для cos(fcyvx) и cos(kfsj/2^)·
Таким образом, БПФ возвращает Фурье-компоненты только до fcyv/2> ко~
гда имеется лишь одна точка на один горб (полупериод) косинусоиды.
Алиасинг. Допустим, наша функция колеблется на расстояниях,
меньших, чем расстояние между точками δχ, в которых она рассчитывается. Тогда
быстрое преобразование Фурье этой функции будет искажать коэффициенты
y^FT, соответствующие большим длинам волн, за счет вклада
высокочастотных волн: ym±Ni Vm±2N и т.д. Рассмотрим частный пример: косинусоиду с
малой длиной волны.
(b) Аналитически покажите, что exp(ifcm±yv^) = exp(ikmxe) в
точках хе, в которых вычисляется значение функции. Покажите, что
cos(fcm+7vx^) = cos(kmxe), таким образом, быстрое преобразование Фурье для
малых т будет давать фиктивный пик на больших длинах волн кт. Численно
проверьте ваши расчеты для преобразования cos(kx) при к > fcyv/2-
Если вы рассчитываете в 7V точках функцию, имеющую
Фурье-компоненты за пределами &лг/2> их вклаД будет добавляться
к Фурье-компонентам для малых волновых векторов. Этот эффект
586
А. Методы Фурье
называется алиасинг и является основным источником ошибок в численных
методах Фурье. Нужно брать достаточно много точек, чтобы избежать этой
проблемы.
Вы должны хотя бы один раз увидеть, как алиасинг влияет на БПФ
функций, не являющихся синусами или косинусами. Сформируйте из 32 точек
волновой пакет у(х) = 1/(\/2πσ) ехр(—χ2/2σ2). Уменьшите ширину пакета
σ. Обратите внимание, что когда пакет становится очень тонким, ряды
Фурье начинают перекрываться. Высокочастотные компоненты накладываются
на более низкие частоты.
Растекание спектра. Зачастую требуется сделать разложение в ряд
Фурье для функций, не являющихся периодическими на некотором интервале.
Возьмите число точек 7V, равное 256 (расчет происходит быстрее для
степеней двойки), и сравните у(х) = coskmx при т = 20 и т = 20.5. Функция
у(х) не является периодической в интервале [0, L) при т = 20.5. Обратите
внимание, что в этом случае ряды Фурье имеют достаточно сложную
структуру. Каждый из двух пиков превращается в целую лестницу. Попробуйте
изучить спектральную функцию (пропорциональную \у\2) и сравнить ее для
т = 20 и т = 20.5. Данный эффект представляет собой огромную проблему
в численных расчетах. Существуют множество различных алгоритмов для
минимизации искажений за счет этого эффекта.
А.8 Белый шум. (Моделирование) (2)
Белый свет представляет собой смесь волн с всевозможными частотами.
Белый шум — это смесь всевозможных звуковых волн с постоянной средней
мощностью на единицу частоты. «Шипение», которое вы слышите на радио
или ТВ между станциями, примерно соответствует белому шуму. Там больше
высоких частот, чем низких, поэтому у него достаточно высокий звуковой
тон.
Скачайте программу по Фурье-преобразованиям и файлы с
соответствующими подсказками на сайте книги [132] в разделе компьютерных
упражнений.
Какая временная последовательность звуковых сигналов соответствует
белому шуму? Выберите Белый шум или сгенерируйте последовательность
независимых случайных чисел у ι = y(£L/N), распределенных согласно
распределению Гаусса26 р(у) = (1/\/2π) ехр(—у2/2а).
Вы увидите зубчатую случайную функцию. Выберите число точек,
равное, например, 1024.
26Мы выбираем числа с вероятностью, задаваемой распределением Гаусса, но на первый
взгляд они выглядят так же, как если бы мы выбирали равновероятные числа, например,
в диапазоне (—1,1).
А. Упражнения
587
Исследуйте Фурье-преобразование шумового сигнала. Фурье-образ
белого шума выглядит удивительно похожим на исходный сигнал. Однако
существуют два важных отличия. Во-первых, он комплексный: у него есть как
реальная, так и мнимая часть. Второе отличие вам предстоит обнаружить
самим.
Исследуйте область вблизи к = О на графике, соответствующем
преобразованию Фурье, и опишите, чем отличается Фурье-преобразование шумового сигнала
от случайной функции. В частности, существует ли симметрия между реальной
и воображаемой частью? Можете ли вы показать, что она будет возникать для
любой вещественной функции?
Теперь исследуем спектральную функцию |у|2.27
Покажите, что спектр достаточно зашумленный, но в среднем он в
грубом приближении не зависит от частоты. (Лучше всего это можно проверить,
меняя последовательность случайных чисел.) Белый шум обусловлен
случайными, некоррелированными флуктуациями во времени.
А.9 Сопоставление функции и ее Фурье-образа. (2)
На трех верхних графиках (а)-(с) на рис. А.б изображены функции у(х),
зависящие от координаты. Для каждого из них выберите, на каком из шести
графиков (1)-(б) показаны Фурье-образы у этих функций? (Сплошная линия
соответствует реальной части Фурье-образа, а пунктирная — мнимой части.)
(После выполнения упражнений А.2, А.4 и А.8, проблем с этим упражнением
возникнуть не должно.)
А. 10 Феномен Гиббса. (Математика) @
В этом упражнении мы рассмотрим ряд Фурье для ступенчатой функции
и для треугольной функции. Данная задача представляет большой интерес,
поскольку эти функции содержат острые углы, которые сложно
аппроксимировать синусоидами.
Рассмотрим функцию у(х), которая равна А при О < χ < L/2 и —А при
L/2 < χ < L. Она представляет собой ступенчатую функцию, имеющую
разрыв при L/2 (рис. А.7).28
(а) В самом грубом приближении ступенчатая функция напоминает
утолщенную синусоиду Asin(2nx/L). Как будет выглядеть в этом приближении
комплексный ряд Фурье (уравнение А.4)?
27Для временного сигнала f(t) средняя мощность на определенной частоте
пропорциональна |/(ω)|2. Если не учитывать коэффициент пропорциональности, то она называется
спектральной функцией. Это название иногда также используется для обозначения
квадрата амплитуды пространственного преобразования Фурье.
28 Она может быть записана через стандартную ступенчатую функцию Хевисайда θ(χ) =
О при χ < О и θ(χ) = 1 при χ > О следующим образом: у(х) = А (1 — 2θ(χ — L/2)).
588
А. Методы Фурье
Рис. А.6. Сопоставление функции и ее Фурье-образа
(b) Покажите, что нечетные коэффициенты комплексных рядов Фурье
ступенчатой функции имеют вид ут = —2Αι/(πιπ) (где т нечетное). Найдите
четные коэффициенты. Проверьте, имеют ли коэффициенты уш при т = ±1 тот
вид, который вы предположили при выполнении задания (а).
(c) Полагая А = 2 и L = 10, постройте частичную сумму для рядов Фурье
(уравнение А.1) при т = — п, —п + 1,... ,п для η = 1, 3 и 5. (Вы должны будете
скомбинировать коэффициенты уш и у_т, представив ряд Фурье в виде
разложения по синусам и косинусам, если ваша программа для построения графиков
не умеет строить комплексные экспоненты.) Сходятся ли эти частичные суммы
к ступенчатой функции? Если вас это не затруднит, постройте частичные суммы
вплоть до η = 100 и обратите особое внимание на поведение функции вблизи
точек 0, L/2 и L. Данное зашкаливание носит название феномена Гиббса, оно
возникает при попытках аппроксимировать функции у{х), имеющие разрыв.
Одним из преимуществ рядов Фурье является то, что они существенно
упрощают взятие производных и интегралов. Как будет выглядеть интеграл
нашей ступенчатой функции? Давайте найдем вначале его ряд Фурье.
А. Упражнения
589
\ /
I
L /
Γ /
L /
Γ /
I/
г
\
\
\
\
\
\
>
1
j CiyncmwM функция 1
| Грубое приближение ]
\
\
4 /
1 . 1
/\γ .1,1,1.1
01 0.21 OAL 0.61 0.81
Рис. А.7. Ступенчатая функция
(d) Получите ряд Фурье для интеграла ступенчатой функции, используя
комплексный ряд Фурье из задания (Ь), а также формулу (А.17) для ряда Фурье,
соответствующего интегралу функции. Постройте графики ваших результатов,
вычисляя частичные суммы вплоть до ±га = п, где η = 1, 3 и 5, для тех же
значений параметров А = 2 и L = 10. Похожа ли производная данной функции на
ступенчатую функцию? Рассчитайте частичную сумму для η = 100 и обратите
внимание на отсутствие зашкаливания.
Литература
[1] Ahlers, G. Critical phenomena at low temperatures / G. Ahlers // Reviews
of Modern Physics. - 1980. - Vol. 52. - Pp. 489-503.
[2] Anderson, P. W. Coherent matter field phenomena in superfluids /
P. W. Anderson // Some recent definitions in the basic sciences. — Yeshiva
University, New York: Belfer Graduate School of Science, 1965. — Vol. 2. —
Pp. 21-40.— Reprinted in [4, p. 229].
[3] Anderson, P. W. Considerations on the flow of superfluid helium /
P. W. Anderson // Reviews of Modern Physics.— 1966.— Vol. 38.—
Pp. 298-310.— Reprinted in [4, p. 249].
[4] Anderson, P. W. Basic notions of condensed matter physics /
P. W. Anderson. — Menlo Park, CA: Benjamin-Cummings, 1984.
[5] Anderson, P. W. Solving problems in finite time / P. W. Anderson //
Nature. - 1999. - Vol. 400. - Pp. 115-6.
[6] Ashcroft, N. W. Solid state physics / N. W. Ashcroft, N. D. Mermin.—
Philadelphia: Hold, Rinehart, and Wilson, 1976.
[7] Bender, С. М. Advanced mathematical methods for scientists and
engineers / С. М. Bender, S. A. Orszag. — New York: McGraw-Hill, 1978.
[8] Bennett, С. Н. Efficient estimation of free energy differences from Monte
Carlo data / С. Н. Bennett // Journal of Computational Physics. — 1976. —
Vol. 22. - Pp. 245-68.
[9] Bennett, С. Н. The thermodynamics of computation—a review /
С. Н. Bennett // International Journal of Theoretical Physics. — 1982. —
Vol. 21.-Pp. 905-40.
Литература 591
[10] Berg, Η. Motile behavior of bacteria / H. Berg // Physics Today. — 2000. —
Vol. 53.— Pp. 24-9.— www.aip.org/pt/janOO/berg.htm.
[11] Bodenschatz, E. Directional solidification of solvent/polymer alloys.—
www.milou.ccmr.cornell.edu. — 2002.
[12] Bortz, A. B. A new algorithm for Monte Carlo simulation of Ising spin
systems / A. B. Bortz, M. H. Kalos, J. L. Lebowitz // Journal of
Computational Physics. — 1975. — Vol. 17. — Pp. 10-8.
[13] Bouchaud, J. Theory of Financial Risk and Derivative Pricing: From
Statistical Physics to Risk Management / J. Bouchaud, M. Potters.—
Cambridge University Press, 2004.
[14] Boundary-layer model of pattern formation in solidification / E. Ben-Jacob,
N. Goldenfeld, J. S. Langer, G. Schon // Physical Review Α.— 1984.—
Vol. 29.-Pp. 330-40.
[15] Buchelj A. Elastic theory has zero radius of convergence / A. Buchel,
J. P. Sethna // Physical Review Letters. — 1996. — Vol. 77. — P. 1520.
[16] Buchel, A. Statistical mechanics of cracks: Thermodynamic limit,
fluctuations, breakdown, and asymptotics of elastic theory / A. Buchel,
J. P. Sethna // Physical Review E. - 1997. - Vol. 55. - P. 7669.
[17] Caratheodory, С Untersuchungen iiber die Grundlagen der
Thermodynamyk / C. Caratheodory // Mathematische Annalen.—
1909. - Vol. 67. - Pp. 355-86.
[18] Caratheodory, С Untersuchungen iiber die Grundlagen der
Thermodynamyk (English translation) / C. Caratheodory // The
second law of thermodynamics, by J. Kestin. — Stroudsberg, Pennsylvania:
Dowden, Hutchinson and Ross, Inc., 1976. — Pp. 229-56.
[19] Cardy, J. Scaling and renormalization in statistical physics / J. Cardy.—
Cambridge University Press, 1996.
[20] Cardy, J. Scaling and Renormalization in Statistical Physics / J. Cardy.—
Cambridge University Press, 1996.
[21] Carlson, J. M. Properties of earthquakes generated by fault dynamics /
J. M. Carlson, J. S. Langer // Physical Review Letters. — 1989. — Vol. 62. —
P. 2632.
592
Литература
Chandler, D. Introduction to modern statistical mechanics / D. Chandler. —
Oxford University Press, 1987.
Chu, С Hysteresis and microstructures: a study of biaxial loading on
compound twins of copper-aluminum-nickel single crystals: Ph.D. thesis /
Aerospace Engineering, University of Minnesota. — 1993.
Coleman, S. Secret symmetry: an introduction to spontaneous symmetry
breakdown and gauge fields / S. Coleman // Aspects of symmetry, selected
Erice lectures.— Cambridge University Press, 1985.— Pp. 113-84.
The cosmic microwave background spectrum from the full СОВЕ FIRAS
data set / D. J. Fixsen, E. S. Cheng, J. M. Gales et al. // The Astrophysical
Journal. - 1996. - Vol. 473. - Pp. 576-87.
Crystal structure of the calcium pump of sarcoplasmic reticulum at
2.6 Angstrom resolution / C. Toyoshima, M. Nakasako, H. Nomura,
H. Ogawa // Nature. - 2000. - Vol. 405. - Pp. 647-55.
Curcic, T. STM images of nanoscale pit decay.—
www.lassp.cornell.edu/cooper_nano. — 1995.
deGennes, P. G. The physics of liquid crystals, 2nd edition /
P. G. deGennes, J. Prost.— Oxford: Clarendon Press, 1993.
Determining computational complexity from characteristic 'phase
transitions' / R. Monasson, R. Zeccina, S. Kirkpatrick et al. // Nature. —
1999. - Vol. 400. - Pp. 133-7.
Bailey, N. P. Digital material: a flexible atomistic simulation code. —
arXiv.org/.- 2006.
Dissipation in two-dimensional superfluids / V. Ambegaokar, B. I. Halperin,
D. Nelson, E. Siggia // Physical Review Letters.— 1978.— Vol. 40.—
Pp. 783-6.
Domb, С Ising model / C. Domb // Phase transitions and critical
phenomena, Vol. 3. — New York: Academic Press, 1974. — Pp. 357-478.
Domb, С Low-temperature series for the Ising model / С Domb,
A. J. Guttman // Journal of Physics C— 1970.— Vol. 8.— Pp. 1652-
60.
Литература 593
Dynamics of interfacial pattern formation / E. Ben-Jacob, N. Goldenfeld,
J. S. Langer, G. Schon // Physical Review Letters.— 1983.— Vol. 51.—
Pp. 1930-2.
Dynamics of superfluid films / V. Ambegaokar, B. I. Halperin, D. Nelson,
E. Siggia // Physical Review B. - 1980. - Vol. 21. - Pp. 1806-26.
Dyson, F. J. Time without end: Physics and biology in an open universe /
F. J. Dyson // Reviews of Modern Physics. — 1979. — Vol. 51. — P. 447.
Elowitz, Μ. Β. A synthetic oscillatory network of transcriptional regulators /
M. B. Elowitz, S. Leibler // Nature. - 2000. - Vol. 403. - Pp. 335-8.
Equilibrium shapes of small lead crystals: Observation of Pokrovsky-
Talapov critical behavior / С Rottman, M. Wortis, J. C. Heyraud,
J. J. Metois // Physical Review Letters.- 1984.- Vol. 52.- Pp. 1009-
12.
Fermi, E. Studies of nonlinear problems. I / E. Fermi, J. Pasta, S. Ulam //
E. Fermi, collected papers, Vol. II. — Chicago: University of Chicago Press,
1965. - P. 978. — (Reprinted from Los Alamos report LA-1940, 1955.).
Choy, T.-S. The Fermi surface database. — . — 2000.
Feynman, R. P. Statistical mechanics, a set of lectures / R. P. Feynman. —
Menlo Park, CA: Addison-Wesley, 1972.
Feynman, R. P. Feynman lectures on computation / R. P. Feynman. —
Boulder, CO: Westview, 1996.
Feynman, R. P. The Feynman lectures on physics / R. P. Feynman,
R. B. Leighton, M. Sands.— Menlo Park, CA: Addison-Wesley, 1963.
Forster, D. Hydrodynamic fluctuations, broken symmetry, and correlation
functions / D. Forster. — Reading, MA: Benjamin-Cummings, 1975.
Frenkel, D. Phase separation in a binary hard-core mixture. An exact
result / D. Frenkel, A. A. Louis // Physical Review Letters.— 1992.—
Vol. 68. - P. 3363.
Geometrical approach to moving interface dynamics / R. С Brower,
D. A. Kessler, J. Koplik, H. Levine // Physical Review Letters.— 1983.—
Vol. 51.-Pp. 1111-4.
594
Литература
[47] Gillespie, D. Т. Exact simulation of coupled chemical reactions /
D. T. Gillespie // Journal of Computational Physics. — 1976. — Vol. 22. —
Pp. 403-34.
[48] Girvan, M. Community structure in social and biological networks /
M. Girvan, M. E. J. Newman // Proceedings of the National Academy of
Sciences. - 2002. - Vol. 12. - Pp. 7821-6.
[49] Goldstein, R. E. Origin of the singular diameter in coexistence curve of
a metal / R. E. Goldstein, N. W. Ashcroft // Physical Review Letters. —
1985. - Vol. 55. - Pp. 2164-7.
[50] Gomes, C. P. Satisfied with physics / C. P. Gomes, B. Selman // Science. —
2002. - Vol. 297. - Pp. 784-5.
[51] Goss, P. J. E. Quantitative modeling of stochastic systems in molecular
biology by using stochastic Petri nets / P. J. E. Goss, J. Peccoud //
Proceedings of the National Academy of Sciences. — 1998. — Vol. 95. —
Pp. 6750-5.
[52] Gottlieb, M. Seven states of matter / M. Gottlieb. — Walker & Company,
1966.
[53] Greiner, W. Thermodynamics and statistical mechanics / W. Greiner,
L. Neise, H. Stocker. — New York: Springer, 1995.
[54] Greywall, D. S. Second-sound velocity and superfluid density in 4He under
pressure near T\ / D. S. Greywall, G. Ahlers // Physical Review Α.—
1973. - Vol. 7. - Pp. 2145-62.
[55] Growth morphologies of the Al-Li-Cu icosahedral phase / J. M. Lang,
M. Audier, B. Dubost, P. Sainfort // Journal of Crystal Growth. — 1987. —
Vol. 83. - Pp. 456-65.
[56] Guggenheim, E. A. The principle of corresponding states /
E. A. Guggenheim // Journal of Chemical Physics. — 1945. — Vol. 13. —
Pp. 253-61.
[57] Hanggi, P. Reaction-rate theory: fifty years after Kramers / P. Hanggi,
P. Talkner, M. Borkovec // Reviews of Modern Physics. — 1990. — Vol. 62. —
P. 251.
Литература
595
Heavy-tailed phenomena in satisfiability and constraint satisfaction
problems / C. P. Gomes, B. Selman, N. Crato, H. Kautz // Journal of
Automated Reasoning. - 2000. - Vol. 24. - Pp. 67-100.
Heller, P. Nuclear magnetic resonance in MnF2 near the critical point /
P. Heller, G. B. Benedek // Physical Review Letters.— 1962.— Vol. 8.—
Pp. 428-32.
Hirth, J. P. Theory of dislocations, 2nd edition / J. P. Hirth, J. Lothe.—
New York: John Wiley & Sons Inc, 1982.
Hodgdon, J. A. Derivation of a general three-dimensional crack-propagation
law: A generalization of the principle of local symmetry / J. A. Hodgdon,
J. P. Sethna // Physical Review B. - 1993. - Vol. 47. - Pp. 4831-40.
Houle, P. A. Acoustic emission from crumpling paper / P. A. Houle,
J. P. Sethna // Physical Review E. - 1996. - Vol. 54. - P. 278.
Ни, W. Ringing in the new cosmology (introduction to the acoustic peaks
and polarization).— background.uchicago.edu. — 2001.
Hull, J. C. Options, futures, and other derivatives / J. C. Hull.— Upper
Saddle River, NJ: Prentice Hall, 2005.
Hysteresis, avalanches, and noise: Numerical methods / M. C. Kuntz,
O. Perkovid, K. A. Dahmen, J. P. Sethna // Computing in Science and
Engineering. — 1999. — Vol. 1. — Pp. 73-81.
Jacobsen, J. Rate theory for correlated processes: Double-jumps in adatom
diffusion / J. Jacobsen, K. W. Jacobsen, J. P. Sethna // Physical Review
Letters. - 1997. - Vol. 79. - P. 2843.
Jarzynski, C. Nonequilibrium equality for free energy differences /
C. Jarzynski // Physical Review Letters. — 1997. — Vol. 78. — Pp. 2690-
3.
Jensen, R. V. Images of the critical points of nonlinear maps / R. V. Jensen,
С R. Myers // Physical Review A. - 1985. - Vol. 32. - Pp. 1222-4.
Kardar, M. Dynamic scaling of growing interfaces / M. Kardar, G. Parisi,
Y.-C. Zhang // Physical Review Letters. — 1986. — Vol. 56. — Pp. 889-92.
Khinchin, A. I. Mathematical foundations of information theory /
A. I. Khinchin. — New York: Dover, 1957.
596
Литература
Kivelson, P. D. Neur-on. — www.neur-on.com. — 2002.
Kuntz, M. C. Crackling noise.— simscience.org/. — 1998.
Landau, L. D. Quantum mechanics, non-relativistic theory, 2nd edition /
L. D. Landau, Ε. Μ. Lifshitz. — Oxford: Pergamon Press, 1965.
Landau, L. D. Statistical physics / L. D. Landau, Ε. Μ. Lifshitz. — Oxford:
Butterworth Heinemann, 1980.
Langer, J. S. Statistical theory of the decay of metastable states /
J. S. Langer // Annals of Physics (NY).- 1969.- Vol. 54.- Pp. 258-
75.
Langer, J. S. Instabilities and pattern formation in crystal growth /
J. S. Langer // Reviews of Modern Physics. — 1980. — Vol. 52. — Pp. 1-28.
Langer, S. A. Nonequilibrium entropy and entropy distributions /
S. A. Langer, E. R. Grannan, J. P. Sethna // Physical Review B. — 1990. —
Vol. 41.-P. 2261.
Langer, S. A. Textures in a chiral smectic liquid crystal film / S. A. Langer,
J. P. Sethna // Physical Review A. - 1986. - Vol. 34. - P. 5305.
Langer, S. A. Entropy of glasses / S. A. Langer, J. P. Sethna // Physical
Review Letters.— 1988.- Vol. 61.— P. 570.— (M. Goldstein noticed the
bounds earlier).
Last, B. J. Percolation theory and electrical conductivity / B. J. Last,
D. J. Thouless // Physical Review Letters.— 1971.— Vol. 27.— Pp. 1719-
21.
Lebowitz, J. L. Modern ergodic theory / J. L. Lebowitz, O. Penrose //
Physics Today. - February 1973. - Pp. 23-9.
Libbrecht, K. Snowflakes: photographed by Kenneth Libbrecht.—
snowcrystals.com. — 2003.
Libbrecht, K. The snowflake: winter's secret beauty / K. Libbrecht,
P. Rasmussen. — Stillwater, MN: Voyageur Press, 2003.
Maier, R. S. Escape problem for irreversible systems / R. S. Maier,
D. L. Stein // Physical Review E. - 1993. - Vol. 48. - Pp. 931-38.
Литература
597
[85] Malkiel, В. G. The random walk guide to investing: ten rules for financial
success / B. G. Malkiel. — New York: Norton, 2003.
[86] Malkiel, B. G. A random walk down Wall street / B. G. Malkiel. — New
York: Norton, 2004.
[87] Markovic, N. Thickness-magnetic field phase diagram at the
superconductor-insulator transition in 2D / N. Markovic, C. Christiansen,
A. M. Goldman // Physical Review Letters.— 1998.— Vol. 81.—
Pp. 5217-20.
[88] Martin, P. C. Probleme к η corps (many-body physics) / P. C. Martin //
Measurements and correlation functions. — New York: Gordon and Breach,
1968.-Pp. 37-136.
[89] Mathews7 J. Mathematical methods of physics / J. Mathews,
R. L. Walker. — Redwood City, CA: Addison-Wesley, 1964.
[90] McGath, G. The self-avoiding random walk. — . — 1996. — BU Center for
Polymer Studies.
[91] A mean-field spin glass with short-range interactions / J. T. Chayes,
L. Chayes, J. P. Sethna, D. J. Thouless // Communications in Mathematical
Physics. - 1986. - Vol. 106. - P. 41.
[92] Melting a copper cluster: Critical-droplet theory / О. Н. Nielsen,
J. P. Sethna, P. Stoltze et al. // Europhysics Letters.— 1994.— Vol. 26.—
Pp. 51-6.
[93] Mermin, N. D. The topological theory of defects in ordered media /
N. D. Mermin // Reviews of Modern Physics. — 1979. — Vol. 51. — Pp. 591-
648.
[94] Mezard, M. Analytic and algorithmic solution of random satisfiability
problems / M. Mezard, G. Parisi, R. Zeccina // Science.— 2002.— Vol.
297. - P. 812.
[95] Nemenman, I. Entropy and inference, revisited / I. Nemenman, F. Shafee,
W. Bialek // Advances in neural information processing systems.—
Cambridge: MIT Press, 2002. — Pp. 471-8.
[96] Newman, M. E. J. Models of the small world / Μ. Ε. J. Newman // Journal
of Statistical Physics. — 2000. — Vol. 101. — Pp. 819-41.
598 Литература
Newman, Μ. Ε. J. Scientific collaboration networks. II. Shortest paths,
weighted networks, and centrality / Μ. Ε. J. Newman // Physical Review
E. - 2001. - Vol. 64. - P. 016132.
Newman, Μ. Ε. J. Power laws, Pareto distributions and Zipf's law /
M. E. J. Newman // Contemporary Physics. — 2005. — Vol. 46. — Pp. 323-
51.— arXiv.org/.
Newman, Μ. Ε. J. Monte Carlo methods in statistical physics /
M. E. J. Newman, G. T. Barkema. — Oxford University Press, 1999.
Newman, Μ. Ε. J. Renormalization-group analysis of the small-world
network model / M. E. J. Newman, D. J. Watts // Physics Letters Α.—
1999. - Vol. 263. - Pp. 341-6.
Nova. Trillion dollar bet.— www.pbs.org/wgbh/nova. — 2000.
Numerical recipes in C++ [C, Fortran, ...], the art of scientific computing,
2nd ed. / W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery. -
Cambridge University Press, 2002.
Observation of Bose-Einstein condensation in a dilute atomic vapor /
M. H. Anderson, J. R. Ensher, M. R. Matthews et al. // Science. — 1995. —
Vol. 269. - P. 198. - .
Obtaining Ising-like expansions for binary alloys from first principles /
A. Zunger, L. G. Wang, G. L. W. Hart, M. Sanatai // Modelling and
Simulation in Materials Science and Engineering. — 2002. — Vol. 10. —
Pp. 685-706.
Onsager, L. Motion of ions—principles and concepts / L. Onsager //
Science. - 1969. - Vol. 166 (3911). - P. 1359. - (1968 Nobel Prize lecture).
Parisi, G. Statistical field theory / G. Parisi. — Redding, MA: Perseus, 1988.
Penrose, R. The emperor's new mind / R. Penrose. — Oxford University
Press, 1989. — (No endorsement of his more speculative ideas implied).
Poon, L. Cat map. — University of Maryland Chaos Group, .
Rajagopal, K. Enforced electrical neutrality of the color-flavor locked phase /
K. Rajagopal, F. Wilczek // Physical Review Letters.— 2001.— Vol. 86.—
Pp. 3492-5.
Литература
599
[ПО] Ralls, К. S. Microscopic study of 1/f noise in metal nanobridges /
K. S. Ralls, R. A. Buhrman // Physical Review В.- 1991.- Vol. 44. -
Pp. 5800-17.
[Ill] Ralls, K. S. Individual-defect electromigration in metal nanobridges /
K. S. Ralls, D. С Ralph, R. A. Buhrman // Physical Review B. — 1989. —
Vol. 40.-Pp. 11561-70.
[112] Reversible unfolding of single RNA molecules by mechanical force /
J. Liphardt, B. Onoa, S. B. Smith et al. // Science.- 2001.- Vol. 292
(5517).-Pp. 733-7.
[113] Rutenberg, A. D. Anisotropic coarsening: Grain shapes and nonuniversal
persistence exponents / A. D. Rutenberg, B. P. Vollmayr-Lee // Physical
Review Letters. — 1999. — Vol. 83. — Pp. 3772-5.
[114] Sander, E. Marlowe the cat starring in the Arnol'd cat map movie.— .
[115] Scaling range and cutoffs in empirical fractals / O. Malcai, D. A. Lidar,
O. Biham, D. Avnir // Physical Review E.- 1997.- Vol. 56.- Pp. 2817-
28.
[116] Schroeder, D. V. Thermal physics / D. V. Schroeder. — San Francisco:
Addison-Wesley Longman, 2000.
[117] Schwarz, U. T. Experimental generation and observation of intrinsic
localized spin wave modes in an antiferromagnet / U. T. Schwarz,
L. Q. English, A. J. Sievers // Physical Review Letters. — 1999. — Vol. 83. —
P. 223.
[118] Selman, B. Local search strategies for satisfiability testing / B. Selman,
H. Krautz, B. Cohen // Dimacs Series in Discrete Mathematics and
Theoretical Computer Science. — 1996. — Vol. 26. — Pp. 521-32.
[119] Series expansions without diagrams / G. Bhanot, M. Creutz, I. Horvath
et al. // Physical Review E. — 1994. - Vol. 49. — Pp. 2445-53.
[120] Sethna, J. P. Frustration, curvature, and defect lines in metallic glasses
and cholesteric blue phases / J. P. Sethna // Physical Review B. — 1985. —
Vol. 31.-P. 6278.
[121] Sethna, J. P. Order parameters, broken symmetry, and topology /
J. P. Sethna // 1991 lectures in complex systems: the proceedings of the
600
Литература
у
1991 complex systems summer school, Santa Fe, New Mexico. — Addison-
Wesley, 1992. — Vol. XV.— P. 243.— www.lassp.cornell.edu.
[122] Sethna, J. P. Equilibrium crystal shapes.— www.lassp.Cornell. — 1995.
[123] Sethna, J. P. Jupiter! The three-body problem. — www.physics. — 1996.
[124] Sethna, J. P. Cracks and elastic theory.— www.lassp.cornell.edu. — 1997.
[125] Sethna, J. P. Quantum electrodynamics has zero radius of convergence. —
. - 1997.
[126] Sethna, J. P. Stirling's formula for n!— www.lassp.cornell.edu. — 1997.
[127] Sethna, J. P. What is coarsening?— www.lassp.cornell.edu. — 1997.
[128] Sethna, J. P. What is the radius of convergence? — www.lassp.— 1997.
[129] Sethna, J. P. Entropy, order parameters, and complexity web site. — . —
2004.
[130] Sethna, J. P. Hysteresis and avalanches.— www.lassp.cornell.edu. — 1996.
[131] Sethna, J. P. Crackling noise / J. P. Sethna, K. A. Dahmen, С R. Myers //
Nature. - 2001. - Vol. 410. - P. 242.
[132] Sethna, J. P. Entropy, Order Parameters, and Complexity computer
exercises: Hints and software. — www.physics. — 2004.
[133] Sethna, J. P. Scaling theory for the glass transition / J. P. Sethna,
J. D. Shore, M. Huang // Physical Review B. - 1991. - Vol. 44. - P. 4943. -
Paper based on discussions with Daniel Fisher, see erratum Physical Review
В 47, 14661 (1993).
[134] Shannon, С. Е. A mathematical theory of communication /
С Ε. Shannon // The Bell System Technical Journal. — 1948. — Vol. 27. —
Pp. 379-423.
[135] Shore, J. D. Logarithmically slow domain growth in nonrandom frustrated
systems: Ising models with competing interactions / J. D. Shore, M. Holzer,
J. P. Sethna // Physical Review B. - 1992. - Vol. 46. - Pp. 11376-404.
[136] Sievers, A. J. Intrinsic localized modes in anharmonic crystals /
A. J. Sievers, S. Takeno // Physical Review Letters.— 1988.— Vol. 61.—
Pp. 970-3.
Литература
601
[137] Siggia, Ε. D. Late stages of spinodal decomposition in binary mixtures /
E. D. Siggia // Physical Review A. - 1979. - Vol. 20. - P. 595.
[138] Statistical mechanics of a discrete nonlinear system / К. О. Rasmussen,
T. Cretegny, P. G. Kevrekidis, N. Gronbech-Jensen // Physical Review
Letters. - 2000. - Vol. 84. - P. 3740.
[139] Swendsen, R. H. Nonuniversal critical dynamics in Monte Carlo
simulations / R. H. Swendsen, J.-S. Wang // Physical Review Letters.—
1987.-Vol. 58.-P. 86.
[140] Tang, L.-H. Finite-size and boundary effects on the I-V characteristics of
two-dimensional superconducting networks / L.-H. Tang, Q.-H. Chen //
Physical Review B. - 2003. - Vol. 67. - P. 024508.
[141] Team, N. S. Wilkinson microwave anisotropy probe. —
map.gsfc.nasa.gov/index.html.— 2004.— Note the wave animations
at map.gsfc.nasa.gov/m_ or/mr_ media2.html.
[142] Thomas, S. B. Studies on glass VI. some specific heat data on boron
trioxide / S. B. Thomas, G. S. Parks // Journal of Physical Chemistry. —
1931. - Vol. 35. - Pp. 2091-102.
[143] Toner, J. Long-range order in a two-dimensional dynamical XY model: How
birds fly together / J. Toner, Y. Tu // Physical Review Letters.— 1995.—
Vol. 75. - Pp. 4326-9.
[144] Trefethen, L. N. How many shuffles to randomize a deck of cards? /
L. N. Trefethen, L. M. Trefethen // Proceedings of the Royal Society of
London A. - 2000. - Vol. 456. - Pp. 2561-8.
[145] Watts, D. J. Collective dynamics of 'small-world' networks / D. J. Watts,
S. H. Strogatz // Nature. - 1998. - Vol. 393. - Pp. 440-42.
[146] Weinberg, S. The first three minutes / S. Weinberg.— New York: Basic
Books (Perseus), 1977.
[147] Wells, H. G. The time machine / H. G. Wells.— several places: Online,
1895.
[148] Wigner, E. The unreasonable effectiveness of mathematics in the
natural sciences / E. Wigner // Communications in Pure and Applied
Mathematics. — 1960. — Vol. 13. — Pp. 1-14. — www.dartmouth.edu/ mate.
602 Литература
149] Wolff, U. Collective Monte Carlo updating for spin systems / U. Wolff //
Physical Review Letters. — 1989. — Vol. 62. — P. 361.
150] Yeomans, J. M. Statistical mechanics of phase transitions /
J. M. Yeomans.— Oxford University Press, 1992.
151] Zinn-Justin, J. Quantum field theory and critical phenomena (3rd edition) /
J. Zinn-Justin. — Oxford University Press, 1996.
152] В.И. Арнольд B.C. Афраймович, Ю. И. Л. Ш. Теория бифуркаций /
Ю. И. Л. Ш. В.И. Арнольд, B.C. Афраймович.— М.: Физматлит, 1980.
153] Жен, П. д. Идеи скейлинга в физике полимеров / П. д. Жен.— М.:
Мир, 1982.
154] Ма, Ш. Современная теория критических явлений / Ш. Ма. — М.: Мир,
1980.
155] Хохлов, А. Г. и. А. Статистическая физика макромолекул / А. Г.
и. А. Хохлов.— М.: Наука, 1989.
Предметный
А
Адиабатический процесс, 99
Алгоритм
Верле, 119
Вольфа, 333, 335
Дэвиса—Патнема, 356
Метрополиса, 332
термостата, 332
Алиасинг, 585
Аллостерические взаимодействия,
251
Аномалия Шоттки, 298
Ансамбль Гиббса, 220
Антиферромагнетик, 310
Апельсиновая корка, 530
Аппроксимация Паде, 324
Атмосфера, 49, 108
Аттрактор, 127, 137, 138, 194, 526, 544
Б
Белый карлик, 305
Белый шум, 418, 419, 586
Бинарный сплав, 311
Биномиальное распределение, 85, 114
Бифуркация, 526, 533, 547
седловая, 535
типа «вилка», 534
транскритическая, 535
Хопфа, 535
Блуждания Леви, 56
указатель
Бозе-конденсация, 280, 282, 283, 299,
300, 323
Бозоны, 265, 269, 271, 276, 287, 295,
296
Большая каноническая
статистическая сумма, 214
Большой
канонический ансамбль, 213, 216
термодинамический потенциал,
214, 221
В
Вариационная производная, 230, 416,
456
Вектор Бюргерса, 374
Вечный двигатель, 150
Вириальное разложение, 323
Волатильность, 69
Волна кручения, 371
Волновое уравнение, 369, 397
Восприимчивость, 423, 459
статическая, 427
Г
Газ твердых сфер, ПО
Гамильтониан, 82, 124
модели Изинга, 309
спина, 291
Гармонический осциллятор, 287
квантовый, 263
604
Предметный указатель
классический, 211
Гемоглобин, 251
Гиперсфера, 87
Гипотеза регрессии Онзагера, 421,
452, 457
Гистерезис, 560
Голдстоуновская мода, 371, 457
Гомотопическая группа, 378
Граф, 27
Гугол и гуголплекс, 107
д
Давление, 96, 99
газа твердых сфер, 111
компьютерное моделирование,
109
Двухатомная молекула, 84
Двухъямный потенциал, 163
Дельта-функция, 19, 82
Демон Максвелла, 160, 177
Дендрит, 479
рост, 496, 499
Детальное равновесие, 279, 320, 331,
345
Детальный баланс, 452
Дефект «ёж», 388
Диаграмма Петри, 337
Диверсификация, 70
Динамическая восприимчивость, 448
Динамические системы, 526
Дисклинация, 384
Дислокация, 373, 486
Дисперсионное соотношение, 289
Диссипативный отклик, 425
Диссипация, 424
Дифракция, 414
Дифференциальная форма, 116, 220
Диффузия, 496
Арнольда, 146
Длина волны де Бройля, 210, 225, 282
Добротность, 458
Доменная стенка, 389
Дробовой шум, 338
Ж
Жидкий кристалл, 359, 365
Жидкость Ферми, 541
Жордановая форма, 318
3
Задача коммивояжера, 354
Закон
Аррениуса, 228, 246
Гутенберга-Рихтера, 504, 519
действующих масс, 224
Кюри, 330
сохранения энергии, 149
Стефана—Больцмана, 294
Закон термодинамики
второй, 150
нулевой, 217
первый, 149, 217
третий, 218, 289
Зародышеобразование, 466, 468, 469,
484, 496
Затухающий осциллятор, 447
Звуковая волна, 369
Зона проводимости, 285
И
Идеальный газ, 84, 103, 210
Излучение
вынужденное, 294, 296
спонтанное, 294, 296
Излучение абсолютно черного тела,
276, 277, 279, 280, 292, 293
Изолированная система, 80
Импульсное пространство, 80
Импульсный шум, 561
Инвариантная мера, 137, 527
Предметный указатель
605
Инверсия симметрии, 399
Инверсная заселенность, 238, 297, 537
Индекс критического замедления, 538
Инстантон, 377, 469
Интегральная формула Коши, 436
Интенсивная величина, 94, 245
Инфляционная модель, 440
Ионный насос, 161
Испарение, 237
К
Калибровочная
инвариантность, 406
симметрия, 370
КАМ-торы, 129
Канонический ансамбль,
квантовый, 260
определение, 204
статистическая сумма, 204
удельная теплоемкость, 206
энтропия, 207
Катализатор, 225
Квазикристалл, 360
Квазичастица, 273, 459
Квантовая статистическая механика,
256
Кельвиновское затухание, 458
Кинетика химических реакций, 336
Конечномерное масштабирование,
558
Контурный интеграл, 387
Конфигурационное пространство, 80
Конъюнкция, 34
Координата реакции, 227
Корреляционная длина, 412
Коэффициенты Эйнштейна, 294, 537
КПД тепловых машин, 150
Критерий Линдеманна, 446
Критическая точка, 246, 313, 481
Критический зародыш, 467
Критическое замедление, 335
Л
Лавина, 348, 506, 517, 560
Лазер, 238, 289, 295, 296, 536
Ламинат, 479, 494
Линейный анализ устойчивости, 499
Линейный отклик, 232, 423
Логическая совместимость, 33
Логическая схема, 178
Логическое выражение, 33, 34
Μ
Магнит, 363
Маргинальная переменная, 542
Марковская система, 316
Мартенсит, 478, 489, 494
Масштабная инвариантность, 41, 509,
515
Матрица плотности, 258, 259, 262
каноническое распределение, 260
приведенная, 402
спиновая, 291
фотонов, 291
Маятник, 117
Мера Юнга, 496
Металлы, 284
Метастабильное состояние, 463-465
Метод Монте-Карло, 314, 332
непрерывный, 338
Метод Эйлера, 118
Механизм Хиггса, 372
Микроволновое реликтовое
излучение, 439
Микроканонический ансамбль, 80,
127, 238
Множители Лагранжа, 242
Модель
Варриджа-Кнопоффа, 504
Гейзенберга, 310
606
Предметный указатель
Изинга, 308, 389, 391, 412, 452,
472, 484, 488, 502, 512, 531,
533, 535, 538
компьютерное моделирование,
327, 332
Поттса, 524
Молекулярный мотор, 57, 239
Момент функции, 44
Мультифрактал, 198
Η
Намагниченность, 363
Нарушение симметрии, 359
Нейтронная звезда, 305
Нематик, 365, 371, 379, 384
Необратимость, 149, 155
Неопределенность, 165, 198
Неравенство Йенсена, 170
Нормальная форма, 535
О
Огрубление масштаба, 473, 510, 548,
552
Определитель Слэтера, 268
Оригами, 489
Осмотическое давление, 99, 160
Отображение
Кот Арнольда, 184
логистическое, 137, 186, 194, 544
Π
Пара дислокаций, 487
Парадокс Гиббса, 159
Парамагнетик, 310
Параметр порядка, 229, 231, 363
Парная корреляционная функция,
443
Паровой двигатель, 149
Перегретая жидкость, 464
Перенормировка, 552
Переохлажденный газ, 464
Перестановка, 266
Переход жидкость—газ, 312
Периодические граничные условия,
60, 276, 367
Перколяция, 73, 501, 507, 556
Персистентная длина, 66
Плазменная частота, 372
Плотность вероятности, 85
Поверхностная диффузия, 476
Поверхностное натяжение, 467
Поверхность Ферми, 285
Подвижность, 48
Показатели Ляпунова, 186
Поле деформаций, 489
Полимер, 42, 66
Полная
дивергенция, 387
производная, 126
Полупроводники, 298
Постоянная Больцмана, 90, 94, 107
Построение Вулффа, 471
Потенциал Леннарда—Джонса, 445
Правило Максвелла, 465, 481
Преобразование
Галилея, 400, 458
Лапласа, 242
Лежандра, 219, 243
Фурье, 50, 414, 424, 565
Принцип
детального баланса, 293
запрета Паули, 268, 275
неопределенности, 582
причинности, 435
Проблема трех тел, 132, 141
Ρ
Равновесие, 79, 148
Равновесная форма кристалла, 471
Размерность Хаусдорфа, 40, 501
Предметный указатель
607
Распределение
Бозе—Эйнштейна, 269, 270
Больцмана, 50, 90, 203, 214, 235
вероятностей, 17
Гаусса, 17, 53, 551, 580
Максвелла, 91, 212
Максвелла—Больцмана, 270, 276
Планка, 294
Пуассона, 114
Ферми—Дирака, 270-272
Реактивный отклик, 425
Реакция
димеризации, 336
термически активируемая, 226
экзотермическая, 226
эндотермическая, 226
Ренормализационная группа, 509,
511, 527, 538, 539, 549, 551,
555
Репрессилятор, 339
Решеточная модель, 308
Решеточный газ, 312
РНК, 340
шпильки, 241
РНК полимераза, 240, 341
С
Свертка, 422, 552, 572
Сверхпроводимость, 539
Сверхпроводник, 371
Сверхтекучая жидкость, 283, 295,
371, 400, 407
Сверхтекучее состояние, 406
Свободная энергия, 96, 201
Гельмгольца, 208, 219, 220
Гиббса, 221, 462
Связная корреляционная функция,
417
Сеть, 27
Сечение Пуанкаре, 129, 145, 186
Симметрия, 359
Симплектическая форма, 125
Симплектический алгоритм, 118
Скейлинг, 521, 532, 538, 559
Скейлинговая функция, 516
Скейлинговый коллапс, 523
Скирмион, 377
Скрытая теплота, 461
Случайное блуждание, 37
компьютерное моделирование, 60
Смешанное состояние, 257, 262
Снежинка, 479, 496
Соотношение
Гиббса—Дюгема, 244
Крамерса—Крёнига, 435, 438, 448
Максвелла, 116
Эйлера, 244, 462
Эйнштейна, 50, 233
Сосуществование фаз, 461, 462, 465
Спектральная функцией, 571
Спин, 449
Спиновая волна, 370
Спинодаль, 465
Среднеквадратичное отклонение, 38
СРТ-преобразование, 155
Статистика, 234, 254
Бозе, Ферми, 265
Максвелла—Больцмана, 105, 273
Статистическая сумма, 204, 208
большая каноническая, 214
Стационарное состояние, 79
Стекло, 134, 161, 528
Стеклование, 162, 529
Стехиометрические коэффициенты,
224
Стехиометрия, 343
Стрела времени, 155
Сфера Ферми, 278, 284
608
Предметный указатель
Τ
Текстура, 377
Телеграфный шум, 241, 242, 343, 449
Температура, 92
отрицательная, 238
Теорема
Байеса, 254
Блоха, 285
КАМ, 132, 141
Коши, 436
Лиувилля, 124, 137, 183
квантовая, 262
Мермина—Вагнера, 372
Нернста, 218, 289
о микроструктуре, 496
о равнораспределении, 50, 91, 212,
277, 280, 456
о спиновой статистике, 265
Фробениуса—Перрона, 319
Теория
возмущений, 322
Гинзбурга—Ландау, 391
гомотопий, 373
среднего поля, 535
Тепловая
машина, 182
смерть Вселенной, 156, 174
Теплопроводность, 65
Термическая волна де Бройля, 106,
229
Термодинамика, 216
законы, 217, 218
Термодинамический
потенциал, 96
предел, 216
Термостат, 95, 201
Ток Джозефсона, 407
Топологический дефект, 373, 379, 384
Топологическое зацепление, 380
Топология, 374
Тор, 367, 374
Траектория пьяницы, 40
Транскрипция, 57, 239, 339
Трансляция, 57, 339
Трение
и флуктуации, 222, 223
Треск, 561
У
Удвоение периода, 546
Удельная теплоемкость, 113, 206
бозонного и фермионного газов,
323
Ультрафиолетовая катастрофа, 278
Универсальность, 41, 506, 507, 509
Универсальный критический индекс,
44
Уравнение
Ван-дер-Ваальса, 481
Гамильтона, 101, 124
диффузии, 44, 187, 233, 419, 571
решение, 50
Клаузиуса—Клапейрона, 245
Ланжевена, 453
Михаэлиса—Ментен, 249
непрерывности, 47, 126
состояния, 104
Хилла, 249, 342
Условная вероятность, 171
Устойчивое многообразие, 513
Φ
Фаза, 322
Фазовая диаграмма, 245, 313, 462
Фазовое пространство, 80
Фазовое расслоение, 472, 488, 496, 533
Фазовый переход, 246, 312, 501
второго рода, 464
квантовый, 525
Предметный указатель
609
первого рода, 464
скачкообразный, 460
Фермент, 225
Ферми-газ, 284, 542
Ферми-жидкость, 273
Фермионы, 265, 271, 284
Ферромагнетик, 310
Флуктуации
трение, 222, 223
числа частиц, 85, 114, 115, 215
энергии, 112, 113, 206
Флуктуационно-диссипационная
теорема, 431, 459
Флуктуационно-диссипационное
соотношение, 113, 429, 430
Фонон, 287, 298, 369
Формула
Планка, 279, 292
Рэлея—Джинса, 279, 280
Стирлинга, 20, 85, 106, 115, 159,
211
Форм-фактор, 414
Фотон, 56, 287, 291
Фрактал, 41, 501
Фрактальная размерность, 40, 195
Фрустрация, 528
Функционал, 229
Функция
аналитическая, 436
Грина, 52
корреляционная, 409, 571
спектральная, 571
Хевисайда, 82, 452, 587
X
Хаос, 81, 186, 526, 544
Хемотаксис, 56
Химическая реакция, 223
Химический потенциал, 96, 98, 2
231, 245, 270, 284
Химическое равновесие, 223
ц
Центральная предельная теорема, 54,
62, 551
Цепи Маркова, 315
Цепное соотношение Эйлера, 116
Цикл Карно, 149, 151, 182
Ч
Частичный след, 215, 252
Черная дыра, 180
Численное решение
дифференциальных уравнений, 118
Число
Авогадро, 85
Лиувилля, 147
намотки, 384
Фейгенбаума, 548
Чистое состояние, 259
Ш
Шум Баркгаузена, 345
Э
Экстенсивная величина, 94, 172
Экстенсивность, 244
Электродвигатель, 149
Элементарное возбуждение, 368
Энергия
нулевых колебаний, 288
Ферми, 284
Энионы, 265
Энтальпия, 221
Энтропия, 94, 96, 148, 154, 207, 289
идеального газа, 103, 106, 211
информационная, 192
квантовая, 261, 291
мера неопределенности, 165
неравновесная, 166, 198
нулевая, 290
610
Предметный указатель
резиновой ленты, 189
смешения, 157
стекол, 160, 187
Шеннона, 148, 167, 193
Эргодичность, 128, 141, 319
Эффект
бабочки, 186
Мейснера, 372