Автор: Лапчик М.П.
Теги: инструменты, приборы и методы астрономических наблюдений, измерений и анализа математика
ISBN: 5-7695-1339-Х
Год: 2004
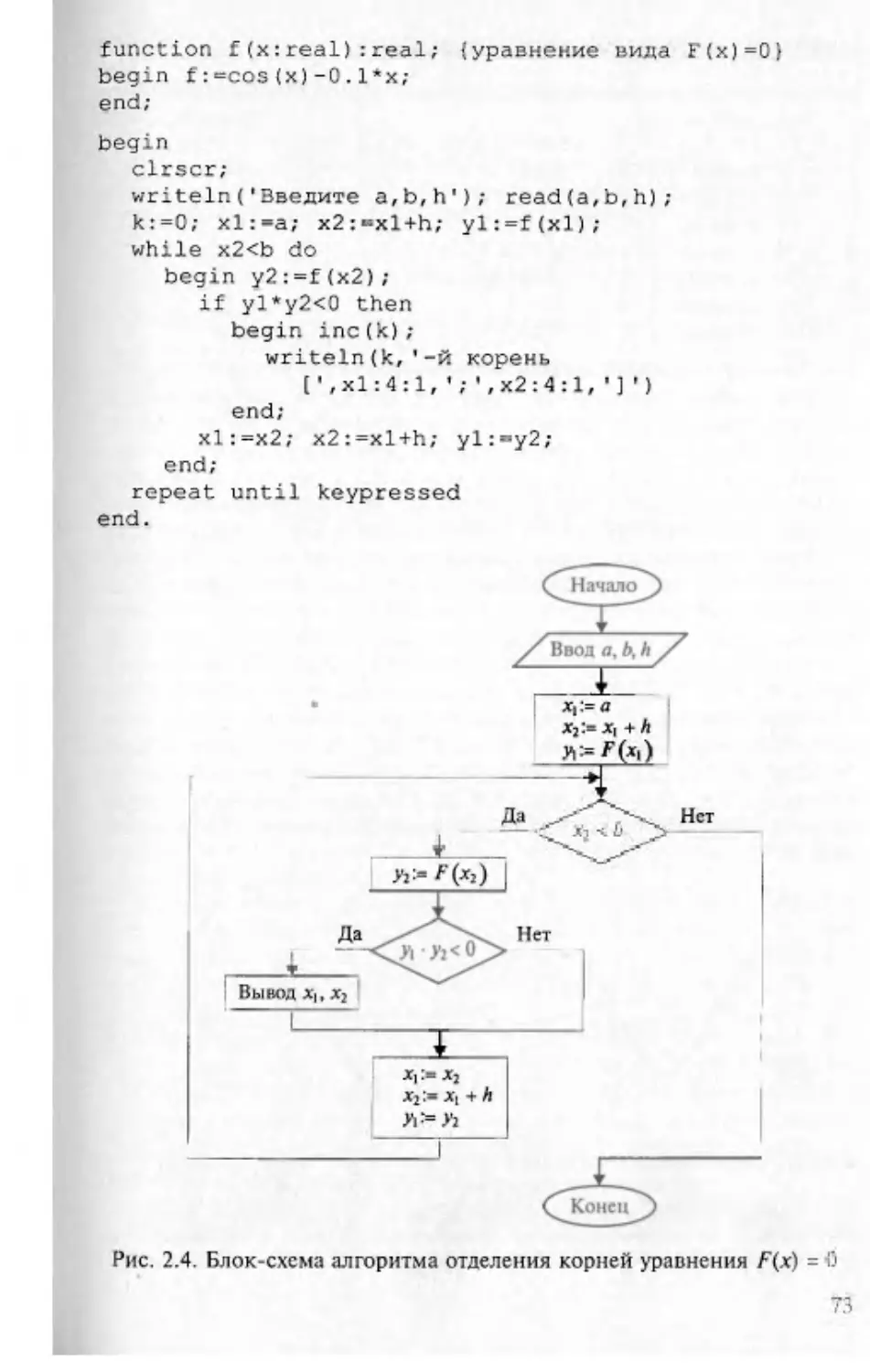
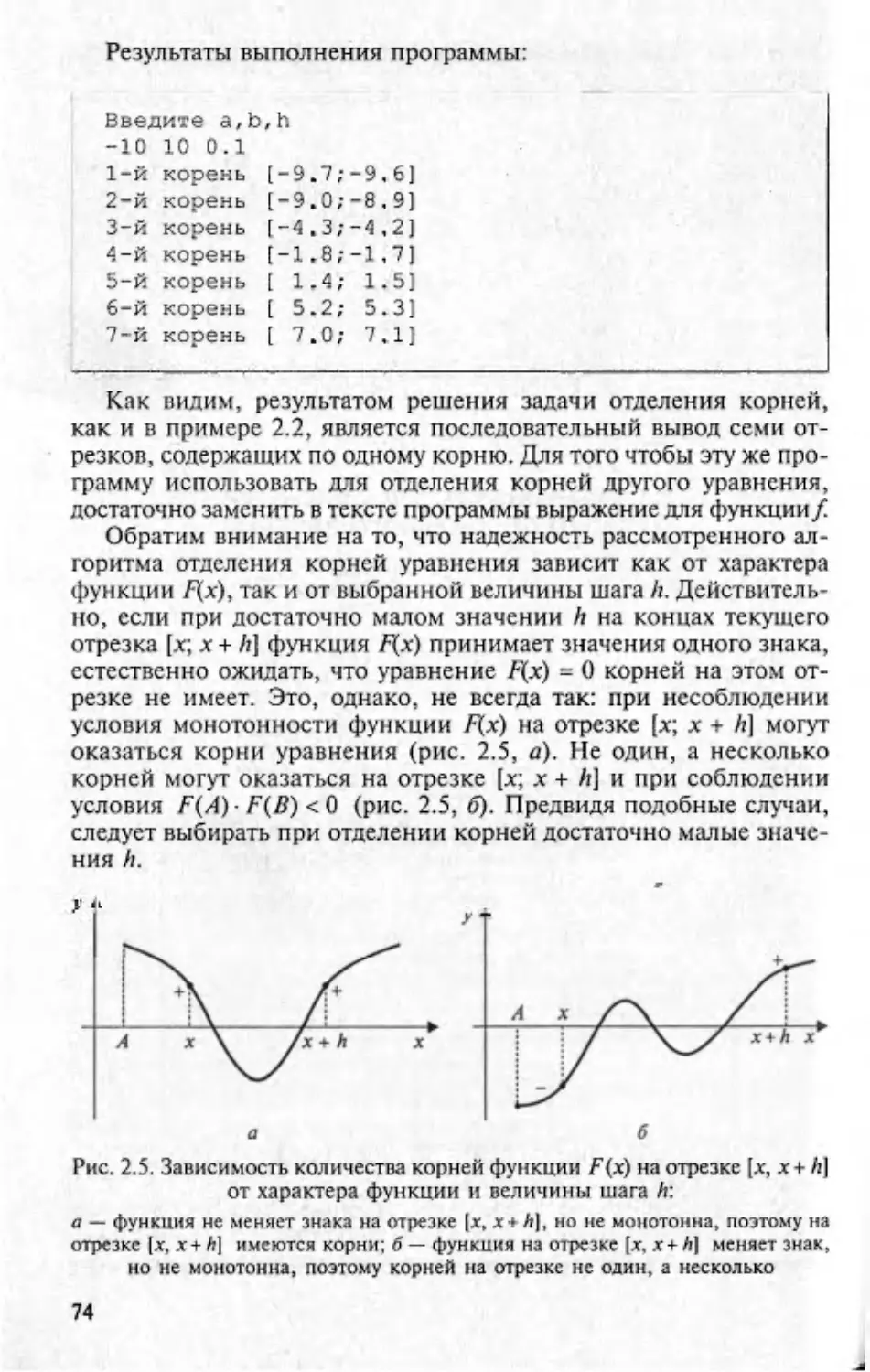
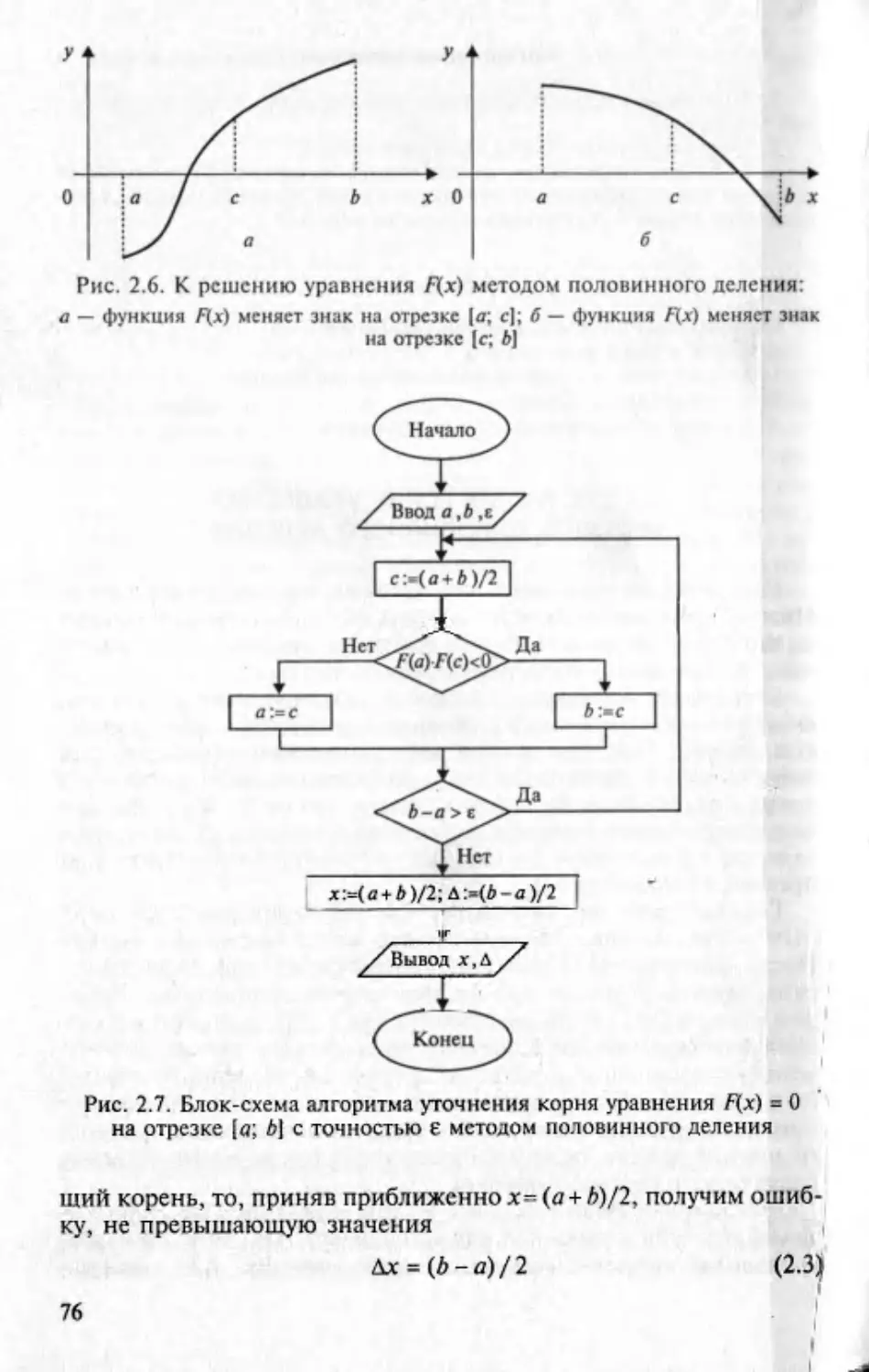
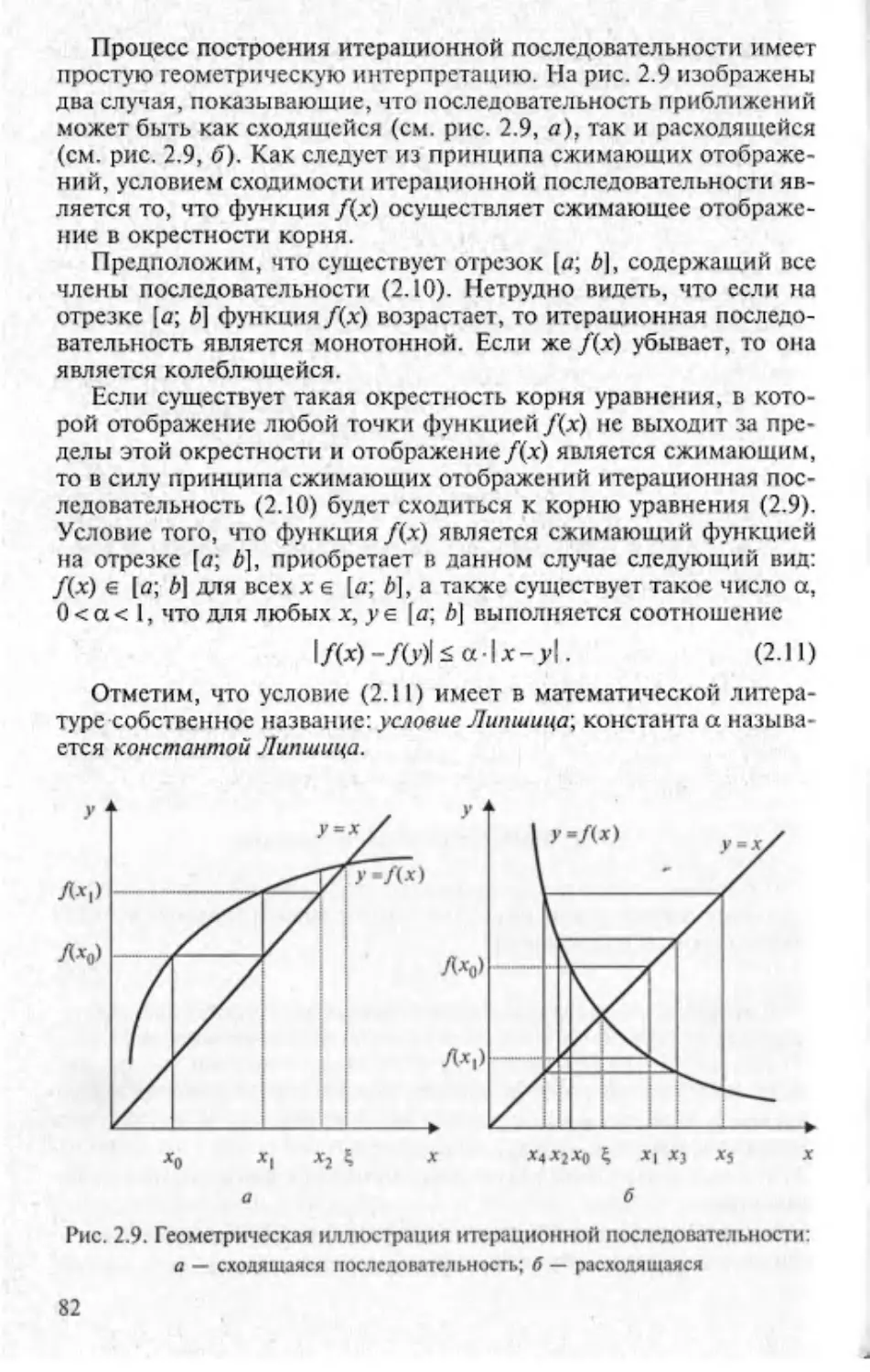
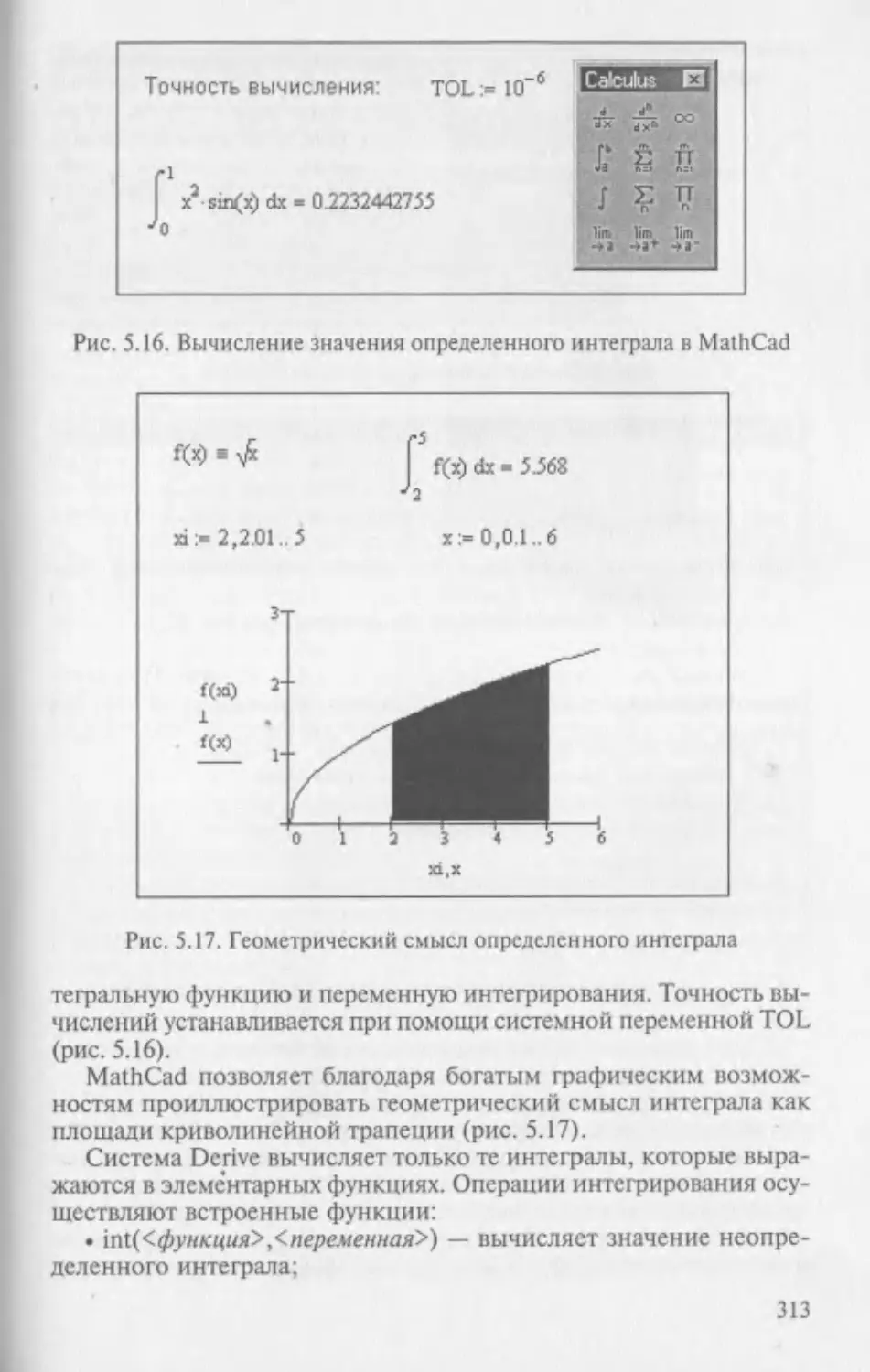
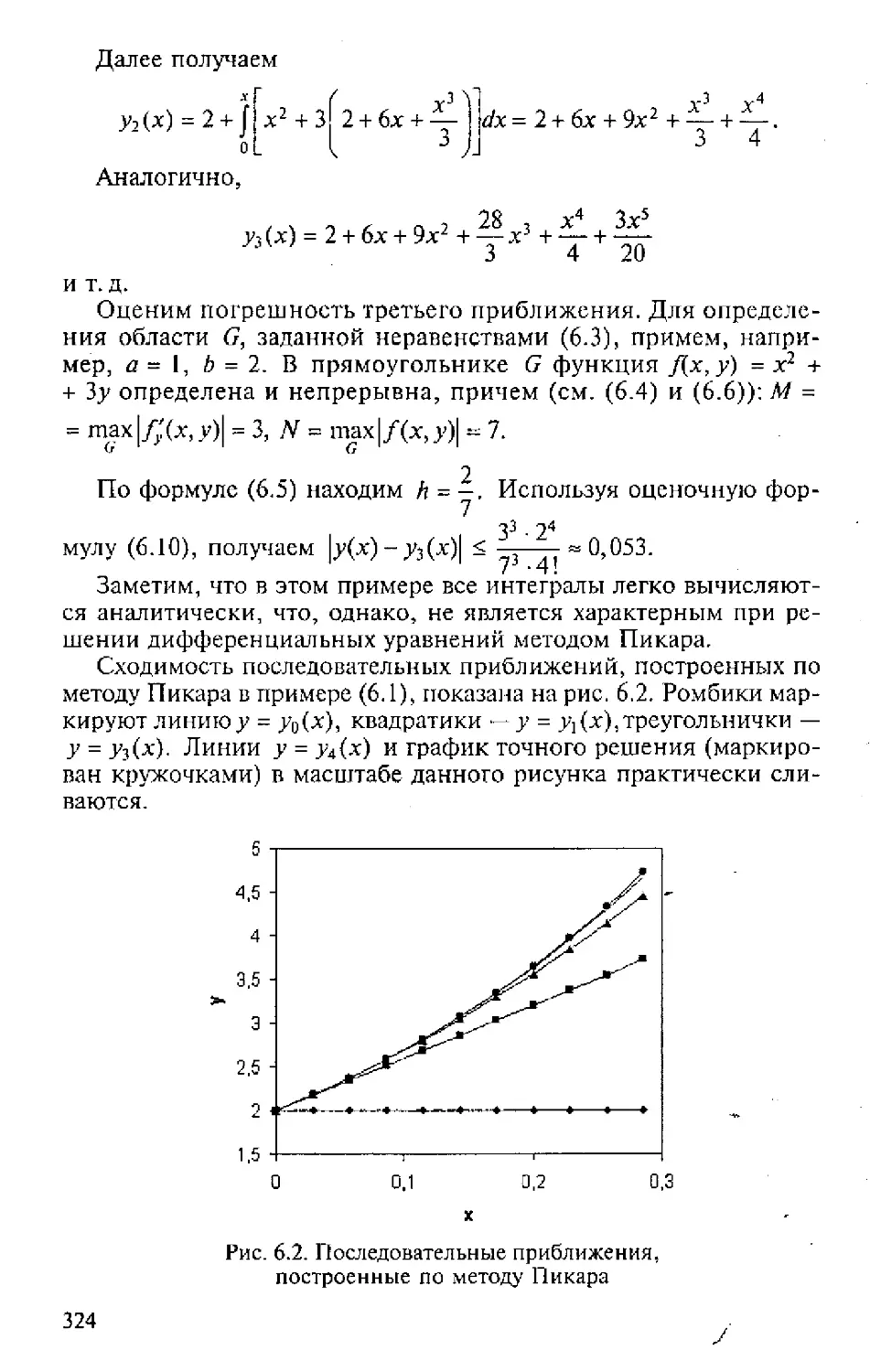
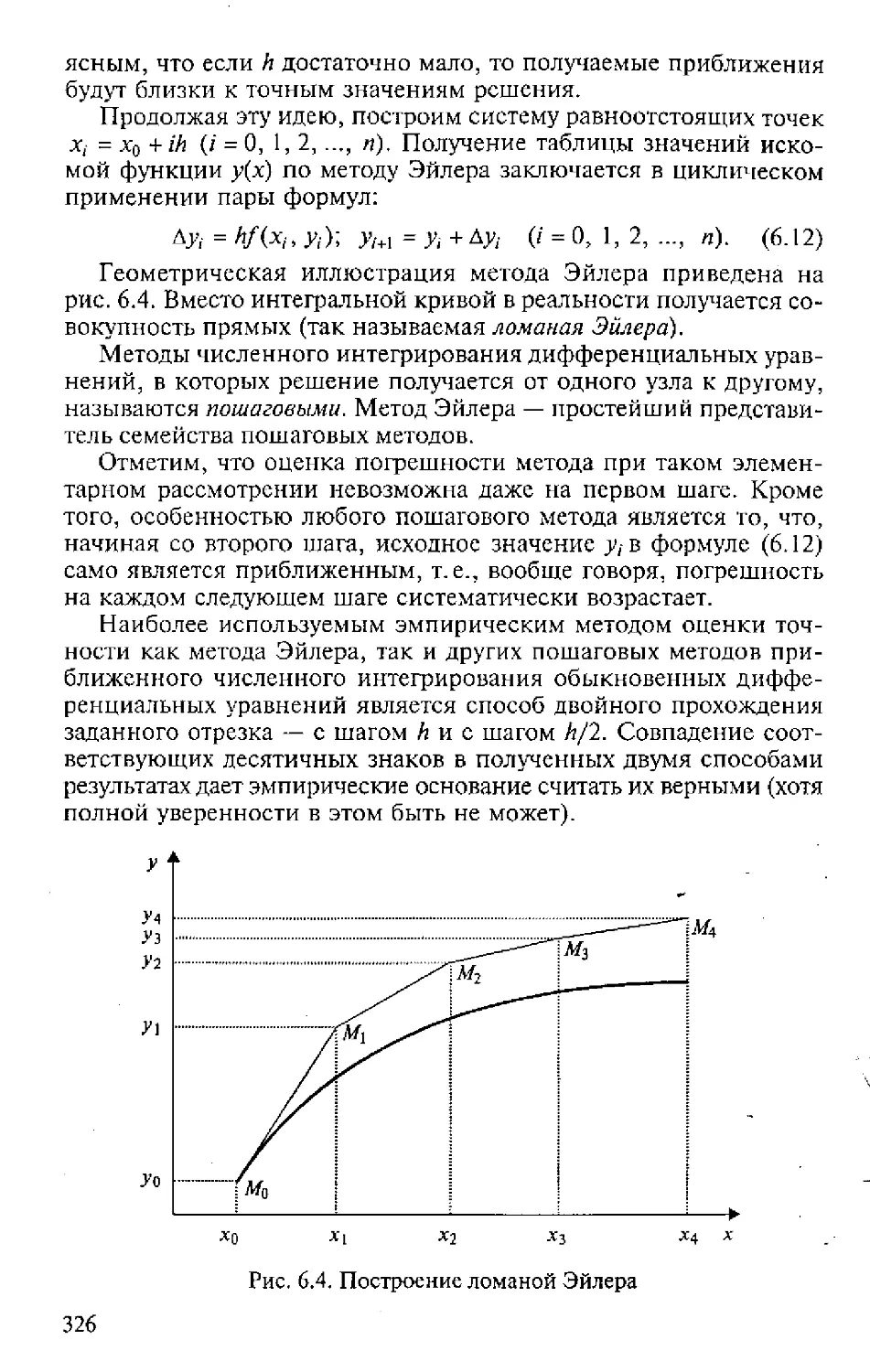
Текст
УДК 520.88
ББК 22.193я73
Л24
Рецензенты:
д-р физ.-мат. наук, проф. Московского
педагогического государственного университета В.А.Горелик;
директор института математики, физики и информатики
при Красноярском государственном педагогическом университете,
д-р пед. наук, профессор Н.И.Пак.
Лапчик М.П.
Л24 Численные методы: Учеб, пособие для студ. вузов /
М.П.Лапчик, М.И.Рагулина, Е.К.Хеннер; Подред. М.П.Лап-
чика. - М.: Издательский центр «Академия», 2004. — 384 с.
ISBN 5-7695-1339-Х
В учебном пособии в сжатом виде и на доступном уровне излагаются
основные теоретические сведения о численных методах решения приклад-
ных задач, рассматриваются вопросы применения инструментальных средств.
Для студентов факультета информатики педагогических вузов, изуча-
ющих систематический курс «Численные методы». Будет полезно студен-
там математических факультетов педагогических вузов, изучающим курс
«Информационные технологии в математике».
УДК 520.88
ББК 22.193я73
Учебное издание
Лапчик Михаил Павлович, Рагулина Марина Ивановна,
Хеннер Евгений Карлович
Численные методы
Учебное пособие
Редакторы Е. Ф. Алферова, Н. С.Лепина-Лавринович
Технический редактор И. И. Горбачева
Компьютерная верстка: Н. В. Протасова
Корректоры Л. А. Котова, Н. С. Потемкина
Изд. № A-749-I. Подписано в печать 12.04.2004. Формат 60х90/16.
Гарнитура «Таймс». Бумага тип. № 2. Печать офсетная. Усл. печ. л. 24,0.
Тираж 5100 экз. Заказ №13086.
Лицензия ИД № 02025 от 13.06.2000. Издательский центр «Академия».
Санитарно-эпидемиологическое заключение № 77.99.02.953.Д.003903.06.03 от 05.06.2003.
117342, Москва, ул. Бутлерова, 17-Б, к. 223. Тел./факс: (095)330-1092, 334-8337.
Отпечатано на Саратовском полиграфическом комбинате.
410004, г. Саратов, ул. Чернышевского, 59.
ISBN 5-7695-1339-Х
© Лапчик М.П., Рагулина М.И., Хеннер Е.К., 2004
© Издательский центр «Академия», 2004
ПРЕДИСЛОВИЕ
Информационные и коммуникационные технологии решитель-
но вторгаются в научно-практическую и образовательную деятель-
ность. Стремительно повышаются требования к уровню подготов-
ки в этой сфере специалистов различных областей. В этой связи
изменяется школьная программа, во все большей степени отра-
жающая прикладной, практический (или, как говорят информа-
тики, пользовательский) подход к применению знаний. Возрас-
тает роль учителей, и прежде всего учителей информатики и ма-
тематики. Одной из важнейших дисциплин профессиональной
подготовки будущего учителя становится вычислительная мате-
матика, которая развивает идеи численного решения задач, воз-
никающих в процессе компьютерного математического модели-
рования реальных явлений в различных предметных сферах.
Данное пособие составлено в соответствии с требованиями
действующего государственного стандарта подготовки учителей по
специальности 030100 «Информатика», что и определяет его со-
держание и структуру. Содержание книги охватывает следующие
разделы: основные пегнятия, связанные с приближенными значе-
ниями величин, и методы оценки вычислительных ошибок (в том
числе и программным способом); методы численного решения
алгебраических и трансцендентных уравнений, а также систем
линейных и нелинейных уравнений; различные способы аппрок-
симации функций; задачи численного дифференцирования и чис-
ленного интегрирования; методы численного решения обыкно-
венных дифференциальных уравнений и краткие сведения о чис-
ленных методах решения уравнений в частных производных. Гла-
вы заканчиваются заданиями к соответствующим лабораторным
работам, каждая из которых снабжена 20 вариантами индивиду-
альных заданий и краткими указаниями к их выполнению.
Характерной особенностью книги является систематическое
рассмотрение вопросов реализации математических методов на
компьютере. Практически все методы проиллюстрированы блок-
схемами вычислительных алгоритмов, для многих из них при-
ведены примеры программ на языке программирования Turbo
Pascal. Наряду с этим, в каждой главе пособия особо рассмат-
риваются примеры применения программных математических
пакетов, которые в настоящее время широко используются в
3
практических вычислениях: Excel, MatLab, MathCad, Derive,
Maple, Mathematica.
При изложении материала авторами учтен опыт чтения лек-
ций и проведения лабораторных работ по курсу «Численные ме-
тоды» для студентов факультетов информатики и математики пе-
дагогических вузов в условиях использования современного про-
граммно-технического обеспечения.
Основное внимание в пособии уделено объяснениям того, как
численные методы работают, и ограничениям при их примене-
нии в связи с особенностями машинной арифметики. Для этого
требовалось найти равновесие между изложением теории и ана-
лизом ошибок и желанием сделать книгу удобочитаемой. Отсю-
да — отсутствие боязни показаться примитивными при рассмот-
рении простых примеров.
Авторы оставляют преподавателям возможность самим опреде-
лять меру полезности «ручных» вычислений. Короткие численные
упражнения можно выполнить с помощью калькулятора, а более
Длинные - с помощью программ для персональных компьютеров
(ПК) или математических инструментов.
Математические обоснования каждого метода изложены с ис-
пользованием элементарных сведений из алгебры и математичес-
кого анализа и должны быть понятны студентам, хотя и не все
обоснования удалось поместить в книгу (здесь уместно напомнить,
что студенты-информатики педагогических вузов не столько изу-
чают фундаментальную математику, сколько знакомятся с ней на
прикладном, пользовательском уровне). В то же время практиче-
ски по всем темам сделаны ссылки на источники более детальных
теоретико-математических сведений (для желающих докопаться
До сути).
Овладению численными методами будет способствовать доста-
точное число подробно рассмотренных примеров, а также упражне-
ний для самостоятельной работы. Нередко различные методы и ал-
горитмы иллюстрируются на одних и тех же примерах. Это позволя-
ет сопоставлять полученные результаты и комментировать вопросы
точности. При этом широко применяются эмпирические (или по-
луэм лирические) подходы к оценке точности численного решения.
Перед авторами стоял вопрос — помещать или не помещать
компьютерные программы в книгу для студентов-информатиков?
Анализ и/или составление программ (и в примерах, и, особенно,
в упражнениях) дает возможность студентам совершенствовать свое
мастерство в программировании. Поэтому предоставление возмож-
ности разбираться в готовых программах, а иногда и составлять
программы самостоятельно (для реализации численных методов)
дает дополнительный стимул, с одной стороны, лучше понять
математику на основе алгоритмики, а с другой — применить тех-
нологию (пакеты).
4
Если содержание или количество учебных заданий, помещен-
ных в лабораторный практикум, покажется избыточным, то пре-
подаватели (кафедра) выберут столько заданий, сколько нужно,
причем именно те, которые возможно выполнить на имеющихся
в распоряжении студентов программно-технических средствах. Ав-
торы приветствуют работу с математическими инструментами, но
только после того, когда соответствующий математический метод
становится понятным. Для читателей, не владеющих пакетами
программ, наряду с примерами рассмотрения использования па-
кетов применительно к конкретным задачам и методам (что дела-
ется в каждой главе) в конце книги приведено приложение, в
котором даны основные сведения о пакетах — хотя бы на уровне
описания назначения и особенностей интерфейса.
Учебное пособие, ориентированное на студентов-информати-
ков педагогических вузов, может быть полезно всем, кто изучает
и применяет численные методы решения математических задач с
помощью ЭВМ.
Авторы в равной мере ответственны за все разделы книги; в то
же время, если рассматривать две основные составляющие учеб-
ного пособия — математику и программные средства, то для
Е.К.Хеннера при неизменном интересе к программам для компь-
ютера приоритетом была все-таки математика, а для М. И. Рагу-
линой — программы и пакетное математическое обеспечение.
М. П.Лапчик принимал участие в подготовке всех разделов кни-
ги, а также осуществлял ее общее редактирование.
ГЛАВА 1
МЕТОДЫ ОЦЕНКИ ОШИБОК ВЫЧИСЛЕНИЙ
1.1. ЭТАПЫ РЕШЕНИЯ ПРИКЛАДНОЙ ЗАДАЧИ
И КЛАССИФИКАЦИЯ ОШИБОК
Анализ ошибок (или, как говорят чаше, погрешностей) явля-
ется неотъемлемой частью процесса решения прикладной задачи.
Часть этих погрешностей связана с вычислениями, которые в наше
время производятся на ЭВМ: в простейших случаях — на микро-
калькуляторах (МК), а в достаточно сложных — на программиру-
емых ЭВМ (компьютерах). С увеличением скорости производства
вычислений и с вовлечением в счетный процесс чисел с боль-
шим количеством значащих цифр, как это делается в ЭВМ, по-
требность в оценке фактической точности результата лишь возра-
стает. При этом следует правильно рассматривать сам термин
«ошибка», который в данном случае выражает объективно неиз-
бежную погрешность, сопровождающую процесс решения зада-
чи, начиная с измерения исходных значений. «Ошибка» в этом
понимании нс есть что-то неправильное, она нс возникает ис-
ключительно в результате промахов вычислителя; от этих ошибок
нельзя избавиться только путем усиления внимания к процессу
измерений и вычислений. Задача анализа ошибок сводится, по
существу, к отысканию их надежных границ и к соблюдению ус-
ловий, обеспечивающих их минимальное распространение.
Возникновение, накопление и распространение ошибок про-
ходят через все стадии решения прикладной задачи, начиная с
получения значений исходных данных. В достаточно общем случае
процесс решения задач с использованием ЭВМ состоит из следу-
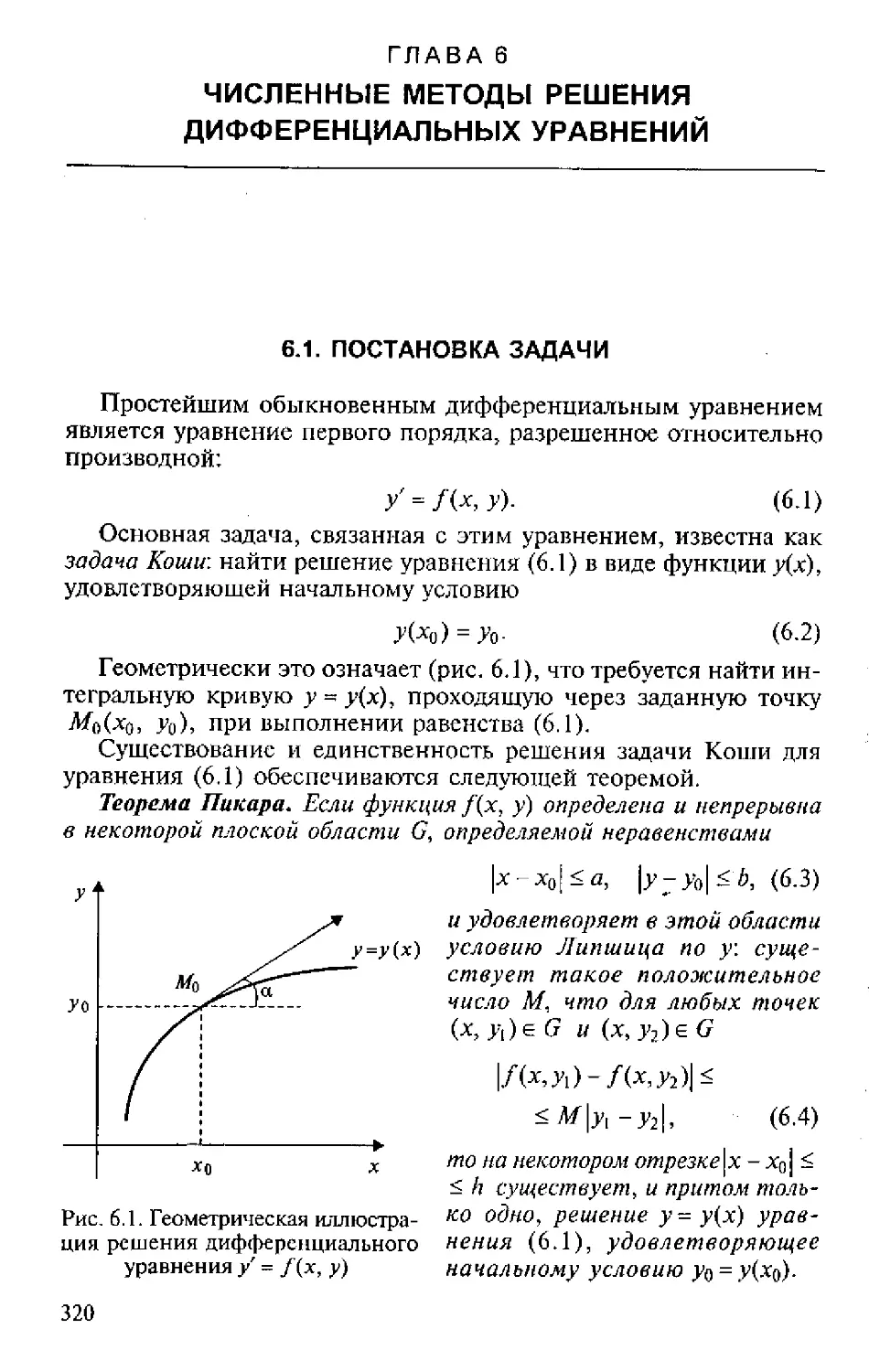
ющих этапов (рис. 1.1):
1) постановка задачи и построение математической модели
(этап моделирования);
2) выбор метода и разработка алгоритма (этап алгоритмиза-
ции);
3) запись алгоритма на языке, понятном ЭВМ (этап програм-
мирования);
4) отладка и исполнение программы на ЭВМ (этап реализа-
ции);
5) анализ полученных результатов (этап интерпретации).
6
Рассмотрим кратко содержание перечисленных этапов реше-
ния прикладной задачи и характер возникающих при этом оши-
бок.
Фабула практических задач изначально связана не с идеальны-
ми, а с реальными объектами — производственными процессами
и явлениями природы, физическими закономерностями, эконо-
мическими отношениями и т.п. По этой причине решение задачи
обычно начинается с описания исходных данных и целей на язы-
ке строго определенных математических понятий. Точную форму-
лировку условий и целей решения называют математической по-
становкой задачи. Выделяя наиболее существенные свойства ре-
ального объекта, исследователь описывает их с помощью матема-
тических соотношений. Этот этап называют построением матема-
тической модели, или моделированием.
Построение математической модели является наиболее слож-
ным и ответственным этапом решения. Если выбранная матема-
тическая модель слишком грубо отражает изучаемое явление, то
какие бы методы решения вслед за этим ни применялись, най-
Рис. 1.1. Общая схема процесса компьютерного математического
моделирования
7
денные значения не будут отвечать условиям реальной задачи и
окажутся бесполезными. Математическая модель может иметь вид
уравнения, системы уравнений или быть выраженной в форме
иных, как угодно сложных, математических структур или соотно-
шений самой различной природы. Математические модели, в част-
ности, могут быть непрерывными или дискретными, в зависимо-
сти от того, какими величинами — непрерывными или дискрет-
ными — они описаны.
По той причине, что математическая модель отражает лишь
некоторые черты реального объекта или явления, в ряде случаев
становятся актуальными вопросы существования и единственно-
сти решения в рамках математической модели. Выяснение в ис-
ходной информации необходимых и достаточных условий для су-
ществования и единственности решения имеет большое практи-
ческое значение, так как определяет цикл тех наблюдений, кото-
рые должны быть запроектированы для количественной реализа-
ции задачи. В числе общетеоретических вопросов можно назвать
также вопрос об устойчивости решений по входным условиям
задачи (такую устойчивость также называют корректностью ре-
шения).
Вслед за построением математической модели исследователь
разрабатывает (или, что бывает чаще, подбирает из числа извест-
ных) метод решения задачи и составляет алгоритмы. Этап поиска
и разработки алгоритма решения задачи в рамках заданной мате-
матической модели называют алгоритмизацией. На этом этапе мо-
гут использоваться любые подходящие средства представления
алгоритмов: словесные описания, формулы, схемы и т.п. Во мно-
гих случаях вслед за построением алгоритма выполняют так назы-
ваемый контрольный просчет — грубую прикидку ожидаемых ре-
зультатов, которые используются затем для анализа решения.
Особые трудности на этапе разработки алгоритма заключаются
в поиске метода решения задачи. Дело в том, что уже для доста-
точно простых моделей чаще всего не удается получить результат
решения в аналитической форме. Пусть, к примеру, задача све-
лась к решению уравнения с одной переменной: х - tgx = 0. При
всей тривиальности этой задачи выразить корни уравнения путем
аналитических преобразований не удается, и весь арсенал мето-
дов «точной» математики оказывается здесь беспомощным. В таких
случаях приходится использовать приближенные математические
методы, позволяющие получать удовлетворительные результаты.
Основными методами решения подобных задач являются числен-
ные методы, при использовании которых результат получается
путем вычислений. По этой причине наиболее естественный путь
реализации численных методов — это использование ЭВМ.
На следующем этапе алгоритм задачи записывается на языке,
понятном ЭВМ. Это — этап программирования. В простейших слу-
8
чаях может оказаться, что на этом этапе вовсе не составляется
новая программа для ЭВМ, а дело сводится, например, к исполь-
зованию имеющегося программного обеспечения.
После отладки и тестирования программы (если ее все же при-
шлось создавать) следует этап реализации — исполнение про-
граммы на ЭВМ и получение результатов решения. Время, требуе-
мое на прохождение этого этапа, зависит от объема вычислений и
быстродействия ЭВМ.
Завершающий этап решения задачи — это анализ, или интер-
претация результатов. На этом этапе происходит осмысливание
полученных результатов, сопоставление их с результатами конт-
рольного просчета, а также с данными, полученными экспери-
ментальным путем. При этом одни результаты могут оказаться
приемлемыми, а другие — противоречащими смыслу реальной
задачи; такие решения следует отбросить. Высшим критерием при-
годности полученных результатов в конечном итоге является прак-
тика.
В условиях использования ЭВМ численные методы выступают
как мощное математическое средство решения практических за-
дач. При этом важно иметь в виду, что сам по себе фактор исполь-
зования ЭВМ не упрощает, а в некотором смысле даже усложняет
(ввиду резкого возрастания количества выполняемых операций)
оценку точности получаемых результатов.
Суть возникающих здесь проблем точно подмечена в извест-
ном принципе Питера: «ЭВМ многократно увеличивает некомпе-
тентность вычислителя». Из этого остроумного замечания следу-
ет, что, используя для решения задачи ЭВМ, вычислитель дол-
жен не столько полагаться на могущество вычислительной техни-
ки, сколько помнить о том, что в конечном итоге он получает на
выходе.
На общую погрешность задачи, как это уже отмечалось, влия-
ет целый ряд факторов. Отметим основные из них, рассмотрев
общий ход решения задачи — от построения математической мо-
дели до производства вычислений.
Пусть R — точное значение результата решения некоторой за-
дачи. Из-за несоответствия построенной математической модели
реальной ситуации, а также по причине неточности исходных
данных вместо R будет получен результат, который обозначим Я[.
Образовавшаяся таким образом погрешность Е] = R - Ry уже не
может быть устранена в ходе последующих вычислений (так назы-
ваемая неустранимая погрешность).
Приступив к решению задачи в рамках математической моде-
ли, мы избираем приближенный (например, численный) метод
и, еще не приступив к вычислениям, допускаем новую погреш-
ность, приводящую к получению результата Т?2 (вместо По-
грешность е2 = R2 - называют погрешностью метода.
9
Действия над числами вносят дополнительную погрешность.
Например, если складывать два числа с одинаковыми погрешно-
стями, то погрешность суммы будет, вообще говоря, больше по-
грешности каждого из слагаемых. Это обстоятельство, а также не-
избежность округлений (в случае использования ЭВМ принуди-
тельное округление диктуется конечностью разрядной сетки ма-
шины) приводят к получению результата А3, отличающегося от
/?2 на величину вычислительной погрешности е3 = Я3 - R}.
Полная погрешность е, очевидно, получается как сумма всех
погрешностей:
£ = R — А3 = (R — R\) + (Л| - Rj) + (Т?2 — А3) = Е| + Е2 + £3.
При решении конкретных задач тс или иные виды погрешно-
стей могут отсутствовать или незначительно влиять на оконча-
тельный результат. Тем не менее, для исчерпывающего представ-
ления о точности окончательного результата в каждом случае не-
обходим полный анализ погрешностей всех видов. Это в полной
мере относится и к неустранимой погрешности — погрешности
математической модели. Располагая несовершенной математичес-
кой моделью, вычислитель должен каким-то способом составить
представление о величине неустранимой погрешности. Понятно,
что в условиях слишком грубой модели не имеет смысла прово-
дить утонченный анализ вычислительных ошибок. Отсюда следу-
ет, что оценка неустранимой погрешности может послужить вес-
ким доводом для снижения требований к точности последующих
вычислений, что, в свою очередь, может сделать их менее трудо-
емкими.
К числу причин, искажающих окончательный результат, сле-
дует отнести также всевозможные промахи, допускаемые иногда в
процессе решения: использование не тех исходных данных, не-
верной программы вычислений и т.п. Возможны также ошибки
из-за сбоев, возникающих в самом компьютере (бывшие обыч-
ным делом в компьютерах первого поколения и исключительно
редкие — для современных ЭВМ). Средством борьбы против про-
махов разного рода служит предварительная, грубая прикидка ожи-
даемого результата. Учитывая быстродействие ЭВМ, часто исполь-
зуют способ двойных вычислений, а также специально организу-
емые системы текущего контроля, связанные обычно с характе-
ром решаемой задачи.
Очевидно, что для исчерпывающего представления о погреш-
ности окончательного результата решения задач следует учиты-
вать влияние всех типов ошибок. Мы рассмотрели этот вопрос
применительно к достаточной общей схеме решения прикладной
задачи, включающей этапы построения математической (или
шире — информационно-математической) модели, выбор мето-
да, алгоритмизации и программирования, интерпретации резуль-
10
татов. Во многих случаях исследователь может выбрать более ко-
роткий путь, исключающий часть из перечисленных выше этапов
и резко сокращающий затраты на программирование. Речь идет об
использовании так называемых компьютерных математических ин-
струментов — программных пакетов, предназначенных как для
производства сложных вычислений, так и для быстрого решения
различных математических, научно-технических, статистических,
экономических и других задач: Excel, MatLaB, MathCad, Derive,
Maple, Mathcmatica и др. Работа с использованием этих пакетов
также предполагает обращение к вопросам точности получения
результатов. Особенность применения специализированных паке-
тов заключается в том, что внутренние механизмы их работы боль-
шей частью скрыты для пользователя.
В любом случае проведение анализа ошибок, как и общее по-
нимание проблемы точности расчетов, невозможно без ознаком-
ления с начальными понятиями методики приближенных вычис-
лений.
Контрольные вопросы
I. Из каких основных этапов состоит процесс решения задачи с по-
мощью ЭВМ? Дайте характеристику каждого этапа.
2. Из каких частей складывается общая погрешность решения задачи?
1.2. ЗАПИСЬ ЧИСЕЛ В ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ
И ОГРАНИЧЕНИЯ ТОЧНОСТИ ВЫЧИСЛЕНИЙ
Арифметические вычисления на ЭВМ выполняются с точнос-
тью, которая до появления этих вычислительных средств достига-
лась на практике лишь в исключительных случаях. И все же точ-
ность расчетов, выполняемых на ЭВМ, всегда объективно огра-
ничена. Эти ограничения связаны с невозможностью представле-
ния в машине всего множества действительных чисел. Точность, с
которой ведут расчеты вычислительные машины, зависит от спо-
соба аппроксимации действительных чисел посредством конеч-
ных машинных представлений.
В ЭВМ используются в основном два способа представления
чисел: с естественным размещением (фиксированной) запятой и в
форме с плавающей запятой. Характерной особенностью машин-
ного представления чисел (в любой из указанных выше форм)
является конечность разрядной сетки, в которой хранятся числа в
машине. Для понимания причин ограничения точности, возника-
ющих из-за конечности представления чисел в ЭВМ, достаточно
использовать десятичную форму изображения чисел, в которой
они воспринимаются человеком.
II
Знак числа Разряды числа
Рис. 1.2. Схема 8-разрядного представления числа с фиксированной запятой
На рис. 1.2 изображена схема представления числа с зафиксиро-
ванной запятой, или естественным размещением запятой, на при-
мере 8-разрядного калькулятора. Десятичная запятая (точка) в этом
случае может оказаться в любом цифровом разряде сетки.
Очевидно, что в форме с естественной запятой 8-разрядная
сетка может размещать лишь числа из диапазона |-(1108-1);
-110’7] u [+11 О*7; +(1IOS-I)J. Важно заметить, что множество
чисел из этого диапазона нс является континуальным (и даже
бесконечным) — это множество конечно. Оно покрывает число-
вую ось двумя участками равномерно расположенных чисел
(с шагом 1 10’7) с границами от -(1 • 10s- 1) до -1 I0’7 и от 1 10’7
до 1 • 10s- I (рис. 1.3).
Числа из интервала (-1 • IO"7; I I0'7) не могут быть помещены в
такой разрядной сетке (кроме нуля), так что если в результате
произведенной операции получится любое ненулевое число из
этого интервала, то в ЭВМ оно будет отождествлено с нулем. По
этой причине числа из этого интервала называют машинным нулем.
Не могут быть помещены в этой сетке и числа, большие по моду-
лю, чем 1 • 10s— 1. При появлении в процессе счета таких чисел
возникает ситуация, называемая переполнением разрядной сетки.
Рассмотренный способ представления чисел хоть и позволяет
решать многие практические задачи, несет в себе, тем не менее,
очевидные ограничения точности. Точность эта может быть увели-
чена лишь за счет увеличения количества разрядов в представле-
нии чисел, т.е. расширения разрядной сетки.
Наиболее совершенные модели калькуляторов и практически
все современные компьютеры используют представление действи-
тельных чисел в так называемой форме с плавающей запятой.
В этом случае число представляется в виде
х = ±М •10р, (1.1)
где М — мантисса; Р — порядок числа, т.е. показатель степе-
ни, в которую нужно возвести 10, чтобы, умножив результат
на мантиссу и присвоив нужный знак, получить данное число
(рис. 1.4).
Абсолютная величина порядка при представлении, изображен-
ном на рис. 1.4, может выражаться максимальным двузначным
числом 99. Это даст огромные диапазоны представления действи-
тельных чисел. Важной особенностью этой системы представле-
12
-(I IO*-!) -I I0-’ О 1 • IO-’ 11O’-I
Зона переполнения
.Машинный нуль
Зона переполнения
Рис. 1.3. Множество чисел, представимых в ЭВМ в форме с фиксирован-
ной запятой
ния чисел является неравномерность их расположения на число-
вой оси.
Для рассмотрения простейших свойств системы чисел с плава-
ющей запятой, позволяющих получить представление об основ-
ных проблемах ошибок машинных вычислений, обсудим эту фор-
му записи чисел более подробно.
Существует несколько способов выделения диапазона, в кото-
ром заключена мантисса. Обсудим два из них.
1. В учебной литературе часто встречается представление ман-
счисления; t — количество разрядов в записи мантиссы; dh d2,...,
dt — целые числа, удовлетворяющие неравенствам
0<</, <0-1 (» = 1, 2
Определенная таким образом мантисса оказывается в диапазо-
не 0 < М < 1. ЗначЬние порядка Р берется из интервала (Рь Р2],
границы которого обусловлены способом физического представле-
ния чисел в машине. Используя эти обозначения, можно вывести,
что в системе с плавающей запятой ровно 2(0 - 1)'''(Р2 - Р\ + I) + 1
чисел. Так, например, при 0 = 2, t = 3, Р{ = -2, Р2 = 3 система бу-
дет состоять из 41 числа, неравномерно покрывающих участок
числовой оси от -3,5 до 3,5.
2. Для хранения двоичных вещественных чисел в современных
ЭВМ соответствующие форматы предписаны стандартом, не за-
висящим от архитектуры ЭВМ и конкретных языков программи-
рования (IEEE Standard 754 Floating Points Numbers, см. (15]).
Как известно, существует несколько типов вещественных ве-
личин. Характеристики некоторых из них приведены в табл. 1.1.
Знак числа Мантисса Знак порядка Порядок
Рис. 1.4. Пример разрядной сетки с представлением десятичных чисел
в форме с плавающей запятой
Таблица 1.1
Тип Длина записи числа, байт Диапазон значений Количество сохраняемых значащих цифр мантиссы в десятичном представлении числа
Real 6 2,9-10~39 — 1,7 - 103R 11-12
Single 4 1,5- ПН3- 3,4- Ю38 7—8
Double 8 5-IO”324 — 1 ,7-10308 15-16
Extended 10 Зз4.ПГ*932_Ь1.104932 19-20
Опишем форматы хранения чисел типов single и double. Отме-
тим предварительно следующее обстоятельство. В указанном выше
стандарте число хранится в такой форме, что его мантисса заклю-
чена в диапазоне 1 < М < 2, т.е. первая цифра мантиссы всегда
равна 1. Эта дополнительная операция сдвига на один разряд («нор-
мализация») делает нормализованный порядок на единицу мень-
ше, чем тот, который использован в предыдущем рассмотрении.
Величина типа single занимает в памяти ЭВМ 4 байта (рис. 1.5).
Знак числа хранится в крайнем левом разряде с номером 31 (как
обычно, разряды нумеруются с 0 и располагаются справа налево).
Порядок в смещенной форме занимает разряды с 23 по 30. Сме-
щенная форма находится так: к настоящему значению порядка
прибавляется число 127 (так называемое «смещение») для того,
чтобы значение смещенного порядка всегда было положительным.
Мантисса занимает все остальные разряды, т.е. с 0 по 22, причем
целая часть мантиссы вообще не хранится (она всегда равна еди-
нице и при вычислениях это учитывается).
Величина типа double занимает в памяти ЭВМ 8 байт (рис. 1.6).
Знак числа хранится в разряде номер 63. Порядок в смещенной
форме занимает разряды с 52 по 62 (смещение в данном случае
равно 1023). Мантисса занимает разряды с 0 по 51 (как и раньше,
целая часть мантиссы, автоматически равная единице, не хранится).
Номера байтов
4 3 2 1
1 1 1 1 1 II 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
31 30 23 22 0
' | Порядок J Мантисса
Знак числа
Рис. 1.5. Способ хранения числа типа single в ЭВМ
14
Обратим внимание, что границы байтов не совпадают с фраг-
ментами, составляющими вещественное число.
Одна из причин накопления ошибок при выполнении ариф-
метических действий в системе чисел с плавающей запятой — это
запись конечных десятичных дробей бесконечными дробями в
двоичной системе счисления. Так, например, во многих случаях в
программах на ЭВМ используется десятичный шаг 0,1. Между тем,
в двоичной системе счисления десятичная дробь 0, I имеет беско-
нечное представление.
В конкретной ЭВМ приходится ограничиваться разрядами дво-
ичного разложения. Поэтому десятичное число 0,1 в машине, ра-
ботающей с двоичными числами, оказывается представленным
приближенно. Не должно удивлять, что при добавлении на ЭВМ
к единице 10 раз по 0,1 получают в ответе не 2, а число, записан-
ное единицей с последующими девятками: 1,99...9.
Нетрудно понять, что если обычным образом выполнять ариф-
метические операции в системе чисел с плавающей запятой, то
очень редко результат будет принадлежать этой же системе. Дей-
ствительно, результат либо выйдет за пределы этой системы чи-
сел (если он окажется больше максимального по модулю нулево-
го элемента этой системы), либо окажется между двумя числами
из этой системы. В первом случае ситуация характеризуется воз-
никновением переполнения или машинного нуля, во втором —
вместо истинного результата возникает значение, которое явля-
ется ближайшим к истинному результату числом из системы чи-
сел с плавающей'запятой. Особенности выполнения арифмети-
ческих операций в системе чисел с плавающей запятой приводят
к тому, что, например, для сложения и умножения сохраняются
законы коммутативности, но законы ассоциативности и дистри-
бутивности для них не выполняются.
Считаться с присущими числам с плавающей запятой ограни-
чениями точности необходимо и при использовании для вычис-
лений языков программирования, как в проведении расчетов, так
и в отображении результатов. Покажем на примере, как можно
обнаружить и исследовать эти ограничения.
Номера байтов
8 7 6 5 4 3 2 1
|1.Ш11||||111Н||||||||||||||1||||1111|1||1111||||1111||ШЙТГ
63 62 52 51 0
| Порядок | Мантисса
Знак числа
Рис. 1.6. Способ хранения числа типа double в ЭВМ
15
Пример 1.1. Исследуем реальную точность вычисления встро-
енных в Turbo Pascal математических функций (на примере функ-
ции sinx) и соотнесем ее с возможностями стандартной процеду-
ры вывода.
Приведенная ниже программа Sin позволяет выполнить ука-
занную работу'. В программе использован форматированный вывод
с заведомо большим, нежели необходимо, количеством значащих
цифр с целью не потерять в отображении результата части цифр
мантиссы. Однако, как уже отмечалось, мантисса отображения
сохраняет лишь 18 значащих цифр.
program Sin;
uses ert;
var x,y: real;
begin
writeln ('введите x’); read(x); y:-sin(x);
writeln('sin x “’,y:40);
repeat until keypressed
end.
Расчеты были повторены при различных вещественных типах
величин х и у. Результаты зависят от типа. Так, для х = 1 получено:
x,y;real sin х - 8.41470984807529021Е-0001
x,y:double sin х •* 8.41470984807896505Е-0001
x,y:single sin х - 8.41470956802368164Е-0001
x,y:extended sin x = 8.41470984807896507E-0001
Если считать, что последнее значение имеет наибольшую точ-
ность (что вполне естественно), то при использовании величины
типа real в мантиссе лишь 12 верных значащих цифр, типа double —
17, типа single — 7 (сомнительные цифры выделены полужирным
курсивом). Все это вполне соответствует данным из табл. 1.1. Есте-
ственно допустить, что разработчики Turbo Pascal для каждой из
встроенных функций согласовали точность вычисления значения
функции с типом переменной, которой присваивается се значе-
ние. В этом случае оказывается, что при использовании типа
extended не все верные цифры результата выводятся процедурой
writeln.
Одной из важных характеристик точности арифметики числа с
плавающей запятой в ЭВМ является значение машинного эпсилон,
т.е. такого наименьшего числа е из системы чисел с плавающей
запятой, что добавление его к единице дает на этой ЭВМ значе-
ние, большее единицы. Значение машинного эпсилон для конк-
ретной ЭВМ можно определить программным путем; соответствую-
щая программа приведена ниже.
16
program epsilon;
uses crt;
const c:singlc=0.5; d:single=l.0; c:singlc=2.0;
var a,eps: single; i:integer;
begin
a:=d; eps:=c; i:=l;
while a+eps>a do
begin
eps:=eps/e; i:=i+l
end;
writcln ('i=i, * 1 2 3eps:single, машинное эпсилон=',
eps:40);
repeat until keypressed
end.
Результат работы программы:
| машинное эпсилон = 5.42101086242752217Е-0020
В программе использован форматированный вывод eps:40
(с заведомо большим, нежели необходимо, количеством знача-
щих цифр) с целью не потерять в отображении результата части
цифр мантиссы. Однако, несмотря на это, мантисса отображения
сохраняет лишь 18 значащих цифр — таково ограничение проце-
дуры writcln.
Все переменные и типизированные константы, заданные в про-
грамме, имеют тип single. При смене типа результат вопреки ожи-
данию (и тому, что написано в ряде руководств по Turbo Pascal)
одинаков для любого из вещественных типов: real, double, single,
extended. Это говорит о том, что данная программа определяет имен-
но машинное (процессорное) эпсилон. Отсутствие реакции на смену
типа величин отражает особенности реализации компилятора.
Контрольные вопросы
1. Какие основные способы представления чисел используются в
ЭВМ?
2. Какие числа называют машинным нулем?
3. Каковы причины возникновения ошибок при проведении расчетов
в системе чисел с плавающей запятой, порождаемых структурой этой си-
стемы?
Упражнения
1. Подсчитать количество чисел в системе с плавающей запятой, у
которой р = 2, t - 2, Р{ = -1, Рг = 1. Изобразите эту систему чисел на
числовой оси.
2. Вычислить границы машинного нуля для системы чисел с плаваю-
щей запятой, у которой р = 10, t = 3, Р\ = -9, Рг = 9.
3. Определить значение машинного эпсилон для вашего компьютера.
17
1.3. АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ
Пусть X — точное значение некоторой величины, а х — наи-
лучшее из известных приближений. В этом случае ошибка (или
погрешность) приближения х определяется разностью X-х. Обыч-
но знак этой ошибки не имеет решающего значения, поэтому
рассматривают абсолютную величину ошибки:
е,=|Х-х|. (I.2)
Величина ех, называемая абсолютной погрешностью приближен-
ного значения х, в большинстве случаев остается неизвестной,
так как для ее вычисления нужно точное значение X. Вместе с тем
на практике обычно удается установить верхнюю границу абсо-
лютной погрешности, т.е. такое (по возможности наименьшее)
число Дх, для которого справедливо неравенство
Дх>рГ-х]. (I.3)
Число Дх в этом случае называют предельной абсолютной по-
грешностью (или границей абсолютной погрешности) приближения х.
Таким образом, предельная абсолютная погрешность прибли-
женного числа х — это всякое число Дх, не меньшее абсолютной
погрешности ех этого числа.
Пример 1.2. Возьмем число п= 3,14159265358.... Если вызватьл
на индикатор 8-разрядного МК, получим приближение этого чи-
сла: л' = 3,1415926. Попытаемся выразить абсолютную погреш-
ность значения л’: еп- = |п- л] = 0,00000005358.... Получили беско-
нечную дробь, непригодную для практических расчетов. Очевид-
но, однако, что еж- < 0,00000006, следовательно, число 0,00000006 -
= 0,6-10 7 можно считать предельной абсолютной погрешностью
приближения, используемого МК вместо числа ек-: Дл'= 0,6-10 7.
Неравенство (1.3) позволяет установить приближения к точ-
ному значению X по недостатку и избытку:
х-Дх < X £ х + Дх, (1.4)
которые могут рассматриваться как одна из возможных пар значе-
ний соответственно нижней границы (НГ) и верхней границы
(ВГ) приближения х
НГх=х-Дх; ВГх=х + Дх. (1.5)
Во многих случаях значения границы абсолютной ошибки Дх,
так же как и наилучшие значения приближения х, получаются на
практике в результате измерений. Пусть, к примеру, в результате
повторных измерений одной и той же величины получены значе-
ния: 5,2; 5,3; 5,4; 5,3. В этом случае естественно принять за наилуч-
шее приближение измеряемой величины среднее значение х= 5,3.
18
Очевидно также, что граничными значениями величины хв дан-
ном случае будут НГЛ. - 5,2, ВГЛ. = 5,4, а граница абсолютной по-
грешности Дх может быть определена как половина длины интер-
вала, образуемого граничными значениями НГЛ. и ВГХ, т.е.
По абсолютной погрешности нельзя в полной мере судить о
точности измерений или вычислений. Качество приближения из-
меряется с помощью относительной погрешности, которая опре-
деляется как отношение ошибки ех к модулю значения X (когда
оно неизвестно, то к модулю приближения х).
Предельной относительной погрешностью (или границей отно-
сительной погрешности) 5х приближенного числа называется от-
ношение предельной абсолютной погрешности к абсолютному
значению приближения х:
, Дх
(1-6)
Формула (1.6) позволяет при необходимости выражать абсо-
лютную погрешность через относительную:
Дх = |х|8х. (1.7)
Относительную погрешность выражают обычно в процентах.
Пример 1.3. Вычислить границу относительной погрешности
приближения к числу л, используемого 8-разрядным МК (см. при-
мер 1.2).
,, 0,6 10~7 „ _ ,.. 7 s ,
Учитывая, что —---------<0,2 10 , можно принять бтг =
3,1415926
= 0,000002 %. Это чрезвычайно высокая точность, если учесть, что
для ординарных технических расчетов считается приемлемым уро-
вень точности от 0,1 до 5 %.
Контрольные вопросы
1. Что такое абсолютная погрешность приближенного значения вели-
чины? граница абсолютной погрешности?
2. Как с помощью границы абсолютной погрешности Дх известного
приближенного значения х можно указать возможные значения его ниж-
ней и верхней границ?
3. Каким образом определяется граница абсолютной погрешности Дх
для приближенного значения х, получаемого в результате многократных
измерений?
4. Что такое относительная погрешность приближенного значения
величины? граница относительной погрешности?
5. Как можно вычислить абсолютную погрешность приближения х,
если известна его относительная погрешность?
19
Упражнения
I. В результате измерения длины стола линейкой с сантиметровыми
делениями установлено, что значение длины находится между деления-
ми 63 и 64 см. Указать границы абсолютной и относительной погрешно-
стей значения длины, если за наилучшее ее приближение принять ее
среднее значение 63,5 см.
2. В результате пятикратных измерений периода колебаний маятника
студент получил результаты (в секундах): 4,8; 5,0; 4,9; 4,8; 5,0.
Основываясь на этих измерениях, установить наилучшее приближе-
ние значения периода и границы абсолютной и относительной погреш-
ностей.
1.4. ПРАВИЛЬНАЯ ЗАПИСЬ И ОКРУГЛЕНИЕ ЧИСЕЛ
Цифра числа называется верной (в широком смысле), если абсо-
лютная погрешность этого числа не превосходит единицы разря-
да, в котором стоит эта цифра.
Пример 1.4. а). Пусть а = 2,91385, Да = 0,0097. В числе а верны в
широком смысле цифры 2, 9, 1.
б). Возьмем в качестве приближения к числу я = 3,141592... чи-
сло я' = 3,142. Тогда |я- л*| < 0,001 = Дл' (рис. 1.7), откуда следует,
что в приближенном значении л'= 3,142 все цифры являются вер-
ными.
в). Вычислим на 8-разрядном МК частное точных чисел 3,2 и
2,3, получим ответ: 1,3913043. Ответ содержит ошибку, поскольку
разрядная сетка МК не вместила всех цифр результата и все разря-
ды, начиная с восьмого, были опущены. (В том, что ответ неточен,
легко убедиться, проверив деление умножением: 1,3913043 -2,3 =
= 3,9999998.) Не зная истинного значения допущенной ошибки,
вычислитель, однако, может быть уверен, что оно не превышает
единицы самого младшего из изображенных на индикаторе раз-
ряда результата. Следовательно, в полученном результате все цифры
верны.
Отметим, что первая отброшенная (неверная) цифра часто
называется сомнительной.
Говорят, что приближенное данное записано правильно, если в
его записи все цифры верные. Это понятно — сохранять в записи
чисел неверные цифры нет смысла. Но важно и другое: если чис-
ло записано правильно, то по одной только его записи в виде
3,141 3,142
______________I______________I______________I____________►
я
Рис. 1.7. Приближение числа я
20
десятичной дроби можно судить о точности этого числа. Пусть, к
примеру, записано приближенное число а= 16,784, в котором все
цифры верны. Из того, что верна последняя цифра 4, которая
стоит в разряде тысячных, следует, что абсолютная погрешность
значения а не превышает 0,001. Это значит, что можно принять
Да = 0,001, т.е. а- 16,784±0,001.
Очевидно, что правильная запись приближенных данных не
только допускает, но и обязывает выписывать нули в последних
разрядах, если эти нули являются выражением верных цифр. На-
пример, в записи Ь- 109,070 нуль в конце означает, что цифра в
разряде тысячных верна и она равна нулю. Предельной абсолют-
ной погрешностью значения Ь, как следует из записи, можно счи-
тать ,\Ь - 0,001. Для сравнения можно заметить, что значение
с = 109,07 является менее точным, так как из его записи прихо-
дится принять, что Дс= 0,01.
Значащими цифрами в записи числа называются все цифры в
его десятичном изображении, отличные от нуля, и нули, если
они расположены между значащими цифрами или стоят в конце
для выражения верных знаков.
Можно сказать короче: значащими цифрами числа являются
все цифры в его правильной записи, начиная с первой ненулевой
слева.
Пример 1.5. 0,2409 — четыре значащие цифры; 24,09 — четыре
значащие цифры; 100,700 — шесть значащих цифр.
Выдача числовых значений в ЭВМ, как правило, устроена та-
ким образом, что нули в конце записи числа, даже если они вер-
ные, не сообщаются. Это означает, что если, например, ЭВМ
показывает результат 247,064 и в то же время известно, что в этом
результате верными должны быть 8 значащих цифр, то получен-
ный ответ следует дополнить двумя нулями: 247,06400.
В процессе вычислений часто происходит округление чисел, т.е.
замена чисел их значениями с меньшим количеством значащих
цифр.
При округлении возникает погрешность, называемая погреш-
ностью округления. Пусть х — данное число, a — результат ок-
ругления. Погрешность округления определяется как модуль раз-
ности прежнего и нового значений числа:
Двч» = |х'*||- 0-8)
В отдельных случаях вместо ДоКр приходится использовать его
верхнюю оценку.
Пример 1.6. Выполним на 8-разрядном МК действие 1:6. На
индикаторе высветится число 0,1666666. Произошло автоматиче-
ское округление бесконечной десятичной дроби 0,1(6) до коли-
чества разрядов, вмещающихся в регистре МК. При этом можно
принять Докр = 0,7 • 10‘7.
21
Рассмотренный случай «принудительного» округления назы-
вают округлением методом отбрасывания. Очевидно, что сам по
себе метод отбрасывания оставляет все сохраняемые цифры ок-
ругленного числа верными.
Если вычисления ведутся с точностью меньшей, чем машин-
ная точность, целесообразнее пользоваться способом симметри-
ческого округления, который приводит к меньшей величине ок-
ругления, чем способ отбрасывания. Симметрическое округление
выполняется по следующим правилам:
если первая слева из отбрасываемых цифр меньше 5, то сохра-
няемые десятичные знаки остаются без изменения;
если первая слева из отбрасываемых цифр больше или равна 5,
то последняя сохраняемая цифра увеличивается на единицу.
Из правил симметрического округления следует, что его по-
грешность не превышает половины единицы последнего сохраня-
емого разряда. Это обстоятельство позволяет вести счет с точнос-
тью большей, чем единица последнего сохраняемого разряда. По
этой причине наряду с понятием «верная цифра в широком смыс-
ле», соответствующем методике округления путем отбрасывания,
используется понятие «цифра, верная в строгом смысле», приме-
няемое в вычислениях с симметрическим округлением.
Отметим, что погрешности принято записывать с одной зна-
чащей цифрой (редко — с двумя). Кроме того, при округлении
погрешности обычные правила округления неприменимы: погреш-
ности, по понятной причине, всегда округляют с завышением (как
это и делается в данной книге).
Цифра числа называется верной в строгом смысле, если абсо-
лютная погрешность этого числа не превосходит половины еди-
ницы разряда, в котором стоит эта цифра.
Пример 1.7. Вычислим х = <'?3б. Получим х- 15,362291. Ок-
руглим результат до десятых методом симметрического округле-
ния: X] = 15,4; Дл'[ = 0,04. Все цифры числа Х| верны -в строгом
смысле.
Абсолютная погрешность числа хь получаемого в результате
округления приближенного значения х, складывается из абсо-
лютной погрешности первоначального числа х (являющегося при-
ближением точного значения X) и погрешности округления. Дей-
ствительно, из неравенства -xj < [Д'-х|+ |х-Х|| < Ах + Локр
следует, что если в результате округления приближенного числа
х получено значение хь то предельной абсолютной погрешнос-
тью числа X! можно считать сумму предельной абсолютной по-
грешности числа х и погрешности округления.
Пример 1.8. Пусть в приближенном значении а = 16,395 все циф-
ры верны в широком смысле. Округлим а до сотых: tq = 16,40.
Погрешность округления Локр = 0,005. Для нахождения полной по-
грешности Дй| нужно сложить ЛоКр с погрешностью исходного зна-
22
чения at, которая в данном случае может быть найдена из усло-
вия, что все цифры н записи а верны: Да = 0,001. Таким образом,
Дй] = Да + Докр = 0,001 + 0,005 = 0,006. Отсюда следует, что в значе-
нии а( = 16,40 цифра 0 не верна в строгом смысле.
Контрольные вопросы
1. Какие цифры в записи приближенного числа называются верными
в широком смысле? верными в строгом смысле?
2. Верно ли утверждение, что компьютер, округляющий числа по
методу отбрасывания, всегда выдает результаты, записанные только вер-
ными цифрами? Почему?
3. Какие цифры в записи приближенного числа называются знача-
щими?
4. Что такое округление числа? погрешность округления?
5. Какие различаются погрешности округления методом отбрасыва-
ния?
6. Из чего складывается полная погрешность округленного числа?
Упражнения
1. Округлить соответственно до двух, трех и четырех знаков после за-
пятой следующие числа: 3,009982; 24,00551; 21,161728.
2. У приближенных чисел 36,7; 2,489; 31,010; 0,031 все цифры верны
в строгом смысле. Указать предельные абсолютные и относительные по-
грешности этих чисел.
3. У приближенных чисел 0,310; 3,495; 24,3790 вес цифры верны в
строгом смысле. Округлить заданные числа до сотых и определить в ок-
ругленных значениях количество цифр, верных в строгом смысле.
1.5. ПРОГРАММНОЕ ОКРУГЛЕНИЕ ДЕСЯТИЧНЫХ ЧИСЕЛ
ПО ЗАДАННОМУ ЗНАЧЕНИЮ АБСОЛЮТНОЙ ПОГРЕШНОСТИ
Обычной практикой, принятой для ЭВМ (в том числе и для
МК), является выдача числовых результатов, округленных мето-
дом отбрасывания. Однако при желании программным путем можно
ввести механизм округления по заданному значению абсолютной
погрешности. Используя управляемое программное округление,
можно также предусматривать и программный вывод результатов
в правильной (с точки зрения теории погрешностей) записи, т.е.
верными значащими цифрами.
В некоторых языках программирования имеется функция
ROUND(a, л), где а — арифметическое выражение, задающее ок-
ругляемое значение, а п — арифметическое выражение, задаю-
щее уровень округления (если значение п — не целое, то его дроб-
ная часть автоматически отбрасывается). Округление с помощью
функции ROUND выполняется следующим образом:
23
а) при n > 0 происходит округление до л-й цифры после запя-
той;
б) при п = 0 — округление до ближайшего целого;
в) при п < 0 — округление до (|л| +1 )-й цифры влево от деся-
тичной точки.
При отсутствии функции ROUND она может быть смоделиро-
вана с помощью функции Int — «целая часть»:
ROUNDS л)
где Sign — «знаковая функция», равная 1 для положительного
значения аргумента, -1 для отрицательного и 0 для нулевого. Ис-
пользуя эту формулу, можно программным путем вести округле-
ние как по заданному уровню округления п, так и по заданной
величине абсолютной погрешности. Во втором случае вначале по
значению абсолютной погрешности требуется определить уровень
Рис. 1.8. Блок-схема алгоритма округления десятичных чисел по задан-
ной величине абсолютной погрешности
24
округления. На рис. 1.8 изображена блок-схема алгоритма округле-
ния числа а с предварительным определением уровня округления
п по заданной величине абсолютной погрешности d.
При всей простоте этого алгоритма при машинном округле-
нии могут возникать некоторые технические проблемы, часто не
позволяющие получать достоверного результата. Коснемся здесь
этих проблем, поскольку процедура округления десятичных чи-
сел с последующим их выводом верными цифрами в естествен-
ной форме записи в дальнейшем будет применяться неоднократно.
Ниже приведена программа okruglenie, которая реализует сим-
метрическое округление десятичных чисел, оставляя лишь вер-
ные (в широком смысле) цифры в соответствии с заданной аб-
солютной погрешностью числа. Для вывода значения округлен-
ного числа в программе умышленно сохранена машинная (нор-
мальная) форма представления десятичных чисел, без «усече-
ния» неверных знаков.
program okruglenie;
{округление десятичного числа "а" по заданной
величине абсолютной погрешности "d” до цифр,
верных в широком смысле)
uses okrugl, crt;
type T=real;
var a,d:T; n:integer;
begin ,
writein;
writein('Введите число и погрешность'); read(a,d);
okr(a,d,a,n);
writein('Округленное число a=',a, ' n=',n);
repeat until keypressed
end.
В программе используется модуль okrugl, который, в свою оче-
редь, обращается к процедуре okr. В основе этой процедуры лежит
алгоритм, изображенный на рис. 1.8. Первый ее аргумент — под-
лежащее округлению число а, второй — абсолютная погрешность d.
Результаты работы процедуры — параметры-переменные b и л;
первый из них — округленное число, второй показывает, на сколь-
ко знаков происходит округление (при d> 1 округление происхо-
дит до л-й цифры до десятичной точки, при d < 1 — до л-й циф-
ры после десятичной точки). В ходе исполнения программы внача-
ле определяется количество оставляемых в числе значащих цифр
л (по разным схемам при d < 1 и d> 1) и затем выполняется
округление по указанной выше формуле. В силу отсутствия в язы-
ке Pascal операции возведения в произвольную степень, для вы-
числения 10” используется функция stcpenlO. Конструкция type Т
позволяет легко менять тип данных (делать это следует одновре-
25
менно в модуле и программе). Оформление конструкции okrugl в
виде модуля связано с тем, что далее в тексте учебника обраще-
ние к ней используется неоднократно.
unit okrugl;
interface
type T=real;
procedure okr(a,d:T; var b:T; var n:integer);
implementation
function stepenlO(n:integer):T;
var i:integer; k:longint;
begin k:=10; for i:=l to (abs(n)-l) do k:=k*10;
if n=0 then stepenlO:=1;
if n>0 then stepenlO:=k;
if n<0 then stepenlO:=1.0/k
end;
procedure okr(a,d:T; var b:T; var n:integer);
var i,k:integer;
begin
n:=l;
if del then
begin
while d<{(1.0/stepenlO(n))+1E-10)
do n:=n+l;
n:=n-l
end
else
begin
while d>=(stepenlO(n)+1E-10)
do n:=n+l;
n : =-n
end;
b:=int((abs(a)* stepenl0(n))+0.5)/stepenlO(n) ;
if a<>0 then b:=b*a/abs(a)
end;
end.
Нуждается в комментарии следующее различие между схемой
на рис. 1.8 и программой: в циклах вместо условий d < 10"" и
d> 10" используются модифицированные условия d < (10"" + е) и
d> (10" + е) соответственно. Это связано с особенностями опера-
ций над вещественными числами: при вычислении 10’" (при п> 0)
в ЭВМ получается приближенное значение, и для правильной рабо-
ты программы следует подстраховаться путем добавления е (точное
значение е особой роли не играет, в программе положено 1 • 1О“10).
26
Если этого не сделать, то при округлении числа 1,23456 (см. при-
мер ниже) при погрешностях, например, 0,1 и 0,2 получится оди-
наковое округленное значение числа, в то время как оно в соответ-
ствии с правилом определения верных цифр должно быть разным.
Результаты работы программы okruglenie для различных набо-
ров исходных данных показаны ниже.
Исходное число Погрешность Результат округления (в виде, полученном ЭВМ) п
1,23456 ЫО*1 1.20000000000073Е+0000 1
1,23456 2-Ю"1 1 .ООООООООООООООЕ+0000 0
1,23456 1-10^ 1.23460000000008Е+0000 4
1,23456 2-Ю-4 1.23400000000038Е+0000 3
1,20034 1-Ю"3 1.20000000000046Е+0000 3
-1,23456 1-10~3 -I.23500000000058E+0000 3
-1,23456 2-ИГ' -I.22999999999956E+0000 2
-1,23432 1-Ю’3 -1.23400000000038Е+0000 3
123456 1-Ю2 1.23499999999881Е+0005 -2
123456 2-Ю2 1.23000000000119Е + 0005 -3
-123 456 2-J.01 -1.23499999999881Е+ 0005 -2
-123 432 2-101 -1.23399999999881Е+0005 -2
Анализ результатов показывает, что алгоритм округления ра-
ботает безупречно, однако в ряде случаев (7, 9, 11 и 12-я строки,
считая сверху) результат искажен из-за приближенного характера
машинного представления числовых данных. На глаз это искаже-
ние безвредно своей очевидностью, однако при «усечении» не-
верных знаков результаты окажутся неверными; очевидно, напри-
мер, что в результате «усечения» результата округления, получен-
ного в последней строке, вместо 123 400 будет выведено 123 300.
Для преодоления этого затруднения воспользуемся приемом,
который применялся выше: перед «усечением» результата округ-
ления добавим к округленному числу значение е= 10~10, причем
со знаком «+», если округляемое число является положительным,
и со знаком «-», если округляемое число отрицательно. Очевид-
но, что выбранное значение е, с одной стороны, не является слиш-
ком малым, чтобы не приводить к искомому результату, а с дру-
гой — не настолько большое, чтобы искажать процедуру округле-
ния (разумеется, при значениях погрешности d, существенно боль-
шей по абсолютной величине, чем е).
27
С учетом сказанного для вывода результатов округления в есте-
ственной форме в программе okruglenie достаточно заменить про-
цедуру вывода
writein('Округленное число а=*,а,’ п=',п);
условным оператором:
if а<0 then begin if n<0 then m:=0 else m:=n;
writein('Округленное число a= ’, а-1Е-10:17:m,
'n«',n);
end
else begin if n<0 then m:-0 else m:»n;
writein('Округленное число a»’,
а + 1Е-10:17:m, ' n=',n);
end;
Разумеется, используемая для восстановления отрицательных
значений уровня округления п вспомогательная целочисленная
переменная т в программе okruglenie должна быть описана. Надо
сказать, что вывод значений уровня округления п в этой програм-
ме сохранен не случайно — по значению п можно контролировать
правильность произведенного округления. Результаты выполнения
модифицированной таким образом программы okruglenie для не-
которых значений из прежнего набора исходных данных показа-
ны ниже (незначащие, т.е. неверные, нули выделены полужир-
ным курсивом).
Введите число и погрешность
1.23456 0.0001
Округленное число а= 1.2346 п=4
Введите число и погрешность
1.23456 0.0002
Округленное число а- 1.235 п-3
Введите число и погрешность
1.20034 0.001
Округленное число а- 1.200 п-3
Введите число и погрешность
-1.23456 0.002
Округленное число а=-1.23 п=2
Введите число и погрешность
123456 100
Округленное число а= 123500 п=-2
Введите число и погрешность
123456 200
Округленное число а= 123000 п=-3
Введите число и погрешность
-123456 20
Округленное число а=-123500 п=-2
28
Вывод значений уровня округления п позволяет, в частности,
избежать ошибки в особых случаях — например, при округлении
целых чисел, в изображении которых оказываются значащие нули,
расположенные между значащими цифрами. Ниже показан при-
мер использования программы okrugicnie, когда в результате ок-
ругления значащие и незначащие нули оказываются рядом и для
их разделения как раз и используется значение п (незначащие нули
выделены полужирным курсивом):
Введите число и погрешность
12000468 1000
Округленное число а= 12000000 п=-4
Для лучшего понимания следует поупражняться с программой
okruglenie, применяя разные варианты сравнения и альтернатив-
ный (на языке Паскаль) способ вычисления 10±я как ехр(±л1п 10),
а также меняя тип данных Тс real на другие вещественные типы.
Контрольные вопросы
1. Почему в функции stepenlO переменная к описана как longint?
2. Какие ограничения существуют в приведенной выше программе
относительно значений величины п при d< 1 и d> I и как эти ограниче-
ния изменятся, если описать переменную к как integer?
Упражнения
1. Замените последовательно в приведенных выше программах тип Т
на другие вещественные типы и исследуйте, как это влияет на возмож-
ности программы.
2. Замените в приведенной выше программе (модуле okrugle) способ
вычисления 10:я с цикла на формулу схр(±л!п 10) и исследуйте, как это
влияет на возможности программы при различных типах данных Т.
3. В Turbo Pascal (как и во многих других языках программирования)
возможен иной, нежели показанный на рис. 1.8 и в приведенных выше
программах, способ округления чисел с помощью функций преобразо-
вания данных из числовой формы в строку (string) и наоборот (в Turbo
Pascal это функции val и str). При этом значение п может быть найдено
по схеме на рис. 1.8, а далее действия выполняются с использованием
указанных функций. С помощью такого приема составить программы
округления чисел: а) в широком смысле; б) в строгом смысле.
1.6. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА ВЕРНЫХ ЦИФР
ПО ОТНОСИТЕЛЬНОЙ ПОГРЕШНОСТИ
ПРИБЛИЖЕННОГО ЧИСЛА
Количество верных значащих цифр в приближенном числе и
величина относительной погрешности этого числа взаимосвяза-
29
ны. Эта связь со всей очевидностью вытекает уже из того, что по
величине х, учитывая формулу (1.7), можно вычислить абсолют-
ную погрешность Ах, которая, как следует из определения верных
значащих цифр, явно влияет на их количество в приближенном
числе.
На практике иногда удобнее пользоваться правилом, устанав-
ливающим взаимосвязь количества верных цифр непосредственно
с величиной относительной погрешности. Рассмотрим этот воп-
рос применительно к приближенному числу х, записанному в
форме с плавающей запятой (1.1) в предположении, что мантисса
М удовлетворяет условию 0,1 < М < 1. У числа в таком виде первый
разряд мантиссы после запятой всегда отличен от нуля (число х в
этом случае называют нормализованным). Заметим также, что для
числа, записанного в указанной форме, справедливо ограничение
|х| < ЮФ (1.9)
Итак, имеются приближенное число х и его относительная по-
грешность 5х. Нужно установить количество верных в строгом смыс-
ле значащих цифр в числе х.
Для каждого известного значения Зх можно подобрать такое
наибольшее натуральное п, чтобы имело место неравенство
8х<10_". (1.10)
Тогда Ах < |х| • 10"" < 10? -10"" = 10f"" < - • 10"(""|)+?, т. е.
1 1 2
Ах <• 10"(""!) • 10р. (1.11)
Сопоставляя теперь (1.9) и (1.11) и используя определение
цифры, верной в строгом смысле, можно сделать вывод, что в
мантиссе приближенного числа х верны в строгом смысле по край-
ней мере п - 1 цифр после запятой (и, стало быть, вее эти циф-
ры — значащие). Таким образом, для того чтобы по заданной ве-
личине относительной погрешности 5х найти количество верных
значащих цифр в числе х, достаточно подобрать наибольшее на-
туральное и такое, чтобы имело место неравенство 5х < 10"", а
потом полученное значение п уменьшить на единицу.
Пример 1.9. Пусть х = 984,6; Зх = 0,008. Очевидно, что
0,008 < 1 • 10“2. Это означает, что число х имеет по крайней мере
одну верную в строгом смысле цифру (это первая слева цифра 9).
Полученный результат легко подтвердить, используя определе-
ние цифры, верной в строгом смысле. Вычислим: х= 984,6-0,008 =
= 7,8768, откуда следует, что в числе 984,6 цифра 9 действительно
верна в строгом смысле.
Полученное правило в отдельных случаях проявляет завышен-
ную «осторожность» — при выполнении условия (1.10) в числе
30
могут оказаться верными все п цифр. Зависит это от величины
первых значащих цифр числа х.
Пример 1,10. Пусть х = 136,4; 5х = 0,008 < 1 • 10~2 (т.е. п = 2).
Согласно правилу в числе 136,4 лишь одна верная в строгом смыс-
ле цифра (л - 1 = 1). Вычислим Дх = 136,4 0,008 < 1,1. Как показы-
вает найденная величина предельной абсолютной погрешности,
в числе 136,4 верны в строгом смысле две цифры: 1 и 3.
В отдельных случаях, когда первая значащая цифра в относи-
тельной погрешности 5х меньше 5, вместо условия (1.10) удается
установить более сильное условие:
5х<--10-и.
2
(1-12)
Легко показать, что в этом случае число х имеет по крайней
мере л верных в строгом смысле цифр. Действительно, с учетом
(1.7), (1.9) и (1.12) имеем Дх < ||х| • НУ" < | 10F • 10"" = ^-10р"я,
т.е. Дх < - • 10‘" • ЮЛ
2
Это означает, что мантисса Л/ нормализованного числа х
(см. (1.9)) имеет по меньшей мере п верных в строгом смысле
цифр.
Пример 1.11. Пусть х = 78,56; 5х = 0,0003. Имеем 0,0003 <
<0,0005 = 10 3, т.е. в числех верны в строгом смысле три циф-
ры. Действительно, в данном случае Дх = 78,56 • 0,0003 < 0,03, что
подтверждает полученный результат.
Контрольные вопросы
1. В значениях хи Дт десятичная запятая одновременно перемещена
на одинаковое количество разрядов влево или вправо. Изменится ли при
этом количество верных цифр в числе х?
2. Как устанавливается количество верных в строгом смысле цифр
по величине относительной погрешности приближенного числа, если
первая цифра относительной погрешности меньше 5? больше или рав-
на 5?
Упражнения
1. По заданным значениям приближенных чисел и их относительных
погрешностей установить количество цифр, верных в строгом смысле:
а) х= 2,364; х=0,07%;
б) у =109,6; у = 0,04%;
в) z=14,307; z= 0,005%.
Округлить значения х, у и z до верных цифр с сохранением одной
запасной цифры.
31
2. Со сколькими верными в строгом смысле десятичными знаками
после запятой нужно взять указанные значения, чтобы относительная
погрешность не превышала О, J %:
а) -/193; б) sin 0,9; в) In 24,6.
3. Составить программу округления приближенного значения хпо его
относительной погрешности 8х.
1.7. ВЫЧИСЛЕНИЕ ОШИБОК АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Получим формулы для учета распространения ошибок при
выполнении основных арифметических действий. Задачу сформу-
лируем в следующем виде:
Имеются приближенные данные с известными оценками ошибок.
С данными производится арифметическая операция. Какое влияние
на ошибку результата оказывают ошибки исходных данных?
Приступая к рассмотрению этого вопроса, нельзя не отметить
чувства неудовлетворенности по поводу самого подхода к делу.
Незнание вычислителем в подавляющем большинстве случаев знака
истинной ошибки принуждает его вводить в рассмотрение пре-
дельные абсолютные величины ошибок и приводит к тому, что
приходится пользоваться формулами, в общем случае сильно за-
вышающими величины ошибок (см. об этом также полразд. 1.11).
Однако ничего другого нс остается, если мы хотим получать хоть
сколько-нибудь гарантированные оценки.
Для простоты записей арифметические операции рассматрива-
ются для двух операндов — получаемые при этом формулы как
раз и используются при поэтапном учете ошибок. При необходи-
мости каждая из формул может быть легко распространена на
общий случай.
Сложение и вычитание. Абсолютная погрешность алгебраичес-
кой суммы приближенных значений не превышает,суммы абсо-
лютных погрешностей этих значений.
Действительно, пусть S=X+ Y — сумма точных чисел, среди
которых могут быть как положительные, так и отрицательные, a s =
= х + у — сумма приближений. Составим разность 5 - s = (X- х) +
+ (У - у) или, переходя к модулям, |5 - s| < jyV -х| + |У -у|, т.е.
es < ех + еу или, тем более, ел < Дх + Ду, откуда следует, что мож-
но принять
Д5 = Дх + Ду, (1-13)
т.е. предельной абсолютной погрешностью алгебраической суммы
можно считать сумму предельных абсолютных погрешностей сла-
гаемых.
Пример 1.12. Даны приближенные значения х = 235,4 и у =
- 79,1834, у которых все цифры являются верными в широком
смысле. Найдем на МК. их сумму: 5=235,4 + 79,1834 = 314,5834. Для
32
оценки точности результата вычислим сумму погрешностей сла-
гаемых: 1-10' + 1 • 10~4 = 0,1001 < 0,2 = As, Величина ошибки пока-
зывает, что в результате уже первый знак после запятой является
сомнительным. Стоило ли терять время на учет в вычислениях всех
знаков после запятой у второго слагаемого?
Из рассмотренного примера следуют поучительные выводы:
1)получение с помощью компьютера результата с большим чи-
слом значащих цифр еще не означает, что все эти цифры верны;
2)при вычислении сумм и разностей чисел с сильно различаю-
щимися абсолютными ошибками с целью экономии времени це-
лесообразно «уравнивать» точность исходных данных путем ок-
ругления более точных данных до точности менее точных (с од-
ной-двумя запасными цифрами). Так, в рассмотренном выше при-
мере имело смысл перед выполнением действия сложения округ-
лить значение у до сотых: 79,18.
Руководствуясь только что указанным правилом, следует иметь
в виду, что при последовательном вычитании и сложении несколь-
ких чисел выгоднее производить действия над числами в порядке
возрастания их абсолютных величин.
Относительные погрешности суммы и разности можно вычис-
лять через абсолютные, пользуясь формулой (1,7), но можно ис-
пользовать и специальные формулы. Получим их:
. Дх + Ду jx| Дх |у| Ду |х| |у|
3(лс+у) = -1-r = r-L-L-f-rr +j-LJ-| гт = гХ±-| Sx+j-bL-Sy; (1.14)
и + И |х-+ И |х| Iх + И 1И Iх + И |х + у|
. Дх + Ду |х| Дх |у| Ду Ы _ |у| с
8(x-y) = -j--Г = 1|ГТ + 1|ТТ = 1 —г^+г-^-ЦЗу. (1.15)
|х~у| |х - у| |х| |х-у||у| |х-у| |х - у|
Формулы (1.14) и (1.15) позволяют сделать полезные для прак-
тического использования выводы.
Пусть слагаемые х и у — одного знака, а 5 = тах(3х,8у). Тогда
из формулы (1.14) следует:
я/ ч Ф1+ 1Я> я я/ х
5(х + у) < —р—1= 3, т. е. 8(х + у) < б.
|х + у|
Это означает, что если приближенные слагаемые имеют оди-
наковый знак, то предельная относительная погрешность их сум-
мы не превышает наибольшей из предельных относительных по-
грешностей слагаемых.
Как видно из формулы (1,15), при вычитании близких чисел
может произойти большая потеря точности. Действительно, когда
вычитаемые числа почти одинаковы, то даже при условии, что их
собственные ошибки малы, относительная ошибка разности мо-
жет оказаться большой.
2 Лапчик
33
Пример 1.13. Найдем разность чисел х= 62,425 и у =62,409, у
которых все цифры верны в строгом смысле. Имеем:
х - у = 62,425 - 62,409 = 0,016.
Граница абсолютной погрешности разности
Л(х - у) = 0,0005 + 0,0005 = 0,001,
поэтому в числе 0,016 из двух значащих цифр верна лишь одна.
Сравним предельные относительные погрешности результата и
исходных данных:
&Г=^| = 0,000008; ^=5^=0,000008; 8(х-у)=^=0,07.
62,425 62,409 0,016
Таким образом, в данном случае предельная относительная
погрешность разности оказалась почти в 8000 раз больше предель-
ных относительных погрешностей исходных данных. Это означа-
ет, что в приближенных вычислениях нужно исключать вычита-
ние близких по величине значений (например, путем преобразо-
вания вычисляемых выражений).
Умножение и деление. Пусть р = х-у — произведение двух при-
ближенных чисел, a q = x/y — их частное. Знаки чисел х и у не
влияют на величину ошибки, поэтому для простоты примем х, у >0.
Имеем: Inp = Inx + Iny, In q = Inx - Iny.
Принимая во внимание (1.13), а также используя приближен-
ную формулу
Д In z=>d'lnz =—, получим Л1пр = Д1п<7 = Д1пх + Д1пу, т.е.
Z
= (|.,6>
Р Я X У
откуда следует
6(ху) = 5(х/у) = 5х + 5у, - (1-17)
т.е. предельной относительной погрешностью произведения (част-
ного) можно считать сумму предельных относительных погреш-
ностей сомножителей (делимого и делителя).
Из формулы (1.16) легко получаются формулы для вычисления
предельных абсолютных погрешностей произведения и частного:
Д(х • у) = хДу + уЛх; (1.18)
... хДу + уДх
М*/У)= у2—‘ (119)
Нетрудно установить, что если хотя бы одно из чисел х или у
неположительны, то в формулы (1.18) и (1.19) они войдут по
модулю (см. табл. 1.2).
34
Пример 1.14. Числа 43,1 и 5,72 заданы верными цифрами. Най-
дем на МК их частное #=7,534965. Для определения числа верных
знаков результата вычислим
. 43,1-0,1 +5,72-0,1
д? = ——-—!—- =
5,722
4,882
32,7184
= 0,15.
Частное q имеет один верный знак (7). Округляя полученный
результат с одной запасной цифрой, получим q = 7,5.
Как следует из формул (1.17), относительная погрешность про-
изведения и частного не может быть меньше, чем относительная
погрешность наименее точного из компонентов действий. В то же
время известно, что величина относительной погрешности при-
ближенного числа определяет количество его верных значащих
цифр (см. подразд. 1.6). По аналогии с тем, как при нахождении
алгебраической суммы не имеет смысла сохранять в более точ-
ных слагаемых излишнее количество десятичных знаков, при ум-
ножении и делении приближенных чисел нет необходимости со-
хранять в более точных данных излишнее количество значащих
цифр.
Для удобства все формулы для вычисления погрешностей ариф-
метических действий сведены в общую таблицу (табл. 1.2). Знак #
обозначает одну из операций: +,-,-, /.
Таблица 1.2
х it у M.V 9 y} S(x # у)
x + y Дх + Ду !х1 = М я 1 1 5х+ 1 1 бу |х + у| |х + у|
x-y Дх + Ду 1Х1 я М я 1 1 5х+ 1 1 5у |х-у| |х-у|
x-y |х|Ду + |у|Дх 8х + 5у
x/y |х| Ду + |у[Дх у2 5х + 5у
Используя приведенные в табл. 1.2 формулы, можно вести по-
операционный учет ошибок арифметических действий на компью-
тере (см. подразд. 1.9). Для этого применяют несложные функции,
примеры которых для языка Turbo Pascal приведены ниже.
function Dsum(da,db;single);single; {предельная
абсолютная погрешность суммы и разности)
begin Dsum:=da+db
end;
35
function Dmult(a,b:T; da,db:single):single;
{предельная абсолюная погрешность произведения}
begin Dmult:=abs(a)*db+abs(b)*da
end;
function Dquot{a,b:T; da,db:single):single;
{предельная абсолютная погрешность частного)
begin Dquot:=da/abs(b)+db*abs(a)/b/b
end;
function Round_R(a:T):single; {погрешность при
округлении с точностью, возможной в типе real)
begin Round_R:=abs(а)*0.5Е-11
end;
function Round_S(a:T):single; {погрешность при
округлении с точностью, возможной в типе single)
begin Round_S:=abs(а)*0.5Е-7
end;
function Round_D(a:T):single; {погрешность при
округлении с точностью, возможной в типе double)
begin Round_D:=abs(а)*0.5Е-15
end;
function Round_E(a:T):single; {погрешность при
округлении с точностью, возможной в типе extended)
begin Round_E:=abs(а)*0.5Е-19
end;
Контрольные вопросы
1. Как объясняется целесообразность сохранения излишних десятич-
ных знаков в более точных слагаемых при сложении нескольких чисел?
2. Каким способом можно быстро оценить относительную погреш-
ность суммы нескольких слагаемых одного знака, если известны относи-
тельные погрешности каждого слагаемого?
3. По какой причине в вычислениях следует избегать вычитания близ-
ких по величине чисел?
4. Как объясняется нецелесообразность сохранения излишних знача-
щих цифр в более точных данных при умножении или делении несколь-
ких чисел?
Упражнения
1. Произвести указанные действия и определить абсолютные и отно-
сительные погрешности результатов (исходные числа заданы верными в
строгом смысле цифрами):
а) 24,37 - 9,18; г) 1,504 - 1,502; ж) 12,64.0,3;
б) 18,437 + 24,9; д) 234,5 - 194,3; з) 72,3 : 0,34;
в) 24,1 - 0,037; е) 0,65.1984; и) 8124,6 : 2,9.
2. Описать на языке программирования функции для вычисления гра-
ниц относительных погрешностей арифметических действий.
36
1.8. ОЦЕНКА ПОГРЕШНОСТЕЙ ЗНАЧЕНИЙ ФУНКЦИЙ
Вычисления по формулам нередко предполагают нахождение
значений различных математических функций. Используя для рас-
четов МК или ЭВМ, вычислитель в этом случае преобразует вы-
числяемое выражение так, чтобы оно содержало лишь стандарт-
ные функции. При этом становится актуальным вопрос о методах
определения погрешностей значений элементарных функций.
Пусть функция Дх) дифференцируема в некоторой окрестно-
сти приближенного значения аргумента х, а ех — абсолютная ошиб-
ка значения аргумента. Тогда абсолютная ошибка значения функ-
ции Су = |/(х + Ах) - /(х)|. Поскольку на практике ошибка ех обыч-
но мала по сравнению со значением х, воспользуемся прибли-
женным равенством: е} ~ \df\ = |/'(х)| ^.Заменим ехна Дх. Это оз-
начает, что можно принять
Д/ = |/'(*)| Дх. (1.20)
Равенство (1.20) позволяет получить целую серию формул для оцен-
ки предельных абсолютных погрешностей значений элементарных
функций. Пусть, например, /(х) = 7х. Тогда Д(-Ух) =
хДх = . Или, аналогично:
14х
A(sin х) = |(sin х)'| Дх = |cos х| • Дх;
Д(соьх) = [(cosx)'| • Дх = |-sin х| - Дх = |sin х| Дх;
A(tgx) = |(tgx)'| • Дх =
1
COS2 X
Дх
COS2 X ’
Д(1п х) = |(1п х)'| Дх = — (х> 0);
Д(ст) = |(с*)'j • Дх - ех - Ахи т. д.
Для вывода формулы погрешности значения функции ху вос-
пользуемся представлением ху = cllnx, а затем формулой погреш-
ности экспоненты и произведения (предполагается, что х > 0):
Д(х}’) = Д(е-,,|пх) = e>,lnj: Д(у Inх) = хг + 1пх Ду
х
Формула (1.20) позволяет сделать важное для практики вычис-
лений наблюдение. Если значение модуля производной функции
/(х) в точке х меньше единицы, то Д/ < Дх, т.е. абсолютная ошиб-
ка значения функции оказывается меньше абсолютной ошибки зна-
чения аргумента. Если же |/'(х)| > 1, то значение функции будет иметь
ошибку, большую ошибки аргумента. Этот факт имеет простое гео-
37
Рис. 1.9. Зависимость абсолютной погрешности значения функции от
модуля ее производной:
а — при <1 Дх > Ду погрешность значения функции меньше погрешнос-
ти значения аргумента, т.е. Дх>Ду; б — при |/'(х)| > 1 погрешность значения
функции превышает погрешность значения аргумента, т.е. Дх < Ду
метрическое толкование. При |У'(лс)| < 1 функция изменяется мед-
ленно, т.е. «коридор» изменений значений функции меньше со-
ответствующего «коридора» изменений аргумента (рис. 1.9, а).
При |/'(х)| > 1 малым отклонениям аргумента будут соответство-
вать большие изменения значений функции (рис. 1.9, б).
Второй случай при достаточно больших значениях |/'(*)| при-
водит к резкой потере точности и потому должен особо учиты-
ваться в практике вычислений.
Формулы для вычисления предельных абсолютных погрешно-
стей значений некоторых функций одной переменной приведены
в табл. 1.3.
Таблица 1.3
/(X) Д/(х) 8/(х)
у/х Дх 2Л
_1_ X Дх X2 8х
sinx |cosx|-Дх |х ctgx| • 5х
COSX |sin х| • Дх |х tgx) • 8х
tgx Ах COS2 X 2|х| я |sin 2х|
Inx Дх X 8х |1пх|
38
Окончание табл. 1.3
м S/(x)
1g X Ax jr In 10 5x |lgx| In 10
е* еЛДх |x| • Sx
1(Н 10* In 10 -Дх In 10-|x| -5x
a resin х Ax Л-Х2 1± s, |arcsinx[Vl -x2
arccosx Ax 7l-X2 И s |arccosx| yl - x2
aretgx Дх 1 + X2 jx| |arctgx| (1 + x2)
ху + IM' Ду) |ylnx|-6y + |y|-3x
Пример 1.15. С помощью МК получаем sin 0,8 = 0,717356091. Если
0,8 — точное значение, то в соответствии с точностью вычисли-
тельного прибора полученный результат имеет точность ±1 -10“9.
Если же 0,8 — приближенное значение, у которого цифра 8 вер-
на, например, в строгом смысле, то предельная абсолютная по-
грешность значения аргумента Дх = 0,05, а погрешность получен-
ного значения синуса в соответствии с формулой оценки пре-
дельной абсолютной погрешности будет A(sinx) = cosхх
х Дх < 0,7 -0,05 - 0,035. Отсюда следует, что во втором случае по-
лученное на МК значение sin 0,8 = 0,717356091 имеет лишь одну
верную значащую цифру. Округляя результат с одной запасной
цифрой, получим 0,72.
В тех случаях, когда производная функция вблизи приближен-
ного значения аргумента имеет большие по модулю значения,
произойдет большая потеря точности (так называемый случай
катастрофической потери точности).
Пример 1.16. Пусть х= 1,5, причем Ах = 0,05, т.е. все цифры в
числе х верны в строгом смысле. Нужно вычислить значение tgx.
С помощью МК получаем: tg 1,5 = 14,10141994. Для определения
верных цифр в результате оценим его абсолютную погрешность:
. . Дх 0,05 Л
Д (tgx) = :— = — = 10, отсюда следует, что в полученном зна-
cos2 х 0,005
чении tg 1,5 ни одну цифру нельзя считать верной.
39
Прокомментируем полученный результат. Заданная точность
исходного значения аргумента определяет «коридор» его возмож-
ных значений: 1,45 < а: < 1,55. Найдем на МК значения tgx для
граничных значений х из этого «коридора»: tg 1,45 = 8,238092753;
tg 1,55 = 48,07848247. Как видно, диапазон изменения tgx состав-
ляет около 40 единиц, что вполне подтверждает отсутствие смыс-
ла в полученном выше результате вычисления.
В подобных случаях надо использовать все имеющиеся возмож-
ности для увеличения числа верных знаков в исходном данном.
Например, если оно получено в результате измерения, то попы-
таться использовать более точный измерительный прибор.
Пусть в условиях примера 1.16 х= 1,4923, Лх = 0,0005. Тогда
tgx = tg 1,4923 = 12,71327341, A(tgx) < 0,0n0°r5 < 0,09, т.е. в полу-
0,006
ченном результате в строгом смысле верны 2 цифры; округляя его
с одной запасной цифрой, получим 12,7.
Используя формулы табл. 1.3, можно составить подпрограм-
мы “функции для вычисления абсолютных погрешностей значе-
ний элементарных функций по заданному значению абсолютной
погрешности аргумента. Ниже приведены описания некоторых
таких функций на языке Turbo Pascal.
function Dsin(x,dx:single):single;
begin Dsin:=abs(cos(x))*dx
end;
function Dtg (x,dx:single) rsingle;
begin Dtg:=dx/sqr(cos(x))
end;
function Din(x,dx:single):single;
begin Dln:=dx/x
end;
function Dexp(x,dx:single):single;
begin Dexp:=dx*exp(x)
end;
Из формулы (1.20) легко получается оценка предельной отно-
сительной погрешности функции через предельную относитель-
ную погрешность значения аргумента:
= IMrl Ах = |/Щ |s
7 ’ ’ |/(*)| " |/(*)|1 1И ~ |/И1 1 ’
т.е.
яг |Я
/=|7wr" ' (I'2I)
40
или
5/ = ?Д^Дх. (1.22)
|/И
Так, пользуясь формулами (1.2L) и (1.22), можно, например,
получить
3(л/х) = —jM-=8x = -5х =
27^ 2 2|х|
Icos X
8(sinx) = ^-Ях|5х = IxctgxISx = Ictgxl Дх;
|sinx| 1 11 ill
5(еЛ) = —|x|5x = |x|5x = Ax; 6(lnx) - •5x;
ex x|lnx| |lnxj
8(xr) = 5(eylllA) = |ylnx]5(ylnx) = |y lnx|[5y + 5(lnx] =
= |lnx| Ay + |y| A(lnx) = |y lnx|5y + |y|8x
и т.д. В зависимости от способа задания исходных данных (с абсо-
лютными или относительными погрешностями) вычислитель
может использовать для подсчета предельных относительных по-
грешностей тот или иной вариант формулы. Наиболее употреби-
тельные из этих формул приведены в табл. 1.3.
Пример 1.17. Значение аргумента х = 0,63 имеет относительную
ошибку около 0,1 %. Оценить величину относительной ошибки
sin 0,63.
Используя соответствующую формулу из табл. 1.3, с помощью
МК получим: 8(sin0,63) = |0,63-ctg0,63| 0,001 = 0,000864 = 0,08%.
Используя величину найденной относительной погрешности,
можно оценить количество верных в строгом смысле значащих
цифр в искомом значении sin 0,63. Поскольку имеет место
0,00864 < 1 • 10'3, то (см. формулу (1.11)) можно сделать вывод, что
в значении sin 0,63 = 0,589145 по крайней мере две цифры после
запятой верны в строгом смысле.
Формулу оценки погрешности значения функции можно по-
лучить для общего случая. Пусть f — дифференцируемая функция п
переменных; — точные значения; хьх2,...,хя— при-
ближенные значения переменных, а ех. (/ = 1, 2,..., л) — их абсолют-
ные погрешности. Тогда абсолютная погрешность значения функции
f в точке (хьх2,...,хл) — это ее приращение ef=\f(Xi,X2,...,X„)~
~/(Х|,х2,...,х„)|. Считая, что погрешности еХ/ значительно мень-
ше абсолютных величин значений Х|,х2,-..,х„, заменим прираще-
ние функции е/ ее дифференциалом:
«у ~|#(х1,х2,...,хя)| =
if'.,
,=1 Эх,
п
1=1
э/
Эх,-
41
Это неравенство усиливается после замены абсолютных погреш-
ностей ех. предельными абсолютными погрешностями Дх,:
•'s £ 1.
Отсюда следует, что можно принять
Я
A/ = S
м
df »
dxt
(1.23)
Формула (1.23) имеет общий характер. Из нее можно получить
не только все формулы для вычисления предельных абсолютных
погрешностей элементарных функций (см. табл. 1.3), но и форму-
лы для предельных абсолютных погрешностей арифметических
действий. Например, пусть/(Х|,х2) = х2. Тогда
Д/ =
Э/
Эх,
ДХ[ +
Э/
дх2
ДХ2 = Х2ДХ( + Х|ДХ2,
что в точности совпадает с формулой (1.18).
Получим общую формулу для относительной погрешности
функции:
(1.24)
Для выражения 8/ через относительные погрешности аргумен-
тов формулу (1.24) можно переписать в виде
5/ = Хк|Ц12-/-8х(.. (1.25)
1 С/Х/
Предположив, что в формуле (1.23) все частные дифферен-
циалы одинаково влияют на образование погрешности д/, полу-
чим:
= п Дх,,
Эх(
откуда
^=-47» 0 = 1>2,...,л). (1.26)
Эх(
Формула (1.26) позволяет решать так называемую обратную
задачу теории погрешностей: по заданной точности значения функ-
42
ции находить необходимые для достижения этой точности допус-
тимые величины погрешностей значений аргументов.
Пример 1,18. Пусть х близко к значению — = 0,7853981.... Уста-
4
новить, какова должна быть точность х, чтобы sin х мог быть полу-
чен на МК с максимальной (машинной) точностью ±1 10“6.
Для /(x) = sinx по формуле (1.26) имеем (здесь п = 1):
А/ 1 Ю"6
Дх = ,——;, т. е. дх =---= 0,2 • 10 s. Отсюда следует, что для
cosx л
11 cos -
4
получения максимальной точности значений синуса при х, близ-
7Г
ких к —,
4
значения аргумента должны иметь не менее пяти верных
(в строгом смысле) знаков после запятой.
Контрольные вопросы
1. В какой зависимости находится абсолютная погрешность значения
функции одной переменной от абсолютной погрешности значения аргу-
мента?
2. Как объясняется резкая потеря точности значения /'(х) для при-
ближенных значений аргумента х на участках с большими по модулю
значениями f'(x) ?
3. Как формулируется обратная задача теории погрешностей?
Упражнения
1. Исходные числовые значения аргумента заданы цифрами, верны-
ми в строгом смысле. Произвести вычисления (на МК или компьютере)
и определить количество верных в строгом смысле цифр в следующих
значениях элементарных функций:
a) log 23,6; в) д) arctg8,45;
б) е2,01; г) arccos0,79; е) 3,42,6.
2. Значение х = 4,53 имеет относительную ошибку 0,02 %. Оценить
количество верных в строгом смысле значащих цифр в значениях:
а) 1пх; б) eJf; в) Xе.
1.9. СПОСОБЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ
ПО ЗАДАННОЙ ФОРМУЛЕ
Наиболее распространенный вид вычислений — это вычисле-
ния по готовой формуле. В компьютере вычисление при любой гро-
моздкости формулы обеспечивается, как правило, одной командой
43
(оператором). Если при этом программно не предусматривается
контроль за вычислительными погрешностями, вычислитель ана-
лизирует результат в конце счета.
Иногда условия вычислительной задачи заставляют вести по-
операционный учет движения вычислительной погрешности. До
появления ЭВМ пооперационный подход к оценке точности вы-
числений по необходимости рассматривался и как способ рацио-
нализации вычислений, ибо позволял на каждом шагу избавлять-
ся от сомнительных цифр, способных лишь загромождать и удли-
нять процесс ручных вычислений.
Однако то, ради чего преимущественно использовался поопе-
рационный подход — исключение сомнительных цифр из после-
дующих вычислений — при широком распространении быстро-
действующих вычислительных устройств с памятью, утратило свой
изначальный смысл.
Уже при вычислениях на микрокалькуляторах, при умелом ис-
пользовании дополнительных регистров памяти, нет необходи-
мости выписывать и заново вводить промежуточные результаты —
даже в случаях вычислений по достаточно громоздким формулам
(для программируемых микрокалькуляторов этих проблем вовсе
не существует).
Для пооперационного учета ошибок в вычислениях по форму-
ле программным путем сохраняется возможность получить досто-
верный окончательный результат методом его итогового округле-
ния на основе предварительно вычисленной погрешности (если,
конечно, возникающие затруднения не заставят вычислителя об-
ратиться к пооперационному анализу движения ошибки — на-
пример, для выяснения причин обнаруженной в итоге катастро-
фической потери точности вычислений).
Рассматривая в дальнейшем приемы вычислений, мы будем
учитывать как пооперационную, так и итоговую методику оценки
точности.
1.9.1. Вычисления по правилам
подсчета цифр
При вычислении этим методом явного учета погрешностей не
ведется, правила подсчета цифр показывают лишь, какое количе-
ство значащих цифр или десятичных знаков в результате можно
считать надежными.
Сами эти правила основываются на выводах, вытекающих из
формул для оценки погрешностей арифметических действий и
функций (см. подразд. 1.7 и 1.8). Приведем эти правила в система-
тизированном виде.
1. При сложении и вычитании приближенных чисел младший
из сохраняемых десятичных разрядов результата должен являться
44
наибольшим среди десятичных разрядов, выражаемых последни-
ми верными значащими цифрами исходных данных1.
Следует избегать вычитания близких по величине чисел, а так-
же при пооперационном применении правила для сложения и
вычитания нескольких чисел подряд стараться производить дей-
ствия над числами в порядке возрастания их абсолютных величин.
2. При умножении и делении приближенных чисел нужно вы-
брать число с наименьшим количеством значащих цифр и округ-
лить остальные числа так, чтобы в них было лишь на одну знача-
щую цифру больше, чем в наименее точном числе.
В результате следует считать верными столько значащих цифр,
сколько их в числе с наименьшим количеством значащих цифр.
3. При определении количества верных цифр в значениях эле-
ментарных функций от приближенных значений аргумента следу-
ет грубо оценить значение модуля производной функции. Если
это значение не превосходит единицы или близко к ней, то в
значении функции можно считать верными столько знаков после
запятой, сколько их имеет значение аргумента. Если же модуль
производной функции в окрестности приближенного значения
аргумента превосходит единицу, то количество верных десятич-
ных знаков в значении функции меньше, чем в значении аргу-
мента на величину к, где к — наименьший показатель степени,
при котором имеет место2 |/'(х)| < 10*.
4. При записи промежуточных результатов следует сохранять на
одну цифру больше, чем рекомендуют правила 1—3. В оконча-
тельном результате эта запасная цифра округляется.
Правила подсчета цифр носят оценочный характер и не являют-
ся методом строгого учета точности вычислений. Обычно их приме-
няют тогда, когда быстро и без особых затрат нужно получить ре-
зультат, не особо беспокоясь о его достоверности. Между тем прак-
тическая надежность этих правил достаточно высока в результате
вычислительной вероятности взаимопогашения ошибок, не учи-
тываемой при строгом подсчете предельных погрешностей.
При операционном учете ошибок вычислений используется
обычная расчетная таблица - так называемая расписка формулы.
1 Когда точность исходных данных такова, что все они имеют десятичные
знаки после запятой, т.е. являются десятичными дробями, правило формулиру-
ется более доступно: при сложении и вычитании приближенных чисел в резуль-
тате следует считать верными столько десятичных знаков после запятой, сколько
их в приближенном данном с наименьшим числом знаков после запятой. Коли-
чество десятичных знаков после запятой перед выполнением действия целесооб-
разно уравнивать, округляя до одной запасной исходные данные с большим
количеством десятичных знаков.
2 Действительно, при этом условии с учетом формулы Д f = |/'(х)|Дх можно
вывести, что увеличение к на единицу означает увеличение Д/примерно в 10 раз,
что в данном случае уменьшает в значении/(х) количество верных десятичных
знаков по сравнению со значением х на единицу.
45
Пример 1.19. Вычислите значение величины
А =
са + 4ь
1п(й + Ь7)
(1.27)
по правилам подсчета цифр для приближенных значений <7 = 2,156
и Ь = 0,927, у которых все цифры верны.
Вычисления приведены в табл. 1.4.
Таблица 1.4
а b еа е° + 4b Л2 а + Ь1 1п(а+ У) А
2,156 0,927 8,637 0,9628 9,600 0,8593 3,0153 1,1037 8,698
Прокомментируем ход вычислений. Сначала вычислим е2,156 =
= 8,63652. Это же дает нам и оценку величины производной
в этой же точке: 22,156 < 1-101, т.е. в полученном значении следу-
ет сохранить на один десятичный знак меньше, чем в значении
аргумента. Округляя с одной запасной цифрой, получаем 8,637
(запасная цифра выделена) и заносим результаты в таблицу. Да-
лее вычисляем ч/0,927 = 0,9628083, причем модуль производной
(1/2 >/й ) меньше единицы, поэтому сохраняем после запятой три
знака и один запасной: 0,9628. При вычислении суммы в числите-
ле находим 8,637 + 0,9628 = 9,5998 и, согласно правилу 1, округ-
ляем результат до тысячных: 9,600. При вычислении /г пользуемся
правилом 2, при нахождении суммы а + № — правилом 1.
При определении количества верных цифр в значении In 3,0153
снова применяем правило 3 (учитываем, что производная функ-
ции Inx при х > 1 имеет значение меньше единицы). Округляя
окончательный результат без запасной цифры, получим А = 8,70
(три верные значащие цифры).
Допустим, что в результате вычисления заданного в приме-
ре 1.19 выражения
(ехр(2,156) + sqrt(0,927))/ln(2,156 + sqr(0,927))
на МК или компьютере было получено значение 8,6873389294998.
Как выделить в полученном числе верные цифры? Сделать это можно
и без подробного поэтапного анализа, который приведен выше.
Действительно, так как выражение А представляет собой дробь,
то последнее действие при его вычислении — деление, а следова-
тельно, результат будет содержать верных значащих цифр не бо-
лее, чем в наименее точном из операндов — числителе или зна-
менателе. Учитывая, что корень квадратный дает верных цифр
столько же, сколько и его аргумент (три), а экспонента в данном
случае теряет не более одного верного знака после запятой (что
вместе с ненулевой целой частью также дает не менее трех знача-
щих цифр), замечаем, что в числителе число верных значащих
46
цифр будет равно трем. Нетрудно видеть, что в знаменателе число
верных цифр благодаря свойствам производной логарифма также
наверняка не менее трех. Следовательно, значение А должно быть
округлено до трех верных знаков: А - 8,70. Там, где возможен по-
добный анализ, при использовании МК или компьютера в не-
посредственных вычислениях по правилам подсчета цифр можно
избежать пооперационного учета количества верных знаков.
Контрольные вопросы
1. Как формулируются правила подсчета цифр?
2. В каких случаях рекомендуется применять правила подсчета цифр?
3. Какие два способа применения правил подсчета цифр возможны в
вычислениях на МК и ЭВМ?
4. Какова последовательность действий на каждом промежуточном
этапе расчетной таблицы в вычислениях по правилам подсчета цифр с
пооперационным учетом ошибок? на заключительном этапе?
Упражнения
Вычислить на МК или компьютере значения заданных выражений по
правилам подсчета цифр двумя способами:
1) с пооперационным анализом результатов;
2) с итоговой оценкой окончательного результата (у числовых дан-
ных все цифры верные):
0,62 + 716/9. 12,47 +712,52 + 14,82 .
а) lg41,3 ’ . sin2 0,97+ cos2 2,63 ’
^6,91 + 3,352). 7W и
’ T626J ’ } е194 --8.042 °’
1.9.2. Вычисления со строгим учетом предельных
абсолютных погрешностей
Этот метод предусматривает использование правил вычисления
предельных абсолютных погрешностей, рассмотренных в подразд. 1.7
и 1.8.
При пооперационном учете ошибок промежуточные результа-
ты, так же как и их погрешности, заносятся в специальную таб-
лицу, состоящую из двух параллельно заполняемых частей — для
результатов и их погрешностей. В табл. 1.5 приведены пошаговые
вычисления со строгим учетом предельных абсолютных погреш-
ностей по той же формуле, что и в примере 1.19, и в предположе-
нии, что исходные данные а и b имеют предельные абсолютные
погрешности Да = \Ь = 0,0005 (т.е. у а и b все цифры верны в
строгом смысле).
Промежуточные результаты вносятся в таблицу после округле-
ния до одной запасной цифры (с учетом вычисленной параллель-
47
но величины погрешности); значения погрешностей для удобства
округляются (с возрастанием!) до двух значащих цифр. Просле-
дим ход вычислений на одном этапе (см. табл. 1.5).
Таблица 1.5
a b ca 4b e° + 4b Z>2 a + i2 ln(<7 + Л2) A
2,156 0,927 8,637 0,9628 9,603 0,860 3,016 1,104 8,70
Дд АЛ A(e°) Д(.4Ь) A(eff + Vz>) A(i2) A(a + b~) Aln(« + Z;2) ДА
0,0005 0,0005 0,0049 0,00027 0,0054 0,0016 0,0021 0,00076 0,016
Используя калькулятор, имеем е2-156 = 8,63652. Подсчитаем пре-
дельную абсолютную погрешность (см. табл. 1.3): Д(е2,156-0,0005) =
= 0,0043182 = 0,0044. Судя по ее величине, в полученном значе-
нии экспоненты в строгом смысле верны два знака после запятой.
Округляем это значение с одной запасной цифрой: с2,156 = 8,6 37
(запасная цифра выделена) и вносим его в таблицу. Вслед за этим
вычисляем полную погрешность полученного результата (погреш-
ность действия плюс погрешность округления: 0,0044 + 0,00048 =
= 0,0049), которую также вносим в таблицу. Все последующие дей-
ствия выполняем аналогично с применением соответствующих
формул для предельных абсолютных погрешностей.
Округляя окончательный результат до последней верной в стро-
гом смысле цифры, а также округляя погрешность до соответ-
ствующих разрядов результата, окончательно получаем: А = 8,7 ± 0,1.
Вычисления по методу строгого учета предельных абсолютных
погрешностей можно выполнить на компьютере с помощью про-
граммы. Если не производить пооперационного учета движения
вычислительной ошибки, то достаточно вычислить значение пре-
дельной абсолютной погрешности окончательного результата, а
затем произвести его округление. Ниже приведена программа вы-
числения по формуле (1.27), в которой значение погрешности
итогового результата вычисляется по формуле, полученной путем
последовательного применения формул для погрешностей ариф-
метических действий и элементарных функций, приведенных в
табл. 1.2 и 1.3:
[le^+V^I 2л/б(Дй+2М/>)+11п(о+£2)| (2е°Да\/Л+Дб)Ф+62)][1п(й+62)]2
дд - J-----!--------------------- . (1.28)
14b{a+b2)
Окончательный результат округляется с использованием мо-
дуля okrugl (см. подразд. 1.5) и выводится в правильной записи
верными в широком смысле значащими цифрами.
program Formula_l__27
uses okrugl,ert;
48
type T=real;
var a,b,da,db,prl,pr2,aa,rezl,rez2,rezult: T;
n,m:intecer;
function Dsum(dx,dy:single):single; (предельная
абсолютная погрешность суммы}
begin Dsum: ==dx+dy
end;
function Dquot(x,у:T;dx,dy:single):single;
{предельная абсолютная погрешность частного}
begin Dquot:=(abs(x)*dy+dx*abs(y))/sqr(y)
end;
function Dmult(x:T;dx:single):single; {предельная
абсолютная погрешность произведения}
begin Dmult:=2*abs(x)*dx
end;
function Din(x,dx:single):single; {предельная
абсолютная погрешность натурального логарифма}
begin Dln:=dx/x
end;
function Dexp(x,dx:single):single; {предельная
абсолютная погрешность экспоненты}
begin Dexp:=dx*exp(х)
end;
function Dsqrt(x,dx:single):single; {предельная
абсолютная погрешность квадратного корня}
begin Dsqrt:=dx/(2*sqrt(x))
end;
function Round_R(a:T):single; {погрешность при
округлении}
begin Round_R:=abs(a)*0.5E-11
end;
begin
writein('Введите a,b,da,db'); read(a,b,da,db);
prl:=exp(a)+sqrt(b); {числитель}
pr2:=ln(a+sqr(b)); {знаменатель}
aa:=prl/pr2;
rezl;=Dsum(Dexp (a, da) , Dsqrt (b, db) ) ; {предельная
абсолютная погрешность числителя}
rez2:=Dln(a+sqr(b),Dsum(da,Dmult (b,db)));
{предельная абсолютная погрешность знаменателя}
rezult:=Dquot(prl,pr2,rezl,rez2);
okr(aa,rezult,aa,n);
49
if aa<0 then begin if n<0 then m:=0 else m:=n;
writeln(1 Округленное число a=',аа-1Е-10:17:m,
' n=',n);
end
else begin if n<0 then m;=0 else m:=n;
writeln('Округленное число a=',
аа+1Е-10:17:m,’ n=',n);
end;
repeat until keypressed
end.
Результат работы программы:
Введите a,b,da,db
2.156 0.927 0.0005 0.0005
Округленное число а=8.70 п=2
В тех случаях, когда для вычислений выгоднее применять каль-
кулятор, можно обойтись и без составления программы. Рас-
смотрим, например, как можно получить итоговую оценку пре-
дельной погрешности результата вычислений на МК по фор-
муле с использованием предельной относительной погрешно-
сти.
Пример 1.20. Значения а = 23,1 и Ь = 5,24 даны цифрами, верны-
ми в строгом смысле. Вычислить значение выражения В =
С помощью МК получаем 5-0,2921247. Используя формулы
относительных погрешностей частного и произведения, запишем:
5 В = 5(Va) + 5А + 5(1па), т.е.
85 = -80 + 86 + 3^.
2 |1пп|
Пользуясь МК (см. также формулу (1.7)), получим 85 =0,003,
что дает Д5 = 5-85 = 0,0008. Это означает, что в результате две
цифры после запятой верны в строгом смысле: В = 0,29 ± 0,001.
Контрольные вопросы
1. Как оформляются вычисления со строгим учетом предельных по-
грешностей при пооперационном учете ошибок?
2. Какова последовательность действий на каждом промежуточном
этапе расчетной таблицы в вычислениях по методу строгого учета пре-
дельных погрешностей с пооперационным учетом ошибок? на заключи-
тельном этапе?
3. Как вычисляются предельные погрешности результата при исполь-
зовании методики итоговой оценки ошибки вычислений?
50
Упражнения
У значений а = 2,674 и b - 31,48 все цифры верны в строгом смысле.
Вычислить значения заданных выражений со строгим учетом границ по-
грешностей двумя способами:
1) с пооперационным учетом границ погрешностей («ручным» и про-
граммным способом, в котором должен быть предусмотрен трассиро-
вочный вывод промежуточных значений погрешности);
2) с итоговой оценкой точности результата:
. ab
а) ,. .;
+ Ь~
lg(«3 + Ьг)’
e-lfb .
В) 1п(1 +а2)’
г) 1g
cos2 а + b
а'Гь + '
1.9.3. Вычисления по методу границ
Если нужно иметь абсолютно гарантированные границы воз-
можных значений вычисляемой величины, используют специаль-
ный метод вычислений — метод границ.
Пусть /(х, у) — функция непрерывная и монотонная в неко-
торой области допустимых значений аргументов тиу Нужно по-
лучить ее значение Дц, Ь), где а и b — приближенные значения
аргументов, причем достоверно известно, что
НГа<й<ВГа; НГ*<Й<ВГ*. (1.29)
Здесь НГ, ВГ — обозначения соответственно нижней и верх-
ней границ значений параметров. Итак, вопрос состоит в том,
чтобы найти строгие границы значения /(а, Ь) при известных
границах значений а и Ь.
Допустим, что функция f(x,y) возрастает по каждому из аргу-
ментов х и у. Тогда
/(НГ0,НГ*) < f(a,b) < /(ВГО,ВГ*).
Пусть теперь f(x, у) возрастает по аргументу х и убывает по ар-
гументу у. Тогда будет строго гарантировано неравенство
/(НГ0,ВГ*) < f(a,b) < /(ВГЙ,НГ*).
Рассмотрим указанный принцип на примере основных ариф-
метических действий. Пусть /(х, у) = х + у. Тогда очевидно, что
НГЙ+НГ* < а+ 6 < ВГа+ВГ*. (1.30)
Точно так же для функции f2(x,y) = х - у (она по х возрастает,
а по у убывает) имеем
НГа - ВГ* <а-Ь< ВГД-НГ*. (1-31)
Аналогично для умножения и деления: НГ0-НГ* < а < ВГЙ • ВГ*; (1.32)
НГа а ВГО ВГ* b НГ*' (1-33)
51
Рассмотрим функцию -----:. Замечаем, что при увеличе-
но - у)
нии х она убывает, а с увеличением у возрастает (разумеется,
при соблюдении условий существования). Следовательно, имеет
место неравенство
I 1 1
1п(ВГа - НГО < 1п(а-&) < 1п(НГя -ВГ6)
Вычисляя по методу границ с пошаговой регистрацией проме-
жуточных результатов, удобно использовать обычную вычисли-
тельную таблицу, состоящую из двух строк отдельно для вы-
числения НГ и ВГ результата (по этой причине метод границ на-
зывают еще методом двойных вычислений). При выполнении про-
межуточных вычислений и округлении результатов используются
все рекомендации правил подсчета цифр с одним важным допол-
нением: округление нижних границ ведется по недостатку, а верх-
них — по избытку. Окончательные результаты округляются по этому
же правилу до последней верной цифры.
+ yfb
В табл. 1.6 приведены вычисления по формуле А =--------z-
1п (а + о)
методом границ. Нижняя и верхняя границы значений а и b опре-
делены из условия, что в исходных данных а = 2,156 и b = 0,927
все цифры верны в строгом смысле (Ду = Ab = 0,0005), т.е. 2,1555 <
< а < 2,1565; 0,9265 < 6 < 0,9275.
Таблица 1.6
а b е“ 4ь с" + 4~Ь Ь2 а + 1л(а + ЬА А
НГ 2,1555 0,9265 8,63220 0,96255 9,59475 0,85840 3,01434 1,10338 8,6894
ВГ 2,1565 0,9275 8,64084 0,96307 9,60391 0,86026 3,01676 ljl0419 8,7041
Таким образом, результат вычислений значения А по методу
границ имеет вид
8,6894 < А < 8,7041.
Способ границ связан со способом строгого учета предельных
абсолютных погрешностей следующим образом. Пусть Х- -- точное
значение некоторой величины, ех — его приближение с известны-
ми границами НГХ и ВГЛ..
„ НГ,+ВГЛ
Примем х равным значению----, тогда абсолютная по-
грешность этого приближения (рис. 1.10) будет заведомо не боль-
н г, - вгх
ше полуразности е.,. = -л-----
52
II I
X x
Рис. 1.10. Связь между абсолютной погрешностью и границами
Так, по результатам вычислений в табл. 1.6 получаем
лЛ 6894 ^ 704.. ^8,704.-8,6894
2 2
что дает А = 8,697 ± 0,008, или при записи цифрами, верными в
строгом смысле,
А = 8,7 ±0,01.
Вычисления по методу границ также можно реализовать про-
граммным путем. При этом можно осуществлять либо поопераци-
онную, либо итоговую регистрацию значений НГ и ВГ результа-
тов. В приведенной ниже программе реализован пошаговый вывод
значений границ в процессе вычисления по формуле (1.27).
program Method_border;
uses crt;
type T=real;
var a,b:T;
da, db, nga, vga,ngb, vgb, Isum, upsum, Imult, upmult, lsum2, aa, upsum2,
Iquot,upquot, ,r:single; n: integer;
{верхняя и нижняя границы погрешности суммы}
procedure BordSum(la,upa,lb,upb:single;
var Is,ups:single);
begin ls:=la+lb; ups:-upa+upb
end;
{верхняя и нижняя границы погрешности произведения)
procedure BordMult(la,upa:single;var Im,upm:single);
begin lm:=sqr(la); upm:=sqr(upa)
end;
{верхняя и нижняя границы погрешности частного)
procedure BordQuot(la,upa,lb,upb:single;
var lq,upq:single);
begin lq:=la/upb; upq:-upa/lb
end;
begin
writein('Введите a,b,da,db’);
read (a, b, da, db) ;
writein;
nga:-a~da; vga:=a+da;
53
writeln(nga:10:4,’ < a < ', vga:10:4);
ngb:=b-db; vgb:=b+db; writeln(ngb:10:4,1 < b <
vgb; 10 : 4) ;
writeln ('нижняя граница eAa=',exp(nga));
writeln ('верхняя граница eAa=',exp(vga));writeln;
writeln('нижняя граница sqrt(b)=',sqrt(ngb));
writeln('верхняя граница
sqrt(b)=',sqrt(vgb));writeln;
BordSum(exp(nga),exp(vga), sqrt(ngb),
sqrt(vgb),Isum,upsum);
writeln ('нижняя граница eAa+sqrt(b) = ’,Isum);
writeln ('верхняя граница eAa+sqrt(b) = ',upsum);
BordMult(ngb,vgb,Imult,upmult)/writeln;
writeln('нижняя граница bA2=1,Imult);
writeln ('верхняя граница bA2=',upmult);
BordSum(nga,vga,Imult,upmult,lsum2,
upsum2)/writeln;
writeln('нижняя граница a+bA2=',lsum2);
writeln ('верхняя граница a+bA2=',upsum2);
BordQuot(Isum,upsum,In(lsum2),In(upsum2) ,
lquot,upquot) ;
aa;=(lquottupquot)/2;writeln;
writeln ('нижняя граница A=' ,lquot);
writeln('верхняя граница A=upquot);writeln;
repeat until keypressed
end.
Результат работы программы:
Введите a,b,da,db
2.156 0.927 0.0005 0.0005
2.1555 < а < 2.1565
0.9265 < b < 0.9275
нижняя граница еАа=8.63220464292705Е+0000
верхняя граница еАа=8.64084259896689Е+0000
нижняя граница sqrt(b)=9.62548711708320Е-0001
верхняя граница sqrt(Ь)=9.63068019164141Е-0001
нижняя граница eAa+sqrt(Ь)=9.59475326538086Е+0000
верхняя граница eAa+sqrt(Ь)=9.60391044616699Е+0000
нижняя граница bA2=8.58402311801910Е-0001
верхняя граница bA2=8.60256254673004Е-0001
нижняя граница a+bA2=3.01390218734741Е+0000
верхняя граница а+ЬА2=3.01675629615784Е+0000
54
нижняя граница In(а+Ьл2)=1.10323564690644Е+0000
верхняя граница In(а+Ьл2)-1.10418218003589Е+0000
нижняя граница А=8.68946647644043Е+0000
верхняя граница А-8.70522117614746Е+0000
Таким образом, результат работы программы вычисления А по
методу границ имеет следующий вид (значения НГ и ВГ округле-
ны соответственно по убыванию и возрастанию до четырех знаков
после запятой):
8,6895 < А < 8,7052.
Сравнивая этот результат с тем, что получено в процессе «руч-
ного» счета (см. табл. 1.6), можно сделать вывод, что с помощью
программного вычисления получен более узкий интервал гранич-
ных значений.
Для сопоставления полученного результата со значением А,
найденным по методу строгого учета границ погрешностей
(см. табл. 1.5), можно найти значение еА:
еА = (8,7052 - 8,6895)/2 = 0,0079.
Тогда окончательный результат будет иметь вид (0 — сомни-
тельная цифра):
А = 8,70 ± 0,01.
Как видно из записи, в результате верны в строгом смысле две
первые значащие цифры: 8 и 7, что в точности совпадает с пре-
дыдущими результатами «ручного» счета.
Вычисления по методу границ можно вести и без пошагового
фиксирования промежуточных результатов. Пусть, например, нуж-
но найти границы значения выражения Z =-----т-, если 4,845 <
1п(х — у2)
< х < 4,855; 1,215 < у < 1,225. Имеем: ------------^-<Z <
У 1п(ВГх-(НГ,)1)
<Z < |п(НГ—(BFV) С помощью МК вычислим значения ниж-
ней и верхней границ Z:
1,807895009 < Z< 1,825100030.
Если нет нужды держать в результате слишком большое коли-
чество значащих цифр, его можно округлить (нижнюю границу —
по убыванию, верхнюю — по возрастанию). Так, округляя грани-
цы Z до сотых, будем иметь
1,80 <Z< 1,83, т.е. Z= 1,81 ±0,01.
55
Контрольные вопросы
1. В чем основное отличие метода границ от вычислений по методу
строгого учета границ погрешностей?
2. Какова последовательность действий в вычислениях по методу гра-
ниц с пооперационным учетом ошибок на каждом промежуточном эта-
пе расчетной таблицы? на заключительном этапе?
Упражнения
У значений а = 2,674 и b = 31,48 все цифры верны в строгом смысле.
Вычислите значения заданных выражений по методу границ («ручным»
и программным способом без пошаговой регистрации значений границ
промежуточных результатов) и сравните ответ с результатами, получен-
ными при выполнении упражнений к п. 1.9.2:
, ah a + Jb , е" -\[b , , cos2c+/>
а Ja + b2’ 1ё(а1+Ь1У В 1п(1+д2)’ Г S '
1.10. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ ПО ФОРМУЛАМ
С ИСПОЛЬЗОВАНИЕМ ИНСТРУМЕНТАЛЬНЫХ ПАКЕТОВ
Оценка точности получения результатов при осуществлении
элементарных арифметических расчетов может быть предусмотре-
на и при использовании инструментальных программных средств:
Excel, Derive, Maple, MatLab, Mathematica, MathCad и др. К со-
жалению, запроса точности исходных данных при применении
этих пакетов не предусматривается. Это означает, что пользова-
тель должен сам организовывать учет ошибок вычислений.
Значительная часть интегрированных программных средств ав-
томатизации процесса решения математических задач принадле-
жит к классу систем символьной математики.
Символьный тип данных — это символы, тексты "и математиче-
ские выражения (формулы).
Целочисленные данные представляются без погрешности, и
арифметические операции над целыми числами системы выпол-
няют также без погрешностей.
Рациональные данные задаются отношением целых чисел и
также представляют результат точно. Количество цифр, представ-
ляющих большое целое число, ограничено лишь его значением,
но не фиксированными форматами.
Для целочисленных операций используются не обычные коман-
ды микропроцессора, ориентированные на фиксированные фор-
маты, а специальные, реализованные программно, алгоритмы вы-
числений с целыми числами произвольной разрядности.
Вещественные числа в системах символьной математики могут
иметь мантиссу с любым, но конечным числом знаков.
56
Вещественные числа всегда имеют некоторую погрешность
представления результатов из-за неизбежного округления их и
существования так называемого «машинного нуля» — наимень-
шего числа, которое воспринимается как нуль. Например, в тер-
минах системы Mathematica говорят о приближении числовых дан-
ных как об их аппроксимации.
Рассмотрим выполнение расчетов средствами наиболее попу-
лярных инструментальных пакетов по формулам на основе уже
рассмотренных нами ранее примеров вычислений.
+ \[b
Пример 1.21. Вычислим значение величины А =------т- при
1п(<2±ш)
заданных значениях параметров а и b с итоговой регистрацией
результатов вычислений по методу систематического учета гра-
ниц абсолютных погрешностей (рис. 1.11) в среде табличного про-
цессора Excel. Для этого воспользуемся формулой (1.28).
Используя результаты, полученные в таблице, изображенной
на рис. 1.11, получаем
А = 8,70 ±0,01.
Пример 1.22. Предыдущее задание может быть выполнено в Excel
и с пошаговой регистрацией границ абсолютных погрешностей
(рис. 1.12).
В ячейках электронной таблицы записываем соответствующие
формулы (см. рис. 1.12). На каждом шаге вычислений выполняется
ручное округление результатов до цифр, верных в широком смысле
(т.е. с одной запасной цифрой). Для этого используется встроен-
ная функция округления ОКРУГЛ(число;количество_цифр).
Результаты расчетов представлены на рис. 1.13.
Окончательный результат: А - 8,70 ± 0,01.
еа + -\[b
Пример 1.23. Вычислим значение А =-----=- методом границ
1п(л + сг)
без пошаговой регистрации промежуточных результатов в среде ма-
тематической системы MathCad; исходные значения а и b прежние.
Воспользуемся формулами
иг - ехР<НГа) + ж; . ехр(ВГд) ± УвГй
А 1п(ВГй+ВГ2) ’ А 1п(НГя+НГ*) ‘
Вычисления показаны на рис. 1.14.
Таким образом, окончательно получаем
8,6895 < А < 8,7052.
Математическая система MathCad позволяет выполнять обыч-
ные вычисления с повышенной точностью — до 20 знаков. Для
перехода в такой режим вычислений нужно числовые константы
57
ixsusaw! ичу’ЕНзСзау-г iti^'Ezc/i-ABstr-rzyi |Е2гЕХР02:лачо^»|^;^_чг?:>'<'.-(21--ог’Е- , гт(А2+е-
A= 8.697339,
ДЛ=1 O.OIlBS]
! A В C < D E F
-1 a b Да/ ДД 2-Jb a + b :
J2 2 156 0 927 0 0005 1 925617 3015329
Рис. 1.11. Вычисления по формуле с итоговой регистр!: ген границ абсолютных погрешностей
;ч\<ЭКРУГЛ1С2‘3)С№УГтГ.(О^^:'ЭкР^Л(Ё2Д|’с<РУГГ(Р2:3] ОКРУГЛ(С2;3) окРУ“Л(Н^:3'|. ОКРУГП12:Зг?.'.- ••• - •.’<
|" ! I 4-------------------- ---
- --------— е —;--- - Л. - -—-— *_____________:_______________________________. ________1____7_____________
I Да А6 д (е-‘ ;. j (*’ ч ,‘£ гi ‘ У -. ъ ••.».',!. Г: д х ••’•• ~ ’•
рЖО^ОД-Щ GZA7 С.'~ЮГ :г--7’117 |Д7<7 G7/C? '|,Л£8'Е?'|'Н7чла&|Нг|-=7).'Н?-2
----------------------1-----------lJ------------1-------------------------------------:
%: СЗ-СЗ |33 32 15Вё\ЬЗ _2) ’Л£2(Г 3-i Al APf;! 13- ?i 'iRSf 3-!7i
Ряс. 1.12. Pc.nnisarfrff нетепл C?CTtviS-|:-tfC«f»t:i • ii I JVIII.-II tlC'ro.I.lU'JLLLCX псирешлостен u Excel
asm';®® ий B-j&J MSiS'F G ••. 1
Hf • -а ь еа +л/Ь Ь 2 д +Z? In^+fc2)
В 2.156 0.927 3.63652 0.96281 9.59933 0.85933 3.01533 1.10371 8.69734
Sa № ш в; Йй а: 8.637 0.983 9.599 0.859 3.015 0 1.104 О ' ! 8.697
Ла ЛЬ Д(е°) Д(^) Д(га + 4Ъ~) А (а + А2) Л1п(й + Д2) <<дл 7
0.0005 0.0005 0.004318 0.00026 0.0046 0.00093 0.001427 0.00047 0.007877
J''”. ! ! 0.00048 М, 0.00480 0.00019! о.ооозз! 0.00033 0.00045 < 0.00491 0.00126 О.ОООЗЗ] 01.0023 0.00034 0.00176 0.000781 0.00822
Рис. 1.13. Расчетная электронная таблица
40
> • 1154 Ь :=
НГ(а) = •- Д>
НГ(а) = 2J555
НГ(Ь)Ь-ДЬ
НГ(Ь) = 0SM5
•1 - НГ(»)
•2ВГ(а)
КГ. А<’>!
к»!*2 + Ь2’1
НГ • »(&!>
Да .« С00С5 ДЬ'-ООСО)
ВГ(а) * а+Да
ВГ(а) • J 1545
ВГ(Ь) > Ъ + ДЬ
ВГ(Ь) = МЯ5
Ы - НГ (Ь)
Ь2 := ВГ(Ъ)
ВГ.^^
h'»l ♦ Ы1'
ВГ « ».WM
I
Рис. 1.14. Реализация метода границ в пакете MathCad
с форматированием результатов вычислений
И
Mathead Рпаллажш - lUnbtfedtl |
sin(o.8) - 0.717fe
twfcliy пи...
Pclynotnal Coeflj
V«idH«5
ffatnK
717356090899522
Transform
—
атгуттм
Рис. 1.15. Вычисление в MathCad значения функции
с увеличенным количеством знаков
в вычисляемых объектах задавать с обязательным указанием деся-
тичной точки, даже если они являются целыми числами. Для это-
го в меню Symbolics выбирается команда Evaluate/Floating Point, в
окне Floating Point Evaluation устанавливается точность вывода ре-
зультата, равная, например, 20 (число цифр результата может со-
держать до 4000 верных знаков) (рис. 1.15).
Система имеет конечную точность вывода результатов вычис-
лений, при которой учитываются только три значащие цифры,
причем последующие нули по умолчанию не пишутся. Точность
вывода результатов можно изменить с помощью контекстного
60
Рис. 1.16. Окно MathCad установки значений встроенных системных
переменных
меню, при этом точность расчетов определяется значением сис-
темной переменной TOL, изменение которой позволяет пользо-
вателю установить необходимую ему минимальную точность вы-
числений или допускаемую погрешность для различных алгорит-
мов аппроксимации (интегрирования, решения уравнений и т.д.;
по умолчанию TOL = 0,001). Системные переменные имеют свои
имена и значения, присваиваемые системой по умолчанию. Их
действие глобальное, т.е. они доступны в любом месте программы
(рис. 1.16).
Пример 1.24. Средствами системы компьютерной математики
Maple вычислим значение выражения по формуле (1.27), приме-
няя пошаговую фиксацию промежуточных результатов вычисле-
ний по методу границ.
Для организации вычислительного процесса потребуется сис-
темная переменная Digits, которая определяет число знаков ман-
тиссы в операциях с плавающей запятой. Вычисления будем осу-
ществлять (см. табл. 1.6) по группам команд (рис. 1.17).
Краткий обзор возможностей применения инструментальных
средств для вычислений по формуле показывает, что во многих
случаях использование этих средств позволяет обеспечить нагляд-
ную организацию вычислительной схемы, автоматизировать сам
процесс вычислений при возможности быстрого варьирования
исходных данных, а также — что особенно важно — получать ре-
зультат в различных форматах представления чисел. Все это делает
применение инструментальных средств для единичных расчетов
61
> * Digits : = б : • nga: = a-da; * vgai »a+da; -ngh : =h-dl»; * vgh: =h+dh ;
«ga-:='2.1555 vga-=2.1565 »gi-~-.9265 vgi-:- 9275
>-Digits r = 6: ngexp:-exp(nga|;vgexp:= exp(vga>; ngexp-~%. 63221 '.’g?w>‘:_,E.64O3^
>•Digits 1 = 5: ngsgrt:= sgrt(ngb) ;vgsgrt:=sgrt(vgh); ngsqrf:=-. 96255
vgsqrt-.— . 96307
> -Digits 1=6 mgexph : =ngexp+ngsqi't ;vgexpb r=vgejq»+vgsgrt; «gexph-—'9.59476
vgsr.pb-=-9.60391
>-Digits; =5:nghb:=ngbft2;vgbh:-vgb*2; л8А5-:=-.85В40
vgbb"=\86026
>-Digits r = 6 :ngsum:=nga+nghh ^-vgsumi^vga+vgbb ; rtgsum-=-3.01390
vgsuw;='3-01676
>-Digits : =6 ingln: = lji(ngstiTi,i) ;vgXn:=ln(vgsum) ; nglr3-.=-1.10323
L vgln •:=!. 10418
>*Digits : =6 :ngA:=ngexph/vgln;vgA:=vgexpb/ngln; »gA-:='8.68949- vgj4':=-B.70527
Рис. 1.17. Окно Maple с результатами пошаговых вычислений
по методу границ
по формулам более предпочтительным по сравнению с примене-
нием МК. или компьютера в программируемом режиме.
Контрольные вопросы
1. Какие встроенные функции округления могут быть использованы
в процессе вычислений с помощью инструментальных средств?
2. Какие инструментальные программные средства являются более
эффективными при использовании различных методов вычислений?
Упражнения
У значений а = 2,674 и b - 31,48 все цифры верны в строгом смысле.
Вычислить значения заданных выражений по методу строгого учета гра-
62
ниц погрешностей и методу границ с использованием инструменталь-
ных средств вычислений и сравнить ответ с результатами, полученными
при выполнении упражнений к п. 1.9.2:
. ab а +• 4b е° -l/b . . cos2 а + b
* Л + Л2> Ш(аа+$г)‘ * ln(l + fl2)’ Г 8 ал + bJa '
1.11. ВЕРОЯТНОСТНЫЕ И ЭМПИРИЧЕСКИЕ МЕТОДЫ
ОЦЕНКИ ОШИБОК ВЫЧИСЛЕНИЙ
Описанные способы оценки погрешностей приближенных вы-
числений — пошаговые вычисления предельных абсолютных по-
грешностей и метод границ, будучи строгими, дают при большом
объеме вычислений многократно завышенную по отношению к
реальности оценку погрешности результатов.
Поясним еще раз механизм этого завышения на простейшем
примере.
Пусть надо оценить погрешность суммы п чисел, каждое из
которых задано приближенно:
5 + Д5 = (<3| + Д[) + (о2 + Д2) +... + (а„ + Д„). (1.34)
Если понимать под Д, предельные абсолютные погрешности
слагаемых, то все, что можно сказать о предельной абсолютной
погрешности суммы, так это то, что она равна сумме предельных
абсолютных погрешностей слагаемых.
Если слагаемых бчень много, то даже при малости каждой Д,
Д5 может оказаться неприемлемо велико. Тем не менее это не оз-
начает реальной неприемлемости результата, поскольку в такой
редакции Д5не есть истинная погрешность суммы, а есть ее оцен-
ка сверху, исходящая из наиболее неблагоприятного стечения об-
стоятельств.
Если понимать под Д/ не предельные абсолютные, а реальные
погрешности слагаемых, картина оказывается иной. Среди них
будут и положительные, и отрицательные, и при сложении про-
исходит то, что в реальности спасает от катастрофически непри-
емлемых погрешностей результата, — так называемая частичная
компенсация погрешностей. Фактически только благодаря ей про-
должительные (иногда многочасовые) решения математических
задач на современных ЭВМ дают достоверные результаты, кото-
рые не тонут целиком в погрешностях.
В некоторых простейших случаях можно провести вероятност-
ную оценку реальной погрешности вычислений. Допустим, что в
сумме (1.34) п велико (иначе вероятностные оценки бессмыслен-
ны) и что совокупность погрешностей слагаемых есть набор неза-
висимых случайных чисел, распределенных по нормальному за-
кону (наиболее правдоподобное предположение) с центром в
63
точке 0 и некоторой дисперсией ст. Тогда статистическая оценка
погрешности суммы такова:
-ле < Д5 < ле,
где е — доверительный интервал, задаваемый с некоторой дове-
рительной надежностью Р,
Как известно из математической статистики, величину е мож-
но оценить следующим образом:
Ун
где t — коэффициент Стыодента, зависящий от доверительной
надежности и объема выборки (в реальности при больших п ко-
эффициент /слабо зависит от Ри при /’=0,99 t~ 3).
Основной вывод, который следует из этой оценки, таков: с
ростом п погрешность суммы растет пропорционально 4п (а не
пропорционально л, как предельная абсолютная погрешность).
Тем не менее вероятностные оценки не получили широкого
распространения и в практических вычислениях не используются.
Это связано с тем, что в любой реальной вычислительной форму-
ле сочетаются различные действия, и вероятностная оценка ито-
говой погрешности становится затруднительной.
Огромную роль в вычислительной практике играют эмпири-
ческие способы оценки погрешностей. Они не имеют под собой
теоретической базы, но почти всегда позволяют получить резуль-
тат, в котором опытный вычислитель практически уверен (хотя
вероятность ошибки отлична от нуля). Так, полуэмпирическими
являются описанные выше вычисления по правилам подсчета
цифр.
Другой достаточно универсальный эмпирический прием зак-
лючается в том, чтобы, решая вычислительную задачу на ЭВМ,
решить ее дважды с различным числом цифр в мантиссе веще-
ственных чисел. Для этого достаточно, применяя Pascal, вначале
объявить все вещественные переменные типом real, а затем, при
повторном решении — double. Значительное несовпадение резуль-
татов сигнал о серьезных проблемах, связанных с организаци-
ей вычислительного процесса или выбором алгоритма.
Далее при рассмотрении конкретных вычислительных процес-
сов мы будем говорить о связанных с ними эмпирических при-
емах контроля точности вычислений.
Контрольный вопрос
Как работает механизм завышения оценки погрешности путем ее за-
мены предельной погрешностью в случае вычисления произведения боль-
шого числа сомножителей?
64
Упражнение
Провести расчеты по формуле (1.27) на компьютере на различных
языках программирования (включая Turbo Pascal), описывая а и b раз-
личными (но, разумеется, одинаковыми в каждом конкретном расчете)
вещественными типами данных. Установить различия результатов и ин-
терпретируйте их.
ЛАБОРАТОРНАЯ РАБОТА № 1
Тема: Методы оценки погрешностей
Задание 1. Число х, все цифры которого верны в строгом смыс-
ле, округлить до трех значащих цифр. Для полученного числа Х| = х
найдите предельную абсолютную и предельную относительную
погрешности. В записи числа х, укажите количество верных цифр
(в строгом и широком смысле).
Задание 2. Вычислите с помощью МК значение величины Z
при заданных значениях параметров а, b и с, используя «ручные»
расчетные таблицы для пошаговой регистрации результатов вы-
числений, тремя способами:
1)по правилам подсчета цифр;
2)с систематическим учетом границ абсолютных погрешностей;
3)по способу границ.
Сравните полученные результаты между собой, прокомменти-
руйте различие методов вычислений и смысл полученных число-
вых значений.
Задание 3. Вычислите значение величины Z при заданных зна-
чениях параметров а, b и с, используя один из инструментальных
пакетов, с пошаговой и итоговой регистрацией результатов вы-
числений двумя способами:
1)по метолу строгого учета границ абсолютных погрешностей;
2) по методу границ.
Задание 4. Составьте программы и вычислите на ЭВМ значе-
ния величины Z при заданных значениях а, b и с с пошаговой и
итоговой регистрацией результатов двумя способами:
1)по методу строгого учета границ абсолютных погрешностей;
2) по методу границ.
Результаты, полученные в заданиях 3 и 4 разными способами,
сопоставьте между собой и сравните с ответами, полученными
при выполнении задания 2.
Пояснения к выполнению лабораторной работы № 1
Исходные данные для выполнения всех заданий содержатся в
табл. 1.7 (числа х, а, Ь, с — приближенные, в их записи все циф-
ры верны в строгом смысле, коэффициенты — точные числа).
3 Лампа ^5
Для выполнения заданий необходимо изучить .материал гл. 1,
подробно разобрав все приведенные в тексте примеры (лучше
всего при этом иметь под руками МК, а также компьютер хотя
бы с одним из инструментальных средств: Excel, MathCad, Maple
и др.).
Для выполнения задания / требуется владение основными оп-
ределениями и понятиями теории приближенных вычислений
(см. подразд. 1.3 и 1.4).
При выполнении задания 2 составляются «ручные» расчетные
таблицы, аналогичные табл. 1.4—1.6 (см. подразд. 1.9).
Для выполнения задания 3требуется владение по крайней мере
одним из инструментальных программных средств (дополнитель-
ные сведения можно получить в Приложении или из источников
[1,7, II]). При этом надо тщательно разобрать примеры, рассмот-
ренные в подразд. 1.9 и 1.11.
При выполнении задания 4 составляются программы для ЭВМ
с использованием процедур и функций, приведенных в примерах
гл. 1. Примеры аналогичных программ имеются в подразд. 1.9.
Поскольку при выполнении заданий 2, 3 и 4 используется одна
и та же расчетная формула, в результате выполнения лаборатор-
ной работы необходимо сделать обоснованный вывод о целесооб-
разности и эффективности использования тех или иных методов
и средств вычислений.
Таблица 1.7
Номер варианта X Z а ь С
1 2,3143 4аЬ Ь-2с 3,4 6,22 0,149
2 0,012147 (Ь-с)1 2а + Ь 4,05 6,723 0,03254
3 0,86138 In 6-о а2 + 12с 0,7219 135,347 0,013
4 0,1385 6 - sin а а + Зс 3,672 4,63 0,0278
5 23,394 lQc + 4b а1 -b 1,24734 0,346 0,051
6 0,003775 (а - с)2 Ji + 3b 4,7 0,0937 5,081
66
Окончание табл. 1.7
Номер варианта X Z а Ъ С
7 718,54 а - sin b Ь2 + 6с 1,75 1,21 0,041
8 9,73491 'Jb-с In а + b 18,0354 3,7251 0,071
9 11,456 In с - !0д Убе 0,113 0,1056 89,4
10 3549 с + sin А с-а2 0,317 3,27 4,7561
11 7,32147 1п(6 + с) b -ас 0,0399 4,83 0,072
12 35,085 Ja + b За -с 1,574 1,40 1,1236
13 7,544 ab - 4с In а + Ь 12,72 0,34 0,0290
14 198,745 а - cos b 13с + Л 3,49 0,845 0,0037
15 37,4781 ас + Ь •Jb-c 0,0976 2,371 1,15874
16 0,183814 1е(д - ь) 4ь-с 82,3574 34,1 7,00493
17 0,009145 Ь + cosc />+ 2а 0,11587 4,25 3,00971
18 1 1,3721 а2 -Ь •Jab + с 3,71452 3,03 0,765
19 0,2538 In о+ 46 ab-c 7,345 0,31 0,09872
20 10,2118 Ь2 + \п с >/с - о 0,038 3,9353 5,75
ГЛАВА 2
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ
УРАВНЕНИЙ
2.1. ПОСТАНОВКА ЗАДАЧИ РЕШЕНИЯ УРАВНЕНИЙ
Решение уравнений — одна из древнейших математических
проблем. Нс счесть приложений математики, в которых решение
уравнений является необходимым элементом решения задачи.
Существует множество классов уравнений — алгебраические и
трансцендентные, дифференциальные, интегральные, функцио-
нальные, операторные и т.д. Конечно, предпочтительными явля-
ются аналитические методы решения, позволяющие получить его
в виде формулы. Примеры уравнений, позволяющих получать ана-
литические решения, хорошо известны из школьной математики.
Из алгебраических это линейные и квадратные уравнения, из
трансцендентных — простейшие показательные, логарифмичес-
кие и тригонометрические уравнения. Простейшие дифференци-
альные уравнения — с разделяющимися переменными, линей-
ные, однородные и некоторые другие — также позволяют полу-
чать аналитические решения. При изучении других классов урав-
нений (интегральных и т.д.) удается выделить некоторые про-
стейшие их разновидности, которые, с известными оговорками,
решаются аналитически. Тем не менее подавляющее большинство
уравнений, встречающихся в приложениях, не могут быть реше-
ны аналитически.
Численные методы решения уравнений являются гораздо бо-
лее мощными, нежели аналитические. Они тоже не всемогущи,
но в умелых руках численные методы позволяют получать реше-
ния множества уравнений, совершенно недоступных для анали-
тических методов. При этом надо заметить, что указанная недо-
ступность может быть обусловлена двумя обстоятельствами: недо-
статочным уровнем математического образования того, кто ре-
шает уравнение, и принципиальной невозможностью; в данном
случае речь идет и о первом, и, что гораздо важнее, о втором
обстоятельствах.
При сопоставлении численных и аналитических методов надо
понимать некоторую условность самого подразделения их на эти
категории. Поясним сказанное двумя примерами.
68
1. При решении квадратного уравнения х2 + рх + q = 0 исполь-
зуют общеизвестные формулы, в которые входит квадратный ко-
рень. Если при некоторых фиксированных значениях коэффици-
ентов понадобятся численные значения корней, то придется ис-
пользовать простейшую численную процедуру.
_ _ . . dy ysin(ax) z
2. Дифференциальное уравнение —- ------ (оно относит-
ся X
ся к простейшим в общепринятой классификации — уравнение с
разделяющимися переменными) можно «решить» в том смысле,
который вкладывается в это понятие в теории дифференциальных
! 5 '"Н Г/1
уравнений, т.е. «в квадратурах»: у = С’схр| I—|. При лю-
бом фиксированном значении С эта формузга определяет функцию
у(х), но интеграл, входящий в нес, не выражается в элементарных
функциях, и вычислять его придется, скорее всего, снова числен-
но. Таким образом, даже в тех случаях, когда можно достаточно
далеко продвинуться в аналитическом решении уравнения, нс ис-
ключено применение на каком-либо этапе численных методов для
того, чтобы получить решение в практически полезном виде.
Часто аналитические методы решения уравнений называют
«точными», а численные — «приближенными». Действительно,
численные методы практически всегда дают приближенный ре-
зультат, но если необходимо довести решение «до числа», то ча-
сто и аналитические методы в реальности позволяют получить
лишь приближенный результат — взять хотя бы приведенный выше
пример с квадратным уравнением. Кроме того, аналитические
методы решения математических задач часто бывают приближен-
ными по существу, оставаясь аналитическими (например, при-
ближение функции отрезком степенного ряда).
В данной главе будут рассмотрены алгебраические и трансцен-
дентные уравнения. В дальнейшем мы рассмотрим уравнения и
других классов.
2.2. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКИХ
И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
Пусть имеется уравнение вида
ад=о, (2.1)
где F(x) — алгебраическая или трансцендентная функция.
Решить такое уравнение — значит установить, имеет ли оно
корни, сколько корней, и найти значения корней (либо точно,
либо, если это невозможно, то с нужной точностью). Мы ограни-
чимся обсуждением методов поиска лишь действительных кор-
ней, не затрагивая проблему корней комплексных.
69
Решение указанной задачи в достаточно общем случае начина-
ется с отделения корней, т.е. с установления:
количества корней;
наиболее «тесных» промежутков, каждый из которых содержит
только один корень.
Следует отметить, что универсальных приемов решения этой
задачи, пригодных для любых уравнений, не существует. Разрабо-
таны методы ее решения для того случая, когда F(x) — много-
член произвольной степени (их можно найти в учебниках алгеб-
ры), здесь мы их рассматривать нс будем.
Если бы мы располагали графиком функции F(x), то пример-
ное положение корней уравнения (2.1) было бы очевидным —
точки пересечения графика с осью абсцисс. Однако построение
графиков функций обычно и начинается с поиска ее нулей, т.е.
возникает замкнутый круг.
Тем нс менее отделение корней во многих случаях можно про-
извести графически. Задачу часто удается сильно упростить, заме-
нив уравнение (2.1) равносильным ему уравнением
Z(x) = /2(x). (2.2)
В этом случае строятся графики функций ft(x) и^(х), а потом
на оси х отмечаются отрезки, локализующие абсциссы точек пе-
ресечения этих графиков.
Пример 2.1. Для графического отделения корней уравнения
sin 2эс - Inх = 0 преобразуем его к равносильному уравнению
sin2x = Inx и отдельно построим графики функций sin 2х и 1пх
(рис. 2.1).
Из графика вполне очевидно, что уравнение имеет единствен-
ный корень 4 и этот корень находится на отрезке (1; 1,5].
При решении задачи об отделении корней бывают полезными
следующие очевидные положения:
Рис. 2.1. Иллюстрация к отделению корней уравнения
70
1.Если непрерывная на отрезке [д; />] функция F(x) прини-
мает на его концах значения разных знаков (т.е. F(a)F(b) < 0),
то уравнение (2.1) имеет на этом отрезке ио меньшей мере один
корень.
2. Если функция А(х) к тому же еще и монотонна, то корень
на отрезке [а; />] единственный.
Вычислим для проверки значения функции F(x) = sin2x - Inx
на концах отрезка [1; 1,5]: /•'(!) = 0,909298; F(1,5) = -0,264344. Как
видно, корень на отрезке [1; 1,5] действительно имеется.
Рассмотренный прием позволяет при желании сузить отрезок,
полученный графическим способом. Так, в нашем примере имеем
Г(1,3) = 0,253138 > 0, так что отрезком, на котором находится
корень, можно считать [1,3; 1,5].
В простейших случаях графическое отделение корней можно
осуществить вручную, однако в более сложных случаях для иссле-
дования вопроса о наличии (и количестве) корней уравнения на
заданном отрезке целесообразнее воспользоваться инструменталь-
ным пакетом или составить программу для компьютера на языке
программирования. Рассмотрим коротко суть идеи для примене-
ния указанных подходов.
Пусть имеется уравнение F(x) = 0, причем известно, что все
интересующие вычислителя корни находятся на отрезке [А; Л],
на котором функция f(x) определена, непрерывна и F(A) F(B) < 0.
Требуется отделить корни уравнения, т.е. указать все отрезки
[а; Л] с [Л; В], содержащие по одному корню.
Будем вычислять значения F(x), начиная с точки х = А, двига-
ясь вправо с некоторым шагом h (рис. 2.2).
Как только обнаружится пара соседних значений Т(х), имею-
щих разные знаки, и функция F(x) монотонна на этом отрезке,
так соответствующие значения аргумента х (предыдущее и следую-
щее) можно считать концами отрезка, содержащего корень.
Рис. 2.2. Иллюстрация к процессу отделения корня
71
Рис. 2.3. Отделение корней функции
с помощью ТП Excel
Пример 2.2. Построить графическую иллюстрацию и локали-
зовать корни уравнения cosx = 0,1 х на отрезке [-10; 10] с ша-
гом 0,1.
Решим эту задачу с помощью Excel (рис. 2.3). Кроме графика
функции у = cos х - 0,1х на экран компьютера выводится таблица
табулирования, из которой и выбирается окончательный резуль-
тат — семь отрезков отделения корня с шагом 0,1: -9,7 < X] < -9,6;
-9,0 < х2 < -8,9; -4,3 < х3 < -4,2; -1,8 < х4 < -1,7; 1,4 < х5 <
< 1,5; 5,2 < х6 < 5,3; 7,0 < х7 < 7,1.
Рассмотрим решение этой же задачи отделения корней уравне-
ния cosx = 0,1х на отрезке [-10; 10] с помощью программы для
компьютера.
Общая схема соответствующего алгоритма изображена на
рис. 2.4. Результатом решения поставленной задачи будут выводи-
мые на экран (или на печать) в цикле значения параметров Х[ и
х2 (концов выделенных отрезков).
По схеме алгоритма отделения корней легко составить про-
грамму.
Ниже приведена программа отделения корней уравнения на
языке Turbo Pascal.
program Separat_root;
uses ert;
var a,b,xl,x2,yl,y2,h:real; n,k:integer;
72
function f (x:real):real; {уравнение вида F(x)=0)
begin f:=cos(x)-0.1*x;
end;
begin
clrscr;
writein(’Введите a,b,h'); read(a,b,h);
k:=0; xl:-a; x2:«xl+h; yl:=f(xl);
while x2<b do
begin y2:=f(x2);
if yl*y2<0 then
begin inc(k);
writein(к,'-й корень
[', xl:4:1,’;’,x2:4:1, 1 ] ’)
end;
xl:=x2; x2:=xl+h; yl:-y2;
end;
repeat until keypressed
end.
Рис. 2.4. Блок-схема алгоритма отделения корней уравнения F(x) = О
73
Результаты выполнения программы:
Введите a,b,h
-10 10 0.1
1-й корень
2-й корень
3-й корень
4-й корень
5-й корень
6-й корень
7-й корень
[-9.7;-9,6]
[-9.0;-8,9)
[-4,3;-4,2)
(-1.8;-!,7)
[ 1.4; 1.5)
[ 5.2; 5.3)
[ 7.0; 7.1)
Как видим, результатом решения задачи отделения корней,
как и в примере 2.2, является последовательный вывод семи от-
резков, содержащих по одному корню. Для того чтобы эту же про-
грамму использовать для отделения корней другого уравнения,
достаточно заменить в тексте программы выражение для функции f
Обратим внимание на то, что надежность рассмотренного ал-
горитма отделения корней уравнения зависит как от характера
функции Дх), так и от выбранной величины шага Л. Действитель-
но, если при достаточно малом значении Л на концах текущего
отрезка [х; х + Л] функция Дх) принимает значения одного знака,
естественно ожидать, что уравнение Дх) = 0 корней на этом от-
резке не имеет. Это, однако, не всегда так: при несоблюдении
условия монотонности функции Дх) на отрезке [х; х + Л] могут
оказаться корни уравнения (рис. 2.5, а). Не один, а несколько
корней могут оказаться на отрезке [х; х + Л] и при соблюдении
условия F(A)- F(B) < 0 (рис. 2.5, б). Предвидя подобные случаи,
следует выбирать при отделении корней достаточно малые значе-
ния Л.
Рис. 2.5. Зависимость количества корней функции F(x) на отрезке [х, х+ Л]
от характера функции и величины шага й:
а — функция не меняет знака на отрезке [х, х + й], но не монотонна, поэтому на
отрезке (х, х+ й] имеются корни; б — функция на отрезке [х, х+ й| меняет знак,
но не монотонна, поэтому корней на отрезке не один, а несколько
74
Контрольные вопросы
1. Что означает «решить уравнение аналитически» и «решить уравне-
ние численно»?
2. В чем заключается задача отделения корней?
3. В чем суть графического метода отделения корней? Какие свойства
функции одной переменной используются для проверки правильности
отделения корня и его единственности на отрезке?
Упражнения
Отделить действительные корни уравнений:
a) Igx + 6 = х2; б) xsinx -1=0:
1) графическим методом (схематически, на бумаге);
2) с помощью ТП Excel;
3) с помощью программы для компьютера.
2.3. УТОЧНЕНИЕ КОРНЯ УРАВНЕНИЯ
МЕТОДОМ ПОЛОВИННОГО ДЕЛЕНИЯ
При решении уравнения, как правило, заранее задастся допу-
стимая погрешность е приближенного значения корня с,. В процес-
се уточнения корней требуется найти их приближенные значе-
ния, отличающиеся от точных не более чем на е.
Описанный в подразд. 2.1 способ табулирования может рас-
сматриваться и как способ уточнения корня (хотя и крайне неэф-
фективный). При этом можно либо постепенно уменьшать шаг
табулирования, приближая его к значению е, либо сделать это
сразу, полагая А = Е. В любом случае получим Ь - а < е. Тогда в
качестве искомого значения корня можно выбрать середину этого
отрезка, т.е. положить Е, = (а + Ь)/2, а граница погрешности Д не
превзойдет значения г/2.
Гораздо более эффективным, чем табулирование с постоян-
ным шагом, является так называемый метод половинного деления.
Пусть уравнение (2.1) имеет на отрезке [а; А] единственный ко-
рень, причем функция F(x) на этом отрезке непрерывна. Разде-
лим отрезок (а; А] пополам точкой с- (а + Ь)/2. Если F{c) 4- 0 (что
практически наиболее вероятно), то возможны два случая:
меняет знак либо на отрезке [a; cj (рис. 2.6, а), либо на отрезке
[с; А] (рис. 2.6, (5). Выбирая в каждом случае тот из отрезков, на
котором функция меняет знак, и продолжая процесс половинно-
го деления дальше, можно дойти до сколь угодно малого отрезка,
содержащего корень уравнения.
Метод половинного деления вполне можно использовать как
метод решения уравнения с заданной точностью. Действительно,
если на каком-то этапе процесса получен отрезок (а; А], содержа-
75
Рис. 2.6. К решению уравнения Дх) методом половинного деления:
а — функция F[x) меняет знак на отрезке |в; с|; б — функция Ц,х) меняет знак
на отрезке (e; ft]
Рис. 2.7. Блок-схема алгоритма уточнения корня уравнения F(x) = О
на отрезке [й; Л] с точностью е методом половинного деления
ший корень, то, приняв приближенно х-(а+ Л)/2, получим ошиб-
ку, не превышающую значения
Дх = (/>-д)/2 (2.3)
76
(заметим, что речь в данном случае идет о погрешности метода, см.
подразд. 1.1). Метод половинного деления требует утомительных руч-
ных вычислений, однако он легко реализуется с помощью про-
граммы на компьютере (блок-схему алгоритма см. на рис. 2.7).
Отметим, что даже если на каком-то этапе деления отрезка
пополам получится F(c) = 0, это не приведет к сбою алгоритма.
Пример 2.3. Уравнение sin 2х - In х = 0 имеет единственный ко-
рень на отрезке {1,3; 1,5] (см. пример 2.1). Решим это уравнение с
точностью до 1 • 10~4 методом половинного деления с помощью
программы для компьютера.
В соответствии с блок-схемой алгоритма, изображенной на
рис. 2.7, программа на языке Turbo Pascal имеет вид:
program divide__half;
uses ert, okrugl;
type T=real;
var a, b,c, eps,x:T;n,m:integer;
function f(x:T):T;
begin f:=sin(2*x)-In(x)
end;
begin
clrscr;
writeln('Введите a,b,eps1);
read(a,b,eps);
repeat
c:=(a+b}/2;
if f(a)*f(c)<0 then b;=c else a:=c;
until b-a<=eps;
x:—(a+b}/2; okr(x,eps,x,n);
if x<0 then begin if n<0 then m:=0 else m:=n;
writeln ( 'x=',x-lE-10;7:m,'
n=',n)
end
else begin if n<0 then m:=0 else m:=n;
writeln (’x=',x+lE-10:7:m, ' n=’,n)
end;
repeat until keypressed
end.
В приведенной программе заданная точность обозначена eps, а
граница погрешности текущего значения корня определяется че-
рез разность b - а. Еще раз напомним, что эта разность отождеств-
лена в алгоритме с погрешностью метода; вычислительная же
погрешность значения х как результат ошибки вычисления по
формуле х= (а + Ь)/2 в программе в явном виде не регистрируется
и связана только с погрешностью машинного представления
77
(см. табл. 1.1). При этом мы исходим из того, что точность машин-
ного представления значительно выше запрашиваемой точности eps
(т.е. полная погрешность значения корня отождествляется с по-
грешностью метода), поэтому выдаваемый программой числовой
результат округляется с помощью модуля okrugl (см. подразд. 1.5)
до цифр, верных в широком смысле, по запрашиваемой точно-
сти eps.
Результат работы программы:
Введите a,b,eps
1.3 1.5 0.0001
х= 1.3995 п--4
Округление значения корня проведено до четырех знаков пос-
ле запятой. Если ввести значение е = 0,000001, результат будет дру-
гой:
Введите a,b,eps
1.3 1.5 0.000001
х— 1.399429 п=б
При алгоритмизации метода половинного деления остановить
процедуру уточнения корня можно и другим способом. Зная допу-
стимое значение погрешности е:
Ь-а
(2-4)
легко вычислить количество шагов JV(e) получения последователь-
, b -а
1п--- Ь-а
ных приближений: N >--------— = 1,4427 • In-. Учитывая, что
In 2 е
W — число целое, окончательно получим
1,4427-In
+ 1,
где, как это принято, квадратные скобки означают целую часть
числа.
Так, для уравнения, рассмотренного в примере 2.1, положив а =
= 1,3; Ь = 1,5 и с = 1 • 10'4, получаем
N =
1,4427-In
1,5-1,3'
0,0001 _
+ 1 = [10,9...] + 1 = 11.
Если же положить е = 1 10-6, то получим N= 18. Зная N, мож-
но в алгоритме заменить цикл с постусловием на цикл с парамет-
ром, ограничив количество делений отрезка числом N.
78
Контрольные вопросы
1. В чем состоит основная идея метода половинного деления?
2. Может ли метод половинного деления дать точное значение корня
уравнения?
Упражнения
1. Уточнить методом половинного деления наименьший по модулю и
отличный от нуля корень уравнения xsinx - 1 = 0 с точностью до 1 10~4,
используя; а) калькулятор; б) программы, приведенные в подразд. 2.2.
2. Разработать алгоритм решения уравнения методом половинного
деления, использующий цикл с параметром и формулу для вычисле-
ния количества последовательных приближений Мг) по заданной ве-
личине Е.
2.4. ИТЕРАЦИОННЫЕ МЕТОДЫ УТОЧНЕНИЯ КОРНЕЙ
Рассмотрим самый мощный класс методов уточнения корней
уравнений. Его достоинство состоит в том, что основная идея рас-
сматриваемых ниже методов является универсальной при прибли-
женном решении уравнений многих классов.
Так называемые итерационные методы уточнения корней урав-
нений основаны на математической теории, которую необходимо
предварительно рассмотреть.
2.4.1. Метрические пространства и принцип
сжимающих отображений
Понятие «расстояние» привычно на уровне геометрической
наглядности. Легко определить привычным образом расстояние
между точками на числовой оси или на координатной плоскости.
Однако в математике это понятие используется гораздо шире.
Способ измерения расстояния р(х, у) между элементами х и у
некоторого множества X (произвольной природы) называется
метрикой. Множество с введенной в нем метрикой р становится
метрическим пространством, если для любых элементов:
1) р(х, у) > 0;
2) р(х, у) = 0 тогда и только тогда, когда х совпадает с у;
3) р(х, у) = р(у, х);
4) р(х, у) < р(х, Z) + p(z, у).
Последовательность {х(я)} точек метрического пространства на-
зывается фундаментальной, если для любого £ > 0 существует такое
число N, что для любых номеров точек тип, для которых
т, п> N, выполняется неравенство р(хш, х„) < е.
79
Метрическое пространство на-
зывается полным, если в нем лю-
бая фундаментальная последо-
вательность сходится (имеет пре-
дел). Примерами полных метричес-
ких пространств, рассмотренных
в курсе математического анализа,
являются:
1) множество точек на чи-
словой оси, расстояние между ко-
торыми определено по формуле
р(х, у) = |х - у|.
Рис. 2.8. Иллюстрация к понятию
«сжимающее отображение» —
расстояние p(Fx, Fy) меньше
расстояния р(х,у)
2) множество точек на координатной плоскости, расстояние меж-
ду которыми определено по формуле р(.х,у) = 7(*! - А'?)2 + (Л ~Уг)'
(здесь хь у, — координаты одной точки, х2, у? — другой).
В наглядном плане полнота пространства означает, что в нем
нет «дыр», в которых может нс быть точек данного пространства.
Так, на числовой оси любой точке соответствует действительное
число. В противоположность этому пространство рациональных чи-
сел не является полным, т.е. существуют фундаментальные после-
довательности рациональных чисел, не имеющие предела в их про-
странстве.
Пусть F— отображение, действующее в метрическом простран-
стве Е с метрикой р; х и у — точки пространства Е, a Fx, Fy —
образы этих точек.
Отображение F пространства Е в себя называется сжимающим
отображением (рис. 2.8), если существует такое число а, 0<а< 1,
что для любых двух точек х, у g Е выполняется неравенство
p(Fx, Fy) S ар(х, у). (2.5)
Точка х называется неподвижной точкой отображения F, если
отображение переводит ее саму в себя: Fx = x.
Важнейшее значение в теории решения уравнений имеет сле-
дующая теорема (доказанная польским математикам С. Банахом и
носящая его имя).
Принцип сжимающих отображений. Если F— сжимающее ото-
бражение, определенное в полном метрическом пространстве, то
для него существует единственная неподвижная точка £ такая,
которая переводится отображением в себя: £= FL,. Эта точка явля-
ется пределом последовательности
Хо, х, = Fx0, х2 = Fx,хя+| = Fx„,... (2.6)
с любым начальным членом х<).
Заметим, что последовательность (2.6) называют итерацион-
ной последовательностью (от лат. iteratio — повторение). Итераци-
80
онная последовательность, образуемая сжимающим отображени-
ем, является сходящейся.
Доказательство этой теоремы приводить не будем (см., напри-
мер, [9]). В процессе доказательства получается и оценка расстоя-
ния между неподвижной точкой отображения Е, и очередным при-
ближением x(i):
(2.7)
Приняв (Л-1)-е приближение за нулевое (£= 1), получаем еще
одно полезное для приложений неравенство:
Р(^ х<*>) S х<*>). (2.8)
1 -а
Здесь а — множитель из условия сжимаемости (2.5).
Контрольные вопросы
1. Какая связь между принципом сжимающих отображений и реше-
нием уравнений?
2. В чем заключается общая идея итерационных методов решения урав-
нений?
Упражнение
•
Вывести достаточные условия сходимости последовательных прибли-
жений хяЯ = F(x„) при решении уравнения х = F(x). Указание, восполь-
зоваться теоремой Лагранжа о конечных приращениях.
2.4.2. Метод простой итерации
Применим принцип сжимающих отображений для уточнения
значения корня уравнения. Для этого заменим уравнение (2.1)
равносильным уравнением
х=/(х). (2.9)
Сделать это можно множеством способов. Простейший и оче-
видный — добавить х к левой и правой частям уравнения (2.1).
Пусть Е, — корень уравнения (2.9), а хд — полученное каким-
либо способом на этапе отделения корней грубое приближение к
корню Подставляя хд в правую часть уравнения (2.9), получим
некоторое число х, = /(х0). Проделаем то же самое с х,, получим
х2 = /(Х|) и т.д. Последовательно применяя рекуррентное соот-
ношение х„ = f(x„.\) для п= 1, 2, ..., образуем итерационную по-
следовательность, совершенно подобную последовательности (2.6):
Хд, х, = /(хо), х2 = /(Х|), .... х„ = /(х,_|), ... (2.10)
81
Процесс построения итерационной последовательности имеет
простую геометрическую интерпретацию. На рис. 2.9 изображены
два случая, показывающие, что последовательность приближений
.может быть как сходящейся (см. рис. 2.9, а), так и расходящейся
(см. рис. 2.9, б). Как следует из принципа сжимающих отображе-
ний, условием сходимости итерационной последовательности яв-
ляется то, что функция Дх) осуществляет сжимающее отображе-
ние в окрестности корня.
Предположим, что существует отрезок [a; Z>], содержащий все
члены последовательности (2.10). Нетрудно видеть, что если на
отрезке [a; Z>] функция /(х) возрастает, то итерационная последо-
вательность является монотонной. Если же /(х) убывает, то она
является колеблющейся.
Если существует такая окрестность корня уравнения, в кото-
рой отображение любой точки функцией Дх) не выходит за пре-
делы этой окрестности и отображение Дх) является сжимающим,
то в силу принципа сжимающих отображений итерационная пос-
ледовательность (2.10) будет сходиться к корню уравнения (2.9).
Условие того, что функция Дх) является сжимающий функцией
на отрезке [а; д], приобретает в данном случае следующий вид:
Дх) е [а; />] для всех х 6 [a; Z>], а также существует такое число а,
0<а< 1, что для любых х, ye [a; Л| выполняется соотношение
1/(х)-/0’Ьа|х-у|. (2.11)
Отметим, что условие (2.11) имеет в математической литера-
туре собственное название: условие Липшица', константа а называ-
ется константой Липшица.
Рис. 2.9. Геометрическая иллюстрация итерационной последовательности:
а — сходящаяся последовательность; б — расходящаяся
82
Однако практически проверить выполнимость условия Липшица
весьма затруднительно. Для этого следовало бы перебрать все воз-
можные пары значений (х, у) из отрезка [a; Z>], что практически
невозможно. Для дифференцируемых функций условие (2.11) мож-
но заменить гораздо более удобным для практического исполь-
зования условием. Для этого применим теорему Лагранжа. Она
гласит, что если функция Дх) дифференцируема на отрезке [а;
, то на нем найдется такая точка с, что будет иметь место фор-
мула
f{b)-f{d) = f'(cY(b-a), (2.12)
называемая формулой Лагранжа (или формулой конечных прираще-
ний).
Сравнивая (2.11) и (2.12), приходим к очевидному выводу: если
существует такое число <у, 0 < q < 1, что для любых х е [л; Ь]
(2.13)
то функция Дх) является сжимающей на отрезке [а; 6]. При этом
роль константы Липшица а играет число q = тах[Д(х)1. Прове-
рить выполнимость условия (2.13) гораздо проще, чем (2.11).
Графической иллюстрацией сходящегося итерационного про-
цесса при выполнении условия (2.13) в случае, когда Д(х) > 0 на
отрезке [a; Z»], является рис. 2.9, а.
Заметим, что условия (2.11), (2.13) (наряду с требованием о
том, что значения функции Дх) не выходят за пределы отрезка
[а; />]) являются достаточными, но не необходимыми для сходи-
мости итерационной последовательности (2.10). Это означает, что
итерационная последовательность может оказаться сходящейся и
при невыполнении этих условий.
Итак, общая схема решения уравнения (2.1) методом итера-
ций такова.
1. Выполнить, полностью или частично, отделение корней.
Выбрать тот корень, который подлежит уточнению, и соответ-
ствующий ему отрезок [а; Ь], содержащий этот корень и не содер-
жащий иных корней данного уравнения.
2. Преобразовать уравнение (2.1) к равносильному ему уравне-
нию вида (2.9).
3. Найти q = тах|/'(х)|и проверить, является ли функция Дх)
|я,й|
сжимающей на отрезке [а; £].
4. Если сжимаемость имеет место, то:
4.1) задаться точностью е нахождения приближенного значе-
ния корня;
4.2) задаться первым членом итерационной последовательно-
сти xq — начальным приближением к корню;
83
4,3) построить следующий член итерационной последователь-
ности (2.9);
4.4) всякий раз, получив очередной член итерационной пос-
ледовательности, проверять, выполняется ли условие, следующее
из (2.8):
1*й+) - х„[ < е, или |х„+1 -х„\ < (п = 0, 1, 2, ...); (2.14)
4.5) если условие (2.14) выполняется, то принять хп за резуль-
тат, иначе вновь выполнить пункт 4.3.
Надо заметить, что принятие х„ в качестве результата, полу-
ченного с точностью е, означает, что вместо полной погрешнос-
ти решения использована погрешность метода.
Очевидно, что способ перехода от уравнения в форме (2.1) к
равносильному уравнению в форме (2.9) (и связанный с этим
вид функции Дх)) является определяющим для сходимости ите-
рационной последовательности. Если подбирать Дх) вслепую,
можно впустую потратить массу времени. Однако есть общие при-
емы, которые позволяют избежать этой ситуации.
Рассмотрим простейший из них. Преобразуем уравнение (2.1)
к равносильному уравнению
х = х-ц-Дх), (2.15)
где ц — отличная от нуля константа.
Таким образом, Дх) =х-ц • Дх). Условие (2.13) приобретает вид
|1 -ц-Г'(х)| < 1, или, иначе,
-1 < 1-цГ(х); 1-пЛ'(х)<1. (2.16)
Если удастся подобрать значение ц так, чтобы условие (2.16)
выполнялось, то метод итераций применим.
Пусть на [а; />] существует единственный корень уравнения Fix) =
- 0. Будем считать функцию Дх) дифференцируемой на отрез-
ке [а; £>1 и сохраняющей на этом отрезке свой знак (фактически
предполагается, что отрезок достаточно мал).
Рассмотрим вначале случай, когда Е'(х) > 0. Второе из нера-
венств (2.16) тогда сводится к условию ц > 0, а первое — к усло-
2
вию ц<—-—. Полагая
Г(х)
В =---= <2'17>
шах г (х) М
[0; й] ! 1
получим из (2.15) итерационную формулу
х„ =х„ч(2.18)
М
84
Обсудим вопрос о критерии выхода из итерационного процес-
са (2.18).
В условие (2.14) входит q = max|/'(x)l.
Имеем:
q = maxjl - щЕ'(х)| = max 1 - .
[a;A] [a;ij M
Поскольку считается, что F'(x) > 0, то q = 1----, где т =
М
= min|F'(x)|.
Если F'(x) < 0 для х е [а; А], то, рассуждая аналогично, полу-
I
чим ц =----и итерационную формулу
М
х„.-х„_1+Д^. (2.19)
М
Отметим одно важное свойство итерационных методов реше-
ния уравнений, называемое самоисправляемостъю. Поскольку на-
чальное приближение х0 выбирается произвольно, то отсюда сле-
дует, что полученное в итерационном процессе л-е приближение
при желании можно считать начальным. Это означает, что если в
процессе вычисления приближений допускались ошибки, то они
не влияют на окончательный результат (при условии, что запра-
шиваемая точность результата существенно ниже реализуемого в
процессе счета уровня точности представления числовых данных).
Указанное свойство метода итераций делает его одним из самых
надежных методов решения уравнений.
Пример 2.4. Уточнить корень уравнения sin 2х - In х= 0 методом
простой итерации на отрезке [1,3; 1,5] с точностью до 1 • 10 ".
Исходное уравнение можно привести к виду х=/(х), потенци-
ально пригодному для итерационного решения, несколькими спо-
собами, например:
1) х- exp(sin2x);
2) х= (-l)"0,5(arcsinlnx + ля), п = 1, 2, ...;
3) х = х - p(sin 2х - In х); ц Ф 0.
Исследуем возможности полученных представлений для при-
менения метода итераций.
В первом случае /(х) = exp(sin2x). Функция /(х) определена и
дифференцируема на отрезке [1,3; 1,5], однако одно из условий
пригодности ее для итерационного решения не выполняется —
уже в левом конце отрезка значение функции /(1,3) = 1,67 выхо-
дит за его пределы.
85
Рассмотрим второе представление. Положим, к примеру, и = - 1 и
получим рекуррентное соотношение
(2.20)
Очевидно, что для всех значений х из отрезка [1,3; 1,5]
/V) =----, 1 , < о,
2х/1 - In2 х
следовательно, функция f(x) монотонно убывает на этом отрезке.
Вычислим ее значение в концах отрезка: /(1,3) = 1,44; /(1,5) = 1,36.
Так как полученные значения входят в отрезок [1,3; 1,5] и функ-
ция /(х) монотонна, то условие принадлежности значений функ-
ции данному отрезку выполняется. Для проверки условия сжима-
емости исследуем модуль производной функции /(х):
ф(х)=|т=ж^-
Найд ем. производную функции ф(х):
<р'(*) =
4х:(1-1п2 х)
1пх
-71 - In2 X J
Замечаем, что производная ф'(х)на отрезке [1,3; 1,5] всюду от-
рицательна. Это означает, что <р(х) на этом отрезке убывает и до-
стигает максимума на левом конце: |/'(1,3)| = 0,38. Таким образом,
можно положить в неравенстве (2.14) </ = 0,38.
Выберем, например, х0 = 1,4 и сделаем несколько итераций;
результаты вычислений внесены в расчетную табл. 2.1 (инстру-
мент в данном случае не столь важен, лишь бы он"обеспечивал
точность вычислений, заведомо большую, чем заданная точность
решения уравнения).
Таблица 2.1
п х„ л arcsin In х„ хя+1 = 2 1 с _ч_ о| 1
0 1,4 1,3992122 0,00049
1 1,3992123 1,39951 11 0,00018
2 1,3995113 1,3993977 0,00006
86
Начало
Рис. 2.10. Блок-схема алгоритма решения уравнения
методом простой итерации
Используя оценочную формулу (2.14) и принимая во внима-
ние исходные значения е = 10"4 и q = 0,38, уже для третьего при-
ближения имеем |х3 -х2| = 0,00006 < 10"*. Отсюда следует, что
х3= 1,3993977 является приближенным решением уравнения с за-
данной точностью ЮЛ Округляя полученный результат до цифр,
верных в широком смысле, окончательно получаем х - 1,3994.
Общая блок-схема алгоритма решения уравнения x=f(x) ме-
тодом итераций приведена на рис. 2.10.
Приведенная ниже программа предусматривает вывод прибли-
жения корня х с округлением с помощью модуля okrugl при до-
стижении введенной точности е (для вычисления значения функ-
ции пришлось арксинус выразить через арктангенс):
program Iterat_2;
uses ert, okrugl;
type T=real;
var a,x,y,p,q,eps:T; n,m:integer;
begin
87
clrscr;
writein('Введите x,eps,q’);
read(x,eps, q) ;
a : =eps* (1-q) /q;
repeat
у: = (pi-arctan((In(x))/sqrt(1-sqr (In (x)))))/2;
p:=x-y;
x: =y;
until abs(p)<=a;
okr(x,eps,x,n);
if x<0 then begin if n<0 then m:=n;
writeIn(’x=',x-lE-10:7 :m,' n=',n)
end;
else begin if n<0 then m:=0 else m:=n;
writein(1x=r,x+lE-10:7:m,' n=',n)
end;
repeat until keypressed
end.
Результат выполнения программы:
Введите х, eps,q
1.4 0 .0001 0.38
х=1.3994 п=4
Рассмотрим третье представление заданного уравнения. В этом
случае f(x) = p(sin 2х - In х). Подберем константу ц из условия (2.17).
Поскольку производная Л?(х) = 2cos2x— на отрезке [1,3; 1,5]
х
отрицательна и монотонно убывает, ее модуль имеет максимум
на правом конце отрезка: |Л/| = 2cos3-j^ =2,65. Следователь-
но, положим ц = --—- = - 0,37. Таким образом, имеем рекуррент-
|М|
ное соотношение
хл+1 =х„+0,37(sin2x„-1пх„). (2.21)
Для использования критерия (2.14) выхода из итерационного
процесса найдем
q = max If'(x)\ = max
1 + 0,37| 2cos2x - —
I X
= 0,081.
Малое значение q обеспечивает быструю сходимость итераци-
онной последовательности.
Выберем вновь х$ = 1,4 и сделаем несколько итераций (табл. 2,2).
88
Таблица 2.2
п -У, хяИ = х„ + 0,37(sin 2х„ - In х„) 1 1
0 1,4 1,3994509 0,000048
1 1,3994509 1,3994297 0,0000018
Как видно из табл. 2.2, уже значение х2 = 1,3994297 соответ-
ствует заданной точности 10"4. Округляя результат до верных цифр,
получим окончательно 1,3994.
Программа на Turbo Pascal даст тот же результат:
program Iterat_3;
uses crt, okrugl;
var a,x,y,p,q,eps:real; n,m:integer;
begin
clrscr;
writeln(’введите x,eps,q');
read(x,eps,q) ;
a:=eps*(l-q>/q;
repeat
y:=x+0.37*(sin(2*x)-In(x));
p:=x-y;
x:=y;
until abs(p)<=a;
okr(x,eps, x,n) ;
if x<0 then begin if n<0 then m:=n;
writeln('x=',x-lE-10:7:m,1
n=’,n)
end
else begin if n<0 then m:=0 else m:=n;
writeln ('x=x+lE-10:7:m, ' n= ',n)
end;
repeat until keypressed
end.
Результат выполнения программы:
Введите x,eps,q
1.4 0.0001 0.1
х= 1.3994 n=4
Контрольные вопросы
1. Какова последовательность действий при решении уравнений ме-
тодом простой итерации?
89
2. Какие условия гарантируют сходимость итерационной последова-
тельности к корню уравнения?
Упражнения
1. Проиллюстрировать сходящийся итерационный процесс при усло-
вии, что -1 < f'(x) < 0 на отрезке [я; Л] (см. рис. 2.9).
2. Уточнить наименьший по модулю отличный от нуля корень урав-
нениях sinx -1 = 0 методом простой итерации с точностью до 1-10 5,
используя: а) ручную расчетную таблицу и калькулятор; б) программы,
приведенные в тексте данного пункта.
3. Разработать алгоритм решения уравнения методом простой итера-
ции, используя цикл с параметром.
2.4.3, Скорость сходимости итерационного процесса
Алгоритм построения итерационной последовательности, при-
меняемый для уточнения приближенного значения корня алгеб-
раического или трансцендентного уравнения, должен быть прост,
надежен и экономичен. Последняя из характеристик связана с
понятием скорости сходимости итерационного процесса.
Определение. Последовательность {х„}, сходящаяся к пределу
имеет порядок сходимости 0 (0 > 1), если существуют числа
с> 0, п0> 0, такие, что для любого п > п0 выполняется неравен-
ство
|*л+1
(2.22)
Сходимость при 0 = 1 называется линейной, а при 0 = 2 — ква-
дратичной. С увеличением 0 вычислительный алгоритм, как пра-
вило, усложняется, а сходимость итерационной последователь-
ности становится более быстрой.
В качестве примера определим порядок скорости сходимости
и простой итерации.
для методов половинного деления
[.Пусть Дл — погрешность значения х„ приближения корня
Ап =|х„- £|, Дл+1 = |х„+! - £|. Для метода половинного деления
справедлива оценка Д„+1 < Очевидно, в этом случае 0 = 1 и
скорость сходимости метода является линейной.
2. Рассуждая аналогично, при оценке скорости сходимости
метода простой итерации получаем оценку |хл+1 Е,| < q\x„ - £|, что
дает право сделать вывод: алгоритм построения итерационной пос-
ледовательности методом простой итерации имеет линейную ско-
рость сходимости.
Надо заметить, что скорость сходимости и скорость решения
задачи — категории существенно разные. Мы могли видеть, какой
несложной математики требует организация процесса уточнения
корня методом половинного деления — метода, обладающего не-
90
высокой (линейной) скоростью сходимости. Метод простой ите-
рации, обладая той же линейной скоростью, требует для своего
применения куда более изощренных предварительных аналити-
ческих исследований. Как мы увидим далее (п. 2.4.4), сходимость
для методов Ньютона — квадратичная, т.е. более высокого поряд-
ка, хотя применение этих методов также предполагает достаточно
скрупулезную аналитическую работу. Очевидно, что разработка и
применение наиболее эффективных методов с высокой скорос-
тью сходимости делает предпочтительным их использование в часто
применяемых алгоритмах (например, встроенных в инструменталь-
ные пакеты). Если же требуется быстро получить уточнение корня
уравнения на установленном отрезке его существования, не теряя
времени на сложные математические доказательства, исследова-
тель вполне аргументировано может предпочесть метод, более мед-
ленный по сходимости, но существенно сокращающий общее
время поиска решения с учетом простоты подготовительного пе-
риода.
Контрольные вопросы
1. Как определяется понятие «скорость сходимости итерационного
процесса»?
2. Какую скорость сходимости для решения уравнения с одной пере-
менной имеют метод половинного деления и метод простой итерации?
3. Как соотносятся скорость сходимости и скорость решения задачи?
Упражнение
Составьте и исследуйте на скорость сходимости алгоритм, построен-
ный аналогично методу половинного деления, но с делением отрезка на
три части.
2.4.4. Методы Ньютона
Наряду с методами половинного деления и простой итерации
существуют и другие, более сложные и более эффективные ите-
рационные методы. Прежде всего к ним относится группа мето-
дов, которые связаны с именем Ньютона. Рассмотрим два из них —
метод касательных и метод хорд.
Оба метода основаны на следующем приеме. Пусть уравне-
ние (2.1) имеет единственный корень на отрезке [а; Ь\. Преобра-
зуем его к равносильному уравнению
х = х - ф(х) • Дх), (2.23)
где ф(х) — любая функция, определенная на отрезке [a; и не
обращающаяся на нем в нуль. Осуществляя различными способа-
ми выбор ф(х), можно получить, в частности, и указанные методы.
91
Метод касательных. Пусть в (2.23) ф(х) = —!—. Таким обра-
Г(х)
зом, итерационная последовательность строится с помощью ре-
куррентного соотношения
*H+i = *«-4^4 (« = °’ 1= 2’ •••)• (2.24)
Вопрос о выборе начального приближения х0 и гарантирован-
ной сходимости итераций решается просто, если функция Дх)
удовлетворяет следующим условиям:
1) является дважды дифференцируемой на отрезке [о; ЭД;
2) обе производные — первая и вторая — не меняют знак на
этом отрезке, т.е. функция Дх) монотонна и не меняет характера
выпуклости; ситуация иллюстрируется одним из вариантов на
рис. 2.И.
В такой ситуации за х0 берется тот конец отрезка [а; ЭД, на
котором функция Дх) и ее вторая производная имеют одинако-
вые знаки, т.е. выполняется условие Д(х0) F"(x0) > 0. Очевидно,
что это левый конец [я; ЭД на рис. 2.12, а и г и правый конец [о; ЭД
на рис. 2.11, би в.
Допустим в дополнение к сделанным ранее предположениям,
что Fr(x) также непрерывна на [л; ЭД. Докажем, что отображение
Г(х)
Ф(х) = х - , соответствующее формуле (2.24), является сжи-
F (х)
мающим в некоторой окрестности корня уравнения Дх) = 0. Для
этого, как показано выше, достаточно, чтобы существовало та-
кое число q (0 < q < i), чтобы в указанной окрестности имело
место неравенство |ф'(х)| < q < 1. Вычислим производную
, _ F'(х)2 - F(x)F'(x) _ F(x)F'(x)
F'(x? ~ Пх)2'"
Рис. 2.1!. Четыре возможности поведения функции Дх) в окрестности корня:
а — функция F(x) убывает и выпукла; б — функция F(x) убывает и вогнута;
в — функция F(x) возрастает и вогнута; г функция F{x) возрастает и выпукла
92
Непосредственно в корне имеем
ЯОТЭ
поскольку ДЕ,) = 0. Далее рассуждаем так: раз непрерывная функция
ф'(х) обращается в нуль в некоторой точке, то существует такая
окрестность этой точки, в которой |ф'(х)| < 1, что и требовалось
доказать.
Для оценки расстояния от очередного приближения хп до кор-
ня можно использовать как общее соотношение (2.14), так и сле-
дующий прием. По формуле Лагранжа
F(x„)-F© = Д(с).(хл-^).
Отсюда получаем
Напомним, что о точке с известно лишь то, что она находится
между хп и поэтому реальная оценка погрешности возможна с
помощью следующего неравенства:
|х„-£|< т = min|F'(x)|. (2.25)
Эта оценка очень удобна, поскольку Дх„), так или иначе, вы-
числяется по мерс нахождения членов рекуррентной последова-
тельности (2.24).
Можно показать (см., например, [5]), что если Дх) имеет на
[a; Z>] непрерывную вторую производную F'(x), то погрешности
на л-м и (л + 1)-м шагах связаны неравенством
|хл+1-^|<|
F'(x„)
Таким образом, вычислитель-
ный алгоритм, заданный формулой
(2.23), имеет квадратичную скорость
сходимости.
Рассмотренный метод называет-
ся методом касательных потому, что
если обратиться к графической ил-
люстрации (рис. 2.12), то точка хь
определяемая по формуле (2.24) при
п = 0, есть точка пересечения каса-
тельной, проведенной к графику
функции у = Дх) в точке с абсцис-
сой Xq, с осью абсцисс.
(х„ -£)2.
(2.26)
Рис. 2.12. Геометрический
смысл метода касательных
93
Каждому следующему члену итерационной последовательно-
сти (2.24) соответствует точка пересечения касательной, прове-
денной к графику функции F(x) в точке с абсциссой, определяе-
мой предыдущим членом последовательности, с осью абсцисс.
Пример 2.5. Уточнить корень уравнения sin2x - 1пх = О на от-
резке [1,3; 1,5] методом касательных с точностью до 1-Ю'4.
Формула (2.24) в данном случае имеет вид
sin 2хя - In х„
2 cos 2хя - 1/х„ '
(2.27)
Для определения точки xq найдем знаки F(x) - sin 2х - In х и
F'(x) = -4cos2x + 1 /х2 на концах отрезка [1,3; 1,5]:
/(1,3) = 0,25>0, Г(1,5) = -0,26<0, /”(1,3) =4,02>0, /71,5)-4,04>0.
Таким образом, Хо= 1,3.
Для проверки критерия (2.25) прерывания итерационного про-
цесса (по сопоставлению искомой точности с погрешностью ме-
тода) необходимо найти
т = min |/'(х)| = min |2cos2x - 1/х|.
|a;i| 1 1 [1Д1.5]1 1
Имеем на концах отрезка /'(1,3) =-2,48, /'(1,5) =-2,65. Отре-
зок столь мал, что вполне очевидна монотонность /'(х) в его пре-
делах (это можно проверить, например, по неизменности знака
второй производной на рассматриваемом отрезке). Таким обра-
зом, можно положить т = 2,4.
Вычислим несколько членов итерационной последовательно-
сти «ручным» способом:
х = , sin(2 1,3) - lnl,3
Х| ’ 2cos(2 1,3) - 1/1,3
= 1,401948.
Сделаем проверку точности достижения корня (см. (2.27)):
|F(x,)| [sin(2 • 1,401948) - In 1,401948| ....
J-----1 = 1-------------------------1 = 0,003 — требуемая точность
т 2,4
еще не достигнута.
_ _ sin(2-1,401948)-In 1,401948
2 ’ 2 cos(2-1,401948)-1/1,401948
= 1,399430.
Снова проверка:
|/(х2)1 |sin(2-1,399430)-In 1,3994301 , 1Л ,
------1 = J1 - 1 • 10 ° — требуемая точ-
т-----2,4
ность достигнута.
Последовательное вычисление членов итерационной последо-
вательности показано в табл. 2.3.
94
Таблица 2.3
п х„ = „ sin 2х„ - 1п 2cos2x„ - ]/xw |x„+i -
0 1,3 1,401948 0,003
1 1,401948 1,399430 0,000001
Итак, можно считать, что в результате <; = 1,399430 все цифры
верны в широком смысле.
Метод хорд. Реализуя метод касательных, при каждой итера-
ции необходимо вычислять значение не только функции F(x), но
и ее производной Fr(x). Однако есть вариант метода Ньютона, в
котором можно ограничиться вычислением только значений Дх),
что иногда упрощает вычислительный алгоритм.
X “ С
Если положить в (2.23) <р(х) =------, а в качестве с взять
Дх) - F(e)
тот конец промежутка [а; 6], на котором F(c) Fr(c) > 0, то прихо-
дим к итерационному методу:
^Я+1 “
сДхл)-хлДс)
F(x„)-F(c) ’
(2.28)
называемому методом хорд (или методом секущих).
В качестве х$ в этом случае следует принять тот конец проме-
жутка [д; Д, который остался после выбора с (т.е. если с = а, то х0 =
= h или наоборот). Далее последовательность строится по форму-
ле (2.28). Оценка степени приближения к корню возможна с по-
мощью неравенства (2.25) (оно было получено с помощью фор-
мулы Лагранжа, не зависящей от рассматриваемых методов).
Геометрический смысл метода (благодаря которому он и полу-
чил название) проиллюстрирован на рис. 2.13. В данном случае с = Ь,
х0 = а, X! соответствует точке пересечения хорды, соединяющей
концы кривой, с осью абсцисс. Далее
находится точка на кривой с абсциссой
хь проводится следующая хорда и т.д.
Можно показать (см., например,
[3]), что этот метод также имеет квад-
ратичную сходимость.
Пример 2.6. Уточнить «ручным»
способом корень уравнения sin 2х -
-1пх-0 на отрезке [1,3; 1,5] методом
хорд с точностью до 1 10-4.
Точка с выбирается так же, как и
точка х0 в примере 2.5, т.е. с - 1,5.
Следовательно, xq = 1,3.
Рис. 2.13. Геометрический
смысл метода хорд
95
Найдем Хр
х = сЛ*о)~лЬ^(<0 _l,5fsin(2-l,3)-lnl,3]-l,3[sin(2-l,5)-lnl,5]_1 397034
1 F(x0)-F(c) [sin(2-l,3)-lnl,3]-[sin(2-l,5)-lnl,5]
Проверим, достигнута ли заданная точность.
|F(x,)( |sin(2 1,397834) - In 1,397834| ......
--------------------=-------------------—г—-’= u,uuz — требуемая точ-
m------------------------------------2,4
ность не достигнута.
Найдем следующее приближение:
_ cF{xi)~x}F{c) _
2 F(x,)-F(c)
1,5[sln(2 1,397834) - In 1,397834] - 1,397834[sin(2 • 1,5) - In 1,5]
[sin(2 1,397834) - In 1,397834] - [sin(2-1,5) - In 1,5]
« 1,399410.
|F(x2)| jsin(2-1,39941)-In 1,3994J| n in 5
~--; = 2 10 — требуемая точ-
m--------------------------------------------2,4-J
ность достигнута.
Последовательное вычисление членов итерационной последо-
вательности показано в табл. 2.4.
Таблица 2.4
н х„ _ cF(x„) - x„F(c) л+' F(x„)-F(c)
0 1,3 1,397834 0,002
1 1,397834 1,399410 0,00002
Итак, можно считать, что в результате £ = 1,39941.0 четыре циф-
ры после запятой верны в широком смысле.
Результат: 1,3994 (записываем лишь верные значащие цифры).
Контрольные вопросы
1. По каким причинам методы хорд и касательных предпочтительнее
метода простой итерации?
2. Каков порядок сходимости метода хорд? метода касательных?
Упражнения
1. Составить программы реализации методов Ньютона (секущих и хорд).
2. Сопоставляя рис. 2.12 и 2.13, построить графические иллюстрации
решений уравнения методами касательных и хорд для всех четырех ситу-
аций, изображенных на рис. 2.11.
96
3. Разработайте алгоритм комбинированного метода хорд и касатель-
ных, с помощью которого приближение к корню осуществляется с двух
сторон. Указание: воспользуйтесь тем, что приближения, возникающие
при применении методов хорд и касательных в ситуациях, изображен-
ных на рис. 2.12, всегда находятся по разные стороны корня.
2.5. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ТОЧНОСТИ НАХОЖДЕНИЯ
КОРНЕЙ УРАВНЕНИЯ
Выше был получен ряд оценок точности, с которой решается
уравнение. Еще раз подчеркнем, что формулы (2.3), (2.14), (2.25)
дают возможность оценить лишь погрешность метода. Они совер-
шенно не учитывают погрешности вычислений, связанные как с
неизбежными округлениями чисел в ЭВМ, так и с действиями
над этими числами, которые после первого же округления стано-
вятся приближенными. В то же время ясно, что если интегральная
погрешность вычислений сравняется или превзойдет погрешность
метода, то произведенные выше в примерах оценки точности най-
денных (приближенных) значений корней потеряют свой смысл.
Для того чтобы избежать такого эффекта, вычисления на ЭВМ
производятся с числами, в которых количество значащих цифр
много больше того, которое диктуется заданной точностью реше-
ния задачи. Теоретически это не дает гарантии, что вычислитель-
ная погрешность не станет катастрофически велика, но практи-
чески в подавляющем большинстве случаев удается решить задачу
с разумной точностью.
Из сказанного выше следует практический вывод: задавая точ-
ность решения уравнения, следует сопоставлять ее с реальными
возможностями вычислительного инструмента. Так, задавая в рас-
смотренных выше примерах е = 1 10-4, можно быть совершенно
уверенным в успехе (если, конечно, работает сам метод), поскольку
точность представления чисел в микрокалькуляторе или компью-
тере заведомо на несколько порядков выше. Но при значениях с,
сопоставимых с «машинным нулем», такой уверенности нет, по-
скольку указанное условие может нарушиться, а при значениях е,
меньших «машинного нуля», задача уточнения корня либо стано-
вится неразрешимой, либо потребует особых приемов работы с
«длинной арифметикой».
Взглянем на проблему точности приближенного решения урав-
нений с другой стороны. До сих пор в рассмотренных выше при-
мерах считалось, что коэффициенты, входящие в уравнения, —
точные числа. Однако в реальных задачах это совсем не так: все
или несколько коэффициентов могут быть числами приближенны-
ми, заданными лишь с некоторой точностью. Тогда вопрос о точ-
ности решения следует согласовывать с точностью коэффициен-
4 Ллпчик
97
тов. Более общее утверждение состоит в том, что совершенно не-
разумно требовать от решения задачи большей точности, чем мо-
гут гарантировать входные данные.
Например, выше несколькими способами решалось уравнение
sin(px) - In х = 0 (при р = 2). Допустим, что вместо «точного» зна-
чения коэффициента р = 2 имеется приближенное значение р -
= 1,999 (в соответствии с правилом записи приближенных чисел
«по умолчанию» это значит, что предельная абсолютная погреш-
ность Др = 5 10-4). Имеет ли смысл при этом искать корень уравне-
ния с точностью е= 1 • 10"4, как это происходило в рассмотренных
выше примерах? Ответ неочевиден. Попробуем получить его дву-
мя способами: «теоретическим» и чисто эмпирическим.
Теоретически задача ставится следующим образом. Имеется
уравнение
F(x,p) = 0,
(2.29)
где р — параметр, известный с точностью Др. С какой максималь-
ной точностью имеет смысл уточнять корень уравнения?
Решение уравнения (2.29) фактически является функцией от
параметра р: ^(р). Та погрешность величины которая определя-
ется погрешностью параметра, в главном приближении имеет вид
д^ = — - Др. Если бы решение уравнения было аналитическим,
t/p
ТО МОЖНО было бы просто ВЫЧИСЛИТЬ производную ф (прир = 2)
и сделать требуемую оценку.
В отсутствие аналитической формулы ^(р) это можно сделать
следующим образом. Если подставить х = £(р) в уравнение (2.29),
то получим тождество Т(Е,(р), р) = 0. ПродиффеРенийРУсм его по Р-
По правилу дифференцирования сложной функции имеем:
ЭТ d^ dF_
ЭС dp + Эр
Отсюда
dp Эр / аг
Таким образом,
3F
др
dF
•Др,
(2.30)
и назначать точность решения уравнения выше той, которая оп-
ределяется равенством (2.30), практически бессмысленно. Прове-
денное выше рассмотрение тесно связано с так называемой об-
ратной задачей теории погрешностей: по допустимой погрешно-
98
сти результатов вычислений оценить возможную погрешность (или
диапазон допустимых значений) начальных данных.
Пример 2.7. Определить, с какой максимальной точностью
уместно уточнять корень уравнения sin(px) - In х = 0 при р = 1,999
и Др = 5-I0"4.
При р = 2, х = 1,399 имеем по формуле (2.30)
Д< =
|х cos(px)|
pcos(px)—
X
Ьр* 0,0026.
При этом использовано решение уравнения, найденное в при-
мерах 2.4, 2.5 для р = 2, причем точность этого решения особой
роли не играет, поскольку для Д£ достаточно получить одну-две
значащие цифры.
Вывод, при той точности, с которой задан коэффициент р в
рассматриваемом уравнении, нет смысла уточнять его корень с
точностью выше, чем е=* 0,0003.
Отметим, что если уравнение содержит не один, а два или
более параметра, значения которых являются приближенными
числами, то анализ, подобный описанному выше, следует прово-
дить по отношению к каждому из них. Это достаточно трудоемкая
работа, и вместо нес, располагая программой для ЭВМ, можно
использовать чисто эмпирический прием для установления степе-
ни влияния точности задания параметров, входящих в уравнение,
на точность достижения корня. Назовем этот прием «шевеление
параметра* и проиллюстрируем на примере.
Пример 2.8. Задача та же, что и в предыдущем примере: опре-
делить, с какой максимальной точностью уместно уточнять ко-
рень уравнения sin(/>x)-Inx = 0 при р= 1,999 и &р = 5-10-4.
Будем уточнять корень уравнения на отрезке [1,3; 1,5] любым
из описанных выше способов — например, методом касательных.
Будем делать это дважды: для р = 1,9985 и р = 1,9995, т.е. в гранич-
ных точках того диапазона значений параметра, который опреде-
ляется точностью его задания. Имеем (вычисления проделаны в
Excel):
/>=1,9985 р= 1,9995
х0= 1,35 х0 = 1,35
х,= 1,4006861 х1 = 1,4001844
х2 = 1,4001905 х2 = 1,3996826
х3= 1,4001902 х3= 1,3996825
х«= 1,4001902 х«= 1,3996825
99
Очевидно, что влияние погрешности параметра р на корень
уравнения проявляется в том, что этот корень лежит в диапазоне
1,3997...1,4002 (или, в другой записи, £ = 1,400010,0003), т.е. при
данной недостоверности значения параметра нет смысла нахо-
дить корень с точностью, более высокой, чем е = 0,0003, — тот же
результат, который был получен выше при «теоретической» оцен-
ке, основанной на равенстве (2.30).
Контрольный вопрос
Какими способами можно увязать точность задания параметров, вхо-
дящих в уравнение, с точностью его решения?
Упражнение
Для уравнения sin2x - ln(gx) = 0 при q = 1,00010.001 определите, с
какой максимальной точностью уместно уточнять значение корня на от-
резке 11,3; 1,5]. Выполните это задание двумя способами, описанными в
подразд. 2.5.
2.6. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ
УРАВНЕНИЙ С ПОМОЩЬЮ ИНСТРУМЕНТАЛЬНЫХ СРЕДСТВ
Часто используемые инструментальные пакеты MathCad, Mat-
Lab, Maple, Derive и др. обладают различными возможностями
для решения уравнений. В зависимости от желания пользователя
результат решения может быть получен в аналитическом (сим-
вольном) или числовом виде. При этом далеко не всегда имеется
информация о том, каким методом решается задача. Точность чис-
лового решения в обычном смысле отождествляется с точностью
представления числовых данных в компьютере. Возможности ин-
струментальных средств для решения алгебраических и трансцен-
дентных уравнений проиллюстрируем несколькими примерами.
Решение уравнения с одной переменной вида/(х) = 0 в системе
MathCad может совмещать графическую иллюстрацию с визуали-
зацией числового значения искомого корня на экране.
Пример 2.9. Определить, имеет ли уравнение Vx + 1 = — корни
на отрезке {-2; 2]; в случае положительного ответа выполнить уточ-
нение корней.
Решим задачу при помощи математической системы MathCad.
С этой целью осуществим графическое отделение корней: постро-
им график функции /(х) = Vx + 1 - —на заданном отрезке вдекар-
х
товой системе координат. Для этого в позиции ввода рабочего до-
100
кумента достаточно ввести выражение, описывающее функцию
/(х), и воспользоваться шаблоном X-Y Plot меню Insert (вставка
объектов, шаблонов) или кнопкой На панели Graph следует
выбрать нужный тип графика и в появившемся шаблоне запол-
нить поля ввода данных (темные прямоугольники): имя перемен-
ной х по оси ОХ, имя функции f{x) по оси ОУ (рис. 2.14), затем
появятся поля ввода для указания предельных значений абсцисс
и ординат, задающие масштаб изображения (если оставить эти
шаблоны незаполненными, то масштабы по осям графика будут
устанавливаться автоматически). Если необходимо построить гра-
фики нескольких функций в одном шаблоне, то имена функций в
поле ввода по оси ОЕследует набирать через запятую. Для постро-
ения графика достаточно вывести курсор за пределы графическо-
го объекта (шаблона) и щелкнуть левой клавишей мыши.
Из графика (рис. 2,15) видно, что уравнение имеет единствен-
ный корень, принадлежащий отрезку [0,5; 1]. Для получения при-
ближенного значения корня система позволяет отобразить в диа-
логовом окне трассировки координаты х и у точки пересечения
графика функции с осью абсцисс (достаточно щелкнуть правой
кнопкой мыши в окне с изображением графика, в появившемся
меню выбрать опцию Trace, установить маркер — перекрещиваю-
щиеся пунктиржяе линии — в точке пересечения графика с осью
абсцисс). Система выдает числовой результат с тремя знаками после
запятой: х= 0,752 (как видно из рис. 2.15, полученное таким путем
значение корня хСоответствует значению у = -0,01).
Символьное (аналитическое) решение линейных и нелиней-
ных уравнений осуществляется при помощи панели символьных
вычислений , на которой необходимо выбрать кнопку L
При этом на экране появится сообщение
где вместо
। solve ,|| —>
I
101
маркеров слева и справа от ключевого слова solve следует задать
соответственно выражение и имя переменной (относительно кото-
рой ищется решение). Результат — значение корня уравнения —
отображается в рабочем документе справа от стрелки и может быть
выражен в различных форматах представления чисел с помощью
команды Result меню Format.
Получить решение уравнения в аналитическом виде можно так-
же, воспользовавшись пунктом Symbolics главного меню: при этом
в рабочем документе MathCad должна быть записана левая часть
уравнения f(x) = 0 и выделена переменная, относительно которой
его следует решать (рис. 2.16).
Для решения одного уравнения с одним неизвестным в систе-
ме MathCad применяют функцию root, которая может использо-
ваться в двух вариантах: root (выражение, имя_переменной) или
гоо((выражение, имя переменной, отрезок). В первом случае перемен-
ной перед использованием функции root необходимо присвоить
числовое значение, которое система будет считать за начальное
приближение при поиске корня (используется комбинация мето-
дов Ньютона и секущих). Во втором случае функция root возвра-
щает значение х, принадлежащее отрезку, при котором выраже-
Рис. 2.15. Графическое отделение корней и символьное решение
уравнения в системе MathCad
102
ние обращается в 0 (используется метод половинного деления).
Примеры использования функции root показаны на рис. 2.17.
Решения получены с погрешностью, заданной системной пере-
менной TOL. При этом по умолчанию система производит вычис-
ления с погрешностью 0,001. При желании значение погрешности
можно изменять как в определенной точке рабочего документа
(1-й способ), так и для всего документа — в меню Math/Options,
причем если значение TOL увеличивать, функция root будет схо-
диться быстрее, но результат будет менее точен, и наоборот.
Функция root может не найти решение (появится сообщение
«Can’t converge to a solution» — отсутствует сходимость) в следую-
щих случаях: уравнение не имеет корней; начальное приближе-
ние расположено слишком далеко от корня; функция имеет точ-
ки разрыва между начальным приближением и корнем; функция
имеет локальный экстремум между начальным приближением и
корнем; уравнение имеет комплексный корень, а начальное при-
ближение задано вещественным числом.
Пример 2.10. Найти положительный корень уравнения
cosx = 0,lx на интервале [-я; л] с точностью 10‘3.
Решим задачу в среде MatLab. Для отделения корней уравнения
необходимо при помощи команды plot(x, у, ‘с’) построить графи-
ки функций у( = cosx и у2 = 0,1х в декартовой системе координат.
Рис. 2.16. Аналитическое решение уравнения относительно выделенной
переменной в MathCad
103
File Edit
SvmboliC? Window Help
Notmal
1 способ
f(x) := - A
x
xO .= 0.5 - начальное приближение корня;
root(f(xq),xO) = 0.754821 - найденное значение соответствует
точности Т01_=0,001
TOL = 10”* - новое значение точности вычислений;
root(f(x(J),x£J) = 0.754878 - уточненное значение корня.
2 способ. Ищем корень уравнения sin 2х = In х на отрезке [1.3; 1,51,
root(sin(2 x) - 1п(х) ,х,1.3,1.5) “ 1.3994
Рис. 2.17. Решение уравнения в MathCad методом секущих
о # г- ©>»:© tg fc ?
» Х«-3:.О1:3; y1scos(x); у2я0.1*x; plot(x ,p11' k * »x»y2 .' k-' >, legend( ' cos(x) *, ‘ )
Рис. 2.18. Графическое отделение корней уравнения в MatLab
104
Предварительно в командном окне следует указать размерности мас-
сивов (они должны совпадать), задающие границы графического
окна. Указанный в апострофах символ ‘с’ задает цвет и тип линии
графика; команда legend позволяет связать с каждой кривой тексто-
вую информацию. По нажатию на клавишу <Enter> будет выведе-
но графическое окно Figure с результатами построения (рис. 2.18).
Из графика видно, что на указанном интервале уравнение имеет
два корня, расположенные на отрезках [-2; -1] и (1; 2]. Для уто-
чнения положительного значения корня с заданной точностью в
D oS I £ И‘- ® 1 ® tg I to ) ?
►> X x-Fzero(‘cos(x)-0.1«x',[1 2]) 1.42755177876459
X x»Fzero(cosCxJ-O.^x' ,1.5) 1.42755177876459
-> X x=Fzero('cos(x)-0.1«x',1.5,0.01) s 1.41514718625761
>> X x=fzero('cos(x)-0.1«x',1.5,0.001) 1.42747455797539
Рис. 2.19. Численное решение уравнения в системе MatLab
» x=Fzero('cos(х)-0.1«х ‘,1.5,0.001,2)
Func euals х F(x) Procedure
1 1.5 -0.0792628 initial
2 1.45757 -0.0327764 search
3 1.54243 -0.125877 search
4 1.44 -0.0135763 search
5 1.56 -0.145204 search
6 1.41515 0.0135067 search
Looking For a zero in the interval [1.4151, 1.56]
7 1.42747 8.41515e-005 interpolation
8 1.43033 -0.0030276 interpolation
1.4275
Рис. 2.20. Уточнение значения корня уравнения в MatLab
I05
системе MatLab используется функция fzero, имеющая следую-
щие форматы записи:
• fzeroffun' ,[xl х2]) — возвращает значение х, при котором
выполняется равенство fun(x) = 0, с заданием интервала поиска
корня (реализован метод деления отрезка пополам);
• fzeroffun',х0) — возвращает уточненное значение х, при ко-
тором достигается нуль функции fun при начальном значении ар-
гумента хО; возвращенное значение близко к точке, где функция
меняет знак, или равно NaN (зарезервированное имя константы
«нечисловая переменная»), если такая точка не найдена;
• fzero(fun',xO,tol) — возвращает результат с заданной точно-
стью lol (реализован метод секущих);
• fzerol/fun’ рсО,tol,trace) — выдает на экран информацию по каж-
дой итерации.
При обращении к функции fzero обязательным параметром яв-
ляется только fun — имя функции. На рис. 2.19 дана иллюстрация
применения перечисленных выше подходов к уточнению корня
уравнения cosx- 0,1х = 0 на отрезке [1; 2]. Точность решения явно
устанавливается только в третьем случае с помощью указания
значения переменной tol.
В двух последних примерах заданы различные значения пере-
менной tol: 10 2 и 10'< Полученные значения корня уравнения
отличаются уже во втором знаке после десятичной точки.
Если при обращении к функции fzero указать любое ненулевое
значение для параметра trace, система выдаст отчет по каждой ите-
рации, содержащий вычисленные значения приближений корня,
значения функции в каждом из приближений, расчетный интер-
вал расположения корня и наименования каждой из операций:
initial— начальное приближение, search — поиск интервала, на
котором функция меняет знак, interpolation — приближение
(рис. 2.20).
Корень уравнения х= 1,4275 при заданной точности 103 полу-
чен на девятой итерации.
Изменить формат вывода результата позволяет команда Свой-
ства меню Файл окна управления (рис. 2.21).
Расчеты в MatLab выполняются с двойной точностью и ис-
пользованием одного из следующих способов представления ре-
зультатов: Short (default)/Short Е — число выводится с четырьмя
цифрами после десятичной точки либо в экспоненциальной фор-
ме с мантиссой из пяти цифр и порядком из трех цифр; Long/
LongE — число с шестнадцатью десятичными цифрами либо в эк-
споненциальной форме с мантиссой из шестнадцати цифр; Hex —
число в шестнадцатеричной системе счисления; Bank — число с
любым количеством знаков до десятичной точки и двумя после
нее; Plus — символическое отображение числа: если положитель-
ное, то будет напечатан «+», отрицательное — «-» и пробел для нуля.
106
MATLAB Окно управления
1-------------------------------Preferences
файл Правка Окно 2
Создать
Открыть...
Выполнить Сценарий...
Загрузить Рабочую Область...
Сохранить Рабочую Область Как
Показать Рабочую Область
Показать редактор Графически)
Показать Инструменты формат;
I
General | Command Window Font | Copying Options |
Числовой формат
Г Short (default)
iL.ong
C Hex
C Bank
Г Plus
C Short E
- Директория Помощи
Установить Маршрут...
Свойства
1 с05г.Ы.т
Г' LongE
Short G
Long G
C~ Рациональный
Г Loose (default) *
(♦ Compact
Редактор Свойств
Г Вкл. Эхо
Р’ Показать Панель инструментов -
С7 Птллпкл
Всегда подключать сетевые директории
ОК
Рис. 2.21. Окно форматирования вывода результата вычислений в MatLab
Вычисление корней полиномов производит функция roots(p), где
р — полином, ввод которого осуществляется с помощью вектора
коэффициентов, начиная с коэффициента при старшей степени.
Пример 2.11. Вычислить корни следующего квадратного урав-
нения х2 - 8х + 5 = 0. Решение приведено на рис. 2.22.
Здесь ans — зарезервированное имя константы, которая полу-
чает значение результатов последней операции (в нашем приме-
ре — корней уравнения: 7,32 и 0,68).
Графическое отделение корней уравнения можно выполнить и
с помощью системы Maple в командном и интерактивном режи-
Рис. 2.22. Вычисление корней квадратного уравнения в MatLab
Рис. 2.23. Отделение корней уравнения в Maple
108
мах (рис. 2.23). В окне документа следует задать выражение, график
которого нужно построить, присвоив его значение некоторой пе-
ременной. Функция plot{f,x = xniin..x,mx), где f — имя функции, xm!n
и *max — диапазон изменения переменной х, возвращает графи-
ческий объект (на одном графике можно изображать несколько
кривых); параметр discont позволяет улучшить качество построе-
ния графиков. Щелчок мыши в поле графика выводит меню дву-
мерной графики, команды которого продублированы в виде пун-
ктов главного меню и кнопок на панели инструментов. Слева от
этих кнопок находится окно, в которое выводятся координаты
точки, отмеченной в данный момент указателем мыши.
Система Maple позволяет получать решение алгебраических и
трансцендентных уравнений в аналитическом виде. Для этого ис-
пользуется функция solve {уравнение, имяпеременной). Если пара-
метр имя_переменной отсутствует, то будут найдены решения от-
носительно всех неизвестных, входящих в уравнение. Функция evalf
{выражение) позволяет получить представление решения в число-
вой форме. Для получения численного решения уравнений также
используется функция fsolve{ypaenenue, переменная, дополнительные
_параметры). В Maple предусмотрена возможность проводить рас-
четы, используя арифметику произвольной точности (арифмети-
кой произвольной точности называют вычисления, в которых вер-
ными считаются все десятичные знаки явно задаваемого количе-
ства десятичных разрядов). Для этого используются команда vpa и
константа digits,* задающая число значащих цифр. На рис. 2.24 по-
казано решение уравнения 7'7'77 = — с максимальной точностью
системы Maple — сначала в аналитической, а затем в числовой
форме. Параметр fulldigits задает точность вычислений, соответ-
ствующую всей разрядной сетке, заданной константой digits.
В системе Derive для решения уравнений в символьном виде
используется команда Algebraically меню Solve — «решение урав-
нений», которая выводит на экран окно для записи уравнения и
выбора из списка переменной, относительно которой ищется рс-
>•S : =solve(sqrt <х <1)-1/х,х);
•twalf (s>
.754877668
(х + 1}=1/х , х-0,1, .2, fnlldigits) ;
..................................................... 7548776662
Рис. 2.24. Решение трансцендентного уравнения в системе Maple
109
Рис. 2.25. Символьное решение квадратного уравнения в системе Derive
Рис. 2.26. Получение числового значения корня уравнения в системе Derive
11: [1.2, 1.18203, 1.17538, 1.17283, 1.1718S, 1.17147, 1.17132]
2: 1.17122
Approximate Expression -???,МТН
а : П • 1 I 51 е ; t; п i е Ч i<jx I pj £ |_oj n |_PJ x ‘ V; 4 Icj + j *
й:В,г]д|Е Z>I I ^Л}Г1М E|O|nlPiEjT|r Ф
|itfirates(sin(x}*tl.25,x,l .2)
Dibits of prcc^ion:
UK Approximate
Рис. 2.27. Реализация итерационных процессов в системе Derive
при решении уравнения sin(x) + 0,25 = 0
ПО
Рис. 2.28. Решение уравнения в системе Mathematics
Рис. 2.29. Запись уравнения в табличном процессоре Excel
Рис. 2.30. Решение уравнения в табличном процессоре Excel
шение данного уравнения. Нажав на кнопку Simplify — «упрос-
тить», получим результат (рис. 2.25).
Численное решение уравнений с одной переменной в системе
Derive реализует команда Numerically. Помимо уравнения и пере-
менной, относительно которой оно решается, задаются пределы
для области решения (рис. 2.26).
Итерационные процессы в системе Derive реализованы функ-
циями Iterates(u,x,xO,n) и lterate(u,xpcO,n). Первая выполняет п ите-
раций при начальном значении х = хО с возвратом результатов
каждой итерации, вторая возвращает результат только последней
итерации (рис. 2.27). Если параметр п не указан, итерации будут
III
проводиться до тех пор, пока значения х на двух последних итера-
циях нс совпадут со значением заданной системной погрешности.
Пример 2.12. Найти действительный корень уравнения № - 2х2 +
+ Зх - 5 = 0.
Воспользуемся системой Mathematics, позволяющей решать
алгебраические и трансцендентные уравнения аналитически и
численно. Для получения численного результата можно исполь-
зовать функции NSolve[eq,var], где ед — уравнение, var — пере-
менная, относительно которой требуется получить решение, и
FindRoot [е<?,{х,х0}], которая возвращает значение корня, начиная
с х = х0 (рис. 2.28).
Табличный процессор Excel для решения уравнений распола-
гает специальным средством Подбор параметра в меню Сервис. Его
алгоритм скрыт от пользователя, но если важен именно резуль-
тат, а не путь к нему, то обращение к стандартному средству оп-
равданно. На рис. 2.29 и 2.30 показаны диалоговые окна Excel при
решении уравнения х2 - sinx= 0: левая часть уравнения записана в
ячейке А1, начальное значение — в ячейке В1 (см. рис. 2.29), ре-
зультат — в ячейке Ы (см. рис. 2.30).
Контрольные вопросы
I. Можно ли изменить точность, с которой функции математических
систем вычисляют корни уравнений?
2. В каких случаях MathCad не может найти корень уравнения?
3. Какие численные методы решения уравнений с одной переменной
реализованы в инструментальных пакетах?
Упражнения
1. Найти методом половинного деления корень трансцендентного урав-
нения Igx - cosx=0 с четырьмя знаками после запятой. Корни отделить
графически.
2. Отделите аналитически корни уравнения х2 - 3,2х = 1. Найти дей-
ствительный корень с точностью 10Л
3. Найти наибольший положительный корень уравнения 4х - 31пх =
= 4 с точностью 10-4, используя метод итераций. Корни отделить графи-
чески.
ЛАБОРАТОРНАЯ РАБОТА № 2
Тема: Решение уравнений с одной переменной
Задание 1. Отделите корни заданного уравнения, пользуясь гра-
фическим методом (схематически, на бумаге). Это же задание
выполните с помощью программы для компьютера и с примене-
нием одного из инструментальных средств.
112
Задание 2. По методу половинного деления вычислите один
корень заданного уравнения с точностью 10~3:
а) с помощью «ручной» расчетной таблицы и калькулятора;
б) с помощью программы для компьютера.
Задание 3. Вычислите один корень заданного уравнения с по-
мощью программы дня компьютера с точностью 10-6, используя
метод простой итерации.
Задание 4. Вычислите один корень заданного уравнения с по-
мощью программы для компьютера с точностью 10'6, используя
один из методов Ньютона.
Задание 5. Вычислите один корень заданного уравнения с точ-
ностью 10-6, используя один из инструментальных пакетов.
Сопоставьте и прокомментируйте полученные результаты.
Варианты заданий приведены в табл. 2.5.
Таблица 2.5
Номер варианта Уравнение Пояснения
1 (0,2х)3 = cos х —
2 x-10sinx = 0 —
3 2'1 = sin х При x < 10
4 2Л - 2 cos х = 0 При x > -10
5 lg(x + 5) = cos x При х < 5
6 >/4x + 7 = 3cosx —
7 xsinx -1 = 0 —
8 8 cos x - x = 6 —
9 sin x - 0,2x = 0 —
10 10cosx-0, lx2 =0 —
11 2 lg(x + 7) - 5 sin x = 0 —
12 4 cos x + 0,3x = 0 —
13 5 sin 2x = 71 -x —
14 l,2x4 + 2x3 -24,1 = 13x2 + 14,2x —
15 2xl-5»2* —
16 2" =10-0,5x2 —
113
Окончание табл. 2.5
Номер варианта Уравнение Пояснения
17 4х4 -6,2 = cos0,6x —
18 3sin8x = 0,7х-0,9 На отрезке |-1; 1|
19 1,2 - In х = 4cos2x —
20 ln(x + 6,1) = 2 sin(x -1,4) —
Пояснения к выполнению лабораторной работы № 2
При выполнении задания 1 отделение корней заданного урав-
нения выполняется с помощью схематического графика на бума-
ге. Во многих случаях задачу графического отделения корня мож-
но упростить, заменив исходное уравнение вида Ь\х) = 0 равно-
сильным ему уравнением /|(х)=/2(х).
Для решения этой же задачи с помощью компьютера сначала
составляется и запускается программа отделения корней уравне-
ния (см. подразд. 2.1). Задание шага может варьироваться в зависи-
мости от величины выбранного участка и характера поведения функ-
ции F\x). Результатом выполнения задания должен быть перечень
отрезков, содержащих по одному корню уравнения. Затем отделе-
ние корней выполняется с помощью одного из инструментальных
пакетов (см. пример 2.2, а также примеры 2.8, 2.9, рис. 2.21).
При выполнении задания 2 сначала уточняется один корень
заданного уравнения по методу половинного деления с заданной
точностью с помощью «ручной» расчетной таблицы и калькуля-
тора. Если корней несколько, в пояснении к заданию указано, на
каком участке выбирается корень, подлежащий уточнению. Фор-
ма расчетной таблицы, которую можно использовать для органи-
зации «ручных» вычислений, показана ниже.
п а ь с = (о + Ь)/2 F(a) Яс) f\b) (b-a)/2
1
Затем эта же задача решается с помощью программы для ком-
пьютера (см. подразд. 2.2).
При выполнении задания 3 исходное уравнение приводится к
виду х = Дх) таким образом, чтобы на выбранном для выполне-
ния задания отрезке [д; Л] функция Дх) удовлетворяла усло-
вию (2.13): существует такое число q, 0 < q < 1, что для любых
хе [а; Л] имеет место |/'(х)| q- Приемы преобразования уравне-
ния к итерационному виду и установление условий сходимости
подробно рассмотрены в п. 2.3.2.
114
При выполнении задания 4 составляется и запускается про-
грамма вычисления одного корня заданного уравнения с точно-
стью 10 6 с использованием одного из методов Ньютона. Суть ал-
горитмов методов Ньютона, а также способы оценки точности
результата подробно рассмотрены на примерах «ручного» счета
(см. примеры 2.5 и 2.6).
При выполнения задания 5 корень заданного уравнения вы-
числяется с использованием одного из инструментальных паке-
тов (см. подразд. 2.5).
После выполнения заданий требуется сравнить полученные
результаты и сопоставить в них верные цифры.
ГЛАВА 3
ЧИСЛЕННЫЕ МЕТОДЫ
РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
3.1. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Множество прикладных и чисто математических задач приво-
дят к необходимости решения систем линейных алгебраических
уравнений. Без преувеличения можно утверждать, что это одна из
важнейших задач вычислительной математики.
Значимость задачи породила целый ряд методов ее решения.
Среди этих методов есть универсальные и специализированные
(т.е. применимые лишь к системам, имеющим некоторые специ-
альные свойства). Методы отличаются друг от друга эффективно-
стью, требованиями к объемам машинной памяти (при реализа-
ции на ЭВМ), закономерностями накопления ошибок в ходе рас-
четов. Нс существует одного метода, который можно было бы во
всех случаях предпочесть всем остальным, и поэтому знакомство
с несколькими методами является обязательным для квалифици-
рованного вычислителя.
Как известно из курса алгебры, число неизвестных в системе
может быть больше числа уравнений или равно ему. Если число
неизвестных больше числа уравнений, то на первом этапе стан-
дартными алгебраическими методами задача сводится к промежу-
точной задаче, в которой число неизвестных равно числу уравне-
ний. С точки зрения вычислителя истинная проблема состоит имен-
но в решении такой системы, и поэтому в данной главе мы огра-
ничимся рассмотрением лишь такой ситуации.
Итак, перед нами система л линейных алгебраических уравне-
ний с п неизвестными:
ДцХ! + а12х2 +... + а|йхя = А;
д2|Х1 + а22х2 +... + а2„х„ = />г;
«л|Х| + а„2х2 +... + а„„х„ = Ь„.
Запись ее в такой форме достаточно громоздка, и при первой
возможности мы будем впредь использовать матричную форму
записи, совершенно равносильную (3.1):
116
Ax = b.
Как обычно, полужирные прописные буквы обозначают мат-
рицу, полужирные строчные — векторы-столбцы.
Методы решения систем вида (3.1) можно разделить на два
класса. К первому относятся точные методы. С помощью таких
методов в принципе можно в результате конечного числа шагов
получить точные значения неизвестных. При этом предполагает-
ся, что и коэффициенты в правой части, и элементы столбца
свободных членов — числа точные, а все вычисления производят-
ся без округлений. Однако практически такое может произойти в
исключительных случаях или может быть связано с решением спе-
циального класса задач (например, когда решениями являются
только целые числа). К подобным методам относятся:
• метод определителей (метод Крамера), хорошо известный из
курса алгебры;
• матричное решение: х = А_|Ь (если известна обратная матри-
ца);
• различные варианты метода исключения неизвестных (мето-
да Гаусса).
Чаше всего точные методы реализуются на ЭВМ, и в процессе
вычислений ошибки округления и погрешности арифметических
действий неизбежны. В силу этого название «точный» не вполне
соответствует существу дела (но является традиционным).
Практическое применение первых двух методов может оказаться
неэффективным или вообще невозможным. Если попробовать ре-
шать «в лоб» систему I'S линейных уравнений с 15 неизвестными с
помощью формул Крамера, то придется вычислить 16 опреде-
лителей порядка 15, что приведет к выполнению примерно
2 • 16 • 15! -14 умножений и сложений. Для выполнения этих вычис-
лений на ЭВМ с быстродействием I06 арифметических операций
в секунду потребуется почти 10 недель непрерывной работы. С прак-
тической точки зрения при достаточно больших размерах систе-
мы матричное решение также является малопривлекательным, по-
скольку задача нахождения обратной матрицы сама по себе не
проще задачи решения системы.
Ко второму классу методов решения систем линейных алгебра-
ических уравнений относятся различные итерационные методы,
основанные на применении принципа сжимающих отображений,
рассмотренного в предыдущей главе.
3.2. МЕТОД ГАУССА
Под названием «метод Гаусса» фигурирует группа методов, объе-
диненных идеей последовательного исключения неизвестных. Наи-
более популярным является метод, основанный на так называе-
117
мой схеме единственного деления', этот метод имеет также и ряд
модификаций.
Кроме решения систем уравнений метод Гаусса весьма эффек-
тивен и для решения некоторых других задач, которые будут рас-
смотрены ниже.
3.2.1. Решение систем уравнений
Будем далее считать матрицу системы (3.1) невырожденной.
Суть метода Гаусса состоит в преобразовании системы (3.1) к
равносильной ей системе с треугольной матрицей, из которой
затем последовательно (обратным ходом) получаются значения
всех неизвестных. Сам по себе метод Гаусса относится к точным
методам. Это означает, что если точно выполнять все требуемые в
нем действия, то будет получено точное решение, поскольку по-
грешность метода в данном случае равна нулю. Понятно, однако,
что из-за вычислительных ошибок (включая ошибки округления,
а также возможные ошибки исходных данных) этот идеал прак-
тически недостижим.
Идея последовательного исключения неизвестных может быть
реализована различными вычислительными схемами (см., напри-
мер, [3, 5] и др.). Ниже рассматривается алгоритм, который полу-
чил название схемы единственного деления.
Подвергнем систему (3.1) следующему преобразованию. Счи-
тая, что Оц * 0 (ведущий элемент), разделим на аи коэффициен-
ты первого уравнения:
*1 +«12*2 +- + а1пХ„ =₽(. (3-2)
Пользуясь уравнением (3.2), легко исключить неизвестное Xi
из остальных уравнений системы (для этого достаточно из каждо-
го уравнения вычесть уравнение (3.2), предварительно умножен-
ное на соответствующий коэффициент при xj).
Затем, оставив первое уравнение в покое, над остальными урав-
нениями системы совершим аналогичное преобразование: выбе-
рем из их числа уравнение с ведущим элементом и исключим с
его помощью из остальных уравнений неизвестное х2. Повторяя
этот процесс, вместо системы (3.2) получим равносильную ей
систему с треугольной матрицей:
' X! + сс12х2 + а13х3 +... + а1ях„ = р,;
*2 + «23*3 + ••• + «2п*п = р2 1
Из системы (3.3) последовательно находят значения неизвест-
ных X^Xn-j,...,^.
118
Таким образом, процесс решения системы (3.1) по методу Га-
усса распадается на два этапа. Первый этап, состоящий в последо-
вательном исключении неизвестных, называют прямым ходом. Вто-
рой этап вычислений — нахождение значений неизвестных —
принято называть обратным ходом.
Процесс решения системы линейных уравнений по схеме един-
ственного деления с контролем ручных вычислений рассмотрим
на примере 3.1. Ручные вычисления по схеме единственного деле-
ния удобно оформлять в виде специальной расчетной таблицы
(табл. 3.1).
Пример 3.1. Решить систему линейных уравнений
2,34^-4,21x2-11,61x3 = 14,41;
8,04xj + 5,22х2 + 0,27х3 = 6,44:
3,92х, - 7,99х2 + 8,37х3 = 55,56.
В раздел А табл. 3.1 вносятся коэффициенты исходной систе-
мы и свободные члены. Для исключения случайных ошибок в
схеме единственного деления предусматривается текущий конт-
роль правильности вычислений; с этой целью в схему вычисле-
ний включены столбец контрольных сумм У и столбец строчных
сумм 5.
Контроль в прямом ходе основывается на следующей идее. После
того как в раздел А внесены коэффициенты и свободные члены
исходной системы, находят контрольные суммы — суммы коэф-
фициентов и свободных членов по строкам — и вносят их в стол-
бец X (в табл. 3.1 это числа 0,93; 7,09; 59,86).
Таблица 3.1
Раздел х| Л'з Свободные члены S 5
А 2,34 8,04 3,92 -4,21 5,22 -7,99 -11,61 0,27 8,37 14,41 6,44 55,56 0,93 7,09 59,86
1 -1,799 -4,962 6,158 0,397 0,398
Л 19,685 -0,938 40,161 27,819 -55,951 31,420 3,895 58,302 3,894 58,302
1 2,040 -2,842 0,198 0,198
29,732 28,756 58,488 58,487
1 0,967 1,967
В 1 1 1 0,967 -4,816 2,293 1,967 -3,816 -3,293
119
В дальнейшем, выполняя преобразования уравнений системы,
над контрольными суммами производятся те же операции, что и
над свободными членами. После выполнения каждого преобразо-
вания находят строчную сумму результатов и помешают ее в стол-
бец 5. Очевидно, что при отсутствии случайных вычислительных
ошибок числа в столбцах 5 и У должны практически совпадать.
Значительное расхождение контрольных значений может ука-
зывать либо на промахи в вычислениях, либо на неустойчивость ал-
горитма вычислений по отношению к данной конкретной системе.
После нахождения контрольных сумм первым преобразовани-
ем в схеме единственного деления является деление элементов
первой строки (включая столбец У) на ведущий элемент 2,34. За-
пись результатов производится в четвертую строку раздела А. Здесь
же впервые выполняют контроль: сравнивают результат1 обычно-
го текущего преобразования контрольной суммы первой строки:
О 93
= 0,397 и строчную сумму: 1 - 1,799 - 4,962 + 6,158 = 0,398. Рас-
хождение в третьем знаке после запятой в данном случае объясняет-
ся накоплением вычислительной ошибки в результате округлений.
Используя четвертую строку раздела А, можно приступить к
преобразованию второй и третьей строк этого раздела (исключе-
нию неизвестного X] из 2-го и 3-го уравнений системы). Результа-
ты этих преобразований образуют соответственно первую и вто-
рую строки раздела А{. Эти преобразования выполняют по следу-
ющему правилу: каждый элемент первой строки раздела At равен
разности соответствующего элемента второй строки раздела А и
произведения его «проекций» на первый столбец и последнюю
строку раздела А; аналогичным способом вторая строка раздела А[
получается из третьей строки раздела А.
Например, для вычисления первого элемента первой строки
раздела А[ берется элемент 5,22 из второй строки раздела Л и из
него вычитается произведение 8,04 (-1,799), т.е. 5,22 + 8,04-1,799 =
= 19,6848 = 19,685. Аналогично второй элемент второй строки раз-
дела Аг образуется вычитанием из числа 8,37 произведения 3,92х
х(-4,962), т.е. 8,37 + 3,92-4,962 = 27,8191 = 27,819.
В общем случае, если b — вычисляемый элемент нового разде-
ла, а — соответствующий элемент предыдущего раздела, причем
рв и pv — соответственно его вертикальная и горизонтальная «про-
екции», можно записать формулу b = a-pBpY. После заполнения
каждой строки нового раздела производится контроль.
Третья строка раздела А] образуется делением первой строки
на ведущий элемент 19,685, после чего аналогичным образом за-
полняются строки раздела А2.
1 Все вычисления в табл. 3.1 для сокращения записей ведутся до трех знаков
после запятой.
120
Разделом Л2 заканчивается прямой ход. В столбце свободных
членов последней строки этого раздела уже получено значение
неизвестного xj=0,967. Значения остальных неизвестных последо-
вательно находят вычитанием из свободных членов соответствую-
щих строк прямого хода, начинающихся с единицы, суммы про-
изведений их коэффициентов на соответствующие значения ра-
нее найденных неизвестных.
Так, для получения х2 проделывают вычисления:
х2 = -2,842 - 2,040 • 0,967 = -4,8157 = -4,816.
Процесс нахождения неизвестных составляет обратный ход (раз-
дел В в табл. 3.2). Контроль в обратном ходе ведется путем сравне-
ния значений неизвестных, получаемых в столбце свободных чле-
нов, с соответствующими числами из столбца X (они образуются
в результате действий, аналогичных действиям по нахождению
значений неизвестных, с той разницей, что вместо свободных
членов используются соответствующие числа из столбца X). Суть
контроля состоит в том, что при безошибочном выполнении вы-
числений числа в столбце X должны быть ровно на единицу боль-
ше соответствующих значений неизвестных из столбца свободных
членов. Этот эффект имеет простое обоснование. Введя в вычисле-
ния столбец X и проделывая с его элементами те же действия,
что и с элементами столбца свободных членов, мы фактически с
самого начала наряда с решением исходной системы параллельно
решали вторую систему, у которой свободные члены образованы
из свободных членов исходной системы, сложенных с коэффици-
ентами соответствующих уравнений. Очевидно, что решениями
второй системы должны быть числа, на единицу большие значе-
ний неизвестных исходной системы.
Вследствие округлений результат решения системы уравнений
(пример 3.1) содержит вычислительную погрешность (наличие
погрешности в ходе вычислений подтвердилось контролем). В этом
можно убедиться, подставив найденные значения неизвестных в
исходную систему:
2,34 2,293 - 4,21 • (-4,816) -11,61 • 0,967 = 14,411;
8,04 2,293 + 5,22 • (-4,816) + 0,27 • 0,967 = -6,441;
3,92-2,293 - 7,99 • (-4,816) + 8,37 0,967 = 55,562.
Значения разностей между свободными членами исходной си-
стемы и результатами подстановки в уравнения системы найден-
ных значений неизвестных называют невязками. В рассмотренном
примере невязки имеют следующие значения:
Е| = 14,41 —14,411 =—0,001;
=—6,44 — (—6,441) = 0,001;
Ej = 55,56 — 55,561 = 0,001.
121
Следует предостеречь от поспешного суждения о погрешнос-
тях результатов по величинам невязок. Различия между ними мо-
гут быть значительными, особенно при неблагоприятных обстоя-
тельствах. Однако существенно то, что, используя невязки, мож-
но уточнить решение системы, вычислив поправки для найден-
ных значений неизвестных. Покажем, как это делается.
Обозначим приближенные значения неизвестных, полученные
в ходе решения системы, как х,- (/=1, 2, п). Исходная система
имеет вил Ах = Ь; если же в нее подставить х вместо х, то в правой
части вместо Ь фактически окажется некоторое Ь: Ах-Б. Вычитая
одну систему из другой, получим А(х - х) = b - Б (правая часть
последнего равенства и есть невязка е). Рассматривая х - х как
неизвестную величину у и решая систему уравнений Ау = Е, полу-
чим новое приближение к точному решению: ? = х + у, где у —
реально полученное (т.е. приближенное) решение новой системы.
Таким образом, можно последовательно уточнять решения систе-
мы, полученной методом Гаусса. На самом деле именно компо-
ненты вектора у (а нс невязки) и позволяют судить о точности
приближенного решения.
За пределами рассмотрения остался вопрос о явном учете вы-
числительных ошибок в ходе реализации схемы единственного
деления, поскольку предусмотренный схемой контроль сам по
себе границ ошибок не устанавливает. Такой учет в принципе
можно было бы организовать и включить соответствующие вы-
числительные процедуры, например, непосредственно в табл. 3.1
(очевидно, что в данном случае речь шла бы исключительно об
учете границ погрешностей арифметических действий). Между
тем понятно, что с увеличением порядка систем и соответствен-
но существенном возрастании числа арифметических операций
вести ручной учет вычислительной ошибки чрезвычайно трудно.
В и. 3.2.3 мы все же обратимся к пооперационному учету вычисли-
тельных ошибок в схеме единственного деления, но уже с помо-
щью программы для ЭВМ.
Контрольные вопросы
I. К какой категории методов вычислительной математики относится
метод Гаусса? Какова структура погрешности результата решения систе-
мы линейных уравнений методом Гаусса?
2. В чем заключается прямой и обратный ход в схеме единственного
деления?
3. На чем основываются подходы к организации контроля вычисле-
ний в прямом ходе, обратном холе? Какого рода вычислительные ошиб-
ки отслеживает этот контроль? Позволяет ли он повысить точность ре-
зультатов?
4. Как можно использовать невязки для уточнения решения системы,
найденного по схеме единственного деления?
122
Упражнения
Решить пользуясь «ручной» схемой единственного деления (см.
табл. 3.1), системы линейных уравнений:
Xi + 10х2 - 5х3 = 1;
а)
2х| + 4х2 - х3 = 2;
Xi + Зх2 + х3 = 3;
1,00х| + 10,00х2-5,00х3 = 1;
б) 1,01Х| + 9,99х2 - 5,01х3 = 2;
0,99х| + 1,01х2 - 4,99х3 = 3.
Вычисления вести на калькуляторе с точностью до трех знаков после
запятой. Подставить найденные решения в исходные системы и вычис-
лить невязки. Чем можно объяснить значительные по величине невязки
для второй системы?
3.2.2. Вычисление определителей и обращение матриц
Приступая в п. 3.2.1 к рассмотрению процесса решения систе-
мы (3.1) по методу Гаусса, мы сделали оговорку, что система
невырождена, т.е. ее определитель отличен от нуля. Но и в том
случае, когда определитель системы отличен от нуля, но очень
мал по абсолютной величине, вычислительная ошибка в ходе
поиска решения может оказаться столь значительной, что полу-
ченное решение потеряет всякий смысл. Поэтому решение систе-
мы линейных уравнений полезно сопровождать вычислением оп-
ределителя этой системы.
Вычисление определителя может представлять и самостоятель-
ный интерес, поскольку такая задача нередко встречается в вы-
числительной математике. Рассмотрим алгоритм вычисления оп-
ределителя в связи с решением системы уравнений методом Гаус-
са по схеме единственного деления.
Обозначим определитель системы (3.1) через D. Что происхо-
дит с ним на каждом шаге реализации метода Гаусса? Ясно, что
после того как мы разделим левую и правую части первого урав-
нения на ведущий элемент оц, определитель преобразованной
системы станет равным О/ап Последующие преобразования пер-
вого шага, связанные с исключением Х| из остальных уравнений
системы, величину определителя не изменяют. На втором шаге,
когда мы разделим обе части (преобразованного) второго уравне-
ния на второй ведущий элемент (обозначим его Дгз*0), определи-
тель полученной системы будет равен £>/(оц-а22(,))- Операции по
исключению *2 из уравнения системы вновь не изменяют величи-
ны определителя D.
Осуществляя аналогичные действия, мы на л-м шаге придем к
системе (3.3). Легко понять, что определитель этой системы будет
равен Д/(аца22(1)-— Но матрица коэффициентов при
неизвестных системы (3.3) — треугольная, с единицами по глав-
ной диагонали. Поэтому ее определитель равен 1.
123
Получаем
P=(eirfl22(1,-..-V'",,) = l.
Следовательно, определитель исходной матрицы
где Аь«й<,\— ведущие элементы схемы единственного
деления.
Отсюда следует практический вывод: если необходимо вычис-
лить определитель некоторой квадратной матрицы, надо решить
систему уравнений с этой матрицей и произвольной правой частью
и воспользоваться формулой (3.4).
Схема единственного деления может использоваться также и
для вычисления элементов матрицы А'1, обратной для невырож-
денной матрицы А. По определению А • А4 = Е, где Е — единичная
матрица. Представим искомую матрицу А’1 и единичную матрицу
в виде совокупности векторов-столбцов:
А*1 = (х(|\ х<2), ..., Е = (е(,\ е(2), ..., е(п>)
(структура векторов е(/) предельно проста: /-й элемент равен едини-
це, а все остальные — нулю). В такой записи соотношение А А’1 =
= Е предстанет в виде совокупности из п систем линейных алге-
браических уравнений вида
Ах<'> = е(/> (/ = 1, 2, ...» л). (3.5)
Решение каждой системы дает соответствующий столбец об-
ратной матрицы.
При нахождении обратной матрицы указанным методом су-
щественно, что все системы, входящие в (3.5), Имеют одинако-
вую матрицу и фактически могут решаться одновременно. Рас-
ширив таблицу схемы единственного деления, можно проиллю-
стрировать получение обратной матрицы рассмотренным мето-
дом.
Пример 3.2. Для матрицы, составленной из коэффициентов си-
стемы, рассмотренной в примере 3.1,
(2,34 -4,21
А = 8,04
3,92
к
5,22
-7,99
-II,6Г
0,27
8,37
/
найти обратную матрицу, пользуясь схемой единственного деле-
ния.
Вычисления показаны в табл. 3.2.
124
Таблица 3.2
Раздел ху х-1 7 = 1 7=2 7=3 5
А 2,34 8,04 3,92 -4,21 5,22 -7,99 -11,61 0,27 8,37 1 0 0 0 1 0 0 0 1 -12,48 14,53 5,30
1 -1,7991 -4,9615 0,4274 0 0 -5,3332 -5,3332
А 19,6848 -0,9388 40,1605 27,8191 -3,4363 -1,6741 1 0 0 1 57,4090 26,2062 57,4089 26,2061
1 2,0401 -0,1746 0,0508 0 2,9164 2,9164
^2 29,7318 -1,8391 0,0476 1 28,9403 28,9406
1 -0,0619 0,0016 0,0336 0,9733 0,9734
В 1 1 1 -0,0619 -0,0483 0,0357 0,0016 0,0475 0,0934 0,0336 -0,0686 0,0433
Выписывая значения найденных элементов (с обратным поряд-
ком расположения строк), получим искомую обратную матрицу:
А*1 =
' 0,0357
-0,0483
-0,0619
\
Сделаем прямую проверку:
0,0934 0,0433 >
0,0475 -0,0686
0,0016 0,0336 ;
Г 1,0041
0,0000
-0,0002
-0,0088 -0,0270'
0,9994 -0,0033
0,0005 1,0003
Поскольку вычисления, показанные в табл. 3.2, реально велись
с заданной в ней точностью (с округлением до второй цифры
после запятой), то наличие невязок, отраженных в матрице А-А’1,
является естественным.
Контрольные вопросы
1. На чем основываются алгоритмы вычисления определителя по ме-
тоду Гаусса?
2. Каким образом схема единственного деления .может использовать-
ся для вычисления элементов обратной матрицы?
Упражнения
1. Пользуясь данными табл. 3.1, вычислить значения определителя
решаемой системы линейных уравнений.
125
2. Найти матрицу, обратную для матрицы, полученной в результате
выполнения примера 3.2.
3.2.3. Программная реализация схемы единственного
деления для решения системы линейных уравнений
и вычисления определителя с пошаговой оценкой
границ абсолютных погрешностей
Для автоматизации учета границ погрешностей достаточно пре-
дусмотреть вызовы соответствующих процедур подсчета ошибок
после каждого арифметического действия (см. подразд. 1.7). Пока-
жем, как это выглядит применительно к схеме единственного де-
ления, рассмотренной в п. 3.2.1.
Алгоритм указанного метода изображен на рис. 3.1. Массив a[i, у]
(1 < i< п, 1 <j< п + 1), называемый ниже «расширенной матрицей
системы» содержит матрицу коэффициентов системы и столбец
свободных членов. Для лучшего понимания следует произвести трас-
сировку алгоритма и сопоставить ее результат с разобранным выше
примером.
Программа, приведенная ниже, реализует алгоритм, изобра-
женный на рис. 3.1. Дополнительно к этому программа содержит
вычисление определителя системы (переменная det) и пошаго-
вые оценки предельной абсолютной погрешности результата по
заданным значениям абсолютной погрешности коэффициентов
системы и свободных членов. Порядок системы задан в виде кон-
станты п. Тип Тосновных вещественных переменных задан в раз-
деле type — для того, чтобы его можно было задавать в одном
месте. Вывод основных результатов организован в естественной
(десятичной) форме с точностью, соответствующей оценке по-
грешности, вывод погрешностей — в нормализованном формате
с плавающей точкой с двумя значащими цифрами в мантиссе.
Следует, однако, сознавать, что вывод результатов решения
системы с указанной выше точностью может стать тормозом в тех
случаях, когда оценка предельной погрешности столь завышена по
сравнению с реальностью, что является бессмысленной. В этом случае
следует отказаться от принятого в программе формата вывода ре-
зультатов. Соответствующие примеры будут рассмотрены ниже.
program Gauss; (Решение системы линейных
алгебраических уравнений и вычисление определителя
по простой схеме Гаусса с пооперационным
вычислением предельной абсолютной погрешности
результатов}
uses ert, okrugl;
const n=3; {порядок системы}
type T=real;
126
Начало
Ввод л (порядок системы) и А (расширенная матрица)
Рис. 3.1. Блок-схема алгоритма метода Гаусса
127
var a:array[1..n,1..n+1] of T; x : array[1..nJ of T;
da:array[1,.n,1..n+1J of single; dx:array[1..n]
of single; r,g,det:T;
dr,dg,Det:single; m, k,i,j :integer;
function ds(da,db:single):single; (погрешность суммы
(разности)}
begin ds:=da+db
end;
function dpr(a,b:T; da,db:single):single;
{погрешность произведения)
begin dpr:=abs(a)*db+abs(b)*da
end;
function dch(a,b:T;da,db:single):single;
{погрешность частного)
begin dch:=da/abs(b)+db*abs(a)/(b*b)
end;
begin
m:=n; {параметр m необходим для обращения
к процедуре округления)
{ввод расширенной матрицы системы)
for k:=l to n do for j:=l to n+1 do
begin writeln(’введите a[ ’ , k, 1 , ' , j , ' ] ') ;
read(a[k,j J);
end;
{вывод элементов расширенной матрицы — для
контроля правильности ввода)
writeln('Расширенная матрица системы');
for k:=l to п do
begin for j:=1 to n+1 do write(a[k,j]:12:4,' ’);
writeln
end;
{ввод абсолютных погрешностей элементов расширенной
матрицы — для контроля правильности ввода)
for k:=l to n do for j:=l to n+1 do
begin writeln ('введите da[',k, ', ',j, ']1);
read(da[k,j])
end;
{вывод абсолютных погрешностей элементов расширенной
матрицы — для контроля правильности ввода)
writeln; writeln(1 Абсолютные погрешности элементов
расширенной матрицы');
for k:=l t*o n do
begin for j:=l to n+1 do write(da[k,j]:12,' ’);
writeln
end;
det:=1.0; {подготовка к вычислению определителя)
128
{Начало 'прямого хода' метода Гаусса}
dr:=0; ddet:=0;
for к:=1 to n do
begin det:=det*a[k,kJ;
ddet:=dpr(det, a [k, k],ddet, da[k,k]);
for j:=k+l to n+1 do
begin a[k,j]:=a[k,j]/a[k,k];
da[k,j]:=dch (a[k,j],a[k,k], da[k,j],da[k,k])
end;
for i:=k+l to n do
for j:=k+l to n+1 do
begin r:=a[k,j]*a [i, k] ;
dr;=dpr(a[k,j],a[i,k],da[k,j],da[i,k]);
a[i,j]:=a[i,j]-r; da[i,j]:=ds(da[i,j],dr)
end;
end;
okr(det,ddet,det,m); if m<0 then m:=0;
writein; writein(1 Определитель системы =',
det:7:m);
writein ('Предельная абсолютная погрешность
значения определителя =',ddet:10);
{Начало 'обратного хода' метода Гаусса}
x[n]:=а[n,n+1]; dx[n]:=da[п,п+1];
for к:=п-1 downto 1 do
begin r:=0,* dr:=0;
for j:=n downto k+1 do
begin g: =a[k,j]*x[j] ;
dg:=dpr(a[k,j],x[j],da[k,j],dx[j]);
r:=r+g; dr:=ds(dr,dg);
end; '
x[k] :=a[k,n+1]-r; dx [k] :=ds(da[k,n+1],dr);
end;
writein; writein(’Результат решения системы');
for i:=l to n do
begin okr(x[i], dx[i], x[i], m) ; if m<0 then
in:=0;
write('x[',i,'] =',x [i] : 7 :m, ' ')
end;
writein; writein('Предельная абсолютная погрешность
ре.зультата') ;
for i : =1 to n do write (’dx [ 1 , i ,'] = ', dx [ i ]: 1'0, ' ');
repeat until keypressed
end.
Пример 3.3. Проиллюстрируем работу программы на той сис-
теме уравнений, которая была рассмотрена в примере 3.1. Грани-
3 Ланчнк
129
цы абсолютных погрешностей коэффициентов системы и свобод-
ных членов примем равными 0,005 (т.е. будем считать, что исход-
ные числовые значения заданы цифрами, верными в строгом смыс-
ле). Тип Т определим как real, константу п в соответствии с раз-
мерностью заданной системы положим равной 3.
Результат работы программы:
Расширенная матрица системы
2.3400 -4.2100 -11.6100 14.4100
8.0400 5.2200 0.2700 -6.4400
3.9200 -7.9900 8.3700 55.5600
Абсолютные погрешности элементов расширенной
матрицы
5.ОЕ-ОООЗ 5.ОЕ-ОООЗ 5.ОЕ-ОООЗ 5.ОЕ-ОООЗ
5.0Е-0003 5.ОЕ-ОООЗ 5.ОЕ-ОООЗ 5.ОЕ-ОООЗ
5.ОЕ-ОООЗ 5.ОЕ-ОООЗ 5.ОЕ-ОООЗ 5.ОЕ-ОООЗ
Определитель системы = 1000
Предельная абсолютная погрешность значения
определителя = 2.ЗЕ + 0002
Результат решения системы
х[1] = 2.3 х[2] = -4. 8 х[3] = 0.S )7
Предельная абсолютная погрешность результата
dx [ 1]= 9.5Е -0002 dx[2] = 2.0Е-0002 dx[3]= 5.ЗЕ-0003
Итак, предельная абсолютная погрешность результатов ДХ] =
= 0,095, Дх2 = 0,02, Дх3 = 0,0053 хотя и существенно больше за-
данной погрешности коэффициентов системы, но не делает ре-
зультат бессмысленным. Так, наибольшая из предельных отно-
сительных погрешностей, оцененных с помощью полученных
выше абсолютных, 5xj = 4%, т.е. является вполне пригодной
для обычных практических расчетов. Тем не менее не следует за-
бывать, что реальные погрешности, скорее всего, существенно
меньше.
Изменение типа Тна double или на single практически не ска-
зывается на приведенных выше результатах. Это обстоятельство
можно считать естественным, учитывая малый порядок и «хоро-
шие» свойства (корректность) рассмотренной системы (о кор-
ректности систем линейных уравнений будет сказано в п. 3.2.4).
Для эмпирического исследования того, насколько вычислен-
ные предельные погрешности отличаются от реальных погрешно-
стей, и как связаны реальные и оцениваемые погрешности с за-
даваемыми погрешностями элементов расширенной матрицы, рас-
смотрим систему уравнений, точное решение которой известно.
130
Пример 3.4. Рассмотрим систему уравнений
xt + х2 + 2х4 = 5;
2Х| + 4х2 л'з + 5х4 - -1;
х3 + Зх2 + 3x4 = —3;
Зх] + 7х2 - Зх3 + 9х4 = -13.
Ее точное решение х( = 9,5, х2 = -2,5, х3 = 5, х4 = ~1.
Применим к ней указанную выше программу, задавая различ-
значения Д границ абсолютных погрешностей элементов
ные
расширенной матрицы (считая при этом, что границы погрешно-
стей для каждого ее элемента одинаковы). Результаты приведены
в табл. 3.3. Отметим, что реальные погрешности, вычисленные как
разности между найденными численно и точными значениями
решений, во всех рассмотренных случаях в пределах достижимой
точности машинных вычислений оказались равными нулю (при
типах данных Т single, real и double).
Таблица 3.3
л Предельные абсолютные погрешности
]-10-' Д, = 49, Д2 = 26, Д3 =34, Д4 = 11
МО-2 Д, -4,9, Д3=2,6, Д3=3,4, Д4 = 1,1
МО 3 Д, =0,49, Д2=0,26, Д3=0,34, Д4 = 0,11
МО 4 . Д, = 0,049, Д2 = 0,026, Д3 = 0,034, Д4 = 0,011
Для систем высокого порядка (а на практике не редкость сис-
темы в сотни уравнений) «точных» решений, разумеется, не по-
лучится, поскольку на результатах начнут сказываться ограниче-
ния машинного представления типа вещественных переменных.
Продемонстрируем это на следующем примере.
Пример 3.5. Сформируем расширенную матрицу системы с по-
мощью следующего фрагмента программы.
for i:=l to n do
begin
a[i,n + 1]:=n;
for j:=l to n-1 do a[i, j]:=d*(-l + 2*random);
a[i,n]:=a[i,n+1];
for k:=l to n-1 do a[i, n]:=a[i, n]-a[i,k]
end;
Легко убедиться, что в итоге возникнет система с точным (в
пределах возможностей машинных расчетов) решением X] = 1, х2 =
= 1, ..., хп = 1. Правые части входящих в нее уравнений равны еди-
нице, а матрица системы образуется с помощью датчика случай-
ных
чисел;
ее элементы лежат в диапазоне
[-d; dj. Если мы хотим,
131
чтобы при различных обращениях получались разные наборы ко-
эффициентов, в начале программы следует поместить обращение
к стандартной процедуре randomize.
В качестве меры отклонения полученного приближенного реше-
ния от точного выберем величину т = max 11 - х,-|, где х,- — прибли-
1<<<л 1 1
женное решение, полученное по программе. Эта величина элемен-
тарно вычисляется в программе по завершении решения системы.
Опишем некоторые результаты численного эксперимента при
значениях параметров л = 40 (т.е. система состоит из 40 уравне-
ний) и d = 4 (т.е. элементы матрицы А — случайные числа в диа-
пазоне [-4; 4]). Величины предельных абсолютных погрешностей,
оцениваемые по описанному выше методу, для такой большой
системы бессмысленно велики, и приводить их здесь не будем.
В табл. 3.4 каждый вариант расчетов выполнен при некотором фик-
сированном наборе элементов матрицы А, т$ соответствует типу
single, тц — real, mD — double, тЕ — extended.
Табл и ца 3.4
№ варианта mS «ц
1 9,7-10L5 1,2-10"9 2,6-10“13 1,11016
2 2,6-10'4 9,4-10“'° 2,0-Ю"13 2,510-16
3 1,4-10-4 6,1-10 9 3,9-10“13 2,1 10“16
На основе данных из табл. 3.4 можно сделать следующие выводы.
1. Для большой системы вычисление предельных абсолютных
погрешностей бессмысленно, так как получаемые значения не
содержат никакой практически полезной информации. В соответ-
ствии с этим, если применять приведенную выше программу для
решения больших систем, то при выводе результатов их не следу-
ет округлять, ориентируясь на вычисленные программой предель-
ные погрешности.
2. Для большой системы существенно, какой используется тип
данных из множества вещественных типов. Хотя даже наиболее
«короткий» тип single в рассмотренном примере дает довольно
высокую точность, эта точность может стать недостаточной — либо
при решении систем еще большего порядка, либо при столкнове-
нии с «плохими» системами даже весьма невысокого порядка (при-
меры последних показаны в п. 3.2.5).
Контрольные вопросы
1. Чем отличается алгоритм, приведенный на рис. 3.1, от алгоритма,
описанного в и. 3.2.1? Существенно ли это отличие с точки зрения полу-
чения решения системы?
132
2. Как в приведенной выше программе организован вывод результа-
тов решения системы? Почему для решения системы и для погрешнос-
тей выбраны различные форматы?
3. При каких обстоятельствах имеет смысл отказаться от программно-
го округления решения системы перед его выводом? Как будет в этом
случае выглядеть соответствующий фрагмент программы?
4. Как эмпирически, пользуясь многообразием вещественных типов в
Turbo Pascal, оценить точность решения системы в случае, когда про-
граммная оценка предельных погрешностей является бессмысленно вы-
сокой?
5. Как, пользуясь процедурой последовательного уточнения решения
системы, описанной в п. 3.2.1, установить эмпирический критерий за-
вершения уточнения?
Упражнения
1. Выполнить программу Gauss для системы примера 3.1 при условии,
что один из коэффициентов при неизвестных или свободных членах имеет
погрешность, существенно более высокую по сравнению с (одинако-
вой) погрешностью других числовых данных. Сопоставить результаты ре-
шения с полученными ранее и сделать выводы.
2. Разработать на основе приведенной выше программы программу
последовательного уточнения решения системы, реализующую проце-
дуру, описанную в п. 3.2.1.
3.2.4. Модификации схемы единственного деления
Описанная в п. 3.2.1 процедура решения системы является про-
стейшим, но далеко не самым эффективным из возможных вари-
антов реализации метода Гаусса. Более того, она при буквальном
следовании приведенному примеру может оказаться непримени-
мой, несмотря на то, что система имеет решение.
Действительно, допустим, что в системе (3,1). коэффициент
йи равен нулю. Тогда переход в первом уравнении к виду (3.2)
невозможен; вместе с тем система может иметь решение даже
тогда, когда в ее матрице равны нулю многие элементы! Следует
модифицировать метод для того, чтобы исключить подобные ка-
зусы.
Самое простое, что можно сделать, если Оц =0, — поменять
местами первое уравнение и любое другое, в котором коэффици-
ент при X! не равен нулю. Далее все идет по описанной выше схе-
ме; если на каком-то промежуточном этапе ведущий коэффици-
ент окажется равным нулю, то снова переставляем уравнения.
Очевидно, что такая перестановка всегда возможна (если сис-
тема имеет решение), потому что, если все коэффициенты в не-
котором столбце матрицы системы равны нулю, то определитель
этой системы также равен нулю, и она решений не имеет. Это
замечание помогает понять и то, каким образом метод Гаусса по-
133
зволяет обнаружить вырожденность матрицы системы: на некото-
ром шаге обнаруживается, что все элементы в некотором столбце
равны нулю.
Отметим, что при вычислении определителя перестановка строк
матрицы может изменить его знак (что легко учесть), а при вы-
числении обратной матрицы требует соответствующих перестано-
вок в получившейся матрице.
При численном решении возникают и дополнительные сооб-
ражения, связанные с приближенным характером вычислений и
стремлением минимизировать вычислительную погрешность. На-
помним, что одна из самых неудачных с точки зрения нарастания
погрешностей вычислительных операций — деление большого
числа на малое. Поэтому для минимизации этого вида ошибок
перестановку уравнений часто бывает целесообразно осуществ-
лять, даже если потенциально ведущий элемент не нуль, но в
соответствующей строке коэффициентов относительно мал. В этом
случае на первое место (на каждом шаге) встает строка, в кото-
рой в оставшихся уравнениях в левом столбце находится макси-
мальный по модулю элемент. Подобный метод, связанный с пе-
рестановками строк, называют методом главного элемента.
Поясним характер действий при осуществлении указанных пе-
рестановок на примере.
Пример 3.6. Рассмотрим систему уравнений
О, ООэс, -4,21х2 - 11,61х3 = 14,41;
< 8,04%| + 5,22х2 +0,27х3 = -6,44;
3,92х, - 7,99х2 + 8,37х3 = 55,56.
Сведем коэффициенты в табл. 3.5.
Сравнивая с табл. 3.1, видим, что такое же, как там, продол-
жение процесса невозможно. Поскольку наибольшим в первой
колонке является число 8,04, стоящее во второй строке, то пере-
ставим первую и вторую строки и продолжим процесс (табл. 3.6).
Далее, следуя высказанной выше рекомендации, переставим
строки в разделе и продолжим решение системы.
Опишем алгоритм перестановки строк в общем виде, имея в
виду возможную программную реализацию. Итак, на некотором
шаге оставшаяся часть системы имеет вид
(*ккхк + + — + ДЬ|ХЛ - Ьк',
<*к+\,кхк + ^t+lX+l^+l + + ак+\,пхп =
й„к хк + а,, к+[хк+1 + ... + й11пхп — Ь„.
Необходимо переставить к-ю строку с той, в которой находит-
ся наибольший по модулю из коэффициентов первого столбца.
134
Табл и ца 3.5
Раздел -V) Л'э Л'З Свободные члены 2 5
А 0,00 8,04 3,92 -4,21 5,22 -7,99 -1 1,61 0.27 8.37 14,41 -6,44 55,56 0,93 7,09 5,86
Табл и ц а 3.6
Раздел *1 *2 х3 Свободные члены X 5
А 8,04 0,00 3,92 5,22 -4,21 -7,99 0,27 -11,61 8,37 -6,44 14,41 55,56 7,09 -1,41 59,86
1 0,649 0,034 -0,801 0,882 0,882
А\ -4,21 -10,53 -11,61 8,24 14,41 58,70 -1,41 56,40 -1,41 56,41
Блок-схема соответствующего алгоритма приведена на рис. 3.2. Этот
алгоритм последовательно применяется к системе, начиная с к = I
и т.д.
Еще более эффективным с точки зрения минимизации вычис-
лительной погрешности является выбор в качестве ведущего эле-
мента (на каждом шаге) наибольшего по модулю числа во всей
матрице коэффициентов системы. Соответствующий вариант ме-
тода Гаусса связан с перестановками не только строк, но и столб-
цов. При перестановке столбцов необходимо запоминать порядок
перестановки. В алгоритмическом плане этот метод существенно
сложнее, и на практике к нему прибегают редко.
Контрольные вопросы
1. Какие ограничения на применение простой схемы единственного
деления могут накладывать произвольные значения коэффициентов при
неизвестных?
2. Почему схемы Гаусса с выбором главного элемента дают более точ-
ный результат, нежели простая схема Гаусса (даже в том случае, когда
простая схема Гаусса формально применима)?
Упражнения
I. Оформить схему, приведенную на рис. 3.2, в виде процедуры на
языке Turbo Pascal, и отладить ее взаимодействие с программой, приве-
денной выше (не выполняющей перестановки строк).
2. Решить, используя рассмотренные в п. 3.2.3 и 3.2.4 методы, систему
линейных уравнений, приведенную в примере 3.4, двумя способами:
135
Начало
Рис. 3.2. Блок-схема алгоритма перестановки строк для оптимизации
метода Гаусса (/ —- номер строки, переставляемой с к-й строкой)
а) без перестановок строк; б) с перестановками строк. Сравнить и про-
комментировать результаты.
3. Разработать алгоритм метода Гаусса с поиском главного элемента
по всей матрице.
3.2.5. Плохо обусловленные системы линейных
алгебраических уравнений
С точки зрения алгебраической теории, для которой все числа
являются точными, система линейных алгебраических уравнений
либо имеет решение, либо нет. Если определитель системы с не-
136
нулевой правой частью равен нулю, то решения не существует,
не равен нулю — решение существует и единственно.
В реальности, когда для решения системы используются чис-
ленные методы, ситуация может быть не столь проста. Предста-
вим, что определитель равен нулю, но в процессе его вычисления
за счет округлений и арифметических действий над округленны-
ми (т.е. неточными) числами компьютер может найти пусть и очень
малое, но ненулевое значение. Тогда есть шанс получить «реше-
ние» системы, у которой его не существует.
Возможна (и реально встречается в приложениях) встречная
ситуация — система имеет решение, но погрешности, обуслов-
ленные различными факторами, оказываются того же порядка или
больше, чем сами решения. Подобные системы называют плохо
обусловленными, или неустойчивыми.
Одной из причин плохой обусловленности может быть боль-
шая чувствительность решения системы к малым изменениям эле-
ментов матрицы А или свободных членов b (или того и другого
одновременно). Если эти элементы являются числами точными,
то в подобной повышенной чувствительности нет ничего необыч-
ного, но если они есть числа приближенные, то решение может
полностью обесцениться.
Пример 3.7. Рассмотрим систему уравнений
1,41х + 5,87у = 13,15;
(2,83х +11,75у = 26,33.
Легко проверить, что ее «точное» решение есть: х = 1, у= 2.
Слово «точное» взято в кавычки, потому что, говоря о точном
решении, мы имеем в виду нс только процедуру его получения
(например, отсутствие округлений при расчетах), но и то, что
коэффициенты — точные числа, без погрешностей.
Теперь предположим, что коэффициенты — числа приближен-
ные (например, возникли в ходе других вычислений или физи-
ческих измерений). Поскольку данный пример — лишь иллюстра-
ция, то проверим, к чему приведет погрешность лишь одного из
коэффициентов, например 1,41. Допустим, что она равна 0,01 (т.е.
относительная погрешность коэффициента невелика, примерно
0,7%). Решим ту же систему, заменив лишь 1,41 на 1,42. Результат
таков: х=-0,61, у= 2,388. Изменения в решении огромны: величи-
на х изменилась более чем на 100% (если считать это изменение
реакцией на погрешность начального данного, то естественно на-
зывать его погрешностью решения). Таким образом, полученное
решение практически бесполезно, в нем нет ни одной верной
цифры.
Данная система плохо обусловлена. Соответствующую неустой-
чивость можно назвать некорректностью, поскольку решение силь-
но реагирует на малые изменения начальных данных. Причину
137
этого в данном примере можно увидеть легко — коэффициенты в
строках матрицы почти пропорциональны, т.е. матрица системы
почти вырождена, ее определитель близок к нулю. Однако если в
системе не два уравнения, а больше, то возможная некоррект-
ность отнюдь не очевидна. Существуют специальные способы оцен-
ки уровня обусловленности системы уравнений, слишком слож-
ные для рассмотрения в данном учебном пособии. Отмстим лишь,
что практическим сигналом о возможном неблагополучии реше-
ния может стать большая величина поправок, полученных в ходе
уточнения решения (см. п. 3.2.1). Поэтому получение по крайней
мерс одной поправки является при решении систем уравнений
методом Гаусса весьма желательным.
При решении плохо обусловленных систем особенно заметно
проявляется длина представления мантиссы используемых веще-
ственных чисел. Для того чтобы это отчетливо продемонстриро-
вать, создадим механизм управления длиной мантиссы — со зна-
чительно большими возможностями, нежели дают стандартные
вещественные типы данных. Соответствующая программа отсече-
ния заданного числа байт мантиссы позволяет, по существу, моде-
лировать ЭВМ с заданной точностью представления веществен-
ных чисел.
Наиболее эффективно реализация указанного отсечения про-
изводится с помощью механизма прямого доступа к памяти. Ис-
ходные версии языка Pascal таким механизмом не располагали.
Turbo Pascal, начиная с версии 6.0, предоставляет программисту
возможность использования величин в той форме, в которой они
непосредственно хранятся в памяти ЭВМ.
Средством прямого доступа к памяти, о котором идет речь,
является Absolute. С его помощью можно разместить переменную
по любому указанному программистом абсолютному адресу в опе-
ративной памяти:
var <имя>:<тип> absolute <адрес>
Если же вместо адреса написать имя другой переменной, то
произойдет совмещение переменных (в том числе и разных ти-
пов), и это может позволить присвоить одной из них полное внут-
реннее изображение другой.
В приведенной ниже программе Round использована конструк-
ция
var x_b: array [1..8] of byte absolute x;
Она вводит массив x__b типа «массив байтов» и совмещает его
с переменной х. Поскольку эта переменная в программе описана
как double, то ее фактический размер равен как раз 8 байт. В про-
цессе исполнения программы каждый элемент этого массива по-
лучает значение одного байта из числа байтов, составляющих пе-
138
ременную л. Важно и то, что если изменить значение элементов
массива х Ь (в программе проводится их обнуление), то это из-
менение окажется в то же время изменением значения перемен-
ной х.
Основу программы составляет функция cut («отсечение»). Па-
раметр х — число типа double, которое подлежит насильственно-
му округлению, параметр п указывает на то, сколько байт следует
отсечь от мантиссы числа х справа. При п= 1 будет отсечен 1 байт,
т.е. относительная погрешность представления числа увеличится
от 2-52 до 2‘44, при п = 2 будет отсечено 2 байта (относительная
погрешность станет равна 2 36) и т.д.
program Round;
uses cr t;
var x;double; i,n:integer;
var x_b: array [1..8] of byte absolute x;
function cut(x:double;n;integer):double;
(Функция реализует отсечение n «правых» байтов
мантиссы в двоичном представлении величины х типа
double; п=1,2...(не более 6)}
var x_b: array [1..6] of byte absolute x;
var i: integer;
begin
for i:= 1 to n do x_b[i]:=0; cut:=x
end;
«
begin
writeln ('введите x,n‘); read(x,n); writeln;
writeln('исходное значение x=',x);
writeln('исходное изображение x1); writeln;
for i:=8 downto 1 do write(x_b[i' ');
x:=cut(x,n);
writeln; writeln(1 преобразованное изображение
x ' , x) ;
for i:=8 downto 1 do writeln(x_b[i], '
writeln; writeln ('значение x после преобразования
x=',x);
repeat until keypressed
end.
Пример работы программы при х= 12345,6789123, п = 3 приве-
ден ниже.
Исходное значение х = 1.23456789123000Е+0004
Исходное изображение х
64 200 28 214 230 153 38 173
139
преобразованное изображение х
04 200 28 2.1 4 230 000
значение х после преобразования
х = 1.23456788940430Е+0004
Вернемся к рассмотрению примеров плохо обусловленных си-
стем. Сконструируем плохо обусловленную систему с известным
решением. Для этого поступим аналогично тому, как в приме-
ре 3.5 была сконструирована система уравнений с помощью дат-
чика случайных чисел. Сделаем в приведенном там фрагменте про-
граммы небольшие изменения:
for i:=l to n do
begin a[i,n+l]:=n;
for j:--l to n-1 do a[i,j]:=l+d*(-l+2*random);
a [i,n] :=a[i,n+1];
for k:=l to n-1 do a [i, n] : =a [i, n]-a [i, k]
end;
Исполнение алгоритма формирует систему с точным (в преде-
лах возможностей машинных расчетов) решением х, = 1, лу = 1, ...,
х„= 1. Правые части входящих в нес уравнений равны единице, а
элементы матрицы системы лежат в диапазоне [1 - d; I +dj. При
очень малых значениях \d\ эта система является плохо обусловленной.
В приведенной ниже программе после каждой операции над ве-
щественными числами делается отсечение т младших байтов ман-
тиссы. В программе для описания вещественных переменных исполь-
зуется самый «длинный» в Turbo Pascal вещественный тип extended.
Управляя величиной т, есть возможность изучать закономерности,
связанные с длиной представления вещественных переменных.
Массивы значений коэффициентов расширенной матрицы и неиз-
вестных описаны «с запасом», на грани возможностей Turbo Pascal
(если не использовать динамические структуры данных). Обраще-
ние к процедуре randomize блокировано для того, чтобы, переби-
рая значение т, иметь дело с одной и той же системой уравнений.
Сняв эту блокировку, можно получать различные системы.
program Gauss2; (Решение плохо обусловленной системы
линейных алгебраических уравнений по простой схеме
Гаусса с управляемой длиной представления
вещественных переменных}
uses ert;
type T-extended;
var a:array[1..70,1..71] of T; x:array[1..70] of T;
k, i, n, j , m :integer; max,g,d,r,det:T;
function cut(у:T;m:integer):T;
(Функция реализует отсечение m «правых» байтов
мантиссы в двоичном представлении величины х
140
вещественного типа)
var y_b: array (1..10) of byte absolute y;
var 1:integer;
begin
for 1:=1 to m do y_b(l]:-0; cut:=y
end;
begin
(задание параметров)
(порядок системы) n: = “;
(коэффициент, определяющий меру обусловленности
системы) d:=**;
(количество отсекаемых байтов в представлении
вещественных чисел) т:=“;
(randomize;)
(формирование расширенной матрицы)
for i:=l to n do
begin a[i,n+l):=n;
for j:=l to n -1 do
a[i, j]:-cut(1+d*(-1+2*random),m);
a[i,n]:=a[i,n+1];
for k:=l to n -1 do a(i,n):*cut(a[i,n]
-a[i,k],m)
end;
det: -1; (подготовка к вычислению определителя)
(ниже - метод Гаусса)
(прямой ход)
for k:=l to n do
begin det:=det*a(k,k];
for j:«k+l to n+1 do
begin a[k,j]:-cut(a[k,j]/a[k,k],m);
end;
for i:=k+l to n do
for j:=k+l to n+1 do
begin r:=cut(a[k,j]*a[i,k],m);
a[i, j ] :-cut(a(i,j] - r, m);
end;
end;
(вывод определителя)
writein;
writein('det=',det) ;
(обратный ход)
x[ n ]:жа[n,n+1];
for k:=n -1 downto 1 do
141
begin r:=0;
for j:=n downto k+1 do
begin g:=cut(a[k,j]*x[j],m); r:=cut(r+g,m);
end;
x[k]:=cut(a[k,n+1] - r, m);
end;
{вычисление максимального отклонения от точного
результата}
max:=abs(l- х[1]);
for i:=2 to n do
if abs(l- x[i])>max then max:=abs(l- x[i]);
{вывод результатов решения}
writeln; writeln;
for i:=l to n do write('x[',ix[i]:20,’ ’);
writeln; writeln; writeln('max=max);
repeat until keypressed
end.
Пример 3.8. Опишем результаты одного из возможных числен-
ных экспериментов с данной программой для л = 40 (число урав-
нений в системе).
При d~ 1 10“3 для одного из вариантов значений коэффициен-
тов системы получено:
• значение определителя системы det = -3,2- 1О-102 (аномально
малое значение определителя — признак «плохой» системы);
• максимальное отклонение (max) компонентов решения х, от
точного результата в зависимости от числа отсеченных младших
байт мантиссы (т):
т 0 1 2 3 4 5 6
max 2,89 IO’14 3,2710-12 6,48-Ю-10 2,43 Л О’7 7,37-Ю"5 1,90 -10 2 2,95
Таким образом, «укорачивание» мантиссы весьма существенно
влияет на точность решения. Отсекая 4 байта, мы в этом примере
еще находимся на уровне точности, которая для многих практичес-
ки важных случаев является приемлемой (относительная погреш-
ность порядка 0,01 %), а отсекая 5 байтов, уже выходим за этот порог.
Разумеется, эти результаты нельзя абсолютизировать. Положив
в той же программе d = 1 -10-5 (т.е. для существенно «ухудшив»
систему) получаем, для того же набора коэффициентов системы:
. det ~ -3,2-IO’180;
• зависимость max от т:
т 0 1 2 3 4 5 6
max 2,26 10~12 4,86 IO’10 1,50Л О'7 3,60-ИГ5 3,12-10 3 1,03 Переполне- ние разряд- ной сетки
142
Рис. 3.3. Зависимость по-
грешности решения си-
стемы уравнений в при-
мере 3.8 от числа отсе-
ченных байтов мантиссы
(линия, маркированная
прямоугольниками, со-
ответствует d = 1 10 3,
кружками — d = 1 10 s)
Очевидно, что при «ухудшении» системы точность падает (с уве-
личением числа отсеченных байтов) значительно быстрее, чем в
предыдущем случае.
Полученные результаты изображены на рис. 3.3. Зависимость
погрешности решения системы уравнений в примере 3.8 от числа
отсеченных байтов мантиссы является практически экспоненци-
альной. Разумеется, это утверждение справедливо лишь для рас-
смотренного примера, но оно убедительно доказывает, что ог-
ромное количество цифр мантиссы в представлении веществен-
ных чисел, кажущееся неопытному вычислителю излишним, не
может игнорироваться без серьезного анализа. В каждой (или по-
чти в каждой) задаче вычислительной математики можно пост-
роить свои примеры того, как даже самый «длинный» из веще-
ственных типов,. существующих в языке программирования, не
справляется с решением задачи.
Контрольные вопросы
1. Какие системы линейных алгебраических уравнений называют пло-
хо обусловленными или неустойчивыми?
2. Чем объясняется важность увеличения длины мантиссы в представ-
лении вещественных чисел при решении плохо обусловленных систем?
3. В чем состоит механизм прямого доступа к памяти в Turbo Pascal и
как он использован в программе, приведенной в п. 3.2.5?
Упражнения
1. Разобрать, как устроена программа Round, и провести с ней экспе-
рименты при различных значениях х и п.
2. Разобрать механизм формирования системы уравнений с плохо обус-
ловленной матрицей, описанный в п. 3.2.5. Убедиться в том, что получа-
емая система при любом наборе коэффициентов имеет решение = 1,
х2 = 1, ..., х„ = 1.
3. Провести эксперименты с программой Gauss2 при различных зна-
чениях числа уравнений, входящих в систему. Сохраняется ли качествен-
ная зависимость, изображенная на рис. 3.2, для различных значений числа
уравнений в системе?
143
3.3. МЕТОД ПРОГОНКИ
Метод Гаусса не является единственным «точным» методом
решения систем линейных алгебраических уравнений. Если мат-
рица системы имеет какое-нибудь особое свойство, то естествен-
но стремление построить метод, использующий это свойство и в
силу этого более эффективный.
Ограничимся одним примером: матрица системы высокого
порядка почти полностью состоит из нулей. Точнее говоря, нену-
левыми элементами матрицы могут быть только элементы глав-
ной диагонали и двух других диагоналей, находящихся над глав-
ной и под ней. Такую матрицу называют трехдиагоналъной. Систе-
ма уравнений с трехдиагональной матрицей — не надуманный
случай, а объект, часто появляющийся при решении некоторых
классов прикладных задач.
Итак, матрица системы Ах = Ъ имеет вид
G| । «]2 0 0 ... О
Я21 °22 й23 0 О
0 «32 а33 «34 ... О
А= . (3.7)
О 0 «43 «44 ... О
0 0 0 0 a„„_i апп
Напомним, что при решении такой системы методом Гаусса
происходит переход к равносильной системе с треугольной мат-
рицей, в которой почти половина элементов равна нулю. Однако
вопреки этому, после первых же шагов нули, уже имеющиеся в
большом количестве в матрице (3.7), будут подвергаться «ненуж-
ным» (но необходимым в методе Гаусса) преобразованиям.
Метод прогонки, который изложен ниже, изначально свободен
от преобразования нулевых элементов матрицы системы и в силу
этого для систем с матрицей вида (3.7) более эффективен, чем
метод Гаусса.
При решении системы вида (3.7) на ЭВМ матрицу (почти пу-
стую для большой системы) целесообразно заменить тремя ли-
нейными массивами, составленными из чисел, стоящих на нену-
левых диагоналях:
а,- = (/ = 2,..., д); р,- = a,j (i = 1,..., л); у; = aiii+l (/ = 1).
При этом экономится значительная часть памяти, и автомати-
чески исключаются манипуляции с нулевыми элементами матри-
цы А (экономия в реальных ситуациях может быть огромной, по-
скольку в системе могут быть сотни уравнений).
144
В новых обозначениях систему уравнений (3.7) можно записать
*-: -
" ’ 1 [if I pi
Pi*i +Yi*2 =b\-,
o-iXi-i + 3,X, + Y/X,+| = bi (i = 2,...,n-1)*< (3.8)
a«*«-i + РЛ = b„.
Будем искать решение системы (3.8) в виде рекуррентной фор-
мулы
Xi = с/+(х/+| + dM (i = 1, 2,..., п -1), (3.9)
в которой с/+| — коэффициенты, подлежащие определению. Для
их нахождения понизим формально индекс в формуле (3.9):
JC/-1 = CiXt + dt = ct (cM|X/t| + dM) + d,
и подставим эту формулу и формулу (3.9) в типичное уравнение
системы (3.8). После несложных алгебраических преобразований
получим
[c/tl(a(c, +р,) + у,]хж +[г/М1(а,с, +p,) + (a,4 -Д)] = 0. (3.10)
Равенство (3.10) будет заведомо выполняться, если обе квад-
ратные скобки, входящие в него, приравнять нулю. Запишем по-
лучившиеся равенства в следующей форме:
- _ • d .bi-ctidi
afci+iii a-iCi+Pi
(3.11)
Равенства (3.11) являются рекуррентными формулами для оп-
ределения коэффициентов с, и d,.
Процедура решения системы уравнений (3.8) методом про-
гонки в целом выглядит так. Вначале по рекуррентным форму-
лам (3.11) находят семейство коэффициентов с, и dt (этап прямой
прогонки), а затем с их помощью по рекуррентным формулам (3.9)
определяют неизвестные х, (этап обратной прогонки).
Для использования тех и других рекуррентных формул необхо-
димы «стартовые» значения величин. Значения с2 и </2, стартовые
для формул (3.11), находят сопоставлением равенства (3.9) при
/= 1 и первого из уравнений, входящего в систему (3.8): с2 =
Pi
d2 = —. Значение х„, стартовое для формулы (3.9), определяют
Pi
при ее сопоставлении с последним из уравнений системы (3.8):
Ьц ая^я
а«ся + Р« ’
145
Пример 3.9. Решить методом прогонки систему уравнений
х, + Зх2 = 5;
-2.x, + 4х2 - х3 = 1;
ч 2х2 - 2х3 + х4 — 3;
х3 + х4 + х5 = -2;
Зх4 -х5 = -1.
Сравнивая с (3.8), выпишем массивы коэффициентов:
а2 = -2, «3 = 2, «4 = 1, а$ = 3;
Р,"= I, р2=4, pj =-2, ₽4 = 1, ₽5 = -1;
у, =3, у2 =-1, Уз =1, У4 = 1;
by = 5, Ьг = 1, Z>3 = з, Ьл = -2, b5 = -1.
Находим с2 и d2: с2 = = -3, d2 = - у- = 5.
Pi Pi
Далее последовательно находим по формулам (3.11) (здесь и
далее вычисления ведутся с точностью, отраженной в записан-
ных значащих цифрах):
с3 = 0,1000; с4 = 0,5555; с5 = -0,6429;
d3 = 1,1000; d, = 2,3333; d5 = -2,7858.
На этом прямая прогонка завершена и начинаем обратную
прогонку. Находим х5:
Далее последовательно находим по формуле (3.9):
х4 =-1,1707; х3 = 1,6830; х2 = 1,2683; х, = 1,1951.
Контрольные вопросы
1. Для каких специфических систем линейных уравнений применяет-
ся метод прогонки? На чем основана более высокая эффективность ме-
тода прогонки по сравнению с методом Гаусса?
2. В чем заключаются этапы прямой и обратной прогонки?
Упражнение
Составить программу решения системы уравнений с матрицей (3.7)
методом прогонки с пооперационным учетом вычислительных погреш-
ностей.
3.4. ИТЕРАЦИОННЫЕ МЕТОДЫ
Как отмечалось в гл. 2, итерационные методы используют для
решения уравнений и систем уравнений любой природы. Рассмот-
146
рим, как это делается применительно к системам линейных ал-
гебраических уравнений.
3.4.1. Метод простой итерации
Приведем систему (3.1) к равносильной ей системе вида х =
= Ах. В развернутом виде новая система выглядит так:
Xi - a!tX| + <Xl2-*2 + + И]ЯХЯ + Рь
х2 = а21 Л'| + а22х2 + + а2лхл + Рг5
(3.12)
►
= «„jXj + ая2х2 +... + аяяхя + р„
или в сокращенной записи х, = Yiaiixj + ('“ 1’ 2, —, л)- Оси-
J-I
стеме со структурой (3.12) говорят, что она «приведена к нор-
мальному виду».
Правая часть системы (3.12) определяет отображение (обозна-
чим его F):
F: у, =£аЛ+р(. (/= 1, 2, ..., п), (3.13)
У=1_
преобразующее точку х (хь х2,..., хя) «-мерного векторного
пространства в точку у у(у\, у2,..., уп) того же пространства.
[Используя отображение (3.13) и выбрав начальную точку
х<°>(Х|<°\ Х2*01,..., хл(0)), можно построить итерационную последо-
вательность точек «-мерного пространства (аналогично методу про-
стой итерации для скалярного уравнения х = /(х)):
! х<°\х^>, ...,х<">, ... (3.14)
I Например, пусть дана система уравнений
I 2х| - х2 - х3 = 1;
F Зх[ - 4х2 + х3 =2;
X] - х2 - х3 = 3.
Перепишем эту систему в виде (3.12) простейшим образом:
Ах = b => (х + Ах) = х + Ь. Равносильность такого преобразования
очевидна. Получим
I fx, =3xt-х2-х3-1;
I х2 = 3х1 - Зх2 + х3 - 2; (3.15)
х3 - Х[ - х2 - 3.
Примем за начальное приближение, например, точку (0; 0; 0)
трехмерного пространства, подставим ее координаты в правую
147
часть системы (3.15) и произведем вычисления. Получим коорди-
наты новой точки (-1; -2; -3). Используя теперь эту точку как
начальную, можно получить следующую точку (1; -2; -2) и т.д.
Тем самым будет получена последовательность точек: (0; 0; 0),
(-1; --2; -3), (1; -2; -2)', ... .
Если отображение F является сжимающим отображением, то
эта последовательность сходится и ее предел является решением
системы (3.15) и тем самым исходной системы.
Рассмотрим условия, при которых отображение (3.13) будет
сжимающим. Решение этого вопроса зависит от способа метри-
зации пространства (т.е. определения расстояния между «-мер-
ными векторами). В отличие от пространства действительных чи-
сел в данном случае существует несколько способов метриза-
ции.
Пусть х (Xj, х2, ..., х„) и у (уь у2,..., у„) — две точки «-мерно-
го пространства. Для применения метода итерации систему ли-
нейных уравнений удобно «погрузить» в пространство с одной из
трех следующих метрик:
а) рДх, у) = maxlx; -у,|; (3.16)
1 <i<n
б) р2(х, у) = Y\xi “ yj; (3.17)
в) р3(х, у) = Х(х;-У/)2. (3.18)
V ; = 1
Сформулируем (пока без доказательства) условия, при кото-
рых отображение (3.13) в пространствах с метриками рь р2, р3
будет сжимающим. Эти условия выражаются через коэффициенты
при неизвестных системы (3.12):
а) в пространстве с метрикой рр
а, = max У Iced < 1, (3.19)
т.е. максимальная из сумм модулей коэффициентов при неизвес-
тных в правой части системы (3.13), взятых по строкам, должна
быть меньше единицы;
б) в пространстве с метрикой р2:
а2 = тах£|а(7| <1, (3.20)
т.е. максимальная из сумм модулей коэффициентов при неизвес-
тных в правой части системы (3.13), взятых по столбцам, должна
быть меньше единицы;
148
в) в пространстве с метрикой ру
«3 = .XXG/<1> (3.21)
\ i=i >1
т.е. сумма квадратов всех коэффициентов при неизвестных в пра-
вой части системы (3.13) должна быть меньше единицы.
Условия (3.19) —(3.21) легко вывести. Рассмотрим, например,
получение условия (3.19).
Напомним, что отображение F называется сжимающим, если
существует такое число а: 0 < а < 1, что для любых двух точек х
и х" выполняется условие
р(Fx, Fx’) < а(х', х") (3.22)
(т.е. расстояние между образами меньше, чем расстояние между
исходными точками).
Для точек х'(х(, х2,..., х') и x'(xf, х2, , х") в соответствии
с (3.16) имеем:
Р1(Гх',ГГ) = тах ^а& (х; -хя). (3.23)
По свойству абсолютной величины имеем:
- Х-)
;=|
<£{а,7||х;-х;|.
Это неравенство лишь усилится, если заменить каждый модуль
|х) - xj| значением рДх', х'):
И
l&jix'j
7=1
*/)
<Р1(х,х')у|сс#|.
Подставляя это в (3.23), получим
p1(fx,,fx')<max£|aff|-p1(x',x'). (3.24)
: ;,i
Сравнивая (3.24) с (3.22), получаем условие (3.19).
Заметим, что каждое из условий (3.19) — (3.21) является доста-
точным для того, чтобы отображение (3.12) было сжимающим.
Условие (3.20) является также и необходимым для сжимаемости
отображения (3.12) (в смысле метрики р2), но ни одно из усло-
вий (3.19) —(3.21) не является необходимым для результативнос-
ти метода итераций.
Контрольные вопросы
1. Каким образом система линейных уравнений преобразуется к ите-
рационному виду?
149
2. Как формулируются условия сходимости итерационного процесса
для пространств с метриками рi pj. р3? Являются ли эти условия необхо-
димыми для того, чтобы итерационный процесс был сходящимся?
Упражнения
1. Доказать, что пространство с каждой из трех метрик (3.16), (3.17)
и (3.18) будет полным метрическим пространством (см., например, [9]).
2. Вывести условия сжимаемости отображения (3.13) в пространствах
с метриками р2 и р3.
3.4.2. Практическая схема решения системы линейных
уравнений методом простой итерации
Как следует из п. 3.4.1, для применения метода итераций сис-
тема (3.1) должна быть сначала переписана в виде (3.12). При этом
гарантией сходимости итерационного процесса может служить
выполнение хотя бы одного из достаточных условий (3.19) —(3.21)
при «погружении» системы в пространство с одной из трех рас-
смотренных выше метрик.
Для обеспечения условий сходимости нужно получить систе-
му вида (3.12) так, чтобы коэффициенты при неизвестных в
правой части системы были существенно меньше единицы. Это-
го можно достичь, если исходную систему вида (3.1) с помо-
щью равносильных преобразований привести к системе, у кото-
рой абсолютные величины коэффициентов, стоящих на глав-
ной диагонали, больше абсолютных величин каждого из других
коэффициентов при неизвестных в соответствующих уравнени-
ях (такую систему называют системой с преобладающими диа-
гональными коэффициентами}. Если теперь разделить все уравне-
ния на соответствующие диагональные коэффициенты и выразить
из каждого уравнения неизвестное с коэффициентом, равным еди-
нице, будет получена система вида (3.12), у которой все |сс^-| < 1.
Выполнение этого условия необходимо, но недостаточно для
удовлетворения условий сжимаемости (3.19) —(3.21). Если после
указанных выше преобразований ни одно из этих условий не вы-
полняется, следует возвратиться к исходной системе и попытать-
ся выполнить преобразования так, чтобы добиться лучшего эф-
фекта. Для этого имеются специальные приемы, но они не уни-
версальны. Иначе говоря, вполне возможно, что для некоторой
конкретной системы метод итераций окажется неприменим.
Результатом установления одного из условий (3.19) —(3.21)
является получение значения а, которое затем находит примене-
ние в формуле (2.8) оценки точности Л-го приближения. После
того как сходимость установлена, можно приступить к выполне-
нию вычислений. Схема алгоритма метода итераций для систем
150
уравнений аналогична схеме метода итераций для одного уравне-
ния (см. рис. 2.10). За начальное приближение обычно берется стол-
бец свободных членов системы (3.12). На основе оценки (2.8), тре-
буя, чтобы р(х<к , х<к> ) < е, получим формулу, по-
1 -а
зволяющую устанавливать момент прекращения итерационного
процесса при достижении заданной точности результата с:
(3:25)
а
Здесь р — метрика, по которой была установлена сходимость и
получено соответствующее значение а.
Пример 3.10. Решить систему линейных уравнений (см. при-
мер 3.2)
2,34^ -4,21х2 -11,61*3 = 14,41;
8,04 X] + 5,22х3 + 0,27*з = -6,44;
3,92*,-7,99*2 +8,37*3 = 55,56
методом простой итерации с точностью е = 1 10“4.
Получим сначала систему с преобладающими диагональными
коэффициентами. Для этого в качестве первого уравнения возьмем
второе, третьего первое, второго — сумму первого уравнения с
третьим:
8,04*| + 5,22х2 + 0,27*3 = -6,44;
6,26*, - 12,20х2 -3,24*3 - 69,97;
2,34х( - 4,21х2 - 11,61*3 = 14,41.
Разделим теперь каждое уравнение на свой диагональный ко-
эффициент и выразим из каждого уравнения диагональное неиз-
вестное:
fxj =-0,649*2 -0,034х3-0,801;
J*2 =0,513х,-0,266х3 -5,735;
[х3 - 0.202*, - 0,363х2-1,241.
Теперь необходимо проверить одно из условий сходимости.
Попробуем установить сходимость по метрике р2 (см. условие (3.20)).
Заметим, что максимальной суммой модулей коэффициентов по
столбцам будет сумма модулей коэффициентов при *2. Однако эта
сумма не удовлетворяет условию (3.20): 0,649 + 0,363 > 1.
Невыполнение одного из условий еще не означает,» что метод
итераций применить нельзя. Попробуем установить сходимость в
пространстве с евклидовой метрикой (см. (3.21)). Имеем: 0,6492 +
+ 0,0342 + 0,5132 + О,2662 + 0,2022 + 0,3632 = 0,422 + 0,001 + 0,263 +
+ 0,071 + 0,041 + 0,131 = 0,929 < 1.
151
Итак, итерационный процесс в евклидовом пространстве схо-
дится, причем ос = ^0,929 = 0,93. Для достижения точности е =
= 1 • 10'4 приближения нужно находить до тех пор, пока будет выпол-
р/1 — /у)
няться неравенство > —-----, где р(ха-|), x(t)) — рас-
а
стояние между двумя последними соседними приближениями в
смысле евклидовой метрики, е = I 10-4, а = 0,93. Поскольку а близко
к единице, то скорость сходимости в данном случае будет невелика.
Алгоритмически итерационные методы решения систем урав-
нений весьма просты, существенно проще метода исключения.
Алгоритм метода простой итерации показан на рис. 3.4. Решаемая
система считается преобразованной к виду (3.12). Алгоритм про-
веряет, реализовано ли достаточное условие сжимаемости (3.21)
(по евклидовой метрике), и при положительном результате при-
ступает к решению системы. В противном случае пользователь по-
лучает сообщение о невыполнении указанного условия. В качестве
начального приближения для итерационного процесса берется
х<°> = р (столбец свободных членов). Для контроля завершения
итераций используется для определенности евклидова метрика
(3.18), и поэтому в качестве а (см. (3.25)) используется величина,
вычисляемая по формуле (3.21).
Алгоритму, приведенному на рис. 3.4, соответствует следую-
щая программа.
program Iterat; {решение системы линейных
алгебраических уравнений методом простой итерации)
uses ert, okrugl;
const n=3; {порядок системы)
type T=real;
var a:array[1..n,1..n] of T; x,y,b:array[1..n] of T;
al,sfeps:T; i, j,k:integer;
begin
writein('ввод данных');
for k:=l to n do
for j:=1 to n do
begin writein('введите a[’,k,',',j,']’);
read(a[k,j ] )
end;
for k:=l to n do
begin writein(’введите b[',k,']’); read(b[k])
end;
writein ('введите eps’); read(eps); al:=0;
for k:=l to n do
for j :,=1 to n do
al:=al+sgr(a[k,j]);
al:=sqrt(al); i:=-l;
152
Начало
Ввод п (порядок системы), {сх^} — матрица коэффициентов,
(Р, ) — столбец свободных членов, е — точность решения >
Рис. 3.4. Блок-схема алгоритма решения системы линейных
алгебраических уравнений методом простой итерации
153
if al<l then
begin
for k:=l to n do x[k]:=b[k];
repeat s:=0; i:=i+l;
for k:=l to n do
begin у [k]:=b[k];
for j : =1 to r. do
у[k]:=y[k]+a[k,j]*x[j];
s:=s+sqr(x[k]-y[k]);
end;
for k:=l to n do x[k]:=y[k];
until sqrt(s)<eps*(1-al)/al;
writeln(1 Итерационный процесс окончен.
Число итераций =',i);
writeln('Решение системы');
for k;=l to n do
begin okr(x[k], eps, x[k], j);
if j<0 then j:=0;
write(’x[',k, '] = ',x[k] : 7 : k, ' ')
end;
end
else wriLein(1 Условие сходимости по
евклидовой метрике не выполняется’)
end.
Результат работы программы:
Итерационный процесс окончен. Число итераций =21
Решение системы
х[1]= 2.2924 х[2] = -4.8172 х[3]= 0.9707
При решении систем уравнений итерационными методами
оценка завершенности итерационного процесса бывает достаточ-
но сложной. На практике можно использовать следующий эмпири-
ческий критерий', если в ходе итераций некоторая десятичная цифра
повторилась в трех-четырех следующих друг за другом итерациях,
то она может считаться верной. Этот прием имеет особенный смысл
для тех случаев, когда нс удастся легко установить выполнение
достаточных условий сходимости, а между тем практическая реа-
лизация итерационного процесса может оказаться результатив-
ной (в смысле отмеченного выше эмпирического критерия).
Для иллюстрации сформулированного выше эмпирического
критерия верности цифры, повторяющейся в итерационном про-
цессе три-четыре раза подряд, приведем результат последователь-
ных итераций при решении той же системы. Повторяющиеся цифри
выделены жирным шрифтом. Видно, что в данном случае указан-
ный критерий справедлив.
154
х[1]=2.9632 х[2]=-5.8158 х[3]=0.6790 Номер итерации = 1
х[1)-2.9504 х[2] —4.3955 х[3]-1.4687 Номер итерации = 2
х[1]=2.0017 х[2]=-4.6121 х[3]=0.9505 Номер итерации 3
х[1]=2.1600 х[2]=-4.9610 х[3]=0.8376 Номер итерации = 4
х(1]-2.3902 x(2J—4.8497 х(3]-0.9961 Номер итерации - 5
х(1]=2.3126 х[2]=-4.7738 х[3]=1.0023 Номер итерации = 6
х[1]=2.2631 х[2]=-4.8152 х[3]=0.9590 Номер итерации = 7
х[1]-2.2915 х[2]—4.8291 х[3]-0.9641 Номер итерации = В
х[1)-2.3003 х[2] — 4.8159 х[3)-0.9749 Номер итерации - 9
х[1]«2.2914 х(2]=-4.8142 х[3)=0.9718 Номер итерации = 10
х[1)-2.2904 х(2]•»-4.8180 х[3)-0.9694 Номер итерации - 11
х[11=2.2929 х(2)—4.8179 х(3]=0.9706 Номер итерации - 12
х[1]=2.2928 х[2]=-4.8169 х(3]=0.9711 Номер итерации = 13
х[1]-2.2922 х[2)=-4.8171 х[3]=0.9707 Номер итерации = 14
х[1]-2.2923 х[2]—4.8173 х(3]-0.9706 Номер итерации - 15
х{1]-2.2924 х[2]—4.8172 х[3)“0.9707 Номер итерации - 16
х[1]=2.2924 х[2)=-4.8172 х[3]=0.9707 Номер итерации = 17
х(1]=2.2924 х[2]=-4.8172 х(3]=0.9707 Номер итерации = 18
х[1]=2.2924 х[2)—4.8172 х[3]=0.9707 Номер итерации - 19
х[1]=2.2924 х[2)=-4.8172 х[3]=0.9707 Номер итерации = 20
х{1)=2.2924 х[2]=-4.8172 х[3]=0.9707 Номер итерации = 21
Итерационный npoifecc окончен. Число итераций = 21
Решение системы
х[1] = 2.2924 х(2] = -4.8172 х[3] = 0.9707
Контрольные вопросы
I. Как привести исходную систему линейных уравнений к системе с
преобладающими диагональными коэффициентами? В чем заключается
смысл такого преобразования?
2. Какова структура погрешности решения системы линейных урав-
нений методом простой итерации?
3. На чем основывается оценка погрешности метода простой итера-
ции для решения систем линейных уравнений?
Упражнения
1. Трансформировать приведенную в п. 3.4.2 программу таким обра-
зом, чтобы она выдавала значения переменных в последовательных ите-
рациях.
2. Изменить приведенную в п. 3.4.2 программу таким образом, чтобы
она использовала иные, нежели евклидов, критерии сходимости итера-
ционного процесса (см. (3.19), (3.20)).
155
3. Решить систему уравнений
12,14л-, + 1,32х, -0,78х3-2,75х4 = 14, 78;
-0,89х| + 16,75х2 + 1,88х3 - 1,55х4 = -12,14;
2,65х, -1, 27х2 - 15, 64х3 - 0,64х4 = -11,65;
2,44х, + 1, 52х2 + 1,93х3 -11,43х4 = 4,26
методом простой итерации с помощью программы для ЭВМ с оценкой
точности:
а) по оценочной формуле (3.25) при различных способах нахожде-
ния входящего в нее коэффициента а;
б) по эмпирическому критерию совпадений значащих цифр в одной
позиции трех соседних приближений.
3.4.3. Метод Зейделя
Будем снова рассматривать исходную систему линейных урав-
нений (3.1) и эквивалентную ей приведенную систему (3.12). При
решении системы (3.12) методом простой итерации каждый шаг
итерационного процесса состоит в переходе от уже имеющегося
приближения значений неизвестных к новому (очередному) при-
ближению. Обозначим элементы имеющегося приближения через
X,, х2,х„, а элементы очередного (вычисляемого) приближе-
ния через j>2j Ун- Вычислительные формулы имеют вид
Уг iX-*/ +Р,- (' = 1, 2, ..., л).
7=1
Основная идея метода Зейделя состоит в том, что на каждом
шаге итерационного процесса при вычислении значения у,- учи-
тываются уже полученные значения >Л-1- Выпишем соот-
ветствующие вычислительные формулы:
)'i = £«17А7 + Рв
7=1
У1 = «2|У| + Х“27А7 +Рг;
7=2
................................. (3.26)
i-1 И
У1 =£зд+£а(2Х7 + РБ
7-1 /=г
Уп - Т^ап]У] + сс„„х„ + Р„.
7-1
Справедливо следующее утверждение: если для матрицы коэф-
фициентов системы (3.12) выполняется хотя бы одно из условий
156
(3.19) —(3.21), то итерационный процесс метода Зейделя сходит-
ся к решению системы при любом выборе начального прибли-
жения Х|0>, х<0), ..., х(„0) (доказательство приводить не будем; см.,
например, [3]).
Таким образом, каждое из условий (3.19) —(3.21) является до-
статочным для сходимости итерационного процесса метода Зейде-
ля. Преимущество этого метода состоит в том, что он обычно обес-
печивает более быструю сходимость, чем метод простой итерации.
Алгоритмически метод Зейделя очень похож на метод простой
итерации, схема которого изображена на рис. 3.4. В методе Зейделя
нет необходимости во втором массиве переменных, обозначен-
ном на рис. 3.4 каку*. Небольшое различие алгоритмических схем
между указанными методами отражено на рис. 3.5.
Пример 3.11. Решить методом Зейделя систему уравнений, рас-
смотренную в примере 3.10.
Как было установлено в примере 3.10, после приведения ис-
ходной системы к виду
X, = -0,649х2 -0,034хз-0,801;
х2 = 0,51 ЗХ| - 0,266х3 - 5,735;
х3 = 0,202Х| - 0,363х2 - 1,241
условие сходимости по евклидовой метрике выполняется.
б
Рис. 3.5. Фрагмент алгоритма метода простой итерации, показанного на
рис. 3.4 (о); модификация того же фрагмента, превращающая алгоритм
на рис. 3.4 в алгоритм метода Зейделя (б)
157
Примем за начальное приближение столбец свободных членов:
xf0) =-0,801; =-5,735; х|0> =-1,241. Покажем, как в данном
случае выполнить первую итерацию по методу Зсйдсля.
Найдем с помощью первого уравнения системы х{°:
xf” = -0,б49х$°> - 0,034xJ0) - 0,801 =
= -0,649 • (-5,735) - 0,034 -(-1,241) - 0,801 = 2,9632
(вычисления ведем с одной запасной цифрой). Далее, при вы-
числении Xj1’ используем уже только что найденное значение х*0:
х"’ = 0,513 • xf1’ - 0,266 • х|0) - 5,735 =
= 0,513 • 2,9632 - 0,266 (-1,241) - 5,735 = -3,8848.
Аналогично при вычислениих,1* используем уже найденные
приближения:
4° = 0,202 • х}0 - 0,363 • xj° -1,241 =
= 0,202 • 2,9632 - 0,363 • (-3,8848) - 1,241 = 0,7678.
Приведем результат решения указанной системы на ЭВМ по
программе, использующей замену, изображенную на рис. 3.5. Как
и в примере 3.10, задаваемая точность е= 1 • 10-4. За начальное при-
ближение принят, как и выше, столбец свободных членов. Иско-
мое решение (совпадающее, естественно, с решением той же си-
стемы, полученным с той же точностью в примере 3.10) достига-
ется за 14 итераций, т.е. существенно быстрее, чем в методе про-
стой итерации.
Результат работы программы:
Итерационный процесс окончен. Число итераций = 14
Решение системы
Х[1]= 2.2924 х(2]« -4.8172 х[3] = 0.9707
Контрольный вопрос
В чем состоит отличие метода Зейделя от аналогичного процесса про-
стой итерации?
Упражнения
Решить систему
12,14Х| + 1, 32х2 - 0,78х3 - 2,75х4 = 14,78;
-0,89х, + 16,75х2 + 1,88хз - 1.55х4 = -12,14;
2,65х, - 1,27х2 - 15,64хз-0,64х4 = -11,65;
2,44х,+1,52х2 +1,93хз-11,43X4 =4,26
методом Зейделя с помощью программы для ЭВМ с оценкой точности:
158
а) по оценочной формуле (3.25) при различных способах нахожде-
ния входящего в нее коэффициента а;
б) по эмпирическому критерию совпадений значащих цифр в одной
позиции трех-четырех соседних приближений.
3.5. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Решение систем нелинейных и трансцендентных уравнений
является в общем случае задачей несравненно более сложной,
нежели решение систем линейных уравнений. Не существует ме-
тодов, которые гарантировали бы успех решения любой такой
задачи.
Как и для отдельных уравнений, наибольшую проблему пред-
ставляет задача отделения решений (корней). Для системы урав-
нений с п неизвестными необходимо, во-первых, понять, сколь-
ко у нее решений, а во-вторых, выделить области «-мерного про-
странства, в каждой из которых есть одно и только одно решение.
Лишь после этого можно говорить о нахождении решений с за-
данной точностью (оцениваемой в соответствии с используемой
метрикой).
Для отделения корней общих методов, гарантирующих успех,
не существует. Для системы с двумя неизвестными можно пытать-
ся использовать геометрические построения (см. приведенный да-
лее пример 3.12). В реальных задачах, являющихся этапами моде-
лирования, исследователь обычно догадывается, где примерно на-
ходятся корни системы (или по крайней мере тот корень, кото-
рый его интересует из содержательных условий модели).
Описанные ниже приемы, явно или неявно, исходят из того,
что задача отделения корней решена и имеется достаточно малая
область «-мерного пространства, в которой находится корень,
подлежащий уточнению. Отметим, что уточнение корней ведется
почти исключительно итерационными методами.
3.5.1. Метод простой итерации
Запишем систему « нелинейных уравнений с п неизвестными
в следующем виде:
/](х1,х2,...,х„) = 0;
f2(xt,x2,...,xJ = 0;
/’л(х1,х2,...,хд) = 0.
(3-27)
159
Метод простой итерации для решения системы (3.26) анало-
гичен методу простой итерации, рассмотренному выше для сис-
темы линейных уравнений. На первом шаге система (3.27) преоб-
разуется к равносильной системе вида
хг = ф|(Х|,х2,...хл);
х2 = Ф2(хьх2,...,х„);
(3.28)
Х„ = фя(х1;х2,...,хл).
Затем выбирается начальное приближение х(0)(Х|(0),..., х„<0)) —
чрезвычайно ответственный шаг, поскольку для систем нелиней-
ных уравнений в отличие от линейных почти всегда успех реше-
ния зависит от того, насколько близко начальное приближение к
корню системы. После этого строится итерационная последова-
тельность
х/*+1) = фДх/*),х/*>). (3.29)
Если отображение, задаваемое системой (3.28), является сжи-
мающим в некоторой окрестности корня, начальное приближе-
ние лежит в той же окрестности и итерации (3.29) нс выходят
за ее пределы, то последовательность {xw} сходится к вектору
x*(x,*,xj,..., х‘), являющемуся решением системы (3.27).
Указанное выше требование сходимости итерационного про-
цесса требует конкретизации, придания ему реально проверяемо-
го вида. Допустим, что все функции ф,(х), входящие в (3.28), диф-
ференцируемы. Обозначим «у = max
Эф,-
dxj
где G — область /i-мер-
ного пространства, содержащая искомое решение /например, л-
мерный куб). В таких обозначениях достаточные условия сжимае-
мости отображения (3.28) можно сформулировать точно так же,
как сформулированы условия (3.19) —(3.21) (соответственно для
метрик (3.16) —(3.18)). Однако в конкретных случаях исследова-
ние сходимости может оказаться значительно сложнее, чем для
систем линейных уравнений. Основные трудности при этом — на-
хождение области G и затем чисел а/у-.
Критерий достижения заданной точности итерационного про-
цесса выражен условием (3.25).
Пример 3.12. Найти приближенное решение системы уравне-
ний
у3 - х2 = 1;
ух3 - х = 4.
160
Приведем систему к виду
у = х/Ькх2;
который позволяет выполнить графическим способом разделение
корней и оценить первое приближение (рис. 3.6). В результате по-
строения серии рисунков в любом из инструментальных пакетов,
имеющих графические средства, и асимптотических оценок визу-
ально обнаруживаем, что система имеет единственное решение,
находящееся в диапазоне 1,25 <х< 1,75; 1,25 <у< 1,75, для кото-
рого удовлетворительным начальным приближением служит точ-
ка х<0) = 1,5; у(0) = 1,5.
Приведем систему к виду, пригодному для итераций. Это мож-
но сделать множеством способов. Перепишем уравнения в виде
у3 - х2 - 1 = 0;
ух3 - х --4 = 0.
Умножим каждое уравнение на некоторый множитель, нерав-
ный нулю: ц(у3 - х2 - 1) = 0; v(yx3 - х - 4) = 0 — равносильность со-
храняется. Множители будут далее использованы для достижения
условия сжимаемости. Теперь прибавим к обеим частям первого
уравнения у,
а второго
х, и вновь получаем систему,
сильную исходной, вид которой соответствует (3.27):
равно-
х = <Р](х,у); у = <р2(х,у),
где <р,(х,у) = x + v(yx3 -х-4); <р20бУ) = У + -*2 ~ 1)-
Найдем частные производные, значения которых определяют
наличие сходимости итерационного процесса:
™ = I + v(3x2y -1); — - vx3; = 2нх; = 1 + Зцу2.
дх ду дх ду
Несколько упрощая ситуацию, заметим, что чем меньше (по
модулю) значения указанных производных в окрестности корня,
Рис. 3.6. Графическое отделение корней (выполнено в Excel)
Лапчик
161
тем больше шансов на сходимость. Множители ц и v позволяют
нам повлиять на указанные значения.
Вычислим значения производных в точке, взятой нами в каче-
стве первого приближения: х(0) = 1,5; у(0) = 1,5. Имеем
Э<Р|
Эх 0
= l + 9,125v;
= 3,375v;
Эу 0 Эх 0
дУ о
= 1 + 6,75р.
Выберем значения ц и v следующим образом: ц = -0,15, v = -O,J.
При таком выборе
=0,08; ^5-
Эх о Эу 0
и выполняется любой из трех сформулированных выше критериев
сходимости. Напомним, однако, что речь идет лишь об одной точ-
ке, а для гарантии успеха необходимо выполнение указанных кри-
териев в некоторой области. Однако в силу непрерывности най-
денных выше производных можно быть уверенными в том, что
указанные критерии выполняются и в некоторой области, содер-
жащей эту точку.
Итерационный процесс над полученной выше системой с вы-
бранными значениями ц и v действительно является сходящимся.
Приведем простейшую программу его реализации и результат ее
работы. Число итераций в программе задается произвольно и яв-
ляется средством эмпирического исследования точности решения.
program Nelin_Iter;
uses ert;
var x,у:real; i:integer;
begin
x : =1,5 ; у:=1.5;
for i:=l to 20 do
begin
x:=x-0.15*(y*x*x*x-x-4);
y:=y-0.1*(y*y*y-x*x-l);
writeIn(’N итерации',i,' x=',x,' y=',y)
end; repeat until keypressed
end.
N итерации 1 x=l. 56562499999927E+0000 y=l.50761816406157E+0000
N итерации 2 x=l.53261636169918E+0000 y=l.49984103393035E+0000
N итерации 3 x=l.55259862590356E+0000 y=l.50350457397144E+0000
N итерации 4 x=l. 54142786480588E+0000 y=l.50123344155872E+0000
N итерации 5 x-! . 54791714627572E+0000 y=l.50250493287240E+0000
N итерации 6 x-1.54421246873426E+0000 y=l.50177049286140E+0000
N итерации 7 x-1.54634510270989E+0000 y=l.50219231670235E+0000
N итерации 8 x=l.54512218456330E+0C00 y=l.50195059558428E+0000
162
N итерации 9 х=1.54582475023199Е+0000 у=1.50208964649573Е+0000
N итерации 10 х=1.54542148538530Е + 0000 у=1.50200992596729Е+0000
N итерации 11 х~1.54565305508913Е+0000 у=1.5Э205574388747Е+0000
N итерации 12 х=1.54552010728730Е+0000 у=1.50202945436104Е+0000
N итерации 13 х=1.545596442741 Э5Е+0000 у=1.50204455480525Е+0000
N итерации 14 х=1.54555261506357Е+0000 у-1.50203588б95877Е + 0000
N итерации 15 х=1.54557777921946Е+0000 у=1.50204086440317Е+0000
N итерации 16 х=1.54556333113760Е+0000 у=1.50203800682903Е+0000
N итерации 17 х=1.54557162661149Е + 0000 у=1.50203964760840Е + 0000
N итерации 18 х=1.54556686372052Е + 0000 у=1.50203870557380Е + 0000
N итерации 19 х=1.54556959836555Е+0000 у=1.50203924645939Е+0000
N итерации 20 х = 1.54556802825391Е +О О О О у=1.50203893591060Е + 0О О О
Ограничимся эмпирическим анализом точности решения. Триж-
ды повторяющиеся в соответствующих разрядах цифры (выделе-
ны жирным шрифтом) с большой степенью достоверности явля-
ются верными.
Зададимся таким вопросом: за сколько итераций достигается
точность 1 -10~5? Эмпирически ответ можно получить, рассуждая
следующим образом. Пятая цифра после запятой в величине х со-
впадает (с учетом округления) с последующими цифрами, сто-
ящими на том же месте в 15-й итерации, а в величине у — в 13-й
итерации, и поэтому указанная точность реализуется в целом за 15
итераций. Результат с указанной точностью: х= 1,54557, у= 1,50204.
Контрольные вопросы
1. По каким причинам задача решения системы нелинейных уравне-
ний принципиально сложнее задачи решения системы линейных урав-
нений?
2. В чем состоит метод простой итерации для решения системы нели-
нейных уравнений?
Упражнения
1. Используя геометрический метод, решите полную задачу отделе-
ния корней для системы уравнений
у - [sin х| -1 = 0;
(у - I)2 + Л-2 -1 = 0.
2. Найдите эти корни с точностью 1 10-4 методом простой итерации.
. 3.5.2. Метод Ньютона
Очевидный недостаток метода простой итерации — необходи-
мость прибегать к искусственным приемам при приведении сис-
темы к виду, пригодному для итераций.
163
При решении систем нелинейных уравнений часто используют
метод Ньютона, являющийся обобщением метода касательных,
рассмотренного в гл. 2. Существенную роль в этом методе играет
специальная матрица — так называемая матрица Якоби (или яко-
биан):
а/.
дх} дх2 дх,,
Э/2 Э/2
J = ch?! дх2 дх,,
э/л
дх2
(3.30)
Очевидно, что построить ее можно лишь при условии, что каж-
дая из функций, входящая в систему (3.27), дифференцируема по
каждой из переменных.
Напомним, что метод касательных применительно к одному
уравнению/(л) = 0 заключается в построении итерационной пос-
ледовательности
f'(Xk ) ‘
Обобщением этой формулы на системы уравнений является
следующая формула (см., например, [2]):
х“+” =х<*> ^j-i(x(*))./(x(*))_ (3.31)
О сходимости метода Ньютона для систем уравнений можно,
не вдаваясь в детали, сказать то же, что и о сходимости метода
касательных для одного уравнения: если начальноелриближение
выбрано достаточно близко к решению системы, то итерацион-
ная последовательность сходится к этому решению, и сходимость
является квадратичной. Более детальное описание условий сходи-
мости можно найти в [3, 12].
Отметим, что метод Ньютона весьма трудоемок, поскольку на
каждом шаге итерационного процесса необходимо найти матри-
цу, обратную матрице Якоби. Чаще всего для этого используют
описанный выше метод Гаусса. Тем не менее для системы, состо-
ящей из двух-трех уравнений, можно найти обратную матрицу
аналитическим методом, известным из курса алгебры. В частно-
сти, при решении системы двух уравнений
Ш*,у) = 0;
1/2(^ у) = о
(3.32)
164
для матрицы Якоби второго порядка обратная матрица имеет вид
0^''
d d
gjl ^22
U d }
(3.33)
где
э/2 ад
^u:=-^-;^i2=-yL;«2i =
ад ад
ij-v Эх Эх ад
(3.34)
Эу дх
Итерационные формулы (3.31) в этом случае примут вид, не-
посредственно пригодный для вычислений:
xk+i = хк - -Ь[off >/, (xt., ук) + d$>f2 (хк, ук)];
t (3.35)
Л+1 = Л - [о^ад (хА, Л) + (xt, л)]
Верхний индекс /с в (3.35) означает, что соответствующая ве-
личина вычисляется в точке (х'*\_/*’).
Отметим эмпирическое правило: если задана абсолютная по-
грешность приближенного решения системы е, то процесс итера-
ции в большинстве случаев можно остановить, когда для каждой
из переменных х; выполнено неравенство |х/4>-x/t-l>|<е.
Пример 3.13. Решить методом Ньютона систему уравнений, рас-
смотренную в примере 3.12.
Имеем
fi(x,y) = / -х2 -1;
/2(х,у) = ух3-х-4.
Величины, входящие в формулы (3.35), принимают вид
Ou = х3; Oj2 = -3y2; o2i =1-Зх2у; а22 = 2х; rf = 2-2x4 -9x2y3.
Возьмем, как и в примере 3.12, за начальное приближение
х0=1,5; у0~1,5. Последовательно находим
/iOWo) = 0,125; /2(х0,у0) = -0,4375;
wfi’ = 3,375; «f20) = -6,75; aff = -9,125; с$> = 3; dm = -76,46875.
Далее по формулам (3.35) получаем х( = 1,5441356; у, =1,46792 —
первое приближение.
Далее приведена простейшая программа, реализующая задан-
ное число шагов итерационного процесса (3.35), для получения
первых 15 приближений по методу Ньютона (только для рассмат-
риваемой в данном примере системы уравнений).
165
program Newton;
uses crt;
var x,y,f1,f2,all,al2,a21,a22,d:real; i:integer;
begin
x:=1.5; y:-1.5;
for i:=l to 15 do
begin
fl:=y*y*y-x*x-l; f2:=y*x*x*x-x-4;
all:=x‘x‘x; al2:=-3*y*y; a21:=l-3*x*x*y;
a22:-2*x; d:*2-2*x*x‘x*x-9‘x*x‘y‘y*y;
x:-x- (all*fl+al2*f2)/d; y:-y-(a21*fl+a22*f2)/d;
writeln('N итерации’,i,* x= ',x,' y= ’,y)
end; repeat until keypressed
end.
Результат работы программы:
N итерации 1 x-1.54413567633856E+0000 y-1.46791990192105E+0000
N итерации 2 x-1.54527011351092E+0000 y-1.48955499620752E+0000
N итерации 3 x-1.54552154520024E+0000 y-1.49763731318126E«0000
N итерации 4 x-1.54556205752306E+0000 y-1.50Q52894444343E+0000
N итерации 5 x-1.54556776551181E+0000 y-1.50152785275895E+0000
N итерации 6 x-1.54556849988512E+0000 y-1.50186698918696E+0000
N итерации 7 x-1.54556858909928E+0000 y-1.50198126602845E+0000
N итерации 8 x-1.54556859957302E+0000 y-1.50201965966517E+0000
N итерации 9 x-1.54556860077901E+0000 y-1.50203254477856E+0000
N итерации 10 x-1.54556860091725E+0000 y-1.50203686743225E+0000
N итерации 11 x-1.54556860093180E+0000 y-1.50203831739054E+0000
N итерации 12 x-1.54556860093362E+0000 y-1.50203880373010E+0000
N итерации 13 x-1.54556860093362E+0000 y-1.50203896685343E+0000
N итерации 14 x-1.54556860093362E+0000 y-1.50203902156682E+0000
N итерации 15 x-1.54556860093362E+0000 y-1.50203903991B60E+0000
Трижды повторяющиеся в соответствующих разрядах цифры
(выделены жирным шрифтом) с большой степенью достовернос-
ти являются верными.
Зададимся тем же вопросом, что и в примере 3.12: за сколько
итераций достигается точность 1 • 10*5? Повторяя проведенное там
рассуждение, получаем ответ: указанная точность реализуется за
10 итераций.
Сопоставляя примеры 3.12 и 3.13, можно сделать вывод: в дан-
ном случае сходимость в методе Ньютона более быстрая, чем в
методе простой итерации (и это — обычное дело). Кроме того, в
методе Ньютона не надо заниматься искусственным подбором
параметров (который может оказаться и невозможным). Однако
166
алгоритмически метод Ньютона в общем виде существенно слож-
нее — прежде всего за счет необходимости нахождения на каждом
шаге итерационного процесса обратной матрицы.
Контрольные вопросы
I. В чем метод Ньютона для решения систем уравнений превосходит
метод простой итерации?
2. В чем состоят основные трудности, связанные с практическим при-
менением метода Ньютона?
Упражнение
Решить систему, предложенную и упражнении к п. 3.5.1, методом
Ньютона. Сопоставить полученные результаты с результатами решения
той же системы методом простой итерации.
3.6. РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ С ПОМОЩЬЮ
ИНСТРУМЕНТАЛЬНЫХ СРЕДСТВ
3.6.1. Табличный процессор Excel
В табличном процессоре Excel для решения систем уравнений
есть два варианта: реализация алгоритмов в электронной таблице
с помощью основных средств табличного процессора и использо-
вание специальных средств.
Первый вариант проиллюстрирован на примере системы урав-
нений
Xj + 2х2 + 2х4 = 5:
2х, + 4х2 - х3 + 5х4 - -1;
Xi + Зх2 + 5х4 - -3;
Зх( + 7х2 - Зх3 + 9х4 = -13.
На рис. 3.7 приведены идентичные тексты в Excel, но один — в
режиме отображения формул, а другой — значений. Из них пре-
красно видно устройство алгоритма.
Второй вариант не столь очевиден. Среди встроенных в Excel
математических программ программы решения систем уравнений,
строго говоря, нет.
Но точно так же, как для решения уравнений в гл. 2 было ис-
пользовано средство Подбор параметра, для решения систем мо-
жет быть использовано средство, предназначенное совсем для
другой цели (для решения задач оптимизации).
Это средство — Поиск решения. Поясним его использование и
приведем примеры применения.
167
168
A-.-' dSIKMi шв&аю» °.... . E Ж
1 г_шение системы линейных алгебраических уравнений Ах=Ь
X метолом Гаусса
A i Ь
4
5 1 1 0 2 i 5
G 2 4 -1 5 -1
,7Т 1 3 0 5 3
ST 3 7 -3 9 -13
9 У Первое преобразование
Ж 1 1 0 2 ! 5
1 ц 0 2 -1 1 i -11
12» 13; 0 2 0 3 1 -8
0 4 •3 3 i -28
14! Второе преобразование
15Д 1 1 0 2 5
18* 0 1 -0.5 0,5 5,5
17» 0 0 1 2 3
18: 0 0 -1 1 6
19^ Третье преобразование
20;' 1 1 0 2 5
0 1 -0.5 0,5 -5,5
111 0 0 1 2 3
ГЦ 0 0 0 3 •3
24? Четвертое преобразование
251 1 1 0 2 5
281 0 1 •0,5 0,5 5,5
23 0 0 1 2 3
28g '295 0 Обр 0 атный ход 0 1 ! -1
303 х4= -1
3J1 хЗ= 5
32| х2= -2.5
33, х1= 9,5
Рис. 3.7. Решение системы линейных
алгебраических уравнений в Excel
Средство Поиск решения активируется в меню Сервис (если это
средство нс установлено, то это необходимо сделать).
Предварительно проводят следующую подготовительную ра-
боту'.
1. Отводят для каждой переменной по ячейке.
2. Вводят формулы для вычисления правых частей уравнений
системы (по одной формуле в ячейку).
После этого запускают Поиск решения. Возможный вид экрана
для подготовки к решению той же системы, что и выше, приве-
ден на рис. 3.8. На этом рисунке под переменные отведены ячейки
A2:D2, под формулы — ячейки А4, Аб, А8 и А10. Какие именно
числовые значения переменных будут введены в ячейки A2:D2,
при решении системы линейных уравнений значения нс имеет
(итерационная процедура, заложенная в Поиск решения, стартует
с этих значений).
Еще один элемент в таблице — целевая функция. Она в данном
случае особой роли не играет, но какую-нибудь формулу ввести
необходимо, иначе Поиск решения работать не может (напомним,
что эта программа нацелена на другой класс задач). Точно так же
Рис. 3.8. Подготовка к решению системы уравнений посредством опции
Поиск решения
Рис. 3.9. Форма Добавление ограничений
170
Рис. 3.10. Результаты поиска решения: Х| =9,5; х2=-2,5; х}=5; х<=-1
неважно, как установлен флажок: «максимальному значению» или
«минимальному значению».
Теперь необходимо ввести то, что в форме на рис. 3.8 именует-
ся ограничениями. Щелкнув по кнопке Добавить, получают дру-
гую форму (рис. 3.9).
В форму, изображенную на рис. 3.9, надо ввести четыре усло-
вия (по числу уравнений системы). На рисунке отражено послед-
нее условие. Ссылка на ячейку А10 обусловлена тем, что в ней —
формула для левой части 4-го уравнения, знак *=’ выбран из меню,
число (-13) введено с клавиатуры (правая часть 4-го уравнения).
После ввода последнего ограничения нажимают кнопку ОК и воз-
вращаются в основную форму Поиск решения. Щелкнув по кнопке
Выполнить, получают результат (рис. 3.10).
Каким методом это решение получено, можно узнать, щелк-
нув по кнопке Параметры (см. рис. 3.8). Там, в частности, есть
знакомый нам метод Ньютона (наверняка сильно видоизменен-
ный, поскольку применяется на самом деле к решению гораздо
более сложной задачи).
Поиск решения можно попытаться применить и к решению си-
стем нелинейных уравнений. В этом случае выбор начального при-
ближения очень важен, в зависимости от него решение может
быть получено или не получено и могут быть получены разные
решения. Применив это средство для решения системы, рассмот-
ренной в примере 3.12, и задав начальное приближение х= 1,5;
у= 1,5, получим х= 1,54556864895469, у= 1,50203907035116 (выписа-
ны все цифры, выведенные программой; опыт работы с Excel гово-
рит, что, за исключением одной-двух последних, все они верные).
3.6.2. Система MathCad
Рассмотрим технологию решения системы уравнений средства-
ми MathCad (рис. 3.11).
171
Решаем систему уравнений:
234x1 - 421x2 - 1161 хЗ 14.41
804x1 + 522x2 + 027 хЗ = -6 44
3 .92 х! - 799x2 + 837 x3 = 5536
Матрица системы:
' 234 -421 -1161
А» 804 522 027
к 392 -7 99 837 >
Вектор-столбец свободных членов
' 14.41 '
Ь-6 44
Решение: x:«A*’b
Проверка точности решения:
' 2293021 '
х- -4815522
, 0967185 ,
Решим эту же систему при помощи встроенной функции: х > ijalv<A,b)
' 2293021 '
х- -4815522
„ 0 967185 ?
Рис. 3.11. Матричное решение системы линейных уравнений в MathCad
Пример 3.14. Решить систему линейных уравнений-из приме-
ра 3.7, используя:
а) матричную форму записи Ах = Ь (см. подразд. 3.1);
б) метод Крамера;
в) метод Гаусса.
При записи уравнений в матричной форме в рабочем докумен-
те MathCad (см. рис. 3.11) вместо обычного знака равенства ис-
пользуется «символьный знак равенства», набираемый комбина-
цией клавиш <Ctrl> + <=>. Если в целях наглядности требуется
текстовый комментарий, то для создания текстовой области нуж-
но воспользоваться клавишей <”>: крестообразный курсор преоб-
разуется в маркер ввода и появляется текстовая рамка; после окон-
чания печати текста нужно щелкнуть мышью вне этой рамки. Ввод
матрицы и вектора-столбца осуществляется с помощью палитры
матричных операций, вызываемой кнопкой панели инстру-
172
ментов. Затем в диалоговом окне Insert Matrix указывается требу-
емое количество строк и столбцов и нажимается кнопка ОК. В по-
явившемся шаблоне заполняются поля ввода в соответствии с ис-
ходными числовыми данными решаемой задачи.
Чтобы получить вектор-решение системы уравнений, необхо-
димо записать вычислительную формулу, в которой присутствует
операция обращения матрицы А и «запустить» вычислительный
процесс, набрав х= (рядом со знаком равенства появится вектор-
решение).'
Убедиться в правильности произведенных расчетов можно,
найдя разность Ах-b: должен получиться вектор, все элементы
которого равны нулю. В противном случае имеет место вычисли-
тельная погрешность. На рис. 3.11 для сравнения показано реше-
ние этой же системы уравнений при помощи встроенной функ-
ции lsoive(A,B), которая возвращает вектор х для системы линей-
ных уравнений.
Система MathCad позволяет получить решение системы линей-
ных уравнений по формулам Крамера (рис. 3.12). По умолчанию
элементы матриц (векторов) в MathCad нумеруются, начиная с
нулевого элемента. Для того чтобы столбцы и строки матрицы
нумеровались, начиная с единицы, следует присвоить встроен-
ной системной переменной ORIGIN значение, равное единице.
Вычисление определителя матрицы системы производится при
помощи палитры мат-ричных операции при нажатии на кнопку Уш
В появившемся поле ввода записывается имя матрицы и набира-
ется знак равенства. Аналогично производятся вычисления опре-
делителей для явно заданных матриц (они обозначены Д1, Д2, ДЗ),
но в этом случае дополнительно следует воспользоваться кноп-
„ р"]
кои L. J и заполнить поля ввода элементами соответствующей мат-
рицы. Сравним полученные значения корней системы уравнений
с результатами матричного решения — они совпали.
В MathCad реализован метод Гаусса (рис. 3.13), причем прямой
и обратный ходы выполняет встроенная функция rref(A) — при-
водит матрицу к ступенчатому виду с единичным базисным ми-
нором; формирование расширенной матрицы системы осуществ-
ляет функция augment(A,b) — она добавляет к столбцам матрицы
системы уравнений справа вектор-столбец свободных членов; век-
тор-решение получается при помощи функции submatrix^A, irjr, icjc),
которая выделяет блок матрицы А с элементами, расположенными
в строках с ir по jr и в столбцах с ic по ус, ir < jr,ic < jc.
Встроенные функции можно набирать с клавиатуры или вос-
.. /5^
пользоваться кнопкой панели инструментов и в появившем-
ся диалоговом окне выбрать нужную функцию.
173
ORIGIN := 1
' 2.34 -4.21 -H.61 0 ( 14.41 )
А := 8.04 5.22 0.27 Ь:= -6.44
, 3.92 -7.99 8.37 ; < 55.56 ,
Вычислим определитель матрицы А: |а| = 1.37 х 103
Определитель отличен от нуля, следовательно,
система имеет единственное решение.
Вычислим определители матриц, полученных заменой соответствующего
столбца исходной матрицы столбцом свободных членов:
' 14.41 -4.21 -H.61 "5 ' 2.34 14.41 -H.61
А! := -6.44 5.22 0.27 Д2:= 8.04 -6.44 0.27
ч 55 56 -7.99 8.37 ; 3 92 55.56 8.37
Д2 = -6.595 х
Л1 - 3.14 х КГ
105
ДЗ :=
( 2.34
-4.21
14.41 >
8.04
5.22
-6.44
V 3.92
-7.99
55.56 )
ДЗ = 1.325 х
103
Находим корни системы уравнений:
Д1
х1 := -—-
|А|
ДЗ
|А|
Х1 = 2.293
£ = -4.816
хЗ = 0967
Рис. 3.12. Решение системы линейных уравнений методом Крамера
в MathCad
Пример 3.15. Решить систему уравнений методом простой ите-
рации (см. пример 3.10) в MathCad (рис. 3.14). Для проверки до-
статочного условия сходимости метода можно ограничиться лю-
бой из норм: функция norml(A) соответствует формуле |Л|| =
= max ^1^1 (см. (3.20)); nomi(A) — это ||Л[]. = max ^|<7„.| (см. (3.19));
погте(А) соответствует (3.21); функция norm 2(A) соответствует
формуле ||Л|| = 1/Amas(AAr), где Хтах(ААг) — максимальное соб-
ственное значение матрицы АА7; Аг— матрица, транспонирован-
ная по отношению к матрице А.
174
ORIGIN - 1
Вводим матрицу системы и вектор-столбец свободных членов:
< 2.34 -4.21 -11.61 > ' 14.41 '
А 8.04 5.22 0.27 b := -6.44
ч 3.92 -7.99 8.37 J < 5556 ;
Формируем расширенную матрицу системы:
Rxn := augiritii'X А ,Ь)
' 2.34 -4.21 -11.61 14.41 41
Rin = 8.04 5.22 0.27 -6.44
ч 3.92 -7.99 8.37 55.56 >
Приводим расширенную матрицу системы к ступенчатому виду:
Sf := tref(Rm)
рОО 2.293
Sf- 0 10 -4.816
< 0 0 1 0.967 >
Формируем вектор-столбец решения системы уравнений:
х := subniatriXSf,l,3,4,4)
' 2.293021
х = -4.815522
< 0.967185 j
Рис. 3.13. Решение системы линейных уравнений методом Гаусса в MathCad
В качестве начального (нулевого) приближения х<0> (для ввода
используется кнопка и матричной палитры) выбираем вектор-
столбец b свободных членов преобразованной системы. При по-
мощи ранжированной переменной А: задаем количество итераций.
На экране представлены заключительные шаги итерационного про-
цесса, на основе которых погрешность вычисляется по формуле
(3,25). Можно убедиться, что чем больше значение переменной к,
тем меньше значение е. Найденное решение совпадает с «ручны-
ми» вычислениями (см, п. 3.3.2),
175
Преобразованная система:
il = -0.649x2 - 0.034x3 - 0.801
х2 = 0.513x1 - 0 266x3 - 5.733
хЗ = 0.202x1 - 0.363x2 - 1.241
Вводим матрицу преобразованной системы и вектор-столбец свободных членов:
( 0 -0.649 —0.034 < -0.801 ' Bi
Г:::1 * ..-1 !*!
А:= Пров с евк 0 513 а -0266 ,0.202 -0.363 0 , еряем достаточное ус лидовой метрикой: Ь:= повие сходимости в -5.735 К ; прсстраг стве L---J п LiQy И4' Пт if*:-"/;
поппе(А) = 0.964
а. := -.Д964 а, = 0.982
Задаем начальное приближение решения:
/о)
k > 1.. 25 - количество итераций;
х № > ъ + А х !'ь - итерационная формула для вычисления приближений
решения;
.. :2с=з‘: </:21 ' Г21- У,
0 2.202373 2.292378 2.292372 2.292371 2.292373 2.292373 2.292373
1 -4.81723 -4.81 7221 -4.81722 -4.817222 -4.817222 -4.817222 -4.817222
:2S: 0.970707 0.970714 0.97071 1 0.97071 0.97071 1 0.970711 0,970711
Проверим, достигнута ли точность s= 0.0001: 0.0001 ----— = 1.85 х 10 6
|х - х I = 5.542 X 10’Т
Рис. 3.14. Решение системы линейных уравнений методом простой
итерации в MathCad
Рассмотрим технологию решения системы нелинейных урав-
нений из примера 3.12 итерационными методами в MathCad. Для
этого используется специальный вычислительный блок:
<Началъные условия>
Given
<Уравнения>
<Выражения со встроенными функциями>
176
Начальные условия задаются операцией присваивания для всех
неизвестных, входящих в систему уравнений. Служебное слово Given
и уравнения в их естественном виде, но с обязательным исполь-
зованием символьного знака равенства, разделяющего левую и
правую части, вводятся с клавиатуры. На рис. 3.15 представлен
фрагмент рабочего документа MathCad, где для решения постав-
ленной задачи применяются две встроенные функции (соответ-
ственно 1-й способ и 2-й способ):
Minerr(v 1 ,v2 vn) — возвращает приближенное решение,
поэтому вычислительный блок обязательно должен содержать про-
верку достоверности результатов;
Find(yl,v2,...,vn) — возвращает точное решение; число ее аргу-
ментов должно быть равно числу неизвестных.
Различие между функциями заключается в том, что первая
пытается найти максимальное приближение к решению (даже если
Начальные приближения решения: х:»15 у>1_5
1-Й способ Вычислительный блок
Given
ух5 - х 4
zl :» Minen(x,y)
< 1 545569")
xi > I • решение системы уравнении.
(, 1502039 )
Проверка: ИО " “*
Х1Г(х10)’-110-4
2-й способ. Вычислительный блок
Given
ух5 - X 4
й.Fmdfx.y)
< 1.545569 'I . решение системы уравнений
' I 1 502039 J
Рис. 3.15. Решение системы нелинейных уравнений в MathCad
177
оно не существует) путем минимизации среднеквадратичной по-
грешности решения, а вторая используется только в случае реаль-
но существующего решения (иначе будет возвращено сообщение
об ошибке).
3.6.3. Система Derive
Для решения систем линейных уравнений в Derive использует-
ся команда System позиции Solve главного меню (рис. 3.16). Она
выводит окно, в котором следует указать количество уравнений.
После нажатия на кнопку ОК появится окно для ввода уравне-
ний и указания переменных, относительно которых ищется ре-
шение (рис. 3.17). Для задания переменных надо щелкнуть мышью
по панели Equation Variables (в окне ввода).
тт : Simplify -Ч
Нажатие на кнопку ———i в окне ввода уравнении позво-
ляет получить вектор решения х (рис. 3.18) в виде рациональных
чисел (символьное представление). Воспользовавшись командой
Approximate пункта Simplify главного меню, можно получить реше-
ние в вещественной форме (она вычисляет заданное выражение).
Системы нелинейных уравнений в Derive решаются численны-
ми методами при помощи файлов внешних расширений, доступ к
которым осуществляется из пункта File главного меню: команда
Open выводит на экран окно с содержимым папки Math, необхо-
димо загрузить файл Solve.mth (рис. 3.19).
Пример 3.16. Решить систему нелинейных уравнений
1х2 - ху - 6,7;
[ху + у- = 4,2.
Пакет Derive располагает внешней функцией Newtons(u,x,xO,n),
позволяющей производить вычисления методом Ньютона — Раф-
сона (см., например, [10]). Для получения начальных приближе-
E DERIVE For Wo
File Edit Author Simp'.
Options
< Nirmericafly... . Ctrl+ShiFt+N
System... Qrh-SMt+5
Number ol Equati л
Equ-Jnn-It 1
Рис. 3.16. Инициализация режима решения систем уравнений в Derive
178
[Authoc 3 equations - 7??.MTH
a p : 7 -fij C , j; i n ? Oj i jJkj X I Ji W £. On p G 7 V ф | X ! f * W J ё ° < : U '-• 1 C ± f-
А В Г ЛЕ Z;H-GJ ‘KiA'n.N'".О II T Г Ф ;X: T! Q ; i j <o >:П л--> 4г J
C quelion
Vari^tiles
Рис. 3.17. Окно Derive для ввода системы линейных уравнений
|В DERIVE tor Window» [Algebra ??? MTH]
jA File :Edit Author o/ropldy Solve Calculus Declare Options Window Help
D Й н| а; . ME'SI = |»i®,|'su,| i^l a| j fz|n|
111&3097t9 122129794 €62295038
X ” ------- у = “ ------- Z = ------
50723386 25361693 684765711
|3 DERIVE IwWmfom-.micba ???.MTHl|
Рис. 3.18. Результат символьного и численного
решений системы линейных уравнений в Derive
F.; File Edit Author' SirripMy Solve Calculus
□ кМй] SiF AF
—1 ------* - Exp-ard Cul+F
Га-tor. . C.mI+F;
бииомпаЬ... Dih6
SubsWiJte lor
Орел
ИИ
; НМ isc.mth
• Nurriber.mth
. К] Numeric.rTilh
|Я] Ode_appr.mih
i- Odel.mth
j [B]OdeZmth
®JOrth_po1mlh
B] Physical .mth
HjP1ot2d.m!h
H] PlotSd.mth
HjPlolparaimth
Wj Piobabil. mill
H Recureqn mth
BSBSSE3IS
ЙТ Vector.mth
feil Zeta nth
Отмена
Рис. 3.19. Окно с файлами расширений Derive
179
Author Expression -SOLVErMTH
я j p r6 I il.nI Bl l |k]x'I ply !;t|oln| pi oj т-»]ф ! X I т
nr: г л i ~ и?’> ) клп n o :i r :•: т г ф ;•, 4'
|NlilllOHS ( |хл2-х“у-6.7.х*у<-у''2--4.2] , Lx.у], [ 1.4,2.7],5>
Рис. 3.21. Окно ввода системы Derive
нЭ Algebra 2:1 SOLVEMTH : | §5 Algebra 2:1 S0LVEJ4TH |
-1.4 2.7 ‘ -3.2 -1.2
-1.5114 2.9477 -3.1451 -1.0186
#14: -1.5074 -1.5074 2.9373 2.9372 #27: -3.1428 -3.1428 -1.0110 -1.0110
-1.5074 2.9372 -3.1428 -1.0110
-1.5074 2.9372 -3-1428 -1.0110
1.4 -2.7 3.2 1.2
1.5114 -2-9477 3.1461 1.0186
#16: 1.5074 1.5074 -2.9373 -2.9372 #29: 3.1428 3.1428 1.0110 1.0110
1.5074 -2.9372 3.1428 1.0110
1.5074 -2.9372 3.1428 1.0110
Рис. 3.22. Результат решения системы нелинейных уравнений в Derive
ний решения можно воспользоваться графическим методом. Из
графика, изображенного на рис. .3.20, можно получить грубые на-
чальные значения, например: (-1,4; 2,7), (1,4; -2,7), (-3,2; -1,2),
180
(3,2; 1,2). Функция Newtons возвращает вектор-решение для задан-
ных п итераций. На рис. 3.21 показано окно ввода (команда Expression
пункта Author меню): в качестве аргументов функции выступают
вектор системы уравнений [х2 - др - 6,7; ху + у2 - 4,2], вектор
переменных [х, у], вектор начальных приближений решения [-1,4;
2,7] и количество итераций, равное 5.
Завершение процесса решения системы уравнений при раз-
личных начальных приближениях вектора решения показано на
рис. 3.22. Из рисунка видно, что итерационный процесс можно
было остановить уже на третьей итерации, когда полученные ре-
шения начинают повторяться: (-1,5074; 2,9372), (1,5074; -2,9372),
(-3,1428; -1,0110), (3,1428; 1,0110).
3.6.4. Система Maple
Решение систем линейных уравнений (см. пример 3.1) матрич-
ным методом в Maple (рис. 3.23) реализуют два класса функций:
1) функции для задания векторов и матриц:
matrix(nun,list) — возвращает матрицу размерности и х т с за-
данными списком элементами, которые перечисляются через за-
пятую построчно (элементы каждой строки заключается в квад-
ратные скобки, а строки разделяются запятыми);
vectorijijist) — возвращает вектор с п элементами, заданными
списком;
2) функции для работы с векторами и матрицами:
muItiply(A,B) — возвращает произведение матриц А и В;
inverse(A) — возвращает матрицу, обратную А.
Решение представляет собой список элементов вектора х.
Этот же метод используется функцией linsolve(A,B), аргумента-
ми которой являются матрица А и матрица (или вектор) В
(рис. 3.24) для решения матричного уравнения вида Ах = В.
" • •. 4”’:
[> .............................‘..............
> [[2.34,-4.21,-11.611 , (8.04,5.22,0.27J, [3.92,-7.99,8.37[J);
[2.34 -4 21 -И. б У
А_= g.M 5.25 .27
13.92 -7.99 8.37 .
> В:—vector( 3.. [14.41,-6.44,55.56]);
5--[]4.41,-5.44,55.56]
> X:-urnItiply(inverse(А),В);
= [2.293020600, -4 815522134, .9671S48739J
К Рис. 3.23. Матричное решение системы линейных уравнений в Maple
I
> Л -«*trl<(3,3,Ц2 34,-4 21,-1141].(«04,5 22,0 27].(3 92,-7 99,В 37)));
2М •421 •1141
8М 122 Л
гп -7>» 8 37 .
> В -MrtorO, (1441.-6.44,55 56));
Л«(|441.-б44,55 %]
> X -1innolvefA.В);
____________________________________Х^(2 29?0Ж€О. -4 815522!^. 967184374]
Рис. 3.24. Решение матричных уравнений в Maple
> ~| -|2 34-ж 4 ?1»у-Ц *1*Ж—14 41,« О4*ж-5 ??*/♦• 17*1—4 44,3 9ft 1 37M-3S 54|
> г*ж -»ol»»(e<.(ж,у,ж|>.
~т-(ж- М71В4Я741.Л--4II55221M.»-2293020600)
> oq7 -(?*ж*у-3*ж'2,ж«?*у-3»ул2(
> гм2 -»olv«<«q2r(ж,у)).
rw2 -(».0^-0).0r- В.ж-1),
О- -1 - J - 1. UM. _U\ ж | - _Z - 1. faM . JJ) (-2 ♦ R^tOfC.Z2 - J - 1. UM - _4?)))
> evAlf(r«z2),
(/-О.Ж-0 ).(y. l,i- 1. ).(>•-2060113294./• 5393444429)
? e^3 -le^rt<(ж-у)/(ж«у>)•»qrt<(»»y)/(xy))-10/3,»*y 2*y-?|:
> r«z3 -4>lve(*47) .
ж>? - (л . «.> - Я. (, - 2 lu-oes У - J ♦ Z IM- JJ\, . - _? - J ♦ 2. Ы.'. JJ)). (» . 1,. ~)
> •valf(r»>3);
(/•4. ж . 5 )_ (/ . 2000000000 ♦ I 2489И60Э I. к • • 2500000000 - i 56)249500 /).(«-• 5000000000,/ - . 40000000001
Рис. 3.25. Решение систем уравнений в символьном виде в Maple
Для решения систем линейных и нелинейных уравнений мо-
жет быть применена функция so!ve({eql,eq2,...},{varl,var2,...}), где
е^— уравнение, var — переменная, по которой ищется решение.
Уравнения и список переменных задаются в виде множества, по-
этому результат будет получен также в виде множества в аналити-
ческом виде (символьной форме).
На рис. 3.25 представлено решение линейной и двух нелиней-
ных систем уравнений:
а) из примера 3.1 — переменная eq. Уравнения перечислены
через запятую;
(2х + у = 3х2;
1х + 2у = 3у2 — пеРеменная ея2\
в)
х-у х + у _ 10.
м х + у + Jх _ у ~ "з"’ — переменная eq3.
ху - 2х - 2у = 2
В случаях б) и в) функция solve формирует множество реше-
ний через функцию RootOf. Это значит, что корни нельзя выра-
182
I к|а| |w| / |///j
> fsolveHy'3-х 2-l,y*x'3-i«4 I, I x,yj) ;
0>= 1.502039049, x= 1.545568601)
> fsolve!(y3-x‘2-l,y*x3-x-41, {x-1 ..2.,y-l. .2.11;
o = 1.502039049, i- 1.545568601 )
> f solve! I 2*abs (x-1) +3*abs (y+2>—17,2 *x + y—7 ), ( x-1. . 3 ,y=2 . . 4 )) ,
(x = 2.000000000, y = 3.000000000)
> fsolve!12*abs(x-1)+3*abs(y+2)-17,2*x+y=71,(x=5. .6,у—5. .-4 )) ;
Си = -4 500000000. x = 5.750000000)
Рис. 3.26. Решение систем нелинейных и трансцендентных уравнений
в числовом виде в Maple
зить в радикалах. Использование функции evalf позволит получить
значения корней в вещественной форме. В случае в) один корень
выражен комплексным числом.
Для получения числового решения систем нелинейных урав-
нений существует функция fsolve({eql,eq2,...},{varI,var2,...}, options),
которая может использовать следующие опции: interval — задается
в виде {д'-а..Ь,у- а..Ь\ и обеспечивает поиск корней в указанном
интервале; complex — находит корни в комплексной форме. На
рис. 3.26 показано решение двух систем уравнений: из примера 3.12
(2|х-1| + ЗЦ + 2| = 17;
Щ<-7 = 7.
Чтобы получить рее решения, для второй системы потребова-
лось явно задавать интервалы поиска корней, т.е. необходим пред-
варительный этап отделения корней.
3.6.5. Система MatLab
Математическая система MatLab ориентирована на выполне-
ние матричных вычислений, поэтому матричное решение систе-
мы линейных уравнений может быть получено двумя способами:
с применением операции обращения матриц — функции iiiv(A)
либо оператора матричного деления \ (использует метод Гаусса).
Как видно из рис. 3.27, в обоих случаях для решения системы
линейных уравнений (см. пример 3.1) получены одинаковые ре-
зультаты.
Элементы матрицы (вектора) перечисляются в квадратных скоб-
ках построчно через запятую и разделяются символом «;» с эле-
ментами следующего столбца. Операции присваивания соответ-
ствует знак равенства.
Чтобы решить эту же задачу методом Крамера (определите-
лей) (рис. 3.28), необходимо сформировать четыре матрицы: ис-
ходную матрицу коэффициентов при неизвестных А и три вспо-
могательных Al, А2, АЗ, причем при вводе необходимо учитывать
183
» А-[2.38,-Й.21,-11.61;8.68.5.22.6.27;3.92.-7.99.8.37]
2.3*88 -*.2188 -11.6188
I.MII 5.2286 8.2788
3.9288 -7.9980 8.3788
• B«(18.M;-6.88:55.56)
В -
18.8188
-6.8808
55.5666
» X-ixw(6)«H
2.2938
-8.8155
8.9672
• X“A\B
x •
2.2938
-8.8155
8.9672
Рис. 3.27. Матричное решение системы линейных уравнений в MatLab
якджл лилтюа!
» А-[2.38.-8.21,-11.61;8.88,5.22.6.27:3.92.-7.99.В.37]
I -
2.3880 -8.2188 -11.6188
8.0800 5.2208 0.2780
3.9200 -7.9900 8.3700
> А1-(18.81,-8.21,-11.61;-6.88,5.22,8.27;55.56,-7.99,8.37]
И -
18.8100 -8.2100 -11.6100
-6.8800 5.2208 8.2700
55.5600 -7.9980 8.3700
» А2-(2.38,18.81,-11.61;0.08.-6.88.0.27:3.92,55.56,0.37]
12 •
2.3800 18.8100 -11.6100
8.0800 -6.8800 0.2700
3.9200 55.5600 0.3700
• АЗ-[2.38,-8.21.18.81:8.68.5.22.-6.88;3.92,-7.99.55.56]
I3 •
2.3800 -8.2100 18.8100
8.8800 5.2208 -6.8800
3.9200 -7.9900 55.5600
• x1-6et(01)/6et(A)
2.2930
► x2-det(A2)/det(А)
i2 -
-8.0155
► x3-det(A3)/det(A>
0.9672
Рис. 3.28. Решение системы линейных уравнений
методом определителей в MatLab
особенность записи элементов: получить матрицу с заменой эле-
ментов первого столбца на свободные члены можно, если при
вводе заменить соответственно 1-й, 4-й и 7-й элементы соответ-
ственно; аналогичные замены производятся для остальных столб-
цов. Вычисление определителя квадратной матрицы осуществляет
функция det(A).
184
(Метод Гаусса также может быть реализован в MatLab (рис. 3.29),
поскольку имеется функция cat(dim,A,B), которая объединяет мас-
сивы А и В (значение параметра dim - 1 соответствует [А; В], т.е.
элементы массива В будут добавлены как строки, а значение dim = 2
соответствует [А, В] — элементы массива В добавляются как столб-
цы) и функция ггеДА), которая приводит матрицу к треугольной
форме (использует метод исключения Гаусса с частичным выбо-
ром ведущего элемента). Полученный результат совпадает с ре-
зультатами решения системы уравнений матричными методами и
методом определителей.
Система нелинейных уравнений в символьном виде решается
при помощи функции solve{eql,eq2,...,eqn,varl,var2i...,vam). При от-
сутствии аналитического решения ищется только числовое реше-
ние. Для задания уравнений в явном виде используются строко-
вые выражения — уравнения заключаются в апострофы.
: sts! й
И. 21 ,-11.61 ;8.04,5.22 ,0.Р/;3.92,-7.99,8.37]
А =
2.34О0 -4.2100 -11.6100
8.04О0 5.2200 0.2700
3.9200 -7.9900 8.3700
» В«[14.41;-6.44;55.56]
8 =
С
14.4100
-6.4400
55,5600
C-c^t(2,A,B)
2,3400
8,0400
3.9200
-4.2100
5.2200
-7.9900
-11.6100
0.2700
8.3700
14.4100
-6.4400
55.5600
ans •
1.0800
0
0
о
1.0000
О
0
О
1.0000
2.2930
-4.8155
0.9672
Рис. 3.29. Решение системы линейных уравнений методом Гаусса в MatLab
Cj S : Т? Г | «С jffl :g ft ? .
» $ = ьи!ие(‘3*к-6«у+ 2’ , ’x*3+y*3-1’,х,у)
ъ -
х: [3x1 syn]
у: [3x1 syfi]
•> ира($.х,6)
ans =
[ .833133]
[ -.527677+.865419*1]
[ -.527677-.865419*i]
» Upa(S.у,6)
ans
[ ,749899]
[ .69U9Ue-1+.432711*1]
[ .69494P-1-.432711*1]
Рис. 3.30. Решение систем нелинейных уравнений в MatLab
185
На рис. 3.30 показано решение системы нелинейных уравнений
Зх-6у + 2 = 0;
х3 + у3 -1 = 0.
Для получения вещественной формы представления корней
(х = 0,833133; у =0,749899) используется функция vpa(S,D), кото-
рая возвращает результат вычислений символьного массива 5 с
числом точных цифр, равным значению аргумента D. Помимо ве-
щественных система имеет два мнимых корня.
3.6.6. Система Mathematics
Решение систем линейных уравнений матричными методами в
пакете Mathematica показано на рис. 3.31. В первом примере реше-
ние выполняется в символьном виде: Х = А’В, где А — матрица
коэффициентов системы, В — вектор свободных членов. Для пере-
множения матриц используется функция для обраще-
ния матрицы — функция /те/зерп]. Во втором примере для реше-
ния системы используется функция LinearSolve[m,b], которая воз-
вращает вектор х решения матричного уравнения.
Ввод значений осуществляется посимвольно с клавиатуры и
после каждой строки нажимается сочетание клавиш <Shift> +
<Enter> (клавиша <Enter> используется для перевода строки), что
инициализирует команду ввода In. Для получения результата дос-
таточно набрать имя вектора X и <Shift> + <Enter>, появится со-
общение о выводе результата операции: Out. Числа в квадратных
Рис. 3.31. Решение системы линейных уравнений в пакете Mathematica
186
h(23]~ NSolve[(xA2 4 у* 2 •• 41, y<x.. 9), (x, y)]
OuipJh ((X-»4.z y-»5.), (Х-»5., у-♦ 4.)) ]
lr>p4]:= NSolveU5»x*6»y-4irZ!=x»y, 3«xt5«y-Z!=yA2,
x»4«y*2nz i.y«z), {x, y, z}]
NSolvs::zsrosol :
Scale of possible solution value -5.31325x IO"14 for
variable у is Coo small. Muse sec this value Co
zero in order co avoid generation of spurious
solutions. This may cause the loss of souse solutions.
0utp4]= {(X-»7., z-»7., y-»7.), '
(X-.2.5, z-»7.S, y-»5.}, {x->0., z-»0., y-*0.}}
Рис. 3.32. Решение систем нелинейных уравнений средствами
пакета Mathematica
скобках указывают на номера ячеек ввода и вывода (нумерация
строго последовательная и ее нельзя менять).
Решение систем нелинейных уравнений в символьном виде осу-
ществляет функция Solve[{eql,eq2,...},{varl,var2,...}] — возвращает ре-
шение системы уравнений относительно переменных var. Для числен-
ного решения используются функции Nsolve[{{eql,eq2,...},{varl,var2,...}].
Решим системы трансцендентных уравнений (рис. 3.32):
а) |^+У2=41;
(.г + у = 9;
б)
5х + бу - 4z = ху;
Зх + 5у - z = у2;
х + 4у + 2z = уг.
В результате проведенных расчетов получены корни:
а) (4; 5), (5; 4); б) (7; 7; 7), (2,5; 5; 7,5), (0; 0; 0).
На основе рассмотренных примеров применения инструмен-
тальных средств — как универсальных (табличный процессор),
так и специального назначения (математические пакеты) — для
решения систем линейных и нелинейных уравнений можно за-
ключить, что этими средствами предоставляются широкие воз-
можности для эффективного решения задач указанного класса,
требуется лишь умело выбирать их оптимальное сочетание.
Контрольные вопросы
1. Какие типы уравнений позволяет решать средство Поиск решения
табличного процессора Excel?
2. Какие встроенные функции MathCad необходимы для решения
систем линейных уравнений?
187
3. Какие функции, позволяющие решать системы нелинейных урав-
нений, реализованы в файле расширений Solve.mtli математической си-
стемы Derive?
4. Какие функции ялра Maple используются при решении систем ли-
нейных уравнений матричным методом?
5. Какие методы решения систем линейных уравнений реализованы в
системе MatLab?
Упражнения
Решить системы линейных и нелинейных уравнений, используя различ-
ные инструментальные средства, и сопоставить полученные результаты:
0,01х, 0,02x, +0,14хз = 1.75;
а) р,98х, +О,34х2-2,О1х3 =-23,67;
0,79х, +0, 2х2 + 0,4х3 =7,35;
3 cos Х| + 2 sin х2 = 1;
х(2 + = 1.
ЛАБОРАТОРНАЯ РАБОТА № 3
Тема'. Численные методы решения систем уравнений
Задание 1. Дана система трех линейных уравнений с тремя не-
известными:
+ G|2-V2 + Фзл’з =
Cl-Vl + a22X2 + а23х3 =
г?31Х] + а32 х2 + СзА'з = Ьз-
(3.36)
Задание 1.1. Решите систему (3.36) методом Гаусса:
а) используя «ручную» схему единственного деления, двумя
способами: без перестановки строк; с перестановкой строк; рас-
четы выполняйте с тремя знаками после запятой (с применением
калькулятора); подставьте найденные решения в исходную систе-
му, вычислите невязки и сравните полученные решения; выбрав
ведущие элементы схемы единственного деления, найдите значе-
ние определителя системы;
б) с помощью программы для ЭВМ с пооперационным уче-
том ошибок.
Задание 1.2. Решите систему (3.36) методом простой итерации
с точностью е = Ю"4 с помощью программы для ЭВМ:
а) с оценкой погрешности метода по одной из метрик с при-
менением оценочной формулы (3.25);
б) с использованием эмпирического критерия близости со-
седних приближений.
Задание 1,3. Решите систему (3.36), используя одно из инстру-
ментальных средств. Сопоставьте найденное решение с решения-
ми, полученными при выполнении заданий 1.1 и 1.2.
188
Задание 2. Найдите решение заданной системы нелинейных
уравнений с прикидкой точности результата с помощью эмпири-
ческого критерия:
а) методом простой итерации;
б) методом Ньютона;
в) с использованием одного из инструментальных средств.
Пояснения к выполнению лабораторной работы № 3
Перед выполнением лабораторной работы необходимо изучить
материал гл. 3 и тщательно разобрать все приведенные в тексте
примеры.
Коэффициенты и свободные члены заданной системы уравне-
ний (3.36) для 20 вариантов к заданию 1 приведены в табл. 3.7.
Для «ручного» решения системы уравнений методом Гаусса
(задание 1.1, а) составляется расчетная схема (см. пример 3.1,
табл. 3.1). Решение с перестановкой строк показано в п. 3.2.4 (при-
мер 3.6).
Задание 1.1, б выполняется с помощью программы для компь-
ютера (см. пример 3.3 в п. 3.2.3), предусматривающей системати-
ческий учет границ абсолютной погрешности вычислений. Грани-
цы абсолютных погрешностей исходных данных — коэффициен-
тов системы и свободных членов — принимаются из предположе-
ния, что исходны^ числовые значения в табл. 3.7 заданы цифра-
ми, верными в строгом смысле. Вычисления производятся для
различных числовых типов данных; полученные результаты необ-
ходимо сопоставить и прокомментировать.
При выполнении задания /.2составляются две программы ре-
шения заданной системы линейных уравнений по методу итера-
ций — с учетом достаточных условий сходимости и без учета этих
условий. Для применения метода итераций с предварительным
доказательством условий сходимости исходная система преобра-
зуется к системе с преобладающими диагональными коэффици-
ентами, а затем к нормальному виду (см. п. 3.4.2). Вслед за этим
производится проверка достаточных условий сходимости (в смысле
одной из метрик); в результате получается значение коэффициен-
та сжатия а, которое используется в программе для проверки окон-
чания цикла (формула (3.25)). При использовании другого подхо-
да (на основе эмпирического критерия совпадения значащих цифр
в одной позиции трех соседних приближений, см. п. 3.4.2) исход-
ную систему достаточно преобразовать в систему с преобладаю-
щими диагональными коэффициентами. Затем с помощью ЭВМ,
вводя различные ограничения на число итераций, проводится
эксперимент по отысканию решения системы с учетом эмпири-
ческого критерия.
189
Таблица 3.7
Номер варианта / й,-3 ь,-
1 0,21 -0,45 -0,20 1,91
1 2 0,30 0,25 0,43 0,32
3 0,60 -0,35 -0,25 1,83
1 -3 0,5 0,5 -56,5
2 2 0,5 -6,0 0,5 -100
3 0,5 0,5 -3 -210
1 0,45 -0,94 -0,15 -0,15
3 2 -0,01 0,34 0,06 0,31
3 -0,35 0,05 0,63 0,37
1 0,63 0,05 0,15 0,34
4 2 0,15 0,10 0,71 0,42
3 0,03 0,34 0,10 0,32
1 -0,20 1,60 -0,10 0,30
5 2 -0,30 0,10 -1,50 0,40
3 1,20 -0,20 0,30 -0,60
1 0,30 1,20 -0,20 -0,60
6 2 -0,10 -0,20 1,60 0,30
3 0,05 0,34 0,10 0,32
I 0,20 0,44 0,81 0,74
7 2 0,58 -0,29 0,05 0,02
3 0,05 0,34 0,10 0,32
I 6,36 11,75 10 -41,40
8 2 7,42 19,03 11,75 -49,49
3 5,77 7,48 6,36 -27,67
1 -9,11 1,02 -0,73 -1,25
9 2 7,61 6,25 -2,32 2,33
3 -4,64 1,13 -8788 -3,75
1 -9,11 -1,06 -0,67 -1,56
10 2 7,61 6,35 -2,42 2,33
3 -4,64 1,23 -8,88 -3,57
1 1,02 -0,73 -9,11 -1,25
11 2 6,25 -2,32 7,62 2,33
3 1,13 -8,88 4,64 -3,75
1 0,06 0,92 0,03 -0,82
12 2 0,99 0,01 0,07 0,66
3 1,01 0,02 0,99 -0,98
1 0,10 -0,07 -0,96 -2,04
13 2 0,04 -0,99 -0,85 -3,73
3 0,91 1,04 0,19 -1,67
190
Окончание табл. 3.7
Номер варианта / e,i ап ь.
1 0,62 0,81 0,77 -8,18
14 2 0,03 -1.11 -1,08 0,08
3 0,97 0,02 -1,08 0,06
1 0,63 -0,37 1,76 -9,29
15 2 0,90 0,99 0,05 0,12
3 0,13 -0,95 0,69 0,69
1 0,98 0,88 -0,24 1,36
16 2 0,16 -0,44 -0,88 -1.27
3 9,74 -10,00 1,71 -5,31
1 0,21 -0,94 -0,94 -0,25
17 2 0,98 -0,19 0,93 0,23
3 0,87 0,87 -0,14 0,33
1 3,43 4,07 -106,00 46,8
18 2 74,4 1,84 -1,85 -26,5
3 3,34 94,3 1,02 92,3
1 0,66 0,44 0,22 -0,58
19 2 1,54 0,74 1,54 -0,32
3 1,42 1,42 0,86 0,83
Г 0,78 -0,02 -0,12 0,56
20 2 0,02 -0,86 0,04 0,77
3 0,12 0,44 -0,72 1,01
Заданием 1.3 предусматривается решение той же системы ли-
нейных уравнений (3.36) с использованием одного из инстру-
ментальных средств (см. подразд. 3.6).
В итоге требуется сопоставить в пределах достигнутой точности
найденное решение с решениями, полученными при выполне-
нии заданий 1.1 и 1.2.
Задание 2 предусматривает решение системы нелинейных урав-
нений тремя способами: а) методом простой итерации; б) мето-
дом Ньютона; в) с использованием одного из инструментальных
средств.
Примеры программ, реализующих методы простой итерации и
Ньютона, приведены в подразд. 3.5, применение инструменталь-
ных средств рассмотрено в подразд. 3.6. Инструментальные сред-
ства могут быть использованы, в частности, для графического от-
деления корней. Варианты систем нелинейных уравнений приве-
дены в табл. 3.8.
191
Таблица 3.8
Номер варианта Система уравнений Номер варианта Система уравнений
1 1х2 - sinx, = 0; U3+^ = i (xt > 0) 11 jx2 - 7x| +1=0; |х2 - 2х2 + х2 - 2х2 = -1 (Х| > 0)
2 f jc, + 31g X| x? = 0; |2x2 - x,x2 - 5X] = -1 (X| > 0, x2 > 0) 12 |х2 - 0,5 In(X] + 1) = 0; [х2 + х2 - 2х2 = 0 (Х| > 0)
3 x2 + x2 + x2 = 1; 2x2 + x2 _ 4x3 = 0; 3x2 - 4x2 + x32 = 0 (л,, x2, x3 > 0) 13 (—- 2х2 = 0; 11 + 2х2 |Х|2 + х22 = 1 (х, < 0)
4 (x2 + x\ = 1; |x2 - x2 = 0 14 {еЛ! + 2х2 = 4; [х2 + Зх2 = 0 (X, > 0)
5 X| + x2 - 2x2x3 = 0,1; x2 - x2 + 3xjX3 = -0,2; x3 + x2 + 2X|X3 =0,3 15 Гх2 + 1,5 cos(X| - 1) = I; |0,6х22 +0,4xj2 = 1 (х2 > 0)
6 jxi cos X| - x2 = 0; lx,2 + xj = 0 (x, >0) 16 Jx( -sin х2 -cos х2 = 0,8; [х2 -0,02 sin X,2 -0,4х, = 0
7 (x2 - 2х1е"Л| = 0; |x2 + x22 = 1 (x, <0) 17 [tg(xrx2 + 0,2) - 2х! = 0; [0,8х2 +2х22 = 1 "(X, >0)
8 i о .и S' 7 s v 11 ГЧ ГЧ " 1 Л Г-J ГЧ 1 18 fsin(0,5х, + х2) -1,2х, =1; |х2 + х2 = 1 (Х| > 0)
9 lx, - 2 sin X| + x2 = 1; }X|2 + x22 = 1 (x, >0) 19 [cos(x, -2)+х2 = 1; [sin Xj +2х22 = 1,5 (х| >0)
10 x2 + x2 + Xj = 1; < x2 + 2x2 - x3 = 0; 2x2 + 2x2 = 0 (X|,x2 >0,x3 <0) 20 /л/3х1 -2sinx2 -3-У2х2 =0,5; [х2+2х2 =1 (х,>0)
ГЛАВА 4
МЕТОДЫ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
4.1. ПОСТАНОВКА ЗАДАЧИ АППРОКСИМАЦИИ ФУНКЦИЙ
В вычислительной математике нередки случаи, когда одну функ-
цию приходится заменять другой, более простой и удобной для
дальнейшей работы. Такую задачу называют аппроксимацией функ-
ций.
Поводом для аппроксимации функции может послужить, в
частности, табличный способ ее задания. Предположим, что в
результате некоторого эксперимента для конечного набора значе-
ний х, величины х из отрезка [a; Z>]
а = х0 < х( < ...Xi... <х„ = b
получен набор значений у, величины у (табл. 4.1). Если допустить,
что между х и у существует функциональная зависимость у = Дх),
можно поставить вопрос о поиске аналитического представления
функции F (очевидно, что в такой общей постановке эта задача
решается неоднозначно). Точки хо,Х|..х„ в этом случае называ-
ются узлами. Если расстояние Л = х/+|-Х/ является постоянным
(т.е. независящим от /), то сетка значений, представленная
табл. 4.1, называется равномерной.
Т а б л и и а 4.1
X -Ч| *1 *2 ... X, ... Хп
Дх) Уо У1 Ут ... У( ... Уп
Повод для аппроксимации может возникнуть даже тогда, ког-
да аналитическое выражение для некоторой функции у= F(x) име-
ется, однако оно оказывается мало пригодным для решения по-
ставленной задачи, потому что операция, которую требуется осу-
ществить над этой функцией, трудновыполнима. Элементарный
пример — вычисление значения трансцендентной функции «вруч-
ную», Действительно, чтобы вычислить, например. In 3,2756, про-
ще всего воспользоваться степенным разложением функции , т.е.
заменить трансцендентную функцию степенной. При этом полу-
чится, разумеется, приближенное значение функции, но если мы
7 Лаичик
193
умеем контролировать погрешность, то можно считать, что мы
получили интересующий нас результат — хотя бы потому, что в
реальности все равно приходится ограничиваться приближенным
представлением значений логарифмической функции.
Другая ситуация, когда может потребоваться аппроксимация
аналитически заданной функции, — вычисление определенных
интегралов. Задача эта, как правило, весьма сложная, часто эле-
ментарными приемами невыполнимая. Как вычислить интеграл
2 •
[----<7х? Он, несомненно, существует, но по формуле Ньюто-
। Л'
на—Лейбница вычислен быть практически нс может, так как пер-
вообразная J---ах не выражается в элементарных функциях (как
и множество других первообразных от элементарных функций).
Аппроксимация подынтегральной функции — один из возмож-
ных приемов (и важно отметить, что цель аппроксимации налага-
ет отпечаток на ее способ).
Классический подход к численному решению подобных задач
заключается в том, чтобы, опираясь на информацию о функции Д,
по некоторому алгоритму подобрать аппроксимирующую функ-
цию G, в определенном смысле «близкую» к F.
Чаще всего задача аппроксимации решается с помощью мно-
гочленов. Вычисления значений многочлена легко автоматизиро-
вать, производная и интеграл от многочлена, в свою очередь,
также являются многочленами. Наряду с многочленами для ап-
проксимации используют ряды Фурье, экспоненциальные и дру-
гие элементарные функции.
Для оценки «близости» функций выбирают тот или иной кри-
терий согласия. Эти критерии основаны на использовании той или
иной метрики, т. с. способа введения расстояния между функциями,
принадлежащими тому или иному классу: р = p(F(x), 6(х)) (см. гл. 2).
Например, для функций, ограниченных на отрезке [д; />], рас-
стояние может быть введено следующим образом: р(Д(х),(7(х)) =
= max|F(x) - 6(х)1; для функций, непрерывных на отрезке [а; А], по
|я; /'1 k к
b ° 2
формуле р(х,у) = J|F(x)-G(x)|Jx или р(х,у) = J[F(x)-<?(х)] dx
(а также многими^другими способами).
Для функций, заданных таблично, достаточно распространен-
ным критерием согласия является критерий Чебышева, который
определяет расстояние р между аппроксимируемой и аппрокси-
мирующей функциями как максимум величины отклонения меж-
ду этими функциями в узлах сетки (см. табл. 4.1):
р = maxj£(x,)-G(x;)|. (4.1)
194
Если р = О, т.е. Г(х/) = (7(х,) = у,, то соответствующий способ
аппроксимации называют интерполяцией, а процедуру вычисле-
ния значений F(x) с помощью G(x) в точках, не являющихся
узлами сетки, — интерполированием.
С геометрической точки зрения график функции G(x) при ин-
терполировании должен проходить через все точки Л)(хо,Уо)>
Д(Х|,Я),..., Ап(хп,у„). Подчеркнем, что для значений х, не явля-
ющихся узловыми, значения функции G(x) ничем не регламен-
тированы, и в принципе могут значительно отличаться от значе-
ний функции F(x)).
Часто процедура аппроксимации связана с другим критерием
согласия:
р = min £ [F(x,) - G(x,)f. (4.2)
' 1-0
Применяемый на его основе способ аппроксимации получил
название метода наименьших квадратов.
Выбор критерия согласия позволяет строить методы, позволяю-
щие однозначно определять параметры аппроксимирующей функ-
ции (если задан ее вид).
Контрольные вопросы
1. В каких случаях может потребоваться аппроксимация функции?
2. Какими критериями пользуются для определения «близости* функ-
ций? На каких критериях основываются интерполяция и метод наимень-
ших квадратов?
Упражнения
I. Функции заданы аналитически: F(x) = х1 - 3, G(x) = |х|. Определить
расстояние между ними на отрезке (-3, 5], пользуясь тремя различными
критериями согласия.
2. Функции F{x) и G(x) заданы таблично:
1 2 3 4 5 6 7 8 9 10
Лх) 0,25 0,28 0,33 0,45 0,65 0,78 0,91 1,09 1,34 1,45
б(х) 3,65 4,56 6,72 8,94 7,40 6,73 5,87 3,34 2,67 0,18
Определить расстояние между ними, пользуясь критериями, указан-
ными в тексте подразд. 4.1.
4.2. СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ
ИНТЕРПОЛЯЦИОННОГО МНОГОЧЛЕНА
Пусть известные значения некоторой функции F(x) образуют
таблицу вида табл. 4.1. Будем решать задачу интерполирования этой
195
функции с помощью построения интерполяционного многочле-
на и-й степени
G(x) = + atx + а2х2 +... + айх”, (4.3)
который в узлах х, принимает табличные значения ур.
G(x0) = у0, G(Xi) - у„ ..., G(x„) = у„. (4.4)
Условия интерполяции (4.4) приводят к системе из п + 1 ли-
нейных алгебраических уравнений с п+ 1 неизвестными — коэф-
фициентами многочлена:
+ д,а-0+... + д,Х =у0;
au + OjX] + ... + а„х” =
(4-5)
й0+Д|Л-„ + ... + а„хп„ = у„.
Решая эту систему относительно неизвестных о0, at, ..., а„, мы и
получим аналитическое выражение полинома (4.3). Система (4.5)
всегда будет иметь единственное решение, поскольку ее опреде-
литель. известный в алгебре как определитель Вандермонда
х0 х02 ... х
Х[ X2 ... X'
х„. х;- ... х;
составленный из попарно различных значений элементов х, (а раз-
личными они в данной ситуации будут всегда), не равен нулю.
Отсюда и вытекают существование и единственность решения си-
стемы (4.5) и, следовательно, многочлена (4.3). -
Совершенно очевидно, что интерполяционный многочлен
меньшей степени, вообще говоря, не существует5, а большей су-
ществует, но не единственен. Поэтому интерполяция стандартно
производится многочленами, степень которых на единицу мень-
ше числа узлов.
Описанный прием можно использовать и для практического
решения задачи построения интерполяционного многочлена: до-
статочно составить и решить систему вида (4.5) и подставить най-
денное решение в (4.3). Такой путь, невзирая на громоздкость
вычислительных действий, которые надо произвести для реше-
ния большой системы линейных уравнений (и — что особенно
1 Разумеется, может случиться, что какие-то коэффициенты в С(х), в том
числе и равны нулю.
196
неприятно — при угрозе потери устойчивости механизма учета
вычислительной ошибки, которая неизбежно возникает с возрас-
танием числа производимых операций), в принципе при исполь-
зовании современных вычислительных средств вполне может быть
применен. Вместе с тем для многочленной интерполяции суще-
ствуют более эффективные приемы, описанные ниже, которые
позволяют обойти решение систем уравнений при построении
интерполяционных многочленов.
Контрольные вопросы
!. На чем основывается доказательство существования и единствен-
ности интерполяционного многочлена для таблично заданной функ-
ции?
2. Какой алгоритм вычислений коэффициентов интерполяционного
многочлена вытекает из этого доказательства?
Упражнение
Для таблично заданной функции
V 0,025 1,327 2,834 3,576 4,396
Лх) -3,298 0,386 2,935 4,129 1,637
построить интерполяционный многочлен путем решения системы ли-
нейных уравнений вцда (4.5). Произвести проверку полученного резуль-
тата, вычислив и сопоставив узловые значения функции. Указание: для
решения системы воспользоваться программами, описанными в гл. 3,
или одним из инструментальных пакетов.
4.3. ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН ЛАГРАНЖА
Пусть функция F(x) задана табл. 4. [. Построим многочлен L„(x),
степень которого не выше, чем /?, и для которого выполнены ус-
ловия интерполяции
Л,(х0) = Уо, L„(xi) = yl.... Lll(x„) = y„. (4.6)
Булем искать L„(x) в виде
4(Х) = /0(х) + /,(х) + ... + /,, (X), (4.7)
где /,(х) — многочлен степени п, причем
«хц- Г ссли/ = '‘;
| 0, если i * к.
(4-8)
Очевидно, что требование (4.8) с учетом (4.7) вполне обеспе-
чивает выполнение условий (4.6).
197
Многочлены li(x) составим следующим образом:
/;(л) = Су(х-х0)(х-х1)-...-(х-х,_1)(х-Ху+|)-...-(х-х„), (4.9)
где С; — коэффициент, значение которого найдем из первой ча-
сти условия (4.8):
С; =--------------------*-------------------- '
(Ху - Хо) •• (Xi - Ху„| )(Х; " Ху+1) •... • (Xi - х„)
(заметим, что ни один множитель в знаменателе не равен нулю).
Подставим С,- в (4.9) и далее с учетом (4.7) окончательно имеем:
L ( ) = у (х - х0 )-...• (х - x,-t )(х - X,tl )•• (X ~ Х„)
(х, -X0)-...-(xf -Xy.jXX; — Х,+| )•-..• (Ху -*л)’
(4.10)
Это и есть интерполяционный многочлен Лагранжа. По таблице
исходной функции /’формула (4.10) позволяет довольно просто
составить «внешний вид» многочлена.
Пример 4.1. Построить интерполяционный многочлен Лагран-
жа для функции, заданной таблицей значений:
X 1 3 4
Дх) 12 4 6
Из таблицы следует, что п = 2 (т. е. степень многочлена будет не
выше 2); здесь х0 = 1, х( =3, х2 =4. Используя формулу (4.10),
получаем
(х-3)(х-4) „(х-1)(х-4) (х-1)(х-3) _
(1-3)(1-4) (3-1)(3-4) (4-1)(4-3)
= 2(х2 - 7х + 12) - 2(х2 - 5х + 4) + 2(х2 - 4х + 3) -
= 2х2 -12х + 22.
Используя обозначение (х) = (х хр)(х-Х])-... (х-х„),
формуле (4.10) можно придать более сжатый вид. Для этого про-
дифференцируем Оп+1 по х:
п:+, ‘ ~ )-•(*- *„)•
7=1
При х = xf имеем (I = 0, 1, ..., и):
П« + | (х.) = (Xi - Хо) ... • (Ху - Ху„, )(ху - х(+1) •... • (Ху - х„).
Тогда формула Лагранжа (4.10) принимает вид
я ГТ (х)
=
(X - Ху)П,,+1<Х' )
198
Контрольные вопросы
]. В какой форме строится интерполяционный многочлен Лагранжа?
2. Как используется при выводе формулы Лагранжа требование со-
впадения его значений со значениями исходной функции в узлах?
»
Упражнение
Для функции, заданной таблицей
X 0,12 . 2,32 2,83 4,57 6,39
р(х) -4,29 0,38 2,93 3,72 1,23
составить интерполяционный многочлен Лагранжа (для расчетов вос-
пользуйтесь калькулятором). Произведите проверку полученного резуль-
тата, вычислив и сопоставив узловые значения функции.
4.4. ОРГАНИЗАЦИЯ РУЧНЫХ ВЫЧИСЛЕНИЙ
ПО ФОРМУЛЕ ЛАГРАНЖА
Непосредственное применение формулы Лагранжа приводит к
большому числу однотипных вычислений. Организация вычисле-
ний существенно улучшается, если пользоваться специальной
вычислительной схемой.
В табл. 4.2 показано построение такой схемы для 4 узлов (/ = О,
1, 2, 3). Таблица составляется заново для каждого нового значе-
ния аргумента х.
Заполнение таблицы начинается с того, что вычисляются и
заносятся в соответствующие клетки все элементарные разности.
Вслед за этим вычисляются произведения Р, разностей по стро-
кам:
Ро =(х- х0)(х0 - Х])(х0 - х2)(х0 - х3);
Р = (х, -х0)(х-х1)(х| -х2)(х, -л3) и т. д.
Таблица 4,2
А А'о Л’! *2 *3 л у,- yJPi
Хо Х-Хо Х0~Х| Хо - х2 х0 - Хз
-V| х ( - х0 Х“Х[ X] - х2 Х| - х3
Х2 х5 - х0 х2 - X] Х-Л'2 х2 - х3
-И *3 - *0 *3 “ Х| х3-х2 Х-Хз
199
Легко видеть, что использованное в табл. 4.2 обозначение Р, —
это знаменатель в формуле Лагранжа (4.11), т.е.
//=(х-х;)П'+1(^) (/= 0, 1, ..., л).
С учетом этого обозначения формула Лагранжа имеет вид
AW = ELi^Sy-
/=о Л
Все необходимые значения последовательно получаются в таб-
лице. Сумма 5образуется сложением элементов последнего столб-
ца. Для получения окончательного значения Т„(х) достаточно ум-
ножить 5 на произведение (х) (произведение диагональных
разностей таблицы).
Пример 4.2. Имеется таблица значений некоторой функции:
X /(х) X /(х)
0,41 1,55 2,63 3,75 2,67 3,84 4,87 5,03
Требуется получить значение этой функции в точке х= 1,91,
пользуясь интерполяционным многочленом Лагранжа.
Вычисления приведены в табл. 4.3. Для нахождения окончатель-
ного результата сумма значений последнего столбца умножается на
произведение диагональных разностей:
/(1,91) = 0,792-5,241 = 4,15.
Таблица 4.3
х = 1,91 Хо Х| х2 Л У>/Р;
хь 1,50 -1,14 -2,26 -3,43 -13,26 2,63 -0,198
1,14 0,36 -1,12 -2,29 1,05 3,75 3,561
*2 2,26 1,12 -0,76 -1,17 2,25 4,87 2,163
*3 3,43 2,29 1,17 -1,93 -17,74 5,03 -0,284
5,242
Контрольные вопросы
1.Как составляется расчетная таблица для ручных вычислений по
формуле Лагранжа?
2. Может ли одна и та же таблица использоваться для повторных вы-
числений (для другого значения аргумента)?
200
Упражнение
Функция задана таблицей:
X 0,12 2,32 2,83 4,57 6,39
/(-V) -4,29 0,38 2,93 3,72 1,23
Вычислить значения этой функции в точках: а) х= 1,36; б) х = 5,82,
используя схему ручных вычислений по формуле Лагранжа (для расчетов
воспользоваться калькулятором).
4.5. ПРОГРАММИРОВАНИЕ ИНТЕРПОЛЯЦИОННОГО
МНОГОЧЛЕНА ЛАГРАНЖА
Рассмотрим способ программной реализации алгоритма вы-
числений по формуле Лагранжа. Для составления программы вы-
числения одного значения интерполяционного многочлена Лаг-
ранжа на ЭВМ воспользуемся формулой (4.10). Основная рабо-
чая часть алгоритма состоит из двойного цикла: во внутреннем
цикле вычисляются п + 1 значений многочленов слагаемых
вида (/ = 0, 1, ..., л)
f = (х - Хр) • ... - (х - х,,)(х - Х,+| )•...- (х - х„)
(*,' - Х0) (.Xi - Х;_[)(Х/ - Х/+1)-...- (X; - Х„)
(в числителе и знаменателе п скобок), а во внешнем — накапли-
вается общая сумма: £„(х) = у/Дх). Блок-схема алгоритма изо-
бражена на рис. 4.1. '"°
Работа внутреннего цикла контролируется с помощью индекса j.
Изменяясь в пределах от 0 до п, индекс j принимает ровно п зна-
чений, «проскакивая» текущее значение индекса /, определяемо-
го во внешнем цикле. Тем самым обеспечивается правильное со-
ставление многочленов — слагаемых формулы Лагранжа. Носите-
лем окончательного результата является переменная f
Ниже приведена программа вычисления значения f с помо-
щью интерполяционной формулы Лагранжа на языке Turbo Pascal.
Ввод исходной таблицы происходит в цикле, причем массивы
значений х и у вводятся не последовательно, а парами соответ-
ствующих элементов.
program Lagrang;
uses ert; •
type mus=array[0. . 10] of real;
label 1;
var x,y:mus;n,i,j:integer;
a, 1, f:real;
201
begin
clrscr;
writcln('Задайте степень многочлена');
readln(n);
writein ('Введите значение аргумента, для которого');
writeln(1 требуется найти значение функции');
readln(а);
writeln('Введите пары значений х и у через
пробел');
for i:=0 to n do read(x[i],у[i]);
f :=0;
for i:=0 to n do
begin
j:=0;
1 :=1;
l:if i=j then inc(j);
if j<=n then begin
1:=1*(a-x[j])/(x[i]”x[j]);
inc(j); goto 1;
end;
l:=y[i]*i;
f:=f+l;
end;
writeln('IlpH a=’,a:5:2,' f (’, a: 5:2, ' ) = ’,f:5:2);
readkey;
end.
Примср работы программы для функции, заданной таблицей
из примера 4.2:
Задайте степень многочлена
3
Введите значение аргумента, для которого
требуется найти значение функции
1.91
Введите пары значений х и у через пробел
0.41 2.63
1.55 3.75
2.67 4.87
3.84 5.03
При а=1.91 f(1.91)=4.15
Контрольные вопросы
I. Каким образом в алгоритме вычисления по формуле Лагранжа ре-
ализуется исключение 7-й скобки в числителе и знаменателе 7-го много-
члена-слагаемого?
202
Начало
Рис. 4.1. Блок-схема алгоритма метода Лагранжа
2. Как следует изменить описанную в подразд. 4.5 программу, чтобы:
а) результат интерполяции выводился с максимальной машинной
точностью;
б) при получении значения многочлена Лагранжа предусматривался
учет вычислительной ошибки на основе заданной точности табличных
данных?
203
Упражнение
Функция задана таблицей:
Л' 0,12 2,32 2,83 4,57 6,39
Ях) -4,29 0,38 2,93 3,72 1,23
Вычислить значения этой функции в точках:
а) л- = 1,36; б) х = 5,82,
используя программу интерполирования по формуле Лагранжа.
4.6. ИНТЕРПОЛЯЦИОННЫЕ ФОРМУЛЫ НЬЮТОНА
Рассмотрим другой способ построения интерполяционного
многочлена. При этом, однако, не следует забывать, что по за-
данной таблице, содержащей значения функции в п + 1 узлов,
интерполяционный многочлен я-й степени единственен (см. под-
разд. 4.2), и поэтому «новые* интерполяционные многочлены от-
личаются от построенного по той таблице многочлена Лагранжа
лишь внешним видом.
Тем не менее, они представляют ценность, поскольку вид (т.е.
форма записи) многочлена определяет порядок и объем вычисле-
ний, что в численных методах существенно.
Часто интерполирование ведется для функций, заданных таб-
лицами с равноотстоящими значениями аргумента. В этом случае
шаг таблицы h = x',+, -xf (/=0, 1, 2, ...) является величиной по-
стоянной.
Для таких таблиц построение интерполяционных формул за-
метно упрощается, и мы ограничимся получением интерполяци-
онных формул Ньютона лишь для этого случая.
4.6.1. Конечные разности
Пусть функция задана таблицей вида табл. 4.1 с постоянным
шагом. Разности между значениями функции в соседних узлах ин-
терполяции называются конечными разностями первого порядка:
Ау,- = У,и-У, (' = 0, 1, «-!)•
Из конечных разностей первого порядка образуются конечные
разности второго порядка
Д2у,- = Ау,+1 - &у, (i= 0, 1, 2).
Продолжая этот процесс, можно по заданной таблице функ-
ции составить таблицу конечных разностей (табл. 4.4).
Конечные разности любого порядка могут быть представлены
через значения функции. Действительно, для разностей первого
204
Таблица 4.4
-Vo Уо Дуо
*1 У1 ДУ1 Д2Уо
Xi У2
Хп-1 Ул-1 ДУл-1 Д2Ул-2
У. Ул
ДяУо
порядка это следует из определения. Для разностей второго по-
рядка имеем
Д2У = Ду+i - Ду = (У+2 - Ун) - (Ун - У) = У,42 - 2у/+, + у.
Аналогично для разностей третьего порядка
Д3У = Д2У/+1 - Д2У/ = (У,43 - 2У/42 + Уг+|) - (Уо-2 - 2у,4, + У, ) =
= У+3 - Зу+2 + Зу+1 - у.
Методом, математической индукции можно доказать, что
Д*У =y,4i -^У+А-1 + -У+л-2 - ...+ (-!)*у. (4.12)
4.6.2. Первая интерполяционная формула Ньютона
Пусть для функции, заданной таблицей с постоянным шагом,
составлена таблица конечных разностей (см. табл. 4.4). Будем ис-
кать интерполяционный многочлен в виде
?„(х) =о0+а|(х-л-о) + й2(х-х0)(*-*1)+
, ч . (4.13)
+ ... + 47л(х-Хо)-...-(Х-Х„_|).
Это — многочлен /г-й степени. Значения коэффициентов
<70, г7(,..., а„ найдем из условия совпадения значений исходной
функции и многочлена в узлах.
Полагая х = хб, из (4.13) находим у = Л(х0) = я0, откуда а$ =у.
Далее, полагая х = Х[, получаем
у, = Д(у) - Go +Gj(X[ — х0), откуда а, = byQlh.
При х = л'2 имеем
205
У? = Лг(х2) = + а, (х2 - х0) + а2(х2 - х0)(х2 - Х(),
т.е. у2 - 2Лу0 - у0 = 2/i2a2, или у2 - 2у( + у0 = 2h2a2,откуда
о2 = tfyfjlh1.
Проведя аналогичные выкладки, можно получить = Д3уо/З!й3.
Исходя из этих формул, методом полной математической ин-
дукции можно доказать, что в общем случае выражение для ак
будет иметь вид
Подставим теперь (4.14) в выражение для многочлена (4.13)
Рп(х) = Уо +^(Х-Хо) + ~Д(Х“Х[))(Х-Х1) + ...
h 2\h2
Л” v
+ -777(х-х(|)-...-(х~хл_1). (4.15)
л!й
Часто эта формула записывается в несколько ином виде. Вве-
х - х0
дем вместо переменной х новую переменную t: -------- = t, или,
h
. . ~ Х-Хг х - х0 - й , . х - х2
напротив, х = х0 + М. Тогда -----L-------у--= /-1, ----- =
h h h
= x——2Й = { _ 2 и т д После этого формула (4.15) примет вид
й
Рл(х) = Р„(х0+/й) =
,д /(Г-1) t(t - 1) •... • (t - п + 1) Л „ (л 1<'1
= Уо + ttyo + -ЧгН дУо + - + ------г------- Л Уо 1
2! л!
Формула (4.16) называется первой интерполяционной формулой
Ньютона.
Эта формула традиционно применяется для интерполирова-
ния в начале отрезка интерполяции, для значений / в интервале
(О, 1). Первую интерполяционную формулу Ньютона называют по
этой причине формулой для интерполирования вперед. Заметим,
что путем переопределения узлов за начальное значение х0 мож-
но принимать любое табличное значение аргумента х (отбросив
«лишние» узлы слева).
Пример 4.3. Построить интерполяционный многочлен Ньюто-
на по следующим данным:
X 0,5 1 1,5 2 2,5
У [,715 2,348 3,127 5,289 8,914
206
Построим таблицу разностей:
Л' У Ду &~У Л’у д4у
0,5 1,715
0,633
1 2,348 0,146
0,779 1,237
1,5 3,127 1,383 -1,157
2,162 0,080
2 5,289 1,463
3,625
2,5 8,914
Таким образом, многочлен Ньютона, представленный в фор-
ме (4.15), имеет вид
,, , , , - 0,633 , 0,146 , „
(х) = 1,715 + (х - 0,5) + 2;(х - 0,5)(х -1) +
I 737 1 I57
+ (X - 0,5)(х - 1)(х -1, 5) - (х - 0,5)(х~ 1)(х - 1, 5)(х - 2) =
= 1,715 + 1,266(х - 0,5)+0,292(х - 0,5)(х I) +
+1,649(х - 0,5)(х - 1)(х -1,5) - 0,771(х - 0,5)(х - 1)(х-1,5)(х - 2).
Представим тот же многочлен в форме (4.16). Введем перемен-
х - хп х 0,5
ную t = —’ и получим
Р4(0,5 + 0,5?) = 1,715 + 0,633г + ^^/(/-l) + ^|y/(Z-l)(Z-2)-
1 157
-^/(/-W-2)(/-3).
4.6.3. Вторая интерполяционная формула Ньютона
Когда значение аргумента находится ближе к концу отрезка
интерполяции, применять первую интерполяционную формулу
становится .невыгодно.
В этом случае применяется формула для интерполирования на-
зад — вторая интерполяционная формула Ньютона, которая ищет-
ся в виде
Л(х) = о0+П|(х-х„)+<72(х-х„)(х-х;,_|)+...+а„(х-х„)-....(х-х1). (4.17)
207
Как и для первой формулы Ньютона, коэффициенты а0, ait
а„ находятся из условия совпадения значений функции и интер-
поляционного многочлена в узлах
&ку„-к
Подставляя (4.18) в (4.17) и переходя к переменной
получим окончательный вид второй интерполяционной формулы
Ньютона:
№) = Р,(х,+<*) = у,+<дх„., + у/ +
+ ^(1П).....« + Д-1>Д,№ (419)
л!
Контрольные вопросы
I. Как находятся конечные разности различных порядков через зна-
чения функции в узловых точках?
2. Почему первую интерполяционную формулу Ньютона нецелесо-
образно применять для интерполирования в конце отрезка интерполя-
ции, а вторую — в начале отрезка интерполяции?
Упражнения
I. Для таблично заданной функции
А' /(х) X /(х)
1,62 8,14 1,65 7,21
1,63 8,02 1,66 6,54
1,64 7,93 1,67 5,01
вычислите значения конечных разностей до третьего порядка включи-
тельно и составьте интерполяционные формулы Ньютона (принять Хо =
= 1,62, - 1,67). Вычислите для контроля значения интерполяционных
многочленов соответственно в точках 1,63 и 1,66; сопоставьте получен-
ные значения с табличными (для вычислений используйте калькуля-
тор).
2. Составьте программу интерполирования по формулам Ньютона.
4.7. ПОГРЕШНОСТЬ МНОГОЧЛЕННОЙ ИНТЕРПОЛЯЦИИ
Если известно аналитическое выражение интерполируемой функ-
ции /(х), то можно получить формулу для оценки погрешности
интерполирования (погрешности метода). Остаточный член интер-
поляционного многочлена Fn(x) имеет вид: Я„(х) = /(х) - F„(x).
208
Предположим, что f(x) имеет все производные до (п + 1)-го
порядка включительно. Введем вспомогательную функцию
«(*) = f(x) - F„(x)~ К- П„+1 (х), (4.20)
где К - постоянный множитель. Как видно, функция w(x) имеет
п + 1 корень (узлы интерполяции х0, хь ..., хк). Подберем коэффи-
циент К так, чтобы н(х) имела (п + 2)-й корень в любой точке
х* * Х( (i = 0, 1, ..., и). Действительно, чтобы было ы(х‘) = 0, т.е.
/(x*)-F(x-) - Кр[л+](х*) = 0, достаточно принять:
к f(x*)-Fn(x*)
П,+1(*)
(4-21)
При этом значении К функция н(х) будет иметь и + 2 корня на
отрезке интерполирования и будет обращаться в нуль на концах каж-
дого из отрезков: [х0; xj], [xt; х2], ..., [х,-; х‘], [х’; xf+i], ..., [x„_j; х„]
(всего отрезков п+ 1).
Применяя теорему Ролля к функции и(х) на каждом из этих
отрезков, убеждаемся в том, что w'(x) имеет не менее п + 1 кор-
ней; далее, применяя ту же теорему к производным, последова-
тельно получаем
и*(х) имеет не менее п корней;
H(Btl)4x) имеет не менее одного корня.
Пусть с, — та самая точка, в которой w(fl+1)(Q = 0. Продиффе-
ренцируем (4.20) «+1 раз: u</i+1)(x) = /(л,1)(х) - К (л +1)!, откуда
/('|+|>(х)~ы<',+1’(х) .
К = -------—-----------—, а при х = £
(л + 1)!
к =
(«4-1)1 ’
Сравнивая (4.21) и (4.22), имеем
Г<"+1>(Е)
/(х*)-/;(х*) = 4—
(п +1)!
Но точка х* — произвольная (правда, £. от х* зависит), поэто-
у(л+1)(£)
му можно написать: Дх) F„(x) = ---------— ГТ л+] (х). Таким обра-
(л + 1)!
зом, если принять Мл+1 = шах |Д',+1) (х)|, то
Хл<Х<Х.. * ।
(4-22)
Мп+{
(п +1)!
(4.23)
209
Оценочная формула (4.23) непосредственно применима для
подсчета погрешности метода интерполирования по формуле Лаг-
ранжа. Используя подстановки / = ——и t = -—— и заменяя
h h
соответствующим образом выражение для (х), можно полу-
чить из (4.23) формулы оценки погрешностей интерполирования
по первой и второй интерполяционным формулам Ньютона
Ь"+1 м
|7?„(х)| < - D(/' 2)' - (Г - «)|; (4-24)
/,и+1 м
(х)| + W + 2) -... • (/ + п)\. (4.25)
(И + 1) ’
Анализ интерполяционных многочленов Лагранжа и Ньютона,
а также оценочных формул (4.23) —(4.25) позволяет сделать по-
лезные практические выводы [2, 5, 12].
Решающее влияние на значение погрешности оказывает вели-
чина (х), которая минимизируется, когда х берется в сере-
дине интервала узловых точек. При этом, когда х ближе к середи-
не между двумя узловыми значениями, выгодно взять четное чис-
ло п - 7т узлов (т узлов слева и т справа от х). Если же х близко к
одному из узловых значений, следует использовать нечетное чис-
ло п = 2т + 1 узлов — узел, ближайший к х и по т узлов слева и
справа от него.
Очевидно, что при составлении интерполяционных формул
Ньютона последние слагаемые практически исчезают, если соот-
ветствующие конечные разности — нули или близкие к нулю чис-
ла. Поэтому в практических вычислениях интерполяционные фор-
мулы Ньютона обрывают на членах, содержащих такие разности,
которые в пределах заданной точности можно считать постоян-
ными.
Связь между конечными разностями и точностью интерполи-
рования по формулам Ньютона подтверждается следующими со-
ображениями. Принимая во внимание, что при малых значениях h
и при условии непрерывности/(пИ)(х) можно приближенно счи-
тать [2, 5] м = ——- где Д"+1у = max 1д',+1у,п| (т.е.Д"+1у — мак-
л*1 Дл+1 ’ 1
симальная из модулей конечных разностей (/?+ 1)-го порядка). При
этом условии оценки (4.24) и (4.25) остаточных членов первой и
второй интерполяционных формул Ньютона принимают следую-
щий вид:
\t(t - !)(( - 2) -...-(/- л)|
R„ (х) = J------——---------L Ду; (4.26)
(л + 1)!
210
' 1 (л + 1)!
(4.27)
Формулы (4.26) и (4.27) удобны тем, что позволяют делать оцен-
ку ошибки метода интерполирования без исследования (л + 1)-й
производной интерполируемой функции f (в частности, когда
аналитическое выражение f вовсе неизвестно).
На окончательную погрешность интерполирования влияет и
вычислительная погрешность. Как можно было видеть ранее (см. гл.
2, 3), полное исследование этих вопросов доставляет немало труд-
ностей. Обращаясь к оценке точности интерполирования, в дан-
ном случае, как и ранее, приходится вполне обоснованно при
использовании всех возможностей современных вычислительных
средств предполагать, что машинная точность реализации вычис-
лений существенно выше задаваемой точности интерполирова-
ния, и что, следовательно, оценка погрешности многочленной
интерполяции может сводиться только к оценке погрешности
метода.
Контрольные вопросы
1. Как производится оценка погрешности метода интерполяции в сле-
дующих случаях: а) интерполируемая функция задана аналитически; б)
интерполируемая функция задана таблично?
2. Какие рекомендации по выбору начальных узлов интерполяции
вытекают из формул оценки погрешностей метода интерполирования?
Упражнения
1. Имеются табличные значения синуса:
X sinx sinx
0,3 0.4 0,5 0,6 0,295520 0,389418 0,479426 0,564642 0,7 0,8 0,9 0,644218 0,717356 0,783327
Составьте таблицу конечных разностей и, используя интерполяцион-
ные формулы Ньютона, найдите значения синуса для следующих про-
межуточных значений х: 0,55; 0,61 (при составлении интерполяционных
формул воспользуйтесь рекомендациями, минимизирующими величину
погрешности метода). Сделайте оценки погрешностей полученных зна-
чений (для вычислений используйте калькулятор или один из инстру-
ментальных пакетов). Сопоставьте значения, найденные интерполирова-
нием, с соответствующими значениями синуса, полученными с помо-
щью многоразрядного вычислительного средства.
Проанализируйте адекватность полученных выше оценок погрешно-
стей метода интерполяции.
211
2. Усовершенствовать программу интерполирования по методу Нью-
тона (см. упражнение 2 к и. 4.6.3), введя оценку погрешности метода по
формулам (4.26) и (4.27).
4.8. МИНИМИЗАЦИЯ ПОГРЕШНОСТИ
МНОГОЧЛЕННОЙ ИНТЕРПОЛЯЦИИ ПУТЕМ СПЕЦИАЛЬНОГО
ВЫБОРА УЗЛОВ ИНТЕРПОЛЯЦИИ
Для анализа способов уменьшения погрешности интерполиро-
вания многочленом заданной степени п обратимся к формуле (4.23).
Входящая в нес величина Мп + । определяется всецело интерполи-
руемой функцией /(х) и не подлежит воздействию со стороны
процедуры интерполяции. Однако величина
|П„+iМ = К* “ А'о)<* -Х1)--(х-х„)| (4.28)
зависит при фиксированном значении х от выбора узлов интерпо-
ляции. Хотя в приведенных выше примерах для простоты исполь-
зовалась интерполяция по равноотстоящим узлам, ниоткуда не
следует, что этот способ оптимален с точки зрения минимизации
погрешности. Задача минимизации путем соответствую-
щего подбора узлов интерполяции решена известным русским ма-
тематиком П.Л.Чебышевым (1821 — 1894).
Ключевую роль в решении этой задачи играют так называемые
> многочлены Чебышева
ТДх) = cos[y? arccos(x)] (/? = 1, 2, ...) (4.29)
(область определения каждого из них — отрезок [-1; 1]). Несмотря
на формальное наличие в определении многочленов Чебышева
тригонометрических функций, на самом деле это обычные алге-
браические многочлены, в чем легко убедиться, йспользуя эле-
ментарные формулы для тригонометрических функций. Так, оче-
видно, что 7](х) = х. Используя тригонометрическое тождество
cos(h + 1)0 = 2 cos 9 cos hQ - cos(/? -1)0,
легко получить рекуррентную формулу для построения многочле-
нов Чебышева любого индекса.
Г,н Дх) = 2x7; (х)-ТлЧ(х). (4.30)
Из нее, в частности, следует:
Т2(х)=2х3-1,Т3(х)=4х3 -Зх, Т4(х)=8х4~8х2 +1, Т5(х) = 16х5-20х3 +5х
и т.д.
Тригонометрическая форма представления многочленов Чебы-
шева (4.29) очень удобна для нахождения корней этих многочле-
212
нов, играющих основную роль в решении проблемы минимиза-
ции величины (4.28). Из уравненияcosp?-arccos(x)]=0 не-
медленно следует выражение для корней многочлена Чебышева
индекса п
(2т + 1)л
Хт =COS-—^-(m = o 1 .. „).
2п
(4.31)
Решение рассматриваемой проблемы содержится в следующей
теореме.
При выборе в качестве узлов интерполяции на отрезке [-/; 7]
корней многочлена Чебышева Tnti(x) величина |П„.|(Х)| (4-28) име-
ет наименьшее возможное значение по отношению к любому другому
выбору узлов интерполяции (с тем же числом узлов).
Доказательство этой теоремы приводить не будем (см., напри-
мер, [3]). Из него дополнительно следует, что при использовании
в качестве узлов интерполирования корней многочленов Чебы-
шева имеет место оценка
1П„ч(А')|5^Г (для любого хе |-1; 1]). От-
сюда получается следующая оценка для погрешности интерполи-
рования при использовании корней многочленов Чебышева:
|Д,(х)
1 2"(л + 1)!
(4.32)
Для перехода от интерполирования с помощью корней много-
членов Чебышева на отрезке [-1; 1] к интерполированию на про-
извольном отрезке [а; Л] достаточно линейным образом отобра-
зить один из этих отрезков на другой. Так, замена переменной
2
[(/>- а)х + (Ь + о)] переводит точки отрезка хе[-1; 1] в точки
отрезка уе [а; 6]. При этом выражение (4.31) для корней много-
членов Чебышева хп, определенных на отрезке [-1; I], переходит
в выражение
У» = | ~ а)х« + (^ + Д)1 (т = °« 1 - •••» л)» (4.33)
определенное на отрезке [й; й].
В табл. 4.5 приведены значения хи для нескольких значений п —
степеней интерполяционных многочленов.
На практике указанный в данном подразделе способ выбора
узлов интерполирования применяется нечасто. Если функция за-
дана таблично, как это было в приведенных выше примерах, то
узлы интерполяции уже заданы самой таблицей; если же интер-
полируется аналитически заданная функция, то относительно
213
Таблица 4.5
Степень интерполя- ционного многочлена Корни многочленов Чебышева х„. (на отрезке [—1; 1])
п = 1 Хо = 0,707106781, X, =-0,707106781
« = 2 х0 = 0,866025404, х, = 0, х2 = -0,866025404
л = 3 х0 = 0,923879533, Х] = 0,382683432, х2 = -0,382683432, х3 = -0,923879533
л = 4 х0 = 0,951056516, X] = 0,587785252, х2 = 0, х3 = -0,587785252, х4 = -0,951056516
л = 5 х0 = 0,965925826, х. = 0,707106781, х2 = 0,258819045, х3 = -0,258819045, х4 =-0,707106781, х5 =-0,965925826
небольшой выигрыш в точности противостоит усложнению алго-
ритма, связанному с нахождением узлов интерполяции по дан-
ному методу.
Контрольный вопрос
Как формулируется задача, приводящая к использованию корней
многочленов Чебышева для интерполяции?
Упражнения
1. Используя рекуррентную формулу (4.30), найти Т6(х) и Т7(х).
2. Найти корни многочлена Г(,(х).
3. Для функции у = х21пх построить на отрезке [2; 4] интерполяци-
онные полиномы Лагранжа 3-й степени:
а) по системе равноотстоящих узлов, включающих концы отрезка;
б) по методу Чебышева.
Оценить погрешность интерполяции в точке х= 2,5, сравнивая точ-
ное значение указанной функции и значения, вычисленные с помощью
полученных многочленов. Которое из приближенных значений точнее и
насколько?
4.9. УПЛОТНЕНИЕ ТАБЛИЦ ФУНКЦИЙ
Интерполирование может применяться для уплотнения табли-
цы задания функции, т.е. вычисления по исходной таблице новой
таблицы с большим числом значений аргумента на прежнем уча-
стке его изменения. Эту операцию называют также субтабулирова-
нием функции. В случае, когда исходная таблица является табли-
214
цей с постоянным шагом, естественно применить интерполяци-
онный многочлен Ньютона. При заданном числе узлов (т.е. при
условии, что конечные разности и степень полинома определены
вручную) для расчетов на ЭВМ формулы Ньютона удобно пред-
ставлять по схеме Горнера. Так, первая интерполяционная форму-
ла Ньютона может быть представлена в виде:
Р„ О) = То + Д ЛУо + ' [ А2 Го + ( Л3Уо + + ~— Л'Э’о Т|- Д (4.34)
I у 3 ( п J) )
Использование схемы Горнера позволяет вычислять значение
Р„(х) в цикле. Если же максимальный порядок используемых
конечных разностей невелик, для вычисления значений Р„(х)
могут использоваться формулы Ньютона в их стандартном виде
(4.16) и (4.19).
Пример 4.4. Дана пятизначная таблица sinx на отрезке [0,15;
0,18] с шагом h = 0,005. Требуется уплотнить эту таблицу с шагом
h = 0,001 на участке [0,155; 0,165].
По исходной таблице составим таблицу конечных разностей
(табл. 4.6). Для сокращения записей конечные разности принято
записывать только значащими цифрами. Замечаем, что конечные
разности второго порядка уже практически близки к нулю в пре-
делах точности таблицы. Поэтому при использовании интерполя-
ционной формулы Ньютона (4.16) ограничимся тремя первыми
слагаемыми
Р„(х) « г0 + t- ДГо + ^7^ Д2Л-
Используя первую формулу Ньютона, в данном случае естествен-
но принять х0 = 0,155. Значение/для каждого значения хнаходит-
ся по формуле } = ———. Блок-схема алгоритма субтабулирова-
h
Таблица 4.6
X sin х 4»’ д2у Д3У
0,150 0,155 0,160 0,165 0,170 0,175 0,180 0,14944 0,15438 0,15932 0,16425 • 0,16918 0,17411 0,17903 494 494 493 493 493 492 0 -1 0 0 -1 -1 1 0 1
215
ния функции на отрезке [я; й] по первой интерполяционной фор-
муле Ньютона при условии, что конечные разности и порядок
полинома определены вручную, показана на рис. 4.2.
Далее приведена программа субтабулирования функции на язы-
ке Turbo Pascal, составленная для примера 4.4 в соответствии с
блок-схемой, изображенной на рис. 4.2. Программа по заданной
таблице функции выводит новую, уплотненную, таблицу со зна-
чениями функции, округленными до шести знаков после запятой.
Кроме того, для вычисляемых значений функции программа вы-
водит также значения соответствующих погрешностей метода,
которые находятся по формуле (4.26). В программе величины а и b
обозначают концы отрезка субтабулирования, h\ — шаг исходной
таблицы, Й2 — шаг уплотненной таблицы, уО — значение функ-
ции в начальной точке субтабулирования (в формуле Ньютона
это Уо)3 у! и у2 — соответствующие (ненулевые) конечные разно-
сти первого и второго порядка.
Все эти значения определяются в программе путем ввода, так
что эта же программа может использоваться для субтабулирова-
ния на других подходящих участках исходной таблицы и с другой
степенью плотности. Граница погрешности метода интерполяции,
Рис. 4.2. Блок-схема алгоритма субтабулирования функции
216
вычисляемая в соответствии с формулой (4.26), в программе обо-
значена е.
program Subtab; (Уплотнение функции, заданной
равномерной сеткой, с применением первой
интерполяционной формулы Ньютона}
uses crt;
var a,b,hl,h2,e,у,yO,yl,y2,t,x:real;
begin
clrscr;
writeln ('Задайте концы отрезка
субтабулирования:1);
readln(a,b);
writeln('Шаг таблицы:');
readln(hl);
writeln('Новый шаг таблицы:');
readln(h2);
writeln(1 Значение функции в начальной точке:');
readln(уО);
writeln('Конечные разности первого и второго
порядков:'); 1
readln(yl,у2);
х: =а;
writeln(' х', ' у' , 1 е1 ) ;
repeat
t: = (х-а) /Ы;
у:=yO+t*yl+t*(t-1)*у2/2;
e:=0.00001*t*(t-l)*(t~2)/6;
writeln(х:б:3,' ’,у:9:б,' ',е:11:8);
x:=x+h2;
until х-(b+h2/10)>0 ;
readkey;
end.
Результаты работы программы:
Задайте концы отрезка субтабулирования:
0.155 0.156
Шаг таблицы:
0.005
Новый шаг таблицы:
0.001 .
Значение функции в начальной точке:
0.15438
Конечные разности первого и второго порядков:
0.00494 -0.00001
217
X У е
0.155 0.154380 0.00000000
0.156 0.155369 0.00000048
0.157 0.156357 0.00000064
0.158 0.157345 0.00000056
0.159 0.158333 0.00000032
0.160 0.159320 0.00000000
0.161 0.160307 -0.00000032
0.162 0.161293 -0.00000056
0.163 0.162279 -0.00000064
0.164 0.163265 -0.00000048
0.165 0.164250 -0.00000000
Интересно заметить, что интерполяция вполне обеспечивает
шесть верных в широком смысле знаков после запятой во всех
полученных в результате субтабулирования значениях функции.
Путем незначительного усложнения программы можно достичь
большей надежности результатов интерполирования по формуле
Ньютона, если предусмотреть при переходе к новому узлу исход-
ной таблицы изменение значений хО, уО и соответствующих ко-
нечных разностей (т.е. каждый встречающийся в процессе субта-
булирования узел исходной таблицы автоматически принимать за
нулевой). Для субтабулирования на концевых участках исходной
таблицы нужное количество конечных разностей в формуле обес-
печивается применением второй интерполяционной формулы
Ньютона. Программа в этом случае составляется аналогично.
Контрольные вопросы
1. Что такое субтабулирование заданной таблично функции?
2. Как удобно преобразовывать интерполяционные формулы Ньюто-
на для циклических вычислений?
Упражнения
1. Уплотнить с помощью программы для компьютера таблицу функ-
ции:
Л' /(*) .V Л-т)
2,65 -3,2456 2,69 12,4348
2,66 -2,8943 2,70 14,3437
2,67 -1,4849 2,71 5.8284
2,68 0,2526 2,72 2,3437
на отрезке (2,66; 2,68] с шагом 0,005, пользуясь интерполяционной фор-
мулой Ньютона. Результат вывести с округлением по оцениваемой в про-
218
грамме погрешности метода (с помощью обращения к модулю okrugl,
см. гл. 1).
2. Сделать представление второй интерполяционной формулы Нью-
тона с помощью схемы Горнера. Пользуясь этим представлением, соста-
вить программу уплотнения заданной выше таблицы функции на участ-
ке [2,71; 2,72) с шагом 0,005.
3. Составить программу субтабулирования по формулам Ньютона,
в которой каждый встречающийся в процессе субтабулирования узел
исходной таблицы автоматически принимается за нулевой (при ин-
терполировании вперед), или конечный (при интерполировании на-
зад).
4.10. ОБРАТНОЕ ИНТЕРПОЛИРОВАНИЕ
4.10.1. Постановка и решение задачи обратного
интерполирования
Рассмотренное выше прямое интерполирование таблично за-
данной функции y=f(x) позволяет, в частности, найти ее значе-
ния в точках, не являющихся узлами интерполяции (в табл. 4.7
одна из таких точек отмечена х‘).
Таблица 4.7
X Хо Х| ... X,- X* xi, | ... Х„
У Уо Л ... Я у Л» 1 ... У„
Как и выше, предполагается естественное упорядочение зна-
чений {х,} по возрастанию.
Можно рассмотреть и обратную задачу. Если значения {у,} в
табл. 4.7 упорядочены по возрастанию или убыванию, то функция
у=/(х) монотонна на промежутке [хь; х„|, и эту же таблицу мож-
но интерпретировать как задание дискретного образа функции
*=ф(У)» обратной по отношению к функции у=/(х). Для этой
обратной функции может быть также поставлена задача интерпо-
лирования: найти значение х’ по заданному значению у*. Эта за-
дача по отношению к исходной называется задачей обратного ин-
терполирования.
Решать ее можно двояко. Если строить на основе данных табли-
цы интерполяционный многочлен для функции х=<р(у), то в ре-
шении задачи.обратного интерполирования нет ничего нового.
Новое появляется в том случае, если для обратного интерполиро-
вания использовать многочлен, построенный для интерполирова-
ния функции y=f(x) (т.е. в данном случае для прямого интерпо-
лирования).
219
Предположим, что узлы {х,} равноотстоящие и образуют сис-
тему с шагом Л и что по данным табл. 4.7 построен один из мно-
гочленов Ньютона (для определенности, первый)
У = Уо +^LU-JCo) + ”7y(x-Ao)(^-X|) +
h 2!Zr
+... + (х - х0) •... (х - х„_,).
п\п
(4.35)
При решении с его помощью задачи обратного интерполиро-
вания в левой части формулы (4.35) возникает известное значе-
ние у*, а сама эта формула становится алгебраическим уравнени-
ем по отношению к х. Если система чисел {>’,-} упорядочена (по
возрастанию или убыванию), то это уравнение имеет единствен-
ное решение на промежутке [xq; х„].
Его решение в общем случае следует искать любым из мето-
дов, описанных в гл. 2. Отметим, что при использовании первого
многочлена Ньютона естественно считать, что у* находится меж-
ду Го иуьт. е. искомое значение х* — вблизи левого конца отрезка
интерполяции.
В случае использования формулы (4.35) наиболее естествен-
ным для такого решения является метод простой итерации. Под-
ставим в (4.35) у - у* и преобразуем получившееся равенство к
виду
1 Гл2Го
АУо [ 2!й
h . . .
х = х0+-г-(у -у0)-
АУо
у
(х - Хо)(х - X,) +... + 0 (х - Хо) - (Л- - х„_,)
п\п
(4.36)
Уравнение (4.36) имеет структуру х = 1Р(х), т.е. по виду при-
годно для применения метода простой итерациц. Естественно в
качестве начального приближения принять значение х(0) = х,-, бли-
жайшее в табл. 4.7 к искомому х*.
Еще ближе к х* будет значение, полученное с помощью ли-
нейной интерполяции по двум узлам, ближайшим кх*. По форму-
ле линейной интерполяции имеем: у = yt + ——— (х -х,-). Поло-
жи -
жив в ней у = у*, получим
Х<°) =х. । Л'''г Л'(у‘ -у,-). (4.37)
Jj'+i У/
Имея начальное приближение, строим итерационный процесс
для решения уравнения (4.36) (до достижения заданной точно-
сти)
220
(i+I) = x0 +~(y' — Уо)~~~
АУп Av.j
4-y-(xw -xr,)(x(^-x,)+...
2! Л
+ -*-l> (4-38)
n\hn 1
С учетом того, что при сделанных допущениях у* близко к у0 а
х* — к Ло, сходимость итерационного процесса при сделанных пред-
положениях весьма вероятна.
Пример 4.5. Используя данные примера 4.3 и построенный там
интерполяционный многочлен, найти с помощью обратного ин-
терполирования значение х*, соответствующее значению у* = 1,957.
Действуя по формуле (4.37), получим ' ' 7
х(0) = о, 5 + —1 415— (] 95^-1/715) = 0,705: kr
2,348 —l,715v ! ’
' -1
Далее строим итерационный процесс по формуле, получен-
ной из формулы (4.38), применительно к данному примеру:
х<*11> = о,5 + -^-(1,957- 1,715)------— -^-^(лл; '- 0,5)х
0,633 v ’ 0,633[ 21- 0,5v ’7
1 777
х(х<*> - 1) + *’(х(А> - 0,5)(х(А) - 1)(х(*> - 1,5)-
(Л'<А’’ " °’ 5)(Л’(А,) " 1)(%<i) ’ ’’ 5)(А'("’ " 2)] =
= 0,6912 - 1,5798[0,1460(х(А) - 0,5)(х(А> - 1^)
-0,8247(х(Л') - 0,5)(х<4> - 1)(х^> 1,5) +
£+)>>3857(х(*) - 0,5)(х{*> - 1)(х<А’’ - 1,5)(х<А) - 2)]. kcP^/nt O .
Последовательные итерации приводят к следующим значениям:
О fc'O= 0,6165"
х<°> = 0,705; х(1) = 0,680447; х® = 0,680927;
х(Э) = 0,680915; х(4) = 0,680916; х(5) = 0,680915,
(вычисления велись на калькуляторе, выписаны избыточные, с
учетом точности исходных данных, значащие цифры). Результат с
учетом точности .представленных в таблице примера 4.3 данных
таков: х* = O^&Sl/ т
Вернемся к общей задаче выполнения обратного интерполи-
рования с помощью многочлена, построенного для прямого ин-
терполированйя. Если узлы {х,} являются равноотстоящими, то
удобнее применять одну из интерполяционных формул Ньютона.
Если же эти узлы нс являются равноотстоящими, то (из обсужда-
емых в данной книге интерполяционных формул) применима
221
формула Лагранжа. В этом случае возникает необходимость реше-
ния уравнения (см. формулу (4.11))
. <6 IL+i W
У = X У/ —-----------
,=0 (х-х,)П„+А)
(4.39)
(неизвестным в нем является х), преобразование которого к виду,
пригодному для применения метода простой итерации, не явля-
ется столь очевидным, как в рассмотренном выше случае. Для ре-
шения уравнения (4.39) можно использовать, например, метод
хорд или метод касательных, обсуждавшиеся в гл. 2.
4.10.2. Приближенное решение уравнений методом
обратного интерполирования
Если для уравнения f(x) = 0 решена задача отделения корня
(т.е. найден отрезок [о; Ь], на котором содержится один корень),
то уточнить его значение можно следующим образом.
Построим на [а; (>] сетку (для удобства с равноотстоящими уз-
лами)
х0 = а, X, = + /?, ..., х„ = ха + nh - b
и протабулируем функцию Дх) на этой сетке. Получим таблицу
вида табл. 4.7 и отыщем в ней пару соседних значений функции
разных знаков. Допустим, что это узлы у, и у1+ Очевидно, что
искомый корень уравнения находится на отрезке [xr-; xi+(Если
случайно окажется, что одно из значений функции у;- = 0, то воп-
рос о дальнейших действиях отпадает, поскольку в этом случае
корень найден точно и равен х,).
Применяя описанные в предыдущем пункте приемы обратной
интерполяции при значении у’=0, получим решение уравнения
с той точностью, которую обеспечивает метод обратной интерпо-
ляции.
Пример 4.6. Найти корень уравнения х2 sin-5 = 0, находя-
щийся на отрезке [3; 8], методом обратной интерполяции с точ-
ностью 1 10-5.
Построим следующую таблицу значений функции:
А' 3 4 5 6 7 8
У -2,05525 -1,04154 -0,03327 0,972261 1,976215 2,979183
Если решать данную задачу с помощью первого интерполяци-
онного многочлена Ньютона, то для его построения естественно
принять отрезок [5; 8], с помощью второго — отрезок [3; 6] (учи-
тывая, что у* = 0).
222
Остановимся на втором варианте. Построим таблицу конечных
разностей
Многочлен Ньютона имеет вид (см. (4.17) —(4.19)):
(х) = 0,97226 + 1,00553(х - 6) - 0,°^74 (х - 6)(х - 5) +
0,00280. Л/ ’ ..
+ —— (х - 6)(х - 5)(х - 4).
• *
Положим значение многочлена равным нулю и преобразуем
получившееся уравнение к виду, пригодному для итераций:
, 0,97226 0,00274 . ...
+-1,00553 "-1,00553 -2! А >(х ) +
0,00280 , ... ..
+ Ч0055ГЗ!(Х-6)(Х'5)(Х-4)-
Начальное приближение найдем по формуле линейной интер-
поляции
х<°» = 5 + а Г77ТГ(0 - ("0.03327)) = 5,03309.
0,97226-(-0,03327)
Точность 1 • 10'5 достигается за две итерации.
Результат: х’=5,03306.
Контрольные вопросы
1. Как формулируется задача обратного интерполирования?
223
2. Как практически решить задачу обратного интерполирования с
помощью многочлена Лагранжа?
Упражнения
I. Написать формулы, стоящие за числовыми выражениями, приве-
денными в примере 4.6. Проделать действия, указанные в этом при-
мере.
2. Реализовать задачу, поставленную в примере 4.6, с помощью:
а) первой интерполяционной формулы Ньютона;
б) интерполяционного многочлена Лагранжа.
4.11. ИНТЕРПОЛЯЦИЯ СПЛАЙНАМИ
При большом количестве узлов интерполяции сильно возрас-
тает степень интерполяционных многочленов, что делает их не-
удобными для вычислений. Высокой степени многочлена можно
избежать, разбив отрезок интерполяции на несколько частей, с
последующим построением на каждой части самостоятельного
интерполяционного многочлена. Однако такое интерполирование
наталкивается на существенный недостаток: в точках стыка раз-
ных интерполяционных многочленов будет разрывной их первая
производная.
В этом случае удобно пользоваться особым видом кусочно-по-
линомиальной интерполяции — интерполяции сплайнами (от англ.
spline — рейка). Суть этого подхода заключается в следующем.
Определение. Функция называется интерполяционным
сплайном порядка т для функции Дх), заданной таблицей
X Xj X,
У То У1 Уп
если:
1) на каждом отрезке [х,;х(+1] (/ = 0, 1, л-1) 5(х) является
многочленом порядка т\
2) 5(х) и ее производные до (т - 1)-го порядка включительно
непрерывны на [х0! хл];
3) 5(xz) = yf (/ = 0, 1, ..., п) — непосредственно условие ин-
терполяции.
Можно доказать, что эти условия достаточны для существова-
ния сплайна порядка т (т> 2), но не гарантируют его единствен-
ности.
Остановимся на построении наиболее популярных в практике
аппроксимации функций кубических сплайнов.
Согласно определению кубический сплайн 5(х) можно пред-
ставить в виде
224
PM, хе [xo. X|];
Л(х), xe [xH xj];
P„(x), xe |хи,х,|,
где каждый из/;(х) — многочлен третьей степени:
/^(х) = а, +Д(х-ху) н-сДх-Х/)2 + Jz(x-x,)3(/= 1, 2, л). (4.41)
Привязку номера многочлена к узлам интерполяции помогает
проследить следующая схема:
Л(х)Р2(х) Р„(х)
I---1----1-------------1----1---1------------------1----1
Хо Х| Х2 х,_| х, хМ| хя_| х„
Последний пункт определения сплайна в сочетании с формулой
(4.41) позволяет немедленно найти коэффициенты а(: yt = S(Xf) =
- Pt(Xi) - at, или
О/ = yt- (4.42)
Условие непрерывности 5(х) в каждом узле приводит к равен-
ствам Р/(х,) = Pi,i(Xi)(j = 1, л - I). В развернутом виде с учетом
(4.41) эти равенства примут вид
о, = ам + />й| (х, - х/И) + см (х, - х(»| )2 + (х, - х1+| )3. (4.43)
Введем обозначение Л, = х, -Х/_|- Понижая в равенствах (4.43)
индекс на единицу’(т.е. заменяя / на /-1) и учитывая (4.42), по-
лучим:
hibj - hfa + hfa = у, - у,.,. (4.44)
Условие непрерывности первой производной кубического
сплайна, входящее в его определение, сводится к требованию
Pi'(Xj) = Pm(xi) (i = 1, ..., л - 1). Дифференцируя формулу (4.41) и
пользуясь введенными выше обозначениями, получим:
^/-i -bj + 2htCt - 3h3d, =0 (/ = 2, .... л). (4.45)
Осталось использовать непрерывность второй производной
сплайн-функции, т.е. условие P'(Xi) = P’t|(х,). Оно порождает ра-
венства
С/-1 “С/ + 3pd, =0 (/ = 2, ...» л). (4.46)
Совокупность равенств (4.44) — (4.46) образует систему Зл - 2 ли-
нейных алгебраПческих уравнений относительно Зл неизвестных
{С/}» {d,} (<= 1. 2, ..., л). Для однозначной разрешимости ее
следует доопределить. Наиболее распространенный способ доопре-
деления — потребовать «гладкости» второй производной сплайна
8 Лмчм
225
на концах отрезка: У^Со) = = 0= что в принятых обозначени-
ях сводится к равенствам PiXx0) = 0, Pt"( = 0, или с учетом (4.43)
Г-оА,‘',=<); (4«)
— и.
Отметим, что первое из уравнений (4.47) совпадет формально
с (4.46) при / = 0, если ввести коэффициент сд (которого нет на
самом деле в наборе {с,}) и положить его равным нулю.
На практике удобно не решать непосредственно систему (4.44) —
(4.47), а предварительно исключить из нее все неизвестные ка-
ких-либо двух групп. Начнем с исключения совокупности пере-
менных {Ь,}. Для этого выразим 6, из (4.44):
Д = + hjCj - hfd,. (4.48)
Д
Перепишем (4.48), понизив индекс на единицу:
= У'~2 + Д-Л-: ~ АД1 i (4-49)
Д-1
Вычтем (4.48) из (4.49) и подставим полученную разность
Д-i - bj в (4.45). После простых преобразований получим
Дс,- + Д сг _1 - 2ДЦ - Д? I4-1 = У‘ ~ У'~] - у*~2 - (4.50)
Д Д_!
Теперь исключим из (4.50) величины Д.. Для этого выразим
d, из (4.46)
4 = ^4-^ 0 = 2, ..., и). (4.51)
ЗД
Подставим это выражение в (4.49), понизив ипдекс там, где
это необходимо. Получим:
Д+|с,+| + 2(Д + Д+| )cz + h;Ci_} = з(Ум, ~У‘ - yi "/'A (4.52)
( Д+1 д )
Система (4.52) содержит лишь неизвестные {сД и является си-
стемой линейных алгебраических уравнений с трехдиагональной
матрицей, которую удобно решать методом прогонки. При этом
необходимое для «обратной прогонки» (см. гл. 3) значение вели-
чины с„ уже известно — см. (4.47).
Найдя неизвестные {<?, }, по формулам (4.51) и первого из урав-
нений (4.47) определим неизвестные {dt}, а затем с помощью
(4.48) неизвестные {Д}. На этом построение кубического сплайна
завершится.
226
Приведем (без доказательства) оценку погрешности интерпо-
ляции кубическим сплайном (см., например, [12]). Ограничимся
случаем равноотстоящих узлов. В этом случае
\f(x)-S(x)\<M^.. (4.53)
где М4 = тах|/(4>(х)|; [а; />] — промежуток интерполяции.
[о; Л] 1 1
Пример 4.7. Построить кубический сплайн для функции у = f(x),
заданной таблицей
X, -1 0 1 2
У: 1/2 1 2 4
с дополнительными условиями: S'(-l) = 5(2) = 0. Найти с помо-
щью 5(х) значение функции y=f(x) при х = 0,3. (Заметим, что в
основу таблицы положена функция у - 2х).
Учитывая, что Q; = с3 = 0, систему (4.52) сведем всего к двум
уравнениям:
3
/с, +с2 = -;
q + 4с3 = 3.
Ее решение (будем в этом простейшем примере вести решение
в простых дробях):
1 7
Ci = -; с2 = —.
1 5 2 10
Далее находим по (4.51) значение коэффициентов :
. 1.1. 7
UI = —, и? = “Т , «3 = —
15 6 30
Теперь по формулам (4.48) находим коэффициенты Д:
, 19 , 23 , 67
а = —; bi - —; bi = —.
30 15 30
Поскольку значения коэффициентов д,- — значения функции
из таблицы (см. (4.42)), то сплайн построен:
7](х) = 1 + — х + -х2 + — х3, хе[-1; 0];
1 30 5 15 L 1
S(x) =
Л(х*) = 2 + ~(х-1) + ^(х-1)2+^(х-1)3, xe[0; 1];
12> 1U о
/>3(х) = 4 + ^(х-2)-^(х-2)3, хе[1; 2].
227
Нетрудно проверить, что условия непрерывности 5(х), S'(x),
S'(x) в точках х = 0 и х = 1 выполнены.
Для нахождения значения интерполирующей функции в за-
данной точке х = 0,3 заметим, что 0,3 е [0; 1], и поэтому исполь-
зуем многочлен Р2(х): /ДОД) ~ 1,2125. Отметим для сопоставле-
ния с той же точностью значение функции, положенной в основу
данного примера: 20,3 - 1,2311.
Интерполяция сплайнами сопряжена с немалым объемом вы-
числительной работы. Весьма необычна и форма окончательного
результата, ибо сплайн имеет различные представления на раз-
личных частичных отрезках интерполяции. Это осложняет доступ
к значениям сплайна в каждой конкретной точке, так как пред-
полагает прежде всего поиск параметров, определяющих соответ-
ствующую формулу сплайна. Эти трудности легко предотвратимы
при использовании компьютера, так как упорядоченное хране-
ние всех необходимых параметров организовать нетрудно, а вы-
полнение однотипных процедур по вычислению параметров сплай-
на и его значений может быть обеспеченно специальными проце-
дурами. Эффективные средства для сплайновой интерполяции
имеются в инструментальных пакетах (см. подразд. 4.15).
Контрольные вопросы
1. Какой недостаток «кусочного* интерполирования с помощью много-
членов Лагранжа и Ньютона устраняется при интерполяции сплайнами?
2. Какие практические трудности интерполирования сплайнами уст-
раняются при использовании компьютера?
Упражнение
Построить кубический сплайн для функции у =f(x), заданной следу-
ющей таблицей:
X,- 1 3 5 7
V/ 3 -2 4 -3
4.12. ПОНЯТИЕ СХОДИМОСТИ ИНТЕРПОЛЯЦИОННОГО
ПРОЦЕССА
Сравнивая интерполяцию по Лагранжу и Ньютону, с одной
стороны, и сплайн-интерполяцию, с другой, видим, что постро-
ение сплайнов — процесс более громоздкий и неудобный. Тем не
менее, в приложениях при большом числе узлов к сплайнампри-
бегают чаще, чем к классическим способам. Одна из причин —
неудобство оперировать в ряде случаев многочленами высокой
228
степени; однако есть и более глубокая причина, связанная со схо-
димостью процесса интерполяции.
Зададим простой вопрос: что происходит с интерполяцион-
ным многочленом Лагранжа (Ньютона), когда число узлов интер-
поляции неограниченно увеличивается на некотором фиксиро-
ванном отрезке [а; £]? Будет ли интерполяционный многочлен
неограниченно сближаться с исходной функцией? Иначе говоря,
будет ли иметь место равенство (которое кажется вполне есте-
ственным): lim £„(/) =/(/) для любой точки х*? Это равенство
выражает свойство сходимости интерполяционного многочлена.
Ответ противоречит интуитивным ожиданиям: вообще говоря,
процесс интерполяции многочленами Лагранжа и Ньютона явля-
ется расходящимся. Вероятно, простейшей иллюстрацией к этому
является пример, построенный известным советским математи-
ком С. Н. Бернштейном: для функции у = |х| на отрезке [я; Л] при
интерполяции по равноотстоящим узлам последовательность ин-
терполяционных полиномов Лагранжа не сходится к этой функ-
ции ни в одной точке, кроме точек-1, 0, 1. Разумеется, подобное
утверждение не является универсальным: есть такие функции и
способы выбора узлов интерполяции что процесс интерполяции
сходится.
В противовес этому процесс интерполяции кубическими сплай-
нами всегда сходится (это практически очевидно из оценки (4.44)),
что усиливает мотивацию предпочтения сплайнов при большом
числе узлов.
Контрольный вопрос
Что означает сходимость интерполяционного процесса? расходи-
мость?
4.13. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
4.13.1. Постановка задачи
Пусть в результате измерений в процессе опыта получена табл. 4.8
некоторой зависимости Дх).
Таблица 4.8
X Х| *2 Х„
яд Л Ут Уп
Нужно найти формулу, выражающую эту зависимость анали-
тически.
229
Можно, разумеется, применить метод интерполяции: постро-
ить интерполяционный многочлен (например, Лагранжа или Нью-
тона), значения которого в точках xl( х2, ..., х„ будут совпадать с
соответствующими значениями f(x) из табл. 4.8. Однако совпаде-
ние значений в узлах иногда может вовсе не означать совпадения
характеров поведения исходной и интерполирующей функций. Тре-
бование неукоснительного совпадения значений в узлах выглядит
тем более неоправданным, если значения функции f(x) в табл. 4.8
получены в результате измерений и являются приближенными.
Поставим сейчас задачу так, чтобы с самого начала обязательно
учитывался характер исходной функции: найти функцию заданного
вида у = F{x), которая в точках jq, х2, .... х„ принимает значения,
как можно более близкие к табличным значениям уь у2, у„.
Практически вид приближающей функции F можно опреде-
лить следующим образом. По данным табл. 4.8 строится точечный
график функции, а затем, как на рис. 4.3, проводится плавная
кривая, по возможности наилучшим образом отражающая харак-
тер расположения точек. По полученной таким образом кривой
устанавливается вид приближающей функции (обычно из числа
простых по виду аналитических функций).
Следует заметить, что строгая функциональная зависимость для
экспериментально полученной табл. 4.8 наблюдается редко, так
как каждая из участвующих в ней величин может зависеть от мно-
гих случайных факторов. Приближающая функция (ее еще назы-
вают эмпирической формулой, или уравнением регрессии у на х) ин-
тересна тем, что позволяет находить значения функции f(x) для
нетабличных значений х, «сглаживая» результаты измерений вели-
чины у. Оправданность такого подхода определяется, в конечном
счете, практической полезностью полученной формулы.
Рассмотрим один из распространенных способов нахождения
эмпирической формулы. Предположим, что приближающая функ-
Рис. 4.3. Сглаживающая аппрок-
симация функцией заданного
вида
ция Fb точках jq, -х2, ..., х„ имеет
значения
У1,У2...У„- (4.54)
Требование близости таблич-
ных значений у,, у2, ..., у„ и зна-
чений (4.54) можно истолковать
следующим образом. Будем рас-
сматривать совокупность значений
функции /(х) из табл. 4.8 и сово-
купность (4.54) как координаты
двух точек «-мерного пространства.
С учетом этого задача приближе-
ния функции/может быть пере-
формулирована следующим обра-
230
зом: найти такую функцию F заданного вида, чтобы расстояние
между точками Л/О’], у2, у„) и Л/(у1э у2, у„)было наи-
меньшим. Если воспользоваться метрикой евклидова простран-
ства, то это условие сводится к требованию, чтобы величина
~ У> )2 + О'г ~У1)2 + — + (Ул - Уя)2 была наименьшей. Легко ви-
деть, что это требование равносильно следующему: чтобы была
наименьшей сумма квадратов
(Я - Й)2 + (Я - Уг)2 + - + (Ул - Ул)2. (4.55)
Итак, задача приближения функции f теперь формулируется
следующим образом: для функции /, заданной табл. 4.8, найти
функцию F определенного вида, чтобы сумма квадратов (4.55)
была наименьшей.
Эта задача носит название задачи приближения функции ме-
тода» наименьших квадратов.
В качестве приближающих функций в зависимости от характе-
ра точечного графика функции f часто используют следующие
функции:
I) у = ах + Ь;
2) у = ах2 + Ьх + с;
3) у = ах1”;
4) у = ое1";
5)У = —’
ах + Ь
6) у = a In х + Ь;
1)у = а — + Ь;
8)У =---
ах + Ь
Здесь а, Ь, с, т — параметры. Когда вид приближающей функ-
ции установлен, задача сводится только к отысканию значений
параметров.
Рассмотрим метод нахождения параметров приближающей
функции в общем виде на примере приближающей функции с
тремя параметрами
у = F(x, а, Ь, с). (4.56)
Итак, имеем F(xh a, b, c) = y’j, i = 1, 2, .... п. Сумма квадра-
тов разностей Соответствующих значений функций /и Рбулет иметь
вид
£[Я - F(xh a, b, с)]2 = Ф(о, Ь, с).
/=1
231
Эта сумма является функцией Ф(а, Ь, с) трех переменных (па-
раметров а, b и с). Задача сводится к отысканию минимума этой
функции. Используем необходимое условие экстремума функции
трех переменных:
“=0; — = 0; “=0,
За ЗЬ За
которое в данном случае примет вид
я
£[y,-F(xf) й, b, c)\Fa(x,, а, Ь, с) = 0;
г=1
a, b, с)\-Рь(х<, a, Ь, с) = 0; (4.57)
f=i
£[у,- -F(x,, a, b, c)} Fc(Xi, а, Ь, с) = 0.
i=i
Решив эту систему трех уравнений с тремя неизвестными от-
носительно параметров а, b и с, мы получим конкретный вид
искомой функции F(x, а, Ь, с). Как видно из рассмотренного приме-
ра, изменение количества параметров не приведет к искажению
сущности самого подхода, а выразится лишь в изменении количе-
ства уравнений в системе (4.56).
Естественно ожидать, что значения найденной функции F(x, а,
Ь, с) в точках х1( •••, х„, будут отличаться от табличных значе-
ний уъ ..., уп. Значения разностей
У, ~ F(xt> a, b, с) = е,- (;' = 1, 2, ..., п) (4.58)
называются отклонениями (или уклонениями) измеренных значе-
ний у от вычисленных по формуле (4.56). Для эмпирической фор-
мулы (4.56) в соответствии с исходной табл, 4.8 можно найти сум-
му квадратов отклонений о = которая в соответствии с прин-
Г = 1
ципом наименьших квадратов для заданного вида приближающей
функции (и найденных значений параметров а, b и с) должна
быть наименьшей. Из двух разных приближений одной и той же
табличной функции, согласно принципу наименьших квадратов,
лучшим является то, для которого о имеет наименьшее значение.
Контрольные вопросы
1. В чем суть приближения таблично заданной функции по методу наи-
меньших квадратов? Чем этот метод отличается от метода интерполяции?
2. Какие элементарные функции чаще всего используются в качестве
приближающих? Как можно определить вид приближающей функции?
232
3. Какое из двух приближений одной и той же таблично заданной
зависимости считается лучшим?
Упражнения
1. По заданным таблицам построить точечные графики и определить
подходящий вид приближающих функций:
а)
X 0,11 0,13 0,14 0,17 0,20 0,25 0,33 0,50
У 1,22 1,24 1,30 1,32 1,41 1,54 1,66 2,02
б)
X 1 2 3 4 5 6 7 8 9
У 520 308 240 204 180 170 159 152 147
2. Для экспериментальной зависимости
/ 0,10 0,32 0,46 0,58 0,74 0,92
/7 0,32 0,58 0,67 0,77 0,84 0,96
построены две приближающие функции: a) w= у7; б) и=(4+ 12/)/15.
Установить, какое из приближений является лучшим.
4.13.2. Нахождение приближающей функции в виде
линейной функции и квадратного трехчлена
Будем искать приближающую функцию в виде:
F(x, а, £>) = ах + Ь. (4.59)
Найдем частные производные по параметрам а и о: — = х,
да
dF
— - 1 и составим систему вида (4.57):
до
X (я- ~ ах> “ ь)х‘ = °; X (я - ах< - = °-
Сумма здесь и далее берется по параметру i в пределах от 1
до п.
Далее имеем:
Ta^x?-5£х,-=°; '^jyi-ayjxi-nb = d,
деля каждое уравнение на п, получим:
f- X +(~ Sxi V " ~ SХ‘У‘’ (- X хНа+b = -Sу> • <4-60)
J Iй ) п \п ) п
233
Введем обозначения:
-£х,=Л/х; = -^х’У>=м*у'' “IX = Л/х2.(4.61)
я п п п
Тогда последняя система будет иметь следующий вид:
Мх2<з + МХЬ - Мху\
Мха + Ь = Му. (4‘62)
Коэффициенты этой системы Мх, Му, Мхг, Mxv — числа,
которые в каждой конкретной задаче приближения могут быть
легко вычислены по формулам (4,61), в которых х,-, у,- — значе-
ния из табл. 4,8. Решив систему (4.62), получим значения пара-
метров а и Ь и, следовательно, конкретный вид линейной функ-
ции (4.59).
В случае нахождения приближающей функции в виде квадрат-
ного трехчлена имеем:
F(x, а, Ь, с) = ах2 + Ьх + с. (4.63)
Находим частные производные:
3F 2 dF 3F .
Эя дЬ дс
Составим систему вида (4.57):
У (ji - ах? - bXj - с)х? = 0;
У (у,- - ах2 - Ьх, - c)Xj = 0;
УСц ~йх/-Z>x,-с) = 0.
После несложных преобразований получается система трех ли-
нейных уравнений с неизвестными а, Ь и с. Коэффициенты систе-
мы, так же как и в случае линейной функции, выражаются толь-
ко через известные данные из табл. 4.8:
Мх<а + МхзЬ + МхгС = Mxiy\
Мxsa + Мxib + Мхс = Мху', (4.64)
Мх2 а + МХЬ + с = Му.
Здесь использованы обозначения (4.61), а также
Мх4=-Ух^; Mj-'^xh Mx2=-Y,xiy<- (4-65)
п п уп
Решение системы (4.64) дает значения параметров а, b и с для
приближающей функции (4.63).
234
Контрольные вопросы
1. Как строится система линейных уравнений, к решению которой
сводится задача отыскания параметров приближающей функции в виде
линейной функции? в виде квадратного трехчлена?
2. По каким формулам вычисляются коэффициенты этих систем че-
!рез табличные исходные данные?
Упражнения
1. Для табличной зависимости
X 1,0 1,5 2,5 3,0 4,5 5,1 6,2
У 67 101 168 202 301 334 404
найти приближающую функцию в виде линейной.
2. Для табличной зависимости
1 2,0 2,2 2,4 2,6 2,8 3,0
до 0,30 0,34 0,38 0,42 0,44 0,48
найти приближающую функцию в виде квадратного трехчлена.
4.13.3. Нахождение приближающей функции
в виде других элементарных функций
Покажем, как на‘хождение приближающей функции с двумя
параметрами F(x, а, Ь) в виде различных элементарных функций
может быть сведено к нахождению параметров линейной функ-
ции.
Степенная функция. Будем искать приближающую функцию в
виде
F(x, а, т) = ахт (4.66)
(так называемая геометрическая регрессия). Предполагая, что в ис-
ходной табл. 4.8 значения аргумента и значения функции положи-
тельны, прологарифмируем равенство (4.66) при условии а>0:
In F - Ina + т Inx. (4.67)
Так как функция F является приближающей для функции f
функция In F будет приближающей для In f. Введем новую пере-
менную и= Inх, тогда, как следует из (4.67), In У7 будет функцией
от и: Ф(а). Примем обозначения:
т = А; 1п а = В. (4.68)
Теперь равенство (4.67) принимает вид
Ф(и, А, В) = Аи + В, (4.69)
235
т.е. задача свелась к отысканию приближающей функции в виде
линейной.
Практически для нахождения приближающей функции в виде
степенной (при сделанных выше предположениях) необходимо
проделать следующее:
1) по данной табл. 4.8 вычислить новую таблицу, прологариф-
мировав значения х и у;
2) по новой таблице найти параметры Лий приближающей
функции вида (4.69) (см. п. 4.11.1);
3) используя обозначения (4.68), найти значения параметров
а и т и подставить их в выражение (4.66).
В некоторых случаях может оказаться, что характер точечного
графика обещает хорошее приближение в виде степенной функ-
ции, но среди табличных значений х и у есть отрицательные, что
делает невозможным их логарифмирование. Трудностей можно
избежать, сделав параллельный перенос значений х и у; после
нахождения значений параметров а и т надлежит снова вернуть-
ся к переменным х и у.
Показательная функция. Пусть исходная табл. 4.8 такова, что
приближающую функцию целесообразно искать в виде показа-
тельной функции
Г(х, а, т) = аеж', а > 0 (4.70)
(так называемая экспоненциальная регрессия). Прологарифмируем
равенство (4.69)
In F = Ina + rnx.
(4.71)
Приняв обозначения (4.68), перепишем (4.71) в виде
In F = Ах + В. (4.72)
Таким образом, для нахождения приближающей функции в
виде (4.70) нужно прологарифмировать значения функции в ис-
ходной табл. 4.8 и, рассматривая их совместно с исходными зна-
чениями аргумента, построить для новой таблицы приближаю-
щую функцию вида (4.59). Вслед за этим в соответствии с обозна-
чениями (4.68) остается получить значения искомых параметров
а, т и подставить их в формулу (4.70).
Если среди исходных значений у есть отрицательные числа,
то, как и в случае построения геометрической регрессии, следует
сделать необходимый параллельный перенос.
Дробно-линейная функция. Будем искать приближающую функ-
цию в виде
F(x, a, b) = —L-. (4.73)
ах + b
Равенство (4.73) перепишем следующим образом:
236
Из последнего равенства следует, что для нахождения значе-
ний параметров а и b по заданной табл. 4.8 нужно составить новую
таблицу, в которой значения аргумента оставить прежними, а
значения функции заменить обратными числами. После этого для
полученной таблицы надо найти приближающую функцию вида
ах + Ь. Найденные значения параметров а и b подставить в фор-
мулу (4.73).
Логарифмическая функция. Пусть приближающая функция име-
ет вид
F(x, а, Ь) = а\пх + Ь. (4.74)
Легко видеть, что для перехода к линейной функции достаточ-
но сделать подстановку 1пх = и. Отсюда следует, что для нахож-
дения значений а и b нужно прологарифмировать значения аргу-
мента в исходной табл. 4.8 и, рассматривая полученные значения
в совокупности с исходными значениями функции, найти для
полученной таким образом новой таблицы приближающую функ-
цию в виде линейной. Коэффициенты а и b найденной функции
подставить в формулу (4.74).
Обратно-пропорциональная зависимость. Если точечный график,
построенный по табл. 4.8, дает ветвь гиперболы, приближающую
функцию можно искать в виде
F(x, а, b) = ~ + b. (4.75)
х
Для перехода к линейной функции сделаем подстановку и = 1/х:
Ф(«, а, b) = au + b. (4.76)
Практически перед нахождением приближающей функции вида
(4.76) значения аргумента в исходной табл. 4.8 следует заменить
обратными числами и найти для новой таблицы приближающую
функцию в виде линейной (4.59). Полученные значения парамет-
ров а и b подставить в формулу (4.75).
Дробно-рациональная функция. Пусть приближающая функция
ищется в виде
F(x, а, b) = х . (4.77)
ах+ Ь
Имеем: Ф (х, а, Ь) = ———-----= а + —, так что задача сводит-
F(x, а, Ь) х
ся к случаю, рассмотренному в предыдущем пункте.
Действительно,. если в исходной таблице заменить значения х
и у их обратными величинами по формулам = 1/х, и = 1/у и
искать для новой таблицы приближающую функцию вида
и = bz + a, то найденные значения а и b будут искомыми для фор-
мулы (4.77).
237
Пример 4.8. Построить приближающую функцию методом наи-
меньших квадратов для зависимости, заданной табл. 4.9.
Таблица 4.9
1,1 1,7 2,4 3,0 3,7 4,5 5,1 5,8
У 0,3 0,6 1,1 1,7 2,3 3,0 3,8 4,6
Точечный график изображен на рис. 4.4. Для сравнения каче-
ства приближений рассмотрим параллельно два способа прибли-
жения заданной функции: в виде линейной функции у - ах + b
и в виде степенной функции у = схт. После нахождения значе-
ний параметров а и Ь, с и т можно найти суммы квадратов укло-
нений (см. п. 4.13.1) и установить, какое из двух приближений
лучше.
Значения параметров а и b линейной функции находятся из
системы вида (4.62), коэффициенты которой вычисляются по дан-
ным из исходной табл. 4.9 в соответствии с обозначениями (4.61).
Для вычисления коэффициентов системы по табл. 4.9 составим
вспомогательную табл. 4.10, в последней строке которой получе-
ны суммы значений по соответствующим столбцам. Заметим, что,
используя регистр памяти калькулятора, суммирование значений
в столбцах можно производить параллельно с вычислениями са-
мих значений.
Разделив полученные суммы на число элементов в столбцах,
имеем в соответствии с формулами (4.60)
Мх = 3,412; 4^=2,175;
Mxv = 9,645; Л/ 2 = 14,056.
Рис. 4.4. Два способа аппроксимации табличной зависимости
238
Таблица 4.10
X У ху X5
1,1 о,з 0,33 1,21
1,7 0,6 1,02 2,89
2,4 1,1 2,64 5,76
3,0 1,7 5,10 9,00
3,7 2,3 8,51 13,69
4,5 3,0 13,50 20,25
5,1 3,8 19,38 26,0!
5,8 4,6 26,68 33,64
27,3 17,4 77,16 112,45
Табл и ца 4.11
и Z UZ и2
0,095 -1,204 -0,114 0,009
0,531 -0,511 -0,271 0,282
0,875 0,095 0,083 0,766
1.099 0.531 0,584 1,208
1,308 0,833 1,090 1,711
1,504 1,099 1,653 2,262
1,629 1,335 2,175 2,654
1,758 1,526 2,683 3,091
8,799 3,704 7,883 11,983
Составим теперь систему вида (4.62)
I 14,056а+ 3,4126 = 9,645;
F 3,412а -Ь- 2,175.
Решив систему, получаем а = 0,921, Ь = -0,968. Отсюда сле-
дует, что приближающая функция у = F(x, а, Ь) имеет вид
у = 0,921.x - 0,968. (4.78)
Для нахождения параметров с и т степенной функции, как
следует из п. 4.13.3, по исходной таблице составляется новая таб-
лица — из логарифмов значений х и у. Обозначим значения новых
переменных соответственно и и z, т.е. и = Inx, z = In у. По число-
вым данным из новой таблицы составляется система уравнений
вида (4.62):
[ М 1А + Ми В = М uz;
[ MUA + B = MZ, <4-79>
коэффициенты которой — числа, вычисляемые по данным из
новой таблицы по формулам вида (4.61), а неизвестные А и В свя-
заны с искомыми параметрами сит соотношениями
А = т\ В = \пс.
Для нахождения коэффициентов системы (4.79) составляем вспо-
могательную табл. 4.11 (используем натуральный логарифм, вычис-
ления ведутся на калькуляторе с тремя знаками после запятой).
Разделив элементы последней строки табл. 4.11 на 8, получаем:
Ми = 1,1; Mz = 0,463; Миг = 0,985; = 1,498.
Составляем систему вида (4.79)
1,498/1 + 1,1 В = 0,985;
1,1/1 + В = 0,463.
239
Та б л ица 4.12
X У 0,921х- 0,968 е. е? 0,257х'-656 £2 *2 е2
1,1 0,3 0,0451 0,2459 0,0650 0,3009 -0,0009 0,0000
1,7 0,6 0,5977 0,0023 0,0000 0,6188 -0,0188 0,0004
2,4 1,1 1,2424 -0,1424 0,0203 1,0954 0,0046 0,0000
3,0 1,7 1,7950 -0,0950 0,0090 1,5851 0,1149 0,0132
3,7 2,3 2,4397 -0,1397 0,0195 2,2432 0,0568 0,0032
4,5 3,0 3,1765 -0,1765 0,0312 3,1021 -0,1021 0.0104
5,1 3,8 3,7291 0,0709 0,0050 3,8165 -0,0165 0,0003
5,8 4,6 4,3738 0,2262 0,0512 4,7225 -0,1225 0,0150
0,2012 0,0425
Ее решение: А = 1,656; В = -1,359.
Находим значения параметров сит:
т = 1,656; с = ехр(-1,359) = 0,257.
Следовательно, приближающая функция в виде степенной
имеет вид
у = 0,257х''656. (4.80)
Для сравнения качества приближений (4.78) и (4.80) вычис-
лим суммы квадратов уклонений (вычисления приведены в
табл. 4.12).
Как следует из табл. 4.12, сумма квадратов уклонений для ли-
нейной функции о = 0,2012, для степенной — <7 = 0,0425. Срав-
нивая качество приближений (в смысле метода наименьших квад-
ратов), находим, что приближение в виде степенной функции в
данном случае предпочтительнее.
Рассмотренный пример показывает, что для решения задачи
приближения функции методом наименьших квадратов требуется
произвести немало вычислений с использованием зйачительного
количества числовых значений, порождаемых главным образом в
процессе самого счета (исходными данными здесь являются толь-
ко числа из табл. 4.9). Очевидно, что наиболее подходящим вычи-
слительным инструментом в этом случае является компьютер.
Составим программу, которая по желанию пользователя рас-
считывает параметры уравнения регрессии одного из трех типов:
1) у = ах + 6;
2) у = охт;
3) у = аетх.
, Исходными для работы программы должны служить данные,
представленные в виде табл. 4.9.
Как было показано выше, несложными преобразованиями дан-
ных расчет параметров уравнений типа 2 и 3 сводится к расчету
240
параметров уравнения первого типа, т.е. к решению системы
вида (4.61). Поэтому основные шаги подлежащего реализации ал-
горитма можно сформулировать так:
1. Ввод исходных данных.
2. Выбор вида уравнения регрессии.
3. Преобразование данных к линейному типу зависимости.
4. Получение параметров уравнения регрессии.
5. Обратное преобразование данных и вычисление суммы квад-
ратов отклонений вычисленных значений функции от заданных.
6. Вывод результатов.
program Regressya;
uses ert;
type mus=array[0..50] of real;
var x,y,u,v:mus; n,i,k:integer;
s,si,s2,s3,s4,a,b,d:real;
begin
clrscr;
writeln(’Введите количество пар элементов
таблицы’);
readln (n);
writeln(1 Введите попарно через пробел х и у');
for i:=l to n do read(x[i], у[i]);
writeln(’1) Y=A*X+B; 2) У=А*ХЛМ;
3) Y=A*EXP(M*X)’);
writeln(1 Введите номер выбранного уравнения');
read In(k);
for i:=l to n do
begin
if k=l then begin u[i]:=x[i]; v[i]:=y[i]; end;
if k=2 then begin u[i]:=ln(x[i]);
v[i]:=ln(y[i]) ; end;
if k=3 then begin u[i]:=x[i]; v[i]:=ln(y[i]);
end;
sl:=sl+u[i]; s2:=s2+v[i];
s3:=s3+u[i]*v[i]; s4:=s4+sqr(u[i]);
end;
d:=n*s4-sqr(si) ; a:=(n*s3-sl*s2)/d; b:=(s4*s2-
sl*s3)/d;
for i:=l to n do
begin
v[i]:=a*u[1]+b;
if (k=2) or (k=3) then v [ i] :=exp(v[i]);
s:=s+sqr(y[i]-v[i]);
end;
writeln('Уравнение регрессии');
241
if k=l then begin writeln(’Y=',a:15:11,'*X + (',
b:15:11, ') ' ) ;
writeln(’S= ',s:15:ll); end;
if k=2 then begin writeln ('Y=exp(b) :15:11*ХЛ’,
a: 15:11) ;
writeln(1S= ',s: 15:11); end;
if k=3 then begin writeln(’Y=',exp(b):15:11,
'*exp(',a,'*X)');
writeln(’S= ',s:15:ll); end;
readkey
end.
В программе для хранения исходных данных используются од-
номерные массивы Л'и К Преобразованные данные заносятся со-
ответственно в массивы U и К
Выполнив расчеты по этой программе для данных табл. 4.9 в
предположении о линейном типе зависимости (при к = 1), полу-
чим следующий результат:
Введите количество пар элементов таблицы
8
Введите попарно через пробел х и у
1.1 0.3
1.7 0.6
2.4 1.1
3.0 1.7
3.7 2.3
4.53.0
5.1 3.8
5.8 4.6
1) Y= А*Х + В; 2) Y= А*ХЛМ; 3) Y= А*ЕХР(М*Х)
Введите номер выбранного уравнения
1
Уравнение регрессии
Y= 0.92191044004*Х + (-0.97101937663)
3= 0.20112760029
Результат работы программы при к = 2:
Уравнение регрессии
Y= 0.25804799057*ХЛ 1.6524291053
3= 0.039226937749
Видно, что рассчитанные уравнения регрессии хорошо согла-
суются с полученными ранее (см. (4.78) и (4.80)). Сравнение сумм
квадратов отклонений показывает, что для рассматриваемых дан-
ных представление эмпирической зависимости в виде степенной
функции является более предпочтительным.
242
Для того чтобы убедиться, что наша программа хорошо рабо-
тает и при к-3, рассмотрим следующий набор данных (табл. 4.13).
Таблица 4.13
X 0,2 0,5 0,9 1,3 1,7 1,7 1,9 2,2
У 0,66 0,95 1,61 2,72 4,55 5,2 5,92 8,73
Результаты работы программы:
Уравнение регрессии
Y= 0.50154189706*ехр(1. 3114 8 94280*Х)
S= 0.38740823363
В завершение отметим, как в некоторых случаях можно улуч-
шить полученную эмпирическую формулу. Простейший прием
состоит в следующем. Пусть у = F(x) — найденная эмпирическая
п
формула, а о = — соответствующая ей сумма квадратов ук-
лонений (см. формулу (4.58)). Рассмотрим функцию у = F(x) + с, где
с - const. Нетрудно показать [5], что формуле у = F(x) + с соответ-
ствует меньшее значение суммы квадратов уклонений, чем фор-
муле у = Дх), если принять
1 л
п ,=1
При этом эффект уточнения будет тем ощутимее, чем сильнее
отличается от нуля значение с.
Контрольные вопросы
1. Каким образом построение приближающих функций в виде раз-
личных элементарных функций сводится к случаю линейной функции?
г 2. Как свести построение геометрической или экспоненциальной рег-
рессии к линейной, если среди табличных значений имеются отрица-
тельные числа?
3. Каким способом можно улучшить найденную эмпирическую фор-
мулу?
Упражнения
1. Набор экспериментальных значений х и у имеет вид таблицы:
X 0,53 0,59 0,71 0,83 0,92 0,98
У 0,08 0,09 0,10 0,11 0,12 0,13
243
Построить методом наименьших квадратов эмпирическую формулу в
Г -А Х
виде дробно-рациональнои функции .
ах + h
2. Построить уравнение геометрической регрессии для табличной за-
висимости:
X -0,20 -0,17 -0,14 -0,08 0 0,13 0,19
У 0,23 0,28 0,33 0,45 0,69 1,12 1,39
Указание. Для построения геометрической регрессии перейти к таб-
лице значений, в которой А'=х + 0,2, Y=y, а потом вернуться к прежним
переменным х и у.
3. Дополнить программу Regressya так, чтобы она давала возможность
вычислять параметры уравнения вида у = alnx + b. Предусмотрите про-
верку исходных данных на наличие неположительных значений в слу-
чае, когда требуется их логарифмирование.
4.14. ЭКСТРАПОЛЯЦИЯ
Вычисление значений таблично заданной функции за предела-
ми диапазона значений аргумента, отраженного в таблице, назы-
вается экстраполяцией. Будучи, с точки зрения формальной мате-
матической теории, ни на чем не основанной, экстраполяция
является, тем не менее, очень полезным приемом эмпирического
исследования процессов и явлений.
Для экстраполяции функций могут использоваться интерполя-
ционные формулы Ньютона — и первая (п. 4.6.2), и вторая (п. 4.6.3).
При этом вычисляются их значения для значений аргументов, лежа-
щих за пределами таблицы. Причем, если х<хф то t - (х - x$)/h < 0, и
в этом случае выгоднее применять первую интерполяционную фор-
мулу Ньютона. Если же х> х„, то t = (х - x„)/h > 0, и здесь удобнее
использовать вторую интерполяционную формулу Ньютона. Таким
образом, по первой интерполяционной формуле Ньютона проис-
ходит интерполирование вперед и экстраполирование назад, а по
второй — интерполирование назад и экстраполирование вперед.
Для экстраполяции часто используют также метод наимень-
ших квадратов. Если таблица значений функции отражает некото-
рую экспериментально установленную зависимость, то построен-
ная по ней указанным методом аппроксимирующая функция вы-
ражает определенную математическую (регрессионную) модель
явления. Применимость всякой регрессионной модели ограниче-
на, особенно за пределами экспериментальной области. Всякая
экстраполяция держится на гипотезе: «предположим, что за пре-
делами экспериментальной области закономерность сохраняется». Так
ли это — всякий раз следует анализировать, причем этот анализ
лежит за пределами математики как таковой.
244
Отметим, что экстраполяция является одним из вариантов прог-
нозирования (вероятно, простейшим). Прогнозирование в более
общих случаях, когда существующая или предполагаемая зависи-
мость между величинами является не простой функциональной, а
вероятностной (например, корреляционной), постоянно приме-
няется при решении реальных задач, носящих порой исключи-
тельно важный характер (прогноз мировых цен на различные виды
сырья, прогноз масштабов эпидемий и т.п.).
Контрольные вопросы
1. В чем состоит сущность экстраполяции?
2. Каковы особенности применения для экстраполяции первой и вто-
рой интерполяционных формул Ньютона?
3. На каком предположении основывается применение для экстрапо-
ляции метода наименьших квадратов?
Упражнение
Для таблично заданной функции
X /(х) X /(х)
1,62 8,14 1.65 7,21
1,63 8,02 1,66 6,54
1,64 7,93 1.67 5,01
методом экстраполяции с помощью интерполяционных формул Ньюто-
на (принять х0 = 1,62, х„ = 1,67) вычислить значения функции в точках
1,61 и 1,68 (для вычислений использовать калькулятор).
4.15. ПРИБЛИЖЕНИЕ ФУНКЦИЙ С ПОМОЩЬЮ
ИНСТРУМЕНТАЛЬНЫХ СРЕДСТВ
Табличный процессор Excel не имеет специальных средств для
интерполяции, поэтому интерполяционные формулы можно ввести
в программу обычным образом, а затем произвести по ним расчет.
Для аппроксимации по методу наименьших квадратов Excel
имеет чрезвычайно удобные встроенные средства. Самый нагляд-
ный способ — использование графического представления дан-
ных. Для этого сначала следует ввести табличные данные и пост-
роить по ним точечную диаграмму. Далее следует:
• щелкнуть мышью по полю диаграммы;
• через главное меню выполнить команды Диаграмма => Доба-
вить линию тренда',
• в открывшемся окне на закладке Тип выбрать одну из шести
функций, предлагаемых для аппроксимации (например, Линей-
ный тренд)',
245
• перейти к закладке Параметры^ установить галочки на флаж-
ках: показывать уравнения на диаграмме и поместить на диаграмму
величину достоверности аппроксимации 1С2. => ОК.
Дадим некоторые дополнительные пояснения.
1. Слово тренд (в переводе — общее направление, или тенден-
ция) — часто употребляемый термин для обозначения линии гра-
фика регрессионной модели.
2. На графиках, которые строит Excel, по желанию исполните-
ля может присутствовать очень полезная величина, полученная в
результате построения трендов. Она обозначена как R2. В статисти-
ке эта величина называется коэффициентом детерминированности.
Именно она определяет, насколько удачным явилась полученная
регрессионная модель. Коэффициент детерминированности всег-
да находится в диапазоне от 0 до 1. Если он равен 1, то функция
точно проходит через табличные значения, если 0 — то выбран-
ный вид регрессионной модели предельно неудачен. Значит, чем
R2 ближе к 1, тем удачнее регрессионная модель.
3. Excel дает возможность пользователю самому задавать тип
регрессионной модели, а не ограничиваться предлагаемым меню
из шести функций. Однако для большого числа практических си-
туаций этих функций бывает вполне достаточно.
4. Выполнив аппроксимацию, можно дополнительно произве-
сти экстраполяцию. Для ее визуального отображения надо доба-
вить в описанный в описанный выше алгоритм еще одно дей-
ствие: на вкладке Параметры в области Прогноз в строке вперед на
установить количество единиц используемого масштаба по гори-
зонтальной оси (например, 2 единицы). Для нахождения числового
значения экстраполированной функции надо провести расчет по
соответствующей формуле. Для вычисления значений при линей-
ной экстраполяции можно использовать стандартную функцию
ПРЕДСКАЗ.
Пример 4.9. Аппроксимировать несколькими способами зави-
симость, приведенную в таблице:
X 25 26 27 28 29 30 31 32 33 34 35 36
У 1,6 1,9 4 4,3 6,5 7,1 9,5 12,1 13,4 18,1 17,6 22,3
Сравнить достоверности различных аппроксимаций, а также с
помощью линейной аппроксимации выполнить экстраполяцию на
два табличных шага вперед.
На рис. 4.5—4.7 показаны три варианта решения, из которых
следует, что наилучшим является степенной тренд (см. рис. 4.6),
поскольку в этом случае коэффициент детерминированности имеет
наибольшее значение.
Процесс интерполяции табличных данных по формуле Лагранжа
средствами MathCad как результат решения примера 4.2 приведен
246
Рис. 4.5. Линейный тренд с графической экстраполяцией.
Экстраполированное значение вычислено в ячейке М4 с
помощью функции ПРЕДСКАЗ
25 . 26
33
34
4.3 I 6£
V 28 1 29 ] 30
JJ6 Ц.9 ' **
36 | 36
9,5 12,1 1347’8,1 17£ 22 3
ттстзтЕнтапзлз____
1 25 28 27 • 28 | 29 ] 30 31 I 32
Рис. 4.6. Степенной тренд
ГЯТТ'ГГ’^Г Г-- I Т-Г7и-ЛГГПГП’Г:1
35 36 I
176 22,3
40
Рис. 4.7. Экспоненциальный тренд
247
в рабочем документе на рис. 4.8. Вводятся векторы узловых точек xi
и yi, вычисляется степень многочлена п с применением функции
length(v), возвращающей число элементов в векторе у. Число узло-
вых точек и их расположение может быть любым, но элементы
вектора xi должны быть расположены в порядке возрастания зна-
чений. Задается формула интерполяции Лагранжа, вычисляющая
значения интерполирующей функции Цх) в заданной точке х =
= 1,91 (в соответствии с алгоритмом, см. п. 4.2.4) и в качестве
проверки правильности произведенных вычислений строится гра-
фик интерполяционного полинома, который действительно про-
ходит через все узловые точки.
Простейшим случаем локальной интерполяции является изоб-
раженная на рис. 4,8 линейная интерполяция, при которой в ка-
честве интерполяционной функции выбирается линейная и узло-
вые точки соединяются отрезками прямых. Для этой цели в MathCad
имеется встроенная функция linterp( УХ, УУ,х) (УХ, ИК — векторы
данных); интерполируемое значение для некоторого х есть орди-
ната у соответствующей точки ломаной.
Функция задана векторами значений:
Calculus S
г >: п
х * ; . г> п
Определим степень многочлена Лагранжа: n := lengU<xi) - 1 п = 3
П и
Формула интерполяции: Цх) yi,
1 =о j = о
Вычислим значение функции в заданной тачке: Ц1.91) - 4.154
Изобразим график исходной функции
и функции 1_(х) с узловыми точками:
+-
1
Рис. 4.8, Интерполирование с помощью многочлена Лагранжа
в MathCad
248
Построим кубический сплайн для функции y=f(x), заданной
этой же таблицей значений; вычислим значения интерполяцион-
ной функции в заданных точках и сравним с точными значения-
ми. В системе MathCad сплайн-интерполяция проводится в два эта-
па: сначала с помощью встроенных функций — cspline(X,Y),
а) Линейная
Функция задана таблицей (векторами) значений: ' 1.0 Г 4 А
Введем переменную z, которая определена 1.8 -1.0
на отрезке [0; 10] и изменяется с шагом 0,1: 2.4 -3.0
3.6 -1.0
z:= 0,0.1 ..10 4.8 -4.16
х = Функция, определяющая линейную 5.2 Y := 0
зависимость: 6.2 3.24
1дп(т) ;= lmtfirp(X\¥ ,z) 7.4 -1J56
Значения в некоторых узловых точках; 8.6 7.96
lin(l.q) = 4 lin(4.S) = -4.16 lir<9.8> 9.44 <98; < Р 'И ,
График линейной аппроксимации:
б) сплайновая
Вычислим элементы вектора
вторых производных интерполяци-
онной кривой в узловых точках:
S := cspline(X.Y)
Функция кубической сплайн_аппроксимации: S(z) := interp(S,X,Y,z)
3(1) = 4 3(4.8) - -4.16 S(9.8) = 9.44
График аппроксимации
кубическим сплайном:
Рис. 4.9. Линейная и сплайн-интерполяция в MathCad
249
Пример А
Представим исходную функцию f(x) в еидв вектора данных на |а; Ь]:
ГСЬ - ») + Ц
h
У1 >
Экстраполяция значений функции f(x) в последующих 70-ти точках по
р := pre dict^y ,5,70)
последним 5-ти значениям:
Аргумент функции (вектора) предсказания: t:= О,.® (4+ Ь10)
График
экстраполяции
Рис. 4.10. Экстраполяция с помощью функции
pspline(X,Y), lspline(X,Y) — находятся векторы вторых производ-
ных интерполяционной функции в узловых точках при приближе-
нии их к кубическому, квадратичному либо линейному сплайну
соответственно, затем для всех табличных данных с использова-
нием встроенной функции interp(S,X, Y,z) вычисляются значения
y~f(x) (см- пример 4.6). На рис. 4.9 изображен график кубической
сплайн-интерполяционной функции, проходящий через узловые
точки.
Экстраполяцию поведения некоторой функции f(x), заданной
на отрезке [а; 6] с постоянным шагом h, в MathCad реализует
встроенная функция predict(y,m,ri), которая возвращает п после-
дующих «предсказанных» значений на основе последних т после-
довательных значений вектора данных v. На рис. 4.10 показаны
примеры «графического» предсказания поведения двух функций
X
/(х) = x-2sinx и g(x) = с5 cos2x.
Функция предсказания использует линейный алгоритм, поэтому
хорошо экстраполирует гладкие функции.
Система MathCad содержит ряд встроенных приближающих
функций, различающихся типом используемой кривой (или по-
верхности). В отличие от функций интерполяции они не требуют,
250
Поимев Б.
с := О d:=3 0» > «р|
1 := 0..(d - с)1О ^:=С + ^ yli:-g(xi)
Экстраполяция значений функции д(х) в последующих 70-ти точках по
последним 7-ми значениям:
pl := predict(yl ,7,70)
Аргумент функции (вектора) предсказания: _ (t+d lO)
предсказания в MathCad
чтобы аппроксимирующая кривая проходила через точки данных,
в связи с чем менее чувствительны к ошибкам данных. Конечный
результат их работы — функция, с помощью которой можно оце-
нить значения в промежутках между заданными точками.
Линейное приближение табличных данных осуществляют две
встроенные функции:
intercept,у) — возвращает величину смещения прямой по оси
ординат или значение свободного члена в уравнении регрессии
по методу наименьших квадратов;
slope(x,y) — возвращает значение углового коэффициента урав-
нения прямой (регрессии).
На рис. 4.11 изображен фрагмент документа MathCad, иллюст-
рирующий процесс осуществления линейной регрессии для век-
торов данных х и у. Вычисленные значения а и b позволяют запи-
сать уравнение приближающей линейной функции вида у = F(x):
/(х) = -0,632х + 0,797 и построить ее график, отобразив и исход-
ные данные (точечный график).
Линейная регрессия общего вида, в результате которой полу-
ченное уравнение есть линейная комбинация некоторых функций
F (линейных и нелинейных) реализована встроенной функцией
linfit(X,Y,F), которая возвращает вектор коэффициентов R, при
251
Линейная регрессия
ORIGIN := 1
Представим значения хи у в виде векторов:
Вычисляем параметры а и Ь:
а := intercapt^x.y)
b slope(x.y)
а = -0.632 Ъ = 0.797
Общее уравнение прямой;
1 := 1.. 8 f(x) := а + Ъ х
Рис. 4.11. Линейная регрессия в MathCad
котором среднеквадратичная погрешность приближения исходных
данных, хранящихся в векторах X и Y, оказывается минимальной.
На рис. 4.12 показан пример проведения линейной регрессии
общего вида для таблицы значений исходных данных, заданных в
виде векторов х и у (вектор х должен содержать абсциссы точек,
упорядоченные по возрастанию). Полученная функция регрессии
имеет вид/(х)- -0,043х2 + 0,856ln(x)-0,659cos(x) + l. На рисун-
ке изображен график этой функции, обозначенный g(n), и отме-
чены точечные значения табличных данных.
Полиномиальная регрессия в MathCad реализована посредством
встроенной функции regress (%, Y,n), которая возвращает вектор зна-
чений полинома порядка п, приближающий данные, хранящиеся
в векторах X и Yno методу наименьших квадратов (рис. 4.13). При-
ближение происходит единственным полиномом, коэффициенты
которого вычисляются глобально, т.е. по всей совокупности за-
данных значений. Функция interp, в свою очередь, возвращает
252
Результаты измерений представлены в виде векторов значений:
Вектор коэффициентов регрессии: r := lirifit(x,y,f)
ад
ь COS(x) J
' 0.043
R = 0 856
ч -0.659 >
Построим график приближения исходных точек при помощи f(x):
i:=O.. 7 п:-0,0.25.. 4 g(n) := f(n)-R
Рис. 4.12. Реализация линейной регрессии общего вида в MathCad
интерполируемое значение х построенного полинома, коэффи-
циенты которого могут быть получены в результате транспониро-
вания вектора coeffs.
В результате получена функция регрессии
у = -82,б45х5 + 91,39х4 - 38,344х3 + 7,908х2 - 0,78х + 0,029.
Требование близости табличных значений и получаемых в ре-
зультате аппроксимации:
* ----------э
У - V)2 = 0.032804
253
В случае, когда данные не связаны единой полиномиальной
зависимостью, лучше применять другую функцию полиномиаль-
ной регрессии loess(vx,vy,span), которая возвращает локальные
приближения исходных данных отрезками полиномов второго
порядка. Величина аргумента span > 0 задает диапазон аппрокси-
мируемых данных (при больших значениях span эта функция при-
ближается к regress). На рис. 4.14 проиллюстрировано приближе-
ние табличных исходных данных (значения х изменяются от 1 до
30 с шагом 1 и определены вводом ранжированной переменной
ух,-, а значения у — равномерно распределенные случайные числа
на интервале [0; 0,5]) двумя способами: полиномами 2-го поряд-
ка /(локальная регрессия) и полиномом 4-го порядка j (глобаль-
ная регрессия). Результат показан на графике.
' 1.92 1 ' -2.4 '
Степень полинома: г;=5 2.95 3.8
Вычисление коэффициентов 33 5.5
полинома 6-й степени: 4.32 7.8
Х:= 5.17 Y > 8.6
Z := regress(X,Y ,г) 6.2 10.2
:= inteip(Z,X,Y,x) 7.24 < S3 > 9.3 „ 7.1 >
coeffs:« submattix(2,3,length(Z) - 1,0,0)
(coeffs/= (-32.643 91.39 -33.344 7.908 -0.78 0.029 )
Стропи график полиномиальной функции и исходных значений:
i:-0..7
Рис. 4.13. Полиномиальная регрессия в MathCad
254
Процедура сглаживания исходных данных осуществляется при
помощи следующих функций:
medsmooth(vy,n) — возвращает вектор — результат сглаживания
вектора данных vy с помощью сглаживания скользящей медианой
(п — нечетное целое число). Функция оставляет первые и послед-
ние (л - 1 )/2 точки неизменяемыми. Длина окна сглаживания, за-
даваемая аргументом п, должна быть мала по сравнению с дли-
ной вектора данных;
ksmooth(vx,vy,b) — возвращает вектор сглаживания, получен-
ный при помощи гауссова ядра, вычисляющего локальные взве-
шенные средние значения исходного вектора данных vy. Пара-
метр b управляет окном сглаживания и должен быть установлен
в несколько раз больше величины интервала между исходными
данными. Функцию следует применять в случаях, когда исход-
ные данные отделены друг от друга равновеликими интервалами;
supsmooth(vx,vy) — возвращает вектор, созданный локальным
(адаптивным) использованием процедуры сглаживания методом
наименьших квадратов.
Приближение полиномами второго порядка (локальная регрессия)
Вектор исходных данных: i > 0.. 30 vx, > i vy, md(0.5) + 2.2
Диапазон окрестности для локального приближения: span :• ОД
Функция локальной регрессии: vs > loess(vx,vy,sp«n)
Функция интерполяции* f(t) > int«rp(vs.vx,vy,X)
Приближение полиномом 4-го порядка к :• 4 х:«tegres«(vx.vy ,1ф
(глобальная регрессия): .
КХ> " mlwp(x.vx,vy,$
График функций приближения
Рис. 4.14. Локальная и глобальная регрессии в MathCad
255
Вектор данных: i:=0..30 4:-i vyfco»(vxj)-md(l.Z) + 0.9
rl > mtdsmooth(vy ,11) r2 := ksmooth^Yx.yy.S) i3 := supsmooth(vx,vy)
Рис. 4.15. Сглаживание данных в MathCad
Аппроксимируемая функция: Fr» > cos(x)
Границы интервала аппроксимации: а,= 0 b:=3 х := а.а + О.5.. b
Вычисление коэффициентов ряда ( с(
Чебышева: = Tcheb^-JJ Т(х) -
0.54
К
Рис. 4.16. Аппроксимация функции многочленом Чебышева в MathCad
256
На рис. 4.15 изображены графики вектора исходных данных vy
и функций сглаживания rl, г2, гЗ, реализующих методы сколь-
зящей медианы, гауссова ядра и метода наименьших квадратов
соответственно. Из графика видно, что наиболее оптимальными
сглаживаниями являются г2 и гЗ, которые практически совпада-
ют (с уменьшением величины п и увеличением значения пара-
метра Ь).
Аппроксимацию с использованием полиномов Чебышева 1-го
и 2-го рода осуществляют встроенные функции Tcheb(n,x) и
Ucheb(n,x) соответственно (л — степень полинома). На рис. 4.16
показано представление функции F\x) на отрезке [0; 5] много-
членом Чебышева первого рода. График иллюстрирует совпадение
исходной функциональной зависимости и полученной с помо-
щью полинома Чебышева Т\х).
Рассмотрим решение примера 4.4 в среде Derive. Для сравне-
ния качества приближения воспользуемся двумя способами при-
ближения: в виде линейной у = ах+ b и в виде логарифмической
у - a In х + b функций. Метод наименьших квадратов реализует фун-
кция FIT(zrr), где m — матрица, состоящая из двух столбцов и
такая, что верхняя се строка содержит аргумент функции и саму
функциональную зависимость, а остальные строки — пары ис-
ходных данных. На рис. 4.17 показана процедура ввода функции в
окне Author Expression. Вычислительный процесс осуществляется
при помощи команды Approximate пункта Symplify главного меню.
Приближающая линейная функция имеет вид: у- 0,921910.x -
-0,971019.
Рис. 4.18 иллюстрирует приближение исходных данных лога-
рифмической функцией, полученное аналогично: у= 2,534041пх-
-0,612298. Нетрудно понять, что наиболее предпочтительным яв-
ляется приближение в виде линейной зависимости.
Функция FlT(m) позволяет реализовать полиномиальную рег-
рессию (рис. 4.19) и регрессию общего вида.
Рис. 4.17. Реализация метода наименьших квадратов в Derive
9 Лапчик
257
Линейная регрессия общего вида представляет собой эмпириче-
скую формулу, полученную методом наименьших квадратов, в виде
линейной комбинации функций: у(х) = й/, (х) + bf2(x) + с/3(х) +....
Теперь решим задачу полиномиальной интерполяции в системе
Mathematica. Введем векторы узловых точек интерполяции и зна-
чений функции в этих точках так, как это показано на рис. 4.20, а.
Функция InterpolatingPolynomial\data,var\ возвращает полином по
переменной var, точно совпадающий со списком данных data (мно-
гочлен Лагранжа). Команда Collect используется для приведения
подобных членов, а знак //N за выражением позволяет выводить
число в формате с плавающей запятой.
Рис. 4.18. Линейная и логарифмическая регрессии в Derive
Рис. 4.19. Полиномиальная регрессия в Derive
258
Встроенная функция Fit\data,{f\, ...,fn},{var\,varn}] возвраща-
ет линейную комбинацию функций fl, ...,fn от аргументов varl,...,
varn по таблице данных data, полученную методом наименьших
квадратов. В примере на рис. 4.20, 6 выполняется регрессия одних
и тех же исходных данных двумя способами: линейной комбина-
цией трех функций и многочленом четвертой степени.
Построение интерполяционного многочлена относительно не-
которой переменной по табличным данным в математической
системе Maple осуществляет команда interp(X, Y,var), где Д' и Y —
векторы таблицы значений. Элементы векторов-значений, задаю-
щие узлы интерполяции, могут быть неупорядочены, но вектор X
нс должен содержать одинаковых элементов, как и на рис. 4.21. По
умолчанию вычисления производятся без обращения к машин-
ной арифметике (автоматический переход к операциям с плаваю-
щей запятой происходит в случае, если в выражении присутству-
ют числа, записанные в формате с десятичной запятой) и для
перехода к расчетам с плавающей запятой используется команда
а
IIЕЗ иыйы-г* спигап
ь>[10]= Fit[((i.o, о.25), (2, o.ni), {3, о.о71), {4, 0.053), —
(5, 0.047)), (Exp[x), Cos[x), хА3), х]
Out[lO]« -0.00718994с" *0.0087197х’ + 0.103358 Соз(х) ill
Fitnil.O, 0.25), (2, 0.111), (3, 0.071), {4, 1 0.053),
(5, 0.04?)), {а, х, хА2, хА3, хА4), х) J 1
Оиг(11 )= 0.632- 0.56825 х * 0.224208 х‘ - 0.04075 х\ 0.00279167 X*
б
Рис. 4.20. Полиномиальная интерполяция (а) и приближение по методу
наименьших квадратов (б) в системе Mathematica
259
evalflex,сГ), где ex — выражение, d — необязательный параметр
количества знаков мантиссы.
Функция spline(X, Y,var,ri) осуществляет сплайновую аппрок-
симацию; здесь п — порядок сплайна (linear — линейный;
quadratic — квадратичный; cubic — кубический; quartic — четвер-
той степени); по умолчанию строится кубический сплайн.
Пусть интерполируемая функция задана таблицей, состоящей
из четырех узлов:
Л' 2 3 5 7
Я*) 4 -2 6 -3
Требуется найти значения коэффициентов, определяющих ку-
бический сплайн. Решение представлено на рис. 4.22.
Получен интерполяционный кубический сплайн 5, определен-
ный на интервале: ]-«>; 3[ и [3; 5[ и [5; + <»[.
Метод наименьших квадратов, проиллюстрированный на
рис. 4.23, реализует функция leastsquare\\yar\,... ,varn], /] ([р])
из пакета статистики stats расширения системы. Входными па-
раметрами являются имена переменных, вид функции и набор
точек.
Г> [-3,-1,-2f-4]; 0. -8.-7], [-3.-1.-2. -4]
> rl;«interp(t,x)/ 101 » 139 2 6943 ri := x + x + x-1 504 42 504
Г > evalf<rl,5}; 3 2 20040 x + 3 3095 x + 13776 x - 1.
f> t2:-[l,2,3,4J, 12,3,4,5] ; t2 ~[1.2. 3,4], [2, 3,4,5]
Г > г2:"interp(12 , x); r2 ?= x + 1
Рис. 4.21. Полиномиальная аппроксимация в Maple
j(Z)| !\!!>
> t:-[2,3,5 7].[4,-2.6.,-3J; t = [2. 3, 5,7]. [4,-2. 6 .-3 J
> Digits:-2 s;«spline(t f x>; s 2 3 13 + 5.1 x - 6.8 x + 1.2 x x <3 68 -51.X + 12 x2-.91x3 x<5 2 3 -73. + 39. x-6.1 x +.29x otherwise
Рис. 4.22. Построение кубического сплайна в Maple
260
Вычисление значений элементарных функций также может быть
реализовано в пакете Maple и с помощью многочленов Чебышева
(см. подразл. 4.8). Для этого используется специальная функция
chebyshev(ex,var,eps) библиотечного модуля (пакета) питарргох,
которая возвращает разложение выражения ех в ряд относительно
переменной var с заданной точностью eps.
Предварительно требуется осуществить загрузку пакета расши-
рения командой *’Н/1(имя_пакета).
На рис. 4.24 показано разложение функции cosx в ряд по поли-
номам Чебышева с различной точностью.
Интерполяцию таблицы значений некоторой функции в сис-
теме MatLab осуществляет команда interpl(X,Y,xi,‘method’).
В результате по исходным данным или векторам значений X, Y
будет получен вектор, содержащий элементы, соответствующие
заданным значениям вектора xi (в качестве xi может быть точка, в
которой требуется получить значение функции).
Параметр method (его можно не указывать) задает метод ин-
терполяции: линейная — linear (действует по умолчанию), или
кубическая — cubic, или кубическая сплайн-интерполяция —
spline.
Для более быстрой интерполяции в случае, когда X — вектор
равномерно распределенных точек, перед наименованием метода
указывается символ звездочка «*». На рис. 4.25 рассмотрен при-
мер, в котором по заданным векторам (таблице значений функ-
ции) получены интерполяционные значения в точке 1,91 двумя
способами: с использованием линейной и кубической сплайн-
интерполяцйй.
> t -(2,3.5,»I,(4.,-2.G.3J;
> with (st at s) .
/-[2. 3.5.7Ц4..2. 6.3)
| aaova. drsmbe.fii. OsJfvatf, й-зСрЫг. ]
> Digit» -3; r -Гit (1-astsquare((x,уj, y-a1-x 3«»2•x‘ 2*аЗ«ж♦a4)]((t]),
, -K9 г3 г U ii2 - 412г rit.6
Рис. 4.23. Реализация метода наименьших квадратов в Maple
[> with(nu*apf>rox)
Г> eh; -ch«by»tiov(co* (ж) , х . О . 0001) ,
ch - 76519768657(0.4)- 2298069699 T(2. x)t-ОСИ5»53277928 T(4.x)- 00004187667601 Т(6.х)
ch: -ch—by*hwv(соя (х) ,ж,0.01) .
• ch - 7651976865 Тс0. х) - 2298069699 Т(2. х) ♦ 004953277923 Т(4. х)
Г> Ch : —C'h«tby»h—V (со* ( X) , Ж . 0 1),
[ сА - 76519768657(0.*)- 22980696997(2. х)
Рис. 4.24. Аппроксимация функции многочленами Чебышева в Maple
261
•J MATLAB Окно управления
Файл Правка Окно ?
- 8 Й ?
» Х=[0.41,1. >5,2.67,3.84];
» V=[2.63,3.75,4.87,5.03];
» yi=interp1(X,Y,1.91,’linear*)
yi -
4.1100
» yi=interp1(X,V,1.91,’spline’)
yi =
4.1539
Рис. 4.26. Визуализация линейной и сплайн-интсрполяции в MatLab
ИMATLAB Окно управления
Файл Правка Окно 7__________________________________________________
<-s I i ГУ. «э, .I дао (!ri ! tei I л
» Х=[0.41,1.55,2.67,3.84];
» V=[2.63,3.75,4.87,5.03];
» p=polyfit(X,V,3)
Р =
-0.1122 0.5271 0.3090 2.4224
Рис. 4.27. Аппроксимация методом наименьших квадратов в MatLab
262
Дополнив документ несколькими командами, получим график
обеих интерполяционных функций, показанный на рис. 4.26.
» xi=0:0.01:4;
» yii=interpl(X,Y,xi, 'spline 1);
» plot(X,Y, ’*k*,xi,yi,'~k',xi,yii, 'k-. 1 ),grid
--------------- " . ........................................
Полиномиальную аппроксимацию методом наименьших квад-
ратов осуществляет функция polyflt(x,y,n), которая возвращает век-
тор коэффициентов полинома р(х) степени п, аппроксимирую-
щего функцию у(х) (рис. 4.27).
Полученные коэффициенты позволяют записать выражение
у = -0,1122х3 + 0,5271х2 -г 0,3090х + 2,4224.
Контрольный вопрос
Какие средства инструментальных программ позволяют автоматизи-
ровать решение задачи аппроксимации?
Упражнения
1. Для таблично заданной функции у-fix):
X 0 1 2 3 5
У 3 4 7 5 6
а) получить формулу многочлена Лагранжа;
б) вычислить, используя интерполяционный многочлен Лагранжа,
значение /(4,5);
в) построить график интерполяционного полинома и отметить на нем
узловые точки.
2. Функция y=f(x) задана таблицей значений;
X 0 0,3 0,6 0,9 1,3 1,6
У 1,1 2,3 2,7 3/ 4,8 7,3
Вычислить /(2,5) и /(4,5), используя:
а) линейную интерполяцию;
б) полиномиальную интерполяцию.
Отобразить на графике исходные данные и интерполяционные функции.
3. Вычислить значения функции у = cos(x + eOTSX) в узлах интерполя-
ции х, = а + hj, где h = (b- а)/10, i = 0, 1, ..., 10 на отрезке [3; 6]. Выпол-
нить экстраполяцию полученного вектора данных в последующих 30 точках
по последним 8 значениям функции. Отобразить графически исходные и
предсказанные данные.
4. Для зависимости, заданной таблицей значений, методом наимень-
ших квадратов получить уравнение и построить график приближающей
функции:
263
X 3,72 4,21 4,17 5,64 2,95 6,85 2,01 1,92 3,57
У 0,51 -2,26 0,63 0,07 -1,78 0,72 -1,67 -2,85 1,45
ЛАБОРА ТОРНАЯ РАБОТА № 4
Тема: Приближение функций
Задание 1. По заданной таблице значений функции
X хо *1 *2 Хз
У Уо У1 У1 Уз
составить формулу интерполяционного многочлена Лагранжа.
Построить его график и отметить на нем узловые точки у,-),
i = О, 1, 2, 3. Это же задание выполнить с помощью инструмен-
тальных программных средств.
Задание 2. Вычислить с помощью калькулятора одно значение
заданной функции для промежуточного значения аргумента с по-
мощью интерполяционного многочлена Лагранжа и оценить по-
грешность интерполяции. Этот же результат получить с помощью
программы для компьютера и с применением математических
пакетов.
Задание 3. Для функции, заданной таблицей узловых значе-
ний, вычислить коэффициенты и составить формулы кубическо-
го сплайна. Результат интерполирования проверить путем вычис-
ления значений сплайна в узловых узлах. Построить график куби-
ческого сплайна и отобразить на нем узловые точки с помощью
одного из инструментальных программных средств.
Задание 4. С помощью программы для компьютера уплотнить
часть таблицы заданной функции, пользуясь интерполяционны-
ми формулами Ньютона.
Задание 5. По заданной таблице значений х и у построить ме-
тодом наименьших квадратов две различные эмпирические фор-
мулы и сравнить качество полученных приближений. Задание вы-
полнить тремя способами: а) с помощью ручных расчетов на каль-
куляторе; б) путем использования программы для компьютера;
в) с помощью табличного процессора Excel или иного инстру-
ментального средства.
Пояснения к выполнению лабораторной работы № 4
Исходные данные ко всем заданиям лабораторной работы со-
держатся в табл. 4.14—4.23, приведенных в конце гл. 4.
При выполнении задания 1 составляют многочлен Лагранжа
по формуле (4.10), производят необходимые вычисления и приве-
264
дение подобных членов (см. пример 4.1). По полученной форму-
ле строится график интерполирующей функции, на котором
отмечаются узловые точки. Это же задание выполняют и с по-
мощью инструментальных пакетов Maple и MathCad (см. под-
разд. 4.15).
Исходные данные для выполнения задания 1 берутся из табл. 4.14.
Задание 2 сначала выполняют с помощью калькулятора по спе-
циальной расчетной схеме (см. табл. 4.2). Для достижения наилуч-
шей точности берут максимально возможное четное или нечетное
число углов, симметричных относительно заданного значения х.
Использование расчетной таблицы показано в примере 4.2. При-
мер использования компьютерной программы для интерполиро-
вания по формуле Лагранжа рассмотрен в подразд. 4.5. Это же за-
дание выполняется и с помощью инструментальных пакетов (см.
подразд. 4.15, рис. 4.8, 4.25).
Поскольку аналитическое выражение интерполируемой функ-
ции в данном случае известно, то оценку погрешности интерпо-
лирования производят по формуле (4.23). Кроме того, имеется воз-
можность сравнить результат интерполирования со значением
функции, вычисленным по ее аналитическому выражению, за-
данному в таблице.
Для определения содержания задания 2 используется табл. 4.15,
из которой по заданному варианту извлекается номер другой таб-
лицы (4.16—4.19), задающей интерполируемую функцию, а так-
же значение аргумента х, для которого требуется вычислить иско-
мое значение интерполяционного многочлена. Так, например, для
варианта 4 задание состоит в вычислении значения функции, за-
данной табл. 4.19 при х=4,8.
Исходными данными для выполнения задания 3 служит таб-
лично заданная функция из задания 1 (см. табл. 4.14). Перед вы-
полнением задания следует внимательно изучить материал под-
разд. 4.11 и разобрать пример 4.7, а также примеры по использова-
нию инструментальных программных средств для сплайновой ап-
проксимации в подразд. 4.15 (рис. 4.9, 4.21, 4.22, 4.26).
Для выполнения задания 4 по заданной таблице функции с
равноотстоящими значениями аргумента составляют таблицу ко-
нечных разностей и определяют порядок интерполяционного по-
линома Ньютона. В зависимости от расположения участка субтабу-
лирования относительно исходной таблицы и потребности в ко-
нечных разностях избирается первая (4.16) или вторая (4.19) ин-
терполяционные формулы Ньютона. Исходные данные для вы-
полнения задания 4 (номер таблицы функции, концы отрезка [а;
6] и шаг Н субтабулирования) берут из табл. 4.15. В программе
субтабулирования необходимо предусмотреть подсчет погрешно-
сти метода по одной из формул (4.26) или (4.27). Перед выполне-
нием задания полезно рассмотреть пример 4.4 из подразд. 4.9.
265
Таблица 4.14
Вариант хо Х1 Л Ji У1 Уз
1 1 0 3 4 -3 5 2 6
2 2 3 5 6 4 1 7 2
3 0 2 3 5 -1 -4 2 -8
4 7 9 13 15 2 -2 3 —4
5 -3 -1 3 5 7 -1 4 -6
6 1 2 4 7 -3 -7 2 8
7 -1 -1 2 4 4 9 1 6
8 2 4 5 7 9 -3 6 -2
9 4 -2 0 3 2 8 5 10
10 -1 1,5 3 5 4 -7 1 -8
11 2 4 7 8 -1 -6 3 12
12 -9 -7 _4 -1 3 „з 4 -9
13 0 1 4 6 7 -1 8 2
14 -8 -5 0 2 9 -2 4 6
15 -7 -5 “4 -1 4 -4 5 10
16 1 4 9 11 -2 9 3 7
17 7 8 10 13 6 -2 7 -10
18 -4 0 2 5 4 8 -2 -9
19 -3 -1 1 3 И -1 6 -2
20 0 3 8 11 1 5 -4 -8
Таблица 4.15
Вариант Задание 2 Задание 4
Таблица X Таблица а В Н
1 4.16 3,8 4.20 0,65 0,75 0,01
2 4.17 3,5 4.21 0,30 0,45 0,025
3 4.18 0,5 4.22 1,45 1,55 0,01
4 4.19 4,8 4.23 1,20 1,40 0,02
5 4.16 4,1 4.21 0,10 0,20 0,01
6 4.17 3,9 4.22 1,10 1,30 0,02
7 4.18 3,3 4.23 1,05 1,25 0,025
8 4.19 4,0 4.20 0,70 0,90 0,02
9 4.16 2,9 4.22 1,25 1,50 0,025
10 4.17 5,3 4.23 1,00 1,10 0,01
И 4.18 4,1 4.20 0,60 0,70 0,01
12 4.19 7,6 4.21 0,15 0,35 0,025
13 4.16 4,4 4.22 1,15 1,25 0,01
14 4.17 2,5 4.20 0,65 0,85 0,025
15 4.18 5,2 4.21 0,20 0,40 0,02
16 4.19 6,8 4.22 1,15 1,25 0,01
17 4.16 0,4 4.21 0,35 0,55 0,01
18 4.17 3,7 4.23 1,05 1,25 0,025
19 4.18 7,5 4.22 1,35 1,60 0,02
20 4.19 8,6 4.23 1,25 1,45 0,01
266
Таблица 4.16
Таблица 4.17
X /<Х) = 1 / X • 1g X + X2
1,3 1,7777
2,1 4,5634
3,7 13,8436
4,5 20,3952
6,1 37,3387
7,7 59,4051
8,5 72,3593
X У(х) = In2,3x-0,8/x
1,2 0,3486
1,9 1,0537
3,3 1,7844
4,7 2,2103
5,4 2,3712
6,8 2,6322
7,5 2,7411
Табл ица 4.18
X /(х) = 2,IsinO,37x
-3,2 -1,9449
-0,8 -0,6126
0,4 0,3097
2,8 1,8068
4,0 2,0913
6,4 1,4673
7,6 0,6797
Таблица4.19 )
X /(x) = l,7^-cos(0,4-0,7x)
2,6 2,1874
3,3 2,8637
4,7 3,8161
6,1 3,8524
7,5 3,1905
8,2 2,8409
9,6 2,6137
Таблица 4.20
X sin х
0,60 0,56464
0,65 0,60519
0,70 0,64422
0,75 0,68164
0,80 0,71736
0,85 0,75128
0,90 0,78333
0,95 0,81342
1,00 0,84147
1,05 0,86742
1,10 0,89121
Табл и ца 4.21
X COS X
0,05 0,99375
0,10 0,99500
0,15 0,99877
0,20 0,98007
0,25 0,96891
0,30 0,95534
0,35 0,93937
0,40 0,92106
0,45 0,90045
0,50 0,87758
0,55 0,85252
Таблица 4.22
X sin х
1,10 0,89121
1,15 0,91276
1,20 0,93204
1,25 0,94898
1,30 0,96356
1,35 0,97572
1,40 0,98545
1,45 0,99271
1,50 0,99749
1,55 0,99973
1,60 0,99957
Таблица 4.23
X cosx
1,00 0,54090
1,05 0,49757
1,10 0,45360
1,15 0,40849
1,20 0,36236
1,25 0,31532
1,30 0,26750
1,35 0,21901
1,40 0,16997
1,45 0,12050
1,50 0,07074
267
Таблица 4.24
1 X 1,73 2,56 3,39 4,22 5,05 5,87 6,70 7,53
У 0,63 1,11 1,42 1,94 2,30 2,89 3,29 3,87
2 X -1.33 -3,84 -3,23 -2,76 -2,22 -1,67 -1,13 -0,60
У 2,25 2,83 3,44 4,31 5,29 6,55 8,01 10,04
3 X 1,00 1,64 2,28 2,91 3,56 4,19 4,84 5,48
У 0,28 0,19 0,15 0,11 0,09 0,08 0,07 0,06
4 X 1,20 1.57 1,94 3,31 2,68 3.05 3,42 3.79
У 2,59 2,06 1,58 1,25 0,91 0,66 0.38 0,21
5 X 1,10 1,74 2,38 3,02 3,66 4,30 4,94 5,18
У 1,73 2,98 3,53 3,89 4,01 4,25 4,32 4,38
6 X 1,74 2,32 2,90 3,48 4,06 4,64 5,22 5,80
У 0,66 0,45 0,36 0,33 0.30 0,29 0,28 0,27
7 X 1,92 2,84 3,76 4,68 5,60 6,52 7,44 8,36
У 1,48 2.69 4,07 5,67 7,42 9,35 11,36 13,54
8 X 1,28 1,76 2,24 2,72 3,20 3,68 4,16 4,64
У 2,10 2.62 3,21 3.98 4.98 6,06 7.47 9,25
9 X -4.84 -4,30 -3,76 -3,22 -2,68 -2,14 -1,60 -1,06
У -0,09 -0,11 -0,13 -0.16 -0,19 -0,26 -0,39 -0,81
10 Л 0,68 1,13 1,58 2,03 2,48 2,93 3,33 3,83
У -2,16 -1.69 -1.36 -1.12 -0,95 -0,75 -0,65 -0,52
11 X 2,4 2,91 3,42 3,93 4,44 4,95 5,46 5,97
У 4,03 3.10 2,44 1,96 1,58 1.29 1,04 0,85
12 X 1,16 1,88 2,60 3,32 4,04 4,76 5,48 6,20
У 0,18 0,26 0,32 0,36 0,40 0,43 0,46 0,48
13 X 1,00 1,71 2,42 3,13 3,84 4,55 5.26 5,97
У 12,49 4,76 2,55 1,60 1,11 0,82 0,63 0,50
14 X -0.64 -0,36 -0,08 0,20 0.48 0,76 - 1,04 1,32
У 29,51 18,86 12,05 7,70 4,92 3,14 2,01 1,28
15 X -2,45 -1,94 -1,43 -0,92 -0,41 0,10 0,61 1.12
У 0,87 1,19 1,68 2,23 3,04 4,15 5,66 7.72
16 X 1.54 1,91 2,28 2,65 3,02 3,39 3,76 4,13
У -2,52 -3,08 -3,54 -3,93 -4,27 -4,57 -4,84 -5,09
17 X 1.2 2,0 2,8 3,6 4,4 5,2 6,0 6,8
У -10,85 -6,15 -4,14 -3,02 -2.30 -1,81 -1,45 -1.17
18 X -1.04 -0,67 -0,30 0,07 0,44 0,81 1,18 1.55
У 10,80 8,08 5,97 4,44 3,31 2,46 1,83 1,36
19 X 0,41 0,97 1,53 2,09 2,65 3,21 3,77 4,33
У 0,45 1,17 1.56 1,82 2,02 2,18 2,31 2,44
20 х 0,80 1.51 2,22 2,93 3,64 4,35 5,06 5,77
у 9,22 6,35 5,31 4,77 4,45 4,23 4,07 3,44
268
При выполнении задания 5 по заданной таблице значений х и у
(см. варианты в табл. 4.24) строится точечный график, с помощью
которого выбираются два наиболее предпочтительных вида при-
ближающей функции. Здесь невозможно указать какой-либо об-
щий метод угадывания наилучшего вида приближения, во многих
случаях удачное решение этой задачи зависит от интуиции и опы-
та исследователя. При использовании компьютера появляется воз-
можность испытания разных способов без сколько-нибудь значи-
тельных усилий.
Исследование точечного графика и выбор вида приближаю-
щей функции как в случае ручного, так и в случае компьютерного
исполнения облегчаются при умелом расположении графика в
системе координат и правильном сочетании масштабов на осях
ОХ н OY, подчеркивающих характер данной зависимости. Следует
заметить, что при построении эмпирической формулы всегда
можно добиться, чтобы исходные значения аргумента и функции
были положительны. Для этого достаточно сделать параллельный
перенос в направлении осей, т.е. фактически перейти к новым
переменным; в записи окончательного результата при этом необ-
ходимо вернуться к прежним обозначениям.
После выбора вида приближающей функции следует присту-
пить к вычислениям. Когда расчеты ведутся с помощью кальку-
лятора (задание 5, а), удобно использовать вспомогательные таб-
лицы вида 4.9 —4.11 (см. пример 4.8). При использовании компью-
тера сначала (задание 5, б) составляется программа с выводом
значений параметров приближающих функций заданного вида и
соответствующих им сумм квадратов уклонений (см. программу в
подразд. 4.13), а затем (задание 5, в) — проводится исследование
заданной табличной зависимости средствами инструментальных
пакетов (см. подразд. 4.15, рис. 4.5 —4.7, 4.11—4.14, 4.17—4.20,
4.21, 4.23, 4.27).
ГЛАВА 5
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
И ИНТЕГРИРОВАНИЕ
5.1. ПОСТАНОВКА ЗАДАЧИ ЧИСЛЕННОГО
ДИФФЕРЕНЦИРОВАНИЯ
Множество прикладных задач, решаемых средствами класси-
ческого математического анализа, сводится к нахождению произ-
водной функции, первообразной или определенного интеграла
от заданной функции.
При аналитическом задании указанной функции ее дифферен-
цирование и(или) интегрирование следует, в первую очередь,
стремиться выполнить аналитически. В классе элементарных функ-
ций, с которыми чаще всего приходится на практике иметь дело,
операция дифференцирования выполняется достаточно просто и
никогда не выводит за пределы этого класса. Операция же нахож-
дения первообразной в этом классе функций, напротив, очень
часто выводит за пределы класса элементарных функций, и по-
этому технически существенно сложнее. Поскольку классический
способ вычисления определенного интеграла по формуле Ньюто-
на-Лейбница требует нахождения первообразной, то те же труд-
ности переносятся и на вычисление определенных интегралов.
При табличном задании функции, для которой требуется осу-
ществить дифференцирование или интегрирование (а такой спо-
соб задания функции в приложениях встречается чрезвычайно
часто), возможности аналитических методов вообще неясны без
уточнения постановки задачи.
В силу указанных факторов численные методы дифференциро-
вания и интегрирования при решении прикладных математичес-
ких задач играют важную роль и поочередно рассматриваются в
этой главе.
Как известно, производная аналитически заданной функции
/(х) в точке х = а определяется следующим образом:
/'(«) = lim/U)~/(Q), (5.1)
x-ta х-а
при этом функция /(х) должна быть непрерывна в окрестности
точки а. Хорошо известная из введения в математический анализ
формула при определенном подходе (когда, скажем, получение
270
аналитического выражения производной по каким-либо причи-
нам затруднительно) может быть использована для быстрого по-
лучения достаточно хорошего приближения к числовому значе-
нию производной в точке а. Для этого строится последователь-
ность значений хПУ сходящаяся к а, и вычисляется соответствую-
щая последовательность значений разностных отношений
dn = 1, 2, 3, ... .
х„ -а
(5.2)
Поскольку последовательность (5.2) сходится к f\a), каждое
новое значение dn будет, вообще говоря, давать все более точное
значение f'(a) (оговорка сделана по известной причине — поме-
хой может стать неустойчивость вычислений). Эта идея может быть
положена в основу программы для компьютера, вычисляющей
приближенное значение производной /'(х) в точке а.
Пример 5.1. В приведенной ниже программе, вычисляющей зна-
чение производной функции /(х) = 7х, последовательность значе-
ний х„ строится по формуле: х„ = а + 0,5я, где а — заданное число,
а п= I, 2, 3, ..., т. Значение т (количество вычисляемых и выво-
димых членов последовательности) определяется, как и значение
а, в процессе ввода, но может быть увеличено в ходе исполнения
программы. Дело в том, что вывод последовательных приближе-
ний устроен так, что после вывода 10 новых приближений про-
грамма делает паузу, а исследователь на основе эмпирического
анализа полученной последовательности приближений принима-
ет решение — прекратить процесс или продолжить вычисления.
program Derivative;
uses crt;
label 1;
type T=real;
var x, b, d, a, c, q:T;
i,tn:integer; ch:char;
begin
clrscr; c:=0.5;
writeln('Введите значение а и tn через пробел');
readln (a, m) ;
writeln ('1 ) ;
writeln ( ' n x', ’ d');
writeln ('________________________________________’) ;
q: =sqrt (a) ;'
i :=1;
1: repeat
x:=a+c;
b:=sqrt(x);
271
d: = (b-q)/с;
с:=c/2;
writein (i:2, ' ',x:12:8,' ', d:20:14);
inc (i);
until i>m;
writein('Продолжить вычисления? Y/N');
ch:=readkey;
if (ch='Y') or (ch='y') then begin
m:=m+10;
goto 1;
end;
readkey;
end.
Ниже приведены результаты двух проходов исполнения про-
граммы для типа real, начиная с т = 10.
Введите значение а и m через пробел
32 10
п х d
1 32.50000000 0.08804575201
2 32.25000000 0.08821638522
3 32.12500000 0.08830219909
4 32.06250000 0.08834523137
5 32.03125000 0.08836677903
6 32.01562500 0.08837756095
7 32.00781250 0.08838295378
8 32.00390625 0.08838565089
9 32.00195313 0.08838699758
10 32.00097656 0.08838767558
Продолжить вычисления? Y/N
11 32.00048828 0.08838801086
12 32.00024414 0.08838817477
13 32.00012207 0.08838826418
14 32.00006104 0.08838832378
15 32.00003052 0.08838844299
16 32.00001526 0.08838844299
17 32.00000763 0.08838844299
18 32.00000381 0.08838844299
19 32.00000191 0.08839035034
20 32.00000095 0.08838653564
Продолжить вычисления? Y/N
272
Для анализа полученных результатов воспользуемся эмпири-
ческим критерием, который ранее (п. 3.4.2) применялся для ите-
рационного процесса (повторившиеся не менее трех раз в одних и
тех же разрядах цифры выделены — см. 14-е приближение). Оче-
видно, что если в качестве результата взять значение 0,088388, то
можно с достаточно высокой степенью уверенности считать все его
цифры верными. Для сравнения отметим, что вычисленное с мак-
симальной точностью восьмиразрядного калькулятора значение про-
изводной функции /(х) = >/х в точке х = 32 равно: 1/(2>/32)=
« 0,08838835. Как видим, это значение вполне соответствует ре-
зультату, полученному в процессе выполнения программы.
Вместе с тем, если с помощью приведенной выше программы
попытаться продолжить процесс построения последовательности
разностных отношений (при том же типе real), то довольно быст-
ро начнет сказываться фактор неустойчивости вычислений. Так,
при попытке выполнить программу для /л= 20 мы сначала (на
15 — 18 шагах) замечаем внезапное совпадение цифр сразу во
всех (!) разрядах, а после 18-го шага начинает проявляться оче-
видный сбой, что служит превосходной иллюстрацией ограни-
ченных возможностей используемого типа числовых данных. По-
нятно, что в этой ситуации продолжать попытки получить более
точное значение результата, не меняя типа данных, не имеет смыс-
ла. Сразу заметим, что и применение более длинных форматов
представления чисел не всегда может добавить ясности к вопросу
о верных знаках. Причины могут объясняться особенностями каж-
дой задачи — в частности, тем, как реагируют на смену типов
числовых данных и с какой точностью вычисляются используе-
мые в расчетах стандартные математические функции: корень квад-
ратный, логарифм, экспонента и т. п. В данном конкретном случае
наряду с явным проявлением ограниченных возможностей исполь-
зуемого типа может сказываться и фактор деления очень малых
чисел. В целом, признавая простоту и эффективность описанного
подхода к вычислению производной, мы должны относиться к
рассмотренному примеру как к полезному напоминанию о том,
что компьютер и стандартное программное обеспечение даже в
совершенно элементарной ситуации не всесильны (читателю на-
стоятельно рекомендуется поэкспериментировать с различными
форматами представления числовых данных; см. упражнения в
конце настоящего пункта).
В силу причин, указанных в начале этой главы, численное диф-
ференцирование применяется, прежде всего, для таблично задан-
ных функций. Задача ставится следующим образом: функция у =
=/(х) задана табл. 5.1 на отрезке [а; />] в узлах а = х0<Х| <
< х2 < ... < х„.| < х„ = Ь. Требуется найти приближенное значение
производной этой функции в некоторой точке х*е [о; />] (х‘е может
быть как узловой точкой, так и расположенной между узлами).
273
Таблица 5.1
X х0 X,
У Уо У| ул
Один из подходов к решению этой задачи заключается в том,
что по таблице значений /(х) строится интерполирующая функ-
ция ф(х) и за значение производной /'(х*) приближенно прини-
мается ф'(х‘), т.е.
/'(x*)«(p'(x‘). (5.3)
При этом задача не может считаться решенной, если нет оцен-
ки погрешности, т.е. величины Я'(х‘) = |/'(х‘)-ф'(х*)|.
Отметим одно чрезвычайно важное обстоятельство — некор-
ректность (в общем случае) этого приема. В процессе построения
интерполирующей функции мы
стремимся сделать ее значения
близкими (в заданной мере) зна-
чениям исходной функции во всех
точках отрезка интерполяции.
В гл. 4 было показано, что эта
задача, вообще говоря, разреши-
ма и что погрешность интерполя-
ции, т.е. максимальное расхожде-
ние между функциями, можно
оценить. Однако близость значе-
ния двух функций не гарантирует
близость значений их производ-
ных, т.е. тангенсов углов наклона
касательных. Это утверждение ил-
люстрируется на рис. 5.1, где
сплошная линия — график исход-
линия — интерполирующей фун-
Рис. 5.1. Иллюстрация некоррект-
ности решения задачи численного
дифференцирования с помощью
интерполяционного многочлена
ной функции /(х), пунктирная
кции ф(х). Из рисунка хорошо видно, что близость (и даже совпа-
дение) значений функций вовсе не означает близости значений
производных, т.е. тангенсов углов наклона качательных А и В.
Контрольные вопросы
1. Как можно построить алгоритм численного нахождения значения
производной аналитически заданной функции в точке на основе опреде-
ления производной? С какими препятствиями в процессе реализации
алгоритма здесь можно столкнуться?
2. Как может быть решена задача численного дифференцирования для
таблично заданной функции с помощью интерполирования? В чем не-
корректность такого способа численного дифференцирования?
I
274
Упражнение
С помощью программы, рассмотренной в подразд. 5.1, найти значе-
ния производных функций в точках:
a) /(*) =-Л -2х, л = -10; б) f(x) = ^7^, х = 0,05.
Произвести численные эксперименты для различных типов представ-
ления числовых данных в языке программирования.
5.2. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ НА ОСНОВЕ
ИНТЕРПОЛЯЦИОННОЙ ФОРМУЛЫ ЛАГРАНЖА
В гл. 4 отмечалось, что по таблице значений функции, постро-
енной по заданной системе из п + 1 узлов, можно сконструировать
единственный интерполяционный многочлен л-й степени. По-
скольку вычисляемый объект (значение производной f'(x*) ) суть
число, то неважно, какую из рассмотренных в гл. 4 интерполяци-
онных формул — Лагранжа или Ньютона — положить в основу
вычислений: результат должен получиться одинаковым.
Итак, применяя для численного дифференцирования на от-
резке {а; />] интерполяционный полином, естественно строить на
этом отрезке систему равноотстоящих узлов а = х0 < х, < х2 < ...
< x„_i <хп = Ь, которыми отрезок делится на п равных частей: xi+1 -
-Xj = h = const (/ = 0, 1, 2, ..., н - 1); шаг интерполирования при этом
имеет значение h = {b - а) / п. В этом случае многочлен Лагранжа
строится на равноотстоящих узлах и имеет более удобный вид.
Примем подстановку:
и с учетом представления (4.11) получим новые выражения для
П,н|М И ПЛ+(<Х')
Используя (5.4), последовательно находим:
х - Хо = ht;
х - х, = х - х0 - h = h(t -1);
х - х2 = х - xQ- 2h = h{t - 2),
т. е. в общем случае:
х - Xj = х - х,| - ih = h(t - i), i = 0, 1, ..., n. (5.5)
Используя (5.5), получаем:
П„+](х) = h^t(t -1)(/ -2)•...•(' -п).
В целях сокращения записей введем обозначение
/(/-!)(/-2) .„•('-») -/1п+и,
275
тогда выражение Ля+1 (х) принимает вид
П„+| (X) = Й-М"+1!. (5.6)
Учитывая, что при постоянном шаге имеет место х,- = х0 + ih,
i = 0, 1, п, последовательно находим:
X/ - х0 = hi, Xi - X! = X; - х0 - h = h(i - I),
Xj-x2 =xf-x0 -2h = h(i-T),Xi-x„ = Xi-xQ-nh = (5.7)
Заметим, что в (5.7) равно п строк (/-я строка отсутствует),
причем значения первых i строк положительны, а остальных —
отрицательны. Используя (5.7), получаем
П «Ц = (*; - *о) ‘ " х,--1 )(х,- - х|Ч1) •... • (х,- - х„) =
= й"7(г -1) •...-1-(-1) ....-[-(л-/)], -
т.е. ...
2П И| (*) = ~ -^j^(5.8)
>едставлений (5.6) и (5.8) формула Лагранжа (4.11)
>ящих узлов принимает дид
” Ц—Ы"-' Ял+|]
’ (M)
Пример 5.2. Составить интерполяционный многочлен Лагран-
жа для функции, заданной своими значениями на равноотстоя-
щих узлах (и = 2, h = 1):
Используя формулу (5.9), запишем:
Lj(-1 + /) = + (-2) + 6 ^-^-2) =
2!f i-1 2\{i-2)
= 2(/ - 1)(7 - 2) т 2/(г 2) t 3r(r - 1) 7/2 - I3r + 4.
Узловые табличные значения функции (4; -2; 6) получаются
по этой формуле соответственно при r = 0; 1; 2.
Следуя (5.3), будем дифференцировать многочлен Лагранжа
(5.9) по х как функцию от /:
/(х)~ L„(x). dt Ху-/!(„_z)!-_
dx
Учитывая, что согласно (5.4) х = хд + /й, а также — = h, полу-
чим окончательно
276
1" (-1)"-' Л/НГ
/'(x)=/'(x0 + ZA) = (!(„_,-
(5.Ю)
Пользуясь формулой (5.10), можно вычислять приближенные
значения производной функции f(x), если она задана на отрезке
[а; А] значениями в равноотстоящих узлах а = х0<Х| < х2 <
<... < x„-i < х„ = b (при этом параметр / пробегает значения от 1
до п).
Аналогично могут быть найдены производные функции f(x)
более высоких порядков.
Пример 5.3. Вычислить приближенное значение производной
функции, заданной таблицей
X 3 4 5
/(X) 2 -1 6
в точке х = 4.
Применяя формулу (5.10), получим (здесь я = 2, й= I)
- 7 1 ^[(/-1)^-2)] _ (-1) d[t(t-2)] ' J_ tf[r(r-l)] _
2! dt 1 dt 2! dt
t = (Z - 2 +t - 1) + (Z - 2 + Z) + 3(Z -1 + Z) - 2z - 3 + 2t - 2 + 6Z - 3 = 10/ - 8.
f Учитывая, что узел x = 4 соответствует значению t = 1 (т. е. Z =
| - х х° ), получаем /'(4) ~ 2.
| п
К Если известно аналитическое выражение функции/(х), то фор-
I мулу для оценки погрешности численного дифференцирования
| можно при этом же условии получить на основе формулы по-
£ грешности интерполирования (см. подразд. 4.7)
' ад вд = <511>
| где £ = £(х) — значение из отрезка [о; А], отличное от узлов и х.
) Учитывая (5.11) и допуская, что Дх) дифференцируема п + 1
/ раз, запишем
г„(х)= л;(х) = —L—Ь^)(^).п;+1(Х) • ^-[/<n+l>(U]|• (5.12)
(и +1)! [ "+l dx J
t. Формула (5.12) значительно упрощается, если оценка нахо-
! дится для значения производной /'(х) в узле х, таблицы. В этом
; случае, учитывая (5.8), получаем (
Г г„(х,) = 7?Дх,) = (-1)"-' A"'!(” ~2 - /(п+|)(^), (5.13)
(п + 1)!
где . промежуточное значение между Xq, хь х2, ..., х„.
277
Обозначив Мп + । = max |/(яИ>(х)|, получим верхнюю оценку
абсолютной ошибки численного дифференцирования в узлах:
irn(x')i5(^7i)!A"'!(w“')!' (5.14)
Контрольные вопросы
1. Как строится интерполяционный многочлен Лагранжа для равно-
отстоящих узлов?
2. Как можно оценить погрешность численного дифференцирования
с использованием интерполяционной формулы Лагранжа?
Упражнение
I. Для функции, заданной таблицей
X 0,22 0,24 0,26 0,28
У -2,43 1,00 2,45 4,57
вычислить значение производной в точке х = 0,23, построив интерполя-
ционный многочлен Лагранжа для равностоящих узлов.
5.3. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ НА ОСНОВЕ
ИНТЕРПОЛЯЦИОННОЙ ФОРМУЛЫ НЬЮТОНА
Запишем для функции Дх), заданной своими значениями в
равноотстоящих узлах х0, xi, ..., х„, первый интерполяционный
многочлен Ньютона
Л(х) = Jo + ^-(х- Хо) + ^771 “ х0)(х - Х|) +-... +
п 2!/г
n\htt
Продифференцировав, получим
(5.15)
Л'(х)=^-+
h
. АЪ’о
2!й2
У П(х-Хк) /(Х-х,)+...+^-^-
J/ n\hn
Подобным путем можно получить и производные функции f(x)
более высоких порядков. Однако каждый раз, вычисляя значение
производной функции f(x) в фиксированной точке х, в качестве х0
следует брать ближайшее слева узловое значение аргумента.
278
Таблица 5.2
/ У, ду д2у Д3у Д4у Д5у
0 1,5 1,844535
0,245461
1 1,6 2,089996 0,023915
0,269376 -0,000450
2 1,7 2,359372 0,023465 0,000077
0,292841 -0,000373 -0,000022
3 1,8 2,652213 0,02 3092 0,000055
0,315933 -0,000318
4 1,9 2,968146 0,022774
0,338707
5 2,0 3,306853
Особенно просто формула (5.16) выглядит для одного из узлов.
Так как в этом случае каждый узел можно считать начальным,
при х = л'о имеем
Рл'(х0) = 1(Ду0 -1д2у0 +|д3у0 +...4-(- Г)''-‘д''у0), (5.17)
Пример 5.4. Пусть /(х) = х2 - 1пх. Выполним интерполирова-
ние на отрезке [1,5; 2,0] с шагом 0,1.
Составим таблицу конечных разностей (табл. 5.2).
Вычислим по формуле (5.17)
/'(х0) =^0 = 1,5) = ^(0,245461-1-0,023915-
-1.0,000450 -1-0,000077 -1 0,000022) « 2,33331.
Для сравнения продифференцируем функцию, лежащую в ос-
нове табл. 5.2, аналитически и найдем ее значение в той же точ-
ке: (х2 - 1пх)' = 2х-1/х = 2,33333 при х= 1,5, т.е. имеет место
высокая степень совпадения «точного» значения с найденным
путем дифференцирования интерполяционного многочлена.
В то же время задача численного дифференцирования в такой
постановке некорректна, из чего следует, что в общем случае нет
оснований ожидать таких хороших результатов.
Для вывода формулы погрешности дифференцирования вос-
пользуемся подходом, рассмотренным в подразд. 5.2. Используя
формулу (5.11) применительно к первому интерполяционному
многочлену Ньютона, запишем
йл(х) = /1"+1
l)(f 2) •...(? и) у(л+1)(^)
(л + 1)!
279
где £, — некоторое промежуточное значение между узлами
х0, X],хп и заданной точкой х.
Предполагая, что f(x) дифференцируема n + 1 раз, получим для
оценки погрешности дифференцирования г„(х) (по аналогии с
формулой (5.12))
/У /7
г„(х) = R' (х) = —2— (^|п+п + ?1и+1] [/<л+1> (£)]}. (5.18)
(и + 1)! at at
Для случая оценки погрешности в узле таблицы (когда х = и
t = 0) будем иметь удобный вид формулы (5.18)
Л"
^(x)^=(-l)"^-/”+1>(^).
н + 1
(5.19)
d
Здесь учтено, что при t - 0 —= (-!)"«!.
dt
Пример 5.5. Оценим погрешность численного дифференцирова-
ния, связанную с примером 5.4. Применяя формулу (5.19), при п =
= 5, имеем: /(й>(х) = max |/<6)(х)| = - 10,54. Таким об-
X6 И.5; 2,01' 1 1,5й
10,54-0,15
разом, |/?5(х)| < ——-——
< 2 -10 5, что вполне согласуется с ре-
альной погрешностью, оцененной выше.
Таким образом, для корректного использования численного
дифференцирования с помощью классических интерполяционных
многочленов (Лагранжа и Ньютона) следует точку, в которой
ищется производная, сделать узлом интерполяции.
Однако здесь явно присутствует логическое противоречие: если
функция задана аналитически (пусть даже и достаточно слож-
ным образом), аналитическое дифференцирование обычно вы-
полнить существенно проще, чем описанную выше численную
процедуру.
Если же функция исходно задана таблично, то становится про-
блематичной оценка погрешности численного дифференцирова-
ния по формуле (5.18), поскольку эта формула включает значе-
ние производной старшего порядка, найти которое при отсут-
ствии аналитической формулы, строго говоря, невозможно. Прак-
тический выход из этого обстоятельства таков: следует воспользо-
ваться аналогией между производными и конечно-разностными
отношениями: /<л+1|(хй) ~ и принять в качестве оценки
Лл+]
погрешности, альтернативной (5.19), оценку (см. [2, 5]):
|К(ХО)| £
Ал+1у0
Л(п + 1)'
(5.20)
280
Применительно к примеру 5.4 эта оценка дает: |/?5'(х0)| £
0,000022 . 1Л 5
< ’ —— = 4-10 , что всего вдвое превышает более коррект-
ную оценку, сделанную в примере 5.5.
Особо отметим простейшую аппроксимацию производных,
основанную на линейной интерполяции. Применительно к любому
внутреннему узлу таблицы имеют место две очевидные аппрокси-
мации — правосторонняя
Х;+1 %l I ^/ + 1
(5.21)
и левосторонняя
Для крайнего левого узла возможна лишь аппроксимация (5.21),
крайнего правого — (5.22). Комбинируя их, получим для случая
1 равноотстоящих узлов (наиболее часто встречающегося в прило-
жениях) симметричную центрально-разностную аппроксимацию
2 п 2 п
1 / X
= — (-^+1 + 37-1)-
(5.23)
Действуя аналогично, можно построить аппроксимации стар-
ших производных. Например, для второй производной симмет-
ричная центрально-'разностная аппроксимация получится в сле-
с ГЧ ч /'Оч-и)-/'(*r-i)
.дующем приближении: f (х,) =---------—--------
Теперь, если мы
хотим ограничиться наименьшим возможным числом узлов в ап-
проксимационной формуле, следует для/'(x, + i) использовать ле-
востороннюю аппроксимацию, а для_/"(Х/_]) — правостороннюю
Ж-ЖЖ) ж,)-Ж.-Д
h h
= -j[/7i)-2/UH Ж-i)]-
2/г
(5.24)
Это трехузельная аппроксимация второй производной. Разуме-
ется, она неприменима для крайних узлов, и для построения со-
ответствующих формул надо брать иную аппроксимацию первой
производной, например
/Ы-/Ы = 1Г Ж)-Ж)) _ Ж)~Жо) =
h h _ h h
= Т^|Ж)-2Ж1) + Жо)] (5.25)
n
281
и аналогично
У'(х„) = р-[/(х„) - 2/(лл_|) + /(хл_2)]. (5.26)
Подобные формулы используются как для простейшего вычисле-
ния значений производных в узлах заданной сетки, так и для других
целей (в частности, в некоторых численных методах решения диф-
ференциальных уравнений, рассматриваемых в следующей главе).
Контрольные вопросы
1. В чем конкретно выражается некорректность численного диффе-
ренцирования при использовании интерполяционных формул Нью-
тона?
2. Какой способ интерполяции приводит к простейшим формулам для
центрально-разностных аппроксимаций производных?
3. Как можно оценить погрешность численного дифференцирования
с использованием интерполяционной формулы Ньютона?
Упражнения
1. Получить формулу, аналогичную формуле (5.16), используя вто-
рую интерполяционную формулу Ньютона.
2. Для функции, заданной таблицей
X 0,22 0,24 0,26 0,28
-2,43 1,00 2,45 4,57
вычислить значение производной в точке х = 0,23, построив интерполя-
ционный многочлен Ньютона, и сделать оценку погрешности по форму-
ле (5.20).
3. Получить формулу для простейшей центрально-разностной аппрок-
симации третьей производной.
5.4. ПОСТАНОВКА ЗАДАЧИ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
При вычислении определенного интеграла
где f(x) — непрерывная на отрезке [а; А] функция, иногда удает-
ся практически воспользоваться формулой Ньютона—Лейбница:
£f(x)dx = F(b)-F(a). (5.27)
Здесь F(x) одна из первообразных функций (т.е. такая функ-
ция, что F'(x)~f(x)). Однако даже в тех практически редких случа-
ях, когда первообразную удается явно найти в аналитической
282
форме, не всегда удается довести до числового ответа значение
определенного интеграла. Если к тому же учесть, что иногда по-
дынтегральная функция вовсе задается таблицей или графиком,
то становится понятным, почему формула (5.27) не исчерпывает
практических приемов вычисления интегралов.
На практике часто применяют различные методы приближен-
ного (численного) интегрирования. Формулы, используемые для
приближенного вычисления интегралов, называют квадратурны-
ми формулами. Простой прием построения квадратурных формул
состоит в том, что подынтегральная функция /(х) заменяется на
отрезке [а; Л] интерполяционным многочленом, например много-
членом Лагранжа 2„(х), и принимается приближенное равенство
ь ь
J f(x)dx = f L„(x)dx. (5.28)
а g
Подобный подход удобен тем, что он приводит к алгоритмам,
легко реализуемым на компьютере и позволяющим получить ре-
зультат с точностью, достаточной для широкого круга практичес-
ких приложений. При этом предполагается, что отрезок [а, 6] раз-
бит на п частей точками а = х0, хн х2,хп = Ь, наличие которых
подразумевается при построении многочлена L„(x). В силу фак-
тической единственности интерполяционного полинома л-й сте-
пени для данной функции и данной системы узлов нс имеет зна-
чения, использовать ли в этой процедуре многочлен Лагранжа
или многочлены Ньютона.
Подставляя в (5.28) вместо L„(x) его представление (4.11),
получим
- j й j---ГЕф)-------dx
« (Х-Х, )П„+1и ) ° (-Х “ *« )Пя+| О'>
Таким образом,
Ь п
]/(х)дх^У1А,, (5-29)
а /=1
где
4=1---------------dx (5.30)
По поводу полученных формул можно заметить, что:
1) коэффициенты А, не зависят от вида функции/(х), так как
они составлены только с учетом узлов интерполяции;
2) если /(х) — полином степени л, то тогда формула (5.17) —
точная, ибо в этом случае А(х) = /(х).
283
Контрольные вопросы
1. Почему формула Ньютона—Лейбница может оказаться непригод-
ной для реального вычисления определенного интеграла?
2. Как связаны задачи численного интегрирования и интерполирова-
ния?
5.5. КВАДРАТУРНЫЕ ФОРМУЛЫ НЬЮТОНА—КОТЕСА
С учетом (5.6) и (5.8) формула (5.30) для «весовых» коэффи-
циентов А, принимает вид
4 = /.,; ,dX а = о, (5.31)
Перейдем в этом интеграле всюду к переменной t. Из под ста-
dx
новки (5.4) получаем: dt = —, т.е. dx-hdt.
h
При х = л'о имеем t = 0, а при х = х„ будет t = ——— = п.
h
Тогда
b-anr (- 1)и“'/|я+|1
4 = — \z ,ч dt = (b - a)Hi
П J .tz.. .4
(5.32)
о
где
1 ? (-l)"-f
н|/!(и-;)!(/-/)
dt (i = 0, 1,..., п).
(5.33)
Числа Н; называют коэффициентами Котеса. Как видно, коэффи-
циенты Котеса нс зависят от вида функции f (д'), а только от числа п
точек разбиения. Окончательно с учетом формул (5.28). и (5.31) по-
лучаем следующий вищ квадратурных формул Ньютона— Котеса:
£ п
J f(x)dx ~(b~ (5.34)
а /=1
дающих на одном участке интегрирования различные представле-
ния для различного числа п отрезков разбиения.
5.6. ФОРМУЛА ТРАПЕЦИЙ
При п= 1 из формулы (5.33) имеем
= -J—Hi=\tdtJ-.
О ' О О 2-
284
Тогда по формуле (5.34) на от-
резке |х0; Х|] получаем интеграл
j f(x)dx =
= (-й - х0)(Я0у0 + Нм) =
= ^(№01). (5/35)
Формула (5.35) дает один из
простейших способов вычисления
определенного интеграла и назы-
вается формулой трапеций. Действи-
тельно, при п - 1 подынтеграль-
ная функция заменяется интерпо-
ляционным многочленом Лагран-
Рис. 5.2. Иллюстрация к вычис-
лению интеграла по формуле
трапеций
жа первой степени (т.е. линейной функцией), а геометрически
это означает, что площадь криволинейной фигуры подменяется
площадью трапеции (рис. 5.2).
Распространяя формулу (5.35) на все отрезки разбиения, по-
лучим общую формулу трапеций для отрезка [я; 6]
}/(х)(/х = й+ +Уз+- + Ь-1+у • (5.36)
а V )
Если аналитическое выражение подынтегральной функции f
известно, может быть поставлен вопрос об оценке погрешности
численного интегрирования по формуле (5.36) (погрешность ме-
тода). В этом случае имеется в виду, что
b ь
J/(x)dx = fz,(x)dx+/?„(/),
а а
где Rn(f) — остаточный член квадратурной формулы (5.36).
Формулу остаточного члена получим вначале для отрезка
[х0;Х|]. Имеем
Ч г *о+л L
л = f f(x)dx - - (Jo + У1) = J /(x)i/x - - [/(x0) + /(x0 + Й)],
ч> 2 2
откуда следует, что естественно рассматривать R как функцию
шага h: R = R(h). Заметим, что 7?(0) = 0.
Продифференцируем R(h) по h
xo+fi ,
Л*) = J f(x)dx '
[/(*о) + /(ХО + А)] -1 [Лх0 + А)] =
= /(хо +й)-у/(х0 +й)--~/(хо)-|/'(хо +й) =
= |[/(хо+ й)-/(хо)]-|/'(хо + й).
285
Замечаем, что Я'(0) = 0. Далее:
R'W = ]-Г(х0 + й) - 1/'(х0 + й) - ^Г(л-0 + й) = ~/'(х0 + й). (5.37)
Выведем сейчас R, последовательно интегрируя Я"(й) на от-
резке [0; й]:
h
f R\z)dz = R"(x )£ = R'(h) - R\Q) = R'(h),
о
откуда с учетом (5.37) имеем
й 1 Л
А'(й) = J R"(z)dz = - -J zf'txQ + z)dz- (5.38)
0 20
Применяя к (5.38) обобщенную теорему о среднем1, получаем
I А h2
R'(fi) = -- /'& )] zdz = - ), (5.39)
2 о 4
где е [х0;х0 +й] и зависит от й. Далее:
JR\z)dz = R(z )|„ = /?(й) - Л(0) - /?(й),
о
откуда с учетом (5.39) и обобщенной теоремы о среднем имеем
л 1 h ъз
R(h) = { R'(z)dz. = Af z2f’&)dz = (5.40)
о 4 о 12
где e [ло;ль+Л].
Таким образом, погрешность метода при интегрировании функ-
ции/ на отрезке [х0, х,] по формуле (5.36) имеет значение
Я = -^/^)Ле[х0;х|]. (5.41)
Из формулы (5.41) видно, что при /'(£)> 0 формула (5.36)
дает значение интеграла с избытком, а при /'(£) < 0 — с недо-
статком.
Для оценки погрешности интегрирования на всем отрезке [о; й]
рассуждаем следующим образом. Общая погрешность складывает-
ся из суммы погрешностей на каждом частичном отрезке, опре-
деляемых по формуле (5.40): R = А(1) + 7?(2) + ... + Л<л). С учетом
(5.41) имеем
1 Если функции Дх) и <р(х) непрерывны и <р(х) не меняет знака на отрезке
ь ь
[а; Ь], то существует такая точка [а; 6], что J/(x)<p(x)<£c = _/'(£)]'чХх)йх.
286
Иго+••+/'№
(.3 1-3
- + |/'(^)| +... +1/'(5.)|] 5 ^»мг,
где Л/2 = max |/'(х)|.
Л61Я;*!1 1
Учитывая, что h-n - b - а, получаем следующий окончатель-
ный вид формулы для оценки погрешности метода интегрирова-
ния по формуле трапеций
(5.42)
1
Пример 5.6. Вычислить интеграл /=jx2sinxcZx по формуле
о
трапеций, разделив отрезок [0; 1] на 10 равных частей, и оценить
погрешность вычислений.
Оценим сначала погрешность метода. Для этого находим вторую
производную подынтегральной функции: /'(х) = (2 - х2)sin х +
+4xcosx. На отрезке [0; 1] f'(x) всюду положительна, причем
ее значение ограничено сверху: |/'(х)| < 3,3. Таким образом, ис-
пользуя формулу (5.42) (а = 0, b= 1, й = 0,1), имеем
з 3.0 12
|А2| < ’ у-- = 0,00275.
Итак, приняв на заданном участке интегрирования п = 10, мы
сможем получить интеграл от заданной функции с погрешностью,
не превышающей 0,003, если будем вести вычисления таким об-
разом, чтобы погрешность округления не исказила окончатель-
ный результат в пределах точно-
сти метода.
Значения подынтегральной
функции в узловых точках при-
ведены в табл. 5.3.
В последней строке таблицы
получены суммы значений у, по
столбцам. Используя значения
этих сумм, в соответствии с фор-
мулой трапеций (5.36) имеем:
7 = 0,1 х (0,4207355 +
+ 1,8302453)= 0,225098.
Учитывая вычисленную рань-
ше ошибку 7?, получаем оконча-
тельно
7= 0,225 ±0,003.
Таблица 5.3
Xi у(' = 0, Ю) >>(/ = 1, 2,9)
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0 0,4207355 0,0009983 0,0079467 0,0265968 0,0623068 0,1198562 0,203271 1 0,3156668 0,4591078 0,6344948
0,4207355 1,8302453
287
В данном случае легко вычислить «точное» значение этого ин-
теграла, пользуясь формулой Ньютона— Лейбница
7= 2sin 1 + cos 1 - 2 = 0,223244275.
Как видим, результат, полученный с помощью приближен-
ной формулы трапеций, в пределах установленной точности впол-
не соответствует этому значению.
Контрольные вопросы
I. Чем объясняется название формулы трапеций?
2. Возможно ли применение формулы (5.35) для оценки погрешно-
сти интегрирования по формуле трапеций в случае, когда подынтеграль-
ная функция задана таблицей?
Упражнение
Составить программу вычисления интеграла по формуле трапеций.
Пользуясь этой программой, выполнить задание из примера 5.6 для п =
= 20, оценить погрешность полученного результата и сравнить его со зна-
чением, полученным по формуле Ньютона—Лейбница.
5.7. ФОРМУЛА СИМПСОНА
При п = 2 из формулы (5.33) последовательно имеем (7 = 0, 1, 2):
, 1 J t(t -1)(? - 2) 1.
° 2„ 2/ 6
1 2 Э
Я, =--р(Г-2) =
2 0 J
I 2 1
Н2=- t(t-l)dt = 7.
4 о 6
Тогда с учетом (5.34) получим на отрезке [х0; х2]
Х2 h
/ f(x)dx =-~Луй + 4у, + у2). 15.43)
ло 4
Геометрически, в соответствии со смыслом интерполяцион-
ной формулы Лагранжа при п = 2, использование формулы (5.43)
означает замену подынтегральной функции f(x) параболой Lj(jc),
проходящей через точки Л/,(х(,у,) (/= 0, 1, 2) (рис. 5.3).
288
Если считать, что п — четное (п = 2т), то, применяя формулу
(5.43) последовательно к каждой паре частичных отрезков
[х2,^2;х2,] (/= 1, 2, т), получим
j f(x)dx = М + 2У1 +у2+ ... + 2у2т_, 1 (5.44)
Формула (5.44) называется формулой Симпсона.
Оценку остаточного члена формулы Симпсона приведем без
вывода:
|Л,|<Л/41М±
1 180
(5-45)
где Л/4 = шах|//к(х)1.
a<x<b '
Как следует из оценки, формула Симпсона оказывается точ-
ной для полиномов до третьей степени включительно (так как
для этих случаев производная четвертого порядка равна нулю). Фор-
мула Симпсона обладает повышенной точностью по сравнению с
формулой трапеций. Это означает, что для достижения той же
точности, что и по формуле трапеций, в ней можно брать мень-
шее число л отрезков разбиения. Последнее обстоятельство весьма
важно для вычислений, поскольку основное время затрачивается
на нахождение значений функции в узлах.
Укажем в заключение весьма простой практический прием,
позволяющий прогнозировать требуемое число отрезков разбие-
ния по заданной точности е.
Пусть задана предельная допустимая погрешность интегриро-
вания в. Желая иметь |ЛЛ| < е, с учетом оценки (5.45) достаточно
потребовать:
\b-a\-hA
180
откуда hA < ----j——, т. е.
\Ь - а| •
, 180е
П < 4 :-----:------
- <з| • Л/4
(5.46)
Формула (5.46) позволяет
оценить величину шага, необхо-
димую для достижения заданной
точности (из формулы видно,
что h имеет порядок л/Ё).
Пример 5.7. Вычислить интег-
рал из примера 5.6 по формуле
Симпсона при том же числе от-
резков разбиения (п = 10).
Рис. 5.3. Иллюстрация
к вычислению интеграла
по формуле Симпсона
I 0 Ла,)'|и«
289
Табл к ца 5.4
X, у 0'=0, 10) у,(/= 2, 4, 6, 8) у,(/ = 1, 3, 5, 7, 9)
0 0,1 0,2 о,з 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0 0,4207355 0,0079467 0,0623068 0,2032711 0,4591078 0,0019966 0,0531936 0,2397124 0,6313333 1,2689896
0,4207355 0,7326324 2,1952255
Для оценки остаточного члена найдем производную четверто-
го порядка от подынтегральной функции f(x) = х2 sinx
f!V (х) = (х2 - 12) sin х - 8х cos х.
Значение |//|Z(*)| на отрезке [0; 1] ограничено числом 14. Ис-
14 0 I4
пользуя формулу (5.45), получаем оценку: | 1 <---— = 0,0000077.
180
Значения подынтегральной функции в узлах в соответствии с
формулой Симпсона (5.44) приведены в табл. 5.4.
Используя значения сумм из последней строки таблицы, име-
ем по формуле Симпсона:
2-0 1
1= —^-(0,4207355 + 0,7326324 + 2,1952255) = 0,2232395.
Округляя результат в соответствии с полученной раньше оцен-
кой, получаем /=0,223240 ± 0,000008.
Сравнивая этот результат со значением интеграла, получен-
ным в примере 5.6, замечаем, что при одинаковом числе отрез-
ков разбиения формула Симпсона дает ответ с более высокой точ-
ностью.
Посмотрим, как можно было бы воспользоваться в данном
случае формулой (5.46). Пусть требуется найти значение заданно-
го интеграла с точностью е = 1 • 10-6. Тогда по формуле (5,46) полу-
чаем
h < 4108 1,10 6 = 0 0598138.
V 14
Отсюда следует, что при использовании формулы Симпсона
для достижения точности 1-10-6 достаточно было бы разбить от-
резок [0; 1] на 20 частей (с шагом Л = 0,05).
290
Контрольные вопросы
1. В чем выражаются преимущества формулы Симпсона перед форму-
лой трапеций?
2. Каким образом при использовании формулы Симпсона можно рас-
считать требуемое число отрезков разбиения для достижения заданной
точности интегрирования е?
5.8. ПОЛУЭМПИРИЧЕСКИЕ ОЦЕНКИ ТОЧНОСТИ ВЫЧИСЛЕНИЙ
ПО КВАДРАТУРНЫМ ФОРМУЛАМ
Как следует из оценочных формул (5.42) и (5.45), оценка по-
грешности метода интегрирования по формулам трапеций и Симп-
сона возможна лишь тогда, когда подынтегральная функция зада-
на аналитически. Однако даже и в этом случае на практике широ-
ко применяется следующий эмпирический прием, пригодный для
каждого из рассмотренных методов интегрирования. Искомый
интеграл вычисляется дважды: при делении отрезка [а; i] на п
частей и на 2и частей (при интегрировании по формуле Симпсона
значение п должно быть четным). Затем полученные значения
интеграла (обозначим их 1п и 12п) сравниваются и совпадающие
первые десятичные знаки считаются верными.
Указанный прием может быть уточнен и, в некотором смысле,
обоснован. Пусть R„ и R2ll — погрешности интегрирования по фор-
муле Симпсона, соответственно при п и 2н отрезках разбиения.
Учитывая (5.45), мЪжно составить приближенную оценку
где h„ и h2n длина отрезков разбиения (шаг интегрирования) в
первом и втором случае. Понятно, что h2n = h„l'l.
Из (5.47) получаем
7?„ «16Я2л. (5.48)
Если I — истинное значение интеграла, то I = In+ R„ и
I = hn + Rin, откуда с учетом (5.48) 1п + 16Я2л hn + Rin, т.е.
(5.49)
Формула (5.49) удобна для практической оценки погрешности
метода Симпсона, но требует двойного счета.
Аналогичное рассуждение применительно к методу трапеций
приводит к оценке
|Т?2л|.1ЦМ (5.50)
291
Из оценочных формул (5.42) и (5.45) следует, что ошибка
интегрирования по методу трапеций и методу Симпсона умень-
шается с уменьшением шага интегрирования (для метода Симп-
сона — значительно быстрее). На основании этого можно сделать
вывод: при последовательном увеличении числа отрезков разбие-
ния значение интеграла будет приближаться к точному. Однако
это утверждение имеет чисто теоретическое значение. Дело в том,
что в процессе практических вычислений при последовательном
удвоении числа отрезков разбиения начинает сильно прогресси-
ровать удельный вес ошибки округления, значение которой с не-
которого момента ставит предел реально достижимой точности
результата интегрирования (подробное исследование влияния ука-
занных ошибок на результат интегрирования имеется в [10]).
Контрольные вопросы
1. Каким образом можно произвести оценку точности интегрирова-
ния по формулам трапеций и Симпсона, не используя аналитическое
выражение подынтегральной функции?
2. Можно ли добиться неограниченного уменьшения погрешности
интегрирования путем последовательного уменьшения шага?
Упражнение
Модифицировать программу вычисления интеграла по формуле тра-
пеций (см. упражнение к подразд. 5.7) для применения метода двойного
счета. Выполнить с помощью этой программы задание из примера 5.6
(при п = 10 и п = 20) с оценкой погрешности полученного результата по
формуле (5.42).
5.9. АЛГОРИТМИЧЕСКАЯ РЕАЛИЗАЦИЯ
ИНТЕРПОЛЯЦИОННЫХ КВАДРАТУРНЫХ ФОРМУЛ
Вычисление интеграла по формулам трапеций и Симпсона легко
программируется. Для организации циклического алгоритма фор-
мулу Симпсона (5.43) удобно переписать в виде
J/(x)dxУо+ (2у] + У2) + (2у3 +у4)+-+(2у2т-! +№„,)] (5.51)
Выражение в квадратных скобках (кроме первого слагаемого)
может быть получено циклическим суммированием двучленов вида
2у,- + у)+| при увеличении параметра i на каждом шаге цикла на 2,
причем верхней границей i должно служить п (л = 2m).
В случае, когда выбор шага интегрирования и оценка погреш-
ности метода производятся «вручную», алгоритм вычисления ин-
теграла по формуле (5.51) представляет собой цикл с постуслови-
292
Начало
Ввод а, Ь, п
Рис. 5.4. Алгоритм вычисления интеграла по формуле Симпсона
ем (рис. 5.4). Соответствующая программа на языке Turbo Pascal
для выполнения задания из примера 5.7 приведена ниже.
program Simpson_l;
uses crt;
const n=10;
type mas=array[0..n] of real;
var y:mas; a, b, S, Integral,h,x:real; i:integer;
begin
clrscr;
writeln('Введите границы отрезка
интегрирования; ') ;
readln(a,b);
writeln(1 Задайте величину шага интегрирования:');
293
readin(h);
{Формирование массива значений подынтегральной
функции}
х:=0;
for i:=0 to n do
begin
y[i] :=sqr(x)*sin(x);
x:=x+h;
end;
S:=(у[0]-y[n])/2; '
i: = l;
repeat
S:=S+(2*y[i]+y[i+1]);
i:=i+2;
until i>--n;
Integral: =2 * (b--a) *S/ (3*n) ;
writeln('Значение интеграла: 1= 1,Integral:11:9);
readkey;
end.
Результат работы программы:
Введите границы отрезка интегрирования:
О 1
Задайте величину шага интегрирования:
0.1
Значение интеграла: 1= 0.223239626
Используя вычисленную в примере 5.7 оценку погрешности
метода, полученный результат следует округлить: I- 0,223240 ±
± 0,000008. Судя по величине погрешности метода и допуская, что
вычислительная погрешность в данном случае не превышает по-
грешности метода, можно утверждать, что в полученном значе-
нии интеграла, по меньшей мере, четыре знака после запятой
верны в строгом смысле.
Рассмотрим подход к программированию формулы Симпсо-
на по методу повторного счета с использованием оценки (5.49).
Если требуемая точность е не достигается (т.е. |/„ - I.2n| > 15е ),
в программе должен предусматриваться повторный счет с ша-
гом, уменьшенным вдвое. По этой причине формировать зара-
нее массив значений подынтегральной функции в узлах не имеет
смысла. Блок-схема соответствующего алгоритма приведена на
рис. 5.5.
Первоначальное значение интеграла 1п принимается равным 0,
значение п = 4 и ведется вычисление значения интеграла /2„. Если
проверка показывает, что требуемая точность не достигнута, 1п
заменяется на 12„, число отрезков разбиения п удваивается, и про-
294
Начало
Рис. 5.5. Алгоритм метода повторного счета по формуле Симпсона
цесс повторяется сначала. Внешний цикл повторяется до тех пор,
пока не будет достигнута требуемая точность.
Практически при использовании описанного подхода следует
помнить о возможном влиянии на окончательный результат оши-
бок округления. Применяя этот прием, необходимо сопоставлять
величину запрашиваемой точности е с возможным диапазоном
ошибки округления.
Приводим программу вычисления интеграла
i
7 = fx2 sinxt/x
о
295
с точностью 1 10"6 по формуле Симпсона в соответствии с алго-
ритмом, изображенным на рис. 5.5 (для округления полученного
результата в соответствии с заданной точностью — погрешностью
метода — использован модуль Okrugl):
program Simpson_2;
uses crt,okrugl;
const n=10;
Label 1;
type mas=array[0..n] of real;
var y:mas; m,nn:integer;
a,b,S,eps,Inti,Int2,h,x:real;
function f(y:real):real;
begin f:=sqr(y)*sin(y);
end;
begin
clrscr;
writein('Введите границы отрезка интегрирования');
readin(a, b);
writein(1 Укажите требуемую точность вычислений
и ’) ;
writein('начальное число отрезков разбиения');
readln(eps,m);
Intl:=0;
1: h:=(b-a)/m;
S:=(f(a)-f(b))/2;
x:=a+h;
repeat
S:=S+2*f(x)+f(x+h);
x:=x+2 *h;
until x-b>=0;
Int2:=2*h*s/3;
if abs(Intl-Int2)<=15*eps then begin
writein('Фактическое число отрезков разбиения =
m) ;
okr(Int2,eps,Int2,nn);
writein('Значение интеграла: ',Int2:17:nn);
end
else begin
m:=2*m;
Inti:=Int2;
goto 1;
end;
readkey;
end.
296
Введите границы отрезка интегрирования
О 1
Укажите требуемую точность вычислений и
начальное число отрезков разбиения
0.000001 10
Фактическое число отрезков разбиения =20
Значение интеграла: 0.223244
Таким образом, в результате применения метода двойного счета
при разбиении отрезка интегрирования на 20 частей получен ре-
зультат: 1= 0,223244 ±10“6.
Сравнивая значения интеграла, вычисленные во всех рассмот-
ренных примерах, можно отметить полное согласование получен-
ных результатов с соответствующими оценками точности. Действи-
тельно, из результата вычисления заданного интеграла по форму-
ле трапеций (пример 5.6) следовало, что верными являются лишь
два знака после запятой: 2, 2. Вычисления по формуле Симпсона
(пример 5.7) подтвердили правильность этих знаков, и добавили
два новых знака: 2, 2, 3, 2. Последнее вычисление по методу по-
вторного счета дали уже пять верных в строгом смысле знаков, в
число которых вошли все найденные раньше: 2, 2, 3, 2, 4.
Контрольные вопросы
I. Каким преобразованием формулы Симпсона облегчается построе-
ние циклического алгоритма для организации вычисления интеграла?
2. В чем суть алгоритма двойного счета при интегрировании по форму-
ле Симпсона? Что вданном случае является условием возобновления цикла?
3. Что может послужить препятствием для достижения запрашивае-
мой точности при использовании метода двойного счета?
Упражнения
1. Составить программу интегрирования по формуле трапеций с ис-
пользованием оценки точности методом двойного счета.
2. Провести численные эксперименты с программой вычисления ин-
теграла по формуле Симпсона с использованием метода двойного счета
для различных форматов представления чисел.
5.10. КВАДРАТУРНЫЕ ФОРМУЛЫ ГАУССА
При переходе от формулы трапеций (5.36) к формуле Симпсо-
на (5.43) точность вычисления интеграла (при фиксированном
значении п) возрастает столь значительно, потому что возрастает
порядок аппроксимации подынтегральной функции Дх) интер-
поляционным многочленом: линейная аппроксимация сменяется
297
< на параболическую. При этом метод трапеций приводит, естествен-
но, к точному значению интеграла, если f(x) линейна на каждом
из отрезков [х,-; xi + J, а метод Симпсона — если /(х) квадратична
на каждом из этих отрезков. Выбор узлов {х,} на исходном отрезке,
с точки зрения теории, произволен (на практике предпочитают
использовать равноотстоящие узлы).
о Существует, однако, иной, связанный с именем Гаусса, под-
ход к построению квадратурных формул, в котором центральное
место играет выбор узлов для интерполирования подынтеграль-
ной функции. Ознакомимся с этим подходом в его простейшей
возможной реализации.
Традиционно при получении квадратурных формул Гаусса в
исходном интеграле выполняется замена переменной, переводя-
щая интеграл по отрезку [а; 6] в интеграл по отрезку [-1; I]:
2х-(£-«) 1 1
t =---------, или х = — (6-a)t + -{b + а). (5.52)
b - а 2 2
Тогда
ь 1 1
//(x)fl'x = -(6-o)j f
а 2 -1
и можно далее, не теряя общности, развивать метод Гаусса при-
1
менительно к интегралу вида j ср(г)Л.
-1
Для разъяснения существа метода Гаусса обратимся к рис. 5.6.
Будем использовать простейшую (т.е. линейную) интерполяцию
|(6- a)t +1 (b + а)Ъу * '*(5.53)
а
Рис. 5.6. Иллюстрация подходов к построению квадратурных формул:
а — фиксированные узлы линейной интерполяции подынтегральной функции
(метод трапеций); погрешность интегрирования характеризуется величиной
плошали 5; б — подвижные узлы интерполяции (метод Гаусса); величина по-
грешности зависит от степени несовпадения площадей 5, + 5, и S2
298
подынтегральной функции. Если в качестве узлов интерполяции
взять концы отрезка [-1; 1] (так делалось при получении формулы
трапеций), то различие в площадях криволинейной трапеции,
ограниченной сверху кривой у = ср(х), и «обычной» трапеции, ог-
раниченной сверху прямой, проведенной через концы указанной
кривой, фиксировано видом функции у - ф(х) (рис. 5.6, а). Одна-
ко если сделать узлы интерполяции «подвижными» (рис. 5.6, б),
то можно выбрать их таким образом, чтобы разность между пло-
щадями криволинейной и «обычной» трапеции была значительно
меньше, чем в случае а. Более того, можно сделать эти площади
равными (5| + 53 = 5'2), т.е. аппроксимировать интеграл точно, но
в уравнения для определения 6 и /2 войдет точное значение ин-
теграла, т.е. практической пользы такой прием не принесет.
Вместо этого сформулируем задачу следующим образом: выб-
рать значения t} и t2 так, чтобы площадь трапеции, ограниченной
сверху прямой, проходящей через точки ф(Л)) и A2{t2, ф((2)),
была равна интегралу от любого многочлена некоторой (наивыс-
шей возможной) степени. Поскольку положение точек At и А2
определяют четыре координаты, то этот многочлен может опре-
деляться максимум четырьмя коэффициентами, т.е. является мно-
гочленом 3-й степени
P3(f) = щ + att + a2t2 + a3t3. (5.54)
Легко установить, что уравнение прямой, проходящей через
точки А[ и А2, имеет вид
Ф2 ~ Ф1 , Дф1~6ф2
У = V2 VI { + 2 VI VV1 , (5 55)
•2 “ Ч '2 ~ Ч
где ф1 = ф(А), Ф2 = фОг)- Таким образом, возникает следующая тех-
ническая задача: выбрать 1\ и /2так, чтобы равенство
Ф2 ~ ф| . , ^Ф1 ~ 6Ф2
6
dt = J (д0 + д1/ + о2(2 +Дз^)Л (5.56)
-11 h ~ 6
имело место при любых значениях а0, а}, а2, а3.
Для ее решения вычислим интегралы в (5.56):
'2 ~ Ч
Подставим в это равенство Ф1 и ф2:
' 2 («О + aifl + °2?|2 + °3?13) - ’ (°0 + fll?2 +«2f22 + #3Z23) = а0 +~а2-
б’ Ч ‘2 - Ч J
Перегруппируем слагаемые в левой части равенства
Оо + 0 щ d2 - 6(2(6 + (2) • аз = ао + -уа2-
299
Для того чтобы последнее равенство выполнялось при любых
значениях а0, at, а2, а3, необходимо и достаточно, чтобы
з ’ Y^(A + - О-
Отсюда следует одно из двух решений
I) ~ ~^з ’?2 _+^з и t} =+7з,Г2--7з’
отличающихся лишь нумерацией значений t\ и t2.
Итак, если взять узлами линейной интерполяции числа
формуле 1 =
то интеграл, вычисленный по
г Ф2 ~Ф1
I _ h
(5.57)
, Л<Р1 -Г,ф2
Г -г—----- 1 •
Z2“/|
dt, '
точно совпадет с интегралом от любого многочлена 3-й степени.
Вычислив интеграл по указанной формуле с учетом (5.57), полу-
чим
Формула
(5-58)
применительно к любой (интегрируемой) функции у = ф(Г) и на-
зывается квадратурной формулой Гаусса. Разумеется, для функ-
ции, не являющейся многочленом не старше 3-й степени, эта
формула дает лишь приближенное значение интеграла, но интуи-
тивно ясно, что это значение, вообще говоря, ближе к истинно-
му, нежели то, которое дает формула трапеций, такжб исходящая
из интегрирования вспомогательной линейной функции вместо
исходной.
Воспользовавшись формулой (5.53), можно для удобства ис-
пользования записать формулу Гаусса применительно к исходно-
му виду интеграла:
г Ib-a b + a} r(b-a Ь + а} ,,
IG=-(b-a) Л------;=- +-- + / —^ + —— . (5.59)
2V L4 2 * ) 2 JJ
Оценка погрешности вычисления интеграла по формуле (5.58)
достаточно громоздка (см., например, [12]). Приведем результат
без вывода:
1 (Ь-а}5 ..
— — Мл-,
135 2
(5.60)
l<z;d] 1 1
300
Разумеется, для повышения точности вычисления интеграла
по методу Гаусса отрезок [а; />] можно так же, как это делалось в
методах трапеций и Симпсона, разделить на несколько (и) частей
и применять формулу (5.59) к каждому из них. Получим (при де-
лении отрезка на равные части) практически используемые фор-
мулы для вычисления интеграла и оценки погрешности
h нЧ '
уХ
2 г=0
h h
2 2-Л
Л h Y
2 + 2^3 ।
(5.61)
\S-IG\<\ (5-62)
4320 • гг
При практическом использовании формулы Гаусса (5.61) спра-
ведливы те же соображения, которые привели к полуэмпиричес-
кой оценке (5.49) точности результата при двойном счете.
Отметим, что формула (5.59) — лишь одна из семейства фор-
мул, называемых формулами Гаусса для вычисления интегралов.
Опираясь на изложенную выше идею, можно строить квадратур-
ные формулы, точные для любого алгебраического многочлена
любой нечетной степени.
Пример 5.8. Вычислить интеграл из примера 5.6 по формуле
Гаусса (5.61) при том же числе отрезков разбиения (п= 10).
Составим таблицу значений функции в точках, входящих в
формулу (5.61) (табл. 5.5).
Таким образом, IG = 0,05 - 4,46488894 = 0,22324447.
Таблица 5.5
х. h h Х‘ + 2 2-Л h h х.- + — + —=• 2 2сЗ У,
0 0,021 13249 0,078868 0,00000944 0,00049005
0,1 0,12113249 0,178868 0,00177304 0,00569215
0,2 0,22113249
0,278868 0,01072537 0,02140672
о,з
0,32113249 0,03255086
0,4 0,378868 0,053091 15
* 0,42113249 0,07250071
0,5 0,478868 0,10566206
0,52113249 0,578868 0,13520907 0,18331848
301
Окончание табл. 5.5
Xi h h Х; + 2 2 Л h h х,+ - + —г 2 2-/3 Уг
0,6
0,62113249 0,22452206
0,7 0,678868 0,28938023
0,72113249 0.34334373
0,8 0,778868 0,42614496
0,82113249 0,49350196
0,9 0,878868 0,59476723
0,921 13249 0,67563779
1,0 0,978868 0,79516236
X = 4,46488894
Сравнивая формулы (5.62) и (5.45) погрешностей методов Га-
усса и Симпсона, видим, что они практически тождественны за
исключением числового коэффициента, благодаря которому оцен-
ка погрешности метода Гаусса благоприятнее в 24 раза. Учитывая
оценку, сделанную в примере 5.7, можно рассчитывать, что пер-
вые 6 цифр, приведенные выше для lG, являются верными, что
подтверждается сравнением с точным значением этого интеграла
(см. пример 5.6).
Контрольный вопрос
На какой основной идее основывается построение квадратурных фор-
мул Гаусса?
Упражнения
1. Составить программу вычисления интеграла на основе квадратур-
ной формулы (5.61).
2. Построить квадратурную формулу Гаусса, базирующуюся на ин-
терполяции подынтегральной функции многочленом второй степени.
5.11. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
МЕТОДОМ МОНТЕ-КАРЛО
Мы видели, что реализация методов численного интегрирова-
ния предусматривает получение суммы, количество слагаемых в
которой определяется числом точек разбиения интервала интег-
рирования.
302
В практических приложениях часто приходится вычислять зна-
чение кратных интегралов. Кратный интеграл вычисляется для
функции многих переменных по замкнутой ограниченной много-
мерной области. Вычислительная схема при этом в основном со-
храняется: интервал, соответствующий изменению каждой пере-
менной внутри области интегрирования, разбивается на фикси-
рованное число отрезков. Таким образом, задается разбиение об-
ласти интегрирования на определенное число элементарных мно-
гомерных объемов. Вычисляются значения подынтегральной фун-
кции для точек, взятых по одной внутри каждого элементарного
объема, и полученные значения суммируются.
Легко понять, что при увеличении кратности интеграла число
слагаемых очень быстро возрастает. Пусть, например, мы разби-
ваем интервал изменения каждой переменной на десять частей.
Тогда для вычисления тройного интеграла придется вычислять
сумму примерно тысячи слагаемых. Для вычисления же 10-крат-
ного интеграла потребуется сумма, количество слагаемых в кото-
рой определяется числом Ю10. Вычисление такой суммы затруд-
нительно даже на самых быстродействующих ЭВМ. В таких ситуа-
циях предпочтительнее использовать для получения значения ин-
теграла вероятностные алгоритмы, т.е. алгоритмы, основанные на
моделировании случайных процессов и явлений. Способы реше-
ния задач, использующие вероятностные алгоритмы, получили
общее название метода Монте-Карло. Прежде чем перейти к воп-
росу о вычисление интегралов методом Монте-Карло, кратко по-
знакомимся с основной идеей вероятностного подхода к постро-
ению алгоритмов.
Все вычислительные алгоритмы, которые мы рассматривали
до сих пор, являлись детерминированными. Это значит, что в
любом таком алгоритме результат, получаемый на очередном шаге,
точно (или с заданной погрешностью) определяется результата-
ми, полученными на предыдущих шагах (в частности, начальны-
ми условиями). При многократной реализации детерминирован-
ного алгоритма с одними и теми же исходными данными и при
отсутствии ошибок результаты, соответствующие одному и тому
же шагу алгоритма, будут совпадать.
Наряду с явлениями, протекающими детерминировано (зако-
номерно, предсказуемо), часто приходится иметь дело с процес-
сами и событиями, характер проявления которых зависит от слу-
чая и заранее непредсказуем. Такого рода события и связанные с
ними величины называют случайными.
Вероятностные алгоритмы нс являются детерминированными.
Основная идея метода Монте-Карло обычно и заключается в мно-
гократном воспроизведении некоторого вероятностного алгорит-
ма (говорят также о многократном повторении случайных испыта-
ний). Значение искомой величины определяется в результате ста-
303
тистической обработки данных, полученных при этих испытани-
ях. Характерной особенностью метода Монте-Карло является ис-
пользование случайных чисел (числовых значений некоторой слу-
чайной величины).
Появление ЭВМ существенно расширило круг задач, доступ-
ных для решения методом Монте-Карло, поскольку высокое бы-
стродействие компьютеров обеспечивает возможность многократ-
ного повторения случайных испытаний и последующую обработ-
ку полученных данных;
В языке программирования Turbo Pascal имеется стандартная
функция random, значениями которой являются случайные чис-
ла, равномерно распределенные на отрезке [0; 1]. Сказанное озна-
чает, что если разбить указанный отрезок на некоторое число рав-
ных интервалов и вычислить значение функции random большое
число раз, то в каждый интервал попадет приблизительно одина-
ковое количество случайных чисел.
В основе оценки искомого значения интеграла /лежит извест-
ное соотношение
I = Усро, (5.63)
где уср — значение подынтегральной функции в некоторой «сред-
ней» точке области интегрирования, а а — (многомерный) объем
области интегрирования. При этом, конечно, предполагается, что
подынтегральная функция (обозначим ее F) непрерывна в обла-
сти интегрирования. Выберем в этой области п случайных точек Л/).
При достаточно большом п приближенно можно считать:
Kp=-ZW).
«i=i
Погрешность вычисления интеграла методом Монте-Карло
пропорциональна корню квадратному из числа случайных испы-
таний и не зависит от кратности интеграла. Именно поэтому при-
менение метода целесообразно для вычисления интегралов высо-
кой кратности.
Ограничимся, однако, иллюстрацией рассматриваемого мето-
h
да для простейшего случая интеграла / = | f(x)dx. В этой ситуа-
ции и равенство (5.63) принимает вид а
т b - а Д .
1 =----£/(х,-), (5.64)
п i=i
где х,- (/ = 1, ..., п) — случайные числа, лежащие в интервале [а; />].
Для получения таких чисел на основе последовательности слу-
чайных чисел х„ равномерно распределенных в интервале [0; 1],
достаточно выполнить преобразование
X, = а + (b - a)* Xi.
Й -
304
Программа вычисления интеграла методом Монте-Карло по
формуле (5.64) будет совсем простой. Приведем эту программу и
осуществим по ней расчеты для интеграла из примера 5.6:
program Могг_е_ Каг 1о;
uses crt;
var х,s,Integral,d:real; a,b,i,n:integer;
function fun(xl:real):real;
begin fun:=xl*xl*sin(xl);
end;
begin
randomize;
writeln('Введите пределы интегрирования1);
read(a,b);
writeln('Введите число случайных испытаний');
readln(n);
s:=0; d:=b-a;
for i:=l to n do
begin
x:=a+d*((b-a)*random+a);
s:=s+fun(x);
end;
Integral:=s*d/n;
writeln('I= 1,Integral:17;11);
repeat until -.keypressed
end.
Для N= 1000 получится следующий результат:
Введите пределы интегрирования
0 1
Введите число случайных испытаний
1000
1= 0.22063635157
Следует учесть, что при решении задач вычислительной мате-
матики методом Монте-Карло точность получаемых результатов
обычно бывает сравнительно невысока. Повышение точности вы-
числений требует значительного увеличения числа реализаций, а
значит, и времени решения. Вместе с тем обоснованность исполь-
зования метода Монте-Карло нередко не только вытекает из его
алгоритмической простоты, но и (как об этом было сказано в
начале настоящего подраздела) обусловлена тем важным обстоя-
тельством, что он оказывается единственным выходом в тех слу-
чаях, когда другие методы приводят к обвальному возрастанию
вычислительных действий.
305
Обратимся к вопросу об оценке точности вычисления интегра-
лов методом Мон ге-Карло. Обозначим через / точное значение
интеграла. Пусть при п испытаниях получено некоторое прибли-
женное значение интеграла rfn). Оценка вида - /| < Я, где R
достоверно известно, не соответствует духу вероятностного под-
хода. Ответ на вопрос о точности вычисления необходимо полу-
чить в следующем виде: с такой-то достоверностью if"’ попадает в
такой-то интервал вблизи такого-то числа. Если указанное число
известно, а достоверность высока, то на практике такой ответ
ничуть не хуже, поскольку в традиционных квадратурных методах
R бывает нелегко определить в реальности; кроме того, традици-
онные оценки, как мы не раз убеждались, дают сильно завышен-
ные значения границ погрешностей.
Действуя в духе математической статистики, проведем серию
испытаний с одним и тем же значением п. В каждой реализации
этой серии получим некоторое приближенное значение интегра-
ла: ^и), ..., (внизу — номер испытания в серии, £ —коли-
чество испытаний в серии). Разумеется, п и к должны быть доста-
точно велики, чтобы утверждения, основанные на математиче-
ской статистике, были применимы.
Числа в указанной последовательности — случайные числа. Из
центральной предельной теоремы теории вероятностей следует,
что распределение чисел i%'\ ..., является асимптотиче-
ски нормальным:
/л 1 ( О'-/)2]
’’(,>=;/2ScxT“wj' (5155)
где /— искомое точное значение; с> — дисперсия распределения.
При этом наилучшей (т.е. несмещенной и состоятельной) ре-
ально возможной оценкой величины / является А — эмпириче-
ское среднее по выборке, а величины о — выборочное средне-
квадратичное отклонение 5
л = (5.66)
*у=| К - L у-|
Доверительный интервал для I определяется неравенствами
Л-Е</<Л + е, (5.67)
где значение е определяется с помощью так называемого, распре-
деления Стьюдента
е = /(РЛ)~ (5.68)
xj К
Здесь t(P, к) — коэффициент Стьюдента, зависящий от дове-
рительной вероятности Р и величины к.
306
Детальную таблицу значений коэффици-
ента Стьюлента можно найти в руководствах
по математической статистике. В табл. 5.6
приведена выдержка из нее, вполне дос-
таточная для практической работы по вы-
числению интегралов.
На практике доверительная вероятность
(надежность) 0,95 считается достаточной
для нс очень ответственных ситуаций,
0,99 — высокой, а 0,999 — очень высокой.
Таблица 5.6
& 0,95 0,99 0,999
10 2,23 3,17 4,59
20 2,09 2,85 3,85
50 2,01 2,68 3,50
100 1,98 2,63 3,39
<ю 1,96 2,58 3,29
Контрольные вопросы
I. В чем особенность задачи численного интегрирования по методу
Монте-Карло?
2. Чем принципиально отличается постановка задачи об оценке точ-
ности вычисления интеграла методом Монте-Карло и по интерполяци-
онным квадратурным формулам?
Упражнения
I. Пользуясь программой, приведенной в данном подразделе, сделать
серию из 10 испытаний, в каждом из которых п = 1000. Пользуясь приве-
денными выше формулами, оценить доверительные интервалы для значе-
ния интеграла при значениях доверительной вероятности 0,95; 0,99; 0,999.
2. Действуя, как указано в упражнении 1, добиться того, чтобы при
вычислении методом Монте-Карло интеграла из примера 5.5 е было нс
более 0,001 при доверительной вероятности 0,95.
5.12. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
И ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ ИНСТРУМЕНТАЛЬНЫХ
СРЕДСТВ
Excel нс имеет специальных средств для проведения указанных
операций. Однако любая из них может быть легко реализована в элек-
тронной таблице и наглядно представлена на экране компьютера.
На рис. 5.7 и 5.8 показано применение Excel для вычисления
интеграла по методу Гаусса, которое было рассмотрено в подразд.
5.10 (см. пример 5.8).
В системе MathCad инструментом для вычисления производ-
ных служит специальный оператор, представленный двумя шаб-
лонами — для вычисления первой производной и для вычисления
и-й производной (рис. 5.9).
Для получения числового значения производной в некоторой
точке достаточно воспользоваться палитрой математических зна-
ков (рис. 5.10).
307
1&АМК lb: «(. «Si|4 ::Sb I»:. Я^!кх~ - | •[
и Вычисление интеграла по методу Гаусса от функции y=x*x*sin(x) на отрезке [0; 1]
-2 ।
3 h= 0,1
4
5 X х1 =х+Ы2-Ь/(2*корень(3)) x2=x+h/2+htf2*Kt3peHb(3)) y(x1) J y(x2)
6 0 =А6+$В$3/2-$В$3/(2*КОРЕН Ь(3)) =А6+$В$3/2+$В$3/(2* КОРЕН Ь(3)) =B6*B6*SlN(B6) |=C6*C6*SIN(C6)
У7^ с? =А6+0,1 = 47+0,1 =А7+$В$3/2-5В $3/(2‘КОРЕН Ь(3)) =А8+Ш13/2-$ВЖ2’ КОРЕН Ь(3)) =A7+$B$3/2+WW* КОРЕН Ь(3)) =А8+$В$ЗЙ+$В$ЗУ(2* КОРЕН Ь(3)) =B7*B7,S1IM(B7) =C7*C7‘SN(C7) =08*B8*S!N(B8) '=C8'C8'S1Ni;C8)
19 =А8+0,1 =A9+$B$3/2-$B$3/(2* КОРЕНЬ(З)) =Д9+$В$3/2+$В$3/(2* КОРЕН Ь(3)) =B9*B9*SIN(B9) !=C9#C9*SIN(C9)
$0, =А9+0,1 =А10+$В$3/2-$В$3/(2* КОРЕН Ь(3)) =А10+$В$3/2+$В$3/(2* КОРЕН Ь(3£| =810‘B10‘SIN(B10) i=C10*C10*SIN(C10)
и® =А10+0,1 =А11 +$В$3/2-$В$3/(2*КОРЕНЬ(3)) =А11 +$В$3/2+$В$ЗЦ2* КОРЕН Ь(3)) =B11 *B11 *SIN(B11) (=011 *011 *SIN(C11)
=А11+0,1 =А12+$В$3/2-$В$3/(2*КОРЕНЬ(3)) =А12+$В$3/2+5В$3/(2’ КОРЕН Ь(3)) =B12*B12*SIN(B12) =012*012*SIW(C12)
1&ЁЙ1 =А12+0,1 =А13+$В$3/2-$В$3/(2*КОРЕНЬ(3)) =А13+$В$3/2+$В$3^2* КОРЕН Ь(3)) =B13*813*SIN(B13) (=C13*013*SIN(C13)
ЙЙЯ R =А13+0,1 =А14+0,1 =А15+0,1 =А14+$В$3/2-$В$ЗД2* КОРЕН Ь(3)) =Д15+$В$3.'2-$В$3;Г2< КОРЕН Ь(3)) =А14+5ВЗЗ/2+ЗВЗЗ/Г2* КОРЕН Ь(3)) =А15+$ЙЗ/2+$В$ЗД:2а КОРЕН Ь(3)) =B14*B14*SIN(B14) i=C14*C14*SIN(C1_4) =B 15*B15*SIN(B15) | =015*C15*SIN(C15 j ~j
=CyMM(D6:D16) |=СУ!*1(Е6:Е16)
Йи Интеграл = =B3/2*(D17+E17) I
J
Рис. 5.7. Режим отображения формул
И М”- Вычисление интеграла по методу Гаусса от функции у=х отрезке (0; 1|
3 Р,1
4 J 5 J к х 1 - к+1С2- 1т/(2*кор е н ь(3)) х2=х+11/2+Ы(2*корень(3)) 6! □ 0.021132487 0,076867513 хИ • 9.43669Е-06; 0,000490054
„ZJ 0,1 0.121132487 0.176867513 0,001773043 0,005692148;
0,2 ; 0.221132487 0,278867513 0,010725373 0,021406721
Й91 0,3 ! 0,321132487 0,378867513 0,032550854 0,053091148:
0,4 1 0,421132487 0,478867513 0,072500712 ^,105662053
ЛЯ 0,5 1 0.521132487 0,578867513 0,135209065 ! 0.183318484:
•13 13. 0,6 i_ 0.621132487 0,7 Т ’ 0,721132487 Q.678867513 0773667513 0,224522055 0,343343712 0,28938023- 0.4261449571
1м 0.0 1 0.821132487 0,878867513 0,493501955 0,594767233;
ЗБ 0,9 ! 0.921132487 0,978867513 0,675637785 0,795162356;
1 i !
i ! 1,989773989; 2,475115388;
i Интеграл = 0,223244469
Рис. 5.8. Режим отображения значений
Рис. 5.9. Производная аналитически заданной функции в MathCad
Вычисление производной функции для заданного значения
аргумента в системе Derive (рис. 5.11) осуществляется следующим
образом;
• при помощи команды Author главного меню активизируется
диалоговое окно Author Expression, предназначенное для записи
выражений; после нажатия на кнопку L.—Z'l—_____i выражение по-
явится в алгебраическом окне (под номером #1);
« команда Differentiate пункта Calculus главного меню активизи-
рует диалоговое окно Calculus Differentiate, в котором необходимо
309
Вычисление значения
производной в точке
х:= 32
Calculus ; .Е|
= 0.0883883476
dx
ГЬ ]_________
" I Derivative Shift+/I
J п л
lim 1im Iwri
-га “>а+ а-
Рис. 5.10. Значение производной в точке
Substitute lot variables m ЙЗ
«1 :
#2 :
#3:
IM:
d
--- чГх
dx
1
2 <х
<2
16
ciojYR^k n'aH|KU^U|^o'in!piohlvb!xM^H
П !: Г;Л Г 3 Н Я 1]К Л ПИ'ЗОП Р,Е|Т|Г|ф'Х'Т|Я^С[Г
Рис. 5.11. Вычисление производной в Derive
Й6: 0.09838834764
указать, по какой переменной будет производиться дифференци-
рование (в общем случае может быть функция нескольких пере-
менных) и порядок производной (по умолчанию 1); нажатие на
кнопку I L'K 1 вызовет запись под номером #2;
• воспользовавшись командой Basic пункта Simplify главного
меню, получим значение производной в символьном-виде — вы-
ражение #3;
• команда подстановки Substitute for пункта Simplify главного
меню активизирует диалоговое окно Substitute for variables in <но-
мер выражения>, в котором вводится числовое значение (точка, в
которой требуется вычислить производную); кнопка br-mpL|z„J ди-
алогового окна запускает процесс вычислений — появится выра-
жение #4;
• команда Approximate пункта меню Simplify активизирует окно
Approximate Expression, позволяющее задать количество десятичных
знаков результата, а по нажатию на кнопку ЁЁЕЕЕЕ1 будет выве-
ден результат — выражение #6.
В системе Mathematica для вычисления производных применя-
ются следующие функции:
310
S Untitled ! -
ЕЕЕИ
tn[t]:= D[Sinfx], x]
Out[l]- Соз [x ]
tn₽]:« D[(x+3)A3* (x*2-4tx), x]
Out[3j= (3 + X)J (-4+ 2x) +3 (3 + x)£ (-4x + x‘)
Рис. 5.12. Дифференцирование в системе Mathematica
Рис. 5.13. Дифференцирование в системе Maple V
• D[/, х] возвращает значение первой производной функции
/(х) по переменной х;
• D[/,{x, »}] возвращает значение производной п-го порядка
функции /(х) по переменной х.
На рис. 5.12 показаны примеры вычисления производных от
функций у = sinх и у = (х + 3)3(х2 - 4х).
Для вычисления производной в пакете Maple следует в команд-
ном окне ввести команду вида: б!Д(<^уихд«я>, <переменная>),
возвращающую значение первой производной функции по не-
которой переменной; эта же команда в виде
<переменная>$п) позволяет получить значение производной п-го
порядка.
Дифференцирование выражения ^/x2cos5jt показано на рис. 5.13.
Полученный результат затем преобразован с помощью команды
simplify (упростить).
Система MathCad реализует вычисление интегралов с помощью
операторов интегрирования палитры математических знаков, име-
ющих шаблоны в виде знаков определенного Н и неопределенно-
го интегралов. В места ввода шаблона (рис. 5.14) записываются
функция, переменная, по которой производится интегрирование
311
Рис. 5.14. Контекстно-зависимое
меню выбора метода интегриро-
вания в системе MathCad
и пределы интегрирования. Воз-
можен выбор метода вычисления
определенного интеграла: доста-
точно поместить указатель мыши
на знак интеграла и нажать пра-
вую клавишу мыши. Теперь мож-
но установить любой из следую-
щих методов: Romberg — Ром-
берга; Adaptive — адаптивный с
изменением шага интегрирова-
ния в зависимости от особенно-
стей функции с выдачей резуль-
тата с погрешностью, заданной
системной переменной TOL;
Infinite Limit — улучшающий ин-
тегрирование при бесконечных
пределах; Singular Endpoint —
учитывающий сингулярность
функции в конечной точке.
Найдем значение определен-
ного интеграла (см. пример 5.6)
по формуле трапеций. Результат
показан на рис. 5.15.
Сравним полученный результат с точным решением. Из палит-
ры математических специальных символов необходимо выбрать
знак интеграла, затем вписать пределы интегрирования, подын-
Подынтегральная функция: Отрезок интегрирования: Число отрезков разбиения: ОД > ? • >0 п:- 10 Ъ:>1 *
Шаг интегрирования: п h - 0.1
Узловые точки: i> 0..п х, :• а + h i
Формула трапеций: Л-1 >*•» £ Уь + (УО + У»)
Значение интеграла -1 1-0225098
Рис. 5.15. Вычисление значения определенного интеграла
по формуле трапеций в MathCad
312
Точность вычисления: TOL:=10“6
Г1
x2sin(x) dx = 02232442755
о
Рис. 5.17. Геометрический смысл определенного интеграла
тегральную функцию и переменную интегрирования. Точность вы-
числений устанавливается при помощи системной переменной TOL
(рис. 5.16).
MathCad позволяет благодаря богатым графическим возмож-
ностям проиллюстрировать геометрический смысл интеграла как
площади криволинейной трапеции (рис. 5.17).
Система Derive вычисляет только те интегралы, которые выра-
жаются в элементарных функциях. Операции интегрирования осу-
ществляют встроенные функции:
• 1т(<функция> ,<переменная>) — вычисляет значение неопре-
деленного интеграла;
313
1
«2: J x SIH<m) dx
И
13s И. 2 23244
Рис. 5.18. Интегрирование в системе Derive
Рис. 5.19. Возможности интегрирования в системе Mathematica
• 1п1(<функция>,<переменная>,<нижний преде.1>,<верх/шй пре-
дел) — вычисляет значение определенного интеграла;
• й'1[(<функция>,<переменная>,<-порядок>) — вычисляет зна-
чение первообразной заданного порядка.
На рис. 5.18 показан пример вычисления значения определен-
ного интеграла в интерактивном режиме. Подынтегральное выра-
жение вводится в окне Author Expresson, затем с помощью ко-
манды Integrate опции Calculus главного меню активизируется со-
ответствующее диалоговое окно, позволяющее определять вид ин-
314
*Л MATLAB Окно улравлем«я
» х-0:О.1:1;
> r1=trapz(sin(x))
r1 -
4.59314548857976
•> r2=quad("sin1,0,1,1e-6)
r2 =
0.45969769656771
>» >"3-quad8('sin‘, 0,1,1e-6)
r3 =
0.45969769413186
Рис. 5.20. Интегрирование в системе MatLab
Рис. 5.21. Интегрирование в пакете Maple
теграла и его пределы интегрирования. Кнопка фиксиру-
ет выбор, а команда Approximate пункта Simplify главного меню
позволяет получить результат.
Система Mathematica для вычисления числовых значений опре-
деленных интегралов использует функцию NIntegrate[<r/>y«K^ufl>,
{< перемен пая >,<нижний предел> верхний предел>}], имеющую ряд
опций, в частности:
• Method->DoubleExponential — применяет алгоритм двойной
экспоненциальной сходимости;
• Method->Trapezodial — применяет метод трапеций.
Применение перечисленных выше опций показано на рис. 5.19.
Численное интегрирование средствами математической систе-
мы MatLab (рис. 5.20) осуществляется при помощи функций:
• 1гарг(<функи,ия>,<переменная>) — возвращает значение ин-
теграла, вычисленное по формуле трапеций;
• суаа^{<функция>,a,b,tol) — возвращает значение определен-
ного интеграла на [д;й] с заданной относительной погрешностью
(по умолчанию tol= 10-3), вычисленное по формуле Симпсона;
315
• циад8(<функция>,a,b,tol) — вычисляет значение определен-
ного интеграла с использованием квадратурных формул Ньюто-
на—Котеса 8-го порядка.
Численное значение определенного интеграла в системе Maple
реализует функция evalf(int(<</jywx^«j?>,x=a..Z>)). На рис. 5.21 при-
ведены результаты интегрирования двух функций:
a) x2sinx; б) .
70,5х2 +2
Упражнения
1. Вычислить значение следующих производных функций в точках:
7х2 +1 х 2 , . tg(x2+0,5)
а) -----— , х = 2; б) — Igx2, х= 1,5; в) —------х= 1.
х +1 3 2х2
2. Вычислить значение определенного интеграла по формуле трапе-
ций в пакете MathCad и оцените погрешность вычислений. Сравните
полученный результат с полученным в среде любого другого инструмен-
тального программного средства:
ч г tg(x2). psin(x2l) . 3f г- . х
а) б) J Л B)JVxsin-.
0.3А +1 I 2ух I 2
ЛАБОРАТОРНАЯ РАБОТА №5
И '
Тема: Численное дифференцирование
и интегрирование
Задание 1. Вычислить с помощью программы для компьютера
значение производной аналитически заданной функции /(х) в
точке х = а.
Задание 2. Вычислить значение производной функции, задан-
ной таблично, используя интерполяционные формулы Лагранжа
или Ньютона, и оценить погрешности метода.
Задание 3. Вычислить интеграл от заданной функции /(х) на
отрезке fa; У] при делении отрезка на 10 равных частей тремя
способами: 1) по формуле трапеций; 2) но формуле Симпсона;
3) по формулам Гаусса. Произвести оценку погрешности методов
интегрирования и сравнить точность полученных результатов.
Задание 4. С помощью программ для компьютера вычислить
значение интеграла заданной функции на отрезке [о; />] двумя
способами: 1) по формуле Симпсона методом повторного счета с
точностью 10-6; 2) методом Монте-Карло. Сопоставить получен-
ные результаты с результатом, полученным с использованием
одного из инструментальных пакетов.
316
Пояснения к выполнению лабораторной работы № 5
Для выполнения задания 1 используются аналитические выра-
жения функции f(x), содержащиеся в табл. 5.7. Значение х=а зада-
ется преподавателем. Программа для приближенного вычисления
значения производной функции в точке рассмотрена в приме-
ре 5.1. Используя программу, произвести численные эксперимен-
ты для различных типов числовых данных. Для сопоставления точ-
ности полученных числовых результатов рекомендуется также вы-
числить значение производной заданной функции в точке х = а с
помощью одного из инструментальных пакетов, а также путем
непосредственного дифференцирования формулы f(x) и после-
дующего вычисления значения f'(a).
Исходные данные к выполнению задания 2берутся из табл. 4.20 —
4.23, которые выбираются в соответствии с номером варианта по
табл. 4.15 в разделе «задание 4» (см. гл. 4). Участок таблицы для
дифференцирования, значение аргумента х, а также используе-
мый метод задаются преподавателем. Для оценки погрешности
метода используются формулы (5.12) —(5.14) или (5.18) — (5.20).
Учитывая, что аналитическое выражение таблично заданной фун-
кции в табл. 4.20—4,23 также известно, предоставляется возмож-
ность — как и при выполнении предыдущего задания — для сопо-
ставления точности полученных числовых результатов вычислить
значение производной заданной функции в точке х = а путем не-
посредственного дифференцирования формулы /(х) и последу-
ющего вычисления значения /'(а); эти вычисления могут быть
выполнены с помощью одного из инструментальных пакетов. Пе-
ред выполнением задания следует прочитать подразд. 5.2, 5.3, 5.12,
разобрать все приведенные в тексте примеры.
Исходные данные для выполнения задания .Уберутся из табл. 5.7.
Отрезок интегрирования разбивается на 10 равных частей и про-
изводится ручное вычисление интеграла по формулам трапеций,
Симпсона и Гаусса. Для расчетов по формулам трапеций и Симп-
сона удобно составить единую таблицу значений подынтеграль-
ной функции по схеме:
х. y/2(i = 0, 10) y.(J~ 1, 2, 3, ..., 9) 2у,. (/= 1, 3, 5, 7, 9)
По каждому из трех столбцов таблицы находятся суммы соот-
ветствующих значений подынтегральной функции (при этом по
столбцу у, для формулы трапеций находится сумма всех элемен-
тов столбца, а для формулы Симпсона — только с четными ин-
дексами). Для расчетов по формулам Гаусса составляется таблица
вида табл. 5.5. Вычисления ведутся с максимально возможной точ-
ностью вычислительного прибора или инструмента.
317
Для оценки погрешности методов используются оценочные
формулы (5.42), (5.45), (5.62). Их применение предполагает ис-
следование модулей соответственно второй и четвертой произ-
водной подынтегральной функции на отрезке [a; ft], В случае, ког-
да исследование общими методами оказывается слишком затруд-
нительным, можно воспользоваться табулированием указанных
производных на заданном отрезке с подходящим шагом на ЭВМ
(по необходимости такая таблица может локально уплотняться на
экстремальных участках отрезка [о; А]).
Перед выполнением задания 4 необходимо изучить подразд. 5.9
и 5.11, тщательно разобраться в сущности и алгоритме метода
повторного счета по формуле Симпсона, а также метода Монте-
Карло. Исходные данные для выполнения задания берутся из
табл. 5.7. Примеры использования для вычисления интегралов ин-
струментальных средств показаны в подразд. 5.12.
Таблица 5.7
Вариант Л*) a b
1 0,37esinjc 0 1
2 0,5 + х 1g х 1 2
3 (х + 1,9) sin(x / 3) 1 2
4 5 — ln(x + 2) X 3cosx 2x + l,7 2 0 3 1
6 (2x + 0,6) cos(x / 2) 1 2
7 2,6x2 In x 1,2 2,2
8 (x2 + l)sin(x -0,5) 0,5 1,5
9 x2 cos(x 14) sin(0, lx - 3) 2 3
10 x1 +1 3 4
11 3x + In x 1 2
12 4xe*2 -1 0
13 14 3x2 + tgx 3x2 + sin x X2 -0,5 0 0,5 1
15 3xeL“-r 0,2 1,2
16 x2tg у 1,5 2,5
318
Окончание табл. 5.7
Вариант /(х) а Ь
17 Тхе’* 0,1 1,1
18 3,1х1п2х 1,4 2,4
19 (х-0,8) In j 2,3 з.з
20 (х-3,1)е'»х 0 1
ГЛАВА 6
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
6.1. ПОСТАНОВКА ЗАДАЧИ
Простейшим обыкновенным дифференциальным уравнением
является уравнение первого порядка, разрешенное относительно
производной:
У' = /(х,У>- (6-1)
Основная задача, связанная с этим уравнением, известна как
задача Коши-, найти решение уравнения (6.1) в виде функции у(х),
удовлетворяющей начальному условию
j(*o) = Jo- (6-2)
Геометрически это означает (рис. 6.1), что требуется найти ин-
тегральную кривую у = у(х), проходящую через заданную точку
М0(х0, у0), при выполнении равенства (6.1).
Существование и единственность решения задачи Коши для
уравнения (6.1) обеспечиваются следующей теоремой.
Теорема Пикара. Если функция f(x, у) определена и непрерывна
в некоторой плоской области G, определяемой неравенствами
Рис. 6.1. Геометрическая иллюстра-
ция решения дифференциального
уравнения у - f(x, у)
|х-х0[<а, |у-у0|<Д (6.3)
и удовлетворяет в этой области
условию Липшица по у: суще-
ствует такое положительное
число М, что для любых точек
(x,yt)EG и (х, у2)еС
|Ж .У1 )-/(*, Л )|^
<Л/|у|-у2|, (6.4)
то на некотором отрезке\х - х0| <
< h существует, и притом толь-
ко одно, решение у = у(х) урав-
нения (6.1), удовлетворяющее
начальному условию уо = у(хо).
320
Число Л/ называется константой Липшица. Если f(x, у) имеет
ограниченную в G производную по у, то М - тах|/Дх, у)|. Ве-
личина Л вычисляется по формуле
b
Контрольные вопросы
1.Что является решением дифференциального уравнения? Что это
означает с геометрической точки зрения?
2. На какие основные группы подразделяются приближенные методы
решения дифференциальных уравнений?
6.2. МЕТОД ПИКАРА
Этот метод позволяет в принципе получить приближенное ре-
шение дифференциального уравнения (6.1) в виде функции, пред-
ставленной аналитически. Метод Пикара можно рассматривать как
применение метода сжимающих отображений, рассмотренного в
гл. 2, к решению дифференциальных уравнений.
Пусть в условиях теоремы существования требуется найти ре-
шение уравнения (6.1) с начальным условием (6.2). Проинтегри-
У х
русы обе части уравнения (6.1) от х0 до х: J dy = | f(x,y)dx, или
Уо хо
у(х) = у0 + ]’ /(х, y)dx. (6.7)
*0
Очевидно, решение интегрального уравнения (6.7) будет удов-
летворять дифференциальному уравнению (6.1) и начальному ус-
ловию (6.2). Действительно, при х = х$ получим: у(х0) = у0 +
41
+ _f f(x,y)dx = y0.
Хо
Вместе с тем, интегральное уравнение (6.7) позволяет приме-
нить метод последовательных приближений. Будем рассматривать
правую часть формулы (6.7) как оператор, отображающий всякую
функцию у(х) (из того класса функций, для которых интеграл,
входящий в (6.7), существует) в другую функцию того же класса:
У(х) = Уо + f f(x, y(x))dx.
хо
Если этот оператор является сжимающим (что следует из усло-
вия теоремы Пикара), то можно строить последовательность при-
ближений, сходящуюся к точному решению. В качестве начально-
го приближения принимается у(х) = у0, и находится первое при-
ближение
У1(х) = у0 + |/(х,у0)г/х.
Хо
Интеграл в правой части содержит только переменную х; пос-
ле нахождения этого интеграла будет получено аналитическое
322
выражение приближения yi(x) как функции переменной х. Далее
заменим в правой части уравнения (6.7) у найденным значением
у, (х) и получим второе приближение
л(х) = Уо + j /(x,y,(x))dx
*0
и т. д. В общем случае итерационная формула имеет вид
У„(х) = Уо + J f(x, y„M)dx (л = 1, 2,...). (6.8)
Циклическое применение формулы (6.8) дает последователь-
ность функций
Уо. У|(х), у2(х), .... у„(х), .... (6.9)
сходящуюся к решению интегрального уравнения (6.7) (а, следо-
вательно, и дифференциального уравнения (6.1) с начальными
условиями (6.2)). Это также означает, что Л-й член последователь-
ности (6.9) является приближением к точному решению уравне-
ния (6.1) с определенной контролируемой степенью точности.
Оценка погрешности к-го приближения дается формулой
|у(х)-Л(х)|<Л/*У-^—(6.10)
(/С + I).
где у(х) — точное решение У определяется равенством (6.6); М—
константа Липшица из неравенства (6.4).
На практике метод Пикара используется очень редко. Одна из
причин — та, что интегралы, которые необходимо вычислять при
построении очередных приближений, чаше всего аналитически
не находятся, а применение для их вычисления численных мето-
дов так усложняет решение, что становится гораздо удобнее не-
посредственно применять другие методы (рассмотренные далее),
которые изначально являются численными.
Пример 6.1. Методом последовательных приближений найти
приближенное решение дифференциального уравнения у' = х2 +
+ Зу, удовлетворяющее начальному условию у(0) = 2. (Заметим, что
эта задача Коши имеет элементарно находимое точное решение:
, . 56 з, 1 5 2 2 .
^>’27е ’Г -Г-27'’
Запишем для данного случая формулу вида (6.8)
y„(x) = 2 + J(x2 + 3y„_,)rfx (л = 1,2, ...).
о
Начальным приближением будем считать функцию у0(х) = 2.
Имеем
y,(x) = 2 + J(x2 + 6)dx = 2 + 6x + ^-.
о
323
Далее получаем
ЛГ С X3 U
у2(х) = 2 + [ х2 + 3 2 + 6х +— Wx = 2 + 6х + 9х2 .
oil 3 JJ 34
Аналогично,
А
ОС у4 Ov-5
Уз (х) = 2 + 6х + 9х2 + — х3 + — +-
3 . 3 4 20
и т.д.
Оценим погрешность третьего приближения. Для определе-
ния области G, заданной неравенствами (6.3), примем, напри-
мер, а = I, b = 2. В прямоугольнике G функция Дх,у) = х2 +
+ Зу определена и непрерывна, причем (см. (6.4) и (6.6)): М -
= тах|/;(х,у)| = 3, N = тах|/(х,у)| = 7.
2
По формуле (6.5) находим h ~ Используя оценочную фор-
33 24
мулу (6.10), получаем |у(х)-у3(х)| < ~ 0,053.
Заметим, что в этом примере все интегралы легко вычисляют-
ся аналитически, что, однако, не является характерным при ре-
шении дифференциальных уравнений методом Пикара.
Сходимость последовательных приближений, построенных по
методу Пикара в примере (6.1), показана на рис. 6.2. Ромбики мар-
кируют линию у - Уо(х), квадратики у = уДх), треугольнички —
у = Уз(х). Линии у = у4(х) и график точного решения (маркиро-
ван кружочками) в масштабе данного рисунка практически сли-
ваются.
Рис. 6.2. Последовательные приближения,
построенные по методу Пикара
324
Контрольные вопросы
1. В какой форме получается приближенное решение дифференци-
ального уравнения по методу Пикара?
2. Что выступает в качестве условий сходимости итерационного про-
цесса по методу Пикара?
Упражнение
Найти приближенное решение дифференциального уравнения
у' = cos у + Зх методом Пикара с начальным условием у(0) = 1,3 (расчет
вести до третьего приближения; сделать оценку точности полученного
решения по формуле (6.10)).
6.3. МЕТОД ЭЙЛЕРА
В основе метода ломаных Эйлера лежит идея графического по-
строения решения дифференциального уравнения, однако этот
метод дает одновременно и способ нахождения искомой функции
в численной (табличной) форме.
Пусть дано уравнение (6.1) с начальным условием (6.2) (т.е.
поставлена задача Коши). Вначале найдем простейшим способом
приближенное значение решения в некоторой точке jq = х0 + И,
где h достаточно малый шаг. Заметим, что уравнение (6.1) совме-
стно с начальным условием (6.2) задают направление касатель-
ной к искомой интегральной кривой в точке М0(х0, у0). Двигаясь
вдоль этой касательной (рис. 6.3)
ние решения в точке xf
У1 = Уо + hf(x0,y0). (6.11)
Располагая приближенным
решением в точке М।(х,, у,),
можно повторить описанную
выше процедуру: построить
прямую, проходящую через эту
точку под углом, определяе-
мым условием tgp = /(Х], yt),
и по ней найти приближен-
ное значение решения в точке
х2 = X] + h. Заметим, что, в от-
личие от ситуации, изображен-
ной на рис. 6.3, эта прямая не
есть касательная к реальной ин-
тегральной кривой, поскольку
точка нам недоступна. Одна-
ко представляется интуитивно
получим приближенное значе-
Рис. 6.3. Иллюстрация первого
шага метода Эйлера
325
ясным, что если h достаточно мало, то получаемые приближения
будут близки к точным значениям решения.
Продолжая эту идею, построим систему равноотстоящих точек
х, = х0 + ih (/ = 0, 1,2, ..., л). Получение таблицы значений иско-
мой функции у(х) по методу Эйлера заключается в циклическом
применении пары формул:
ДУ,- =hf{xiiyi)-> ум =у;+Ду; (i = 0, 1, 2, п). (6.12)
Геометрическая иллюстрация метода Эйлера приведена на
рис. 6.4. Вместо интегральной кривой в реальности получается со-
вокупность прямых (так называемая ломаная Эйлера).
Методы численного интегрирования дифференциальных урав-
нений, в которых решение получается от одного узла к другому,
называются пошаговыми. Метод Эйлера — простейший представи-
тель семейства пошаговых методов.
Отметим, что оценка погрешности метода при таком элемен-
тарном рассмотрении невозможна даже на первом шаге. Кроме
того, особенностью любого пошагового метода является то, что,
начиная со второго шага, исходное значение у, в формуле (6.12)
само является приближенным, т.е., вообще говоря, погрешность
на каждом следующем шаге систематически возрастает.
Наиболее используемым эмпирическим методом оценки точ-
ности как метода Эйлера, так и других пошаговых методов при-
ближенного численного интегрирования обыкновенных диффе-
ренциальных уравнений является способ двойного прохождения
заданного отрезка — с шагом h и с шагом й/2. Совпадение соот-
ветствующих десятичных знаков в полученных двумя способами
результатах дает эмпирические основание считать их верными (хотя
полной уверенности в этом быть не может).
326
Таблица 6.1
к Хк yt Л» = 0,2(cos yk + Зл-()
0 0 1.3 0,05
1 0,2 1,35 0,16
2 0,4 1,52 0,25
3 0,6 1,77 0,32
4 0,8 2,09 0,38
5 1,0 2,47
Одна из принципиальных трудностей всех пошаговых методов
численного решения дифференциальных уравнений состоит в воз-
можности столкнуться с неустойчивостью метода. Оценка погреш-
ности неявно предполагает, что ломаная приближенного реше-
ния (см. рис. 6.4) хотя и не совпадает с интегральной кривой, но
качественно на нее похожа. Чаще всего это именно так, но иногда
(например, при неудачном выборе шага ti) приближенное реше-
ние может быть качественно непохожим на точное (например,
точное монотонно убывает, а приближенное монотонно возра-
стает). Для эмпирического контроля того, не имеет ли места неус-
тойчивость, следует численно интегрировать уравнение с несколь-
кими, значительно отличающимися, значениями шага h, сравни-
вая качественно поведение решений.
Пример 6.2. Решить методом Эйлера дифференциальное урав-
нение у' = cos у + Зх с начальным значением у(0) = 1,3 на отрезке
[0; 1], приняв шар h = 0,2.
Рис. 6.5. Алгоритм метода Эйлера
327
Результаты вычислений с двумя знаками после запятой приве-
дены в табл. 6.1.
Порядок вычислений вполне очевиден: вначале находим
Ду0 = A(cosy0 + Зх0), затем у, = у0 + Ду0 и т. д.
Алгоритм метода Эйлера легко реализовать на ЭВМ. Блок-схе-
ма алгоритма решения дифференциального уравнения вида (6.1)
методом Эйлера изображена на рис. 6.5. Исходными данными яв-
ляются: начальные значения х и у, шаг интегрирования h и пра-
вая граница отрезка интегрирования Ь.
Программа решения дифференциального уравнения методом
Эйлера, составленная в соответствии с алгоритмом, изображен-
ным на рис. 6.5, приведена ниже.
program Euler;
uses ert;
var x,у,h,b:real;
function f(xl,yl:real):real;
begin f:=cos(yl)+3*xl;
end;
begin
clrscr;
writeln('Введите через пробел начальные
значения х и у: 1 ) ;
readin(х,у);
writeln(1 Введите величину шага интегрирования:') ;
readin(h);
writeln('Введите абсциссу правого конца
отрезка: ') ;
readln(Ь);
writeln ('Таблица значений искомой функции:');
writeln(' х ', ' у');
repeat
writeln(х:3:1, ' ' ,у:4:2);
у:=y+h* f (х, у);
х:=x+h;
until x>=b+h/2;
repeat until keypressed
end.
Результаты работы этой программы для задания из примера 6.2,
но с шагом, уменьшенным вдвое (т.е. для h = 0,1) вместе с соот-
ветствующими узловыми значениями из табл. 6.1 (h = 0,2) для удоб-
ства сравнения сведены в табл. 6.2.
Сопоставление приближений, полученных с различным шагом,
показывает, что при выбранном шаге метод Эйлера дает невысо-
кую точность — в пределах одной-двух значащих цифр.
328
Контрольные вопросы
Таблица 6.2
1. В какой форме получается при-
ближенное решение дифференци-
ального уравнения по методу Эй-
лера?
2. Что можно сказать о динамике
погрешности в пошаговом методе
Эйлера?
Упражнения
1. Методом Эйлера найти при-
ближенное решение дифференци-
ального уравнения у'-х2 + Зу, удов-
X х (Л = 0,2) у (Л = 0,1)
0 1,30 1,30
0,1 1,33
0,2 1,35 1,38
0,3 1,46
0,4 1,52 1,56
0,5 1,68
0,6 1,77 1,82
0,7 1,98
0,8 2,09 2,15
0,9 2,33
1,0 2,47 2,53
летворяющее начальному условию
у(0) = 1 на отрезке [0, 2] двумя спо-
собами: а) методом ручного счета с шагом Л - 0,2; б) с помощью про-
граммы Euler с шагом h = 0,1. Сопоставить точность полученных значе-
ний функции.
2. Составить программу решения дифференциального уравнения ме-
тодом Эйлера с двойным прохождением заданного отрезка — с шагом h
и с шагом Л/2 (совпадение соответствующих десятичных знаков в полу-
ченных двумя способами результатах даст эмпирические основание счи-
тать их верными).
6.4. МЕТОД РАЗЛОЖЕНИЯ РЕШЕНИЯ В СТЕПЕННОЙ РЯД
К методу Эйлера можно прийти и иными путями, не исполь-
зуя геометрических построений. Простейший из них таков. Ап-
проксимируем производную у', входящую в уравнение (6.1), пра-
восторонним конечно-разностным отношением в точке Xq (см. фор-
мулу (5.21)), и получим Уо = f (х0,у0). Здесь у, — точное зна-
чение искомого решения в точке Х]. Обозначая через yi прибли-
женное значение решения, получим: У) = у0 + АЛ(хо,Уо) — форму-
ла (6.11).
То же самое можно получить и иным способом, допускающим
в отличие от предыдущего улучшение аппроксимации и контроль
точности. Разложим искомое решение в ряд Тейлора с центром в
точке х0:
у(х) = у0 + y'(x.3)(x-x0) + ^y7x0) (x-x(J)2 +.... (6.13)
Число у0 известно из начального условия (6.2), значение про-
изводной у'(х0) также известно, поскольку из дифференциально-
го уравнения (6.1) следует, что у'(Хо) = /(хо,Уо). Ограничиваясь
в разложении (6.13) первыми двумя членами ряда и положив
х = х]; немедленно получаем формулу метода Эйлера (6.11).
329
Однако при таком подходе возникает возможность улучшить
решение, используя больше членов ряда в разложении (6.13). Уч-
тем еще один член ряда, квадратичный пох-х0. При этом возни-
кает необходимость найти у'(хо). Это можно сделать с помощью
самого дифференциального уравнения (6.1), продифференциро-
вав обе его части
у'(х) = -7- / (х, У(х)) = А'(х, у) + f'(x, у) =
rfx - dx
= А'(х,у) + //(х,у)/(х,у). (6.14)
(использовано правило дифференцирования сложной функции и
само уравнение (6.1)). Положив в (6.13) х = х, и используя (6.14),
получим во втором порядке разложения:
У; = Уо+/(хо,Уо)Л +
+ |[Л'(х, у) + 4'(х,у)/(х,у)] (Х=ХО1 h2. (6.15)
Первые два слагаемых в правой части (6.15) — формула метода
Эйлера, а следующее слагаемое — поправка к ней.
В связи с таким подходом становится понятным, почему метод
Эйлера называют методом первого порядка аппроксимации; ме-
тод, связанный с формулой (6.15), — второго порядка. Продол-
жая разложение в ряд, можно, в принципе, достичь более высо-
кого порядка аппроксимации решения.
Кроме того, становится очевидным, что оценка погрешности
применения метода Эйлера на одном шаге такова (ji — точное
значение решения в точке Xj):
|Й -У]| < Kh2, (6.16)
где К — некоторая константа, вид которой следует из сравнения
(6.15) и (6.16). Тем не менее, следует помнить, что оценка по-
грешности любого многошагового метода на одном шаге не дает
возможности учесть накопление погрешностей при многих ша-
гах, на каждом из которых сказывается погрешность предыдущего
шага.
Формула, аналогичная формуле (6.15), но для любого узла,
имеет вид
Ум =У<+/(х/,у,)й +
+ |[А'(х,у) + 4'(х,у)/(х,у)] (Х=ХЛ у=уд h2. (6.17)
Пример 6.3. Получить рабочую формулу для интегрирования
дифференциального уравнения, рассмотренного в примере 6.2,
во втором порядке аппроксимации.
330
Имеем: f(x, у) = cosy + Зх, f' = 3, fy = - sinу. Таким образом,
с помощью (6.17) получаем
й2
У/н = У, + й(сой у,. + Зх/) + — [3 - sin у, (cos у, + Зх,)].
По причинам, объясненным в начале следующего подраздела,
метод решения дифференциального уравнения путем разложения
в степенной ряд на практике почти не применяется. Однако он
создает теоретическую базу для построения более удобных, прак-
тически используемых методов; некоторые из них будут рассмот-
рены ниже.
Контрольный вопрос
В чем состоят преимущества метода разложения в степенной ряд по
сравнению с методом Эйлера?
Упражнение
Получить формулу третьего порядка по h, аналогичную формуле вто-
рого порядка (6.17). С ее помощью продолжить решение задачи, предло-
женной в примере 6.3.
6.5. МЕТОД РУНГЕ —КУТТА
Отмеченное выше неудобство решения дифференциальных урав-
нений путем разложения решения в степенной ряд связано, прежде
всего, с тем, что в расчетные формулы типа (6.17) входят наряду
с функцией /(х, у), ее частные производные. В формулу 2-го по-
рядка (6.17) входят производные первого порядка, в формулу 3-
го порядка — производные второго порядка и т.д. Поскольку на-
хождение формул для производных — задача не для стандартно
применяемых при решении математических задач систем програм-
мирования, то производные приходится искать вручную и конст-
руировать с их помощью достаточно громоздкие формулы.
Альтернативный путь открывает метод Рунге —Кутта, назван-
ный по имени его создателей. Основная идея этого метода такова:
вместо использования в рабочих формулах частных производных
функции /(х, у) использовать лишь саму эту функцию, но на каж-
дом шаге вычислять ее значения в нескольких точках.
Проиллюстрируем это на примере одного из возможных мето-
дов второго порядка. Для метода Эйлера путем простейшей право-
сторонней аппроксимации производной имеем: у'(х,) = .
h
В это выражение входят значения функции в двух точках. Если
взять в правой части уравнения (6.1) значение /(х, у) в точке с
331
номером i, то придем к методу Эйлера. Однако можно рассудить
и иначе: раз для аппроксимации производной взяты две точки,
то лучшей аппроксимацией правой части уравнения будет полу-
сумма | [/(%,, у,) + /(х,+1
у|+1)]. Тогда для нахождения у/+, полу-
чим равенство
>+i
= > + “[№,>)+ /(>+!,
>7+1 )]• Поскольку оно
представляет собой уравнение для у/+1, то решать его можно ме-
тодом итераций, причем в качестве первого приближения взять
то значение у( + 1, которое определяется методом Эйлера. В итоге
получим
>м =У, +|(й (6.18)
где
Л = hf(xh у,);
ь ч (6.19)
г2 = й/(х,+й, у,+л)
— расчетные формулы нового метода, обеспечивающего пошаго-
вое интегрирование дифференциального уравнения (6.1).
Описанная процедура получения формул (6.18), (6.19) опира-
лась лишь на некие правдоподобные утверждения. Докажем те-
перь, что (6.18) согласуется с (6.17) с точностью до второго по-
рядка по h включительно. Для этого разложим величину
f(Xj + h,yf + hfix/,^)), входящую в (6.18), в ряд вплоть до членов
первого порядка по h
f(x, + й, у, + й/(х/(у()) = f(xh у/) +
+/х(X;, У, )Й + //(%;, У; )hf (Х,, у, ) (6.20)
(учитывая, что й входит в оба аргумента). Подставим (6.20) в (6.18)
й2
>41 = > + ¥(>, >) + у [/х(>, >) + /у(>4 >)/(*!,>)]
— в точности совпадает с (6.17). Таким образом, несмотря на раз-
личный вид, формулы (6.18) и (6.17) согласуются друг с другом
во втором порядке по й включительно. Это, а также то обстоя-
тельство, что в формулы (6.18), (6.19) входят значения лишь са-
мой функции /(х, у), дает основания называть (6.18) формулой
Рунге — Кутта 2-го порядка.
На самом деле, (6.18) — лишь одна из множества возможных
формул Рунге —Кутта 2-го порядка. Попробуем отыскать такие
формулы в семействе формул вида
>н = > + й[а,/(х(, у,) + а2/(х, + Р,й, у, + Р2й/(>, >))], (6.21)
332
где а,, сс2, рь р2 — некоторые коэффициенты, значения кото-
рых следует подобрать так, чтобы (6.21) согласовывалось с (6.17)
с точностью до второго порядка по h.
Разложим f{xi + рй, + р2Л/(х(',у,) в ряд аналогично тому, как
это было сделано при получении (6.20). Получим:
у/+| = X- + й(а, + a2)/(xf,у,) + /г [а2р] Д'(х/5 у() + а2Р2/;(х;,у,)]. (6.22)
Сопоставляя (6.22) с (6.17), получаем ограничения на коэф-
фициенты ctj, се2, рь р2, при выполнении которых будет иметь
место совпадение (6.21) с (6.17):
ОС] +ct2 = 1; a2pi =^; сс2р2 = 1.
Система из трех уравнений с четырьмя неизвестными имеет
бесконечное множество решений, которое можно найти, если по-
ложить, например, переменную а2, входящую во все три уравне-
ния, свободной. Тогда cq = 1 - a2, Pi = ——, (32 = —, и при лю-
2а2 2сс2
бом а2 * 0 имеем вариант формулы Рунге —Кутта второго порядка.
В частности, формула (6.18) получается при о:2 = ^.
Разумеется, разные формулы Рунге— Кутта одного и того же
порядка будут давать при использовании различные числовые зна-
чения, но все они одного порядка точности.
Чем выше порядок формул Рунге —Кутта, тем более точные
значения они дают. На практике соблюдается некоторый компро-
мисс между высоким порядком формул и их громоздкостью, с
одной стороны, и объемом вычислений по ним для достижения
заданной точности, с другой. Ниже приведена одна из самых по-
пулярных формул 4-го порядка, часто называемая просто, без
уточнений, формулой Рунге — Кутта:
У/н +|('i+ 2г2+2г3+г4), (6.23)
где
Л =
, r( h г, А
ri =hf\ х; +-,?/+- ;
S < (6.24)
, ,f h с,)
Ъ =hf х,-+-,у;+у ;
r4 =hf{x; +h,yi + r3),
причем вначале последовательно вычисляются r\, r-i, г3, г4, а лишь
затем ум — по формуле (6.23).
333
Общий недостаток методов Рунге — Кутта — отсутствие про-
стых способов оценки погрешности метода. Погрешность на од-
ном шаге оценить сравнительно нетрудно, гораздо труднее оце-
нить накопление погрешностей на протяжении многих шагов.
Широко используемый на практике для этих методов полуэмпи-
рический способ контроля точности — двойной счет. Допус-
тим, что у„ — точное решение уравнения при х = х0 +nh. Тог-
да для рассмотренного выше метода 4-го порядка уп = у^ + Kh5,
где верхний индекс означает шаг, с которым вычислено при-
ближенное значение. Точно так же при решении с шагом —
у„ = ?пА/2) + j . Отсюда получаем:
VW _ (Л/2)
Л /п
довательно, ошибка при вычислении с шагом —
= ~Kh5. Сле-
16
есть
<б-25>
Из формулы (6.25), в частности, следует, что при достаточно
малом h и малых погрешностях вычислений решение уравне-
ния (6.1), полученное методом Рунге — Кутта 4-го порядка по фор-
мулам (6.23) —(6.24), будет близким к точному.
На рис. 6.6 изображена блок-схема алгоритма пошагового ин-
тегрирования дифференциального уравнения методом Рунге —
Кутта по формулам (6.23) —(6.24) с контролем точности по фор-
муле (6.25). Процедура R_K4 обеспечивает интегрирование урав-
нения на заданном отрезке [а; А] с заданным шагом h. Основная
программа (схема справа) обеспечивает многократное обращение
к процедуре R_K4 с последовательным уменьшением шага вдвое
вплоть до достижения заданной точности е (оцениваемой по фор-
муле (6.25)).
Пример 6.4. Решить дифференциальное уравнение у' = у(1 - х)
на отрезке [0; 0,5] с начальным условием у(0) = 1 и шагом h = 0,05
методом Эйлера и Рунге—Кутта 4-го порядка.
Начнем с того, что получим (для последующего сопоставле-
ния результатов) аналитическое решение уравнения у' = у(1 - х).
При заданных начальных условиях это решение выглядит так:
Пользуясь этой формулой, с помощью табулирования можно
получить таблицу «точного» решения заданного уравнения.
Порядок вычислений по методу Эйлера был продемонстриро-
ван в примере 6.2. Покажем в деталях один шаг вычислений по
методу Рунге —Кутта 4-го порядка. Проведем последовательные
вычисления по формулам (6.24):
334
r^hf(x0, ya)=0,05-l-(l-0)=0,05;
r2=hf(x0+~, й+“^0,05-Г1+^У( l-fo+^ H=0,04997;
2 2 J 2 JI I 2 ))
, ,.( h '2'1 nncfi 0,04997 V <n 0,05"Й л n,n(V7
’3--^ Xq+-, Л+у =0,05. 1+^— • 14 0+-^- = 0,04997;
г4=й/(х0+/г, л+гэ)=0,05/1+0,04997)-(1-(0+0,05))=0,04987.
,a 6
Рис. 6.6. Алгоритм метода Рунге — Кутта:
а — процедура однократного прохождения отрезка [х; Ь] с шагом Л;
б — алгоритм многократного прохождения отрезка [х0; i] с последовательным
уменьшением шага вдвое до достижения заданной точности с
335
Далее действуем по формуле (6.23):
У\ = Уо +|(Л +2г2 + 2г3 +г4) =
6
= 1 +1 (0,05 + 2 • 0,04997 + 2-0,04997 + 0,04987) = 1,04996.
6
Поскольку вычисления достаточно громоздки и трудоемки, то
численные решения заданного уравнения можно найти с помо-
щью программ для компьютера. Программа решения уравнения
по методу Эйлера была приведена в подразд. 6.3. Напишем про-
грамму, реализующую алгоритм однократного прохождения от-
резка интегрирования по методу Рунге —Кутта (см. блок-схему про-
цедуры R_K(x, у, Ь, Л) на рис. 6.6).
Программа состоит из трех фрагментов:
• модуля Rung_Kut4, реализующего сам процесс интегрирова-
ния уравнения на одном шаге;
• внешней по отношению к модулю функции f(x, у) — правой
части дифференциального уравнения (функция вынесена за пре-
делы модуля для большей его универсальности и хранится в фай-
ле по имени f.inc);
• основной (вызывающей модуль) программы Runge_Kutta4.
unit Rung_Kut4;
interface
type T=real;
procedure r_k(x,y,h:T; var z:T);
implementation
procedure r_k(x,y,h:T; var z:T);
{$1 f.inc)
var rl, r2,r3,r4 :T; i,n:integer;
begin
rl:=h*f(x,y);
r2:=h*f(x+h/2,y+rl/2);
r3:=h*f(x4-h/2,y+r2/2);
r4:=h*f(x+h,y+r3);
z:=y+(rl+2*r2+2*r3+r4)/6;
end;
end.
function f(x,y:T):T; {Эта функция должна храниться
как отдельный файл с именем f.inc)
begin f:=y*(l-x);
end;
program Runge_Kutta4;
uses crt, Rung_Kut4;
type T=real;
var x,y,h,b:T; i,n:integer;
336
begin
clrscr;
writeln(’Задайте начальные значения:');
read(x,у);
writeln ('Укажите шаг интегрирования:');
readln(h);
writeln(’и правую границу отрезка
интегрирования:');
readln(b); writeln ( ' х',' у1);
n:=trunc((Ь-х+1Е-10)/h);
writeln(' ’,x:4:2,' ',y:10:6);
for i:=l to n do
begin
r__k(x,y,h,y);
x;=x+h;
writeln(' ',x;4:2,' ',y;10:6);
end;
repeat until keypressed
end.
Для сравнения результаты численного решения уравнения ука-
занными методами и значения «точного» решения, вычисленные
в соответствующих точках (с шестью знаками после запятой), све-
дены в табл. 6.3.
Из табл. 6.3 видно, что результаты, полученные по методу Рун-
ге-Кутта, практически совпадают с «точным» решением — в от-
личие от соответствующих значений, полученных методом Эйле-
ра. Подтвердить истинную точность результатов, полученных ме-
тодом Рунге —Кутта, можно также путем повторения решения с
меньшим шагом, что рекомендуется сделать самостоятельно.
Таблица 6.3
X У
Метод Эйлера Метод Рунге—Кутта «Точное» решение
0,00 1,000000 1,000000 1,000000
0,05 1,050000 1,049958 1,049958
0,10 1,099875 1,099659 1,099659
0,15 1,149369 1,148837 1,148837
0,20 1,198218 1,197217 1,197217
0,25 1,246146 1,244520 1,244520
0,30. 1,292877 1,290462 1,290462
0,35 1,338127 1,334758 1,334758
0,40 1,381617 1,377128 1,377128
0,45 1,423065 1,417295 1,417295
0,50 1,462199 1,454991 1,454991
337
Контрольные вопросы
I. В чем различие одношаговых методов Эйлера и Рунге — Кутта? Как
это различие можно охарактеризовать с графической точки зрения?
2. Как можно реализовать эмпирический критерий оценки точности
решения дифференциальных уравнений применительно к численным
методам Эйлера и Рунге - Кутта?
Упражнения
1. Пользуясь программой Runge_Kutta4, решить дифференциальное
уравнение у' = у2 + Зх с начальным условием у(1) = 3 на отрезке [1; 2]
сначала с шагом h = 0,1, а затем с шагом h = 0,05. Сопоставить и проком-
ментировать полученные решения.
2. Используя программу Rungc_Kutta4, составить программу, реали-
зующую метод Рунге—Кутта 4-го порядка с автоматическим выбором
шага по заданной точности (см. блок-схему на рис, 6.6).
3. Оформить программу Euler, приведенную в предыдущем парагра-
фе, в виде модуля на языке Turbo Pascal, взяв за образец Rung_Kut4.
Назвать полученный модуль Eulcri, а заголовок входящей в него про-
цедуры представить в виде Eul(x, у, h: Т; var z:T).
6.6. МНОГОШАГОВЫЕ МЕТОДЫ
Рассмотренные выше методы пошагового интегрирования диф-
ференциальных уравнений характерны тем, что значение реше-
ния на следующем шаге ищется с использованием решения, по-
лученного лишь на одном предыдущем шаге. Подобные методы
называются одношаговыми. К ним относятся рассмотренные выше
методы Эйлера и Рунге — Кутта. При этом в методах Рунге — Кутта
приходится вычислять значение правой части (т.е. функции f(x,y))
в нескольких точках.
Вполне естественной является идея использования при вычи-
слении значения решения на следующем шаге несколвких преды-
дущих значений решения. Поскольку они к этому моменту уже
известны, это может помочь избежать дополнительных вычисле-
ний значений /(х,у). Методы, использующие эту идею, называ-
ются многошаговыми.
При конечно-разностной аппроксимации дифференциально-
го уравнения у' - f(x,y) многошаговая аппроксимация возмож-
на как для левой части уравнения (т.е. для производной у'), так
и для правой части (функции /(х,у)). Если производную ап-
проксимировать простейшим конечно-разностным отношением:
У I,----5 то возникающее семейство методов собирательно
называется методом Адамса. Этот метод весьма популярен в вы-
числительной практике - прежде всего, в силу более высокой
(вообще говоря) устойчивости, нежели метод Рунге—Кутта.
338
В общем случае формулы метода Адамса имеют следующую
структуру
— . У- = ОоДхм,Ут) + fli/CW,) + - + (6.26) Q
При Oq = 0 метод называется явным, а при ц, О — неявным.
Порядок аппроксимации каждой конкретной реализации ме-
тода Адамса определяется согласием между соответствующей фор-
мулой и разложением решения в ряд Тейлора (см. формулы (6.13) —
(6.17)). Имеет место следующая теорема (доказательство ее приво-
дить не будем, см., например, [12]):
Наивысший возможный порядок аппроксимации явного т-шагово-
го метода Адамса равен т, а неявного (/«+/).
Получим конкретные формулы, реализующие простейшие яв-
ный и неявный методы Адамса.
Явный метод 2-го порядка. Положим в (6.26) а$ = 0 и т = 2.
Получим:
J'+L, У‘ = У/) + Oj/U-bJi-i)-
h
То же самое можно записать иначе:
Ум = у, +й[о1/(хьу,) + а2/(х,- +й,у(х,- +й))]. (6.27)
Разложим (6.26) в ряд по h с точностью до членов 2-го порядка
(пользуясь правилом дифференцирования сложной функции):
У/н =У/ +А(Ц) +й2)/(х,-,у/)-й2о2[А' + /г7]<х=х. ^лГ (6-28)
Сравнивая (6.27) с (6.17), получаем уравнения для коэффици-
ентов а{ и а2
3
2
а^ + <з2 — 1, й2 - “
£
2’
откуда получаем щ =
; д2 = —- Таким
образом, явный метод Адамса 2-го порядка выражается простой
формулой:
й
Ум =У/+^[^(^У^-Ж-ьУм)]. (6-29)
Обсудим на примере этого метода проблему, общую для всех
многошаговых методов — начальные данные для вычислений. Имея
лишь значение у0, невозможно по формуле (6.29) вычислить уь
Потом, когда у, будет найдено, эта проблема исчезнет, так как
для нахождения у2 уже будет все необходимое. Для поиска же у]
необходимо привлечь иной метод, например метод Рунге—Кутта.
При этом для общей согласованности процедуры привлекаемый
метод должен иметь порядок, не меньший, чем метод Адамса,
описываемый формулой (6.29). Таким может быть любой из мето-
339
дов Рунге—Кутта 2-го порядка (например, выражаемый формул
лой (6.19)). Об этой ситуации говорят, что многошаговые методы
не являются самостартующими. Заметим, что для метода Адамса
3-го порядка необходимо привлечь метод Рунге—Кутта не ниже
3-го порядка, причем дважды для получения и у2 и т.д.
Схема применения явного метода Адамса 2-го порядка с при-
влечением метода Рунге —Кутта 2-го порядка приведена на рис. 6.7.
Прежде чем перейти к рассмотрению примеров, отметим, что
интегральная оценка погрешности любого пошагового метода
численного интегрирования дифференциальных уравнений (вклю-
чая и метод Адамса) является на практике полуэмпирической. Она
Рис. 6.7. Алгоритм явного метода Адамса 2-го порядка
340
проводится путем многократного решения уравнения с постепен-
но уменьшающимся значением шага интегрирования.
Программа, приведенная ниже, реализует алгоритм однократ-
ного прохождения отрезка интегрирования по методу Адамса и
соответствует алгоритму, изображенному на рис. 6.7. Ее структура
схожа со структурой программы, приведенной в предыдущем пунк-
те для метода Рунге —Кутта.
unit AdarnS—1 ;
interface
type T=real;
procedure adams (x, y, z, h : T; var v:T);
implementation
procedure adams(x,y,z,h:T; var v:T);
{$1 f.inc}
begin
v:=z+h*(3*f(x,z)-f(x-h,y))/2;
end;
end.
function f(x,y:T}:T; {Эта функция должна храниться
как отдельный файл с именем f.inc}
begin f:=y*(l-x);
end;
program Adamsl;
uses crt., adams_l, RunKut_2;
type T=real;
var x,y,h,b,z,v:T; i,n:integer;
begin
clrscr;
writeln(’Задайте начальные значения:'); read(x,y);
writeln('Укажите шаг интегрирования:’); readin(h);
writeln('и правую границу отрезка
интегрирования:');
readin(Ь);
writeln(' х', ' у');
n:=trunc((b-x+lE-10)/h) ;
writelnf' ',x:4:2,' 'fy:10:6) ;
r_k2(x,y,h, z) ;
writeln(' ',x:4:2,' ',z:10:6);
x:=x+h;
for i:=2 to-n do
begin
adams(x,y,z,h,v);
x:=x+h;
writeln(' ',x:4:2,' ’,v:10:6);
341
у:=z; z : =v
end;
repeat until keypressed
end,
В программе adamsl используется модуль RunKut_2:
unit RunKuL2;
interface
type T=real;
procedure r_k2(x,y,h:T; var z:T);
implementation
procedure rk2(x,y,h:T; var z:T);
{$1 f.inc)
var v:T;
begin
v:=f (x,y); z:=y+h*(v+f(x+h,y+h*v))/2;
end;
end.
Пример 6.5. Выполнить по методу Адамса задание, приведен-
ное в примере 6,4.
Результат работы программы adamsl:
Задайте начальные значения:
О 1
Укажите шаг интегрирования:
0.05
и правую границу отрезка интегрирования;
0.5
X У
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 1.000000 1.049937 1.099746 1.149042 1.197550 1.244985 1.291065 1.335502 1.378014 1.418323 1.456159
Сравнивая с результатами, приведенными в табл. 6.3, делаем
вывод: в данном случае метод Адамса второго порядка дает резуль-
тат лучше, чем метод Эйлера (1-го порядка), но хуже, чем метод
Рунге-“Кутта 4-го порядка, что совершенно естественно.
342
Неявный метод 2-го порядка. Положим в (6.26) т-1. Получим:
Ум~У‘ = ум) + aJCXi, у,-),
п
Проделав элементарные преобразования, подобные тем, что
привели к формуле (6.28), и сравнив их результат с (6.17), полу-
чим уравнения для и йр
. 1
а0 + Д1 - I, ~
откуда следует искомая формула Адамса
И.
Ум =У; + + /(*/, У/)]- (6-30)
На ее примере легко понять основную проблему, связанную со
всеми неявными методами. В отличие от формул типа (6.29), а
также формул Эйлера и Рунге —Кутта (6.30) является не расчет-
ной формулой для нахождения значения искомого решения на
следующем шаге, а уравнением для поиска этого значения, так
как величина у/+1 входит и в левую, и в правую часть этой форму-
лы. Поскольку это уравнение является, вообще говоря, нелиней-
ным, и имеет вид, подходящий для итерационного решения (см.
гл. 2), то так его и следует решать:
Уж ° = У/ + у[/(хж,Уж) + №,У/)], (6.31)
где J— номер итерации. Если шаг h выбран удачно, то итерацион-
ный процесс быстро сходится (обычно h выбирают так, чтобы
требуемая точность была достигнута не более чем за две-три ите-
рации).
Метод (6.31) также не является самостартующим, хотя и по
иной причине, чем метод (6.29). Дело в том, что для вычисления
величины У1 необходимо иметь начальное приближение yf0). Для
его нахождения можно использовать явный метод более низкого
порядка (поскольку более низкий порядок в данном случае — пер-
вый, то возможно привлечение метода Эйлера). Соответствующий
алгоритм с автоматическим выбором шага по заданной точности
решения изображен на рис. 6.8. Под Eul(x,y,li,z) понимается имя
процедуры, выполняющий один шаг по методу Эйлера, создание
которой было предусмотрено при выполнении упражнения в пре-
дыдущем подразделе.
Пример 6.6. Провести вычисления по данному методу для зада-
чи Коши, рассматривавшейся в примерах 6.4 и 6.5.
Имеем уравнение у' = у(1 - х) и начальное условие: у(0) = 1. Точ-
ность, достигаемую в процессе итераций, зададим равной 5 • КГ6,
шаг интегрирования примем равным 0,05.
343
а а — процедура однократного прохожде-
ния отрезка [х; Ь] с шагом й; б — алго-
ритм многократного прохождения от-
резка [х0; Ь] с последовательным умень-
шением шага вдвое до достижения
заданной точности е
Начальное приближение для jj найдем, как и рекомендовалось
выше, с помощью метода Эйлера:
< = >’0 + Wo, Jo) = 1 + 0,05 • 1 • (1 - 0) = 1,05.
Итерационный процесс для нахождения строим по формуле
344
уГ° = >’о + ту[/(*о + M|7)) + Л*о,Уо)]-
Отсюда получаем:
У1” = 1 + [л(0) О - (*о + й)) + у0(I - *о)] =
= 1 + ^[1 -(1 -0,05) + 1(1 -0)] = 1,0499375
(с учетом требуемой точности вычисления ведутся с семью циф-
рами после запятой).
Поскольку требуемая точность не достигнута ([уР - yf0)| = 6-10-5),
то сделаем следующую итерацию:
У|2) = l+|[ji(l)(l-(^o + А)) -ь у0(1 - Ач) )] =
= 1 + [1,0499375 - (1 - 0,05) + 1 • (1- 0)] = 1,0499360.
Поскольку [yf!> - У1(0)| = 1,5 10-6, то требуемая точность достигну-
та, и можно принять, округляя в соответствии с ней, У| = 1,049936
(с одной запасной цифрой).
После этого следует по той же схеме приступить к вычислени-
ям, которые приведут к значению у2, и т.д.
В неявных методах более высокого порядка «несамостартуемость»
проявляется еще сильнее.
Для иллюстрации этого факта ограничимся приведением (без
вывода) формулы неявного метода Адамса 3-го порядка (см., на-
пример, [12]):
h
Ум =Уг +и(5Ж+1,у;-+1) + 8№,у,)-Ж-,,у(..)). (6.32)
При ее применении возникают следующие проблемы:
• метод, за которым стоит формула (6.31), непригоден для вы-
числения yj; для этого следует применить «одношаговый» метод
Рунге —Кутта (причем не ниже 3-го порядка);
• для каждого следующего шага, начиная с вычисления у2,
необходимо иметь начальное приближение у[°[ для итерационно-
го процесса
Ум = y< +^(V(x/+i,y,^rl)) + 8/'(x/, y,)-/U_|,y,_,)). (6.33)
Это начальное приближение рекомендуется искать с помощью
явного метода, порядок которого ниже чем порядок метода, со-
ответствующего) формуле (6.32), т.е. метода Рунге —Кутта 1-го или
2-го порядков, или явного метода Адамса 2-го порядка, рассмот-
ренного выше, см. формулу (6.29). (Впрочем, на практике часто
вполне достаточно принимать в качестве у.®] значение у„ най-
денное на предыдущем шаге).
345
В целом, сравнивая различные методы, можно сделать ряд вы-
водов.
1. Многошаговые методы алгоритмически сложнее, чем мето-
ды Рунге—Кутта того же порядка, из-за необходимости привле-
кать на старте иные методы.
2. Явные многошаговые методы, экономичнее, поскольку ис-
пользуют (после преодоления стартовых трудностей) лишь те зна-
чения правой части уравнения, которые к нужному моменту уже
вычислены.
3. Неявные многошаговые методы обладают большей устойчи-
востью, чем явные, и для некоторых классов уравнений являются
предпочтительными.
Контрольные вопросы
1. В чем состоят принципиальные различия между одношаговыми и
многошаговыми методами?
2. В чем состоит принципиальное различие между явными и неявны-
ми многошаговыми методами?
3. Каким образом можно организовать начальный этап работы при
использовании явного многошагового метода n-го порядка?
4. Каким образом можно организовать начальный этап работы при
использовании неявного многошагового метода w-го порядка?
Упражнения
1. Вывести формулу (6.32), взяв за образец способ, приведший к фор-
муле (6.30).
2. Пользуясь методом (6.32), решить дифференциальное уравнение
у' = у2 + Зх с начальным условием у(1) = 3 на отрезке [1; 1,5] сначала с
шагом h = 0,1, а затем с шагом h= 0,05. Сопоставить и прокомментиро-
вать полученные решения. Испытать различные способы получения на-
чального приближения для итерационного процесса (6.33), выяснить,
влияет ли выбор способа на результат.
3. Составить программу, реализующую неявный метод Адамса 2-го
порядка с автоматическим выбором шага по заданной точности.
6.7. ПОНЯТИЕ О ЧИСЛЕННЫХ МЕТОДАХ РЕШЕНИЯ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ
ПРОИЗВОДНЫХ
Если ^(Х|, х2, ..., х„) — функция нескольких (и>2) перемен-
ных и в дифференциальное уравнение входят производные по
нескольким переменным, то такое уравнение называется диффе-
ренциальным уравнением в частных производных.
Теория таких уравнений существенно более сложна, нежели
обыкновенных дифференциальных уравнений, а возможности
аналитического решения еще более ограничены (хотя и существу-
346
X
0 I
Рис. 6.9. К вопросу о колебаниях
струны
Рис. 6.10. К вопросу о теплопро-
водности в стержне
ет ряд специальных методов, с которыми знакомятся в соответ-
ствующем курсе).
При решении прикладных задач, порожденных математичес-
кими моделями реальных процессов, доминирующими при реше-
нии дифференциальных уравнений в частных производных явля-
ются численные методы, а среди них — метод сеток. Однако даже
этот метод для разных классов уравнений в частных производных
имеет существенные особенности.
Цель данного подраздела — ознакомление на простейшем воз-
можном примере с идеей метода сеток и практическими приема-
ми численного интегрирования дифференциальных уравнений в
частных производных.
В приложениях доминируют те классы указанных уравнений,
которые отражают несколько фундаментальных физических про-
цессов, протекающих во времени и/или в пространстве. Наивыс-
ший порядок производной, входящей в эти уравнения, равен двум,
и поэтому они называются уравнениями второго порядка. Искомая
функция в таких уравнениях зависит, вообще говоря, от четырех
переменных: трех пространственных координат и времени. Однако
в частных, относительно простых, ситуациях число пространствен-
ных переменных может быть меньше трех — если рассматривается
процесс, происходящий в плоскости или вдоль линии.
Другое возможное упрощение связано с тем, что уравнение
может не содержать производной по времени, если рассматрива-
ется стационарный режим.
Напомним некоторые классические уравнения второго поряд-
ка, описывающие фундаментальные физические процессы (см,
например, [2], [3], [12]).
Уравнение колебаний струны описывает процесс, иллюстрируе-
мый рис. 6.9. Конечные точки струны закреплены, а струна туго
натянута. Если в некоторый момент времени вывести струну из
положения равновесия (например, оттянуть ее в некоторой точ-
ке) и отпустить, то струна начнет колебаться.
Процесс описывается дифференциальным уравнением
Э2ы 7
(6.34)
347
где и — смещение точки струны с координатой х в момент t из
положения равновесия; д2 — коэффициент, отражающий свой-
ства материала струны; g ускорение свободного падения. Запись
коэффициента в форме а2 отражает то обстоятельство, что он всегда
положителен (от знака коэффициента в уравнении в частных про-
изводных иногда зависит способ его решения).
Уравнение теплопроводности и уравнение диффузии совпадают по
форме. Для теплопроводности в стержне с теплоизолированными
границами (рис. 6.10) и диффузии в трубке с непроницаемыми
стенками (т.е. в одномерном случае) это уравнение имеет вид
ди д2и
-г- = а Тг
dt дх2
(6-35)
где при описании теплопроводности и(х, /) — температура стрежня
в точке с координатой х в момент времени /, а при описании
диффузии — концентрация диффундирующего вещества.
Трехмерный аналог уравнения (6.35) получается заменой про-
изводной, входящей в правую часть уравнения, соответствующим
оператором Лапласа:
ди _ 2( д2и д2и Э2м''
д! а ^дх2 ду2 dz2 у
(6.36)
Уравнение Лапласа и уравнение Пуассона имеют соответственно
вид
д2и д2и д2и д2и д2и
—т + —т + —г = 0, —г + —г
Эх2 ду2 dz2 дх2 ду2
Э2« .
+ VT = /<Х’У^У
dz2
(6.37)
Эти уравнения описывают многие физические ситуации, свя-
занные со стационарными (т.е. независящими от времени) рас-
пределениями физических полей (электрических, тепловых и т.д.).
Как известно, для выделения частного решения уравнения в
частных производных надо задать некоторое число функций (ана-
логично тому, как для выделения частного решений обыкновен-
ного дифференциального уравнения надо задать два числа, обра-
зующих начальное условие). Для задач с ясной физической интер-
претацией указанные функции распадаются на начальные условия
и краевые условия. Так, для уравнения (6.35) начальное условие
может быть задано следующим образом:
и(х, 0) = 4_0 = /(х), (6.38)
где функция описывает распределение температуры в стержне в
начальный момент времени. Краевые условия для уравнения (6.35)
могут быть записаны несколькими способами. Простейший из
них — задание постоянной (но не обязательно одинаковой) тем-
пературы на каждом конце стержня
«(0, Г) = w[x=0 = w0; u(l, /) = u|,=/ = «о (6.39)
348
X.
Xn— I
Рис. 6.11. Одномерная сетка
Иные варианты задания краевых условий для уравнения (6.35)
изучаются в методах математической физики.
Покажем на примере уравнения теплопроводности в стержне
наиболее распространенные методы численного интегрирования
уравнений в частных производных. В их основе лежит прием диск-
ретизации.
Покроем отрезок [0, /] одномерной сеткой (т.е. разобьем его на
и равных частей, как показано на рис. 6.11) с узлами в точках
х0 =0, = х0 + Дх, ..., х(- = х0 + i Дх, ..., х„ = х0 + и Дх = I.
Искомую функцию м(х, г) будем аппроксимировать ее значе-
ниями в узлах сетки. Конечно, такое представление не дает пол-
ного описания, но в промежуточных точках, если сетка достаточ-
но мелкая, возможна интерполяция.
Для внутренних узлов сетки используем центрально-разностную
аппроксимацию производной, а для крайних узлов — односто-
роннюю (как это было описано в гл. 5)
Эм[ м(х1+[) - ц(х,_]) Эм! м(х,) - м(х0)_
Эх|х=1 2Дх ’ Эх| Дх
2 / х / х (6.40)
Эм = м(х„)-и(хй,)
Эх Дх
Аналогичная аппроксимация вторых производных имеет вид
Э2м 1 Эм Эм
Эх2 2Дх Эх Эх
Х=Х| |_ л~А<г+1
м(х1Ч1)-2м(х,) + м(х,-1).
(Дх)2
Э2м _ 1 Эм
Эх2 Дх Эх
L
Эм
Эх
1_ м(х2)-м(х0)
Дх 2Дх
М(х|)-М(хо)
Дх
м(х2)-2м(х|) + м(х0).
2(Дх)2
Э2М = 1 Эм! _ ЭмI _ м(х„ ) - 2м(х„_! ) + и(Хп_; )
Эх2 Дх Эх L Эх L , 2(Дх)2
X— Хн IA Art-I J
(6.41)
Таким образом, уравнение (6.35) в каждом узле сетки порож-
дает обыкновенное дифференциальное уравнение по времени, а в
целом возникает система таких уравнений:
</М/ _ 2 М,+| - 2и, + М;_]
dt ° (Дх)2
(6.42)
349
где w/ — значение температуры в !-м узле, зависящее от времени.
В систему (6.40) включены лишь уравнения для внутренних уз-
лов, чего при краевых условиях вида (6.38) вполне достаточно.
Для интегрирования системы (6.41) можно использовать опи-
санные выше методы Эйлера, Рунге —Кутта и т.д. Так как им тоже
свойственна дискретизация, то возникает еще одна, временная
сетка. При интегрировании уравнений по времени происходит
продвижение по отдельным временным слоям, а в каждом слое
определяется значение искомой функции на пространственной
сетке. Если для интегрирования по времени используется метод
Эйлера или любой другой одношаговый метод, то для работы со
следующим временным слоем используются значения искомой
функции из предыдущего слоя, для более сложных — из несколь-
ких предыдущих слоев.
Далее будем индексы, соответствующие временной сетке, писать
надстрочно (вверху), а пространственной — подстрочно (внизу).
Таким образом, для одномерного уравнения запись и/ означа-
ет значение функции и(х, i) в j-м временном слое и в 1-м узле
пространственной сетки.
Вернемся к одномерному уравнению теплопроводности (6.35)
и сформулируем простейшую из возможных схем его интегриро-
вания — явную схему первого порядка — по времени, используя
метод Эйлера, и по пространству, используя простейшие ап-
проксимации (6.41). Шаг по времени обозначим А/, по координа-
те — Дх. Величина м*+1 = и((к+1,х,) находится из разностного урав-
нения
u?+l =U? -2и* +и^)(к = 0, 1, ...; i= 1, 2, ..., п- 1)(6.43)
для внутренних узлов пространственной сетки, в силу начального
условия (6.38) л-01 = /(х,). Что касается значений и и* (на
концах стержня), то они зависят от типа краевого,условия; для
случая, когда концы стержня поддерживаются при постоянной
температуре, имеем: и^ = w0; ип = где «о, й, — заданные числа.
Теперь остановимся на вопросе об устойчивости и эффектив-
ности обсуждаемого метода. Устойчивость понимается в том же
смысле, что и для обыкновенных дифференциальных уравнений,
но шансов получить неустойчивый метод для численного интег-
рирования уравнений в частных производных гораздо больше. Су-
ществуют разностные схемы абсолютно неустойчивые, абсолют-
но устойчивые и условно устойчивые. Первые при любых, сколь
угодно малых, шагах так «раскачивают» погрешность, что приво-
дят к результатам, не имеющим ничего общего с реальностью.
Вторые ни при каких шагах не «раскачиваются», хотя, конечно,
чем меньше шаг, тем меньше разница между приближенным и
точным решениями. Третьи устойчивы при одних комбинациях
350
значений Дх и Д/и неустойчивы при других. Исследование пока-
зывает, что разностная схема (6.43) устойчива при
а2 ДГ 1
(Дх)2 ~ 2
(6.44)
и неустойчива в противном случае.
Отметим в связи с критерием (6.44) следующее обстоятель-
ство. При поверхностном ознакомлении с идеей дискретизации
представляется, что чем меньше шаг сетки, тем лучше. Однако в
реальности такой вывод далеко не всегда верен. В самом деле, умень-
шение шага Dx пространственной сетки при фиксированном зна-
чении остальных параметров, входящих в правую часть неравен-
ства (6.44), может привести не к улучшению результатов, а к по-
тере устойчивости разностной схемы. (В этом рассуждении мы не
касаемся сугубо вычислительных погрешностей, накопление ко-
торых с уменьшением шага дискретизации также неочевидно и
может породить иной тип неустойчивости).
Эффективность схемы можно представить лишь при сопостав-
лении ее с другой схемой того же назначения. Прежде всего, под
эффективностью понимают возможность относительно быстро
получить решение с достаточной точностью. Иногда оказывается
не менее важным объем оперативной памяти под массивы, хра-
нение которых неизбежно в данном методе. Схема (6.43) с точки
зрения быстродействия малоэффективна, с точки зрения объема
памяти — вполне удовлетворительна, так как, получив значения
и**' на некотором временном слое, не обязательно сохранять в
ОЗУ значения на предыдущем слое (их можно вывести на диск
или на печать).
Получим более эффективный и устойчивый метод. Он анало-
гичен переходу от метода Эйлера к одному из вариантов метода
Рунге — Кутта 2-го порядка.
Усредним правые части уравнений (6.42) по времени, взяв их
1
с равным весом - в предыдущий и последующий моменты вре-
мени:
ч-+1 = - 2«*+I + и*-') + - 2li< + )• (6.45)
Это, безусловно, лучшая, чем в (6.43), аппроксимация произ-
„ ди
водной —.
UI
Специальное исследование показывает, что схема (6.45) абсо-
лютно устойчива.
Расплатой за устойчивость является то, что (6.45) — неявная
схема, т.е. не формула для непосредственного расчета, как (6.42),
351
а система линейных алгебраических уравнений для величин
и*+1, w)41, которую еще предстоит решать (поскольку не-
известные на (к+ 1)-м временном слое величины «*+1 входят и в
левую, и в правую часть (6.45)).
Заметим, что (6.45) есть система с трехдиагональной матри-
цей. В самом деле, если выписать первое, последнее и некоторое
промежуточное /-е уравнения, перенося неизвестные в левые ча-
сти, получим
1+^ \,4+1 @ А? пк*\_.,к . At / ь j, , k4..Л+1
a2At
2(Дх)2 /+|
=«* ~2U’ +Ui-l <6Л6>
a2\t
2(Дх)2
uk+i
ип-2
=<1 ~2и^ +Н«-2+»"+1 )•
/I / К Л J
Как отмечалось в гл. 2, для решения систем такого типа наибо-
лее эффективен метод прогонки.
Пример 6.7. Решить уравнение (6.35) при а2 = 2 на отрезке [0; 1]
по явной разностной схеме (6.43) с шагом по пространственной
сетке Дх^ 0,2.
Начальное условие
/ m f5’ xgl°; °’5J;
u(x,0) = /(x) =
(-5, хе [0,5; 1];
краевые условия н(0, /) - 5, и(1, /) = -5.
(Отметим интерпретацию этой задачи на языке описания про-
цесса теплопроводности: в начальный момент времени левая по-
ловина стержня имеет температуру 5 °C, правая половина — тем-
пературу -5 °C, а затем происходит процесс перераспределения
температуры при условии, что на левом конце стержня поддер-
живается температура 5 °C, а на правом -5°C.)
Найдем вначале ограничение на шаг по времени, налагаемое
условием устойчивости (6.44) разностной схемы (6.43). Из (6.44)
1 = 0 1=1 1-1 1=3 ! = 4 / = 5
I----------]----------t----------1----------1----------1—
О 0,2 0,4 0,6 0,8 1'
Рис. 6.12. Пространственная сетка, соответствующая разностным
уравнениям (6.47). Указаны координаты и номера узлов
352
(A y)~ (Лг)^
имеем: Д/ < '—При заданных значениях параметров „ , =0,01.
2а1 2а1
Из соображений удобства вычислений примем Дг = 0,005. При
этом разностное уравнение (6.43) примет вид (см. также рис. 6.12)
w*+l = д*+0,25(u*+I - 2иу4+«Д|) (/= 1, 2, 3, 4). (6.47)
Начальное условие приводит к следующим значениям иско-
мой функции на «нулевом» временном слое:
= 5; «2° = 5; и° = -5; д4° = -5.
Краевые условия выражаются равенствами = 5, = -5 (для
любого значения 1с).
Первый шаг в решении поставленной задачи состоит в том, что
по формулам (6.47) последовательно вычисляются и', и'2, и]
(все данные для этого есть). Имеем
и} = и° + 0,25(u° - 2u° + и0°) = 5 + 0,25 (5- 2 5 + 5) = 5;
и!, = w2° + 0,25(и3 - 2д2° + «“) = 5 + 0,25 (-5 - 2 5 + 5) = 2,5;
н’ = «о + 0,25(м° - 2м3° + и») = -5 + 0,25 (-5 - 2- (-5) + 5) = -2,5;
и\ = и4° + 0, 25(ы5° - 2и° + и?) = -5 + 0,25 - (-5 - 2 (-5) - 5) = -5.
Затем вычисляются значения искомой функции в тех же узлах
на втором временном слое и т.д. — до тех пор, пока характер
искомого решения не станет качественно ясен (либо отрезок ин-
тегрирования по времени может быть задан в условии задачи).
Результаты вычислений по пяти временным слоям приведены
в табл. 6.4.
Хотя сделано совсем немного шагов, асимптотика решения при
больших значениях t фактически очевидна (линейная функция).
Отметим, что эта асимптотика вполне очевидна из физического
смысла решаемой задачи. Действительно, если неоднородно на-
гретый в начальный момент стержень достаточно долго держать в
Таблица 6.4
x = 0 x= 0,2 x = 0,4 x - 0,6 x- 0,8 x = 1
t= 0 5 5 5 -5 -5 -5
t = 0,005 5 5 2,5 -2,5 -5 -5
t = 0,01 5 4,375 1,875 -1,875 -4,375 -5
t =0,015 5 3,906 1,563 -1,563 -3,906 -5
t = 0,02 5 3,594 1,367 -1,367 -3,594 -5
/=0,025 5 3,389 1,24 -1,24 -3,389 -5
12 Лапник
353
Рис. 6.13. Эволюция решения во времени. Кривые построены поданным,
приведенным в табл. 6.4, начиная со значения 1= 0,005, с шагом
= 0,005, и сглажены
условиях, когда на его концах поддерживаются постоянные (нео-
динаковые) значения температуры, то процесс теплопроводнос-
ти приведет к установлению линейного распределения темпера-
туры вдоль стержня (рис. 6.13).
Алгоритмически метол, связанный с формулой (6.43), чрезвы-
чайно прост. Соответствующая схема изображена на рис. 6.14. Зна-
чения температуры в узлах пространственной и временной сеток
сведены в двумерный массив. Поскольку формирование значений
начальных и краевых условий может вестись различным образом
(ввод числовых массивов, расчеты по формулам и т. д.), то соот-
ветствующие процедуры детально не прописаны.
Контрольные вопросы
1. В чем состоят различия между начальными и краевыми условиями
для дифференциальных уравнений, описывающих физические процессы?
2. Для каких из классических уравнений математической физики, при-
веденных в начале данного параграфа, понятие «начальное условие» те-
ряет смысл и почему?
3. В чем состоит основная идея метода сеток для численного интегри-
рования уравнений в частных производных?
4. Что стоит за понятиями «эффективность сеточного метода»? «ус-
тойчивость сеточного метода»?
5. В чем состоит принципиальное различие между явными и неявны-
ми сеточными методами?
Упражнения
1. Создать и отладить программу, соответствующую схеме на рис.. 6.14.
С ее помощью:
а) решить задачу, сформулированную в примере 6.7, для простран-
ственной сетки с 20 узлами;
354
Рис. 6.14. Блок-схема численного интегрирования уравнения
теплопроводности по явной схеме первого порядка (6.42)
б) исследова’ть, как влияет количество узлов на точность решения,
пользуясь эмпирическим критерием совпадения значащих цифр.
2. Решить задачу, сформулированную в примере 6.7, с помощью не-
явной разностной схемы 6.44, используя для решения возникающих си-
стем уравнений метод прогонки.
355
3. Разработать схему алгоритма и программу для решения одномер-
ного уравнения теплопроводности по методу, отраженному формулами
(6.43).
6.8. ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ПОМОЩЬЮ ИНСТРУМЕНТАЛЬНЫХ СРЕДСТВ
Решим дифференциальное уравнение из примера 6.2 средства-
ми системы MathCad (рис. 6.15). Для этого присвоим некоторой
функции f(x, у) значение правой части уравнения, введем началь-
ное значение у(0) = 1,3 и определим диапазон изменения индекса
точек. После ввода расчетных формул для нахождения абсцисс
точек х/+] и приближенных решений уравнения в них — формулы
вида (6.12) (результат получен с двумя знаками после запятой)
получим соответственно векторы-значения х и у, позволяющие
построить график решения.
Полученные значения полностью совпадают с ранее выпол-
ненными вычислениями (см. табл. 6.1).
Найдем решение этого же дифференциального уравнения ме-
тодом Рунге— Кутта 4-го порядка. Это можно сделать при помощи
встроенных функций:
rkfixed(y,a,b,n,f) (рис. 6.16), которая возвращает матрицу, име-
ющую два столбца: первый содержит точки, в которых ищется
решение уравнения, а второй столбец содержит значения най-
денного решения в этих точках. Аргументы функции: у — началь-
ное значение; а, b -— граничные точки интервала, на котором
ищется решение; п — число точек (не считая начальной);/(х,у) —
правая часть дифференциального уравнения;
rkadapt(y,a,b,n,f) — функция с автоматическим выбором шага;
rkadapdy,a,b,eps,f,kmax,s), где аргумент eps контролирует погреш-
ность решения при автоматическом выборе шага интегрирования;
ктах — максимальное число узлов сетки, в которых может быть
получено решение; х — наименьшее допустимое значение шага.
На рис. 6.17 показаны результаты применения для решения
дифференциального уравнения первого порядка методом Рунге —
Кутта двух описанных выше функций — с постоянным шагом и с
контролем погрешности при автоматическом выборе шага.
В ядре математической системы Derive отсутствуют встроенные
функции для решения дифференциальных уравнений, однако три
файла внешних расширений (рис. 6.18), доступ к которым осуществ-
ляется из пункта File главного меню, ориентированы на решение диф-
ференциальных уравнений: первого порядка — файл Odel.mth, вто-
рого порядка — файл Ode2.mth и файл Ode_appr.mth содержит не-
которые дополнительные расширения и функции, позволяющие
решать системы нелинейных дифференциальных уравнений.
356
Введем функцию:
Начальное значение:
Шаг =
Диапазон изменения
индекса точек:
f(x,y) = cos(y) -ь З х
Хо := 0 у0 := 1.3
h := 0.2
i;= 0..4
Формулы для получения
таблицы значений: ><+1 = % + h
У1И > У! + h fiXi.yj
< 1.3 '
1.35
1.52
1.77
2.09
< 2.47 ,
График приближенного решения:
Рис. 6.15. Решение дифференциального уравнения
методом Эйлера в MathCad
С помощью команды Open на экран будет вызвано окно с
содержимым папки Math. Для того чтобы решить дифференци-
альное уравнение с заданным начальным условием у(х°) =
(см. пример 6.4) методом Эйлера необходимо прежде всего загру-
зить файл Ode appr.mth. Затем, воспользовавшись опцией Expression
пункта Author главного меню, вызвать диалоговое окно для запи-
си правой части уравнения у’ - у(1 - х) (рис. 6.19).
Нажатие на кнопку ISM&Sgjfl поместит выражение в алгебраи-
ческое окно, после чего необходимо снова активизировать окно
357
ввода выражений и записать в нем функцию вида: EULER
(r,x,y,xO,yO,h,n), реализующую метод Эйлера (рис. 6.20).
При помощи команды Approximaie пункта Simplify главного
меню системы вызывается следующее диалоговое окно (рис. 6.21),
позволяющее ввести значение числа цифр результата вычисле-
ний.
Кнопка I запускает вычислительный алгоритм, резуль-
тат которого отражается в алгебраическом окне (рис. 6.22).
Файл расширений системы Odel.mth содержит функции
LINEARl(^4,x,y,x£(y0) и LINEARl_GEN(p,^,x,y,c). Первая из них
Введем функцию:
Начальное значение:
f(x,y) := cos(y) + 3 х
Уо := 1.3
Шаг =
h := 0.2
Отрезок:
а := 0
Ь:= 1
Количество точек:
b - а
п :=-------
h
Решение:
Z rkfixed(y,a,b,n,f)
13
0.2
1.403
0.4
1.6
0.6
1.869
С.8
2.2
График решения:
1
2.595 J
п = 5
Z =
f О
Рис. 6.16. Решение дифференциального уравнения
методом Рунге — Кутта в MathCad
358
возвращает частное решение, а вторая — общее решение уравне-
ния вида у' + р(х)у = q(x). Воспользуемся этими функциями для
решения уравнения из примера 6.4. Переписав его в виде
у' + (х - l)j = 0 и введя обозначения р(х) = х -1, q(x) = 0 , запол-
ним строку ввода, как показано на рис. 6.23.
a) Z : jkfixed(y,«.b.n,f)
' О 13 '
0 2 1404922
04 1599919
Z =
Об 1.86858
08 2200445
1 2594982,
6) Zl »tksdipt(y.«.b. 10'e.f,13,0.001)
0 1
0 0 1.3
1 0.01 1.302812
2 0.06 1.320891
0 159442 1.375758
4 0.261821 1 456419
5 0.374947 1.571153
6 0.490341 1.712946
7 0.595173 1.861311
8 0 702679 2.031365
9 0 80287 220563
10 0.899109 2.387622
11 0 99286 2.579691
12 1 2.594963
Рис. 6.17. Способы реализации метода Рунге —Кутта в MathCad
Рис. 6.18. Содержимое папки с файлами внешних расширений
359
Кнопка _] запускает вычислительный процесс. Резуль-
тат расчетов появится в алгебраическом окне (выражение #3,
рис. 6.24). Аналогично в окно Author Expression вводится функция
LINEARl_GEN(x-l,O,x,y,c). На рис. 6.24 приведено решение еще
одного дифференциального уравнения: у' = х2 + Зу Переписав его
в виде у' + (-З)у = х2 и введя обозначения: р(х) = -3; q(x) = х2,
получили результат — выражение #5, которое с помощью коман-
ды Expand пункта Simplify главного меню и кнопки диа-
логового окна Expand Expression можно представить в более удоб-
ном виде (см. выражение #6).
Рис. 6.19. Окно ввода математических выражений системы Derive
Рис. 6.20. Ввод функции для решения дифференциального уравнения
в Derive
Рис. 6.21. Диалоговое окно приближенных вычислений системы Derive
360
Математический пакет Maple для получения аналитических и
численных решений дифференциальных уравнений содержит ко-
манду dsolve(ode,var,opt). Здесь ode — дифференциальное уравне-
ние относительно переменных var, параметр opt (дополнительные
условия) позволяет указать способ решения (/ур<?=...) и используе-
мый метод (method = ...). По умолчанию дополнительные условия
opt не указаны. При неполном задании уравнения, например от-
сутствует знак равенства и правая часть, система Maple дополня-
ет уравнение нулевой правой (или левой) частью. Вычисление про-
изводной некоторого выражения ехрг по переменной х осуществ-
ляется при помощи функции difl"(ехргрс). На рис. 6.25 показано ана-
литическое решение дифференциального уравнения у' = у(1 - х).
gAlyetxaZI ОРЕ_АРРЯ МТН
#1: R<x) у (1 - х>
«2: EULER<R<x>. х, у. В. 1. 0.05. 10)
ИЗ:
0 1
0.05 1.05
0.1 1.099875
0.15 1.149369
0.2 1.198217
0.25 1.246146
0.3 1.292876
0.35 1.338127
0.4 1.381616
0.45 1.423065
0.5 1.462199
Рис. 6.22. Решение дифференциального уравнения первого порядка
методом Эйлера в системе Derive
Рис. 6.23. Ввод функции вычисления частного решения
дифференциального уравнения
361
59 Algebra 3:1 0DE1.MTH
02: LINEARl<x - 1. 0. x, y. 0, 1>
2
#3: x - x Z2
3 x 2
56 e 9 x ♦ 6 x ♦ 2
05: у - ---------------------------------
27 27
3-x 2
56 e x 2-x 2
Об: у - ---------------------------------
27 3 9 27
Рис. 6.24. Решение дифференциальных уравнений первого порядка в Derive
Рис. 6.25. Аналитическое решение обыкновенного дифференциального
уравнения в Maple
В первом случае начальное условие не было задано, поэтому в
ответе фигурирует неопределенная константа _С1. Во втором слу-
чае задано начальное условие у(0) = 1.
Для численного решения дифференциальных уравнений при
помощи команды dsolve необходимо указать параметр numeric од-
ним из способов:
dsolveipde, var, type = numeric,opt)',
dsolve( ode, var, numeric, opt).
362
По умолчанию в результате выполнения команды dsolve с па-
раметром numeric будет создана процедура, к которой можно об-
ращаться для вычисления отдельных значений и визуализации
решения дифференциального уравнения.
На рис. 6.26 показано нахождение конкретных значений реше-
ния (выводится 9 значащих цифр результата) дифференциально-
го уравнения у' = у(1 - х) для х = 0,5 с шагом h = 0,05 нескольки-
ми методами: Рунге —Кутта, Эйлера и Адамса соответственно.
> F;=dsolve({eq, ухО ] , numeric);
F — ргос(.гк/45_х) ... endproc
> h:-(k05;evalf(F(0.5) ,9} ;
Л-.05
[z = .5,y(x)= 1.45499172]
> F; -dsolve < {eq, ухО), y(x), numeric, method-classical [foreuler]) ;
F ~ j>Toc(x_classica!) ... end proc
> h-=0.05revalf(F(D.5) ,9} ;
h-Sfi
[x = .5, y(x)= 1.45574545]
> F:-dsolve<{eq, yxO), у (x), numeric r method-classical [adambash]) ;
F ?= proc(x_d<3ffszcaZ) ... end proc
> h:-0.05;evalf(F(D.5),9};
h -.05
[л = .5, y(x)= 1.45499141]
Рис. 6.26. Способы' численного решения дифференциального уравнения
первого порядка в Maple
[> pi —dsolve( (diff (y(x) ,x)=y(x)*(l-x) , y(0)==l) , y(x) ,numeric) :
> odeplot{pr[x,y(x)],-3..4,labels-lx,y]fcolor-black,title-"График
решения”ethickness-2);
Рис. 6.27. Построение графика решения
дифференциального уравнения в Maple
363
> eq : -dlff <«»(x, t) ,t)-2«dlff (u(x,t) .»>»> I
d a2
*?=—«(x.O-2 —»(x,0
* lax2 J
> sol:-pdsolvofcq,Н1ИТ-Х(x)*T(t).build);
2
2 I------- (_C 1»)
(_fjO <v-c>x) сз<» ) Ci
coi CJ(* ) CJt ♦ =—-—I !
(у.С) x)
> 1:-(_C(1)-3,_C1—1/2,_C2-1,_C3—1/2)
> R:—simplify(eval(rhs(sol),1));
I (в!-Тзх), (27Tx)
Рис. 6.28. Решение уравнения теплопроводности
в Maple
В целях визуализации решения дифференциального уравнения
используется команда odeplot{s,vars,a_b,opt), параметры которой:
j— выходная форма записи уравнения, возвращенная командой
dsolve; vars — имена переменных; а_Ь — область изменения неза-
висимой переменной (а и b должны быть вещественными кон-
стантами); opt — дополнительные параметры (могут отсутствовать).
На рис. 6.27 представлен рабочий документ Maple, в котором сна-
чала с помощью команды dsolve происходит поиск решения, за-
тем оно отображается графически.
Для решения уравнений в частных производных используется
команда pdso!ve(eq,f,opt), где eq — уравнение, f — неизвестная
функция, opt — дополнительные параметры (указание на возмож-
ную форму решения HINT = hi, параметр integrate — автоматиче-
ское интегрирование получающейся системы обыкновенных диф-
ференциальных уравнений, build — указание на поиск явного ре-
шения). Пакет Maple ищет общее решение, применяя набор спе-
циальных методов для некоторых видов уравнений и метод разде-
ления переменных в общем случае.
На рис. 6.28 показано нахождение явного представления для
решения уравнения из примера 6.7 через функциональные зави-
симости Х(х) и T(t) и получение частного решения.
Упражнения
I. Найти частное, общее и приближенные решения задачи Коши
/ = /(х.у), у(0) = 0 на отрезке [0; 1] с точностью 10ч:
а ) у = 0,5 sin х -1,2у2 + 1; б) у' = 0,8е ,0+ 0,4х2у.
2. Найти общее решение дифференциального уравнения 6.33.
364
ЛАБОРАТОРНАЯ РАБОТА Ns 6
Тема: Численное решение обыкновенного
дифференциального уравнения первого порядка
Задание. Решить задачу Коши для дифференциального уравне-
ния у = f(x,y) на отрезке [а; Ь] при заданном начальном условии
и шаге интегрирования h.
Задание 1.1. Методом Эйлера с применением «ручных» вычис-
лений с шагом 2h, а также с помощью программы для компьютера
с шагом й. Свести результаты вычисления в одну таблицу и сопо-
ставить точность полученных значений функции. Пользуясь таб-
лицей, сделать ручную прикидку графика интегральной кривой
на бумаге.
Задание 1.2. Методом Рунге —Кутта с помощью программы для
компьютера с шагом h и шагом й/2. На основе результатов двой-
ного счета сделать вывод о точности полученного решения.
Задание 1.3. С помощью одного из инструментальных пакетов
методами Эйлера, Рунге —Кутта 4-го порядка и Адамса, предус-
мотрев вывод полученных решений в виде таблиц и графиков.
Исходные данные для задания содержатся в табл. 6.5.
Таблица 6.5
Вариант У =f(x,y) a b c h
1 ху3- X2 24 5 0,7 0,1
2 Av + 1 - Зу2 2,6 4,6 1,8 0,2
3 cos(l,5x - у2) -1,3 -I 1 0,2 0,2
4 х2 + ху + у2 2 3 1,2 0,1
5 е-<>'г+1>+2х 0 0,5 0,3 0,05
6 cos(l,5y + x)2+ 1,4 1 2 0,9 0,1
7 4,1х-у2 + 0,6 0,6 2,6 3,4 0,2
8 г + 2у 1 + х3у 1,5 2 2,1 0,05
9 у X + COS -р= Vh 2,1 3,1 2,5 0,1
10 -^--0,4 х + 4 3 5 1,7 0,2
11 2,5x + cos(y + 0,6) 1 3 1,5 0,2
365
Окончание табл. 6.5
Вариант У ’•fix,у) а Ь С Л
12 *+2,5/+ 2 1 2 0,9 0,1
13 2 - sin(x + у)2 2 3 2,3 0,1
14 2 + х + 1 х + 2 0,1 0,5 1,25 0,05
15 у x + cos£ 2 -2 -1 3 0,1
16 Jx2 + 0,5/ +1 0 2 2,9 0,2
17 sin(x + y) + 1,5 1,5 2,5 0,5 0,1
18 — + X + 3 х +16,7 1.5 2 1,4 0,05
19 еь + 0,25/ 0 0,5 2,6 0,05
20 0.4Х2 + у2 1 3 1,8 0,2
Пояснения к выполнению лабораторной работы № 6
Первая часть задания (метод Эйлера) выполняется двумя спо-
собами: с помощью ручных вычислений (например, с помощью
калькулятора) и с помощью программы для ЭВМ (см. пример 6.2).
Результаты ручных и машинных вычислений вносятся в одну таб-
лицу (см. табл. 6.2). Значения искомой функции в соответствую-
щих узлах сравниваются между собой и составляется представле-
ние о точности полученного результата. По вычисленной табли-
це функции строится точечный график и проводится плавная
кривая.
По второй части задания составляется программа для компью-
тера, которая пускается дважды — для шага Л и шага Л/2 (на
одном и том же отрезке интегрирования [о; 6]). Путем сравнения
полученных значений делается вывод о точности результата, ко-
торая сопоставляется с точностью интшрирования по методу Эй-
лера.
Для оценки погрешности используется полуэмпирическая фор-
мула (6.24).
При выполнении третьей части задания используется один из
инструментальных математических пакетов. Их применение для
решения задачи Коши методами Эйлера, Рунге—Кутта 4-го по-
рядка и Адамса показано в подразд. 6.8.
ПРИЛОЖЕНИЕ
ИНСТРУМЕНТАЛЬНЫЕ СРЕДСТВА РЕШЕНИЯ
МАТЕМАТИЧЕСКИХ ЗАДАЧ
В данном приложении приведены краткие описания наиболее рас-
пространенных инструментальных пакетов прикладных программ реше-
ния математических задач. По каждой из этих программ существуют под-
робные руководства, к которым можно прибегнуть при необходимости.
Применение этих программ к решению ряда задач вычислительной ма-
тематики описано в соответствующих разделах учебника.
Табличный процессор Excel
Рабочая область Excel изображена на рис. П.1.
Эта программа, чрезвычайно удобная для организации относительно не-
сложных вычислений, является частью популярного пакета Microsoft Office1.
Ячейки в Excel могут содержать следующие типы данных:
1. Символьные (текстовые) данные. Могут включать в себя алфавит-
ные, числовые и специальные символы. По умолчанию символьные дан-
ные при вводе выравниваются по левому краю ячейки. При необходимо-
сти их можно выровнять по правому краю или по центру.
2. Числовые данные. Могут содержать только числовые данные. Исклю-
чением являются десятичные точка (или запятая) и знак числа, стоя-
щий перед ним.'Числовые данные по умолчанию выравниваются при
вводе но левому краю ячейки.
3. Формулы. Формула может включать ряд арифметических, логиче-
ских и других действий, производимых с данными из других ячеек. На
экране после ввода формулы отображается результат вычислений, а сама
формула отображается в строке ввода над таблицей. Ввод формул начи-
нается со знака равенства ( = ).
4. Функции. Функции могут самостоятельно присутствовать в ячей-
ках, а также могут входить в состав формул. Различают математические,
статистические, логические, финансовые и другие функции.
5. Даты.
Excel имеет два окна — программное (внешнее) и рабочее (внутрен-
нее). Внутреннее окно Sheet # содержит рабочую страницу (таких стра-
ниц несколько, они образуют книгу), представляющую двумерную пря-
моугольную таблицу. Справа и внизу на рабочей странице расположены
линейки со стрелками прокрутки, позволяющие с помощью мыши бы-
стро перемещаться по странице.
В окне Excel под зоной заголовка находится область заголовков меню.
Чуть ниже находится основная линейка инструментов. Кнопки линейки
' То, что с помощью Excel можно производить лишь несложные вычисления —
обычное первое впечатление начинающего пользователя-математика. Однако опыт
работы с Excel показывает, что с его помощью можно реализовывать весьма слож-
ные математические процедуры. Некоторые примеры приведены в данной книге.
367
Рис. П.1. Исходный вид окна ТП Excel
инструментов позволяют быстро и легко вызывать различные функции
Excel. Их можно вызывать также через меню.
Чтобы выполнить какое-либо действие с данными, помещенными в
ячейки (ввод, копирование, удаление, форматирование и т.п.), необхо-
димо их выделить. Чтобы выделить ячейку, надо указать на нее и нажать
правую кнопку мыши. При нажатой кнопке можно выделить диапазон
ячеек. После выделения необходимой области следует нажать правую кноп-
ку мыши, вызывая контекстное меню, которое позволяет выполнить ряд
команд: Вырезать, Копировать, Вставить и т.п.
Изменение данных проводят прямо в ячейке. Перемещение или ко-
пирование содержимого ячеек можно осуществить перетаскиванием их
с помощью мыши. Чтобы скопировать (а не переместить), следует дер-
жать нажатой клавишу CTRL.
Создание формулы начинается с ввода знака равенства ( =). Фор-
мула содержит встроенные функции, адреса ячеек, константы. Для
формирования формул есть специальное средство — Мастер функций
(рис. П.2).
Запуск Мастера функций осуществляется либо через меню Встав-
ка\Функция, либо щелчком по кнопке f,. В появившемся меню выбираем
сначала класс функций, затем — конкретную функцию. В классе матема-
тических функций, который нас в данном курсе интересует больше дру-
гих, находятся 50 (!) функций, среди которых, естественно, все эле-
ментарные. При необходимости для каждой функции можно вызвать
справку (как это указано на рисунке), в которой поясняется, как с этой
функцией работать. Разумеется, с помощью Мастера функций можно со-
здавать любые суперпозиции из функций, имеющихся в наличии.
В стандартном режиме Excel, произведя вычисление по формуле, за-
мещает ее в ячейке вычисленным значением. Это не всегда удобно, осо-
бенно в режиме ввода программы и ее отладки. Для того чтобы блокиро-
вать такое действие и сохранить формулы видимыми, следует выполнить
команды Сервис\Параметры и в меню Вид установить флажок формулы.
Впоследствии снятие этого флажка возвращает программу в режим ото-
бражения значений.
Развитый сервис есть и при оформлении дизайна таблицы. Перед пе-
чатью таблиц (кнопка Печать) удобно осуществить предварительный
просмотр (кнопка Предварительный _просмотр в меню Сохранить).
Excel работает с несколькими листами книги. Например, на одном лис-
те можно разместить итоговые оценки класса за несколько лет обучения, а
на пяти следующих — данные за каждый год обучения. Листы книги могут
служить местом для размещения графических иллюстраций, диаграмм.
368
Рис. П.2. Мастер функций
Для отображения числовых данных в графической форме используют
линии, полосы, столбцы, сектора и другие маркеры, а также их объеди-
ненные вариации. Для размещения диаграммы рядом с данными созда-
ют внедренную диаграмму на том же листе. Можно создать диаграмму на
отдельном листе диаграммы. Дзя графического отображения данных есть
специальное средство Мастер диаграмм.
Excel не толькд «дружен» с текстовыми и графическими системами,
но и поддерживает основные действия, характерные для систем управ-
ления базами данных (СУБД). Более того, у него развит аппарат импор-
тирования и экспортирования данных из других программных систем.
В Excel, кроме адресов ячеек, предусмотрен также удобный способ
ссылки на ячейку с помощью присвоения этой ячейке произвольного
имени. Это делается при выделенной ячейке с помощью меню Встав-
ка\Имя\Присвоить... Ввести любое имя, например Сумма. Введенное
имя можно использовать в дальнейшем вместо адреса.
Для форматирования данных в ячейках электронной таблицы исполь-
зуется меню Формат\Ячейки, для настройки ширины и высоты ячеек —
меню Формат\Строка и Формат\Столбец.
Формы представления и диапазон чисел. Числа в Excel могут иметь
различные формы представления — целые числа, десятичные дроби (8,21),
экспоненциальная форма (5,789Е-04). Отметим, что в русифицирован-
ных версиях Excel десятичный разделитель — запятая, а нс точка. Ис-
пользуя общий формат, можно просматривать до 11 разрядов, включая
десятичные запятые и такие символы, как «Е» и « + .» Чтобы использо-
вать числа с большим количеством разрядов, применяют встроенный
экспоненциальный числовой (экспоненциальное представление числа)
или пользовательский формат. Однако независимо от количества отобра-
жаемых разрядов числа хранятся с точностью до 15 разрядов. Если число
имеет больше 15 значащих знаков, то разряды после 15-го преобразуют-
ся в нули.
369
Встроенные функции округления MS Excel
Синтаксис функции Назначение Примеры
ОТБР(число; кол и чество_разрядов) Усекает число до целого, отбрасывая дробную часть ОТБР(8.9)=8 ОТБР(8.999;2)=8.99 ОТБР(-3.4)= -3
ЦЕЛОЕ(число) Округляет число до бли- жайшего меньшего целого с недостатком с учетом значения дробной части ЦЕЛОЕ(8.9)=8 ЦЕЛОЕ(-8.9)= -9 ЦЕЛОЕ(-4.4)= -5 ЦЕЛОЕ(4.0)= -4
ОКРУГЛ(число; кол и чество_разрядов) Округляет число до указан- ного количества десятичных разрядов; отрицательные числа округляются к лево- му краю, положительные — до ближайшего целого ОКРУГЛ(7.89;1)=7.9 О КРУГЛ (-5.48; !) -5.5
ОКРВВЕРХ(число; точность) Возвращает результат окру- гления с избытком до бли- жайшего числа, крапюго заданной точности ОКРВВЕРХ(2.5;1)=3 ОКРВВЕРХ(-2.5;-2)= -4 ОКРВВЕРХ(-2.5;-1.5)= -3
ОКРУГЛ ВВЕРХ(число; количсство_разрядов) Округляет число но моду- лю до ближайшего больше- го целого; отрицательное число — до наименьшего ОКРУГЛВВЕРХ(-2.5;0)= -3 ОКРВВЕРХ(2.5;0)=3 ОКРВВЕРХ(2.55;1)=2.6
ОКРУГЛ ВНИЗ(число; количсство_разрядов) Округляет число до бли- жайшего меньшего по модулю целого ОКРУГЛВНИЗ(-2.5;0)= -2 ОКРУГЛ ВН И 3(-2.55;1)= -2.5
Изменение числа итераций или относительной погрешности. Если в
вычислениях используются итерации, то содержимое листа пересчиты-
вается столько раз, какое значение указано в поле Предельное число ите-
раций, или когда все величины модели изменятся за одну итерацию на
число, меньшее указанного в поле Относительная погрешность. Для это-
го следует воспользоваться алгоритмом:
1. В меню Сервис выберите пункт Параметры и перейдите на вкладку
Вычисления.
2. Установите флажок Итерации.
3. Введите количество итераций, выполняемых при обработке фор-
мул в поле Предельное число итераций.
4. Введите величину относительной погрешности вычислений в поле
Относительная погрешность. Чем меньше погрешность, тем точнее ре-
зультаты обработки формул.
Проведем небольшой эксперимент по точности вычисления значе-
ний элементарных функций и представлению чисел в Excel. В приведен-
ном на рис. П.З фрагменте электронной таблицы слева — формульное
представление, справа — отображение чисел. Итак, при вычислении зна-
чений функций максимальное число значащих цифр равно 14 —15 (за-
тем следует округление), при представлении чисел малых по модулю
максимальное число значащих цифр в мантиссе равно 15 (включая циф-
ру — целую часть числа).
370
1 t.'r - В Г А В
•КОРЕЕЬД 1,3 1,41421356237310000000 1,3!
2 =LOGp) =В1/2 ?- 030100999566396100000 0J65
=SM(2) =В2/2 0,90929742682568200000 ЗДбООаХЮОООШПЮООе-01
4 •EXP (2) =ВЗ/2 4 738905609893065000000 1^25000000000000000006431
5 =B4/2 |5 8,12STrnTT!JITQ7TrriF -П/
Б. =05/2 6 ддиыюозазшюоошшь оз
7 =06/2 ,7 2 Р3125003000000000000Е-82
1 •В7/2 13156250X000X0000006 02
-9 =В8/2 .9 5 /378125000000СПХПЗСОЕ-03
10 =В9/2 10 2 539062500000000300СОЕ-03
11 ’SIM 11 126953125000000000ЭаЗЕ 03
’2 •В11/2 »12 6 Д4765625000000000000Е 04
.13 -B12/2 13 3,i?383i250ooooooooooEe4
14 =В1ЭЛ 14 158691406250000000000Е4М
15 =814/2 7 7 33457031250000000000Е -05
16 1=815/2 3367295156.2500300С020Е-05
17 =816/2 138364257912600000000Е05
1fl =017/2 из 9 31021289302500ПГОЗОЕ-06
•B1S/2 4 35910644531253DOODOE ОБ
[=B19/2 5J1 2 47955322265625000000Е-06
т- =820/2 12397766113261ЗООСОООЕ -06
э ^621/2 , 6,198883056640630000008-07
Рис. П.З. К вопросу о точности вычислений в Excel
Excel имеет и ряд других средств, полезных при организации вычис-
лений и отображении результатов. Весьма совершенны средства графи-
ческого отображения результатов расчетов (графики, различные диаг-
раммы). Много возможностей заложено в Excel для проведения стати-
стических исследований. Команда Поиск -решении в меню Сервис позво-
ляет решать оптимизационные задачи. При использовании макросов Excel
превращается в высокоразвитую среду программирования, но при этом
характеристика «простой» утрачивается полностью.
Математическая система Derive
Derive (разработчик — фирма Soft Warchous) сочетает возможности
проведения числовых и символьных вычислений с простотой требова-
ний к характеристикам ПК, обладает удобным интерфейсом (рис. П.4).
Назначение команд главного меню:
• Author — ввод и редактирование математических выражений;
• Simplify — упрощение символьных выражений; при операциях с чис-
ловыми выражениями позволяет представить результат в виде рацио-
нальных чисел;
• Solve — решение уравнений, систем уравнений, неравенств;
• Calculus — специальные вычисления: производных, интегралов, пре-
делов функций, произведения членов ряда, разложение функции в ряд
Тейлора;
Рис. П.4. Главное меню и панель инструментов системы Derive
371
• Declare — задание новых определений: функций пользователя, пе-
ременных, векторов, матриц;
• Options — задание глобальных опций (установок), которые действу-
ют при решении любой задачи: тип дисплея, гамма цветов, точность
представления результата и пр,;
• Window — работа с окнами: закрыть активное окно, задать тип окна,
стереть окно, перейти в окно с указанным номером, перейти к следую-
щему/предыдущему окну, открыть окно, разделить окно на две части.
Система ориентирована па работу в режиме прямых вычислений. Ввод
математических символов осуществляется путем выбора на панели Author
Expression, либо непосредственным вводом соответствующих обозначе-
ний с клавиатуры. Для храпения числовых и символьных значений ис-
пользуются переменные (имя переменной должно быть уникальным и
начинаться с буквы; выражение может возвращать единственное значе-
ние, вектор либо матрицу) и оператор присваивания:
Имя_переменной := Выражение.
Аналогично задаются функции пользователя:
Имя_функции(список_переменных) := Выражение.
Основные встроенные математические функции системы Derive
Синтаксис Назначение
АВС(х) MIN(x,y,...) МАХ(х,у,„.) SIGN(x) Числовые функции Возвращает абсолютное значение х Возвращает минимальное значение из списка значений аргументов Возвращает максимальное значение из списка значений аргументов Возвращает 1 при х > 0, 0 при х = 0, -1 при х< 0
FLOOR(x,y) FLOOR(x) Функции округления Возвращает наибольшее целое, меньшее или равное значению х/у Возвращает целую часть х
SIN(x)/COS(x) TAN(x)/COT(x) SEC(x)/CSC(x) ATAN(x) Тригонометрические функции Величина угла х задается в радианах', если величина угла задана в градусах, то для преобразования в радианы используется константа deg (pi/l8Oy, Возвращают синус/косинус угла х Возвращают тангепс/котангенс угла х Возвращают секанс/косеканс угла х Возвращает арктангенс угла х
SQRT(x) EXP(x) LN(x) LOG (а, Й) Прочие функции Возвращает значение квадратЕюго корня из х Возвращает значение числа е в степени х Возвращает значение натурального логарифма х Возвращает значение логарифма числа а по основанию Ь
Derive позволяет строить графики функций в декартовой, поляр-
ной системах координат, параметрически заданных функций и гра-
фики поверхностей (ЗВ-графика). Координаты курсора, расположен-
ного в поле графика, непрерывно отображаются в нижней части экра-
на. В качестве примера приведем алгоритм построения графика функции
у = х2 + 4*fx - |х -М| в декартовой системе координат на интервале [0; 3].
1. Выбрать пункт Author главного меню.
2. В диалоговом окне записать выражение (рис. П.5).
372
Рис. П.5. Окно ввода и редактирования выражений
Рис. П.6. Алгебраическое окно
Рис. П.7. Графическое окно
3. Нажать кнопку Iе- ок' I в диалоговом окне ввода и редактирова-
ния выражений (результат показан на рис П.6).
4. Нажать кнопку ’И на панели инструментов (результат показан на
рис. П.7)
5. Еще раз воспользоваться кнопкой панели инструментов графи-
ческого окна, вид которого показан на рис. П.7. Для изменения установок,
принятых по умолчанию, воспользоваться опцией Range пункта Set меню.
Математическая система MathCad
MathCad (разработчик — фирма MathSoft Inc, http://www.mathsoft.com) —
это универсальный интегрированный математический пакет, предназ-
373
каченный для выполнения инженерных и научных расчетов. Его основ-
ное преимущество — естественный математический язык представления
данных. В состав пакета входят: редактор математических формул, биб-
лиотека математических функций, процессор символьных преобразова-
ний, текстовый и графический редакторы.
Назначение команд главного меню (рис. П.8):
• File — работа с файлами, сетью и электронной почтой;
• Edit — редактирование документов;
• View — настройка интерфейса системы;
• Insert — вставка графических объектов, матриц, стандартных функ-
ций;
• Format — форматирование документов;
• Math — управление процессом вычислений, ввод значений сис-
темных переменных;
• Symbolics — выбор операций символьного процессора;
• Window — управление окнами;
• Help — работа со справочной базой данных. г
Вызов встроенных функций осуществляется кнопкой (всплыва-
ющая подсказка — Insen Function) палитры инструментов. В появившемся
затем диалоговом окне, изображенном на рис. П.9, выбирается нужная
категория, затем имя функции.
Рис. 11.8. Главное меню, панель инструментов и палитра
математических знаков MathCad
Рис. П.9. Окно со списком встроенных функций
374
В терминологии MathCad одиночное число называется скаляром, стол-
бец чисел называется вектором, прямоугольная таблица чисел — мат-
рицей. Для вектора или матрицы используется общий термин — массив.
Для того чтобы ввести вектор или матрицу, необходимо в свободном
месте рабочего документа напечатать символ А, сопровождаемый двое-
точием. Теперь можно имя А использовать вместо матрицы (вектора) в
любом выражении (функции).
Встроенные функции округления системы MathCad
Синтаксис Назначение Примеры
ceilfx) Возвращает наименьшее целое, большее или равное х «/<1.5) =2 <•«/(-1.5) = -1 «/<1.455) =2
floor(x) Возвращает наибольшее целое, меньшее или равное х /)оог(1.5) =1 /7оог(-1.5) = -2
round(x,n) Округляет значение вещественного х с точностью до п знаков после десятичной точки (если л < 0, то х округляется слеш от десятичной точки; при л = 0 возвращает округленное до ближайшего целого значения х) mund(\ 1.455,-1) =10 round(: 15.955,-1) =20 гоил</(1.55,1) =1.6 лши</(-1.455,0) =-1 round(-1.455,2) = -1.46
trunc(x) Возвращает целую часть от действительного числа х ггилс(45.78) = 45
Рис. П. 11. Палитра
матричных операций
Рис. П.10. Ввод значений
системных переменных
375
Системные переменные:
TOL — погрешность числовых вычислений < 10-3 по умолчанию);
ORIGIN — нижняя Гранина индекса массива (по умолчанию 0);
п — константа «пи»;
с — основание натурального логарифма.
При помощи пункта Math главного меню возможны установки гло-
бальных определений некоторых системных переменных. Вид экрана с
открытой позицией Math главного меню показан на рис. П.10.
В MathCad развит аппарат применения ранжированных или дискретных
переменных, которые принимают значения из некоторого диапазона. Если
в выражении присутствует дискретный аргумент, то вычислительный про-
цесс будет осуществлен для всех значений аргумента.
Если требуется вычислить набор интерполируемых значений, соответ-
ствующих вектору заданных точек, то можно применить оператор век-
торизации к функции, нажав кнопку ^1. расположенную на палитре
матричных операций (рис. П.11).
Математическая система Maple
Maple (разработчик — фирма Waterloo Maple Software, http://
www.maplesoft.com) — среда для выполнения математических расчетов
преимущественно в аналитическом виде, поэтому Maple называют па-
кетом символьной математики. Символьный процессор Maple широко
используется разработчиками других известных математических паке-
тов. Система обладает развитым языком программирования, что дает
возможность пользователю создавать собственные команды. Хороший
текстовый редактор и прекрасные графические возможности позволя-
ют создавать в среде Maple качественные информационные продукты.
Работа в Maple проходит в режиме так называемой сессии, т.е. пользо-
ватель после приглашения (символ «>») вводит команды, выражения,
которые после нажатия клавиши Enter интерпретируются системой.
Команды главного меню системы Maple (рис. П.12):
• File — работа с файлами: создание, открытие, сохранение, экс-
порт, закрытие, режим автосохранения и вывод на печать;
• Edit — правка и редактирование документа: копирование, выделе-
ние, поиск и замена, вычисление выделенной части или всего документа;
• View — регулирование вида оболочки: выбор разрешения, переме-
щение по гиперссылкам, переключатели;
• Insert — вставка: смена режима (текстовый/набора формул);
• Format — форматирование документа: редактирование стилей, ре-
жимов выравнивания, оформление текста;
• Spreadsheet — работа с таблицами: заполнение, вычисление, масш-
табирование;
• Options — дополнительные установки и параметры: режим вывода
графики, вывод легенды для графика;
• Window — работа с окнами;
• Help — работа со справочной системой.
Стандартная команда Maple состоит из имени команды и ее парамет-
ров, указанных в круглых скобках. В конце каждой команды должен быть
376
Рис. П.12. Интерфейс математического пакета Maple
знак «;» или «:». Точка с запятой означает, что в области ввода после
выполнения этой команды сразу будет выведен результат. Двоеточие ис-
пользуется в случае, когда после выполнения команды нс надо выводить
на экран результат. Для вызова предыдущей команды служит символ «%»,
а операция присваивания имеет вид «: =».
Встроенные функции округления системы Maple
Синтаксис функции Назначение
Round(x) Тгипк(х) Floorfx) Ceii(x) Округление к ближайшему целому Округление отбрасыванием дробной части Округление к меньшему целому Округление к большему целому
Система Mathematica
Mathematica предназначена для обработки математической информа-
ции, относится к классу интегрированных пакетов, позволяющих про-
водить символьные, графические и численные расчеты и писать про-
граммы для проведения таких расчетов (разработчик — фирма Wolfram
Research Inc., http://www.wolfram.com).
Главное меню системы, показанное на рис. ПЛЗ, содержит команды:
• File — работа с файлами;
• Edit — редактирование документа;
• СеЧ — работа с ячейками (основными объектами документа);
• Format — изменение формата (параметров) объектов;
• Input — управление вводом выражений и объектов;
• Kernel — управление действиями ядра символьных операций;
• Find — поиск и навигация по ячейкам документа;
• Window — управление окнами системы;
• Help — работа со справочной базой данных системы.
Для удобства пользователя система обладает возможностью ввода
математических символов, функций и команд с помощью команды меню
File/Palettes (рис. П.14).
Символьные расчеты включают: вычисление пределов последователь-
ностей, дифференцирование, интегрирование, разложение в степенные
ряды, суммирование функциональных рядов, решение обыкновенных
дифференциальных уравнений (ОДУ) и уравнений в частных производ-
ных, различные виды приближения функций, интерполирование.
377
•i-i Mdthemalicd 4.2 (Untitled 1|
File £dt Cet Foim.il Input Kernel Fed Wr.>.-i lief
Рис. П.13. Интерфейс системы Mathematica
Рис. П.14. Палитры пстрограмм ввода системы Mathematica
Рис. П.15. Построение графика функции в системе Mathematica
Графические возможности пакета позволяют строить графики функ-
ций одной переменной, неявно заданных функций, параметрически за-
данные кривые на плоскости и в пространстве, осуществлять техниче-
скую мультипликацию при исследовании динамических систем (на
рис. П.15 показано построение графика функции у = sinx на отрезке
1-10; 10).
Численные расчеты представлены возможностями вычисления пре-
делов, значений производных, интегралов, сумм рядов; нахождения кор-
ней ОДУ и дифференциальных уравнений в частных производных и др.
378
Важным свойством документов, подготовленных в среде пакета, яв-
ляется возможность динамического обмена данными в ходе символьных
преобразований, характерного для табличных процессоров. Система по-
зволяет готовить документы в стиле Notebook с достаточно высоким по-
лиграфическим уровнем исполнения.
Стандартные математические функции системы Mathematica
Синтаксис функции Назначение
Ceiling [х] Floor [х] Quotient [n,w] Round |л'[ Возвращает значение наименьшего целого числа, большего или равного х Возвращает наибольшее целое число, не превышающее х Возвращает целое значение п/т, определяемое как Floor [л,ш] Округляет хдо ближайшего целого
Система MatLab
MatLab (разработчик — фирма MathWorks Inc, http://www.mathworks.com)
содержит инструменты для сбора, анализа и обработки данных, модели-
рования, процедурного и объектно-ориентированного программирова-
ния, разработки приложений. MatLab имеет широкий спектр примене-
ний, стал фактически международным стандартом для технических вы-
числений, Позволяет производить аналитические вычисления, исполь-
зуя команды и функции Maple. Это язык технического программирования
сверхвысокого уровня. Любые вычисления можно выполнять в режиме пря-
мых вычислений, что превращает систему в мощнейший калькулятор.
Интерфейс системы необычайно прост и содержит всего четыре ко-
манды (рис. П.16):
• Файл — работа с файлами;
• Правка — редактирование документа;
• Окно — работа с окнами;
• ? — вызов справочной системы.
Пакет ориентирован преимущественно на работу в командном режи-
ме. В MatLab реализовано четыре типа справочных систем (рис. П.17):
командного режима, в стиле Windows, в HTML-формате (просмотр с
помощью Web-браузера), в виде файлов формата .pdf.
Система содержит несколько системных переменных: pi — число л,
inf — значение машинной бесконечности, ans — хранит результат послед-
ней операции. Все эти переменные можно использовать в математиче-
ских выражениях.
Для вычисления математических выражений достаточно набрать их
по общепринятым правилам и завершить ввод нажатием клавиши Enter:
результат будет присвоен переменной ans и выведен на экран. Операция
присваивания обозначается знаком равенства. Переменные могут быть
простыми, индексированными, сим-
вольными (значения заключаются в
апострофы).
Система ориентирована на про-
ведение вычислений с векторами и
матрицами, поэтому по умолчанию
MATLAB Окно вправления
| Фаап Правка Огне ? j
Рис. П.16. Интерфейс системы MatLab
379
Рис. П.17. Окно справочной системы MatLab
предполагает, что каждая переменная — это либо вектор, либо матрица.
Символ «;» используется для предотвращения вывода на экран выраже-
ния.
По умолчанию включен режим, при котором система различает строч-
ные и прописные буквы. Символы кириллицы допускаются только в тек-
стовых комментариях.
Квадратные скобки используются при задании элементов векторов и
матриц путем перечисления их элементов. При задании матрицы строки
отделяются друг от друга точкой с запятой. Для разделения элементов
строки используются пробелы или запятые.
Круглые скобки применяются для задания приоритета выполнения
операций в математических выражениях, аргументов функций, для ука-
зания подстрочных индексов у индексированных переменных.
Три точки в конце строки указывают на перенос выражения на сле-
дующую строку.
Переменные могут быть числовыми, текстовыми и других типов. Мы
будем оперировать с числовыми (это во всех деталях) и текстовыми (со-
всем немного). Название переменной начинается с латинской буквы,
далее могут быть буквы и цифры (не более 31 символа). Строчные и про-
писные буквы здесь различаются. Числовые переменные — это числа,
векторы, матрицы и многомерные массивы.
Стандартные функции округления системы MatLab
Синтаксис функции Назначение
Fix Ceil Floor Round Округление до ближайшего целого в сторону нуля Округление до ближайшего целого в сторону+" Округление до ближайшего целого в сторону-" Округление до ближайшего по абсолютной величине целого числа
СПИСОК ЛИТЕРАТУРЫ
1. Алябьев В. 3. Эффективная работа в MAPLE 6/7. — М.: Лаборатория
базовых знаний, 2002. — 336 с.
2. Бахвалов Н. С., Жидков Н.П., Кобельков Г.М. Численные методы. —
М.: Лаборатория базовых знаний, 2001. — 632 с.
3. Вержбицкий В.М. Основы численных методов. — М.: Высш, шк.,
2002. - 840 с.
4. Говорухин В., Цибулин В. Компьютер в математическом исследова-
нии. — СПб.: Питер, 2001. — 624 с.
5. Демидович Б.П., Марон И.А. Основы вычислительной математики. —
М.: Наука, 1966. — 664 с.
6. Демидович Б.П., Марон И. А., Шувалова Э.З. Численные методы
анализа. — М.: Наука, 1967. — 368 с.
7. Дьяконов В. П. Компьютерная математика. Теория и практика. — М.:
Нолидж, 2001. — 1296 с.
8. Каханер Д., Моулер К., Нэш С. Численные методы и программное
обеспечение. — М.: Мир, 1998. — 575 с.
9. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функцио-
нального анализа. — М.: Наука, 1989. — 496 с.
10. Мак-Кракен Д., Дорн У. Численные методы и программирование
на Фортране. — М.: Мир, 1997.
11. Мэтьюз Дж. Г, Финк К.Д. Численные методы. Использование
MATLAB. - М.: Вильямс, 2001. - 720 с.
12. Самарский А. А., Гулин А. В. Численные методы. М.: Наука, 1989. —
432 с.
13. Фаддеев Д. К., Фаддеева В.Н. Вычислительные методы линейной
алгебры. — М.: Лань, 2002. — 736 с.
14. Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных диф-
ференциальных уравнений. Нежесткие задачи: Пер. с англ. — М.: Мир,
1990.-512 с.
15. IEEE Standard for Binary Floating Points Arithmetic, ANS1/1EEE
Standard 754 — 1985, Inst. Electrical and Electronics Engineers, Inc., New-
York, 1985.
ОГЛАВЛЕНИЕ
Предисловие.....................................................3
Глава 1. Методы оценки ошибок вычислений........................6
1.1. Этапы решения прикладной задачи и классификация
ошибок.....................................................6
1,2, Запись чисел в вычислительных машинах и ограничения точности
вычислений............................................... 11
1.3. Абсолютная и относительная погрешности...............18
1.4. Правильная запись и округление чисел ................20
1.5. Программное округление десятичных чисел
по заданному значению абсолютной погрешности..............23
1.6. Определение количества верных цифр
по относительной погрешности приближенного числа..........29
1.7. Вычисление ошибок арифметических действий............32
1.8. Оценка погрешностей значений функций.................37
1.9. Способы приближенных вычислений по заданной
формуле...................................................43
1.9.1. Вычисления по правилам подсчета цифр............44
1.9.2. Вычисления со строгим учетом предельных
абсолютных погрешностей................................47
1.9.3. Вычисления по методу границ.....................51
1.10. Приближенные вычисления по формулам с использованием
инструментальных пакетов...................................56
1.11. Вероятностные и эмпирические методы оценки ошибок
вычислений.................................................63
Лабораторная работа № 1. Методы оценки погрешностей.......,....65
Глава 2. Численные методы решения алгебраических
и трансцендентных уравнений....................................68
2.1. Постановка задачи решения уравнений .................68
2.2. Отделение корней алгебраических и трансцендентных
уравнений.................................................69
2.3. Уточнение корня уравнения методом половинного деления.75
2.4. Итерационные методы уточнения корней.................79
2.4.1. Метрические пространства и принцип сжимающих
отображений............................................79
2.4.2. Метод простой итерации..........................81
2.4.3. Скорость сходимости итерационного процесса......90
2.4.4. Методы Ньютона..................................91
2.5. Некоторые замечания о точности нахождения корней
уравнения.................................................97
2.6. Решение алгебраических и трансцендентных уравнений
с помощью инструментальных средств...................... 100
Лабораторная работа № 2. Решение уравнений с одной переменной... 112
382
Глава 3. Численные методы решения систем уравнений........... 116
3.1. Системы линейных алгебраических уравнений........... 116
3.2. Метод Гаусса....................................... 117
3.2.1. Решение систем уравнений...................... 118
3.2.2. Вычисление определителей и обращение матриц.... 123
3.2.3. Программная реализация схемы единственного
деления для решения системы линейных уравнений
и вычисления определителя с пошаговой оценкой
границ абсолютных погрешностей...................... 126
3.2.4. Модификации схемы единственного деления............ 133
3.2.5. Плохо обусловленные системы линейных
алгебраических уравнений.................................. 136
3.3. Метод прогонки..................................... 144
3.4. Итерационные методы................................ 146
3.4.1. Метод простой итерации........................ 147
3.4.2. Практическая схема решения системы линейных
уравнений методом простой итерации ..................150
3.4.3. Метод Зейделя..................................156
3.5. Приближенные методы решения систем нелинейных
уравнений............................................... 159
3.5.1. Метод простой итерации........................ 159
3.5.2. Метод Ньютона................................. 163
3.6. Решение систем уравнений с помошью инструментальных
средств................................................. 167
3.6.1. Табличный процессор Excel..................... 167
3.6.2. Система MathCad............................... 171
3.6.3. Система Derive................................ 178
3.6.4. Система Maple................................. 181
3.6.5. Система MatLab................................ 183
3.6.6. Система Mathematica........................... 186
Лабораторная работа № 3. Численные методы решения
систем уравнений.......................................... 188
Глава 4. Методы приближения функций...........................193
4.1. Постановка задачи аппроксимации функций.............193
4.2. Существование и единственность интерполяционного
многочлена.............................................. 195
4.3. Интерполяционный многочлен Лагранжа................ 197
4.4. Организация ручных вычислений по формуле Лагранжа ..199
4.5. Программирование интерполяционного многочлена
Лагранжа.................................................201
4.6. Интерполяционные формулы Ньютона....................204
4.6.1. Конечные разности..............................204
4.6.2. Первая интерполяционная формула Ньютона........205
4.6.3. Вторая интерполяционная формула Ньютона........207
4.7. Погрешность многочленной интерполяции...............208
4.8. Минимизация погрешности многочленной интерполяции
путем специального выбора узлов интерполяции.............212
4.9. Уплотнение таблиц функций...........................214
4.10. Обратное интерполирование..........................219
4.10.1. Постановка и решение задачи обратного
интерполирования......................................219
4.10.2. Приближенное решение уравнений методом
обратного интерполирования............................222
4.11. Интерполяция сплайнами..............................224
383
4.12. Понятие сходимости интерполяционного процесса.....228
4.13. Метод наименьших квадратов........................229
4.13.1. Постановка задачи...........................229
4.13.2. Нахождение приближающей функции в виде
линейной функции и квадратного трехчлена.......233
4.13.3. Нахождение приближающей функции в виде
других элементарных функций.........................235
4.14. Экстраполяция.....................................244
4.15. Приближение функций с помощью инструментальных
средств.................................................245
Лабораторная работа № 4. Приближение функций................264
Глава 5. Численное дифференцирование и интегрирование ......270
5.1. Постановка задачи численного дифференцирования....270
5.2. Численное дифференцирование на основе
интерполяционной формулы Лагранжа........................275
5.3. Численное дифференцирование на основе
интерполяционной формулы Ньютона.........................278
5.4. Постановка задачи численного интегрирования.......282
5.5. Квадратурные формулы Ньютона —Котеса..............284
5.6. Формула трапеций..................................284
5.7. Формула Симпсона..................................288
5.8. Полуэмпирические оценки точности вычислений
по квадратурным формулам...............................291
5.9. Алгоритмическая реализация интерполяционных
квадратурных формул....................................292
5.10. Квадратурные формулы Гаусса.......................297
5.11. Вычисление определенных интегралов методом
Монте-Карло.............................................302
5.12. Численное дифференцирование и интегрирование
с помощью инструментальных средств .....................307
Лабораторная работа № 5. Численное дифференцирование
и интегрирование..........................................316
Глава 6. Численные методы решения дифференциальных уравнений.320
6.1. Постановка задачи.................................320
6.2. Метод Пикара.................................... 322
6.3. Метод Эйлера.........................Г............325
6.4. Метод разложения решения в степенной ряд..........329
6.5. Метод Рунге —Кутта................................331
6.6. Многошаговые методы...............................338
6.7. Понятие о численных методах решения
дифференциальных уравнений в частных производных........346
6.8. Численное решение дифференциальных уравнений
с помощью инструментальных средств.....................356
Лабораторная работа N? 6. Численное решение обыкновенного
дифференциального уравнения первого порядка.............. 365
Приложение. Инструментальные средства решения математических
задач..................................................... 367
Список литературы.......................................-...381