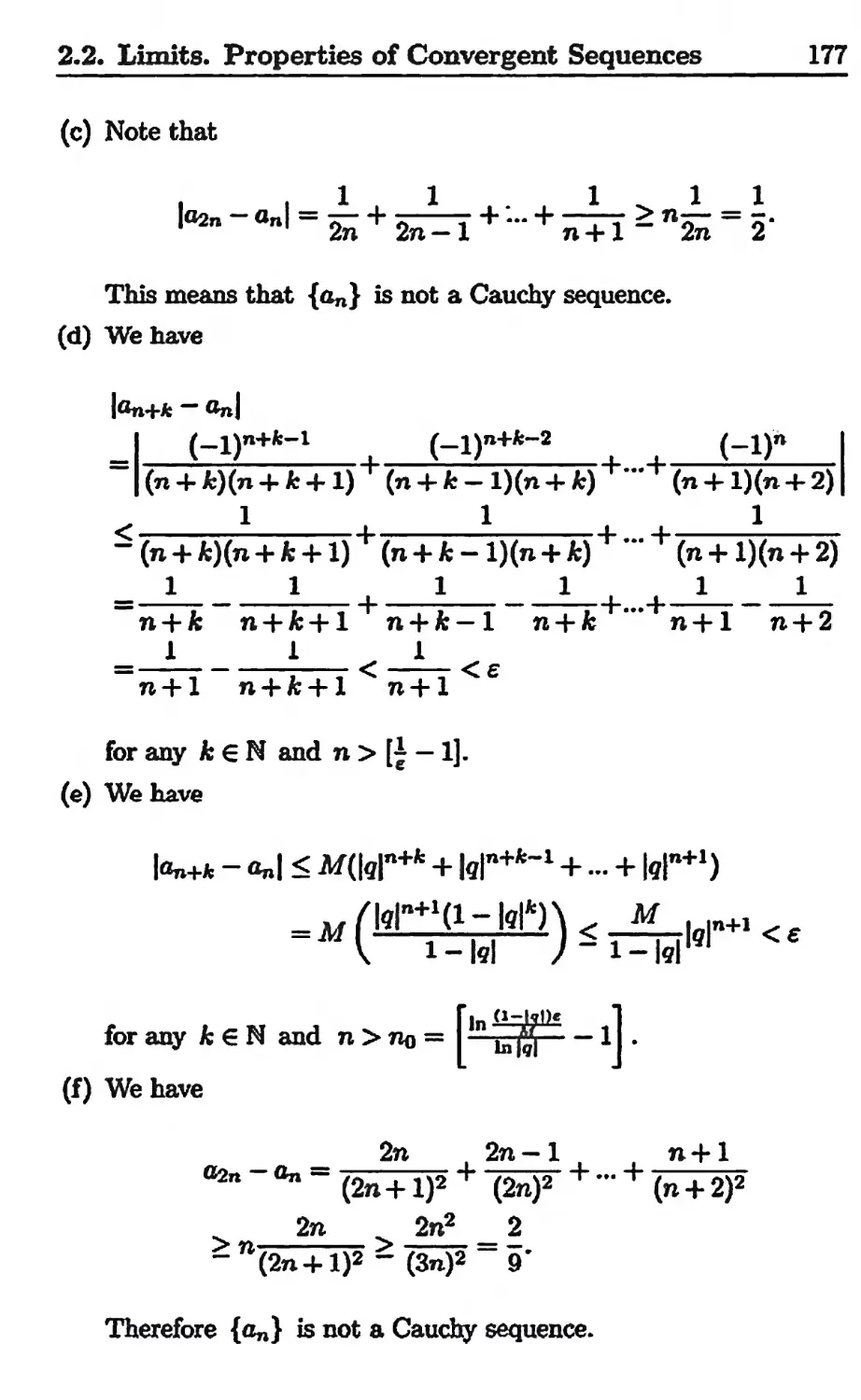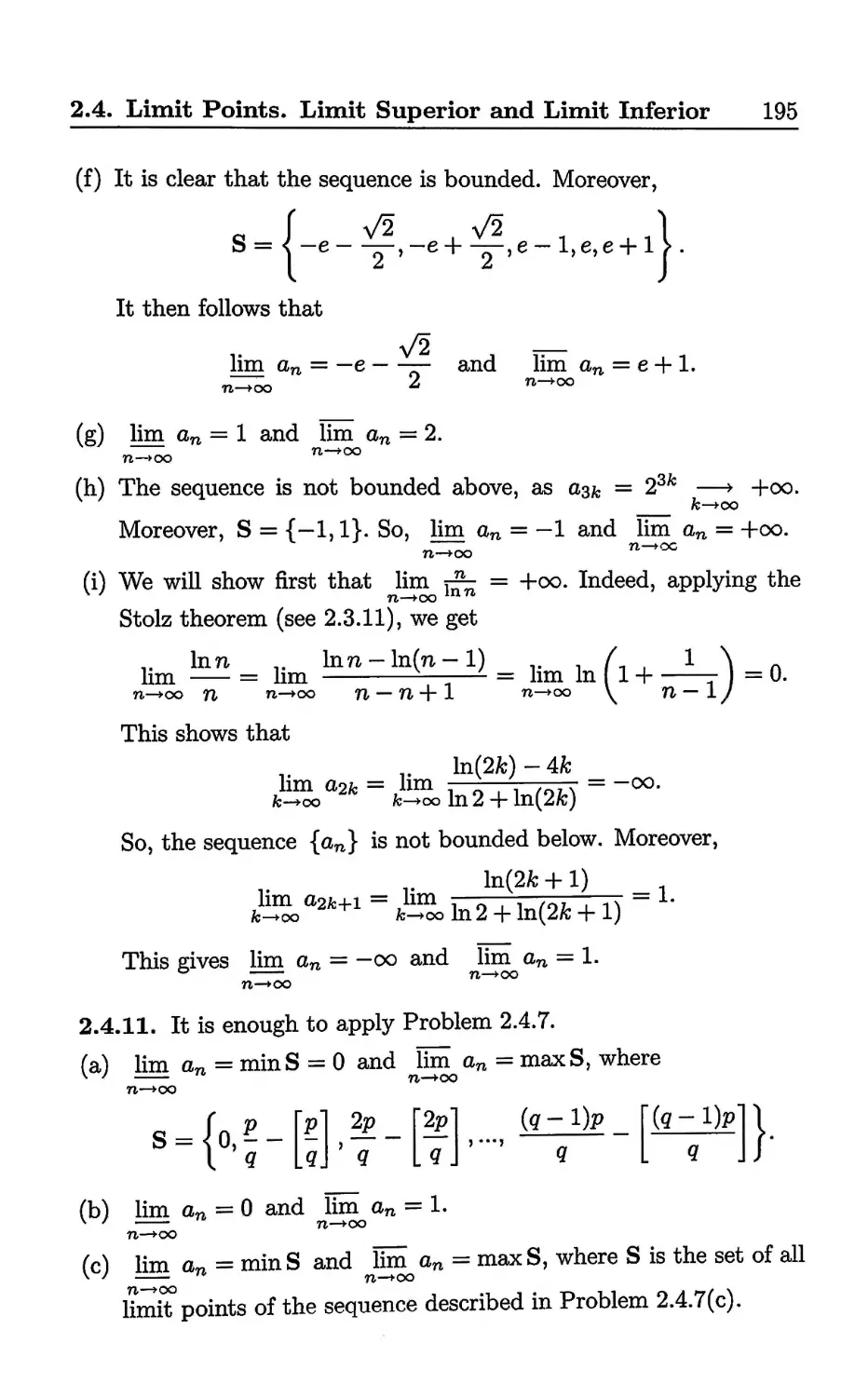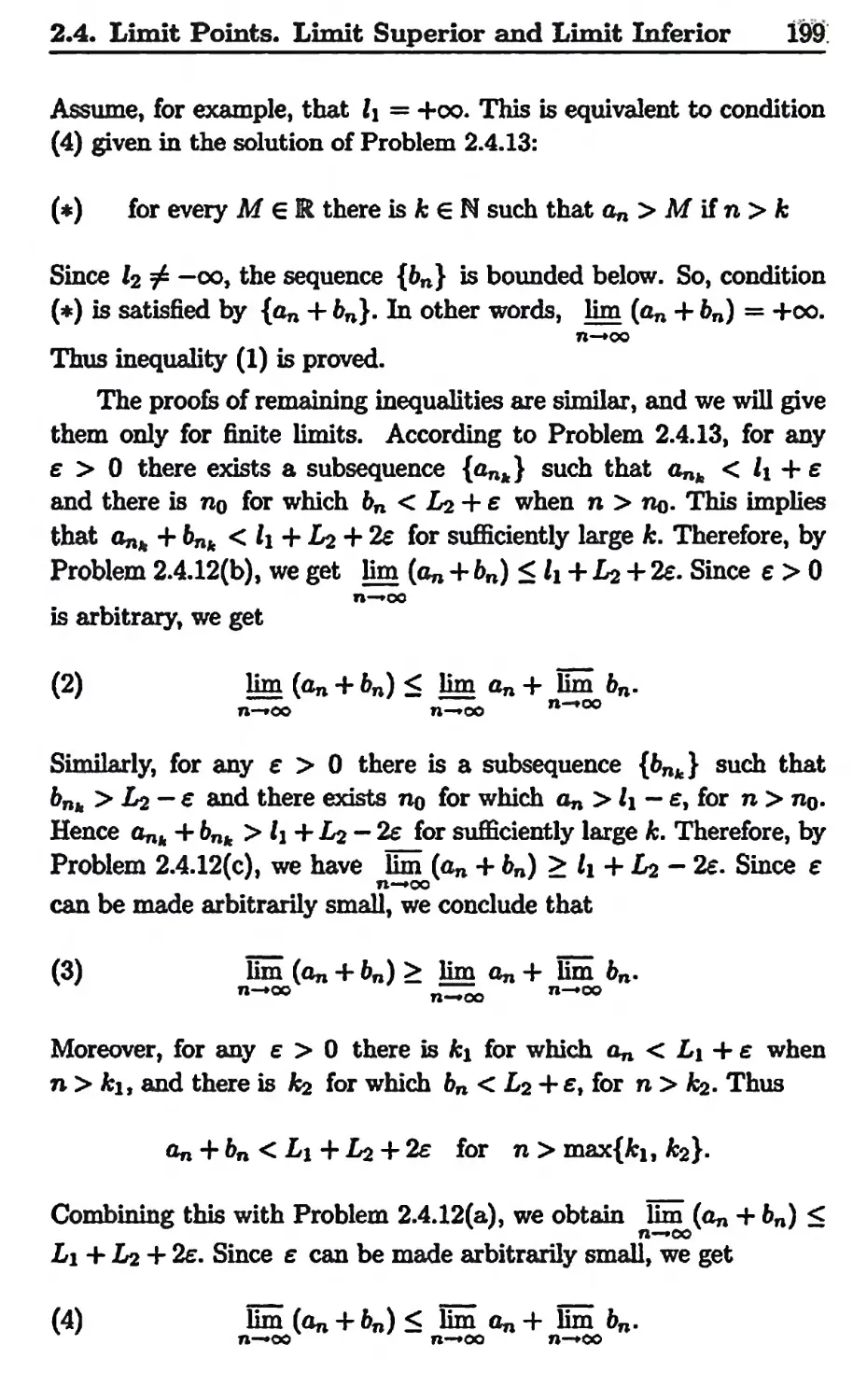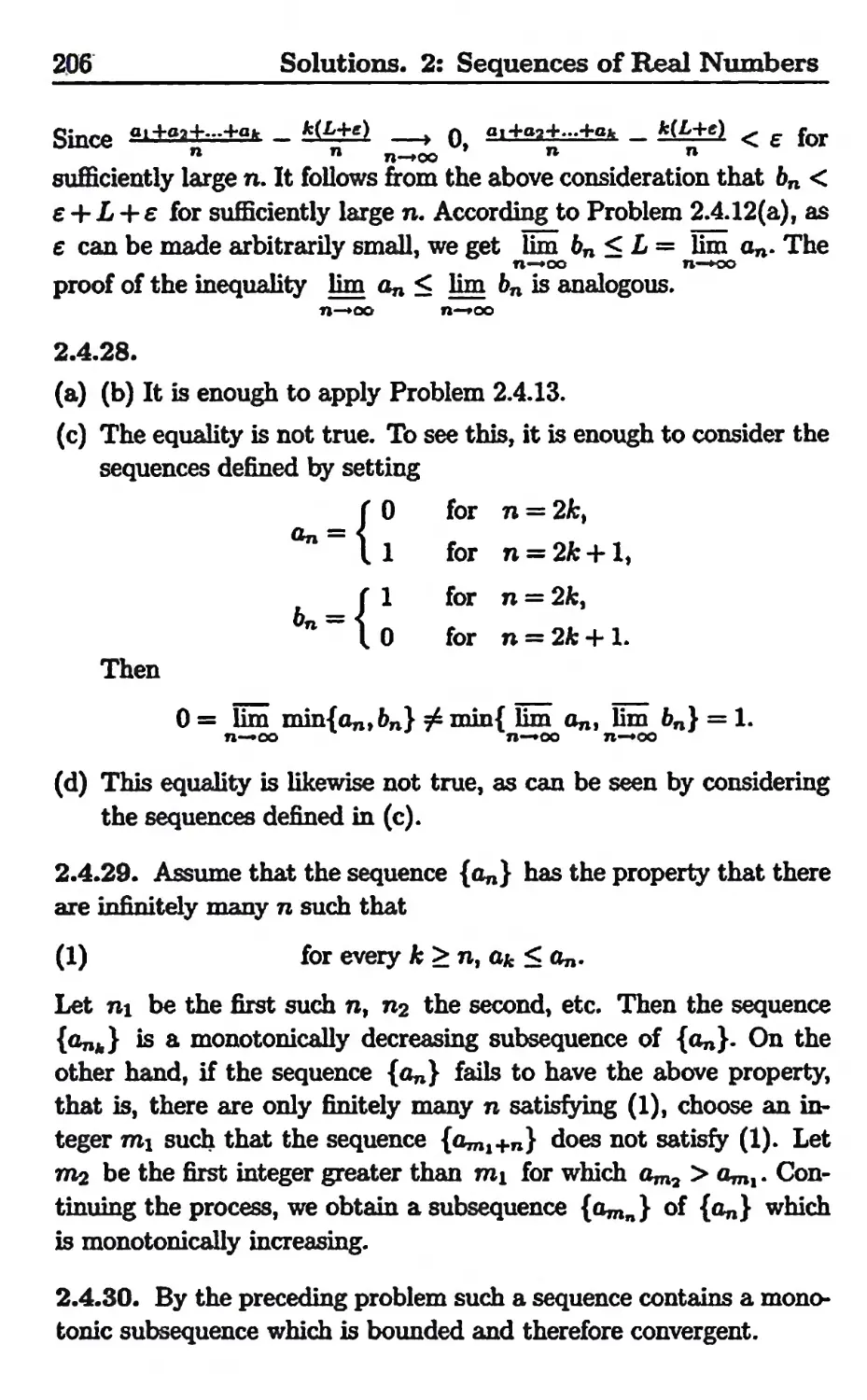STUDENT MATHEMATICAL LIBRARY
Volume 4


11tft (


Problems in
Mathematical
Analysis I
Real N1lll1bers,
Sequences and Series


1


-


-


.


1


w. J. Kaczor
M. T. Nowak

-
] 11 I 1

llP( - 1 - Jr.
111ll r lim
TIn J fun


.
IT


( )-


1


-


--


-


r-


]


11 11 11


AM--


A\ .




Contents


Preface


xi


Notation and Terminology


xiii


Problems


Chapter 1. Real Numbers
1.1. Supremum and Infimum of Sets of Real Numbers.
Continued Fractions 3
1.2. Some Elementary Inequalities 8


Chapter 2. Sequences of Real Numbers
2.1. Monotonic Sequences 19
2.2. Limits. Properties of Convergent Sequences 26
2.3. The Toeplitz 'lransformation, the Stolz Theorem and
their Applications 35
2.4. Limit Points. Limit Superior and Limit Inferior 40
2.5. Miscellaneous Problems 47


Chapter 3. Series of Real Numbers
3.1. S ummat ion of Series 63


vii




...
VIU


Contents


3.2. Series of Nonnegative Terms 72
3.3. The Integral Test 88
3.4. Series of Positive and Negative Terms - Convergence,
Absolute Convergence. Theorem of Leibniz 92
3.5. The Dirichlet and Abel Tests 99
3.6. Cauchy Product of Infinite Series 102
3.7. Rearrangement of Series. Double Series 105
3.8. Infinite Products 112


Solutions


Chapter 1. Real Nwnbers
1.1. Supremum and Infimum of Sets of Real Numbers.
Continued Fractions 125
1.2. Some Elementary Inequalities 136


Chapter 2. Sequences of Real Numbers
2.1. Monotonic Sequences 151
2.2. Limits. Properties of Convergent Sequences 162
2.3. The Toeplitz Transformation, the Stolz Theorem and
their Applications 181
2.4. Limit Points. Limit Superior and Limit Inferior 189
2.5. Miscellaneous Problems 208


Chapter 3. Series of Real Numbers
3.1. S mnm ation of Series 245
3.2. Series of Nonnegative Terms 269
3.3. The Integral Test 302
3.4. Series of Positive and Negative Terms - Convergence,
Absolute Convergence. Theorem of Leibniz 309
3.5. The Dirichlet and Abel Tests 324
3.6. Cauchy Product of Infinite Series 333




Contents


ix


3.7. Rearrangement of Series. Double Series
3.8. Infinite Products


342
360


Bibliography - Books


379




Preface


This book is an enlarged and revised English edition of a Polish
version published in 1996 by the Publishing Bouse of Maria Curie-
Sklodowska University in Lublin, Poland. It is the first volume of a
plauned series of books of problems in mathematical analysis. The
second volume, already published in Polish, is under translation into
English. The series is mainly intended for students who take courses
in basic principles of analysis. The choice and arrangement of the
material make it suitable for self-study, and instructors may find it
useful 88 an aid in o rganj
 ing tutorials and seminars.
This wlmne covers three topics: real numbers, sequences, and
series. It does not contain problems concerning metric and topological
spaces, which we intend to present in subsequent volumes.
The book is divided into two parts. The first part is a collection
of exercises and problems, and the second contains their solutions.
Complete solutions are given in most
 Where no difficulties
couJd be expected or when an analogous problem has already been
solved J only a hint or simply an answer is given. Very often various
solutions of a given problem are possible; we present here only one,
hoping students themselves will find others.


xi




xii


Preface


With the student in mind, we have tried to keep things at an ele-
mentary level whenever possible. For example, we present an elemen-
tary proof of the Toeplitz theorem about the so-called regular tra.n5-
formation of sequences, which in many texts is proved by methods of
functional analysis. The proof presented is taken from 'Theplitzts orig-
Inal paper, published in 1911 in Prace Matematyczno-Fizyczne, Vol.
22. We hope that our presentation of this part of real anal
'sis will
be more accessible to readers and will ensure wider understanding.
AD the notations and definitions used in this volume are standard
and commonly used. The reader can find them, for example, in the
textbooks [12] and [23], in which all necessary theoretical background
can be found. However, to make the book consistent and to avoid
ambiguity, a list of notations and definitions is included.
We have borrowed freeJy from many textbooks, problem books
and problem sections of journals like the American
 fathemat ical
MonthJ.y, MatMmat ics 'Ibday ( Rn
iA.n ) and Delta (Polish). A c0m-
plete list is given in the bibliograp
. It was beyond the authors'
scope to trace aU original soW'Ces, and we may have overlooked some
contri butions. If this has happened, we offer our sincere apologies.
We are deeply indebted to all our friends and colleagues from the
Department of Mathematics of Maria. Curie-Sklodowska University
who offered stimulating suggpst ions. We have had many fruitful con-
versations with M. Koter-M6rgo
 T.Kuczumow, W. Rzymowski,
S. Stachma and W. Zygmunt. Our sincere thanks are also due to
Professor Jan KnyZ for his help in preparing the first version of the
English manuscript. We are pleased to express our gratitude to Pro-
fessor KA7.imi erz Goebel for his encouragement and active interest in
the project. It is our pleasure to thank Professor Richard J. Libera,
University of Delaware, for his invaluable and most generous help
with the English translation and for all his suggestions and correc-
tions which greatly improved the final version of the book.


w. J. Kaczor,
I. T. Nowak




No' ation and
Te minology


. R - the set of aU real numbers
. 14 - the set of all positive real numbers
. Z - the set of all integers
. N - the set of all positive integers
. Q - the set of aU rationaIs
. (a, b) - open interval with the endpoints a and b
. (a, b] - closed interval with the endpoints a and b
. (z] - the integral part of a rea] number :&
. FOr zeR ,


1 for x > 0,
SgDZ = -1 for z < 0,
o for %=0.


. ForneN,
n! == 1 · 2 . 3 - ... · n,
(2n)1I = 2. 4 - 6..... (2n - 2)(2n) and
(2n -1)11 = 1- 3 · 5 · ... · (2n - 3)(2n - 1).
. If A c R is nonempty and bounded from above, then sup A
denotes the least upper bound of A. H a nonempty set A is
not bounded above. then we assume that sup A = +00.


-


xiii




xiv


Notation and Terminology


. If A c R is nonempty and bounded from below t then inf A
denotes the greatest lowet bound of A. H a nonempty set A
is not bounded below, then we assume that inf A = -co.
. A sequence {On} of real numbers is said to be monotonically
in creasing (monotonically d ecreasing) if lIn+l
 On for all
n e N (Bn+l
 On for aU n E N). The class of mono-
tonic sequences consists of the increasing and the decreasing
sequences.
. A number c is a limit point of the sequence {tin} if there is a
subsequence {an.} of {On} converging to c.
. Let S be the set of all the limit points of {an}. The limit infe-
rio. Jim On, and the limit superior, Jim On, of the sequence
n
 "-

{an} are defined 88 follows:
+00 if {On} is not bounded above,
liiii On = -00 if {On} is bounded above and S = 0,
A--t

sup S if {an} is bounded above and S #= 0,
-00 if {an} is not bounded below,
!!m On = +00 if {an} is bounded below and S = 0,
n....oo
infS if {On} is bounded below and S:F 0.
00
. An infinite product IT an is said to be convergent if there
n=l
exists no E N such that On #= 0 for n
 no and tbe sequence
{GnoGno+l · .. · · Ono+n} converges, 88 n --. 00, to a limit Po
other than zero. The number P = 0142 · . . . · Bno-l · Po is
caUed the value of the infinite product.




Problems




Chapter 1


Real Numbers


1.1. Supre m 11m and Infimum of Sets of Real
Numbers. Continued Fractions


1.1.1. Show that


sup{x E Q: x > 0, :r;2 < 2} = V2.


1.1.2. Let A c IR. be a nonempty set. Define -A = {x : -:r; E A}.
Show that


sup ( -A) = - inf A,.
inf(-A) = -supA.


1.1.3. Let A, B c JR be nonempty. Define


A+B = {z = x+y: x eAt y e B},
A-B = {z=z-y: z e A, y E B}.


Show that


sup(A+B) =supA+supB t
sup(A - B) = sup A - infB.
Establish analogous formulas for inf(A + B) and inf(A - B).


3




4


Problems. 1: Real Numbers


1.1.4. Given nonempty subsets A and B of positive real numbers,
define


A.B={z=x.y:xeA, yeB}
X={Z=
:ZEA}.


Show that


sup(A. B) = sup A · supB.
Show also that, if inf A > 0, then
sup(
 ) = m:A
and, if inf A = 0, then sup (i) = +00. Additionally, show that if A
and B are bounded sets of real numbers. then
sup(A · B)
=max{supA.supB, supA.infB, infA-supB, infA.infB}.


1.1.5. Let A and B be nonempty subsets of real numbers. Show
that


sup(AUB) = max{supA,supB}


and


inf(AUB) =min{infA,infB}.


1.1.6. Find the least upper bound and the greatest lower bound of
AI, A 2 defined by setting
{ +1 n(n+l) ( 3 ) }
At = 2(-1)R +(-1) :l 2+fi: neN ,
{ n-l 2n1r }
A2 = n + 1 cos T: n EN.


1.1.7. Find the supremum and the infimum of the sets A and B,
where A = {O.2,O.22,O.222,...} and B is the set of decimal frac-
tions between 0 and 1 whose only digits are zeros and ones.


1.1.8. Find the greatest lower and the least upper bounds of the set
of numbers (ntn 1 )2 , where n E N.




1.1. Supremum and Infimum. Continued Fractions 5


1.1.9. Find the supremum and the infimum of the set of numbers
( n+m ) 2 h M
2""' ,were n, m e .&'1.


1.1.10. Determine the least upper and the greatest lower bounds of
the following sets:


(a)
(b)


A = {
: m. n E N. m < 2n} ,
B = { vn - [vn] : n E N} ·


1.1.11. Find


(a)
(b)
(c)


sup{x E IR : x 2 + x + 1 > O},
inf{z = X+X-l: x> O},
inf{z =
 + 2
 : x > O}.


1.1.12. Find the supremum and the infimum of the following sets:


(a)


{ m 4n }
A= -;+;;:: m,nEN t
B= { 4m
;n2 : mEZ nEN},
C = { m : m, n E N } ,
m+n
D = Cm;: n : m E Z. n E iii } .
E = { I mn : m.n EN } .
+m+n


(b)


(c)


(d)


(e)


1.1.13. Let n
 3 be an arbitrarily fixed integer. Take all the possible
finite sequences (al,". ,an) of positive numbers. Find the least
upper and the greatest lower bounds of the set of numbers


n
E ak
k=l ak + ak+l + ak+2 '
where we put On+l = al and lIn+2 = a2 .




6


Problems. 1: Real Numbers


1.1.14. Show that for any irrational number a and for any positive
integer n there exist a positive integer qn and an integer Pn such
that


I Pn l 1
Q - - <-.
qn nqn
Showa1so that {Pn} and {qn} can be chosen in such a way that we
have


I Pn I 1
a - - < 2".
qn qn


1.1.15. Let Q be irrational. Show that A = {m+na: m, n E Z}
is dense in R, i.e. in any open interval there is at least one element
of A.
1.1.16. Show that {cosn: n EN} is dense in [-1,1].


1.1.17. Let x E R" Z. Define the sequence {xn} by setting
1 1 1
x = (x] + -, Xl = [Xl] + - ,..., Xn-l = [Xn-l] + -.
Xl X2 X n
Then


1
.. +
1
[Xn-l] + -
X n
Show that x is rational if and only if there exists n E N for which
X n is an integer.
Re mar k. The above representation of x is said to be a finite con-
tinued fraction. The expression


X = [x] +
[Xl] +
[X2] +


1


.


1


1


.


1


ao+


1


at +


1


112+


.


1


.. +


1
an-l + -
an




1.1. Supremum and Infimum. Continued Fractions 7


will also be written in the more convenient form
11 11 11
ao + _ I + - , + ... + _ I ·
at 112
I


1.1.18. For positive real numbers ai, a2, ..., an set


Po = ao , qo = I,
P1 = ao a l + 1, ql = ai,
Pk = Pk-l a k + Pk-2, qk = qk-lak + qk-2t with k = 2,3, ..., n,
and define
11 11 11
Ro = ao t Rk = ao + _ I + _ I + ... + _ I ' k = 1,2, ..., n.
al a2 ak
( Rk is called the kth convergent to 00 +
 +
 + ... + I

 ) ·
Show that


Pk
Rk = - for k = 0, I, ..., n.
qk
1.1.19. Show that if Pkt qk are defined as in the foregoing problem
and the ao, a 1 , ..., an are integers, then
Pk-lQk - qk-lPk = (_I)k for k = 1,2, ..., n.
Use this equality to conclude that Pk and qk are co-prime.
1.1.20. For an irrational number x we define a sequence {xn} by
1 1 1
Xl = [ ] ' X2 = [ ] ,... , X n = [ ] ' ... ·
x- X Xl - Xl X n -l - Xn-l
Moreover, we put ao = [xJ, an = (x n ], n = 1,2, ..., and
11 11 11
Rn = ao + _ I + _ I + ... + _ I ·
al a2 On
Show that the difference between the number x and its nth convergent
is given by


( -l)n
x-Rn,= ,
· (qn X n+l + qn-l)qn
where Pn, qn are defined in 1.1.18. Conclude that x is between its
two consecutive convergents.




8


Problems. 1: Real Numbers


1.1.21. Show that the set {sinn: n E N} is dense in [-1,1].


1.1.22. Apply the result in 1.1.20 to prove that for every irrationaI
number x there exists a sequence {
} of rational numbers, with
odd qn, such that


I x - Pn I <
 .
qn qn


(Compare with 1.1.14.)
1.1.23. Derive the following formula for the difference of two consec-
utive convergents:


( -l)n
Rn+l - Rn = .
qnqn+l
1.1.24. Let x be irrational. Show that its convergents Rn defined
in 1.1.20 are successively closer to x, that is,
Ix - Rn+ll < Ix - Rnl. n = 0,1.2,... ·


1.1.25. Prove that the convergent Rn = Pnlqn is the best approx-
imation of x of all rational fractions with deno minat or qn or less.
That is: if rls is a rational number with a positive deno mina tor
such that Ix - rlsl < Ix - Rnl, then s > qn.


1.1.26. Expand each of the following as infinite continued fractions:
. 1n 2 ,/5-1
v
I 2 ·


1.1.27. For a positive integer k, find the representation of Vk 2 + k
by an infinite continued fraction.


1.1.28. Find all the numbers x E (0,1) whose infinite continued
representations have al (see Problem 1.1.20) equal to a given positive
integer n.


1.2. Some Elementary Inequalities


1.2.1. Show that if ak > -1, k = 1, ..., n, are all positive or negative,
then


(1 + at) · (1 + Q2) · ... . (1 + an) > 1 + a) + 42 + ... + an .




1.2. Some Elementary Inequalities


9


Re mar k. Note that if 01 =
 = ... = an = a then we get the well
known Bernoulli inequality: (1 + a)n > 1 + na, a > -1.


1.2.2. Using induction, prove the following result: H aI, tI2, ..., an
are positive real numbers such that a} · 42 · ... · On = 1, then al + lI2 +
... + an
 n.


1.2.3. Let An' G n and Hn denote the arithmetic, geometric and
harmonic means of n positive real numbers aI, a2, ..., an; that is,


.


A _ 41 + a2 + ... + 4n
n- t
n
G n = VIa l · ... · an t
n
Hn = 1 1 1 ·
41 + 42 +... + an


Show that An > G n > Hn.


1.2.4. Using the result (G n < An) in the foregoing problem, establish
the Bernoulli inequality


1.2.5. For n E Nt verify the following claims:
1 1 1 1 2
-+ 1 + 2 +".+- 2 >- 3 '
n n+ n+ n
1 1 1 1
1 + 2 + 3 + ... + 3 1 > 1,
n+ n+ n+ n+


(a)


(b)


(c)


(d)


(l+x)n > l+nx for x>O.


1 1 1 1 1 2
2 < 3n + 1 + 3n + 2 + ... + 5n + 5n + 1 < 3'
1 1
n( V' n + 1 - 1) < 1 + 2 + ... + n
< n ( 1 - + ) , n > 1.
vtnl + 1 n
 1




10


Problems. 1: Real Numbers


1.2.6. Show that for any x > 0 and n E N we have


x" 1
1 + x + 3: 2 + 3: 3 + ... + x2n
 2n + 1 ·


1.2.7. Let {an} be an arithmetic progression with positive terms.
Show that


al + an
..j Blan
 \!a la2...an
 2 ·


1.2.8. Show that


C nq n+l M
v n
 vn!
 2 ' n e 1"4.


n
1.2.9. Let Ok, k = 1,2, ..., n, be positive numbers and let E ak :::; 1.
k=l


Show that


n
E -.!.. > n 2 .
k=l ak


n
1.2.10. Let Ok > 0, k = 1,2, ...n, where n > 1, and set s = E Ok.
Ie=l
Verify the following claims:


(a)


( n ) -1 n
n E Ok 5 n - 1 < .!. L S - Ok ,
k=l S - ale n k=l ak
n S n 2

 > ,
L....J 8 - ak - n - 1
k=l
( n ) -1
n L ale > n+l.
k=l 8 + ak


(b)


(c)


1.2.11. Show that if ak > 0, k = 1, ..., n, and al · G2 . ... · an = 1,
then


(1 + 01)(1 + 112) · ... · (1 + an)
 2 R .




1.2. Some Elementary Inequalities


11


1.2.12. Prove the following Cauchy inequality:
( n ) 2 n n

 akbk <
 a

 I4.


1.2.13. Show that


( t ak ) 2 + ( t bk ) 2
k=l k= l



 n
:5 E(a
 + b
)i.
k=l


11. n
1.2.14. Show that if L ai = L
 = 1, then
k=l k=l


n
L akbk :5 1.

 1


1.2.15. For ak > 0, k = 1,2, ..., n, verify the following claims :


(a)


n n 1
EakE-
n2t
k=l IF 1 ak
n n 1 n
LakL -ak > nL(l-ak),
k=1 k=l ak k= 1
(loga Q l)2 + (lo&a2)2 + ... + (logaan)2 2: .!. t
n
provided al ·
 · ... · an = a :/: 1.


(b)


(c)


1.2.16. For Q > 0, show that


n 1 n n
Eakbk < a Ea
+ : EI4.
k=l k=l k=l


1.2.17. Establish the follov/ing inequalities:
1

 lakl ::; Vii (
 a
 r ::; Vii
 lakl.




12


Problems. 1: Real Numbers


1.2.18. Show that
( n ) 2 n n Of.
Eakbk < Eka
Et,
k=l k=l k=1
( n ) 2 n n
f; T

 k3a


 .


(a)


(b)


1.2.19. Show that
( n ) 2 n n
tf at
 k ar9 k ar-q,


for any real p, q and any positive at J a2, ..., an.


n
1.2.20. Find the minim um of the sum L aI subject to the con-
k= l


n
straint E ak = 1.
k= 1


1.2.21. Let PhfJ2, ...,Pn be given positive numbers. Find the mini -
n n
mum of E Pka
 subject to the constraint E ale = 1.
k
l k=l


1.2.22. Show that
(
 akr
 (n-I) l
 a
+2aI42) ·


1.2.23. Verify the following claims:


(b)


.1 1 1
( n ) 2" ( 71 ) 2 ( n ) :i

 (a1:+bk)2 <
 a
 + tf
 ·
( E a
) 1 - l
 b%r


71
S Elak -blel.
k=l


(a)




1.2. Some Elementary Inequalities


l3


1.2.24. Let Pl,P2,...,Pn be given positive numbers. Find the mini -
mum of
i
 a'f. + (i
 aA) 2 subject to the constraint


n
LPkak = 1.
k=l


1.2.25.. Prove the following Chebyshev inequality: If al > 42 >
...
 an and 61

 > ... > b n (or al S a2 < ... S an and
bl


 ...
 b n ), then


n n n
LOkLbk < nLakbk.
k=1 k=l k=l


1.2.26. Ass umin g ak > 0, k = 1,2, ..., n, and peN, show that
( 1 n ) p 1 n
- Lak
 - La
.
n k=1 n k=l


1.2.27. Establish the inequality
(a+b)2 $ (1 +c)a 2 + (1 +
),;
for positive c and any real a and b.


1.2.28. Show that I va2 + b2 - v'a 2 + & 1 < Ib - cl.


1.2.29. For positive a, b , c, verify the following c la.im
 :
be ac ab
- + - +- > ( a+b+c )
a b c - ,
11111 1
a + b + c
 VbC + vca +
 '
2 2 2 > 9
+ +
b+c c+a a+b - a+b+c'
1J2 - a 2 t? -1J2 a 2 - c2
c + a + a + b + b + c
 0,


(a)


(b)


(c)


(d)


(e)


! (a - b)2 < a + b _ Jab < !. (a - b)2 P rovided b _ < a.
8 a - 2 -8 b




14


Problems. 1: Real Numbers


1.2.30. For ak e R, ble > 0, k = 1,2, ".t n, set
m = min{ i; : k = 1.2. .... n} and M = max{ :: : k = 1.2..... n}.
Show that


m < at + a2 + ... + an < M.
- b 1 + b:z + ... + b n -


1.2.31. Show that, if 0 < al < 02 < ... < On <
 , n > 1, then
sinal + sina2 +... + sin an t
tanal < < an an.
COSOl + cosa2 +... + COSO n


1.2.32. For positive Cl, C2, ..., Cn, and kIt k 2 ,..., k n e N, set


S = max{ k.vcl, kvtC2, ..., k
},
8 = min{ 1c.vcI, Ic
, ..., k
.


Show that


s < (at. a2 . ... · an) leI +1c2i...+kn
 s.


1.2.33. For ak > 0, bk > 0, k = 1,2, .... n, set
M = max {i; : k = 1. 2, ..., n } ·


Show that


at + lJ
 + ... + a;: M
2 < ·
bt + Mb 2 +... + Mn-1b: -


1.2.34. Show that, if x is greater than any of the numbers a}, CI2, ...,
an, then


1 1 1 > n .
+ + ... + + + +
z - al x -
 x - an - x _ 01 C2 on an
n


1.2.35. Let Ck = (
), k = 0,1,2, ..., n, be the binomial coefficients.
Establish the inequality
VC1 + VC2 + ... +
 < V n (2 n - 1).




1.2. Some Elementary Inequalities


15


1.2.36. For n > 2, show that


n ( n ) :s ( 2 n - 2 ) n-l .
II k n-l
k=O


1.2.37. Let ak > 0, k = 1,2, ..., nt and let An be their arithmetic
mean. Show that for any integer p > 1,


n n
EAt:::;;
 1 EAt-lak o
k=l P k=l


1.2.38. For positive ak, k = 1,2, .u, n, we set a = a} + B2 + ... + 4n.
Show that


n-l 2
Eakak+l <
.
k=l


1.2.39. Show that for any rearrangement bl,
, ..., b n of the positive
numbers aI, a2, ..., an,


at a2 an

 +
 +... + b n > n.


1.2.40. Prove the Weierstrass inequalities: If 0 < ak < 1, k =
1,2, ..., n, and al + a2 + ... + an < 1, then


(b)


n n 1
1 + E Ok < II (1 + ak) < n J
k=l k=1 1 - E ak
k=1
n n 1
1 - E ak < II (1 - ak) < n
k=1 k=l . 1 + E ak
k=l


.


(a)


1.2.41. Assume that 0 < Bk < 1, k = 1, 2, .u, nt and set al +
 +
... + an = a. Sho\v that


n
"'" ak > na .
L..J I-ak - n-a
k=l




16


Problems. 1: Real Numbers


1.2.42. Let 0 < ak
 1, k = 1,2, ..., n, and n > 2. Verify the inequal-
ity


n
n 1 nEak
"" < 1:=1

 1+ - n n
k=1 ak E ak+n n ale
1c=1 k=l


.


1.2.43. For nonnegative at, k = 1,2, ..., n, such that al + a2 + ... +
an = 1, show that


(a)


n n
n (1 + ale)
 (n + l)n n ale,
k=l k=l
n n
II (1 - ale)
 (n - l)n II at.
1:=1 k=1


(b)


n
1.2.44. Show that if at > 0, k = 1,2, ..., n, and E l;a = n - 1,
1:=1 4


then


n 1
II -
 (n-l)n.
k=1 ale


1.2.45. Prove that under the assumptions of 1.2.43, we have


n n
n (1 + ale) IT (1- a,:)
k=1 > k=1 > 1
(n + I)n - (n _ l)n ,n ·


1.2.46. Show that for positive alt a2, ..., an,
at + a2 + ... + Cln-2 + an-I + an > n .

 + a3 a3 +
 an-l + an an + at at + a2 - 4


1.2.47. Let t and aI, tI2,..., an be any real numbers. Establish the
inequality



 vial: - tl >
 v'lak - all
L.J 2" - Li 2 k ·
k=l k= 2




1.2. Some Elementary Inequalities


1'1:


1.2.48. Show that for positive al,a2,...,an, and bl,b2,...tbn, we
have


V' (al + bl)(a2 + b2)...(an + b n ) >
a la2...an + V' bl
...bn.


1.2.49. Assume that 0 < al < a2 < ... < an and Pl,iJ2, ...,Pn are
n
nonnegative such that E Pk = 1. Establish the inequality
k=l


( 11 ) ( n 1 ) A2
LPkBk LPk Ck < (]2 '
k=l k=l
where A = !(al + an) and G = ,ja lan.
1.2.50. For a positive integer n, let O'(n) and T(n) denote the sum
of all the positive divisors of n and the number of these divisors,
respectively. Show that

:
 > In.




Chapter 2


Sequences of Real
Numbers


2.1. Monotonic Sequences


2.1.1. Show that
(a.) if a sequence {an} is monotonically increasing t then fun l1n =
R-OO
sup{an: n EN};
(b) if a sequence {an} is monotonically decreasing, then lim 4n =
"-00
inf{an: n eN}.


2.1.2. Let at, 02, ..., a p be fixed positive numbers. Consider the sa--
quences
ar +
 + ... + a; and
8n = X n =
 1 n E N.
P
Show that the sequence {Xn} is monotonically increasing.
Hint. First establish monotonicity of the sequence { 8::'1 }' n
 2.
2.1.3. Show that the sequence {an}t where On = FJ n > 1, strictly
decreases and find its limit.
2.1.4. Let {an} be a bounded sequence which satisfies the condition
an+l ?: an - 2
 ' n E N. Show that the sequence {an} is convergent.
Hint. Consider the sequence {an - 2nl_1 } .


19




20


Problems. 2: Sequences of Real Numbers


2.1.5. Prove the convergence of the sequences:


( 11 1 )
(a) On = -2vn + VT + Vi + ... + ,fii ;
(b) b n = -2 vn+ 1 + (* +
 +...+
).
Hint. First establish the inequalities
1 1 1
2( V n + 1-1) < VT + Vi + ... + ..jii < 2"fii., n E N.


2.1.6. Show that the sequence {an} defined recursively by
3
al = 2' an = y 3 an-l - 2 for n
 2,
converges and find its limit.
2.1.7. For c> 2, define the sequence {an} recursively as follows:
al = t?-, 4n+l = (an - c)2, n
 1.
Show that the sequence {an} strictJy increases.
2.1.8. Suppose that the sequence {a,.} satisfies the conditions
1
o < an < 1, an(l - C£n+l) > 4: for n E N.
Establish the convergence of the sequence and find its limit.


2.1.9. Establish the convergence and find the limit of the sequence
defined by


al = 0, 0.,.+1 = ';6 + an for n > 1.


2.1.10. Show that the sequence defined by
1 1
al = 0, lI2 = 2' an+l = 3(1 + an. + a
_l) for n > 1
converges and determine its limit.




2.1. Monotonic Sequences


21


2.1.11. Study the monotonicity of the sequence
n!
an = (2n + I)!! t n > I,
and determine its limit.


2.1.12. Determine the convergence or divergence of the sequence
_ (2n)!! >
an - (2n + I)!! ' n - 1.


2.1.13. Prove the convergence of the sequences
1 1 1
(a) an = 1 + 2 2 + 32 +... +
, n EN;
1 1 1
(b) an = 1 + 2 2 + 3 3 + ... + n;' n E N.


2.1.14. Show the convergence of the sequence {an}, where
111
an = ..jn(n + 1) + V(n + l)(n + 2) +... + v'(2n - 1)2n '


neN.


2.1.15. For peN, a > 0 and al > 0, define the sequence {an} by
setting
a,,+1 =
 (p - 1)4 n + ;-1 )' n E N.
Determine lim an.
n-oo


2.1.16. Define {an} recursively by
41 = Vi. a,,+1 = ';2 +,;a;; for n
 1.
Prove the convergence of the sequence {an} and find its limit.
2.1.17. Define the recursive sequence {an} as follows:
2(2an + 1)
al = I, an+l = 3 for n E N.
an+
Establish the convergence of the sequence {an} and find its limit.




22


Problems. 2: Sequences of Real Numbers


2.1.18. Determine all c > 0 such that the recmsive sequence {an}
defined by setting


c 1 2
al = 2 ' Bn+l = 2 (c+ an) for n e N
converges. In case of convergence find lirn Bn.
n-X)


2.1.19. Let a> 0 be fixed and define the sequence {an} by setting
a;+3a
at > 0 and an+t = an 3 2 for n E N.
an+a
Determine all al for which the sequence converges and in such a case
find its limit.


2.1.2.0. Let {an} be defined recursively by
1
an+l = 4 _ 3an for n > 1.
Determine for which at the sequence converges and in case of con-
vergence find its limit.
2.1.21. Let a be arbitrarily fixed and let {an} be defined as follows:
01 e R and lln+l = a; + (1- 2a)an +a 2 for n e N.
Determine all al such that the sequence converges and in such a case
find its limit.


2.1.22. For c > 0 and b > a> 0, define the recursive sequence {an}
by setting


a 2 + ab
at = C, 4n+l = n b for n e N.
a+
Determine for which values a, b and c the sequence converges and find
its limit.


2.1.23. Prove the convergence and find the limit of the sequence
{an} defined inductively by
l+an
a] > 0, an+l = 6 7 + an ' n e N.




2.1. Monotonic Sequences


23


2.1.24. For c
 0, define the seque nce {an } as follows:
al = 0, On+l = yc +an, n eN.


Show the convergence of the sequence and determine its limit.


2.1.25. Investigate the convergence of the sequence defined by
al = v'2, 4n+l = y2a n , n E N.


2.1.26. Let kEN be fixed. Study the convergence of the sequence
{an} defined by setting
al = W, an+l =
5an , n E N.


2.1.27. Investigate the convergence of the sequence {an} given by
1 S a} S 2, a
+1 = 3an - 2, n E N.


2.1.28. For c> 1, define the sequences {an} and {b n } as follows:


(a) al= vc (c-l), tln+t= V c(c-l)+an, n2:1;
(b) b 1 = ..fi, b n + 1 = vcr;;, n > 1.


Prove that both sequences tend to c.
2.1.29. Given a> 0 and b> 0, d efine the sequence {an} by setting
o < at < b, Gn+1 = Jm:: :
 Cor n;;?: 1.
Find 1im an.
n-oo


2.1.30. Prove the convergence of {an} defined inductively by
1
an+l = 2 + 1 for n 2: 1
3+-
an


al = 2,


and find its limit.




24


Problems. 2: Sequences of Real Numbers


2.1.31. The recursive sequence {an } is given by setting
al = 1, a2 = 2, an+l = v an-l + van for n > 2.
Show that the sequence is bounded and strictly increasing. Find its
limit.


2.1.32. The recursive sequence {an } is given by setting
al = 9, a2 = 6, CIn+1 = Va n-l + va;: for n > 2.
Show that the sequence is bounded and strictly decreasing. Find its
limit.


2.1.33. Define the sequences {an} and {b n } as follows:
an + b n
 I

0< b l < 01, Bn+l = 2 and b n + 1 = vanbn lor n E N.
Show that {an} and {6n} both tend to the same limit. (This limit
is called the arithmetic-geometric mean of a1 and b 1 .)


2.1.34. Show that the sequences {an} and {b n } given by
a 2 + b 2 an + b
o < b 1 < alt an+l = n b n and b n + 1 = 2 n for n E N
an+n
are both monotonic and have the same limit.


2.1.35. Let the recursive sequences {lln} and {b n } be given by set--
ting
an + b n 2anb n
o < b 1 < aI, lln+l = 2 and bn+1 = b for n E N.
an+n
Prove the monotonicity of these sequences and show that both of them
tend to the arithmetic-geometric mean of al and bl. (See Problem
2.1.33.)


2.1.36. Show the convergence and find the limit of {an}, where
n+l ( 2 22 2 n )
an = 2"+1 I + 2 + ... + -;- for n E N.




2.1. Monotonic Sequences


25


2.1.37. Suppose that a bounded sequence {an} is such that


1 2
a n +2 < a an+l + a CLn for n > 1.


Prove the convergence of the sequence {an}.


2.1.38. Let {an} and {b n } be defined as follows:


an= (l+
r,


( 1 ) n+l
b n = 1 + n for n E N.


Using the arithmetic-geometric-harmonic mean inequalities, show that
(a) an < b n for n e N.
(b) the sequence {an} is strictly increasing,
(c) the sequence {b n } is strictly decreasing,
Show also that {an} and {b n } both have the same limit, defined to
be Euler's number e.


2.1.39. Let


an = (1 +
r for n e N.
(a) Show that if x > 0, then the sequence {an} is bounded and
strictly increasing.
(b) Let x be any real number. Show that the sequence {an} is
bounded and strictly increasing for n > -x.
The number tf& is defined to be the limit of this sequence.


2.1.40. Suppose that x > 0, l E N and I > x. Show that the
sequence {bn}t where


( X ) '+n
b n = 1+;


for n E N,


is strictly decreasing.




26


Problems. 2: Sequences of Real Numbers


2.1.41. Establish the monotonicity of the sequences {an} and {b n },
where


1 1
an = 1 + 2 + ... + n _ 1 -Inn lor n E Nt
111
bra = 1 + 2 + ... + 1 + - - In n for n E N.
n- n


Show that both of them tend to the same limit '1, which is known as
Euler's constant.
Hint. Apply the inequality (1 +
 )n < e < (1 +
 )n+l t which fol-
lows from 2.1.38.


2.1.42. Given x > 0, set 4n = 2V'X, n E N. Show that the sequence
{an} is bounded. Show also that it is strictly increasing if x < 1 and
strictly decreasing if x> 1. Compute lim Bn.
n-co


Moreover 1 put


en = 2n(a,. -1) and d" = 2 n (1- a:) for n E N.
Show that {en} is decreasing and {dn} is increasing and both se-
quences have the same limit.


2.2. L imi ts. Properties of Convergent Sequences


2.2.1. Calculate:


(a)


fun \1 1 2 + 2 2 +... + n 2 ,
n-oo


(b)
(c)
(d)
(e)


. 2
lim n+smn t
n-oo n+cosn
lim 1-2+3-4+...+(-2n)
n-.oo Vn 2 + 1 '
fun (V2 -
)( Vi - if2) · ... · (J2 _ 2ra+
),
n-oo
lim

71.....00 2v;i'




2.2. Limits. Properties of Convergent Sequences 27


,
(f) lim
,
n-oo 2 n
. l ( 1 1 1 )
(g) Ji....

 Jf + J3 + v'3 + J5 + ... + v'2n - 1 + v'2n + 1 '
(h) lim ( / 1 + 2 2 2 + ... + 2 n ) ,
"'-00 n + n + n + n
( - ) Jim ( n 2n nn )
1 3 1 + 3 2 + ... + 3 ·
n-oo n + n + n + n


2.2.2. Let 8 > 0 and p > o. Show that
II
lim n = o.
n-oo (1 + p)'"


2.2.3. For Q e (0,1), calculate fun «n + I)Q - nQ).
n-oo


2.2.4. For Q e Q, calculate lim sin ( n!Q1T).
n-oo


2.2.5. Show that the limit lim sin n does not exist.
R-OO


2.2.6. Show that for any irrational Q the limit lim sin n01r does
R-OO
not exist.


2.2.7. For a e R, calculate
1 (( 1 ) 2 ( 2 ) 2 ( n-l ) 2 )
J
 n a + n + a + n + ... + a + n ·


2.2.8. Suppose an 1= 1 for all n and lim"an = 1. Given a positive
n-oo
integer k, compute


lim l1n + a
 + ... + a
 - k .
R-OO an - 1


2.2.9. Find


lim( 1 1 1 )
+ + ... + .
n-oo 1.2. 3 2. 3. 4 n. (n + 1) · (n + 2)




28


Problems. 2: Sequences of Real Numbers


2.2.10. Calculate


lim II n
-1
n-oo k3 + 1 ·
k=2


2.2.11. Determine


n i e
1im "''' L
n
oo L..J L..." n 3 ·
i===l ;=1


2.2.12. Compute
lim ( 1- 2 )( 1- 2 ) . . ( 1- 2 )
n-oo 2 · 3 3 · 4." (n + 1) · (n + 2) ·


2.2.13. Calculate


. n k 3 +6k 2 +11k+5
J

E (k+3)! ·
11:=1


2.2.14. For x:F -1 and X:F 1, find
n
-1
lim " 2 k ·
n
oo L..." 1 - X
k=!


2.2.15. Determine for which x e R the limit


n
lim II (1 + x 2 ")
n-oo
k=O


exists and find its value.


2.2.16. Determine all x E R such that the limit
lim II " ( 1 + 2. 2 2. )
n-oo X +z-
k=O
exists and find its value.


2.2.17. Establish for which x E Ii the limit


n
lim TI (l + x 3 " + x 2e3 ")
n-oo
k=l


exists and find its value.




2.2. Limits. Properties of Convergent Sequences 29


2.2.18. Calculate


lim I-I! + 2. 21 + ... + n. n!
n-oo (n + I)! ·


2.2.19. For which x e Ii does the equality
n 1999 1
lim =
n.....oo n% - (n - 1)% 2000


hold?


2.2.20. Given a and b such that a
 b > 0, define the sequence {an}
by setting


ab
al = a + b, an = al - , n > 2.
an-I
Determine the nth term of the sequence and compute Jim an.
n-co


2.2.21. Define the sequence {an} by setting
a} = 0, CI2 = 1 and an+1 - 2an + Bn-I = 2 for n > 2.
Determine its nth term and calculate lim an.
n--oo


2.2.22. For a > 0 and b> 0, consider the sequence {an} defined by
ab
al = va 2 + 1J2 and
tlan-J
a n = , n
2.
V a 2 + a
_l
Determine its nth term and find llm l1n.
n-oo


2.2.23. Let {an} be a recursive sequence defined as follows:
tin-I + 3 > 2
al = 0, On = 4 ,n - ·
Find the formula for the nth term of the sequence and find its limit.


2.2.24. Study the convergence of the sequence given by
at =a, an = 1 + ban-I, n
2.




30


Problems. 2: Sequences of Real Numbers


2.2.25. The Fibonacci sequence {an} is defined as followE:


a) = a2 = 1, l1n+2 = an + On+l, n > 1.


Show that


an - pn
an = ,
0.-{3
where Q and {J are roots of x 2 = x + 1. Compute fun
.
n-oo


2.2.26. Define the sequences {an} and {b n } by setting


at = a,
an + b n
an+l = 2 '
Show that lim an = lim b n .
n-oo n-oo



 =6,
6 - an+l +b n
n+l - ·
2


2.2.27. Given a e {I, 2, ..., 9}, compute


n digits


lim a + aa + ... + aa...4 ..
11-00 IOn


2.2.28. Calculate


lim (y'ii_l)n.
n-oo


2.2.29. Suppose that the sequence {an} converges to zero. Find
lim n
an-
n-.oo


2.2.30. Given positive Pit 1'2,... ,Pie and ai, a2,.... ,ale, find
lim Plai+l + P2a2+ 1 +... + Pka
+1
n n n.
R-OO PI al + P2112 + ... + Pkak


2.2.31. Suppose that lim I
"'I I = q. Show that
n
oo n
(a) if q < 1, then lim l1n = 0,
"-00
(b) if q > 1, then lim lanl = 00.
R-OO




2.2. Limits. Properties of Convergent Sequences 31


2.2.32. Suppose that lim V iani = q. Show that
n-oo
(a) if q < 1, then lim an = 0,
n-oo


(b) if q> 1, then lim Ian I = co.
n-co


2.2.33. Given a real number Q and x e (0,1), calculate


lim nQx R .
n-oo


2.2.34. Calculate
lim m(m - 1) · ... . (m - n + 1) n
I X ,
n-oo n.


for mEN and Ixl < 1.


2.2.35. Assume that lim an = 0 and {b n } is a bounded sequence.
n-oo
Show that lim anb n = o.
n-OO


2.2.36. Show that if lim an = a and lim b n = b, then
n-oo n-OC)


lim max{an,b n } = max{a,b}.
n-oo


2.2.37. Let an
 -1 for n E N and let Urn an = O. For peN,
n-oo
find


lim {1 1 + an.
n-oo


2.2.38. Assume that a positive sequence {an} converges to zero.
For natural p
 2, determine


1im {i'l + On - 1 .
n-oo an


2.2.39. For positive al,
, ...,a p , find


n
 ( V (n + al)(n + 42) · ... · (n + ap) - n ).




32


Problems. 2: Sequences of Real Numbers


2.2.40. Calculate
1im( 1 1 1 )
+ + ... + .
n-oo vn 2 + 1 vn 2 + 2 vn 2 + n + 1


2.2.41. For positive 41, lI2, ..., ap, find


lim n ai + a2' + -.. + a
 .
n-.oo p


2.2.42. Compute


2 n1999 n 1999
lim " 2 - + 2
8m 1 cos 1 -
n--.oo n + n +


2.2.43. Find


1
lim (n+ 1 +ncosn) 3 n + n8 i nn_
n-oo


2.2.44. Calculate


..
t ( Jl+
 -1 ) .
k=l


2.2.45. Determine


..
t (
1+ :: -1 ) -
k=l


2.2.46. For positive ak, k = 1,2, ...,p, find


( 1 p ) p
lim - '" v'ik ·
n-.oo p L...J
k=l


2.2.47. Given Q e (0,1), compute


n-l ( ) k
lim
Q+.!. .
n-oo L...J n
k=O




2.2. Limits. Properties of Convergent Sequences 33


2.2.48. Given real :z;
 1, show that
lim (2y'X _l)n = x 2 .
n
oo


2.2.49. Show that


lim (2y'n-l)n = 1.
"
OO n 2 .


2.2.50. Which of the following sequences are Cauchy sequences?
tan! tan 2 tann
an = 2 + 22 + ... + 2 n 1
1 2 2 n 2
an = 1 + 4 + 42 + ... + 4 n '
1 1 1
an = 1 + 2 + 3 + ... + n '
1 1 ( l) n-l 1
Bn = 1.2 - 2. 3 +... + - n(n + 1)'
an = Ql ql + 0'2rr + ... + Qnq" 1


(a)


(b)


(c)


(d)


(e)


(f)


for Iql < 1, IOkl
 M, k = 1,2, ...,
1 2 n
an = 22 + 32 +... + (n+ 1)2.


2.2.51. Suppose that a sequence {an} satisfies the condition
lan+l - a n +21 <
Ian - Bn+ll.
with a
 e (0, 1). Prove that {an} converges.
2.2.52. Given a sequence {an} of positive integers, define
1 1 1
Sn = - + - + ... + -
01 a2 an


and


Un = (1+
) (1 +
)..... (1 + a:).
Prove that if {Sn} converges, then {lnu n } also converges.




34


Problems. 2: Sequences of Real Numbers


2.2.53. Show that the sequence {Rn} of convergents to an irrational
number x (defined in Problem 1.1.20) is a Cauchy sequence.


2.2.54. For an arithmetic progression {an} whose terms are different
from zero, compute


Ii ( 1 1 1 )
m + + ... + .
R-OO Qla2 a2 0 3 ilnt1n+l


2.2.55. For an arithmetic progression {an} with positive terms, cal-
culate


. 1 ( 1 1 1 )
lim - + + ... + .
"-00 vn Viii + Vii2
 + Vii3 .va; + v'D.n +l


2.2.56. Find


(a) lim n( r:fi, - 1),
n-oo


.L.a. n
(b) lim en +e n +...+e ft .
R-OO n


2.2.57. Let {an} be a sequence defined as follows:


al = a, a2 = b, an+l = ptln-l + (1- p)a nJ n = 2,3,...


Determine for which values a, b and p the sequence converges.


2.2.58. Let {an} and {b n } be defined by setting


al = 3, b 1 = 2, lIn+l = an + 2bft and b n + 1 = On + b n .


Moreover, let


an
en = -t n E N.
b n
(a) Show that ICn+l - J21 <
 ICn - V21, n E N.
(b) Calculate Urn Cn.
n-oo




2.3. Toeplitz Transformation and Stolz Theorem 35


2.3. The Toeplitz tr
ns formation, the Stolz
theorem and their applications


2.3.1. Prove the following Toeplitz theorem on regular transforma-
tion of sequences into sequences.
Let {en,1c : 1
 k ::; n, n 2: I} be an array of real numbers such
that:


(i)


Crltk -... 0 for each kEN,
n-too


(ll)
(ill)


n
'"' Cn.k --t I,
L..J n......oo
k=l
there exists C > 0 such that for all positive integers n:


n
E lentkl < c.
k= l
Then for any convergent sequence {an} the transformed sequence
n
{b n } given by b n = E Cr..kak, n
 1, is also convergent and lim b n =
k= 1 n-oo
lim an.
1\-00


2.3.2. Show that if lim an = a, then
n-oo


Ii al + a2 + ... + an
m =a.
n......oo n


2.3.3.
(a) Show that the assumption (ill) in the Toeplitz theorem (Problem
2.3.1) can be omitted if all the numbers Cn.k are nonnegative.
(b) Let {b n } be the transformed sequence defined in the Toeplitz
theorem with Cn.k > 0, 1 ::; k ::; R, n
 1. Show that if lim an =
n-oo
+00, then lim b n = +00.
n...... 00


2.3.4. Show that if lim an = +00, then
n-+oo


1 . al + a2 +... + an
1m = +00.
n-oo n




36


Problems. 2: Sequences of Real Numbers


2.3.5. Prove that if 1im an = a, then
n-+oo


lim nal + en - 1)a2 + ... + 1 · an = a .
n-+oo n 2 2


2.3.6. Show that if a positive sequence {an} coDverges to a, then
lim -tla l..... an = a.
"'-'00


2.3.7. For a positive sequence {an}, show that if lim a n +l = a,
n-oo an
then lim fjan = a.
n-oo


2.3.8. Let lim an = a and lim bra, = b. Show that
n-oo R-OO


lim albn + a2 b n-l + ... + anb l - b
-a .
n-oo n


2.3.9. Let {an} and {b n } be two sequences such that


(i)
(ii)


b n > 0, n E N, and lim. (lit +
 + ... + b n ) = +00,
n-+oo


lim Bn
-=g.
n-+oo b n


Prove that


lim al + CI2 + ... + an
=g.
n-oo b 1 +
 + ... + b n


2.3.10. Let {an} and {b n } be two sequences for which


(i)
(ii)


b n > 0, n E N, and lim (b 1 + h2 + ... + b n ) = +00,
n-+oo


lim an = a.
11-00


Show that


lim. a1b 1 + a2b:l +... + anb n = a.
n-oc bl + h2 + ... + b n




2.3. Toeplitz Transformation and Stolz Theorem 37


2.3.11. Using the result in the foregoing problem, prove the Stolz
theorem.
Let {Xn}, {Yn} be two sequences that satisfy the conditions:


(i)
(ll)


Then


{Yn} strictly increases to + 00,
lim Xn - X n -l
=9.
n
oo Yn - Yn-l


lim Xn
-- g
- .
11-00 Yn


2.3.12. Calculate


(a)


(b)


(c)


(d)


(e)


(f)


(g)


Jim
 ( 1 +
 + ... +
 ) ,
n
oo yn v2 yn


n ( a2 an )
1im +1 a + _ 2 +... + - ,a > 1,
R-OO an n


lim 1 (k l (k + I)! (k +n)! ) k

k+ 1 · + l' + ... + r ,e 1'1,
R-OO n . n.
. 1 ( 1 1 1 )
Jim - - + + ... + ,
n-oo vn .J1i vn + 1 ,f2n
lim lie + 2 1e + ... + nit: k N
n-Poo nk+l ' E,


lim 1 + 1 · a + 2 · a 2 + ... + n · an 1
1 ' a > ,
n-Poo n · a n +


. [ 1 ( k k Ie ) n ]
Jim Ii 1 + 2 +... + n - k 1 ,k E N.
n
co n +


2.3.13. Assume that lim an = a. Find
n
oo


. 1 ( lI2 a3 an. )
lim
 at +
 + /f; + ... +
 ·
n-oo vn v2 v3 v n




38


Problems. 2: Sequences of Real Numbers


2.3.14. Prove that if {an} is a sequence for which
lim (On+l - an) = a,
n ....00


then


lim lln
-=Q.
n-oo n


2.3.15. Let lim an = a. Determine
R-OO


lim ( an lLn-1 a} )
n-oo T + 2 + ... + 2 n - 1 ·


2.3.16. Suppose that lim an = Q. Find
R-OO


( ) 1 - ( an tin-I a l )
a n!..
 1. 2 + 2. 3 +... + n. (n + 1) ,
(b) lim ( lLn an-I ( l) n-l aJ )
n-oo T - 2 1 + ... + - 2 0 - 1 .


2.3.17. Let k be an arbitrarily fixed integer greater than 1. Calculate


lim n r;;;k\ ( nk ) .
n-
 V
n)


2.3.18. For a positive arithmetic progression {an}, find
. 8 n(al . ... . 4n)

1m .
n-oo 01 + ... + On


2.3.19. Suppose that {an} is such tbat the sequence {b n } with
b n = 2an + an-I, n
 2, converges to b. Study the convergence of
{ an}.


2.3.20. Suppose that {an} is a sequence such that lim n%an. = Q
D-OC
for some real x. Prove that
fun % ( )
 %
n a 1 . a2 · ... · an " = ae .
0-00




2.3. Toeplitz Transformation and Stolz Theorem 39


2.3.21. Calculate


(a)


1+ 1 + 1 + 1
lim 2 + ... n=I n
n-oo Inn '
1 1 1 1
lim + 3 + s + ... + 2n-l
n-oo Inn .


(b)


2.3.22. Assume that {an} tends to a. Show that


. 1 ( a l a2 an )
n
 In n T + 2 + ... + -; = a.


2.3.23. Find


(a)


( I ) J.
lim n. n
8-00 nne-n t
1
lim ( (n!)2 ) n ,
8-00 n 2n


lim vn! ' kEN.
n-too n n!


1
r ( n!)3 ) n
(b) n
 n 3n e- n '
(d) n
 ( :
3 )
 ,


(c)


(e)


2.3.24. Show that if 1im an = a, then
n-oo


n
lim 2.... '" ak = a.
n-oo In n L.J k
k=1


2.3.25. For a sequence {an}, consider the sequence {An} of arith-
metic ID e8. nS , i.e. An = BJ+a 2 +...+B n . Show that if limn_oo An = A,
8
then also


n
lim


 = A. I
n-oo In n L-i k
k=1




40


Problems. 2: Sequences of Real Numbers


2.3.26. Prove the converse to the Toeplitz theorem stated in 2.3.1:
Let {Cn,k : 1
 k
 n, n
 I} be an array of real numbers. If for
any convergent sequence {an} the transformed sequence {b n } given
by setting


n
b n = ECn,k4k' n
 1
k=l
is convergent to the same limit, then


(i)


Cnk --+ 0 for each keN,
· R-OO


(ii)


n

 Cn,k --t 1,
L..J n-.oo
Ie=l
there exists C > 0 such that for all positive integers n


(Hi)


n
E len.kl < c.
11:=1


2.4. L imi t Points. Limit Superior and Limit
Inferior


2.4.1. Let {an} be a sequence whose subsequences {a2k}, {02k+l}
and {a3k} are convergent.
(a) Prove that the sequence {an} is convergent.
(b) Does the convergence of any two of these subsequences imply the
convergence of the sequence {an}?
2.4.2. Does the convergence of every subsequence of {an} of the
form {"s.n}, 8 > 1, imply the convergence of the sequence {an}?


2.4.3. Let {Opn}' {4 qn },..., {aan} be subsequences of {an} such
that the sequences {Pn}, {qn},." , {8n} are pairwise disjoint and form
the sequence {n}. Show that, if S, Sp, Sq, ...,8. are the sets of all
the limit points of the sequences {an}, {Bpn}' {a qn }, ..., {Ban}' respec-
tively, then


S = Sp U Sq U ... USa.




2.4. Limit Points. Limit Superior and Limit Inferior 41


Conclude that) if every subsequence {apn}' {a qn }, ..., {a sn } converges
to at then the sequence {an} also converges to a.


2.4.4. Is the above theorem (Problem 2.4.3) true in the case of in-
finitely many subsequences?


2.4.5. Prove that, if every subsequence {an.} of a sequence {an}
contains a subsequence {a nkl } converging to a, then the sequence
{an} also converges to a.


2.4.6. Determine the set of limit points of the sequence {an}, where


(a)
(b)


(c)
(d)
(e)


(I)


an = V4 (-1)n + 2,
an=
(n_2_3[ n;1 ]) (n_a_3[ n;1 ]).
(1- (-I)n) 2 n + 1
an= 2 n +3 '
(1 + cosn1r) ln3n + In n
an = ln2n J
( n1l' ) n
an= cosT J
an = 2;2 _ [ 2;2 ] .


2.4.7. Find the set of all the limit points of the sequence {an} de-
fined by


(a) an = no - [no], aEQ,
(b) an = na - [no], O
Q,
(c) . QEQ,
an = SIn 1r1Kt t
(d) . Q
Q.
an = 8m 1rnct,


2.4.8. Let {ak} be a sequence arising by an arbitrary one-to-one
indexing of the elements of the matrix {.etn - .etm}, n, mEN. Show
that every real number is a limit point of this sequence.




42


Problems. 2: Sequences of Real Numbers


2.4.9. Assume that {an} is a bounded sequence. Prove that the set
of its limit points is closed and bounded.


2.4.10. Determine Jim an and lim an, where
n-oo n-=OO


(f)


an =
2 _ [ 2;2 ] ,
n - 1 n1r
an = n+ 1 cosT'
an = (-l)nn,
an =n(-l}ft n ,
1 · n1r
an = +nmD 2 ,
On = (1 +
) n (- 1)R +Sin
.
an = \1 1 + 2 n (-1)ft,
an = (2005 2
1r r,
Inn - (1 + cosn1r)n
an = In 2n ·


(a)


(b)
(c)
(d)
(e)


(g)
(h)


(i)


2.4.11. Find the limit superior
d the limit inferior of the following
sequences:


(a) an = no - [na], QEQ,
(b) On = no - [nQ], Q
Q,
(c) . QEQ,
an = am 1rna,
(d) an = sin 1rna, a
Q.


2.4.12. For an arbitrary sequence {an}, prove that
(a) if there exists kEN such that for any n greater than k the
inequality an
 A holds, then Jim an $ A,
n-oo




2.4. Limit Points. Limit Superior and Limit Inferior 43


(b) if for any keN there exists nk greater than k such that
an"
 At then Urn an < At


n-OQ


(c) if there exists kEN such that for any n greater than k the
inequality an
 a holds, then lirn an > a,
n-oo


(d) if for any keN there exists nk greater than k such that
an.
 at then Jim an > a.
R-OO


2.4.13. Assume that for a sequence {an} the limit inferior and the
limit superior are both finite. Prove that
(a) L = lim an if and only if
R-OO


(i) for every e > 0 there exists keN such that an < L + E if n > k


and


(ll) for every e > 0 and kEN there is nk > k such that L-E < an lc -


(b) l = Urn an if and only if
n-oo


(i) for every E > 0 there exists kEN such that I - e < an if n > k


and


(ll) for every E > 0 and keN there is nk > k such that lln. < I +e.


Formulate the corresponding statements for infinite limit inferior
and limit superior.


2.4.14. Assume that there is an integer no such that for n > no
the inequality an $ b n holds. Prove that


(a)
(b)


lim an < lim 6,.,
- --
"-00 n-oo


Jim an 5 Jim b n -
"-00 n-oo




44


Problems. 2: Sequences of Real Numbers


2.4.15. Prove that (excluding the indeterminate forms of the type
+00 - 00 and -00 + (0) the following inequalities hold:


lim an + lim b n
 lim (an + b n ) < lim an + lim b n
11,-00 n-oo n-oo n-oo 8-00
S lim (an + b n ) S lim 4n + lim b n -
n-oo n-oo 8-00


Give examples of sequences for which "S" in the above inequalities
is replaced by " < " _


2.4.16. Do the inequalities


lim an + lim b n < lim (an + b n ),
71-00 R-tOO n-oo


lirn (an + 6ft)
 Jim an + lim b n
n-oo 11,-00 8-00


remain valid in the case of infinitely many sequences?


2.4.17. Let {an} and {b n } be sequences of nonnegative numbers.
Prove that (excluding the indeterminate forms of the type o. (+00)
and (+00) - O} the following inequalities hold:
lim an. lim b n
 lim (an. b n )
 lim 4n. lim b n
11,-00 n-oo 11,-00 11,-00 11,-'00

 Urn (an - b n ) < Jim an - lim b n -
n-oo n-oo 8-00


Give examples of sequences for which "
" in the above inequalities
is replaced by "<"_


2.4.18. Prove that a necessary and sufficient condition for the con-
vergence of a sequence {an} is that both the limit inferior and the
limit superior are finite and


lim an = lim On-
n
 n-oo


Prove that the analogous theorem is also true for sequences which
properly diverge to -00 or +00_




2.4. Limit Points. Limit Superior and Limit Inferior 45


2.4.19. Show that, if 1im an = a , a e R , then
n-.oo


lim (an + b n ) = a + Jim b n ,
n-oo n-oo


nm (an + b n ) = a + lim bne
n-oo n-oo


2.4.20. Show that, if lim an = a, a E R , a > 0, and there exists a
n-oo
positive integer no such that b n
 0 for n
 no, then
Jim (an · b n ) = a. Jim b n ,


n-oo


n-oo


nm (an · b n ) = a. nm b n .
n-oo n-oo


2.4.21. Prove that
Jim (-an) = - nm an,
0-00 n-oo


Jim (-an) = - lim an.
n-oo 0-00


2.4.22. Prove that for any positive sequence {an},
lim
=
 I
n
 an lim On
"-00


_ Ii 1 1
m--
n-oo an - lim an.


0-00


(Here +
 = 0, -J+ = +(0).
2.4.23. Prove that, if {an} is a positive sequence such that
- - 1
lim an. lim - = 1,
n-oo 0-00 an


then the sequence {an} is convergent.
2.4.24. Show that, if {an} is a sequence such that for any sequence
{b n },


lim (an + b n ) = lim an + Urn b o


n-oo


0-00


0-00


or


lim (an + b n ) = Jim 4n + lim 6",
n-oo 0-00 0-00
then {an} is convergent.




46


Problems. 2: Sequences of Real Numbers


2.4.25. Show that, if {an} is a positive sequence such that for any
positive sequence {b n },
Jim (an · b n ) = Jim an. Jim b n


n-co


n-co


n-co


or


Jim (an · b n ) = Jim an. Jim b n ,
n-oo n-co R-OO
then {an} is convergent.
2.4.26. Prove that for any positive sequence {an},
lim a n +l < lim ra'il < Jim !It;;- < Jim Bn+l.
_ _ _ vu-n _ vlln _
n-oo an n-co n-oo n-oo an


2.4.27. For a given sequence {an}, define {b n } by setting
1
b n = -(al + C&2 +... + an), n e N.
n


Prove that


Jim an S Jim b n $ Jim b n ::; Jim an.
n-co n-oo n-oo n-oo


2.4.28. Prove that


(a)
(b)


lim (max{an,bn}) = max { fun a,., lim bn } ,
n-co n-oo n-oo
!!!!! (min{ an, b n }) = min { !!!!! an, !!!!! bn } .
»-00 n-
 n-oo


Are the equalities


(c)
(d)


fun (min{an,b n }) = min { lim an, iIiii bn } ,
R-OO R-
 n-oo
lim (max{an,b n }) = max { Jim an, Jim b n }
ft.-CO fl.-OO n-oo


also true?


2.4.29. Prove that every sequence of real numbers contains a mon

tonic subsequence.




2.5. Miscellaneous Problems



1


2.4.30. Use the result in the foregoing exercise to deduce the Bolzano-
Weierstrass theorem:
Every bounded sequence of real numbers contains a convergent
subsequence.


2.4.31. Prove that for every positive sequence {an},
Jim al + a2 + ... + an + an+l > 4.
R-OO an -


Show that 4 is an optimal estimate.


2.5. Miscellaneous Problems


2.5.1. Show that, if lim an = +00 or lim an = -00, then
R-OO n-OQ


( 1 ) an
Urn 1 + - = e.
R-(X) an


2.5.2. For x e R, show that
lim ( 1 +
 ) n = e Z .
n-oo n


2.5.3. For x > 0, establish the inequality
x
2 < In(x + 1) < x.
x+
Prove also (applying differentiation) that the left inequality can be
strengthened to the following:
x 2x
1 < 2 < In(x + 1), x > O.
x+ x+


2.5.4. Prove that


(a)
(b)


lim n( v'4 - 1) = In at a > 0,
n-oo
Urn n( v'ii - 1) = +00.
R-oo




48


Problems. 2: Sequences of Real Numbers


2.5.5. Let {an} be a positive sequence with terms different from 1.
Show that if lim an = 1, then
n-.oo


lim man = 1.
n-.oo an - 1


2.5.6. Let


111
an = 1 + _ 1 1 + _ 2 1 + ... + I' n E N.
.. n.


Show that


lim an=e
R-OO


and


1
0< e - an < -.
nn!


2.5.7. Prove that
( X x 2 XR )
lim 1 + _ 1 1 + _ 2 1 +... +., = ez.
R-oo .. n.


2.5.8. Show that
(a) lim ( ! + 1 1 +... + 2 1 ) = In 2,
n-oo n n + n


(b)
Jim ( 1 1 1 ) ln2
+ + ... + = .
R-OO yn (n + 1) .../ (n + 1)(n + 2) .../2 n(2n + 1)


2.5.9. Find the limit of the sequence {an}, where
an = (1 +
 ) (1 +
 ) · '" · (1 +
 ). n e N.


2.5.10. Let {an} be the recursive sequence defined by
al = 1, an = n(an-l + 1) for n = 2,3,....


Determine


lim rr n ( 1 +
 ) .
R-OO ale
k=1


2.5.11. Prove that Urn (n!e - [n!e]) = o.
R-OO




2.5. Miscellaneous Problems


49


2.5.12. Given positive a and b t show that
lim ( \fii + vb ) II = ,fOb,
n-oo 2


2.5.13. Let {an} and {b n } be positive sequences such that


Um a R = a, lim b n = b,
n-oo R n-too n


where a, b > 0,


and suppose that positive numbers p and q satisfy p + q = 1. Prove
that


lim (Pan + qbn)n = a"b q .
n-oo


2.5.14. Given two real numbers a and b, define the recursive sequence
{an} as follows:


al = a, a2 = b,


n-l 1
4n+l = an + -an-I, n
 2.
n n


Find lim an.
n-oo


2.5.15. Let {an} be the recmsive sequence defined by
01 = 1, a2 = 2, 4n+l = n(an + Crt-1), n > 2.
Find an explicit formula for the general term of the sequence.


2.5.16. Given a and b, define {an} recursively by setting
1 2n-l
al = a, a2 = b, 0n+l = 2n a n -l + 2n an, n > 2.
Determine lim an.
n-co


2.5.17. Let


n 1
an = 3 - t; k(k+ l)(k+ I)!' n E
I.
(a) Show that Urn an = e.
n-oo
(b) Show also that 0 < an - e < (n+l)
n+l)! .




50


Problems. 2: Sequences of Real Numbers


2.5.18. Calculate lirn nsin(21rn!e).
R-OO


2.5.19. Suppose that {an} is a sequence such that an < n, n =
1,2, ... ,and lirn an = +00. Study the convergence of the sequence
n-oo


( 1 -
 r. n = 1, 2, ... ·


2.5.20. Suppose that a positive sequence {b n } diverges to +00.
Study the convergence of the sequence
(l+
r. n=1.2.....


2.5.21. Given the recursive sequence {an} defined by setting


o < al < 1, tln+l = an (1 - an), n > 1,


prove that


(a)
(b)


lim na n = 1,
no-co


lirn n(t - nan) = 1.
n-oo Inn


2.5.22. The sequence {an} is defined inductively as follows:


o < at < 1r,


On+l = sinlln, n
 1.


Prove that lim,fnan = V3.
n-oo


2.5.23. Let


at = 1,


1
CLn+l = CLn + n ,
EOk
k=1


n
 1.


Prove that


lim an = 1.
n-co V2 ln n




2.5. Miscellaneous Problems


51


2.5.24. For {an} defined inductively by


a1 > 0, CLn+l = arctan an, n > 1,


determine lim an.
n-oo


2.5.25. Prove that the recursive sequence defined by


o < a1 < 1, an+J = cosan, n
 1,


converges to the unique root of the equation x = cosx.


2.5.26. Define the sequence {an} inductively as follows:
a) = 0, Cln+l = 1 - sin(an - 1), n > 1.


Find


1 n
Jim - "ak.
n-.oo n L..J
k=1


2.5.27. Let {an} be the sequence of consecutive roots of the equa.
tion tan x = x, x> o. Find lim (an+l - an).
n-'oo


2.5.28. For lal <
 and at e IR, consider the recursive sequence
defined by


6n+l = a sin an, n 2: 1.
Study the convergence of the sequence.


2.5.29. Given al > 0, consider the sequence {C1n} defined by setting
Cln+l = In(! + an), n > 1.


Prove that


(a)
(b)


lim 1U1n = 2,
n-oo


lim n(na.n - 2) = 2 .
n-oo Inn 3




52


Problems. 2: Sequences of Real Numbers


2.5.30. Define the recursive sequence {an} by putting
al = 0 and lJn+! = (
 )...., n > 1.
Study the convergence of the sequence.
2.5.31. Given al > 0, define the sequence {an} as follows:
£In+l = 2 1 - Q " J n > 1.
Study the convergence of the sequence.


2.5.32. Find the limit of the sequence defined by
Bl =.J2, lIn+l = 2
 , n
 1.


2.5.33. Prove that if 1im (On - an-2) = 0, then
n-CX)


lim an - a n -l = o.
R-OO n


2.5.34. Show that if for a positive sequence {an} the limit
lim n ( 1- an+1 )
n-co an
exists (finite or infinite), then


In-L
lim an
n-CX) In n


also exists and both limits are equal.
2.5.35. Given a}, bl E (0,1), prove that the sequences {an} and
{b n } defined by
an+l = al(l- an - b n ) + an, b n + 1 = b 1 (1- an - b n ) +b nJ n > 1,
converge and find their limits.
2.5.36. For positive a and aI, consider the sequence {an} defined
by setting
an+l = an(2 - aan), n = 1,2,....
Study the convergence of the sequence.




2.5. Miscellaneous Problems


53


2.5.37. Show that if at and a2 are p ositive and
lIn+2 = ..;a; + y4n +lt n = 1,2, ...,
then the sequence {an} converges. Find its limit.
2.5.38. Assume that f : Ri -t R+ is a function increasing with
respect to every variable and there exists a > 0 such that


f(x,x, ...,x) >:c for 0 < :c < at
f(x, x, ..., x) < x for x > a.
Given positive a1,a2J ... ,ak, define the recursive sequence {an} by


an = f(an-1' tln-2, ..., an-k) for n> k.
Prove that lim an = a.
n.....oo


2.5.39. Let al and a2 be given positive numbers. Study the con-
vergence of the sequence {an} defined by the recursive relation


an+l = a n eO,,-c n - 1 for n > 1.


2.5.40. Given a > 1 and x > 0, define {an} by setting at =
Q,%, l1n+l = a Bn , n E N. Study the convergence of the sequence.


2.5.41. Show that
12+ ';2+... +
 = 2cos ;'. "
".


n roots


Use this relation to find the limit of the recursive sequence given by
setting


al=V2, tln+l= v2 +an, n > l.


2.5.42. Let {En} be a sequence whose terms are equal to one of the
three values -1, 0, 1. Establis h the formula.
J ( n )
. 1T EIE2...Ek
El 2+E2 V 2 +...+ E ...J2=2sm 4"L 2 k - 1 ,neN,
k= 1




54


Problems. 2: Sequences of Real Numbers


and show that the sequence
an = £) V2 +£2 V 2 +... +£nV2


converges.


2.5.43. Calculate


1 . ( 1 1 1 )
n

 arctan 2 + arctan 2 . 22 + ... + arctan 2n 2 ·


2.5.44. Find lim sin(7r vn 2 + n).
n-oo


2.5.45. Study the convergence of the recursive sequence defined as
follows:
4) = Vi, 02 = -/2 + V3, t1n+2 = -/2 + ';3+an for n
 I.


2.5.46. Show that


JLn;, 1 + 2 V 1 +3 V l + ''' V l + (n-l) '; 1 +n = 3.


2.5.47. Given a> 0, define the recursive sequence {an} by putting


a
al < 0, a n +l = - - 1 for n e N.
an
Show that the ,sequence converges to the negative root of the equation
3: 2 + x = a.


2.5.48. Given a> 0, define the recmsive sequence {an} by setting


a
at > 0, Bn+l = 1 for n e N.
Bn+
Show that the sequence converges to the positive root of the equation
x 2 +x=a.




2.5. Miscellaneous Problems


55


2.5.49. Let {an} be the sequence defined by the recursive formula
2+an
al = 1, lln+l = 1 for n E N.
+a n
Show that the sequence is Cauchy and find its limit.
2.5.50. Show that the sequence defined by
1
lln+l = 2 + -, n e N,
an


al > 0,


is Cauchy and find its limit.
2.5.51. Given a> 0, define {an} as follows:


a
al = 0, l1n+l = for n e N.
2+an
Study the convergence of the sequence.


2.5.52. Assume that
al E 1R and an+l = Ian - 2 1 - n l for n e N.
Study the convergence of the sequence and in case of convergence find
its limit .


2.5.5.3. Show that
(a) if 0 < a < 1, then


n-l . j
lim
 JO = 0,
R-OO L..J n - , .
;=1


(b) if 0 < a < 1, then


nIl
Urn na n
 -:--:' = ,
n-oo L.J 30) 1 - a
j=1


(c) if b> 1, then


n n 1>1- 1 1
lim-" -
R-OO b n L...J j - b - 1 ·
;=1




56


Problems. 2: Sequences of Real Numbers


2.5.54. Calculate
Ii ( . 1r . 1f' . 1f' )
m sin 1 + sm 2 + ... + sm _ 2 ·
n-oo n+ n+ n


2.5.55. Find


(a)


n
ft ( 1+
 ) ,
k=-l


where c > 0,


(b)


n ( k2 )
Jim TI 1-- ,
n....oo cn,3
k=-l


where c > 1.


2.5.56. Determine


qn n k
lim v n ".. TI .
n-oo n! SlD n 'fiA
k=l VIII


2.5.57. For the sequence {an} defined by
an=t(
)-l, n
l,
11:=0
show that lim On = 2.
n-oo


2.5.&8. Determine for which values of Q the sequence


an = (1- (;f) (1- (
f) ..... (1- ( n: 1 f), n > 2,


converges.


2.5.59. For x e R, define {x} = x -[x]. Find lim {(2 + V3)n}.
n-oo


2.5.60. Let {an} be a positive sequence and let Sn = a1 + 42 + ... +
an, n
 1. Suppose that
1
Bn+l
 S «8 n - l)an + an-I), n > 1.
n+l


Determine lim C n .
n-co




2.5. Miscellaneous Problems


57


2.5.61. Let {an} be a positive sequence such that
an. _ 1 . at + fI2 + ... + an
lirn - = 0, 1m < 00.
B-OO n 0-00 n


Find


lim ai +
 + e.. + a;
0-00 n 2 ·


2.5.62. Consider two positive sequences {an} and {b n } such that
Jim an = 0 and lim b n = o.
n-oo a} + B2 + ... + an n-oo b 1 +
 + .n + bft
Define the sequence {en} by setting


en = alb n + a2 b n-l +... + anbtt n E N.


Show that


lim en = o.
n-oo CI + C2 +... +Cn


2.5.63. Find


n 2
lim ( 1 + ! ) e-n.
n-oo n


2.5.64. Suppose that a sequence {an} bounded above satisfies the
condition


1
an+l - an > -2' n e N.
n
Establish the convergence of {On}.
2.5.65. Suppose that a bounded sequence {an} satisfies the condi-
tion


2n
 2
a n +l V

 On,
Establish the convergence of {an}.
2.5.66. Let l and L denote the limit inferior and the limit superior of
the sequence {an}, respectively. Prove that if lim (t1n+ 1 - an) = 0,
n-oo
then each number in the open interval (I, L) is a limit point of {an}.


nEN.




58


Problems. 2: Sequences of Real Numbers


2.5.67. Let I and L denote the limit inferior and the limit superior of
the sequence {an}, respectively. Assume that for any n, 4n+l -an >
-Qn, where On > 0 and Jim an = o. Prove that each number in
n-oo
the open interval (I,L) is a limit point of {an}.


2.5.68. Let {a,..} be a positive and monotonically increasing se-
quence. Prove that the set of all limit points of the sequence
an
I n E N,
n+4n
is an interval (which is reduced to a singleton in case of convergence).


2.5.69. Given at E JR, consider the sequence {an} defined by
{
 for even n,
lIn+l = 1 +an
2 for odd n.
Find the limit points of this sequence.


2.5.70. Is zero a limit point of the sequence {,;n sin n}?


2.5.71. Prove that for a positive sequence {an},
lim ( a 1 +4n+l ) n
 e.
R-OO an


2.5.72. Prove the following generalization of the foregoing result:
For a positive integer p and a positive sequence {an} I
Jim ( a 1 + 4n+ p ) n
 e'P.
n-t)O an


2.5.73. Prove that for a positive sequence {an},
Jim n ( l+4n+l -1 )
1.
R-OO On


Show that 1 is the best possible constant.




2.5. Miscellaneous Problems


59


2.5.74. Let


4n = V 1 + -J 1 + ... + ..ti ·
trr... ."..---



n roots


Find lim an.
n-oo


2.5.75. Let {an} be a sequence whose terms are greater than 1 and
suppose that


lim Inlna n = Q.
11-00 n
Consider the sequence {b n } defined by
b n = J 4 } + -J 4 2 + ... + .jii;;, n e N.
Prove that if a < In2, then {b n } converges; and if a > ln2, then it
diverges to +00.


2.5.76. Assume that the terms of the sequence {an} satisfy the con-
dition
o
 On+m < an +am for n,m EN.
Show that the limit lim
 exists.
11-00


2.5.77. Assume that the terms of the sequence {an} satisfy the con-
dition
o :s a n + m
 an · am for n, mEN.
Show that the limit Jim
 exists.
11-00


2.5.78. Assume that the terms of the sequence {an} satisfy the con-
ditions


lanl < 1,
an +4m -1:S l1n+m < an +a m + 1


for nJm eN.
(a) Show that the limit fun
 exists.
n-oo
(b) Show that if lim
 = g, then
11-00
ng - 1
 an
 ng + 1 for n E N.




60


Problems. 2: Sequences of Real Numbers


2.5.79. Assume that {an} is a positive and monotonically increasing
sequence that satisfies the condition
CIn.m
 nam for n, meN.
Prove that if sup {
 : n E N} < +00, then the sequence {
}
converges.


2.5.80. Given two positive numbers aI, 02, prove that the recursive
sequence {an} defined by


2
Bn+2 = for n E N
tln+1 + 4n


converges.


2.5.81. For bt > 01 > 0, consider the two sequences {an} and {b n }
defined recursively by setting
an + b n _ I b
 JU
Bn+l = ,b n + 1 = V Bn+l n lor n E 1'1.
2
Show that both sequences converge to the same limit.


2.5.82. Let Ok,n, bk,n, n e N, k = 1,2, ..., n, be two triangular
arrays of real numbers with bk,n #= o. Suppose that :",n -. 1
..n n-oo
uniformly with respect to k, that is, for any e > 0 there is a positive
integer no such that


ak,n -1 1 < e
bkn
,


n
for each n > no and k = 1,2, ..., fi. Show that if lim E bk,n exists,
n--+oo k=l
then


n n
lim
 Bk..n = lim.
 ble,n.
n--+oo L...J n-+oo L...J
k=l k=l


2.5.83. Given a:F 0, find
lim E n · (2k - l)a
sm 2 ·
n-+oo n
Ie=!




2.5. Miscellaneous Problems



.1


2.5.84. For a > 0, determine


n
n
E(a
 -1).
Ie=l


2.5.85. Find


n
ft ( 1+ :2 ) .
k=l


2.5.86. For p:/= 0 and q > 0, determine
n (( kq-l )
 )
n

E 1+ n'l -1.
k-:l


2.5.87. Given positive numbers a,b and d such that b> a, calculate
fun a(a+d)...(a+nd)
n
oo b(b + d)...(b + nd) ·




Chapter 3


Series of Real Numbers


3.1. Summation of Series


3.1.1. Find the infinite series and its sum. if the sequence {Sn} of
its partial sums is given by setting


(a)
(c)


n+l
Sn = I n e .N ,
n
8n = arctan n, n e N ,


(b)
(d)


3.1.2. Find the sum of tbe series


00 2n+ 1
(a)
 n 2 (n + l}2 ,

n- vn 2-1
(c) L....J '
"n=1 Vn (n + 1)
00 1
(e) E ·
n=1 (v'ii + ,fn + 1) Vn (n + 1)


2 n -l
Sn = "2 n t n E Nt
(_l)n
Sn = to n. E N.
n


co n
(b) E (2n -1}2(2n+ 1}2 '
n-l °
co 1
(d) E 4n 2 - 1 '
.n=l


"63






A
-



Problems. 3: Series of Real Numbers


3.1.3. Compute the following sums:


(b)


In! + EIn (n+ 1)(3n+ 1)
4 n= 1 n(3n+4)'

ln (2n+ l)n

 (
+ 1)(2n-l)-


(a)


3.1.4. Find the sum of the series
00 1
L ( ) ( r meN.
n= 1 n n + 1 ... n + m
00 1

 meN
L...,; n ( n + m)' ,
n=1
OQ 2

 (n+ 1)(n+ 2)(n+3)(n+4) '


(a)


(b)


(c)


3.1.5. Compute


(a)


00 I
""' . n.w
L.J sm 720 '
n=1


(b)


co 1 [ Inn ]
En n-lnn ·
n- l


3.1.6. Calculate


00 1 3
E sin 2"+1 COB 2 n +1 '
n=1


3.1.7. Find


00 1
E n!(n 4 +n2 + I) '
n=O


3.1.8. Show that


00 n 1

 3,5, .., · (2n + 1) = 2'




3.1. Summation of Series


65


3.1.9. Suppose that {an}
 a sequence satisfying
lim «at + 1)(a2 + l)...(an + 1» = g, U < 9 S +00.
n-tOO
Prove that




 1

 (at + 1)(l12 + 1)...(a,. + 1) = 1 - g'
where we assume that
 = o.


3.1.10. Using the result in the foregoing problem, find the sum of
the series


(a)


00
'" n-l
L..., n! '
n=1
00

 2n-l
L.J l 2 · 4 · 6 · ... . 2n '
n=
00 1
E

n=2 (1-
) (1-
)... (1-
).


(b)


(c)


3.1.11. Let {an} be a recursive sequence given by setting
al > 2, 4n+l = a
 - 2 for n E N.


Show that


E 1 = al - y'a
 - 4 .
1 al · lL2 · ... · an 2
n=


3.1.12. For b >. 2, verify tbat
}': n! = 1 .
n=1 b(b + l)...(b + n - 1) b - 2



.1.13. For a > 0 and b > a + 1, establish the equality

 a(a + l)...(a + n -1) a

 b{b + 1)...(b + n - 1) = b - a-I ·




bt>


¥rODJems. 3: :senes 01 .H.eaJ Numbers


3.1.14. For a > 0 and b > a + 2. verify the following claim:

 a(a + 1)...(4 + n - 1) a(b - I}

 n b(b+ 1)...(b+n -1) = (b- a-l)(b-a- 2)'


00
3.1.15. Let -E -t: be a divergent series with positive terms. For
n=1
b > 0, find the sum


co
?; (
+ b)(



)


(::+1 + b)"


3.1.16. Compute


f( _1)n cos;:n x .
n=O


3.1.17. Given nonzero constants a,b and c, suppose that the func-
tions f and 9 satisfy the condition f(x) = af(bx) + cg(x).
(a) Show that, if Jim aRJ(bnx) = L(x) exists, then
n-.oo


E OO n (b n ) _ f(x) - L(x)
a 9 x - .
C
n=O


(b) Show that, if lim a- n f(b-nx) = M(x) exists, then
n-.oo
E co -n (b - n ) _ M(x) - af(bx)
a 9 x - .
c
w=O


3.1.18. Applying the identity sin:z;
 35m f - 4sin 3 i, show that


(a)


00 .

 3 n .3 X _ X-SlnX
LJ sm 3 n + 1 - 4 '
n=O
00

1.3 X 3.:&
L.-,
Sln 3-- n + 1 =4 SID S.
n=O


(b)




3.1. S umm ation of Series


67


3.1.19. Applying the identity cotX' = 2 cot (2x) + tan x for x
 ki,
k E Z, show that


IX) 1 x 1
"" - tan - = - - 2 cot ( 2x).
L..J 2" 2 n :&
n=O


3.1.20. Using the identity arctanx = arctan(bx) +.arctan \1+:2: t
establish the formulas



 (1- b)bRx
(a)
 arctan 1 + b 2n + 1 x2 = arctan x for 0 < b < 1,
n=O
00 (b - l)b" x
(b) E arctan 1 + lJ2n+lx2 = arccotx for X:F 0 and b> 1.
n=O


3.1.21. Let {an} be the Fibonacci sequence defined by setting


ao = a1 = 1, 4;.+1 = an +an-t, n
 1,


n
and put Sn = E a
. Find
k=O



 (-l)n

S.
n=0 n


3.1.22. For the Fibonacci sequence {an} defined in the foregoing
problem, calculate


E (-l)n .
n=O OnBn+2


3.1.23. For the Fibonacci sequence {an} defined in 3.1.21, deter-
mine the sum of tbe series


00 1
E arctan-.
n=1 tl2n




68


Problems. 3: Series of Real Numbers


3.1.24. Find the sum:


(c)


00 2
Earctan n 2 '
n=1
00 8
Earctan n4 - 2: 2 +5 '
n=1


00 1
(b) Earctan 2 1 '
n=1 n +n+


(a)


3.1.25. Let {an} be a positive sequence that diverges to infinity.
Show that


co

 an+l-On 1
L...J arctan 1 = arctan -.
n=1 + anan+l a}


3.1.26. Prove that any rearrangement of the terms of an infinite
positive series does not change its sum.


3.1.27. Establish the identity
co 1 3 00 1
E (2n-l)2 ="4 E Ji2'
n 1 n= 1


3.1.28. Prove that


(b)


00 1 w2
E 1i2 = 6'
n=l
00 1 1f'4
E fii = 00'
n=l
00
E(-l)ft 2n
1 = i.
,
o


(a)


(c)


3.1.29. For the sequence {an} defined recursively by
al = 2, CLn+l = a
 - Bra + 1 {or n
 1,


co
find E t.
n=1




3.1. S umm ation of Series


69.


3.1.30. Let {an} be defined as !ollows:


al > 0,


eArl - 1
an+l = In for n
 1,.
an


00
and set b,. = al · fI2 ..... an- Find E b n -
n=l


3.1.31. Let {an} be defined by setting
1
al = 1, Cln+l = - Vi
al + lJ2 + ... + l1n


for n>l.
-


00
Determine the sum of the series E an.
n=1


3.1.32. Find the sum of the following series:.


(b)


00
L:(-l)n-I
.
n=l
00
"'(_I)n-l 2n+ 1 .

 n(n+l)
OO ( 1 1 1 )

 x+2n-l + x+2n - x+n ·


.X :F -1, -2,....


(a)


(c)


3.1.33. Calculate


:E<-I)n- 1 1n ( I +
 ) .
n=1


3.1.34. Compute



 <-l)n-lln (1- (n
 1)2 ).


3.1.35. Determine the sum of the series



 (;-1n(1+;)).




70


Problems. 3: Series of Real Numbers


3.1.36. Suppose that a function f is differentiable on (0, 00), that its
derivative I' is monotonic on a subinterval (a. +00), and lim f'(x) =
x-+oo
o. Prove that the limit
n1!..
 (
/(I) + 1(2) + 1(3) +... + I(n -I) +
 /(n) -in I(x)dx )
exists. Consider also the special Ca5e5 of the functions f(:c) -
 and
f(x) = lnx.


3.1.37. Determine the sum of the series
f:(-l)n
n .
n=1


3.1.38. Find


?i (nln
::
 -I).


3.1.39. Given an integer k
 2, sho\v that the series


00 ( 1 1 1 X )
+ + ... + - -

 (u-l)k+ 1 (,,-l)k+ 2 uk -1 uk
converges for only one value of x. Find this value and the sum of the
.
senes.


3.1.40. For the
ence {an} definen by

t.ting
3+ (-l)n
ao = 2, an+l = an + ? '
...


compute


XI

(-l)[!!fl] 1 .
L..J a 2 - 1
n=O n


3.1.41. Prove that the sum of the series
co 1 00 1
(a) E nt ' (b) E (n!)2
n=1 n.=1


is irrational.




3.1. S llmmat ioD of Series


71


3.1.42. Let {En} be a sequence where En is either 1 or -1. Show
00
that the sum of the $el.i
 E
 is an llTational number.
n=l


3.1.43. Show that for any positive integer k the sum ot the series
00 (-l)n
k (n!)k


is irrational.


3.1.44. Suppose that {nk} is a monotonically increasing sequence
of positive integers such that
Iim nk
= +00.
k-oo ntn2". ... · nk-1


oc
Prove that E
 is irrational.
. 1 '
1=
3.1.45. Prove that, if {nk} is a sequence of positive integers such
that


lim nk d
=+00 an
k-cc nl n2 · ... · Rk-l


fun nk > 1
_ 1
.Ie-co nk-l


00
then E t is irrational.
. 1 '




3.1.46. Suppose tbat {nk} is a monotonically increasing sequence
00
of positive integers for which "lim 2V'iik = 00. Prove that E ; is
k-OQ k=l II
irrational.


00
3.1.47. Let E
, where Pn,qn EN, be a convergent series and let
n=l
Pn Pn+l > Pn .
qn - 1 qn+l - 1 - qn
Denote by A the set of all n for which the above inequality is sharp.
00
Prove that E En. is irrational if and only if the set A is infinite.
n=l 9n
3.1.48. Prove that for any strictly increasing sequence {nk} of po

00
itive integers the sum of the series E
nT is irrational.
k=l "




72


Problems. 3: Series of Real Numbers


3.2. Series of Nonn
gative Terms


3.2.1. Determine whether the following series converge or diverge:
oc 00 ( n 2 + 1 ) n 2
(a) L ( V n 2 + 1- V n 3 + 1 ), (b)
 n 2 +n+l '
n=l
f (2n - 3)!! 00 ( n ) n(n+l)
(c) (d) L n+1 '
n=2 (2n - 2)!! '
n=1
f(1-COS;). 00
(
) (f) L(
-l)n,
n=l n=1
00
(g) L(
-l), a>l.
n=1


3_2_2_ Test the following series for convergence=


(a)


00 1 ( 1 )
L-ln 1+- J
n==l n n
00 1
L n 2 -Inn '
n=1
00 1
L (lnn)lnlnn "
n=2


(b)


co


ln n+l

vn n-1'
<X> 1
E (lnn)lnn '
n=2


(c)


(d)


(e)


00 00
3.2.3. Let E Bn, E b n be series of positive terms satisfying
n=1 n=1


C1n+l < bn+l I". >
- b lor n - no.
an n .


00 00
Prove that if E b n converges, then E an . also converges.
n=1 n=1 .


3.2.4. Test these series for convergence:


(a)


00 ft--2

1"
L.J enn! '
n=1


(b)


00

 ",," .
L..J enn!
n=1




3.2. Series of Nonnegative Terms


13.


3.2.5. Determine for which values of Q tbe given series converges.


(8)


co
E< v'Ci - 1)Q, a > 1,
n.=1


OQ
(b) E( v'1i -1)°,
n=l


(c)


00 (( 1 ) "+1 " ) 0

 1+; -e,


00 ( l ) Q
(d) E I-nsin; ·
n-J


00
3.2.6. Prove that, if a series E an with positive terms converges,
n=1


then


co
E (a Qn - 1), where a > 1,
n=1


a1so converges.
3.2.7. Investigate the behavior (convergence or divergence) of the
following series:
(a) f: -In ( ros
 ) , (b) f:e
I:::
 . a,b.c,d e JR,
n= 1 n= l
00 2n
(c)
 (n+a)n;(n+b)n+A ' a.b> O.


00
3.2.8. Suppose a series E an of nonnegative terms converges. Prove
n=1
00
that E v'l1n Bn+l a1so converges. Show that the converse is not true.
n=1
H, however, the sequence {an} is monotonically decreasing,-then the
converse statement does hold.


00
3.2.9. Assume that a positive-term series E an diverges. Study
n=1
the behavior of the following series:


(a)


co

 an
L.Jl+ an '
n=l
00
E 1+
2an '
n=l


(b)


00

1+
 '
00
E 1
a2 ·
n=1 n


(c)


(d)




74


Problems. 3: Series of Real Numbers


00
3.2.10. Assume that a positive term series E an diverges. Denote
n=1
by {Sn} the sequence of its partial sums. Prove that


co
L
 diverges
n=1 n
and
00
L:¥ converges.
n=l n


3.2.11. Show that under the assumptions of the preceding proposi-
tion the series


00
L


=2 SnSn-l


converges for each (J > O.
3.2.12. Prove that under the assumptions of 3.2.10 the series


00
LF
n=l n
converges if a > 1 and diverges if Q
 1.


00
3.2.13. Prove that, if a positive term series E Cn converges and
n=J
00
Tn = E aiel n E N, -denotes the sequence of its re main ders, then
k=n+ 1


(a)


00
L fin diverges,
2 rn-l
n=
00
" an
L.-, converges.
n=2 VT n-l


(b)


3.2.14. Prove that under the assumptions of the foregoing problem


00
E

n=2 T n-l
converges if Q < 1 and diverges if a
 1.




3.2. Series of Nonnegative Terms


75


3.2.15. Show that under the assumptions of Problem 3.2.13 the series
00 "
E On+l ln - Tn converges.
n=)


00
3.2.16. Let E an be a series of positive terms. Suppose that
n=1


lim In an
n .= g.
R-cx) 4n+ 1


00
Prove that E an converges if 9 > - 1 and diverges if 9 < 1 (the
n=l
cases 9 = +00 and 9 = -00 &r.e included). Show that if 9 = 1, then
the te:st
 wcollclw;ive.


3.2.17. Study the behavior of the following series:


(a)


co 1
E 2v'ii I
n=l
co 1
E alon I
n=1-


(b)


00 1 00 1
E 210n ' (c) L 3 lnn '
n
l n-I
DO 1
(e) E alnlnn I a > O.
-n=2


(d)


a> 0,


3.2.18. Discuss convergence of the series


o:c
E a 1 +!+...+!i , a > O.
n=1


3.2.19. Use the result of Problem 3.2.16 to prove the limit form of
the Test of Raabe.
Let an > 0, n E N, and let
lim ( On 1)
n - = T.
A-OO a n +l


co
Prove that E an converges if r > 1 and diverges if r < 1.
n=1


3.2.20. Let {an} be defined recursively by setting
1
at = 112 = 1. an+l = 11n + 2'4n-l for n
 2.
n


co
Study convergence .of the series E t:.
n=1




76


Problems. 3: Series of Real Numbers


3.2.21. Let at and Q be positive. Define the recursive sequence
{an} by putting


Q
an+1 = ane-a" for n = 1,2, .....


00
Determine for which values of Q and {J the series E a
 converges.
n=1


3.2.22. Determine for which values of a the series


00 I

 n.

 (a + 1)(a+2)..... (a+n)


converges.
3.2.23. Let a be an arbitrary positive number and let {b n } be a
positive sequence converging to b. Study the convergence of the series
00 n!a n

 (4 + bt)(2a + bz) 0 no 0 (na + b,.) .
3.2.24. Prove that, if a sequence {4n} of positive numbers satisfies
an+l _ 1 _ ! _
n
- ,
an n nlnn


00
where 7n
 r > 1, then E an converges. On the other hand, if
n- l
l1n+l = 1 _ ! _ 7n
an n nlnn'


00
where 7n 5 r < 1, then E an diverges. (This is the so-called Test
n=1
oj Bertrand.)


3.2.25. Use the tests of Bertrand and Raabe to derive the follQwing
Criterion of Gauss.
H {an} is a sequence of positive numbers satisfying
Bn+l 1 Q 1J n
an = -;; - n
 '


OC)
where A> 1 and {{)n} is abounded sequence. then E an converges
n=1


when Q > 1 and diverges when Q
 1.




3.2. Series of Nonnegative Terms


11


3.2.26. Discuss the convergence of the series
f: o( Q + 1) 0 no 0 (Q + n - 1) f;I({j + 1) 0 nO ° ({j + n - 1)
n=1 n!
(
 + 1) · ... · ('Y + n - 1) ,
where a, {J and '1 are positive constants.


3.2.27. Determine for which values of p.


f: ( in-I)!! ) "
n=l (2n)!!


converges.


3.2.28. Prove the following condensation test of Cauchy.
Let {an} be a monotonically decreasing sequence of nonnegative
00
numbers. Prove that the series E On converges if and only if the
n-l


00
series E 2 n ll2 n converges.
n=1


3.2.29. Test the following series Cor convergence:


(a)


00 1

 n(lnn)o '


(b)


00 1
E nolnnolnlnn °
n =3


3.2.30. Prove the following Theorem of Schlomilch (a generalization
of the Cauchy theorem, see Problem 3.2.28).
If {gk} is a strictly increasing sequence of positive integers such
that for some c > 0 and for all keN, 9"+1 - 9k < C(gk - gk-I) and
if a positive sequence {an} strictly decreases, then


00
E an < 00 if and only if
n=1


00
E(gk+l - 9k)a 91c < 00.
n=1


3.2.31. Let {an} be a monotonically decreasing sequence or positive
00
numbers. Prove that the series E an converges jf and only if the
n==1
fonowing series converges:




78 Problems. 3: Series of Real Numbers


-:0 00 o':'JO
(a) Lana3n) (b) L1ULn 2 , (c) Ln2ana.
n=1 n=l n==1
(d) Apply the above tests to study convergence of the series
in Problem 3.2.17.


3.2.32. Suppose that {lIn} is a positive sequence. Prove tbat
- 1 1
Iim (an) JDn < -
n-oo e
00
implies the convergence of E an.
n=!


3.2.33. Suppose that {an} is a positive sequence. Show that
lim (na n ) m/an < .!
n-oo e
00
implies the convergence of E a".
n=1


3.2.34. Let {an} be a monotonically decreasing sequence of positive
numbers such that


2"
B2n
 9 < 1.
an


00
Show that E l1n converges.
n=1


3.2.35. Let {an} be a monotonically decreasing sequence of nonneg-
00
ative numbers. Prove that if E tin converges, then lim nan = O.
n=1 n-.oo
Show that this coIidition is not sufficient for the convergence of the
series.


3.2.36. Give an example of a convergent series with positive terms
for which the condition lim na n = 0 does not hold.
n-oo


00
3.2.37. Let E an be a convergent positive
ries. Giv
 necessary
n=1
and sufficient conditions for the existence of a positive sequence {b n }




3.2. Series of Nonnegative Terms


79


such that the series


00
Eb n
n=l


and


00
E?
n=1 n


both converge.


3.2.38. Does there exist a po
itive
quence {Un}
uch (,hat t,h




.
nes


00
L an and
n=)


00 1
L n 2 a
n=1 n


both converge.


3.2.39. Show that


00
L.!.' 1 +an+J
n=l n an
diverges for any positive sequence {an}.


3.2.40. Let {an} and {b n } be monotonically decreasing to zero and
IX) 00
such that the series E an and E b n diverge. What can be said
n=1 n=J
00
about the convergence of E en, where en = min{an,b n }?
n=1


3.2.41. Let {an} be a monotonically decreasing sequence of nonneg-
00
ative numbers such that E
 diverges. Assume that
n=l


b,. = min {an t 1n(n 1 + 1) }'


00
Prove that E
 also diverges.
fa.=; 1


3.2.42. Let {an} be a bounded, positive and monotonically increas-
ing sequence. Prove that



(l- a::J


converges.




80


Problems. 3: Series of Real Numbers


3.2.43. Let {an} be an increasing positive sequence diverging to
infinity. Prove that


00 ( )
E 1- an
n=1 Bn+l


diverges.


3.2.44. Let {an} be a positive monotonically increasing sequence.
Show that for any Q > 0


00
E an+l-CLn
n= 1 4n+la



converges.


CXJ
3.2.45. Show that for any positive and divergent series E an there
n=l
exists a sequence {en} monotonically decreasing to zero such that
00
E 4nCn diverges.
n=1


00
3.2.46. Show that for any positive and convergent series E an
n=1
there exists a sequence {en} monotonically increasing to infinity such
00
that E lInCn converges.
n=1


00
3.2.47. Let E an be a convergent series with positive terms. Let
n=1
co
{r ft } denote the sequence of its re m8.in ders. Prove that if E Tn
n=l
converges, then lim nan = O.
n.....oo


3.2.48. Let {an} be a positive sequence diverging to infinity. What
can be said about the convergence of the following series:
00 1 00 1 00 1
(a) E an' (b):E a lnn ' (c) E a lnlnn ?
n=1 n n=1 n n=l n


co
3.2.49. Study convergenr.e of E an, where
n=1
a1 = 1. l1n+l = COStin for n E N.




3.2. Series of Nonnegative Terms


81


3.2.50. Let p be an arbitrarily fixed nonnegative number. Study the
00
convergence of E Unl Whel"e
n=l


at = I, l1n+l = n-Psinan for n E N.


3.2.51. Let {an} be a sequence of consecutive positive solutions of
00
the equation tan x = x. Study the convergence of E c!;-.
n= 1 "


3.2.52. Let {an} be a sequence of consecutive positive solutions of
00
the equation tan VX = x. Study the conver
ence of E t:.
n=1


3.2.53. Let al be an arbitrary positive number and let 4n+l =
00
1n(1 + an) for n
 1. Study the convergence of E an.
n=l


3.2.54. Assume that {an} is a positive monotonically decreasing
00
sequence such that E an diverges. Show that
n=l


lim 41 + 43 +... + 42n-l = 1.
n-OQ 02 + 04 + ... + 02n


3.2.55. Let Sic = 1 + i + ... + t and let kn denote the least of all
positive integers k for which Sic
 n. Find
1im kn+l .
n-.oo kn


3.2.56. Let A be the set of all positive integers such that their dec-
imal representations do not contain zero.
(K) Shuw that, E
 converges.
neA
(b) Determine all a such that E ;to converges.
neA


00
3.2.57. Let E an be a series of positive t.enns and l
t
n=l


In-L
lim an
=9.
n-oo In n




82


Problems. 3: Series of Real Numbers


Prove that if 9 > 1, then the series converges, and if 9 < 1, then the
series diverges (here 9 may he equal to +00 or -00.)
Give examples showing that in the case of 9 = 1 the criteri
n is
indecisive.


3.2.58. Show that the Raabe test (see Problem 3.2,,19) and the test
giv
n in Pruul
JI1 3.2.16 ar

quivw
llL. Murwv
r, show that the
criterion in the preceding problem is stronger than each of the above
mentioned tests.


00
3.2.59. Study the convergence of E an whose terms are given by
n=l


al = V2 t


an=


2- V2 + V2 +...+V2. n > 2.




(TI-l)-roots


3.2.60. Let {an} be a sequence monotonically decreasing to zero.
Show that if the sequence with tenns
(al - an) + (a2 - an) +... + (a n -l - a,a)


00
is bounded, then E an must converge.
n=1


3.2.61. Find a series whose terms On satisfy the following conditions:
1
al = 2 ' an = an+l + 4n+2 +... for n = 1,2,3,....


00
3.2.62. Suppose that the terms of a convergent series E an whose
n=1


sum is S satisfy two conditions:
a)
 a2
 a3
... and 0 < an < a n +l + a n +2 + ..., n E N.
Show that it is possible to represent any number s in the half-closed
00
interval (0, S] by a finite sum of terms of the series E an or by an
n=l
00
infinite subseries E an,., where {an
} is a subsequence of {an}.
k=l




3.2. Series of Nonnegative Terms


83


00
3.2.63. Assume that E an is a series of positive and monotonically
n=l
decreasing terms. Prove that if each number in (O,S), where S de-
notes the sum of the series, can be represented by a finite sum of
00
terms of {an} or by an infinite subseries E an", where {lln,,} is a
1c=1
subsequence of {an}, then the following inequality holds:
On
 a n +l + On+2 + ... for each n E N.


00
3.2.64. Let E an be a divergent series of positive terms and let
n=1
lim r- = 0, where Sn = at + a2 + ... + an. Prove that
n-oo n


8 -1 5 -1 + + 5 -1
Ii at 1 + CZ2 2 ... an n - 1
m -.
R-OO In 8n


3.2.65. Using the preceding problem, show that
Urn 1 +
 + l + ... +

= 1.
n-co Inn


00
3.2.66. Let E an be a convergent series of positive terms. What
n=l
can be said about the convergence of


00
2: at + t&2
 ... + an ?
n=l


n
3.2.67. Prove that if {an} is a positive sequence such that * E ak

1c=1


2n 00
E ak for n E N, then E an < 200 1 .

+1
 1


3.2.68. Prove the following Inequality oj Carleman:
If {fin} is 8. posit.iv
 AAqnenr..e, then


00 00
E VI al · ... · an < e E an,
n=l n=l




84


Problems. 3: Series of Real Numbers


co
provided that E an converges.
n= 1


3.2.69. Show that if {an} is a positive sequence, then, for every
positive integer k,


00 1 00 ( n+k ) n
E V'a l ..... an $ k E an n ·
n=1 n=l


3.2.70. Let {an} be a sequ
nce of positive numbers
 Prove that the
00
convergence of E t implies the convergence of
n=l


f ( n2an ( t Ok ) -2 ) .
n=1 k- l


3.2. '11. Let {an} be a .monotonica1ty inCT'pASing
el}u
nC'.R of pMitiv

00
numbers such that E t diverges. Show that
n= l
00 1

 no,. - en - 1)0,.-1


is also divergent.


3.2.72. Let {Pn} be a sequence of all consecutive prime numbers.
oc
Study convergence. of E -k.
n= J


3.2.73. Study COD vergence of
00 1

 np.. - en - 1)p,.-1 '
where .Pn denotes the nth prime number.


3.2.74. Evaluate


lim
n-oo


00
E knl+1
1:=2
.
00 1
Eki'

2




3.2. Series of Nonnegative Terms


85


3.2.75. Let {an} be a sequence satisfying the following conditions:
o
 an
 1 for all n E N and al ¥= O.


Let


Sn = al + ... + an and Tn = 8 1 + ... + Sn.
00
Determine for which values a > 0 the series E ;.: converges.
n=1 WI


3.2.76. Let k be an arbitrary positive integer. Assume that {an}
is a monotonically increasing sequence Qf positive numbers such that
co
E ,!; converges. Prove that the series"
n=1


f: Ink an and f: Ink n
n=1 t1n n=1 an
are either both convergent or both divergent.


3.2.77. Assume that f : N -. (0,00) is a decreasing function and
rp : N -+ N is an increasing function such that rp( n) > n for all
n e N. Verify the following inequalities:


rp(n)-l ";(1)-1 n-1
(1) E J(k) < L: f(k) + L: j(rp(k»(cp(k + 1) - <p(k»,
1..-=1 k=1 k=l

(n) n
(2) E j(k) > E f(
(k»(cp(k) -
(k - 1».
k=
(I)-l k=2


3.2.78. Prove that under the assumptions of the foregoing problem,
if there exists q such that for all n E N the inequality
j(cp(n»(<p(n + 1) - VJ(n» < q < 1
fen) -


co
holds, then E J(n) converges. On the other hand, if
n=1


!(<p(n»(<p(n) - <p(n -1» > 1

fen) - t n E I
t




86


Problems. 3: Series of Real Numbers


00
then E fen) diverges.
n=1


3.2.79. Derive from the preceding problem the following test for con-
vergence and divergence of positive series.
00
The series E an whose terms are positive and monotonically
n=1
decreasing is convergent when
Jim a2n 1
-=9<-
R-OO an 2


and divergent when


lim a2n 1
- = 9 > -.
n-oo an 2


3.2.80. Derive from Problem 3.2.78 the following test for convergence
and divergence of positive series (compare with Problem 3.2.34).
co
A positive series E an whose terms are monotonically decreas-
»=1
ing is convergent provided that
Jim 2na2n 1
=9<
n-oo On


and divergent provided that
Ii 2n a2" 2
m > .
n
 an


3.2.81. Using Problem 3.2.77, prove the criteria given in 3.2.31.


3.2.82. Prove the following Test of Kummer.
L
t {an} be a positive-valued sequence.
(1) H there are a sequence {b n } of positive numbers and a positive
constant c such that
b n an - bn+l
 c for all n E N,
an+l


00
then E an converges.
n=l




.3.2. Series of Nonnegative Terms


81


co
(2) If there is a positive sequence {b n } .such that E -l; diverges
n=1
and


an
b,. - b n + 1
 0 for aU n E Nt
lLn+l


co
then E an diverges.
n-l


3.2.83. Show that the tests pf d'Alembert (the ratio test), Raabe
(3.2.19) and Bertrand (3.2.24) are special cases of the K umm er test
(3.2.82).


3.2.84. Prove the following converse of the K l1mm"e r test.
Let {an} be a positive sequence.
00
(1) H E On converges, then there exist a positive sequence {b n }
n=l
and a positIve constant c such that


an
b n - b n + 1
 c.
l1n+l _


00
(2) If E an diverges, then there exists a positive sequence {b n }
n=l . .
00
such that E b
 diverges and

1


an
b n - b n + 1
 o.
l1n+ 1


3.2.85. Prove the following tests for convergence and divergence of
.positive series.
(a) Let k be a positive integer and let llm a:+ 1r = g. H 9 < 1, then
n-oo n
00 00
E an converges, and if 9 > I, then E an diverges.
n=1 n= 1
(b) Let k be a positive integer and let lim n ( 0 On -1 ) = g. If
n-OC) n+1c
00 00
9 > k, then E an converges, and if 9 < k, then E l1n diverges.
n= 1 n=l




88


Problems. 3: Series of ReaJ Numbers


3.2.86. Let {an} and {CPn} be sequences of positive numbers. As-
00
sume that CPn = 0 ( I
 n ) . Prove that the convergence of E an im-
n=2


00
plies the convergence of E a
-V'n.
n=2


3.3. The Integral Test


3.3.1. Prove the following integral teat.
Assume that f is a positive and decreasing function OD the m-
oo .
terval [1,00). Then the series E fen) converges if and only if the
n=l


n
sequence {In}, In = J j(z)dx, is bounded.
1


3.3.2. Let I be a positive and dIfferentiable function on (0,00) tiuch
that /1 decreases to zero. Show that the seri



f I'(n) and f I'(n)
n=1 n=1 fen)
either both converge or both diverge.


3.3.3. Let / be a positive and decreasing function on [1.00). Set


N N
SN = L fen) and iN = 1 f(x)dx.
n=l 1
Show that the sequence {SN -IN} is monotonically decreasing and
its limit belongs to the interval [0,/(1)].
3.3.4. Show that the limits of the sequences


(a)
(b)


1 1
1 + 2 + ... + n - In n,
1 1 i nl
1+- 2 +...+-- -dx,
a n Q 1 X Q


o < Q < I,


both belong
o the interval (0, 1).




3.3. The Integral Test


.89



3.3.5. Apply the integral test to study convergence of the series given
in 3.2.29.


00
3.3.6. Let E an be a positive divergent series and let Sn = 01 +
n=1

 + ... + an > 1 for n
 1. Verify the following c] ahT1
 :


(a)


CXJ
E ai..+ 1 diverges,
n=1 SnlnSn


(b)


00
E
 . converges.
,).-1 Sn In 8n


3.3.1. Let J be. a positive and decreasing function on (1, co). Assume
that a function VJ is strictly increasing, differentiable and such that
<p(x) > x for x > 1. Prove that, if there exists q < 1 such that
<p'{:E}{ir(:E»
 q for sufficiently large x, then E fen) converges.
n=l
Prove also that, if
:z:}{
)(z)) 2: 1 for sufficiently large x, then the
series diverges.


3.3.8. Let I, 9 be positive continuously differentiable functions on
(0,00). Moreover, suppose that f is decreasing.
(a) Show that, if "'
 ( -g(x)
l:? - g'(x») > 0, then n
l fen) con-
verges.
n
(b) Show that, if the sequence with terms f 9(
) dx is unbounded
1
and for sufficiently large x, -g(x}
l:? -g'(x} S; 0, then E fen}
n=1
diverges.


3.3.9. Let / be a positive continuously differentiable function on
(0,00). Prove that
(a) if "'
 ( - "':
;) ) > I, then fl fen) converges,
(b) if - %J

»)
 1 for sufficiently large x, then E fen) diverges.
n=1




90


Problems. 3: Series of Real Numbers


3.3.10. Let J be a positive continuously differentiable fun
-tion on
(0,00). Prove that
(a) if Jim ( -
[:? -
) xlnx > I, then E fen) converges,
%-fCO n=1
(b) if ( -
(':? -
) x lnx ::; 1 for sufficiently large x, then F/ ( n)
diverges.


3.3.11. Prove the following converse of the theorem stated in 3.3.8.
Let J be a positive decreasing and continuously differentiable
function on (0,00).
00
(a) If E fen) converges, then there exists a positive continuously
n;:::1
differentiable function 9 on (0, 00) such that
Urn ( _g(x) I'(X) _g/(X) ) > o.
%-00 /(z)


co
(b) 1£ E I( n) diverges, then there exists a positive continuously
71=1
differentiable function 9 on (0,00) such that the sequence with
terms


In 1
Jl g(x) dx, n = 1,2, ...,
is unbounded and for sufficiently large x,
-9(X)

? - g'(x) s o.


3.3.12. For 'Y
 0, study convergence of the series
()O 1

 (lnn)(lnn)'"


3.3.13. Study convergence of the series
co 1
E n1+r..l.n Inn '
n=3




3.3. The Integral Test


91


3.3.14. Let {
n} be a positive monotonically increasing
quence
and let. I h
 A pn.crit.ive a.nd inCTP.a,-=;ing fnn
tinn sat.imying the t'.onc1it.ion


{oo 1
}"1 tf(t) dt < 00.


Show that


00 ( )
""1 1

 1 - -'n+1 f(An) < 00.


3.3.15. Prove the following generalization of the integral test.
Let {>'n} be a sequence strictly increasing to infinity and let /
be a positive continuous and decreasing function on ["\1,00).


(a) H there exists M > 0 such that An+l -"\n > M for n e N
00
and if the improper integral I j(t)dt converges,- then the series
-"\1


00
E /(
R) also converges.
n=l


(b) If there exists M > 0 such that -"n+l -"\n
 M for n e N
00
and if the improper integral f J(t)dt diverges t then the series
'\1


00
E /(An) also diverges.
n=l


3.3.16. Suppose that / ; (0,00) -. R hi a positive cwd differenl,ics.ble
00
function with positive derivative. Prove that E -dn; converges if
n=l


and only if E I-

n) does.
n=1


3.3.17. Define Inix = Inx and Ink X = In(lnk-lX) for k > 1 and
sufficiently large x. For n E N, let cp(n) be the unique positive integer
such that 1

(n) n < e. Does the series
00 1

 n(ln. n)(ln2 n) · ... · (
(n) n)
converge or diverge?




92:


Problems. 3: Series of Real Numbers


3.4. Absolute Convergence. Theorem of Leibniz


3.4.1. For the indicated values of at decide whether the series are
absolutely convergent, conditionally convergent, or divergent:


(a) f: ( nO; 1 ) '" a e R,
n= 1


(b) E(-l)" (1n:)C , aeR,
n= 2


00
(c) E(-I)"Sin;, aE JR,
n=1


(d)


00 1 ( a2 _ 4a _ 8 ) R

 n+l a 2 +64-16 I


a e R \ {-8t2},


(e)


00 n

 n 2 ' a :f: 0,
L..J an
n=l


(f) E(-l)" (In:t" . a> o.
n=1


3.4.2. For a e nt, study convergence and absolute convergence of the.


.
serIes


00 n-I
E na"
l + Inn '
n =n o


where nQ. is an index depending on a such that nan-I + In n :F 0 for
n
 no-


00
3.4.3. Suppose that a series E an with nonzero terms converges.
n=1
Study the convergence of the series


f ( 1- Sin
J ) .
n=l an




3.4. Absolute Convergence. Theorem of Leibniz


93:


3.4.4. Does the condition 1im r- = 1 imply that the convergence
n....oo "
00 00
of E an is equivalent to the convergence of E b n ?
n=l n=l


00
3.4.5. Assume that a series E On converges conditionally and set
n=l
00 00
Pn = JGn
G" , qn = Jan
a" . Show that both E Pn and E qn
n=l n=l


diverge.


00
3.4.6. Assume that a series E an converges conditionally. Let
n-l
00
{Pn} and {Qn} be the sequences of partial sums of E Pn and
n=1
00
E qn, defined in the foregoing problem, respectively. Show that
n=l


lim Pn = 1.
"-'00 Qn


3.4.7. Study convergence and absolute convergence of the series


f: (-
[t] .
n=l


3.4.8. For a e" R, decide whether the series



 (-l)fv;iJ
L.J nO
n= 1


converges absolutely, converges conditionally, or diverges.


3.4.9. Decide whether the series


f: (_l)llnn]
n
n=1


is absolutely convergent, conditionally convergent, or divergent.




94


Problems. 3: Series of Real Numbers


3.4.10. Let


{ +1 for 22.1: < n < 22k+l
£n = -1 for 2 2 k+-;::; n < 22k
2,
where k = 0, 1, 2, .... Discuss the COD vergence of the series


(8)


00
"'


 n t
n=1


00
(b) L en .
n=2 nlnn


3.4.11. Study the convergence of the series

 ( 1) R ,fii · 1

 - (-l)n + v'7i S1n v'fi -


3.4.12. Investigate the behavior (absolute convergence, conditional
convergence) of the following series:


(c)


co
E<-l)"( v'ii _l)ft,
n=1
00
L( _l)n(
 -1), a > I,
n=1
co
L(-1)n(v'ii- 1 ),
n=l


(a)


(b)


(d)



(_l)n (e- (1+
)n).
00 (( l ) n+l )

 (-I)n 1+;; -e.


(e)


3.4.13. For a, b > 0, discuss convergence of the following series:
E<-I)R <:
)a I
n=l
E<_l)n (ln:t ft .
n=1


(a)


(b)




3.4. Absolute Convergence. Theorem of Leibniz 95


00
3.4.14. L
t E (-1)n-1an be an alternating series which satisfies
n=1
the conditions of the Leibniz test, that is, 0 < an+ 1
 an for all
n and lim 4n = o. Denote by Tn the nth re main de! of the series,
n....oo
00
r n = E (-1)k- 1a k. Show that Tn has the same sign as the term
k=n+l
(-l)R4n+l and Irnl < 4 n +l-
3.4.15. Suppose that a sequence {an} tends to zero. Show that the
.
senes


00 00
Ean and E(an+an+l)
n=l n=l
either both .converge or both diverge.
3.4.16. For a sequence {an} convergent to zero and for at b, c such
that a + b + c :F 0, prove that the series


00 00
E an and E(a4n + ba n +l + CQn+2)
n=l n=1
either both converge or both diverge.
3.4.17. Let {an} be a :sequence with lim an - a f 0 and with
n-.oo
nonzero terms. Prove that the series


co OO ( 1 1 )
E(an+l - an) and L - -
n=:1 n=:1 an+l an
either both are absolutely convergent or both do not converge abso-
lutely.




3.4.18. Show that, if a sequence {nan} and a series E n(an-an+l)
n=l


OCI
both converge, then E an also does.
n=1


3.4.19. For a sequence {an} monotonically decreasing to zero, study
the convergence of the series
00
E<-l)n+1 al + a2
... + an .
n=1




96


Problems. 3: Series of Real Numbers


3.4.20. Decide for which values of a the series


OCI
"' < l) R I . . a · a
L...J - n.smasm 2' ..... sin n
n=l


converges absolutely and for which it diverges.


3.4.21. For p
tive a, b and c, study convergence of the
e5



 ( v'li- V'b; ifC ).


3.4.22. Discuss convergence of the following series:


00
(a) E(cosn)R,
n=1


00
(b) E(sinn)n.
n=1


3.4.28. Let {an} be a positive sequence. Prove that
(a) if Jim n ( ":
1 - 1) > 0, then f: (-1 )na,. converges,
n-.oo n=l
(b) if' n ( 0 a,. -1 ) :5 0, then E (-I)na,. diverges (in particular, if
n+l 1
n=
Jim n ( Q an - 1 ) < 0, then the series diverges).
n-.co n+1


3.4.24. Assume that for a positive sequence {an} there exist a e Ii,
t:::> 0 Wlcl a bUW1d
cl
u
nc
 {tin}
uch thaI,
an =1+
+ Pn .
4n+l n n 1 +E=


co
Prove that the series E (-l)na,
 converges for £It> 0 and diverges
n=1


for Q < o.


3.4.25. Discuss the convergence of the series


co n n!e n

(-1) + ' peR.
L.J n B P
n= 1




3.4. Absolute Convergence. Theorem of Leibniz 97°


00
3.4.26. Assume that the series E an converges and {P,,} is a pos-
n=1
itive sequence which increases to +00. Show that
lim alP! + a2P2 + e.. + anPn = o.
n-co Pn


3.4.21. Let {an} be a positive sequence decreasing to zero. Prove
00
that, if the series E 4nbn converges, then
n= 1


lim an(b 1 +
 +... + b n ) = o.
n-+oo


3.4.28. Let Q be a given positive number. Prove that, if the series
00
E
 converges, then
n=1


lim at + 42 + ... + an = o.
n-oo net


3.4.29. T,
t {kn} h
 a
trictly inc:rPA
ing sequence of natural nnm-
. 00 00
bers. Then the series E 4k n is called a subseries of the series E an..
n=1 n=l
Show that, if all the subseries of a series converge, then the series is
absolutely convergent.


3.4.30. Let k, I be integers such that k > 1, I > 2. Must the conver-
00
gent series E an be absolutely convergent if all its subseries of the
n=)
form


00
L ak+(n-l)l
n=l


are convergent?


00
3.4.31. Give an example of a convergent series E an such that
1\- 1


co
E a
 diverges.
n= l




98


Problems. 3: Series of Real Numbers


.00
3.4.32. Does there exist a convergent series E an such that all the
n= 1
00
series of the form E a
, where k is an integer greater than or equal
n=1
to 2, diverge?


3.4.33. Let { an} be a monotonically decreasing and positive se-
OQ
quence such that the series E an diverges. Suppose that the series

=)
00
E Enan, where En
s -lor 1, converges. Prove that
n=1


lim £'1 + £2 + ... + ell < 0 < Hm £1 + S2 + ... + Ere. .
n - - R-tOO n


n-oo


3.4.34. Assume that {an} is a positive monotonically decreasing
co
sequence and that the oorioo E
n4nt where Cn ic 1 or It converges.
n=l


Show that


lim (cl + E2 + ... + cn)an = O.
n-.co


(See 3.2.35.)


00
3.4.35. Suppose that the series E b n converges and {Pn} is a
n=l
monotonically increasing sequence for which lirn .Pn = +00 and
R-OO


00
E .;; = +00. Show that
n=1


lim P1b 1 + P2
 +... + Pnbn < 0 < Jim P1bt + P2
 +... + Pnbn .
n
 n - - n-oo n


00
3.4.36. In the harmonic series E
 let us attach the sign "+", p
n=1
times, consecutively, then the sign "-", q times, consecutively, then
"+" t p times, consecutively, etc.. Show that th
 new series converges
if and only if p = q.


3.4.37. Prove the following generalization of the Toeplitz theorem
(see 2.3.1 and 2.3.3.6).




3.5. The Dirichlet and Abel Tests


99


Let {en,1: : n, kEN} be an array of real numbers. Then for any
convergent sequence {an} the transformed sequence {b n } given by


00
b n = E Cn,kak, n 2: 1,
k=l
is convergent to the same limit if and only if the following three con-
ditions are satisfied:


(i)


en k -I> 0 for each k E Nt
, n....oo


(ii)


co
E C,a,k = I,
k= 1
there exists C > 0 such that for all positive integers n
co
E len,kl
. c.
k=l


(ill)


3.5. The Dirichlet and Abel Tests


3.5.1. Using the Dirichlet and Abel tests, study convergence of the
following series:


(c)


co . 2
E<-l)n SIDn n ,
n=1

 5inn ( 1 1 )

 n 1 + 2 +... + n '
00 1 ( 2 )

 In2n coo 1f n: 1 I
00 . nlr
sm-
E a + .4 n", ' 4 > O.
n=l n smT


(a)


(b)


(d)


00 sin (n + 1.)
3.5.2. Does the series E In In n converge?
n=2 n




10_0


Problems. 3: Series of Real Numbers


3.5.3. For a E It, study convergence of the series


(a)



 sin(na) sin(n 2 a)

 n '
n=1
E Sin(na)
(n2a) .
n=1


(b)


3.5.4. Show that the series


E {,Ul7£:w(na)
n=1
converges for each a E R.


00 sin(na)
3.5.5. Determine whether the series E I a E JR, converg

n=1 n


absolutely.


3.5.6. Show that for a E R and n E N.


t sin(ak) < 2-/i.
k=l k


3.5.7. Prove that the series


co
E(_l)n arctann
n=l Vii


converges.


3.5.8. For x > 1. study convergence of the series


E(-l)R V':x ,
n=1




3.5. The Dirichlet and Abel Tests


101


3.5.9. Prove the following lemma of Kronecker.
00.
Let E an be a convergent series and let {b n } be a monotoni-
n=l
cally incr easing sequence such that lim 6" = +00. Then
R-OQ


(a) f
=o ( .!. ) , (b)
k=n bk b n
where o(b n ) means that lim o(b,.) = o.
n-.oo b n


n
Lak6k = o(6n),
1.:=1


00
3.5.10. Assume that the series E ncn converges. Show that for
n=1
00
every n e N the series E (k + l)Cn+k also converges. Moreover,
1.:=0
00
show that if t n = E (Ie + l)Cn+kl then lim t n = O.
k=O n--.,oo


00
3.5.11. Assume that the partial sums of the series E an form a
n=1
00
bounded sequence. Prove that if the series E Ib n - 6n+ll converges
n=1
00
and lim b n = 0, then for every natural k th
 series E anb
 also
n-
 n=1
converges.


00 00
3.5.12. Prove that if E (b n -b n + 1) converges absolutely and E an
n=l n=l
00
converges, then the series E an6n also conv
rges.
n=1


00
3.5.13. Using Abel's test, show that the convergence of E an im-
n=1
00
plies the convergence of the series E tlnX n for (xl < 1.
n=1


3.5.14. For a given sequence {an} show that if the Dirichlet series


00
"'

L....J n%
1&=1


converges
t .X = :to! then it converges at every x > zo.




102


Problems. 3: Series of Real Numbers


00
3.5.15. Prove that the convergence of the Dirichlet series E

n=l
implies the convergence of the series



 n!a n
L ( ) ( )' x :F 0, -1, -2, ... ·
n=1 X X + 1 au X + n


co
3.5.16. Prove that if the series E anx R converges for Ixl < 1, then
n=1


00 n
L an l':x l1 a1so converges.
n=1


00
3."5.1 '1. Must the convergent series L an be absolutely convergent
'11=1
if all its subseries of the form


00
Eakin. k
 I,l
 2,
n=l


converge'1


3.6. Cauchy Product of Infinite Series


3.6.1. Prove the following theorem oj Mertens.


00 00
If at least one of the two .convergent series E an and E b n
n=O n=O
converges absolutely, then their Cauchy product (that is, tbe series
00
E Cn, where en = aob n + al b n-I + au + 4,1 b O) converges. Moreover,
n=O
00 00 00
if E On = A and E b n = B, then E.Cn = AB.
n=O n=O n=O


3.6.2. Find tbe sum of tbe series


(a)


00
'"'" n-l
L...J nx ,
n=l


Ixl < 1,


co n
(b) E en, where en = E xkyn-k, Ixl < 1, Iyl < 1,
n=O k=O




3.6. Cauchy Product of Infinite Series


103


(c)


00 n 1
Len. where en = L k(k 1)( -k 1)1 .
n= 1 k=l + n +.


3.6.3. Form the Cauchy product of the given series and calculate its
sum.


(b)


00 2 ft 00 1
E--. and E 2 n I'
O n. =0 n.
n= n-
00 1 00 1
E(-l)n n and E
t
n=1 n=1
00 tX7
E(n+l)x n and E(-l)n(n+l)x n .
n=O n=O


(a)


(c)


00
3.6.4. Assume that the series E an is convergent and set An =
n=O
co
ao+al +...+an. Prove that for Ixl < 1 the series E Anxn converges
n=O
and


co 00
LClnx" = (I-x) LAn x ".
n=O n=O


co 2ft
3.6.5. Find the Cauchy product of the series E (-l)n

!)
 , x E JR,
n=O
with itself.
Hint. .Use the equality t (
)2 = (2:).
k=O


3.6.6. For a > 0 and Ixl < 1, verify the claim
( 1 1 x 1.3 x 2 1.3. ... · (2n -1) x" )
- + - + + ... + + ...
a 2 Dr + 2 2 · 4 a + 4 2 · 4 · ... .. (2n) a + 2n
. .
( 1 1 · 3 2 1 · 3 · ... · (2n - 1) n )
)( 1 + 2:1: + 2.4 3; +... + 2.4..... (2n) x +...
1 (1 a+l (a+l)(a+3) 2
- - + x+ %
G 4+2 (4 + 2)(a+ 4)
(a + 1) · ... · (a + 2n - 1) n )
+ ... + ( 2) . . ( 2 ) x + ... ·
a + ... a + n




104.


Problems. 3: Series of Real Numbers


3.6.7. Prove the following theorem of AbeL
00 00
If the Cauchy product E en of the two convergent series E an =

O
O


00
A and E b n = B" converges to C, then C = AB.
n=O


3.6.8. Show that the series


00 ( )
n-l 2 1 1

 (-1) n+l 1+ 2 +'.'+ n


00
is the Cauchy product of the series E ( _l)n-l ; with itaelI t and find
n=l
its sum.


3.6.9. Study the convergence of the Cauchy product of the .series
00
E (_l)n-l
 with jt
lf.
n=l


3.6.10. Prove that if at least one of two positive series is divergent,
then their Cauchy product diverges.


3.6.11. Must the Cauchy product of two divergent series be diver-
gent?


3.6.12. Prove that the Cauchy product of two convergent series
00 00
E an and E b n converges if and only if
n=O n=O


n
lim
 Ok(bn + b n - 1 + ... + bn-k+l) = o.
R-.OO L...J
k=1


3.6.13. Suppose that {an} and {b n } are positive sequences mono-
tonically decreasing to zero. Show that the Cauchy product of the
00 00
series E (-l)"an and E (-l)nb n converges if and only if

 n=O


Jim c n {60 + b 1 +... + 6n) = 0 and Jim 6n{ao + Bl +... + an) = o.
n-.oo .n-.oo




3.7. Rearrangement of Series. Double Series


105


3.6.14. Show that the Cauchy product of


00 (-l)n co (-l)n
E n Q and E nfJ ' Q, P > 0,
n=l n=1


converges if and only if Q + fJ > 1.


3.6.15. Assume that positive sequences {an} and {b n } are mono-
tonically decreasing to zero. Prove that the convergence of the series
00
E an 6 n is a sufficient condition for convergence of the Cauchy prod-
n=O
00 00
uet of the series E (-l)n an and E (-l)nb B , and that the conver-
n=O n=O
co
gence of E (an 6 n)1+o for every Q > 0 is a necessary condition for
n=O
the convergence of this Cauchy product.


3.7. Rearrangement of Series. Double Series


3.1.1. Let, {7fl.k} be B strictly incr
ing zsequence ur pU)itive inte-
gers, and put


6 1 = 4] + B2 + ... + amI'
 = flml+1 + "m 1 +2 + ... + t1m2t....


co 00
Show that if the series E an converges, then E b n also converges
n=1 n=l
and both series have the same sum.


3.1.2. Consider the series


111 1 1 1
1 - 2 - 4 + 3 - 6 - 8 + 5 - ".t


00 ( 1 ) "-1
which is obtained by rearr anging the terms of the series l: - n
n=l
in such a way that each positive term is followed by t\vo negative
terms. Find the sum of this series.




106


Problems. 3: Series of Real Numbers


00 ( 1 ) "-1
3.7.3. Let us rearrange the terms of E - n so that .blocks of
n=l
Q positive terms alternate with blocks of {J negative terms, that is.
1 1 11 1 1 1
1 + 3 + ... + 20 - 1 - 2 - 4 - ... - 21i + 20 + 1 + 2a + 3 +...
1 1 1 1
+ 40 - 1 - 2p + 2 - 2.8 + 4 -... - 4{J + ... .


Find the sum of the rearranged series..


3.7.4. Show that
11111 1 1 1 1 1
1 - 2 - 4 - 6 - 8 + 3 - 10 - 12 - 14 - 16 + 5 - ... = 0..


00 ( 1)"-1
3.7.5. Find a rearrangement of the series L - .. which doubles
n=1
its sum.



 ( -I n ) n-J
3.7.6. Rearrange the terms of L" - - t9 obtain a divergent se-
n.=1


nes.


3.7.7. Study convergence of the series
1 1 1 1 1
1 + V3 - v'2 + J5 + J7 - J4 + .....


obtained by taking alternately two positive terms and one negative"
oo

term of the series E
.
n=l


3.7.8. Prove that any rearrangement of an absolutely convergent se-
ries is convergent and has the AAm e sum.


3.7.9. Assume that a function f : (0, +00) -t (0, (0), decreasing to
zero as x -t 00, is such that the sequence {nf(n)} increases to +00.
00
Let S denote the sum of the series E (_l)n-l fen). Given I., find a
n=1
rearrangement of this series convergent to S + I.




3.7. Rearrangement of Series. Double Series


107


3.7.10. Assume that a function f: (0, +(0)
 (0, (0), decreasing to
2erO as :z: -.. 00 1 satisfies 1im nJ(n) = 9, 9 E (0 1 +00). Let S denote
n-oo
00
the sum of the series E (_l)n-l fen). Given I, find a rearrangement
n=l
of this series convergent to S + I.


00.
3.7.11. Rearrange the terms of E (_l)n--l;!p, p E (O
 I), to increase
n=l
its sum by l.


3.7.12. For Q > 0, using the result in 3..7.10, find a rearrangement
00
of E (_I)n-l
 whose sum is In2 +
 Inc.
n=1


3.7.13. Is it possible to accelerate by rearrangement the divergence of
a divergent series with positive and monotonically decreasing terms?


00
3.7.14. Assume that the series E an with positive terms diverges
n=l
and that llm an = 0.. Show that it is possible to slow down its
n-oo
divergence arbitrarily by rearrangement; that is: for any sequence
{Qn} . satisfying
o < Ql < Q2 < .... < Qn < ....., lim Qn = +00,
n-oo


OC'
there is a r
angement E Bnle such that
k;::l
anI + lIn 2 + ... + an m S Qm for mEN.


3.7.15. Let {Tn} and {sn} be two strictly increasing sequences of
positive integers without common terms. Assume also that every
positive integer appears in one of the two sequences. Then the two
00 00
subseries E aria and E B8n are called complementary subseries of
n=l n=1
00
E tin. We say that the leatrangement shifts the two complementary
n=1
subseries relative to each other if for all positive integers m and n
such that m < n the term arm precedes lIr
 and a 6rn precedes a.ft.
00
Prove that the terms of a conditionally convergent series E. an can
. n=1




108


Problems. 3: Series of Real Numbers


be rearranged, by shifting the two complementary subseries of all its
positive and all its negative terms
 to give a conditionally convergent
series whose sum is an arbitrarily preassigned number.


00
3.1.16. Let E an" be a rearrangement of a conditionally conver-
k=l
00
gent series EOn. Prove that if {nk - k} is a bounded sequence,
n=l
00 00
then E an., = E an. What happens if the sequence {nk - k} is
k- I n=1
unbounded?


oc
3.7.17. Let E a nk be a rearrangement of a conditionally convergent
k=1
00 co DO
series E tln. Prove that E an" = E an if and only if there exists
n=1 k=l n=1
a positive integer N such that each set {nk : 1 < k < m} is a union
of at most N disjoint blocks of successive positive integers.


3.7.18. With an infinite matrix {Oi,k}, i = 1,2, ..., k = 1,2, ..., of
00
real numbers we associate a double series E lli.k- We say that the
i,k=!
double series converges to Sell if, given E > 0, there exists no e N
such that


(8m.n - 81 < £ for m,n> no,


where


m n
Sm,n = E E
,k.
i=l k=l


Then we write


00
S = lim 8m n = '" 4j k.
m.ft-OO ' L....,.
i.k=!
00 00
We say that E Bi.k converges absolutely if E Ia;.k I converges.
i.k=! i,k=!
Note that the terms of an infinite matrix (aa,k)i.k=1.2.... can be or-
00
dered into a
uence {en}, and then the corresponding series E en
n=1
00
is called the ordering of E ai,k into lJ single series. Prove that if
i.k= 1




3.7. Rearrangement of Series. Double Series


109


one of the orderings of a double series converges absolutely, then the
double series converges (a.bsolutely) to the same sum.


00
3.7.19. Prove that if a double series E tIi.k converges absolutely,
i, k....... 1


00
then any of its orderings E en converges and
q-.1


00 00
L 4i.k = Len.
i.k=l n=l


3.7.20. Show that any absolutely convergent double series is conver-
gent.
3.7.21. We say the iterated series j:. (
 Ci,Ic) is absolutely con-
vergent if E ( E lai'kl ) converges; similarly for E ( E ai,/; ) ·
i=l k=1 k=) i=l
Prove that an absolutely convergent iter
ted series is convergent.


00
3. 'T .22. Prove that if the double series E
,k converges absolutely,
i,k= 1


then both the iterated series



 (
 Ci.Ic) and
 (

,Ic )


converge absolutely and


co 00 ( 00 ) 00 ( 00 )
E flit k = E E lli,k = E E tli,1c ·
i,k=! i=l k 1 1e=1 i=l


3.7.23. Prove that if one of the four series


00
L IBi,kl,
i.k=1
00
E{lan,ll + IBn-l,21 + lan-2".31 +... + Jal.nl>
n=l


f; (
 ICi,Ic I) I



 ( tt ICi.lcl) ,




110


Problems. 3::. Series of Real Numbers


converges, then all
he series


'XI
E
,k,
&, 1:- 1
QO
E(Bn,l + Bn-l.2 + l1n-2,3 +... + Bl.n)
n=1


t ( fit;.k ) "
&=1
=I



 (

.k)'


converge to the same sum.


3.7.24. Calculate


00 1
n
 o n!k!{n + k + 1) ·


s. 7.25. Find


00 1
nt l nk(n+ k +2)'


3.7.26. Show that


f n!k! _ 11'2
n,k=O (n+k+2)! - 6.


:c
z(1 - z)
z(1 _ %)2


For 0 < x < 1, consider the infinite matrix
-%l z'l0 _%3 %3
-z2(1- z2) %2(1 - 2: 2 ) -
(l-
3) 2: 3 (1 - :t 3 )
-:c 2 (1 - r)2 z2(1 - %2)2 -x 3 (1 - z3)2. z3(1 - z3)2 . ...


.0 .


3.7.27.


........................................................................


Prove that only one of the iterated series associated with this matrix.
converges (not absolutely).
3.7.28. Study convergence of the following double series:




(a) E xiyk, where Ixl,lyl < I,
i.k=O
OQ 1
(b) E °akD' where a,{3 > 0,
j.k-l

00 1
(c) .E (i+k)P' where p > o.

.k= 1




3°.7. Rearrangement of Series. Double Series


111


3.7.29. Find the sums of the following double series:


(c)


00 1
.L (P+i)k ' where p> -1,
l.k::::2
00 1
i -
- l (2k)i '
00 1
L (4i -1)2k "
i,k=!


(a)


(b)


3.7.30. Given an infinite matrix (b i ,k)i,k=1,2,...t prove- that there. is
oc
only one double series E tli,k such that
i,k= 1


m n
Sm.n = L L ai.k = b m . n , m, n = 1,2,.... ·
i= 1 k= 1


3.7.31. Taking


i+k ( 1 1 )
bi,k = (-1) 2i + 2k '


i, k = 1,2, ...,


in the preceding problem, study convergence of the corresponding
co
double series E lli,k.
i,k=1


00
3.7.32. Show that if Ixl < 1, then the double series E Xik COD-
il k I


verges absolutely. Using this fact, prove that


00 00:rJc 00 00 n 2 00

 Zik = '"" = '"" O(n)x n = 2
 x + '"' x,i
 I
L...i L., 1- xk L..J LJ 1- x n L."
1,1.;;;1 k=1 ...--1 ,&-1 ,,-1


where 6(n) denotes the number of all natural divisors of n.




112


Problems. 3: Series of Real Numbers


00
3.7.33. Show that if Ixl < 1, then the double series E ix ik con-
i,k=1


verges absolutely. Moreover, prove that
00 co k k 00
L i3;il: = L 1
 :cl: = L u(n):c B .
i, k= l 1 1 n=1
wh
re u(n) denotes the sum of all na.t.ural divisors of n.


ex)
3.7.34. Let C(p) = E ;P t P > 1, be the Riemann zeta Junction.
n=1
Set


ex) 1
Sp = '"' - = C;(P) - 1, P > 1.
L...J n P
n=2


Show that


00
(a) LSp = I,
p=2


00 1
(b) L(-l)PS p = 2.
p=2


3.7.35. Prove the following th eorem of Goldbach.
If A = {k m : m,k = 2,3, ...}, then E fall = 1.
nEA


3.7.36. Let , denote the Riemann zeta function. Prove that for any
integer n
 2

{(2){(2n- 2) + {(4){(2n-4) +... + {(2n- 2){(2) = (n +
 ) {(2n).


3.7.37. Using the result in the foregoing problem, find the sums of
the series


00 1 00 1
L no and E n8 .
n=1 n=l


3.8. Infinite Products


3.8.1. Find the value of:


(a)


fi ( 1 -
 ) ,
n= 2


n °o n3 - 1
(b) n 3 + 1 '
n=2




3.8. Infinite Products


113.


00
(c) IT cas
t
 I: 2 t11 (
 + br) t mEN, k E Z,
n=1
00 00
(d) IT cosh ;' t x E JR, (e) II (1 +x 2 ") , Ixl < 1,
n= 1 n=O
1\ (1+ n(n
2»)' 00
(I) (g) II ( _ U n , a > 0,
a PI
n= 1
00 .l 00 9n 2 ,
(h) II en (i) II 9n 2 - 1 ·
1+.1'
n=1 n n=l


3.8.2. Study the convergence of the following infinite products:


(a)


fi (1 + (_
)n ),
IT ( 1 -
 ) ·
n=2


(c)


(b) fi(I+
).


3.8.3. Assume that an > 0, n e N. Prove that the infinite product
00 00
n (1 + an) converges if and only if the series E an converges.
n=l n=l


3.8.4. Suppose that. an
 0 and an i: 1 for n E N. Show that the
00 00
infinite product n (1- an) converges if
d only if the series E an
n=l n=l


converges.


3.8.5. Set


1 1
l12n-l = _ t::z +-,
vn n


1
G2n = - _ t::z ' n e N.
v n .


00
Show that the product IT (1 + an) converges although the series
n=1


00
:E lln diverges.
n=1




114


Problems. 3: Series of Real Numbers


3.8.6. Study convergence. of the products:


(a)


00 1
II cog -
n'
n=)


(b)


00 1
IInSin n ,
n=l


(c)


ft tan (
 +
 ) ,
n=l
00
II
J
n=1


(d)


fr n In ( 1 +
 ) ,
n=1
DO
II ft
.
n=1


(e)


(f)


00
3.8.7. Assume that the series E an converges. Prove that the in-
n=1
00 00
finite product n (1 + an) converges if and only if the series. E a;
n=1 n=1
00
does. Prove also that if the series L: a
 diverges, then the infinite
n=1


00
product n (1 + an) diverges to zero.
n=1


3.8.8. Assume that tbe sequence {an} decreaseg monotonically to
00
zeto. Show that the product n (1 + (-1 )n an ) converges if and only
n=1


00
if the series E a; converges.
n=l


3.8.9. Prove that the product ii ( 1 + (_l)n+l-jn ) diverges al-
0.=1
00
though the series E (_l)R+I-J: converges.
n=l


3.8.10. Show that if the series


f: ( an -

 )
n= l


00
and E )a n l 3
0.=1


00
both converge, then the product n (1 + an) also converges.
n=1




3.8. Inflnite Products


115


00
3.8.11. Does the convergence of the product IT (1 + an) imply the
n=l


00 00
convergence of the series E an and E a
?
n=l n=1
Hint. Consider the product


(1-
) (1 +
 + 2
 ) (1 -
) ( 1 +
 + 3
 ) · ...,


where
 < Q
 l.


3.8.12. Prove the following generalization of the result in 3.8
 10. For
k
 2, if both series


00 ( 1 2 (_l)k-l k )
L an - 2 a n. +... + k an
n=l


00
and L lanl k + 1
n=l


ex)
converge, then the product IT (1 + an) also converges.
n=l


00 00
3.8.13. Prove that the cODvergence of IT (1 + an) and of E a

n=1 n=l


00
implies the convergence of E an.
n=l


00 00
3.8.14. Show that if the products n (1 + an) and n (1 - an)
n=l n=l
00 00
converge, then both series E an and E a
 converge.
n= 1 n;::r 1


3.8.15. Assume that the sequence {an} decreases monotonically to
1. Does the product


1 1
a1 · - · a3 · - · as ....

 a



always converge?




116


Problems. 3: Series of Real Numbers


00 00
3.8.16. Assume that the products n On and n bn with positive
n;::l n=l
factors both converge. Study the convergence of


(c)


co 00
II (an + b n ), (b) II a
,
n=l n=l
00 00
II anb n , (d) II
?
b ·
n=1 n=l n


(a)


3.8.17. Show that for Zn e (0,
), n e N, the products ·


00
II cas Zn
n=1


and


co .
II sm X n
n=l Zn


00
converge if and only if the series E:c
 cul1verg
.
n=l


00
3.8.18. Let E an be a convergent series with positive terms and
n=1
let 8 11 denote its nth partial sum. Show that


ad] ( 1+ S
 ) = fa,..
n=2 n 1 n=l


00
3.8.19. Sho
 that if the infinite product n (1 + an), an > -1,
n=1


converges to P, then the series


00
]; (1 + a1)(1 +
 · '" · (1 + a,.)


also converges. Moreover, if S is its sum, then S = 1- i.


3.8.20. Suppose that the infinite product


00
II (1 + an), where an > 0, n E N,
n=l




3.8. Infinite Products


-111


diverges. Prove that


co
E an -1
n=1 (1 + al) (1 + a2) · ... · (1 + an) - ·


3.8.21. Shuw that.


00 n
E % - 1 for x > 1.
n=1 (1 + x)(1 + x 2 ) · ... · (1 + x n ) -


00
3.8.22. Let an ¥: 0 for n E N. Prove that the infinite product n an
n=l
converges if and only if the following Cauchy criterion is satisfied. For
every E > 0 there is an integer no such that


lan4n+l · ... · 4n+k - 11 < e


for n
 no and keN.


3.8.23. For Ixl < 1, verify the following claim:


00 1
II<l+xn)= 00 ·
n=1 n (1 - x2n-l)
n=1


00
3.8.24. The product n (l+an) is said to be absolutely convergent if
n=1
00 m
n (l+lanl> converges. Show that the product n (l+an) converges
n=l n=l
00
absolutely if and only if the series E an converges absolutely.
n=1


00
3.8.25. Show that every absolutely convergent product n (1 + an)
n= l


is convergent.




118


Problems. 3: Series of Real Numbers


00
3.8.26. Prove that if the product n (1 + an) converges absolutely,
n=1
then


00 00 00
rr (1 + an) = 1 + Lan + L CLn 1 t1n 2
n=1 n=1"1 .n2=1
Rl <n2


+ ... +


nn
L


an! Gn 2 ...BnJi + ... ·


"a. n 2...., r1 k=J
n1 <"2<...<n"


00
3.8.27. Assume that the product n (1 + an) converges absolutely.
n=1
00
Show that the product n (1 + anx) converges absolutely for each
n=l
Z e Ii and it can be expanded in an absolutely convergent series.
That is,


00 00
rr (1 + ClnX) = 1 + LAkZk,
n=1 k=l


where


00
Ale = L CLn 1 l1n 2 u . a n".
nl.t n 2,....n"=1
nl <n2<...<n,.


3.8.28. Establish the equality


co co n(ft+1)
1] (1 +qR:z:) = 1 +
 (1- q)(l-'! q2;. ,... (1- qR) :z:R r JqJ < 1.


3.8.29. Verify the identity


00 00

II (1 .J. q2n-lz) =s 1 + E ( 1- 2)(1-:)..... (1- 2Rt n, Iql < 1.
n= 1 n=l q q


00
3.8.30. Assume that the series E an converges absolutely. Prove
n=1
that if z :F 0, then
00 00 ( 1 )
!!(1 +anx) (1 +
 ) =Bo+
 Bn x n + x n r




3.8. Infinite Products


119


where Bn = An + AIAn+l + A2An+2 + ..., n = 0, 1,2, ..., and


00 00
II (1 +an x ) = Ao + EAk Xk (see 3.8.27).
n=l "--=1


3.8.31. For Iql < 1 and x =F 0, establish the identity
00 00 ( "n-1 ) co ( 1 )
!! (1- rl n ) !! (1 + rln-lx) 1 + rr :z: = 1+
 qn 2 :z:n +:;.; .


3.8.32. For Iql < 1" verify the following cl aim
 :


00 co 00
(a) II(l- q2R) II(I_q2n-l)2 = 1+2E(-1)Rqn2,
n=1 n=1 n=1
00 00 00
(b) II (1- in) II (1 +q2n-l)2 = 1 + 2 E qn 2 ,
n=1 n=l n=l
00 co 00
(c) II (1 - q2R) II (1 + q2R)2 = 1 + E qn2+n.
n=1 n=l n=1


3.8.33. For :t > 0, define the sequence {an} by setting
1 n-l k
n II x-
at = 1 t an = k ' n > 1.
+x x+n '==1 z+


00
Show that the series E an converges and find its sum.
n=1


00
3.8.34. Prove that if the infinite product II (1 + can) converges for
n=1
two different values of c E R \ {OJ, then it converges for each c.
3.8.35. Prove that if the series


00 n
Ean TI(x 2 _k 2 )
n;:;l k=O
converges at :& = $0, Xo f. Z, then it converges for any value of x.




120


Problems. 3: Series of Real Numbers


3.8.36. Let {Pn} be the sequence of consecutive prime numbers
greater than 1.
(a.) Prove the following Euler product formula:


00 ( 1 ) -1 00 1
II 1 - ;; = E
 for x > 1.
n=1 Yn n=l


00
(b) Prove" that the series E .;; diverges (compare with 3.2.72).
n=1


3.8.37. Using DeMoivre's law, establish the identities


(a)


OO ( 20 )
sin x = z II 1- : 2 '
n=1 n1r
00 ( 4
 )
COB:J: = !! 1 - (2n _ 1)211"2 ·


(b)


3..8.38. Applying the result in the foregoing problem prove the Wallis
formula


. (211) I! _ J::
bm (2 l)IIVii = v1r.
R-CO n- .. n


3.8.39. Study convergence of the products


(a)


00
II (1 +
) e-
, :J: > -I,
n=1
00 (1 + *rr:
II 1 +
 ' z > -1.
n=1 ,.


(b)


00
3.8.40. Prove that the infinite product II (1 + an) converges abso-
n=l
lutely if and only if any rearrangement of its factors does not change
its value.




3.8. Infinite Products


121


3.8.41. Find the value of the product
(1+
 ) (1+
 )... (1 +
 )
x (1-
) ... (1- 2P
1 ) (1 + 2a
2 )'"
obtained by rearranging the factors of . n ( 1 + (-
 )" ) in such a way
n=2
that blocks of a factors greater than 1 alternate with blocks of P
factors smaller than 1.


3.8.42. Prove that the convergent but not absolutely convergent m-
eo
finite product n (1 + .an), On > -1, can be rearranged to give a
n=1
product whose value is an arbitrarily preassigned positive number, or
to give 8 product that diverges to zero or to infinity. (Compare with
3.7.15).




Solutions




Chapter 1


Real Numbers


1.1. Supre mum and Infimum of Sets of Real
N11mb ers. Continued Fractions


1.1.1. Set A = {x E Q: z > 0, x 2 < 2} and 8 = supA. We may
assume that s > 1. We will now show that for any positive integer n,
(1) (s-;Y 525 (s+;Y.
Since 8 - * is not an upper bound of A., there exists x. e A such
that 8 -
 < x*. Hence
(s-;Y < (X*)2 <2.
Assume that (8 +
)2 < 2. H s were rational, then 8 +
 E A and
8 + : > Bt which wou1d contradict the fact that 8 = sup A. If s were
irrational then w = J(n+l)at + -L is a rational number such that
, n+l n+l
8 < W < 8+
. Hence w 2 < (8+
)2 < 2 andw E A,acontradictiolL
So, we have proved that (s + *)2
 2. By the left-hand side of (1),
8 2 -
 < 8 2 -
 +

 2, which gives 4
2 <
. Letting n -to Qat
we get 8 2 - 2
 Q.
As above , the ri no 1..t-hand side of ( 1 ) a\ves . .'a -2 > - 1. which
nu n 6 3., - n'
implies 8 2 - 2
 o. Therefore 8 2 = 2.


125:




126


Solutions. 1: Real Numbers


1.1.2. Suppose A is bounded below and set a. = inf A. Then
(1) x > a for all .x e A,
(2) for any E > 0 there is x* E A such that x* < a + E.
Multiplying the inequalities in (1) and (2) by -1, we get
(I') x < -a for. all x e (-A),
(
) for any E > 0 there is x* e (-A) such that x" > -a - E.
Hence -a = sup(-A). H A is not bounded below, then -A is not
bounded above and therefore sup( -A) = - inf A = +00. The other
equality can be established
mi1 arly.
1.1.3. Suppose A and B are bounded above, and put a = sup A
and b = sup B. Then a is an upper bound of A and b is an upper
bound or B. Thus, 4 + b is an upper bound of A + B. Moreover, for
any E > 0 there are x"* E A and y* E B such that x. > a -
 and
y* > b-
 . Therefore, x. +y* > a+b-e. Since z* = .x. +y* E A + B,
the equality a + b = sup(A + B) is proved. H A or B is unbounded
above, then A + B is also unbounded above, and by the definition of
the supremun sup(A + B) = sup A + sup B = +00.
The second equality is an imm ediate consequence of the first one
and of the foregoing problem. Indeed, we have
sup(A - B) = sup(A + (-B» = sup A + sup( -B) = sup A - infB.
Similar arguments can be applied to prove the equalities
inf(A + B) = inf A + inf B,
inf(A - B) = inf A - supB.


1.1.4. Suppose that both sets are bounded above, and put a = sup A
and b = sup B. Since elements of A and B are positive numbers,
xy
 ab for any x e A and y e B. We will now prove that ab is
the least upper bound of A. B. Let E > 0 be arbitrarily fixed. There
exist x1t e A and y'" e B such that x
 > a-E and y" > b-E. Thus
x*y* > ab - e(a + b - e). Since e(a + b - £) can be made arbitrarily
small if c is small enough, we see that any number less than ab




1.1. Supremum and Infimum. Continued Fractions 127


car-n ot be
 upper bound of A. B. Therefore ab = sup(A. B). If
A 01' B is not houndP.tt abov
, thF!n A · B ic; not either. Therefore
sup(A. B) = sup A · supB = +00.
The task is now to prove sup ( lJ = in: A if a' = inf A > O.
Then, for any x E A, the inequality x 2: a' is equivalent to
 5 c!t.
So,
 is an upper bound of *. Moreover, for any e > 0 there is
x* E A such that x* < a ' + E. Hence
111 E
-> =--
x 1f a' + £ a' a' (a ' + E) ·
Since a' (a
 +E) can be made arbitrarily small,
 is the least upper
bound of i . We now turn to the case a' = O. Then the set l is
unbounded (indeed, for "any E > 0 there is x" e 1: for which !£'" >
 ).
Therefore, sup * = +00.
Assume now that A, B are bounded sets of real numbers (pos-
itive or nonpositive) and put a = sup A, b = supB, a' = inf A and
II = infB. H a' and b ' are nonnegative, the desired equality follows
from the above. If a ' < 0 and a, 11 > 0, then xy
 ab for any
x e A and y E B. Take e > 0 so small that a - E > o. Then there is
a positive number x'" in A for which x* > a-E. Moreover, there is
1f" e B such that y. > b - e. Hence
x*y* > x.(b - e) > (a- e)(b- e) = ab -£(a+ b - E).
SO, in this case we have sup (A. B) = ab.
We now consider the case where a', b' < U and a, b > o. Then,
for any x E A and y E B, we have
xy
 max{ab, a'b'}.
Assume first that max{ab. a'b'} = a.'lI. By the definition of the
greatest lower bound, for sufficiently small e > 0, there exist x* E A
and y* e B for which x* < a' +E < 0 and y* < b' +e < o. This gives
x*y* > x*(b' + e) > (a' + e)(b' + e) = a'b' + e(a' + b' + e).
Notice that a' + b' + I! is negative. Therefore a'b' is the least upper
bound of A.B. In the case where max{ab, a'b'} = ab similar reason-
ing yields sup(A. B) = ab. All other cases can be proved analogously.




128


Solutions. 1: Real Numbers


1.1.5. Suppose first that A and B are bounded above. Put a =
sup A and b = sup B. Of course we may assume that a < b. Then, for
any x E AU B, x S b. Moreover, for any e > 0 there is x* e B such
that x* > b - £. It is obvious that x* belongs to A u B. Therefore,
the first equality is valid. H A or B is not bounded above, then
A U B is not either. So, sup(A u B) = +00, and we assume that
max{+oo,c} = max{+oo,+oo} = +00 for any real c. The proof of
the second equality is similar.


1.1.6. We have
Al ={-3.-¥.S}
{ 3 3 3 3
u 4k'- 4k+1 ,-4- 4k+2 ,4+ 4k+3
{ 3k-13k-2 3k-3 }
A2 = 3k + 1 ,- 6k ,- 2(3k _ 1) ; keN ·
Therefore inf Al = -¥' supAI = 5 and inf A2 = -!, SUpA2 = 1.


; kEN}.


1.1.7. sup A = : ' inf A = 0.2, supB =
 , infB = O.
1.1.8. One can show by induction that for n
 11, 2 R > (n + 1)3.
Hence


O (n+l)2 (n+l)2 1
< < = for n
 11.
2 n (n+ 1)3 n+ 1
Therefore 0 is the greatest lower bound of our set.
It is also easy to show that 2" > (n + 1)2 for n
 6. Hence

n;!)2 < 1 for n 2: 6. The numbers 2,
,
,
 (greater than 1) also
belong to our set. Thus the least upper bound of the set is !.


1.1.9. It follows from the foregoing problem that the greatest lower
bound of this set is equal to O. By the inequality mentioned in the
preceding solution, 2 nm > (nm + 1)2 for nm
 6. Since nm + 1

n + m, for n, mEN, we have


(n+m)2 < (n+m)2 < (n+m)2 = 1 if nm
 6.
2"m (nm+ 1)2 - (n+m)2




1.1. Supremum and Infimum. Continued Fractions 129.


For nm < 6 we get the following elements of our set: 1,2, £,
,
; .
Henr.e its ]p.asf; uppeT bound is !.


1.1.10.
(a) It is obvious that 2 is an upper bound for the set A. We will
show there are no smaller upper bounds. Indeed, if E > 0 is ar-
bitrarily fixed, then for any positive integer n* > [ ; ] ,we obtain
2(n,:;1) > 2 - E. The greatest lower bound of A is 0, because

 > 0 f9r m, n
 N. Given £ > 0, there is n such that i < E.
(b) Clearly, 0 < vn - [vnJ < 1. Taking n = k 2 , kEN, we see that
o E B. Thus inf B = O. To show that supB = 11 observe first
that [ vn2 + 2n] = n for each positive integer R. Suppose now
o < £ < 1. A simp le cal culation shows that the inequality
vn 2+2n- [ vn 2+2n] = R > 1-£
1+ ; +1
is satisfied for any integer n> (1;:)2 .
1.1.11.
(a) sup{x E JR: x2 + 2: + 1 > O} = +00,
(b) inf{z = z + z-1 : z > O} = 2,
(c) inf{z = 2% +2: : x> O} =4.
The first two equalities are easily verifiable. To show the third
one, observe that 'Clt

 VOb for G, b > o. Therefore,
2Z +2-! > V2t+z >
 = 2
2 - -
with equality if and only if z = 1. Thus (c) is proved.
1.1.12.
(a) Using the inequality a
b
 Viib for a, b > 0, we get
m 4n >4
-+-
· n m-
with equality for m = 2n. Therefore, inf A = 4. Taking m = 1,.
one can see that the set A is not bounded above. This m eanR
that sup A = +OO





130


Solutions. 1: Real Numbers


(b) Similarly, we get


_! < mn < !
4 - 4m 2 + n 2 - 4 '
with equalities for m = -2n and m = 2n, respective1y. Conse-
quently, infB = -
 and supB = !.
(c) We have infC = 0 and supC = 1. Indeed, 0 < m7.n < 1, and
for any £ > 0 there exist positive integers nl and ml such that
.


1
<E
nl +1


and


ml
1 > 1 - £.
ml+


(d) infD = -1 and supD = 1.
(e) One can take m = n to see that the set is not bounded above.
Hence sup E = +00. On the other hand, for any m, n E N we
have l+

n > l with equali
 {or m = n = 1. Therefore in! E =
1
3.


1.1.13. Setting 8 = al + a2 + ... + an, we get


Ok < al: <: 1 _ 01:+1 _ al:+2
8 - ak+ak+1 +ak+2 - 8 8.


A13 a result,


n
l<E Ok <n-2.
- "=1 ak + 01:+1 + ak+2 -


n
Now, our task is to show that in! E a +a QJt +a = 1 and that
k- l'" "+1 '+2
n
SUp E G +0 a. +0 = n - 2. To this end we take ak = tic, t > O.
1:=1 " Js:+l 1c+2
Then


n
E ale t
L- ak + 4lc+1 + QIc+2 = t + t 2 + t3

1

-2
-l P
+... + t n - 2 + t n - 1 +t n + t n - 1 + t n + t + t n + t+t 2
1 t".-2 t n - 1
= (n- 2) 1 +t+t2 + tn-1 +tn-2 + 1 + t n - 1 +t+ 1 ·




1.1. Supremum-and Infimum. Continued Fractions 131


n
Letting t -+ 0+, we see that sup E 0 +0 Ok +0 = n - 2, and next
k=1 Ie 11+1 1e+3
n
letting t -+ +00, we conclude that inf E a +0 air +4 _ = 1.
k=l Ie k+l 1r+2


1.1.14. Fix n E N and consider the n + 1 real numbers
0, Q - [a]1 2a - [2a], ..., 7Kt - [no:].
Each of them belongs to the interval (0,1). Since the n intervals
[
, ;;1 ), ; = 0, I, ..., n -1 , cover rOt 1), there mUst be one which con-
btinA at least two of th
 points, say nlQ - [nIQ] and n2 Q - [
a]
with 0 ::; nl < n2.
 n. So,


1
In2Q -I
Q] - n}Q + [n}Q]1 < - .
n
Now, it is enough to take qn = n2 - n} and Pn = [n2 Q ] - [nla].
It follows from the above argument that q" < n; that is l the second
inequality also holds..


1.1.15. We will show that in any interval CPt q) there is at least one
element of A. Put 0 < E = q-p. It follows from the preceding problem
that t,hec
 are Pn and qn such that-
Pn 1
Q - - < 2'.
qn qn
Since Q is irrational, lim qn = +00. Therefore
n-oo


1
IqnQ-Pnl < - <E
qn
for almost all n. Now set a = Iqn Q - PnJ. Then at least one of the
numbers ma, m E Z, belongs to the interval (p, q); that is, mqn Q -
mpn. or -mqna + mpn lies in this interval.


1.1.16. Let t e [-1,1). Then there is an x such that t = cosx. By the
result in the foregoing problem, there exist integer sequences {m n }
and {kn} such that x = fun (kn27r + 171n). This and the continuity
n-oo
of the cosine function imply that
t = cosx = cos( lint (kn21r + mn)) = Iim COS171n = lim cos Imnl.
n-oo n-OQ R-OO




132


Solutions. 1: Real Numbers


Hence each number of [-1, 1] is a limit point of the set {cosn: n EN}.
The desired result is proved.


1.1.17. It is obvious that. if there is n for which X n is an integer,
then x is rational. Assume now that z =
 with p E Z and q e N. H
x - [x} :f: 0, then
 - [
] =
, where I is a positive integer smaller than
q. Thus, the den ominato r of %1 = J is smaller than the denominator
of z. This meanR that the denominators of %1.%2,... are successively
strictly decreasing and ca.nn ot constitute an infinite sequence.


1.1.18. We will proceed by induction. It is easily verifiable that
Pk
Rle = - for k = 0, 1,2.
q"
Assume that for an arbitrarily chosen m 2; 2,
Rm = P7n = Pm-lam +Pm-2 .
qm qm-lam+qm-2


Note now that if we replace am in Rm by am + II I t then we get
m+l
the convergent Rm+l. Ther
fore
Pm-I (am + G
"'.) + Pm-2
Rm+l=
qm-I (am + 0..:+1 ) + qm-2
(Pm-16m + Pm-2)a m +l + Pm-l
-
(Qm-l4m. + qm-2)am+l + qm-l


Pm+l
-
qm+l


.


1.1.19. Denote


Ale = Pk-lq" - qk-IPk for k.= 1,2, ..., n.
Then, for k> I,
/:).k = p"-l(qk-lak + qk-2) - Qk-l(P"-lak + Pk-2)
= -(Pk-2Qk-l - Qk-2Pk-l) = -.6"-1 ·
Since dl = PofJI - qOPl = Goa} - (coa] + 1) = -I, we obtain Ale =
(-1)". This implies that Ph and qlc are relatively prime.




1.1. Supremum and Infimum. Continued Fractions 133


1.1.20. k; in the. solution of 1.1.18, we have, for n > 1,


Rn = Pn = Pn-IOn + Pn-2 .
qn qn-lan + qn-2


Analogously


PnXn+1 +Pn-1
x = for n = 1, 2, ... ..
qnXn+l + qn-l


Hence


x-Bra = Pnlln+l +Pn-l _

qnGn+l + qn-l qn
Pn-lqn - qn-lPn (-I)n
- -
- - ,
(qn X n+l + qn-l)qn (qnXn+l + qn-l)qn
where the last equality follows from the result in 1.1.19. Therefore


{ >0
x-R,.
<0


for even n,
for odd n..


Thus z lies between two consecutive coDvergents.


1.1.21. We first prove that if Q is a positive irrational, then the set
{n - ma: n,m e N} is dense in 14. To this end take an interval
( a, b), 0 < a < b. We will show that this interval contains at least
one element of our set. Put E = b - a > O. By the preceding problem
there exists a convergent Rn such that


1
(1) 0 < Rn - Q < 2.
qn
Indeed, take an odd n and observe that
(qn X n+l + qn-l)qn > G.
Since lim qn = +00, for sufficiently large n we have _ q l < E. This
n-oo n
and (1) imply that 0 < Pn - Qqn < t!: < E for sufficiently large
n. Therefore there is no e N such that noCPn - aqn) e (a, b). Now
let t e [-1,1]. There is a positive x such that t = sinz. It follows
from the above considerations that there exist sequences of positive




134


Solutions. 1: Real Numbers


integers {m n } and {kn} for which z = lim (TTtn - 21rk n ). By the
n-.oo
continuity of the sine function,


t = sin x = sine lim (m n - 21rkn» = lim sin mn.
n-.oo n-oo


So, we have proved that any number of the interval [-1,1] is a limit
point of the set {sinn: n EN}.


1.1.22. Let Pn and qn be the integers defined in 1.1.20._ Since Xn+l =
an+l + % J "' > an+l, we get (QnXn+l +qn-I)qn > (qn C n+l +qn-l)qn =
n+.
qn+lqn. Therefore, by 1.1.20,


1
1% - Rn I < .
qnqn+l


Since qn+l = qnBn+l + qn-l > qnBn+l > qn , the desired inequality
follows. We will show now that the sequence {qn} cont&iDS infinitely
many odd numbers. Indeed, it follows from the result in 1.1.19 that
qn and qn+l cann ot be both even.


1.1.23. It is enough to apply the formula given in 1.1.19.


1.1.24. Observe first that the sequence { qn} is strictly increasing.
and qn ;::: n. Moreover, by Problem 1.1.20,


1
Iz -
.I - ( ) ·
qnZn+l + qn-l qn


This and the inequality Xn+l < 4n+l + 1 imply that


1 1
Ix - &at > =.
(qn(an+l + 1) + qn-l)qn (qn+1 + qn)qn


Since tIn+2
 1, we have


1 1
IX-Rn+ll< <.
(qn+ltln+2 + qn)qn+l (qn+l + qn)qn


These inequalities yield the desired result.




1.1. Supremum and Infim um. Continued Fractions 135


1.1.25. Let Ix -
 I < Jx - Rnl < Ix - Rn-ll. Since x lies between
Rn And R,.-1 (
Prohlem 1.1.20)1
I; - Rn-II < IRn-I- Rnl.
Therefore, by the result in 1.1.23,
Irqn-l - sPn-ll 1
<
sqn-l qn-lqn


.


Moreover, we have 6q
-1 < qn_ J 19n because Irqn-l - 8pn-ll
 1.
Hence 8> qn.


1.1.26. Following the algorithm given in 1.1.20, we get
1
ao = (
] = 1. XI = ./2 =
 + 1-
2-1


Therefore, at = [Xl] = 2. Slmllarly,
1
X 2 v'2 -X l and Q 2 =a l =2.
= ( 2 + 1) - 2 -


By induction,


Likewise, .


_ In 11 11 11
v 2 = 1 + i2 + i2 + i2 + ... ·
v'5 - 1 11 11 11
2 = 11 + 11 + 11 + ... ·


1.1.27 . Sin ce k < Vk 2 + k < k+ 1, ao = [ vk 2 + k] = k. As a result,
2:1 = Y k
t k + k. Consequently. 2 < Xl < 2+ l and at = 2. Moreover,
X2 = 1 1 = k + v'k 2 + k.
Vk
 +k-k. - 2
Thus 2k .< X2 < 2k + 1 and 1I2 = 2k. In much the sam e way we
obtain B3 = 2. Now, by induction,
_ I 2 11 11 11 11
v Ie + k = k + 12 + i2k + i2 + i2k + ... ·




136


Solutions. 1-: Real Numbers


1.1.28. Since 0 < x < 1, we have ao = 0 and Xl = l/x. Therefore,
41 = n implies [1/x] = n. Hence, l/x -1 < n S 1/x, which gives
l/(n+ 1) < x
 l/n.


1.2. Some Elementary Inequalities


1.2.t. We will use induction. For n = 1 the inequality is obvious.
Take an arbitrary positive integer n and assume that


(1 + 01) · (1 + 02) · ... · (1 + an)
 1 + al + lI2 + ... + an.


Then


(1 + Gl)(l +
) · ... · (1+ an)(l + Cln+l)

 (1 + al +
 + ... + an)(l + a n +l)
= 1 +al +02 +... +an +l1n+l +4n+l(al +02 +... +4n)
2: 1 + at + 112 +... + an. + l1n+l.
Thus the claim is established.


1.2.2.. Induction will be used.. For n = 1 our statement is clear. We
suppose now that the claim holds for an arbitrarily chosen n. Without
loss of generality we can assume that numbers ai, ..., "n+l satisfying
the condition al ·
 · ... · an+l = 1 are enumerated in such a way
that at


 ...
 an
 an....l. Then at
 land an...1
 t:. Since
02 · a3 · ... · an · (an+ 1 · a1) = 1-, by our induction assumption, we have
42 + aa +... + 4n + (an+l · al)
 n. Hence
at + tI2 + ... + an + On+l > n + f1n+l + at - t1n+l .. G$
= n + a..a+l · (.1 - al) + a
 - 1 + 1
= n + 1 + (an+l - 1)"(1- at)
 n + 1.


1.2
S
 The inequalities follow from the statement proved in Problem
1.2..2
 Indeed, replacing there the numbers OJ by VI
J

...ar. ' we get
An
 G n . The inequality G n > Hn follows from the already proved
inequality An 2: G n provided one replaces aj by its reciprocal t-.
'J




1.2. Some Elementary Inequalities


137


1.2.4. Using the arithmetic-geometric mean
 m

@tY, we have


V' (l + nx). 1.....1
 1 + x


( n factors).


1.2.5.
(a) Apply the arithmetic-harmonic meaJi iij



lj
;,
(b) Use the arithmetic-harmonic mean: mequan
JI
(c) The left-hand

q
ty.can be shown as in (a) and (b). To prove
the right one, let us observe that
1 1 1 1 1 2n 2
3n + 1 + 3n + 2 + ... + sn + 5n + 1 < 3n + 1 + 3n + 2 < 3.
(d) By the arithmetic-geometric mean
e .q
ty,
2 3 4 n+l n
1+2+3+".+ n >n V'n +l.


Hence


1 1 1 \I: 1
1 + 1 + 1 + 2 + 1 + 3 + ... + 1 + ;; > n n +


and


1 +
 +
 +...+; > n( V'n + 1-1).
To prove the other



. we use the arithmetic-geometric
mean inequality and get
1 2 3 n n
2 + 3 + 4 + ... + n + 1 > V'n + 1 ·


This implies
11 1 ( 1 1 )
1 + _ 2 + 3 + ... + - < n 1 -
 + I -
n nn+l n+


1.2.6. By the iPeq
!ditY. On S An we get
n _ 2ft +{/l_ _ . 2n < 1 + ... + z2n
X - X ... X - 2n+l ·




138


Solutions. 1: Real Numbers


1.2.7. The right-hand side of the



 is a direct consequence
of G n
 An. The other one can be proved by induction. This is clear
for n = 1. Now we will prove that the

J;Y: holds for n + 1
provided it does for n. To this end we show that (alOn+l)n+l <
(al · ... · an · tIn+l)2, whenever (alan)R
 (aJ .... · an)2. We have
(ata..+1)'&+1 < at . a..(at . .... a..)2 . (
t ) n+1 .
Hence it is enough to show that
a R + 1
01 ::1
 a
+1 .
R


Note that the last


ty: can be rewritten as
( d ) n-l
al 1 + a1 + (n _ l)d
 a1 + (n - l)d,
where 4n = al + (n - l)d, which is easy to prove by induction.
1.2.8. It is an imm ediate consequence of the foregoing result.
1.2.9. One can apply the arithmetic-harmonic mean. ji1






1.2.10.
(a) By the arithmetic-harmonic m




t3 we have
( n 1 ) -1 1 n
n E-
 -Eakl
1.=1 ale n k=1


and consequently


t .! >
.
k=l ak 8


Similarly, the mequaU
y
( n 1 ) -1 1 n
n E
 - E(s-ak)
Ie 8 - ale n k
=1 =1


implies


n 1 2
'"' > n .

8-ak - B(n-I)




1.2. Some Elementary Inequalities


139


From this and from the equalities


n n 1 n n 1

 k
 -n and E s - ak =8E- -n

 s
 ak = 8
 S - ak k=1 ak 1<=1 at


the desired result follows.
(b) See the solution of part (a).
(c) This follows by the same method as in (a).


1.2.11. Use the

!l


 l
CIr.
 VCik.


1.2.12. We have


n n ( n ) 2
{;a
 h b
-
 akbk


n n
- E a
b; - E akbkajb j
kj=l I:j==1
1 n
= 2 E (atbj - bk a j)2
 o.
k.j=l


1.2.13. This in eqy:aJi ty is equivalent to the following:


n n
2: (aka; + bkbj):S 2: (a
 + bt)! (al + bl)!'
kJ=l kJ=l


which in turn is a direct consequence of the obvious 4t
ity akaj +
bkbj
 (a
 + bi)4(aj + b
)! .
1.2.14. The claim follows from the Cauchy mequanty



1.2.15.
(a) By the Cauchy
e.q
.,.


;


( ) 2
n n 1 n 1
EakE-
 E V ak - =n 2 .
k=l k=lOk k=l ak




140


Solutions. 1: Real Numbers


(b) By (a),


n ra 1 n ra 1 ra
LakL :a k = EakEe-nEak
k=1 1e=1 k 1e=1 Ie=! k k=l
n n

 n 2 -n Ealc =n E(l- ale).
k= 1 k=l


(c) By our assumption, lo
a 1 + lo
a2 + ... + IO&aCln = 1. This and
the Cauchy inequality (Problem 1.2.12) give the desired result.
1.2.16. The inequality is equivalent to


n n n
o
 -4a E akbk + 4 E ai + Q2 E b
 ,
k= 1 k=! k= 1


which holds: for each real a, because


(
n ) 2 n n
.0. = 16 \r.
 akbk -16
 a
 h
 SO.


1.2.17. Applying the Cauchy inequality, we obtain
n n ( n )
 n
Elakl = L1lakl
 Vii La

 ViiElakl.
k=1 k=l k=l k=1


1.2.18.
(a) By the Cauchy inequality,
( n ) 2 ( n ) 2 n n 2
Lakbk = EVkak
 SLkalE
.
Ie=l k=1 k=l k=1


(b) Likewise,
( n ) 2 ( n 3. ) 2 n n
1;
 = t.; k;;k S t.; k3a
 t.;
 .




1.2. Some Elementary Inequalities


141


1.2.19. The Cauchy inequality gives


( n ) 2 ( n ) 2 n n

 at =
a
a :2q

 arq
 at-q.


1.2.20. By the Cauchy inequality,


n n n ( n ) 2
E a
 · n = E a
 E 1
 E ak = 1.
k=l k=l k=l k- l


n
Hence E a


, with equality for o'k =
, k = 1,2,...,n. There-
k=1
fore, the least value we are looking for is
.


1.2.21. In much the same way as in the solution of the last problem
we get


U n ) 2 ( n ) 2 n n
1= Eak = Ev'Pkak

Epka
E
.
=1 k=1 P k=l k=l P


Thus,


n 1
Epka

 n
k=1 E ..L
k=l Pic
with equality for ak = :. Lt :.)-1 . So the least value in question
is ( tl *)-1 .


1.2.22. It follows from the solution of Problem 1.2.20 that


( n ) 2 n
Lak
nEa
.
k=1 11:=1




142


Solutions. 1: Real Numbers


Hence


(
 ak) 2= (a 1 +a2) +
 ak) 2
 (n-I) (a 1 + B2)2+
 a
)
= (n-I) l
 a
 +2a 1112 ) ·


1.2.23.
(8) By the Cauchy inequality,


1 1
C
 (ak + b k )2)
 = (
 (a
 +2akbk +bi»)

n ( n ) I ( n ) i n

 t; a
 +2 t; a
 t; b% + t; b

= ( ta
 ) ! + ( tb
 ) !.
k=1 Ie=l






(b) By (a),
( ta
 ) ! - ( t bi ) !
 ( t(ak-bk)2 ) !.
k=1 k=1 k=l
This and the inequality established in Problem 1.2.17 yield


(
n ) 1 ( n ) ! fa
\,.
 a
 - £; bi
 b lak - bkl.


Similarly,


(
 ) ! ( n ) -1 n

 bi - {; a
 <t; lak-bkl
and the desired result is proved.




1.2. Some Elementary Inequalities


143


n n n
1.2.24. Since E Pkak = 1, we have 1 = E Pkak = E (p,,-a)ak+
k=l k= 1 k=1
n
Q E ale for any real Q. Now t by the Cauchy inequality,
k=1


IS L
 (Pk-O)2+a2)
 a%+(
 akr ·


Hence


n ( n ) 2 ( n ) -1

 aI+ t; a lc
 {; (Pk- o )2+ 0 2 ·


n
Putting a = n
1 E Pie, we obtain the greatest lower bound. There-
k=1
fore,


( ) 2
n n +1
2>
 + 2:ak
 n n n 2 '
1=1 '=1 (n + 1) El Pi - (,
:1 Pic)
where the equality is attained for


n
(n+ l)Pk - E Pk
k=l
ak = 2 ·
(n+l) tl Pi- ( tl Pk )


1.2.25. We will proceed by induction. For n = 1 we get the equality
al b l = al bl. Moreover, if the inequality holds for n, then


n+l n+l n+l
Eak Ebk - (n+ 1) Eakbk
k=1 k=1 k=l


n n n
:s an+l E bk + b n + 1 E ak - n4n+lhn+l - E akbk
k=1 k= 1 k=1


n
= E(b n + 1 - bk)(a/c - On+l) < o.
k=1




144


Solutions. 1: Real Numbers


1.2.26. We will use induction on p. For p = 1 the equality af = af
holds. Ass umin g the inequality to hold for P, we will prove it for
p + 1. Obviously, without loss of generality, we may suppose that the
numbers ak are enumerated in such a way that al <

 ... < an.
Now, by our induction assumption and the result in the foregoing
problem,


( 1 n ) 1>+1 1 n n 1 n
n Eak S;i2 EatEak
 n E a rr 1 .
k=l k=l k=l k=l


1.2.27. We have


(1 + c)a 2 + (1 +
)b2 = a 2 +1J2 + (.reo. -
 b) 2 + 2ab
 (a+ b)2.


1.2.28. Clearly, va 2 + 1J2 + va 2 + c2
 161 + lei
 Ib + el. Hence
11J2 - c2l
 16 - cl ( ya 2 + IJ2 + ya 2 + c2) J which is equivalent to the
desired inequality.


1.2.29.
(a) For any real numbers a, 6, c we have a 2 + 1J2 + c'l > ab + be + ca.
Thus 1J2cfl + a 2 cfl + a 2 1J2 > abc(a + b + c), which is equivalent to
our claim.
(b) The desired result follows from the inequality a 2 + 1J2 + c2

ab + be + ca in much the same way as in (a).
(c) This is a consequence of the arithmetic-harmonic mean inequality.
(d) We have


1J2 - a 2 6 + a 6 + a
= (b-a)= «6+c)-(c+a».
c+a c+a c+a


Putting u = a + b, 11 = b + c and z = c + a J we obtain




1.2. Some Elementary Inequalities


145


b 2 - a 2 cil - b 2 a 2 - t? U 1) Z
+ + = -(V-Z)+-(Z-U)+-(U-V)
c+a a+b b+c z u v
u 2 Vl + V 2 Z 2 + Z 2 U 2 - (U 2 VZ + V 2 UZ + Z 2 UV)


-
-


uvz


_ u 2 (Vl + Z2)+ V 2 (U 2 + %2)+ Z2(U 2 + V 2 )- 2(U 2 V% + V 2 UZ + Z 2 UV)
2uvz



 o.
(e) For a = b the inequality is clear. Assume now that 0 < b < a.
Then


a - b ( va - Vb) ( va + V1}) _
 _ li b a - b
= <va-vo<
2va 2..;0, 2Vb


and thus


(a-b)2 (a-b)2
4a < (Jli - v'b)2 = a + b - 2Jlib < 4b ·


1.2.30. Let m = i:'. Then







m(b 1 + ... + b n ) = b i (b l +
 + ... + b n ) = bi bl + bi
 + ... + bi b,.,
al a2 4n
$ ih
 + b;
 + ... + ;;;:b n = al + ... + an =:; M(
 + ... + b n ).


1.2.31. The inequalities follow from the result in the foregoing prolr
lem and from the monotonicity of the tangent function on (O,1r /2).


1.2.32. Apply the inequality given in 1.2.30 with 4i = In Ci and bi =

, i = 1,2, ".t fi.


1.2.33. Note that


al
 a:
- b $ M, M
 $ M, ..., Mn-1b n $ M
1 2 n
and use the inequality proved in 1.2.30.




146"


Solutions. 1: Real Numbers


1.2.34. By the arithmetic-harmonic mean inequality (see) e.g. 1.2.3),


n < (x - al) + (3; - Cl2) + ... + (3: - an)
1 + 1 ++ 1 - n
Z-BI %-02 ... Z-4n


n:c - (at +
 + ... + an)


.


n


The desired result follows easily.


1.2.35. Observe that


1 + Cl + C2 + ... + en = (1 + 1)" = 2 n 1


and apply the Cauchy inequality (Problem 1.2.12) with Ok = 1 and
bk = VCk, k = 1,2, ..., n..


1.2.36. Since


n ( ) n-l ( )
TIn_TIn
k= O k - k=l k


n-l ( )
and 2 n -2= L
 .
«=1


the claim follows at once from the arithmetic-geometric mean inequal-
ity (Problem 1.2.3).


1.2.37. By the arithmetic-geometric mean inequality (see 1.2.3),
Ap-1A < (P-l)At+A
_1
k k-l - P ,
where Ao = O. It follows that


k = 1,2, ..., n,


At - P 1 Ar1ak
 At - p 1 Ar 1 (kA k - (k - l)AIi:-l)
p- p-
=AP ( l- kp ) + AP-1A (k-1)p <AP ( l- kp )
Ie l ie Ie-I 1 - k 1
p- p- p-
+ k -
 «P-l)At + ALl) = 1 1 «(k -l)ALJ - kAt).
p- p-


Now, adding these inequalities we get our claim.




1.2. Some Elementary Inequalities


147


1.2.38. Assume that Bj = max{al,a2, ...,a n }. Then


n-1 i-I n-J i-I n-I
L Bk a k+l = L akak+l + L ak a k+l
 OJ L ak + £tj L ak+1
11:=1 k=1 k=i k= 1 k=i
a 2 ( a ) 2 a2
= l1j(a - OJ) = 4 - 2 - C£i ::; 4.


1.2.39. One can apply the result in 1.2.2.


1.2.40. The left inequality follows from 1.2.1.
(u.) Obi
rve that


1 - a
 1
l+a k = l < 1 ·
- ak - 6k


Hence


IT (1 + ak) < (IT (1 - a k ») -1 .
k=1 k= 1
Since 41 + 42 + ... + an < 1, applying once again the result in
1.2.1, we get


fI(! +ak) < (1- t ak ) -1.
k= 1 1:=1


(b) Use the same reasoning as in (a).
1.2.41. Apply the inequality given in 1.2.15 (b), replacing ak by
1 - Ok.


1.2.42. Since 0 < o.le
 1 for k = 1,2, ..., nt the inequality


(1)


n n n 1
Lak
IIak.E-
Ok
k- I k=l k=l


holds for n
 2. Now, applying the inequality from 1.2.15 (b) witb
ak replaced by 1:
'" k = 1,2, ..., fi, we get


n l ( n 1 ) n 1
E- n-E
nE ·
k=l ak k=1 1 + a" k=l 1 + a"




148


Solutions. 1: Real Numbers


n
Multiplying both sides of this inequality by n ak and using (1), we
k=l
get our result.


1.2.43.
(a) By the arithmetic-geometric mean inequality (Problem 1.2.3),


"
IT (1 + ak)
k=l
-
-
(n+ l)n


24 1 + B2 + ... + an at + 2a2 + a3 + ... + an
.
n+l n+l
n
at + a2 + ... + 2an > II
· ... · 1 - ak.
n + 1.:=1


(b) The proof of this part runs as in (a).


n n
1.2.44. Observe first that if E 1;0. = n -1, then E 1

 = 1. To
k-l
 k-l

get our result it is enough to apply the inequality given in 1.2.43 (b)
with ale replaced by 1 :
... ·


1.2.45. [M. S. Klamkin, Amer. Math. Monthly 82(1975), 741-742]
We may assume that a) t 02, ..., an are enumerated in such a way
that al = min{al,II2,...,an} and a2 = max{al,a2,...,lln}, and let
An = 1/n be the arithmetic me&n of ai, ...,an. Define a new sequence
{ak} by setting o
 = An,
 = a1 + lI2 - Ant a
 = a; for 3
 i
 n.
We will show that


TI n 1 + ak TI u 1 + a

.
 I ·
k=l 1 - ak k=1 1 - ale
It follows from the definition of the sequence {ak} that (1)
 equiv-
alent to


(1)


(1 + at)'l +
) > (1 + An)(l + at + a2 - An)
(1 - at)(l -
) - (1 - An)(l - at - a2 + An)'
which in turn is equivalent to
(An -- 01 )(An - 02) :5 o.
The last inequality is an imm ediate COnsequence of our assumptions.
Now, we repeat the above procedure for the sequence {ok} to get the




1.2. Some Elementary Inequalities


1
9


sequence {ak}. At least two terms of the sequence {ak} are equal
to an Aft. Moreover, the 8eqnence satisfies an inequa.lity of type (1).
If we repeat this procedure at most n - 1 times, we get the constant
sequence with each term equal to An. In view of (1),
Ii l:a k
 Ii l:An = ( n:l ) n.
k=l 1 aA; k=l 1 All n 1


1.2.46. Let ak! = max{aha2, ...,an}. There is a fraction on the left
side of the inequality whose numerator is equal to akl. The denomi-
nator of this fraction has two terms. Let us denote the greater one by
ak2- Now, take the fraction whose numerator is ak2 and denote by
aka the greater of the two terms of its deno t1') in at or t etc. Note that
(1) a
 > a k " i = 1,2,....
ak£+1 + ak l +2 - 2aka+1
It follows from the above construction that there exists an l such
that ak'+l = ak!. Next, observe that the numbers a", and ak.+1 ap-
pear in our inequality as numerators of either two neighbor fractions
or two fractions which are separated by only one term (we assume
here that the last and the first are neighbor quotients). Moreover,
aki+l appears as a numerator of a fraction that is to the right of the
fraction with the numerator aki. To pass from the fraction with the
numerator Okl to the fraction with the numerator Ok,+ I , I steps are
needed. where l 2: ,g. Hence, by (
) and the arithmetic-geometric
mean inequality,
aiel + a
 +... + ak 1 > llrJ; >
.
2ak2 2ak3 2akl - V 2i - 4


1.2.41. We hav e
i-.. v lale - tl ( 1 1 1 ) v' 11I2 - tl
LJ 2 k
 22 + 23 + ... + 2R v' lal - tl + 2 2
k=1
v lan - till
+... + 2 n
 2i( vial - tl + V)lL2 - tl) + 2i( v' lal - tl
+ V l a 3 - tl) + ... + in< v ial - tl + v ia,. - tl),




150


Solutions. 1: Real Numbers


which implies the desired inequality.
1.2.48. By the arithmetic-geometric mean inequality,
at
 an n bl b:l b n
. .. + . ,..
41 +6 1 B2+b:2 ... an +b n at +b 1 Q2+b-.l ... 4n+ b n
1 ( a1 4n b 1 b n )
< n al + b 1 I ... I an + b
 · at + -b l .. ..... + an + b n = 1.


1.2.49. (V. Ptak, Amer. Math. Monthly 102(1995), 820-821] First,
observe that if we replace each at by cak with c > 0, neither the left
side nor the right side of the inequality is changed. Therefore, we can
assume that G = 1. Then n_ = ! . Observe now that if 4 ) < X < ..!. ,
-n -J - - 01
then x +
 < at +
1 .. Hence
n nIl
LPkak+ LPk- Sa! +- =2A.
n=1 k=l Uk a1
Now, to obtain our claim we may apply the arithmetic-geometric
mean inequality.
1.2.50. Let us arrange all the positive divisors of n into pairs (k, l) in
such a way that kl = n. By the arithmetic-geometric mean inequality,
kt'
 ,fkl. Adding these inequalities, we get
O'(n) > T(n) _ c
2 - "2 v n .




Chapter 2


Sequences of Real
Numbers


2.1. Monotonic Sequences


2.1.1.
(3) Let {an} be an increasing sequence bounded from above. Then
sup{an : n E N} = A < 00. Thus for any n"e N, an $ A. Since
for any e > 0 the number A - E is not an upper bound of the
"set {an : n eN}, there is Bno such that ano > A-E. By the
monotonicity of the sequence, A > an .> A - E for any n > no.
Hence lim an = A.
n-oo
Assume now that {an} is not bounded above. Then for any lI[
there is fino such that 4no > M. Again, by the monotonicity of
the sequence, an > kI for n > no, and therefore lim an = +00.
n-+QC)
(b) See the solution of (a).


2.1.2. We have


Sn < Sn+l
for n > 2.
8n-l 8n


Indeed, by 1.2".19,


(1)


s;
 Sn+lSn-l.


151




152:


Solutions. 2: Sequences of Real Numbers


We will show that {xn} is an incr e.a.sin g sequence. The inequality
Xl $ 3:2 follows from ( tale ) 2 S p t ai (see the solution of
k= t k=1
1.2.20). Assume now that X n -l $ Xn. Then


(2)
Hence, by (1) and (2),


.!!.:.!
Sn-l
 Sn" ·


X n +1 = " +,ysn+1
 " +1 s;
 ..+1

I = Xn.
8 n -l B n"


2.1.3. We have Bn+l = ;
l an < CLn, n > 1. Therefore {an} is a
strictly decreasing sequenCe. Since it is bounded below (e.g. by 0),
lim an = 9 exists. The number 9 satisfies the equation 9 = 19.
n-.oo
Consequently, 9 = Q.
2.1.4. Let b n = an - 2,.1_. . We have b n + 1 -b n = 4n+l-an + in
 o.
Hence the sequence {bra} converges, and so does {an}.


2.1.5.
(a) We will show that the sequence {an} is monotonically decreasing
and bounded below. Indeed.
-1
Gn+l - Cln = vn + Ie v'n + I + v'£.)2 < o.
Moreover, by the ineq uality giv en in the hint (one can prove it
by induction), l1n > 2{ v'n + 1 -
 - 1) > -2.
(b) The proof follows by the same method as in (al.
2.1.6. We first show by induction that
 < 4n < 2 for n E N and
that the sequence {an} is strictly increasing. These two fac ts imply
the convergence of {an}. Let 9 = lim CIn..Because an = J3 an-t - 2
n-.oo
we get 9 = ../39 - 2 ,.and consequently, 9 = 2.


2.1.7. One can e5tablish by induction that On :> 2c. Of course, at <
a:a. Moreover, if an > an-I, then
4n+l = (an - c)2 > (an-l - c)2 = an.




2.1. Monotonic Sequences


153


The last inequality follows from the monotonicity of the function
f(x) = Xl on R+_


2.1.8. By the arithmetic-geometric mean inequality and by our as-
sumptions we get
tin + (1; tIn+l)
 v'an(l- an"-I) >
 .
Hence an - Gn+l > O. Therefore the sequence {an} converges to a
g. Since an(l - On+l) > }, we get g(l - g)
 i. The last inequality
is equivalent to (29 - 1)2 :f 0, which gives 9 =
.
2.1.9. Obviously, 0 $ an < 3 for n
 1. Moreover, lJ
+l - a
 =
-a; +an +6 > 0 for .0
 an < 3. Thus the sequence is monotonically
increasing and bounded above, 50 it converges. By the definition of
the sequence, lim an = 3.
n-oo


2.1.10. We see at once that 0 S an < 1 for n
 1. To prove the
monotonicity of the sequence we will need the following form of the
principle of induction:
Wen) ia troc for all natural numbers.n, if the following two con-
ditions hold:
(i) W(l) is true.
(ll) The truth of W(k) for 1 S k < n implies Wen + 1) is also
true.
Asswne now that tin-I 2: an-2 and an 2: On-I- Then


. l ( 3 3 )
On+l - an = 3 an - a n -l + an-l - a n -2 > o.


Therefore the sequence is convergent. Let 9 denote its Umit. Then
9 =
(l + 9 + g3). Consequently,
-1+v'5 -1-y'S
g=lorg= 2 org= 2 .
Observe that all the terms of the sequence are nonnegative and less
than -1
v'6 . Thus Jim an = -1
V5 .
n-oo




154


Solutions. 2: Sequences of Real Numbers


2.1.11. We have 4n+l = 4n. 2


 < tin, n
 1. Therefore (see the
solution of 2.1.3) we get 9 = o.


2.1.12. Since Bn+1 = an

t
 < lL,u n
 1, the sequenc
 is mono-
tonically decreasing. It is bounded below by zero, 50 it converges.


2.1.13.
(a) Clearly, {an} is monotonically inc reasin g. We will show that it
is also bounded above. Indeed,
1 1 1 1 1 1
an = 1 + 2 2 + 32 + ... +
 < 1 + 1 . 2 + 2 . 3 + .... + en - l)n
= 1 + ( 1 -
 ) + G -
 ) + ... + ( n
 1 -
) = 2 -
 < 2.


(b) Obvious1y, {an} is monotonically increasing. Moreover t
1 1 1 1 1 1
an = 1 + 22 + 33 + .... + nn < 1 + 22 + 32 + ... +
.
Hence it follows from (a) that the sequence is bounded above.


2.1.14. For n
 1, we have


1 1 1
lIn+l-an=- + + <0.
vn (n + 1) v2 n(2n + 1) v (2n + 1)(2n + 2)


Hence the sequence is convergent, as it is monotonically decreasing
and bounded below.


2.1.15. From the arithmetic-geometric mean inequality we get
1'-1 a ,

an p-l = va,
an


a n +l



n
 1.


Therefore


an Q
4n+l - an = -- + _
p p
 1


=-


a
-a <0
p-l - ,
pan


n > 2,


which shows that the sequence converges and Jim an = {Va.
n-.oo




2.1. Monotonic Sequences


155


2.1.16. Clearly, 0 < an < 2 for n
 1.
Ioreover,
a;+l - a; = Van - yGn-l > 0 provided an > a n -1.
Hence the se quence converges to a 9 which satisfies the equation
g= V 2 + vg.
Remark. Using Cardan's formula for real roots of cubic polynomials
one can show that
9 =
 ( 3
(79 + 3 "'249) + 3
(79 - 3 v'249 ) -1).


2.1.17. Note that 4nH = Z (z- "n
3 )' n 2: 1. Now one can
establish by induction that 0 < 4n < 2, n
 1.
Ioreover,
_ _ _ (all + l)(a n - 2) > 0
C,a+l an - an + 3 -.
Hence the sequence converges and lim an = 2.
n-+oc


2.1.18. One can show by induction that the sequence {an} is strictly
increasing. H it were bounded above then there would exist a number
g such that g = lim an. We would also have g2 - 2g + c = o.
n-oo
This equation has a real solution provided c
 1. So, assum e tha t
o < c
 1. Then the seque nce {an} is bounded above by 1- v I - c,
and fun an=l- vf l-c.
n-oo


For c > 1, the sequence is strictly increasing and it does not
converge. So, it diverges to +00.


2.1.19. Since


( a2 - a )
fIn+l = an 1- 2 3a
 + a ' n
 1,


we get


"if an >.;a, then an+l < an,
if 4n < va, then 4n+l > an,
if an = va. then lln+l = va.
Observe now that
a
 +3a
an 3 2 > va if and only if (an - ../0.)3 > 0,
an+a




156


Solutions. 2: Sequences of Real Numbers


which in turn is equivalent to an > va. Finally,


if 0 < a1 <..;a, then {an} is incr easin g and bounded above by ..;a;
if al > ..;a, then {On} is decreasing and bounded below by ..;a;
if at =..;a, then {an} is a constant sequence.
In each of the above cases the sequence converges to va.


2.1.20. One can show by induction that


(3 n - 1 - 1) - (3 n - 1 - 3)al
an = ( ) ( ) for n = 1,2,3,....
3 n - 1 - 3 n - 3 al


Therefore the sequence is not defined tor 41 =
::::
 with n E N.
Moreover, if al = 1, then an = 1 for n = 1,2,3, ... . For other values
of 41, the sequence converges to 1/3.


2.1.21. We have an+l = (an - a)2 + an
 an for n > 1. Hence the
sequence is monotonically increasing. Moreover, if it converges, then
lim an = a. Therefore jf al > at then the given sequenc
 diverges. In
n-.oo
the case where a-I
 a1 ::; a, we have also
-1
 an :; a for 11. > 1.
Thus for such al the sequence converges. Finally, if at < a -I, then
B2 > at and consequently, the sequence diverges.


2.1.22. It is obvious that the sequence may converge either to a or
to b. We will consider the following cases.
1 0 c > b.
Then a2 = c:

 > c = at and by induction an+l > an. Hence
1im On = +00.
n-oo
2° c=b.
Obviously, an = b for n = 1,2,3,....
3° a<c<b.
One can establish inductively that the sequence {an} is monoton-
ically d
iug WId buuud
 b
luw by u. Heure wn Un = u.
n-.oo
4 0 c = a.
Clearly, an = a for n = 1, 2, 3, ... .




2.1. Monotonic Sequences


157


SO O<c<a.
Induction is nsell once again to f;how that {tln} iA monotoni-
cally increasing and bounded above by 6. It then follows that
lim On = a.
n-.oo


2.1.23. Note that an+! = 6 (1- Un
7 ) for n E N. Hence by induc-
tion


if B} < 2, then an < 2, n e Nj
if 01 > 2, then an > 2, n E N.


Moreover,


(On + 3)(a n - 2)
Un+l - Un = - an + 7 ·


Therefore
1 0 if 0 < al < 2, then the sequence is increasing and bounded above
by 2, and Jim On = 2,
n....oo
2° if a1 > 2, then the sequence is decreasing and bounded below by
2, and lim 4n = 2,
n-.oo
3° if 01 = 2, then 4n = 2 for n e N.


2.1.24. Since 0 = al S tI2 and a
+l - a
 = l1n - an-I, we see by
induc
ion that an+l
 an for n e N. The sequence is bounded abov e,
e.g. by ../ 1 + 4c. One can easily establish that lim an = 1+";+4C .
n-.oo


2.1.25. Since fI2 = V2 ...t2 > ...t2 = 01 and a;.'_1-0; = 2(l1n.-O-n-t).
one can show inductively that C£n+ 1
 an for all positive. integers.
The sequence is bounded above by 2, and lim an = 2.
n-.oo


2.1.26. For k = 1, we get an = 6 ft , n e N, and therefore {an}
diverges to +00.
For k > 1,
02 = 1/5
 >
 = al and a
+! - a
 = 5(an - an-I).
It then follows by induction that {an} is strictly increasing. More-
over, an < Ir-
 for n e N. One can easily verify that Jim an =
n-co
"-
.




158


Solutions. 2: Sequences of Real Numbers


2.1.27. We see (by induction) that 1
 an
 2, n E N. The
monotonicity of the sequence follo\vs from the equality a;+1 - a; =
3(an - an-I). Hence for 1 < al < 2 the sequence is monotonically
increasing and its limit is 2. On the other hand t if Q) = 1 or Cl = 2.
the sequence is constant.


2.1.28.
(a) We have al < a2 and a
+l-a
 = Gn-an-l. It follows by induc-
tion that the sequence is monotonically increasing and bounded
above by c. Obviously, lim an = c.
n-co


(b) Since b:z .;;.... Ve ,je > v'C -=
 and
+1 -
 = c(b n - b n - 1 ),
using induction we conclude that the sequence is monotonically
increasing and bounded above by c, which is its limit.
2.1.29. One can establish by induction that 0 < On < b, and next
prove thaI, th
 JSequ
nce hi
l,ricLly iucr
i..ug. Its !in-lit is equal to b.


2.1.30. The sequence is strictly increasing and bounded above, e.g.
by 3. Its limit is 3+fI5 .


2.1.31. We have at < 02 < 03. Moreover, we see that for any n E N,


if an < Bn+l < t1n+2r then lln+2 < Bn+3.
It then follows from the principle of induction stated in the solution
of Problem 2.1.10 that the sequence {an} is strictly increasing. It is
also bounded above by 4, and Um an = 4.
-n--+oo


2.1.32. As in the solution of the foregoing problem, one can
how
that the sequence {an} is monotonically decreasing, bounded below
by 4, and lim an = 4.
n-oo


2.1.33. By the arithmetic-geometric mean inequality, an
 b n . Thus
an + b n
an+l = 2 $ ant n e N.
This means that the sequence {an} is decreasing. On the other hand,
the sequence {b n } is incr easin g because
b n + 1 = v bnan 2::
 = b n , -n E N.




2.1. Monotonic Sequences


159


Moreover, b l < an, b n < ale Therefore both sequences converge. Let
Q = lim. On and fJ = lim b n - Passage to the limit as n ..... co in
n-t>OQ n-.oo
Cn+l = an
bn gives Q = Q;8 or, in other words, a = (J.


2.1.34. Since 2{a; + b
)
 (an + b n )2 t we get an
 bn, n e N.
Therefore


_ a
 +b
 < a
 +anb n _
a n +l - + b - + b - an, n E N,
an nann


which means that the sequence {an} is decreasing.
In much the same way we show that {b n } increases. Moreover,
we see that b 1 < tin, b n < aI, and consequently, both sequences
converge.
Let Q = lirn an, {3 = lim b n . Letting n -to 00 in b n + 1 =
t
R-OO 11.-00
we obtain {3 = Q
.B t or Q = {3.


2.1.35. By the arithmetic-harmonic mean inequality, an
 b n . Hence
an + b n
Bn+l = 2 S an, n E N,
which means tbat {an} decreases. On the otber hand, {bn} increases
because


2a n b n
b n + 1 = b
 b n , n E N.
a n + n
Moreover, b l < en, b n < 4,h and therefore the sequencC3 converge.
Let Q = lim an, {3 = lim b n . Passing to the limit in the equa-
n-oo n-oo
tion Bn+l = an
b" yields Q = 0;8 . Thus Q = {J.
Note also tbat l1n+lb n +l = Cnb n , which m eAn
 that all t he terms
of {anbn} are equal to albl. It follows that Q = P = ya 1 6 1.
2.1.36. We have lln+l = 2


) (an + 1), n E N. Consequently,
-nan + (n+2)
4n+l -an = 2(n+ 1) ·
Now applying the inequality nan > n + 2 for n > 4 (which can be
estab]ished by induction), we see that the sequence is monotonically




160


Solutions. 2: Sequences of Real Numbers


decreasing and hence is convergent. Put Q = lim an. Passage to the
n-oo
limit in the equation Qn+l =- 2
11 1(Bn I 1) giVC8 Q -1.
2.1.37. It follows from the inequality an+2 <
 an+l +
 On that
4n+2 + iOn+l < C&n+l + ; an. Hence the sequence bn. = an+l +
lln is
decreasing, bounded, and therefore convergent. Let b be its limit. We
will show that {an} converg
 to a =
b. Let, t: > 0 be arbitrarily
fixed. Then there exists no E N such that i > Ib n - bl for n
 no-
Consequently,
E I 2 5 2
"6 > an+l + gan - ga > lan+l - al- i1an -
I for n 2; no-
Thus 14n+l - 01 <
 1l1n - aJ + i- We can see by induction that
( 2 ) k (( 2 ) "-1 2 )
lano+lc-al
 3 lano-al+ 3 +"'+3+ 1

( 2 ) " 1- (
)k E ( 2 ) k E

 3 lano - al + 1 _ i 6 < 3 lano - al + 2.
Since (i) Ie lano - at < ; for sufficiently large k, Ian - al < E for n
large enough.


.2.1.38.
(a) bn = (1 + !i> n+l = (1 + !i) an > an.
(b) By the geometric-arithmetic mean inequality G n +l < An+l (see
Problem 1.2.3) with al = 1, C2 = a3 = ... = an+l = 1 +
 ,


n+l ( 1 + ! ) R < 1 + 1 .
n n+l


H
l1



( l ) n ( 1 ) n+l
1 + n < 1 + n + 1 1 n E N.
(c) By the harmonic-geometric mean inequality Hn+l < G n + 1 , n > 1
(see Problem 1.2.3) with al = 1, 02 = a3 = ... = an..... = 1.+ ni l ,


1 ( n )
1 + _ < n+l
n n-l n,




2.1. Monotonic Sequences


161


which in turn gives b n < b n - 1 , n > 1.
To
how tha
 hoth AAqllP.!1c-
 {fin} a.nd {b n } converge it is
enough to observe that al ::; On < b n ::; hI, n E N. Moreover,
fun b n = lim (1 +
 ) On= lim CZn.
n-t>oo n-oo n-.oo


2.1.39.
(3) By th
 gtrow
Lric-ariLhw
Lic W
WI in
quu.liLy G n +l < An+l (

Problem 1.2.3) with at = 1, a2 = 43 = ... = 4n+l = 1+
, n e N,
we see that the sequence is strictly increasing.
H 0 < x
 1, then by the preceding problem,
n ( l ) ft
(1+;)
 1+; <e.


Hz> 1, then there exists a positive integer no such that x
 no.
Consequently, the monotonicity of the sequence {(I +
) n} and
the result stated in the foregoing problem imply
( 1 + ;) n < (1 +
) n < (1 + ,:: ) non < e nQ .
(b) It is enough to apply the. same reaso ning as in (8) and observe
that for z
 0, the sequence is bounded above, e.g. by 1.
2.1.40. Applying the geometric-harmonic mean inequality Gn+l+ 1 >
Hn+l+l (see Problem 1.2.3) with al = 1,
 = a3 = ... = 4n+I+l =
1+
, we get
n+l+l ( 1 X ) n+l 1 xen + I) 1 xen + I)
+n > +n2+nl+x+n> + (n+l)(n+l).
This shows that b n > b n + 1 , n e N.
2.1.41. By the inequality given in the hint,
1 n+l
Bn+l - an = - -log > 0,
n n
1 n+l
b n + 1 - b n = 1 - log < O.
n+ 11
Clearly, al
 an < bn
 b lJ n E N, and consequently, both sequences
converge (to the same limit).




162


Solutions. 2: Sequences of Real Numbers


2.1.42. Monotonicity and boundedness of the sequence {an} are
easily verified. It follows from the equality a
+l = an that its limit
is 1. We now show the monotonicity of {en}- Assume first that x > 1.
Then
en = 2 n (an - 1) = 2"{a
+1 - 1) = 2n(a n +l - l)(an+l + 1)
_ 2"+J. ( n_ 1 ) fZn+l + 1 > p_
- -n+l - 2 ""71+1-
This means that for x > 1, the sequence {en} is strictly decreasing.
The same reasoning applies to the case 0 < x < 1. For x = 1,
tbe sequence is constant. The monotonicity of {£in} can be proved
analogously.
For x > 1, the sequence {en} converges (because it is mono-
tonically decreasing and bounded below by 0). On the other hand.
for 0 < x < 1, the sequence {dn} is monotonically increasing and
bounded above by O. Now, it follows from the equality
dn=

an
that both sequences tend to same limit for all positive x different from
1. If :r; -- 1, then en = dn -= O.


2.2. L jmi ts. Properties of Convergent Sequences


2.2.1.
(a) 1.
(b) 1.
(e) -1.
(d) We have


0< (\1'2 -
)(v'2 - .v2)..... (v'2 - 2n+
) < (V2 -I)".


Th
 the limit of t.he 8equence Us equal tu o.
(e) We will first show that the sequence an = ;: converges to zero.
We have Bn+l = an
 (n

)2 < an for n
 3. Therefore the




2.2. Limits. Properties of Convergent Sequences 163:


sequence is monotonically decreasing. Clearly, it is bounded be-
low hy 7..ero. HPonce it i
 a
onvp.rg
n
 .:;;p.qn
nCf! and jt
 limit 0
satisfies the equation 9 =
 g. Thus 9 = O. We will now find
the limit of our sequence. To this end, set k n = [,jTi]. Then
k n

 < k n + 1, which gives
. n (kn + 1)2
o <: 2v'U < 2 2 k n + 1 ·
Therefore the limit of the given sequence is equal to zero.
(f) Let an = 2

 . Then lln+l = an
 (
tnl) < Un, n E Nt which
implies (see the solution of Problem 2.1.3) that 9 = o.
(g) Set
1 ( 1 1 1 )
a,a =
 v'f + J3 + v'3 + J5 + ... + v2n - 1 + v2n + 1 ·


Then an = Y.l;
 - I , w hich is a consequence of tbe
uality
1 - ../2k-l-v2k+l So Iim an -

.j2k -l+
 - -2 ·
 n-oo - 2.
(h) It follows from the inequalities
( I? ) 1 / 1 2 n
+ .., + ... + n n 2 + n
 n 2 + 1 + n 2 + 2 + up + n 2 + n
1

 (1 + 2 + ... + n) q 1
n-+
and from the squeeze law that the limit is
 .
(i) As in (h) we show that this limit is also equal to
 .
2 2 2 S t - n a Th 0" + 1 - ( !!.:t! ) 8 1 M
· .. e an - h+p)n . en an - n p+l . oreover, we
have lim ( n;:-I )$ ..1. 1 = .ll . Consequently, the sequence {an} is
n-oo YT Y J
monotonica.lly decreasing beginning with some value no of tbe index
n. It is also bounded below, e.g. by zero. Its limit 9 satisfies the
equality 9 = P
l g. Therefore 9 = O.
2.2.3. We have (( Q
O«n+l)O-no=no 1+
 ) -1)
< nO ( (1 +
) - 1) = nl
o .




164


Solutions. 2: Sequences of Real Numbers


Thus the limit of the sequence is equal to zero.
2.2.4. Let Q =
, with p e Z and q E N. For n > q the number
nlQ1l' is a multiple of 1f', which me3ns that the terms of the sequence,
b eginning with some value no of the index n, are.all equal t«? zero.


2.2.5. If the limit existed then we would .get
0= lim (sin(n+2)-sinn)=2sinllim cos(n+l),
n-oo n-too


and consequently, Iim COB n = O. SimilarlY1
n-.oo


0= lim (cos(n + 2) - cosn) = -25m 1 lim sin(n + 1),
n-.oo n--.oo


which is impossible because 5in 2 n+cos 2 n = 1, n E N. Therefore the
limit 1im sin n does not exist.
n--oo


2.2.6. See the solution of the foregoing problem.


2.2.7. We have
1 (( 1 ) 2 ( 2 ) 2 ( n-l ) 2 )
J

 n a + n + a + n + -U. + a + n
= lim ( n-l a2 + n(n-l) a+ 1 +22 + ...+ (n -1)2 )
n-OQ n n 2 n 3
1
= a 2 +a+ 3.


The last equality follows from the fact that 1 2 + 2 2 + ... + n 2 =
!!f n+l )(2n+l)
6


.


2.2.8. We have
an + a; + ... + a
 - k = (an - 1) + (a
 - 1) + ... + (a
 - 1).


Moreover ,


llID. . a
 - 1 =: l
 I 1 2 k
...or =: J 1"., .
"-00 an - 1
Therefore the limit is equal to 1 + 2 +... + k = k(
+l) .




2.2. Limits. Properties of Convergent Sequences 165


2.2.9. Using the equality
1 1 1 1 1 1
k(k+I)(k+2) = 2 .1£- k+l + 2 . k+2'
one can show that the limit is equal to
 .
2.2.10. Since
k 3 - 1 (k - l)«k + 1)2 - (k + 1) + 1)
k3+1 - (k+l)(k 2 -k+l)


keN,


,


we get


rr n k3 - 1 2 n 2 + n + 1 2
k3 + 1 = 3. n 2 + n n
 3.
11:=2


2.2.11.
.
2.2.12. Since 1 - 1i{';+l) =
(1- 2
3) (1- 3
4} "'" (1- (n+ 1)
 (n + 2») =
. ::
 n-=:O
.


2.2.13. We have


k 3 + 6k 2 + Ilk + 5 ;;: (k + l)(k + 2)(k + 3) - 1.


Hence
. n J:3+6k2+11k+5 . n ( 1 1 ) 5
lim - lim -- --
n_co L (k+3)! - n_co L k! (k+3)! - 3"
k=l k=l


2.2.14. Observe that

-1 1 1
L 2 k 1 2 1r for k = 1,2, ..., n.
l_x 2ft = I-x - -I-x
Therefore


n 2 k - 1
limE X -
Ie -
n--oo 1 - :£2
k=1


x.
I-x
1
I-x


for Ixl < 1,


for Jxl > 1.




166


Solutions. 2: Sequences of Real Numbers


2.2.15. For z 1= 1,
(1 - x)(1 + x)(l + 3: 2 )..n · (1 + x 2 ") _
1-%


1 1)"+1
-x-
l-x '


and consequently,


n
Un = II (1 +:£2") =
k;:O


. 1 - z2"+1
I-x
2n+l


for n = 0, 1,..., x:/: 1,
for n = 0, 1,..., .X = 1.


Finally,


for x < -1,
for z - -1,
for Ixl < 1,
for x
 1.


-co
o
lim OyJ = 1
r&-OO
I-x
+00


2.2.16. For x :F 1,
n ( 2 ) n (x 2 " + 1)2
a.. = n 1 + x 2 " + x- 2 " = n X2"+1 + 1
k
 k
O
(x + l)(x -I)(x + 1)(x 2 + 1) . ... · (x
t. + 1)
(x - 1)(x 2n + 1 + 1)
x + 1 X 2 "+1 - 1
- x-I · x2n+1 + 1 ·


Hence x+l
for Ixl < 1,
x-I
x+l for Ixl > 1,
llm On = 3;-1
n-:)O
0 for x = -1,

oo for :£ = 1.


2.2.17. Let x be different from 1. Then
( 3k I) 3" )( 3k ) 3"+J
1 ak 2 1 3" 1 + r + X-" x" - 1 x-I
+ x +x = Ir = It ·
r-I z3-1
Thus


11 3"+1 1
n 3 " ,, 3 k X -
( 1 + x + X-" ) = x 3 _ 1 ·
k=l




2.2. Limits. Properties of Convergent Sequences 167


Let 9 denote the limit of the sequence. Theil
1
l-x 3
+00
g=


1-00


for Ixl < I,
for Ixl > 1,
for x = -1,
Cor :& = 1.


1


2.2.18. Clearly, k. k! = (k + I)! - k!, kEN. Hence
Iim 1. I! + 2. 2! +... + n. n! = lim (n + 1)1 - 1 = 1.
n
oo (n + I)! n-oo (n + I)!


2.2.19. Note first that the problem is me anin gful for x
 O. B}f 2.2.3,
the denominator n Z - (n -lrr tends to zero if 0 < x < 1.
Ioreover,
If x < 0, then the denominator also tends to zero. For x = 1 it
equals 1. Therefore the sequence diverges to infinity (+00 or -00) for
x < 1, x:/: O. Now let x > 1 and set k = [x].. Then k
 1 and


l-(l-
r < l-(l-
r <l-(l-
r+1.
It follows from these inequalities that there exist a and {3 such that


Q < n (1- ( 1 -
 r) < P.


which in turn gives
on x - 1 <nX(l- (1-
 )''') <pn x - 1 .
Hence if z - 1 < 1999, then the sequence diverges to +00. If x-I >
1999, the sequence converges to zero. Now let x = 2000. By the
binomial formula,


n 1 qQ
 1
1im - .
n-oo n 2000 - (n - 1)2000 2000




168


Solutions. 2: Sequences of Real Numbers


2.2.20. We have


a,. =


a R + 1 _ b n + 1
an - b n
n+l
a


if a > b,


if a = b.


n


Hence lim an = a...
"-QU


2.2.21. It can be shown by induction that an = (n - 1)2. Conse-
quently, Jim an = +00.
n
oo


2.2.22. We show by induction that an - _, ,
 b'J . Thus lim an - O.
va n n



2.2.23. One can show that an = 1- (
)n-l . Therefore lim an = 1.
n-tQO


2.2.24. It is easy to verify that Bn+l = 1 +b+...+6'1-1 +bna. Hence
an+!= l
b +(a- l
b )b" for b
l,
n+a for b= 1.


Thus if b .;;;. 1, a. e R, the sequence diverges to +00. If b .f 1 and
a = 11 b ' the sequence converges to 11 b . In the case a :F l
b and
161 < 1, it also converges to 1:" . In the rem aining cases the sequence
is divergent. Namely, if b :$ -1 and a :f: 1 1 6 ' the sequence has
neither finite nor infinite limit. If b > 1 and a > 1 1 II ' the sequence
diverges properly to +00. Finally, if b> 1 and a < 1:1) ' the sequence
diverges properly to -00.


2.2.25. The formula for the nth term of the Fibonacci sequence can
be proved by induction. We may assume that Q :> {3. Then 0: = 1+ 2 {5
and {J = 1- 2 ../5 .. Moreover,


a" 1-
r S via" - pn Sa" 1 +
r.
Since lim 1
 l n = 0, we get lim -Clan = Q.
n
oo R-OO




2.2. Limits. Properties of Convergent Sequences 169


2.2.26. Note first that b n + 1 = an
3bn . From this Bn+l - b n + 1 =
!(lln - bn), which means that the sequence {an - b n } is a geometric
progression with the ratio i. Hence this sequence converges to zero.
Now it is enough to show that the sequence {an} converges. Assume
first that a
 b. Then {an} monotonically increases and an < b n < b.
Therefore it converges. It follows from the above that {b n } also
converges and lim an = lim b n . The same reasoning applies to the
n-.oo 11-00
case 4 > b.


2.2.27. We have


n digits n d
g its

 ,.. -,
a + aa + ... + OO...a = a(1 + 11 + ... + 11...1)
= a(lon-l + 2 · 10n-2 + ... + n . 10°)
= a«l + 10 +... + 10n-1) + (1 + 10 + ... + 10n-2)
+ ... + (1 + 10) + 1)
_ ( Ion - 1 lon-l - 1 10 2 - 1 10 - 1 )
- a 9 + 9 +...+ 9 + 9
10(10 n - 1) - 9n
= a 81 ·
Therefore the limit is 1:: .
2.2.28. Note that the sequence with terms viii, n
 3, is monoton-
ically decreasing and its limit is 1. Now it is easy to check that
(V'R-l)R< G f for neN.
Thus lim ('\fR - 1)" = O.
n-oo


2.2.29. Since lim On = 0, b eginnin g with some value no of the
r
-OU
index n, lanl" < (
)n. Consequently, lirn a: = o.
n-oo


2.2.30. Let max{al,a2,...,ak} = ale Dividing the denominator and
numerator by ar we show that
lim . Plai+l +P2a;+1 +... +Pk a k+ 1 _
n n n - a'e
n-co Pial + P202 + ... + Pkak




170


Solutions. 2: Sequences of Real Numbers


2.2.31.
(a) Let
 > 0 be so small that q + c < 1. Then there exists no e N
such that


a n + 1 1
< q + E for n
 no.
a ra


Hence


Ju,al < (q + £)fJ-noIClnol, n
 no_
This implies lim lanl = 0, that is, lim l1n = o.
n-oo n-oo
(b) Let E. > 0 be so small that q - € > 1. Then, be ginnin g with
some value n) of the index n, Ian 1 > (q - £)n-n 1 la n1 I. Since
full (q - c)"-nl = +00, we get liw lanl = +00.
"-00 n-oc


2.2.32.
(a) Take € > 0 small enough to get q + £ < 1. Then there exists
no e N such that lanl < (q+e)JI , n
 no- Therefore lirn. an = o.
1& -0\1
(b) We have Ian 1 > (q - E)n for n > Rt- HE> 0 is small enough,
then q-e > 1 and therefore lim (q-c)R = +00. So, lim lanl =
n-oo ra-oc
+00.


2.2.33. Setting a" = nO x" t we get
lim l1 n +J = lim ( n+ l ) Q x =x, where 0 < x < 1.
n-oo an n-oc n
Hence, by Problem 2.2.31, the sequence tends to zero.
2.2.34. Let an denote the nth term of the sequence. Then
4n+ I m. - n I I I
= X --to x.
an -n+ 1 n-oo
By Problem 2.2.31 the 5equence converges to zero.


2.2.35. Assume that Ib n I < M for n e N. Since Urn a.,. = 0, for
n-::Xi
any e > 0 there exists no E N such that lara 1 < ;1 for n > no.
Hence


lanbnl < E Cor n > no.
This means that lim 4nbn = o.
. n-oo




2.2. Limits. Properties of Convergent Sequences 171


2.2.36. \Vithout loss of generality we can assume that a
 b. Sup-
p
 firRt that f1 < h. T...et E > 0 be so small that a + E <: b - E. By
the definition of the limit of a sequence, an < a + E < b - E < h 1l for
n sufficiently large. Hence max{a n , b n } = b n , and consequently,
lim max{a,uh,,} = lim b n = b = max{a,b}.
n-oo n-.:)O


If a = b, then for any E > 0 there exists no such that for n > no,
the inequalities Ian - al < E and Ib n - al < E hold. This m eans that
I max{a n , b n } - al < E.
In this way we have proved that
lim max{an,b n } = max{a,b}.
n-
 .


2.2.37. Since Jim aJl = 0, for any E e (0, 1) we have
n-oc


{I I - E <
 1 + an < {II + E for n sufficiently large.
This implies that lirn {1 1 + an = 1.
n-oo


2.2.38. Put XJ) = {it + an. It follows from the foregoing problem
that lim:E n = 1. Consequently,
n-.oo


11m (11 + an - 1 = Urn X n - 1
t&-
 an fI-:)c
 - 1
= Urn X n - 1 = 1
n-oc (x n - l)(X
-l + ... + 1) P


(1)


By Pro blem 1.2.1,
n ( VI + al +"2: ...+ap -1)
< n ( ( 1 +
 ) ( 1 +
) · on · (1 +
) - I )
= v' (n + al)(n + a2) · ... · (n + a p ) - n.


2.2.39.




172


Solutions. 2: Sequences of Real Numbers


Moreover, by 1.2.4 we get


n ( ( 1 +
 )( 1 +
;n · ... · (1 +
 ) - 1 )


(2)


E ai 4 j
p 1 al + ... + Op i<j al · ... · Op 1
+ + 2 + ... + -
n n n P


=n


E BiBj
< a1 + ... + lip i<j 41 · ... · lip
- p + np + ... + pnP-J ·
Combining (1) and (2) with the result in the foregoing problem, we
show that the limit is 41 +(1
;...+Qp .


2.2.40. Note that
n+ 1 < 1 1 1.. n+ 1
yn 2 + n + 1 - vn 2 + 1 + ,fn 2 + 2 +... + Vn 2 + n + 1 S yn 2 + 1 ·
This and the squeeze law for sequences imply that .the limit is 1.


2.2.41. Let a denote tbe largest of the numbers al)!&2, ..., ape Then


a a
 +
 + ... + a p n
_ < n <a.
'\IP- p -


By the squeeze law for sequences,


. n a
 +
 + ... + a;
lim = a = max{Cl,C2, ...tOp}.
n-oo p


2.2.42. Since


n l999 n l999
1 < n 2sin 2 1 +COS2 1 $ V'2,
- n+ n+


it follows that


2 n19W n 1WY
lim n 2 . + 2 _ 1
SID 1 cos 1 - ·
n-.oo n+ n+




2.2. Limits. Properties of Convergent Sequences 113


2.2.43. We will apply the squeeze law for sequences. We have


I I
1 < (1 + n(1 + cosn» 2 n + n. i Dn <; (I + 2n) 2 n + n. i Dn.


We will now show that


(*)


lirn (1 + 2n) 2ft+
.lan = 1.
n -.00



deed,


t 1-
1 < (1 + 2n) 2 n + nll i D n < (1 + 2n) n.
Hence (*) follows from the squeeze law. Thus the limit we are looking
for is 1.


2.2.44. By the harmonic-geometric-arithmetic mean inequality (see
1.2.3), for z > -1 we have
:1; 2 l+z+1 z
1+ = 1
 v( l +x)l= vl +x
 =1 +-.
2+z _ 1 - +1 2 2
T%


Now, putting z =
, k = 1,2,...,n, and adding the obtained in-
equalities, we get


n
 " ( r:-:-T ) n k
(*) {;2+


 V 1 +fi2-1
 t;2n2 .


Moreover,



 Ie n(n + 1) 1
L...J 2n 2 = 4n 2 n
 4
k= 1


and
t
 = t k > 1 tk = n(n+ 1) __!.
Ic:=l 2 +
 k=1 2n 2 + k - 2n 2 + n k=l 2(2n 2 + n) R-fOO 4
Therefore, by (*) and the squeeze law,


lim
 ( VI + !:... - 1 ) = !.
n.....oo L.J n 2 4
°k=l




174


Solutions. 2: Sequences of Real Numbers


2.2.45. One can apply reasoning analogous to that used in the so-
lution of the preceding problem. Let x > -1. By the harmonic-
geometric-arithmetic mean inequalit)"
1 x _ 3 < -3/(1 .1:)1 .1 < 1 + x + 1 + 1 = 1
.
+ 3 + 2z - --L + 1 + 1 - v + - 3 + 3"
l+:c
Substituting X =
, we get


n k'J n ( 3
 ) n k 2
(*) L 3 +n;k2 :5L V 1 + Ji3 -1 :5L 3n 3 '
k=J ns- k=l k- l


Moreover,



 k 2 = n(n+ 1)(2-n+ 1)
 !
L..J 3n 3 18n 3 n-
 9
k::= 1


and


n Jr.2 n k,2 1 n


 - ""' > ""' k 2
L-i 3 + 2 k 2 - L-i 3n 3 + 2k 2 - 3n 3 + 2n 2

k=l
 k=l k=1
n(n + 1)(2n + 1) 1
= -to -.
6(3n 3 + 2n2) n-
 9
By the above, together with (*) and the squ
.le law,
" ( k 2 ) 1
Jim
 3 1 + - - 1 =-.
n-oo L.,,; n 3 9
k- I


2.2.46. Clearly, lim v'iik = 1 for k = 1,2, ...,p. So we find that
fI,-OO


( 1 p ) p
lim -":tiik = 1.
n-co p L...i
k=l


2.2.41. For sufficiently large no and for n > nOt we have 0 < Q +
* < Q + i!o < 1. Thus
. '1-1 ( 1 ) k . 1 _ (Q + 1.)7. 1
lim
a+- -lirn n _
n-oof:o n -n-oo l-(Q+
) -I-a.




2.2. Limits. Properties of Convergent Sequences 175


2.2.48. The equality is obvious Cor x = 1. Assume now that x > 1.
To ca1culate the limit, we will apply the squeeze law for 8equenc.es.
We have


0< (\IX_l)2 = t9" -2\IX+ 1.


Hence


(*)


(2 VX -1)'1 < (v'X2yl. = x




Moreover,


( 2\I'X-l ) n=x2 (
- 1 ) " =X2 ( 1+ (
- 1 _1 )) ".
\i.X v0 v'X 0
Now, by the Bernoulli inequality we get
(2vX-l)n
x2(1+n( :X -
 -1))
_ 2 (1 _ (v'X-l)2 )
-x n \JX2 -
" 2
X


(**)


Also, by the Bernoulli inequality,

 = (
-1+ l)n
 1 +n(
-1) > n(
-1)_


Consequently,


?
X"
( tIX - 1)2 < 2"-
n


Therefore, by (**),


( * * *) (2 \IX - 1) n > x 2 ( 1 _
2 ) .
n\JX2
Combining (*) and (* * *) with the squeeze law, we see that
lim (2 tIX _l)n = x 2 .
'1-00


2.2.49. As in the solution of the foregoing problem, we may establish
the inequalities


{2
-1)n (
-1)2
1 > ? > l-n \fii2 ·
n- n




116


Solutions. 2: Sequences of Real Numbers


Now, it is enough to show that
lim n (
-1)2 =0.
n...oo



To this end, note that for n 2: 3,
n- (
-1+ l)n > n(n-
(n- 2) (
-1)3.


Hence


05 n( yr,i-l)2 $ n ( n-l

n _ 2» )! ·
So, 1im n(:tn - 1)2 = o.
n-.oo


2.2.50.
(a) We have
I _ I - arctan(n + 1) arctan(n + k)
4n+k On - 2n+l + ... + 2n+k
< ; ( 2n
1 +... + 2n
1c ) < 2: 1 ·
For arbitrarily fixed e > 0, let no = [log2
 - 1). Then for any
Ie E N and n> no we get lan+k - ani < e.. T
erefore {an} is a
Cauchy sequence.
(b) One can show by induction that 4 R > n 4 for all n
 5. Hence
111
lan+k-anl < (n+l)2 + (n+2)2 +...+ (n+k)2 .
Consequently,
lan-l-k - tin I
1 1 1
< n(n+l) + (n+l)(n+2) +...+ (n+k-l)(n+k)
1 1 1 1 1 1
= n - n + 1 + n + 1 - n + 2 + ... + n + k - 1 n + Ie
1 1 1
=-- <-<e
n n+1e n
for any kEN and n > [
].




2.2. Limits. Properties of Convergent Sequences 177


(c) Note that


1 1 1 1 1
I
n - ani = 2n + 2n -1 +:.. + n + 1
 n2; = 2.


This m eAn
 that {an} is not a Cauchy sequence.
(d) We have


lan+k - anI
I (_1)"+"-1 (_1)R+k-2 (-l)n I
= (n + k)(n+ Ie + 1) + (n + Ie -l)(n+ Ie) +...+ (n + 1)(n+2)
< I 1 1
- (n+ k)(n+ k + 1) + (n+ k -l)(n+ k) +... + (n + l)(n + 2)
1 1 1 1 1 1
= - + - + + -
n + k n + k + 1 n + k - 1 n + k ... n + 1 n + 2
1 1 1
= - < <e
n+l n+k+l n+l


for any kEN and n > [
 - 1].
(e) We have


IBn+k - ani
 M(lqlft+k + Iqln+k-l +... + Iqln+l)
= M ( Iqln+l{l-Iqlk» ) < M Iq)R+l < E
1 - Iql - 1 - Iql


[ In (
 ]
for any keN and n>no= lnq -1.
(I) We have


2n 2n-l n+l
tl2n - an = (2n + 1)2 + (2n)2 +... + (n + 2)2
> 2n > 2n2 _

-n(2n+l)2 - (3n)2 - g.


Therefore {an} is not a Cauchy sequence..




178


Solutions. 2: Sequences of Real Numbers


2.2.51. By the given condition,


lan+k - ani = lara+k - all+k-J + "n+k-I - O-n+k-2 +.... + U n +l: - ani
< >'(JCln+k-l - Cln+k-21 + la,l+k-2 - a n +k-31 + ... + la'i - an-l D
< (A k + A k - J + ... + >.'l. + A)lu n - an-II
< ().k + >.k-l + ... + ).2 + ).).,a- 2 Ia2- - aJ I
).n-l(l_ ).k) >.n-l
= 1 _ >. la
 - all < 1 _ ). 1a. 2 - at I.


[ In .11-.\ ) ]
Hence for arbitrarily fixed c > 0, for n > 1 + r


Q] T ,and for an:y
kEN, we bave 1a,I+k - a,a I < E.


2.2.52. Since {Sn} is convergent., it is a Cauchy sequence. We will
show that {lnO'n} is also a Cauchy sequence. By the inequality in
2.1.41,


( 1 ) ( -. 1 )
lnun+k -wun = In 1 + +... + In 1+
an+k- an+l
1 I
<:: + ... + < E
an+k a n +l


for kEN and for sufficiently large n.


2.2.53. By the reSult.in 1.1.23,


Rn+k - RYI
=(Rn+k-R,.+k-I)+(R,&+k-l-R,I+k-2)+". + (Rn+l - R,I)
. n ( (_1)1:-1 (_t)k-2 1 1 )
=(-1) + +...- + .
qn-t-k-l qll+k qra;-k-2qn-t-k-l qrl+ 1 Q'1-t-2 qnqn-t- 1


Hence, by the monotonicity of the sequence {qn} and the fact that
qn ;:: n (see the solution of 1.1.24),


1
 1
IRn+k - Rnl
 < --;-.
qn+iqn n-




2.2. Limits. Properties of Convergent Sequences 179


2.2.54. Let d denote the common difference of the given progression.
Assume first that d #: o. Then
1 ( 1 1 ) 1
ak a k+l = a; - ak+l d .


Hence


. ( 1 1 1 ) 1
lim + +...+ =-.

-oo Qla2 a203 a n C1n+l aid
For d = 0, the arithmetic progression is a constant sequence and
therefore


1im ( 1 1 1 )
+ + ... + = +00.
n-oc a] 02 lI2 0 a BnUn+l


2.2.55. Let d denote the common difference of the given progression.
Assume first that d:/: O. Since
1 _ Vak+1 - VBk

 + -/a k+l d


t


we have
. 1 ( 1 1 1 ) 1
nl!."Jo .,fn .Jiil +.fii2 + .fii2 +.;as + --- + va; + ..ja..+l = .,fir
For d = 0, the arithmetic progression is a constant sequence and
therefore the limit is equal to +00.


2.2.56.
(a) By Problem 2.1.38,
( l ) n ( 1 ) "+1
l+ n <e< l+ n ·


Thus
(*) 1 < n(
-1) < n ((1+
 y+* -1).
Now using the Bernoulli inequality (see 1.2.4) one can show that
( 1 )
 1
1+- n < 1+-.
n n 2




180


Solutions. 2: Sequences of Real Numbers


Hence


(( 1 ) 1+-!- ) 1 1
n 1 +
 -I < 1 + n +;2.
Therefore, by (*) and by the squeeze law J


lim n( tie - 1) = 1.
R-.OO


(b) For an arbitrarily fixed n,

 2. n ( 1) J.
en + en +... + en _ e - en
- J. ·
n n(e.. - 1)
Hence in view of (a) we get


I
 !1
lim en + en + ... + en
= e - 1.
n-+oo n


2.2.51. We have lIn+l - an = -p(an - an-I). Therefore.
On = a + (b - a) + (a3 - a2) + ....+ (an - an-I)
= a + (b - a)(I- p + p2 +... + (_1)Rpn-2).


H b = a, then {an} is a constant sequence convergent to a. H a:l= b,
then the sequence is convergent provided (PI < 1, and its limit is
+ 6-0
a l+p .


2.2.58. Observe that


an+2b n en+2
Cn+l = an+b n - en+l.


Hence


v'2-1 1
len+l - Vii = en + l ien - Vii < (Vi -l)len - Vii < "2len - '-"21.
Consequently, by induction,


1
ICn+l - '-"21 < F'cl - v'21,
wbich means that the limit of {en} is v'2.




2.3. Toeplitz Transformation and Stolz Theorem 181


2.3. The Toeplitz Tr ans formation, the Stolz
Theorem and their Applications


2.3.1. If all the terms of the sequence {an} are equal to a, then by
n
(ii), Jim b n = a lim E Cn,k = a. Thus it is enough to consider the
n
OQ n-tOQ k=l
case where the sequence converges to zero. Then, for any m > 1 and
n
m,


n m-I n
(.) Ib n - 01 = L Cn,kak
 L ICn.k).lakl + L )Cn,kl. Jakl.
k- ] k=l k=m


The convergence to zero of {an} implies that for a given £ > 0 there
exists nl such that


E
Ian I < 2C for n
 nl.
Of course, the sequence {an} is bounded, say by D > O. It follows
from (i) that there exists n2 such that for n 2= 712,


R1- 1
L Ic..,kl < in.
k=1


Next putting m = nl in (*), we get


R.-I n
" E '" E E
1 6 nl
 D
 ICn,kl + 2C L.J ICn.kl < 2' + 2' = E
k= 1 k=n1


for n
 max{nl,n2}. Hence lim b n = o.
n-oo


2.3.2. Apply the Toeplitz theorem with Cn,k = !' k = 1,2, ..., n.


2.3.3.
(a) H Cn.k are nonnegative, then (ill) follows from (n).
n
(b) By (ii) in Problem 2.3.1, E Cn,k >
 for sufficiently large n,
k=l
say n> no. It follows from the divergence of {an} to +00 that,
given M > 0, there exists nl such that an
 2M if n > nl.




182


Solutions. 2: Sequences of Real Numbers


Without loss of generality we can assume that all the terms 4n
are positive. Set 1t2. = max{no, n.}. Then


n n:l JI n:!
E Cn,kQk = E Cn,kak + E Cn,kQk
 E Cn,kQk + !vI
 lvI,
k=1 k- l k::;:n3+1 Ic=l


and so {b n } diverges to +00.
2.3.4. This is a special case of 2.3.3. Take Cn.k =
 for k = 1,2, n.t n.
2.3.5. Apply the Toeplitz theorem (2.3.1) with Cn,k = .2(n

+1) .
2.3.6. Use the harmonic-geometric-arithmetic mean inequality (see
1.2.3») the squeeze principle for sequences and the result in 2.3.2.
2.3.1. Apply the foregoing problem to the sequence { G::I. }.
2.3.8. H b i: 0, we take Cn,k = bn
b+1 and see that condition (i) in
2.3.1 is satisfied. In view of 2.3.2' condition (ii) is also satisfied. In
this case the desired result follows from the Toeplitz theorem. For
b = 0, setting Cn.k = l+bn;
+1 yields
lim Qt-(l + b n ) + a2(1 + b n - 1 ) +... + an(l + bl) = a.
n-oo n


Thus, by 2.3.2,


Jim alb
 + Q2b n -t +... + anbl = o.
n-oo n


2.3.9. We apply the Toeplitz theorem to the sequence {t-} with
en k = b hi: b .
· 1+"+ n


2.3.10. One can apply the Toeplitz theorem with Cn.k = bJ +
':.rbn ·
2.3.11. For n > 1:, we put


X n - Xn-l
an = J
Yn - Yn-l
and apply the result in the foregoing problem.


b n = Yn - Yn-l




2.3. Toeplitz Transformation and Stolz Theorem 183


2.3.12.
(a) In 2.3.10 we put X n = 1 +
 +...+ ..in , Yn =
 and show that
the limit is 2.
(b) Set


a 2 an a n + 1
X n = a + _ 2 +... + -, Yn = ·
n n
B eginnin g with some value of the index n, the sequence {Yn} is
strictly increasing. By 2.2.31 (b) we see that lim Yn = +00.
n-oo
Therefore


n ( a2 an ) 1
lim +1 a + _ 2 +... + - = 1 .
n-ex) an n a -


(c) We can apply the Stolz theorem (see 2.3.11) to the sequences
- k l (k+l)! (k+n)! 1:+1
X n - . + }I + ... + I ' Yn = n ·
. 11.
We have


lim X n -X n -l = lim (n+ 1). (n+ 2)..... (n + k)
n-oo Yn - Yn-l R-ex) nk+l - (n _1)k+l
= lim (1 +
) · ... · (1 +
) = lim (1 +
) .... · (1 +
)
n-co n(l_(l_
 )k+1) n-col+(l-
)+..+(l-!Jk
1
-
- k+I.
(d) Set X n = * + ... + k , Yn =
. Then
1 + 1 _ 1
Jim :en - %n-l = lim 'V2: '-t2n-C v'n-I
n-oo 'Un - Yn-l n-oo
 - vn - 1
=lim(Jn+ vn-l ) ( 1 + 1 _ 1 )
n-oo J2n -I 2n - 1 -I n - 1
= lim (2..+
_ ,-n + rn::I+
_

n-oo\V2 V
 V
 V
 V2n=l I
= 2(V2 -1).
Hence by the Stolz theorem the limit is 2(,f2 - 1).




184


Solutions. 2: Sequences of Real Numbers


(e) Taking X n = lk + 2 k + ... + n k and Yn = nk+l, we see that


:en -Xn-I n k 1
Yn - Yn-l = nk+l - (n - 1)1:+1 n
 k + 1 ·


Now it is enough to apply the Stolz theorem.
(f) By the Stolz theorem,


lim 1 + 1 . 4 + 2 . 4 2 + ... + n . an = 1 .
R-OO n · a n + 1 a-I


(g) One can also apply the Stolz theorem with
Zn = (k + l)(lk + 2" +... + n") - nk+l and Yn = (k + l)n k .


Then


X n - X n -l (k + l)n" - nk+l + (n - l)k+l 1
- -. -
Yn - Yn-l - (k + l)[n k - (n -1)1:] n-too 2.


2.3.13. Applying the Stolz theorem to

 an c
X n = al + V2 + ... + .;n and Yn = y n,


we see that


. 1 ( 02 a3 an )
lim 7:: al +
 +
 + ... +
 = 2a.
n-oo yn y2 v3 yn


2.3.14. In the Stolz theorem we set X n = Bn+l and Yn = n.


2.3.15. Applying the Toeplitz transformation to {an} with en,k =
2 n - 1JJ + 1 , we see that


1im ( an an-I a 1 ) 2
n-oo T + 2 + ... + 2n-1 = a.




2.3. Toeplitz Transformation and Stolz Theorem 185


2.3.16.
(a) Using the Toeplitz transformation to {an} with
1
Cn.k = (n + 1 - k)(n + 2 - k)'
we can show that
lim ( an Bn-I at )
n-oo 1. 2 + 2. 3 +..- + n( n + 1) = a.
(b) As in the proof of (a), we can apply the Toeplitz theorem to {an}
- th 3 ! _l ) "-Ic d h that th !imi - t - 2
WI Cn.k = 2 2n-1E an s ow e IS aa.


2.3.17. Set an = (
k). In view of 2.3.7 it is enough to calculate
lim An+l . We have
n-oo 4n


«':.
lk) (nk + l)(nk + 2) · ... - (nk + k)
(
) = (n+l)(nk-n+l)(nk-n+2).....(nk-n+k-l).
Therefore the limit is equal to (k-
;k-I .
2.3.18. Let {an} be an arithmetic progression with the common
difference d > o. Set


nn(al · ... · an)
Cn= ·
(al + ... + an)n


Then


Cn+l (n + 1)C1n+l ( Gt+o;;+Qrt. ) n
en = al + CI2 + ... + Ctn+l a1 +
.;
fI+l
= 2an+l ( 2a1 + (n - l)d ) n ---t 2e- 1 .
al + C1n+l 2li-t + nil n-oo
Hence by 2.3.7, the limit equals 2e- 1 . If d = 0, the limit is 1.
2.3.19. Since b n = 2an + an-It an = bn-;n-s and an-l-
b n _ 1 ;a n - 2 _ Thus an = 2bn-bn
1+an-2 . Repeated application of this
procedure n - 1 times gives
2 n - 1 b n - 2 n - 2 b n _l +... + (_1)n-221
 + (-1)n-1at

= .
2 n




186


Solutions. 2: Sequences of Real Numbers


Thus by 2.3.16 (b), lim an = ! b.
n-oo


2.3.20. Put en = (a) · ... · aR)n RZ . Then
Cn+l ( 1 ) R%
= 1 + - (n+ I)Zan+l --t> e%a.

 n n-oo
Therefore by 2.3.7, lim nZ(al .l12 · ... · an)
 = eZa.
R-OO


2.3.21.
(a) We apply the Stolz theorem with Xo = 1 +
 + ... +
 and
'Yn = In n. This gives
X n - X o -l 1 1
= n --. ,
Yn - Yn-l In ( 1 + -L ) n-oo
0-1


because lim In (1 +
 )n = 1, which follows from the inequalities
0-00
(1 +
)o < e < (1 +
 )R+I (see 2.1.41).
(b) The limit is
 (see the solution of ( a».
2.3.22. We apply the Stolz theorem to
al 42 4,1
X n = T + 2 +... + -;;: and Yn = Inn.
Consequently,


X n - X n -l an
= n --+ a.
Yn - Yn-l In ( 1 + -L ) R-OO
n-l


2.3.23. Use the result in 2.3.7.
(8) 1,
(b) e- 2 t
(c) e- 2 t
(d) e 3 .
(e) We have


1r'1i { e
lim V"'_
R-OO V1i! - 0


for k = 1,
for k > 1.




2.3. Toeplitz Transformation and Stolz Theorem 187


2.3.24. By the Stolz theorem (see 2.3.11).


n
I:9f
I . ,..= 1
1m
n-oc in n


1 - an + I
- 1m
'I-:)C In (1 + 1;) ra+1


= (I.


2.3.25. One can easily verif.y that


01 = At, 02 = 2A 2 - At. a'l = nA" - (n - l}An-l'


n> 2.
-


Thus


n
E9f
I . k= a
1m
ft.-DO In n


_ I . 4Aa + AA 2 +.n +
A"_I + An A
-1m =.
n-oo In n


where the last equalit). Collows from the foregoing problem.


2.3.26. (0. Toeplitz. Prace
18tematyczno-Fizyczne, 22(1911), 113-
119] Le
 {a'l} be the sequence all of whose terms are equal to 1. Then
n n
Um On = 1 and 6n = E Ct..k O " = E C,1.k- Hence 1 = Um b n =
n-QO k=1 k=1 n-oo
n
lim E Cn.Ic- Thus (ll) holds. Now let {

}} be a sequence whose
ft-OOk=1
kth term is 1 and whose other terms are all O. Then lim o

) = 0
n-oo
and 0 = 1im 6n = lint en,lc. Therefore (i) also holds. Suppose that
n-
 n-oc
(ill) is not satisfied. Then for any C > 0 there exists nc such
ne
that E lC,ac,kl 2: C. In fact, given C > 0, there are infinitely many
k=1
such indices ne- Now let nl be the least positive integer such that
ft.
E ICot.lel > 10 2 . We define the first na terms of {an} by setting
k=1


sgn Cn..k = £gn Ok and


1
lakl = w.


Then


'I, "I 1
bRa = L cn.."a" = L jijlCnh/t1 > 10.
k==1 k=1




188


Solutions. 2: Sequences of Real Numbers


By (i), there exists no such that


ft!
E ICn,kl < 1 for n
 no.
Ie=!


Consequently,


nl 1
E Cn,kale < 10 for n
 no.
k=l


Now we take the least integer
 such that n2
 max{no,nl} and
n2
E ICn 2 .kl > 1()4 + 1 + 10. Define the consecutive terms of {an} by
k=l
setting


1
sgnCn 2 ,Ic = sgnall: and la",1 = 1()2 for nl + 1
 k
 n2.


Then


R2 Rl 71 2
b R2 = E Cn 2 .k B k = E Cn 2 ,k B k + E Cn 2 ,k a lc
k=l k=l k
 1+1
nl 1 n2
= ECn 2 ,k a ", + 10 2 E ICn 2 .kl.
k- l k=nJ+l
It follows from the above that


b n2 > --to + 1
 (104 + 1 + 10 -1) = 10 2 .


We can construct inductively the sequence {an} whose terms with
indices from nk-l + 1 through nk are equal either to + 1
1c or - 1
1c ;
then the transformed sequence {b n } satisfies


b nJc > 101e for k = 1,2,3, ... .


Thus the sequence {an} converges to zero whereas the transformed
sequence {b n } has a divergent subsequence {b nJc }. This is a contra-
diction, and so (ill) holds true.




2.4. Limit Points. Limit Superior and Limit Inferior 189


2.4. Limit Points. Limit Superior and Limit
Inferior


2.4.1.
(a) First, let us show that the given subsequences have a common
limit. Suppose that lim a2k = a, lim a2k+l = b and lim a3k =
k-+oo k-+oo k-+oo
c. Then fun a6k = a = c and lim a6k+3 = b = c. Therefore
k.-.oo k-oo
a = b = c. Now we prove that the sequence {an} also converges
to a. Given any E > 0, there exist positive integers k 1 and k 2
such that


k > k 1 implies lCL2k - al < E,
k >
 implies la2k+l - al < E.


Hence


n > no = max{2kl,2k2 + I} implies Ian - al < E.


(b) No. Consider the sequence {an} defined by an = (-1)n. Then
Jim a2k = 1, Jim Q2k+l = -1. But lim an does not exist.
k-oo k-co n.-.oo
Now take the sequence {On} defined as follows
{ 0 if n = 2 k , k = 0,1,2,... I
4n=
1 otherwise.
Then lim a3k = 1 and lim a2k+l = 1, but lim a2k does not
k-oo k-oo k-oo
exist. Of course, the sequence {an} is divergent.
Finally, consider the third sequence
{ 0 if n is a prime number,
an = 1 if n is a composite number.
For this sequence we have 1im a3k = 1 and lim a2k = 1, but
k....oo k-oo
lim 42k+ 1 does not exist, because the sequence {CL2k+l} contains
k-oo
a subsequence with prime indexes and a subsequence with com-
posite indexes.(Note that there are infinitely many prime num-
bers. Otherwise, if 1'1,1'2, ...,Pn are prime, 1'1 < 1'2 < ... < Pn,
and no prime greater than Pn does exist, then PI · 112 · ... · Pn + 1 >




190


Solutions. 2: Sequences of Real Numbers


Pn is also prime, because it has no prime divisors except for itself
and 1. This is a contradiction.)


2.4.2. No. Define the sequence {an} by putting
{ 0 if n is a priole number,
a-II = 1 if n is a cOlnposite t1UDlber.
Then every subsequence {a.... n }, S > 1, n
 2, is a constant sequence
and therefore it is convergent. The sequence {4n} is divergent (see
the solution of Problem 2.4.1 (b) ).


2.4.3. Evidently, SpuSqU....US s c S. To obtain the inclusion in the
otbcr direction, assume :r tI. SpUSqU....uS s . Tb£'n there exist positive
numbers ept£qt.", £It and positive Integers n p, nqt".' nt' such that


n > np implies Ix - a pn I> Ept
n>n q implies Ix - 0"..1 > Eq,
...
n>n 3 implies Ix - a".,. I > E..


Setting E = min{Ep,E q , ...,E.} and m = Inax{Pn", 9n.,... t Bn,.}, we
obtain Ix --ani> E for n > m, This implies that z. cannot be a limit
point of the sequence {fly,}. Therefore
S C Sp U Sq U ... US..
It follows £roln the equality S = Sp U Sq U ... U S5 just proved that,
if eVCQr subsequence {a p ,.} t {a qn } t ..., {a
,,} converges to at then the
sequence {4,.} also converges to o.
2.4.4. No. Define the sequellce {a,,} by the follo\viug formula:
{ 0 jf n = 2 k . k = 0.. 1, 2, ... ,
a ra =
1 otherwise.
Every subsequence
{a2k-l}, {02(2k-1)}, {a2:1(2k-I)}' ..., {a2"'(2k-n}t...

onverges to 1, whereas the sequence {a,,} diverges.




2.4. Limit Points. Limit Superior and Limit Inferior 191


2.4.5. Assume that the sequence {an} does not converge to Q. Then
there exists E > 0 such that for any positive integer k there is nA: > k
satisfying IOnlt - al
 E. If we assume that nk is the minimum of
such numbers, then the sequence {nk} is monotonically incrcasing.
Moreover, Hm nk = +00. Such a sequence {an.} does not contain
k-oo
any subsequence converging to a, which contradicts our hypothesis.
Therefore {o,,} converges to o.


2.4.8.
(8) It is obvious that 1 is the only limit point of the sequence. Hence
S is a singleton, S = .{ 1 }.
(b) We have 03k = 0, O:Sk+l = 1, 03k+2 = o. Hence, by Problem
2.4.3, tbe set S of the limit points of this
quence has two nlem-
bers, S = {O, I}.
(c) We bave


1
G2k = 22k + 3
Hence S = tOt 2}.
(d) We have
210 (6k) + In (2k)
a2k = In(4k)
Therefore S = {I, 3}.
(e)


22k+2 + 1
and Q2k+1 = 22k+1 + 3 .


In (2k + 1)
and a2kH = In (2(2k + 1»"


OGle = 1,
00"+3 = -1,


- (0 5) 6k+ 1
061:+1 _. ,
( 0 5) Ok+'1
QOk+,s = - · ,


06k+2 = (_O.S)6k+2.
- (0 5) 61.:+5
OOk+5 -. ·


Thus S = {-I,D, I}.
(f) We have


071c = 0,


2
R7k+1 = '7'
1
a7k+5 = -,
7


1
071:+2 = 7'
2
°7k+6 = '7.


4
a7k+3 = -,
7


4
07#:+4 = 7'




192


Solutions. 2: Sequences of Real Numbers


Therefore S = {O,
 ,
 J
}.


2.4.'1.
(a) Let Q =
, P E Z.q eN, where p and q are co-prime. Then
4kq = 0 and 4kq+1 = kp+ ': - [kp+ [
 ] +r] =
 - [
 ].
where l = 1.2,....q-l and r =
 - [
] . Thus
S = { O.
 _ [
] .
 _ [
] . .... (q
 l)p _ [ (q
 l)P ] }.
(b) We will show that every real number x e (0, 1] is
 limit point of
the sequence {nQ- [no]}. By Problem 1.1.20. there exist Pn E Z
and 9n E N such that 0 < Q - 2!!. q <
 q l . Since lim qn = +00,
n" n-oo
lim (Qqn - Pn) = O. Let x e (0,1) and let E > 0 be so small
n-oo
that 0 < x - E < X + e < 1. Now suppose that nl is so large that
1
o < aqna - Pnl < - < E.
qnl


Then there is no E N satisfying


(1) no(aqns - PntJ e (x - £. X + e).
(see the solution of Problem 1.1.21). It follows from (:1) that
[no a qn1 - noP n l1 = 0, or equivalently, 1lOPns = [11009nl). There-
fore the term noaqns - (noaqna) from the range of our sequence
belongs to the interval (x - e,x + e), which means that x is a
limit point of the sequence under consideration. Similarly, one
can show that 0 and 1 are also limit points.
(c) Assume first that a is a rational number of the interval (0,1).
Let Q =
, where p and q are co-prime and P < q. Then a2kq =
a2kq+q = 0, and
. 1p1r
 I 2 " .
02kq+1 = sm - lor = 1, ,.... q - 1, q + 1, ..., 2q - 1.
q
Hence


S = {o .
 . 2p1r . (q - l)p7I' }
, sm ,5lIl . ..., SIn .
q q q




2.4. Limit Points. Limit Superior and Limit Inferior 193


If Q E Z, then the sequence is constant. Taking a e Q \ Z, we
can write


Q = (oj + (Q - (Q» and Q - [a] E (0, 1).
Sot sin R7rQ = (-1)1 0 ) sin(o- (o])n1l", and this case can be reduced
to the foregoing special case.
(d) Let t e [-1, 1] be an arbitrarily chosen number. Then there
exists % e IR+ such that sin:e = -t. We can restrict our consid-
eration to the case Q > 0, because the sine is an odd function.
Since Q is irrational, there exist sequences of positive integers
{Pn} and {qn} such that

 = n
 (Pn -qnj).
(See the solution of 1.1.21.) Therefore % = lim (211'pn - O1I'Qn).
n-oo
Hence, by continuity and periodicity of the sine function, we get
_to = sin x = lim sin(211pn - Q1rqn) = - lim sinQ1fQn.
n-oo n-oc


It follows from tbe above consideration that every number in the
interval (-1 t 1] is a limit point of the sequence.
2.4.8. We will show that in any inte rval ( 0t b) there is at least one
term Qf our sequence. Since Urn ( .vn + 1 - .v;i) = 0, there exists
n-oo
no e N such that

n + 1 -
 < b - at n > r1Q.
Let mo be a positive integer satisfying 9'1710 > .vno - a and let
A = {n eN:
- {Ymo
 a}. The set A is nonempty (e.g., no e A)
and bounded above. Putting nl = maxA and n2 = nl + 1, we get
VR2 -
mo > (1 and .vn2 > a + eVmo >
. Therefore n2 > no.
Hence 9'R2 < 9'RI + b - G

mo + a + b - 0, or equivalently,
a < 9'R2 - .vmo < b.
2.4.9. Boundedness of the set of the limit points of a bounded se-
quence is evident. Let S denote the set of limit points of the sequence
{on}. If S is finite, then it is closed. Assume that S is infinite and
let s be its limit point. Define the sequence {Sic} of members of S




194


Solutions. 2: Sequences of Real Numbers


in the. following way: for s) take any member of S different from
8. For 82 choose any member of S different from s and such that
1 8 2 - 81 < !I S I - sl, and inductively, I S k+l - sl <
 ISk - sl, Sk+l i= s.
Such a sequence {Sk} satisfies the following condition:
1
ISk - sl < 2k-l ls1 - sl, kEN.
Since Sk is a limit point of the sequence {an}, there exists On,. such
that la nle - ski < 2k
l lsl - sl. Hence


1
Janie - sl :5 Ian. - ski + ISk - 81 < 2k-2 1s1 - sl,
which implies that S is a limit of the subsequence {an.}. Therefore
8 e s.


2.4.10. Let S denote the set of limit points of {an}.
(a) The sequence {an} is bounded. By 2.4.6, S = {O,
 , i,
}.
Therefore lim an = 0 and lim On =
 .
n-OQ R-OO
(b) We have S = {-I, -
, !' I}, which together with the bounded-
ness of the sequence gives lim an = -1 and Urn = 1.
R-OO R-OO
(c) The sequence is unbounded and the set of its limit points is empty.
Therefore


lim an = -00 and
n-oo


lirn an = +00.
n-oo


(d) The sequence is unbounded above because its subsequence a2k =
(2k)2k diverges to infinity. The subsequence with odd indexes
tends to zero. This shows that


lim an = 0 and
n
oo


lim an = +00.
n-



(e) The sequence is unbounded because a4k+l = 4k + 2 --+ +00
k-oo
and a4k+3 = -4k - 2 -+ -00. Consequently, Jim 4n = -00
k-oo n-OQ
and litn an = +00.
n....oo




196


Solutions. 2: Sequences of Real Numbers


(d) lim an = -1 and lim On = 1.
n
 n-oo


2.4.12.
(a) H the set S of the limit points of {an} is empty, then Jim an =
8-00
-00
 A. Now assume that S is nonempty. Since S is closed (see
Problem 2.4.9), supS = Jim an = L e S. It follows from the
R-OO
definition of a limit point that there exists a subsequence {an lc }
converging to L. Therefore, for any E > 0 t there is ko E N such
that


L - E < an., S A for k > ko.
Since e is arbitrary, we get L
 A.
(b) If the sequence {an} is not bounded below, then Jim 4n =
n-.oo
-00 < A. So, assume that the sequence {an} is bounded below,
that is, there exists B E R such that Ora
 B for all n E N.
Moreover, by asswnption, there is a sequence nk, nk > k, such
that a nk
 A. Thus, by the Bolzano-Weierstrass theorem (see
2.4.30), the sequence {Cln IJ } contains a convergent subsequence.
Let 9 denote its limit. Then B
 9 < A. Therefore the set S of
the limit points of the sequence {an} is nonempty and Jim an =
n-oo
infS < g < A.
(c) It is enough to apply the argument presented in the proof of (a).
(d) It is enough to use analysis similar to that in the proof of (b).
2.4.13.
(a) Let L = Jim On. Suppose that (i) is not satisfied, contrary to
n-oo
what is to be proved. Then there is E > 0 such that for any
keN there is 11 > k Cor which Un
 L +
. TlllJ
1 by Prubl
w
2.4.12 (d), Jim an 2: L + £, which contradicts our hypothesis.
n-oo
Now suppose that (ii) is not satisfied. Then there are e> 0 and
kEN such that an S L - £ for all n> k. By 2.4.12(a), we get
Jim On < L - £. which again contradicts our hypothesis. Thus
"-00
we have proved that L = Jim an implies (i) and (ii).
R-OC
Now we prove that conditions (i) and (ii) imply Jim Un = L.
n-oo




!.4. Limit Points. Limit Superior and Limit Inferior 197


It follows from (i) that the sequence {an} is bounded above.
On the other hand, it follows from (ii) that the sequence con-
tains a subsequence which is bounded below. According to the
Bolzano-Weierstrass tbeorem (see 2.4.30), tbe sequence contains
at least one convergent subsequence. Therefore the set S of all
limit points of {an} is nonempty. We will show that L = sup s.
Indeed, if s is an element of S, then by (i), s :5 L + E. By the
arbitrariness of E we get s < L. Moreover, from condition (ii),
we see that for any E > 0 there is a subsequence of the sequence
{an} converging to s which satisfies the inequality L-E
 s. Of
course i e S. In this way the second implication is also proved.
Thus the proof is complete.
b) This follows by the same method as in (a).
Now we state necessary and sufficient conditions for infinite limit
superior and inferior. The limit superior of {an} is +00 if and
only if the sequence is not bounded above. Therefore


(1)
every kEN there exists nk > k such that an. > M.
The limit superior of {an} is -00 if and only if the sequence
is bounded above, say by L, and the set of its limit points is
empty. Therefore there is a finite number of terms of {an} in
every bounded interval [M,L]. Hence On < M for all sufficiently
large R. This implies that
Jim an = -00 if and only if for every MeR there is
(2) n-oo
kEN such that for every n > k, 4n < M.
Similar arguments give
lim tin = -00 if and only if for every MeR and for


lim an = +00 if and only if for every MER and for
R-OO


(3) n-oo


every kEN there exists nk > k such that an,. < M,


Jim On = +00 if and only if for every M e 1R there is
(4) n
oo
kEN such that for every n > kt an > M.




198


Solutions. 2: Sequences of Real Numbers


2.4.14. We prove only inequality (a), because the proof of (b) is
analogous. Inequality (a) is obvious in the case of lim bra = +00
n-.oo
or Um an = -00. H Um an = +00, then, combining condition (4)
n-oo n-.oo
given in the solution of Problem 2.4.13 with the inequality an
 bn,
we get Jim b n = +00. Similarly, if Jim b n = -00, then combin-
0-00 n
oo
ing condition (3) given in the solution of Problem 2.4.13 with the
inequality On :S bn, we obtain Urn an = -00.
n....oo


Assume now that both limits are finite and let


lirn 4n = 11 and lim bra = 12.
8-00 8-00


We wish to show that 11
 1 2 . Suppose, contrary to our aim, that
12 < 11. Let e > 0 be so small that 12 + E < 11 - E. Then there is c
such that 12 + E < C < 11 - E. By (ii) of Problem 2.4.13(b), we have
b nlc < 12 + E < c. On the other hand, by (i) we get c < 11 - E < an.
Hence, in particular I c < an,., and therefore the inequality b nlr < link
holds for infinitely m
QY nk, contrary to our hypothesis.


2.4.15. Set


Jim an = 11, Jim b n = 12,
n-oo n-oo


Jim an = L 1 , Jim b n =
.
n
oo n-.oo


We show first that


(1)


Um (an + bra)
 Urn an + lim b n .


n
oo


n-oo


n-oo


Assume that 11 and 1 2 are finite. Then, by Problem 2.4.13 (b), for
any E > 0 there is k l such that an > II - e for n > k l , and there
exists k2 for which b n > 1 2 - E if n > k2. As a result,


an + 6n > '1 + '2 - 2e for n > max{kl'
}.
Combining this with Problem 2.4.12(c), we obtain Urn (an + b n )

n....oo
11 + 1 2 - 2£. Letting e -t 0+ J we get (1).
If 11 or 12 is -00, then inequality (1) is obvious. Now we show
that if one of the limits 11 or 12 is +00, then Jim (an + bn) = +00.
n-oo




2.4. Limit Points. Limit Superior and Limit Inferior 199:


Assume, for example, that II = +00. This is equivalent to condition
(4) given in the solution of Problem 2.4.13:


(*) for every MER there is keN such that an > M if n > k


Since 12 :f: -00, the sequence {bn.} is bounded below. So, condition
(*) is satisfied by {an + b n }. In other words, lim (an + b n ) = +00.
n-.oo
Thus inequality (I) is proved.
The proofs of re maini ng inequalities are similar, and we will give
them only for finite limits. According to Problem 2.4.13, for any
E > 0 there exists a subsequence {an..} such that an A2 < 11 + E
and there is no for which b n <
 + E when n > no. This implies
that an" + bn lc < 11 +
 + 2e for sufficiently large k. Therefore, by
Problem 2.4.12(b), we get lim (an + b n )
 11 +
 + 2e. Since e > 0


n-oo


is arbitrary, we get


(2)


!!m (an + b n )
 !!m an + liiii b n .
R-OO n-oo n-.oo


Similarly, for any £ > 0 there is a subsequence {b nlc } such that
b n .. >
 - e and there exists no for which 4n > II - E, for n > no.
Hence tin.. + b nlc > I) +
 - 2e for sufficiently large Ie. Therefore, by
Problem 2.4.12(c), we have lim (an + b n ) 2: 11 +
 - 2e. Since £
n-oo
can be made arbitrarily small, we conclude that


(3)


lirn (an + b n )
 Jim an + Um b n .
R-'OO n-oo n-oo


Moreover, for any E > 0 there is kl for which an < Ll + E when
n> kIt and there is
 for which b n < L2 +E, for n >
. Thus


an + b n < L 1 + L,. + 2e for n > max{k ll 1e2}.


Combining this with Problem 2.4.12(a), we obtain Jim (an + b n ) :S
n-oo
Ll +
 + 2e. Since E can be made arbitrarily small, we get


(4)


liiii (an + b n )
 liiii an + liiii b n .
R-OO n-oo n-.oo




200


Solutions. 2: Sequences of Real Numbers


Now we give examples or sequences {an} and {b n } Cor which the
inequalities (1 )-(4) are strict. Let
0" jf n = 4k,
1 if n = 4k + 1,
a.n=
2 if n=4k+2,
1 if n=4k+3,
2 if n = 4k,
1 if n = 4k + 1,
b n =
1 if n=4k+2,
o if n=4k+3.
In this case the inequalities given in the problem are of the form
0<1<2<3<4.


2.4.16. No. It is enough to consider sequences {a
'}, m = 1,2,3.... I
defined by setting


{ I for n = m,
O m-
n-
O for n:F m.


Then


r;::-:- ( 1 2 ) 1 0 _ 1 - I - . - 2
11m an + an + -.. = > = 1m an + 1m an + ... .
"--00 n-oo 71-00
Now let


{ -I for n = m,
O m-
n -
o for n #: m.


In this case
lim (a
 +0: + ...) = -1 < 0 = Urn a
 + lim a; + ....
n-
 n-
 n-



2.4..17. Let


lim an = 'it
n-oo


Jim b n = l2.
-
n-oo


-
Jim an = Lit
n-OQ


lim b n = L2.
R-oo


We will only show the inequality
(1) , 1 1 2 S lirn (a n 6 n) S , 1 L 2.
n....oo


The same reasoning applies to the other C&CieS.




2.4. Limit Points. Limit Superior and Limit Inferior 201


Assume first that 11 and 12 are positive. Then, by Problem
2.4.13(b), for any £ > 0, there exists no such that


an > 11 - e, b n > 12 - e for n > no.


Consequently, anb n > ' 1 ' 2 - e( '1 + ' 2 ) + E. 2 for e so small that 11 -
E > 0 and 12 - £ > o. Therefore, on account of Problem 2.4.12(c),
Jim (anbn) > , 1 1 2 - e(ll + '2) + e 2 . Letting E -t 0+, we get
n-oo


(i)


' 1 ' 2
 lim (anbn).
"-00


1£ 11 = 0 or 12 = 0, then inequality (i) is obvious. H II = +00 and
l2 = +00, then (by condition (4) in the solution of Problem 2.4.13),
for any preassigned positive number M, we can find no such that
an >,fM, b n >,fM for n > no.


Therefore anb n > M, which means that Urn (anbn) = +00.
n-co
Assume now that one of the limits, say 11, is infinite and the
second one is finite and positive. Then for any 0 < E < 12 and any
M > 0 there exists a positive integer no such that for n > no we have
M
b n > l2 - e, an > I ·
2-£


Hence anb R > M for n > no. Therefore lim (anbn) = +00, and
n-oo
inequality (i) is proved.
Now our task is to prove that


(ii)


lim (anbn)
 'lL2.
R-OO


H 11 and
 are finite, then on account of Problem 2.4.13, one can
find a subsequence {nk} such that lIn" < 11 + e and b R " <
 + E.
This gives
O-nlcb nlc < '1L2 + E(ll +
) + il.
Therefore Um (anbn)
 '1L2+E(11 +
)+E2. Letting e -Jo 0+ yields
n-oo
(n). H 11 = +00 or
 = +00, then inequality (ii) is apparent.




202


Solutions. 2: Sequences of Real Numbers


Now we give examples of sequences {an} and {b n } for which all
the inequalities are strict. Let


1 for n = 4k,
2 Cor n = 4k + 1,
an= 3 for n=4k+2,
2 for n=4k+3,


3 for n = 4k,
2 for n = 4k + 1,
b n =
2 for n=4k+2,
1 for n=4k+3.
In this case our inequalities are of the form 1 < 2 < 3 < 6 < 9.
2.4.18. Assume that lim an = lim an = g. Then, by 2.4.13,
n-oo n-oo
(i) for any E > 0 there is keN such that an < g+e ifn > k; and
(i') for any E > 0 there is keN such that 9 - E < an if n > k.
Thereby 9 is a limit of the sequence {an}.
On the other hand, if lim an = g, then (i) and (ii) in Problem
R-tOQ
2.4.13(a) and (b) are satisfied with L = 9 and l = g. Consequently,
lim an = Jim an = g.
n-oo n-oo
Assume now that 1im an = +00. Then statements (1) and (4) in
n-oo
the solution of Problem 2.4.13 are obvious. If lim an = Jim an =
R
 n-oo
+00, then condition (4) means that Urn an = +00. Similar argu-
n-DO
ments apply to the case lim 4n = -00.
n-oo


2.4.19. By Problem 2.4.15,
Jim an + Jim b n $ Urn (an + b n )
 Urn an + lim bna
n-too R-OO R-oo n-oo n-oo


On the other hand, on account of the last problem, a = lim On =
n-too
Jim an. Therefore Jim (an + b n ) = a + Jim b n . The proof of the

oo
oo
oo
second equality runs as before.




2.4. Limit Points. Limit Superior and Limit Inferior 203:


2.4.20. Using the inequalities given in Problem 2.4.17, we can apply
the same method as in the solution of the preceding exercise.


2.4.21. We will apply Problem 2.4.13. Let Jim an = L" Then con-
n--.oo
ditions (i) and (ll) in 2.4.13 (a) are fulfilled. Multiplying both sides
of the inequalities in (i) and (ii) by -I, we get:
(i) for every e > 0 there is keN such that for every n > k we
have -L - E < -an; and
(ll) for every E > 0 and for every kEN there exists nk > k for
which -Cln,. < -L+E"
By 2.4.13(b), we obtain
!!!!! (-an) = -L = - lliii an.
n--.oo n-oc


The proof of the second equality runs as before. In the case of infinite
limits it is enough to apply statements (1)-(4) given in the solution
of Problem 2.4.13.


2.4.22. We will apply Problem 2.4.13. Let lim an = L. Then by
n-... OQ
conditions (i) and (ii) in 2.4.13(a), we have
(i) for every E > 0, there exists keN such that for every n > k
we have an < L + eL2; and
(ll) for every E > 0 and for every kEN there exists nk > k for
which L - E
2 < Bn".
Assume first that L:/: o. Then by (i),
1 1 1 £L2 1
-> =-- >--E
an L+EL2 L L(L+EL2) L ·
Assume now that 0 < E < i. Then by (ii),
1 1 1 elf 1
-< £L2= L + ( L2 ) <- L +E.
an . L- - L L-E-
2 2


The above conditions imply (by 2.4.13(b»
lim .!.=!=
 .
n
 an L lim an
R-OO




204


Solutions. 2: Sequences of Real Numbers


Now suppose that Jim 4n = O. Given M > 0, by (i) in Problem
R-OO
2.4.13(a), there exists an integer k such that an < if for n > k.
Therefore c!; > M for n> k, which in turD, by statement (4) given .
in the solution of Problem 2.4.13, means that lim t = +00. Finally,
"-00
suppose Jim an = +00. Then for any E > 0 and for any kEN there
n-.oo
exists nlc > k such that an. >
 (see statement (1) in the solution of
Problem 2.4.13(a». The above inequality is equivalent to _ 0 1 < £. Of
ft.
course -e < a l n . Thus both conditions given in 2.4.13(b) are fulfilled
for the sequence { a 1 n } with I = 0, which m ean
 that Jim c!; = o.
"-CO
The proof of the first equality is finished. The proof of the second
equality is similar.


2.4.23. It follows from our hypothesis that 0 < lim On < +00. The
"-'00
equality lim an. lim a l = 1 combined with the preceding problem
"-00 R-OO n
yields


nm 1 lim
n-oo an = Urn ...L = - lln.
n-oo
n-oo an


Therefore, by Problem 2.4.18, the sequence {an} is convergent.


2.4.24. Assume that {an} is a sequence such that for any sequence
{6,,} the first equality holds. Take b n = -On. From Problem 2.4.21
it follows that


0= !!!!! (an + (-an» = !!!!! an + ill!! (-an) = lim an - lim CIn.
n-
 n-oo "-00 "-00 ft-



From this, by Problem 2.4.18, we conclude that the sequence {an}
is convergent.


2.4.25. Assume that {an} is a positive valued sequence such that
for any positive valued sequence {b,,} the first equality holds. Take
b n = ;t;. Hence, by Problem 2.4.22, we get


1 = lim ( an. ..!.. ) = !!!!! an. ill!! ( ..!.. ) = ill!! an.
 a,. .
n-.oo an R-OO n-oo an n-oo
n-.oo




2.4. Limit Points. Limit Superior and Limit Inferior 205


From this it follows that both the limits superior and inferior of {an}
are positive and lim On = lim an. Therefore the sequence {an} is
n-oo n-oo
convergent (see 2.4.18).
2.4.26. Evidently, Jim
 < lim
. Now we will show that
n-oo n-.....oo
Jim nlQ; < Jim On+l . If Jim On+1 = +00, then the inequality is
n-oo v -n n-oo On n-oo Cn
obvious. So, assume that Jim a:+ 1 = L < +00. Then for any e > 0
"-00 n
there exists k such that
CIn+l < L+e for n> k.
an -


Hence



 = On . an-I ..... Bk+l < (L + e)n-k.
ak an-I 11n-2 ak
Consequently,


-..

 < \fQk(L+e)n(L+e).
-II
v'lik(L + e)ft" --+ 1,
n-oo
-Ir

(L+E)n < l+e
for sufficiently large n. From what has already been proved, we have


Since



 < (1 +e)(L+e) = L+ (L+ l)e+£2
for sufficiently large n. Combining this with Problem 2.4.12(a), we
obtain Jim
 S L+(L+ l)e+e2. Since e can be made arbitrarily
n-oo
small, Jim nlQ; S L = Jim 4 n + l . To prove lim 4n+1 < lim

"-00 v
 "-00 On - an -
n-oo n-oo
it is enough to apply Problem 2.4.22 and the inequality just proved
to the sequence {t}.
2.4.27. We first prove that Um b n S Urn On. To this end, assume
n-oo n-oo
that Jim an = L < +00. (For L = +00 the above inequality is
n-oo
clear). Then, given e > 0, there exists kEN such that On < L + e
for n > k. Hence
b - at + 02 + ... + ale + ak+t + ... + an
n-
n
at + a2 + ... + ak k(L + £) L
< - + +e.
n n




206 0


Solutions. 2: Sequences of Real Numbers


Since
 - k(L+
) -+ 0, OI+a2+...+aar - k{L+e) < E for
n n n....oo n n
sufficiently large n. It follows from the above consideration that b n <
e + L + E for sufficiently large n. According to Problem 2.4.12(a), as
£ can be made arbitrarily small, we get lim 6n
 L = lim an. The
n-oo n-eooo
proof of the inequality Jim an
 Iim b n is analogous.
fa-CO n-.oo


2.4.28.
(a) (b) It is enough to apply Problem 2.4.13.
(c) The equality is not true. To see this, it is enough to consider the
sequences defined by setting
4n={

bn={



for n = 2k.
for n = 2k + 1,


for n = 2k,
for n = 2k + 1.


Then


o = iIiii mintOn, b n } :f:. mint iIiii On, iIiii bra} = 1.
n-oo n-oo n-oo


(d) This equality is likewise not true, as can be seen by considering
the sequences defined in (c).
2.4.29. Assume that the sequence {an} has the property that there
are infinitely m;l.n y n such that


(I)


for every k > n, o'k S an.


Let nl be the first such n, n2 the second, etc. Then the sequence
{anJ,} is a monotonically decreasing subsequence of {an}. On the
other hand, if the sequence {On} fails to have the above property,
that is, there are only finitely 11\8.ny n satisfying (1), choose an in-
teger ml sucl}. that the sequence {Om 1 +n} does not satisfy (1). Let
7n2 be the first integer greater than ml for which lIm 2 > Om l . Con-
tinuing the process, we obtain a subsequence {am,,} of {an} which
is monotonically increasing.


2.4.30. By the preceding problem such a sequence contains a mono-
tonic subsequence which is bounded and therefore convergent.




2.4. Limit Points. Limit Superior and Limit Inferior 207


2.4.31. Assume first that lim 4,,+.1 = +00. Then, by 2.4. 14(b) 1
n-oo Cln
Jim at + ... + an + lln+t
= +00.
n-oo an


Now let


Urn lln+l = Q < +00.
n-oc an
Then, given e > 0, there exists k such that
(1) an+l < a + E for n
 k.
an


In other words,


an 1
(2) > for n
 k.
lln+l a + e
Hence, for sufficiently large n, we have
b n = 0) + ... + an + an+l 2: Ok + ... + an + lln+l
an On
ale an-2 Bn-I ak+l an-2 an-I
= .. . + .. .
... ...
Ok+l an-l an alc+2 On-l On
+ ... + an-2 . an-I + an-I + 1 + 4n+l
an-I On. an an
( 1 ) n-k ( 1 ) n-k-l 1 an+l
> + + ... + + 1 + .
- a+E O+E O+E an
If 0 < Q < I, then the above inequality and Problem 2.4.14(b) yield
Jim 6n = +00.
n-.oo


On the other hand, if a
 1, then by Problems 2.4.14 (b) and
2.4.19 we conclude that
( 1 ) n-k+1
1- -
(3) Jim b n > 0 + lirn Q+
 1 = a + Q + E .
R-OO - R-OO 1-- a+e-l
Q+



In case Q = 1 (e > 0 can be arbitrary) we get Urn b n = +00. H
n-.oo
Q > 1, then (3) implies
- 1 1
lim b n 2: 1 + Q + 1 = 2 + (0 -1) + 1
 4.


 Q- 0-
4 is an optimal estimate because it is attained for the sequence an =
2", n E N.




208


Solutions. 2: Sequences of Real Numbers


2.5. Miscellaneous Problems


2.5.1. Assume first that lim 0" = +00. Put b n = (a,,). Then b n

n-oo
an < b n + 1. Hence
( 1 ) "" ( 1 ) an ( 1 ) 6n + 1
l+ b n +l < 1+0;; < 1+;;;; ·
Thus the result in 2.1.38 and the squeeze principle imply
( 1 ) an
Urn 1 + - = e.
n-oo an


Moreover,


( 1 ) aft
Urn 1- - = e- I ,
ft-OO On


because


( 1 ) aft 1
lim 1- - = Hm ( ).... =e- I .
n-oo 11,. .n....oc 1 + 1
0"-1


This implies that


( 1 ) Gn
Jim 1 + - = e,
h--OO an


if {an} diverges to - 00.


2.5.2. One can apply the foregoing problem with an =
, Z:F O.
2.5.3. By 2.1.39, 2.1.40 and 2.5.2, (1 +
)n < e
 < (1 + ;)'+n for
I > % > 0, I e N. Hence for any positive x and for any positive integer
n, n
1 < In (1 + i) < ; if I> z. Taking n = 1 we get 1o(1+:r) < x
for x > o. Now, set l = [x] + 1. Then we obtain
( X ) :£
In l+n > 2
.£ .
n
Therefore In(l + z) > 2
Z for % > o.
Consider now the function f(x) = In(1 + z) - 2
Z ' :t > O. We
have


%2
/'(:J:) = (.1' + 1)(.1' + 2)2 > 0 for x> O.




2.5. Miscellaneous Problems


209


Hence


2x
f(x) = m(l + x) - 2 > 1(0) = 0 for z > o.
+x


2.5.4.
(a) Assume first that a> 1. Set an =
 -1. By the inequality in
2.5.3,


2an 1
2 < -lna = In(an + 1) < tin..
an+ n
Therefore the squeeze principle implies that Jim n( \10, -1) =
n-oo
lna for a > 1. We see at once that the claim holds if a = 1.
To prove it for 0 < a < 1, it is enough to apply the above with
! > 1.
(b) Put Un = vtn - 1. Th
u (Un + 1)" = 11... Ht:uce by 2.5.3, In 11 =
nm{an + 1) < 00n. Consequently, Urn nan = +00.
n-..oo


2.5.5. Using differentiation we can show that, for x > -1, 1
% $
In(I+x) S x. Since lim an = 1, an > 0 b eginnin g with some value of
n-O(;
the index n. It follows that 1
;:::1 $lnan = In(l+(a,.-I)) $ an-I.
Dividing the inequalities by an - 1 and using the squeeze principle
yields the desired result.


2.&.6. By the delluitiou (
2.1.38), e = liw (1 + ;) n . Moreover,
n-oo


(1+
f = 1+ (
)
 + (;)
 +...+ (
)
 +...+ (:)

1 ( 1 ) 1 ( 1 ) ( Ie - 1 )
= 1 + 1 + 2! 1 - n +... + k! 1 -
 ... 1- n
1 ( 1 ) ( n-I )
+ ... + n! 1 - n ... 1 - n ..


Hence


(i)


(1+;f <an.




210


Solutions. 2: Sequences of Real Numbers


On the other band,
(1+;f > 2+ i (1-;) + it (1-;) (1-;)
1 ( 1 ) ( k-l )
+ ... + k! 1 - n .. · · · 1 - n .


Passage to the limit as n -+ 00 gives


(ii)


e > ak.


By (i) and (ii), the limit of the sequence {an} is e. Moreover,
111
On+rn - 4n = (n + I)! + (n + 2)! + ... + (n + m)!
1 { 1 1 I }
< (n + I)! 1 + n + 2 + (n + 2)2 + ... + (n + 2)m-1
1 n+2
< (n + I)! n + 1 ·


Keeping n fixed and letting m -t 00, we get
< 1 n+2
e - On - (n + 1)1 n + 1.
This and (ii) imply that 0 < e - an < n!;y.
2.5
 1. We know (See 2.5.2) that e% = lim (1 +
) n t % E JR. For a
n-oo
fixed Z E Rt put an = (1 + iT +
 + ... +
 ) . We get


Ian - (1 +
rl = t ( 1- ( 1- ! ) . .... ( 1- k -1 )) %k
n k=2 n n k!

 ( ( 1 ) ( Ie - 1 )) Ixlk
::: f:; 1 - 1 - n · ... · 1 - n k! ·


By 1.2.1,


( 1 ) ( k - 1 ) Ie-I j k( k - 1)
1 - - ..... 1-
 1-
 - = 1- for 2 < k
 n.
n rl
n 2n




2.&. Miscellaneous Problems


211


Therefore
lan-(I+!)"lst k(k-I)lzlA: =.!..t IzlA: "
n k:s2 2n k! 2n k=2 (k - 2).


n

Since Urn in E
2 r = 0 (which follows easily from the Stolz
"-00 k=2
theorem. see 2.3.11), we get Urn On = lirn (1 +
)n = e?
n -00 n....oo


2.&.8.
(a) By 2.1.38, n:!:i < In (1 +
) <
. So for n> 1 we get
2n+ 1 1 1 1 2n
In < - + 1 +... + _ 2 < In 1 ·
n n n+ n n-
Thus the desired result follows from the continuity or the loga-
rithm £unction and the squeeze principle.
(b) We have
1 1 1 1
+ ... + < + ... +
n+ 1 2n + 1 vn (n+ 1) v 2 n (2n+ 1)
111
< - + 1 +... + _ 2 ·
n n+ n
Therefore the claim follows from (a).
2.5.9. Analysis similar to that in the proof of 2.5.3 gives
x2
(.) z-2<ln(1+z)<z for %>0.
n
Set 6ft = IDa,. = E In (1 +
). By (*),
k::sl
k Jil ( k ) k
'2 - 2 4 < In 1 + 2' < 2.
n n n n
This and the equaJities
tk = n(n 2 + I) , t
 = n(n+ 1
(2n + I)
kml A
t
imply that Urn 6ft = l. Finally, the continuity of the logarithm
n-.co
function yields Urn an =
.
n-oo




212


Solutions. 2: Sequences of Real Numbers


2.5.10. One can show by induction that


an = n + n(n - 1) + ... + n(n - 1) · ... .2+ n(n - 1) . ... · 2 · 1
n! n! n! n!
= (n - I)! + (n - 2)! +... + If + Of.


Hence


lim TI n ( 1 +
 ) = lim ( a 1 + 1 . ... . On + 1 )
R-OO ale n-oo a) an
k=l
Ii an + 1 lim (1 1 1 )
= m I = + _ 1 1 + ... + -. = e,
n-oo n. R-OO . n.


where the last equality follows from 2.5.6.


2.5.11. By 2.5.6,


lIOn
e = 1 + _ 1 1 + ... + -. + I' where 0 < Bn < 1.
. n. nn.


Therefore 0 < n!e - [n!e] = P: <
, which proves our claim.


2.5.12. By the arithmetic-geometric mean inequality, the monotonic-
ity of the logarithm function and the inequality proved in 2.5.3, we
get


1 r;- 1 ( 1 1 )
-In vab < In-( vta+ Vb) = In -( y'Q-l) + -( V'b -1) + 1
n - 2 2 2
<
 « tIii -1) + < V'b -1») .


To get the desired result it is enough to multiply these inequalities
by n and use the result in 2.5.4 (a).


2.5.13. Note first that if lim a: = a > 0, then fun an = 1.
R-OO R-OO
Assume now that {an} and {b n } are sequences whose terms are
different from 1. By Problem 2.5.5,
lim nlna n = 1.
R-OO n(an - 1)


(*)




2.5. Miscellaneous Problems


213


The assumption lim a: = a > 0 and the continuity of the logarithm
n-oo
function imply that lim nlnan = mo. Thus, by (*),
n-cx:>


lim n(an - 1) = lim nlna n = ma.
n-co n-oo


Observe that these equalities re mA-in valid if 4n = 1. Finally,


lim nln(pan + qb n ) = lim n(p(an -1) + q(b n -1» = lnaPb q .
n-oo n-co


2.5.14. We have an+1 - an = -
(4n - an-I). Consequently,


an = a+ (b-a) + ...+ (an - Bn-I)
= a+ (b - a) (1-
 +
 -... + (_1)n-2 (n
 I)! ).
Finally, by 2.5.7, lim an = b - (b - a )e- I .
n-oo


2.5.15. Consider the sequence {b n }, where 6n =
, and apply the
same method as in the solution of the foregoing problem to conclude
that an = n!.
2.5.16. As in the solution of 2.5.14, lIn+l - an = -
(4n - an-I).
-I
Thus lim an=2b-a-2(b-a)e T .
n-oo


2.5.17. (a) We have


n ( 1 1 ) 1
fin =3- (; "k- k+1 (k+1)!
n k+l-k n 1
= 3 -
 k(k + I)! +
 (k + l)(k + I)!
n 1 n 1 n 1
= 3 -
 kki + {; (k + I)! + h (k + l)(k + I)!
n+ 1 1 1
= E - k l + ( 1)( )' .
k= O. n + n + 1 ·
Therefore, by 2.5.6, Um an = e.
n-oo




214


Solutions. 2: Sequences of Real Numbers


(b) By (a) and 2.5.6,


1
o < an - e < en + l)(n + I)! ·
Re mark . It is interesting to note that this sequence tends to e
faster than the sequence considered in Problem 2.5.6.


2.5.18. It follows from 2.5.6 that e = 1 + -fi +... + ;!r + Tn, where
lim n!r n = O. Moreover,
R-too


(*)


1 I 1
1 < n.T R < -.
n+ n


So,


Jim nsin(2wn!e) = lim nsin(2wn!T n )
R-tQO R-tOO


. I sin(211'n!rn) Ii 2 ' 2
= Jim n27rn Tn 2 I = m n 1rn.r n = "Ir.
n-too 1Tn.T R n-too
The last equality follows from (*).
2.6.19. We will show that lim (1-
)n = O. By assumption, for
n-co
an arbitrarily chosen M > 0 we have an > M if n is large enough.
Hence


an M
o < 1 - - < 1 - -.
n n


Consequently,


0< (l-
r < (l-
r.
So, by 2.4.12, 2.4.14 and 2.5.2, we get
OS Jim ( 1- Bn ) R
 Jim ( 1- 4n ) R
 e- M .
n....oo n n-.oo n


Letting M -to 00 yields


( tln ) R - ( an ) "
O:S Um 1 - -
 lim 1 - -
 O.
R-too n R-OO n


Therefore lim (1 -
)n = 0, as claimed.
R-CO




2.5. Miscellaneous Problems


215


2.5.20. We will show that lim (1 +
 ) 8 = +00. Given M > 0, we
8-00
have bra > M for sufficiently large n. So, as in the solution of the
foregoing problem, we get


lim ( 1+
 ) n
 lim ( 1 +
 ) n = eM.
n-.oo n n-oo n


Since M can be arbitrarily large, we see that lim (1 +
)n = +00.
n.-.oo


2.5.21. It is easy to see that the sequence {an} is monotonically
decreasing to zero.
(a) We have 0... 1 - t = l!a -+ 1. So, by 2.3.14, fun no 1 = 1.
+1 n n n.....oo 8.....00 n
(b) By (a),


(1 ) n ( ..1- - 1 ) nan ..l.. - n
1im n - nan = lim nOn = lim On .
"....00 In n n-oo In n 8.....00 In n


Using the Stolz theorem (see 2.3.11), we obtain


(1 ) n ( 1 - -L - 1 )
lim. n - nan = lim Gn+J On
"....00 In n n....oo n In (1 +
)
n ( 1 -1 )
= lim I-on n = lim n4n = 1.
n-oo In (1 +
) 8.....00 I-an


2.5.22. It is easy to see that the sequence { an} is monotonically
decr easing to zero. Moreover, an application of I'Hospital's rule gives


Z2 - 8in 2 Z 1
Jim
%-0 z 2 sin 2 z = 3.


Therefore


lim ( 1 _ ..!.. ) _ !
n-oo a
+l a
 - 3.
Now, by the result in Problem 2.3.14, lim na
 = 3.
n .....00




216


Solutions. 2: Sequences of Real Numbers


2.5.23. Clearly, the sequence is monotonically increasing. We will
show that it diverges to +00. We have
a
+1 = ( an + 1 ) 2 > ( an +
 ) 2 > a: +

o} + ... + l1t, na,. n


and


2 2 2 2 2 2n
t12n - an > 2 1 + 2 2 + ... + - > 2 1 > 1.
n- n- n n-
Thus {a
} 15 not a Cauchy
uence. Since it increases, it must
diverge to +00. Moreover,
(.) 1 < Gra+1 < 1 +
.
- an - na"


By the Stolz theorem


2 ( 2 _ 2 )
" On " n 4 n +, an I " n ( 2 2 )
Inn 21 = 11m ( 1 ) " = 1m - 2 0n+l-a;
ft-OC nn 11-00 21n 1 + - "-00
'1
Ii n ( 2an 1 ) 1
- m" - + -
- n-oo 2 a, + a2 + ... + an (a1 + a2 + ... + on)2 - ,
because


n 1
o < < -.
(a. + Q2 + ... + an)2 n '


and agam, by Stolz's theorem,
. . nan . " (n + 1)a,.+1 - na,.
1m =lm
R-DC al + 02 + ... + an fl
OO a n + 1
= lint ( n + 1- n an ) = 1.
n-oo lZn+l
The last equality fonows &om (*). Indeed, \\'e have
a 1 + !tf:.!
1 < n + 1 - n n < nG"
- "n+ 1 - 1 + n
.. ·
Since Um On = +00,
n-OQ


1 + !!.%!
lim na,. = 1.
n-oo 1 + --L
'fiG..




2.5. Miscellaneous Problems


217


2.5.24. By the inequality arctanx < x for x > 0, the sequence is
monotonically decreasing. Moreover, it is bounded below by zero.
Hence it converges, say, to g, which has to satisfy the equation 9 =
arctang. Thus 9 = O.
2.5.25. Note that all the terms of the sequence {an} belong to the
interval (0, 1). Denote by X'o the unique root of the equation cos X' =
z. If z > :1:0, then cos(cosx) < z. The function f{x) = cos(cosx)-x
is monotonically decreasing, because f'(x) = sinxsin(cosx) -1 < 0
for x E JR. Thus, for x > Xo, cos(cosx) -x < f(xo) = o. Analogously,
if x < xo, then cos( cos x) > x.
Assume first that a} > Xo. It follows from the above that 03 =
cos(cosal) < at. Since the function y = cos(cosx) is monotonically
increasing in (0,
), we get 65 < a3. It can be shown by induc-
tion that the sequence {a2n-l} is monotonically decreasing. On
the other hand, 62 = coo 61 < cos Xo = xo, which implies that
64 = 005( 0050 2) > a2, and consequently, {B2n} is monotonically
increasing.
Similar arguments can be applied to the case where 0 < 61 < xo.
lf al = xo, then all the terms of the sequence {an} are equal to xo.
In all these cases the sequences {tI2n-l} and {tI2n} both tend to the
unique root of the equation cos( cos x) = x. It is easily seen that Xo
is such a root.


2.5.26. We get, inductively,
an = 1- (_l)n-l sin(sin(... sin 1)...),
"-- ......

(n-l) times


n> 1.


Hence


n-l
n -1- E (_l)k-l sin(sin(... sin 1)...)
L- ....

n
1

1
 (Ic-I) times
n L..Jak = n
k=I
We will show now that


.


n-l
E (_l)k-l sin(sin(...sin 1)...)
k - l


- ....


(*)


lim
n-oo


(k-l) times
n


= O.




218


Solutions. 2: Sequences of Real Numbers


H n - 1 is even, then


- sin 1 + sin(sin(... sin 1)...)



"..
en-I) times
n


n-l
E (_l)k-l sin(sin(... sin 1)...)
k - l ....

- "..


<


(k-l) times
n


< o.


n
Obviously, for odd n - 1, (*) also holds. Finally, lim
 E ak = 1.
n-co k=l


2.5.27. Clearly, an e (n7r, n1r+
)J n = 1,2, ..., and thus lim an =
D-OO
+00. Moreover t


lim tan( 1r + n1l" - an) = lim 1 = lim ..!.. = o.


 2
OO


OO



By the continuity of the arctan function we get lim ( ; +n1l"-an) = o.
n-oo
Therefore


lim (an+l - an -11")
n-oo
= lim ( ! + n1l' - an - (
 + (n + 1)11" - an+l )) = O.
n-oo 2 2


Consequently, lim (an+l - an) = 1f'.
n
oo


2.5.28. Observe that without loss of generality we can assume that
lall < ; . Indeed, if not, then by assumption la21 <
 . Consider
first the case where 0 < a < 1 and 0 < al

. Then an+l =
asinan < an. This means that {an} is monotonically decreasing
and, since it is bounded, it converges. Its limit is equal to zero,
which is the unique root of the equation x = asinx, 0 < a S 1.
Assume now that 1 < a S
 and 0 < al $ i. Then the equation
x = asinx has two nonnegative solutions 0 and Xo > O. H al < :to,
then {an} is monotonically increasing and bounded above by Xo.
Indeed, a:z = asinal > ale Moreover, tI2 = asinal < asinxo = Xo
and, inductively, an < tin + 1 < Xo. Similarly, Xo < at S ! implies
that an > Cln+l > xo. Hence lim On = :to for 1 < a < i. If
n-oo
-!
 a < 0, al > 0, then we consider the sequence {b n } defined
by setting b l = ai, bn+1 = -asinb n . Obviously, b n = (_!)n- 1 an.. It




2.5. Miscellaneous Problems


219


follows from the above that in the case where 0 < 41 S f we have


llman=O
n-oo


if lal:$ 1,


1 . if 1 < 7r
1m an =:co < a - _ 2 '
"-00
71"
Um 4n does not exist if -
 2
 a < -1.
n-.oo
If -i
 al < 0, then one can consider the sequence given by b l =
-ai, b"+1 = asinb n , and apply the foregoing. U al = 0, then all the
terms of the sequence are also equal to O.


2.5.29.
(a) Note that an > 0 and On+1 = 1n(1 + 4n) < lIn. Therefore the
sequence converges to a 9 which satisfies 9 = In(l+g), 60 9 = O.
We now show that Urn Ran = 2. Using differentiation, one can
R-OO
prove that (see also 2.5.3)
2x
 %3
<1n(1+3:)<z--+- for %>0.
2+% 2 3
This implies that
1 1 1 1 1 1
(.) - - - + 1 I < < - + -.
On On an (1 - 2 4n + 3a
) On+l an 2
Putting


1 1
b n = -- +
4n an (1 -
a,. + ia
)
we see that Jim b n = I. S ummin g both sides of (*), we get
n-oo


1 1 1 1 1 1
- + - +...+ - +b1 +
 + ...+bn < - +... + - +
01 02 an C2 4n On+l
1 1 1 n
<-+-+...+-+- .
al a2 an 2


Consequently,
1 b1 + b2 + · · · + b n 1
(n + l)a. + n + 1 < (n + 1)4,.+1
1 n
< (n+l)ol + 2(n+l).




.220.


Solutions. 2: Sequences of Real Numbers


H Ii 1 1
ence m ( n + l ) a = 2.
n-oo n+l


(b) We have


(1)


2
n n--
lim (na n - 2)- 1 = Jim nan In 4 n .
n-oo n n 8-00 n


n- 2
To prove that lim In
ft exists we will use the Stolz theorem
8-00
(see 2.3.11). We get


n - .1... 1 - 2 +..1..
lim an _ lim a,,+1 a"
n-oo Inn - n-oo In (1 +
) ·
Since lim 4n+1 = Um 10(I+o n ) = 1 and lim n In ( 1 + 1. ) = 1,
n-tOQ an 8-00 an n-oo n
we see that
lim n - t li n(2CLn+l - 2an + 4n4n+l)
n-.oo In n = n-
 a 2 .
n


(2)


Now it is enough to show that lim 2o n + 1 -2o;+onCJn+1 exists. To
n-oo an
this end, we use the inequality (which can be proved by differen-
tiation)
Z2 z3 x 4 x 2 z3
x- 2"+ 3 - 4 < In(l +x) <x- 2" +3' z> o.
Thus
13 1 4 Is 13 1 4
6 an - 6 an - 4 an < 2an+l - 2an + tlnOn+l < 6 an + 3an.
This gives


lim 2lLn+l - 24,a + l1n4n+l _ 1
R-OO a 3 - 6.
n
Combining this with (1) and (2), we see that lim n(
n-2) = 2 3 .
n-.oo n n


2.5.30. Set f(x) = (ifl: and F(z) = f(f(x» - z. We first show
that F'(x) < 0 for positive x. We have


( ) (il
+z
F'(x) = i 10 2 4-1.




2.5. Miscellaneous Problems


221


Hence


( 1 ) (i)
+z 1
F'(x) < 0 if and onl.y if 4 < In 2 4 .


It is a simple matter to verify that the funct.on on the left-hand side
of the last inequality attains its maximum value of e I
 4 at x -
.
This implies that F' (x) < 0, which m ea'l$ that F strictly decreases
on (0, +00). Moreover, F(
 ) = o. Therefore F(x) > 0 for 0 < x < i
and F(x) < 0 for x>
 . -Consequently,


1
fe/ex») < x for x > 2.


Since B2 = 1 > !, it follows that 04 = f(/(02» < Q21 and inductively,
we find that {a2n} strictly decreases. Thus. it tends to a 91 such
that /(/(91» = 91- The convergence of {a2n-l} to a 92 satisfying
J(J(92» = 92 can be established in much the same way. Clearly,
9 _",,_1
1 - :I
 - 2.


2.5.31. Observe first that 0 < an < 2 for n
 2. H an > I, then
CIn+l < 1. Set lex) = 2 1 -% and F(x) = f(/(x» - x. One can show
that F'(x) < 0 for 0 < x < 2. Therefore


F(z) < F(l) = 0 for 1 < x < 2,
F(x) > F(l) = 0 for 0 < x < 1.


Next, as in the proof of the foregoing problem, we show that if 41 < 1,
then the sequence {i12n} is monotonically decreasing and the se-
quence {02n-l} is monotonically increasing, and both tend to the
same limit 1. Similar considerations apply to the case 41 > 1.


2.5.32. Observe first the all the terms of the sequence are in the
interval (1,2). Since the function F(x) = 2
 - x is monotonically
decreasing on this interval, F(x) > F(2) = 0 for x E (1,2). Therefore
the sequence is monotonically increasing and its limit 9 satisfies 9 =
2
 t 50 9 = 2.




222


Solutions. 2: Sequences of Real Numbers


2.5.33. We apply 2.3.14 to the sequence {an + On-I} and obtain
lim On+On-l = o. Next we consider the sequence b n = (-l)nan.
n-.oo n
Since lim (b n - b"-2) = 0, we see that
n-oo


O Ii bn + b n - I Ii an - an-l
= m = m .
n....oo n
oo n


2.5.34. By the Stolz theorem (see 2.3.11),


In .l.. In 1 - In -L -n In an+l
lim an - 1 . On+l an - lim art
-1m - n
"....00 In n n....oo In( n + 1) - In n n....oo In (1 +
)
lim In £In+ 1
=- n .
,,
oo an


If lim n ( I - 0:+ 1 ) = 9 is finite, then fun ( ':+1 - 1 ) = o. Now
n
oo n n
CQ n
the desir ed r esult follows from the inequalities
n
t - 1 < nln ( 1 + ( an+l _ 1 )) < n ( an+l - 1 ) .
1 + On+l - 1 - -
an an an


If 9 = +00, then the right inequality shows that lim nIn 0:...1 =
n.....oo n
-00, and consequently, lim
n
 = +00. Finally, if 9 = -00, then
n-oo
for any M > 0 there is no such that CI:
l > !;f + 1 for n > no. Hence
nln t1n+l > In ( 1 +
 ) n . M.
an n n
oo


Since M can be arbitrarily large, we see that Jim

 = -00.
n-oo


2.5.35. By the definition of the sequences,


D.n+l + hn+l = (at + b1)(1 - (an + b n ) + (an + b n ).
Set dn = an + b n . Then dn+l = d 1 (1- dn) + dn and by induction we
show that dn = 1- (1- d1)n. Likewise,
a,. = * (1 - (1- dI)'t) and b n =
 (1 - (1 - dl)n) .




2.5. Miscellaneous Probl eJll9


223


Since 11- d 1 1 < 1, we get
. . fll
Iman=
n-oo 0) + 6 1


and


6 1
11m 6n. = .
"...oc; 41 + 6 1


2.5.36. Define the sequence {b n } by setting 6ft = oa,.. Then hn+l =
bn{2-6n) = -(bra -1)2 + 1. Hence 6n+l -1 = -(6n -1)2. Obviously,
the sequence {an} converges if and only if {b n - I} does or, in other
words, when Ib l - 11 = lao,l - 11
 1. Moreover, if a, = !' then
lim On = 0, and if 0 < (0) < 2, then lim an = !
n"'
 n-



2.5.37. This result is contained 88 a special case in Probl
m 2.5.38.


2.&.38. One can show that the function 1 is continuous at (a,a. ...,a)
and /(0" a, ..., a) = o. Define the se.quence {bn} by setting
bl =
 =... = bk = min{41,a2,...,ak},
b n = l(b n - 1 , b n -2' ..., bn-k) for n > k.
Note that if min{al,02, ...,ak} < a, then {6n} is strictly increasing
and bounded above by o,. On the other hand, if min{al,a2t ...,ak} >
a, then {bn} is strictly decreasing and bounded below by CI. Hence, in
both cases, the sequence {bn} converges and lim b n = a. Moreover,
fa-CO
the monotoniclty of / with respect to every variable implies an
 bra
for n EN. Now define the sequence {en} by setting
CI = C2 =... = CJc = max{at, Cl 2, ...,Ok},
Cn = I(Cn-I,Cn-2....,Cn-k) for n> k.
As above, we show that lim en = a and en $ On for n e N.
R-OC
Finally, by the squeeze principle,. lirn an = G.
n-.oo


2.5.39. We have 0,3 = B2e Q2 - a1 , 04 = a3e G3 - a2 = 02eQ.3-01 and,
inductively, Gn+l = a2e
n -01 for n
 2. Suppose 9 is the limit of the
sequence. Then


e OI
(.) -9 = e 9 .
Q2
Note that if "a
 = e t then the equation (.) has only one solution
9 = 1. If e:; > e this equation has two solutions, and if 0 < e:; < e




2



Solutions. 2: Sequences of Real Numbers


it has no solutions. Consider first the case where 0 < e:: < e. Then
the sequence {an} diverges because in this case (*) does not have
any solutions. Moreover, one can show that the sequence {an} is
monotonically increasing and therefore diverges to +00.
Consider now the case where e:; = e. Then a2 = e C1 - 1
 al
and, inductively, a n +l
 an. Moreover, if al :::; I, then one can show
by induction that also an
 1. Hence, in such a case, lim an = 1. H
n-.oo
al > 1, then {an} is monotonically increasing and diverges to +00.
Next, consider the case where e;; > e. Then (*) has two solutions,
say !/l,92, where, e.g. 91 < 92. Assume that al < gl. Then


eat
ea.! - -al > 0
a2


or, in other words, B2 > ale It follows by induction that {an} is
monotonically increasing and bounded above by 91, which is its limit.
H 91 < a1 < 92, then {an} is monotonically decreasing and bounded
below by 91, which is also its limit. H al = 91 or al = 92, then the
sequence is constant. Finally, if al > 92, then the sequence increases
to +00.


2.5.40. (This problem and its solution is due to Euler in a more
general case. See also [13]). Applying differentiation, we show that
lnx S ; for z > o. Hence

 lnlln = Cln-Ilna, n > 1, and
consequently, an
 Bn-IIn a e . Therefore, if a > e
, the sequence
{an} is monotonically increasing. We will show that in this case,
lim an = +00. We have a n +l - tin = a Cn - an. So for a > e!,
n-.oo
we consider the function g(x) = a Z - x. This function at tslin
 its
minim um at x = _ lne lno ) < e It follows that a%-x > 1+10(10(1) > 0
o In 0 · In 0 I
and consequently, Bn+l - an > l+II
(
nQ) > O. Since the difference
between two consecutive terms is greater than a positive number, the
sequence diverges to infinity.
Now we will consider the case where 1 < a < e
. We first show
that in this case the equation a Z - x = 0 has two positive roots.
The derivative of the function g(x) = a Z - x vanishes at the point
2:0 > 0 such that a%o = I; a . The function 9 attains its minim um
value at xo, and 9(xo) = a%O -Xo = h
a -xo = l-i:
nc < 0, because




2.5. Miscellaneous Problems


225


if 1 < a < e!, then 1.:a > e. Since 9 is a continuous function on
Rt it possesses the intermediate value property. Thus the equation
Q,z = % has one root in the interval (0, %0) and the other in (:rOt +00).
Denote these roots by Q and 11.. respectively. Note that since gee) =
a,e - e < (e!)" - e = 0. the number e is between Q and p.
II z > p, then Q,Z > a/J = (J and g(x) > O. This m eans that
in such a case the sequence {an} is monotonically increasing and
bounded below by {J. Hence lim On = +00.
,,-.cc
If Q < % < Pt then Q < cr < (J and g(x) < o. Consequently,
the sequence {an} is bounded and monotonically decreasing. Thus
it converges to Q.
For either z = Q or x = p, we get a constant sequence.
Now if 0 < % < a J then 1 < a Z < Q and g(z) > O. Therefore the
sequence {an} increases to Q.
Finally, if G = e! , then the number e is the only solution of the
equation a
 = x, and the function 9 attains its minimum value of 0
at e. Thus Cor 0 < x
 e, we get 0 < o/
 5 e and g(x)
 gee) = o.
This implies tbat the sequence {an} is monotonically increasing and
its limit is equal to e. On the other hand, if z > e, the sequence
mcre.ases to infinity.
We can summarize the results as Collows:


Um an =
"-00


+00
+00
fJ


Q


+00


e


if Q. > e
 and % > 0,
if 1 < (I < e! and % > {J,
if 1 < a < e t and z = fJ,
if 1 < a < e! and 0 < x < {J,
if a = e! and x > e,
if (I = e! and 0 < % < e.
-


2.5.41. The equality can be proved by induction. We have Urn tin =
h -"00
2 (compare with t.he solution of 2.1.16).




226 Solutions. 2: Sequences of Real Numbers


2.5.42. [20] Note first that
an S V 2 + ../2 +... + v'2 < 2.
L

.....


n roots


Observe that if El = O. then all the terms of the sequence {an} are
equal to zero. Assume now that EJ -1= o. We will show by induction
that the given equality holds. It is ev ident for n = 1. So suppose that
J ( n )
. 7r Et£2...Ek
a,,=£l -2+£2 V 2 +...+£nv'2=2Sm iL 2k-1 ·
1e=1
Then
( n+l ) ( n+l )
2 _ 2 _ 2 . 1r
 £2...£1e _ _ 2
 7r
 E2...£k
4n+l - sin 4 L.J 2k-2 -. cos 2 + 2 L.,., 2k-1
k=2 k=2
( ta+l ) ( n+1 )
= _ 2 !
 £)...£k = 4 · 2 !
 El..
Ek - 2
cos 2
 2k-l sm 4 L.J 2k-l ·
k=1 k=l
which completes the proof of equality. Now, by the continuity of the
sine function,


( 00 )
. . 7r EI...Ek
J.!..
 an = 2 sin 4 L 2k-1 ·
k=l


2.5.43. One can show by induction that
1 1 n
arctan 2 + .n + arctan 2n 2 = arctan n + 1 ·
Therefore lim (arctan
 + ... + arctan 2
2 ) = : .
n-oo


2.5.44. We hav e
sin 2 (", v'n 2 + n) = sin 2 (", v'n 2 + n - 1m) = sin 2 A -I.
I + 1 + 1. n-too
n


2.5.45. One can show by induction that the sequence is monotoni-
cally increasing and bounded above, e.g. by 3. Henc e it is a conver-
gent sequence whose limit 9 satisfies 9 = ../2 + J3+9 and 9 e (2,3).




2.5. Miscellaneous Problems


227


2.5.46. [13] We have
3 = vI +2.4 = ../1 +2Ji6 = VI +2"1+3

= V I +2+ V I +3 Vl +4V36 .


and, inductively,


(1) 1+2 1+3 V l+... ../ I+n o/ (n+2)2=3.


Therefore


(2) 3
 1+21+3 V I+... "/ I+(n-I) Vn +1.
Now we will use the foll owing ( easily verifiable) inequality:
(3) v I +ZQ
 va " l +z, x 2= 0, Q> 1.
By (3) with x = n and Q = n + 2 ,
../ 1 +n o/(n+2)2 < vn+2vl +n .


Hence
V I +(n -1) " 1 + n v'(n + 2)2 < " I + v n + 2 (n -1)vl +n
< (n + 2)1 ../ 1 + (n -l)vn+ I ,
where the last inequality follows from (3) with Q = "fn + 2. In View
of (1), repeating this argument n times gives


(4) 3 $ (n+2)2- n 1 +2 V I +3 V l + ... " 1 + (n -1) vn + 1.
Combining (2) with (4) yields
lirn 1+2 ' 1+3 -' l+... " 1+(n-l) vn +I=3.
n-.cc V V




228


Solutions. 2: Sequences of Real Numbers


2.5.41. The equation z2 + z - a = 0, a > 0, has two roots Q and
{J such that Q > 0 > p. Furthermore, we have


a a-an-QOn
On+l - Q = - - 1 - Q =
an an
= a - (1 + a)(an - a) - Q(1 + Q) _
an


-(I + Q)(an - Q)
an


.


Since a + 13 = -1, we see that an+l - Q = {3 a
:Q . Likewise, C£n+l -
{J = Q On-a . Thus
an


tln+l - {J Q an - {3
4n+l - Q = {3 an - a'


and inductively,


an - {J = (
 ) n-l at - {j .
4n - Q {3 41 - Q
Since I i I = I
Q < I, we get J

 (» r- 1 = 0, and consequently,
lim an = {J.
n-.oo


2.5.48. Let Q and {j be the roots of :r;2 + x - €I = 0, a > O. Then
Q > 0 > 13. In much the same manner as in the solution of the
foregoing problem we get


( ) n-1
an - Q = Q al - Q .
an - f3 {3 41 - fJ


Thus Jim On = Q.
n
oo


2.5.49. For any positive integer k, we have


I 1 1
lan+l+k - an+ll = 1 + Bn+k - 1 + On
1
< 4lan+k - ani.


_ ICn+k-a.n1
- (1 + CLn+JJ (1 + an)


Now by induction we get
14n+1+k - 4n+11 ::; (i) n lak+1 - all.




2.5. Miscellaneous Problems


229


Moreover,


10k+1 - oIl
 10/c+l - Ok I + lak - ale-II +... + I
 - all
1 4

 l la2 - all = - 3 1a2 - all.
1--
4


Thus {an} is a Cauchy sequence. Its limit is V2.


2.5.50. One can proceed as in the solution of the foregoing problem
and show that lim On = 1 + ,;2.
n .....00


2.5.51. Let lex) = 2
Z ' X > 0, and F(z) := fe/ex)). Then F'(x) >
o for x > o. It is easily verified that at < a3 and a4 < a2. More-
over, since F is strictly increasing, we see that the sequence {lI2n}
is strictly decreasing and the sequence {a2n+ I} is strictly increasing.
The sequence {an} is bounded. Thus both its subsequences {G2n}
and {4 2n+l} converge. One can check that they have the same limit
v I + a-I.


2.5.52. If al
 .0, then lI2 = 1 - al > 1 and a3 = a2 -
 >
. By
induction, an+l = an - 2nl_1 for n
 2. Consequently,


( 1 1 1 )
Bn+1 = - 2 n - 1 + 2 n - 2 +... + 2 + 02,
and therefore Jim a,. = -al if al $ O. Now if 01 E (0,2), then
n-CX)
42 E [0,1) and inductively, we see that a n +l .E [U, 2 n1 _ 1 ], which implies
that in this case lim an = O. Finally, if al
 2, then
 = al -1
 1.
n-oo
By induction, we get a n +l = an - 2n
1 ' and consequently, as in the
first case, we show that fun an = 01 - 2.
n-oo


2.5.53.
(a) We have


7& 2: - 1 jai _ a 2a 2 3a 3 (n - l)a n - 1
. - 1 + 2 + 3 +... + 1
n-J n- n- n-
j=l
_ 1 (
 2(n - 1)a 2 3(n - 1)a 3 (n - 1)2a n - l )
- 1 1 + 2 + 3 + ... + 1 ·
n- n- n-




230


Solutions. 2: Sequences of Real Numbers


Since


. n -1 = . ( n - j + j -1 ) < ' ( I + . -1 ) = .2
3n_j J n-j n-j -3 1 J ,
we obtain
n-I ja i < a + 22a'l + 3 2 a 3 + ... + (n - 1)2a n - 1

 n-j - n-l ·
,=1


Now it is enough to observ(! that, by the. result in Pr()blem 2.3.2,
. . a + 22a 2 + 3 2 0 3 + ... + (n - 1)2a n - 1 0
1m = ·
n-oo n-l


(b) Observe that


n 1 n n-l n-l n-l k Ie
na"
 --:-- =

an-J =
 n a k = """ alt + """ a
L-" 30) L-" 3 L..J n - k

 n - k
;=1 j=1 kaD 1:=0 Ic=O


and apply (a).
(c) Apply (b) with a = i.


2.5.&4. Since for positive x, x -
 < sin x < X, we see that


n n 3 n n
E 1f' E 71' E .7r E 7r
- < sIn < .
k=l n + k 1c=1 6(n + k)3 1:=1 n + k k=1 n + k


n
It is easy to check that Urn E 6(n
I:):J = O. Moreover, by 2.5.8 (a),
71-0() Ie:::l
n
Urn E n:1c = 1f' In 2. Therefore the limit is 1r In 2.
-n-oo k=1


2.5.55.
(a) Let an = fi ( 1 + £.r ) . In view of the inequality (see 2.5.3)
Ie=l
or:. < In(! +z) < X for z> 0, we get


n k 2 n k 2
E 3 k2 < loan < E 3'
k=1 en + lc=1 en




2.5. Miscellaneous Problems


231


n
Hence, by the equality E k 2 = n(n+l
(2n+l) ,
k;:l
n(n + 1)(2n + 1) In n(n + 1)(2n + 1)
6(cn3 + n2) < an < 6cn 3 ·
Therefore lim an = elc .
n-.oo


(b) One can show that the inequality %
1 < In(l +x) < x also holds
if -1 < x < o. Therefore, as in the proof of (a), we get
n ( k2 )
lim TI 1 - - = e-/c.
R-OO cn 3
k=1


2 5 56 S .
 · · z3. %3 %&
.. · mee lor pOSItive x, z - "6 < SlDX < x - 6' + iT' we see
that


vn 3n n! n ( k2 ) Vn3n n. k
(1) II 1-- < II sm
n! (n,fii)n 6n 3 n! _ n..jii
k=1 k-I


and


vn 3n fa k vn3n nl n ( k'2 k 4 )
(2) II sin < II 1 - - +
nl n./ii nl (nVii)n _ 6n 3 Sfn 6 .
k=1 k-I
It follows from (1) and from the result in the foregoing problem that
the limit is greater than or equal to e-r,. We will now show that
. n ( k2 k 4 ) -Ii
n1.!..
 II 1 - 6n 3 + 5!n ti S; e .
k=l


Indeed,
n ( k2 k4 ) n ( 1;,2 k4 )
In II 1 - 6 3 + 5' 6 < E - 6n 3 + 5' 6
k- l n .n 1:=1 .n
_ _ n(n + 1)(2n + 1) + n(n + 1)(2n + 1)(3n 2 + 3n - 1)
- 300 3 30 · S!n 6 ·
Finally, by (2) and the squeeze principle,
. "n 311 n. k -Ii
lim TI am ..;n =e ·
n-oo n! k- l n n




232


Solutions. 2: Sequences of Real Numbers


2.5.57. We will first show that 4n =.

l 4n_l + 1, n
 2. We have

 1
 k!(n - 1 - k)!(n - k)
an = L..J - = L..J + 1
k=O (
) k=O (n - l)!n
n-l 1 n-l k (n - 1- k)!k!
= E (n-I) - E n (n-I)! +1
"- 0 k k=O
n-l k 1
= an-I - E n (n-I) + 1.
k=O k


(1)


Moreover,
n-l k 1 n-l n - 1 - kIn - 1 n-l k 1
E n (n-I) = E n (n-I) = n an-I - E n (n-I) ·
k=0 It: 11;=0 k k=O Ie
Therefore


n-l kIn - 1
E - (n-I) = 2 an-I.
k=On k n
Finally, by (1), 4n = 4,,-1 - ;n l tin-I + 1 = n2
1 4n-l + 1, which
establishes our first assertion. From this we deduce that lim an = 2.
ft-CO


2.5.58. H Q = 0, then obviously lim an = O. If a > 0, then 0 <
D-DO
4n < 1 -
n

)Q , and consequently, lim an = o. Assume now that
n-oo
Q < o. Then


an = <_l)n-I (n-a_l) ( G r u -I).....(( n:I r a -1).


Therefore, if we take a = -1, we obtain the divergent sequence an =
(_l)n-l. H we take Q < -1, we get


((
ra -1) (( n
p ra -1) > ( ; -1) ( n
p -1) =1


for 1 < p < n. Moreover, ( ; ) -u - 1 > 2 - 1 = 1. Therefore
Ian I > (n- a -1) ( ( n: 1 ) -co -1) n
 +00.




2.5. Miscellaneous Problems


233


Likewise, we can see that if -1 < Q < 0, then
1a,,1 S (n- O -1) ( ( n
 1 ) -0 -1) n
 O.


n
2.&.59. We have (2 + v'3)n = E (k)(v'3)k2 n - k . If we group the
k=O
terms with odd and even indices, respectively. we can write
(2 + v'3)" = An + -.l3Bn and (2 - vi)n = An - V3 B n.
Hence lim (An + JaB n ) = +00 and lim (An - JaB") = O. Also,
n"'oo n...oo
lim t/3 B n = t.
n-oo An
Since the An are integers and 1
ft < I, it tollows that [JaBia] =
Aft - 1 for sufficiently large n. Consequently,
{J3B n } --t 1 or {An + v'3Bn} = {v'3Bn} --t 1.
n--oo "-CO


2.5.60. The sequence {8n} is monotonically increasing. If it were
bounded above it would converge, and then
Urn fin = Urn (Sn - 8 n - l ) = o.
n-oo n-oo


Suppose now that Urn 8n = +00. By our assumption, Sn+l4n+l +
n-DO
an S SnGn+On-lt and consequently, Bnan +4n-l
 $2 Q 2+01- Hence
< an-I < 820.2 + 01
4n_4n+ 8n - 8n ·
Finally, lim an = O.
n-oo


2.5.81. By assumption, for any E > 0 there is a positive integer no
such that On < £ n if n > no. Hence
0 2 1 + 4 + ... + a
 oJ + 4 + ... + a
 a
o+l + ... + o

= +
n 2 n 2 n 2
< of + a.
 + ... + a
 + nE (tln o +l + ... + On)
n 2 n 2 .




234


Solutions. 2: Sequences of Real Numbers


By 2.4.14 and 2.4.19,
2 2 2
Jim at + G2 + ... + an < Jim at + ... + an
2 _E ·
ft-CO n n-oo n
3 3 2
This obviously implies that lim t11+ 0 2-t;...+t&n = o.
n-oo n


2.5.62. We will apply the Toeplitz theorem (see 2.3.1). Set
An = al +ll2:.+...+an, Bn =
'+b:l.:+...+bn, C n = CI +C2+...+en


and


A an-k+lBk

k= ·
· alB n + C12 B n-t + ... + anBt
Now we will show that the positive numbers dn.k satisfy conditions
(i) and (ii) in 2.3.1: (see also 2.3.3 (a». For fixed k.
d,. k < 4n-k+l --. o.
, - at + lL2 + ... + t1n-k+l n-oo


n
Clearly, E lln,k = 1. Observe also that
IF 1
en albn + tt2bn-l +... + anb 1 A b l ,I b:2 A bn
-= =
I-+u.n2'-+".+u.nn-.
On BIBn + Cl2 B n-l + ... + anBl · Bl ' B 2 . ' Bn
. .
Finally, by the Toeplitz theorem, lim l?- = lim If- = o.
n-oo" n-oo n
.....2 2 .

2.5.63. We know that x - T < In(l +3:) < x -
 +
 for :£ > o.
2
Put an = (1 +
)n e- n . Then -! < lnan < -
 +

 , which implies
1im. In' an = - i. 'l'herefore the limit is equal to e- i .
n...oo


2.5.64. We have l1n+l - an > -
 > - n(nt_l) = - n:l +
 for
n > 1. Let b n = an - n': 1 · Then the sequence {b n } is monotonically
increasing and bounded above; hence it converges. Therefore {an}
also converges.
2.5.65. By the assumption CIn+l 2V'2
 Bn, we see that
6n+l2-

 l1n2- 2 n "' l .
Hence the sequence bn = an2- 2". I is monotonically increasing and
bounded. So, it converges. Obviously, lim b n = lim an.
n-co n-oo




2.5. Miscellaneous Problems


235


2.5.66. Let a e (I. L). Suppose, contrary to our claim, that a is not a
limit point of {an}. Then there is a neighborhood of a which contains
only finitely many terms of the sequence. Let E > 0 be so small that


(.) l<o-E<a<a+E<L and 4n
la-Eta+e] for n>nl.
By the assumption, Ia,a+l - ani < E for n > ft2. By 2.4.13 (b), we
know that there exists on, such that an. < I + £ < 4 for nk >
max{n..n2}. Hence an ar +l
 anI, + lan.+l - an. I < 0+ €. Thus by
(.), Gn lr +l < a-E. Therefore, by 2.4.12 (8), L
 0 - E < L, a
contradiction.


2.6.67. Let a e (It L). Suppose, contrary to our claim, that a is not a
limit point of {an}. Then there is a neighborhood of a which contains
only finitely many terms of the sequence. Let E > 0 be so small that


(.) l<o-E<a<a+E<L and an,[a-€,a+E] for n>nl.


By the assumption.


(..)


an - On+l < On < £ for n> n2.


It follows from 2.4.13 (a) that there is tin. such that an. > L-£ > Q.
Hence, by C..), we get G n .+l = 4n.. + (0.,.,,+1 - on.J > G - E. Now,
by (.), Bn.+1 > 0 + E for nk > max{nh n2}. Thus by 2.4.12 (c),
I
 a + £ > a > I, a contradiction.


2.5.68. We will use the result proved in the solution of the laSt prob-
lem. By the monotonicity of {On},


Gn+1
n+l+on+1


On > -an > -1 .
n+tJ n - (n+l+a n +l)(n+On) - n


Thus, by the result in the preceding problem, the set of all limit points
of the given sequence is the interval (I, L], where


I:: Um On
n-=oc. n + a,.


and L = Urn an .
n.
n+an




236


Solutions. 2: Sequences of Real Numbers


2.5.69. Note that
l a 2 +1 - 1 1 =!. a 2 - 2 = !. I I -I a2n-l - 2 1 = ! l a 2 1 - !.
n 3 2 n 3 2 2 3 4 n- 3.
This implies that the sequence has the two limit points:
 and
.
2.5.70. We know, by 1.1.14, that for any positive integer n there
exist a positive integer qn and an integer Pn such that
I Pn I 1
21r - - < 2".
qn qn
Thus IPn I < (21r + 1 )q,
, and consequently,
1 v'IPnl sinPnl = 1 v'lPnl sin (21rqn - Pn)1
 v'IPnl sm 1:. 1 5 v
 I ,
qn qn
Since the sequence {qn} is unbounded, it contains a subsequence
divergent to infinity. Therefore zero is a limit point of {an}.


2.5.71. It is enough to show that there is a subsequence {D.n
} for
which


( nk(a 1 + tlnA:+l» ) n k > 1.
(nk + l)an"
Suppose that the above condition does not hold. Then there exists
no such that


neal + an+l) < 1 if >
(n + l)an n - no.
Hence -!!L.. + 0'1+1 <!!xL for n > no Thus
n+l n+l n -.
an _ an-I < _ al
n n-l n'
On-I On-2 at
- <-
n-l n-2 n-2'


.
.
.


On o +l _ 6no < _ 01 .
no+l no 110+1
S umming the above inequalities, we get

 < 4no _ a1 ( 1 1 +... + .!. ) .
n no no+ n




2.5. Miscellaneous Problems


237


Therefore, by 2.2.50 (c), lim
 = -00, which is impossible because
n-co
tin > o.


2.5. '72. In much the same way as in the proof of the foregoing prob-
lem we show that there is a subsequence {a"
} for which
( nk(OI + anir+.J ) "" > 1
(nk + p)an.. -.


2.6.7'3. Suppose that our claim does not hold. Then there exists an
no such that for n
no. n ( I+:::t. - 1) < 1. The last inequality
can be rewritten as n
J <
 -
".t: . This, in turn, implies (see the
solution of 2.5.71) that
1 1 olJO On
no + 1 +... + ; < no - n.
Hence lirn
 = -00, which contradicts the fact that {an} is a
n-oo
positive sequence.
To show that 1 is the best possible constant, take an = n In n.
Then


I . ( 1 + (n + 1) In( n + 1) )
1m n -n
n-.oo n In n
= Um l+(n+l)ln(n+l)-nlnn
n.....
 In n
= fun 1+ln(n+l)+In(I+
)" =1.
"-00 In n


2.6.7'4. Note that Q
 = 1 + an-I and 01 = 1. Clearly, the sequence
strictly increases. We will show by induction that it is bounded above
by
(1 + v'5). Indeed, if O n-I < 1( 1 + VS), then G
 = 1 + tin-I <

 + i v'5. Therefore an < ,j
 + 4 v'5 = 4 + 4 v'5. and {an} converges
to l(l +
).
2.&.75. [20] Obviously, the sequence {6ft} is strictly increasing. As-
sume first that Q < In 2. Then, by assumption, there is no e N
01'''1, tJ..ot 1",/1ftll \" 911
,) it 91 '"'> 91_-". An..i....IAft..I.. "
 .ft2" =1'




238


Solutions. 2: Sequences of Real Numbers


n
 no. We have
b,. = Va l + "0 + ..; a no + "0 + ,;a;;
al + ... + V On o -l + Ve 2ftO + ... + J e 2ft


<
-


al +.. + Va",, -I + e 2fto V I +..0 +..If.


<
-


By tbe foregoing problem,


6n



2 n o 1 + v'5
Ba +.. + lln o -1 + e 2.


This means that {bra} is bounded above and convergent. Assume
now that Q > In 2. By assumption, given e > 0, there is an no such
that In(ln4n) > n(Q + £) for n
 no. Setting Q + E = InP, we get
an > ell" for n
 no, where {J > 2. Thus
b,. = Ja l + V02 +... + Va"" +..0 +,;a;;
. I _ I
 " ( I! ) ft
> Val +..0 + V Ono-l + e '''-ft(JH > e 'I ·


In this case, tbe sequence {6ft} diverges to infinity.
Note, additionally, that if 0 < On
 1, then, although In In On
is not defined, the sequence {6n) is monotonically increasing and
bounded above by .1+ 2 ..{5 , and is convergent.


2.5.76. (20) It follows from the 8SSUIDption that 0
 On
 not. Thus
the sequence {
} is bounded. Denote by L its limit superior. Then
there is a sequence {mk} of positive integers such that lim c:;. = L.
k-oo ·
For an arbitrarily fixed n e Nt we can write mk = nil: + Tic. where
Tic e to, 1, ..., n - I}. Thus, by the assumption, Om.. S 11cf1n + G,o.e
Hence


Om. < I" Cr.
- _ an+-.
mk nile + rk mk




2.5. Miscellaneous Problems


239


Letting k .... 00, we get


(.)


L<

- ,
n


which implies


_ 1 . On < 1 - On
00- Im-
- .
n
oo n n
 n
As a result the sequence {
} converges.


2.&.77. Analysis similar to that in the solution of the preceding prob-
lem can be applied.


2.5.78. (20] The sequences {an + I} and {I - an} satisfy the as-
sumption of Problem 2.5.76. Hence lim at
+l and Urn I- n G n exist
n
oo n-co
and are finite.
(a) By the abovey since lim ¥- = 9t lim ':- = 9.
"-00 "-00
(b) The inequalities follow immediately from (.) in tbe solution of
2.5.76.


2.5.79. We will show that the sequence {
} converges to A =
sup{
 : n eN}. Let p be an arbitrarily fixed positive integer. Then


On _ Bpl n +rn > a".ln
- ,
n pin + rn - pin + r n
where r n e {O, 1, ..." - I}. So, by our assumption, lim


.
n-.oo
This, in turn, implies that Jim

 Um
. Thus the convergence
"-00 p-OG
of the seq uence { !!A } has been established Moreover awn. n. > !!A
n · t mn - n
implies that


A> Urn
 > lirn
 =inrsup

- n
 n - 1'-00 P p '
p l
> e nf t1pom > e nf am A
_ 1 sup _ I SUp - = .
P ".eN pm "m m


2.5.80. We first show the boundedne8S of the given sequencee Indeed,
if _ 0 1 < Cn,Gn+1 < Ot then _ a t
 Gn+2 = Q +;
 a. Thus, by the
- - .. n+l




240


Solutions. 2: Sequences of Real Numbers


principle of'induction stated in the solution of Problem 2.1.10, the
sequence {an} is bounded. Put


I = lim llnt
n-oo


L = iiiii an.
n-oo


Then for an arbitrarily fixed E > 0 there exist nl, n2 e N such that


(i)
(ii)


an < L + E for n > nl,
On > , - £ for n > 712.


By (i), Bn+2 = 0"":"+1 >
t n >-nl . Since the positive £ can be
arbitrarily small, we get. I
 !. In much the same way (ii) implies
that L st. Thus I = t. Let {nk} be a sequence of positive inte-
gers such tbat lim On.+2 = L. We can assume that the sequences
"-00
{an.+l}, {an,J and {lln.-l} converge to lit 12, and 1 3 , respectively.
In fact, if this is not the case, we can choose subsequences which do.
By the definition of {an},
2 2
'1 + '2 = - = 21 and '2 + '3 = -,

 '1
and since 1
 '1,'2,13
 L, we get '1 = '2 = I and 12 = 13 = L.
Hence I = L. This and the equality I = t imply that the sequence
{an} converges to 1.


2.5.81. Since 0 < at S 61, there exists f/) e [0, i) such that al =
6 1 COS VJ. Now, one can show by induction that, for 'P '/: O.
b 1 sin VJ hI sin cp
11n+1 = 2" tan
 and ""+1 = 2" sin f.; . n E N.
Therefore lim an = lim 6n = 6 1
n "' .. H f/) = 0, i.e. al = hI, then
YI-OC n-oo
the given sequences {On} and {b n } are constant.
2.5.82. (18] By assumption, }::: = 1 + Ek
n, where Ek.n tends to
zero,. uniformly with respect to k. Thus


(*)


n n n
Eak.n = E b 1c.n + EEk
nbk.n.
Ie=t k=1 k= 1




2.5. Miscellaneous Problems


241


Since lim t bk.n exists, there is an M > 0 such that I t bk.n l <
n

k=l Ie- I
M, n e N. Moreover, for any E > 0, IEk.nl < -b for k = 1,2, ...t n,
provided n is sufficiently large. Hence I t £k.-nbk.fl i < E. which means
1:=1
n
that 1im E £k.nbk.n = O. Thus, by (.),
n--oo kc:1


n ,.
lim
 0k,n = lim
 bk.n.
n-co L.J n-oo L...,
k- l kc:l


2.5.83. We have
. $21:-1 )4
SID n 3
J2k-l )0
n 3


--t 1 uniformly with respect to k.
n-oo


Thus. by the foregoing problem,
1 . E n · (2k - 1)0 lim E n (2k - l)a
1m SID = = o.
n-
 n 2 n-


k=1 k=1


2.5.84. It follows from 2.5.5 that, if the sequence {%,,} converges to
h all'" -I 1 This . Ii that
zero, t en ... In a -.. unp es
6ft n--oo


a;.\ - 1
---+ 1
:.\ In a n--oo
n


uniformly with respect to k. Now applying Problem 2.5.82 we get
n n k 1
lim
 ( 0.;\ -1 ) = lim lno
 _ 2 = -Ino.
"-00 L...ti n--oo L...ti n 2
k=1 k=1


2.5.85. If {xn} is a positive sequence that converges to zero, then,
by Problem 2.5.3, !!!.(
+Zft) --t 1. Applying 2.5.82, we see that
fI 91-00
n ( k ) n k 1
lim
ln 1+ 2 = Urn
2=- 2 .
n-oo L..., n n-.oo L..., n
k= I k= I
n
Thus lim n (1 +
) = ej.
71-00 k=1




Wt2


Solutions. 2: Sequences of Real Numbers


2.5.86. One can sbow that if {Xn} is a positive sequence that con-
verges to zero, then


(*)


1.
(1 + x n ) P - 1 --+ 1
1xn R-OO
p


Set


k q - 1
Ck,n = n q t k = 1,2, ..., n.
Then CIe.n 5 max{
,
4 }' and consequentlYt {CIe.n} converges to
zero, uniformly with respect to k. Putting ak,n = (1 +Ck,n)
 -1 and
b/c,n =
 Ck,nt and using . 2.5.82, we obtain


( 1. )
n k'/-l PIn kq-1
lim 1+ -1 =-lim
n.....oo E ( n q ) p "-00 E nil "
k=l k=l


By the Stolz theorem (see 2.3.11),


n Wl-l n q - 1 nq-1
lim
 = lim = lim
n-ooL....J n q n-oo n q - ( n - l)q n-oo nil - n q ( 1-
 ) q
k-I n
q-I 1
-lim n __
- n-OOnll-n'l(l-q
+ 1l(1l;1)
_.".) - q"


2.5.87. Set an = lfc:1

::J:::2 · Then
a (1 +
)... (1 +n
)
On = b (1 +
 + < : -1» (1 + 2
 + (
-1»... (1 + n : + (
-1»).
Now let x =
 - 1. Then x > 0 and
a 1
an --
- b (1 + 1

 ) (1 + 1':;
 ) ... ( 1 + 1+";.
 ) "


Since


Z d +... + x d < ( 1 + Z d ) ... ( 1 + x d ) '
1 + - 1 + n- 1 + - 1 + n-
o a G a




2.5. Miscellaneous Problems


243:


we get


Hence


a
4,& <: ( ) .
bx J
: + 1+

 +... + 1+


Jim On == 0, because
n-oo


Ii ( 1 1 1 )
m d + d +... + d = +00.
n---oo 1 + - 1 + 2- 1 + n-
a a a




Chapter 3


Series of Real Numbers


3.1. Summation of Series


3.1.1.
(a) We have 41 = 8 1 = 2 and 4n = 8n -Sn-l = - n(n 1 _1) ' n > 1. So
00
we get the series 2 - E n(nt_l) , whose sum is S = lim Sn = 1.

2 n-



00
(b) As in the solution of (a), we get a,a =:In, E 2n
1 = 1.
0=1


(c) By a similar argument, 4n = arctann - arctan(n -1), and con-
sequently, tanan = n 3 _ 1 n+1 . Therefore an = arctan n:i_In+l and
00
E arctan n2_1n+l = -i.
n=l


(d) al = -1, an = (-1)"
::
) for n> 1. Moreover,


00
" 2n - 1
-1 + L.-( _1)" ( 1) = o.
2 n 71,-
n=


3.1.2.
(a) We have an =
 - (n;ljlJ . Thus 8n = 1 - (n':l)
 and S =
liw 8n = 1.
n-.oo


.245




246


Solutions. 3: Series of Real Numbers


(b) Similarly, an = 1 ( {2n
1)3 - (2n
1)" ) · It then follows that 8n =
l (1- (2n
1)3 ) and S = nl!.
Sn = l.


(c) an = .J
l - v'
1 . Therefore Sn =
1. .and S = J.!..
 Sn = 1


(d) an =
 ( 2n
1 - 2';+1 ) . Thus S = lim Sn =
.
R-OO


( ) vn+ 1 - nIl CIS Ii S 1
e an = n(n+l) =
 - vn+i . onsequent y, = n-
 n. = ·


3.1.3.


(a) 5n = Inl-ln4+ ln2 + ln4 -lnt-In 7 +ln3 +In 7 -ln2
-In 10 +... + Inn + In(3n - 2) -In(n -1) -In(3n + 1)
1'1+1
+ In(n+ 1) + m(3n+ 1) -Inn -In(3n+4) = In 3n+4 -
Hence S = In 1.
(b) S = 1n2.
3.1.4. (a) We have
1
On=
n(n + l)...(n + m)
1 ( 1 1 )
= m n(n + l)...(n + m -1) - (n + l)(n + 2)...(n + m) -
Hence 8n =
 ( 1'2'
_,'m - (n+l)(n+
).__(n+m» ) - So, 8 = m:"l -
(b) Since an =
 (
 - n
m) , 8 =
 (1 +
 + -.. +
 ) ·
(c) We have


n 2 2
-
-
(n + l)(n + 2)(n + 3)(n + 4) (n + l)(n + 2)
11 ( 1 1 )
- 2 (n+ l)(n+ 3) - (n+ 2)(n + 4)
11 ( 1 1 )
+ "4 (n + l)(n + 4) - (n + 2)(n + 3) -


1
(n + 3)(n + 4)




3.1. S umm ation of Series


247


Now, as in (b), after simple calculations we get S = 16.


3.1.5.
(a) For n
 5. we have



 . 'If' . 71" . '1r . 1r . 'It

n = 8m 720 +sm 360 +sm 120 + 81n3i) + SID '6.


(b) Observe that 0
 n
.:n < 1, n e N. Th
 S = o.


3 1 6 S . . I 3 1 ( · I · I )
· .. moo 4n = SID 2..+1 COS 2n+1 = '2 SID 2n-1 - 8m 2" t we see
that S = isinl.


3.1.7. Note that
1
n!(n 4 + n 2 + 1)
_ ! ( n _ n-l + 1 )
- 2 (n + l)!«n + l)n + 1) n!(n(n - 1) + 1) (n + I)! ·


Hence


l ( n fa 1 )
Sn = 2 ("+ 1)!«" + 1)"+ 1) +1 +
 (k+ 1)1 I


and by 2.5.6, we get S = 1im Bra = Ie.
R-OO


3.1.8. Note that for n> 1,
1 (2n + 1) - 1
G n =-.
2 3 · 5 · ... · (2n + 1)
1 ( 1 1 )
= 2 3. 5 · ... · (2n - 1) - 3. 5 · ... · (2n + 1)


and 41 = !. It follows that


1 1 ( 1 1 )
Sn = 3 + 2 3 - 3. 5 · ... · (2ft + 1) I
which implies the desired result.




248


Solutions. 3: Series of Real Numbers


3.1.9. As in the solution of the last problem, we have


an
-
(al + 1)(a2 + l)...(an + 1)
1
-
(al + 1)(a2 + I)...(an-l + I)


an+l-l
(al + 1)(a2 + 1)...(a,. + 1)
1
(al + 1)(
 + l)...(an + 1)


for n> 1. Hence 8n = 1 - (OJ+l)(42;1)...(On+l) .


3.1.10.
e a) If we take an = n - 1 in the last problem, we have 9 = +00, and
50 the sum of the given series is equal to 1.
(b) Here we take an = 2n -1, and, as in (a), the sum of the given
series is equal to 1.
(c) We take an = -
. Then
lim (112 + 1)(03 + l)...(an + 1»
n--oo
= lim (2 -1)(2 + 1) (3 - 1)(3 + 1) (n -l)(n + 1) = !
2 2 3 2." 2 2 .
R-OO n


Thus, by the result in 3.1.9, the sum of the given series is equaJ
to 1.


3.1.11. By definition, the sequence {an} increases to infinity. More-
over, we have a
 - 4 = a;-l(a
-1 - 4), and it can be shown by
induction that a; - 4 = a¥. 01..... a;_t(ai - 4). Hence


(1)


Jim an = ..; a"f - 4 .
n-.oo at ·
 · ... · an-I


Note also that for n > 1,
at · C&2
... · an =
 ( at · C&2
.. an-I - al ·


. · an ) ·
Thus by (1) the sum of the given series is equal to
..!.. + !.
 _ !. ..ja"f - 4 = at - .jay - 4 .
a] 2 at 2 2




3.1. S umm ation of Series


249


3.1.12. Observe that


1 I! 21
b = 6-2 (6-2)6'
21 2! 31
b(6 + 1) = (6 - 2)b - (b - 2)b(b + 1) ,


.
.
.


n! n!
6(b + l)...(b + n - 1) = (6 - 2)6(6 + 1)...(6 + n - 2)
(n + I)!
(b - 2)b(b + 1)...(6 + n - 1).


Summing the above equalities, we obtain


s _ 1 _ en + I)!
n - 6 - 2 (6 - 2)6(6 + 1)...(b + n - 1) ·


Hence, by 2.5.87, lim 8n = 6
2 .
"--00


3.1.13. For n = 0, 1, ...t put On = CI a :

: ::: J and define An =
an(a. + n + 1). Then An-l - An = ClnC6 - a-I). n = 0, I, ...t where
we additionally set A_I = 0 and a_I = 1. S umm ing both sides of
the above equalities from n = 0 to n = N, we get


N
a- AN = A_I - AN = (6-a-l) L4n = (6- a-l)SN+l,
":to


or equivalently, a - ON(O + N + 1) = (b - a - 1)5N+l. Therefore
( 1- (O+l)...(O+N+l» ) = ( 6- -1 ) 5
a 6(6 + 1)...(6 + N) a N+l


and, by 2.5.87, we see that Um SN+I = b-. :-l.
N-oo


3.1.14. By the foregoing problem,


(*)


1+
 a(a+l)...(a+n-l) =1+ a = b-l .

 6(b+l)...(6+n-l) 6-0-1 b-a-l




250


Solutions. 3: Series of Real Numbers


Replacing a by a + 1, we see that


(**) 1
 (a+l)...(a+n) b-l
+
 b(b + 1)...(b + n - 1) = b - a - .
,.


Subtracting (*) from (**), we obtain


f (a+l)...(a+n-l)
n=1 n b(b + l)...(b + n -1)
_ b-l b-l _ (b-1)
- b - a - 2 - b - a-I - (b - a - l.)(b - a - 2.) ·


n
3.1.15. Set An = "(G2+b)(


5):::(;ft+l +bj and Sn = E Ak. Then
k=t
-AL = Ok +6 ' or equivalently, Ako k + J " + Akb = Ak-1ak- S limm ing
Air:": 1 0"+1
both sides of these equalities from k = 2. to k = n, we get


(*)


An4n+l + Sn b - Atb = Ala2.


Now note that


O A Cl2.. a3..... Cln+l
< nl1n+l = a1- ( )( ( )
42 + b a3 + b)... lLn+l + b
1
= 41 (1 + ;!;) (1 + *) ... (1 + on 6 +1 ) .


Hence, by 1.2.1,


at
0< Antln.ft < n+l .
bE...!..
k=2 Ok
Therefore, by assumption, lim Anl1n+l = o. It then follows from (*)
n-OQ
that lim Sn = Al(
a2) = T.
n-oo


3.1.16. By the trigonometric identity 4
:z = cos3x + 3.cosx, we
get




3.1. Summation of Series


251


4005 3 X = cos3x + 3cosz,
4cos 3 3x = cos3 2 x + 3cos3x,
4OO5 3 3 2 x = cos3 3 x + 3cos3 2 x,


.
.
.


4005 3 g"X = COS3"+lX + 3OO83"x.


Multiplying both sides of these equalities by 1, -1, -b, ..., (-1)" 3 1 " ,
respectively, and then s ummin g them we obtain 4S n = 3cosx +
(_l)n 3
 cos3n+1x. Thus S = I cosx.


3.1.17.
(a) By assumption,


f(x) = a/(bx) + cg(x),
af(bx) = a 2 f(b 2 x) + acg(bx),
a 2 f(b 2 x) = a 3 f(b 3 z) + oo 2 g(b 2 x},


.
.
.


a n - 1 /(b"-IX) = an j(bnx) + a n - 1 cg(b n - 1 x).
Hence f(x) = an f(bnx) + c (g(x) + ag(bx) +... + a n - 1 g(b n - 1 x») .
00
Since lim an f(bn
) = L(x), E ang(bnx) = f(x)-L(z) _
n-

O c
(b) As in (a),
/(x) = af(bx) + cg(x),
a- 1 /(b- 1 %) =-/(%) .J a- 1 cg(b- 1 %),
a- 2 J(b- 2 x) = a- 1 /(b- 1 z) + ca- 2 g(b- 2 x},


.
.
.


a-R/(b-nx) = a 1 - R /(b l - n x) + B-ncg(b-nx).


Thus
af(bx) = a- n f(b-nx) - c (g(x) + a- 1 g(b- 1 z) +... + a-ng(b-nx»




252


Solutions. 3: Series of Real Numbers


and consequently,



..!.. ( =- ) = M(x) - af(bx) .
L..J ang b n c
n=O


3.1.18. We may apply the foregoing problem to the functions /(x) =
sin x, g(z) = sin 3 i with a = 3, b =
 and c == -4. The desired
results follow from the equalities 1im 3 ft sin 3:r:.. = x = L{x) and
n-+oo
1im 3- n sin3"'x = 0 = M(x).
"-"00


3.1.19. One can apply 3.1.17 to f(x) = cotx, g(x) = tanz, a =
2, b = 2 and c = I, and then use the equality
Jim ..!.. cot -=- = !..
n-+oo 2'i 2" z


3.1.20. We apply 3.1.17 to


(1- b)x
f(x) = arctanx, g(z) = arctan 1 + bx 2 ' a = c = 1,
and use the following:


lim arctan(bnz) = {
 .
n....oo -SIgn X
2


for 0 < b < 1,
for b > 1.


3.1.21. Since On+l = an + an-I, we have Bn+l4n = a
 + an-Ian
for n
 1. S ummin g these equalities, we get


(*)


8n = anan+l, n.
 o.


One can prove, by induction, th
t


(i) an =
 e +2 ./5 ) n+1 - e
 ./5 ) ,,+1 ,n
 0,
(ii) an-lOn+l - a; = (_1)n+l, n
 1.




3.1. Su mm ation of Series


253


Combining (*) with (ii) yields

=t (-l)k =t (-l)k =l_t ak-lak+1-a

k=O Sk k=O ak a k+l k=l ak Q k+l
-1- t ( 01:-1 _ ak ) _ an
- "-I Ok Bk+l - an+l ·


By (i),


n_ * ( ( 1+2
 ) n+1 _ ( l-fS ) R+1 )
lim -n = lim
(ill) n-oo On+1 n-oo -js ( (
+2
 ) n+2 _ ( 1- 2 Y! ) R+2)
2
= 1 + vlS 8
00 (_1)ft
Hence E T = 1+2.;5 .
n=O


3.1.22. It is easy to check that


(*)


(_1)"+1 :: lIn+IBn+2 - tlnBn+a,


n> O.
-


Thus


n ( 1) 1c n
8n = E - = - E ak+l a k+2 - ak a k+3
k=O Ok O k+2 1;=0 4k a k+2
= _ t ( a k + 1 _ Ok+3 ) = -3 + an+2 + an+3 .
k=O Ole ak+2 l1n+l 4n+2
Now, by (iii) in the solution of the foregoing problem, lim 8n =
"-00
.../5 - 2.


3.1.23. By (*) in the solution of the preceding problem,


arctan
42n+l


1


_ arctan 1 = arctan 42"+2 - Q2n+l
O2n+2 O2n+l t12n+2 + 1


t12n
= arctan = arctan
l12n a 2n+3


1


.


02n+3




254


Solutions. 3: Series of Real Numbers


S ummin g up these equalities gives
1 ra+l 1 1
arctan - = E arctan - + arctan ·
al k=l a2k. 0-2n+3


00
So, E arctg a J = : .
1 2n
n=


3.1.24.
(a) Note that arctan
 = arctan n
l - arctan n
l ' n > 1. Hence
00
E arctan
 = arctan 2 + arctan 1 + arctan! =
1T, where the
n=1
last equality follows from the fact that arctan a + arctan
 =

for a > o.
(b) For n e N, arctan n
+
+1 = arctan
 - arctan n
l . Hence we
DO
see that 2: arctan n",+ln+l = arctan! = lwo
n=1
(c) Since for n> 1, arctan n"-
:
+5 = arctan (n!1)2 -arctan tn';l)
 '
00
we get, as in (a), E arctan ia4_
::Z+5 = arctan 2 + arctan 2 +
n=l
arctan
 =
 w + arctan 2.


3.1.25. To obtain the desired result one can apply the trigonometric
identity


:r;-y
arctan x - arctan y = arctan 1 .
+xy
It is worth noting here that the results in the preceding problem are
contained as special cases of this one.


00

3.1.26. Let E b n be a rearrangement of E lln. Moreover, let Sn =
n=1 n=l
Bl +
 + ... + an, S
 = bt +
 + ... + b n and S = lim Sn. Clearly,
n-oo
S

 S. So {S
} converges, say to 8', and 5'
 S. By similar
arguments, S < 5'.


3.1.2'7. Since


2n 1 n 1 n 1
B2n = E k2 = E (2k)2 + E (2k-l)2
k=l
 1 k=1




3.1. S 1 1 JnTJI ation of Series


255


and lim 82n+l = lim S2n, we get
n.....oo R-OO


00 1 00 1 1 00 1
L n 2 = L (2n-l)2 + 2 2 L
'
n=l n=1 n=l


3.1.28. Following A. M. Yaglom and 1. M. Yaglom, Uspehi Matern.
Nauk (N.S.) 8 (1953) no. 5(57), pp. 181-187 (in Russian), we present
elementary proofs of these well known identities.
(a) For 0 < x < It the inequalities sinx < x < tanx hold. Thus
cot 2 x <
 < 1 + cot 2 x. Putting x = 2

1 with k = 1,2, ..., m,
and s ummi ng from k = 1 to k = m we obtain


( . )
 2 k1r (2m + 1)2
 1
 2 k1r
1 .LJ cot 2 1 < 2 L-, k2 < m+ L-, cot 2 1 -
k= 1 m + 1r k=l k=l m +
We now show that

 2 k1f _ m(2m-l)

co
 2 1 - 3 ·
k=l m+


(ll)


Let 0 < t < ; . By DeMoivre's law
cosnt + isinnt = (cost + isint)R = sinn t(cott + i)R
= sinn t t (
 ) ik cot ri - k t.
k=O k
'laking n = 2m + 1, and equating imaginary parts, we get
(iii) sin(2m + l)t = sin 2m + 1 tPm(cot2 t),


where
(iv) Pm(x) = Cmt 1)xm - Cm 3 + 1)xm-l +...:1:: 1.
Substituting t = 2':
1 in (iii) gives Pm(Cot 2 2

1 ) = o. So,
Zk = cot 2 2
1 ' k = 1,2, ..., m, are the zeros of Pm and their
sum is


(v)


m k:rr ( 2m+l ) m(2m - 1)

 cot 2 - 3 -
L....J 2 1 - ( 2m+l ) - 3 ·
k=1 m + 1




256


Solutions. 3: Series of Real Numbers


This, (i) and (ll) imply


m(2m-l) (2m + 1)2
 1 m(2m-l)
3 < 71"2 .LJ k2 <m+ 3 ·
k=l


Multiplying th
 inP.q11a1iti
 hy (2m
1)
 anrl np.xt lP.tting m-+
00 yield equality (a).
(b) To prove the second identity, note that


m r
+l)
E XiX; = 2 (2m+!) .
i.;=l 1
i:f;j


where XIc, k = 1,2, ..., m are the zeros of the polynomial (iv). It
then follows by (v) that


m k1r
L cot 4
11:=1 2m+ 1
= ( m(2m _1» 2 _ 2 2m (2m -1)(2m - 2)(2m - 3)
3 5!
_ m(2m -1)(4m 2 + 10m - 9)
45


.


The inequality cot 2 x < :z < 1 + cot 2 :£ (see (a» implies that
cot 4 z <
 < 1 + 2 cot 2 x + cot 4 x for 0 < :z; < ; . Consequently,


m(2m - 1)(4m 2 + 10m - 9) (2m + 1)4
 1
< L,-

 w 4
1

2 2m -1 m(2m - 1)(4m 2 + 10m - 9)
< m+ m 3 + 45 ·


Th11R (b) iR prnved.
Re mark. It is worth noting here that the above procedure can
00
be applied to calculate the sum of the series E n
lr ' where kEN.
n=l




3.1. S umm ation of Series


25't


(c) It follows from DeMoivre's formula, that for m = 4n, n E N,
cosmt = cosmt - (;) cosm- 2 tsin 2 t +... +sinmt,
· mt ( m ) m-l t . t ( m ) t . m-l t
SIn = 1 cos SID +... - m _ 1 cos sm ,

d consequently,
cot m t - (';) cot m - 2 t + ... - (m
2) cot 2 t + 1
cot mt = (':) cotm-1 t _ (';) cot m - 3 t + .... - (m
l) cot t .
It follows from the last equality that
4k1r + 1r
:Ck = cot 4m ' k = O,...,m -1,
are the roots of the equation
m ( m ) m-l ( m ) m-2 ( m ) 1 0
z - 1 z - 2:C + ... + m _ 1 x + = t
which implies that


(1)


m-l
E cot 4k1r + 1r = m.
k =O 4m


Since m = 4n,
m-l 2n-l m-l
L cot 4k1r + 1r = L cot 4k1r + 1r + L cot 4k1l" + 11"
k=O 4m k- O 4m k= 2n 4m
2n-) 4k + 2n AI.-

 1f' 1f'

-1r
= L..J cot 4 - L..J cot 4 ·
k=O m k=l m


This and (1) give
1f' 31r 51T' 71f'
cot- -cot-+cot- -cot-
4m 4m 4m 4m
t (2m - 3)1f' t (2m - 1)1r
+...+00 4m -co 4m =m.


(2)


Since


cot a -cot,B = tan(P - a) (1 + tana l tanP ) 1




258


Solutions. 3: Series of Real Numbers


we get from (2) that m is equal to
tan 2: (
 + tan,..!t..l tan;m. +... + tan !2n.-3J.! Itan $2," -I
,, ) ·
4"1 4m 4rn 4m
Hence, by the inequality
 > cla-; for 0 < % < w /2,
(3) m < tan ;: (
 + ,..!t..l;m. +... + !2rn-3)}(2m- I I" ) ·
4m 4"1 4", .Im
011 tbe other hand, we have
sin({J - Q)
cot Q - cot P = . . 13 '
Sin Q Sin
and as above, using the inequality
 < tti:' z t we obtain
. " ( 1 1 )
m = sm 2m sin .l!.. sin.!!t. +... + · !2m-3)Jr . !2m-I)1f
4m .lm sin -1m 8m -1m
. 7r ( 1 1 )
> sin 2m .JL 3,,- +... + 12m-a!! j2m-I)1r ·
4m 4rrl 4m 4m


This and (3) yield
( m m ) w2 1 1
-- <-+ +
tan:fm 216m 2 2. 3 ... (2m - 3)(2m -1)
r
< 16m sin S ·


Letting m. --+ 00 we get
co
1 1 1" m 1 "
2 · 3 + 5. 7 + ... = 2 L.., ( -1) 2m + 1 = 8'
"12=0


3.1.29. We have tln+l-l = an(an-l ) . Hence (I. t I = -
+
 1 .
"+1- .." ...-
Summing these equalities from n = 1 to n = Nt we get
(.) .!. + .!. + .n + ..!... = 1 _ 1 .
al 42 ON aN+1 - 1
It is easy to check tbat the sequence {an} inc reases and diverges to


infinity. Thus (.) implies E t = 1.
n=1




3.1. Summation of Series


259


3.1.30. By the definition or the sequence.,



I -1 = 41e a2 ,
eG.'J - 1 = "2e 03 t


.
.
.


Hence


e a , - 1 = at + ala2ea

= ... = al + ala.l + ... + at · ... · an + al · ... · 0,..+1 e GII + 2 .


00
This implies that E b n == eO' -1, because
n.e1


Um (01 · ... · a,a+le Ofl + 2 ) = o.
n-.oo


Indeed, {an} is bounded below by zero, is monotonically decrc
ingt
and converges to zero.


3.1.31. We have Sn+1 = 8n + On+1 = Sn + -J: - J2. Consider
the function /(z) = z +
 - Vi, % > o. If the sequence {Sn}
were convergent to S, we would get 1(9) = S. The only solution
of this equation is
.
{oreover, the function % ..... /(/(x» - % is
monotonically decreasing on the interval (
t 1). So, if x e (
t 1),
then


1 1
/(/(x» - :r < /(/( "J2») - "J2 = 0,
and since I is monotonically decreasing on the interval (0,1), we a1so
have /(f(x» > -J2 for % e (-J2t 1). Finally,
1 1
J2 < 1(/(x» < x for :z: e (J2,1).


This meaJ1
 that the sequence {8 2n - l } is monotonical1y decreasing
and bounded below. Thus it converges, and its limit is
. FUrther-
more, n
 B2n = n

/(S2n-l) = / (-J2) = -J2. So, the sum of the
given series is equal to -J2.




260


Solutions. 3: Series of Real Numbers


3.1.32.
(a) Note that
111
52n = 1 - 2 + 3 - ... -

1 1 1 ( 1 1 1 )
= 1 + 2 + 3 + ... + 2n - 1 + 2 + 3 + ... + n
1 1 1
= 1 + 2 + ... + _ 2 ·
n+ n+ n
So, by 2.5.8 (a), we have 1im 82n = In 2. Clearly,
n-oo
Jim S2n+l = lim ( 5.!n + 2 1 1 ) = 1n2.
11.-00 n-oo n +


(b) We have n1:t
) =
 + n
l . Hence by (a),
co I) 1 co 1 00 1
E<-l)n-l _11.+ = EC-l)n-l- + E(-l)n-I
n=1 n(n+ 1) n=1 n n=l n+ 1
= In2 - (ln2 -1) = 1.


(c) Denote by Sn the nth partial sum of the given series. Then
1 1 1 1
8 2n = + + ... + +.
z+2n+l z+2n+2 x+4n-l z+4n
As in the proof of 2.5.8, one can show that Urn S2n = In 2.
"-'00
Obviously, lim S2n+l = In2.
n-oo


3.1.33. We have
2 3 4 5 2n 2n+ 1
S2n = In 1- In 2 + In 3 - In 4 +... + In 2n _ 1 -In 2n
= In 2 · 4 · ... · 2n -In 3 · 5 · ... · (2n + 1)
1 · 3 · ... · (2n - 1) 2 · 4 · ... · 2n
-In ( 1 ( (2n)!! ) 2 )
- 2n+l (2n-l)!! ·


By the Wallis formula., i = fun 2n
1 ( 2

iJ! ) 2 . Hence Jim S2n =
n-.oo n......oo
In
.




S.I. S umm ation of Series


261


3.1.34. We have

 (-1)n-lln(1- (n
1)2 )
=
 (_1)n-l (In (1 + n
 1 ) +In (1- n
 1 ))
= - f( _1)n-lln ( 1 +
 ) - f( _1)n-l1n ( 1 +
 ) ·
n= 2 n= l


It follows from the foregoing problem that the sum of the series is
In 2 - 21n ; .
3.1.35. The nth partial sum of the given series can be written 88
1 1
Sn = 1 + 2 + ... + n - (In 2 -In 1 + In 3 -In 2
1 1
+... + In{n+ 1) -lnn) + 1 + 2 +... + n -In(n+ 1).
Thus, by Problem 2.1.41, the sum of this series is equal to the Euler
constant 'Y.




3.1.36. [20] Write F(x) = f j(t)dt. It follows from the Taylor theo-
1
rem that there exist Xk, Yk such that k < xk < k +
, k +.l < 'Uk <
k + 1 and


F (k + n - F(k) =
f(k) +
f'(%k)'
-F (k+ D +F(k+ 1) =
/(k+l) - ijl'(Yk).
S umming the above equations from k = 1 to k = n - 1 yields
1 1
2 / (1) + 1(2) + 1(3) + ... + J(n - 1) + 2 J (n) - F(n)
=i (f'(Yl) -/'(:£1) + 1'(Y2) -/'(:£2) + ... + I'CYn-l) -/'(:£n-l» ·
The limit of the expression on the right-hand side of the last equality
exists, because the series -1'(Xl) + fl(Yl) - 1'(x2) + jl(Y2) - ... is

nvergent (the terms have alternating signs and their absolute values
converge monotonically to 0).




262


Solutions. 3: Series of Real Numbers


Hwe take f(x) =
,then we can prove the existence of the limit
J

 (1+
 +
 +... +
 -Inn).
(Compare with 2.1.41 (a).) Taking I(x) = lnx, we can show that thE
sequence {In n! - (n + 4) In n + n} converges. (By Stirling's formuls
its limit is In
.)
3.1.31. Applying the foregoing problem to f(x) = I
% , X > 0, WE
can show the existence of the limit
1im ( In 1 In 2 In n (In n)2 )
_ 1 + _ 2 +... + - - 2 = s.
n-.oo n


Hence


lim 8 2n = lim ( _ In 1 + In2 _.... + 1n2n )



oo 1 2

= Jim ( _ ( In! ln2 1n2n _ (ln2n)2 )
n--oo 1 + 2 +... + 2n 2
2 ( 1n2- 1n4 In2n ) (In2n)2 )
+ 2+4+".+ 2n - 2
=-8+ 11m ( lnl + 1n2 +...+ Inn _ (lnn)2 )
n-
 1 2 n 2
. ( ln2 1n2 1n2 ) (In 2)2
+ J!.
 T+2+".+n- ln2lnn - 2
= In2 (7-
2 ) I
where 'Y is the Euler constant.
3.1.38. By Stirling's formula, n! = On v 21rn (
 )11. ,where lim an =
n--oo
1. Hence
1 (2n + 1)2n 1 (2n + 1) 2n 2 2n (n!)2
So = 2 In ({2n -1)!!)2e2n = 2 ln «2n)!)2e2n
= !.In (2n + 1)2n22na;
'Im (
)2n = l In (( 2n + 1 ) 2n Q
 ) .
2 a
n4nn (
) n e2n 2 2'1 2Q2n
Therefore lim 8n =
 (1-ln2).
n-.co




"3.1. S ummat ion of Series


263


8.1.89. Assume that the given series converges for z and y, and write


N ( 1 1 1 X )
SN(X) =
 (n-l)k+l + (n-l)k+2 +...+ nk-l -7ik ·


N
Then SN(:':) - SN(Y) = Yk:t: E
. Therefore the convergence of the
n=l
series implies that x = y. Now, we find the unique value z for which
the series converges. We know, by Problem 2.1.41, that the sequence
On = 1 + ! + ... + r!k - In( nk) converges to the Euler constant '1.
Hence


N 1 N k-l
SN(k - 1) = aN + In(Nk) - L - - E
n=:1 nk n=1 nk
= aN +lnk+ ( inN - E
 ) .
n=1
This implies that lim SN(k-l) = '1+lnk-7 = Ink. Thus x = k-l,
N-oo
and the sum of the given series is equal to In k.


3.1.40. One can easily check by induction that


a2n = 3n+ 2 for n = 0,1,2, ...,
42n-l = 3n + 1 for n = 1, 2, ... .


Thus


(*)


s =
 ( -l ) (
] 1 =
 (-1)"
 (-1)°
2N L....., a2 _ 1 L..J 2 _ 1 + LJ 2 - 1
n=O n n=O C2n n=1 42n-l
N N
_ "'(_1)" 1
 ( _I)n 1
- L.J (3n + 1)(3n + 3) + L.J 3n(3n + 2)
n=0 ngl


li N ( I 1 ) IN ( 1 1 )
= 3 +2 L (-1)ft 3n+1 - 3n+3 +2 E (-1)n
- 3n+2
n=1 n=1
tIN ( 1 1 ) IN ( 1 1 )
=3+2
 (-1)" 37i- 3n+3 +2
 (-1)" 3n+1 - 3n+2




264


Solutions. 3: Series of Real Numbers


1 1 N n 1 (_l)N+l 1. N n ( 1 1 )
= 3-6+ E(-1) 3;+ 6(N + 1) +2" E(-1) 3n+ 1 - 3n+2 ·

2
l
On the other hand, by 3.1.32 (a), we get


( 3N 1 )
-ln2 == fun E<-l)n-
N-.oo n
n=l
( N ) ( N-l ( ))
- 1im -1 n1-. _ lim -1 n 1 _ 1
- N-co
( ) 3n N-oo
 ( ) 3n+ 1 3n+ 2
1 ( N-l ( 1 1 ))
= --1n2- lim "(_l)R - .
3 N....oo
 3n+ 1 3n+ 2


N-l ( )
This implies lim E (-l)n 3n
1 - 3ra
2 =
 1n2. Finally, by
N-.co n=0
(*), lim S2N =
 -lln2 + ! +
In2 - t = i. Moreover, since
N-+oo
Iim S . Jim S Jim ( _I ) N+l Iim S . th f
2N+l = 2N + (3N+4)2-1 = 2N, e sum 0
N
oo N-oo N-oo N-co
the given series is l.


3.1.41.
(a) Suppose, contrary to our claim, that the sum S of the given series
q I co !
isarationa1number-
.Then (q-l)!p=q!S= E;r+ E
.
n=1 n=q+l
00
This implies that E
 is an integer. On the other hand,
n=q+l



 q! 1 1 1
o <
1 n!
 q+ 1 + (q+ 1)(q+ 2) + (q+ 1)(q+2)2 +...
= q+2 <

(q+l)2 -4'


a contradiction. Thus S is irrational.
(b) The 83I11 e method as in (a) can be applied..




3.1. .S 1lmm ation of Series


265:


3.1.42. On the contrary, suppose that the suIIi S of the series is &
rationa1 number
. Then


q I 00 I
(q _ l)!p = qfS = '" q.fn + " q.En .
L..J n! LJ n!
n=1 n;::q+l


00
This implies that E 9
i' is an integer. On the other hand,
n=q+l


00 I 00 I
" q.En < "'!!.: 1

 I -
 .<.
n n.
n=q+l n=q+l


00
To obtain a contradiction, it is enough to show that E g:t is not
n=q+l


equal to zero. We have


00 I 1 00 I 1
" Enq. > _ " !!.: _
L...J I - +1 L-i '> q+l
n=q+1 n. q n=q+2 n.


1 >0
q(q+l) - J


which proves that S is irrational.


3.1.43. Reasoning similar to the above can be applied.


00
3.1.44. Suppose, contrary to our claim, that E
 = E q ' p, q e N.
- I i
1-
By assumption, there exists a positive integer k such that if i
 k
then nl n2.
:.n'-1 > 3q. Thus


k-l co .

 nl"-2 · ... · nk-lq
 nl
 · ... · nk-lq
L.J + L-, = pnln2. ... · nk-l-

l

k



Moreover,


00 .

 nl n 2 · ... · nk-lq 1 (1 1 1 ) 1

 < - + - + + ... < t
i=k 7Jj 3 nk nknk+l


a contradiction.




266


Solutions. 3: Series of Real Numbers


3.1.45. If the sum were a rational number
, then for any positive
00 let -1
integer k 1 , we would have E * = ; - E *. Thus the sum
k=kt k= l
co
E q.n1'1\2

..nkl-l would be a positive integer, and we would get
k=kl


(*)


00 1 1
E->
k=kl nk - q. n) · n2 · ... · nkl -1 ·


Set Jim n::l = I > 1 and take E > 0 SO small that a = l - E > 1.
k-oo
Then th
e exists an index ko such that if k > ko, then


nk > a > 1.
nk-I -
Since J

 na."
'
A:-l = +00, there is k 1 > ko such that nJ...
.';:"1-1 >
:3 1 & Thus by (**)


(**)


00 00
E -.!. sE / = Q < 1 .
k=kt nk ;=0 Q nks (Q -l)nkl q. nl · n2..... nkl-1
which contradicts (*).


00
3.1.46. On the contrary, suppose that E r!- ::: E q 1 where p and q
k=l Jr


are positive integers. Then


00 1 1
nln2... n k-l E
 -
;=0 nk+; q


for all k
 2. (See the solutions of the preceding problems.) Set
Ok = 2
. By assumption, lim ale = +00. We claim that there
k-oo
exists an Tl such that aj
 ar 1 for j = 1,2, ".t rl - 1. Indeed, if
01 S 02, then rl = 2. If it is not the case, then we take the least
integer"l > 2 such that al
 ar 1 . In fact, there exist an infinite
sequence of integers rk with the above property, that is, OJ
 ar"
for j = 1, 2, ..., Tk - 1. To find T2 we apply the above procedure to
the sequence {ak}n
rl and so on. Denote by T the least positive
integer such that a,.+i > q + 1 for j = 0, 1, 2,... and aj S a,. for




3.1. S ultJQ1 ation of Series


267


j = l,2,...,r - 1. ObServe also that since n r S n,.+j, a,. S a

j for
j = 0, 1,2. ... . It follows from the above that


2+22+...+2'"- ·
nln2... R r-1 < Or

+J Rr+j


2:1(2'" -2)
< ar+
r+J = tJ;
;"1 < (q + 1)-(;+1).
°r+j


Hence


00 00
,,1 ,, < ) -U+I) 1
nl n 2...n,.-1 L... . <
 q + 1 = -,
i=O
+J j=O q
a contradiction.


oc
3.1.47. Since the series E Ea. q .. converges, lim q P:l = O. It then
n=1 n--oo ..
00
follows from the given inequality that o='=-.
 E
. Suppose that
n=m
the set A is finite. Then there is an index m such that


00 m-I
S=L
=L
+ Pm .
n=1 qn n=1 qn qm - 1


Therefore S is rational. Assume now that


oio
S = L
 =
 e Q.
n=1 qn q


Then


n 00
Tn =
 - L
 = L

 Pn+l ·
q k=1 qk k=n+l qk qn+1 - 1
Multiplying the inequality by 6n = q. ql ..... qn, we get
b b Pn+1
n+ITn+l = "r n 9n+J - q. ql · ... · qn+l
qn+l

 bnrnqn+l - b,.r n (qn+l - 1) = bnr n .


This m eAns that the sequence {bnTn} of positive integers is mono-
tonically decreasing. Thus, beginnip g with some value of the index
n, all its terms are equal, which implies that the set A is finite.




268


Solutions. 3: Series of Real Numbers


3.1.48. Clearly, we can write n! = 2 Q {n) pen), where
(n) is odd.
More precisely, a theorem of Legendre asserts that a(n) = n -1I(n),
where lI(n) denotes the sum of ones in the binary expansion of n.
tx) ft. oc 2"
Moreover, we have E
.f = E 6n fir' where 6ft = 1 if n = nk and
k==1 n= I
00
6,. = 0 otherwise. Suppose, contrary to our claim, that E 6 ft 5- =
n=1

, p, q E N. Write q = 2 8 t, where t is odd. Take N = 2 r >
max{t,2-+ 2 }. It then follows tbat (J(
) e N. Therefore 2.{J(N)
 =
¥-p e N. A simple calculation shows tbat Nt = 2N-I{J(N) (which
also follows directly from the Legendre theorem). lvlultiplying the
equality


N 2 ft 00 2"

="6n-+
 6n-
q L-, n! L", n!
n=1 "=N+I


by 2-(j(N), we get


(.)


N 2 n oc 2"
211j3(N)!!.=2.fJ(N)E6 n ,+2"(3(N) E 6 n - , .
q n. n
n=1 n=N+1


Note tbat


N 2" N IJ(N)2"
2.PC N) E 6 n , = 2" E 8n 2 o (n) PC r
I n. I n
n= n=
Since pen) divides peN), we see that the first term on the right-hand
side of (*) is an integer. To get a contradiction, we will show that
00 2"
0< 2'{J(N) E 6nnr < 1. Indeed,
n=N+J


oc 2" 00 2n
28fJ(N) '" 6 - = 2.-N+1 NI " () -
L", n n! ·
 n n!
n=N+1 n=N+l
OG N! 2 .+2 00 ( 2 ) n-N-I
=
+2 E 6 n 2 n - N - 1 - < E
n=N+l n! N + 1 n=N+l N + 2
2,,+2 N + 2 28+3
= N + 1 N < N + 1 < 1.




- -r. .-8----- n.______


3.2. Series of Nonnegative Terms


269


3.2. Series of Nonnegative Terms


3.2.1.
(a) We have
an = vn 2 + 1- (ln 3 + 1
1
= vn 2 + 1 + -Vn 3 + 1
3n 4 - 2n 3 + 3n 2
x (n 2 + 1)2 + (n2 + 1) (I(n a + 1)2 + (n 3 + 1)
n3 + 1 .


Hence


lirn
 = !.
n-.oo 1. 2
n
By the comparison test the series diverges.
(b) Um tfii; = Urn ( 1- n3+
.+I ) n =
, and the root test gives
R-OO n-.oo
the divergence of the series.
(c) One can verify by induction that
(2n - 3)11 > 1 for n > 2.
(2n - 2)11 2n - 1


So by the comparison test, the given series is divergent.
(d) The series is convergent because lim
 = !.
n-.oo


(e) I-cos
 = 2sin 2 -k < 2
" t and therefore the series is convergent.
(f) Um
4n = 0, which proves tbe convergence of the series.
n-oo
(g) By Problem 2.5.4 (a),


. y'a-l
bm 1 = In a,
n-oo -
n


and therefore the series is divergent.


3.2.2.
(a) The series converges because
 In (1 +
) < ,!,.




270


Solutions. 3: Series of Real Numbers


(b) The convergence of the series follows from the inequality

 In n + 1 < 2 for n > 1.
vn n - 1 v'fi(n - 1)
(c) Using the inequality Inn < n, we get n 3 .!.nn <
. Hence
the given series converges.
(d) We have


1 1
-
- .
(lnn)lnn nlnlnn
Thus the series is convergent.
(e) Applying methods of differential calculus, one can prove that for
sufficiently large :& the inequality (In mz)2 < lnz holds. There-
fore


111
- >-
(in n)lnlnn - e(ln Inn) 2 n
Cor sufficiently large n. This proves the divergence of the series.


3.2.3. Put en = t. By our assumption,
an+a 4n
Cn+l = S - = Cn, n
 no.
b n +l 6ft
Thus the sequence {en} is monotonically decreasing for n
 no. This
implies that the sequence is bounded, i.e. there exists C > 0 such
00 00 00
that 0 < en < 0, n E N. Hence E On = E enb" < 0 E b na which
n=1 n=l n=1
completes the proof of our statement.


3.2.4.
(a) By Problem 2.1.38, we get
( I ) n-'2 ( ) 2 1
l.In.+l _ 1 + n . n _

- < - 1 ·
an e n+l ::2"
n
Now the convergence of the series follows from the convergence
test given in the foregoing problem.
(b) Similarly, by Problem 2.1.38, we obtain
4 n +l (1 +
)n (1 +
)n
= >
an e (1 +
)n+J


1
n+i
=-r.
n




3..2. Series of Nonnegative Terms


2'11


H the given series were convergent then, by Problem 3.2.3, the
00
5eries E * would also be convergent. Thus the given aeries
net
diverges.


3.2.5.


00 00
(a) By Problem 2.5.4 (a), the series E (
 - 1)° and E # ei-
n=) n=l
ther both converge or both diverge. Therefore the given series is
convergent for Q > 1 and is divergent for Q S 1.
(b) It follows from the solution of Problem 2.5
4 (b) that In n <
n( v'ii - 1). Thus for n > 3 and Q > 0,
..!.. < ( In n ) .. < ( vn _ I)Q .
n Q n
This implies that the given series is divergent for 0 < a < 1. Let
Wj u.h>u uu
rve that for u :5 0 t.lu
 n

ary condit.ion Un -. 0
for & series to be convergent is not satisfied. For Q > 1, by
Problem 2.5.5, the given series converges if and only if the series
00 Q
E ( I
 n ) does. The convergence of the latter series follows from
n=1
Problem 3.2.3, because for sufficiently large n we have
t1n+l = ( nln(n + 1) ) Q < 2 Q ( n ) Q.
an (n+ l)lnn - n+ 1
(c) By 2.5.5, the given series converges if and only if the series

 (In (1 + ;t+1 )"
converges. By.the inequality 2':% < m(l + x) < x, which is valid
if Z' > 0, see Problem 2.5.3, we get
(In ( 1 +
 r+ 1 - 1)" < :.. for a > 1


pnd


(In(I+
r+1 -1)" > (2n11)Q for O<a$l.




272


Solutions. 3: Series of Real Numbers


Therefore the given series is convergent for Q > 1 and divergent
for O. < (). S 1. Fnrthermore, let l1S observe th
t for 0
 0 the
necessary condition for a series to be convergent is not satisfied.
Cd) It is easily verifiable that
I-nsin.! 1
lim n __
A-CO '* - 6.
n


Hence the given series is convergent if and only if the series
co
E n
o is convergent. Therefore our series is convergent for
n= l
a > t and divergent for Q

.
3.2.6. By Problem 2.5.5, we get 1im ::
':
 = 1, and so our series
n-oo
00
converges if and only if the series E an does.
n=l


3.2.'1.
00
(a) The convergence of the series E -In (COB *)
n= 1
fact that


follows from the


1im -In (cos
 )
1 = 1.
"....00 2n3"


(b) He:/: 0, then


. 0 Ip n+b S
lim ee l a n+ d = e c :/= o.
n....oo
Thus the given series diverges.
H c - 0 and d
 0, then the necessary condition an -. 0 for
convergence does not hold.. If c = 0 and .
 < 0, then
e cln:+b = e
e
 Inn = e
n
.


Therefore, in this case, our series converges if
 < -1 and di-
verges if

 -1.
(c) We have


n 2n 1
(n+ a)n+b(n + b)n+B - (n + a)b (1 + : )n (n + b)c (1 +
 )n.


co
Thus the series in question converges if and only if E nG\b does.
n=1




3.2. Series of Nonnegative Terms


273


00
3.2.8. The convergence of the series E v'an 4n+1 is an immediate
n =1
consequence of the inequality "O nan+1
 4(Bn + On+l). Moreove r,
if the sequence {an} is monotonically decreasing then van On + I

00
1In+1. Consequently, the convergence of E an follows from the con-
n=1


:)0
vergence of the series E v'4 nBn+t.
n=l
Now t let us consider the sequence {an} defined by setting


{ I if n is odd,
On= 1
4 if n is even.
n


Then


n 2n 1 n 1
E ..ta kak+! < E ..ta kak+! = 4 E /ii'
«=1 Ic=l k
l


OCI co
Therefore the series E va nBn+1 converges, whereas the series E On
r&.=1 n=1
diverges.


3.2.9.
(a) Let us first notice that if the z,equence {On} is bounded above,
say by M > 0, then


an > 4n .
l+an - l+M


00
Therefore the series E 1 ::" is divergent. On the other hand,
n=1
if the sequence {4n} is unbounded above, then there exists a
subsequence {an.} divergent to infinity. Thus


Ii On.. - 1
m -,
k....oo 1 + an.


and therefore the necessary condition for convergence fails to
hold.




274


Solutions. 3: Series of Real Numbers


00
(b) The series E l':;On can converge or diverge. To show this let
n=1
us consider the following example:
{ I if n = m 2 , m = 1,2, ... ,
a,. = 1
'2 otherwise.
n


00
The series E an diverges. We have
n.=l


n n 1 n 1 n 1
L a
 <L l k 2 + L k k2 <2L k2 '
k= 11+ ale k=l + k=l + - t=J 1+


00
Hence, in this case, the series E l:
n converges. H we take
n=l
00 00
an =
, we see that both series E an and E l'::an can di-
n-I n.-l
verge.
(c) The convergence of the series in question follows from the inequal-
ity


an < On = 1:..
1 + n 2 a n - n2an n 2
(d) If the sequence {an} is bounded above, say by M, then
an > an
l+a
 - l+k[2.
Therefore, in this case, the series in question is divergent. But, if
00
for example On = n 2 , then the series E 1:::1 converges.
n=1 "


3.2.10. For any positive integers n and p,


nj:r

 ak
Bn+l + Bn+2 +... + CIn+p > k=n+l
Sn+l Sn+2 Sn+p - Sn+p


_ Sn+p - Sn
- Sn+p


.


Since lim Sn;p Sft = 1, the sequence of partial sums of the series
p-+oo n+p
00
E
 is not a Cauchy sequence. Thus this series diverges.
n=1




3.2. Series of Nonnegative Terms


275.


On the other hand,



< On

 - SnSn-l


Sn - 5n-l
-
8n 8 "-1


1 1
- Sn-l - Sn '


and therefore


n+p Ok n+p ( 1 1 ) 1 1 1
L - < L - - = - - < -.
k=n+l Sf: - k=n+l Sk-l Sk Sn, 8P1+p Sn


00
Hence the series E
 is convergent by the Cauchy criterion.
n-J "


3.2.11. We have


an Sn - 8n-l
(J - {J.
Sn S n_1 SnS
_1
Let p be a positive integer such that ! < {J. Then, for sufficiently
p
large n, the inequality


an Q'R
{3 < .!.
Sn S n_ l S S
1& ::'-1
holds. Therefore it is enough to establish the convergence of the series
with terms
. To this end we will show that the inequality
S."S!_I
Sn -
n-1 '5 p ( : -lr )
Sn S :_l 8:;-1 51:
is satisfied. The last inequality is equivalent to
1- SS:l S P (1- .
r ) ·
This follows imm ediately from the easily verifiable inequality l-:J;P <
pel - x), which is valid if 0 < x < 1. Indeed, it is enough to set
.L
% = ( 5;:' ) P . Therefore (see the solution of the foregoing problem)
the convergence of the series in question is established Cor {3 > O.




216


Solutions. 3: Series of Real Numbers


3.2.12. Let us first assume that Q> 1. Then for n
 2,


a,. < a"
So - S SQ-l.
11 n n-l


Thus the convergence of the given series follows from the last problem.
Now, let Q
 1. Then for sufficiently large n, we have


. This
:;: n
and Problem 3.2.10 imply the divergence of our series for Q < 1..


3.2.13.
(a) By assumption, the sequence
and tends to zero. Moreover,
an


{r n} is monotonically decreasing


T n -1 - Tn


.


Tn-l


Tn-l


Hence for any positive integers n and p,


an+l On+ p Tn - Tn+l T n + ,, -l - rn+ J'
+ ... +
 + ... +
Tn Tn+p-l Tn Tn+p-l
Tn - Tn+p 1 Tn+p
> - -
- .
Tn r n


Given nt we have llm ( 1- r;","p ) = 1. Therefore the divergence
p--oo ,.
of our series follows from the Cauchy criterion.
(b) We have


"j Tn-l


(v Tn - l - vr;)(V Tn - 1 + vr;)
"';T n-l


an


r n -l - Tn


"jTn-l
< 2( v T n-l - v:;:;).
Applying this inequality one can show that the sequence of partial
00
sums of the series E ..t
ft is a Cauchy sequence. Thus the
1 n-1
n-
series converges.


3.2.14. We first assume that Q > 1. Then, for sufficiently large n,
1 1
> .
n -
T n-l rn-l


The divergence of the series in question is now derived from part (a)
of the foregoing problem.




3.2. Series of Nonnegative Terms


277


Let a < 1. Then there exists a positive integer p such that Q <
1 -
. Hence


an an rn-l - Tn *
Q < 1 1 - T n-}-
Tn-l (Tn-I) -p rn-l
Applying the inequality l-x P
 p(l-x), which is valid if 0 < x
 1,
1
with :c -:' ( rn ) j we g et
rn-J '
:n "5 p ( r:_l - T: ) ·
rn-l
The convergence of the given series follows from the Cauchy criterion.


3.2.15. For 0 < Q < 1,


1 - an+lln2 Tn - 0
1m an+1 -.
n.-.oo
rO
n


00
Therefore the convergence of the series E 4n+lln2 TII follows from
n= 1
the foregoing problem.
3.2.16. We know (see, e.g., Problem 2.1.38) that
( l ) n ( l ) ft+l
(*) l+fi <e< l+ n ·
Assume that 9 > 1 and let E > 0 be so small that 9 - E > 1. Then
there exists no such that n In a:
1 > 9 - € for n > no. Thus by (*),
nln an > (g - e) > nln ( 1 + ! ) ,
4n+l n
and consequently,


1
l1n+l ( n+l)9- C
< J .
an nfJ-



00
Therefore the series E an is convergent by the test proved in Prob-
n=l
lern 3.2.3
 Similar arguments apply to the case 9 = +00. Analogous
reasoning can be used to prove the divergence of the series if g < 1.
The following examples show that the test is inconclusive if 9 = 1.
00
Taking an =
,we see that 9 = 1 and E
 diverges.
n=l




278


Solutions. 3: Series of Real Numbers


On the other band, It'ttil1g ClJA = 11 12 . \ve get the cOl1ver a ent.
" , " 0
:x
series E an (see Problcln 3.2.29). To shO\\' that in this case 9 = 1,
u=1
let us first obse rve that
n 111 '1 h;7 11 = In ( 1 + ! ) II + 211 In In(;, + I) .
(
,+ I) 'u 2 {,,+ I) n 11 1.
As tit£' first. t.crm of the Sl1m tends to 1. it iN enough to 8110W ..bat
Ihl1 271 In In ::
.) = O. To this end!! note that
" -3;;


I . ( Inen. + 1) ) " I . (I Ira '1
.1 ) " 0 1
1111 = 1m + = e = .
..-x In n I,-X In n


3.2.17.
(8) \Ve have
litlt n In alt = Urn ,.( ,.In + I - vn) In 2 = +00.
n-x. ""+1 JI-Xo
The convergence of the
rit
 follows fron1 the preceding probleru.
(b) Similarly,
lint ,., In a" = linl In ( 1 + .!. ) " · In 2 = 1112 < 1.
II-X' a,,+1 r.-x "-


Helice the series diverg
.
( (
) I.,ike\\ise,


lin1 11111 '1." = In 3 > 1.
"._
 a..t I .
whicb proves the (
onvcrgence or thl
 series.


(d)


. . J a" I
un " 11 = nu.
n-cx (1"+1
Th
r('rorc the scri('S is convcrg(,l1t. for It > t: ulld divergent for
a < c. For a = e. the series in question is th(' hnnnonic divergent
series.
(c) \Vc bave (S<..'e the solution or 3.2.16)
1 . I alA I . I 111(" + 1)
1m r. II = In1 II II I · In a = O.
la -x: a,,+ I n-'X II '"




3.2. Series of Nonnegative Terms


2"7{f


Therefore, by the convergence test given in the foregoing problem,
the series let divergent for any a > 0_


3.2.18. Since


Ii In a'i . - 1 - I In 1
m n = 1m 7L n a 11+1 = -,
n-co "n+l n-
 a


the series is convergent for 0 < a <
 and divergent for a >

(compare with 3.2.16). H a =: then (see, e.g_, Problem 2.1.41)


I
1 - eJ+!+.......* ....
lID I =e,
n--:>o -
n


where 'Y is the Euler constant. The comparison test and the diver-
:)C
gence of the harmonic series L
 imply the divergence of the series
n=_
in question for a =
.


3.2.19. Applying the inequality 1
% :S In{t + x)
 x, which is valid
if x > -1, we get


n ( ...!!u- 1 )
On+J - < n in ( 1 + an _ 1 ) < n ( an - 1 ) .
1 + ( ...!!n- - 1 ) an+ 1 Cln+ 1
On+l


By this inequality, the Raabe test and the test given in Problem 3.2.16
are equivalent for a finite r _ It also follows from the above inequality
that if lim nln
 = +00, then lim n (
 - 1 ) = +00. We
n-oo n+& n-oc n+J
will now show tbat the other implication is also true. Indeed, if
lim n ( 0 an - 1 ) = +00, then for any A > 0 there is 7!{) such that
no .
 "-10'
On _ 1 >.d for n > TI{). Hence
0fJ+J n


n In an = In ( 1 + an _ 1 ) n > In ( 1 +
 ) n t A.
Bn+l a n +l n n-



Since A can be arbitrarily large, we see that lim n in
 = +00.
n-OO n+ I
Similar arguments apply to the case r = -00.




2S0.



Solutions. 3: Series of Real Numbers


3.2.20. Since the sequence {tIn} is monotonically increasing,
O ( -t 1 ) 1 a n -l 1
< n 1 - = n a < n.
Gn+l n


By the Raabe test, the series diverges.
3.2.21. By the definition of the sequence,


n-I
- E a:
an = ale 'ua! for n = 1,2,....


00 (X)
We will Gmt, ::;how that E u
 is -iliv
rgeIJL. Indeed, if E a: =
n=1 n=1
S < +00, then lim an = B) e- S > Ot and so Jim a
 > 0; this
n-oo n-oo
would contradict the necessary condition for the convergence of-the
00
series. Therefore the series E a
 diverges and, by the foregoing,
n:::l


lim an = O.
R-OO


Now assume that (J > Q. We will prove that in tills case the series
in question is convergent. To this end, we will show tbat


(*)


a;-O > a(n - 1) for n > 1.


This inequality is obvious for n = 1. Assume that it holds for an
arbitrarily fixed. R. Then, by the definition of the sequence, we obtain


-Q -Q aa G -a ( 0 -Q
0nT I = an en> an 1 + oa'l) :::= an + Ot > 0tt1.


Thus (*) holds for any positive integer n. This inequality is equivalent
(for n 1= 1) to
a
 < (o(n -l»-!.
Hence, by the comparison test, the given series converges for {3 > Q.
Let (J
 Q. It has already been shown that lim On = O. Therefore,
A-CO
for sufficiently large nt 0 < an < 1. Thus a
 < a
. This inequality
00
and the convergence of the series E a
 imply the convergence of
n=1
00 13
E an.
n=!




3.2. Series of Nonnegative Terms


281


3.2.22. Note that
Ii ( an 1) I " n
m n - = 1m Q = Q.
n-.oo a n + 1 n-oo n + 1
By the Raabe test, the series in question is convergent for a > 1 and
divergent for 0 < a < 1.
For a = 1 the given series reduces to the divergent harmonic series
00
E n
l .
n=l


3.2.23. By


li ( an 1) I - nbn+l b
m n - = 1m =-
n-.oo On+l n-oo (n+ l)a a
and the Raabe test, the series is convergent for b > a and divergent
for b < a. In the case where b = at the cODvergence of the series
depends on the sequence {b n }. Indeed, if {b n } is a constant sequence,
00
then the given series is the harmonic series E n
l .
n=l
We will now show that if b n = a + in(

l) ' then the series is
convergent. In fact,


n!
an = ( 2 ) ( 2 ( 2 ) .
2 + 1ii2 3 + Iii3) · .... n-+ 1 + In(n+1)


Thus


4n(n - 1) 1n(n -1) - Cn+lnlnn
=an ( n-l)ln(n-l)- (n+1)nl
n ) .
n + 2 + In(n+2)
Calculation shows that
lim ( n -1) In(n -1) _ (n + 1)n
n ) = 1.
n-co n + 2 + 10(n+2)
Therefore, for sufficiently large n,
an(n -1)ln(1
 -1) - an+l1
lun > (1- c:)u n
 o.
Hence the positive sequence an(n - 1) In(n - 1) is monotonically
decreasing and so is convergent. This, in turn, implies the convergence




282


Solutions. 3: Series of Real Numbers


oCtile series with the terms an(n-l) In(n-l)-an+tn In n. B
. thp last.


incqualit
. and by tbe cornparison tcst t the series E,l" cOllverges.
n;1


3.2.24. By BSSW11))tion!
a,. « n - 1) In n- - 1) - 11,1+ 17I1n 1. = (1'" - 1 )on .
No\v if 7n
 r > 1, then
(*) 11..«n - 1) In ". - 1) - tl fI +1" In n
 (r - J )a n .
Combining (.) with the inequalit). (11 - 1) In( n - 1) > (n - 1) In n - 1,
we get


(*.) ora(n-l)ln(n-l) -a n +lnln1l
 (r- 1)0" > o.
This means tbat tbe sequence {"n.< n - 1) 111(71 - I)} is rnonotonica1ly
decre&.ing and so convergent. Therefore tbe seri
 \\itb the terms
a,,(n - 1) In(n - 1) - o"+I71lnn is convergent. B). C..), the series
:)0
E an is also convergent.
n=1
IC '1" :5 r < 1, theu un(n - 1) 111 71 -1) - 0,,+ In In 7t :5 (r -l)a,a.
Hence
a,,(n - 1) In(n -1) - a"+l nlnn < (r + In (1-
 )"_1) an.
Since


( ( 1 ) "-1 )
lim r + In 1 - - = r - 1 < 0.
n-oo 71
the sequence {a..+1 n In n} is monotonicll11y increasing (except for
finitely Dlany n). Therefore there is AI > 0 such that an + I n In n >
AI. Thus (1,.+ I > n 1

 n ' which proves the divergen(:e of the series
:xi
EOn.
n=1


3.2.25. We havt'


( ) ..,.. + ,1'1
I . 0" 1 . IS n A - 1
1m n - 1 = nn iJ = n.
n-
 On+1 n-.')C 1 - !!. - -:i
,. n
Therefore the Raabe te;t implies the cOllvergence of tile series for
Q > 1 and its divergence for Q < 1. In case () = 1, the divergence




3.2. Series of Nonnegative Terms


283


of the series follows from the test given in the foregoing problem,
because.


a n +l = 1 _ ! _ fJ. n = 1: _ .! _ in
an n n" n nlnn'
where 'Yn = iJ;;>.I!!l ft
 r < 1 for some f.


3.2.26. We will apply the criterion of Gauss from the preceding prob-
lem. We have


lln+l = n 2 '+(lk+ P )n+QP' =1_ 1 +'Y- Q -P _
.
an n 2 + (1 + ')')n + "'f n n 2 .
Therefore the scri
 in question converges if
 .. g: <,. and diverges
if Q + /3,
 j'.


3.2.27. As in the foregoing proof, we will use the Gauss criterion.
We bave


a n +l = 1 _1_ {)n
an n n 2 ·
Hence the series converges if p > 2- and diverges if p < 2.


_ 00
3.2.28. Let Snl $n denote the nth partial s nms of the series E an
n=1


00
and E 211a2-" t respectively. Then for n
 2 k t
n=1 .


k -
Sn
 Bl +(az+a3)+...+(
k+...+a21r+I-t)
 at + 2a 2-+...+2 el2 Jr = Sk.
For n > -2 k ,
Sn > 41 + l12' + (a3 + 04) + ... + (ll2 1t - 1 +1 + ... + a2")
. 1:-1 _ 1-
> 02 + 2a4 + ... + 2 Q2 Jc - ?Sk.
..,


-
Thus the sequences {Sn} and {Sn} are either both bounded or both
unbounded.


3.2.29.
(a) We will apply Cauchy's condensation test (3.2.28). Since the
condensed series is
00 2 n 00 1

 2'>(ln2 n )CI =
 (nln2)CI '




284


Solutions. 3: Series or Real Numbers


the given series converges for Q > 1 Bud divcrg('S Cor 0 < Q < 1.
"X.
If Q < Ot the divergence of E ii{tn l " )0 follows immediately from
n::2
the comparison t.est.
(b) By the equality


oc 2"
 1

2nln2nlnln2n =
nln2In(nI1l2)
and by (8), the given series is convergent.


3.2.30. Reasoning similar to that in the proof of the Cauchy con-
densation test (3.2.28) can be applied. For n
 9k,
Sr.
 59. < (al +...0 9 ,_1 ) + (a!11 +...+a g2 -1 )+...+(a QIt +...+0 9 ".1 -1)
::; (al + ...a yl -l) + (92 - 91 )a 91 +... + (gk+1 - 9,;)Oq".
For n > 9k,
cS n
 cS g "
 c(a ga +l + ... + 092) +... + c(ag._a+ 1 +... + ag,,)



 C(92 - 91 )a!h +... +C(Yk - 9k-1 )09., > (0:1- g'J, )0 92 +... +(91:+ 1 - 9k )a 9 ".
These inequalities prove our assertion.


3.2.31.
(a) It is enough to appl). the Schlomilch theorem (3.2.30) witb 9n =
3".
(b) Applying the Scbloluilch lheorem with g" = n 2 , we get the
0Ci :x)
equiconvergencc or the series E a,. aud E (2n + 1 )a,.2. Since
n=1 n:cl


1 . (2n + 1 )a,,2 2
1m = ,
"-DC' nan 2



 :!Co
the series E (211 + 1)0,.2 and E 'U1'J
 are also equiconvergent.
net "=1
(C) Compare witb (b).
00 oc
(d) By (b), the series E 2
 and E in are equicoDvergent. The
,.=1 ,.=1
latter is convergent, e.g. b}' the root test. To dctemune the




3.2. Series of Nonnegative Terms


285


ex: oc
divergence or convergence of tbe series E
, E:pk "and
".::1 ..=.
oc
E aJ!' I) ' the Cauchy condensation theorem or the test given in
n=1
(a) can be applied. We \vill now study the behavior of the series
with terms atn
.." . If 0 > 1, then the convergence of this series is
00
equivalent to the convergence of E a

'.. . It is easy to check that
n.=1
the last series diverges, e.g. by the root test. This establishes
00
the divergence of the seriE's E oJn
n II for a > 1. Observe that
n=2
if 0 < a
 1, then the neccs.4ilary condition for convergence is not
satisfied.


3.2.32. By Problem 2.4.13 (8), there exists an E > 0 such tbat
(a.,.)rn'n <e- I -!:, n>k.
Hence '
n In an < -1 - E, and so an < nil.., . The comparison test
00
yields the convergence or L an.
n=1


3.2.33. Analysis similar to that in the solution of the preceding prob-
lem gives
o < 1 for '" > k and for an E > O.
fa - 71(ln fl.) I +e




Therefore, by Problem 3.2.29(a), the series E an is convergent.
n=1


3.2.34.


5%"0"" _I - S2 n u -I = (a2"11 + 02"0 + 1 + ... + 42"0 +1-1)
+ (C2"0+& +... + Q2 n u+ 2 _1) +... + (02"0+.-' +... +
nO+._I)

 2'10 02 "0 + 2nn+IC2Ao+J +... + 2no+k-I
"o+lr_a

 g(an o + O-nn+1 +... + lIno+k-I).
Hence, for sufficiently large k,


2"0+" -I
(I-g) E an Sg
n=2"0


2"0 -I 2"0+1t-1
E Cn- E an
n"=no n=no+A:


2"0 -1
$. 9 Lan.
n=no




286


Solutions. 3: Series of Real Numbers


00
Thus the sequence of partial sums of E an is bounded, and so the
n=l


series converges.


oc;
3.2.35. Assume that the series E an converges. Then
n=l .
2" 2"+1
lim
 ak - lim
 Ck - O.
n-oo L....ti n-oo L-i
k=n+l k=n+l
Hence, by the monotonicity of {an},


2n 2n 1
E ak 2: E
n = M2n = 2 (2na 2 n )
k=n+1 k;;:n+l


and


2n+l 2n+l n + 1
L: ak > L: a:ln+1 = 2n + 1 (2n + 1)4211+1'
$: -:.n +l k- n+l
It follows from the above that lim nafl = O.
R-OC


Let an = n In(
+ 1) . Then the series with the terms an diverges
and


fun fun 1: 0
na.n= -= ·
n-
 n-oo In(n + 1)


3.2.36. Let


1
for n = k 2 , k = 1,2, ... ,
n
an = 1
- otherwise.
n 2
00
The series E an is convergent but the limit lim na,. does not exist.
n=J R-oc)


3.2.37. The r.onc1itinn we A.r
 Innking for i
 the t:onvergence of the
00 00
series E
. Indeed, if E
 converges, then we take b n =
n=1 n=l

.
Now assume that there is a sequence {b n } such that both series
00 00
E b n and E
 converge. Then
1&=1 n=l n
va;; = Jbn
 <
 (b n + :: ).




3.2. Series of Nonnegative Terms


287


.)C.
81ld so the series E van converg
.
IU:: I


3.2.38. Asswne that there is a sequence {all} such tbat both series
.:)C

E a" and E nJn; converge. Let
..=1 11= I


A = { lilt eN: 1.
 .)1 } and A' = N \ A.
n
 n;a n .
Then E t < +00 and so E t = +00 (of course A can be an
n.EA ,,_EA'
empty set).
Now observe that a". > t Cor nIl e A'. Therefore the series
:x:-
I: a,. diverges, contrary t.o our ass\1Jnptiol1.
,,=1


3.2.39. \Ve have
t!. 1 +4,,+1 = f...!.- + t an+! .
I "(In I 71",. I "na,.
,,= n= n=


.x
\Ve willsho\v that the convergence of the series E ':;,... impli
 the
.. On
n=.
X
divergence of E ,,
.. . 8
. the Cauch)" crit.erion, there is keN such
ra=1
k+n k+n
that for any positivC' integer " t E U
': I < !. Thu't I.:k E
;
.I <
.=k+1 · i=k+l ·
!. Thereforo. for " > k t


k+"

 "i+t 1 k+1I. 1
L..J < 4 . n < _ 2 .
I. I nOi
'=ft"+


By the rclation bct\vcen arithnletic and geometric Uleans,


"k+n+ I 1
ak+1 < 2.


Ok+1
and so Uk+n+l < 2 ·
"


TllUS


1
"
(k + 1I. + l)aA'+IJ+1 > (k + n + I )Ok+1 ·
x.
Therefore the series E 1I
.. diverges.
"=1




2.88


Solutions. 3: Series of Real Numbers


3.2.40.
n eN).
terms


00
Of course the series E en can diverge (e.g. if an ::; b n for
n=1
Surprisingly, it can converge. Indeed, take the series with


1111111 1
1, 22' 22' 22' 22' 22' 72' 82' 9 2 ' ...


and


11111111 1
1, 22' 32' 42' 52' 62' 72' 82' 82' ..., 82'....
.....


8 2 +1 times
Each of these series contains infinitely many blocks of terms whose
sums are greater than 1. Therefore each of them diverges. In this
00
case en =
, and SO E en converges.
n:;l


3.2.41. We will use the Cauchy condensation theorem (3.2.28). The
00
divergence or E ": is equivalent to the divergence of the :series with
n=1
the terms



.. = min {tl2 n , n
2 }.


00
In turn, the series E
n diverges if and only if the condensed series
n=1


with terms


2 n b:t2 n = min { 2n
.. t
 2 }
diverges. We will now show that the latter series diverges. Indeed, if
00 00
aseries E tin is divergent, then E min{dn,c}, where c> 0, is also
n=l n=1
divergent. H min{dn,c} = c for infinitely maIJ Y n, then the series
00
E min{dn,c} diverges. H min{d,.,c} = c for finitely many n, then
0=1
00
the divergence of the series follows from the divergence of E dn.
n=l


3.2.42. We have


1 _ l1n = On+l - On < Bn+ 1 - an .
4n+1 lIn+l - a1




3.2. Series of Nonnegative Terms


289




This and the convergence of the telescoping scri
 E (4n+l - On)
,.=1
imply the convergence of the series in question.


3.2.43. We have


1- a r . = 0,.+1 - an .
a,. + 1 a n + I
Setting b,. = 4,,+1 - an and Sn = b l +.... + bu. we obtain s ".; =
n 01
On:. -Oq . Thus the divergence of our series follows from 3.2.10.
"+1


3.2.44. If the sequence {an} is unbounded, then the convergence of
the series in question follows from Problem 3.2.11. To see this one can
apply arguments similar to that given in the
lution of the preceding
problem. Now assuule that the sequence {on} is bounded. Then
an+1 - an < 1 ( )
n - Q on+ I - an ·
On+1Qn 424.


Hence the convergence of our series follows from the cOllvergence or
OC'
the telescoping series E (1',1+1 - an).
n=1


3.2.45. It is enough to take en = -J;, where 8n is the nth partial


sum of E Gr., and apply 3.2.10.
n=1


3.2.46. One can set en = "," t where rra = 0'1+1 + 0n+2 + ."1 and
..-I
w;e 3.2.13 (b).


3.2.47. The sequence {Tn} b monotonically decreasing. Hence by
3.2.35, lim nr n = o. Therefore
n-oo


Um nOn = Urn n(rn-I - Tn) = Urn ((n-l)rn_1 - nrf) +rn-I) = O.
n-
 n-
 n-



3.2.48.
(a) Since Urn On = +00, a,. > 2 for n large enough. The con-
n-oo
vergence of the series in question follows from the inequality
c!n <
 t which holds for sufficiently large n.
"




290


Solutions. S: Series of Real Numbers


(b) As in (a), n can be chosen so large that I I
 n < :s l
 n . Thus b)9
. "
3.2.17 ( c) t our series converges.
(c) The series can be either divergent or convergent. Its behavior
depends 011 the sequence {an}. If a,. = In n, n
 2, t.hen the
:X.
series E a illt ." diverges (see 3.2.2 (e)). On the otbpr hand! if
fie 1 ..
a" = n, then for n > e
,
1 1 1
I 1 - I I 1 < -. where 0 > 1.
a unra eh""'U'" 'n U
"


In this case the series in qu
tion is convergent.


3.2.49. The series diverges because tbe necessary condition an -9 0
for convcrgence is not satisfied (see 2.5.25).
3.2.50. \Ve assUltle first that p = o. Then b}. 2.5.22. Urn JUan =
n-:x.
v'3 and so our series diverges. No\\. suppo
 that p > O. Then
lint Un = O. lIenee lirn a.. + I = Ihn ..ill 011 · J.. = o. The serieJJ
n-x n-:x. 0" n-x 0,. nr
converge:; by tbe ratio test.
3.2.51. Observe that. a" e (n.7r. n7r + ; ). Hel1c(
 ;!T <
t and so
"
x;
the series E u\- con\rerges.
,,=1 "


3.2.52. Set b , . = .;0:;;; then b,. E (rur. '/l.7r +
). Hence the series
Ole .X
E c!- = E .,fr converges (see the solution of t.he foregoing problem).
n=1" ,,= I "


3.2.53. Tbe series diverges because tin1 nail = 2 (s
 2.5.29).
n-



3.2.54. For simplicity we introduce the following notation:
L" = a. + 0:) + ... + 0211-1 and AI" = a
 + a.a + .... + 02n.
By tbe mOl1otonicit)e of {a,.},
(*) L" > A/tt and Ln - fll
 AlII.


n
Hence 2A/ n = AI,. + AJ n
 }'l,. + L,. - a. = E aka Thus
k -4)
-..


(..)


lin1 AI" = +00.
n-x




3.2. Series of Nonnegative Terms


291


Combining (*) and (**), we anive at
Ln _ 1 = Ln - M n < at ---+ o.
M n /vl n - M n n-oo


3.2.55. By the definition of kn.. we have 0
 Sk n - n < t;. It is
known that llm (S"" -lnk n ) = 77 where 7 is the Euler constant (see
n-.co
2.1.41). Therefore
lim (n-lnkn) = Um (n+l-Ink n + 1 ) =7-
n-too n-.oo


Hence


lim ( l-In kn+J ) = 0,
n-oo kn


and so


lim kn+l = e.
n-ex;) k,.


3.2.56.
(a) [A. J. Kempner, Amer. Math. Monthly 23(1914),48-50] A k-digit
number from A can be written in the form
IOIc-l al +10k-202+...+0Aa where 0 < Bi
.9
 i = l,2,...,k.
For a given k, there are gk k-digit numbers in At and each of
them exceeds IOk-l. Therefore
1 00 gk
E ;; < E lOk-l = gO.
nEA k=1


(b) As in (a) we have


1 00 gk
E n Q < E 10 0 (1;-1) ·
nEA k=l


Therefore if Q > lOglO 9
 then the series E r!o converges. More-
nEA


ovp.r, Rin
.e


1 co gk 00 911:
E no > E (1()k -1)0 > E l()ka '
nEA Ie=1 k= 1"




292


Solutions. 3: Series of Real Numbers


the series E ;!n diverges if Q
 logll) 9.
neA
Remark. Let Ak denote the subset of positive integers t.hat do not
contain the digit k in their decimal expansion. In much the same way
one can show tha
 the series E r!u converges if Q > lOglO 9.
fJEAk


3.2.57. Assume that. -00 < 9 < 1 and take E > 0 so small that
9 + E < 1. Then, for sufficientl)' large n, In t < (g + E) In n and
an >
. Therefore the series diverges. If 9 = -00, then (for n large
enough), In t < -1.10 n. Thus an > n and the series diverges. The
00
same proof works for 9 > 1. Let us consider two series: E
 and
n=1


f2 ..b:
" . The first one diverges and the second converges, although
for both 9 is equal to 1.
3.2.58. The equivalence of these tests has been sbown in the solution
of Problem 3..2.19. By 2.5.34, if the Raabe criterion is decisive, then
so is the criterion from tIle foregoing problem. To show that the
converse is not true, we consider the series with terms a r . defined by
setting a2n-1 =
, a2n = 4

 .


3.2.59. Let b" = J 2 + V 2 + ... + .J2. Then b" = 2 cas 2 Q "+ I (com-



......


n-root.s
pare with 2.5.41). By the definition of {an}, we have a; = 2 - b n - h
d 2 - 11' L T} h -. ·
an so On = sin 2..... 1 < 2". iUS t c series ID questIon converges.


3.2.60. Assume K is a positive number such that
(al - an) + (02 - an) + ... + (On-I - an)
 K for n eN.
Hence Cor ever). n e N we have 01 + ... + an - no,. < K. Let meN
be arbitrarily chosen. By tbe monotonicity of the sequence {an} and
by its cODvergence to zero, there exists n.() e N such that
1
(*) an S 2 0m for 11
 no.
We have


Ql + ... + am - man + Dnl+l + ... + 0" - (n - m)a ll
 K.




3.2. Series of Nonnegative Terms


293


Again. by the mono tonicity of {an},
4m+1 +... + tin
 (n - m)a,. and a1 +... + am 2: mam.
Therefore m(am-an) =mam-man S al+a2+...+0m-man
 K.
This and (*) imply imam S m(am - an) S K. Finally,
8m = al + a2 + ... + am = 8m - mam + mam
 K + mam
 3K.


3.2.61. From the relations
an = CLn+l + l1n+2 + 4n+3:+...,


On+l = tln+2'+ Bn+3 +...


we gather that "n+l =
 Un. Nuw, by inductiun, Un = 2 1n , 1& e N.


3.2.62. (20] Let Tn.k = an + lln+l + ... + 4n+k, n = 1',2',.., k =
0,1,.2; ..., and let lim Tn,k = Tn, n = 1,2,... Assume that 8 E (0, S)
k-oc
and that Bra! is the first term of the sequence {an} for which Bn 1 < 8.
Either there exists a k 1 such that rnl.kt < 8 ::; Tnl.kl+l", or rnt S 8.
In the second case we have 8
 an 1 -l
 Tn)
 8, and SO Tn. = B.
In the first case we determine the first term 4n 2 with n2. > nt. + kl
,
T n1 .kl +
 < s. Either there exists a
 with


Tntel:l + Tn2,k2 < 8 S Tnl,kt + rn2,k2+1,


or r n1 .k 1 + T n2 = 8. This procedure can be repeated, and if the first
case occurs at every step, then s = T n1 .k 1 + rn2.k2 +....


8.2.63. (2n] SnppO.
J
nnt.rary to our
laim7 that there is kEN suc.h
00 00
that ak = 2p+ E an, where p> O. Then ak-p = p+ E an =
n=k+l n=k+l
00
E Enant where En equals either zero or one. By the monotonicity
n=l
00 00
of {an}, En = 0 for n S k. Hence Gk -p = E Enan:s E an =
n=1 n==k+l


BI: - 2p, a contradiction.


3.2.64. By the Stolz theorem (see 2.3.11), we obtain
8 -1 + S -l + + 8 -1 5 -1
lim al 1
 2 .u an n = lim an n 1 = 1.
n-+co lnSn n-oo -In (1 - anS; )
The last equality follows, e.g., from 2.5.5





294


Solutions. 3: Series of Real Numbers


3.2.65. Set an = 1
, n E N.


QO
3.2.66. Since (l1+02:...+ 0 n >
J the series E
 isdiver-
n=l
gent for any positive sequence {an}. The divergence is independent
00
of the behavior of the series E CIn.
n=l


3.2.67. By assumption,


a2
 aI,


2" 2 ft - I
E ale

-1 E ale.
k=2n-l+l k I


Jlence, by induction,

alc
 2 (1+
) (1+
)... (1+
-1 ) a1.


Moreover t


( 1 ) ( 1 ) ( 1 ) ntlln(l+:!.) nf,1 ;i-
t + 2 1 + 22 ... 1 + 2R- 1 = e Jrm1 2
 e"al 2 < e.


3.2.68. Put. en = l:t
ln = n ( n:l ) n t n e N. Then
(*) CI ..... en = (n+ l)n and en < nee
Using the geometric-arithmetic mean inequality, we arrive at
1 alCI +... + linen
V'
 l · ... · an = 1 V'a lCl · ... · 4nCn < ( 1) ·
n+ n n+".:
Therefore
N N

 <
 alCI -I- ... + O-nen
Z-..J V'a l · ... · an - L.J ( 1)

1
1 nn+
( 1 1 1 )
= GIC] 1 .2 + 2. 3 +... + N(N + 1)
( 1 t 1 ) 1
+tI2C2 2.3 + 3.".4 +...+ N(N +1) +...+CNCN N(N +1)
1 1 1
< aici + G2C2 2 + a 3C 3 3 +... + aNCNY;
 2aJ' + eCt2 +... + faN-




3.2. Series of Nonnegative Terms


295


The last inequality follows from (.) . Letting N .... 00, we obtain the
desired inequality.


3.2.69. Writing


(n + 1)" · ... · (n + Ie - l)n(n + k)"
en = nn-I ..... (n + k - 2)n-l(n + k -1)"-1
( n+k ) n
= n n(n + 1) · ... · (n + k - I),


we get CI ..... en = (n + 1)" ..... (n + k)n. Hence, 88 in the solution
of the preceding problem, we obtain


N N


 alCI + ... + OnCn
L-, 1
G I · ... · On
 L.., 1 n(n + 1) · ... · (n + k)
n= n=
=41Cl ( 1.2....\I+k) +...+ N(N+I),
,,'(N+k» )
+C12C:l ( 2.3... \2 + k) +... + N(N + I) .
... (N +k» )
1
+ ... + o'NCN N(N + 1) · ... · (N + k)
1 ( 1 1
< i ki OICI + 2.3.....(1+k)o2C2
+... + N(N + I). ..
. (N +k_I) 4 N CN).


The last inequality follows from Problem 3.1.4 (a). Since


1 ( '+k ) '
CI = ,
l(1 + 1) · ... · (l + k - 1) l


letting N -t 00, we obtain the desired inequality.




296


Solutions. S: Series of Real Numbers


3.2.70. Let Tn = 41 +02 +... +an and"let Sn denote the nth partial
sum of the series in question. Then


S 1
 n 2 (Tn - Tn-I) < 1
 n 2 (Tn - Tn-I)
N=-+L-, -+L..-,
41 n=2
 - 41 "=2 Tn T n-1
1 .v n 2 N n2 1 N-I (n + 1)2 N n 2
=-+E -E-=-+E -E-
111 n=2 Tn-I n=2 Tn al "=1 Tn n=2 Tn
5 N-t 2n N-l 1 5 N 2n N 1
< - + " - + " - < - +
 - +
 -.
- 0 1 L-,
 L-., T. - a l L-J 7: L-., 7:
n=2 n n=2 n ra=1 n n=1 n



Ioreovert by the Cauchy inequality (see 1.2.12),


( N ) 2 N 2 N
,,
 <" na1J

<S .kf
L-,7: -L.J
 L..J a - N
n= J n n=l n n= 1 n


00
with AI = E t. Hence
n=1


N
E¥:svs;.m.
n= . II


Consequently, S,\J S t + 2.;sNv'M + M, and so


SN S ( JM +


2
2Al + .!.
BI


.


3.2.71. The arithmetic-harmonic nlean inequality (see, e.g., 1.2.3)
yields


2'
E nan-(n
I)O"-1
"=2"-1 + I
21:-1


>


2"-1


2.
E (non - (n -l)On-I)
n=2"-I+1
2"-1 1
- >
- 2ka21r - 2k-162.-1 - 20:lt ·




3.2. Series of Nonnegative Terms


297


Hence


2
 1 2 k
E > ·
L I na,. - (n -l)On-1 - 4a2'
n=2
- +1


Therefore


Ie 2'
S2.
E 4 ·
,= I °2'
The divergence of the series follows from the Caucby condensation
theorem (see 3.2.28).


00
3.2.72. We will show that the series E f- is divergent. If it were
n=t "
oc
not, then there would be an n such that E ;t; < 4. Let G =
m=-n+l
PI · P2 · ... · l'n. Then the number 1 + ka with keN can be written as
a product of primes. This unique factorization does not contain any
of the numbers Pit .",Pn. Hence


00 1 ;)() ( 00 1 ) ' 00 ( 1 ) '
E 1 ka < L L - < L 2 = I,
k=1 + 1=1 n'
n+l 'Pm '=1


a contradiction.


3.2.73. It is enough to apply tbe results from the foregoing problem
and from Problem 3.2.71.


3.2.74. \Ve get


00

 1 I ( 2"+1 2n+1 )


 2ft+T 1 + 3,.+1 + .1"+1 +... 1
1 - A" =2 1 -
1m oc = 1m I ( 2" 2" ) = -.
n....oo
..L "-00 2" 1 + 3h + i" + ... 2
L..J k"
k=2


because the sums in parentheses tend to 1 as n tends to infinity.
Indeed,


2n+1 2"+1 OQ 1
3 n + 1 + 4 n +! + ... = 2 ft +! L kn+1 ·
k=3




298


Solutions. 3: Series of Real Numbers


Moreover,


00 1 1 00 1 :)C 1
L k n +1 = 3 n + 1 + L (2k)n+1 + L (2k + l)n+l
k=3 k=2 k= 2
1 eo 1 1 1 1 00 1

 3 n + 1 + 2 L (2k)ra+l = 3 n +1 + 22n+1 + 2" L k"+I ·
k=2
 3
Therefore


CIC ( 2 ) "+1 1
2n+l
 1 < 3 + F
L.J kn+l - ( 1 _ ....L ) ,
k=3 2"


and so


0Ci
2n+J
 1
 0

 kn+1 R-OO ·
#:=3




3.2.75. Assume first that the series E an converges. Then the
n=1
convergence of the series in question foUows from the inequality


"
oc
t!r. If the series E an diverges, then there exists a strictly increasing
"=1
sequence {nm} of positive integers such that Sn..-l
 m < 8 n ",.
Then


m(m + 1)
Tnm = 51 + ... + S"fft
 8'&1 +... + S'.m > 2 ·


Hence


00 I;x) mm+l- J oc;

 an = ""' ""' ak <
 8","+1-1 - 8","-1
L-, T.a L.,

 - L., T!!
n=n2 n 1R=2 k="m k m=2 nm

 1 00 1
<"-<"

 T.0 L-, ( "1:1+". ) 0.
m=2 n", m=2 2


Therefore the series in question is convergent if Q > i. This series can
be divergent if Q :51. Indeed, it is enough to take an = 1. n eN.
3.2.78. By Problem 3.2.35, lim f- = O. Take 0 < K < 1. Then
'1-00 "
there is no such that n
 Ka.,. for n
 110. Hence
Ink an
 Ink ( .!. ) ink n .
an K an




3.2. Series of Nonnegative Terms


299


co
Thus the convergence of the series E In=:"" implies the convergence
n=1
oc
of E I
: It . To prove the other implication put
n= 1


1 1 = {n eN: an:S nk+2 } and 12 = N \ 11.
Then for n e 11 we have In an
 (k + 2) In n, and so the conver-
gence of E I
: n implies the convergence of E In::" . Moreover,
nQs


for sufficiently large n in 1 2 ,
Ink an anrl:t 1
< <
.
On C1n n li+T
Hence
 In" aft. < 00 because t+ 2 > 1
LJ Aft · + I ·
nEI2


3.2.77. We have
\O(n)-1 cp(1)-1
E j(k)= E I(k) + (j(cp(I» + j(cp(l) + 1) +... + f(cp(2) -1»
1c=1 1:=1
+... + (j(rp(n -1» + f(cp(n -1) + 1) +... + j(cp(n) -1»

(I)-1 n-l
< E J(k) + E j(cp(k») (<<p(k + 1) - «,O(k».
k= I k=1
Inequality (1) is proved. The proof of (2) is analogous.
3.2. '18. Assume first that
j(cp(n)(cp(n + 1) - cp(n» < q < 1
fen) -.
Then, by (1) in the preceding problem,
ep(!)-!
S¥'(n)-l < E j(k) + q8 n - l -
Ic:!


.,0(1)-1
Therefore, in view of tp(n) > n, (1 - q)Sn-1 < E j(k). The
k=1
DO
convergence of E j(n) is proved. To prove the second part of the
n=1




300


Solutions. 3: Series of Real Numbers


statement we can use inequality (2) from the foregoing problem and
proceed analogously.


3.2.79. One can apply the result from the preceding problem with
cp(n) = 2n.
3.2.80. We apply the result from Problem 3.2.78 with <pen) = 2 n .
3.2.81. Apply the result from Problem 3.2.77 with
rp(n) = 3 11 , cp(n) = n 2 and tp(n) = n 3 t


respectively.


3.2.82.
(1) We have anb n -an+lbn+l 2: can+l. Therefore {anbn} is a mono--
tonically decreasing sequence with positive terms, and so it is
00
convergent. Thus the telescoping series E (anbn -
+lbn+l)
n=1
00
converges. The convergence of E an follows from the compari-
n=l
son test.
(2) We have


1
On+l >

- 1 ·
an -
b n


00
Therefore the divergence of E an follows from the test given in
n=1
J>robl
 3.2.°3.


3.2.83. To derive the d'Alembert test (the ratio test) we take b n =
1 for n = 1,2,.... Setting bn. = n for n = 1,2, ..., we get the
Raabe test. Putting bra. = nlnn for n = 2t3J ..., we arrive at the
Bertrand test.


3.2.84. [J. Tong, Amer. Math. Monthly, lOl(1994),450-452]
00
(1) Let S = E an and let
n=l


n
S - E ak
b - k=l
n-


r n


=-.


an an




3.2. Series of Nonnegative Terms


"301


Of course, b n > 0 for n E N. Moreover,


b - ar
 _ b _ r WI _ r 71 +1 _ 4r&+1 - 1
n n+l - - - ·
C&n+l tLn+l lIn+l Qn+l


(2) In this case set


n
Eak
b - k-=l _ 8ft
n - -.
an an
co
Then the series E
 diverges (see, e.g., Problem 3.2.10). More-
n=l
over ,


bra .a,. _ 6..+1 = S.", _ S"+1 = -Un+1 = -1.
C n +l 4n.+l l1n+l 4n+l


3.2.85.
(a) It is enough to a.pply the ratio test to each of the. series:


00 00 00
E Bkn' E Bl+kn, ..., E a(k-l)+kn.
n=1 n=O n=O


(b) It is enough to apply the Raabe test (
 3.2.19) to each of the
series given in the solution of (a). -
3.2.86. By assumptioD. there exists a positive constant K such that
1
f/'n
 K Inn ' n 2= 2.
Let us define th
 sets of positive integers N 1 and N2 as follows:
1\1. = {n: a,.

 } and N 2 = N\N..
For sufficiently large n e N 1,


In ...L
l--K- 1o-;K ( e K ) fit: e 2K
(1) a
-"'n
 a,. JiiIi = a,. ta n = 11.
 11. 2 .
Furthermore, for 5UfIiciently large n e N2,
a 1 -V'n K ( 1 )
 :lK
(2) ';". =:; a;JiiIi =;: =:; n JiiIi = ,!JK.


.




302


Solutions. 3: Series of Real Numbers


00
Comb ining (1) and (2.) with the convergence of the series E an, we
n=2
arrive at


E a
-rpn < +00 and
nENl


E a
 -tpn < +00.
nEN2


3.3. The Integral Test


3.3.1:. For k-l S x
 k, k
 2, we have f(x) e:.l(k). On the other
hand, for k 5 x
 k + 1, we have f(x)
 f(k). Hence
l k+l l k
f(x)rh
 l(k) :5 J(x)dx, k = 2.
"3
....
k k-l
S nmmilJg both sides of the above inequalities from k = 2": to k = n,
we get
inH f(x)dx 51(2) + f(3) + ... + fen) 5 1" f(x)dx,
which proves the integral test.
"I
3-S-
.. Note that !i is a positive and monotonically decreasing func-
tion. Therefore, by the integral test. convergence of the given series
is equivalent to boundedness of the sequences {I f'ex) dx} and
{l
 dx } · Since
[ J'(x)dx = fen) - f(l) and 1"
f:l dx = Inf(n) - Inf(I),
either both sequences are bounded or both sequences are unbounded.
N+l
3.3.3. We have SN-IN-(SN+t- 1 N+l) = f f(x)dx-f(N+l)

N
n
O. Moreover, fen)
 f f(x)dx
 f(n - 1) for n = 2
3,..... N.
n-l
S nmm ill g these inequalities from '" = 2 to J't. = Nt we g

 SN-
1(1) S IN :5 SN - feN). Hence 0 < feN)
 SN - IN
 j(l.), which
completes the proof.




3.3. The Integral Test


303


3.3.4. Convergence of the given sequences follows from the foregoing
problem. It remains to show that the limits of these sequences belong
to (0,1).
(a) Since /(%) =
 is a strictly decreasing function on the interval
(0,00), SN-IN<S2-12</(l)=1 for N>2 and
1(2) + /(3) + ... + /(N - 1) + feN)
> 1(2) + 1(3) + ... + I(N - 1) > iN I(z)dx,
or equivalently, SN -/(1) > IN - 12. Finally,
o < 1-12 S N lim (SN -IN)
 S2 -12 < 1.
-00


(See also 2.1.41 and 3.1.36).
(b) The proof is analogous to that in (a).


3.3.&.
00
(a) Convergence of the series E n(ln1n)D is equivalent to bounded-
n=2
n
ness of the sequence J ;r(
 z)O dx. For Q:/: I,
2


n
f 1 (lnn)-O+l (1n2)-O+1
dx- -
:r(lnz)Q - -Q+l -Q+l.
2
Thus the series converges if Q > 1 and diverges if 0 < a < 1.
Clearly. if Q S O. then the series diverges. Finally, if Q = 1, then
n n
J i1hd3: = melon) -1n(ln2). Hence the sequence f i1hcU is
2 2
unbounded and therefore the series diverges.
(b) In this case. we have


,n 1
J3 zlnzln(lnz) dx = In(ln(lnn» -In(ln(ln3)).


Thus by the integral test the series is divergent.




304


Solutions. 3: Series of Real Numbers


3.3.6.
(8) We have


N N S S N 1 5 ....., 1
On+1 = "+1 - n > dx

 Sft InSft ?; Sft InS ft - ?; 8ft %lnz
= InlnSN+l -lolnSl --t 00.
N-!)Q


(b) As in (a), we have


N N S S N S..
E ar; =E ft- 2 11 - 1 <E f 1 2 dx
n=2 Snln Sn n=2 Sr. In Sri - "=2)S,,-1 xlo X
1 1 1
=- + ---. .
lnSN InSI N-OG InS.


3.3.1. If


cp/(Z)/(cp(X» < q < 1 for x> % 0,
I(x) -


then



(
)
 z
f I(t) dt = f cp'(t)/(cp(t» dt =:; q f J(t) dt.


o)




Hence


1 &P(,J:) (1
 I Ip(Z) )
(1 - q) /(t)dt
 q j(t)dt - I(t)dt
sp(xu) :to
(zo)
(l 'P(ZO) 1 ",(%) ) 1 '1'(%0)
= q .1'0 I(t)dt - z I(t)dt $ q Zo I(t)dt.


00
Thus by the integral test, the series E fen) is convergent.
n=l


Now if


.p'(z)J(<p(X» > 1 for z > :c (),
I(x) -




3.3. The Integral Test


305



a)

then f I(t) dt
 f I(t) dt. As a consequence,
rp(zo) zo



z) cp(zo)
f /(t)dt
 f /(t)dt.
z zo


Moreover, since for any n there exists kn e N such that n < cp(n) <
n + k'At we have


In+k.. - In = [+.... /(t)dt
 (ft) /(t)dt
 (
) /(t)dt.
Therefore {In} is not a Cauchy sequence, and consequently, it is not
bounded. So by the integral test the series diverges.
.3.8.
(a) II 6m (-g(x)1Jtif - 9'(x» > 0, then there exist Xo and 6 > 0

-+oo
such that


-g(z)
&? - g'(z)
 6 for z
 Xo.
Therefore -(g(:I:)/(%»)'
 6/(%), %
 Xo. Consequently, for suf-
ficiently large R, we get
[ /(z)d3::S i [ -(/(z)g(x»'dz
ZO

11.
= 6 (g(Zo)!(ZO) - g(n)j(n» S "69(ZO)/(Zo).
Thus by the integral test, the series converges.
(b) As in (a), we get -(g(x}/(:»'
 0 for x
 %0. Thus the
fnnction 91 is monotonically increasing on (ZO, oo)t and conse-
quentlYt 9(x)f(x)
 g(Xo)/(xo) if x
 zo. This means that
n
I(z)
 I(z;l:
%o) for % > %0. Therefore the sequence f f(x)d%
1
n
is unbounded because, by assumption, the sequence J k dz is
1
unbounded.




306


Solutions. 3: Series of Real Numbers


8.3.9. It is enough to apply the result in the preceding problem to
g(%) = ,;.
3.8.10. In 3.3.8, we substitute g(z) = z1n%.
3.3.11.
(a) Set


00
f J(t)dt
9(%) = z 1(%) .
.&1
Then -g(%)7(Zf - g'(x) = 1 > O.
(b) Put


s
f I( t)dt
1/2
9(:':) = 1(%) ·
" n 1
Then J ic>d:e = In J j(t)dt - In f J(t)dt, which means that
1 1/2 1/2
n
the sequence f 9(
f dz is unbounded. Moreover,
1


-g(Z)

: - g(z) = -1 < 0.


3.3.12. We will apply the t
 proved in 3.3.9. Taking f(x) =
(1nz)-(1u
)", % > 1, we get
-z
(
: = (lnzp-l(-y lnlnz + 1).
If "'I
 1, then Um (lnZ)"-1(7lnlnz + 1) = +00, and consequently,
z-oo
the series is convergent. On the other hand, if 0 S 1 < I, then we
have Jim (InZ)7- 1 (7 In Inx + 1) = 0, which means that the series is
=-00
divergent.
3.3.13. Set


1
/(%) = r+&ti. ' % > e..
.In



Copy'
l"h!d 1
latl
rl:!




308


Solutions. 3: Series of Real Numbers


(b) The right inequality in (*) implies the divergen
e of the series
00
E f(>'n).
n=l


00
3.3.16. Assume first that the series E /(
) converges. Then, by
n=1
00
the Integral test, the improper integral J /ttj dt also converges. In-
1
tegration by parts and then integration by substitution give


(*)


1 00 1 dt = lim t _ 1 + 1 00 tll(t) dt
1 J(t) t-oo J(t) J(I) 1 12(t)
= fun t _ 1 + (00 I-I(t) dt.
t-oo f(t) 1(1) J 1(1) t 2


We will now show that


(**)


Jim t = o.
t-oo f(t)


2t
The convergence of the improper integral implies lim J
 dx - o.
t-oo t J \t6J
2t 2t
Since! Jr:t) = I(
t) I dx < f
 dx, the equality (**) holds. Thus
t t
00
/-1 (t)
the improper integral J
 dt converg
.
1
Moreover, we have


co f-1(n) 00 I n + 1 f-l(t) _ 1 00 I-l(t)
E ( 1)2 :s E 2 dt - 2 dt < 00,
n=1 n + n=1 n tIt


oo

which m e8nS that the series E

n= 1
series E J-
Jn) also converges.
n-rl


converges. Obviously, the


To prove the implication in the other dire.ction, assume that thE
series E J-
jn) converges. In much the same way we can show that
n=l




3.4. Absolute Convergence. Theorem of Leibniz 309



 -1

the integral f 9dt converges, and consequently, f l et) dt also
Ill) t
00
converges. Thus by the integral test the series E ,tn) is convergent.
n=l


3.3.17. First observe that the function f{J can be defined, in the same
way, on the \vhole interval [e,oo). Then cp(x) = 1 for x E [e. ee).
tp(x) = 2. for x E [ee t ee
) . For simplicity set e 1 = e and e k = ee lr - 1
for k > 1. Thus we have
<p(x) = k for x E [e k ,e k + 1 ) .


Let


l'
lex) = ;
x(1n 1 X)( 1n 2"X) · ... · (lncp(z) x)


then


1
f( x ) for x E [ e h , ef
 .01 ) .
= x(lnl x)(ln2-x) · ... · (Ink x)
Now, by the integral test, our series diverges because, for n > e k ,


1 n 1 e-1e 1 i2 1 L e3 1
1.. = f(x)dx
 f(x)dx = In dx +.. (In )(1 ) th
e e e X X e 2 X Z n2 x
l"
1 1
+ ... + dx = k - 1.
alr-1 x(In
)(ln2.x) · ... · (lnk-l x)


3.4. Absolute Convergence. Theorem of Leibniz


3.4.1.
(a) We have


lim" an I n = 101.
n
oo n+ 1
Thus the- series converges absolutely if lal < 1 and diverges if
Jal > 1. U lal = 1:, then the series diverges because
lim I an n. 1 1
= bm n = -.
n
oo n+l n-.oo (1+*) e




310


Solutions. 3: Series of Real Numbers


(b) Set I(x) = (In;)" for x > o. Then f'ex) = (In:l:)a-;Ja-ID:I:) < 0
for x > max{l, ea.}. Thus by the Leibniz test the series converges
for every a E JR. We will now decide whether the series converges
absolutely, that is, whether the series E Jln,
)O converges.. By
n=2
the theorem of Cauchy (
ee 3.2.28), the convergence of this series
00
is equivalent to the convergence of E nG(ln
)'a. Thus our series
n=2
converges absolutely if a < -1.
(e) If a > 0, then by the Leibniz test the series converges. H a < 0,
then


E oo ( _ 1) " · Q E oo ( l) R+l · lal
- sm-= - sm-.
n n
n= 1- n= l
Applying the Leibniz test again, we see that the series converges
for all a e R. The series does not converge absolutely if a :F 0,
because


sin .l!J.
lim 1 n = laJ.
n-co -
n


(d) The series converges if and only if -1 < :::Hs
a:186 < 1; that is,
if a E [-4.,
) U [3
 00). Clearly, the series converges absolutely if
a E (-4,
) u (3
 00).
(e) Since


Iim n I n': I = 0 if tal >
',
11----00 an
the series converges absolutely if tal > 1. If lal
 1, then the nec-
essary condition for convergence is not satisfied because lim I in 3
n-oo a n
= +00.
(f) Observe that


(In n)ln n
lim = lim n lo In n-o = +00.
n-oc n Q n-oo


Thus the nec essary condition for convergence is not satisfied.


3.4.2. If lal < 1, then for sufficiently large n,
a n - 1
< I I R-l
nan-1 + Inn a ·




3.4.. Absolute Convergence. Theorem of Leibniz 311
......


Thus the series converges absolute1y. If lat
 I, then


a n - 1 1 ( 1 )
na n - 1 + in n =;; 1 + In n .
.,0"- 1
Therefore for sufficiently large n the terms of the series are positive t
an
 by the comparison test t its divergence follows from the divergence
00
of E
 .
n=l


3.4.3. A5sume fi.rb
 that an > 0 for all n e N.. Using differentiation,
one can show that sin x > x -:;. for z > O. Hence 1- ai:
 <
a;.
00
Since a
 < an for sufficiently large n, the series E a
 is conver-
n=l
gent, which in turn implies the convergence of the given series. If
we drop the assumption 4n > 0, then the series can diverge or con-
verge. Indeed, take an = (_1)1\ r!o with Q > O. Then the series
El ( 1 - m::" ) diverges if 0 < a $ ! and converges if a > 4.
3.4.4. No, as the following example shows:
(_l)n 1 (-l)YJ
an = + ,b,. = t n
 2.
n nlnn n


3.4.5. We have an = Pn - qn and Ian I = Pn + qn. Note also that
00 00
Pn and qn are nOWlegative. Thus both the series E Pn and E fin
n=1 n=l
()O 00
div
et because E On converges and L Illnl diver
..
n=l n=1


3.4.6. Set Sn = 01 + ... + On. By the foregoing problem, we have
lim
 = lim ( 1 +
 ) = 1.
ft-OO QI) ft-OO Qn


3.4.7. The series does not co nverge absolutely. We will show that it
converges (conditionally). To this end we group tbe terms with the
same sign and we obtain
00 (-1)[1] 3 OQ ( 1 1 1 )
= _ + -1 n _ + +

 n 2
( ) 3n 3n + 1 3n + 2 ·




312


Solutions. 3.: Series of Real Numbers


Thus the cODvergence follows from the Leibniz theorem.
3.4.g
 Clearly, the series converges absolutely if a > I and diverges
if a :5 o. We will show that if 0 < a :S 1, then the series converges
conditionally. Observe that the first three terms of the series are
negative. the next five terms are positive, etc. Now grouping the
00
terms of the sam e sign we get the alternating series E (-l)ftA nt
n=1


(n+l)
-l
where An = E -b. Moreover t for a t= 1,
k_ n2


1 l cn + 1o )2 1 1 1
An < -;- + -dt = ') + 1 «n + 1)2-20 - n 2 ;-2a").
n- Q n 2 to n- O - a
Hence (see 2.2
3), lirn An = 0 if
 < a < 1. For a = 1= we have
R-OO
n;l < An <
, and consequently, lim An = 0 for! < a
 1.
n-()()
We will now show that for such a the sequence {An} is monotonically
decreasing. Indeed l
(n+l)2-1 1 (n+2)2-1 1
A - A +1 = "" - -
 -
n n.




k=n2 k=('&.Tl)

(n+l)2-1 1 (n+l)2+1 1
= E J(ti - L (k' +2n+ 1)0
k= n 2 k'=n 2
(n+l)2- 1 ( 1 1' ) 1 1
= E kji- (k+2n + 1)" - «n+2)2-2)0 - «n+Z)2-1)a
k=n2
2n ( 1 1 ) 1
= E (n 2 +k)0 - «n+l)2+k)o - «n+2)2-2)o
k=O
- > (2n + 1 ) ( - )
«n+2
2-1)0 (n 2 :2n)A «n+ 1); + 2n)A
1 1
«n + 2)2 - 2)4 (n + 2)2" -1)0 t
where the last inequality follows from the monotonicity of the function
1 1
g(x) = (n: 2 -+x)0 «n+ 1)2-+ x )0




3.4. Absolute Convergence. Theorem of Leibniz 313


-


on the interval [O,2n]. Hence, for sufficiently large n,
( 1 I ) 2
An-At>+l >(2n+l) (n 2 +2n)o - «n+l)2+2n)0 - (n+l)2a
=
( n+
 )((1+ :) -0 -(1+
 +
) -) _ (1 +
) -2a}

 n- 2o (2a - 1) > 0,
because (1 + x)-Q > 1 - ax and (1 + X)-4 < 1 - ax + !.(o.i J ) x2 for
at Z > o. (These two inequalities can be proved by differentiation.)
00
Thus by the theorem of Leibniz J the se
 E (_1)n An converges if
tt=1

 < Q
 1.
If 0 < a

, then since An > (2n + 1) (n2
2")Q t the nccessa.ry
.XiI
condition for the convergence of E ( -1)" An is not satisfied.
n=J


3.4.9. As in the solutions of 3.4.7 and 3.4.8, we group the terms of
the same sign and rewri te the series in the following form:

(_l)n-l ( (e n -:] + 1 +... +
) ·
We also observe that
1 -.!... [en] - [ en-I I _ _ [en 1]
(en-I] + 1 +... + (en] > [e n ] - 1 (en].
Moreover, since


( [ en-I] ) 1
Urn 1 - = t - -
n-C() [en] e'


the n
 condition for the convergence of the series.is not satisfied
and therefore the series diverges.


3.4.10.
(8) Observe that the series can be written in the fonn


OCJ
L(-l)"A n ,
n=O


where


2"+I_J
1
An = E "k.

=2"




314


Solutions. 3: Series of Real Numbers


Since An > 2 n 2nA -1 --t i, the series diverges.
n
oo
(b) As in (a), the series can be written in the form


00 2,,+1_1 1
E(-I)nAn, where An = E kink .
n-l k=2"


Moreover,


0< A.. < 2" 2"
2" .
This implies Um An = o. We will now show that {An} mono-
n-oo
tonica1ly decreases. Indeed,


2-+ 2 -1 2n+l_l
1 1
A,.+1 = E kink = E (2"+1 +1)1n(2"+1 +1)
k=2n+1 1=0
2--1 ( 1 1 \
=
 (2"+1+21) 1n(2"+1 +21) + (2"+1+21+1)1n(2"+1+21+1)}
2--1 2 2--1 1
< E (2"+1 +21)In(2"+1 +21) < E (2" +1)1n(2" +1) =A...
1=0 1=0


8.4.11. We have
(l)n
 · 1 (l)n ( 1 (-I)n ) . 1
- (-I)n+Viism
= - -(-I)n+Vii sm

= (-I)nsin2... + (-I)n sin 2... _
 sin 2....
,fR n-l .;n n-l ,fii
By the Leibniz test, both the series
00
E( _1)n sin 2...
n=2 ,fii


and E (-I)" sin 2...
nm2 n - 1 ..jR


converge. But the series
E oo ,fR . 1
sm-
n=2 n - 1 ../ii
diverges, so the given series also diverges.


Copyr:gh!cd rnate.;al




3.4. Absolute Convergence. Theorem of Leibniz 315


3.4.12.
(a) The 5eries converges 8b501utely (see 3.2.i (f».
(b) Convergence of this series follows from the test of Leibniz. The
series converges conditionally (see 3.2.1 (g».
( c) Clearly, the sequence {
}, n
 3, is monotonically decreasing
and therefore the series converges. However, it does not converge
absolutely {see 3.2.5
 (b».
(d) Convergence follows from the monotonicity of {(1+ *)n} and
from the fact that the limit of this sequence is e (see.2.1.38). To
prove that the series does not converge absolutely, we use the
inequality


} 1 2 1 3
In(l+x <x- 2 x + 3 x, x>O,
with x = *, and we get (1 +
)n < el-tn+ 3
:J . Hence
e-(l+
 r >e(l-e-in+sh»e(l-e-tn) for n>l.
It follows from 2.5.4 (a) that, for sufficiently large n,
4n(1-e-in) >
 .


'X) n
Therefore the series E (e - (1 +
 ) ) diverges.
n=1
( e) The convergence of this series follows from tbe monotonicity of
the sequence {(1 +
) n+l} and from the fact that e is its limit
(see 2.1.38). In view of 3.2.5 (c), the series does not converge
absolutely.


3.4.13.
(a) The function


(In x)C
J(x) = :rP ' x E (e l . +00),


monotonically decr eases to zero as x -+ 00. Therefore by the
Leibniz test, the series converges. We claim that if b > 1, then




316
..


Solutions. 3: Series of Real Numbers


the series converges absolutely. B)r the theorem of Cauchy (see
3.2.28), it is enough to shOW' the convergence of


00 a
L2"
.
n=l


Now by the root test this series converges if b > 1 and diverges
if 0 < b < 1. Clearly, if b = 1, this series diverges.
(b) Note that


(lnn)lnn e(lnn)(lnlnD) n tn1nn
6 = b = b.
n n n
Hence tbe n
 condition for convergence is Dot satisfied.


3.4.14. By the monotonicity of {an}, we have
r2n = (02n+l - G2n+2) + (02n+3 - G2n+4) + ... > 0,
r2n+l = (-«2n+2 + a2n+3) + (-a2n+4 + 02n+S) + ... < 0


and


r2n = 42ra+l + (-02n+2 + a2f1+3) + .... < 02n+lt
- r2n+l = 02n+2 + (-G2n+3 + Q2n+4) + ... < 42n+2.


3.4.15. Note that


n n

(alc + lIk+l) - 2
 Ok = 4ta+l - al --+ -0\..
L..J
 n....oo
k= 1 k=1


3.4.16. Observe that


n n
E(OOt + 001:+1 + C4k+2) - (0 + b + c) E ak
k=1 k=1
= b{4n+l - 01) + c{
+1 + tlq+2 - B) - 42) -. -001 - C(OI + (2).
n-oo


3.4.11. By assumption) there exist positive constants c and 0 such
that for sufficiently large n, C < Ian I s C. Hence
I 1 1 I 1
4n+J - 0; =s &IOn+1 - ani.
I 2 1 1 1
t4n+l - an
 C - - .

+1 4n




3.4. Absolute Convergence. Theorem of Leibniz 317


Thus our claim follows from the comparison test.


_ 00
3.4.18. Let 8n and 8n denote the nth partial sum of E an and
n=1


00
E n(an - Bn+l), respectively. Then
n=1


n n n n
Sn = L k{ak - ak+l') = L kak - L(k + l)ak+l + L ak+l
k=1 k=l k=l k=l
= -(n + 1)a n +l + Sn+lt
which proves our claim.
3.4.19. Convergence follows from the Leibniz test..
3.4.20. H lal < r, then the series converges absolutely. Indeed. since
I sin zl
 lxi,
In! sin asin j · ... · sin ; I
 lain.
We now turn to the ca.se lal
 1. We claim that in this case the
series diverges because the necessary condition for convergence is not
satisfied. In fact, for a fixed a there exists no such that
 S 1.
Then, setting C = (no - I)! I sin a sin
 · ... · sin no':. 1 I and using the
ine q uali ty !!!!.: > 1 - =.: z > 0 we g et
z 6 ' ,
I' " · a · a I C · lal . lal
n.smasm o .....sm- = no.....nsm-.....sm-
"" n no n

 Cno · ... · nsin
 · ... · sin
 = C ft (1 - 6
2 )
k=no

C n n ( l-
 ) =C (no-l)(n+l)
 C no - 1 >0.
k k2 non n tCO no
=no


3.4.21. By 2.5.4 (&),
. \/li- V"

 . ( va- 1 v'b-l+
-1 )
lim 1 :;lim 1 - 1
n
oo - n....oc - 2-
n n n
1 a
= lna - 2(lnb + lne) = In JbC .




318


Solutions. 3: Series of Real Numbers


Hence if G > ../&t then, beginning with some value of the index n,
the terms of oW' series are positive, and by the comparison test it
diverges. If a < ../&, then the terms of the series are negative and it
also diverges. For (J =
t we have
f: ( v'4- V'b; tIC ) = -
 f (2
_
f.
"=1 n=l


Since


Jim ( 2t1b -1
 20'(:+ 1 ) 2 = (lnb-lnc):I,
n-+oo 2ii


00
the convergence of our series follows from the convergence of E
.
n=1


3.4.22.
(a) By 1.1.14 t there exist a sequence of integers {PII} and a sequence
of positive integers {fin} for which
I - Pn I 1
11' - qn <
.
Hence icosp,.1 = Icos(1rqn-Pft)1 > cosi; = 1-2sin2
 >
1 -
. Thus
( 1 ) PA P 1
(J cas p,. n Pn > 1 - 2 > 1 - ....!!.-.
2qn qn 2qn
This meA nR that the subsequence {(COSPn)
} of {cos n n} does
not converge to zero. Therefore the necessary condition for con-
vergence is not satisfied.
(b) By Problem 1.1.22, we know that the sequences {Pn} and {qq}
mentioned in (8) can be chosen in such a way that all the terms
or {
} are odd. Then by the inequality
I ! -
 < 1-
2 fln q

we get JsinPnl = IC06(
-m -Pn) J > COS q
 > 1- k. Thus, as
in (a), the sequence (sinpn)JJ,. d
 not converge to zero, and
consequently! the series diverges.




3.4. Absolute Convergence. Theorem of Leibniz 319


3.4.23.
(8) By 855umption (5ee also 2.4.13 (b», there are no and Q such that
n ( an - 1 ) > a > 0 for .n
 no.
an+l
Hence a::, < n
Ot < 1, which means that, b eginnin g with the
value no of the index n, the sequence {an} monotonically de-
creases. We will show that lim an = O. It follows from the
n-oo
above that
a n +l an ano+t n · (n - 1) · ... · no
Gra+l
 · · ... · · a.,
 < a.,J{)'
an an-l 4n o (0 + n) · ... · (a + no)
= O. Indeed,


lim n · (n - 1) · ... · no _ I " 1 - 0
- 1m - J
n-oo (a +n)..... (a+ no) n-oo (1 +;) · .... (1 +
)
because (see 1.2.1)


( a ) ( Q ) . a a
1 + - ..... 1 + - :> 1+ - +... + -
 00.
no n no n n-+oo


00
So by the Leibniz test, the series E (-I)Qan converges.
n=l
(b) By the assumption n ( ..::. - 1) < 0, the seQuence {a..} mono-
00
tonically increases and consequently the series E (-l)n an di-
n=l
verges, because the necessary condition for convergence is not
satisfied.
3.4.24. By assumption, lim n ( a an - 1 ) = Q. For Q:F 0, the test
n-oo "+1
proved in the foregoing problem can be applied. For Q = 0, the
necessary condition for convergence is not satisfied. Indeed, we ha.ve
1 1- a} 112 an-I
- = -- . ---- .
 . ... .
an al 0:2. as an.
t: ( /31 ) ( /32 ) ( Pn-l )
= at 1 + 11+E 1 + 2 1 +£" ... 1 + (n _l)l+E -.




320


Solutions. S: Series of Real Numbers


-


Moreover, there exists IJ such that
Pnl
 p" Hence
> at >

an - (1 + Jk ) (1 +
 ) ... (1 +
 ) - elM t


oc
where A = E n J \. .
n=1


3.4.25. By 2..5.34) the existence of the limit lim n In o.,.
 is equiva-
n-oo +1
lent to the existence of lim n ( 04... - 1 ) t and both limits are equal.
ft-OO ....+1
Set an. = ;
: . Then lim n In
4. = P - _ 2 1 . Hence, by 3.4.23, the
"-00 +.
series CODverges if p >
 and diverges if p <
 . In the case p = l
the n ecessary condition for convergence is not satisfied because, by
Stirling's formula, Jim 4n =
.
ft
CO


3.4.26. Let Sn = at + 02 + ... + On. We use the so-called 8Um17WJtion
bu pam (Abel'" transformation) to obtain


n-J
DIPl + Q2P2 + .n + CnPn = E Sk(Pk - Pk+l) + SnPn,
k-l


and we get


n-l
OlPI + 42})2 + ... + 4nPn _ S
 S Pk+l - Pi
- Q-
 k ·

 bl

Now it is enough to apply tbe Toeplitz theorem (see 2.3.1).


oc
3.4.27. Apply the result in the last problem to the series E tlnbn
n=1
and take Pn = -!;.
3.4.28. The result is contained as a special case in the preceding
problem.


3.4..29. If the series were not
utelr convergent t then the sub-
series of aU positive terms and the subseries of all negative terms
would diverge (see 3.4.5).




3.4. Absolute Convergence. Theorem of Leibniz 321


3.4.30. (20] No, as the fonowing example shows.
00
Take a conditionally convergent series E bn and set
n=1



 b:J
al = bl. 42 = 43 = 2!' a4 = as = ... = Qg = 3i pUt
01l+21+...+(n-l)l+l = aU+2!+...+(n-l)!+2
bra
= ... = BII+21+...+(n-l)I+n! = "....
n.


00
Then the series E On converges conditionally. But for each k > 1
n-1
and I
 2 the subseries


Ok + Bt+l + Oi+21 + ...
converges. Indeed, for n
 I there are
! terms of the form
.
Grouping these terms. we get the convergent series


1 00
constant + I E bn.
n=no


3.4.31. Consider the sene:J
1 1 1 1 1 1
1 + -V2 +
 -
 + ... + -Vii + ... + _s
 - _31::: + .... ·
2 2 2 2 v2 n n nyR yn
.......

.....-


n times


3.4.32. Yes. Consider the series
1 1 1 1 1 1
1 + 2ln2 + 21n2 - In2 + .... + nlnn +... + nlnn - Inn + .....
........- ......

n times


Then


N2
N-2
E a
=
n=1


N
1 + E ( ft.-lllnA! n + ID
 n ) if k is event
n=2
N
1 +
 ( 1 1 ) if k is odd.
LJ fI . -1ln . n - 1n
 n
n 2


Gopy
 q.-ten l
lCltena




3..4. Absolute Convergence. Theorem of Leibniz 823.


Assume that Em = 0 and that the terms Em+b Em+2,...., En have
the same sign. Then (*) and the mOt1otonicity of the sequenc.e {aq}
imply that


IEnanl < E,


n
 m + 1.


3.4.35. The proof is analogous to that of 3.4.33. We set En =
P1bl +... +Pnbn and assume that Urn Plbl+.
+Pnbn = 2a > O. Then
n-OC'J
for n > no we have P 1 b 1 + ... + Pnbn > an, and consequently,


1 1
b 1 +... +b n = -(Plb 1 ) +... + -(Pnb n )
PI P1
n-l ( 1 1 ) 1 n 1
=EEk -- +En->constant+Q E -,
k= 1 Pk Pk+J Pn k= n o+2 Pk


a contradiction.


3..4..36. We first show that if p = q, then the series converges. We
have


Sip
 (1 +
 +... +
) - ( p
 1 +... +
)
1+1 ( 1 1 )
+ ... + (-1) (l- l)p + 1 +... + lP ·
Therefore Sip is a partial sum of an alternating series. By the Leibniz
test the limit lim Sip exists. Clearly, each partial sum of the form
1-00
S'p+k, k = 1,2, ...,p -1, tends to the same limit as 1-. 00.
Assume now that our series converges. Then, by 3.4.34,


1im np - nq = 'P - q = 0,
n-QO np + nq P + q


which implies that p = q.


3.4..37. We note first that if conditions (i)-(iii) are satisfied, then for
any convergent sequence {an}, the transformed sequence {b n } is well
defined. Now the proof runs in much the same way as in the solutions
of Problems 2.3.1 and 2.3.26.




324


Solutions. 3: Series of Real Numbers


3.5. The Dirich1et and Abel Tests


3.6.1.
(a) Since Bin: n = -/n<l- cos(2n». it is enough to consider the Series


OQ 1 00 1
L(-l)"ji and L(-l)"n cos(2n).
n=l n=1


By the Leibniz telt J the fust seri
 converges. Co

gen

 of the
second one follows from the Dirichlet test (see, e.g., [12], p.l05).
Indeed, by the fonnula (which can be proved by induction)


(1)


ft . no (n
J)Q

 1._ = smT cos
L.-, COS M.I . CJ.
k=1 SID '2


for G:F 2l7f', I e Z,


we obtain


I t<-1)J:OOS<2k) = tOOS(C2r- 2 )k)
k..l It.z:-I
sin (w-2)n cog (n+l)(",-2)

 2
cosl


-
-


< 1 .
- cosl


00
TherefOre the sequence or partial sums of E (-1)"cos(2n) is
nz=1
bounded. Moreover, {
} tends monotonically to zero. Thus the
00
series. E (-l)"
 cos(2n) converges.
ft.K I
(b) The sequence


1 +
 + ... +

On=
n
of arithmetic bl
 of {
} converges to zero (see 2.3.2). More-
over t it is easy to check that the sequence { an} monotonically
decreases. By the formula (which can be proved by induction)


(2)


n sin
 sin (n+l)

"'sinka= 2 2
L....J . 4
Ie_I 8m '2


for o:f: 2l1f', I e Z,




1.5. The Dirichlet and Abel Tests


325


we get



 sm . k _ I sin
 sin n;-l I 1
L-i - · 1 $ . 1 .
k=l sm 2 sm 2
Therefore by the Dirichlet test the series converges..
:c) Observe that
cos (1r n: 1 ) =008 (n1r- nn; J = (-ltcos (1r- n:l )
7r
= (_l)n+l cos I "
n+
Thus the given series can be rewritten in the form
00 11'

(_l)n+l cos n+i .
L-i In 2 n
n=2
The convergence of the above series follows from
he Abel test
00
(see, e.g., [12]t p.l06), because the series E (_l)n+l ln
n con-
n -2
verges (by the Leibniz test) and {cos l
n } is a monotonic and
bounded sequence.
:d) We have


.. n

sm-
4
nO. + sin
W"


sin !!1!
4
nO


( !in 7 )
1 n4
- . n ·
1 + fil:?


The series


00 . n1t
E smT
, a > 0,
n Cl
n=1
converges (by the Dirichlet test). Now we will study the series
(with positive terms)



 II&in2 n1l'
- "'T

 n 20
L...J sin T ·
n=l 1 + nO
There exist positive constants Co and Co such that


sin 2

1 " 1
n ;l O n
Co.
_ < j n1r < va. _ 2 '
ntlO-U 1 + 1J D T n a
nO


n =1= 4k. kEN.


Therefore tbe series converges if a >
 and diverges if 0 < a < !.




326


Solutions. 3-= Series of Real Numbers


3.5.2. We have
N - ( 1 ) N - 1 N - 1
E S1D n+ii = E smnCOSii + E cosnsmii .
n -.2 In In n n=2 In in n n=2 In In n
By formula (2) given in the solution of 3.5.1(b) and by the Dirich.
00
let test we see that the series E I



 converges. "Since the

n=2
quence {cas
 } is monotonic and bounded, the series E si
:,::!
n=2
converges, 1;>y the Abel test. Finally, the convergence of E C08 1n n a :i:-!-
n=2
follows from formula (;1..) given in the solution of 3.5.1(a) and from thE
Dirichlet test.


3.5.3.
(a) We have
n n I
2 Esin(k 2 a)sin(ka) = E[cos(k(k-l)a) - c05(k(k+ 1)a)]
k=l k=1 I
= 11 - cas (n(n + l)a)1 $ 2.


Thus the convergence of the series follows from the Dirichlet test.
(b) As in (a), the Dirichlet test can be applied.
3.5.4. In view of the formula
cas nsin (na) = ! sin (n(a + l» + ! sin (n(a -1» t
on 2 n "
 n
the convergence of our series follows directly from the Dirichlet tes1
(use formula (2.) in the solution of 3.5.1(b».


3.5.5. H a = k1f. k E Z, then all terms of the series are equal to zero
H a ¥: k7r then, by the inequality I sin xl
 sin2
x =
(1- cos2x)
we get



 I sin (na)1

.
! _!
 cos(2na) .
L.J n 2:" L.J n 2 L...J n
n=1 n=1 n=1
Hence in this case the series does not converge absolutely.




3.5. The Dirichlet and Abel Tests


327


3.5.6. Assume first that 0 < a < 11", and set m = [1] . Then, for
sufficiently large n,



 sin(ak) <
 sin(Gk) 1
 sin(ak)
L., k -
 k +
 k .
1c2: 1 h= 1 k=m+ 1


Since I sin tl < It I Cor t i: 0,


(.)



 I Sin(ak) 1

 = < c
L...J k < L.J k ma - v 1r .
k=1 k=1


Moreover. from (2) in the solution of 3.5.1(b) and from the inequality
sint >
t, 0 < t <
,we get


(**)


n sin(ak) 1 1
E k
 (m+ 1)1 sin !!I < !!:Ii = -Ii.
k=m+l 2 W' (&


Combining (*) with (**), we see that the desired inequality holds
for a e (0,11'). Clearly, since the sine function is odd, it a1so holds
for a E (-11',0). Moreover, since sink1r = 0 and the sine function is
periodic, the inequality holds for every a E R.


3.5.7. The convergence of the series follows from the Abel test, be-
00
cause the series E (-1)" -7: is convergent and {arctan n} is a mono-
ncd
tonically increasing and bounded sequence.


Of)
3.5.8. By the Abel test the series converges. Indeed, E (-I)n

n=1
converges, and the sequence {V1DZ} is bounded, strictly d ec
qjng
if z > e, and strictly increasing if 1 < z < e.


3.5.9.
00
(a) Observe first that, by the Abet test, the series E i:' converges.

=1
00
Moreover, since the series E an is convergent, the sequence
n=1




328;


Solutions. 3: Series of Real Numbers


00
{r n }, r n = E ak, tends to zero. Hence for p > n,
k -n


p p p p
L ale = L Tie-ricH = L!:! - L TIc+l
k==n ble k=n bk k= n bk k=n bk
p ( )
Tn
 1 1 Tp+l
= - + L." rk - - -
b n k b" bk-l b p
'=n+l
( 1 1 1 1 ) 2en
<e -+---+- =-
_n b n b n b p b p b n '


where E q = sup Irkl. Consequently,
k > n


f:?
 2£..i- n
 0 ( i- n) .
k=n 'k


(b) See 3.4.26.


3.5.10. Note that


00 co k

)k+ I}Cn+k = L k -1 (n+ k -l}Cn+k-l.
k=0 k=l n+


00
Thus the Abel test implies the convergence of E (k+ l)Cn+k for each
1:=0
n E N. Setting Tn = nen + (n + l)Cn+l + ..., we get


00 00
t n = E(k + l)Cn+k = E(k - n + l)Ck
k=O k=n
00 00 1 00 1
= Lkc/.: - (n-I) E k kc k = Tn - (n-I) E k(TIc - TlcH)
k=n
=n k=n
1 00 ( 1 1 )
= -Tn + (n - 1)
 - - rk.
n k L-, l k-l k
=n +




3.6. The Dirichlet and Abel Tests


329


Hence


1 00 ( 1 1 )
Ifni :$ -Irnl + sup Irkl(n - 1) L k _ 1 - k
n k
,,+l kZlln+l
1 n-l

 -Irnl + sup Irk I .
n k > n+l n


This together with Iim,. n = 0 yields lim tn = o.
n-oo n-oo


3.&.11. By snmmR tion by partst


n ,,-1
Sn = L 4tb
 = E Ai(
 -I{+I) + Anb
,
i= 1 i= 1


00
where An denotes tbe ntb partial sum of the series E an. Given
n=l
£ > 0, there is no such that Ibil < e for i
 1lQ. So if m > n
 no
and IAnl
 L.. then


m-l
ISm - 5nl = L Ai(b
 - b
+1) - Anb
 + Amb



i
n


m-l
$ E IA j IIb
 - b
+ll + I A n 6 :' + IArnb
 I


1=:...


( m-l )
S L ?: Ib i - bi+lllb
-1 + b
-2b;+1 +... + b
;111 + 1141 + Ib
1
t:z:n
( m-l )
SL
-I
Ib;-bi+1I+
 ·
' -n


00
Hence the C9nvergence of E anbn follows from the Cauchy criterion.
n=t


3.5.12. By s umma tion by parts,


Q n-l
(*) 5n = LBi
 = E Ai(bi -
+1) + Anbn,
im:1 i=l




330


Solutions. 3: Series of Real Numbers


00
where All denotes the nth partial sum of E G n . Since tbe series
n=l
00
E (b n - b n + 1 ) converges absolutely and the sequence {An} is
n=1
00
bounded, the series E An(b n - b n + 1 ) converges absolutely. The
n=1
00
convergence of E (b n - b n + 1 ) implies that lim b n exists, because
n=l. n-.oo
(bt. -
) + (
 - li:J) + ... + (b n -l - b n ) = b l - b n . Consequently,
oc
1im A,.b n .also exists and, by (*), E an6n converges.
n-+oo n=1


3.5.13. For 0 < x < Ji the sequence {x n } is monotonically decreas-
ing and bounded, and therefore th
 Abel test can be applied. For
-1 < x < 0 both the sequences {
n} and {x2.n-l} are monotonic
00 00
and bounded. Consequently, E
nz2n and E a2n_ l Zl n - 1 are
n=1 n=1
convergent. The convergence of our series follows from the equality


'00 00 00
E anxn = E
nX2n + E B2n_l X2n - 1 .
n=1 n= l n=l


3.5.14. Observe that if x > XOt then


00 00 1
" an
 an .
L..J n
 =
 n
o · n:%-zo.
n=1 n=1


Now it is enough to apply the Abel test.
3.5.15. We have


f: n!an = f: an . n!n Z .
n=l x(x + l)...(z + n) n=l n% x(x + l)...(x + n)
Note that for sufficiently large n all the numbers :e(%+
;.

:J:+n) have
the same sign. We will show that they form a monotonic sequence.
To this end, observe that the ratio of the (n + l)th term to the nth
term is


en + 1) (
):I:

+n+l


e(2:+i) In(l+-!-)
l+

n


.




3.5. The Dirichlet and Abel Tests


331


Now set Rn = e(.1:+J)JQ(1+
) -1- :1::1 . By the result in 2.5.7 we see
that


R" = (x+ 1) (In (1 +
) -
) +
(x+ 1)21n 2 (1 +
)
+
(x+ 1)3ln 3 (1 +
 ) +...
:;
 (_ X;1 +
(x+ 1)2+0(
))
+
 (x + 1 )3ln 3 ( 1 + ;) + ...,
where 0 (an) denotes an expression whose value divided by an re-
maing bounded as n..... 00. This implies that for sufficiently large n,
Rn is positive if x(x + 1) > 0 and negative if x(x + 1) < o. Couse-
quentJyt for all sufficiently large n the ratio of two consecutive terms
of { :<{:I'+f:
.
Hn) } is either greater tluw 1 or less than 1. We will
now show that this sequence is convergent for Z:F 0, -1, -2, .... To
this end, write


n!n2: 1 n n-l (1 + i)Z
:r(% + 1)...(% + n) = x x + n n 1 + F ·
Assume first that x > 1. For such x we have (1 + *)% > 1 + f.
Consequently,


In ij (11:
z = E (x In (1+
) -In (1 +
)),
k-l k=l


where aU terms of the sum are positive. Moreover t note that


lim zln (1 + 1) -In (1 + f) _ :rex -1)
k-co -b - 2 ·


As a result, the existence of the limit
lim In " n - 1 (1 + i}Z
n-oo 1 +

k%:l "




3"32


Solutions. 3: Series of Real Numbers


00
follows from the convergence of the series E -b. Thus the sequence
k=1
under consideration converges for x > 1.
. %
Assume now that :c E (0, I). Then for such x we have (1 +
 ) <
1 +
. Therefore one can apply the above reasoning to the sequence
with terms


n-l (1 + i):':
-inTI 1+
 ·
k=l k
Finally, we consider the case x < 0, x ¥= -1, - 2, -3, .... Let ko be
a positive integer such that 1 + % > 0 for k
 1:0. To show that the
sequence


IT (1 + HI:
k=ko 1 + i


converges, note that
(1+
 r' >1+i for k


and proceed as in the case x > 1.


3.5.16. It follows immediately from the Abel test that for Ix I < 1
00 oc
the convergence of E lI,aX R implies the convergence of E Bnx 2n
n=1 n=l
(see 3.5.13). Since { 1-
2n } is monotonic and bOW1ded, the equality


00 xn co ( 1 1 )
an = anz n + anx2n
E l-x n E l-x 2n l-x2n
n=1 n=l


00 n
and the Abel test imply the convergence of E an .'::r'. .
n=1


00
3.5.17. [20] No. Let E b n be a conditionally convergent series. Put
n=1
co
F(x) = 22: 2 and define the new series E an by setting
n=l


6 1 b
al = a2 = 2' ale = F(rn) _ ;(m _ 1) for F(rn-l) < k ::; F(rn).




Cauchy Product of Infinite Series


333


I series is a1so conditionally convergent. Now we show that every
:eries of the form


ak + Qkl + akP + ...
rerges. Note first that for any positive integer m there exists a
lue tm. tm = [logt F
m) ] . such that
kl fnt S F(rn) < kl'nt+ 1 .
»llows from the definition of t m that, beginning with some value
l1e index m, the subseries (*) has t m - t m -l terms of the form
)
F(m-l) . Grouping tllt
j
 terum, W
 tramsCurul (.) into the
ci



00

 t m -t m -l b
constant +
I F(m) _ F(m -1) m'



 series converges-by Abel's test, because the sequence with terms
t m - t m -1
Cm= _
F(m) - F(m - 1:)
Lono
oni
ally decr easin g. Indeed,
(2m -1) log ,:2"- 1 d (2m + 1) log,.2.+ 1
t:m > 2m3 _ 2(m-l)2 an Cm+l < 2(m+l)2 _
2 ·
.ce for sufficiently large m we have Cm+l < Cm, because
. (2m + i) log I 2,+ 1 2
2 _ 2(m-l)2
lim · -- 0
m
oo (2m -1)log,2:-1 "2.:(m+I)
 _
2 - ·


I. Cauchy Product of Infinite Series


00
.1. Assume that the series E an converg
 absolutely. Let An'
n=O


00


00


00




334


Solutions. 3: Series of Real Numbers
_ _ -A


Write


B = Bn + Tn, where lim rfl = O.
n ....00


Consequently

en = BAn - (aorn + Qtrn"'l + ... + anro).
We will now show that


(.)


lim (aor n + 0trn-l + ... + anro) = O.
n-QO


1b this end, let £ > 0 be chosen arbitrarily and let m, M be such
that


00
ITnl
 m for n
 Ot M = E Ian I.
n=O
There exist keN and I E N such that if n
 k, then Irnl < rn
and if n
 I + It then Ja'+11 +... + lanl <
. There!ore for n
 l +k
weget
laoTn + o]r n -l + ... + OnTol

 (Iaollrnl + ... + la,Urn-rl) + (l a ,+1H r n.-I-ll + ... + 14nl1rol)
E
< (Iaol + 1011 +... + la,1) 2M + (lal+J t + ... + JanDm
E' €
< M 2M + 2m m = f,
which proves (.).
Note that it follows from the above analysis that if both the
series converge absolutely, then their Cauchy product also converg(JJJ
absolutely.
3.6.2.
(a) It foUows from the Mertens theorem that if Ixl < 1, then the
00
Caucl1y product of the series E x n with itself converges. More-
n=O


over,


en = x n + xx n - 1 + ... + zn = (n + l)x 7l .


Hence


f nx"-1 = ( 1
 3: ) 2 ·
n.=1


(b) l
% . I:U .




3.6. Cauchy Product of Infinite Series


335


00 00
(c) The series is the Cauchy product of E n(n 1 +1) with E
. The
n=1 n=1
sum of the first series is 1- (see 3.1
4 (b», and the sum of the
second is e -1 (see 2.5.6). Therefore, by the Mertens theorem,
the sum of our series is e - 1.


3.6.3.
(a) We have
n 2k 1 1 n ( n ) k 1 1 ( l ) n
c,.=
 k! ' 2n- k (n- k)! = n! £; k 2 2n-k = n! 2+ 2 ·
By 2.5.1: the sum of the Cauchy product is et.
(b) The Cauchy product is the series
00 1 n (-3)k
L. sn+J L k .
n=1
 k=l
By 3.1.32 (a), its sum is -
 In2.
(c) We have


2n+1
C2n+l- = x2n+l E (-l)k(k + 1)(2n + 1- k + 1)
-k=O
= x2n+l (t( -:l)k(k + 1)(2n + 1- k + 1)
k=O
+ 3: 1 (-l)k(k+ 1)(2n+ l-k+l»)
k=n+l
=-X2n+l ( t( -l)k(k + 1)(2n + 1: - k+ 1)
k=O
- 'to <-1)k'<k'+1)(2n+l-k'+1») =0.


Moreover, since C2n+l = 0, we get


2n
C2n = x 2n E(-1)2n-k(k+ 1)(2n - k + 1)
k=O




336


Solutions. 3: Series of Real Numbers


....


( 2n-t
=%2n E<-I)k(k+l)(2n-l-k+ 1)
k=O
+ 2f: J (_I)"(k+I)+(2R+I» )
k.-zO
= x 2n (O+ (-n) + (2n+ 1» = (n + 1)x 2n .
Finally, by 3.6.2 (a),


OQ 1
L(n + l)x2n = (I _ x2)2 '
n::()


00
3.8.4. Observe that the series E Anxn is the Cauchy product of
nZlZ(l
00 OCI
E z'" with E Cnx ft . Therefore it is convergent for Ixl < 1 and its
n.=O n:zO
co
sum is 11 % E anx".




3.6.15. To prove the equality given in the hint it is enough to equate
the coefBcients of x n in the Cormula (I + x)"(l + z)n = (1 + 2;)2n..
Consequently,
c" = (-I)"x 2 " (R
)2
 (
) 2 = {_1)"x 2n {n
)2 (
).


3.6.6. In view of the relation
en = ( ! 1 · 3 . .n · (2n - 1) +! 1 1 · 3. ... · (2n - 3)
a 2 · 4 .. ... · 2n 2 a + 2 2 .. 4 .. ... · (2n - 2)
1 1 · 3 · h. · (2n - 1» ) n
+ ... + 2 2 4 2n :t t
a + n ... ... ..
it is enough to prove the equality
! 1 · 3 · ... .. (2n - 1) +! 1 1 · 3 .. .... · (2n - 3)
a 2 .. 4 .. ... · 2n 2 t1 + 2 2 · 4 · .n . (2n - 2)
1 1.3...n. (2n -1) (a+ 1)(0+ 3)...(a+ (2n -1)
+ ... + = ( .
0+2n 2.4........2n Q a+2)(a+4)...(a+2n)




3.6. Cauchy Product of Infinite Series


337


To this end, we decompose the right-hand side expression into partial
fractions:


(a + 1) (a +3)...(a + (2n -1» _ Po 01 an
( )( ) ( ) - - + 2 + ... + ·
a a + 2 a + 4 ... a + 2n a. a + a + 2n
Multiplying both sides of this equality by a(a + 2) (a + 4)...(0 + 2n)
and substituting a = 0, a = -2
 ..., a = -2k, ..., a = -2n, we get


(2n - 1)!!
Qo = (2n)!! t
-1(2n - 3)'1
0'1 = -2"(2n - 2)!! ,...t
(-2k + 1)( -2k + 3)...( -.1)1. 3...(2(n - k) -1)
Qk= - ..
-2k« -2k + 2)...( -
) · 2. 4...(2(n - k»
(2k - 1)!!(2(n - k) - I)!!
-
- (2k)II(2(n - k»11
(2n - 1)!!
an = (2n)!! 1
which gives the desired equality.


t ...,


00 00
3.6.7. Let An' Bn' C n denotethenthpartialsumsof E an, E b n
n=O n=O


00
and E Cn, respectively. It is easy to check that
n=O


C n = aoBn + alBn-l- +... + anBo.


Therefore


Co + Cl" + ... + On = AoBn + AJ-Bn-I' + ... + AnBo.
Dividing both sides of the last equality by n+ 1, using 2.3.2 and 2.3.8,
we obtain C = AB.


00 00
3.6.8. Let E en be the Cauchy product of E (_l)n-l
 with it-
n= 1 n=1
self. rl'hen
( ) n-l ( 1 1 1 1 )
en = -1 1 . n + 2(n - 1) +... + ken - k + 1) +... + n · 1 ·




338


Solutions. 3: Series of Real Numbers


Since


1 1 ( 1 1 )
ken - k + 1) = n + 1 k + n _ k + 1 for k = 1,2, ..., n,
we can write


( l) n-l 2 (1 1 1 1 )
en = - n + 1 + 2 + 3 + ... +;; ·


00
We know that E (_l)n-l
 = 10 2 (see 3.1.32 (8» and that the series
n..z:: 1
00
E (-l)n- l ntT (1 + ! +... +
) is convergent (see 3.4.19). Thus, by
n-l
the result in the preceding problem,


00 ( )
n-l 2 1 1 2

(-1) n+l 1+2+"'+; = (ln2) ·


00 00
3.6.9. If E en is tbe

u
..
rO<J.u
 of the series E (-1)
-1*
n=l ,,;:;;1
with itself, then


( ) n-t ( 1 1 1 )
en = -1 1 .
 +... + .jk +... + Vii 1 ·
.yn k. v' n-k+l n.
Since each term in the parenthesis is greater than
,we see that
co
lenl> 1 for n > 1. It then follows that E en is a divergent series.
n=l


3.6.10. We have
en = ao 6 n + Qlb n - 1 +... + anbo > aobnt


00
and consequentlyt if the series E b
 diverges, then the Qa
y_.

n=O . .
co
uct E en also diverges.
n=O


3.8.11. No. Consider the following two divergent series:


00 ( 3 ) " 00 ( 3 ) "-1 ( 1 )
1-
 2 and l+
 2 2"+ 2"+1 .




3.6. Cauchy Product of Infinite Series


339


Then


n-l
£;. = aob,J. + boan + L Okbn-kt
k=l
where tJo = bo = 1, an = - (
 )n , b n = (
)n-l (2
 + 2 n \I ). Hence


( S" ) n-l ( 0 1 ) ( 3 ) n
c,. = 2 2?' + 2"+ 1 - 2
( 3 ) n-1 n-l ( 1 ) ( 3 ) "
- 2 h 2 T1 - k + 2"-"+1 = 4 ·


3.6.12. Let An' Bn' C n denote the nth partial sums of the series
00 00 00
E an, E b n and E Cn, respectively_ Then
,&-=0 n;;: O n=O


C n = CloBn + arBn-l- +.... + a"Bo-


As a result,


n
E ak(b n + b n - 1 + ... + b n -k+l)
k= 1
= al(B n - B n - 1 ) + o2(B n - B n -2) + .. + on(Bn - Bo)
= Bn(An - 00) - atBn-l - a2 B n-2 - ... - anBo = BnAn - Cn.


00 oc:
3.6.13. Let E C n be the Cauchy product of the series L ( -l]n an
n=O n=O


00
with E (-I)nb n . Then
n=O


en = (-l)t1(a o b n + at b n -l + ... + anb o ).


00
Assume first that the series L Crt converges. Then lirn C n = o. By
n=O n-oo
the monotonicity of the sequences {an} and {b n }, we get
lenl
 bn(ao +... + an) and lenl > an(bo +... + b n ).


So
lim an(b o + b 1 +... + b n ) = 0 and lim bn(ao + al +... + an) = O.
n-oo n-.cc




340


Solutions. 3: Series of Real Numbers


Assume now that these two equalities hold. Then, by the preceding
problem, it is enough to show that


n
lim "(-I)kak«-l)nbn+(-l)"-lbn_l +....+( -l)'l.-k+lb n _k+l) =0.
n-ooL..,
k=1


Note that
I( -1)"b n + (-1)n-1b n _ 1 +... + (_l)n-k+lb n _k+ll :5 b n -k+ll


and consequently,


n
E(-l)k Ok «-I)nb n + (-1)n- 1 b n _ 1 +... + (_l)n-k+lb n _k+l)
k= 1


n

 E a k b n-k+l.
k=1


n
Now we show that lim E akbn-k+l = o. Indeed,
n-oo k=l


2n
o < E Ok b 2n-k+l :5 (a 1 + ... + an)b n + (61 + ...6,,)a nl
k=1


2n
which implies that lim E ak
n-k+l = O. In much the same way
n-oo k=1
2n-l
we show that lim E ak
n-k = 0, which completes the proof.
B-oo k=l


3.6.14. Observe first that it is enough to consider the case where
both Q and P do not exceed 1. We will now show that
11m .!. ( 1 + n\. + ... + .; ) = 0
R-OO n Q v n'"
if and only if a + fJ > 1. By the Stolz theorem (see 2.3.11),
lim 1 (1 1 1 ) lim 1
- +-+ +- ::=
n-oo n Q 2{j." nP n-oo nP{n Q - (n - 1)0)
=lim 1 Q _
n-.oo na+/J (1- (1-
) )




3.6. Cauchy Product of Infinite Series


341


By L'Hospital's rule,
1 t a+fJ
lim a =lim
%-'+00 xa+p (1- (1-
)) t-O+ 1- (1 - t)a
. (Q + {J)t a + 8 - 1
=lim .
t-O+ a(l - t)o-I


Hence


o if Q: + P > 1,
= 1 if Q + 13 = 1,
a
+00 ifa+p<l.
Now the desired result follows from the preceding problem.


Ii 1
n-
 n o + fJ (1- (1- *)Q)


00
3.6.15. Assume that the series E 4nbn converges. By the result in
n=O
3.6.13, it is enough to show that
lim an(b o + 61 + -.. + b n ) = 0 and Urn bn(ao + 01 + ... + an) = o.
n
oo n-oo
For an arbitrarily fixed E> 0 there is ko E N such that ako+lb
+l +
a
+2bko+2. + ... < ; - Thus for n > ka,
E
an(b 1 + ... + b n } < an(b.. +... + bko) + 2-
On the other hand, since lim an = 0, there is nl > ko such that
n-co


E
an < . if n> nl,
2(bo + ... + bAo)
which in turn implies that an(bo + ... + b n ) < E for n > nt. Hence
we have proved that lim an(bo +... + b n ) = o.
n-oo
Assume now that the Cauchy product is convergent. It then
follows from 3.6.13 that lim an (bo J ... I b n ) - O. As 0. result, for
n-.oo
sufficiently large n,
(n + l)anb n < an(bo +... + b n ) < 1,
and consequently,


( 1 ) 1+0
{a n b n )l+a < n + 1: ·




342


Solutions. 3: Series of Real Numbers


3.7. Rearrangement of Series. Double Series


()Co
S.7.1. Let 8n = 01 + a2 + ... + an be the nth partial sum of E
.
n=l
Then
6 1 + b:2 + ... + b n = 8m,. for n
 1.
Since each subsequence of a convergent sequence converges to thE
same limit, lim 8m,. = lim Sn.
I'J-OC n-:xJ


3.7.2. Denote by {Tn} the sequence of partial sums of the rear-
ranged .series. Then
T 3n = ( 1 - D -
 + G - n - ij + ...
( 1 1 ) 1
+ 2n-l - 4n-2 -4;
1 1 1 1 1 1

 2 - 4 + 6 - 8 + ... + 4n - 2 - 4n
1 ( 111 1 1 )
= 2 1 - 2 + 3 - 4 + ... + 2n - 1 - 2n ·


Therefore, by 3.1.32 (8), we get lim T 3n =
 1n2. or course, lim T3r
n-co n-OC
= fun T 3n + l ::: lim T3n+2. It then foUows tha.t
IJ,-QO n-OO


111111 1
1 - 2 - 4 + 3 - 6 - 8' + 5 - ... = 2 In 2.


3.'1.3. Let {Tn} be the sequence of partial sums of the rearrange(
series. Set f(n) = 1 +
 + A + ! + ... + n:l +
. Then
1 1 1 1 1
TQ+

 1 + 3 + ... + 2a - 1 - 2' - 4' - ... - 2P
= j(2a -1) -
 j(O' - 1) -
 j(8) = j(20') -
/(O') -
/(.8).


Now we will prove by induction that
1 1
Tn(Q+p) = f{2na) - 2 /(na) - 2!(n{J).




3.'1. Rearrangement of Series. Double Series


343


As we have already shown, the equality holds (or n = 1. If it holds
for an n e N, then


1 1 1 1
7(11+1)(0+11) = 1(2t1Q) - 2/(no) - '2/(n(J) + 2na + 1 + 2no + 3
111 1
+ ... + 2(n + 1)0 - 1 2np + 2 2n,B + 4 -... - 2(n + 1),8
1 1
= J(2no) - 2/(na) - 2 /(nfJ) + /(2(n + 1)0 - 1)
1 1 1 1
- 2/«n + I)Q - 1) -j(2na) + 2/(na) - 2 J «n + l)P) + 2/(nfl)
1 1
== j(2(n + 1)0) - 2 / ({n + 1)0) - '2/(n + 1){3.
Hence, by 2.1.41,
lim Tn(a+.8) = Iim ( /(2no) - 1n(2na) - - 2 1 /(na)
n-oo n-oc
1 1 1 )
+ 2 ln (na) - '2!(n P ) + 2 In (nP)
+ n
 ( 1n(2na) -
(In(7IQ) + 1n(n,8» )
. 2na 1 0
= limln =ln2+-ln-.
"-00 v n 2a {j 2 fJ
ObviousJy, for k = 1,2,3, ..., (Q + P) - 1, we have lim T n (o+6)+i' =
n-oo
lim Tn(a+p). Consequently, the sum of the series is In2 + llD!A.
n-co P


3.7.4. Note that this
t is contained 88 8 special case (0 = 1 and
p Ie 4) in the preceding problem.


3.7.5. It is enough to apply the result in 3.7.3 with a = 4 and fJ = 1.
3.7.6. Consider the series
11111111
(1) 1 - 2 + 3 + 5 - 4 + 7 + 9 + IT - 6 + ...


00 1-1\"-1
o bta-ined by rearranging the terms of E
 in such a way that
n=l
n., n = 1,2,3,... , positive terms are followed by one negative term.


Copy' c:"ted ,'letter,;!




344


Solutions. 3: Series of Real Numbers


Collecting the terms of series (1) in the following way:
( 1 _ ! ) + ( ! + ! _ ! ) + ( 1 + 1 + .!.. _ ! ) +
2 3 5 4 7 9 11 6 ... ,
we get
OO ( 1 1 1 1 )
(2)
 2 + 2 + ... + 2 - - ·
L.J n -n+l n -n+3 n +n-l 2n
n-l
Let Sw. and Tn denote the nth partial sums of the series (1) and (2),
respectively. Then
1'1 ( k 1 ) 1 n 1
Tn =S
+n > E k2 +k-l - 2k > 4 E k n:::' +00.
kzl k=l


3. "/.7. Grouping the terms of our series, we tewti te it in the form


CO ( 1 1 1 )

 v'4n - 3 + v'4n - 1 - v'2ii ·


Moreover,


111
+ -

4 n - 3 v4n -1 ..f2R
_ v(4n - 1)2n + V(4n - 3)2n - y(4n - 3)(4n - 1)
-
4n - 3 v4 n-lv'2ii
2..f2R - van - 1 2..f2R - J4ii 2 - V2
> _
 > _t;:;:::= .
v4 n-1v2n v4 n-1v2n v 4 n - 1
Thus Urn
 :c: +00, where {8n.} denotes the bequence or partial
n-.oo
sums of the rearranged series. Consequently, the series diverges.


00
3. 7.8. Assume that the series E On converges absolutely, let Sn
n=1
denote its nth partial sum, and set S:= Jim Sn- Denote by {Tn}
11-00
the sequence or partial sums of a rearranged series. It follows from
00
the absolute convergence or E On that, given E > 0, there is n e N
n.=1
such that


(1)


IOn+ll + lan+21 +... < E.


Gopy
 f:..tf
 1'lClt,:
,.a




3.7. Rearrangement of Series. Double Series


345


Let m be 50 large that all the tenns a1J
, ...,an appear in Tm.
Then, by (1),


IS - Tml < IS - Snl + ISn - Tml < 2e.


3.7.9. [4] Assume first that l > 0 and let n = d + u, d > u; then
00
rearrange the series E (_l)n-lf(n) so that the nth partial sum of
n=l


a new series is


Tn = Td+u = (/(1) - /(2) + 1(8) - ... - f(2
»
+ (f(2u + 1) + f(2u + 3) +... + f(2d - 1»).


This sum contains u negative terms, and all re maining terms, d in
number, are positive. The sum in the second grouping contains d-
u terms, and consequently, this sum is between (d - u)f(2u) and
(cl- u)f(2d). Since the sum in tbe first parenthesis converges to S
as u -t 00, the change in the sum is equal to the limit of the second
parenthesis. Set lIe u) = d - u. Then
(1) lI(u)f(2d) < f(2u+l)+f(2u+3)+...+/(2d-l) < v(u)f(2u),


and the monotonicity of the sequence {nj(n)} implies
( ) u j(2u + 211(u) 1
2 u+ II(U) < f(2u) <.
Choose lIe u) such that


(3)


lim lI(u)f(2u) = I.
U-()Q


(One can take, e.g., II(U) = I [ /(
 ) ] .) Then lirn v(u) = 0, because
-" U-CIC) U


1= lim _ 2 1 v(u) 2uj(2u) and lim 2uf(2u) = +00.
u-
 u u-

Thus (2) implies that lim 1{2u+2
 u ) = 1. As a result, (1) and the
u-oo 1{2u
squeeze principle give


lim (/(2u+ 1) + /(2u + 3) +... + f(2d -1» = I..
u-co


So, we have proved tbat lim T2u+lI ( u ) = S + I.
u-oo .




346


Solutions. 3: Series of Real Numbers


 -.. _

Ai:jlld
 -----t:I


..._



Now note that if 2u + v(u) < k < 2(u + 1) + II(U + 1), then
o S Tt -72u+...(u) + f{2u+ 2) S T2u+2+II(U+l) - T2u+II(u) + /(211,+ 2)..
Since j(2u + 2) -+ 0 88 1.& -. 00, we see that lim Tk = S + I.
k-

In the case where i < 0, we can interchange d and u and proceed
analogously.


8. '7..10. Given € > 0, beg;nning with BOme value no or the index n,
we have


g-f f( ) g+€
< n < .
n n
Consider the rearranged series whose nth partial sum is (see the s0-
lution of 3.7.9)
Tn = Td+
 = (J(I) - 1(2) + /(3) - ... - f(2u»
+ (f(2tJ + 1) + J(2u + 3) + ... + 1(2d - 1).


(1)


Moreover, assume that the number d of positive terms" is such that
lim
 = k. Then, in the case where d > U t
t.&-oc
111
2u + 1 + 2u+ 3 +.... + 2d-1
( 1 1 1 )
= 1+ 2 +".+ 21£+1 +."+ 2d_l - ln (2d-l)
- (1 +
 + ... + 2u
 1 -1n(2u - 1»)
( 1 1 1 ) 2u-l
- 2; + 2u + 2 + ... + 2d - 2 - In 2d - 1 ·
By 2.1.41 eacb of the first two parentheses tends to the Euler constant

. As in 2.5.8 (a») we may show that the third parenthesis tends to
i In k. Hence
.. ( 1 1 1 ) 1
ta
 2u + 1 + 2u + 3 + ... + 2d - 1 = 2 In k.
Consequently, (1) implies that


lim (f(2u + 1) + 1(2u + 3) + ... + J(2cl- 1» = _ 2 1 9 In k.
u-oo




3.7. Rearrangement of Series. Double Series


347


Thus the change in the sum S of the series is
 gin k. Analogous
reasoning can be applied to the case d < u.
.


3.7.11. It is enough to apply the rearrangement described in the
solution of Problem 3.7.9° with II(U) = 1(2-u)P].


3.7.12. Take the rearrangement described in the solution of Problem
3.7.10 with 1im
 = Q.
u-oo




3.7.13. No. Indeed, let L an" be a rearrangement of a divergent
k=l
00
series E an. The monotonicity of the sequence {an} implies that
n=l


an! + 4n 2 + ... + anm < a1 + a2 + ... + am.


So, it is not possible to accelerate the divergence of this series.


3.7.14. [20] Choose a subsequence {ar,,} of {an} such that aT" <
min(2- n , Qn - Qn-l), n = 1.,2, ..., where Qo = O. Then


Or! + a r2 + ... + a rn
 Qn and 4,.1 + 4 r2 + ... + aT" < 1.


Thus since lim Qn = +00, the sequence {Qn -(arl +flr 2 +...+Clr,,)}
R-QO .
00
also diverges to infinity. Now, we add the terms of E an which do
n=l
not appear in the sequence {a rn } to the sum lIr. + a r2 + ... + Or" in
such a way that


Bt.+02+...+a r1 -1 +a r1 +0.,..+1 +...+lli+a,... + Br"+J +...+a,." S Qn,
and as is the last term aUowed. That is, if we add a term which does
not appear in the sequence {4r,,} and whose index is greater than i,
then the above inequality does not hold.


3.7.15. (W. Sierpinski, BulL Intern. Acad. Sei. Cracovie, 1911,
00 00
149-158] Let L Pn and L qn be the complementary subseries of
n=) n=]
00
a conditionally convergent series E 4n consisting of all successive
n=l
nonnegative and negative terms, respectively. Let a be an arbitrarily




348


Solutions. 3: Series of Real Numbers
.,


00
chosen real Dumber. Since the series E Pn diverges to +00, there
n=1
exists a least index k J for which


PI + P2 + ... + Pic, > u.


Next. we choose the least index 81 for which


PI + P2 +.n + Pk J + qJ +(/2 + ... +qnl < CT.
Then we find the least index k2 for which


PI + P2 + ... + Pic! + ql + fJ2 + ... + qnl + Pk l + I + ... + Pk
 > (1


and the least R2 such that


PI +P2+...+Pkl +q.+92+...+qnl +Plcl+l +...+Pk 2 +9n t +1 +...+qn:l < CT.


Continuing this pr
, we define two sequences k t ,k2)." and nit

,... and the corresponding rearrangement of our series. Let Son be
the nth partiaJ sum of this rearrangement. Then


Sn
a for n<k 1 but SQ
(1 for kl $n<k 1 +ot.


FUrthermore)
Sn :S u for
SA
 (1 for


km +nm
 n < km+l + 11m,
km.+l + 11m
 n < km+l + Rm+lt


where m = 1 t 2, .... By the definition of the sequences {k".} and
{nm} we also get


IS
+2 -1+
 - 0'1 < Pkm+l t
1 Slc m + I +lIm - 0'1 < Pk"'+1 t
ISkm+)+n.n.+l - 0'1 < PkPlt+1 for I = 1,2,.., 11rn+J - 11m - 1,
ISk",+1 +11"'+1 - 111 < 19"","11,
IS
+,+I+n"'+1 - 0'1 < iqnm+11 for I =:; 1,2, ..., km+2 - km+l - 1.
Since lim Pn:;: Iim qn = 0, we conclude that lim Sn = u.
Fa-CO 11......00 ft-OO




3.7. Rearrangement of Series. Double Series


349


3.7.16. Denote by {8m} and {Tm} the sequences of partial sums
co 0()
of E Un and E Un,., respectively. Since {nk - k} is a bOWlded
n=1 k=l
sequence, there is I e N such that k - I
 nk < k + I for all kEN.
H m > l and nk $ m - I, then k - I.
 nk $ m - I. Hence k $ m,
and consequently,
(1) {I, 2, ".t m -I} c {nI, n2, ..., n m }.
Indeed, if s is a positive integer not greater than m - " then there
exists a unique kEN such that s = nk. It then follows from the
above that k < m, or in other words, 8 e {n}, n2, ..., n m }. By (1-),
we see that each Clnt with n = 1,2, ..., m -I, appears in Tm. On the
other hand, if k < m, then nk < k.+l < m+l, and consequently, all
the terms Cln 1 ,a n2 ,...,o.,.", appear in Sm+l. Hence


ISm - T ml =:; lam-I+II + ... + ICZm+zI for 1R > l.
Therefore lim 8m = lim Tm.
m-oo m-oo


H the sequence {nk - k} is Wlbounded, then the examples given
in Problems 3.7.2 - 3.7.0: show that the rearranged series may diverge
or may change the sum of the series. Now we give an example of a
rearrangement that does not change the sum of the series. To this
end, we take a sequence {nk} obtained by the permutation of positive
integers that interchanges !!(
+l) with n(
+3>' and leaves the other
integers unchanged. Since n(
+3) _ n(
+1) = n, the sequence {nk-k}
is unbounded. Moreover,
{ 0,
Tm - 8m =
an(n+3-)/2 - 4n{n+l)/2t


if m = n(
+3) ,
if n(;+1:) $ m < n(
+3) .


3.7.17. [R. P. Agnew, Pruc. AlIlt
r. Math. Suc. 6(1955), 563-564]
m
We will apply the Toeplitz theorem (see 3.4.37). Set 8m = E ak and
k=l
m
Tm = E anJr. Asswne that m is so large that 1 E {nl,
,...,nm},
k=l
and arrange all the members of the set {nt, n2, ..., 11m} to form an
increasing sequence
1, 2,3.,..., PO,JRJQt,m + 1,Ot,m + 2
 ".,Pl,mt




350


Solutions. 3: Series of Real Numbers


ct2.m + It Q 2.m + 2, ...,{J2,m, ...,Qjwn,m + 1, Ctjrn,m + 2, ...,f3j,ra.mt
where


0< /Jo,m < Qi,m < Pl,m < Q2,m < ... < f3Jm,rn.
Hence the partial sum T m of the rearranged series can be written in
the following way:
Tm = SPo.m + (SPl.", - SQ1.m) +... + (SPJ",.m - SOjm. rn ).


00
Consequently, T m = E Cm.kSk, where
k=l


I,
Cm,k = -1,
o


if k = {l"rnt .1 -= 0, 1", ...,jm,
if k = Q',m, l = 1, 2
 ".,;m,
otherwise.


Since lim /30 m = +00, lim Cm,k = 0 for every kEN.
Ioreover t
m_1'Jn ' na-nn
00 00
L Cm.k = 1 for m = 1,2, ..., and E 1c,II.kl = 2.B m - 1, where B'II
k= 1 k=1
denotes the number of disjoint blocks of successive integers in the
set {nl' 112, ...t n,,&}. Finally, by the Toeplitz theorem, lim Tm =
m-oo
lim 8m if and only if there is N such that Bm
 N for all mEN.
m-oo


00
3.7.18. Assume that the series E c,& is absolutely convergent and
n=J
its sum is S. Then for any e > 0 there is ko such that


E
ICI + C2 + ... + Cko - 51 < 2 and


oc
1: ICII <
.
l::ko+l


Let m, n be so large that for each l E {I, 2, ".t ko} there exist i and
k, i e {l,2, ".t m}, k E {I, 2., .h' n}, such that Cl = at.k. Then


co
IS'R,n - 51 < ICI + C2 + ... + Cko - 81 + .L led < E.
l=ko+ 1


Hence the convergence of the double series to S is proved. Likewise,
the absolute convergence of this double series can be established.




3.1. Rearrangement of Series. Double Series


351


3.7.19. Set


00
S. = L 1Bi)kl,
j .1'= 1


00
T. = E lenl,
n=1


m n
S;',n :: L L

,kl,
i:x I 10:=1


n

=EJCkl.
k=1


Arbitrarily fix € > 0 and I E N. Take m, n so large that an tbe terms
of Tt are in S:n,n and'S. - S;".n I < E. Then 7',- $ S:n,n < S" + E t
00
which m eang that the series E en is absolut
ty.convergent. Denote
"==1
00
by Tn and T tbe nth sum and the sum of E
, respectivel
". To
n=l
prove the identity


ex: 00
L 02.1. = Eent
i,k:l ft-l
fix E > 0 and take I so large that
1 7 t - T"J < ; and IT, - TI <
.


In n
H Sm,.,. = E E 4i.k and if m, n are SO large that all tenns of 7i
i::s: 1 k= I
are in Sm.n, then


ISm." - Tt < iT -7}f + IT. -'IiI < E.


3.7.20. This is a coronary or the two preceding problems.
3.1.21. Assume that, e..g., the iterated series E ( f ta..kl ) con-
i=J k-l
ore 00
verges, and set E 100,kl = O'i and E (Ii = (1'. Therefore, each of
k-I i
l
the series E
.t, i;::- 1 1 2, ..., converges, and E 4i,k ! = ISil $ Dj.
k=l k
1
Ole
This and tbe converg
.of E Ui imply the absolute
vergmxce of
. ...... i-I ... -
.t; Si. ConsequentlY, !; Si =
 (fl Bo.It) ·




352


Solutions. "3: Series of Real Numbers


00 00 171 11.
3.7.22. Let E a;,k = $, E ICli,kl = S., and set Sm.n = E E ai,k
i,k=1 f,k=l i=1 k=1
m n
and S;",n = E E Ia.;,kl. We first show that the iterated series
i=1 k=1



 (
 la i . kl )


converges to S.. Indeed, given E > 0, there is no such that S. - E <
S;",n < S* for m, n > no. Let m be fixed for the moment. Then the
sequence {S:',n} is monotonically incr easin g and bounded. Thus it
is convergent, lim S:n n = S:n, o.nd consequently, S* -c
 S:n
 S"
n-oo '
for m > no. This means that lim ( lim S;" n) = S*. We know from
m-.oo n-oo ·
the preceding problem that absolute CQDvergence of the iterated series
00
implies its convergence. Thus E ai,k converges for each it say, to
k=1
Sj. We will now show that for every c> 0 there is ml such that


I(SI + 82 + ... + 8m) - 81 < E for m > mi.


By the absolute convergence of the double series,
ISm... - SI <
 and IS:'... - S., <
 for m, n > mI.
Therefore, for m > ml,


m fX)
1(8) + 52 + ... + 5na) - 81 = L L aitk - S
i=1 k=l


m 00
S 1 8 m.n - 51 + E E Ui,k :s; ISnl,n - 81 + IS" - S
,nl < E_
i=l k=1a+l


The proof of the convergence of the oth
r iterated series is
aIogous.


00
3.7.23. Note that the series E (an,1 + 0.,.-1,2 + CIn-2,3 +.... + al tn )
n=l
is an ordering of the double series. H one of tbe series


00
L Illi,kl,
i,k;::!


00
E(la n ,ll + IBn-l,21 + lan-2tal + ... + lal,nl)
n- )




3.7. Rearrangement of Series. Double Series


353


converges, then our claim follows directly from 3.7.18. 3.7.19 and
3.7.22. Hence it is enough to show that the absolute
nvergence of
one of the itera1ed series implies the absolute convergen
 of any or-
dering of the double series. To this end, assume that. f ( E jOi,tl )
i=l k
1
converges. say, to S.. Let {en} be a sequence obtained by an enu-
meration of the infinite matrix (lJi.l;)i
k=1
2..... Then for LEN there
exist m, n so large that


m n
ICII + I C 2f +... +
ClI :5 E E f
.kl
 S..
i
J k= 1


00
Thus the series E en converges 81)solute
Yt which in turn implies
n=1
the absolute convergence of tbe double series (see 3.7.18).


m
3.7.24. Since E e::> = 2m
 we get
k==O


m
'" J 2 tr1
L.J ;;m = ;;a. Hence
n
k=O
k+n=m


m 1 2 m
n
 o n!k!(n + k + 1) = (m + 1)1'
J:+n=m


Consequently, by 3.7..23,


()Q 1 00 'rJl 1
E n!kl(n+k+l) = E E n!k!(n+k+l)
!I. k=O m=O n,k-O
I:+n;:m

 2 m 1
 2m+l 1 2
= E (m+l)! =2 E (m+l)! =2(e -1),
m
 mzO
where tbe last equality follows from 2.5.7.
3.1.25. We have (see 3.7.23)
00 1 00 1 OQ 1 ( 1 1 )
"
I nk(n+k+2) =
 n?; n+2 k - n+k+2
(X) 1 ( 1 I 1 )
=
 n(n+2) 1 + 2 + 3 + ...+ n+2




354


Solutions. 3: Series of Real Numbers


1 00 ( l 1 ) ( 1 1 )
= 2
 ;;: - n + 2 1 + 2 + 0" + n + 2
1 { II 1 ( 1 1 1 ) 1 ( 1 1 )
=2 1+ 2 + 3 + 2 1+ 2 + 3 + 4 + 3 4+ 5
1: ( 1 1: ) } " 7:
+ 4" 5 + 6 +... = 4.


3.7.26. It follows from 3.7.23 that


00 n!k! 00 k! 00 ( n! (n + I)! )
L (n+k+2)! =L k+l L (n+k+l)! - (n+k+2)!
n. A.-O k=O ,
 o
00 k! O! 00 1
= L k + 1 (k + 1)! = L (k + 1)2 .
k=O k=O


Hence, by 3.1.28, the desired equality is proved.


3.7.27. Observe that the sum of each row series of the matrix is
finite. Indeed, the sum of the first row is x, of the second is x(l- x),
of the third is x( 1 - X)2, etc. Moreover,


.
x + x(l- x) + x(l - x)2 + .. = 1.


On the other hand, the sums of the col umn series are alternately equal
to 1- and - - i
 Therefore the other iterntcd series diverges. By 3.7.23,
we conclude that the iterated series cann ot converge absolutely.


3.7.28.


00 00
(a) The absolute convergence of E Xi and E yk imply the absfr
i=O k=O
Jute convergence of the iterated series i
 (Eo xiyk ) . because
f ( E I

lfl ) = f: Ixil (
 ) = (l-Izt)l(l-fiif> . Consequently,
&=0 k=O 1=0
the given double series is absolutely convergent.
(b) Considering the iterated series, we see that our series converges
if and only a > 1 and {3: > 1.




S.7:. Rearrangement of Series. Double Series


355


(c) Collecting the terms for which i + k = n, we get
co 1 00. 1
.L (i+k)p = }:)n-l) W' .
t., k 1 n=2


Thus the double series converges if p > 2: and diverges if p S 2.


3.7.29.
(a) It is enough to calculate the sum of the iterated series. We have


00 ( 00 1 ) 00 ( 1 1 ) 1
E E (p + ")k = E " . +. 1 = + 1 ·
i=2 k=2 'A i=2. P + t P t - P

) As in (a), we compute the sum of the iterated series:


00 ( 00 1 ) 00 1 OO ( 1 1 )
L ?: (2k)i = L 2k (2k -1) = L 2k-l - 2k
1:=1 I -
 k=l k=l
00
= E(-l)k-l! = In 2.
k=l k
The last equality follows from 3.1.32(a).
(c) As in (b), we have
00 ( 00 1 ) 00 1 1
k t; (4i - 1)210 = k (4i -2)4i = 4 In 2.


m n
3.7.30. Since Sm.n = E E ai,k = bm,n, we see that
i=1 k=1


al,l = 8l. 1 = bl,l,
al,ft = SI.n - 81.n-l = 61-.n - bl.n-t, n > 1,
Om,1 = Sm,! - 8m-lt l = b m ,! - b m -l.!, m> 1.
Similarly, for n, m > 1j we get
am.n = Sm.n - 8m-l.n - (Sm.n-l - 8 m -1,n-l)
= bm,n - b m - 1 . n - (b m . n - 1 - bm-l.n-l), n, m > 1.




356


Solutions. S: Series" of Real Numbers


3.7.31. We have Sm." = (_l)m+n (
 + in). So, for £ > 0, there
is no such that if m, n > no, then
ISm,nl < &.
Therefore the double series converges to zero. However, both the
iterate4 :series diverge. Indeed,


ft

 n_' k - S . S . 1 _ ( _ l) i+n! +( _ l) i+n 1


, - I,n - ..-." - 2i
-l t
k=1


0()
whim implies that every series. E Oi,
, i e N, diverges.
k:l


3.7.32. We have


00 ( 00 ) 00 I I'
?:
):tlik =
 1
I.xli .

l '-- I ,
1


By the ratio test, the .seriEs
 on the right-hand side of this equality
converges. This means that the i
l:lted series converges absolutely.
Thus by 3.7.23,


00 C)Q Ie

tk ,",x
L-,x =
l-zk.
itA:= 1 "- 1
Collecting the pairs (i, k) with the same value of tbe product ik, we
get


00 00
E xik = E6(n)x n ,
i.k=-l
1
because the number of divisors of n is equal to the number of the
pairs (it k) Cor which it = n. Moreover, for n = 2t3, ...,


Sntn - 8 n - l ,n-1
= :E" + z2n + ... + x(ft-l)n + zn
 + x n (n-l) + ... + 2:"0 2 + z'B
2
x" -
n; 2
= 2 1 n +zn.
-:I:


Obviouslyt 8 1 ,1 = oX = 2
:: + x. Hence, on account of
8n t .", = (Sn.n - Sn-I,n-l) + (Sn-l,n-l - Sn-2,n-2) + ... + SI.1 ,




8.7. Rearrangement of Series. Double Series


357


we see that



 k
 n


E z
 E x - x E n':l
-
 + x
. l-x k - I-x n ·
k=l n=l n=1


3.7.33. As in the solution of the foregoing problem, we show that the
iterated series converges absolutely. Thus the first equality follows
directly from 3.7.23. To prove the o
her equality we consider the
ordering of the double series described in the solution of 3.7.32.


3.7.34.
(a) By 3.7.23,


00 00 1 00 1 .00 1 .
ES,,= Ezn+ E3r'+."= E k(k-l) =1.
p 2 n=2 n=2 k=2


(b) As in (a),


00 00 1 1
L(-I)"8" = L k(k 1) = 2.
p=2 k=2 +


3.7.35. Let B denote the set of all integers which are not powers.
Then


A = {k n : n.E Nt n
 2, k e B }.


00
Since fl:l == E ;b-, n
 2, applying 3.7.23 and 3.7.34, we get
;i.-I


1 co 1 00 00 1
E n-l =EEnJ=ELE

nEA nEAj=l kEBn=2j=1
00 oc 1 00 00 1
= LLL k n ; =LL k n =1.
keB ;=1 n=2 k=2n
 :


8.7.36. [G. T. Williams, Amer. Math. Monthly, 60 (1953), 19-25]
The left-hand side of the equality is equal to
N N ( 1 1 1 1 1 1 )
(.) J
oo E E k2 .2n-2 + k4 .2n-4 + ... + k 2n - 2
 ·
j

 l J J J




358


Solutions. 3: Series of Real Numbers


Summing the expression in the parentheses, we get


(**)


. N N j'Z-2n _ k 2 - 2n 1
N
moo E E k 2 _.
-2 + (n -1) -2n ·
J "=l k=l' J
k
j


Note that


N N -2-2n k 2 - 2n N N
2n N N k 2 - 2n

E J k 2 =P =?:E ;2_j2 -
E k2_j

) =1 k=l } =1 k=1. } =1 k=l
k
 k
 k

NN 1 1 NN 1 1
= EE j'ba-2k2 _]"2 + EE k 2n - 2 j2 -k 2
j=lk=l j=lk=l
k
 k

N 1 N 1
= 2 E pn-2 E k2' _ j'Z '
j=l k==l
k:pj


Hence


=lim
N-oo


N j2....2n _ k 2 - 2n I
E k 2 "- -2 +(n-l)

k=l J J
k:#j
N 1 N 1 N 1
2 L -2n-2
 k 2 _ "2 + (n-l) E-=?;".
' "=1) k=l J ' "=1)
k;#j


N
lim

N-ooL.-J
;=1


(* * *)


Now, observe that
_N 1 N 1 N 1
2J L k2- _ ;2 = E k - ; - E k + ;
k;J k=l k=l
k=Fj k
j kt-j
;-1 1 N 1 NIl
=E k - . + E k- . -E k+ . +

k=J 1 k -; +l 1 k=t" 1 J
j-l 1 N-j 1 N+j 1 1 N+j 1 1 N-j 1 1
=-L k +E k - E k +f==-Ek+-:+Ek+

k=l k=1 1..-=;+1 '.J 1c:=1 J 1c:=1 1




3.7. Rearrangement 01 Series. Double Series


359


3 ( 1 1 I )
= - - + + ... + - .
2; N - j + 1 N - j + 2 N + 1
Thus by (. * *),


N N j2-2n _ Jil-2n 1
L L k 2 - -2 +(n-l)

j=l k-J J J
k
i
iN} N 1 ( 1 1 )
= (n + 2) L:
 - L: -2fl-1 N - . + 1 +... + N +. ·
i=1 J ;=1 3 J 1
Moreover, since 0 < 'N-
+1 +... + N
j < N-=t+1 ' we see that


N 1 ( 1 1 )
O<
 j2"_l N-j+l +...+ N+j
N N
2" 1 1 <2,,1 1
< L.J -2n-2 N - . + 1 - LJ -: N - - + 1
j
l J J ;=1 J 1
2 N ( 1 1 )
= N+l ?: -:+ N-'+l
)::::;1 J ,
4 N 1 4
= N + 1 E -: 5 N + 1 h + In(N + 1»,
;::::;1 1


where" is the Euler constant (see 2.1.(1). Finally, by (*),
. N N ( l 1 11 11 )
N
co
 L k2 pn-2 + ki j2fl-4 +... + 1.2 n - 2 fi
J=lk=l


1 NIl
= Jim (n + 2 ) "
 = (n + - 2 ){{2n).
N -'OQ L..J J
j=1


3.7.37. Substituting n = 2 in tbe identity given in the foregoing
problem, we get


«2)«2) = (2 +
)«4).




360


Solutions. 3: Series of Real Numbers


Since '(2) =
 {see 3.1.28 (a», we obtain (see a1so 3.1.28 (b»
co 1 4
(4) = E 4 =
.
n=ln 90
Likewise, taking n = 3, we find that
00 1 1f'6
(6) = E TIft = 945 .
8=1


S imilarl
y,


00 1 7r 8
C(8) = E n8 = 9450 .
n=1


3.8. Infinite Products


3.8.1.
(a) We have
Pn = Ii ( 1 -
 ) = Ii (k - 1)
k + 1) = n + 1
k= 2 k k=2 k 2n


1
.-. -
n-.oo 2.


(b)


n (k-l)(k 2 +k+l)
II (k+ 1)(k 2 - k+ 1)
k-2
= II n (k-l)«k+l)2-(k+l)+1) = 2(n2+n+l) --+
.
( k + 1) ( k 2 - k + 1) 3n(n + 1) 8-00 3
k=2


(c) For x = 0 the value of the product is 1. H x ¥: 2 m ( ; + k1r) I
then cos -fm 1= 0 and sin fn :f: o. Hence


n n t . :Z: . .
II x II Sln 2
 - 1 Slnz smx
C05-= - = --+.
2 k 2 sin
 2n5in
 n-oo Z
1.:=1 1.:=1 2 2


(d) On account of the formulas


sinh(2z) = 2sinhxcoshx and


. sinhx
lun = 1,
%-0 X




3.8. Infinite Products


361


as in (c), we get
00 { sinh x
TI cosh
 = :z:
n=1- 1


if x ;i: 0,
if x = o.


(e) We have
TI n ( xr- ) _ TI n 1 - X21e+1 1- x2ft+l 1
1+. - l_x 21c - I-x n
 I-x .
k=O k=O


(f)


n ( 1 1 ) TI n (k + 1)2 2(n + 1) 2"
TI + k(k+2) = k(k+2) = n+2 n
'
k=1 k=]
(g) Since


n n ( 1'*
TI
 E
Ie
-
a
 = alc
l ,
k=l
the continujty of the exponential function and 3.1.32 (a) imply
00 ( _ I) "
that n a n = a-1D
.
n.=1


(h)


n
n 1 E i "
TI e1i e k =l E i-Inn n
- - e*=l ·
k=1 1 + * - n + 1 - n + 1.
Thus by 2.1.41,


00 1-
TI en -..,
1 .i-e.,
n=1 + n
where 'Y is the Euler constant.
(i) We have
n (3k)2' n (3k)3 33n(n!)3
Pn = !! (3k -1)(3k + 1) = !! (3k - 1)3k(3k + 1) = (3n + I)! '
Using the Stirling formula


on! = an v2 1m (;) n, where


lim an = 1,
n-oo




362


Solutions. 3 0 : Series of Real Numbers


we get


. . 33n(2
)3/2n3n+3f2e-3n
nl!.
 Pn = n
 (211")1/2(3n + 1)3n+l+1/2 e -3n-l
( 3 ) 3n ( ) 3/2, 2
2 lim n n 11"
= 7re = .
R-CO 3n + 1 3n + 1 3v'3


3.8.2.
(a)


2n ( ( _1)1c ) 3 2 5 4 ( 1 )
P2n = II 1 + = - · - · - · - . .... 1 + -
k=
o k 2345 2n
= l' + 1:.. -.. 1,
2n n-oo
3 2 5 4. 2n-l 2n--2
1'2n-1 = 2: · 3 · :4 · 5 · ... · 2n - 2 · 2n - 1 = 1.


(b) We have


n ( 1 ) 3 I n+ 1
Pn = IT 1 + k = 2 · 2 · 3 · ... · n = n + 1- n
 +00,
k=1


00
so that n (1 +
 ) diverges.
n=1


("0
(c) The product IT (1-
 ) diverges, because
n=1


n ( )
11.23 n-11
Pn = II. 1- k = 2 · 3. 4 . ... . n = n n
 o.
k =2


3.8.3. Note first that for nonnegative an,


(1) at + a2 + ... + an < (1 + (1)(1 + lI2)...(l + an).


Moreover, the inequality ez
 1 + x,

 0, gives


(2) (1 + (1)(1 + a2)...(1 + an) ::;; e41+C2+...+an.




3.8. Infinite Products


363


The inequalities (1) and (2) together with the continuity of the expo-
00
nential function show that the convergence of the product n (1 +
)
n..:l
00
is equivalent to the convergence of the series E an.
n=1


00
3.8.4. Asmme that the series E an converges. Then for sufficiently
'1=1


00
large Nt E On < !. It follows from 1,2.1 that
n=N
n n 1
II (1- Ok)
 1 - L air > 2'
k=N k=N


n n
Since Pn = n (I-at) = PN-1 n (1-0l;), we see that the sequence
k=l k=N
{ "P="- I} is monotonically decreasing and bounded below. Conse-
quently, it converges, say, to P. Then P E [41 IJ. Thus Um Pn =
n-oc
PN-I P :F O.


00
To prove tbe other implication t assume that E an diverges.
"=1
If tbe sequence {an} does not converge to zero
 then the sequence
{l - an.} does not converge to 1 and the necessary condition for
00
oonvergence of n (1 - an) is not satisfied. So we may 88SUI11e that
n=1
lim Otto = 0, and consequently, 0 $ On < 1 beginning with some
n--+oo
value N of the index n. In view of the formula (see 2.5.7)
( x 2 z3 ) ( X4 xS )
e- z = 1 - x + 2f - 3! + 4f - Sf + ...,
we get I-x
 e- z for 0
 x < It because all the terms in parentheses
are nonnegative. Hence
ft ft
- E 4,.
o
 II (1 - Qk)
 e k=1J , n
 N,
k=.N


n 00
and consequently, lim n (1 - QAJ = O. Therefore, n (1 - an)
n-oo It:=N "=1










364


Solutions. .3: 'Series of Real Numbers


3.8.5. Note that


2n n
n (1 + ak) = n (1 + 02k-l)(l + a2k)
k=l k=l
= Ii ( 1 + 2... + ! ) ( 1 - 2... ) = Ii ( 1 _ 1 ) .
k= 1 ..fk k .../k k=l k.vk


Thus, by 3.8.4, the product converges.


3.8.6.
(a) Since cos
 = 1- (1- COB
 ) and 1-
 1- cos
 > 0, n e N,
we can apply the result in 3.8.

 Thus the convergence of the
00
product follows from the convergence of the series E (l- cos
 )
n=l
(see 3.2.1 (e».
(b) As in (a), the convergence of the product follows from the con-
00
vergence of E (1- nsin
) (see 3.2.5 (d».
n=l
(c) We have


( 1r 1 ) 1 + tan..! 2 tan .1
tan -+- =
 =1+ . n 1 .
4 n I-tan; I-tan n


S ince 2 tan '\ ;> 0 for n > 2.and
I-tan - .
n


2 tan 1
lim I-t
 n = 2,
n-oo -
n


by 3.8.3 the product diverges.
I- n ln i 1 +;J.; :) 1
(d) In view of lim n = 2' the convergence of the product
n-oo n
follows from 3.8.4;.
(e) The divergence of the product follows from the divergence of the
00
series E ( vn -l) (see 3.2.5.(a».
n=1




3.8. Infinite Products


365


(f) Since lim .
 = I, it follows from 2.5.5 that nm.._ao
.. =
ft
 · n-I
1. Thus the convergence of tbe product follows from the coover-
00
gence of the series E I:: .
n=2


00
3.8.7. By assumption, the series E On converges and, without loss
n=1
of generality. we can assume that lanl < 1. Since
lim an -met + an) =!
n
co
 2


(1)


00 00
and the series E an converges, the convergence of E
 is equiv-
n-l n=1
00
alent to the convergence of E In(t + an), which in turn is equivalent
n=1


00
to the convergence of n (1 + On).
n==1


00
Note that if E
 diverges, then by (1),
neat


1
On -In(l + On) > 4
 for sufficiently large fi.


00
Thus the series E In(l + an) diverges to -00, which means that
nat


00
IT (1 + On) diverges to zero.
fllat


3.8.8. The result follows imm ediately from 3.8.7.


3.&9. Apply 3.8.7 or 3.8.8.
3.8.10. We use the equality
lim IIn(l+Gn)-On+

1 =!
n-oo IGnP 3


and proceed as in the solution of 3.8.7.


Copy' c:"ted ,'letter,;!




366


Solutions. 3: Series of Real Numbers


3.8.11. No. By t.he test in the foregoing problem, we see that the
product given in the hint converges if 1 < Q. On the other hand, the
series


1 ( 1 1 ) 1 ( 1 1 ) 1
-2Q' + 20 + 220- - 30 + 30 + 3 20 -
 + ...


and


( 1 ) 2 ( 1 1 ) 2 ( 1 ) 2 ( 1 1 ) 2 ( 1 ) 2
-
 + 2Q"+ 2 20 + -
 + 3Q+ 3 2a + -
 +...


both diverge if Q

.
3.8.12. Observe that if Iim On = 0, then
n-+oo


11n( 1 ) 1 2 1 3 ( - ) } .tc let
lim + 4n - an + 2 a n - 3 a n +... + k an ! 1
n--oc 1a,.l k + J :z k + 1 ·


3.8.13. By the Taylor formula,


1
m(t + an) = an - 2(1 +(In)2
 = an - ena
,
where I < en < 2t if Ian I < I. Thus if nIt n2 are sufficiently large
and nl < n2) then


"2 n:l"2 ( 2 )
L In(t + an) = L a,. - e L a
, where e E 9' 2 ·
71 :;;''' 1 n=n, n=n,


00
Hence the convergence of E On follows from the Cauchy criterion.
'IJ.= 1 .


00 00
3.8.14. H the products n (I +
) and n (1 - an) both converge)
n
1 n
1
00 00
then n (l-a
) also converges. Consequently, the series E a
 con-
n- I n=)
verges (see 3.8.4). Now the desired result follows from the preceding
problem.




368


Solutions. 3: Series of Real Numbers


S.8.18. Observe that
Gl Ii ( 1+ SOl: ) =Gl ft 58. =8...
k=2 k-l k=2 1:-1


3.8.19. See Problem 3.1.9.
3.8."'0. See Problem 3.1.9.
3.8.21. Appty the foregoing problem with On = z'l.


00
3.8.22. ASStJrne first that the product n On converges , that is,
n=1
"
1im P" = P :F 0, where Pya == n O.k. This implies that there is
....-..00 b1
a > 0 such that IPn I
 a for n E N. The convergent sequence {Pn}
is a Cauchy sequence. Thus for every £ > 0 there is an integer no
such that IPR+A: - PR-Il < EQ if n
 no and Ie E N. Therefore
I P,,+
 I EQ
Pn-l -1 < lPn-II
 £ for n
 no.
Assume now that for every E > 0 there is an integer no such that
(.) lanGn+l ..... On+. - 11 < E
for n
 no and kEN. Taking £ = I, we get
( ) 1 P"-1 3
.. 2 < PlIO < 2 for n > no.
Next using (.), with e replaced by i
"O l ' we find an integer fl.l such
that


I Pn+J; I 2e
Pft-l -1 < 31 P nol (or n
 nl, kEN.
Hence if n > max{no, Ol}, then
I I 2e I Pn-t l
P,,+, - P"-1 < '3 Pno < £.
This means that {Pn} is a Cauchy sequence. Moreover, it follows
&om (**) that its limit is different &om zero.


CO
>y
lgl.tcd material




3.8. Infinite Products


369


3.8.23. We have


2..
2n 2n 1 2k n (1-x 2k )
II (l+x k )= II -x =k=l
1 - x lc 2n
k=1 k=1 II (1 - xk)
k=1


,


2n
n (l - x2k)
k=1


-
-


2n
n (l-x 2k )
k=n+l
n
n (1- x2k-l)
k=1


.


-
-


n n
n (1- X2k) n (1- .z21:-1)
k=l k= l


Now, the desired result follows from the Cauchy criterion (3.8.22).


3.8.24. This is a consequence of 3.8.3.


3.8.25. Note that for al,a2, ...,an E Rt


1(1 + at)(l +
)...(l + an) - 11
 (1 + lal 1)(1 + la2J)...(1 + lanD - 1


and apply the Cauchy criterion (3.8.22).
3.8.26. Set Pn = (l+at)(1+a2)...(1+an), n E N. Then Pn-Pn-l =
Pn-1Cln and


Pn = PI + (P 2 - PI) +... + (Pn - P n - 1 )
= p) + P t a 2 + P 2 a 3 + ... + Pn-lt1n.


Thus


Pn = (1 + al) + a2(1 + at) + a3(1 + al)(l + a2)
+... + an(l + al)(l + CI2)...(l + an-I),
or equivalently,
Pn = (1 + al) + (a2 + ala2) + (a3 + a)a3 +
a3 + ala2 a a)
+ ... + (an + 4lCn + ... + On-Ian + 41l12an
+... + Bn-2lLn-l4n + ... + QllL2...4n-llLn).


00
Note that absolute convergence of II (1 + an) implies the absolute
n=1
00
.convergence of the series 1 + a} + E an(l + al){! + a2)...(1 + an-I).
n=2




370


Solutions. 3: Series of Real Numbers


This series is an ordering of a double series whose terms form tb
infinite matrix


a) a:z
al
 al. a a
Blll2 B 3 Bi' a 2 a 4


43;
a2 a S-.
ala3 a jJ


44
alD.4
Q2 Q 3l14 · · ·


. . .


. . .


. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .


By 3.7.18 the double series converges absolutely, and by 3.7.22 th
iterated series given in the problem coDverges. Consequently, th
desired equality holds.


00 00
3.8.27. Dy the absolute convergence of E an, the series E an3
n=l n=l
converges absolutely for every :& E nt Now it is enough to apply tb
result in the preceding problem.


co
S.8.2R. OhvinnR)Y. fnr Iql < rAnd !r. E R. thp. prnrlllr.t n (1 +q7' X :
n=1
converges absolutely. Taking an = qn in the foregoing problem, WI
00
get J(x) = IT (1 + qRx) = 1 + A1x + A 2 x 2 + .... Now observe tha
n=l
(l+qx)f(qx) = f(x). So equating coefficients of like powers, we obtaiJ
q qn
Al = 1 and An = An-I" l for n = ,2;3,....
. _ q , _ qft
Finally, by induction, we can show that


n(n+1)
q 2
An= .
(1 - q)(1- q2) · ... · (1- qn)


00
3.8.29. Set f(x) = n (l+Q2n-lx) and note that (l+qx)f(q2x) =
n=l
j(x), and apply reasoning similar to that in 3.8.28.


3.8.30. We have
Q(I+ t1n X) (1+
) = (1+
 Ak
) (1+

: )
00 ( 1 ) 00 ooA
=l+
 Ak
+Xk + H Ad' H; .




3.8. Infinite Products


371


00 00
The absolute convergence of E AkXk and E
 implies the abso-
1c=1 1:=1
lute convergence of their Cauchy product (
 the solution of 3.6.1).
Observe that. this Cauchy product is an ordering of the double series
corresponding to the matrix
AlAI A
A2
A2Al (x +
) A3A
 (x +
)
A3 A l (:t 2 +
) AaA2 (x2 +
)


A3
3
A.As (x + ; )
As.A3 (x 2 - +
) ...


. . .


. . .


. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .


Therefore, by 3.7.18 and 3.7.22, we get
00 ooA
L AkZk L 7 = (AlAI + A:lA2 + AsAa + ...)
"=1 k=l
+(A 2 A I + As"A 2 +...) (z +
) + (AsAI +
A2+.") (Z2 +
 ) +....
3.8.31. (4] By 3.8.30,
00 ( q2n-l ) 00 ( 1 )
II (1+q2n-lx) 1+ x =Bo+ LBn xn+
 ·
n=l n=1
.Setting



 ( 2n-l )
F(z) = n (1 +q'ln-Iz) 1 + q z
and using the equality qxF(q2x) = F(x), we get
BI = Boq, Bn = B n _ 1q 2n-l ,


and inductively,


2 -
Bn = Boq'l , n = 1,2, ....


Thus


F(z) = Bo (1 +
qn2 (zn+
) ) .
To determine Bo we may use the results in 3.8.29 and 3.8.30.
n 00
Pn = n (1 - q2k) and P = n (1- erR). Then
k;l n=l


Put


n 2 (n+I)2+.1
Boqn2 = Bn = An + AlAn+! + ... = qn + qR P. + ... ·
.rn 1 n+l




372


Solutions. 3: Series of Real Numbers


Ifl


Hence


q2n q
n
PnBo - 1 < p2 + p2 + ... ·
Now t letting n -+ 00, we get Bo = -}.


3.8.32. Apply 3.8.31 with
(a) % = -1.
(b) :t = 1.
(c) :e = q.
3.8.33. Observe that for n > 1,
1 ( Ii x - k Ii % - k )
On = 2 hi Z + k - 1.,.1 .:r + k .


Hence


n 1 n 1 1 no x-k
Sn = Laic = ) +z + La" = 2 - 2 n x+k "
k=1 k:2 1e=1
If % is a positive integer, then for sufficiently large n, 8n = t. WE
now show that for x 1= 1,2, ".t lim Sn =
. Note that for k largE
n-oo
eno
 ! :;l l = 1-

' " Hence, by the result iD 3.8.4,


lim n n I X-k l -o
n-..oo x + k - ,
k=l
which in turn gi
 lim S.,., = ! t 88 we have claimed.
'Q-oo


OlD
3.8.34. Assume that tbe product n (1 + aI,a) converges for c = CO
n-=l
and C = CI t where Co ¥: CI- Then the products
Ole n °c (1 + Cla,.)

n(l+CIBn)
 and
n.wl n.=1 1 + coan
also converge. Moreover,


(1 + Cl4n)
l = 1 + CoCco - Cl) 2 ( 1 + )
1 + CoOn 2 an Eta t




3.8. Infinite Products


373


oc
where En -+ 0 as n -+ 00. Thus, by 3.8.3 and 3.8.4, the series E a:
n=l
00
converges. Next, by 3..8.13, E an aJso converges. Consequently, for
n=-l
I 00 00
. each C E ,both series E (can)2 and E CCn converge. Hence our
n=1 11=1
claim follows from 3.8.7.
OQ '11
3.8.35. Clearly, the series E On n (r - k 2 ) converges to zero if 3;
n=1 kz()
is an integer. Assume now that it converges for a noninteger value
ZO. For z e R, consider the sequence whose terms are given by


n
n (z2 -
)
bn = k:<'
n (xg - k 2 )
Ic



Then


,.. 2 k 2 t} ( 2 _2 )
X - X -

bn=II
_k2 =II 1+ 2_k 2 ..
k=O 0 k=O %0
From this, we conclude that, beginning with some value of the index
ft, the sequence {bn} is monotonic. Moreover, since the product
00 2 2
n
:=2 converges, the sequence {bn} is bounded. We have also
k-:O


oc; n OC) n
E an II (x 2 - 1;2) = E an II (x
 - k 2 )b n .
n=1 kzz:O Q=J k

Therefore, by the Abel test, the series under consideration converges
for any % E R.


3.8.36.
(a) We have


( I ) -1 CQ 1
1 - - = 1 + E -.

 k= 1

Multiplying the first N equalities, we obtain
Ii ( 1 ) -lOC, 1 PN 1 00, 1
(i) II 1 - - = 1 + E
 = E k% + E k%'
n=1
 k=1 k=1 1:=1'111 +1




374


Solutions. 3: Series of Real Numbers


where E' denotes s nmma tion over the integers which in their
prime factorization contain only prime numbers Pl,P2, ...,PN.
Hence


N ( 1 ) -1 PH 1 co I 1 co 1
0< II 1- - -
 - =
 - <
 -.
L.J k:z:
 k% L.J /eX
n=l
 k==l k:::;PN+l k=PN+l


00
Since Jim E b = 0, we get
N-oo k -P N+l


00 ( 1 ) -1 00 1
II 1 - -:- = E z.
n=1
 n=1 n


(b) By (i) in the solution of part (a),


N ( 1 ) -I 'PN 1
II 1-- > Lk.
n=1 Pn
=1


Therefore the divergence of E
 implies that fi ( 1 - ,L ) di-
n=l n=l
verges to zero, which in turn is equivalent to the divergence of
oc
the series L -!: (see 3.8.4).
n=1


3.8.31. [18]
(a) By DeMoivrets law, cosmt + i sin mt = (cost + isint)m, with
m=2n+l,weget


sin(2n + 1)t = (2n + 1) c0g2" t sin t - en: 1) ccxrn- 2 t sins t
+ ... + ( _l)n sin
+l t.


So we can write


(1)


sin(2n+ l)t.= sint W(sin
t),


where W( u) is a polynomial of degree < n. Since the function
on the left-hand side of the equality vanishes at tic = 2

1 ' k =




3.8. Infinite Products


375


1,2, ..., n, which belong to the interval (0, :; ), the polynomial
W(u) vAni
hpj; At 'Ilk = sin2"-tk, k = lJ 2) .... n
 Cnnsequent.ly.


W(u} = A IT ( 1 - .
 ) .
k=1 sm tk


Bence, by (l)y
sin(2n+l}t=AsintTI ( 1- .s
n2;. ) .
k=1 sm 2n+l


(2)


The ta:;k is now to find A. We have A -= lim sin(
n+1)t =- 2n+ 1.
t-O Sin £
Substituting this value of A into (2) and taking t = 2n
 1 ' we get


(3)


n ( .:2:r )
... x sm.. 2n+l
smx = (2n + l)sm 2 1 n 1- . 2 kfr ·
n + k=1 sm 2n1-1


For fixed x e R and mEN such that Ixl < (m + 1:)1r, take n
greater than m. Then, by (3)t


(4)


sinx = Pm.nQm.n,


where


m ( .- 2- % )
. X SIn 2n+l
Pm.n = (2n + 1) sm 2n + f n 1 - · 2 k-:r '
1e= 1 SlD 2n+l
n ( .-2 % )
SID 2n+ 1
Qm.n = n 1 - 5m 2 k7r ·
k;::m+l 2n+1


Letting n --to 00, we obtain


(5)


lim Pm.n = x n m ( 1 - k
2 2 ) .
,
-oo "'1f
k=l


It follows from (4) that for x ¥= k1r, lim Qm.n = Qm. To esti-
R-DO
mate Qm, we note that by the above assumptions,
(xl kTr < n-rr ! k _
o < 2 1 < 2 1 - 2 1 < no for - m + It ..., n.
n+' n+ n+
.




376


SoJutions. 3: Series of Real Numbers


Taking into account the inequality
u < sinu < U, 0 < u < i,
we see that Ii (1 -
) < Q....n < 1. Since the pr04uct
k=m+l
Ii (1 - ::
 ) oonverge8, we have
n=1


fI (1 -
 ) S Q... $ 1.
k-m+l


Consequently,


(6)


Iim Qm = 1.
m-co


Finally, the desired equality follows from (4) , (5) and (6).
(b) Apply (a) and the identity sin2x = 2sinxcos:£.
3.8.38. Substitute x = i in the formula stated in 3.8.37 (a).
3.8.39.
(a) The convergence of the given prOduct is equivalent to the con-
00
vergence of the series E (In (1 +
) -
). The absolute con-
n=l
vergence of this series follows from the equality


1im I ln (1 + :) - :1 _ !
n
oc
 - 2-


(b) We have


(1 +
):e _ 1 x(x - I) ( 2.. )
1 + £ - + 2n 2 + 0 n2 ·
n
So the absolute convergence of the produCt follows from 3.8.3.


00
3.8.40. Clearly, the product n (1 + an), On > -1, converges if and
n=1
00
only if the series E m(! + an) converges. Moreover, if P is the
n.-l
va1ue of the p
u
 and S is the sum of the seri
, tben P = e S .




3.8. Infinite Products


377


Assume now that the product converges absolutely. Then in view
of the p.(}1Jality


(1)


lim IIn(l + an)1 = 1 (because Urn an = 0)
n-co Ian I n-OC)


00
the series E In(! + an) converges absolutely. Consequently (see
n=1
3.7.8), any of its rearrangements converges to the same sum. Finally,
by the remark at the b eginnin g of this solution, any rearrangement
of the factors of the product does not chang e its value.


uu
Assume now that the value of the product n (1 + an) does not
n=1
depend on the order of its factors. This means that the sum of the
00
series E In(l + an) is also independent of the order of its terms.. By
n=1
Riemann's theorem, tbe series converges absolutely, which in view
00
of (1:) implies the convergence of E Ian I. Thus the desired result is
n=l
proved.


3.8.41. [20] Set Rn =
 . I .
 . ... .


l =
\f!. Then


( 1 + n ( 1 + i) ... ( 1 +
) =
,
(1- n (1- n... (1- 2{J
 1) =
.


Hence the (Q + lJ)nth partial product is equal to !k.. n . By the Wallis
ntJ
Cormula (see 3.8.38),


I . (2n + 1)!! 2
1m --
n-.oo (2n)!!Vii -
'


and therefore


lim Rna - _

n-oo Rna - V p.




378


Solutions. 3: Series of Real Numbers


oc
3.8.42. H the product n (1 + an) converges, but not absolutely,
n=1
00
then the series E In(l + an) converges conditionally (see the solu-
11=1 .
tion of 3.8.40). On account of the Rie m8J1n theorem, its terms can
be rearranged to give either a convergent series whose sum is an ar-
bitrarily preassigned real number S, or a divergent series (to +00 or
to -00). Thus our claim follows from the relation P = e S (see the
solution of 3.8.40).




Bibliography - Books


References
[1] J. BanaS, S. W
chowicz, Zbi6r zadart z analizy matematYCZJ1ej, Wy-
· dawnictwa Naukowo- T
hni cznet Warszaw&, 1994.
[2] W. I. Bernuk, I. K. Zuk, O.W. Melnikov, Sbomik olimpiadnych zadaC
po matematike, Narodnaja Asveta, Minsk, 1980.
(3) P. Biler, A. Witkowski, Problems in Mathematical Analysis,
farcel
Dekker, Inc, New York and Basel, 1990.
[4] T. J. Bromwich, An Introduction to the Theory of Infinite Series,
Macmillcw iWd Co., Liwitec.1, London, 1949.
[5] R. B. Burckel, An Introduction to Classical Complex Analysis, Aca,-
demic Press, New York San Francisco, 1979.
[6] B. P. Demidovic, Sbomik zadal i upminenij po matematiceskomu anal-
izu, Nauka, MoSkva, 1969.
[7) A. J. Dorogovcev, Matematiceskij a1U1liz. Spravoa"oe posobe , Vyscaja
Skola, Kiev, 1985.
[8] A. J. Dorogovcev, MatematiCes1ij analiza Sbornik zadac, VyseajaSkola,
Kiev. 1987.
[9] G. M. FichteIiholz, Differential- und Integralrechnung, I,ll, 111.. V.E.B.
Deutscher Verlag Wiss., Berlin, 1966-1968.
[10] G. H. Hardy, A Course of Pure Mathematics, Cambridge University
Press, Cambridge, 1946.
[11] G. H. Hardy, J. E. Littlewood, G. Polya, Inequalities, Cambridge Uni-
versity Press, Cambridge, 1967.


379




380


Bibliography - Books


(12) G. Klambauer, Mathematical Analysis, Marcel Dekker, Inc., New York,
1975.
[13} G. KJambauer, Problem8 and Propositions in Analysis, Marcel Dekker.
Inc., New York and Basel, 1979.
[14] K. Knopp, ThelJTie und Anwendung der UMndlichen Reihen, Springer-
Verlag, Berlin and Heidelberg, 1947.
[15] L. D. Kudriavtsev, A. D. Kutasov, V. I. Chejlov, M. I. Shabunin,
,
Problemas de Andlisis Matem6tico. Limite, Continuidad, Derivabili-
dad, Mir. Moskva, 1989.
[16] K. Kuratowski. Introduction to Calculus, Pergamon Press, Oxford-
Edinburgh-New York; Polish Scientific Publishers, Warsaw, 1969.
[11] D. S. Mitrinovic, Elementary lncqualitiu, P. Noordhoff Ltd
, Gronin-
gen, 1964.
[18] D. S. Mitrinovic, D. D. Adamovic, Nizovi i Redovi. Definicije, stavovi,
zadaci, problemi (Subo-Croatian). Nauena Knjiga, Belgrade. 1971..
[19] A. Ostrowski, Aufgabensammlung zur Infinituimalrechnungl Band 1:
Funktionen einer Yariablen, BirkhiU5er Verlag, Basel und Stuttgart,
1964.
120] G. P61ya, G. Szego, Problems and theorems in analysis 1, Sprlger-
Verlag, Berlin Heidelberg New York, 1978.
[21] Va. I. Rivkind, ZadaCi po matematiCeskomu. analizu, VySejSaja 9kola.
Minsk. 1973.
[22] W. I. Rozhkov, G. D. Kurdevanidze, N. G. Panfilov, Sbomik zadaC
matematiceskich olimpiad, Izdat. Univ. Druzhby Narodov, Moskva,
1987.
[23] W. Rudin, Principles of Mathematical Analysis. McGraw-Hill Book
Company, New York. 1964.
[24] W. A. Sadownicij, A. S. Podkolzin. ZadaCi studenceskich olimpiad po
matematike, Nauka, Moskva, 1978.
[25] W. SierpiDski, A
tyka teoretyczna, PWN, Warszawa. 1959.
[26] w.
ie1"piiiRki, Dzi.aln.nin nip.J
km£r.%MlP, C
lnik, Wan;?Awa, 1948.
[27] H. Silverman, Comple::& variables, Houghton Mifflin Company. Boston,
1975.
[28) G. A. Tonojan, W. N. Sergeev, Studenceskije matematiceskije olimpia-
dy, Izdatelstwo Erevanskogo Universiteta, Erivan, 1985.




,Problems in Mathematical Analysis I
Real NUl11bers, Sequences and Series
W J. Kac or and M. T. No\\'ak


We learn b} duing. We learn 111atheillaucs br doing problenl
.
Th}
 hook is the first volume of a
crie
 of hooks of problem

in 111atheillatkal anal)rsi
 It i
 Inainl) )ntt.'nd
d for
(Udl'nts
stud) Il1g the bask principles of analysis. Ho\\cver, ghcn its
organi/auon, level. and scl
cuon of problen1s, it \\,Quld also
be an ideal choice for tutorial or probl('lll-so1ving C\eminar
,
paniLularl) those gear
d to\\ard the PUUhun e'\am. The vol-
tllnc is al'-to '\u iLahle for self-stud}.
Each SCLuon of the book begins with ft'lativd} '-til11plc C\.l'r-
ch
, } el III a)' aL
o conlall1 quite challenging problcl11S. Very
oftcn a few C(Jn

culhe exercises are concerned \vith differ-
ent a'-tpl'crs of ont' mathcll1atical prohk"m or thcorem. Thb
pfl'
eIHation of Inatcrial is designed to help Mudent cOlnpre-
hcnslon and to encourage then1 to
k their o\\n qucstiOll

and to Mart rcsl'arch. The collection of probl
lns in the b ok
i
 al
() intcnd
d to help teachers \vho \\ i
h to incorporate the
pr()hleln
 into Il"UUrC\. Soluti{)n
 for all the prohll'111S are
provided


ISBN 0-8218-2050-8


9 780821 820506
STML/4


Al\ts 011 tbi" \\'ch