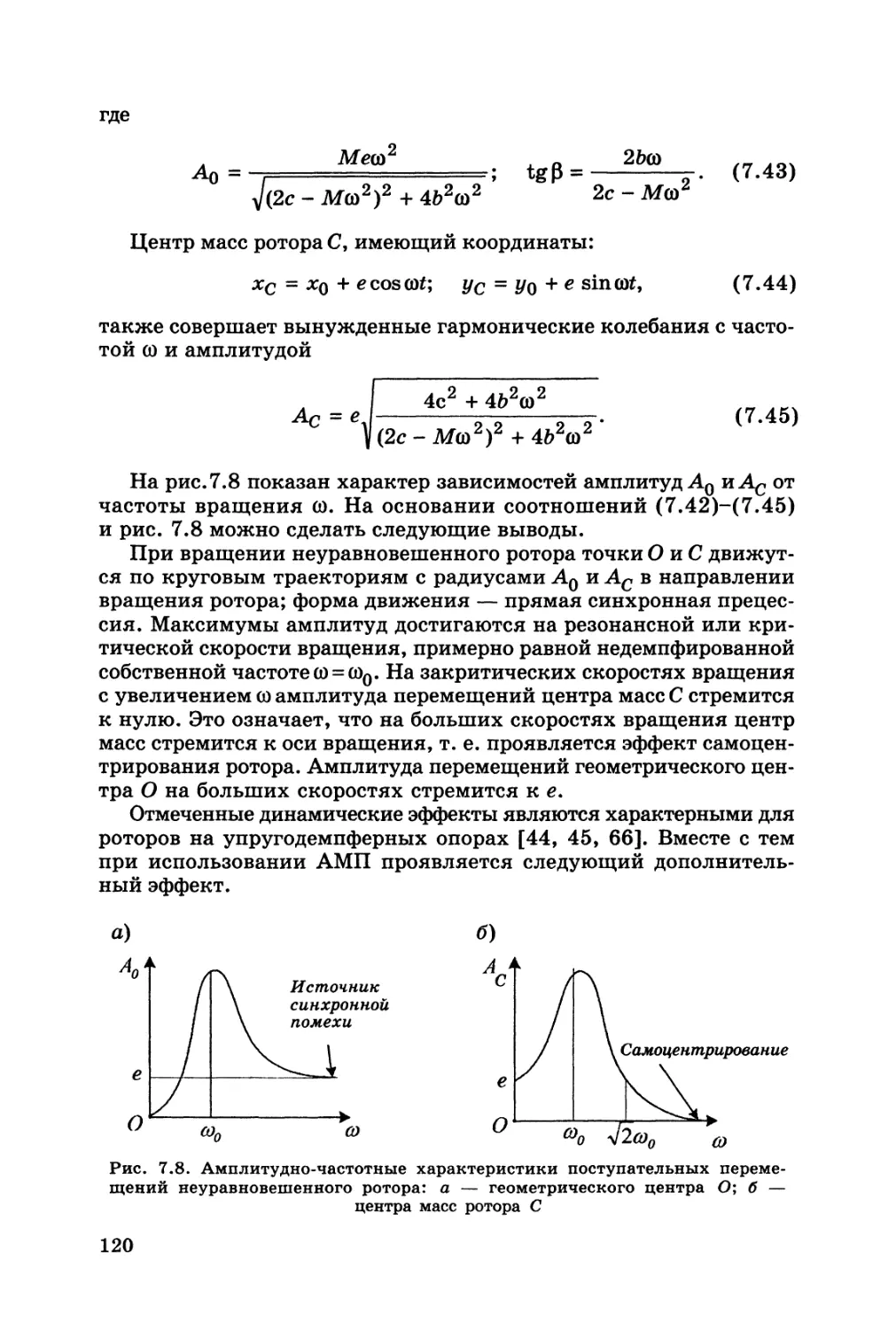
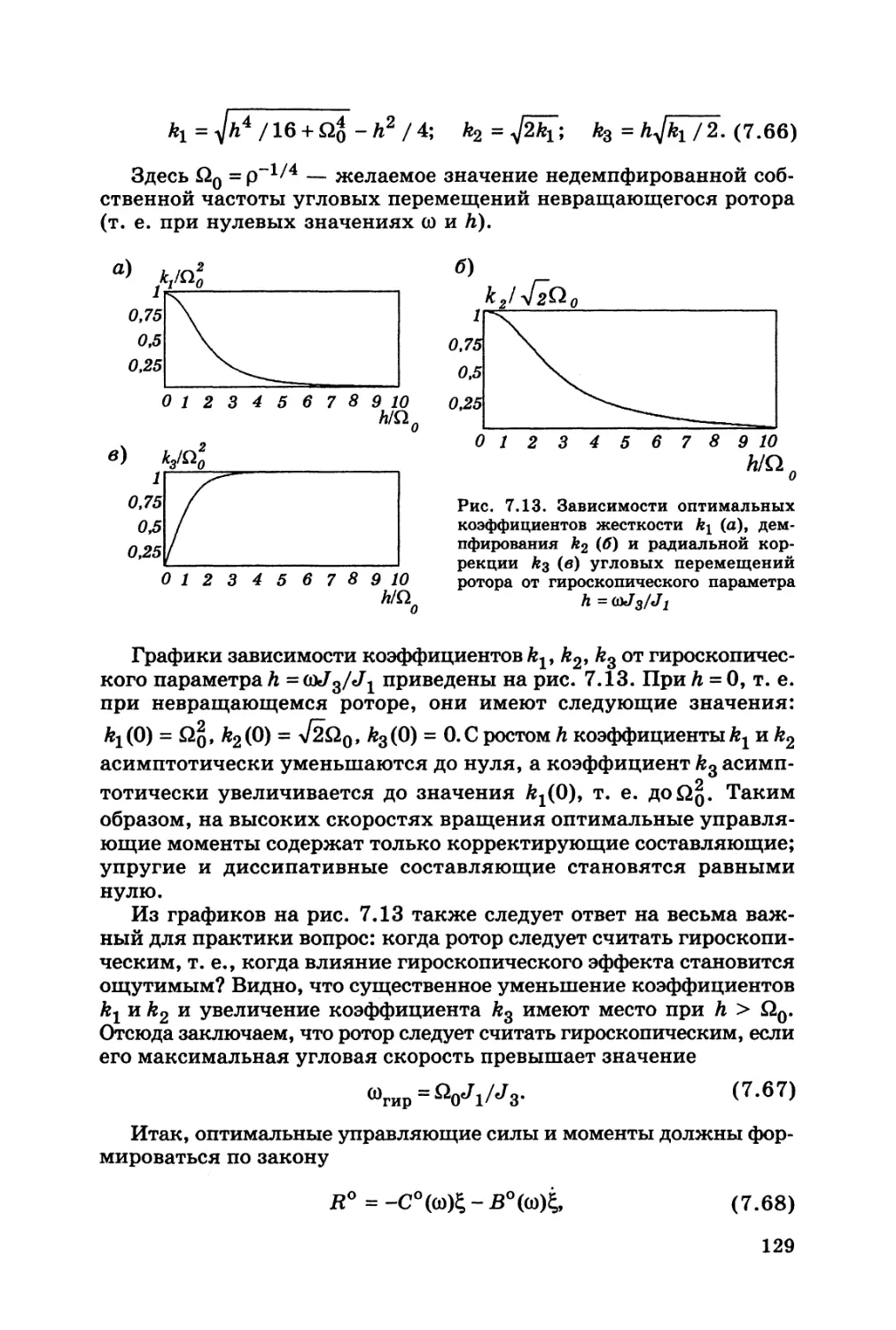
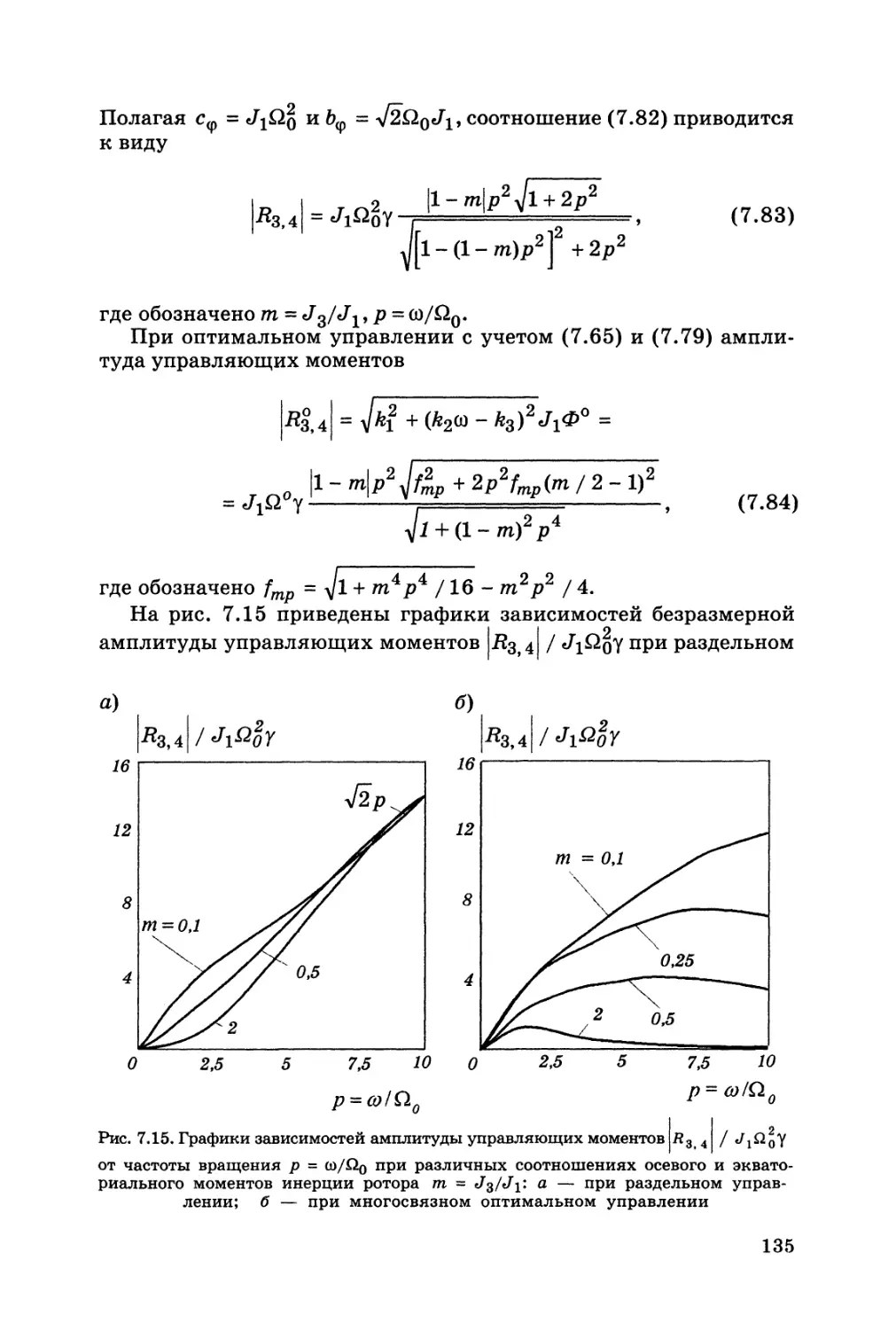
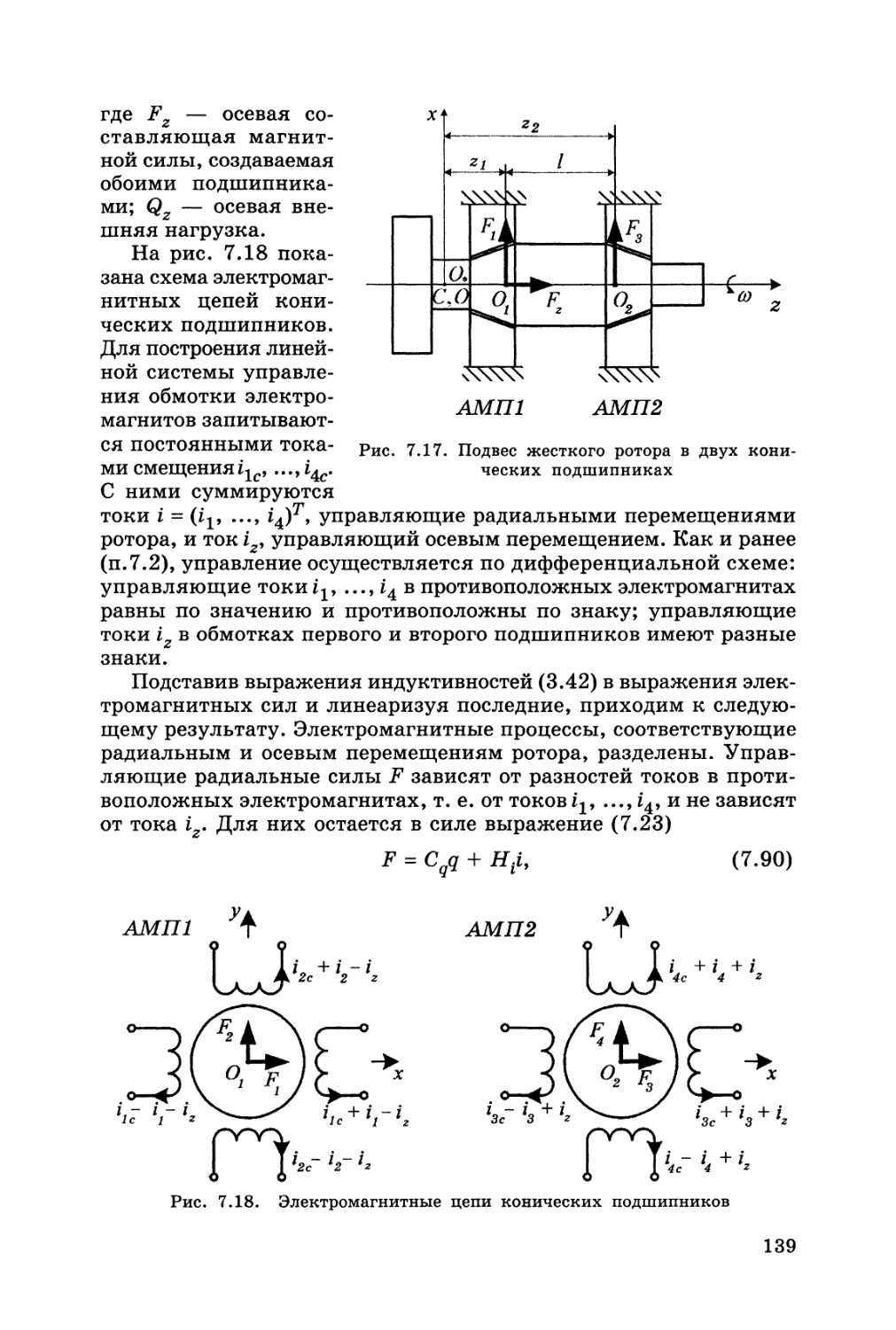
Автор: Журавлев Ю.Н.
Теги: детали машины общее машиностроение машиноведение машиностроение механика
ISBN: 5-7325-0655-1
Год: 2003
Текст
Ю. Н. ЖУРАВЛЕВ
Активные
магнитные
подшипники
Теория, расчет, применение
ПОЛИТЕХНИКА
ИЗДАТЕЛЬСТВО
Санкт-Петербург 2003
УДК 62-233.2
ББК 34.445
Ж91
Федеральная целевая программа “Культура России"
(подпрограмма “Поддержка полиграфии и книгоиздания России")
Рецензенты: доктор физико-математических наук, профес-
сор Р. Ф. Нагаев; кафедра «Теория механизмов и машин»
Псковского политехнического института
Журавлев Ю. Н.
Ж91 Активные магнитные подшипники: Теория, расчет, при-
менение. — СПб.: Политехника, 2003. — 206 с.: ил.
ISBN 5-7325-0655-1
В книге рассматриваются нетрадиционные активные магнитные под-
шипники, которые могут эффективно работать в экстремальных усло-
виях, т. е. в условиях высоких скоростей, вакуума, высоких или низких
температур, стерильности, агрессивной среды и т. д. Ротор вращается в АМП
без механического контакта и износа. Также не требуется смазка. Ус-
тойчивый подвес ротора осуществляется силами магнитного притяже-
ния со стороны управляемых электромагнитов.
Особое внимание уделено таким малоосвещенным в литературе во-
просам, как описание систем подвеса в безразмерном пространстве состо-
яний, оптимизация геометрии АМП и законов управления, взаимное воз-
действие АМП и приводного электродвигателя, эффект автовращения ро-
тора в АМП, создание бесподшипниковых электрических машин и т. д.
Книга рассчитана на широкий круг инженерно-технических и науч-
ных работников, студентов и аспирантов технических специальностей.
УДК 62-233.2
ББК 34.445
YURI N. ZHURAVLYOV
ACTIVE MAGNETIC BEARINGS: theory, desing, applications
The present book deals with a nonconventional Active Magnetic Bearing
(AMB) that might efficiently operate in extreme conditions: higt speed, vacuum,
sterility, etc. The rotor revolves in AMB's without any mechanical contact and
wear. Lubrication is not required either. The stable suspension of the rotor is
provided by magnetic attractive forces exerted by controlled electromagnets.
Although the subject of AMB is not new there are few papers and books,
such as this, which cover the entire field including survey, mathematical modeling,
design of magnetic circuits and control laws, analysis of dynamics and stability for
rigid and elastic rotors, digital control, dynamic aspects of realization, and application
problems. Special attention is paid to the dimensionless state space description of
systems, optimization of geometry and control laws, mutual influence between
AMB and a driving electromotor, effect of autorotation of a rotor in AMB, bearing-
less electrical machines, ets.
The book is intended for readers who are interested in solution of bearing
problems and it is a suitable book for design engineers as well as for students
at technical universities.
ISBN 5-7325-0655-1
© Издательство «Политехника», 2003
Моей жене Вере и дочерям
Наталии и Екатерине, актив-
ный магнетизм которых прида-
ет моей жизни устойчивый ди-
намизм
ПРЕДИСЛОВИЕ
Основным элементом многих машин является ротор,
вращающийся в подшипниковых опорах. Рост скоростей враще-
ния и мощностей роторных машин при одновременной тенденции
к уменьшению массовых и габаритных показателей выдвигает про-
блему повышения долговечности подшипниковых узлов как пер-
воочередную. Кроме того, в целом ряде областей современной тех-
ники требуются подшипники, способные надежно работать в экс-
тремальных условиях: в вакууме, при высоких и низких темпера-
турах, сверхчистых технологиях, в агрессивных средах и т. п. Созда-
ние таких подшипников также является актуальной технической
проблемой.
Решение указанных проблем может осуществляться как совер-
шенствованием традиционных подшипников качения и скольже-
ния, так и созданием нетрадиционных подшипников, в которых
используются иные физические принципы действия.
Традиционные подшипники качения и скольжения (жидкостные
и газовые) к настоящему времени достигли высокого технического
уровня. Однако природа протекающих в них процессов ограничи-
вает, а иногда делает принципиально невозможным применение
этих подшипников для достижения указанных выше целей. Так,
существенными недостатками подшипников качения являются
наличие механического контакта между подвижными и неподвиж-
ными частями и необходимость в смазке дорожек качения. В под-
шипниках скольжения механический контакт отсутствует, но не-
обходимы система подачи смазочного материала для создания сма-
зочного слоя и герметизация этого слоя. Очевидно, что совершен-
ствование узлов герметизации может лишь уменьшить, но не пол-
ностью устранить взаимное проникновение смазочного материала
и внешней среды.
От указанных недостатков свободны подшипники, в которых
для создания опорных реакций используются магнитные и элект-
рические поля. Среди них наибольший практический интерес пред-
ставляют активные магнитные подшипники (АМП). Работа АМП
основана на известном принципе активного магнитного подвеса
ферромагнитного тела: стабилизация тела в заданном положении
осуществляется силами магнитного притяжения, действующими на
3
тело со стороны управляемых электромагнитов. Токи в обмотках
электромагнитов формируются при помощи системы автоматичес-
кого управления, состоящей из датчиков перемещений тела, элект-
ронного регулятора и усилителей мощности, питающихся от внеш-
него источника электрической энергии.
Первые примеры практического использования активных маг-
нитных подвесов в измерительных приборах относятся к 40-м
годам XX столетия. Они связаны с именами Д. Бимса и Д. Хри-
зингера (США) и О. Г. Кацнельсона и А. С. Эдельштейна (СССР).
Первый активный магнитный подшипник был предложен и экспе-
риментально исследован в 1960 году Р. Сикссмитом (США). Ши-
рокое практическое применение АМП в нашей стране и за рубе-
жом началось в начале 70-х годов XX столетия.
Отсутствие в АМП механического контакта и необходимости
смазки делает их весьма перспективными во многих областях тех-
ники. Это, прежде всего: турбины и насосы в вакуумной и криоген-
ной технике; машины для сверхчистых технологий и для работы
в агрессивных средах; машины и приборы для ядерных и косми-
ческих установок; гироскопы; инерционные накопители энергии;
а также изделия для общего машиностроения и приборостроения —
шлифовальные и фрезерные высокоскоростные шпиндели, текстиль-
ные машины, центрифуги, турбины, балансировочные станки, виб-
ростенды, роботы, точные измерительные приборы и т. д.
Однако, несмотря на имеющиеся успехи, АМП внедряются на
практике значительно медленнее, чем это ожидалось из прогнозов,
сделанных в начале 1970-х годов. Прежде всего, это объясняется
замедленным восприятием промышленностью новшеств, в том
числе и АМП. Как и любое новшество, чтобы быть востребован-
ным, АМП нуждаются в популяризации.
К сожалению, на момент написания этих строк активным
магнитным подшипникам посвящена лишь одна книга [99]:
G. Schweitzer, Н. Bleuler and A. Traxler «Active magnetic bearings»,
ETH Zurich, 1994, 244 p., изданная на английском и немецком
языках. Небольшая по объему, эта книга ориентирована в первую
очередь на читателя, делающего первые шаги в понимании тех
проблем, которые возникают при создании АМП. Предъявляя весьма
скромные требования к инженерной и математической подготовке
читателя, авторы выстраивают основные идеи и понятия в такой
продуманной последовательности, которая позволяет начинающе-
му легко войти в курс дела и концептуально овладеть новой для
себя областью. Несомненно, указанная книга является заметным
явлением, а ее популяризаторскую роль трудно переоценить.
Читатель может спросить, стоило ли писать настоящую моно-
графию, а не ограничиться переводом на русский язык цитирован-
ной выше книги [99]. Во-первых, начиная с 1992 года меня при-
глашали прочитать лекции по АМП в университетах России, Фин-
ляндии и Швеции. Из этих лекций выросла книга. Во-вторых,
4
многие мои коллеги высказывали желание получить книгу об АМП,
написанную для разработчиков машин с АМП. В-третьих, я также
сознавал, что многие инженеры, которые вовсе не специализируют-
ся в области АМП, нуждаются в книге, исследующей такой объект
управления, как электромагнит.
Цель этой книги состоит в том, чтобы вооружить инженеров
методами математического моделирования, синтеза и анализа АМП
и способствовать тем самым возбуждению интереса к этой новой
области техники. Не сомневаюсь, что книга будет также полезна
для студентов многих технических специальностей, особенно при
курсовом и дипломном проектировании. При написании книги
я опирался на 20-летний опыт работы в области АМП в качестве
научного руководителя научно-исследовательской лаборатории маг-
нитных опор при Псковском политехническом институте Санкт-
Петербургского государственного технического университета.
Книга содержит 10 глав. В главе 1 дается краткое описание
всех возможных видов электромагнитных подвесов, цель которого —
расширить кругозор читателя. Глава 2, нацеленная на пользовате-
лей АМП, вводит читателя в технику активных магнитных под-
шипников — это история развития, конструкции, характеристики,
проблемы освоения и несколько примеров практических приложе-
ний. В главах 3 и 4 приводится методика расчета магнитных це-
пей подшипников. Электромагнит как объект управления изуча-
ется в главе 5. В главе 6 решаются задачи синтеза регулятора
и анализа динамики одностепенного магнитного подвеса. Это гла-
ва о том, как следует управлять подвесом и что может помешать
получить требуемые динамические качества. Центральное место
занимает глава 7, в которой рассматриваются задачи управления
подвесом жесткого ротора, имеющего пять степеней свободы, ис-
следуется взаимодействие подвеса и приводного электродвигателя,
а также затронут вопрос создания бесподшипниковых электричес-
ких машин. Влияние упругих изгибных деформаций ротора на
динамику подвеса рассматривается в главе 8. Глава 9 посвящена
цифровому управлению подвесом. В заключительной главе 10 рас-
сматривается ряд динамических аспектов, связанных с реализаци-
ей подвесов роторов в АМП.
Что касается списка литературы в конце книги, то я не пытался
включить в него все исторически заметные статьи по АМП и про-
шу прощения у тех исследователей, чьи вклады в эту область не
упомянуты.
Поскольку круг вопросов весьма широк, оказалось невозмож-
ным сохранить одну систему условных обозначений по всей кни-
ге. Однако в каждой главе использована постоянная система обо-
значений.
Я благодарен своим учителям профессорам Давиду Рахмилье-
вичу Меркину и Анатолию Сауловичу Кельзону — они во многом
способствовали появлению этой книги. Я хотел бы поблагодарить
5
моих коллег по лаборатории магнитных опор и университету,
в особенности Федора Георгиевича Кочевина, Михаила Вадимовича
Афанасьева, Валентина Васильевича Андреева, Сергея Владимиро-
вича Смирнова, Сергея Геннадьевича Стебихова и Игоря Иванови-
ча Морозова, чьими усилиями созданы многие машины с АМП.
Мне были также полезны беседы и совместная работа с профессо-
ром Камилом Шамсуддиновичем Ходжаевым и доцентами Вла-
димиром Александровичем Андреевым, Валерием Георгиевичем
Боговым и Вячеславом Григорьевичем Мацевичем. Я хотел бы
также отметить вклад дипломников и аспирантов, которые с боль-
шим энтузиазмом работали со мной в области АМП, — это Григо-
рий Михайлович Крайзман, Николай Вадимович Хмылко, Аркадий
Григорьевич Хростицкий, Николай Михайлович Ильин, Александр
Михайлович Ветлицын и Павел Васильевич Киселев. Особого упо-
минания заслуживает техническая помощь по подготовке рукопи-
си к изданию Елены Владимировны Журавлевой и Андрея Семено-
вича Леонтьева.
За помощь в финансировании издания книги хочу поблагода-
рить Псковскую инженерную компанию и Псковский политехни-
ческий институт.
1. КЛАССИФИКАЦИЯ
ЭЛЕКТРОМАГНИТНЫХ ПОДВЕСОВ
1.1. ПРИНЦИПЫ ЭЛЕКТРОМАГНИТНОЙ ЛЕВИТАЦИИ
Идея использовать электрические и магнитные поля для
левитации (или подвеса) тел существует уже в течение многих
веков. Интерес к ней возродился в нашем столетии в связи с раз-
витием приборостроения и машиностроения для измерительной,
ядерной, космической, криогенной и других видов современной тех-
ники.
Из физики известно, что на электрический заряд Q, движущий-
ся со скоростью v в электромагнитном поле с электрической на-
пряженностью Е и магнитной индукцией В, действует сила
F = Q(E + vxB). (1.1)
Первое слагаемое
Fe = QE (1.2)
описывает силу электростатического взаимодействия. Второе сла-
гаемое с учетом того, что произведение заряда Q на скорость v
есть электрический ток I, описывает силу взаимодействия тока
с магнитным полем (силу Лоренца):
Fm = IxB. (1.3)
В зависимости от способа создания различают:
токи в проводнике от внешнего источника тока;
амперовы токи в постоянном магните;
токи в ферромагнитном материале, индуцированные постоян-
ным магнитным полем;
токи в проводнике, индуцированные переменным магнитным
полем.
При использовании постоянных магнитов магнитная сила мо-
жет быть как силой притяжения, так и силой отталкивания. Сила
взаимодействия между ферромагнетиком и источником магнитно-
го поля всегда является силой притяжения. Электропроводный
неферромагнитный материал и источник переменного магнитного
поля всегда отталкиваются. Два проводника, несущие ток, могут
как притягиваться, так и отталкиваться.
Проблемам электромагнитной левитации тел посвящено
огромное число работ. Первый систематический анализ возмож-
ных принципов левитации тел с использованием электрических и
магнитных полей был проведен в 1956 году А. Боердийком [84].
7
В 1964 году П. Джери составил полный библиографический обзор
работ этого направления [90]. На русском языке подробный обзор
в 1968 году составил В. Б. Метлин [60]. Обзор исследований
(до 1985 г.), посвященных движению твердого тела в электричес-
ких и магнитных полях, можно найти в работе Ю. Г. Марты-
ненко [58].
Электрические и магнитные подвесы в зависимости от принци-
па действия принято разбивать на девять типов [60, 84]: электро-
статические; на постоянных магнитах; активные магнитные;
LC-резонансные; индукционные; кондукционные; диамагнитные;
сверхпроводящие; магнитогидродинамические.
Последующие параграфы данной главы посвящены краткому
изложению принципов действия и основных технических характе-
ристик каждого из перечисленных типов подвесов.
1.2. ЭЛЕКТРОСТАТИЧЕСКИЙ ПОДВЕС
В основе работы электростатического подвеса (ЭСП) ис-
пользуются силы притяжения между проводящими поверхностя-
ми, имеющими различные электрические потенциалы. Одна поверх-
ность принадлежит подвешиваемому проводящему телу, другие по-
верхности — системе электродов. В межэлектродном пространстве
обычно создается вакуум.
Для создания одноосного электростатического подвеса незаря-
женного тела его помещают в электрическое поле, созданное двумя
парами электродов Sp S2, S3, S4 (рис. 1.1). Электроды S3 и S4
заземлены, а на электроды Sx и S2 подаются напряжения
и и2 так, чтобы обеспечить бесконтактный подвес тела вдоль вер-
тикальной оси у. Пусть площади всех электродов одинаковы
и равны А, а в положении у = 0 тело находится на одинаковом
Рис. 1.1. Четырехэлектродный электростатический подвес
8
расстоянии 3 от электродов. Тогда выражение для силы, действую-
щей на тело, будет иметь вид [58]
ш = тг-
16л
(1.4)
При постоянных Uj и и2 производная dF/dy на интервале (-3,8)
всюду положительна, поэтому положение равновесия подвеса тела
будет неустойчивым. Данный факт является следствием извест-
ной теоремы Ирншоу [88] о невозможности устойчивого положе-
ния равновесия активного элемента в статическом силовом поле,
если сила и расстояние связаны законом обратных квадратов.
Следует заметить, что диэлектрическое тело с диэлектрической про-
ницаемостью меньшей, чем диэлектрическая проницаемость среды,
может иметь устойчивое положение равновесия в электростатичес-
ком поле.
Устойчивость ЭСП достигается использованием системы уп-
равления потенциалами электродов. При этом используются либо
внешняя система управления с емкостными или оптическими дат-
чиками положения тела, либо пассивная или резонансная система
с последовательно включенными индуктивностями.
Положительные качества ЭСП — высокое быстродействие сис-
темы регулирования и отсутствие магнитного поля и тепловых
потерь. Недостатки ЭСП — необходимость высоких напряжений и
глубокого вакуума, малая грузоподъемность. Основное применение
ЭСП — подвеска роторов гироскопов [58].
1.3. ПОДВЕСЫ НА ПОСТОЯННЫХ МАГНИТАХ.
ЗАПРЕТ ИРНШОУ
В подвесах на постоянных магнитах (ППМ) магнитное
поле создается постоянными магнитами или электромагнитами по-
стоянного тока без регулирования. Подвешиваемое тело частично
или полностью выполняется из ферромагнитного материала и мо-
жет нести постоянные магниты. Подвес тела (или частичная раз-
грузка механических опор) осуществляется за счет магнитных сил
отталкивания или притяжения. Наиболее подходящими материа-
лами для изготовления постоянных магнитов являются литые и ме-
таллокерамические сплавы альнико, ферриты бария, а также са-
марий-кобальтовые сплавы [68].
На рис. 1.2 приведена схема системы «магнит — ферромагне-
тик», предложенная Драйсдэйлом и Джоллем в 1924 году для
разгрузки упорного подпятника ротора ваттметра.
Подвес ферромагнитного тела в соленоиде показан на рис. 1.3.
В горизонтальных направлениях подвес неустойчив. Устойчивость
подвеса в вертикальном направлении в ряде случаев достигается
9
<^<SSSSSSSS>\ Постоянный
магнит
Ферромагнитный
s' подшипник
Рис. 1.3. Электромагнитный подвес соле-
ноидного типа
N
S
Рис. 1.2. Разгрузка упорного под-
пятника с помощью постоянного
магнита
без специального регулятора. Объясняется это тем, что на тяговой
характеристике соленоида есть участок ab, на котором положение
равновесия может быть устойчивым. Соленоид может питаться как
постоянным, так и переменным током. По значению тока в обмотке
можно судить о нагрузке на подвешенное тело. На данном принципе
созданы весоизмерительные устройства, плотномеры, расходомеры,
стабилизаторы переменного тока и т. п., описание и расчеты которых
можно найти в работах О. Г. Кацнельсона и А. С. Эдельштейна [42].
Осевой подшипник системы «магнит—магнит» (рис. 1.4), предло-
женный Изааксоном в 1936 году, состоит из закрепленного на валу
подвижного цилиндрического магнита, который расположен между
двумя неподвижными магнитами. Все магниты имеют осевую намаг-
ниченность. Подвес устойчив в осевом направлении, но без механи-
ческих подшипников неустойчив в радиальных направлениях.
На рис. 1.5 показана схема радиального магнитного подшип-
ника, предложенная в 1954 году Баерманом. Закрепленный на валу
кольцевой магнит вставлен с зазором внутрь неподвижного коль-
цевого магнита. Оба магнита имеют радиальную намагниченность.
В осевом направлении такой подвес неустойчив.
Подвесы на постоянных магнитах отличаются большой просто-
той и высокой экономичностью. Вместе с тем им присущи следую-
щие недостатки: низкая механическая прочность; малая удельная
грузоподъемность (для ферри-
тов не более 0,5 Н на 1 см2
опорной поверхности); не рассе-
ивают механическую энергию
при колебаниях подвешенного
£^3 тела, поэтому нуждаются в спе-
циальных демпферах.
Особо следует отметить прин-
Рис. 1.4. Осевой подшипник на посто-
янных магнитах
ципиальную невозможность
осуществления полной устой-
10
N
S
Ротор
S
N
N
S
S
—N.___
w\\\\\x
Рис. 1.6. Пример на первый
взгляд вполне работоспособ-
ной, но в силу запрета Ирн-
шоу не реализуемой и поэто-
му ошибочной конструкции
полного магнитного подвеса
на постоянных магнитах
Рис. 1.5. Радиальный
подшипник на постоян-
ных магнитах
чивой неконтактной подвески с использованием только постоян-
ных магнитов. Этот факт вытекает из уже упоминавшейся в п. 1.2
теоремы Ирншоу [88], а также из исследований Браунбека [85].
Последний в 1939 году показал, что устойчивая подвеска тела в по-
стоянном магнитном поле возможна лишь в случае, если магнит-
ная проницаемость материала, из которого изготовлено тело, мень-
ше магнитной проницаемости окружающей среды, т. е. для диа-
магнетиков и сверхпроводников. Тем не менее в литературе иног-
да появляются ошибочные описания на первый взгляд вполне рабо-
тоспособных конструкций полной подвески на постоянных магнитах
(схема такой курьезной конструкции, заимствованная из работы
[89], приведена на рис. 1.6). Отметим также, что интересная кон-
струкция подвеса тороидального ротора на постоянных магнитах,
в которой неустойчивая степень свободы соответствует вращатель-
ному движению, предложена В. А. Андреевым [83].
Вследствие отмеченных недостатков опоры на постоянных магни-
тах используются в основном для разгрузки механических опор или
в сочетании с активными магнитными опорами, а также в измери-
тельных устройствах.
1.4. ЭЛЕКТРОМАГНИТНЫЙ ПОДВЕС
С РЕЗОНАНСНОЙ ЦЕПЬЮ
Электромагнитный подвес с резонансной LC-цепью (или
LC-подвес) является одним из наиболее простых и не требующим
специального регулятора подвесом. Схема LC-подвеса приведена
11
Рис. 1.7. Электромагнитный резонансный LC-подвес: а — принципиаль-
ная схема; б — резонансная кривая
на рис. 1.7, а. Подвешиваемое ферромагнитное тело устанавлива-
ется между двумя одинаковыми электромагнитами с зазором 8.
В цепи обмоток электромагнитов, питаемых переменным напряже-
нием, включены последовательно конденсаторы. Емкость С кон-
денсаторов подбирается такой, чтобы в центральном положении
тела действующие значения токов в каждой обмотке, имеющей
индуктивность Lo, находились на ниспадающей ветви резонансной
кривой (точкаLq , Lp... на рис. 1.7, б). Наиболее выгодное значе-
ние тока Iq = Im / V2, где 1т — максимальное значение тока на
резонансном пике.
В положении равновесия силы притяжения электромагнитов
F^ и F2 равны между собой. Пусть равновесие тела нарушилось,
и тело переместилось на расстояние у вправо. Тогда индуктив-
ность Lj возрастет, £2 — уменьшится. Изменение же токов и сил
будет обратное: ток^ и силаТ^ уменьшатся, 12 и^2 — возрастут.
Результирующая сила притяжения при этом будет направлена влево,
и положение равновесия восстановится.
Простота конструкции LC-подвесов сопровождается и целым
рядом существенных недостатков: малая грузоподъемность; по-
вышенные потери энергии на вихревые токи и перемагничивание;
малые рабочие зазоры. Поэтому сфера их применения ограничива-
ется с лабонагруженными роторами.
1.5. АКТИВНЫЙ МАГНИТНЫЙ ПОДВЕС
На рис. 1.8 показаны принцип действия и функцио-
нальные компоненты простейшего одноосного (одностепенного) ак-
тивного магнитного подвеса (АМП). Датчик измеряет смещение
12
Рис. 1.8. Принцип действия активного магнитного подвеса
подвешиваемого ферромагнитного тела из заданного положения рав-
новесия. Сигнал измерения обрабатывается регулятором. Усилитель
мощности, питаемый от внешнего источника электроэнергии, преоб-
разует этот сигнал в управляющий ток в обмотке электромагнита,
который вызывает силу магнитного притяжения таким образом,
что нарушенное положение равновесия восстанавливается. Устойчи-
вость подвеса, также как и необходимые жесткость и демпфирование,
достигаются соответствующим выбором закона управления.
Активный магнитный подвес по сравнению с подвесом на по-
стоянных магнитах и LC-подвесом имеет следующие основные пре-
имущества: грузоподъемность АМП значительно выше и состав-
ляет 40-80 Н на 1 см2 площади опорной поверхности; высокая
механическая прочность; возможность осуществления устойчивой
неконтактной подвески тела; возможность изменения жесткости
и демпфирования в широких пределах. К недостаткам АМП сле-
дует отнести: наличие внешнего источника электроэнергии и от-
носительно более высокие сложность и стоимость, вызванные на-
личием электронного блока управления. В силу своих неоспори-
мых преимуществ именно данный вид подвеса наиболее широко
применяется в технике (история развития АМП и сферы его при-
менения будут рассмотрены в следующей главе).
1.6. ИНДУКЦИОННЫЙ ПОДВЕС
Принцип действия индукционного подвеса (ИП) осно-
ван на том, что подвешиваемое электропроводное тело помещается
в высокочастотное переменное магнитное поле электромагнита,
а подвеска осуществляется за счет сил отталкивания основного
поля и вихревых токов, наведенных этим полем в подвешивае-
мом теле (рис. 1.9). Возможен также обращенный вариант ИП,
когда электромагнит, питаемый высокочастотным напряжением,
парит над электропроводной поверхностью.
13
Рис. 1.9. Индукционный подвес
Следует отметить, что если подвеши-
ваемое тело имеет большую магнитную
проницаемость, то кроме отталкивающей
силы индукционного характера суще-
ствует значительная сила, притягиваю-
щая тело к электромагниту. Поэтому
применение ИП для подвешивания фер-
ромагнитных тел нецелесообразно.
Важной областью применения ИП
является бестигельная плавка сверх-
чистых металлов. Суть ее заключается
в том, что кусок металла нагревается и плавится индукционным
путем за счет энергии магнитного поля подвеса [60].
Разновидность ИП, состоящая из неподвижного электропровод-
ного рельса и установленного на движущемся экипаже постоянно-
го сверхпроводникового магнита, используется при создании вы-
сокоскоростного наземного транспорта с магнитной подушкой
(см. п. 1.11).
Простота конструкции, способность работать в агрессивных сре-
дах и вакууме, а также при больших скоростях, возможность со-
здания опор без трения — свойства, которые позволяют применять
ИП в устройствах различного назначения — от оборудования точ-
ного физического эксперимента до энергомашиностроения и транс-
порта. Существенный недостаток — большие энергетические за-
траты (до 100 Вт на 1 Н нагрузки) — является основным препят-
ствием широкому практическому внедрению ИП.
1.7. КОНДУКЦИОННЫЙ ПОДВЕС
Принцип действия кондукционного подвеса (КП) основан
на вытеснении проводника с током из магнитного поля (рис. 1.10).
По роду тока КП делятся на подвесы постоянного тока и подвесы
переменного тока (магнитное поле и ток должны совпадать по фазе).
Также как и индукционные подвесы, КП чаще всего используются
для бестигельной плавки чистых металлов, но могут быть использо-
ваны и в транспортных устройствах.
Основной недостаток КП — необходимость в источнике тока
больших значений. Размещение источника тока вне подвешивае-
мого тела требует наличия
контактного или бесконтакт-
ного устройства для переда-
чи энергии. Размещение ис-
точника тока на подвешива-
емом теле приводит к зна-
чительному увеличению соб-
ственного веса и снижению
Рис. 1.10. Кондукционный подвес
эффективности подвеса.
14
1.8. ДИАМАГНИТНЫЙ ПОДВЕС
Принцип действия диамагнитного подвеса (ДП) осно
ван на том, что диамагнетик, помещенный в магнитное поле
намагничивается в направлении, обратном направлению поля
и выталкивается из магнитно-
го поля (рис. 1.11). Лучшие диа-
магнетики — графит и висмут.
Грузоподъемность ДП чрезвы-
чайно мала. Области возмож-
ного применения ДП — кине-
матические датчики и датчики
для измерения мгновенных уси-
лий [60].
Рис. 1.11. Диамагнитный подвес
1.9. СВЕРХПРОВОДЯЩИЙ ПОДВЕС
Сверхпроводящий подвес (СП) включает в себя сверх-
проводник, установленный на подвешиваемом теле, и обычный или
сверхпроводящий электромагнит. Принцип действия СП основан
на том, что магнитное поле не проникает в тело сверхпроводника
и он, таким образом, представляет собой идеальный диамагнетик,
который отталкивается магнитным полем. Это обстоятельство сни-
мает запрет Ирншоу и позволяет создавать подвес сверхпроводя-
щего тела без внешней системы стабилизации [46]. Управляемый
сверхпроводящий подвес исследован в работе [19].
Практическое применение СП ограничено криогенными дви-
гателями для привода гелиевых насосов и другими устройствами
в установках глубокого холода. Громоздкость и дороговизна та-
ких установок не позволяют применять СП в качестве самостоя-
тельных опор.
1.10. МАГНИТОГИДРОДИНАМИЧЕСКИЙ ПОДВЕС
Развитие ядерной и МГД-энергетики и металлургии при-
вело к созданию насосов, дозаторов, перемешивателей и других
машин, работающих с жидкими металлами и ионизированными
газами при температурах до 1200 °C (натрий, калий, литий и др.).
Применение здесь обычных подшипников сопровождается значи-
тельными трудностями. Логичным решением является исполь-
зовать в качестве смазочного материала сам рабочий агент, т. е.
жидкий металл или газ. Однако последние обладают малой вяз-
костью, а образуемый ими смазочный слой — малой грузоподъем-
ностью. Наложение на смазочный слой магнитных полей, а так-
же пропускание через него электрического тока могут значитель-
15
но увеличить несущую способность таких опор, называемых
магнитогидродинамическими опорами. Более подробные сведения
о таких опорах заинтересованный читатель может найти в обзо-
ре [60].
1.11. ЭЛЕКТРОМАГНИТНЫЙ ПОДВЕС
В ВЫСОКОСКОРОСТНОМ НАЗЕМНОМ ТРАНСПОРТЕ
Актуальность разработок по созданию высокоскорост-
ного наземного транспорта для скоростей 500 км/ч и более широ-
ко известна благодаря печати. Работы по созданию магнитного
подвеса вагона ведутся по двум направлениям (см., например,
[22, 30]). В первом — это разработка магнитного подвеса с при-
тяжением — используется принцип активной магнитной опоры
(п. 1.5). Обычные (или сверхпроводящие) электромагниты, уста-
новленные на вагоне, притягиваются к ферромагнитному рельсу
и подвешивают вагон (рис. 1.12, а). Для стабилизации подвеса
применяют систему управления, регулирующую ток магнита. При
использовании обычных электромагнитов воздушный зазор мал
(порядка 1 см). Для увеличения зазора обычные магниты можно
заменить на сверхпроводящие, однако при этом возрастают труд-
ности управления током в сверхпроводящем магните, которое не-
обходимо для стабилизации подвеса.
Во втором направлении — разработка магнитного подвеса с от-
талкиванием — используется принцип индукционной опоры (п. 1.6).
Для подвешивания вагона используется сила отталкивания,
возникающая между токопроводящим полотном (обычно алюми-
ниевым) и движущимся над ним магнитом под действием поля
наведенных вихревых токов. Однако при малых скоростях (менее
Рис. 1.12. Магнитные подвесы вагона высокоскоростного наземного транс-
порта: а — вагон на магнитном подвесе с притяжением (или на актив-
ном магнитном подвесе); б — магнитный подвес вагона с отталкиванием
(или индукционный подвес):
1 и 2 — неуправляемые магниты
б)
Токопроводящее
полотно
16
80 км/ч) подъемная сила недостаточна, поэтому необходима до-
полнительная колесная подвеска. Данной системе присуща устой-
чивость равновесия, поэтому отпадает необходимость в системе ста-
билизации. Применение сверхпроводящих материалов позволяет
увеличить воздушный зазор до 30 см. На рис 1.12, б магниты 1
обеспечивают подъемную силу и стабилизацию вагона относитель-
но полотна по вертикали, а магниты 2 — стабилизацию по гори-
зонтали.
1.12. ВЫВОДЫ
Сравнивая преимущества и недостатки рассмотренных
выше различных типов электромагнитных подвесов, можно заклю-
чить, что наибольший практический интерес для широкого про-
мышленного использования в подшипниковых узлах роторных
машин представляет активный магнитный подвес. Подшипники,
работающие по принципу активного магнитного подвеса и обычно
называемые активными магнитными подшипниками, и будут яв-
ляться предметом дальнейшего рассмотрения.
2. ВВЕДЕНИЕ В ТЕХНИКУ
АКТИВНЫХ МАГНИТНЫХ ПОДШИПНИКОВ
2.1. ИСТОРИЧЕСКАЯ СПРАВКА
Первые примеры практического использования актив-
ных магнитных подвесов относятся к 40-м годам XX столетия.
Они описаны в работах Д. Бимса [9] по созданию ультрацентрифуг
и роторных вакуумметров, Д. Хризенгера [87] по подвеске моделей
в аэродинамических трубах и О. Г. Кацнельсона и А. С. Эдель-
штейна [42] по созданию весоизмерительных приборов. Подробное
описание конструктивных и схемных решений, использованных
в перечисленных работах, приведено в [60].
Классическим примером первых подвесов может служить ва-
куумметр Д. Бимса (рис. 2.1), сыгравший большую роль в разви-
тии исследований по магнитным подвесам. Ротор 6, представляю-
щий собой ферромагнитный шарик, подвешен внутри стеклянного
вакуумного баллона 5 с помощью электромагнита 4. Ток в элект-
ромагните управляется по сигналу индуктивного датчика 2 систе-
мой автоматического регулирования САР. Так как магнитная ин-
дукция на оси сердечника электромагнита максимальна, то невра-
щающийся шарик устойчив и в горизонтальных направлениях.
Вращающийся же шарик перейти собственную частоту горизон-
тальных колебаний без демпфирования не может. Роль демпфера
горизонтальных колебаний шарика выполняет намагниченная
стальная игла 7 с поплавком 3, помещенные в стакан 1 с маслом.
При колебаниях игла следует за шариком и демпфирует их. Раз-
гон ротора осуществляется обмотками 3, создающими вращающее-
ся магнитное поле. Частота вращения шарика измеряется опти-
ческим способом. Давление в баллоне измеряется по скорости сниже-
Рис. 2.1. Роторный вакуумметр Д. Бимса
ния частоты вращения ротора
на выбеге. Симметричность и
однородность шарика и акси-
альная симметричность маг-
нитного поля электромагнита
обеспечивают практическое от-
сутствие вихревых токов и
тормозящего момента.
Описанный подвес нахо-
дит широкое применение при
создании различного рода цент-
рифуг [60]. Интересно отме-
тить, что с помощью такого
подвеса Д. Бимс в 1954 году по-
лучил максимальную частоту
вращения шарика диаметром
0,4 мм, равную 48 млн об/мин
18
(окружная скорость 1000 м/с). В 1961 году была достигнута фан-
тастическая частота вращения 100 млн об/мин.
С 1960-х годов активные магнитные подвесы стали применять-
ся в активных магнитных подшипниках вращающихся валов.
Первый радиальный АМП был предложен и испытан в 1960 году
Р. Сикссмитом [69]. Работа Р. Сикссмита показала реальную воз-
можность использования магнитных подвесов в опорных узлах
валов и послужила новым импульсом к проведению интенсивных
разработок АМП и их практическому применению в самых различ-
ных областях техники.
В России (бывшем СССР) первые существенные практические
успехи были достигнуты во Всесоюзном научно-исследователь-
ском институте электромеханики (ВНИИЭМ, Москва) при созда-
нии уникальных электромеханических комплексов для космичес-
кой техники, используемых для управления ориентацией орбиталь-
ных станций «Салют» и «Мир» [17, 80]. Другим направлением
деятельности ВНИИЭМ в области АМП являются крупные энерге-
тические машины: электровентиляторы, электрогазодувки, турбо-
компрессоры, электронасосы, турбогенераторы [1, 25]. Первые успе-
хи по применению подвесов в области приборостроения и средств
автоматики были получены в Московском авиационном институ-
те [16, 23, 24, 52, 62], Московском энергетическом институте [41,
58] и Научно-исследовательском институте прикладной матема-
тики и кибернетики (НИИ ПМК, г. Нижний Новгород) [20, 21, 28,
51, 54, 72, 94]. Первый высокоскоростной шлифовальный электро-
шпиндель с АМП был создан и испытан в Псковском политехни-
ческом институте [38, 76]. Работы по созданию шпинделей с АМП
проводились в Экспериментальном научно-исследовательском ин-
ституте металлорежущих станков (ЭНИМС, Москва) [15].
Среди зарубежных разработчиков АМП следует особо выде-
лить французскую фирму Societe de Mecanique Magnetique (S2M) —
первую в мире коммерческую фирму, специализирующуюся на вы-
пуске АМП для машин самого различного назначения. Фирму S2M
основал в 1976 году X. Хаберманн, ему же принадлежит большое
число приоритетных конструктивных решений [91, 92]. Подроб-
ный обзор разработок фирмы S2M до 1980 года выполнен Г. А. Лу-
чиным [56].
Одними из первых разработчиков машин с АМП также являют-
ся Г. Лиард [92], Р. Каттерлоер [93], Д. Лиман [96], Ф. Матсумура
и К. Накагава [97], Г. Швайтцер и X. Ульбрих [100].
В настоящее время разработкой и производством АМП занима-
ется целый ряд фирм. Среди них:
ПИК (Псковская инженерная компания), Россия;
НИИ ПМК, г. Нижний Новгород, Россия;
MBI (Magnetic Bearings, Inc.), США;
JMB (Japan Magnetic Bearings Co., Ltd), Япония;
Mecos Traxler AG (Mechanics Control Systems), Швейцария;
19
AVCON (Advanced Controls Technology, Inc.), США;
Center for Magnetic Bearings, University of Virginia, США;
Revolve Technologies Inc., Канада;
High Speed Technology, Финляндия.
Большую роль в развитии АМП сыграли международные сим-
позиумы по магнитным подшипникам, состоявшиеся в Швейца-
рии в 1988 и в 1994 годах, в Японии в 1990 и в 1996 годах, в США
в 1992 и 1998 годах, а также международные конференции по
применениям АМП, проводившиеся университетом штата Вирд-
жиния (США): ROMAG'91, MAG'92, MAG'93, MAG'95, MAG'97.
Организаторами симпозиумов и конференций являются профессо-
ра: G. Schweitzer (Швейцария), Т. Higuchi (Япония) и Р. Allaire
(США).
Анализ публикаций показывает, что развитие АМП идет в сле-
дующих направлениях:
расширение сфер применения АМП;
методы управления АМП для гироскопических и гибких рото-
ров (оптимальное, адаптивное, нелинейное, цифровое и другие виды
управления);
прецизионные АМП;
гибридные АМП (с использованием постоянных магнитов);
динамика роторов в АМП;
идентификация параметров систем с АМП;
бездатчиковые АМП;
бесподшипниковые электродвигатели (совмещение АМП с элек-
трической машиной);
микроАМП;
сверхпроводящие подвесы;
усилители мощности;
потери в АМП;
страховочные подшипники.
2.2. ПРИНЦИП ДЕЙСТВИЯ
Активный магнитный подшипник — это управляемое
электромагнитное устройство, которое удерживает вращающуюся
часть машины (ротор) в заданном положении относительно не-
подвижной части (статора). Магнитные силы притяжения, действу-
ющие на ротор со стороны электромагнитов, управляются с помо-
щью электронной системы управления. Поэтому конструктивно
АМП состоит из двух основных частей (рис. 2.2):
электромеханической части, или собственно подшипника;
электронной системы управления.
Подшипник включает в себя ротор, подвешенный в магнитном
поле, закрепленные на статоре электромагниты и датчики положе-
ния ротора. Механический контакт между ротором и неподвиж-
20
Электронная система управления
Рис. 2.2. Принцип действия активного магнитного подшипника
ным статором отсутствует. Смещения ротора из заданного поло-
жения равновесия измеряются датчиками положения. Сигнал
с датчиков обрабатывается электронной системой управления та-
ким образом, что магнитные силы возвращают ротор в исходное
положение. При отключенном подвесе, а также в случае аварийно-
го сбоя в системе управления ротор опирается на страховочные
(или аварийные) подшипники. Эти подшипники (чаще всего это
шарикоподшипники) устанавливаются с зазором, поэтому в нор-
мальном режиме они не вращаются.
Электронная система управления включает в себя регулятор
и усилители мощности. Используя информацию, поступающую
с датчиков положения, эта система управляет положением ротора
путем изменения токов в электромагнитах. Соответствующий вы-
бор закона управления токов поз-
воляет обеспечить устойчивое
положение ротора и его цент-
ровку в зазоре, а также полу-
чить желаемые значения жест-
кости и демпфирования подве-
са. Конструктивно электронная
система управления оформляет-
ся в виде электронного блока,
соединенного кабелями с под-
шипниками и источником элек-
тропитания.
Рис. 2.3. Схема ротора как твердого
тела
21
a)
Рис. 2.4. Варианты полного магнитного подвеса ротора: а —
в двух радиальных и одном осевом АМП; б — в двух кони-
ческих АМП; в — обращенная конструкция с двумя кони-
ческими АМП
Ротор как твердое тело имеет шесть степеней свободы. Его пе-
ремещения относительно статора могут происходить в четырех ради-
альных направлениях Xv Ур Х2, Y2, одном осевом направлении Z
и во вращательном движении на угол ср2 вокруг продольной
оси (рис. 2.3). Вращение ротора <р2 является его рабочим движе-
нием. Поэтому полный (неконтактный) магнитный подвес ротора
должен ограничивать его перемещения и воспринимать нагрузки в пя-
ти направленияхХр Ур Х2, У2, Z.
В зависимости от направления воспринимаемой нагрузки АМП
могут быть радиальными, осевыми (или упорными) и радиально-
упорными (или коническими).
Полный магнитный подвес ротора может быть создан при
помощи одного осевого и, как минимум, двух радиальных АМП
(рис. 2.4, а) либо при помощи двух конических АМП (рис. 2.4, б).
На рис. 2.4, в показан обращенный вариант подвеса, в котором
неподвижный статор расположен внутри вращающегося ротора.
2.3. КОНСТРУКЦИИ ПОДШИПНИКОВ
Мировой практикой разработано и испытано большое
число конструктивных вариантов АМП. Однако нет оснований
полагать, что существует конструкция, которая была бы пригодна
Для всех без исключения приложений. При создании конкретных
Устройств всегда имеется возможность для отыскания новых кон-
СтРУктивных решений. Вместе с тем разработаны конструкции
22
Рис. 2.5. Конструктивные варианты радиального
подшипника: а — с поперечным направлением
потока; б — с продольным направлением потока
(назовем их классическими), которые с успехом используются
в большинстве приложений [13, 24, 62, 75, 99]. Рассмотрим эти
конструкции.
Радиальный подшипник. В зависимости от направления маг-
нитного потока в теле ротора относительно его продольной оси
возможны два конструктивных варианта радиального АМП:
с поперечным направлением потока (рис. 2.5, а);
с продольным направлением потока (рис. 2.5, б).
Подшипники с поперечным направлением потока более просты
в изготовлении и имеют меньшие продольные размеры. Для умень-
шения потерь на вихревые токи статор и магнитоактивная часть
ротора (цапфа) выполняются шихтованными. Данный тип под-
шипников является классическим и получил наиболее широкое
применение.
В подшипниках с продольным направлением потока нет необ-
ходимости, чтобы ротор был шихтованным. Такие подшипники при-
меняются главным образом в тех случаях, когда ротор должен быть
цельнометаллическим (например, в условиях глубокого вакуума).
Конструктивная схема классического радиального АМП представ-
лена на рис. 2.6. Подшипник содержит силовую часть, измеритель-
ную часть и страховочный (аварийный) подшипник. Силовая часть
служит для восприятия нагрузок в радиальных направлениях и со-
стоит из статора и укрепленной на валу 1 цапфы 6. Цапфа располо-
жена внутри статора с радиальным зазором 8. Статор состоит из
многополюсного кольцевого шихтованного пакета железа 4 и обмо-
ток полюсов 5. Цапфа представляет собой пакет железа в форме
полого цилиндра. Пакеты статора и цапфы набираются обычно из
листовой электротехнической стали толщиной 0,1-0,5 мм.
23
Рис. 2.6. Конструктивная схема радиального активного магнитного подшипника
Чтобы вызвать силу в любом радиальном направлении, статор
должен иметь не менее трех пар полюсов. Обычно используется
восьмиполюсная конструкция (четыре пары полюсов), в которой
обмотки каждых двух соседних полюсов соединяются между собой
и вместе с этими полюсами образуют электромагнит. В результате
статор содержит четыре электромагнита: два из них удерживают
цапфу по оси Ох, два других — по оси Оу. Очевидно, что восьмипо-
люсная конструкция более удобна при решении задачи управле-
ния, чем шестиполюсная. В случае больших подшипников целесо-
образно использовать большее число полюсов — 16, 24, 32 — это
позволит уменьшить габаритные размеры подшипника. Для умень-
шения потерь на гистерезис соседние полюса соседних электромаг-
нитов имеют одинаковую полярность.
Измерительная часть подшипника содержит датчики переме-
щений ротора в радиальных направлениях Ох и Оу. По принципу
действия датчики могут быть индуктивными, индукционными (вих-
ревыми), емкостными и оптическими. Чаще других используются
индуктивные датчики. Такой датчик состоит из статора 3 и укреп-
ленного на валу мерительного кольца 2, конструкции которых ана-
логичны конструкциям силового статора и цапфы соответственно.
Разница состоит лишь в значительно меньшей толщине пакетов
железа и большем числе полюсов и обмоток.
Страховочный подшипник 7 может быть либо шарикоподшип-
ником, либо подшипником скольжения. Он служит для двух це-
лей: опирания ротора при отключенном АМП и обеспечения выбе-
га ротора кратковременно или до полной остановки в случае ава-
рийного отказа АМП. Зазор в страховочном подшипнике обычно
равен половине рабочего зазора в АМП. Шарикоподшипник может
закрепляться как на валу, так и в корпусе машины. Подшипник
скольжения содержит вкладыш, выполненный из графита, бронзы,
фторопласта, тефлона.
24
Рис. 2.7. Конструктивная схема осевого активного
магнитного подшипника
Радиально-упорный АМП имеет коническую расточку статора
и коническую цапфу; в остальном его конструкция аналогична
рассмотренной конструкции радиального АМП.
Осевой подшипник. Осевой АМП двустороннего действия
(рис. 2.7) содержит укрепленный на валу 1 сплошной (нешихто-
ванный ) ферромагнитный диск 2, расположенный между двумя
кольцевыми электромагнитами 3 и 6 с обмотками 4 и 5. Для
измерения осевых перемещений ротора служит датчик 7. При дей-
ствии на ротор значительной постоянной осевой нагрузки (напри-
мер, силы тяжести) можно использовать осевой АМП односторон-
него действия, имеющий один электромагнит.
2.4. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
Основными техническими характеристиками АМП яв-
ляются: предельная частота вращения ротора; рабочий зазор; не-
сущая способность; габаритные размеры и масса; жесткость; точ-
ность позиционирования оси ротора; потери на трение; энергопо-
требление; эксплуатационная надежность.
Предельная частота вращения ротора зависит только от проч-
ности на разрыв материала цапфы или диска. Известно [79], что
для электротехнических сталей допустимая окружная скорость
составляет 200 м/с. Поэтому, например, при диаметре цапфы 20 мм
ротор может вращаться с частотой до 200 000 об/мин. Еще боль-
шие скорости вращения можно получить за счет использования
аморфного железа, допускающего окружную скорость 350 м/с.
Рабочий зазор в АМП на один-два порядка больше, чем в газо-
вых подшипниках. Так, характерные значения радиального зазо-
ра: 5= 0,3 мм при диаметре цапфы 70 мм; 8= 0,6 мм при диаметре
цапфы 320 мм. В специальных случаях зазор может достигать
25
нескольких десятков миллиметров. Относительно большие зазоры
облегчают технологию изготовления и снижают чувствительность
подшипника к эксплуатационному загрязнению.
Несущая способность АМП зависит от габаритных размеров
и используемого материала и достигает 60 Н на 1 см2 площади
полюса для электротехнических сталей и 100 Н на 1 см2 — для
кобальтовых сталей. Примерно такой же несущей способностью
обладают газостатические подшипники; несущая способность под-
шипников качения значительно выше. В оценочных расчетах можно
руководствоваться следующими значениями удельной несущей спо-
собности: для радиального АМП — 20 Н на 1 см2 площади диа-
метрального сечения цапфы; для осевого АМП — 40 Н на 1см2
площади полюсов.
Габаритные размеры и масса АМП существенно больше, чем
подшипников качения при одинаковой несущей способности. Раз-
меры радиального АМП можно оценить через площадь диамет-
рального сечения цапфы, равной отношению требуемой несущей
способности к удельной несущей способности (20 Н/см2). Отсюда,
зная диаметр цапфы, можно найти ее длину. Наружный диаметр
АМП приблизительно вдвое больше диаметра цапфы. Масса АМП
примерно равна произведению объема статора АМП на удельную
плотность стали.
В качестве примера в приложениях 1-3 приведены стандарты
Псковской инженерной компании на активные магнитные под-
шипники.
Жесткость АМП, определяемая как отношение амплитуды ре-
акции подшипника к амплитуде колебаний цапфы, зависит от па-
раметров системы управления и от частоты возмущения. Мини-
мальное значение жесткости имеет место на частоте возмущения,
равной собственной частоте подвеса (Оо, и составляет cmin = ^(00’
где М — масса ротора. Значение (00 зависит от параметров систе-
мы управления и обычно находится в пределах 50-500 Гц. Стати-
ческая жесткость АМП за счет введения в регулятор интегрирую-
щего звена может быть чрезвычайно высокой, в десятки раз превы-
шающей значение cmin.
Точность позиционирования оси ротора в АМП относительно
статора определяется главным образом качеством сигнала датчи-
ка положения и жесткостью подвеса. При использовании индук-
тивных датчиков может быть достигнута точность до 0,5 мкм.
Важной особенностью АМП является возможность создания
контролируемых микроперемещений ротора в зазоре путем пода-
чи в систему управления соответствующего задающего сигнала (см.
рис. 2.2). Это свойство может быть использовано, например, для
микроперемещений режущего инструмента, создания микроосцил-
ляций ротора и т. п.
Потери на трение в АМП вызваны потерями на вихревые
токи и перемагничивание в пакетах ротора. Эти потери мень-
26
ше в 5-20 раз по сравнению с подшипниками качения и в 100-
200 раз по сравнению с гидродинамическими подшипниками. Их
покрытие осуществляется двигателем, приводящим ротор во вра-
щение.
Энергопотребление АМП — это электрическая мощность, по-
требляемая подвесом от источника электроэнергии и обусловлен-
ная потерями в обмотках электромагнитов и усилителях мощнос-
ти, приблизительно равная ДР = Вт, где М — масса рото-
ра, кг. Так, в машине с ротором массой 1000 кг и гидродинамичес-
кими подшипниками потребление мощности на трение и снабже-
ние маслом составляет 150 кВт. При использовании АМП эта
мощность равна всего 1 кВт.
Энергопотребление АМП зависит также от типа привода вра-
щательного движения ротора. Длительная постоянная нагрузка,
как в случае ременной передачи, повышает расход электроэнергии.
Наиболее подходящим приводом в этом смысле является асин-
хронный электродвигатель.
Существенное (в несколько раз) снижение энергопотребле-
ния может быть достигнуто за счет использования гибридных
АМП, разработанных фирмой AVCON. Эти подшипники отличают-
ся от классических тем, что основное магнитное поле в зазоре
создается не токами смещения в обмотках, а встроенным в под-
шипник постоянным магнитом (более подробно они рассматрива-
ются в п. 5.9).
Эксплуатационная надежность АМП определяется, прежде все-
го, надежностью электронной схемы и системы электроснабжения.
Повышение надежности электронной схемы достигается путем ре-
зервирования отдельных электронных элементов и цепей, а также
обмоток электромагнитов. При внезапном прекращении электро-
снабжения питание системы управления может осуществляться
либо от запасных аккумуляторных батарей, либо от встроенного
в машину специального генератора малой мощности. При поврежде-
нии кабеля подвода тока к АМП выбег ротора до полной останов-
ки происходит на страховочных подшипниках. Эксплуатационная
надежность АМП с резервным исполнением очень высока и со-
ставляет 99 % в течение 10 лет работы.
2.5. ПРЕИМУЩЕСТВА И НЕДОСТАТКИ
Преимущества АМП вытекают из двух основных прису-
щих им особенностей:
отсутствия механического контакта между вращающейся и не-
подвижной частями машины;
наличия электронной системы управления.
Перечень преимуществ АМП и вытекающих из них положи-
тельных технических следствий приведен в табл. 2.1.
27
Таблица 2.1. Положительные свойства АМП
Преимущество Следствие
Отсутсте Отсутствие изнашивания Отсутствие смазки Высокие скорости враще- ния Низкое энергопотребление Возможность работы в экс- тремальных условиях Большой зазор Наличие эле Контролируемость положе- ния оси ротора Регулируемость жесткости и демпфирования подвеса Возможность использова- ния датчиковых сигналов для контроля параметров рабочего процесса ше механического контакта Неограниченный ресурс Снижение расходов на обслуживание и ремонт Отсутствие системы подготовки и подачи смазочного материала (насосов, фильтров, уплот- нений, сборников и т. д.) Экологическая чистота Снижение габаритных размеров машины Высокоскоростные технологии Снижение эксплуатационных расходов за счет экономии электроэнергии Малая отдача теплоты в окружающую среду Малый коэффициент трения Работа в вакууме Работа при низких и высоких температу- рах (от -150 до +450 °C) Работа в условиях радиации Работа в агрессивных средах Сверхчистые технологии Невосприимчивость к загрязнению ктронной системы управления Возможность создания контролируемых мик- роперемещений ротора в зазоре Вращение ротора вокруг оси инерции (са- моцентрование ротора) и отсутствие вибраций вследствие дисбаланса Возможность создания системы активного гашения колебаний ротора Высокая точность позиционирования Облегченный переход через критические ско- рости Отсутствие шума и вибраций Контроль скорости вращения Контроль нагрузки на подшипники Контроль положения ротора Контроль дисбаланса и балансировки ротора
К недостаткам АМП можно отнести:
необходимость во внешнем источнике электроэнергии;
сложность электронного блока управления;
относительно низкая несущая способность;
относительно высокая стоимость;
необходимость в персонале высокой квалификации для техни-
ческого обслуживания.
Взвешивая положительные свойства и недостатки АМП, можно
отметить следующее. АМП никогда не смогут полностью вытес-
нить традиционные подшипники качения и скольжения. Они на-
ходят и будут находить применение там, где возможности тради-
ционных подшипников исчерпаны.
28
2.6. ОПЫТ И ПРОБЛЕМЫ
ПРОМЫШЛЕННОГО ОСВОЕНИЯ
Промышленное, серийное освоение АМП началось в 70-х
годах XX столетия. Области их применения весьма разнообразны.
Обширный опыт накоплен по эксплуатации центрифуг: газовая
центрифуга для обогащения урана на 60000 об/мин в условиях
вакуума и радиоактивного излучения, сверхвысокоскоростная
центрифуга для проверки сцепляемости защитных покрытий на
800 000 об/мин и многие другие.
Разработки АМП не в последнюю очередь вызваны развитием
космической техники. Подшипники антенн и маховиков гироси-
ловых стабилизаторов ориентации спутников должны длительное
время работать в таких экстремальных условиях, как высокий
вакуум, невесомость, переменные температуры. Регулировка и ре-
монт их, само собой разумеется, невозможны. Применение АМП
оказывается здесь очень перспективным.
При создании высоковакуумных турбомолекулярных насосов
большой проблемой является борьба с испаряющимися из шари-
коподшипников смазочными веществами, которые загрязняют ва-
куум. Применение АМП позволило достигнуть абсолютно свобод-
ного от углеводородов вакуума.
Установка АМП в центробежный электрокомпрессор для обес-
печения циркуляции газовой среды в замкнутом контуре газового
технологического лазера позволило полностью исключить загряз-
нение внутренней среды лазера.
С помощью АМП успешно решается задача обеспечения абсо-
лютной стерильности насосов и мешалок для медицинской, фарма-
цевтической и пищевой отраслей техники.
Способность АМП работать при низких температурах позволя-
ет использовать их в криогенных турбинах и насосах.
В шлифовальных и фрезерных шпинделях необходимо обеспечить
высокие скорости вращения ротора и большую статическую жест-
кость подшипников. Этим требованиям вполне удовлетворяют АМП.
В текстильной промышленности очень актуальна проблема сни-
жения уровня шумов. Использование АМП в прядильных верете-
нах позволяет снизить уровень шумов в прядильных цехах на 15 дБ.
В балансировочных станках необходимы очень точные подшипни-
ки. С помощью АМП ось вращения ротора может стабилизироваться
с точностью до 0,5 мкм, при этом токи в катушках электромагнитов
одновременно содержат информацию об имеющемся дисбалансе.
Малое энергопотребление и способность работать в вакууме при
высоких скоростях позволяют использовать АМП в супермахови-
ках для накопления кинетической энергии.
В больших турбинах важной проблемой является обеспечение пе-
рехода ротора через критические резонансные частоты. Использование
АМП позволяет успешно демпфировать такие колебания. Кроме того,
замена гидродинамических подшипников на АМП позволяет суще-
ственно снизить эксплуатационные расходы за счет экономии энергии.
29
Насосные станции на газовых магистралях зачастую распола-
гаются в местах, труднодоступных для проведения технического
обслуживания насосов (доставки и замены масла в подшипниках,
замены изношенных частей и т. д.). Установка АМП в насосах
для перекачки газа дает большой экономический эффект за счет
отсутствия смазки и износа.
Важным применением АМП из-за малого трения и отсутствия
смазки являются опоры подвижных частей в точных измеритель-
ных приборах, гироскопах, роботах, испытательных стендах и т.д.
При этом подвижная часть, подвешенная в АМП, может совершать
как вращательное, так и поступательное рабочее движение.
Таков далеко не полный перечень возможных применений АМП.
Сферы и масштабы их применения постоянно расширяются. Вмес-
те с тем нельзя не отметить, что на пути широкого промышленно-
го освоения АМП имеется целый ряд объективных трудностей.
1. В отличие от подшипников качения и скольжения для АМП
трудно создать разносторонне используемую стандартизованную се-
рию. В каждом отдельном случае в зависимости от размеров, скоро-
сти, нагрузок, требуемой жесткости и точности, характеристик окру-
жающей среды и системы электропитания выбирается конструкция
и рассчитываются параметры подшипников и системы управления.
2. Создание машин с АМП затрудняется его многоплановостью,
обусловленной необходимостью одновременного решения комплекса
задач механики, электромеханики, систем управления и электро-
ники, а также задач по обеспечению функциональной сущности
машины. Такая работа может быть выполнена, как правило, лишь
группой подготовленных специалистов.
3. Промышленность воспринимает всякие новшества, в том числе
и АМП, замедленно в силу объективной инерционности и консерва-
тизма.
4. Прогресс в традиционных подшипниках создает конкурен-
цию для АМП (например, использование керамики в шарикопод-
шипниках создало серьезную конкуренцию для использования АМП
в металлообрабатывающих шпинделях).
Все это приводит к тому, что «... идеи АМП претворяются на
практике значительно медленнее, чем это можно было бы ожидать
из прогнозов в отношении АМП двадцать лет назад из-за встре-
тившихся на пути внедрения трудностей» [62]. С этим заключе-
нием отечественных авторов перекликается мнение зарубежных
специалистов [102] : «... для широкого промышленного внедре-
ния АМП потребуются мужество и творческая энергия инженеров
и конструкторов, а также положительное отношение к новшествам
со стороны промышленности».
2.7. ПРИМЕРЫ ПРАКТИЧЕСКИХ ПРИЛОЖЕНИЙ
Рисунки 2.8-2.12 иллюстрируют лишь небольшую часть при-
меров успешного применения АМП; необходимые пояснения даны
в подрисуночных подписях.
30
Рис. 2.8. Радиальный активный магнитный подшипник с индуктивным датчи-
ком перемещений (число полюсов подшипника 8, число полюсов датчика 16,
внутренний диаметр 50 мм, тяговое усилие 400 Н)
Рис. 2.9. Высокоскоростной шлифовальный электрошпиндель с активными
магнитными подшипниками (выполнен на базе серийного электрошпинделя
ШО-120-0,4, частота вращения 120 000 об/мин, мощность 0,4 кВт; содержит
два радиальных и один осевой АМП, статическая жесткость подвеса 30 Н/мкм,
точность позиционирования оси ротора 0,5 мкм, используется на операциях
чистового шлифования дорожек качения шарикоподшипников)
31
Рис. 2.10. Центробежный электрокомпрессор для обеспечения циркуляции
газовой среды в замкнутом контуре технологического лазера и блок управле-
ния магнитным подвесом (объемный расход газа 1 м3/с, степень сжатия 1,5, ча-
стота вращения ротора 36 000 об/мин, мощность 5,5 кВт, масса ротора 6,9 кг,
содержит два радиально-упорных конических АМП, применение которых исклю-
чает загрязнение внутренней среды лазера)
Рис. 2.11. Турбодетандер для сжижения гелия (частота вращения ротора
140 000 об/мин, мощность 2,5 кВт, функции активных магнитных под-
шипников совмещены с нагрузочным индукторным электрогенератором)
32
Рис. 2.12. Низкочастотный электродинамический вибратор с магнитным под-
весом подвижной части (пример использования магнитного подвеса для посту-
пательно движущихся объектов; служит для поверки акселерометров в инфра-
низком диапазоне частот 0,1-5,0 Гц, максимальная амплитуда 250 мм, коэффи-
циент нелинейных искажений 0,6 %, несущая способность магнитного подвеса
60 Н, коэффициент трения в подвесе менее 0,0002, на снимке видна только одна
конструктивная часть подвеса — светлый цилиндр с отверстиями, содержащий
два радиальных АМП, вибратор используется как составная часть Националь-
ного Стандарта вибрационного движения Российской Федерации — нижнее фото)
33
3. РАСЧЕТ РАДИАЛЬНОГО ПОДШИПНИКА
В настоящей главе приводятся методика расчета маг-
нитной цепи, расчет обмоток, тепловой расчет, расчет индуктивнос-
тей радиального АМП и показываются особенности расчета кони-
ческого АМП. Из большого числа возможных конструктивных ва-
риантов рассматривается только один (так называемый классичес-
кий) вариант радиального АМП с поперечным направлением маг-
нитного потока (см. п. 2.3).
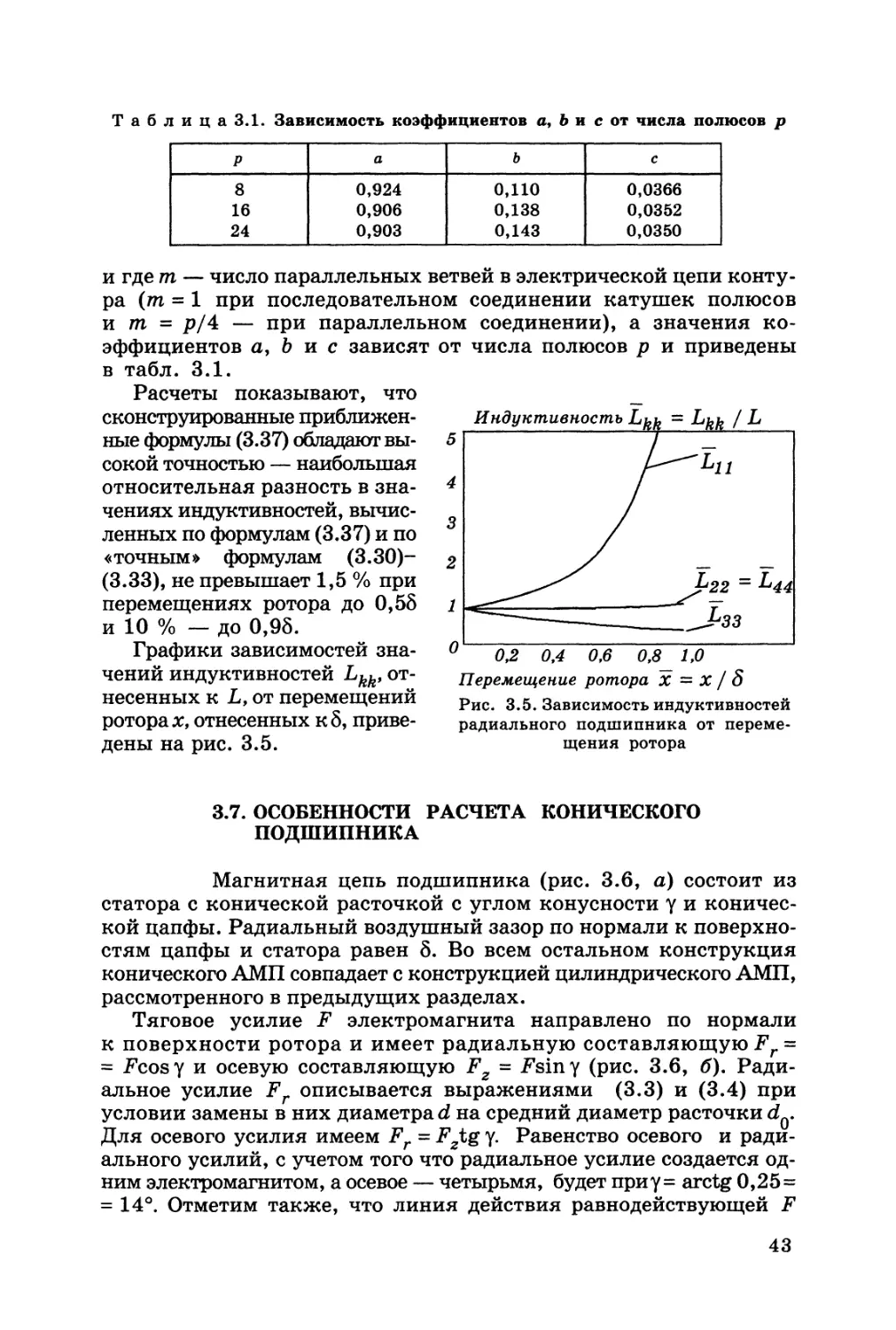
3.1. ГЕОМЕТРИЯ ПОДШИПНИКА
Геометрия магнитной цепи радиального АМП показа-
на на рис. 3.1.
Рис. 3.1. Геометрия реального подшипника
3.2. ТЯГОВОЕ УСИЛИЕ
Известно [8], что магнитная сила притяжения, действу-
ющая на элемент площади ферромагнитного тела dA в однород-
ном магнитном поле с индукцией в зазоре В,
d2
dF =------dA,
2|i0
(3.1)
где = 4 л • 10~7 Гн/м — магнитная постоянная.
Отсюда следует, что электромагнит с плоским зазором создает
тяговое усилие F = 0,4 • 106В2А, или 40 Н/см2 при В = 1 Т.
Тяговое усилие электромагнита, создаваемое, например, полюса-
ми 1 и 2 (см. рис. 3.1), определяется интегральной суммой проек-
ций элементарных сил на ось Ох
34
B2 Id
2цо 2
oq+Да а2 + Да
J cos a da + J cos a da
ai a2
(3.2)
где a — угловая координата, отсчитываемая от оси Ох.
Учитывая, что а! =-22,5° - Да/2, а2 = 22,5° - Да/2, нетрудно
установить, что выражение в круглых скобках приводится к виду
4cos 22,5° sin (Да/2) = 3,695 sin (Да/2). Аналогичным образом вы-
числяется тяговое усилие для АМП с числом полюсовр = 16, 24,..., 32.
Обобщающая формула для тягового усилия радиального АМП при-
нимает вид
„ В2 paid . Ла
F = — ------sin—, (3.3)
2ц0 4 2
где а — коэффициент числа полюсов, а = 0,924 прир = 8, а = 0,906
при р = 16, а = 0,903 при р = 24.
Поскольку полюсный угол Да = t/(d/2) мал, можно положить
sin (Да/2) = t/d и привести выражение (3.3) к виду
(3.4)
8g0
Чтобы найти удельное тяговое усилие на единицу площади ди-
аметрального сечения цапфы f - F/ld, нужно задаться шириной
полюса t. Пусть полюс занимает половину полюсного деления, т. е.
t = nd/2p. Тогда имеем
f = F/(ld) = 15,6aB2 Н/см2. (3.5)
В частном случае восьмиполюсного подшипника f = 14,4В2 Н/см2.
3.3. ОПТИМИЗАЦИЯ ГЕОМЕТРИИ
АМП, как и любой другой тип подшипника, должен об-
ладать заданной несущей способностью Втах. Применительно
к АМП под несущей способностью понимается максимальное тяго-
вое усилие, которое может развиваться в течение длительного вре-
мени без перегрева обмотки. В ряде случаев статическая нагрузка
на подшипник Q известна точно, в других случаях — приближен-
но. Однако всегда значение Втах должно быть больше Q настоль-
ко, чтобы оставался запас для отработки динамических нагрузок.
Также должна быть учтена возможность непредвиденных
нагрузок. При отсутствии особых обстоятельств коэффициент за-
паса, равный Fm8iX/Q = 2, может быть принят как вполне
приемлемый.
35
Во всех случаях вполне естествен оптимизационный подход, при
котором в заданном объеме, занимаемом подшипником, реализу-
ется максимальное тяговое усилие. Отправной точкой в процедуре
оптимизации геометрии является индукция в зазоре В. Она, в свою
очередь, зависит от магнитных свойств используемой стали. В от-
личие от электрических машин магнитное насыщение в АМП не
допускается, поскольку оно вызывает потерю управляемости.
Поэтому максимальное значение магнитной индукции в стали не
должно быть больше чем 1,4 Т для электротехнической стали
и 1,8 Т — для кобальтовой стали. Индукция в зазоре Втах при
этом будет на 10-15 % меньше, чем в стали, из-за наличия пото-
ков рассеяния и составлять 1,2 Т при использовании электротех-
нической стали и 1,6 Т — кобальтовой стали. Очевидно, что при
индукции в зазоре В = Втах подшипник должен развивать тяговое
усилие, равное требуемой несущей способности Fmax. Плотность
тока в проводниках катушек при этом должна быть равна допус-
тимому значению Jmax.
Рассмотрим для определенности восьмиполюсный АМП и сфор-
мулируем задачу оптимизации его геометрии следующим об-
разом. Пусть задан объем, занимаемый пакетом стали, т. е. зада-
ны внешний диаметр D и длина пакета I. Пусть также заданы
зазор 3 и допустимая плотность тока /тах. Требуется найти диа-
метр цапфы d и ширину полюса t, при которых тяговое усилие было
бы максимальным, а индукция в зазоре при этом была бы равна
Индукцию в зазоре найдем из закона Ампера для магнитной
цепи, по которому МДС, создаваемая катушками обоих полюсов,
равна сумме падений магнитных напряжений в двух воздушных
зазорах и в стали. Магнитная цепь не насыщена, поэтому для
простоты магнитным сопротивлением стали пренебрегаем. Тогда
имеем
Утах ^Си “ 23,
Но
(3.6)
где /?Си — коэффициент заполнения площади паза А медью (ориен-
тировочно &Си = 0,3-Ю,5).
Площадь, занимаемая обмоткой в пазу,
Отсюда следуют выражение для индукции в зазоре
(3.8)
36
и выражение для тягового усилия
91 D
F(d,t) = CFCl\ —
. \2/ Л2
(151 J t
2 2 J '
(3.9)
где Ср и Ср — константы, определяемые соотношениями:
Св = MofeCu/max . q = Р°£. (3.10)
28 8jliq
Задача оптимизации геометрии подшипника математически сво-
дится теперь к задаче на условный экстремум: требуется найти
максимум функции F(d,t) при дополнительном условии B{d,t) =
= Bmax, которое можно записать в виде уравнения
Ф(<М) = (----г¥— -^-^^ = 0. (3.11)
v 12 2 Д 2 ) Св
Метод решения такой задачи хорошо известен. Формируем функ-
цию Ф(<М) = F(d,t) + X<p(d,Z), где X — множитель Лагранжа. Три
неизвестные d, t и Л находятся из совместного решения уравнения
(3.11) и двух уравнений:
= ЭФОМ) _
М д!
Решение задачи дается соотношениями:
i = 0,22П-0,9937втах/Св; (3.13)
d = 0,52) + 0,273f; (3.14)
Св >Втах/(л2)2/64). (3.15)
Видно, что в оптимальном подшипнике внутренний диаметр d
должен быть немного больше половины наружного диаметра D.
Ширина полюса t в зависимости от соотношения между вы-
бранными значениями параметров Втах, / х и 5 может менять-
ся в определенных пределах. Обычно эти параметры выбирают
так, чтобы полюс занимал примерно половину полюсного деления,
равного nd/8.
Требуемое значение несущей способности ^max может быть дос-
тигнуто соответствующим выбором длины пакета стали Z. Про-
дольный размер статора lc - I + 2t0 где tQ = (nd/8 - t)/2 — длина
лобовой части обмотки.
В приложении 1 приведены результаты оптимизации геометрии
подшипника при Bmax = 1 Т.
37
3.4. РАСЧЕТ ОБМОТКИ
Радиальный АМП имеет четыре электромагнита, поэто-
му его обмотка содержит четыре электрические цепи. Каждая цепь
содержит р/4 полюсных катушек. Катушки в цепи могут вклю-
чаться последовательно или параллельно. Очевидно, что при па-
раллельном включении требуется больший ток, но меньшее на-
пряжение. Потери на перемагничивание в роторе будут меньше,
если МДС двух соседних полюсов соседних электромагнитов име-
ют одинаковое направление. Схема соединения катушек обмотки
восьмиполюсного АМП показана на рис. 3.2. Схемой реализуется
последовательность полярностей полюсных наконечников вида
NS—SN—NS—SN.
Максимальный ток в проводнике катушки imax должен быть
согласован с максимальным током, который может развивать уси-
литель мощности. С другой стороны, ток imax должен вызывать
максимальное тяговое усилие Fmax и максимальную магнитодви-
жущую силу
2zlZmax = AnaxW- <ЗЛ6>
При известном токе гтах по формуле (3.16) легко вычисляется
число витков на полюс п. Далее последовательно определяются
площадь сечения проводника
а0 = *тах/Лпах’ (3.17)
омическое сопротивление катушки
B = pnZm/a0
(3.18)
Рис. 3.2. Соединение катушек радиального АМП: а — расположение
катушек; б — последовательное включение; в — параллельное
включение
б)
ИН1К2 hK3H4 13Н5К6 Ч К7 Н8
38
и мощность тепловых потерь одного электромагнита
Pl = i2Rp/4:. (3.19)
Здесь р = 0,018 Ом • мм2/м — удельное сопротивление меди; 1т —
средняя длина проводника катушки,
lm = 2l + 2nd/p. (3.20)
3.5. ТЕПЛОВОЙ РАСЧЕТ
Тепловой расчет АМП заключается в определении мак-
симальной температуры проводника катушки и сравнении ее с до-
пустимой температурой для используемого класса изоляции. Рас-
чет основан на законе Ома для установившегося теплового потока
АТ = РЛт, (3.21)
где ДТ — перепад температуры на тепловом проводнике; Р —
рассеиваемая мощность; RT —тепловое сопротивление.
Рассмотрим характерный случай, когда токи в катушках всех
четырех электромагнитов одинаковы и равны: i = imax/2. Тогда в об-
мотке АМП будет выделяться мощность
Р = 4Л = /4ахЯ/4. (3.22)
На рис. 3.3 показана расчетная схема тепловой цепи подшип-
ника. Обмотка представлена в виде теплового источника мощнос-
тью Р. Отбор теплоты происходит двояко: через воздух с темпе-
ратурой Та и через корпус машины с температурой корпуса Th.
Одна часть теплоты передается от обмотки непосредственно в ок-
ружающий ее воздух через тепловое сопротивление
«Си-а =1/(аАСи_а), (3.23)
где а = 12 Вт/(м2 • К) — коэффициент теплопередачи от обмотки
в воздух; Aqu_o —площадь поверхности лобовых частей обмотки.
Другая часть теплоты передается от обмотки на железный сер-
дечник через электроизоляционный слой между обмоткой и сер-
дечником, обладающий тепловым сопротивлением
R^/tA^), (3.24)
где Az — толщина изоляции;
X- — коэффициент теплопро-
водности изолирующего мате-
риала [Х = 0,16 Вт/(м • К) для
изоляционной бумаги]; А- —
суммарная площадь внутрен-
ней поверхности пазов и на-
ружной поверхности полюсов.
Рис. 3.3. Тепловая цепь радиального
АМП
39
Тепловое сопротивление железного сердечника значительно меньше,
чем электроизоляционного слоя, поэтому им можно пренебречь. Отбор
теплоты от железного сердечника, имеющего температуру TFe, про-
исходит двумя путями: в воздух через тепловое сопротивление
ЯРе_а = 1/(аАГе_а), (3.25)
где AFe _ а — площадь контактирующей с воздухом части наруж-
ной поверхности сердечника, и в корпус машины через тепловое
сопротивление T?Fe _ h (последнее зависит от конструкции узла
крепления подшипника в корпусе).
В случае, если сердечник подшипника запрессован непосредствен-
но в металлический корпус машины, то тепловым сопротивлением
BFe _ h можно пренебречь, температура сердечника TFe будет равна
температуре корпуса Th, и температура обмотки
^Си = ( ^Си — а ^1? + Яр а + ^Си — а^\)/(^Си — а + ty' (3.26)
В другом предельном случае, когда тепловое сопротивление пе-
рехода от сердечника к корпусу jRFe __ h очень большое, решение
задачи имеет вид
•^Си “ + ^Си — a (fy + ^Fe — а)/(^Си — а + + ^Fe — а)* (3.27)
Тепловой расчет заканчивается сравнением температуры обмотки
ТСи с допустимой температурой для используемого класса изоля-
ции ( 110 °C для эмалевой изоляции).
3.6. ИНДУКТИВНОСТИ ПОДШИПНИКА
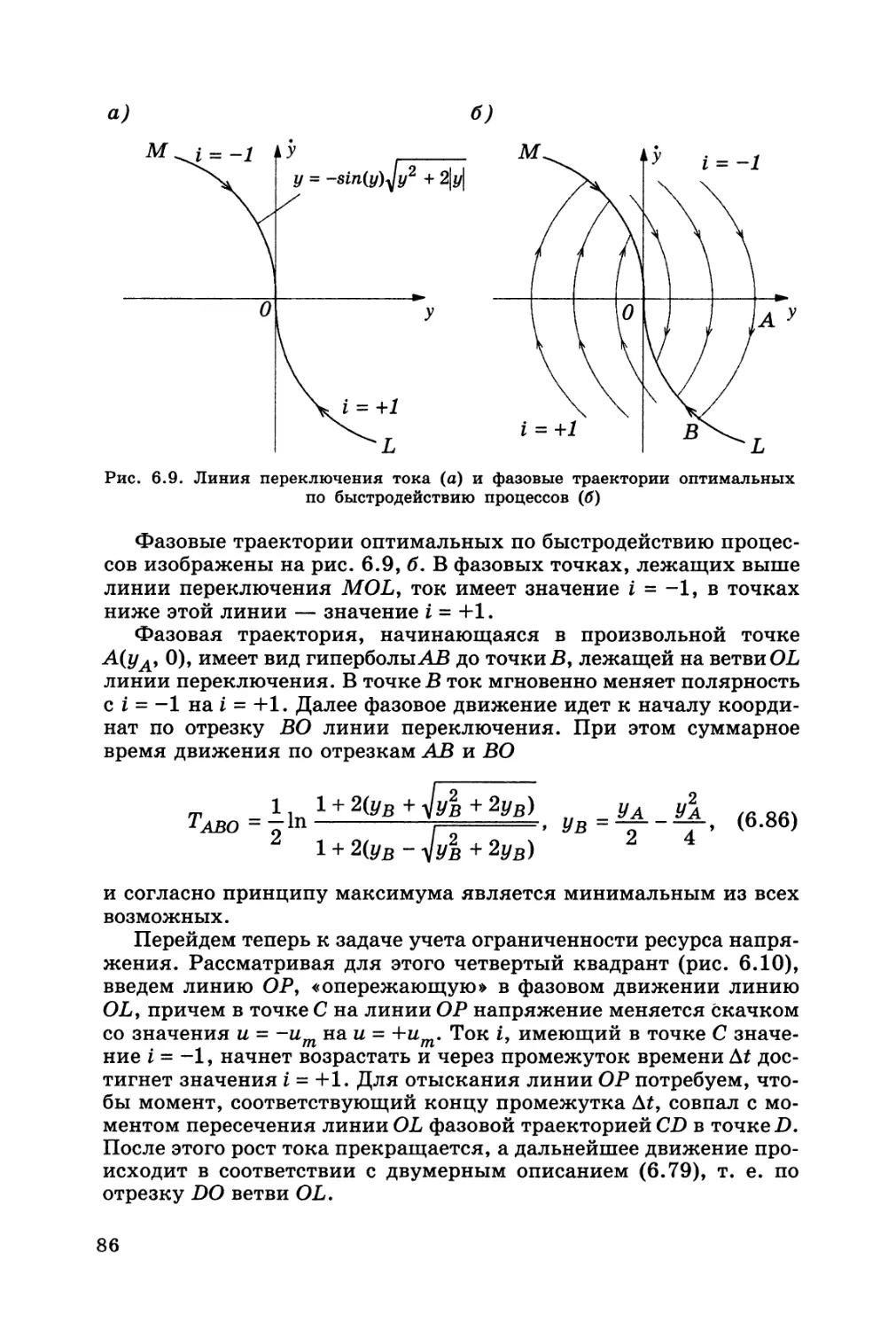
Радиальный АМП содержит четыре электромагнита.
В данном разделе дается вывод выражений для самоиндуктивнос-
тей Lkk и взаимоиндуктивностей Lks (k *s; k, s = 1, ..., 4) электро-
магнитов как функций перемещений ротора х и у. Эти выражения
будут необходимы в дальнейшем для описания электромагнитных
процессов в АМП.
Обратимся вновь к рис. 3.2, на котором показана электромаг-
нитная цепь АМП с числом полюсов р = 8. Катушки полюсов
имеют равное число витков п, соединены попарно последовательно
(рис. 3.2, б) и образуют четыре электромагнитных контура е тока-
ми i2, i3, i±. Первый контур с полюсами 1 и 2 и третий контур
с полюсами 5 и 6 удерживают ротор по оси х, второй контур с полю-
сами 3 и 4 и четвертый контур с полюсами 7 и 8 — по оси у.
Рассматривается случай короткого подшипника; магнитным со-
противлением железа, потоками рассеяния, магнитным гистерези-
сом и вихревыми токами пренебрегаем.
Эквивалентная схема цепи показана на рис. 3.4, где ek = nik —
МДС одной катушки в /?-м контуре, k =1, ..., 4; — магнитная
40
Рис. 3.4. Эквивалентная схема электромагнитной цепи радиального
подшипника
проводимость воздушного зазора под i-м полюсом, i = 1, ..., 8; Ф^ —
магнитный поток через полюс и зазор.
Самоиндуктивность &-го контура и взаимоиндуктивность &-го
и s-го контуров определяются как
hk=^sk/^ <3-28>
где, например, для k - 1 и s = 2 потокосцепления ?пи нахо-
дятся при = niv е2 = е3 =е4 = 0 и составляют:
= п(Ф2 - Фг); Т21 = и(Ф3 - Ф4). (3.29)
Магнитные потоки Ф- легко могут быть найдены по методу
узловых потенциалов [8]. В результате получаем:
= n2[^2fe-i + g2k “ f^2fe-i “ &2k)2 I G]> 30)
Lks = (~Vk+Sn2(g2k-l -^2k)(^2s -&2s-l) I G>
где G — суммарная магнитная проводимость зазоров,
G =£1 +£2 + - + Я8. (3.31)
Магнитная проводимость зазора под i-м полюсом определяется
интегралом
Л a'i
где ot- и af — соответственно угловые координаты начала и конца
f-й полюсной дуги; h — высота зазора под элементом площади dA,
h =8 - xcos а - i/sin а. (3.33)
41
Таким образом, индуктивности АМП описываются выражения-
ми (З.ЗО)-(З.ЗЗ). Вполне очевидно, что использование этих выра-
жений при описании электромагнитных процессов чрезвычайно
неудобно. Поэтому возникает задача конструирования приближен-
ных аналитических выражений. Для этого разложим функцию 1/Л
в степенной ряд
h 1 = 3 1 1 + (х cosa + у sin a) + (х cosa + у sin a)2 + • • L (3.34)
где x и у — безразмерные перемещения ротора,
X = х / 8; у = у /8.
(3.35)
Отбрасывая слагаемые со степенями х и у выше второй, после
интегрирования получаем
Si = {Да + x(sina" - sina£) + i/(cosa- - cosaf) +
23
+ — [Да + i (sin 2a* - sin 2a •) 4- — (cos 2a'z - cos 2aJ) +
2 2 2
—2 i
+ [Да + — (sin 2а'г - sin 2a')]} (
A A
(3.36)
где, например, aj = -22,5° - Да / 2, aj = -22,5° + Да / 2 и т. д.
Учитывая, что подынтегральное выражение (3.32) является ги-
перболической функцией х и у, приближенные выражения для ин-
дуктивностей целесообразно конструировать также в виде гипер-
болических функций х и у. Потребуем также, чтобы разложение
приближенных выражений в степенной ряд по х и у совпадало с раз-
ложением «точных» выражений (З.ЗО)-(З.ЗЗ) с точностью до
квадратических членов.
Обобщая результаты на АМП с числом полюсовр, равным 8, 16,
24, приходим к следующим приближенным выражениям для ин-
дуктивностей радиального АМП:
Ln = L / (1 - ах - by2); L22 = L /(1-ау - bx2);
L33 = L / (1 + ах - by2); L44 = L / (1 + ау - bx2); L13 = Ley2;
^24 = Lex2; L^4 = L23 = ~^i2 = “Am = Lexy, (3.37)
где L — индуктивность контуров при центральном положении
ротора,
L = J_£"WAa, (3.38)
тп2 8 3
42
Таблица 3.1. Зависимость коэффициентов а, Ъ и с от числа полюсов р
р а b с
8 0,924 0,110 0,0366
16 0,906 0,138 0,0352
24 0,903 0,143 0,0350
и где т — число параллельных ветвей в электрической цепи конту-
ра (т = 1 при последовательном соединении катушек полюсов
и т = р/4 — при параллельном соединении), а значения ко-
эффициентов а, b и с зависят от числа полюсов р и приведены
в табл. 3.1.
Расчеты показывают, что
сконструированные приближен-
ные формулы (3.37) обладают вы-
сокой точностью — наибольшая
относительная разность в зна-
чениях индуктивностей, вычис-
ленных по формулам (3.37) и по
«точным» формулам (3.30)-
(3.33), не превышает 1,5 % при
перемещениях ротора до 0,58
и 10 % — до 0,98.
Графики зависимостей зна-
чений индуктивностей Lkk, от-
несенных к L, от перемещений
роторах, отнесенных к8, приве-
дены на рис. 3.5.
Перемещение ротора X = X / 8
Рис. 3.5. Зависимость индуктивностей
радиального подшипника от переме-
щения ротора
3.7. ОСОБЕННОСТИ РАСЧЕТА КОНИЧЕСКОГО
ПОДШИПНИКА
Магнитная цепь подшипника (рис. 3.6, а) состоит из
статора с конической расточкой с углом конусности у и коничес-
кой цапфы. Радиальный воздушный зазор по нормали к поверхно-
стям цапфы и статора равен 8. Во всем остальном конструкция
конического АМП совпадает с конструкцией цилиндрического АМП,
рассмотренного в предыдущих разделах.
Тяговое усилие F электромагнита направлено по нормали
к поверхности ротора и имеет радиальную составляющую Fr =
= Feos у и осевую составляющую Fz - Fsiny (рис. 3.6, б). Ради-
альное усилие Fr описывается выражениями (3.3) и (3.4) при
условии замены в них диаметра d на средний диаметр расточки
Для осевого усилия имеем Fr = Fztg у. Равенство осевого и ради-
ального усилий, с учетом того что радиальное усилие создается од-
ним электромагнитом, а осевое — четырьмя, будет приу = arctg 0,25 =
= 14°. Отметим также, что линия действия равнодействующей F
43
Рис. 3.6. Конический подшипник: а — геометрия; б — диаграмма сил
пересекает продольную ось ротора не в центре О подшипника,
а в точке С, смещенной от точки О в сторону основания конуса на
расстояние
9 \
dp ! I2
2 6d0cos2Y>
(3.39)
tgy.
Перейдем к индуктивностям конического АМП. Очевидно, что
выражения (3.30) для индуктивностей цилиндрического АМП спра-
ведливы и для конического АМП, однако выражение (3.32) для
магнитной проводимости зазора под i-м полюсом будет иным:
, л //2 <
podA ц0 г f r(z)
gi = —— =-------- docdz, (3.40)
1 J h cosy J J h
Ai -1/2 a-
где r(z) — текущий радиус расточки; h — высота зазора под эле-
ментом площади dA,
h = 8 - (xcosa + z/sina)cosy - zsiny. (3.41)
Аналогично тому, как были сконструированы приближенные
выражения (3.37) для индуктивностей цилиндрического АМП, по-
лучаются следующие приближенные выражения для индуктивно-
стей конического АМП [32]:
Ьц - L / (1- ах - by2 - z sin у); L22 = L / (1- ay - bx2 - z sin y);
44
L33 = Ь / (1 + ax - by2 - z siny); L44 = L / (1 + ay - bx2 - z siny);
Ь13 ~ Ley2; L24 = Lex2; L14 = L23 = “^12 = ~^34 = Lexy, (3.42)
где z = z / 3 и где
1 pn2 |iodoZAa
m2 8 Scosy
(3.43)
Заметим, что если oebz будет направлена от вершины к основа-
нию конуса, то в формулах (3.42) следует положить у < 0.
4. РАСЧЕТ ОСЕВОГО ПОДШИПНИКА
В данной главе приводится процедура расчета геомет-
рических параметров и обмотки осевого АМП, выводятся выраже-
ния для индуктивностей и рассматривается способ учета вихревых
токов.
4.1. ГЕОМЕТРИЯ ПОДШИПНИКА
Геометрия магнитной цепи осевого АМП показана на
рис. 4.1.
Рис. 4.1. Геометрия осевого подшипника
4.2. РАСЧЕТ МАГНИТНОЙ ЦЕПИ
Предполагается, что площади обоих полюсов — внут-
реннего и наружного — одинаковы и равны А. Тогда, учитывая
(3.1), тяговое усилие осевого АМП
F = В2А / ц0 = 0,8 • 106В2А. (4.1)
Задавшись несущей способностью Fmax и максимальной индук-
цией в зазоре Втах, определяем из (4.1) площадь полюса
А = Ростах / ^тах* (4*2)
Отсюда следуют значения толщины внутреннего полюса
46
I 2
+ (4.3)
V 4 я 2
и толщины наружного полюса
t= ^2 _М--. (4.4)
2 2 V 4 я
Площади путей магнитного потока в стенке статора и в диске
не постоянны, а пропорциональны расстоянию до оси вращения.
Чтобы не было насыщения, минимальные значения этих площадей
должны быть больше или равны площади полюсов. Из этого усло-
вия находим толщину стенки статора
^3 > А / + tj) (4.5)
и толщину диска
t4>2*3. (4.6)
Тем самым определена ширина паза под обмотку
bQ^(D2-d1)/2-t1-t2. (4.7)
Используя закон полного тока и пренебрегая магнитным со-
противлением железа, находим высоту паза
^0 = 2J33 / НоЛпах^Си^О’ (4.8)
где, как и ранее, ;тах — допустимая плотность тока; /?с— коэф-
фициент заполнения площади паза медью (&Си = 0,4 * 0,6).
В приложении 3 приведены результаты расчета магнитной цепи
подшипника при Bmax = 1 Т.
4.3. РАСЧЕТ ОБМОТКИ
Зная максимальный ток усилителя мощности imax, по-
следовательно находим:
площадь сечения провода
*тах/Лпах’ (4.9)
число витков обмотки п ~ *CtAA)/aO* (4.10)
среднюю длину витка = + 2tr 4- 60); (4.И)
47
омическое сопротивление обмотки
R = pnlm/a0; (4.12)
мощность тепловых потерь в обмотке при i = *тах/2
Р = й4ах/4. (4.13)
Тепловой расчет обмотки осевого АМП производится по той же
методике, что и для обмотки радиального АМП (п. 3.5).
4.4. ИНДУКТИВНОСТИ ПОДШИПНИКА
Найдем индуктивности 1-го (левого) иЬ22 2-го (пра-
вого) электромагнитов (см. рис. 4.1) в предположении, что оста-
ются в силе все упрощающие допущения, сделанные для радиаль-
ного АМП в п. 3.6.
Принципиальное различие состоит в том, что в осевом АМП
геометрия воздушного зазора и, следовательно, индуктивности за-
висят от осевого перемещения z и угловых перемещений ф„ и
диска и не зависят от поступательных перемещении х и у.
Электромагнитная цепь каждого электромагнита представляет
собой последовательное соединение магнитных проводимостей воз-
душных зазоров под внутренним полюсом и под наружным
полюсом £2, содержащее МДС обмотки ш. Для такой цепи имеем
Lkk=n2g1g2/(g1+g2'),k = i,2- (4-14)
Магнитные проводимости зазоров определяются интегралами
2л А/2 л п 2л D2/2
f f pdpda r f pdpda
*1=HO J J J (4.15)
0 c^/2 0 с^/2
где p, a — полярные координаты; h — текущая высота зазора,
h = 3 - z - <pxp sin a 4- ф^р cosa (4.16)
для первой цепи и
h = 3 + z + фд-psina - ф^рсоэа (4.17)
для второй цепи.
Из соотношений (4.14)-(4.17) с точностью до квадратических
членов в разложениях в ряды по степеням z, фх и ф^ получаем:
ill = - -Z -^-2----2'; £22 = Ь°--2--Г. (4.18)
1-2 -аф(Фх +<рр 1 + а-аф(<р; + <рр
48
Здесь Lq — индуктивность при центральном положении диска,
Lq =ц0«2^/(28),
(4.19)
— безразмерный коэффициент, определяемый соотношением
аф = (df + Dl +dl + D%) / (З232), (4.20)
и 2 = z 15 — безразмерное осевое перемещение диска.
4.5. УЧЕТ ВИХРЕВЫХ ТОКОВ
Статор и диск осевого АМП выполняются из ферромаг-
нитного токопроводящего материала. Любое изменение магнитно-
го потока в таком материале приводит к индуцированию вихре-
вых токов. Эти токи, как известно, препятствуют причине, их вы-
зывающей, т. е. изменению основного потока. В отличие от ради-
ального подшипника, геометрия осевого подшипника не позволяет
использовать шихтованный материал. В связи с этим возникает
задача учета влияния вихревых токов в осевом АМП.
В качестве иллюстрации на рис. 4.2. показан характер влия-
ния вихревых токов на частотные характеристики электромагни-
та. Эксперимент проводился с радиальным АМП (шихтованный
сердечник) и осевым АМП (сплошной сердечник). Видно, что вих-
Рис. 4.2. Экспериментальные частотные характеристики электро-
магнита с шихтованным 1 и сплошным 2 сердечниками: а — схе-
ма электромагнита; б — амплитудно-частотные характерис-
тики; в — фазочастотные характеристики
49
Короткозамкнутая и = Usintot
A\\\\><\\\\\\V
Рабочая
обмотка
Рис. 4.3. Моделирование влияния вихревых токов на частотные характе-
ристики электромагнита со сплошным сердечником при помощи коротко-
замкнутой обмотки: а — схема электромагнита; б — амплитудно-частотные
характеристики; в — фазочастотные характеристики:
1 — экспериментальная; 2 — расчетная
ревые токи на высоких частотах препятствуют стремлению ампли-
туды тока в обмотке к нулю и уменьшают угол сдвига фаз между
током и напряжением на 45°.
Для учета влияния вихревых токов будем использовать следу-
ющий подход. Вихревые токи циркулируют по замкнутым конту-
рам в каждом элементарном объеме материала, и число таких
контуров бесконечно большое. Для приближенного решения зада-
чи вполне естественно заменить их одним короткозамкнутым кон-
туром, через который проходил бы весь магнитный поток, при
этом материал магнитопровода можно условно считать нетоко-
проводящим.
На рис. 4.3, а показан электромагнит со сплошным сердечни-
ком, влияние вихревых токов в котором моделируется дополни-
тельной короткозамкнутой обмоткой. Эта обмотка характеризует-
ся двумя параметрами: числом витков пкз и омическим сопротив-
лением Лкз. Физически очевидно, что одним из этих параметров
можно задаться, другой же параметр следует найти из эксперимен-
та. Наиболее удобным в расчетах является случай, когда коротко-
замкнутая обмотка имеет такое же число витков, что и рабочая
обмотка. Эксперименты показывают, что для осевого подшипника
омическое сопротивление короткозамкнутой обмотки примерно на
порядок выше, чем омическое сопротивление рабочей обмотки R.
В дальнейшем будем полагать, что
п=п, Д=10Л. (4.21)
XVO XVO
На рис. 4.3, б и 4.3, в сравнивается вид частотных характерис-
тик осевого АМП — полученных из эксперимента и расчетом при
50
моделировании влияния вихревых токов короткозамкнутой обмот-
кой. Видно, что имеется количественное (по амплитуде) и каче-
ственное (по фазе) совпадение результатов.
В заключение отметим, что при описанном способе моделирова-
ния влияния вихревых токов каждый электромагнит содержит не
одну, а две обмотки — рабочую и короткозамкнутую, между кото-
рыми имеется индуктивная связь. Индуктивность рабочей обмот-
ки дается выражением (4.18). В силу (4.21) этим же выражени-
ем описываются как индуктивность короткозамкнутой обмотки,
так и взаимная индуктивность этих двух обмоток.
5. ЭЛЕКТРОМАГНИТ КАК ОБЪЕКТ УПРАВЛЕНИЯ
В активных магнитных подвесах управление механи-
ческим движением подвижного элемента (ротора) осуществляется
при помощи электромагнитов. Целью данной главы является ма-
тематическое описание электромагнита как объекта управления, т. е.
установление взаимосвязей между механическим движением по-
движного элемента и электромагнитными процессами, протекаю-
щими в электромагните.
5.1. СХЕМАТИЗАЦИЯ ПОДВЕСА
ОДНОСТОРОННЕГО ДЕЙСТВИЯ
Схема одностепенного магнитного подвеса односторон-
него действия показана на рис. 5.1. Ферромагнитное тело (якорь)
массой т должно удерживаться на расстоянии 8 от полюсов элек-
тромагнита. Текущее значение воздушного зазора между телом и
полюсами
q(t) = 8 - y(t), (5.1)
где y(t) — смещение тела из заданного положения, или управляе-
мая координата.
На тело действуют две силы: сила тяжести Q = mg и магнит-
ная сила F. К обмотке электромагнита, имеющей число витков п,
сопротивление г и ток i, приложено управляющее напряжение и.
Ток i вызывает магнитный поток Ф, поэтому потокосцепление об-
мотки Т = пФ.
Механическое движение на основании второго закона Ньютона
описывается дифференциальным уравнением
my = F-Q. (5.2)
52
Магнитная силаГ может быть определена из рассмотрения элек-
тромагнитных процессов. Согласно второму закону Кирхгофа эти
процессы описываются дифференциальным уравнением
бРР
---+ п = и.
dt
(5.3)
5.2. МАГНИТНАЯ ЭНЕРГИЯ И КОЭНЕРГИЯ
Уравнение (5.3) содержит две переменные: ток i и пото-
косцепление гР. Если считать, что вихревые токи и магнитный гис-
терезис отсутствуют, то между этими переменными для каждого
значения координаты у имеется однозначная зависимость, пред-
ставляемая диаграммой намагничивания Т - i (рис. 5.2). Отсюда
следует, что для описания электромагнитных процессов можно
использовать либо пару переменных у и 'Р, либо пару переменных
У и i.
В электромеханике [57, 81] с переменными у и Т связывается
понятие магнитной энергии
= f ify^dY,
О
(5.4)
а с переменными у и i — понятие магнитной коэнергии
W(y,i) = ^(y.ijdi. (5.5)
О
Потокосцепление ¥
Рис. 5.2. Диаграмма намагничивания электромагнита
при постоянном зазоре
53
Различие между магнитной энергией и коэнергией поясняет
рис. 5.2. Из этого же рисунка следует
Wm + W = Vi. (5.6)
5.3. МАГНИТНАЯ СИЛА
Чтобы найти силу F, умножим обе части уравнения (5.3)
на idt и запишем его в виде
uidt = ri?dt + zdT. (5.7)
Левая часть уравнения (5.7) представляет собой энергию, полу-
чаемую от внешнего источника за время ск. Слагаемое ri2dt есть
энергия, идущая на нагрев обмотки. Слагаемое idT есть прираще-
ние энергии системы, которое затрачивается на совершение силой F
механической работы на элементарном перемещении dy и на при-
ращение магнитной энергии dWm, т. е.
idT = Fdy + dWm. (5.8)
Из аналитической механики [55] известно, что при вычислении
обобщенной силы, соответствующей какой-либо обобщенной коор-
динате, варьируется только эта координата, а все другие координа-
ты остаются неизменными. Поэтому, если используется пара пере-
менных у и 4х, то работа силы F на перемещении dy должна вычис-
ляться по определению при 4х = const. Тогда dT = 0 и из (5.8)
следует
F = -dWm/dy. (5.9)
Следует еще раз подчеркнуть, что при выводе формулы (5.9)
потокосцепление 4х считается постоянным именно по определе-
нию, а не как некоторые не подкрепленные объяснением гипотети-
ческие частные случаи 4х = const (или i = const), вводимые некото-
рыми авторами (см., например, [8] и [81]). В методическом смысле
это принципиально.
В другом случае, когда используется пара переменных у и I,
работа силы F на перемещении dz/ должна вычисляться также по
определению при i= const. Выразив предварительно из (5.6) диф-
ференциал dWm = -сПУ + Tdi + zdT и подставив его в (5.8), имеем
Fdy = dW - Tdz. В данном случае dz = 0, поэтому получаем
F = dW /ду. (5.10)
Таким образом, магнитная сила может определяться как через
магнитную энергию, так и через коэнергию.
Насыщение в магнитной цепи АМП отсутствует, поэтому пото-
косцепление и ток связаны линейной зависимостью
54
'Р = L(y)i,
(5.11)
где L(y) — индуктивность электромагнита.
Для рассматриваемого электромагнита, используя формулу (4.18)
для индуктивности осевого АМП, имеем
L(y) = cL/^-y), (5.12)
где cL = iIq7i2A/2 — конструктивный параметр.
С учетом (5.11) и (5.12) выражения (5.4) и (5.5) принимают вид:
IT2 1 9 1 2 W = -L(y)i2 (5.14) 2 2 о - у
Из (5.9) и (5.10) следуют две формы выражения для магнитной
силы:
r=A =2«t= (515’ 2 (5.16) dy 2 (8-y)2
5.4. ДВЕ ФОРМЫ УРАВНЕНИЙ ПОДВЕСА
Математическое описание объекта управления «элект-
ромагнит — подвижный элемент» зависит от выбора независимых
переменных, определяющих его состояние. Так, если используются
переменные у и 4х, то согласно (5.2), (5.3), (5.11), (5.12) и (5.15)
объект управления описывается следующей системой дифференци-
альных уравнений:
тпу = 'Р2/(2с£)-С;
'V + rQ-yYV/cL =и.
(5.17)
В случае, если используются переменные у и i, уравнения объек-
та управления имеют вид:
my = cLi2(b- у) 2 / 2- Q;
С£(3 - уУХ(1)' +cL(6- y)~2iy + ri = и,
(5.18)
где обозначено (i)e -di / dt.
55
Отметим, что обе системы уравнений (5.17) и (5.18) нелиней-
ны. Структура уравнений (5.17) несколько проще, чем уравнений
(5.18). Однако чаще всего используется представление (5.18), по-
скольку ток измеряется значительно проще, чем потокосцепле-
ние. Поэтому в дальнейшем будем использовать только пред-
ставление (5.18).
Уравнения (5.18) описывают простейшую нелинейную элект-
ромеханическую систему третьего порядка, в которой механиче-
ское движение подвижного элемента и электромагнитные про-
цессы в электромагните взаимосвязаны. Первое уравнение, опи-
сывающее механическое движение, содержит магнитную силу, за-
висящую от квадрата тока. Второе уравнение, описывающее элект-
ромагнитные процессы, содержит перемещение и скорость под-
вижного элемента.
5.5. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ
Известно, что линейные системы управления обладают
высокими динамическими качествами и просты в реализации.
В связи с этим линеаризуем уравнения подвеса (5.18) в окрестно-
сти положения равновесия.
В рассматриваемом подвесе (см. рис. 5.1) тело должно быть
застабилизировано на расстоянии q = 8 от поверхности полюсов,
т. е. в положении, где координата у = 0. Это положение тела будет
равновесным, если магнитная сила равна силе тяжести, т. е. F =
= Fc= Q, а ток и напряжение имеют постоянные значения или зна-
чения смещения:
i = ic = ^2&2Fc I cL\ u = uc = ric, (5.19)
которые определяют номинальную или рабочую точку системы.
Теперь предположим, что подвес функционирует вблизи рабочей
точки, так что справедливо представление
|г/| «8; F = Fc + Fv(t)\ i = ic + iv(t); u = uc + uv(t), (5.20)
где Fv(t), iv(t), uv(t) суть малые отклонения соответствующих
переменных от их номинальных значений (условие малости управ-
ляющего напряжения uv(t) не является обязательным).
Применив процедуру линеаризации к уравнениям (5.18), полу-
чаем линеаризованные уравнения подвеса вида:
ту = Fv; Fv=cyy-^hiiv; (5.21)
L(iv)* + hty + riv = uv; (5.22)
56
где
и =Г—1 С^с _ Lic .
у Ыо" з3 82 ’
(5.23)
h cLlc _ Lic
1 UJ0" 82 8
(5.24)
и где L — индуктивность в положении равновесия,
L = cL /8.
(5.25)
Коэффициент Су связывает магнитную силу и перемещение тела.
Как и жесткость пружины, работающей на растяжение-сжатие, он
измеряется в ньютонах на метр. Однако, если сила упругости пру-
жины всегда направлена в сторону, противоположную перемеще-
нию, и стремится вернуть тело в положение равновесия, то рас-
сматриваемая составляющая магнитной силы направлена в сторо-
ну перемещения и, следовательно, стремится дестабилизировать си-
стему. Поэтому коэффициенту, являющийся положительным, на-
зывают «отрицательной» позиционной жесткостью магнитного
подвеса.
Коэффициент h-L связывает магнитную силу и ток; он измеряет-
ся в ньютонах на ампер и называется токовой жесткостью подвеса
или регулировочным коэффициентом.
Первое слагаемое в (5.22) есть ЭДС самоиндукции, второе сла-
гаемое — ЭДС движения и третье слагаемое — падение напряже-
ния на активном сопротивлении обмотки. Правая часть в (5.22)
содержит управляющее напряжение, приложенное к обмотке элек-
тромагнита.
5.6. НЕУСТОЙЧИВОСТЬ ОБЪЕКТА УПРАВЛЕНИЯ
Согласно (5.21) движение тела в линейном приближе-
нии описывается дифференциальным уравнением
my-cyy = hiiv. (5.26)
Характеристическое уравнение объекта управления (5.26)
ms2 - су = 0 (5.27)
имеет два вещественных корня = -jCy/m и s2 = / zn’
один из которых положителен. Поэтому при отсутствии управле-
ния, т. е. при iv & 0, объект управления (5.26) неустойчив. Ма-
57
леишее отклонение тела из положения равновесия приведет к
экс-поненциальному росту координаты г/, так что тело либо уда-
рится о магнит, либо упадет вниз. Это явление знакомо каждому,
кто обращался с постоянными магнитами.
5.7. УРАВНЕНИЯ ПОДВЕСА ДВУСТОРОННЕГО
ДЕЙСТВИЯ
В предыдущих разделах рассматривался магнитный под-
вес одностороннего действия. Он находит практическое применение
только в тех случаях, когда сила тяжести подвешиваемого тела Q
заведомо превышает значения возможных динамических нагрузок.
Рис. 5.3. Магнитный подвес двустороннего
действия
Во всех остальных случаях
используется подвес двусто-
роннего действия, в котором
используются два проти-
воположно расположен-
ных электромагнита, созда-
ющих две противоположно
направленные магнитные
силы притяжения F1 и F2
(рис. 5.3).
Допустим, что ферромаг-
нитное тело массой т долж-
но удерживаться на одина-
ковом расстоянии 8 от обоих
электромагнитов. Текущее
положение тела определяет-
ся, как и ранее, координа-
той у. На тело действует кроме магнитных сил и F2 внешняя сила
Q = Q(z/,z/, 0, которая может иметь постоянную составляющую, за-
висящую от перемещения у и скорости у, переменную составляю-
щую и зависящую явно от времени t вынуждающую составляющую.
Используя те же предпосылки, что и при выводе уравнений (5.18),
и вводя индексы 1 и 2 для обозначения величин, принадлежащих
соответственно 1-му и 2-му электромагнитам, приходим к уравне-
ниям магнитного подвеса двустороннего действия вида:
тпг/
2 [(5 -у)2
СТ Ст
+ е" 2 11У + П1 = “1;
3-1/ (3-у)2
(5.28)
~ + Л2 = U2-
8 + У (& + у)2
58
Линеаризацию уравнений (5.28) проведем в рабочей точке
У = °; he = he = h? ulc = u2c = UC- <5-29)
Значение тока смещения ic может быть выбрано, вообще гово-
ря, произвольно. Обычно на практике принимается значение
*е=*тах/2, (5.30)
при котором обеспечивается равенство ресурсов положительных
и отрицательных значений управляющих токов.
Линеаризованные уравнения подвеса двустороннего действия
имеют вид:
ту = Fv + Q; Fv = суу + Au(ilv - i2v); + huy + rilv = ulv;
L(i2v)‘ - huy + ri2v = u2v, (5.31)
где, как и ранее, су и hu — соответственно «отрицательная» жест-
кость подвеса и токовая жесткость одного электромагнита, опреде-
ляемые как
Су = 2Li2 / 52; hu = Lic / 5. (5.32)
Уравнения (5.31) можно упростить путем перехода к разност-
ным iv, uv и суммарным Iv, Uv токам и напряжениям по фор-
мулам:
zv = hv — hv’ Iv = ilv hv’ uv = “lv ~ u2v’ Uv = ulv + u2v (5-33)
В результате дифференциальная система четвертого порядка
(5.31) распадается на не связанные между собой систему третьего
порядка относительно разностных переменных
ту =FV+ Q; Fv=cyy + hutv; L(iv)* + 2huy + riv = uv(5.34)
и уравнение первого порядка относительно суммарных переменных
LIv+r/v = t7v. (5.35)
5.8. ПОЧЕМУ НУЖНЫ ТОКИ СМЕЩЕНИЯ
Данный вопрос в случае подвеса одностороннего дей-
ствия не возникает, поскольку в нем ток смещения ic, однозначно
определяемый формулой (5.19), вызывает постоянную магнитную
силу, которая компенсирует силу тяжести Q.
Однако этот вопрос актуален для подвеса двустороннего дей-
ствия, поскольку в нем, как это было отмечено выше, в выборе
значений токов смещения существует определенный произвол. Из
линеаризованных уравнений (5.31) видно, что при нулевых токах
59
смещения линейная составляющая магнитной силы Fv становится
равной нулю. Объясняется это тем, что согласно (5.16) магнитная
сила является параболической функцией тока, а производная та-
кой функции в нулевой точке равна нулю. Поэтому для линеари-
зации магнитной силы токи смещения не должны быть нулевыми.
Они не должны быть также чересчур малыми, поскольку с их уве-
личением растут токовые жесткости и, как следствие, подвес ста-
новится более управляемым. Как это будет показано в дальней-
шем, с ростом токовых жесткостей требуемые динамические каче-
ства подвеса достигаются при меньших коэффициентах усиления
обратных связей и в результате система управления становится
более помехозащищенной.
Иными словами, токи смещения нужны для линеаризации маг-
нитной силы в целях построения линейной системы управления.
Создаваемое ими магнитное смещение вызывает в подвесе предва-
рительный силовой натяг. Управление силой происходит за счет
увеличения натяга в одном направлении при одновременном его
уменьшении в противоположном направлении. Поэтому токи сме-
щения иногда еще называют токами натяга.
Однако с ростом токов смещения растут потери энергии, иду-
щей на нагрев обмоток. Кроме того, должен оставаться запас по
току для отработки динамических нагрузок. Из этих соображений
вытекает формула (5.30) по выбору значения токов смещения.
На рис. 5.4 показаны два способа создания магнитного смеще-
ния: при помощи отдельной обмотки смещения (рис. 5.4, а) и по
дифференциальной схеме (рис. 5.4, б). При первом способе каж-
дый электромагнит содержит обмотку смещения и управляющую
обмотку. Обмотки смещения обоих электромагнитов включены
в одну электрическую цепь и питаются от общего источника.
Управляющие обмотки включены последовательно так, что маг-
нитные потоки, вызываемые током смещения и управляющим то-
а)
Рис. 5.4. Создание магнитного смещения: а — при помощи отдельной обмотки
смещения; б — по дифференциальной схеме
60
ком, суммируются в одном магните и вычитаются в другом. При
втором способе (рис. 5.4, б) обмотка каждого электромагнита пи-
тается от своего усилителя мощности током, который складывает-
ся из тока смещения и тока управления.
Достоинство первого способа состоит в том, что для его реализа-
ции требуется в два раза меньше усилителей мощности. Однако
энергетически этот способ менее выгоден. Например, в предельном
случае, когда требуется реализовать максимальное тяговое усилие,
максимальный ток будет течь в обмотках обоих электромагнитов;
при втором же способе — в обмотке только одного электромагни-
та, в другом электромагните ток будет равен нулю.
5.9. МАГНИТНОЕ СМЕЩЕНИЕ НА ПОСТОЯННЫХ
МАГНИТАХ. ГИБРИДНЫЕ ПОДШИПНИКИ
Магнитное смещение, необходимое для линеаризации маг-
нитной силы, можно создать как токами смещения, так и при по-
мощи постоянных магнитов. Главная выгода второго способа оче-
видна: магнитное смещение реализуется при нулевом потребле-
нии энергии. Постоянные магниты, выполненные из редкоземель-
ных материалов, имеют малые размеры и способны создавать в воз-
душных зазорах магнитные поля смещения высокой интенсивности.
Обмотки электромагнитов используются при этом только в целях
управления. Подшипники, в которых магнитное смещение создает-
ся постоянными магнитами, называются гибридными.
На рис. 5.5 приведена конструкция радиального гибридного
подшипника, разработанная фирмой AVCON. Подшипник состо-
ит из двух одинаковых модулей, между которыми установлен коль-
цевой постоянный магнит с осевым намагничиванием. Создавае-
мые постоянным магнитом потоки смещения, энергетизируя воз-
душные зазоры под полюсами, протекают в теле ротора в про-
Колъцевой
постоянный
Рис. 5.5. Радиальный гибридный подшипник
61
дольном направлении. Обмотки полюсов создают потоки управ-
ления, которые протекают в теле ротора в поперечном направле-
нии. По сравнению с обычным АМП гибридный подшипник имеет
меньшие размеры, массу и энергопотребление. Поэтому, несмот-
ря на то что постоянные магниты дороги, чувствительны к вне-
шним воздействиям и требуют бережного обращения, гибридные
подшипники в ряде случаев более выгодны, чем обычные АМП.
5.10. АДЕКВАТНОСТЬ ЛИНЕЙНОЙ МОДЕЛИ ПОДВЕСА
Линейная модель подвеса получена в предположении ма-
лости отклонений переменных от их номинальных значений или
значений смещений. В действительности эти отклонения могут
быть немалыми. Поэтому возникает вопрос о степени адекватности
исходной нелинейной модели (5.28) и ее линеаризованного анало-
га (5.31).
Расчеты и эксперименты показывают, что ошибки, вносимые
линеаризацией, весьма малы даже в том случае, если перемещения
подвешиваемого тела сравнимы с зазором. Сочетание простоты и высо-
кой степени адекватности является причиной широкого и успеш-
ного применения линейной модели подвеса в самых разнообраз-
ных приложениях. Конечно, в предельных режимах, таких как
насыщение магнитной цепи, нулевой ток или нулевой зазор, линей-
ная модель подвеса теряет смысл.
5.11. УРАВНЕНИЯ ЛАГРАНЖА—МАКСВЕЛЛА.
ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИ
В пп. 5.1-5.7 дано математическое описание односте-
пенного магнитного подвеса, в котором механическое движение
подвижного элемента определяется единственной координатой у,
а протекание электромагнитных процессов определяется током i
в случае подвеса одностороннего действия или токами и i2
в случае подвеса двустороннего действия [с равным успехом вмес-
то токов можно использовать потокосцепления (см. п. 5.4), но
этот случай мы намеренно опускаем]. Ротор как твердое тело име-
ет пять степеней свободы, поэтому его подвес является многосте-
пенной электромеханической системой. Такие системы описыва-
ются уравнениями, имеющими структуру уравнений механики; они
называются уравнениями Лагранжа—Максвелла. Выводы этих урав-
нений даны в работах [57, 77].
Для описания механического движения должны быть введены
обобщенные координаты; обозначим их через ..., qn, где п —
число степеней свободы механической системы. Составим выраже-
ния для кинетической Т и потенциальной 77 энергии системы:
62
J n n
T = •’ ViMM n = n{q1,...,qn), (5.36)
i=l/=l
где ay(gp ..., <7Л) — обобщенные коэффициенты инерции.
Пусть подшипники содержат т электромагнитных контуров
с токами ip im, активными сопротивлениями Гр гт и входны-
ми напряжениями ..., насыщением и магнитным гистерези-
сом пренебрегаем. Составим выражение для магнитной коэнергии
w = (5.37)
2 fc=ls=l
vj\eLks(q^ ..., qn) — индуктивности контуров ( при/? = s их называют
самоиндуктивностями и при k Ф s — взаимными индуктивностями).
При отсутствии в электрических цепях конденсаторов уравне-
ния Лагранжа—Максвелла имеют вид:
<1ЪТ_ЪТ ЪП_
, ~ . -X ' -х “ *"*/ • **/ ~ ~ ,
dt ddi да; dq; J 7 7 dq;
' Г (5.38)
d dW . , . ,
— ^ + rkik = uk, j = l,...,n; k =
dt dik
где Rj — обобщенные магнитные (пондеромоторные) реакции под-
шипников; Qy — непотенциальные обобщенные силы.
Учитывая (5.37), выражение дляЛу и второе уравнение в (5.38)
принимают вид:
8=1 8=17=1 J
Система (5.38) содержит п уравнений второго порядка относитель-
но координат qv ..., qn и ш уравнений первого порядка относитель-
но токов ip ..., im. Общий порядок системы равен 2п+тп. Из уравне-
ний (5.38) можно вывести следующие электромеханические аналогии.
Токи ik имеют смысл обобщенных скоростей (если принять фор-
мально электрические заряды за квазициклические обобщенные
координаты). Магнитную коэнергию можно формально отнести
к кинетической энергии. Напряжения uk играют роль обобщенных
сил (по сути, это сторонняя ЭДС в /?-м контуре). Слагаемые rkik
играют роль диссипативных сил.
63
6. УПРАВЛЕНИЕ ОДНОСТЕПЕННЫМ
МАГНИТНЫМ ПОДВЕСОМ
6.1. УПРАВЛЕНИЕ ПО ТОКУ И НАПРЯЖЕНИЮ
Неконтактный магнитный подвес ротора имеет пять ка-
налов управления — четыре радиальных и один осевой. Обычно
используется раздельное управление подвесом, при котором каж-
дый канал управляется автономно по сигналу своего датчика по-
ложения и имеет одну управляемую координату, т. е. одну степень
свободы. Исходя из этого в данной главе в качестве объекта уп-
равления будет рассматриваться одностепенной подвес двусторон-
него действия (рис. 5.3), описанный в п. 5.7.
Рассматриваемый объект управления неустойчив. Чтобы его
стабилизировать, а также придать ему желаемые динамические
качества, в канал управления вводится регулятор. Это — динами-
ческое звено, на вход которого поступает сигнал с датчика положе-
ния, а выходной сигнал — ток или напряжение - подается на
электромагнит и управляет магнитной силой.
Если управляющей переменной является ток, то такой способ
управления называется управлением по току, если же напря-
жение — то управлением по напряжению [99]. При управлении
по току усилителем мощности служит усилитель тока, а объект
управления описывается одним первым уравнением второго по-
рядка в (5.28). При управлении по напряжению усилителем мощ-
ности служит усилитель напряжения, а объект управления описы-
вается системой уравнений (5.28), имеющей четвертый порядок.
На практике используются оба принципа управления. Сравни-
вая их, отметим, что при управлении по току используется не пол-
ное описание объекта управления — предполагается, что требуемое
значение тока управления будет обеспечиваться точно в любой
момент времени. При подвесе легких роторов и наличии достаточ-
ного ресурса напряжения такой подход вполне оправдан и широко
используется на практике. При подвесе же тяжелых роторов или
весьма ограниченном ресурсе напряжения приходится учитывать
инерционность электромагнитных процессов и использовать пол-
ное описание объекта управления, т. е. использовать управление
по напряжению.
В данной главе рассматриваются задачи синтеза линейных, не-
линейных, оптимальных и адаптивных регуляторов при обоих спо-
собах управления, обсуждаются вопросы фильтрации шумов изме-
рения и построения наблюдателя состояния, показывается возмож-
ность построения бездатчикового подвеса, дается анализ устойчи-
вости подвеса в малом и большом с учетом влияния ограниченно-
сти ресурсов управления, приводятся передаточные функции и
частотные характеристики подвеса.
64
6.2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПОДВЕСА
Как уже отмечалось в п. 6.1, математическое описание
подвеса зависит от выбранного способа управления — по току или
по напряжению.
При управлении по напряжению. Исходная нелинейная мо-
дель подвеса описывается уравнениями (5.28), а ее линеаризован-
ный аналог — уравнениями (5.34) и (5.35). Так как магнитная
сила Fv от суммарного тока Zv не зависит, то вполне естественно
потребовать, чтобы Iv(t) = 0. Необходимым условием для этого
является выполнение тождества Uv(t) = 0. Поскольку решение
однородного уравнения LIV + rlv = 0 с течением времени стремит-
ся к нулю, то следует положить
— ~^2v = 4v — *2v — (^*1)
Соотношениям (6.1) и (5.34) отвечает так называемая диффе-
ренциальная схема управления электромагнитами в подвесе дву-
стороннего действия (рис. 6.1). По этой схеме управляющая пере-
менная, ток (рис. 6.1, а) или напряжение (рис. 6.1, б), второго
электромагнита равна по значению, но противоположна по знаку
управляющей переменной первого электромагнита. Следовательно,
подвес имеет два управляющих входа, но одну управляющую пере-
менную — ток i или напряжение и первого электромагнита.
Используя соотношения (6.1) и (5.34), получаем линейную мо-
дель подвеса в виде дифференциальной системы третьего порядка:
ту - суУ “ = Q; L(i)9 + / 2)у + ri = u, (6.2)
Рис. 6.1. Дифференциальная схема управления электромагнитами: а — при
управлении по току; б — при управлении по напряжению
65
где и hj — соответственно «отрицательная» позиционная и то-
у
ковая жесткости подвеса,
су = 2Li^ / З2; = 2ЛХ. = 21лс / 3, (6.3)
и где функцию управления выполняет напряжение и.
Модель (6.2) справедлива при следующих ограничениях
-8 < у < 8; - ic < i < ic; -ит<и< ит, (6.4)
где, как правило, ит » ric.
Теперь дадим описание системы (6.2) в пространстве состоя-
ний, т. е. приведем ее к нормализованному виду:
х = Ах + Ви +
У = Сх;
2 = Вх,
(6.5)
где х — вектор состояния; и — входная или управляющая пере-
менная; /(О — вектор возмущений; у — выходная или управляе-
мая переменная; z —измеряемая переменная; А, В, С, В, В^ — по-
стоянные матрицы.
Выбирая в качестве компонент вектора состояния у, у, i и учи-
тывая, что непосредственному измерению доступны у и i, имеем:
X = (у, у, i)T; f(t) = Q(t); С = (1,0, 0);
(10 0)
Ноо1М=
1
о
~hi/2L
о
0
где Т — индекс транспонирования матрицы.
Наконец, в ряде задач более удобно использовать безразмерную
форму записи уравнений. Введением безразмерных переменных
T = t/T0; у' = у/&, i' = i/ic; u' = u/rtc; Q' = Q/(m8/tf) <6-7>
и характерного безразмерного параметра подвеса
2Li*T$
т82
(6.8)
где То — постоянная времени электромагнита,
То = L / г,
(6.9)
66
уравнения (6.2) приводятся к виду
У - Х2у - %2i = QCO; (i)*+y + i = u, (6.10)
где штрихи в обозначениях безразмерных величин опущены, а верх-
ние точки означают дифференцирование по безразмерному
времени т.
Введением еще одного безразмерного времени
t' = 4 = tx/T0 (6.11)
уравнения (6.10) преобразуются к виду
y-y-i = Q(t)/%2-, (О* +У + 1 /Х = и / %. (6.12)
Обе модели (6.10) и (6.12) справедливы при следующих огра-
ничениях
-1<у<1; -1<г<1; -ит<и<ит. (6.13)
Удобство уравнений (6.10) и (6.12) заключается в том, что чис-
ло параметров объекта управления снизилось до одного — харак-
терного параметра подвесах.
При управлении по току. Исходная нелинейная модель подвеса
в этом случае описывается первым уравнением в системе (5.28),
где функцию управлений выполняют токи и Z2- Линейная мо-
дель описывается уравнением
ту - суу = hfi + Q(t) (6.14)
при ограничениях
-8 < г/< 8; -ic<i<ic, (6.15)
где управлением служит ток I.
Приводя систему (6.14) к нормализованному виду (6.5), имеем
x = (y,yf; u = i; f(t) = Q(t); C = D = (l,0);
(о Л (о) (o')
A = , л ; B= ; Bf = . (6.16)
\Cy / m Oj \hi / m) ’ (l/mj
В безразмерных переменных (6.7) и (6.11) уравнение (6.14)
может иметь две формы записи:
У-Х2У = Х21 + <Ж), (6.17)
если используется безразмерное время т = t/Тц, и
у-у = i + Q(t)/%2, (6.18)
67
если используется безразмерное время t = t* X/TQ, при ограничениях
—1 < г/< 1; (6.19)
6.3. СИНТЕЗ УПРАВЛЕНИЙ
С ПОЗИЦИЙ ОБРАТНЫХ ЗАДАЧ ДИНАМИКИ.
ПД, ПИД И ПИДДТ-РЕГУЛЯТОРЫ
В обратных задачах динамики, как известно, отыскива-
ются силы, обеспечивающие заданный закон движения системы.
Движение системы при этом может быть задано либо в виде яв-
ных функций времени, либо в виде дифференциальных уравнений,
решение которых совпадает с желаемой траекторией. Управляю-
щие переменные, токи или напряжения, по существу являются «си-
лами», которые опосредованно обеспечивают желаемое движение
подвешенного тела. Поскольку текущие значения управлений фор-
мируются регулятором не в виде явной функции времени, а на
основе обратных связей по компонентам вектора состояния, то
желаемое движение наиболее целесообразно задавать в виде диф-
ференциальных уравнений или дифференциальной программы [11,
33, 35, 50, 64, 65].
При управлении по току. Применим этот метод вначале к под-
весу с управлением по току (6.14). Допустим, что мы хотим, чтобы
свободное движение подвешиваемого тела, описываемое уравне-
нием
ту - суу = hti, (6.20)
в точности совпадало при одинаковых начальных условиях со сво-
бодным движением механического линейного осциллятора с вяз-
ким трением, описываемого уравнением
ту + by + су = 0, (6.21)
или
у + 2£cooi/ + (Оду = 0, (6.22)
где с — жесткость пружины; b — коэффициент вязкого трения
демпфера; соо и £ — соответственно частота недемпфированных
свободных колебаний и безразмерный параметр затухания:
0)0 = у[с~/~пг; = Ъ / (2тиа)0). (6.23)
Заметим, что поскольку параметры 0)0 и £ имеют более ясный
физический смысл, чем параметры с и &, в дальнейшем будем
пользоваться уравнением (6.22). Назовем его уравнением требуе-
мого движения.
68
Очевидно, что для совпадения движений систем (6.20) и (6.22)
при одинаковых начальных условиях г/(0) и у(0) необходимо и до-
статочно, чтобы текущие значения ускорений y(t) обеих систем были
одинаковы. Выражая из (6.22) ускорение у и подставляя его в (6.20),
получаем закон управления током вида
i = -(*1У + k2y), (6.24)
где и k2 — коэффициенты усиления обратных связей соответ-
ственно по перемещению и скорости:
= (т(П$ + су) / fy; k2 = ЯСрот / hi. (6.25)
Регулятор, реализующий закон управления (6.24), называется
пропорционально-дифференциальным, или ПД-регулятором. Нетруд-
но убедиться, что уравнение замкнутой системы управления, полу-
чающееся в результате подстановки (6.24) в (6.20), в точности
совпадает с уравнением требуемого движения (6.22). При этом
предполагается, что перемещение и скорость тела могут быть из-
мерены точно в любой момент времени. Такой подвес выполняет
функцию упругодемпферного элемента, имеющего жесткость с и ко-
эффициент вязкого трения Ь.
На практике часто требуется, чтобы положение тела не изменя-
лось при изменении статических нагрузок, т. е. чтобы подвес обла-
дал высокой статической жесткостью. Добиться этого можно вве-
дением дополнительной обратной связи по интегралу от переме-
щения или интегрального управления. Для этого вводится инте-
гральная переменная а, определяемая как
t
а = у, или a(t) = а(0) + y(t)dt. (6.26)
о
Теперь, задаваясь дифференциальной программой вида
у + 2£соог/ + ОАоУ + d3o = 0. (6.27)
где d — положительное число, приходим к закону управления
током
i = ~(^1У + k2y + k3a). (6.28)
Последнее слагаемое в (6.28) описывает дополнительную об-
ратную связь по интегралу с коэффициентом усиления
k3 = md3/ht. (6.29)
Регулятор, реализующий закон управления (6.28), называется
пропорционально-интегрально-дифференциальным или ПИД-регу-
69
Рис. 6.2. Структурная схема системы управления по току
с ПИД-регулятором
лятором. Структурная схема системы управления по току с ПИД-ре-
гулятором показана на рис. 6.2. Объект управления представляет
собой инерционное звено с передаточной функцией 1/(тиз2), охва-
ченное внутренней положительной обратной связью с коэффициен-
том усиления, равным «отрицательной» жесткости подвеса су.
Измеренное перемещение у сравнивается с нулевым задающим сиг-
налом, сигнал ошибки обрабатывается ПИД-регулятором, и выход-
ной сигнал регулятора — ток i — подается на вход объекта управ-
ления.
Значения программных коэффициентов соо, £ и d в (6.27) долж-
ны быть выбраны так, чтобы прежде всего обеспечивалась асимп-
тотическая устойчивость подвеса. По критерию Гурвица система
(6.27) будет устойчива при выполнении неравенства
d3 < 2;cog. (6.30)
В диапазоне значений, отвечающих неравенству (6.30), их вы-
бор может быть произведен либо исходя из обычных инженерных
рассуждений, либо в результате решения задач оптимизации
(см. п. 6.4).
При управлении по напряжению. Теперь применим метод об-
ратных задач динамики к подвесу с управлением по напряжению
(6.2). Для этого декомпозируем систему (6.2) на механическую
my-Cyy^hji (6.31)
и электромагнитную
L(i)* + (ht / 2)у + ri = и (6.32)
подсистемы. Задачу синтеза закона управления будем решать
в два этапа: вначале найдем ток i = i°, обеспечивающий движение
70
тела согласно программе (6.27); затем найдем напряжение и°, ре-
ализующее требуемые значения тока i°.
Решение первого этапа задачи дается выражением (6.28), в ко-
тором следует положить I = г°, т. е.
i° = ~(кгу + k2y + А3о). (6.33)
Точное решение второго этапа задачи дается функцией и0, кото-
рая описывается левой частью второго уравнения в (6.2) после
замены в нем тока i на ток i° при условии, что в начальный
момент i(0) = i°(0).
Так как программное значение i°(0) задано соотношением (6.33)
при t = 0, а текущее значение 1(0) может быть произвольным, то
неизбежно отклонение
te(t) = i°(t)-i(t). (6.34)
В связи с этим возникает задача о приближении к управлению
и0. Сформулируем ее так. Требуется подобрать такое напряжение
и = и°, чтобы уменьшение начального отклонения Ai(f) до нуля про-
исходило по закону, заданному в виде дифференциального уравне-
ния
(Ai)e + XAi = 0, (6.35)
где X — положительное число.
Решение уравнения (6.35) имеет вид
Ai(t) = Д/(О)е"Ч (6.36)
Отсюда следует, что при Ai(0) * 0 программное движение тела
будет осуществляться не точно, а приближенно, причем степень
приближения возрастает с увеличением %. Значение X следует на-
значать так, чтобы процессы в электромагнитной подсистеме (6.32)
протекали заметно быстрее, чем в программной механической под-
системе (6.27). Количественные рекомендации по выбору зна-
чения X будут даны в п. 6.4.
Таким образом, для отслеживания программных значений тока
i°(t) вводится следящая система, требуемый закон отслеживания
в которой с учетом (6.34) и (6.35) задан дифференциальным урав-
нением
(i)e+Xj = (i0)* +Xi°. (6.37)
Применяя, как и ранее, метод обратных задач динамики, выра-
зим из (6.37) производную (i)* и подставим ее в уравнение (6.32).
Используя (6.33) с учетом (6.25) и (6.29), получаем следующий
закон управления напряжением
71
Рис. 6.3. Структурная схема системы управления по напряжению
с ПИДДТ-регулятором
U° = ~(gry + g2y + gtf + g4a + &5У)’ (6.38)
где^р ...,#5— коэффициенты усиления обратных связей соответ-
ственно по перемещению, скорости, току, интегралу от перемеще-
ния и ускорению:
= L^k(/под + су) + md? j / ; g2 = Ь(тпо)о + cy 4- 2Cf^0km) / ht -
- 12; g3 = Lk - r; g± = Lkrrtd? / g§ = 2ЬС^0т / fy. (6.39)
Регулятор, реализующий закон управления (6.39), назовем про-
порционально-интегральным регулятором с двойным дифференциро-
ванием и обратной связью по току, или сокращенно ПИДДТ-регу-
лятором. Структурная схема системы управления по напряжению
с ПИДДТ-регулятором показана на рис. 6.3.
6.4. СИНТЕЗ ЛК-ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Активные магнитные подшипники обладают ограничен-
ными ресурсами управления по силе, току и напряжению. Поэтому
желательно, чтобы расходование ресурсов управления было мини-
мальным. С другой стороны, подшипник должен удерживать ротор,
находящийся под действием возмущающих сил, с заданной точно-
стью. Очевидно, что с ростом точности позиционирования растут
значения управляющих переменных. Здесь должен быть найден
оптимальный компромисс, который может быть сформулирован
72
в виде экстремума некоторого функционала качества, учитываю-
щего оба отмеченных фактора. Теория управления располагает
большим числом методов оптимизации [7, 19, 43, 63]. Практика
показывает, что одним из наиболее подходящих в указанном смысле
для магнитных подвесов является метод линейно-квадратической
(ЛК) оптимизации (линейная система управления при квадрати-
ческом функционале качества) [37, 39, 105, 106].
ВВЕДЕНИЕ В ЛК-МЕТОД
В дальнейшем используется следующая интерпретация
этого метода. Для линейной системы
х = Ах + Вщ
У = Сх
требуется найти управление и = zz°, которое при переводе системы
из произвольного начального состояния в нулевое состояние дос-
тавляет минимум интегральному квадратическому функционалу
/ [*/Т(0*/(0 +puT(f)u(t)]dZ, (6.41)
0
где р — положительный весовой скаляр.
Отметим, что при малых р допускаются большие значения уп-
равления и («дешевое» управление), при больших жер значениям
будут малыми («дорогое» управление); чем меньше р — тем выше
точность позиционирования и быстродействие системы.
Известно, что оптимальное управление формируется по линей-
ному закону
и° = -Gx; G = р~1ВтР, (6.42)
где G — матрица коэффициентов усиления обратной связи; Р —
симметрическая матрица, являющаяся единственным положительно
определенным решением алгебраического матричного уравнения
Лурье—Риккати [63]
СТС + АТР + РА - р~хРВВтР = 0. (6.43)
Заметим, что оптимальное управление (6.42) автоматически обес-
печивает ассимптотическую устойчивость замкнутой системы х =
= (А - BG)x.
Заметим также, что в уравнениях (6.40)-(6.43) векторы х, у и и
могут быть комплексными векторами, матрицы А, В и С — комп-
лексными матрицами, матрица Р — комплексной эрмитовой
73
матрицей; в этом случае индекс Т обозначает сопряженное транс-
понирование. Комплексное представление часто используется в за-
дачах динамического анализа роторных систем [31, 66, 71, 74].
Поскольку порядок системы при комплексном представлении сни-
жается наполовину, решение задач существенно упрощается. Ком-
плексное представление будет использовано ниже в п. 7.5.
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ТОКОМ
Для системы управления по току (6.40) с учетом (6.16)
задача ЛК-оптимизации (6.40)-(6.43) имеет аналитическое реше-
ние, приводящее к закону управления
i° =-(k?y + k$y),
(6.44)
где коэффициенты усиления обратной связи, как это нетрудно убе-
диться, определяются соотношениями:
fef = mfe2[l + (1 +1 / (pfe4))1/2| / hf,
(6.45)
= 42mk[l + (1 + 1/ (pfe4))1/2]1/2/hlt
где k — модуль полюсов объекта управления (рис. 6.4, а),
ления KJ и тс2; б — оптимальной замкнутой системы sj и s2 при «дорогом»
управлении (о>о = Л); в — оптимальной замкнутой системы «1 и з2 при «деше-
вом» управлении (cdq » k) — распределение Баттерворса второго порядка;
штриховой линией показана траектория полюсов при увеличении «д
74
Отсутствие доступной физической трактовки у весового пара-
метра р затрудняет непосредственное использование выражений
(6.45). Поэтому целесообразно заменить р некоторым другим бо-
лее понятным для инженеров параметром. Приравнивая для этого
характеристический полином оптимальной замкнутой системы
(6.31) и (6.44)
ф(з) = s2 + (&2^i / rn)s + k^hi / m-k2 (6.47)
к полиному программной системы (6.22)
ф(з) = s2 + 2£(d0s + (Do, (6.48)
получаем:
р = 1 / (Wq - fe4); ; = 72(1 + *2/“о)/2, (6.49)
откуда следует
kf = тп(соо + k2) / k$ = ту/2((О0 + k2) / ht. (6.50)
Соотношения (6.50) содержат варьируемый параметр соо, имею-
щий ясный физический смысл, — это недемпфированная собствен-
ная частота подвеса. Из условия положительности р в (6.49) сле-
дует неравенство
соо > k = jcy /т. (6.51)
Случаю 0)0 = k, при котором р и £ = 1, соответствует наибо-
лее «дорогое» и энергетически наиболее выгодное управление. По-
люса замкнутой системы кратны, вещественны и отрицательны
(рис. 6.4, б):
Si = S2 = -^jcy I m. (6.52)
Траектория полюсов оптимальной замкнутой системы на ком-
плексной плоскости с увеличением со0 показана на рис. 6.4, в штри-
ховой линией. Они асимптотически приближаются к прямым ли-
ниям, проведенным из начала координат под углами ±45° к отри-
цательной действительной полуоси. При соо » k полюса равноуда-
лены от начала координат на расстояние соо и образуют распреде-
ление Баттерворса второго порядка радиусом о0 [43]. Этому случаю,
при котором р—>0и£—»>/2/2, и соответствует «дешевое» уп-
равление. Расчеты показывают, что с точностью до 10 % в значе-
ниях коэффициентов усиления k° и k£ распределение полюсов Бат-
75
терворса реализуется при (о0 > 2^су / т. На практике в зависимо-
сти от требований к подвесу значения соо обычно составляют
20-500 Гц.
Соотношение (6.44) описывает оптимальное ПД-управление.
Оптимальное ПИД-управление током реализуется по закону
i° = ~(k°y + k£y + *30), (6.53)
в котором о — интегральная переменная, определяемая соотноше-
нием (6.26).
Чтобы найти оптимальные коэффициенты усиления обратных
связей, зададимся характеристическим полиномом замкнутой сис-
темы вида
<р(а) = (s + a0)(s2 + 2£(oos + (Do), (6.54)
где (Xq — модуль дополнительного интегрального полюса s3 = -а0,
размещаемого вблизи начала координат; обычно принимается
а0 = О,1соо. (6.55)
В результате получаем
ki = ти(соо + k2 + 2£cooao) / hz;
*2 = тп(2С<00 + a0) / hi', fej = пмоо«о / hi- (6-56)
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ НАПРЯЖЕНИЕМ
К настоящему времени в литературе отсутствуют сведе-
ния о существовании аналитического решения задачи ЛК-оптими-
зации применительно к системе управления по напряжению (6.2).
В связи с этим рассмотрим только два предельных случая: «доро-
гое» управление (при р —> ©о) и «дешевое» управление (при р —> 0).
Найдем для этих случаев оптимальные значения коэффициентов
усиления обратных связей в законе управления напряжением
«° = ~(ё1У + ^2 У + + ^4°)-
(6.57)
Воспользуемся для этого корневым методом. Вначале вычис-
лим полюса объекта управления л1, л2 и л3 из решения характери-
стического уравнения
а3 + Tq ха2 - суг / mL = 0.
(6.58)
Можно показать, что объект управления имеет один неустой-
чивый действительный положительный полюс и два устой-
76
a)
Im(s)
6)
nt Refs)
Im(s)
S2-^2
Refs)
^2
X
0
0
s5 =Яз
«3
Рис. 6.5. Распределение полюсов
при управлении по напряжению:
а — объекта управления (при
X2 > 4/27); б — оптимальной
замкнутой системы при «дорогом»
управлении (р —»«=); в — опти-
мальной замкнутой системы при
«дешевом» управлении (р —»0) —
распределение Баттерворса тре-
тьего порядка; штриховой лини-
ей показана траектория по-
люсов при увеличении vq
чивых полюса л2 и л3, причем последние могут быть либо дей-
ствительными отрицательными (при %2 < 4/27), либо комплекс-
но-сопряженными (при %2 > 4/27), где % — характерный безраз-
мерный параметр подвеса, введенный ранее соотношением
(6.8). На рис. 6.5, а показано типичное распределение полюсов
объекта управления при %2 > 4/27. Пусть
= +ах; п2 = -а2 + яз = "а2 ~ $2> (6.59)
где ар а2, Рг — положительные числа; j — мнимая единица.
Теперь составим характеристический полином ср($) замкнутой
системы (6.31) и (6.32) при управлении (6.57). Корни полинома
ср($), называемые полюсами замкнутой системы, зависят от весово-
го параметра р.
Известно [43], что прир—»<* («дорогое» управление) два полюса
з2 и з3 оптимальной замкнутой системы совпадают с двумя устой-
чивыми полюсами л2 и л3 объекта управления; третий же полюс
совпадает с зеркальным отображением неустойчивого полюса
в левой полуплоскости (рис. 6.5, б), т. е. = -Лр s2 = Tt2, «3 = ^3.
Интегральное управление учтем введением малого по модулю до-
полнительного четвертого полюса з4= -а0. Тогда характеристичес-
кий полином замкнутой системы можно записать в виде
77
<p(s) = (s - sx)(s - s2)(s - s3)(s - s4).
(6.60)
Приравнивая полином замкнутой системы (6.31), (6.32), (6.57)
полиному (6.60), находим коэффициенты усиления обратных свя-
зей при «дорогом» управлении (р—»<*)
gi = {cyL(a0 + ах + 2а2) + тпь[(а0 + ах)(а2 +Р2) +
+ 2а0а1а2]}/й/;
g$ = mb[a2 + 2аха2 + 02 + а0(ах + 2а2)]/ ht;
g3 = L(a0 +ах +2a2)-r;
g4 = 7nLaoax(a2 + P2).
(6.61)
Также известно, что при р -^0 («дешевое» управление) полюса
оптимальной замкнутой системы образуют распределение Баттер-
ворса третьего порядка радиусом v0 (рис. 6.5, в). Отсюда следует,
что при малых р и учете интегрального управления введением
малого по модулю дополнительного полюса s4= ~а0 полином (6.60)
может быть представлен в виде
<p(s) = (s + a0)(s + v0)(s2 + vos + v|). (6.62)
Приравнивая полином замкнутой системы (6.31), (6.32), (6.57)
полиному (6.62), получаем коэффициенты усиления обратных связей
при «дешевом» управлении (р-»0):
g° = b[m(vo + 2aovo) + cy(2v0 + a0)]/ ht;
g2 = 2mLv0(v0 + a0) / fy;
g3 = L(2v0 + a0) - r;
g4 = mLaoVo.
(6.63)
ОПТИМАЛЬНЫЕ ЗНАЧЕНИЯ ПАРАМЕТРОВ
ПРОГРАММНОГО ДВИЖЕНИЯ
При синтезе управлений с позиций обратных задач ди-
намики (п. 6.3) программное движение системы задавалось диффе-
ренциальными уравнениями (6.27) и (6.37), содержащими варьи-
руемые параметры 0)q, d, X. В случае оптимального управления,
как это следует из (6.62), могут варьироваться два параметра —
радиус распределения полюсов vQ и модуль интегрального полюса
78
а0. Из условия равенства характеристических полиномов замкну-
тых систем вытекают следующие соотношения связи между этими
группами параметров:
«О = vo + a0v0'> С = 7(1 + а0 /vo) / 2; d3 = aovg; X = v0. (6.64)
При выполнении соотношений (6.64) оба варианта системы уп-
равления подвесом будут иметь одинаковые характеристические
полиномы и, следовательно, одинаковые переходные характерис-
тики (но частотные характеристики у них могут быть разные).
С помощью соотношений (6.64) легко решается проблема опти-
мального выбора параметров программного движения подвеса.
6.5. СИНТЕЗ НЕЛИНЕЙНЫХ УПРАВЛЕНИЙ
В основу синтезированных в пп. 6.3 и 6.4 линейных
систем управления подвесом заложен принцип магнитного сме-
щения. Токи смещения протекают по обмоткам даже тогда, когда
внешние нагрузки отсутствуют и магнитная сила вовсе не требует-
ся. Потребляемая энергия при этом идет на нагрев обмоток и
усилителей мощности. В связи с этим возникает задача синтеза
закона управления, который минимизировал бы потери электри-
ческой энергии. Решение данной задачи, как это будет видно из
дальнейшего, приводит к нелинейному закону управления.
К нелинейным законам управления приходим также в случа-
ях, когда объект управления линеен, но требуемое движение зада-
ется либо нелинейными дифференциальными уравнениями, либо
в виде условия максимального быстродействия.
В настоящем параграфе решается задача синтеза оптимального
в смысле минимума потерь электроэнергии алгоритма управления
подвесом, показывается, как организовать автоколебательное дви-
жение тела в подвесе заданной амплитуды и частоты, рассматрива-
ется релейное управление с организацией скользящих режимов,
синтезируется оптимальное по быстродействию управление.
МИНИМИЗАЦИЯ ПОТЕРЬ ЭЛЕКТРОЭНЕРГИИ.
ВНЕШНЯЯ ЛИНЕАРИЗАЦИЯ
Допустим, что требуется реализовать движение тела, за-
данное дифференциальным уравнением (6.27). Магнитную силу
F°, реализующую такое движение, назовем программной управля-
ющей силой. Она должна формироваться по закону
F° = -тп(2£й)01/ + cDqZ/ + d3o) (6.65)
79
на основе обратных связей по у, у, а. Из исходной нелинейной мо-
дели подвеса (5.28) видно, что ток создает положительную силу,
а ток i2 — отрицательную. Логично заключить, что для минимиза-
ции потерь электроэнергии в те моменты времени, когда F° > О,
должен быть включен первый электромагнит, а второй электромаг-
нит выключен; и наоборот, если F0 < 0. Данное рассуждение приво-
дит к закону управления с переключением электромагнитов вида:
й = (5-y)y/2F° / cL; i2 = 0 при F°(f) > 0;
й = 0; i2 = (8 + y)^2|F0| / cL при F°{t) < 0.
(6.66)
Структурная схема алгоритма управления (6.66) показана на
рис. 6.6. Часто в литературе [99] алгоритм управления (6.66)
называют внешней или схемной линеаризацией магнитной силы
(заметим, что этот термин не совсем точен, поскольку функция F°
не обязательно должна быть линейной).
Хотя данный способ управления и минимизирует потери элект-
роэнергии, но он имеет и один существенный недостаток — низкие
Рис. 6.6. Структурная схема алгоритма управле-
ния, минимизирующего потери электроэнергии
(внешняя линеаризация магнитной силы)
80
динамические качества при отсутствии постоянной нагрузки.
В этом случае в положении равновесия требуемая сила F° = 0;
тело будет совершать высокочастотные автоколебания в окрестно-
сти положения равновесия; для отработки даже небольших дина-
мических нагрузок требуются значительные амплитуды токов. По-
этому алгоритм управления (6.66) целесообразно использовать
только при наличии постоянной нагрузки на подвешиваемое тело.
ОРГАНИЗАЦИЯ АВТОКОЛЕБАНИЙ ТЕЛА
С ПОМОЩЬЮ ПОДВЕСА
До сих пор рассматривались случаи, когда уравнениям
требуемого движения тела отвечали линейные асимптотически ус-
тойчивые системы вида (6.22), (6.27). Однако могут встретиться
случаи, когда желаемая динамическая система должна быть нели-
нейной и, более того, иметь неустойчивое положение равновесия. В ка-
честве иллюстрации рассмотрим задачу организации гармоничес-
ких колебаний тела по закону y(t) = Ysin Qt с заданными амплиту-
дой У и частотой Q. Практическим примером такой системы явля-
ется осевой магнитный подвес ротора сверлильной головки при ус-
ловии, что ротор в некоторые промежутки времени должен совершать
осевые колебания для дробления стружки при сверлении.
Организовать данный режим можно либо подачей на элемент срав-
нения (см. рис. 6.2) соответствующего задающего сигнала yc(t), либо
возбуждением автоколебаний. В последнем случае желаемая систе-
ма должна быть автоколебательной с мягким возбуждением автоко-
лебаний. Пусть это будет известная система Ван-дер-Поля [14]
У-(01-02Л + ®о1/ = О, (6.67)
имеющая неустойчивое положение равновесия, но устойчивый пре-
дельный цикл y(t) = Ysin Qt с параметрами
Q = (оо; Y = 2^ /₽2. (6.68)
Данный режим реализуется при нелинейном законе управле-
ния током
i = -[(mwo + су)у + (fi2y2 - Р1)у]- (6.69)
РЕЛЕЙНОЕ УПРАВЛЕНИЕ. СКОЛЬЗЯЩИЙ РЕЖИМ
В разделе 6.3 решалась задача отыскания напряжения
и = и°, которое уменьшает отклонение А/ = i° - i действительного
тока i от программного i° до нуля по закону, заданному линейным
81
дифференциальным уравнением (6.35). Однако это не единствен-
но возможный подход.
Вполне правомерно рассмотреть задачу о максимальном быст-
родействии системы отслеживания программного тока, т. е. потре-
бовать, чтобы отработка ошибки &i(t) до нуля происходила за ми-
нимально короткое время. Решение задачи очевидно:
+ ит при Д/(/) > 0;
- ит при &i(t) < 0,
(6.70)
где ит — максимальное значение напряжения.
Алгоритм управления (6.70) описывает релейную систему, ко-
торая в зависимости от знака ошибки слежения увеличивает или
уменьшает ток i до программного значения 1° с максимально воз-
можной скоростью. Структурная схема алгоритма управления (6.70)
приведена на рис. 6.7.
Переключение релейного элемента происходит при перемене знака
отклонения Д/. Уравнение Д/ =0, которое, учитывая (6.33), имеет
вид
^1У + ^2У + М + ^ = 0, (6.71)
описывает гиперплоскость переключения в пространстве фазовых
координату, у, о, /.Релейный элемент обладает очень высоким, но
не бесконечно большим быстродействием. Поэтому перевод систе-
мы из произвольного начального состояния в нулевое состояние
будет происходить в режиме скольжения вдоль гиперплоскости
переключения (6.71) и сопровождаться высокочастотными авто-
колебаниями. Эти автоколебания, сохраняющиеся и после дости-
жения системой нулевого состояния, обычно имеют очень малую
амплитуду и не оказывают заметного влияния на функционирова-
ние подвеса. Несомненным достоинством релейной системы уп-
равления подвесом является высокая степень инвариантности
к параметрическим и силовым возмущениям, т. е. высокая робаст-
ность [49].
Рис. 6.7. Структурная схема релейной системы отсле-
живания программного тока
82
ОПТИМАЛЬНОЕ ПО БЫСТРОДЕЙСТВИЮ УПРАВЛЕНИЕ
Интерес к созданию оптимального по быстродействию
регулятора продиктован постоянно ведущимся поиском алгорит-
мов управления, обеспечивающих наибольшие быстродействие
и жесткость подвеса. Известно [12, 63], что оптимальное по быст-
родействию управление релейно. Также хорошо известны трудно-
сти задачи синтеза такого управления для объектов с порядком
выше второго, обладающих к тому же неустойчивостью и комплекс-
ными полюсами, к каковым и относится магнитный подвес. Ниже
излагаются результаты работы [2], в которой использован некий
компромисс в преодолении указанных выше трудностей.
Используя описание (6.12), будем исходить из системы уравне-
ний третьего порядка в безразмерных переменных
(О* = -y-i / х +U / X
при ограничениях
-1 < у < 1; - 1 < i < 1; -ит<и<ит. (6.73)
В переменных состояниях = (х1? х2, х3)т = (г/, у, i)T система(6.72)
принимает вид
х = А3х + В3и, (6.74)
где
'0 1 0 ' " о"
А3 - 1 0 1 ; в3 = 1
.0 -1 -1/Х, J/xJ
Полюса объекта как собственные числа матрицы А3 при %2 > 4/27:
= ^(2ch ?1); Х2>3 = "^(ch I+1; 1'47shI’ <6-75)
О О О
где параметр ср удовлетворяет равенству
ch ср = 27х2 / 2 - 1.
(6.76)
По условиям задачи напряжение может принимать только по-
стоянные максимальные значения и = ± ит. Тогда общее реше-
ние системы (6.74) при начальных условиях х(0) = (*/О’£/О’*о)Г име’
ет вид
83
'y(t)'
y(t)
j(t) ,
+ h3(t)
+ ^2 (t)
У0
Уо + io
1Z. .
~У0 ~~(l0 ~u)
\ X J
Уо + io
lz. >
-~(iq ~u)
X
(6.77)
- (Уо + io? + ~Уо + —^fio ~ u)
* -x
где функции hs(t) (s = 1, 2, 3) являются чисто действительными и
удовлетворяют системе
"1 Xi
1 ^2
J ^3
e^2t
(6.78)
Неустойчивость объекта, вытекающая из того, чтоХ^ > 0, нали-
чие комплексных полюсов Х2 3, а также необходимость одновре-
менного учета ограничений (6’73), существенно усложняют задачу
синтеза оптимального по быстродействию управления. Для пре-
одоления этих трудностей будем решать задачу в два этапа. Вна-
чале, предполагая неограниченность ресурса напряжения (и^—>«0,
рассматриваем двумерный объект с управлением по току и для
него синтезируем оптимальный по быстродействию закон управ-
ления. Затем отыскиваем и анализируем корректирующую по-
правку, вносимую ограниченностью значения ит.
Итак, пусть —> ©с. Тогда управляющий ток i = х3 может
мгновенно менять полярность с i = +1 на i = -1, и наоборот,
а динамическая модель (6.74) редуцируется к двумерной модели
х = А2х + В2г, (6.79)
где
г . т Го fоЛ
х = (х1,х2Г =(у,у)т; А2 = ; В2 = . (6.80)
JL \JJ \ >
Объект (6.79) имеет полюса Х-^ = 1, Х2 = -1, один из кото-
рых (Хх) — неустойчив.
84
Учитывая, что ток может иметь только постоянные значения
i = ±1, общее решение системы (6.79) имеет вид
^(О^
(у о + х
+ ch t +
uo ;
Уо
У о +С
sht.
(6.81)
При отыскании оптимального по быстродействию управления
для системы (6.79) будем использовать традиционный подход [12].
Он приводит к релейному закону i = ±1. Чтобы найти линию пере-
ключения тока, приведем уравнения (6.79) к виду
dy dy
— = У, — = y + i.
dt У dt ”
(6.82)
Исключая d£ из уравнений (6.82), получаем при i = ±1 диффе-
ренциальное уравнение ydy = (у + 1 )dy, порождающее семейство ги-
перболических фазовых траекторий (рис. 6.8, а)
у2 = у2 +2у + с. (6.83)
Аналогично при i = -1 получаем (рис. 6.8, б)
у2=у2-2у + с. (6.84)
Процесс должен заканчиваться в начале координат (у = у = 0).
Поэтому линия переключения тока MOL (рис. 6.9, а) образуется
ветвями гипербол (6.83) и (6.84) при с = 0, которые вливаются
в начало координат и описываются уравнением
у = -sign (у)у/у2 +2|j/|. (6.85)
85
Рис. 6.9. Линия переключения тока (а) и фазовые траектории оптимальных
по быстродействию процессов (б)
Фазовые траектории оптимальных по быстродействию процес-
сов изображены на рис. 6.9, б. В фазовых точках, лежащих выше
линии переключения MOL, ток имеет значение i = -1, в точках
ниже этой линии — значение i = +1.
Фазовая траектория, начинающаяся в произвольной точке
А(уА, имеет вид гиперболы АВ до точки В, лежащей на ветви OL
линии переключения. В точке В ток мгновенно меняет полярность
сг = -1на/ = +1. Далее фазовое движение идет к началу коорди-
нат по отрезку ВО линии переключения. При этом суммарное
время движения по отрезкам АВ и ВО
Глво = -In 1 + 21;'д + + 2ув). КВ - — - — <6.8в>
2 l + 2toB-7i/B+2KS) 2 4
и согласно принципу максимума является минимальным из всех
возможных.
Перейдем теперь к задаче учета ограниченности ресурса напря-
жения. Рассматривая для этого четвертый квадрант (рис. 6.10),
введем линию ОР, «опережающую» в фазовом движении линию
OL, причем в точке С на линии ОР напряжение меняется скачком
со значения и = -ит на и = +ит. Ток i, имеющий в точке С значе-
ние i = -1, начнет возрастать и через промежуток времени At дос-
тигнет значения i = 4-1. Для отыскания линии ОР потребуем, что-
бы момент, соответствующий концу промежутка At, совпал с мо-
ментом пересечения линии OL фазовой траекторией CD в точке В.
После этого рост тока прекращается, а дальнейшее движение про-
исходит в соответствии с двумерным описанием (6.79), т. е. по
отрезку DO ветви OL.
86
Рис. 6.10. Линия переключения напряжения (ОР)
Решение данной задачи возможно, если воспользоваться реше-
нием (6.77) и уравнением гиперболы (8.63) при с = 0. Однако,
даже если будет найдено абсолютно точное решение задачи, оно не
имеет практической ценности. Объясняется это тем, что в силу
неустойчивости объекта такая система функционирует на границе
устойчивости. Малейшая ошибка в измерении перемещения или
скорости, при которой переключение напряжения произойдет чуть
Рис. 6.11. Потеря устойчивости подвеса вследствие ран-
него переключения напряжения
87
раньше, чем будет достигнута линия ОР, приведет к потере устой-
чивости подвеса. Это иллюстрируется рис. 6.11, где С' — точка
переключения напряжения; D' — точка достижения током зна-
чения i = +1, из которой движение происходит по неограниченной
траектории, минуя начало координат.
Чтобы избежать рассмотренной неприятной ситуации, необхо-
димо создать запас по устойчивости. Этот запас может быть дос-
тигнут, например, если линию переключения тока OL назна-
чить в качестве линии переключения напряжения. В этом случае
оптимальный по быстродействию (точнее, квазиоптимальный) ал-
горитм управления напряжением имеет вид
+ ит при у < у* иу = у*<0;
- ит при у>у»ъу = у*>Ъ, (6.87)
где
У* = — sign (г/)д/г/2 + 2|у|. (6.88)
Анализ динамического поведения синтезированной системы уп-
равления показывает наличие устойчивого предельного автоколе-
бательного цикла в малой окрестности состояния равновесия. Пе-
риод Та и амплитуда z/a автоколебаний при ит >10 с высокой сте-
пенью точности:
. 40% 5%
У&~2и2т
(6.89)
В заключение отметим, что в диапазоне реальных значений па-
раметров х и ит амплитуда уа очень мала, поэтому автоколебания
заметного влияния на работоспособность подвеса не оказывают.
6.6. ОПТИМАЛЬНОЕ ПО УСТОЙЧИВОСТИ
УПРАВЛЕНИЕ
В данном параграфе рассматривается ситуация, когда
качество работы подвеса отражает критерий оптимальности в виде
максимальной области притяжения стабилизируемого состояния
равновесия в фазовом пространстве (МОП-критерий). Системы, удов-
летворяющие этому критерию, принято называть оптимальными
по устойчивости. Применительно к магнитным подвесам метод
МОП-оптимизации предложен и разработан В. С. Воронковым
[20, 21]. По этому методу управление и(х) считается оптималь-
ным по устойчивости, если с его помощью достигается максимум
области притяжения
v[u*(x)j = тахцейУ[и(х)] = Vm (6.90)
88
стабилизируемого состояния равновесия х = 0 в фазовом простран-
стве системы управления. Здесь V — область притяжения, или
область асимптотического приведения переменных состояния объек-
та в начало координат; Q — область допустимых управлений.
Суть метода заключается в выделении из пространства состоя-
ний объекта подпространства неустойчивых состояний с последую-
щим построением стабилизирующей обратной связи только по
неустойчивым модальным координатам.
Для иллюстрации метода рассмотрим одностепенной подвес
с управлением по току, описание которого дается дифференциаль-
ным уравнением в безразмерных переменных (6.13). Считая, что
вынуждающая сила отсутствует (Q з 0) и опуская штрихи в обо-
значениях безразмерных переменных, уравнение объекта предста-
вим в виде
{/-!/ = /, (6-91)
где точки означают дифференцирование по безразмерному времени
t' Tq. Запишем (6.91) в нормализованной форме
где
х = Ах + Bi,
(6.92)
х = (хп х2)т = (у, у)т; А = Г ; В =
Диагонализируем уравнение (6.92). Для этого введем замену
переменных
x = Sz, (6.93)
где S — матрица перехода к новому базису внутреннего описания.
В новом базисе уравнение (6.92) примет вид
z = Az + Bi, (6.94)
где А = S-1AS; В = S~lB.
Из алгебры известно, что если столбцами матрицы S являются
собственные векторы и S2, соответствующие собственным чис-
лам и Х2 матрицы А, то тогда А = S-1AS = Л = diag(X1,X2).
Собственные числа матрицы А как решения уравнения det (XJ -
- А) = 0: = 1, Х2 = -1. Решая уравнения (kkI - A)Sk = 0, k = 1, 2,
находим собственные векторы = (1, 1)т и S2 = (l, -1)г. Форми-
руя матрицу S из столбцов Sx и S2 и вычисляя обратную ей мат-
рицу имеем:
S =
1
1
1
-1
s-Л1 1
2(1 -1
(6.95)
89
Теперь А = Л, В = (1, - 1)т / 2, и уравнения (6.94) принимают
диагональный вид:
2i=2i+i/2; (6.96)
*2 = -*2 / 2- (6.97)
Уравнение (6.96) описывает подпространство неустойчивых со-
стояний, а уравнение (6.97) — подпространство устойчивых состо-
яний. Согласно МОП-методу оптимальная обратная связь должна
формироваться только по неустойчивой модальной координате
zr = (хх + х2)/2:
i = = -р(*1 + х2) / 2, Р > 2 (6.98)
с учетом ограничений -1 < i < 1 и исходя из условия устойчивости
при Р > 2.
Вполне очевидно, что МОП-управление (6.98) перемещает неус-
тойчивый полюс Xj = 1 объекта в устойчивую левую полуплоскость
и не оказывает при этом никакого влияния на размещение устой-
чивого полюса Х2 = “1. Поэтому при данном управлении полюса
замкнутой системы не могут быть размещены произвольным обра-
зом. Например, при р = 4 замкнутая система имеет полюса = $2 =
= -1, т. е. реализуется случай ЛК-оптимального «дорогого» управ-
ления (см. п. 6.4). Однако случай ЛК-оптимального «дешевого»
управления, при котором «i>2 = (“1 - j)wo^2 / 2, по МОП-методу ре-
ализован быть не может.
В заключение параграфа отметим, что еще одной особенностью
МОП-метода является существование множества законов управле-
ния, на котором достигается критерий качества (6.90).
6.7. АДАПТИВНОЕ УПРАВЛЕНИЕ
В задачах синтеза управлений, рассмотренных в пп. 6.3-
6.6, использовалось предположение, что параметры подвеса извест-
ны точно и неизменны во времени. Однако нередко встречаются
случаи, когда в процессе функционирования подвеса его параметры
могут существенно изменяться.
Например, при включенном электродвигателе к «отрицательной»
жесткости подвесасу добавляется «отрицательная» жесткость элек-
тродвигателя, вызванная магнитными силами тяжения ротора в ра-
диальном направлении (см. п. 7.10). Другими примерами могут
служить влияние сил резания в металлообрабатывающих шпинде-
лях, гидро- или газодинамических сил в насосах и компрессорах,
изменения массы веретена при намотке нити и др. В таких
случаях вполне естественно возникает задача об адаптивном управ-
90
лении, способном обеспечить постоянство динамических качеств
подвеса в широком диапазоне изменения его параметров.
Следует указать еще одну причину актуальности адаптивного
управления. Дело в том, что каждый неадаптивный регулятор пос-
ле своего изготовления должен быть настроен. Эта настройка осу-
ществляется методом проб и ошибок и требует больших трудоза-
трат персонала высокой квалификации. Поэтому весьма желательно
построить такой регулятор, который вовсе бы не нуждался в настрой-
ке после изготовления и мог бы использоваться для различных
подшипников без перенастройки. Единственным параметром, ко-
торый должен характеризовать такой регулятор, могла бы слу-
жить собственная частота подвеса <оо.
Таким образом, во всех перечисленных случаях возникает задача
управления при существенно неполной информации об объекте уп-
равления, т. е. задача адаптивного управления. Из большого числа
методов теории адаптивного управления [63] остановимся на мето-
де синтеза систем управления, устойчивых при бесконечно боль-
шом коэффициенте усиления, используя при этом идеи работы [50].
Рассмотрим вначале подвес с управлением по току. Уравнение
подвеса запишем в виде
У = f(y, У, (6.99)
а условие существенной неполноты информации об объекте управ-
ления сформулируем так. Пусть о функции /(г/, у, i) известно лишь
то, что при всех возможных значениях ее аргументов частная про-
изводная по управляющему току i положительна, т. е.
df(y, у, 0 /di > 0. (6.100)
Пусть также задана программная функция f = f °, реализующая
требуемый закон движения тела. Используя, например, (6.27), имеем
f°(y, у, ст) = -((ЛдУ + 2£(001/ + d3CT). (6.101)
Теперь задача сводится к следующему. Для каждого момента t
и соответствующего ему состояния y(t), y(t), о(0 требуется найти
такое значение i°(t), при котором
f(y, y,i°) = f°(yt У, а). (6.102)
При наличии полной информации о подвесе, т. е. при известной
функции f(y, у, I), потребное значение i°(0 можно было бы найти
на основе аналитического решения уравнения (6.102), как это и
делалось в предыдущих параграфах.
В рассматриваемом же случае уравнение (6.102) можно решить
лишь алгоритмически. Алгоритм решения имеет вид [50]:
91
(i)e = Р1Д/; = P1>0. (6.103)
Действительно, при сделанном допущении относительно функ-
ции f(y, у, i), для каждого момента t = t' справедливо предельное
равенство
lim i(t) = f(y, у, i°) = f°(y, у, о), (6.104)
T—>oo
где т — быстрое время.
Этот факт является следствием того, что следящая система, от-
вечающая алгоритму (6.103), устойчива.
Подставляя в (6.103) выражения для f° и f из (6.101) и (6.99),
будем иметь:
(0* = рхД/; Д/ = -(РоУ + 2£cooz> + d3o + у). (6.105)
Структурная схема контура управления, построенная по (6.105),
представлена на рис. 6.12.
Существенной особенностью алгоритма (6.105) является то об-
стоятельство, что для его реализации не нужно использовать яв-
ную функциональную зависимость f(y, у, Г). Эта зависимость может
оставаться неизвестной. Структура алгоритма управления не со-
держит в явном виде параметров объекта управления. Отсюда вы-
текает, что алгоритм управления (6.105) является в полном смысле
адаптивным, поскольку его динамические свойства адекватны тре-
буемым динамическим свойствам подвеса. Практическое осуще-
ствление алгоритма основано на измерении ускорения у.
Относительно реализации алгоритма управления (6.105) отме-
тим следующее. Можно показать, что данному алгоритму отвечает
следящая система
T1(0*+i = i° (6.106)
с постоянной времени
тх =[рх(Э//дО]-1. (6.107)
Точность отслеживания существенно определяется величиной
Р1. При конечном значении Р1 требуемый закон движения тела
Рис. 6.12. Структурная схема адаптивного ПИД-регулятора тока
92
будет осуществляться приближенно. Степень приближения возра-
стает с увеличением рр Значение рх следует выбирать из следую-
щего условия: процессы в системе (6.106) должны протекать су-
щественно быстрее (в 5-10 раз), чем в программной системе (6.27).
Отсюда следует нижняя оценка
Р > (6.108)
Э//Э1
а также тот факт, что система управления сохраняет устойчивость
при бесконечно большом значении рг
Рассмотрим теперь подвес с управлением по напряжению. Урав-
нение подвеса запишем в виде
У = f[y,y.i(u)], (6.109)
где в отличие от (6.99) правая часть является неявной функцией
управляющей переменной и.
Однако, поскольку
= (6.110)
ди di ди
остаются справедливыми все приведенные выше рассуждения и по
аналогии с (6.105) приходим к следующему алгоритму управле-
ния напряжением
й = р2Д/; Д/ = -(«оУ + 2С“оУ + + у), р2 > 0- (6.111)
Структурная схема контура управления, реализующая алго-
ритм (6.111), может быть представлена схемой, изображенной на
рис. 6.12, при замене в ней pj и i на р2 и и соответственно. Данно-
му алгоритму отвечает следящая система
т2и + и = uQ
с постоянной времени
df di
Р23Г
di
(6.112)
(6.113)
6.8. ФИЛЬТРАЦИЯ ШУМОВ ИЗМЕРЕНИЯ.
НАБЛЮДАТЕЛИ СОСТОЯНИЯ
Во всех задачах управления подвесом, рассмотренных
в предыдущих разделах, используется основное допущение: все пере-
менные состояния (у, у, i, а, у) могут быть измерены точно в лю-
бой момент времени. На самом деле это не так. На практике не-
93
посредственному измерению с помощью соответствующих датчиков
поддаются только перемещение тела у и ток L Надежных способов из-
мерения скорости у и тем более ускорения у применительно к вра-
щающимся роторам до настоящего времени не существует. Поэто-
му скорость у, ускорение у, как и интеграл от перемещения о, не
измеряются, а вычисляются.
Наиболее простой и распространенный способ вычисления ско-
рости и ускорения — это использование дифференцирующих зве-
ньев. Однако при таком подходе возникают трудности, связанные
с проблемой шумов измерения, неизбежно содержащихся в сигнале
датчика положения. Амплитуда сигнала на выходе дифференциру-
ющего звена, как известно, пропорциональна частоте. Поэтому, если
не принять мер по ограничению частотного диапазона, уровень вы-
сокочастотных составляющих шума измерения, усиленных диффе-
ренцирующими звеньями, будет бесконечно большим, и такая сис-
тема не будет работоспособной. Для борьбы с шумами измерения
канал управления снабжается фильтром нижних частот (ФНЧ).
Обычно используется быстродействующий демпферный фильтр вто-
рого порядка с передаточной функцией
(О?
Wf (s) = - 2--=Л-----5-, (6.114)
где (0^ — собственная частота фильтра.
Сигнал шума, проходящий через фильтр (6.114), существенно
подавляется в диапазоне частот со > оу Однако вместе с подавлени-
ем шумов в той же степени подавляется и полезный сигнал изме-
рения у. Это приводит к тому, что формирование управляющей
переменной в регуляторе осуществляется на основе обратной связи
не по действительным значениям у, у, у, а по их приближенным
оценкам у, у, у, определяемым как:
y(s) = Wf(s)y(s); Р(8) = sWf(s)y(s); ij(s) = s2Wf(s)y(s). (6.115)
На рис. 6.13 показана схема прохождения сигнала измерения
перемещения у, просуммированного с сигналом шума измерения
ут, через ПД-регулятор тока, снабженный фильтром (6.114). Уп-
равляющий ток i при этом складывается из приближенной оцен-
ки i и сигнала шума /ш. Чтобы наличие фильтра (6.114) не при-
водило к существенному ухудшению динамических качеств подве-
са, значение (0^ должно быть не менее чем на порядок больше
собственной частоты подвеса (Dq, т. е.
(0/ >1Осоо. (6.116)
Рассмотренный выше способ фильтрации шумов измерения прост
в реализации, но обладает существенным недостатком — вместе
94
Рис. 6.13. Структурная схема ПД-регулятора тока с фильтром нижних частот
при наличии шума измерения уш
с подавлением сигнала шума в одинаковой степени подавляется
и полезный сигнал. Стремление преодолеть этот недостаток приве-
ло к созданию теории оптимальной фильтрации, или фильтра Кал-
мана—Бьюси [43].
Основным понятием в теории оптимальной фильтрации явля-
ется наблюдатель состояния. Это — динамическое звено, являю-
щееся, по сути, моделью объекта управления, на вход которого по-
даются измеряемая и управляющая переменные, а выходами явля-
ются переменные восстановленного состояния. Подавление шума
измерения в наблюдателе происходит без ослабления выходных
переменных.
По определению для линейной системы
z = Dx, J
где г — измеряемая переменная, наблюдателем полного поряд-
ка является система
х = Ах + Ви + N(2 -Dx), (6.118)
в которой N есть матрица коэффициентов усиления наблю-
дателя. Наблюдатель (6.118) может быть представлен также
в виде
х = (А - ND)x + Ви + N2. (6.119)
Из (6.119) следует, что динамические свойства наблюдателя
определяются распределением его полюсов, являющихся корнями
характеристического полинома
A(s) = det[sl - (А - NjD)]. (6.120)
Построим, к примеру, наблюдатель полного порядка для подвеса
с управлением по току (6.16). Потребуем, чтобы характеристичес-
95
кий полином наблюдателя (6.120) являлся полиномом Баттер-
ворса второго порядка
Д(з) = s2 + л/2 (DHs + со2 (6.121)
с радиусом распределения полюсов сон. Тогда элементы матрицы
коэффициентов усиления наблюдателя N = п2)т-
п1 = Т2~(Он» и2=со2+Л2. (6.122)
Наблюдатель будет обладать достаточным быстродействием, если
назначить
сон = (3-5)соо. (6.123)
Структурная схема канала управления по току с наблюдателем
полного порядка (6.118) и ПД-регулятором представлена на
рис. 6.14. Входами наблюдателя служат измеряемая переменная
2 = у + 1/ш» состоящая из полезного сигнала у и шума измерения
г/ш, и управляющий ток L Выходными переменными наблюдателя
являются восстановленные значения перемещения у и скорости у.
Поэтому такой наблюдатель можно назвать наблюдателем поло-
жения и скорости (НПС). Выходные переменные наблюдателя ис-
пользуются в качестве входных переменных регулятора для фор-
мирования управляющего тока/.
Рис. 6.14. Структурная схема канала управления по току с наблюдателем по-
ложения и скорости и ПД-регулятором
96
Уравнения наблюдателя в операторной форме записи имеют вид:
ч Д(а) z ч lus + по
y(s) = -7-7 z/(«) + . ym(s);
A(s) A(s)
о
* v A(s) , v n2s + n-tk
y(s) = -±-!-sy(s) + 21 уш(8).
A(s) A(s)
(6.124)
Из (6.124) следует, что в установившемся режиме перемеще-
ние и скорость восстанавливаются точно без ослабления. Поскольку
в передаточных функциях, связывающих y(s) и y(s) с шумом из-
мерения уш(8), порядок числителя на единицу меньше порядка зна-
менателя, наблюдатель ослабляет шум измерения на обоих выхо-
дах подобно инерционному звену первого порядка.
Ряд алгоритмов управления подвесом, синтезированных в пре-
дыдущих разделах 6.3-6.6, предполагает использование обратной
связи по ускорению. В связи с этим рассмотрим задачу построе-
ния наблюдателя положения, скорости и ускорения (НПСУ). Для
ее решения необходимо, чтобы ускорение входило в число компо-
нент вектора состояния системы. Такое возможно только в случае
подвеса с управлением по напряжению. Тогда имеем:
X = (у, У, у)Т; z = y + ym; D = (1, 0, 0);
0 1
0
rk2 /L
(6.125)
Потребуем, чтобы характеристический полином наблюдателя
(6.120) был полиномом Баттерворса третьего порядка с радиусом
распределения полюсов сон:
Д($) = s3 +2(онз2 +2со2$ + (о3. (6.126)
Приравнивая (6.120) и (6.126), находим элементы матрицы N:
Г о Г q Г 9
^=2^--; п2=2(з)^--п1; п3 = (»*-~(n2-кл). (6.127)
JL Ju Л/
Структурная схема наблюдателя положения, скорости и ускоре-
ния (НПСУ) представлена на рис. 6.15. Данный наблюдатель об-
ладает теми же динамическими свойствами, что и наблюдатель
НПС — он «точно» восстанавливает положение, скорость и уско-
рение, но ослабляет шум измерения на всех трех выходах подобно
инерционному звену первого порядка.
97
Выходы
Рис. 6.15. Структурная схема наблюдателя положения, скорости и ускорения
В заключение параграфа заметим, что оба синтезированных на-
блюдателя имеют полный порядок, т. е. они восстанавливают все
компоненты вектора состояния. Вместе с тем для упрощения можно
построить наблюдатель пониженного порядка, в котором, напри-
мер, не восстанавливается перемещение у.
6.9. БЕЗДАТЧИКОВЫЙ ПОДВЕС
В п. 6.8 было показано, что на основе измерения только
одной компоненты вектора состояния — перемещения у — можно
с помощью наблюдателя восстановить все остальные переменные
состояния. В связи с этим возникает вопрос — можно ли восстано-
вить состояние подвеса, если измерять только ток i? Ответ на этот
вопрос положителен, поскольку матрица восстанавливаемости [43]
' D '
DA
(6.128)
для системы с управлением по напряжению (6.125) при D = (0, 0,1),
как нетрудно убедиться, имеет полный ранг.
Это означает, что подвес может быть осуществлен без датчика
положения тела, а лишь на основе измерения тока. Такой подвес
называется без датчиковым. Он может функционировать лишь при
наличии наблюдателя состояния. Входными переменными наблю-
дателя являются ток i и управляющее напряжение и, а выходны-
ми переменными — оценки перемещения у, скорости у и тока i.
Процедура построения наблюдателя для бездатчикового подве-
са абсолютно идентична процедуре построения наблюдателя НПСУ,
изложенной в п. 6.8, поэтому здесь не приводится.
98
Бездатчиковый подвес уступает по динамическим качествам
обычному подвесу с датчиком положения. Вместе с тем он об-
ладает одной интересной особенностью, состоящей в том, что при
нагружении подвешиваемого тела постоянной нагрузкой оно пере-
местится в направлении, противоположном направлению нагруз-
ки. Иными словами, бездатчиковый подвес обладает «отрицатель-
ной» статической жесткостью. Объясняется это тем, что бездатчи-
ковый подвес является, по существу, системой стабилизации не
положения тела, а тока смещения. Поэтому, чтобы создать магнит-
ную силу, компенсирующую постоянную нагрузку при постоян-
стве и равенстве токов в обмотках электромагнитов, должно про-
изойти соответствующее изменение зазоров под полюсами электро-
магнитов.
Благодаря отмеченной особенности бездатчиковый подвес обла-
дает более высокой несущей способностью, чем обычный подвес.
Поэтому его выгодно применять в случаях больших статических
нагружений.
6.10. УСТОЙЧИВОСТЬ В МАЛОМ И БОЛЬШОМ.
ВЛИЯНИЕ ОГРАНИЧЕННОСТИ
РЕСУРСОВ УПРАВЛЕНИЯ
В пп. 6.3 и 6.4 синтез законов управления выполнялся
в предположении, что подвес функционирует в малой окрестности
положения равновесия и что исчерпания ресурсов управления по
току и напряжению не происходит. Однако практически в любом
подвесе имеется режим, при котором отклонение ротора от положе-
ния равновесия нельзя считать малым — это режим «всплывания»
ротора со страховочных подшипников при включении подвеса. На-
чальное отклонение ротора в этом режиме равно зазору в страховоч-
ном подшипнике 80, который сравним с зазором в магнитном под-
шипнике 8.
Если усиление в контуре управления достаточно большое, то при
большом начальном отклонении ротора значение управляющего сиг-
нала, тока или напряжения будет превосходить максимально воз-
можное значение. Усилитель мощности при этом входит в насыще-
ние. Это означает, что происходит исчерпание ресурса управления.
Система управления подвесом должна быть спроектирована так,
чтобы после включения подвеса ротор плавно «всплыл» со страхо-
вочных подшипников и застабилизировался в центральном по-
ложении. Это означает, что область возможных положений рото-
ра -80 < у < 80 должна быть областью притяжения к положению
равновесия. Иными словами, система управления подвесом долж-
на быть устойчива как при малых, так и при больших возмущени-
ях положения ротора (в малом и большом), т. е. быть абсолютно
устойчивой.
99
Рис. 6.16. Фазовые портреты подвеса в случаях: а — абсолютной устойчивости;
б — неустойчивости в малом; в — устойчивости в малом и неустойчивости
в большом
На рис. 6.16 показано движение изображающей точки подвеса
на фазовой плоскости у у в трех типичных случаях. На рис. 6.16, а
отражен случай абсолютной устойчивости подвеса: изображающая
точка движется из начального положения М0(50, 0) в центр О по
траектории, имеющей вид сходящейся логарифмической спирали.
Центр О в этом случае — устойчивый фокус.
На рис. 6.16, б показан случай, когда подвес неустойчив в ма-
лом. Такой случай может встретиться при настройке подвеса —
когда усиление в контуре управления слишком мало, чтобы ком-
пенсировать «отрицательную» жесткость подвеса. В этом случае
фазовые траектории имеют вид расходящихся из центра О лога-
рифмических спиралей. Изображающая точка, двигаясь из произ-
вольного начального положения М(у0, 0), достигнет упора, ее ско-
рость погасится до нуля, затем будет двигаться в обратном на-
правлении до другого упора и т. д. Ротор при этом будет либо
совершать циклическое движение малой частоты с ударами о стра-
ховочный подшипник, либо оставаться в одном из крайних поло-
жений.
На рис. 6.16, в показан случай устойчивости в малом и неус-
тойчивости в большом. На фазовой плоскости имеется неустойчи-
вый предельный цикл с амплитудой ау < 80. Если изображающая
точка находится внутри области, ограниченной предельным цик-
лом, то она придет в начало координат, если находится снаружи —
то выйдет на циклическое движение от упора до упора.
Отсюда следует, что устойчивость подвеса в малом является не-
обходимым, но недостаточным условием работоспособности подве-
са. Для этого также нужно, чтобы область возможных перемещений
-80 < у < 80 была свободна от предельных циклов. В связи с этим
возникает задача отыскания предельных циклов, которые могут су-
ществовать вследствие ограниченности ресурсов управления.
Вначале рассмотрим подвес с управлением по току. Будем ис-
пользовать уравнение движения (6.17), записанное в безразмерных
100
переменных. Полагая, что значение управляющего тока заключено
в пределах-tmимеем:
У - Х2У = X2i(&
[£, при - 1т < £< 1т;
i(^) ~ 1 . /е.. |j-i
Sign(^)im при |£| > im;
£ = ~(^1У + k2y)
(6.129)
при естественных ограничениях на перемещение
-30<1/<50 ; 30<1, (6.130)
где 80 — зазор в страховочном подшипнике.
В системе (6.129) управление / является нелинейной функцией
дополнительной переменной £. Эта переменная, в свою очередь, фор-
мируется по линейному закону на основе обратной связи по у и у.
Предполагается, что коэффициенты усиления и /?2 выбраны
так, что система (6.129) устойчива в малом, т. е. при |£| < im. Струк-
турная схема системы (6.129) может быть представлена в виде
последовательного соединения линейной части системы и нели-
нейного звена типа насыщения (рис. 6.17).
Применение метода гармонической линеаризации [7, с. 546] по-
казывает, что система (6.129) имеет один неустойчивый предель-
ный цикл с амплитудой перемещения
йу ~
(6.131)
Обычно im = 1, поэтому согласно (6.131) ау > 1. Отсюда следует,
что подвес с управлением по току (6.129) обладает абсолютной
устойчивостью. Однако этот вывод
не совсем соответствует практике,
поскольку в действительности при
больших усилениях наблюдается
потеря устойчивости в большом.
Данное расхождение может быть
объяснено неполнотой модели под-
веса (6.129), не учитывающей инер-
ционность установления тока при
ограниченном ресурсе напряжения.
Рассмотрим поэтому подвес с уп-
равлением по напряжению. Исполь-
зуя уравнения движения (6.10) и по-
лагая, что значения тока и нап-
ряжения ограничены в пределах
-i <i <i^ и -ит <и <ит, имеем:
т т т тп’
Рис. 6.17. Структурная схема под-
веса с учетом ограниченности ре-
сурса управления по току
101
y-X2y~x2i(^) = 0;
^г+У + Ъ = «(£/);
^2 при-1т <^2 <1т-,
. zc \* |н ।
[sign(£2)im при |^| > im;
,е. при ~ит ^“т;
и(^/) — 1 • zc \ |е I
[sign(^)um при |^| > ит;
=-(g/У + ё2У + ёзК^г))
(6.132)
при сохранении ограничений (6.130) на перемещение у.
В системе (6.132) управление и является нелинейной функцией
дополнительной переменной^, которая формируется на основе об-
ратной связи по г/, у, i. В свою очередь, ток i также является
нелинейной функцией другой дополнительной переменной Обе-
им нелинейностям отвечает нелинейное звено типа насыщения.
Структурная схема системы (6.132) представлена на рис. 6.18.
Рис. 6.18. Структурная схема подвесасучетом ограниченности
ресурсов управления по току и напряжению
При дальнейшем анализе
будем рассматривать ЛК-оп-
тимальный вариант закона уп-
равления, в котором согласно
(6.63) и (6.64) безразмерные ко-
эффициенты усиления обрат-
ной связи:
gi = «о /х2 +2соо;
g2 =2<о§/%2;
£3=2о)0-1, (6.133)
где 0)0 — безразмерная соб-
ственная частота подвеса.
Очевидно, что замкнутая си-
стема (6.132), (6.133) асимпто-
Рис. 6.19. Графики зависимости ресурса
напряжения ит от собственной часто-
ты (00 оптимального подвеса (% = 2,1),
при котором ау = 3/2:
------- — расчетный метод гармонической ли-
неаризации; х—Х---Х-— — экспериментальный
102
тически устойчива в малом. При im = 1 амплитуда предельного
цикла ау зависит от трех параметров: %, соо, ит. Чтобы подвес был
абсолютно устойчив, амплитуда ау должна быть больше зазора
в страховочном подшипнике 50.
На рис. 6.19 в качестве примера приведены расчетные и экс-
периментальные графики зависимости ит от со0. При значениях
напряжения, лежащих выше соответствующих кривых, зона пе-
ремещений -5/2 < у <5/2 свободна от предельных циклов, т. е.
подвес абсолютно устойчив. При меньших напряжениях подвес
неустойчив в большом.
6.11. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ
ХАРАКТЕРИСТИКИ ПОДВЕСА. ЧАСТОТА СРЕЗА
В данном параграфе рассматривается реакция подвеса
на гармоническую вынуждающую силуф(£) = Qo sin (Of. Амплитуда
силы Qo при этом может быть либо постоянной (например, при
кинематическом возбуждении колебаний вследствие вибраций ста-
тора подшипника с частотой со), либо, если(?(£) вызвана неуравно-
вешенностью ротора, пропорциональна квадрату частоты враще-
ния со2. Ограничимся случаем подвеса с ЛК-оптимальным ПД-регу-
лятором тока (п. 6.4).
Будем использовать безразмерное описание (6.18). Вводя без-
размерную вынуждающую силу = Qq sin со7', где (% = QqTq /
/ (т8%2); t' = / TqI co' = <oTo / %, и опуская штрихи в обозначе-
ниях безразмерных величин, уравнение подвеса запишем в виде
у - у = i + Qo sin (6.134)
Оптимальный ПД-закон управления (6.34)
i = -(k1y + k2y) (6.135)
содержит безразмерные коэффициенты усиления обратной
связи:
= (Oq + 1; k2 = ^2(COq + 1), (Oq > 1. (6.136)
Чтобы найти амплитуды и фазовые углы переменных
y(t) = Ау sin(cot + Vy); Ф) = A sin(cof + \|//), (6.137)
запишем операторные выражения
y(s) = Wy(s)Q(s); i(s) = Wi(s)Q(s), (6.138)
содержащие передаточные функции подвеса:
103
Wj,(s) = 1/(s2 + A2s + *1-1);
Wz (s) = -(ft2s + ) / (s2 + *2S + - !)•
(6.139)
По своему физическому смыслу передаточные функции (6.139)
являются операторами динамических податливостей подвеса. За-
менив оператор s на /со, где j — мнимая единица, получаем ком-
плексные амплитудно-фазовые частотные характеристики W
и ТУД/со), из которых находятся амплитудно-частотные характе-
ристики
Ау(со) = |и^О(о)|ео; Ai(o)) = |Wz(jco)|Qo (6.140)
и фазочастотные характеристики подвеса
Уу(<й) = arg Wy(j(0); уг((о) = arg Wz(». (6.141)
На рис. 6.20 в качестве примера показаны частотные характе-
ристики подвеса при различных значениях собственной частоты
0)0 (значению (00 = 1 соответствует случай «дорогого» управления).
Рассмотрим еще одну характеристику — частоту среза подвеса.
Она играет важную роль в задачах, связанных с использованием
магнитных подвесов в упругих конструкциях, имеющих слабодем-
пфированные собственные частоты и формы (гибкие роторы, упру-
гие элементы корпусов и др.). В таких задачах часто возникает про-
блема обеспечения устойчивости подвеса. Как правило, потеря ус-
Рис. 6.20. Частотные характеристики подвеса при
ЛК-оптимальном ПД-регуляторе (со' = (dTq/x):
1 ~ О) 0 = I; 2 — (О q — 2} 3 О) 0 = 5
104
тойчивости происходит благодаря энергетической подпитке упру-
гих колебаний вследствие незапланированного наличия положи-
тельной обратной связи в подвесе по какой-либо из собственных
форм и выражается в так называемом «пении» элемента конструк-
ции с соответствующей собственной частотой. Однако если коэф-
фициент усиления амплитуды сигнала на частоте, равной указанной
собственной частоте, меньше единицы, то энергетической подпитки
упругих колебаний со стороны подвеса не будет.
Частоту, начиная с которой модуль передаточной функции ра-
зомкнутой системы становится меньше единицы, принято назы-
вать частотой среза и обозначать соср. Для ее определения соста-
вим передаточную функцию разомкнутой системы (6.134)-(6.136):
H(s) = ~(k2s + kt) / (s2 -1), (6.142)
выполним в ней замену s = jw и из равенства |/Z(jcocp)| = 1 находим
С0ср = й)0{1 + [2(1 +1 / со|)]1/2}1/2. (6.143)
В частном случае «дорогого» управления, когда соо = 1, имеем
соср = 1,73соо. В случае «дешевого» управления, когдасоо »1, име-
ем <оср= 1,55соо. И, наконец, в случаях, когда по какой-либо причи-
не система имеет коэффициент усиления обратной связи по скоро-
сти А?2 меньше оптимального значения (6.136), частота среза так-
же снижается и, как это следует из (6.142), соср —> (00 при k2 —> 0.
7. ДИНАМИКА ЖЕСТКОГО РОТОРА
В АКТИВНЫХ МАГНИТНЫХ ПОДШИПНИКАХ
7.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Как уже отмечалось в п. 2.2, полный (неконтактный)
подвес ротора может быть осуществлен путем использования либо
двух радиальных и одного осевого АМП, либо двух конических
АМП. Наибольшее распространение получила первая схема, по ко-
торой подвес ротора в направлении оси вращения (осевой подвес)
осуществляется независимо от подвеса в радиальных направлени-
ях (радиальный подвес). Осевой подвес является одностепенным
(см. пп. 5 и 6), влияние на его динамику со стороны радиального
подвеса практически отсутствует, поэтому специально исследовать
его нет необходимости. Вместе с тем осевой АМП оказывает опре-
деленное дестабилизирующее влияние на радиальный подвес из-за
«отрицательной» жесткости при угловых перемещениях ферромаг-
нитного диска; это обстоятельство будет учтено ниже. Поэтому
основным объектом исследования в данной главе является ради-
альный подвес ротора, хотя наряду с этим будет рассмотрен и под-
вес ротора в конических АМП.
По поводу содержания главы отметим следующее. Активные
магнитные подшипники выполняют роль упругодемпферных эле-
ментов (см. п. 6.3). Поэтому целый ряд известных динамических
явлений (прецессия оси, критические скорости, самоцентрирование
и др.), имеющих место при использовании механических упруго-
демпферных опор и описанных в большом числе публикаций (см.,
например [31, 44, 45, 66, 74]), проявляются и при использовании
АМП. Вместе с тем АМП как управляемые элементы вносят свою
специфику в виде дополнительных динамических явлений, таких
как синхронная помеха, потеря устойчивости, перманентный резо-
нанс, автовращение и др. [41, 47, 48, 99, 105]. Поэтому в данной
главе основное внимание уделяется именно этим специфическим
явлениям; описание же известных положений из динамики рото-
ров приводится лишь для более полного понимания этих явлений.
В п. 7.2 дается математическое описание ротора и подшипни-
ков. Ротор схематизируется в виде абсолютно твердого тела (учету
упругих деформаций будет посвящена глава 8). Используется ли-
неаризованная модель подшипников.
В п. 7.3 приводится процедура синтеза регулятора при наибо-
лее простом и распространенном раздельном способе управления,
т. е. когда каждый из четырех каналов управляется автономно;
перекрестные связи между каналами отсутствуют; каждый канал
выполняет функцию упругодемпферного элемента.
В п. 7.4 дан анализ динамики подвеса при раздельном управ-
лении. На примере симметричного подвеса анализируются свобод-
ные и вынужденные колебания при поступательных и угловых
106
перемещениях ротора. Отмечаются особенности динамики несим-
метричного подвеса. Анализируется влияние несовпадения точек
измерения и точек управления. Показывается, что из-за ошибок
в вычислении скоростей и наличия интегрального управления подвес
может терять устойчивость; приводится вывод критериев ус-
тойчивости.
В п. 7.5 излагается процедура синтеза ЛК-оптимального управ-
ления подвесом гироскопического ротора. Задача имеет замкнутое
аналитическое решение, которое приводит к многосвязному регу-
лятору, настройка которого зависит от частоты вращения. Дина-
мика ЛК-оптимального подвеса анализируется в п.7.6.
В п. 7.7 содержится ответ на весьма важный вопрос — в каких
случаях следует отдать предпочтение более сложному в реализа-
ции оптимальному многосвязному управлению и в каких — более
простому раздельному управлению?
В п.7.8 рассматриваются особенности управления подвесом ро-
тора, имеющего неодинаковые экваториальные моменты инерции
и являющегося, по сути, нестационарным объектом управления.
В п.7.9 решается задача синтеза системы управления подвесом
ротора в двух конических АМП, выполняющих функции радиаль-
но-упорных подшипников.
В п. 7.10 ставятся вопросы взаимовоздействия подвеса и при-
водного электродвигателя. Анализируется дестабилизирующее воз-
действие электродвигателя на подвес. Приводится оценка тормо-
зящего воздействия на привод со стороны подвеса вследствие не-
уравновешенности ротора. Дается описание эффекта автовраще-
ния ротора в подвесе и показывается, при каких условиях под-
шипники могут выполнять роль приводного двигателя.
Заключает главу п. 7.11, в котором рассматриваются вопросы
совмещения электрической машины и магнитного подшипника, т. е.
проблемы создания бесподшипниковых машин.
7.2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
МОДЕЛИРОВАНИЕ РОТОРА
Рассматривается жесткий ротор массой М9 вращаю-
щийся с постоянной угловой скоростью й) в двух радиальных
активных магнитных подшипниках АМП1 и АМП2 (рис.7.1).
Свяжем с ротором систему осей Ox'y'z' так, чтобы ось Oz' со-
впадала с его геометрической продольной осью, а поперечная ось
Ох' проходила через центр масс С (рис. 7.2). Пусть Cx"y"z" —
система главных центральных осей инерции ротора с главными
центральными моментами инерции: экваториальными
и осевым J2„ = J3- Статическая неуравновешенность масс ротора
характеризуется линейным параметром — эксцентриситетом
ОС = е. Динамическая (моментная) неуравновешенность характери-
107
Рис. 7.2. Координатные оси жесткого ротора
зуется угловым пара-
метром = Y (для про-
стоты считаем уу, = 0).
В начальный момент
оси подвижной системы
Ox'y'z' совпадают с ося-
ми неподвижной сис-
темы О* xyz.
Для определения по-
ложения ротора будем
использовать две груп-
пы обобщенных коорди-
нат и, как следствие, две
формы записи диффе-
ренциальных уравнений
движения. Первая груп-
па включает в себя ко-
ординаты х0 и у$ полю-
са О и углы малых поворотов фх и (р^ вокруг осей х и у соответ-
ственно. Запишем их в виде вектора
k = (£1, ^2> ^4)Т = (*0> У0> <Рх> <Pyf- (7.1)
Вторая группа обобщенных координат включает в себя коорди-
наты центров опорных участков ротора О х и О2 (или точек управле-
ния) в осях х и у и представляется вектором
9 = (91, 92» 9з, ?4)Г = (*1> У1> х2’ У2)Т• (7.2)
Введем также вектор координат центров датчиковых участков
ротора О1т и О2т (или точек измерения)
108
Чт “ (#1тп’ Ч2т* ЧЗт’ Ч4т) ~ (х1т> У1т* х2т> У 2т) • (7.3)
Чтобы установить связь между векторами q и qm предполо-
жим, что точки управления и О2 имеют продольные координа-
ты 2^ и 22(22 > 2-^). Расстояние между точками управления I = 22 - 2±.
Точки измерения и О2т имеют продольные координаты
г1т и г2гг&2т > 21т)' Расстояние между точками измерения 1т =
= 22т ~ 21т. Рассматривается общий случай, когда расположение
точек управления и точек измерения не совпадает, т. е. 2р
z2m * z2. Тогда имеем следующие линейные преобразования:
Ч “ ~ % Ч* Чт = %т& Чт ~ Ч^Ч~ %%т Чт (7.4)
с матрицами преобразований
10 0^
0 1 -2Х 0
1 0 0 z2
0 1 -22 0
0 - 21 0
22 0 -2!
10-1
0 10
(ZT)-X = (Z-Y;
22 - 2Хт
ZmZ~l = i
т I
о
г2 ~ г2т
0
о
22 ~ 21т
о
22 “ 22т
21m - Zi 0
г1т ~ 21
г2т “21 0
0 г2т ~ 21
(7.5)
Заметим, что при совпадении точек управления и точек измере-
ния матрица есть единичная матрица.
Для вывода дифференциальных уравнений движения ротора
будем использовать уравнения Лагранжа второго рода (см. п. 5.11):
ddT дТ
dtdys ду$
rs, 8 = 1,...,4,
(7.6)
где обобщенными координатами ys могут быть как координаты так
и q ; Ys — обобщенная сила; Т — кинетическая энергия.
Кинетическая энергия твердого тела дается известным выраже-
нием [55, с.157]
7 = +2M(U0 x(O) rc +0) ©° СО], (7-7)
109
где Во — скорость полюса О; CD — угловая скорость тела; гс —
радиус-вектор ОС центра масс; 0° — тензор инерции тела в точ-
ке О.
Наиболее простая развернутая запись формулы (7.7) получает-
ся при пользовании осями Ox'y'z', неизменно связанными с рото-
ром. Будем считать, что перемещения ротора и параметры неурав-
новешенности малы, так что величины х0, z/0, е имеют тот же поря-
док малости, что и зазор в подшипниках, и что справедлива замена
sin а «а, cos а»1, где а = фх, фу, у . При сделанных предположениях
проекции вектора угловой скорости на оси Ox'y'z' даются соотно-
шениями [55]:
со х' = <рх cos (of + у у sincof;
0)^' = -фх sinotf + coscof;
®г' =о)-фхф!/.
(7.8)
Тензор инерции ротора в точке О при сделанных выше предпо-
ложениях о характере неуравновешенности масс имеет вид
0 0
Jl -Jy'z' >
- Jу’2> J3
(7.9)
где Jy'2' = У(«71“«7з) — центробежный момент инерции ротора.
Схема, моделирующая моментную не-
Рис. 7.3. Моделирование
моментной неуравновешен-
ности ротора
уравновешенность ротора, показана на
рис. 7.3. К ротору в плоскости у"г' при-
крепляются две одинаковые точечные
массы Дтп в точках с координатами
(0, -Ь, с) и (0, Ь, -с). Центробежный мо-
мент инерции по определению равен
Jy'z' = -2ЬсДтп, поэтому
у = 2bcAm/(J3 - Ji). (7.10)
Учитывая, что х'с = е, у'с = 2'с = 0,
имеем
(Bq хСО) Гс =eo)(-x0sinttrt + z/ocosart). (7.11)
Так как Vq = Xq + i/q, выражение кинетической энергии (7.7)
в координатах £ принимает вид
110
Т = —[M(xq + z/q) + 2Meco(z/o cos art - x0 sin art) + J1 (фх + ф^) +
+ е/з(со^ - 2йхрхфр - 2ajy(J / - е/з)(-фх sin art + фу cosart)j. (7.12)
Используя преобразования (7.4), запишем выражение кинети-
ческой энергии в координатах q
Т = ^{m^xf + у2) + т2(х2 + у2) - 2m12(xix2 + УхУ2) +
2Месо г
+ 2Ьо(У2 ~ У1)(х2 - xj + —-—[(х22х - x1z2)sincot +
q 2( J 4 — eTg )ую Г
+ 0/1г2 - У2г1)cos“Ч +-----j-----[(^ ~ У2)sin+
+ (х/ - x2)coscot]|, (7.13)
где т^, тп12, т2 — инерционные коэффициенты; Ло — гироскопи-
ческий коэффициент:
Jx+Mz2 Jx+Mz^ Jx + Mzx J30) . ..
mi -----p----’ p’ m2 ---------. «0 -
Преобразовав уравнения Лагранжа (7.6) с учетом (7.12), полу-
чаем хорошо известные [66] дифференциальные уравнения движе-
ния ротора в координатах
Mxq = + Р1 + Мею2 cosort; MyQ = R2 + Р2 + Мею2 sin art;
^срх + Ы2фу = R3+P3+ (Jx - J3)yai2 coscot; Jx<$y + =
= 1?4 + P4 + (Jx - J3)Yco2 sincot. (7.15)
В матричной записи уравнения (7.15) имеют вид
J^ + H^ = l? + P + Pv(t), (7Л6)
где R = (Rr, ..., Р4)т; Р = (Рг,..., Р4)г; Pv(t) = [Meco2cos cot, Мeco2sin art,
(J; - J3)ya)2cosart, (Jr - J3)Y0)2sin art]T — соответственно векторы
обобщенных электромагнитных реакций подвеса, внешних сил и воз-
мущающих сил; = diagfМ, — инерционная матрица;
— кососимметричная гироскопическая матрица с двумя ненуле-
выми элементами (И-)34 = ~(Н^)43 = J3co.
Ill
Заметим, что первые два уравнения в (7.15) описывают посту-
пательные движения ротора, последние два уравнения — угловые
движения, причем между угловыми движениями (рх и <ру имеется
гироскопическая связь. Физически эта связь означает, что при уг-
ловом движении ротора, например, против хода часовой стрелки
вокруг оси у со скоростью ф^, на него будет действовать гироско-
пический момент окГзфу, стремящийся повернуть ротор вокруг осих
по ходу часовой стрелки.
Обобщенные электромагнитные реакции подвеса R создаются
управляющими магнитными силами подшипников
F = (FV ...,F4f = (FxVFyl,Fx2,Fy2,)T, (7.17)
которые приложены к ротору в точках управления О1 и О2 (см.
рис. 7.1). ВекторыRn F связаны соотношениями:
R = ZTF; F = (Z~X)TR. (7.18)
Структура обобщенных внешних сил Р в зависимости от типа
привода вращательного движения и характеристик внешней среды
может быть самой различной. Среди них могут быть позиционные,
диссипативные, циркуляционные и вынуждающие силы (учету по-
зиционных сил, действующих на подвес со стороны электродвига-
теля, посвящен п. 7.10).
Подстановка выражения кинетической энергии (7.13) в уравне-
ния Лагранжа (7.6) приводит к дифференциальным уравнениям
движения ротора в координатах qz
т1х1 - ^12*2 + Мл - У2) = Fi + Qi + Qvi(O;
т1У1 “ ^12^2 - hQ (А - *2) = *2 + $2 + Qv2 (0;
- 7п12хх + т2х2 - Мл - л) = *з + ®з + Qv3(0;
" ^12Л + т2У2 + *0(*1 " *2) = Л + ©4 + Qv4(0,
(7.19)
или в матричной записи
Jq + Hq = F + Q + QV(Z). (7.20)
Здесь F, как и ранее, магнитные силы подшипников; Q =
= (Qp •••, Q4)T — обобщенные внешние силы; Qv(t) — обобщенные
возмущающие силы,
2
Qv (t) = —-— (z2 cos (fit, z2 sin (fit, - zr cos cot, - z± sin cot)T +
(e71 — о )V0) T
+ —1—_2_! (sin (of t - cos (at, - sin (fit, cos co£) ; (7.21)
J, H — соответственно инерционная и гироскопическая матрицы:
112
0 - т12 0 * 0 1 0 -1
J = 0 7П1 0 -т12 ; н = й0 -1 0 1 0
-/п12 0 т2 0 0 -1 0 1
0 - т12 0 тп2 1 0 -1 0
Из (7.19) видно, что между движениями хх и х2, происходящи-
ми в плоскости xz, также как между движениями у^ и z/2, происхо-
дящими в плоскости j/2, имеется инерционная связь. Движения же
в разных плоскостях связаны гироскопически.
ОПЫТНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
Приведем описание
одного из наиболее удобных и
точных методов опытного оп-
ределения экваториального
и осевого J3 моментов инерции
ротора.
Ротор подвешивается на
двух нерастяжимых нитях
длины йн (рис. 7.4). Расстоя-
ние от центра тяжести С до
каждой из нитей одинаково и
Рис. 7.4. Опытное определение момен-
тов инерции ротора
равно ас. Предполагается, что
величины hH и ас имеют одинаковый порядок. Ротору придаются
свободные поворотные колебания малой амплитуды в горизонталь-
ной плоскости и измеряется их период т. Экваториальный момент
инерции вычисляется по формуле
Mga2t2
=----5---»
4лгЛн
(7.22)
где М — масса ротора; g — ускорение силы тяжести.
Аналогично может быть определен и осевой момент инерции^.
МОДЕЛИРОВАНИЕ РАДИАЛЬНЫХ ПОДШИПНИКОВ
Схема электромагнитных цепей подшипников представ-
лена на рис. 7.5.
Для построения линейной системы управления на обмотки по-
даются напряжения смещения и1с, ..., и4с, которые вызывают токи
смещения Цс, ..., i4c. Управляющие напряжения и = (ut, ..., и^)т
и токи i = ..., суммируются с напряжениями и токами
смещения. Как и в случае одностепенного подвеса (п. 6.2), уп-
113
АМП2 у। и +и
Рис. 7.5. Электромагнитные цепи радиальных подшипников
равление осуществляется по дифференциальной схеме, согласно ко-
торой управляющие токи и напряжения в противоположных элек-
тромагнитах равны по значению и противоположны по знаку. Токи
i1 и /3 создают магнитные силы и в направлении оси х, а
токи i2 и i4 — силы F2 и F± в направлении оси у. Тогда для
магнитных сил подшипников F и обобщенных магнитных сил R
имеем:
F = Cqq + Hji-, R = ZTF = C^, + ZTHli, (7.23)
VReC^=Z^CqZ; Cq = diag(cxV cyl, cx2, cy2); Ht = diag(Aa, hi2, hi3, h^).
Здесь Cq и H. — соответственно матрицы позиционных «отри-
цательных» жесткостей и токовых жесткостей каналов управле-
ния радиальных АМП с элементами
cas = 2Lsa&s I §2; his = 2Lsasics / 8S, s = 1, 2, 3, 4. (7.24)
О О Lu ' O' lu О О Си • О7 7 7 7 V J
Уравнения для управляющих токов имеют вид
L(iY + Sq + R*i = и, (7.25)
где£, S, R* — соответственно матрицы индуктивностей, коэффици-
ентов связи «ЭДС движения — скорость» и активных сопротивле-
ний обмоток:
L = diag(Lp L2, L&, L4); S = diag(ftt|/2, h^/2, h^/29 h^/2);
R* = diag(rp r2, r3, r4).
УЧЕТ ОСЕВОГО ПОДШИПНИКА
Как уже отмечалось в п. 7.1, осевой АМП оказывает
дестабилизирующее влияние на радиальный подвес из-за «отрица-
тельной» жесткости при угловых перемещениях ферромагнитного
114
диска. Пусть электромагниты осевого АМП имеют токи смещения
и 12. Тогда, учитывая (4.18)-(4.20), со стороны осевого АМП на
ротор будет действовать дестабилизирующий момент
_ 1 ^11 г2 . dL22 г2
1 2
= О)Р,
₽ = <Px’<P{/>
где Со = Ьоа<р(А2 +^2) — «отрицательная» жесткость осевого АМП
при угловых перемещениях ротора. Следовательно, при учете де-
стабилизирующего влияния осевого АМП вместо соотношений (7.23)
для магнитных сил подшипников F и обобщенных магнитных сил
R нужно использовать следующие соотношения:
F = (Cq + Cqc)q + Hzi; R = (Q + Co)^ + ZT Hti, (7.26)
где C°c = (Z-1)TC0Z-1; Co = diag(0, 0, c0,c0).
Следует отметить, что в большинстве приложений дестабилизи-
рующее влияние осевого АМП на радиальный подвес пренебрежи-
мо мало.
7.3. СИНТЕЗ РЕГУЛЯТОРА
ПРИ РАЗДЕЛЬНОМ УПРАВЛЕНИИ
При раздельном управлении каждый из четырех кана-
лов z/p х2, z/2 управляется автономно по сигналу своего датчика
положения; перекрестные связи между каналами отсутствуют. Про-
стота регулятора и удобство его наладки являются причинами при-
менения раздельного управления в подавляющем большинстве при-
ложений.
Для описания объекта управления обратимся к уравнениям
(7.19). Полагая в них zn12 = 0 и hQ = 0, т. е. пренебрегая инерцион-
ной и гироскопической связанностью, и учитывая (7.23), прихо-
дим к четырем независимым между собой уравнениям вида (6.20).
Этим уравнениям отвечают четыре парциальные системы или че-
тыре не связанных между собою одностепенных подвеса. В мат-
ричной записи эти уравнения имеют вид
Mqq-Cqq = Hii, (7.27)
где = diag(m1, т2, m2)-
Синтез управлений одностепенным подвесом подробно рассмот-
рен в пп.6.3 и 6.4. Здесь остановимся лишь на особенностях, свя-
занных с заданием программного движения и описанием замкну-
той системы управления.
115
Как и в п. 6.3, потребуем, чтобы каждый из четырех каналов
управления выполнял функцию упругодемпферного элемента с за-
данными коэффициентами жесткости cs и демпфирования bs. Тог-
да по аналогии с (6.22) программное движение ротора зададим
уравнениями
qs + 2^Xsgs + k2sqs =0, s = l, 4, (7.28)
или в матричной записи
<7 + £<j+AQ = 0, (7.29)
где^=(11а§(2^1Х1, ..., 2£4Х4); A = diag(X|,..., %4). ЗдесьXs— недемп-
фированная парциальная собственная частота канала управления;
— параметр затухания. Программные управляющие силы име-
ют упруговязкий характер:
Fs =~(csqs +bsqs), s = l,...,4, (7.30)
где Ья = 2CX4m..
r-1 О О О ' О О О
При = Х2, Ci = ^2’ Х3 = ^4’ Сз = ^4 п°Двес ротора будет обладать
изотропными упругодемпферными свойствами. При равенстве между
собой всех четырех парциальных собственных частот и парамет-
Рис. 7.6. Парциальные системы управления под-
весом ротора в плоскости xz: а — система управле-
ния перемещением х^ б — система управления
перемещением Х2
116
ров затухания область резонансных частот будет наиболее узкой
и, как следствие, динамические качества подвеса будут наиболее
высокие.
На рис. 7.6 в качестве примера изображены расчетные схемы
первой и третьей парциальных систем. Они получаются путем
замены рассматриваемого канала управления упругодемпферным
элементом при одновременной замене другого подшипника шар-
нирной опорой. Заметим, что на практике по такой схеме обычно
осуществляется предварительная настройка регулятора подвеса.
Решив (7.29) относительно ускорениями подставив его в (7.27),
приходим к ПД-закону управления током
i = -(K-fl + K2q)
(7.31)
с диагональными матрицами коэффициентов усиления обратной
связи по перемещениям и скоростям в точках управления:
Кх = Hi1 (MqA + Cq); К 2 = H[lMq^
(7.32)
Расположения точек измерения и точек управления, как уже
говорилось, могут не совпадать. Для парциальных систем соотно-
шения связи между координатами q и qm (7.4) теряют силу; вмес-
то них, как это следует из рис. 7.6, надо теперь записать:
g = Tmgm;Tm = diagf—-----—,------1--,---1--1 (7.33)
ч22 21т 22 21т 22т 21 ^2^
Тогда закон управления (7.31), построенный на основе обрат-
ной связи по перемещениям qm и скоростям qm в точках измере-
ния, принимает вид
(7.34)
В силу диагональности матриц К у К2 и Тт отчетливо обнару-
живается раздельность управления (7.34).
Остается дать описание замкнутой системы управления. Ис-
пользуя (7.20), (7.23), (7.31) и (7.4), приходим к дифференциаль-
ным уравнениям замкнутой системы с раздельным управлением
в координатах q
Jq + (H + D)q + (К - Cq)q = Q + Qv(f),
где
D = Н,К9Ттг Я"1; К = HjKiT Z Z~l.
i л m ш 1 i 1 m m
(7.35)
(7.36)
Заметим, что дополнительно к инерционной и гироскопической
связанности каналов управления, присущей объекту управления
117
(7.20), в замкнутой системе (7.35) добавляется еще связанность
движений х^ с х2 и с у2 за счет несовпадения расположения
точек управления и точек измерения.
Нетрудно установить, что в координатах дифференциальные
уравнения замкнутой системы при раздельном управлении имеют
вид
+ Kg = Р + Pv(t), (7.37)
где
= ZT(HiKlTmZm - CqZy, = ZTHlK2TmZm. (7.38)
Следует отметить, что уравнения (7.35) и (7.37), строго говоря,
не являются «точными», поскольку они получены в предположе-
нии, что перемещения qm и скорости qm, входящие в закон управ-
ления (7.34), могут быть измерены точно в любой момент времени.
Кроме того, в них не учитывается возможность введения обратных
связей по интегралам от перемещений (или интегральное управле-
ние). Отмеченные обстоятельства будут учтены ниже при анализе
устойчивости подвеса.
7.4. ДИНАМИКА ПОДВЕСА
ПРИ РАЗДЕЛЬНОМ УПРАВЛЕНИИ
СХЕМАТИЗАЦИЯ СИММЕТРИЧНОГО ПОДВЕСА
Рассмотрим симметричный подвес ротора, схема которо-
го изображена на рис. 7.7. Предполагается, что точки измерения
совпадают с точками управления, так что: 2^ z2~z2m ~
= 1/2. Активные магнитные подшипники выполняют роль упруго-
демпферных элементов, имеющих жесткость с = тпХ2 и коэффици-
ент вязкого трения Ь = 2£Хтп, где, как и ранее, X— недемпфиро-
У
Рис. 7.7. Симметричный подвес ротора при раздельном
управлении
118
ванная парциальная собственная частота каналов управления;
т = (J^ + MZ2/4)/Z2 — инерционный коэффициент. Пусть внешние
нагрузки отсутствуют. Тогда уравнения подвеса (7.37) принима-
ют вид:
Мх0 + 2&х0 + 2сх0 = Меся2 coscoZ;
Му$ + 2Zn/0 + 2сг/0 = Meco2 sincoZ;
(7.39)
J/Фх + (А13фу + &фФх + СфФх = (^1 - ^3)Y“2 COSCOZ;
Jfiy - (Ик13фх + ЬфФ^ + Сффу = (Jx - J3)YW2 sin art,
где = bl2/2 = tyml2 и = cl2/2 = X2ml2/2 — коэффициенты демп-
фирования и жесткости при угловых перемещениях.
Вследствие симметрии подвеса поступательные перемещения
ротора Xq и yQ не связаны с угловыми перемещениями фх и ф^; это
позволяет рассматривать их раздельно.
ПОСТУПАТЕЛЬНЫЕ ПЕРЕМЕЩЕНИЯ.
СИНХРОННАЯ ПОМЕХА
Два первых уравнения в (7.39) формально не свя-
заны, и каждое из них определяет поступательные колебания в со-
ответствующем направлении. Недемпфированная собственная ча-
стота поступательных перемещений по любому из радиальных
направлений
сю0 = у]2с / М = Xfan / М.
(7.40)
Свободные поступательные колебания ротора (при е = 0) не
зависят от скорости вращения и происходят по закону
x0(t) = Сое п°‘ sin(pot + ос0),
(7.41)
где Ро = a)ovl~d) — частота свободных колебаний; = £ф0)0 —
показатель затухания; = £соо / Л — параметр затухания поступа-
тельных колебаний; Со, а0 — постоянные, зависящие от началь-
ных условий.
Траектория точки О — прямая линия.
Вынужденные колебания геометрического центра ротора О под
действием статической неуравновешенности происходят по за-
кону:
x0(Z) = AqCos (cdZ - Р); z/0(Z) = Aosin (coz ~ P), (7.42)
119
где
Месо2
7(2с - Мео2)2 + 4Ь2й)2
tg₽ =
25<в
2с - Мео2 ’
(7.43)
Центр масс ротора С, имеющий координаты:
ХС = х0 + ecoscof; ус - i/о + е sinojf, (7.44)
также совершает вынужденные гармонические колебания с часто-
той со и амплитудой
4с2 + 4&2®2
(2с - Мео2)2 + 4Ь2(О2 '
(7.45)
На рис. 7.8 показан характер зависимостей амплитуд Ац иАс от
частоты вращения (0. На основании соотношений (7.42)-(7.45)
и рис. 7.8 можно сделать следующие выводы.
При вращении неуравновешенного ротора точки О иС движут-
ся по круговым траекториям с радиусами Aq и Ас в направлении
вращения ротора; форма движения — прямая синхронная прецес-
сия. Максимумы амплитуд достигаются на резонансной или кри-
тической скорости вращения, примерно равной недемпфированной
собственной частоте со = (00. На закритических скоростях вращения
с увеличением со амплитуда перемещений центра масс С стремится
к нулю. Это означает, что на больших скоростях вращения центр
масс стремится к оси вращения, т. е. проявляется эффект самоцен-
трирования ротора. Амплитуда перемещений геометрического цен-
тра О на больших скоростях стремится к е.
Отмеченные динамические эффекты являются характерными для
роторов на упругодемпферных опорах [44, 45, 66]. Вместе с тем
при использовании АМП проявляется следующий дополнитель-
ный эффект.
Рис. 7.8. Амплитудно-частотные характеристики поступательных переме-
щений неуравновешенного ротора: а — геометрического центра О; б —
центра масс ротора С
120
На больших скоростях прецессионные перемещения оси ротора,
измеренные датчиками и пропущенные через пропорциональные и
дифференцирующие звенья регулятора, создают в каналах управ-
ления так называемую синхронную помеху. Амплитуда этой поме-
хи в результате дифференцирования растет с увеличением скорос-
ти вращения. При достижении некоторой скорости синхронная
помеха начинает насыщать усилитель мощности — и подвес теря-
ет управляемость. Поэтому при создании подвесов высокоскорост-
ных роторов возникает проблема компенсации синхронной помехи
(см. п. 10.5).
УГЛОВЫЕ ПЕРЕМЕЩЕНИЯ.
ПЕРМАНЕНТНЫЙ РЕЗОНАНС
Угловые перемещения ротора описываются двумя пос-
ледними уравнениями в (7.39). Эти уравнения связаны гироскопи-
ческими членами. Присо= 0 гироскопическая связанность исчезает,
и недемпфированная собственная частота угловых перемещений
невращающегося ротора относительно любой из поперечных осей
О0 = 7СФ = ^ml2 /2Jr. (7.46)
На рис. 7.9 приведены численные соотношения между значени-
ями соо, Qo и X для различных геометрических форм ротора.
Рассмотрим теперь вращающийся ротор. Положив в (7.39)
Ьф = О и записав характеристическое уравнение угловых перемеще-
ний в виде (£2q - Q2)2 - (hQ.)2 = 0, находим из него две недемпфи-
рованные собственные частоты угловых перемещений ротора:
а) ______________
I ' "I со0 = 0,8162.
rvs rvs Qo-1,41Л
Q0/(00 = ^3=l,73
6)0 = 0,732.
Qo = 1,582.
Q /<w =2,16
0 0
G)o =1,582,
&о=О,73Л
Рис. 7.9. Соотношения между недемпфированными собственными частотами
поступательных перемещений (Oq, угловых перемещений и парциальных
перемещений X для различных геометрических форм ротора при со = 0: а —
длинный цилиндр; б — г — массивные диски
121
Рис. 7.10. График зависимостей недемпфированных собствен-
ных частот угловых перемещений ротора от угловой скорости
при различных отношениях моментов инерции J3/J1
Qx = (y/4Q^ + Л2 - Л) / 2; Q2 = (д/4£20 + + Л) / 2. (7.47)
Здесь, как и ранее, h = (oJ3/J1 — гироскопический параметр.
На рис. 7.10 приведены графики зависимостей Qx и Q2 от угло-
вой скорости (О при различных значениях отношения моментов
инерции Jg/Jp При со=О обе собственные частоты одинаковы и
равны Qo. С ростом (о собственная частота уменьшается и при
h » 2Q0 становится равной Qx = Qq / Л. Собственная частота Q2
с ростом (О увеличивается и при h » 2Q0 принимает значение й2 =
= h + Очевидно, что Qx —> 0, Q2 —> Л ПРИ 00 •
На рис. 7.11 изображены собственные формы недемпфирован-
ных угловых колебаний ротора. Геометрическая ось ротора Ozf
совершает кососимметричные (конические) вращательные движе-
ния вокруг неподвижной оси Oz. С более высокой частотой Q2
Рис. 7.11. Собственные формы недемпфированных угловых ко-
лебаний гироскопического ротора (&2 > &i): а — высокочастот-
ная прямая прецессия (нутация); б — низкочастотная обратная
прецессия
122
вращение оси Oz' происходит в сторону вращения ротора; такое
движение называется прямой угловой прецессией, или нутацией.
С меньшей частотой ось Oz' вращается в сторону, противопо-
ложную направлению вращения ротора; такое движение называ-
ется обратной угловой прецессией.
Заметим, что с учетом демпфирования корни характеристичес-
кого уравнения становятся комплексными числами; их называют
полюсами замкнутой системы. Недемпфированным собственным
частотам и Q2 отвечают полюса
53 4=-a±/Q2’ (7.48)
где ос= &(p/2J1 — показатель демпфирования.
Вынужденные угловые колебания вследствие моментной неурав-
новешенности возникают в форме прямой синхронной прецессии
геометрической оси ротора Oz' с амплитудой
о
ф = (^1-^з)¥<« (7.49)
^[С<Р ~ (J1 ~ J3>2]2 + (b<p“)2
и прецессии главной оси инерции ротора Cz" с амплитудой
Сф + (&фсо)2
Фс = Y Jf------------------------2
У [СФ -(J1 - J3)“ J +(Ьфй)2
(7.50)
На основании формул (7.47) - (7.50) и рис. 7.10 можно сде-
лать следующие выводы. Система имеет две собственные частоты
Q1 и Q2, которые зависят от скорости вращения о. Скорость со = £2+,
совпадающая с большей собственной частотой Q2, называется кри-
тической скоростью прямой прецессии. Скорость (о = Q_, равная
меньшей собственной частоте Qp называется критической скорос-
тью обратной прецессии. Критические скорости определяются из
рис. 7.10 как точки пересечения кривых &2(со) и ^(со) с прямой
Q = со; согласно (7.47):
й+ = = ^/(Ji+Jg). (7.51)
Из первого соотношения в (7.51) и рис. 7.10 видно, что при
J1 < критическая скорость прямой прецессии отсутствует.
Амплитуды угловых колебаний, вызванных моментной неуравно-
вешенностью, достигают максимума вблизи критической скорости
прямой прецессии (о = Q+. При Jr1 < J$ резонансные колебания
отсутствуют. Критическая скорость обратной прецессии при
колебаниях от неуравновешенности не реализуется. Она может
123
проявиться лишь в случае, когда на ротор действует периодичес-
кая с частотой вращения со нагрузка неизменного направления.
Как и при поступательных перемещениях, на закритических ско-
ростях возникает синхронная помеха у и происходит само-
центрирование ротора Аф —> 0 (см. рис. 7.8).
В связи с тем что интенсивность угловых колебаний зависит от
разности J1 - J3, отметим следующее. Моменты инерции для по-
лого цилиндра с массой М, наружным радиусом R, внутренним
радиусом г и длиной I вычисляются по формулам:
= M(R2 + г2 + /2/3)/4; J3 = M(R2 + r2)^. (7.52)
Поскольку для тонкого диска (Z 0) = 2, в общем случае
имеем 0 < J3/J1 2. Случай = J3 для магнитных подшипников
является нежелательным в силу следующего обстоятельства. Как
уже было установлено выше, в этом случае на высоких скоростях
собственная частота Q2 примерно равна частоте вращения со (см.
рис. 7.10). Хотя резонансные колебания от неуравновешенности
в силу (7.49) отсутствуют, они могут вызываться другими источ-
никами возмущений с частотой со (со стороны электродвигателя,
шумами измерений и т. д.). Демпфирование колебаний (коэффи-
циент Ьф) осуществляется за счет обратной связи по скорости.
Измерение же скорости на высоких частотах сопряжено с опреде-
ленными трудностями (см. п. 6.7), поэтому при = J3 подвес
будет функционировать в режиме перманентного резонанса.
НЕСИММЕТРИЧНЫЙ ПОДВЕС
Подвес, в котором подшипники расположены несиммет-
рично по отношению к центру масс ротора, будем называть несим-
метричным. В этом случае уравнения поступательных и угловых
перемещений ротора будут взаимосвязаны жесткостными и демп-
фирующими членами. Подвес
Рис. 7.12. Зависимости собственных
частот несимметричного подвеса рото-
ра от скорости вращения при J%<
имеет четыре собственные часто-
ты Qp ..., Q4, которые являются
корнями характеристического
уравнения системы (7.37) или
(7.35).
На рис. 7.12 показан харак-
тер зависимостей собственных ча-
стот от скорости вращения. Ин-
дексы (+) и (-) обозначают соот-
ветственно прямую и обратную
прецессию. Невращающийся ро-
тор имеет две недемпфированные
собственные частоты и
124
На этом же рисунке изображены собственные формы. В собствен-
ных формах, отвечающих собственным частотам (низшей) и Q4
(высшей), превалируют угловые перемещения, а в двух других —
поступательные перемещения.
При > J3 имеются две критические скорости прямой прецес-
сии QK1 и Qk2, а при < J3 — только одна Qr1. На каждой
критической скорости возбуждение возможно как от статической,
так и от моментной неуравновешенности. На закритических ско-
ростях вращения амплитуда колебаний геометрического центра О
стремится к е, а амплитуда угловых колебаний геометрической оси
Oz' стремится к у. Это означает, что в несимметричном подвесе,
как и в симметричном, происходит самоцентрирование ротора
и возникает синхронная помеха.
ВЛИЯНИЕ НЕСОВПАДЕНИЯ ТОЧЕК ИЗМЕРЕНИЯ
И УПРАВЛЕНИЯ
Пусть расстояние lm = z2m - 21т между точками измере-
ния О1/п и O2zn не Равн0 расстоянию I = z2 - z^ между точками
управления и О2. Введем параметр = (Z - lm) /(I + 1т) ,
характеризующий степень несовпадения расположения точек изме-
рения и управления. Этот параметр вносит дополнительную связан-
ность в уравнения движения, что приводит к некоторому изменению
значений собственных частот. Расчеты показывают, что в этом слу-
чае недемпфированные собственные частоты невращающегося рото-
ра и Q2 (см- рис.7.12) примут новые значения:
1Д 1 +
4
Ml2
4Ji
А™
т
; Q2 = Q2 1 -
,2 Г"»
. (7.53)
Обычно мало, и его влиянием можно пренебречь.
УСТОЙЧИВОСТЬ ПОДВЕСА
Чтобы судить об устойчивости подвеса, описываемого диф-
ференциальными уравнениями (7.37), нет необходимости в отыс-
кании корней характеристического уравнения, — для этого доста-
точно проанализировать структуру сил, входящих в эти уравне-
ния. Система (7.37) содержит следующие силы: упругие потенци-
альные силы-ЙГ^ с симметричной матрицей диссипативные силы
с симметричной матрицей и гироскопические силы
с кососимметричной матрицей G^. На основании известных тео-
рем Кельвина—Тета—Четаева [59, с. 159] можно заключить, что
система (7.37) асимптотически устойчива.
125
Однако следует учесть, что система (7.37) получена в предположе-
нии, что скорости qm могут быть измерены точно в любой момент
и что отсутствует обратная связь по интегралу от qm. В реальных
подвесах для вычисления скоростей qm и фильтрации шумов изме-
рения используются либо дифференцирующие звенья с фильтра-
ми нижних частот, либо наблюдатель состояния (см. п. 6.7). Повы-
шение статической жесткости подвеса осуществляется введением
интегрального управления (см. п. 6.3). Оба эти обстоятельства
должны учитываться при анализе устойчивости реального подвеса.
Для этого вновь обратимся к уравнениям симметричного под-
веса (7.39). Собственная частота(оо поступательных перемещений
ротора от угловой скорости (о не зависит, поэтому устойчивость
этих перемещений в реальном подвесе сохраняется.
Угловые перемещения имеют две зависящие от со недемпфиро-
ванные собственные частоты, определяемые формулой (7.47): вы-
сокую Q2 и низкую Qi (см. рис. 7.10). Демпфирование собствен-
ных частот в (7.39) обеспечивается диссипативными членами Ьффх
и йффу. В реальном подвесе из-за указанных выше факторов при
достижении определенной скорости вращения диссипация может
быть разрушена, что приводит к потере устойчивости. Разрушение
демпфирования высокой собственной частоты Q2 сопряжено с ошиб-
ками в измерении скоростей фх и ф^, низкой собственной частоты
Qj — с интегральным управлением.
Ограничимся приближенным анализом. Для этого введем до-
пущение, что Q2 » £Ц и что быстрое собственное движение <р2(0
с частотой &>2 и медленное собственное движение фх(0 с частотой
разделены. Тогда, учитывая (7.48), быстрому движению при
отсутствии ошибок в измерении скоростей соответствует характе-
ристическое уравнение (s - s3)(s - з4) = s2 + 2as + а2 + = 0- По-
лагая, что в реальном подвесе используется фильтр нижних час-
тот с передаточной функцией (6.80), уравнение быстрых движений
запишем в операторной форме
2 (2as + a2
s2 +V2(0^S + 0)2
ф2 =°>
(7.54)
где, как и ранее, a = b^/2Jv
Условие устойчивости системы (7.54) по критерию Гурвица имеет
вид
V2a)^a - За2 - П2 > 0. (7.55)
По формуле (7.55) с учетом (7.47) можно найти скорость вра-
щения о, при достижении которой быстрое нутационное движение
ротора становится неустойчивым.
126
Учитывая (7.48), медленному движению при отсутствии интег-
рального управления соответствует характеристическое уравнение
(s - 8i)(s - s2) = s2 + 2ocs + ос2 + Q2 =0. При введении интегрально-
го управления медленные движения опишем уравнением
(s2 + 2as + а2 + Q2 + df / s)<pr = 0. (7.56)
Условие устойчивости системы (7.56) по критерию Гурвица имеет
вид
2a(a2 + Q2) - df >0. (7.57)
7.5. СИНТЕЗ ЛК-ОПТИМАЛЬНОГО РЕГУЛЯТОРА.
МНОГОСВЯЗНОЕ УПРАВЛЕНИЕ
Используя метод ЛК-оптимизации для случая описания
систем в комплексном пространстве состояний (см. п. 6.4), най-
дем ЛК-оптимальное управление подвесом жесткого ротора в ра-
диальных АМП. Описание объекта управления существенно зави-
сит от выбора управляющих переменных; в качестве последних
могут быть магнитные силы, токи и напряжения.
Наиболее простое описание имеет место, когда управляющими
переменными являются обобщенные магнитные силы R. В этом
случае, как это будет показано ниже, задача ЛК-оптимизации име-
ет аналитическое решение без наложения каких-либо ограничений
на расположение подшипников и датчиков по длине ротора [34, 37,
105, 106]. Аналитическое решение имеется также и в случае, когда
управляющими переменными являются токи, но при одном суще-
ственном ограничении — подвес должен быть симметричным [105].
Сравнительный анализ показывает, что оба способа оптимиза-
ции (сил и токов) приводят к одинаковым результатам. В связи
с этим ограничимся рассмотрением только случая, когда управля-
ющими переменными являются обобщенные магнитные силы R.
Обратимся к уравнениям (7.15) и представим объект управле-
ния в виде совокупности трех систем: двух систем с одной степе-
нью свободы
х0 = А; Уо ~ А (7.58)
и гироскопической системы с двумя степенями свободы
Фх + ЙФ</ = /з; ф</ - лФх = Л’ (7.59)
где f1 = R^/M; f2 - = R^/J^, f4 = R^/Ji — новые управля-
ющие силы и моменты; h = (oJ3/Jr1 — гироскопический параметр.
Применяя к каждой из двух систем (7.58) процедуру ЛК-опти-
мизации (6.40) - (6.43), легко установить, что оптимальные управ-
ляющие силы должны формироваться по закону:
127
7?i = -М(а20х0 + 2£шохо); «2 = -М^оУо + 2Ыо), (7.60)
где C0q = р-1/4 — желаемое значение недемпфированной собствен-
ной частоты поступательных перемещений ротора; £ = V2 / 2 — опти-
мальный фактор затухания.
Рассматривая теперь гироскопическую систему (7.59), предста-
вим ее в комплексной форме
Ф-/ЛФ = Л (7.61)
где <р = <рх + jq>y; f = f3 + jf4; j = уП.
Применяя к системе (7.61) процедуру ЛК-оптимизации (6.40) -
(6.43), имеем:
х = (ф,ф)г, У = ф, u = f, В = (0,1)г, С = (1,0);
(7.62)
Комплексное матричное уравнение Лурье-Риккати (6.43) по-
рождает четыре скалярных уравнения
Р2 + р! - р = °;
Р2Р3 - ppi + лрр4 = °;
рзРа - hPP2 = °;
Рз - 2рр2 = °.
которые имеют следующее аналитическое решение:
4 з ь 2 г 2
Тз ft + ЬР4‘> Р2 = —^Р4> Рз = ~гР4>
р2й3 рй2 h
pi =
Р4 =
(n4h3
р fl р fl
64 + 4
(7.63)
(7.64)
„2*4 I1'2
р и
8
В результате получаем, что оптимальные управляющие момен-
ты должны формироваться по закону:
Я3 = ~Ji(ki(px + /?2Фх + ^зФг/)» ^4 ~ "“«ЛС^Фг/ + ^Фг/ ~ ^зФх)»(7-65)
где — соответственно оптимальные коэффициенты жест-
кости, демпфирования и радиальной коррекции угловых перемеще-
ний ротора:
128
= 7^4/16 + Qo ~h2 14; k2 = hJkt/2. (7.66)
Здесь Qq = p"1/4 — желаемое значение недемпфированной соб-
ственной частоты угловых перемещений невращающегося ротора
(т. е. при нулевых значениях со и h).
Графики зависимости коэффициентов kv k2, k2 от гироскопичес-
кого параметра h = coJg/Jj приведены на рис. 7.13. При h = 0, т. е.
при невращающемся роторе, они имеют следующие значения:
^(0) = Qq, Л2(0) = ^2й0, (0) = 0. С ростом h коэффициенты и k2
асимптотически уменьшаются до нуля, а коэффициент k3 асимп-
тотически увеличивается до значения /^(О), т. е. дойд. Таким
образом, на высоких скоростях вращения оптимальные управля-
ющие моменты содержат только корректирующие составляющие;
упругие и диссипативные составляющие становятся равными
нулю.
Из графиков на рис. 7.13 также следует ответ на весьма важ-
ный для практики вопрос: когда ротор следует считать гироскопи-
ческим, т. е., когда влияние гироскопического эффекта становится
ощутимым? Видно, что существенное уменьшение коэффициентов
kx и k2 и увеличение коэффициента /?3 имеют место при Л > Qo.
Отсюда заключаем, что ротор следует считать гироскопическим, если
его максимальная угловая скорость превышает значение
^гир = /J3« (7.67)
Итак, оптимальные управляющие силы и моменты должны фор-
мироваться по закону
В° = -С°(0))£ - В°(0))£, (7.68)
129
где
В°(со) = diag[2MC(00, 2MCo)o, ^^(w),
0 0 0
С°«о) = 0 М(й1 0 0 . (7.69)
0 0 (<о) J 1&3 ((D)
0 0 - Jjftg (ft)) ^1*1 ((d).
Теперь, используя соотношение (7.23) для подшипниковых сил
F и формулы преобразований (7.18) и (7.4), получаем закон фор-
мирования управляющих токов, реализующих оптимальные силы
и моменты, вида
i° = -[*1 бСОЛЪп + (7.70)
где коэффициенты усиления обратных связей по перемещениям
qm и скоростям qm в точках измерения задаются матрицами:
(со) = Hz-;(Z-1)TC°((0)Z-2 + H^CgZZ^-,
K^) = H[t(Z-1)TB°(a>)Z^. (7.71)
Закон управления (7.70) является многосвязным и зависящим
от угловой скорости со. Многосвязность проявляется в том, что
каждый из четырех каналов управления, кроме двух основных об-
ратных связей по перемещению и скорости в своей точке измере-
ния, имеет четыре перекрестные связи: по перемещениям в осталь-
ных трех точках измерения и по скорости в расположенной в той
же плоскости точке измерения. Так, первый канал, кроме основ-
ных обратных связей по х1т и имеет перекрестные связи по
У 1т* х2т* У2т и х2т* Общее число обратных связей равно 24 вместо
8 при раздельном управлении. При этом все 24 коэффициента
усиления обратных связей в общем случае зависят от угловой
скорости. Это говорит об относительной сложности в реализации
регулятора, отвечающего закону управления (7.70). Вопрос о том,
в каких случаях оправдано использование такого регулятора, бу-
дет обсуждаться в п. 7.7.
7.6. ДИНАМИКА ПОДВЕСА ПРИ МНОГОСВЯЗНОМ
ОПТИМАЛЬНОМ УПРАВЛЕНИИ
Уравнения замкнутой оптимальной системы управления
подвесом (7.58), (7.59) при законе управления (7.70) и при учете
возмущающих сил от неуравновешенности ротора имеют вид:
130
xq + 2£соохо + woxo = есо coscot;
Уо + 2^о0Уо + woJ/o = е®2 sinctf;
(/.72)
Фх + hipy + /?2Фх + ^1Фх + ^зФг/ = (1 “ тп)усо coscot;
(ру - h(px + k2tyy - /?3<РХ + ^ср^ = (1 - тп)усо2 sin cot,
где т = J3/J± и где коэффициенты kv k2 н k2 зависят от угловой
скорости со (точнее, от гироскопического параметра h = сос/д/Л^ = сотп)
согласно (7.66) и рис. 7.13.
Видно, что в оптимальном подвесе (7.72) отсутствует связь меж-
ду поступательными перемещениями х0, yQ и угловыми перемещени-
ями срх, ср^ независимо от степени несимметрии подвеса и степени
несовпадения расположения точек управления и измерения.
Подвес при невращающемся роторе имеет две недемпфирован-
ные собственные частоты: поступательных перемещений соо и уг-
ловых перемещений Qq = ^/^(О). При раздельном управлении
и симметричном подвесе соотношение между значениями соо и
определяется геометрией ротора и расстоянием между подшип-
никами (см. рис. 7.9). В рассматриваемой системе значениями соо
и Qo можно задаваться произвольно. Наибольший интерес пред-
ставляют два случая. В первом из них соо = Qo, поэтому область
резонансных частот будет наиболее узкой. Во втором случае зна-
чения (00 и задаются согласно (7.40) и (7.46), т. е. как и при
раздельном управлении. Тогда движение невращающегося ротора
будет такое же, как и при раздельном управлении, т. е. наиболее
«естественным», а перекрестные связи будут функционировать лишь
при вращающемся роторе.
Перейдем к анализу динамических свойств оптимального под-
веса. Поскольку поступательные и угловые перемещения в нем не
связаны, их можно анализировать по отдельности. Анализировать
динамику поступательных перемещений нет необходимости, так
как все результаты анализа этих перемещений, описанные в п. 7.4
для симметричного подвеса при раздельном управлении, целиком
справедливы и для системы (7.72).
Займемся динамикой угловых перемещений. Вновь вводя комп-
лексную переменнуюф = срх + /ф^, «спрессуем» два последних урав-
нения в (7.72) в одно комплексное уравнение
ф + (/?2 - ;Л)ф + (kr - /7?з)ф = (1 - тп)у(О2е7(0^. (7.73)
Решая комплексное характеристическое уравнение системы
(7.73)
s2 + (k2 - jh)s + кг- jk3 =0, (7.74)
131
находим полюса этой системы:
$! = -а + jQj; $2 ~ ~
(7.75)
где
а = 7*1 / 2; Qi = 7*1 / 2 + Л2 / 4 - h / 2; Q2 = 7*1 / 2 + *2 /4 +
+ Л/2. (7.76)
Здесь а — показатель демпфирования; и Q2 — соответственно
собственные частоты обратной прецессии и прямой прецессии (ну-
тации), Q2 -
Заметим, что Qi = Q2 = 7*1 (0)/2 при со = 0. С ростом со соб-
ственная частота Qp как и показатель демпфирования а, уменьша-
ется и стремится к нулю, а собственная частота Q2 растет и стре-
мится к значению Q2 = *• Очевидно, что исходная действительная
(не комплексная) система двух последних уравнений в (7.72) име-
ет четыре полюса:
«1, з = -а ± уйр з2> 4 = -а ± /&2. (7.77)
Im (s)
Рис. 7.14. Траектории полю-
сов многосвязной оптимальной
системы управления угловыми
перемещениями ротора с рос-
том скорости вращения
Траектории этих полюсов с ростом
со показаны на рис. 7.14.
Перейдем к вынужденным коле-
баниям от моментной неуравновешен-
ности. Отыскивая частное решение си-
стемы (7.73) в виде
<р = Фс°е>‘, (7.78)
где Ф° — комплексная амплитуда,
и подставляя (7.78) в (7.73), нахо-
дим модуль амплитуды угловых пе-
ремещений
.о-И-
7^0 +(1-ТП)2<04
(7.79)
где, как и прежде, т =
Из (7.79) следует, что амплитуда
угловых перемещений геометрической
оси ротора Ф° с ростом со монотонно
увеличивается от нуля до у и не имеет
резонансного пика. Это означает, что,
как и при раздельном управлении,
в оптимальном подвесе на высоких
132
скоростях вращения происходит самоцентрирование ротора и в ка-
налах управления возникает синхронная помеха. Однако в отли-
чие от раздельного управления в оптимальном законе управле-
ния (7.70) коэффициент усиления k2 при скоростях qm с ростом
0) стремится к нулю. Поэтому на высоких скоростях сигнал от
угловой синхронной помехи не дифференцируется и, следователь-
но, не увеличивается с ростом со. Таким образом, оптимальный
подвес (7.72) имеет только одну критическую скорость, равную
недемпфированной собственной частоте поступательных переме-
щений (0q.
Перейдем к анализу устойчивости. В п. 7.4 было показано, что
потеря устойчивости подвеса с раздельным управлением на высо-
ких скоростях вращения может наступить как из-за ошибок в вы-
числении скоростей перемещений, так и вследствие использования
интегрального управления. При этом ошибки в скоростях разру-
шают демпфирование быстрых собственных движений с собствен-
ной частотой Q2, а интегральное управление — медленных собствен-
ных движений с собственной частотой Qp
В оптимальном подвесе, как уже отмечалось выше, коэффици-
ент k2 при скоростях qm с ростом со стремится к нулю, поэтому
ошибки в вычислении скоростей к потере устойчивости не приво-
дят. Интегральное же управление и в оптимальном подвесе может
разрушить демпфирование медленных движений <p1(t). Представив
уравнение этих движений в виде
(s2 + 2as + a2 + Q2 + df / = 0, (7.80)
приходим к условию устойчивости
df < 2a(a2 +Q2), (7.81)
из которого можно найти граничное значение угловой скорости со.
Следует отметить, что проблема устойчивости оптимального
подвеса может быть полностью снята либо за счет исключения
интегрального управления, либо за счет уменьшения коэффициен-
та до нуля с ростом со (по аналогии с коэффициентами k1 и k2).
7.7. РАЗДЕЛЬНОЕ ИЛИ МНОГОСВЯЗНОЕ
УПРАВЛЕНИЕ?
Как уже отмечалось выше, при раздельном способе уп-
равления радиальным подвесом ротора каждый из четырех кана-
лов управляется автономно по сигналу своего датчика положения,
перекрестные связи между каналами отсутствуют. Регулятор, отве-
чающий раздельному управлению, имеет постоянную настройку
и прост в реализации, что весьма важно в практических задачах.
133
Оптимальное же управление предполагает наличие перекрест-
ных связей между каналами управления, причем коэффициенты
усиления обратных связей не являются постоянными величинами,
а зависят от скорости вращения ротора. Поэтому регулятор, обес-
печивающий оптимальное управление, является многосвязным и
имеет зависящую от скорости вращения переменную настройку.
Очевидно, что практическая реализация такого регулятора суще-
ственно сложнее, чем при раздельном управлении.
В связи с этим возникает естественный вопрос — в каких слу-
чаях применение оптимального многосвязного управления целесо-
образно, а в каких нет? Заметим, что этот вопрос актуален лишь
для подвесов гироскопических роторов, т. е. у которых согласно
(7.67) со > в подвесах же негироскопических роторов
целесообразность использования раздельного способа управления
совершенно очевидна.
При сравнении двух систем управления будем исходить из сле-
дующей предпосылки: подвес должен быть устойчив на рабочих
скоростях вращения ротора и отрабатывать возможные возмуще-
ния с наименьшими значениями управляющих переменных.
В предыдущих разделах показано, что проблема обеспечения
устойчивости подвеса при оптимальном управлении решается ав-
томатически; при раздельном же управлении имеются определен-
ные трудности. Перевод ротора из произвольного возмущенного
состояния в нулевое состояние с наименьшими значениями управ-
ляющих сил, а значит токов и напряжений, осуществляется по
определению оптимальным управлением. Достоинством оптималь-
ного управления является также более низкий уровень сигнала
синхронной помехи на высоких скоростях вращения.
Отмеченные выше положительные свойства оптимального уп-
равления все же не могут служить основанием для заключения о не-
целесообразности раздельного управления. Чтобы сделать такое
заключение, нужно сравнить уровни амплитуд управляющих сил
при отработке дисбалансного возмущения (амплитуды токов при-
мерно пропорциональны амплитудам сил).
Для определенности вновь обратимся к симметричному подвесу
ротора (см. п. 7.4). Будем полагать, что значения собственных
частот поступательных перемещений соо и угловых перемещений
невращающегося ротора одинаковы при обоих способах управ-
ления. Поэтому уровень амплитуд управляющих сил 7^ иТ?2, выз-
ванных статической неуравновешенностью е, в обеих системах бу-
дет одинаковым. Уровень же амплитуд управляющих моментов
и вызванных моментной неуравновешенностью у, будет разным.
При раздельном управлении согласно (7.39) и (7.49) амплиту-
да управляющих моментов
|Яз,4| = Ф^ф +(®М2- (7-82)
134
Полагая сф = и fyp = a/2Qq Ji, соотношение (7.82) приводится
к виду
|*3,41 = ^OY
|1 - т\р2у11 + 2р2
1 - (1 - т)р2 j + 2р2
(7.83)
где обозначено т = р = co/Qo.
При оптимальном управлении с учетом (7.65) и (7.79) ампли-
туда управляющих моментов
|-Кз,4| - 7^1 + (^2W ~ ^з)2^1Ф° =
|1 - m\p2yjf2p ч- 2p2fmp(m / 2 - l)2
Y--------=========----------
^1 + (1 - m)2 p4
(7.84)
где обозначено fmp = y/l + m4p4 /16 - m2p2 / 4.
На рис. 7.15 приведены графики зависимостей безразмерной
амплитуды управляющих моментов |в3)4| / JiQqY пРи раздельном
p = Р = <^о
Рис. 7.15. Графики зависимостей амплитуды управляющих моментов |R3 41 / JxQqY
от частоты вращения р - cd/Q0 при различных соотношениях осевого и эквато-
риального моментов инерции ротора т = J3/J1: а — при раздельном управ-
лении; б — при многосвязном оптимальном управлении
135
управлении (рис. 7.15, а) и амплитуды |Яз,4| / при опти-
мальном управлении (рис. 7.15, б) от безразмерной скорости вра-
щения ротора р = oj/Qq при различных соотношениях осевого и
экваториального моментов инерции т = J3/Jv
Анализ формул (7.83), (7.84) и графических зависимостей при-
водит к следующим результатам. При раздельном управлении
амплитуда |^з,4| с Ростом 00 увеличивается монотонно и неогра-
ниченно, и при co»Qo ее увеличение происходит по прямой линии
|в3л| = V^JjQoYCo; влияние соотношения моментов инерции т =
= J%/Ji заметно лишь при низких скоростях вращения 0 < со < 2,5£2О.
При оптимальном управлении амплитуда существенно зависит
от соотношения моментов инерции; с ростом со амплитуда моментов
асимптотически стремится к значению = - 2 / (J3 /
По результатам анализа можно сделать следующие выводы.
Оптимальное управление характеризуется более низким уровнем
амплитуд управляющих моментов, а значит токов и напряжений,
чем раздельное управление. Эффективность оптимального управ-
ления возрастает с увеличением отношения осевого и экватори-
ального моментов инерции т = Jg/Jp Наибольшая эффективность
достигается в случае т = 2, т. е. когда ротор выполнен в форме
массивного диска. При значениях т < 0, 1 применение оптималь-
ного управления нецелесообразно.
7.8. УПРАВЛЕНИЕ ПОДВЕСОМ РОТОРА,
ИМЕЮЩЕГО НЕОДИНАКОВЫЕ
ЭКВАТОРИАЛЬНЫЕ МОМЕНТЫ ИНЕРЦИИ
До сих пор рассматривались жесткие роторы, имеющие
одинаковые экваториальные моменты инерции Jx„ = Jy" = J Од-
нако на практике могут встретиться случаи, когда это правило не
выполняется. Например, роторы некоторых типов ультрацентри-
фуг несут массивный элемент в форме эллипсоидального тора, име-
ющего существенно неодинаковые экваториальные моменты инер-
ции. Такие роторы, обладающие подвижной анизотропией, являют-
ся нестационарными объектами управления — их движение в непо-
движной системе координат описывается дифференциальными
уравнениями с периодическими коэффициентами. Рассмотрим осо-
бенности управления подвесом таких роторов.
Предположим, что модель ротора, описание которой приведено
в п.7.2, имеет экваториальные Jx" = Jp Jy" = J2 и осев°й J3
136
моменты инерции. В рассматриваемой
задаче существенно, что Пусть
J2 > J2 (рис. 7.16).
Известно, что ротор, имеющий неодина-
ковые экваториальные моменты инерции
и установленный в упругие опоры, может
терять устойчивость. Условие устойчиво-
сти выражается неравенством [66, с.153]:
Рис. 7.16. Пример ротора,
имеющего неодинаковые
экваториальные моменты
инерции
[сф - (о2^ - J3)] [сф - <o2(J2 - J3)] > 0, (7.85)
где сф — обобщенный коэффициент пово-
ротной жесткости опор.
Из этого неравенства следует, что при
J3 > Jl > J2, т. е. когда вращение происходит вокруг оси с макси-
мальным моментом инерции, ротор всегда устойчив. При J3 <
имеется диапазон неустойчивых частот вращения.
Допустим, что по условиям задачи неравенство (7.85) не вы-
полняется. Требуется найти закон управления радиальным подве-
сом ротора, имеющего неодинаковые экваториальные моменты инер-
ции, который обеспечивал бы наряду с устойчивостью такое же
оптимальное динамическое поведение, как и в случае, если бы ро-
тор имел одинаковые экваториальные моменты инерции.
Движение рассматриваемого ротора при отсутствии внешних
нагрузок описывается системой линейных дифференциальных урав-
нений с периодическими коэффициентами [35]
A(t)l + B(t)i = R, (7.86)
A(t) =
М
о
о
о
о
м
о
о
B(t) = co
о
о
о
о
о
о
о
о
О
О
«Ли + ai(0
a2(t) J
О
О
- 2л2(0
- J3 + 2ai(t)
о
о
а2(£)
-аг(0
О
О
(t)
2a2(t)
т
Как и ранее, через R обозначены обобщенные электромагнитные
реакции подвеса. Время t входит в матрицы A(t) и B(t) через
параметры нестационарности системы = [(J\ - J2)/2]cos2ort
и a2(t) = [(- J2)/2]sin2(D£. Величина Jm = (J1 + J2)/2 есть среднее
значение экваториальных моментов инерции.
Программный динамический режим подвеса зададим в виде
левых частей дифференциальных уравнений оптимальной замкну-
той системы управления (7.68)
137
+ +B°(w)]^ + Co((d)^ = 0 (7.87)
с заменой в них J\ naJm. Выразив из (7.87) ускорения £ и подста-
вив их в (7.86), получим алгоритм формирования программных
оптимальных управляющих сил и моментов
R° = + В°(со) - B(i)]t (7.88)
Дальнейшее решение задачи по отысканию управляющих то-
ков полностью совпадает с решением аналогичной задачи (7.64)-
(7.67) и здесь не приводится.
Подытожим полученные результаты. Существенное отличие
алгоритма управления нестационарным подвесом по сравнению
со стационарным подвесом состоит в необходимости измерения
текущих значений параметров нестационарности a^G) и a2(t). Это
означает, что измерительная система оптимального подвеса наряду
с измерением перемещений qm и угловой скорости (0 и с вычисле-
нием скоростей qm должна измерять угол поворота ротора ф2 = cot
(описание датчика угла поворота приведено в работе [3]). При
условии точной реализации алгоритма (7.88) обеспечивается пол-
ная компенсация нестационарности ротора, вызванной неодина-
ковостью экваториальных моментов инерции. Движение рото-
ра в подвесе при этом будет таким же, как если бы он имел
одинаковые экваториальные моменты инерции.
7.9. УПРАВЛЕНИЕ ПОДВЕСОМ РОТОРА
В КОНИЧЕСКИХ ПОДШИПНИКАХ
В данном разделе решается задача синтеза системы уп-
равления подвесом жесткого ротора в двух конических АМП, ко-
торые выполняют одновременно функции двух радиальных и од-
ного осевого АМП, т. е. радиально-упорных подшипников (п.3.7).
На рис. 7.17 представлена схема подвеса. Ротор теперь имеет
пять степеней свободы. Перемещения ротора в радиальных на-
правлениях будем по-прежнему определять векторами обобщен-
ных координат £= (х0, z/0, фх, ф^)т и q= (хр у19 х2, у2)т, введенными
в п.7.2. Перемещения ротора в направлении продольной оси z
будем определять координатой zQ точки О.
Движения ротора в радиальных направлениях описываются, как
и ранее, системой дифференциальных уравнений (7.16) или (7.20).
Используемое в них обозначение радиальных магнитных сил под-
шипников F = ..., F^)T сохраним и в дальнейшем. Осевое дви-
жение ротора описывается дифференциальным уравнением
MzQ = Fz +Q2i (7.89)
138
где Fz — осевая со-
ставляющая магнит-
ной силы, создаваемая
обоими подшипника-
ми; Qz — осевая вне-
шняя нагрузка.
На рис. 7.18 пока-
зана схема электромаг-
нитных цепей кони-
ческих подшипников.
Для построения линей-
ной системы управле-
ния обмотки электро-
магнитов запитывают-
АМП1 АМП2
СЯ ПОСТОЯННЫМИ ТОКа- Рис. 7.17. Подвес жесткого ротора в двух кони-
МИ смещенияi-^c, ..., i^c. ческих подшипниках
С ними суммируются
токи i = (ip ..., i4)T, управляющие радиальными перемещениями
ротора, и ток iz, управляющий осевым перемещением. Как и ранее
(п.7.2), управление осуществляется по дифференциальной схеме:
управляющие токи ip ..., i4 в противоположных электромагнитах
равны по значению и противоположны по знаку; управляющие
токи iz в обмотках первого и второго подшипников имеют разные
знаки.
Подставив выражения индуктивностей (3.42) в выражения элек-
тромагнитных сил и линеаризуя последние, приходим к следую-
щему результату. Электромагнитные процессы, соответствующие
радиальным и осевым перемещениям ротора, разделены. Управ-
ляющие радиальные силы F зависят от разностей токов в проти-
воположных электромагнитах, т. е. от токов ip ..., i4, и не зависят
от тока iz. Для них остается в силе выражение (7.23)
F = Cqq + H.i, (7.90)
AM III
Рис. 7.18. Электромагнитные
АМП2
цепи конических подшипников
139
Рис. 7.19. Упрощенная структурная схема системы уп-
равления подвесом ротора в конических подшипниках
где
Cq = z3c’ *4с); Hi = ^pdiag(ilc, i2c, i3c, i4c). (7.91)
С другой стороны, управляющая осевая сила^ зависит от сум-
мы токов в электромагнитах каждого из подшипников, т. е. от
тока 12, и не зависит от токов i±. Имеем
Fz = czz0 + <7-92)
где
2Lsin2yv>.2 , 2Lsinv
cz — “о z у hz ~ 7 (7.93)
5 *=1 ° k=l
Таким образом, задача синтеза закона управления подвесом рото-
ра в конических подшипниках сводится к решению двух уже рас-
смотренных выше задач. Это задача синтеза закона управления ра-
диальным подвесом (т. е. отыскание токов ip /2, *3, i4), рассмотренная
в пп. 7.3 и 7.5, и задача синтеза закона управления одностепенным
осевым подвесом (т. е. отыскание тока i2), рассмотренная в главе 6.
На рис. 7.19 приведена упрощенная структурная схема систе-
мы управления коническими подшипниками. Ток iz суммируется
согласно схеме на рис. 7.18 с токами i3 и i4 второго подшипника
и вычитается из токов 4 и i2 первого подшипника.
В заключение отметим, что все результаты анализа динамики
подвесов, полученные в главах 6 и 7, остаются справедливыми при-
менительно и к подвесу ротора в конических подшипниках.
7.10. ВЗАИМОВОЗДЕЙСТВИЕ ПОДВЕСА
И ПРИВОДНОГО ЭЛЕКТРОДВИГАТЕЛЯ
В данном разделе рассматривается взаимовоздействие
радиальных АМП и приводного электродвигателя.
Наряду со своим основным назначением — созданием враща-
ющего момента и приведением ротора во вращение — приводной
140
электродвигатель является также источником сил, действующих
в радиальных направлениях и оказывающих воздействие на под-
вес. Среди них могут быть позиционные, диссипативные, циркуля-
ционные и вынуждающие составляющие. Здесь ограничимся уче-
том только одного класса сил — позиционных сил магнитного
тяжения. Природа этих сил та же, что и позиционных магнитных
сил с «отрицательной» жесткостью в магнитном подвесе (п. 5.6).
Ротор электродвигателя, по сути, является железным сердечником,
помещенным в магнитное поле. Смещение ротора из положения
равновесия в радиальном направлении сопровождается появлени-
ем магнитной силы, которая пропорциональна смещению и на-
правлена в сторону смещения. Очевидно, что такая сила оказывает
дестабилизирующее влияние на подвес.
С другой стороны, активные магнитные подшипники, удержи-
вая ротор в радиальных (и осевом) направлениях, могут генериро-
вать момент М2 относительно оси вращения z и тем самым вли-
ять на закон вращения ротора <p2(t). Так, если момент М2 отрица-
тельный, а приводной электродвигатель маломощный, то могут воз-
никнуть проблемы при разгоне ротора. Если момент М2 положи-
тельный, то подвес может обеспечивать вращение ротора без
участия приводного двигателя (так называемый эффект автовра-
щения или авторотации). Из выражения
(7.94)
’Эф, Эф,
следует, что для возникновения момента М2 требуется, чтобы ин-
дуктивности подшипников Lkk зависели от угла поворота ротора
ф2. Это будет только в том случае, если координата (р2 войдет в
выражение высоты зазора в подшипнике h (п.3.6). Можно указать
следующие причины зависимости h от (р2: прецессия ротора в зазо-
ре подшипника под действием неуравновешенности; эксцентрич-
ное расположение центра цапфы относительно центра мерительно-
го кольца датчика радиальных перемещений ротора; некруглость
цапфы, т. е. отклонения геометрии профиля поперечного сечения
цапфы от идеальной окружности. При этом заметим, что некруг-
лость расточки статора подшипника не приводит к зависимости h
от ф , поэтому не может быть причиной возникновения момента
М2. Возмущающие моменты вследствие некруглости цапфы иссле-
дованы в работе [40].
ВОЗДЕЙСТВИЕ ЭЛЕКТРОДВИГАТЕЛЯ НА ПОДВЕС
Данную задачу рассмотрим на примере симметричного
подвеса ротора электродвигателя, имеющего длину магнитоактив-
ной части /р, в двух радиальных АМП (рис. 7.20, а). При посту-
пательном перемещении ротора на величину х0 в направлении оси х
141
Рис. 7.20. Учет воздействия электродвигателя на подвес: а — схема
подвеса; б — воздействие при поступательном перемещении ротора;
в — воздействие при угловых перемещениях ротора
(рис. 7.20, б) на него будут действовать в том же направлении
равномерно распределенные по длине lD силы магнитного тяжения,
имеющие равнодействующую
^>D = cjDxO’ (7.95)
где cD — коэффициент «отрицательной» жесткости электродви-
гателя при поступательном перемещении ротора.
Значение cD зависит от типа электродвигателя; для асинхрон-
ных электродвигателей согласно [79] имеем
2
cD = 0,3 ' (7.96)
где Rd — радиус расточки; BD — максимальная индукция; 8П —
радиальный зазор.
При угловом перемещении ротора на величину относительно
оси у (рис. 7.20, в) на него будут действовать линейно распреде-
ленные по длине lD силы магнитного тяжения, создающие в на-
правлении углового перемещения момент
142
MD = SD<Py, (7.97)
где^р — коэффициент «отрицательной» жесткости электродвига-
теля при угловых перемещениях ротора,
gD=cDl2D/12. (7.98)
Исходя из изложенного влияние электродвигателя на матема-
тическую модель подвеса сводится к следующему. При выключен-
ном электродвигателе управляющие магнитные силы подшипни-
ков F определяются формулой (7.23) с учетом (7.24). При вклю-
ченном электродвигателе в формуле (7.23) для F матрицу
позиционных «отрицательных» жесткостей Cq следует заменить
матрицей
С*=Сд+С*, (7.99)
где матрица
1 + ki 0 1 — ki О
О 1 — ki 0 1 + ki
учитывает влияние электродвигателя на подвес. Здесь обозначено
fy=zf>/3Z2. (7.101)
Теперь проанализируем влияние, оказываемое электродвигате-
лем на динамику подвеса. Рассмотрим для этого поступательные
перемещения ротора. Задача сводится к исследованию одностепен-
ного подвеса (п.6). При выключенном электродвигателе, учитывая
(6.14), уравнение подвеса имеет вид
ту ~ суУ = fyi + QG), (7.102)
где у = Хр т = М/2; су = сх1; й. = hxl.
При включенном электродвигателе подвес описывается уравне-
нием
ту - (су + c*D)y = hti + Q(0, (7.103)
где Ср=Ср/2 — дополнительная составляющая «отрицатель-
ной» жесткости подвеса, вызванная влиянием электродвигателя.
Подвес должен обладать устойчивостью как при выключенном,
так и при включенном электродвигателе. Пусть закон управления
подвесом (6.44) синтезирован без учета влияния электродвигате-
143
ля, т. е. для системы (7.102), и при выключенном электродвигате-
ле обеспечивает собственную частоту > k = ^су / т. Включение
электродвигателя в этом случае приводит к снижению собствен-
ной частоты подвеса до значения со о = , где kD = / т.
При kD > й)0 такой подвес теряет устойчивость.
Пусть теперь закон управления подвесом (6.44) синтезирован
с учетом влияния электродвигателя, т. е. для системы (7.103),
и при включенном электродвигателе обеспечивает собственную ча-
стоту ооо - В этом случае при выключенном электро-
двигателе собственная частота подвеса возрастает до значения
** I 21 2
(00 = + ^D-
В обоих случаях включение-выключение электродвигателя при-
водит к ухудшению динамических качеств подвеса. В первом слу-
чае возникает опасность потери устойчивости подвеса. Во втором
случае значение собственной частоты сп0 может оказаться непри-
емлимо большим. Можно указать следующие пути решения про-
блемы: подбор компромиссного значения 0)0; соответствующее из-
менение значений коэффициентов усиления обратной связи при
включении — выключении электродвигателя; использование адап-
тивного управления (см.п.6.7).
ТОРМОЗЯЩЕЕ ВОЗДЕЙСТВИЕ ПОДВЕСА
НА ПРИВОД НЕУРАВНОВЕШЕННОГО РОТОРА.
ЭФФЕКТ ЗОММЕРФЕЛЬДА
Вычислим электромагнитный момент М2, действующий
относительно оси вращения со стороны подвеса на неуравновешен-
ный ротор. Для простоты ограничимся случаем симметричного
подвеса ротора в двух радиальных подшипниках (п.7.4). Будем
рассматривать поступательные перемещения ротора под действи-
ем статической неуравновешенности, характеризующейся эксцент-
риситетом центра масс е. Движение ротора описывается двумя пер-
выми дифференциальными уравнениями в (7.39), решение кото-
рых имеет вид (7.42).
Момент М2 найдем как среднее значение за один оборот ротора
(ф2 = 2л) работы упругодемпферных реакций подвеса на переме-
щениях Xq и yQ:
1 2л/а)
М2 = — |[(-2сх0 - 2&х0)х0 + (“2q/o ~ 2ьУо)Уо]d* = -2feA^o). (7.104)
о
144
Используя (7.43) и учитывая, что 2с = М(Oq, 2b = 2M^Q($Q,
имеем
М2 = -Ме2о$
2^об(о/(оо>)5
(1 - / ®1)2 + (Х0<о / (00)2
(7.105)
Знак минус в (7.105) показывает,
что подвес оказывает тормозящее
воздействие на привод неуравнове-
шенного ротора. Величина М2 увели-
чивается с ростом частоты вращения
со и при со » соо изменяется пропор-
ционально со по линейному закону
\М2\ = Ме2соо2^о(со/соо). На рис. 7.21
в качестве иллюстрации приведены гра-
фические зависимости безразмерного
Рис. 7.21. Зависимость тормо-
зящего момента, действующе-
го со стороны подвеса на не-
уравновешенный ротор, от ча-
стоты вращения при опти-
мальном значении параметра
затухания:
1 — (Do = k = — «дорогое
управление»; 2— <оо = 5/г —«де-
шевое управление»
тормозящего момента \М2\/ Ме2С0д
от безразмерной частоты вращениясо/соо
при оптимальном значении парамет-
ра затухания £0 = ^2(1 + k2 / сод) / 2,
определяемого формулой (6.49).
При разгоне ротора маломощным
двигателем из-за наличия тормозящего
момента М2 может проявиться эффект
Зоммерфельда: двигатель не может набрать необходимую скорость,
застряв на некоторой промежуточной частоте. Снижение момента
М2 может быть достигнуто за счет более тщательной балансировки
ротора, а также путем снижения собственной частоты соо и пара-
метра затухания подвеса.
В заключение заметим, что к выражению (7.105) для момента
М2 можно прийти и другим путем — используя формулу (7.94).
МАГНИТНЫЙ ПОДШИПНИК
В РОЛИ ПРИВОДНОГО ДВИГАТЕЛЯ.
ЭФФЕКТ АВТОВРАЩЕНИЯ
В некоторых приложениях весьма привлекательной яв-
ляется идея использовать магнитный подшипник в роли привод-
ного двигателя. Для этого нужно создать условия, при которых
среднее за один оборот значение момента М2, определяемое форму-
лой (7.94), было бы положительным. Тогда подвес будет автома-
тически поддерживать вращение ротора. Данное явление называ-
ется эффектом автовращения (авторотации) ротора в подвесе.
145
Впервые эффект автовращения ротора в магнитном подвесе был
обнаружен и исследован Г. Г. Денисовым, Ю. И. Неймарком
и О. Д. Поздеевым (НИИ ПМК, г. Нижний Новгород). В 1962 году
ими был сделан доклад на данную тему на секции навигационных
систем Президиума Академии Наук СССР. Эффект автовращения
может проявляться не только в магнитном, но и в сверхпроводя-
щем и электростатическом подвесах [58]. Известно практическое
использование данного эффекта для поддержания стационарной
частоты вращения ротора гироскопа в навигационной системе
«Микрон» [103].
На рис. 7.22 изображена схема простейшего магнитного подве-
са, демонстрирующая эффект автовращения ротора [103]. Ферро-
магнитный ротор имеет форму шара, на котором выполнена огран-
ка двумя лысками. Высота зазора h при такой форме ротора зави-
сит не только от смещения у,но и от угла поворота (р2. Поэтому
индуктивность электромагнита также зависит от у и (р2, и согласно
(7.94) на ротор кроме управляющей магнитной силы Fy будет дей-
ствовать момент М2. Очевидно, что при постоянном токе в обмот-
ке I = const постоянная составляющая момента М2 за один оборот
будет равна нулю. Однако поскольку в сигнале датчика зазора
содержится информация как о смещении у, так и об угле поворота
cpz, то ток I будет иметь переменную составляющую, зависящую от
угла <р2. В связи с этим момент М2 будет содержать положитель-
ную постоянную компоненту или вращающий момент. Вращающий
момент зависит от разности фаз тока и угла поворота, которая,
в свою очередь, зависит от частоты вращения ротора.
Для разгона ротора с помощью подвеса ему нужно первоначаль-
но придать небольшую угловую скорость. Затем подвес автомати-
чески разгонит ротор до установившейся угловой скорости, на ко-
торой вращающий момент будет равен тормозящему моменту; при-
родой последнего могут быть аэродинамическое трение, неуравно-
вешенность ротора и т. д.
Рис. 7.22. Схема магнитного под- Рис. 7.23. Ротор подшипника с некруг-
веса, демонстрирующая эффект ав- лой цапфой
товращения ротора
146
Вернемся к ротору в двух радиальных подшипниках и обсу-
дим вопрос о возможности его автовращения. Очевидно, что если
на цапфе и мерительном кольце подшипника выполнить про-
дольные лыски по аналогии с лысками на сферическом роторе, а дат-
чик положения модернизировать в датчик зазора, то будет наблю-
даться такой же эффект автовращения ротора, что и описан выше
(см. рис. 7.22).
Вместе с тем можно указать еще одно обстоятельство, когда
может проявиться эффект автовращения ротора в радиальных под-
шипниках. Допустим, что ротор слегка погнут. Пространственное
положение оси вращения ротора, как известно, задается осью, про-
ходящей через центры мерительных колец. Вследствие погнутости
ротора центр цапфы располагается эксцентрично относительно цен-
тра мерительного кольца. При вращении ротора цапфа будет со-
вершать биения, поэтому высота зазора h будет зависеть от угла
поворота ф2. Однако, чтобы момент М2 имел положительную по-
стоянную составляющую, необходимо, чтобы токи в обмотках так-
же зависели от угла ср2. Причиной такой зависимости в данном
случае является неуравновешенность ротора. При определенном
сочетании разностей фаз перемещений цапфы, токов и угла поворо-
та положительная составляющая момента М2 может оказаться
больше его тормозящей составляющей (7.105). Подшипник при
этом будет поддерживать вращение ротора. Данный эффект на-
блюдался автором при подвесе длинного тонкого вала в радиаль-
ных подшипниках в лаборатории магнитных опор Псковского по-
литехнического института.
Рассмотренные выше способы организации автовращения рото-
ра в подвесе имеют два недостатка: вращающий момент суще-
ственно зависит от угловой скорости ротора; при невращающемся
роторе вращающий момент равен нулю, поэтому требуется перво-
начальный подразгон ротора. Ниже описывается еще один способ
организации автовращения ротора в радиальных подшипниках,
свободный от указанных недостатков. Способ основан на исполь-
зовании датчика угла поворота ротора.
Пусть подшипник имеет идеально круглое мерительное кольцо
и некруглую цапфу (рис. 7.23). Свяжем с поперечным сечением
цапфы полярную систему координат г, 0, полюс которой совпадает с
центром От мерительного кольца, а угол 0 отсчитывается от свя-
занного с цапфой луча ОтК. Представим зависимость г(0) для кон-
тура цапфы в виде ряда Фурье
г(0) = г0 + £ r„ Sin (710 + Р„), (7.106)
п
где г0 — среднее значение радиуса цапфы; rn, Pn, п = 1, 2,... —
амплитуда и начальная фаза n-й гармоники некруглости, причем
г1 есть эксцентриситет центра цапфы относительно центра мери-
тельного кольца, г2 характеризует овальность и т. д.
147
Учитывая, что 0 = а - ф2, для высоты зазора вместо (3.33) спра-
ведливо следующее выражение
h = So - sin[n(a - ф2) + ₽n]- xcosa - i/sina, (7.107)
n
где 80 — средний радиальный зазор.
Используя методологию п. 3.6, индуктивности подшипника с не-
круглой цапфой представим в виде
£11 = CL
80 + «X hn sin(ra(Pz " Pn ) ~ ах1
^22 = CL
+ hn sin(n<p2
n
-1-1
~5--Pn)-ai/i
Li
£33 ~ CL Sq
+ a^ft„sin(ncp2
n
-1-1
- nn - P„) + axi
(7.108)
£44 ~ CL So
+ a^ft„sin(n(p2
n
-i-i
Злп „ .
— -p„) + ai/1
XU
где hn = 2rnsin(nAa/2)/(nAa) — параметры некруглости цапфы.
Токи в обмотках подшипника формируются следующим обра-
зом:^ = ic + ii + ij; ^2 = Ч + *2 + Ч’ ^3 = Ч “ *1 + Ф А = Ч “ *2 + Ч>
где ic — ток смещения; и i2 — токи, управляющие подвесом
ротора; ,..., ц — токи, обеспечивающие автовращение ротора. Син-
тез управлений и i2 описан в пп.7.3 и 7.5. Токи, обеспечиваю-
щие автовращение ротора, формируем в виде функции угла пово-
рота
ifef<Pz> = ±XZ'»cos[ra<P2 - nn(k - рД (7.109)
к. )
п у
Постоянная составляющая момента Мг, развиваемая подшип-
ником [40],
2я 4 z \
М° = ~ X Т*1 К + d<?z = ;^~^Tihni*n.(7.110)
о fe=A Фг' 8о п
Заметим, что знак плюс перед суммой в (7.109) соответствует
торможению ротора, знак минус — разгону. Момент М® не зави-
148
сит от частоты вращения ротора. Подвес вовлекает ротор во вра-
щение из неподвижного состояния либо при смене знака в (7.109)
затормаживает его. Из множества возможных гармоник в (7.106)
практический интерес представляют две из них: п = 1 — эксцент-
ричное расположение круглой цапфы относительно мерительного
кольца и п = 2 — овальная цапфа.
Согласно алгоритму (7.109), токи ^(ф2) формируются на осно-
ве измерения угла поворота ротора <р2. При изменении угла <р2
система управления автоматически изменяет токи таким образом,
что в результате образуется вращающееся магнитное поле, которое
вовлекает некруглую цапфу во вращение.
7.11. СОВМЕЩЕНИЕ ЭЛЕКТРИЧЕСКОЙ МАШИНЫ
И МАГНИТНОГО ПОДШИПНИКА.
БЕСПОДШИПНИКОВЫЕ МАШИНЫ
Мощные высокоскоростные электрические машины (дви-
гатели и генераторы) требуются во многих областях современной
техники. Возникающие в таких машинах подшипниковые пробле-
мы во многих случаях успешно решаются путем использования
активных магнитных подшипников. Однако наряду со многими
достоинствами АМП обладают существенным недостатком: они
имеют относительно большие габаритные размеры. Поэтому их
применение вызывает необходимость увеличения длины вала. Ро-
тор становится более гибким, что приводит к снижению критичес-
ких скоростей и затрудняет получение высоких скоростей враще-
ния. Укорочение же электрической машины приводит к снижению
ее мощности. Весьма эффективный способ сделать электрическую
машину наиболее компактной — это возложить функции подшип-
ников на саму электрическую машину. Такие машины обычно на-
зываются бесподшипниковыми.
Термин «бесподшипниковая машина» вовсе не означает, что от-
сутствуют подшипниковые силы. Эти силы необходимы во всех
случаях для удержания ротора в заданном положении. В данном
же случае они генерируются самой электрической машиной; под-
шипники же, как таковые, отсутствуют.
На рис.7.24 показаны два конструктивных варианта электри-
ческой машины. Обычная машина (рис. 7.24, а) создает только
вращающий момент; ее ротор опирается на два радиальных под-
шипника. В бесподшипниковой машине (рис. 7.24, б) генерирует-
ся не только вращающий момент, но и радиальные магнитные
силы, необходимые для подвеса ротора. Чтобы обеспечить подвес
ротора по пяти степеням свободы, машина состоит из двух частей.
Все дальнейшие рассуждения будут касаться только одной части.
Идея совместить электрическую машину с магнитным подшип-
ником не нова [101]. Большинство предлагаемых решений осно-
вано на использовании части полюсов многополюсной электричес-
149
a)
б)
АМП Машина АМП
Рис. 7.24. Конструктивные варианты электрической машины: а —
обычная машина с АМП; б — бесподшипниковая машина
Машина + АМП Машина + АМП
1 I Г I I Т1 II I I I I тт
I I I I I I I____п~1~1 I гп
СПТТО <ШШ>
кой машины в качестве полюсов активного магнитного подшипни-
ка. Данный принцип использовался при создании бесподшипнико-
вой синхронной машины, асинхронной машины и индукторного ша-
гового двигателя. Во всех этих решениях простота конструкции
сопровождается следующими недостатками. Магнитная индукция
под подшипниковыми полюсами модулируется рабочим магнитным
потоком машины; вследствие этого в подшипниках генерируются
радиальные возмущающие силы, вызывающие вибрацию ротора. Мощ-
ность таких машин заметно ниже мощности обычных машин при
одинаковых габаритных размерах. Из-за большого числа пар полю-
сов для получения высоких скоростей вращения требуется высоко-
частотный источник рабочего питания машины.
Преодолеть отмеченные недостатки позволяет другой подход,
при котором для создания радиальных подшипниковых сил ис-
пользуется рабочий магнитный поток, предназначенный для созда-
ния вращающего момента. Перед тем как перейти к описанию
конструкций, реализующих данный подход, рассмотрим магнит-
ные силы в обычной машине переменного тока.
Рис. 7.25. Распределение ради-
альных магнитных сил в двух-
полюсной машине переменного
тока
Известны два вида магнитных сил:
лоренцевы и максвелловы. Лоренце-
ва сила действует на проводник с то-
ком, расположенный в магнитном
поле. В электрической машине лорен-
цевы силы направлены тангенциаль-
но и создают вращающий момент.
Максвелловы силы возникают в маг-
нитных цепях на поверхностях ма-
териалов с различной магнитной про-
ницаемостью. Они направлены пер-
пендикулярно к поверхности ротора
и пропорциональны квадрату индук-
ции в зазоре. На рис. 7.25 показано
распределение радиальных максвел-
ловых сил в двухполюсной машине
при синусоидальном распределении
150
магнитной индукции. Рав-
нодействующая этих сил
вследствие угловой симмет-
рии распределения индук-
ции равна нулю. Это оз-
начает, что с помощью
только рабочих обмоток,
предназначенных для со-
здания вращающего мо-
мента, осуществить управ-
ляемый подвес ротора в ра-
диальных направлениях
невозможно. Следует заме-
тить, что смещение ротора
из центрального положе-
ния вызывает асимметрию
в распределении индукции
Рис. 7.26. Генерирование радиальной силы
Fy рабочей обмоткой Na и управляющей
обмоткой Ny
и радиальную магнитную
силу, направленную в сто-
рону смещения. Эта си-
ла имеет «отрицательную»
жесткость и оказывает дестабилизирующее влияние на подвес
(п.7.10). Задача сводится к преобразованию «отрицательной» же-
сткости в положительную.
Данная задача решается путем наложения на рабочий магнит-
ный поток машины управляющих магнитных потоков, создавае-
мых специальными дополнительными управляющими обмотками.
Управляющие потоки ослабляют рабочий поток в той области,
куда направлено смещение ротора, и усиливают его в противопо-
ложной области. В результате возникает радиальная восстанавли-
вающая магнитная сила. Число полюсов рабочей обмотки и уп-
равляющей обмотки р2 должно быть различным (обычно р2 =Pi ± 2).
Максимальной радиальной магнитной силой обладают четырехпо-
люсные машины с двухполюсной управляющей обмоткой (/^ = 4,
Р2 = 2)-
На рис. 7.26 иллюстрируется принцип генерирования радиаль-
ной силы в бесподшипниковой машине. Для простоты изображена
двухфазная машина. Статор имеет четырехполюсные рабочие об-
мотки NaH Nbn двухполюсные управляющие обмотки Nx и N .
Для генерирования радиальной силы^ на потоки у4, создаваемые
рабочей обмоткой Д^, накладывается поток создаваемый управ-
ляющей обмоткой Д^. Индукция В+ увеличивается, В_ уменьшает-
ся, и в результате создается радиальная сила в направлении оси у.
При изменении направления тока в обмотке Ny радиальная сила
будет иметь противоположное направление. Радиальная сила!7*
в направлении оси х создается обмотками и Nх.
Данный принцип может быть реализован в синхронных и асин-
хронных бесподшипниковых машинах. В пазы статора уклады-
151
ваются две трехфазные обмотки: четырехполюсная рабочая и двух-
полюсная управляющая (возможен также вариант двухполюсной
рабочей и четырехполюсной управляющей обмоток [101]). Рабо-
чая обмотка создает вращающееся магнитное поле и приводит во
вращение ротор. Фазные токи в управляющей обмотке формиру-
ются системой управления подвесом ротора. Для этого машина
снабжается датчиками положения ротора в направлениях осей х
и у. Как и в обычных подшипниках, сигналы с датчиков поступа-
ют на регулятор, который вырабатывает требуемые значения ради-
альных сил Fx и Fy и фазных токов в управляющей обмотке.
Однако в отличие от обычных подшипников, в которых сила и ток
связаны линейной зависимостью (5.21), в электрической машине
радиальная сила зависит не только от фазных токов в управляю-
щей обмотке, но и от значения и направления магнитного потока
рабочей обмотки. Поэтому, чтобы вычислить требуемые значения
фазных токов в управляющей обмотке, нужно машину снабдить
датчиком вектора магнитного потока (значения и направления).
Исследования показывают [101], что ошибка в измерении направ-
ления вектора потока не должна превышать 10°. В синхронных
машинах данная проблема решается достаточно просто, в асин-
хронных же машинах из-за наличия скольжения возникают опре-
Рис. 7.27. Бесподшипниковая синхронная индукторная машина
152
деленные трудности. При точном измерении вектора потока вра-
щающий момент и радиальные силы не зависят друг от друга, т. е.
полностью разделены.
Другим примером полной разделенности вращающего момен-
та и радиальных сил может служить бесподшипниковая син-
хронная индукторная машина, исследованная П. В. Киселе-
вым и Ф. Г. Кочевиным. Схема машины показана на рис. 7.27.
Машина состоит из статора, в пазы которого уложены трехфазная
обмотка якоря и обмотка возбуждения, и зубчатого ротора. В обыч-
ной машине обмотка возбуждения запитывается постоянным то-
ком ZB и создает постоянную составляющую магнитного потока.
При вращении зубчатого ротора в обмотке якоря наводится перио-
дическая ЭД С за счет периодического изменения магнитной прово-
димости магнитной цепи якоря (либо при питании обмотки якоря
трехфазным током создается вращающий момент и ротор втяги-
вается в синхронизм). В бесподшипниковой машине обмотка воз-
буждения состоит из четырех секций, которые образуют четыре
электромагнита. Расположение электромагнитов и схема соедине-
ния их катушек такие же, как и в радиальном подшипнике (см.
рис. 3.2). Поэтому подвес ротора в машине осуществляется точно
так же, как и в подшипнике: токи в секциях обмотки возбужде-
ния складываются из постоянного тока 1в и управляющих токов
и i2 с соответствующим знаком (см. рис. 7.27). Синтез управлений
i1 и /2 может быть выполнен по любой из процедур, описанных
в пп.7.3 и 7.5. Полная разделенность вращающего момента и
радиальных сил достигается за счет того, что в процессе управле-
ния подвесом увеличение индукции в какой-либо области зазора
сопровождается уменьшением индукции на такое же значение
в диаметрально противоположной области.
8. ДИНАМИКА ГИБКОГО РОТОРА
В АКТИВНЫХ МАГНИТНЫХ ПОДШИПНИКАХ
8.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
В главе 7 рассмотрен подвес жесткого (недеформируемо-
го) ротора в АМП. Однако любой ротор является упругодеформи-
руемым телом, способным совершать изгибные колебания. При
совпадении скорости вращения ротора с любой из собственных
частот изгибных колебаний наступает явление резонанса; такие
скорости вращения называются критическими. Амплитуды коле-
баний и нагрузок на подшипники на критических скоростях могут
достигать опасных значений. Они могут быть снижены за счет
демпфирования, а при наличии мощного двигателя за счет быстро-
го перехода ротором критической скорости. Независимо от типа
используемых подшипников переход ротором критических скоро-
стей создает определенные технические трудности. С этой точки
зрения наиболее предпочтительным является ротор, у которого
максимальная рабочая скорость вращения меньше первой крити-
ческой скорости. В динамике машин такой ротор традиционно при-
нято называть жестким, в противном случае — гибким. Динамике
гибких роторов в упругодемпферных механических опорах посвя-
щена обширная литература [31, 44, 45, 66, 71].
Следует отметить, что такое традиционное разделение роторов
на жесткие и гибкие не может быть распространено на случай,
когда используются АМП. Объясняется это тем, что изгибные ко-
лебания ротора в подвесе, который является управляемой систе-
мой, могут проявляться не только при достижении критической
скорости, но и не во вращающемся состоянии. На практике не
редки случаи, когда невращающийся, но подвешенный в АМП ро-
тор «поет» с частотой, равной одной из собственных частот изгиб-
ных колебаний, находящейся и акустическом диапазоне. Такое
«пение» обычно приводит к насыщению усилителей мощности.
Причина этого явления, как это будет показано ниже, заключается
в потере устойчивости подвеса по соответствующей собственной
форме колебаний. Энергетическая подпитка изгибных колебаний
ротора со стороны подвеса может быть лишь при условии, если
данная собственная частота меньше частоты среза шср системы
управления подвеса (п. 6.11). Поэтому применительно к АМП ро-
тор следует считать жестким, если его первая собственная частота
изгибных колебаний больше частоты среза подвеса; в противном
случае — гибким. Очевидно, что при таком определении понятием
«гибкий ротор* охватывается более широкий класс роторов, чем
при вышеупомянутом традиционном определении.
Интуитивно ясно, что осуществление подвеса гибкого ротора
является более сложной задачей, чем жесткого ротора. Сложность
154
заключается в том, что магнитные подшипники должны удержи-
вать воображаемый «твердый скелет» гибкого ротора в заданном
пространственном положении и одновременно не позволять разви-
ваться изгибным деформациям ротора относительно этого «скеле-
та». Если жесткий ротор как объект управления имеет пять степе-
ней свободы, то гибкий ротор имеет бесконечное число степеней
свободы. При деформациях в гибком роторе кроме сил упругости
возникают силы внутреннего трения в материале вала и на повер-
хностях соприкосновения вала и насаженных на него деталей.
Под действием сил внутреннего трения гибкий ротор может те-
рять устойчивость [10, 59, 66]. Неуравновешенность ротора может
вызвать недопустимо большие амплитуды колебаний и нагрузок
на подшипники.
В данной главе решается задача управления подвесом гибкого
ротора в АМП с учетом перечисленных выше факторов и анализи-
руются динамические свойства подвеса. В п. 8.2 приводятся диф-
ференциальные уравнения движения гибкого ротора в АМП с уче-
том сил внутреннего трения (по гипотезе Фойхта), гироскопичес-
ких сил и нагрузок от неуравновешенности масс. Для описания
движения коротких роторов используется теория изгиба Тимошенко,
длинных роторов — техническая теория изгиба. Активные маг-
нитные подшипники считаются короткими, поэтому их реакции
представляются в виде сосредоточенных сил. В п. 8.3 изложена
методика определения собственных частот и собственных форм
ротора с учетом жесткостей подшипников. В п. 8.4 формулируется
стратегия управления подвесом гибкого ротора, согласно которой
в п. 8.5 приводится методика решения задачи синтеза управления
подвесом. В п. 8.6 осуществляется замена исходной динамической
модели замкнутой системы управления подвесом, имеющей распре-
деленные параметры, ее приближенным аналогом, имеющим ко-
нечное число степеней свободы, с использованием разложения движе-
ния ротора по собственным формам и метода Галеркина. В п. 8.7
дан динамический анализ подвеса гибкого ротора в АМП: анали-
зируется структура действующих на ротор сил; оценивается влия-
ние на устойчивость несовпадения точек управления и измерения,
а также внутреннего трения; показываются способы стабилизации
подвеса.
8.2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ
Наиболее полное описание изгибных деформаций рото-
ра дает теория изгиба Тимошенко [6]. Эта теория, учитывающая
деформацию сдвига, обычно используется для коротких стержней,
характерный поперечный размер которых составляет не менее од-
ной десятой части длины. При описании движения длинных рото-
ров можно пренебречь деформацией сдвига и использовать техни-
ческую теорию изгиба.
155
КОРОТКИЙ РОТОР
Ротор представляется прямым стержнем (балкой Ти-
мошенко) с распределенными по длине параметрами, вращающим-
ся в двух радиальных АМП с частотой со (рис. 8.1). Начало О
неподвижной системы осей Oxyz поместим на левом конце рото-
ра; ось Oz совместим с продольной осью жесткости ротора. Ротор
имеет длину I и распределенные параметры: массу р(з), экватори-
альный j(z) и осевой jQ(z) моменты инерции, податливость сечений
на изгиб (3(z) = l/EI(z) и на сдвиг b(z) = kx/GA(z); параметры
неуравновешенности — линейный e(z) и угловой у(^); коэффици-
ент линейного внутреннего трения x(z). Здесь Е и G —соответ-
ственно модуль Юнга и модуль сдвига; I(z) — момент инерции
площади сечения вала; A(z) — площадь сечения вала; kx — коэф-
фициент, учитывающий неравномерность распределения касатель-
ных напряжений по сечению (для круглого сечения kx = 1,185).
На ротор действуют внешние распределенные силы px(z), py(z) и
моменты mx(z), my(z). Магнитные подшипники создают распреде-
ленные управляющие силы fx(z), fy(z).
Положение ротора определяется поперечными перемещениями
x(z, t), y(z, t) и углами поворотов фх(з, t), ф^(г, t) сечений. Уравнения
движения ротора по аналогии с [74] запишем в операторной форме:
tfpix - сотг2т]у + + М = Fx + рх‘>
R]f\y - соЛ2Пх + 'Xfihfhy - + n2 Пу = Fy + Ру•
(8.1)
Здесь т]х = (х, (ру)т, Пу = (А/» <Рх)г — векторы перемещений сечений;
Рх = ^х' О)7’ Fy = (fy’ — векторы магнитных сил подшипников;
Pv - Р„ = (Р„, — векторы внешних нагрузок;
X х у у у X
///////////
АМП1 Датчик 1
77777777777' 77777
АМП2 Датчик 2
Рис. 8.1. Гибкий ротор в активных магнитных подшипниках
156
jRx = diag(p, у), B2 = diag(O, j0) — операторы инерции; Nr - diag(O,
-d2/dz2) — дифференциальный оператор; tV2 — алгебродифферен-
циальный оператор,
-Ь-1Э2 /Эз2 rt/az
- / Эз д"1 - Р-1Э2 / Эз2
(8.2)
Краевые условия запишем для случая, когда концы ротора сво-
бодны от нагрузок:
= q = x,y. (8.3)
Здесь и в дальнейшем штрихи обозначают дифференцирование
по z. Левые части уравнений (8.1) содержат распределенные по
длине гироскопические силы — исо/?2т]х,силы внутреннего
трения X^(f]x - coriz/) и - (0Г|х) и упругие силы N2x\x и N2x\y.
Будем считать, что внешние нагрузки складываются из состав-
ляющих, зависящих от перемещений и скоростей, и вынуждающих
составляющих, зависящих от неуравновешенности:
Рх = + (р^о)2 coscof, (у - 7o)Y°)2 cosart)T;
Ру = ру(^д’^ + (pew2 sincot, (j - j0)y(02 sin(O£)T.
ДЛИННЫЙ РОТОР
В случаях, когда длина ротора в десять и более раз пре-
вышает характерный диаметр вала, можно пренебречь деформаци-
ей сдвига и использовать техническую теорию изгиба. В этих слу-
чаях угловые перемещения сечений связаны с прогибами соотно-
шениями
фх = -ду/дг; <ру = dx/dz. (8.5)
Уравнения движения длинного ротора с учетом инерции пово-
ротов сечений, гироскопических сил и сил внутреннего трения име-
ют вид [31]:
д Э2
рх-— (jx' + со/0 z/') + + о»/") + Elx"] = fx+px-
dz
Э Э2 д
РУ - (Jy' + + уу [%(у" + ®х") + Ely"] = fy + Ру- — тх.
Э
dzm^
(8-6)
157
При свободных от нагрузок концах ротора краевые условия будут:
g"(0, t) = g"'(0, t) = 0; q"(l, t) = g"'(Z, t) = 0; q = x,y. (8.7)
ПОДШИПНИКИ
Подшипники будем считать короткими, поэтому их ре-
акции представим в виде
fx=8(2-21)F1+3(2-z2)F3;
fy = 8(2 - 2X)F2 + 8(2 - 22)F4,
(8.8)
где 8(2 - 2S), (s = 1, 2) — дельта-функция; F^,..., F± — сосредоточен-
ные силы, определяемые линейным соотношением (7.23),
F = (FV ...,F4)T = Cqq = Hii. (8.9)
Здесь q = (xv yv x2, y2)T = [х(гх), у(гг), x(z2), y(z2)]T — вектор
перемещений ротора в точках управления; i — вектор управляю-
щих токов; Cq, Ht — постоянные матрицы позиционных и токо-
вых жесткостей подшипников.
Как и в случае жесткого ротора, датчики положения измеряют
перемещения ротора в точках измерения с координатами z^m и z2zn
(см. рис. 8.1), не совпадающими в общем случае с координатами
и z2 точек управления. Измеряемая переменная задается векто-
ром qm = (xlm, ylm, Х2т, y2m)T = [x(zlm), y(zlm), x(z2m), y(z2m)]T.
8.3. СОБСТВЕННЫЕ ЧАСТОТЫ
И СОБСТВЕННЫЕ ФОРМЫ РОТОРА
Допустим, что, как и в случае подвеса жесткого ротора
(см. п.7.3), известны значения программных жесткостей подшип-
ников и с2. Тогда свободные колебания невращающегося рото-
ра без учета сил трения в плоскости xz описываются уравнением
+ (^2 + = 0 (8.10)
при граничных условиях (8.3) и с матрицей жесткостей подшипников
Со = diag[8(z - 21)с1 + 8(2 - z2)c2, 0]. (8.11)
Отыскивая решение уравнения (8.10) в виде
r|x(z,0 = r|(z)cosco£ (8.12)
(здесь О) — неизвестная частота колебаний), получаем дифференциаль-
ное уравнение для амплитудной вектор-функции r|(z) = [w(z), <p(z)]T
158
(?V2 + С0)г] - (02Я1т] = О
(8.13)
при граничных условиях
П"(0) = т]"(0 = 0.
(8.14)
Методы решения данной краевой задачи хорошо известны [18,
73]. В дальнейшем будем полагать, что вычислены первые п соб-
ственных частот соа и собственных форм
na(2) = [wa(2),(pa(z)]7’, а = 1, ...,п (8.15)
из их бесконечного числа. Здесь wa(z) обозначает собственную форму
линейных перемещений сечений ротора, <pa(z) — угловых переме-
щений. В случае длинного ротора, учитывая (8.5), имеем (ра =
= dwaldz. Число п должно быть выбрано таким, чтобы программ-
ное значение частоты среза подвеса 0)ср удовлетворяло соотноше-
нию con<(Dcp<con+/.
Заметим, что две первые собственные частоты и 0)2, отвечаю-
щие формам колебаний «твердого скелета» ротора, полностью опре-
деляются жесткостями подшипников и с2; ПРИ отсутствии под-
шипников они равны нулю. Влияние жесткостей подшипников на
другие собственные частоты, отвечающие изгибным формам коле-
баний, неодинаково: с ростом номера частоты оно существенно
уменьшается. Собственные формы вычисляются с точностью до
произвольного множителя. Кроме того, они обладают известным
свойством попарной ортогональности по кинетической и потенци-
альной энергиям. Соответствующим выбором произвольного мно-
жителя каждую форму можно пронормировать. В дальнейшем бу-
дем полагать, что этот множитель выбран так, что собственные
формы обладают свойством ортонормированности:
I I
J^ltlanpdz = 5^; J(N2 + C0)naTlpdz = co^S^,
о о
где 8ар — символ Кронекера,
1 при а = Р;
0 при а ф Р; а, Р = 1,
(8.16)
(8.17)
В качестве иллюстрации на рис. 8.2 изображены собственные
формы w^z), ..., w§(z) с указанием значений собственных частот
(Ор ..., со5 вала постоянного сечения в двух радиальных АМП.
Вал имеет диаметр 22 мм, длину I = 0,57 м, массу М = 16 кг,
распределенную массу р= 2,8кг/м, изгибную жесткость сечения
EI = 247 Н-м , жесткости подшипников <4 = с2 = 7,3-104 Н/м.
На этом же рисунке пунктирными линиями изображены собствен-
ные формы ^(z), ..., £5(z) и указаны значения собственных частот
159
Рис. 8.2. Собственные формы wa(z), ^(z) и собственные
частоты wa, ра вала постоянного сечения:
——— — wa(z), toa в подшипниках с жесткостями <?i = с2 =
= 7,3«104Н/м; — — — — £a(z), Ра безопорного вала
Рр ..., р5 свободного от подшипников вала. Собственные формы
J;a(z) определяются выражениями [18]
(z) = (cos у- z) I cos у- + (ch z) / ch , a = 1,3,5,;
(2) = (sin “ z) I sin -y + (sh -у- 2) / sh , a = 2,4,6,...
-Z / 2<z<l I 2,
(8.18)
160
причем функции (8.18) обладают свойством ортонормированности
Z/2
ji^pdz = 5ар, а,р = 1,2........... (8.19)
-//2
Здесь га — корни уравнения chr cos г = 1, причем г« = г2 = 0, г3 =
= 4,73, г4 = 7,853, rk =it(2k - 3)/2 при k = 5, 6, ... . Собственные
частоты безопорного вала определяются по формуле
ра =4Ж а = 1’2’-- <8-20)
z2 V р
Двум нулевым собственным частотам и р2 (при = г2 = 0) соот-
ветствуют формы движения вала как твердого тела: поступательная
^l(z) = 1 / yfM и поворотная = 2 / 7^7, ^1 = /12 — эква-
ториальный момент инерции. Собственным частотам р3,р4, ... со-
ответствуют чисто изгибные формы колебаний.
Из рис. 8.2 видно, что подшипники оказывают существенное
влияние лишь на две первые собственные частоты, делая их не
нулевыми. Небольшое влияние они оказывают на две первые соб-
ственные формы и на третью собственную частоту. Собственная
форма с номером а имеет а - 1 узловых точек (узлов), остающихся
неподвижными при колебаниях ротора с собственной частотой соа.
8.4. СТРАТЕГИЯ УПРАВЛЕНИЯ ПОДВЕСОМ
Очевидно, что основным назначением подвеса является
удержание ротора в заданном пространственном положении отно-
сительно неподвижного статора с заданной точностью. Если ротор
жесткий, то его пространственное положение в радиальных на-
правлениях полностью определяется четырьмя обобщенными ко-
ординатами £ = (х0, у0, (рх, ф^)7 или q = (хр yv х2, у2)т (п.7.2).
Пространственное положение гибкого ротора определяется соглас-
но (8.1) двумя бесконечно мерными векторами Т]х и т^, т. е. гибкий
ротор имеет бесконечное число степеней свободы.
При подвесе ротора в двух радиальных подшипниках число
точек управления равно четырем: по две точки в каждой из плос-
костей xz и yz. При таком числе точек управления жесткий ротор
является полностью управляемым объектом, гибкий же ротор —
не полностью управляемым объектом. Поэтому гибкий ротор как
объект управления можно представить в виде композиции двух
частей — управляемой и неуправляемой. Под управляемой частью
будем подразумевать воображаемый «твердый скелет» ротора, гео-
метрия которого совпадает с геометрией ротора в предположении,
что ротор абсолютно жесткий. Неуправляемой части отвечают упру-
161
гие изгибные и сдвиговые деформации элементов ротора относи-
тельно «твердого скелета». Управляемая и неуправляемая части
оказывают взаимное влияние друг на друга.
Поэтому стратегия управления подвесом гибкого ротора зак-
лючается в одновременном решении двух основных задач: 1) обес-
печение надлежащего подвеса «твердого скелета» ротора; 2) эф-
фективное демпфирование упругих изгибных колебаний. Вторая
задача приобретает особую важность, если ротор является закри-
тическим, т. е. если он должен переходить одну или несколько
критических скоростей вращения.
Можно указать три причины, заложенные в самой природе подве-
са гибкого ротора (т. е. без учета внешних нагрузок), способствую-
щих развитию изгибных колебаний вплоть до потери устойчивос-
ти: несовпадение расположения точек управления и точек измере-
ния; наличие сил внутреннего трения; неуравновешенность ротора.
Синтез управления подвесом гибкого ротора может выпол-
няться как традиционными методами, рассмотренными частично
в пп. 6 и 7, так и более современными методами теории опти-
мального управления по критериям типаЯ^-нормы передаточной
функции и теории ц-синтеза [5, 86, 95, 98].
По поводу выбора метода синтеза отметим следующее. Эффек-
тивность демпфирования изгибных колебаний во многих случаях
зависит не столько от типа регулятора, сколько от взаимного рас-
положения точек управления, точек измерения и узлов собствен-
ных форм ротора. Например, если центры подшипников располо-
жены в узлах какой-либо собственной формы, то демпфирование
колебаний по этой форме будет нулевым при любом законе управ-
ления. Поэтому в дальнейшем ограничимся рассмотрением толь-
ко одного наиболее распространенного подхода [36], включающего
в себя следующие этапы:
синтез закона управления подвесом «твердого скелета» ротора;
составление динамической модели замкнутой системы управле-
ния подвесом гибкого ротора;
анализ динамических качеств замкнутой системы: устойчивость,
реакции на возмущения и т. д.;
внесение необходимых корректив в закон управления или в кон-
струкцию подвеса.
8.5. СИНТЕЗ УПРАВЛЕНИЯ ПОДВЕСОМ
«ТВЕРДОГО СКЕЛЕТА» РОТОРА
Согласно изложенному в п.8.4 подходу, задача синтеза
управления подвесом гибкого ротора начинается с отыскания за-
кона управления подвесом «твердого скелета» ротора. Решение
данной задачи полностью совпадает с решением задачи синтеза
управления подвесом жесткого ротора, рассмотренной в главе 7.
Если ротор не гироскопический, то используется раздельное управ-
ление (см.п.7.3) по закону (7.34). Если ротор гироскопический, то
162
в ряде случаев целесообразно использовать ЛК-оптимальное мно-
госвязное управление (см. п. 7.5) по закону (7.66). Остаются в
силе и все выводы по результатам анализа устойчивости и реак-
ций на возмущения, сделанные в пп.7.4, 7.6, 7.7.
8.6. ДИСКРЕТНАЯ МОДЕЛЬ ПОДВЕСА
Исходная динамическая модель замкнутой системы уп-
равления подвесом гибкого ротора в АМП описывается системой
дифференциальных уравнений в частных производных (8.1) при
краевых условиях (8.3) с учетом выражений магнитных сил (8.8)
и (8.9) и закона управления током (7.34). Задачу анализа дина-
мики подвеса можно существенно упростить, если заменить исход-
ную модель с распределенными параметрами ее приближенным
дискретным аналогом, имеющим конечное число степеней свобо-
ды. Существует несколько путей такой замены: переход к много-
массовой модели, использование метода конечных элементов, раз-
ложение движения ротора по собственным формам. Остановимся
на последнем методе, который совмещает простоту и возможность
физически наглядной интерпретации результатов анализа.
Вернемся для этого к п.8.3 и допустим, что вычислены первые п
собственных частот соа и собственных форм:
<Pa(2)]T; ^у<№ = 1>а(2)’ « = 1» •••> п (8.21)
с учетом программных жесткостей подшипников и с2. Заметим,
что в силу свойства ортонормированности (8.16) wa(z) измеряется
в кг-1/2, <pa(z) — в м"1. кг-1/2. Движение ротора представим в виде
разложения по собственным формам
п п
Лх(^Д) = Л ха (^Р^а(О> 0 = У, Лиа (^Р'а (0> (8.22)
а=1 а=1
гдеХа(£), Уа(£) — модальные координаты.
Для их определения используем проекционные условия Галер-
кина [73]:
I
|[flifi* - (о7?2П|/ + х^1(Пх - «Пу) + n2^x - Fx~ pxhxad2 = 0;
о
I
J [-R^ - <о7?2т]х + - (ОПх) + N2^y “ Fy~ PyK«d2 = °’
0
(8.23)
a = 1, ...,n.
163
Пусть внешние силы Pv и Р„ содержат только вынуждающие
Л у
нагрузки от неуравновешенности, а магнитные силы подшипников
формируются по закону:
Fl - ^2 “ с1У1т Ь1У1т>
*3 “ ~с2х2т ~ ^2х2т^ ^4 ~ ~с2У2т “ ^2У2т9
(8.24)
где согласно (7.30) cs = 7?sms^ bs = 2^sXsms— программные коэф-
фициенты жесткости и демпфирования подшипников; xsm, ysm —
перемещения в точках измерения, 8=1,2.
Подставив в (8.23) соотношения (8.22), (8.24) и учитывая свой-
ство ортонормированности собственных форм (8.16), приходим
к уравнениям движения гибкого ротора в модальных координа-
тах:
X + (WTBWm + D)X + tiiHY + QX + ®ОУ = E®2 cos®*;
' „ f(8.25]
Y - шНХ + (WTBWm + D)Y - (oDX + £1Y = E<a2 sin®*.
Здесь X = (Xj, ХП)Л Y = (Yv Уn)T — векторы модальных
координат; й = diag(®2, ...,®2) — матрица квадратов собственных
частот; В = diag(dp &2) — матрица коэффициентов вязкого трения
подшипников; W и Wm — 2 х п матрицы значений собственных
форм в точках управления и точках измерения соответственно,
WlOx) ta2(z1)...ir„(z1)
_IO1(Z2) W2(z2)...Wn(z2)
w2(zlm)...wn(zlm)
w2(z2m)...wn(z2m)
;(8.26)
E = en)T— вектор обобщенных неуравновешенностей рото-
pa; Н = (йар) — пхп гироскопическая матрица; D = (dap) — п хп
матрица коэффициентов внутреннего трения с элементами:
I
еа = J[рewa + (7 - 7о)усра](Ь;
о
i i
М = J /оФаФ^; J ХФаФра*; а,Р = 1,
о о
.,п.
(8.27)
Уравнения (8.25) могут быть приведены к одному матричному
уравнению вида
Z + BZ + HZ + CZ + PZ = Q(t). (8.28)
Здесь Z — вектор модальных координат размерности 2n; Q(t) —
164
вектор возмущений той же размерности; В, Н, С, Р — блочные
квадратные 2п х 2п матрицы:
; Q(0 = со2
Ecos mt
Esin со£
WTBWm + D
О
О
WTBWm + D
О
-шН
О - _ 0 mD
Q ’ соЛ О
(8.29)
В =
mH — Q.
О ’ ~ О
где нуль обозначает нулевую п х п матрицу.
Итак, динамика замкнутой системы управления подвесом гиб-
кого ротора при раздельном способе управления по току прибли-
женно описывается уравнением (8.28). Этому уравнению отвечает
механическая система с дискретными параметрами, имеющая 2п
степеней свободы.
8.7. ДИНАМИЧЕСКИЙ АНАЛИЗ
Об устойчивости системы (8.28) можно судить по рас-
пределению на комплексной плоскости корней характеристическо-
го полинома
A(s) = detps2 + (В + H)s + С + р], (8.30)
где I — единичная матрица.
Далее, задавшись параметрами неуравновешенности e(z) и y(z),
можно рассчитать амплитуды перемещений, токов и нагрузок на
подшипники. По результатам численного анализа при необходи-
мости можно внести коррективы в закон управления и конструк-
цию подвеса. Внесение корректив существенно упрощается, если
использовать известные теоремы Кельвина-Тета-Четаева о влия-
нии структуры сил на устойчивость динамических систем; эти тео-
ремы превосходно изложены в книге Д. Р. Меркина [59].
СТРУКТУРА СИЛ
Заметим, что в уравнении (8.28) матрицаС — симмет-
ричная, матрица Н — кососимметричная; матрицы же В и Р в силу
несимметричности матрицы D и неравенства матриц W Ф Wm при
несовпадении расположения точек управления и измерения несим-
метричны. Поэтому, чтобы использовать метод структурного ана-
лиза в строгой постановке, нужно разбить матрицы В и Р на сим-
метричные и кососимметричные части [59]. В дальнейшем ограни-
165
чимся приближенным (качественным) анализом. Для этого будем
считать, что матрицы D и WTBWm диагональные. Тогда матрица
В будет также диагональной, а матрица Р — кососимметричной.
В такой постановке слагаемые в левой части уравнения (8^28)
характеризуют следующие силы: потенциальные (упругие) силы CZ,
диссипативные силы В Z, гироскопические силыН£ и неконсерва-
тивные (циркуляционные) силы PZ.
Очевидно, что система (8.28) при действии только потенциаль-
ных силС£ устойчива. Устойчивость системы сохраняется при до-
бавлении гироскопических сил HZ и диссипативных сил с пол-
ной диссипацией. Однако из-за несовпадения расположения точек
управления и измерения среди сил BZ кроме диссипативных сил
с полной диссипацией могут быть ускоряющие силы. Эти силы,
как и неконсервативные силы PZ, которые являются позиционны-
ми составляющими сил внутреннего трения во вращающемся гиб-
ком роторе, могут разрушать устойчивость системы.
ВЛИЯНИЕ НЕСОВПАДЕНИЯ ТОЧЕК УПРАВЛЕНИЯ
И ИЗМЕРЕНИЯ НА УСТОЙЧИВОСТЬ
Рассмотрим случай невращающегося ротора. Условием
устойчивости системы (8.28) является положительная определен-
ность матрицы В, которая при сделанных выше упрощающих пред-
положениях имеет место при
+ W22W22m) + daa > °’ a= "•> <8-31)
Здесь daa является положительным коэффициентом, вычислен-
ным согласно (8.27) и характеризующим диссипативные
свойства сил внутреннего трения при колебаниях с собственной
частотой соа.
Если между центрами подшипников и их датчиками отсутству-
ют узлы колебаний, то значения всех собственных форм в точках
управления wa(zs) и в точках измерения wa(z$m), s = 1, 2, будут
одного знака и в силу условия (8.31) подвес будет устойчив. При
наличии же узла между этими точками знаки величин wa(zs)
и wa(zsm) будут разными и, следовательно, ротор может оказаться
неустойчивым по соответствующей собственной форме.
Причина данного явления вполне понятна. Информация с дат-
чика, который расположен так, что между ним и подшипником
имеется узел колебаний, неверна не только по значению, но и по
направлению. Поэтому обратная связь в каналах управления на
данной собственной частоте становится положительной. Система
управления подвесом не гасит эти колебания, а, наоборот, подпи-
тывает их. Подпитки не будет только в том случае, если данная
собственная частота лежит выше частоты среза системы.
166
б)
Рис. 8.3. Узкополосный заградительный фильтр
типа антивибратора: а — электрическая схема;
б — амплитудно-частотная характеристика
Наиболее надежный способ избежать такого явления — это ис-
пользование для каждого подшипника не одного, а двух симметрично
расположенных относительно подшипника датчиков. Тогда суммар-
ный сигнал с этих датчиков будет показывать истинное перемещение
ротора под центром подшипника. В этом случае координаты точек
управления zs и точек измерения zsm будут совпадать и условие
устойчивости (8.31) будет выполняться для всех собственных форм.
Стремление сделать ротор более коротким и жестким приводит
к конструктивным схемам с одним датчиком на подшипник. В этих
случаях необходимы тщательный расчет собственных частот и форм
ротора при заданных программных жесткостях подшипников и по-
иск такого расположения подшипников и датчиков по длине ро-
тора, при котором между ними не было бы узлов колебаний с соб-
ственными частотами, лежащими ниже частоты среза системы уп-
равления. На практике, однако, не всегда можно обеспечить такое
взаимное расположение подшипников и датчиков. В связи с этим
возникает вопрос — как можно застабилизировать неустойчивую по
собственной частоте сор систему?
Можно указать несколько способов решения данной проблемы.
Из условия устойчивости (8.31) видно, что наиболее простой способ —
это уменьшение программных коэффициентов демпфирования под-
шипников и Ь2« Недостатком такого способа является ухудше-
ние динамических качеств подвеса «твердого скелета» ротора.
Другой способ заключается в уменьшении коэффициентов дем-
пфирования и Ъ2 не во всем диапазоне частот, как по первому
способу, а только в узкой полосе частот в окрестности неустойчи-
вой собственной частоты top. Для этого в канал управления встав-
ляется узкополосный настроенный на частоту top заградительный
фильтр типа антивибратора. На рис. 8.3 приведены электрическая
схема и амплитудно-частотная характеристика такого фильтра
с передаточной функцией [7]
s2 + (Ор
=__________________
ul(s) s2 + 2£ptops + top
(8.32)
167
Крышка Упругий элемент Грузик Вязкий заполнитель
х х
\WWSJWitM7SSSSSSA0.
Рис, 8.4. Механический демпфер изгибных колебаний ротора
Недостаток данного способа прежний — ухудшение динамичес-
ких качеств подвеса «твердого скелета» ротора.
Наконец, третий способ — это установка на ротор механическо-
го демпфера, настроенного на частоту со^. На рис. 8.4. показана
схема демпфера, которая успешно испытана на практике (в испы-
таниях участвовали инженеры В. В. Андреев, И. И. Морозов
и С. В. Смирнов). В выходном конце вала делается полость, кото-
рая заполняется вязким заполнителем и закрывается крышкой.
К крышке с внутренней стороны жестко прикреплен упругий эле-
мент (валик), на котором закреплен грузик. Жесткость на изгиб
упругого элемента и масса грузика подбираются так, чтобы частота
свободных колебаний грузика равнялась частоте (Dp. При такой на-
стройке и соответствующем выборе вязкости заполнителя может
быть достигнуто эффективное демпфирование изгибных колебаний
ротора. Стабилизация подвеса осуществляется за счет добавления
к слагаемому dpp в (8.31) некоторого положительного слагаемого,
зависящего от параметров демпфера. Динамические качества подве-
са «твердого скелета» ротора при этом остаются неизменными.
ВЛИЯНИЕ ВНУТРЕННЕГО ТРЕНИЯ
НА УСТОЙЧИВОСТЬ
Данная проблема применительно к гибким роторам с упру-
годемпферными опорами подробно изучена и отражена в литературе
[59, 66]. Здесь остановимся лишь на основных особенностях пробле-
мы применительно к магнитным подвесам гибких роторов [10, 36].
Учитывая, что = d22 = 0, запишем приближенные уравнения
только для модальных координат и Y3 (без учета гироскопичес-
кого эффекта):
*3 + + М^З + + fyCOYg - 0;
У3 + (be + bi)Y3 + (»|У3 - &/(оХ3 = 0,
(8.33)
где Ье и bt — соответственно коэффициенты внешнего (в подшип-
никах) и внутреннего (в материале вала) вязкого трения,
168
Ье = blw3<zl)w3(2lm) + b2w3(22>3(22m)’ bi = d33- <8-34>
Из уравнений (8.33) видно, что при вращении ротора внутрен-
нее трение создает не только зависящие от скоростей диссипатив-
ные силы btX^ и bjYs, но и неконсервативные позиционные силы
с кососимметричной матрицей коэффициентов
f 0 Ь^
О J
Условие устойчивости системы (8.33) имеет вид [59, с. 217]
со < <0* =(1 + —)о)3. (8.35)
bi
Если скорость вращения ротора будет больше граничного значе-
ния со*, то произойдет потеря устойчивости. Значение со* зависит от
соотношения между коэффициентами внешнего трения Ье и внут-
реннего трения fy; силы внешнего трения отодвигают границу ус-
тойчивости в сторону высших скоростей.
Следует отметить, что имеется существенное различие в наи-
меньших значениях со* = co^in ПРИ установке ротора в упруго-
демпферные опоры и магнитные подшипники. При использовании
упругодемпферных опор коэффициент внешнего трения Ье не мо-
жет принимать отрицательные значения: Ье= 0 при расположении
опор в узлах третьей формы и Ье > 0 — при расположении опор вне
узлов. Поэтому в случае упругодемпферных опор = со3.
При использовании магнитных подшипников, как это показано
в п. 8.7., коэффициент внешнего тренияЬе> 0 — если подшипник и
датчик расположены по одну сторону от узла; Ье = 0 — если либо
подшипник, либо датчик расположены в узле; Ье < 0 — если узел
расположен между подшипником и датчиком. Отрицательность Ье
не означает, что подвес невращающегося ротора неустойчив, так как
условие устойчивости согласно (8.31) и (8.34) имеет вид
Ье+Ь-> 0. (8.36)
Теперь предположим, что&е= -(1 -е)&р гдее — малое положи-
тельное число. При данном значении Ье подвес, будучи устойчи-
вым при невращающемся роторе, потеряет устойчивость при дос-
тижении ротором скорости вращения co^in = есо3. Это означает, что
при использовании магнитного подвеса потеря устойчивости под
действием сил внутреннего трения может произойти на частоте
вращения, которая меньше собственной частоты со3. Увеличение ско-
рости G)^in может быть осуществлено теми же способами, что и при
169
стабилизации подвеса в случае несовпадения точек управления
и измерения.
Остается отметить, что рассчитать значение коэффициента внут-
реннего трения по формуле
I
<*зз = J ХФзФз^ (8.37)
о
практически невозможно, так как обычно неизвестно распределе-
ние параметра внутреннего трения %(z) по длине ротора. В связи с
этим рассмотрим косвенный метод расчета. Допустим, что извест-
но значение логарифмического декремента изгибных колебаний по
третьей (первой изгибной) собственной форме свободного от опор
ротора Д3 как натурального логарифма отношения двух последо-
вательных через периодт3 = 2тг/(О3 амплитуд любого сечения рото-
ра. Тогда имеем
^33 = Аз^з/71- (8.38)
Значение декремента Д3 можно либо определить опытным пу-
тем, либо приближенно назначить с помощью справочных таблиц.
9. ЦИФРОВОЕ УПРАВЛЕНИЕ ПОДВЕСОМ
9.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Законы управления подвесами, рассмотренные в гла-
вах 6-8, могут быть реализованы при помощи как аналоговой,
так и цифровой техники. Аналоговая обработка сигналов на базе
операционных усилителей [7] характеризуется простотой реализа-
ции и относительно низкой стоимостью. Однако к настоящему
времени благодаря стремительному развитию микроэлектроники
аналоговое управление подвесами роторов вытесняется цифровым
[99, 104]. Аналоговые регуляторы используются теперь главным
образом в подвесах легких роторов. В данном параграфе остано-
вимся на преимуществах и основных проблемах цифрового управ-
ления.
Можно отметить следующие преимущества цифрового управле-
ния по сравнению с аналоговым.
1. Универсальность. Можно использовать один и тот же циф-
ровой регулятор в различных подвесах, лишь внося некоторые из-
менения в программы.
2. Возможность более высоких уровней управления. Благодаря
гибкости программного обеспечения могут быть легко реализова-
ны более сложные, чем ПИД, алгоритмы управления. Это особенно
удобно на стадии разработки.
3. Системное расширение. Цифровой регулятор (наряду с ос-
новным назначением — стабилизацией подвеса) может осуществ-
лять активный контроль за состоянием роторной системы: часто-
той вращения, вибрацией, нагрузкой на подшипники, компенсаци-
ей синхронной помехи и др.
На рис. 9.1 показана структурная схема цифровой системы уп-
равления подвесом. Она включает в себя непрерывную часть (уси-
лители мощности, электромагниты, датчики) и цифровой регуля-
тор. Выходные аналоговые сигналы датчиков y(t) при помощи ана-
лого-цифрового преобразователя (АЦП) в моменты времени t = tk =
= kT преобразуются в последо-
вательность импульсов y(k),
модулированную сигналом
y(t). Здесь k = 0, 1, 2,... —
дискретное время; Т — пе-
риод дискретности по време-
ни (период квантования). Сиг-
нал y(k), преобразованный
в цифровой код, обрабатыва-
ется цифровым вычисли-
тельным устройством (ЦВУ)
Рис. 9.1. Структурная схема систем управ-
ления подвесом с цифровым регулятором
в соответствии с заложенны-
ми в нем алгоритмами и про-
171
граммами. Выходной сигнал ЦВУ u(k), являющийся цифровым
представлением сигнала управления, при помощи цифроаналого-
вого преобразователя (ЦАП) декодируется и преобразуется из им-
пульсного сигнала в аналоговый сигнал управления u(t). При та-
ком преобразовании выходной сигнал, как правило, фиксируется
на постоянном уровне в течение периода дискретности Т (фикса-
тор нулевого порядка).
Процессы преобразования (аналог-цифра и цифра-аналог) и вы-
полнения арифметических вычислений сопровождаются временным
запаздыванием, которое вызывает отставание по фазе выходного
сигнала по отношению к входному. Стремление повысить быстро-
действие регулятора приводит к его удорожанию, поэтому здесь
нужен компромисс.
Другая важная проблема цифрового управления — это пра-
вильный выбор периода дискретности Т. Интуитивно ясно, что
значение Т должно быть как можно меньше. Однако это не совсем
так. Период дискретности должен быть в несколько раз больше
временного запаздывания. Кроме того, при очень малых Т возни-
кает целый ряд вычислительных проблем, что приводит к появле-
нию дополнительных шумов на выходе. С другой стороны, увели-
чение Т сужает частотный диапазон подвеса и уменьшает запас
устойчивости. Установлено [99], что частота дискретизации долж-
на быть в пять и более раз выше верхней границы желаемого
частотного диапазона. Поэтому при выборе Т должен быть также
найден компромисс. Обычно в системах АМП значение Т ле-
жит в интервале от 0,1 до нескольких миллисекунд. Представляет
также практический интерес случай, когда значение?7 не постоян-
ное, а синхронизировано с вращением ротора [99].
Еще одна особенность цифрового управления — это переход от
дифференциальных к разностным уравнениям. Такой переход выз-
ван тем, что переменные объекта являются функциями непрерыв-
ного времени, а переменные цифрового регулятора изменяются
только в дискретные моменты времени tk = kT. Очевидно, что разли-
чие в описании объекта управления приводит и к различиям в мето-
дах синтеза и анализа системы управления подвесом.
В последующих параграфах рассматривается математические ос-
новы синтеза и анализа дискретной системы управления током одно-
степенного подвеса с использованием метода пространства состояний
и метода ^-преобразования (теории цифровых систем управления
посвящена обширная литература; см., например, [43, 53, 61, 63, 78]).
9.2. ДИСКРЕТНОЕ ОПИСАНИЕ ОБЪЕКТА
Рассматривается одностепенной подвес с управлением
по току, описание которого дается дифференциальным уравнени-
ем в безразмерных переменных (6.13). Считая, что вынуждающая
сила отсутствует (Q = 0), и опуская штрихи в обозначениях безраз-
мерных величин, уравнение объекта запишем в виде
172
У-У = 1,
(9.1)
где точки над у означают дифференцирование по безразмерному
времени f [здесь %— характерный безразмерный параметр
подвеса (6.8)].
Пусть подвес снабжен идеальным квантователем с периодом
квантования Т и фиксатором нулевого порядка, сохраняющим
постоянное значение управляющего тока в течение периода Т, т. е.
i(t) = i(k) = const при kT < t < (k + 1)T. (9.2)
Задача сводится к определению изменения состояния системы
(9.1) за один период квантования путем интегрирования урав-
нения
У-У = № (9.3)
при начальных условиях z/(0) = y(k) и у(0) = y(k). Отыскивая реше-
ние уравнения (9.3) как сумму общего решения однородного урав-
нения и частного решения неоднородного уравнения, находим, что
в момент времени tk +1 = (k +1)Т перемещение и скорость примут
значения:
y(k + 1) = y(k)chT + y(k)shT + i(k)(chT - 1);
y(k + 1) = y(k)shT + y(k)chT + i(k)shT.
Вводя векторы состояния x(k) = [z/(A), y(k)^ и x(k +1) = [y(k +1),
iT
y(k +1)] , получаем дискретное описание объекта в виде разно-
стных уравнений, записанных в матричном виде:
x(k + 1) = Ax(k) + Bi(k); y(k) = Сх(/г), (9.5)
где
(chT
[shT
shT\
chT)
chT -1\
8ЙТ J
c = (1, 0).
(9.6)
B =
9.3. НЕУСТОЙЧИВОСТЬ ДИСКРЕТНОГО ОБЪЕКТА
Известно, что дискретный объект (9.5) будет устойчив,
если собственные числа матрицы А находятся внутри единичного
круга. Из физических соображений ясно, что в силу неустойчивос-
ти непрерывного объекта (9.1) дискретный объект (9.5) также дол-
жен быть неустойчив. Отыскивая собственные числа матрицы А
как корни уравнения det(XI - А) = 0, имеем = chT + shT = ет9
Х2 = chT - shT = е~т. Видно, что > 1 при любом Т > 0, т. е.
дискретный объект действительно неустойчив.
173
Для стабилизации объекта вводится цифровой регулятор, фор-
мирующий управляющий ток i(k) в каждый дискретный момент
времени t = tk, т. е. используется дискретное управление.
9.4. ДИСКРЕТНОЕ УПРАВЛЕНИЕ
ПРИ ПОЛНЫХ ИЗМЕРЕНИЯХ
В данном параграфе используется предположение, что
непосредственному измерению доступны как перемещение y(t), так
и скорость y(t)9 так что в дискретные моменты времени t = tk век-
тор состояния x(k) считается известным. Используя ПД-регулятор
i(k) = -fry(k) - f2y(k) = -Fx(k), (9.7)
где F = f2), и прикладывая управление (9.7) к объекту (9.5),
получаем уравнение замкнутой дискретной системы
x(k 4-1) = Аох(/г), (9.8)
где Aq =A-BF.
Коэффициенты усиления fr и f2 и период квантования Т должны
быть выбраны так, чтобы система (9.8) была устойчива. Для этого
собственные числа матрицы Aq, являющиеся корнями многочлена
Д0(Х) = detQJ - Aq) = Х2 + ЬХ + с;
b = ft(chT - 1) + /2shT - 2chT; с = /i(chT - 1) - f2shT + 1, (9.9)
должны размещаться внутри единого круга.
Очевидно, что наряду с обеспечением устойчивости цифровой
регулятор должен придавать подвесу определенные динамические
свойства, такие как заданные быстродействие, статическую и дина-
мическую жесткости, качество переходных процессов, «затраты»
управления и др. Исходя из этого при синтезе дискретного управ-
ления, т. е. при выборе значений f2 и Т, могут быть использова-
ны различные подходы. Из их числа наиболее интересны три вида
управления: 1) финитное; 2) ЛК-оптимальное для непрерывного
объекта; 3) ЛК-оптимальное для дискретного объекта.
ФИНИТНОЕ УПРАВЛЕНИЕ
При таком управлении, называемом еще управлени-
ем с конечным временем регулирования, матрица F выбирается
так, чтобы переход в состояние х = 0 заканчивался не более чем за
п тактов, где п — размерность вектора х (в данном случае п = 2).
Для этого выберем F так, чтобы матрицаAq имела все собственные
числа нулевыми. При этом характеристическое уравнение будет
174
0,500 0,062
-4,021 -0,500
иметь вид X2 = 0. Тогда по теореме Гамильтона — Кэли Aq = 0,
и в результате имеем х(2) = Aqx(0) = 0 при любом х(0).
Приравнивая в (9.9) коэффициенты Ъ и с нулю, находим:
fr = (2chT - l)/2(chT - 1); f2 = (2chT + l)/2shT. (9.10)
При выполнении соотношений (9.10) условие устойчивости под-
веса обеспечивается автоматически, а отработка переходных про-
цессов осуществляется не более чем за два такта.
Рассмотрим пример. Пусть Т = 0,25. Тогда = 16,917, /2 = 6,062,
, Х1 = Х2 = 0. Используя начальные условия
х(0) = (1; 0)т, вычисляем i(0) = -Fx(0) = -16,917, х(1) = Аох(О) =
= (0,500; -4,021)т, i(l) = -Fx(l) = 15,920, х(2) = = Аох(1) =(0; 0)г,
Д2) = -Рх(2) = 0. Как и следовало ожидать, переходный процесс
закончился за два такта.
Следует отметить, что финитное управление является достаточ-
но эффективным, но ему присущ один существенный недостаток,
заключающийся в очень быстром увеличении «затрат» управле-
ния по мере приближения к нулю периода квантования Т.
ЛК-ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
ДЛЯ НЕПРЕРЫВНОГО ОБЪЕКТА
При таком управлении матрица F цифрового регулято-
ра находится из решения задачи ЛК-оптимального управления для
непрерывного объекта (см. п. 6.4). Для этого достаточно в соотно-
шениях (6.43) формально положить m - = k = 1. В результате
имеем:
/1 = cog +1; f2 = ^(cog +1), (9.11)
где — безразмерная недемпфированная собственная частота под-
веса, связанная с размерной частотой масштабным множителем
То / %. Такой подход обычно называется цифровым перепроекти-
рованием.
Период квантования Т должен быть выбран так, чтобы систе-
ма (9.8) с учетом (9.11) была устойчива. На рис. 9.2 (кривая 1)
приведен график зависимости максимально допустимого значе-
ния периода квантования Ттах от собственной частоты подве-
са <оо; при значениях Т, лежащих выше кривой 5г’тах(<00), подвес
неустойчив.
Следует заметить, что в отличие от финитного управления,
при котором значения /2 и Т связаны соотношениями (9.10),
175
при данном управлении в вы-
боре Т допустим определенный
произвол. Например, назначив
(00= 4, имеем =17, f2- 5,831,
а значение Г, как следует из
графика на рис. 9.2, может быть
выбрано любым из диапазона
О < Т < < 0,35. Если принять
Т = 0,25, то имеем:
( 0,497 0,069^1
Ап =
и (-4,042 -0,442/
Х1>2 = 0,028 ± /0,245.
Переходный процесс в дан-
ной системе заканчивается за два
такта и мало отличается от про-
цесса, рассмотренного выше.
Рис. 9.2. Зависимость максимально допус-
тимого значения периода квантования
ГШах 07 собственной частоты подвеса
1 — при полных измерениях; 2 — при нали-
чии дискретного дифференцирующего звена
ЛК-ОПТИМАЛЬНОЕ
УПРАВЛЕНИЕ
ДЛЯ ДИСКРЕТНОГО
ОБЪЕКТА
Будем использовать следующую интерпретацию метода
линейно-квадратической (ЛК) оптимизации применительно к дис-
кретному объекту (9.5). Примем за показатель качества работы
подвеса величину
J =£[/(*) +pi2(fe)], (9.12)
fc=0
где р — положительный весовой скаляр.
Показатель (9.12) минимизируется, если управляющий ток фор-
мируется по закону
i(k) = -Fx(k), (9.13)
где
F = (/р /2) = (р + ВТРВГХВТРА. (9.14)
Здесь матрицы Р и F суть пределы, к которым сходятся после-
довательности Р8 и Fs, строящиеся по рекурренции [63]:
Ps =ATPs_1A-ATPs_1B(p + BrPs_/B)-1BrPs_;A + СТС; Ро = 0; (9.15)
Fs = (р + BTPSB)-1BTPSA, s = l,2....... (9.16)
Данную процедуру проиллюстрируем примером, где Т = 0,25,
р = 0,004 (или соо = р~1//4 = 4):
176
s.. 1 2 3456789 10
fY. 8,10 23,95 11,35 8,64 8,87 8,85 8,78 8,77 8,77 8,77
f2. 1,96 9,69 5,35 4,07 4,15 4,14 4,11 4,11 4,11 4,11
Из примера видно, что последовательность Fs сходится к опти-
мальной матрице F = (8,77; 4,11) при s > 7. Оптимальная замкну-
тая система (9.8) имеет полюса “ 0,38 ± /0,31. Используя на-
чальные условия х(0) = (1; О)7, вычисляем:
У(0)=1,
i/(l) = 0,76,
i/(2) = 0,33,
1/(3) = 0,07,
i/(4) = -0,03,
i(0) =-8,77,
Z(l) =-1,41,
i(2) = -3,17,
i(3) = 2,04,
i(4) = 0,77.
Переходной процесс в системе закончился за четыре такта.
9.5. ДИСКРЕТНОЕ УПРАВЛЕНИЕ
ПРИ НЕПОЛНЫХ ИЗМЕРЕНИЯХ
Как уже отмечалось, в реальных подвесах непосредствен-
ному измерению доступно лишь перемещение y(t), скорость же y(t)
либо вычисляется с помощью дифференцирующего звена, либо вос-
станавливается наблюдателем состояния. Ниже рассматриваются
оба этих способа применительно к дискретному объекту (9.5).
ДИСКРЕТНОЕ ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО
При аппроксимации скорости выражением y(k) = [y(k) -
- y(k -1)] / Т и использовании ПД-управления (9.7) имеем
i(k) = -fry(k) - f2y(k) = -gly(k) + g2y(k - 1), (9.17)
где
gl=fl+f2/T'> g2=f2/T^ (9.18)
Регулятор (9.17) вносит дополнительную третью переменную
состояния y(k - 1), поэтому управление замкнутой системы с диф-
ференцирующим звеном имеет вид
^ + lf
y(k + l)
'chT-gjCchT-l)
shT - ^jshT
1
shT
chT
0
£2(chT -l)Yi/(/o
£2shT y(k)
.(9.19)
177
Система (9.19) будет устойчивой, если ее матрица имеет соб-
ственные числа внутри единичного круга. На рис. 9.2 (кривая 2)
приведен график зависимости максимально допустимого значения
периода квантования Ттах от собственной частоты подвеса соо для
системы (9.19) с учетом (9.11). Видно, что наличие дискретного
дифференцирующего звена требует меньших значений периода кван-
тования Т.
ДИСКРЕТНЫЙ НАБЛЮДАТЕЛЬ СОСТОЯНИЯ
В данной ситуации система (9.5) замыкается обратной
связью, задаваемой соотношением
i(k) = -Fx(k), (9.20)
гдех(^) является выходом наблюдателя состояния,
x(k +1) = Ax(k) + Bi(k) + - Cx(fe)]. (9.21)
Здесь F и N — соответственно матрицы коэффициентов усиле-
ния регулятора и наблюдателя, выбираемые так, чтобы матрицы
А - BF и А - NC имели собственные числа внутри единичного
круга (выбору F посвящен п. 9.4). Структурная схема системы
приведена на рис. 9.3.
Подчеркнем, что в отличие от простого правила (9.13) соотно-
шения (9.20) и (9.21) в силу алгоритма
x(k) = Ax(k -1) + Bi(k -1) + N[y(k -1) - Cx(k -1)] (9.22)
требуют для формирования управления знания результатов изме-
рений и вычислений не в тот же самый момент, а только в предше-
ствующий.
Рис. 9.3. Дискретная система управления подвесом с на-
блюдателем состояния
178
Ошибка восстановления наблюдателя e(k) = x(k) - x(k) удовлет-
воряет уравнению
e(k + 1) = (А - NC)e(k). (9.23)
Отсюда следует, что устойчивость и быстродействие наблюдате-
ля определяются собственными числами матрицы А - NC или по-
люсами наблюдателя.
Специальный интерес представляет ситуация, когда все полюса
наблюдателя равны нулю. В этом случае
det[XI - (А - NC)] = = 0. (9.24)
Тогда по теореме Гамильтона — Кэли (А - NC)n = 0, поэтому
е(п) = (А - NC)ne(0) = 0 для любого е(0). Это означает, что восста-
новление ошибки до нуля происходит не более чем за п шагов.
Поэтому такой наблюдатель называется финитным. Пусть N = (п19
п2)т. Тогда из уравнения (9.24) при п = 2 следует:
и1 = 2chT; п2 = (2ch2T - l)/shT. (9.25)
Уравнение замкнутой системы (с наблюдателем) имеет вид
+ -BF Yx(k)\
I —- I II . • (У.^ОI
^(/e + l); I^C A-NC-BF)[x(k))
Подстановка соотношения x(k) = x(k)-e(k)B (9.26) дает
x(k + 1) = (A - BF)x(k) + BFe(k). (9.27)
Из (9.23) и (9.27) следует, что полюса замкнутой системы обра-
зуются полюсами регулятора (собственные числа матрицы А - BF)
и полюсами наблюдателя (собственные числа матрицы А - NC).
Определенный интерес представляет случай, когда все полюса
регулятора и наблюдателя равны нулю, т. е. когда реализуется
финитная система управления. В такой системе наблюдатель вос-
станавливает состояние за два такта, после чего регулятор, как это
следует из (9.27) при e(k) = 0 и k > 2, переводит систему в нулевое
состояние за другие два такта.
Ниже приводятся результаты расчета переходного процесса в фи-
нитной системе управления при Т = 0,25 и матрицах F = (16,917;
6,062) и^ = (2,063; 4,464)т, вычисленных согласно (9.10) и (9.25),
и начальных условиях х(0) =(1; О)71, х(0) = 0:
е(0) = 1, И0) = 1, Ц0) = 0,
е(1) =-1,03, у(1) = 1.03, i(l) = -62,3,
е(2) = 0, у(2) = -0,82, i(2) = 105,
е(3) = 0, 1/(3) =-1,35, i(3) = -42,3,
е(4) = 0, У(4) = 0, i(4) = 0.
179
Столь высокое быстродействие наблюдателя и регулятора,
конечно же, сопровождается весьма большими «затратами» управ-
ления.
9.6. ДИСКРЕТНОЕ ИНТЕГРАЛЬНОЕ УПРАВЛЕНИЕ
Для придания подвесу с дискретным управлением вы-
сокой статической жесткости (астатизма) введем дополнительную
интегральную переменную <?, определяемую как
q(k +1) = q(k) + y(k), (9.28)
где y(k) = Cx(k) = Xj (k) — восстанавливаемое наблюдателем значе-
ние наблюдаемой переменной, а управление формируем по закону
i(k) = -Fx(k) - faq(k). (9.29)
В этом случае уравнение замкнутой системы имеет вид
x(k + I)' ' A -BF -B/3Yx(^
х(А +1) = NC A-NC-BF -В/з x(k) (9.30)
0 0 10 1
Коэффициент усиления /3 выбирается так, чтобы собственные
числа матрицы системы (9.30) размещались внутри единичного
круга.
9.7. МЕТОД ^-ПРЕОБРАЗОВАНИЯ
Применяя метод ^-преобразования к системе разностных
уравнений (9.5) при нулевых начальных условиях, имеем
У(2)=Я(2)Д2), (9.31)
где г — комплексная переменная преобразования; H(z) — переда-
точная функция объекта, определяемая как
H(z) = C(zI- А)~1В = ^^= ^ЬГ-1)(2 + 1) (9 32)
Ф(г) z2 - (2chT)z +1
Корни полинома 'F(z) называются нулями объекта. Рассматри-
ваемый объект имеет один нуль Vj = -1. Корни полинома ф(з)
называются полюсами объекта. В данном случае объект имеет два
полюса: = chT + shT = ет; п2 = chT - shT = е~т, которые совпада-
ют с собственными числами матрицы А и один из которых (л^) —
неустойчив.
180
Заменяя в (9.31) с учетом (9.32) комплексную переменную z на
оператор £ сдвига на такт вперед, получаем операторное уравнение
(9.33)
из которого вытекает эквивалентное системе (9.5) разностное урав-
нение
y(k + 2) - (2chT)i/(/? + 1) + y(k) = (chT - 4- 1) + (9.34)
Перейдем к задаче синтеза регулятора на основе метода z-npe-
образования. Пусть объект описан операторным уравнением (9.33),
возможно измерение выходной последовательности y(k) и требует-
ся построить стабилизирующую обратную связь, определяемую урав-
нением
«=<)^), (9.35)
где г(£) и 6(£) — многочлены от £.
Замкнутая система окажется устойчивой, если ее характеристи-
ческий многочлен
A(z) = 0(z)r(z) + T(z)O(z) (9.36)
будет иметь все корни (полюса замкнутой системы) внутри еди-
ничного круга. Многочлены r(z) и 0(z) всегда могут быть выбраны
так, чтобы полюса размещались произвольным образом. Единствен-
ное ограничение: выполнение требования строгой реализуемости
обратной связи degr(z) > degO(z), эквивалентного требованию не-
упреждающего характера обратной связи.
Назначаем
r(z) = z2 + гг2 + r0; 6(z) = 0xz + 60 (9.37)
и попробуем организовать финитное управление. Для этого потре-
буем, чтобы все четыре полюса замкнутой системы были равны
нулю, т. е. чтобы A(z) = z4. Из этого тождества получаем
гг = 2chT; r0 = (4ch2T 4- 2chT - l)/[2(chT - 1)];
= (8ch3T 4- 4ch2T - 4chT - l)/2ch2T;
60 = -(4ch2T 4- 2chT - l)/2sh2T. (9.38)
Согласно (9.35) и (9.37), обратная связь задается уравнением
i(k) = -r^k - 1) - rQi(k - 2) - ^y(k - 1) - &Qy(k - 2). (9.39)
При формировании управления (9.39) используются только преды-
дущие измерения y(k - 1) и y(k - 2) и вычисления i(k - 1) и i(k - 2).
Теперь попробуем обеспечить A(z) = z3. Это возможно при
r(z) = z 4- r0; 6(z) = 6xz 4- 60, (9.40)
181
где
r0 = (2chT + l)/[2(chT + 1)]; ©г = (4ch2T + 2chT - l)/2sh2T;
60 = -(2chT + l)/2sh2T, (9.41)
и законе управления
i(k) = -rQi(k - 1) - ^y(k) - $Qy(k - 1), (9.42)
в котором кроме предыдущих значений y(k - 1) и i(k - 1) исполь-
зуется и текущее измерение y(k).
Рассмотрим пример. Пусть Т = 0,25. Тогда согласно (9.41)
имеем г0 = 0,754, = 41,67,60 = -24. Используя начальные условия
х(0) = (1; 0)г, рекуррентно вычисляем
1/(0) = 1,
1/(1) = -0,28,
1/(2) = -0,78,
Х/(3) = 0,
f(0) = -41,67
i(l) = 66,98,
f(2) = -24,75
Z(3) = 0.
Как и следовало ожидать, переходной процесс закончился за
три такта.
Заключим параграф описанием дискретного пропорциональ-
но-интегрально-дифференциального регулятора, который широ-
ко используется на практике (см., например, [53]). На рис 9.4
изображена структурная схема регулятора, воздействующего на
сигнал ошибки e(k) = -y(k). Пропорциональное управление
заключается в простом умножении сигнала ошибки на констан-
ту fv т. е.:
i(k) = fre(k), или I(z) = frE(z). (9.43)
При аппроксимации производной e(k) выражением ё(к) = [е(&) -
- e(k -1)] / Т и коэффициенте усиления по производной /2 разност-
ное уравнение дается соотношениями:
у г = о e(k) = -y(k) /1 ' *(fe) / I(k)
, 'V E{k)=-Y(k) y(k) Y(k) T z f3T г + 1
2 z — 1
Рис. 9.4. Структурная схема дискретного ПИД-регулятора
182
„ e(k) - e(k - 1) TZ ч /2 2 -1 „z ч
i(k) = /2 ~---------> или №) = —------Е^' (9.44)
Т Т z
При вычислении интеграла по методу трапеций и коэффициен-
те усиления по интегралу /3 для интегрального управления имеем:
i(k) = i(k -1) + /3 tg(fe) + е(& ~ Х^Г, или Цг) = E(z). (9.45)
2 2 2 -1
Данный регулятор формирует обратную связь (9.35) при г(г) =
= 2^-2, 0(2) = +g2 + я3)з2 + (g3 - 2g2 - gx)z + g2, где gx = fx,g2 = f2/T>
Синтез регулятора, т. e. определение значений/р /2 и /3 может
быть выполнен любым из известных методов, часть которых ис-
пользовалась выше.
10. ДИНАМИЧЕСКИЕ АСПЕКТЫ
ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ
ПОДВЕСОВ РОТОРОВ
10.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Техническая реализация подвесов роторов в АМП со-
пряжена с решением большого комплекса конструкторских и тех-
нологических задач механики, электромеханики, автоуправления,
измерительной техники и промышленной электроники. Деталь-
ный анализ этих задач, несомненно, составляет важный предмет
отдельного обсуждения, однако он выходит за рамки данной кни-
ги. Поэтому в настоящей главе внимание уделяется лишь тем
аспектам технической реализации, которые могут оказывать за-
метное влияние на динамическое поведение подвеса.
В п. 10.2 рассматриваются вопросы обеспечения механической
прочности вращающихся магнитоактивных элементов подвеса, да-
ется оценка предельной окружной скорости из условия прочности
и оценка частоты вращения, при которой происходит полное ос-
лабление натяга между валом и насаженным на него элементом
подвеса. В п. 10.3 описывается динамическое поведение ротора в
страховочных подшипниках после внезапного выключения маг-
нитного подвеса. В п. 10.4 даны описание индуктивного датчика
перемещений ротора и анализ источников шумов измерений. Зак-
лючительный п. 10.5 посвящен описанию компенсатора синхрон-
ной помехи.
10.2. ПРОЧНОСТЬ ВРАЩАЮЩИХСЯ
ЭЛЕМЕНТОВ ПОДВЕСА.
ПРЕДЕЛЬНАЯ ОКРУЖНАЯ СКОРОСТЬ
И ОСВОБОЖДАЮЩЕЕ ЧИСЛО ОБОРОТОВ
К вращающимся элементам подвесов роторов относят-
ся пакеты железа цапфы и мерительного кольца радиального АМП
и ферромагнитный диск осевого АМП. В расчетах на прочность
эти элементы могут схематизироваться диском постоянной тол-
щины, имеющим центральное отверстие и посаженным с некото-
рым натягом на вал. Расчетам напряжений и деформаций во
вращающихся дисках посвящена обширная литература (см., на-
пример, [6] и список литературы в [26]). Поэтому в данном пара-
графе рассмотрим только те аспекты, которые непосредственно от-
носятся к изучаемой проблематике, положив в основу результаты
упомянутых выше работ.
Пусть диск (рис. 10.1, а) имеет внутренний радиус г = а, наруж-
ный радиус г = Ь, плотность материала р и частоту вращения со.
Напряженное состояние в диске считаем плоским (двухмерным)
184
Рис. 10.1. Напряжения во вращающемся диске: а —
схема диска; б — напряженное состояние в элементе
диска
и осесимметричным. Рассмотрим элемент диска, показанный на
рис. 10.1, б. На этот элемент наряду с радиальными ог и окружны-
ми главными напряжениями, распределенными по боковым гра-
ням, действует объемная нагрузка qr = рсо2г, вызванная центро-
бежными силами инерции. Предполагается, что диск посажен на
вал с радиальным натягом 8а, благодаря которому на внутреннем
контуре диска (г = а) действует сжимающее напряжение вга = -р.
Обозначим перемещение элемента диска в радиальном направле-
нии iz(r). При сделанных предположениях распределение напря-
жений и деформаций в диске согласно [26] определяется выраже-
ниями:
ar(r) = -агаВх + ст0(г) = -агаВ2 + Q2;
u(r) = -ага -^(В2 - iiBJ + -^(Q2 - рйх),
(10.1)
где Вг =
+ а2
2 »2 2 т 2 о . _
а st Ь \ г> а ° х гх 3 + Ц 2[
~2 2 (1 2^ “ 72 2 + 2’ “ о [
Ъ - а г Ъ - а г й L
2] гч 3 + ц 2^2 , 2и Я2&2 1 + Зц 2
------г ;Q2=-~pw Р +<* +-Т"-'ТТТГ
J О L О + J1
185
Рис. 10.2. Эпюры радиальных (а) и окружных (б) напряжений в диске постоянной
толщины при ога = 0:
1 - а/b = 0,5; 2 - а/Ъ = 0,2; 3 - а/b = 0 (сплошной диск без центрального отверстия)
Здесь Е — модуль упругости материала диска; ц — коэффици-
ент Пуассона. Выражения (10.1) справедливы и для сплошного
диска (без центрального отверстия), если положить а = 0.
На рис. 10.2 в относительных координатах показаны эпюры
напряжений в диске при отсутствии напряжений натяга вга. Оба
напряжения ог и а0 являются растягивающими. Преобладающими
являются окружные напряжения, принимающие наибольшие зна-
чения на внутреннем контуре диска (при г = а); эти значения
растут с увеличением радиуса центрального отверстия, т. е. с уве-
личением отношения а/b. При а ~ Ь, т. е. в случае очень тонкого
кольца, окружные напряжения принимают максимально возмож-
ные значения
^0тах = = Р^окр» (10.2)
где 1?оКр = до — окружная скорость диска.
Отсюда следует приближенная верхняя оценка допустимой ок-
ружной скорости
[ц>кр] < (10-3)
где [а] — допускаемое напряжение.
Результаты многочисленных экспериментов (ссылка на них да-
ется в [26, с. 115]) показывают, что при оценке прочности дисков
целесообразно использовать запас прочности по напряжениям вида
= qb / атах> (Ю.4)
где ов — предел прочности материала; отах — максимальное на-
пряжение в диске.
Допустимая величина kG обычно регламентируется в пределах
1,3 - 1,8. Заметим, что здесь используется гипотеза прочности по
наибольшим нормальным напряжениям; вместе с тем могут ис-
пользоваться и другие гипотезы.
186
Если диск посажен на вал с радиальным натягом и требует-
ся, чтобы при вращении он не был меньше заданного значения 8а,
то должно выполняться условие совместности деформаций дис-
ка и вала
ид(а)-ыв(а) = 5а,
(10.5)
где ид(а) и ив(а) — радиальные перемещения диска и вала под
действием посадки и центробежных сил.
Если пренебречь деформацией вала, то связь между выборкой
натяга и частотой вращения, как это следует из (10.1), определяет-
ся соотношением
8
- Р0^2
4£
(10.6)
Данное соотношение дает нижнюю оценку частоты вращения,
при которой натяг исчезает полностью, известную как освобождаю-
щее число оборотов. При более точных расчетах следует использо-
вать уравнение (10.5).
10.3. СТРАХОВОЧНЫЕ ПОДШИПНИКИ
Страховочные (аварийные) подшипники служат для
обеспечения надежного выбега ротора при аварийном отказе маг-
нитного подвеса. Это могут быть как подшипники качения, так
и фрикционные подшипники с бронзовыми, графитовыми или теф-
лоновыми вкладышами. Во многих случаях использование смазки
в них не допускается.
Надежных методов расчета страховочных подшипников до на-
стоящего времени не выработано. Причиной этого, в первую оче-
редь, является сложность описания и моделирования физических
процессов взаимодействия вращающихся и неподвижных элемен-
тов подшипника в условиях отсутствия смазочных материалов
и сравнительно больших радиальных зазоров между цилиндричес-
кими поверхностями. Опубликованные экспериментальные резуль-
таты малоинформативны из-за отсутствия должного критерия на-
дежности таких подшипников и к тому же малочисленны из-за
дороговизны экспериментов. Поэтому в данном параграфе ограни-
чимся кратким анализом динамических эффектов в страховочных
подшипниках.
В зависимости от типа подшипника различают два вида взаи-
модействия цилиндрических поверхностей: подвижная поверх-
ность скользит относительно неподвижной в режиме сухого тре-
ния (рис. 10.3, а) и через подшипник качения (рис.10.3, б).
187
Рис. 10.3. Взаимодейстие поверхностей в страховочных подшипниках: а —
в режиме сухого трения; б — через подшипник качения
Динамика роторов при взаимодействии поверхностей в режиме
сухого трения исследовалась в работах [4, 28, 29, 99]. Из этих
работ следует, что при таком взаимодействии возможно возникно-
вение отрывных (ударных) и безотрывных (маятниковых и обкат-
ных) динамических режимов. Наиболее опасным является режим
обката. Механизм его возникновения следующий [29]. Ротор, вой-
дя в соприкосновение с подшипником, под действием сил сухого
трения начинает прецессировать с возрастающей скоростью в сто-
рону, противоположную вращению, скользя по поверхности под-
шипника. При этом движение ротора относительно неподвижной
поверхности со скоростью в точке контакта V = JR(o + 8Q (где (о —
угловая скорость вращения ротора, Q = 0 — угловая скорость пре-
цессии, R — радиус ротора, 8 — радиальный зазор) за весьма малое
время может перейти в качение без проскальзывания (обкат) по
этой поверхности, при котором V = 0. При возникшем обкате
прецессионное движение имеет скорость Qo = -Лсо/8. Нагрузка на
подшипник N = znSQ2 + mgcosG, где т — ротора, может ока-
заться недопустимо большой, поскольку R » 8. Например, для
ротора массой 50 кг, вращающегося с частотой 3000 об/мин при
R = 30 мм и 8 = 0,2 мм, имеем N ~ 2-107 Н.
При описании движения ротора рассмотрим простейший слу-
чай плоско-параллельного движения при действии силы тяжести
mg и кулоновых сил сухого трения с постоянным коэффициентом
трения Л Введем полярные координаты 8, 0 с началом в центре
подшипника О. В этом случае уравнения движения ротора в пре-
делах зазора (р < 8) имеют вид [29, 99]:
тр - mpQ2 - mg cos 0 = 0;
(Ю.7)
188
трв + 2mp0 + mgsin0 = О;
Jeb = М,
(10.8)
(10.9)
где J — осевой момент инерции ротора; М — суммарный момент
двигателя и сил сопротивления вращению.
Движение ротора может быть двух типов: с ударами о подшип-
ник и при постоянном контакте с подшипником (безотрывное).
При ударном взаимодействии скорости ротора до и после удара
связаны соотношением
р+ = -/гр - /(1 + fe)p ,
(10.10)
где 0 < k < 1 - коэффициент восстановления скорости.
Знаком минус обозначены скорости до удара, знаком плюс —
после удара.
При безотрывном движении р = 8,р = р = 0и имеют место уравнения:
N = т802 + mg с os О > 0;
т80 + mg sin 0 + fN sig nV = 0;
J(b + fRN = M.
(10.11)
(10.12)
(10.13)
В зависимости от начальных условий движения (р, р, 0, 0, со при
t = 0) и значений параметров возможны три типа движений:
ударные, обкатные и маятниковые. Последние предпочтительнее
в силу малости значений нагрузки N. Численные исследования
[99] показывают, что выход ротора на обкат происходит за весь-
ма короткое время, в течение которого скорость вращения со резко
падает, скорость прецессии Q = 0 резко возрастает и большое коли-
чество кинетической энергии ротора рассеивается в теплоту. Пос-
ле выхода ротора на обкат обе скорости практически не изменя-
ются, а рассеивание энергии прекращается из-за отсутствия про-
скальзывания в точке контакта. С уменьшением коэффициента тре-
ния f расширяется область возмущений, не приводящих к обкату.
При взаимодействии поверхностей в режиме подшипника каче-
ния (см. рис.10.3, б) характерными видами движения являются маят-
никовые и ротационные колебания ротора [67]. Рассмотрим про-
стейший случай плоскопараллельного движения неуравновешенно-
го ротора при действии силы тяжести mg и сил сопротивления
двух видов: вязкого трения с коэффициентом демпфирования h
и трения качения, которое пропорционально силе нормального дав-
ления N с коэффициентом пропорциональности X = a/R, где а —
плечо трения, R — радиус наружного кольца подшипника. Неурав-
новешенность ротора характеризуется эксцентриситетом е = О'С
центра масс С, причем пусть е « 5, где 8= ОО' — радиальный зазор
между наружным кольцом и корпусом.
189
Вводя полярные координаты р, 6 и рассматривая случай безот-
рывного движения (р = 3 = const), приходим к уравнениям движе-
ния ротора вида:
N = ти302 + mgcosB + /песо2 cos(co£ - 0) > 0; (10.14)
тпЗё + mgsinG + Л80 + kN sin0 = /песо2 cos(co/ - 0); (10.15)
Ju + fRN = М. (10.16)
Расчетные и экспериментальные исследования [67] показыва-
ют, что при имеющих место на практике сочетаниях параметров
ротор выходит на установившийся режим маятниковых колеба-
ний. Эти колебания происходят как с частотой вращения, так и с час-
тотами, дробными этой частоте (субгармонические колебания по-
рядка 1/2, 1/3, ...).
Основной резонанс имеет место на собственной частоте =(g/5)1/2.
Амплитуды перемещений при таких колебаниях на соответствую-
щих резонансах могут быть большими, однако усилия на корпус
не достигают при этом больших значений.
Очевидно, что рассмотренный выше случай плоскопараллельного
движения может реализоваться лишь при строгой симметрии ротора
и действующих на него сил. В реальных роторах условие симметрии,
как правило, не выполняется. Поэтому их движение представляет
собой суперпозицию поступательной и конической форм прецессий.
В заключение данного параграфа выразим надежду, что буду-
щие исследования позволят не только уточнить характер сил вза-
имодействия в страховочных подшипниках, но и выработать мето-
ды расчета этих подшипников.
10.4. ДАТЧИКИ
В главах 6 и 7 было показано, что в самом общем слу-
чае алгоритм управления подвесом ротора строится на основе об-
ратных связей по перемещениям, скоростям перемещений, интегра-
лам от перемещений, ускорениям, токам, углу поворота и угловой
скорости ротора. Информация о текущих значениях этих величин
может быть получена либо путем непосредственного измерения при
помощи соответствующих датчиков, либо путем вычислений.
Важнейшим элементом, от которого зависят динамические ка-
чества подвеса, являются датчики перемещений (положения) рото-
ра. Они могут быть индуктивными, индукционными (вихревыми),
емкостными и оптическими [82]. Поскольку поверхность, переме-
щение которой измеряется, совершает вращательное движение, ка-
чество выходного сигнала датчика зависит от качества этой повер-
хности. Любые отклонения геометрии поверхности от идеальной
окружности и наличие неоднородностей материала вызывают шумы
190
измерений с частотами, кратными частоте вращения. Шумы могут
также индуцироваться электромагнитными полями электродвига-
теля, электромагнитов и импульсных усилителей. Наличие шумов
измерения снижает разрешающую способность датчика, сужает ча-
стотный диапазон и уменьшает точность позиционирования оси
ротора. Вопросы фильтрации шумов измерения обсуждались в п. 6.8.
Наряду с низким уровнем шумов, датчик перемещений должен
иметь высокую чувствительность и линейную зависимость выход-
ного сигнала от измеряемого перемещения.
Измерение скоростей является более трудной задачей, чем изме-
рение перемещений. Датчик скорости может быть построен, напри-
мер, на принципе выделения зависящей от скорости ЭДС движения
из напряжения на обмотке электромагнита при поддержании по-
стоянного значения тока [это видно из структуры уравнения (5.22)].
Однако такой датчик очень чувствителен к электромагнитным
помехам и не нашел практического применения. Другие принци-
пы измерения скорости также не внедрились в практику подвесов.
Поэтому скорости перемещений не измеряются, а вычисляются либо
дифференцированием выходных сигналов датчиков перемещений,
либо с помощью наблюдателей состояния. Таким же образом вы-
числяются ускорения. Очевидно, что интеграл от перемещения вы-
числяется через операцию интегрирования. Способы измерения тока,
угла поворота и угловой скорости хорошо известны [3, 82]. Здесь
рассмотрим лишь один тип датчика перемещений — индуктивный
преобразователь с трансформаторным мостом (рис. 10.4), прове-
ренный во многих практических приложениях и детально иссле-
дованный В. Г. Мацевичем.
Функциональная схема преобразователя (рис. 10.4, а) включает
в себя генератор несущей частоты сон, трансформатор с двумя одина-
ковыми обмотками, индуктивный датчик перемещения у с двумя
диаметрально противоположно расположенными обмотками, фазочув-
ствительный выпрямитель и масштабный усилитель. Вторичные об-
мотки трансформатора и обмотки датчика образуют трансформатор-
ный мост. В центральном положении ротора (у = 0) мост сбаланси-
рован и выходное напряжение Uab = 0. В смещенном положении
ротора, как это следует из схемы замещения (рис. 10.4, б), имеем
— Zg
Unb = Е--1--,
ab Zx+Z2+2Z
(10.17)
где Е — ЭДС вторичной обмотки трансформатора; Z, Z19 Z2 —
комплексные сопротивления вторичной обмотки, первой и второй
обмоток датчика соответственно.
Несущая частота сон обычно высока (несколько килогерц), по-
этому активные сопротивления обмоток пренебрежимо малы по
сравнению с их индуктивными сопротивлениями. Кроме того, транс-
форматорный мост проектируется так, чтобы индуктивность вто-
191
I
Рис. 10.4. Индуктивный преобразователь с трансформаторным мостом: а — функ-
циональная схема; б — схема замещения; в — диаграмма выходного сигнала
ричных обмоток трансформатора была значительно меньше ин-
дуктивности обмоток датчика. При сделанных допущениях фор-
мула (10.17) принимает вид
uab = - L2)/(Lr + L2),
(10.18)
где Zq и L2 — индуктивности обмоток датчика.
Магнитная цепь датчика конструктивно ничем не отличается
от магнитной цепи радиального подшипника. Поэтому, используя
формулы (3.37) для индуктивностей радиального подшипника,
можно записать:
У
L1-Ll-a~-b—~
3 §2
п-1
; L2 = L l + a^-b^
1 4 £ ^2
2 "1 1
5 5 2
(10.19)
где, как и ранее, L — индуктивность обмоток датчика при централь-
ном положении ротора; 8 — радиальный зазор; а = 0,9; b = 0,15.
Подставив (10.19) в (10.18), получаем
192
( 9 Л
О QF
I7afr=-^- 1 + 0,15—j/. (10.20)
8 52J
Отсюда следует, что выходной сигнал моста не зависит от ин-
дуктивности обмоток датчика. Он также практически не зависит
от перемещений ротора в перпендикулярном направлении, поскольку
неравенство 0,15х2/82 « 1 справедливо даже прих = 8. Линейная
зависимость выходного сигнала от измеряемого перемещения у име-
ет место практически по всей высоте рабочего зазора (рис. 10.4, в).
Поэтому с высокой степенью точности можно записать
0.9Е 0,451Zi^td
Vab = =- 0,9 < г// 8 < 0,9, (10.21)
о о
где U1 — напряжение на первичной обмотке трансформатора;
К — коэффициент трансформации.
Ъыходной сигнал моста Uab демодулируется фазочувствитель-
ным выпрямителем и усиливается масштабным усилителем. Вно-
симые этими звеньями нелинейные искажения обычно малы, по-
этому выходной сигнал индуктивного преобразователя также яв-
ляется линейной функцией у в широком диапазоне перемещений
ротора, т. е.
Un=Cny, (10.22)
где Сп — коэффициент передачи преобразователя, зависящий от
параметров выпрямителя и усилителя.
10.5. КОМПЕНСАТОР СИНХРОННОЙ ПОМЕХИ
Как уже отмечалось в п. 7.4, на высоких частотах вра-
щения, в два-три раза превышающих собственные частоты посту-
пательных перемещений оо0 и угловых перемещений Qo, появляют-
ся проблемы подавления синхронной помехи в каналах управле-
ния радиальным подвесом. Суть явления такова. Любой ротор,
даже после самой тщательной балансировки, обладает неуравнове-
шенностью масс. Поэтому его главная центральная (продольная)
ось инерции Сз" не совпадает с геометрической осью Оз' (см. рис. 7.2);
она смещена в радиальном направлении на значение эксцентриси-
тета е = ОС (статическая неуравновешенность) и наклонена на
угол у (моментная неуравновешенность). Радиальный подвес, как
известно, стремится удержать (застабилизировать) геометрическую
(но не главную центральную) ось в заданном пространственном
положении. Однако на высоких скоростях происходит самоцент-
рирование ротора — он вращается не вокруг геометрической оси,
а вокруг главной оси инерции. Геометрическая ось при этом со-
вершает прецессионное движение с частотой вращения со в направ-
193
(10.24)
лении вращения вокруг главной оси инерции. Это движение скла-
дывается из поступательного движения по круговой траектории
радиуса е и конического вращательного движения вокруг центра
масс С с амплитудой у (см. рис. 7.11). Точки измерения на гео-
метрической оси ротора Olzn и О2т будут при этом двигаться по
круговым траекториям с соответствующими радиусами:
Р1 = е ± Чт^ Р2 = е Т W’ (10.23)
где выбор знака зависит от направления угла наклона у* Коорди-
наты точек измерения в осях х и у будут изменяться по гармони-
ческому закону
х1т = Picosort; у1т = PiSincot;
х2т = P2C0S(0*; У 2т = P2sinC0*-
Для простоты далее будем рассматривать первый подшипник
(АМП1) радиального подвеса с раздельным управлением по току
при ПД-законе управления (7.34). Формирование управляющих
токов в этом подшипнике происходит по закону:
Ч ~ ~(^1х1т + ^2^1тп)’ *2 = ~^1У1т + £2У1т)> (10.25)
где коэффициенты усиления обратных связей по перемещению gr
и скорости перемещения g2 суть соответствующие элементы диа-
гональных матриц К1Тт и К2Тт в (7.34). Гармонические переме-
щения (10.24) точки измерения О1/п вызывают гармоническую
синхронную помеху:
if = cos art - g^picosinart] = -A cos (art + P);
1% = -[£;pi sin art - g^piOJcos art] = -A sin (art + P),
где амплитуда помехи А и начальная фаза Р определяются как:
А = Рп/gi + (cog2)2; Р = arctg(a»g2 I Si)- (10.27)
Видно, что амплитуда помехи растет с увеличением скорости
вращения. При достижении некоторой скорости синхронная поме-
ха начинает насыщать усилители мощности, в результате чего подвес
теряет управляемость и, как следствие, также и устойчивость.
Способ компенсации помехи очевиден — нужно в каналы уп-
равления ввести компенсирующие сигналы:
11 = +Acos(art + Р); i2 = +Asin(art + р) (10.28)
и просуммировать их с управляющими сигналами if и i2.
Основная трудность заключается в необходимости формирова-
ния гармонических сигналов (10.28), амплитуда и фаза которых
194
Рис. 10.5. Функциональная схема компенсатора синхронной
помехи
зависит от частоты вращения ротора. Один из способов компенса-
ции описан в работе [42]. Здесь рассмотрим несколько иной прин-
цип. Функциональная схема устройства (компенсатора), реализую-
щего данный принцип, показана на рис. 10.5. Данная схема, явля-
ющаяся результатом коллективного творчества Ф. Г. Кочевина,
М. В. Афанасьева, С. В. Смирнова и С. Г. Стебихова, успешно
апробирована на практике.
Входным сигналом компенсатора служит выходной сигнал дат-
чика перемещения ротора. По достижении входным сигналом оп-
ределенной амплитуды и частоты блок слежения за амплитудой
и частотой (БС) вырабатывает команду на включение компенсато-
ра. Входной сигнал через нормирующий усилитель (НУ) подается
на фазовый детектор (ФД). Частота и фаза генератора управляе-
мого напряжения (ГУН) при помощи ФД синхронизируется с вход-
ным сигналом. Управляемый аттенюатор (УА) изменяет амплиту-
ду выходного сигнала ГУН посредством БС (выход А) в соответ-
ствии с входным сигналом.
ПРИЛОЖЕНИЯ
СТАНДАРТЫ ПСКОВСКОЙ ИНЖЕНЕРНОЙ КОМПАНИИ
НА АКТИВНЫЕ МАГНИТНЫЕ ПОДШИПНИКИ
ПРИЛОЖЕНИЕ 1. РАДИАЛЬНЫЕ ПОДШИПНИКИ
Условные обозначения:
d — диаметр цапфы;
D — наружный диаметр
статора;
I — длина пакета статора;
L — длина (осевой раз-
мер) подшипника;
t — толщина пакета цапфы;
р — число полюсов;
5 — радиальный зазор;
п — допустимая скорость
вращения;
F — несущая способность
(без принудительного ох-
лаждения обмотки);
М — масса статора.
d D 1 L t А S, 71, F, м,
мм шт. мм 103 об/мин Н кг
15 44 8 14 3 8 0,1 252 20 0,07
20 52 10 16 4 8 0,14 190 30 0,12
25 58 12 20 5 8 0,15 150 50 0,18
30 66 16 24 6 8 0,18 125 70 0,3
35 72 18 27 7 8 0,2 ПО 90 0,4
40 80 20 30 8 8 0,2 95 120 0,52
45 86 22 34 9 8 0,2 85 150 0,65
50 94 24 36 10 8 0,25 75 180 0,84
55 102 26 38 11 8 0,3 68 210 1,1
60 ПО 28 42 12 8 0,3 63 250 1,32
70 130 30 46 14 8 0,4 54 360 2
80 148 32 50 16 8 0,5 47 450 2,7
90 164 34 56 18 8 0,6 42 600 3,6
100 176 38 52 10 16 0,6 38 710 3,4
ПО 186 42 56 11 16 0,6 34 850 4,1
120 196 48 62 12 16 0,6 31 1000 5,1
140 216 54 70 13 16 0,7 28 1400 6,5
160 236 62 82 14 16 0,8 23 1800 8,4
196
ПРИЛОЖЕНИЕ 2. РАДИАЛЬНО-УПОРНЫЕ (КОНИЧЕСКИЕ)
ПОДШИПНИКИ
1. Угол конусности равен 14°, при котором = ^рад = F.
2. d — наименьший диаметр цапфы.
3. Остальные параметры те же, что и у радиального подшипника
(см. Прилож. 1).
ПРИЛОЖЕНИЕ 3. ОСЕВЫЕ ПОДШИПНИКИ
Условные обозначения:
d — внутренний диаметр электромагнита;
D — наружный диаметр электромагнита;
t — толщина наружного полюса;
8 — воздушный зазор;
L — длина (осевой размер) электромаг-
нита;
п — допустимая скорость вращения;
F — несущая способность;
М — масса электромагнита.
r t L
8
d D t 5 L п, 103 об/мин F, Н м,
мм КГ
15 30 1 0,1 12 200 35 0,02
20 40 1,5 0,15 14 150 70 0,05
25 50 2 0,2 16 120 120 0,1
32 60 2,5 0,2 16 100 176 0,15
38 70 3 0,25 18 86 250 0,23
48 80 3,5 0,25 20 75 330 0,32
54 90 4 0,3 22 66 420 0,5
60 100 4,5 0,35 24 60 520 0,62
68 110 5 0,4 26 55 640 0,8
76 120 5,5 0,45 28 50 770 1,1
84 130 6 0,5 30 46 920 1,3
92 140 6,5 0,55 32 42 1100 1,6
100 150 7 0,6 34 40 1230 2
108 160 7,5 0,6 36 38 1400 2,3
124 180 8,5 0,7 40 33 1800 3,2
197
СПИСОК ЛИТЕРАТУРЫ
1. Активные электромагнитные подшипники для крупных энергетических
машин И ВНИИЭМ. Техн. Информ. — ОАБ.149.649. — М., 1988. — С. 10.
2. Андреев В. А., Журавлев Ю. Н. Квазиоптимальное по быстродействию
управление активным магнитным подвесом // Тр. Псков, политехи, ин-та. —
1999. - № 3. - С. 226 - 232.
3. Андреев В. А., Толчеев В. Н. Цифровой измеритель динамической не-
стабильности скорости вращения механизмов // Измер. техника. — 1978. —
№ 8. — С. 63 - 64.
4. Артоболевский И. И., Костицын В. Т., Раевский Н. П. Об одном состо-
янии вала, вращающегося в подшипнике без смазки с зазором // Изв. АН
СССР. ОТН. — 1949. — № 2. — С. 168-173.
5. Барабанов А. Е., Первозванский А. А. Оптимизация по равномерно-час-
тотным показателям (Н^-теория) // Автоматика и телемеханика, — №9. —
1993. — С. 3-32.
6. Беляев Н. М. Сопротивление материалов. — М.: Наука, 1965. — С. 856.
7. Бесекерский В. А., Попов Е. П. Теория систем автоматического регули-
рования. — М.: Наука, 1975. — С. 768.
8. Бессонов П. А. Теоретические основы электротехники. — М.: Высш,
шк., 1973. — С. 752.
9. Бимс Д., Спитцер Р., Уэйд К. Роторный вакуумметр с магнитным под-
весом // Приборы для науч, исслед. — 1962. — № 2. —- С. 3 - 7.
10. Боговой В. Г., Журавлев Ю. Н., Хростицкий А. Г. Исследование дина-
мики гибкого ротора в активных магнитных подшипниках // Нелинейн.
колебания механ. систем: Тез. докл. Всесоюз. конф. — Ч. 1. — Горький: ГГУ,
1987. — С. 160-163.
11. Бойчук Л. М. Метод структурного синтеза нелинейных систем автома-
тического управления. — М.: Энергия, 1971. — С. 112.
12. Болтянский В. Г. Математические методы оптимального управления. —
М.: Наука, 1966. — С. 308.
13. Буль Б. К., Гаврилов Г. Г. Классификация устройств, использующих
принцип магнитного подвеса на постоянных магнитах и электромагни-
тах постоянного тока // Изв. вузов. Электромеханика. — 1970. — №7. —
С. 744-751.
14. Бутенин Н. В., Неймарк Ю. И., Фуфаев Н. А. Введение в теорию нели-
нейных колебаний. — М.: Наука, 1987. — С. 382.
15. Васильев А. В., Бетин В. Н., Айзеншток Г. И. Электромагнитные опо-
ры с внешней автоматической стабилизацией // Станки и инструмент. —
1985. — № 9. — С. 16-18.
16. Васильев В. С., Сердюк Г. Б. Установка с магнитной подвеской вала
для исследования моментов токоподводов приборов с подвижной системой //
Измер. техника. — 1977. — №6. — С. 56.
17. Вейнберг Д. М., Верещагин В. П., Данилов-Нитусов Н. Н. Системы
магнитного подвеса в исполнительных органах управления ориентаци-
ей космических аппаратов // Изв. АН СССР. МТТ. — 1981. — № 3. —
С. 152- 157.
18. Вибрации в технике: Справ, в 6 т. — М.: Машиностроение, 1978. —
Т. 1. — С. 352.
19. Воронков В. С. Устойчивость управляемого сверхпроводящего подвеса //
Изв. вузов. Приборостроение. — 1981. — №8. — С. 69-74.
20. Воронков В. С. Стабилизация вала в активных магнитных подшипни-
ках И Изв. АН СССР. МТТ. — 1991. - № 4. - С. 63-70.
21. Воронков В. С., Поздеев О. Д. Оптимизация системы стабилизации
магнитного подвеса // Изв. вузов. Приборостроение. — 1979. — № 9. —
С. 53- 57.
198
22. Высокоскоростной наземный транспорт с линейным приводом и маг-
нитным подвесом / Под ред. В. И. Бочарова и В. Д. Нагорского. —
М.: Транспорт, 1985. — С. 279.
23. Вышков Ю. Д. Виброзащитные свойства устройства электромагнитной
подвески // Изв. вузов. Приборостроение. — 1985. — №9. — С. 49 - 54.
24. Вышков Ю. Д., Иванов В. И. Магнитные опоры в автоматике. — М.:
Энергия, 1978. — С. 163.
25. Галкин В. И., Болыпева А. А. Радиальная магнитная стабилизация
ротора торцевого типа в рабочем поле электродвигателя // Изв. вузов. Элек-
тромеханика. — 1980. — № 1. — С. 181 - 185.
26. Демьянушко И. В., Биргер И. А. Расчет на прочность вращающихся
дисков. — М.: Машиностроение, 1978. — С. 247.
27. Грибов А. Н., Журавлев Ю. Н., Мацевич В. Г. Вибровозбудитель низко-
частотной вибрации с активной магнитной подвеской подвижной части //
Совр. пробл. совершенствования средств измерений механ. величин. — Л:
Энергоатомиздат, 1986. — С. 77-82.
28. Денисов Г. Г., Неймарк Ю. И., Поздеев О. Д. Экспериментальное иссле-
дование колебаний безопорного вращающегося вала // Динамика машин. —
М.: Машиностроение, 1969. — С. 127-138.
29. Денисов Г. Г., Неймарк Ю. И., Сандалов В. М. Об обкатке ротора
по жесткому подшипнику // Изв. АН СССР. МТТ. — 1973. — № 6. —
С. 4-13.
30. Денисов Г. Г., Кугушева Е. К. Об устойчивости вагона с магнитной
подвеской // Машиноведение. — 1987. — №4. — С. 43 - 48.
31. Диментберг Ф. М. Изгибные колебания вращающихся валов. — М.:
Изд-во АН СССР, 1959. — С. 247.
32. Журавлев Ю. Н. Электромагнитные силы в радиально-упорном кони-
ческом электромагнитном подшипнике // Электричество. — 1982. — № 11. —
С. 61 - 63.
33. Журавлев Ю. Н. Синтез системы управления активной магнитной опо-
рой с позиций обратных задач динамики // Изв. вузов. Приборостроение. —
1987. — № 5. — С. 47 - 52.
34. Журавлев Ю. Н. Синтез линейной оптимальной системы управления
магнитным подвесом жесткого ротора // Машиноведение, 1987. — № 4. —
С. 49 - 56.
35. Журавлев Ю. Н. Динамика механических систем с активными магнит-
ными опорами // Машиноведение. — 1988. — № 5. — С. 70 - 76.
36. Журавлев Ю. Н. Управление динамикой гибкого ротора в активных
магнитных подшипниках // Изв. вузов. Приборостроение. — 1988. — №6. —
С. 7-12.
37. Журавлев Ю. Н. Оптимизация силовой характеристики управляемого
подвеса гироскопического ротора // Изв. вузов. Приборостроение. — 1991. —
№ 10. — С. 68 - 72.
38. Журавлев Ю. Н., Ветлицин А. М., Хмылко Н. В. Экспериментальное
исследование электромагнитных опор для высокоскоростных роторов // Станки
и инструмент. — 1982. — №5. — С. 13 - 14.
39. Журавлев Ю. Н., Хмылко Н. В. Динамическая оптимизация линейной
системы управления активной магнитной опорой // Изв. вузов. Электроме-
ханика. — 1987. — № 12. — С. 74-81.
40. Журавлев Ю. Н., Хмылко Н. В., Хростицкий А. Г. Возмущающие мо-
менты в активном радиальном электромагнитном подшипнике // Изв. ву-
зов. Электромеханика. — 1983. — №7. — С. 82 - 88.
41. Карпов А. А., Трегубов В. А. Частотные характеристики магнитных
опор роторов электрических машин при разгоне. — М.: Моск, энергет. ин-т,
1986. — С. 12.
42. Кацнельсон О. Г., Эдельштейн А. С. Автоматические измерительные
приборы с магнитной подвеской. — М.: Энергия, 1970. — С. 216.
199
43. Квакернаак X., Сиван Р. Линейные оптимальные системы управления. —
М.: Мир, 1977. — С. 650.
44. Кельзон А. С., Журавлев Ю. Н„ Январев Н. В. Расчет и конструирова-
ние роторных машин. — Л.: Машиностроение, 1977. — С. 288.
45. Кельзон А. С., Циманский Ю. П., Яковлев В. И. Динамика роторов в упру-
гих опорах. — М.: Наука, 1982. — С. 280.
46. Козорез В. В. Динамические системы магнитно-взаимодействующих сво-
бодных тел. — Киев: Наукова думка, 1981. — С. 140.
47. Кочановский П. В., Кочетов Д. А., Лебедев В. М. Компенсация син-
хронных возмущений в магнитном подвесе ротора. — Тр. ВНИИЭМ, 1987. —
Т. 84.
48. Кочетов Д. А., Кравцова Е. В., Позняк Э. Л. Устойчивость и вынужден-
ные колебания вращающегося ротора в электромагнитном подвесе активного
типа. // Нелинейн. колебания механ. систем: Тез. докл. Всесоюз. конф. — 4.1.
Горький: ГГУ, 1987. — С. 208.
49. Крапивин В. С., Востриков А. С. К синтезу инвариантной системы ста-
билизации магнитного подвеса // Изв. вузов. Электромеханика. — 1985. —
№ 2. — С. 67 - 73.
50. Крутько П. Д., Петров Б. Н., Попов Е. П. Построение алгоритмов уп-
равления как обратная задача динамики // ДАН СССР. — 1979. — Т. 247. —
№ 5. — С. 1078-1081.
51. Кувыкин В. И. Влияние вихревых токов на силовые характеристики
магнитных подшипников с периодической структурой поля // Изв. вузов.
Электромеханика. — 1986. — № 9. — С. 11-17.
52. Кузин А. В., Вышков Ю. Д. Оптимизация управления в многокомпонент-
ной системе электромагнитной подвески // Изв. вузов. Приборостроение. —
1987. — № 11. — С. 44-49.
53. Куо Б. Теория и проектирование цифровых систем управления. — М.:
Машиностроение, 1986. — С. 447.
54. Линьков Р. В., Урман Ю. М. Влияние системы регулирования подвеса
на условие движения несбалансированного ротора неконтактного гироскопа //
Изв. АН СССР. МТТ. — 1986. — № 4. — С. 5 - 12.
55. Лурье А. И. Аналитическая механика. — М.: Физматгиз, 1961. — С. 824.
56. Лучин Г. А. Создание магнитных опор для роторов турбомашин //
Энергет. машиностроение (НИИЭинформэнергомаш). — 1982. — № 3 (2-82-03). —
С. 30.
57. Львович Ю. А. Основы теории электромеханических систем. — Л.: Изд-
во ЛГУ, 1973. — С. 196.
58. Мартыненко Ю. Г. Движение твердого тела в электрических и магнит-
ных полях. — М.: Наука, 1988. — С. 368.
59. Меркин Д. Р. Введение в теорию устойчивости движения. — М.: Наука,
1971. — С. 312.
60. Метлин В. Б. Магнитные и магнитно-гидродинамические опоры. — М.:
Энергия, 1968. — С. 190.
61. Мита Ц., Хара С., Кондо Р. Введение в цифровое управление. — М.:
Мир, 1994. — С. 256.
62. Осокин Ю. А., Станкевич Н. Н. Разработка и применение электромагнит-
ных подвесов в приборостроении // Изв. вузов. Приборостроение. — 1982. —
№ 2. — С. 56-59.
63. Первозванский А. А. Курс теории автоматического управления. — М.:
Наука, 1986. — С. 616.
64. Петров Б. Н., Крутько П. Д. Обратные задачи динамики управляемых
систем. Линейные модели // Изв. АН СССР. Техн, кибернетика. — 1980. —
№ 4. — С. 147-156.
65. Петров Б. Н., Крутько П. Д. Обратные задачи динамики управляемых
систем. Нелинейные модели // Изв. АН СССР. Техн, кибернетика. — 1980. —
№ 5. — С. 149-155.
200
66. Позняк Э. Л. Колебания роторов // Вибрации в технике. — М.: Маши-
ностроение, 1980. — Т. 3. — С. 130 - 189.
67. Позняк Э. Л., Гладышева Т. Н., Ковалев В. Б. Маятниковые колебания
несимметричного жесткого ротора в подшипниках с зазорами // Проблемы
машиностроения и надежности машин. — 1990. — № 4. — С. 33 - 40.
68. Постоянные магниты: Справ./Под ред. Ю. М. П я т и н а — М.: Энер-
гия, 1980. — С. 488.
69. Сикссмит Р. Электромагнитный подшипник // Приборы для науч,
исслед. — 1961. — № 11. — С. 30-32.
70. Сорин В. М. Устойчивость ротора в электромагнитном подвесе с уче-
том инерционности электрических цепей // Тр. ЛПИ. — 1969. — № 307. —
С. 46 - 53.
71. Тондл А. Динамика роторов турбогенераторов. — Л.: Энергия, 1971. —
С. 387.
72. Урман Ю. М. Уводящие моменты, вызванные несферичностью ротора
в подвесе с аксиально-симметричным полем // Изв. АН СССР. МТТ. — 1973. —
№ 1. — С. 24-31.
73. Филиппов А. П. Колебания деформируемых систем. — М.: Машино-
строение, 1970. — С. 736.
74. Фридман В. М. Колебания электрических машин // Вибрации в тех-
нике. — М.: Машиностроение, 1980. — Т. 3. — С. 519 - 538.
75. Фролов Б. В. Сравнительный анализ силовых электромагнитных опор //
Изв. вузов. Электромеханика. — 1985. — №2. — С. 73 - 76.
76. Харламов Б. В. Электрическая машина с магнитным подвесом ротора //
А. с. СССР № 1152067. — Бюлл. изобр. — 1985.
77. Ходжаев К. Ш. Колебания нелинейных электромеханических систем //
Вибрации в технике. — М.: Машиностроение, 1979. — Т. 2. — С. 331-347.
78. Шамриков Б. М. Основы теории цифровых систем управления. — М.:
Машиностроение, 1985. — С. 296.
79. Шаров В. С. Сверхвысокоскоростные асинхронные электродвигатели. —
М.-Л.: Госэнергоиздат, 1963. — С. 152.
80. Шереметьевский Н. Н., Данилов-Нитусов Н. Н., Вейнберг Д. М. Про-
блемы создания шарового двигателя-маховика для управления положением
космического объекта // Докл. ВЭЛК. — М., 1977. — С. 9.
81. Шмитц Н., Новотный Д. Введение в электромеханику. — М.: Энергия,
1969. — С. 336.
82. Шрамков Е. Г. Электрические измерения. — М.: Высш, шк., 1972. — С. 520.
83. Andrejev V. A. Interaction of permanent cylindrical magnets with axial
magnetization // Proc, of 4-th Int. Symp. on Magnetic Bearings. — 1994. —
Zurich. — P. 165-170.
84. Boerdijk A. H. Technical aspekts of levitation // Philips Res. Rep. — 11. —
1965. — P. 45 - 56.
85. Braunbek W. Freischwebende Korper im elektrischen und magnetischen
Feld 11 Z. fur Phisic. — 112. — 1939. — S. 753- 765.
86. Carrere F., Font S., Due G. control design of flexible rotor magnetic
bearing system // Proc, of 4-th Int. Symp. on Magnetic Bearings. — 1994. —
Zurich. — P. 65 - 70.
87. Chrisinger J. E. Magnetic suspension and balance system for wind tunnel
application // Jorn. of Roy. Aeronaut. Soc. — 67. — 1963. — P. 717-724.
88. Earnshaw S. On the nature of the molecular forces // Trans. Cambridge
phil. Soc. — 1842. — vol. 7. — P. 97-112.
89. Frictionless bearing uses magnets // Oil and Gas Jorn. — 63. — 1965. —
July 12. — P. 85.
90. Geary P. J. Magnetic and electric suspensions // BSIRA. — R314. —
London. — 1964. — P. 162.
91. Haberman H. Entwicklungsstand und Anwendungsbereich der aktiven
Magnetlager // Schmiertech. Tribol. — 1979. — 26. — №2. — S. 49 - 53.
201
92. Haberman Н.» Liard G. An active magnetic bearing system // Precis Eng. —
1980. — 2. — № 3. — P. 139 - 140.
93. Katterloher R. Magnetlager auch im Maschinenbau: Aufbau, Eigenschaften,
Anwendungen // Maschinenmarkt. — Wurzburg, 81 (1975) 19. — S. 315-317.
94. Komarov V. N. Regulating the magnetic gyroscope’s motionm// Proc, of
4-th Int. Symp. on Magnetic Bearings. — 1994. — Zurich. — P. 19 - 22.
95. Lin C. F. Advanced control systems design // PTR Prentice Hall. — 1993. —
P. 664.
96. Lyman J. Virtually zero powered magnetic bearing // IEEE. Appl. Magn.
Workshop-Milwaukee, Wise. — N.Y., 1975. — P. 1 - 15.
97. Matsumura F., Nakagawa K. Theory and Experiment of Magnetic Bearing
Combining Radial Control and Thrust Control // Trans. Inst. Elec. Eng. Jap. —
1986. — В 106. — №. 2. — P. 135 - 142.
98. Nonami K., Ito T. ц — synthesis of flexible rotor magnetic bearing
systems // Proc, of 4-th Int. Symp. on Magnetic Bearings. — 1994. — Zurich. —
P. 73 - 78.
99. Schweitzer G., Bleuler H., Traxler A. Active magnetic bearings //
Hochschulverlag AG an der ETH Zurich. — 1994. — P. 244.
100. Schweitzer G., Ulbrich Y. Magnetic bearings — a novel type of suspension //
Vibr. Rotating Mach 2-nd Int. Conf., London: Cambridge, 1980. — P. 151 -156.
101. Schob R., Bichsel J. Vector control of the bearingless motor // Proc, of
4-th Int. Symp. on Magnetic Bearings. — 1994. — Zurich. — P. 327 - 332.
102. VDI nachrichten. — Nr. 11/12. — Marz. — 1982. — S. 11-16.
103. Voronkov V. S., Denisov G. G. The effect of body’s autorotation in active
magnetic bearings // Proc, of 4-th Int. Symp. on Magnetic Bearings. — 1994. —
Zurich. — P. 339 - 342.
104. Williams R. D., Wayner P. M., Ebert J. A. Reliable, high-speed digital control
for magnetic bearings // Proc, of 4-th Int. Symp. on Magnetic Bearings. — 1994. —
Zurich. — P. 1-6.
105. Zhuravlyov Y. N. Linear-Quadratic optimal control of active magnetic
bearings for high speed rotor // Proc, of 6-th Int. Symp. on Magnetic Bearings.
USA: Cambridge, 1998. — P. 587 - 596.
106. Zhuravlyov Y. N. On LQ-Control of Magnetic Bearing // IEEE Transactions
on control systems technology. — Vol. 8. — №. 2. — March 2000. — P. 344 - 350.
ОГЛАВЛЕНИЕ
Предисловие.......................................................... 3
1. Классификация электромагнитных подвесов........................ 7
1.1. Принципы электромагнитной левитации............................. -
1.2. Электростатический подвес....................................... 8
1.3. Подвесы на постоянных магнитах. Запрет Ирншоу................... 9
1.4. Электромагнитный подвес с резонансной цепью................. 11
1.5. Активный магнитный подвес................................... 12
1.6. Индукционный подвес......................................... 13
1.7. Кондукционный подвес........................................ 14
1.8. Диамагнитный подвес......................................... 15
1.9. Сверхпроводящий подвес....................................... -
1.10. Магнитогидродинамический подвес................................ -
1.11. Электромагнитный подвес в высокоскоростном наземном транспорте 16
1.12. Выводы......................................................... 17
2. Введение в технику активных магнитных подшипников............ 18
2.1. Историческая справка......................................... -
2.2. Принцип действия............................................ 20
2.3. Конструкции подшипников..................................... 22
2.4. Технические характеристики.................................. 25
2.5. Преимущества и недостатки................................... 27
2.6. Опыт и проблемы промышленного освоения...................... 29
2.7. Примеры практических приложений............................. 30
3. Расчет радиального подшипника................................ 34
3.1. Геометрия подшипника......................................... -
3.2. Тяговое усилие............................................... -
3.3. Оптимизация геометрии....................................... 35
3.4. Расчет обмотки.............................................. 38
3.5. Тепловой расчет............................................. 39
3.6. Индуктивности подшипника.................................... 40
3.7. Особенности расчета конического подшипника.................. 43
4. Расчет осевого подшипника.................................... 46
4.1. Геометрия подшипника......................................... -
4.2. Расчет магнитной цепи........................................ -
4.3. Расчет обмотки.............................................. 47
4.4. Индуктивности подшипника.................................... 48
4.5. Учет вихревых токов......................................... 49
5. Электромагнит как объект управления.......................... 52
5.1. Схематизация подвеса одностороннего действия................. -
5.2. Магнитная энергия и коэнергия............................... 53
5.3. Магнитная сила.............................................. 54
5.4. Две формы уравнений подвеса................................. 55
5.5. Линеаризация уравнений...................................... 56
5.6. Неустойчивость объекта управления........................... 57
5.7. Уравнения подвеса двустороннего действия.................... 58
5.8. Почему нужны токи смещения.................................. 59
5.9. Магнитное смещение на постоянных магнитах. Гибридные подшип-
ники ............................................................ 61
5.10. Адекватность линейной модели подвеса....................... 62
5.11. Уравнения Лагранжа — Максвелла. Электромеханические аналоги.... -
6. Управление одностепенным магнитным подвесом.................. 64
6.1. Управление по току и напряжению.............................. -
6.2. Математические модели подвеса............................... 65
203
6.3. Синтез управлений с позиций обратных задач динамики. ПД, ПИД
и ПИ ДДТ-регуляторы................................................ 68
6.4. Синтез ЛК-оптимального управления............................. 72
Введение в ЛК-метод.......................................... 73
Оптимальное управление током................................. 74
Оптимальное управление напряжением........................... 76
Оптимальные значения параметров программного движения........ 78
6.5. Синтез нелинейных управлений.................................. 79
Минимизация потерь электроэнергии. Внешняя линеаризация....... -
Организация автоколебаний тела с помощью подвеса............. 81
Релейное управление. Скользящий режим........................ -
Оптимальное по быстродействию управление..................... 83
6.6. Оптимальное по устойчивости управление........................ 88
6.7. Адаптивное управление......................................... 90
6.8. Фильтрация шумов измерения. Наблюдатели состояния............. 93
6.9. Бездатчиковый подвес.......................................... 98
6.10. Устойчивость в малом и большом. Влияние ограниченности ресурсов
управления......................................................... 99
6.11. Передаточные функции и частотные характеристики подвеса. Час-
тота среза.........................................................103
7. Динамика жесткого ротора в активных магнитных подшипниках......106
7.1. Вводные замечания.............................................
7.2. Математическая модель.........................................107
Моделирование ротора......................................... -
Опытное определение моментов инерции.........................113
Моделирование радиальных подшипников......................... -
Учет осевого подшипника......................................114
7.3. Синтез регулятора при раздельном управлении...................115
7.4. Динамика подвеса при раздельном управлении....................118
Схематизация симметричного подвеса........................... -
Поступательные перемещения. Синхронная помеха................119
Угловые перемещения. Перманентный резонанс...................121
Несимметричный подвес........................................124
Влияние несовпадения точек измерения и управления........... 125
Устойчивость подвеса......................................... -
7.5. Синтез ЛК-оптимального регулятора. Многосвязное управление....127
7.6. Динамика подвеса при многосвязном оптимальном управлении......130
7.7. Раздельное или многосвязное управление?.......................133
7.8. Управление подвесом ротора, имеющего неодинаковые экваториаль-
ные моменты инерции................................................136
7.9. Управление подвесом ротора в конических подшипниках...........138
7.10. Взаимовоздействие подвеса и приводного электродвигателя......140
Воздействие электродвигателя на подвес.......................141
Тормозящее воздействие подвеса на привод неуравновешенного
ротора. Эффект Зоммерфельда..................................144
Магнитный подшипник в роли приводного двигателя. Эффект авто-
вращения ....................................................145
7.11. Совмещение электрической машины и магнитного подшипника. Бес-
подшипниковые машины..............................................149
8. Динамика гибкого ротора в активных магнитных подшипниках...... 154
8.1. Вводные замечания............................................. ~
8.2. Математическое описание......................................155
Короткий ротор......................................... 156
Длинный ротор.......................................... 157
204
Подшипники................................................ 158
8.3. Собственные частоты и собственные формы ротора .............. “
8.4. Стратегия управления подвесом.............................. 161
8.5. Синтез управления подвесом «твердого скелета» ротора....... 162
8.6. Дискретная модель подвеса.................................. 163
8.7. Динамический анализ ........................................165
Структура сил .............................................. -
Влияние несовпадения точек управления и измерения на устой-
чивость .........................................................166
Влияние внутреннего трения на устойчивость ................ 168
9. Цифровое управление подвесом................................. 171
9.1. Вводные замечания ........................................... -
9.2. Дискретное описание объекта ................................ 172
9.3. Неустойчивость дискретного объекта ......................... 173
9.4. Дискретное управление при полных измерениях ................ 174
Финитное управление ........................................ -
ЛК-оптимальное управление для непрерывного объекта ....... 175
ЛК-оптимальное управление для дискретного объекта ......... 176
9.5. Дискретное управление при неполных измерениях ............. 177
Дискретное дифференцирующее звено .......................... -
Дискретный наблюдатель состояния ......................... 178
9.6. Дискретное интегральное управление ........................ 180
9.7. Метод ^-преобразования ...................................... -
10. Динамические аспекты технической реализации подвесов роторов. 184
10.1. Вводные замечания .......................................... -
10.2. Прочность вращающихся элементов подвеса. Предельная окружная
скорость и освобождающее число оборотов .......................... -
10.3. Страховочные подшипники ...................................187
10.4. Датчики ................................................... 190
10.5. Компенсатор синхронной помехи ............................. 193
Приложения. Стандарты Псковской инженерной компании на активные
магнитные подшипники............................................ 196
Приложение 1. Радиальные подшипники .............................. -
Приложение 2. Радиально-упорные (конические) подшипники ......... 197
Приложение 3. Осевые подшипники .................................. -
Список литературы ............................................... 198
С О N T E N S
Preface..................................................................... 3
1. Classification of Electromagnetic Suspensions........................... 7
1.1. Princi pies of an Electromagnetic Levitation........................
1.2. Electrostatic Suspension.............................................. 8
1.3. Suspension with Permanent Magnets. Earnshaw's Theorem................. 9
1.4. Electromagnetic Suspension with a Resonance Circuit................. ц
1.5. Active Magnetic Suspension........................................... 12
1.6. Inductive Suspension................................................. 13
1.7. Conductive Suspension................................................ 14
1.8. Diamagnetic Suspension............................................... 15
1.9. Superconductive Suspension............................................ _
1.10. Magnetohydrodynamic Suspension.....................................
1.11. Electromagnetic Suspension in Transportation........................ 16
1.12. Conclusions......................................................... 17
2. Introduction to the Active Magnetic Bearing Technique.................. 18
2.1. Historical Review..................................................... _
2.2. Principle of Action.................................................. 20
2.3. Components in Bearing Systems....................................... 22
2.4. Technical Characteristics............................................ 25
2.5. Advantages and Disadvantages......................................... 27
2.6. Experience and Problems in Manufacturing and Applying................ 29
2.7. Examples from Industrial Applications................................ 30
3. Design of Radial Bearings.............................................. 34
3.1. Geometry............................................................
3.2. Carrying Force........................................................ _
3.3. Optimization of Geometry............................................. 35
3.4. Coil Design.......................................................... 38
3.5. Thermal Calculations................................................. 39
3.6. Bearing Inductances.................................................. 40
3.7. Conical Bearing Design............................................... 43
4. Design of Axial Bearings............................................... 46
4.1. Geometry.............................................................. _
4.2. Magnetic Circuit Design............................................... _
4.3. Coil Design.......................................................... 47
4.4. Bearing Inductances.................................................. 48
4.5. Eddy Currents Effect................................................. 49
5. The Electromagnet as a Controlled Actuator............................ 52
5.1. Configuration of a Suspension with One Electromagnet.................. _
5.2. Magnetic Energy and Coenergy........................................ 53
5.3. MMagnetic Force..................................................... 54
5.4. Two Form of Suspension Equations.................................... 55
5.5. Linearization of Equations.......................................... 56
5.6. Instabiliity of the Plant........................................... 57
5.7. Equations of a Saspension with Two Electromagnets................... 58
5.8. Why Bias Currents are Nesessary?.................................... 59
5.9. Permanent Magnets instead of Bias Currents. Hybriol Bearings........ 61
5.10. Adequacy of a Linear Suspension Model.............................. 62
5.11. Lagrange-Maxwell's Equations. Electromechanical Analogies.......... _
6. Control of a One-Dgree of Freedom Suspension System................... 64
6.1. Introduction. Current Control and Voltage Control................... _
6.2. Mathematical Models of the Suspension............................... 65
6.3. Control Design as an Inverse Problem of Dynamics. PD, PID and PIDDC-Controllers 68
206
6.4. Design of the LQ-Optimal Control..................................... 72
6.5. Design of Nonlinear Control.......................................... 79
6.6. Stability-Optimal Control............................................ 88
6.7. Adaptive Control..................................................... 90
6.8. Filtering of the Measurenent Noise. State Observers.................. 93
6.9. Sensor less Suspension............................................... 98
6.10. Stability in the Small and in the Large. The Effect of Current and Voltage Limi-
tatioms.................................................................... 99
6.11. Transfer Functions and Frequency Responses of the Suspension. Cutoff
Frequency................................................................. 103
7. Dynamics of a Rigid Rotor in Active Magnetic Bearings ................ 106
7.1. Preliminary Remarks..................................................
7.2. Mathematical Model.................................................. 107
7.3. Design of the Decentralized Control................................. 115
7.4. Dynamics of the Decentralized Control Suspension System............. 118
7.5. Design of the LQ-Optimal Controller. Centralized Control............ 127
7.6. Dynamics of the Centralized Optimal Control Suspension System....... 130
7.7. Decentraized or Centralized Control?................................ 133
7.8. Control Suspension System for the Rotor Having Unequal Equatorial Momebts
of Inertia................................................................ 136
7.9. Design of the Controller Bearings................................... 138
7.10. Mutual Influence Between Magnetic Bearings and a Driving Electromotor 140
7.11. Combination of an Eiectrical Machine with Magnetic Bearings........ 149
8. Dynamics of an Elastic in Active Magnetic Bearings.................... 154
8.1. Introduction......................................................... -
8.2. Mathematical Description............................................ 155
8.3. Natural Frequencies and Natural Modes of the Rotor................... -
8.4. Control Strategy for the Suspension System.......................... 161
8.5. Design of the Controller for Suspending the «Rigid Skeleton» of the Elastic
Rotor....................................................................... 162
8.6. Discrete Model of the Control Suspension System..................... 163
8.7. Dynamic Analysis...................................................... 165
9. Digital Control......................................................... 171
9.1. Preliminary Remarks.................................................... -
9.2. State Description of the Discrete-Time Suspension System.............. 172
9.3. Instability of the Discrete-Time System............................. 173
9.4. Discrete-Time Control with Complete Measurements...................... 174
9.5. Discrete-Time Control with Incomplete Measurements.................... 177
9.6. Discrete-Time Integral Control...................................... 180
9.7. z-Transformation Method................................................ -
10. Dynamic Aspects of Realisation......................................... 184
10.1. Preliminary Remarks................................................... -
10.2. Strength of High-Speed Rotors. Achievable Circumeferential Speed and
Separating Speed............................................................. -
10.3. Retainer Bearings.................................................... 187
10.4. Sensors.............................................................. 190
10.5. Compensator of Synchronous Disturbances............................ 193
Appendix: Standards of the Pskov the Engineering Company on Active Magnetic
Bearings.................................................................. 196
A 1. Radial Bearings......................................................... -
A 2. Radial-Axial (Conical) Bearings........................................ 197
A 3. Axial Bearings.......................................................... -
References.................................................................. 198
Сведения об авторе
Юрий Николаевич Журавлев
родился 16 ноября 1941 года в д. Ники-
тина Гора Хвойнинского р-на Новго-
родской обл. В 1968 г, закончил Ленин-
градский институт водного транспор-
та. В 1974 г. защитил кандидатскую
диссертацию на тему «Снижение вибро-
активности судовых роторных машин»,
в 1989 г. — докторскую диссертацию
на тему «Динамика роторов в уп-
равляемых магнитных подшипниках».
Доктор технических наук, профессор, за-
ведующий кафедрой сопротивления ма-
териалов Псковского политехническо-
го института, Заслуженный деятель
науки РФ, член-корреспондент Между-
народной академии наук высшей шко-
лы. Автор 120 научных и методических
работ. Научные интересы: динамика
и прочность машин, ротородинамика,
электромеханика, автоматическое уп-
равление, магнитная левитация.
НАУЧНО-ПРАКТИЧЕСКОЕ ИЗДАНИЕ
Журавлев Юрий Николаевич
АКТИВНЫЕ МАГНИТНЫЕ ПОДШИПНИКИ
Теория, расчет, применение
Заведующая редакцией Е. В. Шарова. Редактор М. И. Козицкая.
Переплет художника А. А Ларушкина. Технический редактор Т. М. Жилич.
Корректоры Н. В. Соловьева, 3. С. Романова. Верстка Н. В. Макаренко
ЛР № 010292 от 18. 08. 98.
Сдано в набор 11. 01. 02. Подписано в печать 31. 10. 02.
Формат издания 60 х 90 1/ie« Гарнитура SchoolBook.
Печать офсетная. Бумага офсетная. Усл. печ. л. 13.0.
Уч.-изд. л. 11,9. Тираж 1000 экз. Зак. 4117.
ФГУП «Издательство «Политехника».
191011, Санкт-Петербург, Инженерная ул., 6.
Отпечатано с готовых диапозитивов в ГП «Типография им. П. Ф. Анохина».
185005, г. Петрозаводск, ул. «Правды», 4.