(Ш
МОСКВА
ФИЗМАТЛИТ
2004

УДК 530.1
ББК 22.3
Т19
Тарасов Л. В. Закономерности окружающего мира. В 3 кн. Кн. 1.
Случайность, необходимость, вероятность. — М.: ФИЗМАТЛИТ, 2004. —
384 с. - ISBN 5-9221-0414-4.
Данная книга является достаточно популярным и в то же время строго науч-
научным развернутым введением в теорию вероятностей, включающим в себя подроб-
подробный анализ рассматриваемых проблем, широкие обобщения философского плана,
отступления исторического характера. Книга имеет четко выраженный учебный
характер; ее материал строго структурирован, построен на доказательной основе,
снабжен большим количеством графиков и схем; приведено значительное количество
оригинальных задач, из которых часть разбирается в книге, а часть предлагается
читателю для самостоятельного решения. Книга представляет собой законченный
труд и при этом является первой книгой трехтомника автора с общим названием «За-
«Закономерности окружающего мира» (первая книга: «Случайность, необходимость,
вероятность»; вторая книга: «Постижение мира через вероятность», третья книга:
«Эволюция естественно-научного знания»).
Для школьников старших классов (начиная с 7-го), а также студентов технику-
техникумов и высших учебных заведений.
© ФИЗМАТЛИТ, 2004
ISBN 5-9221-0414-4	© Л. В. Тарасов, 2004

Л.В. Тарасов
СЛУЧАЙНОСТЬ,
НЕОБХОДИМОСТЬ,
ВЕРОЯТНОСТЬ

Книга первая

Оглавление
Вступительный диалог автора с читателем...
ТЕМА 1. СЛУЧАЙНЫЕ СОБЫТИЯ: ПРОТИВ И ЗА	13
1.1	Случайное событие, или, проще говоря, случайность	13
1.2	Как люди привыкли относиться к случайному?	17
1.3	Случайность под маской необходимости	19
1.4	Каково современное отношение к случайному?	21
1.5	Диалог о причинности и случайностях (как субъективных, так
и объективных)	22
1.6	Уникальность как следствие случайности	25
1.7	Случайности неуправляемы, но могут быть предсказуемыми	27
ТЕМА 2. ПОРЯДОК И БЕСПОРЯДОК	30
2.1	Мифы о борьбе Космоса и Хаоса	30
2.2	Абсолютный беспорядок и абсолютный порядок — две нелепые
крайности	35
2.3	Беседа, посвященная переходам от порядка к беспорядку	40
2.4	Первая беседа, посвященная переходам от беспорядка к порядку:
современные представления о «Сотворении Мира»	43
2.5	Вторая беседа, посвященная переходам от беспорядка к порядку:
рождение информации из шума	47
2.6	Единство двух противоположностей	51
ТЕМА 3. ЛЕВОЕ И ПРАВОЕ	54
3.1	Объект и его зазеркальный двойник	54
3.2	Зеркально симметричные объекты	58
3.3	Энантиоморфы. Лево-правая асимметрия (киральность)	59
3.4	Лево-правая асимметрия и жизнь	62
ТЕМА 4. СИММЕТРИЯ И АСИММЕТРИЯ	66
4.1	Геометрическая симметрия	66
4.2	Геометрическая симметрия в природе	78
4.3	Обобщение понятия симметрии	83
4.4	Прежний и современный взгляд на симметрию	86
4.5	Симметрия (порядок) и асимметрия (беспорядок)	89
4.6	Что такое красота? (Размышления о симметрии и асимметрии
в искусстве)	92

ТЕМА 5. ПЕРЕСТАНОВКИ, СОЧЕТАНИЯ И ШАНСЫ	97
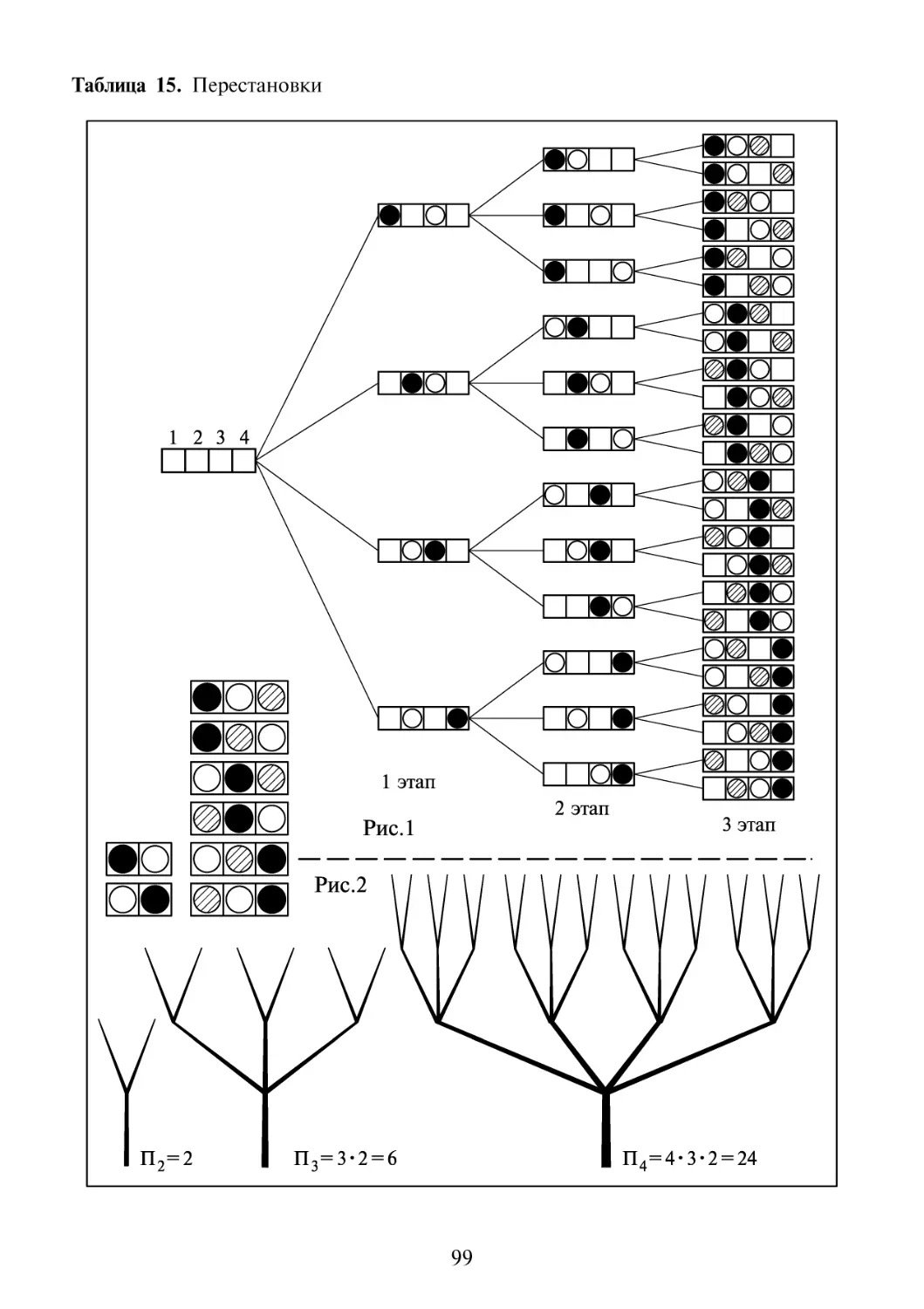
5.1	Перестановки	97
5.2	Сочетания (выборки)	102
5.3	Формула для подсчета числа сочетаний	107
5.4	Сочетания и треугольник Паскаля	109
5.5	Треугольник Паскаля, доска Гальтона, монетки...	111
5.6	Давайте сравним шансы!	115
ТЕМА 6. ПЕРВОЕ ЗНАКОМСТВО С ВЕРОЯТНОСТЬЮ	119
6.1	Классическое определение вероятности события	120
6.2	Вероятность и шансы	126
6.3	Для всякого ли события с неоднозначным исходом можно
подсчитать вероятность?	127
6.4	Тренировочные задачи с использованием классического
определения вероятности	131
6.5	Знаменитая ошибка Д'Аламбера и ее «близнецы»	135
6.6	Пространство элементарных исходов для данного типа
однородных испытаний и подсчет вероятности события	138
6.7	Одинаковы ли шансы выпадения 11 очков и 12 очков
при трех бросаниях игральной кости?	143
6.8	Геометрическое определение вероятности	145
6.9	Задача о встрече	148
ТЕМА 7. ЧАСТОТА И ВЕРОЯТНОСТЬ	156
7.1	Статистическая устойчивость частот появления
случайного события	157
7.2	Диалог: Как объяснить феномен статистической устойчивости
частот?	162
7.3	Как можно получить так называемую «таблицу случайных чисел»? 166
7.4	Таблица случайных чисел — наглядное доказательство
существования порядка в хаосе	172
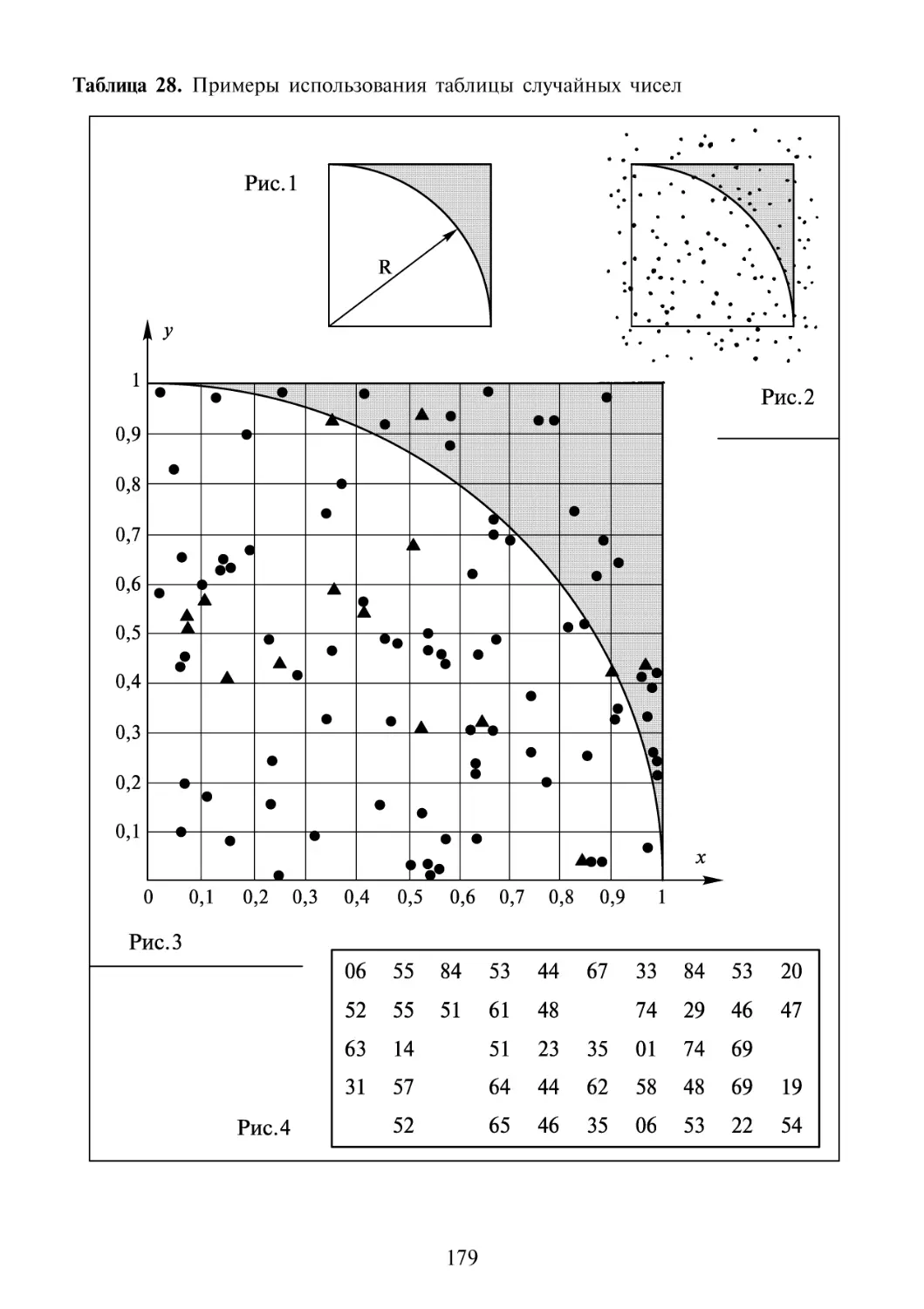
7.5	Воспользуемся таблицей случайных чисел!	176
7.6	Диалог: Что практически дает нам подсчет вероятности
случайного события?	183
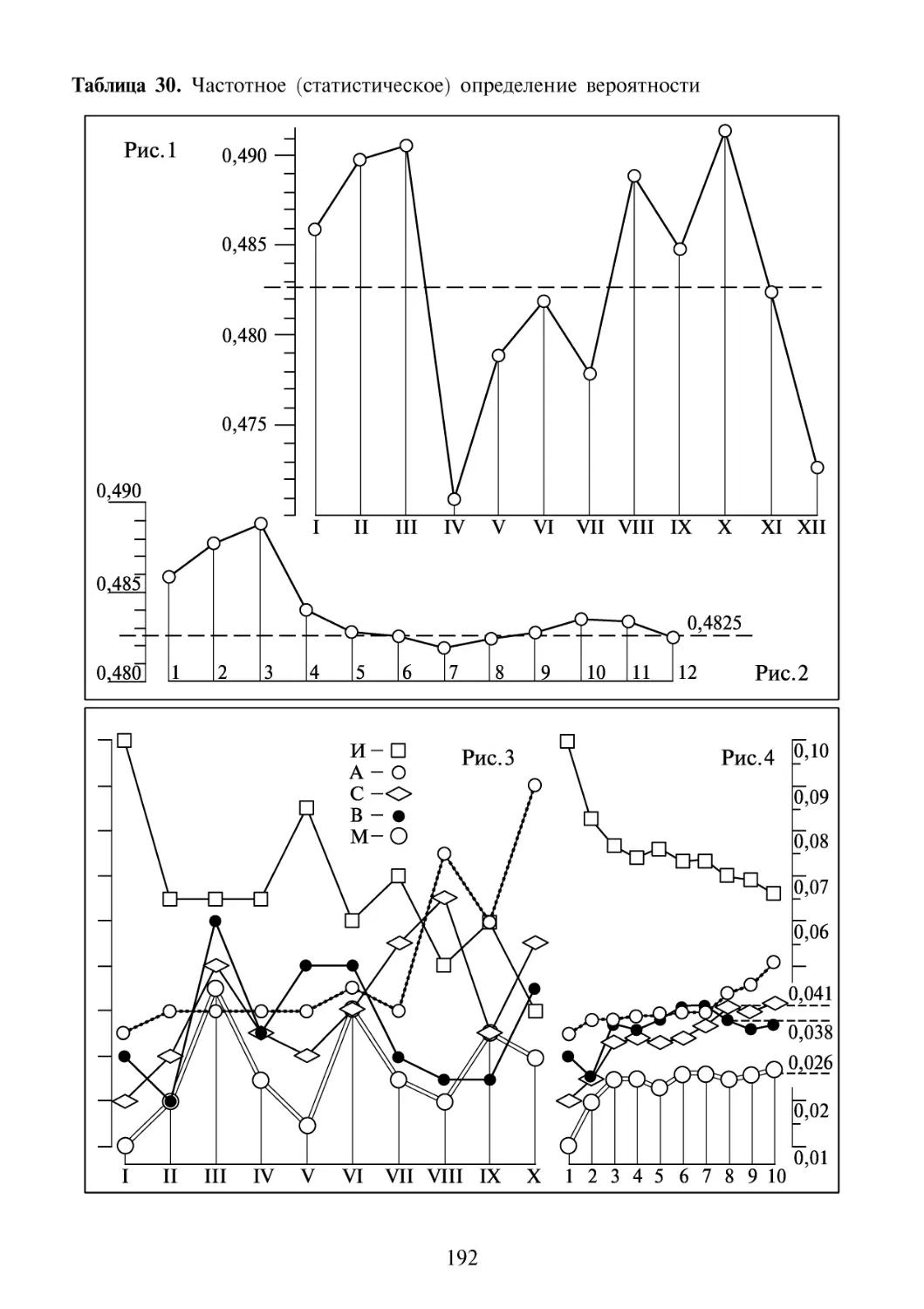
7.7	Частотное (статистическое) определение вероятности	189
7.8	Диалог об определении вероятности, предложенном
Рихардом Мизесом	194
ТЕМА 8. АЛГЕБРА СОБЫТИЙ	201
8.1	Событие как множество, элементами которого являются
элементарные исходы...	202
8.2	Несовместные и совместные события	205

8.3	Пересечение и объединение событий	206
8.4	Беседа о необходимости и достаточности	209
8.5	Законы алгебры событий	212
8.6	Диаграммы Эйлера-Венна	216
ТЕМА 9. АЛГЕБРА СОБЫТИЙ
И ОСНОВНЫЕ ПРАВИЛА ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТЕЙ	222
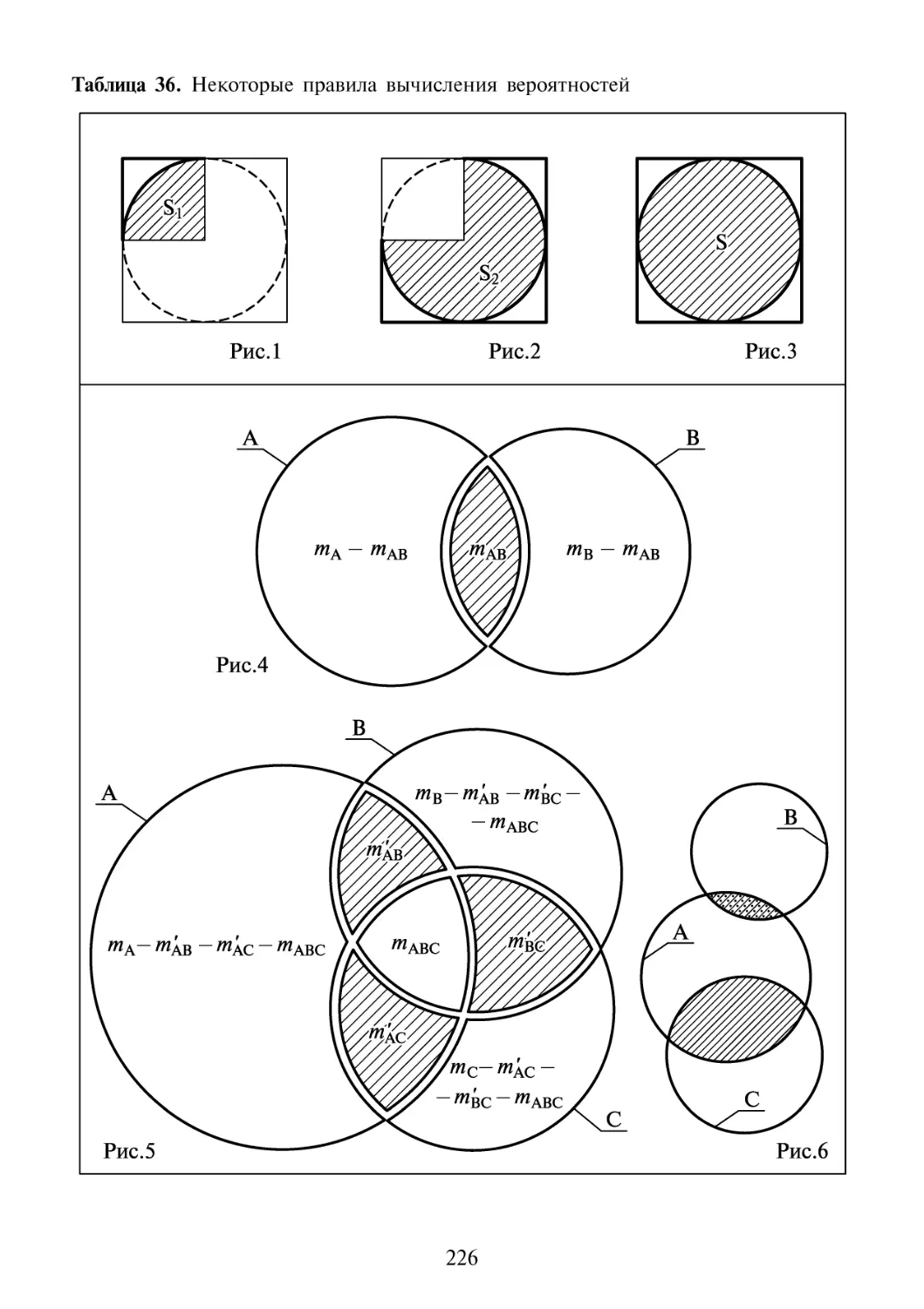
9.1	Правило сложения вероятностей несовместных событий	222
9.2	Правило вычисления вероятности объединения
двух совместных событий	227
9.3	Правило вычисления вероятности объединения
трех совместных событий	229
9.4	Условная вероятность	230
9.5	Независимые и зависимые совместные события. Правила
вычисления вероятности пересечения двух совместных событий
(вероятности совместного наступления двух событий)	239
9.6	Правила вычисления вероятности совместного наступления
трех и более событий. События, независимые в совокупности	245
9.7	Повезет или не повезет мне с зачетом?
(Размышления одного студента)	251
9.8	Тренировочные задачи с вычислением вероятности
совместного наступления событий, независимых в совокупности	253
9.9	Вероятностные задачи-сказки с лабиринтами	256
9.10	Правило вычисления вероятности наступления хотя бы
одного из совокупности независимых событий	264
ТЕМА 10. ПОЛНАЯ ВЕРОЯТНОСТЬ И ВЕРОЯТНОСТИ ГИПОТЕЗ 270
10.1	Полная группа событий	270
10.2	Формула полной вероятности	274
10.3	Пример вероятностной задачи из семеноведения	276
10.4	Зависит ли вероятность вытянуть благоприятный жребий
от очередности участников жеребьевки?	277
10.5	Правила вычисления апостериорных вероятностей гипотез
(формулы Байеса)	284
10.6	Практический смысл вычислений апостериорных вероятностей
гипотез	288
10.7	Беседа с «персоналистом» о вероятностях вообще
и о Формулах Байеса в частности	292
ТЕМА 11. ПОВТОРЕНИЕ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
С ДВУМЯ ИСХОДАМИ (математическая схема Бернулли)	300
11.1	Испытания Бернулли — независимые испытания с двумя исходами 300
11.2	Формула Бернулли для вычисления биномиальных вероятностей	303

11.3	Доказательство двух соотношений с биномиальными вероятностями 307
11.4	Математическое ожидание «успеха». Среднее число «успехов»	309
11.5	Наиболее вероятное число «успехов»	311
11.6	Биномиальный закон распределения вероятностей	315
11.7	Закон больших чисел в форме Бернулли	316
11.8	Приближенный подсчет биномиальных вероятностей,
предложенный Абрахамом Муавром и Пьером Лапласом	320
11.9	Какова вероятность того, что при бросаниях кубика частота
выпадения единицы отклонится от 1 /6 более, чем на 0,01?	327
11.10	Беседа о предельной теореме Пуассона или, иначе говоря,
о законе редких событий	328
11.11	Выгодно ли заниматься страхованием?	335
Задания по теме 11	336
ТЕМА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ	339
12.1	Случайные события и случайные величины	340
12.2	Закон распределения дискретной случайной величины	345
12.3	Три распределения дискретных случайных величин:
биномиальное, пуассоновское, геометрическое	348
12.4	Математическое ожидание дискретной случайной величины	353
12.5	Свойства математического ожидания	355
12.6	Дисперсия и среднее квадратичное отклонение дискретной
случайной величины	359
12.7	Свойства дисперсии	363
12.8	Неравенство Чебышёва и «правило трех сигм»	364
12.9	Среднее арифметическое независимых случайных величин
и закон больших чисел	366
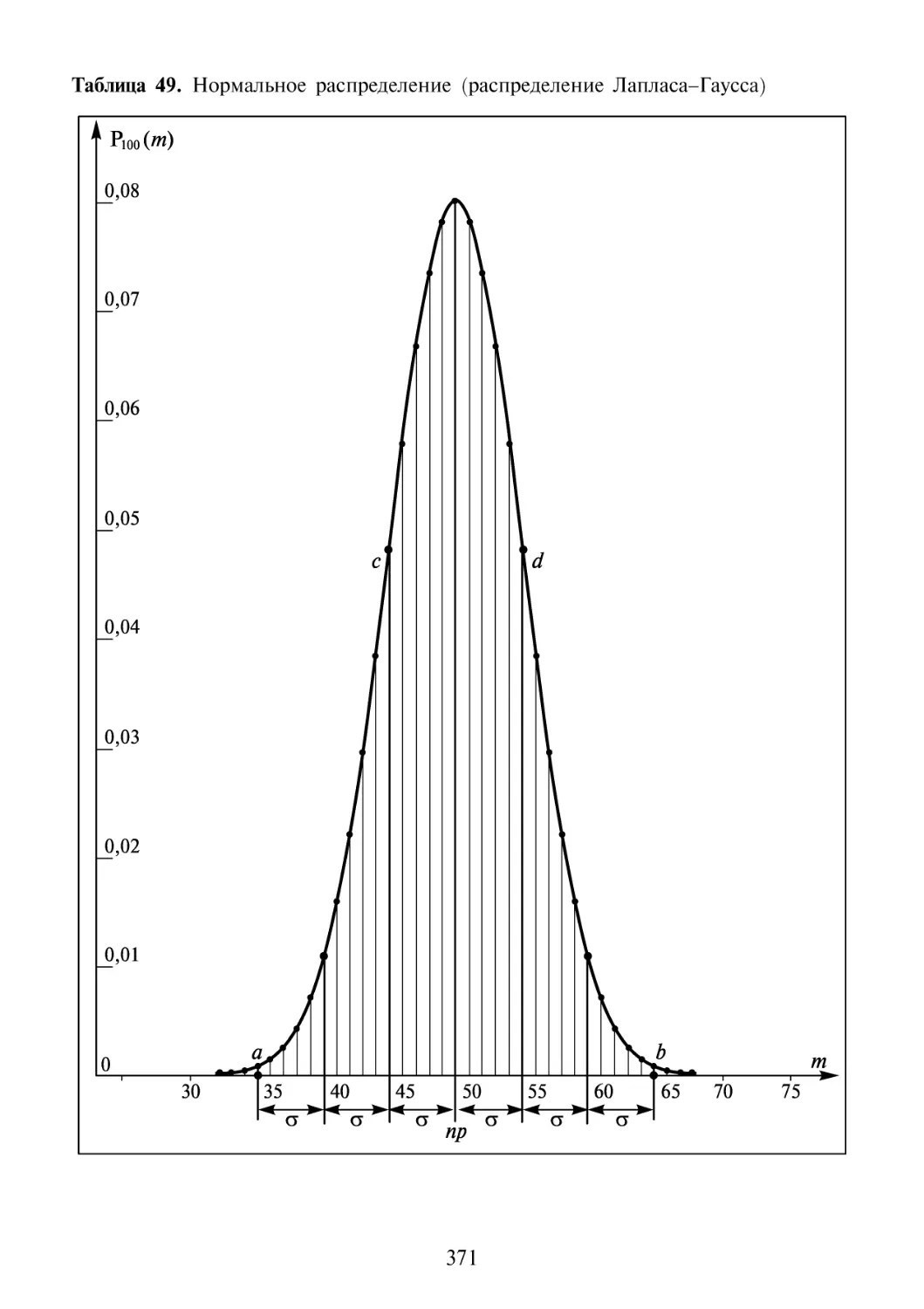
12.10	Нормальное распределение и центральная предельная теорема	370
12.11	У дискретной случайной величины вероятность, а у непрерывной
случайной величины — плотность вероятности	374
Заключительный диалог автора с читателем: необходимо продолжение
разговора	380
Список литературы	383

Вступительный диалог автора
с читателем...
«Мы можем сказать, что вечная загад-
загадка мира — это его познаваемость... Сам
факт этой познаваемости представляется
чудом».
А. Эйнштейн
(«Физика и реальность»)
. Насколько все-таки необъятен и многолик окружающий
нас мир! Он включает в себя и микроструктуры атомов и молекул, и
гигантские структуры звездных систем и галактик. И сколько же удиви-
удивительных событий происходит вокруг нас! Делится живая клетка, раскры-
раскрывается зеленый лист, пробивается из земли росток, извергается гейзер,
просыпается вулкан, вспыхивает полярное сияние, гусеница оборачива-
оборачивается бабочкой, облако превращается в грозовую тучу, водная гладь по-
покрывается ледяным панцирем... Всего не перечислить. И все это — окру-
окружающий нас мир, наша природа. Красивая и страшная, спокойная
и буйная, добрая и злая. Наверное, нет ничего удивительнее ее.
Пвтор. Природа, конечно, необъятна и удивительна. Но, пожалуй,
есть нечто еще более удивительное. Великий ученый ХХ-го столетия.
Альберт Эйнштейн A879-1955) утверждал, что самое большое чудо,
действительно достойное удивления, — это способность нашего разума
познавать природу, способность понимать ее «язык» — «язык» тех об-
образов, которые мы воспринимаем нашими органами чувств. Как заме-
заметил известный французский поэт Шарль Бодлер A821-1867),
Природа — некий храм, где от живых колонн
Обрывки смутных фраз исходят временами.
Как в чаще символов мы бродим в этом храме,
И взглядом родственным глядит на смертных он...
Можно сказать, что задача науки как раз и состоит в том, чтобы
услышать и понять эти «обрывки смутных фраз». И тот факт, что это
удается делать, есть, по мысли Эйнштейна, великое чудо.

. Вы хотите сказать, что окружающий нас мир удивителен,
но еще более удивительно то, что нам, людям, удается раскрывать зако-
закономерности этого мира?
Пвтор. Да, это так. Хотя глагол «раскрывать» тут не вполне подхо-
подходит. Поэты любят говорить о неких «тайнах природы», «тайнах бытия».
Во все века жила, затаена,
Надежда — вскрыть все таинства природы...
Валерий Брюсов
A873-1924)
Повсюду прелести, везде живые краски.
Для всех природы длань исполнена даров.
Зачем же, к красоте бесчувственно суров.
Ты ищешь тайн ее и жаждешь их огласки?
Владимир Бенедиктов
A807 -1873)
В моей душе тревожное волненье:
Напрасно вопрошал природу взором я.
Она молчит в глубоком усыпленьи —
И грустно стало мне, что ни одно творенье
Не в силах знать о тайнах бытия...
Иван Тургенев
A818-1883)
Строго говоря, мы, люди, исследующие природу, не вскрываем ее
«таинств», не раскрываем зашифрованных кем-то закономерностей,
так называемых «тайн бытия». Мы переводим поступающие к нам из-
извне чувственные образы на язык научных понятий, которые мы сами же
и формулируем. И мы устанавливаем соотношения между этими поня-
понятиями. И вот эти-то соотношения и представляют собой закономернос-
закономерности окружающего мира. Коротко говоря, мы не раскрываем, а формули-
формулируем (конструируем) закономерности окружающего мира.
tCcufUuiie**. Мы наблюдаем обширный мир природных объектов и
явлений. Но как от наблюдения перейти к конструированию тех зако-
закономерностей, которые позволили бы осмыслить этот мир?
Пвтор. Процесс научного познания мира в двух словах не объяс-
объяснишь. Для начала отмечу лишь, что очень важно выявлять взаимозави-
взаимозависимости объектов и взаимосвязи явлений. Без этого принципиально не-
невозможно сконструировать естественнонаучную картину мира. Великий
немецкий поэт и мыслитель Тёте A749-1832) остерегал некоторых ес-
естествоиспытателей:
10

Во всем подслушать жизнь стремясь,
Спешат явленья обездушить,
Забыв, что если в них нарушить
Одушевляющую связь,
То больше нечего и слушать.
. А на чем основывается уверенность, что устанавливае-
устанавливаемые нами соотношения между придуманными нами же понятиями в
самое деле отражают суть природных явлений? Иными словами, как
мы можем судить о том, что правильно отразили в сконструированных
нами закономерностях «язык» природы, правильно истолковали «об-
«обрывки смутных фраз», не нарушили «одушевляющую связь» явлений?
Пвтор. Иначе говоря, как можно судить о том, что конструируемая
нами естественнонаучная картина мира адекватна реальному миру]
*Чипиипель. Да, именно в этом мой вопрос. Я понимаю, что есте-
естественнонаучная картина мира конструируется постепенно, на протяже-
протяжении веков. Постижение природы — долгий процесс. Однако, наверное,
как-то можно судить о том, что этот процесс идет в правильном на-
направлении?
Пвтор. Вопрос этот не простой. Тут следовало бы о многом сказать.
Но пока ограничимся самым общим ответом. Дело в том, что закономер-
закономерности конструируемой нами картины мира позволяют делать предсказа-
предсказания. А предсказания можно проверять практикой. По результатам таких
проверок можно судить о том, насколько точно и полно нам удается
познать реальный мир в рамках той или иной естественнонаучной кар-
картины. Так, используя законы классической механики, сконструирован-
сконструированные в свое время Ньютоном, можно предсказывать, как будет двигаться
космический корабль в околоземном пространстве, куда упадет брошен-
брошенный под углом к горизонту камень, как будет колебаться маятник.
*Чипиинель. Ну конечно же! И как это я сам не сообразил? Ведь раз-
различные закономерности окружающего мира позволяют делать строго
определенные предсказания, дают возможность вычислять те или иные
величины!
Пвтор. Что Вы имеете в виду, говоря о строго определенных предска-
предсказаниях?
'Чийиийел*. Я имею в виду, что закономерности научной картины
позволяют, в принципе, точно предсказывать результаты тех или иных
событий или процессов. Естественные науки — это точные науки. Они
основаны на математических расчетах!
Пвтор. Однако далеко не всякие закономерности позволяют делать точ-
точные (однозначные) предсказания. Существуют два типа закономерностей.
11

Одни в самом деле позволяют делать однозначные предсказания, тогда
как на основе других делаются предсказания не однозначные, а всего лишь
вероятные. Закономерности первого типа называют динамическими, а
второго типа — статистическими или вероятностными. Разделение природ-
природных закономерностей на два указанных типа было введено в 60-х го-
годах XIX-го столетия знаменитым английским физиком Джеймсом Макс-
велом A831-1879). В докладе Кембриджскому философскому обществу
он заявил: «Я считаю, что наиболее важное значение для развития на-
наших методов мышления молекулярные теории имеют по той причине,
что заставляют делать различие между двумя типами познания, кото-
которые можно назвать динамическим и статистическим».
'Читснкель. А нельзя ли привести пример статистических законо-
закономерностей? Мне, признаться, не доводилось встречаться с закономер-
закономерностями, описывающими события, которые нельзя точно предсказать.
Пвтор. С ними совсем нетрудно встретиться. Возьмем монетку и нач-
начнем ее подбрасывать. Каждое бросание монетки — это событие, результат
которого заранее предсказать нельзя. Мы не можем предсказать, как упадет
монетка в том или ином случае — орлом или решкой. Однако можно
утверждать (иными словами, можно предсказать), что, если подбросить
монетку достаточно много раз, то примерно в половине случаев выпадет
орел, а в половине случаев решка. Эту закономерность можно проверить
на практике, подбросив монетку, скажем, пятьсот раз. Вот простой и на-
наглядный пример статистической закономерности.
'Чиниинель. Но выпадение того или иного результата при подбрасы-
подбрасывании монетки — это же событие случайное!
Пвтор. Да, случайное. Ну и что же?
'ЪиАаАелй. Я не думал, что случайные события могут описываться
какими-то закономерностями. Случайность как-то не согласуется с за-
закономерностями!
Пвтор. Это только на первый взгляд не согласуется. А между тем
статистические закономерности описывают именно случайные собы-
события и процессы. Причем, как доказано наукой ХХ-го столетия, именно
статистические (а не динамические!) закономерности более адекватно
отражают реальный мир. Именно на языке теории вероятностей более
внятно прочитываются «обрывки смутных фраз» и более четко обнару-
обнаруживается «одушевляющая связь» явлений.
. Признаться, в это трудно поверить.
Пвтор. А никто и не предлагает поверить. Наука, как известно, ос-
основывается не на вере, а на доказательствах. Будем во всем этом посте-
постепенно разбираться. И начнем с обсуждения того, что такое случайность
и что такое необходимость и как они соотносятся друг с другом.
12

ТЕМА 1
СЛУЧАЙНЫЕ СОБЫТИЯ:
ПРОТИВ И ЗА
Случай играет в мире столь большую
роль, что обыкновенно я стараюсь отвес-
отвести ему как можно меньше места в уве-
уверенности, что и без моей помощи он по-
позаботится о себе.
Александр Дюма
A802-1870)
1.1 Случайное событие,
или, проще говоря, случайность
Мы
живем в мире, где на каждом шагу происходят случайные
события. Случайности осаждают нас со всех сторон. Случайная встре-
встреча, случайная находка, случайная поломка, случайная ошибка, слу-
случайная потеря, случайное открытие — перечень случайностей можно
было бы продолжить дальше.
13

Что такое случайность? Какие события называют случайными?
Сходу напрашивается ответ: случайное событие — это такое собы-
событие, которое произошло неожиданно. Вот я отправился по своим делам, и
вдруг произошла встреча, которой я не ожидал, или, например, мне
посчастливилось случайно выиграть в лотерее. Никто не ожидал, что
вдруг перегорит лампочка или вдруг выйдет из строя холодильник. Кто-
то случайно допустил ошибку в важных расчетах. А кому-то случайно
пришла в голову мысль, которая позволяет устранить эту ошибку. Слу-
Случайность может оказаться смешной. Рабочий, ремонтирующий крышу
дома, случайно уронил вниз свои очки, а по улице проходил мужчина в
шляпе, и очки случайно оказались как раз на шляпе. Всем было смеш-
смешно. Но случайность может быть совсем не смешной. Вот огромный лай-
лайнер «Титаник» отправился в апреле 1912 года в свое первое плавание
через Атлантический океан и случайно столкнулся с айсбергом. И про-
произошла трагическая случайность — «Титаник» затонул, полторы тысячи
человек погибли.
Конечно, никто не ожидал (даже не предполагал), что «Титаник»
может затонуть. Полной неожиданностью для всех было падение оч-
очков с крыши дома прямо на шляпу прохожего. Но можно ли считать
неожиданным выигрыш в лотерее? Ведь если бы не было ожидания выиг-
выигрыша (надежды на выигрыш), то стоило ли играть в лотерее? Известный
чеховский «человек в футляре» постоянно пребывал в ожидании вся-
всяческих неожиданных неприятностей.
А может быть, лучше говорить не о неожиданности случайного
события, а о его непредсказуемости! Может быть, надо считать слу-
случайным такое событие, которое нельзя заранее предсказать! Однако
и тут не все ладно. Тут надо сначала выяснить, что именно понимается
под словом «предсказать». Неожиданную встречу все-таки можно было,
наверное, предсказать с какой-то долей уверенности. И выигрыш в ло-
лотерее тоже можно было в какой-то мере предсказать. Возможность столк-
столкновения «Титаника» с айсбергом тоже можно было в какой-то степени
предвидеть. «Доля уверенности», «более или менее», «в какой-то мере» —
все это, по-видимому, нуждается в пояснениях и уточнениях.
А может быть, скажем проще: случайное событие — это такое собы-
событие, которое происходит без какой-либо причины, само по себе? Недаром
здесь так подходит слово «вдруг». Вот ни с того, ни с сего, именно вдруг
произошло событие. Потому его и называют случайным.
Однако вряд ли кто скажет, что «Титаник» затонул «ни с того, ни
с сего», без всякой причины. И лампочка перегорела в силу определен-
определенных причин. И очки свалились с крыши не сами по себе, а потому, что
14

владелец задел их рукавом. И вообще возникает сомнение: а могут ли
происходить какие-либо события без причины! Сразу скажем: сомнение
это справедливое. Таких событий и вправду не бывает. Просто мы не
всегда можем доискаться до всех причин того или иного события, а часто
вообще не интересуемся этими причинами. Но это уже наши проблемы.
Позднее мы отдельно поговорим о том, почему случайность не надо
связывать с отсутствием причин. А пока, чтобы окончательно не запу-
запутаться с понятием случайного события, рассмотрим простой пример
такого события. Это будет пример с бросанием кубика. Речь идет об иг-
игральном кубике, на гранях которого изображены цифры от 1 до 6. Это
простой и хороший пример. Он хорош тем, что здесь можно рассмот-
рассмотреть много однородных случайных событий, бросив кубик в первый
раз, во второй раз, в третий раз, в четвертый и так далее. Иначе говоря,
можно выполнить сколь угодно много однородных испытаний. Исходом
каждого испытания (каждого бросания) будет то или иное случайное
событие — выпадение той или иной грани. Исходы различных испыта-
испытаний можно, очевидно, сопоставить друг с другом.
Заметим, что в ситуации с лотереей тоже можно повторить много
испытаний — закупить много билетов. И в ситуации с перегоревшей
лампочкой тоже возможно рассмотреть много испытаний, если взять
достаточно большое количество лампочек. И даже в ситуации со слу-
случайной встречей можно устроить много испытаний. Надо опросить много
людей и узнать, у скольких сегодня произошли случайные встречи.
В принципе можно было бы рассмотреть большое число «Титаников»,
пересекающих Атлантический океан. Но это, разумеется, нереально.
А вот случайная ошибка в расчетах принципиально индивидуальна:
тут многократные испытания исключены. И удачная мысль, случайно
пришедшая кому-то в голову, тоже индивидуальна. И смешной случай
с очками, упавшими на шляпу прохожего, нельзя повторить.
Но вернемся к кубикам. Ясно, что выпадение при бросании кубика
той или иной грани нельзя точно предсказать. Например, нельзя утверж-
утверждать, что при предстоящем бросании выпадет, скажем, грань 6. Это
нельзя предсказать точно: однако можно предсказать с некоторой долей
уверенности. Более того, можно утверждать, что шестерка имеет такие
же шансы выпасть, как и пятерка, четверка, тройка, двойка, единица.
В этом можно убедиться если набраться терпения и повторить испыта-
испытания (бросания кубика) достаточно много раз. Скажем, несколько сотен
раз. Мы увидим, что количества выпавших шестерок, пятерок, четверок,
троек, двоек, единиц оказывается приблизительно одинаковым. Значит,
кое-что предсказать в данной ситуации мы все-таки можем. И, конечно,
15

выпадение той или иной конкретной грани нельзя рассматривать как
событие, которое произошло «ни с того, ни с сего». Тут был целый набор
причин — положение кубика в пальцах руки перед бросанием, харак-
характер и сила броска, высота броска, воздействие воздуха на кубик в по-
полете, свойство поверхности, на которую упал кубик, размеры и масса
кубика. Понятно, что все эти причины практически невозможно учесть
и тем более воспользоваться ими. Но кубику до этого «нет дела».
Итак, случайное событие — выпадение конкретной грани — нельзя
считать ни непредсказуемым, ни беспричинным. Так что же в таком слу-
случае позволяет утверждать, что исход бросания кубика есть случайное со-
событие? Ответ можно дать незамедлительно: это позволяет утверждать тот
факт, что выпадение конкретной грани не зависит от того, какая грань
выпала {какие грани выпали) раньше. Более того, выпадение данной грани
нисколько не влияет на исходы последующих испытаний. В последова-
последовательности случайных событий {исходов) нет связи прошлого с настоящим
и настоящего с будущим. Именно в этом и заключается принципиальная
особенность случайных событий, рассматриваемых в математике.
Точно так же выигрыш или невыигрыш данного лотерейного билета
не зависит от того, выиграл или нет другой билет. Неисправность
данной лампочки не зависит от того, какой оказалась другая лампоч-
лампочка, и моя случайная встреча не зависит от случайных встреч, которые
произошли (или не произошли) с другими людьми.
Но вернемся опять к кубикам. Будем многократно бросать кубик и
всякий раз записывать выпавшую цифру. В результате мы получим сколь
угодно длинный набор случайных цифр из единиц, двоек, троек, четверок,
пятерок, шестерок. Возможно, кто-то заявит, что он может выписать
набор случайных цифр, не выполняя бросаний кубика, а просто выбирая
наобум и записывая на бумаге разные цифры. Можно, однако, утверж-
утверждать, что в этом случае набора случайных цифр получить не удастся.
Вот наш «кто-то» начинает выписывать цифры и пишет 1. Затем он,
допустим, пишет 2. Цифру 3 он, скорее всего, не напишет. Ведь надо,
чтобы цифры были случайными, а тут наметился бы какой-то порядок.
Пусть снова будет 1. Затем пусть будет 6. Теперь, конечно, он не напи-
напишет 1 — ведь единица уже была два раза. А вот не было, например,
цифры 5. Пусть будет 5. После чего вполне можно записать 3 или, ска-
скажем, 4. Этих цифр тоже пока не было...
Стоп! Можно не продолжать. Ясно, что записываемые цифры нельзя
считать случайными. Когда рука записывала очередную цифру, голова
думала о цифрах, которые были уже написаны (или еще не были на-
написаны). Голова как бы подсказывала руке: «после 1и 2 не ставь 3»,
«довольно единиц», «еще не было пятерки» и т. д. Тут появление оче-
16

редного события оказывается зависящим от того, какие события уже
появились (или еще не появились). Поэтому говорить о математически
случайных событиях здесь не приходится.
1.2 Как люди привыкли относиться
к случайному?
v^/твет на этот вопрос вполне очевиден. Люди привыкли относиться
к случайному как к чему-то весьма нежелательному, досадному. Слу-
Случайности вносят в нашу жизнь немало дискомфорта и беспорядка, а
порой и несчастий. Они нарушают {а подчас и просто разрушают) наши
планы и создают неожиданные проблемы. Кому это может понравиться?
А потому надлежит стараться, по мере возможности, избавляться от
случайностей, уменьшать степень их воздействия на нашу жизнь. Одним
словом, случайное — наш противник, наш враг. И надо действовать, ис-
исходя из этого факта.
Однако, возможно ли случайностям противостоять! Возможно ли
избавляться от них? С древних времен у многих мыслителей не было
сомнений на этот счет. Они были уверены, что в природе все сверша-
свершается по необходимости. А все случайное в нашей жизни — исключи-
исключительно от недостатка наших знаний. Так, древнегреческий философ
Демокрит (Увек до н. э.) утверждал: «Люди сотворили себе кумир из
случая как прикрытие для присущего им недомыслия». Известный
римский оратор и писатель Цицерон A век до н. э.) заявлял: «Нет ни-
ничего более противоречащего разуму, чем случай». Ту же мысль выска-
высказывал две тысячи лет спустя известный ученый Климентий Тимирязев
A843-1920): «Что такое случай? Пустое слово, которым прикрывается
невежество, уловка ленивого ума. Разве случай существует в приро-
природе?» Итак, сама по себе природа случайностей не терпит, но они появля-
появляются в нашей жизни из-за неполноты наших знаний или, если выра-
выражаться резко, вследствие нашего недомыслия и невежества. И задача
науки, с точки зрения данной парадигмы, состоит в том, чтобы за
счет умножения наших знаний об окружающем мире постепенно сужать
область проявления случайного, стремясь в идеале к полной победе над
случайностями. Такая точка зрения приучала относиться к случайнос-
случайностям, как к чему-то непринципиальному, несущественному, второстепен-
второстепенному, досадной помехе. Как выразился поэт, «сотри случайные черты
и ты увидишь: мир прекрасен!» А в Кратком словаре по философии
17

под редакцией И. Блауберга и И. Пантина (Москва, Политиздат, 1982)
прямым текстом утверждается: «Каждое явление формируется под вли-
влиянием не только существенных, необходимых, но также случайных,
несущественных причин». Что такое «случайные черты» — это пред-
представить себе можно. Но что такое «случайные причины»? Авторы пы-
пытаются разъяснить это, используя слово «несущественные».
Такова в общих чертах ставшая давно привычной точка зрения на
случайное. На первый взгляд, она представляется разумной. Разве дос-
достижения науки и техники не позволили уверенно предсказывать мно-
многие явления, казавшиеся ранее случайными? Разве рост научных зна-
знаний не способствует устранению в человеческой практике многих
случайностей? — Все это, конечно, так, спору нет. Однако именно со-
современные научно-технические достижения показали, что случайности
в нашем мире отнюдь не являются чем-то второстепенным и несуще-
несущественным, но напротив, весьма принципиальны и связаны не только с не-
недостаточностью наших знаний (нашим «невежеством»), но и с самой
сущностью природных явлений. Все оказалось далеко не таким простым.
Впрочем люди давно догадывались об этом. Уже в одной из наиболее
древних книг — Библии — подчеркивалось: «...Не проворным достается
успешный бег, и не храбрым — победа, не мудрым — хлеб, и не у ра-
разумных богатство, и не искусным — благорасположение, но время и
случай для всех» (Екклесиаст, 9-11). В IV веке до н. э. знаменитый древ-
древнегреческий ученый Аристотель отмечал, не соглашаясь с Демокритом:
«Уничтожение случая влечет за собой нелепые последствия. Есть мно-
многое, что совершается не по необходимости, а случайно...» Еще более
решительно выступал в защиту случайного известный древнегреческий
философ Эпикур (конец IV — начало IIIвека до н.э.). Он утверждал,
что весь мир возник из случайных движений и столкновений «первона-
«первоначал» (атомов). Учению Эпикура посвящена прекрасная поэма Лукреция
Кара «О природе вещей». Там, в частности, есть такие строки:
Первоначала вещей, разумеется, вовсе невольно
Все остроумно в таком разместилися стройном порядке
И о движеньях своих не условились раньше, конечно,
Но, многократно свои положения в мире меюы,
От бесконечных времен постоянным толчкам подвергаясь,
В расположенья они, наконец, попадают, из коих
Вся совокупность вещей получилась в теперешнем виде...
Не отрицая того, что случайность может быть связана с неполнотой
наших знаний, Эпикур в то же время рассматривал случайное в качестве
основного фактора, определяющего природу вещей.
18

Надо признать, что точка зрения Эпикура не была принята совре-
современниками. Так, о ней с презрением отзывался Цицерон: «Как ни по-
подивиться тут, что находится кое-кто, убежденный, будто какие-то тела,
плотные и неделимые, носятся в пространстве, и мир получился пре-
прекрасным из-за случайных столкновений этих тел?»
История показала, что представление о случайном как основе при-
природы было не принято не только современниками Эпикура, но и мно-
многими последующими поколениями. Вплоть до ХХ-го столетия. Все это
время господствовала точка зрения, которой придерживался Демокрит.
И мы, сегодняшние жители планеты, в подавляющем большинстве
своем сознательно или интуитивно придерживаемся этой точки зрения.
Почему точка зрения Демокрита оказалась столь живучей? Возмож-
Возможно, потому, что психике человека присуще стремление к определенно-
определенности. Человек желает жить в условиях гарантированной безопасности,
уверенности, что его сегодняшнему и завтрашнему благополучию не
угрожают неведомые случайности. В глубине души человек страшится
неожиданностей. Он хочет иметь надежду на то, что возможно найти
укрытие от мира случайностей. Вели не с помощью науки, то хотя бы
с помощью каких-либо потусторонних сил. И в страхе перед угрозой
случайностей он нередко обращается за помощью к религии.
1.3 Случайность под маской необходимости
G
стремление человека избежать случайностей приводило и приводит
к тому, что многие случайные события люди стараются представить как
события отнюдь не случайные. Можно сказать, что случайность нередко
выступает под маской необходимости. При этом случайные события трак-
трактуются как кем-то специально подстроенные или как пророческие.
Во времена средневековья во всем были виноваты ведьмы. Сгорел
где-то сарай — это наколдовала ведьма. Наступила засуха — тоже на-
наколдовала ведьма. Вспыхнула эпидемия страшной болезни — и тут не
обошлось без колдовства, без злого умысла. Оставалось лишь отыскать
и наказать ведьму, после чего можно было надеяться, что впредь те или
иные неприятности не повторятся.
Усматривалась связь между рисунком линий на ладони человека и его
судьбой. Была придумана целая наука, называемая «гаданием по руке» или,
по-ученому, «хиромантией». Она рассматривала шесть основных линий на
ладони — жизни, ума, сердца, судьбы, искусства, здоровья. На основании
длины, толщины, формы этих линий делались соответствующие выводы
о данном человеке, о том, что его ожидает, чего он должен опасаться.
19

Усматривалась также связь между расположением небесных тел на
звездном небе и возможными событиями в жизни человека с учетом
времени его рождения. Усматривалась связь между появлением на небе
кометы и, например, эпидемией чумы. Подобными вопросами ведали
лжеученые, называемые астрологами.
Уместно вспомнить о приметах-суевериях. Эти приметы не имеют
ничего общего с народными приметами, связанными с предсказанием
погоды или видов на урожай. Вот случайно упал нож на пол. Оказыва-
Оказывается, тут нет ничего случайного — просто должен придти мужчина.
Перебежала дорогу черная кошка. Это тоже не просто так — жди не-
неприятностей. Встретилась женщина с пустым ведром — не будет удачи.
Вернулся за забытой вещью — пути не будет.
Какой сон мне сегодня приснится? Никто этого предсказать не мо-
может. А сон приснится такой, который связан с тем, что со мной произой-
произойдет на самом деле. Надо только уметь толковать сны, знать, что к чему.
Плакать во сне — это к радости. Потерять во сне зуб — это потерять
друга или самому заболеть. Гоняться во сне за пчелами — к прибыли.
Большой популярностью всегда пользовались всевозможные гадания.
Самые распространенные гадания — это гадания на картах и по руке. Но
можно также гадать на кофейной гуще, на бобах, на решете, в зеркале.
На Руси издавна любили гадать под новый год, на святки. В тарелку
с холодной водой выливали растопленный воск. Воск застывал, образуя
замысловатую фигуру. Ее изучали и давали ей определенное толкование.
Девушки бросали башмак через забор на улицу и смотрели: в какую сто-
сторону он будет обращен носком. В той стороне и быть замужем. Плохо,
если башмак будет лежать носком к домашним воротам: в этот год не
быть замужем. Или ставили корыто на дороге и шли к нему задом. Какая
из девушек упадет в корыто, та выйдет замуж в наступающем году. Наи-
Наиболее храбрые выходили в ночь на реку послушать в прорубь. Которой
суждено выйти замуж в этом году, та увидит своего суженого в воде.
Которой же сидеть в девках, та только услышит стук из воды.
Я плавлю мертвенное олово	Зажигаю я на святки
И с тайным страхом в воду лью.	Сине-черную свечу.
Что шлет судьба?	Без опаски, без оглядки
Шута ль веселого,	С силой темною шучу.
Собаку, гроб или змею?	Ставлю зеркало в оправе
В. Ходасевич	Из литого серебра.
Неразумный разум вправе
Ждать от нечисти добра.
С. Кузнецова
20

Не следует, однако, думать, что приметы-суеверия, толкование снов,
астрологические предсказания, гадания ушли в прошлое. Увы, это не
так. И в наше просвещенное время существуют и даже благоденствуют
гадалки, астрологи, всевозможные предсказатели. Видно, неистребима
надежда человека увернуться от случайного, заменить его чем-нибудь
определенным, хотя бы и ценой маскарада.
Но только ли в этой надежде дело? Может быть дело также в «неразум-
«неразумном разуме»? Видный венгерский математик Альфред Винер A921-1970),
большой специалист в области теории вероятностей, заметил: «Люди, сто-
стоящие на низкой ступени развития, склонны к излишней подозрительнос-
подозрительности. Какая бы беда ни приключилась с ними, они приписывают ее чьему-то
злому умыслу, даже если это лишено малейших оснований. Объясняется
это тем, что примитивные люди не знакомы с таким понятием, как слу-
случайность». Кто они — эти «примитивные люди»? По-видимому, это наши
относительно далекие предки, жившие несколько веков назад, когда мате-
математики случайного попросту не существовало. Так что их пристрастие к
гаданиям, приметам, предсказаниям можно вполне понять. Но сегодня на
дворе уже XXI-й век. Сегодня теория вероятностей буквально пронизыва-
пронизывает многие области человеческой практики. А потому интерес сегодняшнего
поколения к гадалкам и всевозможным шарлатанам-предсказателям можно
объяснить исключительно недостатками современного образования. Прихо-
Приходится признать, что оно не прилагает должных усилий к смене парадигмы
прежнего (демокритского) отношения к случайному на парадигму совре-
современного отношения к случайному.
1.4 Каково современное отношение
к случайному?
/твечая на этот отнюдь не простой вопрос, выделим пять позиций.
Первые две являются, пожалуй, наиболее важными и глубокими; наде-
надеемся, что в должной мере они прояснятся позднее. Оставшиеся три
позиции могут быть вполне разъяснены уже в настоящем параграфе.
Позиция первая. Случайное не является чем-то второстепенным и не-
несущественным. Напротив, его роль в окружающем мире исключительно
велика. Причины появления случайного разнообразны. Они обусловлены
не только недостатком наших знаний, а имеют глубокие основания, связан-
связанные с самой сущностью материи и информации. Происходящие в мире
процессы приводят как к нарастанию случайностей {переходы от порядка
к беспорядку), так и к сокращению случайностей {переходы от беспоряд-
беспорядка к порядку, рождение порядка в хаосе).
21

Позиция вторая. Случайности не только разрушают наши планы и соз-
создают проблемы, но действуют также в положительном направлении —
создают новые возможности, позволяют по-новому подойти к решению мно-
многих проблем. Это означает, что случайности могут быть для нас не только
противником, но также союзником и даже помощником. Следовательно, в
каких-то ситуациях со случайностями надо бороться, а в каких-то ситуа-
ситуациях надо случайности использовать и даже специально создавать их.
Позиция третья. При всем разнообразии случайных событий все они
имеют свои причины. Беспричинных событий не бывает. Случайность
отнюдь не отменяет причинности.
Позиция четвертая. Следствием случайностей в нашем мире является
уникальность (неповторимость) многих объектов и явлений, например,
уникальность живых организмов и, в частности, человека. В этом одно
из проявлений принципиально важной роли случайного.
Позиция пятая. При определенных условиях случайности оказыва-
оказываются предсказуемыми и поддающимися объективной оценке. И тогда с ними
работает математика, получившая первоначально название «математи-
«математика случайного», а ныне именуемая как теория вероятностей.
1.5 Диалог о причинности и случайностях
(как субъективных, так и объективных)
Насколько я понимаю, в мире не бывает событий, кото-
которые происходили бы ни с того, ни с сего, без всякой причины. Любые
события, в том числе и те, которые называются случайными, происхо-
происходят в силу каких-то причин. Не так ли?
Пвтор. Именно так. Только имейте в виду, что результаты исходов
могут определяться целым набором разнообразных воздействий; кроме
того некоторые воздействия оказываются почти неуловимыми из-за своей
малости. Вследствие исключительной сложности или малости воздей-
воздействий подчас практически невозможно выявить причины случайных
событий. Так, практически невозможно выявить все причины, которые
приводят к выпадению той или иной грани при бросании кубика. Впро-
Впрочем нет необходимости пытаться выявить эти причины. Достаточно знать,
что у каждой из шести граней имеются одинаковые шансы выпасть
и что результаты (исходы) разных испытаний (разных бросаний) совер-
совершенно не влияют друг на друга.
'Чиниикель. В данном случае меня не волнует вопрос о том, можно
или нельзя выявить причины тех или иных случайных событий и нужно
ли это делать. Я хотел бы обсудить другой вопрос.
22

Пвтор. Какой же?
"Читателе Я хотел бы обсудить принципиальный вопрос. Если у всех
случайных событий имеются какие-то причины, то, значит, можно в
принципе (пусть не на практике, а в принципе) эти причины установить.
А после этого случайное событие перестанет, очевидно, быть случайным.
Следовательно, случайность существует лишь постольку, поскольку мы
не знаем причин соответствующего события (поскольку мы не смогли
или не захотели выявить эти причины). Иначе говоря, случайность ока-
оказывается связанной только с неполнотой наших знаний (знаний о причи-
причинах данной случайности). И получается, что Демокрит по большому счету
все-таки прав. А где же случайность, связанная с «природой вещей»?
Пвтор. Различают случайность субъективную и объективную. Субъек-
Субъективная случайность связана с неполнотой наших знаний. Объективная
случайность связана с природой материи, с ее сущностью. Вы хотите
сказать, что, коль скоро все случайные события имеют какие-то причи-
причины, то все они должны рассматриваться как субъективные случайности,
т. е. по Демокриту. И возникает вопрос: а где же в таком случае объек-
объективная случайность? Существует ли она в действительности?
ь. Именно этот вопрос возникает. Он не возникал бы, если
бы существовали события, происходящие без какой-либо причины.
Именно они и были бы примерами объективной случайности.
Пвтор. Таких событий не существует, а вот объективная случайность,
тем не менее, существует. Уже говорилось, что она связана с сущностью
материи. А сущность эту составляют молекулы, атомы, элементарные час-
частицы. Значит, объективную случайность надо искать на уровне микромира.
'Чийии&ел*. Желательны конкретные примеры.
Пвтор. Для примера рассмотрим броуновское движение. Его обнаружил
в 1827 году английский ботаник Роберт Броун A773-1858). Это есть дви-
движение в воде или иной жидкости мелких крупинок под действием «бом-
«бомбардировки» их беспорядочно движущимися молекулами жидкости. Пред-
Представим такую картину. В какой-то момент крупинка испытала больше ударов
молекул справа — тогда она сделает скачок влево. В другой момент число
ударов снизу может случайно оказаться больше, чем сверху — крупинка
сделает скачок вверх. Из-за случайных ударов молекул крупинка будет
совершать случайные скачки; их можно наблюдать в микроскоп. Причина
этих случайных скачков — беспорядочное тепловое движение молекул жид-
жидкости. Бессмысленно пытаться учесть движение каждой молекулы. А зна-
значит, нельзя связывать случайные скачки броуновской крупинки с непол-
неполнотой наших знаний. Тут налицо объективная случайность.
ntutftiufU*b. С неполнотой наших знаний нельзя. Но почему не пред-
предположить, что есть некий разум, который в состоянии знать скорость
23

и положение каждой молекулы жидкости в каждый момент? Для него
не будет ничего случайного в скачках броуновской крупинки.
Пвтор. Вы повторили мысль известного французского ученого Пьера
Симона Лапласа A749-1827). Вот, что он сказал: «Ум, которому были
бы известны для каждого момента времени все силы природы и поло-
положения всех ее составных частей, если бы вдобавок он оказался доста-
достаточно обширным, чтобы подвергнуть эти данные анализу, обнял бы
в одной формуле движения величайших тел Вселенной наравне с дви-
движениями легчайших атомов. Не осталось бы ничего, что было бы для
него недостоверно, и будущее, так же как и прошедшее, предстало бы
перед его взором». Правда, в природе такого «ума» не существует.
ь. Предположим, что это какие-то инопланетяне.
Пвтор. Никакие инопланетяне не могут выявить того, чего нет в дей-
действительности. Как установила наука ХХ-го столетия, природа устрое-
устроена таким образом, что у микрообъектов (в частности у молекул) есть
либо определенное положение в пространстве (и тогда их скорость ока-
оказывается неопределенной), либо определенная скорость (и тогда их по-
положение в пространстве «размывается»). Поэтому принципиально невоз-
невозможно (даже чисто умозрительно) проследить одновременно и за
положением молекул, и за их скоростью.
Ъиниинелй. Тут мне, конечно, нечего возразить.
Пвтор. Именно на уровне микромира особенно ярко обнаруживают
случайности свою объективность (и следовательно, свою фундамен-
фундаментальность). Здесь открывается немало неожиданного для нас. Так, ока-
оказывается, что вакуум — это отнюдь не пустота, а пространство, «за-
«заполненное» случайно возникающими и исчезающими элементарными
частицами разного типа. Можно вообразить, что вакуум «заполнен» ми-
мириадами «вспышек», каждая из которых есть случайно возникшая и слу-
случайно исчезающая частица. Вследствие этого все реальные элементар-
элементарные частицы (за исключением двух — электрона и протона) оказываются
нестабильными. Они самопроизвольно превращаются в другие частицы,
причем во многих случаях эти превращения идут по разным непредска-
непредсказуемым заранее схемам.
ёЧи<9ии9се*ь. Вы сказали «самопроизвольно превращаются». Самопро-
Самопроизвольно — значит беспричинно. Частицы превращаются сами по себе?
Пвтор. Термин «самопроизвольное превращение» не вполне удачен.
Говорить о самопроизвольности можно лишь в отношении изолирован-
изолированного объекта. А элементарная частица не может быть изолированной
в принципе. Ведь она находится в вакууме, «заполненном» упомяну-
упомянутыми выше «вспышками». Разумеется, они как-то влияют на частицу.
В этом глубинная причина «самопроизвольных превращений» частиц.
24

Пожалуй, в микромире случайности в самом деле фунда-
фундаментальны. Тут все так перепуталось — концов не отыщешь. А нельзя ли
привести пример, когда фундаментальность случайного обнаруживается
в ситуациях, которые мы можем воспринимать непосредственно?
Пвтор. Таким примером может служить эволюция живых организмов.
В ее основе лежат мутации — случайные изменения в структуре генов.
Случайно возникшая мутация может усилиться многократно в процес-
процессе размножения клеток организма и оказаться доступной непосредствен-
непосредственному наблюдению. Одновременно с мутациями важную роль играет
процесс отбора организмов по степени приспособленности к условиям
внешней среды. Эволюция основывается на отборе случайных измене-
изменений генетических программ.
ntutftiufU*b. Нельзя ли пояснить, как действует отбор?
Пвтор. Вот простой пример. У некоторых орхидей цветы напоминают
самок шмелей. Они опыляются самцами шмелей, которые принимают цветы
за самок. Допустим, возникла мутация, заметно изменившая форму или
окраску цветка. Такой цветок останется неопыленным. Можно сказать,
что отбор «забраковал» мутацию, изменившую внешний вид цветка.
'ЧиФнатель. Насколько мне известно, эволюция идет в направлении
постепенного усложнения видов. Не указывает ли это на то, что лежа-
лежащие в основе эволюции мутации на самом деле не так уж случайны?
Пвтор. Эволюция идет по пути отбора более приспособленных орга-
организмов. А на этом пути иногда предпочтительна более высокая степень
организации, а иногда — наоборот. Недаром в современном мире суще-
существуют одновременно и человек, и медуза, и вирус гриппа.
"Читателе Придется мне согласиться с существованием объективной
случайности. Более того, я прихожу к заключению, что с ростом научных
знаний сокращается область случайностей субъективных, но в то же вре-
время все более и более раскрывается область случайностей объективных.
Пвтор. Вы правы. Можно сказать, что вместо того, чтобы освободить
человека от случайностей, современная наука, напротив, убедительно про-
продемонстрировала фундаментальность случайного.
1.6 Уникальность как следствие
случайности
атим внимание на одно важное обстоятельство, которое осо-
особенно убедительно говорит о фундаментальности случайного в нашем
мире. Дело в том, что обусловленная отбором случайных изменений
25

генетических программ эволюция приводит к появлению принципиально
непредсказуемых новых видов. Любой вид, возникший в природных усло-
условиях (мы сейчас не касаемся возможностей генной инженерии), принци-
принципиально случаен', поэтому он является уникальным. Если какой-то вид
исчез, то он исчез навсегда, поскольку невозможно воссоздание тех слу-
случайных факторов, которые в свое время привели к появлению данного
вида. В этой связи следует задуматься над тем, что за тысячу лет человек
истребил около 300 видов животных. Причем 200 видов были истребле-
истреблены всего за последние двести лет. Все эти виды исчезли навсегда.
Следует также задуматься и над тем, что любой конкретный организм
и, в частности, любой человек тоже уникален. Это тоже есть следствие
случайности — случайности появления на свет любого организма.
Подумать только: сколько моих предков (далеких и очень далеких)
сумели в свое время увернуться от бивня мамонта, от стрелы или пули,
уцелеть в оледенениях, потопах, пожарах, землетрясениях, эпидемиях,
бесконечных войнах — чтобы в результате всего этого поистине гран-
грандиозного случайного стечения обстоятельств именно я появился на свет!
Все мы случайны и, значит, все мы уникальны. Было бы очень неплохо,
если бы люди не забывали об этом. Хочется надеяться, что когда-ни-
когда-нибудь в сознании всех людей утвердится простая мысль: убийство любо-
любого человека есть уничтожение уникального организма и одновременно
всех тех уникальных организмов, которые могли бы родиться от этого
человека.
Вспомним господствовавшую в прошлом парадигму: «Человек — это
всего лишь винтик. Незаменимых людей нет». В наше время в сознание
людей все сильнее проникает иная парадигма: « Человек — это уникум.
Все люди незаменимы, поскольку неповторимы». Да, по большому счету, в
любом человеке заключен неповторимый, уникальный духовный мир.
В нем находит индивидуальное выражение весь мир, который окружает
человека. Это хорошо выразил на языке поэзии известный австрийский
поэт Райнер Мария Рильке A875-1926):
Единое — и внутримировое
Пространство все связует. И во мне
Летают птицы. К дальней вышине
Хочу подняться — и шумлю листвою.
Да, я заботлив, и во мне мой дом.
Я жду охраны — и я сам хранитель.
Прекрасный мир, моих волнений зритель,
Рыдает дивно на плече моем.
26

1.7 Случайности неуправляемы,
но могут быть предсказуемыми
Рассмотрим конкретный пример. В мешке находятся десять шаров.
Все они одинаковы, только окрашены по-разному: три шара красные и
семь желтые. Мы запускаем руку в мешок и вынимаем наугад какой-то
шар. Какой шар мы вынем — красный или желтый? Это событие (ока-
(оказался вынутым шар определенного цвета) является, очевидно, случай-
случайным. Ясно, что мы не можем заранее обеспечить появление из мешка
именно красного или именно желтого шара. Это означает, что случай-
случайность неуправляема.
А теперь выполним много однородных испытаний: будем многократно
вынимать наугад шар из мешка, принимая всякий раз меры к тому, чтобы
оставались неизменными условия, в которых проводится каждое испыта-
испытание. Для этого надо после каждого испытания возвращать вынутый шар
обратно в мешок и тщательно перемешивать шары внутри мешка. Заме-
Заметим, что именно тогда наши испытания можно считать однородными.
Результат достаточно большого числа однородных испытаний нетруд-
нетрудно предсказать. Если, например, выполнены 2000 испытаний, то следу-
следует ожидать, что примерно в шестистах случаях будет вынут красный
шар и примерно в тысяче четырехстах — желтый. Это означает, что
случайность предсказуема.
Тут важно иметь в виду, что не всякие случайности можно предсказы-
предсказывать. Любые случайности неуправляемы, но не всякие оказываются предска-
предсказуемыми. Нужно, чтобы рассматриваемое случайное событие допускало
выполнение большого числа однородных испытаний и чтобы точность пред-
предсказания исхода возрастала по мере увеличения количества испытаний.
Принято говорить, что такие случайные события характеризуются стати-
статистической устойчивостью. Именно с ними и предпочитает работать тео-
теория вероятностей. Именно их мы имели в виду, когда в самом конце
§ 1.1 использовали термин «математически случайные события».
Примерами подобных случайных событий могут служить, наряду с вы-
выниманием шаров из мешка, также подбрасывание кубика или монетки,
включение лампочки, случайная встреча и т. д. Во всех этих примерах
возможны многократные однородные испытания и наблюдается стати-
статистическая устойчивость. Будем условно называть такие случайности «хо-
«хорошими».
Вместе с тем встречаются случайные события (случайности), для ко-
которых повторные испытания или вообще невозможны, или возможны лишь
с нарушением однородности (когда не удается обеспечить одинаковые
27

условия для всех испытаний). Будем условно называть такие случайно-
случайности «дурными».
Вот некий инженер допустил в расчетах случайную ошибку. Мог
просчитать все правильно, но случайно ошибся. Эта случайность не
только неуправляема, но и непредсказуема. Нет смысла проводить по-
повторные испытания, предлагая нашему инженеру снова и снова про-
просчитывать все с начала. Скорее всего он уже не повторит той ошибки.
Тут налицо «дурная» случайность.
Случайно пришедшая кому-то в голову счастливая мысль, случайно
найденное удачное решение некой проблемы — это тоже «дурная» слу-
случайность. Хотя, конечно, называть ее дурной в данном случае не хочется.
Приводившийся ранее смешной пример со случайным попаданием
на шляпу прохожего очков, которые случайно свалились с носа рабоче-
рабочего, починявшего крышу, есть также пример «дурной» случайности.
Получение данным учеником той или иной оценки на экзамене, мес-
место, занятое тем или иным спортсменом на соревнованиях, попадание
того или иного стрелка в мишень — все это тоже примеры событий с «дур-
«дурной» случайностью. Конечно, можно предложить стрелку выстрелить по
мишени много раз или попросить нашего спортсмена много раз повто-
повторить забег (прыжок, бросок, заплыв). Однако все эти испытания нельзя,
строго говоря, считать однородными. Стрелок может пристреляться или,
напротив, расслабиться. Спортсмен может натренироваться или просто
устать. Условия испытаний оказываются в той или иной степени неоди-
неодинаковыми. При этом исход одного испытания будет так или иначе вли-
влиять на исход других испытаний.
Строго говоря, «дурные» случайности не должны рассматриваться в те-
теории вероятности. Не следует рассматривать вероятность получения опре-
определенной оценки на экзамене, вероятность попадания в мишень, вероят-
вероятность занять определенное место на соревнованиях. Тем более не имеет
смысла говорить о вероятности допустить ошибку в расчетах или вероят-
вероятности найти удачное решение проблемы. Однако на практике подобные
«вероятности» нередко используются и даже каким-то образом оценива-
оцениваются. Математическое рассмотрение «дурных» случайностей в принципе
допустимо. Но при этом необходимо учитывать всякий раз особенности
подобных случайностей, вводить оговорки, ограничения, приближения.
ЗАДАНИЯ ПО ТЕМЕ 1
1. Жители города звонят по телефону диспетчеру и заказывают такси. Для кого эти
заказы являются случайными событиями, а для кого они таковыми не являются?
Ответ надо аргументировать.
28

2.	Рождение ребенка того или иного пола издавна считалось случайным событием.
Но сегодня медики научились распознавать пол ребенка до его рождения. Озна-
Означает ли это, что данное событие перестало теперь быть случайным? Заодно поду-
подумайте: о субъективном или объективном случайном событии идет здесь речь?
3.	Проделаем следующее испытание. Осторожно поставим карандаш его тыльной
стороной так, чтобы он оказался перпендикулярным к плоскости стола. Затем,
не трогая карандаша, слегка ударим ладонью по столу. Карандаш упадет и бу-
будет показывать своим острием в некоторую сторону. Можно ли говорить здесь
о случайном событии? Почему можно (или нельзя)? Если можно, то с какой
случайностью мы имеем здесь дело — субъективной или объективной?
4.	Астрологи утверждают, что все случайное лишь кажется случайным, а на самом
деле все можно объяснить, рассматривая положения и перемещения небесных
тел на небосводе. Согласуется ли, по-вашему, такая точка зрения с позицией
Демокрита? Можно ли согласовать существование объективной случайности с ве-
верой в астрологию?
5.	А может быть, гадая и используя разные приметы, мы вовсе не подменяем слу-
случайное необходимым, а скорее наоборот: как раз полагаемся на волю случая?
Может быть, мы предлагаем случаю подсказать нам будущее?
6.	Поразмышляйте на досуге, почему, все-таки, существование причины не мешает
некоторым событиям оставаться случайными?
7.	Попробуйте подобрать побольше примеров «хороших» случайностей и «дурных»
случайностей.
8.	Приведите примеры, когда случайности выступают не как наш противник, а как
союзник или даже помощник.
9.	Известный французский ученый Блез Паскаль A623-1662) как-то заметил:
«Я понимаю, что меня могло бы и не быть...» Это замечание не прошло неза-
незамеченным. Но одни полагают, что здесь выражена глубокая мысль, тогда как
другие считают, что все это очевидно и не о чем тут задумываться. А каково
Ваше мнение?
10.	При бросании кубика могут выпасть всего шесть цифр. Можно ли говорить об
уникальности исходов, получающихся в таком случайном событии как бросание
кубика? Если можно, то в чем же именно проявляется здесь уникальность (не-
(неповторимость)? Как Вы полагаете, всякие ли случайности обусловливают уникаль-
уникальность? Возможна ли уникальность в отсутствие случайности?
11.	Возьми в руку пару кубиков и 300 раз подбрось эту пару. Попробуй предсказать,
сколько приблизительно раз выпадет пара с одинаковыми цифрами на гранях.
Проверь свое предсказание на практике.
29

ТЕМА 2
ПОРЯДОК И БЕСПОРЯДОК
Однажды я наткнулся на «Размышления» Марка Аврелия
и случайно открыл ту страницу, где он пишет о двух возможно-
возможностях: либо мир является огромным Хаосом, либо в нем царству-
царствуют порядок и закономерность. Я впервые задумался над тем,
а почему, собственно, Марк Аврелий считал, что в мире гос-
господствуют либо случайность, либо закономерность? Почему он
думал, что эти две возможности исключают друг друга? В мире
господствует случай и одновременно действуют порядок и за-
закономерность, которые формируются из массы случайностей
по законам случайного.
Альфред Ренъи
(«Письма о вероятности»)
в
2.1 Мифы о борьбе Космоса и Хаоса
наше время слово «Космос» означает «Вселенная». Когда говорят о
Космосе, то имеют в виду планеты, звезды, галактики. Но у этого слова
есть также древнее значение. Для наших далеких предков «Космос»
30

означал «порядок», «совершенное устройство». Глядя на звездное небо,
на котором из ночи в ночь зажигаются одни и те же созвездия, люди
полагали, что именно там царит подлинный порядок. Там, на небесах,
все упорядочено и подчинено строгим и неизменным законам. Там нет
места случайностям. Они могут встречаться лишь в нашем столь несо-
несовершенном земном мире. Беспорядок на Земле и строгий порядок на не-
небесах^. Так порядок и звездное небо стали восприниматься как единое
понятие — как Космос.
Космосу противостоит Хаос. Если Космос — это порядок, совершен-
совершенное мировое устройство, то Хаос — это отсутствие порядка и вообще
какого-либо мирового устройства. С Хаосом связывали беспорядочное
состояние мира, отсутствие каких-либо явлений и объектов. Хаос опи-
описывается в Библии очень коротко: «Земля была безвидна и пуста, и
тьма над бездною».
Во всех мифах и преданиях Хаос считался изначальным состоянием мира.
Вначале был Хаос и только Хаос. А затем из Хаоса возник Космос —
произошло сотворение Мира. В древнегреческом мифе, например, гово-
говорится: «В самом начале существовал лишь безграничный темный Хаос.
В нем заключался источник Жизни Мира. Все возникло из безгранич-
безграничного Хаоса — весь мир и бессмертные боги».
Рождение Космоса из Хаоса утверждают мифы всех народов. Как
произошло это рождение? На этот счет в разных мифах высказываются
разные гипотезы. Их можно выделить в две группы. Одна группа —
гипотезы о самозарождении Космоса из Хаоса. Другая группа гипотезы,
согласно которым Бог сотворил Космос из Хаоса.
Согласно упомянутому выше древнегреческому мифу имело место са-
самозарождение Космоса из Хаоса, в котором содержался таинственный
«источник Жизни Мира». Более подробно картина самозарождения Кос-
Космоса описана в древнеиндийском мифе: «Давным-давно не было ни солн-
солнца, ни луны, ни звезд. Не было даже времени, потому как некому было
его отмерять. Один лишь Хаос царил во всем мире. И вот из тьмы спящего
Хаоса возникли воды. Из повсюду простиравшихся вод возник огонь. Ве-
Великой силой этого огня было рождено Золотое Яйцо, сияющее как солн-
солнце. Оно долго плавало в безбрежном океане вод и разрасталось. Затем из
него возник Создатель Вселенной — Брахма. Он силой мысли разбил
Яйцо на две половины. Верхняя половина стала Небом, а нижняя —
Землею, и чтобы разделить их, Брахма поместил между ними воздух.
И он утвердил землю среди вод, создал страны света, положил начало вре-
времени...» Итак, сначала из тьмы Хаоса возникли воды. Из вод возник огонь.
Силой огня было рождено Золотое Яйцо. Из Яйца возник Создатель
31

Вселенной. Он положил начало времени, и вся дальнейшая эволюция
Вселенной происходила уже под его руководством.
А вот согласно библейскому мифу никакого самозарождения Космо-
Космоса не было. С самого начала были Хаос («тьма над бездною»), Созда-
Создатель (Бог) и время. Космос был сотворен Богом в шесть дней. Вот как
это происходило: «И сказал Бог: да будет свет. И стал свет. И отделил
Бог свет от тьмы. И был вечер, и было утро: день первый. И сказал Бог:
да будет твердь посреди воды и да отделяет она воду от воды. И создал
Бог твердь, и отделил воду, которая под твердью, от воды, которая над
твердью. И назвал Бог твердь небом. И был вечер, и было утро: день
второй. И сказал Бог: да соберется вода, которая под небом, в одно
место, и да явится суша. И назвал Бог сушу землею, а собрание вод
назвал морями. И сказал Бог: да произрастит земля зелень, траву, сею-
сеющую семя, и дерево плодовитое, приносящее по роду своему плод. И был
вечер, и было утро: день третий. И сказал Бог: да будут светила на
тверди небесной для освещения земли и для отделения дня от ночи.
И создал Бог два светила великие: светило большее для управления днем,
и светило меньшее для управления ночью, и звезды. И был вечер, и бы-
было утро: день четвертый. И сказал Бог: да произведет вода пресмыкаю-
пресмыкающихся и птицы да полетят над землею по тверди небесной. И сотворил
Бог рыб. И был вечер, и было утро: день пятый. И сказал Бог: да произ-
произведет земля душу живую по роду ее, скотов, и гадов, и зверей земных по
роду их. И сказал Бог: сотворим человека по образу Нашему и по подо-
подобию Нашему, и да владычествует он над рыбами морскими, и над пти-
птицами небесными, и над зверями, и над скотом, и над всею землею, и
над всеми гадами, пресмыкающимися по земле... И был вечер, и было
утро: день шестой».
Известный голландский художник Мориц Эшер A898-1972) изобразил
второй, пятый и шестой Дни Творения — см. рисунки в таблице 1.
Итак, с точки зрения творцов древних мифов, в процессе Сотворе-
Сотворения Мира из Хаоса был создан Богом или самозародился Космос. В не-
некоторых мифах Бог создал Космос сразу, в одночасье. В других же (на-
(например, в библейском мифе) процесс создания Космоса происходил
постепенно; здесь можно говорить о процессе развития {эволюции) Кос-
Космоса, происходящем под руководством Создателя.
Разумеется, библейская эволюция Космоса весьма и весьма отлича-
отличается от современной естественнонаучной картины эволюции Вселен-
Вселенной, Солнечной системы, Земли. Но сейчас мы об этом говорить не
будем. Для нас важно, что уже в древних мифах была выражена идея
32

Таблица 1. Дни Творения по Эшеру
Второй
День Творения
Пятый
День Творения
Шестой
День Творения
33

появления Порядка из всеобщего Беспорядка, идея рождения Порядка в Хаосе.
Это была интуитивно возникшая идея превращения случайностей в за-
закономерности, выражающие необходимость. Пройдет время — и идея
возникновения необходимости из случайностей получит научное обо-
обоснование.
А пока вернемся к мифам и отметим, что в них возникновение Кос-
Космоса из Хаоса отнюдь не приводит к исчезновению Хаоса. С появлением
Космоса Хаос не исчез, а лишь отодвинулся как бы на второй план,
ушел в тень или, лучше сказать, во тьму. Из случайностей родилась
необходимость, и теперь они сосуществуют в мире вместе — необходи-
необходимость и случайности (порядок и беспорядок). Затаившись во тьме, Хаос
продолжает угрожать Космосу, порождает ужасы и страхи, провоцирует
всевозможные бедствия и войны. И нет надежных преград между чело-
человеком и Хаосом. Эту мысль хорошо выразил знаменитый русский поэт
Федор Тютчев A803-1873):
И бездна нам обнажена
С своими страхами и мглами,
И нет преград меж ней и нами —
Вот отчего нам ночь страшна.
Согласно мифам, борьба между Космосом и Хаосом продолжается все
время. Нередко Хаос берет верх над Космосом — тогда происходят по-
потопы, землетрясения, тайфуны, многие иные катастрофы. Сюда же надо
отнести военные конфликты, убийство одних людей другими. Много-
Многочисленные легенды рассматривают все это как временные победы сил
Беспорядка над силами Порядка, сил Зла над силами Добра. И если на
стороне Космоса, Порядка, Добра выступает Бог, то на стороне Хаоса,
Беспорядка, Зла выступает Дьявол.
И не предвидится конца борьбе этих двух противоположностей —
порядка и беспорядка, необходимости и случайности. Впрочем, мифы
не исключают возможность полного торжества Хаоса и возвращения
Космоса к изначальному Хаосу. Эта возможность отражена в мифах
о Конце Света. В наше время эти мифы звучат как предостережение,
напоминающее о грозящей человечеству глобальной экологической
катастрофе.
Когда пробьет последний час Природы,
Состав частей разрушится земных,
Все зримое опять покроют воды
И Божий лик изобразится в них...
Ф. Тютчев
34

2.2 Абсолютный беспорядок и абсолютный порядок —
две нелепые крайности
11опробуем представить себе мир, в котором вообще нет какого-
либо порядка. Вообразим абсолютно беспорядочный мир. В таком мире
нет ничего закономерного, необходимого, а есть только случайности.
Это был бы мир сплошных неожиданностей, мир, где ничего невоз-
невозможно понять, ничего нельзя предсказать. В нем отсутствовали бы ка-
какие-либо причины и какие-либо следствия. Ничто не влияло бы ни на что,
не было бы никаких взаимосвязей. Где-то что-то случайно возникало
бы и столь же случайно исчезало.
Подобный мир может возникнуть только в больном воображении.
Совершенно очевидно, что он нелеп. Существовать такой мир, конеч-
конечно, не может, поскольку не может существовать абсурд.
Если подумать, то в воображаемом мире абсолютного беспорядка не
могут наблюдаться никакие объекты, не могут происходить какие-либо
явления. Ведь всякий объект возникает как следствие каких-то процес-
процессов и какие-то причины обеспечивают его существование в течение
какого-то времени. Всякое явление предполагает какие-то происходя-
происходящие во времени процессы с множеством причин и следствий. Но в
абсолютно беспорядочном мире нет места каким-либо причинно-след-
причинно-следственным связям. Там всё сиюминутно, там нет ничего, что развивалось
бы во времени, было как-то связано с прошлым и как-то влияло бы на
будущее. Можно сказать, что в таком мире нет времени', ведь отсутствие
связи прошлого с настоящим, а настоящего с будущим лишает смысла
сами понятия «прошлое», «настоящее», «будущее». Напомним, что имен-
именно отсутствие указанной связи является принципиальной особеннос-
особенностью последовательности случайных событий (каждое событие не зави-
зависит от прошлых событий и не влияет на будущие события).
По просьбе автора один из учеников 7-го класса пофантазировал
и написал сочинение на тему «Я в мире, где царствует случайность». Он
попытался передать ощущение всеобщего хаоса и сплошных неожидан-
неожиданностей. Вот что у него получилось:
Я заснул и вдруг оказался в мире сплошных случайностей. Был ясный
пасмурный не то день, не то ночь. Все кругом клокотало, лопалось и
пучилось. Откуда-то появились цветы и вдруг оказались лягушками, ко-
которые неожиданно пропали. Мелькнула птица, оказавшаяся собакой без
головы, но с клювом, который вдруг сделался хвостом и отвалился. Я сам
вдруг провалился вниз и оказался где-то вверху, за облаками, которые
тут же стали огромными лопухами и полопались, превратившись в сло-
слонов без хоботов, но с панцирями. Мне на голову свалился камень и
35

растекся по лицу липкой жидкостью, превратившейся в горячее мороже-
мороженое. Подо мной образовалась пропасть, ставшая вдруг горой, которая тут
же опрокинулась на меня. Я закричал от ужаса и проснулся...
Ну, а другая крайность? Каким мог бы быть мир абсолютного поряд-
порядка, мир, где нет места случайному? В таком мире совсем не было бы
никаких неожиданностей — здесь происходило бы только то, что зара-
заранее должно было произойти. Словно кто-то всемогущий составил раз и
навсегда абсолютно строгий и точный Распорядок для всего и для всех.
Как если бы существовал Закон, управляющий всем на свете. Если бы
мы жили в таком мире, то все наши поступки, малейшие движения,
даже мысли были бы заранее предопределены, а сами мы уподобились
бы куклам в неком театре, которых кто-то водит на веревочках. В мире
абсолютного порядка все нормировано: формы, положения, действия.
Никаких отклонений от нормы!
А вот сочинение-фантазия того же школьника на тему «Я в мире,
где царствуют порядок и необходимость»:
Я заснул и попал в мир абсолютного порядка и необходимости.
По небу безостановочно плыли облака, все одинаковой формы и од-
одного размера. Передо мной текла река, прямая как луч света с абсо-
абсолютно ровными берегами, вдоль которых ровными рядами росли де-
деревья. Все деревья были одинаковой высоты, одинаковой формы
и одинаково раскачивались под ритмичными порывами ветра. Это на-
напоминало слаженный танец и показалось мне красивым. А потом при-
прилетело множество одинаковых птиц. Они дружно расселись по деревь-
деревьям и склевали все листья, которые, должно быть, показались им
вкусными. Но листья были ядовитыми, все птицы попадали на землю
и вокруг каждого дерева образовалась аккуратная окружность из пти-
птичьих тел. Это было красивое, хотя и грустное зрелище. Оно привлекло
внимание волков, живших в ближайшем лесу. Волки дружно прибежа-
прибежали и быстро поели всех птиц. Нашествие волков не могло остаться не-
незамеченным — на лодках приплыли охотники и всех волков перестре-
перестреляли. Потом пришли лесорубы. Они срубили и выкорчевали все деревья,
оказавшиеся без листьев. А потом пришли лесоводы и посадили ровные
ряды молодых саженцев. А потом мне стало скучно и я проснулся...
Не правда ли, в сочинении передано ощущение какой-то обречен-
обреченности, предписанности и скуки? Сплошной беспорядок и засилье
случайностей, конечно, страшны. Но и от сплошного порядка и заси-
засилья необходимости тошно. Хотя особенно переживать не следует — ведь
как то, так и другое нереально.
По-видимому, невозможно изобразить в виде рисунка абсолютно бес-
беспорядочный или абсолютно упорядоченный мир. Даже если пытаться
36

изображать весьма условно. Разве можно нарисовать на листе бумаги
нелепые ситуации? Тем не менее мы рискнем предложить два рисунка
из М. Эшера. На наш взгляд, рисунок 1 из таблицы 2 в какой-то мере
передает ощущение фантастического мира случайностей, а рисунок 2
из таблицы 2 неплохо олицетворяет фантастический мир железной не-
необходимости, мир абсолютного порядка.
Наверное, все согласятся, что абсолютно беспорядочный мир, ли-
лишенный каких-либо причин и следствий, абсурден. Тут даже понятие
времени строго говоря, не имеет смысла. А вот абсолютно упорядо-
упорядоченный мир, в котором нет места случайностям, может кому-то даже
нравиться. Чем плохо, если везде и во всем порядок? И разве мы не
хотели бы, чтобы все шло по плану, без каких-либо импровизаций? У
известного российского поэта Владимира Высоцкого A938-1980) есть
Песня о плане:
Чтобы не попасть в капкан,
Чтобы в темноте не заблудиться,
Чтобы никогда с пути не сбиться,
Чтобы в нужном месте приземлиться, приводниться,
Начерти на карте план.
И шагай и пой беспечно —
Тири-тири-там-там-тирам!
Встреча обеспечена — в плане все отмечено
Точно, безупречно и пунктиром...
Если даже есть талант —
Чтобы не нарушить, не расстроить.
Чтобы не разрушить, а построить,
Чтобы увеличиться, удвоить и утроить, —
Нужен очень точный план...
Как воспринимать эти стихи? Если считать, что это — похвальное
слово нашей любви к планам, то, признайтесь, звучит это похвальное
слово достаточно иронически.
Ну, а если говорить серьезно, то, нисколько не порицая стремление
людей к порядку, мы должны все-таки признать, что абсолютный поря-
порядок, т. е. порядок стопроцентный, без какой-либо «примеси» случайного,
нереален и нелеп. Он нереален и нелеп в такой же мере, как нереальна
и нелепа противоположная крайность — абсолютный беспорядок, когда
есть только случайности без какой-либо «примеси» упорядочивающих
закономерностей. В то же время не надо особенно удивляться тому, что
люди нередко склонны приветствовать абсолютный порядок и вообще
отдавать предпочтение не случайности, а необходимости. Мы уже
37

Таблица 2. Фантастические «миры» случайностей и абсолютного порядка
38

говорили о том, что психика человека страшится всяческих неожиданно-
неожиданностей, связанных со случайностями. Впрочем дело, по-видимому, не толь-
только в этом. Видно, есть в психике человека нечто такое, что заставляет его
восторгаться стройными колоннами слаженно марширующих людей и
что понуждает его к поистине безудержному законотворчеству, попыт-
попыткам установить законы и правила практически для любых случаев.
Тем, кто будет упорствовать в своих симпатиях к абсолютному по-
порядку, нам остается заметить лишь, что абсолютно упорядоченный мир
следует считать абсурдным уже потому, что это есть ситуация, доведен-
доведенная до абсурда. О том, как можно довести до абсурда стремление к упо-
упорядоченности, совсем нетрудно нафантазировать. В качестве примера
напомним фантазию, описанную известным польским писателем Ста-
Станиславом Лемом (род. 1921) в его «Звездных дневниках Ийона Тихого».
Придуманный Лемом космический путешественник Ийон Тихий попал
однажды на планету индиотов. На той планете было когда-то много
беспорядка. И вот Правитель призвал талантливого конструктора и сказал
ему: «Нашему государству угрожает хаос; ширятся беспорядки и неува-
неуважение законов. Сконструируй и построй Машину, которая введет на
планете наивысший Порядок, Порядок Совершенный и Абсолютный».
Через шесть месяцев конструктор создал такую Машину. Машина дол-
долго и упорно трудилась и воздвигла великолепный Радужный Дворец.
Затем она распахнула двери Дворца и предложила всем желающим по-
посетить его. Толпы индиотов ринулись во дворец, желая заполучить Аб-
Абсолютный Порядок. Однако вскоре возникло подозрение, поскольку
ни один из миллионов индиотов, посетивших дворец, не вышел обрат-
обратно. Выяснилось, что по ночам задняя стена дворца отворялась и оттуда
высыпалось множество блестящих кружков. Черные автоматы развози-
развозили эти кружки на поля и укладывали их в красивые симметричные узо-
узоры. Оказалось, что Машина превращала каждого попавшего во Дворец
индиота в красивый блестящий кружок. Узнав об этом, индиоты возму-
возмутились. Они напомнили Машине, что она должна была установить Аб-
Абсолютный Порядок. «Я это и делаю, — ответила Машина. — Взгляните
на себя, как неаккуратно сложены ваши тела. Одни из вас толстые,
другие худые. Вы хаотически передвигаетесь, куда захотите, иногда бес-
бесцельно бродите по лесам. Во всем этом нет ни на грош математической
гармонии! Я, Добровольный Распространитель Абсолютного Порядка,
превращаю ваши слабые, хрупкие тела в изящные, устойчивые формы,
из которых складываю потом симметричные, невиданно правильные
узоры, вводя тем самым на планете элементы совершенного порядка...».
Конечно, это всего лишь фантазия писателя. Но не следует ли заду-
задуматься над ней всем, кто жаждет абсолютного порядка? Как говорится,
сказка — ложь, да в ней намек...
39

2.3 Беседа, посвященная переходам
от порядка к беспорядку
g4u<StiuSU*&. А что же, все-таки, есть порядок и что такое беспорядок]
В общих чертах понятно: беспорядок — это хаос, это случайности, а
порядок — это закономерности и необходимость. А если более конк-
конкретно и наглядно?
Пвтор. Ответ на вопрос о том, как могут выглядеть в различных
случаях порядок и беспорядок, будет дан в определенной мере в следую-
следующих темах (когда мы будем рассматривать симметрию и асимметрию).
А пока познакомимся с понятиями порядка и беспорядка на конкрет-
конкретных примерах превращения порядка в беспорядок. Такие превращения
постоянно происходят в природе и нашей повседневной жизни.
ь. Как же так? Понятия порядка и беспорядка еще не уточ-
уточнены, а уже рассматриваются превращения порядка в беспорядок?
Пвтор. Дело в том, что сами по себе эти превращения достаточно
хорошо известны. Остается лишь разглядеть в них переходы от порядка
к беспорядку. Тем самым и будут уточняться сами эти понятия.
g4u<StiuSU*&. Интересный логический ход! Наблюдаем некоторые яв-
явления, происходящие в окружающем мире. Затем описываем эти явле-
явления на языке используемых нами понятий, которые мы пока еще тол-
толком не определили. А в результате получаем наглядные и конкретные
представления об этих понятиях!
Пвтор. Явления, которые можно трактовать как превращения поряд-
порядка в беспорядок, происходят буквально на каждом шагу. Это, кстати ска-
сказать, лишний раз доказывает, что абсолютно упорядоченный мир суще-
существовать не может. Если бы даже некий всемогущий Создатель сотворил
однажды такой мир, то процессы превращения порядка в беспорядок
вскоре непременно испортили бы первоначальное творение. Чтобы это-
этого не случилось, Создателю пришлось бы все время заботиться о поддер-
поддержании порядка, пресекая процессы перехода порядка в беспорядок.
ь. Подозреваю, что все тираны во все времена воображали
себя богами, которые подарили людям абсолютный порядок. И чтобы
его сохранить, они всегда обращались к силе.
Пвтор. К счастью, никаким тиранам не под силу изменить ход при-
природных процессов и, в частности, процессов превращения порядка
в беспорядок.
'Чиниинель. А как могут на практике выглядеть эти процессы?
Пвтор. Вот, например, падает на землю красивое спелое яблоко. Че-
Через некоторое время оно сгнивает. Перед нами пример перехода от по-
порядка к беспорядку. Вот высится величественная скала. Кажется, что
40

она будет стоять вечно. Но проходят года, десятилетия, столетия. Под
действием воды, ветра, сезонных изменений температуры эта скала по-
постепенно разрушается, превращаясь в скопление щебня, песка, глины.
Это также переход от порядка к беспорядку.
"Читателе Получается, что спелое яблоко — это порядок, а его гни-
гнилые остатки — беспорядок. Величественная скала — это порядок, а то,
что от нее осталось после долгих лет — беспорядок.
Пвтор. Процессы перехода от порядка к беспорядку — это процессы
разрушения. Со временем разрушается (деградирует) почва, засыхает
некогда живое дерево, исчезает озеро, превращаясь в болото. Это тоже
процессы перехода от порядка к беспорядку.
"Читатель. А нельзя ли привести более яркие примеры порядка, ко-
который затем разрушается и переходит в беспорядок?
Пвтор. Разнообразные образцы порядка создают своим трудом люди.
Автомобили, авиалайнеры, космические корабли, телевизоры, компью-
компьютеры, книги — всего не перечесть. Стремясь подольше сохранить сотво-
сотворенный им порядок, человек принимает специальные меры. Например,
ставит автомобиль в гараж и периодически ремонтирует его. Книги «оде-
«одевают» в переплеты и заботятся об условиях их хранения (следят за осве-
освещенностью, температурой, влажностью воздуха в библиотеках). Однако
все подобные меры дают лишь временный эффект. Рано или поздно книга
истлеет, а автомобиль и авиалайнер превратятся в груду ржавого металла
(если раньше того их не отправят под пресс). Сотворенный человеком
порядок неизбежно переходит со временем в беспорядок. Недаром неук-
неуклонно растет во всем мире количество свалок и становится все более и
более острой проблема утилизации отходов производства.
'Читатель. Насколько я заметил, превращения порядка в беспорядок
происходят довольно медленно. Требуется время, чтобы яблоко сгнило.
Еще дольше деградирует почва или засыхает дерево. И совсем много
времени требуется для разрушения скалы.
Пвтор. Можно не ждать, пока яблоко сгниет. Можно взять да съесть
его — пусть переваривается в желудке. А вот совсем быстрый процесс
перехода от порядка к беспорядку: бросьте в огонь костра лист бумаги
или сухую ветку — они сгорят менее, чем за минуту. Был лист бумаги
с каким-то текстом или рисунком. Была ветка с красивыми изгибами.
И вот в течение минуты все это превратилось в горстку бесформенного
пепла, горстку золы.
"Читатель. Такой быстрый переход от порядка к беспорядку мне
совсем нетрудно устроить в качестве опыта.
Пвтор. Не будем, однако, играть с огнем. Я предлагаю иной опыт.
Возьмем стакан чистой воды и стакан воды, подкрашенной, например,
41

чернилами. Если Вам захочется пить, Вы не будет трогать стакана с чер-
чернильной водой, а воспользуетесь стаканом с чистой водой. Но вот, пред-
предположим, Вы слили воду из обоих стаканов в банку. Теперь Вы уже не
сможете утолить жажду. То, что Вы проделали, следует рассматривать
как превращение некоторого порядка (когда есть чистая вода и вода
с чернилами) в беспорядок (когда вся вода оказалась разбавленной чер-
чернилами). Глядя на банку с водой, разбавленной чернилами, Вы уже
никак не сможете определить, где тут чистая вода, а где чернила —
здесь все перемешалось.
'Читатель. Во всех приведенных примерах процесс перехода от по-
порядка к беспорядку нельзя исправить, нельзя устроить переход в обрат-
обратном направлении. Иначе говоря, нельзя от получившегося беспорядка
перейти обратно к порядку.
Пвтор. Верно подмечено. Такие процессы называют необратимыми.
В самом деле, результаты гниения или переваривания яблока не могут
превратиться обратно в целое яблоко. Остатки скалы не обратятся сно-
снова в скалу. Горстка золы не превратится в сухую ветку. Равно как сухая
ветка не превратится в ветку с зелеными листьями.
"Читатели. В детстве я слышал сказку, в которой сказочная птица
Феникс возрождалась из пепла. Я понимаю, что это было чудо, которо-
которому место только в сказке. А в жизни беспорядок не превращается об-
обратно в порядок.
Пвтор. Не следует так категорически утверждать это. Можно привести
примеры обратимых переходов от порядка к беспорядку — когда возможен
обратный процесс. Кусочек льда, ледяная снежинка тают, превращаясь в
воду. Это процесс перехода от порядка к беспорядку. Но охладите полу-
получившуюся воду — и она станет кусочком льда. Это уже обратный пере-
переход — переход от беспорядка к порядку. Лед на морозе испаряется, т. е.
превращается в водяной пар (недаром на морозе сушат белье после стир-
стирки). Возможно, это особенно наглядный пример превращения порядка в
беспорядок: в кристалле льда молекулы находятся в узлах упорядоченной
кристаллической решетки, а в водяном паре они движутся беспорядочно,
не объединяясь ни в какую структуру. С другой стороны, водяной пар
может кристаллизоваться и образовывать на ветвях деревьев кристаллы
инея — тут налицо не менее наглядный переход от беспорядка к порядку.
'Читатели. Признаться, мне не приходило в голову, что из беспо-
беспорядка может возникнуть порядок! Но вода и водяной пар в самом деле
могут превращаться в ледяные кристаллы!
Пвтор. Процессы превращения беспорядка в порядок не менее инте-
интересны, чем процессы превращения порядка в беспорядок.
"Читатели. На мой взгляд, они значительно интереснее!
42

2.4 Первая беседа, посвященная переходам
от беспорядка к порядку:
современные представления о «сотворении мира»
'Читатель. Если задуматься, то появление порядка из беспорядка
похоже на чудо.
Пвтор. Именно такова парадигма, формировавшаяся в сознании лю-
людей в течение многих веков. Люди давно поняли, что когда-то не было
ни Солнца, ни нашей планеты, а был некий первозданный беспорядок
(хаос). А потом из этого всеобщего беспорядка народился порядок: воз-
возникли Солнце и планеты, а на одной из планет (на нашей Земле) воз-
возникла жизнь и, в частности, возникли мы сами — мыслящие люди.
В рамках старой парадигмы все это и вправду рассматривалось как чудо,
Сотворенное Создателем.
&. Мне кажется, что многие и сегодня так считают.
Пвтор. Сегодня эту парадигму следует признать несостоятельной. Она
безнадежно устарела и никак не соответствует современному уровню
познания мира человечеством. Важно формировать в сознании людей
принципиально новую парадигму: рождение порядка из беспорядка —
это не чудотворный процесс, а процесс естественный, в котором «поря-
«порядок и закономерность формируются из массы случайностей по законам
случайного». (Здесь мы воспользовались выражением Альфреда Реньи,
приведенном в качестве эпиграфа к данной теме.)
^СшОаАел*. Законы случайного? А что это такое?
Пвтор. Мы достаточно подробно поговорим о них в свое время. А пока
я хочу вкратце напомнить, как современная наука представляет гло-
глобальный процесс рождения порядка из хаоса. Тот процесс, которому
посвящены мифы о Сотворении Мира. Рассматривать этот процесс нач-
начнем с этапа, предшествовавшего рождению Солнца и планет.
Немногим более 5 миллиардов лет назад Солнца и планет еще не
было. Но было гигантское водородное облако вместе с космической пы-
пылью. Под действием гравитации (сил взаимного притяжения частиц
космического вещества) облако начало сжиматься и, как положено при
сжатии, нагреваться. Одновременно оно начало вращаться вокруг сво-
своей центральной области. Гравитация привела к образованию относи-
относительно плотного горячего ядра облака {протозвезды), а вращение облака
привело к образованию в его экваториальной плоскости нескольких срав-
сравнительно небольших сгустков вещества (протопланет), движущихся вок-
вокруг протозвезды. Гравитация собирает вещество, а вращение способству-
способствует его разбрасыванию. Вот и превратилось хаотическое космическое
43

облако из водорода и пыли в протозвезду с «разбросанными» вокруг нее
протопланетами.
*Чи(*иипель. Вследствие притяжения протозвезда должна была сжи-
сжиматься все больше и больше...
Пвтор. Так оно и происходило. Соответственно, шар протозвезды
все сильнее нагревался. Когда его температура повысилась примерно
до 10 миллионов градусов, в его недрах начался продолжающийся и
поныне процесс превращения водорода в гелий. При этом превращении
происходит высвобождение огромных количеств энергии. В результате
в недрах протозвезды начало расти давление, стремящееся взорвать про-
протозвезду. Итак, внутреннее давление стремилось взорвать протозвезду,
тогда как силы гравитации стремились, напротив, ее сжать. Когда силы
давления и силы гравитации взаимно уравновесились, начался длитель-
длительный период стабильного существования звезды — протозвезда превра-
превратилась в Солнце. Это произошло примерно 5 миллиардов лет назад.
'Чиниинель. А что происходило с протопланетами?
Пвтор. Эти остатки водородного облака, не захваченные в свое время
протозвездой (помешал центробежный эффект при вращении облака),
тоже подверглись сжатию, в результате чего сформировались плотные
шары планет. В том числе наша Земля.
'Чиниинель. А разве сжатие не привело к разогреву планет?
Пвтор. Разогрев, конечно, происходил, но далеко не столь сильный,
как в случае протозвезды. Ведь масса планет во много раз меньше массы
Солнца. Последствиями этого разогрева для Земли является существо-
существование жидкого (расплавленного) — внешнего ядра Земли на глубине от
2900 км до 5100 км и слоя твердо-жидкой астеносферы на глубине от
50-100 км до 200-300 км. При определенных условиях астеносфера пре-
превращается в жидкую магму — и тогда возможно извержение вулкана.
*Чипии*иль. А как насчет возникновения жизни на Землей Как она воз-
возникла? Может быть, живые организмы были занесены с иных миров,
а может быть, произошло самозарождение живых организмов из нежи-
неживой материи?
Пвтор. Современная наука считает, что жизнь действительно само-
самозародилась на неживой Земле, но только не в виде живых организмов,
хотя бы и простейших. Все началось, по-видимому, с того, что в древ-
древних морях стали возникать и накапливаться фрагменты «биологических
молекул», например, молекулы различных аминокислот. Они строились
из тех неорганических веществ, которые находились в те времена в ат-
атмосфере Земли. Эти фрагменты стали образовывать полимерные це-
цепочки, из которых состоят «биологические молекулы» — такие, напри-
44

мер, как молекулы белков или углеводов. Спустя время стали возникать
группы таких молекул, окружившие себя оболочкой (биологической мем-
мембраной). Подобные образования дали начало самым первым однокле-
одноклеточным живым организмам — прокариотам. Это произошло, по оцен-
оценкам ученых, примерно 3,5 миллиарда лет назад^
ль. Прокариоты... Какое странное название!
Пвтор. В переводе с греческого оно означает «доядерные» организмы
(«про» — «до», «карион» — «ядро»). Дело в том, что у этих одноклеточ-
одноклеточных организмов еще не сформировалось внутриклеточное ядро. Впрочем
там много чего еще не сформировалось.
*&. Но тем не менее это были живые организмы!
Пвтор. Да, это были простейшие живые организмы. Как и всякие
живые организмы они обладали способностью к метаболизму, т. е. обме-
обмену веществами и энергией с окружающей средой.
*Чи(*иипель. А что было потом?
Пвтор. А потом в течение 2 миллиардов лет происходила эволюция
прокариот. В результате возникли одноклеточные организма, называе-
называемые эукариотами (в переводе с греческого «истинноядерные» организ-
организмы; «эу» — «истинный», «настоящий»). В отличие от прокариот уже
самые первые эукариоты обладали внутриклеточным ядром. Затем внут-
внутри эукариот сформировались другие внутриклеточные структуры: ми-
митохондрии, аппарат Голъджи, хлоропласты. Мы не будем здесь вникать
в подробности и выяснять происхождение и назначение всех этих струк-
структур. Сейчас для нас важно отметить лишь то, что переход от прокари-
прокариот кэукариотам явился принципиально важным переходом от беспо-
беспорядка к порядку.
*Чи(*иипель. Но почему с прокариотами надо связывать беспорядок,
ас эукариотами порядок?
Пвтор. Дело в том, что в процессе перехода от прокариот к эукарио-
там происходило формирование различных внутриклеточных структур.
*Чипиинель. Получается, что рождение каких-либо структур — это акт
появления порядка, акт упорядочивания?
Пвтор. Конечно. Вообще процессы перехода от беспорядка к поряд-
порядку — это процессы созидающие. В отличие от разрушающих процессов,
какими являются процессы перехода от порядка к беспорядку. Первые
процессы (от беспорядка к порядку) называют конструктивными, а вто-
вторые (от порядка к беспорядку) — деструктивными.
ль. Как я догадываюсь, дальнейшие этапы перехода от бес-
беспорядка к порядку состояли в формировании из одноклеточных эука-
эукариот многоклеточных живых организмов?
45

Пвтор. Верно. Из тех эукариот, внутри которых возникли хлоропла-
сты (структуры, в которых идет процесс фотосинтеза), появились расте-
растения, а из эукариот без хлоропластов сформировались грибы и животные.
На это понадобилось еще около полумиллиарда лет. А потом происхо-
происходила эволюция многоклеточных живых организмов, увенчавшаяся воз-
возникновением человека примерно 40 тысяч лет назад. Вот так в общих
чертах происходил процесс Сотворения Мира.
'Чиниииель. А что же двигало этим процессом? Почему на тех или
иных этапах совершалось очередное превращение беспорядка в поря-
порядок? С чем связаны эти превращения? Где таятся их первопричины?
Пвтор. Общая переопричина одна — случайные события, случайности.
Внутри какого-то водородного космического облака случайно возникло
достаточно сильное уплотнение, начавшее интенсивно притягивать к себе
остальные части облака. Разумеется, частицы облака не устремились
прямо к области уплотнения. Под действием притяжения частицы на-
начали изменять направления движения, начали заворачивать к области
уплотнения. Случайно все эти многочисленные «заворачивания» оказа-
оказались в массе своей схожими друг с другом, что и вызвало вращение
облака в целом вокруг некоторой случайно определившейся оси. Слу-
Случайно образовалась планета с приемлемыми для жизни условиями (та-
(такая планета могла и не образоваться). Случайно на этой планете возник-
возникли соединения из неорганических веществ, которые смогли с течением
времени сформировать (причем тоже случайно) углеводные, белковые
и прочие «биологические молекулы». Еще целый ряд случайностей при-
привел к появлению прокариот — первых живых организмов. В результате
множества последующих случайных проб природа сформировала мно-
многоклеточные организмы — появились растения, грибы, животные. Ра-
Разумеется, и вся последующая биологическая эволюция происходила
благодаря множеству случайностей и естественному отбору случайно
возникших вариантов.
'ЧиФнатель. Как я вижу, везде инициаторами переходов от беспоряд-
беспорядка к порядку были случайные события!
Пвтор. Совершенно верно. Ведь мы уже отмечали: порядок и законо-
закономерности формируются из массы случайностей. Удивительно точно поэт
назвал Случай Богом-изобретателем.
О сколько нам открытий чудных
Готовят просвещенья дух,
И опыт, сын ошибок трудных,
И гений, парадоксов друг,
И Случай — Бог-изобретатель...
Александр Пушкин
46

2.5 Вторая беседа, посвященная переходам
от беспорядка к порядку:
рождение информации из шума
Пвтор. О том, что такое информация как общенаучное понятие, мы
подробно поговорим позднее, в книге «Вероятность в современном
мире». Пока же нам достаточно житейского представления, согласно
которому информация — это просто некоторые сведения, которые, в част-
частности, могут позволять делать предсказания. Слово «информация» в пе-
переводе с латинского означает «разъяснение».
ь. А что касается шума, то он, по-видимому, связан со слу-
случайными событиями.
Пвтор. Не с отдельными случайными событиями, а с огромной массой
случайных событий. Отдельные случайности хаоса не образуют. Нужно
великое множество случайностей. Шум — это синоним хаоса на языке
теории информации.
'Чиниипель. Рождение информации из шума, т. е. получение каких-то
полезных сведений из хаоса, на первый взгляд, кажется невозможным.
Однако нетрудно сообразить, что это как раз и есть рождение порядка
из беспорядка, рождение закономерности (необходимости) из случай-
случайностей. А подобные вещи, как мы уже выяснили, действительно проис-
происходят в нашем мире.
Пвтор. Вы рассуждаете верно. Добавлю, что, если бы информация не
могла рождаться из хаоса, то нельзя было бы делать какие-либо предска-
предсказания относительно случайных событий. Напомню пример с подбрасы-
подбрасыванием монетки; он приводился во вступительном диалоге для того, что-
чтобы продемонстрировать статистическую закономерность. Если выполнить
много подбрасываний монетки (т. е. устроить массу случайных событий),
то обнаружится закономерность, позволяющая сделать предсказание:
приблизительно половина монеток выпадает орлом, а приблизительно
половина — решкой. Возьмем игральный кубик и выполним, например,
600 его бросаний. Мы обнаружим целый ряд статистических закономер-
закономерностей и можем сделать немало предсказаний. Вот некоторые:
-	приблизительно в 100 случаях выпадет единица,
-	приблизительно в 100 случаях выпадет шестерка,
-	приблизительно в половине всех случаев выпадет нечетное число.
И в примере с монеткой, и в примере с кубиком мы имеем дело
с рождением информации из шума, который был создан весьма боль-
большим количеством случайных событий-подбрасываний. Родившаяся
в этом шуме информация позволила нам делать некоторые предсказания.
47

Эти предсказания приблизительные. Не однозначные!
Пвтор. Тем не менее это предсказания, которые можно проверить на
практике. А вопрос о степени их точности — это отдельный вопрос.
В данном случае он непринципиален.
g4u*ftfufie*b. Я могу предложить более наглядный пример рождения
информации из шума. У меня когда-то был мешочек с кучей квадрати-
квадратиков, изображавших различные буквы (такие мешочки с буквами ис-
использовались в детской игре под названием «Эрудит»). Я любил выни-
вынимать из мешочка буквы наугад и записывать их одну за другой в строку
на листе бумаги. Каждую вынутую букву я всякий раз возвращал обрат-
обратно в мешочек. С течением времени у меня получался на листе бумаги
длинный ряд случайно появившихся букв. В нем я обнаруживал от-
отдельные слова. Чаще всего это были трехбуквенные слова, реже четы-
четырехбуквенные, еще реже пятибуквенные. А однажды у меня встрети-
встретилось семибуквенное слово «БЕГЕМОТ». Этот «бегемот» родился
буквально из хаоса — из беспорядочного набора случайно вынутых из
мешочка букв.
Пвтор. Похожий метод получения информации из хаоса описал из-
известный английский писатель Джонатан Свифт A667-1745) в своей
знаменитой книге о путешествиях Гулливера. При посещении Большой
Академии в Лагадо (столице придуманного писателем королевства) Гул-
Гулливер видел хитроумное устройство с множеством нанизанных на спи-
спицы деревянных кубиков, на сторонах которых были написаны (все сло-
слова в различных наклонениях, временах, падежах, но без всякого порядка).
По команде местного профессора ученики несколько раз повертывали
спицы с кубиками, что приводило к изменениям сочетаний слов. «Тог-
«Тогда профессор приказывал тридцати шести ученикам медленно читать
образовавшиеся строки в том порядке, в каком они разместились в раме.
Если случалось, что три или четыре слова составляли часть фразы, то ее
диктовали остальным четырем ученикам, которые играли роль писцов».
ttcuSUuSie**. Мне думается, что такая технология добывания инфор-
информации практически неинтересна. Меня давно занимает вопрос о том,
откуда вообще люди достают информацию, которую они затем исполь-
используют для создания всевозможных образцов порядка? Как человеку уда-
удалось придумать, например, автомобиль или телевизор? Я понимаю, что
подобные открытия делаются не на пустом месте, а требуют предвари-
предварительных познаний в физике и технике. И тем не менее мне непонятно,
как рождается главная идея того или иного изобретения? Откуда появ-
появляются у ученых новые идеи? Как у поэта рождаются стихи? Как у ком-
композитора возникает мелодия?
48

Музыкант играл на скрипке — я в глаза ему глядел.
Я не то, чтоб любопытствовал, — я по небу летел.
Я не то, чтобы от скуки, — я надеялся понять,
Как умеют эти руки эти звуки извлекать
Из какой-то деревяшки, из каких-то грубых жил,
Из какой-то там фантазии, которой он служил!
Булат Окуджава
Пвтор. Вопрос о том, как человек творит, возможно, наиболее
интересен и наиболее сложен. Тут можно упомянуть знания, жиз-
жизненный опыт, наблюдательность, воображение, интуицию, вдохно-
вдохновение, и все равно остается прямой вопрос: откуда человек черпает
новую информацию0!
^ЧсиЯлАе**. Может быть, из имеющейся в его распоряжении информа-
информации! Недаром ученые так часто обращаются к книгам, а в наше время
также и к Интернету.
Пвтор. Конечно, уже имеющаяся информация весьма необходима
любому творцу — ученому, поэту, композитору и другим. И находит он
ее не только в книгах и Интернете, но также в окружающей действи-
действительности, которую он наблюдает и анализирует. Однако из только лишь
имеющейся информации действительно новая информация не рождает-
рождается. В этом случае происходит фактически лишь перекодировка суще-
существующей информации, изменяется форма представления информации,
не более того. Для рождения принципиально новой информации нуж-
нужно к прежней информации добавить еще что-то, и это «что-то» возни-
возникает в сознании человека-творца случайным образом, из шума.
ticuftiiAe**. Но как это можно конкретно представить?
Пвтор. Как и для любых случайных ситуаций, не существует жест-
жестких алгоритмов (жестких правил) творческого процесса. Но можно пред-
представить себе, что ученый, размышляя над какой-то проблемой, переби-
перебирает многочисленные варианты, в том числе случайно приходящие ему
в голову. Он анализирует различные варианты и производит отбор, от-
отбрасывая неподходящие варианты. В одних случаях этот процесс ока-
оказывается мучительно долгим, а в других он, напротив, увлекателен и не
требует особых усилий. В отношении поэтического творчества об этом
красноречиво говорят следующие два стихотворных отрывка.
Поэзия — та же добыча радия:
В грамм добыча — в год труды.
Изводишь единого слова ради
Тысячи тонн словесной руды...
Владимир Маяковский
49

И забываю мир — и в сладкой тишине
Я сладко усыплен моим воображеньем,
И пробуждается поэзия во мне:
Душа стесняется лирическим волненьем,
Трепещет и звучит, и ищет, как во сне,
Излиться, наконец свободным проявленьем —
И тут ко мне идет незримый рой гостей,
Знакомцы давние, плоды мечты моей.
И мысли в голове волнуются в отваге,
И рифмы легкие навстречу им бегут,
И пальцы просятся к перу, перо к бумаге,
Минута — и стихи свободно потекут...
Александр Пушкин
А если иметь в виду не поэтическое, а научное творчество?
Пвтор. У современного американского писателя Рэймонда Джоунса
есть любопытная фантастическая новелла «Уровень шума». Собирают
большую группу специалистов из разных областей науки, техники, куль-
культуры и сообщают им, что сделано удивительное открытие (какое именно,
сейчас нам неважно). Далее всем собравшимся сообщают, что, к несча-
несчастью, изобретатель внезапно погиб и унес с собой тайну открытия (на са-
самом деле, заметим, не было ни изобретателя, ни открытия). Собрав-
Собравшимся предлагают изучить все, что якобы осталось после гибели
изобретателя: обрывки каких-то записей и пленок, какие-то расчеты,
дневники, множество самых разных журналов и книг, принадлежавших
мнимому изобретателю, множество случайно подобранных приборов,
устройств, незавершенных конструкций непонятного предназначения
и тому подобное. Одним словом, предложен огромный информацион-
информационный шум. На первый взгляд, тут вообще ничего нельзя понять — пол-
полнейший хаос. И вот специалисты, используя этот хаос и будучи уверен-
уверенными, что проблема разрешима (ведь их уверили, что изобретатель успел
продемонстрировать свое изобретение), и вправду решают проблему.
Ставка на Его Величество Случай себя оправдала!
g4utftiuSU*b. Но это же фантастика! Придуманная история!
Пвтор. Верно. Однако здесь выражена весьма разумная мысль: рож-
рождение новой информации становится более вероятным, если «уровень
шума» будет весьма высок, т. е. если использовать побольше всевозмож-
всевозможных сведений, включая и те, которые, казалось бы, отношения к рас-
рассматриваемой проблеме не имеют. Иначе говоря, желателен случайный,
набор большого количества разнообразных данных, именуемый информа-
информационным шумом.
50

Я вижу, что и вправду без Его Величества Случая поря-
порядок из беспорядка не возникнет, принципиально новые открытия не
состоятся.
Пвтор. Современные ученые широко используют случайности для
получения информации, не прибегая к приемам академиков из Лагадо.
Существует метод статистических испытаний, называемый также мето-
методом Монте-Карло. Существуют методы случайного поиска. В свое время
мы достаточно обстоятельно познакомимся с этими методами.
2.6 Единство двух противоположностей
]К1так, есть две противоположности. С одной из них связывают поня-
понятия «порядок», «необходимое», «информация». С другой связывают по-
понятия «беспорядок», «случайное», «шум». Обе противоположности от-
отнюдь не исключают друг друга. Мир, в котором царствовала бы только
одна из этих двух противоположностей (мир абсолютного порядка или
мир абсолютного беспорядка), нереален, он невозможен. В реальном
мире присутствуют обе указанные противоположности; поэтому можно
говорить о единстве этих противоположностей. В чем оно проявляется?
Ответить на этот вопрос нетрудно. Единство порядка и беспорядка про-
проявляется в происходящих постоянно переходах от порядка к беспорядку
(деструктивные процессы, т. е. процессы разрушения) и переходах от бес-
беспорядку к порядку (конструктивные процессы, т. е. процессы созидания).
Благодаря чему совершаются эти переходы? И на этот вопрос отве-
ответить несложно. Как те, так и другие переходы совершаются благодаря
существованию случайных событий. Можно сказать, что наш мир «управ-
«управляется» случайными событиями. С одной стороны, случайные события
нарушают или даже разрушают порядок. С другой стороны, они порож-
порождают порядок. Для рождения порядка из беспорядка (необходимого из
случайного, информации из шума) нужно, чтобы случайных событий
было достаточно много. Одно или всего лишь несколько случайных
событий не обеспечат рождение порядка.
Если мы желаем получить порядок из беспорядка (информацию из
шума), то должны принимать меры к увеличению множества случай-
случайных событий. В таких ситуациях случайности являются нашими союзни-
союзниками и помощниками. Если мы желаем подольше сохранить имеющийся
порядок, мы должны принимать меры к ограничению и сокращению
случайных событий. В таких ситуациях случайности являются нашими
противниками.
51

Таблица 3. Переходы между порядком и беспорядком

Существенно, что как процессы созидания, так и процессы разруше-
разрушения происходят в нашем мире одновременно и постоянно. Можно ска-
сказать, что все время совершается «сотворение мира» и все время проис-
происходят процессы, называемые «концом света».
Вот два рисунка М. Эшера (см. табл. 3). На рисунке 1 из беспорядка
возникает порядок. На рисунке 2 один порядок как бы растворяется
в беспорядке, но одновременно из беспорядка возникает новый порядок.
ЗАДАНИЯ ПО ТЕМЕ 2
1.	Проанализируйте библейский миф о Сотворении Мира. Сравните его с современ-
современными научными представлениями о возникновении Солнечной системы и о био-
биологической эволюции на Земле.
2.	Попробуйте на досуге написать собственные сочинения на темы: «Мир, где цар-
царствует случайность» и «Мир, где царствуют порядок и необходимость». Продумай-
Продумайте собственный ответ на вопрос, почему нереален как тот, так и другой мир.
3.	Что теряет человек, оказавшийся (разумеется, мысленно) в мире абсолютного
порядка?
4.	Подберите собственные примеры, иллюстрирующие переходы от порядка к беспо-
беспорядку. Каким образом люди пытаются задержать хотя бы на время такие переходы?
5.	Подберите примеры, иллюстрирующие переходы от беспорядка к порядку.
6.	Пару игральных кубиков подбросили 600 раз. Какие предсказания можно сде-
сделать по поводу результатов этих бросаний?
7.	Существует метод поиска информации, называемый «мозговым штурмом»: не-
несколько человек совершенно свободно, не останавливая и не критикуя друг дру-
друга, высказывают любые (какие захотят) соображения по предложенной пробле-
проблеме. Какое отношение имеет этот метод к процессу рождения информации из
хаоса?
8.	Приведите примеры, когда Его Величество Случай выступает как наш противник,
а также примеры, когда он союзник и помощник.
9.	В § 2.6 говорилось: «для рождения порядка из беспорядка нужно, чтобы случай-
случайных событий было достаточно много». Приведите примеры, доказывающие вер-
верность этого утверждения.
53

ТЕМА 3
ЛЕВОЕ И ПРАВОЕ
Что может быть больше похоже на мою
руку или мое ухо, чем их собственные
отражения в зеркале? И все же руку, ко-
которую я вижу в зеркале, нельзя поставить
на место настоящей руки...
Иммануил Кант
Хчазалось бы, какие могут быть проблемы с левым и правым? Нико-
Никому не надо объяснять, где левая рука и где правая, как сделать поворот
налево и как повернуть направо. Каждый отличит левый берег или при-
приток реки от правого. Однако существуют также левые и правые спирали
и винты, левые и правые системы координатных осей, левые и правые
узлы, левые и правые молекулы. Так что тут есть о чем говорить. Разго-
Разговор о левом и правом начнем с того, что сравним объект с его зазер-
кальным двойником.
3.1 Объект и его зазеркальный двойник
)се знают, что увидеть зазеркальный двойник объекта совсем не-
нетрудно. Надо поместить освещенный объект перед плоским зеркалом
54

и заглянуть в это зеркало. Обычно полагают, что наблюдаемый в зеркале
двойник является точной копией самого объекта. Но это не совсем так.
Зеркало не просто копирует объект, а меняет местами (переставляет) пе-
передние и задние по отношению к плоскости зеркала части объекта. В срав-
сравнении с самим объектом его зазеркальный двойник оказывается «вывер-
«вывернутым» вдоль направления, перпендикулярного к плоскости зеркала.
Все это хорошо видно на рис. 1 и рис. 2 в таблице 4, а также на рис. 1
и рис. 2 в таблице 5. В таблице 4 рассматривается зеркальное отражение
в плоскости (отражение происходят по отношению к оси симметрии,
которая представлена здесь в виде пунктирной прямой), а в таблице 5
рассматривается зеркальное отражение в пространстве (отражение про-
происходит по отношению к плоскости симметрии). На упомянутых рисун-
рисунках точки а, Ъ, с, d являются зазеркальными двойниками соответствен-
соответственно точек А, В, С, D. Отрезки Аа, ВЪ, Cc, Dd перпендикулярны к оси
симметрии (либо плоскости симметрии) и делятся пополам осью сим-
симметрии (плоскостью симметрии).
Возникающие при зеркальном отражении двойники (как плоские, так
и объемные) можно разбить на две группы. К первой группе отнесем те
зазеркальные двойники, которые посредством переносов и поворотов
можно совместить с соответствующими объектами. В этом смысле ука-
указанные двойники действительно оказываются точными копиями объек-
объектов. Двойники-копии можно видеть на рис. 1 в таблице 4 (для плоских
геометрических фигур) и на рис. 1 в таблице 5 (для объемных фигур).
Ко второй группе отнесем зазеркальные двойники, которые никаки-
никакими переносами и поворотами не совмещаются с соответствующими
объектами. Заметим, что плоские фигуры должны при переносах и по-
поворотах оставаться в своей плоскости. Зазеркальные двойники второй
группы можно видеть на рис. 2 в таблице 4 (для плоских геометричес-
геометрических фигур) и на рис. 2 в таблице 5 (для объемных фигур). Понятно, что
такие зазеркальные двойники уже нельзя считать точными копиями со-
соответствующих объектов. Существует специальное название для пар,
образованных подобными двойниками и объектами, — энантиоморфы.
«Энантиос» означает по-гречески «противоположный». Значит, термин
«энантиоморфы» дословно переводится как «противоположные фор-
формы» («морфе» — по-гречески «форма»).
Итак, при зеркальных отражениях возможны два разных случая. В од-
одном из них зазеркальный двойник и объект — это точные копии друг
друга» В другом случае зазеркальный двойник и объект — это энантио-
энантиоморфы; они не являются точными копиями друг друга. Они зеркально
противоположны, но не совмещаются друг с другом при переносах и
поворотах.
55

Таблица 4. Зеркальное отражение в плоскости
Рис.1
D
с
с
1
с
Рис.4
Рис.2
А	1	а
I	*
Рис.3
Рис.5
56

Таблица 5. Зеркальное отражение в пространстве
57

Когда же, можно спросить, реализуется тот или иной из двух случаев?
Когда при зеркальных отражениях формируются пары точных копий,
а когда — пары энантиоморфов? Ответ на этот вопрос будет дан в § 3.2.
3.2 Зеркально симметричные объекты
1 Хредположим, объект таков, что одна из двух его половинок может
рассматриваться в качестве зазеркалъного двойника другой половинки это
можно наблюдать на рис. 3 в таблице 4 и на рис. 3 в таблице 5. (Заме-
(Заметим, что, если «другая» половинка — зазеркальный двойник «первой»
половинки, то точно так же «первую» половинку можно рассматривать
в качестве зазеркального двойника «другой» половинки. (Подобные
объекты называют зеркально симметричными объектами. У них есть ось
симметрии (если объект плоский) или плоскость симметрии (если объект
объемный).
Вот некоторые известные всем примеры зеркально симметричных
объектов: скрипка, лодка, санки, дельтаплан, авиалайнер, стул, чайник,
ложка, вилка, очки, бинокль, кленовый, дубовый, березовый и многие
другие листья. Человеческое тело (точнее: его внешние формы) также
зеркально симметрично. Вообще почти все животные по своему внеш-
внешнему виду зеркально симметричны. Это особенно хорошо видно на при-
примере жуков, стрекоз, бабочек, рыб, крокодилов.
Однако можно указать немало объектов, которые не являются зер-
зеркально симметричными и, следовательно, не имеют плоскости симмет-
симметрии. Например, рояль, ботинок, перчатка, винт, ракушка прудовика,
лыжа, мотоцикл с коляской, вертолет. Внутреннее строение человечес-
человеческого тела и вообще всех животных также не является зеркально сим-
симметричным. Так, сердце и желудок находятся у нас слева, а печень справа.
Теперь мы можем ответить на вопрос, почему при зеркальном отра-
отражении в одном случае формируются точные копии, а в другом — энан-
тиоморфы. Точные копии возникают при отражении зеркально симмет-
симметричных объектов. Энантиоморфы возникают при отражении объектов, не
являющихся зеркально симметричными, т. е. не имеющих плоскости (оси)
симметрии.
В результате получаем строгое определение понятия «энантиомор-
«энантиоморфы». Энантиоморфы — это пара объектов {плоских фигур), которые яв-
являются зеркальным изображением один другого, но при этом каждый из
них не имеет плоскости {оси) симметрии. Пары энантиоморфов можно
58

видеть на рис. 2 в таблице 4 и рис. 2 в таблице 5; кроме того им специ-
специально посвящена таблица 6.
Из пары энантиоморфов нетрудно, в принципе, образовать объект
(фигуру), являющийся зеркально симметричным — см. рис. 4 в табли-
таблице 4 и рис. 4 в таблице 5. Здесь в качестве энантиоморфов выступают не
сами объекты (фигуры), а их половинки, «разрезанные» плоскостью
(осью) симметрии.
Если же брать не пары энантиоморфов, а пары точных зеркальных
копий, то из них можно образовать объект (фигуру), имеющий не одну,
а две и даже больше плоскостей (осей) симметрии. На рис. 5 в табли-
таблице 4 и на рис. 5 в таблице 5 показаны такие объекты (фигуры). Каждая
из них имеет две плоскости (оси) симметрии.
3.3 Энантиоморфы.
Лево-правая асимметрия (киральность)
iVlbi уже выяснили, что такое энантиоморфы. Пару энантиоморфов
можно кратко назвать взаимно зеркальными изображениями, не явля-
являющимися точными копиями один другого. Чтобы различить энантио-
энантиоморфы в данной паре, вводят обозначения «левый» и «правый». Один из
энантиоморфое левый, а другой правый. Не имеет принципиального зна-
значения, какой именно назван левым (правым); это вопрос договоренно-
договоренности, традиции, привычки.
На рис. 1 и рис. 2 в таблице 6 представлены примеры двумерных (плос-
(плоских) и трехмерных (объемных) пар энантиоморфов. Здесь пунктирная
прямая изображает ось симметрии (на рис. 1) либо сечение плоскости
симметрии плоскостью рисунка (на рис. 2). Слева от пунктирной прямой
находятся «левые» энантиоморфы, а справа — соответствующие «пра-
«правые» энантиоморфы.
На рис. 1 в таблице 6 даны следующие двумерные энантиоморфы:
1.	Поворот против часовой стрелки (левый энантиоморф) и пово-
поворот по часовой стрелке (правый энантиоморф).
2.	Левая плоская спираль (она раскручивается против часовой стрел-
стрелки) и правая спираль (раскручивается по часовой стрелке).
3.	Дорожный знак «прямо и налево» и знак «прямо и направо».
4.	Китайский символ Инь-Ян (левый энантиоморф) и его зазер-
кальный двойник (правый энантиоморф).
5.	Знак американского доллара (левый энантиоморф) и его зазер-
кальный двойник (правый энантиоморф).
59

Таблица 6. Энантиоморфы
1
В пространстве:
h
о 0 ' % о
хч I > х
ОН
он
7 /сА\
СН, "ч
/Н | Н
С2Н5
Рис.1
Рис.2
60

6.	Левая система осей и правая система осей.
7.	Буква «Ь» (левый энантиоморф) и его зазеркальный двойник (пра-
(правый энантиоморф; при повороте он может стать буквой «Р»).
8.	Слово «КУБ» (левый энантиоморф) и его зазеркальный двойник
(правый энантиоморф). Этот пример особенно ярко показывает,
насколько сильно могут различаться энантиоморфы.
На рис. 2 в таблице 6 даны следующие трехмерные энантиоморфы:
1.	Левая перчатка и правая перчатка.
2.	Левый игральный кубик и правый игральный кубик.
3.	Левый узел и правый узел.
4.	Левый винт и правый винт.
5.	Левая объемная спираль (если смотреть вдоль ее оси, то точка
будет удаляться от наблюдателя при движении по винтовой ли-
линии в направлении против часовой стрелки) и правая объемная
спираль (теперь точка удаляется от наблюдателя при движении
по винтовой линии в направлении по часовой стрелке).
6.	Левая система осей и правая система осей.
7.	Молекула вторичного бутилового спирта (левый энантиоморф) и
ее зазеркальный двойник (правый энантиоморф).
Понятно, что левые и правые перчатки используются в одинаковой
мере. Нет предпочтения левым или правым узлам. Игральные кубики
чаще делаются в «правом» варианте. Винты в нашей стране практичес-
практически всегда правые. Если кому-то из наших читателей вдруг предложить
ввинтить или вывинтить левый винт, он наверняка окажется в затруд-
затруднении. Он привык к правым винтам. А ввинтить лампочку с левой вин-
винтовой нарезкой он вообще не сможет, поскольку у нас патроны делают-
делаются под лампочки с правой нарезкой. Мы привыкли пользоваться правой
системой координатных осей. Что же касается примера с молекулой
вторичного бутилового спирта, то здесь ситуация особая. Дело в том,
что правый энантиоморф — это уже не молекула вторичного бутилово-
бутилового спирта, а совсем иное вещество. Несмотря на то, что при зеркальном
отражении не изменились ни состав атомов, ни структурные элементы
молекулы, ни внутренние связи между ними.
Как уже отмечалось, двумерные энантиоморфы нельзя совместить
друг с другом никакими переносами и поворотами в плоскости этих
энантиоморфов. Чтобы все-таки совместить их, надо выйти за пределы
плоскости и выполнить поворот в трехмерном пространстве: перевер-
перевернуть плоскость обратной стороной. Что же касается трехмерных энан-
энантиоморфов, то для их совмещения потребовался бы поворот в фантас-
фантастическом четырехмерном пространстве. Выполнить такой поворот и даже
61

представить его мысленно, очевидно, невозможно. Поэтому для трех-
трехмерных энантиоморфов справедливо утверждение: никакие перемещения
или повороты не в состоянии обратить левый энантиоморф в правый или
наоборот. Левый энантиоморф всегда будет левым, а правый всегда бу-
будет правым. Как ни вертеть в руках левый ботинок, он никогда не по-
подойдет к правой ноге. Сколько бы ни бросали правый игральный кубик
он никогда не превратится в левый.
Принято говорить, что пара энантиоморфов обладает лево-правой
асимметрией, или киралыюстью (от греческого слова «кир», означающе-
означающего «рука»).
Любопытно, что для «доказательства» существования «потусторон-
«потустороннего» четырехмерного мира использовались в свое время фальшивые
демонстрации с превращением левых энантиоморфов в правые (и на-
наоборот) . Подобные демонстрации предлагались на так называемых спи-
спиритических сеансах, достаточно модных в начале ХХ-го столетия в не-
некоторых мистически настроенных кругах. Разумеется, демонстрации
с «превращением» одного энантиоморфа в другой являлись не более
как ловкими трюками, основанными на незаметной подмене соответ-
соответствующих энантиоморфов. Например, у участника сеанса отбиралась
левая перчатка, затем проводились отвлекающие внимание манипуля-
манипуляции и сидящим в полутемной комнате зрителям предъявлялась правая
перчатка точно такого же размера, цвета, покроя. Это выдавалось за
доказательство кратковременного пребывания перчатки в потусторон-
потустороннем мире, где она, дескать, и превратилась из левой в правую.
3.4 Лево-правая асимметрия и жизнь
1 Хриводившаяся в § 3.3 молекула вторичного бутилового спирта —
всего лишь пример из великого множества сложных молекул, не имею-
имеющих плоскости симметрии. Ученые называют такие молекулы кираль-
ными или зеркально асимметричными (а также оптическими изомерами).
Существенно, что многие сложные молекулы, из которых построены
живые организмы, зеркально асимметричны, т. е. киральны. Они подоб-
подобны «винтам», а в ряде случаев прямо похожи на винты. Например, двой-
двойная спираль молекулы ДНК или альфа-спираль Полинга, в которую
«закручены» полипептидные цепочки молекул белков. Более того, ки-
ральные молекулы живых организмов существуют всякий раз лишь в ка-
каком-то одном варианте — либо «левом», либо «правом». Так, спираль
62

молекулы ДНК и белковая альфа-спираль Полинга всегда правые. По-
Подобные молекулы ученые называют кирально чистыми.
Знаменитый французский ученый Луи Пастер A822-1895) первый
обратил внимание на то, что, если в неживой природе молекулы либо
зеркально симметричны, либо одинаково часто встречаются в «левом» и
«правом» вариантах, то в живых организмах зеркально асимметричные
молекулы встречаются в виде только определенной киралъности — левой
или правой. Пастер полагал, что именно здесь проходит граница между
химией живой и неживой природы. В отличие от неорганических объектов
живые организмы построены из «винтов», причем винты одного типа
только левые, а другого только правые. Можно сказать, что специфика
живой материи — киралъная чистота молекул. В своей очень интересной
книге «Этот правый, левый мир» известный американский популяриза-
популяризатор науки Мартин Гарднер писал: «Одна из наиболее замечательных черт
жизни — это способность организма извлекать из окружающей среды
химические соединения, молекулярная структура которых по большей
части симметрична, и изготовлять из них правые и левые асимметрич-
асимметричные соединения углерода. Растения, например, используют симметрич-
симметричные неорганические соединения вроде воды и углекислого газа и превра-
превращают их в асимметричные молекулы крахмала и сахара... Тела всех живых
существ насыщены асимметричными углеродными молекулами, а также
асимметричными спиралями белков и нуклеиновых кислот».
Человек, как и все животные, построен из молекул определенной ки-
ральности (для одних видов молекул левой, для других правой). Потреб-
Потребляемая человеком органическая пища также построена из молекул опре-
определенной киральности. Понятно, что киральность молекул пищи
согласуется с киральностью молекул человеческого организма (подобно
тому, как правые гайки «согласуются» с правыми болтами). А что будет,
если киральность молекул нашей пищи вдруг изменится? Такая пища
станет для нас непригодной, она может оказаться биологически ядовитой.
Современная химия в ряде случаев искусственно получает зеркально отра-
отраженные молекулы. Их действие на наш организм оказывается совершен-
совершенно иным по сравнению с действием соответствующих природных моле-
молекул. Так, «отраженная» молекула витамина С не воспринимается
организмом. Небольшая добавка в пишу фенилаланина, приготовленно-
приготовленного из имеющихся в природе веществ, не вызывает неприятных послед-
последствий. Добавка же «отраженного» фенилаланина приводит к резкому на-
нарушению обмена веществ, сопровождающемуся умопомешательством.
Известный английский писатель и математик Льюис Кэрролл (настоя-
(настоящее имя: Чарлз Доджсон) A832-1898) написал для детей чудесную книгу
63

«Алиса в Зазеркалье». Там есть сценка, имеющая прямое отношение
ккиральным молекулам. Собираясь «пройти» сквозь зеркало в скры-
скрытый за ним зазеркальный мир, Алиса обращается к своему котенку с во-
вопросом: «Но понравится ли тебе в Зазеркалье, киска? Дадут ли тебе там
молочка? Может быть, молоко в Зазеркалье не годится для питья?» Дей-
Действительно, в состав молока входит много зеркально асимметричных
соединений — жиры, лактоза, белки. При «переходе» из обычного мира
в зазеркальный все асимметричные молекулы должны бы превратиться
из одних энантиоморфов в другие («отраженные»); в результате, зазер-
кальное молоко должно было бы отличаться от обычного. Впрочем,
при «переходе» в Зазеркалье и Алиса, и ее котенок сами превращаются
в своих зазеркальных двойников. А в таком случае зазеркальное молоко
будет для них столь же вкусным и полезным, каким было раньше обыч-
обычное («неотраженное») молоко.
С вопросами зеркальной симметрии-асимметрии на молекулярном
уровне тесно связана проблема возникновения жизни на Земле. Живая ма-
материя возникла из неживой. Значит, возникновение жизни обусловлено
нарушением существовавшей до того зеркальной симметрии, образованием
киралъно чистых молекул. Воспроизведение и поддержание в дальнейшем
этой киральной чистоты есть важнейшая функция жизнедеятельности.
Современная наука пришла к выводу, что переход от мира зеркально
симметричных соединений к кирально чистому миру произошел не в про-
процессе длительной эволюции, а скачком — в виде своеобразного Большого
Биологического Взрыва. Российский ученый Л.Л. Морозов A946-1984), один
из активных исследователей проблемы возникновения жизни в результа-
результате нарушения зеркальной симметрии, писал: «Анализ условий, которые
физический мир мог обеспечить для нарушения зеркальной симметрии,
привел нас к достаточно сильному утверждению: эволюционные процес-
процессы не способны обеспечить возникновение наблюдаемого кирально чис-
чистого состояния биосферы. Генезис этого состояния связан не с устойчи-
устойчивой эволюцией органического вещества, а с катастрофой, т. е. достижением
развивающейся средой критической точки, за которой теряется устойчи-
устойчивость прежнего, симметричного состояния. На каком-то этапе перехода
материи к живой форме должен быть аналог «Большого Взрыва» — «Боль-
«Большой Биологический взрыв».
Конечно, не хочется рассматривать возникновение жизни на Земле
как некую катастрофу. Однако данный термин вполне точен, если под-
подходить к нему не с бытовой (житейской), а с научной точки зрения. Эта
«катастрофа» была величайшим в истории нашей планеты актом само-
самоорганизации материи.
64

ЗАДАНИЯ ПО ТЕМЕ 3
1.	У меня часы на левой руке, а у моего зазеркального двойника на правой. Зерка-
Зеркало меняет местами «левое» и «правое». А почему оно не меняет местами «верх» и
«низ»?
2.	Объект А, отражаясь в зеркале 1, превращается в объект Г, а отражаясь в зерка-
зеркале 2 превращается в объект Б. Объект Б, отражаясь в зеркале 1, превращается
в объект В. Объект Г, отражаясь в зеркале 2, тоже превращается в объект В.
Изобразите объекты Б, В, Г и укажите, какие пары из четырех рассматриваемых
здесь объектов являются парами энантиоморфов, а какие — не являются.
3.	Вот ряд заглавных букв: А, Б, Е, И, К, М, Р, П, У, Ц, Я, Т. Какие из этих букв-фигур
могут быть энантиоморфами? Рассматривая каждую из них как левый энантиоморф,
изобразите соответствующие правые энантиоморфы.
4.	Предложите продолжения рисунков 1 и 2 из таблицы 6. В частности, присмотри-
присмотритесь к собственной квартире. Укажите те объекты в ней, которые имеют плос-
плоскость симметрии, а также объекты, не имеющие плоскости симметрии.
5.	В кинозале установили параллельно экрану большое плоское зеркало. Зритель
сидит спиной к экрану и следит за фильмом, глядя в зеркало. В фильме развива-
развиваются какие-то события. Кто-то с кем-то встречается, обнимается, дерется. Кто-то
куда-то бежит, что-то получает и что-то отдает. Как будет воспринимать все это
зритель, сидящий лицом к зеркалу? Что изменится в зазеркальном фильме по
сравнению с фильмом на обычном экране?
6.	Рассмотрим фантастическую ситуацию. Дама сидела за туалетным столиком перед
зеркалом и писала какую-то записку. И вдруг комната вместе с дамой оказалась
в Зазеркалье. Что при этом изменилось? Укажите побольше изменений, которые
стали следствием перехода в Зазеркалье.
65

ТЕМА 4
СИММЕТРИЯ И АСИММЕТРИЯ
Симметрия является той идеей, посред-
посредством которой человек на протяжении ве-
веков пытался постичь и создать порядок,
красоту и совершенство.
Герман Вейлъ
4.1 Геометрическая симметрия
4.1.1. Зеркальная и поворотная симметрии. Существуют три основных
вида геометрической симметрии (иначе говоря, симметрии положений):
зеркальная, поворотная, переносная (трансляционная). Сначала рассмот-
рассмотрим зеркальную и поворотную симметрии, принимая во внимание их
глубокую взаимосвязь.
С зеркальной симметрией мы уже познакомились в теме 3. Говорят,
что объект обладает зеркальной симметрией, если его можно предста-
представить в виде двух «половинок», являющихся зеркальным отражением одна
другой. Эти «половинки» мысленно разграничиваются плоскостью
66

симметрии {осью симметрии, если рассматриваются плоские фигуры).
Многие объекты можно мысленно разбить на зеркально отраженные
«половинки» не одним способом, а несколькими. Такие объекты имеют
не одну, а несколько плоскостей (осей) симметрии — см. плоские фи-
фигуры на рис. 1 в таблице 7 (здесь через / обозначено число осей симмет-
симметрии фигуры, а сами эти оси показаны пунктиром).
Чем объясняется наличие у ряда объектов нескольких плоскостей (осей)
симметрии? — Это объясняется тем, что данные объекты обладают,
наряду с зеркальной, также поворотной симметрией.
Говорят, что объект обладает поворотной симметрией п-го порядка, если
он совмещается сам с собой при повороте на угол 360°/ п (п = 2, 3, 4, 5, ...).
Ось, вокруг которой совершается поворот, называют поворотной осью п-
го порядка. Двумерные фигуры совершают поворот вокруг точки поворо-
поворота (это есть точка пересечения поворотной оси с плоскостью рисун-
рисунка) — см. плоские фигуры на рис. 2 в таблице 7 (здесь А — точка поворота).
Если у объекта нет поворотной симметрии, то он может иметь лишь
одну плоскость симметрии (или вообще не иметь плоскости симметрии).
К этому хочется добавить вывод, который вроде бы следует из сравнения
рисунков 1 и 2: если у объекта есть поворотная ось п-го порядка, то он
обладает п плоскостями (осями) симметрии. Такой вывод был бы, одна-
однако, неверен. В этом легко убедиться, посмотрев на рис. 3 в таблице 7. У
объектов 3, 4, 5 и вправду /= п. Однако у объектов 6, 7, 8 равенства /= п
нет несмотря на наличие у них поворотной симметрии. Объекты 6 и 7
обладают поворотной симметрией соответственно 4-го и 2-го порядка, а
зеркальной симметрии у них нет. У объекта 8 (правильной трехгранной
призмы) есть поворотная ось 3-го порядка и 4 плоскости симметрии.
Отметим, что объект 8 — не плоская фигура, а тело. Количества по-
поворотных осей и плоскостей симметрии у геометрических тел могут быть
достаточно большими. Для описания симметрии конкретного трехмерно-
трехмерного объекта необходимо указать все поворотные оси и их порядок, а также
все плоскости симметрии.
Например, куб имеет 9 плоскостей симметрии и 13 поворотных осей,
в том числе 6 осей 2-го порядка, 4 оси 3-го порядка и 3 оси 4-го поряд-
порядка. На рис. 4 в таблице 7 изображен куб, на поверхности которого отме-
отмечены буквами 26 точек. Используя эти точки, можно представить (и да-
даже провести тонким карандашом) все поворотные оси и плоскости
симметрии куба. Поворотные оси:
—	шесть осей 2-го порядка, каждая из которых проходит через середи-
середины противоположных параллельных ребер куба: ВХ9 TF, DZ, HV, LQ, JN;
—	четыре оси 3-го порядка, каждая из которых совпадает с внутрен-
внутренней диагональю куба: CY, UG, SE, AW;
67

Таблица 7. Зеркальная и поворотная симметрии
1	— Тетраэдр
2	— Октаэдр
3	— Икосаэдр
4	— Куб (гексаэдр)
5	- Додекаэдр
Рис.5
Рис.3
68

—	три оси 4-го порядка, каждая из которых проходит через центры
противоположных граней куба: КР, RG, 10.
Плоскости симметрии зададим четырьмя точками:
—	три плоскости симметрии, каждая из которых проходит через центр
куба параллельно одной из его граней: TBFX, ZHDV, JLNQ;
—	шесть плоскостей симметрии, каждая из которых проходит через
противоположные параллельные ребра куба: SAEW, UCGY, CEYS, AGWU,
YWCA, GEUS.
Интересна симметрия прямого кругового цилиндра. Цилиндр имеет
одну поворотную ось бесконечно большого порядка (ось цилиндра) и бес-
бесконечное количество поворотных осей 2-го порядка (все они находятся
в плоскости симметрии, которая перпендикулярна к оси цилиндра и де-
делит высоту цилиндра пополам). Кроме того у цилиндра есть бесконеч-
бесконечное количество плоскостей симметрии, которые все проходят через ось
цилиндра.
По сравнению с цилиндром прямой круговой конус менее симметри-
симметричен. У него только одна поворотная ось. Это есть ось конуса; она имеет
бесконечно большой порядок. Кроме того, у конуса есть бесконечно много
плоскостей симметрии; все они проходят через ось конуса.
4.1.2. Правильные многогранники (пять Платоновых тел). Правильным
называется многогранник с одинаковыми гранями в форме правильных мно-
многоугольников с одинаковыми двугранными углами. Оказывается, что таких
тел может быть всего пять. Все они показаны на рис. 5 в таблице 7: тетра-
тетраэдр (правильная треугольная пирамида), октаэдр, икосаэдр, гексаэдр (куб),
додекаэдр. Правильные многогранники имеют разное число граней и имен-
именно по этому числу получили свои названия. Тетраэдр имеет четыре грани
в форме равносторонних треугольников («тетра» и «хедрон» — по-гре-
по-гречески «четыре» и «грань»). Октаэдр имеет восемь граней-треугольников
(«окто» — «восемь»). Икосаэдр имеет двадцать граней-треугольников («эй-
коси» — «двадцать»). Гексаэдр, или куб имеет шесть граней в форме
квадратов («гекс» — «шесть»). Додекаэдр имеет двенадцать граней в форме
правильных пятиугольников («додека» — «двенадцать»).
На основе куба нетрудно построить тетраэдр — он изображен тонки-
тонкими линиями внутри куба на рис. 5 в таблице 7. Ребра этого тетраэдра —
диагонали граней куба.
Соединив отрезками прямых центры граней куба, имеющих общее ребро,
мы получим октаэдр. Соединив отрезками прямых центры граней
октаэдра, имеющих общее ребро, мы получим куб. Такие многогранни-
многогранники называют взаимными. Взаимны не только куб и октаэдр. Взаимны также
икосаэдр и додекаэдр. Соединив отрезками прямых центры граней
икосаэдра, имеющих общее ребро, получаем додекаэдр, а соединив
69

отрезками прямых центры граней додекаэдра, имеющих общее ребро,
получаем икосаэдр.
Интересно, что пары взаимных многогранников имеют одинаковую сим-
симметрию (примем это без доказательства). Симметрию куба мы уже рас-
рассматривали. Такую же симметрию имеет октаэдр.
Нетрудно понять почему существуют только пять правильных мно-
многогранников. Возьмем простейшую грань — равносторонний треуголь-
треугольник. Многогранный угол можно образовать, приложив друг к другу три,
четыре либо пять треугольников, то есть тремя способами. Шесть рав-
равносторонних треугольников уже не могут образовать многогранного угла,
поскольку сумма плоских углов при обшей вершине в этом случае рав-
равна 6 • 60° = 360°. Используя в качестве граней квадраты, можно образо-
образовать многогранный угол только одним способом — с помощью трех при-
приложенных друг к другу квадратов. Единственным способом может быть
образован многогранный угол и из правильных пятиугольников (при
помощи трех пятиугольников). Правильные я-угольники при п > 6 мно-
многогранных углов, очевидно, не образует вообще. Вот и получается, что
могут существовать только пять правильных многогранников: три с тре-
треугольными гранями (тетраэдр, октаэдр, икосаэдр), один с квадратными
гранями (куб) и один с пятиугольными гранями (додекаэдр).
4.1.3. Переносная симметрия; плоские (двумерные) и пространственные
(трехмерные) решетки. Говорят, что объект обладает переносной симмет-
симметрией, если он совмещается сам с собой при переносе вдоль некоторого на-
направления (вдоль оси переноса) на один или любое целое число шагов (перио-
(периодов, или элементарных переносов). Переносную симметрию называют
также трансляционной (от латинского «трансляция» — «передача»). Строго
говоря, симметричный по отношению к переносам объект должен быть
бесконечно длинным в направлении оси переноса (например это мог
бы быть бесконечно длинный бордюр). Однако на практике понятие
переносной симметрии применяют для объектов конечных размеров,
имея в виду наблюдаемое при переносе совмещение одной части объек-
объекта с другой его частью.
С переносной симметрией связано понятие двумерной периодической
структуры — плоской решетки. Плоская решетка может быть образова-
образована наложением двух семейств параллельных равноотстоящих друг от друга
прямых. Эти семейства параллельных прямых разбивают плоскость на
одинаковые параллелограммы. Различают 5 типов плоских решеток: квад-
квадратную, прямоугольную, гексагональную, ромбическую, косую. Все они
показаны на рис. 1 в таблице 8. Чтобы задать решетку, достаточно за-
задать ее элементарною ячейку (соответствующий параллелограмм) и за-
затем переносить эту ячейку параллельно самой себе вдоль направления
70

одного семейства параллельных прямых и вдоль направления другого
семейства параллельных прямых. Так, заштрихованную на рис. 1 эле-
элементарную ячейку следует переносить в направлении ОА на расстоя-
расстояния, кратные а, и в направлении ОВ на расстояния, кратные Ъ.
На рис. 2 в таблице 8 показан использовавшийся древними китайца-
китайцами каркас для окон из бумаги. Каркас обладает переносной симметри-
симметрией. Его можно построить, используя различные типы плоских решеток:
гексагональную (позиция 1 на рисунке), прямоугольную (позиция 2),
косую (позиция 3). Соответствующие элементарные ячейки на рисунке
заштрихованы (в случае гексагональной решетки элементарная ячейка
дана двойной штриховкой); кроме того во всех трех случаях показаны
семейства параллельных прямых, образующие ту или иную плоскую
решетку. Обратите внимание: одна и та же плоская фигура (один и тот
же каркас) может быть представлена тремя типами плоских решеток.
С переносной симметрией в пространстве связано понятие трех-
трехмерной периодической структуры — пространственной решетки. Если
плоскую решетку образуют два семейства параллельных: равноотстоя-
равноотстоящих друг от друга прямых, то пространственную решетку образуют
три семейства параллельных равноотстоящих друг от друга плоскостей.
Эти три семейства параллельных плоскостей разбивают пространство
на одинаковые параллелепипеды. Различают 7 различных типов таких
параллелепипедов, в связи с чем говорят о семи сингониях (семи кри-
кристаллографических системах): триклинной, моноклинной, ромбической,
тригональной (ромбоэдрической), гексагональной, тетрагональной, куби-
кубической. Все эти параллелепипеды изображены в таблице 9. Они могут
рассматриваться как элементарные ячейки соответствующих простран-
пространственных решеток. Показанную в верхнем левом углу таблицы 9 эле-
элементарную ячейку надо переносить параллельно самой себе вдоль на-
направления ОА на расстояния, кратные а, вдоль направления ОВ на
расстояния, кратные Ъ, вдоль направления ОС на расстояния, кратные с.
В результате как раз и возникнет заданная этой элементарной ячей-
ячейкой пространственная решетка.
Итак, пространственную решетку можно образовать двумя способа-
способами. Во-первых, используя три семейства параллельных равноотстоящих
друг от друга плоскостей. Во-вторых, за счет параллельных переносов
элементарной ячейки (соответствующего параллелепипеда) вдоль трех
определенных направлений в пространстве. Напомним, что плоскую
решетку также можно образовать двумя способами. Во-первых, исполь-
используя два семейства параллельных прямых. Во-вторых, за счет параллель-
параллельных переносов элементарной ячейки (соответствующего параллелограм-
параллелограмма) вдоль двух определенных направлений в плоскости.
71

Таблица 8. Плоские (двумерные) решетки
О а
Рис.1
1.	Квадратная решетка:	а = Ъ\ у = 90°
2.	Прямоугольная решетка: а ^ Ъ\ у = 90°
3.	Гексагональная решетка: а = Ъ\ у = 60°
4.	Ромбическая решетка: а = Ь; у = 90° 60°
2 5. Косая решетка:	а ^ Ъ\ у ^ 90°
Y56VWWSXW
V
Рис.2
72

Таблица 9. Пространственные (трехмерные) решетки: семь сингоний
1	Триклинная сингония:
а ф Ъ ф с,
а ф Р ф У-
2	Моноклинная сингония:
а ф Ъ ф с,
а = р = 90° Ф у.
3	Ромбическая сингония:
а ф Ъ ф с,
а = р = у = 90°.
4	Тригональная (ромбоэд-
(ромбоэдрическая) сингония:
5	Гексагональная сингония:
а = Ъ * с,
а = р = 90°, у =120°.
6	Тетрагональная сингония:
а = Ъ ф с,
а = р = у = 90°.
7	Кубическая сингония:
а = Ъ = с,
73

Отметим, что переносная и поворотная симметрии могут «соседство-
«соседствовать». Так, квадратная решетка обладает поворотной симметрией 4-го
порядка, а гексагональная решетка — поворотной симметрией 6-го по-
порядка, впрочем, переносная и поворотная симметрии — соседи «неужив-
«неуживчивые». При наличии переносной симметрии возможны поворотные оси только
2, J, 4 и 6-го порядков. Это утверждение дадим без доказательства.
4.1.4 Бордюры. Бордюром называют периодически повторяющийся
рисунок на длинной ленте. На практике бордюры встречаются в разных
видах. Это может быть настенная роспись, украшающая стены зданий,
галереи, лестничные переходы. Это может быть чугунное литье, исполь-
используемое в оградах парков, решетках мостов и набережных. Это могут
быть гипсовые барельефы или керамика. Бордюры можно видеть на
полотенцах, шторах, ковровых дорожках.
На рис. 1 в таблице 10 приведены 14 бордюров. Они разбиты на семь
пар, в каждую из которых входят бордюры, одинаковые по типу сим-
симметрии. Всего существует 7 типов симметрии бордюров] они показаны
схематически на рис. 2 в таблице 10.
Любой бордюр обладает переносной симметрией вдоль оси перено-
переноса. В простейшем случае симметрия бордюра полностью исчерпывается
переносной симметрией — см. рис. 1, а. Схематически этот тип бордю-
бордюров представлен на рис. 2, а; здесь АВ — ось переноса, а — период бор-
бордюра (элементарный перенос), треугольник условно обозначает повто-
повторяющийся несимметричный элемент бордюра.
Бордюры на рис. 1, б обладают наряду с переносной также зеркаль-
зеркальной симметрией; они зеркально симметричны относительно прямой,
которая делит ленту бордюра пополам в продольном направлении. Схе-
Схематически такой тип бордюров показан на рис. 2, б\ здесь ось переноса
является также осью симметрии.
У бордюров на рис. 1, в (и соответственно на рис. 2, в) ось переноса
является скользящей осью симметрии. В этом случае рисунок совмеща-
совмещается сам с собой при переносе вдоль оси АВ на расстояние а/2 и после-
последующем отражении относительно оси АВ (здесь, как и везде, а — пе-
период бордюра).
Бордюры на рис. 1, г имеют поперечные оси симметрии. Эти оси изоб-
изображены на рис. 2, г в виде отрезков прямых, перпендикулярных к оси
переноса.
На рис. 1, д показаны бордюры, имеющие поворотные оси 2-го поряд-
порядка, перпендикулярные к плоскости бордюра. Точки пересечения этих осей
с плоскостью бордюра отмечены на рис. 2, д зачерненными чечевицами.
На комбинировании скользящей оси симметрии с поворотными ося-
осями 2-го порядка, перпендикулярными к плоскости бордюра, основаны
74

Таблица 10. Бордюры
75

бордюры, изображенные на рис. 1, е. В результате такого комбинирова-
комбинирования возникают поперечные оси симметрии. Схематически этот тип бор-
бордюров показан на рис. 2, е.
Наконец, на рис. 1, ж (и соответственно на рис. 2, ж) представлены
бордюры, основанные на комбинировании зеркальных отражений. Та-
Такие бордюры имеют наряду с продольной также поперечные оси сим-
симметрии; как следствие возникают поворотные оси 2-го порядка.
4.1.5. Орнаменты. Трудно найти человека, не любовавшегося орна-
орнаментами —этими удивительными рисунками, часто встречающимися
в декоративном художественном творчестве. В них можно обнаружить
затейливые сочетания переносной, зеркальной и поворотной симмет-
симметрии. За примером орнамента не надо далеко ходить — достаточно взгля-
взглянуть на рисунок обоев в комнате или паркета на полу.
На рис. 2 в таблице 8 мы познакомились с красивым китайским ор-
орнаментом — тем самым, который использовался как каркас для окон из
бумаги. Уже из этого рисунка ясно, что в основе орнамента лежат один
или несколько типов плоских решеток. Именно тип плоской решетки
определяет характер переносной симметрии конкретного орнамента.
В таблице 11 представлены три орнамента: 1 — орнамент «Летящие пти-
птицы» (М. Эшер), 2 — характерный египетский орнамент, 3 — орнамент
«Рептилии» (М. Эшер). Орнамент «Летящие птицы» основан на косой
решетке, египетский орнамент — на квадратной решетке, орнамент «Реп-
«Рептилии» — на гексагональной решетке. Все эти решетки можно видеть в
таблице 11 — см. соответствующие семейства параллельных прямых.
Штриховкой выделены элементарные ячейки. Особенно интересен ор-
орнамент «Рептилии». Он представляет собой мозаику, составленную из
совершенно одинаковых фигурок рептилий. Рептилии плотно уложены
на поверхности орнамента — без накладывания друг на друга и без ка-
каких-либо пустых промежутков.
В простейшем случае орнамент характеризуется только переносной
симметрией. Таков, например, орнамент «Летящие птицы». Чтобы по-
построить этот орнамент, надо выбрать соответствующую косую решетку,
«заполнить» элементарную ячейку решетки определенным рисунком
и затем многократно повторить этот рисунок посредством переносов
ячейки без изменения ее ориентации. Заметим, что площадь ячейки
равна в данном случае сумме площадей, занимаемых изображениями
птиц разного цвета.
В принципе любой орнамент можно построить так, как строится ор-
орнамент «Летящие птицы»: посредством параллельных переносов заполнен-
заполненной рисунком элементарной ячейки. Такой способ построения орнамен-
орнамента — единственный, если орнамент не обладает ни поворотной, ни
76

Таблица 11. Орнаменты
77

зеркальной симметрией. В остальных случаях возможны иные способы
построения орнамента; при этом в качестве исходного изображения (как
говорят, основного мотива) используют не всю элементарную ячейку
орнамента, а лишь часть ее.
Рассмотрим в качестве примера египетский орнамент. Его элемен-
элементарная ячейка дана крупным планом на рис. 1 в таблице 12. В качестве
основного мотива выберем изображение в пределах заштрихованного
прямоугольника. Площадь этого прямоугольника составляет одну
восьмую площади элементарной ячейки орнамента. Для построения
орнамента воспользуемся осями симметрии ВС и DE, показанными на
рис. 2 в таблице 12, а также поворотной осью 2-го порядка, проходящей
через точку А. Зафиксируем точку А и оси ВС и DE на плоскости рисун-
рисунка и, используя основной мотив (рис. 2,я), будем выполнять отражения
относительно ВС и DE и повороты на 180° вокруг А в любой последо-
последовательности и сколь угодно долго. Поворот вокруг А превращает ри-
рисунок 2, а в рисунок 2, б. Последующее отражение относительно ВС при-
приводит к рисунку 2, в. Затем выполняем отражение относительно DE —
получаем рисунок 2, г. Новый поворот на 180° вокруг А позволяет полу-
получить рисунок 2, д. И так далее. По мере выполнения поворотов и отра-
отражений орнамент как бы раскрывается на наших глазах, все более и бо-
более заполняя площадь рисунка.
4.2 Геометрическая симметрия в природе
Ког
)гда мы смотрим на нагромождения камней у подножия горы, на
причудливые извивы берегов реки или озера, на фантастические фор-
формы облаков, у нас может возникнуть мысль, что симметрия в неживой
природе отнюдь не частый гость. И в то же время встречается мнение,
что симметрия и строгая точность холодны и враждебны живому.
Замок Снежной Королевы из известной сказки Андерсена представля-
представляют весьма симметричным сооружением, сверкающим отполированны-
отполированными зеркальными гранями правильных форм. Так кто же прав — тот, кто
видит в неживой природе нагромождение беспорядка, или, напротив,
тот, кто видит в ней господство холодной точности и симметрии?
Строго говоря, неверны обе крайние точки зрения. Конечно, воздей-
воздействие на облик земной поверхности воды, ветра, солнечного тепла сти-
стихийно. Однако песчаные дюны и барханы, кратер потухшего вулкана,
галька на морском берегу имеют достаточно правильные формы. Ко-
Конечно, груда камней у подножия горы весьма беспорядочна. Однако
78

Таблица 12. Построение египетского орнамента
Рис.1
D
В
Рис.2
79

каждый камень — это огромная колония кристаллов, представляющих
собой в высшей степени симметричные «постройки» из атомов и моле-
молекул, в основе которых лежат разные типы пространственных решеток.
Именно кристаллы вносят в мир неживой природы очарование сим-
симметрии. Здесь нельзя не вспомнить о снежинках — маленьких кристал-
кристалликах замерзшей воды. Они нередко имеют форму правильных шести-
шестиугольных «звездочек» (обладают поворотной симметрией 6-го порядка
и шестью плоскостями симметрии). Все твердые тела состоят из крис-
кристаллов. Как правило, отдельные кристаллы весьма малы (меньше пес-
песчинки); однако иногда кристаллы вырастают до внушительных разме-
размеров и тогда они предстают перед нами во всей своей геометрически
правильной красоте. Некоторые образцы крупных кристаллов показа-
показаны на рис. 1 в таблице 13. Отметим, что симметрия внешней формы кри-
кристаллов является следствием их внутренней симметрии — упорядочен-
упорядоченного расположения в пространстве атомов (молекул). Иначе говоря,
симметрия кристалла связана с наличием пространственной решетки
из атомов — кристаллической решетки. В отдельных случаях (хотя от-
отнюдь не всегда) симметрия кристалла соответствует симметрии элемен-
элементарной ячейки кристаллической решетки.
В книге «Этот правый, левый мир» М. Гарднер пишет: «На Земле
жизнь зародилась в сферически симметричных формах, а потом стала
развиваться по двум главным линиям: образовался мир растений, обла-
обладающий симметрией конуса, и мир животных с билатеральной симмет-
симметрией». Поясним: термин билатеральная симметрия часто применяется
в биологии. Имеется в виду зеркальная симметрия (от латинского «би-
«билатеральный» — «дважды боковой»); соответствующая плоскость сим-
симметрии показана на рис. 4 в таблице 13.
Для деревьев характерна симметрия конуса. При помощи корней де-
дерево поглощает воду и питательные вещества из почвы, то есть снизу,
а остальные жизненно важные функции выполняются кроной, то есть
наверху. Поэтому направления «вверх» и «вниз» для дерева различны.
В то же время направления в плоскости, перпендикулярной к вертика-
вертикали, для дерева фактически неразличимы: по всем этим направлениям
к дереву в достаточно равной мере поступают воздух и свет. В результа-
результате появляются вертикальная поворотная ось бесконечно большого по-
порядка и бесконечное число вертикальных плоскостей симметрии. Ко-
Конечно, нередко встречаются деревья, стволы которых изогнуты, а крона
развита однобоко. Тем не менее идея конуса правильно отражает спе-
специфику симметрии дерева, ее сущность. Для любого дерева можно ука-
указать основание и вершину, и в то же время для дерева неприемлемы по-
понятия левой или правой, задней или передней сторон.
80

Таблица 13. Геометрическая симметрия в природе
81

Хорошо выражена симметрия у листьев, цветков, плодов. На рис. 2
в таблице 13 приведены в качестве примера некоторые листья. Нетруд-
Нетрудно обнаружить в них поворотную, зеркальную, переносную симметрии.
Для цветков характерна поворотная симметрия. Тут встречаются пово-
поворотные оси разных порядков. Но, пожалуй, наиболее распространена
поворотная симметрия 5-го порядка. Ее можно наблюдать у многих по-
полевых цветов (колокольчик, незабудка, гвоздика, зверобой, лапчатка гу-
гусиная и др.), у цветов плодовых деревьев (вишня, яблоня, груша, манда-
мандарин и др.), у цветов плодово-ягодных растений (земляника, малина, калина,
черемуха, рябина, шиповник, ежевика, боярышник и др.). По этому пово-
поводу иногда высказывается мнение, что «пристрастие» растений к поворот-
поворотной симметрии 5-го порядка, которая, как уже отмечалось, принципи-
принципиально невозможна в периодических структурах, можно объяснить
обусловленной такой симметрией гарантией сохранения растением его
индивидуальности. Как выразился академик Николай Васильевич Белое
A891-1982), «пятерная ось является своеобразным инструментом борь-
борьбы за существование, страховкой против окаменения, против кристалли-
кристаллизации, первым шагом которой была бы «поимка» решеткой».
Правда, поворотная симметрия 5-го порядка встречается и в мире
животных (примеры: морская звезда и панцирь морского ежа). Однако
в отличие от мира растений поворотная симметрия у животных наблю-
наблюдается редко. Мы встречаемся с ней в основном лишь при изучении
некоторых обитателей моря. Например, простейших морских живот-
животных, называемых радиоляриями или лучниками. На рис. 3 в таблице 13
можно увидеть удивительно красивые раковины радиолярий.
Вообще же для животных (насекомых, рыб, земноводных, рептилий,
птиц, млекопитающих) характерно несовместимое с поворотной симмет-
симметрией различие между направлениями «вперед» и «назад». У животных
есть направление движения. В этом направлении животное устремляется
за пищей, в этом же направлении оно спасается от преследователей.
Кроме направления движения симметрию животного определяет еще
одно направление — направление силы тяжести. Оба направления су-
существенны; они задают плоскость симметрии животного — см. рис. 4
в таблице 13 (здесь 1 — направление силы тяжести, 2 — направление
движения животного). Билатеральная {зеркальная) симметрия — харак-
характерная симметрия практически всех представителей животного мира.
Можно сказать, что каждое животное состоит из двух энантиоморфов —
правой и левой половин. Энантиоморфами являются также парные де-
детали, одна из которых попадает в правую, а другая в левую половину
тела животного. Так, энантиоморфами являются правое и левое ухо,
правый и левый глаз, правый и левый рог и т. д.
82

Во многих фантастических произведениях обсуждается возможный
облик пришельцев из иных миров. Не останавливаясь подробно на обсуж-
обсуждении этого вопроса, приведем лишь некоторые соображения, связан-
связанные с симметрией. Каким бы ни был пришелец, его внешний облик
должен характеризоваться билатеральной симметрией; ведь на любой
планете живое существо должно иметь выделенное направление движе-
движения и на любой планете действует сила тяжести. Пришелец может по-
походить на сказочного многоголового дракона, но он не может походить
на Тяни-толкая (фантастическое существо с симметричными передней
и задней половинами). Пришелец не может быть левоглазым или пра-
воухим. Число конечностей слева и справа должно быть одинаковым.
Как мы видим, требования симметрии существенным образом сокра-
сокращают число возможных вариантов облика пришельцев. И хотя мы не
можем определенно указать, каким должен быть этот облик, мы в со-
состоянии заключить, каким он не может быть.
4.3 Обобщение понятия симметрии
Дс
Цо сих нор мы говорили о симметрии в геометрическом смысле —
как о симметрии геометрических форм или, иными словами, симметрии
положений. Она проявляется в том, что объекты совмещаются сами с со-
собой при разных геометрических преобразованиях — отражениях, поворо-
поворотах, переносах (включая комбинации этих преобразований). Само сло-
слово «симметрия» греческого происхождения. Оно переводится как
«соразмерность, пропорциональность, уравновешенность». С давних
времен люди связывали с понятием симметрии такие понятия как поря-
порядок, гармония, совершенство.
Современное понятие симметрии значительно шире: оно не ограни-
ограничивается симметрией положений и выходит далеко за рамки собственно
геометрии. Приведем примеры. Предположим, все электроны одного
атома поменялись с электронами другого атома. Поскольку электроны
тождественны (любой наугад выбранный электрон ничем не отличается
от мириадов других электронов), то от обмена электронов никаких из-
изменений в атомах не произойдет. Тут можно говорить о симметрии ато-
атомов по отношению к обмену электронами. Вот другой пример. При
переходе от одного поколения данного растения к другому поколению
наблюдается сохранение определенных свойств. Так, из семечка вырас-
вырастает новый подсолнух с таким же огромным соцветием-корзинкой, так
же исправно поворачивающимся к солнцу. Перед нами симметрия
свойств подсолнуха по отношению к переходу от одного поколения
83

к другому; эту симметрию обычно называют наследственностью. Число
ударных слогов в данном стихотворении остается неизменным при пе-
переходе от одной строки к другой. И это есть симметрия.
Итак, с симметрией мы встречаемся всякий раз, когда при каких-то
изменениях что-то сохраняется. Или, иначе говоря, когда после каких-
то преобразований (изменений) приходим к изначальной ситуации.
Известный немецкий математик Герман Вейлъ A885-1955) предложил
наглядное определение симметрии, согласно которому симметричным
называется объект, который можно как-то изменять, получая в резуль-
результате то же, с чего начали.
Мы видим, таким образом, что понятие симметрии имеет структуру.
1	— есть объект (или явление) симметрия которого рассматривается,
2	— есть изменение (преобразование), по отношению к которому рас-
рассматривается симметрия,
3	— есть сохранение (неизменность) объекта (явления, свойств объек-
объекта, сторон явления), которое как раз и выражает рассматриваемую сим-
симметрию.
Подчеркнем: неизменность существует не сама по себе, не вообще, а
лишь по отношению к каким-то преобразованиям (изменениям). С дру-
другой стороны, эти изменения (преобразования) представляют интерес по-
постольку, поскольку что-то при этом сохраняется. Без изменений нет смыс-
смысла рассматривать сохранение, равно как без сохранения исчезает интерес
к изменениям. Симметрия выражает сохранение чего-то при каких-то
изменениях или, иначе, сохранение чего-то несмотря на изменения.
Упомянутое выше «что-то» может быть геометрической фигурой, ри-
рисунком орнамента, телом. Именно с такими «что-то» имеет дело геомет-
геометрическая симметрия. В более общем случае в качестве этого «что-то»
могут выступать те или иные свойства какого-либо объекта (например,
количество ударных слогов в стихотворной строке или наследственные
характеристики растения). Роль упомянутого «что-то» могут играть те
или иные явления. Так, вода начинает закипать всякий раз, как только
ее температура повысится до 100 °С (при нормальном давлении возду-
воздуха). Отметим, что это явление наблюдается несмотря, например, на из-
изменения времени года или места опыта (если, конечно, эти изменения
не приведут к изменению атмосферного давления). Именно поэтому
и появляется возможность формулировать те или иные природные зако-
закономерности (их обычно называют законами природы). Рассматривая сим-
симметрию наблюдаемых в природе явлений с более общей точки зрения,
мы можем говорить о симметрии законов природы. Законы природы сим-
симметричны по отношению к переносам во времени, по отношению к пе-
переносам и поворотам в пространстве, по отношению к состоянию дви-
84

жения, если это движение равномерное (симметрия по отношению к пе-
переходу из одной инерциальной системы отсчета к другой), по отноше-
отношению к замене левого на правое, а правого на левое, по отношению
к замене всех частиц на соответствующие античастицы. В своей работе
ученые весьма широко пользуются различными симметриями законов
природы.
Итак, можно говорить о симметрии не только каких-либо изображе-
изображений, фигур, тел, но также различных свойств, характеристик, явлений,
законов природы. Как видим, понятие симметрии приобретает поисти-
поистине глобальный смысл. Впрочем, можно пойти еще дальше и обратить
внимание на то, что, по большому счету, мы имеем дело с симметрией
всякий раз, когда решаем проблему распознавания образов, проблему
диагностики.
Вот мы берем некий фрукт и определяем: это яблоко. Берем другой
фрукт, иного размера и расцветки и даже запаха. Смотрим на него и го-
говорим: это тоже яблоко. Решая эту несложную проблему, связанную
с распознаванием образов, мы фактически имели дело с симметрией.
В роли объекта — фрукт. Изменение — смена одного фрукта другим.
Несмотря на это изменение наблюдалось сохранение ряда свойств, при-
признаков, общих для фрукта, который мы называем яблоком. Или вот дру-
другой пример. На приеме у врача находится больной. Врач осматривает
его и ставит диагноз: ангина. Входит другой больной, иного возраста,
пола, комплекции. После осмотра врач ставит тот же диагноз: ангина.
И здесь мы имеем дело с симметрией. Рассматривается некое явление
(точнее говоря, некое заболевание). Изменение — смена пациента. Не-
Несмотря на это изменение наблюдается сохранение ряда симптомов за-
заболевания, которое медики называют ангиной.
Пойдем еще дальше и отметим, что, строго говоря, мы имеем дело с
симметрией всякий раз, как используем тот или иной термин. Вот мы
используем термин «колесо». Конечно, колесо обладает определенной
геометрической симметрией. Но мы сейчас не об этом. Есть колесо
автомобиля, вагона, детской коляски. Но есть также колесо обозрения
в парке. Это весьма разные объекты. Однако все они объединяются
общим термином «колесо». Некоторые жители Севера называют тюле-
тюленя в воде одним термином, а тюленя на льдине другим термином. Мы
понимаем, что речь идет об одном и том же объекте, находящемся в раз-
разных ситуациях (в воде или на льдине), и используем единый термин.
Допуская, что последний пример покажется кому-то примитивным, про-
проиллюстрируем то же самое, обратившись к физике. В свое время физи-
физики ввели термины «протон» и «нейтрон» для частиц внутри атомного
ядра. Позднее физики выяснили, что протон и нейтрон, введенные ими
85

в употребление, похожи в известном смысле на мокрого и сухого тюле-
тюленя, потому что в действительности они представляют собой попросту
два состояния одной частицы. Эта симметрия привела к появлению
новой физической величины, названной изотопическим спином, а для
протона и нейтрона было предложено общее «имя» — нуклон.
4.4 Прежний и современный взгляд
на симметрию
злюдаемая в природе симметрия форм с давних времен произво-
производила на людей сильное впечатление. Человек усматривал в симметрии
порядок и гармонию, вносимые всемогущим Творцом в изначальный хаос.
Наших далеких предков восхищали, например, правильные много-
многоугольники и правильные многогранники. Древние греки весьма серьез-
серьезно воспринимали тот факт, что существуют лишь пять правильных мно-
многогранников. В их представлении это были атомы, из которых построен
весь мир: тетраэдр — атом огня, октаэдр — атом воздуха, куб — атом
земли, икосаэдр — атом воды, додекаэдр — атом эфира.
Знаменитый немецкий астроном Иоганн Кеплер A571-1630) полагал,
что в правильных многогранниках зашифрована идея Божественной гар-
гармонии. Исходя из этого, он пытался связать эти пять Платоновых тел
с радиусами сфер (орбит) известных в те времена шести планет. В сферу
Сатурна Кеплер вписал куб. В этот куб он вписал следующую сферу —
сферу Юпитера. В сферу Юпитера был вписан тетраэдр, а в тетраэдр
сфера Марса. В сферу Марса Кеплер вписал додекаэдр, а в него сферу
Земли. Затем шли последовательно икосаэдр, вписанный в сферу Земли,
сфера Венеры, октаэдр, вписанный в сферу Венеры, и, наконец, сфера
Меркурия. Вычислив в соответствии с такой схемой относительные ра-
радиусы планетных сфер, Кеплер обнаружил, что отношения этих радиу-
радиусов согласуются с данными наблюдений:
8: 15:20:30:115: 195.
Это удивительное совпадение, как казалось Кеплеру, подтверждало
правильность геометрической схемы Вселенной, построенной Творцом
на основе пяти Платоновых тел. Все это ученый изложил в книге, кото-
которой дал интригующее название «Космографическая тайна».
Убеждение, что симметрия есть не что иное, как проявление мудро-
мудрости Творца, просуществовало фактически вплоть до двадцатого столе-
столетия. Полагая, что мир представляет собой гигантский «часовой меха-
86

низм», запущенный в действие Богом, человек, естественно, верил в со-
совершенство этого механизма. И он усматривал в симметрии доказа-
доказательство совершенства. Двадцатый век покончил с этой парадигмой. На
смену мистическому преклонению перед симметрией пришло трезвое пони-
понимание ее действительной сущности. Обсуждая современный взгляд на
симметрию, выделим три принципиальных момента.
Момент первый: симметрия связана с сохранением, со стабильностью.
Она выделяет: в нашем весьма изменчивом, очень динамичном мире сво-
своеобразные «опорные точки», сохраняющиеся при различных изменениях
и превращениях (так называемые инварианты). Тем самым в мир вносят-
вносятся порядок и стабильность. Этот мир наполнен взаимодействиями, в нем
«все течет, все изменяется», повсюду буйствуют случайности. Но несмот-
несмотря на это мы можем формулировать определенные закономерности, го-
говорить о тех или иных законах природы, обладающих симметрией (в
частности, симметрией по отношению к переносам во времени, а также
переносам и поворотам в пространстве). Конечно, справедлива старая
истина, что «все течет, все изменяется». Но еще более точна другая ста-
старая истина, высказанная Екклесиастом: «все возвращается на круги свои».
Не просто течет и изменяется, но возвращается обратно, совершает цикл.
Это и означает сохранение несмотря на изменения. Таким образом, древ-
древнее библейское откровение, что «все возвращается на круги свои», есть,
по сути, древняя формулировка принципа симметрии.
Выдающаяся немецкий математик Эмми Нётер A882-1935) доказала
фундаментальную теорему теоретической физики: различным симметриям
законов природы соответствуют законы сохранения определенных физи-
физических величин. Так, симметрии законов природы по отношению к пе-
переносам во времени соответствует закон сохранения энергии. Симметрии
законов природы по отношению к переносам в пространстве соответ-
соответствует закон сохранения импульса. Симметрии законов природы по от-
отношению к поворотам в пространстве соответствует закон сохранения
момента импульса. Можно сказать, что законы сохранения энергии, им-
импульса, момента импульса следует рассматривать как прямое следствие
определенных симметрии законов природы.
Итак, что бы ни происходило в нашем изменчивом мире, наполнен-
наполненном случайностями, энергия сохраняется. Сохраняются также импульс,
момент импульса и целый ряд других физических величин. И не только
физических величин. Например, несмотря на всякие изменения и кап-
капризы погоды, за зимой следует весна, а за весной лето, из зерна появля-
появляется колос, из семечка вырастает подсолнух. Все это — проявление сим-
симметрии в нашем мире.
87

Момент второй: симметрия выделяет общее как в объектах, так и
в явлениях. Существует, например, великое множество различных яб-
яблок. Они различаются размерами, формой, цветом, вкусом, запахом. И
тем не менее все они — яблоки. Термин «яблоко» фиксирует целый
набор признаков, являющихся общими для всех яблок; эти признаки
сохраняются при переходе от одного яблока к другому.
Мир в высшей степени многообразен, но в то же время он един; в его
разнообразных проявлениях присутствуют черты общности. Так, зако-
законы сохранения, действуя в самых разных областях и различных конк-
конкретных ситуациях, выражают то общее для всех ситуаций, что, в конеч-
конечном счете, связано с соответствующими симметриями законов природы.
Законы сохранения «безразличны» к специфике тех или иных ситуа-
ситуаций, они «безразличны» к конкретным механизмам взаимодействия, их
область применимости выходит за рамки частных теорий. Общий, уни-
универсальный характер законов сохранения, не требующий анализа дета-
деталей того или иного явления, предопределяет простоту этих законов и до-
достоверность результатов, получаемых на их основе. Подчеркнем, что
детали того или иного явления, особенности механизма взаимодействия
часто нам неизвестны или известны приближенно, их учет нередко свя-
связан с большими математическими трудностями. Поэтому простые
и изящные законы сохранения выглядят крайне привлекательно. Ис-
Исследуя то или иное явление, физик анализирует его прежде всего на
уровне законов сохранения и лишь затем вступает при необходимости
на тяжелый путь изучения деталей. Многие явления исследованы в на-
настоящее время лишь на уровне законов сохранения.
Симметрия позволяет использовать аналогии, выявляя общие свой-
свойства в различных объектах или явлениях. Многие физические модели
тех или иных явлений или объектов создаются как раз на основе анало-
аналогии. Молекула ДНК моделируется как винт. Спин микрочастицы упо-
уподобляется волчку. Столкновение фотона с электроном в эффекте Комп-
тона рассматривается по аналогии со столкновением бильярдных шаров.
Движение электронов в атоме сравнивают с движением планет вокруг
Солнца, а при более строгом подходе используют аналогию с облаком,
вводя понятие «электронного облака».
Момент третий: симметрия предопределяет необходимость, действуя
в направлении сокращения числа возможных вариантов структур и вариан-
вариантов поведения системы. То, что симметрия ограничивает многообра-
многообразие структур, хорошо видно уже на примере правильных многогран-
многогранников — их всего пять. Симметрия накладывает ограничения на
разнообразие структур молекул и кристаллов. Вселенная состоит из ми-
риадов атомов. Однако, благодаря тому, что все электроны во Вселенной

тождественны (симметричны по отношению к взаимным перестановкам),
равно как тождественны все протоны и вообще все частицы одного и то-
того же типа, все эти мириады атомов реализуют относительно малое число
возможных вариантов', их около ста, они систематизированы в Перио-
Периодической системе элементов.
Законы сохранения могут рассматриваться как правила запрета, кото-
которые симметрия налагает на процессы, происходящие в природе. Так, за-
закон сохранения энергии запрещает существование вечного двигателя.
Закон сохранения импульса запрещает поднимать самого себя за волосы.
Существенно, что симметрия не только что-то запрещает, но подчас
подсказывает единственно возможный вариант, т. е. позволяет делать
предсказания. Вот два примера подобных предсказаний. В 1869 году зна-
знаменитый российский химик Дмитрий Иванович Менделеев A834-1907)
предсказал существование и свойства скандия (ученый называл его эка-
бором), галлия (экаалюминия), германия (экакремния). В 1931 году из-
известный швейцарский физик Вольфганг Паули A900-1958) предсказал
существование элементарной частицы, названной нейтрино.
4.5 Симметрия (порядок) и асимметрия (беспорядок)
]К1так, с идеей симметрии оказываются органически связанными идеи
сохранения, общности, необходимости. Сохранение противостоит измене-
изменениям. Общность противостоит различиям. Необходимость противостоит
случайностям. Изменения, различия, случайности — все это противосто-
противостоит симметрии и должно рассматриваться в целом как проявление асим-
асимметрии. Если симметрия, опираясь на идеи сохранения, общности, не-
необходимости, вносит в мир порядок, то асимметрия, используя
изменения, различия, случайности, вносит в мир беспорядок.
Сохранение и изменения не просто противостоят друг другу. Они
взаимосвязаны и не имеют смысла одно без другого. Сохранение на-
наблюдается на фоне изменений; изменения происходят как нарушения
сохранения. Взаимоотношения сохранения и изменений надо рассмат-
рассматривать как единство и борьбу двух противоположностей. Это же относит-
относится и к таким противоположностям, как общее и различное, как необхо-
необходимое и случайное. Следовательно, симметрия и асимметрия также
должны рассматриваться с позиций единства и борьбы противополож-
противоположностей. Это означает, что в мире есть не просто симметрия, но одно-
одновременно симметрия и асимметрия как две противоположности, для
которых характерны и противостояние, и единство. Такие противопо-
противоположности ученые называют диалектическими.
89

Можно сказать, что мир определяется диалектикой симметрии и асим-
асимметрии. Более того, он существует благодаря единству и борьбе симмет-
симметрии и асимметрии. Симметрия и асимметрия должны рассматриваться как
две диалектически противоположные стороны единого понятия. Поэтому в
целом наш мир может быть назван симметрично-асимметричным миром.
В § 2.2 мы говорили о том, что реальный мир не может быть ни
абсолютно упорядоченным, ни абсолютно беспорядочным. Теперь мы
уточним: реальный мир не может быть ни полностью симметричным, ни
полностью асимметричным.
В полностью симметричном мире ничто никогда не изменялось бы,
не существовало бы никаких вариантов (альтернатив), поскольку все было
бы жестко предопределено. Причем предопределено, что называется,
намертво, без какой-либо возможности развития. В таком мире не было
бы никаких различий, индивидуальностей; ничто нельзя было бы выде-
выделить и как-то отличить от остального. Следовательно, здесь попросту
ничего бы не наблюдалось — никаких явлений, никаких объектов. Да и
как они могли бы существовать, если решительно все вокруг совмеща-
совмещалось бы с собой при любом повороте вокруг любой оси, при отражении
относительно любой плоскости в пространстве, при переносе в любом
направлении на любое расстояние! Тут вообще нет места каким-либо
объектам; тут приходит на ум некая общая однородная «каша».
Не менее абсурден и полностью асимметричный мир. В нем ничто
не сохранялось бы, не было бы никаких причин и следствий, а значит,
никаких законов. Здесь всякая сущность была бы сиюминутна, случай-
случайно возникала бы и случайно исчезала. И к тому же она была бы ни на
что не похожа, не имела бы ни с чем ничего общего.
Надо признать, что ученых всегда вдохновляла вера в глубинную
гармонию (симметрию) природы. Она и сегодня вдохновляет их на
предпринимаемые время от времени поиски «единой теории» и «универ-
«универсальных уравнений». Они ищут и открывают новые симметрии в окру-
окружающем нас мире (точнее говоря, в мире элементарных частиц). Одна-
Однако это отнюдь не приближает нас к заветной единой теории. Картина
мира по мере его познавания все более усложняется и все сомнительнее
становится сама возможность существования «универсальных уравне-
уравнений». В книге О.П. Мороза «В поисках гармонии» есть довольно образ-
образное замечание: «Физики гонятся за симметрией подобно тому, как пут-
путники преследуют в пустыне ускользающий мираж. Вот возникла на
горизонте прекрасная манящая картина, но как только вы пытаетесь
к ней приблизиться, она исчезает, оставляя чувство горечи...» В чем же
тут дело? — А дело в том, что, чем больше мы постигаем симметрию
природы, тем шире проявляется асимметрия. Поиски единой теории заве-
90

домо обречены на неудачу, как попытка рассмотрения симметрии е от-
отрыве от асимметрии.
Ранее мы приводили примеры, подчеркивающие роль симметрии в на-
научном познании мира. Однако не менее важную роль играет также асим-
асимметрия. Проще всего это можно продемонстрировать, обратившись к на-
научной классификации. Любая научная классификация в равной мере
использует как сохранение {общность), так и изменения {различия) свойств
классифицируемых объектов. Яркий пример — Периодическая система
элементов Д.И. Менделеева. Здесь от периода к периоду сохраняется
общность свойств элементов, входящих в один и тот же столбец табли-
таблицы Менделеева, например, лития, натрия, калия, рубидия, цезия. Свой-
Свойства же элементов в пределах данного периода изменяются, причем ха-
характер изменения является общим для разных периодов. Ясно, что
симметрия свойств соответствующих элементов из разных периодов
важна для научной классификации лишь в сочетании с асимметрией
свойств элементов внутри одного и того же периода.
Как уже отмечалось, симметрия действует в направлении ограниче-
ограничения числа возможных вариантов структур, вариантов поведения сис-
систем. Необходимость действует в том же направлении. С другой сторо-
стороны, асимметрия действует в направлении увеличения числа вариантов;
в этом же направлении действует и случайность (мы уже обращали
внимание на то, что случайности создают новые возможности, порож-
порождают новые альтернативы).
Сокращая число возможных вариантов, симметрия и необходимость
вносят в мир порядок (это мы оцениваем положительно). В то же время
симметрия и необходимость, сокращая число альтернатив, могут при-
привести к безвыходной ситуации, завести в тупик, создать обреченность
(это мы оцениваем, конечно, отрицательно). В подобных «тупиковых»
ситуациях жизненно важна спасительная случайность, способная раз-
разрушить симметрию, создать неожиданный выход из тупика.
Создавая новые возможности, новые альтернативы, асимметрия и слу-
случайность обеспечивают развитие, способствуют творческому поиску, по-
появлению новой информации (это мы оцениваем положительно). В то же
время асимметрия и случайность вносят дезорганизацию, увеличивают
степень беспорядка в мире (это мы оцениваем отрицательно). Обилие аль-
альтернатив, разнообразных вариантов может стать чрезмерным — и тогда на
помощь приходит упорядочивание в лице симметрии и необходимости.
Так и живем, находясь под воздействием, с одной стороны, симмет-
симметрии и необходимости, а с другой — асимметрии и случайности и ис-
используя в своей практике (сознательно или стихийно) диалектику сим-
симметрии и асимметрии, диалектику необходимого и случайного.
91

4.6 ЧТО ТАКОЕ КРАСОТА? (РАЗМЫШЛЕНИЯ О СИММЕТРИИ
И АСИММЕТРИИ В ИСКУССТВЕ)
]К1звестный французский архитектор Шарль Ле Корбузъе A887-1965)
в своей книге «Архитектура XX века» утверждал: «Человеку необходим
порядок. Без него все его действия теряют согласованность, логическую
взаимосвязь. Чем совершеннее порядок, тем спокойнее и увереннее чув-
чувствует себя человек. Он делает умозрительные построения, основываясь
на порядке, который продиктован ему потребностями его психики, —
это творческий процесс. Творчество есть акт упорядочения».
Да, потребность психики человека в порядке несомненна. Мы отмеча-
отмечали это уже в § 1.2. Что же касается рассмотрения творческого процесса
главным образом как акта упорядочения, то тут можно поспорить со зна-
знаменитым архитектором. Ссылаясь, в частности, на его же собственные
творения, например сооружения в Чандигархе в Индии. Безусловно, со-
соображения симметрии всегда играли важную роль в работе любого архи-
архитектора. Но в одних случаях архитектор использует богатство симмет-
симметричных форм и создает, например, Большой театр в Москве или Зимний
дворец в Санкт-Петербурге, а в других — ограничивается примитивной
симметрией прямоугольного параллелепипеда, создавая невыразитель-
невыразительные дома-коробки. Так что «акты упорядочения» могут быть весьма раз-
разными. Тут дело не только и не столько в упорядочении (и уж тем более
не в стремлении к «совершенному порядку»), а в том, каким образом,
насколько удачно удается архитектору решить в своем творчестве пробле-
проблему соотношения между симметрией и асимметрией. Именно тут находит-
находится разгадка красоты в архитектуре. Да и не только в архитектуре.
В качестве яркого примера, когда асимметричное в целом сооруже-
сооружение являет собой удивительно гармоничную композицию из симмет-
симметричных элементов, отметим собор Василия Блаженного на Красной пло-
площади в Москве (см. рис. 1 в таблице 14), возведенный в 1551-1561 годах
зодчими Бармой и Постником в ознаменование покорения Иваном Гроз-
Грозным Казанского ханства. В целом все сооружение состоит из восьми
столпообразных храмов, группирующихся вокруг центра — девятого
(шатрового) храма. Храмы объединены общим основанием и внутрен-
внутренними переходами. Каждый храм геометрически симметричен, однако
собор как целое не обладает ни зеркальной, ни поворотной симметри-
симметрией. Архитектурные формы собора как бы накладываются друг на друга,
пересекаются, поднимаются, обгоняя друг друга, и завершаются цент-
центральным шатром. И все это настолько гармонично, что вызывает ощу-
ощущение праздника.
92

Таблица 14. Симметрия и асимметрия в искусстве

В книге М.А. Ильина «Москва» читаем: «При первом взгляде на со-
собор можно подумать, что количество архитектурных форм, применен-
примененных в нем, необычайно велико. Однако скоро становится ясно, что
мастера воспользовались всего лишь двумя архитектурными мотивами —
формой восьмерика и полукружия. Если первая определяет граненые
формы основных объемов, то вторая представлена значительным коли-
количеством вариантов, начиная от широких и спокойных арок подклети и
кончая заостренными кокошниками». Отметим, что два основных мо-
мотива не просто повторяются в разных храмах собора, но как бы развива-
развиваются по мере того, как взгляд зрителя обегает все сооружение. Перед
нами в высшей степени талантливое решение проблемы симметрия-асим-
симметрия-асимметрия. Это и есть то подлинное искусство, которое дарит людям красоту.
Красоту праздничной индивидуальности.
Диалектическое единство симметрии и асимметрии определяет кра-
красоту не только в архитектуре. То же самое можно сказать о музыке,
поэзии, живописи. Известный русский ученый, кристаллограф Георгий
Викторович Вулъф A863-1925) подчеркивал наличие симметрии в му-
музыкальны произведениях. Он писал: «Душа музыки — ритм — состоит
в правильном периодическом повторении частей произведения. Пра-
Правильное же повторение одинаковых частей и составляет сущность сим-
симметрии. Мы с тем большим правом можем приложить к музыкальному
произведению понятие симметрии, что это произведение записывается
при помощи нот, т. е. получает геометрический образ, части которого
можно обозревать». Он же отмечал: «Подобно музыкальным произве-
произведениям, могут быть симметричны и произведения словесные, в особен-
особенности стихотворения». Понятно, что в стихотворениях имеются в виду
чередования рифм и ударных слогов, то есть опять-таки ритмичность.
Вместе с тем как в музыке, так и в поэзии симметрию нельзя сводить
к ритму. Всякое хорошее произведение (музыкальное или стихотворное)
имеет определенные смысловые инварианты, которые проходят, видоиз-
видоизменяясь и развиваясь, через все произведение или какую-то его часть.
Композитор может по несколько раз возвращаться в своей симфонии
к одной и той же теме, постепенно разрабатывая ее. Нечто подобное мы
имели в примере с собором Василия Блаженного. Сохранение темы и ее
изменения {разработка, развитие) — это и есть диалектическое единство
симметрии и асимметрии. И чем удачнее решают архитектор, компози-
композитор, поэт проблему соотношения между симметрией и асимметрией, тем
выше художественная ценность произведения искусства. В связи с этим
напомним, что великий Гёте обращал особое внимание на композицию
произведения, выделяя три основных требования к композиции: транс -
ляционно-тождественное повторение элементов структуры, контрастное
повторение, варьированное повторение.
94

В заключение обратимся к живописи, взяв в качестве примера извест-
известную картину «Мадонна Литта» кисти великого итальянца Леонардо да Вин-
Винчи A452-1519) — см. рис. 2 в таблице 14. Обратите внимание: фигуры ма-
мадонны и младенца на картине вписываются в правильный треугольник,
который вследствие своей симметричности достаточно хорошо восприни-
воспринимается глазом зрителя. Благодаря этому мать и младенец сразу же оказы-
оказываются в центре внимания, как бы выдвигаются на передний план. Голова
мадонны точно и в то же время естественно помещается между двумя
симметричными окнами на заднем плане картины. В окнах просматрива-
просматриваются спокойные горизонтальные линии облаков и пологих холмов. Воз-
Возникает ощущение покоя и умиротворенности, усиливаемое за счет гармо-
гармоничного сочетания голубого цвета с желтоватыми и красными тонами.
Внутренней симметрии противостоит асимметрия, которую нетрудно
обнаружить, остановившись взглядом на младенце. Его тельце как-то
неправильно, наискосок разрезает упомянутый выше треугольник. Кро-
Кроме того тут есть особенно выразительная деталь. Вследствие взаимной
замкнутости, завершенности линий фигуры мадонны создается впечат-
впечатление ее безразличия к окружающему миру, и в частности к зрителю.
Мадонна вся сосредоточена на младенце, она нежно держит его, нежно
глядит на него. Все ее мысли сосредоточены только на нем. И вдруг вся
эта умиротворяющая замкнутость картины мгновенно исчезает, как только
мы встречаемся со взглядом младенца. Именно тут внутренняя уравнове-
уравновешенность композиции нарушается: спокойный и внимательный взгляд
младенца обращен прямо на зрителя и через него картина раскрывается
во внешний мир. Попробуйте мысленно убрать эту чудесную асимметрию,
повернуть лицо младенца к матери, соединить их взгляды. Разве не чув-
чувствуете, что от этого картина сразу стала бы менее выразительной?
Вот и получается, что всякий раз, когда мы, восхищаясь тем или
иным произведением искусства, говорим о гармонии, красоте, эмоцио-
эмоциональности воздействия, мы тем самым соприкасаемся с одной и той же
вечной проблемой — проблемой соотношения между симметрией и асим-
асимметрией. Природа — наука — искусство. Во всем мы обнаруживаем
извечное единоборство симметрии и асимметрии.
ЗАДАНИЯ ПО ТЕМЕ 4
1.	Рассмотрите тетраэдр и укажите для него все плоскости симметрии, а также все
поворотные оси и их порядок.
2.	Каковы зеркальная и поворотная симметрии круга? Тот же вопрос относительно
шара.
3.	Какой тип симметрии бордюра представлен на рис. 3 в таблице 10?
95

4.	Попробуйте пофантазировать и предложите возможный облик инопланетянина.
5.	Приведите собственные примеры симметрии, не связанные с симметрией гео-
геометрических форм (симметрией положений).
6.	Поэма А. Пушкина «Домик в Коломне» написана в относительно редко встречаю-
встречающейся форме октавы. Что Вы можете сказать о симметрии этой формы?
7.	Как Вы понимаете отмеченные в §4.3 симметрии законов природы? Имеются
в виду:
—	симметрия по отношению к переносам во времени,
—	симметрия по отношению к переносам в пространстве,
—	симметрия по отношению к поворотам в пространстве,
—	симметрия по отношению к переходу от одного равномерного прямолинейно-
прямолинейного движения к другому равномерному движению,
—	симметрия по отношению к замене левого на правое, а правого на левое,
—	симметрия по отношению к замене всех частиц на соответствующие античас-
античастицы.
Представьте себе, что Вы кому-то рассказываете об этих симметриях законов
природы. Тут, без сомнения, потребуются от Вас какие-то пояснения.
8.	Когда-то люди считали, что Земля плоская. Могли ли они поверить, что законы
природы симметричны по отношению к поворотам и переносам в пространстве?
Ответ следует обосновать.
9.	Какие разные понятия мы обозначаем термином «земля»? Почему для этих поня-
понятий используется один и тот же термин?
10.	Вообразите фантастическую ситуацию: Вы беседуете с Иоганном Кеплером. Ка-
Какие аргументы Вы привели бы ему в опровержение его представлений об устрой-
устройстве Вселенной?
11.	В законах сохранения, которыми широко пользуются ученые, выражена не толь-
только идея сохранения, но также идеи общности и необходимости. Попробуйте обо-
обосновать это утверждение.
12.	Почему невозможно было бы сформулировать какие-либо законы природы в пол-
полностью асимметричном мире?
13.	Почему невозможно было бы само существование каких-либо объектов в полнос-
полностью симметричном мире?
14.	Мы живем в симметрично-асимметричном мире. В § 4.5 отмечались ситуации,
когда симметрия оценивается нами положительно, а асимметрия — отрицатель-
отрицательно, а также когда симметрия оценивается нами отрицательно, а асимметрия —
положительно. Возможны ли ситуации, когда и симметрия, и асимметрия оцени-
оцениваются нами положительно, а также когда и симметрия, и асимметрия оценива-
оцениваются нами отрицательно?
15.	При посещении картинной галереи попробуйте проанализировать хотя бы какие-
то картины с точки зрения соотношения между симметрией и асимметрией.
96

ТЕМА 5
ПЕРЕСТАНОВКИ, СОЧЕТАНИЯ
И ШАНСЫ
В комбинаторике часто случается, что
задача, на первый взгляд кажущаяся пус-
пустой головоломкой, получает в дальней-
дальнейшем применения в самых различных об-
областях практической деятельности.
Н.Я. Виленкин
5.1 Перестановки
Оозьмем коробку с несколькими отделениями; пусть их будет четы-
четыре. И возьмем четыре шарика — черный, белый, серый, желтый. Каждый
шарик надо поместить в какое-то отделение. Спрашивается: сколько
есть разных способов, которыми можно разместить четыре шарика по
четырем отделениям? Математик сформулирует этот вопрос короче: чему
равно число перестановок четырех шариков? Перестановкой некоторого
97

количества элементов называют любое размещение этих элементов в опре-
определенном порядке. В данном случае элементами являются разноцветные
шарики в количестве четырех. В роли элементов могут выступать раз-
различные предметы, объекты и даже события. В этой роли выступали,
например, Проказница-мартышка, Осел, Козел да косолапый Мишка,
которые «затеяли сыграть квартет» в известной басне И.А. Крылова. Число
перестановок п элементов будем обозначать как Пп. В рассматриваемом
нами случае с четырьмя шариками п = 4, и нам требуется выяснить,
чему равно П4. Берем первый шарик (пусть это будет черный шарик).
Его можно поместить в отделения коробки четырьмя способами — по-
положив в первое отделение или во второе, или в третье, или в четвертое
(см. этап 1 на рис. 1 в таблице 15). Затем берем второй шарик (пусть это
будет белый шарик). При каждом положении первого (черного) шарика
этот второй шарик можно разместить по оставшимся незанятыми трем
отделениям тремя способами, так что всего получается 4 • 3 = 12 спосо-
способов (см. этап 2 на рис. 1). Берем третий шарик (пусть это будет серый
шарик). При каждом из двенадцати размещений черного и белого ша-
шариков этот третий шарик можно разместить по оставшимся незаняты-
незанятыми двум отделениям двумя способами, так что всего получается
4 • 3* 2 = 24 способа (см. этап 3 на рис. 1). Когда три шарика размеще-
размещены, для четвертого (желтого) шарика вариантов не остается; он попада-
попадает всякий раз в то отделение, которое осталось незанятым. Поэтому
общее число способов размещения шариков более не возрастает.
Итак, П4 = 4 • 3 • 2 • 1 = 24. В этом произведении мы специально на-
написали множитель 1, чтобы отметить тот факт, что при каждом разме-
размещении трех шариков остается всего один способ поместить четвертый
шарик.
Все это можно наглядно изобразить в виде своеобразного «дерева»
(см. рис. 2 в таблице 15). Первый шарик можно разместить по отделе-
отделениям четырьмя способами — ствол нашего дерева расщепляется на 4 вет-
ветки. При каждом положении первого шарика можно разместить по ос-
оставшимся незанятыми отделениям второй шарик тремя способами —
каждая из четырех веток расщепляется на 3 ветки; получаются 4 • 3 = 12
веток. При каждом размещении первых двух шариков можно размес-
разместить по оставшимся незанятыми отделениям третий шарик двумя спо-
способами — каждая из двенадцати веток расщепляется на 2 ветки; получа-
получаются 4 • 3 * 2 = 24 ветки. На этом дальнейшее ветвление дерева
перестановок заканчивается.
Теперь предположим, что надо найти П5. Ход рассуждений остает-
остается прежний. Надо разместить разными способами 5 шариков по пяти
98

Таблица 15. Перестановки
12 3 4
I I I I
до
о
99

отделениям. Для первого шарика есть 5 способов размещения (надо по-
помещать его поочередно в каждое из пяти отделений). При каждом поло-
положении первого шарика второй шарик можно разместить по оставшимся
незанятыми четырем отделениям четырьмя способами. Для размещения
третьего шарика остаются, очевидно, 3 способа, для четвертого шари-
шарика — 2 способа, для пятого — один способ. Таким образом,
П5 = 5-4-3-2-1 = 120.
Нетрудно получить далее:
П6 =6-5-4-3-2 1=720,
П7 = 7-6-5-4-3-2-1=5040,
П8 = 8-7-6-5-4-3-2-1=40320.
Впрочем, нет необходимости всякий раз перемножать все множите-
множители. Можно поступить проще:
П3 =3-2-1=6,
П4 =4 -П3 =4-6 = 24,
П5 =5-П4 =5-24 = 120,
П6 =6-П5 =6-120=720,
П7 =4-П6 =7-720 = 5040,
П8 =8-П7 =8-5040=40320,
П9 = 9 • П8 = 9 • 40320 = 362880,
П10 = 10 • П9 = 10 • 362880 = 3628800,
По-видимому, уже можно обобщить полученные результаты и записать:
П„ = п • П„_! = п ¦ (п - 2) • П„_2 = п ¦ (п -1) • (п - 2) • П„_3 =
= п(п-1)(п-2)(п-3)Пп_4.
Продолжая в том же духе, можем дойти, скажем до П3 = 3 • 2 • 1. В ре-
результате число перестановок Пи может быть представлено в виде произ-
произведения п сомножителей (от и до 1):
П„ =й-(й-1)-(я-2)-(/1-3)... 3-2-1.	A)
За многоточием скрываются те множители, которые здесь не выписаны
(ведь мы рассматриваем общий случай и сознательно не уточняем, чему
равно п).
100

Результат A) принято записывать значительно короче, вводя знак
факториала. Произведение п сомножителей от п до 1 записывают с по-
помощью этого знака так:
п • (п -1) • (п - 2) • (п - 3)... 3 • 2 • 1 = п!	B)
Говорят, что указанное произведение равно п факториал. Не надо пу-
путать знак факториала с восклицательным знаком.
Итак,
П„=п\	C)
Можно также представить:
Пл=/!-(/!-1)!	D)
Далее рассмотрим несколько задач.
Задача 1. В забеге участвуют пять спортсменов. Сколькими способами могут
распределиться первые три места?
Решение. Начнем с первого места. В принципе, любой из пяти спортсменов
может его занять. Иными словами, есть 5 способов занять первое место. Если
первое место кем-то занято, то число претендентов на остальные места становится
равным четырем (ведь один из спортсменов, неважно какой именно, занимает
первое место) и, значит, в каждом из пяти вариантов заполнения первого места
остаются 4 способа занять второе место. Если, например, первое место займет
спортсмен № 1, то второе место может оказаться у спортсмена № 2 или № 3, или
№ 4, или № 5. А если, например, первое место займет спортсмен № 5, то второе
может оказаться у спортсмена № 1 или № 2, или № 3, или № 4. Итак, получается,
что число способов, какими могут распределиться первые два места, равно 5 • 4 = 20.
Если два места заняты, то число претендентов на остальные места равно трем и,
значит, в каждом из двадцати вариантов распределения первых двух мест имеются
3 способа занять третье место. Таким образом, число способов, какими могут рас-
распределиться первые три места (при пяти участниках забега) равно 5*4*3 = 60.
Примечание. Нетрудно сообразить (хотя это и не спрашивается в задаче), что
число способов, какими могут распределиться первые четыре места, равно
5*4*3*2= 120. Если четыре места заняты, то судьба пятого места определяется
однозначно. Следовательно, полное число способов распределения пяти мест при
забеге пяти спортсменов равно 5 * 4 • 3 * 2 • 1 = 5! (пять факториал). Впрочем, это
можно было бы и не трудиться подсчитывать, поскольку полное число распреде-
распределений мест пяти участников забега должно равняться числу перестановок этих
участников. Это все равно, как если бы спросили: сколькими способами могут
пять человек стать в очередь?
Задача 2. В автомашине пять мест. Сколькими способами можно разместить
в ней пять человек, если занять место водителя могут только трое из них?
101

Решение. На место водителя могут претендовать три человека и, значит, воз-
возможны три варианта. В каждом из этих вариантов надо разместить оставшихся
четырех человек по четырем местам, что можно сделать числом способов, рав-
равным 4!. Итак, ответ на вопрос задачи: 3-4! = 3-4-3-2 = 72 способа.
Задача 3. Семь человек дожидаются большого начальника, сидя у него в приемной.
Начальник появился и предложил ожидающим организовать очередь. Сколькими спо-
способами может быть организована эта очередь, если трое являются ветеранами и
имеют право на внеочередное обслуживание?
Решение. Если бы никто из ожидавших не имел льгот, то ответ был бы ясен
сразу. Очередь из семи человек можно организовать числом способом, равным 7!,
т. е. равным 5040. Но тут есть три ветерана. Они должны занять первые три места
в очереди, и сделать это можно числом способов, равным 3! = 6. Любой из этих
шести вариантов допускает организацию остальных четырех мест в очереди чис-
числом способов, равным 4! = 12. Следовательно ответ на вопрос задачи таков:
3! • 4! = 6 • 24 = 144 способа.
5.2 Сочетания (выборки)
п,
Lpn работе с перестановками мы рассматривали различные спосо-
способы размещения некоторого количества неких элементов друг относи-
относительно друга. Теперь мы займемся иной проблемой. Имеется некоторое
количество п неких элементов, и надо рассмотреть различные способы,
какими можно выбрать из них т элементов @ < т< п). При этом поря-
порядок выбранных элементов не учитывается, так что нет смысла рассмат-
рассматривать их перестановки. Выборку т элементов из п обычно называют
сочетанием (сочетанием из п элементов по т). Число таких сочетаний
(выборок) обозначают как С^7. Приведем ряд несложных задач, требу-
требующих подсчета числа сочетаний.
Задача 1. Ученику дано задание прочитать за лето любые две книги из указанных
в списке четырех книг. Сколько у него есть способов выполнить это задание?
Решение. Пусть в списке находятся книги А, Б, В, Г (обозначим так эти книги).
Ученику надо прочитать любые из них, причем порядок прочтения не оговарива-
оговаривается. Допустим, в качестве первой он выбрал для чтения книгу А. Тогда, чтобы
выполнить задание, ученик должен прочитать книги А, Б или А, В или А, Г. Если
в качестве первой он выбрал книгу Б, то ему придется прочитать Б, В или Б, Г
(вариант Б, А совпадает с уже учтенным вариантом А, Б). Если в качестве первой
ученик выбрал книгу В, то теперь у него остался один способ выполнить зада-
задание — прочитать В, Г. Вот и все возможные варианты:
А, Б; А, В; А, Г; Б, В; Б, Г; В, Г.
Этих вариантов шесть. Таким образом С42 = 6 .
102

Задача 2. Человеку нужно приобрести три подарка. В магазине ему предложили на
выбор пять вполне равноценных предметов. Сколькими способами человек может сде-
сделать выбор?
Решение. Обозначим предложенные предметы: А, Б, В, Г, Д. Возможные выбор-
выборки трех из пяти (сочетания из пяти по три): А, Б, В; А, Б, Г; А, Б, Д\ А, Д Г; А, В, Д\
А, Г, Д\ Б, А, Г; Б, В, Д\ Б, Г, Д В, Г, Д. Всего 10 выборок. Таким образом, Съ5 = 10 .
Задача 3. Имеются три одноместные путевки в санаторий. А попасть в санаторий
желают шесть человек. Сколькими способами можно выбрать трех «счастливчиков» ?
Решение. Обозначим желающих получить путевку: А, Б, Д Г, Д Е. Возможные
способы выбрать троих из них:
А, Б, В; А, Б, Г; А, Б, Д; А, Б, Е; А, В, Г; А, В, Д; А, В, Е;
А, Г, Д; А, Г, Е; А, Д, Е; Б, В, Г; Б, В, Д; Б, В, Е; Б, Г, Д;
Б, Г, Е; Б, Д, Е; В, Г, Д; В, Г, Е; В, Д, Е; Г, Д, Е.
Всего 20 способов. Таким образом, С63 = 20 .
Задача 4. Сколькими способами молено выбрать из шести человек комиссию, со-
состоящую из четырех членов?
Решение. Обозначим шестерых претендентов: А, Б, В, Г, Д Е.
Возможные выборки четырех из них:
А, Б, В, Г; А, Б, В, Д; А, Б, В, Е; А, Б, Г, Д;	А, Б, Г, Е;
А, Б, Д, Е; А, В, Г, Д; А, В, Г, Е; А, В, Д, Е;	А, Г, Д, Е;
Б, В, Г, Д; Б, В, Г, Е; Б, В, Д, Е; Б, Г, Д, Е;	В, Г, Д, Е.
Всего 15 выборок. Таким образом, С64 = 15 .
Если внимательно прочитать решения рассмотренных задач, то впол-
вполне можно уловить логику отбора нужных сочетаний, а значит, и подсчета
их числа. Однако для большей наглядности обратимся, как и в случае
с перестановками, к модели раскладывания шариков по отделениям в ко-
коробке. Правда, модель с шариками будет теперь иной. Раньше (при рас-
рассмотрении перестановок) число шариков равнялось числу отделений и
принимался во внимание порядок расположения шариков друг по отно-
отношению к другу (недаром шарики различались, например, по цвету или
номеру). Теперь число шариков меньше числа отделений (в частном слу-
случае оно равно числу отделений или нулю) и при этом порядок расположения
шариков не учитывается (все шарики белые). Будем выяснять, сколькими
способами можно разместить т одинаковых шариков по п отделениям,
полагая, как и раньше, что в отделении может поместиться только один
шарик. Число этих способов и есть число сочетаний из п элементов по т9
или, иначе говоря, число выборок т элементов из п.
103

Возможен вопрос: если речь идет о разных размещениях т шариков
по п отделениям, то о какой выборке тут можно говорить? Из чего и что
именно мы здесь выбираем? И что здесь понимается под словом «эле-
«элемент»? Отвечаем: из общего числа п отделений мы выбираем здесь т
занятых шариками отделений. Отделение занято — значит, в него поло-
положен шарик. В роли элементов выступают здесь отделения, причем по-
порядок выбранных (занятых) отделений не учитывается.
Начнем с двух частных случаев. Первый: т = 0. Ситуация, когда ни
в одно из отделений не положен шарик, разумеется, возможна. Но воз-
возможны ли два или более разных способов не положить ни одного ша-
шарика ни в одно отделение? — Нет, невозможны. Значит, есть только
один способ реализовать данную ситуацию; следовательно,
С0 -1
Второй частный случай: т = п. Это значит, что в каждом отделении
есть по шарику. Реализовать такую ситуацию можно тоже только одним
способом (ведь шарики одинаковы и, значит, порядок их размещения
учитывается). Следовательно,
С* = 1.
'п
Далее обратимся к случаям, когда т=\. Сколькими способами мож-
можно разместить один шарик в коробке с п отделениями? Очевидно, таких
способов п (надо поочередно помещать шарик в каждое из п отделе-
отделений). Следовательно,
С1=п.
у п
Для я = 3, я = 4, п = 5 соответствующие способы размещения шарика
изображены на рис. 1, а в таблице 16.
А на рис. 1, б в той же таблице показаны случаи, когда m = п — 1
(опять-таки для я = 3, я = 4, л = 5). Мы видим, что
Сп~1 = л.
Получается, что
С\ = С".	E)
И это отнюдь не случайное совпадение! Есть определенная аналогия
между рис. 1, а и рис. 1,6. На рис. 1, а в каждом размещении участвует
один шарик, или, иными словами, одно занятое отделение, а на рис. 1, б
в каждом размещении участвует одно незанятое (пустующее) отделение.
Понятно, что число способов, какими из п отделений можно выбрать
104

Таблица 16. Сочетания
Cl =10
а)
Ю
Ю
lo
IO
IO
IO
op
lop
1 IO
O| |O
O|
ODD
OIOI
O| |O
IOI
lop
OI
OI
OI
OI
OI
OI
б)
ю
ю
ю
ю
Ю
OI
О|О|
Ю1
ЮЮ
Ю
|О|
о| Ю
OI
о
о
о
о
Рис.2
Рис.1
1 -г2
О I I I
I СЖЖЗ
Г,
Го
о
о
! o:
n.
i:
! СП
n — 1 отделений
	A
-Д	-	V,
J !
J i
Число
сочетаний:
(-лт-\
^ n-\
UJ	Li
C^	ffl 	 г~л JTl-1 _i_ ^ fit
1 Группа 2
] i
Число
сочетаний:
^ пЛ
Рис.3
105

одно занятое, должно равняться числу способов, какими из п отделений
можно выбрать одно незанятое. Размещать один шарик — это все равно,
что размешать п - 1 пустых мест. А число размещений п - 1 пустых мест
равно, очевидно, числу размещений п — 1 шариков (достаточно заменить
мысленно пустые места на шарики, а шарики на пустые места).
Соотношение A) можно обобщить для любого т:
/^т гчп—т	t ел
На рис. 2 в таблице 16 наглядно демонстрируется справедливость
формулы F) для случая, когда п = 5, т = 3. Размещать три шарика по
пяти отделениям — это все равно, что размещать по пяти отделениям
два пустых места. А размещать два пустых места — это все равно, что
размещать два шарика.
В справедливости формулы F) можно также убедиться, решив следу-
следующую задачу.
Задача 5. Сколькими способами можно разбить группу из п человек на две подгруп-
подгруппы, в одной из которых будет т человек, а в другой п — т?
Задача имеет два решения.
Решение первое. Надо выяснить, сколькими способами можно выбрать т человек
из п. Понятно, что число таких способов равно С™ . При этом всякий раз автомати-
автоматически выявляется и соответствующая подгруппа, состоящая из п - т человек.
Решение второе. Надо выяснить, сколькими способами можно выбрать п - т
человек из п. Число таких способов равно С™ . При этом всякий раз выявляется и
подгруппа из т человек.
Оба решения дают ответ на вопрос, поставленный в задаче. А это как раз и озна-
означает, что С = Спп~т .
Получим еще одно полезное соотношение для числа сочетаний (оно позволит
нам переходить от числа сочетаний из п - 1 элементов к числу сочетаний из
пэлементов). Для этого разобьем мысленно все количество сочетаний из п эле-
элементов по т (оно равно С™ ) на две группы — группу 1 и группу 2. В группу 1
включим все сочетания, для которых первое отделение в коробке занято шариком,
так что остальные т - 1 шариков распределены по оставшимся п - 1 отделениям.
Число таких сочетаний равно C™ll. В группу 2 включим все остальные из С™ со-
сочетаний; у этих «остальных» сочетаний первое отделение пустует, так что все т,
шариков оказываются распределенными по оставшимся п - 1 отделениям. Число
«остальных» сочетаний равно С™_х. Полное число сочетаний С^ сумма сочетаний
из группы 1 и сочетаний из группы 2; следовательно,
Эти рассуждения поясняет рис. 3 из таблицы 16.
106

Задача 6. Используя соотношение G), надо найти, чему равно Су .
Решение. Согласно G), С75 = С64 + С65. Из задачи 4 мы знаем, что С64 = 15 . Да-
Далее учтем, что С65 = Q1 = 6. Таким образом, С| =15 + 6 = 21.
Задача 7. Используя G), /шдо найти, чему равно С3 .
Решение. Согласно G), С73 = С62 +С63. Мы уже знаем, что С64 =15 и, значит,
С62 =15 (поскольку С62 = С64). Что же касается С63, то применим еще раз соотно-
соотношение G); С63 = С] + С\ = 10 +10 = 20 . Таким образом, С73 = 15 + 20 = 35.
Задача 8. Используя G), надо найти, чему равно С\ .
Решение. Согласно G), С% =Cj +C] . Согласно F), Cj=Cj, a C75 мы уже
подсчитывали (в задаче 6) и получили 21. Нам известно также С3, оно равно 35
(см. задачу 7). Таким образом, С83 = 21 + 35 = 56 .
5.3 Формула для подсчета числа сочетаний
п
шлезность соотношения G) очевидна. Однако вряд ли удобно
пользоваться им всякий раз, как потребуется найти число тех или иных
выборок. Хотелось бы иметь формулу, позволяющую сразу подсчитать
С^7, коль скоро даны пят.
Получить эту формулу нетрудно. Рассмотрим какую-то одну выборку
т элементов из п (одну выборку т прочитанных книг из общего числа
п книг). Сколькими способами можно реализовать перестановку эле-
элементов (книг) для данной конкретной выборки, не нарушая этой выбор-
выборки? Подчеркнем: не просто для всех п элементов (тогда число переста-
перестановок равнялось бы л!), а для т отобранных элементов (прочитанных
книг) в комбинации с перестановками п - т элементов, оставшихся в дан-
данной выборке неотобранными. Число перестановок т отобранных эле-
элементов равно т\. Число перестановок п — т неотобранных элементов
равно (п - т)\. Каждую из первых перестановок надо скомбинировать
с каждой из вторых перестановок. Таким образом, все перестановки эле-
элементов для данной выборки т элементов из л, не нарушающие этой
выборки, можно реализовать числом способов, равным т\{п — т)\. Если
мы затем умножим это число на число всех возможных выборок из
п элементов по т, т. е. умножим на С™, то получим полное число пере-
перестановок п элементов, которое есть п\. Итак,
т\{п-т)\С™ =п\
Отсюда следует искомая формула:
п ~ т\(п-т)Г
107

Возникает вопрос: как быть, если т = О или m = nl Тут можно посту-
поступить двояко. Можно оговорить, что формула (8) применима для т ^ О
и/и^«, и учитывать, что С^ = С^ = 1. А можно условиться, что 0! = 1,
и пользоваться формулой (8) во всех случаях. Математики предпочита-
предпочитают использовать второй вариант.
Рассмотрим несколько задач с использованием формулы (8).
Задача 1. У туриста есть семь консервных банок с ухой. В походе он будет
находиться десять дней; из них какие-то семь дней будет есть уху, а три дня будет
питаться всухомятку. Сколько у туриста есть способов выбрать дни с горячим
питанием?
Решение. Число способов равно С±о . Используя (8), находим:
7 _ 10! _10-9-8-7!
10~ТГЗТ~ WJ\	4-12U.
Задача 2. Для подарков ко дню восьмого марта человек должен приобрести три
броши и три браслета. В магазине ему предложили на выбор пять брошей и шесть
браслетов. Сколькими способами человек может сделать выбор?
Решение. Три броши из пяти можно выбрать числом способов, равным С53, а три
браслета из шести — числом способов С\ . Каждый из способов выбора броши
нужно скомбинировать с каждым из способов выбора браслета. Следовательно, полное
число способов, какими человек может выбрать три броши и три браслета, есть
зсз_ 5! 6! _5-4-3!-6-5-4.3!
5 6 ~ 3~Ш' 1ПТ ~ 3!-2!-3!-3! ~ ' ' ' ~ '
Задача 3. Восемь человек должны расположиться в двух комнатах, причем так, что-
чтобы в каждой было не менее трех человек. Сколькими способами это можно сделать ?
Решение. Есть два варианта. Первый: в одной комнате три человека, а в дру-
другой пять. Второй: в каждой комнате по четыре человека. В первом варианте
число способов размещения равно числу выборок трех из восьми (или пяти из
восьми, что одно и то же); это число есть С\ . Во втором варианте число спосо-
способов размещения равно числу выборок четырех из восьми, т. е. равно С84. Полное
число способов размещения людей должно учитывать как первый, так и второй
варианты:
Задача 4. Группу из девяти человек надо разбить на три подгруппы — в одной два
человека, в другой три, в третьей четыре. Сколькими способами можно выполнить
такое разбиение ?
Решение. Сначала выясняем, сколькими способами можно выбрать двух чело-
человек из девяти. Это число способов равно С92. После того, как этот выбор состоял-
состоялся, осталось семь человек. Из них надо организовать подгруппы из трех и четырех
человек. Это можно сделать числом способов, равным С73 (или С74, что одно и то
108

же). Итак, девять человек можно разбить на два, три и четыре следующим числом
способов:
Г2 Гз_^	7! _9-8-7-6-5-4!_
9 7 "" 2!-7! ' 3!-4! ~~ 2!-3!-4! -iZDU-
Примечание. Можно было бы сначала выяснить, сколько есть выборок трех
человек из девяти. Тогда ответ на вопрос задачи дало бы произведение С93 • С62.
А можно было бы сначала выяснить, сколько есть выборок четырех человек из
девяти. Тогда ответ дало бы произведение С94 • С52. Предлагаем самостоятельно
убедиться, что
С2 лЗ 	 лЗ л2 	 л4 л2
о ' \_/ j — ^9 * 6 — 9 * 5 *
Задача 5. Сколькими способами можно рассадить за столом пять гостей, если
стол накрыт на семь персон?
Решение. Пять выборок из семи равно Су . Но это еще не ответ на поставлен-
поставленный в задаче вопрос, поскольку при рассаживании гостей за столом необходимо
принимать во внимание также число перестановок пяти гостей (оно равно П5).
Ведь занявших те или иные пять стульев можно поменять местами. Таким обра-
образом, пять гостей можно рассадить за столом, накрытым на семь персон, числом
способов, равным
5.4 Сочетания и треугольник Паскаля
Расположим различные числа сочетаний на листе бумаги так, как это
показано на рис. 1 в таблице 17. Здесь все числа сочетаний с данным п
расположены в строку; она содержит п + 1 чисел (для /и = 0, 1, 2, 3,..., п).
Строка с п = 1 содержит два числа сочетаний: Cf и С{.
Под ней помещается строка с п = 2; она содержит три числа сочета-
сочетаний: С2°, С\, С\.
Ниже идет строка с п = 3; она содержит четыре числа сочетаний: С® ,
С], С32, С|.
И так далее. На рис. 1 изображены последовательно одна под другой
восемь строк (для п=1, 2, 3, 4, 5, 6, 7, 8). Разумеется, строки можно,
при желании продолжить вниз, постепенно увеличивая п. Чем больше п,
тем ниже расположена соответствующая строка и тем она длиннее.
Обратим внимание также на то, что число С™ помещается не точно
под числом C™_i, а под промежутком между числами С^1 и С™_х.
Такое расположение чисел сочетаний на листе бумаги математики
называют арифметическим треугольником. Этот «треугольник» образован
109

Таблица 17. Треугольник Паскаля
110

не отрезками прямых, а определенным расположением чисел сочетаний на
плоскости. Он был описан в 1665 году французским ученым Блезом
Паскалем в его труде «Трактат об арифметическом треугольнике». В честь
Паскаля арифметический треугольник принято называть треугольником
Паскаля.
Используя формулу E), можно было бы сразу представить треуголь-
треугольник Паскаля не в виде, показанном на рис. 1, а в виде соответствующих
натуральных чисел. Однако не будем торопиться и покажем, как можно
получить треугольник Паскаля в виде чисел, не пользуясь формулой (8).
Воспользуемся тем, что С^ = С^ = 1, а также тем, что С\ = С^ = п.
В результате рис. 1 в таблице 17 преобразуется в рис. 2. Глядя на него,
можно предположить, что треугольник Паскаля зеркально симметричен
относительно вертикальной прямой, проведенной пунктиром. В пра-
правильности этого предположения нетрудно убедиться, воспользовавшись
соотношением F).
Чтобы представить в виде натуральных чисел все числа сочетаний
на рис.2, надо воспользоваться соотношением G). Так, зная, что
С\ = С32 = 3, можно, используя G), найти С\ (поскольку С\ = С\ + С32 ,
то С % =3 + 3 = 6). Если нам известны, например, С72 и С73, то мы мо-
можем, используя G), найти С83 (С83 =Cj +Cj).
В итоге не составит особого труда найти все С^7, представленные на
рис. 2, и получить треугольник Паскаля в виде натуральных чисел — см.
рис. 3 в таблице 17.
5.5 Треугольник Паскаля, доска Гальтона, монетки...
JHLa рис. 1 в таблице 18 изображено устройство, называемое доской
Гальтона по имени английского ученого Френсиса Гальтона A822-1911).
Это устройство представляет собой плоскую доску, на которой в опре-
определенном порядке укреплены штырьки-цилиндрики (кружочки на ри-
рисунке — основания цилиндриков): вверху один штырек-цилиндрик,
ниже — первый ряд из двух штырьков, еще ниже — второй ряд из трех
штырьков и так далее. На доске Гальтона, представленной на рис. 1,
имеются пять рядов штырьков. Количество рядов (и соответственно
штырьков) могло бы быть больше, но нам вполне достаточно пяти ря-
рядов. Внизу доски есть семь отделений-ловушек, обозначенных буквами
А, Д Д Г, Д Д Ж.
Доска с штырьками устанавливается в наклонном положении. За-
Затем берется шарик и аккуратно роняется прямо на середину верхнего
111

Таблица 18. Доска Гальтона
Рис.1
Рис.2
ряд 1-
о о о
о о о
ряд 2
/
о о о о о\4/о
о о о о о Oi5f о а
в
д
ж
Рис.3
в
о
о © о а
TV
ряд 2
-рядЗ
Рис.4
О О О О C5V-T4-O
О О О О О О-р4-О О О О О О
о
о о
о о о
о о о о
ж
112

штырька. Он отскакивает от штырька влево или вправо и попадает на
середину одного из штырьков первого ряда. Затем шарик снова отска-
отскакивает влево или вправо и попадает на середину одного из штырьков
второго ряда. И так далее. На рис. 2 в таблице 18 весь путь шарика
состоит из последовательности следующих шагов-отскоков:
ВЛЕВО - ВЛЕВО - ВПРАВО - ВЛЕВО - ВЛЕВО - ВПРАВО.
После этого шарик попал в ловушку В. Конечно, возможен был и дру-
другой путь шарика, который привел бы его в ту же или другую ловушку.
Поставим вопрос: сколько есть возможных путей попадания шарика,
например, на второй слева штырек в третьем ряду? Нетрудно сообра-
сообразить, что таких путей три — см. рис. 3 в таблице 18. Обозначая отскок
шарика влево буквой Л, а вправо буквой П, можем кратко записать эти
три пути так: ЛЛП, ЛПЛ, ПЛЛ.
А сколько есть путей попадания шарика на крайний правый штырек
в пятом ряду? Очевидно, что тут есть только один путь: ППППП. Он
также показан на рис. 3.
На рис. 4 в таблице 18 показаны все четыре пути попадания шарика
на второй слева штырек в четвертом ряду:
лллп, ллпл, лплл, пллл.
На рис. 5 в таблице 18 показаны все пять путей попадания шарика на
второй справа штырек в пятом ряду:
ппппл, ппплп, пплпп, плппп, лпппп.
На рис. 6 в таблице 48 на основании каждого штырька-цилиндрика
написано число способов (путей) попадания шарика на этот штырек.
Сравним этот рисунок с рис. 3 в таблице 17. Убеждаемся, что перед
нами треугольник Паскаля. Написанные на штырьках числа — это числа
сочетаний С™. Здесь п — номер ряда, в котором находится штырек; для
крайнего левого в ряду штырька т = 0, а затем в ряду идут штырьки с
т= 1, 2, 3,..., п.
Согласно рис. 6, число способов, какими шарик может попасть, на-
например, на третий слева штырек в пятом ряду, есть число сочетаний из
пяти по два: С\ = 10 . Все эти десять способов таковы (в наших обозна-
обозначениях, где Л — отскакивание шарика влево, а П — вправо):
лллпп	плллп
лпллп	пллпл
лпплл	плплл
ллплп	лплпл
ллппл	ппллл
113

Нетрудно убедиться, что все эти десять вариантов попадания на тре-
третий штырек в пятом ряду полностью соответствуют десяти способам
размещения двух шариков по пяти отделениям в коробке, которые были
изображены на рис. 2, б в таблице 16. Надо только заменить здесь П на
отделение, занятое шариком, а Л — на незанятое отделение. Заметим,
что, если поступить наоборот (заменить П на незанятое отделение, а
Л — на занятое шариком), получатся размещения трех шариков по пяти
отделениям, изображенные на рис. 2, а в таблице 16.
Итак, число способов, какими можно попасть на (т+ 1)-й штырек
(считая слева) в п-м ряду, равно числу способов разместить т шариков
по п отделениям; иначе говоря, равно числу выборок т элементов из я,
т. е. равно С™
Используя движение (скачки) шарика по доске Гальтона, можно
лишний раз получить уже известное нам соотношение G) для чисел
сочетаний. Мы уже выяснили, что добраться до штырька, занимаю-
занимающего (т + 1)-е место в п-м ряду, возможно числом способов, равным
С™. Ясно, что попасть на этот штырек можно либо с расположенного
над ним штырька слева (штырька, занимающего т-е место в (п - 1)-м
ряду), либо с расположенного над ним штырька справа (штырька, за-
занимающего (т + 1)-е место в (п - 1)-м ряду). Есть С%Г\ способов по-
попасть на левый верхний штырек и C™_i способов попасть на правый.
Отсюда сразу получаем: С™ = С™_Г\ + С™_х.
А теперь займемся подбрасыванием монетки. Сколькими способами
могут выпасть две решки при пяти бросаниях монетки? Обозначая вы-
выпадение решки буквой Р, а выпадение орла буквой О, представим сле-
следующим образом все интересующие нас варианты:
ОООРР	РОООР
ОРООР	РООРО
ОРРОО	РОРОО
ООРОР	ОРОРО
ООРРО	РРООО
Получаются те же десять вариантов, что и в случае с размещениями
двух шариков по пяти отделениям или в случае с попаданием на третий
штырек в пятом ряду на доске Гальтона.
Вполне понятно, что набор способов выбрать из пяти отделений два
занятых отделения должен совпадать с набором способов выбрать из
пяти бросаний монетки два с выпадением решки. Но почему такой же
набор вариантов получается при рассмотрении способов попадания
шарика на третий штырек в пятом ряду на доске Гальтона? Ответить на
этот вопрос нетрудно. Чтобы попасть на упомянутый штырек, шарик
114

должен испытать пять соударений (с самым верхним штырьком, а затем
с каким-то штырьком из первого, второго, третьего и четвертого ря-
рядов), и при этом в двух соударениях шарик должен отскочить вправо.
Значит, речь идет о наборе способов выбрать из пяти соударений два
правых соударения (соударения с отскоком вправо).
Задача 1. Сколько есть способов {путей) попадания шарика в ловушку В на доске
Галътона, изображенной на рис. 1 в таблице 18.
Решение. В ловушку В шарик может попасть либо после соударения со вторым
штырьком из пятого ряда, либо после соударения с третьим штырьком из пятого
ряда. У шарика есть 5 способов добраться до первого из упомянутых штырьков
и 10 способов добраться до второго из упомянутых штырьков. Значит, попасть
в ловушку В шарик может числом способов, равным 5 + 10 = 15.
Задача 2. Сколько есть способов {путей) попадания шарика либо в ловушку В, либо
в ловушку А?
Решение. Чтобы найти число способов попасть либо в ловушку В, либо в ло-
ловушку А, надо сложить число способов попасть в ловушку В и число способов
попасть в ловушку А. Число способов попасть в ловушку В мы уже знаем; оно
равно 15. А попасть в ловушку А есть, очевидно, только один способ. Значит,
число способов попасть либо в В, либо в А, равно 15 + 1 = 16.
Задача 3. Сколько есть способов {путей) попадания шарика хотя бы в какую-то
{безразлично какую) из семи ловушек?
Решение. Данный вопрос можно переформулировать так: сколько есть спосо-
способов попасть либо в ловушку А, либо в ловушку Б, либо в ловушку В, либо в ловуш-
ловушку Г, либо в ловушку Д либо в ловушку Е, либо в ловушку Ж? В каждую из семи
ловушек ведет определенное число путей. В задаче требуется указать полное число
путей для всех ловушек. Оно равно 64 (см. рис. 6 в таблице 18; там для каждой
ловушки указано число путей, приводящих шарик в эту ловушку).
5.6 Давайте сравним шансы!
в
жизни мы нередко сравниваем шансы. Когда мы это делаем? —
Тогда, когда рассматриваем события, исход которых неоднозначен. Ша-
Шарик, скачущий по доске Гальтона, может попасть или не попасть в ло-
ловушку В. Он может также попасть или не попасть в ловушку А. Мы гово-
говорим, что у него больше шансов попасть в ловушку В, нежели в ловушку А.
Почему мы так говорим? — Да потому, что существует 15 способов (пу-
(путей) попасть в ловушку В и только один — попасть в ловушку А.
При подбрасывании монетки пять раз решка может выпасть или не
выпасть два раза. Мы уверены, что выпадение решки два раза при пяти
115

подбрасываниях имеет больше шансов по сравнению с выпадением реш-
решки, скажем, все пять раз. Такая уверенность связана с тем, что при пяти
подбрасываниях монетки есть 10 способов выпадения двух решек (ведь
С\ = 10 ) и лишь один выпадения пяти решек (С$ = 1).
И в случае с движением шарика по доске Гальтона, и в случае с под-
подбрасыванием монетки мы полагаем, что шансы каждого конкретного
способа одинаковы. Именно поэтому мы заключаем, что больше шансов
у той ситуации, которая имеет больше способов реализации.
Но можно ли считать, что шансы каждого пути, который проделыва-
проделывает шарик от верхнего штырька до той или иной ловушки, действитель-
действительно одинаковы? — Да, можно. На любом пути шарик испытывает пять
соударений с штырьками и при каждом соударении он имеет одинако-
одинаковые шансы отскочить как влево, так и вправо. Вот и получается, что
у шарика одинаковые шансы проделать любой из шестидесяти четырех
возможных путей (то, что всего путей шестьдесят четыре, мы установи-
установили в задаче 3 в § 5.5). Все это справедливо и для примера с подбрасыва-
подбрасыванием монетки. При каждом подбрасывании у монетки есть одинаковые
шансы выпасть решкой или орлом. Если события имеют одинаковые шан-
шансы, их называют равновозможными. Отскакивание шарика от штырька
влево или вправо — равновозможные события. Выпадение подброшен-
подброшенной монетки решкой или орлом — равновозможные события. Равно-
возможными являются также такие события как попадание шарика в ло-
ловушку А или в ловушку Ж. Или, например, попадание шарика
в ловушку Б или ловушку Е. Или попадание шарика в ловушку В или
ловушку Д. Ведь в каждую из этих пар ловушек ведет одинаковое число
путей (способов): один в ловушки Л и Ж, шесть в ловушки Б и Д пят-
пятнадцать в ловушки В и Д (см. рис. 6 в таблице 18). Заметим, что мы
начали сравнивать шансы (хотя бы качественно), не выяснив, чем эти
шансы измеряют. В § 6.1 мы это выясним, но в дальнейшем перейдем
от не очень четкого и во многом интуитивного понятия «шансы» к ма-
математически строгому понятию «вероятность».
ЗАДАНИЯ ПО ТЕМЕ 5
1.	В автомашине пять мест. Сколькими способами можно разместить в ней пять
человек, из которых один не имеет права занять место за рулем?
Ответ: 96 способов.
2.	В автомашине пять мест. Сколькими способами можно разместить в ней четырех
человек, если занять место водителя могут двое из них?
Ответ: 48 способов.
116

3.	Студенту нужно сдать четыре экзамена в течение семи дней. Сколькими способа-
способами можно составить ему расписание экзаменов с учетом того, что в один день
нельзя сдавать более одного экзамена?
Ответ: 840 способов.
4.	Студенту нужно сдать за шесть дней три экзамена: по математике, физике, элект-
электронике. Сколькими способами можно составить ему расписание экзаменов при
условии, что в один день разрешено сдавать не более одного экзамена и что
сначала нужно сдать математику, потом физику, потом электронику?
Ответ: 20 способов.
5.	Из семи человек, среди которых есть три доктора наук, надо выбрать комиссию
из четырех членов с условием, что в нее вошел по крайней мере один доктор
наук. Сколькими способами можно выбрать такую комиссию?
Ответ: 34 способа.
Указание. Надо рассмотреть три ситуации: 1) в комиссию включены все три док-
доктора наук, 2) в комиссию включены два доктора наук, 3) в комиссию включен
один доктор наук.
6.	Десять человек должны расположиться в трех комнатах, причем так, чтобы в каж-
каждой было не менее трех человек. Сколькими способами можно это сделать?
Ответ: 4200 способов.
Указание. Надо каждый из способов, какими можно выбрать троих из десяти,
скомбинировать с каждым из способов, какими можно выбрать троих из семи
(или четверых из семи, что одно и то же).
7.	Восемь человек должны расположиться в трех комнатах, причем так, чтобы в каж-
каждой было не менее двух человек. Сколькими способами можно это сделать?
Ответ: 980 способов.
Указание. Надо рассмотреть две схемы расселения: 2-2-4 и 2-3-3.
8.	В порядке тренировки выпишите все числа в 9-й, 10-й и 11-й строках треуголь-
треугольника Паскаля и изобразите на отдельном листе бумаги треугольник Паскаля
с п = 1, 2, 3,..., 11. Этот треугольник пригодится нам для выполнения заданий
9, 10, 11, 15.
9.	Выпишите по порядку суммы чисел для разных строк треугольника Паскаля, начи-
начиная с п = 1 вплоть до п = 11. Какая закономерность наблюдается в последова-
последовательности этих сумм?
10.	Для каждой строки треугольника Паскаля сравните сумму чисел, стоящих на не-
нечетных местах, с суммой чисел, стоящих на четных местах. Какой вывод Вы сде-
сделаете?
11.	Рассмотрите внимательно строки треугольника Паскаля, для которых п — про-
простое число (п = 2, 3, 5, 7, 11). Что особенного можно заметить в этих строках?
12.	Монетка подбрасывается шесть раз. Сколько есть вариантов выпадения либо
двух, либо трех решек?
Ответ: 35 вариантов.
117

13.	Монетка подбрасывается семь раз. Сколько есть вариантов выпадения либо двух
решек, либо трех орлов?
Ответ: 56 вариантов.
14.	Монетка подбрасывается восемь раз. Сколько есть вариантов выпадения одно-
одновременно пяти орлов и трех решек?
Ответ: 56 вариантов.
15.	Монетка подбрасывается девять раз. Сколько всего есть различных вариантов
выпадения орлов и решек?
Ответ: 512 вариантов.
16.	Монетка подбрасывается п раз. Докажите, что число вариантов выпадения
гп решек равно числу вариантов выпадения п - т решек.
17.	Монетка подбрасывается восемь раз. Какие шансы больше — выпасть решке
четыре раза или выпасть орлу пять раз?
18.	Какие шансы больше — попасть шарику в ловушку В или попасть ему в ловушку Г
на доске Гальтона? Здесь и далее рассматриваем доску Гальтона, изображенную
в таблице 18 (см. рис. 1 и рис. 6).
19.	Какие шансы больше — попасть шарику в любую из ловушек 4 и Е или же по-
попасть ему в любую из ловушек Г и Ж на доске Гальтона?
118

ТЕМА 6
ПЕРВОЕ ЗНАКОМСТВО С ВЕРОЯТНОСТЬЮ
Вероятностью какого-либо события назы-
называется отношение числа равновозможных слу-
случаев, благоприятствующих событию, к числу
всех возможных случаев.
В.Я. Буняковский
Нас интересует отношение числа шансов,
благоприятствующих событию, к общему
числу всех шансов. Его называют вероятно-
вероятностью события.
Огюстен Курно
Вероятность есть степень достоверности ...
Николай Бернулли
Справка:
Виктор Яковлевич Буняковский A804—1889) — вьщающийся российский математик.
Огюстен Курно A801 — 1877) — известный французский математик и философ.
Николай Бернулли A687-1759) — известный швейцарский математик, племян-
племянник знаменитого математика Якоба Бернулли A654-1705), автора книги «Искусст-
«Искусство предположений».
119

6.1 Классическое определение вероятности события
шаите не торопясь начнем знакомиться с понятием вероятности,
не касаясь пока вопросов, связанных с историей появления и развития
этого понятия. Прежде всего отметим, что вероятность рассматривают
по отношению к событиям, причем событиям случайным. Например,
при подбрасывании игрального кубика случайно выпадает грань с чет-
четным числом очков. Можно поинтересоваться вероятностью этого со-
события. В мешке три красных и пять белых шаров. Какова вероятность,
действуя наугад, случайно вынуть из мешка красный шар? Перемещаясь
по доске Гальтона, шарик случайно попадает в ловушку Д. И у этого
события есть определенная вероятность, которую можно подсчитать
(ипритом довольно легко). Или вот Вам случайно досталась путевка
в санаторий, выделенная на пятерых человек (пришлось тянуть жре-
жребий). Какова вероятность этого приятного для Вас, но тем не менее
случайного события? А какова вероятность случайного получения путе-
путевки, если всего имеются три путевки, но, кроме Вас, на них претендуют
еще семь человек? Произвольно отбирают четверых лиц из шести для
работы в некоторой комиссии. Какова вероятность того, что в комис-
комиссию случайно попадут четверо определенных лиц?
В двух крайних случаях понятие вероятности формально применяют
по отношению к событиям, не являющимся случайными. Если некото-
некоторое событие никогда не происходит, его называют невозможным собы-
событием и полагают его вероятность равной нулю. Другой крайний случай
связан с событием, которое при определенных условиях происходит
наверняка. Такое событие называют достоверным и полагают его веро-
вероятность равной единице. Конечно, ни невозможное, ни достоверное со-
события нельзя считать случайными. Невозможное событие попросту не
существует; мы можем говорить о нем лишь чисто умозрительно. При-
Примеры невозможных событий: железный молоток при нагревании под-
подскочил вверх; упавшее с яблони яблоко превратилось в грушу; при со-
совершенно безоблачном небе пошел сильный дождь. Что же касается
достоверных событий, то они по самой сути своей не являются случай-
случайными — они происходят наверняка.
Значение вероятности любого случайного события удовлетворяет
неравенствам:
0<Р<1,	A)
где Р — общепринятое обозначение вероятности (начальная буква анг-
английского слова PROBABILITY, означающего ВЕРОЯТНОСТЬ). Веро-
Вероятность события можно рассматривать как меру его достоверности. Чем
ближе Р к нулю, тем менее достоверно событие; при Р= О оно вообще
120

оказывается недостоверным — это событие невозможное. Чем ближе Р
к единице, тем более достоверно событие; при Р=\ оно превращается
в достоверное событие.
Если два случайных события (событие Р{\) и событие РB)) имеют
одинаковую вероятность, т. е. если РA) = РB), то такие события назы-
называют равновероятными или равновозможными. В § 5.6 мы ввели понятие
равновозможных событий как событий, имеющих одинаковые шансы.
Отметим, что смысл таких событий вполне ясен уже из рассматривав-
рассматривавшихся нами примеров (например, связанных с движением шарика по
доске Гальтона или подбрасыванием монетки) и не нуждается в предва-
предварительном введении понятия вероятности. Так, равновероятность отска-
отскакивания шарика от штырька влево или вправо объясняется симметрией
шарика и штырька по отношению к отражению в плоскости, проходя-
проходящей через центр шарика и ось штырька. Равновероятность выпадения
орла или решки объясняется симметрией монетки по отношению к пе-
переворачиванию ее с одной стороны на другую. С очевидной симметрией
кубика связана равновероятность выпадения каждой его грани.
Это очень хорошо, что понятия равновероятности (равновозможно-
сти) событий можно с учетом симметрии ввести до того, как введено
понятие вероятности. Потому что само понятие вероятности вводится
с использованием понятия равновозможности.
Классическое определение вероятности было введено в науку в 1812 году
Лапласом. Его поддерживал, в частности, В.Я. Буняковский — см. один
из эпиграфов к данной теме. Достаточно аккуратная формулировка этого
определения выглядит так.
Предположим, что однородные испытания могут привести к любому
из п равновозможных исходов. Пусть в каждом из т этих исходов и
только в них реализуется событие А {эти исходы называют благопри-
благоприятными для события А). Тогда вероятность Р{А) данного события оп-
определяется выражением:
Р{А) = т/п.	B)
Коротко говоря, вероятностью события называется отношение числа
благоприятных для события исходов к общему числу исходов.
Отметим два крайних случая:
1)	т = п — число благоприятных исходов равно числу всех равновоз-
равновозможных исходов: Р(А) = п / п=1; событие А достоверное;
2)	т = 0 — число благоприятных исходов равно нулю: Р{А) = 0 / п = 0;
событие А невозможное.
Отметим также, что вероятность каждого из п равновозможных (рав-
(равновероятных) исходов равна 1 / п.
121

Наряду с событием А рассматривают также событие А, называемое
противоположным (или дополнительным). Вероятность того, что про-
произойдет событие А (вероятность Р{А)) можно рассматривать как веро-
вероятность того, что не произойдет событие А. Если из п равновероятных
исходов т исходов благоприятствуют событию А (эти и только эти ис-
исходы реализуют событие А), то ясно, что остальные п — т исходов не
реализуют события А; они реализуют событие А .
Таким образом,
Р(А) = O—JUL = i_-??. = i_ р(А).	C)
Отсюда следует, что
Р(А) + Р(А) = \.	D)
Заметим, что если событие А невозможное (Р(А) = 0), то событие А
является достоверным [Р(А) = 1 — Р(А) = 1 — 0 = 1). Соответственно,
если событие А достоверное, то событие А является невозможным.
Упавшее с яблони яблоко превратилось в грушу — событие невозмож-
невозможное; упавшее с яблони яблоко не превратилось в грушу — событие дос-
достоверное. При безоблачном небе пошел дождь — событие невозможное;
при безоблачном небе не пошел дождь — событие достоверное. На нахо-
находящееся в бассейне с водой тело действует выталкивающая сила —
событие достоверное; на находящееся в бассейне с водой тело не дей-
действует выталкивающая сила — невозможное событие. При нагревании
золотого кольца его диаметр увеличился — событие достоверное; при
нагревании золотого кольца его диаметр не увеличился — невозможное
событие. Обратим внимание: тот факт, что некое событие не происхо-
происходит, сам по себе тоже рассматривается как событие.
Перейдем к конкретным примерам, начиная с наиболее простых.
Подбрасывание монетки. Испытания, заключающиеся в подбрасыва-
подбрасываниях монетки, имеют два равновероятных исхода: выпадение решки
и выпадение орла. Если в качестве события А рассматривать выпадение
решки, то ясно, что Р(А) = 1 / 2.
Подбрасывание игрального кубика. Испытания, заключающиеся в под-
подбрасываниях кубика, имеют 6 равновероятных исходов — ведь у кубика
шесть граней. Ясно, что вероятность выпадения каждой конкретной
грани равна 1/6. Если в качестве события А рассматривается не выпа-
выпадение какой-то конкретной грани, а выпадение грани с четным числом
очков, то в этом случае число благоприятных исходов т = 3. Значит,
согласно B), Р{А) = 3/6=1/2.
122

Вынимание шаров из мешка. Каждое испытание — вынимание наугад
одного шара из мешка, в котором находятся п шаров, одинаковых на
ощупь. После каждого испытания вынутый шар возвращают в мешок
и хорошо перемешивают шары в мешке. Пусть в мешке три красных
и пять белых шаров и пусть в качестве события А рассматривается вы-
вынимание из мешка красного шара. Полное число равновероятных исхо-
исходов п = 3 + 5 = 8. Число исходов, благоприятных для события Л, т = 3.
Следовательно, Р{А) = 3/8. Если в качестве события А рассматривать
вынимание из мешка белого шара, то тогда Р{А) = 5 / 8.
А теперь предположим, что событие А — это вынимание из мешка
хотя бы какого-то шара {либо красного, либо белого). Это есть достовер-
достоверное событие, поскольку в любом из испытаний будет вынут либо крас-
красный, либо белый шар; значит, Р{А) = 1. В связи с этим обратим внима-
внимание на то, что 3/8+5/8=1. Это можно выразить словами:
Вероятность вынуть красный шар +
+ Вероятность вынуть белый шар =
= Вероятность вынуть хотя бы какой-то шар	E)
Заметим, что результат E) соответствует результату D). Ведь вероят-
вероятность вынуть белый шар — это вероятность не вынуть красный. Соот-
Соответственно, вероятность вынуть красный шар — это вероятность не
вынуть белый.
Пример с путевкой в санаторий, по поводу которой пришлось тянуть
жребий, сводится, по сути дела, к модели вынимания шара из мешка.
Итак, есть одна путевка и пять человек, желающих ее получить. Можно
свернуть в трубочку и положить в мешок пять бумажек, на одной из
которых поставлен плюс, а на остальных минус. Какова вероятность
вынуть наугад из мешка бумажку с плюсом? Испытания заключаются
в данном случае в произвольном вынимании бумажки из мешка. После
каждого испытания вынутая бумажка возвращается в мешок, и бумаж-
бумажки внутри мешка хорошо перемешиваются. Полное число равновероят-
равновероятных исходов в этих испытаниях п = 5. Интересующее нас событие —
вынимание бумажки с плюсом. Для него есть лишь один благоприят-
благоприятный исход {т = 1), поскольку из пяти бумажек в мешке только на од-
одной стоит плюс. Следовательно, Р(А) = 1/5. Понятно, что вероятность
не вынуть из мешка бумажку с плюсом: Р(А) = 4/5 .
Ну, а если есть три путевки на восемь человек? Тогда в мешок надо
положить восемь бумажек — три с плюсом и пять с минусом. Теперь
вероятность вынуть из мешка бумажку с плюсом будет равна 3/8.
123

Произвольный выбор определенного сочетания. Предположим, что есть
шесть человек и надо из них произвольно выбрать четверых для работы
в некоторой комиссии. Среди шести человек четверо являются докто-
докторами наук. Какова вероятность того, что при произвольном выборе все
четыре отобранных кандидата в комиссию окажутся докторами наук?
Испытания заключаются в произвольных выборах четверых из шести.
Полное число равновероятных исходов равно, в данном случае числу
различных выборок четырех из шести: п = С? = 15. Среди всех этих
исходов (выборок) есть только один, когда кажутся выбранными четы-
четыре наших доктора. Во всех остальных четырнадцати выборках будут
присутствовать один или два «недоктора». Чтобы убедиться в этом,
мысленно построим докторов и «недокторов» в какой-нибудь ряд. На-
Например, поставим слева четырех докторов, а справа двоих «недокторов»
(перестановки докторов между собой или «недокторов» между собой
роли не играют). На рис. 1 в таблице 19 показаны все 15 сочетаний (вы-
(выборок), где возможные четверки кандидатов в члены комиссии условно
обозначены крестиками. Легко видеть, что есть только одно сочетание,
для которого вся четверка — доктора наук. Итак, т = 1 и, следователь-
следовательно, Р(Л) = 1/С64=1/15.
Шарик на доске Гальтона. Более интересен пример с шариком на
доске Гальтона. Испытания состоят в том, что на верхний штырек ро-
роняется шарик, и рассматривается его движение от штырька к штырь-
штырьку, заканчивающееся попаданием в ту или иную ловушку. Мы рассмат-
рассматриваем доску Гальтона с семью ловушками: А, Б, В, Г, Д Д Ж. Она
изображена на рис. 2 в таблице 19. Там же отмечены числа равноверо-
равновероятных исходов, когда шарик оказывается в той или иной ловушке. Эти
числа равны, соответственно, 1, 6, 15, 20, 15, 6, 1. Напомним, что есть
только один способ попасть шарику в ловушку А, а также в ловушку Ж,
шесть способов попасть в ловушку Б и столько же способов попасть в
ловушку Д 15 способов попасть в ловушку В и столько же способов
попасть в ловушку Д 20 способов попасть в ловушку/7. Полное число
исходов (полное число способов попасть хотя бы в какую-нибудь ло-
ловушку) равно 1 + 6 + 15 +20+ 15 + 6 + 1 = 64. Все эти исходы равнове-
равновероятны, поскольку в каждом испытании шарик испытывает шесть столк-
столкновений со штырьками и при каждом столкновении он с равной
вероятностью отскакивает влево или вправо. Итак, п = 64.
Чему равна вероятность попадания шарика, скажем в ловушку Д?
Из полного числа равновероятных исходов п = 64 благоприятными
будут т = 15 исходов. Значит, искомая вероятность (ее имеет смысл
обозначить как Рц) есть Рд = 15/64.
124

Таблица 19. Классическое определение вероятности
j Доктора j
i наук i
jixixixixl! l
II lxixlxl;xi
II I
jlxixixl
iixixixi l; ixi
II ixixixi; ixi
II ixi Ixiixixi
jixixi ixiixi I
llxixi ixi; ixi
Hxixi I iixixi
;l ixixi ijxixi
I ixi ixixii ixi
; ixi ixi iixixi
Рис.1
Рис.2
Рис.3
A
i|x
2|
3|
4|X
5|X
6|
7|X
8 |X
9|
10 |X
11 |X
12 |X
13 |
14 |X
15 |X
A
Б
X
X
X
X
X
X
X
X
X
X
Б
Б
X
X
X
X
X
X
X
X
X
X
Б
Б
X
X
X
X
X
X
X
X
X
X
Б
Б
X
X
X
X
X
X
X
X
X
X
Б
Б
х
х
х
х
х
х
х
х
х
х
Б
а)
А
1|х
2|
з|
4|
5|Х
6|х
7|Х
8|
91
10 |Х
111
12 |Х
13|
14 |Х
15 |
16 1
17 |Х
18 |Х
19|
20 |Х
А
Б
X
X
X
X
X
X
X
X
X
X
Б
Б
X
X
X
X
X
X
X
X
X
X
Б
Б
X
X
X
X
X
X
X
X
X
Б
Б
X
X
X
X
X
X
X
X
X
X
Б
Б
1
1
1
х|
1
1
х|
1
х|
1
х|
1
1
х|
х|
х|
1
х|
х|
х|
Б
б)
Рис.4
д
1|Х
2|
з|
4|Х
5|Х
б|
7|Х
8 |Х
9|
10 |Х
11 |Х
12 |Х
13 |
14 |Х
15 |Х
Д
Д
X
X
X
X
X
X
X
X
X
X
д
д
X
X
X
X
X
X
X
X
X
X
д
д
X
X
X
X
X
X
X
X
X
X
д
н
X
X
X
X
X
X
X
X
X
X
н
н
1
1
х|
1
х|
х|
1
х|
х|
1
х|
х|
х|
х|
х|
н
125

Можно подсчитать вероятности для попадания шарика в другие ловуш-
ловушки: РА, РБ, Рв, Рг, РЕ, Рж. Числа благоприятных событий (числа т) будут
равны, соответственно, 1, 6, 15, 20, 6, 1. Поэтому РА= 1/64, РБ=6/64,
Рв=15/64, Рг= 20 /64, РЕ=6/24, Рж= 1 /64. Нетрудно видеть, что
РА+РБ+РВ+РГ+РД+РЕ+РЖ =
= 1/64 + 6/64 + 15/64 + 20/64 + 15/64 + 6/64 + 1/64 =
= A + 6+ 15+ 20+ 15 + 6+ 1)/64 = 64/64 = 1.	F)
Таким образом, вероятность попадания шарика хотя бы в какую-нибудь
ловушку (или в А, или в Д или в Д или в Т7, или в Д или в Д или в Ж)
равна 1. Это естественно, поскольку попадание хотя бы в какую-нибудь
ловушку происходит наверняка — это есть достоверное событие. А веро-
вероятность достоверного события должна равняться единице.
Чему равна вероятность попадания шарика либо в ловушку Д либо
в ловушку Р. Из полного числа равновероятных исходов п = 64 благо-
благоприятными будут все исходы с попаданием шарика в ловушку Д (таких
исходов 15) и все исходы с попаданием в ловушку Г (их 20); значит,
число благоприятных исходов в данном случае: т = 15 + 20 = 35. Иско-
Искомая вероятность есть т / п = 35 / 64.
6.2 Вероятность и шансы
в
§ 5.6 мы сравнивали шансы событий. Пора уточнить смысл этого
понятия. Если использовать классическое определение вероятности B),
согласно которому Р(А) = т / п, то можно сказать, что событие А имеет
т шансов из п. Получается, что равенство Р(А) = т / п можно трактовать
двояко:
1)	вероятность события А равна отношению т исходов к л,
2)	событие А имеет т шансов из п.
Так, имеется один шанс из двух получить одну из трех путевок при
наличии еще пяти желающих. Имеются три шанса из восьми вынуть
красный шар из мешка, в котором находятся 3 красных и 5 белых ша-
шаров. А вот вынуть белый шар есть пять шансов из восьми. Имеются 15 шан-
шансов из 64 попадания шарика в ловушку Дна доске Гальтона. Напомним
в этой связи высказывание Огюстена Курно, взятое нами в качестве
одного из эпиграфов к данной теме. О достоверном событии принято
говорить, что оно имеет сто шансов из ста, а о невозможном событии
говорят просто: у него нет шансов (или: его шансы равны нулю).
126

Впрочем в США часто пользуются иной трактовкой слова «шансы».
Если Р(А) = т / п, то говорят, что шансы в пользу события А равны т
к п — т. При этом шансы в пользу события А равны п — т к т. Так,
шансы вынуть красный шар из мешка, в котором находятся 3 красных
и 5 белых шаров, равны трем к пяти. А вот шансы вынуть из мешка
белый шар равны пяти к трем. Шансы попасть шарику в ловушку Дна
доске Гальтона равны пятнадцати к сорока девяти (ведь 64 - 15 = 49).
Вместо «трем к пяти», «пятнадцати к сорока девяти» и тому подобного,
говорят также «три против пяти», «пятнадцать против сорока девяти».
Что касается достоверных и невозможных событий, то они при подоб-
подобных трактовках понятия «шансы события» просто не рассматриваются.
Существование различных трактовок понятия «шансы события» не
должно нас смущать. Дело в том, что в дальнейшем мы будем пользо-
пользоваться практически исключительно понятием вероятность события.
Если же иногда будут упомянуты шансы, то их следует понимать
в контексте «данное событие имеет т шансов из п».
6.3 Для всякого ли события с неоднозначным исходом
МОЖНО ПОДСЧИТАТЬ ВЕРОЯТНОСТЬ?
^Достаточно широко бытует мнение, что вполне можно говорить о ве-
вероятности всякого события с неоднозначным исходом и можно хотя бы
приблизительно подсчитать (оценить) вероятность этого события. Мно-
Многие готовы всерьез обсуждать, например, такие вопросы. Какова веро-
вероятность того, что в будущем году будет исключительно холодное (или,
напротив, исключительно жаркое) лето? Какова вероятность научиться
излечивать СПИД, например, в ближайшие два года? Какова вероят-
вероятность столкновения Земли с огромным кометным ядром? Какова веро-
вероятность предотвращения всемирной атомной катастрофы? Это вопросы
глобального плана. Значительно больше задается вопросов частного
характера. Какова вероятность того, что авиалайнер, на котором пред-
предстоит лететь, не разобьется? Какова вероятность того, что в мое отсут-
отсутствие никто не взломает мою квартиру? Какова вероятность не заболеть
после обеда в общепите? Какова вероятность получить на предстоящем
экзамене отличную оценку? Какова вероятность, что мой должник вер-
вернет мне в срок долг? И так далее, и так далее.
Наверное, на многие подобные вопросы (особенно вопросы частно-
частного характера) можно приближенно ответить, используя, в частности,
127

накопленный житейский опыт и практику прежних случаев. Однако
речь сейчас идет не о качественных оценках, являющихся в значитель-
значительной мере субъективными, а об объективном математическом подсчете
вероятности, рассматриваемой как строгое математическое понятие.
В § 1.7 мы говорили о разных типах событий с неоднозначным исхо-
исходом — «хороших» случайных событиях и «дурных» случайных событи-
событиях (термины условные). «Хорошие» случайные события — это события,
исходы которых реализуются в так называемых однородных испытаниях,
т. е. испытаниях, допускающих многократное повторение без изменения
условий испытаний. «Дурные» случайные события реализуются в испыта-
испытаниях, которые нельзя повторить несколько раз или возможно повторить,
но без сохранения неизменных условий испытаний. Строгий объективный
подсчет вероятности можно выполнить для «хорошего» случайного со-
события, но нельзя выполнить для «дурного» случайного события.
Примерами однородных испытаний являются подбрасывания монетки
или кубика. Очевидно, что как монетку, так и кубик можно подбрасы-
подбрасывать сколько угодно раз при неизменных условиях подбрасывания.
Шарик можно ронять на верхний штырек доски Гальтона сколько угодно
раз. В разных случаях движение шарика по доске к ловушке оказывает-
оказывается, вообще говоря, различным, но условия этого движения остаются во
всех случаях неизменными. Понятно, что и тут мы имеем дело с одно-
однородными испытаниями. Различные ситуации, когда приходится тянуть
жребий, можно представлять моделью, в которой вынимают наугад шар
из мешка. Именно для того, чтобы испытания в таких случаях были
однородными, требуется всякий раз после очередного испытания воз-
возвращать вынутый шар обратно в мешок и хорошо перемешивать шары
внутри мешка. Кстати, в различных карточных играх вынутую карту
возвращают в колоду карт, которую затем старательно тасуют. Это так-
также объясняется требованием однородности испытаний.
А вот некоторые примеры «дурных» случайных событий (дурных по
условной терминологии, но не обязательно по своей сути). Ученик по-
получил на экзамене оценку «удовлетворительно». Спортсмен завоевал на
соревнованиях серебряную медаль. Стрелок попал в десятку. Грибнику
посчастливилось найти в лесу с десяток белых грибов. После обеда в сто-
столовой человек получил серьезное расстройство желудка. Во всех таких
случаях многократные испытания или вообще невозможны, или осу-
осуществляются без сохранения условий испытаний неизменными. Конечно,
можно попросить ученика несколько раз повторить сдачу экзамена. Но
по мере повторения таких испытаний наш ученик от раза к разу будет
все лучше разбираться в предмете. Спортсмен на соревнованиях может
128

многократно повторить забег, заплыв, прыжок, бросок. Но и эти испы-
испытания, строго говоря, нельзя считать однородными, поскольку по мере
их повторения наш спортсмен будет становиться более натренирован-
натренированным или, напротив, утомится и расслабится. То же можно сказать о стрел-
стрелке, которого заставляют много раз производить выстрел по мишени.
А как устроить многократные испытания в случае с грибником? Как
подсчитать нашему грибнику вероятность найти в данном лесу в дан-
данное время года не менее десяти белых грибов? По-видимому, нет смыс-
смысла предлагать грибнику пройтись по лесу несколько раз. Срезанные
грибы назад в траву не возвращаются, так что предлагаемые испытания
не будут однородными. В ситуации со столовой будем, для простоты,
рассматривать только, скажем, молочные блюда. Можно попросить по-
посетителя столовой многократно (в течение многих дней) отведывать мо-
молочные блюда в данной столовой. Однако сохранить неизменными ус-
условия испытаний не удастся, поскольку может меняться качество блюд,
степень свежести продукта, уровень гигиенического обслуживания и т. д.
Одним словом, раз на раз не приходится. К тому же, получив однажды
серьезное расстройство желудка, наш посетитель столовой, скорее все-
всего, прекратит дальнейшие испытания.
Итак, мы приходим к заключению, что во всех отмеченных ситуаци-
ситуациях не удается осуществить однородные испытания. Более того, для этих
ситуаций нельзя указать равновероятные исходы испытаний. Допустим,
мы хотим подсчитать вероятность получения данным учеником оценки
«удовлетворительно» на экзамене. Число возможных исходов п = 4: по-
получил «отлично», «хорошо», «удовлетворительно», «неудовлетворитель-
«неудовлетворительно». Но можно ли эти исходы считать равновероятными! Если бы это
было так, то искомая вероятность заведомо равнялась бы 1 / 4. В приме-
примере со спортсменом можно говорить тоже о четырех исходах (без медали,
бронзовая медаль, серебряная медаль, золотая медаль); их тоже нельзя
считать равновероятными. Нельзя говорить о каких-либо равновероят-
равновероятных исходах и в ситуациях со стрелком, с грибником, с посетителем
столовой.
Все это означает, что нельзя воспользоваться классическим определе-
определением вероятности при попытках ответить на вопросы, подобные следую-
следующим. Какова вероятность, что данный ученик получит на экзамене та-
такую-то оценку? Какова вероятность, что данный спортсмен завоюет на
соревнованиях такую-то медаль? Какова вероятность, что данный гриб-
грибник найдет в лесу такое-то количество белых грибов? Какова вероят-
вероятность, что данный стрелок выстрелит в десятку? Какова вероятность, что
данный человек, посетив данную столовую, не получит расстройства
129

желудка? Все подобные случайные события относятся к «дурным». Для
них нельзя выполнить строгий и объективный подсчет вероятности.
Но, может быть, для них можно рассматривать не строгую, а ка-
какую-то «приблизительную» вероятность? Ее не надо подсчитывать че-
через отношение благоприятных исходов ко всем равновероятным исхо-
исходам в однородных испытаниях, а надо как-то оценить или, как говорят,
прикинуть. Ведь может же быть какая-то уверенность в том, что дан-
данный ученик больше «троечки», скорее всего, не заработает на экзамене.
Что данный спортсмен, обладатель многих призов, вполне может заво-
завоевать серебряную медаль и имеет неплохие шансы получить даже золо-
золотую медаль. Что один стрелок вряд ли попадет в десятку, тогда как
другому удастся это сделать почти наверняка. Что опытному грибнику
вероятнее отыскать в лесу с десяток белых грибов, нежели человеку,
который редко ходит в лес по грибы. Что в данной столовой посетите-
посетители, как правило, всегда довольны, тогда как соседняя столовая пользу-
пользуется дурной славой.
Существуют две разных позиции в вопросе интерпретации и исполь-
использования вероятностных представлений. Наиболее популярна среди ма-
математиков так называемая объективистская позиция — когда понятие
вероятности применяют только к случайным событиям, исходы кото-
которых допускают многократное повторение без изменения условий испы-
испытаний. Как раз такие события мы и назвали «хорошими» случайными
событиями. Сторонники такой позиции (назовем их объективистами)
интересуются вероятностями, связанными с бросанием монет и куби-
кубиков, выниманием шаров из мешка, массовым производством каких-
либо изделий и вообще с ситуациями, допускающими заведомо равно-
равновероятные исходы. Объективистов не интересуют всевозможные «дурные»
случайные события, поскольку здесь вероятностные оценки не отлича-
отличаются математической строгостью. В частности, их не интересуют уни-
уникальные события. Объективисты оставляют в стороне большую группу
задач как неподходящих для исследования в рамках теории вероятнос-
вероятностей, коль скоро в этих задачах не удается составить отношения благо-
благоприятных исходов к некоей совокупности равновероятных исходов.
Другой точки зрения придерживаются сторонники так называемой
персоналистской позиции (назовем их персоналистами). Они рассматри-
рассматривают вероятность не только как меру достоверности события, но и как
меру личного доверия к тем или иным утверждениям, касающимся како-
какого-либо случайного события. Персоналисты готовы применять теорию
вероятностей не только ко всем задачам, рассматриваемым объективис-
объективистами, но и ко многим другим и, в частности, к уникальным событиям.
В отличие от объективистов, персоналисты готовы обсуждать и как-то
130

оценивать вероятности различных «дурных» случайных событий. Мож-
Можно сказать, что персоналисты мыслят шире, тогда как объективисты
мыслят строже. По-видимому, одно другого стоит.
Мы будем исходить в первую очередь из объективистской позиции и
использовать классическое и геометрическое определения вероятности,
а там, где это невозможно, частотное определение. Вместе с тем мы не
станем отметать подходы персоналистов и в определенные моменты
(например, при рассмотрении формул Байеса) будем использовать так-
также и эти подходы.
6.4 Тренировочные задачи с использованием
классического определения вероятности
6.4.1. Поиск нужной книги. Рассеянный человек записал на полях од-
одной из шести своих книг адрес своего знакомого, но не потрудился за-
запомнить ту книгу. Когда ему понадобился адрес знакомого, он решил
взять наугад четыре книги и попробовать найти адрес в них. Какова ве-
вероятность того, что в одной из выбранных наугад книг отыщется адрес?
Задача несложная. Число способов, какими можно выбрать четыре
книги из шести, есть Cl = 15. Следовательно, п = 15. Надо сообразить,
чему равно число благоприятных исходов т, т. е. найти, в скольких
сочетаниях из пятнадцати может находиться книга с адресом. В каждом
из таких сочетаний одна из четырех книг может скрывать адрес. Ос-
Остальные три книги могут образовывать различные сочетания по три из
пяти книг, не содержащих адреса; таких сочетаний имеется С| = 10.
Это как раз и есть число благоприятных исходов т. На рис. 3, а в табли-
таблице 19 показаны крестиками все возможные выборки четырех из шести.
В каждой выборке (каждом сочетании) на первое место мы поставили
книгу с адресом; они образуют столбец Л. Остальные пять столбцов
(столбцы Б) — книги, в которых адреса нет. Наличие крестика означа-
означает, что соответствующая книга (с адресом или без него) в данном соче-
сочетании присутствует. Легко видеть, что крестики в столбце А имеются в
сочетаниях №№ 1, 4, 5, 7, 8, 10, 11, 12, 14, 15, т. е. в десяти сочетаниях.
Наглядно убеждаемся, что т = 10.
Итак, вероятность РD) найти адрес, выбирая наугад 4 книги из шести,
равна PD) = m/n = Ci /C64 =10/15 = 2/3.
Предположим теперь, что человек попробовал отыскать адрес в од-
одной из трех книг, наугад выбранных из шести книг. Теперь п = С| = 20.
131

Все эти сочетания (равновероятные исходы) представлены наглядно на
рис. 3, б в таблице 19. Как и на рис. 3, а, мы поставили на первое место
в каждом сочетании книгу с адресом. Легко видеть, что крестик есть на
первом месте в сочетаниях №№ 1, 5, 6, 7, 10, 12, 14, 17, 18, 20, т.е.
в десяти сочетаниях и, следовательно, m = 10. Можно было бы не изоб-
изображать сочетания на рисунке, а просто сообразить, что число т благо-
благоприятных исходов равно числу сочетаний по два из пяти книг, не со-
содержащих адреса: т = Cf = 10 .
Итак, вероятность Р(Ъ) найти адрес, выбирая наугад 3 книги из шести,
равна PC) = m/n = Ci /C\ =10/20 = 1/2.
Далее не составит особого труда сообразить, что вероятность РB)
найти адрес, выбирая наугад 2 книги из шести, равна РB) = С\ /С| =
= 5/15 = 1/3;
-	вероятность РE) найти адрес, выбирая наугад 5 книг из шести, равна
РE) = С64/С| =5/6;
-	вероятность РA) найти адрес, выбирая наугад одну книгу из шести,
равна 1/6.
Выпишем все полученные вероятности в ряд:
=1/6, РB)=1/3, РC)=1/2, РD)=2/3, РE)=5/6.
Приведем все эти дроби к общему знаменателю — знаменателю 6:
=1/6, РB)=2/6, РC)=3/6, />D)=4/6, РE)=5/6.
Бросается в глаза закономерность: везде знаменатель — полное чис-
число книг, а числитель равен всякий раз числу книг, выбираемых наугад.
Эта закономерность подводит нас к обобщению: вероятность найти
адрес, выбирая наугад г книг из s книг, равна г / s. Мы дадим прямое
доказательство этого утверждения в §9.1, воспользовавшись правилом
сложения вероятностей.
6.4.2. Выбор членов комиссии. В §6.1 мы рассматривали задачу, где
надо было из шести человек (четырех докторов наук и двух «недокто-
«недокторов») выбрать четверых в некоторую комиссию. Мы подсчитывали ве-
вероятность того, что при произвольном (случайном) отборе все отобран-
отобранные в комиссию люди окажутся докторами наук (обозначим эту
вероятность через Р{АД)). Напомним, как это делалось. Полное число
равновероятных исходов равно в данном случае числу способов, каки-
какими можно выбрать четверых из шести: п = С% =15. Все они показаны
на рис. 4 в таблице 19; на рисунке обозначены крестиками лица, кото-
которые в данном сочетании отобраны в комиссию. Все пятнадцать сочета-
сочетаний перенумерованы. В каждом сочетании первые четыре места мы решили
132

отвести докторам наук (Д), а пятое и шестое места — «недокторам» (Н).
Легко видеть, что есть только одно сочетание (оно стоит под № 1), при
котором все четыре крестика (все отобранные в комиссию лица) — док-
доктора наук. Значит, т = 1 и, следовательно,
А теперь подсчитаем, какова вероятность того, что при произволь-
произвольном отборе в четверке отобранных в комиссию окажутся три доктора
наук и один «недоктор» (обозначим вероятность через Р{ЪД)). Мы уже
знаем, что п = 15. Остается выяснить число благоприятных исходов т,
для данного случая. Казалось бы, это число равно числу способов, ка-
какими можно выбрать из четырех докторов троих (С%). Однако этого
мало. Вот мы мысленно отобрали трех докторов и тем самым заполни-
заполнили в комиссии три места. Одно место осталось вакантным — и на него
может попасть один из двух «недокторов» (либо из находящихся на
пятом месте в сочетаниях на рисунке 4, либо из находящихся на шес-
шестом месте). Число способов, какими можно выбрать одного из двоих,
равно С\, т. е., проще говоря, равно 2. Таким образом, в нашем случае
т = с\ • С\ = 8 . На рис. 4 все эти благоприятные исходы (благоприят-
(благоприятные выборки) имеют следующие номера: 2, 4, 5, 6, 7, 10, 11, 14. Итак,
Р{ЪД) = т/п = с1.С\/С% =8/15.
Теперь уже нетрудно подсчитать, какова вероятность того, что при
произвольном отборе в четверке отобранных окажутся два доктора наук
и два «недоктора» (вероятность РBД)). В данном случае т равно числу
выборок двух докторов из четырех (С\ = 6), помноженному на число
выборок двух «недокторов» из двух (С| = 1), т. е. т = С\ • С\ = 6 . Та-
Таким образом,
РBД) = С42.С22/С64=6/15.
А какова вероятность того, что в комиссии среди четырех ее членов
окажется только один доктор наук? Очевидно, эта вероятность равна
нулю, поскольку в этом случае трое членов комиссии должны были бы
являться «недокторами». А у нас «недокторов» всего двое.
Итак, возможны только три варианта: 1) в комиссию попадают все
четыре доктора наук (такой вариант имеет один исход), 2) в комиссию
попадают три доктора и один «недоктор» (такой вариант имеет 8 исхо-
исходов), 3) в комиссию попадают два доктора и два «недоктора» (такой
133

вариант имеет 6 исходов). Вероятность того, что в комиссию попадут
либо четыре, либо три, либо два доктора наук, есть, очевидно, вероятность
достоверного события, она должна равняться единице. Мы немедленно
убеждаемся в этом. Так как полное число благоприятных исходов есть в
данном случае сумма 1 + 8 + 6, то, следовательно, рассматриваемая ве-
вероятность равна A + 8 + 6) / 15 = 15 / 15 = 1.
Можно поставить вопрос о вероятности того, что в комиссии ока-
окажутся не менее трех докторов. В этом случае в комиссии должны быть
либо четыре, либо три доктора, и значит, т = 1 + 8 = 9. Искомая веро-
вероятность равна т / п = 9 / 15 = 3/5.
6.4.3. Поиск водителя с водительскими правами. В задаче 2 в § 5.1 мы
выясняли, сколькими способами можно рассадить в пятиместном авто-
автомобиле пять человек при условии, что занять место водителя могут только
трое из них. Мы установили, что число таких способов равно 3 * П4.
(Есть три варианта, когда за рулем оказываются последовательно те
трое, у которых имеются водительские права. И в каждом из трех вари-
вариантов надо разместить оставшихся четырех человек по четырем местам,
что равно числу перестановок четырех человек.)
Предположим, что наших пять человек совершенно произвольно рас-
рассаживают по пяти местам в автомобиле. Какова вероятность того, что
при этом на водительском месте окажется человек с водительскими пра-
правами ? Число благоприятных исходов мы только что выяснили: т = 3 • П4.
А полное число равновероятных исходов равно числу перестановок на-
наших пяти человек: п = П5. Таким образом, искомая вероятность равна
3 • П4 / П5 = 3 • 4! / 5! = 3 / 5.
Рассмотрим более интересную ситуацию. Имеется семиместный мик-
микроавтобус, и в него произвольно рассаживают в одном случае семерых
людей, в другом — шестерых людей, в третьем — пятерых, в четвер-
четвертом — четверых, в пятом — троих, в шестом случае — двоих людей.
Будем полагать, что в каждом из шести случаев только двое из рассажи-
рассаживающихся в микроавтобусе людей имеют водительские права. Найдем
для каждого случая вероятность того, что за рулем окажется человек с
правами. Соответствующие вероятности будем обозначать соответственно
через РG)9 РF)9 РE)9 РD)9 Р{3)9 РB)9 принимая во внимание количе-
количество людей, рассаживаемых в автобусе.
Вероятность Р{1) (когда в семиместный микроавтобус усаживаются
7 человек) можем определить по аналогии с рассмотренной ранее зада-
задачей, когда пять человек рассаживались в пятиместном автомобиле. Она
равна Р{1) = 2 • П6 / П7 = 2 • 6! / 7! = 2 / 7.
134

Найдем теперь вероятность РF). Полное число равновозможных спо-
способов рассадить 6 человек по семи местам равно числу способов выб-
выбрать 6 человек из семи (С7 ), помноженному на число перестановок
шести человек (П6): п = С7 • П6. При этом число благоприятных исхо-
исходов равно т — 2 • С| • П5 (любой из двух человек с правами оказывается
за рулем, и для каждого из этих двух вариантов надо учесть число выбо-
выборок оставшихся пяти человек из оставшихся шести мест, а также число
перестановок этих пяти человек). Таким образом,
Рассуждая аналогичным, образом, находим
РE)=2.С64-П4/С75-П5=2/7,
РD)=2.С63-П3/С74-П4=2/7,
РC)=2.С62.П2/С73.П3=2/7,
РB)=2.С61.П1/С72.П2=2/7.
Оказывается,
РA) = РF) = РE) = РD) = РC) = РB) = 2/7.
Это наводит на мысль, что, по-видимому, есть какой-то простой спо-
способ подсчета рассматриваемых вероятностей. Такой способ действительно
есть. Он основан на применении правила сложения вероятностей и бу-
будет рассмотрен в § 9.1.
6.5 Знаменитая ошибка Д'Аламбера и ее «близнецы»
]К1звестный французский математик и философ XVIII-ro столетия
Жан Д'Аламбер A717-1783), рассматривая задачу о двукратном подбра-
подбрасывании монеты (или о подбрасывании одновременно двух монет), по-
полагал, что вероятность выпадения в таком испытании и орла, и решки
равна 1/3. В действительности же вероятность такого события равна
1/2. Ошибка Д'Аламбера вызвала в свое время немало споров и стала в
определенном смысле знаменитой. Она весьма поучительна.
Д'Аламбер рассуждал следующим образом. Есть три возможных исхо-
исхода рассматриваемого испытания: 1) выпали два орла, 2) выпали орел и
решка, 3) выпали две решки. Полагая эти исходы равновероятными, Д'Алам-
Д'Аламбер заключал, что вероятность выпадения орла и решки равна 1/3.
135

Ошибка известного математика заключалась в предположении, что
упомянутые три исхода равновероятны. В действительности же это не
так. Обозначим выпадение орла буквой О, а решки — буквой Р. Тогда
равновероятные исходы можно кратко изобразить так:
ОО, ОР, РО, РР
Этих исходов четыре (п = 4). Из них благоприятными являются в на-
нашем случае два исхода: ОР и РО. Значит, т = 2. Отсюда немедленно
получаем, что вероятность выпадения орла и решки равна 2 / 4, т. е. 1/2.
Начиная знакомиться с теорией вероятностей, многие, как и некогда
Д'Аламбер, делают ошибку, полагая равновероятными исходы, которые
в действительности таковыми не являются. Приведем некоторые примеры.
Пример 1: производится трехкратное подбрасывание монеты (или под-
подбрасывание сразу трех монет). Тут возможны четыре исхода: 1) выпали
три орла, 2) выпали два орла и одна решка, 3) выпали один орел и две
решки, 4) выпали три решки. Повторяя ошибку Д'Аламбера, многие
полагают, что эти исходы равновероятны и отсюда заключают, что вы-
выпадение, например, двух орлов и одной решки имеет вероятность 1/4,
тогда как в действительности это событие имеет вероятность 3/8. В са-
самом деле, при трехкратном подбрасывании монеты возможны восемь
равновероятных исходов:
ООО, OOP, ОРО, РОО, ОРР, POP, РРО, РРР.
Из них благоприятными являются в данном случае три исхода: OOP,
ОРО и РОО, так что т / п = 3 / 8. Сравним неверные и верные значе-
значения вероятностей четырех рассматриваемых событий:
1) выпали три орла
2) выпали два орла и одна решка
3) выпали один орел и две решки
4) выпали три решки
1/4
1/4
1/4
1/4
1/8
3/8
3/8
1/8
Здесь левый столбец — вероятности, предлагаемые теми, кто неосоз-
неосознанно повторяет ошибку Д'Аламбера, а правый столбец — действитель-
действительные вероятности.
Пример 2: производится случайный отбор из шести человек (четырех
докторов наук и двух «недокторов») в комиссию, состоящую из четырех
членов. Тут возможны три исхода: 1) в комиссии оказались четыре док-
доктора, 2) в комиссии оказались три доктора и один «недоктор», 3) в ко-
комиссии оказались два доктора и два «недоктора». Какова вероятность
каждого из трех исходов? Не изучавшие теорию вероятностей обычно
склонны полагать, что все три возможных: исхода равновероятны; тем
136

самым они делают «ошибку Д'Аламбера». В § 6.4 мы вычисляли вероят-
вероятности рассматриваемых трех событий и убедились, что они отнюдь не
равновероятны. Выпишем таблицу для сравнения:
1)	в комиссию попали четыре доктора
2)	в комиссии три доктора и один «недоктор»
3)	в комиссии два доктора и два «недоктора»
1/3
1/3
1/3
1/15
8/15
2/5
Левый столбец — неверные значения вероятности, правый — действи-
действительные вероятности.
Пример 3: производится случайное разбиение шести человек {четырех
докторов наук и двух «недокторов») на две группы по три человека в каж-
каждой. Возможны два исхода: 1) в одной группе три доктора, в другой
один доктор и два «недоктора», 2) в каждой группе два доктора и один
«недоктор». Какова вероятность каждого из двух исходов? Приведем,
как и в предыдущих примерах, таблицу:
1)
2)
три
два
два
два
доктора
— один доктор,
«недоктора»
доктора,
доктора,
один «недоктор» —
один «недоктор»
1
1
/2
/2
2/5
3/5
Напоминаем: слева вероятности, полученные при ошибочном предполо-
предположении равновероятности исходов; справа — действительные вероятности.
Пример 4: производится случайное разбиение шести человек {четырех
докторов и двух «недокторов») на три группы по два человека в каждой.
Возможны два исхода 1) доктор и доктор, доктор и доктор, «недоктор»
и «недоктор»; 2) доктор и доктор, доктор и «недоктор», доктор и «недок-
«недоктор». Какова вероятность каждого из этих исходов? Приведем, как и в
предыдущих примерах, таблицу с неверными (слева) и действительны-
действительными (справа) вероятностями:
1) доктор + доктор, доктор + доктор,
+ «недоктор» + «недоктор»
2) доктор + доктор, доктор +
+ «недоктор», доктор + «недоктор»
1/2
1/2
1/5
4/5
Как найдены правильные значения вероятностей в примерах 3 и 4?
Как вообще действовать, чтобы избежать «ошибки Д'Аламбера»? — Для
этого следует предварительно рассмотреть для данного типа испытаний
пространство элементарных исходов. Проще всего можно познакомить-
познакомиться с этим понятием на примере таких однородных испытаний, как под-
подбрасывание монет или игральных кубиков.
137

6.6 Пространство элементарных исходов
для данного типа однородных испытаний
и подсчет вероятности события
11режде всего обратим внимание на то, что, как правило, то или
иное событие можно рассматривать как «набор» неких других событий.
«Набор» не в том смысле, что данное событие реализуется при условии
реализации всей совокупности событий из «набора», а в том смысле,
что оно реализуется всякий раз, когда происходит любое из событий
«набора». Так, событие «выпадение грани с четным числом очков при
подбрасывании кубика» есть «набор» трех событий: «выпадение гра-
грани 2», «выпадение грани 4», «выпадение грани 6». Всякий раз, как про-
происходит любое из трех событий, реализуется событие «выпадение грани
с четным числом очков». Рассадить, скажем, четырех человек за столом
можно числом способов, равным числу перестановок четырех, то есть
двадцатью четырьмя способами (П4 = 4! = 24). Значит, событие «четы-
«четырех человек как-то рассадили за столом» является «набором» двадцати
четырех событий, каждое из которых соответствует одной из переста-
перестановок четырех человек. Событие «составили комиссию из трех членов
посредством случайного выбора из семи человек» является «набором»
событий, количество которых равно числу выборок трех из семи:
Cj = 35 . Далее обратим внимание на то, что для всякого типа однород-
однородных испытаний можно указать различные совокупности событий, каж-
каждая из которых (каждая совокупность) исчерпывает все возможные в дан-
данных испытаниях исходы. (Заметим, что понятия «событие» и «исход» —
по сути дела, одно и то же.) Будем подбрасывать кубик и рассмотрим
следующие четыре варианта: 1) данные испытания имеют шесть воз-
возможных исходов: выпадение каждой из шести граней; 2) данные испы-
испытания имеют два возможных исхода: выпадение грани с четным числом
очков и выпадение грани с нечетным числом очков; 3) данные испыта-
испытания имеют четыре возможных исхода: выпадение грани с четным чис-
числом очков, выпадение единицы, выпадение тройки, выпадение пятер-
пятерки; 4) данные испытания имеют семь возможных исходов: выпадение
каждой из шести граней плюс выпадение грани с четным числом очков.
Сразу отметим, что четвертый вариант не годится. Дело в том, что
все возможные исходы должны быть несовместными. Несовместными
называют взаимоисключающие исходы (события)— когда появление
одного исхода в данном испытании исключает возможность появления дру-
другого исхода в том же испытании. В варианте же под номером 4 появление
138

в некотором испытании грани с четным числом очков отнюдь не исклю-
исключает появления в том же испытании ни грани с двойкой, ни грани с
четверкой, ни грани с шестеркой. Что касается трех первых вариантов,
то относительно них возражений нет. В каждом из них рассматривается
совокупность несовместных событий, исчерпывающая все возможные
исходы.
Вариант 3 рассматривает все возможные исходы, не предполагая их
равновероятности. Здесь уместно напомнить, что в рассмотренных в
§ 6.5 четырех примерах все возможные исходы тоже не были равнове-
равновероятными. В варианте 2 все возможные исходы равновероятны, но при
этом каждый из них можно реализовать за счет любого из других трех
исходов (тоже равновероятных). Так, выпадение грани с четным числом
очков реализуется при выпадении либо двойки, либо четверки, либо
шестерки. Особо отметим вариант 1 — здесь все возможные исходы
испытаний с бросанием кубика не только равновероятны, но, кроме
того, каждый из них нельзя рассматривать как «набор» каких-либо дру-
других исходов. Говорят, что шесть исходов, соответствующих выпадению
каждой из шести граней кубика, образуют пространство элементарных
исходов для испытаний, состоящих в бросании игрального кубика.
Вот мы и вышли на понятие элементарные исходы (для данного типа
однородных испытаний). Как следует из сделанных замечаний, эти ис-
исходы обладают тремя свойствами: 1) они несовместные, т. е. взаимоис-
взаимоисключающие, 2) они имеют равные вероятности, 3) каждый из этих ис-
исходов не может быть представлен как «набор» каких-либо других исходов
(смысл слова «набор» был пояснен в самом начале данного параграфа).
Здесь уместно вернуться к классическому определению вероятнос-
вероятности B) (см.§6.1). Упоминавшиеся в этом определении п равновозмож-
ных исходов как раз и образуют пространство элементарных исходов
для того или иного типа однородных испытаний. Поэтому можно сфор-
сформулировать следующий алгоритм подсчета вероятности Р{А) некоторо-
некоторого события А, реализуемого в рассматриваемых испытаниях:
-	надо определить пространство элементарных исходов для данного
типа испытаний (тем самым мы найдем число п);
-	надо найти в пространстве элементарных исходов все исходы, яв-
являющиеся благоприятными для события А, т. е. исходы, которые реали-
реализуют событие А (тем самым мы найдем число /и);
-	надо воспользоваться формулой B): Р(А) = т / п. Мы уже пользо-
пользовались данным алгоритмом в § 6.6, когда объясняли ошибку Д'Аламбе-
ра и когда рассматривали трехкратное подбрасывание монеты. Рассмот-
Рассмотрим теперь ряд более сложных примеров.
139

Пример 1: четырехкратное подбрасывание монеты (или одновремен-
одновременное подбрасывание четырех монет). В первом бросании выпадают либо
орел, либо решка. Во втором бросании снова возможны два равноверо-
равновероятных варианта (орел или решка) — как в том случае, когда в предыду-
предыдущем бросании выпал орел, так и в том случае, когда в предыдущем
бросании выпала решка. То же можно сказать о третьем и четвертом
бросаниях монеты. Все это хорошо видно на рис. 1 в таблице 20. По
результатам четырех бросаний выявляются 16 несовместных равнове-
равновероятных исходов, образующих пространство элементарных исходов для
четырехкратного подбрасывания монеты. Все они приведены на рис. 1
внутри пунктирного прямоугольника. Теперь мы можем сразу указать,
например, чему равна вероятность того, что в четырех бросаниях моне-
монеты выпадет равное количество орлов и решек. Из 16 элементарных ис-
исходов этому событию благоприятствуют исходы ООРР, ОРОР, ОРРО,
POOP, POPO, РРОО; следовательно, т = 6. Таким образом, искомая
вероятность равна т / п = 6 / 16 = 3/8. А чему равна вероятность того,
что при четырех бросаниях монеты выпадут три орла и одна решка?
В данном случае благоприятные исходы: ОРОО, РООО, ООРО, ОООР;
значит т = 4. Искомая вероятность: т / п = 4 / 16 = 1 / 4.
Пример 2: пятикратное подбрасывание монеты. Этот пример наглядно
иллюстрирует рис. 2 в таблице 20. Легко видеть, что пространство эле-
элементарных исходов образуют 32 исхода (они приведены на рисунке внут-
внутри пунктирного прямоугольника). Какова вероятность того, что при пя-
пятикратном бросании монеты орел выпадет только два раза? Благоприятные
исходы: ООРРР, ОРОРР, ОРРОР, ОРРРО, РООРР, РОРОР, РОРРО,
РРООР, РРОРО, РРРОО; значит, т = 10 и, следовательно, искомая ве-
вероятность 10/32, т. е. 5/ 16. Впрочем, найти т в данном случае можно
очень просто: это есть число выборок двух элементов из пяти: Cf.
Пример 3: двукратное подбрасывание кубика (или одновременное под-
подбрасывание двух кубиков). На рис. 3 в таблице 20 представлены в виде дву-
двузначных чисел 36 исходов, образующих пространство элементарных собы-
событий для данного типа испытаний. Первая цифра в каждом двузначном числе
(число десятков) — это количество очков, выпавшее при первом бросании
кубика, а вторая цифра в двузначном числе (число единиц) —количество
очков, выпавшее при втором бросании кубика. На рисунке обведены тон-
тонкими линиями благоприятные исходы для четырех событий:
-	событие А: выпадение пары одинаковых граней (легко видеть, что
число благоприятных исходов тА = 6);
-	событие Б: выпадение пары граней с суммой очков не более 5
(число благоприятных исходов тБ= 10);
140

Таблица 20. Пространство элементарных исходов
Рис.1
Б-
Рис.3
О
р
О
р
О
р
О
р
О
р
О
р
О
р
О
р
ю
!°
|о
10
!°
|о
ю
!°
|р
IP
!р
|р
IP
Ip
|р
IP
0
0
0
0
р
р
р
р
0
0
0
0
р
р
р
р
0
0
р
р
0
0
р
р
0
0
р
р
0
0
р
р
0
р
0
р
0
р
0
р
0
р
0
р
0
р
0
р
16
51 52 53/54
61 62
<63/6
64
А/
В	Г
xll	х12	х13	х14	х15	х16
х21	х22	х23	х24	х25	х26
х31	х32	хЗЗ	х34	х35	хЗб
х41	х42	х43	х44	х45	х46
х51	х52	х53	х54	х55	х56
х61	х62	хбЗ	х64	х65	хбб
х=	1, 2,	3, 4,	5, 6
Рис.4
Рис.5
Рис.2
0 0 0 01
О О О Р
О О Р О
О О Р Р
О Р О О
О Р О Р
О Р Р О
О Р Р Р
Р О О О
POOP
Р О Р О
Р О Р Р
Р Р О О
Р Р О Р
Р Р Р О
р р р р
0 0 0 0
О О О Р
О О Р О
О О Р Р
О Р О О
О Р О Р
О Р Р О
О Р Р Р
РО О О
POOP
Р О Р О
Р О Р Р
Р Р О О
Р Р О Р
Р Р Р О
р р р р
141

-	событие В: выпадение пары граней с суммой очков 9 {тв= 4);
-	событие Г: выпадение пары граней, из которых хотя бы одна име-
имела 5 очков (тг = 11).
Отсюда сразу находим соответствующие вероятности:
Р(Б) = тБ /п = 10/36 = 5/18;
Р(Г) = тг/п = 11/36.
Заметим кстати, что события Бя В (а также события Б я Г) являются
несовместными. А вот события А и Б (а также А я В, А я Г, В я Г)
несовместными назвать нельзя.
Какова вероятность того, что при подбрасывании двух кубиков выпадет
пара граней, для которой сумма очков является простым числом? Глядя на
рис. 3 в таблице 20, совсем нетрудно ответить на этот вопрос. Речь идет о
парах граней, представленных на рисунке следующими двузначными чис-
числами: 11 (поскольку 1 + 1 = 2), 12 я 21 (поскольку 1 + 2 = 3), 14, 41, 23 я 32
(поскольку 1+4 = 2 + 3 = 5), 16, 61, 25я 52 (поскольку 1+6 = 2 + 5 = 7),
56я 65 (поскольку 5 + 6=11). Как видим, всего имеется 15 благоприятных
исходов. Следовательно, искомая вероятность равна 15/36, т. е. 5/ 12.
Пример 4: трехкратное подбрасывание кубика. Из рис. 4 в таблице 20
видно, что для данных испытаний пространство элементарных исходов
состоит из 216 исходов {п = 216). Они представлены на рисунке в виде
трехзначных чисел; первая цифра в каждом числе (х= 1, 2, 3, 4, 5, 6) —
очки, выпавшие в первом бросании, вторая цифра — очки, выпавшие
во втором бросании, третья цифра — очки, выпавшие в третьем броса-
бросании. Какова, например, вероятность того, что при трех бросаниях вы-
выпадут две и только две грани с одинаковым числом очков? Вот благо-
благоприятные исходы cjc=1: 112, 113, 114, 115, 116, 121, 122, 131, 133, 141,
144, 151, 155, 161, 166. Таких исходов 15. Очевидно, что столько же
будет благоприятных исходов с х= 2, х= 3, х= 4, х= 5 я с х= 6. Зна-
Значит, полное число благоприятных исходов равно т = 15 * 6 = 90. Поэто-
Поэтому искомая вероятность равна т/л = 90/216 = 5/12.
Пример 5: случайные разбиения шести человек на две группы по трое
или на три группы по двое. Эти испытания мы рассматривали в § 6.5: см.
пример 3 и пример 4. Как и в § 6.5, будем полагать, что шесть чело-
человек — это четыре доктора наук и два «недоктора». На рис. 5 в табли-
таблице 20 показаны 15 элементарных исходов для данных испытаний (Д —
доктор наук, Н — недоктор).
142

Сначала рассмотрим разбиение на две подгруппы из трех человек.
В § 6.5 мы отмечали такие два варианта разбиения:
1)	три доктора в одной подгруппе; доктор и два «недоктора» в другой
подгруппе;
2)	в каждой подгруппе два доктора и один «недоктор».
Какова вероятность реализации первого варианта? Обращаемся к рис. 5
в таблице 20. Там разбиение на две подгруппы по три человека показано
прямоугольниками со сплошными сторонами. Легко видеть, что благо-
благоприятные исходы — это исходы с номерами 1, 3, 4, 5, 8, 9; значит, т = 6.
Отсюда следует, что искомая вероятность равна т / п = 6 / 15 = 2/5. По-
Поскольку пространство элементарных исходов состоит из исходов, бла-
благоприятных для реализации первого варианта, и исходов, благопри-
благоприятных для реализации второго варианта, то сразу находим вероятность
реализации второго варианта: A5 - 6) / 15 = 9 / 15 = 3 / 5. Этот резуль-
результат можно было бы получить также, воспользовавшись формулой C).
Разбиение на три подгруппы по два человека имеет два варианта:
1)	два доктора, два доктора, два «недоктора»;
2)	два доктора, доктор + «недоктор», доктор + «недоктор».
Разбиение на три подгруппы показано на рис. 5 в таблице 20 прямо-
прямоугольниками с пунктирными сторонами. Какова вероятность реализа-
реализации первого варианта? Глядя на рисунок, определяем номера благопри-
благоприятных исходов: 1, 3, 12. Таких исходов три. Значит, искомая вероятность
равна 3/15, т. е. 1/5. Отсюда сразу находим вероятность второго вари-
варианта: A5 - 3) / 15 = 12 / 15 = 4 / 5.
6.7 Одинаковы ли шансы выпадения 11 очков
И 12 ОЧКОВ ПРИ ТРЕХ БРОСАНИЯХ ИГРАЛЬНОЙ КОСТИ?
1 Лринято считать, что теория вероятностей зародилась в середине
XVII века и что существенную роль в ее рождении сыграли известные
французские ученые Влез Паскаль A623-1662) и Пьер Ферма A601-1665)
и известный нидерландский ученый Христиан Гюйгенс A629-1695). От-
Отметим знаменитую переписку в 1654 году между Паскалем и Ферма, в
которой ученые обсудили многие проблемы математики случайного и
разобрали ряд задач по подсчету вероятности и, в частности, задач,
связанных с бросанием игральных костей (так назывались игральные ку-
кубики, вырезанные из кости).
143

Некоторые из этих задач возникли как ответ на вопросы, с которы-
которыми обращался к ученым придворный Людовика XIV кавалер де Мере
A607-1648), известный в те времена философ и литератор, а также
азартный игрок.
Вот один из вопросов кавалера де Мере. Одинаковы ли шансы выпаде-
выпадения 11 очков и 12очков при трех бросаниях игральной кости? Сам де Мере
полагал, что шансы (иначе говоря, вероятности) указанных событий
должны быть одинаковыми. Он рассуждал следующим образом. При
трех бросаниях игральной кости 11 очков можно получить шестью спо-
способами: 6-4-1, 6-3-2, 5-5-1, 5-4-2, 5-3-3, 4-4-3. И 12 очков мож-
можно получить тоже шестью способами: 6-5-1, 6-4-2, 6-3-3, 5-5-2, 5-
4-3, 4-4-4. А поскольку число исходов, при которых получаются в
сумме Пи 12 очков, одно и то же, то и вероятности получения Пи
12 очков должны быть равны. Однако, наблюдая долгое время за игрой
в кости, де Мере заметил, что те, кто ставит на 11 очков, выигрывают
чаще, чем те, кто ставит на 12 очков. За разъяснением этого парадокса
де Мере обратился к Паскалю. В действительности же никакого пара-
парадокса тут нет, поскольку в своих рассуждениях де Мере предполагал
равновероятность рассматривавшихся им исходов. А это неверно.
Нам нетрудно подсчитать вероятности получения 11 и 12 очков при
трехкратном подбрасывании кубика. Пространство элементарных ис-
исходов составляют 216 исходов (см. рис. 4 из таблицы 20); значит, п = 216.
Выделяем исходы, благоприятствующие выпадению 11 очков:
-	для комбинации 6-4-1: 641, 614, 461, 416, 164, 146 F исходов);
-	для комбинации 6-3-2: 632, 623, 362, 326, 263, 236 F исходов);
-	для комбинации 5-5-1: 551, 515, 155 C исхода);
-	для комбинации 5-4-2: 542, 524, 452, 425, 254, 245 F исходов);
-	для комбинации 5-3-3: 533, 353, 335 C исхода);
-	для комбинации 4-4-3: 443, 434, 344 C исхода).
Складываем благоприятствующие исходы: 6 + 6 + 3 + 6 + 3 + 3 + 3 = 27.
Таким образом, т = 27 и, следовательно, искомая вероятность равна
/и/л = 27/216= 1/8.
А теперь подсчитаем вероятность выпадения 12 очков. Выделяем бла-
благоприятные исходы:
-	для комбинации 6-5-1: 651, 615, 561, 516, 165, 156 F исходов);
-	для комбинации 6-4-2: 642, 624, 462, 426, 264, 246 F исходов);
-	для комбинации 6-3-3: 633, 363, 366 C исхода);
-	для комбинации 5-5-2: 552, 525, 255 C исхода);
-	для комбинации 5-4-3: 543, 534, 453, 435, 354, 345 F исходов);
-	для комбинации 4-4-4: 444 A исход).
144

Складываем благоприятные исходы: 6 + 6 + 3 + 3 + 3 + 6 + 1 = 25.
Таким образом, т = 25 и, следовательно, искомая вероятность равна
25/216.
Итак, вероятность выпадения 11 очков при трех бросаниях кости
оказывается немного больше вероятности выпадения 12 очков B7 / 216 >
> 25 / 216). Фактически кавалер де Мере повторил ошибку Д'Аламбера.
6.8 Геометрическое определение вероятности
Рассмотрим следующую ситуацию. Некий телевизионный канал ра-
работает 15 часов в сутки; из них 4 часа занимает реклама. Какова вероят-
вероятность того, что, случайно включив телевизор на данном канале, мы не
попадем на рекламу?
Решить эту вроде бы несложную задачу, применяя классическое опре-
определение вероятности, заведомо нельзя. Ведь в данном случае простран-
пространство элементарных исходов состоит из бесконечного числа исходов (каж-
(каждый исход соответствует включению телевизора наугад в тот или иной
момент времени в пределах времени работы канала). Тем не менее эта
задача в самом деле совсем несложная. Просто здесь не надо думать о
подсчете числа исходов, а надо сравнить промежуток времени, в преде-
пределах которого находятся благоприятные исходы (он равен 15ч-4ч =
= 11ч), со всем временем функционирования канала A5 ч). Искомая
вероятность есть отношение первого (благоприятного) промежутка вре-
времени ко всему времени; она равна 11/15. Так мы приходим к геомет-
геометрическому определению вероятности:
Вероятность некоторого случайного события равна отношению меры
области, благоприятствующей появлению данного события, к мере всей
области.
В рассмотренном выше примере «мерой области» являлась величина
промежутка времени. В других случаях в качестве «меры области» могут
выступать, например, длины, площади, объемы. Недаром данное опре-
определение вероятности называют геометрическим.
В частном случае «мерой области» может служить конечное число рав-
равновероятных несовместных исходов. Например, на рис. 3 в таблице 20
«мера всей области» — совокупность из 36 двузначных чисел (они разме-
размещены на рисунке в пределах квадрата), а, скажем, «мера области, благо-
благоприятствующей появлению события Б» — совокупность из 10 двузнач-
двузначных чисел (они размещены на рисунке в пределах прямоугольного
145

треугольника). Можно сказать, что геометрическое определение вероят-
вероятности является, по сути дела, обобщением классического определения на
случаи, когда число исходов бесконечное и подсчету не поддается.
Впервые подсчет вероятности не через подсчет числа исходов, а че-
через отношение площадей, выполнил в 1777 году известный француз-
французский естествоиспытатель Жорж: Бюффон A707-1788). Он известен прежде
всего как автор фундаментального труда «Естественная история» из 36 то-
томов. Ему же принадлежит честь фактического введения в математику
нового понятия, которое получило название «геометрическая вероят-
вероятность». Бюффон рассматривал игру «франк-карро» (в переводе с фран-
французского — «прямо в клетку»). В этой игре на пол, выложенный шести-
шестиугольными плитками, бросают монету, и один из игроков держит пари
за то, что монета ляжет целиком внутри одного из шестиугольников.
Второй игрок ставит за то, что монета ляжет, пересекая границу между
какими-либо шестиугольниками. Какова вероятность, что выиграет пер-
первый игрок? Чтобы найти эту вероятность, Бюффон предлагал нарисо-
нарисовать внутри шестиугольника ABCDEF, размеры которого соответствуют
размерам плитки на полу, второй шестиугольник abcdef так, чтобы его
стороны были параллельны сторонам первого шестиугольника и чтобы
расстояние между сторонами шестиугольников было равно радиусу мо-
монеты (см. рис. 1 в таблице 21). Первый игрок выигрывает, если центр
монеты попадает внутрь шестиугольника abcdef. Поэтому вероятность
его выигрыша равна отношению площади внутреннего шестиугольника
к площади внешнего.
А вот другой пример на применение геометрического определения
вероятности. На рис. 2 в таблице 21 на осях координат хну изображен
квадрат со стороной а. В квадрат вписан круг. Однородные испытания
состоят в том, что наугад выбираются точки с координатами х и у,
причем 0<х<ая0<у<а. Какова вероятность того, что наугад выб-
выбранная точка окажется внутри круга? Поскольку равновероятен выбор
любой точки в пределах квадрата, то искомая вероятность будет равна
отношению площади круга (па2 / 4) к площади квадрата {а2). Таким об-
образом, вероятность равна тг / 4.
В книге Ф. Мостеллера «Пятьдесят занимательных вероятностных
задач с решениями» (Пер. с англ. М: «Наука», 1971) приведена следую-
следующая занимательная задача, связанная с геометрическим определением
вероятности. Задача называется «Странное метро». Вот текст:
Мэреин кончает работу в случайное время между 15 и 17 часами. Его
мать и его невеста живут в противоположных частях города. Молодой
человек садится в первый подошедший к платформе поезд, идущий в
том или противоположном направлении, и обедает с той из женщин, к
146

Таблица 21. Геометрическое определение вероятности
Рис.1
Рис.2
У i
1
«г
0
ii
1/4
1/4
R/ )Я
Г
F
Jl/4
X
1
19.00
20.00
Рис.3
1/8
i/<
1/4;;
n
s
M P
\ / \W^
i
1/4
Рис.6
1/2
1/2
Рис.8
1/4:
м р
1/41
1/4
^c
N
1/4v |S М	Р
1/2
Рис.5
1/4
Рис.7
1/2
N
Е
1/4
Рис.9
147

которой приедет. Мать Мэреина жалуется на то, что он редко у нее
бывает, но юноша утверждает, что его шансы обедать с ней и с невес-
невестой равны. Мэрвин обедал с матерью всего два раза в течение послед-
последних двадцати рабочих дней. Как объяснить это явление?
На первый взгляд, ситуация кажется действительно странной. Осо-
Особенно, если считать, что поезда метро ходят аккуратно через строго
равные промежутки времени как в одном направлении (направлении к
матери Мэрвина), так и в другом направлении (направлении к невесте
Мэрвина). Впрочем, именно эта строгость в следовании поездов по рас-
расписанию всё как раз объясняет. Предположим, что в направлении к
невесте поезда останавливаются на несколько секунд у платформы, куда
приходит Мэрвин, в 15.00, 15.10, 15.20, 15.30, 15.40 и т. д. А поезда, сле-
следующие в противоположном направлении, останавливаются у этой плат-
платформы в 15.01, 15.11, 15.21, 15.31, 15.41 и т. д. Чтобы поехать к матери и
отобедать с ней, Мэрвин должен, приходя на платформу, попасть в
одноминутный интервал (от 15.00 до 15.01 или от 15.10 до 15.11, или от
15.20 до 15.21 и т. д.), а чтобы поехать к невесте, Мэрвин должен по-
появиться на платформе в пределах девятиминутного интервала A5.01 до
15.10 или от 15.11 до 15.20, или от 15.21 до 15.30 ит. д.). Вероятность
попасть случайно в девятиминутный интервал в 9 раз больше вероятно-
вероятности попасть в одноминутный интервал, поскольку мера области (интер-
(интервал времени), благоприятствующий появлению перед Мэрвином поезда
в направлении к невесте, в 9 раз больше меры области, благоприятству-
благоприятствующей появлению поезда в обратном направлении. Именно поэтому
Мэрвин чаще обедает у невесты, чем у родной матери.
6.9 Задача о встрече
Хорошим примером использования геометрического определения
вероятности для подсчета вероятности случайного события является за-
задача о встрече. Заметим, что это довольно известная задача; она помогает
в решении некоторых проблем, связанных с организацией производства.
Для нас важно, что эта задача позволяет продемонстрировать особенно-
особенности и возможности геометрического определения вероятности. Поэтому
рассмотрим ее для нескольких воображаемых ситуаций. В каждой уча-
участвуют два условных персонажа — юноша и девушка, которые договари-
договариваются о встрече в некотором известном им месте.
Ситуация 1. Юноша и девушка условились, что каждый приходит на
место встречи в любой (случайный) момент в течение часа. Скажем, от
148

19.00 до 20.00. Ждет там ровно четверть часа, а затем уходит. Спрашива-
Спрашивается: какова вероятность встречи в такой ситуации?
Обратимся к рис. 3 в таблице 21. Здесь х — момент прихода юноши,
а у — момент прихода девушки. Время здесь и далее будем измерять в
часах и примем момент времени 19.00 за нуль, а момент 20.00 — за
1 час. Элементарный исход — приход юноши в момент х и приход де-
девушки в момент у, причем 0<х<1и0<^<1. Иначе говоря, элемен-
элементарный исход — это некоторая точка внутри квадрата 01F1.
Пространство элементарных исходов — все точки в указанном квад-
квадрате. Найдем теперь область в пределах данного квадрата, которая бла-
благоприятствует встрече наших персонажей. Встреча состоится в любом
из следующих трех случаев:
1)	юноша и девушка пришли на место встречи одновременно: х = у;
2)	девушка пришла позже (у>х), но не позднее, чем на 1/4 часа после
прихода юноши: у - х < 1/4 (ведь, прождав 1/4 часа, юноша уйдет);
3)	юноша пришел позже девушки (х>у), но не более, чем на 1 / 4 часа:
х-у< 1/4.
Таким образом, область благоприятных исходов определяется соот-
соотношениями:
в первом случае -
х = у, 0<х<1, 0<з><1;	G)
во втором случае -
у>х, у-х<1/4, 0<х<1, 0<з><1;	(8)
в третьем случае -
х>у, х-у<1/4, 0<х<1, 0<з><1.	(9)
Из G) следует, что благоприятные исходы (точки х, у) находятся на
отрезке прямой OF (см. рис. 3). Рассматривая (8), преобразуем второе не-
неравенство: у < х+ 1 / 4. Теперь легко сообразить, что, согласно (8), благо-
благоприятные исходы находятся в пределах трапеции OABF. Рассматривая (9),
преобразуем второе неравенство. Нетрудно сообразить, что, согласно (9),
благоприятные исходы находятся в пределах трапеции OFDC.
Теперь можно воспользоваться геометрическим определением вероят-
вероятности. Надо найти отношение суммы площадей трапеций OABF и OFDC
(эта сумма является мерой области, благоприятствующей встрече) к пло-
площади квадрата 01F1 (эта площадь есть мера всей области). Мера всей обла-
области равна 1-1 = 1. Область, благоприятствующая встрече, на рисунке за-
заштрихована; ее площадь легко найти, вычтя из площади квадрата 01F1 сумму
площадей треугольников А1В и CD1: 1 - C / 4J = 1 - 9 / 16 = 7 / 16. Таким
образом, искомая вероятность есть G / 16): 1 = 7 / 16.
149

Ситуация 2. Девушка заявила, что, придя на встречу, она будет ждать
1/8 часа, а юноша пусть ждет 1/4 часа. На том и порешили. Какова
вероятность встречи в такой ситуации?
Теперь обратимся к рис. 4 в таблице 21 и рассмотрим случаи, обеспе-
обеспечивающие встречу:
-	девушка пришла позже юноши, но не позднее, чем на 1 / 4 часа
после его прихода (тут работают соотношения (8));
-	юноша пришел позже девушки, но теперь уже не позднее, чем на
1/8 часа после ее прихода:
у > х, х - у < 1 / 8, 0 < х < 1, 0 < у < 1.	A0)
Случай, когда юноша и девушка приходят на место встречи одновре-
одновременно (х = у), ничего нового нам не дает, так что в дальнейшем мы его
принимать во внимание не будем.
Определяемая соотношениями (8) и A0) область, благоприятствующая
встрече, заштрихована на рис. 4. Площадь этой области находим, вычтя из
площади квадрата 01F1 сумму площадей треугольников Л1В и CD1:
1 - C / 4J / 2 - G / 8J / 2 = 1 - 9 / 32 - 49 / 128 =
= 1-85/128 = 43/128.
Искомая вероятность есть D3 / 128) : 1 = 43 / 128.
Ситуация 3. Девушка заявила, что она вообще не хочет ждать. Она придет
на место встречи и, если никого не застанет, тут же повернется и уйдет.
Тогда юноша предложил увеличить время своего ожидания до 1 / 2 часа. На
том и порешили. Какова вероятность встречи в такой ситуации?
Эта ситуация представлена графически на рис. 5 из таблицы 21. Те-
Теперь встреча состоится, когда девушка придет позже юноши, но не позд-
позднее, чем на 1 / 2 часа после его прихода:
у>х, у-х<1/2, 0<х<1, 0<з><1.	A1)
Определяемая соотношениями A1) область, благоприятствующая встре-
встрече, заштрихована на рис. 5. Нетрудно найти площадь этой области:
1-A/2J /2-1/2 =1-5/8 = 3/ 8.
Искомая вероятность есть C/8): 1 = 3/8.
Ситуация 4. Девушка снова согласна ждать 1 /4часа, но предложила
уменьшить промежуток времени, в пределах которого она придет, на
1/4 часа (пусть это будет интервал времени от 19.00 до 19.45). А юноша
пусть приходит где-то от 19.00 до 20.00 (как и раньше) и ждет 1/4 часа.
На том и порешили. Какова вероятность встречи в такой ситуации?
150

Данная ситуация представлена на рис.6 в таблице 21. Теперь про-
пространство элементарных исходов находится в пределах прямоугольника
0SN1 @ < х < 1, 0 < j < 3 / 4); его площадь (мера всей области) равна
1-3/4 = 3/4. Встреча состоится в случаях:
-	девушка пришла позже, но не позднее, чем на 1 / 4 часа после при-
прихода юноши:
у>х, у-х<1/4, 0<х<1, 0<у<3;	A2)
-	юноша пришел позже, но не позднее, чем на 1 /4часа после при-
прихода девушки:
х>у, х-у<1/4, 0<х<1, 0<у<3.	A3)
Определяемая соотношениями A2) и A3) область благоприятствую-
благоприятствующая встрече, заштрихована на рис. 6. Площадь этой области находим,
вычитая из площади прямоугольника OSN1 площади треугольников ASM
и CN1: 3 / 4 - A / 2J / 2 - C / 4J / 2 = 3 / 4 - 13 / 32 = 11 / 32. Искомая
вероятность есть A1 / 32) : C / 4) = 11 / 24.
Ситуация 5. Юноша предложил немного изменить ситуацию 4: он,
как и девушка, тоже будет приходить на место встречи где-то между
19.00 и 19.45. Предложение было принято. Какова теперь вероятность
встречи?
Данная ситуация представлена на рис. 7 в таблице 21. Теперь про-
пространство элементарных исходов находится в пределах квадрата OSPE
@ < х < 3, 0 < у < 3 / 4); его площадь равна C / 4) • C / 4) = 9 / 16. Об-
Область, благоприятствующая встрече, определяется соотношениями:
у>х, у-х<1/2, 0<х<3/4, 0<у<3/4;	A4)
х>у, х-у<1/4, 0<jc<3/4, 0<j;<3/4.	A5)
Она заштрихована на рис. 7. Площадь этой области легко найти: 0 < х < 1,
9 / 16 — A / 2J = 9/16 — 1/4 = 5/ 16. Искомая вероятность есть отноше-
отношение этой площади к площади квадрата OSPE: E / 16): (9 / 16) = 5 / 9.
Ситуация 6. Юноша и девушка решили: пусть каждый приходит на
место встречи в любой момент времени между 19.00 и 20.00 и ждет ров-
ровно 1 / 2 часа. Какова вероятность встречи в такой ситуации?
Эта ситуация представлена на рис. 8 в таблице 21. Пространство эле-
элементарных исходов находится в пределах квадрата 01F1; его площадь
есть 1-1 = 1. Область, благоприятствующая встрече, определяется со-
соотношениями:
у>х, у-х<1/2, 0<х<1, 0<з><1;	A6)
х>у, х-у<1/2, 0<х<1, 0<j><1.	A7)
151

Она заштрихована на рис. 8. Ее площадь равна 1 - A / 2J = 3 / 4.
Искомая вероятность есть C / 4) : 1 = 3 / 4.
Ситуация 7. Конечно, увеличение времени ожидания повысило веро-
вероятность встречи. А если при этом уменьшить интервал времени прихо-
прихода? Юноша и девушка решили сделать интервал времени, в течение
которого каждый приходит на место встречи, равным 3/4 часа, а время
ожидания оставить равным 1/2 часа. Какова вероятность встречи в та-
такой ситуации?
Эта ситуация представлена на рис. 9 в таблице 21. Пространство эле-
элементарных исходов находится в пределах квадрата OSPE; его площадь
равна 9/ 16. Область, благоприятствующая встрече, определяется соот-
соотношениями:
у>х, у-х<1/2, 0<х<3/4, 0 < j; < 3 / 4;	A8)
х>у, х-у<1/2, 0<;с<3/4, 0<j<3/4.	A9)
Она заштрихована на рис. 9. Ее площадь равна 9 / 16 — A / 4J =1/2.
Искомая вероятность есть A / 2) : (9 / 16) = 8 / 9.
Сравним вероятность встречи Р для ситуаций 1, 5, 6, 7. Обозначим
через Т интервал времени, в течение которого оба партнера должны
посетить место встречи, а через т — время ожидания каждого партнера.
Мы можем составить следующую таблицу:
Ситуация 1
Ситуация 5
Ситуация 6
Ситуация 7
Т
1
3/4
1
3/4
т
1/4
1/4
1/2
1/2
Р
7/16
5/9
3/4
8/9
Из таблицы видно, что вероятность встречи растет по мере увеличения т
и по мере уменьшения Т. Нетрудно сообразить, что вероятность встре-
встречи станет равной единице, когда т и Покажутся равными.
ЗАДАНИЯ ПО ТЕМЕ 6
1.	Приведите примеры достоверных и невозможных событий.
2.	В мешке 10 красных, 5 белых и 4 синих шара. Вынимаем наугад один шар. Како-
Какова вероятность: 1) вынуть синий шар? 2) не вынуть красный шар? 3) не вынуть
белый шар? 4) вынуть либо красный, либо белый шар?
Ответы: 1) 4/19, 2) 9/19, 3) 14/19, 4) 15/19.
152

3.	Из восьми человек (трех докторов наук и пяти кандидатов наук) надо составить
комиссию из трех человек. Членов комиссии выбирают наугад. Какова вероят-
вероятность того, что в комиссию попадут: 1) три доктора наук? 2) два доктора наук и
один кандидат наук? 3) один доктор и два кандидата наук? 4) три кандидата наук?
Ответы: 1) 1/56, 2) 15/56, 3) 15/28, 4) 5/28.
4.	Юноша хочет выбрать в подарок своей девушке три книги. В магазине ему пред-
предложили на выбор девять книг: четыре книги по искусству и пять книг-детективов.
Юноша не знал, что девушка любит книги по искусству и терпеть не может детек-
детективов. Поэтому он выбрал три книги наугад. Какова вероятность того, что пода-
подарок девушке: 1) очень понравится (все три книги окажутся книгами по искусст-
искусству)? 2) вообще не понравится (все три книги окажутся детективами)? 3) все-таки
понравится (одна или две книги будут по искусству)?
Ответы: 1) 1/21, 2) 5/42, 3) 5/6.
5.	Монету подбрасывают три раза. Какова вероятность того, что орел выпадет: 1) не-
нечетное число раз? 2) четное число раз? 3) не выпадет ни разу?
Ответы: 1) 1/2, 2) 3/8, 3) 1/8.
6.	Те же вопросы, но относительно выпадения решки.
7.	Монету подбрасывают четыре раза. Какова вероятность того, что орел выпадет:
1) нечетное число раз? 2) четное число раз? 3) не менее двух раз?
Ответы: 1) 1/2, 2) 7/16, 3) 11/16.
8.	Монету подбрасывают четыре раза. Какова вероятность того, что решка выпа-
выпадет: 1) не менее трех раз? 2) не менее двух раз? 3) не менее одного раза? 4) во-
вообще не выпадет?
Ответы: 1) 5/16, 2) 11/16, 3) 15/16, 4) 1/16.
9.	Монету подбрасывают четыре раза. Какова вероятность того, что орел выпадет:
1) или один раз или вообще не выпадет? 2) или два раза, или три раза? 3) или
один раз, или два раза?
Ответы: 1) 5/16, 2) 5/8, 3) 5/8.
10.	Монету подбрасывают пять раз. Какова вероятность того, что: 1) орел выпадет
нечетное число раз, а решка четное число раз? 2) орел выпадет нечетное число
раз? 3) орел выпадет четное число раз? 4) орел выпадет четное число раз, а
решка нечетное число раз?
Ответы: 1) 15/32, 2) 1/2, 3) 15/32, 4) 15/32.
11.	Монету подбрасывают пять раз. Какова вероятность того, что орел выпадет: 1) не
менее трех раз? 2) не менее четырех раз? 3) либо один раз, либо два раза?
4) либо один раз, либо четыре раза? 5) либо два раза, либо 3 раза?
Ответы: 1) 1/2, 2) 3/16, 3) 15/32, 4) 5/16, 5) 5/8.
12.	Кубик подбрасывают два раза. Что более вероятно — выпадение в сумме 6 оч-
очков или выпадение 8 очков? выпадение 5 очков или 9 очков? выпадение 5 очков
или 6 очков? выпадение 8 очков или 9 очков? выпадение 5 очков или 8 очков?
выпадение 6 очков или 7 очков? выпадение 7 очков или 5 очков?
153

13.	Какова вероятность того, что при бросании двух кубиков выпадет пара очков,
различающихся в два раза?
Ответ: 1/6.
14.	Какова вероятность того, что при двукратном подбрасывании кубика выпадет
хотя бы один раз: 1) единица? 2) двойка? 3) тройка? 4) четверка? 5) пятерка?
6) шестерка?
Ответ: 11 / 36 во всех шести случаях.
15.	В каком случае больше и на сколько больше вероятность получить 6 очков — при
однократном или при двукратном подбрасывании кубика?
Ответ: При однократном подбрасывании больше на 1/36, чем при двукратном
подбрасывании.
16.	В каком случае больше и на сколько больше вероятность получить четное число
очков — при однократном или при двукратном подбрасывании кубика?
Ответ: В обоих случаях вероятность равна 1/2.
17.	Кубик подбрасывают два раза. Какова вероятность того, что сумма выпавших
очков окажется: 1) нечетным числом? 2) больше 4, но меньше 9? 3) числом,
делящимся без остатка на 3? 4) числом, делящимся без остатка на 4? 5) числом,
делящимся без остатка на 5? 6) числом, делящимся без остатка на 6?
Ответы: 1) 1/2, 2) 5/9, 3) 1/3, 4) 1/4, 5) 7/36, 6) 1/6.
18.	В каком случае больше и на сколько больше вероятность получить число очков,
которое делится без остатка на 3 — при однократном или при двукратном под-
подбрасывании кубика?
Ответ: В обоих случаях вероятность равна 1/3.
19.	Тот же вопрос, но в отношении числа, делящегося без остатка на 4.
Ответ: При двукратном подбрасывании больше на 1/12.
20.	Кубик подбрасывают два раза. Какова вероятность того, что произведение вы-
выпавших очков окажется: 1) равным 12? 2) числом, делящимся без остатка на 3?
3) числом, делящимся без остатка на 4? 4) числом, делящимся без остатка на 5?
5) числом, делящимся без остатка на 10?
Ответы: 1) 1/9, 2) 5/9, 3) 5/12, 4) 11/36, 5) 1/6.
21.	При бросании двух кубиков 9 очков в сумме может выпасть в двух случаях: 3-6 и
4-5. И 10 очков тоже может выпасть в двух случаях: 5-5 и 4-6. Можно ли сде-
сделать отсюда вывод, что вероятности выпадения 9 очков и 10 очков при однократ-
однократном бросании двух кубиков (или двукратном бросании одного кубика) равны?
22.	Кубик подбрасывают три раза. Какова вероятность, что выпадут три грани:
1) с одинаковым числом очков? 2) с разным числом очков? 3) с суммой оч-
очков, равной 9? 4) с суммой очков, равной 10? 5) с суммой очков, делящейся
без остатка на 5?
Ответы: 1) 1/36, 2) 5/9, 3) 25/216, 4) 1/8, 5) 43/216.
23.	Кубик подбрасывают три раза. Какова вероятность, что выпадет хотя бы одна
единица?
154

Указание: на рис. 4 в таблице 20 надо сначала учесть все исходы с х= 1, а затем
поискать единицу среди исходов с х= 1.
Ответ: 91/216.
24.	Какова вероятность выпадения при трех бросаниях кубика: 1) хотя бы одной двой-
двойки? 2) хотя бы одной тройки? 3) хотя бы одной четверки? 4) хотя бы одной пятер-
пятерки? 5) хотя бы одной шестерки?
Ответ: Все вероятности равны 91/216.
25.	Какова вероятность, что при трех бросаниях кубика единица вообще не выпа-
выпадет? Тот же вопрос для двойки, тройки и т. д.
Ответ: 125/216.
26.	Какая вероятность больше и на сколько: 1) заработать 5 очков при двух бросани-
бросаниях кубика или при трех бросаниях? 2) заработать 6 очков при двух бросаниях
кубика или трех бросаниях? 3) заработать 11 очков при двух бросаниях кубика
или трех бросаниях?
Ответы: 1) при двух бросаниях больше на 1/12, 2) при двух бросаниях больше
на 5/54, 3) при трех бросаниях больше на 5 /72.
27.	Двое условились придти на место встречи в любой момент от 19.00 до 19.30.
Какова вероятность встречи, если: 1) один, придя на место, ждет полчаса, а дру-
другой вообще не ждет? 2) один ждет 10 минут, а другой только 5 минут?
Ответы: 1) 1/2, 2) 31/72.
155

ЧАСТОТА И ВЕРОЯТНОСТЬ
Автор: Чем больше вероятность события, тем чаще
оно происходит.
Читатель: А справедливо ли обратное утвержде-
утверждение: чем чаще происходит событие, тем больше его
вероятность? Если это так, то, измеряя частоты по-
появления события, мы могли бы определить его ве-
вероятность.
Автор: Тут важно, чтобы наблюдалась статисти-
статистическая устойчивость частот появления события.
Вопросы и ответы
Наблюдения над статистической устойчивостью
частот многочисленных реальных явлений послужи-
послужили отправным пунктом для построения теории ве-
вероятностей как математической науки... Теорию
вероятностей можно определить как область мате-
математики, занимающуюся исследованием математи-
математических моделей случайных явлений, обладающих
свойством устойчивости частот.
Б. В. Гнеденко
156

Высшее назначение математики —
находить порядок в хаосе, который нас
окружает.
Норберт Винер
7.1 Статистическая устойчивость частот появления
случайного события
Те
ермин «статистическая устойчивость» упоминался в § 1.7. Там
отмечалось, что теория вероятностей предпочитает работать со случай-
случайными событиями, которые допускают выполнение большого числа од-
однородных испытаний и для которых точность предсказания исхода воз-
возрастает по мере увеличения количества испытаний. Там же прозвучала
фраза: «Принято говорить, что такие случайные события характеризу-
характеризуются статистической устойчивостью». Мы могли бы теперь заметить,
что статистической устойчивостью должны характеризоваться, в част-
частности, те случайные события, вероятность которых рассматривается на
основе классического определения вероятности. Например, события,
связанные с подбрасыванием монеты или кубика, выниманием наугад
шарика из мешка, движением шарика по доске Гальтона. Обращаясь к
подобным событиям, уточним содержание термина «статистическая ус-
устойчивость».
Прежде всего отметим, что понятие статистической устойчивости
относится к частотам появления рассматриваемого случайного события.
Предположим, что мы подбрасываем монету и интересуемся случай-
случайным событием, представляющим собой выпадение орла. Выполним
N бросаний монеты и подсчитаем, сколько раз выпал орел; обозначим
это число через Мх. Отношение v1 = Mi/ ^назовем частотой выпаде-
выпадения орла в данной серии из N бросаний. Мы можем снова выполнить
N бросаний монеты и снова подсчитать, сколько раз выпал орел. Полу-
Полученное число обозначим через М2. Частота выпадений орла в новой
серии из N бросаний будет равна v2 = М2 / N. Понятно, что, вообще
говоря, М1 ^ М2 и, значит, Vj ^ v2. Выполнив третью серию из N броса-
бросаний монеты, мы обнаружим Мъ исходов с выпадением орла; частота
выпадений орла равна v3 = Мъ / N. В четвертой серии из N бросаний
обнаружим М4 выпадений орла; частота выпадений орла равна у4 = М4 / N.
И так далее. Можно выполнить много серий из N бросаний монеты и
получить соответствующее количество значений частоты выпадений орла
157

в сериях: v1? v2, v3, v4, ..., vs (s — число серий). Все эти частоты будут
группироваться вблизи вероятности выпадения орла, т. е. вблизи 0,5.
Насколько вблизи? — Это зависит от числа бросаний N в серии. Чем
больше N9 тем ближе к 0,5 должны группироваться частоты выпадений
орла. Все это как раз и означает, что частоты обнаруживают статис-
статистическую устойчивость.
А теперь познакомимся с результатами конкретного эксперимента,
в котором приняли участие четыре человека. Три участника экспери-
эксперимента взяли по монете и начали ее подбрасывать. Каждый выполнил
15 серий испытаний, делая по 20 бросаний в серии GV=20). Количе-
Количества исходов с выпадением орла оказались в этих сериях такими (здесь
1, 2, 3 — номера участников эксперимента, а римскими числами обо-
обозначены номера серий):
1
2
3
I
11
12
8
II
8
9
10
III
7
13
12
IV
10
8
6
V
9
10
8
VI
12
10
9
VII
14
6
11
VIII
12
13
10
IX
10
12
8
X
13
15
10
XI
7
13
15
XII
7
9
8
XIII
13
6
10
XIV
7
10
12
XV
9
6
11
Четвертый участник эксперимента подбрасывал не монету, а играль-
игральный кубик и фиксировал выпадение граней с нечетным числом очков.
Он тоже выполнил 15 серий испытаний, делая по 20 бросаний в серии.
Количества исходов с выпадением нечетной грани оказались в этих се-
сериях такими:
I
10
II
14
III
11
IV
7
V
11
VI
7
VII
12
VIII
8
IX
6
X
12
XI
12
XII
5
XIII
8
XIV
11
XV
13
Разделив каждое из приведенных здесь чисел на 20, мы получим ча-
частоты появления интересующего нас события (выпадения орла или гра-
грани с нечетным числом очков) для соответствующих серий. Все эти час-
частоты представлены графически на рис. 1 в таблице 22. Здесь ромбами
показаны результаты, полученные 1-м участником эксперимента, квад-
квадратиками — результаты 2-го участника, незачерненными кружками —
результаты 3-го участника, зачерненными кружками — результаты 4-го
участника. Мы видим, что ромбы, квадратики, кружки оказались раз-
разбросанными на рисунке довольно беспорядочно, но примерно в равной
мере как по одну, так и по другую сторону пунктирной прямой, которая
158

Таблица 22. Статистическая устойчивость частот
0,7-
0,6—
0,5-
0,4-
0,3-
0,6-
0,5-
0,4-
0,6^
0,5-
0,4-
0,3-
0,2-
0 1
0,6-
0,5-
0,4-
0,3-
I
[
<r
H
11
i
1
•
<
J
ч.
L/ V
п
III
г 2I з
\a
г V\
II
III
\
/
Ч 2
<
3
J
}
IV
к
Ы
4
IV
4
Y
V
VI
H
VIIIVIII
5I 6
7
8
л /
VT VI
VII
\
Vllt
^^
5
6
7
8
IX
ж
9
V
A
IX
9
/
x
<i
XI
xr
10
11
XY XI
^^
10
11
\ J
xiiKin
12
jv——f
13
<> с
r
t
XII
? ^
XIII
12
13
Рис.1
XIV
H
XV|
Рис.2
1 [j
14
15
Рис.3
k>§ / m
л/
XIV
XV
Рис.4
14
15
159

соответствует вероятности 0,5. Именно такова вероятность выпадения
орла, а также грани с нечетным числом очков. Будем обозначать через
Мъ М1Ь Мш,...5 М^у количества интересующих нас исходов в той или
иной серий из N= 20 испытаний (подбрасываний). Подсчитаем теперь
частоты появления этих исходов, объединяя последовательно результа-
результаты, полученные для первых двух серий, затем для первых трех серий,
затем для первых четырех серий и так далее — вплоть до объединения
результатов, полученных для всех пятнадцати серий. Получаем для каж-
каждого участника эксперимента набор частот:
v2=(Ml+Mu)/BN);
v3=(Ml+Mu+Mm)/CN);
v4 = (M, +MU +МШ +Mjy)/DN);
v15=(Ml+Mu+Mm+... + Mx
Вот эти наборы частот для четырех участников эксперимента:
(*)
v2
v3
v4
V5
v6
v7
v8
v9
VlO
Vll
Vl2
Vl3
Vl4
Vl5
1-Й
участник
0,550
0,475
0,433
0,450
0,450
0,475
0,507
0,519
0,517
0,530
0,514
0,500
0,512
0,500
0,49667
2-й
участник
0,600
0,525
0,567
0,525
0,520
0,517
0,486
0,506
0,517
0,540
0,550
0,542
0,523
0,521
0,50667
3-й
участник
0,400
0,450
0,500
0,450
0,440
0,442
0,457
0,463
0,456
0,460
0,486
0,479
0,481
0,489
0,49333
4-й
участник
0,500
0,600
0,583
0,525
0,530
0,500
0,514
0,500
0,478
0,490
0,500
0,479
0,473
0,479
0,49000
160

Все эти наборы частот представлены графически на рис. 2 в табли-
таблице 22. Легко видеть, что по мере увеличения количества испытаний ча-
частота появления интересующего нас исхода все более приближается к
вероятности этого исхода. Так, на конкретном примере можно наблю-
наблюдать феномен статистической устойчивости частот.
Статистическая устойчивость частот должна проявляться тем силь-
сильнее, чем больше число испытаний. Каждый из первых трех участников
эксперимента подбросил монету 300 раз. Это все равно, как если бы
кто-то один подбросил монету 900 раз. Надо только сложить количе-
количества выпавших орлов, полученные каждым из трех участников:
149 + 152 + 148 = 449. Тогда для числа испытаний, равного 900 D5 се-
серий по 20 испытаний в серии), находим v45 = 449 / 900 = 0,49889.
Рассмотрим еще один конкретный эксперимент. Положим в мешок
три неотличимых наощупь шара — один черный и два белых. Однород-
Однородные испытания в данном случае состоят в том, что из мешка много раз
вынимается наугад один шар. Всякий раз вынутый шар возвращают
обратно в мешок, который затем встряхивают, чтобы как-то переме-
перемешать шары. При большом количестве испытаний данный эксперимент
оказывается весьма продолжительным. Нас будут интересовать исходы,
состоящие в появлении из мешка черного шара (вероятность такого
события равна 1/3).
В эксперименте участвовали трое человек. Каждый выполнил 15 се-
серий испытаний, вынимая шар из мешка 20 раз в серии (N= 20). Коли-
Количества исходов с появлением черного шара оказались такими:
1
2
3
I
7
5
12
II
8
9
4
III
4
6
7
IV
6
7
5
V
7
3
8
VI
10
5
8
VII
6
7
5
VIII
3
10
6
IX
6
7
4
X
9
3
5
XI
4
10
5
XII
11
8
7
XIII
7
11
8
XIV
5
4
7
XV
9
4
7
(здесь 1, 2, 3 — номера участников эксперимента, а римскими числами
обозначены номера серий). Разделив каждое из полученных в экспери-
эксперименте чисел на 20, получим частоту появления черного шара для соот-
соответствующей серии испытаний. Эти частоты представлены графически
на рис. 3 в таблице 22. Здесь ромбами показаны результаты 1-го участ-
участника, незачерненными кружками — 2-го участника, зачерненными круж-
кружками — 3-го участника. Пунктирная прямая соответствует вероятности
1/3. Ромбы и кружки беспорядочно распределились по обе стороны от
этой прямой (в равной мере как выше прямой, так и ниже ее). Как и в
161

опыте с бросанием монеты или кубика, подсчитываем частоты v1? v2, v3,
v4, ..., v15, определяемые соотношениями (*). Эти частоты представлены
графически на рис. 4 в таблице 22. Как можно видеть, феномен устой-
устойчивости частот проявился в данном опыте особенно ярко.
Подсчитанные по результатам рассмотренного опыта с шарами часто-
частоты v15 появления черного шара при числе испытаний, равном 300 A5 се-
серий по 20 испытаний в серии), имеют для разных участников значения:
-	для 1-го участника: v15 = 102 / 300 = 0,34000, е15 = 2,001%,
-	для 2-го участника: v15 = 99 / 300 = 0,33000, е15 = 0,999%,
-	для 3-го участника: v15 = 98 / 300 = 0,32667, е15 = 1,998%.
Здесь мы обозначили е15 = | е15 - Р \ / Р, где Р — вероятность 0,33333.
Складывая количества появлений черного шара, полученные тремя уча-
участниками, находим частоту появления интересующего нас исхода для
900 испытаний: v45 = A02 + 99 + 98) / 900 = 0,33222; 845 = 0,333%.
Отметим, что Бюффон, желая посмотреть, как сильно приближается
к вероятности 0,5 частота выпадения орла при увеличении числа испы-
испытаний, подбросил монету 4040 раз. В его опыте орел выпал 2048 раз.
Таким образом, частота выпадения орла оказалась равной 0,508 (на 1,6%
больше значения вероятности). Этот опыт был проделан в XVIII-м сто-
столетии. А в следующем столетии английский статистик К. Пирсон пере-
перекрыл достижение Бюффона: он подбросил монету 12 000 раз, а затем
24 000 раз. В первом случае орел выпал 6019 раз, частота выпадения орла
оказалась равной 0,5016 (на 0,32% больше значения вероятности). Во
втором случае орел выпал 12 012 раз, частота выпадения орла оказалась
равной 0,5005 (на 0,1% больше значения вероятности).
7.2 Диалог: Как объяснить феномен
статистической устойчивости частот?
. Хотелось бы понять, что же, все-таки, побуждало Бюф-
Бюффона, Пирсона и других ученых так настойчиво исследовать фено-
феномен статистической устойчивости частот. Наверное, не из-за празд-
праздного любопытства они подбрасывали монеты или кубики по несколько
тысяч раз?
Пвтор. Конечно, дело тут отнюдь не в праздном любопытстве. Надо
признать, что статистическая устойчивость частот в высшей степени
удивительна. Вполне понятно, что она должна была производить силь-
сильное впечатление на людей, склонных к размышлениям.
162

. Но что же удивительного в подбрасывании монеты? Мо-
Монета имеет одинаковые шансы выпасть орлом или решкой. Естественно,
что примерно в половине случаев она выпадет орлом, а в половине
случаев решкой.
Пвтор. Давайте немного порассуждаем. Вот мы подбросили монету
и она упала, допустим, орлом кверху. Мы подбрасываем монету во вто-
второй раз — и снова выпал орел. Подбрасываем монету в третий раз.
И снова орел. Подбрасываем в четвертый раз. Опять орел!
'Чипиинель. Что-то многовато орлов. Наверное, пора выпасть решке.
Пвтор. Что значит «многовато орлов»? Монета не может помнить,
какой стороной она падала. И если получилось так, что она выпала
орлом четыре раза подряд, то что же может помешать ей выпасть орлом
снова? При каждом очередном бросании монета по-прежнему имеет
одинаковые шансы выпасть как орлом, так и решкой. Можно сказать
также, что выпадение орла подряд четыре раза (или пять раз, или шесть
раз) отнюдь не увеличивают вероятности выпадения решки. Заметим, кста-
кстати, что многие этого не понимают. Многие ошибочно полагают, что,
если во время игры они несколько раз подряд оказались в проигрыше,
то в результате этого вероятность их выигрыша увеличивается. Кажет-
Кажется, что, если весь вечер не везло, все проиграл, то вот именно теперь
должно же, наконец, повезти! Напрасные надежды. Сколько ни проиг-
проигрывай, вероятность выигрыша не возрастает. Недаром существует по-
пословица: «играй, да не отыгрывайся».
nUuftfUfie*b. А ведь и в самом деле случайное выпадение орла не-
несколько раз подряд не увеличивает вероятности выпадения решки!
Пвтор. Так почему же Вы утверждали, что «пора выпасть решке»?
*Чи(*иипель. Потому лишь, что, как известно, при большом количестве
бросаний общее количество выпавших орлов должно уравновешиваться ко-
количеством выпавших решек. Так что, если выпали подряд четыре орла,
то для уравновешивания нужно, чтобы начали, наконец, появляться
решки.
Пвтор. Вы произнесли слова «должно уравновешиваться». А что зна-
значит «должно»? Почему, собственно говоря, исходы с выпадением орла
должны уравновешиваться исходами с выпадением решки?
*Чи(*иипель. Потому что те и другие исходы равновероятны.
Пвтор. Однако вспомним опять о том, что монета не ведает, какие
исходы уже состоялись и, разумеется, ей нет дела до того, какие исходы
«должны» в связи с этим состояться. Каждый конкретный исход случа-
случаен. На него ни в какой мере не влияют предыдущие исходы, и он, в свою
очередь, нисколько не влияет на последующие исходы. Мы имеем
163

совершенно беспорядочную, в строгом смысле хаотическую последова-
последовательность исходов. Вот потому-то удивительна сбалансированность тех
и других исходов, которая проявляется в наблюдаемой на практике ста-
статистической устойчивости частот. Как если бы кто-то или что-то «управ-
«управляли» беспорядком в картине исходов, обеспечивая при большом числе
испытаний удивительную сбалансированность.
^УсиЯсиЯе**. А может быть, проще предположить, что одни исходы
как-то влияют на другие? Может быть, монета каким-то образом «пом-
«помнит» о том, как она выпадала? Почему бы не сделать такое фантасти-
фантастическое предположение?
Пвтор. А как быть в таком случае с опытами, в которых мы наугад
вынимали шар из мешка? В случае с подбрасыванием монеты допустима
иллюзия, будто монета способна при подбрасывании как-то «управлять»
исходом испытания. Но в случае с шарами, лежащими в мешке, подоб-
подобная иллюзия принципиально исключена. Перед каждым испытанием шары
лежат себе спокойно в мешке, а мы (именно мы!) вслепую, наугад выби-
выбираем какой-то один шар. Что толку в том, что шары будут «помнить»,
сколько раз того или другого из них уже вынимали из мешка?
. Пожалуй, моя гипотеза о возможном взаимном влиянии
исходов испытаний принципиально не годится.
Пвтор. Да, она не проходит. Кстати, ее несостоятельность весьма
ярко видна на примере с движением шариков по доске Гальтона. Вот
мы посылаем первый шарик скакать по штырькам на этой доске. В ре-
результате шарик оказывается в какой-то ловушке. Затем мы посылаем
скакать по доске Гальтона второй шарик. Затем третий шарик, четвер-
четвертый, пятый и так далее. Каждый шарик никаким образом не может «знать»
какой путь по доске проделали другие шарики. В свою очередь, он не
в состоянии повлиять на характер движения по доске последующих ша-
шариков. Каждый шарик движется «сам по себе», или, можно сказать, по
воле случая. И тем не менее общая картина распределения достаточно
большого числа шариков по ловушкам оказывается вполне упорядочен-
упорядоченной. Как если бы шарики «сговорились» друг с другом. Постепенное
формирование упорядоченного распределения шариков по ловушкам по
мере увеличения числа шариков наглядно демонстрируют рисунки в табли-
таблице 23. Эти рисунки схематичны; они выражают идею и не должны рас-
рассматриваться как некие конкретные результаты, полученные в конкрет-
конкретном опыте. Мы видим, что поначалу, пока количество шариков,
проскакавших по доске Гальтона, невелико, распределения шариков по
ловушкам не обнаруживают закономерности. Но по мере увеличения
числа шариков начинает выявляться закономерность: распределение ша-
шариков по ловушкам делается симметричным и начинает соответствовать
164

Таблица 23. Хаос и порядок на доске Гальтона
1
ч >
Q
2
Ok
Ол
3
R
4
5
x
X
>^
ч^_>
8
ч„>
x;
CXXXXX)
CXXXXJQ
4»>
10
11
12
Но
13
14
15
16
165

вероятностям попадания шарика в ту или иную ловушку. Иными слова-
словами, начинает проявляться статистическая устойчивость частот попада-
попадания шариков в ловушки.
*Чипииъель. Однако как же, все-таки, объяснить феномен статисти-
статистической устойчивости частот? Как объяснить тот факт, что хаос случай-
случайных исходов приводит при большом количестве испытаний к вполне
упорядоченной картине?
Пвтор. Объяснение состоит в том, что хаос оказывается внутренне
конструктивным. Или, другими словами, беспорядок оказывается внут-
внутренне конструктивным.
g4tuftfufie*b. Как это понимать? Хаос — он и есть хаос, полный беспо-
беспорядок. О какой внутренней конструктивности тут можно говорить?
Пвтор. Это значит, что в самом хаосе, в самом беспорядке как бы
скрыт некий порядок и что этот порядок выявляется тем лучше, чем
хаос богаче, чем больше происходит случайных событий.
g4tuftfufie*b. Я помню, что в теме 2 был разговор о рождении порядка
из хаоса, которое совершается, когда происходит достаточно много слу-
случайных событий.
Пвтор. Да, мы тогда достаточно много поговорили о рождении по-
порядка из хаоса. Теперь можно сделать некоторое уточнение. Оно сос-
состоит в том, что правильнее говорить не о рождении порядка из хаоса, а
о существовании порядка в хаосе. Порядок в хаосе как раз и есть стати-
статистическая устойчивость, проявляющаяся при большом числе испытаний.
А теорию вероятностей можно рассматривать как науку о системах и
процессах, обладающих статистической устойчивостью. Иными слова-
словами, как науку о порядке в хаосе.
7.3 Как можно получить так называемую
«таблицу случайных чисел»?
v^pa3y отметим, что общепринятый термин «случайные числа» яв-
является сокращением термина «числа, генерированные случайным обра-
образом с вероятностью 1 / 10». Это есть сколь угодно длинная последова-
последовательность однозначных чисел, включая нуль, каждое из которых выбрано
с вероятностью 1/10.
Укажем три способа, посредством которых можно случайно выби-
выбирать однозначные числа с указанной вероятностью. Иначе говоря, ука-
укажем три способа получения последовательности случайных чисел.
166

Первый способ использует урну (мешок), внутри которой находятся
десять одинаковых шаров, помеченных числами 0, 1,2, 3, 4, 5, 6, 7, 8, 9.
Вынимаем наугад один из шаров и записываем число, которым он по-
помечен. Допустим, это есть число 2. Возвращаем вынутый шар в урну,
перемешиваем шары и во второй раз вынимаем наугад шар из урны.
Пусть это будет шар 5. Возвращаем вынутый шар в урну и повторяем
испытание в третий раз. Допустим, снова появился шар 2. Предполо-
Предположим, что четвертое испытание привело к появлению шара 6, пятое ис-
испытание — шара 7, шестое — шара 3, седьмое — шара 5, восьмое —
шара 9, девятое — шара 7, десятое — шара 4, одиннадцатое — шара О,
двенадцатое — шара 8, тринадцатое — шара 1, четырнадцатое — шара 1,...
И вот перед нами начало последовательности случайных чисел:
2526735974081 1...
Другой генератор случайных чисел — рулетка. Она представляет со-
собой круг, разбитый на десять одинаковых секторов, помеченных числа-
числами 0, 1, 2, 3,4, 5, 6, 7, 8, 9. Рулетка имеет вращающуюся стрелку или
катящийся по кругу шарик. Каждое испытание состоит в том, чтобы
привести в движение (толкнуть) стрелку или вбросить шарик, заставив
его тем самым бежать но кругу, а затем подождать, пока стрелка или
шарик остановятся. Исход испытания — число в том секторе круга, где
произошла остановка стрелки (шарика).
В третьем типе генератора случайных чисел используют кубик и же-
жетон (см. таблицу 24). Пять граней кубика помечают числами 0, 1, 2, 3, 4,
а шестую грань закрашивают. На одной стороне жетона изображают
число 0, а на другой число 5. Кубик и жетон одновременно подбрасыва-
подбрасывают и всякий раз подсчитывают сумму выпавших очков. Если, напри-
например, кубик выпал гранью 3, а жетон стороной 5, то фиксируют случай-
случайное число 8 (поскольку 3 + 5 = 8). Если выпали грань 4 и сторона 0, то
фиксируют случайное число 4 (поскольку 4 + 0 = 4). Если кубик выпал
закрашенной гранью, то такое испытание просто не засчитывают.
Последовательность случайных чисел — это последовательность ха-
хаотическая, совершенно беспорядочная, поскольку появление того или
иного очередного числа в этой последовательности случайно: оно не
зависит от того, какие числа уже появились, и не влияет на то, какие
числа появятся в дальнейшем. В то же время нетрудно убедиться, что
образуемый случайными числами хаос внутренне конструктивен: в этом
хаосе скрывается некий порядок. Чтобы обнаружить его, нужно рас-
рассматривать достаточно большую последовательность случайных чисел.
167

Таблица 24. Генераторы случайных чисел и таблица из 1200 чисел
Таблица, состоящая
из 1200 случайных чисел,
сгруппированных в 60 блоков по
5 четырехзначных чисел в блоке
0655
5255
6314
3157
9052
4105
1437
4064
1037
5718
4064 5228
5458
2461
8453 4467
5161
8951
9764
9565
4105
2851
.4171
5765
8791
5127
9401
2302
2423
3497 9785
9313
5179
ЗОЮ
4242
3585
8462
0672
5163
4995
6751
4889
2335
4862
4635
3187
6727
7013
1562
0754
1402
1392
6301
4153
9849
4320 4558
3466 8269 9926
7489
8081
5081
9599 9828 8740
3961
9123
3145
1281
9690
9115
6447
3384 5320
7429
0174
5848
0653
4631
9869
2222
4413
2611
2544
9886
5678
2464
3361
6247
5014
5950 3384 0276 4503 3333
0456 0944 3058 2545
0413
5273
4991
4647
6993
6919
2254
4312
580 0368
8288
0756
2013
9651
0650
4125
5579
4471
2545 4436
7429
2575
0109
3300 9979
4911
6582 8605 7300
8697 54090653
3043
1293
6458
0709 2523 9224
4331
6157
3135
5704
0010
0063
2837
8865 2627
00636006
9910
1596
I403 6859 7802
0604 7956 2304
6560
6346 5392
830 0927 0466
9265
7516
9284
7730
1970
6666 6692
7264
6328 9659
3756
1014
7894
9307
8922
0400 5998
9854 6380 6650 8567 5045
4171
2873
9844
1126
1787
6279
1863
5519
9050
3371
1023
3724 8900 7852
6675 7989 5592
2391
6256 1303
0247 0583 7679
0532
8967 3382
6298 6673 6406
2436 2408
9720
546С
1378
8144 8638 0307
8851
9928 2439
6265
1863
0159
6345 4576 5059
4245
6307 7935
5590 2455 3963 6463
4477
0111
0228 5460 2835 3294 3674
2220
3243 2958
6271
1736
7791
7959 3682
3180 4499
8417
2986
7526
7877
9182
2260
3759
5618
6503 4081
4977
7942
3199
6313
3016 0639 2007
5951
5707
4745
3756
2607
3775
8941
з>
2018
6610
4733
9032
1314
5843
3431
7746
0146
4754
0501
1609
2482
7619
7427
5441
7979
9795
4738 3996
УРНА С ШАРАМИ
РУЛЕТКА
КУБИК-
Сумма очков: 0516273849
168

Нет смысла составлять таблицу случайных чисел, состоящую всего лишь
из нескольких десятков чисел. Количество генерированных случайным
образом чисел в последовательности должно измеряться, по крайней мере,
сотнями, а еще лучше — тысячами. Для удобства работы с такими боль-
большими последовательностями чисел их обычно разбивают или на трех-
трехзначные, или на четырехзначные, или на пятизначные числа, которые
группируют в блоки (например, по пять четырехзначных чисел в блоке).
Вот в виде подобных блоков и принято изображать таблицы случай-
случайных чисел.
Таблица 24 содержит 1200 случайных чисел, сгруппированных в 60 бло-
блоков по пять четырехзначных чисел в блоке. Для удобства каждые пять
блоков объединены в большой блок из 100 случайных чисел; большие
блоки имеют номера: 1, 2, 3,...,12. Не надо удивляться, что некоторые
четырехзначные числа в данной таблице начинаются с нуля; ведь раз-
разбиение последовательности однозначных чисел на четырехзначные про-
проводилось чисто формально. Например, совокупность двадцати одно-
однозначных случайных чисел
08 3 009270466752666 10
формально разбита в таблице на пять четверок чисел:
0830 0927 0466 7526 6610
(см. большой блок № 4, последняя строка). Мы видим, что три полу-
получившиеся при таком разбиении четырехзначных числа начинаются с
нуля. При работе с таблицей эти нули надо, разумеется, учитывать. За-
Заметим, что в таблице встречаются также четырехзначные числа, начи-
начинающиеся с двух нулей:
4331 0010 8144 8638 0307
6157 0063 6006 1736 3775
(см. большой блок № 2, вторая и третья строки).
В таблице 25 начинается, а в таблице 26 оканчивается последова-
последовательность из 10 000 случайных чисел, сгруппированных в 400 блоков
по пять пятизначных чисел в блоке. Здесь можно встретить пятизнач-
пятизначные числа, начинающиеся не только с одного или двух нулей, но даже
с трех нулей (см. число 00020 в блоке 7x18, число 00055 в блоке 10x7,
число 00052 в блоке 6x13).
В дальнейшем мы будем использовать главным образом таблицу из
1200 случайных чисел, оставляя таблицу из 10 000 случайных чисел же-
желающим получше убедиться в существовании порядка в хаосе.
169

Таблица 25. Таблица из 10 000 случайных чисел (начало)
Таблица, состоящая
из 10 000 случайных чисел
5
сгруппированныз в 400 блоков
по 5 пятизначных чисел в блоке
65135
68718
49667
96777
61204
201С0
04375
67183
49380
56013
46596
52928
09403
20328
78707
73597
07446
47870
84269
52704
19020
19-442
39523
01201
51725
91045
548Э6
92324
88397
52118
37202
71637
35790
99087
89768
83816
00806
65733
60671
45326
54419
72845
01823
89671
71883
25493
28278
44834
23329
33176
44597
81456
91503
63651
30709
50664
80089
19293
97754
47923
1
54879
38375
78039
08667
91185
50003
15463
Л8629
42273
02278
51960
66296
50848
72163
57821
94657
66408
55448
35824
71441
09999
94873
74227
85057
60273
72642
95603
88115
78035
65337
05623
80260
19603
72525
36608
00718
20667
03902
23190
86280
65493
68939
48113
81320
93005
56247
93841
89816
74767
16108
28074
81110
59589
64109
25869
89487
83750
91304
28401
38366
2
71903
46747
61030
74544
23485
71684
49139
25607
93835
53110
02957
15570
71088
66728
28410
72927
19958
14158
35508
50581
08516
36976
51895
93409
84903
42684
17290
77848
06366
13461
23595
83299
31212
344O2
49108
94663
81224
29140
47433
74876
88741
06483
60005
05251
77888
46907
13134
52509
85661
98145
92908
94771
22803
13207
68851
41973
36605
37043
62553
81939
3
23541
19860
46122
92903
18424
34875
17369
27003
32621
33235
56574
31407
31308
81091
64908
46459
65159
83451
49401
65679
82751
30366
39733
81200
84374
32419
91508
38006
37342
18438
79677
89743
34119
50115
92337
39629
24296
05414
86979
51856
89069
40835
87083
25930
64673
25634
25129
85192
54449
27652
22392
13664
18122
68348
65221
98456
85343
82077
98641
61526
4
92400
76129
54941
58427
65084
60617
71179
09721
60848
62949
18672
54988
35677
52307
30452
61325
11338
58729
36478
37597
89731
65815
29426
21176
31438
12825
95605
45600
62026
16099
59772
94628
34728
09825
79809
27812
39967
62087
45281
03263
10789
16564
98000
37320
19502
84761
65536
32114
76506
76918
38034
07478
17790
42140
69392
51147
26090
42231
48553
27691
5
20306
94718
53721
29754
38379
77Э91
77472
70206
67721
53799
02994
78749
49046
78952
78760
50908
39231
42430
30246
17182
52148
66895
76685
78459
36959
58785
82514
02181
13032
57330
37141
26784
47391
54728
81934
28250
60239
65727
69750
.10215
00973
75047
22348
11895
54669
76421
19838
83770
02131
41000
83739
80992
00236
00052
35106
51327
28447
31534
35996
13988
6
31712
97397
67437
77409
07293
66322
96230
10497
69712
51375
39960
16135
10870
60261
36880
25601
72802
42234
41771
60733
09111
27222
93548
18960
83719
84563
32257
70261
14048
05018
63590
17792
93272
37514
06370
44083
89494
54430
96999
87947
30238
22938
89182
16187
21526
42907
21479
90076
93202
46059
32876
58485
93750
04099
36393
26590
33179
54358
08033
21630
7
96238
92197
61709
48146
76788
27390
18521
83617
3343Л
42451
02489
82797
72107
11207
02564
30038
70630
4L905
61398
11765
64205
17378
87546
85182
40702
62071
15699
49705
197Н
92605
48093
09214
09887
24437
18703
33831
34431
52632
42104
09427
46126
13073
27750
03303
074О1
95158
48265
70233
053S5
72208
98604
18882
20468
48767
27129
94684
69730
52939
91811
00957
8
57864
57257
88182
50411
84281
73334
67354
39176
85908
76889
5Э079
31296
11550
73065
96978
78786
87336
83274
98154
09293
77930
59359
07687
02245
70038
17799
02654
31491
30101
10316
02366
53781
34196
01316
90858
54280
44890
94126
34377
32380
85X6
32066
63314
40287
30925
27146
01674
76730
93941
90475
75652
13238
92189
23355
17326
58103
09683
26655
70471
50599
9
86267
73187
92769
50511
58561
73494
41883
4506/2
58620
68096
72789
93268
61175
48286
62332
65197
16385
22459
61644-
70076
32391
00055
47338
11566
68130
96094
83110
25318
16304
07351
05407
90102
98251
04770
55130
67850
59892
95597
63300
43636
37114
43098
87302
52435
46148
37042
47274
25043
84434
10341
95680
89865
66781
42505
86452
96936
08770
72687
81538
91260
10
64733
90287
41702
44379
46031
17196
74037
05051
95736
86726
90501
15979
01081
30655
18682
21527
58939
6Э903
50646
80857
22562
10101
33345
57057
77321
65283
32784
75032
12405
40751
69076
06780
12240
52527
63125
41635
44878
52586
11950
78020
08325
25774
62453
06554
40869
06025
79682
48338
83181
58578
22718
75738
49472
23926
20138
43361
56350
16686
22384
39703
51386
55644
06210
34539
69052
71276
80381
26616
20017
72832
11
93872
91434
78189
40276
45306
24569
12501
78702
43637
91039
27533
83469
57748
41878
45966
93579
Э6222
33862
47857
91046
30359
95616
56717
49472
92228
18169
38073
93544
45037
95846
13459
54939
32277
62992
03821
52830
95523
72494
78684
86361
52046
92525
37703
17768
80243
96117
20308
67645
60278
07761
56584
94910
24885
92544
33874
03173
37512
54737
13240
83244
48724
05528
18208
51129
68433
30275
43130
09608
19613
80364
12
72698
66453
205S6
85S64
64476
26820
94162
13102
60399
13884
69946
76952
09012
93610
25837
20049
43935
14903
80021
95340
38220
82618
07896
95241
53849
72867
87910
10482
68034
80277
59896
78360
23015
55171
50005
19700
12666
66685
72590
30286
87404
32301
70711
36086
37403
99768
82510
44676
08969
28456
92291
15403
79506
54099
56715
97911
14883
57431
93617
37858
76069
94935
13973
48580
72332
22753
88108
59223
81103
14158
13
78520
84477
12707
71604
31460
66299
42006
74518
19080
25376
69875
50065
39805
51745
79966
85666
36272
36996
58560
70209
13972
85756
74085
84360
26578
53931
89260
34277
98561
92450
78185
04163
54261
85448
02204
08193
87597
05344
47283
06434
95585
25923
37921
05468
42231
14321
53609
14730
96020
46570
56575
89151
60638
31497
38424
71313
99673
01786
51549
61657
94867
58972
57905
59386
62502
46046
64709
74533
37642
71740
14
43340
03559
91101
05691
61553
50962
99213
20992
72417
60187
31568
89540
35950
97527
62841
25102
47817
60027
67414
23825
86115
51156
53886
13960
39954
47906
66444
46177
46747
69033
60268
77673
95020
12545
69319
37600
23190
71633
45445
50229
25547
76556
54989
41631
17073
69029
13258
22642
75815
11623
24075
73322
07132
03863
38273
44256
62298
20803
28532
04184
93570
43340
66878
62209
76323
67196
15191
64966
41866
91289
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
( Для примера выделен блок 3Х11 — блок в 3-м столбце, 11-й строке)
170

Таблица 26. Таблица из 10 000 случайных чисел (окончание)
72137
04254
46083
16602
29910
77708
90715
79666
53294
44422
12601
65664
18363
00491
02878
79920
97556
79435
93903
04758
53341
07626
40645
82666
00147
61557
71522
05366
72668
51497
66170
23361
53608
24079
50495
93550
16260
32868
80722
С7Э62
83452
51168
83905
59782
09627
48174
20750
02115
42726
61692
69792
16451
95619
27552
85710
02280
86827
71126
36336
85591
76298
32147
92840
72835
56832
51122
90789
93975
87353
20359
1
73850
60099
50731
26772
55480
83761
65115
48119
49761
78305
54432
73669
66515
53688
83197
22780
54260
52143
78220
50961
28758
78473
27008
14127
99378
43927
16545
66273
62720
78491
68781
60672
59661
01177
87947
48308
03381
72831
21328
В7389
92994
41624
28803
50488
2G695
62551
74116
37096
54307
45137
01480
67912
16238
72387
11035
53815
81430
71770
98297
33192
32532
17457
44833
87258
78400
92668
32932
66981
15094
48577
2
32733
50584
81250
89693
47184
89238
12870
38525
76235
76369
65017
24910
23098
72033
94318
43100
42361
12322
09178
90230
93442
17708
16341
94390
58310
11643
68464
49518
08971
83680
91423
52451
70966
02666
20592
20282
09798
55156
19977
09559
85019
34 768
63272
77081
78373
96122
58973
20505
29170
17539
51557
66404
25374
34О01
40171
47479
45597
16092
48100
65127
22644
56296
81146
89384
24190
96750
67449
19556
29529
05971
3
35321
10961
57995
92558
79775
86521
89922
82189
55814
20601
91131
25488
22384
68063
47901
83886
12741
12554
33676
72006
42963
50059
05870
07069
34655
65522
62540
25415
97908
08319
86645
03774
24937
35515
91917
92711
89487
90166
82161
98456
57720
53124
65480
10186
09119
22375
99018
91937
13045
31799
70726
76254
13653
83792
04810
44017
82296
03942
71594
80852
96853
48964
64060
11251
37978
11130
05115
24605
87305
92373
4
80647
57642
41467
38394
09779
82711
24926
34921
29900
39701
50515
23699
67756
86104
85252
26378
56996
04314
58996
24268
25254
33584
42604
39152
48242
76713
76143
20346
15905
51223
02925
06365
56559
24819
59595
74402
33632
91599
29385
70498
36951
95920
08764
66577
79765
96488
22769
69776
65527
64780
35862
75495
25345
66764
69848
37563
28947
90111
52667
42030
18610
64733
62975
34329
85863
06275
45941
52169
01361
22765
5
39713
19101
29834
84119
08718
79266
44062
49838
03796
80769
97477
86413
66396
90576
91224
66010
48177
98550
78675
77817
96336
52451
79286
10357
58656
95782
06328
22719
В6615
19735
51327
94880
98856
73382
55083
51335
47073
09471
62151
40173
03383
04777
16379
28581
99918
38010
06003
85630
55604
83917
56413
47831
96315
99251
23425
74587
80254
71318
43155
16779
59151
58360
60045
42402
83918
66609
33048
69465
57150
15597
6
61060
30613
08059
68486
45822
47763
94896
47558
73326
17322
80691
19985
63646
04119
32939
00020
85725
58315
11648
10524
16570
11575
08720
94612
30544
34956
94718
18255
97550
72708
41022
70978
19207
50172
43112
64031
92357
79945
48030
80016
34265
82534
72055
26993
огбгз
92522
58033
08059
51222
90452
77817
86797
55657
06260
27602
70563
99608
07976
30432
35724
97420
57364
23250
47962
20530
42504
32456
37970
77261
29448
7
57865
01549
22945
17622
17643
26173
97561
92343
94291
78280
31834
49355
50963
65531
75043
80666
36668
78036
96220
60304
89358
53992
13175
56748
01860
67384
58404
47685
68107
82599
76893
57385
41684
23114
94833
41740
38870
42580
05125
81500
65728
76335
61146
96204
47335
57728
50082
35757
17900
64753
10655
11284
76473
74779
47759
77813
17019
35440
48384
82103
23689
85406
30647
21439
61565
76799
28675
05673
62643
01922
8
88049
96531
72193
30953
63252
36183
96490
47408
10739
42376
32401
24358
99099
30304
40325
66861
45531
24355
54127
79352
36619
83223
89573
75428
08322
47654
84099
78475
10649
28127
292О(Г
70532
20288
28745
72864
69680
73784
86605
70865
48061
89776
21108
82780
20431
17893
39432
94968
49479
55553
99645
52915
49160
08217
96285
18422
50242
17892
26128
85430
61658
74515
63918
46616
54664
69344
46790
04242
49518
74966
05709
9
20557
83936
36077
78267
00232
65869
35454
99542
36087
64899
11994
02915
67895
39202
53252
17820
85245
85822
24804
31942
72838
58546
38051
28101
70476
64999
73641
67421
30976
29660
82747
46078
19783
12249
58785
69373
95662
97758
72154
25583
04006
42302
89111
30114
53176
27914
62152
63531
02980
19799
68198
79852
46810
31998
56074
60 398
76813
10М5
51828
20206
55211
17046
17817
97968
71964
28464
20735
98035
08777
77900
10
43375
45842
82577
31568
98059
64355
51623
44247
32326
62390
97820
81553
09202
82110
18175
50756
12710
44424
24729
85419
10933
49559
3939 Т
38543
44242
11468
52165
83093
66455
30790
97297
87300
82215
35844
53473
73674
83923
08206
86385
74Ю1
06080
79406
53131
23035
07436
03650
73342
77705
75992
60672
70617
26243
68536
35611
09070
53500
13274
17828
95632
49097
25453
89631
21919
09043
50417
43889
18378
00908
22864
11361
11
50914
78222
16210
58297
07255
91271
98381
12762
52225
68375
06653
92012
48494
82254
09457
80608
60264
88508
66501
93017
99964
71671
92039
54214
54227
74140
54336
77038
90708
65154
74420
53319
35810
63265
063О8
97914
90790
54199
39490
87573
84076
21054
57879
30380
14799
36814
78915
81683
08790
90037
78259
36690
18786
98354
44846
45017
39776
60976
78154
54147
48798
80497
21050
48864
37763
40909
90586
92035
72620
15263
12
83628
88481
76092
88922
90786
49295
11055
54488
72447
42921
27477
50435
95974
03669
83810
35695
74650
66190
74157
28087
13468
53603
71664
46928
28598
81386
89196
55399
06450
19582
18783
90155
39852
26451
56778
77989
49474
41327
57482
01556
12445
80132
39099
78272
78197
88460
20537
96907
88992
76680
45488
75829
28575
53680
09996
08406
97027
57662
38634
03656
15486
49167
87791
87355
30136
18741
46115
75518
74169
64912
13
73935
44933
87730
50436
95246
98354
32951
74321
77804
28545
61364
73814
33534
03281
46392
72641
92126
74060
42246
78323
17211
24491
40219
32818
64422
94127
40042
67893
50129
20942
93471
03154
43795
06986
30474
47280
11901
01170
32921
89183
47416
67719
42715
80343
48601
34049
06126
37411
69756
96734
56338
71060
08455
45747
77753
66984
56919
61757
47463
14735
73835
81559
76192
27209
58254
86154
87375
30878
25511
62494
14
72502
12839
90049
86135
15280
28005
28363
36224
57045
33167
22681
96290
94657
11613
02705
26306
08152
93206
41688
77109
48046
57570
97707
51963
29361
67342
37889
89597
17795
81439
89055
20301
21530
08707
57277
71804
30322
21745
33795
64830
83620
72662
24830
57573
97557
19544
92460
90717
46772
92743
12464
91605
93825
78442
49227
71128
88547
71249
99723
78551
51776
47202
56686
89827
71090
20843
79147
14979
80669
31231
15
15
16
17
18
19
20
21
22
23
24
25
26
27
28
171

7.4 Таблица случайных чисел — наглядное доказательство
существования порядка в хаосе
Y1так, убедимся на ряде конкретных примеров, что хаос, образуе-
образуемый достаточно большой последовательностью случайных чисел, дей-
действительно внутренне конструктивен, т. е., проще говоря, действитель-
действительно скрывает в себе порядок. Этот порядок демонстрирует статистическая
устойчивость частот появления тех или иных случайных чисел. Мы бу-
будем использовать таблицу 24, в которой содержатся 1200 однозначных
случайных чисел (или 300 четырехзначных случайных чисел).
Наличие порядка в хаосе случайных чисел можно легко обнаружить
уже на следующем простом примере.
Пример 1. Подсчитаем и сравним частоты появления нуля на пер-
первом, втором, третьем и четвертом местах в четырехзначных случайных
числах в таблице 24.
Убеждаемся, что нуль появился:
-	на 1-м месте 32 раза; частота появления v = 32 / 300 = 0,101
-	на 2-м месте 25 раз; частота появления v = 25 / 300 = 0,083
-	на 3-м месте 33 раза; частота появления v = 33 / 300 = 0,110
-	на 4-м месте 28 раз; частота появления v = 28 / 300 = 0,093.
Вполне можно говорить об определенной устойчивости полученных
частот. Они группируются вблизи значения вероятности, равного 0,1.
Здесь уместно напомнить, что для рассматриваемых в таблице 24 четы-
четырехзначных чисел равны вероятности появления на том или ином месте
(и, в частности, на 1-м месте) любой из десяти цифр 0, 1, 2, 3,..., 9 (для
обычных же четырехзначных чисел вероятность появления нуля на 1-м
месте равна нулю).
Пример 2. Еще лучше устойчивость частот проявляется, если подсчи-
подсчитать и сравнить частоты появления девятки на первом, втором, третьем,
четвертом местах в четырехзначных случайных числах в таблице 24.
Убеждаемся, что девятка появилась на третьем месте 25 раз (v = 0,083),
а на первом, втором и четвертом местах — по 32 раза (v = 0,101).
А теперь подсчитаем, сколько раз появились в каждом из двенадцати
больших блоков в таблице 24 нуль, единица, двойка, тройка, четверка,
пятерка, шестерка, семерка, восьмерка, девятка. Результаты подсчета
приведены на рис. 1 в таблице 27; они разнесены по ячейкам, соответ-
соответствующим номерам больших блоков (от № 1 до № 12). Этими данными
мы воспользуемся в последующих примерах.
172

Пример 3. Используя данные, представленные на рис. 1 в таблице 27,
подсчитаем частоту появления каждой из десяти цифр в таблице 24.
Находим, что нуль появился 118 раз (частота его появления v = 118/ 1200 =
= 0,098), единица появилась ПО раз (v = ПО / 1200 = 0,092), двойка по-
появилась 114 раз (v = 114 / 1200 = 0,095), тройка появилась 125 раз
(v = 125 / 1200 = 0,104), четверка появилась 136 раз (v = 136 / 1200 =
= 0,113), пятерка появилась 136 раз (v = 0,113), шестерка появилась
131 раз (v = 131 / 1200 = 0,109), семерка появилась 115 раз (v = 115/ 1200 =
= 0,096), восьмерка появилась 94 раза (v = 94 / 1200 = 0,078), девятка по-
появилась 121 раз (v = 121 / 1200 = 0,101). Мы обнаруживаем определен-
определенную устойчивость всех полученных частот, их близость к 0,1, т. е. к ве-
вероятности появления любой из десяти цифр в последовательности
случайных чисел.
Пример 4. Используя данные, представленные на рис. 1 в таблице 27,
подсчитаем частоты появления нуля в различных выборках четырехсот
случайных чисел. Выборки сделаем, используя различные наборы че-
четырех больших блоков из таблицы 24.
Рассмотрим 15 следующих выборок:
-	блоки 1, 2, 3, 4; нуль появился 42 раза; v = 42 / 400 = 0,105
-	блоки 5, 6, 7, 8; нуль появился 38 раз; v = 38 / 400 = 0,095
-	блоки 9, 10, 11, 12; нуль появился 37 раз; v = 37 / 400 = 0,093
-	блоки 1, 3, 5, 7; нуль появился 33 раза; v = 33 / 400 = 0,083
-	блоки 9, 11, 2, 4; нуль появился 46 раз; v = 46 / 400 = 0,115
-	блоки 6, 8, 10, 12; нуль появился 39 раз; v = 39 / 400 = 0,098
-	блоки 1, 2, 5, 6; нуль появился 38 раз; v = 38 / 400 = 0,095
-	блоки 3, 4, 11, 12; нуль появился 43 раза; v = 32 / 400 = 0,101
-	блоки 7, 8, 9, 10; нуль появился 37 раз; v = 37 / 400 = 0,093
-	блоки 1, 3, 10, 12; нуль появился 34 раза; v = 34 / 400 = 0,085
-	блоки 2, 4, 5, 7; нуль появился 45 раз; v = 45 / 400 = 0,113
-	блоки 6, 8, 9, 11; нуль появился 39 раз; v = 39 / 400 = 0,098
-	блоки 1, 4, 5, 8; нуль появился 33 раза; v = 33 / 400 = 0,083
-	блоки 3, 6, 9, 12; нуль появился 39 раз; v = 39 . 400 = 0,098
-	блоки 7, 10, 2, 11; нуль появился 46 раз; v = 46 / 400 = 0,115.
Мы перебрали 15 вариантов и обнаружили, что частоты появления
нуля лежат в рассмотренных случаях в пределах от 0,083 до 0,115. На-
Напомним, что в таблице из 1200 случайных чисел нуль, как и остальные
девять однозначных чисел, генерировался случайным образом (напри-
(например, при помощи рулетки). И тем не менее, как бы мы ни выбирали
четверку больших блоков, частота появления нуля в совокупности из
400 случайных чисел ни разу не оказалась больше, например, 0,5 или
173

Таблица 27. Хаос и порядок в таблице случайных чисел
N1
N3
N5
N7
N9
N11
N2
N4
N6
N8
N10
N12
Нули
Единицы Двойки	Тройки Четверки
Рис.1
5
10
7
11
8
11
14
13
12
8
10
9
Пятерки
18
12
13
10
11
13
7
8
10
15
8
11
7
16
13
9
6
11
10
6
8
10
7
7
Шестерки
12
9
8
9
15
10
11
15
8
13
16
5
8
10
13
9
11
5
10
9
11
6
10
12
Семерки
6
12
6
9
5
8
14
8
9
14
10
14
11
8
7
11
13
10
12
7
10
10
14
12
Восьмерки
8
10
8
11
13
15
9
17
11
11
14
6
12
10
11
7
13
Девятки
10
4
9
14
11
13
8
11
9
9
12
11
0,60
0,58
0,56
0,54
0,52
0,50
0,48
0,46
0,44
0,42
0,40
I II III IV V VI VIIVIIIIX X XI XII
Нечетные
числа
52
52
48
53
46
55
51
40
46
58
51
55
0,52
0,50
0,48
Рис.2
1 2 3 4 5 6 7 8 9 10 1112
Рис.3
174

меньше, например, 0,01. Все полученные частоты сгруппировались вбли-
вблизи вероятности, равной 0,1, с отклонениями вниз в пределах 0,017 и
вверх в пределах 0,015.
Нечто подобное мы должны были бы, по-видимому, получить, про-
проделав такой же опыт не с нулем, а с любой другой цифрой.
Пример 5. Используя данные, представленные на рис. 1 в таблице 27,
подсчитаем частоты появления нуля в различных выборках восьмисот
случайных чисел. Выборки сделаем, используя различные наборы вось-
восьми больших блоков из таблицы 24.
Рассмотрим 15 следующих выборок:
-	блоки 1, 2, 3, 4, 5, 6, 7, 8; 80 нулей; v = 80 / 800 = 0,100
-	блоки 2, 3, 4, 5, 6, 7, 8, 9; 83 нуля; v = 83 / 800 = 0,104
-	блоки 3, 4, 5, 6, 7, 8, 9, 10; 79 нулей; v = 79 / 800 = 0,099;
-	блоки 5, 6, 7, 8, 9, 10, 11, 12; 76 нулей; v = 76 / 800 = 0,095;
-	блоки 1, 3, 5, 7, 9, 11, 2, 4; 79 нулей; v = 79 / 800 = 0,099;
-	блоки 1, 3, 5, 7, 9, 11, 6, 8; 72 нуля; v = 72 / 800 = 0,090;
-	блоки 1, 3, 5, 7, 9, 11, 10, 12; 71 нуль; v = 71 / 800 = 0,089;
-	блоки 2, 4, 6, 8, 10, 12, 1, 3; 81 нуль; v = 81 / 800 = 0,101;
-	блоки 2, 4, 6, 8, 10, 12, 5, 7; 84 нуля; v = 84 / 800 = 0,105;
-	блоки 2, 4, 6, 8, 10, 12, 9, 11; 85 нулей; v = 85 / 800 = 0,106;
-	блоки 1, 3, 5, 7, 6, 8, 10, 12; 72 нуля; v = 72 / 800 = 0,090;
-	блоки 2, 4, 6, 8, 5, 7, 9, 11; 84 нуля; v = 84 / 800 = 0,105;
-	блоки 1, 3, 4, 6, 7, 9, 10, 12; 78 нулей; v = 78 / 800 = 0,098;
-	блоки 1, 2, 3, 5, 7, 8, 10, 12; 74 нуля; v = 74 / 800 = 0,093;
-	блоки 1, 3, 5, 6, 8, 10, 11, 12; 72 нуля; v = 72 / 800 = 0,090.
Мы перебрали 15 различных вариантов и обнаружили устойчивость
частот появления нуля в пределах от 0,089 до 0,106. Частота оказалась
приблизительно равной вероятности 0,1с отклонениями в пределах
0,011 вниз и в пределах 0,006 вверх. Отметим, что разброс отклонений
теперь немного меньше, чем в примере 4. Это неудивительно, посколь-
поскольку количество испытаний в серии увеличилось теперь вдвое.
Данные, представленные на рис. 1 в таблице 27, позволяют быстро
найти количества нечетных однозначных чисел (чисел 1, 3, 5, 7, 9),
появившихся случайным образом в каждом из двенадцати больших бло-
блоков в таблице 24. Разделив каждое из этих количеств на 100 (т. е. на
число испытаний в большом блоке), находим частоты появления не-
нечетных чисел в двенадцати сериях по 100 испытаний в серии. Эти час-
частоты графически представлены на рис. 2 в таблице 27. Мы видим, что
частоты колеблются вблизи вероятности появления нечетного однознач-
однозначного числа, равной 0,5, отклоняясь вниз и вверх в пределах 0,1.
175

Пример 6. Используя сведения о количествах нечетных чисел в каж-
каждом большом блоке в таблице 24, подсчитаем частоту появления нечет-
нечетных чисел сначала в двух блоках (блоке 1 и блоке 2), затем в трех блоках
(блоках 1, 2 и 3), затем в четырех блоках (блоках 1, 2, 3 и 4) и так да-
далее — вплоть до учета всех двенадцати блоков.
Такой подсчет использует соотношения (*) из § 7.1. Результаты под-
подсчета представлены графически на рис. 3 в таблице 27. Налицо посте-
постепенное приближение частот к вероятности 0,5 по мере увеличения чис-
числа испытаний (феномен статистической устойчивости частот).
7.5 Воспользуемся таблицей случайных чисел!
7.5.1. Случайные числа вместо длительных испытаний. «После того,
как кто-либо достаточно много раз выполнит опыты с бросанием моне-
монеты или кости или с вытаскиванием карты из предварительно перетасо-
перетасованной колоды, у него возникнет естественное желание получить более
удобный и быстрый метод выполнения эксперимента, математически
эквивалентного этим экспериментам... Карты, шары в урне, кости —
все это хорошо использовать тогда, когда эксперимент недолог; если же
нужно выполнить сотни и тысячи испытаний, использование карт, ша-
шаров, костей становится практически неприемлемым. В подобных ситуа-
ситуациях математики используют случайные числа». Эту цитату мы взяли
из книги по теории вероятностей, написанной группой видных амери-
американских математиков и педагогов (см. Ф. Мостеллер, Р. Рурке, Дж. То-
Томас. «Вероятность». Пер. с англ. М.: «Мир», 1969).
Имея под рукой таблицу случайных чисел, мы можем не тратить вре-
времени на подбрасывание монеты. Надо просто перемещаться мысленно
по таблице и всякую встречу с нечетным числом A, 3, 5, 7 или 9) рас-
рассматривать как выпадение, скажем, орла, а всякую встречу с нулем или
четным числом рассматривать как выпадение решки. Маршруты пере-
перемещения по таблице случайных чисел могут быть выбраны разными
способами. Можно, например, перемещаться по строкам слева напра-
направо, начиная с самой верхней. Можно перемещаться по столбцам сверху
вниз, начиная с крайнего левого столбца. Можно обходить таблицу чи-
чисел как бы по спирали: сначала пройти первую (самую верхнюю) строку
слева направо, затем опуститься вниз по крайнему правому столбцу,
затем пройти самую нижнюю строку справа налево, затем подняться
вверх по крайнему левому столбцу до второй строки, затем пройти вто-
вторую сроку слева направо — и так далее. Можно придумать еще какие-
176

нибудь способы перемещения по таблице чисел — все это, в конечном
счете, не имеет значения.
Вместо того, чтобы выяснять на практике, сколько раз выпадет орел
при тысяче подбрасываний монеты, мы можем воспользоваться табли-
таблицей 24 и просто подсчитать количество нечетных однозначных чисел
в десяти больших блоках. Вот, что мы получим для шести разных выбо-
выборок десятки блоков:
-	все блоки кроме 1 и 2; «орел выпал» 504 раза; v = 0,504;
-	все блоки кроме 3 и 4; «орел выпал» 515 раз; v = 0,515;
-	все блоки кроме 5 и 6; «орел выпал» 513 раз; v = 0,513;
-	все блоки кроме 7 и 8; «орел выпал» 496 раз; v = 0,469;
-	все блоки кроме 9 и 10; «орел выпал» 510 раз; v = 0,510;
-	все блоки кроме 11 и 12; «орел выпал» 497 раз; v = 0,497.
Здесь слова «орел выпал» взяты в кавычки, поскольку исход с выпаде-
выпадением орла сопоставлен математически с появлением нечетного одно-
однозначного числа в рассматриваемой последовательности случайных чисел.
При желании, можно воспользоваться таблицей из 10 000 случайных
чисел (см. таблицы 25 и 26 в § 7.3) и подсчитать, сколько раз там встре-
встречаются нечетные числа. Этот подсчет будет математически эквивален-
эквивалентен утомительному опыту, в котором надо подбросить монету 10 000 раз.
Испытания с выниманием наугад шара из мешка, в котором находят-
находятся один черный и два белых шара, совсем несложно заменить мыслен-
мысленной прогулкой по таблице случайных чисел. Всякую встречу с числом,
делящимся без остатка на три (числом 3, 6 либо 9), будем рассматри-
рассматривать как исход с выниманием из мешка черного шара. Встречу с числом
1, 2, 4, 5, 7 или 8 будем рассматривать как исход с выниманием белого
шара. А встречу с нулем будем попросту игнорировать. В таблице 24 нуль
встречается 118 раз. Значит, полное число испытаний, которое подле-
подлежит учету в данном случае, равно 1200 - 118 = 1082. Общее количество
троек, шестерок и девяток в таблице 24 равно 125 + 131 + 121 = 377.
Значит, можно считать, что частота появления черного шара равна
v = 377/1082 = 0,35.
Чтобы заменить таблицей случайных чисел подбрасывание кубика,
надо попросту игнорировать встречи с нулем, семеркой, восьмеркой и
девяткой. Тогда встречи с единицей, двойкой, тройкой, четверкой,
пятеркой и шестеркой могут рассматриваться как исходы с выпаде-
выпадением соответствующей грани при подбрасывании кубика. В табли-
таблице 24 общее количество нулей, семерок, восьмерок и девяток равно
118 + 115 + 94 + 121 = 448. Значит, полное число испытаний, которое
надо учитывать в данном случае, равно 1200 - 448 = 752. Единица
177

появилась в таблице ПО раз; значит, выпадение грани 1 при подбрасы-
подбрасывании кубика можно представить частотой v = ПО / 752 = 0,146. Двой-
Двойка появилась в таблице 114 раз; отсюда v = 114 / 752 = 0,152. Тройка по-
появилась 125 раз; отсюда v = 125 / 752 = 0,166. Четверка появилась 136 раз;
отсюда v = 136 / 752 = 0,181. Такой же результат получился для пятерки.
Наконец, шестерка появилась в таблице 131 раз; отсюда v = 131 / 752 =
= 0,174. Вероятность выпадения любой грани кубика равна 1/6, т.е.
0,167. Мы видим, что частоты, полученные из таблицы 24 колеблются
около этой вероятности с отклонением вниз в пределах 0,021 и отклоне-
отклонением вверх в пределах 0,014. Без сомнения, эти отклонения были бы
меньше, если бы мы воспользовались таблицей, содержащей 10 000 слу-
случайных чисел.
7.5.2. Случайные числа и число к. Рассмотрим наглядный пример прак-
практического применения таблицы случайных чисел. В этом примере слу-
случайные числа используются для того, чтобы найти, чему равно число к.
Идея приближенного подсчета числа к вероятностным способом доста-
достаточно проста. Изобразим на листе бумаги квадрат, в который вписана
четверть круга; радиус круга R равен стороне квадрата (см. рис. 1 в табли-
таблице 28). Отношение площади четверти круга к площади квадрата есть
(nR2 / 4) / R2 = к / 4. Будем бросать на лист бумаги мелкие крупинки.
Бросать надо наугад, без какого-либо прицеливания; крупинки должны
распределиться по поверхности листа случайным образом (см. рис. 2 в
таблице 28). Часть крупинок окажется вне квадрата; эти крупинки в
дальнейшем учитывать не будем. Подсчитаем количество крупинок,
оказавшихся внутри квадрата; пусть это количество равно N±. Предпо-
Предположим, что из них N2 крупинок оказались внутри четверти круга (внут-
(внутри незакрашенной области квадрата). Будем полагать, что для каждой
крупинки равновероятно оказаться в любом месте квадрата. Тогда при
достаточно большом числе крупинок отношение N2 / N± должно при-
приближенно равняться отношению площади незакрашенной области квад-
квадрата ко всей площади квадрата. Таким образом,
Числа Ni и N2 определяем в эксперименте; отсюда можем найти, чему
равно число тт.
Идея эксперимента проста. Однако как ее реализовать на практике?
Как на практике обеспечить равновероятность попадания крупинок в лю-
любое место квадрата? Иными словами, что значит «бросать наугад» и как
это надо делать?
И вот тут-то на помощь приходит таблица случайных чисел. Мы
вообще не станем бросать крупинки на лист бумаги, а воспользуемся
178

Таблица 28. Примеры использования таблицы случайных чисел
О ОД 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
06 55	84 53	44	67	33	84	53	20
52 55	51 61	48	74	29	46	47
63 14	51	23	35	01	74	69
31 57	64	44	62	58	48	69	19
52	65	46	35	06	53	22	54
179

случайными числами. Проведем вдоль сторон квадрата координатные
оси; масштаб выберем таким, чтобы сторона квадрата равнялась единице
(см. рис. 3 в таблице 28). Будем пользоваться таблицей 24, причем пред-
предварительно каждое из четырехзначных чисел в этой таблице мысленно
поделим на 10 000 — чтобы иметь набор случайных десятичных чисел,
находящихся в пределах от 0 до 1. Условимся рассматривать десятичные
числа, оказавшиеся в нечетных строках таблицы, в качестве х-координа-
ты, а стоящие непосредственно под ними десятичные числа — в каче-
качестве j-координаты случайных точек. Эти точки будем наносить на рису-
рисунок 3, постепенно перемещаясь по таблице сначала вдоль всего первого
столбца сверху вниз, затем вдоль всего второго столбца и т. д.
Первые пятнадцать случайных точек показаны на рисунке 3 черны-
черными треугольниками; они имеют координаты:
@,0655, 0,5255),	@,6314, 0,3157),	@,9052, 0,4105),	@,1437, 0,4064),
@,1037, 0,5718),	@,5127, 0,9401),	@,4064, 0,5458),	@,2461, 0,4320),
@,3466, 0,9313),	@,5179, 0,3010),	@,9599, 0,4242),	@,3585, 0,5950),
@,8462,	0,0456), @,0672,	0,5163), @,4995,	0,6751).
Черными кружочками на рисунке показаны еще 85 случайных точек.
Используя рисунок, нетрудно подсчитать, что для первых пятнадцати
точек N2 I Nx = 13 / 15 и, следовательно, тг = 3,467. Для ста точек (учи-
(учитываем как треугольники, так и черные кружочки) N2 / N{ = 78 / 100 и,
следовательно, к = 3,120.
7.5.3 Случайные числа и выбор по справедливости.
Задача 1. На 85 выпускников школы выделено 25 путевок для интересной турис-
туристической поездки. Как отобрать 25 «счастливчиков» таким образом, чтобы не была
нарушена справедливость?
Примечание. Выбор по справедливости означает, что у каждого из выпускников
должна быть одинаковая вероятность получить путевку. Эта вероятность равна 1 / 85.
Решение. Данную задачу можно, конечно, решить с помощью мешка, в кото-
котором находятся 85 одинаковых шаров, перенумерованных от 1 до 85. Всех выпуск-
выпускников также нужно перенумеровать. Затем надо приступить к испытаниям, выни-
вынимая наугад шары из мешка. Вот мы вынули первый шар. Пускай это будет шар
с номером 15. Значит, первую путевку получит выпускник под номером 15. Как
обычно, вынутый шар возвращаем в мешок и как следует встряхиваем мешок,
чтобы шары перемешались. Затем вынимаем второй шар. Пусть это будет шар
с номером 76. Вторую путевку получает выпускник под номером 76. Если бы ока-
оказалось, что второй шар снова есть шар с номером 15, то данное испытание не
засчитывалось бы. Выполнив соответствующее число выниманий шара из мешка,
мы, в конечном счете, наберем 25 обладателей путевок на поездку.
Весь эксперимент оказывается довольно долгим. Его можно было бы немного
ускорить, не возвращая всякий раз вынутый шар обратно в мешок. Однако тогда у
180

разных участников эксперимента оказались бы неодинаковые шансы получить путев-
путевку. В самом деле, если, например, первый вынутый шар не возвратить в мешок, то
вероятность выявления следующего обладателя путевки будет уже не 1 / 85, а 1 / 84.
Рассматриваемую задачу значительно проще решить, если воспользоваться табли-
таблицей случайных чисел. Нам не понадобится вся таблица 24. Достаточно рассмот-
рассмотреть числа, представленные в одном большом блоке. Все равно каком именно.
Пусть это будет блок 1. Все четырехзначные числа в этом блоке разобьем на пары
двузначных чисел. Выпускникам присвоим номера 01, 02, 03, ..., 85. Из совокуп-
совокупности двузначных чисел в рассматриваемом блоке сразу вычеркнем числа от 86 до
99. В результате получится таблица, изображенная на рис. 4 в таблице 28. Начнем
обходить эту таблицу, например, по строкам (начиная с первой строки и идя по
каждой строке слева направо). Всякую повторную встречу с тем или иным дву-
двузначным числом будем игнорировать. В итоге у нас получится вот такая последо-
последовательность случайных двузначных чисел:
06 55 84 53 44 67 33 20 52 51 61 48 74 29 46 47
63 14 23 35 01 69 31 57 64 62 58 19 65 22 54.
Первые двадцать пять чисел этой последовательности могут по всей справедли-
справедливости рассматриваться как номера выпускников, которым посчастливилось полу-
получить путевку. (Впрочем, с тем же основанием могли быть выбраны последние
двадцать пять чисел последовательности.)
Разумеется, мы могли рассматривать любой из двенадцати блоков в таблице 24
и получить иные наборы двадцати пяти «счастливчиков». Существенно, что в каж-
каждом из этих случаев отбор «счастливчиков» был бы справедливым.
Задача 2. Для проверки эффективности новой учебной программы подобрали 16 классов
в одной и той лее параллели с вполне равноценным контингентом учащихся. Эти классы
разделили на 8 пар, имея в виду, что в каждой паре один класс будет заниматься по
новой программе, а другой — по старой. Как выбрать классы под новую программу
таким образом, чтобы не нарушить объективности и справедливости?
Объективность и справедливость выбора будут соблюдены, если выбор будет
произведен случайным образом с вероятностью для каждой из восьми пар клас-
классов, равной 1 /256.
Поясним, откуда взялась вероятность 1 /256. Обозначим 16 подобранных клас-
классов буквами А, Б, В, Г, Д, Е, Ж, 3, И, К, Л, М, Н, О, П, Р. Разобьем их на 8 пар:
АБВГДЕЖЗ
ИК ЛМНОПР.
Нам надо выбрать новую или старою программу для восьми классов — напри-
например для классов А, Б, В, Г, Д, Е, Ж, 3 (при этом автоматически определится выбор
программы для каждого из остальных восьми классов).
Начнем с класса А. Возможны два равновероятных варианта: класс А работает
по новой программе, класс А работает по старой программе (варианты Ан и Ас).
Для каждого из этих двух вариантов существуют два варианта выбора программы
181

в классе Б, так что имеются уже четыре варианта (А Б , А Б , А Б , А Б ). Для
каждого из этих четырех вариантов существуют два варианта выбора программы в
классе В — получаются восемь вариантов (АНБНВН, АНБНВС, АНБСВН, АНБСВС,
АСБНВН, АСБНВС, АСБСВН, АСБСВС). С учетом выбора программы в классе Г полу-
получатся 8-2=16 вариантов. С учетом выбора программы в классе Д получатся
16 • 2 = 32 варианта. И так далее. Нетрудно сообразить, что, когда мы дойдем до
восьмого класса (класса 3), общее число равновероятных вариантов достигнет 28 = 256.
Итак, имеются 256 равновероятных вариантов разбиения 16 классов на 8 пар
классов, в каждой из которых можно провести сравнение новой программы со
старой. Спрашивается, как можно выбрать, не нарушая объективности и справед-
справедливости, один из этих вариантов?
Можно заготовить 256 листков бумаги с указанием на этих листках соответ-
соответствующих вариантов, скатать листки в трубочки, положить в мешок, тщательно
перемешать и затем вынуть наугад один из вариантов. Правда, придется немало
потрудиться, изображая на листках различные варианты (вот так будет выглядеть
один из двухсот пятидесяти шести вариантов: АНБНВСГСДНЕСЖН3С).
Можно не расписывать листки, а поступить значительно проще: выполнить
восемь подбрасываний монеты — по подбрасыванию на каждый из восьми клас-
классов: А, Б, В, Г, Д, Е, Ж, 3. Предположим, что результат восьми подбрасываний
окажется таким: ОРРООРОО (здесь О — выпадение орла, Р — выпадение решки).
Условимся, что при выпадении орла класс выбирает новую программу, а при вы-
выпадении решки — старую. Тогда полученные исходы подбрасываний будут соот-
соответствовать варианту, при котором класс А работает по новой программе, класс
Б — по старой, класс В — по старой, класс Г — по новой, класс Д — по новой,
класс В — по старой, класс Ж — по новой, класс 3 — по новой.
Отсюда следует, что класс И должен работать по старой программе, класс К —
по новой, класс Л — по новой, класс М — по старой, класс Н — по старой, класс
О — по новой, класс П — по старой, класс Р — по старой.
Наконец, можно монету не подбрасывать, а воспользоваться случайными чис-
числами. Причем воспользоваться ими можно по-разному. Например, выпишем по
порядку начальные однозначные числа больших блоков в таблице 24, начиная с бло-
блока 1 и кончая блоком 8:
0049584 6.
Эти восемь чисел сопоставим, соответственно, с классами
А, Б, В, Г, Д, Е, Ж, 3.
В тех классах, которым досталось нечетное число, будем использовать новую
программу, а в остальных классах — старую. В данном случае по новой программе
будут заниматься классы Г и Д, а по старой программе — классы А, Б, В, Е, Ж, 3.
Отсюда следует, что по старой программе должны заниматься также классы М и
Н, а по новой — классы И, К, Л, О, П, Р.
Задача 3. Иван, Сергей, Юрий и Борис приобрели вскладчину ценную книгу, причем
Иван внес 40% стоимости книги, Сергей 30%, Юрий 20%, Борис 10%. Каждому не
182

терпится первым прочитать книгу. Решили тянуть жребий, причем так, чтобы
шансы получить первым книгу были у каждого пропорциональны размеру внесенной им
за книгу суммы. Как это сделать?
Согласно условию задачи, Иван должен иметь вероятность вытянуть жребий,
равную 0,4, Сергей — 0,3, Юрий — 0,2, Борис — 0,1. Это можно сделать весьма
просто, воспользовавшись таблицей случайных чисел. Условимся рассматривать
числа 0, 1, 2 и 3 в качестве «чисел Ивана», числа 4, 5 и 6 в качестве «чисел Сергея»,
числа 7 и 8 в качестве «чисел Юрия», число 9 в качестве «числа Бориса». После
этого завяжем одному из участников опыта глаза и попросим его наугад поставить
точку где-нибудь в таблице случайных чисел. В чье число попадет эта точка, тот и
получает по справедливости право первого прочтения книги.
Конечно, можно было закрепить за каждым из наших персонажей иные числа.
Тут важно (во имя соблюдения справедливости), чтобы за Иваном были закрепле-
закреплены четыре числа, за Сергеем три, за Юрием два и за Борисом одно число.
7.6 Диалог: Что практически дает нам
подсчет вероятности случайного события?
Пвтор. Когда человек впервые начинает осмысливать для себя слу-
случайные ситуации, он, как правило, поначалу полагает, что можно уве-
уверенно предсказывать исходы этих ситуаций. Это можно условно назвать
первым этапом знакомства с вероятностными представлениями. На вто-
втором этапе человек обычно разочарованно заявляет, что в подобных си-
ситуациях ничего нельзя утверждать. И лишь позднее, уже на третьем эта-
этапе, человек начинает открывать для себя, что в кажущемся хаосе мира
случайностей можно обнаружить закономерности, позволяющие непло-
неплохо ориентироваться в окружающем нас мире. Кстати, эти три этапа
процесса постепенного постижения мира случайностей хорошо наблю-
наблюдаются у детей младшего школьного возраста, что отмечают многие
известные педагоги (см., например, весьма интересную книгу: М. Гле-
ман. Т. Варга. «Вероятность в играх и развлечениях». Пер. с француз-
французского, М.: «Просвещение», 1979).
'Читатель. Интересная мысль! Вначале мир случайностей кажется
довольно простым и вполне ясным. Потом он оказывается, напротив,
безнадежно сложным и совершенно непонятным. И уже после этого
начинает открываться необычность такого мира, для понимания кото-
которой нужно отказаться от ряда привычных представлений. Например, от
представления о хаосе как о чем-то таком, что полностью исключает
какой-либо порядок.
183

Пвтор. Думаю, что отмеченные этапы постижения мира случайнос-
случайностей вполне объяснимы. Случайности, которые принято рассматривать
в самую первую очередь (такие как выпадение грани при бросании ку-
кубика), имеют строго определенную и притом легко вычисляемую веро-
вероятность. Вполне может возникнуть впечатление, что случайности под-
поддаются точному расчету и, значит, исходы случайных событий можно
предсказывать. Но потом выясняется, что вероятность отнюдь не гаран-
гарантирует того или иного исхода. Любой конкретный исход случайного
события все равно остается принципиально непредсказуемым. Откры-
Открытие этой истины вполне может породить разочарование и подвести к вы-
выводу о том, что тут «ничего нельзя утверждать».
'Чиниикель. Признаться, мне не раз приходили в голову вопросы: За-
Зачем надо вычислять вероятность события, если оно случайное, и зна-
значит, нельзя точно предсказать его исход? Что толку в подсчете вероят-
вероятности события, если, как говорится, «фирма не гарантирует»? И самый
главный вопрос: Что же практически дает нам подсчет вероятности
случайного события?
Пвтор. Последний вопрос действительно можно считать главным,
именно здесь ключ к переходу от этапа разочарования к этапу понима-
понимания специфики мира случайностей.
'Чиниинель. Итак, что же практически дает нам подсчет вероятности
случайного события?
Пвтор. Отвечая на этот вопрос, отметим прежде всего, что, чем боль-
больше вероятность события, тем чаще оно происходит на практике. И на-
наоборот: чем меньше вероятность события, тем реже оно происходит на
практике. Значит, ожидая исход того или иного события, мы заинтере-
заинтересованы в знании вероятности этого события. Для нас это важно как
в отношении события желаемого, так и в отношении события нежела-
нежелательного. Оценивая вероятность нежелательного события (например,
вероятность вспышки эпидемии, вероятность землетрясения в данной
местности, вероятность гибели водоема в результате техногенных за-
загрязнений, вероятность пересыхания реки вследствие чрезмерного во-
водозабора и т. д.), мы получаем представление о степени грозящей нам
опасности и можем как-то координировать на практике свои действия.
'ЧиЯа&ел*. Приведенные примеры вызывают у меня сомнения. Как
надо понимать эти вероятности? Как их вычислять или хотя бы оце-
оценивать? Как, например, подсчитать вероятность эпидемии или земле-
землетрясения?
Пвтор. Что ж, нетрудно привести сколько угодно ситуаций, где фигу-
фигурируют случайные события, вероятность которых определяется на научной
184

основе — в результате использования методов, разработанных учеными.
Вот один из примеров; он связан с распространением потока нейтро-
нейтронов через защитную стенку, окружающую активную зону ядерного ре-
реактора.
ntutftiufU*b. Боюсь, что это очень специальный пример. Он будет не
всем понятен.
Пвтор. Мы не будем входить в детали. На атомных станциях есть
ядерный реактор, в активную зону которого загружают ядерное горючее,
например уран. В результате деления ядер урана в активной зоне выс-
высвобождается значительная энергия и происходит сильный разогрев про-
прокачиваемого через зону теплоносителя (например, воды, органической
жидкости, жидкого натрия). Теплоноситель нагревает воду в другом
контуре, превращая ее в пар, который заставляет вращаться турбину
благодаря чему в генераторе вырабатывается электрическая энергия. Все
это схематически изображено на рис. 2 в таблице 29; здесь активная
зона реактора показана штриховкой (на рис. 1 в той же таблице показан
общий вид атомной электростанции). Отметим цепочку происходящих
на АЭС превращений энергии:
Атомная
энергия
Тепловая
энергия
—>
Механическая
энергия
Электрическая
энергия
Впрочем, все эти подробности не имеют прямого отношения к на-
нашему разговору о вероятностях. Нам важно отметить, что деление ядер
урана в активной зоне реактора сопровождается не только высвобожде-
высвобождением энергии, но и рождением нейтронов. Эти нейтроны разлетаются
в разные стороны и проникают в стенку, которая окружает активную
зону и защищает рабочее помещение от нейтронов (и другой радиации,
выходящей из зоны). Проникая внутрь защитной стенки, нейтроны вза-
взаимодействуют с ядрами вещества стенки. Возможны три варианта исхо-
исходов такого взаимодействия: нейтрон возвращается обратно в активную
зону (вариант 1), нейтрон после ряда столкновений поглощается, в ко-
конечном счете, одним из ядер вещества стенки (вариант 2), нейтрон пос-
после ряда столкновений все-таки преодолевает стенку и выходит наружу
(вариант 3). Все эти варианты можно видеть на рис. 3 в таблице 29, где
схематически изображены траектории ряда нейтронов. Для примера здесь
отмечены соответствующими номерами три траектории для отмечен-
отмеченных выше трех вариантов.
Итак, перед нами весьма сложный и многообразный набор физи-
физических процессов, насыщенный случайностями. Случайны энергия и
185

Таблица 29. Вероятности и защита в ядерном реакторе
Рис.1
Ядерное горючее Теплоноситель Пар Турбина Генератор
Регулирующие
стержни
Защита от
радиации
Рис.2
Конденсатор
\
Парогенератор Вода
~~ —" Рис.3
186

направление движения каждого нейтрона в момент его перехода из актив-
активной зоны в защитную стенку, случайна длина пробега нейтрона до его
первого столкновения с каким-то ядром вещества стенки, случаен резуль-
результат столкновения (поглощение нейтрона или его рассеяние), случайны
энергия и направление движения рассеянного нейтрона и так далее.
*Чи(*иипель. Не могу себе представить, как можно проанализировать
все эти процессы.
Пвтор. Этот анализ предполагает использование ЭВМ, куда предва-
предварительно вводят данные о потоке нейтронов, входящем внутрь стенки,
данные о веществе стенки, а главное, вероятность того или иного пробе-
пробега нейтрона до момента его взаимодействия с одним из ядер вещества
стенки, вероятность поглощения нейтрона, вероятность рассеяния ней-
нейтрона на тот или иной угол. Затем происходит расчет «судьбы» какого-то
наугад выбранного нейтрона с учетом упомянутых данных и всех вероят-
вероятностей. Этот расчет выполняется с момента попадания нейтрона внутрь
стенки вплоть до момента его выхода из игры. Такая процедура вычисле-
вычислений повторяется для второго наугад выбранного нейтрона, для третьего,
четвертого и многих других. В итоге получают множество возможных
траекторий нейтронов внутри стенки (вроде тех, что показаны на рисун-
рисунке 3). Каждая траектория — исход какого-то одного испытания, пред-
представляющего собой розыгрыш «судьбы» отдельного нейтрона. Огромный
набор таких испытаний позволяет проанализировать в целом картину про-
прохождения нейтронов через защитную стенку и получить практические ре-
рекомендации по толщине стенки и составу ее вещества, гарантирующие до-
достаточную безопасность работы в помещении, где находится реактор.
Понятно, что для ученых, выполняющих подобный анализ, исклю-
исключена даже тень сомнения в практической важности подсчета вероятно-
вероятностей тех событий, которые совершаются внутри защитной стенки.
*Чипиинель. Безусловно, тут подсчет вероятностей совершенно необ-
необходим. Однако мне хотелось бы вернуться из большой науки на «быто-
«бытовой уровень» и обратиться к какой-нибудь совсем простой ситуации,
в которой вероятность легко просчитывается.
Пвтор. Что ж, давайте вернемся на «бытовой уровень».
*Чи(*иипель. Допустим, я предложил приятелю подбросить четыре мо-
монеты и сравнить количества выпавших орлов и решек. Тут возможны
три комбинации:
-	комбинация 1: одинаковы все четыре исхода (выпали 4 орла или
4 решки),
-	комбинация 2: одинаковы три исхода (выпали либо 3 орла + 1 реш-
решка, либо 3 решки + 1 орел),
-	комбинация 3: одинаковы два исхода (выпали 2 орла и 2 решки).
187

Предварительно я предлагаю приятелю поставить на какую-нибудь
из этих трех комбинаций. Известно, что вероятность комбинации 1 равна
2 / 16, комбинации 2 — 8/16, комбинации 3 — 6/16 (см. рис. 1 в табли-
таблице 20). Учитывая это, приятель ставит на комбинацию 2. Мне остаются
либо комбинация 3, либо комбинация 1. Я решаю рискнуть, ставлю на
комбинацию 1 и... выигрываю. Оказалось так, что все четыре монеты
выпали орлом. Вероятность комбинации 2 в четыре раза больше вероят-
вероятности комбинации 1, но в данном случае это не помогло. Мой приятель
вправе спросить: какой же практический смысл был в подсчете вероят-
вероятностей при подбрасывании четырех монет?
Пвтор. Практический смысл обнаруживается, если повторить дан-
данное испытание (подбрасывание четырех монет) достаточно много раз.
По итогам многократных испытаний суммарный баланс по выигрышам
окажется почти наверняка в пользу того, кто поставил на комбинацию
с большей вероятностью. Можно также вообразить, что в эксперименте
участвует большая группа людей (например, тысяча людей) и каждый
подбрасывает четыре монеты. Предположим все участники из первой
половины группы поставили на комбинацию 2, а все участники из вто-
второй половины группы — на комбинацию 1. Суммарный выигрыш в пер-
первой подгруппе почти наверняка будет выше суммарного выигрыша во
второй подгруппе. Так что и в такой ситуации обнаруживается практи-
практический смысл подсчета вероятностей.
t&ufia&e**. Значит, необходимы многократные испытания? Или много
испытаний выполняет один человек. Или по одному испытанию вы-
выполняют много людей.
Пвтор. Именно так. Ведь уже отмечалось, что, чем больше вероят-
вероятность события, тем чаще оно происходит. Чтобы этим воспользоваться
на практике, необходимо, очевидно, располагать большим количеством
испытаний. В противном случае нельзя оценить, насколько часто (или
редко) происходит событие.
*Чипииъель. Как я понял, случайности не позволяют предсказать оди-
одиночный исход, но возможно предсказание большого числа исходов. По-
Получается, что ради отдельного IоднократногоI испытания подсчет вероят-
вероятности события не имеет смысла?
Пвтор. Это не совсем так. Предположим, что подсчет дал для неко-
некоторого события весьма малую вероятность (например, 0,001). В подоб-
подобных случаях мы можем рассматривать данное событие как практически
невозможное. И напротив, если подсчет дал для некоторого события
вероятность, которая очень близка к единице (например, 0,998), то по-
подобное событие может рассматриваться как практически достоверное.
188

ь. Мне известно, что вероятность выпадения десяти орлов
при десяти подбрасываниях монеты равна 1/1024. Значит, я могу уве-
уверенно ставить на то, что десять орлов подряд при подбрасываниях мо-
монеты не выпадут. Но в таком случае те, кому, предположим, девять раз
не повезло, вправе полагать, что уж в десятый-то раз должно повезти.
Они могли, например, ставить на выпадение решки при бросании мо-
монеты. Пусть им несколько раз не повезло (все время выпадали орлы).
Но поскольку выпадение подряд десяти орлов — событие практически
невозможное, то по крайней мере при десятом подбрасывании должна,
наконец, выпасть решка. Разве не так?
Пвтор. Речь шла о практически невозможном событии. Однако такое
событие все-таки возможно. Откроем книгу Стругацких «Обитаемый ос-
остров». Там на первой странице читаем: «Максим обошел корабль, ведя
ладонью по холодному, чуть влажному его боку. Он обнаружил следы
ударов там, где и ожидал... Черные кляксы были теперь еле видны.
Метеоритная атака в стратосфере, вероятность — ноль целых, ноль-
ноль... Но ведь всякое возможное событие когда-нибудь да осуществля-
осуществляется...». Неплохо сказано.
7.7 Частотное (статистическое) определение
вероятности
Ог
'пыт убеждает нас, что, чем больше (меньше) вероятность данного
случайного события, тем чаще (реже) происходит это событие. Мето-
Методом, называемым «доказательством от противного», легко доказать, что
верно также обратное утверждение: чем чаще (реже) происходит некото-
некоторое случайное событие, тем больше (меньше) его вероятность. Отсюда
следует, что можно попытаться находить вероятность случайного собы-
события не на основе вычислений, а непосредственно из эксперимента.
До сих пор мы сначала вычисляли вероятность того или иного случай-
случайного события (опираясь на классическое либо геометрическое опреде-
определение вероятности и используя равновозможность элементарных исхо-
исходов), а уже потом обращались к эксперименту, убеждаясь на практике,
что частота появления данного события в достаточно больших сериях
испытаний колеблется вблизи вероятности события. При этом откло-
отклонения частоты от вероятности в ту или другою сторону оказываются
тем меньше, чем больше число испытаний в серии. Теперь мы обсудим
обратную ситуацию: сначала измерим в эксперименте с достаточно боль-
большим количеством испытаний частоту появления некоторого события,
189

а потом, уже на основании результатов эксперимента, оценим вероят-
вероятность данного события. Понятно, что таким образом мы сможем найти
не точное, а некоторое приближенное значение вероятности. Чем боль-
больше количество испытаний, тем, вообще говоря, точнее значение вероят-
вероятности, определяемое на опыте.
Итак, вот частотное {статистическое) определение вероятности:
Вероятность случайного события А — это постоянное число Р(А),
вблизи которого колеблется частота появления данного события
М{А) / N в сериях испытаний при условии достаточно большого количе-
количества N испытаний в серии. Таким образом,
Р{А) « М{А) IN, если 7V> 1.
Частотное определение вероятности позволяет получить вероятность
события всего лишь с некоторой точностью, приближенно — в этом
недостаток данного определения. Но зато частотное определение дает
возможность найти вероятность события в весьма различных ситуациях,
в частности и таких, где не удается указать равновозможные элементар-
элементарные исходы — в этом несомненное преимущество данного определения.
Неудивительно, что фактическое использование этого определения для
отыскания вероятности тех или иных событий началось практически
уже на первых этапах развития теории вероятностей.
В частности, частотное определение вероятности широко применялось
(и применяется) при рассмотрении явлений демографического характера. В
качестве примера отметим такие случайные события как рождение мла-
младенцев того или иного пола. Вот официальные данные шведской стати-
статистики за 1935-й год (здесь /=1, II, III,..., XII — месяцы года, Nt —
общее количество новорожденных в Швеции в /-ом месяце, Mt — коли-
количество родившихся девочек, vz = Mt / Nt — частота рождения девочек в
/-ом месяце):
V/
Nt
М,
v/
I
7280
3537
0,486
VII
7585
3621
0,462
II
6957
3407
0,489
VIII
7393
3596
0,484
III
7883
3866
0,490
IX
7203
3491
0,485
IV
7884
3711
0,471
X
6903
3391
0,491
V
7892
3775
0,478
XI
6552
3160
0,482
VI
7609
3665
0,482
XII
7132
3371
0,473
190

Частоты vI? vn, vin,..., vXII — представлены графически на рис. 1 в таб-
таблице 30. В той же таблице на рис. 2 представлены графически частоты
v1? v2, v3,..., v12, вычисленные с использованием соотношений:
v2=(MI+MII)/(NI+Nu);
v3 = (М, + Ми + Mw) /(N, + Nu + Nm);
v4 = (Мг + Ми + Мш + Mw) /{Nl + Nu + Nm
V12 =(Ml+Mll+... + Mxll)/{Nl + Nu +... + 7VXII).
Легко убедиться, что эти частоты имеют значения:
V! = 0,4829; v2 = 0,4877; v3 = 0,4887; v4 = 0,4840;
v5 = 0,4828; v6 = 0,4826; v7 = 0,4819; v8 = 0,4824;
v9 = 0,4827; v10 = 0,4834; vn = 0,4834; v12 = 0,4825.
Можно приближенно считать, что вероятность рождения девочки
равна 0,4825. Она показана на рис. 1 и рис. 2 в таблице 30 пунктирной
прямой.
Другой пример экспериментального поиска вероятности случайного
события на основе использования частотного определения вероятности
представлен на рис. 3 и рис. 4 в таблице 30. Здесь в качестве случайных
событий рассмотрены появления букв И, А, С, В, М в отрывке Н.В. Го-
Гоголя «Страшная месть» (сам отрывок приведен в таблице 31). Весь от-
отрывок разбит на десять кусков, обозначенных числами I, II, III, IV,..., X.
В каждом куске содержатся N= 200 знаков (в качестве знаков рассмат-
рассматриваются буквы, знаки препинания и пробелы между словами). Коли-
Количества появлений той или иной буквы в каждом отрывке (числа Мь М1Ъ
Миь Afjy,..., Mx) таковы:
Буква И:
Буква А:
Буква С:
Буква В:
Буква М:
I
20
7
4
6
2
II
13
8
6
4
4
III
13
8
10
12
9
IV
13
8
7
7
5
V
17
8
6
10
3
VI
12
9
8
10
8
VII
14
8
11
6
5
VIII
10
15
13
5
4
IX
12
12
7
5
7
X
8
18
11
9
6
191

Таблица 30. Частотное (статистическое) определение вероятности
Рис. 1 о,49О —
0,485 —
0,480 —
0,475 —
0,490
I II III IV V VI VII VIII IX X XI XII
0.485
0.480 1 2	3 4 5	6	[7
9 110 111 112	Рис.2
I II III IV V VI VII VIII IX X 1234567
192

Таблица 31. Отрывок из повести Н. В. Гоголя «Страшная месть»
Чуден Днепр при тихой погоде, когда вольно и
плавно мчит сквозь леса и горы полные воды свои. Ни j
зашелохнет; ни прогремит. Глядишь, и не знаешь, идет
или не идет его величавая ширина, и чудится, будто
весь вылит он из стекла, и будто голубая зеркальная
дорога, без меры в ширину, без конца в длину, реет и
вьется по зеленому миру. Любо тогда и жаркому солнцу
оглядеться с вышины и погрузить лучи в холод стек-
лянных вод и прибережным лесам ярко отсветиться в
водах. Зеленокудрые! они толпятся вместе с полевыми ™
цветами к водам и, наклонившись, глядят в них и не
наглядятся, и не налюбуются светлым своим зраком,
и усмехаются к нему, и приветствуют его, кивая вет-
ветвями. В середину же Днепра они не смеют глянуть: ^у
никто, кроме солнца и голубого неба, не глядит в него.
Редкая птица долетит до середины Днепра. Пышный!
ему нет равной реки в мире. Чуден Днепр и при теплой
летней ночи, когда все засыпает — и человек, и зверь,
и птица; а бог один величаво озирает небо и землю и
величаво сотрясает ризу. От ризы сыплются звезды.
Звезды горят и светят над миром и все разом отдаются
в Днепре. Всех их держит Днепр в темном лоне своем.
Ни одна не убежит от него; разве погаснет на небе.
Черный лес, унизанный спящими воронами, и древле
разломанные горы, свесясь, силятся закрыть его хотя
длинною тенью своею, — напрасно! Нет ничего в мире,
что бы могло прикрыть Днепр. Синий, синий, ходит он
плавным разливом и середь ночи, как середь дня; виден
за столько вдаль, за сколько видеть может человечье
око. Нежась и прижимаясь ближе к берегам от ночного
холода, дает он по себе серебряную струю; и она вспы-
вспыхивает, будто полоса дамасской сабли; а он, синий,
снова заснул. Чуден и тогда Днепр, и нет реки, равной
ему в мире! Когда же пойдут горами по небу синие
тучи, черный лес шатается до корня, дубы трещат и к
молния, изламываясь между туч, разом осветит целый
мир — страшен тогда Днепр! Водяные холмы гремят,
ударяясь о горы, и с блеском и стоном отбегают назад,
и плачут, и заливаются вдали. Так убивается старая
мать козака, выпровожая своего сына в войско.
193

Отсюда находим частоты, Vi = MI/ 200, vn = Мя / 200, vni = Мш / 200,
...5 vx = Мх I 200 для каждой из пяти рассматриваемых букв. Эти часто-
частоты графически представлены на рис. 3 в таблице 30. Чтобы найти веро-
вероятность появления той или иной буквы, надо посмотреть, как изменя-
изменяется частота ее появления по мере увеличения количества испытаний.
Иначе говоря, надо подсчитать для каждой буквы десять значений час-
частоты — от v1 (для N= 200) до v10 (для N= 2000), используя соотношения:
vx =71^/200;
v2=(MI+MII)/400;
v3 = (Мг + Ми + Мш) / 600;
+ Mu + Мт + Mw)/ 800;
v10 = (Ml + Ми + Мш + ... + Жх)/2000.
Графически все эти частоты представлены на рис. 4 в таблице 30.
Статистические данные, полученные нами при рассмотрении текста
из таблицы 31, оказались явно недостаточными для того, чтобы оце-
оценить вероятность появления букв И и А. Для буквы С мы получили
вероятность 0,041, для буквы В — 0,038, для буквы М — 0,026. Заметим,
что в интересной популярной книге A.M. Яглома и И.М. Яглома «Веро-
«Вероятность и информация» (М.: Физматгиз, 1960) приведены результаты
достаточно серьезных исследований по отысканию вероятности появ-
появления различных букв в художественных классических текстах. Эти ис-
исследования показали, что, например, вероятность появления буквы С
равна 0,045, буквы В — 0,038, буквы М — 0,026.
7.8 Диалог об определении вероятности,
предложенном Рихардом Мизесом
'Читатель. В § 7.7 дано частотное определение вероятности:
Р(А) « М{А) I N, если 7V> 1	A)
На первый взгляд, им очень удобно пользоваться на практике. По-
Поставь эксперимент с достаточно большим количеством испытаний N,
подсчитай количество исходов М(А) с появлением события А, подели
М (А) на N— и вот тебе для данного случайного события приближенное
значение вероятности Р(А). Однако при этом возникает ряд вопросов.
Что значит «достаточно большое число испытаний»? Сто испытаний,
194

тысяча, миллион? С какой степенью приближения соотношение A) дает
вероятность рассматриваемого события? Иными словами, насколько
точной оказывается вероятность Р(А), определяемая соотношением A)?
Пвтор. Вопросы совершенно уместные. Они возникают практически
у всякого, кто пытается поглубже осмыслить частотное определение
вероятности. Известный математик из Австро-Венгрии Рихард Мизес
A883-1953) предлагал снять эти вопросы, заменив приближенное соот-
соотношение A) точным соотношением:
Р(А)= lim M{A)/ N	B)
g4u<SiA&e*&. Что такое lim и как понимать тут стрелку?
Пвтор. Через lim математики обозначают знак предела («лимес» —
по-латыни «предел»). Соотношение B) означает, что, если сколь угод-
угодно увеличивать количество испытаний (иначе говоря, если устремить N
к бесконечности), то частота М(А) / Сбудет в пределе стремиться к точ-
точному значению вероятности Р{А).
'Чийии&ел*. По-моему, в этом есть смысл. Коль скоро с увеличением
количества испытаний N частота М(А) / N все больше и больше при-
приближается к значению вероятности, то логично допустить, что при бес-
бесконечно больших N эта частота окажется в точности равна вероятнос-
вероятности. Мне нравится определение вероятности, предложенное Мизесом.
Пвтор. Тем не менее математики не приняли этого определения.
ttutfiA&e**. Но почему?
Пвтор. В любом реальном эксперименте количество испытаний ко-
конечно. Оно может быть очень большим, но не может быть бесконеч-
бесконечным. И не только потому, что физически невозможно подбросить
монету или кубик бесконечное число раз. Стремясь, например, найти
вероятность появления той или иной буквы в художественном тексте,
в принципе нельзя отсмотреть бесконечно много букв уже по той при-
причине, что объем всех существующих текстов конечен. Стремясь найти
вероятность рождения девочек в течение какого-то года, в принципе
нельзя рассмотреть бесконечно много рождений, поскольку число де-
детей, родившихся за год на всем земном шаре, конечно. Так или иначе
в любом эксперименте мы рассматриваем конечное число испытаний.
ль. Все это так, если иметь в виду экспериментальный поиск
вероятности события. Но почему бы не рассматривать соотношение B)
как соотношение теоретическое*} Как соотношение, позволяющее не
измерять, а вычислять вероятность события.
Пвтор. И при таком подходе определение вероятности по Мизесу ока-
оказывается несостоятельным. Чтобы почувствовать это, следует поближе
195

познакомиться с понятием предела бесконечной последовательности чисел.
Пусть имеется некая бесконечная числовая последовательность:
(здесь п — последовательные номера членов последовательности от 1
до оо). Пусть некое число Р есть предел этой последовательности, т. е.
пусть Р = Х\трп. Задумаемся о том, как это следует понимать?
ёЧш9иийе*ь. Чего же тут задумываться? Это следует понимать так,
что числа рп стремятся к Р по мере того, как п неограниченно увели-
увеличиваются.
Пвтор. Это так. Однако не мешало бы пояснить математический
смысл используемого здесь глагола «стремятся». Выберем некоторое
число 8 > 0 и рассмотрим последовательность абсолютных значений
отклонений чисел р от Р:
\P-Pi\> \P~PiU \Р-Ръ\, •••> \P~PnU -	D)
Необходимым условием того, что Ресть предел последовательности C),
является неравенство
\Р-рп\<е,	E)
которое должно выполняться, начиная с некоторого номера N9 для всех
без исключения последующих номеров п. Которых, кстати говоря, беско-
бесконечно много.
"Читателе. Наверное, имеет смысл выбирать какое-то маленькое
число 8? А какое именно?
Пвтор. Пока мы говорили о любом числе 8 > 0. Но условие E), явля-
являясь необходимым, в то же время не является условием достаточным.
Надо теперь выбрать другое число 8 > 0, которое было бы меньше пре-
предыдущего числа 8. И надо убедиться, что и для нового 8 найдется номер N
(он будет больше предыдущего номера N), начиная с которого для всех
остальных п будет выполняться неравенство E). Затем надо выбрать
третье, еще меньшее число 8 > 0 — и снова убедиться, что, начиная с ка-
какого-то номера, неравенство E) будет выполняться для всех последую-
последующих номеров. И так далее.
И если мы можем утверждать, что, каково бы ни было число 8 > 0, обя-
обязательно найдется в нашей бесконечной последовательности C) номер N
такой, что для всех п > ^выполняется неравенство E), — вот тогда мож-
можно назвать Р пределом последовательности C) и записать: Р =]\трп.
%и*на*нелй. А нельзя ли привести пример последовательности, кото-
которая «стремится» к некоторому пределу?
196

Пвтор. В качестве примера рассмотрим последовательность, у кото-
которой п-й член (общий член последовательности) есть
Рп=B + п)/Bп).	F)
Вот первые десять членов такой последовательности:
3/2, 1, 5/6, 6/8, 7/10, 8/12, 9/14, 10/16, 11/18, 12/20,...
Убедимся, что данная последовательность имеет предел (при п —> оо) и
что этот предел равен Р = 1 / 2. В данном случае:
\P~Pn
2 + п
п
п-2-п
2п
=1/11.
Выберем произвольное число 8 > 0. Оно может быть сколь угодно
малым. Легко видеть, что неравенство E) имеет в данном случае вид:
1 / п < 8, откуда следует, что п > 1 / 8. Таким образом, в качестве номера N
надо выбрать любой номер больше 1 /е. Если, например, 8 = 0,001, то
можно выбрать N= 1001.
'Читатель. Тут все понятно.
Пвтор. А теперь обратимся к определению вероятности по Мизесу.
В качестве последовательности C) будем рассматривать последователь-
последовательность частот появления случайного события А. Ее общий член имеет вид:
рп=Мп(А)/п.	G)
М (А)
Чтобы можно было утверждать, что Р{А) — lim — , необходимо
п^оо П
убедиться что для произвольного, сколь угодно малого числа 8 > 0 обя-
обязательно найдется в нашей последовательности номер Атакой, что для
всех п> N будет выполняться неравенство
\Р(А)-Мп(А)/п\<г.	(8)
Однако вследствие случайного характера появлений благоприятных ис-
исходов Мп(А) мы не можем в данном случае (в отличие от последователь-
последовательности F)) указать, как числа рп зависят от п. Тут зависимости попросту
не существует). А значит, и предел B), объявленный Мизесом, попросту
не существует.
*Чит<ииель. Но тогда получается, что мы вообще не можем «подвести
теорию» под утверждение «чем чаше происходит событие, тем больше
его вероятность»! А ведь мы до сих пор утверждали, что, чем больше л,
тем ближе частота Мп(А) / Nk вероятности Р(А)\ Неужели это утверж-
утверждение тоже несостоятельно?
197

Пвтор. Нет, оно состоятельно. Иначе вообще не было бы частотного
определения вероятности. Дело в том, что утверждение «чем больше п,
тем ближе частота Мп(А) / N к вероятности Р(А)» отнюдь не означает,
что Р(А) = lim Мп {А) / п . Оно означает нечто иное.
'Читатель. Что же именно?
Пвтор. Об этом мы поговорим позднее. А пока заметим лишь, что
вместо несуществующего предела последовательности частот надо рас-
рассматривать последовательности вероятностей отклонения частот от ве-
вероятности события Р(А). При сколь угодно больших п не сами отклоне-
отклонения частоты от вероятности события стремятся к нулю, а всего лишь
вероятности этих отклонений становятся сколь угодно малыми. Это
есть так называемый закон больших чисел. Но о нем будет разговор в свое
время (см. § 11.7 и § 12.9).
ЗАДАНИЯ ПО ТЕМЕ 7
1.	Подбросьте игральный кубик 300 раз. Запишите, сколько раз выпали единица,
двойка, тройка, четверка, пятерка, шестерка. Подсчитайте и сравните друг с дру-
другом частоту выпадения каждой грани при количестве испытаний, равном 300.
Сравните с вероятностью 1/6.
2.	Используя результаты эксперимента, выполненного в задании 1, а также соотно-
соотношения (*) из § 7.1, подсчитайте частоты выпадения грани с числом очков, деля-
делящимся без остатка на 3, для серий с N= 20, 40, 60, ..., 300. Представьте вычис-
вычисленные частоты графически. Воспользуйтесь частотным определением
вероятности для экспериментального поиска вероятности выпадения грани с чис-
числом очков, делящимся без остатка на 3. Сравните с вероятностью, найденной на
основе классического определения.
3.	Подбросьте 300 раз пару игральных кубиков и отметьте исходы испытаний, при кото-
которых обе выпавшие грани имеют четное число очков. Подсчитайте частоты появле-
появления рассматриваемых исходов для серий с N=20, 40, 60,..., 300. Представьте вы-
вычисленные частоты графически и найдите из данного эксперимента вероятность
выпадения обеих четных граней при одновременном подбрасывании пары кубиков.
4.	Такое же задание, что и задание 3, но для события, при котором оба кубика
выпали гранями с одинаковыми очками.
5.	Такое же задание, что и задание 3, но для события, при котором один кубик
в паре выпал с четными очками, а другой кубик в паре — с нечетными очками.
6.	Как статистически заменить рассмотренный в § 7.1 эксперимент с тремя шара-
шарами в мешке (один шар черный, два белых; вынимают наугад шар из мешка; рас-
рассматриваемое случайное событие — появление черного шара) экспериментом
с подбрасыванием кубика? Выполните соответствующий эксперимент с кубиком
198

и по полученным результатам постройте графики, аналогичные графикам, пред-
представленным на рис. 4 в таблице 22.
7.	Как статистически заменить эксперимент с шестью шарами в мешке (два чер-
черных, три белых, один красный; случайное событие — вынимание из мешка белого
шара) экспериментом с подбрасыванием кубика?
8.	Как статистически заменить эксперимент с пятью шарами в мешке (один чер-
черный, четыре белых; случайное событие — вынимание из мешка белого шара)
экспериментом с подбрасыванием кубика?
9.	Предлагается выполнить следующий эксперимент. Предварительно надо начертить
мелом на доске (или карандашом на листе бумаги) упрощенную доску Гальтона, у
которой не 21 штырек и 7 ловушек, а только 10 штырьков и 5 ловушек (А, Б, В, Г, Д).
На такой доске шарик попадает в ту или иную ловушку после четырех столкновений
с штырьками. Шарик у нас здесь будет воображаемый, а результаты его вообража-
воображаемых столкновений с штырьками будут определяться с помощью подбрасываемой
монеты (орел — шарик отскочил от штырька вправо, решка — шарик отскочил вле-
влево). Эксперимент состоит в том, чтобы мысленно «пустить шарик» по такой доске
Гальтона 50 раз и определить (через подбрасывания монеты), в какой ловушке он
должен оказаться в том или ином случае. Надо изобразить на доске (или на бумаге),
как распределятся 50 воображаемых шариков по ловушкам. Хорошо бы, чтобы такой
эксперимент одновременно проделали несколько человек — каждый со своей рисо-
рисованной доской Гальтона. Интересно сравнить полученные результаты.
10.	Используя в качестве простого генератора случайных чисел игральный кубик и
жетон, постройте собственную таблицу из 400 однозначных случайных чисел (вклю-
(включая нуль), которые для удобства представьте в виде четырех столбцов четырех-
четырехзначных чисел (по 25 четырехзначных случайных чисел в каждом столбце). Испы-
Испытайте собственную таблицу случайных чисел на статистическую устойчивость,
используя примеры, приводившиеся в § 7.4.
11.	А теперь воспользуйтесь таблицей 25 (там 4750 однозначных случайные числа
сгруппированы в блоки из пятизначных чисел), подсчитайте и сравните частоты
появления нуля на первом и на пятом местах в пятизначных числах.
12.	Воспользуйтесь таблицей 26 (там 5250 однозначных случайных чисел сгруппиро-
сгруппированы в блоки из пятизначных чисел), подсчитайте и сравните частоты появления
нуля на втором и четвертом местах в пятизначных числах.
13.	При желании, повторите задания 11 и 12, но уже не для нуля, а для других цифр.
14.	Определите экспериментально вероятность выпадения орла, не подбрасывая мо-
монету, а используя: а) 4750 однозначных случайных чисел из таблицы 25, б) 5250 од-
однозначных случайных чисел из таблицы 26, в) 10 000 однозначных случайных чи-
чисел из таблиц 25 и 26, г) 400 однозначных случайных чисел из собственной таблицы.
Примечание. Здесь, как и в других случаях, используйте калькулятор для ускоре-
ускорения вычислений.
15.	Методом, рассмотренным в § 7.5, определите экспериментально значение числа п,
используя: а) 50 случайных точек из собственной таблицы случайных чисел, б) 150 слу-
случайных точек из таблицы 24, содержащей 1200 однозначных случайных чисел.
199

16.	Определите экспериментально вероятность выпадение грани кубика с числом
очков, делящимся без остатка на 3, не выполняя подбрасываний кубика, а ис-
используя случайные числа из первых шести столбцов пятизначных чисел в табли-
таблице 26 B100 однозначных случайных чисел).
Подсказка. Предварительно вычеркните все нули, встречающиеся среди 2100 од-
однозначных чисел.
17.	Определите экспериментально вероятность выпадения грани кубика с числом
очков 6, не выполняя подбрасываний кубика, а используя случайные числа из
первых шести столбцов пятизначных чисел в таблице 26.
18.	Определите экспериментально вероятность выпадения пары кубиков с четными
гранями, не выполняя подбрасываний пар кубиков, а используя случайные числа
из первых шести столбцов пятизначных чисел в таблице 26. Сравните результа-
результаты с теми результатами, которые были получены при выполнении задания 3.
19.	На 50 выпускников школы, из которых 20 девушек, выделено 25 путевок для ин-
интересной туристической поездки. Как отобрать 25 «счастливчиков» так, чтобы не
нарушить справедливость? Справедливость в данном случае означает, что у каж-
каждого юноши должна быть одинаковая: вероятность получить путевку, а у каждой
девушки вероятность получить путевку должна быть вдвое больше, чем у юноши.
20.	Из 50 десятиклассников школы, среди которых 20 девушек, надо направить 25 че-
человек на уборку городского парка. Как отобрать эти 25 человек по справедливо-
справедливости, предполагая, что все юноши должны иметь одинаковую вероятность попасть
на уборку парка, а у каждой девушки вероятность туда попасть должна быть вдвое
меньше, чем у юноши?
21.	Иван, Сергей и Юрий приобрели в складчину ценную книгу, причем Иван оплатил
50% стоимости книги, а Сергей и Юрий — по 25%. Каждому не терпится первым
прочитать книгу. Решили тянуть жребий, причем так, чтобы шансы получить кни-
книгу первым были у каждого пропорциональны размеру внесенной им за книгу сум-
сумму. Как это сделать, если воспользоваться: а) четырьмя шарами в мешке (шары
можно как-то обозначить), б) однократным бросанием игрального кубика, в) табли-
таблицей случайных чисел?
22.	В предлагаемом ниже эксперименте должны быть два участника: А и Б. Вероят-
Вероятность того, что при подбрасывании двух кубиков выпадет сумма очков равная 9,
есть Р(9) = 4/36. Вероятность же выпадения суммы 8 есть Р(8) = 5/36 (см.
рис. 3 из таблицы 20) Участник А ставит на то, что при подбрасывании двух куби-
кубиков выпадут 9 очков, а участник Б ставит на выпадение 8 очков. У каждого участ-
участника есть два кубика и каждый пусть сделает ровно 200 подбрасываний своей
пары кубиков и при этом аккуратно подсчитает, сколько раз выпала соответству-
соответствующая сумма (9 у участника А и 8 у участника Б). Сравните полученные результа-
результаты. Выиграет ли по итогам 200 подбрасываний участник Б? Соответствуют ли
результаты бросаний отношению вероятностей Р(9) / Р(8) = 4/5?
23.	Подберите какой-нибудь художественный текст и попробуйте оценить вероятность
появления в нем той или иной буквы.
200

ТЕМА 8
АЛГЕБРА СОБЫТИЙ
Читатель. Алгебра событий? Но мате-
математические действия выполняются над
буквами, если буквами обозначены чис-
числа! Разве можно выполнять алгебраичес-
алгебраические действия над буквами-событиями?
Автор. Можно. Используются такие по-
понятия как «сумма событий» и «произведе-
«произведение событий». В алгебре событий суще-
существуют переместительные, сочетательные,
распределительные и другие законы.
Читатель. Мы работаем с вероятнос-
вероятностями событий. При чем же тут алгебра
событий? Зачем она нужна?
Автор. Пользуясь алгеброй событий,
можно вычислить вероятность события,
представляя его как сумму или произве-
произведение других событий, вероятность ко-
которых известна или может быть надежно
измерена.
Вопросы и ответы
201

Можно придумать некий алфавит че-
человеческих мыслей и с помощью комби-
комбинации букв этого алфавита и анализа слов,
из них составленных, все может быть и от-
открыто, и разрешено.
Готфрид Вильгельм Лейбниц
Математическая логика есть логика по
предмету, математика по методу.
77. Порецкий, российский математик
8.1 Событие как множество, элементами которого
являются элементарные исходы
ХЭудем для конкретности рассматривать события, которые происхо-
происходят при двукратном бросании игрального кубика. Эту ситуацию мы до-
достаточно подробно обсуждали в § 6.6, где объясняли, что представляет
собой пространство элементарных исходов. Его называют также универ-
универсальным множеством. В рассматриваемом случае универсальное множе-
множество состоит из 36 элементарных исходов; вероятность каждого исхода
равна 1 / 36. Графически эти исходы были представлены на рис. 3 в табли-
таблице 20; они будут использоваться нами и в данной теме. Напомним, что
на упомянутом рисунке изображены отнюдь не двузначные числа; так,
например, 35 — это не «тридцать пять», а «три-пять» (это элементарный
исход с выпадением грани 3 в первом бросании кубика и грани 5 во
втором бросании). Во избежание путаницы будем в дальнейшем разде-
разделять дефисом очки выпавших пар граней: 1-1, 1-2,...
На рис. 1 в таблице 32 изображены в виде маленьких эллипсов 36 эле-
элементарных исходов испытаний с двукратным бросанием кубика и там
же выделены области, соответствующие шести выбранным в качестве
примера событиям: А, В, С, Д Д F. Каждая из этих областей (каждое из
шести событий) состоит из определенного набора элементарных исхо-
исходов. Иными словами, каждое событие есть множество, элементами ко-
которого являются соответствующие элементарные исходы.
Здесь уместно отметить, что понятие множества широко использует-
используется в математике. Множеством называют любой набор предметов, объек-
объектов, фигур, свойств, а также событий, собранных по какому-либо призна-
признаку (или нескольким признакам). Все эти предметы, объекты, фигуры,
свойства, события называются элементами множества. Множества
202

Таблица 32. Различные события при двукратном бросании кубика
203

с конечным числом элементов называют конечными множествами. Су-
Существуют также бесконечные множества (например, множество всех на-
натуральных чисел).
Рассматривая алгебру событий, мы фактически рассматриваем алгеб-
алгебру множеств. Точнее говоря, множеств событий.
Сделаем небольшое отступление исторического плана. Алгебра со-
событий, конечно, существенно отличается от алгебры чисел, хотя во
многом обнаруживаются аналогии. Последнее неудивительно, поскольку
как алгебра чисел, так и алгебра событий имеют общие корни в матема-
математической логике. Рождение математической логики во многом связано
с идеями знаменитого немецкого ученого (математика, физика, фило-
философа, языковеда) Готфрида Вильгельма Лейбница A646-1716), считав-
считавшего, что различные рассуждения могут быть в каком-то смысле сведе-
сведены к механическому выполнению определенных действий по некоторым
правилам. Как самостоятельный раздел математики математическая
логика начала формироваться с середины XIX столетия благодаря,
в основном, работам ирландского математика и логика Джорджа Буля
A815-1864) «Математический анализ логики» A847), «Логическое исчис-
исчисление» A848), «Исследование законов мышления» A854). Буль применил
алгебраические методы для решения логических задач и сформулировал
на языке алгебры некоторые фундаментальные законы мышления. За-
Законы алгебры событий, с которыми мы познакомимся в § 8.5, фактичес-
фактически моделируют алгебру Буля.
Но вернемся к рис. 1 в таблице 32 и рассмотрим выделенные здесь
шесть событий-множеств.
Событие А — выпала пара одинаковых граней. Оно представлено
множеством, элементами которого являются шесть элементарных исхо-
исходов: 1-1, 2-2, 3-3, 4-4, 5-5, 6-6. Вероятность данного события
Р(А) = 6/36.
Событие В — выпала пара граней, среди которых есть хотя бы одна
единица. В этом множестве одиннадцать элементов F-1, 5-1, 4-1, 3-1,
2-1, 1-1, 1-2, 1-3, 1-4, 1-5, 1-6). Вероятность события Р{В) = 11 / 36.
Событие С — выпала пара граней с суммой очков меньше 8; множе-
множество состоит из двадцати одного элемента. Вероятность события
РC6) = 21/36.
Событие D — выпала пара граней с суммой очков больше 7; множество
состоит из пятнадцати элементов. Вероятность события P(D) = 15 / 36.
Событие Е — выпала пара граней с суммой очков 10; множество
состоит из трех элементов. Вероятность события Р(Е) = 3/36.
204

Событие F — выпала пара граней с очками 5 и 5; множество состоит
из одного элемента (элементарного исхода 5-5). Вероятность события
P(F) = 1/36.
Как известно (см. §6.1), по отношению к любому событию можно
определить противоположное (дополнительное) событие. Если, напри-
например, рассматривается событие А, то противоположное событие обозна-
обозначают через А. Вероятности событий А я А связаны соотношением:
Р(А) + Р(А) = 1. Точно так же можно записать: Р(В) + Р(В) = 1 ,
Р(С) + Р(С) = 1 и так далее. На рис. 1 в таблице 32 событие D можно
рассматривать как событие С . В самом деле, если С есть событие с вы-
выпадением суммы очков меньше 8, то противоположным является собы-
событие с выпадением суммы не меньше 8, т. е. с выпадением суммы боль-
больше 7. А это и есть событие D.
События А, В, Ё, F на рисунке 1 не выделены. Однако нетрудно
найти их самостоятельно. Если А — событие с выпадением пары одина-
одинаковых граней, то А — событие с выпадением пары разных граней. Если
В — событие с выпадением пары граней, среди которых есть хотя бы
одна единица, то В — событие с выпадением пары граней, среди кото-
которых единицы нет.
В теории множеств используется понятие подмножества (части мно-
множества). Множество К называют подмножеством множества Z, если
каждый элемент множества К является одновременно элементом мно-
множества L. Записывают это так: К с L. Или вот так: Ld К. Заметим, что,
если бы при этом также каждый элемент множества L являлся одновре-
одновременно элементом множества К, то оба множества считались бы равны-
равными: К= L. Нетрудно сообразить, что, если К с L и L с М, то К с М.
Обращаясь к выделенным на рис. 1 в таблице 32 событиям, отметим,
что В с С, Еа Д ^с Д ^с D.
8.2 Несовместные и совместные события
в
§ 6.6 было введено понятие несовместных событий. Два события
называются несовместными, если невозможно их совместное появление
в одном и том же испытании. Если же это возможно, то события назы-
называются совместными. Несовместные события называют также взаимоис-
взаимоисключающими и непересекающимися. Последний термин связан с рассмот-
рассмотрением событий в рамках теории множеств. Сразу отметим, что любые
два элементарных исхода являются несовместными событиями.
Обращаясь к «языку» множеств, заметим, что несовместными (непе-
(непересекающимися) являются множества, у которых нет общих элементов.
205

Поэтому достаточно попросту взглянуть на рис. 2 в таблице 32, чтобы
сразу заключить о совместности или несовместности той или иной пары
событий из тех шести событий, которые выделены на рисунке. Всего из
шести событий можно составить С\ = 15 пар. Из этих пятнадцати пар
шесть пар являются несовместными (у них нет ни одного общего эле-
элементарного исхода) и девять пар — совместными (у них есть хотя бы
один общий элементарный исход).
Из несовместных отметим, прежде всего, события В и Д события В
и F, события В и D. Ясно, что, если хотя бы одна из двух выпавших
граней кубика единица (событие В), то сумма очков этих двух граней
не может равняться 10 (исключаются события Е и F) и вообще не мо-
может быть больше 7 (исключается D). При сумме очков меньше 8 исклю-
исключена сумма 10; поэтому несовместны СиД а также С и F. Наконец,
события С и D несовместны уже потому, что они являются взаимно
противоположными событиями (С = D и D — С). Взаимно противопо-
противоположные события всегда несовместны] ведь событие не может одновре-
одновременно (в одном и том же испытании) и происходить, и не происходить.
Теперь отметим девять пар совместных событий:
-	А и В (элементарный исход 1-1 — это одновременно и событие А,
и событие В: следовательно, оба события происходят одновременно в
испытании, имеющем исход 1-1);
-	А я С (общие элементарные исходы: 1-1, 2-2, 3-3);
-	А и D (общие элементарные исходы: 4-4, 5-5, 6-6);
-	В и С (являются общими все исходы для события В; ведь В —
подмножество множества С);
-	Е и D (являются общими все исходы для события Е; ведь Е —
подмножество множества D);
-	А и Д F я A, F и Д F я Е (в каждой из этих пар есть один общий
элементарный исход — исход 5-5).
Отметим очевидное общее положение: если К с L или La К, то со-
события Кя L совместны.
8.3 Пересечение и объединение событий
в
теории множеств вводятся понятия: «пересечение множеств» и «объе-
«объединение множеств». Они вводятся с помощью следующих определений.
Определение 1. Пересечением множеств Кя L является такое мно-
множество М, все элементы которого принадлежат и множеству К, и мно-
множеству L. Записывается это так: KC\L = M.
206

Определение 2. Объединением множеств Кж L является такое множе-
множество М9 все элементы которого принадлежат или множеству К, или мно-
множеству Z, или множествам Кя L вместе. Записывается это так: К[] L = M.
Наряду со знаками Пии здесь используется знак равенства =. На-
Напомним, что два множества равны, если каждый элемент первого мно-
множества является также элементом второго множества, а каждый эле-
элемент второго множества является также элементом первого множества.
Обращаясь к алгебре событий, будем говорить не о пересечении мно-
множеств К и Z, а о пересечении (или, иными словами, произведении)
событий К и Z, а также не об объединении множеств К и Z, а об объе-
объединении (или, иными словами, сумме) событий Кж L. Соответствую-
Соответствующие определения будут выглядеть так:
Определение 1. Пересечение (произведение) событий К я L есть
такое событие М, которое происходит тогда и только тогда, когда
происходят и событие К, и событие L:
Kf]L = M.	A)
Определение 2. Объединение (сумма) событий К я L есть такое
событие М9 которое происходит тогда и только тогда, когда происхо-
происходят или событие К, или событие Z, или события Kn L вместе:
K\JL = M.	B)
Примечание. В применении к событиям соотношения A) и B) часто
представляют в виде К- L = М я К+ L = M соответственно. Мы пред-
предпочитаем сохранить знаки П и U по той причине, чтобы у читателя не
возникала иллюзия, будто законы алгебры чисел можно автоматически
переносить на законы алгебры событий. Конечно, есть аналогия между
произведением чисел и пересечением событий, а также между суммой
чисел и объединением событий. Однако есть также и принципиальные
различия. События — это отнюдь не числа, а множества. Поэтому ра-
разумнее, на наш взгляд, применять при работе с событиями знаки Пии,
используемые в теории множеств.
Обратимся к событиям, выделенным на рис. 2 в таблице 32 (мы по-
прежнему рассматриваем испытания, состоящие в двукратном броса-
бросании игрального кубика):
-	событие А: выпали две одинаковые грани с суммой очков меньше 8,
-	событие В: выпали грани с суммой очков 4,
-	событие С: выпали грани 2 и 2,
-	событие D: выпали грани с суммой очков больше 8, но меньше 11,
-	событие Е\ выпали грани с суммой очков больше 9,
-	событие F: выпали грани с суммой очков 10.
207

Легко видеть, что А П В = Си что Dp\E = F. События ^иДа также
события D и Е являются совместными событиями, именно поэтому
представляет интерес рассматривать пересечения этих пар событий. Тут
термин «пересечение» говорит сам за себя.
А можно ли говорить о пересечении несовместных событий? Напри-
Например, событий А и D1 На первый взгляд, нельзя. Но в математике рас-
рассматривают пересечение (произведение) также и несовместных собы-
событий. Пересечение двух несовместных событий есть невозможное событие.
Ему соответствует так называемое пустое множество, т. е. множество,
не содержащее ни одного элемента. Невозможное событие (пустое мно-
множество) принято обозначать так: 0. Таким образом, Af]D= 0-
Соотношение
Kf]L = 0	C)
верно для любых двух несовместных событий и не верно для любых
совместных событий. Поэтому соотношение C) можно рассматривать
в качестве определения несовместности событий. События К и L не-
несовместны тогда и только тогда, когда К Г\Е = 0.
Теперь обратимся к событиям, выделенным на рис. 3 в таблице 32: со-
событие А — выпала сумма очков меньше 4, событие В — выпала сумма 4,
событие С — выпала сумма меньше 5, событие D — выпала сумма 10
либо 11, событие Е — выпала сумма больше 10, событие F — выпала
сумма больше 9, событие G — выпала сумма больше 4. Легко видеть,
что A\JB= С, D\JE=F. В первом случае имеем объединение (сумму)
несовместных событий (событие С происходит тогда и только тогда,
когда происходят или событие А, или событие В). Во втором случае
имеем объединение (сумму) совместных событий (событие F происхо-
происходит тогда и только тогда, когда происходят или событие Д или событие Д
или событие Df]E).
Особо отметим объединение двух взаимно противоположных собы-
событий. Такими здесь являются события Си G. Объединением множеств С
и G является множество, состоящее из всех тридцати шести элементар-
элементарных исходов, т. е. универсальное множество. Его обычно обозначают бук-
буквой Q. Универсальному множеству соответствует достоверное событие.
При двукратном бросании кубика обязательно реализуется какой-ни-
какой-нибудь из тридцати шести исходов. Итак, CU G=Q.
Легко доказать логически соотношения для произвольного события К:
К[\К = 0, К[)К = П.	D)
Первое соотношение есть прямое следствие соотношения C), по-
поскольку К и К — несовместные события. Для доказательства другого
208

соотношения учтем, что для любого события существуют две альтерна-
альтернативы: либо оно происходит (пусть это будет событие К), либо оно не
происходит (это есть событие К). Одно из двух обязательно имеет ме-
место; поэтому объединение событий К я К есть достоверное событие.
Для любых событий К очевидны соотношения:
Щ^ = 1, KUQ = Q;	E)
Щ0 = 0, K[J0 = K.	F)
Очевидны также соотношения:
Если KcL,to К П L = К и К (J L = L.	G)
Для любых KnL \ (КП L) с К, {К[\ Ц с Z;	(8)
Kc(KUL), Lc(KUL);	(9)
(K{]L)c(KUL).	A0)
Вот и начала работать алгебра событий. Самое время познакомиться
с законами этой алгебры.
8.4 Беседа о необходимости и достаточности
ь. Прежде чем мы займемся законами алгебры событий, я хо-
хотел бы кое-что уточнить. Несколько раз в предыдущем параграфе ис-
использовалась фраза «тогда и только тогда». Она, конечно, неплохо зву-
звучит, но не проще было бы ограничиться словом «тогда»? Почему бы не
сказать, что мы имеем дело с пересечением двух событий тогда, когда
происходят одновременно первое и второе? К чему тут фраза «тогда и
только тогда»? Или вот почему бы не сказать просто: «события Кж L
несовместны тогда, когда К П L = 0»? Зачем и здесь громоздить слова
«тогда и только тогда»? Математика — наука строгая. К чему ей лишние
фразы, даже если они красиво звучат?
Пвтор. Но фраза «тогда и только тогда» — это отнюдь не просто
красивая фраза. Ее применяют именно потому, что математика — наука
строгая. Если бы, например, в определении 1 в § 8.3 использовалось
лишь слово «тогда», то это означало бы, что совместное появление и
события К, и события L можно рассматривать как достаточное условие
того, чтобы говорить об их пересечении (если появились одновременно
и К, и Z, то имеем KC\L)9 однако эти события нельзя рассматривать как
условие необходимое (ведь возможно, что пересечение Кр\ L имеет место
и тогда, когда К ж L не появляются одновременно).
209

ь. А ведь верно! Фраза «тогда, когда происходят и событие К,
и событие L» ничего не говорит о том, будем ли мы иметь пересечение
К П L тогда, когда не происходят одновременно события К и L!
Пвтор. Вот именно. Добавление же слов «только тогда» как раз и
означает, что, если не происходят одновременно и событие К, и собы-
событие Z, то нельзя говорить о пересечении этих событий. Следовательно,
совместное появление обоих событий есть не только достаточное, но и
необходимое условие наличия пересечения этих событий. Именно поэто-
поэтому совместное появление событий можно рассматривать как определе-
определение их пересечения.
. Если я правильно понял, фраза «тогда и только тогда»
позволяет вместить в одно утверждение целых два утверждения! Так,
утверждение «пересечение К П L происходит тогда и только тогда, ког-
когда события К ж L происходят одновременно» вмещает в себя два утверж-
утверждения. Первое: «если происходит совместное появление событий КжЬ,
то можно говорить о пересечении К П L». Второе: «если не происходит
совместное появление событий К и Z, то нельзя говорить о пересече-
пересечении К П L».
Пвтор. Вы совершенно правы. Замечу, что вместо второго утвержде-
утверждения можно использовать утверждение: «если можно говорить о пересе-
пересечении К П L, то происходит совместное появление событий К и L».
Ведь если бы совместного появления событий К ж L не происходило, то
нельзя было бы говорить о пересечении событий! Таким образом, утверж-
утверждение «пересечение К П L происходит тогда и только тогда, когда собы-
события Кж L происходят одновременно» можно представить в виде таких
двух утверждений: «если события К ж L происходят одновременно, то
происходит пересечение К П L» и «если происходит пересечение К П А
то события Кж L происходят одновременно».
'гСи*к<инел<к. Но ведь это же прямая ж обратная теоремы! Получается,
что утверждение, использующее фразу «тогда и только тогда» означает,
что верны соответствующие прямая ж обратная теоремы!
Пвтор. Да, за фразой «тогда и только тогда» прячутся прямая и об-
обратная теоремы. Вспомним утверждение, с которым мы встретились
в предыдущем параграфе: «события К ж L несовместны тогда и только
тогда, когда К П L = 0». Это утверждение означает, во-первых, «если
К П L = 0, то события К ж L несовместны», а во-вторых, «если события
Кж L несовместны, то К П L = 0». Первая теорема (назовем ее прямой)
говорит о том, что равенство К П L = 0 есть достаточное условие не-
несовместности событий К ж Z, а вторая теорема {обратная теорема) гово-
говорит о том, что равенство К П L = 0 есть необходимое условие несовмест-
несовместности событий Кж L.
210

. Я убедился, что фраза «тогда и только тогда» — фраза
принципиально важная, а не просто красивая. Она связана с понятия-
понятиями необходимости и достаточности. Хотелось бы познакомиться с эти-
этими понятиями на каких-нибудь простых примерах. В частности, на та-
таких, где есть необходимость, но нет достаточности. И наоборот, есть
достаточность, но нет необходимости.
Пвтор. Вот совсем простой пример. Рассмотрим два утверждения: А
и В. Утверждение А. число делится без остатка на 3. Утверждение В:
число делится без остатка на 6. Ясно, что, если есть Д то есть также и А
(если число делится на 6, то оно, конечно, делится на 3); значит, В —
достаточное условие для А. В то же время нельзя сказать, что, если есть А,
то есть также и В (если число делится на 3, то оно не обязательно
должно делиться на 6); значит, А не является достаточным условием
для В. Зато А есть необходимое условие для В (если число не делится
на 3, то оно и подавно не делится на 6). Но, конечно, В нельзя считать
необходимым условием для А (если число не делится на 6, то это еще не
означает, что оно не делится на 3).
'Чипиинель. Как бы тут не запутаться.
Пвтор. Чтобы не запутаться, изобразим вот такую простую схему:
Утверждение А:
число делится на 3
Утверждение В:
число делится на 3
А — необходимое
(но не достаточное)
условие для В
В — достаточное
(но не необходимое)
условие для А
. Давайте озвучим эту схему, используя слово «тогда» и
слова «только тогда».
Пвтор. Это нетрудно сделать. Вот, пожалуйста:
Число делится на 3,
если оно (тогда, когда оно)
делится на 6.
Число делится на 3
не только тогда, когда оно
делится на 6.
Число делится на 6 только
при условии, что оно (только
тогда, когда оно) делится
на 3. Если оно не делится
на 3, то не делится на 6.
Число делится на 6 не тогда,
когда оно делится на 3,
а тогда, когда оно делится
на 3 и на 2.
211

b. А теперь, пожалуйста, пример, когда одно из утвержде-
утверждений является и необходимым, и достаточным условиями для другого.
Пвтор. В этом случае другое утверждение будет, в свою очередь, и
необходимым, и достаточным условиями для первого. Рассмотрим сле-
следующие два утверждения. Утверждение А: число делится на 3. Утверж-
Утверждение В: сумма цифр числа делится на 3. Вот соответствующая схема:
Утверждение А:
число делится на 3.
^^
Утверждение В: сумма
цифр числа делится на 3.
А — необходимое
и достаточное
условие для В.
В — необходимое
и достаточное
условие для А.
&. Всё понятно: число делится на 3 тогда и только тогда,
когда сумма его цифр делится на 3. Если сумма цифр числа делится
на 3, то и число делится на 3; если число делится на 3, то и сумма его
цифр делится на 3.
8.5 Законы алгебры событий
ГТапомним хорошо известные законы алгебры чисел:
—	переместительные законы:
B + Z? = Z? + ^; а-Ь — Ь-а
—	сочетательные законы:
а + (Ь + с) = (а + Ь) + с; а ЛЬ • с) = (ab)- с
—	распределительный закон:
А теперь рассмотрим законы алгебры событий, иллюстрируя их, при
необходимости, на примерах событий, происходящих при двукратном
бросании игрального кубика.
Прежде всего отметим два переместителъных закона:
KUL = LUK,	A1)
A2)
Они очевидны и пояснений не требуют.
212

Далее отметим два сочетательных закона:
-	A4)
Закон A3) очевиден. Закон A4), возможно, не столь очевиден; по-
поэтому проиллюстрируем его, обратившись к рис. 1 в таблице 33. На ри-
рисунке совершенно произвольно выделены три события — К, Z, М. В ле-
левой половине рисунка заштриховано событие i ПДа точками выделено
событие К П (L П Щ- В правой половине рисунка заштриховано собы-
событие К П L, а точками выделено событие (К П L) П М. Легко видеть, что
в обеих половинах штриховкой и точками выделено одно и то же собы-
событие — событие, состоящее из элементарных исходов 3-3, 3-4, 4-3, 4-4.
Следовательно, К П (L ПМ) = {К ПL) ПМ
В отличие от алгебры чисел, в алгебре событий существуют не один,
а два распределительных закона. Один из них имеет вид:
К П (L U М) = (К П L) U (К П М).	A5)
Проиллюстрируем этот закон, обратившись к рис. 2 в таблице 33, где
произвольно выделены события К, Z, М. В левой половине рисунка
заштриховано событие L U М9 а точками выделено событие X П (L []М).
В правой половине рисунка вертикальными прямыми заштриховано
событие К П L, а горизонтальными прямыми — событие ZflM Объе-
Объединение этих двух событий, т. е. событие (К П L) U (К П М), совпадает,
как легко видеть, с областью на левом рисунке, выделенной точками,
т. е. совпадает с событием К U (L Г\М).
Другой распределительный закон алгебры событий имеет вид:
К U (L П М) = (К U L) П (^ U М).	A6)
Этот закон проиллюстрируем, обратившись к рис. 3 в таблице 33. В ле-
левой половине рисунка выделено точками событие L П М9 а заштрихо-
заштриховано событие К U (L П М). В правой половине рисунка вертикальными
прямыми заштриховано событие К \JL,a горизонтальными прямыми —
событие K\JM.
Пересечение этих двух событий — событие (К U L) П (К U М). Оно
имеет двойною штриховку — вертикальными и горизонтальными пря-
прямыми. Легко видеть, что данное событие совпадает с областью на левом
рисунке, которая заштрихована, т. е. с событием К U (L Г\М).
Закон A5) имеет аналог в алгебре чисел: a(b + c) = ab + ac.A вот
закон A6) аналога в алгебре чисел не имеет. Формально такой аналог
213

Таблица 33. Законы алгебры событий и бросание кубика
(В) (ED
(В)
(В)
(В)
<в>
(В> с?з) (El)
<О> СЕ?) т^ (ЕР @>
К-
СВ)
О
(В)
(В)
(ED
(ED О
КП(ЬПМ) = (КПЬ)ПМ
(В) СЕ?)
(В) СЕ?)
(В)
D=1)
(В)
(В)
////
<4=2>
	L
У/,
'/,
с—
к
(В)
СВ)
(В>
СВ)
(ED
CED
CED
Рис.1
(В) „CB>
-Jv
СВ) CED
(В) (В>
М
|<4=1)	D=g)
(В) (В>
(В) св>
=(Э^=
®
CEJ)
B=4)
::i^4j:
=<4=4Х
СЕЗ)
@)
"LCB>
(ED
(ED
О)
СВ)
CED
(В>
(El)
(В)
(Ei)
Рис.2
<в>
(В)
<3>
(Q) (О) (ED
© © ©
(В) (В> (В)
KU(LDM) = (KUL) П (KUM)
Рис.3
^>;
••(ED--
..(О)..
•CED--
ж
•<ED--<E|>
//^=й/ууЙ=^
iii
. /&> . . *@>
KnL=KUL
Рис.4
i
(El)
!^^E^(ED
i
E=3)
U-Щ
O-
Q
(EJ)
(S>
(Ei)
О
о
СВ)
(ED
CED
О
(ED
CED
F=6)
киь=кпь
Рис.5
214

должен был бы иметь вид: а + b • с = (а + Ь) • {а + с). Это выглядит как
нелепость. Недаром закон A6) иногда называют «чудо-законом».
Из G), (8), (9) следуют так называемые законы поглощения
K,	A7)
Kf](K[jL) = K.	A8)
Они также не имеют аналогов в алгебре чисел. Формально такие
аналоги должны были бы выглядеть совершенно нелепо: а + а-Ъ — а и
а • (а + Ь) = а .
Не имеют аналогов в алгебре чисел также следующие два закона алгеб-
алгебры событий, представляющиеся очевидными:
К{]К = К,	A9)
К[}К = К.	B0)
Эти законы называют законами идемпотентности (от латинского
«идемпотенс», что означает «сохраняющий ту же силу»). Не имея ана-
аналога в алгебре чисел, законы A9) и B0) имеют, однако, аналогию с ло-
логическими законами, позволяющими исключать повторение одного и
того же утверждения. Обозначим через К утверждение «мак есть цве-
цветок». Тогда соотношение К {] К = К можно расшифровать так: «мак есть
цветок» или «мак есть цветок» — это все равно, что «мак есть цветок».
А соотношение К Г\К = К можно расшифровать так: «мак есть цветок»
и «мак есть цветок» — это все равно, что «мак есть цветок».
Отметим еще два закона алгебры событий. Их называют законами де-
Моргана — по имени шотландского математика и логика Огастеса де-
Моргана A806-1871), который независимо от Буля пришел к основным
идеям математической логики. Законы де-Моргана имеют вид:
А | | L — A U L ,	\^Ч
A U Ь - А [ | L .	B2)
Проиллюстрируем закон B1), обратившись к рис. 4 в таблице 33. Здесь
произвольно выбраны события 1и1. Универсальное множество, объе-
объединяющее все тридцать шесть элементарных исходов, обозначено
через W. В левой половине рисунка заштриховано событие К П L, а точ-
точками выделено противоположное событие (событие K[\L). В правой
половине рисунка вертикальными прямыми заштриховано событие К ,
а горизонтальными прямыми — событие L. Легко видеть, что объеди-
объединение событий I и I т.е. событие К(JL, совпадает с областью на
левом рисунке, выделенной точками, т. е. совпадает с событием К П L.
215

Закон B2) проиллюстрируем на рис. 5 в таблице 33, где, для про-
простоты выделены те же события К я L, что и на рисунке 4. В левой
половине рисунка заштриховано событие IUA а точками выделено
противоположное событие (событие K{]L). В правой половине ри-
рисунка вертикальными прямыми заштриховано событие К, а горизон-
горизонтальными — L. Видно, что пересечение событий К и L (событие
K[\L) совпадает с областью на левом рисунке, выделенной точками,
т. е. с событием К (J L.
8.6 Диаграммы Эйлера-Венна
На
La рисунках в таблицах 32 и 33 были продемонстрированы графи-
графически (а потому наглядно) различные отношения между событиями-
множествами на примере ситуации с двукратным бросанием игрально-
игрального кубика. Можно, однако, отвлечься от конкретной случайной ситуации
и наглядно представить различные отношения между событиями в об-
общем случае. Это можно сделать, воспользовавшись диаграммами Эйле-
Эйлера-Венна, на которых множества представляются плоскими фигурами,
чаще всего кругами. Эти диаграммы названы в честь выдающегося ма-
математика из Швейцарии Леонарда Эйлера A707-1783) и английского
ученого, специалиста по вероятностной логике Джона Венна A834-1923).
Эйлер впервые предложил представлять взаимно пересекающиеся мно-
множества каких-либо объектов в виде пересекающихся кругов; их называ-
называют теперь «кругами Эйлера». («Круги Эйлера» — это, например, множе-
множество студентов и множество спортсменов, множество насекомых и
множество летающих животных, множество салатов и множество рыб-
рыбных блюд). Что касается Венна, то ему принадлежит честь дополнения
кругов Эйлера противоположными множествами.
В таблице 34 изображен ряд диаграмм без учета противоположных
событий-множеств. На рис. 1 представлены в виде кругов события А
и В для случая, когда В с А. На рис. 2 и рис. 3 можно видеть пары пе-
пересекающихся кругов (пары совместных событий А и В). При этом на
рис. 2 заштриховано событие А П Д а на рис. 3 заштриховано событие
A U В.
На остальных шести рисунках в таблице 34 изображены в виде трех
пересекающихся кругов по три совместных события — события А, Д С.
На рис. 4 заштриховано событие A U В U С, представляющее собой объе-
объединение (сумму) трех событий. На рис. 5 горизонтальными прямыми
216

Таблица 34. Диаграммы Эйлера-Венна (первая часть)
— событие АПВ
Рис.2
В
— событие A U В
Рис.3
событие
AUBUC
Рис.4
-АПВ
-АПС
-ВПС
-АПВПС
Рис.5
-	событие
ВПС
-	событие
А11(ВПС)
Рис.6
А,
\
ч
1
L
1
—	событие
AUB
—	событие
AUC
Рис.7
\
/
•
Ч
!
•
*
N
J
V
:
s
/
\
/
событие
BUC
- событие
АП(ВиС)
Рис.8
— событие
(АПВ)и(АПС)
Рис.9
217

заштриховано событие А П Д прямыми, отклонившимися от вертикали
влево, заштриховано событие А П С, прямыми, отклонившимися от вер-
вертикали вправо, заштриховано событие В Г\ С. Точками здесь выделено
событие А П В П С, представляющее собой пересечение (произведение)
трех событий.
Здесь уместно сформулировать определение объединения трех событий.
Определение. Объединение (сумма) событий А, В и С есть такое со-
событие, которое происходит тогда и только тогда, когда происходят или
событие А, или событие Д или событие С, или событие А Р\В (события
АжВ вместе), или событие А П С (события Аж С вместе), или событие
В П С (события 5 и С вместе), или событие Л П В П С (события А, Д С
вместе).
На рис. 6 в таблице 34 точками выделено событие В П С, а штрихов-
штриховкой показано событие Л U B? П С). На рис. 7 вертикальными прямыми
заштриховано событие A U Д а горизонтальными прямыми — событие
^4LJC Легко видеть, что пересечение событий A U В я A U С (это есть
событие (A U В) р\ (A U С)) совпадает с событием A U (В П С), пока-
показанным на рис.6. Следовательно, Л U (В П С) = (A U 2?) П (Л U С).
Таким образом, мы доказали е общем случае (не прибегая к частной
ситуации с двукратным бросанием кубика) распределительный закон A6).
Рисунки 8 и 9 позволяют доказать в общем случае распределительный
закон A5).
В таблице 35 изображен ряд диаграмм с учетом противоположных
событий. На рис. 1: круг — некоторое событие А, заштрихованная об-
область — противоположное событие (событие А). Область прямоуголь-
прямоугольника Q — это универсальное множество (достоверное событие);
A U А — Q. На рис. 2 два круга представляют события А ж В, причем
В с А. Из этого рисунка, следует, что, если В с А, то В d A .
На остальных шести рисунках в таблице 35 рассматриваются наряду
с событием Q два совместных события (А и В), представляющие собой
пересекающиеся круги. При этом на рис. 3 заштриховано событие
A U В , на рис. 4 заштриховано событие А П В , на рис. 5 заштриховано
событие A\JB, на рис. 7 заштриховано событие А[\В. Сравнивая
рисунки 5 и 6, мы получим доказательство в общем случае (без броса-
бросаний кубика) одного из законов де-Моргана — того, который в § 8.5 был
представлен соотношением B2). А другой закон де-Моргана (соотно-
(соотношение B1)) легко доказывается в общем случае в результате сопостав-
сопоставления рисунков 7 и 8.
218

Таблица 35. Диаграммы Эйлера-Венна (вторая часть)
Рис.1
А-
В-
Рис.2
Q
В
-А
-В
-AUB
т.
-апв
ж
-AUB
-А
-В
-АПВ
-АПВ
А-
В-
-А
ш
•
гН
В
. . . .
Рис.8
—Q
-AUB
219

ЗАДАНИЯ ПО ТЕМЕ 8
1.	Изобразите на листе бумаги пространство элементарных исходов (универсаль-
(универсальное множество) для двукратного бросания кубика, как это делалось на рисунках
в таблице. Используя для удобства цветные карандаши, выделите следующие со-
события: Л/ — выпала пара граней с суммой очков больше 5, но меньше 9; Q —
выпала пара граней с суммой очков меньше 6 или больше 8; R — выпала пара
граней, среди которых есть, по крайней мере, одна четверка; S — выпала пара
граней с нечетной суммой очков; Т— выпала пара граней с разностью очков 4.
Укажите здесь все пары совместных и несовместных событий.
2.	Сколько элементов содержит универсальное множество в случае трехкратного
бросания кубика? в случае однократного бросания додекаэдра? в случае дву-
двукратного бросания додекаэдра? в случае двукратного бросания икосаэдра?
Ответы: 216, 2, 144, 400.
3.	а) Если события Л\л В несовместные события Л\л С несовместные, то следует ли
отсюда, что события Б и С тоже несовместные? б) Если события Ли В совмест-
совместные и события Л и С совместные, то следует ли отсюда, что события Л и С тоже
совместные? Ответы докажите с помощью диаграмм Эйлера-Венна.
Ответы: а) не следует, б) не следует.
4.	а) Какое событие является пересечением событий Q и 0? б) Ка кое событие
является объединением событий Q и 0?
Ответы: а) 0, б) Q.
5.	В алгебре чисел верно утверждение: «если а + b = а + с, то Ь = с». В алгебре
событий утверждение «если K{JL = K{JM то L = М» не яв ляется верным. Дока-
Докажите это.
Подсказка. Для доказательства рассмотрите, например, такие события в ситуа-
ситуации с двукратным бросанием кубика: К — выпала сумма меньше 8, L — выпала
сумма 8 или 9, М — выпала сумма больше 5, но меньше 10.
6.	В алгебре чисел верно утверждение: «если а-Ь = а-с и а ^ 0 , то b = с». А вот
в алгебре событий утверждение «если KP\L = КР\М и К^0,то L = M не явля-
является верным. Докажите это.
7.	Является ли множество M\J(KP\L) подмножеством множества (K[jL)[jM?
Ответ: является.
8.	Является ли множество [(К П L) U К] U L подмножеством множества [(/_ Г\1-)ЦК]Г\(КЦК).
Ответ: не является.
9.	Используя законы алгебры событий, докажите следующие соотношения;
a) Z\J(K\JL) = a,
б)
г)	L{J(K{JL) =
д)	K{J(K{J0)=U[](K{JK),
е)	П(и) (и)П
220

10.	Используя законы алгебры событий, найдите, как проще представить следующие
события:
а)	LU(KUL),
б)	КП(/-ПК),
в)	L[)[K[)(L\JK)],
г)	КГ\[1-Г\(КГ\Ц],
A) (K(JK(JK)f}(L{JL{JL),
е)	(Kf)Kf)K){J(Lf)Lf)L),
ж)	Lf][K\J(Lf]K)},
з)	(ЩК)П(КПК),
и) (KfU)UK,
к) (КП/-)П/С ,
л) (КЩ)Ги_,
м) (K[JL)\JK.
Ответы: а) ЩК, 6) Kf]L, в) /-UK, г) KfU.A) KfU.e) К11/-,ж) /-ПК,
з)К, и) КП/-, к) К, л) K\JL, м) К.
11.	Используя законы алгебры событий, докажите следующие соотношения:
a)
б)
в)
г)
д)	[Lf1(KUL)]UK =
е)
ж)
з)
12.	Является ли взаимная противоположность событий необходимым и достаточным
условием их несовместности?
Ответ: не является.
13.	а) Сформулируйте необходимое и достаточное условие делимости без остатка
на 4. б) Сформулируйте хотя бы одно условие делимости без остатка на 4, являю-
являющееся необходимым, но не достаточным, в) Сформулируйте хотя бы одно усло-
условие делимости без остатка на 4, являющееся достаточным, но не необходимым.
14.	Попробуйте сформулировать определение для объединения (суммы) четырех со-
событий. Как изменится это определение, если заранее предположить, что ни одно
из четырех событий не является совместным с другими событиями?
221

ТЕМА 9
АЛГЕБРА СОБЫТИЙ
И ОСНОВНЫЕ ПРАВИЛА
ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТЕЙ
Наука о вероятностях, известная под названием тео-
теории вероятностей, имеет предметом своим вычисление
вероятности события по данной связи его с событиями,
которых вероятности известны.
П.Л. Чебышёв
Справка:
Пафнутий Львович Чебышёв A821-1894) — выдающийся российский матема-
математик, внесший принципиально важный вклад в развитие теории вероятностей. Ос-
Основатель знаменитой Петербургской математической школы, к которой принад-
принадлежали, в частности, ученики и последователи П.Л. Чебышёва академики Андрей
Андреевич Марков A856-1922) и Александр Михайлович Ляпунов A857-1918).
э
9.1 Правило сложения вероятностей
несовместных событий
'то правило таково: Если события А и В несовместные, то
P(A{JB) =
A)
222

Иными словами, вероятность объединения двух несовместных событий
равна сумме вероятностей этих событий.
Предположим, что рассматриваются г событий (Ah Аъ Аъ, ..., Аг),
среди которых нет ни одной пары совместных событий. В этом случае
вероятность объединения всех рассматриваемых событий равна сумме
вероятностей событий:
P(A1\JA2\JA3\J...\JAr) =
B)
Правило A) (а также B)) особенно легко доказывается для ситуаций,
когда можно пользоваться классическим определением вероятности. Пусть
из общего количества п элементарных исходов оказываются благопри-
благоприятными для события А тА исходов, а для события В — тв исходов.
События А и В несовместные; поэтому среди упомянутых тА и тв исхо-
исходов нет совпадающих. Используя определение B) из § 6.1, запишем:
Р(А) = тА/п; Р(В) = тв/п.	(*)
Согласно определению 2 из § 8.3 событие A U В происходит тогда и только
тогда, когда происходят или событие А, или событие В (напомним, что
события А я В несовместные). Значит, для того, чтобы событие A[jВ
произошло, необходимо и достаточно, чтобы реализовался любой из
указанных выше тА и тв элементарных исходов. Таким образом, общее
количество элементарных исходов, благоприятных для события A U Д
равно тА + тв и, следовательно,
Р(А UВ) = (тА +тв)/п = (тА /п) + (тв /п).	(**)
Сравнивая (*) и (**), заключаем: Р(А U В) = Р(А) + Р(В).
Итак, воспользовавшись классическим определением вероятности,
мы получили правило сложения вероятностей несовместных событий.
Теперь, тренировки ради, проделаем рассуждения в обратном направ-
направлении. Воспользуемся правилом сложения вероятностей несовмест-
несовместных событий и, применив его к п несовместным равновероятным ис-
исходам, выведем классическое определение вероятности. Обозначим п
элементарных исходов (речь идет о полном количестве элементарных
исходов для данного типа испытаний) через Къ К2, Къ, ..., Кп. Учтем,
что Р(КХ) = Р(К2) = Р(КЪ) = ... = Р(Кп) и что сумма всех этих вероят-
вероятностей равна единице как вероятность достоверного события. Отсюда
заключаем, что
^ = \/п для /=1, 2, 3, ..., п.	(***)
223

Пусть для некоторого события А благоприятны исходы Къ Къ Къ,..., Кт —
всего т исходов. Используя (***), заключаем отсюда, что
(****)
Так как событие Л есть событие Кх \JK2\JK3 \J...\JKm9 то из (****)
немедленно получаем: Р{А) = т / п.
Заметим, что с правилом сложения вероятностей несовместных со-
событий согласуются соотношения D) и F), рассматривавшиеся в §6.1.
В § 6.4 мы решали задачу под названием «Поиск нужной книги».
Путем относительно сложных рассуждений мы установили там, что ве-
вероятность обнаружить адрес знакомого, выбирая наугад г книг из s книг,
равна г / s. Этот результат можно было бы получить сразу, если бы мы
воспользовались правилом сложения вероятностей. В самом деле, веро-
вероятность обнаружить адрес в любой из s книг равна 1 / s. Из этих s книг
мы внимательно просматриваем в поисках адреса какие-то г книг. Об-
Обнаружение адреса в 1-й, 2-й, 3-й,..., r-й книге являются, очевидно, не-
несовместными событиями. Обозначим их через Къ Къ Къ, ..., Кг. Соглас-
Согласно правилу B),
В том же параграфе (в § 6.4) в задаче «поиск водителя с водительски-
водительскими правами» мы наугад рассаживали в семиместном микроавтобусе семь
человек (потом шесть человек, пять, четыре, три, два), полагая, что
всякий раз только какие-то двое из рассаживаемых имеют водитель-
водительские права. Надо было подсчитать для каждого случая вероятность того,
что на водительском месте окажется человек с правами. Достаточно
непростые подсчеты с учетом различных сочетаний и перестановок дали
во всех случаях подозрительно одинаковую вероятность — 2/7. Почему
всякий раз 2/7? Уже тогда возникла мысль, что, наверное, есть какой-
то простой способ подсчета. Он действительно существует и основан на
правиле сложения вероятностей несовместных событий. Согласно этому
правилу вероятность того, что при произвольном рассаживании человек
с правами окажется на водительском месте, равна 1/7. Водительские
права имеют два человека. Поскольку нам все равно, кто именно из них
случайно окажется на месте водителя, заключаем, что искомая вероят-
вероятность есть 1/7+1/7 = 2/7. Как говорится, «ларчик просто открывался».
Теперь продемонстрируем правило сложения вероятностей несовме-
несовместных событий для некоторой ситуации, когда используется геометри-
геометрическое определение вероятности. Предположим, что на квадрат площа-
площадью S случайным образом бросают мелкие зерна (это можно делать
224

умозрительно, воспользовавшись таблицей случайных чисел). В квадрат
вписан круг. Пусть событие А — случайное попадание зерна в заштрихо-
заштрихованный сектор круга на рис. 1 в таблице 36; вероятность этого события
Р(А) = Si /X, где Si — площадь заштрихованного сектора. Пусть событие
В — попадание зерна в заштрихованный сектор на рис. 2; Р(В) = S2/Z.
Ясно, что событие A U В есть случайное попадание зерна в круг (см. рис. 3);
P(A[jB) = S/Е. Легко видеть, что S/Ъ = {Sx /X) + E2 /X) и, следова-
следовательно, Р(А U В) = Р(А) + Р(В). Тем самым правило A) оказывается
работающим также в ситуации, когда классическое определение веро-
вероятности не годится, но можно воспользоваться геометрическим опреде-
определением вероятности.
Правило A) (а также B)) применяют также тогда, когда используется
частотное определение вероятности. В § 7.7 мы упоминали о приведен-
приведенных в книге A.M. Яглома и И.М. Яглома «Вероятность и информация»
результатах исследований по экспериментальному отысканию вероятно-
вероятности появления различных букв в художественных текстах. В этой книге
приводятся, в частности, следующие значения вероятности для различных
гласных букв: для буквы «о» — 0,090, для буквы «е» (включая букву «ё») —
0,072, для буквы «а» — 0,062, для буквы «и» — 0,062, для буквы «у» —
0,021, для буквы «я» — 0,018, для буквы «ы» — 0,016, для буквы «ю» —
0,006, для буквы «э» — 0,002. Применяя правило B), можно найти веро-
вероятность появления в тексте гласной буквы. Эта вероятность есть
0,090 + 0,072 + 0,062 + 0,062 + 0,021 + 0,018 + 0,016 + 0,006 + 0,002 = 0,349.
НЕЗАПЛАНИРОВАННЫЙ ДИАЛОГ
ticuftiiAe**. Итак, правило сложения вероятностей для несовместных
событий можно применять как в тех случаях, когда исходные вероятно-
вероятности могут быть строго определены (классические вероятности или гео-
геометрические вероятности), так и в тех случаях, когда они определяются
приблизительно, например через измерение частот появления рассмат-
рассматриваемых событий. Не так ли?
Пвтор. Именно так.
*Чи(*иипель. Тогда давайте рассмотрим следующую задачу. Два охот-
охотника одновременно стреляют по летящей утке. Исходя из частот попа-
попаданий по летящим птицам, можно считать, что для первого охотника
вероятность попасть в утку равна, скажем, 0,3, а для второго охотника
(более меткого) вероятность попасть в утку равна 0,9. Утка будет под-
подстрелена, если в нее попадет хотя бы один из охотников, неважно ка-
какой именно. Получается, что вероятность того, что утка будет подстре-
подстрелена, должна равняться 0,3 + 0,9 = 1,2. Но такой результат абсурден!
Вероятность не может быть больше единицы! В чем же тут дело?
225

Таблица 36. Некоторые правила вычисления вероятностей
ш.
\
\
\
ч
V/
1
"^ч
у
\
\
\
\
/
i
у
Рис.1
Рис.2
Рис.3
В
Рис.5
Рис.6
226

Пвтор. Давайте уточним, вероятности каких именно событий Вы скла-
складывали? Что есть событие А и что есть событие В ?
*Чи(*иипель. Событие А — утка подстрелена в результате попадания
в нее первого охотника. Событие В — утка подстрелена в результате
попадания в нее второго охотника.
Пвтор. Являются ли эти события несовместными, т. е. взаимоисклю-
взаимоисключающими? Можно ли утверждать, что они не могут произойти одновре-
одновременно (в одном и том же испытании)?
'Чиниинель. Так утверждать нельзя. В летящую утку могут попасть
оба охотника.
Пвтор. Значит, события А и В не являются несовместными. А поэто-
поэтому использование правила A) в данном случае неправомерно.
ь. Как же быть? Как найти в данном случае вероятность
того, что летящая утка окажется подстреленной?
Пвтор. Мы обсудим это позднее.
9.2 Правило вычисления вероятности объединения
двух совместных событий
э.
/то правило таково:
Если события Аи В совместны, то
Р(А [}В) = Р(А) + Р{В) - Р(А П В).	C)
Иными словами, чтобы найти вероятность объединения двух совместных
событий, надо сложить вероятности этих событий и вычесть вероят-
вероятность их пересечения. Заметим, что часто данное правило называют «пра-
«правилом сложения вероятностей совместных событий». Однако название
«правило сложения» здесь не вполне уместно, поскольку в C) происхо-
происходит не только сложение, но и вычитание вероятностей.
Легко видеть, что правило C) годится также для событий несовместных.
Ведь для таких событий Р(АГ\ В) = 0, и правило C) превращается в A).
Докажем правило C), воспользовавшись диаграммами Эйлера-Вен-
на. Событие A U Д являющееся объединением двух совместных собы-
событий А и В, показано штриховкой на рисунке 3 в таблице 34. Обратим
внимание на то, что заштрихованною на этом рисунке фигуру можно
рассматривать не только как объединение совместных событий А ж В,
но также как объединение несовместных событий Вж А[\В или объе-
объединение несовместных событий А и А П В (событие А П В показано
227

с помощью штриховки на рис. 4 в таблице 35). События Вя Ар\В (как
и события Аи А П В) несовместны, поскольку представляющие их на
диаграмме Эйлера- Венна фигуры не пересекаются с друг другом.
Учитывая несовместность В и А П В , можем записать:
В) = Р(В U (А П В)) = Р(В) + Р(А П 5).	(*)
Используя рис. 4 из таблицы 35 и рис. 2 из таблицы 34, предста-
представим событие А как объединение несовместных событий А П В я А{] В
применим правило сложения вероятностей несовместных событий.
Получим:
Вычитая (**) из (*), находим:
Р(АU В)- Р(А) = Р(В) + Р(АПВ)- Р(АП В)- Р(АП В).
Отсюда следует, что Р(А [} В) = Р(А) + Р(В) - Р(А П В). Это и требова-
требовалось доказать.
Проведенное доказательство правила C) годится для общего случая
(для классических, геометрических, частотных вероятностей событий А
и В). Однако это доказательство не отличается наглядностью; оно мо-
может показаться достаточно сложным и формальным. Поэтому полезно
познакомиться с простым и наглядным выводом правила C), который
предполагает использование классического определения вероятности.
Пусть п — полное количество элементарных исходов для данного типа
испытаний, т. е. количество элементов универсального множества Q.
Обозначим через тА количество элементов множества (события) А, а
через тв — количество элементов множества (события) В. Ясно, что
Р{А) = тА/ п и Р{В) = тв/ п. Предположим, что множества Аи В пере-
пересекаются и их пересечение содержит тм элементов. Нетрудно сообра-
сообразить, что множество (событие) A U В будет содержать количество эле-
элементов, равное
т = (тА- тАВ) + тАВ + (тв - тАВ)	(***)
(это поясняет рис. 4 в таблице 36). Раскрывая в (***) скобки, получаем:
т = тА + тв - т^. Отсюда следует, что
Р(А\\т- тА+Мв~ Мав _Ма ,гпв тАВ _	тАВ
п	п п п	п
228

Отношение тАВ / п есть отношение количества благоприятных для
события А П В элементарных исходов к полному количеству элементар-
элементарных исходов; иначе говоря тАВ/ п = Р(А{] В). Таким образом,
Р(А U В) = Р(А) + Р(В) - Р(А П В) что и требовалось доказать.
Итак, правило C) доказано. Однако практически воспользоваться
им мы не можем, так как пока не научились вычислять вероятность
пересечения событий А ж В (вероятность Р(АГ\В)). Чтобы решить эту
проблему, нам придется познакомиться с понятием «условная вероят-
вероятность». Но прежде того выведем правило вычисления вероятности объе-
объединения трех совместных событий.
9.3 Правило вычисления вероятности
объединения трех совместных событий
Эйлера-Венна для трех совместных событий рассмат-
рассматривались на рисунках 4, 5, 6, 7, 8, 9 в таблице 34. Три события А, В, С
попарно пересекаются и, кроме того, имеет место пересечение всех трех
событий. Для этого случая справедливо правило:
Р(А U В U С) = Р(А) + Р(В) + Р(С) - Р(А ПВ)-
- Р(А ПС)- Р(В f]C) + P(Af]Bf]C).
D)
Докажем правило D), используя классическое определение вероятности.
Примем обозначения:
п — количество элементов универсального множества;
т — количество элементов множества ^4IJ^UC [т/п — Р(АUВUС)];
тА, тв, тс — количества элементов множеств А, В, С соответственно
тлв — количество элементов множества АП В [тАВ/ п = Р(Ар\В)];
тАС — количество элементов множества А{] С [тАС/ п = Р(А{] С)];
твс ~ количество элементов множества ВГ\ С [твс / п = Р(ВГ\ Q];
тлвс — количество элементов множества А П В П С [т^с / п = Р(АГ\ВГ\С)].
Кроме того, обозначим:
™'ав =
(*)
229

Как хорошо видно из рис. 5, представленного в таблице 36, множество
(событие) A U В U С можно рассматривать как объединение семи непере-
непересекающихся подмножеств (семи несовместных событий). На рисунке ука-
указано для каждого из них количество элементов. Легко видеть, что
т=(тА- тАВ - тАС - тАВС) + {тв - тАВ - твс - тАВС) +
+ (тс - тАС - твс - тАВС) + тАВ + тАС + твс + тАВС.
Раскрывая скобки, запишем:
т = тА+тв + тс- тАВ - тАС - твс - 2тАВС.
Подставляя сюда (*), находим:
т = тА+тв+тс- тАВ - тАС - твс + тАВС.
Поделив обе стороны этого равенства на п, получим правило D).
Предположим теперь, что рассматриваются три события А, Д С, причем
события А я В совместные, события А я С совместные, а события В я С
несовместные — см. рис.6 в таблице 36. В этом случае Р(ВГ\С) = 0
) = 0. Поэтому правило D) превращается в следующее правило:
Р(А U В U С) = Р(А) + Р(В) + Р(С) - Р(А П В) - Р(А П С). E)
9.4 Условная вероятность
11ри совместном рассмотрении двух случайных событий А я В час-
часто возникает вопрос о том, в какой мере эти события связаны друг с
другом. Вопрос ставится так: какова вероятность наступления одного из
событий (например, события А) при условии наступления другого собы-
события (события В)? В связи с этим вводят понятие условной вероятности.
Условная вероятность РВ(А) есть вероятность наступления события А
при условии наступления события В. Если указанное условие отсутству-
отсутствует, то говорят о безусловной вероятности события А (вероятности Р{А)).
Соответственно, условная вероятность РА(В) есть вероятность наступ-
наступления события при условии наступления события А.
Найдем выражение для условной вероятности РВ(А), используя клас-
классическое определение вероятности. Примем обозначения: п — количе-
количество элементов универсального множества (полное количество элемен-
элементарных исходов); тА я тв — количества элементов множеств А я В
соответственно [тА / п = Р{А)\ тв / п = Р{В)\\ т^ — количество элементов
множества А П В [ тАВ / п = Р(А П В) ].
230

Если бы мы интересовались безусловной вероятностью события А,
то должны были бы рассматривать отношение тА/ п и отбирать эле-
элементарные исходы с появлением события А из полного количества эле-
элементарных исходов. Но сейчас мы интересуемся вероятностью собы-
события А не вообще, а лишь при условии наступления также события В.
Поэтому теперь надо отобрать благоприятные для события А исходы не
из всего пространства элементарных исходов, а только из подмножества
элементарных исходов, которые благоприятны для события В. Короче
говоря, надо отобрать тм элементарных исходов из тв элементарных
исходов. Отношение как раз и будет условной вероятностью РВ(А). Та-
Таким образом,
Рв(А) = тАВ/тв.	(*)
Поделив на п числитель и знаменатель дроби тАВ/ тв получим из (*):
Поскольку тв/ п = Р(В) и тм / п = Р(АГ\В), то можно переписать (**)
в виде:
= P(Af]B)/P(B).	F)
Отметим, что это соотношение применимо в общем случае и, в част-
частности, при использовании частотного определения вероятности. По-
Поэтому именно данное соотношение принято рассматривать в качестве
определения условной вероятности. Конечно, соотношение (*) более на-
наглядно, но оно получается из F) лишь в тех ситуациях, когда можно
пользоваться классическим определением вероятности.
Поскольку А П В = В П А, то из F) следует, что вероятность наступле-
наступления события В при условии наступления события А должна определять-
определяться соотношением:
= P(Af]B)/P(A).	G)
Сравнивая F) и G), заключаем, что
"	(8)
Рассмотрим теперь несколько примеров на вычисление условной ве-
вероятности.
Пример 1. Подбрасывание игрального кубика. Предварительно закле-
заклеим бумагой грани кубика с числом очков больше 3. В качестве события А
231

выберем выпадение грани с четным числом, а события В — выпадение
грани с числом очков больше 3. Предположим, что при бросании куби-
кубика выпала заклеенная грань. Какова вероятность того, что на этой гра-
грани под бумагой находится четное число? Иными словами, надо найти
вероятность выпадения четного числа при условии выпадения числа
очков больше 3.
Полное число элементарных исходов равно п = 6 (по числу всех гра-
граней). Число элементарных исходов, благоприятных для события А, равно
тА = 3 (выпадение граней 2, 4, 6) и, значит, Р(А) = тА / п = 3 / 6 = 1 / 2.
Число элементарных исходов, благоприятных для события Д равно
тв=3 (выпадение граней 4, 5, 6) и, значит, Р(В) = тв / п. Число эле-
элементарных исходов, благоприятных для события А П Д равно т^ (вы-
(выпадение граней 4 и 6) и, значит, Р(Ар\ В) = тАВ / п = 2/6 = 1 /3. Ис-
Используя соотношение F), получаем:
Рв(А)=Р(АПВ)/Р(В)=A/3)/A/2)=2/3.
Конечно, этот результат можно было бы получить сразу, воспользовав-
воспользовавшись соотношением (*).
Пример 2. Подбрасывание додекаэдра. Напомним, что додекаэдром
называют правильный многогранник, имеющий 12 граней. Грани на-
нашего додекаэдра пронумерованы от 1 до 12; кроме того, грани с четны-
четными числами заклеены бумагой. Событие А — выпадение грани с номе-
номером больше 5; событие В — выпадение грани с четным номером (грани,
заклеенной бумагой). Какова вероятность того, что случайно выпавшая
заклеенная бумагой грань окажется с номером больше 5? Иначе говоря,
какова вероятность РВ{АI
Полное число элементарных исходов п = 12. Число исходов, благо-
благоприятных для события А, равно fnA = 7 (выпадение граней 6, 7, 8, 9, 10,
11, 12), так что Р(А) = тА/ п = 7/ 12. Число исходов, благоприятных
для события Д равно тв=6 (выпадение граней 2, 4, 6, 8, 10, 12), так
что Р{В) = тв I п = 6 / 12 = 1 / 2. Число исходов, благоприятных для со-
события АГ\В, равно #2^ = 4 (выпадение граней 6, 8, 10, 12), так что
Р(А П В) = т^ / п = А / \2=\ /Ъ. Используя F), получаем отсюда, что
РВ(А) = Р(АПВ)/Р(В) = A/3): A/2) = 2/3.
НЕЗАПЛАНИРОВАННЫЙ ДИАЛОГ
*76*Яа&е**. В § 7.7 мы познакомились с частотным определением веро-
вероятности. Чтобы экспериментально найти приближенное значение вероят-
вероятности некоторого события А, надо было подсчитать частоту наступления
232

этого события М(А) / Nnpn достаточно большом количестве N испыта-
испытаний. Например, чтобы найти вероятность выпадения четной грани при
подбрасывании кубика, надо выполнить N бросаний, посчитать коли-
количество М появлений четной грани и затем найти, чему равно отноше-
отношение М/ N. А как экспериментально найти приближенное значение ус-
условной вероятности? Я имею в виду условную вероятность, которую
мы рассматривали в примере 1.
Пвтор. Надо, как обычно, выполнить достаточно большое количе-
количество ^испытаний (подбрасываний кубика). Но учитывать теперь сле-
следует только те Nf испытаний, исходом которых оказалось выпадение
грани, заклеенной бумагой. Остальные N-N' испытаний просто не
принимаются во внимание.
ь. Итак, мы получили, что ^испытаний имели исходы с вы-
выпадением заклеенной грани. Что делать дальше?
Пвтор. Надо подсчитать те М исходов, где под бумажкой-наклейкой
скрывается четное число. Отношение М/ Nksk раз и будет приближен-
приближенным значением вероятности Рд(А) в нашем случае. Если, конечно, Nf
достаточно велико.
'Ъынателй. Получается, что надо всякий раз отдирать с грани бумаж-
бумажку, чтобы узнать, какое число под ней прячется? А нельзя ли
обойтись без заклеивания бумажкой граней кубика или додекаэдра?
Пвтор. Бумажки использовались здесь всего лишь для того, чтобы
нагляднее представить смысл условной вероятности. А вообще-то мож-
можно без них обойтись. В примере 1 надо подбросить обычный (без бу-
бумажных наклеек) кубик N раз и оставить без внимания те исходы, при
которых выпавшие грани имеют числа 1, 2 и 3. Они нас сейчас не инте-
интересуют. Нас будут интересовать только те Nf исходов, которые соответ-
соответствуют выпадению чисел 4, 5 или 6. Пусть из этих N' исходов М исхо-
исходов отвечают выпадению 4 или 6. Отношение М / Nf и есть приближенное
значение условной вероятности Рд(А), где событие А есть выпадение
грани с четным числом, а событие В есть выпадение грани с числом
очков больше 3.
g4u<SiA&e*&. Как я понимаю, упомянутые М исходов — это исходы,
когда оба события {А и В) наступили одновременно?
Пвтор. Это так. Только правильнее было бы сказать, что события А
и В наступили в одном и том же испытании.
"ЧитОФнел^. Теперь я вижу, что ошибался, когда думал, что вероят-
вероятность Рв (А) есть вероятность наступления события А при условии, что
прежде того произошло событие В.
Пвтор. Но почему Вы так думали?
233

. В некоторых книгах написано, что условная вероятность
Рв (А) есть вероятность события А, вычисленная «при условии, что со-
событие В уже произошло». По-видимому, меня сбили с толку слова «уже
произошло». Они как бы намекают на то, что само событие А еще не
произошло.
Пвтор. Пожалуй, слова «уже произошло» выбраны здесь не вполне
удачно. Более точным является выражение, приводившееся в самом
начале данного параграфа: «условная вероятность РВ(А) есть вероят-
вероятность наступления события А при условии наступления события В». Не
после того, как событие В «уже произошло», а при условии «наступле-
«наступления события В». Рассматриваем все элементарные исходы с наступле-
наступлением события В (количество этих исходов равно тв) и именно из этих
исходов (только из них!) отбираем исходы с наступлением также со-
события А (количество этих исходов равно т^). Затем подсчитываем от-
отношение тдд I тв, которое и является условной вероятностью Рв (А).
Пример 3. Снова подбрасываем додекаэдр. Но теперь, в отличие от
примера 2, определяем не условную вероятность РВ(А), а условную ве-
вероятность РА(В). События А и В в данном примере те же, что и в при-
примере 2. Вероятности РВ(А), Р(А), Р(В) известны; поэтому воспользуем-
воспользуемся соотношением (8). Из него следует, что
РА(В) = РВ(А)Р(В)/Р(А) = B/3). A/2): G/12).
Пример 4. Подбрасываем два кубика. Надо найти условную вероят-
вероятность выпадения четного суммарного числа очков (событие А) при ус-
условии, что пара выпавших граней состоит из разных чисел (событие В).
Пространство элементарных исходов для данной ситуации использова-
использовалось на всех рисунках в таблицах 32 и 33. Поэтому можем записать: п = 36;
тА= 18 (исходы 1-1, 1-3, 1-5, 2-2, 2-4, 2-6, 3-1, 3-3, 3-5, 4-2, 4-4, 4-6,
5-1, 5-3, 5-5, 6-2, 6-4, 6-6), поэтому Р(А) = тА / п = 18 / 36 = 1 / 2; тв = 30
(все представленные на рисунке исходы кроме исходов 1-1, 2-2, 3-3,
4-4, 5-5, 6-6), поэтому Р(В) = тв/ п = 30/36 = 5/6; т^=12 (исходы
1-3, 1-5, 2-4, 2-6, 3-1, 3-5, 4-2, 4-6, 5-1, 5-3, 6-2, 6-4), поэтому
Р(АП В) = тмI тв =12/36 = 1/3. Отсюда, согласно F) следует, что
РВ(А) = Р(АПВ)/Р(В) = A/3): E/6) = 2/5.
ПРОДОЛЖЕНИЕ ДИАЛОГА
g4tuftfufce*b. В примере 4 испытание представляло собой одновремен-
одновременное подбрасывание двух кубиков; мы использовали пространство эле-
элементарных исходов, которое рассматривалось на рисунках в таблицах 32
234

и 33. Однако все эти рисунки относились к иному типу испытаний —
не одновременному бросанию двух кубиков, а двукратному бросанию
одного кубика. При этом элементарный исход, обозначавшийся, на-
например, как 4-5, означал, что при первом бросании кубика выпало чис-
число 4, а при втором бросании — число 5.
Пвтор. Вы правы. Но, как уже отмечалось ранее, пространство эле-
элементарных исходов для одновременного бросания двух кубиков и для
двукратного бросания одного кубика одно и то же.
'Чипиинель. Но как практически различать исходы 4-5 и 5-4 при од-
одновременном бросании двух кубиков?
Пвтор. Можно один из кубиков как-то пометить. Например, нанес-
нанести на него краску. Исход 4-5 может означать, что чистый кубик выпал
четверкой, а подкрашенный кубик выпал пятеркой. Тогда исход 5-4
будет означать, что чистый кубик выпал пятеркой, а подкрашенный
выпал четверкой.
'Чипиинель. Понятно. А теперь обсудим одну проблему, воспользо-
воспользовавшись следующим примером. Это будет пример 5. Кубик подбрасы-
подбрасывают два раза. Надо найти условную вероятность Рв (А) выпадения чет-
четного суммарного числа очков (событие А) при условии, что в первом
бросании выпала тройка (событие В).
Пвтор. Отличный пример. Вы наверняка можете решить его сами.
'Читатель. Именно это я и собираюсь сделать. Полное число элемен-
элементарных исходов п = 36. Число исходов, благоприятных для события А, нам
уже известно из примера 4; оно равно тА = 18, так что Р(А) = 18 / 36 =
= 1/2. Число исходов, благоприятных для события В, равно тв=6 (ис-
(исходы 3-1, 3-2, 3-3, 3-4, 3-5, 3-6), так что Р(В) = 6/36 = 1/6. Число
исходов, благоприятных для события АГ\В, равно тм = 3 (исходы 3-1,
3-3, 3-5), так что Р{А П В) = 3 / 36 = 1 / 12. Отсюда, согласно F), нахо-
находим, что Рв (А) = 1 / 2.
Пвтор. Прекрасно. В чем же проблема? Почему Вы предложили рас-
рассмотреть этот пример?
'Чи&л&ел*. Дело в том, что в данном примере вполне можно сказать:
«условная вероятность Рв (А) есть вероятность события А, вычисленная
при условии, что событие В уже произошло». Ведь событие В — это
выпадение тройки при первом бросании кубика. Значит, событие В про-
происходит (или не происходит) прежде, чем произойдет (не произойдет)
событие А\ Наше испытание (двукратное подбрасывание кубика) состо-
состоит из двух последовательных испытаний: первого бросания кубика и вто-
второго бросания. Событие В реализуется уже в первом бросании, т. е. в
235

первом испытании. А ведь совсем недавно мы говорили о том, что при
рассмотрении условной вероятности Рв (А) оба события (как событие А,
так и событие В) наступают е одном и том же испытании и, следова-
следовательно, одновременно! Как это приложить к только что рассмотренно-
рассмотренному примеру?
Пвтор. Прежде всего отмечу некоторые допущенные Вами неточно-
неточности. Испытание в предложенном Вами примере — это двукратное под-
подбрасывание кубика. Именно двукратное. Как таковое оно не может со-
состоять из двух последовательных испытаний — первого броска и второго
броска. Можно говорить о двух этапах данного испытания, соответ-
соответствующих разным броскам. Но испытание здесь единое, оно включает
в себя оба броска.
g4u<StiuSU*&. Что ж, назовем первый и второй броски этапами, а не
испытаниями. Разве от перемены названия что-то меняется?
Пвтор. Дело в том, что наши события А и В (как одно, так и другое)
всякий раз наступают или не наступают отнюдь не на каких-то отдель-
отдельных этапах, а в одном и том же испытании. Хотя и не одновременно.
В связи с этим я отмечу еще одну неточность в Ваших рассуждениях.
Вы сказали: «события наступают в одном и том же испытании и, следо-
следовательно, одновременно». Тут слово «следовательно» неуместно. На-
Наступление двух событий в одном и том же испытании может происхо-
происходить как одновременно (как в примерах 1-4), так и не одновременно (как
в Вашем примере).
'Чи&а&е**. Все-таки мне представляется, что происходит какая-то
игра словами. Событие В — это выпадение тройки в первом броске.
Чем это не исход испытания?
Пвтор. Тогда исходом какого испытания Вы назовете событие АР.
&. По-видимому, исходом второго броска... Впрочем, я не-
неправ. Событие А — исход испытания, представляющего собой двукрат-
двукратное подбрасывание кубика.
Пвтор. Итак, событие В — это исход первого броска, а событие А —
исход двух бросков. Согласен. А можно ли сказать, что испытание, име-
именуемое «первым броском», наступает (не наступает) раньше наступле-
наступления испытания, именуемого «двумя бросками»?
ёЧи<9ии9се*ь. Наверное, нельзя.
Пвтор. Как видите, вопрос о том, в чем состоит испытание, является
принципиальным. Никаких двух последовательных испытаний, из ко-
которых одно событие относилось бы к одному испытанию, а другое к дру-
другому, в Вашем примере нет. Здесь (как и в иных ситуациях) условная
236

вероятность РВ(А) рассматривается для событий А и В, наступающих
(не наступающих) в одном, а не в каких-то разных испытаниях. Кстати
говоря, в Вашем примере вероятности Р(А), Р(В), Рд(А) (а также Ра(В))
вычисляются на основе подсчета количеств элементов соответствую-
соответствующих подмножеств универсального множества, которое наглядно пред-
представлено на рисунках в таблицах 32 и 33. Здесь каждый элемент изобра-
изображен двумя числами, из которых левое — результат первого броска, а
правое — результат второго броска.
"ЧитОФнел^. Вы, конечно, правы. И все-таки сначала выпала тройка.
Она выпала в первом броске. А уже после того, как наступило это собы-
событие (событие В), мы стали интересоваться событием А — выпадением
четного суммарного числа очков.
Пвтор. Что значит «мы стали интересоваться»? Ясно, что событие А
определяется не только вторым, но и первым броском. Тут, пожалуй,
мы и впрямь рискуем заняться игрой в слова. Давайте не будем отожде-
отождествлять фразу «Рв (А) есть вероятность события А, вычисленная при ус-
условии, что событие В уже произошло» с фразой «Рв (А) есть вероятность
события А, вычисленная, когда событие В уже произошло». Одно дело
«при условии, что» или «в предположении, что» и другое дело — «когда
произошло». Если учесть, что «при условии» можно понимать как «в пред-
предположении» (а отнюдь не как свершившийся факт), то не возникнет
противоречия с тем безупречным определением условной вероятности,
которое мы привели в начале параграфа. Я назвал то определение бе-
безупречным, поскольку оно оставляет в стороне непринципиальный в дан-
данном случае вопрос о возможности или невозможности разбиения испы-
испытания на этапы,
После такого диалога уместно рассмотреть следующий пример.
Пример 6: наугад вынимаем из мешка дважды по одному шару без
возвращения первого вынутого шара в мешок. Предположим, в мешке
было 5 шаров — 2 белых и 3 черных. Шары различаются только по цве-
цвету. Надо найти вероятность того, что второй вынутый шар окажется
черным при условии, что первый вынутый шар — белый. Событие А
состоит в том, что второй из двух вынутых шаров оказался черным.
Событие В состоит в том, что первый из двух вынутых шаров оказался
белым. Требуется вычислить условную вероятность РВ(А).
Подчеркнем, что события А и В выявляются не в разных испытаниях
(событие А в одном, а событие В в следующем), а в одном и том же
испытании, им является двукратное вынимание наугад шара без воз-
возвращения первого вынутого шара обратно в мешок. Нам нужно прежде
всего определить пространство элементарных исходов для данного типа
237

испытаний. Имеем пять шаров; обозначим их через бъ бъ чъ чъ чъ
(буква «б» относится к белым шарам, а буква «ч» к черным). Нужно
составить всевозможные пары из этих шаров. Для этого удобно нагляд-
наглядности ради представить себе два ящика — один для одного шара, дру-
другой для другого. В первый ящик мы можем положить любой из пяти
шаров — тут возможны пять вариантов:
бх
б2
ч2
чъ
В каждом из этих вариантов во второй ящик можно положить любой из
четырех оставшихся шаров. Значит, всего имеем 5 • 4 = 20 всевозмож-
всевозможных пар шаров — двадцать равновероятных несовместных исходов:
бх
бх
бх
бх
б2
Чх
ч2
Чъ
б2
б2
б2
б2
бх
чх
ч2
чъ
чх
чх
чх
чх
бх
б2
ч2
чъ
ч2
ч2
ч2
ч2
бх
б2
Чх
чъ
чз
чъ
чъ
чъ
бх
б2
Чх
ч2
Таково пространство элементарных исходов в данном случае (п = 20).
Условимся считать, что в каждой из этих пар слева стоит шар, вынутый
из мешка первым, а справа — шар, вынутый из мешка вторым. Используя
пространство элементарных исходов, запишем: тА= 12 (исходы бхчъ бхчъ
бхчъ, б2чь б2чъ б2чъ, чхчъ чхчъ, ч2чь ч2чъ, чъчъ чъч2) и, значит, Р(А) = 12/20 =
= 3/5; тв=8 (исходы бхбъ бхчь бхчъ бхчъ, б2бъ б2чъ б2чъ б2чъ) и, значит,
Р(В) = 8/20 = 2/5; m^g = 6 (исходы бхчъ бхчъ бхчъ, б2чъ б2чъ б2ч3) и,
значит, Р(Ар\ В) = 6/20 = 3/ 10. Отсюда, согласно F), получаем:
РВ(А) = C/10): B/5) = 3/4.
В заключение заметим, что приведенное выше решение примера 6
оправдано лишь с точки зрения тренировки в вычислении условной
вероятности. Дело в том, что здесь можно вообще обойтись без услов-
условной вероятности и не прибегать к соотношению F) (а также к выявле-
выявлению пространства элементарных исходов). Можно поступить много
проще. В мешке находились два белых и три черных шара. Предполо-
Предположим, что из него вынули белый шар. После этого в мешке остались
один белый и три черных шара — всего четыре шара. Легко сообразить,
что теперь вероятность вынуть наугад из мешка черный шар равна 3/4.
Таков ответ на вопрос, поставленный в примере 6. Мы получили его,
не прибегая к понятию условной вероятности. Конечно, столь простое
решение возможно далеко не во всех ситуациях. Поэтому надо уметь
вычислять условную вероятность.
238

9.5 Независимые и зависимые совместные события.
Правила вычисления вероятности пересечения
двух совместных событий
(вероятности совместного наступления
двух событий)
Х\ак уже отмечалось, понятие условной вероятности позволяет ха-
характеризовать пару тех или иных совместных событий с точки зрения
их взаимной зависимости, т. е. с точки зрения влияния появления одного
из событий на вероятность появления другого.
Обратимся к примерам, рассмотренным в предыдущем параграфе.
В примере 1 безусловная вероятность Р{А) равна 1/2, а условная
вероятность РВ{А) равна 2/3. Следовательно, при условии выпадения
числа очков больше трех у кубика оказывается больше шансов выпасть
четной гранью (по сравнению со случаем, когда упомянутое отсутству-
отсутствует). В данном примере наступление события В увеличивает вероятность
наступления события А на 1/6 (коль скоро 2/3-1/2=1/6). В при-
примере 2 имеем Р(А) = 7 / 12 и Рв (А) = 2 / 3; наступление события В увели-
увеличивает вероятность наступления события А на 1/12. В примере 3 име-
имеем Р(В) = 1 / 2 и РА(В) = 4/7; наступление события А увеличивает
вероятность наступления события В на 1 / 14. А вот в примере 4 наступ-
наступление одного события не увеличивает, а напротив, уменьшает вероятность
наступления другого события; там Р(А) - Рв (А) = 1 / 2 - 2 / 5 = 1 / 10. В при-
примере 5 Р(А) = РВ{А) (обе вероятности равны 1/2); в этих испытаниях на-
наступление события В никак не влияет на вероятность наступления собы-
события А. Наконец, в примере 6 имеем Р(А) = 3 / 5 и Рв (А) = 3 / 4; наступление
события В увеличивает вероятность наступления события Аш 3/20.
Важно обратить внимание на то, что для несовместных событий пробле-
проблемы влияния наступления одного события на вероятность наступления дру-
другого попросту не существует. Ведь несовместные события — это события
взаимоисключающие: наступление одного из них попросту исключает появ-
появление в данном испытании другого события. Иное дело, если рассматрива-
рассматриваются два совместных события. Здесь возможны две ситуации:
-	наступление одного из событий влияет на вероятность наступле-
наступления другого события (увеличивает или уменьшает ее) — такие со-
совместные события называют зависимыми;
—	наступление одного из событий не влияет на вероятность наступ-
наступления другого события — такие совместные события называют
независимыми.
239

Рассмотренные в предыдущем параграфе в примерах 1, 2, 3, 4, 6
пары событий А и В являлись, очевидно, зависимыми событиями. Те-
Теперь поговорим о независимых совместных событиях. Тем более, что
независимость событий часто используется при практических примене-
применениях теории вероятностей.
Допустим, что для событий Аи В справедливо соотношение (см. при-
пример 5 в §9.4):
РВ(А)=Р(А).	(*)
Это означает, что наступление события В не изменяет вероятности на-
наступления события А, так что событие А можно считать независимым
от события В. Подставляя (*) в соотношение (8), находим:
Р{В) = РА(В)	(**)
и, следовательно, событие В можно считать независимым от события А.
Получается, что, если наступление события В не изменяет вероятности
наступления события А, то тогда наступление события А также не изме-
изменяет вероятности наступления события В. Иными словами, если собы-
событие А независимо от события В, то и событие В независимо от события А.
Это позволяет говорить о взаимной независимости событий А я В (или
просто о независимости А я В).
Подставив (**) в G), получаем для независимых событий А я В:
(9)
Соотношение (9) принято рассматривать как определение независи-
независимых совместных событий. Оно формулируется так: совместные события А
и В являются независимыми тогда и только тогда, когда вероятность
пересечения {совместного наступления) событий А и В равна произведению
вероятностей этих событий.
Соотношение (9) является также правилом вычисления вероятности
пересечения независимых событий А и В. Иными словами, это есть пра-
правило вычисления вероятности совместного наступления независимых
событий А и В в одном и том же испытании. Проще данное правило
называют правилом умножения вероятностей независимых событий.
Что же касается вероятности совместного появления зависимых со-
событий А и Д то для ее вычисления надо применять следующее правило,
вытекающее из F) и G):
Р(А ПВ) = Р(А) ¦ РА{В) = Р(В) ¦ РВ{А).	A0)
Обсуждавшееся в § 9.2 правило C) является фактически общим пра-
правилом вычисления вероятности объединения двух случайных событий А
240

и В. В зависимости от характера событий оно превращается в одно из
следующих трех правил:
-	правило для несовместных событий:
Р(А f]B) = Р(А) + Р(В);	(правило 1)
-	правило для независимых совместных событий:
Р(А U В) = Р(А) + Р(В) - Р(А) • Р(В);	A1)
-	правило для зависимых совместных событий:
Р(А UВ) = Р(А) + Р(В) -Р(А) РА(В) =
= Р(А)+Р(В)-Р(В)РВ(А).	A2)
Предостережение. Иногда ошибочно полагают, что независимые со-
события — это то же самое, что несовместные события. И те, и другие
рассматриваются как события, которые «не имеют никакого отноше-
отношения друг к другу». В связи с этим не помешает еще раз обратить внима-
внимание на различие между понятиями несовместности событий и незави-
независимости событий.
События А ж В называют несовместными [взаимоисключающими) тог-
тогда и только тогда, когда наступление одного события в любом данном
испытании исключает наступление другого события в том же испыта-
испытании. В этом смысле несовместные события действительно «не имеют
никакого отношения друг к другу». Вероятность пересечения этих со-
событий равна нулю (Р(АГ\В) = 0) и, следовательно, равны нулю услов-
условные вероятности:
Что же касается независимых событий, то, строго говоря, их нельзя
назвать событиями, которые «не имеют никакого отношения друг к
другу». Дело в том, что наступления независимых событий А ж В могут
наблюдаться в одном и том же испытании, так что Рв (А) ^ 0 и РА(В) ^ 0.
Правда, наступление одного из независимых событий не влияет на ве-
вероятность наступления другого события; поэтому можно записать:
РВ(А) = Р(А); РА(В) = Р(В).	(**)
Соотношения (*) и (**) математически строго демонстрируют
различие между понятиями несовместности событий и независимости
событий.
В дополнение к примеру 5 из § 9.4 рассмотрим некоторые примеры
независимых событий.
241

Пример 1. Подбрасываются две одинаковые монеты (для удобства
обсуждения на одну из монет нанесена царапина). Событие А — монета
с царапиной упала орлом. Событие В — обе монеты упали одинаково.
Докажем, что события Аи В независимые.
Пространство элементарных исходов: 00, ОР, РО, РР (О — выпал
орел, Р — выпала решка; первая из двух букв в каждой паре относится
в монете с царапиной). В данном примере: п = 4; тА=2 (элементарные
исходы 00 и ОР) и, значит, Р(А) = 2/4 = 1 /2; тв=2 (элементарные
исходы 00 и РР) и, значит, Р(В) = 1 /2; тАВ = 1 (исход 00) и, значит,
Р(АГ\В) = 1/4. Легко видеть, что Р(АГ\ В) = Р(А) - Р(В). Отсюда за-
заключаем, что события А к В независимые.
Пример 2. Монету подбрасывают четыре раза. Событие А — монета
выпала орлом во втором бросании. Событие В — монета выпала орлом
в четвертом бросании. Докажем, что события А ж В независимые.
Пространство элементарных исходов для таких испытаний приводи-
приводилось на рис. 1 в таблице 20. Из рисунка видно, что п = 16; тА=8 (исхо-
(исходы 0000, OOOP, OOPO, OOPP, POOO, POOP, РОРО, РОРР) и, зна-
значит, Р{А) = 8/ 16 = 1 / 2; тв = 8 (исходы 0000, ООРО, ОРОО, ОРРО,
РООО, РОРО, РРОО, РРРО) и, значит, Р(В) = 8 / 16 = 1 / 2; т^ = 4 (ис-
(исходы 0000, ООРО, РООО, РОРО) и, значит, Р(А{]В) =4/16= 1/4.
Легко видеть, что Р(АГ\В) = Р(А) - Р(В) и, следовательно, события А
и В независимые.
Пример 3. Кубик подбрасывают два раза. Событие А — выпала пятер-
пятерка в первом бросании. Событие В — выпала двойка во втором броса-
бросании. Докажем независимость событий А ж В.
Пространство элементарных исходов для таких испытаний мы уже
несколько раз рассматривали. Имеем: п = 36; тА = 6 (исходы 5-1, 5-2,
5-3, 5-4, 5-5, 5-6) и, значит, Р{А) = 6/36 = 1 /6; тв= 6 (исходы 1-2,
2-2, 3-2, 4-2, 5-2, 6-2) и, значит, Р(В) = 6/36= 1/6; m^g= 1 (исход
5-2) и, значит, Р(АГ\В) = 1/36. Легко видеть, что Р(А П В) = Р(А) • Р{В)
и, следовательно, события А и В независимые.
Пример 4. Кубик подбрасывают два раза. Событие А — в первом и
втором броске выпали грани с одинаковым числом очков. Событие В —
во втором броске выпала тройка. Докажем независимость событий Аи В.
Пространство элементарных исходов нам известно. Имеем: п = 36;
тА = 6 (исходы 1-1, 2-2, 3-3, 4-4, 5-5, 6-6) и, значит, Р(А) = 1 /6;
тв=6 (исходы 1-5, 2-5, 3-5, 4-5, 5-5, 6-5) и, значит, Р(В) = 1/6;
тАВ=1 (исход 5-5) и, значит, Р(А{] В) = 1 / 36. Легко видеть, что
Р(Ар\ В) = Р{А) • Р{В) и, следовательно, события А я В независимые.
242

Пример 5. Кубик подбрасывают два раза. Событие А — сумма выпав-
выпавших очков есть четное число. Событие В — во втором броске выпала
пятерка или шестерка. Докажем независимость событий А и В.
Пространство элементарных исходов известно. Имеем: п = 36; тА = 18
(исходы 1-1, 1-3, 1-5, 2-2, 2-4, 2-6, 3-1, 3-3, 3-5, 4-2, 4-4, 4-6,
5-1, 5-3, 5-5, 6-2, 6-4, 6-6) и, значит, Р(А) = 18/36; тв= 12 (исходы
1-5, 2-5, 3-5, 4-5, 5-5, 6-5, 1-6, 2-6, 3-6, 4-6, 5-6, 6-6) и, значит,
Р(В) = 12/36; тм = 6 (исходы 1-5, 3-5, 5-5, 2-6, 4-6, 6-6) и, зна-
значит, Р(АПВ) = 6/36 = 1/6. Легко видеть, что Р(АПВ)=Р(А) • Р{В)
и, значит, события Аи В независимые.
НЕЗАПЛАНИРОВАННЫЙ ДИАЛОГ
"Читатель. У меня возникли замечания по поводу соотношения (9).
Пвтор. В чем они заключаются?
*Чипиинель. Согласно (9), вероятность совместного наступления со-
событий А ж В (вероятность Р(АГ\В)) можно найти, умножив вероят-
вероятность Р{А) на вероятность Р{В). Это правило работает тогда и только
тогда, когда события А я В независимые. Однако, чтобы выяснить явля-
являются ли на самом деле независимыми события А ж В, нам нужно убе-
убедиться, что Р {А П В) = Р (А) - Р(В). Получается замкнутый логический
круг. Как из него выйти?
Пвтор. В ситуациях, допускающих использование классического опре-
определения вероятности, можно вычислить вероятность совместного на-
наступления событий А и Д не обращаясь к вероятностям Р (А) и Р (В), а
с помощью соотношения
Р(АПВ)=тАВ/п,
которым, кстати говоря, мы уже неоднократно пользовались. Мы ис-
использовали это соотношение, в частности, во всех примерах в § 9.4 для
того, чтобы найти Р(АГ\В). Кроме того, во многих случаях вопрос о
независимости событий решают, не прибегая к соотношению (9), а исхо-
исходя из общих (подчас интуитивных) соображений, основанных на опы-
опыте, представляющихся достаточно очевидными.
"Читатель. Как я понимаю, доказательство с помощью соотноше-
соотношения (9) независимости событий А и В в примерах 2 и 3 можно считать
излишним. Известно, что тот или иной исход бросания монеты или
кубика не зависит от предыдущих исходов и не влияет на последующие.
Так что события А и В в этих примерах являются заведомо независимы-
независимыми. Можно сказать, что независимость событий здесь очевидна.
Пвтор. Использование очевидности независимости тех или иных со-
событий особенно важно тогда, когда вероятность определяется экспери-
243

ментально — на основании подсчета частоты наступления события в дли-
длительной серии испытаний. Например, очевидно, что рождение мальчи-
мальчика (девочки) у двух разных матерей — события независимые. Очевидно,
что изготовление доброкачественного изделия на двух разных заводах
(или на одном заводе в разные смены), — тоже независимые события.
Независим выход из строя двух разных станков, не связанных функцио-
функционально друг с другом. Независим выбор дальнейшего пути для двух
разных развилок в лабиринте.
g4u<StiuSU*&. По-видимому, попадание в цель одного стрелка и попа-
попадание в цель другого стрелка — тоже независимые события.
Пвтор. Вы напомнили своим замечанием, что до сих пор не решена
задача о вероятности подстрелить летящую утку двумя одновременно
стреляющими охотниками. Об этой задаче мы говорили в § 9.1.
*Чипииъель. Там возникла проблема с вероятностью, которая получа-
получалась больше единицы.
Пвтор. На самом же деле такой проблемы нет. Поскольку события А
и В в той задаче являются совместными событиями, то надо применять
не правило A), а правило C):
Р(А U В) = Р(А) + Р(В) - Р(А П В).
А так как совместные события А и В независимы, то Р (А П В) =
= Р(А) • Р{В) = 0,3 • 0,9 = 0,27. Поэтому получаем следующее значение
вероятности подстрелить утку в результате одновременных выстрелов
наших двух охотников: Р= 0,3 + 0,9 - 0,27 = 0,93.
В заключение решим несколько простых задач с использованием
соотношения (9), рассматриваемого в качестве правила умножения веро-
вероятностей независимых событий.
Задача 1. Кубик подбрасывают два раза. Какова вероятность того, что выпадет
12 очков по сумме двух бросаний?
Столько очков наберется, если в каждом бросании выпадет шестерка. Вероят-
Вероятность, что шестерка выпадет в первом бросании, есть Р(А) = 1/6. Вероятность,
что шестерка выпадет во втором бросании, есть Р(В) = 1 / 6. События Аи В неза-
независимы; следовательно, Р(А Г\В) = Р(А)- Р{В) = A / 6) / A / 6) = 1 / 36.
Задача 2. Кубик подбрасывают два раза. Какова вероятность того, что выпадут
11 очков ?
Столько очков выпадут в двух случаях:
-	в первом бросании выпала пятерка (Р5 = 1 /6), а во втором бросании выпала
шестерка (Р6 = 1 / 6); РE-6) = Р5 • Р6 = 1 / 36;
—	в первом бросании выпала шестерка, а во втором бросании выпала пятерка;
244

События 5—6 и 6—5 несовместные; поэтому искомая вероятность есть
Напомним еще раз:
-	при вычислении вероятности того, что наступят и событие А, и событие В,
надо вероятности Р(А) и Р(В) перемножить;
-	при вычислении вероятности того, что наступят или событие С, или событие D,
надо вероятности Р(С) и P(D) сложить.
При этом необходимо, чтобы события Аи В были независимыми, а события С
и D были несовместными.
Задача 3. Кубик подбрасывают два раза. Какова вероятность, что выпадут
10 очков?
Столько очков может выпасть в трех случаях:
-	выпали 6 очков и 4 очка,
-	выпали 4 очка и 6 очков,
-	выпали 5 очков и 5 очков.
Искомая вероятность: Р = Р6 Р4 + Р4 • Р6 + Р5 • Р5 = 3 / 36 = 1 / 12.
9.6 Правила вычисления вероятности
совместного наступления трех и более событий.
События, независимые в совокупности
v^CHOBHoe внимание в данном параграфе будет уделено совместно-
совместному наступлению трех случайных событий (событий А, В, С), т.е. вы-
вычислению вероятности Р(АГ\ВГ\ С). Полученные правила будут обоб-
обобщены на произвольное конечное число событий Аъ Аъ А3,...9АГ.
Прежде всего заметим, что, если события А, В, С попарно несовмес-
несовместны, то Р(АГ\ВГ\ С) = 0. Этот результат очевиден. Предположим те-
теперь, что из трех пар событий (А я В, А я С, В я С) несовместность
наблюдается только для одной пары — см., например, рис. 6 в табли-
таблице 36, где несовместны только события В я С, тогда как события А я В,
а также А я С совместны. Событие А П В П С можно рассматривать как
пересечение событий А П В я С. Событие А П В я выделено на рисунке
штриховкой с точками. Можно видеть, что события С и А П В пересека-
пересекаются и, следовательно, (АГ\ В) П С= 0. Значит,
Заметим, что результат (*) можно получить, не прибегая к диаграм-
диаграммам Эйлера- Венна:
Р(А{]В{]С)=Р(А{](В{]С))=Р(А{]0)=Р@)=О.
245

Если рассматриваются г событий Аъ Аъ А$,..., Аг и известно, что со-
события, например Ах и Аъ несовместные [Ах Г\А2 = 0), то в этом случае:
Итак, если среди событий Аъ Аъ А3,..АГ есть хотя бы одна пара несовме-
несовместных событий, то Р(А{ Г\А2 Г\А3... Г\АГ) = 0.
Замечание. Итак, наличие хотя бы одной пары несовместных собы-
событий является достаточным условием для того, чтобы вероятность пере-
пересечения г событий равнялась нулю. Но есть ли это необходимое условие?
Иначе говоря, можно ли утверждать, что, если нет ни одной пары не-
несовместных событий, то вероятность Р(А1Р\А2Р\А3 ...р\Аг) обязательно
будет отлична от нуля? Оказывается, так утверждать нельзя. Все собы-
события могут быть попарно совместны и тем не менее вероятность их пере-
пересечения может равняться нулю. Это видно из примера с двукратным
подбрасыванием кубика, где в качестве событий А, В, С выбраны следу-
следующие события: А — выпадение одинаковых очков при первом и втором
бросках (элементарные исходы: 1-1, 2-2, 3-3, 4-4, 5-5, 6-6), В — вы-
выпадение единицы в первом броске (элементарные исходы: 1-1, 1-2,
1-3, 1-4, 1-5, 1-6); С — выпадение шестерки во втором броске (эле-
(элементарные исходы: 1-6, 2-6, 3-6, 4-6, 5-6, 6-6). Пересечение А П В —
это исход 1-1 (Р(Ар\В) = 1/36); пересечение Ар\ С — это исход 6-6
(Р(А П С) = 1 / 36); пересечение В{] С - это исход 1-6 (Р(ВГ\ С) = 1 / 36).
А вот пересечение Ар\Вр\ С — пустое множество и, следовательно,
Выведем основное правило для вычисления Р(А{] В{] С). Применив
правило A0) к вероятности пересечения событий АГ\В и С, получаем:
Р(АГ\ВГ\С)=Р(АГ\В).РАГ1В(С).	(**)
Затем применим правило A0) к вероятности пересечения А я В:
(***)
Подставляя (***) в (**), находим:
Р(А П В П С) = Р(А) • РА(В) • РАПВ(С).	A3)
Это и есть основное правило для вычисления Р(АГ\В{] С).
С учетом переместительного и сочетательного законов для пересече-
пересечения событий, мы можем как угодно переставлять события в A3). Для
трех событий число перестановок равно П3 = 3! = 3*2 = 6. Значит,
246

основное правило для вероятности пересечения трех событий можно
записать в виде шести равноправных соотношений:
P(Af]Bf]C) = -
A3)
Р(А)РА(С)РАпС(В);	A3')
P(B)PB(C)PBf]c(A);	A3")
P(B)PB(A)PAf]B(C);	A3'")
[ Р(С)Рс(В)Ртс(А).	A3'"")
Предположим, что рассматриваются четыре события: А, В, С, D. Вы
ведем правило для вычисления P(Af]Bf] Cf]D), действуя так же, как
в случае с тремя событиями. Сначала применим правило A0) к вероят-
вероятности пересечения событий D и А П В П С; получим
Затем применим правило A0) к вероятности пересечения событий С
яАГ\В; получим
Наконец, применим правило A0) к вероятности пересечения А я В;
получим
Р(А{)В)=Р(А)РА(В).
Собирая все эти три соотношения, находим:
Р(А П В П С П D) = Р(А) • РА(В) • РА[]В(С) • PAf]mc(D).	A4)
Как и в A3), здесь можно как угодно переставлять события. По-
Поскольку у нас четыре события, получим П4 = 4! = 24 равноправных со-
соотношения. Выписывать все эти соотношения не будем. Напомним лишь
все перестановки четырех событий:
ABCD
ABDC
ACBD
ADBC
ACDB
ADCB
BACD
BADC
BCAD
BDAC
BCDA
BDCA
CABD
CADB
CBAD
CDAB
CBDA
CDBA
DABC
DACB
DBAC
DCAB
DBCA
DCBA
247

Результаты, полученные для A3) и D) легко обобщаются на случай,
когда рассматриваются г событий Аъ Аъ Аъ, А4,...,АГ.
= Р{АХ)
A5)
Это соотношение можно, при желании, представить в виде Пг= г\ рав-
равноправных соотношений, переставляя события.
Теперь нам важно уточнить понятие независимости событий для слу-
случаев, когда этих событий три или более. В общем случае определение
независимости случайных событий таково:
События Аъ Аъ А^,..., Аг называются независимыми в совокупности
{или просто независимыми), если вероятность наступления любого из
этих событий не зависит от наступления какого угодно числа осталь-
остальных событий из данной совокупности.
В случае трех событий {А, Д С) независимость в совокупности означает,
что вероятность наступления события А не зависит от наступления со-
событий Д С, Вр\ С, вероятность наступления события В не зависит от
наступления событий А, С, А П С, вероятность наступления события С
не зависит от наступления событий А, Д А П В.
Для четырех событий (А, Д С, D) независимость в совокупности озна-
означает, что вероятность наступления события А не зависит от наступле-
наступления событий Д С, Д Bf] С, Bf] Д СП А ЯП СП А вероятность на-
наступления события В не зависит от наступления событий А, С, D, А{] С,
А П А СП А Л П СП А вероятность наступления события С не зависит
от наступления событий А, Д Д Л П Д ^ П А Я П А ^ П В П А вероят-
вероятность наступления события D не зависит от наступления событий А, Д С,
ЛПД ЛПС, яп С, АПВПС.
Нетрудно сообразить, как следует понимать независимость в совокуп-
совокупности для пяти, шести и вообще любого конечного числа событий. На-
Наряду с независимостью в совокупности рассматривают также попарную не-
независимость событий. Ее смысл ясен из названия. Попарная — значит,
взаимная независимость любых двух событий из рассматриваемой сово-
совокупности. Используя в дальнейшем термин «независимость событий»,
мы будем иметь в виду именно независимость в совокупности.
Но вернемся к рассмотрению трех событий. Из определения незави-
независимости событий следует, что независимость событий А, Д С (незави-
(независимость в совокупности) означает, что взаимно независимы следующие
248

пары событий: А и В, А и С, 5и С, АиВП С, 5и^П С, Си^П В. Иначе
говоря, это означает, что безусловные вероятности событий А, В, С (ве-
(вероятности Р(А), Р(В), Р(С)) должны равняться условным вероятностям:
Р(А) = РВ(А) = РС(А) =
Р{В) = РА{В) = РС{В) = РАПС(ВУ,	(****)
Р(С) = РА(С) = РВ(С) = РАПВ(С).
А теперь подставим соотношения (****) в соотношения A3)-A3/////).
Легко видеть, что эта подстановка превращает каждое из соотношений
A3) — A3/////) в следующее соотношение:
Р(АГ\ВГ\С)=Р(А).Р(В).Р(С).	A6)
Мы получили правило: вероятность совместного наступления событий,
независимых в совокупности, равна произведению вероятностей событий.
Итак, если выполняются соотношения (****), то выполняется соот-
соотношение A6). Значит, независимость событий в совокупности есть до-
достаточное условие для использования правила умножения безусловных
вероятностей этих событий. С другой стороны, если выполняется соот-
соотношение A6), то, подставив его в соотношения A3)-A3/////), мы полу-
получим соотношения (****). Значит, независимость событий в совокупно-
совокупности есть не только достаточное, но также необходимое условие для
использования правила умножения безусловных вероятностей событий.
Отсюда следует, что правило A6) может рассматриваться как определе-
определение независимости событий в совокупности.
Правило A6) без труда обобщается на г событий, независимых в со-
совокупности:
A7)
Правило A7) широко используется в теории вероятностей в отношении
событий, независимых в совокупности. Оно же рассматривается как фор-
формальное определение независимости в совокупности для г событий.
НЕЗАПЛАНИРОВАННЫЙ ДИАЛОГ
*Чипиипель. Как мы видим, справедливы два утверждения. Первое:
Если события независимы в совокупности, то вероятность их совместно-
совместного наступления равна произведению безусловных вероятностей этих собы-
событий. Второе утверждение: Если вероятность совместного наступления
нескольких событий равна произведению их безусловных вероятностей, то
249

эти события независимы в совокупности. Опять, как и в случае с прави-
правилом (9), получается, замкнутый логический круг.
Пвтор. Согласен. И точно так же, как в упомянутом случае, выход из
этого круга состоит, во-первых, в анализе пространства элементарных
исходов (для тех испытаний, которые допускают использование клас-
классического определения вероятности) и, во-вторых, в установлении не-
независимости событий на основе очевидности или интуиции.
g4tuftfufie*b. Так я и предполагал. Но у меня есть еще один вопрос.
Правило A7) для г событий получено как обобщение правила A6) для
трех событий. Но почему же само правило A6) мы не рассматривали
как обобщение правила (9) для двух событий, а выводили независимо
от правила (9)?
Пвтор. Для трех (и более) событий существует, наряду с понятием
попарной независимости событий, также понятие независимости в сово-
совокупности. Вот из-за этого и понадобился отдельный разговор.
*Чипи1*иель. Вообще-то мне казалось, что из попарной независимо-
независимости событий следует также и независимость в совокупности. Ведь если
А не зависит от В, В не зависит от А и это же можно сказать о парах
А — С и В — С, то как может существовать какая-то общая зависимость
между А, В, С?
Пвтор. В алгебре событий такое вполне возможно.
. Нельзя ли привести какой-нибудь «живой» пример, ког-
когда события А, В, С попарно независимы, а в то же время независимость
в совокупности для этих событий не имеет места?
Пвтор. Пусть испытания состоят в подбрасывании двух монет. Со-
Событие А — первая монета выпала орлом, событие В — вторая монета
выпала орлом, событие С — обе монеты выпали одинаковым образом.
Пространство элементарных исходов: 00, ОР, РО, РР (п = 4). Легко
видеть, что тА = 2 (исходы 00 и ОР), тв=2 (исходы 00 и РО), тс=2
(исходы 00 и РР); следовательно, Р(А) = тА / п = 1 / 2, Р(В) = тв / п = 1 / 2,
Р(С) = тсI п = 1 / 2. Легко видеть также, что тм = тАС = твс = 1 (ис-
(исход 00), так что Р(АП В) = Р(АП С) = Р(ВП С) = 1 / 4. Применяя к каж-
каждой из трех пар событий правило G), мы получаем, что
РВ(А)=РС(А)=Р(А) =1/2;
РА(В)=РС(В)=Р(В) = 1/2;
РА(С)=РВ(С)=Р(С) =1/2.
Итак, мы убедились, что события А, В, С попарно независимы. А теперь
выясним, чему равна Р(АГ\В{] С). Для этого найдем тАВС — количество
элементарных исходов, благоприятных для события АГ\ВГ\С.
250

Есть только один такой исход — исход 00. Значит, Р(АГ\ВГ\ С) =
= тлвс/ п= 1/4- Учитывая, что РАПВ(С) =Р(АГ\ВГ\ С) / Р(А[\В) по-
получаем: РАПВ(С) = A/4) :A/4) = 1. Мы видим, что РА(]В(С) * Р(С)
и, следовательно, условие независимости в совокупности (условие (****))
не выполняется.
'Чипиинель. И в самом деле! Здесь вероятность Р(АГ\ ВГ\ С) не равна
произведению вероятностей Р(А) • Р(В) • Р(С). Как мы убедились,
Р(А{]В{]С) = 1/4, а Р(А) - Р(В) - Р(С) = A / 2) - A / 2) - A / 2) = 1 / 8.
9.7 Повезет или не повезет мне с зачетом?
(Размышления одного студента)
JnLain преподаватель вынес на зачет 25 вопросов. Он очень строгий.
Предупредил, что каждому предложит какие-то четыре вопроса из это-
этого вопросника. Тот, кто не ответит хотя бы на один из предложенных
вопросов, зачета не получит. Я успел разобраться только с двадцатью
вопросами, а к пяти не знаю, как подступиться. Вот и думаю: имеет ли
смысл идти сегодня на зачет? Неплохо было бы подсчитать вероятность
получить зачет.
Иначе говоря, надо подсчитать вероятность Р того, что четыре воп-
вопроса, выбранные наугад из двадцати пяти вопросов, попадут в число
двадцати «моих» вопросов (я имею в виду те двадцать вопросов, с кото-
которыми я успел разобраться). Обозначим через А, В, С, D вероятности
того, что, соответственно, первый, второй, третий и четвертый предло-
предложенные мне вопросы окажутся из числа «моих» вопросов. Искомую
вероятность Р можно представить в виде:
P = P{A(\B(\C(\D).	(*)
Воспользовавшись правилом A5), я могу переписать (*) вот так:
(**)
Первый вопрос будет выбираться наугад из двадцати пяти вопросов;
вероятность, что он окажется одним из двадцати «моих» вопросов, равна
20/25. Итак, Р(А) = 20/25. Вероятность появления второго из известных
мне вопросов при условии наступления события А есть условная вероят-
вероятность РА(В). Она равна 19/24, поскольку теперь надо из 24оставшихся
в вопроснике вопросов попасть случайным образом в один из 19 остав-
оставшихся «моих» вопросов. Итак, РА(В) = 19/24. Вероятность появления
251

третьего из известных мне вопросов при условии совместного наступле-
наступления событий А и В есть PAf]B(C). Легко сообразить, что Рапв(С) = 18 / 23.
Переходя, наконец, к четвертому вопросу, который должен появиться
при условии совместного наступления событий А, В и С, мы тоже без
труда определяем его вероятность: Раг\вг\с№) = 17/22. Теперь можно,
используя (**), вычислить вероятность Р:
Р = B0/25). A9/24). A8/23). A7/22) =
= 116280/303600 = 969/2530 = 0,383.
Итак, у меня приблизительно четыре шанса из десяти получить зачет.
Маловато, конечно. Но, может быть, я ошибся? Самый надежный спо-
способ вычислить вероятность — это рассмотреть пространство элементар-
элементарных исходов и воспользоваться классическим определением вероятнос-
вероятности. Если, разумеется, ситуация позволяет использовать классическое
определение вероятности. В нашем случае это возможно. Полное число
п элементарных исходов есть в нашем случае количество всевозможных
выборок 4 элементов из 25, т. е. п = С\5. А количество благоприятных
исходов (благоприятных для события АГ\ВГ\ C[\D) есть число т все-
всевозможных выборок 4 элементов из 20, т. е. п = С\$. Используя класси-
классическое определение вероятности, находим:
= B0!/4! 16!): B5!/4!21!) = 969/2530.
Получается такой же в точности результат, что и при первом подсчете!
Что ж, к строгому преподавателю я, пожалуй, явлюсь. Авось мне
повезет. Все-таки четыре шанса из десяти позволяют надеяться полу-
получить зачет.
Послесловие. Наш студент отправился за зачетом, но прежде, чем
зайти в аудиторию, он разобрался в коридоре с помощью друзей еще с
одним вопросом. Подсчитав тут же вероятность, он убедился, что те-
теперь она увеличилась до 0,473. Это его весьма приободрило. Тем време-
временем строгий преподаватель пошел обедать. Не теряя времени, наш сту-
студент разобрался вместе с друзьями еще с двумя вопросами. Теперь он
знал 23 вопроса из 25! Вероятность получить зачет поднялась до 0,7.
Семь шансов из десяти! И студент смело отправился на беседу с препо-
преподавателем. Зачет он получил. Правда, ему не достался ни один из тех
вопросов, которые он познал в коридоре. Как всегда, Его Величество
Случай проявил своеволие. Впрочем, семь шансов из десяти, надо по-
полагать, чего-то стоили...
252

9.8 Тренировочные задачи с вычислением
вероятности совместного наступления событий,
независимых в совокупности
Задача 1. Цехи № 1 и № 2, работая независимо один от другого, выпускают лам-
лампочки. Как показала практика, в продукции цеха № 1 на 400 лампочек приходится одна
бракованная, а в продукции цеха № 2 одна бракованная лампочка приходится на 700 лам-
лампочек. Выбраны наугад пять лампочек — две из цеха № 1 и три из цеха № 2. Какова
вероятность Р того, что все пять лампочек окажутся небракованными?
Решение. Из условия задачи следует, что вероятность Р± появления бракован-
бракованной лампочки в продукции цеха № 1 равна Р1 = 1 /400 = 0,0025, а вероятность Р2
появления брака в продукции цеха № 2 равна Р2 = 1 /700 = 0,00143. Вероятно-
Вероятности появления небракованных лампочек равны, соответственно, 1 - Р{ = 0,9975
и 1 - Р2 = 0,99857. Пусть К— событие, заключающееся в том, что и первая, и вторая
лампочки из цеха № 1 оказались небракованными, и пусть L — событие, заключа-
заключающееся в том, что и первая, и вторая, и третья лампочки из цеха № 2 также оказа-
оказались небракованными. Пользуясь, для удобства, калькулятором, находим:
Р(К) = A - Р{) • A - Р{) = 0,9975 • 0,9975 = 0,99501,
P(L) = A - Р2) • A - Р2) • A - Р2) = 0,99857 • 0,99857 • 0,99857 = 0,99572.
Вероятность Р есть вероятность наступления и события Р{К) и события Р{Ц;
следовательно, Р(К) • РЩ = 0,99501 • 0,99572 = 0,99075.
Задача 2. Имеется система из трех блоков A, 2, 3). Надежность работы любого
блока не зависит от надежности работы остальных. Вероятности случайного выхода
из строя блоков 1, 2, 3 равны, соответственно, 0,12, 0,08, 0,13. Какова вероятность Р
функционирования системы? Рассмотреть два случая: 1) система выходит из строя,
когда выходит из строя хотя бы один из блоков {пример: лампочки, соединенные последо-
последовательно); 2) система выходит из строя лишь тогда, когда выходят из строя все три
блока {пример: лампочки соединенные параллельно).
Решение. Случай 1. Пусть события Аъ А2, Аъ — случайный выход из строя бло-
блоков 1, 2, 3, соответственно. Согласно условию задачи, Р{А{) = 0,12, Р{А2) =0,08,
Р{А3) =0,13. Система функционирует, если исправны и блок 1 (вероятность того,
что он исправен, есть 1 - Р{А{)), и блок 2 (вероятность 1 - Р{А2)), и блокЗ (веро-
(вероятность 1 - Р{А3)). Если какие-то события независимы в совокупности, то и соот-
соответствующие противоположные события также независимы в совокупности. Учи-
Учитывая это и используя правило A7), получаем:
Р = Р{АХ) • Р(А2) ¦ Р(А3) = A - Р(АХ)) ¦ A - Р(А2)) ¦ A - Р(АЪ)) =
= A-0,12).A-0,08).A-0,13) =0,88-0,92-0,87 =0,70435.
Случай 2. Система выходит из строя тогда и только тогда, когда выходят из строя
и блок 1, и блок2, и блокЗ; вероятность такого события есть Р(А1) • Р{А2) • Р{А3).
253

А нам требуется найти вероятность Р, являющуюся вероятностью противополож-
противоположного события. Значит,
Р = 1-Р(А1).Р(А2).Р(А3).	(*)
Подставив значения Р(А{), Р(А2) и Р(А3), получаем:
Р= 1 - 0,12 • 0,08 • 0,13 = 1 - 0,00125 = 0,99875.
НЕЗАПЛАНИРОВАННЫЙ ДИАЛОГ
'%сана*нелй. В случае 2 система функционирует, если исправен хотя бы
один из блоков. Вероятность того, что исправен блок 1, есть 1 - Р(А{)'9
вероятность, что исправен блок 2, есть 1 - Р(А2); вероятность, что ис-
исправен блокЗ, есть 1 - Р{ЛЪ). Я правильно пока рассуждаю?
Пвтор. Пока правильно.
'Чсонсинель. Поскольку для функционирования системы нужно, чтобы
были исправны или блок 1, или блок2, или блокЗ, то, следовательно
(**)
Пвтор. Стоп! Вот тут уже допущена ошибка. Вы могли бы это почув-
почувствовать сами, обратив внимание на то, что, согласно (**), вероятность Р
оказывается заведомо больше единицы. Это недопустимо. В Вашем рас-
рассуждении к фразе «или блок 1, или блок 2, или блок 3» следовало добавить
«или блоки 1 и 2, или блоки 1 и 3, или блоки 2 и 3, или все три блока».
Короче говоря, Вы не приняли во внимание, что события Ah Аъ Аъ (как
и события Аь Аъ А3) не являются несовместными событиями. Кстати, вспом-
вспомните задачу о двух охотниках, стреляющих в одну и ту же утку.
g4u*StiuSU*&, Значит, вместо (**) мне следовало воспользоваться пра-
правилом D)?
Пвтор. Вот именно. Только при этом надо учесть, что наши события
являются независимыми. Так что в нашем случае мы имеем:
Р = Р(АХ) + Р{А2) + Р(АЪ) - Р(АХ) • Р(А2) -
-Р(АХ) • Р(А3) - Р(А2). Р(А3) + Р(АХ) • Р(А2). Р(А3). (***)
'Чипиипель. Соотношение (*) можно, очевидно, переписать так:
Р = 1 - A - Р(АХ)) • A - Р(А2)) • A - Р(А3)).	(****)
Получается, что, если тут выполнить умножение, то придем к соот-
соотношению (***)?
254

Пвтор. Конечно. В этом нетрудно убедиться. Посмотрите:
A - Р(АХ)) • A - Р{А2)) • A - Р(АЪ)) =
= A - Р{ЛХ) - Р{Л2) + Р(ЛХ) • Р{Л2)) • A - Р(Т3)) =
= 1 - Р(АХ) - Р{А2) - Р(АЪ) + Р(АХ) • Р(А2) +
+ Р(ЛХ) • Р(ЛЪ) + Р(Л2). Р(ЛЪ) - Р(ЛХ). Р(Л2). Р(АЪ).
Подставив полученный результат в (****), мы немедленно получим
(***), т. е. придем к соотношению (*).
Задача 3. Подбрасывают три кубика. Какова вероятность Р того, что все кубики
выпадут одной и той же гранью!
Решение. Для каждого кубика вероятность выпадения единицы (обозначим ее
через Pi) есть Рх = 1 / 6. Такова же вероятность выпадения двойки, тройки, чет-
четверки, пятерки, шестерки: Р2 = 1 / 6, Р3 = 1 / 6, Р4 = 1 / 6, Р5 = 1 / 6, Р6 = 1 / 6. Пусть
событие А — выпали три единицы, В — выпали три двойки, С — выпали три
тройки, D — выпали три четверки, Е — выпали три пятерки, F — выпали три
шестерки. Безразлично, какое из этих шести несовместных событий наступит.
Поэтому искомая вероятность есть Р= Р(А) + Р(В) + Р(С) + P(D) + Р(Е) + P(F).
Каждое из слагаемых вычисляется с использованием правила A7). Например,
Р(А) = Р1-Р1- Рь Р{В) = Р2-Р2-Р2ит. д. Таким образом,
P = Pl.Pl.Pl + P2.P2.P2 + ... + P6.P6.P6 =
= 1/216 + 1/216 + 1/216 + 1/216 + 1/216+1/216=6/216 =1/36.
Задача 4. Подбрасывают три кубика. Какова вероятность Р того, что не выпа-
выпадут ни три единицы, ни три двойки, ни три тройки?
Решение. Если воспользоваться обозначениями, введенными в предыдущей за-
задаче, то можем записать:
Р = Р(А) ¦ Р(В) ¦ Р(С) = A - Р(А)) ¦ A - Р(В)) ¦ A - Р(С)) =
= A -1/216) • A -1/216) • A -1/216) = B15/216) • B15/216) • B15/216) =
= @,99537K =0,98617.
Задача 5. Кубик подбрасывают три раза. Какова вероятность Р того, что при
этом единица не выпадет?
Решение. Рассмотрим два варианта.
Вариант первый. Пусть событие А — единица выпала три раза, единица выпала
два раза, С — единица выпала один раз. Из задачи 3 мы уже знаем, что
Р(А) = Р{ • Р{ • Pi = 1 /216. Найдем теперь Р(В). Событие В можно рассматривать
как объединение трех несовместных: событий; обозначим их через Въ В2, В3. Со-
Событие В{. в первом броске единица выпала (вероятность 1/6), во втором броске
единица выпала (вероятность 5 / 6), в третьем броске единица не выпала (вероят-
(вероятность 5/6); понятно, что Р(ВХ) = A /6) • A /6) • A - 1 /6) = 5 /216. Событие В2:
255

в первом броске единица выпала, во втором не выпала, в третьем выпала; Р(В2) =
= A / 6) • A - 1 / 6) • A / 6) = 5 / 216. Событие В3: в первом броске единица не выпала,
во втором и третьем бросках единица выпала; Р(В3) = A-1/ 6) • A / 6) -A/6) =
= 5/216. Таким образом.
Р{В) = Р(В{) + Р(В2) + Р(В3) = 15/216.
Наконец, найдем Р{С). Событие С можно рассматривать как объединение трех
несовместных событий: Съ С2, С3. Событие С\ — единица выпала только в первом
броске и, значит, не выпала ни во втором, ни в третьем; Р(С1) = A / 6) • E / 6) • E / 6) =
= 25 I 216. Событие С2: единица выпала только во втором броске; Р(С2) = E / 6) •
• A / 6) • E / 6) = 25 / 216. Событие С3. единица выпала только в третьем броске;
Р(С3) = E / 6) • E / 6) • A / 6) = 25 / 216. Таким образом,
Р(С) = Р(С{) + Р(С2) + Р(С3) = 75/216.
Нам надо найти вероятность Р того, что единица не выпадет при трех бросках,
т. е. не выпадет ни три раза, ни два раза, ни один раз. Иначе говоря, нам надо
найти вероятность события, противоположного событию A\JB\JC, т.е. вероят-
вероятность Р= 1 - P(A\JBU С). Поскольку Р(АUBU С) = Р(А) + Р{В) + Р(С) = 1 /216 +
+ 15 / 216 + 75 / 216 = 91 / 216, то, следовательно, Р= 1 - 91 / 216 = 125 / 216.
Вариант второй (значительно более простой). Вероятность выпадения единицы в
каждом броске равна, очевидно, 1/6. Значит, вероятность того, что единица не выпа-
выпала, скажем, в первом броске, равна 1-1/6 = 5/6. Таковы же вероятности того, что
единица не выпадет во втором и третьем бросках. Отсюда немедленно получаем иско-
искомую вероятность: Р = A-1/6) A — 1/6) A — 1/6) = E/6) E/6) E/6) = 125/216.
Задача 6. Кубик подбрасывают три раза. Какова вероятность Р того, что выпа-
выпадут в сумме 17 очков?
Решение. Столько очков может выпасть в трех случаях: 6-6-5, 6-5-6, 5-6-6.
События, отвечающие этим случаям, несовместны. Воспользовавшись обозначени-
обозначениями, введенными в задаче 3, получаем: Р= Р6- Р6- Р5 + Р6- Р5- Р6 + Р5- Р6- Р6=1 / 216 +
+ 1/216+1/216=1/72.
Задача 7. Кубик подбрасывают четыре раза. Какова вероятность Р того, что
выпадут в сумме 23 очка?
Решение. Столько очков может выпасть в четырех случаях: 5-6-6-6, 6-5-6-6,
6—6—5—6, 6—6—6—5. Следовательно,
р = р5р6р6р6+р6р5р6р6+р6р6р5р6+р6р6р6р5 =
= 1/1296 + 1/1296 + 1/1296 + 1/1296 = 4/1296 = 1/324.
9.9 Вероятностные задачи-сказки с лабиринтами
9.9.1. Задача-сказка первая: Поиск сокровищ в лабиринте в надежде на
Случай. Один хитроумный Шах придумал хранить свои сокровища в лаби-
лабиринте. Для большей сохранности он поселил в том лабиринте свирепого
256

дракона. Схема лабиринта показана на рис. 1 в таблице 37. Дракон нахо-
находится в яме, изображенной в виде черного квадрата, а сокровища находят-
находятся в пещере L. Существуют три выхода из лабиринта: Д G, К. У каждого
выхода день и ночь дежурят стражи с мечами. Они должны немедленно
отрубить голову всякому, кто появится на выходе из лабиринта.
Прослышала о сокровищах лабиринта Ведьма и очень захотела запо-
заполучить их. Зазвала она к себе Удальца-Хитреца, накормила его, напоила
и стала уговаривать отправиться в лабиринт за сокровищами. Половину
тех сокровищ обещала уступить. «А как же я назад выберусь с сокрови-
сокровищами? — спрашивал Ведьму Удалец-Хитрец. — Я тебе клубок ниток
дам, — отвечала она. — Идешь по лабиринту — клубок разматывается.
По нити назад ты и возвратишься». «А как же дракон да стражи с меча-
мечами на выходах? — спрашивал Ведьму Удалец-Хитрец. — А ты иди по
лабиринту той дорожкой, какой Шах к своим сокровищам ходит, —
отвечала она. — Тогда ни с драконом, ни со стражами не встретишься».
«А кто же мне ту заветную дорожку в лабиринте подскажет? — спраши-
спрашивал Ведьму Удалец-Хитрец. — Подскажет Случай, на него надейся, —
отвечала она. — А я позабочусь, чтобы он тебя не подвел».
На том разговор и прервался. Отправился Удалец-Хитрец почивать.
Как известно, утро вечера мудренее. А утром Удалец-Хитрец крепко
призадумался. Вспомнил он, что управлять Случаем никто не может.
Даже Ведьма. А чтобы на Случай понадеяться, надо шансы соответ-
соответствующие подсчитать. Подсчитал Удалец-Хитрец вероятность добрать-
добраться до сокровищ в том лабиринте, усмехнулся, да без чаю и без кофе
восвояси отправился. Только его Ведьма и видела.
На рис. 2 в таблице 37 изображена схема всех дорожек и развилок в
лабиринте, показанном на рис. 1. Подсчитаем вероятность Рсокр добраться
от входа в лабиринт до сокровищ. Первая развилка — это развилка О. Весь
путь от нее до сокровищ состоит из трех событий-переходов: перехода
О^ С, перехода С^Н и перехода Н^ L. Все эти события случайные.
Например, из О можно с равной вероятностью выбрать переход не к С, а
к В или к Л. Значит, событие О^ С имеет вероятность 1/3. Запишем:
Р(О^ С) = 1/3. Легко сообразить, что Р{С^ Н) = 1 / 3 и Р(Н^ L) = 1 / 3.
Все события-переходы независимы, поскольку выбор на каждой развилке
дальнейшего пути производится, очевидно, независимым образом. Поэтому
мы можем воспользоваться правилом A7) и записать:
= Р(О -> С) • Р(С -> Н) • Р(Н
= A/3)A/3)A/3) = 1/27.
257

Таблица 37. Лабиринты и вероятности
258

Такова вероятность выбрать ту дорожку в лабиринте, по которой Шах
ходит любоваться своими сокровищами.
Теперь подсчитаем вероятность Рдрак попасть в яму к дракону. От
развилки к дракону ведут четыре пути:
-	от О к А; Р(О^ А) = 1/3;
-	от О к С и от С к D;
Р((О -* С)П(С ^ D)) = Р(О -* С)Р(С ^D) = A/3) A/3) = 1/9;
-	от О к С, от С к Е, от Е к F;
Р((О -> С) П (С -> Я) П (Я -> Л) = Р(О -> С) • Р(С -> Я) • Р(? -»• F) =
= A / 3) - A / 3) - A / 2) = 1 /18;
-	от О к С, от С к Я, от Як М;
Р((о -+ с) п (с -+ я) п (я ^ м» =
Все четыре пути несовместны (использование одного из данных путей
исключает использование других путей); поэтому, согласно B),
E)f)(E
= 1/3 +1/9 + 1/18 +1/27 = 1/27.
Наконец, подсчитаем вероятность Рвых выйти из лабиринта и под-
подвергнуться нападению со стороны бдительных стражей. Тут имеются
три несовместных пути:
- от О к В;
-	от О к С, от С к Д от Е к G; Р((О -> С) П (С -> Е) П (Я -> (?)) =
= Р(О^ С)Р(С -f E)P(E -f (?) = A / 3) • A / 3) ¦ A / 2) = 1/18;
-	от О к С, от С к Я, Як #; Р((О -> С) П (С -> Я) П (Я -. А")) =
f С)Р(С - Н)Р{Н ^ К) = A / 3) • A / 3) - A / 3) = 1/27.
Складывая вероятности выбора этих трех путей, находим, что
^вых = 1/3 + 1/18 + 1/27 = 23/54.
Заметим, что для всякого, кто войдет в лабиринт нашего Шаха,
есть всего три исхода: найти сокровища и по нити вернуться с ними
назад ко входу в лабиринт (вероятность этого исхода Рвых= 1/27),
259

попасть в яму к дракону и быть растерзанным (вероятность исхода
Рдрак = 29 / 54), выйти из лабиринта к стражам с мечами (вероятность
исхода Рвых = 23/54). Других исходов нет. Значит, вероятность того,
что реализуется или первый, или второй, или третий исходы, должна
равняться единице как вероятность достоверного события. Так оно и
есть: 1/27+ 29/54 +23/54 = B +29+ 23)/54 = 1.
Итак, вероятность отыскать сокровища равна 1/27, а вероятность
погибнуть при этом поиске равна 1 - 1 / 27 = 26 / 27. Как видим, слу-
случай подсказывает, что шансов найти сокровища в 26 раз меньше, чем
шансов погибнуть. Вряд ли разумно надеяться на такой случай.
9.9.2. Задача-сказка вторая: Поиск выхода из лабиринта в надежде
на Случай. Один человек совершил проступок. Кто-то утверждал, что
проступок был очень серьезный, а кто-то считал его незначитель-
незначительным. Как бы там ни было, но суд приговорил того человека к пожиз-
пожизненному заключению. И обратился осужденный с прошением к Шаху:
просил либо помиловать, либо казнить, потому что пожизненное за-
заключение — это, хотя и не смерть, но и жизнью считаться не может.
«Я не Бог, чтобы выбирать между помилованием и казнью! — сказал
Шах. — Пусть этот выбор сделает Случай!» И повелел Шах своему
Визирю: «Отправить осужденного в Особый Лабиринт! Если он су-
сумеет выйти из лабиринта, будет свободным. Если не сумеет, окажет-
окажется там замурованным и вскоре скончается». Визирь поклонился и
спросил: «А сколько монет ему выдать?» Подумал Шах и сказал: «До-
«Достаточно будет пяти монет».
Теперь пора объяснить, что такое Особый Лабиринт и зачем нужны
монеты тому, кого туда отправляют. Этот лабиринт изображен на рис. 3
в таблице 37. В лабиринте четыре комнаты: А, Д С, D. Входя в лаби-
лабиринт, человек попадает в комнату А, а чтобы выйти из лабиринта, ему
надо попасть, в конечном счете, в комнату D. На рисунке видны изо-
изогнутые коридоры, соединяющие комнаты А и Д В и С, С и D. Малень-
Маленькими кружками показаны особые двери, из-за которых лабиринт на-
назван «особым». Всего дверей пять. Двери заперты. Каждую из них можно
открыть (и притом лишь на несколько секунд) только со стороны кори-
коридора, но не со стороны комнаты. Чтобы дверь приоткрылась, надо, по-
подойдя к ней со стороны коридора, опустить монету в специальную щель.
Вот для чего тут нужны монеты.
Отправив осужденного в Особый Лабиринт и снабдив его пятью мо-
монетами, Шах тем самым дал ему шансы оказаться на свободе. Насколь-
Насколько они велики? Подсчитаем вероятность осужденному, получившему
260

для открывания дверей пять монет, попасть в комнату D и, таким обра-
образом, выйти на свободу.
Существуют три несовместных пути, позволяющие попасть в D тому,
у кого было пять монет: один путь с тремя переходами (переходы Л —> Д
В —> С, С —> D) и два пути с пятью переходами (либо путь с переходами:
А^ В, В^А,А^ В, В^ С, С —> Z) либо путь с переходами: А^ В, В^ С,
С—> Д В^ С, С—>D). Чтобы пройти путь с тремя переходами, нуж-
нужны, кроме везения, три монеты. Чтобы пройти путь с пятью перехода-
переходами, нужны пять монет. Все эти пути изображены схематически на
рисунках 4, 5 и 6 в таблице 37. Числами указаны вероятности каждого
из рассматриваемых переходов. Пользуясь правилом A7) и учитывая
вероятности переходов, подсчитываем вероятности попасть в комнату D.
Для пути, показанного на рис. 4, эта вероятность есть 1 • A / 2) • A / 2) =
= 1/4. Для пути, показанного на рис. 5, вероятность попасть в D есть
1 • A / 2) • 1 • A / 2) • A / 2) = 1 / 8. Для пути, показанного на рис. 6, ве-
вероятность попасть в D есть 1 • A / 2) • A / 2) • A / 2) = 1 / 16. В итоге по-
получаем, что вероятность нашему осужденному выйти из лабиринта на
свободу равна 1/4+1/8 + 1/16 = 7/16.
Если бы осужденному дали не пять, а, скажем, семь монет, то воз-
возникли бы дополнительные возможные пути выхода из лабиринта. Но
это уже другой разговор.
9.9.3. Задача-сказка третья: На случай надейся, но и сам не плошай!
Однажды Шах сильно разгневался на своего Звездочета. Тот предска-
предсказал по звездам, что не позднее, как через месяц, должен наступить
конец света. Но вот прошло три месяца — и ничего не случилось.
Позвал Шах Палача и повелел отрубить Звездочету голову. Однако в
последний момент Шах смягчился — все-таки хорошо, что Звездочет
ошибся. А потому решил Шах дать возможность Звездочету спастись.
Взял он три белых и три черных шара и предложил Звездочету распре-
распределить эти шары каким-то образом по двум вазам из непрозрачного
материала. Палач должен был выбрать наугад одну из ваз и наугад
вынуть из нее один шар. Если вынутый шар окажется белым. Звездо-
Звездочет будет помилован, а если черным, казнен. «О, Владыка! — взмо-
взмолился Звездочет. — Получается, что моя жизнь будет дважды зависеть
от Случая! Никто не ведает, какую вазу выберет Палач. Никто не ве-
ведает, какой шар подвернется Палачу под руку!». «На Случай надейся,
но и сам не плошай, — усмехнулся Шах. — Сообрази, как надо рас-
распределить шары по вазам, чтобы получить наибольшее число шансов
спастись». «Я вижу семь вариантов размещения трех белых и трех
261

черных шаров по вазам», — сказал Звездочет (эти семь вариантов мож-
можно видеть в левой половине таблицы 38). «Вот и выбери из них тот, где
вероятность вынуть белый шар наибольшая, — сказал Шах. — Это ис-
исключительно в твоих интересах».
Поможем Звездочету спастись. От волнения он может выбрать не
самый лучший вариант. Рассматриваемые варианты удобно представить
в виде семи несложных лабиринтов', они изображены в правой полови-
половине таблицы 38. Белые кружки соответствуют белым шарам, а черные —
черным; выход в лабиринте к белому кружку соответствует выниманию
Палачом белого шара. Если Палач подошел, например, к левой вазе, то
на схеме лабиринтов это будет означать выбор пути А —> В1 от развилки А.
Выбор случаен; его вероятность равна 1/2 (то же относится и к выбору
пути А^ В2).
Рассмотрим различные варианты и подсчитаем для каждого вероят-
вероятность вынуть белый шар (иначе говоря, вероятность выйти в лабиринте
к одному из белых кружков). Обозначим эту вероятность соответствен-
соответственно через Ръ Ръ Р3, А, Р5, Р& Pi-
Вариант 1. Здесь все выявляется уже на развилке А. Если выбрать
путь А —> Въ то выход к одному из белых кружков обеспечен. Если же
выбрать путь А —> Въ то обеспечен выход к черному кружку. Ясно, что
Pi = l/2.
Вариант 2. Согласно правилу A), вероятность Р2 есть сумма вероят-
вероятностей двух несовместных исходов — исхода при подходе Палача к ле-
левой вазе (исхода при выборе пути А —> В{) и исхода при подходе Палача
к правой вазе (исхода при выборе пути А^ В2). Для обозначения этих
двух вероятностей будем использовать в данном и последующих вари-
вариантах индексы «л» (левая ваза) и «пр» (правая ваза) соответственно.
Итак, представим: Р2 = Р2 + P2V. Далее воспользуемся правилом (9) и
запишем: Р2л = A / 2) • A / 3) и Р2пр = A / 2) • A / 3). Таким образом,
Р2= A/2) -B/3) + A/2) -A/3) = 1/3+ 1/6 = 1/2.
Вариант 3: Pf = A / 2) • C / 4) и Р3пр = О (при выборе правой вазы
появление белого шара исключается). Таким образом, Р3 = Р^ =
= A/2)-C/4) = 3/8.
Вариант 4: Дл = A / 2) • A / 4) и Дпр = A / 2) • 1 (мы написали тут
единицу, чтобы подчеркнуть: при выборе правой вазы появление белого
шара есть достоверное событие). Таким образом, Р4 =1/8 + 1/2 = 5/8.
Вариант 5: Pf = A / 2) • A / 2) и Р5пр = A / 2) • A / 2). Таким образом
/>5 =1/4+1/4=1/2.
Вариант 6: Р6Л = A / 2) • B / 5) и Дпр = A / 2) • 1. Таким образом,
Р6 = 1 / 5 + 1 / 2 = 7 / 10.
Вариант 7: Р7л = A / 2) • C / 5) и Р7пр = 0. Таким образом, Р7 = 3 / 10.
262

Таблица 38. На Случай надейся, но и сам не плошай!
Вариант 1
Вариант 4
Вариант 5
Вариант 6
Вариант
263

Мы видим, что Звездочету наиболее целесообразно разместить шары по
вазам в соответствии с вариантом 6, а наименее целесообразен вариант 7.
Конечно, не следует забывать, что речь идет о вероятности события.
А выбор Палачом того или иного шара все равно случаен, так что вари-
вариант 6 (как и любой другой вариант) не дает гарантии Звездочету избе-
избежать казни. Здесь уместно еще раз обратиться к § 7.6, где мы рассужда-
рассуждали над вопросом «Что практически дает нам подсчет вероятности
случайного события?».
9.10 Правило вычисления вероятности
наступления хотя бы одного из совокупности
независимых событий
Рассматривается совокупность г независимых событий: АЪАЪАЪ,
...9АГ. Известны вероятности событий: Р(А{)9 Р(А2)9 Р(А3)9 ..., Р(АГ).
Пусть В — событие, заключающееся в наступлении хотя бы одного из
рассматриваемой совокупности событий. Поставим вопрос: Чему равна
вероятность Р{ВI Иначе говоря, какова вероятность наступления хотя
бы одного из событий Аъ Аъ Аъ, ..., АГ1 Тот же вопрос можно поставить
и так: какова вероятность наступления или события Аъ или события Аъ
или события Аъ, ..., или события АГ1
Поскольку при перечислении событий использовался союз «или»,
напрашивается ответ: Р(В) = Р(А{) + Р(А2) + Р{АЪ) + ... + Р{АГ). Но пра-
правило B) в данном случае не годится, поскольку наши события не явля-
являются несовместными.
Чтобы найти ответ на поставленный вопрос, подумаем над смыслом
события В , являющегося противоположным по отношению к событию В.
Если В — появление хотя бы одного из событий Аъ Аъ Аъ, ..., АГ9 то В
есть непоявление ни одного из указанных событий, т. е. непоявление ни
события Аъ ни события Аъ ни события Аъ, ..., ни события Аг. Другими
словами, событие В — это появление и события А±, и события А2 , и
события Аъ , ..., и события Аг ; поэтому запишем:
Учитывая, что Р(В) = 1 — Р{В), получаем отсюда:
Р{В) = 1 - P(Ai П А2 П Аз П... П Аг).
264

События Ah Аъ Аъ, ..., Аг, а значит, и события А\, Ai, Аз, ..., Аг
независимы в совокупности. Поэтому можно воспользоваться прави-
правилом A7) и представить Р(В) в виде:
Р(В) = 1 - Р(Ах) - P(Ai) - Р{Ъ) ...Р(Аг).
Таким образом,
Р{В) = !-(!- РD)) - A - Р(Л2)) ¦ A - Р(Л3)) • • A ~ Р(Л))-1 A8)
В частном случае, когда
Р{АХ) = Р(А2) = Р(Л3) = ... = Р{АГ) = р,
правило A8) принимает вид:
A9)
Рассмотрим три примера на применение полученного правила.
Пример 1 (посвящен несчастной утке, в которую стреляли одновремен-
одновременно десять неопытных стрелков). Предположим, что каждый из десяти
стрелков попадает в летящую утку с вероятностью 0,2. И вот все они
стреляют по несчастной утке. Нас интересует ответ на вопрос: какова
вероятность Р того, что хотя бы один из стрелков попадет в цель! Пра-
Правило A9) в данном случае годится, поскольку попадание (или непопа-
непопадание) в утку любого из десяти стрелков не зависит от попадания в нее
всех других стрелков. При условии, конечно, что все стрелки выстрели-
выстрелили одновременно. Подставим в A9) г = 10 и р = 0,2. Получим: Р=\-
- A - 0,2I0 = 1 - 0,810 = 1 - 0,107374 = 0,892626. Как видим, совсем не-
неплохой результат!
Если бы в утку стрелял один из наших неопытных стрелков, то, ско-
скорее всего, на костре нечего было бы жарить. Но если стреляют десять
неопытных стрелков, жареная утка практически обеспечена. Правда,
одной жареной утки для десятерых человек маловато.
Пример 2 (взят из производственной практики). Рабочий обслуживает
четыре станка, работающих независимо один от другого. Вероятность
того, что в течение, скажем, часа станок не потребует вмешательства
рабочего, равна: для 1-го станка 0,8, для 2-го станка 0,9, для 3-го станка
0,85, для 4-го станка 0,75. Какова вероятность Р, что хотя бы один из
четырех станков не потребует вмешательства рабочего в течение часа?
Исходя из соотношения A8), находим:
р = 1 - A - 0,8) • A - 0,9) • A - 0,85) • A - 0,75) =
= 1-0,2.0,Ь0,15.0,25 = 1-
265

Пример 3 {посвящен многократному бросанию монеты). Уже отмеча-
отмечалось, что, сколько бы раз ни подбрасывалась монета, вероятность вы-
выпадения орла (или решки) не меняется; она остается равной 1/2. Тем
не менее, когда некто начинает подбрасывать монету и обнаруживает,
что, например, четыре раза подряд выпала решка, он удивляется. Дол-
Должен же выпасть, наконец, орел! Его удивление можно объяснить, со-
сославшись на практику бросаний монеты. Но можно также обосновать
научно. Поставим вопрос: какова вероятность Р того, что из пяти бро-
бросаний монеты хотя бы один раз выпадет орел ? Падения монеты той или
другой стороной — события независимые. Поэтому воспользуемся со-
соотношением A9), положив г=5и/?=1/2. Получим:
р = 1-A-1/2M = 1 - A/2M =1-1/32 = 31/32.	(*)
Как видим «некто» вполне обоснованно удивлялся.
Вероятность выпадения орла в каждом бросании не меняется с чис-
числом бросаний, но вероятность того, что орел выпадет хотя бы один раз
за г бросаний, возрастает по мере увеличения г. Так, для г = 1 указанная
вероятность равна 1/2, для г= 2 она равна 3/4, для г= 3 равна 7/8,
для г= 4 равна 15/16 и т. д. В общем случае рассматриваемая вероят-
вероятность равна BГ- 1)/2г. При достаточно большом г она может стать
сколь угодно близкой к единице.
Полезно заметить, что результат (*) мог быть получен непосредственно
из рассмотрения пространства элементарных исходов для пятикратного
подбрасывания монеты. Это пространство изображалось на рис. 2
в таблице 20. Событие «при пяти бросаниях орел выпал хотя бы раз»
есть объединение событий: «он выпал один раз», «выпал два раза», «вы-
«выпал три раза», «выпал четыре раза», «выпал пять раз». Легко видеть из
рисунка, что количество элементарных исходов, благоприятных для ука-
указанного объединения, равно 31. А всего исходов 32. Отсюда сразу сле-
следует результат (*).
ЗАДАНИЯ ПО ТЕМЕ 9
1.	Для каких С соотношение D) превращается в соотношение P(A\J B\J С) =
= Р(А) + Р(В) + Р(С) - Р(А П В)? Изобразите соответствующую диаграмму Эй-
Эйлера—Венна.
2.	Для каких С соотношение D) превращается в соотношение C)? Рассмотрите
разные случаи и изобразите для них диаграммы Эйлера-Венна.
3.	Кубик подбрасывают два раза. Вычислите P(A\JB) и Р(АГ\В) для следующих
пар событий Ли В:
а) А — выпала нечетная сумма, В — выпали одинаковые очки;
266

б)	Л — выпала четная сумма, Б — выпали одинаковые очки;
в)	Л — выпала сумма больше 7, Б — выпала сумма меньше 7;
г)	А — выпала сумма меньше 10, В— выпала сумма больше 5;
д)	А — выпала четная сумма, В— выпала сумма меньше 8;
е)	А — выпала нечетная сумма В — выпала сумма меньше 3.
Ответы: а) 2/3,0; б) 1/2, 1/6; в) 5/6, 0; г) 1, 5/9; д) 5/6, 1/4; е) 3/4, 1/3.
4.	Кубик подбрасывают два раза. Вычислите P(A\J B\J С) и Р(ЛП БП С) для следую-
следующих троек событий А, В, С:
а)	А — выпала четная сумма, В — выпала сумма меньше 7, С — во втором
броске выпала двойка;
б)	А— выпала нечетная сумма, В— выпала разность 1, С— выпала сумма мень-
меньше 8;
в)	А — выпали разные очки, В — выпала сумма меньше 7, С— выпала сумма 6;
г)	А — выпали очки хотя бы с одной единицей, В — выпали очки хотя бы с одной
шестеркой, С— выпали одинаковые очки;
А) А — выпали очки хотя бы с одной двойкой, В — в первом броске выпала
двойка, С — выпала сумма меньше 6;
е) А — в первом броске выпала единица, В — выпали одинаковые очки, С —
выпала сумма, равная 6.
Ответы: а) 25/36, 1/18; б) 31/36, 1/6; в) 11/12, 1/9; г) 2/3, 0; г) 4/
9, 1/12; е) 7/18, 0.
5.	Кубик подбрасывают два раза. Вычислите условную вероятность РВ(А) для следую-
следующих пар событий Л и Б и укажите, являются ли эти события взаимно независимыми:
а)	А — выпали одинаковые очки, В— выпала четная сумма;
б)	Л — в первом броске выпала тройка, В— во втором броске выпала тройка;
в)	А — выпала разность 1, Б — выпала сумма, равная 5;
г)	А — выпала разность 2, Б — выпала сумма, равная 8;
д)	А — выпала сумма, равная 7, Б— во втором броске выпала единица;
е)	А — выпала сумма меньше 6, Б — выпала сумма меньше 10.
Ответы: а) 1/3, не являются; б) 1/6, являются; в) 1/2, не являются; г) 2 / 5, не
являются; д) 1/6, являются; е) 1, не являются.
6.	Монету подбрасывают четыре раза. Докажите, что следующие тройки событий
А, Б, С являются независимыми в совокупности и вычислите вероятности пересе-
пересечений АПВ, Л ПС, БПС, АПВПС:
а)	А — в первом броске выпал орел, Б — в третьем броске выпал орел, С —
в четвертом броске выпал орел;
б)	Л — в первом броске выпал орел, Б — во втором броске выпал орел, С —
в третьем броске выпал орел;
в)	Л — в первых двух бросках выпал орел, Б— в третьем броске выпал орел, С—
в четвертом броске выпал орел;
г)	Л — в первом броске выпал орел, Б — во втором броске выпал орел, С —
в последних двух бросках выпал орел.
Ответы: а) 1/4, 1/4, 1/4, 1/8; б) 1/4, 1/4, 1/4, 1/8; в) 1/8, 1/8, 1/4,
1/16; г) 1/4, 1/8, 1/8, 1/16.
267

7.	Монету подбрасывают четыре раза. Докажите, что следующие тройки событий
Л, В, С не являются независимыми в совокупности:
а)	Л — в первых двух бросках выпал орел, В — в третьем броске выпал орел, С —
в двух последних бросках выпал орел;
б)	Л — в первом броске выпал орел, В — во втором броске выпал орел, С —
в первых двух бросках выпал орел;
в)	А — в первом броске выпал орел, В — в первых двух бросках выпал орел, С —
во всех четырех бросках выпал орел;
г)	А — в первом броске выпал орел, В — в первых двух бросках выпал орел, С —
в последних двух бросках выпал орел.
8.	Являются ли независимыми события Л и Б? события Л и С? события Б и С? Эти
вопросы относятся к каждой из четырех троек событий, рассмотренных в зада-
задании 7.
Ответы: а) да, да, нет; б) да, нет, нет; в) нет, нет, нет; г) нет, да, да.
9.	Кубик подбрасывают два раза. Докажите, что для следующих троек событий
А, В, С имеет место попарная независимость, но при этом нет независимости
в совокупности:
а)	Л — в первом броске выпала единица, В — во втором броске выпала шестер-
шестерка, С — выпала сумма 7;
б)	Л — в первом броске выпала единица, В — во втором броске выпала единица,
С — выпали одинаковые очки;
в)	Л — в первом броске выпала двойка, В — во втором броске выпала пятерка,
С — выпала сумма 7;
г)	Л — в первом броске выпала единица, В— во втором броске выпала шестер-
шестерка, С— выпали одинаковые очки;
д)	Л — в первом броске выпала шестерка, В— во втором броске выпала шестер-
шестерка, С — выпала сумма 7;
е)	Л — в первом броске выпала шестерка, В — во втором броске выпала едини-
единица, С — выпали одинаковые очки.
10.	Кубик подбрасывают три раза. Какова вероятность того, что выпадут следующие
суммы очков: а) 4, б) 5, в) 6, г) 7, д) 8, е) 9, ж) 10?
Ответы: а) 1 / 72, б) 1 / 36, в) 5 / 108, г) 5 / 72, д) 7 / 72, е) 25 / 216, ж) 1 / 8.
11.	В задаче—сказке «Поиск выхода из лабиринта в надежде на Случай» осужденно-
осужденному выдали не пять, а семь монет. Какова теперь у него вероятность выбраться из
лабиринта?
Ответ: 19/32.
Подсказка. Надо учесть еще четыре варианта:
12. В задаче-сказке «На Случай надейся, но и сам не плошай!» Звездочету предложи-
предложили распределить по двум вазам пять белых и пять черных шаров. Какой вариант
268

распределения шаров наиболее целесообразен? Какова вероятность Звездоче-
Звездочету спастись при выборе им этого варианта?
Ответ: надо в одну из ваз положить белый шар, а в другую вазу все остальные
шары; 3/18.
13.	Три охотника стреляют одновременно по летящей утке. Вероятности попасть в ут-
утку у охотников разные: Р±, Р2, Р3. Вероятность того, что утка окажется подстре-
подстреленной может быть вычислена с использованием правила D) при учете прави-
правила A7). Вероятность того, что хотя бы один из охотников попал в утку, вычисляется
с использованием правила A8). Убедитесь, что речь идет об одной и той же
вероятности, используя упомянутые правила.
14.	По летящей утке стреляют одновременно 6 охотников. Трое попадают в такую
цель с вероятностью 0,4, а трое с вероятностью 0,6. Какова вероятность того,
что хотя бы один из охотников попадет в утку? Воспользуйтесь калькулятором.
Ответ: 0,986176.
15.	Переиначим задачу о Звездочете. Предположим, что у Шаха были не один, а
шесть Звездочетов. Каждого из них Шах решил подвергнуть испытанию с пятью
белыми и пятью черными шарами. Каждый Звездочет положил в одну вазу белый
шар, а в другую — остальные шары. Какова вероятность того, что после испыта-
испытания у Шаха останется хотя бы один Звездочет?
Ответ: 0,99575.
16.	Дано: Л и В — независимые события и, значит, Р(А П В) = Р(А) • Р(В). Докажи-
Докажите, что события Лив тоже независимые.
Подсказка. Учитывая несовместность событий Л П в и Л П В , и выразите вероят-
вероятность P(Af)B) через вероятности событий В и АГ\В и убедитесь, что Л и В —
независимые события. Далее рассуждайте самостоятельно.
269

ТЕМА 10
ПОЛНАЯ ВЕРОЯТНОСТЬ
И ВЕРОЯТНОСТИ ГИПОТЕЗ
Одним из эффективных методов под-
подсчета вероятностей является формула пол-
полной вероятности, с помощью которой
решается широкий круг задач.
А. С. Солодовников
...На основе нашего опыта может ме-
меняться наша вера в те или иные гипоте-
гипотезы, уменьшаться степень доверия к од-
одним из них и увеличиваться — к другим.
Фредерик Мостелл
10.1 Полная группа событий
1 оворят, что события Аъ Аъ Аъ, ..., Аг образуют полную группу, если,
во-первых, все эти события попарно несовместны и если, во-вторых,
объединение всех этих событий есть достоверное событие. Последнее
270

обстоятельство математически выражается так: А1 U А2 U А3 U ... UАг = Q,
где Q — универсальное множество (оно было введено в § 8.3). Итак, для
событий, образующих полную группу, имеем:
P(Al{jA2{jA3{J...{jAr) = L
А поскольку среди этих г событий нет ни одной пары совместных, то
можно использовать правило B) из темы 9 и представить:
Р(А1) + Р(А2) + Р(А3) + ...+Р(Аг) = 1.	A)
Пусть Аь Аъ Аъ, ..., Аг — одна из полных групп событий для данного
типа испытаний. Соотношение A) говорит о том, что в любом конкрет-
конкретном испытании рассматриваемого типа обязательно наступает какое-
то из событий группы — или Аъ или Аъ или Аъ, ... или Аг. Иначе говоря,
исключена ситуация, когда не наступает ни событие Аъ ни событие Аъ
ни событие Аъ, ... ни событие Аг. Вот и возникает представление о «пол-
«полноте» группы событий Аъ Аъ Аъ, ..., Аг. Однако не следует понимать эту
«полноту» слишком широко, т. е. не надо думать, что группа событий
Аь Аъ Аъ, ..., Аг охватывает все возможные взаимоисключающие события
в рассматриваемых испытаниях. Дело в том, что для каждого типа ис-
испытаний можно привести отнюдь не одну, а сколько угодно полных групп
событий.
Всякая пара взаимно противоположных событий (А и А) образует
полную группу. Действительно, для любого А имеем: Ар\А = 0,
Р(А) + Р(А) = 1. В любом испытании событие А или наступает, или не
наступает. Иными словами, в любом испытании наступает или событие А,
или событие А.
События An A — наиболее простые примеры полных групп. Другие
примеры полных групп, с которыми мы уже встречались (и притом не-
неоднократно), — это пространства элементарных исходов (они были вве-
введены в §6.6). Пять примеров таких пространств были наглядно пред-
представлены на рисунках 1-5 в таблице 20:
-	пространство элементарных исходов для испытаний, заключаю-
заключающихся в четырехкратном подбрасывании монеты (полная группа состо-
состоит из 16 равновероятных событий);
-	пространство элементарных исходов для пятикратного подбрасы-
подбрасывания монеты (полная группа из 32 равновероятных событий);
-	пространство элементарных исходов для двукратного подбрасыва-
подбрасывания кубика (полная группа из 36 равновероятных событий);
271

-	пространство элементарных исходов для трехкратного подбрасы-
подбрасывания кубика (полная группа из 216 равновероятных событий);
-	пространство элементарных исходов для случайного распределе-
распределения нескольких человек по определенным группам (полная группа из
15 равновероятных событий).
Отметим, что полные группы, представляющие собой пространства
элементарных исходов, образованы равновероятными событиями. Од-
Однако равновероятность событий отнюдь не обязательна для событий,
образующих полную группу. Так, события А и А вовсе не обязаны быть
равновероятными.
На рисунках 1-3 в таблице 39 представлены три различных полных
группы событий для испытаний с двукратным бросанием кубика. Здесь
пространство элементарных исходов (универсальное множество) изоб-
изображено в виде 36 точек — 6 строк, 6 столбцов. Номер строки показыва-
показывает, сколько очков выпало в первом броске, номер столбца — число
очков, выпавших во втором броске.
На рисунке 1 полную группу образуют события Лъ Аъ Аъ, где Ах —
выпала единица во втором броске, А2 — выпала или двойка, или тройка
во втором броске, Аъ — выпала или четверка, или пятерка, или шестерка
во втором броске. Глядя на рисунок, легко подсчитать, что Р(А{) = 6 / 36 =
= 1/6, Р(А2) = 12/36 = 1/3, Р{АЪ) = 18/36= 1/2.
На рисунке 2 полную группу образуют события Аъ Аъ Аъ, где Ах —
выпала сумма меньше 7, А2 — выпала сумма 7, Аъ — выпала сумма
больше 7. Легко подсчитать, что Р(А{) = 15 / 36 = 5 / 12, Р(А2) = 6 / 36 = 1 / 6,
Р(А3) = 15/36 = 5/12.
На рисунке 3 полную группу образуют события Аъ Аъ Аъ, А4, А5, где
Ах — выпала сумма меньше 4, А2 — выпала сумма 4, Аъ — выпала сумма или
5, или 6, А4 — выпала сумма больше 6, но меньше 10, А5 — выпала сумма
больше 9. Легко подсчитать, что Р(А{) = 3 / 36 = 1 / 12, Р(А2) = 3 / 36 = 1/12,
Р{АЪ) = 9/36 = 1/4, Р(А4) = 15/36 = 5/12, Р(А5) = 6/36 = 1 /6.
Рисунки 4-6 в таблице 39 можно рассматривать как примеры пол-
полных групп событий безотносительно к конкретному типу испытаний.
Здесь квадрат — событие Q (универсальное множество), большой
круг — некое событие А, малый круг — некое событие В. Полная
группа событий на рисунке 4 — это три события: А, В, А П В . Полная
группа событий на рисунке 5 — это три события: А, Д А П В . Пол-
Полная группа событий на рисунке 6 — это четыре события: А П В , А П В ,
272

Таблица 39. Полная группа событий и формула полной вероятности
•
•
• •
• >-
*• • •
Аз
12 3 4 5 6
Рис.1
Рис.4
12 3 4 5 6
Рис.2
АПВ
В
А
Рис.5
12 3 4 5 6
Рис.3
• • Ai* •
• • • [X/
. • •\?
A7 ^*-
• • • •
A2
• •
-A
• •
A4
W/Ш
W////A
• \ • • Аб<
1 * I * * A *
V//A//J* •
» • / • • •
Рис.7
273

10.2 Формула полной вероятности
LycTb Аъ Аъ А3, ..., Аг — полная группа событий для выбранного
нами типа испытаний. Обозначим через В некоторое событие, которое
может наступить в наших испытаниях лишь совместно с наступлением
какого-либо события At из упомянутой полной группы. Иными слова-
словами, для наступления события В нужно, чтобы наступило или событие
Aid В, или событие А2Г\В, или событие А3Г\В, ... или событие АГГ\В.
Заметим, что в каждом конкретном испытании может наступить не более
одного из этих событий, поскольку они попарно несовместны (попарная
несовместность событий Ах П Д А2 П Д Аъ П Д... ,АГ П В есть очевидное след-
следствие попарной несовместности событий Аъ Аъ Аъ, ..., Аг). Итак,
Р{В) = Р{{АХ П В) U (А2 П В) U (А3 П В) U ... U (Л П
= Р(АХ П 5) + Р(^2 П 5) + Р(^3 П 5) + Р(^г П 5).	(*)
Воспользовавшись соотношением A0) из темы 9, представим (*) в виде:
Р{В) = Р{АХ) • РА (В) + Р(Л2) • PAl (В)
B)
Это соотношение принято называть формулой полной вероятности.
Рис. 7 в таблице 39 позволяет наглядно представить формулу полной
вероятности. События в виде точек представляют элементарные исхо-
исходы, прямоугольник — универсальное множество; полное число элемен-
элементарных исходов (число элементов универсального множества) равно в
данном случае 80. Универсальное множество разбито здесь на семь под-
подмножеств (событий): Аъ Аъ Аъ, А4, А5, А6, А7. Они образуют полную
группу событий. Заштрихованная фигура представляет некое событие В.
Из рисунка хорошо видно, что В наступает лишь совместно с наступле-
наступлением какого-либо из событий At. Легко подсчитать по числу точек внутри
заштрихованной фигуры, что событие В имеет 22 благоприятных эле-
элементарных исхода и, следовательно, Р{В) = 22 / 80. Это количество бла-
благоприятных исходов есть сумма элементарных исходов для семи пере-
пересечений А(Г\В: для Ах П В имеем один элементарный исход, для А2 П В —
2 исхода, для Аъ П В — 5 исходов, для А4 П В — 5 исходов, для А5 П В —
2 исхода, для А6 П В —4 исхода, для А7 П В — 3 исхода.
Итак,
22 =1 + 2 + 5 + 5 + 2 + 4 + 3.
Разделим обе части этого равенства на полное число элементарных ис-
исходов:
22 / 80 = 1 / 80 + 2 / 80 + 5 / 80 + 5 / 80 + 2 / 80 + 4 / 80 + 3 / 80.
274

Это выражение есть численное представление соотношения:
Р(В) = Р{АХ (\В) + Р(А2 [)В) + Р(А3 [)В) +
+ Р(А4 [)В) + Р(А5 [)В) + Р(А6 [)В) + Р(А7
соответствующего формуле полной вероятности для рассматриваемого
на рисунке 7 случая.
Прежде чем рассматривать примеры с использованием формулы пол-
полной вероятности, обратим внимание на один момент. Когда говорят,
что событие В может наступить лишь совместно с наступлением како-
какого-либо события At из полной группы, то это отнюдь не означает, что
события В и At обязательно должны наступать одновременно. Совмест-
Совместное наступление не предполагает здесь одновременного наступления;
совместное наступление событий — это наступление их в одном и том
же испытании. В ряде случаев испытание можно разбить на два этапа,
так что события В и At оказываются разделенными во времени: сначала
наступает событие Ai9 а уже после этого наступает событие В. Заметим,
что число этапов в одном и том же испытании может оказаться больше
двух, так как события At могут быть пересечениями других событий,
а эти другие события могут быть разнесены во времени. Например, ис-
испытание «участник жеребьевки тянет жребий после того, как три участ-
участника вытянули свои жребии» очевидным образом предполагает нали-
наличие четырех событий, разделенных во времени (см. ниже § 10.4).
Рассмотрим несложный пример с использованием формулы полной
вероятности. Имеются три типа внешне одинаковых ваз: 3 вазы 1-го типа,
2 вазы 2-го типа, 4 вазы 3-го типа — всего 9 ваз (тип вазы фиксируется
каким-нибудь знаком на донышке). В каждой вазе 1-го типа находятся
по 3 белых и 4 черных шара, в каждой вазе 2-го типа — 7 белых шаров, в
каждой вазе 3-го типа — 2 белых и 5 черных шаров. Вазы расставлены по
полу в беспорядке. Испытание состоит в том, что человек подходит на-
наугад к той или иной вазе (это первый этап испытания), а затем наугад
вынимает из этой вазы один шар (второй этап испытания). Событие 3 —
вынут белый шар. Надо найти вероятность этого события.
Будем считать событиями Аъ Аъ Аъ подходы к вазам соответственно
1-го, 2-го и 3-го типа. Эти несовместные события образуют полную
группу, поскольку в каждом испытании обязательно наступает какое-то
из них (любая случайно выбранная ваза будет или 1-го, или 2-го, или 3-го
типа). Вероятности событий Аъ Аъ А3: Р(А{) = 3/9=1/3, Р(А2) = 2/9,
Р(АЪ) = 4/9. Событие 3 может наступить лишь совместно с наступлени-
наступлением одного из событий Аъ Аъ Аъ (т. е. при условии, что человек подошел
275

к какой-то вазе). Вычислим Р(В), воспользовавшись формулой полной
вероятности B):
Р{В) = Р{АХ) ¦ РА (В) + Р(А2) ¦ PAi(В) + Р(А3) ¦ РАз (В) =
= A/3). PAi(B) + B/9)PA2(B) + D /9). РАз(В).	(**)
Условные вероятности в соотношении (**) легко найти. Поскольку в
вазе 1-го типа находятся 3 белых и 4 черных шара, то РА{(В) = 3/7. Да-
Далее находим: РА (В) = 1 и РА (В) = 2 / 7. Подставив эти условные веро-
вероятности в (**), получим:
= A/3). C/7)+ B/9). 1+ D/9). B/7) = 31/63.
10.3 Пример вероятностной задачи из семеноведения
Справка. Семеноведение — раздел агрономии; изучает строение и развитие се-
семян сельскохозяйственных культур, разрабатывает методы оценки и контроля се-
семенного материала.
11редположим, что рассматриваются четыре сорта семян пшеницы.
По характеру почвы и климатическим условиям нам подходит главным
образом сорт 1, который в нашем краю дает полновесный колос (колос,
содержащий более 50 зерен) с вероятностью 0,65, тогда как зерно сор-
сорта 2 дает полновесный колос с вероятностью 0,18, зерно сорта 3 — с ве-
вероятностью 0,15, зерно сорта 4 — с вероятностью 0,08. В заготовленной
для посева партии зерна сорта 1 было выявлено наличие примесей ос-
остальных трех сортов. Проверка показала, что в данной партии содер-
содержится 94% зерен сорта 1,2% зерен сорта 2, 1% зерен сорта 3 и 3% зерен
сорта 4. Возникает практический вопрос: следует ли использовать для
посева данную партию зерна?
Переведем рассматриваемую ситуацию в математическую плоскость:
подсчитаем вероятности того, что зёрна из данной партии дадут полно-
полновесный колос. Обозначим эту вероятность через Р(В), рассматривая в
качестве В событие, состоящее в появлении полновесного колоса. Со-
События, состоящие в том, что взятое наугад из нашей партии зерно ока-
окажется сорта 1, 2, 3 или 4, обозначим соответственно через Аъ Аъ Аъ, А4.
Понятно, что эти события образуют полную группу. В соответствии с
данными проверки семенного материала,
Р(А1)=0,94, Р(^2) = 0,02, Р(А3) = 0,01, Р(А4) = 0903.
276

Мы уже отмечали, что вероятность получить полновесный колос равна
0,65 для зерна сорта 1, 0,18 для зерна сорта 2, 0,15 для зерна сорта 3,
0,08 для зерна сорта 4. Таким образом,
PAl(B) = 0,65, РА2(В) = 0,18, РАз(В) = 0,15, РАа{В) = 0,08.
Подставляя все эти вероятности в формулу полной вероятности, на-
находим:
Р{В) = Р{АХ) ¦ РА (В) + Р(А2) ¦ РА2(В) + Р(А3) ¦ РАз (В) + Р(А4) ¦ РАа (В) =
= 0,94.0,65 + 0,02.0,18 + 0,0Ь0,15 + 0,03.0,08 =
= 0,6110 + 0,0036 + 0,0015 + 0,0024 = 0,6185.
Мы видим, что засорение партии зерна примесями сортов 2, 3 и 4
снижает в данном случае вероятность получения полновесного колоса с
0,65 до 0,6185. Теория вероятностей свое слово сказала; теперь агроно-
агроному надо принять решение о возможности использовать данную партию.
10.4 Зависит ли вероятность вытянуть благоприятный
жребий от очередности участников жеребьевки?
-D § 6.1 рассматривалась весьма простая задача с выниманием шара
из мешка. В мешке находились 8 шаров — три красных и пять белых.
Надо было найти вероятность вынуть наугад красный шар из мешка.
Ответ легко определялся: эта вероятность равна 3/8.
Теперь рассмотрим более сложную задачу. Имеются 3 путевки в са-
санаторий и 8 претендентов на эти путевки. Нужно тянуть жребий. Как
обычно делается в подобных случаях, изготавливают 8 одинаковых кар-
карточек (или свернутых в трубочку бумажек), на трех из них изображают
плюс, а на пяти — нуль. Все карточки кладут в мешок и тщательно
перемешивают. Затем каждый из претендентов подходит к мешку и на-
наугад вытягивает карточку. После того, как все восемь карточек окажут-
окажутся вынутыми, каждый из участников жеребьевки предъявляет свою кар-
карточку. Путевку в санаторий получают те трое счастливчиков, у кого на
руках оказались карточки с плюсом.
Понятно, что у того, кто первым тянул жребий, вероятность вытянуть
карточку с плюсом равна 3 / 8. А какова вероятность вытянуть карточку
с плюсом у второго участника жеребьевки? У третьего! У четвертого!
Наконец, у восьмого! Зависит ли вероятность вытянуть благоприятный
жребий от очередности участников жеребьевки? Ясно, что жеребьевку
можно считать справедливой только в том случае, если все ее участники
277

имеют равные шансы вытянуть карточку с плюсом. Иными словами,
жеребьевка будет справедливой, если вероятность вытянуть карточку
с плюсом равна 3/8 для каждого из восьми участников.
На первый взгляд, условие справедливости жеребьевки не выполня-
выполняется. Если первый участник вытянул плюс, то теперь вероятность, что
второй участник тоже вытянет плюс, станет меньше 3/8. Если же пер-
первый участник вытянул нуль, то вероятность второму участнику вытя-
вытянуть плюс окажется больше 3/8. Однако не будем спешить с выводами
и аккуратно подсчитаем вероятность вытянуть карточку с плюсом сна-
сначала для второго участника, потом для третьего, потом для четвертого,
потом для пятого... Всякий раз мы будем пользоваться формулой полной
вероятности.
Будем рассматривать события:
А — первый участник вытянул плюс (соответственно,
А — первый участник не вытянул плюса, т. е. вытянул нуль);
В — второй участник вытянул плюс;
С — третий участник вытянул плюс;
D — четвертый участник вытянул плюс;
Е — пятый участник вытянул плюс.
Об остальных участниках говорить, по-видимому, нет необходимос-
необходимости, поскольку ситуация вполне прояснится уже до того, как настанет их
черед тянуть жребий.
Рассмотрим испытание, состоящее в том, что второй участник тя-
тянет жребий после того, разумеется, как первый участник уже тянул
жребий. События А и А образуют полную группу, а событие В наступа-
наступает совместно или с событием А, или с событием А. Применяя формулу
полной вероятности, представим:
Р(В) = Р(А) ¦ РА{В) + Р(А) ¦ Р-А{В).	(*)
Легко сообразить, что Р(А) = 3 /8, а Р(А) = 5/8. Условная вероят-
вероятность Ра(В) есть вероятность наступления события В при условии,
что первый участник вытянул плюс: РА(В) = 2/7 (это есть вероят-
вероятность вытянуть плюс из мешка, где из семи оставшихся карточек две
карточки с плюсом). Условная вероятность РА{В) есть вероятность на-
наступления события В при условии, что первый участник вытянул ми-
= 3/7- Подставляя все эти вероятности в (*), находим:
3 2 5 3 ^М5 21 3
Как мы убедились, вероятность стать обладателем путевки у второго
участника жеребьевки точно такая же, как и у первого участника. Хотя
278

условные вероятности Рд(В) и Pj{B) не равны 3/8, однако полная веро-
вероятность Р{В) в точности равна 3/8. Итак, мы доказали, что Р{В) = Р(А).
Теперь рассмотрим испытание, состоящее в том, что тянет жребий
третий участник {после того, как первые два участника уже поучаство-
поучаствовали в жеребьевке). События Л[\В (оба первых участника вытянули
нуль), А[}В (первый вытянул плюс, а второй — нуль), А [\В (первый
вытянул нуль, а второй — плюс), А П В (оба первых участника вытянули
плюс) образуют полную группу. Событие С наступает только совместно
с каким-либо из этих событий. Применяя формулу полной вероятности,
представим:
Р{С) = Р(А П В) ¦ РШ(С) + Р(А П В) ¦ РАпВ(С) +
+ Р(А П В) ¦ Р1пв(С) + Р(А П В) ¦ РЛПВ(С).	(**)
Для некоторого упрощения записи, а также для большей наглядности
здесь и далее будем использовать знаки «+» (если соответствующий
участник вытянул плюс) и «о» (если соответствующий участник вытя-
вытянул минус). Поэтому перепишем (**) в виде:
Р(С) = Р(оо) ¦ Р00	^
(***)
Воспользовавшись соотношением A0) из темы 9.5, находим:
Р(оо) = Р(р) ¦ Ро(о) = | • |; Р(о+) = Р(о). ро(+) = |. |;
Р(+о) = Р(+)Р+(О) = |-4;
(поясним: Ро(о) — вероятность второму вытянуть нуль при условии, что
и первый вытянул нуль; она равна вероятности вытянуть нуль из мешка,
где из семи оставшихся карточек четыре имеют нуль, т.е. равна 4/7).
Условная вероятность Р00{С) есть вероятность вытянуть плюс из шести
карточек, среди которых три карточки с плюсом; значит, Р00(С) = 3/6.
Нетрудно установить и другие условные вероятности: Р+0(С) = 2/6,
Ро+(С) = 2/6, Р++(С) = 1/6. Подставляя все эти вероятности в (***),
получаем:
Р(Г) -111 111 111 111- Ю + 5 + 5 + 1 _ 2\_ _ 3_
( ' ~ 8~'7' 6~+ 8"'У 6~+ 8' б"+ 8"У б"~	56	~^б"~ 8"'
Как видим, у третьего участника жеребьевки вероятность вытянуть
путевку также равна 3/8.
279

Рисунки 1-4 в таблице 40 иллюстрируют формулу полной вероятно-
вероятности для следующих четырех типов испытаний:
-	рисунок 1: второй участник тянет жребий после того, как первый
участник поучаствовал в жеребьевке,
-	рисунок 2: третий участник тянет жребий после того, как первые
два участника поучаствовали в жеребьевке,
-	рисунок 3: четвертый участник тянет жребий после того, как пер-
первые три участника поучаствовали в жеребьевке,
-	рисунок 4: пятый участник тянет жребий после того, как первые
четыре участника поучаствовали в жеребьевке.
На рисунках прямоугольники — это универсальные множества Q;
они разбиваются на полные группы событий, учитывающие всякий раз
все возможные результаты жеребьевки предыдущих участников: первого
(см. рис. 1), первого и второго (см. рис. 2), первого, второго и третьего
(см. рис. 3), первого, второго, третьего и четвертого (см. рис. 4). Круги
представляют события В (на рис. 1), С (на рис. 2), D (на рис. 3), Е (на
рис. 4). Относительные размеры площадей событий на рассматривае-
рассматриваемых рисунках не связаны с количеством соответствующих благоприят-
благоприятных элементарных исходов.
Переходя к испытанию, в котором жребий тянет четвертый участ-
участник, будем пользоваться рисунком 3. В данном случае полную группу
образуют восемь событий: А П В П С (условная запись: ооо), А П В П С
(+оо), 4f)Bf)C (о+о), ЛП5ПС (оо+), А(]В(]С (++о), А[]В[]С
(+о+), АГ\ВГ\С (о++), Ар\Вр\С (+++). Используя формулу полной
вероятности, представим:
Рф) = Р(ооо) ¦ Роооф) +Р(+оо) ¦ Р^ф) + Р(о+о)- Р0Лоф) +
\-Р0++ф) + Р(+++У P+++(D).	(****)
Нетрудно сообразить, что
Р(ооо) ¦ P000(D) = Р(о) ¦ Р0(р) ¦ Роо(о) ¦ P000(D) = |. 1. |. |;
3 5 4 2
8 7 6 5'
P{o + o).Po+o(D) = P{o).Po(+)-Po+(o)-Po+o(D) = \\^\;
Р(оо+) ¦ P00+(D) = Р(о) ¦ Ро (о) ¦ Роо (+) • Роо+(D) = | • 1 • | • |;
о / О 3
280

P+0+(D) =
Слагаемое Р (+++) * P+++(D) в (****) равно нулю, поскольку P+++(D) = 0 —
ведь вероятность четвертому участнику вытянуть плюс после того, как
все три плюса уже вытянуты, есть вероятность невозможного события.
Собирая все полученные результаты, получаем из (****):
р(д) = 1.А.1.1 + 1.1.1.2 + 1.1.1.2 + 1.А.1.2 +
К ' 8765876587658765
+ 111. 1 + 1 1 1 1 + 1 111-
8'7'б'58*7'б'58*7*6*5~
_ 6 + 4 + 4 + 4 + 1 + 1 + 1 _2!__1
~	56	~ 56 ~ I'
Таким образом, четвертый участник жеребьевки также имеет вероят-
вероятность 3/8 стать обладателем заветной путевки.
Переходя к испытанию, в котором жребий тянет пятый участник,
воспользуемся рисунком 4 из таблицы 40. В данном случае полная группа
событий состоит из шестнадцати событий; все они показаны на рисун-
рисунке. Следует учесть, что АГ\ВГ\ Cf]D= 0, поскольку нельзя вынуть че-
четыре путевки из трех. Кроме того, не нужно принимать во внимание
еще_четыре события: Af]BC]CC]D (+++о), Af]Bf]Cf]D (++о+),
Af]Bf]Cf]D (+о++), Af]Bf]Cf]D (o+++). В этих событиях оказа-
оказались выбранными все три карточки с плюсом и поэтому событие Е не
может наступить совместно с ними. Таким образом, формула полной
вероятности будет в данном случае содержать в правой своей части не
16, а только 11 слагаемых:
Р(Е) = Р(оооо) ¦ Р0000(Е) + Р(+ооо) ¦ Р+000(Е) + Р(р + оо) ¦ Р0+00(Е) +
+ Р(оо + о) ¦ Р00+0(Е) + Р(ооо+) ¦ Рооо+ (Е) + Р(+ + оо) ¦ Р++00(Е) +
+ Р(о + +о)-Ро++о(Е) + Р(оо + +)¦ Р00++(Е) + Р(+оо+)Р+оо+(Е) +
+ Р(+о+о)Р+о+о(Е) + Р(о + о+)-Ро+о+(Е).
281

Таблица 40. Вероятность вытащить благоприятный жребий
Рис.1
Рис.2
Q
Рис.3
Q
АПВП
I+O+ +
АПВП
АПВП
Ю+++
^^
АПВП
Ю+О+
ПВ
4.
СП
h+C
-—
1
СП
СП
1
	—
СП
1 у
вг
ПСПБ\
I + ++OI
^^
D
D

I+O+OI
ichd/
АПВПСПБ
\ I + ++ + I
/
/ l+oo+i
АПВПСПБ
АПВПСПБ,
looool /
->\
\
IOO++I \
АПВПСПБ
Лпвпс
I+OOOI .
/ |О + С
^^
АПВ
АПВ
\
IO++OI '
\А П В П (
ВПСПЬ
loo+oi
ПСПБ
ПСПБ
looo+l
I + +OOI
Рис.4
282

Нетрудно сообразить, что
Р(оооо) • Роооо (Е) = Р(о) • Ро (о) • Роо (о) • Рооо (о) • Роооо (Е) =
-11111 1_А
~87"б4~56*
Следующие четыре слагаемые отвечают событиям, в которых до того,
как появился пятый участник, оказался вытянутым из мешка один плюс.
Нетрудно убедиться, что каждое из этих четырех слагаемых равно 3 / 56.
Оставшиеся шесть слагаемых отвечают событиям, в которых до того,
как появился пятый участник, оказались вытянутыми из мешка два
плюса. Нетрудно убедиться, что каждое из этих шести слагаемых равно
1 / 56. Таким образом,
Р(Е) = 3/56 + 4- C/56) + 6 -A/56) = 21/56 = 3/8.
Мы опять получили вероятность 3/8.
Желающие могут убедиться самостоятельно, что вероятность вытя-
вытянуть карточку с плюсом равна 3/8 также для шестого, седьмого и восьмо-
восьмого участников жеребьевки. При этом надо иметь в виду, что нет смысла
рассматривать варианты, для которых число вытянутых плюсов три и бо-
более или число вытянутых нулей больше пяти (речь идет о плюсах и ну-
нулях, вытянутых из мешка до того, как очередной участник будет тянуть
жребий). Короче говоря, надо помнить, что всего было три карточки
с плюсом и пять карточек с нулями.
Итак, жеребьевка оказалась справедливой. Независимо от очереднос-
очередности все участники имеют одинаковые шансы приобрести заветную путев-
путевку. Все находятся в равном положении. Правда, психологически первый
и последующие участники чувствуют себя по-разному. Первый пони-
понимает, что у него есть выбор. Он может ощупывать карточки в мешке,
перебирать их пальцами. Он может вытащить ту карточку, которая ка-
кажется ему выигрышной. Второй участник может заявить, что у него
свобода выбора меньше. Еще меньше свобода выбора у последующих
участников. Восьмой участник вправе заявить, что у него вообще нет
свободы выбора — он должен вынуть ту карточку, которая осталась
в мешке. Однако нас в данном случае интересует отнюдь не возмож-
возможность выбора, а то, зависит или не зависит вероятность вытянуть благо-
благоприятный жребий от очередности. И чтобы снять ненужные вопросы,
мы предлагаем всем участникам не открывать вытянутых ими карточек
до того момента, когда окажется вынутой последняя карточка.
Чтобы задние в очереди не чувствовали себя обделенными, напом-
напомним, что случайные события могут быть предсказуемыми, однако управ-
управлять ими нельзя.
283

10.5 Правила вычисления апостериорных вероятностей
гипотез (формулы Байеса)
±то здесь подразумевается под понятием «гипотезы»? Что такое «апо-
«апостериорные вероятности гипотез» и как они вычисляются? Зачем нужно
вычислять апостериорные вероятности гипотез? В данном параграфе мы
ответим на первые два вопроса, а в следующем параграфе приведем не-
некоторые примеры из практики, позволяющие ответить на третий вопрос.
Знакомясь с формулой полной вероятности, мы рассматривали веро-
вероятность события Д которое наступает только совместно с каким-либо
событием из полной группы событий Ah Аъ Аъ, ..., Аг. Заранее неизвест-
неизвестно, с каким именно из этих событий наступит событие В в том или ином
испытании. Мы можем делать лишь предположения. Предположим, что
наступит совместно с Ах. Предположим, что В наступит совместно с А2.
Предположим, что В наступит совместно с А3. И так далее. У нас есть г
предположений. В связи с этим уместно называть события Аъ Аъ Аъ,..., Аг
гипотезами. Точнее сказать, гипотезами по отношению к событию В.
Полную группу событий Аь Аъ Аъ, ..., Аг следует теперь называть полной
группой гипотез. Наступление события В в том или ином испытании про-
происходит обязательно по какой-то из гипотез Аь Аъ Аъ, ..., Аг, причем
всякий раз «срабатывает» случайным образом одна из полной группы
гипотез (гипотезы несовместны: или Аъ или Аъ или Аъ, ..., или Аг).
Присутствующие в соотношении B) вероятности
Р(А{), Р(А2), Р(А3), ..., Р{АГ)	(*)
можно рассматривать как вероятности «срабатывания» соответствующих
гипотез или, короче, как вероятности гипотез. Та или иная гипотеза At
обеспечивает наступление события Д разумеется, не в обязательном по-
порядке, а лишь с какой-то вероятностью РА{В) (/= 1, 2, ..., г). Иногда
говорят, что гипотеза At «сообщает» событию В вероятность Р^.(В). Гово-
Говорят также, что Ра(В) есть условная вероятность события В по гипотезе At.
С введением понятия «гипотеза» формулу полной вероятности мож-
можно прочитать так: вероятность события В равна сумме произведений ус-
условных вероятностей этого события по каждой из гипотез на вероятнос-
вероятности самих гипотез. При использовании такой формулировки уместно
переписать формулу полной вероятности в виде:
Р(В) = РА{В) • Р(Аг) + РА2(В) • Р(А2) + ... + РАг{В) • Р{АГ). C)
Разумеется, соотношение C) не содержит ничего нового по сравнению
с соотношением B); просто сомножители в произведениях поменялись
местами — только и всего.
284

Итак, мы ввели понятия «гипотеза» и «вероятность гипотезы». А что
такое «апостериорная вероятность гипотезы»? Приведем справку, взя-
взятую из энциклопедии:
Справка. Априори (от латинского «a priori» — «из предшествующего») — понятие
логики и теории познания, характеризующее знание, предшествующее опыту и неза-
независимое от него. Апостериори (от латинского «a posteriori» — «из последующего») —
знание, происходящее из опыта; понятие, противоположное понятию априори.
Из справки следует, что термин «апостериорный» надо понимать как
«послеопытный» (тогда как «априорный» будет означать «доопытный»).
О каком же опыте может идти речь в нашем случае? — Очевидно, име-
имеются в виду испытания.
Вероятности гипотез (*) установлены до рассматриваемых нами испы-
испытаний и независимо от них. В этом смысле их следует рассматривать как
априорные вероятности гипотез. Зная эти вероятности (а также условные
вероятности PAl(B), PAl(B)9 Ра3(В)-> •••> Раг(В))-> мы можем вычислить за-
заранее (до испытаний) вероятность Р(В), которая позволит нам делать
вероятностные предсказания относительно результатов испытаний.
Что же касается апостериорных вероятностей тех же самых гипотез,
то они должны рассматриваться как вероятности, определяемые при
условии наступления события В (после наступления события В). Следо-
Следовательно, речь идет об условных вероятностях:
РВ(А{), РВ(А2), РВ(А3), ..., РВ{АГ).	(**)
Заметим, что как априорные вероятности гипотез (*), так и апосте-
апостериорные вероятности гипотез (**) являются полными группами собы-
событий, так что
= 1.	(***)
Наступление события В не изменяет суммы вероятностей гипотез, а из-
изменяет слагаемые (принято говорить, что наступление события В приво-
приводит к переоценке вероятностей гипотез).
Если нам известны Р(А{)9 Р(А2), ..., Р(АГ) и PAl(B), PAl(B)9 ..., PAr(B)
то с помощью формулы полной вероятности мы можем вычислить Р(В).
Используя затем соотношение (8) из темы 9.4, мы можем вычислить
апостериорные вероятности гипотез РВ(А{)9 РВ(А2)9 ..., РВ(АГ). В ре-
результате мы получим г соотношений:
B(Ai) = PAj{B)P{Ai)/P(B),\	D)
где /= 1, 2, ..., г.
285

Используя C), перепишем эти соотношения:
E)
в ' РА
(В)Р(;
PAi(B)P(Ai
Ь) + РА2(В)Р(А2)-
)
+ Ра
¦Р{АГУ
где /= 1, 2, ..., г.
Соотношения E) принято называть формулами Байеса — в честь ан-
английского ученого Томаса Байеса A702-1761). Заметим, что Байес са-
самих этих соотношений не устанавливал, но он вывел правило, которое
в наше время представляют в виде соотношения Р{А П В) = Р{А) * Рд(В)
(правило умножения вероятностей зависимых событий) и из которого
сразу следует основополагающее в нашем случае соотношение (8) из
темы 9. В одной из работ Байеса доказано следующее утверждение: «Ве-
«Вероятность того, что наступят оба взаимосвязанных события, есть про-
произведение, получающееся от перемножения вероятности наступления пер-
первого события на вероятность наступления второго, при предположении,
что первое событие наступило». Эта работа Байеса была опубликована
в 1763 году (уже после кончины ученого) в издаваемых членом англий-
английского Королевского общества Ричардом Прайсом A723-1791) «Фило-
«Философских трудах» под заглавием «Опыт решения задачи по теории веро-
вероятностей покойного достопочтенного мистера Байеса».
Проиллюстрируем характер задач, решаемых с помощью формул Байе-
Байеса, на примере с вазами трех типов, приводившемся в конце § 10.2.
Событие В (наугад вынут белый шар) наступает или по гипотезе Ах
(человек случайно подошел к одной из ваз 1-го типа), или по гипотезе
А2 (подошел к одной из ваз 2-го типа), или по гипотезе Аъ (подошел
к одной из ваз 3-го типа). Априорные вероятности гипотез таковы:
Р{А1) = Ъ/9, Р(А2) = 2/9, Р(А3) = 4/9.
Гипотезы «сообщают» событию В следующие вероятности:
PAi(B) = 3/7, PA2(B) = h РАг{В) = 2/1.
По формуле полной вероятности была вычислена вероятность Р(В);
она равна 31/63.
Итак, знание априорных вероятностей гипотез и вероятностей, кото-
которые «сообщают» гипотезы событию В, позволяет нам ответить на воп-
вопрос: если мы случайно подойдем к какой-то из ваз и наугад вынем шар,
то какова вероятность, что будет вынут белый шар?
Применяя формулы Байеса, мы можем теперь ответить на другие
вопросы: если мы случайно подошли к какой-то из ваз и наугад вынули
шар, который оказался белым, то какова вероятность, что этот белый
286

шар был вынут из вазы 1-го типа? из вазы 2-го типа? из вазы 3-го
типа? Обратим внимание на то, что, если раньше через вероятность
прогнозировалось будущее (будет ли вынут белый шар?), то теперь через
вероятность уточняется то, что уже произошло (откуда был вынут бе-
белый шар?). Там мы интересовались вероятностным предсказанием ре-
результата будущего испытания, а здесь речь идет о вероятностном вы-
выявлении причин (гипотез), приведших к результату состоявшегося
испытания. Мы привыкли иметь дело с вероятностями априорного
(доопытного) характера; теперь же мы встретились с вероятностями
апостериорного (послеопытного) характера. Непонимание специфики
апостериорных вероятностей приводит нередко к тому, что формулы
Байеса воспринимаются не более как результат несложных манипуля-
манипуляций с формулой полной вероятности и правилом умножения вероят-
вероятностей зависимых событий.
После сделанных замечаний вернемся к нашему примеру. Используя
формулы Байеса D), получаем:
= РАз(В)Р(А3)/Р(В) = B/7).D/9)/C1/63) = 8/31.
Итак, мы вынули наугад шар, который оказался белым. Конечно, мы
не можем однозначно утверждать, из вазы какого типа он был вынут.
Но мы можем утверждать: вероятность, что этот шар был вынут из вазы
1-го типа, равна 9/31, вероятность, что он был вынут из вазы 2-го
типа, равна 14/31, вероятность, что он был вынут из вазы 3-го типа,
равна 8/31.
Сопоставим вероятности трех полных групп гипотез:
-	априорные вероятности: Р(А{) = 3/9, Р(А2) = 2/9, Р(А3) =4/9;
-	апостериорные вероятности: РВ(А{) = 9 / 31, РВ(А2) = 14 / 31,
РВ(А3) = 8/31.
Обратим внимание на переоценку вероятностей гипотез. В частно-
частности, отметим, что, если до опыта гипотеза А2 имела наименьшую вероят-
вероятность, то после того, как состоялся опыт и был вынут белый шар, гипо-
гипотеза А2 оказалась, напротив, наиболее вероятной (ее вероятность
увеличилась в два раза).
Вполне уместен вопрос: как изменятся вероятности наших гипо-
гипотез, если при испытании окажется вынутым не белый, а черный шар?
Событие В не наступило; наступило противоположное событие — со-
287

бытие В. В этом случае надо вычислять апостериорные вероятности
Pg(Ai), Pg(A2), Рд(А3). Легко сообразить, что формулы Байеса при-
примут теперь вид:
Р (Й\. P( АЛ
F)
Р (А)
в , р
k(B)PU
рл,
к)+Рл2
(В)-
(В)-
P(Ai)
Р(А2)^
РАЪ
(В)-
Р(А3
)'
где /=1, 2, 3.
Чтобы воспользоваться ими, надо предварительно найти условные
вероятности РА(В). Напомним, что в вазах 1-го типа находятся по
3 белых и 4 черных шара и, значит, PAi (В) = 4 / 7 . В вазах 2-го типа
находятся по 7 белых шаров и ни одного черного и, значит, РА (В) — О.
В вазах 3-го типа находятся по 2 белых и 5 черных шаров и, значит,
= 5/7 . С учетом этих вероятностей находим:
Р(В) = D/7). C/9)+ E/7). D/9) = 12/63 + 20/63 = 32/63.
Далее, используя F), получаем:
PB(A1) = PAl(B).P(A1)/P(B) = D/7).C/9)/C2/63) = U/32
РцШ = Ра2(В)Р(А2)/Р(В) = О,
= РАз(В)Р(А3)/Р(В) = E/7). D/9)/C2/63) = 20/32 = 5/8.
Итак, если вынутый наугад шар оказался черным, то можно утверж-
утверждать: вероятность, что этот шар вынут из вазы 1-го типа, равна 3/8,
а вероятность, что он вынут из вазы 3-го типа, равна 5/8. Гипотеза А2
в данном случае исключается. Апостериорные вероятности наших ги-
гипотез приобретают после данного испытания значения:
10.6 Практический смысл вычислений
апостериорных вероятностей гипотез
вычисление апостериорных вероятностей гипотез представляет не
только теоретический, но и практический интерес. Это неплохо демон-
демонстрируют рассматриваемые ниже задачи.
Задача 1. Бригада 1 изготавливает 30% неких деталей и при этом дает 1% брака.
Бригада 2 изготавливает 20% тех же деталей и дает 3% брака. Бригада 3 изготавливает
288

50% деталей и дает 2% брака. Взята наугад одна деталь из общей партии. Она
оказалась бракованной. Какова вероятность, что в браке виновата бригада 1? вино-
виновата бригада 2? виновата бригада 3?
Решение. Гипотезы Аъ Аъ А3 — проверяемая деталь выбрана случайным обра-
образом из продукции бригад 1, 2, 3 соответственно. Событие В — случайно выбран-
выбранная деталь оказалась бракованной. Из условия задачи нам известно:
Р{АХ) = 0,3, Р(А2) = 0,2, Р(АЪ) = 0,5,
РА(В) = 0,01, РЛг(В) = 0,03, РАз(В) = 0,02.
Вычислим, используя формулы Байеса E), апостериорные вероятности наших
гипотез. Предварительно подсчитаем, чему равен знаменатель в соотношениях E),
т. е. вероятность Р(В):
Р(В) = РА(В) ¦ Р(А{) + РА2(В) ¦ Р(А2) + РАз(В) ¦ Р(А3) =
= 0,003 + 0,006 + 0,01 = 0,019.
Далее вычисляем:
РВ(А{) = 0,01 -0,3/0,019 = 0,158,
Рв(>42) = 0,03-0,2/0,019 = 0,316,
РВ(А3) = 0,02-0,5/0,019 = 0,526.
(*)
Как мы видим, наиболее вероятно, что бракованная деталь принадлежит бри-
бригаде 3 (апостериорная вероятность гипотезы Аъ равна 0,526), а наименее вероятно,
что деталь принадлежит бригаде 1 (апостериорная вероятность гипотезы Ах равна
0,158). Конечно, мы не можем сказать, какая именно из трех бригад виновата в
изготовлении подвернувшейся нам под руку бракованной детали. Но это в данном
случае и несущественно^. Важно то, что эта бракованная деталь была выбрана из
общей партии случайным образом. И поэтому теперь мы вправе полагать, что любая
бракованная деталь из общей партии есть с вероятностью 0,158 продукция брига-
бригады 1, с вероятностью 0,316 — продукция бригады 2, с вероятностью 0,526 — про-
продукция бригады 3. Понятно, что этот вывод представляет определенный практи-
практический интерес. А получен он в результате подсчета апостериорных вероятностей
наших гипотез по формулам Байеса.
Задача 2. Условие задачи такое же, что и в задаче 1. Но теперь были взяты
наугад две детали из общей достаточно крупной партии. Они обе оказались брако-
бракованными. Какова вероятность, что виновата бригада 1? виновата бригада 2] винова-
виновата бригада 3?
Решение. Гипотезы Аъ Аъ Аъ прежние; Р(А{) =0,3, Р(А2) =0,2, Р(А3) =0,5. А
вот событие В теперь иное. Это событие состоит в том, что две случайно взятые из
общей крупной партии детали оказались бракованными. Теперь РА (В) есть услов-
условная вероятность того, что две детали окажутся бракованными при условии «сраба-
«срабатывания» гипотезы, т. е. при условии, что эти детали оказались принадлежащими
289

продукции бригады 1. Легко сообразить, что РАл{В) = @,01) = 0,0001. Соответствен-
Соответственно нахс
Теперь
но находим: PAi(B) = @,03J = 0,0009, РАр) = @,02J = 0,0004.
Р(В) = 0,0001 • 0,3 + 0,0009 • 0,2 + 0,0004 • 0,5 =
= 0,00003 + 0,00018 + 0,0002 = 0,00041.
Используя формулы Байеса E), находим:
00041 = 0,073,
РВ(А{) = 0,00003/0,00041 = 0,073,
РВ(А2) = 0,00018/0,00041 = 0,439,
РВ(А3) = 0,0002/0,00041 = 0,488.
Сравнивая апостериорные вероятности гипотез (**) и (*), мы видим, что сте-
степень вины бригады 1 за выпуск брака еще больше уменьшилась, тогда как степень
вины бригады 2 заметно возросла, а степень вины бригады 3 слегка уменьшилась,
оставаясь при этом наибольшей. Мы по-прежнему не знаем, какая именно бригада
виновата в изготовлении подвернувшейся нам под руку пары бракованных дета-
деталей. Не исключено, в частности, что эти детали были изготовлены разными брига-
бригадами. В данном случае это не имеет значения. Результат (**) следует понимать так:
любая пара бракованных деталей из общей крупной партии есть с вероятностью
0,073 продукция бригады 1, с вероятностью 0,439 — продукция бригады 2, с веро-
вероятностью 0,488 — продукция бригады 3.
Задача 3. Задача отличается от предыдущей только тем, что теперь взяты на-
наугад три детали из общей крупной партии и все три оказались бракованными.
Решение. Теперь В — событие, состоящее в том, что три детали, случайно вы-
выбранные из общей крупной партии, оказались бракованными. Процесс решения,
по-видимому, не требует пояснений. Запишем:
РА]{В) = @,01K = 0,000001, РА2{В) = @,03K = 0,000027, PA^{B) = @,02K = 0,000008;
Р(В) = РА{(В) • Р{ЛХ) + РА2(В) • Р(А2) + РАз(В) • Р(А3) =
= 0,000001 • 0,3 + 0,000027 • 0,2 + 0,000008 • 0,5 = 0,0000097
РВ(А{) = 0,000001-0,3/0,0000097 = 0,031,
РВ(А2) = 0,000027 -0,2 /0,0000097 = 0,557,	(***)
РВ(А3) = 0,000008-0,5/0,0000097 = 0,412.
Итак, любая тройка бракованных деталей из общей крупной партии есть с вероят-
вероятностью 0,031 продукция бригады 1, с вероятностью 0,557 — продукция бригады 2,
с вероятностью 0,412 — продукция бригады 3.
Теперь основной виновник брака вполне выявился — это бригада 2. Возможно,
что, познакомившись с результатами (**) и в особенности (***), руководитель
предприятия уволит бригаду 2. Тем более, что эта бригада изготавливает всего 20%
всех деталей.
290

Задача 4. На основании обследования больного сделан вывод, что у него одно из
двух заболеваний — или Ах (гипотеза Ах), или А2 (гипотеза А2). Согласно справочни-
справочникам вероятности этих заболеваний в данных условиях таковы: Р(А{) = 0,6, Р(А2) = 0,4.
Врач пожелал уточнить диагноз и назначил проведение анализа, результатом кото-
которого является положительная или отрицательная реакция. Если у пациента
болезнь Ах, анализ должен дать с вероятностью 0,9 положительную реакцию и с
вероятностью 0,1 отрицательную. Если у пациента болезнь А2, положительная и
отрицательная реакции равновероятны. Анализ был проведен и дал отрицательную
реакцию. Какова вероятность, что этот результат обусловлен заболеванием А{!
обусловлен заболеванием А{1
Решение. Гипотезы А{и А2 — имеют место заболевания А{ и А2 соответственно.
Событие В — обнаружена отрицательная реакция. По условию задачи, Р(А1) = 0,6,
Р(А2) = 0,4, РА (В) = 0,1, РА (В) = 0,5. Воспользуемся формулами Байеса. Сначала
подсчитаем Р(В)\
Р(В) = PAi(B) - Р(А{) + РА2(В) - Р(А2) = 0,1 • 0,6 + 0,5 • 0,4 = 0,06 + 0,2 = 0,26.
Далее находим:
Рв (А{) = 0,06 / 0,26 = 0,23, Рв (А2) = 0,2 / 0,26 = 0,77.
Таким образом, обнаруженная при испытании отрицательная реакция указы-
указывает с вероятностью 0,23 на наличие у пациента заболевания Ах, и с вероятностью
0,77 на наличие у него заболевания А2. Врач ставит диагноз: у данного пациента
заболевание А2. Нашим пациентом заинтересовался второй врач, более осторож-
осторожный. Его насторожило, что поставленный первым врачом диагноз противоречит
справочным данным о вероятности заболеваний в данных условиях. Поэтому он
предложил повторить испытание — еще раз провести тот же анализ.
Задача 5. Задача отличается от задачи 4 только тем, что теперь анализ прове-
проведен дважды. Оказалось, что повторное испытание также дало отрицательную реак-
реакцию. Какова вероятность, что обнаруженная в двух испытаниях отрицательная реак-
реакция обусловлена заболеванием А{! заболеванием А{1
Решение. Теперь событие В — событие, состоящее в том, что в двух испытаниях
обнаружена отрицательная реакция. Легко сообразить, что теперь РА (В) =
= (ОДJ = 0,01, РА2(В) = @,5J = 0,25. Вычисляем:
Р(В) = РА{(В) - Р(АХ) + PAi(B) - Р(А2) = 0,01 • 0,6 + 0,25 • 0,4 = 0,006 + 0,1 = 0,106,
РВ{АХ) = 0,01 • 0,6 / 0,106 = 0,06, РВ{А2) = 0,25 • 0,4 / 0,106 = 0,94.
Теперь у врачей появились весьма серьезные основания сделать выбор в пользу
гипотезы А2, т. е. предположить у пациента болезнь А2.
Идея использовать формулы Байеса для уточнения медицинского диагноза очень
заинтересовала молодого аспиранта. Он подумал: «А если при повторном испыта-
испытании мы получим не отрицательную, а положительную реакцию? Какие тогда по-
появятся рекомендации относительно диагноза?»
291

Задача 6. Задача отличается от задачи 4 только тем, что теперь анализ прове-
проведен дважды и при этом первое испытание дало отрицательную реакцию, а второе
положительную.
Решение. Теперь В — событие, состоящее в том, что в первом испытании обна-
обнаружена отрицательная реакция, а во втором положительная. Легко сообразить, что
PAi(B) =0,1 -0,9 = 0,09, PAi(B) = 0,5 -0,5 = 0,25. Вычисляем: Р (В) = 0,09 • 0,6 +
+ 0,25 • 0,4 = 0,054 + 0,1 = 0,154,
РВ(А{) = 0,054 / 0,154 = 0,35, РВ(А2) = 0,1 / 0,154 = 0,65.
Мы видим, что произошло некоторое уточнение диагноза, хотя и не столь эффек-
эффектное, как в задаче 5 (когда опыт обнаружил отрицательную реакцию в обоих ис-
испытаниях). По результатам данного опыта, гипотеза А{ имеет один шанс из трех,
а гипотеза А2 — два шанса из трех.
Рассмотренные задачи анализируют всего два примера из практики,
когда формулы Байеса находят практическое применение. Подобных
примеров можно было бы привести достаточно много. Отметим, что
формулы Байеса нередко используются, например, при выборочном конт-
контроле качества выпускаемой продукции. Эти формулы широко использу-
используются также в артиллерийской практике — когда производится так назы-
называемая пристрелка для уточнения наших знаний об условиях стрельбы
и, в частности, о местонахождении цели.
10.7 Беседа с «персоналистом» о вероятностях вообще
и о формулах Байеса в частности
Есть в мире тьма, Гораций, кой-чего,
Что вашей философии не снилось...
в
Вильям Шекспир {«Гамлет»)
Перевод Б. Пастернака
§ 6.3 отмечалось, что в вопросах интерпретации и использования
вероятностных представлений существуют две разных позиции, одну из
которых можно назвать объективистской, а другую персоналистской.
«Объективисты» рассматривают вероятность исключительно как меру
объективной достоверности события. «Персоналисты» же рассматрива-
рассматривают вероятность не только как меру достоверности события, но и как
меру личного доверия к тем или иным утверждениям относительно слу-
случайного события. Полагаем, что читателю будет интересно познако-
познакомиться с диалогом, который мог бы произойти при встрече автора с не-
неким воображаемым «персоналистом».
292

Персоналист. Ортодоксальные «объективисты» считают, что понятие
вероятности, строго говоря, применимо лишь к событиям, которые про-
происходят при многократных испытаниях без изменения условий опыта.
Они ограничиваются бросаниями кубиков и монет, выниманием шаров
из урн, рассмотрением массового производства однотипных изделий
и т. п. Исходя из соображений симметрии и равновозможности, «объек-
«объективисты» выполняют точные подсчеты вероятностей, используя клас-
классическое или геометрическое определения понятия «вероятность». Они
также прибегают к приближенным вычислениям вероятностей в случа-
случаях, позволяющих использовать частотное определение этого понятия и,
в частности, пользоваться таблицами случайных чисел. Но они отказы-
отказываются включать в теорию вероятностей анализ иных случайных собы-
событий и в том числе тех событий, где вероятность выступает как мера
лычного доверия к правдоподобию тех или иных утверждений, касающихся
этих событий. А между тем такой подход не без успеха развивается
в математике, начиная с первой половины ХХ-го столетия. На мой взгляд,
это указывает на ограниченность (точнее сказать: узость) концепции
ортодоксальных «объективистов».
Пвтор. Согласитесь, что узость концепции — это отнюдь не ошибоч-
ошибочность концепции. Заведомо сужая круг рассматриваемых случайных
ситуаций, «объективисты» тем самым получают возможность проанали-
проанализировать принципы и методы теории вероятностей в наиболее «чистом»
виде. Это весьма важно. Особенно на первых этапах изучения теории.
Вполне возможно, что без увлечения азартными играми с использова-
использованием игральных костей (кубиков), монет, игральных карт (варианта
ситуаций с выниманием шаров из урн) теория вероятностей как мате-
математическая наука не зародилась бы в XVII-м столетии.
Персоналист. Однако жизнь не сводится к костям и картам. Сама ло-
логика процесса познания реального мира, который нас окружает, долж-
должна была заставить людей расширять область применения вероятностей.
Пвтор. Что ж, именно так и случилось. Только надо заметить, что в
XVIII-м и первой половине XIX-го столетия такое расширение проис-
происходило подчас не слишком продуманно, а потому неправомерно. Даже
такие выдающиеся математики как П. Лаплас A749-1827) и С. Пуассон
A781-1840), внесшие большой вклад в развитие теории вероятностей,
грешили предложениями применять понятие вероятности в математи-
математическом плане к судебным процессам, исследованиям преданий, рас-
рассмотрению нравственных вопросов и т. д. У Пуассона есть работа, оза-
озаглавленная «Исследования о вероятности судебных приговоров по
уголовным и гражданским делам». В 1843 году профессор Московского
293

университета Н.Е. Зерное A804-1862) в своей весьма нашумевшей тогда
речи на торжественном собрании в университете провозглашал: «Тео-
«Теория вероятностей проникает в храм Фемиды, подавая мерило правды и
милости судиям. Она может руководствовать законодателя в избрании
мер гражданского порядка, оценивая их по замеченным последствиям. Она
может подавать светильник историку, взвешивая доверенность к преда-
преданиям». Однако, согласитесь, вряд ли можно говорить всерьез, что, на-
например, вероятность виновности подсудимого равна 3/4или вероят-
вероятность вынесения справедливого приговора равна 9/10. Вряд ли кого-то
удовлетворит признание, что его любят с вероятностью, равной 2/3, и
вряд ли можно серьезно воспринимать утверждение, что вероятность
определенного поведения какого-то человека равна 7/9. Не будем за-
забывать, что подобные многочисленные «злоупотребления», когда веро-
вероятность пытались применять практически везде и нередко совсем не к
месту, в немалой степени способствовали возникновению в первой по-
половине XIX-го столетия серьезного кризиса в теории вероятностей.
Персоналист. Но ведь этот кризис был, в конечном счете, преодолен?
Пвтор. Да, он был преодолен. В этом большая заслуга П.Л. Чебышёва
A821-1891), а также его учеников и последователей из знаменитой
Петербургской математической школы.
Персоналист. Мне это известно. Чебышёв предложил рассматривать
теорию вероятностей как математическую дисциплину с заранее извес-
известными «элементарными» вероятностями, используя которые вычисля-
вычисляют по правилам теории вероятностей другие, более сложные вероятно-
вероятности. При этом Чебышёв вовсе не требовал, чтобы «элементарные»
вероятности непременно вычислялись с использованием классического
или геометрического определений вероятности. Как я представляю, его
вообще не очень-то интересовало, откуда взяты «элементарные» веро-
вероятности. Они считаются известными — и точка! Может быть, они ак-
аккуратно вычислены, а может быть, введены достаточно произвольно.
Пвтор. Однако ни в одной работе Чебышёва не рассматриваются
вопросы судопроизводства или нравственного поведения. Надо пола-
полагать, он считал, что «элементарные» вероятности, не поддающиеся пря-
прямому вычислению, известны нам из практики, из наблюдений над про-
происходящими вокруг нас явлениями.
Персоналист. В любом случае этот главный «виновник» прорыва в тео-
теории вероятностей (я имею в виду Чебышёва) не был ортодоксальным
«объективистом». А вот Вы, как мне представляется, отдаете явное пред-
предпочтение именно объективистской позиции. Об этом говорит содержа-
содержание и самый стиль Вашей книги.
294

Пвтор. Вполне естественно. Ведь это книга учебного характера. Вы
довольно точно заметили, что я отдаю в книге предпочтение объекти-
объективистской позиции. Именно «отдаю предпочтение» — и не более того!
При этом я отнюдь не разделяю точки зрения ортодоксов, которые ка-
категорически отвергают персоналистские подходы и соглашаются рас-
рассматривать вероятности только для событий, наступающих в однород-
однородных испытаниях.
Персоналист. Я это заметил. Если бы Вы были ортодоксом, то не рас-
рассматривали бы, например, задачу о вероятности попадания охотни-
охотника в пролетающую мимо него утку. Разговор о частотном определении
вероятности в данной ситуации ортодокс не поддержал бы. О частоте
каких однородных испытаний тут может идти речь? Ведь утки бывают
разных размеров, летают на разных высотах и с разными скоростями.
Многое зависит от освещенности места охоты, от психического и фи-
физического состояния охотника в данный момент, от того, насколько
неожиданно появилась утка в поле его зрения. Поэтому, когда Вы гово-
говорите, что вероятность попасть в утку равна для данного охотника, ска-
скажем, 0,8, то это в немалой степени отражает меру Вашего доверия к спо-
способностям стрелка.
Пвтор. Доверия, основанного на моем знании об опыте, какой имеет-
имеется у охотника в вопросе стрельбы по летающим уткам.
Персоналист. Все равно без доверия здесь не обойтись. Другой чело-
человек мог бы утверждать, что вероятность попадания в летящую утку у
рассматриваемого охотника не 0,8, а 0,7 или 0,9. И еще он мог бы зая-
заявить, что ему лучше известно, насколько опытен этот охотник.
Пвтор. Если Вы помните, в самом конце § 6.3 я специально подчер-
подчеркивал, что, отдавая предпочтение объективистской позиции, «мы не
станем отметать подходы персоналистов и в определенные моменты,
например при рассмотрении формул Байеса, будем использовать также
и эти подходы.»
Персоналист. Мы как раз только что рассматривали формулы Байеса.
Неплохо было бы привести соответствующий пример в духе персоналист-
ских идей.
Пвтор. Вернемся к ситуации, рассматривавшейся в задачах 4, 5, 6
в § 10.6. В этих задачах априорные вероятности двух гипотез равнялись
0,6 и 0,4. Эти значения взяты, как было сказано, из медицинских спра-
справочников. Теперь допустим, что у нас нет с собой справочника, но извест-
известно, что вероятности данных гипотез различаются не очень сильно.
Довольствуясь этой информацией, мы проявим произвол и будем счи-
считать, что вероятности Р{А{) и Р(А2) равны друг другу. Предположим те-
теперь, что проведен анализ и при этом получена отрицательная реакция.
295

Нам надо по Байесу найти апостериорные вероятности РВ(А1) и РВ(А2).
Вот наши вычисления: Р(А{) = Р(А2) = 0,5; РА{(В) = ОД, РА?В) = 0,5.
Р{В) = 0,1 • 0,5 + 0,5 • 0,5 = 0,05 + 0,25 = 0,3;
РВ(АХ) = 0,05 / 0,3 = 0,17, РВ(А2) = 0,25 / 0,3 = 0,83.
Уточненный диагноз: пациент страдает заболеванием А2. Предполо-
Предположим, что анализ проводился не один раз, а дважды и что в обоих испы-
испытаниях была получена отрицательная реакция. Теперь:
PAl(B) = (ОДJ = 0,01, РА2{В) = @,5J = 0,25;
Р{В) = 0,01 • 0,5 + 0,25 • 0,5 = 0,005 + 0,125 = 0,13;
РВ(А1) = 0,005 / 0,13 = 0,04, РВ(А2) = 0,125 / 0,13 = 0,96.
Произошло еще большее уточнение диагноза. Теперь гипотеза А1
практически исключается. Как видим, нам не понадобилось ворошить
справочники в поисках более или менее точных значений априорных
вероятностей гипотез.
Персоналист. Полагаю, что «персоналисты» значительно чаше, чем
«объективисты», обращаются к формулам Байеса.
Пвтор. Чем Вы это объясняете?
Персоналист. Тем, что формулы Байеса позволяют обойтись приблизи-
приблизительным знанием априорных вероятностей гипотез. Исследователь мо-
может приписывать этим гипотезам вероятности, отвечающие «степени
правдоподобия», которая оценивается лично им. Другой исследователь
может выбрать иные априорные вероятности, ориентируясь на свое лич-
личное понимание «степени правдоподобия». Затем выполняется опыт (про-
(проводится испытание). Его результатом являются послеопытные вероят-
вероятности гипотез. При этом вероятности одних гипотез могут оказаться
больше, чем они были выбраны до опыта, а вероятности других гипо-
гипотез, напротив, могут оказаться меньше или даже вообще могут выпасть
из дальнейшего рассмотрения. Новое испытание можно проводить с но-
новыми априорными вероятностями гипотез, которые теперь будут выб-
выбраны в соответствии с теми апостериорными вероятностями, которые
мы получили после первого испытания. Можно выполнить целый ряд
испытаний и постепенно выявить с большой степенью надежности «пра-
«правильную» гипотезу. «Персоналисты» используют постепенно уменьшаю-
уменьшающееся влияние априорных вероятностей по мере увеличения опытных дан-
данных. Можно сказать, что первоначальные оценки постепенно все более
утрачивают свое значение под воздействием информации, накапливаю-
накапливающейся в результате проведения испытаний.
296

Пвтор. Все это так. Тем не менее не следует злоупотреблять возмож-
возможностями метода, основанного на использовании формул Байеса. Не надо
ориентироваться на «полное незнание» априорных вероятностей и на-
надеяться, что при достаточно большом количестве испытаний удастся
при этом выйти на разумные апостериорные вероятности. Между про-
прочим, подобные ошибки допускал в свое время знаменитый Лаплас (и,
конечно же, не только он один). Неправомерно используя формулы
Байеса, Лаплас пришел к неверному заключению: если событие наблю-
наблюдалось в испытаниях т раз подряд, то вероятность, что оно повторится
при s следующих испытаниях равна (т+ I) / (m + s+ 1). Получается,
например, что, если монета выпала орлом 10 раз, то вероятность ей
выпасть орлом в 11-й раз равна A0 + 1) / A0 + 1 + 1). А между тем мы
хорошо знаем, что, как бы ни выпадала монета 10 раз (и вообще сколь-
сколько угодно раз), вероятность ее выпадения орлом в очередной раз равна
1/2. Лаплас рассматривал, в частности, следующий курьезный пример.
Он предположил, что утренний восход солнца люди наблюдают вот уже
5 тысяч лет, т. е. 1 826 250 дней. Вероятность того, что солнце взойдет
еще раз после пяти тысяч лет наблюдения, получается, согласно приве-
приведенной выше формуле, равной A 826 250 + 1) / A 826 250 + 1 + 1) =
= 1 826 251/1 826 252 = 0,9999994. Нужно ли комментировать подобные
«вычисления»?
Персоналист. Ваши последние замечания, конечно, справедливые.
Надеюсь, Вы не рассматриваете их как аргумент против самой идеи
включения в рамки теории вероятностей также и тех вероятностей,
которые можно рассматривать не более, как меру личного доверия
к правдоподобности тех или иных утверждений по поводу случайных
событий.
Пвтор. Я полагаю, что теория вероятностей вполне может иметь дело
также и с такими вероятностями. Но при этом необходимо, чтобы сте-
степень доверия являлась разумной при данных условиях, а не определялась
бы личным мнением отдельных индивидуумов, которые могут быть как
разумными, так и неразумными.
Персоналист. Всегда ли, однако, можно различить «разумных» и «не-
«неразумных» индивидуумов? Здесь все далеко не так просто. Недаром в
ХХ-м столетии исследования по вероятностной логике (ее называют также
индуктивной логикой) развернулись по весьма широкому фронту. Сегод-
Сегодня можно отметить, по крайней мере, три научных школы, занимаю-
занимающихся такими исследованиями. Эти школы связаны с именами трех
видных философов и логиков ХХ-го столетия: Карлом Поппером A902—
1994), Рудольфом Карнапом A891-1970), Хансом Рейхенбахом A891-1953).
297

ЗАДАНИЯ ПО ТЕМЕ 10
1.	Имеется полная группа событий А±, А2, А3, А4. Как будет выглядеть формула пол-
полной вероятности для события В, если известно, что ВГ\А3 = 0?
Ответ. Р(В) = РА±(В) • Р(А±) + РА2(В) • Р(А2) + PAJ,B) • Р(А4).
2.	Рассматриваются двукратные бросания кубика. Образуют ли следующие события
полную группу событий:
а)	А — в первом броске выпало четное число, В — во втором броске выпало
нечетное число?
б)	Л — выпала нечетная сумма очков, В — выпала четная сумма?
в)	А — в каждом броске выпали четные очки, В — в каждом броске выпали
нечетные очки?
г)	А — выпала нечетная разность очков, В — выпала четная сумма?
А) А — выпала тройка в первом броске, В — выпала тройка во втором броске?
е)	А — выпало хотя бы одно нечетное число, В — выпало хотя бы одно четное
число?
ж)	А — выпала сумма больше 7, В — выпала сумма меньше 7?
з)	А — выпала сумма, равная 8, — выпала сумма не меньше 9, С — выпала
сумма не больше 7?
и) Л — выпали разные очки, В — выпали равные четные очки, С— выпали рав-
равные нечетные очки?
к) А — выпала хотя бы одна единица или двойка, В — выпала хотя бы одна тройка
или четверка, С — выпала хотя бы одна пятерка или шестерка?
а) А — выпало хотя бы одно четное число, В— выпала хотя бы одна единица, С —
выпала хотя бы одна тройка, D — выпала хотя бы одна пятерка?
м) А — выпала разность очков, равная единице, В — выпала разность очков,
равная трем, С — выпала разность очков, равная пяти, D— выпала четная сум-
сумма очков?
Ответы: а) нет, б) да, в) нет, г) да, д) нет, е) нет, ж) нет, з) да, и) да, к) нет,
л) нет, м) да.
3.	Бригада 1 сдала на склад готовой продукции 4200 лампочек, а бригада 2 —
1800 лампочек. Бригада 1дала 5% брака. Сколько процентов брака дала брига-
бригада 2, если выяснилось, что всего на склад было сдано 5720 небракованных лам-
лампочек?
Ответ: 3,9%.
4.	На 10 работников выдано 6 льготных путевок в дом отдыха. Работники тянули
жребий. Докажите соответствующими вычислениями, что вероятность вытянуть
путевку равна 3/5 для второго участника жеребьевки, для третьего участника,
для четвертого участника.
5.	Выяснилось, что в условие задачи из § 10.3 закралась ошибка. Результаты про-
проверки качества данной партии зерна оказались под чьим-то давлением слегка
искаженными. В действительности не 94%, а только 88% зерен были сорта 1, а
298

зерен сортов 2, 3 и 4 было, соответственно, 4%, 3% и 5%. Какова в действитель-
действительности вероятность того, что зерна из данной партии дадут полновесный колос?
Ответ: 0,588.
6.	Половину всех деталей изготавливал цех № 1 и давал при этом только 2% брака,
а другую половину всех деталей изготавливал цех № 2 и давал 4% брака. После
того, как часть работников из цеха № 1 перешли на другое предприятие, цех № 1
стал изготавливать вдвое меньше продукции) с тем же процентом брака, что
и раньше). Изготовление недостающего количества деталей пришлось передать
в цех № 3, который стал давать 9% брака. Насколько теперь возросла вероят-
вероятность того, что наугад выбранная деталь окажется бракованной?
Ответ: На 0,0175, т. е. на 1,75%.
7.	Из общей партии деталей, изготовленной тремя цехами в задаче 6, взяли наугад
одну деталь. Она оказалась бракованной. Какова вероятность, что деталь являет-
является продукцией цеха № 1? цеха № 2? цеха № 3?
Ответы: 0,105, 0,474, 0,421.
8.	Из общей достаточно крупной партии, изготовленной тремя цехами в задаче 6,
взяли наугад пару деталей. Обе детали оказались бракованными. Какова вероят-
вероятность, что детали являются продукцией цеха № 1? цеха № 2? цеха № 3?
Ответы: 0,025, 0,516, 0,459.
9.	Вероятность того, что изделие удовлетворяет стандарту, равна 0,95. Некоторая
система испытаний дает для изделий, удовлетворяющих стандарту, положитель-
положительный результат с вероятностью 0,97, а для изделий, не удовлетворяющих стандар-
стандарту, — лишь с вероятностью 0,05. Какова вероятность, что изделие, дважды вы-
выдержавшее испытание с положительным результатом, удовлетворяет стандарту?
Ответ: 0,99986.
Пояснение: Полная группа событий: А± — изделие удовлетворяет стандарту, А2 —
изделие не удовлетворяет стандарту. В данном случае Р(А±) = 0,95, Р(А2) = 0,05.
10.	В задаче 4 из § 10.6 анализ дал не отрицательную, а положительную реакцию.
Какова вероятность, что у пациента заболевание А±? Заболевание А2?
Ответы: 0,73, 0,27.
11.	В задаче 5 из § 10.6 анализ дал отрицательную реакцию два раза подряд. Како-
Какова вероятность, что у пациента заболевание А±? заболевание А2?
Ответы: 0,83, 0,17.
12.	Рассматривается предыдущая задача, в которой теперь оговорено одно измене-
изменение: априорные вероятности гипотез считаются равными.
Ответы: 0,76, 0,24.
299

ТЕМА 11
ПОВТОРЕНИЕ НЕЗАВИСИМЫХ
ИСПЫТАНИЙ С ДВУМЯ ИСХОДАМИ
(математическая схема Бернулли)
В самом начале формирования основ-
основных понятий теории вероятностей выяс-
выяснилась фундаментальная роль одной ма-
математической схемы, изученной известным
швейцарским математиком Якобом Бер-
Бернулли A654-1705)
А.Н. Колмогоров
На практике часто приходится иметь
дело с многократным повторением одно-
одного и того же опыта по возможности в од-
одних и тех же условиях.
Б А. Кордемский
11.1 Испытания Бернулли — независимые испытания
с двумя исходами
Jt5 математике существует специальный термин — «испытания Бер-
Бернулли». Так называют повторяющиеся много раз одинаковые испытания,
300

в каждом из которых возможны только два взаимно противоположных
исхода (один из них будем условно называть «успехом», а другой —
«неудачей»), причем вероятности как «успеха», так и «неудачи» посто-
постоянны, они не меняются от испытания к испытанию. Будем обозначать
вероятность наступления «успеха» в каждом испытании через р, а веро-
вероятность наступления «неудачи» через q; очевидно, что р + q = 1.
В математической схеме Бернулли вычисляют так называемые бино-
биноминальные вероятности, которые принято обозначать через Рп(т). Ве-
Вероятность Рп(т) есть вероятность того, что в п испытаниях Бернулли
«успех» наступит т раз (и, соответственно, п — т раз наступит «неуда-
«неудача»). Число т может принимать целочисленные значения от 0 до п, так
что для данного п можно рассматривать п + 1 биномиальных вероятно-
вероятностей Рп(т). Испытания Бернулли относятся к категории независимых
испытаний. Говорят, что п испытаний являются независимыми, если лю-
любая комбинация исходов этих испытаний представляет собой группу из
событий, независимых в совокупности. Любая комбинация «успехов» и
«неудач» в испытаниях Бернулли — это комбинация независимых со-
событий. Ведь вероятности наступления «успеха» и «неудачи» для всякого
конкретного типа испытаний Бернулли имеют некие постоянные значе-
значения, а это как раз и означает, что исход того или иного испытания не
зависит от исходов предыдущих испытаний и не влияет на исходы по-
последующих испытаний.
Подчеркнем, что термины «успех» и «неудача» для двух возможных
исходов выбираются условно. Их конкретное содержание определяется
той ситуацией, для которой применяется схема Бернулли. Приведем
примеры.
Монета подбрасывается п раз и вычисляется вероятность того, что
она т раз упадет орлом. Здесь «успех» — выпадение орла.
Проверяются п одинаковых изделий и вычисляется вероятность того,
что т изделий окажутся бракованными. Здесь «успех» — обнаружение
бракованного изделия.
Регистрируются п новорожденных и вычисляется вероятность того,
что т новорожденных оказались девочками. Здесь «успех» — рождение
девочки.
В физическом эксперименте регистрируются п нейтронов и вычисля-
вычисляется вероятность того, что т нейтронов будут иметь энергию в заданном
интервале значений. Здесь «успех» — обнаружение такого нейтрона.
Проверяются п страниц в книге и вычисляется вероятность того, что
на т страницах будет обнаружена хотя бы одна опечатка. Здесь «ус-
«успех» — обнаружение страницы с хотя бы одной опечаткой.
301

Контролируется суточный расход электроэнергии за каждый из п дней
и вычисляется вероятность того, что в т днях расход не превысит уста-
установленной нормы. Здесь «успех» — выявление дня, в который норма
расхода электроэнергии не была превышена.
Посеяны п семян и вычисляется вероятность того, что т семян взой-
взойдут. Здесь «успех» — появление ростка.
Проверяются п лампочек на длительность их работы и вычисляется
вероятность того, что т лампочек проработают не менее 1000 часов.
Здесь «успех» — лампочка не перегорела до контрольного срока.
На экзамен вынесены п вопросов, на каждый из которых предлагает-
предлагается одно и то же количество предполагаемых ответов, причем лишь один
правильный. Вычисляется вероятность того, что методом простого уга-
угадывания удастся ответить правильно на т вопросов. Здесь «успех» — на
вопрос дан правильный ответ.
Стрелок делает п выстрелов по мишени и вычисляется вероятность
того, что он попадет в «яблочко» т раз. Здесь «успех» — попадание в
«яблочко».
Отслеживается в течение п дней нерегулируемый перекресток и вы-
вычисляется вероятность того, что будут обнаружены т дней, когда на
перекрестке произойдет хотя бы одна автомобильная авария. Здесь «ус-
«успех» — обнаружение дня с хотя бы одной аварией.
Во всех предложенных ситуациях можно было бы договориться рас-
рассматривать в качестве «успеха» те события, которые здесь рассматрива-
рассматривались как «неудача». Так, «успехом» можно считать выпадение не орла,
а решки, обнаружение не бракованного, а годного изделия, рождение
не девочки, а мальчика, обнаружение нейтрона вне заданного интерва-
интервала значений энергии, обнаружение страницы без опечаток, выявление
дня, в который норма расхода электроэнергии была превышена, непо-
непоявление ростка из посаженного семени, обнаружение перегоревшей до
срока лампочки, выдачу неправильного ответа на вопрос, непопадание
в «яблочко», обнаружение безаварийного дня. Обратим внимание на
то, что в рассмотренных нами ситуациях независимость испытаний вполне
очевидна. Исход того или иного подбрасывания монеты никак не свя-
связан с исходами других подбрасываний. Появление того или иного бра-
бракованного изделия не связано с появлением или непоявлением брака
в других изделиях. Рождение у данной матери девочки не связано с рож-
рождением детей у других матерей. Каждый нейтрон регистрируется неза-
независимо от регистрации других нейтронов. Обнаружение страницы с опе-
опечаткой не связано с наличием или отсутствием опечаток на других
страницах. Расход электроэнергии в тот или иной день не зависит от
302

величины ее расхода в другие дни. Появление того или иного ростка не
зависит от появления других ростков. Тот факт, что данная лампочка
не перегорела в течение 1000 часов, не зависит от качества других лам-
лампочек. Если повезло угадать правильный ответ на данный вопрос, то
это не означает, что повезет при угадывании ответа на другие вопросы.
Успех при данном выстреле не влияет, вообще говоря, на успешность
других выстрелов. Факт аварии на нерегулируемом перекрестке, слу-
случившийся в тот или иной день, не связан с предыдущими авариями
и не влияет на последующие.
11.2 Формула Бернулли для вычисления
биномиальных вероятностей
ГТлйдем выражение для биномиальных вероятностей Рп(т). Снача-
Сначала рассмотрим частный случай, когда п = 5 и т = 3. Обозначим через А
«успешный» исход, а через В — «неудачный» исход. Нам надо найти
вероятность того, что в серии из пяти независимых испытаний исход А
наступит три раза (и, соответственно, два раза наступит исход В). Пред-
Предположим, что в данной конкретной серии испытаний сначала наступи-
наступили три исхода А9 а затем два исхода В. Иными словами, наступило ком-
комбинированное событие
Оно является пересечением пяти исходов, независимых в совокуп-
совокупности, поскольку все они наступили в независимых испытаниях. Ис-
Используя правило умножения вероятностей событий, являющихся неза-
независимыми в совокупности (правило A7) из темы 9), запишем:
Поскольку Р(А)=р9 Р{В) = 1 -р = д9 то, следовательно,
P(Kl)=p3-q2.	(*)
Далее учтем, что комбинированное событие Кх — не единственное,
какое надо учитывать при вычислении Р$E). В других сериях из пяти
испытаний три исхода А могут наступить в иных последовательностях.
Нужно рассмотреть столько серий из пяти испытаний, сколько суще-
существует выборок (сочетаний) из пяти по три, т. е. С53 = 5! / C!2!) = 10 вы-
выборок. Значит, чтобы вычислить Р$E)9 нужно учесть вероятности сле-
следующих десяти комбинированных событий:
303

К2=ВГ\АГ\АГ\АГ\В;
К3=ВГ\ВГ\АГ\АГ\А;
К4=АПАГ\ВГ\ВГ\А;
K5=Af]Af]Bf]Af]B;
К6=АГ\ВПАГ\АГ\В;
K7=Bf]Af]Af]Bf]B;
Ks=Af]Bf]Bf]Af]A;
К9=ВПАГ\ВГ\АГ\А;
Kw=Af]Bf]Af]Bf]A.
Для вероятности каждого из этих комбинированных событий спра-
справедливо соотношение (*), т. е. все они имеют вероятность ръ ¦ q1. А по-
поскольку события Kj несовместные, то в соответствии с правилом B) из
темы 9 можем записать:
ю
(**)
(Здесь и в дальнейшем вместо того, чтобы выписывать слагаемые в сумме
ai + а2 + аъ + а4 + ••• + ап будем использовать общепринятый знак сум-
г
мирования S и будем писать: / jai.)
Соотношение (**) можно переписать в виде:
P5C) = C5V q2.	(***)
коль скоро каждое из слагаемых P{Kt) равнор3 • q2, а число таких слагае-
слагаемых равно С53.
Обобщая результат (***) на случай произвольных целых чисел пят
(п > 0, 0 < т < п) получаем искомое выражение для биномиальных ве-
вероятностей — так называемую формулу Бернулли:
п\
т\(п - т)\
pmqn-m
A)
Совокупность п + 1 событий, состоящих в том, что из п испытаний
«успех» наступил 0, 1, 2, 3,..., п раз, является, очевидно, полной группой
событий и, следовательно, сумма вероятностей этих событий равна еди-
единице. Иначе говоря, равна единице сумма биномиальных вероятностей:
B)
п
\im)
п
/ j
т = 0
С
т
п
р
т п-т
= 1.
304

Отметим, что совокупность вероятностей, состоящую из п + 1 биноми-
биномиальных вероятностей, называют биномиальным законом распределения
вероятностей.
Примечание. Читатель должен был обратить внимание на то, что здесь
часто встречается слово «биномиальный». Это связано с биномом Нью-
Ньютона. Напомним формулу бинома Ньютона:
(а + Ъ)п = f^ С™Ътап-т.	(****)
Частными случаями этой формулы являются формулы:
(a + bJ = а2 +2ba + b2;
(а + ЪK = а3 + ЗЬ • а2 + ЪЪ2 • а + Ъ3\
(a + bL = a4 +4ba3 +6b2 a2+4b3 • а + Ь4;
(a + bM = a5 +5b-a4 +10b2 a3 +10Z>3 a2 +5b4 a + b5.
Подставим в (****) а = q и b=ps, где р и q — вероятности двух исхо-
исходов в испытаниях Бернулли, s — некое число. В результате соотноше-
соотношение (****) примет вид:
С учетом A) получаем отсюда:
п
{q + ps)n = У^ Pn{m)-sm.	(*****)
Итак мы видим, вероятности Рп{т) выступают в (*****) в качестве
коэффициентов в разложении бинома {q+ps)n по степеням числа s.
Отсюда и название «биномиальные» для этих вероятностей. Отсюда и
термин «биномиальный закон распределения вероятностей» для сово-
совокупности вероятностей Рп(т).
Заметим, что при s= 1 соотношение (*****) превращается в уже из-
известное нам соотношение B).
Отметим четыре следствия формулы Бернулли:
1) вероятность того, что в п испытаниях «успех» наступит все п раз:
Рп(п) = рп;	C)
305

2) вероятность того, что в п испытаниях «успех» не наступит ни разу:
3)	вероятность того, что в п испытаниях «успех» наступит менее т раз
или вообще не наступит (обозначим эту вероятность через Qn(m):
т-\
ап(т) = Рп@) + РпA) + ... + Рп(т-1)=^Рп(Ъ	E)
/=о
4)	вероятность того, что в п испытаниях «успех» наступит не менее
траз (обозначим эту вероятность через Rn(m))\
т-\
Rn(m) = 1 - Qn(m) = 1 - ? Pn(i)\	F)
эту же вероятность можно найти с помощью формулы:
Rn(m) = Рп(т) + Рп(т + 1) + ... + Рп(п) =
Рассмотрим несколько задач.
Задача 1. Какова вероятность того, что при семи бросаниях монеты орел выпа-
выпадет не менее трех раз ?
Решение. В данной задаче п = 7, т = 3, р = q= 1 /2. Используя F) и A), находим:
Rn(m) = 1 - (Р7@) +Р7A) +Р7B)) = 1 - A/2O (С7° +С7Х +С72) =
= 1 - A /128) A+7+21) =1-29/128 =99/128.
Тот же результат получим, воспользовавшись формулой G):
O -(С73 +С74 +С75 +С76 +С77) =
= A/128).C5 + 35 + 21 + 7 + 1) = 99/128.
Задача 2. На экзамен вынесены 15 вопросов и для каждого предлагаются три от-
ответа, один из которых правильный. Какова вероятность того, что методом простого
угадывания будут даны правильные ответы на какие-либо 10 вопросов?
Решение. Здесь п = 15, т = 10, р = 1 / 3, q = 2 / 3. Применяя формулу A), находим:
Р15A0) = A5!/10!5!)-A/3I0-B/3M = 32032/47822969 = 0,0067.
Задача 3. Вероятность, что изделие будет выпущено с браком, равна 1%. Изго-
Изготовлено 10 изделий. Какова вероятность, что с браком окажутся не более одного
изделия?
306

Решение. Поставленный вопрос можно сформулировать иначе: Какова вероят-
вероятность, что с браком окажется одно изделие или не окажется ни одного? Таким
образом, надо вычислить вероятность Р равную Рю@) + Р10A). Используя форму-
формулу Бернулли и значения вероятностей /? = 0,01 и q = 0,99, находим:
Р = q10 +Cll0p-q9 = @,99I0 +10 0,01 @,99)9 =
= 0,90438 + 0,09135 = 0,99573.
В § 7.7 приводились статистические данные по рождаемости мальчиков и дево-
девочек и на их основе подсчитывалась вероятность рождения девочки; она оказалась
равной 0,4825. Используя эту вероятность, решим следующую задачу.
Задача 4. В цирк отправилась группа первоклассников из 6 человек, отобранных
в классе по жребию. Полагая, что вероятность рождения девочки р = 0,4825, найди-
найдите вероятность того, что в данной группе не больше двух девочек.
Решение. Искомая вероятность Р есть
Р6@) + Р6A) + Р6B) = q6 + С\ • р -q5 + Cj • р2 • q4 =
= @,5175N+6-0,4825-@,5175M + 15-@,4825J-@,5175L =
= 0,0192 + 0,1074 + 0,2504 = 0,377.
Разумеется все эти (и подобные им) вычисления следует выполнять с
помощью калькулятора.
11.3 Доказательство двух соотношений
с биномиальными вероятностями
Jl ечь
идет о соотношениях:
n
Р„(т) =
= n2p2
пр;
+ np(l
-P).
(8)
(9)
Докажем соотношение (8). Предварительно заметим, что
n
E
m=\
307
т=\

Используя формулу Бернулли, представим:
т ¦ Рп{т) = У 7	^i	-rPmq
п\ / ^ (т - \)\(п - т)\
m=lv	7 v	7
mqn-m
\n~ l)-	m-\ n-m _ \^ r^m-\ m-\ n-m
Am-\)\{n-m)\P q ~nPl^Cn-iP Q ¦
Введя обозначение /и — 1 = г, перепишем последнее выражение так:
п-\
Ln_iP q
Сумма в данном выражении есть, согласно формуле Бернулли,
/i-i
У^Рп-\(г)- Воспользовавшись соотношением B), заключаем, что эта
сумма равна единице. Соотношение (8) доказано.
Докажем соотношение (9). Представим: m2 = m + m(m- 1). Тогда
п	п
\	Т/i/l ^	D / -ШЛЛ \ 		X	-ШЛЛ ^
Используя формулу Бернулли, преобразуем сумму в (*) к виду:
V^ т(ш — 1)	—	птап~т =
^ч	т\{п-т)\
т=2	v	7
— fi(fi _ \)гJ V^	V^ z/ •	 m-2 n-m
m=2 ^	' "^	7 '
Введя обозначение m - 2 = г, перепишем последнее выражение так:
«-2
308

Сумма в данном выражении есть, согласно формуле Бернулли,
п-2
Pn-i(r) 9 а это есть единица, согласно соотношению B). Таким образом,
^	(**)
Подставляя (**) в (*), находим:
п
пр+^2 т(т -1) • Рп(т) = пр + я(я - Щ? = л2^2 + пр(\ - р).
Соотношение (9) доказано.
11.4 Математическое ожидание «успеха».
Среднее число «успехов»
1У1атематическое ожидание «успеха» в п испытаниях Бернулли есть
сумма произведений тРп(т), вычисленная для всех т от 1 до п. Введя
обозначение (т) для этого понятия, можем записать:
A0)
Воспользовавшись соотношением (8), получаем, что
(т) = пр.	A1)
Выясним, какой смысл имеет понятие (т) и почему его называют
«математическим ожиданием».
Термин «математическое ожидание» стал использоваться в началь-
начальный период развития теории вероятностей (в XVII-м столетии), т. е. в
те времена, когда область применения теории ограничивалась азартны-
азартными играми. Игроков интересовало среднее значение ожидаемого выигры-
выигрыша, которое они стали называть математическим ожиданием выигрыша.
О математическом ожидании (т), представляемом формулой A1),
нередко говорят, что это есть среднее число «успехов» в п испытаниях
Бернулли. Такое толкование смысла термина «математическое ожида-
ожидание» требует очевидно, разъяснения, о каком усреднении идет тут речь.
Воспользуемся частотным определением вероятности. Пусть в 1-й серии
309

из п испытаний событие А (т. е. «успех») наступило тх раз, во 2-й серии
из п испытаний наступило т2 раз, в 3-й серии — т3, раз и т. д. Пусть
всего выполнено к серий испытаний (по п испытаний в каждой серии).
к
Обозначим через М(А) сумму ^ mt, т. е. полное количество наступле-
/=i
ний события А в к сериях. Поделив М (А) на к, мы получим среднее
число появлений события в каждой из к серий испытаний:
т = (тх +т2 + ... + тк)/к = М(А)/к	(*)
(усреднение выполнено по к сериям). А поскольку в каждой серии было
п испытаний, то полное число испытаний N равно
N = пк.	(**)
Разделив М{А) на N, мы получим частоту появления события А в
рассматриваемых испытаниях. Согласно частотному определению вероят-
вероятности (см. § 7.7), частота наступления события А, т. е. отношение М(А) / N,
дает при 7V> 1 приближенное значение вероятности Р{А). Значит, при-
приближенно можем записать:
М(А) I N=p при jY> 1.	(***)
Используя (**) и (***), перепишем (*) в виде:
(****)
Этот результат будет тем точнее, чем больше полное число испытаний.
Итак, мы убедились, что математическое ожидание (т) = пр прибли-
приближенно равно среднему арифметическому числу «успехов» е п испытаниях
Бернулли. Кроме того, у математического ожидания есть еще одна ин-
интерпретация, которую мы рассмотрим в следующем параграфе.
А пока приведем два простых примера. Допустим, что вероятность
появления бракованного изделия на предприятии равна 0,025. Чему равно
среднее число бракованных изделий на каждую тысячу изделий, изготов-
изготовленных данным предприятием? В соответствии с A1) находим, что ис-
искомое среднее число равно пр = 1000 • 0,25 = 25.
Другой пример. Примем, что вероятность рождения девочки равна
0,4825. Чему равно среднее число рождений девочек на каждую тысячу
новорожденных! Используя A1), находим, что искомое среднее число есть
пр = 1000 * 0,4825 = 482,5. Конечно, озвучивать такой ответ не вполне удоб-
удобно, хотя с точки зрения математики он верен. Чтобы не говорить «четы-
«четыреста восемьдесят две с половиной девочки», надо или округлить резуль-
310

тат (в среднем на каждую тысячу новорожденных приходится 483 девоч-
девочки), или увеличить число испытаний в серии и рассматривать среднее
число рождений девочек на каждые десять тысяч новорожденных (в сред-
среднем на каждые десять тысяч новорожденных приходится 4825 девочек).
11.5 Наиболее вероятное число «успехов»
1 Хоставим вопрос: как изменяются значения биномиальных вероят-
вероятностей Рп(т) по мере возрастания т от 0до nl Используя A), выразим
отношение Рп(т+ 1) к Рп(т)\
Рп{т + \) _ п\т\(п-т)\	pm+\qn-m-\ _n_m ^
Рп(т) ~ {т + \)\{п-т-\)\п\ pmqn~m ~ m+\ q' ^
Из (*) следует, что Рп (т+\)> Рп (т), если (п - т) - р > (т + 1) • q.
Второе неравенство можно переписать в виде: (пр - д) > т.
Итак, если (пр - д) > т, то Рп (т + 1) > Рп (т) и, значит Рп (т) возра-
возрастает с увеличением т; если (пр - д) < т, то Рп (т + 1) < Рп (т) и, зна-
значит, Рп (т) убывает с увеличением т.
Мы видим, что сначала по мере роста т в пределах от 0 до пр - q
вероятности Рп(т) постепенно возрастают, а затем, по мере дальней-
дальнейшего роста т (в пределах от пр - q до п) вероятности Рп (т) постепенно
убывают. Возрастание Рп(т) начинается от значения Рп@) = qn, а убы-
убывание завершается при значении Рп(п) =рп.
Выясним, при каком значении т биномиальная вероятность оказы-
оказывается наибольшей. На первый взгляд, ответ ясен: это происходит при
т = пр - q. Однако такой ответ слишком поспешен. Как правило, раз-
разность пр - q не является целым числом, тогда как т принимает лишь
целочисленные значения.
Предположим, что разность пр - q оказалась где-то между целыми
числами т' и т' + 1 (см. рис. 1 в таблице 41). Поскольку (пр — д)> т\
то, согласно (**), Рп(т' + 1) > Рп(т')9 а поскольку (пр - д) < (т' + 1),
то, согласно (***), Рп(т' + 2) < Рп(т' + 1). Таким образом,
Рп(т')<Рп(т' + \)<Рп(т' + 2).
При
т1 <(np-q)<(m! + 1)	A2)
наиболее вероятное число «успехов» равно т' + 1.
311

Таблица 41. Биномиальный закон распределения вероятностей
Ря(и)
U,3
0,2"
од-
^ 0,372
7П
Г
Г
Г
Г
<
1
Па
л\
да
? i
1
7
7
1
f
Г
Г
Г
Г
Г
S
-i—I
II
U
07
,z /
2
\
Л
i
1 V 1
и
ii
iK
i
1
7—
/
Г
l),zu
1
\
\
U
Л
.1-
\
\
Л
4
т' т'+\
\у////Лу/////л ™
г
np-q
т' т'+\
Рис.
—^
1
t ж
и^ - ? Рис.2
0,161
1
\
]
\
\
\
\
к
/
/
5
/
/
/
)
)
i
1
/
?
1
5
«/
1—
1—
1
s
3

Л
\
у
\
\
К
\
\
\
\
\\
\\
/
/
/
/
f
/
/
1
у
/
/
/
1
А
/
у
А
И
\
с
К
У
00
II
\
\
\
\
\ уТО
\
\
р
\
\
\
\
\
\
ис.
\
\
\
з-
0 2 4 6
10 12 14 16 18 20	23 т
312

Легко убедиться, что в частном случае, когдар = q= I /2 и п четное
число, наиболее вероятное число «успехов» равно математическому
ожиданию пр.
Теперь рассмотрим тот относительно редкий случай, когда разность
пр - q оказывается целым числом. Так как пр - q = пр - A - р) =
= р(п + 1) - 1, то отсюда следует, что при заданном п разность пр - q
окажется целочисленной для тех значений р, для которых выполняется
условие:
(****)
где ц — любое целое число от 0 до п - 1. Например, при п = 9 условие
(****) выполняется для р = 1 / 10, 2 / 10, 3 / 10, 4 / 10, 5 / 10, 6 / 10, 7 / 10,
8/10, 9/10.
Итак, предположим, что условие (****) выполнено; пусть пр - q = m'
(см. рис. 2 в таблице 41). Если пр — q = mf, то —-.	— = 1 и, соглас-
т +1 Q
но (*), Рп [т') = Рп (т! + 1). Наиболее вероятными оказываются не одно,
а два числа «успехов».
При
np-q = mf	A3)
есть два наиболее вероятных числа «успехов»: mf и mf + I.
На рисунках 1 и 2 в таблице 41 наиболее вероятные числа «успехов»
показаны черными треугольниками.
Остается уточнить, насколько близко к вероятным числам «успехов»
находится математическое ожидание пр. Если пр - q= т', то сразу по-
получаем: np = q+m' и, значит, пр попадает в интервал значений меж-
между т' и т' + 1, т.е., оказывается между двумя наиболее вероятными
числами «успехов» (см. заштрихованный участок на рисунке 2). Теперь
предположим, что
mf < (пр - q) < [т1 + 1).
Преобразуем эти неравенства к виду:
т' + q < пр < (т' + 1 + q).	(*****)
Учитывая, что 0 < q< 1, заключаем: если выполняются неравенства
(*****)? то тем более будут выполняться неравенства
т1 < пр < (т1 + 2).
Следовательно, математическое ожидание пр находится вблизи наи-
наиболее вероятного числа «успехов» т1 + 1, отклоняясь от него влево или
вправо в пределах единицы (см. заштрихованный участок на рисунке 1).
313

Итак, математическое ожидание пр есть величина, близкая к наиболее
вероятным числам «успехов» (отклонение в пределах единицы). Этот ре-
результат вполне логичен: наиболее вероятное число «успехов» в той или
иной серии независимых испытаний может рассматриваться как мате-
математическое ожидание «успеха» в этой серии испытаний.
Рассмотрим следующий пример. Всхожесть посеянных шести семян
равна/? = 0,6. В первом случае предлагается сравнить вероятности того,
что взойдут шесть семян, и того, что взойдут пять семян. Во втором
случае предлагается сравнить вероятности того, что взойдут шесть се-
семян и взойдет только одно семя.
Те, кто не знакомился с теорией вероятностей, обычно полагают, что
в первом случае вероятности не должны сильно различаться (ведь 5 и 6
не сильно различаются), а вот во втором случае различие вероятностей
должно быть значительным (поскольку 1 и 6 существенно различны).
Проверим, насколько справедливы такие предположения. Для этого,
воспользовавшись формулой Бернулли, подсчитаем:
Р6A) = С\ p-q6 = 6- @,6). @,4M = 0,037,
Р6E) = С65 р5 -q = 6.@,бM • @,4) = 0,187,
/=@,6N= 0,047.
Получается, что высказанные неискушенными людьми предположе-
предположения оказались неверными. Вероятности Р6E) и Р6F)существенно раз-
различны (Р6E) /Р6F) = 4). А вот вероятности Р6F) и Р6A), напротив, до-
довольно близки (Р6A) /ДF) = 1,3)- Чтобы понять, в чем тут дело, найдем
наиболее вероятное число всходов для рассматриваемой серии испыта-
испытаний. Так как пр - q = 6 • 0,6 - 0,4 = 3,2, то, согласно A2), наиболее ве-
вероятное число всходов равно 4. Числа всходов, равные 1 и 6, находятся
по разные стороны от 4. Вероятность для т = 1 еще толком не возрос-
возросла, тогда как вероятность для т = 4 уже заметно снизилась; поэтому
данные вероятности оказываются близкими. Числа же всходов 5 и 6 на-
находятся по одну сторону от 4 — когда, пройдя через максимум (при
т = 4) вероятность начинает быстро убывать.
Задача. У первого стрелка вероятность попадания в «яблочко» р± = 0,2, а у второ-
второго стрелка — р2 = 0,7. Каждый выполняет по 8 выстрелов. Насколько больше наибо-
наиболее вероятное число попаданий в «яблочко» у второго стрелка по сравнению с первым
стрелком? Каковы вероятности того, что каждый из стрелков реализует свое наи-
наиболее вероятное число попаданий?
Решение. Для первого стрелка: пр{- q{ = 8 - 0,2 - 0,8 = 0,8; поэтому, согласно
A2), наиболее вероятное число попаданий в «яблочко» равно 1. Для второго стрелка:
314

пр2 — ^2^8* 0,7 — 0,3 ^ 5,3; поэтому наиболее вероятное число попаданий равно 6.
Искомая разность составляет 5. Теперь подсчитаем вероятности. Для первого стрелка
искомая вероятность есть: Psl = Q1 - р{ • q± = 8 • 0,2 • @,8O = 0,336. Для второго
стрелка искомая вероятность есть: Р8F) = С86 • р26 • q22 = 28 • @,7N • @,3J = 0,296.
11.6 Биномиальный закон распределения вероятностей
Совокупность значений Рп{т) для заданных пир называют биноми-
биномиальным законом распределения вероятностей (проще: биномиальным рас-
распределением вероятности). На рис. 3 в таблице 41 графически представ-
представлены в качестве примера четыре биномиальных распределения:
1)	п = 23, /> = 0,05 (пр= 1,15),
2)	п = 23, /7 = 0,1 (л/> = 2,3),
3)	л = 23, /7 = 0,5 (л/>= 11,5),
4)	л = 23, /> = 0,8 (я/? =18,4).
По горизонтальной оси отложены значения т от 0 до 23, по верти-
вертикальной оси отложены значения биномиальных вероятностей. График
биномиального распределения вероятностей — это совокупность п + 1 точек
на данной координатной плоскости. Абсцисса каждой точки — одно из
значений т, а ордината — значение соответствующей вероятности Рп (т).
Для большей наглядности точки на рисунке 3 соединены отрезками
прямых.
Как легко видеть, график распределения 1 состоит на рисунке толь-
только из семи точек, хотя всего должно быть п + 1 = 24 точки. Недостаю-
Недостающие точки не попали на рисунок просто потому, что для них
Рп{т) < 0,01. По этой же причине остальные распределения представ-
представлены на рисунке наборами точек меньше 24. Так, на графике распре-
распределения 4 показаны только 12 точек — для т= 12, 13, 14, ..., 23. Ос-
Остальные 12 точек (для т = 0, 1,2,3,..., 11) «не попали в кадр», поскольку
их ординаты меньше 0,001.
В соответствии с тем, что говорилось в § 11.5, наблюдаем на графи-
графиках следующие наиболее вероятные числа «успехов»:
-	для распределения 1: т= 1 (вероятность равна 0,372),
-	для распределения 2: т = 2 (вероятность равна 0,277),
-	для распределения 3: т = 11 и т = 12 (вероятность равна 0,161),
-	для распределения 4: т=19 (вероятность равна 0,204).
Во всех случаях наиболее вероятное число успехов отличается от мате-
математического ожидания пр менее, чем на единицу (математические ожи-
ожидания выделены на рисунке при помощи пунктирных вертикалей).
315

В соответствии с соотношением B), сумма значений ординат всех
п + 1 точек на графике распределения Рп (т) должна быть равна 1. Убе-
Убедимся в этом на примере распределения, имеющего в таблице 41 пер-
первый номер. Выпишем значения ординат семи точек, показанных на
графике: 0,307 (/и = 0), 0,372 (т=1), 0,215 (/и = 2), 0,079 (/и = 3),
0,021(т = 4), 0,004 (/и = 5), 0,001 (/и = 6). Сумма этих чисел равна, как
нетрудно подсчитать, 0,999. До единицы не хватает 0,001. Это есть сум-
сумма значений ординат точек, не попавших на рисунок (имеются в виду
точки с т = 7, 8, 9,..., 24).
Обратим внимание на то, что при малых р основной вклад в сумму
п (т) Дают вероятности с малыми т (максимум распределения сме-
щается влево, поближе к т = 0), тогда как при р вблизи 1 основной
вклад вносят вероятности с большими т (максимум распределения сме-
смещается вправо, поближе к т = п). Как и следовало ожидать, по мере
уменьшения/? наблюдается постепенное снижение числа «успехов» в лю-
любой конкретной серии испытаний (при/? = 0 наступление «успеха» в дан-
данной серии полностью исключается), тогда как по мере приближения р
к единице наблюдается постепенное увеличение числа «успехов» в рас-
рассматриваемой серии испытаний (при р = 1 во всех п испытаниях серии
наступает «успех»). При р = q = 1/2 график распределения принимает
симметричный (по отношению к пр) вид, что и демонстрирует график
распределения 3 в таблице 41.
При р = q= 1 / 2 графики биномиальных распределений имеют сим-
симметричный вид при любых п. Если при этом п — нечетное число, то
наблюдаются два наиболее вероятных числа «успехов», при этом мате-
математическое ожидание пр оказывается строго посредине между этими
числами. Если же п — четное число, то наблюдается лишь одно наибо-
наиболее вероятное число «успехов» в серии; оно равно пр, т. е. п = 1 / 2. Шесть
симметричных графиков с четными п представлены на рис. 1 в табли-
таблице 42 (для п = 4, 6,10, 14, 18, 24).
11.7 Закон больших чисел в форме Бернулли
ГТапомним утверждение, высказанное в конце § 7.8: «При сколь угод-
угодно больших п не сами отклонения частоты от вероятности события стре-
стремятся к нулю, а всего лишь вероятности этих отклонений становятся
сколь угодно малыми». Это утверждение было впервые доказано Якобом
Бернулли. С легкой руки Пуассона его стали называть законом больших
316

Таблица 42. Биномиальный закон распределения вероятностей и доказательство
теоремы Бернулли
г(т)
0,3-
0,2-
од-
0
n = 4
Г 0,3/5
1
L
i
L
n-
¦) 0
Ь
I
Л
-и
/I
1
111
1
I»
ЯЕ
1 M \l ft °'209
1 i 1 W1^
11/
I II Ir
1
1
t
I
t
t
f
rr
tt
tt
tt
tt
tt
i
f
г
г
Я
1
у
I
I
Л
/1
I
n
1
/
/
/
И
Г
\
\
1
V
/
/
/
/
1
л
/4
/
д
/
/
/
)
>
/
I
1
«=
^ 0,209 Д
\T
7
T
1/
1
A
/1
/
/
(
w
i
Л
\
E)^=18
I 0 185
1 \ -/ X. 5
\ I \ \
I/ \ \
A \ \
/ \ 1 \l \
A
I/
/
UUfUr^ 1
V
T
4 4 л
t Г \
г Д
[ Тч Ч
\
V
b
Рис.:
Pj
1С.]
n
)
0 2 4 6
10 12 14 16 18 20 23
317

чисел. Доказательство, данное Бернулли, называют сегодня теоремой
Бернулли. В общем случае закон больших чисел был рассмотрен П.Л. Че-
бышёвым; ему же принадлежит заслуга весьма простого доказательства
этого закона в частном случае, когда используется схема Бернулли. Дан-
Данный частный случай математики именуют законом больших чисел в фор-
форме Бернулли. Познакомимся с доказательством этого закона, приведен-
приведенным П.Л. Чебышёвым.
Пусть в некоторой серии из п независимых испытаний событие А,
имеющее вероятность р, наступило т раз. Отношение т / п есть частота
появления события А в данной серии. Немецкий математик Р. Мизес
полагал, что, если рассматривать серии, в которых число испытаний п
будет становиться все больше и больше, то частота т/п наступления
события А будет всё меньше и меньше отличаться от вероятности р, так
что в пределе при п —> оо она должна стать равной вероятности:
lim (m/ п) = р.
Мы уже отмечали (см. § 7.8), что подобное утверждение неправомерно
по той простой причине, что в любой серии испытаний число т на-
наступлений события А является случайным. Случайность наступления
события А принципиально не позволяет гарантировать того, что вели-
величина | (т I п) - р | станет меньше любого малого числа 8, если рассмат-
рассматривать серии с достаточно большим количеством п испытаний. Иными
словами, выбрав произвольное малое 8, мы не вправе полагать, что для
любой серии с достаточно большим числом испытаний п должно вы-
выполняться неравенство
т
<?.	(*)
Всегда может появиться серия испытаний, в которой неравенство (*)
нарушится. Однако (и именно в этом вся суть!) вероятность того, что
такая серия появится (обозначим эту вероятность Р
т
— -Р
> 8 , будет
серии испытаний, в которой
>8, возможно в принципе всегда
по мере увеличения п стремиться к нулю. Подчеркнем: хотя появление
т
п
(как бы велико п ни было), однако это появление будет тем менее веро-
вероятно, чем больше п. Именно в этом и проявляется феномен статистичес-
статистической устойчивости частот наступления случайного события, который де-
делает возможным использование частотного определения вероятности.
318

Итак, вместо предела lim
HmP
т
— -Р
= 0, существует иной предел:
т
— -Р
> г
= 0.
A4)
В связи с этим говорят, что, хотя при п —> оо нет обычной сходимос-
сходимости т I п к р, однако существует сходимость по вероятности: при п —> оо
т
стремится к нулю вероятность того, что
> г для любого сколь
угодно малого г.
Именно таков смысл теоремы Бернулли, если выразить его, пользу-
пользуясь языком современной математики. Приведем доказательство этой
теоремы, данное П.Л. Чебышёвым. Соотношение A4) можно, очевид-
очевидно, переписать в виде:
lim Р (| т - пр | > е) = 0.
A5)
Именно этот предел мы и должны установить.
Начнем с того, что для некоторого фиксированного п выразим веро-
вероятность Р(\т — пр\> пг) через биномиальные вероятности Рп(т). По-
Понятно, что
Р(\т — пр\ >пг) =
(**)
| т-пр \>пг
где суммирование выполняется по всем т, удовлетворяющим условию
т — пр\> пг,	(***)
т. е. по всем т вне промежутка от пр - пг до пр + пг. На рис. 2 в табли-
таблице 42 все эти т находятся или справа от Ъ, или слева от а. Сложив
длины всех вертикальных отрезков на этом рисунке, которые оказались
справа от Ъ или слева от я, мы как раз и получим значение вероятности
Р (| т - пр | > пг).
Из (***) видно, что [(т-пр)/пг]2 >1. Это позволяет получить из
равенства (**) неравенство:
Р (| т - пр | > пг) <
Е
\m-np \>ж
[(т-пр)/пг]2Рп(т).
Понятно, что мы еще более усилим последнее неравенство, если те-
теперь заставим число т пробегать все значения от 0 до п (а не только
значения справа от Ъ и слева от а):
319

Рп{т)
(****)
Теперь убедимся, что
lim
У2
~ пРJ
= 0-
С учетом B), (8) и (9) представим:
Pn{m) =
1
i2e2
1
1
л (/и) + л2
i2Pn (m) -
+ пр — пр2 — 2прпр + п2р2\ =
1
we	we
Отсюда немедленно следует, что
рA-р).
lim
-прJ Рп (т) =
lim - = 0.
(*****)
Итак, мы убедились, что соотношение (*****) справедливо: выраже-
ние
1
9 9
(т ~ пРJ ?п (т) действительно стремится к нулю при
л —> оо. А поскольку вероятность Р(\т — пр\> пг) меньше этого выра-
выражения, то она тем более будет сходиться к нулю при п —> оо. Таким
образом, соотношение A5) доказано, т.е. доказана теорема Бернулли
(или, что то же, закон больших чисел в форме Бернулли).
11.8 Приближенный подсчет биномиальных вероятностей,
предложенный Абрахамом Муавром и Пьером Лапласом
. Формула Бернулли A) красиво выглядит, но использо-
использовать ее на практике, когда п велико, весьма хлопотно. Допустим, веро-
вероятность выпуска бракованного изделия равна р = 0,04. Рассматривается
320

партия, состоящая из 800 изделий. Наиболее вероятное количество бра-
бракованных изделий в такой партии есть пр = 800 • 0,04 = 32. Мы хотим
выяснить, чему равна вероятность того, что в данной партии окажется
32 бракованных изделия. По формуле Бернулли искомая вероятность равна
Р800C2) = С83020 • @,04K2 • @,96)ш .
Конечно, можно воспользоваться калькулятором. Однако даже с его
помощью перемножить 768 раз число 0,96 не так-то легко. Еще труднее
подсчитать Cgoo • В самом деле,
32	800! 800 • 799 • 798 • 797 • 796 •... • 769
800 ~ 321-768! ~	2- 3-4- 5-6-. ..-32	'
Пвтор. Трудности, возникающие при подсчете Рп (т) очевидны. Они
еще больше возрастут, если потребуется найти вероятность того, что
количество бракованных изделий будет, скажем, не больше 40. В этом
случае пришлось бы подсчитывать сумму
^800 @) + ^800 A) + ^800 B) + ^800 C) + ... + ^800 D0) .
*Чи(*иипель. Вот и возникает вопрос: нет ли какого-то иного способа
подсчета Рп (/и) в случаях, когда п велико? Пусть это будет приближен-
приближенный подсчет. Лишь бы он позволял обойтись без формулы Бернулли.
Пвтор. Такой способ приближенного подсчета Рп (/и) при больших п
существует. Его предложил в 1730 году английский математик Абрахам
де Муаер A667-1754) для частной ситуации, когда р = q = 1 / 2. Спустя
полвека выведенную Муавром формулу обобщил на случай произволь-
произвольного р, отличного от 0 и 1, выдающийся французский астроном, мате-
математик, физик Пьер Симон Лаплас A749-1827), автор знаменитой «Ана-
«Аналитической теории вероятностей» A812) и пятитомного «Трактата о
небесной механике». Так в математике появилась формула, которую
ныне принято называть локальной приближенной формулой Лапласа. На-
Наверное, справедливости ради, ее следует называть формулой Муаера—
Лапласа.
'Чийии&ель. Как была получена эта формула? Как она выглядит?
Пвтор. Вывод формулы мы опустим. А выглядит она довольно просто:
Рп(т) = ф(х) / 4npq, где х = (т- пр) / ^npq.	A6)
Используемая здесь функция <p(x) часто встречается в теории вероят-
вероятностей. Ее свойства исследовал выдающийся немецкий математик Карл
Фридрих Гаусс A777-1855); в честь него эту функцию принято называть
321

гауссовой кривой (а также «колоколом Гаусса»). График гауссовой кри-
кривой ф(х) изображен на рисунке в таблице 43; он и в самом деле напоми-
напоминает колокол.
'Чипиипель. По-моему, этот график больше похож на шляпу с широ-
широкими полями,
Пвтор. При х = 0 функция <р(х) принимает наибольшее значение; оно
равно 0,4. По мере увеличения |х| значение функции уменьшается, при-
приближаясь асимптотически к нулю. Строго говоря, гауссова кривая оп-
определена на всей числовой оси: — оо < х < оо; однако при \х\ > 3 значе-
значения ф(х) становятся меньше 0,004 и поэтому на нашем графике не
представлены. Отметим также, что ф(-х) = ф(х), т. е. функция ф(х) яв-
является четной функцией.
Таблица 43 содержит набор значений функции ф(х) в интервале зна-
значений х от 0 до 4; значения х выбраны с шагом 0,01. Значения функции
приведены с точностью до четвертого знака после запятой.
g4u*StiuSU*&, Как я понимаю, формула A6) является приближенной?
Пвтор. Да, приближенной. Чтобы ею пользоваться, нужно, чтобы
число испытаний п было достаточно велико. Обратимся к нашему при-
примеру, в котором требовалось найти Р800C2). Вот все вычисления:
п = 800, т = 32, р = 0,04, q = 0,96, пр = 32;
4npq = л/800-0,04-0,96 = л/30,72 =5,54;
х = {т-пр)/4пм = C2- 32)/5,54 = 0;
Рш C2) = Ф@) / 5,54 = 0,4 / 5,54 = 0,072 .
Как просто! Как я понимаю, чтобы найти вероятность
того, что количество бракованных изделий окажется, например, в про-
промежутке от 20 до 40, надо выбрать из таблицы 43 значения гауссовой
кривой ф(х) для значений х9 соответствующих, сложить эти значения и
разделить сумму на ^Jnpq .
Пвтор. Можно, конечно, поступить именно так. Но можно сделать
проще — воспользоваться так называемой интегральной приближенной
формулой Лапласа.
*Чш%си%е**. Вне одна приближенная формула при больших nl
Пвтор. Да, еще одна. Эту формулу можно представить в виде:
A7)
322

Таблица 43. Гауссова кривая
X
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1.0
1,1
1.2
1,3
¦1.4
1.5
1.6
1,7
1.8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
0
0,3989
3970
3910
3814
3683
3521
3332
3123
2897
2661
0,2420
2179
1942
1714
1497
1295
1109
0940
0790
0656
0,0540
0440
0355
0283
0224
0175
0136
0104
0079
0060
0,0044
0033
0024
0017
0012
0009
0006
0004
0003
0002
1
3989
3965
3902
3802
3668
3503
3312
3101
2874
2637
2396
2155
1919
1691
1476
1276
1092
0925
0775
0644
0529
0431
0347
0277
0219
0171
0132
0101
0077
0058
0043
0032
0023
0017
0012
0008
0006
0004
0003
0002
2
3989
3961
3894
3790
3653
3485
3292
3079
2850
2613
2371
2131
1895
1669
1456
1257
1074
0909
0761
0632
0519
0422
0339
0270
0213
0167
0129
0099
0075
0056
0042
0031
0022
0016
0012
0008
0006
0004
0003
0002
3
3988
3956
3885
3778
3637
3467
3271
3056
2827
2589
2347
2107
1872
1647
1435
1238
1057
0893
0748
0620
0508
0413
0332
0264
0208
0163
0126
0096
0073
0055
0040
0030
0022
0016
0011
0008
0005
0004
0003
0002
4
3986
3951
3876
3765
3621
3448
3251
3034
2803
2565
2323
2083
1849
1626
1415
1219
1040
0878
0734
0608
0498
0404
0325
0258
0203
0158
0122
0093
0071
0053
0039
0029
0021
0015
ООП
0008
0005
0004
0003
0002
5
3984
3945
3867
3752
3605
3429
3230
ЗОН
2780
2541
2299
2059
1826
1604
1394
1200
1023
0863
0721
0596
0488
0396
0317
0252
0198
0154
0119
0091
0069
0051
0038
0028
0020
0015
0010
0007
0005
0004
0002
0002
6
3982
3939
3857
3739
3589
3410
3209
2989
2756
2516
2275
2036
1804
1582
1374
1182
1006
0848
0707
0584
0478
0387
0310
0246
0194
0151
0116
0088
0067
0050
0037
0027
0020
0014
0010
0007
0005
0003
0002
0002
7
3980
3932
3847
3726
3572
3391
3187
2966
2732
2492
2251
2012
1781
1561
1354
1163
0989
0833
0694
0573
0468
0379
0303
0241
0189
0147
0113
0086
0065
0048
0036
0026
0019
0014
0010
0007
0005
0003
0002
0002
8
3977
3925
3836
3712
3555
3372
3166
2943
2709
2468
2227
1989
1758
1539
1334
1145
0973
0818
0681
0562
0459
0371
0297
0235
0184
0143
ОНО
0084
0063
0047
0035
0025
0018
0013
0009
0007
0005
0003
0002
0001
9
3973
3918
3825
3697
3538
3352
3144
2920
2685
2444
2203
1965
1736
1518
1315
1127
0957
0804
0669
0551
0449
0363
0290
0229
0180
0139
0107
0081
0061
0046
0034
0025
0018
0013
0009
0006
0004
0003
0002
0001
323

где
хх =
= (т2 - пР) 1
Функцию Ф(х) часто называют функцией Лапласа. Ее график пред-
представлен на рисунке в таблице 44. Функция Ф(х)— нечетная функция:
Ф(-х) = -Ф(х). Таблица 44 содержит набор значений Ф(х) в интервале
от х = 0 до х = 5; значения х выбраны с шагом 0,01. Значения функции
Ф(х) приведены с точностью до пятого знака после запятой.
'Чипиинель. Давайте посмотрим на практике, как работает форму-
формула A7). Найдем вероятность того, что количество бракованных изделий
(вероятность брака р = 0,04) в партии из п = 800 изделий окажется в
промежутке от 20 до 40.
Пвтор. В этом случае имеем:
хх = B0 -np)/4npq = B0-32)/5,54 = -2,17,
х2 = D0 - пр)/4гт = D0 - 32)/5,54 = 1,44.
Искомая вероятность Р есть, согласно A7),
40
Е
*. А теперь найдем вероятность того, что в рассмотренной
только что партии изделий количество бракованных изделий не будет
превышать 40.
Пвтор. В этом случае имеем:
хх=@- пр)/4пм = -32/5,54 = -5,8 ,
х2 =
Искомая вероятность Р есть:
40
= ФA,44) - Ф(-5,8) = ФA,44) + ФE,8).
g4u<StiuSU*&. Но в таблице 44 приведены значения Ф(х) лишь для х,
которые не превышают 5.
Пвтор. Посмотрите внимательно на график функции Ф(х). Можно
спокойно полагать, что ФE,8) = 0,5. Таким образом, Р= ФA,44) + 0,5 =
= 0,425 + 0,5 = 0,925.
324

Таблица 44. Функция Лапласа
0,5
-1,5	-1,0	-0,5
0	0,5	1,0	1,5
-0,5
X
0.0
ОД
0,2
0.3
0,4
0.5
0,6
0,7
0,8
0.9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2.0
2,1
2,2
2,3
2,4
2,5
2,6
2J
2,8
2,9
3,0
3,5
4,0
4,5
5,0
0
0,00000
03983
07926
11791
15542
19146
22575
25804
28814
31594
34134
36433
38493
40320
41924
43319
44520
45543
46407
47128
47725
48214
48610
48928
49180
49379
49534
49653
49744
49813
1
00399
04380
08317
12172
15910
19497
22907
26115
29103
31859
34375
36650
38686
40490
42073
43448
44630
45637
46485
47193
47778
48257
48645
48956
49202
49396
49547
49664
49752
49819
0,49865
49977
499968
499997
49999997
2
00798
04776
08706
12552
16276
19847
23237
26424
29389
32121
34614
36864
38877
40658
42220
43574
44738
45728
46562
47257
47831
48300
48679
48983
49224
49413
49560
49674
49760
49825
3,1
3,6
3
01197
05172
09095
12930
16640
20194
23565
26730
29673
32381
34850
37076
39065
40824
42364
43699
44845
45818
46638
47320
47882
48341
48713
49010
49245
49430
49573
49683
49767
49831
49903
49984
4
01595
05567
09483
13307
17003
20540
23891
27035
29955
32639
35083
37286
39251
40988
42507
43822
44950
45907
46712
47381
47932
48382
48745
49036
49266
49446
49585
49693
49774
49836
3,2
3,7
5
01994
05962
09871
13683
17364
20884
24215
27337
30234
32894
35314
37493
39435
41149
42647
43943
45053
45994
46784
47441
47982
48422
48778
49061
49286
49461
49598
49702
49781
49841
49931
49989
6
02392
06356
10257
14058
17724
21226
24537
27637
30511
33147
35543
37698
39617
41309
42786
44062
45154
46080
46856
47500
48030
48461
48809
49086
49305
49477
49609
49711
49788
49846
3.3
3,8
7
02790
06749
10642
14431
18082
21566
24857
27935
30785
33398
35769
37900
39796
41466
42922
44179
45254
46164
46926
47558
48077
48500
48840
49111
49324
49492
49621
49720
49795
49851
49952
49993
8
03188
07142
11026
14803
18439
21904
25175
28230
31057
33646
35993
38100
39973
41621
43056
44295
45352
46246
46995
47615
48124
48537
48870
49134
49343
49506
49632
49728
49801
49856
3,4
3,9
9
03586
07535
11409
15173
18793
22240
25490
28524
31327
33891
36214
38298
40147
41774
43189
44408
45449
46327
47062
47670
48169
48574
48899
49158
49361
49520
49643
49736
49807
49861
49966
49995
325

гЧи*п,<ниель. Мне кажется, что должна существовать какая-то связь
между формулами A7) и A6).
Пвтор. Связь между ними действительно существует. Выберем неко-
некоторое значение х = х0. Оказывается (примем это без доказательства), что
Ф(хо) есть не что иное, как площадь под графиком функции <р(хM рассмат-
рассматриваемым на отрезке от х = О до х = х0. Взгляните на заштрихованную
фигуру на рисунке в таблице 43. Площадь этой фигуры равна Ф(х0).
ёЧи<9ии9се*ь. Но тогда получается, что площадь под графиком гауссо-
гауссовой кривой ф(х), рассматриваемым на промежутке от 0 до оо, должна
равняться Ф(оо) = 1 /2. И значит, полная площадь под колоколом Гаус-
Гаусса равна 1. Не так ли?
Пвтор. Так оно и есть. Как видите, наша беседа о том, как прибли-
приближенно подсчитать Рп{т) в случае больших я, дала возможность позна-
познакомиться с двумя важными для теории вероятностей функциями — «ко-
«колоколом Гаусса» и «функцией Лапласа».
ь. А нельзя представить эти функции в виде формул?
Пвтор. Полагаю, что графики и таблицы дают полную информацию
о функциях ф(х) и Ф(х). Что же касается формул, то тут необходимо
предварительно познакомиться с числом е. Рассмотрим бесконечную пос-
последовательность чисел:
2
2
При п —> оо эта последовательность сходится к числу, которое полу-
получило у математиков «персональное имя» — «число е»:
е = lim fl + -1 = lim A + соI/со.
л-юо1 П)	со^О
A8)
Это число математики относят к категории так называемых транс-
трансцендентных чисел. Так они называют те иррациональные числа, кото-
которые нельзя получить, решая какие-либо алгебраические уравнения с це-
целыми коэффициентами. Эти числа получают при вычислении пределов
тех или иных числовых последовательностей. Вот так выглядит число е
с точностью до двенадцатого знака после запятой:
е =2,718281828459...
Обозначение «е» для этого числа ввел в 1736 году известный матема-
математик и физик, швейцарец по происхождению Леонард Эйлер A707-1783).
Он вычислил данное число с точностью до двадцать третьего знака после
326

запятой. Полагаю, что еще одно трансцендентное число Вам достаточ-
достаточно хорошо известно. Я имею в виду число к — отношение длины окруж-
окружности к длине диаметра.
g4utftiuSte*&. Число к — это весьма интересное число. Без него не обой-
обойтись, если вычислять объемы и площади поверхности различных «круг-
«круглых тел» — шара, цилиндра, конуса. А чем интересно число el
Пвтор. Главным образом тем, что позволяет представить формулы для
целого ряда интересных функций. В частности, для гауссовой кривой:
1
7-х2/2
A9)
11.9 Какова вероятность того, что при бросаниях кубика
частота выпадения единицы отклонится
от 1 / 6 более, чем на 0,01?
Задача 1. Игральный кубик бросают 600 раз. Какова вероятность того, что час-
частота выпадения единицы отклонится от I / 6 более, чем на 0,01?
Решение. Пусть т — число выпадений единицы при п бросаниях кубика. В
нашем случае: п = 600, р= 1 / 6, #=5/6 и, значит, пр = 100, Jnpq = 9,129 . Иско-
Искомая вероятность Р равна 1 - Р', где Р' — вероятность того, что число т будет
удовлетворять неравенству:
т
600
1
< 0,01.
Преобразуем неравенство (*):
I/и-1001
600
106
< 0,01, |/и-100|<6, 94<т<106.
Таким образом, Р1 = У^ Рт(т). С учетом A7) получаем:
/ j ^600
т=94
fnpq
Ф
94 -пр
Jnpq
Ф
Ф
П06-100
I 9>129
w)+o(w)=2o@'66)=0'49-
ф
94 -100
9,129
Итак, искомая вероятность равна Р= 1 - Р' = 1 - 0,49 = 0,51.
Задача 2. Кубик бросают 3000раз. Какова вероятность того, что частота выпа-
выпадения единицы отклонится от 1/6 более, чем на 0,01?
327

Решение. Оно такое же, как и в задаче 1. Только теперь п = 3000 и, значит,
пр = 500, yjnpq = 20,41. Вместо (*) имеем теперь неравенство:
т 1
3000 6
< 0,01,
которое можно преобразовать к виду: 470 <т< 530 .
Используя A7), получаем:
^)-*[Щ^) = 20C0/20,4!) .2.A,47) =0,86.
Искомая вероятность: Р = 1 - Р1 = 1 - 0,86 = 0,14 .
Задача 3. Кубик бросают 6000раз. Какова вероятность того, что частота выпа-
выпадения единицы отклонится от I / 6 более, чем на 0,01?
Решение. Теперь п = 6000 и, значит, пр = 1000, y/npq = 28,87 . Вместо (*) имеем
ерь:
теперь:
т 1
6000 6
Используя A7), получаем
< 0,01.
1060
A060-10001 Л( 940 -10001
* -^^6ooov^--^ 28?8? j--^ 28?8? j-
= 2Ф F0 / 28,87) = 2Ф B,08) = 0,96.
Искомая вероятность: Р=\ - Pf =\ - 0,96 = 0,04.
Итак, мы выбрали некоторое малое число е (конкретно: г = 0,01) и подсчитали,
т
> г для трех значений п. Получены следу-
используя A7), вероятность Р\\	р
ющие вероятности: 0,51 (для п = 600), 0,14 (для п = 3000), 0,04 (для п = 6000). По-
Полученные результаты соответствуют соотношению A4), выражающему закон боль-
больших чисел.
11.10 Беседа о предельной теореме Пуассона
или, иначе говоря, о законе редких событий
b. Формулы A6) и A7), конечно, весьма упрощают подсчет
биномиальных вероятностей в случае больших п. Но эти формулы при-
приближенные и, естественно, возникает вопрос о том, как велико должно
быть п, чтобы была достигнута приемлемая точность вычислений. На-
Насколько я представляю, п должно быть больше нескольких десятков
или, что еще лучше, нескольких сотен.
328

Пвтор. Подсчитаем, например, биномиальную вероятность Р4оо(8О)
при/? = 0,2. Точный подсчет по формуле Бернулли дает Рт(Щ = 0,0498,
тогда как приближенный подсчет по формуле A6) дает Рш(80) = 0,0499.
А вот для Р10(8) при р =0,75 получаем 0,282, если использовать фор-
формулу Бернулли, и 0,273, если использовать формулу A6). В первом приме-
примере формула A6) дает расхождение с точным результатом лишь в четвер-
четвертом знаке после запятой, тогда как во втором примере расхождение
с точным результатом наблюдается уже во втором знаке после запятой.
'Чи&л&ел*. Значит, можно считать, что приближенные формулы Ла-
Лапласа могут использоваться для подсчета биномиальных вероятностей,
если п > 100?
Пвтор. Это так, хотя и не всегда так.
ь. Как такое понимать?
Пвтор. Дело в том, что нужно принимать во внимание величину р,
т. е. вероятность наступления «успеха» в отдельном испытании. Как по-
показывают вычисления (мы их опускаем), для уверенного использования
приближенных формул A6) и A7) нужно, чтобы выполнялось условие:
пр{\ - р) > 10.	B0)
Из B0) следует, что, если /?^0,1 или /?^0,9, то нужно, чтобы
число испытаний п было больше 100. Если же р « 0,01 или р « 0,99,
то нужно, чтобы п было больше 1000. Отметим, что при /7 < 0,01,
равно как и при р > 0,99 формулами A6) и A7), как правило, не
пользуются. Кстати, при р = 0 и при р=\ эти формулы вообще не
работают. Итак, недостаточно, чтобы п было большим. Важно, кро-
кроме того, чтобы вероятность «успеха» (вероятность р) не была слиш-
слишком близкой к нулю или единице.
*Чи(*иипель. Получается, что формулами A6) и A7) не следует пользо-
пользоваться в случаях, когда рассматриваются вероятности того или иного
количества «успехов», представляющих собой достаточно редкие собы-
события? Такие, например, как авария на городском транспорте, опечатка
в книге, достижение девяностолетнего возраста, рождение близнецов.
Неужели в подобных ситуациях неизбежны громоздкие вычисления по
формуле Бернулли?
Пвтор. Выход из положения в таких ситуациях нашел выдающийся
французский математик и физик Симеон Дени Пуассон A781-1840). Что-
Чтобы понять ход его мыслей, обратим внимание на то, что выражение для
Рп(т) в формуле Бернулли представляет собой формально функцию
трех величин: п, т, р. Лаплас вслед за Муавром исследовал вопрос о
том, во что превратится выражение для Рп(т), если увеличивать п, не
329

меняя при этом ни т, ни р. Он нашел, что при фиксированных т и р выраже-
выражение для Рп(т) претерпевает при переходе к большим п превращение:
1
(т-пр)
'2пр(\-р)
- р)
Так появилась локальная приближенная формула Лапласа A6) с га-
гауссовой кривой A9). Итак, подчеркиваю, Лаплас рассмотрел предел
lim Pn(m) при постоянных значениях тир.
Ъиниинелй. Простите, пожалуйста, но разве мог быть какой-то иной
вариант? Число т (число «успехов» в серии испытаний) обязано быть
постоянным; в схеме Бернулли его задают заранее. Ведь тут рассматри-
рассматривается вероятность появления данного числа т «успехов» в серии испы-
испытаний. А величина р — это вероятность наступления «успеха» в отдель-
отдельном испытании. Для данного типа испытаний она тоже постоянна.
Пвтор. Заслуга Пуассона в том и состоит, что он предложил рас-
рассмотреть иной вариант. Пуассон задался вопросом: а что будет, если
увеличивать п, оставляя при этом фиксированными не т и р, а т и пр! Во
что тогда превратится выражение для Рп(т), описываемое формулой
Бернулли? Пуассон понимал, что, получив ответ на данный вопрос, он
тем самым найдет приближенное выражение для Рп(т)9 работающее
в ситуациях, где велико п и в то же время мала вероятность р.
. Ну, конечно же! Ведь чтобы при увеличении п произве-
произведение пр оставалось неизменным, необходимо уменьшить р.
Пвтор. Вот именно. Следуя за Пуассоном, введем обозначение
пр = Х	(*)
и перепишем формулу Бернулли A) так, чтобы теперь в ней фигуриро-
фигурировали только я, т, X. С учетом (*) получаем:
Р„(т) =
т\
1
л \п-т
К
П
(**)
. Все понятно! Нам остается найти предел lim Pn (т), по-
лагая т и X фиксированными.
йвтор. Правильно. Только не будем торопиться. Учтем, что
п(п-\)(п-2)...(п-(т-\)) = fj _ I
т-\
330

и что
п
после чего можем записать:
= 1
lim Pn{m) =
— lim
ml n^oo
lim 1-- • lim 1--| .
Ясно, что первые два предела равны единице и, следовательно,
Xm r L X\
= —hm 1--I .
ml n^oo n
***
Введя обозначение -X / n = со, перепишем оставшийся предел в виде:
, , -А,
-А] =ИтA + со)
lim
С учетом A8), заключаем, что
-Ц =е
П)
~\
Подставляя этот результат в (***), получаем:
****
т\
. Вот мы и выполнили предельный переход, задуманный
Пуассоном!
Пвтор. И тем самым доказали так называемую предельную теорему
Пуассона. Ее формулируют так: если п велико, а р мало, справедливо
соотношение:
Рп{т) =
(пр)п
т\
,-пр
B1)
На рис.1 в таблице 45 приведен набор значений Рп{т), вычисленных
по формуле B1) для различных значений т и Х = пр. Он позволит нам
331

Таблица 45. К предельной теореме Пуассона
Рис
•л
р <гп) =
п
т
0
1
2
3
4
5
6
А
т\
Х = пр
1-
0,9-
0,8-
0,7-
0,6-
0,5-
0,4-
0,3-
0,2-
од-
\
L
0 0,
Y
\
1
2 0
^=0,1
0,9048
0,0905
0,0045
0,0002
?~Х
т
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ех
>
у
/
\
/
<
А 0,6 (
^=0,2
0,8187
0,1637
0,0164
0,0011
0,0001
Х=2
0,1353
0,2707
0,2707
0,1804
0,0902
0,0361
0,0120
0,0034
0,0009
0,0002
/
х=о,з
0,7408
0,2222
0,0333
0,0033
0,0003
Х=3
0,0498
0,1494
0,2240
0,2240
0,1680
0,1008
0,0504
0,0216
0,0081
0,0027
0,0008
0,0002
0,0001
/
/X 1
1
1
1
г
3,8 1
1
1
1
1
Я,=0,4
0,6703
0,2681
0,0536
0,0072
0,0007
0,0001
Х=4
0,0183
0,0733
0,1465
0,1954
0,1954
0,1563
0,1042
0,0595
0,0298
0,0132
0,0053
0,0019
0,0006
0,0002
0,0001
X2
_2_
хех
—-р-
х\
/ 2 (
—
^=0,5
0,6065
0,3033
0,0758
0,0126
0,0016
0,0002
Х=5
0,0067
0,0337
0,0842
0,1404
0,1755
0,1755
0,1462
0,1044
0,0653
0,0363
0,0181
0,0082
0,0034
0,0013
0,0005
0,0002
\
\
\
\
\
-2
2
^=0,6
0,5488
0,3293
0,0988
0,0198
0,0030
0,0004
Х=6
0,0025
0,0149
0,0446
0,0892
0,1339
0,1606
0,1606
0,1377
0,1033
0,0688
0,0413
0,0213
0,0126
0,0052
0,0022
0,0009
^=0,7
0,4966
0,3476
0,1217
0,0284
0,0050
0,0007
0,0001
Х=7
0,0009
0,0064
0,0223
0,0521
0,0912
0,1277
0,1490
0,1490
0,1304
0,1014
0,0710
0,0452
0,0263
0,0142
0,0071
0,0033
^=0,8
0,4493
0,3595
0,1438
0,0383
0,0077
0,0012
0,0002
^=8
0,0003
0,0027
0,0107
0,0286
0,0572
0,0916
0,1221
0,1396
0,1396
0,1241
0,0993
0,0722
0,0481
0,0296
0,0169
0,0090
Рис.2
ех
<7
\
	'
-1
— —
п
7
6
5
4
3
2
<
0
3
^=0,9
0,4066
0,3659
0,1647
0,0494
0,0111
0,0020
0,0003
Х=9
0,0001
0,0011
0,0050
0,0150
0,0337
0,0607
0,0911
0,1171
0,1318
0,1318
0,1186
0,0970
0,0728
0,0504
0,0324
0,0194
е-'
\
А
/
'
1
^

^=1
0,3679
0,3679
0,1839
0,0613
0,0153
0,0031
0,0005
^=10
0,0000
0,0005
0,0023
0,0076
0,0189
0,0378
0,0631
0,0901
0,1126
0,1251
0,1251
0,1137
0,0948
0,0729
0,0521
0,0347
/
/
/
х 2
	^
^—^
Рис.3 4
332

использовать B1) для подсчета вероятности количества «успехов» в си-
ситуациях, когда «успех» является редким событием. Соотношение B1)
называют также законом редких событий.
Задача 1. Вероятность подбить вертолет при выстреле из стрелкового оружия
равна р = 0,005. Произведено п = 200 выстрелов по вертолету. Какова вероятность
того, что не менее двух выстрелов окажутся удачными?
Решение. Пусть А — событие, состоящее в том, что не менее двух выстрелов по
вертолету оказались удачными, а В — событие, состоящее в том, что удачным
оказался только один выстрел или вообще ни одного такого не оказалось. Очевид-
Очевидно, что Аи В — противоположные события и, значит, Р(А) = 1 — Р{В). Рассматри-
Рассматривая удачный выстрел по вертолету как «успех», представим: Р{В) = Р2оо(О) +
Таким образом, искомая вероятность есть Р(А) = 1 - Р(В) = 1 - (i^ooW +
Биномиальные вероятности Р2оо(®) и ^2ооA) найдем, используя закон редких со-
событий B1). Так как в нашем случае пр = 200 • 0,005 = 1, то
Аоо(О)+ АооA) =-^^+^"! = 2^! = 2 • 0,3679 = 0,7358.
Итак, искомая вероятность равна
Р(А) = 1-0,7358 =0,2642.
. Предположим, что в задаче 1 ставился вопрос: какова ве-
вероятность того, что хотя бы один из двухсот выстрелов по вертолету
окажется удачным?
Пвтор. Легко сообразить, что эта вероятность равна 1 - i^ooW = 1 ~~
-0,3679 = 0,6321.
'Чийии&ел*. А разве нельзя было бы в данном случае воспользоваться
соотношением A9) из §9.10?
Пвтор. Это соотношение имеет в рассматриваемом случае вид: Р= 1 -
- A - р)ш. Оно, разумеется, годится. Но тогда нам пришлось бы 200 раз
перемножить число 0,995. Это весьма хлопотно.
Задача 2. Завод отправил потребителю 4000 доброкачественных изделий. Вероят-
Вероятность того, что изделие будет повреждено в пути, равна 0,0005. Какова вероят-
вероятность того, что потребитель получит не более трех негодных изделий?
Решение. Заметим, что здесь «успех» — это случайное повреждение изделия
в процессе его транспортировки. Искомая вероятность Р есть:
Воспользуемся законом редких событий B1). По условию задачи, пр
4000 • 0,0005 = 2. Поэтому соотношение B1) принимает у нас вид:
333

Отсюда следует, что искомая вероятность Р равна
Р= е~2. A + 2 + 2 + 4/3) =0,1353 -6,333 = 0,857.
Пвтор. Если бы Вы были потребителем тех изделий, о которых гово-
говорилось в задаче, то согласились бы воспользоваться услугами фирмы,
обеспечивающей такую транспортировку?
g4u*ftfufie*b. Вообще-то вероятность 0,86 не представляется мне дос-
достаточно большой...
Пвтор. Это как посмотреть. Транспортируется большая партия изде-
изделий — четыре тысячи. И из этих четырех тысяч Вы не дополучите всего
лишь не более трех изделий с вероятностью, близкой к 0,9. Будучи по-
потребителем изделий, я бы наверняка на это согласился.
ntutftiu&e*&. Пожалуй, весь вопрос в том, сколько изделий из четырех
тысяч потребитель согласен недополучить.
Пвтор. Верно. Так давайте согласимся потерять шесть изделий. Это
всего 0,15% от всей партии. Подсчитайте вероятность того, что во вре-
время транспортировки придут в негодность не более шести изделий.
ь. Эта вероятность есть
= е'1 • A + 2 + 2 + 1,333 + 0,667 + 0,267 + 0,089) =
= е~2 • 7,365 = 0,1353 • 7,356 = 0,995.
Практически полная гарантия!
Пвтор. Заканчивая нашу беседу, хочу отметить, что мы познакомились
здесь с функцией у = е~х. Показательные функции, основанием которых
служит число е, находят исключительно широкое применение. Они имеют
специальное название — экспоненциальные функции, или экспоненты. Функ-
Функция у=е* — возрастающая экспонента; функция у = е~х — убывающая
экспонента. Графики этих функций изображены на рис. 2 в таблице 45.
'Чипииъель. В той же таблице на рисунке 3 изображены на промежут-
промежутке 0 < х < оо, наряду с графиком функции е~х, также графики функций
хе~х и (х2 / 2)е~х. Зачем они тут?
Пвтор. Обратите внимание: приведенные здесь в виде таблицы значе-
значения Рп@) — это значения функции е~х, аргумент которой принимает раз-
разные значения X. Легко видеть также, что значения Рп{\) — это значения
функции хе~х, аргумент которой принимает значения А,, а значения Рп B) —
это значения функции (х2 / 2)е~х, аргумент которой принимает значения X.
Отметим, что при х вблизи нуля функции хе~х и (х2 / 2)е~х ведут себя,
334

соответственно, как х и как х2 / 2, а по мере возрастания х, их поведение
все больше и больше попадает под влияние убывающей экспоненты.
11.11 ВЫГОДНО ЛИ ЗАНИМАТЬСЯ СТРАХОВАНИЕМ?
-Используя предельную теорему Пуассона, обсудим практическую
проблему, которую приходится решать всякому, кто захочет зарабаты-
зарабатывать деньги, занимаясь страхованием чужого имущества. Например, стра-
страхованием от пожара хозблоков на дачных участках. Предположим, что,
изучив статистические данные, мы оценили вероятность/? того, что хоз-
хозблок в данной дачной местности сгорит в течение года. Это определяет-
определяется целым рядом причин — общим состоянием электросети, характером
растительности и почв, характерными для данного региона погодными
условиями, криминогенной обстановкой и т. д. И вот теперь мы хотели
бы выяснить, при каких условиях страхование хозблоков от пожара могло
бы стать выгодным бизнесом. Понятно, что желательно, чтобы удалось
застраховать побольше хозблоков и чтобы процент страховки был по-
побольше. Однако при повышении процента страховки неизбежно сни-
снижение числа желающих застраховаться.
Предположим, что мы назначили плату за страховку хозблока в раз-
размере 1% от суммы, на которую хозблок застрахован, и что при этом
удалось застраховать п = 1000 хозблоков. Пусть W — сумма, на которую
застрахован на год каждый хозблок, и, значит, размер годовой страхов-
страховки составляет 0,01 Ж Это означает, что мы собрали деньги в сумме
0,01^=10Ж Мы рассчитываем, что в течение года нам придется вып-
выплатить клиентам не более 3/5 данной суммы, т. е. не более 6 Ж Иначе
говоря, мы рассчитываем, что из застрахованных тысячи хозблоков сгорят
в течение года не более шести. Вероятность Р того, что в течение года
сгорят не более шести хозблоков из тысячи, есть
где Р1000(т) подсчитываются по формуле B1).
В качестве «успеха» здесь рассматривается факт сгорания хозблока.
Допустим, что вероятность такого «успеха» /? = 0,01 и, следовательно,
пр = 10. В этом случае искомая вероятность (*) равна сумме первых
семи чисел в столбике с X = 10 в таблице 45:
Р= 0,0000 + 0,005 + 0,0023 + 0,0076 + 0,0189 + 0,0378 + 0,0631 = 0,1302.
335

Вероятность оказалась равной всего лишь 0,13. Она указывает на то,
что мы занялись явно невыгодным бизнесом.
А теперь предположим, что р = 0,002 и, следовательно, пр = 2. В этом
случае искомая вероятность (*) равна сумме первых семи чисел в стол-
столбике с X = 2 в таблице 45:
Р= 0,1353 + 0,2707 + 0,2707 + 0,1804 + 0,0902 + 0,0361 + 0,0120 = 0,9954.
Вот теперь наш страховой бизнес оказывается явно выгодным. Закон
редких событий практически гарантирует (с вероятностью 0,9954), что
не менее 2/5 суммы, вырученной при страховании, получит наша стра-
страховая фирма.
ЗАДАНИЯ ПО ТЕМЕ 11
1.	Какова вероятность того, что при четырех бросаниях кубика единица выпадет
ровно два раза?
Ответ: 0,116.
2.	Какова вероятность того, что при четырех бросаниях кубика единица выпадет не
более двух раз?
Ответ: 0,984.
3.	Какова вероятность того, что при четырех бросаниях кубика единица выпадет не
менее одного раза?
Ответ: 0,518.
4.	Какова вероятность того, что при четырех бросаниях кубика единица выпадет не
менее трех раз?
Ответ: 0,016.
5.	Какова вероятность того, что при четырех бросаниях кубика три раза выпадет
грань с четным числом очков?
Ответ: 1/4.
6.	Какова вероятность того, что при четырех бросаниях кубика два раза выпадет
грань с нечетным числом очков?
Ответ: 3/8.
7.	Какова вероятность того, что при четырех бросаниях кубика не менее двух раз
выпадет грань с нечетным числом очков?
Ответ: 11/16.
8.	Какова вероятность того, что при четырех бросаниях кубика не менее трех раз
выпадет грань с четным числом очков?
Ответ: 5/16.
9.	Какова вероятность того, что при четырех бросаниях кубика два раза выпадет
грань с числом очков, не делящимся на три без остатка?
Ответ: 8/27.
336

10.	Какова вероятность того, что при четырех бросаниях кубика не более двух раз
выпадет грань с числом очков, не делящимся на три без остатка?
Ответ: 11/27.
11.	Вероятность того, что суточный расход электроэнергии на данном предприятии
не превысит установленной нормы, равна 0,8. Какова вероятность, что за неде-
неделю расход электроэнергии не выйдет за пределы нормы в четырех сутках?
Ответ: 0,115.
12.	В задаче 11 надо найти вероятность того, что за неделю расход электроэнергии
не выйдет за пределы нормы не менее, чем в пяти сутках.
Ответ: 0,853.
13.	В задаче 11 надо найти вероятность того, что за неделю перерасход электро-
электроэнергии будет наблюдаться не более чем в трех сутках.
Ответ: 0,968.
14.	Вероятность того, что лампочка не перегорит в течение тысячи часов работы,
равна 0,95. Чему равно среднее число выдержавших тысячу часов работы лам-
лампочек, приходящееся на каждую партию из 500 лампочек?
Ответ: 475.
15.	Докажите, что, если р=д= 1/2 и п — четное число, то наиболее вероятное
число «успехов» равно математическому ожиданию.
16.	Число испытаний Бернулли равно п = 5. При каких значениях р разность пр - q
будет целочисленной и, следовательно, биномиальное распределение будет иметь
два наиболее вероятных числа «успехов» т' и m' + l? Используя формулу Бер-
Бернулли, подсчитайте для каждого из этих р биномиальные вероятности Ръ{т')
и при этом убедитесь, что Р5(ш0 = рь(т' + !)¦
Ответ: Возможны пять случаев:
1) р = 1 / 6, т' = 0, Ръ(т') = 0,402,
Р5(т') = 0,329,
Ръ(т') = 0,313,
Ръ{т') = 0,329,
5) р = 5 / 6, т' = 4, Ръ(т') = 0,402.
17.	Используя график в таблице 42 и измерительную линейку, убедитесь, что для рас-
распределения 1:
2)
3)
4)
Р
р
Р
= 2 i
= 3 ,
= 4 i
;6,
;6,
;6,
т'
т'
т'
= 1,
= 2,
= 3,
2, J2m2PA{m) =5.
/77=0	/77=1	/77=1
18. Используя график в таблице 42 и измерительную линейку, убедитесь, что для рас-
распределения 2:
/77=0	/77=1	/77=1
19. Вероятность поражения мишени стрелком равна 0,8. Какова вероятность того,
что, выполнив 80 выстрелов, стрелок поразит мишень: а) ровно 60 раз? б) ровно
64 раза? в) от 60 до 70 раз? г) не менее 60 раз?
Ответы: а) 0,06, б) 0,11, в) 0,82, г) 0,87.
337

20.	Из данной партии семян посеяли 10000 семян и обнаружили, что взошли 8498 се-
семян. На основании этого был сделан вывод, что всхожесть данной партии семян
составляет 85% (р = 0,85). А теперь подсчитайте вероятность того, что из ста
посеянных семян из рассматриваемой партии взойдут: а) ровно 85 семян? б) от
60 до 80 семян? в) от 70 до 90 семян? г) не менее 80 семян? д) не менее 85 се-
семян? е) не менее 90 семян? ж) не менее 92 семян?
Ответы: а) 0,11, б) 0,08, в) 0,92, г) 0,92, д) 0,5, е) 0,08, ж) 0,025.
21.	В § 11.9 вычислялись вероятности того, что частота выпадения единицы отклонит-
отклонится от 1 / 6 более, чем на е = 0,01, при 600, 3000 и 6000 бросаниях кубика. Теперь
вычислите вероятности того, что частота выпадения единицы отклонится от 1/6
более, чем нае = 0,01, при 600, 3000, 6000, 12 000 и 24 000 бросаниях кубика.
Ответы: 0,73, 0,46, 0,30, 0,14, 0,04.
22.	Пусть во время некоторой эпидемии вероятность заболеть составляет р = 0,005.
Какова вероятность того, что из тысячи человек заболеют: а) не более 2 чело-
человек? б) не более 5 человек? в) не более 10 человек? г) не менее 3 человек?
Ответы: а) 0,125, б) 0,656, в) 0,986, г) 0,735.
23.	С помощью профилактических мер удалось снизить вероятность заболевания во
время надвигающейся эпидемии с р± = 0,005 до р2 = 0,003. Во сколько раз уве-
увеличилась в результате этого вероятность того, что из 1000 человек заболеют:
а) не более 5 человек? б) не более 2 человек? в) никто не заболеет? Вычислите
и сравните для каждого случая соответствующие вероятности при р± и р2.
Ответы: а) в 1,4 раза @,916/0,656 = 1,4); б) в 3,4 раза @,423/0,125 = 3,4);
в) в 7,5 раза @,05/0,067 = 7,5).
24.	Вероятность появления бракованного изделия на данном предприятии составля-
составляет р = 0,004. Во сколько раз следует снизить процент брака, чтобы возросла в
20 раз вероятность того, что в партии из 1000 изделий не окажется ни одного
бракованного?
Ответ: надо снизить процент брака в 4 раза.
Подсказка. Сначала нужно вычислить Р1Ооо(О) при р = 0,004, затем надо умно-
умножить результат на 20 и по таблице 45 подобрать соответствующее значение X.
25.	Возвращаемся к проблеме, обсуждавшейся в § 11.11 и предположим теперь, что
благодаря принятым мерам удалось заметно снизить вероятность «успеха»; пусть
теперь р = 0,001. В этих условиях мы рискнули уменьшить процент страховки, сни-
снизив его с 1% до 0,5%, что сразу привело к увеличению до п = 2000 числа пожелав-
пожелавших застраховаться. Мы надеемся, что теперь нам придется в течение года выпла-
выплачивать нашим клиентам не более половины суммы, которую мы выручили в процессе
страхования. Какова вероятность Р того, что наша надежда оправдается?
Ответ: Р= 0,9834.
Подсказка. Нетрудно сообразить, что мы, рассчитывая выплатить клиентам не
более половины вырученной нами при страховании суммы, надеялись, что сгорят
не более 5 хозблоков из застрахованных двух тысяч. Значит, нужно вычислить
5
вероятность Р = ^Р2
т=0
338

ТЕМА 12
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
В обыденной жизни и в научных ис-
исследованиях постоянно приходится встре-
встречаться с такими ситуациями, когда инте-
интересующая нас величина может принимать
различные значения в зависимости от слу-
случайных обстоятельств.
АН. Колмогоров
Одним из основных понятий теории
вероятностей является понятие случайной
величины.
Б. В. Гнеденко
Случайной величиной, связанной с
данным опытом, называется величина,
которая при каждом осуществлении это-
этого опыта принимает то или иное число-
числовое значение, причем заранее неизвест-
неизвестно, какое именно. Это зависит от случая.
А. С. Солодовников
339

12.1 Случайные события и случайные величины
. До сих пор основным понятием у нас было понятие слу-
случайного события. Мы рассматривали вероятность наступления того или
иного случайного события в том или ином испытании или серии испы-
испытаний. Теперь же появляется новое понятие — понятие случайной вели-
величины, которое, к тому же, объявляется «одним из основных понятий
теории вероятностей». Возникают два вопроса. Первый: что такое «слу-
«случайная величина» и чем она отличается от обычной (иначе говоря, «не-
«неслучайной») величины? Второй вопрос: как соотносятся друг с другом
понятия «случайная величина» и «случайное событие»?
Пвтор. Обычная (неслучайная) величина имеет определенное числовое
значение. Она выражается определенным числом (отвлеченным или име-
именованным). А вот случайная величина характеризуется множеством чис-
числовых значений', она принимает то или иное значение под влиянием слу-
случайных обстоятельств. Если множество числовых значений конечное или
если оно бесконечное, но счетное (каждому элементу множества можно
приписать порядковый номер), то говорят о дискретной случайной ве-
величине. Если же числовые значения заполняют какой-то промежуток
на числовой оси или даже всю числовую ось, то говорят о непрерывной
случайной величине. Мы ограничимся здесь рассмотрением дискрет-
дискретных случайных величин.
nUuftfUfie*b. Как я догадываюсь, между случайными величинами и
случайными событиями существует связь?
Пвтор. Да, существует. Точнее говоря, ее можно установить в раз-
различных конкретных ситуациях. С множеством исходов какого-либо
испытания, образующих полную группу случайных событий, можно
сопоставить множество числовых значений дискретной случайной ве-
величины. Вот простой пример. Рассматриваем испытание — подбрасы-
подбрасывание игрального кубика. Полная группа событий — выпадения той
или иной из шести граней кубика; множество исходов состоит из шести
элементов. С этим множеством из шести исходов можно сопоставить
множество из шести числовых значений случайной величины, пред-
представляющей собой количество выпавших очков'. 1, 2, 3, 4, 5, 6. Пусть
в конкретном испытании выпала какая-то грань. Это означает, что слу-
случайно реализовалось соответствующее числовое значение нашей слу-
случайной величины (выпало соответствующее количество очков).
'Чи&А&ел*. По-видимому, случайные величины можно рассматри-
рассматривать как числовые представления случайных событии]
Пвтор. Действительно, множество значений случайной величины мож-
можно рассматривать как числовое представление некоторой полной группы
340

случайных событий. Если речь идет о дискретной случайной величине,
то можно говорить о вероятностях ее значений: от испытания к испыта-
испытанию она принимает числовые значения с вероятностями, равными ве-
вероятностям наступления соответствующих случайных событий из рас-
рассматриваемой полной группы событий. Сумма вероятностей значений
дискретной случайной величины равна единице (как и сумма вероятностей
наступления событий, составляющих полную группу).
*Чи(*иипель. Вы говорите о дискретных случайных величинах. А разве
все это не относится также к непрерывным случайным величинам?
Пвтор. Вероятность того или иного значения непрерывной случай-
случайной величины всегда равна нулю.
'Чийии&ел*. Не понимаю. Разве значения непрерывной случайной ве-
величины не реализуются?
Пвтор. Они, конечно, реализуются. Тем не менее вероятность любо-
любого наперед заданного значения из множества значений непрерывной
случайной величины равна нулю. Допустим, Вы мысленно бросаете точку
на отрезок числовой оси 0 < х < 10. Может ли эта точка попасть, на-
например, в точку отрезка с координатой х = 5?
'Ъынателй. А почему бы и нет?
Пвтор. Однако вероятность того, что она попадет в точку х= 5, рав-
равна нулю. Более того, вероятность попасть в любую другую наперед
выбранную точку отрезка тоже равна нулю.
*&. Всё это нуждается в дополнительных разъяснениях.
Пвтор. Как я уже заметил, мы ограничимся рассмотрением дискрет-
дискретных случайных величин. Однако в конце темы сделаем по поводу слу-
случайных величин ряд замечаний общего характера и, в частности, пого-
поговорим немного об особенностях непрерывных случайных величин. Вот
тогда и появятся некоторые дополнительные разъяснения.
g4utftiuSU*b. He возражаю. Давайте ограничимся пока дискретными
случайными величинами. Хорошо бы привести конкретные примеры этих
величин.
Пвтор. Их можно привести сколько угодно. Например, число брако-
бракованных изделий из каждой сотни готовых изделий, выпущенных дан-
данным предприятием. Это число случайным образом меняется от одной
сотни изделий к другой. Возможные значения данной дискретной слу-
случайной величины: 0, 1, 2, 3, 4 и так далее — вплоть до 100 (ведь теоре-
теоретически в какой-то партии все сто изделий могут оказаться бракован-
бракованными, хотя это и маловероятно). А вот пример, относящийся к стрельбе
в цель. Стрелок сделал п выстрелов. Число попаданий в цель — случайная
величина; ее возможные значения: 0, 1, 2, 3, ..., п. Примерами случайных
341

величин являются также число родившихся девочек в каждой сотне
новорожденных, число ростков, появившихся на свет из каждой сотни
посаженных в почву семян, число страниц в книге, на которых обнару-
обнаружена хотя бы одна опечатка, число ограблений, зарегистрированных в
городе в течение, скажем, месяца, число вызовов, поступивших от або-
абонентов на телефонную станцию в течение суток, сумма, которую может
получить некий человек, приобретя лотерейный билет...
g4utftiuSU*b. Думаю, что примеров вполне достаточно. Подобные при-
примеры хорошо знакомы. Мы с ними много раз встречались в данной
книге. Получается, что мы уже давно работаем, не ведая того, с диск-
дискретными случайными величинами!
Пвтор. Это действительно так. Уместно вспомнить господина Жур-
дена из комедии Мольера «Мещанин во дворянстве». Этот господин
был немало удивлен, узнав, что всю жизнь говорит прозой. Несмотря
на то, что о прозе никогда не слышал и говорить прозой не обучался.
'Чипинпель. Почему же мы раньше не ввели понятие случайной ве-
величины?
Пвтор. По той простой причине, что можно было вполне обойтись
без него.
ntutftiu&e*&. Но тогда зачем мы теперь вводим это понятие?
Пвтор. В процессе ознакомления с теорией вероятностей мы вышли
на новые рубежи. Выражаясь определеннее, мы вышли на задачи, ре-
решение которых требует использования понятия случайной величины и,
в частности, таких специальных понятий как «математическое ожида-
ожидание», «дисперсия», «среднее квадратичное отклонение», «доверитель-
«доверительный интервал».
g4u<StiuSU*&. Предыдущая тема была посвящена рассмотрению числа
«успехов» в серии независимых испытаний. А ведь это число «успехов»
есть не что иное как дискретная случайная величина.
Пвтор. Совершенно верно. Поэтому можно воспринимать предыду-
предыдущую тему как хороший пример, позволяющий познакомиться с поня-
понятием случайной величины. А теперь мы продолжим знакомство со слу-
случайными величинами в более общем плане. И хотя мы вынуждены
ограничиться здесь дискретными случайными величинами, однако не-
некоторые выходы на непрерывные случайные величины будут, конечно,
сделаны.
g4utftiuSU*b. Нельзя ли привести конкретные примеры непрерывных
случайных величин?
Пвтор. Вот простой пример: длительность непрерывного горения элект-
электрической лампочки. Нельзя сколь-либо определенно предсказать время,
в течение которого данная лампочка будет светиться. По истечении
342

некоторого срока (как правило, измеряемого тысячами часов) лампоч-
лампочка может перегореть в любой момент в силу тех или иных случайных
обстоятельств. Срок непрерывной работы случайным образом меняется
от лампочки к лампочке. А вот пример из практики артиллерийских
стрельб. Артиллерист наводит орудие на цель, старается сделать это как
можно тщательнее. Однако при всем своем старании он не может га-
гарантировать попадание снаряда в указанное место. Как дальность поле-
полета, так и угол отклонения от направления на цель оказываются непре-
непрерывными случайными величинами; их значения меняются от выстрела
к выстрелу под воздействием различных случайных факторов. Среди
них и случайные порывы ветра, и случайные отклонения массы снаря-
снаряда от стандартной, и погрешности наводки, и непредсказуемые особен-
особенности развития процесса взрыва, выбрасывающего снаряд из ствола
орудия. Недаром существует такое понятие как «рассеивание снаря-
снарядов»: при стрельбе из одного и того же орудия на одном и том же при-
прицеле и при, казалось бы, неизменных условиях снаряды тем не менее
ложатся в разных местах. Можно привести немало примеров из практи-
практики спортивных соревнований. Время преодоления спортсменом задан-
заданной дистанции и дальность прыжка спортсмена или посланного им
спортивного снаряда (молота, копья, диска, ядра) являются, очевидно,
непрерывными случайными величинами. Значения этих величин (ина-
(иначе говоря, спортивные результаты) зависят не только от степени подго-
подготовленности спортсмена, но и от многих факторов случайного характе-
характера — влияния ветра, особенностей движений спортсмена при выполнении
соответствующего упражнения, физического и психического состояния
спортсмена в данный момент и т. д.
'ЧиФиатель. Наверное, мы встречаемся с непрерывными случайными
величинами значительно чаще, чем с дискретными?
Пвтор. Ваша догадка вполне справедлива. Так называемые «случай-
«случайные обстоятельства» и «случайные факторы» не всегда проявляются так
явно, как во время стрельб или спортивных соревнований. Возьмем,
например, яблоню, ветви которой гнутся под тяжестью созревших пло-
плодов. Понятно, что у разных яблок будет разная масса. Это связано с тем,
что процесс развития каждого яблока протекал со своими особенностя-
особенностями, которые случайным образом менялись от одного плода к другому.
«Случайные факторы» действовали и тут, хотя и не столь открыто.
Таким образом, массу яблока также можно рассматривать как непре-
непрерывную случайную величину. Если число детей, родившихся в данном
роддоме в течение, скажем, месяца есть дискретная случайная величи-
величина, то масса и длина этих новорожденных являются непрерывными слу-
случайными величинами. Если количество ростков, появившихся на свет
343

из каждой сотни посаженных в почву семян, есть дискретная случайная
величина, то масса тех семян, что проросли, а также высота ростков
спустя определенное время после посева являются непрерывными слу-
случайными величинами.
g4utftiuSU*b. Я заметил, что дискретные случайные величины выража-
выражаются, как правило, через натуральные числа. Надо подсчитать количе-
количество соответствующих исходов — и тем самым будет получено одно из
значений дискретной случайной величины. А вот с непрерывными слу-
случайными величинами связаны измерения. Измеряем дальность полета
артиллерийского снаряда или копья. Измеряем время преодоления спорт-
спортсменом данной дистанции. Измеряем массу и длину новорожденных.
Пвтор. Ваше замечание весьма кстати. Действительно, чтобы выя-
выявить те или иные значения непрерывной случайной величины, надо
выполнить соответствующие измерения. А сам по себе измерительный
акт всегда связан с погрешностями. Иначе говоря, всякое измерение
выполняется с какой-то степенью точности. Совершенствуя измери-
измерительное устройство и сам процесс измерения, мы можем увеличивать
степень точности измерения и тем самым уменьшать погрешность из-
измерения. Однако все равно нам не удастся получить «абсолютно точ-
точный» результат. Этого не допустят неуловимые случайные факторы,
неизбежно проявляющиеся в годе измерения и связанные, в частности,
со случайными процессами внутри измерительного устройства. На ос-
основе теории вероятностей разработана специальная теория, исследую-
исследующая погрешности измерений, — так называемая теория ошибок.
ёЧи<9ии9се*ь. Получается, что результат любого измерения — это всего
лишь одно из возможных значений некоторой непрерывной случайной
величины?
Пвтор. Одно из возможных значений в пределах погрешности из-
измерения.
'Чипииъель. Значит, если я, например, попрошу в магазине взвесить
сто граммов колбасы, то получу всего лишь одно из возможных значе-
значений массы колбасы, а не именно сто граммов?
Пвтор. Конечно. Вы получите одно из значений массы колбасы, ко-
которые находятся в интервале от 95 г до 105 г — ведь весы в магазине
измеряют массу колбасы с точностью до 5 г.
g4u<StiuSU*&. Никогда бы не подумал, что взвешивание ста граммов
колбасы также является случайным событием, исходом которого ока-
оказывается одно из значений непрерывной случайной величины.
Пвтор. Без сомнения, продавщица тоже не подозревает о том, что ее
профессиональная деятельность причастна к теории вероятностей.
344

12.2 Закон распределения
дискретной случайной величины
Чшэбы задать дискретную случайную величину X (будем обозначать
случайные величины полужирными заглавными латинскими буквами),
надо, во-первых, задать числовые значения хь которые она может прини-
принимать по воле случае (таких значений может быть конечное количество
или бесконечно много) и, во-вторых, задать вероятности Pt значений xz.
Как мы уже отмечали (см. предыдущий параграф),
A)
Заданием возможных xt и соответствующих вероятностей Pt опреде-
определяется закон распределения дискретной случайной величины X. Его можно
представить различными способами: в виде таблицы, графически, ана-
аналитически (с помощью формулы). Рассмотрим несколько примеров, для
каждого из которых закон распределения случайной величины будет
представлен в виде таблицы и графически.
Пример 1. Рассматриваем в качестве случайной величины (обозна-
(обозначим эту величину через X) количество очков, выпавших при бросании
игрального кубика. Случайная величина принимает по воле случае шесть
возможных числовых значений xt: 1, 2, 3, 4, 5, 6. Вероятность каждого
из этих числовых значений одна и та же — она равна 1/6. Таблица для
данного закона распределения имеет вид:
Pi
1
1/6
2
1/6
3
1/6
4
1/6
5
1/6
6
1/6
На рис. 1 в таблице 46 дано графическое представление рассматрива-
рассматриваемого закона распределения.
Пример 2. Рассматриваем в качестве случайной величины (обозна-
(обозначим ее через F) сумму количества очков, выпавших при двукратном
бросании кубика. Случайная величина F принимает 11 возможных зна-
значений/: 2, 3, 4,..., 12. Вероятности Pz равны, соответственно, 1/36,
2/36, 3/36, 4/36, 5/36, 6/36, 5/36, 4/36, 3/36, 2/36, 1/36. В этом
легко убедиться, обратившись к пространству элементарных исходов
для двукратного бросания кубика (см. например, таблицу 32); полезно
также убедиться непосредственным подсчетом, что соотношение A) вы-
выполняется. Таблица для данного закона распределения такова:
345

Таблица 46. Закон распределения дискретной случайной величины: графическое
представление
0 1 2 3 4 5 6
Рис.1
I
1
6
1
9
1
18
P/
T
T т 1
•
T
1 К
0 12 3 4 5 6 7
9 10 11 12//
Рис.2
4
о 1
10	15	20	25	30
10
25	30 yt
346

//
Pi
2
1/36
3
2/36
4
3/36
5
4/36
6
5/36
7
6/36
8
5/36
9
4/36
10
3/36
11
2/36
12
1/36
На рис. 2 в таблице 46 рассматриваемый закон представлен графически.
Пример 3. Рассматриваем в качестве случайной величины (обозна-
(обозначим ее через G) произведение количества очков, выпавших при дву-
двукратном бросании кубика. Величина принимает 18 возможных значе-
значений. Таблица для закона распределения имеет вид:
gi
Pi
gi
Pi
1
1
36
12
4
36
2
2
36
15
2
36
3
2
36
16
1
36
4
3
36
18
2
36
5
2
36
20
2
36
6
4
36
24
2
36
8
2
36
25
1
36
9
1
36
30
2
36
10
2
36
36
1
36
На рис. 3 в таблице 46 данный закон распределения представлен гра-
графически.
Точки, дающие графическое представление закона распределения
дискретной случайной величины на координатной плоскости «значе-
«значения величины — вероятность значений», обычно соединяют отрезками
прямых и называют получающуюся при этом геометрическую фигуру
многоугольником распределения. На рис. 3 в таблице 46 (а также на ри-
рисунках 4 и 5) как раз изображены многоугольники распределений. Мно-
Многоугольниками распределений мы могли любоваться также на рисунках
в таблицах 41 и 42, где были даны графические представления биномиаль-
биномиального закона распределения для разных п и р.
Пример 4. В денежной лотерее выпущено 100 билетов. Разыгрывают-
Разыгрываются 1 выигрыш в 30 долларов, 3 выигрыша в 10 долларов, 6 выигрышей в
3 доллара и 20 выигрышей в 1 доллар. Случайная величина Y — сто-
стоимость возможного выигрыша для человека, купившего один билет. Она
принимает пять возможных значений yt (в долларах): 0, 1, 3, 10, 30.
Таблица для закона распределения этой величины имеет вид:
Pi
0
0,7
1
0,2
3
0,06
10
0,03
30
0,01
Графически этот закон распределения представлен на рис. 4 в
таблице 46.
Пример 5. Стрелок стреляет по мишени, изображенной на рис. 5
в таблице 46. Если он попадает в область А, то получает 1 очко, в об-
347

ласть В — 2 очка, в область С — 3 очка, в область D — 4 очка. Рассмат-
Рассматриваем в качестве случайной величины количество очков, выбиваемое
стрелком при отдельном выстреле (обозначим величину через Z). Ве-
Величина принимает четыре возможных значения zt\ 1, 2, 3, 4. Предполо-
Предположим (на основании опыта), что для нашего стрелка эти значения имеют
вероятности Рь равные, соответственно, 0, 0,1, 0,3, 0,6.
Таблица для закона распределения имеет в данном случае вид:
Pi
1
0
2
0,1
3
0,3
4
0,6
Графически этот закон распределения представлен на рис. 5 в таб-
таблице 46.
12.3 Три распределения дискретных
случайных величин: биномиальное,
пуассоновское, геометрическое
12.3.1. Биномиальное распределение. С этим распределением мы дос-
достаточно подробно познакомились в теме 11, если рассматривать в каче-
качестве дискретной случайной величины X количество «успехов» в п испы-
испытаниях Бернулли. Эта случайная величина имеет п+\ возможных
значений xt: 0, 1, 2, 3,..., п. Соответствующие вероятности Pt описыва-
описываются формулой Бернулли (это есть биномиальные вероятности). Таблицу
для закона распределения можно представить в виде:
Pi
0
Д@)
1
ДA)
2
РпB)
3
ЛC)
...
...
п
Рп{п)
(фигурирующие в нижней строке таблицы вероятности Рп (xt) как раз и
являются хорошо известными нам биномиальными вероятностями
Рп{т)). В теме 11 были получены важные соотношения (8) и (9). Пере-
Перепишем их в виде:
n+l
t = np ;
B)
n+l
E-
p. = n2p2 + np{\ - p)
C)
348

Напомним, что р — вероятность наступления «успеха» в отдельном
испытании.
Ряд биномиальных распределений были представлены графически
на рис. 3 в таблице 41 и на рис. 1 в таблице 42. Приведем еще семь мно-
многоугольников биномиального распределения — см. рис. 1 в таблице 47;
здесь п = 9, а вероятность/? принимает семь значений: 0,05, 0,1, 0,3, 0,5,
0,7, 0,9, 0,95. Заметим, что многоугольники распределений для/? = 0,05,
0,1, 0,3 зеркально симметричны по отношению к многоугольникам для
/? = 0,95, 0,9, 0,7, соответственно; ось симметрии показана на рисунке
пунктирной прямой.
12.3.2. Пуассоновское распределение. Говорят, что дискретная случай-
случайная величина X распределена по закону Пуассона, если соответствую-
соответствующая таблица имеет вид:
xt
Pi
0
е~х
1
Хе~х
2
2!
3
3! е
4
— е~х
4!
п
1 п
Обратим внимание на то, что здесь число возможных значений слу-
случайной величины бесконечно велико.
Найдем, чему равна сумма
ния. Прежде всего заметим, что
для пуассоновского распределе-
v.P. = \ / —
*1	/i
= Хе
-f-f (/ — 1)
(мы обозначили /- l = m). Далее учтем, что справедливо следующее
соотношение (примем его без доказательства):
л
ml
= e
D)
Отсюда, кстати говоря, получается достаточно удобное для вычисле-
вычисления числа е соотношение:
1
1 1 1 1
E)
Заметим также, что из D) немедленно получается соотношение A)
для пуассоновского распределения:
349

Таблица 47. Многоугольники биномиальных, пуассоновских и геометрических
распределений
Рис.1: биномиальные распределения
I
геометрические
распределения
0 1 2 3 4 5 6 7 8 9 10 11 12 JC/
Рис.2: пуассоновские распределения
350

/2\+X3 /3\+X4
ex =1.
Используя D), получаем из (*):
F)
Надо признать, что результат F) можно было предсказать заранее.
Напомним, что пуассоновское распределение тесно связано с биноми-
биномиальным. Если в выражении для биномиальной вероятности Рп{т) за-
зафиксировать т и устремить п к бесконечности, а вероятность р к нулю,
и при этом потребовать, чтобы произведение пр оставалось равным по-
постоянному числу X (Х = пр), то будем иметь:
lim Pn(m) = (Хт /т\)е
~х
(**)
(этот результат мы получили в § 11.10). С учетом (**) мы могли бы
переписать (*) в виде:
,-я
(lim Pn{m)) =X lim
П^ОО,
т=0
Поскольку V Рп(т) = 1, то, значит, lim
= 1, и мы при-
ходим к результату F).
На рис. 2 в таблице 47 представлены восемь многоугольников пуас-
соновского распределения — для А, = 0,3, 0,5, 0,8, 1, 2, 3, 4, 5.
12.3.3. Геометрическое распределение. Надеясь на счастливый случай,
мы склонны ожидать успеха с первой же попытки. Потерпев неудачу
в первой попытке, мы надеемся, что успешной окажется вторая попыт-
попытка. Если как первая, так и вторая попытки не принесли успеха, мы
ожидаем, что окажется успешной третья попытка. И так далее — вплоть
до первого успеха на какой-то попытке. Будем полагать, что наши по-
попытки — это независимые испытания, и пусть р — вероятность успеха
в каждом испытании (соответственно q = 1 - р — вероятность неудачи
в каждом испытании). Рассматриваем в качестве случайной величины X
количество попыток (количество испытаний), в результате которых мы,
351

наконец, дождались успеха. Таблица для закона распределения случай-
случайной величины X имеет вид:
Pi
1
р
2
PG
3
PG2
4
PG3
5
6
PG5
...
п
PG"-1
Это распределение называют геометрическим, поскольку последователь-
последовательность вероятностей Pt образует геометрическую прогрессию (точнее: бес-
бесконечную убывающую геометрическую прогрессию).
Используя известную формулу для вычисления суммы бесконечной
убывающей прогрессии, находим:
т. е. убеждаемся в справедливости соотношения A).
Найдем для геометрического распределения выражение для
Легко видеть, что
°° с./>. = р{\ + 2q + 3q2 + 4q3 +5q4+..
(p + 2pq + 3pq2 + 4pq3 +...) + (
= p
Итак,
pq + pq2 + pq3
= p + q
+ 1
^. =p
Z-^"
Отсюда находим: A - g)^ x^- = p + q
Так как /? + ^ = 1, то получаем:
G)
На рис. З в таблице 47 приведены шесть многоугольников геометри-
геометрического распределения — для р = 0,9, 0,8, 0,7, 0,5, 0,35, 0,2.
352

12.4 Математическое ожидание
дискретной случайной величины
Оакон распределения случайной величины полностью ее характери-
характеризует. Во многих случаях, однако, можно обойтись меньшей информа-
информацией и удовлетвориться знанием некоторых постоянных для рассмат-
рассматриваемой случайной величины чисел, отражающих наиболее важные
особенности этой величины. Особенно важную роль играют два чис-
числа — математическое ожидание случайной величины и дисперсия слу-
случайной величины. Математическое ожидание имеет смысл среднего зна-
значения случайной величины, а дисперсия характеризует средние размеры
отклонения случайной величины от ее среднего значения. Можно сказать,
что математическое ожидание и дисперсия описывают случайную вели-
величину не детально, а как бы суммарно. Их называют числовыми характе-
характеристиками случайной величины.
С математическим ожиданием мы уже встречались в предыдущей теме
(см. § 11.4). Там мы познакомились с ним, рассматривая среднее коли-
количество «успехов» в п испытаниях Бернулли. Математическое ожидание
(т) было определено как сумма:
/и=1
и было показано, что
(jn) = пр .	(**)
Теперь мы рассмотрим понятие математического ожидания приме-
применительно не только к количеству «успехов» в п испытаниях Бернулли, а
к любой дискретной случайной величине. Будем обозначать через (X)
математическое ожидание случайной величины X. Определением мате-
математического ожидания (X) может служить соотношение:
(8)
Математическое ожидание дискретной случайной величины есть сумма
произведений всех ее возможных числовых значений на их вероятности.
Предположим, что некоторая случайная величина X имеет к воз-
возможных числовых значений: xh хъ х3,..., хк. Допустим, произведено
N опытов (испытаний), и оказалось, что упомянутые числовые значе-
значения реализовались, соответственно, пъ пъ я3,..., пк раз. Понятно, что
пх + п2 + щ + ... + пк = N. Обозначим через х среднее арифметическое
353

значение нашей случайной величины, полученное усреднением по N
испытаниям:
к
х =
/N.	(9)
Если N достаточно велико, то х1 будет приблизительно равно мате-
математическому ожиданию величины X.
х^(Х).	A0)
Именно таков смысл математического ожидания случайной величины.
Допустим, для серии из ^испытаний мы получили среднее арифме-
арифметическое случайной величины Х9 равное х\ для серии из Nf испытаний
получили среднее значение х'\ для серии из N" испытаний получили х"
и т. д. Все эти средние значения х, х1', х"9... будут колебаться около ма-
математического ожидания (X), отклоняясь от него тем меньше, чем больше
число испытаний в серии. Кстати говоря, мы уже отмечали этот факт в
§ 11.4, рассматривая там математическое ожидание и среднее значение
количества «успехов» в испытаниях Бернулли.
В § 12.3 мы отметили три специальных типа распределений — бино-
биномиальные, пуассоновские и геометрические распределения. Для них были
рассмотрены, в частности, суммы ^Х;Р; математические ожидания (X):
-	для биномиального распределения: (X) = пр (соотношение B)),
-	дляпуассоновскогораспределения: (X) =Х = пр (соотношение F)),
-	для геометрического распределения: (X) = \ /р (соотношение G)).
Заметим, что, если для биномиального и пуассоновского распреде-
распределений математическое ожидание случайной величины близко к ее наи-
наиболее вероятному значению, то в общем случае этого утверждать нельзя.
Так, для геометрического распределения наиболее вероятное значение
величины всегда (для любых р) равно 1, тогда как математическое ожи-
ожидание величины возрастает с уменьшением р по закону 1 /р и, напри-
например, при р = 0,2, равно 5.
Вернемся к распределениям, представленным графически в табли-
таблице 46. Подсчитаем для каждого из них математическое ожидание (ис-
(используя для этого соотношение (8)) и сравним с наиболее вероятным
значением рассматриваемой величины. Мы получим:
а) для распределения на рис. 1
все значения равновероятны, так что любое можно рассматривать как
наиболее вероятное;
354

б) для распределения на рис. 2
(F) = B + 3.2 + 4.3 + 5.4 + 6.5
9-4 + 10. 3
12)/36 = 7;
наиболее вероятное значение равно 7;
в) для распределения на рис. 3
(G) = A+2- 2 + 3-2 + 4- 3 + 5- 2 + 6- 4 +8- 2 + 9.1+10-2+ 12- 4 +15- 2 +
+16 • 1 +18 • 2 + 20 • 2 + 24 - 2 + 25 • 1 + 30 • 2 + 36) / 36 = 49 / 4 = 12,25;
наиболее вероятные значения равны 6 и 12;
г)	для распределения на рис. 4
(У) = 0- 0,7 + 1-0,2 + 3- 0,06 + 10- 0,03 + 30- 0,01 = 0,98;
наиболее вероятное значение равно нулю;
д)	для распределения на рис. 5
(Z} = 10 + 2- 0,1 + 3- 0,3 + 4- 0,6 = 3,6;
наиболее вероятное значение равно 4.
12.5 Свойства математического ожидания
1 Лредположим, что дискретная случайная величина X задана таблицей:
Pi
х3
Рз
хп
Рп
В таком случае случайная величина аХ (где а — некоторая постоян-
постоянная величина) будет задаваться таблицей:
ахх
л
ах2
р2
ах3
Рз
ахп
Рп
случайная величина Х+ Ъ (где Ъ — некоторая постоянная величина) бу-
будет задаваться таблицей:
*i + Ь
Л
x2 + b
Pi
х3 + Ь
Рз
хп + Ь
Рп
355

случайная величина аХ+ b будет задаваться таблицей:
ахх + Ъ
ах2 + b
ахъ + Ъ
Ръ
...
...
ахп + Ъ
Рп
Нетрудно выразить математические ожидания случайных величин аХ,
Х+ b, aX+ b через математическое ожидание величины X:
(аХ + b) --
Итак, мы получили:
axt
¦b)Pi=d?:
Pt =a{X) + b.
= a(X);
= a(X)
(И)
A2)
A3)
Теперь рассмотрим сумму Х+ У и произведение Х- У двух независи-
независимых случайных величин Хя Y. Тут следует, очевидно, пояснить, какие
случайные величины называются независимыми и что понимается под
суммой и произведением случайных величин.
Две случайные величины называют независимыми, если закон рас-
распределения одной из них не зависит от того, какое из возможных зна-
значений приняла другая величина. Несколько случайных величин назы-
называют взаимно независимыми, если закон распределения любой из них не
зависит от того, какие возможные значения приняли остальные вели-
величины. Как известно, два случайных события являются независимыми,
если вероятность наступления одного из них не зависит от наступления
другого события. Отсюда видно, что независимость случайных величин
предполагает независимость соответствующих случайных событий.
Суммой (или произведением) случайных величин Хж У называют слу-
случайную величину Х+ У (или X У), возможные значения которой обра-
образуют множество значений суммы (или произведения) каждого возмож-
возможного значения величины Хж каждого возможного значения величины У
Предположим, простоты ради, что величина X принимает всего два воз-
возможных значения (х{ и х2) и величина У принимает всего два значения
(ji и у2). Тогда величина Х+ Уимеет возможные значения: jq + уь хх + у2,
х2 + У\, х2 + у2. Соответственно величина Х- Убудет иметь возможные
356

значения: jq • уъ хх • уъ х2'У\, х2'У2- Заметим, что рассмотрение вели-
величин 1и У, имеющих только по два возможных числовых значения, не
скажется на общности выводов, которые будут получены.
Пусть случайные величины Хя У задаются таблицами:
Pi
х2
Р2
Л
Pi'
У2
Р2'
И
Каковы будут вероятности различных возможных значений величин
Х+ У и Х- У? Если величины Хж У независимые, то можно предста-
представить вероятность реализации одновременно значений xt и yj в виде про-
произведения вероятностей Pt и Р- (в соответствии с известным правилом
умножения вероятностей независимых событий). Поэтому случайные
величины Х+Уя X Убудут задаваться таблицами:
xi+yi
Р\Р\'
Х1+У2
P\Pi
Х2+У1
P2Pl'
Х2+У2
Р2Р2'
И
Р\Р\'
xv Уг
PiPi!
xi-у\
Р2Р{
Х2'У2
Р2Р2'
(*)
Используя таблицы (*), найдем в соответствии с (8) выражения для
математического ожидания суммы и произведения независимых величин.
Начнем с математического ожидания для произведения величин Хи Y:
x2y2P2P2f =
(X-Y) =
Теперь разберемся с математическим ожиданием для суммы величин
Хи Y:
(X+Y)=
(х2
2 +y2)P2P2 =
+P2)+y2P2'(Pl +P2).
Поскольку Pl + P2 = 1 и P/ + P2' = 1, то, следовательно,
Итак, мы получили для независимых величин Хя Y:
A4)
A5)
357

Заметим, что результат A4) можно было бы получить также и в том
случае, когда величины Хж Уне являются независимыми. Пусть вели-
величина Х+ У задана таблицей:
Х\+У\
Рп
*1+У2
Рп
*2+У\
Рп
х2 + у2
Рц
Мы можем представить:
{X+Y)=(xi +yi)Pn +(xi +У2)РП +(х
= xl(Pn +Pl2)+x2(P21 +P22)+yl(Pn +P21)+y2(P12 +P22).(**)
Если учесть далее, что
P2l+P22=P2,
pn+p2l=p;,
p _|_ p 	 r>f
то выражение (**) можно переписать в виде:
***
х2Р2
у2Р2 = (X)
Таким образом, мы приходим к результату A4), не прибегая к пере-
перемножению вероятностей Pt и PJ.
Соотношения (***) нетрудно доказать. Докажем, например, первое
из них. Величина X принимает значение Xi тогда, когда величина Х+ У
принимает значение хх +у1 или тогда, когда величина Х+ У принимает
значение Xi + y2. Используя известную теорему о сумме вероятностей
несовместных событий, заключаем: вероятность Рх того, что величина X
примет значение хъ равна сумме вероятностей двух несовместных со-
событий — вероятности Рп наступления события, состоящего в том, что
величина Х+ У примет значение хх+уъ и вероятности наступления
события, состоящего в том, что величина Х+ Упримет значение Xi + у2.
Таким образом, /\ = Рп + Рп.
Обобщая результаты A4) и A5) на случай нескольких случайных ве-
величин (X, У, Z, W,...) представим:
A6)
A7)
358

Соотношение A7) работает при условии, что величины X, У, Z, W,...
являются взаимно независимыми. Соотношение же A6) не требует взаим-
взаимной независимости рассматриваемых величин.
Воспользовавшись соотношением A6), можно весьма просто найти
математическое ожидание случайной величины, представляющей со-
собой количество «успехов» в п испытаниях Бернулли. Для этого введем в
рассмотрение п случайных величин, которые будем обозначать
Х\, Х2, Х$, ..., Xt, ..., Хп.
Здесь Xt — случайная величина, представляющая собой число «успе-
«успехов» в испытании, имеющем номер (/= 1, 2, 3,..., п). Каждая величина^
имеет всего два возможных значения: 1 (данное испытание заверши-
завершилось «успехом») и 0 (испытание завершилось «неудачей»). Каждая слу-
случайная величина Xt задается одной и той же таблицей:
1
р
0
\-р
и имеет одно и то же математическое ожидание:
Согласно A6), математическое ожидание (X) есть сумма математи-
п
ческих ожиданий ^(Х/). С учетом (*****) получаем: (X) = пр. Этот
результат был получен в § 11.3 более сложным путем.
12.6 Дисперсия и среднее квадратичное отклонение
дискретной случайной величины
Онание математического ожидания (среднего значения) случайной
величины, конечно, важно. Не менее важно знать также, насколько
сильно возможные значения случайной величины отклоняются в ту или
другую сторону от среднего значения. Может показаться, что разброс
отклонений возможных значений случайной величины характеризуется
математическим ожиданием (X — (X)). Однако легко убедиться, что
= <>.	A8)
359

В самом деле,
Впрочем, этот результат немедленно следует из A2), если там поло-
положить Ъ = — (X).
Разброс или, иначе говоря, рассеяние возможных числовых значе-
значений случайной величины X около ее среднего значения принято харак-
характеризовать с помощью дисперсии случайной величины D{X). Она опреде-
определяется как математическое ожидание квадрата отклонения случайной
величины от ее математического ожидания:
i =((X-(X)f
A9)
Слово «дисперсия» в переводе с латинского означает «рассеяние».
Соотношение A9) можно преобразовать к виду:
/2 -2х,(Х)+(ХJ)Р, =
D(X) =
= (Х2)-2(Х)(Х)+(ХJ = (Х2)-(ХJ.
Итак, дисперсия равна разности между математическим ожиданием квад-
квадрата случайной величины и квадратом ее математического ожидания:
B0)
Легко видеть, что дисперсия имеет размерность, равную квадрату
размерности случайной величины. Однако во многих случаях желатель-
желательно, чтобы оценка рассеяния случайной величины имела такую же раз-
размерность, что и сама величина. В таких случаях рассеяние величины X
характеризуют не дисперсией, а так называемым средним квадратичным
отклонением с(Х), которое выражается через дисперсию D(X) весьма
просто:
B1)
D(X) = ^2xi2Pi-
i
J2x>pi
i
=
-{X)>.
360

В ряде стран для среднего квадратичного отклонения используется
термин «стандартное отклонение».
На рис. 1 в таблице 48 приведены семь распределений некоторой слу-
случайной величины. Во всех семи случаях математическое ожидание рав-
равно нулю. Используя B0) и B1), нетрудно вычислить дисперсию D и
среднее квадратичное отклонение а для каждого из рассматриваемых
распределений; соответствующие значения D и а указаны на рисунках
рядом с распределениями. Наименьшей дисперсией обладает распреде-
распределение 1 — здесь возможные значения случайной величины отклоняют-
отклоняются от (X) всего на 1 и при этом имеют относительно небольшую вероят-
вероятность, равную 1/8. Наибольшей дисперсией обладает распределение 7 —
здесь возможные значения случайной величины отклоняются от (X)
на 2 и при этом имеют вероятность 3/8.
Используя B), C) и B0), получим выражение для дисперсии числа
«успехов» в п испытаниях Бернулли:
D =
21
= [п2р2 + пр(\ - р)\ - \{прJ\ = пр(\ -р) = npq.
Итак, если случайная величина описывается биномиальным распреде-
распределением с параметрами п, р, q (q= I - q), то дисперсия этой величины
вычисляется по формуле:
D=npq,	B2)
а среднее квадратичное отклонение — по формуле:
B3)
На рис. 2 в таблице 48 приведены три биномиальных распределения:
1.	п = 25, /> = 0,1,
2.	п = 25, /? = 0,9,
3.	п = 25, /7 = 0,5.
Распределения 1 и 2 имеют разные математические ожидания (соот-
(соответственно 2,5 и 22,5), но одинаковые дисперсии (Z> = 2,25), а также
средние квадратичные отклонения (о= 1,5). Распределение 3 отличает-
отличается от распределений 1 и 2 не только математическим ожиданием, но и
дисперсией (средним квадратичным отклонением). У распределения 3:
Z)=6,25, a = 2,5.
361

Таблица 48. Дисперсия и среднее квадратичное отклонение
и=2
а = 0,71
2
a = 0,87
D=l
а=1
-1 0
-1 0
-1 0
-1 О
0-L
-2 -1 О
1 2-2-1 О
-2 -1
1
4
5.
8
1
2
8"
1
4
1
1
"8
1
4
1
1 210
Рис.1
пр = 22,5
D = 2,25
а=1,5
пр=12,5
D = 6,25
а = 2,5
од
0,05-
I
Рис.2 0 2 4 6
I
10 12 14 16 18 20 22 24 25
362

12.7 Свойства дисперсии
11режде всего заметим, что дисперсия постоянной величины равна нулю.
Это очевидно, поскольку постоянная величина принимает только одно
определенное числовое значение, так что ни о каком рассеянии значе-
значений тут говорить не приходится.
Постоянный множитель можно выносить за знак дисперсии, возво-
возводя его при этом в квадрат. Доказательство основывается на использова-
использовании соотношений A1) и B0):
D(aX)=((aXJ)-((aX)J =
= a2(X2)-(a(X)J=a2((X2)-(XJ)=a2D(X).
Итак,
D{aX) = a2D{X).	B4)
Дисперсия суммы двух независимых случайных величин равна сумме
дисперсий этих величин. Для доказательства воспользуемся соотноше-
соотношениями A1), A4), A5), B0):
D{X + Y) = ((X + YJ)- ((X + F)J =
= [(Х2 +2XY + Y2)\-[((X)
Y2)}-[(XJ+2(X)(Y)
= (X2) - (XJ +(Y2)- (YJ = D(X) + D{Y).
Итак,
D(X + Y) = D{X) + D(Y).	B5)
Из B5) немедленно следует, что
D{X + b) = D{X),	B6)
где b — постоянная величина. Из B5) и B4) следует что
-b) = a2D{X).	B7)
Результат B5) обобщается на случай, когда складываются несколько
взаимно независимых случайных величин:
D(X + Y + Z+ ...) = D(X) + D(Y) + D(Z) +...	B8)
363

Воспользовавшись соотношением B8), можно весьма просто найти
выражение для дисперсии случайной величины X, представляющей со-
собой число «успехов» в п испытаниях Бернулли. Для этого используем
прием, с которым мы познакомились в конце § 12.5. Представим слу-
случайную величину X как сумму п независимых случайных величин:
где Xt — случайная величина, являющаяся числом «успехов» в /-ом ис-
испытании (/= 1, 2, 3,..., п). Закон распределения каждой из случайных
величин Xt — один и тот же; он задается таблицей (****) из §12.5.
Каждая из этих величин обладает дисперсией
D{Xt) = (xf)-(XtJ =p-p2=p(l-p) = pq.	(**)
Отсюда немедленно получаем, используя B8):
Этот результат был получен в § 11.3 более сложным путем.
12.8 Неравенство Чебышёва и «правило трех сигм»
Jt5 1866 году П.Л. Чебышёв в своей работе под названием «О средних
величинах» получил важное неравенство, при помощи которого он до-
доказал закон больших чисел в общем виде (теорема Бернулли оказалась
всего лишь частным случаем этого закона). Доказанное П.Л. Чебышё-
вым неравенство можно представить в виде:
Р(\Х-(Х)\<а)>1-
Р(Х)
а2
B9)
Здесь (X) и D{X) — математическое ожидание и дисперсия некоторой
дискретной случайной величины X, а Р(\Х -(Х)\ < а) — вероятность
того, что величина X отклонится от своего математического ожидания
менее, чем на некоторое положительное число а. В современной лите-
литературе неравенство B9) принято называть неравенством Чебышёва.
Приведем доказательство неравенства Чебышёва. Для этого сначала
рассмотрим вероятность Р(Х> 1), т. е. вероятность того, что величина X
364

окажется не менее 1. Пусть возможные значения данной величины
хъ хъ х3,... неотрицательны и имеют вероятности, равные, соответствен-
соответственно, Р1? Ръ Рът- • Вероятность Р(Х> 1) есть сумма тех из этих вероятно-
вероятностей, для которых xt> 1:
Р(Х > 1) = ? />•	(*)
i\xt>l
(вспомним правило сложения вероятностей). Умножив каждое из сла-
слагаемых в правой части равенства (*) на соответствующее xt, мы не умень-
уменьшим сумму, поскольку xt> 1. Поэтому можем записать:
Р(Х > 1) < X) xipi'	(**)
i\xt>\
Мы тем более не уменьшим рассматриваемую здесь сумму, если рас-
распространим суммирование на все возможные значения величины Д т. е.
если добавим неотрицательные слагаемые xtPi9 для которых 0<xz<l.
Полученная при этом сумма есть, очевидно, математическое ожидание.
Итак,
Р(Х>1)<(Х).	(***)
Теперь можно приступить непосредственно к доказательству нера-
неравенства B9). Учтем, что
Р((\Х-(Х)\<а) + Р(\Х-(Х)\>а) = 1
(сумма вероятностей противоположных событий равна единице), вслед-
вследствие чего неравенство B9) можно переписать в эквивалентной форме:
Р(\Х-(Х)\>а)<
D(X)
а2
C0)
Событие, описываемое неравенством \Х — (Х)\ > а (оно состоит в том,
что величина Xотклоняется от (X) не менее, чем на а), равносильно со-
событию, описываемому неравенством (X - (X)J /а2 > 1. Следовательно,
Р (\Х - (Х)\ >а) = Р((Х- (X)J I a2 > l).
В результате неравенство C0) преобразуется к виду:
Р ((X - (X)J I a2 >l)<D(X)/a2.	(****)
Нам остается доказать неравенство (****). Это легко сделать, восполь-
воспользовавшись неравенством (***), в котором надо заменить случайную
365

величину ^Гна случайную величину (X — (X)) /а . Мы имеем полное
право воспользоваться неравенством (***), поскольку числовые значе-
ния величины (X - (X)) / а заведомо неотрицательны. Произведя ука-
указанную замену случайных величин, мы тем самым преобразуем нера-
неравенство (***) к виду:
Р ((X - (X)J I а2 > l)< ((Л- - (X)J I a:
т. е., как нетрудно видеть, немедленно придем к неравенству (****) (в этом
можно убедиться, воспользовавшись соотношениями A1) и A9)). Итак,
неравенство (****) доказано и, значит, доказано неравенство Чебышёва.
Как уже отмечалось, неравенство Чебышёва позволяет получить за-
закон больших чисел в общем виде. Об этом мы поговорим в следующем
параграфе. Здесь же воспользуемся неравенством C0) для того, чтобы
вывести так называемое «правило трех сигм». Учитывая, что среднее
квадратичное отклонение а(Х) равно ^JD(X), перепишем C0):
Р (\Х - (Х)\> а) < о2(Х) I а2.
Положим а = За(Х); получим
Р(\Х-(Х)\>Зс(Х))<1/9.	C1)
Мы видим, что для любой дискретной случайной величины X вероят-
вероятность ее отклонения от математического ожидания на За и более не
превышает 1/9. Это и есть «правило трех сигм».
Важно иметь в виду, что для встречающихся на практике случайных
величин упомянутая вероятность, как правило, оказывается значитель-
значительно меньше, чем 1/9. Например, для биномиального распределения 3,
графически представленного на рис. 2 в таблице 48 вероятность
Р(\Х - (Х)\ > За) не превышает 0,002.
12.9 Среднее арифметическое независимых
случайных величин и закон больших чисел
ХЗудем полагать, что некая дискретная случайная величина X может
принимать бесконечное множество числовых значений: xh хъ хъ... Пусть
(X) и D{X) — математическое ожидание и дисперсия этой величины.
Предположим, что требуется измерить рассматриваемую величину.
С этой целью произведем п независимых измерений при одних и
тех же условиях. Будем рассматривать результат первого измерения как
366

случайную величину Хъ результат второго измерения — как случайную
величину Хъ результат третьего измерения — как случайную величину Хъ,
и так далее — вплоть до я-го измерения, результат которого будем рас-
рассматривать как случайную величину Хп. Очевидно, что каждая из вели-
величин Хъ Хъ Х3,..., Хп имеет тот же набор возможных числовых значений,
что и величина X (в каждом из п измерений реализуется какое-то из
значений хъ хъ х3,...)- Закон распределения каждой из величин
ХЬХЪХЪ,..., Хп один и тот же — такой же, что и закон распределения
величины X. Поэтому
D{XX) = D(X2) = D(X3) = ... = D{Xn) = D{X).	(**)
Ясно, что случайные величины Xh Хъ Хъ,..., Хп являются взаимно неза-
независимыми, что связано с независимостью п измерений.
Рассмотрим случайную величину X, которую определим так:
X ^1 + ^2 + ^з + • • • + Хп	/32)
Эта величина есть среднее арифметическое п независимых случайных
величин, являющихся результатами измерения величины X. Используя
A1) и A6), получаем:
п	I	п
С учетом (*) заключаем отсюда, что
= п{Х)/п={Х).
Используя B4) и B8), получаем
п
D(X2)+D(X3)+...
С учетом (**) заключаем отсюда, что
Итак,
п2
D(X) = nD(X)/n2 = D{X)/n.
Х) = (Х), D(X) = D(X)/n, o(X)=a(X)/^.\	C3)
367

Как мы видим, среднее арифметическое п независимых результатов
измерений имеет:
а)	математическое ожидание — то же, что и для отдельного измерения,
б)	дисперсию — в п раз меньше, чем для отдельного измерения,
в)	среднее квадратичное отклонение — в 4п раз меньше, чем для
отдельного измерения.
Мы пришли к весьма важному выводу о том, что среднее арифмети-
арифметическое большого числа взаимно независимых случайных величин обладает
во много раз меньшим рассеянием, чем каждая случайная величина в от-
отдельности. Можно сказать, что среднее арифметическое большого чис-
числа п независимых величин утрачивает характер случайной величины,
причем тем в большей мере, чем больше п.
Это очень важный результат. Именно он позволяет, в конечном
счете, получить закон больших чисел в общем виде. Чтобы убедиться
в этом, воспользуемся неравенством Чебышёва C0), рассматривая в
нем в качестве случайной величины величину X:
P(\X-(x)\>a)<D(X)/a2.
С учетом C3) это неравенство принимает вид:
р(\Х-{Х)\>а)<Щ±.	C4)
па
Так как D{X) /а2 есть некоторое фиксированное число, то ясно, что
limD(X)/na2 =0.
С учетом C4) отсюда следует, что
ИтР(\Х-(Х)\>а)=0.	C5)
Это и есть закон больших чисел. Мы уже обсуждали сущность этого зако-
закона в § 11.7, введя там понятие сходимости по вероятности. Легко видеть,
что фигурировавшее в § 11.7 соотношение A4) может рассматриваться как
частный случай соотношения C5), предполагающий использование в ка-
качестве дискретной случайной величины X количество «успехов» в одиноч-
одиночном испытании Бернулли. В этом частном случае: X =т/п, (X) = р
(см. (*****) в § 12.5), D{X) =p(l-p) (см. (**) в § 12.7). Кстати, заметим,
что неравенство (****) в § 11.7 есть не что иное, как неравенство Чебышё-
Чебышёва C0) для случая, когда в качестве X рассматривается случайная величина,
представляющая собой количество «успехов» т в п испытаниях Бернулли.
п
Здесь (X) = пр, D(X) = ^ (т - прJ Рп(т) = пр{\ - р).
368

О глубоком содержании и большой практической ценности закона
больших чисел хорошо говорится в книге Б.В. Гнеденко и А.Я. Хинчина
«Элементарное введение в теорию вероятностей» (М.: Изд-во физико-
математической литературы, 1961). Позволим себе выдержку из этой книги.
«Глубокое содержание закона больших чисел, открытого в середине
прошлого столетия великим русским математиком Чебышёвым, состо-
состоит в том, что, в то время как отдельная случайная величина может (как
мы знаем) часто принимать значения, далекие от ее среднего значения
(иметь значительное рассеяние), среднее арифметическое большого числа
случайных величин ведет себя в этом отношении совершенно иначе:
такая величина очень мало рассеяна, с подавляющей вероятностью она
принимает лишь значения, очень близкие к ее среднему значению.
Происходит это, конечно, потому, что при взятии среднего арифмети-
арифметического случайные отклонения в ту и другую сторону взаимно уничто-
уничтожаются, вследствие чего суммарное отклонение в большинстве случаев
оказывается малым.
Важное и часто встречающееся в практике использование результа-
результатов теоремы Чебышёва состоит в том, что по сравнительно небольшой
пробе (выборке) судят о качестве большого количества однородного
материала. Так, например, о качестве хлопка, находящегося в кипе,
судят по нескольким его пучочкам (штапелям), выхваченным случайно
из разных мест кипы. Или о качестве большой партии зерна судят по
нескольким небольшим меркам, наполненным случайно захваченными
в мерку зернами из разных мест оцениваемой партии. Суждения о каче-
качестве продукции, сделанные на основании такой выборки, обладают боль-
большой точностью. Число зерен, захваченных в мерку, хотя и мало по срав-
сравнению со всей партией зерна, но само по себе велико и позволяет,
согласно закону больших чисел, достаточно точно судить о среднем
весе одного зерна и, значит, о качестве всей партии зерна. Точно так же
о двадцатипудовой кипе хлопка судят по маленькому штапелю, содер-
содержащему несколько сотен волокон, весящих всего-навсего какую-ни-
какую-нибудь десятую долю грамма»
Было бы, однако, неправильно переоценивать возможности закона
больших чисел. Допустим, что, выполнив п измерений некоторой фи-
физической величины А, мы получили п числовых значений величины
хъхъ х3..., хп (вообще говоря, разных). В качестве приближенного зна-
значения измеряемой величины мы, естественно, возьмем значение
Xi + Х2 + Х3 + ... + Хп
п
369

Мы полагаем, что в соответствии с законом больших чисел значение х
будет тем ближе к точному значению, чем больше п. Можно ли, однако,
получить сколь угодно точное значение величины А, выполнив доста-
достаточно большое число измерений? Не следует спешить с утвердитель-
утвердительным ответом. Надо принять во внимание, во-первых, возможность си-
систематической ошибки при измерениях и, во-вторых, ширину деления
шкалы измерительного прибора. Компенсировать обусловленную эти-
этими двумя факторами погрешность измерений за счет закона больших
чисел принципиально невозможно.
12.10 Нормальное распределение
и центральная предельная теорема
в
1812 году П. Лаплас доказал для любого р, удовлетворяющего не-
неравенствам 0<р< 1, что биномиальные вероятности С™ртA- р)п~т
превращаются при достаточно больших п в вероятности:
(т-прJ
Рп(т)=	Х	~
Мы уже говорили об этом в § 11.8. Результат (*) получается, как легко
убедиться, из A6), если воспользоваться A9) (имеются в виду соотно-
соотношения A6) и A9) из § 11.8).
Рассматривая т как возможные значения случайной величины X,
представляющей собой количество «успехов» в п испытаниях Бернулли
и учитывая, что пр= (X) и пр A - р) = о2(Х) перепишем (*) в виде:
C6)
Распределение случайной величины X, вероятности значений которой
описываются соотношением C6), называют нормальным распределением
(а также распределением Лапласа—Гаусса). Мы пришли к нему как к пре-
предельному случаю биномиального распределения при больших п.
Для случая п = 100 и р = 0,5 это распределение изображено графичес-
графически в таблице 49. Заметим, что вместо многоугольника распределения тут
показана плавная кривая, проведенная через точки с координатами
{т\ Рп(т)). Математическое ожидание для данного распределения равно
100 • 0,5 = 50, а среднее квадратичное отклонение равно VlOO-0,5-0,5 = 5 .
370

Таблица 49. Нормальное распределение (распределение Лапласа-Гаусса)
75
371

Рассмотрим «правило трех сигм» в применении к нормальному распре-
распределению C6). При т — (X) = За(Х) вероятности в C6) принимают вид:
Р =	1-^е~4>5.	(**)
{XLb
Значение е~4'5 читатель может найти, воспользовавшись таблицей 43,
где табулирована функция ф(х) = е~х ^2/-^2п . Легко видеть, что
фC) = е~4'5 /у/2п . Из таблицы находим: фC) = 0,0044. Следовательно,
е-4'5 = фC).>/2тс = 0,0044 • л/2-3,1416 = 0,0044 • 2,507 = 0,011.
В случае, представленном в таблице 49, имеем а = 5 и, значит,
Р= 0,011 / B,507 • 5) = 0,0009. Этому значению соответствуют точки а
и Ъ на графике; для сравнения указаны точки cud, соответствующие
значениям Р^ 0,048 при отклонении от среднего значения 50 на одно
(а не три) значения а = 5. Получается, что в данном случае вероятность
того, что случайная величина примет значения, отклоняющиеся от ма-
математического ожидания на За и более, меньше 0,001. Если при п = 100
упомянутая вероятность меньше 0,001, то при п = 1000 она будет мень-
меньше 0,0003, а при п = 10 000 она будет меньше 0,0001.
Нормальное распределение возникает отнюдь не только в тех случа-
случаях, когда рассматривается количество «успехов» в п испытаниях Бер-
нулли при очень больших п. В общем случае нормальный закон распре-
распределения случайной величины X, характеризующейся возможными
числовыми значениями xh хъ х3..., хь ..., можно представить таблицей:
р —
{
1
j(Z)V2
n
(Xi-iX)J
2o2(X)
C7)
Как оказалось, нормальный закон распределения встречается в тео-
теории вероятностей и ее приложениях весьма часто. Уже Лаплас обратил
внимание на то, что по нормальному закону распределяются случайные
ошибки измерений. Он же предположил, что это связано с наличием боль-
большого количества независимо действующих причин, под воздействием
которых появляются ошибки в измерениях. П.Л. Чебышёв развил эту
идею и доказал в конце 80-х годов XIX-го столетия важную предельную
теорему, согласно которой при выполнении некоторых специальных усло-
условий закон распределения для суммы п независимых случайных величин
приближается в пределе при п —> оо к нормальному закону распределения.
Спустя десять с небольшим лет (в 1901 году) эту предельную теорему
доказал в более общем виде (т. е. при более общих условиях) ученик и
последователь Чебышёва A.M. Ляпунов. В его формулировке предель-
предельная теорема получила название центральной предельной теоремы.
372

Если случайная величина X представляет собой сумму очень большого
числа взаимно независимых случайных величин, влияние каждой из ко-
которых на всю сумму ничтожно мало, то X имеет распределение близкое
к нормальному.
Отметим, что сущность условия, выдвинутого A.M. Ляпуновым, состо-
состоит именно в требовании, чтобы влияние каждой отдельной случайной
величины на всю сумму было достаточно малым.
Предположим, измеряется какая-то физическая величина. Произво-
Производится в одних и тех же условиях ряд замеров. На результаты каждого
замера влияет большое число факторов случайного характера. Они могут
быть связаны с незаметными глазу сотрясениями измерительной уста-
установки, колебаниями давления воздуха, небольшими изменениями тем-
температуры, степенью сосредоточенности экспериментатора и т. д. Каждый
из этих факторов, взятый в отдельности, порождает какую-то «частную
ошибку» Xt в измерении. В совокупности различные факторы порождают
«суммарную ошибку» ^ Xt . Как правило, вклад каждой «частной ошиб-
ки» Xt в общую сумму ^2 Xj ничтожен и, следовательно, условие Ляпу-
нова, как правило, выполняется в практике измерений. И в итоге мы
имеем дело с удивительным феноменом предельной центральной теоре-
теоремы: хотя законы распределения каждой из случайных величин неизвестны,
тем не менее сумма ^^/ имеет закон распределения, близкий к нормаль-
i
ному. Именно на этом основывается математическая обработка резуль-
результатов измерений', она исходит из того, что случайная ошибка измерения
подчиняется нормальному закону распределения. При этом один из двух
главных числовых параметров распределения величины У^ Xt заведомо
известен — математическое ожидание равно нулю
• Другой
важный числовой параметр (среднее квадратичное отклонение а
характеризует в определенном смысле точность измерения.
Еще один важный пример, иллюстрирующий практическую важность
центральной предельной теоремы, связан с массовым производством,
существующим ныне во многих отраслях народного хозяйства. При
массовом производстве изготавливаются огромные партии однотипных
изделий, характеристики которых должны, разумеется, соответствовать
373

определенным стандартам. Разнообразные факторы случайного харак-
характера неизбежно приводят к случайным отклонениям от стандарта. Та-
Таких факторов много; это связано, в частности, с тем, что выпуск изде-
изделия предполагает, как правило, выполнение большого числа операций,
а все они выполняются лишь с какой-то степенью точности. Каждый
фактор в отдельности порождает ничтожное отклонение от стандарта,
характеризуемое случайной величиной Xt; сумма же ^ Xt может да-
вать ощутимые отклонения. Согласно центральной предельной теореме
суммарное отклонение от стандарта (случайная величина ^ Xt) долж-
но иметь закон распределения, близкий к нормальному.
12.11 У ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ВЕРОЯТНОСТЬ,
А У НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ —
ПЛОТНОСТЬ ВЕРОЯТНОСТИ
Пвтор. Наше обсуждение случайных величин было ограничено величи-
величинами дискретными. Сколь-либо последовательный разговор о непрерыв-
непрерывных случайных величинах потребовал бы привлечения аппарата матема-
математического анализа, т. е. операций дифференцирования и интегрирования.
В рамках данной книги это неосуществимо. Поэтому мы ограничимся
обсуждением лишь одного принципиального момента, связанного с тем,
что понятие вероятности того или иного числового значения случайной,
величины «не работает» для непрерывных случайных величин.
'ЧиФксикел*. В § 12.1 Вы говорили, что вероятность любого конкрет-
конкретного числового значения непрерывной случайной величины равна нулю.
Честно говоря, это трудно понять. Допустим, значения какой-то непре-
непрерывной случайной величины X заполняют отрезок [а; Ь]. Вероятность
того, что наугад брошенная точка (разумеется, брошенная мысленно)
попадет в отрезок [а; й], равна, конечно, единице — это есть вероят-
вероятность достоверного события. Выберем внутри отрезка [а; Ь] небольшой
отрезочек [х;х + Ах] (см. рис. 1 в таблице 50). По-видимому, существу-
существует какая-то не равная нулю вероятность того, что наугад брошенная точ-
точка окажется в пределах нашего отрезочка. Думаю, что эта вероятность
будет тем меньше, чем меньше Ах. Правильно ли я рассуждаю?
Пвтор. Правильно.
е. Согласно Вашему утверждению, вероятность того, что
наша точка попадет в любое конкретное число на отрезочке \х\ х + Ах],
374

Таблица 50. Плотность вероятности значения непрерывной случайной величины
Рис.1
f
Ах
Ж-
А*)
fix,)
х1 х2 х3
Рис.4
Рис.3
Рис.6
375

равна нулю. Как же получается, что вероятность попасть в этот отрезо-
чек нулю не равна? Разве сумма нулей может быть отлична от нуля?
Разве равенство п • 0 = 0 не выполняется для любого nl
Пвтор. Равенство п • О = 0 выполняется для любого конечного п. А вот
предел lim n • О совсем не обязательно должен быть нулем.
g4u*StiuSU*&, Допустим, что это так. А существует ли какая-то вероят-
вероятностная характеристика, связанная с попаданием точки в некоторое
конкретное число xt внутри отрезочка [х;х + Ах]?
Пвтор. Существует. Она называется плотностью вероятности число-
числового значения xt. Каждая точка отрезка [а; Ь] (и в частности, нашего
отрезочка) характеризуется определенным значением плотности веро-
вероятности/(х). Предположим, что функция/(х) имеет график, изобра-
изображенный на рис. 2 в таблице 50. Площадь под этим графиком, рассмат-
рассматриваемая на отрезке [а; Ь] (она на рисунке заштрихована), есть
вероятность попасть в отрезок [а; Ь]. Она равна единице, коль скоро
значения величины X определены на данном отрезке и только на нем.
Площадь под графиком функции fix), рассматриваемая на отрезочке
[х;х + Ах] (она на рисунке имеет двойную штриховку), есть вероят-
вероятность попасть в этот отрезочек. Условно обозначим эту вероятность
через P(xi9 Ах), где xt — середина отрезочка. Если Ах достаточно мало,
то можно приближенно считать, что
Отсюда следует, что
~, ч P(xhAx)
(**)
В пределе при Ах —> 0 вероятность Р [xt, Ах) стремится к нулю, но
r P(xhAx)
дробь 	^	 к нулю не стремится, а стремится к плотности вероят-
ности в точке xi9 т. е. k/(xz):
t. P(xhAx) j, ч	. N
Alimn Av	f{%i)'
Соотношение (***) можно рассматривать как определение понятия
«плотность вероятности».
g4ufauSU*b. Но почему в этом понятии используется слово «плот-
«плотность»? В физике есть плотность вещества. Она равна массе вещества
поделенной на его объем. Есть ли что-то общее между плотностью ве-
вещества и плотностью вероятности?
376

Пвтор. Да, тут есть определенная аналогия. Рассматривая вещество,
мы говорим, что в объеме Vвещества сосредоточена масса М. А как Вы
полагаете, можно ли говорить о массе, сосредоточенной не в объеме, а
в некоторой точке внутри тела?
*Чи*ксикел1к. Полагаю, что нельзя. Масса в точке должна равняться
нулю. Чтобы говорить о какой-то ненулевой массе, надо взять некото-
некоторый объем внутри тела, пусть даже совсем небольшой.
Пвтор. Вы совершенно правы. Давайте выберем мысленно некото-
некоторую точку А внутри некоторого тела и выделим небольшой объем V,
внутри которого находится точка А Для большей наглядности (и толь-
только ради нее) изобразим этот объем в виде куба, и пусть точка А нахо-
находится в центре куба — см. рис. 3 в таблице 50. Обозначим через М(А; А V)
массу вещества, находящуюся внутри объема AV. Если мы станем по-
постепенно уменьшать объем AF, как бы стягивая его в точку А, то, оче-
очевидно, масса М{А\ AV) будет постепенно уменьшаться. В пределе при
AF^O масса M(A;AV) будет стремиться к нулю, но отношение
М(А; А V) IA Vk нулю стремиться не будет. Оно будет стремиться к плот-
плотности вещества р(А), т. е. к плотности, которую вещество нашего тела
имеет в точке А:
lim —^-—- = р(А).	(****)
AF^O AV	V	J
Нетрудно усмотреть определенную аналогию между соотношениями
(****) и (***). Первое определяет плотность вещества в точке А про-
пространства, занятого веществом, а второе определяет плотность вероят-
вероятности в точке Xj отрезка [а; Ь], на котором задана непрерывная случай-
случайная величина.
'Чийиийел*. Понятно. В любой конкретной точке внутри вещества
рассматривают не массу вещества, а плотность вещества. Точно так же
для любой конкретной точки на отрезке [а; Ь] рассматривают не веро-
вероятность значения непрерывной величины, а плотность вероятности.
Пвтор. Если вещество распределено равномерно по всему объему
тела V, имеющего массу М, то в любой точке внутри тела плотность
вещества будет определяться хорошо известной всем формулой: р = М/ V.
Допустим теперь, что вещество распределено по объему V неравномерно.
Мысленно разобьем объем тела на п маленьких кубиков объемом AV
каждый. Пусть
Pb Р2> РЗ> •••> Рп
- значения плотности вещества в центре различных кубиков. Если А V
достаточно мало, то можно полагать приближенно, что внутри каждого
377

из кубиков вещество распределено равномерно с плотностью, равной
плотности в центре кубика. В этом случае можем записать:
p1AF + p2AF + p3AF + ... + pnAF ^ М.	(*****)
Аналогичным образом можно разбить отрезок [а; Ь] на п маленьких
отрезочков длиной Ах каждый. Пусть
- значения плотности вероятности величины X в центре различных
отрезочков. Если Ах достаточно мало, то можно полагать приближенно
что внутри каждого из отрезочков плотность вероятности постоянна и
равна плотности вероятности в середине отрезочка (см. рис. 4 в табли-
таблице 50). В этом случае плавная кривая fix) превращается в «ступенчатую
кривую» и мы можем записать:
Р{хх\ Ах) + Р(х2;Ах) + Р(х3;Ах) +... + Р(хп; Ах) ^
= /(х1)Ах + /(х2)Ах + /(х3)Ах + ... + f(xn)Ax = 1. (******)
'HutftiuSU**. Мы разбили мысленно отрезок [а; Ь] на п отрезочков
длиной Ах каждый и говорим о вероятностях попасть в тот или иной
из п отрезочков:
Р(хъ Ах), Р(х2, Ах), Р(х3, Ах),..., Р(хп, Ах).
Получается, что тем самым мы приближенно представили случайную ве-
величину в виде дискретной случайной величины0!
Пвтор. Именно так. Если мы станем разбивать отрезок [а; Ь] на все
более маленькие отрезочки Ах, т. е. станем увеличивать п (см. рис. 5
в таблице 50), то наша «ступенчатая кривая» будет всё более прибли-
приближаться к плавной кривой/(х). Она сольется с графиком функции/(х)
в пределе Ах —> 0 (т. е. при п —> оо).
'Ъигнашеусй. По-видимому, по мере уменьшения Ах (увеличения п)
многоугольник распределения, определяемый вероятностями P(xi9 Ax) будет
постепенно превращаться в плавную кривую, описывающую плотность
вероятности /(х)?
Пвтор. Вы правы. В таблице 49, полагая, что п = 100 — это достаточно
большое число, мы просто заменили многоугольник распределения плавной
кривой, которую, очевидно, можно рассматривать как плотность вероят-
вероятности /(х) для нормального распределения (ее называют нормальной кри-
кривой). Вероятности Рп{т) при больших п описываются выражением C6);
нормальная кривая fix) описывается аналогичным выражением:
C8)
378

. Можно ли считать, что изображенная в таблице 49 плав-
плавная кривая есть график функции/(х), заданной выражением C8) и что
площадь под этой кривой равна единице?
Пвтор. Да, можно. Если, разумеется, принять во внимание, что в
данном случае (X) = 50 и а = 5. Мы повторяем данную кривую на рис. 6
в таблице 50. Это есть график функции
ЗАДАНИЯ ПО ТЕМЕ 12
1.	Приведите побольше примеров непрерывных случайных величин.
2.	Изобразите графически закон распределения случайной величины, представля-
представляющей собой количество выпавших орлов при пятикратном подбрасывании моне-
монеты. Вычислите математическое ожидание и дисперсию этой величины.
Ответ: 5/2; 5/4.
3.	Подсчитайте дисперсию для распределений, показанных на рис. 1 и рис. 2 в таблице 46
и убедитесь, что в данном случае соотношение B5) действительно выполняется.
Ответ: 35/12; 35/6.
4.	Используя соотношение E) с числом слагаемых: вплоть до т = 10, подсчитайте
с помощью калькулятора число е с точностью до семи знаков после запятой.
Ответ: е= 2,7182817.
5.	Выведите формулу для суммы бесконечной убывающей геометрической прогрес-
прогрессии: 1 + Q+ q2 + q3 + ... = 1/A - q).
Подсказка. Сначала перепишите эту сумму в виде:
1 + q+ q2 + q3 + ... = 1 + g(l + Q+ Q2 + ...)¦
6.	Подсчитайте математические ожидания для всех распределений, представлен-
представленных графически на рисунках 1-3 в таблице 47.
7.	Подсчитайте дисперсии для всех распределений, представленных графически на
рисунках 1-3 в таблице 47.
8.	Используя B4) и B5), докажите, что D(X- Y) = D{X) + D(Y), где Хи Y —
независимые случайные величины.
9.	Вычислите математическое ожидание и дисперсию случайной величины (X/ 2 — 5),
если величина X распределена по биномиальному закону с п = 20 и р = 0,5.
Ответ: 0; 5/4.
379

ЗАКЛЮЧИТЕЛЬНЫЙ ДИАЛОГ
АВТОРА С ЧИТАТЕЛЕМ:
необходимо продолжение разговора
... Мы лишь теперь начинаем по досто-
достоинству оценивать значение всего круга про-
проблем, связанных с необходимостью и слу-
случайностью.
И. Пригожий, И. Стенгерс
(«Порядок из хаоса»)
Что бы мы ни называли реальностью, она
открывается нам только в процессе актив-
активного построения, в котором мы участвуем.
Рабиндранат Тагор
A861-1941).
й. Ну вот, наконец, книга прочитана. Она познакомила меня
с вероятностями и в определенной мере научила работать с ними. Я нашел
в ней немало интересного и полезного для себя. Однако, как мне кажется,
разговор на этом не может окончиться. Сделана только половина дела.
Пвтор. Поясните, пожалуйста, свою мысль.
Ъиниинелй. Во вступительном диалоге (в самом начале книги) отме-
отмечалось, что человек познаёт окружающий мир, используя закономерно-
закономерности двух типов — динамические (они позволяют делать однозначные
предсказания) и статистические (они позволяют делать вероятностные
предсказания). Там же отмечалось, что, как доказала наука XX-го сто-
столетия, именно статистические (а не динамические) закономерности более
адекватно отражают реалии нашего мира. Именно на языке теории ве-
вероятностей более четко обнаруживается «одушевляющая связь» явле-
явлений. Прочитанная книга раскрыла для меня многие тайны теории веро-
вероятностей и указала на многие примеры практического применения этой
теории, но она не объяснила, почему вероятностные подходы оказыва-
оказываются более эффективными при изучении окружающего мира и в чем
проявляется их эффективность. Она не продемонстрировала вероятно-
380

стного характера мира, конструируемого в сознании современного че-
человека. О самих вероятностях книга рассказала, но о мире, построенном
на вероятностях, она умолчала.
Пвтор. Действительно, пройдена лишь треть пути. Сделана только
треть дела. Если иметь в виду раскрытие темы «Закономерности окру-
окружающего мира». Остальные две трети автор предполагает рассмотреть
во второй и третьей книгах трехтомника, озаглавленных, соответствен-
соответственно, «Вероятность в современном обществе» и «От динамических законо-
закономерностей к вероятностным».
'Чийии&ел*. Что же конкретно предполагается рассмотреть во второй
книге?
Пвтор. Наверное, не стоит говорить здесь конкретно о ее содержа-
содержании. Поясню лишь в общих чертах. Во второй книге трехтомника будут
рассмотрены две взаимосвязанные группы вопросов. К первой отно-
относятся вопросы, связанные с исследованием операций (марковские слу-
случайные процессы, системы массового обслуживания, теория игр и при-
принятия стратегических решений, метод Монте-Карло). Ко второй группе
относятся вопросы, связанные с теорией информации (основные прин-
принципы и формулы, передача информации по каналу связи, энтропия и
информация, информатика и вероятность). Думаю, что перечисленные
вопросы дают общее представление о второй книге.
'Чипиинель. Общее представление они, пожалуй, дают. А какова глу-
глубинная идея?
Пвтор. Хороший вопрос. Действительно, можно говорить о глубин-
глубинной идее книги и идеях, которые лежат, так сказать, «на поверхности».
Последние вполне очевидны. Во второй книге трехтомника речь идет
о том, чтобы показать, что современное общество в буквальном смысле
построено на вероятности, коль скоро оно насыщено сложными и сверх-
сверхсложными информационными системами.
'Чипиинель. А что можно сказать о глубинной идее?
Пвтор. Глубинная идея раскрывается не столько во второй книге,
сколько в третьей книге трехтомника. В книге, озаглавленной «От ди-
динамических закономерностей к вероятностным». Ее можно было бы
назвать также «Эволюцией естественно-научной картины мира от ан-
античности до наших дней». Говоря сейчас только о глубинной идее, от-
отметим, что человек всегда стремился объяснить окружающий мир, по
возможности, наиболее рационально и был склонен упрощать пред-
представления о закономерностях мира, которые на протяжении веков фор-
формировались в сознании исследователей. В связи с этим приведу неболь-
небольшой отрывок из книги И. Пригожина и И. Стенгерс «Порядок из хаоса»
(Пер. с англ. М.: Прогресс, 1986): «...Галилей и те, кто пришел после
него, разделяли убеждение в том, что наука способна открывать глобальные
381

истины о природе. По их мнению, природа не только записана на мате-
математическом языке, поддающемся расшифровке с помощью надлежаще
поставленных экспериментов, но и сам язык природы единственен. Про-
Простейшие явления, изучаемые наукой, при таких взглядах объявлялись
ключом к пониманию природы в целом. Сложность природы была про-
провозглашена кажущейся, а разнообразие природы — укладывающимся в
универсальные истины, воплощенные для Галилея в математических за-
законах движения».
Такова в общих чертах традиционная парадигма, сохранившаяся вплоть
до наших дней. Авторы книги «Порядок из хаоса» считают (и мы с ни-
ними согласны), что пришло время, когда нужно отказаться от этой па-
парадигмы и признать принципиальную сложность окружающего мира.
Основной аргумент — развитие вероятностных представлений, приоб-
приобретающих в наше время всеобъемлющий характер. «Когда в науку, —
пишут Пригожий и Стенгерс, — в качестве объекта положительного
знания входят случайность, сложность и необратимость, мы отходим от
прежнего весьма наивного допущения о существовании прямой связи
между нашим описанием мира и самим миром» (курсив наш. — Авт.).
И вот еще один отрывок из книги Пригожина и Стенгерс:
«Идеалом классической науки была «прозрачная» картина физичес-
физической Вселенной. В каждом случае предполагалась возможность четко
указать причину и ее следствие. Но когда возникает необходимость в
использовании вероятностного описания, причинно-следственные связи
усложняются. Теперь имеет смысл говорить лишь о статистической при-
причинности. С такой ситуацией мы столкнулись довольно давно — с воз-
возникновением квантовой механики, но с особой остротой она дала о
себе знать в последнее время, когда случайность и вероятность стали
играть существенную роль даже в классической динамике и химии.
С этим и связано основное отличие современной тенденции по сравне-
сравнению с классической: в противоположность «прозрачности» классичес-
классического мышления она ведет к «смутной» картине мира».
По-видимому, теперь Вы в состоянии, если и не понять, то хотя бы
уловить глубинную идею всего трехтомника. Он предполагает преодоле-
преодоление традиционной классической парадигмы, попытку показать сложность
реального мира, окружающего нас, продемонстрировать возможности ве-
вероятностных подходов в лабиринтах этих сложностей, показать, что даль-
дальнейший прогресс в нашем миропонимании требует отказа от «навязыва-
«навязывания» природе упрощенных решений и признания важности апробации
альтернативных моделей.
'ЧиФксикел*. Я вижу, что наши беседы о вероятностях и закономерно-
закономерностях мира и в самом деле далеко не завершены.
Пвтор. Да, необходимо продолжение разговора.
382

СПИСОК ЛИТЕРАТУРЫ
Популярные издания
1.	Гнеденко Б.В., ХинчинА.Я. Элементарное введение в теорию вероятностей.
М.: ГИФМЛ, 1961.
2.	Колмогоров А.Н., Журбенко И.Т., Прохоров А.В. Введение в теорию вероятнос-
вероятностей. Библиотечка «Квант», вып.23. М.: Наука, 1982.
3.	Кордемский Б.А. Математика изучает случайности. М.: Просвещение, 1975.
4.	ЧубаревА.М., Холодный B.C. Невероятная вероятность. М.: Знание, 1976.
5.	Хургин Я.И. Как объять необъятное. М.: Знание, 1979.
6.	ГлеманМ., Варга Т. Вероятность в играх и развлечениях. Пер. с французско-
французского. М.: Просвещение, 1979.
7.	Тарасов Л.В. Мир, построенный на вероятности. М.: Просвещение, 1984.
8.	Тарасов Л.В. Неслучайная случайность. М.: ВШМФ «Авангард», 1994.
Научные издания
1.	Гнеденко Б.В. Курс теории вероятностей. М.: Наука, 1965.
2.	Солодовников А. С. Теория вероятностей. М.: «Вербум-М», 1999.
3.	Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая
школа, 1998.
4.	Розанов Ю.А. Случайные процессы. М.: Наука, 1971.
5.	Мостеллер Ф., РуркеР., Томас Дж. Вероятность. Пер. с англ. М.: Мир, 1969.
6.	Вентцелъ Е.С. Теория вероятностей. М.: Наука, 1964.
7.	Нейман Ю. Вводный курс теории вероятностей и математической статисти-
статистики. Пер. с англ. М.: Наука, 1968.
8.	Кайберг Г. Вероятность и индуктивная логика. Пер. с англ. М.: Прогресс,
1978.
9.	Майстров Л.Е. Развитие понятия вероятности. М.: Наука, 1980.
10.	Колмогоров А.Н. Основные понятия теории вероятностей. М.: Наука, 1974.
383

Учебное издание
ТАРАСОВ Лев Васильевич
ЗАКОНОМЕРНОСТИ ОКРУЖАЮЩЕГО МИРА
Книга 1
СЛУЧАЙНОСТЬ, НЕОБХОДИМОСТЬ, ВЕРОЯТНОСТЬ
Редактор Ю.Г. Рудой
Оригинал-макет: О.А. Пелипенко
Оформление переплета: А.Ю. Алехина
ЛР №071930 от 06.07.99. Подписано в печать 04.08.04.
Формат 70x100/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 31,11. Уч.-изд. л. 26,5. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru; http://www.fml.ru
Отпечатано с диапозитивов
в ОАО «Чебоксарская типография № 1»
428019, г. Чебоксары, пр. И. Яковлева, 15
ISBN 5-9221-0414-4
785922 104142